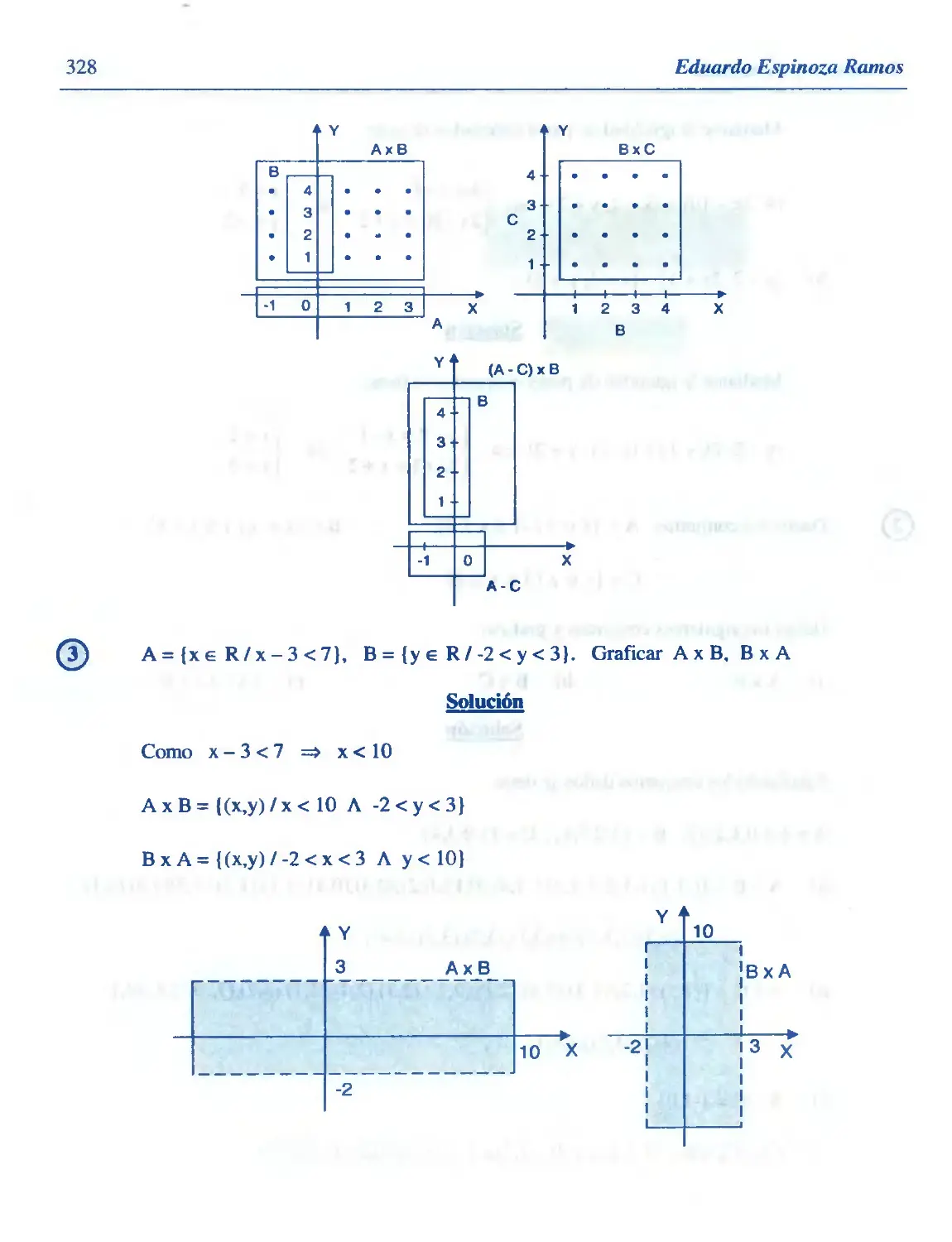
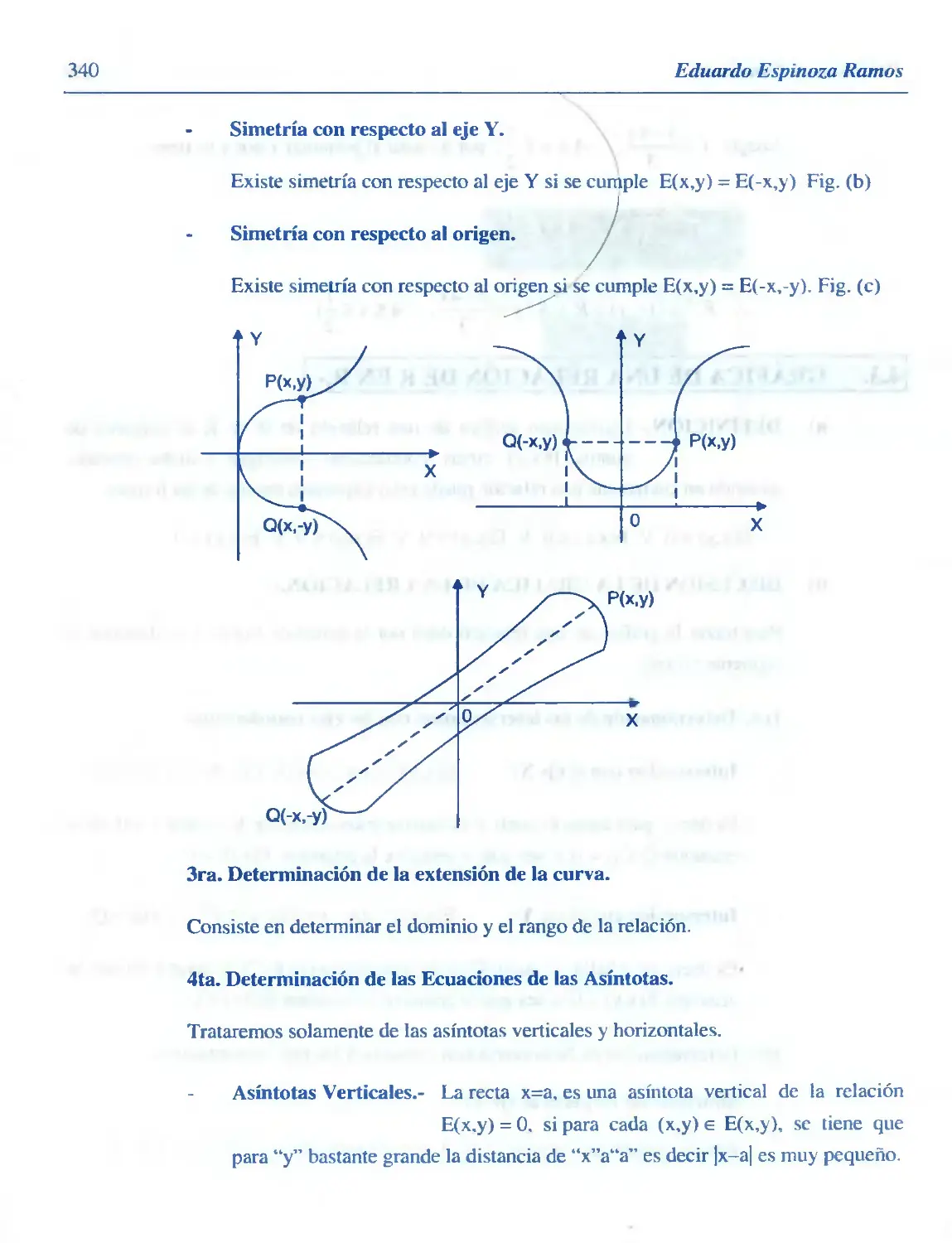
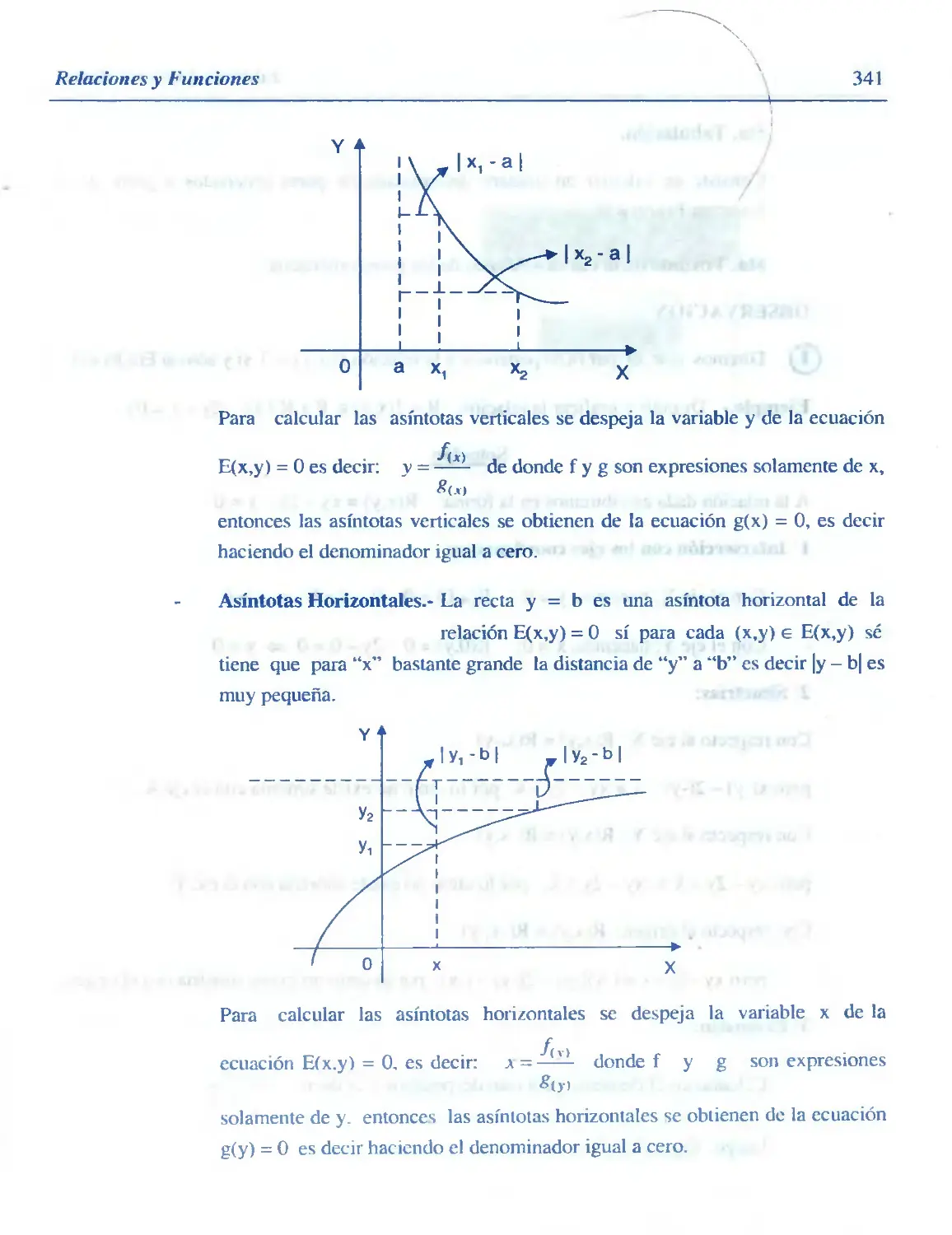
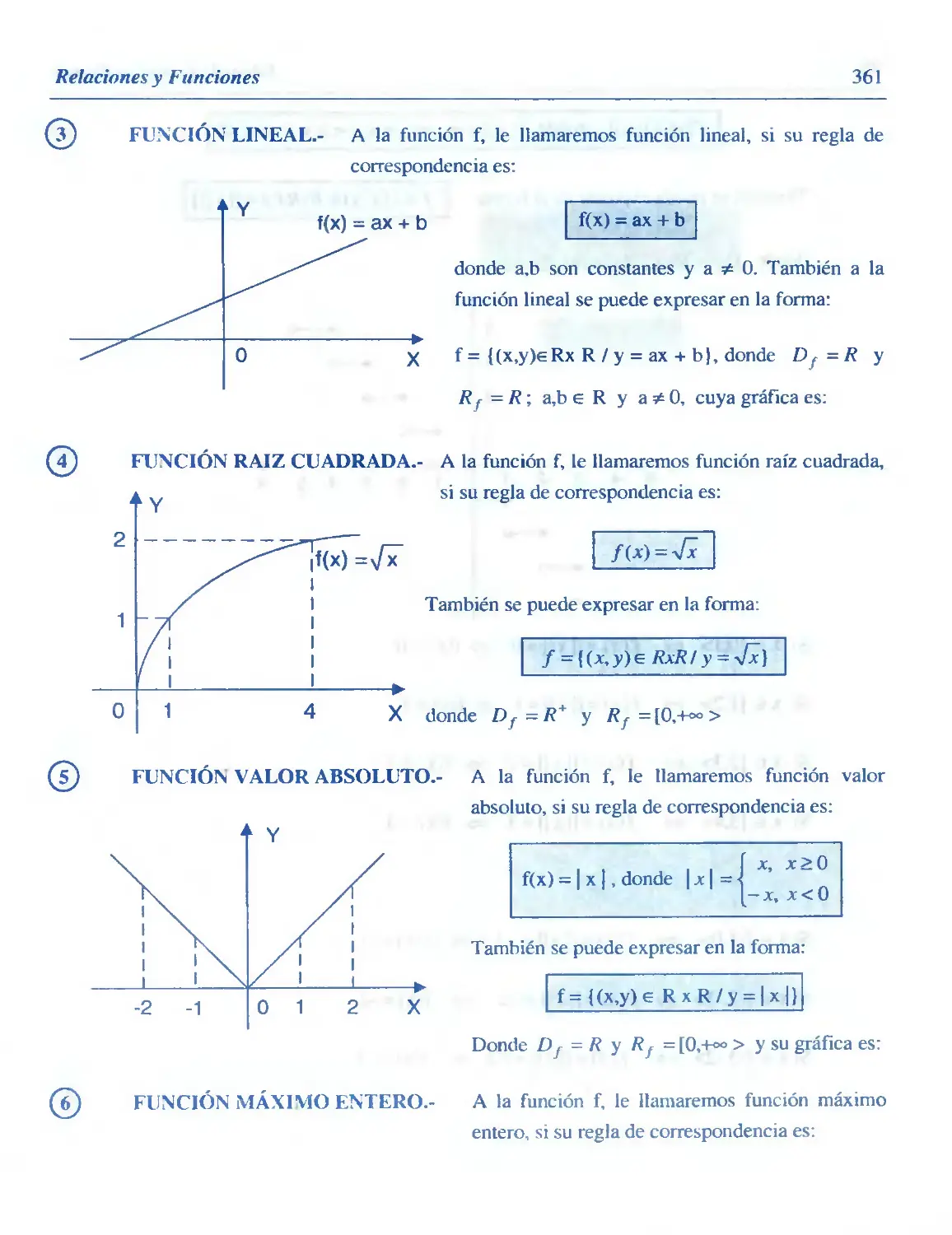
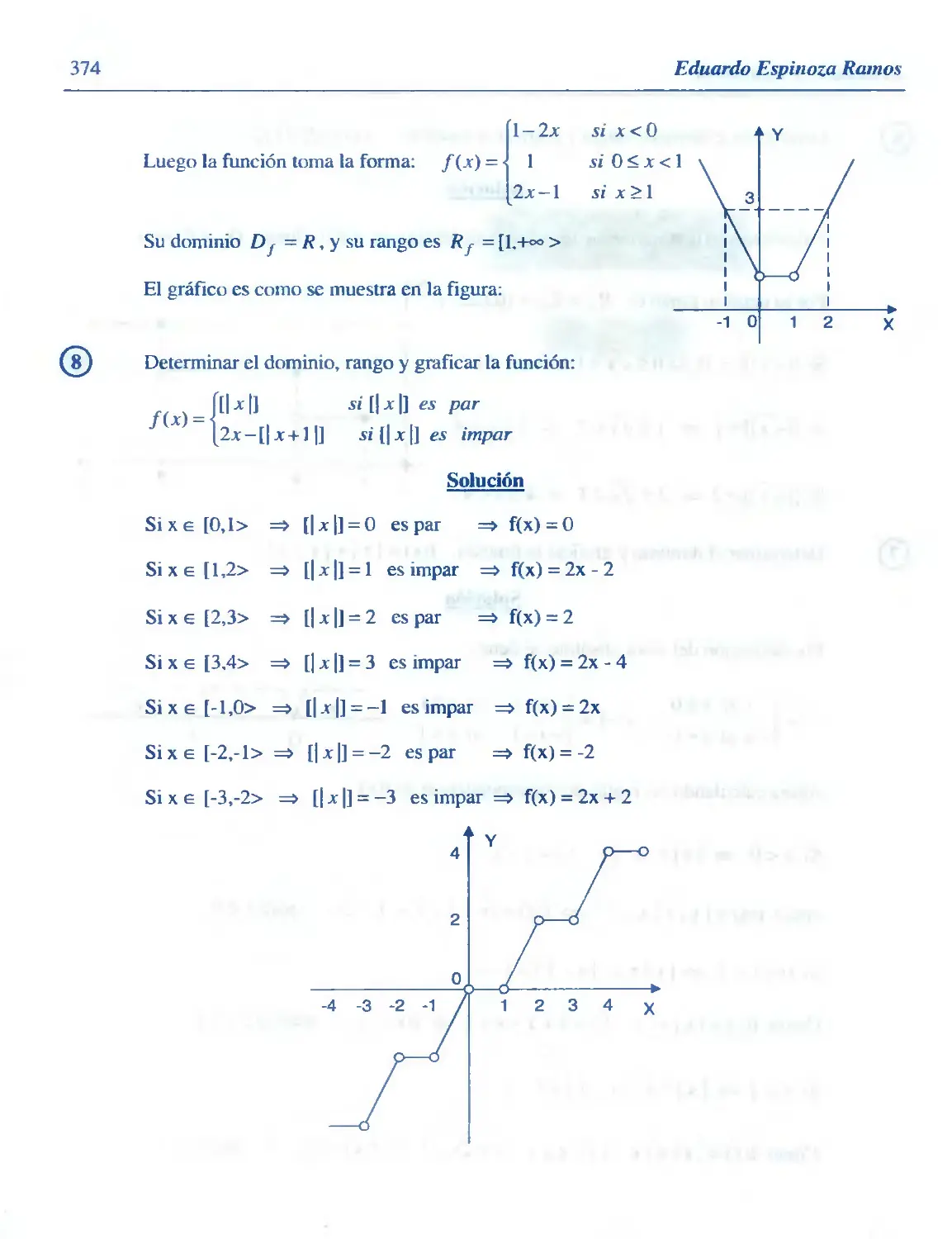
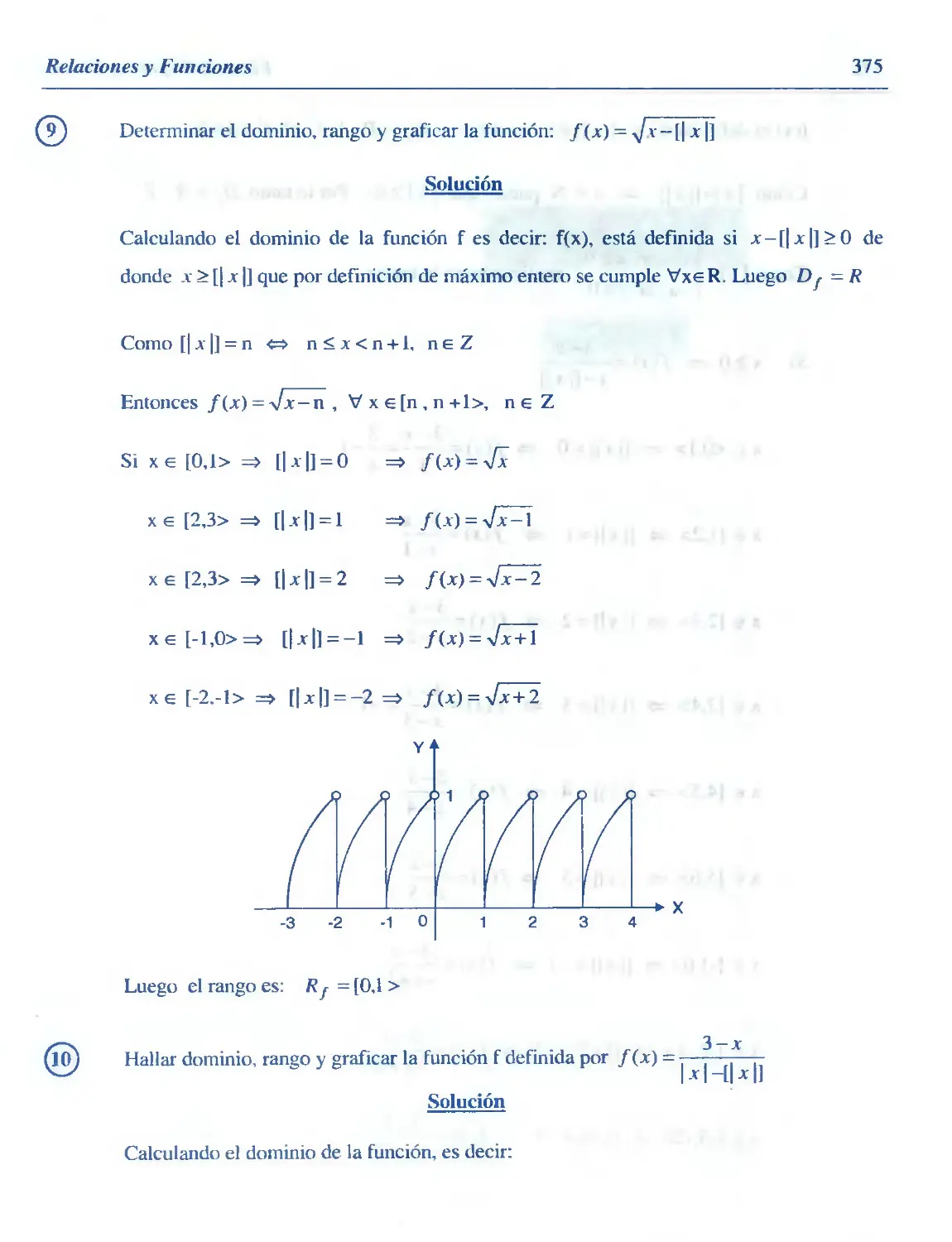
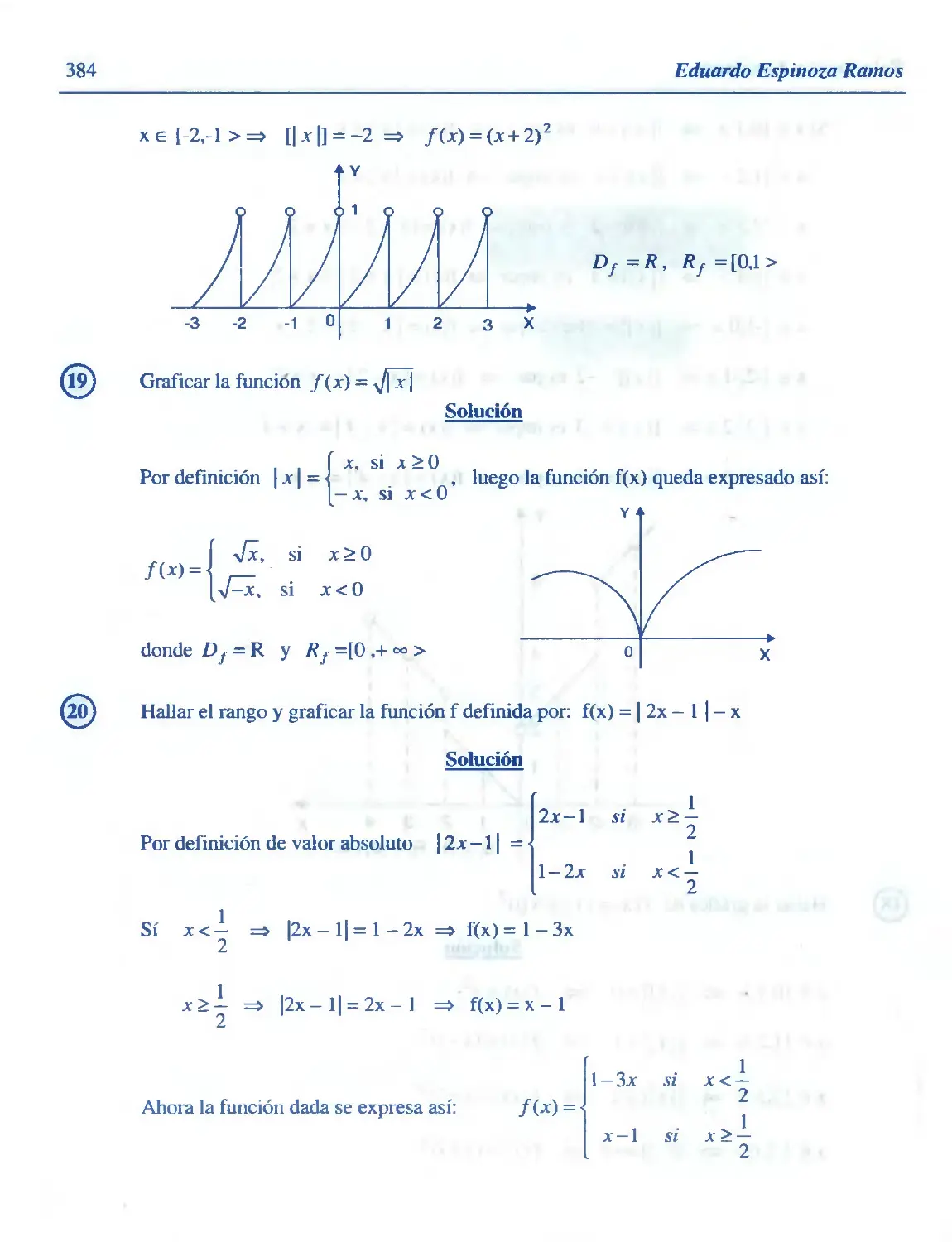
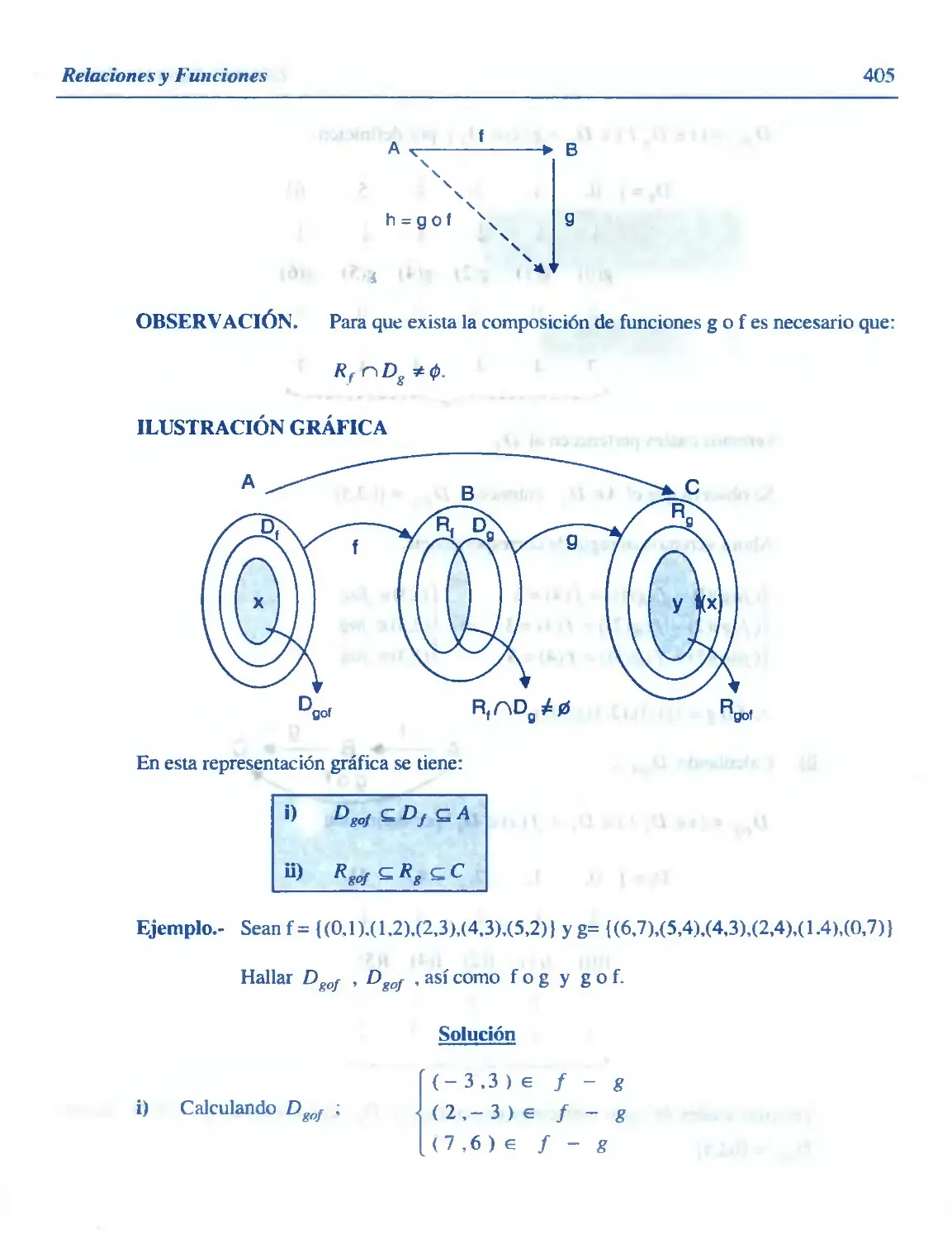
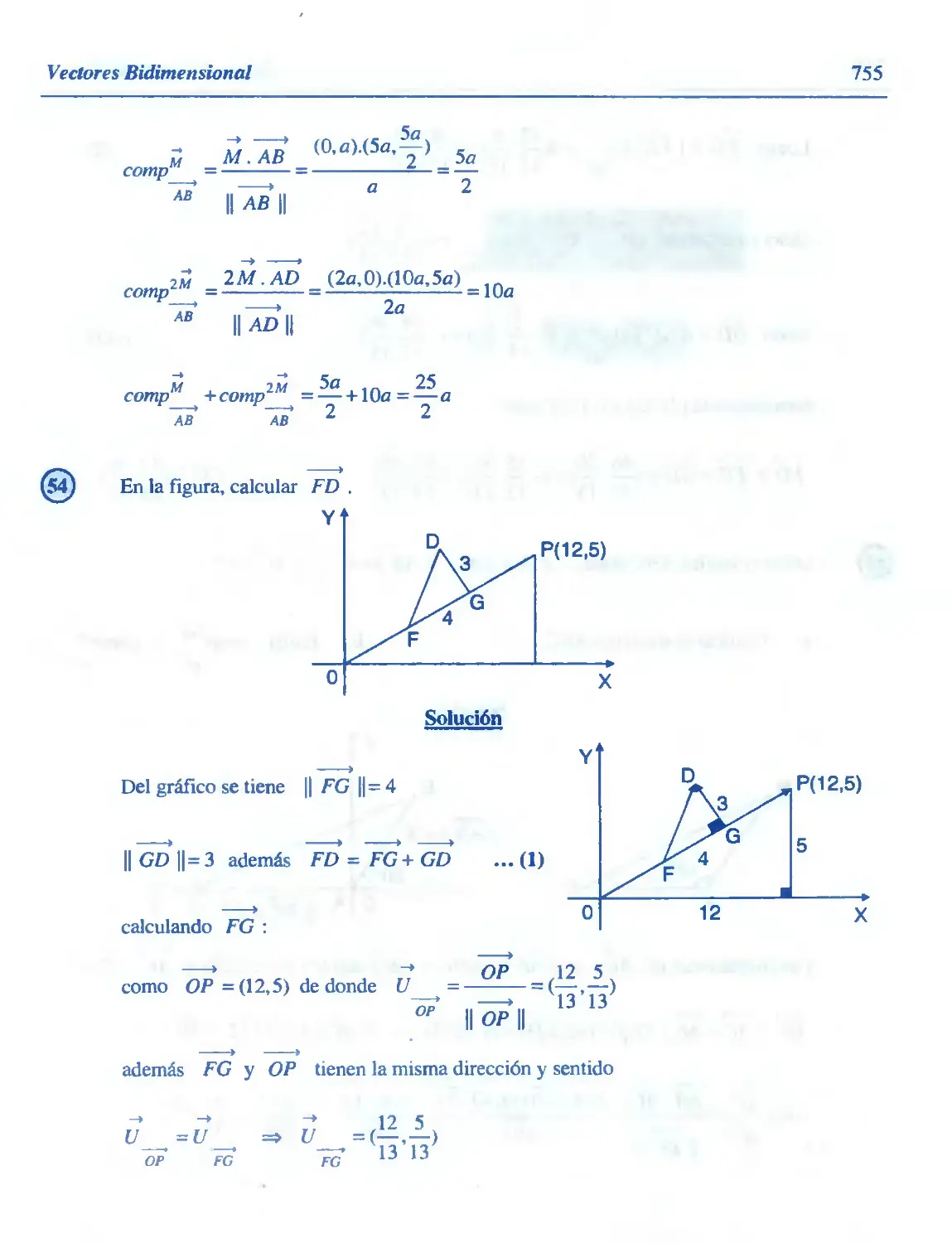
Similar
Text
MATEMÁTICA BÁSICA
n
/«^u" /n\ n-k.k
(a+b= (Ja b
k
Eduari o Es i inoz : Ramos
MATEMÁTICA
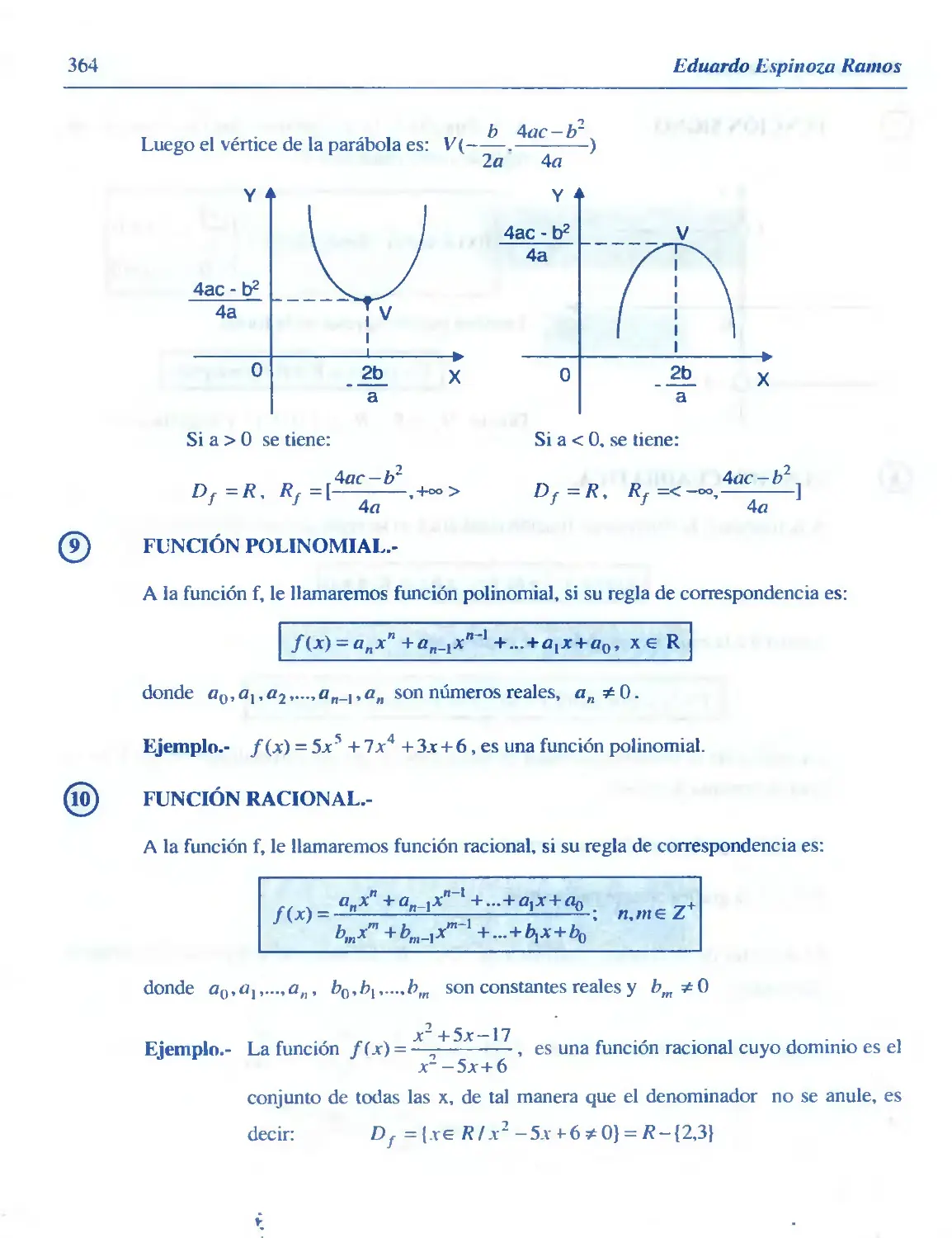
BÁSICA
♦ LÓGICA ♦ CONJUNTOS
oo xn
♦ N° REALES n=o n! ♦ RELACIONES Y FUNCIONES
♦ INDUCCIÓN MATEMÁTICA ♦ N° COMPLEJOS
♦ TEORÍA DE POLINOMIOS ♦ VECTORES EN R2
EDUARDO ESPINOZA RAMOS
LIMA - PERÚ
IMPRESO EN EL PERÚ
05 - 05 - 2005
2o EDICIÓN
DERECHOS RESERVADOS
Este libro no puede reproducirse total ó parcialmente por ningún método
gráfico, electrónico o mecánico.
incluyendo los sistemas'de fotocopia.
registros magnéticos o de alimentación de datos, sin expreso consentimiento
del autor y Editor.
RUC
Ley del Libro
Ley de Derechos del Autor
Registro comercial
Escritura Publica
N°10070440607
N° 28086
N°13714
N°10716
N° 4484
PROLOGO
La presente obra titulada "Matemática Básica" en su segunda edición contiene
esencialmente los temas que generalmente se desarrolla en los primeros cursos en las carreras de
ciencias. Ingeniería. Economía, Administración, Medicina, etc., así como también en los Institutos
Superiores.
En la actualidad el contenido científico de un libro debe complementarse con el aspecto
didáctico que es tan importante como el contenido científico, por tal motivo en el presente trabajo
se expone en forma Teórica y Práctica en donde en cada capítulo comienza con enunciados claros
de las definiciones y Teoremas juntos con sus respectivos ejemplos seguidos de una colección de
problemas resueltos y problemas propuestos.
En las definiciones importantes así como los Teoremas y Propiedades son explicados en
forma clara y amena ilustrado con gráficos y ejemplos en forma graduada.
La presente obra consta de ocho capítulos: Lógica, Conjunto, Sistema de los Números
Reales, Relaciones y Funciones, inducción Matemática, Números Complejos, la Teoría de
Polinomios y Vectores en R~ que es el capítulo que se ha agregado a la edición anterior así mismo
se ha incluido la divisibilidad de los números enteros, se ha incluido mas problemas y aplicaciones
a la economía.
El presente texto es básicamente para estudiantes recién ingresantes a las Universidades
en las especialidades de Ciencias Matemáticas. Físicas, Ingeniería y Economía y a toda persona
interesada en fundamentar sólidamente sus conocimientos matemáticos.
Deseo expresar mi más profundo agradecimiento a mis colegas de las diversas
universidades en donde presto mis servicios, quienes con su apoyo moral y sugerencias han hecho
posible la realización de este libro en su 2da edición.
Agradezco por anticipado la acogida que brinden a la presente obra.
Eduardo Espinoza Ramos
DEDICATORIA
Este libro lo dedico a mis hijos:
RONALD, JORGE Y DIANA
que Dios ilumine sus caminos para que puedan
ser guías de su prójimo
ÍNDICE
CAPITULO I
LÓGICA
1.1. Introducción 1
1.2. Elementos de Lógica Simbólica 2
1.3. Proposiciones Lógicas 3
1.4. Definición 3
1.5. Conectivos Lógicos 3
1.6. Clases de Proposiciones Lógicos 4
1.7. Proposiciones Compuestos Básicos 4
1.8. Proposiciones Compuestas 8
1.9. Jerarquía de los Conectivos Lógicos 9
1.10. Tautológicas, contradicciones y contingencias 9
1.11. Implicación Lógica y Equivalencia Lógica 12
1.12. Proposiciones Lógicamente Equivalente 13
1.13. Principales Leyes Lógicas o Tautológicas 13
1.14. La Inferencia Lógica o Argumento Lógico 18
1.15. Definición 18
1.16. Teorema 19
1.17. Inferencia Validas Notables 20
1.18. El Método Abreviado 21
1.19. Métodos de Demostración 25
1.20. Forma o Método Directo de Demostración 25
1.21. Forma o Método Indirecto de Demostración 26
1.22. Definición 26
1.23. Circuitos Lógicos 28
1.24. Diseño de Circuitos Eléctricos en Serie 28
1.25. Diseño de Circuitos Eléctricos en Paralelo 29
1.26. Lógica Cuantificacional 33
1.27. Cuantificadores Existencial y Universal 33
1.28. Negación de Proposiciones en Cuantificadores 35
1.29. Ejercicios Desarrollados 36
1.30. Ejercicios Propuestos 49
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
2.12.
2.13.
2.14.
2.15.
2.16.
2.17.
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
3.1.
3.2.
3.3.
3.4.
Definición
CAPITULO II
TEORÍA DE CONJUNTOS
Definición
Relación de Pertenencia
Diagrama de VENN - EULER
Determinación de Conjuntos
Conjuntos Numéricos
Conjunto Finito
Conjunto Infinito
Relaciones entre Conjunto
Igualdad de Conjuntos
Propiedades de la Igualdad de Conjunto
Conjuntos Especiales
Representación Gráfica de los Conjuntos
Ejercicios Propuestos
Operaciones con Conjuntos
Conjunto Potencia
Propiedades del Conjunto Potencia
Intervalos
Operaciones de Conjuntos Aplicados a los Intervalos
Familia de Conjuntos
Número de Elementos de un Conjunto
Propiedades del Número de Elementos de un Conjunto
Ejercicios Propuestos
Introducción
CAPITULO III
SISTEMA DE NÚMEROS REALES
Definición
Axioma de Sustitución
Axioma Distrib
utivo
69
69
69
70
71
72
73
73
73
76
76
77
79
80
83
103
104
107
108
112
117
117
125
140
141
143
143
3.5. Teorema de la Igualdad para la Suma 143
3.6. Teorema de la Igualdad para la Multiplicación 143
3.7. Teorema de Cancelación para la Adición 143
3.8. Teorema de Cancelación para la Multiplicación 144
3.9. Sustracción de Números Reales 144
3.10. División de Números Reales 144
3.11. Ejercicios Desarrollados 145
3.12. Representación de los Números Reales 149
3.13. Desigualdades 150
3.14. Axioma de la Relación de Orden 151
3.15. Definición 151
3.16. Teorema 151
3.17. Teorema 152
3.18. Teorema 152
3.19. Teorema 153
3.20. Teorema 153
3.21. Teorema 154
3.22. Ejercicios Desarrollados 154
3.23. Ejercicios Propuestos 162
3.24. Inecuaciones 168
3.25. Conjunto Solución de una Inecuación 170
3.26. Resolución de una Inecuación 170
3.27. Inecuación de Primer Grado en una Incógnita 170
3.28. Inecuación de Segundo Grado en una Incógnita 172
3.29. Inecuaciones Polinómicas 177
3.30. Inecuaciones Fraccionarias 181
3.31. Inecuaciones Exponenciales 183
3.32. Inecuaciones Irracionales 185
3.33. Ejercicios Desarrollados 196
3.34. Ejercicios Propuestos 221
3.35. Valor Absoluto 238
3.36. Propiedades Básicas para resolver Ecuación e Inecuaciones donde
interviene Valor Absoluto 239
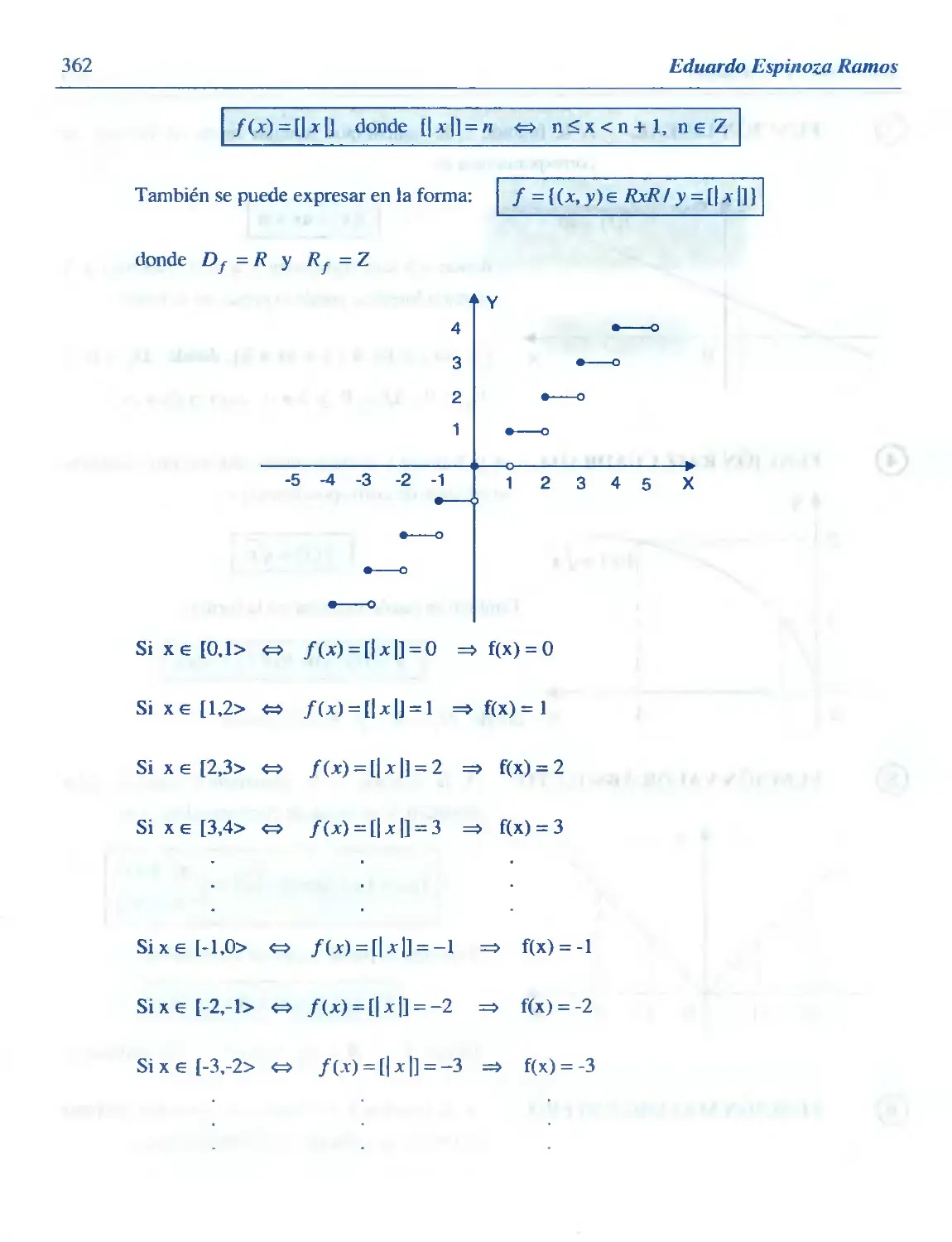
3.37. Máximo Entero 242
3.38. Propiedades del Máximo Entero 244
3.39. Inecuación Logarítmica 249
3.40. Ejercicios Desarrollados 254
3.41. Ejercicios Propuestos 293
3.42. Aplicaciones de las Inecuaciones a la Administración y Economía 314
3.43. Ejercicios Propuestos 318
CAPITULO IV
RELACIONES Y FUNCIONES
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
4.7.
4.8.
4.9.
4.10.
4.11.
4.12.
4.13.
4.14.
4.15.
4.16.
4.17.
4.18.
4.19.
4.20.
4.21.
4.22.
4.23.
4.24.
4.25.
4.26.
4.27.
4.28.
4.29.
4.30.
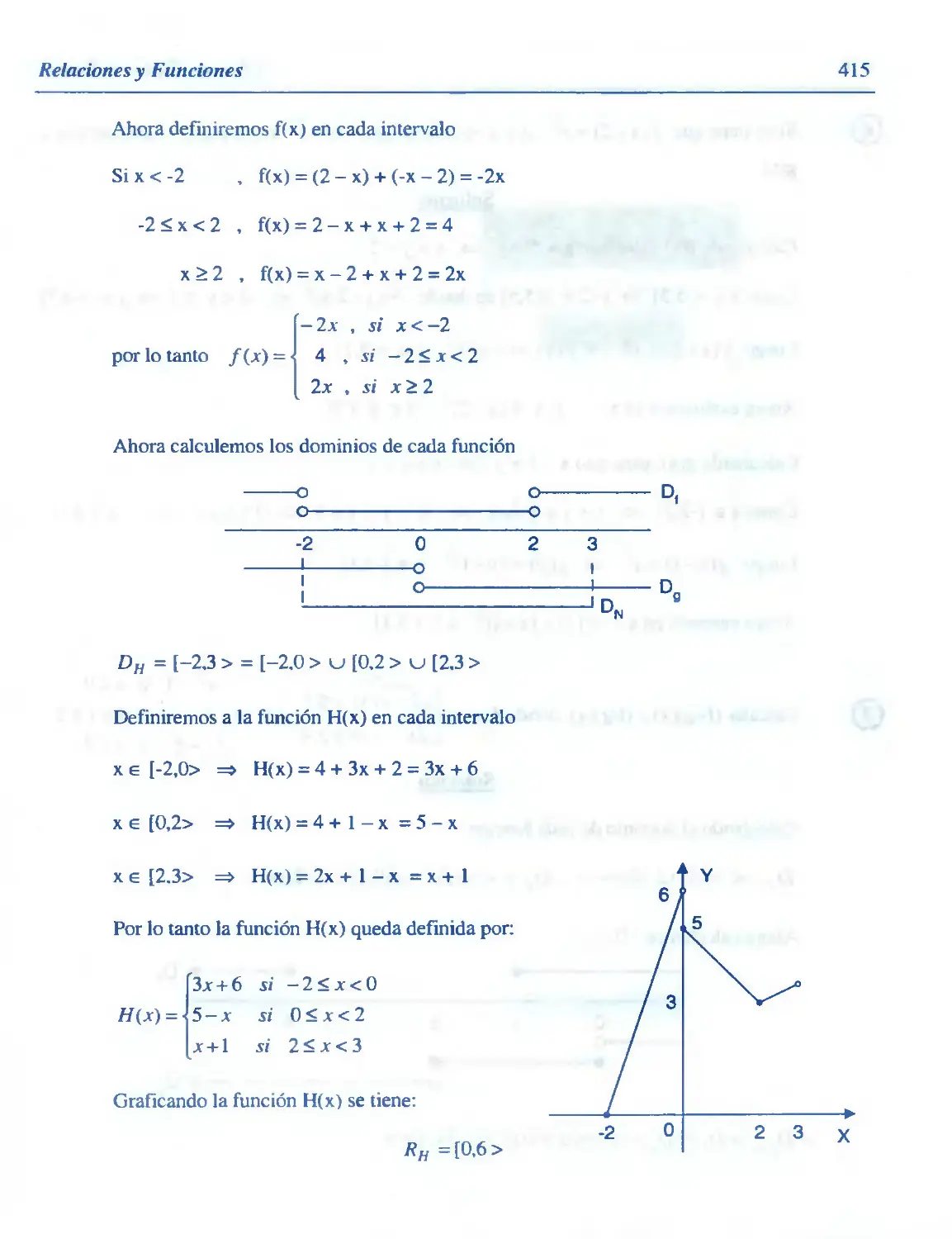
Introducción
Relaciones Binarias
Gráfica de una Relación de R en R
Ejercicios Desarrollados
Ejercicios Propuestos
Funciones
Dominio y Rango de una Función
Criterio para el Calculo de Dominio y Rango de una Función
Aplicación de A en B
Funciones Especiales
Evaluación de una Función
Funciones Definidas con Varias Regla de Correspondencia
Trazado de Gráfica Especiales
Ejercicios Desarrollados
Ejercicios Propuestos
Operaciones con Funciones
Composición de Funciones
Propiedades de la Composición de Funciones
Ejercicios Desarrollados
Ejercicios Propuestos
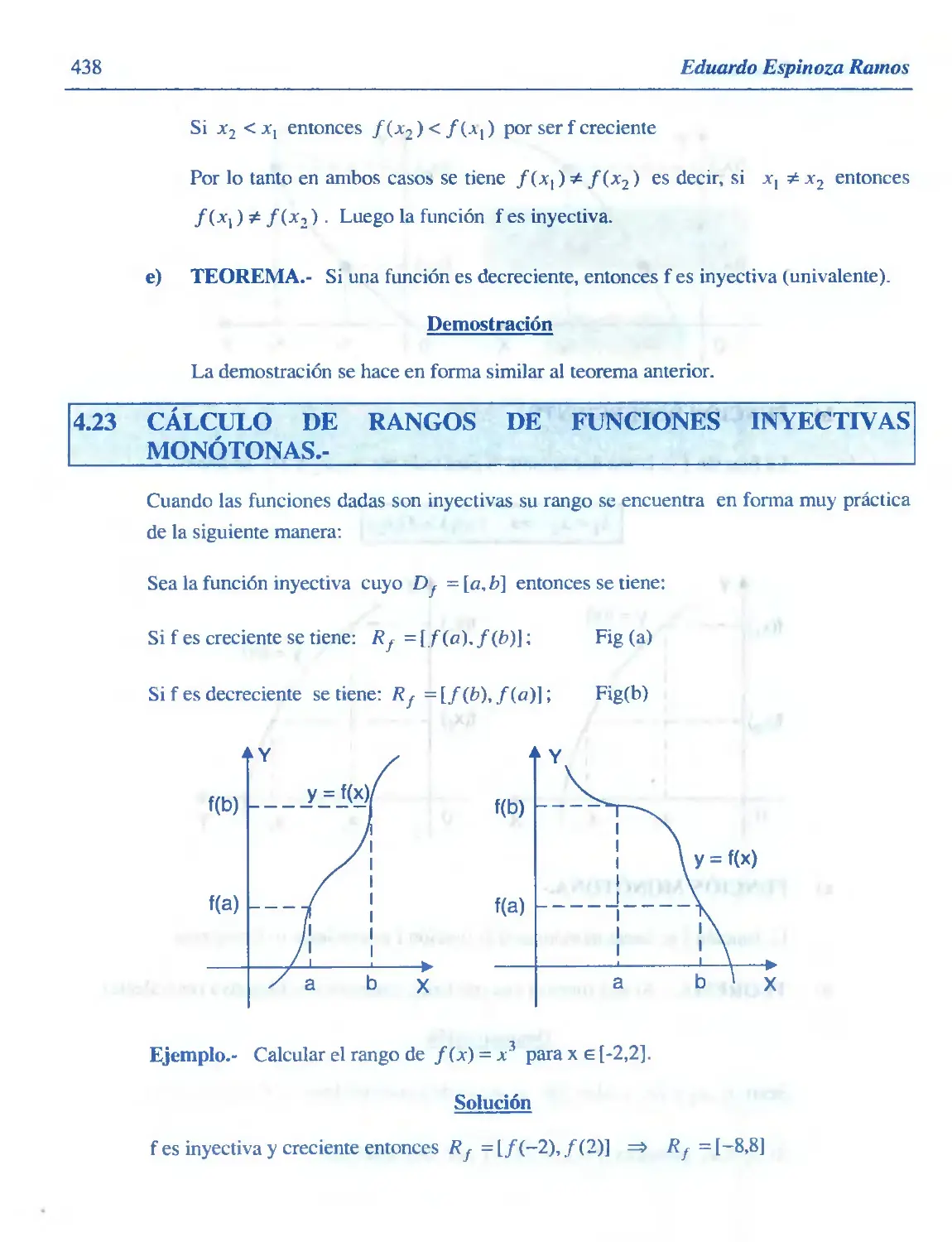
Función: Inyectiva, Suryectiva y Biyectiva
Funciones Crecientes, Decrecientes y Monótonas
Cálculo de Rango de Funciones Inyectivas Monótonas
Función Inversa
Función Inversa de una Composición
Ejercicios Desarrollados
Ejercicios Propuestos
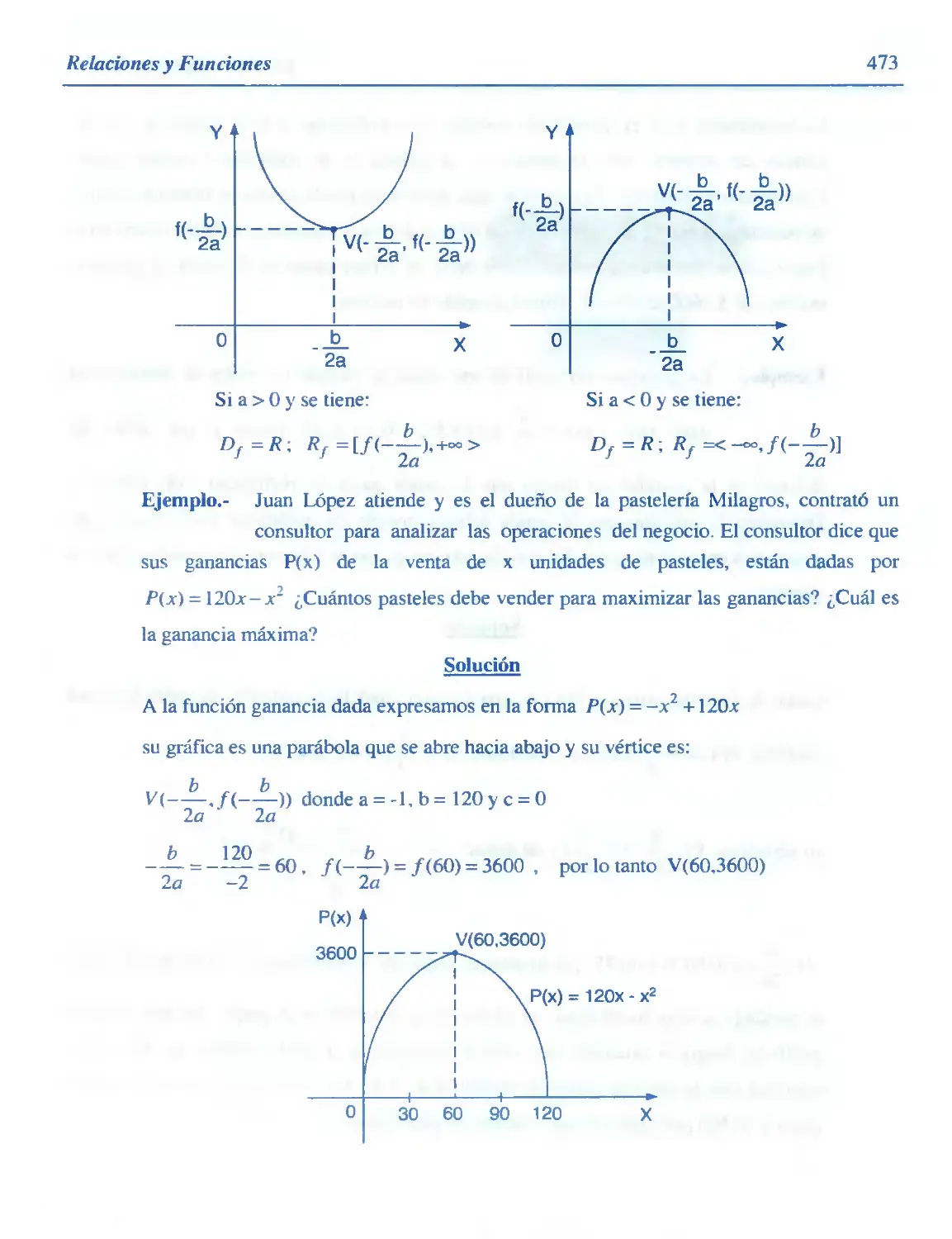
Aplicaciones de las Funciones en Administración y Economía
Ejercicios Desarrollados
Ejercicios Propuestos
323
332
339
343
353
356
357
358
359
360
365
365
366
370
388
399
404
411
411
423
433
436
438
439
441
441
454
466
477
483
CAPITULO V
INDUCCIÓN MATEMÁTICA
.1.
.2.
.3.
.4.
.5.
.6.
.7.
.8.
.9.
.10.
.11.
.12.
.13.
.14.
.15.
.16.
.17.
.18.
.19.
.20.
.21.
.22.
.23.
>.24.
».25.
.26.
.27.
.28.
.29.
.30.
.31.
Introducción
Conjuntos Acotados
Axioma del Supremo o Axioma de la Mínima Cota Superior
Principio Arquimediano
Principio del Buen Orden
Menor Elemento y Mayor elemento de A cz R
Proposición
Sub Conjuntos Inductivos de R
El Principio de Inducción Matemática Completa
Teorema 1 (Primer Principio de Inducción)
Teorema 2 (Segundo Principio de Inducción)
Definición
Ejercicios Propuestos
Sumatorias
Propiedades de la Sumatoria
Fórmulas de la Sumatoria
Notación del Producto de n Números
Ejercicios Propuestos
Divisibilidad en Z
Máximo como Divisor M.C.D.
Lema
Mínimo Común Múltiplo
Regla para averiguar si un número dado es primo
Criba de Erastóstenes
Ejercicios Propuestos
La Función Factorial
Números Combinatorios
Principales Propiedades de los Coeficientes Binomiales
El Triángulo de BLAISE PASCAL
Potencias de un Binomio
Ejercicios Propuestos
490
491
492
493
495
495
496
496
498
499
499
500
507
511
511
516
520
523
529
534
538
539
540
541
542
543
544
546
548
548
551
CAPITULO VI
NÚMEROS COMPLEJOS
6.1. Ecuaciones sin Solución en R 557
6.2. Definición 557
6.3. Definición 557
6.4. Plano Complejo 558
6.5. Definición 558
6.6. Ejercicios Propuestos 558
6.7. Cero y Opuesto de un Número Complejo 559
6.8. Operaciones con Complejos 560
6.9. Unidad Imaginaria 560
6.10. Forma Estándar o Binómica de Números Complejos 566
6.11. Teorema 566
6.12. La Conjugación en C 566
6.13. Módulo de un Número Complejo 567
6.14. Ejercicios Desarrollados 568
6.15. Ejercicios Propuestos 589
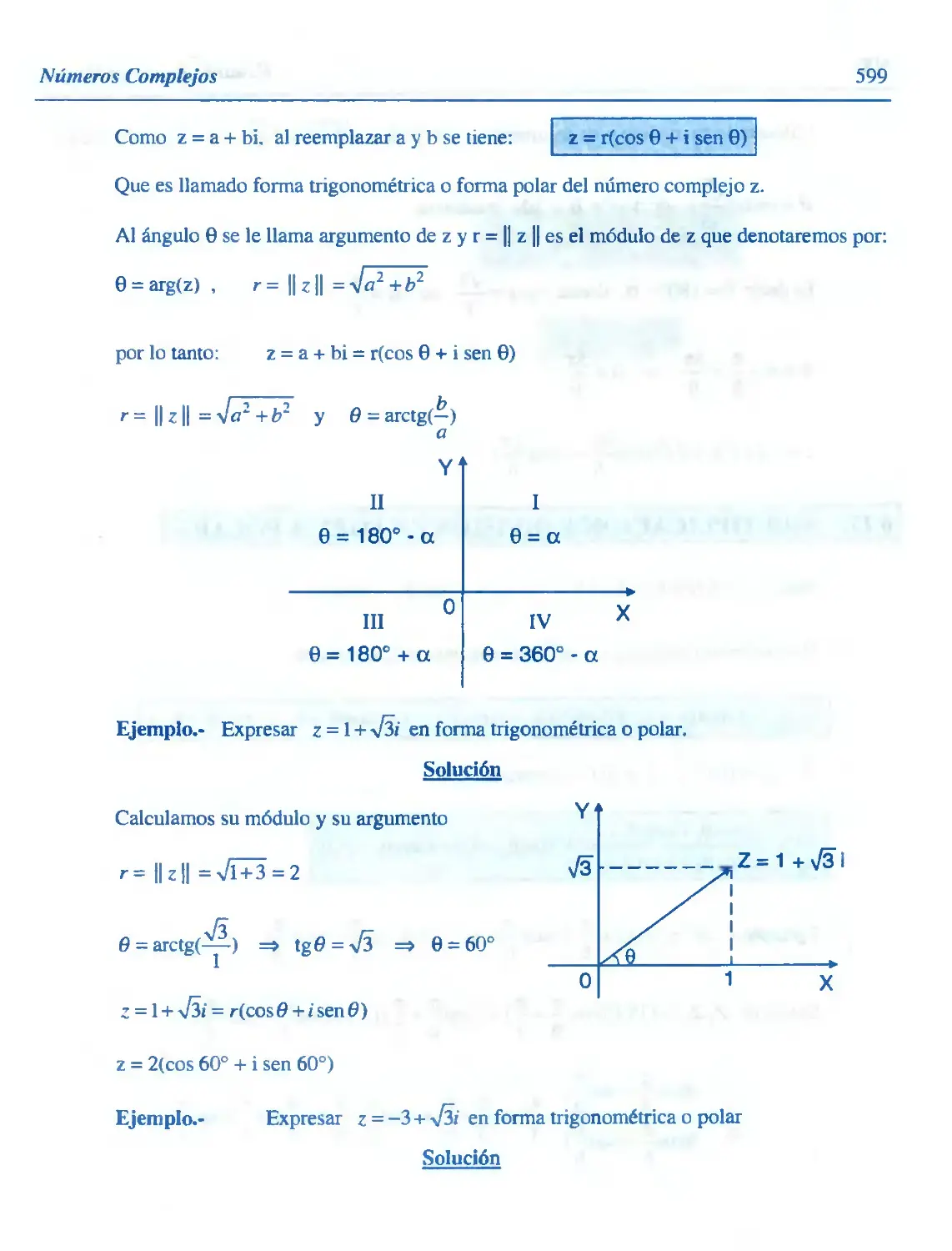
6.16. Forma Trigonométrica o Polar de un Número Complejo 598
6.17. Multiplicación y División en Forma Polar 600
6.18. Potencia y Raíces de Números Complejos 601
6.19. Exponenciales Complejas (Fórmula de Euler) 604
6.20. Logaritmos en C 605
6.21. Exponencial Compleja General 606
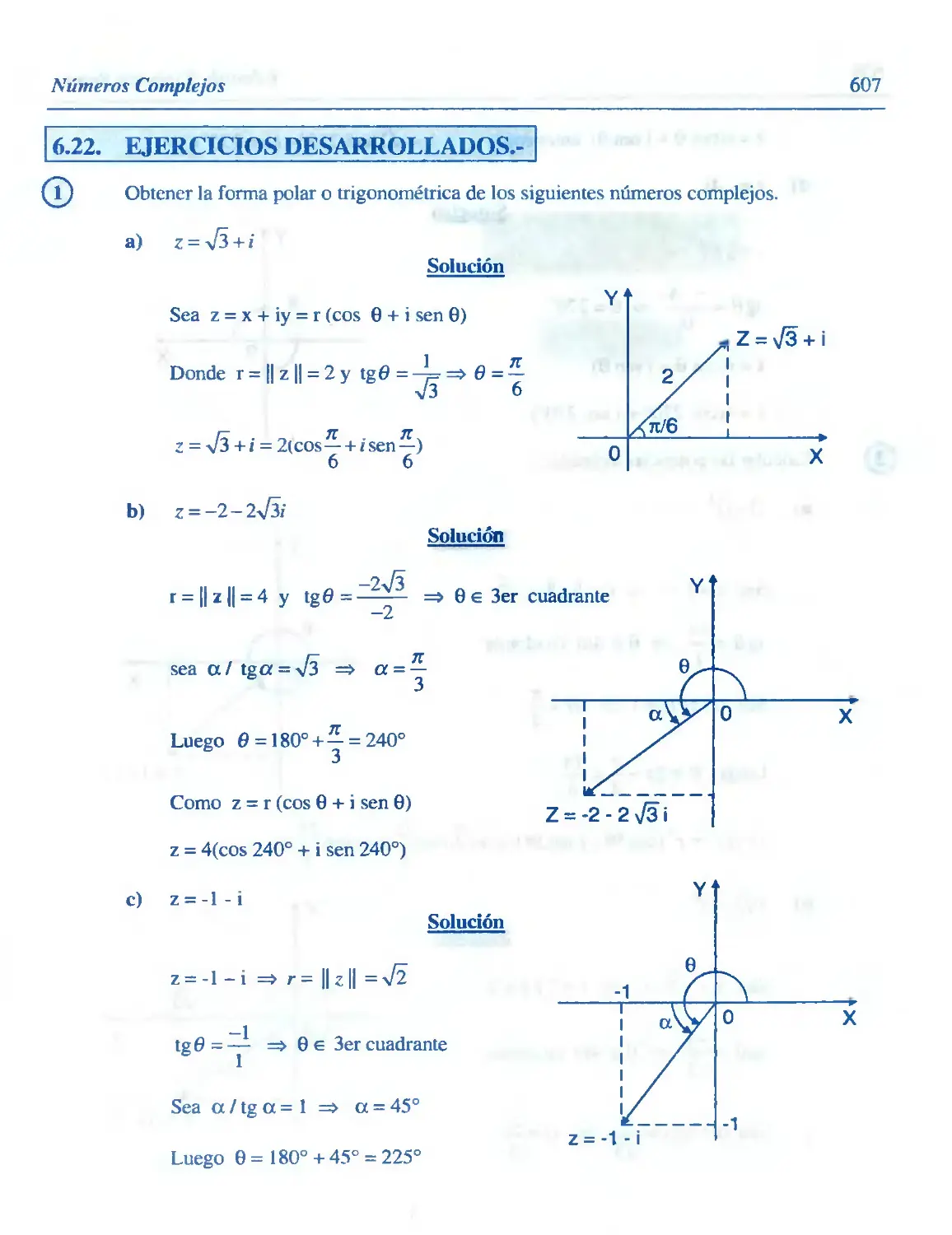
6.22. Ejercicios Desarrollados 607
6.23. Ejercicios Propuestos 619
6.24. Miscelánea de Ejercicios 623
CAPITULO VII
teoría de ecuaciones
7.1. Definición 635
7.2. Ecuaciones Polinómicas de Segundo Grado 637
7.3. Raíces y Discriminante de una Ecuación Cuadrática 637
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
7.10.
7.11.
7.12.
7.13.
7.14.
7.15.
7.16.
7.17.
7.18.
7.19.
7.20.
7.21.
7.22.
7.23.
7.24.
7.25.
7.26.
7.27.
7.28.
7.29.
7.30.
7.31.
7.32.
Relación Entre Raíces y Coeficientes de una Ecuación Cuadrática
Ecuaciones Reducibles a Cuadráticas
Ecuaciones Irracionales
Algoritmo de la División
Teorema (Algoritmo de la División para Polinomio)
La División Sintética
Teorema del Resto
Teorema del Factor
Raíces de un Polinomio
Teorema Fundamental del Algebra
Número de Raíces de una Ecuación Polinómica
Definición
Raíces Enteras
Forma Factorizada de un Polinomio
Relación Entre los Coeficientes y las Raíces de una Ecuación Polinómica
Naturaleza de las raíces de Polinomios Reales
Raíces Racionales de un Polinomio
Teorema del Limite Superior de las Raíces Reales (LAGRANGE)
Variación de Signos de un Polinomio
Regla de los Signos de Descartes
Ecuaciones Binómicas
Ecuaciones Trinómicas Bicuadradas
Ecuaciones Recíprocas
Ecuaciones Polinomicas de Tercer Orden
Ecuaciones Cuartica
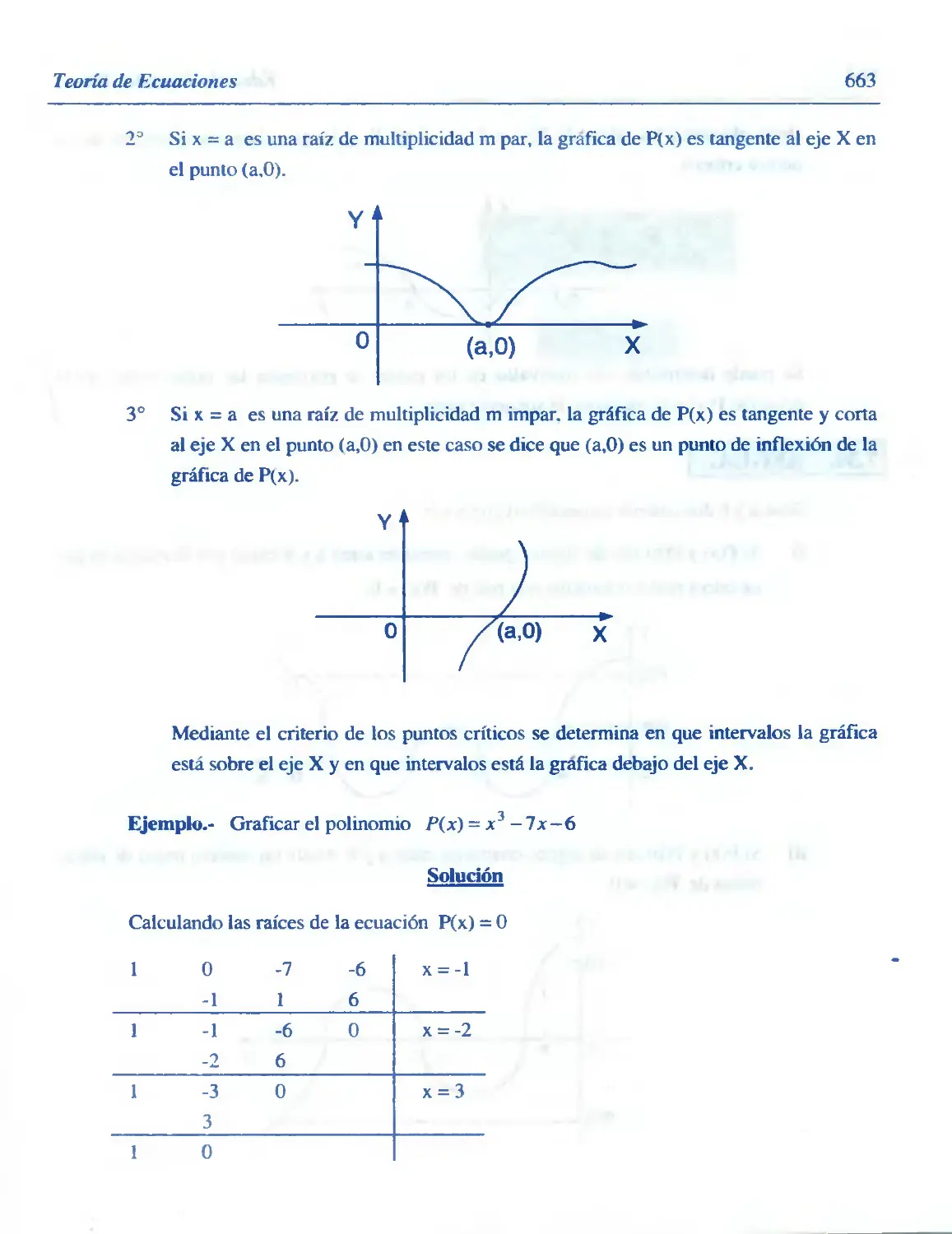
Gráfica de un Polinomio
Regla
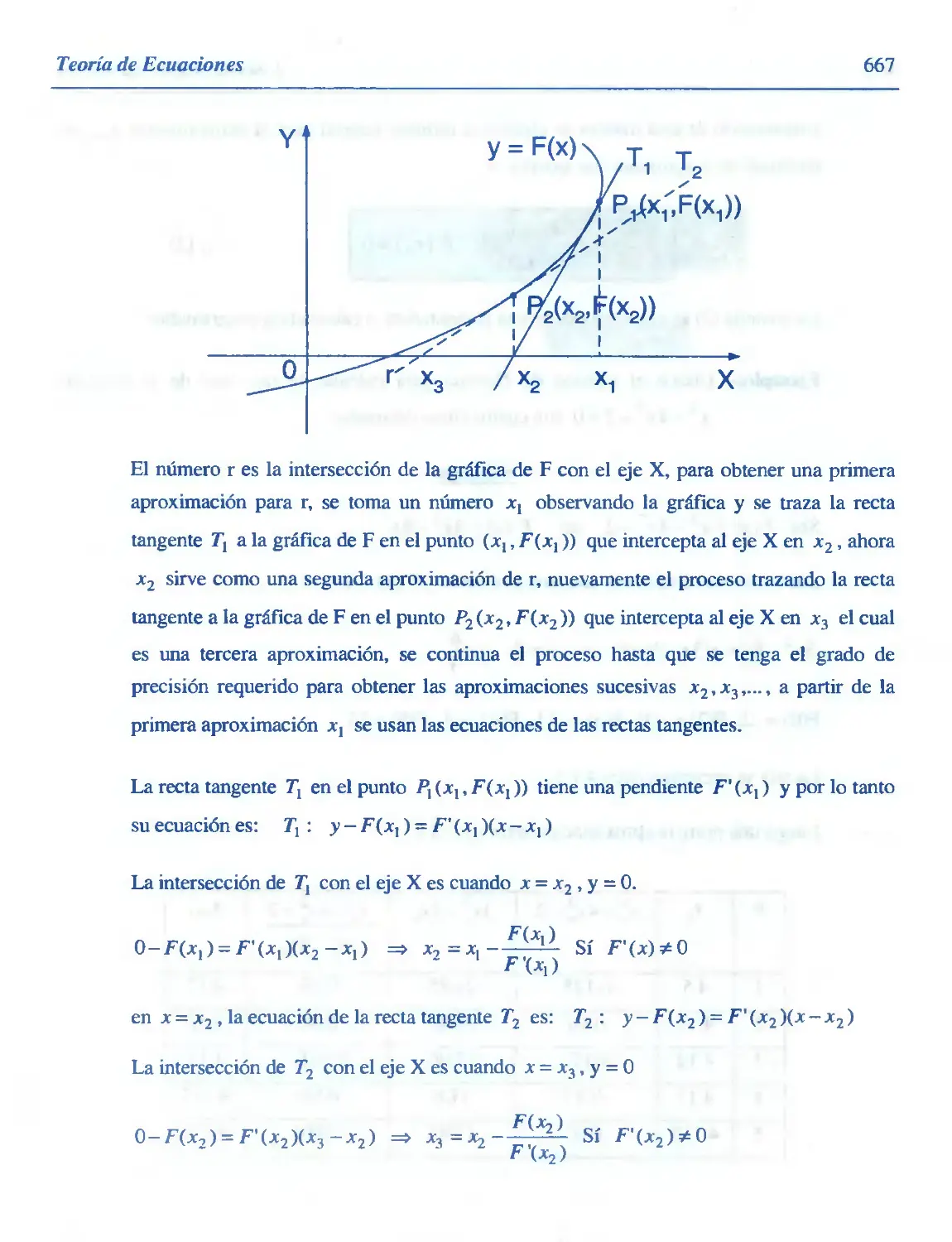
Solución Numérica de Ecuaciones con el Método de Newton
Ejercicios Propuestos
638
639
640
642
643
643
645
646
646
646
647
647
648
649
650
651
653
653
654
654
654
655
656
657
660
662
664
666
669
CAPITULO VIII
VECTORES EN R2
8.1. Conceptos Básicos 682
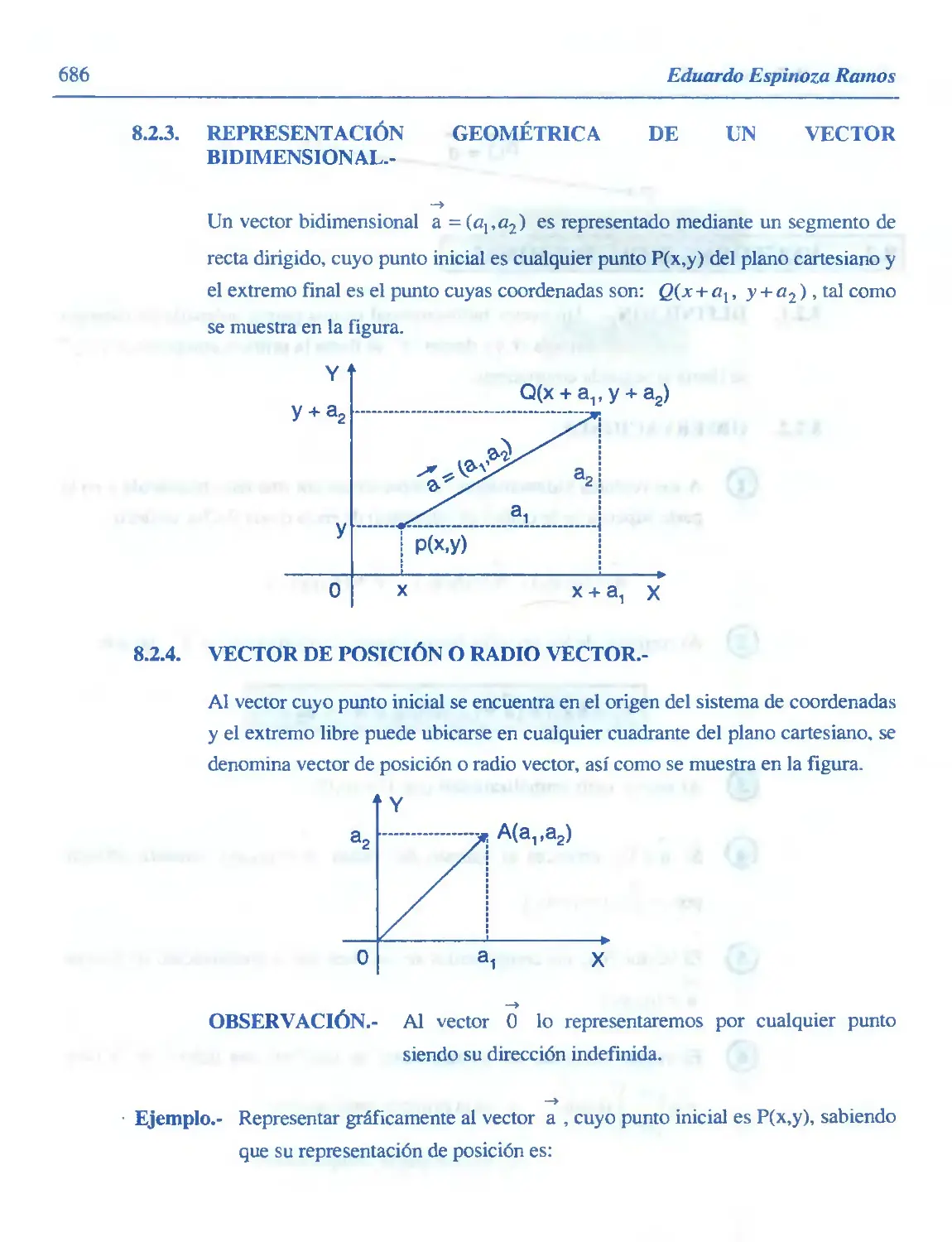
8.2. Vectores Bidimensional 685
8.3. Operaciones con Vectores 687
8.4. Longitud o Módulo de un Vector 694
8.5. Propiedades del Módulo de un Vector 696
8.6. Vector Unitario 697
8.7. Teorema 697
8.8. Dirección de un vector en R2 698
8.9. Producto Escalar de Vectores 700
8.10. Propiedades del Producto Escalar de Vectores 701
8.11. Vectores Paralelos y Ortogonales 702
8.12. Criterio de Colinealidad 703
8.13. Interpretación Geométrica de la Ortogonalidad de Vectores 704
8.14. Teorema 705
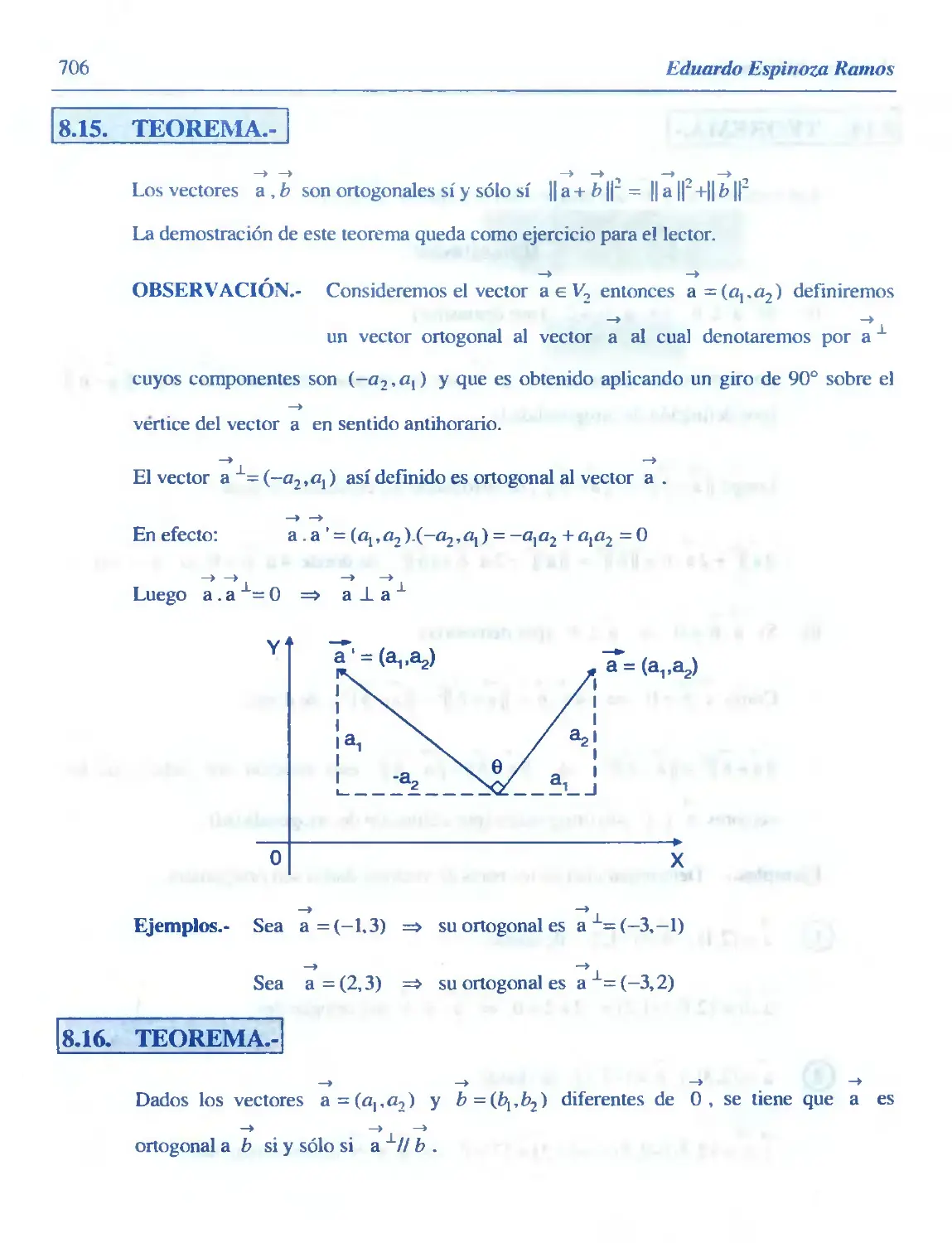
8.15. Teorema 706
8.16. Teorema 706
8.17. Corolario 707
8.18. Combinación Lineal de Vectores 708
8.19. Teorema 709
8.20. Teorema 710
8.21. Dependencia en Independencia Lineal de Vectores en R2 710
8.22. Vectores Fundamentales 712
8.23. Propiedades de los Vectores Ortogonales Unitarios 713
8.24. Definición 714
8.25. Proyección Ortogonal y Componente 714
8.26. Definición 715
8.27. Propiedades del Vector Proyección y Componente 716
8.28. Relación entre Proyección y Componente 717
8.29. Ángulo entre Dos Rectas 718
8.30. La Desigualdad de Cauchy - Schwarz 720
8.31. Área de: Triángulo y Paralelogramo 721
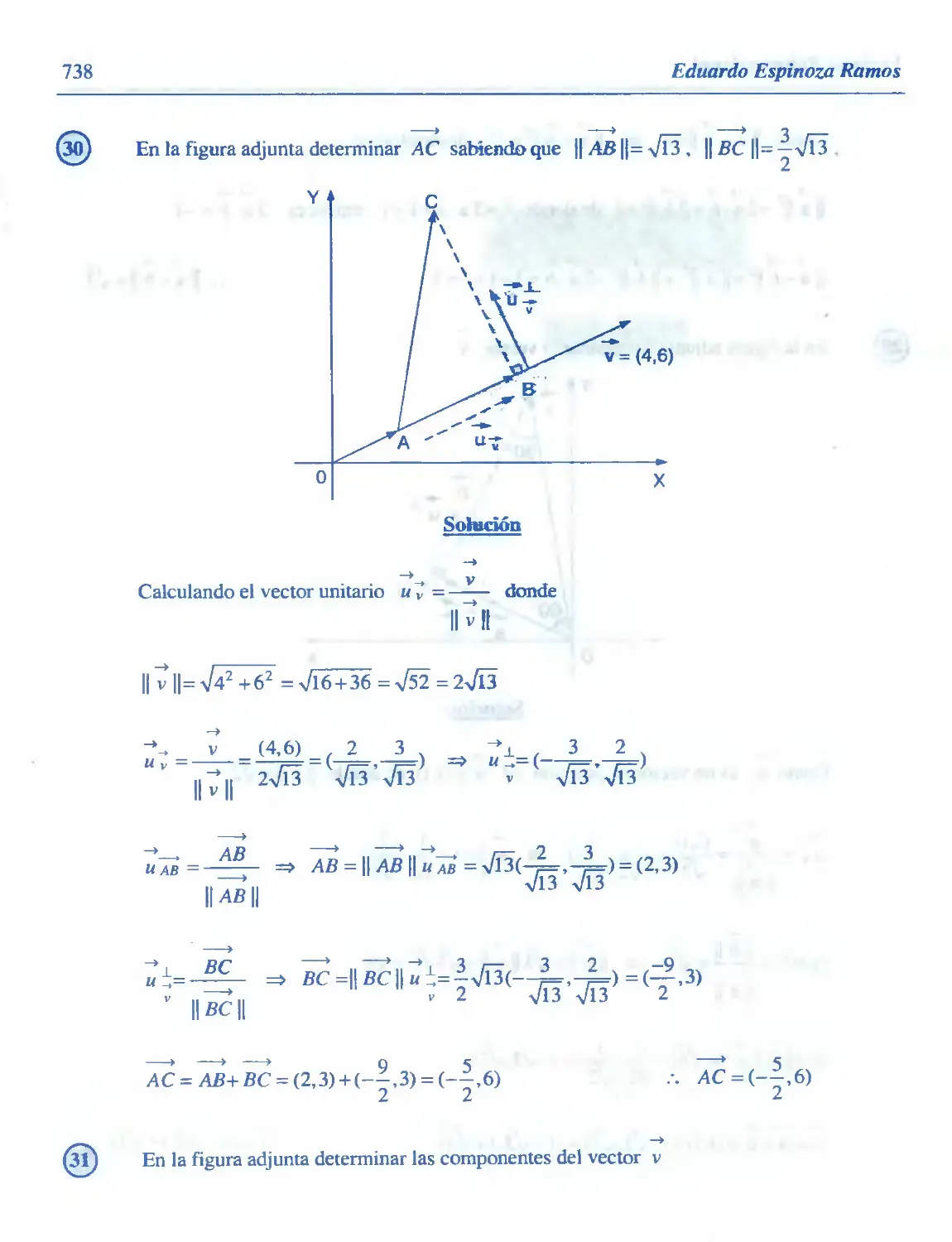
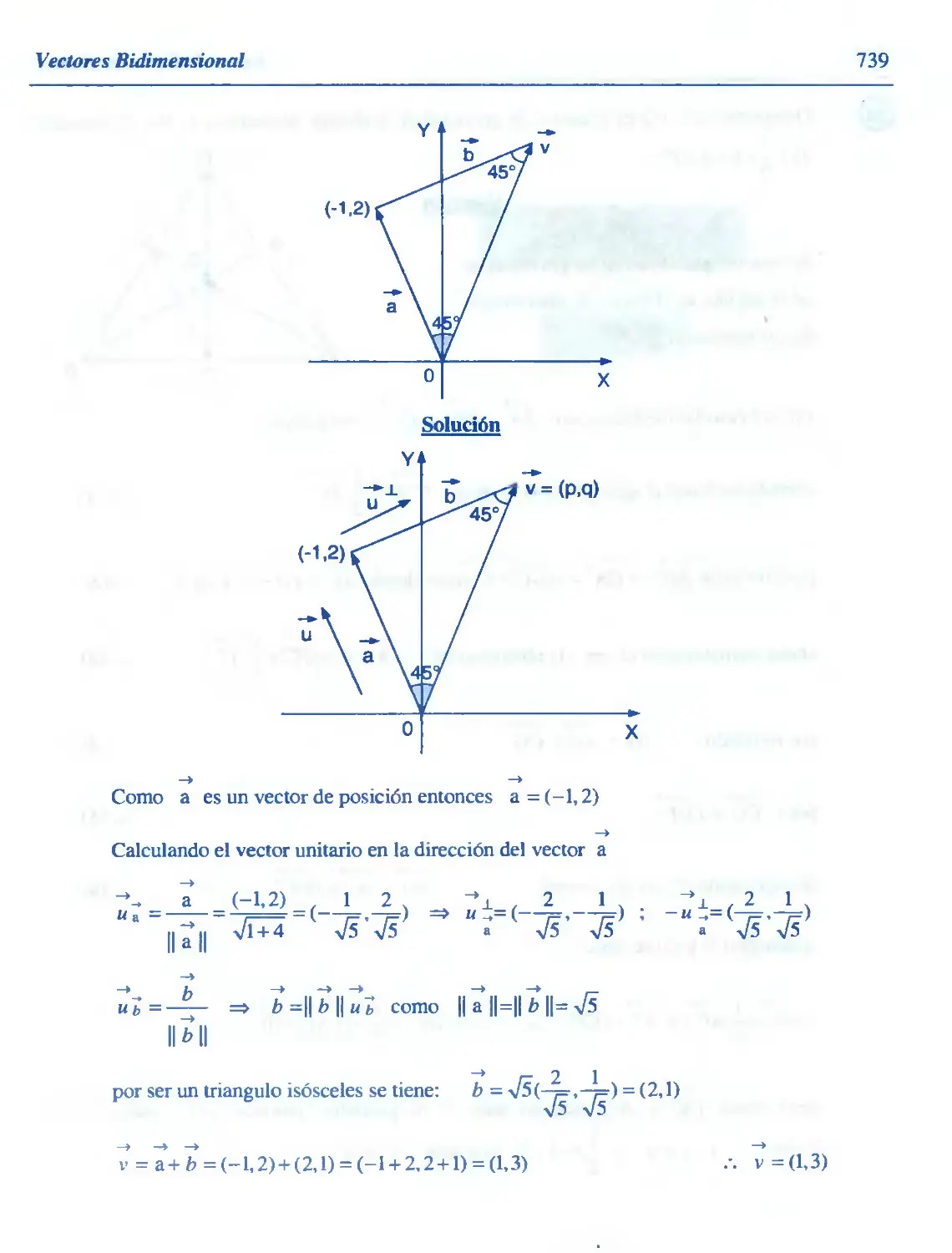
8.32. Ejercicios Desarrollados 722
8.33. Ejercicios Propuestos 760
BIBLIOGRAFÍA 784
Lógica
1
CAPITULO I
LÓGICA
1.1. INTRODUCCIÓN.-
Lógica es el estudio de los procesos válidos del razonamiento humano. En la actualidad,
el estudio serio de cualquier tema tanto en el campo de las Humanidades como el de las
ciencias y la técnica requieren conocer los fundamentos y métodos del razonamiento
lógico preciso que permite al estudiante o profesional extraer y depurar sus conclusiones
evitando el riesgo de modificar en forma equivocada la información que posee. Esto es
aun más en esta era de la computación, herramienta que es empleada en todos los campos
del desarrollo de una sociedad y con la velocidad a la cuál se procesan los datos cualquier
error de lógica puede originar problemas técnicos, sociales y económicos.
Siendo muy importante, en la matemática moderna el análisis del lenguaje con un criterio
lógico: la Lógica tiene como fin de conducimos a un hábil manejo del lenguaje
matemático y el empleo de métodos eficaces de razonamiento.
Existen dos tipos importantes del razonamiento: El inductivo y el Deductivo.
El razonamiento inductivo es el razonamiento por el cuál una persona en base a sus
experiencias específicas, decide aceptar como válida un principio general.
El razonamiento deductivo es, en cambio, el medio según el cuál dicha persona utiliza el
principio general aceptado previamente para decidir sobre la validez de una idea, que a su
vez habrá de determinar el curso de su acción.
Dado que las proposiciones son preceptos válidos de razonamiento deductivo, en el
desarrollo de nuestro estudio veremos lo esencial de la lógica proposicional, a través del
uso y manejo de una simbología adecuada.
2
Eduardo Espinoza Ramos
1.2. ELEMENTOS DE LÓGICA SIMBÓLICA,
a) ENUNCIADO.- Se denomina enunciado a toda frase u oración.
Ejemplo.- ff) 11 es un número primo. \2J París está en Italia.
© ¿Qué hora es? © ¡Viva el Perú!
© 5>9 © 6+2=8
© x2 <9 ® jc2 + v2<4
Los enunciados que matemáticamente tienen significado son aquellos que pueden
ser considerados como verdaderos o falsos (proposiciones); algunos enunciados no
es posible afirmar si es verdadero o falso, como por ejemplo, las interrogaciones, las
exclamaciones o las preguntas.
b) ENUNCIADOS ABIERTOS.- Son expresiones que contienen variables y no
tienen la propiedad de ser verdadero o falso.
Ejemplo.-
(T) x < 7, es un enunciado abierto, porque no podemos afirmar si es verdadero o
falso, solamente cuando a la variable x se le dá un valor numérico podemos
decir si es verdadero o falso.
Así por ejemplo: para x = 3, 3 < 7 es verdadero
para x = 9, 9 < 7 es falso
(Y\ x2 + y2 = 16, también es un enunciado abierto.
c) VARIABLE.- Es una cantidad susceptible de variar en un determinado campo o
recorrido, a las variables representaremos por las letras
minúsculas x,
y, z. t, u, v, a estas variables se les dá el nombre de variables indeterminados.
Ejemplo.-
CO y = y¡x-5 es un número real, si x es un número real que sea mayor o igual a
5 El campo o recorrido dt-x es x>5.
Lógica
3
En la ecuación x2 + y2 - 16
El campo o recorrido dexes - 4 < x < 4
El campo o recorrido de y es - 4 < y < 4.
1.3. PROPOSICIONES LÓGICAS.-
Llamaremos proposiciones lógicas a todo enunciado abierto que pueden ser califícado
como verdaderas o bien como falsas, sin ambigüedades
NOTACIÓN.- Las proposiciones lógicas serán denotadas generalmente con letras
minúsculas p, q, r, t, ..., etc. A la veracidad o falsedad de una
proposición se denomina valor de veidad.
Ejemplos de Proposiciones Lógicas.-
(7) p: 15-4=11, verdadero (V)
(2) q: Lima es la capital del Perú, verdadero (V)
(3) r: 107 + 301=48, falsa (F)
{4) t: 7 es un número par, falsa (F).
1.4. DEFINICIÓN.-
Se llama valores de verdad de una proposición a sus dos valores posibles; verdadero o
falso, estos posibles valores se puede esquematizar en una tabla de verdad en la forma.
P
V
F
1.5. CONECTIVOS LÓGICOS.-
Son expresiones que sirven para unir dos o más proposiciones, entre los más importantes
conectivos lógicos tenemos:
La conjunción, disyunción, implicación, bicondicional, negación, contradicción, esto
mostraremos en el siguiente cuadro.
©
4
Eduardo Espinoza Ramos
Nombre
Conjunción
Disyunción
Implicación
Bicondicional, equivalencia
doble implicación
Negación
Contradicción
Expresión
y
ó
Sí,.... entonces,...
... Sí y sólo sí,...
No
... no equivalente,...
Símbolo Lógico
A %
V
>
-
É
1.6. CLASES DE PROPOSICIONES LÓGICAS.-
a) PROPOSICIONES SIMPLES Ó ATÓMICAS.-
En una proposición que no contiene ningún conectivo lógico.
Ejemplo.-^) 6 es par. (2) 2 + 5 = 7
b) PROPOSICIONES COMPUESTOS O MOLECULARES.-
Es una proposición que contiene al menos un conectivo lógico.
Ejemplo.- (Y) 5 es primo y 2 es par.
(2) Si 5 es par entonces 2 es impar.
QQ Si n es par entonces n es divisible por 2.
1.7. PROPOSICIONES COMPUESTAS BÁSICOS.
a) LA NEGACIÓN.- Dado una proposición P, llamaremos la negación de P, a otra
proposición que denotaremos por -P, y que se le asigna el
valor opuesto a p, y su tabla de verdad es:
P ^
V F
F V
El principio lógico de la negación es:
Lógica
5
b)
Si una proposición es verdadera V, su negación es falsa F y recíprocamente, si dicha
proposición es falsa F, su negación es verdadera V.
La proposición ~P es leída así "no P", "no es cierto que P"
Ejemplo.- (\) 2 es primo V
Su negación es: 2 no es primo F
fa) 5 es par F
Su negación es: no es cierto que 5 es par V
(3) Dada la proposición P: 5x7 =35
Su negación es: ~P: no es cierto que 5 x 7 = 35
LA DISYUNCIÓN.- La disyunción de dos proposiciones p y q es la proposición
compuesta que resulta de unir p y q por el conectivo
lógico "o" en el sentido inclusivo y/o y que el principio lógico es "La proposición
p v q es falsa únicamente en el caso en que p y q son ambas falsas, en cualquier otro
caso es verdadera". La tabla de verdad para la disyunción es:
P q pvq
V V V~
V F V
F V V
F F F
Ejemplo.- Hallar el valor de p v q donde p: 7 es mayor que 9; q: 4 es menor que 5
Solución
P q pvq
F V V
c) LA CONJUNCIÓN.- La conjunción de dos proposiciones p y q es la proposición
compuesta que resulta de unir p y q mediante el conectivo
lógico "y" que se simboliza p a q, donde el principio lógico es "La conjunción p a q
es verdadero V, sólo cuando p es verdadero y q es verdadero V, en todos los demás
casos es falso". Su tabla de verdad es:
6
Eduardo Espinoza Ramos
P Q PAq
V V V~~
V F F
F V F
F F F
Ejemplo.
Sí p: 4 < 7 y q: 6 es número par. Calcular el valor de verdad de p a q
Solución
p q pAq
V V V~~
d) LA CONDICIONAL (IMPLICATIVA).- La implicación o condicional de dos
proposiciones p y q es la proposición
compuesta mediante el conectivo lógico "si,..., entonces, ..." y se simboliza p >
q, donde el principio lógico es "La proposición implicativa es falso únicamente en el
caso que la proposición p es verdadera y la proposición q es falsa, siendo verdadera
en todos los demás casos. Su tabla de verdad es:
p q p-»q
V V V~~
V F F
F V V
F F V
La proposición p es llamado antecedente y la proposición q es llamado consecuente.
Antecedente
Premisa
Hipótesis
>q
Consecuente
Conclusión.
Tesis.
OBSERVACIÓN.
fl) Una implicación es verdadera si el antecedente es falso, cualquiera que sea el
consecuente.
(2) Una implicación es verdadera si el consecuente es verdadero, cualquiera que
sea el antecedente.
Lógica
1
Ejemplo.- Sea p : Cristóbal Colón descubrió América. ; q : 6 + 3 = 8
Hallar el valor de verdad de p > q
Solución
Para calcular el valor de verdad de la proposición p > q, primero calcularemos el
valor de verdad de las proposiciones dadas.
p : Cristóbal Colón descubrió América es verdadera V
q : 6 + 3 = 8, es falsa F
P Q P~»q
V F F
e) LA BICONDICIONAL (Equivalente ó Doble Implicación).-
La doble implicación o bicondicional de dos proposiciones p y q es la proposición
compuesta mediante el conectivo lógico "si y sólo si" y se simboliza p <—> q son
verdaderos V o son falsos F, en otros casos es falso F. Su tabla de verdad es:
p
V
V
F
F
q
V
F
V
F
p<->q
V
F
F
V
f) LA DISYUNCIÓN EXCLUSIVA.- La disyunción exclusiva de dos
proposiciones p y q es la proposición
compuesto mediante conectivo lógico "o" y se simboliza p A q, donde ambas
proposiciones p y q tengan valores de verdad opuestos y es falsa si ambas tiene
idénticos valores. Su tabla de verdad es:
P q pAq
V V F
V F V
F V V
F F F
Eduardo Espinoza Ramos
Ejemplo.- Sea p : k es par ; q : k es impar. Hallar el valor de verdad de p A q.
Solución
Para calcular el valor de verdad de p A q, primero veamos lo siguiente:
(T} Si k es par, si puede ser impar (Si p es V ; q es F)
\2) Si k es impar, no puede ser par (Si p es F ; q es V)
De las notaciones (1) y (2) vemos que p A q es verdadera.
En efecto:
P q pAq
V F V
F V V
1.8. PROPOSICIONES COMPUESTAS.-
Mediante los conectivos lógicos se pueden combinar cualquier número finito de
proposiciones cuyos valores de verdad pueden ser conocidos, construyendo su tabla de
verdad, en dicha tabla se puede indicar los valores resultantes de estas proposiciones
compuestas, para todas las combinaciones posibles de valores de verdad de las
proposiciones compuestas.
Ejemplo.- La tabla de verdad de la proposición compuesta de:
[(p > q) a (q > r)] > (p > r)
Solución
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
p—>q
V
V
F
F
V
V
V
V
q—>r
V
F
V
V
V
F
V
V
P »r
V
F
V
F
V
V
V
V
[(P-
—> q) a (q—
V
F
F
F
V
F
V
V
->r)] >(p >r)
V V
V F
V V
V F
V V
V V
V V
V V
Lógica
9
1.9. JERARQUÍA DE LOS CONECTIVOS LÓGICOS.-
Si se tiene una proposición compuesta con varios conectivos lógicos, para realizar las
operaciones primero se debe colocar los paréntesis adecuadamente empezando con las
proposiciones que se encuentran dentro de los paréntesis anteriores, luego siguen todas las
negaciones y se avanza de izquierda a derecha (los corchetes son considerados como
paréntesis).
Ejemplo.- Hallar la tabla de valor de verdad de la proposición:
[p v (q > ~r)] a [(~p v r) < > - q]
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
[P
V
V
V
V
F
F
F
F
v (q-
V
V
V
V
F
V
V
V
>
F
V
V
V
F
V
V
V
~r)] a [(-
F
V
V
F
F
F
V
V
-pvr)
V
F
V
F
V
V
V
V
<—>
F
V
V
F
F
F
V
V
-ql
F
F
V
V
F
F
V
V
■-*" "«-—.
1.10. TAUTOLOGÍAS, CONTRADICCIONES Y CONTINGENCIAS.-
a) TAUTOLOGÍA.- Son proposiciones compuestos que siempre son verdaderos
cualquiera que sea el valor de las proposiciones componentes.
Ejemplos de Tautología.-
\\J p v - p (principio del tercio excluido)
@ [(p > q) a p] * q @ - fp ■ -p)
En electo teneme-
10
Eduardo Espinoza Ramos
©
p
V
F
p v ~p
V V F
F V V
Es Tautología
©
p
V
V
F
F
q
V
F
V
F
l(p—>q) a p]
V V V
F F V
V F F
V F F
V
V
V
V
q
V
F
V
F
Es una Tautología
©
p
V
F
~P
F
V
- (p a ~p)
V F
V F
Es una tautología
b) CONTRADICCIONES.- Son proposiciones compuestas que siempre son falsas,
cualquiera que sea el valor de las proposiciones
compuestas.
Ejemplo de contradicciones.-
(l) p a ~p (principio de contradicción)
© ~(pv~p)
En efecto tenemos:
©
(5) (p >q)A(pA~q)
p -p p a ~p
V F F~
F V F
Es una contradicción
Lógica
11
©
p
V
F
~P
F
V
~ (p v ~p)
F V
F V
©
Es una contradicción
P
V
V
F
F
q
V
F
V
F
(p >q) a (pA~q)
V F F
F F V
V F F
V F F
Es una contradicción.
c) CONTINGENCIA.- Son proposiciones compuestas que no son ni tautología ni
contradicciones, es decir, son proposiciones que en algunos
casos es F, y en otros es V.
Ejemplos de Contingencia.
© P*~>q
0 (p >q) >p
En efecto tenemos:
©
©
pAq
p q p <—► q
V V V
V F F
F V F
F F V
©
Es una contingencia
p
V
V
F
F
q
V
F
V
F
pAq
V
F
F
F
Es una contingencia
12
Eduardo Espinoza Ramos
®
p
V
V
F
F
q
V
F
V
F
(p—>q)—*v
V V V
F V V
V F F
V F F
Es una contingencia
1.11. IMPLICACIÓN LÓGICA Y EQUIVALENCIA LOGICA.-
A toda proposición condicional p —> q que sea tautología le llamaremos implicación
lógica (o simplemente implicación) en éste caso a la condicional denotaremos por
p=>q
Ejemplo de Implicación lógica se tiene:
puesto que:
[((~p) v q) a ~q] => ~p
p
V
V
F
F
q
V
F
V
F
K(~P) v q) a ~q] => -p
V F F V F
F F V V F
V F F V V
V V V V V
Es una tautología. Por lo tanto es una implicación lógica.
ii) A toda bicondicional p <-> q que sea tautología se le llama equivalencia lógica (o
simplemente equivalencia) y en éste caso a la bicondicional denotaremos por p<=> q.
Ejemplo de equivalencia lógica se tiene: [p a (p v q)] <=> p
puesto que:
p
V
V
F
F
q
V
F
V
F
[p a (pvq)] <=>
V V V V
V V V V
F F V V
F F F V
P
V
V
F
F
Es una tautología. Por lo tanto es una equivalencia lógica.
Lógica
13
1.12. PROPOSICIONES LÓGICAMENTE EQUIVALENTES.-
Cuando sus tablas de verdad de dos proposiciones p y q son idénticos se denominan
equivalentes (o lógicamente equivalentes) en este caso se simboliza en la forma p=q.
Ejemplo.- Las proposiciones (p > q) y (~q > ~p) son lógicamente equivalentes.
puesto que sus tablas de verdad son idénticos. En efecto:
p q p—>q -q—>~p
V V V F~V F"
V F F V F F
F V V F V V
F F V V V V
Idénticos'
->q = ~q >~p
OBSERVACION.-
fl) La equivalencia de este ejemplo es muy importante, porque viene a ser la base del
llamado método de demostración por Reducción al absurdo, en una forma indirecta
de un proceso de demostración que se va utilizar en el desarrollo del curso.
(l) Un par de proposiciones equivalentes p = q resulta siempre una equivalencia
lógica p <=> q y viceversa, por esta razón cuando se tiene una equivalencia lógica
entre p y q, también se dice p = q.
1.13. PRINCIPALES LEYES LÓGICAS O TAUTOLÓGICAS.
Las llamadas leyes lógicas o principios lógicos viene a ser formas preposicionales
tautológicas de carácter general y que a partir de estas leyes lógicas se puede generar otras
tautológicas y también cualquier tautología se puede reducir a una de las leyes lógicas,
entre las principales leyes lógicas mencionaremos.
14
Eduardo Espinoza Ramos
Io LOS TRES PRINCIPIOS LÓGICOS CLÁSICOS.-
flj Ley de identidad.
\P »P
< "una proposición sólo son idénticos así mismo"
[P* >P
[2j Ley no contradicción.
~(p a -p) "una proposición no puede ser verdadero y falso a la vez"
(3j Ley del Tercio excluido.
p v -p "una proposición es verdadero o es falso no hay una tercera posibilidad"
2° ELIVALENCIAS NOTABLES.-
\l) Ley de la doble negación.
~(-p) = p "la negación de la negación es una afirmación"
(2) Ley de la Idempotencia.
a)pAp = p b)pvp = p
\3J Leyes conmutativas.
a) (pAq) = (qAp) b) (pvq)^(qvp)
c) p < > q = q < > p
(4) Leyes Asociativa.
a) p a (q a r) s (p a q) a r b) pv(qvr) = (pvq)vr
c) p <—> (q < ► r) = (p <—» q) <—» r
(5) Leyes Distributivas
a) p A(qvr)s(p Aq) v(p at) b) p v (q a r) = (p v q) a (p v r)
c) p >(qAr) = (p >q)A(p >r)
d) p > Iq v r) = (p ~>q)v(p > r)
Lógica
15
(ó) Leyes De Morgan.
a) ~(pAq) = ~pv~q b) ~(p v q) = - p a ~q
(7j Leyes del Condicional.
a) p >q = -pvq b) -(p >q)=pA~q
Q$) Las Leyes del Bicondicional.-
a) (p< »q) = (p >q)A(q > p)
b) (p <—> q) s (p a q) v (~p v -q)
Qh Leyes De La Absorción.
a) pA(pvq) = p b pA(~pvq) = pAq
c) p v (p a q) = p d p v (~p a q) = p v q
\W) Leyes De Transposición.
a) (p »q)s~q >-p b) (p<—>q) = ~q<—>~p
(ln Leyes De Exportación.
a) (pAq) »r = p > (q > r)
b) (P, Ap2 A...A/7J >r=(px Ap2 A... A/>„_,) »(/>„ > Ó
HL2) Elementos Neutros para la Conjunción y Disyunción.
a) p a V s p. V neutro de la conjunción.
b) pvF^p, F neutro de la Disyunción.
(l3) También:
a) (p v q) a (p v -q) = p b) (p a q) v (p a -q) = p
OBSERVACIÓN.- Estas Leyes son muy útiles para simplificar los problemas, puesto
que es válido reemplazai una proposición por su equivalente sin
alterar el resultado.
16
Eduardo Espinoza Ramos
Ejemplo.- Simplificar las proposiciones siguientes aplicando las leyes lógicas.
(l) [(pv-q)Aq] >p
Solución
I(P v -q) a q] > p = ~[(p v ~q) a q] v p
= [~(P v -q) v -q] v p
= Kp v -q)] v (p v -q)
= pv~q
(5) ~[~(p a q) > ~q] v q
Solución
~1~(P a q) > -q] v q = [ -(p a q) a - (-q)] v q por (7b)
= ~t(P a q) v í-q)] v q por (6a)
= [~(p a q) a ~(~q)] v q por (6b)
= [(-p v -q) a q] v q = q v ((-p v ~q) a q) por (3b)
= qv [q a (~p v ~q)] = q por (9b)
{3J Comprobar que las tres proposiciones siguientes son equivalentes:
a) - [(q v ~p) v (q a (r v ~p))]
b) (p a -q) a [~q v (-r v p)]
c) ~(-q > ~p) a [q > ~(p > r)]
(4) Determinar si (a) y (b) son proposiciones equivalentes:
a) p >(rv~q)
b) (q > ~p) v (~r —^ -p)
Dejamos el desarrollo de este ejercicio al lector.
© [((-p) a q) > (r a ~r) 1 a ~q
Solución
[((~p) a q) > (r a ~r)] a ~q = [((~p) a q) > F] a ~q
= K(~P) a q) v F] a -q
= [(P v -q) v F] a -q
= (p v -q) a -q = ~q
Ejemplo.- Determinar si a) y b) son proposiciones equivalentes:
a) p > (r v ~q)
Determinaremos la equivalencia mediante la tabla de verdad
b) (q > -p) v (~r > ~p)
Solución
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
P
V
V
V
V
F
F
F
F
—>
V
F
V
V
V
V
V
V
(r v -p)
V
F
V
V
V
F
V
V
(q—>
F
F
V
V
V
V
V
V
-P) v (~r
V
F
V
V
V
V
V
V
—»-í)
V
F
V
F
V
V
V
V
Idénticos ^
j
Otra manera es mediante la simplificación.
a) p > (r v ~q) = (~p) v (r v ~q)
b) (q- >~p)v(~r »~p) = (~qv~pjvrv~p)
= (~q) v (~p v ~p) v r
= (~q) v (~p) v r
= (~p) v (r v ~q)
Luego de (1) y (2) se tiene: a) = b)
18
Eduardo Espinoza Ramos
1.14. LA INFERENCIA LÓGICA O ARGUMENTO LÓGICO.-
Al proceso de pasar de un conjunto de premisas a una conclusión se denomina inferencia
lógica o Argumento lógico.
La inferencia lógica es una condicional de la forma:
(pt Ap2 A...Ap„) >q ...(a)
donde las proposiciones P\,p2,— P„ son llamadas premisas y que originan como
consecuencia otra proposición q llamada conclusión.
OBSERVACIÓN.- Una inferencia lógica puede ser una tautología, una contingencia o
una contradicción y por lo tanto se tiene:
flj Si la condicional (a) es una tautología se denomina argumento válido o inferencia
válida.
(2) Si la condicional (a) no es una tautología se denomina FALACIA.
Ahora veremos como se determina el valor de verdad de un argumento lógico.
1.15. DEFINICIÓN.-
El argumento (a) es verdadero si q es verdadero cuándo todas las premisas p¡, p2,..., p„
son verdaderos, en cualquier otro caso el argumento (a) es falso.
NOTACIÓN.- También el argumento (a) se denota por:
Pl,/>2'-'/>« >(7 ™(P)
Ejemplo.- Determinar si pvq es una consecuencia válida de ~p »~q,~q >r, ~r
Solución
En este problema las premisas ~p > ~q, ~q > r, ~r y la conclusión es p v q, por lo
tanto se debe demostrar que (~p > ~q) a (~q > r) a ~r > p v q es una
tautología.
Lógica
19
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
U-P *
V
V
V
V
F
F
V
V
~q) a (-
V
V
V
F
F
F
V
F
-q—
V
V
V
F
V
V
V
F
»r)] a [
F
V
F
F
F
F
F
F
F
V
F
V
F
V
F
V
—>
V
V
V
V
V
V
V
V
(p v q)]
V
V
V
V
V
V
F
F
Es una tautología
Como es una tautología es una inferencia válida.
1.16. TEOREMA.-
Si el argumento (a) es válida y las premisas pi,p2,...,p„ son verdaderas, entonces la
conclusión q es verdadera.
Demostración
Si el argumento (a) es válido, la condicional p, a p2 a ...a pn >q es una tautología
en que (p, Ap2 A — AP«) es verdadera (puesto que cada P\,p2,—,p„ son verdaderos)
de donde se tiene que la única posibilidad para la conclusión q es que sea verdadera, pues
si fuese falsa, la condicional seria falsa y la inferencia no seria válida, contradiciendo la
hipótesis.
OBSERVACIÓN.- Una inferencia no se modifica si una o varias de las proposiciones
componentes p,, p2,—, p„, q se reemplaza por otra u otras que sean equivalentes.
NOTACIÓN.- Al argumento (p, a/?2 a...ap„) >q, también se denota en la
forma siguiente:
P\
Pi
Pí
Pn
20
Eduardo Espinoza Ramos
Ejemplo.- Demostrar que el argumento es válido.
P
p—>q
••• q
Solución
Se debe demostrar que la condicional
[p a (p > q)] > q es una tautología
[pA(p >q)] »q s~[pA(p >q)]vq
= [~pv~(p >q)]vq
= (~p v q) v ~(~p v q)
= (~p v q) v (p a -q)
= ~(p a ~q) v (p a ~q) = V es tautología
También puede haberse demostrado con la tabla de verdad.
p
V
v"
F
F
q
V
F
V
F
[p a (p >q)] > q
V V V V V
V F F V F
F F V V V
F F V V F
—___ ^yc,y Es una tautología
1.17. INFERENCIAS VÁLIDAS NOTABLES.-
Ley De Módus Pones.- [(p >q>Aq]=>q
también se simboliza p > q
_P
.-. q
Ley De Módus Tollens.- [(p > q) a (~q)] => (~p)
también se simboliza p > q
~q
©
Lógica
21
(3) Ley Del Silogismo Hipotético, [(p >q)AÍq >r)]=>(p > r)
También se simboliza: p >q
q >r
.-. p >r
\4j Ley Del Silogismo Disyuntivo, [(p v q) a (~p)] => q
También se simboliza: p v q
~P
•"• q
{5J Ley Del Dilema Constructivo, [(p > q) a (r > s) a (p v r)] => (q v s)
También se simboliza: p > q
r > s
p vr
.: q v s
CSj Ley De Simplificación.
a) p a q => p
También se simboliza:
P
q
de.
- P
b) p a q => q
P
q
••- q
1.18. EL MÉTODO ABREVIADO.-
El desarrollo de la tabla de valores de la inferencia (p, ap2 a...apn) >q es muy
laborioso cuando se desea saber su validez, esto se puede evitar mediante el "método
abreviado" que es fácil de manejar y de gran precisión.
El método abreviado consiste en analizar la única posibilidad de ser falsa la
implicación p > q, es decir:
22
Eduardo Espinoza Ramos
O sea que la implicación es falsa F sólo cuando el antecedente es verdadero V y el
consecuente falsa F.
Ahora haremos un análisis a la inferencia, (p, a/?2 a —aP„) »0
mediante los siguientes pasos:
Io Asignar el valor de verdad V a cada una de las premisas p,, p2,—, p„ y falso F a la
conclusión, como el antecedente es verdadero y por ser una conjunción n premisas
entonces cada premisa p¡, p2,..., pn es verdadera es decir:
(Pi Ap2 a...ap„) >q
V (?) F
t t
2° Deducir el valor de cada una de las variables proporcionales teniendo en cuenta las
reglas a, v, >, ~ que se pueden presentar en cada premisa.
3° Si cada una de las variables proporcionales tiene un sólo valor, entonces la
inferencia no es válida, es decir no hay implicación puesto que la conjunción de
premisas es V y la conclusión es F.
4° Si una variable proporcional llega tener dos valores a la vez (V y F), entonces
quedará demostrado que no es posible que la conjunción de premisas es V y la
conclusión es F, por lo tanto hay implicación y la inferencia es válida
Ejemplo. Analizar la inferencia [(p >q) a (r »~s) a (~q v ~s)] > (~p v ~r)
Solución
[(p -¡—mj) a (r -^—> ~s) a (~q y ~s)] > (~p v ~r)
t * * í ¡
^ v v v ^ i i
T T
'?) F
Analizando la conclusión (~p v -r)
~p v ~r
F ▲ _ AF
~ p es F I p es V
de donde
\~resF \r es V
ahora analizaremos cada premisa
p 1 > q de donde p es V
q es V
y T '4 '
vt^
> ~s de donde r es V
V ~s es V entonces S es F.
~q v s de donde - q es V
s es F entonces q es F
VI * I F
OJ
como se puede apreciar que q es V por una parte y q es F por otra parte, lo cual es una
contradicción por lo tanto la inferencia es válida.
Ejemplo.- Analizar la inferencia [(p >q) a (~p > r) a (p v ~p)] > (p v r)
Solución
[(p > q) a (~p > r) a (p v ~p)] > (p v r)
lili
T T T I I
I I
v__V J/ V ^ T T
V (jF) F
Analizando la conclusión p v r
p v r de donde \
es F
es F
24
Eduardo Espinoza Ramos
Ahora analizamos cada una de las premisas.
P
U*
> q de donde p es F
q es V
~P
A
QJ
* r de donde -p es F entonces p es V
F
como podemos apreciar p es F por una parte
p es V por otra parte
lo cual es una contradicción, por lo tanto la inferencia es válida.
Ejemplo.- Analizar la inferencia: [(-p <—> (~q v r)) a (r > s)] ■
Solución
[(~p <—> (~q v r)) a (r > s)]
-»(s >-p)
Y
V
Y
V
>(s >-p)
I I
I I
I I
T T
V (FI
Analizando la conclusión s > ~p
s es V
» ~p de donde < entonces p es V
~ p es F
U¿
Ahora analizamos cada una de las premisas.
~p < > (~q v r) ~q v r
X de donde I k entonces
F (y) 1 F f' (?) ' F
q es V
r es F
Lógica
25
r es F
r —> s de donde
L-Ó—1
Como se tiene una contradicción. Luego la inferencia no tiene validez.
1.19. MÉTODOS DE DEMOSTRACIÓN.-
En la demostración de teoremas y proposiciones que se presentan en el álgebra y el
análisis se aplican ordenadamente los pasos lógicos agotando todas las premisas
(antecedentes o hipótesis) para verificar la conclusión (consecuente o tesis).
Existen dos formas o métodos de demostración matemática, la directa y la indirecta.
1.20. FORMA O MÉTODO DIRECTO DE DEMOSTRAC1ÓN.-
En la tabla de verdad de la implicación p > q.
Si p es falso, la proposición p > q es válida cualquiera que sea el valor de q, entonces
no se tendrá nada que demostrar, es decir que interesan los casos de antecedente
verdadero.
Sí a partir de la verdad de p o de un conjunto de premisas de la forma.
(p, Ap2 a...a/7„) >q ...(1)
se deduce la verdad de la conclusión de q, se dice que se ha usado una demostración
directa.
Ejemplo.- Mediante el método directo comprobar la validez de la inferencia lógica.
[~p a (p v q)] > q
Solución
[~p a (p v q)] > q = ~[~p a (p v q)] v q
= [pv ~(p v q)] v q
= (p v q) v ~(p v q)
V v '
V
= tautología.
26
Eduardo Espinoza Ramos
1.21. FORMA O MÉTODO INDIRECTO DE DEMOSTRACION.-
A esta forma de demostración también se denomina demostración por contradicción o por
reducción al absurdo, este método consiste es negar la conclusión q y considerarla como
una premisa, y a una de las premisas p,, p2,..., p„ negarla digamos a px y construir el
siguiente argumento lógico
((-q) a p2 a ... a pn) » ~ p, ... (2)
ahora probaremos que el argumento lógico(2) es equivalente al argumento lógico (1).
((~q) Ap2 A...Apn) >~pl =~[~q Ap2A...Ap„]v-p,
s [q v - p2 v... v - pn ] v - p,
= [- p, v - p2 v ... v - p„ ] v q
= ~[PiAP2a... Ap„]vq
= (p, a p2 a ... a pn ) ► q (argumento 1)
1.22. DEFINICIÓN.-
Cuando en una demostración se emplea el argumento lógico (2) se dice que se está
aplicando el método indirecto o método por reducción al absurdo.
Ejemplo.- Por el método indirecto comprobar la validez a la inferencia lógica siguiente:
[~p a (p v q)] > q
Solución
Negaremos la conclusión q y la consideremos como premisa y negaremos a la premisa ~p
y considerarla como conclusión.
Lógica
27
t(-q) a (p v q)] > p = -[(-q) a (p v q)] v p
= [qv ~íp v q)] v p
= (p v q) v ~(p v q)
v j
Y
V
= tautología
Ejemplo.- Probar que él número no es racional.
Solución
La comprobación lo haremos por el método de reducción al absurdo.
1ro. Suponemos que es racional.
2do. Si es racional => 3 m, n e Z primos entre sí tal que >/2 = ™
n
2
3ro. Sí>/2=— => 2 = ^r- => m2=2n2 ...(a)
n n
4to. Como m2 -2n2, con n entero => m2 es par, por lo tanto m es par.
5to. Como m es par => m = 2k, para algún k entero.
6to. Reemplazando en (a) se tiene: 4k2 =2n2 => n2 =2k
7mo. Comow2=2Jt2 => n2 es par, por lo tanto n es par.
8vo. Como n es par => n = 21, para algún 1 entero.
9no. De 5to. y 8vo. se tiene m = 2k, n = 21 de donde m y n tiene un factor común 2,
lo cual contradice a la hipótesis de que m y n son primos entre sí.
lOmo. Conclusión, por lo tanto no es racional.
28
Eduardo Espinoza Ramos
1.23. CIRCUITOS LÓGICOS.-
A un ensamblaje de interruptores automáticos que permiten el paso de la corriente
eléctrica o la interrumpen de denomina circuitos eléctricos.
A un interruptor se puede representar por medio de una proposición p y viceversa, de tal
manera que el valor de verdad de la proposición p se identiñque con el "paso de la
corriente" en este caso se dice que el "circuito está cerrado" y cuando el valor es "falso"
con la interrupción de la corriente en este caso se dice que el circuito está abierto.
/
o p » o ' P o
Circuito cerrado Circuito Abierto
(pasa corriente V) (no pasa corriente F)
OBSERVACIÓN.- Para diseñar los circuitos eléctricos, se usa la siguiente notación.
Él 1 indica "pasa corriente"
El 0 indica "no pasa corriente"
Luego en circuitos eléctricos se usan como notación.
"El 1 en lugar de V"
"El 0 en lugar de F'
En el diseño de esquemas de circuitos eléctricos para representar a proposiciones
compuestas y viceversa consideramos dos clases de instalaciones, en serie y en paralelo.
1.24. DISEÑO DE CIRCUITOS ELÉCTRICOS EN SERIE.-
Consideremos dos interruptores p y q conectados en serie.
p » q ► o
Pasa corriente
Lógica
29
Se observa que este circuito admite paso de corriente cuando estos dos interruptores p y q
están cerrados, en cualquier otro caso no hay paso de corriente, es decir ésta situación
corresponde a la tabla de verdad de la conjunción p y q.
p
1
1
0
0
q
i
0
i
0
pAq
1
0
0
0
En la tabla de verdad se observa que basta que uno de los interruptores esté abierto "O"
para que no circule la corriente en todo el circuito
p:1
q:0
A la expresión p a q se le llama la "Función Booleana del circuito en serie".
1.25. DISEÑO DE CIRCUITOS ELÉCTRICOS EN PARALELO.
Consideremos dos interruptores p y q instalados en paralelo.
pasa corriente
Se observa en el circuito para que circule corriente es suficiente que alguno de los
interruptores o ambos p o q esté cerrado "1" y no hay paso de corriente si ambos
interruptores están abiertos (ambos con el valor '"O")-
Este circuito corresponde a la tabla de verdad de la disyunción p v q, es decir:
30
Eduardo Espinoza Ramos
p
1
1
0
0
q
i
0
i
0
pvq
1
1
1
0
A la expresión p v q se denomina la función Booleana del circuito en paralelo.
©
no pasa corriente
NOTACIÓN.- A un interruptor p representaremos simplemente como
o p o
Ejemplo.-
p/vq p q
pvq
OBSERVACIÓN.- A una tautología se representa mediante un circuito siempre
cerrado (donde la corriente siempre está circulando). En las computadoras no son de
utilidad.
Ejemplos.-
Construir el circuito lógico de las funciones Booleanas.
a) p >q
Solución
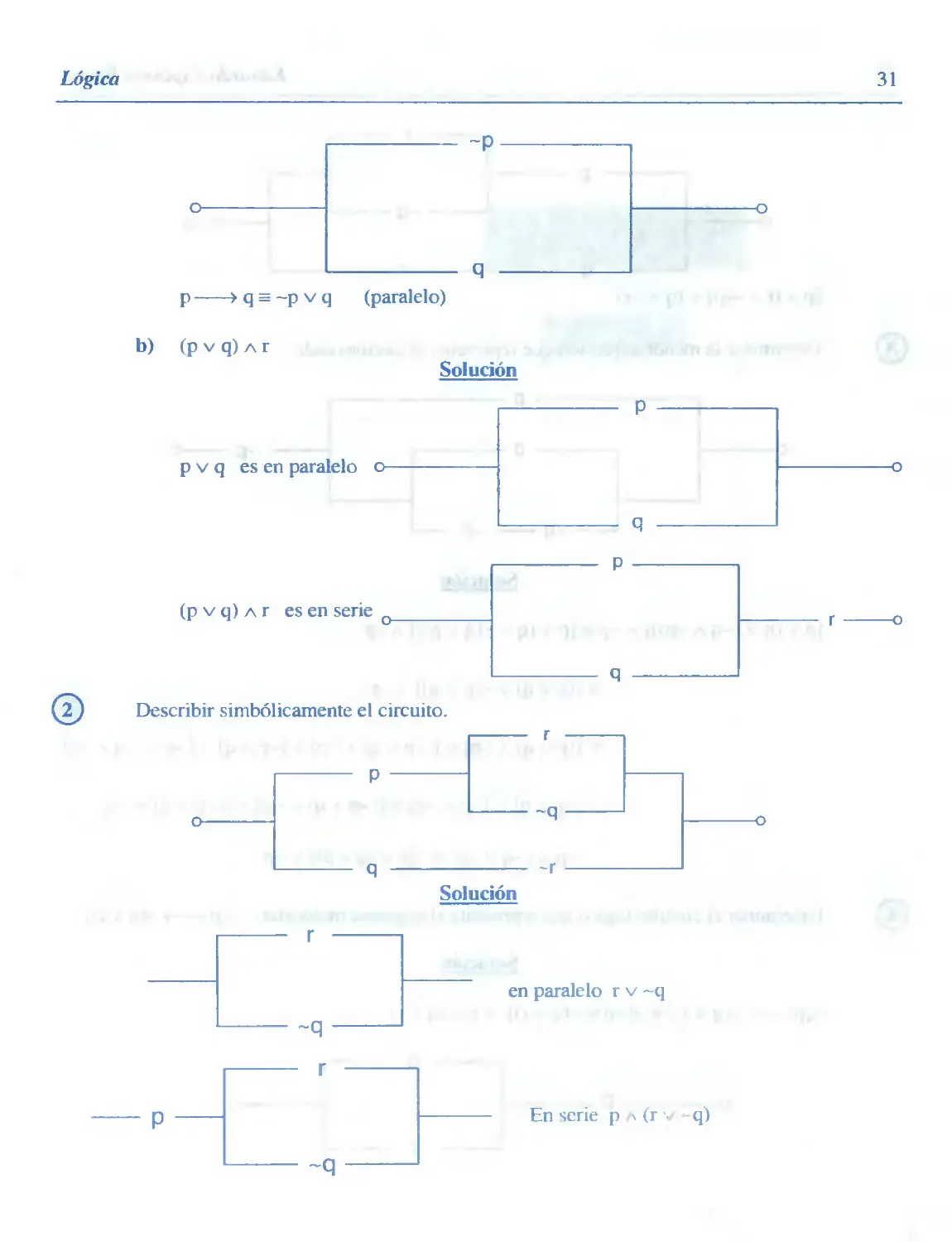
Lógica
31
p > q = ~p v q (paralelo)
b) (p v q) a r
Solución
p v q es en paralelo o-
©
(p v q) a r es en serie
Describir simbólicamente el circuito.
r o
Solución
en paralelo r v ~q
~q
En serie p x (r •■ q)
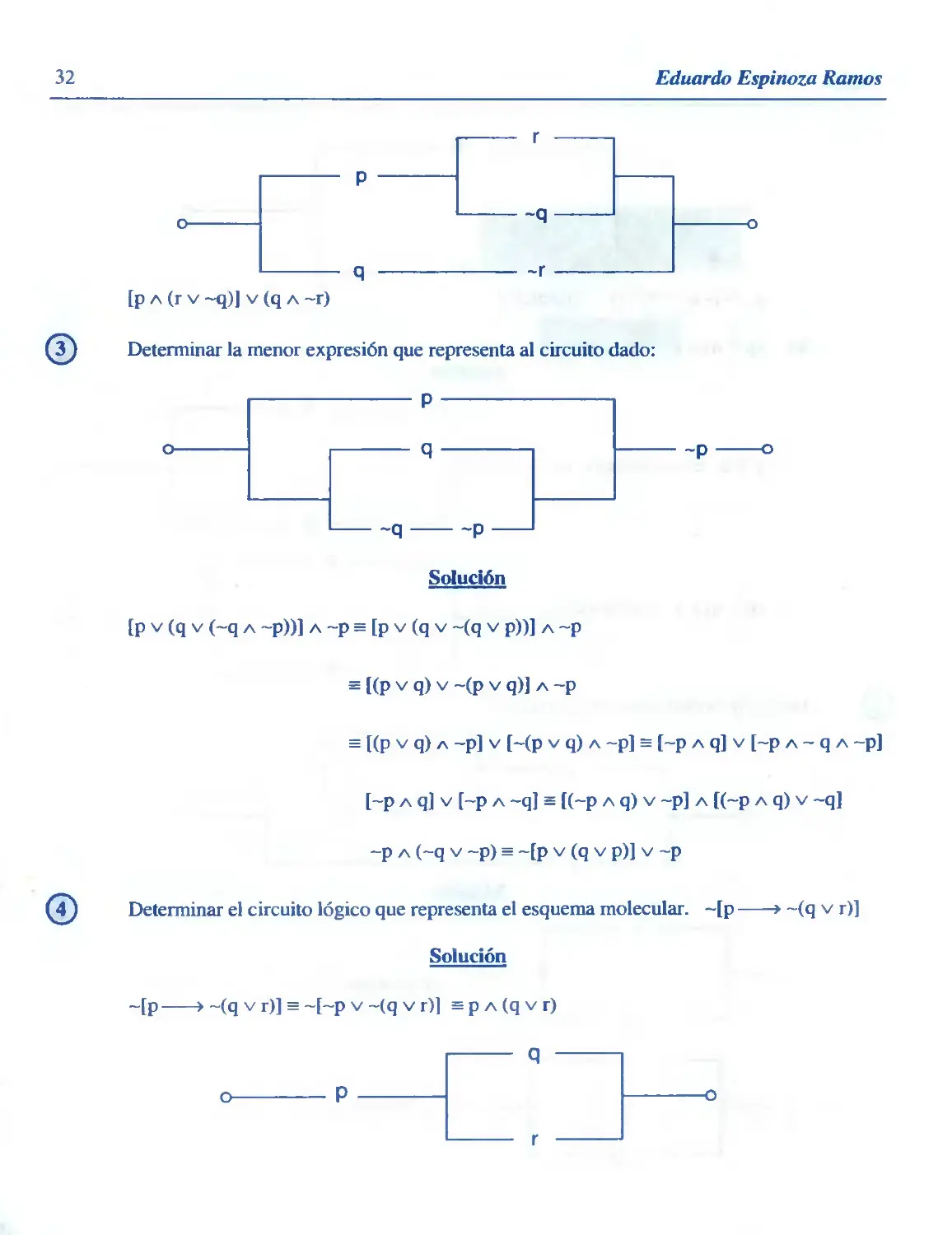
32
Eduardo Espinoza Ramos
®
©
[p a (r v ~q)] v (q a -r)
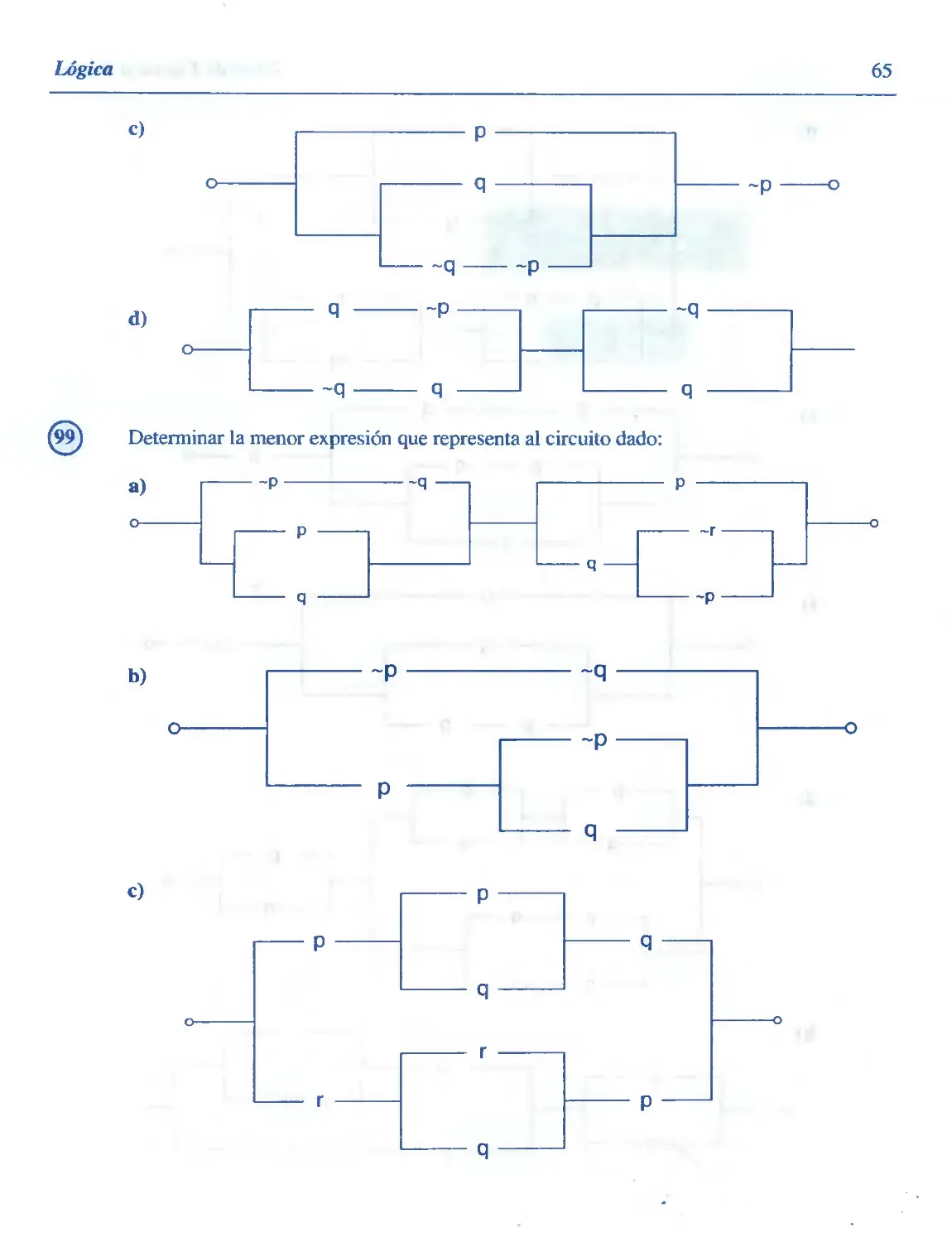
Determinar la menor expresión que representa al circuito dado:
P
q
-q
~P
-P
Solución
[p v (q v (~q a -p))] a -p = [p v (q v ~(q v p))] a ~p
= [(P v q) v ~(p v q)] a -p
= [(P v q) a -p] v [~(p v q) a -p] s [~p a q] v [~p a - q a ~p]
[~p a q] v [~p a -q] = [(~p a q) v -p] a [(~p a q) v -q]
-p a (~q v -p) = ~[p v (q v p)] v ~p
Determinar el circuito lógico que representa el esquema molecular. ~[p -
Solución
~[p > ~(q v r)] = ~[~p v ~(q v r)] = p a (q v r)
q
~(q v r)]
Lógica
33
1.26. LÓGICA CUANTIFICACIONAL.-
FUNC1ÓN PROPOSICIONAL.-
A todo enunciado abierto de la forma P(x) se denomina función proposicional la cual
tiene la propiedad de convertirse en una proposición al ser sustituido la variable x por una
constante "a" especifica, al conjunto de todos los valores convenidos para la variable x se
denomina dominio de la variable.
De acuerdo a la definición de enunciado abierto, la función proposicional sobre D es toda
expresión P(x) donde P(a) es verdadero o falso para todo a e D.
Ejemplo.- P(x) = x + 1 < 9, si x pertenece al conjunto de los enteros, entonces P(x) es
una función proposicional cuyo dominio es los enteros.
Si x = -2 € Z, -2 + 1 < 9 es verdadero
x= lOe Z, 10+1<9 es falso
por lo tanto P(x) es una función proposicional.
1.27. CUANTIFICADORES EXISTENCIAL Y UNIVERSAL.-
Se ha visto un método que nos permite que a partir de una función proposicional P(x) se
puede obtener proposiciones, sin embargo se tiene otro método completamente distinto
que permite obtener proposiciones a partir de una función proposicional, dicho método es
llamado cuantificadores.
Ejemplo.- Sea la función proposicional P(x): x es un número primo — (1)
Si a la función proposicional le anteponemos "para todo x" se obtiene:
"para todo x, x es un número primo" ... (2)
La frase "para todo x'" se denomina el cuantificador universal y se simboliza por: V x
que se lee para todo x.
34
Eduardo Espinoza Ramos
Luego (2) se puede escribir en la forma. V x: x es un número primo ... (3)
aclarando (1) es una función proposicional
(3) es una proposición.
A un cuantifícador universal puede ser reemplazado por:
Vx: P(x) o V x / p(x) ó (V x) (P(x))
y en todas estas notaciones, se lee "para todo x, tal que se verifica P(x)" es decir:
V se lee "para todo"
El cuantificador El cuantificado
Notación:
Vjc : P(x)
Vjc / P(x)
(Vjc) (/>(*))
Ejemplo.- V x: x + 4 = x
El cuantificador universal no es el único cuantificador que permite obtener proposiciones
a partir de funciones proposicionales, existe otro llamado cuantificador existencial.
Sí en (1) P(x): x es un número primo antes ponemos la frase "existe x tal que" es nuevo
cuantificador, se obtiene:
"Existe x tal que x es un número primo" ... (4)
Al cuantificador existencial x "existe x tal que" se simboliza 3 x. de donde (4) se escribe
3 x: x es un número primo ... (5)
un cuantificador existencial puede ser representado por 3 x: P(x) o 3 x/P(x) o (3x) (P(x))
y en todas éstas notaciones se lee:
"Existe por lo menos un x, tal que se verifique P(x)" es decir: 3 se lee existe
Lógica
35
El cuantificador El cuantificado
Notación
3x: P(x)
3.1 / P(x)
(3x)(P(x))
Ejemplo.- Sea el conjunto A = {-2.-1,2,3.4} se tiene:
3xe A: x2-2x = S
3xe A/ jc2-2jc = 8
(3a:e A)(jc2-2jc = 8)
1.28. NEGACIÓN DE PROPOSICIÓN CON CUANtlFICADORES.
Proposición
V x : P(x)
3x: P(x)
V x e A : P(x)
3 x e A : P(x)
La negación
~ [V x : P(x)] =3x:~ P(x)
-[3 x : P(x)] = V x : -P(x)
~[V x e A : P(x)] = 3 x e A :
~[3 x e A : P(x)] = V x € A :
-P(x)
-P(x)
®
©
©
©
Ejemplo.- Negar la proposición, Vxe N/x + 3>5
Solución
~[VxeN/x + 3>5] = 3xeN/x + 3<5
Ejemplos.- Negar cada una de las siguientes proposiciones si el conjunto de referencia
es los reales R.
(V x)(3 ytfP(x) > (q(y) > r(x)j]
(V x)(3 y)(3 z) [P(x,y) > q(x) a r(z)]
(3 x)(V y)(3 z)RP(x) > q(y)) v r(z)]
(V x)(3 y)(V z)[~(r(\) v ~P(x)) v q(z)J
36
Eduardo Espinoza Ramos
Solución
© -(V x)(3 y)[P(x) > (q(y) > r(x))] = (3 x)(V y)[P(x) a ~(q(y) > r(x)]
= (3 x)(V y)[P(x) a (q(y) a -r(x))]
® ~(V x)(3 y)(3 y)(P(x,y) > (q(x) a r(z)) = (3 x)(V y)(V z)[P(x,y) a ~(q(x) a r(z))]
= (3 x)(V y)(V z)[P(x,y) a (-q(x) v -r(z))]
® -(3 x)(V y)(3 z)[~(P(x) > q(y)] v r(z)] = (V z)(3 y)(V z)[P(x) > q(y)) a -r(z)]
(4) ~(V x)(3 y)(V z)[~(r(x) v -P(x)) v q(z)] = (3 x)(V y)(3 z)[r(x) v ~p(x)) a ~qtz)]
11.29. EJERCICIOS DESARROLLADOS.-
fT) Determinar el valor de verdad de cada una de las siguientes proposiciones:
a) Sí 5+4= 11, entonces 6 + 6= 12
Solución
Es verdadera puesto que el antecedente es falso mientras que el consecuente es verdadero.
b) No es verdad que 3 + 3 = 7 sí y solo sí 5 + 5=12
Solución
Es falso puesto que se está negando una proposición verdadera.
c) Lima está en Chile o La Paz está en Ecuador.
Solución
Es falso puesto que ambas componentes son falsas
d) No es verdad que 2 + 2 = 5 o que 3+1=4
Solución
Es falso puesto que se está negando una proposición verdadera.
Lógica
37
2J Determinar el valor de verdad de cada una de las siguientes proposiciones:
a) 4 + 8=12 y 9-4 = 5
Solución
Es verdadera V, porque es una conjunción cuyas dos proposiciones son verdaderas.
b) 8 + 4=12 y 8-3 = 2
Solución
Es falso F, puesto que es una conjunción con una proposición simple falsa.
c) 8 + 4=12o7-2 = 3
Solución
Es verdadera V, puesto que es una disyunción con una proposición simple
verdadera.
d) La UNMSM está en Arequipa o está en Lima.
Solución
Es verdadera V, puesto que es una disyunción exclusiva con una proposición simple
verdadera.
e) La UNÍ está en Lima o está en Trujillo.
Solución
Es verdadera V, puesto que es una disyunción exclusiva con una proposición simple
verdadera.
f) Sí 5 + 2 = 7, entonces 3 + 6 = 9
Solución
Es verdadera V, puesto que es una implicación con las dos proposiciones simples -
verdaderas.
g) Sí 4 + 3 = 2, entonces 5 + 5=10
Solución
Es verdadera V, por ser una implicación en donde el antecedente es falso F, y el
consecuente es verdadero V de dos proposiciones simples.
38
Eduardo Espinoza Ramos
®
©
h) Si 4 + 5 - 9, entonces 3 + 1=2
Solución
Es falso F, puesto que de una proposición verdadera V no puede implicar una
proposición falsa F.
i) Si 7 + 3 = 4, entonces 11-7 = 9
Solución
Es verdadera V, puesto que las proposiciones que intervienen en la implicación son falsas.
Evaluar la tabla de verdad de la proposición compuesta. ~(p a q) <—> (~p v ~q)
Solución
p
V
V
F
F
q
V
F
V
F
~(pAq)<—»(~p v ~q)
F V V F F F
V F V F V V
V F V V V F
V F V V V V
Construir la tabla de verdad de la siguiente proposición:
~Hp v (~q > p)] v ~[(p <—> ~q) > (q a ~p)]
Solución
Primero simplificaremos la proposición por la ley de Morgan:
—{[p v (~q » p)] a [(p <—> ~q) > (q a ~p)]} de donde se tiene:
[p v (~q » p)] a [(p <—> -q)—-» (q a -p)]
p
V
V
F
F
q
V
F
V
F
[p v (~q
V V
V V
F V
F F
» p)] a [(p <—> -q) > (q a ~p)]
V V F V F
V F V F F
V V V V V
F F F V F
'+*-
El valor de verdad
Lógica
©
Determinar la proposición [((~p) v q) a ~q] > ~p es una tautología.
Solución
p
V
V
F
F
q
V
F
V
F
[(~pvq) a ~q] >
V F F V
F F V V
V F F V
V V V V
~P
F
F
V
V
-▼>.
Es una tautología
©
Verificar que las siguientes proposiciones son contradicciones:
a) (p a q) a ~(p v q) b) ~[p v (~p v ~q)]
Solución
p
V
V
F
F
q
V
F
V
F
(pAq) a -(p v q)
V F F V
F F F V
F F F V
F F V F
- [p v (~pv~q)]
F V V F
F V V V
F F V V
F f V V
Contradicción
Contradicción
©
Demostrar que las proposiciones dada es una tautología: [(p v -q) a q] -
Solución
p
V
V
F
F
q
V
F
V
F
[(pv~q) a q]
V V V
V F F
F F V
V F F
» P
V V
V V
V F
V F
-*^.
-*p
Es una tautología
40
Eduardo Espinoza Ramos
©
®
Verificar que la proposición dada es una contingencia [~p a (q v r)] <—> [(p v r) a q]
Solución
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
[~P
F
F
F
F
V
V
V
V
A
F
F
F
F
V
V
V
F
(qvr)]
V
V
V
F
V
V
V
F
* 3
F
F
V
V
V
F
F
V
[(P v r)
V
V
V
V
V
F
V
F
a q]
V V
V V
F F
F F
V V
F V
F F
F F
Determinar si las proposiciones [p -
equivalentes.
i j £s una contingencia
-* (r v ~q)] y [(q > ~p) v (~r > -p)J son
Solución
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
[p
V
V
V
V
F
F
F
F
>
V
F
V
V
V
V
V
V
(rv-q)]
V
F
V
V
V
F
V
V
[(q >
F
F
V
V
V
V
V
V
~p) v (~r
V
F
V
V
V
V
V
V
—>~p)]
V
F
V
F
V
V
V
V
Idénticas
Por lo tanto son equivalentes es decir: [ p——» (r v ~q)] = [(q > ~p) v (~r > ~p)]
Determinar si las proposiciones [(~p v q) v (~r a ~p)] y ~q > - p son equivalentes.
Solución
Lógica
41
©
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
[(~P) v q) v (-
V V
V V
F F
F F
V V
V V
V V
V V
-r a ~p)]
F
F
F
F
F
F
F
V
-q >~p
V
V
F
F
V
V
V
V
. Idénticas —J
Por lo tanto son equivalentes es decir: (~p v q) v (~r a ~p) = ~q » ~ p
Determinar los esquemas más simples de la proposición: ~[~(p a q) » -q] v p
Solución
~[~(p a q) > ~q] v p por la condicional
~[~(~(p a q) v -q)] v p por la negación
~[(p a q) v ~q] v p por conmutatividad en la conjunción
por absorción
por Morgan
por absorción
.-. ~[-(p a q) > ~q] v p = p v q
~[~q v (p a q)] v p
4~q v p] v p
(~p a q) v p
pvq
De la falsedad de la proposición: (p * ~q) v (~r > s) determinar el valor de verdad
de los esquemas moleculares
a) (~p a -q) v -q
c) íp »q) »(pvq)A~q
b) (~r v q) <—> (~q v r) a s
Solución
42
Eduardo Espinoza Ramos
Determinaremos el valor de verdad de p, q, r y s
(p > ~q) v (~r > s) F falso
y r por la disyunción
->~q
por implicación
p es V y -q es F
por negación
P es V y q es V
-»s
por implicación
-r es V y s es F
por negación
r es F y s es F
Por lo tanto:
p es V, q es V , r es F, s es F
a) (~p A~q)v~q
F
F
+
F
i
ta
El valor de verdad es F
c)
(P-
-*q)-
i
V
V
-»(p v q) a ~q
v: v
i
+
+
F
F
El valor de verdad es F
b) (~r v q) •
V
V
F
(~q v r) a s
♦ !♦ "
F¡ F
i
+
á
v El valor verdad V
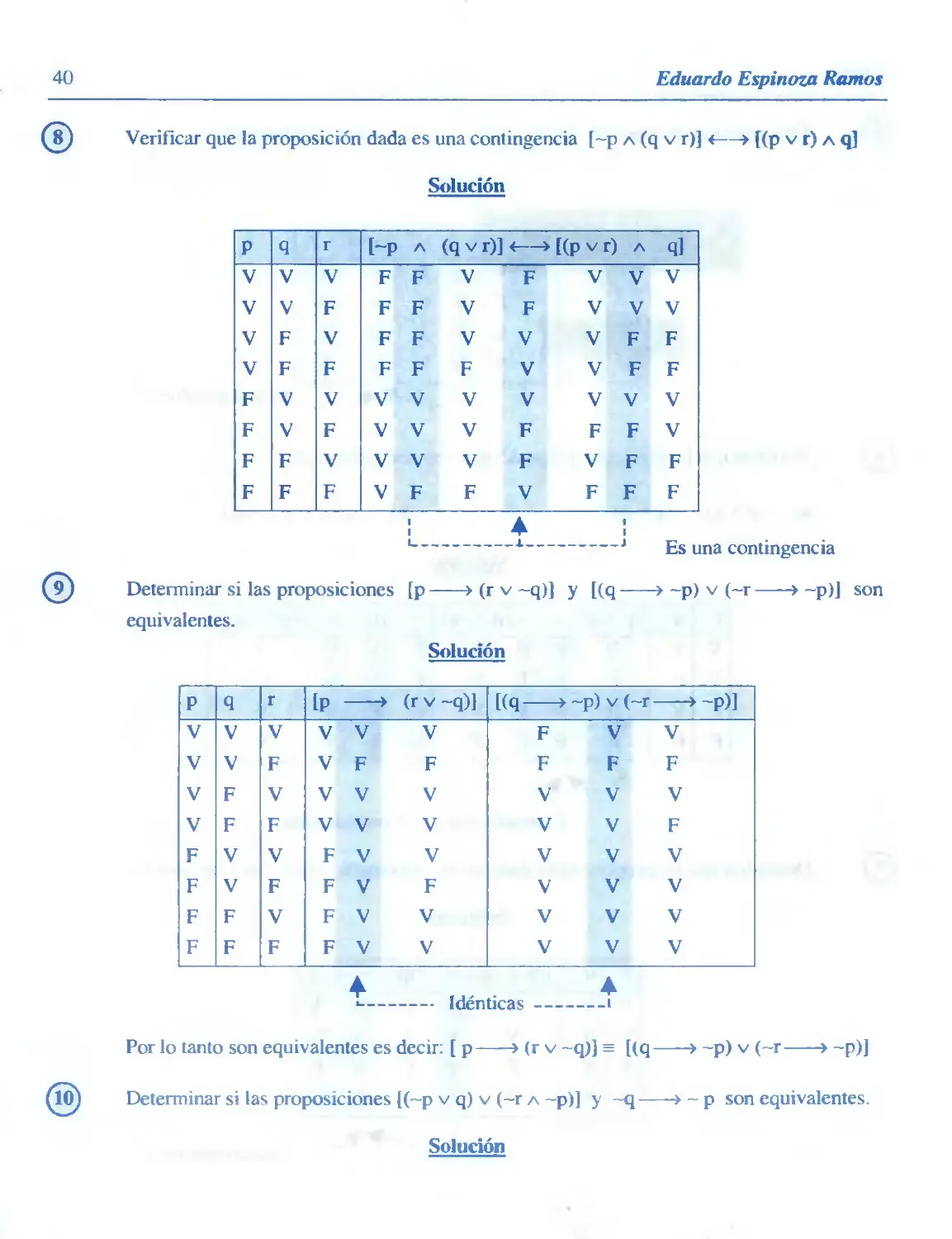
fI3) El valor de verdad de: ~[(~p vq)v (r > q)] a [(~p v q) > {q a -p)] es verdadera.
Hallar el valor de verdad de p, q, y r
Solución
Lógica
43
[(-p v q) v (r » q)] a [(-p v q) > (q a -p)] es V
_T
por conjunción
~[(~pvqjv(r >q)] es V
1
[(~pvq) >(qA~p)] esV
por negación
por implicación
(~p v q) v (r » q) es F
(~P v Q) es P
por disyunción por disyunción
(~p v q) es F
(r » q) esF
por disyunción
~p es F y q es F
(q a ~p) es F
por conjunción
p es V y q es F
q es F y -p es F
por implicación
por negación
r es V y q es F
q es F y p es V
por negación
p es V y q es F
por lo tanto el valor de verdad de
p es V
q es F
r es V
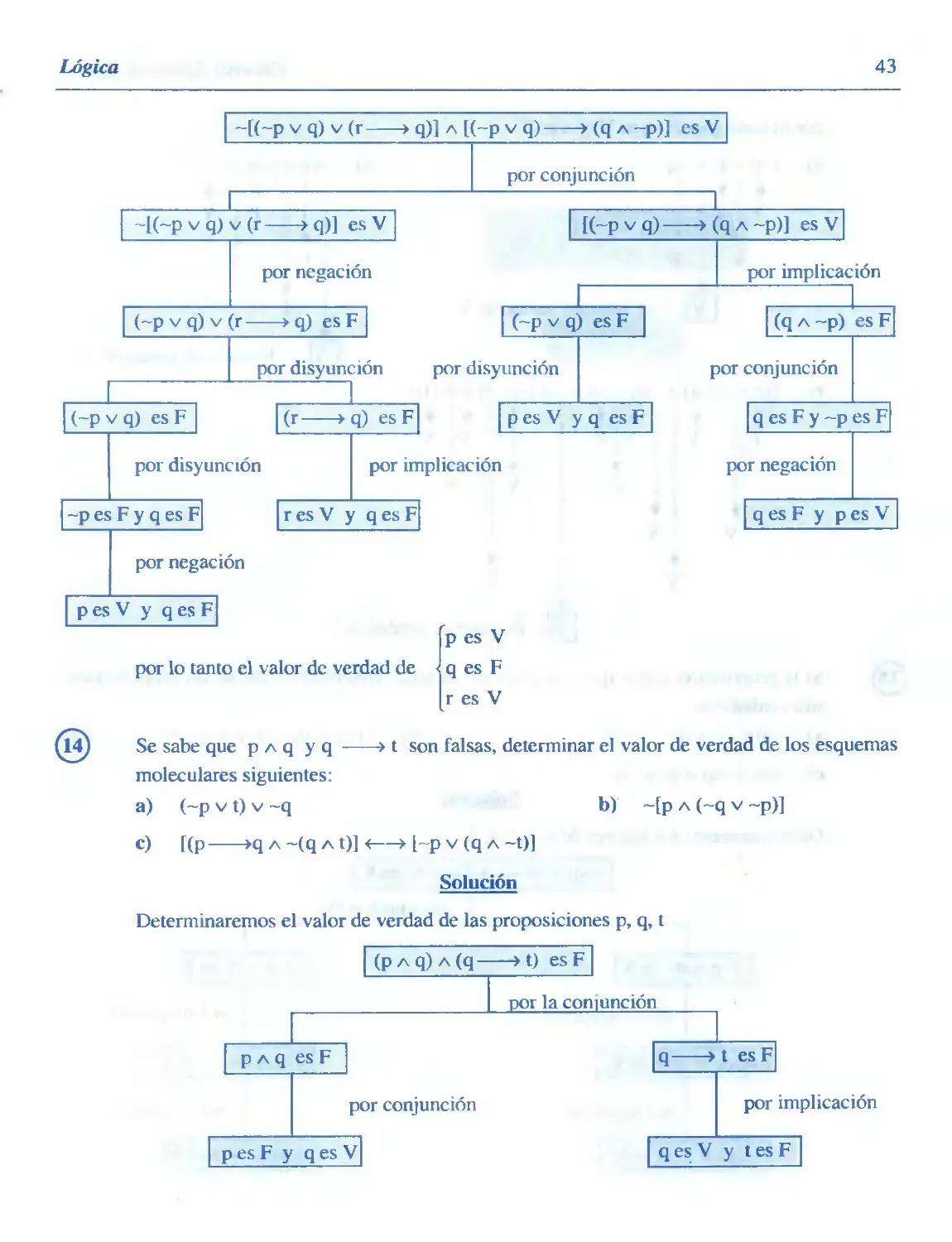
Se sabe que p a q y q » t son falsas, detenninar el valor de verdad de los esquemas
moleculares siguientes:
a) (-pvt)v-q b) ~[pA(~qv~p)]
c) [(p >q a ~(q a t)] <—> l~p v (q a ~t)]
Solución
Determinaremos el valor de verdad de las proposiciones p, q, t
(p a q) a (q > t) es F
por la coniunción
p a q es F
por conjunción
p es F y q es V
q > t es F
por
im
q es V y t es F
44
Eduardo Espinoza Ramos
por lo tanto p es F, q es V y t es F
a) (~p v t) v ~q
V ¡ F
i
♦
V
b) ~[p a (~q v -p)]
I
F
I v| el valor de verdad es V
F ¡ V
i
+
V
F
| V| El valor de verdad es V
c) [(p »q)A-(qAt)]
F
V
V
v! f
I
+
F
V
V
[~p v (q a -t)]
v! v
i
+
V
V
V
T
I V| El valor de verdad es V
Si la proposición (~p a q) > (~s v r) es falsa. Determinar cuál de las proposiciones
son verdaderas:
a) ~[(p >q) >t] b) -(-p a q) a [(-r v r) a s]
c) [(p v ~q) a p] v ~q
Solución
Determinaremos los valores de p, q, r, s
(~p a q) es V
porco
. x
V P A H)
nj
-p es V y q es V
por nega<
p es F y q es V
unción
:ión
-s v r) es F
por implica
ción
(~s v r) es F
por dis
yur
-s es F y r es F
por negací
s es V y r es F
Lógica
45
por lo tanto \
p es F , q es V
s es V , r es F
a)
1(P-
+
F
->q)-
i
V
->r]
b) [~(~ p a q)] a [(-r v r) a s]
+
V
F
V
V
+
V
F
F
v¡ F
I
+
+
V
V
El valor de verdad es V
F El valor de verdad F
c) [(p v ~q) a p] v ~q
+ ! +
F¡ F
I
+
F
F
| F| El valor de verdad es F
Por lo tanto únicamente es verdadero la a)
Determinar el esquema más simple de la proposición [(p a q) v (p a ~q)] v (~p a ~q)
Solución
[(p a q) v (p a ~q)] v (~p a ~q) por distribución respecto a a
[((p a q) v p) a ((p a q) v ~q)] v (~p a ~q) por absorción
[p a (~q v p)] v (~p a ~q) por conmutatividad en v
[p a (p v ~q)] v (~p a ~q) por absorción
p v (~p a ~q) por absorción
pv-q
por lo tanto [(p a q) v (p a -q)] v (~p a -q) = pv~q
46
Eduardo Espinoza Ramos
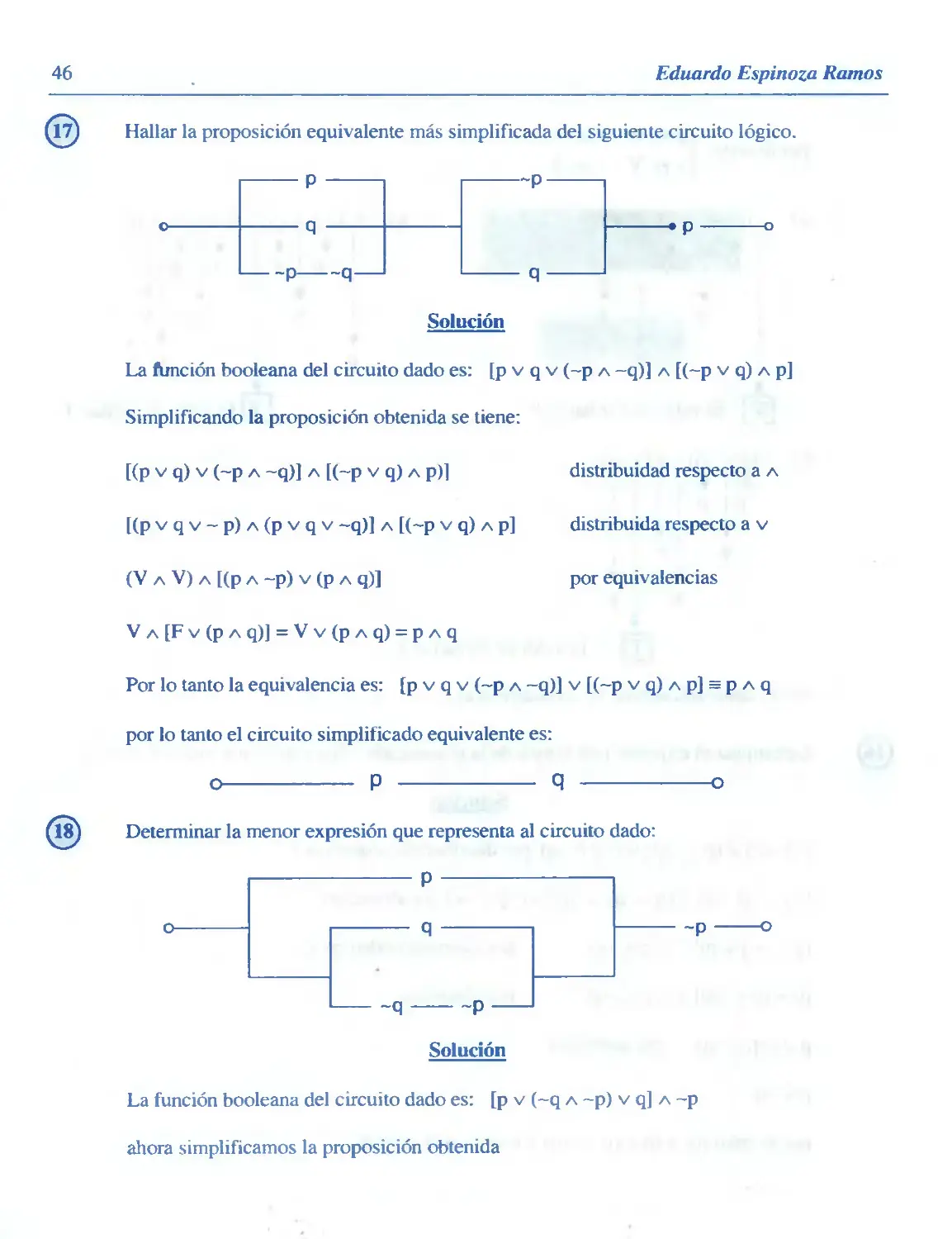
[li) Hallar la proposición equivalente más simplificada del siguiente circuito lógico.
n«
distribuidad respecto a a
distribuida respecto a v
por equivalencias
Solución
La función booleana del circuito dado es: [p v q v (~p a -q)] a [(~p v q) a p]
Simplificando la proposición obtenida se tiene:
[(P v q) v (~p a ~q)] a [(~p v q) a p)l
[(p v q v - p) a (p v q v -q)] a [(~p v q) a p]
(VAV)A[(PA-p)v(PAq)]
V a [F v (p a q)] = V v (p a q) = p a q
Por lo tanto la equivalencia es: [p v q v (~p a -q)] v [(~p v q) a p] = p a q
por lo tanto el circuito simplificado equivalente es:
O P Q o
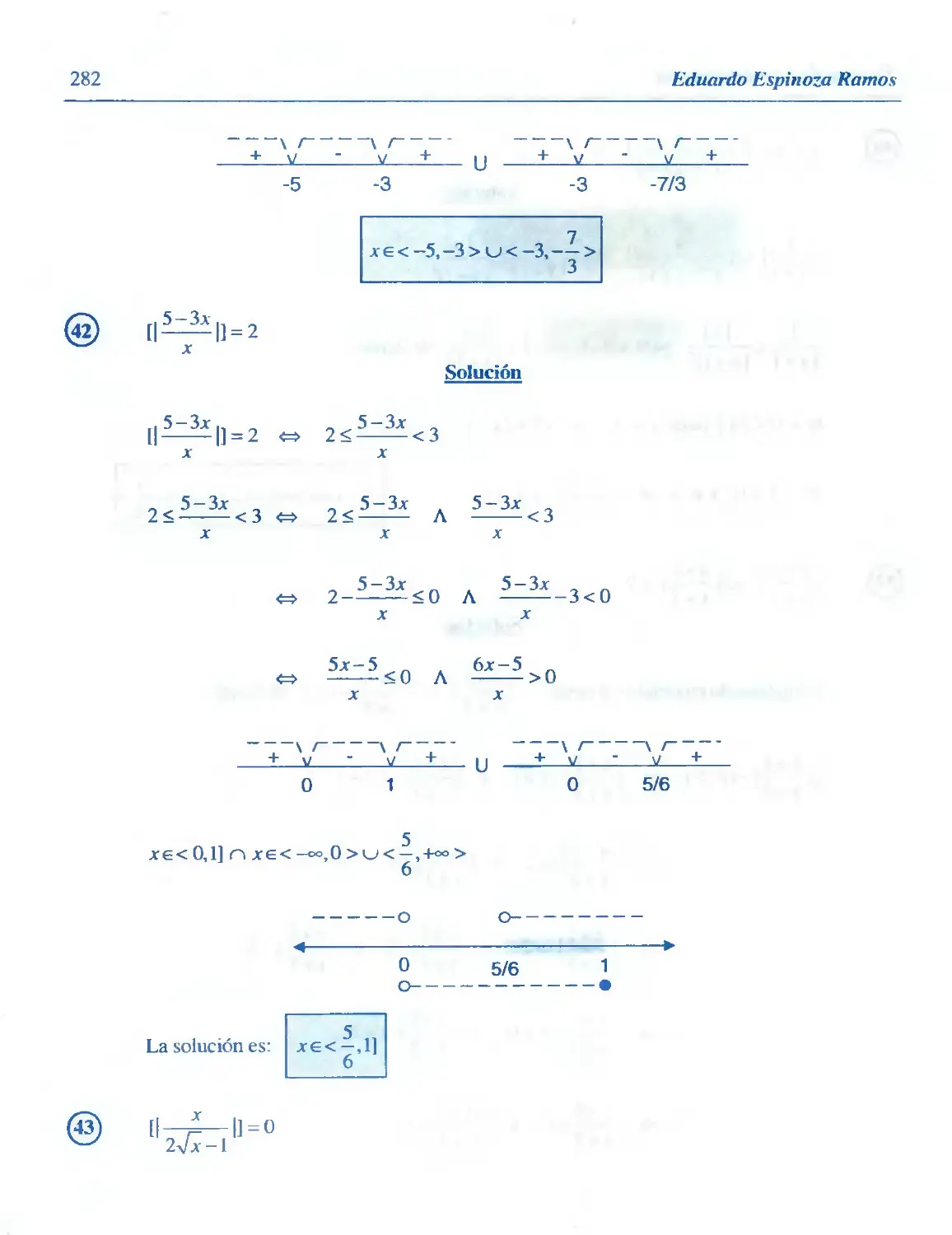
Determinar la menor expresión que representa al circuito dado:
P
q
~q
~P
Solución
La función booleana del circuito dado es: [p v (~q a ~p) v q] a -p
ahora simplificamos la proposición obtenida
Lógica
[p v (~q a ~p) v q] a ~p s [p v q v ~p] a -p
= [(p v ~q) v q] a ~p
s (V v q) a ~p s q a ~p
Determinar la menor expresión que representa al circuito dado:
p q
Solución
La función booleana del circuito dado es: [(-p a ~q) v (p a (~p v q))]
ahora simplificando la proposición obtenida
[(~p a -q) v (p a (~p v q))] s [(-p a -q) a (p a q)] = p <—> q
Determinar la menor expresión que representa el circuito dado:
r
Solución
La función booleana del circuito dado es: (p v q) a [(~q a (r v -q)) v (p a q)] a
simplificando la proposición obtenida
(p v q) a [(~q a (r v ~q» v (p a q)] a r = (p v q) a [~q v (q a p)] a r
= (pvq)A[~qvp]Ar
= [p v (q a ~q)] a r
= (pvF)Ar=pAr
48
Eduardo Espinoza Ramos
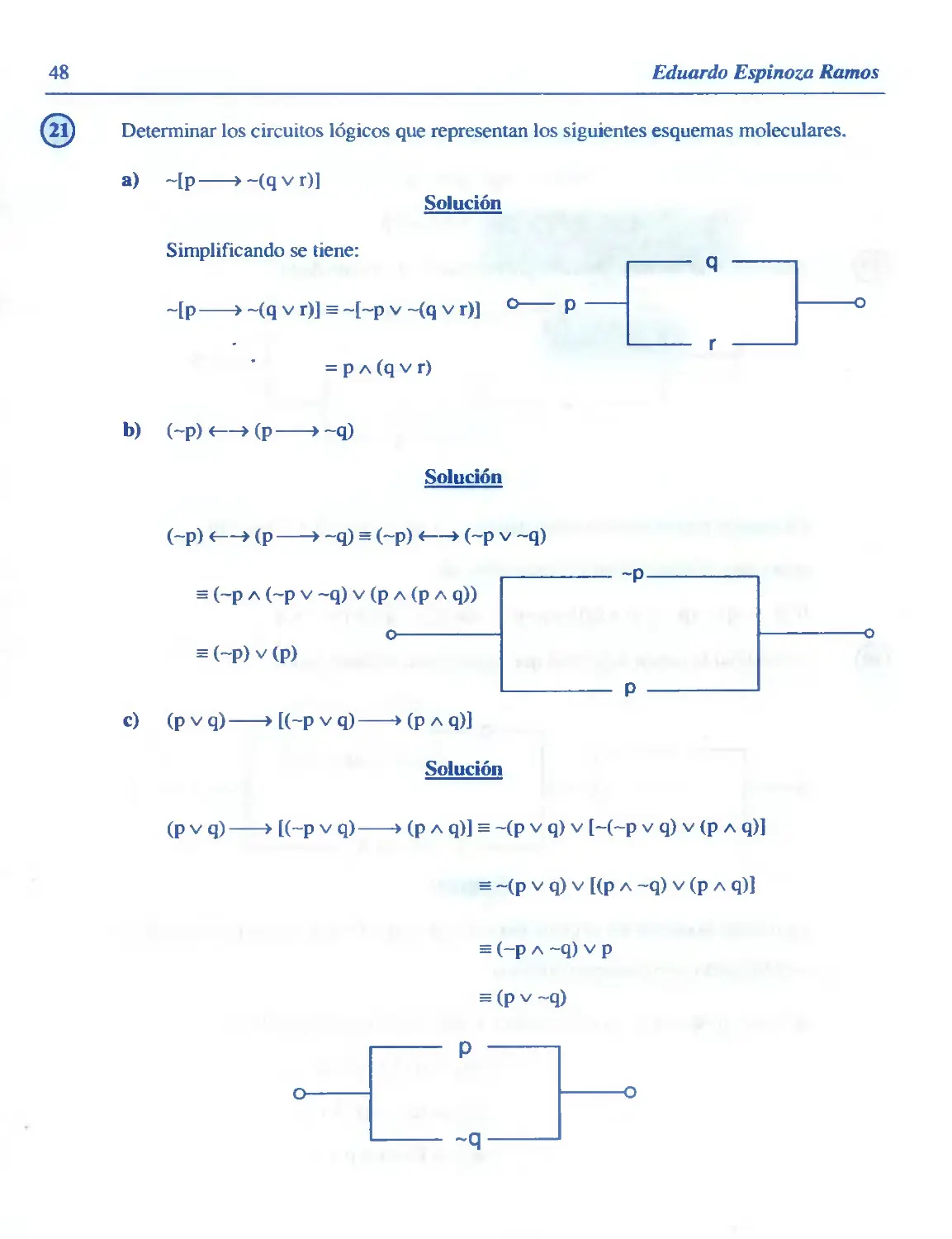
Determinar los circuitos lógicos que representan los siguientes esquemas moleculares.
a) ~[p >-(qvr)]
Solución
Simplificando se tiene:
~[p > ~(q v r)] = ~[~p v ~(q v r)] ° P
= p a (q v r)
b) (~p)<—>(p >~q)
Solución
(~p) <—»(p > -q) = (~p) <—> (-p v -q)
s (~p A (~p v -q) v (p a (p a q))
o
= (~P) v (p)
c) (pvq) >[(~pvq) >(pAq)]
Solución
(p v q) > [(~p v q) > (p a q)] = ~(p v q) v [-(~p v q) v (p a q)]
= ~(p v q) v [(p a -q) v (p a q)]
s (-p a -q) v p
= (p v ~q)
~q
Lógica
49
1.30. EJERCICIOS PROPUESTOS.-
(1) Determinar cuales de los siguientes enunciados son proposiciones:
a) S+ 7 =16-4 b) 3x6=15+1 y 4-2*23x5
c) ¿El silencio es fundamental para estudiar?
d) ¡Estudia lógica simbólica!
e) Nosotros estudiamos en la Universidad Peruana.
f) Los hombres no pueden vivir sin oxígeno.
g) ¡Arriba Callao!
h) 5 + x = 7 i)2 + x*3 + x
(2) Determine cuáles de los siguientes enunciados son enunciados abiertos:
a) x es hermano de y b) 28<15
c) x + y + z*l d) 9x + 3>12
e) Tenga calma, no se impaciente
g) x es ingeniero y Juan es matemático,
h) La UNAC sobresalió en el deporte en el 2000.
(y) ¿Cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas?
a) Sí 3 + 3 = 6, entonces 4 = 4
b) Si 5(7) = 35, entonces 10-3 = 13
c) Si 19 - 7 = 3. entonces 4(5 + 3) = 32
d) Si 2 = 3 entonces 8 es un número primo.
e) Si 3(7) es un número natural, entonces 17 es un número primo.
f) Si x = 2, entonces 3x = 6
50
Eduardo Espinoza Ramos
(4j Determinar el valor de verdad de las siguientes proposiciones:
a) (3 + 5 = 8)v(5-3=4) b) (3 + 8 = 11) v (7-3 > 1)
c) (5-3 = 8) > (1-7 = 6) d) (4 + 6 = 9)<—>(5-2 = 4)
(Sj Dados las siguientes proposiciones: p: 5 > 10
q: si x +1 = 0, entonces x es un número real
r: "El punto medio de un segmento, equidista de los extremos del segmento"
t: Sí x + 3 = 0, entonces x = -3
Hallar el valor de verdad de las siguientes proposiciones.
a) KpAq) >r]A~t b) [(p <—» q) >~rAt]v(pvr)
(ó) Si P(x): x2 -16 = 0; q(x): x - 12 = 0, r(x): x2 > 9 . Hallar el valor de verdad de:
a) [p(2)A~q(2)]<—>r(4)
b) [~p(4) »r(5)]v~q(4)
c) [(p(l) a p(3)) <—> (r(2) v p(3)] > [~(p(2) v q(2))]
(?) Si P(x): jc3 = 27 ; q(x): x2 = 9; r(x): x < 10. Hallar el valor de verdad de:
a) (p(l) > q(12)] <-^ [r(-3) v -r(3)]
b) [p(0) a ~q(-1)] v [r(-5) > (r(-6) v r(0)]
c) [(p(3) v p(2)) <-^ (r(2) a ~q(3))] <-^ [~q(3) v -p(-3)]
(s) Construir la tabla de verdad de las siguientes proposiciones:
a) (p<—»~q)<—>(q >p) b) (pA-q) >(~pvq)
c) [(p v-r) a (p v r)] a [(q >p)A(qvp)] d) ~(p v -q) a (~p v r)
e) ~[p a (~q » p)] a [~(p <—> ~q) > (q v~p)]
Lógica
51
\9J Construir la tabla de verdad de las siguientes proposiciones:
a) (p a q) v (~p) => (p v q) b) (p => q) => r
c) (p => q) ==> (q ==> p) d) ((~p) v q) => (~q => ~p)
e) (p a r) => (~q v r) f) (p a q) v r <=> (~p v ~q) a (~r)
(lO) Hallar las tablas de verdad de las siguientes proposiciones:
a) p »(pv~q) b) [(pv~q) > (q > p)]
c) [pv(q > ~r)] a l(~p v r) <—> ~q] d) ~l~(p a q) » ~q] v p
e) ~{[(p >q)v(q > r)] > (r >p)}
(il) Deducir el valor de verdad de:
a) (p >r) >((pvq)A~q] b) (-pA-q)v-q
c) [(~r v q) a q] < > [(~q v r) a s]
fl2) Indicar cuál es la tabla de verdad de cada una de las siguientes proposiciones:
~[(p v q) a (-p v ~q)]
fl3) Determinar cuál de las siguientes proposiciones son tautología
a) [(pv-q)Aq] >p b) [(pAq)vq]<—>q
c) [~p a (q a ~r)J <—> f(~p a q) v ~(p v r)]
(14) Por medio de una tabla de valores, establecer, si cada una de los siguientes esquemas
moleculares es tautología, contingencia o contradictoria.
a) -[~p > ~(~q a ~p)J v ~(~p v-q) b) [(p v ~q) a ~p] a (~q > p)
c) ~(p > q) <—> ~(~q > ~p)
d) lp >(q >r)]<—H(pA~r) >~q]
e) lpA(-q >p)]A~l(p >~q) > (q v ~p)]
f) f-p a (q v ~r)] < > l(~p a q) v ~(p v r)]
52
Eduardo Espinóla Ramos
(15) Determinar mediante la tabla de verdad, cuales de las siguientes proposiciones son:
tautologías, contradicciones o contingencias
a) (p >q)A(q » p) b) [(pvq)A-q] >p
c) ~[(pvp) >p] d) ~(pvq)Ap
e) [p >(q—^r)jA[(qvp) > r]
nó) Determinar cuáles de las siguientes proposiciones son tautología, contradicciones y
contingencias,
a) ~(~p)<—»-[-(-p)] b) (-pvq)A(-q > p)
c) (p v q) a r <—> ~(p a r) a ~(q a r)
d) [(pAqAr) »s]<—>[(pAq) > (r > s)]
Mm Dadas las proposiciones siguientes:
a) ~(pAq)<—>(pv~q) b) ~(p > q) <—>(pv-q)
c) -(p <—> q) <—> (~p <—» -q)
indicar cuál o cuáles es una contradicción
U8) ¿Algunos de las siguientes proposiciones es una tautología?
a) ~[~(p v q) » -q] <—»(p > q)
b) ~[(-p) <—> q] <—> (p > q)
c) ~[(p a q) v (p a (~p v q))] <—> (p > -q)
U9) Determinar cuál de las siguientes proposiciones son tautologías, contingencias o
contradictorias.
a) [(p a ~q) a (~p > r)] ► (p v ~q)
b) íp v (q > -r)] a [(~p v r) <—» -q]
c) [(~p a q) > -r] <—» [r a ~(p v ~q)]
d) ~{(pAq)v[pA(~pvq)]} <—> (p > ~q)
Lógica
53
(20) ¿Cual de las siguientes esquemas no señalan una tautología?
a) (p a q)<=> (q v p; b) (p a q) <=> (~p a ~q)
c) (p a q) <=> (q a p) d) (p > q) <=> (~p a -q)
(21) Determinar la validez del esquema: ~[~(~pA~q) »~(pvq)]<—>[~(~pvq)]
Í22) ¿Cuál de las siguientes proposiciones es una tautología.
a) (pAq)vlpA(~pvq)]<—>(p >~q)
b) ~[~(p v q) > ~q] <—> (p > q) c) ~(~p > q) < > (p < > q)
(23) Construir la tabla de verdad y determinar cuáles son tautología, contradicción o
contingencia.
a) (p »q)<—»[(r »q)A(q > p)]
b) (p > (q v ~r)] a -tp <—>r]
^4) ¿Cuales de las siguientes proposiciones es una tautología?
a) ~{(pAq)v[pA(~pvq)]) < > (p > ~q)
b) ~(-p<—»q)<—»(p<—>q) c) [(pv-q)Aq] >p
d) ~[(~p v q) > q] <—> (p > q)
e) [~p a (q v ~r)] < > [(~p a q) v ~(p v r)]
(25J Simplificar las siguientes proposiciones:
a) {[(-q) —> (~q)] > [(~p) > (~q)] ] > ~(p a q)
b) [(p > q) v ~p] a (~q > p) c) -{[~(~p a q) v ~q] > [~(p v ~q)]}
d) (~p v ~q) a f-p a (q -> p)] e) [(p => q) => (p a q)] v (p a r)
f) ~[-(p a q)-> ~q] v p g) [(~p a q) => (q => p)] a p
feo) Simplificar las siguientes proposiciones:
54
Eduardo Espinoza Ramos
a) [(~p a q) > (r a ~r)] a ~q
b) K~q > ~p) > (~p > ~q)] a ~(p a q)
c) [(p a q) v (p a ~q)] v (~p a -q) d) (p Aq) v(~p A~q) v p
e) t => [(p => q) => q] a [~p a (q => p)] f) [~(p => q) => ~(q => p)] a (p v q)
g) [(p a -q) a (q => p) a r] v p
(27) Si ~[(~p v q) v (r > q)] a [(~p v q) > (q a -p)] es verdadera, hallar los valores de
verdad de p, q y r.
(28) Si la proposición (p > ~q) > (r > ~s) es falsa. Hallar el valor de verdad de las
proposiciones p,q,r,s.
(29) Si la proposición ~(p a q) a (q <—> p) es verdadera; entonces hallar los valores de verdad
de p y q respectivamente.
(3<j) Si la proposición (p => ~q) v (~r » s) es falsa. Hallar el valor de verdad de los
siguientes esquemas moleculares.
a) (p => q) => [(p v q) a ~q] b) (~r vq)o [(~q v r) a s]
c) (~p a -q) v -q
(31) Determinar el valor de verdad de las proposiciones p y q si se conoce la información
siguiente:
a) (p a q) <=> (p v q) es verdadero b) ~(p a q) es verdadero
(32) Determinar el valor de verdad de las proposiciones p y q si se conoce que el valor de
verdad del siguiente esquema [~(~p => q) => ~(p » ~q)] ==* (p > q) es falso.
(33) Si p y q son verdaderos ¿para qué valores de r, el esquema siguiente es
verdadero? (r > p) o (~q => r)
{M) Si se tiene los siguientes datos: p es verdadero; r => ~p es verdadero y w => t es
verdadero, hallar el valor de verdad de ~r y de t.
Lógica
55
Si el esquema (p a q) > (p » r) tiene valor de verdad, falso, halla el valor de verdad
de los esquemas.
a) [(p a q) v (q v ~r)] <=> (p v ~r) b) (pv~q)=> (~r a q)
c) ~(q v r) v (p v q)
Si la proposición (~p a q) =* [(p a r) v t] es falsa, hallar el valor veritativo de:
a) ~[(~pv~q) »(rv~t)] b) (~q v ~r) v [~t v (p v q)]
c) (~p => t) =* (~q => r)
Si la proposición (p a q) => (q => r) es falsa y se tiene los esquemas moleculares.
a) -(qvr)v(pvq) b) (p v ~q) => (~r a q)
c) [(P a q) v (q a ~r)] <=> (p v ~r)
Cuáles son falsas
Si la proposición (~p a q) => [(p a r) v t] es falsa. Hallar el valor de verdad de cada una
de las siguientes proposiciones.
a) (~p => t) =* (~q =* r) b) (~q a ~r) v [~t a (p v q)]
c) ~[(~p v -q) => (r v ~0]
Sean p.q,r,s,t proposiciones. Si [(~p) a q] => [(r => p) v t] es una proposición falsa, hallar
el valor de verdad de: ~(q v ~r) v ~[t =* (~q a p)]
Si la proposición (~p Aq)^ (~s v r) es falsa, de las proposiciones siguientes, cuales son
verdaderas?
a) ~[(p => q) => r] b) ~[(~p a q) a (~r v r)] a s
c) [(p v ~q) a p] v (-q)
Admitiendo la falsedad de: ~[p v q v r] => ~(M a N a t). Hallar el valor de verdad de:
a) [(pAM)=>(qvN)]At b) [(p=>q)=>(q=> M)] <=> (r => t)
c) ([(pvq) >íias)] A(-q >~i)} =>[(p—^q) a (q > M)]
56
Eduardo Espinoza Ramos
(42) Admitiendo la falsedad de la proposición: (p a q) => [(r v s) => (t => w)] hallar el valor
de verdad de:
a) (p => w) a (r => q) b) ~(p a t) => (~s => p)
c) üq =* ~(t v r)] a [p => ~(r a w)]} « [(p =* ~q) v ~t]
(43) Si la proposición (~p a q) »[(p a q) v t] es falsa. Hallar el valor de verdad de:
a) ~[(~pv~q) >(rv~t)] b) (~p > t) > (~q > r)
c) (~q v ~r) v [~t a (p v q)J
(44) Si q >t ypAq son falsas. Determinar el valor de verdad de:
a) (-pvt)v-q b) ~[p a (~q v ~p)]
c) [(p > q) a ~(q a t)J <—> [~p v (q a ~t)]
(4£¡) Si la proposición (~p a q) > (~s v r) es falsa. Determinar el valor de verdad de:
a) ~[(p >q) >r] b) ~(~p a q) a [(~r v r) a s]
c) [fp v -q) a p] v ~q
(46) Si la proposición (~p » q) v (s > ~r) es falsa. Determinar el valor de verdad de las
proposiciones.
a) ~(pvq)v~q b) ~[(pvq)A~q] >~(p > q)
c) [(r > q) a q] <—> [(~q v r) a s]
U7) Si la proposición (q a ~p) > [(p a r) v t] es falsa, calcular el valor de verdad de la
proposición: (~p »t) »(~q > r)
M8) Sabiendo que (q > t) y (pAq) son falsas, determinar el valor de verdad de:
a) ~[pA(~qv~p)] b) (~pvt)vs
c> i-pv(qA-t)]* > ffp >q)A~(qAt)]
Lógica
57
(49) Si el esquema (~p > ~q) v (r A q) es falsa, determinar el valor de verdad de:
a) (p >q) >(rA~q) b) -q >[(p<—>q)Ar]
(50) Si [(r > s) a t] > (p v q) es falsa determinar el valor de verdad de:
a) ~r v (~s > -t) b) (p <—> t) v [q a (~r v s)]
c) [(r A s) v (t > s)] a (p a r)
[Si) Dado los esquemas preposicionales denotados por A, B y C respectivamente:
A: p <—» ~(q a r) ; B: -p A ~r ; C: -(p a q) v -r
Determinar si A > C y B > C son implicaciones (tautología)
(52) Si la proposición (~p a q) =* [(p a q) v t] es falsa. Hallar el valor de verdad de:
a) ~[(~p v ~q) => (r v ~t)] b) (~q a ~r) v [~t a (p v q)]
(53) Si el esquema indicado: [(~p v q) v [(p —» q) a t]] a q es verdadero, indicar el valor de
verdad de:
a) p =* q b) t v q c) ~q v (t v p)
(54) Si la proposición [íp v t) —» (p a q)] es falsa, dar el valor de verdad de las siguientes
proposiciones.
a) [(~p a ~t) a (q -> r)] b) [(pvt)H(~pv~q)] c) [fp v t) A (p a q)]
(55) Si la siguiente proposición lógica ~[(p a q) => (q <=> (r v s))] es verdadera, hallar los
valores de verdad de p, r, q, s.
(56) De la falsedad de la proposición: (p -» ~q) v (~r —» s) determinar el valor de verdad de
los esquemas moleculares.
a) (~p a ~q) v -q b) (~r vq)«(~qvr)AS c) (p -» q) -» (p v q) a ~q
(57) De la falsedad de (p => ~q) v (~r => ~s), hallar el valor de verdad de las siguientes
proposiciones.
a) ~(~qv~s)=5~p b) ~(~r a s) =* (~p =* q) c) p => ~(q => ~(s =í> r))
58
Eduardo Espinoza Ramos
(60
Hallar los valores de verdad de: p, q, r si: [(-p v q) v (r =* q)] a [(~p v q) =* (q a ~p)]
es falso.
Si la proposición: [~(p => q) a (~r v s)] =* r es falso, halle los valores de verdad de: p, q
yr-
Si: ~p v [(p Ar)^(r« q)] es falso, halle el valor de verdad de: [(p => q) v r] <=> (p a r)
(61) Si [-(p => q) a -r] => [p a (q v r)] es falsa, halle los valores de verdad de: p, q y r.
(62) De la proposición compuesta: ~[(p a q a r) => s] =* (~p v s) se conoce que es falso,
señale el valor de: p, q, r y s.
(¡63) Si la proposición "s" es falsa, y el siguiente esquema: (~p Aq)« [fq => r) v (p a ~s)] es
una tautología, hallar los valores de verdad de p, q y r.
(64) Demostrar si las siguientes fórmulas son lógicamente equivalentes:
a) -pAq = ~(pvq) b) p a ~p = ~[(p v p) «=> p]
c) -q v p = ~(-p Aq)E-p«(p=> -q)
d) ~[(p a q) a ~r] s ~[(-p a -q) a (p v r)]
e) ~(p=>q) = ~p « q = p «=> -q = ~(-p «=> ~q)
(65) Probar que son equivalentes p => q y (~p) v q
(66) Probar la equivalencia de las siguientes proposiciones:
a) -(p => q) y p a (~q) b) ~(p a q) y (~p) v (-q)
c) ~(p v q) y (~p) a -q d) p => q y -q => -p
e) (p =* q) a (q => r) y p=>r
yST\ Demostrar que las bicondicionales siguientes son equivalencias lógicas.
a) (p >q)«=>(~p)vq
b) (p<—»q)«(p >q)A(q >p) c) (pAq)vp <=>p
d) (pvq)Ap«p e) ~(p >q)<=>(pA-q)
Lógica
59
Determinar el valor de verdad de los siguientes enunciados considerando como universo a
los números reales.
a) {Vjce R/x3 =x] b) {3xeR/2x = x}
c) {3xeR/x2 +3x-2 = 0} d) {3xe R/x2 -2jc + 5 = 0)
e) {Vxe R/2x + 3x = 5x} f) {3xe R/2x2+x = 15]
g) {VxeR/x-3<x} h) {VxeR/x + 3<6}
i) {3xeR/x + 3<6} j) {Vxe R/x2 -10<8]
Evaluar ~{~(p v -q)} <=> {~[(r a p) > (p a ~p)]} sí: p: {Vxe R/x° =1};
q:{3xeQ/3x2=x-5] ; r: {3 jte Z/jc2 -2jc-1 = -1, >/4=jc}
Sean las proposiciones /?: {Vxe £)/—h jc > 0}, q: {3 x e I / x + 0 = 7t},
r: {Vxe tf / x2 +1 = 0}. Hallar el valor de [(p > q) a r] <=> ~q
De las siguientes proposiciones, hallar el valor de verdad.
a) (Vxe R/|x| = x)a(3xé R/x+1 í x)
b) (~3xe R/ x2 *jt)v(~Vxe z/x+ 1 *x-l)
c) (~Vxe N/|x|*0) »(~3xe Q/|x|*0)
¿Cuáles son equivalencias lógicas?
a) ~(q > ~p) o(qvp) b) [f~p a ~q) v ~q] <=> [(p v q) a q]
c) ~(p > q) <=> [(p v q) a ~q]
Sea U el conjunto universal y p, q, r las proposiciones:
U= {-10,-9 80}, UcZ(numerosenteros) ; p: {Vjce U, 3ye Ulx-x2 <-2y}
60
Eduardo Espinoza Ramos
q: {3ye U, V x e U/x-5y<3x-y} r: {V ze í/,3ye U,3xeU I x1 + y2 < z2}
Evaluar (~p v r) <—> (p a -q)
Determinar el valor de cada uno de las siguientes proposiciones:
a) [3xeZ/x2 = x) b) {VxeZ/x-7<x}
c) {3xeZ/x + 5 = 5} d) {VxeZ/x + 8>x}
e) {VxeZfx2 >x] f) {VxeZ/x+l=x}
Si U = {x e R / 2 < x < 10} y p: (Vjte U)(3ye í/)(Vze U)/-x-y>-<z2,
q: (Vxe í/)(3 z e í/)(3 z e U)(x+ y < z2), hallar el valor de verdad de (~pv~q) => (pAq)
Si U = {1,2,3,...,99}, determinar cuáles de los siguientes proposiciones son verdaderos.
a) {3xe U/x + 5 = 2x} b) {VxeU/x+leUJ
c) {3xe U/|x-8|>5} d) {V x e U /20-3x <0}
Hallar el valor de verdad de la fórmula, [fp v q) > (~r v ~w)] <=> (q > r) sí
p: 3 xeQ/x+3 = y¡2+3, q: 3xe I/x + 0 = 7t
r: Vxe N/x + 2.5 = 5, w: 3 x£Q/x + 0 = yfl
Hallar el valor de verdad de: [(~p a -q) > (r v q)] a [~(p a q) <—> r]
Sí U= {xe Z/-100<x< 100} ; p: (Vxe U)(3 y e U)(V z e U)(x + y-z>30)
q: (Vxe U)(V y e U)(V z e U)(2x + z - 4y < 800)
r: (3 x e U)(V y e U)(3 z e U)(5x < z - y + 50)
Si x puede tomar cualquier valor 1,2,3, demostrar mediante contraejemplos la falsedad de
las siguientes proposiciones.
a) {(Vx)/x2 =x) b) {3x/x = 2x}
Lógica
61
c) (Vx/x + 2 = 5) d) {Vx/x+l>3)
e) ~{3x/jc2=4) f) (3x/x>4)
(80) Si x, y pueden ser cualquiera de los números 1 y 2, determine el valor de verdad de las
siguientes proposiciones:
a) (3 x)(V y)(x < y + 2) b) (V x)(3 y)( x + y < 5)
c) ((VxXVyX*2+y2<l) d) (Vjc)(3>>)(x2>v)
e) (3 x)(3 y)(x + y = 2)
Q$l) Cuales de las siguientes proposiciones son verdaderas o falsas. Si U = (1,2,3) es el
universo y sí x, y e U
a) 3x,3y/x2 <y + l b) Vx,3y/x2 + y2 <12
c) Vx,Vy/x2+y2 <12 d) 3x,3y,Vzfx2 + y2 <2z2
e) 3x,\/y,3z/x2+y2<2z2,zeU
(82) Determinar el valor lógico de las siguientes proposiciones.
a) 3xeR/x2+l = 0 b) 3xeR/x2=l
c) (V x e R)(V yeR)/x + y = 7 d) (Vxe z)(3 yez/x-y>0)
WÍ) Sean A= {1,2,3.4), B = (1,4,5.8) ¿cuáles de las afirmaciones siguientes son verdaderas?
a) 3 x,y e A/x + y > z, V z e B b) ~[V xe A, 3 y e B/x>y]
c) VxeB, 3yeA/x-yeA d) VreA, VyeB/x + y<10
(84) Si A = {0,1,2,3,4} hallar el valor de verdad de las siguientes proposiciones:
a) P: 3 x e A / 2x + 1 = 5 b) q: V n e Z+ / 3n es divisible por 3
c) r: 3xe R/x2+7<0 d) 5 : V .ve Q/x2 >x
62
Eduardo Espinoza Ramos
(85
(86)
©
(89)
(90)
Si M = {-1,1,2,7} cual es el valor de verdad, de las siguientes proposiciones:
a) V x e M, 3 y e M / jc2 > y b) 3xeM, VyeM/jc>y2>0
c) 3 x e M, 3 y e M / (x < 3) v (y2 > 2)
Dadas las proposiciones P: 3 xe Z/(4x + 2)(3x - 7) = 0; q: V xe Z / (jc2 > 0) v (je -1) < 0,
r: 3 x e N / (4x + 2)(3x - 7) = 0, señale el valor de verdad de p, q, r y además
f(p a q) =* (p v r)] => r
Sea M = {0,1,2,3} el dominio de x e y, señale el valor de verdad de:
a) Vx,3y/ (x2-y2<10) v(jt2<;y + l)
b) Vx, Vy/(x2-y2>-10) A(jc2>y + 1)
Negar las siguientes proposiciones para el conjunto z.
a) Vxez/x+l>x
c) 3 jce z/x2 =x
Negar las siguientes proposiciones.
a) 3x/x + 7<y
c) (3 x / p(x)) > (Vy / ~p(y))
e) 3x/q(x)_ 5x + 7<10
Negar los enunciados del ejercicio 56)
b) 3 xe z/x2+l=0
d) V jtez/jc2-l>0
b) (Vx/p(x))A(3y/q(y))
d) (p v -q) > (p a ~r)
f) 3x/5x + 8<4
fel) Negar los siguientes enunciados,
a) {3x/p(x)v-q(x)}
c) {Vx,3y/x.y = 0}
e) {(3 y)(p(x)) > (V x)(~q(x))}
b) {Vx/p(x) >q(x)}
d) {(VxXp(x))A(3x)(q(x))}
f) {(3x)(~p(x))v(Vx)(q(x))}
Lógica
63
g) {3x,3y/p(x)v~q(y)} h) {V x, 3 y/p(x,y) >q(y)|
i) {3x,3y/p(x)Aq(y)} j) {Vx, 3u, Vz/p(x,y,z)}
(92) Negar cada una de las proposiciones siguientes:
a) {3x/x + 7>2} b) {Vx/x + 0 = x}
c) {Vx/x2+7>x2+3) d) {3x/~(x*x)}
e) ~{Vx/x2=x} f) ~{3x/x + 3 = x}
(93¡) Negar las proposiciones del ejercicio 52) y verificar que estas negaciones resultan ser
proposiciones verdaderas.
(94) Si x puede ser cualquier número natural, determine el valor de verdad de las
proposiciones:
p: (Vjc)(jc2 > x) => (Vx)(x < 3x) ; q: (Vx)(jt2 > jc) => (3 x)(x = x)
r: (3 x)(x + 3 = 5) «=> (Vx)(x + 1 > x)
(95) Verifique la validez de los siguientes argumentos:
a) p a q b) (p a q) > (r a s)
~p—>q (~q)v(~s)
••- (~p)v(~q)
c) pA(pvq) d) r—>~q
pvq- *t p- »q
r >s -r- »s
.-. s •■• p >s
Demostrar, por la tabla de valores o por el método abreviado si los esquemas representan
o no reglas de inferencia válidas.
a) p—>q b) p >~q
~q >~r pv(~q)
64 Eduardo Espinoza Ramos
c) p-
q-
->q
-+p)
.-. p <--
e) p <—» q
rvq
~r
d) (p >q)A(r >s)
p vr
.". q v s
f) q >p
q >(rvs)
-(-q v -s)
->(s >p)
g) P
q
r »s
»q
»r
h) (p v -q)
r >-p
s<—>p
-»s
.-. pv(q >~r)
i) q >(~pvr)
j) P
rvs
-P«-
(-p v -s) > (~p a -r)
.\ q v r
Determinar los circuitos lógicos que representan a los siguientes esquemas moleculares.
a) (~p)<—»(p >~q) b) pA(qv~p)
c) ~[pv >-(qvr)] d) {[(rv q) a p] v-r) Aq
e) (pvq) »[(~pvq) >(pAq)] f) [(p > q) v p]A[(p »q)v -p]
Representar mediante funciones boolianas los siguientes argumentos:
a)
b)
Lógica
65
c)
d)
~q
— p
q
~q p
~P
~q
(99) Determinar la menor expresión que representa al circuito dado:
a)
o—
-P
b)
~P
~q
~P
c)
66
Eduardo Espinoza Ramos
d)
e)
P q
- r 1 ' q
P q
p q —
P °
0
-P-
-q-
g)
—q-
—q-
—P-
- p-
-~q-
h)
~q
~q
q
Lógica
67
-p.
flOOj Determinarlos circuitos lógicos que representan a los siguientes esquemas moleculares.
a) {[(rvq)Ap] v~r} Aq
b) ~[(p v ~q) v (p a -r) v -(r v q v ~p)]
Í101J Simplificar los siguientes circuitos lógicos:
a)
- q -
—P-
—q-
P "
-q-
b)
c)
—P-
—P-
- q-
—q-
—p-
—q-
~P
68
Eduardo Espinoza Ramos
d)
-q-
q —
-p
Dado el circuito lógico, hallar el circuito lógico más simple posible.
- q ~r —
-p— r
~r
Simplificar el siguiente circuito
P
q
.~p ~q.
~P
q
Representar mediante funciones Booleanas los circuitos.
q
a)
—P-
~r-
-q o
b)
~P
~q
Teoría de Conjuntos
69
CAPITULO II
1 TEORÍA DE CONJUNTOS
2.1. DEFINICIÓN.-
Un concepto se dice que es primitivo, cuando dicho concepto se acepta sin definición, en
la matemática son conceptos primitivos, el de conjunto, de elemento y la relación de
pertenencia, sin embargo debido a su gran importancia en todas las ramas de la
matemática aceptaremos las siguientes definiciones.
2.2. DEFINICIÓN.-
Entenderemos por conjunto a toda agrupación, colección o reunión de objetos de
cualquier especie siempre que exista un criterio preciso que nos permita que un objeto
pertenece o no a dicha agrupación. Los objetos que "pertenecen a un conjunto" se llama
elementos del conjunto.
NOTACIÓN.- A los conjuntos representaremos con las letras mayúsculas A.B.C,..., y a
sus elementos representaremos con letras minúsculas a,b,x
23. RELACIÓN DE PERTENENCIA (e ).-
La relación de pertenencia es el símbolo que relaciona a los elementos de un conjunto con
el mismo conjunto:
(elemento) e (conjunto)
Si un objeto x es un elemento o pertenece al conjunto A, escribiremos
x e A
y leeremos "x pertenece al conjunto A".
Si x no es un elemento del conjunto A. escribiremos
xg A
y leeremos "x no pertenece al conjunto A"
70
Eduardo Espinoza Ramos
OBSERVACIÓN.-
flj Sea A el cejijunto formado por los nombres de los siguientes países, Perú, Chile,
Ecuador, Colombia, podemos escribir entonces
Perú e A
Colombia e A
Argentina g A
Brasil £ A
Al conjunto A expresaremos en cerrando entre llaves a sus elementos:
A =,{Perú, Chile, Ecuador, Colombia}
Q2) Sea A el conjunto formado por las letras n, m. p. q, t del mismo modo podemos
escribir:
pe A
qe A
w g A
zíA
Al conjunto A expresaremos encerrando entre llaves a sus elementos: A={n,m,p',q,t}
2.4. DIAGRAMAS DE VENN-EULER.-
Para facilitar nuestra compresión intuitiva de los conjuntos, los representaremos
gráficamente mediante los llamados "Diagramas de VENN", estos diagramas son curvas
cerradas de la forma.
Teoría de Conjuntos
71
En el interior de estás curvas cerradas, representaremos mediante puntos a los elementos
del conjunto.
Ejemplo.-
(lj Sea A= {1,10,12,15}. El conjunto A será representado mediante el diagrama de Venn
©
Sea A = {-1,3,-5,0}, su diagrama de VENN es
2.5. DETERMINACIÓN DE CONJUNTOS.-
Un conjunto está bien determinado, cuando se conoce con exactitud que elementos
pertenecen o no al conjunto. Cuando se conoce qué elementos pertenece o no al conjunto
se dice que el conjunto está bien definido, un conjunto se puede definir por extensión y
por comprensión.
Definición de un conjunto
-► Por Extensión
-► Por Comprensión
POR EXTENSIÓN.
Ejemplo.-
Cuando se nombra cada unn de los elementos del conjunto se
dice que el conjunto ha sido definido por extensión.
Ql) El conjunto A de los números naturales que son mayores o iguales a cero y menor o
igual a 10 queda definido por extensión si escribimos.
A= {0.1.2,3,4,5,6.7,8,9,10}
72
Eduardo Espinoza Ramos
{2j El conjunto A de los números naturales que dividen simultáneamente a los números
8 y 12, queda definido por extensión si escribimos A = {1,2,4}
Observe que 3g A, pues 3 no divide a 8 a pesar que 3 divide a 12.
POR COMPRENSION.-Un conjunto se define por comprensión, cuando se da una
propiedad P. que sólo lo satisfacen los elementos del conjunto.
Ejemplos.-
(j^ A = {x/x es una vocal} y se lee: "A es el conjunto de las x tal que x es una vocal"
(5) A = {x e N/0< x <9} y se lee "A es el conjunto de las x perteneciente a los
naturales tal que los x sean mayores que cero y menores que 9.
2.6. CONJUNTOS NUMÉRICOS.
En matemática los conjuntos numéricos característicos que se estudian son: Los números
naturales, los números enteros, los números racionales, los números irracionales, los
números reales y los números complejos.
El conjunto de los números naturales N = {1,2,3,...}
El conjunto de los números enteros Z = {..., -3,-2,-1,0,1,2,3,...}
El conjunto de los números racionales Q = {—/meZ a ne Z, m*0}
n
El conjunto de los números irracionales I = {x/x tiene representación decimal
infinita no periódica}
El conjunto de los números reales R = {x/x es racional o x es irracional}
El conjunto de los números complejos C = {a + bi/ae R a be R, i = v-1}
Teoría de Conjuntos
73
OBSERVACIÓN.- El conjunto de los números reales, es la reunión de los números
naturales, enteros, racionales e irracionales, es decir:
R=NuZuQuI
A los números reales se representa mediante una recta que se denomina recta real.
- oo-* 1 1 1 ►+(»
x 0 x
x<0 x>0
2.7. CONJUNTO FINITO.-
Es el conjunto que está formado por un número limitado de elementos
Ejemplos.- fl) A = {x/x es una vocal}
(¿) B={xe N/5<x<12)
Qn C= {x/x es un día de la semana)
2.8. CONJUNTO INFINITO.-
Es el conjunto que está formado por un número infinito de elementos.
Ejemplo.- (V) A={xe Z/xes impar)
(2) B = {x/x es número natural)
2.9. RELACIONES ENTRE CONJUNTOS.-
a) INCLUSIÓN DE CONJUNTOS.- (Sub - conjuntos)
Se dice que el conjunto A es un subconjunto B, o que A está contenido en B, o que
A es parte de B, si todo elementos de A pertenece al conjunto B se escribe AcBy
se lee "A está incluido en B, o A está contenido en B o A es parte de B".
Está definición en forma simbólica se expresa.
AcB » {Vxg A, x e A => xeB)
74
Eduardo Espinoza Ramos
De la misma definición se sigue que es suficiente que exista al menos un elemento
del conjunto A que no sea elemento de B para que A no sea subconjunto de B, en
este caso se denota: A ct B
AcB AcB ACB
Ejemplo.- Si A = {1,3,5} y B = {1,2,3,4,5,6,7} entonces A c B. En efecto se
observa por simple inspección que todo elemento de A es también
elemento de B.
Ejemplo.- Consideremos los siguientes conjuntos: A={ 1,3,5,7}, B={ 1,3,5,7,9,11}
M = {a,b,c,d,e}, N = {b,c,d,m,n}. Podemos afirmar que:
i) AcB, porque todos, los elementos de A están en B.
ii) M (2 N, por que algunos elementos de M no están en N.
Estos representaremos usando diagrama de VENN - EULER.
AcB
b) SUBCONJUNTO PROPIO.
McN
Diremos que A es un subconjunto propio de B, o
parte de B, si se verifica AcB y además existe
algún x e B tal que xí A.
Ejemplo.- El conjunto A = {2,4,6} es un subconjunto propio de B = {1,2,3.4,5,6}
puesto que AcB además le B, 3e B, 5e B tal que lg A, 3« A, 5 « A.
Teoría de Conjuntos
75
c) PROPIEDADES DE LA INCLLSIÓN.-
fl) $cA. V conjunto A, donde <J>es el conjunto vacío.
Q2) AcA, (propiedad reflexiva)
Qn A c B a B c C => AcC (propiedad transitiva)
(4) Sí A cB y BcA => A = B (propiedad antisimétrica)
Demostración
(7) Io V x, x e (> => x e A, def. C
2° p > q (es una tautología)
F FoV
3o (¡icA, por definición de C
(2) Io Suponiendo que V x, x e A hipótesis
2° Como p > p es una tautología
3o Sí x e A => x 6 A es verdadero por la parte 2°
4° A c A de 3° y def. C
(3) 1° A c B hipótesis
2° V x, x e A => x e B, Io def. C
3° Be C.hipótesis
4o V x, x e B => x e C, 3° def. C
5o Por la Ley Transitiva (p > q) a (q ——> r) => p > r (ley del silogismo
hipotético)
6o V x e A => x e C, de 2°, 4° y 5°
7° AcC, 6o def. C
76
Eduardo Espinoza Ramos
2.10. IGUALDAD DE CONJUNTOS.
DEFINICIÓN.- Dos conjuntos A y B se dice que son iguales sí y sólo sí A c B y Bcz A.
En forma simbólica se tiene:
A = B t=> AcB a BcA
Se lee "El conjunto A es igual al conjunto B, si y sólo si A está contenido en B y B está
contenido en A"
2.11. PROPIEDADES DE LA IGUALDAD DE CONJUNTOS.-
(T) A = A, V A (reflexiva) (T) A = B => B = A (simétrica)
(3) A = ByB = C => A = C (Transitiva)
Demostración
©
©
©
r
2°
i°
2°
3o
4°
1°
2o
3o
4o
5o
6o
7°
8o
9o
AcA por reflexividad de inclusión.
A = A 1° y definición de igualdad.
A = B por hipótesis
AcB a BcA
BcA a AcB
l°def.de =
2° y la ley conmutativa
B = A 3o y definición de =
A = B por hipótesis
AcB a BcA,
B = C por hipótesis
BcC a CcB
AcB a BcC
A c C 5o transitiva incl
CcB a BcA,
Ce A,
1° definición de =
3 o definición de =
2° y 4o y transitiva de inclusión
usión.
4° y 3o y transitiva.
7o transitiva inclusión.
A = C,6° y 8° definición de =.
Teoría de Conjuntos
11
2.12. CONJUNTOS ESPECIALES,
\\) CONJUNTO VACÍO (Nulo).- Es el conjunto que no tiene elementos y se
representa simbólicamente por la letra griega <¡)
(phi) y .se define como:
<¡)= {x/x #x}
y se lee: para cualquier x tal que, x es diferente de x, no se satisface para algún
elemento
Ejemplo.-
(lj A = {xe R/x2 +1 = 0} es un conjunto vacío, pues la ecuación x" +1 = 0 no tiefle
raíz real, luego A = $.
{2} A={xeN/2<x<3} es un conjunto vacío, porque no existe un número natural
que sea mayor que 2 y menor que 3, luego A = <¡).
(3) A = {xe Z/I5x2 -11jc+2 = 0) es un conjunto vacío, pues al resolver la ecuación
T 2 1
15jc~ — 1 Ijc + 2 = 0 se obtiene x — — ,jt=-que son números enteros por lo tanto A=<b.
5 3
OBSERVACIÓN.- El conjunto vacío <¡) está incluido en todo conjunto es decir (t><=A, VA
(l) CONJUNTO UNIVERSAL.- Es el conjunto tomado como base o conjunto fijo,
para la determinación de otros conjuntos y se
denota por U. También al conjunto universal se le llama el universo.
Los conjuntos más importantes en matemática son los conjuntos numéricos: R, N,
Z, Q, 1, C en ese orden.
Ejemplos.-
(T) El conjunto universal U={xeZ/-3<x<9} es universo de los
conjuntos A= {-3,0,2,5}, B = {-2,1,3,7}, C = {-1,0,2,5,8} porque todos los
elementos de los conjuntos A, B y C pertenecen al conjunto U.
78
Eduardo Espinoza Ramos
2j Dado el conjunto universal U ={xe Z+/x<40]. Determinar los siguientes
conjuntos.
a) A = {x/x2 <28}
Solución
Tabulando el conjunto universal U = {1,2,3,4,5,...,39,40]
1 e A puesto que 1 < 28
2 e A puesto que 2~ < 28
3 e A puesto que 32 = 9 < 28
4 e A puesto que 42 = 16 < 28
5 e A puesto que 5" = 25 < 28
6í A puesto que 62 = 36 £ 28
por lo tanto el conjunto A está dado por: A = {1,2,3,4,5 J
b) B={x + 2/x<9}
Solución
Para x=l => x + 2 = 3eB
x = 2 => x + 2 = 4e B
x = 3 => x + 2 = 5e B
x = 4 => x + 2 = 6e B
x = 5 => x + 2 = 7e B *
x = 6 => x + 2 = 8eB
x = 7 => x + 2 = 9«B
Luego se tiene: B = {3,4,5,6,7,8}
¿) CONJUNTO UNITARIO.- Se llama conjunto unitario, al conjunto que consiste de
un sólo elemento.
Teoría de Conjuntos
79
Ejemplos.- a) A = {x e R/x + 2 = 0} = {-2}
b) A={xe N/l<x<3} = {2}
c) A = {xeZ* /x2-\ = 0} = {\]
(T) CONJUNTOS COMPARABLES.- Dos conjuntos A y B son comparables
sí: AcB v BcA.
Los conjuntos A y B no serán comparables sí: AcB a BcA.
Ejemplos.-
a) Si A={a.e,i) y B = {a.c.i.o.u} de donde A es comparable con B para que AcB.
b) Si M = {1,5,7,8} y N = {2,5,6,8,9} los conjuntos M y N no son comparables
pues M C N a N C M.
(5) CONJUNTOS DISJUNTOS.- Si dos conjuntos A y B no tienen elementos
comunes, se dice que A y B son disjuntos.
En forma simbólica se expresa: A es disjunto con B si y solo si, 2 x/x e A a x e B
Ejemplos.- a) Los conjuntos A= {1,3,5,7} y B = {2,4,6,8} son disjuntos.
b) Los conjuntos A={a,b,c,d} y B={r,s,t,u} son disjuntos.
2.13. REPRESENTACIÓN GRÁFICA DE LOS CONJUNTOS.-
Para mostrar a los elementos de los conjuntos o visualizar relaciones entre estos, existen
los llamados diagrama de VENN - EULER que son regiones del plano limitados por
líneas geométricas.
Al conjunto universal se acostumbra representar por medio de un rectángulo.
U
AcB
80
Eduardo Espinoza Ramos
2.14. EJERCICIOS PROPUESTOS.-
Clj Determinar por extensión los siguientes conjuntos.
a) A = {xe N/x<3 v 5<x<7} b) B = {x2 -1/jce Z a -1 < jc<3}
c) C= {3-5x/xe Z, -2<x<5 a 3<x<8}
d) D = {xeZ/x3-x2 -10jc-8 = 0) e) £ = {jce N/6x3 -3\x2 +3jc+10 = 0}
f) F = {xeZ/x2 >0 a x2 <20) g) £ = {jc/jc3 -19jc2 -36jc+ 1440 = 0}
h) // = {jce/?/(jc2+16jc)2=172}
(l) Determinar por extensión los siguientes conjuntos:
a) A = {x/x3-7x + 6 = 0] b) B = {x/6x2-5x + l = 0)
c) C = {jc/2jc3-3jc2-7jc + 3 = 0} d) D = {x/2x3 +x2 +jc-1 = 0}
e) E = {jc/jc4+jc3-6jc2-jc + 5 = 0}
f) F = {x/x4 +2x3 -3lx2 -32x+60 = 0]
(3) Hallar el conjunto solución del siguiente conjunto: A = {xl (Ax +24* -6x —1 = 0}
Rpta. a = {-I,-I.Ij
(4_) Determinar los elementos de cada conjunto.
a) A = {números naturales x que satisfacen jc' = 16 }
b) B = {números enteros x que satisfacen x~ = 16 }
c) C={xe N/2x + 3=15} d) D= {x e Q/(2x-l)(x-2) = 0}
e) E = {xeZ/x2-2x-3 = 0] f) G= {x e N/5 < x< 12}
Teoría de Conjuntos
81
\Sj Determinar por comprensión el siguiente conjunto T = {-1,1,2}
Rpta. T = {xeZ/x3 -2x2 -jc+2 = 0}
fó) Determinar por comprensión los siguientes conjuntos:
a) A= {-7,-3,1,5,9,...} b) B = {-1,1,2,^,5,...}
c) C= {2,3,6.11,18,...}
\7J Si A = {2,3,5,7}, diga cuál de las siguientes afirmaciones son verdaderas ó falsas
a) 5eA b) 3cA c) |7)cA d) {3,5} e A
QO Si A={xeN/x<2 v x = 7}, hallar todos los subconjuntos propios de A.
nn Dados los siguientes conjuntos A={7x + 2/xeZ}, B={7x-26/xeZ),
C = {4x +1/xeZ} y D= {2x + 1 / x e Z}, analizar y justificar debidamente su
conclusión en los siguientes casos.
a) A = B b) C = D
Rpta. a) A = B b) C*D
(m) Sean U = {1,2,3.4,5,6,7.8,9}, A = {2,4,6,8}, B = {1,3,5,7,9} y C = {3,4,5}. Al hallar
un subconjunto x de U tal que xcC, x <z A, xdB, cuántas soluciones existe.
Rpta. tres
(ll) Cuántos de los siguientes conjuntos son vacíos:
a) A={xeU/x*U} b) fí = {jceZ/x3 =3}
c) C = {x<eR/-eR) d) D = {xeQ/x2-x = 2)
x
e) E = {x<eN/x2 +1 = 0} f) F = {aeZ/12v1+4v2-3x-1 = 0}
82
Eduardo Espinoza Ramos
(12) ¿Cuál de los siguientes conjuntos es el conjunto vacío?
a) {x/x es un entero par y jT=9} b) [xsZ+/x<0]
c) (xe Z/x+18=18) d) {xeZ/6x2+5x-4 = 0}
e) {xeZ+ /x2-3x-4 = 0] f) (xeN/x«)
(l3¡) Dado A y B determinar si A = B en los siguientes ejercicios.
a) A = {-2,0,2} y B = {xe Z/x3-4x = 0]
b) A={l,-2} y B = {xe Z/(x - l)(x + 2)(2x-3) = 0}
c) A = {xeZ+ /l<x<6] y B = {1,2,3,4,5,6}
ML4) Si A, B y C son conjuntos tal que AcBcC. ¿Cuál es la relación entre C - B y C - A?
Rpta. C-BcC-A
(ÍS) Si A = {1,2,3,4,5}, B = {2,3,4}, C = {2,4,5}, D = {2,4}. ¿Cuál de las siguientes
proposiciones son verdaderas?
a) AcB b) AcD c) CcA
d) BcA c) BcC f) DcB
g) AcA h)B*C i) DcA
@ SeanA = {x/x3-17jc2+71jc-55 = 0};B = {x/jc4-15jc3+37jc2-16jc + ll0 = 0}esAcB
U7) Sea U={ 1,2,3,4,5,9} el conjunto universal, si A = {x2 / xe U] hallarAyA' porextensión
(18) Sea A={^-/xbZ/0<x<4] y B = (—/jreZ, -2 < x < 3} determinar cual de
las relaciones se cumplen AcB,BcA,A=B.
(19) Sí A = {jce N/x3-3jc2-6jc+8 = 0} y fí = {^±!/jce Z, -4 < x < 3}. Determinar cual
de las relaciones se cumplen AcB,BcA,A = B.
Teoría de Conjuntos
83
(20) Sea U = {x e N / 1 < x < 5}, A = {x e U / x es par}, B = {x e U / x es impar} y
C = {.ve A/jE = 2",net/}u{12}. Si D={xeU/xeU => xe B|n(xe A/xes
múltiplo de 4} ¿cuantos subconjuntos de C contienen a D?
2.15. OPERACIONES CON CONJUNTOS.-
(T) UNIÓN DE CONJUNTOS.- La unión de los conjuntos A y B es el conjunto
formado por todas los elementos de A y todos los
elementos B.
A la unión de los conjuntos A y B denotaremos por: AuB y se lee "A unión B".
En forma simbólica:
AuB = (xeU/xeA o xeB]
La parte sombreada de los siguientes diagramas es una representación gráfica de la
unión.
U
A y B no disjuntos
A y B disjuntos
Donde U representa al conjunto universal y la parte sombreada representa la unión
AuB
Ejemplo.-
(T) Sí A=(xeN/1<x<6) y B = {x eN/3 < x < 8}. Calcular A u B
Solución
Calculando los elementos de cada conjunto A y B: A = {2.4,5}, B ={-< 5,6,7}
AuB= {2,4,5} u {4,5,6.7} = {2,4.5,6,7}
(T) Sí A = {x e N/x es par} y B = {x e N /x es impar} entonces
A u B = {x e N/x es par v x es impar} = N
84
Eduardo Espinoza Ramos
a) PROPIEDADES DE LA UNIÓN DE CONJUNTOS.-
(7) AuA = A (T) Au<}> = A
(3) AuU = U (T) AuB = BuA
(?) (AuB)uC = Au(BuQ (ó) AcAuB
(?) BcAuB (?) AcCaBcC=>AuB <rC
Demostración
Ql) i) AuAcA por demostrar
Io x e A u A, por hipótesis
2o xeAvxeA, 1° definición de U
3o por la tautología de PvP o P podemos afirmar
que: xeA v xeA => xeA
4o x e A kj A =* x e A, 3o definición U
5o AuAcA, 4o definición C
ii) AcAuA por demostrar
lc x e A, por hipótesis
2° Sí x e A => (x e A v x e A), por tautología p«pvp
3o xe A => xeAuA, 2° definición U
4o AcAuA, 3o definición C
5o de i), ii) se tiene AuA = A definición de =
(2) i) Au(])cA por demostrar.
Io xe Auf por hipótesis
2° xeA v x e 0, Io definición U
3o x.e A, 2° definición de <b
4° xe Au<(> => xe A, Io y 3o
5° Aui|icA, 4° definición C
Teoría de Conjuntos
85
ii) AcAui(i por demostrar
1° x e A, por hipótesis
2° xeAvxE(¡), 1° definición <¡)
3o x g A u <¡), 2o definición U
4° xe A => xe Au<(>, l°y4°
5° AcAuí 4o definición U
de i) y ii) se concluye que A u <¡) = A definición de =
3j i) AuUcU por demostrar
Io x e A u U , por hipótesis
2o x e A v x e U, Io definición U
3o x e U, 2° y definición de U
4o xeAuU=>xeU, Io y 3o
5° AuUcA, 4r definiciónC
ii) UcAull por demostrar
Io x e U, por hipótesis
2° xeAvxeU, L° definición U
3o xeAuU, 2° definición U
4o xe U => xe AuU, Io y 3o
5o UcAull, 4o definición C
6o :. AuU = U, por i), ii) definición =
4) i) AuBcBuA por demostrar
1° xeAuB, por hipótesis
2° xeAvxeB, Io definición U
86
Eduardo Espinoza Ramos
3o x e B v x e A, 2o y tautología pvqoqvp
4o x e B u A, 3o definición U
5o xeAuB=>xeBuA, Io y 4o
6o AuBcBuA,5° definición C
ii) BuAcAuB por demostrar
Io x e B u A, por hipótesis
2° xeBvxeA, Io definición U
3o x e A v x e B, 2° y tautología pvq <=> qvp
4o xeAuB, 3o definición U
5o xeBuA=>xeAuB, Io y 4o
6o BuAcAuB,5° definición C
/. A u B = BU de i), ii) y definición =
(5} i) (AuB)uCcAu (Bu C) por demostrar
Io xe(AuB)uC, por hipótesis
2° xeAuBvxeC Io definición U
3o xeAvxeBvxeC, 2° definición U
4o x e A v (x e B v x e C), 3o propiedad asociativa
5o x e A v x e B u C, 4o definición U
6o x e A u (B u C), 5o definición U
T x e (A u B) u C => x e A \j (B u C), Io y 6o
8o (AuB)uCcAu(BuC), T definición C
ii) Au(BuC)c(AuB)uC, por demostrar
Io xeAu(BuC), por hipótesis
Teoría de Conjuntos
87
1° xgAvxgBuC, Io definición U
3o xgAvxgBvxgC, 2° definición U
4o (x g A v x g B) v x e C, 3o definición propiedad asociativa
5o x e A u B v x e C, 4o definición U
6o x e (A u B) u C, 5o definición U
7o xe Au(BuC) => xe (AuB)uC, Io y 6o
8o Au(BuC)c(AuB)uC, T definición C
.-. (AuB)uC = Au(BuC), de i), ii) definición =
Qó) 1 ° Sea x e A por hipótesis
2o Perop >(pvq), Vq es una tautología
3o xeA => xeAuB, Io y 2o
4o AcAuB, 3o definición C
Qn Io x e B por hipótesis
2o Pero p > (p v q), V q es una tautología
3o xe B => xe AuB, l°y2°
4o BcAuB, 3o definición C
(?) Io AcC, por Hipótesis
2o x e A => x e C, 1 ° y definición C
3o BcC, por hipótesis
4o x e B => x g C, 3o definición C
5o (x e A v x e B) => x g C, 2o y 4o
6o x g A u B => x g C, 5o definición U
7o AuBcC, 6o definición C
88
Eduardo Espinoza Ramos
(5) INTERSECCIÓN DE CONJUNTOS.- La intersección de los conjuntos A y B
es el conjunto de todos los elementos
comunes al conjunto A y al conjunto B, y que denotado por "A n B" y se lee "A
intersección B".
En forma simbólica:
AnB={xeU/xeA a xeB}
La parte sombreada de las siguientes diagramas es una representación gráfica de la
intersección.
U
A y B no disjuntos A y B disjuntos
Ejemplo.- SíA= {xe Z/-2<x<6} y B = {xe Z/0< x < 10}. Hallar A nB
Solución
Calculando los elementos de los conjuntos A y B.
A= {-1,0,1,2,3,4,5} y B= {1,2,3,4,5,6,7,8,9} .-. An B = {1,2,3,4,5}
a) PROPIEDADES DE LA INTERSECCIÓN DE CONJUNTOS.-
(l) AnA = A (5) An<}> = <}>
(5) AnB=BnA (í) AnU = A
(i) (AnB)nC = An(BnC) (ó) AnBcA
0 AnBcB (?) AcB=>AnCcBnC, VC
(9) SíAcCyBcD=*AnBcCnD
(10) Si AcB=>AnB = A " (n) Au(BnC) = (AuB)n(AuC)
(l2) An(BuC) = (AnB)u(AnC)
Teoría de Conjuntos
89
Demostración
ClJ i) AnAcA por demostrar
Io x e A n A, por hipótesis
2° xeAaxgA, Io definición n
3o Por tautología p a p <=> p se tiene
4o x e A, de 2o y 3o
5o xeAnA =>xeA, Io y 4o
6o AnAcA, 5°y definición c
ii) AcAnA por demostrar
Io x e A, por hipótesis
2° por tautología p <=> p a p
3o xe A a xe A, Io y 2o
4o x e A n A, 3o definición n
5o x e A => x e A n A, Io y 4o
6o AcAnA, 5o definición c
/. A n A = A, i), ii) definición =
(2) i) A n 4> c 4> por demostrar
Io xeAn<¡>, por hipótesis
2° x e A a x e <)», Io definición n
3o x e <)», 2o y p a q <=> q
4o xe An<) => xe <¡>, Io y 3o
5o A n <)> e <)», 4o definición c
ii) <)» c A n <)»
como <{> es subconjunto de cualquier conjunto entonces fcAnji.
Luego por lo tanto: A n <¡) - <)> de i), ii) y definición =
90
Eduardo Espinoza Ramos
(3J i) AnBcBnA, por demostrar
Io xeAnB, por hipótesis
2° x e A a x e B, Io definición n
3o xeB/\ xeA,2°yp/\qsqAp
4o x e B n A, 3o definición n
5o xeAnB=>xeBnA, Io y 4o
6o AnBcBnA,5° definición c
ii) BnAcAnB, por demostrar
Io x e B n A, por hipótesis
2° xeBaxeA, Io definición n
3o xeAaxgB, 2°ypAq = qAp
4o x e A n B, 3o definición n
5o xeBnA=>xeAnB, Io y 4o
6o B n A e A n B, 5o definición e
.-. A n B = B n A, i), ii) definición =
(4) i) (AnB)nCcAn(BnC) por demostrar
Io x e (A n B) n C, por hipótesis
2o x e A n B a x e C, Io definición n
3o xeAAxeBAxeC, 2° y definición n
4o x e A a (x e B a x e C), 3o propiedad asociativa.
5o x e A a x e (B n C), 4o definición n
6o x e A n (B n C), 5o definición n
7o xe (AnB)nC => xe An(BnC), Io y 6o
8o (AnB)nCcAn(Bn C), T definición c
ii) An(BnC)c(AnB)nC, por demostrar
Io xeAn(BnC), por hipótesis
2° xeAAxeBnC, Io definición n
3° xgAaxgBaxgC, 2° definición n
4o (xgAaxgB)axgC, 3o propiedad asociativa
5o x e A n B a x e C. 4o definición n
6o x g (A n B) o C. 5o definición n
7o xg An(B nC) => XG(AnB)nC, Io y 6o
8o An(BnC)c(AnB)nC, 7° definición e
.-. (A n B) n C = A n (B n C), i), ii) definición =
Io xeAhB, por hipótesis
2° x g A a x g B, 1 definición n
3o por tautología p a q <=> p se tiene.
4o x g A, 2° y 3o
5o xg AnB => xg A. Ioy4o
6o AnBcA. 5odefiniciónc
Io A cr B, por hipótesis
2° xgA=>xgB, 1c definición cr
3o x g A n C, por hipótesis
4° x e A a x g C, 3o definición n
5o x g B a x g C, 2o y 4o
6o x e B n C, 5o definición n
T XGAnC=>XGBoC, 3o y 6o
8 AnCcBnC, T definición e
92
Eduardo Espinoza Ramos
\7j Io AcC, por hipótesis
2° x e A => x e C, Io definición c
3o BcD, por hipótesis
4o x e B => x e D, 3o definición c
5o x e A a x e B, 2° y 4o
6o x e A n B, 5o definición n
7o x e C a x e D, 2o y 4o
8o xeCnD, 7o definición n
9o xeAnB=>xeCnD, 6o y 8o
10° AnBcCnD, 9o definición <=
n$) i) AnBcA por demostrar
1° AcB, por hipótesis
2° xeA=>xeB,l° definición e
3o x e A n B, por hipótesis
4o x e A a x e B, 4o definición n
5o x e A, 2o y 4o y p a q => p es tautología
6o x e A n B => x € A, 3o y 5o
T AnBcA, 6o definición c
ii) AcAnB por demostrar
Io AcB, por hipótesis
2° x e A, por hipótesis
3o x e A a x e B, 2o y Io definición c
4o x e A n B, 3o definición n
Teoría de Conjuntos
93
5o xeA =>xeAnB, Io y 4o
6o AcAnB, 5o definición <=
/. A n B = Apor i), ii) y definición =
2) i) Au(BaQc(Aufi)n{Aii)C), por demostrar
Io x e A u (B n C), por hipótesis
2° x e A v x e (B n C), Io definición u
3o x e A v (x e B a x e C), 2o definición n
4o (xe A v xe B) a (xe AvxeC), 3o y pv(qA r) = (pv q) A(pv r)
5o xe(AuB)ax6(AuC), 4o definición u
6o xE(AuB)n(Au C), 5o definición n
7o xe Au(BnC) => xe (AuB)n(AuQ, Io y 6o
8o Au(BnC)c(AuB)n(Au C), T definición c
" ii) (AuB)n(AuQcAu(Bn C), por demostrar
Io x e (A u B) n (A u C), por hipótesis
2o x e (A u B) a x e (A u C), Io definición n
3o (x e A v x e B) a (x e A v x e C), 2o definición u
4o x e A v (x e B a x e C), 3o pv(q a r) = (p v q) a (p v r)
5o x e A v x e (B n C), 4o definición n
6o x e A u (B n C), 5o definición u
1° xe (AuB)n(AuC) => xe Au(BnC), Io y 6o
8o (AuB)n(AuQcAu(BnC), T definición c
.-. Au(BnC) = (AuB)n(Au C), i), ii) definición =
94
Eduardo Espinoza Ramos
® LA DIFERENCIA DE CONJUNTOS.-
La diferencia de los conjuntos A y B es el conjunto de elementos que pertenecen a
A, pero que no pertenecen a B. a la diferencia de los conjuntos A y B denotaremos
por "A - B" y se lee "A menos B'\ En forma Simbólica:
A-B = {xeU/xeA a xíB)
La parte sombreada de los diagramas siguientes es una representación gráfica de la
diferencia.
A y B no disjuntos A y B disjuntos
Ejemplo.- Sí A = {2.3,4,5*9} ]f&.s> (1,2,5,7,8}. La diferencia es A - B = {3,4,9}
a) PROPIEDADES DtE LA DIFERENCIA DE CONJUNTOS.-
© A-A = $ © A-<)> = A
® <)>-A = $ © A-B*B-A
© An(B-C) = CAríB)-(AnQ ® (A-B)cA
© Si AeB => A-C<=B-C, VC ® AcB => A-B = <))
© Bn(A-B) = <}> (lo) Si A y B disjuntos=> AnB=<}>
Demostración
Dejamos como ejercicio para el lector.
Teoría de Conjuntos
95
(4) COMPLEMENTACIÓN DE UN CONJUNTO.-
a) DEFINICIÓN.- Si A es un subconjunto de B, al complemento del conjunto
A con respecto al conjunto B se define como la diferencia
B - A y que denotaremos por
CBA = B-A.
La parte sombreada del siguiente diagrama es la representación gráfica del
complemento de A con respecto a B.
' U
b) DEFINICIÓN.- El complemento de un conjunto A es el conjunto de
elementos que no pertenecen al conjunto A, es decir: la
diferencia del conjunto universal U y el conjunto A, al complemento del
conjunto A denotaremos por: A o CA y se lee "complemento de A"
En forma simbólica
A'=Ca=U-A = [x/x(eU a xíA)
La parte sombreada del siguiente diagrama es una representación gráfica del
complemento de A.
U
Ejemplo.- Sí U = {x e N / x < 10} y A = {x e N / 5 < x < 8}. Hallar A
Solución
Calculando los elementos se tiene: U = {1,2,3,4,5,6,7,8,9,10}, A = {5,6,7}
A =U-A = {1,2,3,4,8,910}
96
Eduardo Espinoza Ramos
Ejemplo.- Sí U = N, A = {x e N / x es par}, entonces:
A'=U — A = {xe NIx es impar}
c) PROPIEDADES DEL COMPLEMENTO DE UN CONJUNTO.-
(T) (A)'=A (5) AvA'=U
(5) AnA'=(|) @ V'=<Sf
(?) A-B = /4nB' (?) AcB => B'cA"
Demostración
(l) i) (A')'c:A, por demostrar
1 ° jc e (A)', por hipótesis
2° jcí A', Io definición de complemento
3° x e A, 2° definición de complemento
4o xe(A'y => xe A, Io y 3o
5o (A')' c A , 4o definición c
ii) A c (A*)', por demostrar
1° x e A, por hipótesis
2o xiA', 1° definición de complemento
3° jce (A")', 2° definición de complemento
4o xe A => Jce(A')', Io y 3o
5° A c: (A")', 4° definición c
/. (A')'-A de i), ii) y definición =
Teoría de Conjuntos
97
{2J i) A^jA'aU, por demostrar
1° xe A^jA' , por hipótesis
2° xeAv jc e A',\° definición u
3° x e A v x £ A, 2° definición de complemento.
4° x e U, 3o definición de conjunto universal U
5o .veAu/V =>xeU, Io y 4o
6o Au/l'cí/, 5o definición c
¡i) U a A kj A', por demostrar
Io x e U, por hipótesis
2° xeAvxeA, Io definición U
3o x e A v jce A' ,2o definición del complemento
4° x e A u A', 3° definición U
5o xeU=> *eAu/V, Ioy4o
6° U c A u A', 5o definición c
.-. Au¿1-Í/ por i), ii) definición =
f3) i) An/Vc<)> por demostrar
1 ° x e A n /V, por hipótesis
2° x e A a jre /V,l° definición n
3o x e A a x £ A, 2o definición del complemento
4° xEf, 3o definición <)>
5o xeAnA' => x e <>, Io y 4o
6° A n /*' c <)), 5o definición c
98
Eduardo Espinoza Ramos
ii) $ c: A n A' por demostrar, pero como el conjunto vacío <)> es
subconjunto de todo conjunto entonces fcAnA
/. A n A' = <)), de i), ii) y definición =
(4) i) U'czty por demostrar
1° .teí/', por hipótesis
2° x e U, Io definición de complemento
3o x e <)>, 2° definición <)>
4o jceí/' => xe <|>, Io y 3o
5o l/'c:<t>, 4° definición c
ii) <)> c: U' por demostrar, como el conjunto vacío <)> es subconjunto de
cualquier conjunto entonces <t>c U' por lo tanto í/'=<)) de i), ii) y
definición =
(Sj i) A-Bcz Ar\B', por demostrar
1° x e A - B , por hipótesis
2° xcAaxíB, Io definición -
3° x e A a jce B', 2° definición de complemento
4° jc e A n B', 3o definición n
5o xeA-B=> Ae^ní', l°y4°
6o A-ficAnB',5° definición c
ii) Ar\B'czA-B, por demostrar
Io JteAnF, por hipótesis
2° xe A a jce B', \° definición n
3o x e A a x e B, 2° definición de complemento
Teoría de Conjuntos
99
4o x e A - B, 3o definición -
5o xe AnB' =* xgA-B, Io y 4o
6o Aní'cA-í, 5° definición <=
.". A — B = A n B' de i), ii) definición =
\6) Io A c B, por hipótesis
2° xeA=>xeB, 1c definición c
3 o xgB', por hipótesis
4o x £ B, 3o definición de un complemento
5o x«A, 4o y 2o definición <=
6° jce A', 5o definición de un complemento
7o A-efl' => ;ceA\ 3o y 6o
8o £'<=/V, 7° definición <=
d) TEOREMA (Leyes de Morgen).-
Sean A y B dos subconjuntos del conjunto universal U y designaremos a los
respectivos complementos por A'=CuA, B'=CVB, se verifican
a) (AKjB)'=A'r¡B' b) (¿nfl)' = Aufl'
Demostración
a) i) (/\u BVcA'nB', por demostrar
Io ie(i4uB)', por hipótesis
2° xíAuB, Io definición de complemento
3o x e A a x e B. 2° definición u
4 xg A' a *efí', 3o definición de complemento
100
Eduardo Espinoza Ramos
5o a e A'r>B', 4o definición de n
6o jce(i4u£)' => JceA'nfl', Io y 5o
7o (^uB)'c A'nfl", 6° definición c
¡i) A'r\B'cMuB)', por demostrar
1° .aeA'nfi', por hipótesis
2° xe A' a jceB', 1° definición n
3° x g A a x g B, 2o definición de complemento
4° xíAuB, 3° definición u
5° x e (A u B)', 4° definición de complemento
6o jceA'nB" => xfz(A\>jB)\ Io y 5o
7o A'nB"c(Aufi)', 6o definición c
.•. (Au £)' c: A'nB", de i), ii) y definición =
b) i) A'nB'c(Aufi)', por demostrar
1 ° x: e (A n B)', por hipótesis
2° aí AnB, Io definición de complemento
3° xíAvxíB,2° definición den
4o jce /V v xe B' ,3° definición de complemento
5 ' jce i4'uB', 4° definición u
6o Jce(AnB)' => xe AkjB', Io y 5o
7o (A n B)'c A'uB' 6o definición c
Teoría de Conjuntos
101
ii) A'\uB'a (A n B)', por demostrar
Io agí4'uB', por hipótesis
2° x g A' v íeí'.r definición de u
3o x £ A v x g B, 2o definición de complemento
4o x{AnB, 3o definición de r\
5° jcg (AnB)', 4° definición de complemento
6o A-e/Vufl' =* jt£(/\nB)', Io y 5o
7o ¿'ufl'c (A n B)'. 6o definición c
.*. (v4 n B)'= /Vufí', por i), ii) definición =
(5) DIFERENCIA SIMÉTRICA.- Sean A y B dos subconjuntos de U, a la diferencia
simétrica A y B denotado por A A B se define por:
AAB = {xeU/xe(AuB) a xe(AnB)}
= (A u B) - (A n B) = (A - B) u (B - A)
La notación A A B se lee "La diferencia simétrica de A y B".
En el diagrama de VENN - EULER, mostraremos la diferencia simétrica de A y B
que es la parte sombreada de la figura.
U
A A B = (A - B) u (B - A)
Ejemplo.- Sean A = {1,2.3,4,6} y B = {2,3,5,7}. Hallar A A B
102
Eduardo Espinoza Ramos
Solución
Calculando AuB = ( 1,2,3,4,5,6,7} ; A n B = {2,3}
A A B = (A u B) - (A n B) = {1,2,3,4,5,6,7} - {2,3}= {1,4,5,6,7}
a) PROPIEDADES DE LA DIFERENCIA SIMÉTRICA.-
(?) AAA = <|> (T) AA<)> = A
0 AAB = BAA (?) (A A B) AC = AA(BAC)
(?) (A A B) n C = (A n C) A (B n C)
(ó) (A A B) u (B A C) = (A u B u C) - (A n B n C)
Demostración
(T) AAA = (AuA)-(AnA) = A-A = <)> :. AAA = $
(5) AA<}> = (Au<l))-(An<l)) = A-<l> = A .-. AA<J)=A
(T) AAB = (AuB)-(AnB) = (BuA)-(BnA) = BAA
.-. AAB=BAA
(4) Para demostrar (A A B) A C = A A (B A C), aplicamos:
A A B = (A - B) u (B - A) como A - B y B - A son conjunto
disjuntos, entonces la unión deA-ByB-Aes reemplazando por la
suma (+)
AAB = (A-B)u(B-A) = (A-B) + (B-A) = Anfi' + finA'
Ahora haremos la demostración correspondiente.
(AAB)AC = [(A n B') u (B n A' )]AC
= Pní,)u(finA,)]-CuC-[MnB,)u(Bn^')]
= [(AnB')u(BnA')]nC'uCn[(AnJ!')u(BnA')]'
= [(AnB')nC']u[(BoA')oC,]uCn[(AnB,),n(Bn/\')']
Teoría de Conjuntos
103
= A n B'c^CkjB n /t'nC'uC n [(¿'ufl) n (£"u¿)]
= A n B'nC'ufl n A'nC'uC n [(A'uB) n B'u( yl'ufi) n /\ ]
^AnB'nCuflnA'nCuCnP'nB'JuíAnfi)]
^[Anfi'nC'uBn/l'nC'luIA'nB'nCuíAnBnOI
= An B'nC'+B n A'nC'+A'nfl'nC + AnínC
= [/lnBnC + /in B'nC J + [B n (A'nC) + C n B'nA']
= i4n[BnC+Fr>C'] + [(BnC') + Cnfl']n/V
= An[BnC + (BuC)'l + [BAC]nA'
= An[5uCn(BnQ'J'+(BAC)n/l'
= A^I(BAC)'HBAC)^IA• =AA(B AC)
.-. (A A B) A C = A A (B A C)
2.16. CONJUNTO POTENCIA (O CONJUNTO DE PARTES DE UN
CONJUNTO).-
Dado el conjunto A, llamaremos conjunto potencia de A al conjunto formado por todos
los subconjuntos de A incluyendo al conjunto vacío <|>.
Al conjunto potencia de A denotaremos por P(A) y de acuerdo a la definición P(A) se
expresa:
P(A)={x/xcA)
OBSERVACIÓN.- Para todo conjunto A valen ty c A y A c A. luego <)> y A son
subconjuntos de A, o sea que son elementos de P(A) por lo tanto,
para cualquiera conjunto A se verifica (|) e P(A), A e P(A)
104
Eduardo Esfj'moza Ramos
OBSERVACIÓN.- Un elemento de P(A) es un subconjunto de A, es decn
x e P(A) «xcA
2.17. PROPIEDADES DEL CONJUNTO POTENCIA.-
Para cualquier conjunto A, se cumple:
(7) Sí AcB « P(A) c P(B) (2) SíBcAwBe P(A)
(5) Sí A = B <=> P(A) = P(B) (4) P(AnB) = P(A)n P(B)
(?) P(A) u P(B) c P(A u B)
Demostración
(T) i) AcB=> P(A)cP(B)
1° A c B, por hipótesis
2° x e P(A), por hipótesis
3o xcA, 3o definición P(A)
4° xcB, 3° y 1 ° propiedad transitiva
5o x e P(B), 4o definición P(A)
6o x e P(A) => x e P(B), 2o y 5o
7o P(A) c P(B), 6o definición c
ii) P(A)cP(B) =>AcB
Io x e A, por hipótesis
2° {x}cA, Io
3o {xj g P(A), 2o definición P(A)
4o P(A) c P(B), por hipótesis
5o {x} e P(B), 3o y 4o definición c
Teoría de Conjuntos
6o |x|cB. 5o definición P(B)
7° x e B, 63 definición B
8o xe A => xe B, Ioy7o
9o AcB. 8o definición <z
(T) Io Be A. por hipótesis
2o BeP(A), Io definición P(A)
(T) i) P(A)cP(B), por demostrar
1° A = B por hipótesis
2° x e P(A) por hipótesis
3o xcA, 2° definición de P(A)
4° xcB, de 3o y Io
5o x e P(B), 4° definición P(A)
6o x e P(A) => x e P(B), 5o y Io
T P(A) c P(B), 6o definición c
ii) P(B) cz P(A) por demostrar
Io A=B, por hipótesis
2o x e P(B), por hipótesis
3o xcB, 2° definición de P(B)
4o xcA, Io y 3o
5o x e P(A), 4o del P(A)
6o x e P(B) => x e P(A), Io y 5o
7o P(B) cz P(A), 6D definición <z
.-. P(A) = P(B), de i), ii) y definición =
i) P(A nB)c P( A) n P(B) por demostrar
Io xeP(AnB), por hipótesis
2o xc (AnB), Io definición P(AnB)
3o xcA a xcB, 2° propiedad
4o x e P(A) a x e P(B), 3o del P
5o x e P(A) n P(B), 4o definición n
6o x e P(A n B) => x e P(A) n P(B),
T P(A n B) a P(A) n P(B), 6o definición <=
i¡) P(A) n P(B) d P(A n B), por demostrar
Io x e P(A) n P(B). por hipótesis
2o xe P(A) a xe P(B), Io definición n
3o xcA a xcB, 2o y definición P
4o xcAnB, 3o definición n
5o x e P(A n B), 4o definición P
6o x e P(A) n P(B) => x e P(A n B), Io y 5o
T P(A) n P(B) c P(A n B), 6o definición <=
.-. P(A n B) = P(A) r\ P(B) de i), ii) definición =
Io x e P(A) u P(B), por hipótesis
2o xe P(A) v xe P(B), Io definición u
3o xcA vxcB, 2° definición P
4° xcAuB, 3o definición u
5o x e P(A u B). 4o definición P
Teoría de Conjuntos
107
6 xeP(A)uP(B) =>xeP(AuB), Io y 5o
7o P(A) u P(B) <= P(A u B), 6o definición <=
Ejemplos.-
(T) Dados los conjuntos A={3} y B={2,3,5}. Determinar P(A), P(B), P(AuB), P(An B)
Solución
P(A)={{3}.<M, P(B)={{2},{3},{5},{2,3},{3,5},{2,5},{2,3,5}.<!)}
AuB=(2,3,5), AnB={3}
P(AuB)={{2},{3},{5},{2,3},{2,5},{3,5},{2,3,5},<S)}
P(AnB)={(3),<i}
2.18. INTERVALOS.-
Los intervalos son conjuntos de números definidos mediante la relación de orden en el
campo de los números reales.
Los intervalos son de varios tipos:
a) INTERVALOS CERRADOS: [a,b], a < b.-
Es el conjunto de los números reales "x" para los que se satisfacen a < x < b y se
denota por: [a,b]. En forma simbólica.
[a,b] = {xe R/a<x<b}
Su representación gráfica es:
a b
OBSERVACIÓN.- Se dice x e [a,b] <=* a < x < b
b) INTERVALOS ABIERTOS: <a,b>, a < b.-
Es el conjunto de los números reales "x" para los que se satisfacen a < x < b y se
denota por <a,b>. En forma simbólica.
108
Eduardo Espinoza Ramos
<a,b> ={xe R/a<x<b}
Su representación gráfica es:
a b
También se tiene los siguientes conjuntos de números reales, los cuales se
denominan, intervalos abiertos por la izquierda, e intervalos abiertos por la derecha
respectivamente.
Su representación gi
Su representación gi
<a,b] = {xe R/a<x<b}
áfica es:
a b
[a,b>={xe R/a<x<b}
■áfica es:
—• e-
a b
También se tiene los intervalos infinitos que son:
<a,+°°> ={xe R/x>a}
[a,+°°>= {x e R/x > a}
<-o°,b> ={xe R/x<b}
<-00,b] = |xe R/x<b}
2.19. OPERACIONES DE CONJUNTOS APLICADOS A LOS
INTERVALOS.-
Es este caso el conjunto de los números reales R será considerado como el conjunto
universal.
Ejemplos.-
(7) Si A = <-°°.2], hallar Ca = X
Teoría de Conjuntos
109
Solución
&4 = {jce/?/*£<-°°,2]} = {xe R/~(xe <-°o,2]}
= {xe R/~(x<2)} = {xe R/x > 2} =<2,+°o>
1»
A = <-oo,2] +oo
oo 2 R
O
CA = A" = <2,+oo>
El complemento de A está formado por todo lo que no está en A dentro del conjunto
universal R.
(5) Si A = <2,+°o>, Hallar Ca = A'
Solucién
fiA = A'={xe Rfx£<2,+<>°>} = {xe R/~(xe <2,+°°>)}
= {xe R/~(x>2)J = {xe R/x<2} = <-°°,2]
<
CA = A' = <-co,2]
-co
(
>
)—
A = <2,+oo>
+00
R
(3) Sí A = <l,ll]yB = [7,18>. HallarAuB y AnB
Solución
AuB=|xeR/xe <1,11] v xe [7,18>} =<1,11] u [7,18> = <1,18>
•- O
O ■* ws ^
+00
-+-
-+-
•00
1
O-
11
18
-o
R
AuB = <l.l8>
110
Eduardo Espinoza Ramos
AnB={xeR/xe <1,11] a xe [7,18>} =<1,11] n [7,18> = [7,11]
f , o
° ! 1
-00
+
7
11
—i—
18
AnB = [7,ll]
(4) SiA = <-7,-l>u<0,6], B = <-°°,l]u[4,8>. Hallar
a) t\ = A' b) AnB c) C(AuB)
Solución
a) CA = /\,= {jte/?/jce<-7,-l>u<0,6]}={xG R/-(xe <-7,-l> u<0,6])J
= (xe R/~(xe <-7,-l>) a ~(xe <0,6])}
= {x e R / -(-7 < x < -1} a -(0 < x < 6)}
= JxgR/(x<-7v x>-1) a (x<0 ax>6)}
A = <-7,-l>u<0.6]
O O O •
+00
■00
-7
6
o
£4 = A'=< -oo,-7] u[-l,0]u < 6.+«° >
b)
-00
o-
1
h h
l 1
1
f"
+00
8
-o
-7 -10 1
A n B = <-7,-l> U <0,1J u [4.6]
Teoría de Conjuntos
111
c)
-O B
-• A
H h
+00
R
AuB = <-oo,8>
C(i4uB) = (i4uB)'={jce R/xe<-°°,8>} = {x e R/~(xe <-°=,8>)}
{xe R/~(x<8)}= {xe R/x>8| = [8,+°°>
S>
AUB = <-co,8>
-co
8
+ CO
R
C(AUB) = [8,+oo>
(ff) Si A=<-°°,-4]u[4,6> y B = [-12,-6>u<5,7], encontrar la diferencia simétrica A A B
Solución
A A B = (A u B) - (A n B) por definición de diferencia simétrica, ahora
calculamos A u B y AnB
f-
I
I
I
-co -121
é-
4 i
T~
I"
-6-
—t—
-4
f
i
-o
i
5|
—O
16
+ 00
R
-12 -6
A u B = <-°o,-4] u [4,7]
• o
B
I A
I
+co
-«—
-00
-12
-4
-•
I 4
•—
R
A n B = [-12,-6> u <5,6>
112 Eduardo E.ipinoza Ramos
C(A n B) = <-°o,-l2> u [-6,5] u [6,+°°>
AAB = AuB-AnB = (AuB)n C(A n B)
• f •
+00
-co -12 -6 -4 ¡4 5 6 7 R
•-
• f ' ' f
i T i i T i i
¿ é i i i i i
-12 -6-44567
A A B = <-°°,-12> u [-6,-4J u [4,5] u [6,7]
2.20. FAMILIA DE CONJUNTOS.
Llamaremos familia de conjuntos al conjunto cuyos elementos son también conjuntos.
A una familia de conjuntos denotaremos por [A, },>,, donde cada A¡ es un conjunto.
Ejemplo.- (T) {A¡} ,<,<3 ={Al,A2,A3)
© ÍA-W,=Mi.A,,í4s....}
Ejemplo.- Determinar los componentes de las siguientes familia de conjuntos.
(i) IAJisís4 donde A¿ ={í + n/«e Z+ impar a w<5}
Solución
{í4,},<iS4 ={Al,A2,A3,A4} de donde Ax -{\ + n/ne Z + impar a« < 5} = {2,4}
A2 =(2 + n/«£ Z* impar a« <5} = {3,5}
A3 ={3 + m/«e Z+ impar An< 5} = {4,6}
A4 = {4 + n/«e Z+ impar a«<5} = {5,7}
Teoría de Conjuntos
113
a) LNION DE FAMILIA DE CONJUNTOS.
NOTACIÓN.-
2
© a^=|Ja © ^u^u...ua,=(Ja
1=1
DEFINICIÓN.- La unión de familia de conjuntos es dado por:
n
I \A¡= {x/xe A¡, para algún /}
i=i
OBSERVACIÓN.-
n n
© Sí JcelU <=> 3i/xeA¡ © xelU <=> \fi/xeA,
i=i í=i
Ejemplos.- Sea {A,} ls/s5 donde At■ = [ x +1 e NI x < i y .v e N}.
5
Hallar a) Ai<uA3^A5 b) \\a¡
í=i
Solución
a) A, = {x + leN/x<l a xe N} = {2)
A3=[x + leN/x<3 a xeN} = {2,3,4}
A5 = {* + le N/x<5 a xe W} = (2.3.4,5,6}
4, uA3uA, ={2,3,4,5,6}
5
b) I Ji4,-=í4jU A, uAjUí44u A¡={ 2,3,4,5,6}
i=i
114
Eduardo Espinoza Ramos
b) INTERSECCIÓN DE FAMILIA DE CONJUNTOS.
NOTACIÓN:
(T) A¡nA2nA3 = (|A \¿) A nA2 nAin...nAn = (|A
1=1 1=1
DEFINICIÓN.- La intersección de familia de conjuntos es dado por:
n
I i A¡: = [x/xe A¡, para todo /}
i=i
OBSERVACIÓN:
(T) *eP)A <=* Vi/jceA,- © *éP|A <=> 3i7jc«A,-
i=i i=i
Ejemplo.- Sea la familia {A }i</<5 donde A¡ = {jc + 1/jc < i, xe N]
n
Hallar a) AinA3nAs b) {AluAs)nA3 c) l JA
i=i
d) (A-A3)n(A^^2) e> (A5-/\3)n(/\4-A)
Solución
Ax ={jc + 1/jc<1, xeN} = {2] A2 = [x + l/x<2, *eJV} = {2,3}
A3={x + lfx<3, Jie N} = {2,3,4] At ={jc + 1/jc<4, í€ A/} = (2,3,4,5)
A5 = {jc + 1/jc<5, xe N} = {2,3,4,5,6}
a) Aj nA3 nA5 ={2}
b) A, u As = {2.3,4,5,6}, (AluA5)nA3=[2,3.4}
n
c) IU = A uA2u Ai uAjUA¡= {2,3,4,5,6}
i=i
Teoría de Conjuntos
115
d) A,-A3=0, (A, -A3)n(Al uA2) = <J>n(A uA2) = <|>
e) A5-A,={5.6}. At-A=l3'4'5} .-. (Aj - A,)n(Ai-M,) = {5J
c) COMPLEMENTO DE FAMILIA DE CONJUNTOS.-
NOTACIÓN.- © C(A uA2) = Ca, n&42
12 12
© C(|jA) = f>.
1=1 i=i
12 12
© C(|jA) = nCA
1=1 1=1
n n
OBSERVACIÓN.- jteC(ljA) <=> *S|)A <=> Ví/jcí A,
i=i i=i
í=i i=i
C(PjA) <=> í« Ha <=> 3i7jh2A,-
d) PROPIEDADES GENERALES DE FAMILIA DE CONJUNTOS.-
Sea E cualquier conjunto, entonces:
n n n n
® En(\jAi) = [J(E^A¡) © £u((Ja) = IJ(£^A)
1=1 1=1 1=1 1=1
n h n n
® £n(p|A) = P)^^A) © £u(p|A)-p|(£^A)
i=i i=i i=i i=i
© ííf|A> = |JítA) © C(|jA) = f>CA)
1=1 i=i 1=1 i=i
Demostración
116
Eduardo Espinazo Ramos
n
(T) Io jce£n(M/i,) por hipótesis
í=i
n
2° xe E a xel JA, Io definición n
1=1
3o xcEa xgA¡, para algún i, 2° del u
4o x e E n A,;, 3o definición n
n
5° jc e I J (£ n A;), 4o definición u
i=i
n n
6o xeEn(IU) => JteH(EnA;), l°y5°
í=i í=i
n n
7° EníMAJcMíEn/i,), 6o definición<
i=i í=i
n
8° jcel KEnA;) por hipótesis
i=i
9o x e E r\ A,,, para algún i, 8o definición u
10° xeE a .*e A,. 9o definición n
11° xcEa jccMa., 10o definición u
/=i
n
12° jre En(l Ja.-), ' 1° definición n
Teoría de Conjuntos
117
n n
13° .reljtEn/lf) => jceErnlU). 8o y 12°
i=i i=i
n n
), 13° definición cz
¿=i i=i
n n l,
15° E ni] A¡ a M (£ n A,,), T y 14° definición =
f=i í=i
2.21. NUMERO DE ELEMENTOS DE UN CONJUNTO.-
DEFINICIÓN.- Sea A un conjunto cualquier, al número de elementos distintos que
forman dicho conjunto denotamos por n(A) llamado cardinalidad del
conjunto.
NOTA: n(A) se lee "el número de elementos del conjunto A".
Ejemplos.- Sí A = {1,3,5,6}, B = {a.b,c,d,e}, C = {2,4,2,4,2}, D =ty
Solución
n(A) = 4, n(B) = 5, n(C) = 2, n(D) = 0
2.22. PROPIEDADES DEL NUMERO DE ELEMENTOS DE UN
CONJUNTO.-
(T) Si A y B son conjuntos cualquiera, entonces: n(AuB) - n(A) + n(B), sí AnB = <J)
Demostración
Supongamos que: A tiene x elementos => n(A) = x
B tiene y elementos => n(B) - y
Por hipótesis no hay elementos comunes a ambos conjuntos.
AuB tienen x + y elementos, esto es: n(A u B) = x + y - n(A) + n(B)
.-. n(A u B) = n(A) + n(B)
118
Eduardo Espinoza Ramos
\2J Si A y B son conjuntos cualquiera, entonces n(A - B) = n(A) - n(A r\ B)
Demostración
Sea M=A-B = AnB',N = AnB, se tiene: M vN = {Ar\B')v(Ar\B) = A
M r\N = (Ar\B')r>i(Ar>iB) por asociatividad y conmutatividad de n
= A n (B'niB) r\ A pero como B'nB = <(>, se tiene
MnN = f luego por la propiedad (1) se tiene:
n(A) = n(M u N) = n(M) + n(N) = n(A - B) + n(A n B)
de donde n(A - B) = n(A) - n(A n B)
(5) n(A uB) = n(A) + n(B) -n(A n B)
Demostración
Como A u B = (A - B) u B y (A - B) n B = <)>, entonces
n(A u B) = n(A - B) + n(B) por la propiedad (1)
= n(A) - n(A n B) + n(B) por la propiedad (2)
= n(A) + n(B) - n(A n B)
/. n(AuB) = n(A) + n(B)-n(AriB)
(4) n(AuBuC)= n(A) + n(B) + n(C)-n(An B)-n(A nQ-n(B nC) + n(A nBnC)
Demostración
Sea E = B u C. entonces por la propiedad (3) se tiene:
n(A u E) = n(A) + n(E) - n(A r\ E) entonces:
n(A u B u C) = n(A) + n( B u C) - n(A n (B u O)
= n(A) + n(B) + n(C)-n(B nC)-n((AnB)u(AnC))
= n(A) + n(B) + n(C) - n(B nC)- [n(A n B) + n(A nC)-n(A n B nC)J
.-. n(AuBuCj = n(A) + n(B) +n(Q - n(AnB)- n(A nC)-n(B nC)+ n(AnBrC)
leorm de Conjuntos
119
Ljimplo.-
\J l na persona come plátano o naranja cada mañana durante el mes de marzo, si come
larunja 25 mañanas y plátano 18 mañanas ¿Cuantas mañanas come plátano y
" iranjas?
Solución
Sea U = {mes de marzo} conjunto universal => n(U) = 31
A = {mañanas que come plátano) => n( Aj - 18
i = {mañanas que come naranja) => n(B) = 25
bbiquemos la información en un diagrama de Venn - Euler.
jj Mañanas que comen plátano y naranjas = x
n(A u B) = n(A) + n(B) - n(A n B)
31 = 18-x + 25-x-x
3x = 43-31 = 12 de donde x = 4
Rpta. 4 mañanas come plátano y naranja
7) Sean A y B dos conjuntos tales que n( A u B) = 24 y n(A - B) = 10, n(B - A) = 6.
Hallar 5[n(A)l -4{n(B)]
Solución
llbiquenios los datos un diagrama de Venn - Euler.
Calculando se tiene:
5[n(A)M[n(B)]=5(18)- 4(14) = 90 - 56 = 34
En una investigación realizada a un grupo de 100 personas, que estudiaban varios
idiomas fueron los siguientes: Español 28, Alemán 30, Francés 42. Español y
Alemán 8, Español y Francés 10. Alemán y Francés 5 y los tres idiomas 3
a) ¿Cuántos alumnos no estudiaban idiomas?
®
120
Eduardo Espinoza Ramos
b) ¿Cuántos alumnos tenían como francés el único idioma de estudio?
Solución
Ilustraremos el problema en un diagrama de Venn - Euler, para facilitar la solución.
En el diagrama se observa que:
n(EnAnF) = 3 ; n(AnF) = 5
n(EnF)=10 ; n(EnA) = 8
n(F) = 42 ; n(A) = 30
n(E) = 28
n(AuEuF) = n(A) + n(E) + n(F) - n(A n E) - n(A n F) - n(E n F) + n(A n E n F)
= 28 + 30 + 42 -8-10-5 + 3 = 80
por lo tanto a) No estudian idiomas = 100-80 =20
b) Sólo francés 30
4J En un instituto de investigación trabajan 67 personas. De estas 47 conocen el ingles,
35 el alemán y 23 ambos idiomas. ¿Cuántas personas en el instituto no conocen el
ingles ni el Alemán?
Solución
Para facilitar la solución utilizamos el diagrama de Venn - Euler.
I = ingles, A = Alemán
En el diagrama se observa que n(In A) = 23,
n(A) = 35, n(I) = 47 por conocer N(I u A)
Hallaremos «(/'nA') = n((/uA)') = «(t/)-«(/uA) = 67-n(IuA) ...(1)
edemas n(I u A) = n(I) + n(A) - n(I n A) = 47 + 35 - 23 = 59 ... (2)
reemplazando (2) en (1) se tiene: n(U) - n(I u A) = 67 - n(I u A) = 67 - 59 = 8
por lo tanto 8 personas no conocen el Ingles y Alemán.
Teoría de Conjuntos
121
5J Sea A un conjunto tal que n(A) = 3p + q, B es un conjunto tal que n(B) = 2q + 3, y
los dos tienen elementos comunes n(AnB)=p+q - 4 ¿cuántos elementos tiene AAB?
Solución
Debemos de calcular n(A A B) = ?
n(A A B) = n[(A uB)-(An B)l = n(A u B)-n(A n B)
= n(A) + n(B) - n(A n B) - n(A n B)
n(A A B) = n(A) + n(B) -2n(A o B)= (2p + q +2q + 3) - 2(p + q - 4)
= 3p + 2q + 12 - 2p - 2q + 8 = p + 20
7T) De 120 alumnos de una universidad se obtuvo la información siguiente:
72 alumnos estudian Análisis Matemático.
64 alumnos estudian Biología.
36 alumnos estudian Ciencias Sociales.
12 alumnos estudian las tres asignaturas.
¿Cuántos alumnos estudian exclusivamente dos asignaturas?
Solución
Sean A = {estudiantes de Análisis Matemático}
B - {estudiantes de Biología}
C = {estudiantes de Ciencias Sociales}
Ilustraremos mediante el diagrama de Venn-Euler.
Las variables x,y,z representan a los estudiantes
que estudian exclusivamente dos asignaturas.
Las variables a, b, c representan los estudiantes de
una sola asignatura, de acuerdo a los datos del
problema se tiene:
122
Eduardo Espinazo. Ramos
a + x + y+ 12 = 72
b + x + z+12 = 64
c + y + z+12 = 36
(a + b + c) + 2(x + y+ z)= 136 ...(1)
como son 120 alumnos, del diagrama se tiene: a + b + c + x+y+z+12 = 120 de donde
(a + b + c) + (x + y + z)= 108 ...(2)
ahora al restar (2) de (1) se tiene: x + y + z = 136 - 108 = 28
por lo tanto, los estudiantes que estudian exclusivamente dos asignaturas son 28
7) En una ciudad de 10,000 habitantes adultos el 70% de los adultos escuchan radio, el
40% leen los periódicos y el 10% ven televisión, entre los que escuchan radio el
30% lee los periódicos y el 4% ven televisión, el 90% de los que ven televisión, lee
los periódicos, y solo el 2% de la población total adultos lee los periódicos, ven
televisión y escuchan radio se pide:
a) Cuántos habitantes no escuchan radio, no lee periódicos ni ven televisión.
b) Cuántos habitantes leen periódicos solamente.
Solución
Consideremos los siguientes conjuntos:
A = {conjunto de personas que escuchan radio)
B = {conjunto de personas que leen periódicos) .
C = {conjunto de personas que ven televisión)
Personas que escuchan radio 70% de 10.000 es 7,000
gersonas qye leen periódicos 40% de 10,000 es 4,000
Personas que ven televisión 10% de 10,000 es 1,000
Paja facilitar la solución utilizaremos diagramas de Venn.
Teoría de Conjuntos
123
U
a) Observando el diagrama se tiene:
n(A u B u C) = 4820 + 1900 + 1200 + 700 + 200 + 80 +20
= 4820 + 3100 + 1000 = 8920, además se conoce que n(U) = 10,000
Los que no leen periódicos, no escuchan radio, ni ven T.V. estará dado por:
n(U) - n(A u B u C) = 10,000 - 8920 = 1080 es decir 1,080 personas adultas,
no leen periódicos, no escuchan radio, ni ven T.V.
b) Según el diagrama de Venn -Euler las personas que leen periódicos solamente
son 1,200.
\8J En una encuesta realizada a 154 personas, se obtuvieron las siguientes
informaciones: 6 personas cenan y desayunan pero no almuerzan
5 personas desayunan y almuerzan solamente
8 personas almuerzan solamente
Él número de personas que realizan las tres comidas es el séxtuplo de las que sólo
desayunan y el triple de las que solo cenan, nadie declara almorzar y cenar
solamente. ¿Cuántas personas cenan por lo menos?
Solución
Sean A = {conjunto de personas que almuerzan}
C = (conjunto de personas que cenan}
D = {conjunto de personas que desayunan}
124
Eduardo Espinoza Ramos
Sea x el número de personas que desayunan solamente entonces las personas que
realizan las tres comidas es el séxtuplo de los que desayunan solamente 6x y esto es
el triple de los que quiere decir que los que cenan solamente es 2x.
Para facilitar la solución usaremos los diagramas de Venn - Euler.
Además se tiene que: n(U) =154
Donde U = A u C u D, donde n(c) = 6x + 6 + 0 + 2x = 8x + 6
n(AuCuD)=n(U) = 154, de donde al observar el diagrama de Venn - Euler se tiene:
6x+6+2x+ 0 + 8 + 5 + x= 154, simplificando 9x + 19 = 154 => 9x = 135 => x = 15
las personas que cenan por lo menos es: n(c) = 8(15) + 6= 120 + 6= 126
En una encuesta realizada en una población sobre su preferencia de tres diarios A, B
y C se encontró el 42% leen el diario A, el 34% leen B, el 28% leen C, el 17% lee A
y B. el 15% lee A y C, el 8% lee B y C y el 66% leen al menos uno de los tres
diarios. Determinar:
a) Que tanto por ciento leen un solo diario.
b) Que tanto por ciento leen exactamente dos de los diarios.
c) Que tanto por ciento ninguno de los tres diarios
Solución
©
Teoría de Conjuntos
125
U
n(A) = 42, n(B) = 34, n(C) = 28 "
n(AnB) = 17, n(AnC) = 15, n(BnC) = 8
y n(AuBuC) = 66
Sea x el porcentaje de personas que leen los tres diarios.
Sí n(AuBuC) = n(A) + n(B) + n(C) - n(AnB) - n(AnC) - n(BnC) + n(AnBnC)
66 = 42 + 34 + 28 - 17 - 15 - 8 + x de donde 66 = 62 + x => x = 2
En el diagrama: n(A) = a + (17 - x) + (15 - x) + x = 42 => a = 12
n(B) = b + (17-x) + (8-x) + x = 34 => b=ll
n(C) = c + (15-x) + (8-x) + x = 28 => c = 7
Luego: a) Leen un solo diario a + b + c = 30%
b) Leen exactamente dos de los tres diarios 15+ 17 + 8-3x = 34%
c) No leen ninguno de los tres diarios 100-66 = 34%
2.23. EJERCICIOS PROPUESTOS.
(T) Dados los conjuntos A = {a,e,d}, B = {e,f,g} y C = {l,ej,k}. Hallar Au(BnC)
(5) Sí U= {a,b,c,d,e}, A uB = {a,b,c,d}, AnB={a,c} y A-B={b}. Hallar AyB
(5) Sean los conjuntos A = {xe N/x = -(k2-l), fce/V}, B = {xe NI x2 =8jc},
C = {jre N/x2 -32jc + 192 = 0}. Hallar el resultado de (B - A) n C
{4) Consideremos los conjuntos siguientes: A = {x e N/x es divisor de 12},
B= {x e N / x es divisor de 18} y C= {x e N / x es divisor de 16}.
Hallar a) (A-B)n(B-C) b) (A-B)u(B-C)
126
Eduardo Espinoza Ramos
(?) Dados los conjuntos A = {5,6,7,8}. B = {6,7,1,2}. C = {4.5,7,9} y U = {1,2,3,4.5,6.7,8.9}
calcular:
a) AuB b) (AnB)uC c) An(B-C) d) C-(Ar\B)'
(ó) Dados los conjuntos A = {1,2,3,4), B = {2,3,5,7}, C = {1,4,6,8} yU={xeN/x<8}
calcular
a) AuB b) AnB c) (AuB)nC
d) (A-B)' respecto aU e) [C-(AuB)\ respecto a U
(7) Sí A={xe N/x<5 v x=7}, B={2x + 1/xe N a x<3)
Hallar a) AuB b) AnB c)A-B d) B-A
(?) Sean A = {{1.2,3},3,1}, B = {1.2,3}, C= {2,3.4} y D = {{2,3}, 1.2,5}. Hallar:
a) AuB b)AuC c)AuD
d) AnB e) AnC f) AnD
g)A-B h)A-C i)A-D
(5) Sí AuB ={1,2,3,4}, AnB ={1,3} y A-B = {2}. HallarAyB
Rpta. A = {1,2,3} y B= {1,3,4}
(lo) Si U= {a,b,c,d,e}, A u B = {a,b,c,d}, AnB = {a,c} y A-B={b}. Hallar AyB
Rpta. A = {a,b,c}, B = {a,c.d}
Mi) Si A= {x e Z/x es divisor de 60} ; B = {x 6 Z/x es divisor de 42} y
C={xe Z+ /xes múltiple de 2, menor que 20}. Verificar las siguientes igualdades
a) Au(BnC) = (AuB)n(AuC) b) An (BuC) = (An B) u (A n C)
(U) Si A={xe R/-3<x<5}, B = {x e R12 < x < 7} y C=(xe R/4<x < 5}. Hallar:
a) AuBuC b) (A-B)n(AuC)
Teoría de Conjuntos
127
Si P={x e N/x es divisor de 12}, Q= {x 6 N /x es divisor de 24}
R = {\ e N/x es divisor de 36} ¿Cuál de las siguientes proposiciones son verdaderas?
a) PnQ = PnR b) PnQ = R c) Q-R = P
d)PuR = Q c)P-Q = R
Simplificar los siguientes conjuntos:
a) (<-2,3] u <0,4>) - [2,6] b) <0,4> u <-2,3] - [2,6]
c) (<-2,3] u C[2,6]) u (<0,4> n [<-~>,2> u <6,+~>>])
Si U= {-3,-2,-1,0,2,3} el conjunto universal y sean A = {-1,0,1}, B = {-2,-1,0,1,2},
C = {-3,1,2}. Determinar cada uno de los siguientes conjuntos.
a) B' b) A c) (Anfl)' d) A'ufí'
e) Bc\C f) {Br\C)~
Sea l = {1,2,3,4,5,6,7,8,9,10} el universo. A = {1,2,3,4,5} y B = {2,4.6,8,10}.
Determinar los siguientes conjuntos.
a)AuB b)AnB c)A-B d) B-A
e) CA f) CB g) C(AuB) h) CAnCB
Si U = {1.2,3,4,5,6}, A = {1,4,5.6}, B = {2.4,6}. Determinar los siguientes conjuntos:
a) A b) B¡ c) Ar\B' d) Ar\B
e) A'nfi' f) (A'nfi')' g) AnB h) A'ufi'
Sea U={xeN/x<7} el conjunto universal, siendo los subconjuntos
deU, A = {A-eí//jc1 <8}, B = {x e U/x es múltiplo de 3}, C = {xe U / x2 > 25}.
D= {xe U/x es par}. Hallar F-[(C"uD')- A\
128
Eduardo Espinoza Ramos
(19) Sean U= {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, A ={ 1,2,3,4}, B = {1,4,13.14}, C ={2,8},
D= {10,11,12}. Hallar:
a)AuB b)AuC c) BuD d)D^C
e) CA f) (CA)uB g) CAuCB h) C(AuB)
i) CAr>CB j) C(AnD) k) C(AuC) I) (AuB)-D
II) (AnB)-D m) (A-B)u(B-A) n) (AuB)-(AnB)
o) (A - B) n (B - A)
(20) Siendo Z el conjunto universal y sean los conjuntos A= {x e Z/x es número par},
B={xeZ/xes número primo}, C={xeZ/xesun cuadrado perfecto}. Hallar
a) Ar>fí' b) C-(BuA) c) (Aufl)'nC
(21) Sean U={xeN/2<x< 12}, A = {x e U/x es impar, x *3}, B={x e U/5<x< II},
• C={xeU/xes múltiplo de 3}. Calcular (A'-B)' A(B'uC)"
(S) Dados los conjuntos A={ 1,2,5,7,8}, B={ 2,3,4,7,9}, C={ 1,3,5,6,8} y U= {xe N/x <9}.
Hallar
a) puB)-(AnC)]' b) [(AnB)-(AuC)]'
c) [(A-B)u(A-C)]' d) [(A-B)n(A-C)]'
e) [(C-F)-(A'uC)]' f) (A'-B')A(£VjC)'
(23) Si M ={Jte NIx3, <30), N = {x2 e N lx<3] y el universo es U= {1,2,3,4,6,7,9}. Hallar
a) (M r\N)' — (.M uW)' b) Hacer un diagrama de Venn - Euler.
(24) Dados los conjuntos A= {2,3,5,6,8} y B = {0,1,2,4,5.7,9} Si m es el número de
subconjuntos no vacíos de A que son disjuntos con B y n él número de subconjuntos no
vacíos de B que son disjuntos con A. Hallar m + n. Rpta. 38
Teoría de Conjuntos
129
Sea U = {x e N/O <x < 10} y los subconjuntos A = {x e U/x es primo},
B={\e U/x es cuadrado perfecto}, C={xe U/x es impar}. Hallar:
a) (AuB)'-C b) (A-C)'n,B
c) (AAB)-(AAC) d) (AnC)'-(BuC)'
Dado los conjuntos A = {xeZ/~[ x <-2 v x>3}}. B= {xe N/~(-l <x<3=>x = 5)}
y C = {x e Z/ (x < -2 v x > 2) -» x > 1}. Hallar el resultado de (B n C) A (A n B)
Sean los conjuntos A={xeN/7 - x = 3v x < 3}, B = {xe N/5-x>2 a -(6jr-2)>2},
C = {x e N / x cuadrado perfecto, x < 10}. Hallar
a) (AuB)n(C-A) b) (A-B)u(BnC)
c) (AnB)-(A-C) e) (AAB)n(BnC)
Dado el conjunto universal U={xe N/x< 50} y los subconjuntos:
- —i ~ i
A = { /xeU a x es N° primo}; B-{ /xeU a x es N° impar}
C = rX l/xe U a x es N° par}. Hallar
a)AnB b)AAB c)AAC
d) (AAB)AC' e) (AuB)A(AuC)
Determinar los conjuntos X e Y si se tiene que X A Y ={ 1,2,3,4,5}, X'= {2,3,5,7},
y= |1,4.7} siendo el universo U= {1,2,3,4,5,6,7,8}
Sea U = {x e N/0< x < 10} y los subconjuntos A = {x e U/x es primo},
B={xe U/x es cuadrado perfecto}, C={xe U/x es impar}. Hallar
a) C(AuB)-C b) C(A-C)nB
c) (AuB)-(AuC) d) C(AnC)-C(BuC)
130
Eduardo Espinoza Ramos
®
Sí A-{xeZ / x' +Ax — 5x) y B = [.veZ/3v, y '= jc} . Hallar el complemento de B
con respecto a A es decir: A - B.
Rpta. A-B = {-1.-2,2}
Simplificar y expresar en términos de reuniones de intervalos:
a) [2,7>A<0,1> b) <1,4> A(<2,6>u<0,l>)
c) [2,9] n (E <-°°,-3] u [3,6]) - <2,8J) d) (<-°°,5>u <6.12>) A {1,7}
Determinar los elementos de A y B sabiendo que A A B = {1,2,3,4,5}, CEB = {\,7,4).
CEA = {2,3,5,7}, E = {1,2,3,4,5,6,7,8}
En las siguientes proposiciones dadas indicar cuáles son verdaderas o falsas y justificar su
respuestas.
a) {x,y,z} = {z,x,y} b) {x,x,x} = {x} c) {<|>}=<t>
d) {{x,y}}c{z,{x,y},w} e) {x,y} e {x,{x,y}} f) {x,y} c {x,{x,y}}
g) {x,y} c {z,{x,y},y} h) {x,y] <= {z,{x,y},w} i) {x,y.z} = {y,x.w,x,z}
j) ac{a} k) {a}<={{a}} e) {a}e{{a}}
Dibujar el diagrama que aparece a continuación, tantas veces como sea necesario, para
representar, por sombreado, cada uno de los conjuntos que a continuación se indican.
a) AnB
e) C A n C B
i) A n C A
c) AnBnC
g) E (A n B)
I) An(BuC)
d) AuB
h) t(Au B)
U) Au(BnC)
Teoría de Conjuntos
131
(36) Verilicar mediante diagí ama de Venn - Euler que se cumple:
a) AuB = BuA b) AnB=BnA c) (AnB)nC) = An(BnC)
d) lAuB)uC = Au(BuC) e) An(BuC) = (AnB)u(AnC)
O C^ntB=C(AuB) g) A-B = AnCB h) CAuCB=C(AnB)
\yf) Mostiar. utilizando diagrama de Venn -Euler que se cumplen las siguientes propiedades:
a) (AnB)uC = (AuC)n(BuC) b) (A uB)-C = (A-C) u(B-C)
c) (AnB)-C = (A-C)n(B-C) d) AcB oCBcCA
e) Ac(AuB) f) Bc(AuB) g) AnBcA h) AnB<=B
(38) Simplificar las siguientes proposiciones:
a) Anf b)AnU c) AuÍA d)A-<)>
e) Au$ f) AuU g) AntA h) C(CA)
i) G(AnU) j) C(A n<J» k) C(Au<J>) 1) C(AuU)
(39) Sea A ={<J>,1,{1}}. Hallar P(A)
^0) Si A = {<)>,1,{ 1}} Hallar P(A), P(PíA))
Wl) Sean los conjuntos siguientes A=( 1,2,3},fi = { \e Z/x2 ~x-6 = 0), C={xeN/2<x<6},
D = C - (A n B). Determinar el conjunto potencia de P(P(A)).
62) Sea A = |1,{(})),<)>} y B = {2,{1 },{2},<t>}, calcular los elementos de:
a) AAB b) P(AnB)
(43) Sí A = {2,<}>}. Determinar los elementos de P(P(A))
(44) Dados los conjuntos A = {xe N / x3 -2x2 -5.v + 6 = 0}, B = [xe N llx2 -7v + 3 = 0}.
C = (2,3} sí D = (A - B) u C Hallar el número de elementos de P(D).
132
Eduardo Espinoza Ramos
(45) Demostrar que: a) AcB =} AnMcBnM, VM
b) AcB=>MuAcMuB,VM
(4ó) Probar que: a) AcB<=>Ar>CB = <¡) b) CAdCB <=>CBnA = (|)
(¡¥n Muestre que: AnB = A => AcB
(48) Sean A, B cS entonces BcA <=> S-AcS-B.
(49) Sean A, Be S, entonces A = B ** S-A = S-B.
Q¡0) Muestre que:
a) AcBcCoAuB = BnC b) (A - B) r> C = (A r> C) - (B n C)
c) (Ar>C)-B = (A-B)n(C-B) d) An(B-C) = (AnB)-(AnC)
fel) Demostrar las siguientes propiedades:
a) A = (AnB)u(An(B) b) A-(B-C) = (A-B)u(AnC)
c) Au(B-C) = (AuB)-(C-A) d) A n(B-C) = (An B)-(AnC)
e) (AuB)-C = (A-C)u(B-C) f) A-(B uC) = (A-B) - C
g) (A n E B) u (B n E A) = (A u B) r> E (A n B)
h) (Au(B)n(BntA) = (AnB)ut(AuB)
(52) Dados los conjuntos A y B, demostrar que:
a) SíA-B = (|>yB-A = <t>=>A = B b) SíAAB = <¡>=>A = B
(53) Demostrar que: [A n B nC] u [(A-B)-C] = [A-(B -Q] n [A-(C-B)]
(54) Demostrar que: A'AB'=AAB
(55j Si A,B,C son conjuntos y C c A', entonces demostrar que: {[(Cufl)nA]uC" }nfl = Br\C
(56) Probar que: A-(Bn¡A') = A
Teoría de Conjuntos
133
(57) Demosti arque:
a) A'AB = A =>A<=B b) McAjMcB =>McAnB
c) AnB = <¡) <=> Br^A'=B d) A<=B<=>A-B = <)>
e) Ar\Bc(B~A)' => B<=A f) A = CXB => AAB = X
(58) Demostrar que: A n (B A C) = (A n B) A (A n C)
(59) Demostrar por definición que: P((A n B) u C) = P(A uC)n P(B n C)
(60) Probar que sí B cz A, entonces:
a) A-BeP(A-B) b) B-AeP(A-B)
(61) En una encuesta realizada en un grupo de 100 estudiantes, la cantidad de personas que
estudiaban varios idiomas fueron las siguientes: Ruso 28, Ingles 30, Latín 42, Ruso e
Ingles 8, Ruso y Latín 10, Ingles y latín 5, los tres idiomas 3.
a) ¿Cuántos alumnos no estudian ningún idioma?
b) ¿Cuántos alumnos tenían al Latín como único idioma de estudio?
c) ¿Cuántos estudiantes aprendían Ruso o Ingles pero no Latín?
Rpta: a) 20 alumnos b) 30 alumnos c) 38 alumnos
(62) Un club deportivo tiene 48 jugadores de fútbol, 25 de basket y 30 de béisbol, si el total de
jugadores en 68 y solo 6 de ellos figuran en los tres deportes:
a) ¿Cuántos figuran exactamente en un deporte?
b) ¿Cuántos figuran exactamente en dos deportes?
Rpta: a) 39 b) 23
(63) Entre los varones que llegaron en un avión internacional; 40 fueron peruanos y 60
comerciantes, de los peruanos el 75% tenían bigote y la mitad eran comerciantes; 5 de
cada 6 comerciantes tienen bigotes; de los peruanos con bigote la mitad eran
comerciantes. Hallar:
134
Eduardo Espinoza Ramos
a) El número de peruanos y comerciantes con bigotes.
b) El número de peruanos o comerciantes con bigotes.
Rpta: a) 15 b) 65
Un club está constituido por 78 personas, de ellas 50 juegan fútbol, 32 basket y 23 voley.
Además 6 figuras en los tres deportes y 10 no practican ningún deporte. Si x es el total de
personas que practican exactamente un deporte, y es el total de personas que practican
exactamente dos deportes. Hallar x - y. Rpta: 12
De 120 personas de cierta universidad se obtuvo la información:
72 alumnos estudian el curso A.
64 alumnos estudian el curso B.
36 alumnos estudian el curso C.
12 alumnos estudian los tres cursos.
¿Cuántos alumnos estudian exclusivamente dos cursos? Rpta: 28
En el ensamblaje de autos de cierta planta, han resultado 120 unidades con fallas, los
fallas son de embrague, dirección y caja de cambios. Sabiendo que 68 fallan en el
embrague por lo menos, 32 en la dirección por lo menos 40 fallan solamente en el
embrague, 5 tienen fallas en embrague y dirección pero no en la caja de cambios, 17
tienen fallas en la dirección y caja de cambio pero no en el embrague.
a) ¿Cuántos autos les falla sólo la caja de cambios?
b) ¿Cuántos autos tienen fallas en la caja de cambios por lo menos?
Rpta: a) 29 b) 69
De una encuesta a 58 personas sobre un producto en sus tres tipos se obtienen los
siguientes resultados: 10 usan solo el tipo A, 15 solo usan el tipo B, 12 sólo usan el tipo
C, 8 usan el tipo A y B. 5 usan el tipo B y C, 15 usan el tipo A y C. Rpta: 1
Teoría de Conjuntos
135
¿Cuántos de los 2000 alumnos están inscritos en matemática básica pero no en física I,
sabiendo que, 1050 están inscritos en matemática básica, 750 en física 1, 650 en Básica y
matemática I, 350 en física I y Básica. 300 en matemática I y física I, 1150 en matemática
I, y 200 llevan las tres materias. Rpta: 700
Una encuesta de 200 votantes, revelo la siguiente información conveniente a tres
candidatos A, B y C de un cierto partido que se presentaban a tres diferentes cargos:
28 a favor de A y B
98 a favor de A o B pero no a C
42 a favoi de B pero no de A o C
122 a favor de B o C pero no de A
64 a favor de C pero no A o B
14 a favor de A y C pero no de B
¿Cuántos votantes estaban a favor?
a) De los tres candidatos b) ¿Solamente de uno de los candidatos?
Rpta: a) 8 b) 142
De un grupo de 100 alumnos, 49 no llevan el curso de aritmética; 53 no llevan álgebra y
27 no llevan álgebra ni aritmética ¿Cuántos alumnos llevan uno de los cursos?
Rpta: 48 llevan solo un curso
Supóngase que Juan come huevos o tocino en el desayuno cada mañana durante el mes de
Enero (31 días). Si come tocino durante 25 mañanas y huevos durante 18 mañanas,
cuántas mañanas come solamente huevos? Rpta: 6
De 150 personas consultados sobre el deporte que practican manifestaron lo siguiente: 82
juegan fútbol, 54 juegan básquet, 50 solo juegan fútbol, 30 sólo juegan sólo básquet.
además, el número de personas que juegan sólo básquet y tenis es la mitad de las que
juegan sólo fútbol y tenis: el número de personas que juegan sólo fútbol y básquet es el
triple de las que juegan los 3 deportes las personas que no practican ningún depone son
tantos como las que practican sólo tenis. Hallar:
136
Eduardo Espinoza Ramos
a) El número de personas que practican sólo dos deportes.
b) El número de personas que no practican ninguno de los tres deportes.
Rpta: a) 36 b) 17
En una investigación efectuada a 370 personas, se determino que: 20 personas leen
solamente la revista A, 40 personas leen solamente la revista B y C, 10 personas leen
solamente la revista A y B Él número de personas que leen las revistas A. B y C es: el
doble de las que leen solamente la revista B, el cuadruplo de las que leen solamente la
revista C y es 8 veces mayor de las que leen solamente las revistas A y C. Hallar él
número de personas que leen:
a) Solamente la revista B b) Solamente la revista C.
Rpta: a) 80 b) 40
En la edición de un libro hay un resultado de 120 ejemplares con fallas, en el papel, fallas
de Impresión, fallas en encuademación; si se sabe que 68 libros tienen la primera falla,
por lo menos 32 tienen la segunda falla; por lo menos 40 libros tiene la primera falla
solamente, 5 tienen la primera y segunda falla, pero no la tercera falla, 17 tienen la
segunda y tercera, pero no la primera, 4 tienen las tres fallas, se pregunta:
a) ¿Cuántos libros tienen solamente la tercera falla?
b) ¿Cuántos libros tienen la tercera falla por lo menos?
En la biblioteca de un colegio se realizó una encuesta sobre los libros que más leen los
alumnos, obteniéndose los siguientes resultados:
350 alumnos leen los libros de letras
380 alumnos leen los libros de ciencias
350 alumnos leen los libros de artes
además, el número de alumnos que leen sólo asignaturas de artes es — de los que leen
4
solo asignatura de ciencias, él número de alumnos sólo leen libros de letras es — de los
que leen sólo libros de ciencias y letras.
Teoría de Conjuntos
137
El numero de alumnos que leen las tres asignaturas es — de los que leen sólo libros de
4
artes y letras y - de los que leen sólo libros de artes y ciencias ¿cuántos alumnos leen
solamente los libros de ciencias?
¿76J Una agencia de turismo realiza una encuesta entre 5000 personas para ver las preferencias
en materia de viajes a Cuzco, Iquitos y Trujillo; 2400 personas desean viajar por lo menos
al Cuzco, 3000 por lo menos a Trujillo, 2100 por lo menos a Iquitos. 1000 a Trujillo y
Iquitos, 800 al Cuzco y a Iquitos, 1500 a Trujillo y el Cuzco y 500 están dispuestos a
realizar tres excursiones se preguntan:
a) ¿Cuántos indicaron que no realizaran ningún viaje?
b) ¿Cuántos no mostraron interés por el viaje a Iquitos?
c) ¿Cuántos desean hacer dos excursiones siempre que ninguna sea el Cuzco?
d) ¿Cuántos están dispuestos a realizar dos viajes diferentes?
e) ¿Cuántos viajarán al Cuzco si y sólo si no lo harían a Iquitos ni a Trujillo?
J7/ En una encuesta realizada en una Universidad sobre las marcas de cigarros que gustan a
los estudiantes, se obtuvieron los siguientes resultados.
28 estudiantes consumen Premier.
22 estudiantes consumen Ducal.
25 estudiantes consumen Winston.
11 estudiantes consumen Premier y Ducal.
15 estudiantes consumen Premier y Winston.
14 estudiantes consumen Ducal y Winston.
8 estudiantes consumen, Premier, Ducal y Winston.
a) ¿Cuántos estudiantes prefieren los cigarrillos Premier o Ducal?
b) ¿Cuántos fueron los estudiantes encuestados?
138
Eduardo Espinoza Ramos
uS) En una encuesta tomada a 160 ahorristas sobre el destino de sus futuros prestamos se
verifico que 120, se comprarían casa y que 90 se comprarían auto. ¿Cuántos se disponían
a comprar las dos cosas?.
(79) De un grupo de 120 personas, 45 no estudian ni trabajan; 30 estudian, 9 estudian y
trabajan. ¿Cuántas personas trabajan solamente?
feo) Consideremos tres conjuntos A, B, C tales que Ac C, Be C, n(C) = 120, n(A uB) = 90,
n(A n B) = 30 y n(A) = n(B) + 30. Hallar:
a) n[(C-B)nA] b) n[(A u B) - (A n B)]
(8l) Si A es un conjunto de 8n elementos, B es un conjunto de 5n elementos, y 2n - 1
elementos comunes, hallar la suma de los números de elementos de: (AnB)n(A- B)
y (AuB)n(A-B).
(55) Demostrar que: n([A A B) u C) = n(A) + n(B) + n(C) - n(AnC)- n(B n C) - 2n(A n B)
+ 2n(A nBnC)
(SS) Demostrar que: n([AAB]-C)=n(A)+ n(B) - n(AnC)- n(BnC) - 2n(AnB) + 2n(AnBnC)
(84) Si x el máximo número de elementos deAuBuC y sea z el máximo número de
elementos de DnEnF, sí n(A)=9, n(B) = 7, n(C) = 10, n(D) = 4, n(E) = 2 y n(F) = 9.
Hallar x + z
(85) Sean A y B dos conjuntos tales que: n(A uB) = 24, n(A - B) = 10, n(B - A) = 6. hallar
5n(A) - 4n(B).
Qtó) Si los conjuntos A y B son tales que: n(A uB) = 30, n(A - B) = 12 y n(B - A) = 10,
hallar n(A) + n(B).
(87) Se sabe que "U" es un conjunto universal: n(B) = 28, n(C) = 19, n(A n B) = 14,
n(A'nBnC) = 5, n(AnC") = 12, n(AnB'nC) = l, n(A n B n C) = 6, n(U) = 50.
calcular n[(AuC)nBl
Teoría de Conjuntos
139
(88) Si n( A) = 4, n(B) = 3 y n(A n B) = 2, hallar la suma de nlP(A) u P(B)] + n[P(A u B)]
(89) Dado el conjunto U y los subconjuntos A, B y C, se tiene los siguientes datos: n(U) = 44,
n(A) = 21, n(B)=17, n(A n B) = 12, #i(AnBnC') = 3, n(A n B n C) = 5 y
n(AuBuC) = 6. Hallarn(C).
(90) A es un conjunto de 8n elementos, B un conjunto de 5n elementos y tiene 2n - 1
elementos comunes. Si n(A - B)-n(B - A) = 12 ¿Cuántos subconjuntos propios tiene
AnB?
(91) Si A es un conjunto de 8n elementos, B un conjunto de 5n elementos y tiene 2n - 1
elementos comunes, halla la suma de los números de elementos de: (AnB)n(A-B) y
(AuB)n(A- B).
(92) Sean A y B conjuntos tales que n( A) = 6, n(B) = 3, n(A n B) = 2. Hallar n[P(A A B)]
(93) Si n(P) = 15, n(Q) = 22, n(P uQ)= 30, hallar n(PnQ)
($4) Si n(A u B) = 14, n(A n B) = 6. halle n(A) + n(B).
(95) Si n(A) = 18, n(B) = 20, n(An B) = 4, calcular n[(A uB)n(A-B)]
(96) Si n(M) = 7x, n(R) = 9x, n(M n R) = 5x + 3, además n(M u R) = 63, calcular
n[(Af u/f)u(/?nAf")]
(97) M y N son dos conjuntos tales que: n(M u N) = 16, n(M n N) = 7, n(M) + 3 = n(N)
¿Cuántos subconjuntos propios tiene N - M?
(98) Si A={2x/xe Z, 3<x<9}, B = {3n/n e Z, 5 <n< 10}, calcule
n[(A n B)] + n[(A u B)]
(99) Si A={xeN/xes impar, x < 25}, B = {y / y e N, y < 20} ¿cuántos elementos tiene
P(A A B)
Si A ={2,3,4,5 50}, B = {2n/ne Z, l<n<30}, calcule n[(A u B) - (A n B)]
140 Eduardo Espinoza Ramos
CAPITULO III
3. SISTEMA DE NÚMEROS REALES.-
3.1. INTRODUCCIÓN.-
El sistema de los números reales que ahora conocemos, fue obtenido después de muchas
reflexiones por parte del hombre.
Desde el comienzo de nuestra civilización, ya se conocían los números enteros positivos,
o sea 1, 2, 3,... Los números enteros tan grandes como 100,000 se utilizaban en Egipto en
épocas tempranas, como es 300 A.C.
La aritmética que desarrollaron los antiguos Egipcios y Babilonios con los números
enteros positivos mediante los cuáles podían efectuarse las operaciones de adición y
multiplicación, aunque la división no se desarrollo por completo.
En estos dichos pueblos usaron ciertas fracciones, es decir que los números racionales
también aparecieron en una temprana etapa de nuestra civilización (un numero racional es
cociente de dos enteros).
Los que tuvieron mas éxito en el desarrollo de la aritmética y el álgebra fueron los
babilonios, ellos tenían una notación para los números, muy superior al de los Egipcios,
esta notación, análoga a nuestro sistema decimal, excepto por el hecho de que su base es
60 en lugar 10, una buena notación es el pre - requisito para el desarrollo de los
matemáticos.
Sistema de Números Reales
141
Nuestro sistema decimal de los números llamados análogos fue creado por los Hindúes e
introducido en Europa Occidental en el siglo XII mediante la traducción de textos Árabes.
Sin embargo, esta notación demoro demasiado en una aceptación generalizada, mucho
más tarde fue la aceptación de los números negativos, que se prolongo hasta finales del
siglo XVI se descartaba las raíces negativas de las ecuaciones.
En contradicción de la geometría que desarrollaron los Griegos solamente para su
satisfacción intelectual y en su modelo del sistema lógico, con el desarrollo del calculo,
los números irracionales tales como , tuvieron que sustentarse sobre una
fundamentación lógica, esto se logró en la ultima parte del siglo XIX,. Ahora tenemos un
sistema de axiomas, que describen completamente los números reales partiendo de estas
axiomas podemos deducir todas las propiedades de los números reales.
Esto es el método usado en la Geometría Euclideana, se acepta un cierto numero de
proposición a los que se llama axiomas o postulados o hipótesis y basándose en esos
axiomas se prueban todas las Teoremas de la Geometría.
3.2. DEFINICIÓN.-
Llamaremos sistema de los números reales a un conjunto R, provisto de dos operaciones
adición (+) y multiplicación (.) (leyes de composición interna), y una relación de orden
denotado por "<" y el axioma del supremo, es decir:
Io LEY DE COMPOSICIÓN INTERNA:
+: R x R > R
(a,b) > +(a,b) = a + b
Además debe cumplirse los axiomas siguientes:
Aq Cerradura: , Va, b e R => a + b e R
A¡ Conmutatividad: a + b = b + a, Va.beR
A, Asociatividad: (a + b) + c = a + (b + c), V a,b,c € R
142
Eduardo Espinoza Ramos
• : RxR >R
(a,b) > a.b
A3 Identidad aditiva: VaeR. 3 Oe R/a + 0 = 0 + a = a
Aj Opuesto Aditivo: V a e R, 3 - a € R, y es único, tal que: a + (-a) = (-a) + a = 0
2° LEY DE COMPOSICIÓN INTERNA:
Además debe cumplirse los axiomas siguientes:
M0 Cerradura: V a, b e R => a.b e R
Ai, Conmutativa: a.b = b.a. V a,b e R
M2 Asociativa: (a.b).c = a.(b.c), V a,b,c e R
M3 Identidad Multiplicativa: VaeR, 3 1 ^0, le R, tal que: 1.a = a
Af4 Inverso Multiplicativo: Va*0, 3 a~l e R, tal que: a.a~y =a~l.a = l
3o RELACIÓN DE ORDEN:
O, V a,b e R una y solamente una de las relaciones se cumple a<b, a = b, b<a (ley de
tricotomía).
02 Sí a < b y b < c entonces a < c (transitiva).
03 Sia<b=> a + c<b + c, V a,b,c e R.
04 Sí a < b, o 0 entonces a.c < b.c
OBSERVACIÓN:
i) A los números a_ y b los llamaremos sumando, y al numero a + b suma de a y b.
ii) En a.b; a los números a y b los llamaremos factores y al número a.b producto de a y
b.
iii) El opuesto es único, así mismo el inverso es único.
Sistema de Números Reales
143
3.3. AXIOMA DE SUSTITUCIÓN.-
Si a y b pertenecen a un conjunto B y si a = b, entonces en toda relación se puede
sustituir al elemento a por el elemento b sin que altere el significado de la relación.
3.4. AXIOMAS DISTRIBUTIVAS.-
a) a.(b + c) = a.b + a.c, Va,b,ce R distributiva a izquierda
b) (a + b).c = a.c + b.c, Va,b,ce R distributiva a derecha
3.5. TEOREMA DE IGUALDAD PARA LA ADICIÓN.-
Sí a = b entonces a + c = b + c, para todo a, b, c e R
Demostración
Io a = b. por hipótesis.
2° a + c = a + c, propiedad reflexiva.
3o a + c = b + c, Io, 2o y axioma 1.3
3.6. TEOREMA DE IGUALDAD PARA LA MULTIPLICACIÓN.-
Sí a = b entonces a.c = b.c, para todo a, b, c e R
Demostración
Io a = b por hipótesis.
2° a.c = a.c, propiedad reflexiva.
3o a.c = b.c, Io, 2o y axioma 1.3
3.7. TEOREMA DE CANCELACIÓN PARA LA ADICIÓN.-
a I '-¿ . ■ i -I
Sean a,b,c e R; Sí a + c = b + c entonces a = b
Demostración
Io a + c = b + c. por hipótesis.
2o a + c+ (-c) = b + c+ (-c), Io y teorema 1.4
144
Eduardo Espinoza Ramos
3o a + (c + (-c)) = b + (c + (c)), 2o y A2
4o a + O = b + O, 3o axioma A4
5° a = b, 4o axioma A,
3.8. TEOREMA DE CANCELACIÓN PARA LA MULTIPLICACIÓN.-
Sean a,b,c e R; Sí a.c = b.c y c * 0, entonces a = b
Demostración
Io a.c = b.c,
2o c*0,
3o 3 - e R/(a.c).- = (b.c).-,
c ce
4o a.(c.-) = b.{c.-),
c c
5o a.l=b.l,
6o a = b,
... por hipótesis.
... por hipótesis
...2o, Io y axioma A/4
... 3o y axioma M2
...4o y axioma A/4
... 5o y axioma M3
3.9. SUSTRACCIÓN DE NÚMEROS REALES.-
DEFINICIÓN.- Para cualquier números reales a,b g R, definiremos a la sustracción
de números reales por:
a - b = a + (-b)
3.10. DIVISIÓN DE NÚMEROS REALES.
DEFINICIÓN.- Para cualquier números reales a,b g R, donde b * 0, definiremos al
cociente de números reales por:
b
Sistema de Números Reales
145
3.11. EJERCICIOS DESARROLLADOS.
(l) Para cada número real a e R, demostrar que a + a = 2a
Demostración
©
1°
2o
3o
40
5o
a = a.l
a + a = a.l +a.l
a+ a = a.(l+l)
a + a = a.2
a + a = 2a
Para cada número real a € R,
1°
2o
3o
40
5o
6o
T
8o
a.O = a.0 + 0
a.0 = a.0 + (a +
a.0 = (a.0 + a) +
a.0 = (a.0 + a.l)
a.O = a(0+ 1) +
a.O = a.l +(-a)
a.O = a + (-a)
a.0 = 0
(-a))
(-a)
+ (-a)
(-a)
... Por M3
... P
... 2o
... 3o
... 4o
y
y
y
y
demostrar que
axioma 1.4
axioma 1.3.a
por M3
por A/3
a.0 = 0
Demostración
... Por A3
... P
... 2°
... 3o
... 4o
... 5o
6C
... 7°
y
y
y
y
y
y
y
por A4
por A2
por Ai 3
por axioma 1.3.a
por A3
por M3
por A4
(3) Para cada número real a e R, demostrar que: -a = (-lj.a
Demostración
Basta demostrar que a + (-l)a = 0, porque (-1 ).a, y -a son inversos aditivos de a por A4
146
Eduardo Espinoza Ramos
Luego a + (-l)a= l.a + (-l)a, ... por axioma 1.3
a + (-l)a = (l+(-l))a, ... por axioma 1.3.b.
a + (-l)a = 0.a, ... por AA
a + (-1 )a = 0, ... por ejercicio 2.
.-. -a = (-l)a
\4J Para cada número real a e R, demostrar que -(-a) = a
Demostración
Io a + (-a) = 0 ... por A4
2° (-a) + (-(-a)) = 0 ... por A,
3o (-a) + (-(-a)) = a + (-a) ... Io, 2o
4o -(-a) = a ... 3o y por teorema 1.6
(s) Para cada número real a,b e R, demostrar que (-a).(-b) = a.b
Demostración
Io (-a).(-b) = [(-l)a][(-l)b] ... por el ejercicio 3
2o (-a).(-b) = (-l)[a((-l)b)] ... Io y M2
3o (-a).(-b) = (-l)[(-l)al.b ... 2o y Ai,, M2
4o (-a).(-b) = (-l)[(-a)].b ... 3o y ejercicio3
5o (-a).(-b) = [(-l)(-a)].b ... 4o y M2
6o (-a).(-b)=a.b ... 5o y ejercicio4
Q>) V a,b e R, demostrar que a.(-b) = -(a.b)
Demostración
Io a.(-b) = a.((-l).b) ... por ejercicio 3
Sistema de Números Reales
147
2o a.(-b) = (a.(-l)).b ... Io y por M2
3° a.(-b) = ((-l)a).b ... 2o y por M,
4o a.(-b) = (-l)(a.b) ... 3o y por M2
5° a.(-b) =-(a.b) ... 4o y ejercicio 3
6o -(a-b) = (-l)(a.b) ... Por el ejercicio 3
T -(ab) = ((-l)a).b ... 6o y por M2
8° -(ab) = (-a).b ... 7° y ejercicio3.
9° a(-b) =-(ab) = (-a).b ... 5o y 8o
(Y) V a,b e R, demostrar que a.(b - c) = a.b - a.c
Demostración
Io a.(b - c) = a.(b + (-c)) ... definición de sustracción
2° a.(b - c) = a.b + a.(-c) ... 1 ° y axioma 1.3.a
3o a.(b - c) = a.b + (-(a.c)) ... 2o ejercicio 6
4o a.(b - c) = a.b - a.c ... 3o definición de sustracción
©
Pan
1°
2o
3o
i a e R, demostrar sí a * 0,
a-1 =(<T').l
fl-^Ufl-1)
«-=!
entonces
a
Demostración
... por M3
... r y a/,
... 2° definición de división
148
Eduardo Espinoza Ramos
(5) V a,b e R, a.b * O, demostrar que (aJb) ' = a xb '
Demostración
Io (aJb).—— = 1
(ab)
2o (aJb).(aJbyl = 1
.. por A/4
.. Io y definición de división
3o (ab).(a~l b~l) = (a).(arl .{b).{b'x)
por M 2
4° (^).(a-,2?-1) = (a.-!-).(fc.i)
o b
3o, A/2 y definición de división.
5o (fl2?).(fl-'2?-1) = (l)(l) = l
6o (a£).(íTl.¿r,) = l
4o y A/4
de 5o
7° (ai>).(ai>)_1 = (ai>)(a_12T1)
de 2o y 6o
i _ „-i t-i
8o (ab)~l=a-lb
7° y teorema 1.7
®> ,..„.„. ^ , a c a A + bjc
V a,b,c,d e R, b * 0, d * 0, demostrar que: — + — =
b d bjd
Demostración
b d
... por definición de división
2o - + - = {ab-l).(d.-) + {cA-lUb.-) ... Io y por MA
b d
3o - + - = {ab~lHdA~l) + (cjd~1).{bb}) ... 2° y definición por división.
b d
Sistema de Números Reales
149
4 - + - = (fl^).(fc"'^_1) + (fc.í-)(fc~1-¿~1) ... 3o, M2
b d
5° - + — = (a¿i)Xb.dri+(b.cUb.drl ... 4o y ejercicio9
b d
a c _i
6 — + — = (cul+b.c).(bd) ... de5° y axioma 1.3.b.
b d
a c ad + b.c ,„ ,-..., , ,. . .,
7 — + — = ... 6 y definición de división
b d bd
3.12. REPRESENTACIÓN DE LOS NÚMEROS REALES.-
Entre los números reales y los puntos de una recta se puede establecer una
correspondencia, es decir:
Si sobre una recta se fija su origen "O", una unidad, y un sentido positivo, entonces, a
cada punto de una recta le corresponde un número real y recíprocamente, a cada número
real le corresponde un único punto de la recta, al número real correspondiente a un punto
de la recta se le llama abscisa del punto.
-3-2-1012345
NOTACIÓN PARA LOS CONJUNTOS DE NUMEROS.-
N: Conjunto de los números naturales.
Z: Conjunto de los números enteros.
Q: Conjunto de los números racionales.
1: Conjunto de los números irracionales.
R: Conjunto de los números reales.
C: Conjunto de los números complejos.
150
Eduardo Espinoza Ramos
CONJUNTO DE LOS NÚMEROS REALES
Q
racionales
[ z+fJV = U.2,...,ii,..}
| ° [N0 ={0,1,2 «,.
Z enteros negativos
Decimales periódicos = Ojabc =
entero positivo
abe
999
Decimales periódico mixto = 0.abcde ■■
abe
abede—ab
99900
Decimales exactos = 0.abc = -
1000
Q = [-/ a,bsZ, b*0)
b
I ¡ propios:
Irracionales ¡ trascendentes = {e, n,...}
3.13. DESIGUALDADES.-
La correspondencia entre los números reales y los puntos de una recta pueden usarse para
dar una interpretación geométrica de la relación de orden entre los números reales.
La relación a < b significa que sobre una recta numérica el punto A corresponde al
número "a", que se encuentra a la izquierda del punto B correspondiente al número "b".
A B
El símbolo < se lee "Es menor que". También usaremos los símbolos siguientes:
>, que se lee
<, que se lee
>, que se lee
"Es mayor que".
"Es menor o igual que".
"Es mayor o igual que".
Sistema de Números Reales
151
3.13.a DEFINICIÓN.-
i) Un número real "a" es positivo sí, a > 0.
ii) Un número real "a" es negativo sí. a < 0.
3.13.b DEFINICIÓN.-
Llamaremos desigualdad a una expresión que indica que un número es mayor o
menor que otro. Por ejemplo: 5 < 9.
3.14. AXIOMA DE LA RELACIÓN DE ORDEN.-
V a.b.c e R., se tiene:
Ot Orden de tricotomía: una y sólo una de las siguientes posibilidades se cumple:
a = b v a<b v a>b
02 Orden transitivo: sía<b a b<c =>a<c
O, Orden de adición: sía<b => a + c<b + c
04 Orden Multiplicativo: sía<byc>0 => a.c<b.c
En base a estos axiomas daremos las siguientes definiciones:
3.15. DEFINICIÓN.-
i) a<b <=> b-aes positivo. ii) a > b <=> a - b es positivo
iii) a<b<=>a = bva<b iv) a>b<=>a>bva = b
3.16. TEOREMA.-
V a,b,c,de R; Sía<c Ab<d <=> a + b<c + d
Demostración
1 ° a < c por hipótesis
2° a + b < b + c lJy03.
152
Eduardo Espinoza Ramos
3o b < d por hipótesis
4o b + c < c + d 3°y03
5o a + b < c + d 2°,4°y02
3.17. TEOREMA.-
Para a,b e R, si a < b => -a > -b
Demostración
Io a<b poi hipótesis
2o b - a > 0 1° y definición 1.14 i.
3o (b - a) + (-b) > 0 + (-b) 2o y 03
4o -a + (b + (-b)) >-b 3o, A2 y A,
5o -a + 0 > -b 4o y A4
6° -a > -b 5o y A,
3.18. TEOREMA.-
Sí a, b, c e R, donde a < b a c < 0 => a.o b.c
Demostración
1° a<b por hipótesis
2o c < 0 por hipótesis
3o - c> 0 2o y definición l. 14.0
4o - a.c < -b.c 1 °, 3° y 04 y ejercicio 6
5° a.o b.c 4o y teorema 1.16
Sistema de Números Reales
153
3.19.
TEOREMA.-
Para
1°
i
3
4o
5o
6o
a e R, a * 0
=> a2 >0
a*0
a>0 va<0
si a > 0 => a.a > 0.a
a2 >0
sí a < 0 => -a > 0
(-a)(-a) > 0. (-a)
Demostración
por hipótesis
i° y ol
2°y o4
3o y ejercicio 2
2o y definición 1.15i
5o y o4
7° a' > 0 6°, ejercicio 2 y 5
3.20. TEOREMA.
Para a e R, a * 0 entonces a ' tiene el mismo signo que "a" es decir:
i) Sí a>0 => a~l >0 ii) Sía<0=> a"1 <0
Demostración
i) 1° a>0 por hipótesis
2° a_1<0 hipótesis auxiliar
3o a.G-1 < 0 1°, 2° y teorema 1.18
4° 1 < 0 3°yiW4es absurdo
5o a"'>0, por2o y 4°
6o Sí a>0 => g"1 >0 Io y 5o
ii) Su demostración es en forma similar.
154
Eduardo Espinoza Ramos
3.21. TEOREMA.-
Para a,b e R, donde a y b tienen el mismo signo, sí a<b=> a'1 >b '
Demostración
Como a y b tienen el mismo signo entonces se tiene dos casos:
i) a>OAb>0 ii)a<OAb<0
i) Io a < b por hipótesis
2o a > 0 a b > 0 por hipótesis
3o <r'>0 a fc"'>0 2°, teorema 1.20
4o axTx <bxx~x 3°yl°;04
5o (a.<T' )b~l < (fc.a_1 )b'1 3o y 4o; 04
6o (axi~l )b~l < (bb"1 )a~l 5o y M2
Io 12>_1<1^_1 6°yM4
8o b'1 <a~l 7°yA/3
9o sí a<b => a~l >b~l Ioy 8o
i¡) Su demostración es en forma similar.
3.22. EJERCICIOS DESARROLLADOS.-
(J) Si a>b>0, Demostrar que: a2 >b2, dondea.be R.
Demostración
Por hipótesis se tiene a>b>0 => a>0 a b>0
Como a>b=>a + b>2b>0=>a + b>0 -..(a)
a>b => a-b>0 .-(P)
Sistema de S'úmeros Reales
155
de (a) y (B) se tiene: (a + b)(a - h) > 0.(a - b)
dedonde a2 -b2 >0 => a2 >b2 .-. Sía>b>0=> a2 >b2
Qt) Sía.b>0 y a2 >b2 =>a>b
Demostración
Por hipótesis se tiene a2 >b2 => a2 -b2 >0 dedonde (a + b)(a-b)>0 ... (a)
como a>0 a b>0 => a + b>0, dedonde >0 ••• (P)
a + b
de (a) y (B) se tiene > 0, de donde a - b > 0 entonces a > b.
a + b
(.3) Sib>a>0 yc>0. Demostrar: > —
^ 3 b+c b
Demostración
Como b>a>0 => a.b>0 ... (1)
b > a y o 0 => b.o a.c ... (2)
en (2) sumando a.b > 0 en ambos lados, a.b + b.c > a.b + a.c
a + c a
b.(a + c) > a.íb + c) , de donde: > —
b + c b
(4) Si a,b,c,d>0 y — >— Demostrar > —
v-/ b d b + d d
Demostración
Q C
Como — >—, dondeb,d>0 => a.d >b.c ••• (1)
b d
Además o 0, d > 0 entonces c.d > 0
Sumando c.d > 0, a ambos miembros en (1): a.d + c.d > b.c + c.d
156
Eduardo Espinoza Ramos
=>
a2 +b2 -2ai>>0
a2 +c2 -2o.c>0
b2+c2-2bjc>0
Q + C C
d.(a + c) > c.(b + d), de donde: > —
b + d d
\5j Para a,b,c números reales. Demostrar que a2 +b2 +c2 >ab + a.c + bx:
Demostración
V a.beR, (a-bf >0
Vo.ce/?, (a-c)2>0
Vfe.ce /?, (¿-c)2>0
2(o2 +b2 + c2)-2(a.b + a.c + b.c)>0
dedonde a2 +b2 +c2 >ab + a.c + b.c
\J¿J V a,b e R+, demostrar que >yjaJb
Solución
Como a,be R+ => 4a-S e R
Sí yfa-S 6 R => (yfa-Sf>0, dedonde a + b-2yfay¡b>0 => a + b>24ab
2
(7) Demostrar que sí a < b. Entonces o < < fe
Demostración
Como a<b=>a + a<a + b=>2a<a + b ... (1)
a<b=>a + b<b + b=>a + b<2b ... (2)
a + b
de (1) y (2) por transitividad se tiene: 2a < a + b < 2b :. a< < b
[SJ Demostrar que si, a2 +b2 = 1, c2 +d2 = 1, entonces: 1 > a.c + b.d. para a.b.c.d e R
Sistema de Súmeros Reales 157
Demostración
Va.ceR, (a-c)2 >0 => a2+c2>2a.c ...(1)
Vb.de R, (b-d)2 >0 => b2+d2>2b.d ...(2)
sumando (1) y (2) se tiene: o2 +fe2 +c2 + ¿/2 >2(ax: + b.d)
2 > 2(a.c + b.d) .-. 1 > a.c + b.d
(?) Va.b.cde R+ yne Z+ , demostrar que: a2n +b2" +c2n +d2n >4(abcd)nl2
Demostración
a.be R* => o",fe" e K+,pero a"-b" e R, entonces:
(a"-¿")2>0 => o2"+fe2">2a"fe" ...(1)
c.d e R+ => c",rf" e /?+, pero c" -d" e R, entonces:
(c"-d")2>0 => c2"+¿/2" >2c"í/" ...(2)
Sumando (1) y (2) se tiene: a2" +b2" +c2" +d2n >2{a"b" +c"d") ...(3)
(yfw-yf^d")2 >0 => anbn+cnd">2yjanbnc"dn ...(4)
o2" + fe2" + c2n + d2n > 4y¡a"bncnd"
.-. fl2" + ¿>2n +c2" +d2" >4(abcd)"'2
(lO) Si a + b + c = 1. donde a.b.c > 0. Demostrar que (1 - a)(l - b)(l - c) > 8abc
Demostración
Como a,b,c>0 => 4a.-Jb,-Jc >0 entonces:
158
Eduardo Espinoza Ramos
yfb-yfc e R
y¡a-y¡C £/?=>•
4a-4b e R
b + c>2-Jbc
a + c> 2yfac
a + b>2-Jab
(b + c)(a + c)(a + b) > 8abc
Pero sí a + b + c = 1
l-a=b+c
l-b = a + c
l-c+a+b
(1)
... (2)
Reemplazando (2) en (1) se tiene: (1 - a)( 1 - b)( 1 - c) > 8abc
(ll) Si a,b,c,d e /?+, Demostrar que: (ab + cd)(ac + bd) > 4abcd
Demostración
Como a,b,c,de R* => ab>0, cd>0, ac>0, bd>0
De donde -Jab - -Jcd e R, y 4ac - yfbd e R, entonces:
Uyfab-yfcdf>0
\(y¡ac-yfbd)2>0
multiplicando se tiene:
\ab + cd>2yjabcd
\ac + bd>2yjabcd
(ab + cd)(ac + bd) > 4abcd
, , „+ . a c , a a + c c
Sean a,b,c,d e R tal que — < — , demostrar que: — < < —
b d b b+d d
Demostración
ci c
Como < => a.d < b.c por que b,d e /?* a.d < b.c, sumando a.b, a ambos
b d
miembros ad + ab < be + ab, factorizando
a(b + d) < b(a + c), de donde
a a + c
b b + d
...(1)
En ad < be sumando cd, a ambos miembros ad + cd < be + cd,
Sistema de Números Reales
159
Factorizando d(a + c) < c(b + d), de donde:
a + c c
< —
b + d d
(2)
~ /lx ,-,, a a + c a + c c
De (1) y (2) se tiene: — < a < —
b b+d b+d d
De donde por transitividad se tiene: — < < —
b b + d d
\\ój Si a,b,c y d, son números reales cualesquiera. Demostrar que: a +b +c +d > 4abcd
Demostración
Como a.b,c.d e R => a2,b2,c2,d2 e R, además:
Uf-b'eR
\c2-d2eR
(a2-b2)2>0
(c2-rf2)2>0
4 . 1.4 ^o„2. 2
de donde al efectuar se tiene: a +b >2a b
c4+d4>2c2d2
... (1)
... (2)
Sumando (1) y (2) miembro a miembro se tiene:
a4 + b4 + c4 + d4 >2(a2b2 +c2d2)
... (3)
Como ab, cd e R => ab - cd e R, entonces: (ab-cd) >0 de donde
a2b2+c2d2 >2abcd => 2{a2b2 +c2d2)>4abcd
..(4)
de (3) y (4) por transitividad se tiene: a4 +b4 +c4 +d4 > 4abcd
Cl4) Si a > 0, a e R, demostrar que: a + — > 2
^-^ a
Demostración
Como a>0 => %/a>0, de donde Va—¿= e R por lo tanto
y/a
160
Eduardo Espinoza Ramos
(yfa —-¡=)2 -0 • desarrollando se tiene: a-2 + — > 0 de donde a + — > 2
y¡a a a
„+ j be ac ab ^ ,
Si a,b,c, e R , demostrar que: — + — + —>a+b+c
abe
Demostración
Por hipótesis se tiene que a.b.c > 0. entonces
— > 0, — > 0, — > 0 entonces aplicando el ejercicio 14).
b c c
r. • a b _ „ b c ^ „ a c „
Setiene: -+—>2, - + ->2, —+ —>2
b a c b c a
(1)
Ahora a (1) multiplicamos por c.a.b respectivamente.
ac be _
— + —>2c
b a
ab ac „ nac „bc „ab _
— + — >2a => 2— + 2— + 2—>2c + 2a + 2fe
c b b a c
ab be _,
— + —>2¿>
„,fcc ac ab, „,
2(— + — + —)>2(a + b + c)
abe
be ac ab
— + — + —>a+b+c
abe
a + b a b
Si a > 0, b > 0, demostrar que: < +
a+b+l b+l a+l
Demostración
Como a > 0, b > 0, entonces a + 1 > 1, b + 1 > 1 luego se tiene:
ía + l>l
¿> + l>l
a+b+l>b+l
a+b+l>a+l
ahora inviniendo cada una de las desigualdades: < y <
a + b + \ b + l a + b + l a + \
Sistema de Números Reales
161
multiplicando a las desigualdades por a y b respectivamente.
a ^ a b ^ b
< y <
a+b+\ b+l a+b+l a + l
Sumado estas dos desigualdades se tiene: < +
a+b+l b+l a+l
1 4
Si a,b g R, b ?t 0, demostrar que: — < —-
a2+ab + b2 3b2
Demostración
Completando cuadrado en a2 +ab + b2 setiene: a2 +ab + b2 =(a + — )2 +-— ... (1)
2 4
h h
Como a,b e R => a + — e R, de donde (a + —)2 > 0
2 2
J 3b2 . , b, 3b2 ^ 3b2
Sumando setiene: (a + —)'-t > ...(2)
4 2 4 4
Ahora de (1) y (2) se tiene.
h ré: fl in\7prtiinri« __
a2+ab + b2 3b2
2 3b2 14
a"+ab + b > como b*0 invertimos — -<
L , 1 t
Si a > 0 y b < 0, Demostrar que: < —
a a
Demostración
Como a > 0, b < 0 => ab < 0, sumando "a" a ambos miembros se tiene:
a + b.a < a, de donde a(b + 1) < a ... (1)
Como a > 0 => — > 0, ahora multiplicamos a (1) por —
a' a~
., „ a{b + \) a ,._ , b + l 1
Obteniéndose ■-<—^ simplificando .". —— < —
a2 a~ a a
162
Eduardo Espinoza Ramos
(Í9) Si a>0, b>0 tal que a + b=l, demostrar que: ab< —
Demostración
Como a > 0, b > 0 => a-be R, de donde:
(a-fe)2 >0 => a2-2ab + b2 >0 sumando4ab.
a2 +2ab + b2 >4ab dedonde: (a + b)2 >4ab
pero como a + b = 1, se tiene 1 > 4ab, por lo tanto ab< —
4
®Si a > 0, b > 0, 3a * 5b, demostrar que: — + — > 2
5b 3a
Demostración
Como 3a*5b => 3a-5b*0 y 3a-5be R entonces (3«—5¿>)2 >0
Desarrollando se tiene: 9a2 -30ab + 25b2 > 0
Sumando 30ab, a ambos miembros: 9a" + 25b2 > 30ab multiplicando por
I5ab
9a2+25b2 30ab ... 3a 5b
de donde: — + — > 2
I5ab \5ab 5b 3a
3.23. EJERCICIOS PROPUESTOS.
fl) Si a y b son números reales positivos, demostrar que: (— + — )(a + b)>4
^"^ a b
(2) Si a,b,c son números reales positivos, demostrar que: (— h 1- — )(a + b + c) >9
^■^ abe
(3) Si a,b,c,d son números reales positivos, demostrar que:
(- + - + - + -)(a + b + c + d)>\6
a b c d
Sistema de Números Reales
163
(4) Si a y b dos números reales positivos tal que a > b, demostrar que: — + — > ^r + 3
b a a-
(¿) V a e R, a ■*■ 0, demostrar que: a2 + — > 6
a~
(ó) Sia.b.ce R+ . demostrar que: (b + c)(a + c)(a + b) > 8abc
\7J Si a,b e R, demostrar que: a3b + ab3 <a4 + b4
(5) Si a,b,c e R, demostrar que: a2 +b2 + c2 + 3>2(a + b + c)
{9j Si 0 < a < 1, demostrar que a2 <a
(lO) Si a,b,c son números reales positivos y — < — < —. Demostrar que:
^^ abe
d d+e+f f
— < —< —
a a+b+c c
Ul) Demostrar que si a,b,c son números positivos y no iguales entre si, entonces:
(a + b + c)(a2 +b2 +c2)>9abc
(J2) Si a,b,c son números positivos y no iguales entre si. Demostrar que:
(a + b + c)(a~l +b~l +c"') >9
(l3\ Si a y b son números reales diferentes de cero. Demostrar que:
a2 16ír „_8o 32b
—- +—— + 24> — +
b2 a2 b a
(u) Si a2 + b2 =1. Demostrar que: -^2<a + b<^¡2
Sug. U-;y)2>0 => 2(x2+y2)>(x+y)2
(i?) Si a + b = c, a>0, b>0, demostrar que: a2'3 + b2'3 > c2'3
s~\ abe
U6) Si a + b > o 0, demostrar que: + >:
l + <7 l + b l+(
164
Eduardo Espinazo Ramos
(l7) Si a,b,c > O, demostrar que: 3abc <a3 +b3 +c3
®Si c> 0, d > 0, 2d * 3c, demostrar que: — > 1
3c Ad
(19) Si a > 0, b > 0, a * b, demostrar que: —= + —=>!
(20) Si a,b,c e R, demostrar que: b2c2 +c2a2 +a2b2 > abc(a + b + c)
[2u Sea a + b = 2. donde a y b son números reales, demostrar que: a4 + b4 > 2
Q.2) Si a2+b2+c2-l y x2 + y2 +z2 =1, demostrar que: ax + by + cz< 1
C23) Si a > 0, b >0, demostrar que: —+ -T> — + —
^-^ b2 a2 a b
uÁ\ Si 0<a<l, demostrar que: a2 <a
^5) Si a,b > 0, demostrar que: -Job > -
C26)
a + b
-3 . u3
Si a > 0, b > 0, demostrar que: > ( )3
2 2
Q.7J Si a > 0, a * 1, demostrar que: a3+ — >a2+ —
^^ a a~
(28) Sia>0 y b>0, demostrar que: 4(o3 + b3) > (a + b)3
Q9) Si a y b son números reales, demostrar que: yj(a + c)2 + (b + d)2 < Va2 + b2 + ve2 + d2
foo) Si a,b,c e R+ , demostrar que: (a + b + c)3 >27 abe
Si a.b.c y d son números reales cualesquiera. Demostrar (ab + cd)~ <(a +c )(b +d~)
Sistema de Números Reales
165
Si a,b e R. demostrar que: a4 + b4 >-{a + bf
© Si a >0 y b>0, demostrar que: (u + -f + (fr + -)2 >l((g + fc) +4)2
^■^ a b 2 a + b
(34) Si a>0, b>0 tal que a + b=l, demostrar que: (o + — )2 +(b + -)2 > —
^5) Si a,b.c,d e R, demostrar que: ac + bd<J(a2+b2)(c2+d2)
(36) Si a.b e R tal que a + b - 1, demostrar que: a4 + b4 > -
o
{y?) Si a.b e R tal que a + b = 3, demostrar que: a4 +b4 > —
38
8
Si a.b.c.de /?+, demostrar que: —(a + b + c + d)>4Jabcd
4
^S¡) Si ai,a2,...,an , £>,,£>2 ^n61^ tal 1ue: a2 +al+... + a2 =1 ,b2 +b2+... + b2 =1.
demostrar que: o,fe, +o2fe2 +... + anbn < 1
fao) Demostrar que si -l<a<0 entonces a3 >a
Un Si-a>Oy (a-b)2 > (a + b)2, entonces b >0
(42) Si a, b e R, tal que 2a +4b - 1, Demostrar que: a2 +b2> —
(43) Sia>0. b>0 => fl3+fe3 >a2fe + flfo2
-V, + JC, +A\ + ...+ X,
^4) Si xl,x2 -v„e R y si p = ^jxl.\2—x„ y a = — ———-. demostrar que:
P<a.
©a b c a b+a+c c
Si a,b.c.m,n.p e R / m > 0, n > 0. p > 0: — < —<— entonces: — < < —
m n p m m+n+p p
166
Eduardo Espinoza Ramos
®_ , a, +a-, +... + a„
Probar que si o, < a2 <... < an entonces a, < — = < an
®a3 -b3
Demostrar que si 0 < a < b < c entonces: < a + b + c
3c(b-a)
M8) Probar que: a4 +b* +c4 + d4 >4\abcd \ para a,b,c,d e R
wl9) Si a,b,c> 0, demostrar que: 2(a3 + b3 + c3) > bc(b + c) + ac(c + a) + ab(a + b)
Demostrar que: a~b~ +b~c~ +a c" >abc(a+b + c) V a,b,c e R
(51
x" 1
V x e R y n par, demostrar que: — < —
M x2n+l 2
©Demostrar que si r>0ya<b entonces a a < < b
\ + r
(53) Si a y b son números positivos y distintos, demostrar que: — + —r- > — + —
^^ b2 a2 a b
\S4j Consideremos x, y, z, w números reales, demostrar que:
2
x +y + z +w~ >—{xy + xz + xw+yz + yw+zw)
(55) Si a y b son números desiguales positivos demostrar que: a + b < h —
v~' b a
(Sé) Si a,b y c son números positivos distintos. Demostrar que: (a + b + c)" < 3(o " + b +c~)
Si a y b son números positivos distintos, demostrar que: (a +b )(a + b)>(a +b~)
\5S) Si x,y son números distintos, demostrar que: (x4 + y*)(x2 + v2) > (jc3 + y3)"
(59) Si x,y,z son números positivos distintos, demostrar que:
xy(x + y) + yz(y + z) + xz(x + z) > 6xy/
Sistema de Números Reales
167
(60) Demostrar que: a < b < 1 =* <
^ fl-1 b-\
(¡6l) Sean a,b,c,x,y,z números positivos distintos, demostrar que:
(a2 + b2 + c2)(x2 + y2 +z2) > (ax + by + czj2
_. 3 .3
(62) Demostrar que: 0<d<c =* >d2(c-d)
4 .3
(63) SíO<d<c => d3(c-d)< -<c2(c-d)
(64) Si x > 0 , y > 0, z > 0, demostrar que:
a) xyz =1 =* x + y + z > 3
b) xyz =lAX + y + z = 3 <=> x = y=z=l
(65) Demostrar que: x>0, y>0, z>0 =* —h— + —>3 (sug: = 1 y ejercicio 64)
v—' y z x y z x
(66m Demostrar para todo a y b real yfab < —= \]a2 +b2
(67) Si x e y e R, demuestre que: |x| + |y|> |x + y|
(68) Si xi,x2,—,x„ € /?+ tal que x,.jr2...j:n =1 . Entonces jc, +x2 +... + xn > 1
(69) Si a,b e R, demostrar que: (a+b)4 <8(a4+b4)
2 ,
m)) Si a>0. probar que: . >q + 1
Va2 + g
Si a,b,c e fl+ ,y si o~ +/T + c~ =8 , demostrar que: a~+b +c >16
1 1 -> ■>
Si a>0, b >0, demostrar que: (— + —)(a-+b-)>4
cr b
4
168
Eduardo Espinoza Ramos
(73) Demostrar que sí a,b,c nos números reales positivos entonces > yfabc
(74) SíVa,be R talque a>0 Ab>0 y a<x2<b => yfa < x<yfb v-Jb <x<->fa
(75) Si jc, , x2, -., xn e R, tal que xl.x2-—xn =1. Demostrar que jc, +jc2 +... + xn >n
(76) Si a,beR+, Demostrar que (o2 +b2)(a + b)2 >Sa2b2
111,1 1 l
a b c a~ b c
77J Si a + b + c = 0, Demostrar que: (— + — + -)' = — + — + —
78) Si o,¿e /?+ , Demostrar que —+ — ^
a' ir (g+¿)~
3.24. INECUACIONES,
3.24.1 DEFINICIÓN.- Una inecuación es una desigualdad en las que hay una o más
cantidades desconocidas (incógnita) y que sólo se verifica
para determinados valores de la incógnita o incógnitas.
Ejemplo.- La desigualdad: 2x + 1 > x + 5, es una inecuación por que tiene una
incógnita "x" que se verifica para valores mayores que 4.
3.24.2 INTERVALOS.- Los intervalos son sub-conjuntos de los números reales que
sirven para expresar la solución de las inecuaciones, estos
intervalos sé representan gráficamente en la recta numérica real.
Consideremos los siguientes tipos de intervalos:
a) Intervalo cerrado.- a < b
-E 3-
[a,b] = {xe R/a<x<b} a b
b) Intervalo abierto.- a < b
"*—^ ^P~
<a,b>= {xe R/a<x <b} SL b
Sistema de Números Reales
169
c) Intervalo cerrado en a y abierto en b.
[a,b>= {x€ R/a<x<b}
d) Intervalo abierto en a y cerrado en b.
<a,b] ={xe R/a<x<b}
e) Intervalo infinitos.-
-*
[a,+<*>> ={xe R / x > a]
-4-
>
<a,+<*>> = {xeR/x>a}
+—e-
<-<x,,b] = {x€ R/x<b}
<-oo,b> ={xg R/x<b}
<-oo,+o<» = { X/X G R }
-e-
b
<-<*>, a> u <a,+<*>> = [x g R / x ^ a}
Nota.- (7)
Sí x e [a,b] <=> a < x < b
-o
a
Ejemplo.- Demostrar que: sí x g [2,4] entonces 2x + 3 € [7,11]
Solución
x g [2,4] =* 2 < x < 4, multiplicando por 2
4 < 2x < 8, sumando 3
7 < 2x + 3 < 11
Sí7<2x + 3<11 => 2x + 3g[7,11]
Por lo tanto, sí x e [2,4] => 2x + 3g[7,11]
170
Eduardo Espinoza Ramos
©
Sí x e <a,b> <=> a < x < b
Ejemplo.- Demostrar que: Sí 2x-6e <-4,4> =* x e <1,5>
Solución
2x - 6 e <-4,4> =* -4 < 2x - 6 < 4. sumando 6
2 < 2x < 10 dividiendo entre 2
1 < x < 5 , entonces x e <1,5>
Por lo tanto, sí 2x-6e <-4,4> =* xe<1.5>
3.25. CONJUNTO SOLUCIÓN DE UNA INECUACION.-
Se llama conjunto solución de una inecuación a todos los números reales que la
verifiquen, es decir, que dichos números reales dan la desigualdad en el sentido prefijado.
3.26. RESOLUCIÓN DE UNA INECUACIÓN.
El resolver una inecuación consiste en hallar un conjunto solución: es decir, encontrar el
intervalo donde están los valores que puede lomar la incógnita para que verifique la
inecuación.
3.27. INECUACIÓN DE PRIMER GRADO EN UNA INCÓGNITA.
Las inecuaciones de primer grado en una incógnita, son de la forma:
ax + b>0 o ax + b<0 o ax + b > 0 o ax + b < 0, a * 0
Para resolver estas inecuaciones se debe considerar a > 0, es decir, sí a > 0, entonces:
b , b
X> O JC<
a a
Su representación gráfica es
—e
b_ x
a
/ \
-*• o
-e-
a
Sistema de Números Reales
171
Luego la solución es dado en la forma: xe <—,+°o> ó xe <-«>,— >
a a
Ejemplos.- Resolver las siguientes inecuaciones.
(T) 3x-4<x + 6
Solución
Las inecuaciones de primer grado en una incógnita, se resuelve, expresando la inecuación
en la forma:
En un sólo miembro se pone la incógnita, en el otro miembro los números, es decir:
3x - x < 6 + 4, simplificando se tiene: x < 5, es decir: x e <-<*>,5>
© * La solución es: x e <-°°,5>
5
(5) 3(x - 4) + 4x < 7x + 2
Solución
Poniendo en un sólo miembro la incógnita y en el otro miembro los números:
3x - 12 + 4x < 7x + 2 => 3x + 4x - 7x < 2 + 12 simplificando 0 < 14
esta desigualdad obtenida es cierta, entonces la solución de la inecuación dada , es el
conjunto de todos los números reales (x e R).
(5) 5x-4(x + 5)<x-24
Solución
En forma análoga a los ejemplos anteriores en un sólo miembro ponemos las incógnitas y
en el otro miembro los números: 5x - 4x - x < -24 + 20 simplificando 0 < - 4
Como la desigualdad obtenida no es conecta, entonces no hay ningún valor de x, que
verifique que la inecuación dada. Por lo tanto la solución es el vacío (<|>).
(4) 2 < 5 -3x < 11
Solución
Aplicando la propiedad de transitividad: a < b < c <=> a < b a b < c
172
Eduardo Espinosa Ramos
2 < 5 - 3x < 11 <=> 2<5-3xa5-3x<11
<=> 3x<5-2a5-11<3x
<=> x< 1 a-2<x "*
e-
La solución es: xe<-2,l]
3.28. INECUACIÓN DE SEGUNDO GRADO EN UNA INCOGNITA.-
Las inecuaciones de segundo grado en una incógnita son de la forma:
ca■ +bx + c>0 ó ax +bx+c<0, a*0
donde a,b,c e R, siendo a * 0, la solución de estas inecuaciones, se obtiene mediante las
propiedades de los números reales o también por medio de la naturaleza de las raíces del
trinomio ax2 +bx + c = 0.
a) CARÁCTER DE LAS RAICES DEL TRINOMIO DE SEGUNDO GRADO.
Consideremos el trinomio de segundo grado
ax2 +bx+c~0, con a>0 ...(1)
al analizar el valor numérico de la ecuación (1) dando valores reales a x se presentan
tres casos:
1" Caso.- Si A = b~ —Aac > 0, entonces hay dos valores reales diferentes r, < r2
que anulan al trinomio ax +bx + c = 0.
Es decir: a(x- r, )(x- r2) = 0 , si se hace variar x a lo largo de la recta real resulta:
i) Cuando x toma valores menores que r,, los factores (.r-r,) y (x — r2) son
negativos, luego el trinomio ax2 +bx + c, tiene el mismo signo del coeficiente
de "a".
ii) Cupndo x toma valores intermedio entre r, y r2; entonces el factor (a —r,) es
positivo y el factor (x - r2) es nega
signo opuesto del coeficiente de "a"
positivo y el factor (x-r2) es negativo, luego el trinomio ax +bx + c , tiene
Sistema de Números Reales
173
iii) Cuando x toma valores mayores que r2, entonces los factores {.x — r,),
(x—r2) son positivos, luego el trinomio ax2 +bx + c, tiene el mismo signo
del coeficiente de "a".
2° Caso.- Si A = b -4ac = 0, entonces hay un sólo valor real rl—r2=r, que
anulan el trinomio ax~ +bx + c , luego como (x — r) es positivo, el
signo del trinomio ax" +bx + c es el mismo del coeficiente de "a".
3o Caso.- Si A = b~ -4ac<0, entonces se tiene dos valores no reales
rl=a + fii y r2 -a-fii que anulan el trinomio ax' +bx + c , y para
cualquier valor de x, el trinomio: ax" +bx + c tiene el mismo signo del
coeficiente de "'a".
NOTA.-
Sí ax" +bx + c — 0 entonces x = -
>±^
4ac
2a
b) RESOLUCIÓN DE UNA INECUACIÓN DE SEGUNDO GRADO.-
Para resolver una inecuación cuadrática de las formas ax2 +bx + c>0 ó
ax2 +bx: + c < 0, donde a,b,c e R, a # 0, por medio de la naturaleza de las raíces
primero se resuelve la ecuación ax" +hx+c = 0, y de acuerdo a la naturaleza de las
raíces se presenta tres casos:
1° Caso.- Si la ecuación ax2 +bx+c = 0, tiene dos raíces reales diferentes
r, < r7 .
-3-
-g-
i) Si la inecuación es de la forma ax2 +bx + c> 0, con a > 0, la solución es todos
los valores de x que pertenecen al intervalo < —°o, r, > U < r2,+°° >
ii) Si la inecuación es de ¡a forma ax2 +bx + c<0 con a > 0, la solución es todos
lo valores de x que pertenece al intervalo < rt. r2 >.
174
Eduardo Espinoza Ramos
2° Caso.- Si la ecuación ax +bx + c = 0, tiene una raíz real única r, =r-, =r.
+
-+-
i) Si la inecuación es de la forma: ax2 + bx + o 0. con a > 0.
La solución es todos los valores de x * r, es decir: x e <-<*>,r> U <r,+°°>
ii) Si la inecuación es de la forma: ax2 + bx + c < 0, con a > 0.
No se verifica para ningún valor real de x; la solución es el <|>
3o Caso.- Si la ecuación ax~ +bx + c = 0, tiene dos raíces no reales.
i) Si la inecuación es de la forma: ax + bx + o 0, con a > 0.
La solución es todos los valores reales de x.
ii) Si la inecuación es de la forma: ax" + bx + c < 0 , con a > 0.
No se verifica para ningún valor real de x; la solución es el <(>
RESUMIENDO EN EL SIGUIENTE CUADRO.
Forma de la Inecuación
ax2 +bx + c>0, a>0
ax2 +bx + c<0, a>0
Raíces de la Ecuación
ax' +bx + c = 0
Raíces diferentes
r, <r2
Raíz Real Única r
Raíces no reales
Raíces diferentes
r, <r2
Raíz Real Única
Raíces no reales
Conjunto Solución
< -oo, r, >U <r2,+°° >
R-{r]
R
<r],r2>
■e-
0
Sistema de Números Reales
175
©
©
Ejemplos.- Resolver las siguientes inecuaciones.
2.v2-x-10>0
Solución
Resolveremos la inecuación usando propiedades de los números reales:
a.b>0 <=> (a>0Ab>0)v(a<0Ab<0)
2jr-Jt-10>0 => (x + 2)(2x-5)>0
(x + 2)(2x - 5) > 0 <=> (x + 2 > 0 a 2x - 5 > 0) v (x + 2 < 0 a 2x - 5 < 0)
<=> (x > -2 a x > 5/2) v (x < -2 a x < 5/2)
O—
-O
-e-
o-
-e—
-2
-o
o >
2
La solución es: xe <—«>,-2 >U < — ,-h» >
Otra forma de resolver esta inecuación, es por la naturaleza de sus raíces de la ecuación
■> 5 i
1x" —a —10 = 0, de donde r,=-2, r2= — , luego rí<r2 y como 2x~ -a-10>0,
de acuerdo al cuadro la solución es:
xe <-oo,— 2>U <— .+oo >
2
a^+8a-65<0
-©-
H&-
5_
2
Solución
Usando propiedades de los números reales.
a2 <b,b>0 <=> -yfb<a<Jb
completando cuadrados en x ~ + 8a — 65 < O, se tiene:
176
Eduardo Espinoza Ramos
x~ +8jc + 16< 65 + 16 => (x + 4)' < 81, aplicando la propiedad
U + 4)2<81 <=> -JÍ\<x + 4<Js\
<=> -9<x + 4<9 <=> -13<x<5
La solución es x e <-13,5>
Ahora resolveremos la inecuación por medio de la naturaleza de las raíces de
x' + 8jc -65 = 0, es decir: (x + 13)(x-5) = 0 de donde r, =-13, r2=5
-e e—►
-13 5
de acuerdo al cuadro es: xe<-13,5>
(5) a2+20* +100 >0
Solución
Mediante propiedad de los números reales se tiene:
jr+20.v + 100>0 => U + 10)2>0 entonces:
Vxg R; x?t-10, (jc + 10)"" >0, por lo tanto la solución es; xe R-{-10}
Ahora veremos de acuerdo a la naturaleza de las raíces: x~ +20jc + 100 = 0=> r = -10,
multiplicidad 2, y como x2 + 20jc +100 > 0, de acuerdo al cuadro de solución es:
(í) x2+-x + — <0
v-/ 5 100
xg R-{-10}
3 9
-<U
)
Solución
Aplicando la propiedad de los números reales: VxeR. jc~>0
t 3 9 3 -, 3 2
lueeo x~+—x + <0 => (x + —)*<0 pero (_v + —) >0, entonces no existe
5 100 10 10
ningún valor real para x que verifique a la inecuación, es decir: (¡>.
Sistema de Números Reales
177
7 3 9
Ahora resolvemos mediante la naturaleza de las raíces de la ecuación x +—x + 0,
5 100
3 -,3 9
de donde r = de multiplicidad dos, pero se tiene que x~+ — x + <0 y de
10 5 100
acuerdo al cuadro la solución es: (¡>.
3.29. INECUACIONES POLINOMICAS.
Una inecuación polinómica en una incógnita, es de la forma siguiente:
P{x) = anxn +... + aix + a0>0 ó P{x) = anx" +... + «,x+a0 <0
donde a0,ai,...,an son constantes y an *0, neZ+
a) RESOLUCIÓN DE UNA INECUACIÓN POLINÓMICAS.-
Una inecuación polinómicas de la forma P(x) > 0 o P(x) < 0, se resuelve de acuerdo
a la naturaleza de sus raíces de la ecuación polinómica P(x) = 0, en una forma
sencilla y rápida, considerando an > 0.
Para esto hallaremos primero las raíces del polinomio
P(x) = anx" +... + alx + a0 =0, y como éste polinomio es de grado n entonces tiene
n raíces, los cuáles pueden ser reales diferentes, reales de multiplicidad y no reales.
Io CASO.- Cuando las raíces de la ecuación polinómica p(x) = 0, son reales
diferentes. Es decir: r, < r2 < ... < rn_} < rn
a) En los intervalos consecutivos determinados por las raíces del polinomio
P(x) = 0, se alternan los signos "+" y "-" empezando por asignar el signo (+)
al intervalo < r , °° >.
v i \ i \ i \ i ;-
+ \/ - x/ + V I \L ±_
XXX X
'n-3 'n-2 'n-1 'n
178
Eduardo Espinoza Ramos
©
b) Si la inecuación polinómica es de la forma: P(x) = anx" +... + alx + a0 >0,
an > 0; al conjunto solución será la unión de los intervalos a los cuales se le
ha asignado el signo "+".
c) Si la inecuación polinómica es de la forma: P(x) = anx" + ... + atx + a0 <0,
an > 0; el conjunto solución, será la unión de los intervalos a los cuales se le
ha asignado el signo "-".
NOTA.- Explicar el método de Ruffini
Ejemplo: Resolver las inecuaciones siguientes:
x5 +3*4 -5x3 -15jc2 +4jc + 12 >0
Solución
Expresamos el Io miembro de la inecuación en forma factorizada
(x + 3)(x + 2)(x- l)(x + l)(x-2) = 0
Luego las raíces son:
r, = -3 , r2=-2, r3=-l,
r4 = 1, r5 = 2
1 3
1
1 4
2
1 6
-1
1 5
-2
1 3
-3
1 0
-5
4
-1
12
11
-5
6
-6
0
-15
-1
-16
22
6
-6
0
4
-16
-12
12
0
12
-12
0
1
2
-1
-2
-3
-3 -2-11 2
Como P(x) > 0, la solución es la unión de los intervalos donde aparecen el signo (+).
Es decir: x e <-3,-2> U <-l,l> U <2,+°o>
Sistema de Números Reales
179
(2) 2*3-3*2-1Ly + 6<0
Solución
Hallaremos las raíces de la ecuación 2jc3 - 3jc2 -1 l.v + 6 = 0
2
2
2
-3
-4
-7
6
-1
1
-11
14
3
-3
0
6
-6
0
-2
3
V2
2 0
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos
donde aparecen el signo (-). Es decir: xe <-°°,-2>E/ <— ,3>
2° CASO.- Si algunas de las raíces del polinomio P(x) = 0 son reales de
multiplicidad de orden mayor que 1 se tiene:
a) Cuando el orden de la multiplicidad de una de las raíces del polinomio P(x) - 0
es par, en este caso a la raíz no se considera para la determinación de los
intervalos y para dar la solución se sigue el mismo proceso del Io caso.
b) Cuando el orden de la multiplicidad de una de las raíces del polinomio
P(x) = 0, es impar, en este caso a la raíz se considera para la determinación de
los intervalos y para dar la solución se sigue el mismo proceso del 1 ° caso.
Ejemplo.- Resolver las inecuaciones siguientes.
(T) (x-l)2(x+2)(x + 4)>0
Solución
Resolviendo la ecuación (jc-1)2(jc + 2)(jc + 4) = 0, de donde rx =-4, r2=-2, y
r3 = 1, de multiplicidad 2.
Luego las raíces del polinomio son:
/-, =-2, r2=-, r3=3
\ r~ v 1 \ 1—--"
: v ± j¿ v + »
-2 1/2 3
180
Eduardo Espinoza Ramos
-—v i \ /
-± tf : X-
-4 -2 1
Como la inecuación es de la forma P(x) > 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir: x e <-oo,-4> U <-2.+°°> - {1}
(2) (2jc + 1)(3x-2)3(2jc-5)<0
Solución
l 2
Resolviendo la ecuación (2jc + 1)(3jc-2)1(2jc-5) = 0, de donde r, - —, r2=— de
multiplicidad 3, r3 = — \/~ + \ \ +
-1/2 2/3 5/2
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos
1 2 5
donde aparecen el signo(-). Es decir: xe <-°°,— >(/<—,— >
3o CASO.- Cuando alguna de las raíces del polinomio P(x) = 0 no son reales, en
este caso a estas raíces no se consideran en la determinación de los
intervalos y para dar la solución se sigue el mismo procedimiento de los
casos anteriores.
Ejemplo.- Resolver las siguientes inecuaciones.
(T) (jr-7)(*2+i6)Or-i6)or+i)<0
Solución
Resolviendo la ecuación: (x2 -7)(jc2 + 16)(jc2 - 16)(.v2 +1) - 0, de donde
r, = -4 , r2 - -yjl , r3 = -Jl , r4 = 4 . r5 = -4/ , rb - 4/ , r7 = 1 , rH = -í
_ / N n —N / N r
+ \i - m + m : \l ± w
-4 -\fT \TF 4
Como la inecuación es de la forma P(x) < 0, la solución es de la unión de los intervalos
donde aparecen el signo (-), es decir: x e < —4,—J7 > U < v7,4>
Sistema de Números Reales
181
©
(l + x + x2)(2-x-x2)>0
Solución
La inecuación la expresaremos así: (x2 + x + l)(x2 + x- 2) < 0
ahora resolviendo la ecuación (jc +x + l)(x2 +x—2) = 0 de donde: /-,=-2, r2=''
-1 + >/3i -l->/3/
r, = , r.
\ /
+ ^
'^ZL
-2 1
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos
donde aparecen el signo (-), es decir: x e [-2,1]
3.30. INECUACIONES FRACCIONAR1AS.-
Una inecuación fraccionaria en una incógnita es de la forma:
PW>0 ó ^<0, Q(x)*0
Q(x)
Q(x)
donde P(x) y Q(x) son monomios o polinomios diferente de cero.
Para resolver una inecuación fraccionaria debe tenerse en cuenta que las inecuaciones:
P(x) P(x)
> 0 o < 0, son equivalentes a las inecuaciones
Q(x) Q(x)
P(x).Q(x) > 0 ó P(x).Q(x) < 0 es decir: Sí Q(x) * 0 =* Q2(x) > 0 , de donde se tiene:
Sí ^1>0 => P(x)-Q {x)>0.Q2(x) => P(x).Q(x)>0
CU) CW
©
Sí ^><0
Q(x)
P(x).Q¿(*)^n„2
CW
<0.Q¿(x) => P(x).Q(x)<0
Ejemplo.- Resolver las inecuaciones siguientes:
(jc2-1)(* + 3)(j;-2)
(*-5)(* + 7)
>0
182
Eduardo Espinoza Ramos
©
Solución
. . ., (*2-1)(.í + 3)(jc-2) .
La inecuación > 0, es equivalente a la siguiente inecuación.
(x-5)(.v + 7)
(jr2-l)(jt + 3)(Jt-2)(jc-5)(.r + 7)>0, para x *-7,5
ahora hallaremos las raíces de la ecuación (jc2 -1)(x + 3)(x- 2)(x -5)(x + 7) = 0.
De donde r¡ = — 7, r2 = -3, r3 = -1, r4 = 1, r5 = 2 , r6 = 5, que son reales diferentes.
\ / \ / \ / \ / \ / \ /
± y : y ± s¿ : ^ ± v : v ±
-7-3-1125
P(x)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
donde aparecen el signo (+) es decir: x e <-oo,-7> U <-3,-1 > U < 1,2> U <5,+«»
jc-2 x+l
<
x + 3 x
Solución
La inecuación dada se expresa en la forma, mayor que cero o menor que cero, es decir:
x-2 x+\ x(x-2)-(x + \)(x + 3)
<0 => <0, dedonde:
x + 3 x jc(jc + 3)
-6jc-3 _ 2jc + 1 n . ,
< 0 => > 0, que es equivalente a:
x(x + 3) jrU + 3)
(2x + l)(x + 3)x > 0, para x ^ -3,0 ahora encontramos las raíces de la ecuación.
(2x+l)(x + 3)x = 0, dedonde r,=-3, r2 = —, r3=0
\ i \ i \ i
^ M + <J - V + fc
-3 -1/2 0
Como la inecuación es de la forma: (2x + l)(x + 3)x > 0,
Sistema de Números Reales
183
®
la solución es la unión de los intervalos donde aparecen el signo (+), es decir:
xe <-3,—>t/<0,+<»>
2
x x-l 2x
- + <■
.V — 1 X X + \
Solución
x x — 1 2x
La inecuación dada expresaremos en la forma: + < 0
JC-1 X X+l
x-(x + l) + (x- l)(x - 1)(jc +1) - 2 x2 (x: -1)
(x-\)x(x + \)
< 0, simplificando
2x--jt + l
(*-!)*(* +1)
< 0, que es equivalente a la inecuación.
(2x2 -x + l)(x-l)x(x + l)<0. para x*-l,0,l
ahora encontramos las raíces de (2x -x + l)(x-l)x(x + l) = 0, de donde sus raíces son:
i n i 1 + yfi' l-^1
/■,=-!, r2=0, r3=l, r4 =—-—, r5 =—-—
\/ + v
\rT
-1
P(x)
Como la inecuación es de la forma < 0, la solución es la unión de los intervalos
Q(x)
donde aparecen el signo (-), es decir: x e <-«>,-1> U <0, 1>
3.31. INECUACIONES EXPONENCIALES.-
Las inecuaciones exponenciales en una incógnita son de la forma:
C/U)>flgu) v <,/»*><<,««*)
184
Eduardo Espinoza Ramos
donde f(x) y g(x) son expresiones enx,aefi+,a#l.
Para resolver estas inecuaciones, se consideran dos casos:
1" CASO.- Si a > 1, entonces los exponentes de la inecuación dada son desiguales en el
mismo sentido prefijado, es decir:
Si
Si
afM
a"*
>ag{x)
<agM
<=>
<=>
f(x)
f(x)
>g(x)
<g(x)
2o CASO.- Si 0 < a < 1, entonces los exponentes de la inecuación dada son desiguales en
sentido contrario al prefijado, es decir:
Si afM >as(x) <¿> f(x)<g(x)
Si a}M <ag{x) <=» f(x)>g(x)
Ejemplos.- Resolver las siguientes inecuaciones:
Q 3/3(5-v+D/3 < ^JgX^U/5
Solución
5a+1 3( t+1) 5-r+l 6jt+6
La inecuación dada es equivalente a: 3 9 < 9 10 =* 39<3'°
5jc +1 6x + 6
como a = 3 > 1 entonces < —■—-
9 10
50jc + 10<54jc + 54 => -44<4,v => x>-ll => xe<-ll,+°°>
.•. La solución es: x e <-l l,+°o>
® [(0>2)(v+1)(,-2,]i>(0^8)^
8
Solución
La inecuación dada se puede escribir en la forma:
(*+'X*-2) nnl9n U4QU-2)
(0,2) *"3 > UAJ1_£» 3jr-l dedonde. (f)2j c-3 >(0,2)12A-4,
8
Sistema de Números Reales
185
comoa = 0.2< l,se tiene: U + 1)U-2)<12-4 =» (jr+IXjf-2)-l2x + 4<0
jc-3 x-3
IIjc2 -39a: + 14
efectuando operaciones y simplificando tenemos: > 0, esta inecuación es
x-3
equivalente a: (IIjc2 -39.r + 14)(jt-3)>0 para x* 3.
Ahora hallando las raíces de : (11 x 2 - 39* +14)(.v - 3) = 0, de donde:
39->/905 , 39 + >/905
r. = , r-, = 3 , r, =
1 22 3 22
\ /—~—v / v /—-~
v + V - v + »
39-V905 3 39+\/905
22 22
P(x)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
Q{x)
a a ■ • , x a ■ 39->/905 , _. 39 + >/905
donde aparece el signo (+) es decir: x e < , 3 > U < , +°° >
3.32. INECUACIONES IRRACIONALES.-
Las inecuaciones irracionales en una incógnita son de la forma:
F(x.JP2(x),fáOQ ^PB(*))>0 ó FUy¡P2(x),^ix~) ^P„U))<0
donde P2 (jc), Pi (x),..., Pn (x) son monomios o polinomios diferentes de cero.
Para que la solución de la inecuación sea válida debe resolverse antes lá condición
J^(jc)>0, i = 2,3,---.n en las expresiones con una radical par. cuyo conjunto solución
constituirá el universo o dentro del cuál se resuelve la inecuación dada. Debe observarse
que yjP(x), quiere decir, (+-Jp(x)) y si se desea la raíz negativa se escribirá
expresamente como (-y¡P(x)); es decir:
ü) Jñ.
186
Eduardo Espinoza Ramos
para resolver las inecuaciones radicales se debe tener en cuenta las siguientes
propiedades:
(l) 0<x<y <=> 0<y¡x<yjy Q) 0<x<y <=> 0<yjx<yfy
(D 0<x<y <=> 0<Jx<Jy
{4j i) Si n es un entero positivo par.
a,) V P(x)>0 .-. !¡jP(x) >0 <=> P(x)>0
a2) ¡lJP(x) = 0 <=> P(x) = 0
<J3) <^U) <^Q(x) <=> 0<P(x)<Q(x)
ii) Si n es entero positivo impar.
bx) !¡¡P{x)>0 <=> P(x)>0
b2) !¡jP(.x) <0 » P(x)<0
*3) #WS^GW <=> P(x)<Q(x)
Las propiedades fc,), fe2 ) indican que y]P(x) tienen el mismo signo que P(x) si n es
impar.
OBSERVACIÓN.- Cuando en una expresión existen k radicales par entonces se
calculan los universos relativos Í71,Í72,...,Í7k para cada radical
y el universo general será U = Í7, ní/2 f^...r\Uk .
Daremos algunos ejemplos de ilustración de estas propiedades, para después estudiar las
diversas formas de inecuaciones irracionales.
Ejemplos.- Resolver las siguientes inecuaciones
® ^[x~+5>-2
Sistema de Números Reales
187
Solución
Como Vjc + 5 > -2 es válida para todo x tal que xeU: x + 5 > 0 => x > -5
=> U = [-5,+°°>, luego el conjunto solución es [-5,+°°>
0 Vjc + 7>0
Solución
Como Vjr + 7 > 0 entonces el conjunto universal es x + 7 > 0 => x > -7 => U = [-7,+°°>
Además -Jx + 7 > 0 « x + 7>0 => xe <-7,+°°>.
Luego el conjunto solución es x e [-7,+<*>> A <-7,+°°> .•. x e <-7,+°°>
0 a/jc^^O
Solución
Como *Jx—5 < 0, el conjunto universal es x - 5 > 0 => x > 5 => U = [5,+°°> y como
0< -Jx-5 <0»-\/jc-5 =0 => x-5=0=> x = 5 e U, luego el conjunto solución es {5}.
0 >/7:8<0
Solución
Como -8 < 0 es absurdo entonces la solución es <¡>.
0 yfx~+9>0
Solución
Como -n/jc + 9 > 0 es verdadero V xeU: x + 9 > 0 es decir U = [-9,+°°>, luego el
conjunto solución es x e [-9,+°°>.
0 n/8-2jc<VÍ3
Solución
El conjunto universal es 8 - 2x > 0 => x < 4 de donde U = <-°°,4].
1 ;— 5 5
V8-2jc<v13 » 8 - 2x < 13 => jc>— de donde Jte[—,+°°>. Luego el
2 2
conjunto solución es: U n[—,-k» >= [—,4]
188
Eduardo Espinoza Ramos
© yfx^3 + yf4^c>-3
Solución
Calculando los universos relativos.
(/,: x + 3 > 0 => x > -3 => xe [-3,+°°>
í/2:4-x>0=>x<4 => x e <-°°,4]
í/ = {/,n(/2= [-3,+oo > n < -°°,4] = [-3,4]
como la suma de dos positivos es siempre mayor que un negativo.
Jx + 3 + ^4-x>-3 es valido V xe U = [-3,4].
(s) yfx~^7>3
Solución
Sea U: x - 7 > 0 => x > 7 =>xe [7,+°°>
■Jx-7 >3 <=> x - 7 > 9 => x > 16 =>xe <16,+°o>
el conjunto solución es x e U n <16,+°°> = <16,+°°>
0 -y¡x~^5>0
Solución
-yfx — 5 > 0 <=> yJx — 5 < 0 el conjunto solución es <¡>.
(lO) Vjc2-jc-12<Vjc2-6jc + 5
Solución
Calculando los universos relativos.
i/, : x2-jt-12>0 => (x-4)(x + 3)>0 \/ w
± V. I tf_
í/, =< -°°,-3] C/ [4,+°° >
ÍA : jc"-6jc + 5>0 => (x-5)(x-l)>0 \/ w
+ v i¿_
[/ =<-oo,l] (/ [5,+°o>
Sistema de Números Reales
189
U=UlnU2 = <-oo-3] U [5,+«=>
\/jc2-jc-12<>/jc2-6jc + 5 » jc2-jc-12<jc2-6jc + 5
de donde 5x<17 => jc<— => ae< -»,—1
5 5
Luego el conjunto solución es: jce [/ a <—«»,—]=<—«»,—3]
%/jc2-4(jc- 2)2(jc3-13jc + 12) >
(jc + 4)3 ( jc3 + 8jc2 + 4jc - 48)
Solución
Como vjc2-4 tiene el mismo signo que jc2—4 y (jc + 4)3 tiene el mismo signo que
x + 4 entonces la inecuación dada es equivalente.
37jc2-4(x-2)2(jc3-13x + 12)^() ^ (jc2 -4)(jc-2)2(jc3 -13jc + 12) >q
(jc + 4)3(jc3+8jc2+4jc-48) ~ (jc + 4)Crl + 8jc2 + 4jc - 48)
Como V x e R, (jc-2)2 >0 entonces
(x2 -4)(x-2)V -13X + 12) ^0 ^ (x2-4){x3 -13x+12) ^Q
(jc + 4)(jc3 + 8jc2 + 4jc - 48) (jc + 4)(jc3 + 8jc2 + 4jc - 48)
U+2)(,-2)(,-l)U2+,-12)^0 2> ,4
(jc + 4)( jc - 2)(jc + 6)( jc + 4)
U + 2)(x-l)U-3)
(,Y+6)(JC + 4)
> 0, para x * 2, - 4
\ / \ / \ / \ / \ r~-
M + M - M + M - )L ±_
-6 -4-2 1 3
Luego el conjunto solución es: x e <-6,-4> u [-2,1] u f3,+°°>
190
Eduardo Espinoza Ramos
^/jc + 7U + 2)4(jc + 3)^"-7a + 12 ^IO-jc
^jc + 9(jc-8)3(jc3-27)(jc2-14x + 48)
Solución
Los radicales pares nos da el universo U. 10-x>0 A x + 9>0 => x < 10 A x >-9
X e <-9,10] => U = <-9,10] (no se incluye el -9 por que anula al denominador)
como los radicales pares son positivos la inecuación es equivalente a:
#¡^7^+2)4(jc + 3)^jc2-7a + 12 47Í(P7 ffc+7(jt + 2)4(s+3)&t2-7jc + 12
ty!x + 9(jt-8)3U3 -27)(jc2 -14jc + 48) ~ (jc-8)3(jc3-27)(jc2-14jc+48)
como los radicales impares tienen el mismo signo que las cantidades subradicales
entonces:
(*+7)(* + 2)4(Jt+3)(jr-7jc+12) ^n „ , _.4 ^n
— ■ , '-± —<0, como para todo x e R (jc + 2)* >0
( jc - 8)3 ( jc - 3)( jc2 + 3jc + 9)( jr - 6)( jc - 8)
U+7)(jc + 3)(jc-3)(a:-4) ^. _ „ . ,.„ _,
< 0, para x * 3, 8 simplificando tenemos
(jc-8)3(x-3)(jc-6)(jc-8)
_ / v r--~\ i \ r---
(> + 7)U + 3)U-4) i^-a -—* ¿-^ : * ±
— <0, x*3,8 -7-3 4 6
x e [-7,-3] u [4,6> luego el conjunto solución es: x e U n ([-7,-3] u [4,6>)
.-. xe[-7,-3]u[4,6>u|-2)
ahora veremos como resolver diversas formas de la inecuación con radicales aplicando
criterios de acuerdo a cada tipo de inecuación irracional.
Io Para las inecuaciones irracionales de las formas:
a) -Jp(x) > Q(x). La solución se obtiene así:
4PM>Qíx)<^ (P(x)>0 A [0U)<O V (/>(*)>0 A P(x)>Q2(x))])
Sistema de Números Reales
191
b) yJP(x) ^ Q(x); la solución se obtiene así:
y]P(x) > Q(x) <=> [P(x) > 0 A (Q(jc) < 0 V [P(jc) > 0 A P(x) > Q2(x)])]
2° Para las inecuaciones irracionales de las formas:
a) y]P(x) < Q(x); la solución se obtiene así:
^/PÜ) < Q{x) <=> [(/>(*) > 0 A (C(JC) > 0 A P{x) < Q 2 (*))]
b) ^P(x) < Q(x); la solución se obtiene así:
yfpjx) < Q{x) » />(*) > 0 A [Q(x) > 0 A />(*) < 02 W]
3o Para las inecuaciones irracionales de la forma:
a) t]P(x) + yJQ(x) > 0 ; La solución se obtiene así:
JP(x)+jQ(x)>0 => (P(x)>0 A Q(x)>0) V (P(x)>0 A Q(x)>0)
b) \]P(x) + yJQ(x) > 0; La solución se obtiene así:
VpÜ)+VgÜ)>0 => P(x)>0 AQ(x)>0
4o Para la inecuación irracional de la forma:
^P(x) + y¡Q(x) > K , K > 0; La solución se obtiene así:
^/PÜ)+^/GÜ)>^ => [{P(x)>0aQ{x)>0)aP{x)>(Ic-JQ(x])2]
5° Para las inecuaciones irracionales de la forma:
tJP(x) + -jQ(x) < 0; La solución se obtiene así:
JP(xj + jQ(x~)<0 => P(x) = 0 A Q(x) = 0
OBSERVACIÓN.-
Consideremos otros casos más generales.
192
Eduardo Espinoza Ramos
Io Caso.- Si n es impar positivo mayor que uno.
rwq/5w>0 ^ P(x).Q(X)>Q
R(x) R(x)
b) ™<0 « -™-<0
c) ^/PÜ)<^/GW ** P(x)< Q(x)
2o Caso.- Si n es par positivo
a) ¡¡}P(x)Q(x) > 0 <=> P(x) >0 A Q(x)>0
b) ¡t¡P(x)Q{x) < 0 <=> P(x) >0 A Q(x)<0
c) , PU) >0 <=> Q(x)>0 A -^>0
!¡jQ(x)R(x) R(x)
d) r-^f) <0 <=> Q(x)>0 A ^<0
qQ(x)R(x) R{x)
e) ^P(jc) > G(jc) <=> (P(jc) > 0 A [£>(*) < 0 V (Q{x) > 0 A />(*) > £>" (*))]
f) ^/P(I) < G(a:) <=> />(*) > 0 A [0(jc) > 0) A P(x) < Q" (x)]
Ejemplo.- Resolver las siguientes inecuaciones
(T) Vjc2-14jc + 13>jc-3
Solución
Vx2-14x + 13>jc-3 <=> x2-14jc + 13>0 A [jc-3<0 V
(x2-14jc+13>0 A jc2-14jc + 13>(jc-3)2)]
<=> jc2-14jc + 13>0 a[.v<3 v (jc2 -14* +13 >0 a jc<-)]
Sistema de Números Reales
193
9 1
<=> jc2-14a + 13>0 a[jc<3 v .ve<-«.,l] U[13,oo> ajc<-]
2
«=> x2-14jc + 13>0 a[jc<3 v jc< —1
2
<=> jc2-14x + 13>0 A jc<3
<=> (x-13)(x-l)>0 A xS3
<=> x€ <-°°,l]u[13,+°°> A x<3 .-. x e <-°°,l]
@ ylx2-\4x + l3<x + l
Solución
Aplicando la parte b) del Io caso:
>/jr-14x + 13<jc + l<=>(jc2-14jc + 13>0 A [jc + 1>0) A (jc2 -14x + 13<(jc + 1)21)
<=> ((x-13)U-l)>0 A[x>-1) A ((jc-13)U-1)<(jc + 1)2])
3
<=> ((jc-13)(jc-1)>0 a [jc>-1) ajc>-]
4
3
<=> x e <-l,l] u[l3,+oo> Ajc> —]
4
3
«=> Jte<-,1] u[13,+°o>
4
® &&
Solución
Aplicando la parte b), del 3o caso: y]P(x) + y¡Q(x)>0 <=> P(x)>0 A Q(x)>0
194
Eduardo Espinoza Ramos
<=> (x - 4)(x - 1) > O, x * 1 A (5 - x)(x + 3) > O, x * 3
<=> (x - 4)(x - 1) > O, x * 1 A (x - 5)(x + 3) < 0. x * -3
~~\ I \ I \ / \ /
±—s¿ : y ± w a ± u : v + »
-3
xe <-°o,l>u [4,<=o> A xe <-3,5]
-3 1
O
-O •-
-e e-
La solución es: x e <-3,l> U [4,5]
OBSERVACIÓN.- Si n es un numero positivo impar, entonces:
© !^P(x)<!^Qix) <=* P(x)<Q(x) © n[P(x)<?lQ(x) <¿> P(x)<Q(x)
© !¡[ñx) > ¡>JQ(x) <=> P(x)>Q(x) @ n[P(x) > ufooO <=> P(x)>Q(x)
Ejemplo.- Resolver la inecuación . > 0
SÍJ^iUxTs
Solución
El conjunto de referencia o conjunto universal se obtiene del radical par y diferente de
cero: x2 -1 >0, dé donde x2 > 1 => x>l v x<-l .\ x g <-«,-l> u <l,+«>>
luego el radical par resulta positivo y puede simplificar quedando la inecuación
yÍ3^Tx
—P= > 0, que de acuerdo a las observaciones, las expresiones del subradical tiene el
Vx + 5
3-.v „ . . . x-3 ___x ' * '
mismo signo
>0, dedonde <0 ±—V 1 i¿ ±_
x + 5 x + 5 _5 3
x e <-5,3>
Sistema de Números Reales
195
Luego la solución de la inecuación es: x e <-5,3> o (<-°°,-l> u <l,+°°>)
.•. x e <-5,-1>u<1,3>
^/x2-9.U3+8jc2+4jc-
48).
Ejemplo.- Resolver la inecuación '—-— > 0
5/ 3
(jc + 4f(jc--13x + 12)
Solución
De acuerdo a las observaciones indicadas se tiene que vjc2 -9 tiene el mismo signo que
x2 -9 y que (jc + 4)5 tiene el mismo signo que x + 4, por lo tanto la inecuación dada
resulta equivalente a la inecuación:
> 0 factorizando el numerador y el denominador
(x2 -9)(jc3 +8jc2 + 4*-48)
(jr + 4)(jr,-13x + 12)
(x + 3)(jc-3)(x-2)U + 6)U + 4) ^Q ^ (a+3)(x-2)U + 6)(x + 4):;0 ^ ^ 3
(jc + 4)(jc-1)(jc + 4)(jc-3) ~ (jc + 4)2(jc-1)
\ / \ / \ / \ / \ /—--
(jc+3)(jc-2)(jc + 6)(jc+4)^ _^—H ±—tí :—« ±—« : X ±—
x_l ~U -6 -4 -3 1 2
.-. x u [-6,-4] u [-3,1 > u [2,+°°> - {3}
OBSERVACIÓN.- Si n es un numero positivo par, entonces:
(T) tfP(x) < !¡¡Q(x) <=> 0 < P(x) < Q(x) (I) ?jP{x) < !¡JQ(x) <=> 0 <P(x)< Q(x)
Ejemplo.-
Solución
Aplicando la observación a) se tiene:
V x +
-2x n^ 32-2jc
<=> 0<jc<-
2 x + 2
32-2.V
<=> x > 0 a jc <:
x + 2
196
Eduardo Espinoza Ramos
<=> x>0 a a--32 2x<0
x+2
<=> X>0 A
■^+4*-32
x + 2
<0
« x>0 a íx+***-4)<0-
x + 2
<=> x > 0 a x e <-°o,-8] u <-2,4]
\ / \ / \ /
-^—tí ±—tí :—«—1—
-8 -2 4
.-. x e [0.4]
333. EJERCICIOS DESARROLLADOS.-
©
Resolver la inecuación cuadrática: - 4x- + 4a: + 3 > 0
Solución
La inecuación dada expresaremos en la forma: 4x " — 4x: — 3 < 0
factorizando (2x + l)(2x - 3) < 0, aplicando la propiedad de números reales:
(2x + l)(2x - 3) < 0 <=> (2x + 1 > 0 A 2x - 3 < 0) V (2x + 1 < 0 A 2x - 3 > 0)
13 13
<=> (x>— A jc<-) V (a<— A x> —)
2 2 2 2
o-
-o
V
—o
o—
-1/2
3/2
-1/2 $ 3/2
1 3
La solución es: xe<—,—>
2 2
Ahora resolvemos mediante la naturaleza de las raíces la ecuación 4jr-4A--3 = 0,de
donde r, = —, r,= —
1 o - O
ZY
-1/2 3/2
Como la inecuación es de la forma 4a2-4a-3<0, la solución es la unión de los
intenalos donde aparece el signo {-), es decir:
1 3
Ae<—,—:
2 2
Sistema de Números Reales
197
(Í) a5+8.y4+12a3-a-2-8a— 12>0
®
Solución
Aplicaremos el criterio de las raíces de la ecuación: jc5 + 8a4 +1 2jc3 - jc 2 — 8jc -12 = 0
La ecuación que queda es:
x2 +x + l = 0, cuyas raíces
-l±y/3i
son: r=
1
1
1
1
8
1
9
-2
7
-6
1
12
9
21
-14
7
-6
1
-1
21
20
-14
6
-6
0
-8
20
12
-12
0
-12
12
0
1
-2
-6
Luego las raíces reales son: r, = —6, r2 = -2, r3 = 1
\ /—--\ r-
-i¿ ± )¿
^Z
-6 -2 1
Como la inecuación es de la forma P(x) > 0. la solución es la unión de los intervalos
donde aparece el signo (+), es decir:
x e <-6,-2> u <!,+«>
12jc4-56ji3+89jc2-56X + 12 < 0
Solución
Encontrando las raíces de la ecuación
12a-4 -56jc3 +89jc2 -56t + 12 = 0 dividiendo entre x2
12*2-56*+ 89-— + ^- = 0 => 12(jc2+4r)-56(jc + -) + 89 = 0
XX' X" X
...(1)
Sea z-x+- => z2=a2+—r- + 2 ^ v2+—- = z2-2
x
Reemplazando en la ecuación (1) se tiene:
12(z2 -2)-56z + 89 = 0, entonces: 12z2 -56^ + 65 = 0 => (6z-13)(2z-5) = 0
198
Eduardo Espinoza Ramos
de donde z = —, z = —
6 2
13 1 13 3 2
para z = — => jc+—= — => 6x2 -13jc + 6 = 0, de donde /¡= —, J"2= —
6x6 23
para z = -
jc + —= — => 2jc2 -5jc + 2 = 0, de donde r,=—, r¿=2
2 x 2
ordenando las raíces en la recta numérica
"\
"V
£2¿
-\
1/2 2/3 3/2 2
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos
donde aparece el signo (-), es decir:
12 3 „
xe <—,—>u<—,2>
2 3 2
(4) x(2x + 1 )(x - 2)(2x - 3) > 63
Solución
Hallaremos las raíces de la ecuación:
x(2x + 1 )(x - 2)(2x - 3) - 63 = 0, entonces x(2x - 3)(2x + 1 )(x - 2) - 63 = 0
(2jc2 -3a)(2a-2 -3jc- 2) -63 = 0
Sea z = 2jc2-3jc => z(z-2)-63 = 0
z2-2z-63 = 0 =* (z-9)(z + 7) = 0, de donde z = 9, z = -7, entonces:
Para z = 9 =* 9 = 2jcz-3a- => 2x2 -3x-9 = 0 , de donde: r. = —, r,=3
2
Para z = -7
, 3± 47/
-7 = 2jc'-3a- => 2x2-3jc+7 = 0, de donde: r= —
\ t
-3/2
Sistema de Números Reales
199
©
Como la inecuación es de la forma P(x) > 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
jce<-°°,— >u<3,+«>
2
x jc —3
1-jc~2~jc
Solución
La inecuación dada se escribe en la forma:
x jc-3
1-jc~2-jc
<0
jc(2-jc)-U-3)(1-x)
(1-jc)(2-jc)
< 0, simplificando
-2*+ 3
(1-jc)(2-jc)
<0
2a--3
(a-IXa-2)
> 0, entonces la inecuación
2a-3
> 0, es equivalente a la inecuación
(jc-1)(jc-2)
(2x - 3)(x - l)(x - 2) > 0 para x * 1,2 encontrando las raíces de la ecuación
(2x - 3)(x - l)(x - 2) = 0, se tiene: r,=l, r2 — -, r3=2
v + v
3/2
P(v)
como la inecuación es de la forma > 0, la solución es la unión de los intervalos
Qix)
donde aparecen el signo (+), es decir:
A:e<l,—] u<2,+«>
2
© x:
^-^ x +
x-2 x + \
<
3 x
Solución
La inecuación dada se escribe en la forma:
200
Eduardo Espinoza Ramos
x-2 x + l
jc + 3
-ójc-3
<0
jc(jc-2)-(jc+1)U + 3)
x(jc + 3)
< 0, simplificando
<0
2jc+1 _ , . ., 2x + \ _ . ,
> 0. entonces la inecuación — — > 0 es equivalente a la
jc(jc + 3) x(x + 3) x(x + 3)
inecuación (2x + l)x(x + 3) > 0, para x * -3,0, ahora encontraremos las raíces de la
ecuación: (2x + l)(x + 3)x = 0, de donde r, = -3 , r2= —, r3 = 0.
w
-± VL
V +
-3 -1/2 0
Como la inecuación P(x) > 0, la solución es la unión de los intervalos donde aparecen el
signo (+) es decir:
1
xe< -3,— > u< 0,+oo >
2
®
©
a2-5jc+6
a-2+jc-42
>0
Solución
jc2-5jc + 6^„ (x-2)(x-3) n
— > 0 <=> > 0, esta inecuación es equivalente a:
jc2+jc-42 (jc + 7Xjc-6)
(x-2)(x-3)(x + 7)(x - 6) > 0 para x * -7,6, ahora encontraremos las raíces de la ecuación,
(x - 2)(x - 3)(x + 7)(x - 6) = 0, donde r, = -7 , r2 = 2 , r3 = 3, r4 = 6 .
\ /
Jt S£_
\ /
-7
Como la ecuación es de la forma
2 3
P{x)
Qix)
> 0 la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
x e <-£», -7> u [2,3] u <6,+°°>
-jc3+jt2+22A--40
x(x + l)
>0
Sistema de Números Reales
201
Solución
La inecuación dada escribiremos en la forma:
a3-a:2-22* + 40^0 ^ {x-2){x-4){x + 5) ^Q
jc(jc + 7) jc(jc + 7)
La inecuación < 0, es equivalente a:
jc(jc+7)
(x - 2)(x - 4)(x + 5)x(x + 7 ) < 0, para x * -7.0
ahora encontramos las raíces de la ecuación
(x - 2)(x - 4)(x + 5)x(x + 7) = 0 de donde: r, = -7 , r2 = -5, r3 = 0, r4 = 2 , r5 = 4
-\ / \ / \ / \ / \ /
-X ±—ü :—ti ±—tí : tí ±-
P(v)
Como la inecuación es de la forma < 0, la solución es la unión de los intervalos
<2U)
donde aparecen el signo (-), es decir:
24-4*
— >u
15
Solución
x e <-oo,-7> u [-5,0> u [2,4]
0 1+_*zf^>0
v-x jc2-2jc-15
■- ^ a -u- . r jc2-6jc + 9 _ U-3)2
La inecuación dada escribiremos en la forma: — > 0 <=> > 0
J-lx-lS (jc-5)(jc + 3)
v- „)2
pero (jc-3) > 0, x * 3, entonces: > 0 <=> > 0 para x * 3
v2.„ _, U~3)z .n _ 1
(jr-5)(jt + 3) (jc-5)(jc + 3)
1
■ > 0 , x * -3, 5 <=> (x - 5)(x + 3) > 0, para x * -3, 5,
(a-5)(jc + 3)
ahora encontraremos las raíces de (x - 5)(x + 3) = 0, de donde r, = -3, r2 = 5 .
202
Eduardo Espinoza Ramos
T2¿_
Como la inecuación es de la forma
Pjx)
CU)
> 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
x e <-»,-3> u <5,»>
3jc + 5
2jc+1
<3
Solución
A la inecuación dada escribiremos en la forma:
3* + 5 -^ -3jc + 2^„ 3jc-2 „
3<0 <=> <0 <=> >0
2a + 1 2jc + 1 2jc + 1
^^>0 <=> (3x-2)(2x+l) =>0, para x*--
2x+\ v 2
©
ahora encontramos las raíces de: (3x - 2) (2x + 1) = 0, donde r, = —, r2 = —
\ /-■
+ V
\¿ ±_
-1/2 2/3
Píx)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
Q(x)
donde aparecen el signo (+), es decir:
(2jc2-8jc + 8)(jc + 3)>()
Solución
1 r2
2 3
jc+6
(2^-8, + 8)U + 3)s() ^ 2(v-2)^ + 3)^)U_2)2s()|VxeR
jc + 6
jc+3
jc + 6
r+6
>0 <=> (x + 3)(x + 6) > 0, para x*-6
Sistema de Números Reales
203
Luego las raíces de (x + 3)(x + 6) = 0 son r, = - 6 , r-, = -3
\ / \ /
+ x/ : M +
P(x)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
x e <-°o,-6> u [-3,+°o> u {2}
(\-x-x~)(2-x-x2)
(3-a-)(2-jc)
>0
Solución
{l-x-x2)(2-x-x2) Or+x-Wc2 + x-2)^n
(3-x)(2-x)
U-3)(v-2)
(.V+x-i)Qr+jt-2)
(.t-3)U-2)
>0 <=> {x2 +jc-1)(.v- +.v-2)(.t-3)(a-2)>0, para x * 2,3
ahora encontramos las raíces de: (x + jr-l)(jr~ +jc-2)(jc-3)(jc-2) = 0, dé donde
r, =-2, r2
-1-^5 -1 + VS , _ ,
—-z • ^3= ñ ' r4=1> r5=2. r6=3
\ r
+ M
-\ / \ / \ / \ / v /
■J + \J - \1 + \l ~ M +
-1 - \¡5 -1 + \/5 1
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
Q(x)
donde aparecen el signo (+), es decir:
„, r-l—v/5 -í + yf5, „ „
xe< -°°,-2]u[ —, —lu[l,2 > u < 3,-h» >
5 i 5 t
-r-l x -2
A"4+l .T4+2
204
Eduardo Espinoza Ramos
Solución
Vxe R, x +1>0, jc4 + 2 > 0, entonces la inecuación dada se puede escribir en la
forma: (jc — 1)(jc4 + 2)<(jc5 -2)(.t4 +1), efectuando operaciones y simplificando se
tiene: x4 (jc +1) < 0, luego encontrando las raíces de
jc4(jc + 1)=0 setiene r,=—1, r2 = 0, multiplicidad4.
punto critico de
multiplicidad par.
Como la inecuación es de la forma p(x) < 0, la solución es:
x e <-<*>,-1>
(jc -2a+4)(jc-1)
(2a + 1)(jc + 4)
<0
Solución
La inecuación < 0, es equivalente a:
(2jc + 1)(jc + 4)
? 1
(jc -2.T + 4)U--lX2jr+l)U + 4)<0, para x*-4,—
ahora encontramos las raíces de la ecuación.
(jc2-2jc + 4)(jc-1)(2a + 1)(jc+4) = 0, de donde.
i| = —4 , r2— , r3 = 1, r4 = 1 + v3t, r5 = 1 - V3i
\ /-■
+ \/
\l +
Como la inecuación es de la forma
donde aparece el signo (-), es decir:
-1/2
P(x)
CU)
< 0, la solución es la unión de los intervalos
jte<-«>,-4>u<—.1 >
2
Sistema de Números Reales
205
jc + 5 x-l
<
x - 6 x - 3
Solución
jc + 5 x-l .v + 5 Jc-l _ ,
< <=> < 0, efectuando operaciones se tiene:
jc —6 jc —3
-6 jc-3
3jc-7
< 0 <=> (3x - 7)(x - 6)(x - 3) < 0, x *■ 3,6
U-6)(jc-3)
ahora encontramos las raíces de la ecuación
(3x-7)(x - 6)(x- 3)= 0, de donde r, = —, r2 -3, r3-6
\ l \ i \ i
_i¿ ± )L : )¿ ±.
7/3 3
P{x)
Como la inecuación es de la forma < 0, la solución es la unión de los intervalos
Q(x)
donde aparece el signo (-), es decir:
jce<-oo,— 1 u<3,6>
3
(A-3)(.T + 2r(A + l)(A-4)
a(jc + 2Xjc2-3)(jc + 3)
>0
Solución
(jc + 2)2 >0, para x *■ -2, la inecuación dada es equivalente.
^ = -j=r- > 0, la cual es equivalente a:
(jc + 2)jc( jc + 3)(jc + V3)U - V3)
(jc-3)U + 1)(jc-4)a(jc + 3)(jc + >/3)(a— >/3)(jc + 2) >0, x*0,-3,-2, ■& , S
ahora encontramos las raíces de la ecuación,
( jc + 2)(jc - 3)(jc + 1)(jc - 4) jc(jc + 3)(.x + >/3)( jc - >/5) = 0, de donde
206
Eduardo Espinoza Ramos
r, = -3, r2 - -2, r3 = —JS, r4 = -1. r5 = 0 , r6 = yfí , r7 = 3, r8 = 4
--\ / \ r~--\ i \ f~-~-\ i \ i \ i \ i
_± sz : v ± i¿ : )¿ + v \j + v \j +
-3
-2 -n/3
v/3
P(x)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
Q(x)
donde aparecen el signo (+), es decir:
xe< -oo,-3 >u<-2,—v/3 >u<-1,0> u< >/3,3> u<4,-h» >
©
x-2 xL
x+2 x2+2
Solución
x-2 xl
x-2 x1
x+2 x2 + 2 x + 2 x2+2
< 0, de donde
-Ax¿+2x-4
(jc+2)(jc2 + 2)
<0 <=>
2^-x + 2
(x + 2){x2+2)
>0
VxeR, 2jc-jc+2>0 y x~ + 2 > 0, entonces se simplifica la inecuación > 0
x + 2
Luego >0 « x + 2>0, para x * -2. La solución es:
x+2
x e <-2,+°°>
®
jc + 4 x
■>-
x-1 x+\
Solución
jc + 4 x x + 4 x n . . .
> <=> >0, de donde
x-1 x + \ x-1 x + l
12x + 4
(jc-7)U + 1)
>0 c=> (3x+l)(x-7)(x+1)>0, para x*-1,7
ih -i i encontramos las raíces de la ecuación (3x + l)(x - 7)(x + 1) = 0, de donde
Sistema de Números Reales
207
r, = -1, r2 = —- , r3 = 7
_i¿ ± V!
'^T
-1/3
P(jc)
Como la solución es de la forma >0, la solución es la unión de los intervalos
Q{x)
donde aparecen los intervalos donde aparece el signo (+), es decir:
Jte<-1,— >u<7,+°°>
3
19
2x1-6x + 3,
x2 -5 a-+ 4
>1
Solución
2jc~-6jc + 3
x2 -5jc + 4
■>1 <=>
2^-6^ + 3
í2-5j+4
1 > 0, de donde
>0 <=> (x2-jr-l)(jr2 -5jc + 4)>0 parax*l,4;
.r -5jc + 4
ahora hallaremos las raíces de la ecuación.
7 7 l->/5
(x -x-l)(x -5x + 4) = 0, de donde r, = .
r2 = 1, r3 =
1 + JE
, r4 -4
z^:
V + V
-\ /
1 -\¡5
1 + \/fí
P(x)
Como la inecuación es de la forma > 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
l-S , l + >/5
jce<-°°, >u<l, >u<4,+°°>
(20) ^z!<_^<^li
^~^ x + 4 x+4 v + 4
Solución
208
Eduardo Fspinoza Ramos
2x — \ x x + l 2x-\ x \ x + \
<- < — <=> <. A <
v + 4 x + 4 x + 4
2jc— 1 x
■<0 A
x + 4 v + 4
x + l
x+4 a+4
x + 4 a + 4 x + 4 a+4
ecuaciones son equivalentes a:
< 0, de donde < 0 A > 0 , estas
A--4
A+4
(x llix + 4) < 0 A x + 4 > 0. para x ^ -4 ahora encontraron las raíces de las
ecuaciones, (x - 2)(x + 4) = 0 A x + 4 = 0, de donde r, = —4 r-, = 1 A r} = -4
\ i \ i
+ v : u ±_
-\ /
_M +.
-4 1 -4
de acuerde a la forma de la inecuación la solución es: xe <-4,l> A xe [-4,+°°>
xe <-4,l>
\lx2-x-2<5-x
Solución
Aplicando la propiedad: yjP(x) < Q{x) <=> (P(x) > 0 A [Q(x) > 0) A (P(a) < Q1 (x)])
y¡x2-x-2<5-x <=> (a:2-a-2>0 A [5-*>0 A jt2 - x-2< (5-a)2])
<=> (a2-a-2)>0 A [5-a>0 A v2 -a-2<25-10v + a2])
« (í-2)(a+1)>0 A (a<5 A *<3)
-e—► a<-
-é-
x e <-oo,-l] U [2,5] A x e <-oo,J>
5
-o
o
-e-
o
-e e-
2 3
o
-e-
x e
i n *
Sistema de Números Reales
209
I 3^-4" I 2^:
VíO.8) 4 >V(0.64) 5
Solución
3.T-4 4.T—1
La inecuación dada es equivalente a: (0.8) l6 > (0.8) 40
como a = 0.8 < 1, entonces los exponentes son desiguales en sentido contrario, es decir:
3jc — 4 4jc — 4
< , efectuando y simplificando.
16 40
3;r-4 x-l
<- =>
8 5
4lA-2x-x2 <x
x< —, la solución es:
7
12
XS< —00, >
7
Solución
Aplicando la propiedad siguiente:
yfPÜ) < Q(x) « (/>(*) > 0 A \Q{x) > 0 A P(x) < Q1 (*)])
>/24-2x-JC2 <x « (24-2jc-x2 >0 A[jc>0 A 24-2x-x2 <x2])
« {x2+2x<24 A [x>0 A 2jc2+2jc>24])
« ((jc + 1)2 <25 A [jc>0 A (x + -)2 >—])
2 4
« (-6<;r<4 A U>0 A (jc> 3 V x<-4)])
<=> x e [0,4] A x e <-°°, -4> U <3,+°°>
x e <3,4]
6i-4 2x-3 3j-4 4i-2
(0.25)~.(0.5) 4 < (0.0625) 6 .(0.125) 9
Solución
210
Eduardo Espinoza Ramos
12a-8 2.1-3
6ji-8 4r-2
La inecuación dada es equivalente a: (0.5) 3 .(0.5) 4 < (0.5) 3 .(0.5) 3
I2t-g 2j-3 6x-8 4j-2
Operando tenemos: (0.5) 3 4 <(0.5) 3 3
Como a = 0.5 < 1, entonces los exponentes son desiguales en sentido contrario a la
, . 12a—8 2*-3 6a—8 4*-2
inecuación, es decir: + > h
12a—8 2*-3 10a—10 ,.,. J 2a + 2 2a—3 „
+ > , simplificando: + >0
8a + 8 + 6*-9
12
>0
14x- 1 >0
a > — ; la solución es:
14
A€< — ,+oo>
4
@ -n4r^ > (42x.8*-3 )2/5
Solución
*+i
La inecuación dada es equivalente a: 2.2 - >(24r.23v y)'/5. de donde
x+ll I4x-18
2 2 > 2 5 , como a = 2 > 0. entonces:
a + 11 14a-18
>
5x + 55>28x-36
x < — La solución
23
91
jre<-o°,— >
23
®o- 1 , X. 3 a + 2 6
Si — < x < 1, Demostrar que: — < < —
2 8 a + 3 7
Solución
= 1 (se obtiene dividiendo)
a + 3 a + 3
< a < 1
< r + 3<4
1 1 2
— < < —
4 a + 3 7
Sistema de Números Reales
211
(28)
2 1 1
— < < —
7 jt+3 4
5 jc+2 3
— < <— =>
7 Jt+3 4
1—<1 <1 —
7 jc + 3 4
3 5 x+2 3 6
— < —< < —< —
8 7 jc+3 4 7
3 jc + 2 6
-< < —
8 jc+3 7
(27) VT^<^5+7
Solución
yfl^x<ij5 + x « (1-jc>0 A a + 5>0) A(>/rTJ¡:)2<(</jt + 5)2
<=> (jc<1 A jc>-5) A (1-jc<Vjc + 5) ... (1)
Vjc + 5>1-jc « [(jc + 5>0 A 1-jc<0) v (jc + 5>0 A jc + 5>(1-jc)2]
» [(jc>-5A jc>1)v(jc>-5 A jc + 5>1-2jc + jc2)]
« [(jc>-5 A jc>1)v(jt>-5 A x2-3jc-4<0)]
« [(jc>-5A jc>1)v(jc>-5 A xe [-1,4])]
« [(jc > -5 A jc > 1) v jc e [-1,4]]
« [jc>-5 A jc >-l] => jc>-1 => jce[-l,«> ...(2)
ahora (2) en (l) se tiene: (x < 1 A x > -5) A x e [-1 ,+<*>>
xe [-5, 1] A x e [-!,+<*» I .-. xe [-1,1]
V3jc + 7-Vjt-2>9
Solución
Calculando el campo de existencia 3.v + 7 > 0 a jc - 2 > 0 <=> x-~^: A * - 2
por lo tanto x e [2,+°°> es el campo de existencia
212
Eduardo Espinoza Ramos
®
y/3x+l >9 + ylx-2 » jc€[2,+°o> A [3jc + 7<81 + 18>/jc-2 + x-2]
« xe[2,+oo> A (x-36<9\lx-2)
«• xe[2,+oo> A jc2-153jc + 1458<0
. , !53^2 17577
« jce[2,+°o> A (x y<
2 4
153-Vi 7577 153 +Vi 7577
« xe[2,+»>A <jc<
153->/l7577 153 +Vi 7577
xe< , >
VI+T + Vjc-2
49^-41
>0
Solución
Calculando el campo de existencia
(x-1 >0 a x-2>0) a (9-Jt2 >0 a x>0)
(x> 1 a x>2) a (jc2 <9 a x>0)
(x > 1 a x > 2) a (-3 < x < 3 a x > 0)
x e [2,31 es el campo de existencia.
x>2 a 0<x<3. de donde
Como Vjt + l+V*-2>0, Vxe[2,3]
y¡X+\+Jx-2 „ yjx + l+y/x-2
>o =•
V9-X2 -VI
>0.
y¡g-x2 _Vjc V* + l + V-*-2 'V* + l+Vx-2
simplificando . > 0 <=> y¡9-x2 -y]x>0
V9-x2-Ví
de donde
\<9-x-
Sistema de Números Reales
213
1 i 37
x2 + a - 9 < O => (x + —)2 < — (completandocuadrados)
, * ^2 37
{x+2} <T
yfyf 1 >/37
<x + —<
Luego la solución es: x e < —
2 2 2
V37+1 >/37-l
-<x<
> a [2,3]
.-. xe[2, >
V 2 - J3 + x < ^4 + x
Solución
V2-V3 + A <j4 + x <=> (2-V3 + jc>0 A 4+a>0) A (2 - y¡3 + x < 4 + je)
« (yj3 + x<2 A a>-4) A (V3 + jr>-jc-2) ... (1)
yj3 + x<2 «. (3 + jc>0 A 3 + jc<4)
« (x>-3Ax<l) => xe[-3,l] ...(2)
y¡3 + x>-x-2 » x+3>0 A [-a-2<0 V (a + 3>0 A x + 3>(* + 2)2)]
« x>-3 A [a>-2 V (v>-3 A a-2+3a + 1<0)]
3 5
«. a>-3 a [a>-2 v (*>-3 a (x + -)2<-)]
j5+3 >/5-3xl
<=> a>-3 a [a>-2 v (a>-3 a —<*<—-—)]
c* a
c>-3 a [a>-2 V jt€<
y¡5+3 y¡5-3
2 ' 2
v5+3
<=> A">-3 A A£< ,+o°>
2
214
Eduardo Espinoza Ramos
xe< ,+«>
... (3)
Luego de (2), (3) en (1) se tiene:
V2->/*+3 <yl4 + x « (xe[-3,l] a x>-4) a *e< ,+«>>
2
>/5+3
« Jte[-3,1] a xs< ,+«>
yfS+3
xs< —,1]
3 13 1
— < +
x 4(x-l) 4jc+12
Solución
A la inecuación dada expresaremos así:
13 1 3^_ 13(jc+3).t+4-v-l)-12(Jc-lX.y+3) ^n
+ > 0, efectuando operaciones > 0
4(jc-1) 4(jc+3) jc 4(x-1Xjc+3)jc
13x2+39x+jc2-jc-12(jr+2jc-3)
4jc(jc-1)(jc + 3)
>0, simplificando
2jc2+14jc + 36
4x(jt-l)(x +3)
>0
x¿+lx + lE
jc(jc-1)(jc+3)
>0
,_, 2 - .o ^ jr+7jr + 18
VxeR, x +7jc + 18>0 entonces: «•
1
jc(jt-l)U+3) jc(jc-!)(* +3)
>0
1
a(a-!)(* +3)
>0 <=> A(jt-l)(jt + 3)>0,para x* 1.-3,0
resolviendo la ecuación x(x - 1 )(x + 3) = 0, de donde, r, = -3, r2 - 0, r, = 1
Sistema de Números Reales
215
-\ r---\ i \ i
V + V - V +
como la ecuación es de la forma > 0 la solución es la unión de los intervalos donde
Q(x)
aparecen los signos (+), es decir:
x e <-3,0> u <!,+<»>
3 1 3
+ >_
JC —1 JC + 1 X
Solución
La inecuación dada escribiremos en la forma:
3 1 3 n 3r+3jc + .r -*-3.r+3^„
- + >0 <=> >0
jr-1 v + 1 x
.V(JC-1)(A+1)
V+2JC + 3 „
<=> >0
a(a-1)U + 1)
como V x e R, .v~+2x + 3>0, entonces
.v" + 2x + 3
a(a-1)(a + 1)
>0 <=>
1
A(t-l)(r+l)
•>0
1
jrív-lXt + 1)
>0 <=> x(x-l)(x+1)>0. para x*-1,0.1
Ahora resolviendo x(x - l)(x + 1) = 0, de donde r, = —1, r2 = 0 , r^=\
-\ r--~\ /-■
y/ + v
_i¿ ±_
-1
0
1
P(-0
Como la inecuación es de la forma > O la solución es la unión de los intervalos
Q(x)
donde aparecen el signo (+). es decir: x e <-1.0> U <I.+°°>
216
Eduardo Espinoza Ramos
2a-25 2x + \\ 1
+ >-
2(x2+2;t-3) 2(*--l) x + 3
Solución
La inecuación dada escribiremos en la forma:
2a-25 2* +11 1
> 0, factorizando en el denominador
2(;r+2v-3) 2(t2-l) Jt + 3
2x-25 2x + ll 1 n .
+ > 0, efectuando operaciones
2U + 3)U-1) 2íx-1)(jc+1) v+3
(2A-25)(A + l) + (2A + llXx+3)-2(.r-l)u + D
2(x-l)(x+\)(x + 3)
x2 -3* +5
> 0, simplificando se tiene:
> 0, como V x e R, x~ - 3x + 5 > 0, entonces:
U-1)(a+ !)(* +3)
a"-3a + 5 „ 1
>0 c=> >0
(jc-1)(jc + 1X* + 3) (r-l)U + l)U + 3)
1
U-1)(a + 1)(a+3)
>0 <=> (x-l)(x+l)(x + 3)>0, Xít-3,-1, 1
encontrando las raíces de (x - 1 )(x + l)(x + 3) = 0, donde r, = — 3, r2 - — 1, r3 = 1
\ r---\ i \ /---
V + V ' V +
Como la inecuación es de la forma > 0 la solución es la unión de los intervalos
CU)
donde aparece el signo (+), es decir:
xe <-3,-l>u<l,+°°>
U-1)2-U + 2)2^Q
(jc-2)2-(jc + 1)2 "
Solución
Sistema de Números Reales
217
Por medio de la diferencia de cuadrados se tiene:
[U-1)-(a-+2)][(a--1) + U + 2)]
l(x-2)-{x+l)]Hx-2) + (x + D]
> 0, simplificando.
-3(2*+ 1)
-3(2a-1)
>0 <=> (2x +l)(2x-1)>0 para x*-
encontrando las raíces de (2x + l)(2x - 1) = 0, de donde, r, = —, r, = —
1 o -o
+ i/
v^:
-1/2
1/2
Como la inecuación es de la forma
P(x)
Q(x)
>0 la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
a4 + 5 a3 -20a- 16
Solución
1 1
jce<-oo—>u<—,+°°>
2 2
a3 + 2a2-13a+ 10
Factorizando tanto en el numerador y denominador.
(a-2)(a + 2)(a- + 1)(a- + 4) n ^ , „
^0, para x?t-5,1,2
(a + 5)(a-2)(a-1)
la inecuación dada es equivalente a:
(x - 2)(x + 2)(x + l)(x + 4)(x + 5)(x - 2)(x - 1) < 0 para x ^ -5,1,2
(a-2)2(a + 2)(x+1)(a + 4)(a+5)(a + 1)<0 para x^-5,1,2
comoVxeR, x*2, (a-2)2 >0 entonces
(x + 2)(x + l)(x + 4)(x + 5)(x - 1) <0 , para x * -5,1,2
encontrando las raíces de (x + 2)(x + l)(x + 4)(x + 5)(x - 1) = 0, de donde:
218
Eduardo Espinoza Ramos
-5, r2=-4, r-¡=-2. r.=-\, r5=\
_i¿
_j¿ ± i¿
V"
-5
-2
Como la inecuación es de la forma
donde aparecen el signo (-), es decir:
G(a)
<0 la solución es la unión de los intervalos
x e <-°o,-5> u <-4,-2> u < -1,1>
yix-l -yi-X
-,6jc-1
2.v+l .(.v-2)
>(3"+,y
Solución
La inecuación dada expresaremos en la forma
32Jr_1+4_Jr_6jr+1 >3(2x+lX*-2)jdedonde. 3-5,+4 > 3lS-3x-2
como a = 3>0 => -5* + 4>2;c -3jc-2, de donde
2a2— 2a-6<0 <=> a2 + a-3 <0, completando cuadrados a2+x + —<3 + —
4 4
, 1,2 13 VÍ3 1 VÍ3
(x + —) <— <=> <* + —<
2 4 2 2 2
VÍ3 + 1 VÍ3-1 , , ,
< x < , de donde
jce<-
Vl3 + 1 VÍ3-1
®
x 1 2x
- +— >•
a2-5a + 6 2x 3-4a + a2
Solución
A la inecuación dada expresaremos en la forma
1 2x
- +
a2-5a + 6 2x 3-4* + .
> 0, efectuando las operaciones:
2,2(.-l) + U-2)U-3)(*-l)-4*2U-2)^0 desarrollando;
2x(x-3)(x-2)(x-l)
Sistema de Números Reales
219
.3 . o„2
2xi - 2.r- + x3 - 6x- +1 1a: - 6 - Ax5 + 8
2a(a-3)(a-2)(a-1)
■ > O , simplificando
, ,v 3-VÍ7v 3 + >/T7,
3 ii . /: (a-3)(a + )(a + )
x —lije+ 6 „ 0 9 ~
<0 <=> - - <0
a(a-3)(a-2)(a-1)
a(a-3)(a-2)(a-1)
(A + )(A + )
para x * 3 se tiene - < 0
a(a-2)(a-1)
\ i \ i \ i \ r
—n ± \i : u. + v
-3-v/7 -3 + v/7 0
P{x)
Como la inecuación es de la forma < 0 la solución es la unión de los intervalos
CU)
donde aparece el signo (-) es decir:
xe<-
3 + yf¡7 -3 + >/Í7 _ , .
>u< ,0>u<l,2>
1 a-3 2
— < < —
5 A + l 3
Solución
Aplicaremos la propiedad siguiente: a<b<c <=> a<bAb<c
1 a—3 2 1 a-3 a a-3 2
— < <— <=> —< A < —
5 v+1 3 5 A+l A+l 3
<=> >0 A <0
A+l 5 A+l 3
5a-15-a-1 . A 3a-9-2a-2 _
<=> >0 A <0
5(a + 1)
3(a + 1)
x~4 n a X~U n
<=> >0 A <0
A+l A+l
220
Eduardo Espinoza Ramos
<=> (x-4)(x+ 1)>0, x*-l A (x-ll)(x+1)<0, x*-l
ahora encontrando las raíces de (x - 4)(x + 1) = 0, de donde r, =—1, r2 =4,
r3 = -1, r4 = 11
TV1
^1V
A
VVI
-1 4 -1
de acuerdo a la forma de la inecuación la solución es:
11
x e <-oo,-l> U <4,+«» A x e <-l.l 1>
M
XA
a4-16
—\j
©
-1
o
5x2 +36
a4-16
«->-
-O
4
o
11
_o
.-. x e <4,11>
Solución
A la inecuación dada escribiremos en la forma
x4 5x2 +36
x4-16 jc4-16
<0 <=>
x4 -5x2 -16
*4-16
<0, factorizando
(*;-9K*;+4)<o« 4^<o
U2-4)(a2+4) a--4
(x+3)(x-3)
< 0 <=> (x + 3)(x - 3)(x + 2)(x - 2) < 0, para x * -2.2
(x + 2Xx-2)
ahora encontrando las raíces de:
(x + 3)(x - 3)(x + 2)(x - 2) = 0 de donde r, = -3, r2 = -2, r3 = 2, r4 = 3
—\ /-■
+ ^
-3
i \ r
)¿ ± )¿.
2 2
P(a)
como la inecuación es de la forma
. CU)
donde aparecen los signos (-), es decir:
< 0, la solución es la unión de los intervalos
x e <-3,-2> u <2,3>
Sistema de Números Reales
221
(A-9)2n(l-A-3)2n+,(.r4-9)<0, sin> l.ne N
Solución
Para x* 9, (x-9)2">0, (l-x3)2" >0, parax * 1.
Entonces a la inecuación dado se puede simplificar, es decir: (1 - x3 )(a4 -9) < 0
Factorizando (x-l)(x2 + x + l)(x-j3)(x+j3)(x2 +3)>0. x*l,9
como V x e R, x2+x + l>0, a-2+3>0
entonces (x-l)(x-yf3)(x + yf3)>0, x * 1,9
ahora encontrando las raíces de: (x-1)(x--J3)(x + v3) = 0
de donde: r, = —s/3 , r2 - 1, r3 = -s/3 ~
\ y----\ /--
_i¿ ± vi
W
-y/3
1
n/3
Como la inecuación es de la forma P(x) > 0, la solución es la unión de los intervalos
donde aparece el signo (+), es decir:
xe<->^,l> u < S,+°° > -{9}
3.34. EJERCICIOS PROPUESTOS.
I.
©
©
©
Resolver las siguientes inecuaciones
5x-2<10x + 8<2x+ 16
1 „ 1 1
-<3x—<-
5 4 3
x 3.v 5
- + ——< , a> b>0
Rpta. <-2,l>
1 7
Rpta. [—,—]
V 60 36
a~—b" a + b a — b
Rpta. <-
5a + 5b
l + 3a-3fc
®— + 4> — + 2a, a>b>0
3a 6b
Rpta. < -»,
24ofc
5a + i2ab-4b
Eduardo Espinoza Ramos
©
©
2v + <4
4
V X V
— + — >1+— , ob>a>0
a b c
Rpta. < -o°,2 >
abe
Rpta. <
ac + bc — ab
,+oo>
(?) 2x-6-
3a+8
38
Rpta. <-°°,— >
7
(?) 3(x - 5) - 4(4 - 3x) > 2(7 - x) - 3(x - 5) Rpta. <3,+°°>
II. Resolver las inecuaciones siguientes:
©
©
©
©
©
©
©
©
©
®
(íi)
2.v2-6a- + 3<0
2a2+6a-9<0
9a2+54v>-76
-4a2+4a + 3>0
4x2+9a+9<0
4a2-4a + 7>0
a4-2a2-8<0
-4a-2-8 <-12a-
a2-2>/3a--2>0
3a2-8v + 11>4(x-1)
3r2-10.»+3<0
3-yfe 3+yft
Rpta. < , >
-3-W3 -3 + 3>/3
Rpta. < , >
9 + yf5 V5-9
Rpta. <-°°, >u< ,+oo>
1 3
Rpta. <—.—>
2 2
Rpta. <J>
Rpta. C.S. = R
Rpta. <-2.2>
Rpta. <-oo,l>u<2,+oo>
Rpta. <-°o,yf3-^Í5 >u<>/3 + \/5,+°°>
Rpta. V x e R
Rpta. <-.3>
Sistema de Números Reales
223
(12) a(3a + 2)<(a + 2)2
Rpta. <-1.2>
®
4vj!-8a + 1<0
_ . 2->/3 2 + ^
Rpta. < , >
(14) 5x2 -14a + 9SO
®
jT+3x+2>0
Rpta. [1,-
Rpta. <-o°,-2> u <-!,+<»>
U6)
1-2x-3a¿ >0
Rpta. [-1,-]
17)
3a--5x-2>0
Rpta. <-«»-—>u<2,+oo>
(18) (x~ + 2x)(x2 -1) - 24 > O
(19) x(x-3)(x-l)(x + 2)> 16
Rpta. <-°°,-3> u <2,+<»>
1-V33 1 + V33
Rpta. <-°°, >u< ,+=»>
®
©
©
®
a4+2a-3-a-2+4a:-6<0
(a-+a-6)(4jc-4-a-'!)<0
2a-3+3a:2-11a-6>0
rJ-3r--13.v+I5>0
a4-4a-3-a2+16a--12>0
a-5 +3a4 -5a3 -I5.v2 +4.v + 12>0
a5 -6a4 -a3 +29a2 + 8a-15<0
-1-V5 . -1 + V5
Rpta. <-°°, >'vj<-l,
Rpta. <-3,l>
Rpta. <-o°,-3] u [2,+°°>
Rpta. [-3,—]u[2.+°°>
Rpta. <-3,l>u<5,+°°>
Rpta. <-°°,-2> u <1,2> u <3,+°°>
Rpta. <-3,-2>u<-l,l>u<2,+oo>
>u<3,5>
224
Eduardo Espinoza Ramos
(27) (x2 -2x-5)(x2 -2x-7)(x2 -2x-4)>0
Rpta. <-°°,l-2yf2>KJ<l-yÍ6,l-S>KJ<l + yj5,l + yÍ6>KJ<l + 2-j2,+<>°>
(28) x5 -2*4 -15a 3 > O Rpta. <-3,0> u <5,+°°>
(2$) (a3-5a2+7a-3)(2-a)>0 Rpta. [2,3]
60) (x - a)(x - b)(x - c)(x -d)<0, si a<b<c<d Rpta. <a.b> u <c.d>
(5l) (x2+6x-l)(x3-2x2-2x + 4)(x + 5)5 >0
Rpta. < -00,-3-V¡0 > u < -5.-V2 > u< -3 + y[ÍO,y¡2 > u < 2,+°° >
62) (6a-+3)2(jc2-1)3(3a--5)7 <0 Rpta. <-°°,-1>u<1,->
v-x 3
(33) (3-x)3(x2-l)2(l-x)5x>0 Rpta. <-0,l>u<3,+oo>
(Sí) a-4-2a-2-3jc-2>0 Rpta. <-°°,-l] u [2.+°°>
(35) a-4-3a:3+5a-2-27a--36<0 Rpta. <-l,4>
@ a4<a2 Rpta. <-l,l>-{0}
(37) (2a2-4a-1)(3a2-6a + 4)U2+4a-2)>0
/- 2-J6 r 2 + >/6
Rpta. <-oo,-2-v6 >u< ,-2 + v6>u< ,+oo>
2 2
(38) jc5+8a4+12a3-a2-8a-12>0 Rpta. <-6,-2>u<1,+°°>
(55) (a2-1)(x2+9)(a + 4)(a--5)>0 Rpta. <-oo,-4>u<-1,1>u<5,+o°>
(40) (x + 2)(x + 3)(x - 4)(x - 5) > 44 Rpta. V x e R
61) a6 + 6a4 + 9a-2 + 4 > O Rpta. V x e R
Sistema de Números Reales
225
(42) x4-3a2-6a-2 <O Rpta. <\-y[2,\ + y[2>
(43) a-5-6a-4-17x3+17x2+6x-1>0
.l>u<4 + >/r5,-i-oo>
@ x4-2x2+8x-3>0 . Rpta.<-oo,-l-V2>u<-l + >/2,+~>
®4 o 3 «2 ,n -^n o . r-l->/Í3 3->/5" -1-VÍ3 3-^5.
r -2a -5x +10x-3<0 Rpta. [ , ]u[ , 1
2 2 2 2
(4ó) (x - 7)(x - 3)(x + 5)(x + 1) > 1680 Rpta. <-°°,-7] u [9,+°°>
(47) (x + 9)(x - 3)(x - 7)(x + 5) < 385 Rpta. l-l-yífÍ,-4] u[2,-l + >/7Í]
III. Resolver las inecuaciones siguientes:
®-* + l ■* r.
< Rpta. <-oo -3> u <2,+oo>
2-x 3+x
(2) > Rpta. <-,2]u< —,+=»>
W 3a-7 3-2a .2 3
(3) £±l>i_±l Rpta. <2,+°°>
A-2 x2
O 1
®-—-> Rpta. <-00,-4>u[— ,2>
.r + 4 a-2 2
±j—1 < ^—- Rpta. <-2,0> u <0,+°°>
A'' +2 X~ + 1
®-^HÍ<— — Rpta. <-°o,_l>u<0,l>
- .i. 1 ,- _ 1
(T) £±1>£J1 Rpta. VxeR
W A4+l A4+l
226
Eduardo Espinoza Ramos
®
®
®
©
©
fS5í
x~ -2x ^ x + &
jc-4 ~ 2
1 3a+ 1 „
-< <4
X X
•
a2+8^5a-8
x + 4 " 5
x+4 x-2
1 >~r
x +4a + 4 x -4
1 2
<
x+l 3x-l
1 2x2-3a + 3
— <
Rpta. <-°°,4>
Rpta. <-°°,0>u<l,+°°>
Rpta. <-4,6]
Rpta. Vx€ R-{-2,2}
Rpta. <-«>,-l>u<-,3>
3
3 7
. . Rpta. <-°°,— >u<0,— >u< 2,+°o>
^^ 2 (a-2)(2x + 3) 2 6
®2x-\ 3x-l A x-1 _ „ 5
+ <4 + Rpta. <-2,— >u<-l,l>u<5,+oo>
x+\ x+2 x-1 4
© Vt^-t^ Rp|a- ♦
x+4 jr + jt + 4
Ü6.
2
^—?U"+5)(* 3)>0 Rpta. <-»,-5>u<-3,->/2>u<0,>/2>u<3,+oo>
- x(x2+2)U+3)
®(6a + 3)2(a2 + 1)3(3a-5)7 n D 4 , , 3 5
- ^— —-—— >0 Rpta. <-°°,-6>u<-6,— >u<-,+oo>
(a + 6)2(2a-+3)17 2 3
® (4"2>'(*:t2)'(2,r8)'<° «** <-^,4>-(-i,-ii
w (x + l)2(2x + 5)13 2 2
®^^<^^ Rpta. <^~,-3>u<--,5>
x-5 x+3 7
^ 7 - + —!— <-2 Rpta. <-3.-2>u<l,4>
.v-4 jt + 2
Sistema de Números Reales
227
© (*2+*-<**;-*-6)>0
W U2-4XJt2-2)
Rpta. <-°<\-3>u<—s/2,>/2 >\j<3,+°°>
(22)
jT-2x + 3
jt2-4.r + 3
>-3
Rpta. <-~rl >\u<— ,2>kj<3,°°>
2
(23)
5 1
-+ >2
x+3 x-l
Rpta. <-3,-l>u<l,2>
(24)
2>^1>I
jc x
Rpta. [1,0>
(25
jr-2x + 3
jt2 -4.r + 3
>-3
Rpta. <-oo,l>vj<—,2>lj<3,-h»>
(26
2.t4+7jt3+8jr+6.r+l
6x5 + 17x4 + 23x3 + 18x2 + 7jt+1
>0
-5-yfÍ7 , 1 1 -5 + VÍ7
Rpta. < ,-lxj<—,— >u< ,+°o>
2 2 3 2
(27
7 6
x-l a--1
<5
Rpta. <-oo,-l>u<—,l>u<2,+oo>
(28
12x5 - 35a4 -53a3 + 53a2 + 35* -12
v6 +15x5 + 78a4 + 155.Í3 + 78 x2 +15x +1
<0
-5-yffl 4 3 -5 + yflí „ /r , _ /r
Rpta. <-«., >u<—,— >u< ,2->/3>vj<1,2 + >/3>
F 2 3 4 2
(29
2a-1 A+2 x-l
+ >-
a + 4 3-jt a + 3
Rpta. <-°°,-4> u <-3,3>
30
l + x*
1 4 S
x-x + r -jt
+ 9
(l-jr-)(l-A) (1-a)-(1 + x)
Rpta. < -oo, -1 - >/3 > U < -1 + -^3, I>u<1.2>u<2,+oo>
228
Eduardo Espinoza Ramos
4x4 -20a2 +8 D „ /r „ , , , rr
— <8 Rpta. <-V6,-2>u<-l,l>u<2,V6>
a4-5 a2+4
(A-1)2(A2-1)(A4-1)^„
>0 Rpta. <2,+oo>
(a4+1)(a-2)
(a2 +5a + 6)(a4 -16)(x2 -4a-12)
(l-3jt)3(A--l)(A-2+l)
<0
Rpta. <-oo,-3>u<-2,->u<l,2>u<6,+<»>
4 x-2 4
-<— Rpta. <0,2>u<4,+oo>
4-x 5
3a2 + 7a+ 5
a2+3a + 2
<2 Rpta. <-2,-l>
= ^ < 0 Rpta. <-4,-3] u [3,4>
(jc2-4)(x2-16)
(l + A-+A2)(2-A--jt2)(A:4-2A-2-3jt-2)
(2x2 -4x-l)(3x2 -6a + 4)(x2 + 4a-2)(a2 -7)
<0
Rpta. <-~,->/7>u<-l-—,-2]u[-l,->/6 + 2>u<-—l,l>u[2,>/7 >u<>/6 + 2,+<»>
2 2
®x 12 A + l „ t 5 12
< — < Rpta. <-,— >
A + l 19 x + 2 11
Q, (a--3)U+2)2(a- + 1)U-4) ?0
^ a(a- + 2)(x2 - 3)(jt + 3)(a2 + 4)
Rpta. < -oo,-31 u < -2,S > u [-1,0 > u < >/3,3] u [4,+°° >
®2a -3a+ 3 ^_j_ Rpta. <-*>,--> u<2,+<~>
(a— 2)(2a + 1) 2 2
Sistema de Números Reales
229
2 3 x + 5
— + >-
a + 1 x-\ l-x2
2 > 2a
-5a + 6 2-x (3-a)(1-a)
Rpta. <l,+°°>
Rpta. <-°°,-6] u <2,3>
3 13 1
-< + -
x 4(a-1) 4a+ 12
_ . r 31 + ^89 „ r>/889-31 „
Rpta. [ ,-3>u[- ,0>u<!,+«>>
(x2+4x + 4)(a-9)2
(11-x)(a2+5)
3 1 3
+ > —
x-l x+l x
x-l
x+2
<1
U2-5)U2+7)
(a2+X+1)(a2-3a+2)
3a
x'-x-6
x2 -3a + 2
a2-4x + 3
>1
<2
2a-25 2a + 11 1
2(a-2+2a-3) 2(x2-1) a+ 3
a2 + 4x + 4
x¿~4x-5
2a-a2-1
A2-A4
■>0
<0
(2a2-8a + 8)(a+3)
-v + 6
<0 Rpta. <ll,+oo>u{-2,9}
Rpta. <-1,0> u < 1 ,+°°>
Rpta. <-2,+oo>
>0 Rpta. <—>°,->/5]u< 1,2 >uh/5,-K»>
Rpta. <-2,2->/Í0>u<3,2 + >/Í0>
Rpta. <-°°,3> u <4,+°o> - {1}
Rpta. <-3,-1>u<1,+°°>
Rpta. <-°°,-l>u<5,+°°>
Rpta. <-1,0>u<0,1>
> O Rpta. <-°°,-6> u [-3,+°o> m
230
Eduardo Espinoza Ramos
©
©
®
©
©
a: -2a+1
A-l
2* + l
>0
>3
x + l
a2+4a + 9
a2-4*-5
x2+x + 2
a(a2-a-2)
<0
<0
2 3
<
3jc-2 a: + 2
32 ^ x
*2_4~x-2
2 + x-x2 ^
jt2-2jc+l
*3-jc2-8a + 12
*2+5*-14
*2+8*-12-*3
7a-a2-6
a2+3a+2 a-
4
A+2
<0
>0
-2
A-2 A+2
1 2 3
+ >
x+l x + 3 a + 2
X+l 0 1-A
1-A X
*2+8a+24._
Rpta. <l,+«»
Rpta. [-2,-l>
Rpta. <-l,5>
Rpta. <-oo,-l>u<0,2>
„ 2 10
Rpta. <-2,—>u<—,+oo>
Rpta. [-4,-2> u <2,6]
Rpta. [-1,1>U<1,2]
Rpta. <-o°,-7> u [-3,2>
Rpta. [-3,1> u <6,+°°> U {2}
Rpta. <-°°,-2> u <0,2>
Rpta. <-3,-2>u<-l,l>
Rpta. <-oo,-l>u<0,—>u<l,+oo>
2
A+2
Rpta. <-2,+°°>
Sistema de Números Reales
231
©í-° °v-3 1
——>— Rpta. <-°o,-2>u<-,1]u[4.-k>o>
x+2 4.Y-1 4
(68) <0 Rpta. <-2,— >u<-l,l>u<5,+°°>
W a-1 t + 1 x + 2 4
a4-3a3-6a2-28a-24 „ /-n 3a
(69) — — — <0 (70) — >1
^-/ 40 + (a-1)U-3)(a- + 4)(a- + 6) ^^ x2-x-6
(71) _^ + ^^<__ (72) _L + ^_<2
7
a —
3a2
x~
30
4 a + 2
+ 7a-6
-x-6
2x
<
>
>
7
jt + 1
3a2 + 16a
x~ -
-4a-
A'
-12
12
®
©
®
©
©
(0.5) 2 > (0.0625) 5
27-1 <9x+3
2x+l 2x-2
(0.2) 2 < (0.0016) 5
25r+8<]6.t+5
n2jt-3 -,4-v
3 3 >72^r-2,
35,-l
X-2 JC + 4
(73) "\ >~. (74) 2-^>^
A'-l A —2
,__. ^ - ,_,, a2+10a + 16
(75) —; > — (76) >10
2a2+7v + 5 a2+6a-i-5 ^-^ JC-1
a2-3a+ 2^ „ /CN a2
(77) * >0 (781 + 4>a + 10
W a-2+3a + 2 W a-2
65) ^<a + 6 65) 1+ '"8A~ <0
x-6 ^^ a2+4a + 3
IV. Resolver las inecuaciones siguientes:
1
Rpta. <—,-h»>
4
Rpta. <-°°,9>
Rpta. <-<»,->
Rpta. <-oo,i2>
_ t -l->/33 -l + >/33^
Rpta. < . >
232
Eduardo Espinoza Ramos
© [(0.5)*2 (0.5)6 r2~3 < ^^ Rpta. V x e R
8*
© 9u-»2 > JL_ R ta y x e R
W 9t+3.3
® x*^**í < x^322*+5 Rpta. <-eo,-l>u<l,+~>
0 yÍ2r+*<ll9^ Rpta. <—,,-—]
@ V81í+15 <V243^10 Rpta. <110,+oo>
3(.r-2)2 , ,
V2293+33 V2293-33
(11) (256) 2 >29u"9) .83^+,.2565u-16) Rpta. <■
86 86
/r>, 729*2.243x 2436.275t_6 „ . ,
(12) > Rpta. <-oo,-l>u<2,+oo>
(tt) 3 .32x>27 Rpta. <l.+<*»
x-5 x-9
(Í3) 2 2 >8 3 Rpta. <-oo,l3>
812x
3x¡32x
x-5
2 2 >í
(0.216)"
5
(42)*2-'
274x
>27
x-9
! 3
ix+3 / 2x+l
4 >V(0.36) 6
1
> (64)*"'
(15J (0.216) 4 >V(0.36) 6 Rpta. <-<»--—>
(16) (4')**-' >(64)*-' Rpta. <-°°,-l >u<l,->
© [(0.3)(x"1,(x-2) ]x~3 > [(0.09)*"-* /'~9 Rpta. V x e R
I 2j+I ,
(18) 3J(0.00032)5jr"2 <V(0.2) 2 Rpta. <—,+oo>
+f^-X+fV
19) X+M—) ^ r+-2/(0.2)-v"'! Rpta. <-oo.-3>u<-2,-l|
Sistema de Números Reales
233
i i ■/^T
(^(0.16)^=í .^(0.0256)^) 2 < ^0.004096
^(0.008)*-' > *-Jj(.0.04Y+3 Rpta. < 1,2> u [3,5]
x+^¡(0.04)2x-1 > ^/(0.2)2jr-' Rpta. <-3,0>u[-,3]
■>2a-3wo4-j:>
2
+^f(0.0016)**3 >*-^(0.2)4jc+1 Rpta. <-—,-2>u<5.-h»>
171
*-$4*I*Zx+fé* Rpta. <-l,2]u<5,+oo>
^(O.Ol)^2 < ^(O.l)2*-3 Rpta. <-3,-1 > u [3,+°°>
'^(OM)2*"1 >{¡(.OÍ)2"-1 Rpta. <-3,0>u<-,3>
(—)r(-)4j[2+1<(-)x+2(—)x2_:u Rpta. <-<~-2]u[--,+~>
250 5 5 625 2
r (i} 2 - r(^r Rpta" <"3'3>
)2-,r"2 Rpta. <-oo,-3>u<-2,-l]
(2^X2-')<J^5^ R <_h+00>_{_!}
25x-\ r 2
15^"' < ^/(0.2)^+1 @ (0.1)*_3<10x+3
2^(0.00032)*+2 < -^(i)3-1 (g) [(0.5)*2 .(0.5)6]('2-3) > ^^
234
Eduardo Espinoza Ramos
V. Resolver las ecuaciones siguientes:
© .. +y]x2-2x-4>2 Rpta. <-°°,1->/5>u<1 + >/5,°°>-{1±>/6)
y]x2-2x-4
© Jx + 5 + y¡x<5 Rpta. [0,4>
© ^x + yl2x-l +^Jx-yl2x-Í<y/2 Rpta. [-,1>
© Jx-9tfx + ll&>0 Rpta. [0,+oo>
© x+2< 3/x3+8 Rpta. <-2,0>
© n/T^4->/8^>1 Rpta. [4, ]
© y]j¿*-l<Jx+l Rpta. [1,2>
© >/2a-9<3-x Rpta. «})
© Jto-J-HJ-to+W^ Rpta [26]U {18}
®(x-4)Jx*-2x+2 ^„ _ .
^ ^- <0 Rpta. <-oo,4]
a2+2
(Íí) >/jc2-2x-15>a + 1 Rpta. <-oo,-3]
^2) >/3x-6>-V4jt-12 Rpta. [3.+<~>
(l3) >/5jt-3->/Jt::T>0 Rpta. [l,+«»
í¡) yff^-^>0 Rpta. [64.+00>
v->^ x-l
Jx^6x-Jx > 3/JTT^ Rpta. [7,8> u {0}
8-x
Sistema de Números Reales
235
C26)
\M -3 + >/6-a < Vjc-Í-1 Rpta. <3,+oo>
yJx-l + Jx-3>Jx + l Rpta. <—,5]
© £^±£31^ Rpta. p. 84+16^]
^
@ y¡4-yf[^-yÍ2^>0 Rpta. [-2, 13 5]
(20) V.v2-14.v + 13>A-3 Rpta. <-°°,3]
O Vx2 + 3x+ 4
y¡2\+^x2-4
> 0 Rpta. <-oo,-2] u [2,+°°>
V-a + 2 < V-4* + 2 + V-9a + 6 Rpta. <-«>,-]
^625-a-2^aJ^4(a+4)8(a-2 -l)2
a-3 -2*2 -a +2
<0 Rpta. [-25,-2] u<-l,l>u {25}
>/T-l
lx + 6 I a+2
yfx + l Rpta. <1,2>
Rpta. <-oo,-6] u <1,2>
Va2-14a-13<a + 1 Rpta. <-,l]u[13,+<~>
4
Gn) ^^ZlJ^ < 0 Rpta. <-oo,-4] u <2,3>
Vat-4x + 3
(S) J^±2S,-4 Rpta.*
^^ V2-^/A:+4
236
Eduardo Espinoza Ramos
1 x x-2
-< <-
x-2 x + 4 x + l
|jc2-9|-2jc
|jc + 5|+5
<0
4 x + 4 „
< <2
x — 4 x — 4
3Jt+4(3*"4-l)<3x-81
^2-3ffll>o
[>/2Í->/7^4
' ~3X-4 >Jc2-2Jc-29
>-Vl6-j
¿
32-2*
jc+2
>>£
\4JZ~2-:
>x-5
^-s V 2-Vx-4
(37) Vjc2-6jc + 5+Vjc2-7jc + 10<0
@ Vjc2-6jc + 5+Vjc2-7jc+10>0
(S) yJ4-^x + U<^Jx + 5
y¡x2 -Ix-rtjx* -6x2 +9x)
(jt-l)4(jt-2)5
<0
Rpta. <8,+°°>
Rpta. <>/ÍO-l, l + >/ÍO>
Rpta. <18,+o°>
Rpta. <0,4>
Rpta. <-5,-2] u [4,5>
Rpta. [-4,-1] u {4}
Rpta. [0,4]
Rpta. [-4,-2] u [2.3]
Rpta. x = 5
Rpta. <-o°,l] u<5,+°°>
Rpta. [-5,3]
Rpta. [-3,0] u <2,5]
41
x + 4
>¿c
Rpta. <2,4]
Sistema de Números Reales
237
@ >/3-3.v<>/21 + 4jt-.v2 Rpta. [-2.1J
(£) Vv:-A-12U-5)(2jt2-3jt-2)<0 Rpta. <-o°.-3] u [4,5]
(53)
x2-16
V24-2jc-jc2
9-x
-^
9
-VÍ3 + 5 >/Í3-5
@ j4-JTx~-j2^x>0 Rpta. <-15,"VU+ >U<^£Z£,1]
>0 Rpta. <-oo,-4>
^ Vl-v-4|-|x-l|
(4ó) yjx2-3x + 2>2-x Rpta. <2,+oo>
@ ^2~^"^>^nó Rpta. [7,8>u{0}
<1 Rpta. [-6,3]
®£í_?- + líL^ > o Rpta. <_2,i> u [3,5]
V Jt + 2 Vjc + 1
/Vjc* 5jc V3jc >jc_10 Rpta. [8,9>^{OJ
(Sí) N *" ,4jC 5 >x-6 Rpta. [-5,-3] u {5]
(S) ylx2-x-l2(x-5)(2jc2 - 3jc - 2) < O Rpta. <-°°,-3] u [4,5]
K/jT+.v 2+3^ t 1 Rpta_ <_2^_2]^[l,2V2>
(54) N^' S-t + 4 2>JC_6 Rpta. [-2,0] ^ [4,5]
238
Eduardo Espinoza Ramos
V *-l V* + 3
Vjc2 —jc + 1 <y]4-x
y¡x2+l(x2-4x + l)
Rpla. <-3,l>u[4,5]
Rpta. <S,yÍ3>
4x + 4
>0
Rpta. <-l,2->/3 >u<2 + >/3,°o>
Jx + 3+Jx-6 >^6-x
60) ^
2a-15>*+1
@ >/2x-1+V3jc-2>>/4jc-3 + >/5jc-4
V2jc + 3 + V3x-2->/2x+5<>^í
W \ 3-a/7^2 jc-8
62} Jx2-2x-y]x2+4x>2
yfx^l + ylx-2
^7-yfx
£0,a>0
3.35. VALOR ABSOLUTO.-
a) DEFINICIÓN.- Al valor absoluto del número real x denotaremos por | x |, y se
define por la regla.
1*1=
x si jc>0
-x si x<0
Ejemplo.- |7| = 7, | -7 | = -(-7) = 7
b) PROPIEDADES DEL VALOR ABSOLUTO.-
(7) | a | > 0, V a e R (?) | a | > a V a e R
® |a| = |-a| © |ab| = |a||b|
(5) if^ifL^bítO (£) | a + b | < | a | + | b | (desigualdad triangular)
Sistema de Números Reales
239
Demostraremos la 6° propiedad, las demás dejamos para el lector.
\a+b\2= \(a + b)2 \=(a + b)2 =a2 +2ab + b2
<|a|2+2|fl||¿| + |¿|2=(|fl| + |¿|)2
|o+fc|2<(|c| + |¿|)2 entonces .-. |a + b |< |a| +|b |
336. PROPIEDADES BÁSICAS PARA RESOLVER ECUACIONES E|
INECUACIONES DONDE INTERVffiNE VALOR ABSOLUTO.
(T) ja | = 0 t=> a = 0
(i) I a I = b t=>[b>0A(a = bv a = -b)]
@ |a| = |b|«a = bva = -b
M) Sí b > 0, entonces:
i) |a|<b <=> -b<a<b ¡i) |a|<b t=> -b<a<b
(¿) Si a, b e R se verifica
i) |a|>be=>a>bva<-b ¡i) |a|>b<=>a£bva<-b
0 i) \at4a1 ü) \a\2 = a2
La demostración de estas propiedades dejamos para el lector.
Ejemplo.- Resolver la ecuación 14x + 3 | =7
Solución
14x + 3 I = 7 t=> 4x + 3 = 7 v 4x + 3 = -7
5
C=> X= 1 V JC ——
2
Luego para x = 1, x = — son soluciones para la ecuación dada.
240
Eduardo Espinoza Ramos
Ejemplo.- Resolver la ecuación |2x + 2| =6x-18
Solución
|2x + 2| = 6x-18 « [6x-18>0 A (2x + 2 = 6x-18 v 2x + 2 = -6x + 18)]
<=> [x > 3 A (x = 5 v x = 2)]
—£
2 3
Luego la solución de la ecuación es x = 5.
Ejemplo.- Resolver la ecuación | x — 2 | = | 3 - 2x |
Solución
| x - 2 | = | 3 - 2x | <=> x-2=3-2xvx-2 = -3 + 2x
<=> x = — vx=l, la solución es: {1,—}
|4jt + l|-|jt-l|
Ejemplo.- Hallar el valor de la expresión: , síxe<0,l>
Solución
|4jc + 1| =
1
4jc + 1 , x> —
-4jc-1 , x<
4
|x-l| =
JC-1 , JC>1
1-JC , Jt<l
si x e <0,1> => | 4x + 1 | = 4x + 1 , | x — 1 | = 1 — x
|4jc + 1|-|jc-1| 4jc + 1-(1-.v) 5x _
Luego: J '—! = = — = 5
x xx
|4jc + 1|-|jc-1|
= 5, para x e <0,1>
Sistema de Números Reales
241
Ejemplo.- Resolver la ecuación |2x + 2| = 6x-18
Solución
|2x + 2| = 6x-18 <=> [6x- 18 >0 A (2x + 2 = 6x- 18 v 2x+ 2 =-6x + 18)]
« [x>3 A (x = 5 v x = 2)]
2 3 5
Luego la solución de la ecuación es x = 5.
Ejemplo.- Resolver la ecuación | x - 2 | = | 3 - 2x |
Solución
I x-2 | = |3-2x| t=> x-2=3-2xvx-2 = -3 + 2x
<=> x = — vx=l, la solución es: {1,—}
3 3
| 4jc +11 — I jc — 11
Ejemplo.- Hallar el valor de la expresión: , sí x e <0,1>
Solución
|4jc+1|
4jc + 1 , x>
-4jc-1 , x< —
4
\x-l\=\
1 ' [l-jc , x<l
si x e <0.1> => 14x + l | = 4x + 1 , | x - 1 | = 1 - x
|4jc + 1|-|jc-1| 4jc + 1-(1-jc) 5jc .
Luego: = = — = ->
x xx
|4jc + 1|-|jc-1| _ ..
.-. !—! 1 = 5, para xe <0,1>
242
Eduardo Espinoza Ramos
Ejemplo.- Resolver la inecuación | 2x - 5 | < 3
Solución
|2x-5|<3 <=> -3<2x-5<3 <=> 2<2x<8
<=> l<x<4 <=> x£ <1,4>
Luego la solución es x e <1,4>
2x-5
Ejemplo.- Resolver la inecuación: | 1 < 3
x-6
Solución
,2jc-5. 2jc-5 2jc-5 2x-5
| 1 < 3 <=> -3 < < 3 <=> -3 < A < 3
jc —6 jc —6 jc —6 jc —6
5x-23 _ A jc-13 _
<=> >0 A >0
x-6 jc-6
<=> (5x - 23)(x - 6) > 0 A (x - 13)(x - 6) > 9, x * 6
_w N/ N/ N/
a : ^ ± ^ ± v : i¿ ±
23/5 6 6 13
23
jce<—oo,— >u<6,+°°> A <—t»,6>u<13,+oo>
-O O
-e e e-
23/5 6 13
O O--
La solución es: jce<—°°,— >u<13,+°°>
5
3.37. MÁXIMO ENTERO.-
Si x es un número real, el máximo entero de x representaremos por [| jc |] y es el mayor
de todo los entero menores o iguales a x, es decir:
Sistema de Números Reales
243
[| jc |] = máx {n e Z / x > n}
Para calcular el máximo entero de un número real x, se observa todos los enteros que se
encuentran a la izquierda de x (o que coinciden con x, en caso que x sea entero) y el
mayor de todos ellos es el máximo entero [| x |], por ejemplo:
1 1 1 h-^H 1 1 ►
-1 0 1 2x3 4 5
De donde [|x|] =2
Ejemplo.- Hallar [|3.7|]
<•—I 1 1 1 H»H 1 ►
De donde [| 3.71] = 3 _., Q 1 2
Si x se encuentra entre dos enteros consecutivos de la forma:
3 3.7 4
+—e-
-e-
-e-
n+1
Entonces:
[|x|]=n <=> n<x<n + l, neZ
Ejunplo.- Sí [| x |] = 5 <=> 5 < x < 6
[|jc|] =-5 <=> -5<x<-4
NOTA.- Como se podrá observar siempre se toma él número entero más próximo a la
izquierda.
OBSERVACIÓN.- Por definición de máximo entero se tiene:
[|x|] = n <¡=> n < x < n + l, neZ
<=> x € [n, n+l>, ne Z
[|x|] = n <=> xe [n,n+1>, ne Z
Ejemplo.-[| x |] = -4 « -4 < x < -3 =* x e f-4.-3>
Ejemplo.-[| x |] = 2.15, es absurdo, puesto que todo máximo entero es un numero entero.
244
Eduardo Espinoza Ramos
3.38. PROPD2DADES DEL MÁXIMO ENTERO.-
(T) [| x |] € Z, por definición Q2) [|x|] = x <=> xeZ
(5) V x e R, [| x |] < x, por definición (?) [| x |] < x < [| x |] + 1, V xeR
© 0<x-[|x|]<l, VxeR ® [|[|x|]|] = [|x|], VxeR
@ [|x + n|] = [|x|] + n, neZ
En efecto: Sea [| x |] = k, keZ, entonces k < x < k + 1
=> k + n<x + n<(k + n)+l
=> [|x + n|] = k + n = [|x|] + n
(D [|x|]<n » x<n+l, neZ (5) [|x|]<n o x<n, neZ
(lO) [|x|]>n <=> x > n, neZ, xeR @ [| x |] > n <=> x > n + 1
@ Vx,y€R, síx<y « [| x |] < fly |]
@ [|x + y|]>[|x|] + [|y|]
Í[|jc|] = wi m<x<m+\
[|>|] = « n<y<n + l
m + n<x + y<(m + n) + 2
entonces [|x + y|] = m + n o m + n+1
por lo tanto [| x + y |] > m + n .-. [| x + y |] > [| x |] + [| y |]
(H) Sí neZ+ => [|nx|]>n[|x|]
En efecto: Sea [|x|] = m => m < x < m + 1
=> nm < nx < mn + n
=> [|nx|]>nm .\ [| nx |] >n [| x |]
Sistema de Números Reales
245
15) SixeRy neZ+, entonces [|Ü^|] = [|-|]
(16) Si a y b e Z, x e R, entonces se cumple:
i) a<[|x|]<b=>a<x<b+l ii) a<[|x|]<b=>a<x<b
iü) a<[|x|]<b => a + 1 < x < b
Ejemplo.-
ClJ Resolver la ecuación [| 3x + 1 |] = 2
Solución
12 12
[|3x + l|] = 2 => 2<3x+l<3 => -<x<— entonces *e [-,— >
3 3 3 3
(2) Resolver la inecuación [| 5x |] < 3
Solución
3 3
[|5x|]<3 => 5x<3 => x<- .: jre<-°°,->
5 5
© [|2x|]<x
Solución
Sí x < 0 => 2x < x => [| 2x |] < 2x < x
Es decir [| 2x |] < x .\ 5, =< -°°.0 >
Sí 0 <x < - => 0 < 2x < 1 => [I 2x I] = 0 < x
2
Es decir [| 2x |] < x .". S2=<0,->
2
Si x>- => 2x>l => [|2x|]>l esdecir: [|2x|]*x .: Si=<¡>
2
.-. 5=<-°°.0>u<0,->
2
246
Eduardo Espinoza Ramos
© [|2x|]<[|4x|]
Solución
P P 1 P
Sea [|4x|] = P <=> P<4x<P+l => — <2x<— + -< — + 1
2 2 2 2
P P
=> [12x I] = — a -eZ
2 2
[| 2x |] < [| 4x |] => — <P => 0<— => 0<P => 0<[|4x|] => 4x>l
.-. x>— => Cs = [—,+»>
4 4
© [|-5x|]<[|x|]
Solución
Sí
1 Í0<5x<l ,
0<x<- => i => -1 <-5x<0 => [ -5x ] = -l y -1<0
5 \üx|] = 0
.-. S.=<0,->
1 5
Sí x>- => -5x<x => [| -5x |] < [| x |] .". 52=[-,-H»>
.-. S = <0,-h»>
© [|x-l|]<[|x|]
Solución
Sí x > 1; supongamos que: [| x |] = k
=> [|x-l|] = k-l <k=[|x|] de donde 5, =[1,-k>°>
Sí x < 1, entonces [| x - 1 |] < 0 a [| x |] < 0
entonces [| x - 1 |] < [| x |] :. S2 =< -°°,1 > .\ S = R
© ([|x|]-2)(x-2)(x+l)>0
Solución
Sistema de Números Reales
247
a) Si x < 2 => [| x |] - 2 < O, luego resolveremos
-(x - 2)(x + 1) > 0 es decir (x - 2)(x + 1) < 0 de donde 5, =< -1,2 >
b) Sí 2 < x < 3, entonces [| x |] - 2 = 0 de donde 52 = <¡>
c) Si x > 3 => [| x |] - 2 > 0 luego resolveremos (x - 2)(x + 1) > 0
53 = [3.+00 > n(< -oo,-l > u[2,+oo >) .-. 53 = [3,-t-°° >
.-. S = <-1.2>u[3,+°°>
® (jc3 -l)(x2 + lyj\\x\]-x >0
Solución
[| x |] - x > 0, entonces [| x |] > x, pero por definición se tiene: [| x |] < x,
V x e R => [| x |] = x e Z
Luego resolveremos (jc3 — l)(x + 1)>0 => x>l .: S — Z+
® ([|x-2[|x|]|])(x-l)(x+l)>0
Solución
[|x-2[|x|]|] = [|x|]-2[|x|]=-[|x|]
i) Si x < 0, => -[| x |] > 0, entonces resolveremos
(x-l)(x+l)>0 /. 5, =<^o,-l]
ii) Si 0<x<l => [|x|]=0 entonces 52=[0,1>
iii) Si x>l => [|x|]>0, entonces resolveremos (x-l)(x+l)<0 53={l}
.-. S = <-oo,-l]u[0,l]
® 11^11 = 2
v-y -v + 3
Solución
248
Eduardo Espinoza Ramos
Se conoce que [|x|] + n <=>n<x<n+l
jc+2
jc+3
x+2 _ „ , 1
= 2 <=> 2< —<3 *=> 2<1
x + 3 x + 3
<3
@
$=> 1<—■—-<2 <¿> 1< A <2
jc + 3 jc + 3 x + 3
<=> 1 + <0 A 2+ >0
jc + 3 x + 3
x+4 „ . 2jc + 7 „
<=> <0 A >0
x+3 x+3
<=> [(x + 4)(x + 3) < 0 A (2x + 7)(x + 3) > 0], x*-3
<=> jce[--4,-3> A ¿ce<-°°,— >U <-3,+°°>
2
Luego la solución es: xe [—4,— >
iíí!z!,,>.
Resolver la inecuación [| 1] > 4
Solución
Aplicando la propiedad siguiente: Sí y e Z, [| x |] > y <=> x > y
4e Z,
1*1-1
>4 » i^bi>4
|x | - 1 > 20
*=> | x | > 21 <=> x>21 V x<-21
La solución es: x 6 <-°°,-21] u [21,+°°>
Resolver la inecuación [|| x \ —2x |] = 0
Solución
Sistema de Números Reales
249
Por definición de máximo entero se tiene:
|||.v|-2.v|] = 0 *=> 0<|x|-2x<l « 2x<|x|<l+2x
ahora por la propiedad transitiva (a<b<c í=> a<b A b<c)
se tiene: 2x < | x | < I + 2x <=> 2x < | x | A | x | < 1 + 2x „.(1)
A ■ I I í *' X-0
ademas se conoce que: | x \ =<
[-x, x<0
Io Si x>0 =>|x| = x reemplazando en (1) se tiene:
2x<0Ax<l+2x =>x<0Ax>-l => xe<-l,0]
La primera parte de la solución es: xe [0,+°°> A <-l,0] => x = 0
2o x < 0 => | x | = -x reemplazando en (1) se tiene:
2x <-x A -x < 1 +2x => x <0 A x>— => xe<—,0]
3 3
la segunda parte de la solución es: x e <-°°,0> A <—,0] => xe<—,0>
3 3
Por lo tanto la solución de [|| x|-2x|] = 0 es: *e<—,0>u{0}=<—,0]
3.39. INECUACIONES LOGARÍTMICAS.
Para el estudio de las inecuaciones logarítmicas es necesario recordar lo siguiente:
En primer lugar la definición de logaritmo es decir:
logfcA = x «. N=bx, N>0 a b>0
En segundo lugar las propiedades del logaritmo
a) log,,AB = logbA + logbB b) \ogh — = \ogbA-logbB
250
Eduardo Espinoza Ramos
c) \ogbAR=n\og,,A
e) logfcl = 0
d) \ogh<ljA=-logbA
n
f) log„¿7 = l
g) log„ N =
logfcO
En tercer lugar se observa la gráfica y = logfc x cuando b > 1 y 0 < b < 1. También
dentro del campo de los números reales, sólo tiene logaritmo los números reales positivo:
ahora gratificamos la ecuación y = logfc x .
y = 'ogbx
Y'
0
y = 'ogbx
/i *
1 *
b>l
2 X
Al observar la gráfica se tiene los siguientes casos:
Io CASO.- Cuando la base es b > 1. en la gráfica podemos observar:
i) Los números mayores que 1 tiene logaritmo positivo.
ii) Los números entre 0 y 1 tiene logaritmo negativo, entonces para cualquier
JC|.x2 e R+ se tiene
Síb>l y 0<a,<x2 <=> logfc x, <logfc x2
De donde deducimos las relaciones siguientes:
a) Sí x > 0, b > 1; N e R => logfc x>N <=> x>b"
b) Six>0, b> 1: Ne R => loa, x<N <=> x<bn
Sistema de Súmeros Reales
251
2 CASO.- Cuándo la base es 0 < b < 1, en la gráfica podemos observar:
i) Los números mayores que 1 tiene logaritmo negativo.
¡i) Los números entre 0 y 1 tiene logaritmo positivo, entonces para cualquier jc, , x2 de
R+ se tiene:
Sí 0 < b < 1 y 0 < X, < x2 <=> logt x. > logfc x2
de donde deducimos las relaciones siguientes:
Síx>0, 0<b<lyNeR=> log,, x> N *=> 0 < v < b V
Síx>0, 0<b<lyEeR=> \ogbx<N <=> x>bN
OBSERVACIÓN.- Resumiendo, para la solución de las inecuaciones logarítmicas se
obtiene de la siguiente manera:
. ,1
\ogba>\ogbc <=> , :n^b<l
{a>c si b > 1
a<c si 0<l
Ia>bc si b > 1
a<b' si 0<¿<1
Ejemplo.- Resolver las inecuaciones siguientes:
(T) log;(2x + 4)>log2(5x + 3)
Solución
Calculando el campo de existencia de los logarítmicos dados
3 3
2x + 4>0 a5x + 3>0 de donde x >-2 a x>— .: U =<—,-H>
5 5
como la base es 2 > 1. entonces se tiene:
1 1
log,(2jt + 4)>log2(5jc + 3) <=> 2x + 4>5x + 3=> x<- => x6<-°°,->
252
Eduardo Espinoza Ramos
3 13 1 3 1
La solución es: jre<—.-k» >n<-°°,— >=<—_ > .-. S =<—,—>
5 3 5 3 5 3
© log,(2x + 5)<-2
3
Solución
Calculando el campo de existencia del logaritmo
2x + 5 >0, entonces x>—— de donde U =<—,+«>>
2 2
como la base es — < 1, entonces se tiene:
3
log,(2jc + 5)<-2 <=> (2x + 5>(-)~2 => 2x + 5>9=>x>2 => x 6 <2,+°°>
3
Luego la soluciones: xe<—,+°°>n<2,+°o>=<2,-K>o> .". S = <2,+°°>
® log2(|jc-2|-l)>l
Solución
Calculando el campo de existencia del logaritmo
| x — 2 | - 1 > 0 => | x — 2 | > 1 => x-2>l v x-2<-l => x>3vx<l
de donde U = <-°°, 1 > u <3,+°°>
como la base es 2 > 1, entonces se tiene:
log2(|x-2|-l)>l => |x-2|-l>2'
=> | x — 2 | > 3 =>x-2>3vx-2<-3 => x>5 vx<-l
x e <-°o,-l> u <5,+°°>
La solución es: x 6 (<-°°, 1> u <3,+°o>) n (<-■»,-1> vj <5,+°°>)
.-. S = <-<*>,-1 > u <5,+«>>
Sistema de Números Reales
253
© ,og>(^l)>l
jc + 15,
>1
Solución
jc+15
El logaritmo dado está bien definida sí x > 0 y x & 1 además > 0
x—1
Luego el campo de existencia es U = <l,+°°>
, ,-«c + 15^ , jc + 15 , .v+15 «...
log^í )>1 => >x => x>0, de donde
x-l x—1 A-l
x + \5-x2+x „ jc2-2.v-15 _. J , , (jt-5)U + 3) „
>0 => <0 de donde -<0
x-l x-l x-l
de donde x e <1 ,+°°> u <1,5>
La solución es: x e <l,+°°>n (<-°°,-3> u <1,5>) = <1,5> .\ S=<1,5>
{5J Resolver la inecuación log1/3(2v + 5)<-2
Solución
Aplicando la propiedad siguiente: x>0, 0<b<l, N e R, logbAr<7v" <=> x>bN
5
para nuestro caso 2x + 5 > 0 => x> —
logi/3(2jc + 5)<-2 <=> 2x + 5x-r2
2x + 5>9 « 2x>4 => x > 2 , la solución es: x e <2,+°°>
(ó) Resolver la inecuación log2(| x-2|— 1) >1
Solución
Aplicando la propiedad siguiente: x > 0, b > 1. N e R, \ogh x> N <=> x>b
para nuestro caso se tiene | x - 2 | - 1 > 0
254
Eduardo Espinoza Ramos
| x-2 |> 1 <=> x-2>l vx-2<-l <=> x>3vx<l
log2(|jt-2|-l)>l <=> |x-2|-l>2
| x - 2 | > 3 <¡=> x-2>3vx-2<-3 <=> x>5vx<-l
La solución es x e <-°o,-l> u <5,+°°>
3.40. EJERCICIOS DESARROLLADOS.-
Resolver las siguientes ecuaciones:
(T) U2+2|=2jc + 1
Solución
Por definición de valor absoluto | x2 + 2 | = x2 + 2 ... (1)
AI reemplazar en | x ~ + 21 = 2x +1 se tiene:
x2+2 = 2a+1 dedonde a2-2jc + 1 = 0
(a-1)~ =0 entonces x=l. Luego la solución es: x=l
© |jc2-jc-6|-jc + 2
Solución
\x2-x-6\=x + 2 <=> [x + 2>0 A(x2-x-6 = x + 2 v x2-x-6 = -x-2)]
<=> [a>-2 A (a2-2x-8 = 0 v x2=4)]
<=> [x>-2 A (a = 4, a =-2 v a = ±2)]
l
La solución es el conjunto {-2,2,4} „ o a
© a2-2|a-1-3 = 0
Sistema de Números Reales
255
Solución
La ecuación dada se expresa así:
2|jc|=.í2-3 *=> [jc2-3>0 A (2jc = ;c2-3 v 2jc = -*2+3)]
<=> Lv2>3 A ía-2-2x-3 = 0 v a-2+2jc-3 = 0)]
<=> (x>VJ V a<-V3) A (jc = 3,-1 Vx=-3,1)
-* 1 1 1 1 1 1 ► La solución es {-3.3)
-3 ->/3 "I 1 >/3 3
0 |x-4| = |x-2|
Solución
Aplicamos la propiedad: |a| = |b| <=> a = b V a = -b
| x — 4 | — | x — 2 | *=> x-4 = x-2 Vx-4 = -x + 2
<=> -4 = -2 V 2x = 6
<=> <[> V x - 3, La solución es x = 3
© | x - 2 | = | 3 - 2x |
Solución
| x — 2 | = | 3 — 2x | «=> x-2 = 3-2xVx-2 = -3 + 2x
<=> x = — V x=l, La solución es: {1.—}
3 3
0 2|v+21-|2A+1-l|=2A+,+l
Solución
Aplicando la definición de valor absoluto
,x+2h{ *+2 • **:2 I2--.NÍ2"'-,1 x>-'
\-x-2 , -v<-2 1_2'+' . a<-1
256
Eduardo Espinoza Ramos
~-\ i \ /
+ Sj - M +
|jc + 2| =-jc-2
para x < -2 => ■!
[12x+i -l|=l-2xtl
reemplazando en la ecuación 2'*+2' -12JC+I -11 = 2JC+I +1, se tiene:
2'x~2 - (1 - 2x+l) = 2 *+1 +1. simplificando 2~x~2 =2 =>-x-2=l=>x = -3
Luego x < -2, la solución es x = -3
í|x + 2| =x + 2
Para -2<x<-l -, ,
12^-11 =1-2X+I
reemplazando en la ecuación 2x+2 - (1 - 2 x+1) = 2 *+1 +1, simplificando
2JC+2 =2 => x + 2 = l => x = -l, como -2<x<-l entonces x = -l no es solución
| jc + 2 i =x + 2
Para x>-1 _ ,
|2*+I-1|=2*+1-1
reemplazando en la ecuación se tiene: 2X -{2X -1) = 2JC+ +1, simplificando
2X+2 = 2X+2 => x + 2 = x + 2,VxeR
Luego la solución para x > -1 es R A [-1,°°> = [-l.°°>
Por lo tanto la solución de la ecuación es: x = -3 y [-l,+°o>
Q 1^-91 + 1^-41=5
Solución
A la ecuación |jc2-9| + |jc2-4| =5 expresaremos en la forma:
|x + 3||x-3| + |x-2||x + 2| = 5 ...(1)
Sistema de Números Reales
257
', >2 «3 <4 "5
1 1 1 1 ►
-3-2 2 3
analizando en cada intervalo /,, i = 1, 2, 3, 4, 5
¡\x + 3\=-x-3 ; \x-3\=3-x
Para x <-3 => i , , -"(2)
[|a + 2|=-jc-2 : \x-2\=2-x
Reemplazando (2) en (1) se tiene: (-x - 3)(3 - x) + (-x - 2)(2 - x) = 5
efectuando y simplificando x~ —9 => x = ± 3
luego como x < -3 la solución es: x e <-°°,-3> A {± 3} = <|>
í|* + 3| =x + 3 ; I a- — 31 =3-x
Para -3<x<-2 =» V ' ...(3)
[|jc + 2| =-x-2 ■ \x-2\ =2-x
Reemplazando (3) en (1) se tiene: (x + 3)(3 - x) - (x + 2)(2 - x) = 5
efectuando operaciones y simplificando: 9-a-" —4 + a-' =5 => 5 = 5 es valido Vxe R
luego la solución es:
[-3,-2> n R = [-3.-2>
Í|a- + 3| =jc + 3 ; I a- — 31 =3-j:
Para -2<x<2 =» V ' ..-(4)
[|jc + 2| =x + 2 ; \x-2\ =2-x
Reemplazando (4) en (1) se tiene: (x + 3)(3 - x) + (x + 2)(2 - x) = 5
9-a-2+4-a-2=5 => x = + 2
luego la solución es: [-2,-2> n {±2} = {-2}
Í|a- + 3|=a+3 , |a-3|=3-a-
para 2<x<3=>-¿ , , „, „ ••■(•»
y [|a- + 2|=jc + 2 , |a-2| =a-2
reemplazando (5) en (1) se tiene: (x + 3)(3 - x) + (x + 2)(x - 2) = 5
efectuando y simplificando 5 = 5 es valido V x e R
258
Eduardo Espinoza Ramos
®
Luego la solución es: [2,3> r> R = [2,3>
d ^ f|jc + 3|=jr + 3 , |jr-3|=jr-3
Para x>3 => i
[\x + 2\ = x + 2 , | a -21 = x-2
Reemplazando (6) en (1) se tiene: (x + 3)(x - 3) + (x + 2)(x - 2) = 5
(6)
efectuando y simplificando: x = 9
Luego la solución es:
x = ±3
[3,+<~>n{±3) = {3}
Por lo tanto la solución de la ecuación es: [-3,-2> v {-2} u [2,3> v {3}
[-3,-2] u [2,3]
(D |jc2-4|=-2jc + 4
Solución
Por la propiedad: | a ] = b <=> b > 0 A (a = b v a = -b)
|jc2-4|=-2a + 4 <=> -2jc + 4>0 A (jc2-4 = -2a + 4 v x2 -4 = 2jc-4)
<=> x<2 A (x2+2jc-8 = 0 v .v2-2jc = 0)
<=> x<2 A ((x + 4)(x-2) = 0 v x(x-2) = 0)
<=> x < 2 A (x = 2, -4 vx= 0,2)
Luego [-4, 0, 2) son las soluciones de la ecuación dada
|jc2+3| = |2jc+1|
Solución
Por la propiedad: |a| = |b| <=> a = bva = -b
|x2+3| = |2j: + 1| <=> jc2+3 = 2a- + 1 v jc2+3 = -2jt-1
<p> jc2-2a + 2 = 0 v jc2+2jc + 4 = 0
<=> <|> v <|> = <|>
La solución es él <|> puesto que V x e R, a~-2a + 2>0. jT+2a+4>0
Sistema de Números Reales
259
(10) | v-+6a- + 1|=2jc + 6
Solución
Por la propiedad: |a| = b <=> b > 0 A (a = b v a = -b)
| y2+6a + 1|=2a + 6 <p> 2jc+6>0 A [x2 + 6a + 1 = 2a + 6 v x2 +6jc + 1 = -2jc-6]
<=> x>-3 A (a2+4a-5 = 0 v jc2+8jc + 7 = 0)
<=> x>-3 A (x= 1,-5 v x = -l.-7) I
*—i—i—!—i—i—►
Luego la solución es {-1,1} .. _ „ . .
-I -o -o -1 1
© ,££,-.
Solución
,3a + 8. „ 3a + 8 d „ 3a + 8 d 3
=8 <=> = 8 V = -8, para a*-
2.V-3 2a-3 2a-3 2
3
<=> 3x + 8 = 8(2x-3) v 3x + 8 =-8(2x-3), x*-
<=> 13x = 32 v 19x = 16, Luego la solución es: x = —, x - —
13 19
@ 11 x | - S | = 2x - 3
Solución
11 x | - 5| = 2x - 3 <=> 2x-3>0A(|x|-5 = 2x-3v|x|-5 = -2x + 3)
<=> x>- A (|a|=2x + 2 V |a|=-2x + 8)
3
Como x>- => |x| = x=>x = 2x + 2vx = -2x + 8
2 ' '
8 8
=> x = -2 v a = -, por lo tanto la solución es x- —
3 3
260
Eduardo Espinoza Ramos
(13) |jc-4|2-5|jc-4|+6 = 0
Solución
Factorizando se tiene: (|x-4|-3)(|x-4|-2) = 0
<=> |x-4|-3 = 0 v |x-4|-2 = 0
<=> |x-4| = 3 v |x-4| = 2
<=> (x-4 = 3vx-4 = -3)v(x-4 = 2vx-4 = -2)
<=> x = 7vx=lvx = 6vx = 2, las soluciones son: {1,2,6,7)
(14) Hallar el valor de la expresión: ' si x e <2,5>
Solución
Por la definición de valor absoluto se tiene:
7
4j: + 7 si x>— ( _
4 . . je-7 si x> 7
|4* + 7| = 4 ; \x-l\=\
„ . 7 \l-x %\ x<l
-Ax — 1 si x<— l
l 4
ahora para x e <2,5> <=> |4x + 7| = 4x + 7, |x - 7| = 7 - x
|4jc + 7|-|jc-7| 4jc + 7-(7-jc) 5x c
comoxe<2,5> <^> l— - = - = — = 5
—! - = 5 si x e <2,5>
15 x + 41 _ 14 + 2x I
Hallar el valor de la expresión: si x e <0,3>
Solución
Aplicando la definición de valor absoluto
Sistema de Números Reales
261
|5a+4| =
5a + 4 si x> —
-5a-4 si x<
; 14 + 3jc | =
4 + 3jc si x>
3
—4-3* si x< —
3
ahora para x e <0.3> <=> | 5x + 4 | = 5x + 4, 14 + 3x | = 4 + 3x
|5jc + 4|-|4-3jt| 5jc + 4-(4 + 3x) 2x „
como x e <0,3> <=> i !—' = = — = 2
|5a- + 4|-|4 + 3jc|
(16) Hallar el valor de la expresión:
= 2 si x e <0,3>
|5jc-20|-|3jc-20|
si x e <-3,-2>
Solución
Aplicando la definición de valor absoluto
, Í5jc-20 si x>4
|5a-20|= . ; 3jr-20 =
|20-5jc si a-<4
3jc-20 si x> —
3
™ -, 20
20-3jc si x< —
3
ahora para x e <-3,-2> <=> |5x - 20| = 20 - 5x, |3x - 20| = 20 - 3x
|5jc-20|-|3jc-20| 20-5jc-(20-3jc) _ 2x
como x e <-3,-2> <=>
|5jc-20|-|3jc-20|
x
= -2 si x e <-3.-2>
[YJJ Resolver la inecuación |a"-4|<5
Solución
Por la propiedad: |a|<b <=> -b<a<b donde b > 0
| r-4|<5 <=> -5<jr2-4<5
262
Eduardo Espinoza Ramos
<^> —1 <jc2 <9 <=> -l<rnr<9
<=> xeRn-3<x<3
<=> -3 < x < 3, Luego la solución es
x e <-3,3>
|9-*2|>3
Solución
Por la propiedad | a | > b <=> a > b V a < -b
|9-jc2|>3 «• 9-jc2 >3 v 9-jc2 <3
<=> x2 <6 v x2 >12
<=> -yf6<X<yf6 U JC > VÍ2 U JC <-VÍ2
I
r~"
i
i
■ ^ -\/F \/íF \/Í2"
Luego la solución es:
l^l<2
x + l
xe< -00--VÍ2] u [-a/ó,a/ó] u [VÍ2,+°° >
Solución
Mediante la propiedad: |a|<b <=> -b<a<b
| 1<2 <=> -2< <2
A: +1 * +1
3jc — 3 3x — 3
<=> -2< A <2
x + ]
x+l
5jc —1 a-5 „ ,
<=> >0 A <0, para Xit-1
a- + 1 jr + 1
« (5x-l)(x+ 1)>0 A (x-5)(x+l)<0, x*-l
Sistema de Números Reales
263
VV1
-\ I
^vl
^cv
1/5
*e<-°°,-l >U <—,+oo > A jce<-l,5>
O
-1
O-
1/5
5
-O
Luego la solución es
xe<— ,5>
Resolver: e [-,1]
x + 4 3
Solución
jc + 4 3
3 * + 4
1<x+4<3
-3 < x < -1, luego la solución es x e [-3,-1 ]
Resolver I 1 > I 1
1 2jc-1 x-2
Solución
i 5 . . 1 . 5 1 1 „
> <=> > para x * ,2 se tiene
2.V-11 x-21 |2jc-1| \x-2\ 2
5|x-2| > |2x - 1|, elevando al cuadrado 25(jt-2)2 > (2jc-1)2 efectuando y simplificando:
\ / --
7v2-32jc + 33>0 <=> (7x- U)(x-3)>0
HL
11/7
Como (7x - 1 l)(x - 3) > 0, se toma los intervalos donde aparecen el signo (+), es decir
<-oo,—]u[3,+°°>. Luego la solución es:
7
Ui ,1 í1!
< -~, —] U [3, +°o > -{-}
7 2
264
Eduardo Espinoza Ramos
(24
Resolver la inecuación: | jc — 11~ +21 jc -11 -3 < 0
Solución
Completando cuadrados se tiene:
(|jc-1|+1)2 <4 <=> -2<|x+ 1 |+ 1 <2
<=> -3 < | x + 1 | < 1
<=>-3<|x+l|A|x+l|<l <=> RA-l<x+l<l
<=> R A -2 < x < 0,
la solución es x e <-2,0>
@ |x-3|2-3|jc-3|-18>0
Solución
Factorizando se tiene:
(| x - 3 | - 6)(| x - 3 | + 3) > 0 <=> (|x-3|>6A|x-3|>-3)v(|x-3|<6A|x-3|<-3)
<=> (|x-3|>6AR)v<J>
<=> (x-3>6vx-3<-6)AR
<=> (x > 9 v x < -3) A R
<=> (x < -3 v x > 9)
La solución es x e <-°°,-3> kj <9,+°°>
libido
2-jc
Solución
Por la definición de valor absoluto | x |=
x, x > 0
- jc, jc < 0
Si x < 0 => | x | = -x, reemplazando en la ecuación dada se tiene
Sistema de Números Reales
265
-JC-1
>0
x + l
>0
x+l
2-x x-2
de donde (x + l)(x - 2) = 0
> 0 <=> (x + 1 )(x - 2) > 0, para x * 2
x-2
r, =-1, r2 -2
vv
JC + 1
como > 0 la solución es la unión de los intervalos donde aparecen el signo (+) es
x-2
decir:
xs (<-°°,-l]u<2,+°°>) A <-°°,0]
.-. xe <-oo,-l]
-(I)
Si x > 0 => | x | = x, reemplazando en la ecuación dada se tiene
jc —1 „ Jt-1 „ ,
>0 => <0 de donde
2-x
x-2
\ /
je—1
Si <0 <=> (x-l)(x-2)<0 para Xit2
x — 2
Entonces (x - 1 )(x - 2) = 0 => r¡ = 1, r2 = 2
x-l
Como <0 => la solución es: xe [0,+°°> A [1,2> = [1,2>
x-2
.-. xe [1,2>
(2)
La solución de la inecuación es la unión de (1) y (2) es decir: x e <-<»,-1] u [1,2>
| —í— | < | —^— |
2a + 3 3a + 7
Solución
I—1— I Él—5— I
2a:-+3 3jc + 7
1 K_ 1*1
|2jc + 3| |3jc + 7|
7 3
Para .v * —, —, se tiene: | 3x + 7 | < | x 11 2x + 3 |
(1)
266
Eduardo Espinoza Ramos
\ l \ /--
_J¿ ± V.
^Z
-7/3
-3/2
a) si a<—
3
|3r + 7| =-3.v-7
U\=-x
|2a + 3| = -2a-3
... (2)
reemplazando (2) en (1) se tiene: -3x- 7 < (-x)(-2x - 3) de donde 2x~ + 6a +7 > 0
pero como V x e R, 2x~ + 6a: + 7 > 0
la solución es:
>AR= <
7 3
b) Si —<x<— =>
3 2
|3a + 7|=3a+7
|a|=-A
| 2a+ 31=-2a-3
(3)
reemplazando (3) en (1) se tiene: 3x + 7 < -x(-2x - 3) de donde 2x - 7 > 0
2.t2-7>0 => (>/2a:+V7)(>/2a:-V7)>0
ZY
^
.n/7
n/7
7T
7 3 ¡7 ¡7
La solución es: <—,— > A (<-«>,-,— 1 U [,—,+°°>)
3 2 \2 \2
-!-#
c) Si —<a<0
7
|3a+7| =3a + 7
|a|=-a
|2a + 3| =2v + 3
... (4)
Sistema de Números Reales
267
reemplazando (4) en (1) se tiene: 3x + 7 < (-x)(2x + 3) de donde 2t~ + 6a + 7 < 0
como V x e R, 2a" + 6 v + 7 > 0 entonces la solución es:
<—,0> A (¡>-(¡>
d) Si x>0
|3.v + 7| = 3a + 7
| a | = x
|2a + 3| = 2a + 3
... (5)
reemplazando (5) en (1) se tiene: 3x + 7<x(2x + 3) => 2x"-7>0
2a2-7>0 <=> (V2a + n/7)(^a-V7)>0
\ /-■
+ V
"V2 \/§
La solución es:
[0,+°°>n
«^.-^ju^.-»^.
+oo>
7 i ¡T fT
luego la respuesta es: < -<*>,— > u < —'-W—1 u U—■
+oo>
i-U| -
Solución
Íjc-1, sia>1
Aplicando la definición de valor absoluto: | x — 11 = < ; | x \ ■
11—JC, SÍ X<1
x, si a > 0
—A, SÍ A < 0
a) Si x < 0
■4 (D-
0
| JC— 1 | =1-A"
-©-
... (2)
reemplazando (2) en la inecuación dada. > 0
l-(--v)
1 + A
•>0
como >0 <=> x+ 1 >0. x?t-l <=> x>-l
Y + l
268
Eduardo Espinoza Ramos
La solución para este caso es: <-°°,0> A <-<*>,-1 > = <-1,0>
b) Si 0<x<l => \\
1 jt-lM-*
... O)
reemplazando (2) en la ecuación dada:
A>0 => -^— >0 <=> (2x-l)(x-l)>0 parax* 1
1-jt
a—1
ahora mediante el criterio de los puntos críticos se tiene:
\ / \ /
+ V : \L ±_
1/2 1
La solución para este caso es:
iai)>Ajf<-»,-] V <l,+oo» = [0,-]
2 2
c) Si x > 1
1*1=-*
| jc — 11 =jc-1
(4)
reemplazando (4) en la inecuación dada:
x-l-x 1
> 0 <=> > 0 <=> x - 1 > 0 para x * 1 de donde x > 1.
1-jc x-l
La solución para este caso es:
[l,+°°> A <l,+oo> = <l,+oo>
Por lo tanto la respuesta es:
< -1,0 > u [0,-1 u < 1,-k» > = < -1,-1 u < l,+«> >
@ |2a2 -3jc-9|<2|jc2 -2jc-3|
Solución
Se conoce que:
2a-2 - 3a— 9 = (2jc + 3X* - 3)
(1)
[x¿-2x- 3 = (a + 1)(a-3)
Reemplazando (1) en la inecuación dada
Sistema de Números Reales
269
|2a:-3a-9| <2|.v2-2a-3| <=> | (2x+ 3)(x-3) |<2 | (x + l)(x-3) |
de donde: |2x + 3||x-3|<2|x+l ||x-3| para x * 3
se tiene: | 2x + 3 | < 2 | x + 1 |, elevando al cuadrado:
4.v2 +12a +9 < 4a2 +8jc+4 => 4x < -5 de donde:
.v < — — ; luego la solución es:
4
xe<-°°—>
4
(28) |--2|<11
Solución
Mediante la propiedad: |a|<b<=>-b<a<b __
|--2|<11 «- —11 < —— 2<11 «- -9<-<13
mediante la propiedad: a<b<c <=> a<b Ab<c
-9<-<13 «- -9<- A -<13
9a + 1 13a-1
<=> >0 A >0
"V
+ v
-1/9 0
0 1/13
La solución es: .ve (<-«>,— >u<0,-B»>)n (< -°°,0>u<—,+°°>)
9 13
1 1
jte<—°°, — >u<—,+o°>
9 13
m) |3x + 2|<|2x-l| + |x + 3|
Solución
270
Eduardo Espinoza Ramos
Aplicando la desigualdad triangular
V x e R: | 3x + 2 | = | (2x - 1) + (x + 3) | < | 2x - 1 | + | x + 3 |
Por lo tanto la solución es: V x e R
4jr+2j:+3-9>0
Solución
Se conoce: 4v = 22x, 2r+3 = 8.2*
4*+2A+3-9>0 <=> 22a+8.2^-9>0
22a+8.2*-9>0 «. (2A+9)(2t-l)>0
(2*+9)(2A-l)>0 <=> (2A+9>0 A 2l-l>0) V (2A+9<0 A 2A-1<0)
<=> (2*>-9 A 2r>l) V (2r<-9 A 2r<l)
<=> x e (R A [0,+°°>) V (0 A <-°°,0])
<=>
x e [0,+°°>
Demostrar que: Sí | x - a | < R => x e [a - R, a + R]
Solución
Si |x-a|<R=>-R<x-a<R
=» a-R<x<a + R
=> x e [a - R, a + R]
~ „, i . i i 2jc + 3 , 7
Demostrar que: Si | x + 4 | < 1 => | 1 < —
jc-1 4
Solución
A 1 -' 2X+3 1 f 2X+3
A la expresión expresaremos en la torma:
x-l
jt-1
= 2 + -
x-l
(1)
Sistema de Números Reales
271
Como | x + 41 < I => -I<x + 4<1 sumando -5 se tiene:
=> -6 < x - 1 < -4 inviniendo
— < < —, multiplicando por 5
4 x-l 6
5 5 5
=> —< <— sumando 2
4 x + l 6
3 „ 5 7 7
=> —<2 + <-< —
4 x-l 6 4
3 2x+3 7 ,2jc + 3. 7
=> —< <— => < —
4 jc-1 4 jc-1 4
12£Z1!±Í<0
x2-2x-3
Solución
Por deñnición de valor absoluto: 12x: — 11=
2x-\ , x>
1-2* , x<
t
1/2
Sí jc<- => |2x-l |=l-2x
2
Reemplazando en la inecuación dada:
1-2jc + 1 2jc—2
-<0 <=> . >0 => (x-l)(x-3)(x+l)>0
^-2jc-3
(jc-3(jc + 1)
para x * -1,3- Mediante el criterio de los puntos críticos se tiene:
^li
-1
272
Eduardo Espinoza Ramos-
La solución para este caso es: x:e< —<»,— > A (< —1.1] U < 3,+°° >)
xe<-l,— >
2
Si x>-
2
|2x - 1| = 2x - 1, reemplazando en la inecuación dada
2a-1 + 1
x" -2jc-3
<0 <=>
U-3)(jc+1)
<0 => x(x-3)(x+1)<0, x*-l,3
Mediante el criterio de los puntos críticos se tiene:
-\ / \ /--
_V ± \L
~ii^
La solución para este caso es: jte [—,+°° > n (< -°°.-l > u [0,3 >)
•"• XG^,3>
Por lo tanto la solución de la inecuación es:
xe< -1,— > u í—,3 >=< -1.3 >
2 2
Solución
A la inecuación expresaremos en la forma
\x2-x\-2 n |jc||x-1|-1 „
' '—>0 <=> ' " ,—■—>0
|a|-1 |jc|-1
Ahora aplicamos la definición de valor absoluto.
x si x>0
UN
-x si jc<0
\*-l\=
{x-l, si jc> I
1-jc. si x<l
(1)
\ /
+ x/
para x<0 =>|x| = -x, | x — 1 | = 1 — x
... (2)
Sistema de Números Reales
273
-a(1-a)-2
-.v-l
>0
x — x — 2
*+l
<0
U-2)(jr + l)
x + l)
<0
, (a-2)(jc + 1) „ „ „
para x * 1, - - < O => x - 2 < 0. x * -1
x + l
=> x e <-°°.-1>u<-1,2]
Luego la solución para este caso es: x e <-°°,0> n (<-eo,-l>u<-l,l])
x e <-°°,-l> u <-l,0>
para 0 < x < 1, => |x| = x, | x - 1 | = 1 - x
reemplazando (3) en (1) se tiene:
...(a)
... (3)
-v(l--v)-2
.v-l
>0
x — x' — 2
>0
x--x+2
x-l
-<0
pero como VxeR, a ' - .* + 2 > 0
1
x-\
<0 => x-l <0
x * 1 => x < 1, luego la solución para este caso es: xe fO,l> n<-°°,l> = [0,1> ... ((1)
para x > 1 =>|x| = x, | x — 1 | = x — 1
reemplazando (4) en (1) se tiene:
«*-¡)-2>o =» x2-*-2>o =* (v-2)u + 1)>o
x-l x-l v-l
=> (x-2)(x+l)(x-1)>0, parax* 1
Ahora por el criterio de los puntos críticos se tiene
___v
x e [l,+«»n(l-l,l>u [2.+°°>)
V + V
_U ±_
-1
x e [2,+°°>
... (Y)
274
Eduardo Espifioza Ramos
Por lo tanto la solución general de la inecuación es: la unión de (a), ((1) y (y)
x e <-£»,-1> u <-1.0> v^ [0,1> u [2,+°°>
'4*-yl-5,o
Solución
A la inecuación dada expresaremos en la forma.
'4"2i-5,0 =* '*»*-4,'-5*o ...a)
\ /
+ \1
0
x2 -4x—S
-\rv-
4
... (2)
0
Aplicando la definición de valor absoluto:
. . \ x si x>0 . . \x-4 si a>4 + v
*H n 'lA~4H,i a n
[-*■ si x<0 [4-x si x<4 U
Para x<0 =>|x| = -x,|x-4| = 4-x
-jí(4-je)-5
Reemplazando (2) en (1 j se tiene: > 0
l+x x+l
U-5)(t + l)^0 ^ X-5>0 => x>5
*+l
La solución para este caso se tiene: xe <-°°,0> n [5,+°°> = <)) ...(a)
Para0<x<4 =>|x| = x, |x-4| = 4-x ...(3)
Reemplazando (3) en (1) se tiene:
-*(4-*>-5>o ^ 4"-"2-5>o =» ilzi£±l>o
1-x l-jc x-1
•> 1
como Vxe R, jT-4a + 5>0 => >0 => x - 1 > 0, x * 1
JC-1
entonces x > 1, por lo tanto la solución para este caso es:
Sistema de Números Reales
275
xe [0,4> n <l,+°o> .-. xe <1,4>
para x>4 =>|x| = x,|x-4| = x-4
reemplazando (4) en (1) se tiene:
... (P)
... (4)
v(a-4)-5
>0
az-4a-5
>0
a"-4a-5
>0
l-.v l-.v jt-1
para x * 1. (x - 5)(x+l)(x-l) >0, ahora mediante el criterio de los puntos críticos se tiene:
■\ / \ /
v + i¿_
_sz +.
la solución para este caso es: x e [4,+°°> r> ([-l.l>u [5,+°°>)
x e [5,+°°>
La solución general es la unión de (a), ((1), y (y)
.-. x e <1,4> u [5,+°° >
?-:
8a- 19 - jc2 I
<0
Solución
A la inecuación dada se puede expresar en la forma:
\2-x\-x2
8t-|9-.v2|
<0 <=>
l-x-21-
8a-| a2-91
< 0 (propiedad del valor absoluto)
\2-x\-x2 „ |*-2|-a2
<0 <=> —'- '— — <0
(7)
8a-19-a2 |
8a-|a- + 3||jc-3|'
... (1)
ahora aplicando la definición de valor absoluto.
|a + 3
"l-v-3 .
A>-3
x < -3
|a-2|
-_o
z-x
x>-\ i,-3i =í*-3 •x>-3
x<2 |3-a , a<3
276
Eduardo Espinoza Ramos
© © ©—►
-3 2 3
Sí x < -3, => | x + 3 | = -x - 3. | x - 2 | = 2 - x, | x - 3 | = 3 - x ... (2)
Ahora reemplazamos (2) en (1) se tiene:
T - o 2
2—x—x „ 2—x—x
<0 => <0
8jc-(-jc-3)(3-jc) 8jc + (3 + jc)(3-jc)
2-x-x2 ,„ x2 + x-2
<0 <=> — <0
8x + 9-x2 x2-8x-9
U + 2)U 1)^0 ^ (x + 2)(x-l)(x-9)(x+l)<0. xíí-1,9
(jc-9)(jc + 1)
\ / \ / \ / \ /
+ M - V + y - \/ +
-2-11 9
de donde xe [-2.-l>u [l,9>
La solución para el caso en que x < -3 es: x e (f-2,-l> u [1.9>) n <-°°,-3> = <]>
para - 3 < x<2 => | x + 3 | = x + 3, | x - 2 | = 2 - x, | x - 3 | = 3 - x ... (3)
reemplazando (3) en (1) se tiene:
2-*-x2 <0 ^ 2-v-"2<o => x;+x-2>o
8jc-(jc + 3)(3-jc) 8x-9 + x2 x2 + 8jc-9
(.v+2)(.r-l)
(x + 9)(x-l)
>0 <=> (x + 2)(x- l)(x + 9)(x- 1)>0, para x * -9,1
\ i \ / --
U + 2)(x + 9)(jt-l)2 >0, x*-9,l ± V I V. ±-
-9 -2
de donde xe <-°°,-9> u [-2.1>u <l.+oo>
La solución para este caso en que -3 < x < 2 es:
Sistema de Números Reales
277
x e (<-°°,-9> u [-2.1 > u < 1 ,+<»> n [-3.2>
.-. xe [-2,l>u<l,2>
para 2 < x < 3 => | x + 3 | = x + 3, | x - 2 | = x - 2, | x - 3 | = 3 - x
reemplazando (4) en (1) se tiene:
y-2-jT
8a--(y + 3)(3-a:)
-<0
x-2-x¿
8v-9 + jc2
como a-~-a-+2>0 VxeR
<0
1
x- -x + 2
x2+8x-9
•>0
>0
1
.t-+8jr-9
>0
1
U + 9)U-1)
a-+8a-9
>0 => (x+9)(x-1)>0, x*-9,l
+ v
-9 1
de donde x e <-°°,9> u <l.+°o>
La solución para este caso en que 2 < x < 3 es:
xe <-°°,-9>u<l,+°°>n [2,3> = [2,3>
para x > 3 => |x + 3| = x + 3, |x-2| = x-2, | x - 3 | = x - 3
reemplazando (5) en (1) se tiene:
8v
x-2-x2
-(a: + 3)(.v-
como a" — .v4
— <0
-3)
2>0,
=>
Vx
X-
8a--
=>
-2-
-x~
K~
+ 9
1
<0
x -x+2
x2-%x-9
<0
1
a-8x-9
de donde x e <1.9>
<0
x--8a-9
<0 « <x-9)(x + 1)<0, x*9.-l
... (a)
... (4)
- (P)
... (5)
\ /
id
-1
278
Eduardo Espinoza Ramos
La solución para este caso es: x e <-l,9> n [3,+°o> = [3,9>
... (Y)
la solución es: x e [-2,1> u <1,2> u [2,3> u [3,9>
.-. xe [-2,1>u<1,9>
jc + 3
x+l
| <4x + 3
Solución
|^—| <4x + 3 <=> (4x + 3>0 A -4x-3<^-<4x + 3)
x+\ x+l
i ^ . , A , * + 3 x + 3 .
<=> (x>— A (-4x-3< A <4.v + 3))
4 x+l x+\
<=> (x>-- A (:^+4x + 3>0 A 4x + 3-^í^>0))
4 x + l x+l
3 A 2x^+4x + 3
<=> (x>— A (
4 x + l
>0 A
x(2x + 3)
x + l
>0))
« (jr>_2 A (_L>0 A i^±^>0))
4 x + l x + l
puesto que 2x + 4x + 3 > 0
T"
-3/4
A
-> A <*-
44 fc-
-3/2 -1 0
r"
-é-
o--
-3/4
-*> A
-3/2
o
-1
-o
0
o--
xe<—,+°o> A <0,+°o>=<0,+°°>
4
.*. x e <0,+oo>
Sistema de Números Reales
279
v jc-3
>
| .v2 + 41 x2 + x + 4
Solución
Aplicando la propiedad: V x e R, x~ > 0 de donde
a2+4>0 A jc2+jc + 4>0, entonces
| a:" + 41 = x" + 4 luego reemplazando se tiene:
,. r —3
— >^ <=> a-(a2+a + 4)>(a:-3)(a2+4)
jT+4 x +x + 4
<=> a-3 +A-2 +4a> a-2 -3a2 + 4a-12
« a2 > -3 => V x e R
JA||x|-|-i2_Miz£MT+v^I^0
V |r + 2|+l | jc-l l-f-4
Solución
.i
.HH-'-i2_l|i-v|-3|+^ emonces
\ |v + 2|+l l.v-ll+4
v|lAl-.|-12j|l-vl-3l^ A 9 _^Q
|a + 2|+1 |a-1|+4
,|U-l|-12^||l-*|-3| A 9_^Q
¡a + 2|+1 |a--1|+4
además como '— > 0, entonces:
|a-1|+4
,11,1-11-12^11^1-31^ A ^ dedonde
;a+2|+1 |a-I|+4
X*'A'~ '~ " > 0 A a < 9 como I x + 2 | + l > 0 entonces
|x+2|+l
280
Eduardo Espinazo Ramos
x|x-l |- 12>0 A x<9
Por definición: | x \
(1)
f x, x>0
l~\-x, x<0 '
entonces
six<0=> x|-x-l|-12>0 => x|x+l|-12>0
:>-l
como |jt + 1|
_J x + l , x>-l
~\-x-l , v<-l
x e <-oo,0> = <-oo,-]> u [-1,0>
si x e <-oo,-l> => | x + 1 | = -x - 1 como
x| x+ 1 |- 12 >0 =* ~x2-x-l2>0 => a2+* + 12<0
=> 3 x e R, tal que a2+a + 12<0; por lo tanto <j>
si xe [-1,0>=> |x+ 1 | = x+ 1 => x(x + 1)- 12 >0
a2+a-12>0 => (x + 4)(x-3)>0
-4 3
Luego x e [-1.0> A <-°°,-4] U [3,+ °°> = <j>
Ahora si x>0 => x|x-l|-12>0 Ax<9
=> x(x-l)-12> 0 Ax<9
=> a2-a-12>0 A v<9 => (x-4)(x + 3) >0 Ax<9
+ V
i2vl
-3
x e <-°°,-3] u [4,+°°> n x < 9
x e <-°°.-3] u [4.9]
A
.-. como x > 0 n x e (<-°o,-3] u [4.9])
.-. x e [4,9]
Sistema de Números Reales
281
i ' i i x i
v + 1 jT+2jc + 1
Solución
l—í—-l < l^—^—l « r-LTT<rMF
x + l x~+2x + \ |-v + l| |x + l|2
1 U| Ijtl
< parax^-1 => \<r^—— de donde
|jt + 1 |jc + 1|2
|jm-1|
|x+l|<|x| para x*-l => x2 +2x + l<x2, x*-l
2x+l<0, x*-l => a< —, x*-l
2
/. jre<-oo,-l >u<-l,— X
2
x + 3 x + 3
Solución
Completando cuadrados se tiene: | 12 -21 1 +1 > 1 de donde
x+3 x + 3
^1|-1)2>1 « |^|-1>1 v |^±1|-K-1
x+3 x+3 x+3
i x + l , _ , jc + l . „
*» | >2 v | -|<0
x + 3 x + 3
I rl>2
X + 3
x + l .v+1 „
> 2 v < -2
x + 3
x + 3
x + l „ „ jc + 1 _ _
2>0 v + 2<0
x+3 x+3
x + 5 3x + 7
<0 v <0
jt + 3
x + 3
282
Eduardo Espinoza Ramos
—\ r
+ v
u
—\ /
+ V
-3 -7/3
A-e<-5,-3>u<-3,—>
3
x
Solución
[|1Z3£|] = 2 « 2<^<3
x x
2<1Z^<3 « 2<^í A ^<3
jc xx
« 2-^<0 A ^-3<0
5*-5 6jc-5
<=> <0 A >0
/ y / -
+ \¡ - \i +
/ v /---
_± i¿ : i¿ +_
0 5/6
U
jce<0,l] n jre<-o°,0>u<—,+<»>
6
o--
O 5/6
O
1
-•
La solución es:
xe<-,l]
6
© fe11'0
Sistema de Números Reales
283
Solución
[|—í—1] = 0 <=> 0<—j£—<1
2Vv-l 2Vjc-1
0<—¡í—<1 <=> 0<—j¿— A —í—<1 ...(1)
2V.V-1 2Vjc-1 2V*-1
la expresión esta definida para 2>/x-l*0, x>0
2\/Jv*l => 4**1 => a
* -
1
Por lo tanto analizaremos en: [0,— > u < — ,-H» >
4 4
si a>— entonces en (1) se tiene: a>0 A x<2-Jx-\
v>0 A x-2-Jx + l<0
a>0 A (a/a-1)2<0 =>xe<))
sí0<a<- => *<0 A x>2yfx-l => x<0 A (^-l)2^
4
=>x<0Ax>0 -•. x = 0
© [|--v|]>0
Solución
[|-jr|]>0 => [|-Jr|]>l <=> -x>l
como -x > 1 => x < -1 =>xe <-«,-1 ]
@ [|-x|]<0
Solución
[| -x \] < 0 <=> -x <0 => x > 0 => x e <0,+o°>
284
Eduardo Espinoza Ramos
(46) [|2jr-l|] = -3
(47
Solución
[[2jc —1|J = —3 <=> -3<2x-l<-2
<=> -2<2x<-l
<=> -1<jc<— => jce[-l,— >
2 2
[|VÍ + 1|] = -1
Solución
< 0. La solución es <]) puesto que vjc +1 > 0
(48) [|*2-2a-8|] = -
Solución
Como -íZ => no tiene solución.
2
© [|V*-[|*l]D = o
Solución
[| Vjc-[|jc|] |] = 0 <=> 0<Va-[|a|]<1
<=> 0<jc-[|jc|]<1
<=> [|jc|]<jc<[|jc|] + 1 , Vxe R
(50) [|*2|]<15
Solución
[|a-2|]<15 => [1 jc2 |]< 16 => x2<16 => -4<x<4
/. x e <-4,4>
286
Eduardo Espinoza Ramos
i) si x > O
2x <2 « * ,<!
-l\x\Y
-l\*\Y
-^ i<o => fzf±íNl<0 =» JNL<o
*-[|*|] *-[|*|] Jc-[|x|]
11 m11,,^0 ** «1*11^0 A *-[|*|]<0) V ([|*|]<0 A *-[|*|]>0)
x-[\x\]
<=> ([|*|]>0 A *<[|*|]) V ([|x|]<0 A [|*|]>.x)
<í=> (x>0 AxeZj) V(x<lA«í)
<í=> (jceZ„) V (jc<1)
<í=> x e <-°o,l> .-. x e <0,+°°> n (<-°o,l>) = <0,1>
ii) Si x<0, ieZ~ => |x| = -x
0
-*-[|*|]
<2 =>0<2 => x<0, jceZ
.. xe Z u<0,l>
/. x e Z"
Demostrar que V x e R; | x |> ^/[| x31]
Solución
Por propiedad: V x e R, [| x |] < x < [| jc |] +1
Sixe R => Jt3e/?,
LuegoV x3efi: [|jc3 |]<a:3 <[|x3 |] + 1 => [|jc3 |]<jc3
además V x e R: x < | x | => x3 < \ x3 \
Luego (2) en (1) se tiene: V x e R, [|x3 \]<x3 < \x\3 . => [|x3 |]< | x|3
..(1)
..(2)
m¿\]<\x\
\x\> ^[|^|],
Vxe R
Sistema de Números Reales
287
(55) [|a[|*|]|] = a
Solución
Se conoce que [| x |] e Z entonces como [| x [| x |] |] = x e Z
Es decir x e Z => [|a|] = agZ => a{|a[]6Z
Luego: [|a[|x|]|] = a => [|a.a|] = a
|| v2 \\ = x => x2 = x => x(x -1) = 0 => x = 0, x = 1
por lo tanto [[ jc[| .v |] |] = v => x e {0,1
(56) [||a|+1|]<2
Solución
Aplicando la propiedad [| x + n |] = n + [| x |], neZ
I||*|+l|]<2 ^ [||a||] + 1<2 ^ [\\x\\]<\
como íIIaI 1<1 => x I < 1 => -1 <x < 1
x e <-!,!>
57
,l^i|H3
Solución
Aplicando la propiedad [| x |] < a => x < a + 1
'£
3a-+
-9a
+2I1£3
l-4(3v-
3a-2
+Vo
-
-2)
=>
3a
3a
\ -
+ 1
-2
<4 =>
3\ + I-
3\ + l
31-2
12a + 8
-4<0
3a-2
<0
a-I
3a-2
3a-2
<0
> 0, aplicando el criterio de los puntos críticos.
288
Eduardo Espinoza Ramos
60
\ f
+ *
2/3
1
jc-1 2
Como la inecuación es > 0, entonces la solución es: x e < —°°, — > u < 1, +°° >
3jc-2 3
@ [|jc2-2jc-2|]<13
Solución
Por la propiedad: si [| jc |] < a => x<a
[|jc2 -2a:-2|]<13 => jc2-2jc-2<13 => x2-2x + \<\6
(jc-1)2<16 =>-4<x-1<4=>-3<x<5 .-. x e <-3,5>
® 2[|jc + 1|]2-11[|jc|]<^1
Solución
Como [|jc + 1|] = [|a-|] + 1 entonces: 2([|jc|]+1)2 -11[|jc|]<-4 desarrollando
2[|jc|]2 +4[|x|J + 2-11[|jc|]<-4
2[|jc|]2-7[|x|] + 6<0 =* (2[|*|]-3)([|*|]-2)<0
Z^Z
3/2
como (2[| jc |] - 3)([| jc |] — 2) < 0 entonces: [|jc|]e[-,2] => [|jc|] = 2 => 2<x<3
x e [2,3>
[| 2jc-| jc | U = jc
Solución
Se sabe por propiedad que si [|a|]eZ A [| a |] = a => aeZ
Luego como [| 2jc- ] jc 11] = jc =>xeZ=>2x-|x| = x
De donde | x | = x => jte Zq
:. La solución es {0,1,2....,n}
Sistema de Números Reales
289
(61
Hhrii-J^ioG
2x V x
Solución
Calculando los valores de x en donde la expresión esta definida, es decir:
>0 A a>0 de donde x e [l,+°°>
ahora calcularemos [| — |] cuando xe [l.+°°>
2x
como x e [ I .+»> => x > 1 => 2x > 2 inviniendo
0< — <— => [| —1] = 0, por lo tanto:
2x 2 2x
mo v?"<n/i
lo/I =» |o-J— |<VÍ
^
*-i
<A => A -A+1>0
como a~-a + 1>0. VxeR entonces para x e [1,-H»>, a~-x + 1>0
Por lo tanto la solución es: x e [l,+°°>
(62) logI/3(2.v + 5)<-2
Solución
Aplicando la propiedad: logaA<fo síO<a<l <=> x> a
1,-2
logI/3(2\+5)<-2 <=> 2t + 5>(-)
2x + 5>9=>2x>4=>x>2 => xe <2,+°°>
(63) log,(3Y + 2)-log2(l-2v)>2
290
Eduardo Espinoza Ramos
Solución
loga*>fo,a>l <=> x>a A jc>0
log2 (3* + 2) - log2 (1 - 2*) > 2
log,(^)>2
\-2x
,3* + 2x „ 3jc + 2
log2(——)>2 « —-
\-2x \-2x
>0 A
3a+2
1-2*
>2¿
3* + 2 „ A 3* + 2 A n
<=> <0 A 4>0
2x-\
1-2*
3* + 2 Hjc-2 n
<=> <0 A <0
2*-l
2*-l
I2»¿
_>¿ +.
\ r
+ V
_5¿ +.
2/3 1/2
2/11 1/2
2 1. 2 1
*e<—,—> A *e<—,—>
3 2 11 2
2 1
xe<—,—>
11 2
log1/5(2jc~ -3jc + 5)<log|/5(jir + 2a + 1)
Solución
loga P(x) < log0 Q(x) <=> P(x) > Q(x) A (P(x) > 0 A Q(x) > 0), 0 < a < 1
log1/5(2jc -3* + 5)<log1/5(jc + 2*+l), 0<-<l
\7
2x2 -x + 5>x2+2x + ] A (2jT-3jc + 5>0 A a-z+2* + 1>0)
a" -5v + 4>0 \ x *-I
Sistema de Números Reales
291
(x-4)(x- 1)>0 n x*-l
xe <-°o,l>u<4,+oo> x^-1
\ /
+ V
x e <-ooj-i> u <-l,l> u <4,+«o>
logi(^)>l
x-l
Solución
_tf ±.
x + 3
La variable x debe cumplir x > 0 A > 0
x-l
O
-3
0
O--
.x + 3.
Como x > 1 aplicamos la propiedad: log^í ) > 1
x-l
x+3 i
> x = x
x-l
v + 3
jc —1
jc + 3
JC-1
-x>ü
x+3—x +x
~l
>0
x~ — 2jc - 3
<0
(jc-3)(jc+1)
<0
_X +.
x-l x-l
x e <-°o,-l>u<l,3>
La solución es: xe <l,+°°> n (<-°°,-l>u<1.3>)
x-9
Hallar el menor de los números M tales que: | 1 < M , sí x e [2,5]
x-6
Solución
x e <1,3>
^—^ = 1 —, como xe [2.5] => 2<x<5
v-6 x—6
-4<x-6<-l =>
.v-6 4
292
Eduardo Espinoza Ramos
I<__L<, ^ I+i,£z^2
4 x-6 4 x-6
4 jc-6
M= 2
067) Hallar el mayor número M de tal manera que: > M , si x e [-2,2]
^-^ jc3 + 27
Solución
jc2 + 6a: +14 = (jc + 3)2 + 5 entonces: si x e [-2,2] => -2 < x < 2
l<x+3<5 => 1<(jc + 3)2<25 de donde 6<U + 3)2 + 5<30
6<jr+6jc + 14<30
- (1)
como xe[-2,2] =>-2<x<2 => -8<jc3<8
19<jc3+27<35
±<_i_<±
35 jc3 + 27 19
... (2)
_, , , „ 6 jT+6jc + 14 30
de (1) y (2) se tiene: —< = <
35 x
3+ 27 19
|*2+6jc + 6| 6
.x3 + 27 ~35
M =■
35
(68) Hallar el número mayor de m y el número M tal que para todo xe [— ,1] se cumple:
x+2 w
m < < M
: + 3
Solución
A la expresión escribiremos en la forma: = 1
x+3 x+3 x+3
como Jte [-,1] => — <x<l sumando 3
Sistema de Números Reales
293
7 112
— < x + 3 < 4, inviniendo — < < — , multiplicando por - 1
2 4 x + 3 7
2 1 ^ !
— < <— sumando 1
7 x + 3 4
.2,1,1 5 x+2 3
1 — <1-—— <1— entonces — < < —
7 x + 3 4 7 .v + 3 4
de donde
5 M 3
m—— y M-—
7 4
3.41. EJERCICIOS PROPUESTOS.-
Hallar los valores de x que satisfacen a las siguientes ecuaciones.
© | 2x + 3 | + 4 = 5x
Rpta. x = —
3
@ | 3x - 1 | = 2x + 5
Rpta. 1--.6}
©
©
©
©
©
©
r= 1^-161
x -1 x + 4
i 'i-i
.v -1 x
U-4)2-2 |jt-41-15 = 0
| 2x + 9 | = x - 1
|jc2-3r-7|=3
|-«|,3
\ + 4
Rpta. {-}
Rpta. {2.-2 +2>/2}
Rpta. {-1.9}
Rpta. <)>
Rpta. {-1,-2,4,5}
Rpta. {-5,-2}
(?) | 3x + 1 | = 7 - x
Rpta. M.-}
294
Eduardo Espinoza Ramos
©
®
©
©
©
©
©
©
®
®
®
©
©
®
©
®
®
| 4 - 8x | = | x -1 2x + 1
|3x-5| + x-7 = 0
15x - 3 | = | 3x + 5 |
| 2x - 6 | = 14 - 5x |
|6x + 3| = |18 + x|
|3x-l | = |5x-15|
| 5x + 3 | = 3x - 1
\\x2-l\-x\=x
|2x-3| + 2 = |x-6|
|3x-l|-|x + 2|=l
| jc —4 |2 -5| x-4|+6 =
2|jc2 -2|+5 = 6|2x2 -
| 6x + 3 | = | 18 + x |
3||* + 1|-4|2-5||jc+1
||x|-3| = |3x + 2|
||*+2|-l|2-5||* + 2
|2x-3|-l=|x-3|
II
0
-3|
|-4|=2
-l|-6 = 0
Rpta.
Rpta.
Rpta.
Rpta.
Rpta. |
Rpta. {
Rpta. <|
Rpta.
Rpta.
Rpta.
Rpta. {
Rpta.
Rpta.
Rpta. {
Rpta.
Rpta. |
Rpta.
7 3
-1,3}
,->
2 10
1 3'7}
-3,3}
2,7}
>
[1.-1 + V2, 1 + V2}
.-..1.
4.2.
1,2.6,7}
[±y¡2. ±2}
-3.3}
-7,-3,1,5}
4 4
-9,5}
H¿
Sistema de Números Reales
295
(27) ||jr-5.v + 15|-*2+8|=3A + 9 Rpta. {-.16}
@ |x+l| + 2|x-2| = |x-8| Rpta. {-|,H}
@ 3|x+l|-2|x-2| = 2x-l Rpta. {-.8}
(30) 2||.v-5|+2|2-11|| x-5|-2|+12 = 0 Rpta. {3,7}
II. Hallar el valor de las siguientes expresiones:
®|12 + 5a|-|12-4a| , „
——! - sí xe <1,3> Rpta. 9
|7a+10|-|5i-10|
—i si x e <0,1> Rpta. 6
2a
|9a + 8|-|2a-8| , D . 11
—!—! ! si x e <1,2> Rpta. 11
|2a+3|-|3-a| síxe<Q>1> Rpta>3
|6v + 4|+2|2-3a| . d . 1
! ! si xe <2,3] Rpta. 1
12a
|6a + 32|-4|8-a|
5a
|4a + 1|-|a-1|
sí x e <-3.-2> Rpta. 2
sí x € <0,l> Rpta. 5
A"
|7jí + 2|-|3a + 2| , D . .
'- ■—! sí x e <0.3> Rpta. 4
x
3|3v-8|-|3jc + 24| . c A w . ,
— !— si x e <-5.-4> Rpta. -6
296
Eduardo Espinoza Ramos
si x e <0,3>
X
Resolver cada una de las siguientes inecuaciones.
X+1 I A
<4
2a-3
5a + 4|-|4 + 4a|
6-5a. <J_
3 + a- 2
4 + -| <5
A
A + -| <6
A
a'+3a + 11
a-2
5--|<l
|<3
A
x*i|
A
3-2a
2 + a
A + 3
6-3a
2\\
A + l
A-l.
<6
|<4
|<2
>6
->1
Rpta. 1
10
Rpta. <-«>,— >u<2,+°o>
9
9 5
Rpta. [—,-]
11 3
Rpta. <-o°,— >u<l,+o°>
Rpta. [-4,-2] u [2.4]
Rpta. [-5,-1]
Rpta. <-,—>
6 4
Rpta. [-3-2>/2,-3 + 2a/2]u[3-2a/2,3 + 2>/2]
11 5
Rpta. <-°°, >u<—,<«>
F 2 6
3 3
Rpta. <—,-1>u<-1,— >
2 4
3 3
Rpta. <—,-1>u<-1,— >
2 4
Rpta. <-°o,0>u<0,->
2
52
4-14 - jt |
|a|+4
<0
Rpta. <-l,0]
Sistema de Números Reales
297
3 + .x 2
Kpta. < -oo.-3 > u < -3.—]u[l,°°>
13
i^u.
4- \
Rpta. <-o°,l] u [3,4> u <4, °°>
55
|_í±!|>!
6-2a 2
Rpta. [0,3> u <3, «>
(56)
I——I >-6
a-2
Rpta. <-oo.2> u <2, «>
O»7) I r-4| <-2v + 4
Rpta. <-4.0>
58
■ a+3.
-I <5~x
A+2
Rpta. <-oo,22-VT7>u<-2.1 + 2>/2>
(59
|3a-1¡+2a
|a + I|-3a-
>0
Rpta. <-oo,->
3
(60) | x - 2 | < 2x
Rpta. [— .oo>
©
®
©
|3.v-l|+ 2a ^
|v+l|- 3v
| 3x - 9 | < x + 1
. A — 2 . A" + 3
A + 4 A - 6
Rpta. <-«>,->
Rpta. <2,5>
Rpta. <6, co>
64
|a2+3a|+a2-2>0
2, ,1
Rpta. < -oo,—] u l—, °° >
v . 3 2
65
i+3 . 3
>
x +16 a - 4
Rpta. <-oo,4>
(66) |4x2 -Rx + 4| <4a + 10
3-7T5 3 + VÍI
Rpta. [— — >
298
Eduardo Espinoza Ramos
&
8>
®
®
©
©
©
| x + 5 | > 2x - 3
a) I^^O
a~ -2a — 3
b) 14x - 3 | > x + 2
| jc2 -4| >-2a + 4
| 2x + 1 | > 2 + x
| 4x + 3 | > x + 2
| 3x + 8 | > 8x - 3
Demostrar que:
a) Sí | x | < 3 =>
Rpta. <-<=o,8>
Rpta. <-1.3>
Rpta. <-oo,— >u<5,°°>
Rpta. <-oo,-4> u <0,2> u <2, <*>>
Rpta. <-«>,-1 ] u [ 1, °°>
Rpta. <-■*>,-! >u<—, «>
Rpta. <-o°,—]
1 11 k^ e-I -il , 9 A + 5 7
-e<—, > b) Si | x — 3 | < 1 =* —< < —
x
-7 4 10 5 a + 1 3
c) Sí |x|<2 => | —| <- d) Sí |x|<l => | —1<2
A' + 4 2 x - 2
e) Sí|x-3|<1 => |^-^|<7 f) Sí | x - 21 < 1 => |x2-4|<5
jc —1
g) Sí |x|<3 =* 1^1 <7 h) Sí |x-4|<l => i<-í-<l
a-4 4 2 a-2
i) Sí | x - 3 | < 1 => ¿ < —^—- < -> j) Sí |x|<l => |^-|<-
8 a+4 6 a+3 2
k) Sí|a-2| <- =>|x2-4| <-|a-2| l) Sí | x-5 | < 1 => i<-i-<l
3 v-3
©Sabiendo que: b >0 y I x - a | < 2b probarque: e<-,l>
a - a + 2b 5
Sistema de Números Reales
299
Demostrar que si x. a e <-<»,-11 U [ 1, °°> entonces: | 1 < | a — a \
x a
-|2+3|*|<^
2 2 4
|a|+2|<|a-2|
a--2|- -3|a-2|-4<0
a-1|2 +21 a— 11 -3 <0
v-2|2 -2|a--2|-15>0
i- i i 15
4
2<|a-|2+|a-|
t3-1|2-|a-3-1|-3<0
*-3|2 -3|a— 3|-18>0
a— 1|2 + 51 a— l|-36>0
86) 2|x+1 |-3|x-2| + |x-5[>x + 2
x- 1 |>|x|-2
_ x-3| + 2|x|<5
(89) *2+2| v+3|-10<0
Rpta. -1 <x< 1
Rpta. <-°°,-2] u [2, co >
Rpta. <-2,6>
Rpta. <0,2>
Rpta. <-3,7>
3 3
Rpta. <—,—>
2 2
Rpta. <-co,-1 ] u [ 1, <»>
_ . 1-VÍ3 3 + VÍ3.
Rpta. [ ,- ]
Rpta. <-oo,-3> u <9. co>
Rpta. <-co,-3> u <5,+°°>
Rpta. < -oo, -5 > u [1, —]
Rpta. R
Rpta. <—,2>
F 3
Rpta. [1-VÍ7,-1 + n/5]
90
U-5|-| r-2| + |\|2>7
Rpta. < -oo,-V6] u [2V2.4^o >
300
Eduardo Espinoza Ramos
\
(n) *2-|3a-+2|+jc>0 Rpta. <-~>.-2->/2]u[l+V3.+°° >
(92) |3x-2|<|x + 6| Rpta. <-l,4>
(93) |a + 2|<|x|2 Rpta. <-co,-l>u<2,+oo>
®i, ■> o ,. -,1 ■> -,. « . 1 + 748T 1-748T 22
3a--2a + 1 > 3 a- + v-7 Rpta. <-°°, >u<— ,— >
12 12 5
($5) |x-l| + |x + l|<4 Rpta. <-2,2>
(96) |2x2-4a—6|>|2.r2-3jc-9| Rpta. <-~>,-]
(97) |x + 6|>|x + 9| + |x-2| Rpta. <>
(98) |4x + 2|>|x-l| + 3|x+l| Rpta. [1 + ^13,oo>
@ |3jt -2*2-7a--2| > |a-3+6jc2-9a-14| Rpta. <-°°,-2> u <3, «>
(lOO) |10-3a- + a2 |<|í2+a-6| Rpta. [4,oo>
, , 11
I2a" +a--1| < I2a~ -a-1| Rpta. <-°°,—=>u<0,-=>
v2 v2
|x-6|-|x-3|<|x-l| Rpta. < ^>°.-2] u 1^-,+°° >
(|a—1| + |a-2|)(|1-a:|-|a-2|) < a2-6 Rpta. <-°o,-l] u [3,oo>
.1.2 15 3^30. r25 3^30,
< Rpta. <-°°, ]u[—, ]
'ó-3a |a + 3| 7 35 7 35
, x . .v + 12 „t 3^33, rV33-3 _^
I 1< Rpta. <-«>, ]u[ ,3>u<3.4]
jt-3 4 2 2
/ \ 3 -5 + ^33
(106) 2.v+l< Rpta. <-«,-2>u<-2. >
|a + 2| 4
Sistema de Números Reales
301
3 5
■ <-
|2a-3| x2+x+l
n t ,13 + 5^ -13 + 5n/Í3,
Rpta. [ , ]
W 'PTíi'4
Rpta. <-oo,-l>u<-l,0>u< ,l>u<I,+oo>
,m) U2-2a-48|(|a-2-2a-|-|*-12|)
|a-2|-6
Rpta. {-6} u <-4,-31 u [4, «>
[U0) H2-*|-a<0
U-x-l-2
Rpta. <2. «>
[11D -M,*1
\+\x\ x
1 + yfE
Rpta. <-°o,0>u[ ,t>o>
2
W '¿T1*1^'
Rpta. f-l-Vó.— >u<— ,-1 + Vó >u<2,oo>
2 2
[113) |-^-|>|.v + 3|
Rpta. [-l--v/7,-V6]i^[l + -v/7,2>uh/6,+oo>
a+1 1
<
| jc2 + 11 x
Rpta. <0,1>
U2-16L x2
jc + 4 | jc — 11
Rpta. <-oo,-4>u[—,l>u<l.-H»>
[116) i^l±iM<3,
|4a|
Rpta. [!.+<»>
x+4 x-2
■>-
|a2+4a + 4| a2+4
Rpta. R-{-2}
118
lUI+il
■>A-1
Rpta. <-°o,N/2>
302
Eduardo Espinoza Ramos
119) lií—^i>0 Rpta. V xe R-{--}
' J | 2a + 51 F 2
[120) |x + l|-2|x| + 3|x-2|<6 Rpta. <-,—>
fl2l) —'* ~ 7<0 Rpta. <-oo,2-a/7]u[1,3]u[2 + a/7,+oo>
|a-5|+jT
122) 3|2a + 6|-|a + -| <6 Rpta. <-°o.-3] u [-1,--] u<0,~6 + >'61]
[123) | ilzl^ | + ?<í±4) < 0 Rpta- [.4j.3> u <3i51
[124) |_^Z]_|<|_L| Rpta. <—,V{l}
jc"-4jc + 8 *-l 2
125) | —1>|-!-| Rpta. [-^,^]-{0}
X A-2
126) 2~I2~VI~A>0 Rpta. <-oo,-i>u<-l,2>
U2-a|-2
127) 1^1 -4-V+20 > 4 R <_0^] u [_2,2] u [4,+°o>
' 1*1+1
128) I6*"* l^>_i Rpta. <-4,0> u <0,4> u <5,7>
' 4-|a|
129) (|a+2| + |a-2|K|1-a-|-|2-a|)>a2-6 Rpta. [-1,3]
(130) |x-l|-|x| + |2x-3|>x + 2 Rpta. <-°°,->u<6,+°°>
Sistema de Números Reales
303
(|a-J+2)(|a|-2Wa-2+4
(| v2 + 3M.vWa-2+5
>0
Rpta. <-oo.-2] u <1,2] u <3 +°°>
31 v | -a; j < 1
A + 1 A + 1
1 1
Rpta. <—,—>
4 2
|Hil|>2
A-3
Rpta. <-,5>-{3)
(a + 3)(a-5)|a|
|a|2+2
<0
Rpta. <-3,5>- {0}
. 3x-x~ .
—\2x
x+2
Rpta. <°o,_]-{-2}
(a + 3)(a-5)|a|
|a|2+2
<0
Rpta. <-3.0>u<0,5>
138) (|x|-l)(2x+l)(|x| + 3)>0
Rpta. [-1,—]u[l.+oo>
139) |6a-2+9a-3|<|2a2-9a + 2|
11 2 1
Rpta. <—,— >u<—,—>
2 4 5 2
140) |a-2-5|2-|a2-5¡<12
Rpta. [-3,-1 ]u [1,3]
141) (|a-2| + |a-3|)(|2-a|-|3-.v|)>|a2-1| Rpta. $
\x2-2\+x^.
U42J - ■ <3
A + 2
Rpta. <-°°,4] - {-2}
(143) l*-6|-*+2l* + 2|<3
Rpta. <-oo,2>u<—,+°°>
[144) U-4| + |2x+3|s,
|a-1|-1
Rpta. <0.2>
304
Eduardo Espinoza Ramos
(148)
|a-5| + |a + i1^3
A"-]
1 A - 8 I -A+ I A- + 4 j
A + 2
1^1-3^2-^1
<3
Rpta. <-°°,l> u f3,+oo>
Rpta. <-oo,-2>u< — .+<*>>
. 13, r13 c
Rpta. <-5, ]uf—,5>
v 5 5
5-|a| |a|+1
(VU-1|-3->/5-|í-4|)(a/|a-1|-3+V5-|a-4|)<a-6 Rpta. 14,7]
(VI a-- 21 -4-^/6-1A-3 |)(VI A--21 -4 + V6-1 a -3 [) < IA-21 -5 Rpta. [-3,-2]u [6.9]
|a- + 1|.||a-1|-2]_i+ i a
|a-1|
a-3
|jT+4| jT+a + 4
>0
Rpta. <-^,-3]u[-(l + VT7),3>u[-(3 + >/r7),+oo>
1 ~>
(ísT) HU + l|-2|-6_j|A±3RT + v^^
\¿y V l*"2|+5 |a + 1|+2
154) 1 <
|4-a| + |2a + 3|
|a-1|-1
1
<2
Rpta. [4,91
l^+2|(A-2+A-12)<Q
<2
|a2+2a + 3| + |a2-1|<6
I A' + A-+ 1 I
(155) ^-3^U-l|+4 ,Q
|a-1|+a-2+10a + 27
^
|A2+^|(.r2-5A + 6)
<0
158) |x-l|-|x| + |2x-3|>x + 2
A2+3-|15 + 2y-A2
|v2-9|-8
<0
(A2-9)(A^+A+1)
I a2+91+3
|a2-1|
>0
(í-2)(.r-4)
<1
Sistema de Números Reales
305
\x + 5\-4x+\x-2\
\*2+2\
>0
@ ||x|-|2x + 3||<||x|-|2x + 2||
x+2\-x2
<0
|a + 5|+8
\3x+2\yjx2+5
-x2 + 6a- - 3
>0
165) |jr-4|+8 >|a-2|+4a
[167) |3a2+-5,+ 2|^0
a" +5
l-v-212,
| a - + 41 x(a + 2) + 2(.y + 3)
169) |x-l|-|x + 2| + |x + 4|<8
170
-2|a-| + |a¿-a|+1
a' -5a+ 6
<0
I a-2 —161 x2+4
a + 4 |a-1|
(172) -v2+3-|a2-2a-15|<0
19-a2 |-8a
A2 + | A | -3
(174 1<
i+|a|
x -a"+4a
|a2-3a+2|
>0
4<(^2)2+|a + 2|-2<
|a+2|+2
íl76) l*-3'+7-*>o
|a + 3|-2
ll77) |2v-x2|-3 ^
|a2-2a-I5|-a2-3
178
l-vl
11-vMI
<A-1
fe\ |a-2-a|-2|a2cos^|+1^0
^~y a2-5a-6cos7T
(180
lui+n
>2a + 1
(181) | 2X~l l<l^l
a2-4a+ 8 l-x
(182) \l-M\ >2
[183) l*l-|2»-H>0
A(A-l)
||v- + l|+3|
185) v2+a + 1-|a3-1| >0
306
Eduardo Espinoza Ramos
U86) *-l*+ll-H<0
II x |-11
[187) i^fiM <|a|-4
\x\
188
190
n/|a-3|-|a-1|
a2-9
In/I-SI-^
<0
|a2-4|
>0
189) l£Zilli^zl)>o
Va - 6a
[191) ü^zílhñl >0
x2-\2-x\
U92) i^lMl<|.v|-4
I «I
(Í94) a2+a + 1-|a3-1|>0
193) |v'a:-6v + 9-3|>>/33¡:
195) |a -5a + 7|>a:2-1
196
3-|jt-4v|
|a-5|+a2
<0
Í97) (a2-6a+8)a/i2-|4-a2|<0
198
||a-1|+2|-|a-1|2
A- + 2
>0
199) (|4a-a21-5)>/a-(a-1)(a-3);:0
|a|-1
(200)
l£=±l>-i
4-|a|
(201) |£1Z^|<.2
A-l A-l
(202)
|a-3|3+2(a-3)2-5|a-3|-6
(.v-2)2-2|a-2|-24
<0
U03J '47' + '2* + 3'<2
|a-1|-1
(204) |^_8|<|I-6| + U-2|
(205) 1^^21-4^
a2+5
(206
A - A" + 4A
|a2-3a + 2|
>0
a--16
vU-4Hv-i|
>0
(208) {4x~f '-5>0
|a|-i
Sistema de Números Reales
307
IV. Encontrar el menor número M con la propiedad de que para todo x e R se cumple:
(T) 2.v-.r2<M Rpta. M=l
(T) 1-4a-a2<AÍ Rpta. M = 3
© 2-x2n-xU3<M Rpta. M=-
(4) 2a2/3 -a4'3 < M Rpta. M = 1
(?) 1 + 6.v-jt<AÍ Rpta. M= 10
(ó) 3 + 36a-12.v2 <M Rpta. M = 30
V. Encontrar el número mayor M con la propiedad de que para todo x e R se cumple:
(T) AÍ<3 + 4—- Rpta- M =
■2 x "r 6
9
(¿) M <x2l5-xu5-2 Rpta. M= —
(3) M < 9a-2 -48.v-36 Rpta. M = -100
(4) M < 5a 2 - 20a +16 Rpta. M = -4
(5) Si 2x + 3 e [7,11] encontrar el valor M que satisface a la siguiente desigualdad
^^-<M Rpta. Af=--
a-7 5
(ó) Si a€ [-,-] encontrar el mayor valor M que satisface a la desigualdad M <
Rpta. -
2 2 x-2
5
3
(i) Sí — 6 fr|< -00,1 > U < 2, +0° >]. Hallar el menor valor de M tal que | 1 < M
^s x 2a + 5
308
Eduardo Espinoza Ramos
g) Sí |x - 3| < 1. Hallar el número M tal que: ] 1 < M
JC+1
®
®
(Sí
Hallar M tal que sí | x | < 2 => \^—^-\<M
x + 4
Encontrar un número M positivo tal que:
Encontrar un número M positivo tal que:
Encontrar un número M positivo tal que:
(Í3) Encontrar un número M positivo tal que:
VJ4) Encontrar un número M positivo tal que:
(i5) Encontrar un número M positivo tal que:
xi-2x¿+3x-4| <M
— |<M sí jce[-,-]
x-2 2 2
a2-3a + 4|<M sí xe [-2,2]
x2 + 4*-3| < M sí x e [-2,4]
x + 2
\<M sí x e [5,8]
A--4
x3 +2x2-3x-6\<M sí xe [-2,5]
116) Encontrar un número M positivo tal que: \x -2x +x -3x-5\<M síxe [-3,-1]
(l7) Encontrar un número M positivo tal que: |
az-6a + 2. , 9
\<M si A-e[—,4]
x + 5 2
[18) Encontrar un número M positivo tal que: I —
V-/ a-2+4a- + 4
<M sí xe [-1,3]
3 T ,
H19) Encontrar un número M positivo tal que: | — \ <M sí x e [0,4]
®x +6a + 14
Hallar el mayor número N tal que: | ; \>N si x e [-2,2]
a-3+27
®Si — e (< -00,1 > U < 2, +00 >), Determinar el menor número M tal que | 1 < M
x x + 4
Sistema de Números Reales
309
(22) Determinar el número M tal que: | | < M , V x e <1,3>
^■^ .v —4
©x3 +14
Hallar el menor número M tal que: I — 1 < M , sí x e [-1,2]
*2-4x + 14
(24) Hallar un número M tal que: sí | x | < 1 => | 1 < M
VI. Resolver las siguientes ecuaciones:
0 [|3a|] = jc + 2 Rpta. x=l
(¿) [|3a|] = 2jc + 2 Rpta. x=2,-
0 [|lJf~2|+3|] = 5 Rpta. <-7,-5]u [9.11>
0 [|2-|a||] = 1 Rpta. [-1,0>u<0,1]
0 [|3v-5|] = 2jc + 1 Rpta. {6,y}
0 [| yfJ^I |] = 2 Rpta. <-6,-1 ]
0 [|U-1|-1|] = 2 Rpta. <-9,-6]u [8,11>
® [ll^lll^-i Rp^. d>
Ix I
0 [|2a|] + [|4jc|] = 3 Rpta. [~>
® [||^||] = 5 Rpta. [^-ii>u<-H.-Z1
(n) r||J^||] = 3 Rpta. [-3,-2>u<-^,-J]
310
Eduardo Espinoza Ramos
12
[1^11 = 3
23 17
Rpta. < ,-9]u[6.—>
2 2
(U) [||2a2-1||] = 1
Rpta. < -J|.-l] u (0} u [1 J|:
14
jc + 3
Rpta. <—,8]
(S) [|i^i^|] = 4
Rpta. [-1,0>U<0,1]
fió) [|2-|x||] = l
Rpta. [7,9>
17
[1^11 = 4
A+3
r 13 16
Rpta. [ , >
2 3
18
[|x2-2a|] = 3
Rpta. <l->/5,-l]u[3,l + >/5>
19
[|2x|]-|x-l| = 2x-3
Rpta. {-2,y,y,4}
(20)
U2|]-H=3
Rpta. <S,-2]v[2,S>
(21
[[|x-2| + |2x-l|-2|]_1
5 2, r8 11
Rpta. <—,—]^[-,— >
3 3 3 3
(22) [|a-1|]2+2[|a-|]2=57
VII. Resolver las siguientes inecuaciones:
Rpta. [-4,-3>
© 0<2
x + 2
Rpta. <-°°,-2> u <-l,3>
® [|4a2-5a-4|]<1
Rpta. <—,2>
4
® [||2v2+5.v|-2|]<l
,3 1
Rpta. <-3,— >u<-l,—>
2 2
Sistema de Números Reales
311
© \\\-x\\-\\<2
© [|a2-1|]>0
© [\S-2x\\ <fi
® [U2-1|]<0
5-x
® [|jt2-4|]<-l
® [||^-1||]<1
^-^ A+l
(fi) [i^-ni^i
Rpta. <-3,0|
Rpta. <-o°,-l] u [l,+°°>
Rpta. <0,+°°>
Rpta. <-j2,y¡2>
Rpta. <0,5>
Rpta. <-2,2>
Rpta. < -o», — > u < 6, +00 >
3
Rpta. <-°°,-51 u [5,+°°>
12
Í141
15
Í16^
[|2a-^|]>1
A'
(B) [|a-|]2-2[|a|]-2<0
>/Ñ=3
[|a2-2a-19|]
<0
n/[|a|12-12([|a|]2-[|a|]-6)>0
[|a-2-2a-3|
<0
(Í7) [|a-2[|a|]|](a2-4)>0
(w) ( [|a|]-2h/|a-2+2|(a2-4a- + 3)>0
Rpta. [-2.0>u[-,+°°>
Rpta. [0.2]
Rpta. <l-2>/5,-3]u[3,l + 2>/5>
Rpta. <-°°,-3> u <4,+°°>
Rpta. [2,3>
18) [|a--2|1.(.v2-a- + 2)>0
20) 'I-'"-2 so
6-f|A|]
312
Eduardo Espinoza Ramos
£
21) , " * <0 (22) ([|v|]-a)(jc-2)(a-3)2>0
a--[|a|]-4 ^s
23) 44^-<l 6$) . . V.2"* >0
\2-a-
[|a|]-1 ^ |a| [|a-1|]-9
(|a-5|+2a+>/a:^5-[|a-2|]a + 5)(a-^) /¿-t-t
3_<0 (28) V2? '*' <0
29) (*2+4A- + 5WA~I(2*+SenA)(A- + 2)50 fi¡) [|-^li|]<4
([Ull--)U -2a-3)
VIII. Resolver la inecuación logarítmica.
lu 2 ^ ^ ^^ 4* + 2
(?) log1/2|2.v-3|>-3 Rpta. <-|,Ü>h|}
2 2 2
(¿) log2(A:-3>/I+7 + 3)<l Rpta. [-l,0>u<3.15>
®| a2 + 4a I +3 „ _ , 2
log7' , , ' , >0 Rpta. [-,+o°>
a-+|a-5| 5
(5) log,[ **~U ]<-l Rpta. [2,^>u<4,+~>
w " 2v2-4a-6 4
(?) log[|2jf~3*]>l Rpta. <-(yf2l-3),l>
^^ x+l 2
© logu-4,(3-v)<2 Rpta. 4
Sistema de Números Reales
313
(?) log,(2v + 6)<-2
Rpta. <2.+°°>
(5) log2|3-4jc|>3
d * 5 11
Rpta. <-oo,— >kj<—,+o°>
4 4
flOJ Iog5|3-4A|>2
Rpta. <-«>,— >u<3,+°°>
© log6[|^-||+35]>2
Rpta. <— ,5>u<5,+°° >
®24-2a-jT ,
^^Z m )>!
16
Rpta. <-3,l>u<3,4>
@ -oS.C^)2.
Rpta. <-l + V6, 2>u<2,5]
(Í4) log6(A-3>/A:+T + 3)<l
Rpta. [-l,0>u<3,15>
U5) log5(3A-5)>log5(7-2v)
12 7
Rpta. <—,—>
5 2
(16) log,(A--4v + 3)>-l
Rpta. [0.1>u<3.4]
(rf) iog2í|jc-2|-n>i
Rpta. <-<*>,-1> u <5,°°>
18
,3-2a\
1-A
•og|^(- )^0
Rpta. <0,l>u[2,+oo>
(19) log.(2 + A)<l
20) log, (a- -4) > log, (4a - 7)
(2l) log2(A2) + log2(A-4)>3
22) log, (8-2*) > 3
314
Eduardo Espinoza Ramos
3.42. APLICACIONES DE LAS INECUACIONES A LA
ADMINISTRACIÓN Y ECONOMIA.-
Muchas veces la resolución de problemas expresado en palabras nos conducen a
inecuaciones como ilustraremos en los siguiente ejemplos. \
(lj El producto Interno Bruto (PIB) de un país está proyectado en t2 +2/ +50 miles millones
de dólares, donde t se mide en años a partir del año en curso. Determínese el instante en
que el PIB del país sea igual o exceda $ 58 mil millones.
Solución
El (PIB) del país será igual o excederá $ 58 mil millones cuando t2 + 2/ + 50 > 58
Para obtener la solución de la inecuación expresaremos en la forma: /~+2f-8>0,
donde al factorizar se tiene (t + 4)(t - 2) > 0.
Aplicando el criterio de los puntos críticos se tiene:
\ i \ /
± i¿ : u ± ».
El conjunto solución de la inecuación es <-°o,-4] 'o [2,°°> como t debe ser positivo,
entonces se considera t > 2 es decir que, el PIB será igual o excederá por vez primera a
los $ 58 mil millones, cuanto t - 2 es decir dentro de dos años.
CT) Para una compañía que fabrica termostatos, el costo combinado de mano de obra y
material es de $ 5 por termostato. Los costos fijos (los costos de un periodo dado sin
importar la producción) son de $ 60.000. Si el precio de venta de un termostato es de $ 7
¿Cuantos debe venderse para que la compañía obtenga utilidades?
Solución
Como:
ganancia = ingreso total - costo total
Entonces debemos encontrar el ingreso total y el costo total y después determinar cuando
su diferencia es positiva.
Sistema de Números Reales
315
Sea q = el número de termostato que deben ser vendidos entonces su costo es 5q
Lugo el costo total para la compañía es 5q + 60,000, el ingreso total de q termostatos
será 7q y como: Ganancia = Ingreso total - costo total > 0 I
i
entonces: 7q - (5q + 60,000) > 0, de donde 2q> 60,000 entonces q> 30.000
por lo tanto se deben vender al menos 30,001 termostato para que la compañía obtenga
utilidades.
¿) El fabricante de cierto artículo puede vender todo lo que produce al precio de $ 60 cada
artículo. Gasta $ 40 en materia prima y mano de obra al producir cada artículo y tiene
costos adicionales (fijos) de $ 3,000 a la semana en la operación de la planta. Encuentre el
número de unidades que debería producir y vender para obtener una utilidad de al menos
$ 1,000 ala semana.
Solución
Sea x = número de artículos producidos y vendidos a la semana.
Como el costo total de producir x unidades es de $ 3,000 más $ 40 por artículo, es decir:
(40x + 3,000) dólares el ingreso obtenido por vender x unidades a $ 60 cada una será de
60x dólares, por lo tanto
Utilidad = ingresos - costos = 60x - (40x + 3,000) = 20x - 3,000
como debe tener una ganancia de al menos $ 1,000 al mes, tenemos la inecuación:
utilidad > 1000 de donde 20x - 3000 > 1000 entonces x > 200
por lo tanto, el fabricante debe producir y vender al menos 200 unidades cada semana.
4j La gerencia de la misma Antamina, un gran consorcio, ha estimado que necesita x miles
de dólares para adquirir 100,000(-l + \¡\ + 0.001a) acciones de la compañía telefónica.
Determinar el dinero que necesita Antamina para adquirir un mínimo de 100,000 acciones
de telefónica.
Solución
Calculamos la cantidad de dinero que Antamina necesita para adquirir un mínimo de
100,000 acciones resolviendo la inecuación.
316
Eduardo Espinoza Ramos
100.000(-1 + Vi +0.001jt)> 100,000 de donde -1 +Vi+ 0.001* >1
entonces Vi+ 0.001* >2 elevando al cuadrado 1+0.001x >4 =f> 0.001x>3
x > 3000, por lo tanto Antamina necesita al menos $ 3 000,000
(5) Un constructor debe decidir si renta o compra una maquina excavadora. Si renta la
máquina el pago mensual sería de $ 600 (con base en un año), y el costo diario (gas,
aceite y conductor) sería de $ 60 por cada día que sea utilizada. Si la compra, su costo fijo
anual sería de $ 4,000, y los costos por operación y mantenimiento serían de $ 80 por
cada día que la máquina sea utilizada ¿Cuál es el número mínimo de días al año que
tendría que usarse la máquina para justificar la renta en lugar de la compra?
Solución
Determinaremos expresiones para el costo anual de la renta y el de la compra, así
encontraremos cuándo el costo de la renta es menor que el de la compra.
Sea d = el número de días de cada año en que la máquina es utilizada.
Si la máquina rentada, el costo total anual consistiría en el pago de la renta, que es
(12)(600) y los cargos diarios de 60d, si la máquina es comprada, el costo por año será
4000 + 80d, queremos Costo renta < costo compra
12(600)+ 60d< 4000+ 80d => 7200 + 60d < 4000 + 80d, de donde
3200 < 20d => 160 < d, por lo tanto, el constructor debe utilizar la máquina al menos
161 días para justificar su renta.
fó) Las ventas mensuales x de cierto artículo cuando su precio es P dólares están dadas por
P = 200 - 3x. El costo de producir x unidades del mismo artículo es C = (650 + 5x) dólar
¿Cuántas unidades de este artículo deberán producirse de modo que la utilidad mensual
sea por lo menos de 2,500 dólares?
Solución
Sea R = el ingreso en $ obtenido por vender x unidades al precio de P dólares por unidad,
es decir: R = x (precio por unidad) = x(p) = x(200 - 3x) =* R = 20Qx-3x~
Sistema de Números Reales
317
C = el costo en $ de fabricar x unidad, es decir: C = 650 + 5x
Como utilidad = Ingresos - costos = (200* - 3x2) - (650 + 5x)
= 195.r-3.r2-650
como la utilidad debe ser al menos de $ 2,500, es decir:
utilidad > 2,500, de donde 195 * - 3x2 - 650 > 2,500, simplificando
x2 -65.r + 1050 < 0, factorizando se tiene:
(x - 30)(x - 35) < 0, aplicando puntos críticos
\ i \ i
+ v : \¡ + ►
30 35
La solución es 30 < x < 35
Luego para obtener una utilidad de al menos $ 2,500 al mes, el fabricante debe producir y
vender cualesquiera unidades de 30 a 35.
7j Una compañía de publicidad determina que el costo por publicar cada ejemplar de una
cierta revista es de $ 1.50. El ingreso recibido de los distribuidores es de $ 1.40 por
revista. El ingreso por publicidad es de 10% del ingreso recibido de los distribuidores por
todos los ejemplares vendidos por arriba de 10,000 ¿Cuál es el número mínimo de
revistas que deben ser vendidas de modo que la compañía obtenga utilidades?
Solución
Sea q = número de revistas vendidas
El ingreso total recibido de los distribuidores es 1.40q y el recibido por publicidad es
(0.10)[( 1.40)(q - 10,000)] el costo total de la publicación es 1.50q
como utilidad - ingreso - costo > 0
1.40q + (0.10)[(1.40)(q-l 0,000)] - 1.50q>0 => 1.4q + 0.14q-1400-1.5q>0
0.04q-1400>0 => 0.04q>1400 => q> 35,000
318
Eduardo Espinoza Ramos
por lo tanto el número total de revistas debe ser mayor que 35,000, es decir que al menos
35,001 ejemplares deben ser vendidos para garantizar utilidades.
£) Un peluquero atiende un promedio de 100 clientes a la semana y íes cobra $ 3 por corte
por cada incremento de $ 0.5 en la tarifa, el peluquero pierde 10 clientes ¿Que precio
deberá fijar de modo que los ingresos semanales no sean menores de los que él obtiene
por una tarifa de $ 3?
Solución
Sea x = el número de incremento de $ 0.5 en la tarifa por encima de $ 3
$ (3 + 0.5x) = el precio del corte
100 - lOx = número de clientes por semana.
Ingreso total a la semana = (número de clientes) precio del corte
= (100 - 10x)(3 + 0.5x) dólares
el ingreso correspondiente a 100 clientes son de 100 x $ 3 = 300
luego los nuevos ingresos semanales deben ser al menos 300 dólares, es decir:
(100-10x)(3+ 0.5x) >300, simplificando x(x-4)<0, aplicando puntos críticos
~~~\ i \ /
+ * : m +
0 4
por lo tanto la solución es 0 < x < 4
esto quiere decir que debería subir a lo más 4 x 0.5 = $ 2
El peluquero debería cobrar una tarifa máxima de$3 + $2 = $5 por corte, para obtener
al menos los mismo ingresos que los correspondientes a 100 clientes cobrándoles $ 3 por
corte.
[3.43. EJERCICIOS PROPUESTOS.-
Mn Determine el costo mínimo C (en dólares) dado que 5(C - 25) > 1.75 + 2.5C
Rpta. $ 50.70
Sistema de Números Reales
319
©
(¿) Determine la ganancia máxima P (en-dólares) dado que: 6(P - 2500) < 4(P + 2400)
Rpta. $ 12,300
(5) Determine el costo mínimo C (en dólares) dado que: 2(1.5C + 80) < 2Í2.5C - 20)
Rpta. $ 100
Deteimine la ganancia máxima P (en dólares) dado que: 12(2P - 320) < 4(3P + 240)
Rpta. $ 400
Q5) La compañía Davis fabrica un producto que tiene un precio unitario de venta de $ 20 y un
costo unitario de $ 15. Si los costos fijos son de $ 600,000, determine el número mínimo
de unidades que deben ser vendidos para que la compañía tenga utilidades.
Rpta. Al menos 120,001
(ó) El administrador de una fabrica debe decidir si deberán producir sus propios empaques,
que la empresa ha estado adquiriendo de proveedores externos a $ 1.10 cada uno. La
fabricación de los empaques incrementaría los costos generales de la empresa en $ 800 al
mes y el costo del material y de mano de obra será de $ 0.60 por cada empaque ¿Cuántos
empaques deberá usar la empresa al mes para justificar la decisión de fabricar sus propios
empaques? Rpta. Producir al menos 1601 empaques al mes
\7j La publicidad indica que cierto auto rinde 20 millas por galón en la ciudad y 27 millas por
galón en la carretera, y que la capacidad del tanque de gasolina es de 18.1 galones.
Suponga que existen las condiciones ideales de manejo y determine la distancia que
puede recorrer un auto de estas características con el tanque lleno.
Rpta. [362,488.7]
(SJ Una mujer de negocios quiere determinar la diferencia entre los costos de comprar y
rentar un automóvil. Ella puede rentar un automóvil por $ 400 mensual (con una base
anual). Bajo este plan el costo por milla (gasolina y aceite) es de $ 0.10. Si comprarse el
cano, el gasto fijo anual sería de $ 3,000 más $ 0.18 por milla ¿Cuál es el menor número
de millas que deberá conducir por año para que la renta no sea más cara que la compra?
Rpta. 22,500
320
Eduardo Espinoza Ramos
(9j Un fabricante puede vender todas las unidades que produce al precio de $ 30 cada una.
Tiene costos fijos de $ 12,000 aTmes; y además, le cuesta $ 22 producir artículo ¿Cuántas
unidades debe producir y vender al mes la compañía para obtener utilidades?
Rpta. más de 1,500
UO) La comisión mensual de un agente de ventas es de 15% de las venias por arriba de
$ 12,000. Si su objetivo es lograr una comisión de al menos $ 3,000 por mes ¿Cuál es el
volumen mínimo de ventas que debe alcanzar? Rpta. S 32,000
(11) El costo unitario de publicación de una revista es de $ 0.65 se vende al distribuidor en
$ 0.60 cada una, y la cantidad que recibe por publicidad es el 10% de la recibida por todas
las revistas vendidas arriba de las 10,000. Encuentre el menor número de revistas que
pueden ser publicadas sin pérdida, esto es, que la utilidad > 0 (suponga que toda la
emisión será vendida) Rpta. 60,000
(12) Una empresa automotriz desea saber si le conviene fabricar sus propias correas para el
ventilador, que ha estado adquiriendo de proveedores externos a $ 2.50 cada unidad. La
fabricación de las correas por la empresa incrementará sus costos fijos en $ 1,500 al mes,
pero sólo le costara $ 1.70 fabricar cada correa ¿Cuántas correas debe utilizar la empresa
cada mes para justificar la fabricación de sus propias correas?
Rpta. más de 1,875
(13) Una compañía invierte $ 30,000 de sus fondos excedentes a dos tasas de interés anual: 5 y
6.75%. Desea una ganancia anual que no sea menor al 6.5% ¿Cuál es la menor cantidad
de dinero que debe invertir a la tasa de 6.75 por ciento? Rpta. $25,714.29
(14) La fabricante de cierto artículo ha estimado que su ganancia en miles de dólares está dado
por la expresión -6a2 + 30jc-10 donde x (miles) es el número de unidades producidas.
¿Qué nivel de producción el permitirá obtener una ganancia de al menos $ 14,000?
Rpta. Entre 1,000 y 4,000 unidades
Q5) Una pelota se lanza hacia arriba, de modo que su altura después de t segundo es
128r-16r+4 pies. Determine el tiempo durante el cuál la pelota está arriba de una
altura de 196 pies. Rpta. 4 segundos
Sistema de Números Reales
321
El costo de publicar cada ejemplar de la revista semanal compra y venta es de $ 0.35. Los
ingresos del representante de ventas, ^on de S 0.30 por ejemplar y los ingresos de la
publicidad conesponden al 20% de los ingresos obtenidos por ventas que exceden los
2,000 ejemplares ¿Cuántas copias deberá publicar y vender cada semana para obtener
ingresos semanales del al menos $ 1,000? Rpta. 112,000, o más
L'n fabricante tiene 2.500 unidades de un producto cuyo precio unitario es de $ 4. El
próximo mes el precio por unidad se incrementará en $ 0.50. El fabricante quiere que el
ingreso total recibido por la venta de las 2,500 unidades no sea menor que $ 10,750 ¿Cuál
es el número máximo de unidades que puede ser vendido este mes?
Rpta. 1,000
Al precio de P por unidad, x unidades de cierto artículo pueden venderse al mes en el
mercado, con P = 600 - 5x ¿Cuántas unidades deberán venderse cada mes con objeto de
obtener ingresos por los menos de $ 18,000? Rpta. 60 unidades
Un fabricante puede vender todas las unidades de un producto a $ 25 cada una. El costo C
(en dólares) de producir x unidades cada semana está dado por C = 3,000+20jt-0.1jc2
¿Cuántas unidades deberán producirse y venderse a la semana para obtener alguna
utilidad? Rpta. más de 150
Un granjero desea delimitar un terreno rectangular y tiene 200 yardas de cerco disponible.
Encuentre las dimensiones posibles del terreno si su área debe ser de al menos 2,100
yardas cuadradas.
Rpta. 30 < x < 70, si x yardas es la longitud de un lado del terreno.
Un peluquero atiende en promedio a 120 clientes a la semana cobrándoles $ 4 por corte
por cada incremento de $ 0.50 en el precio, el peluquero pierde 8 clientes. ¿Qué precio
máximo deberá fijar para obtener ingresos semanales por lo menos $ 520?
Rpta. $ 6.50
Un accionista invierte $ 100 a un interés anual del R por ciento y otros $ 100 al 2R por
ciento anual. Si el valor de las dos inversiones debe ser de al menos $ 224.80 después de
2 años ¿Qué restricciones deben establecerse sobre R? Rpta. R > 4
322
Eduardo Espinoza Ramos
Para producir 1 unidad de un producto nuevo, una compañía determina que el costo del
material es de $ 2.50 y el-denrano de obra de $ 4. El gasto general, sin importar el
volumen de ventas, es de $ 5,000. Si el precio para un mayorista es de $ 7.40 por unidad,
determine el número mínimo de unidades que debe ser vendido para que la compañía
obtenga utilidades.
El margen de ganancia para un auto usado era de al menos 30% de su precio total al por
mayor. Si el auto fue vendido en $ 6,500 ¿Cuál fue el precio máximo al por mayor?
t minutos después de introducir un bactericida experimental en cierto cultivo, el número
de bacterias está dado por —^ 1-2,000. Determine el momento en que el número de
í +1
bacterias esté por debajo de 4,000.
Un editor puede vender 12,000 ejemplares de un libro al precio de $ 25 cada uno, por
cada dólar de incremento en el precio, las ventas bajan en 400 ejemplares ¿Qué precio
mínimo deberá fijarse a cada ejemplar con objetivo de lograr ingresos por lo menos de
$ 300,000?
Una fabrica de camisetas produce N camisetas a un costo de mano de obra total de $ 1.2N
y un costo total por material de $ 0.3N. Los gastos generales para la planta son $ 6,000. Si
cada camiseta se vende en $ 3 ¿Cuántas camisetas deben venderse para que la compañía
obtenga utilidades?
Suponga que los consumidores comprarán q unidades de un producto al precio de +1
q
dólares por unidad ¿Cuál es el número mínimo de unidades que debe ser vendido para que
el ingreso por ventas sea mayor que $ 5,000?
En cierto estanque se crían peces (se introducen n de ellos allí). Si se sabe que la ganancia
de peso promedio de cada pez es de (600 - 3n) gramos. Determine las restricciones de n
si la ganancia total en peso de todos los peces debe ser mayor que 28,800 gramos.
Un supermercado se encuentra con grandes existencias de manzanas que debe vender
rápidamente. El gerente sabe que si las manzanas se ofrecen a P centavos por libra,
venderá x libras, con x = 1000 - 20P ¿Qué precio deberá fijar con el fin de obtener
ingresos por lo menos de $ 120?
Relaciones y Funciones
323
CAPITULO IV
RELACIONES Y FUNCIONES
4.1. INTRODUCCIÓN.-
a) PAR ORDENADO.-
Llamaremos "par ordenado" de números reales a la expresión (a.b) donde a es
llamada la primera componente y b es llamada la segunda componente.
Ejemplo.- Son pares ordenados, (3,5), (-2,7), (etc).
b) IGUALDAD DE PARES ORDENADOS--
Los pares ordenados (a,b) y (c,d) diremos que son iguales si sus correspondientes
componentes son iguales, esto es:
(a,b) = (c,d) <=> a = c A b = d
Ejemplo.- Los pares ordenados (5,6) y (5,4) no son iguales sus segundas
componentes son diferentes.
Luego diremos que dos pares ordenados son diferentes si una de sus componentes
correspondientes son diferentes esto es:
(a,b)*(c,d) <=> a^c y/o b*á
Ejemplo.- Detenninar el valor de x e y de tal manera que (5x+2y, -4) = (-1, 2x- y)
Solución
Para calcular el valor de x e y aplicamos el concepto de igualdad de pares
ordenados:
324
Eduardo Espinoza Ramos
5x+2y = -l
(5x + 2y,-4) = (-l,2xs-y) <=> .„
[2x-y = -4
c) PRODUCTO CARTESIANO DE CONJUNTOS.-
x = -l
v = 2
Consideremos dos conjuntos A y B arbitrarios; llamaremos producto cartesiano de A
y B, al conjunto formado por todos los pares ordenados (a,b) de tal manera que la
primera componente a pertenece al conjunto A y la segunda componente b pertenece
al conjunto B.
La notación del producto cartesiano de A y B es: AxB. Simbólicamente el producto
cartesiano se representa:
AxB = {(a,b)/ae A A be B}
Nota:
(a,b) EAxBoaeAAbeB
Ejemplo.- Sean A = {1,3,5} y B = {2,4} Entonces:
A x B = {(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)}
También puede determinarse AxB mediante el método del "diagrama del árbol" el
cual nos permite observar el conjunto de pares ordenados, este método consiste en
disponer los elementos de A y B del modo siguiente
A B AxB
(1.2)
4
2
4
2
(1.4)
(3.2)
(3,4)
(5.2)
(5,4)
Relaciones y Funciones 325
OBSERVACIÓN.- Cuando los conjuntos A y B son finitos entonces:
nf A x B) = n(A).n(B)
donde: n(A): es el número de elementos del conjunto A.
n(B): es el número de elementos del conjunto B.
n(A x B): es el número de elementos del conjunto A x B.
Ejemplo.- Si A={2,4) y B = {1,3,5} entonces: AxB={(2,l),(2,3),(2,5),(4,l),(4,3),(4,5)}
De donde: n(A x B) = n(A).n(B) = (2)(3) = 6
Además se tiene:
B x A = {(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)} de donde se observa queAxBíBxA
d) PROPIEDADES DEL PRODUCTO CARTESIANO
©
©
©
©
©
AxB^BxA, no siempre se cumple
Ax(BuC) = AxB u AxC
Ax(B-C) = AxB-AxC
SíAcB =*AxCcBxC,VC
Si AcCy BcD => AxBcC)
íD
©
©
©
Ax(|) = (|)xA = <¡)
Ax(BnC) = AxBnAxC
(AxB)xC = A x (B x C)
e) REPRESENTACIÓN GEOMÉTRICA DEL PRODUCTO CARTESIANO.-
En el producto cartesiano A x B, a cada uno de los conjuntos A y B lo
representaremos sobre dos rectas perpendiculares, en donde los elementos del
conjunto A se. representa sobre el eje horizontal y los elementos del conjunto B se
representan sobre el eje vertical, de tal manera que las líneas verticales que pasan
por los elementos de A y las líneas horizontales que pasan por los elementos de B al
interceptarse se obtienen los pares ordenados de A x B.
326
Eduardo Espinoza Ramos
Ejemplos.-
-4—4—4
AxB
J_
I
I
l
±
I I I
i 1 r
i 1 r
12 3 4 5
Sí A= {1,3,5} y B = {2,4} entonces:
Ax B = {(1,2),(1,4),(3.2)(3,4X5.2)(5,4)}
A los elementos del conjunto A lo representaremos
en el eje horizontal y a los elementos del conjunto B
"♦ lo representaremos en el eje vertical.
OBSERVACIÓN
Como los conjuntos A y B son arbitrarios, entonces consideremos los siguientes casos:
(\j Si A = B, el producto cartesiano denotaremos por AxB = AxA — A
{2) Si A = B = R entonces AxB = RxR = R2 este producto nos representa al plano
cartesiano.
f) DIAGONAL DE UN CONJUNTO.-
Dado un conjunto A * <t>, a la diagonal del producto cartesiano AxA denotaremos
por 1A y es definido por:
IA = U*.;y)e AxAly = x)
Ejemplo.- Sí A = {1,3,5} entonces:
A x A = {(1,1),(1,3)(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5)}
Entonces: IA = {(1,1), (3,3), (5,5)}
g) EJERCICIOS DESARROLLADOS.-
(V) Determinar los valores x e y, en cada caso:
a) (4,2x-10) = (x-l,y + 2)
Solución
Relaciones y Funciones
327
Mediante la igualdad de pares ordenados se tiene:
Í4 = jc-1 í* = 5
(4,2x-10) = (x-l.y + 2) => \ => i
b) (y-2,2x+l) = (x-l,y + 2)
Solución
Mediante la igualdad de pares ordenados se tiene:
|>-2 = *-l Íjc = 2
(y-2,2x+l) = (x-l,y + 2) => T =>
[2x+\ = y + 2 [y = 3
1) Dados los conjuntos A={xez/-l<x<3) ; B={xez/l<x<4)
C={xe z/1 <x<4}
Hallar los siguientes conjuntos y graficar:
a) AxB b) BxC c) (A-C)xB
Solución
Tabulando los conjuntos dados se tiene:
A ={-1,0,1,2,3}. B= {1,2,3,4}, C= {1,2,3,4}
a) A x B = {(-1.1),(-1,2),(-1.3),(-1.4).(0,1 ).(0.2).(0.3),(0,4).( 1,1).( 1,2),( 1,3X1,4),(2,1),
(2,2)(2,3) (2.4)(3,1 ).(3,2),(3,3),(3,4)}
b) B x C = {(1,1),(1,2),( 1,3),(1,4),(2,1),(2,2))>(2,3),(2,4),(3,1),(3,2),(3,3)1(3,4),(4,1),
(4,2),(4,3),(4,4)}
c) A-C={-1,0}
(A - C) x B = {(-1,1),(-1,2).(-1,3),(-1,4),(0,1 ),(0,2),(0,3),(0,4)}
328
Eduardo Espinoza Ramos
©
AxB
♦ Y
4-
3
2
1 ■
BxC
-i 1 1 h-
12 3 4
B
4
3
2-
1
(A - C) x B
B
A-C
A={xe R/x-3<7}, B = {y e R/-2< y < 3}. Graficar Ax B, B x A
Solución
Como x-3<7 => x<10
AxB= ((x,y)/x< 10 A -2<y<3}
B x A = {(x,y) / -2 < x < 3 A y < 10}
'Y
3
AxB
10
BxA
10 X -2¡
3 X
Relaciones y Funciones
329
(4) Para A y B subconjuntos arbitrarios de R, geométricamente visualizar, como superficie, el
producto cartesiano A x B en el espacio bidimensional R2, entonces:
Y'
•{
.
AxB
^ j
A
X
B<
A
AxB
AxB
Yt
^
V
J
>
A
(¿) Que parte del plano cartesiano se obtiene si se representa gráficamente los siguientes
productos cartesianos.
a) <0,+°°> x <0.+°°>
b) <-°°,0> x <-°°,0>
c) <-°°.0> x <0.+°°>
d) <0,+°°> x <-°°,0>
Solución
a) <0,+°°>x <0,+°°> => {(x,y)/x>0 A y >0}
b) <-oo.0> x <-°°,0> => {(x,y)/x <0 A y <0}
c) <-°°.0> x <0,+°°> => {(x,y)/x <0 A y >0}
d) <0,+«»> x <-«.()> =$■ {(x.y)/x >0 A y <0)
330
Eduardo Espinoza Ramos
h) EJERCICIOS PROPUESTOS.
I. En cada caso determinar los valores de x e y.
© (x,4) = (-2,y) © (4,2x-10) = (x-l.y + 2)
® (y-2,2x+l) = (x-l,y + 2) @ (5x + 2y, -4) = (-1,2x - y)
© (x+4,6) = (10,y-x) © (x + 5,3 - y) = (7,2)
© (x + y,3) = (5.y-x) © (x-7y.2x-6y) = (15,-10)
© (3x - 8y, 4x + 3y) = (4 - 2x - lOy, 2x + 4y + 7)
@ (5x + 2y,-4) = (-l,2x-y) @ (x3 -19, x2y-6) = (y3, xy2)
U2) (2x-y. x + y + 3) = (x + y+l,2x + y)
v—/ 2 2 2 2
Relaciones y Funciones
331
II. En cada caso hallar los conjuntos y graficar:
(7) Dado los conjuntos: A ={xe z/-l <x <3}, B ={xe z/ 1 <x <4}, C= {xez/ 1 <x <4J;
Hallar los conjuntos y graficar:
a) AxB b) BxC c) (A-C)xB
Q) Sea A = (xs R/l<x<3} y B = {y e R/2 <y <4}. Hallar A x B y graficar
(?) SeanA=(a.b}, B ={ 1.2,3,4,5} y E= {3,5,7,9}. Hallar (AxB) n(AxE)
(4) Repiesentar al conjunto producto cartesiano: {xe R / |x| < 5} x {xe R / -2 < x < 3}
Sombreando el área apropiada en el sistema bidimensional.
(?) Dado los conjuntos A = {xe N/x = ^^-, keN], B = {xe NI x2 -14x+40 = 0},
4
C = {x€ N/x~ -1 = 0}. entonces el número de elementos del conjunto
|(AnB)uC]x(B-C)es.
(?) Si A={xe R/2<x<5} y B = {x-eR/1 <x<4}. Graficar Ax B, luego graficar BxA.
(7) Si A={xe R/2<x<5} , T= {x eR/1 <x <4). Graficar Tx A, luego graficar AxT.
(i) Sí 4 = {^^/(,v-2)U + 3)(A— 5) = 0} y B = {— + 3/ v(x + 2)(t-4) = 2} Vxe R
\_^ 3 2
Hallar A x B, B x A y graficar.
(9) Si A = {ve NIk = ^—-, keN], B = [xe N /x2+1<12]. Hallar (A n B) x (B - A)
(w) Sí A = [x2-l/0<x<5, xez], B = {x2 +\/-5<x<-3, xe z},
C = {.v3+4/(.v-l)(v + 2)U-3) = 0, -ve;}. Hallar AxB, AxC, BxC
@ Si A = {-/xez A -2<x<4}, B = {xeN/x<2 A xe {3,2,4,5}}
Hallar y graficar AxB y BxA
332
Eduardo Esptnoza Ramos
(12) Si A={3x+l/(xe N Ax<3) V(xe z A O < x < 5)}
Calcular la diagonal del producto A x A y luego grafique.
(l?) Dado A= |xe </-12<x + 6<20} y B = {xe z/10<x2 <400}
Cuantos elementos tiene A x B.
(14) Dados los conjuntos: A={xeN/x<3) , B = {x eN /x es par y x < 5},
C = {x e N /x es impar y x <4J. Hallar el conjunto (AnB)x(C- A)
(j5) Sí A = {xez+/x =——, kez*} y fl = {xe z+/x2+1< 12}. Hallar (AnB) x (B-A)
Ué) Si A y B son dos conjuntos arbitrarios demostrar que: AxB=<¡) <=> A = <[) VB = <¡>
(l7) Demostrar que: A x (B u C) = (A x B) u (A x C)
(15) Demostrar que: A x (B n C) = (A x B) n (A x C)
(19) Demostrar que: (A - B) x C = (A x C) - (B x C)
(20) Demostrar que: Sí AcB entonces AxBcBxB
(21) Demostrar que: Sí A c: B entonces AxAcAxB
(22) Demostrar que: A x (E - B) = (A x E) - (A x B)
(S) Demostrar que: (A n B) x (E n F) = (A x E) n (B x F)
(2) Demostrar que: (AxE)u(BxF)e(AuB)x(Eu F)
(25) Demostrar que: AcB y EcD implica que AxEcBxD
4.2. RELACIONES BINARIAS,
a) DEFINICIÓN.- Consideremos dos conjuntos A y B no vacíos, llamaremos
relación binaria de A en B o relación entre elementos de A y B a
todo subconjunto R del producto cartesiano A x B, esto es:
R es una relación dé A en B « Re AxB
Relaciones y Funciones
333
Ejemplo.- Sean A ={2,4} y B = {1,3,5} entonces
A x B = {(2,1),(2,3),(2,5),(4,1),(4,3),(4,5)}
Los siguientes conjuntos de pares ordenados son relaciones de A a B:
/?,={(2,1),(2,5)}, fl2={(2,3),(4,l),(4,5)}, R3 = {(2,1), (4,3), (2,3)}. RA=AxB
Pero los siguientes conjuntos de pares ordenados no son relaciones de A en B:
R5 = {(1,2), (4,1), (4,5)}, R6 = {(2,1), (4,1), (3,4)} puesto que (1,2) É A x B, (3,4) ¿AxB
por lo tanto /f5gA.vB, R6 g: A xB.
OBSERVACIÓN.-
(Y) Si A = B. entonces R es una relación en A o, R es una relación entre elementos de A.
(2) La definición 1.1 establece una comparación entre elementos de pares ordenados,
motivo por el cuál se le llama "relación binaria".
Q3) Si R es una relación entre elementos de A y B, al conjunto A le llamaremos conjunto
de partida y al conjunto B le llamaremos conjunto de llegada.
(4J Generalizando: una relación R, entre los elementos del conjunto de los números
reales R, está determinado por una función proposicional P(x,y); esto es:
E={(x,y)e RxR/P(x,y)}
QQ Cuando el par ordenado (a,b) satisface a la función proposicional P(x,y) de la
relación R, diremos que (a,b) e R en caso contrario (a,b) e R.
Mí) Si A tiene p elementos y B tiene q elementos entonces 3 2" relaciones entre A y B
donde n = pq.
Ejemplos.- Sí A = {1,3} y B = {2.4} entonces A x B = {(1,2),( 1,4),(3,2),(3,4)}
El número de relación que se obtendrá de A x B es 22'2 =24 =16 es decir: que se
puede formar 16 relaciones:
334
Eduardo Espinoza Ramos
{(1.2)}, {(1,2),(3,2)}, {(1,4)}, {(3,2)}, {(3,4)}, {(1,2),(1,4)}, {(1,4).(3,2)}, {(1,2),(3,4)},
{(1,4),(3,4)}, {(3,2),(3,4)}, {(1,2),(1,4),(3,2)}, {(1,2),(1,4),(3,4)}, {(1,4),(3,2),(3,4)}.
{(1,2),(3,2),(3.4)}, {(1,2),(1,4),(3,2),(3,4)}, $
b) DOMINIO Y RANGO DE UNA RELACIÓN BINARIA.
Consideremos una relación R de A en B: es decir que RcAxB.
El dominio de la relación R denotado por DR es el conjunto definido por:
DR = [ae A/3beB A (a,b)eR]
El rango de la relación R denotado por RR es el conjunto definido por:
RR={beB/3aeA A (a,b)e R)
Ejemplo.- Si R={(1,4),(1,5),(2,3),(2,4),(2,5)} entonces DR={1,2}, RR ={3,4,5}
OBSERVACIÓN.-
Para determinar el dominio de una relación, primero se despeja "y" enseguida se analiza
los valores que pueden tomar "x" para que la variable "y" sea real.
Para determinar el rango de una relación se despeja "x", enseguida se analiza los valores
que puedan tomar "y" para que la variable "x" sea real.
Ejemplo.- Determinar el rango y dominio de la siguiente relación:
R = {(*, v)e RxRIx2 + y2 + lOy-75 = 0}
Solución
En primer lugar despejamos la variable "y" para obtener el dominio, es decir:
x2 + y2 +10y-75 = 0, completando cuadrado
(y + 5)2 =100-jc2 dedonde y =-5±y!\00-x2
Ahora analizaremos los valores que pueda tomar x para que "y" sea número real es decir:
100-x2 >0 dedonde: x2<100 => -10<x<10 /. D, =[-10,10]
Relaciones y Funciones
335
Ahora despejamos la variable "x" para obtener el rango, como x2 +y2 + 10y-75 = 0
-lOv-.v" entonces analizando los valores que puede tomar "y" para que
x sea número real se tiene: 75 — lOy — y2 >0
donde (y + 5)2 <100 => -10<y + 5<10 => -15<y<5 .-. Rf =[-^5,5]
c) PROPIEDADES DE LA RELACIÓN BINARIA.-
Las relaciones binarias gozan de las siguientes propiedades:
(T) PROPIEDAD REFLEXIVA.- Una relación R en A, düemos que es
reflexiva si (a,a) e R para todo a e A esto es:
R es reflexiva en A <=> V a e A, (a,a) e R
(¿) PROPIEDAD SIMÉTRICA.- Una relación R en A diremos que es simétrica
si (a,b) e R implica que (b,a) e R, esto es:
R es simétrica <=> V (a.b) e R => (b,a) e R
(3) PROPIEDAD TRANSITIVA.- Una relación R en A, diremos que es
transitiva sí:
(a,b) e R A (b,c) e R implica que (a,c) e R, esto es:
R es transitiva <=> V a,b,c e A, l(a,b) e R A (b,c) e R => (a,c) e R]
(4) PROPIEDAD ANTISIMÉTRICA.- Una relación R en A, diremos que es
antisimétrica sí:
V a,b e A, (a,b) e R y (b,a) e R implica que: a = b, esto es:
R es antisimétrica <=> V a,b e A, [(a,b) e R A (b,a) € R => a = b]
(?) PROPIEDAD DE EQUIVALENCIA.-
Una relación R en A, diremos que es de equivalencia si es: reflexiva, simétrica
y transitiva.
Ejemplo.- Si A = {1,2,3,4,5,6} las relaciones en A.
336
Eduardo Espinoza Ramos
a) /?, = {(1,1), (2,2), (3.3), (4,4), (5,5), (6,6)} es reflexiva en A.
b) R2 ={(1,1), (3,3), (4,4), (5,5), (6,6)} no es reflexiva en A por que falta (2,2).
Ejemplo.- Si A = {2,3,5,7}, las relaciones en A
a) /?, = {(5,3),(2,7),(3,5),(7,2),(2,2)} es simétrica porque (*, y)e /?, => (v, x) e /?,
b) R2 = {(5,3), (2,7), (3,5), (2,2)) no es simétrica porque falta (7,2).
Ejemplo.- Si A = {1,3,7,9} las relaciones en A.
a) /?, ={(7,l),(2,2),(l,2)}no es transitiya porque (7,1)e R2 A (1,2)e R2 => (7,2)e R2
Ejemplo.- Si A = {1,2,3,4,5} la relación R en A dado por
R = {(1,1),(2,2),(3,3),(4,4),(5,5)} es una relación de equivalencia porque
es reflexiva, simétrica y transitiva en A.
Ejemplo.- Sea Z = conjunto de los números enteros y la relación R definida sobre
Z en R = {(x,y) e ZxZ/x-y = 3m, meZjes una relación de
equivalencia. En efecto:
fl) R es reflexiva porque: a-a = 0 = 0.3 VaeZ es decir: (a,a) e R, V a e Z
(2) R es simétrica porque: Sí a - b = m.3 => b - a = -(a - b) = (-m).3
V a,b e Z => (a,b) e R => (b,a) e R ,
(3) R es transitiva porque: Sí a - b = m.3 y b - c = m .3 entonces
a - c = (a - b) + (b - c) = m.3 + rrí .3
a - c = (m + rrí )3 => a - c =m.3, V a,b,c e Z
es decir: (a.b) e R A (b,c) e R => (a,c) e R, V a,b,c e Z.
Por lo tanto R es una relación de equivalencia.
Relaciones y Funciones
337
d) DETERMINACIÓN DE UNA RELACIÓN BINARIA.
Teniendo en cuenta que una relación es un conjunto de pares ordenados, entonces a
una relación determinaremos por extensión o por compresión.
\
Ira. POR EXTENSIÓN.- j
Una relación queda determinada por extensión cuando se menciona cada uno de los
pares ordenados de la relación. /
Ejemplos.-
a) Rx ={(1,2),(2,3),(3,4),(4,5)j , R2 ={(a,b),(c,dUe,f)}
b) Si A ={2,3,6,9} y B = {1,4,5,6,12}
Expresa por extensión cada una de las relaciones:
(7) R= {(x,y)e AxB/y =2x}
Solución
R={(2,4),(3,6),(6,12)}
(5) R = {(x,y)e AxB/x + y=12}
Solución
R={6,6}
2da. POR COMPRENSIÓN.-
Una relación queda determinada por comprensión cuando se da una propiedad que
caracteriza a todos los pares ordenados que conforman la relación.
Ejemplos.-
a) Si A = Zconjunto de los números enteros la relación R={(x,y)eZx Z/y = x}
es una relación expresada por comprensión.
b) Si U=(xeN/x<7). Determinar por comprensión la relación:
R={(3,1).(4.2),(5,3),(6,4),(7,5)}
338
Eduardo Espinoza Ramos
Solución
Se observa que la diferencia entre la primera componente y la segunda componente
es dos unidades por lo tanto expresaremos por coipprensión:
R={(x,y)e UxU/x-y = Í)
e) RELACIÓN INVERSA.-
Si R c A x B es una relación de A en B; entonces a la relación inversa de R lo
denotaremos por R~l y está definido por:
/?"' ={(y,x)e BxA/(x,y)e R]
Ejemplo.- SÍR={(3,2),(3,1),(4,2),(4,5),(6,8)} => Rl -{(2,3), (1,3), (2,4), (5,4), (8,6)}
Ejemplo.- Hallar la inversa de las siguientes relaciones,
a) R={(x,y)e RxR/x + 3y= 12}
Solución
Para determinar la inversa de una relación se despeja x, es decir: x = 12 - 3y
Luego se permuta x por y es decir: y = 12 - 3x
R~l = {(x,y)eRxR/y = 12-3x)
b) R = {(x,y) eRxR/3x + 4y = 5 A 1 < x < 7}
Solución
5-4v
Primeramente despejamos x de 3x + 4y = 5 es decir: x = , 1 < x < 7
5-4y
Ahora veremos como va variando y; como 1 < x < 7 => 1< — < 7
3
3<5-4y<21 => -4<y<-
Relaciones y Funciones
339
5-4v 1
Luego jr = —, -4 < y < —, por lo tanto al permutar x por y se tiene:
y- , -4<jc< —
3 2
-i ., . „ „, 5-4/ _ ^ 1.
R = {(x,y)eR x R/y = —/-, -4<Jt<-}
4.3. GRÁFICA DE UNA RELACIÓN DE R EN R.
a) DEFINICIÓN.- Llamaremos gráfica de una relación de R en R al conjunto de
puntos P(x,y) cuyas coordenadas satisfagan a dicha relación,
teniendo en cuenta que una relación puede estar expresada en una de las formas:
E(x,y) = 0 V E(x,y)<0 V E(x,y)>0 V E(x,y)<0 V E(x,y)>0.
b) DISCUSIÓN DE LA GRÁFICA DE UNA RELACIÓN.-
Para trazar la gráfica de una relación dada por la ecuación E(x,y) = 0, daremos el
siguiente criterio.
Ira. Determinación de las intersecciones con los ejes coordenados.
Intersección con el eje X: E(x,y) n eje x = {(x, y) e R " I y = 0} = P
Es decir: para hallar el punto P de intersección con el eje X se hace y = 0 en la
ecuación E(x,y) = 0, o sea que se resuelve la ecuación E(x.O) = 0
Intersección con el eje Y: E(x,y) n eje v = ((\, v)e /?' Ix = 0} = Q
Es decir: para hallar el punto Q de intercesión con el eje Y se hace x = 0 en la
ecuación E(x,y) = 0, o sea que se resuelve la ecuación E(0,y) = 0.
2da. Determinación de la simetría con respecto a los ejes coordenados.
Simetría con respecto al eje X.
Existe simetría con respecto a eje X si se cumple E(x,y) = E(x,-y). Fig. (a)
340
Eduardo Espinoza Ramos
Simetría con respecto al eje Y.
Existe simetría con respecto al eje Y si se cumple E(x,y) - E(-x,y) Fig. (b)
Simetría con respecto al origen.
Existe simetría con respecto al origen si se cumple E(x,y) = E(-x,-y). Fig. (c)
Q(-x,-y)
3ra. Determinación de la extensión de la curva.
Consiste en determinar el dominio y el rango de la relación.
4ta. Determinación de las Ecuaciones de las Asíntotas.
Trataremos solamente de las asíntotas verticales y horizontales.
Asíntotas Verticales.- La recta x=a, es una asíntota vertical de la relación
E(x.y) = 0. si para cada (x,y) e E(x,y), se tiene que
para "y" bastante grande la distancia de "x"a"a" es decir |x-a| es muy pequeño.
\
Relaciones y Funciones
341
Y '
0
l-J
r_
a
i\
i
i
_x_
i
i
i
_x
x,-a|
i
i
*2
► 1 *2 - a 1
X
Para calcular las asíntotas verticales se despeja la variable y de la ecuación
E(x,y) = 0 es decir: y = de donde f y g son expresiones solamente de x,
entonces las asíntotas verticales se obtienen de la ecuación g(x) = 0, es decir
haciendo el denominador igual a cero.
Asíntotas Horizontales.- La recta y = b es una asíntota horizontal de la
relación E(x,y) = 0 sí para cada (x,y) e E(x,y) sé
tiene que para "x" bastante grande la distancia de "y" a "b" es decir |y - b| es
muy pequeña.
Y
„|y,-M wlya-bi
Para calcular las asíntotas horizontales se despeja la variable x de la
f
ecuación E(x.y) = 0. es decir: a --^- donde f y g son expresiones
Si
}>
solamente de y. entonces las asíntotas horizontales se obtienen de la ecuación
g(y) = 0 es decir haciendo el denominador igual a cero.
342 Eduardo Ettpinoza Ramos
bpi
5ta. Tabulación.
Consiste en calcular un número determinado de pares ordenados a partir de la
ecuación E(x,y) = 0.
6ta. Trazado de la curva.- Mapeo de los pares ordenados.
OBSERVACIÓN
(T) Diremos que el par (a.b) pertenece a la relación E(x,y) = 0 sí y sólo sí E(a,b) — 0.
Ejemplo.- Discutir y graficar la relación: R = {(x,y) e RxR/xy-2y-x = 0)
Solución
A la relación dada escribiremos en la forma: R(x,y) = xy - 2y - x = 0
Io Intersección con los ejes coordenados:
Con el eje X; hacemos, y = 0 ; R(x,0) = 0-0-x = 0 => x = 0
Con el eje Y; hacemos, x = 0; R(0,y) = 0-2y-0 = 0 => y = 0
2° Simetrías:
Con respecto al eje X: R(x,y) = R(x,-y)
pero x(-y) - 2(-y) - x * xy - 2y - x, por lo tanto no existe simetría con el eje X.
Con respecto al eje Y: R(x,y) = R(-x,y)
pero xy - 2y - x * -xy - 2y + x, por lo tanto no existe simetría con el eje Y.
Con respecto al origen: R(x,y) = R(-x,-y)
pero xy -2y- x * (-x)(-y) - 2(-y) - (-x), por lo tanto no existe simetría con el origen.
3o Extensión:
x
Calculamos el dominio, para esto despejamos y es decir: v =
x-2
Luego DR =/?-{2}
Relaciones y Funciones
343
Calculamos el rango, para esto despejamos x es decir: x -
Luego RR = /?-{U
4° Vsíntotas:
2y_
y-\
Asíntota Vertical: se despeja y: v = la ecuación de la asíntota vertical es x=2
x — 2
Asíntota horizontal: se despeja x:
2y
x , la ecuación de la asíntota horizontal es y = 1.
y-\
5° Tabulación:
X
Y
0
0
1
-1
3
3
4
2
-1
0.3
-2
0.5
-3 -2 -1
-1 -
._i L.
4.4. EJERCICIOS DESARROLLADOS.
\AJ Hallar el dominio y rango de la relación: R = [(x,y)e RxR/ xy2 -jr + 3y2 +1 = 0}
Solución
Calculando el dominio de la relación R, para esto despejamos y de la ecuación
.vy2-A + 3v2+l = 0 => U + 3)v2 = jc —1 => y =
x-\
\+3
344
Eduardo Éspinoza Ramos
Analizando los valores que pueda tomar x para que y sea real, en esite caso debe
x — 1
cumplirse: > 0. \ / \ /
jc + 3 + v - v + p
-3 1
Luego DR -< —oo,-3 > U[l,+°° >
Ahora calculamos el rango de la relación R.
Para esto despejamos x de la ecuación: xy2 -x + 3y2 +1 = 0
y-l
Luego los valores que puede tomar y para x sea real es que y * ± 1
Por lo tanto RR = R - [ -1,1}
(2) Hallar el dominio y el rango de la relación: R = [(x, y)e RxR/x2y2 -4x2 -4y2 =0}
Solución
Sea x2y2-4x2-4y2 =0 ...(1)
Para calcular el dominio de la ecuación (1) despejamos y = ±.
4x2
x2-4
Ahora analizaremos los valores que pueda tomar x para que y sea real, en este caso debe
x2 1 1
cumplir: — >0 => — >0 => >0
x2-4 x2-4 (x + 2)(x-2)
\ I \ /
+ >¿ : v. ± w
La solución es x e <-°°,-2> u <2,+°°>
Para x = 0 también se verifica. Por lo tanto: DR= < -°°,-2 > u < 2,+00 > u {0}
Relaciones y h unciones
345
Ahora calculamos el rango de la relación para esto despejamos x de la ecuación (1)
, analizando los valores que pueda tomar y para que x sea real, en este caso
,=±.-4¿
Vr-4
4y2
se tiene —-^—>0
y2-4
-> 4v2 1
VyeR, y">0 => y = 0 se cumple, / >0 => >0
r-4 (y-2)(y + 2)
\ i \ /
± V I J¿ + >.
-2 2
La solución es y e <-°°,-2> ¡u <2.+°°>
Por lo tanto: RR-< -«,-2 > o < 2,-H» > u {0}
(3) Sí A ={2,3,6,9,11} y B = {1,4,5,6,12,14}
Expresar por extensión cada una de las siguientes relaciones:
a) R= {(x,y)e AxB/y = 3x}
Solución
R={(2.6)}
b) R={(x,y)e AxB/x + y=12}
Solución
R={(6,6),(11,1)}
c) R= {(x,y)e AxB/y = x}
Solución
R={(6,6)}
346
Eduardo Espinoza Ramos
\4j Si el universo es U = {1,2,3,4,5} determinar por comprensión cada una de las relaciones:
a) R = {(1,1),(2,2),(3,3),(4,4),(5,5)}
Solución
R= {(x,y)e UxU/y = x}
b) R={(3,1),(4,2),(5,3)}
Solución
R={(x,y)e UxU/y = x-2}
[5y La relación R = {(x,y) eZxZ/x-y = 2k, keZJ. Es una relación de equivalencia
Solución
a) Reflexiva: Six = y => y-x = 0
=> x - x = 2(0), 0 e Z
Luego V (x,x) e R .: R es reflexiva.
b) Simetría: Como x - y = 2k, multiplicando por -1 se tiene: y - x = 2(-k), -k e Z
Luego (y,x) e R .\ R es simétrica
c) Transitiva: Sí(x,y)eR => jt-;y = 2Jfc1, k¡ e Z
(y,z)eR => y-z = 2k2, k2eZ
x-z = 2{kl+k2), kl+k2eZ
Luego (x,z) e R .". R es transitiva. Por lo tanto R es de equivalencia.
^T) La relación R definida por: R = {(x,y) e RxR/|x-y|<4),Resde equivalencia.
Solución
a) Reflexiva: VxeR, |x-x| = 0<4 => (x,x) e R .-. Res reflexiva
Relaciones y Funciones
347
b) Simétrica: (x,y) eR => | x — y | < 4
=> | y - x | < 4 => (y,x) e R .-. R es simétrica.
c) R no es transitiva: para esto tomemos dos pares ordenados
(7,4) eR => | 7 -4 | = 3 < 4
(4,1) e R => |4-1 | = 3<4
(7.1) eR => | 7 - 1 | = 6 í 4, luego R no es transitiva.
Por lo tanto R no es de equivalencia.
7J Determinar sí la relación: R = [(x,y)/yíx + -Jy —í, x,ye R+] es reflexiva, simétrica y
transitiva.
Solución
a) Reflexiva: Sí .ve R+ => -Jx + -Jx * 1, x * —.
4
Luego (x.x) é R => R no es reflexiva.
b) Simétrica: Sí(x,y)eR => y[x + -Jy=\
yfy + yfx = l => (y,x)e R
Por lo tanto R es simétrica.
c) Transitiva: Sí(x,y)e R entonces: -Jx + Jy=l
(y,z) e R entonces Jy + -Jz = 1
>/í + Ví = 2(l-Vy)^l
=> (x,z) g R, por lo tanto no es transitiva.
348
Eduardo Espinazo Ramos
QQ Discutir y graficar la relación: R-[{x, y)e RxR/x2y-4y + x = 0]
Solución
La relación dada también se escribe así: R(x, y) = x~y — 4y + x-0
Ahora haremos la discusión correspondiente:
Ira. Intersección con los ejes coordenados
Con el eje X, hacemos y = 0; R(x,0) = 0-0 + x = 0 => x = 0
Con el eje Y, hacemos x = 0; R(0,y) = 0-4y+ 0 = 0 => y = 0
2da. Simetrías
Con respecto al eje X: R(x,y) = R(x,-y).
Pero x2 (—y) — 4(—y) + x*x2y — 4y + x, por lo tanto no existe simetría en el eje X
Con respecto al eje Y: R(x,y) = R(-x,y)
Pero x2y — 4y + x*(—x)2y-4y-x, por lo tanto no existe simetría con el ejeY.
Con respecto al origen: R(x,y) = R(-x.-y)
x2y-4y + x = (-x)2 - 4(->) - x, por lo tanto si existe en el origen.
3ra. Extensión.
—x
Calculamos el dominio, para esto despejamos y, y =
x2-4
el dominio es: R = {-2,2}
Calculamos el rango, para esto despejamos x
, n -1 + Jl + I6y2
x y-4y + x = 0 => x = ; y ^ 0
el rango es todos los reales R, puesto que y = 0, x = 0, la ecuación se verifica.
Relaciones y Funciones
349
4ta. Asíntotas
Asíntotas Verticales: se despeja y, y ■■
x2-4
, las ecuaciones de las asíntotas
verticales se obtienen de la ecuación x~ - 4 = 0 de donde x = -2, x = +2 es decir:
x = ± 2 son las asíntotas verticales.
Asíntotas horizontales, se despeja x, x ■
-I±yjl + I6y2
2>
La ecuación de la asíntota horizontal es y = 0
5ta. Tabulación.
X
y
-4
0.3
-2.5
1.1
-1.5
-0.9
-1
-0.3
0
0
1
0.3
1.5
0.9
2.5
1.1
4
-0.3
-2.5
1 1.5
(9} Discutir y graficar la relación: /? = {(*, y)e RxRIx2 y2 -4x2 -4y2 =0}
Solución
A la relación dada escribiremos en la forma: R(x, y) = x2 y2 - 4x -4y =0
Ahora haremos la discusión correspondiente.
350
Eduardo Espinoza Ramos
Ira. Intersecciones con los ejes coordenados.
Con el eje X, hacemos y = 0 de donde R(x,0) = 0 -4;r2 - 0 = 0 => x = 0
ConelejeY, hacemosx = 0 dedonde /?(0,_v) = 0-0-4y2 =0 => y=0
2da. Simetrías:
Con respecto al eje X: R(x,y) = R(x,-y)
Como x2y2 -4x2 -4y2 = x2{-y)2 -4x2 -4(->)2
Por lo tanto existe simetría en el eje X.
Con respecto al eje Y: R(x,y) = R(-x,y)
Como x2y2 -4x2 -4y2 =(-x)2y2 -4{-x)2 -4>2
Por lo tanto existe simetría en el eje Y.
Con respecto al origen: R(x,y) = R(-x,-y)
Como x2y2 - 4a;2 - 4y2 = (-x)2{-y)2 - 4(-xf - 4(-y)2
Por lo tanto existe simetría en el origen.
3ra. Extensión.
I 4jt2
Calculamos el dominio para esto despejamos y, y = ±-|—=
U -4
4 2 j \ / \ /
y es real sí — >0 => >0 1—* = * ± ►
x2-4 (jt-2)(jt+2) _2 2
x e <-oo,-2> u <2,+oo> por lo tanto .-. Dp -< -°°.-2 > u < 2, +<» > u {0}
| 4.y2
Calculamos el rango, para esto despejamos x, x = ± —e—
\y -4
Relaciones y Funciones
351
x es real si
4y-
v2-4
>0
1
(v-2)(v + 2)
>0
^V
^v
y e <-oo,-2> u <2.+oo>. p0r lo tanto /. RR = < -°°,-2 > u < 2.+°o > u {0}
4ta. Asíntotas.
Asíntotas verticales: se despeja y = ±.
4jt
IjT-4
Las asíntotas verticales se obtiene de la ecuación a2-4 = 0 => x = ± 2
4y¿
Asíntotas horizontales: se despeja x = ± I—
Las asíntotas horizontales se obtienen de la ecuación v ~ — 4 = 0 => y=±2
5ta. Tabulación.
X
y
+ 3
+ 6yf5
5
±4
+ 4>/3
3
0
0
Discutir y graficar la relación. R = [(x, y) e RxR I yx - 4 y -x =0}
Solución
352
Eduardo Espinoza Ramos
A la relación dada escribiremos en la forma: R(x. y) = yx~ —4y — x~ =0
Ahora haremos la discusión correspondiente
Ira. Intersección con los ejes coordenados.
Con el eje X, hacemos y = 0, de donde R(x,0) = 0-0-x2 -0 => x = 0
Con el eje Y, hacemos x = 0, de donde /?(0, >) = 0-4>-0 = 0 => y = 0
2da. Simetrías
Con respecto al eje X: R(x,y) = R(x,-y)
pero yx2 —4y — x2 *—yx~—4(—y) — x
por lo tanto no existe simetría en el eje X.
Con respecto al eje Y: R(x,y) = R(-x,y)
como yx2 -Ay-x2 = y(-x)2 -4y-(-x)2
por lo tanto existe simetría en el eje Y.
Con respecto al origen: R(x,y) = R(-x,-y)
pero yx2-4y-x2 *-y(-x)2 -4(->)-(-x)2
por lo tanto no existe simetría en el origen.
3ra. Extensión.
x2
Calculamos el dominio, para esto despejamos y de donde y = —= , y es real
x -4
si x * ± 2, luego entonces .*. DR=R-{-2,2}
4y
Calculamos el rango, para esto despejamos x., x - ±
\y-l
--~\ i \ r---
x es real si: > 0
y-1 0 1
Relación es y Fu n cion es
353
y e <-oo,0] u<l,+°°>, -•. RR =<-°°,0] u<l, +<» >
4ta. Asíntotas
Asíntotas verticales, se despeja y, y = — , las asíntotas verticales se obtienen
de la ecuación a"-4 = 0 =$ x = ±2.
x2-4
Asíntotas horizontales, se despeja x
obtienen de la ecuación y-l=0 => y=l
5ta. Tabulación.
H£-
las asíntotas horizontales se
X
y
0
0
±i
-0.3
±1.5
-1.2
±2.5
2.7
±3
1.8
-2 "2
4.5. EJERCICIOS PROPUESTOS.
(íj Hallar el dominio y rango de las relaciones
a) R = {(x, y)e RxR/y = x1 -4x, y < 0}
c) R = {(x.y)sRxR/x2 =y-l)
b) R = {(x,y)e RxR/y = y¡4-x2 }
d) R = {(x,y) e RxR / xy -2y-x=0}
e) R = {(.v, y)e RxR/ x+ y = 1}
2 ..2
f) R = {(x,y)<ERxR/x¿y~+xy = 5]
354
Eduardo Espinoza Ramos
g) R = {(x,y)eRxR/y = —- } h) R = {(x,y)e RxRI(x2 -4)y = y2)
2x~ -3x-5
i) R = {(x,y)eRxR/x2y2-2x+y2-4 = 0)
j) R = {(x,y)eRxR/(x2-6x + 5)y2 =4>-l}
\2J Sí U = {jte Z* Ix impar A x< 8}. Tabular las siguientes relaciones en U
a) R = {(x,y)e UxU/x = 3 V y = 5} b) R= {(x,y) e U x U/x +y = 8}
c) R={(x,y)e UxU/xy = 21} d) R={(x,y)eUxU/x divide a 20}
\3J En el conjunto de los naturales N se define una relación R de la siguiente forma:
R = [(x,y)e NxN/x2 +at=>2 +>}
es decir si es una relación de equivalencia, justifique su respuesta.
M) En R se define las siguientes relaciones, V x,y e R
a) R={(x,y)e RxR/|x-l | = |y-l |) b) R = {(x,y)e RxR/x2 -x = y2 -y).
Demostrar que son relaciones de equivalencia.
(s) Siendo A = {1,2,3,4,5,6} estudiar las propiedades de las relaciones binarias.
a) R=((x,y)eAxA/x + y>0) b) R = {(x.y) e Ax A/x-y <2)
c) R= {(x,y)e Ax A/x<y}
Rpta. a y c es de equivalencia, b) es reflexiva
^T) En A = {1,2,3,4} se considera la relación R = {(x,y) eAxA/x = y V x + y = 3}
Es de equivalencia. Rpta. Si
(?) En Z define la relación R: /? = {(Jt,y)e ZxZ Ix2 + x = y2 + y). Graficar R.
Qíj) Clasificar la relación R definida en Z x Z mediante (a,b)R(a',b') <=> ab'=ba'
Rpta. R es de equivalencia.
Relaciones y Funciones
355
{9j Definimos en el conjunto Z x (Z - 0) la siguiente relación (a,b) R (c,d) *=> ad = be
Es una relación de equivalencia Rpta. R es una relación de equivalencia
(lO) Demostrar que la relación dada por: R= {(a,a),(b,b),(c,c),(d,d).(a,c),(c,a),(b.d),(d.b)}
En el conjunto A = {a,b,c,d} es una relación de equivalencia.
Ql) Discutir y graficar las relaciones siguientes:
a) ry2-3y2 -1 = 0 b) y2(x2 -4) = x + 2
c) y = d) v = -
3-Jt ' 2jt2-3jt-5
e) x2y2-x2+y2+l=0 f) x2y2 +4jT -4y2 =0
g) xy-2x-y-2 = 0 h) y~(;c+l) = 4
Discutir y graficar las relaciones siguientes:
a) xv" +x\-6x-3-0
c) >-
jT-4
e) x' +xy~ — y~ —0
g) vx~ -25y-x = 0
b)
d)
f)
M
3jc2-8jc + 4
■V
x2+]
>_2jt2-5jt + 2
jcU + 3)
>_U + 2)(r-2)
jc2-3jc + 2
v =
Or-1)-
Discutir y graficar las relaciones siguientes:
a) v= b) y = r
Jt + l 2(jc2-1)
c) v= 2a"~5v + 2 d) xy2_4r2-3v2+12.v = 0
' 3a2-10.*+ 3
356
Eduardo Espinoza Ramos
®(2jc-1) -4
Discutir y graficar la relación R definida por: R = { (jc, y) e RxR I y = — —}
jc2-7jc + 10
4.6. FUNCIONES.
Se va a introducir el concepto de función, hablando libremente una función f de un
conjunto A en un conjunto B es una regla (procedimiento o mecanismo) que nos
transporta de un conjunto a otro de manera que asociamos cada elemento de A un único
elemento en B.
a) DEFINICIÓN.- Consideremos dos conjuntos cualquiera A y B, a la relación
binaria f de A en B le llamaremos función de A en B, si y
sólo si, verifica:
Io
»
f CA
(a,b) e
xB
f A (a,c) e f
=>
b =
= c
esto quiere decir, que dos pares ordenados distintos no pueden tener la misma
primera componente.
f
A
Gráficamente:
f es función, sí b = c
OBSERVACIONES:
(T) Una función f de A en B denotaremos por: f: A > B; o A——> B y se lee "f
es una función de A en B", donde el conjunto A le llamaremos conjunto de partida y
el conjunto B le llamaremos conjunto de llegada.
\2) Si el par (a,b) e f, escribiremos b = f(a) y se dice que b es la imagen de "a" por f o
también, que b = f(a) es el valor de f en el punto a.
(3) Sí A = B = R, a la función f: R > R, se denomina función real de variable real
(4) Teniendo en cuenta la parte 2) se tiene la siguiente notación:
y = f(x) <=> (x,y) e f
Relaciones y Funciones
357
donde y = f(x) se lee "y es función de x" ó "y es la imagen de x por f'.
(x,y) e f se lee "el par (x,y) pertenece a f'.
Ejemplo.- f(l) = 3 » (1,3) e f
(¿) De la parte 4), a la función f se puede escribir en la forma:
f={(x,y)e RxR/y = f(x)}
donde la ecuación y = f(x) es llamada regla de correspondencia.
OBSERVACIÓN.- Una consecuencia inmediata de la definición a), es que toda
función es una relación pero no toda relación es una función.
Ejemplo.- La relación: R = {(1,2),(2,3),(3,4),(2,5)} no es una función, puesto que para
el elemento 2 existen dos elementos 3 y 5 tales que (2,3),(2,5) e R, que
contradice a la definición de función.
b) DEFINICIÓN GEOMÉTRICA.- f es una función <=> cualquier recta
perpendicular al eje X corta a la gráfica de f en
un sólo punto. Es decir: Gf(f) nL= {punto}
G,(/) nL={p},
f es función
G2(h) nL=(P,Q)
=> h no es función
4.7. DOMINIO Y RANGO DE UNA FUNCION.-
Sea f: A > B una función de A en B, llamaremos dominio de la función f, al conjunto
de todas sus primeras componentes, al cual denotaremos por Df , es decir:
358
Eduardo Espinoza Ramos
Df={xe A/3 ve B A (x,y)e f]cA
y llamaremos rango de la función f al conjunto de las imágenes de todos los elementos de
A, mediante f al cual denotaremos por Rf es decir:
Rf ={yeB/3xe A A (*,v)e /)cí
X
/
,.
y
Ejemplo.- Sea f = {(1,2),(3,4),(5,6).(7,8)} su dominio y rango es: Df ={1,3,5,7};
Rf = {2,4,6,8}
4.8. CRITERIO PARA EL CALCULO DEL DOMINIO Y RANGO DE
UNA FUNCIÓN.
El dominio de una función f se determina analizando todos los valores posibles que pueda
tomar x, de tal manera que f(x) sea real, salvo el caso en que dicho dominio sea
especificado.
El rango de una función f se determina despejando la variable x en función de "y", luego
se analiza todos los valores posibles que pueda tomar "y", de tal manera que x sea real.
Ejemplo.- Hallar el dominio y rango de la función / ( jc) = V2 + jc -x2
Solución
Calculando el dominio: como y = f(x,) entonces:
y = V2 + x — x2 luego "y" es real si, 2 + x -x2 >0, dedonde
jc2-jc-2<0 => (x-2)(x + l)<0
+ V
-1
Relaciones y Funciones
359
Luego el dominio es: .\ Df =[-1,2]
Calculando el rango: como y = \2 + x — x2 , y > 0
l±^9-4y2
y~ =2 + x-x , despejamos x, es decir: x =
2^ _ ..2 .9 3 , ,3
Luego x es real si 9-4y >0 => y < — => —<y<
4 2 2
Por lo tanto Rf = [0,+~>n[—,-] = [0,-] de donde .-. Rf =[0,-]
1 2 2 2 T 2
Ejemplo.- Hallar el rango de la función: f(x) = x2 -4jc + 7 , x e [2,3]
Solución
En este caso el dominio esta especificado x e [2.3] ahora calculando el rango: como
>' = /(*) = x2 — 4a:+ 7 . Despejamos x es decir: x= = 2±yjy — 3
x = 2±Jy^3 e [2,3] => 2<2±V^I3<3
0 < +V.V-3 < 1 => 0 < ^jy-3 < 1 => 0 < y - 3 < 1
3 < y < 4 => ye [3.4] por lo tanto .-. Rf = [3,4]
4.9. APLICACIONES DE A EN B.
A una función f, le llamaremos aplicación de A en B, si y sólo si: Df = A.
EN FORMA SIMBÓLICA: Un conjunto fcAxB es una aplicación de A en B <=>
V x e A, 3 y e B, tal que y = f(x).
OBSERVACIÓN.- Una aplicación es un caso particular de una función, luego toda
aplicación es una función, pero toda función no siempre es una
aplicación.
360
Eduardo Espinoza Ramos
NOTA.- Algunos autores consideran a la función y aplicaciones como sinónimos, en
estos apuntes, a las aplicaciones las consideraremos como casos particulares de
las funciones.
Ejemplo.- Sean A ={1,3,5}, B = {2,4,6}, calculando AxB
A x B = {(1,2),(1,4),(1,6U3,2),(3,4),(3,6),(5,2),(5.4),(5.6)}
a) El conjunto f= {(1,4),(3,2)} es función donde Df ={1,3} y R¡ ={4,2} pero f no es
una aplicación de A en B puesto que D**A.
b) El conjunto f = {(1,2),(3,4),(5,6)} es una función donde: D¡ ={1,3,5} y
Rf — {2,4,6} como Df — A entonces fes una aplicación de A en B.
4.10. FUNCIONES ESPECIALES.-
®
©
FUNCIÓN CONSTANTE.-
Y
c
A la función f, le llamaremos función constante, si su
regla de correspondencia es:
f(x) = c, donde c es una constante.
f(x) = c También a la función constante, se puede definir por:
f = {(x,y)e RxR/y = c,cconstante}
FUNCIÓN IDENTIDAD.-
Y f(x) = x
X donde su dominio es Df = R , su rango es Rf -{c}
y su gráfica es:
A la función f, le llamaremos función identidad, si su
regla de correspondencia es:
f(x) = x
—►
X
También a la función identidad se define:
f= {(x,y)e RxR/y = x}, donde Df=R, Rf=R
y su gráfica es:
Relaciones y Funciones
361
©
©
©
©
FUNCIÓN LINEAL.- A la función f, le llamaremos función lineal, si su regla de
correspondencia es:
f(x) = ax + b
f(x) = ax + b
donde a.b son constantes y a * 0. También a la
función lineal se puede expresar en la forma:
X f = {(x.y)eRx R /y = ax + b), donde Df=R y
Rj = R; a,b e R y a *■ 0, cuya gráfica es:
FUNCIÓN RAÍZ CUADRADA.- A la función f, le llamaremos función raíz cuadrada,
si su regla de correspondencia es:
i
2
1
0
^Y
/ \
/ I
I
1
^^TÓó^v/7
4 X
/w=Ví
También se puede expresar en la forma:
f = \(x,y)eRxR/y = J¿}
X donde Df =R+ y Rf = [0,-k» >
FUNCIÓN VALOR ABSOLUTO.
Y
A la función f, le llamaremos función valor
absoluto, si su regla de correspondencia es:
f(x) = | x |, donde | x \
_ í x, xZO
\-x, x<0
También se puede expresar en la forma:
0 1 2 X
FUNCIÓN MÁXIMO ENTERO.
f={(x,y)e RxR/y = |x|}
Donde Df - R y Rf = [0,-k>° > y su gráfica es:
A la función f, le llamaremos función máximo
entero, si su regla de correspondencia es:
362
Eduardo Espinoza Ramos
/M=[|-*D donde [|jc|] = n <=> n<x<n+l, neZ
También se puede expresar en la forma:
f={(x,y)eRxR/y = [\x\]}
donde Df = R y Rf = Z
-5 -4 -3 -2 -1
12 3 4 5 X
Sixe[0,l> <=> /(x) = [|jc|] = 0 => f(x) = 0
Sixe[l,2> <=> /(x) = [|;c|J = 1 =>f(x)=l
Si x e [2,3> <=> f(x) = [| x |] = 2 => f(x) = 2
Si x e [3,4> <=> /(jc) = [| jc |] = 3 => f(x) = 3
Sixe[-1,0> <=> /U) = [|jr|] = -1 => f(x) = -l
Sixe[-2,-l> <=> /U) = [|x|] = -2 => f(x) = -2
Sixe[-3,-2> <=> /(-t) = [|jc|] = -3 =» f(x) = -3
Relaciones y Funciones
363
©
FUNCIÓN SIGNO.-
A la función f. le llamaremos función signo, si su
regla de correspondencia es:
f(x) = sig(x), donde sig(x) =
n „i
m
i
.V
0
x*0
, jc = 0
X También puede expresar en la forma:
t
■1
f={(x,y)e RxR/y = sig(x)}
Donde Df=R, Rf ={-1,0,1} y su gráfica es:
FUNCIÓN CUADRÁTICA.-
A la función f, le llamaremos función cuadrática, si su regla de correspondencia es:
f(x) - ax +bx + c, a,b,c e R, a * 0
También a la ecuación cuadrática se expresa así:
f = {(x,y)<ERxR/y = ax2+b\ + c, a,b,ce R. a*0}
La gráfica de la función cuadrática es una parábola con eje perpendicular al eje X en el
cual se presenta dos casos.
Si a > 0 la gráfica se abre hacia arriba.
Si a < 0 la gráfica se abre hacia abajo.
El dominio de la función cuadrática es: D ¡ = R, El rango se determina completando
cuadrados.
Como f(x) = ax~ +bx + c
, o b b2 b-
f(x) = a(x- + — x + —-) + c
a 4«" 4í7
b ■> 4ac-b'
f(x) = a(x + —)- +
2í7 4í7
364
Eduardo Espinoza Ramos
■ - - j i -l . ,,, b 4ac-b x
Luego el vértice de la parábola es: V( . )
Y '
4ac-b2
4a
0
i
2b_ X
a
Si a > 0 se tiene:
~ „ Aac-b2
Df=R, Rf=[ ,+°°>
f f 4a
Si a < 0, se tiene:
„ „ „ 4ac — b2^
Df=R, «,=<-,— ]
J 4a
(5) FUNCIÓN POLINOMIAL.-
A la función f, le llamaremos función polinomial, si su regla de correspondencia es:
f{x) = anx"+a„_lxn +... + alx + a(), xe R
donde a0, ax,a2,...,an_i,a„ son números reales, an *■ 0.
Ejemplo.- f(x) = 5jc5 + 7jt4 + 3x + 6, es una función polinomial.
FUNCIÓN RACIONAL.-
A la función f, le llamaremos función racional, si su regla de correspondencia es:
„n-l
bmxm+bm_1xm-i+... + bix+b0
donde a0,a¡,...,an, fc0,¿, ,...,£,„ son constantes reales y bm*0
jc2+5jc-17
Ejemplo.- La función f(x) =:
, es una función racional cuyo dominio es el
x~ — 5jr+6
conjunto de todas las x, de tal manera que el denominador no se anule, es
decir: Df = {xe Rlx1 -5.v f6*0} = fi-{2,3}
»■
Relaciones y /-'unciones
365
4.11. EVALUACIÓN DE UNA FUNCION.-
Consideremos una función f con regla de correspondencia.
y = f(x), x€.Df
Si x toma valores específicos, por ejemplo: x = a0, entonces y0 = /(a0) se dice que la
función ha sido evaluada, en otras palabras es:
Cuando x = x0 el valor de la función es /(a0 )
Ejemplo.- Si f(x) = 2x3 + x2 + x + 2 , el valor de f en el punto x = 2 es f(2) es decir:
/(2) = 2(2)3+(2)2 +2 + 2 = 16 + 4 + 2 + 2 = 24
Ejemplo.- Si /(a) = a"+a + 1 entonces f(z) = z2+z + l
Ejemplo.- Si /(a) = 5jc , probar que f(x + y) = f(x).f(y)
Solución
/<*+>■) = 5**-" =5A.5V =/(a)./(v)
.-. f(x + y) = f(x).f(y)
4.12. FUNCIONES DEFINIDAS CON VARIAS REGÍ AS DE
CORRESPONDENCIA.
En las funciones definidas con dos o más reglas de correspondencia, su dominio y rango se
determinan de la siguiente forma:
Suponiendo que la función f es definida por:
I/2(a). a6D/o
el dominio de f(x) se detemiinan así:
Df=Df^Dh
366
Fduardo R\¡iii t . Rtwo\
el rango de la función f(x) se calcula por:
Rf=RhKjRh
Esta forma de calcular dominio y rango de una función con dos reglas de
correspondencia, también se extiende a funciones de tres o más reglas de
correspondencia.
Í2a-+1 si x>\
I x2 - 2 si x < 0
Solución
Ejemplo.- Calcular el dominio y rango de la función: /(.v) =
Calculando su dominio se tiene:
Í/,(a) = 2a + 1. si" .v>1
}/2(a-) = jT-2. si x<0
[D, = [!.+«=>
lDf2 = <-
3,0 >
Luego su dominio de f(x) es: D, = D, u D, = [1,+°° > u < -°°.0 >
.: Df = < -oo,0 > u [K+oo >
Ahora calcularemos el rango:
Si x>l=> y = 2x+l despejamos x: a- = > 1 => y > 3 de donde: y e [3,+<»>
Si x<0 => y = x2 - 2, despejando x se tiene: x = --Jy + 2 < O => -Jy + 2 > O => y > -2
de donde: y e <-2,+°o>
Luego el rango de la función f es dada por: R, = < -2,+°o > u [3.+<=° > — < -2.+°° >
4.13. TRAZADO DE GRÁFICOS ESPECIALES.
Cuando se conoce una función y = f(x), en base a esta función, se puede construir otra
función en una forma rápida mediante el siguiente criterio:
f(x) + c
ler. Si se tiene la gráfica de y = fíx) entonces la
gráfica de la función:
F(x) = f(x) + c se obtiene desplazando
verticalmente la gráfica de y = f(x) en c
unidades, siendo hacia arriba si c > O y
hacia abajo si c < 0.
Relaciones y Funciones
367
2do. Si se tiene la gráfica de y = f(x) entonces la gráfica de la función F(x) = f(x - c) se
obtiene desplazando horizontalmente la gráfica de y = f(x) en c unidades, siendo
hacia la derecha si c > 0 y hacia la izquierda si c < 0.
f(x-c)
c<0
y = f(x)
f(x-c)
c>0
3er. Si se tiene la gráfica de y = f(x) entonces la gráfica de la función F(x) = f(x - h) + k
se obtiene desplazando horizontal y verticalmente la gráfica y = f(x) en h y k
unidades respectivamente.
f(x - x) + h
si h<0
k>0
y = f(x)
f(x-h) + k, h<0, k<0
f(x-h) + k, h>0, k<0
4ta. Si se tiene la gráfica y = fíx) entonces la gráfica de la función F(x) = af(x), a > 0 se
obtiene de la siguiente manera:
i) Si a > 1 la gráfica está estirándose verticalmente en un factor a en base al eje X.
ii) Si 0 < a < 1, la gráfica está encogiéndose verticalmente en su factor a.
368
Eduardo Espinoza Ramos
5ta. Si se tiene y = f(x) entonces la gráfica de la función F(x) = f(ax), a > 0 se obtiene
de la siguiente manera:
i) Si a > 1, la gráfica se encoge horizontalmente en un factor "a" en base al eje Y.
ii) Si 0 < a < 1, la gráfica se estira horizontalmente en un factor "a" en base al eje Y.
f(ax) si a > 1
y = f(x)
f(ax) si 0 < a < 1
6ta. Si se tiene la gráfica y = f(x) entonces la gráfica de la función F(x) = -f(x) se obtiene
haciendo rotar la gráfica y = f(x) alrededor del eje X.
Relaciones y Funciones
369
7ma.Si se tiene la gráfica y - f(x) entonces la gráfica de la función F(x) = f(-x) se
obtiene haciendo rotar la gráfica y = f(x) alrededor del eje Y.
y = f(x)
8va. Si se tiene la gráfica y = f (x) entonces la gráfica de la función F(x) = -f(-x) se
obtiene haciendo rotar la gráfica y = f(x) alrededor del eje X y el eje Y.
Ejemplo.- Graficar la función F(x) = ~Jx-2 + 2
Solución
La gráfica de F{x) — ylx — 2 + 2 se construye a partir de la función f(x) — \fx,
trasladando a la derecha 2 dos unidades y hacia arriba dos unidades.
f(x) =N/x~
i
2
0
f(x)=N/x-2 + 2
l
l
l
i »
2 X
—►
X
Ejemplo.- Graficar la función F(x) = | x - 3 | +3
Solución
La gráfica de F(x) = | x - 3 | + 3 se construye a partir de la función f(x)
trasladando u la derecha 3 unidades y hacia arriba 3 unidades.
= |x|
370
Eduardo Espinoza Ramos
Y"
0
F(x) = |x|
X
F(x) = |x - 3| + 3
[4.14. EJERCICIOS DESARROLLADOS.-
Qj Determinar el dominio y rango de la función /(a) — yjx2 — 1
Solución
Como v = /(*) = va2 -1 => y = Vjc2 -1 - Luego analizamos los valores que x puede
tomar para que "y" sea real, y como _y = VA2-l entonces "y" es real si Jt~-1>0
=> x~ >1 => x<-l V x>l por lo tanto el dominio es: D, = <-°°,—l]u[l,<»>
©
Ahora calculamos el rango, y para esto despejamos x y = ylx2 -l,y>0^ x = ±yjy2 +1 ,
Luego analizamos los valores que "y" puede tomar para que x sea real y como
jt = ±yjy2 +1 entonces x es real Vv e R .
Por lo tanto el rango de f es : Rf = [0,+°° > n R = [0,+°° >
Calcular el rango de /(.v) = 2jc2 +5jc-6
Solución
Como y = /(jc) => v = 2x ~ +5.r-6 es una función cuadrática en estos casos el rango se
determina completando cuadrados:
n 5 ?5 25 73 5,
v + 6 = 2(x~ +—x—) de donde y + — = 2(.x+—)
2 16 8 8 4
Relaciones y Funciones
371
5 73 73
Lueso V(—, ) por lo tanto el rango de f es: Rf = \ ,+°»>
4 8 f 8
(3^ Determinar dominio, rango y construir la gráfica de la función /(*) =
4jc -1
2.x+ 1
Solución
r- ,r- j ,-, x 4,V2-1 (2jt + l)(2.V-l) „ , 1
Factori7ando y simplificando se tiene: f(x) = = = 2x — 1. x* —
2x + \ 2x+\ 2
Luego como f(x) = 2x-l , x * — su dominio es: Df = R — {—}
9 j ^
Ahora calculando el rango, para esto despejamos x: y = 2x -1 => v =
y + l
11 v+1 1 1
como \e<-°°,— >u<—,°°> entonces e<—°°—>u<—,°°>
2 2 2 2 2
y+l 1 „ 1 v+1 „
—00 < < — V < < °° entonces -<» < y < — 2 v — 2 < y < °°
2 ? 9 ?
Por lo tanto Rf = < -°°,-2 > u < -2, °° >
i
-1/2
/
V
1 Y
-2
., » 4x2- 1
f(x) = 2x + 1
/
/ ,
' X
\A) Determinar el dominio y rango de la función /( v) =
Solución
2x
7^4
La función f(x) está bien definida si:
372
Eduardo Espinoza Ramos
©
x'-4
>0 entonces
U + 2Xjt-2)
> 0, ahora resolvemos la inecuación.
_tf ± i¿_
y/ +
-2 0 2
Luego D¡ - < -2,0] u < 2,+°o >
Para determinar el rango despejamos x, como y = f(x)
2x
Entonces y
- i 2x
~\x2-¿
y>0 => y =
jt2-4
de donde y"x" -2x — 4y~ =0, y>0
21^4 + 16/
: = —i ,y>0
2y
racionalizando jt = -
-16/
-8/
2/(2+^4 + 16/) 2 + ^4+16}
x es real si y solo si y e R. Luego R, = [0,+°» > A R = [0,+» >
Jt-3
Determinar dominio, rango y graficar la función: f(x) — sig{ )
jt + 4
Solución
Aplicando la definición de la función signo se tiene:
y>0
jt + 4
-1 SI <0
0 si
jt + 4
. Jt-3
Jt + 4
= 0 al resolver cada una de las inecuaciones se tiene:
/(Jt) = iií(i-4) =
Jt + 4
1 si -^>0
Jt + 4
-1 , si -4< Jt<3
0 , si Jt = 3
1 , si jt<-4 Vjt>3
-4
Su dominio es: D, =< -°°,- 4>u<-4,°°>
Su rango es Rf ={-1,0,1}
Relaciones y Funciones
373
©
©
Determinar el dominio rango y graficar la función: f(x) = [| yjx |]
Solución
Calculando su dominio se tiene: f(x; está definida si x > 0, luego Df = [0,°° >
Y'
Por lo tanto su rango es: Rf = Z0 = {0,1,2,...}
Sí [| >/* |] = 0 =>0<>/x<l=>0<Jt<:l
Sí [| Vj^|] = 1 => l<yfx<2 => 1 < x < 4
—I
Si[|^|] = 2 => 2<yfx~<3 => 4<x:<9
1
X
Determinar el dominio y graficar la función: f(x) = | x | + | x - l |
Solución
Por definición del valor absoluto se tiene:
_ J x si x > 0
\-X SÍ A<0'
A-l
x — l si x > l
^O
-x + l si x < l
Ahora calculando las reglas de correspondencia de f(x)
Six<0 => | x | = -x, | x- l | = l -x
0
como
f(x) = | x | + | x - l | => f(x) = -x + l - x = l - 2x, , para x < 0
Si0<x<l => | x | = x, | x - l | = l - x
Como f(x) = | x | + | x - l | = x + l - x = l => f(x) = l, , para 0 < x < l
Six>l=>|x| = x, [ x - l | = x - l
Como f(x) = | x | + | x - l | = x + x - l = 2x - l => f(x) = 2x - l, para x > l
374
Eduardo Espinoza Ramos
Luego la función toma la forma: /(_*) =
1-2* si x<0
1 si" 0 < jc < 1
2jc-1 si x>1
Su dominio D, = R, y su rango es R¡ = [l.-H» >
El gráfico es como se muestra en la figura:
U$) Determinar el dominio, rango y graficar la función:
ítU ll si [\ x |] es par
\2x — [|x +11] si [| Jt[] es impar
Solución
Sixe[0,I> => [| x |] = 0 es par =>f(x) = 0
Sixe[l,2> => [| jc |1 = 1 es impar =>f(x) = 2x-2
Si x e [2,3> => l| x |1 = 2 es par => f(x) = 2
Si x e [3,4> => [| jc |] = 3 es impar => f(x) = 2x - 4
Si x e [-1,0> => [| x |] = -1 es impar => f(x) = 2x
Sixe [-2,-l> => [|jt|] = -2 es par => f(x) = -2
Si x e [-3,-2> => [| x \] = -3 es impar => f(x) = 2x + 2
Y
Relaciones y Funciones
375
m/) Determinar el dominio, rango y graficar la función: f(x) = >/v-[| jc |]
Solución
Calculando el dominio de la función f es decir: f(x), está definida si jc-[|jc|]>0 de
donde .v > [| x |] que por definición de máximo entero se cumple Vxe R. Luego Df—R
Como [| a- |] = n <=> n < a < n +1, neZ
Entonces /(jc) = ylx — n , V x e [n , n +1>, n e Z
Si xe [0,1> => [|a|] = 0 => f(x) = yfx~
xe [2,3> =» [|jr|] = l =* f(x) = yfx^\
xe [2,3> => [|jc|] = 2 =* f(x) = Jx~^2
xe[-l,0>=> [|a|] = -1 => f(x) = y¡x + l
xe [-2.-l> => [|jc|] = -2 => f(x) = y[x+2
-3-2-10 12 3 4
*■ X
Luego el rango es: Rj = [0,1 >
MO) Hallar dominio, rango y graficar la función f definida por /(jc) =
Solución
Calculando el dominio de la función, es decir:
3-jc
M-[|*|]
376
r
Eduardo Espinoza Ramos
Como | x|= [|x|] => x e N puesto que | x | > 0. Por lo tanto D¡ = R-Z
. íx si x > 0
\— x si x<0'
Como \x = i , analizamos en la forma
sí x>o => fix) = JLJL^
xe <0,1> => [|jt|] = 0 => /(jc)=^—^ = —-1
X X
xe[l,2> =» [|x|l = l => /W-^-4
x-1
3-x
xe [2,3> =» [|x|] = 2 =* /(*) =
jc-2
xe [3,4> => [|*|] = 3 =* /U) = ^-4 = -l
jc-3
xe [4,5> => [|jc|] = 4 =* /(jc) = 1-4
x-4
3-x
x e [5.6> => [| jc |] = 5 => /(jc) =
xe [-1,0>=> [|.v|] = -l => /(*) =
xe [-2,-l> => [|jc|] = -2 => /(*) =
xe [-3,-2> => [|v|J = -3 => /(*) =
jt-5
3-x
-jc + 1
3-a-
-x + 2
3-x
-x + 3
Relaciones y Funciones
377
®
Luego el rango es : R f = < -**>,—1 > u {-1} u < 0,+°° >
Determinar el rango y graficar la función definida por
f(x) = \\lx 15|] + 2.v, sixe<-l,0>
x-l
Solución
Por la propiedad [| x + n |] = n + [\ x \], n e Z
/íx)=a^n+2*=n^^~^rn=íi7~?-i]+2x
x-l x-i x-l x-l
/(-v) = 7 + [| -|] + 2jt
x-l
Ahora definimos [| 1] es decir:
x-l
Comoxe<-l,0> => -1 <x<0 => -2<x-l<-l => -l<
1 1
< —
x-l 2
=> -8<-^-<^l => 4< <8
x-l x-l
378
Eduardo Espinoza Ramos
=> [I -|] =4,5,6.7
x-\
8 8
Además [| 1] = « => n< <n+l
x-l x-l
1 A-1 !
< <-
n +1 8 n
8 .^8
<-JC+l< —
n + 1 «
, 8
-1+ <-x<\-
n + \
«-8 n-7
<JC<
8
/! + ]
« « +1
r«-8 n-7 , „ „ _ „ _
xe [ , > entonces x e <-l,0> para n = 4, 5, 6, 7
n «
Luego f(x) = 7 + n + 2x, n = 4, 5, 6, 7. Ahora definimos f para cada valor de n
/(*) =
2x+7 + 4 = 2jc + 11 si" jcg<-1,-3/5>
2jc + 7 + 5 = 2jc + 12 sí xe<-3/5,-l/3>
2jc+7 + 6 = 2*+13 si xe [-1/3,-1/7 >
2jc+7 + 7 = 2jc + 14 si xe[-l/7,0>
f Y
, Graneando la función f se tiene:
-3/5
-1/3 -1/7
14
96/7
89/7
37/3
34/3
54/5
49/5
9
0
Relaciones y Funciones
379
_ Q 49 r54 34 37 89 r96
7 5 5 3 3 7 7
fl2) Hallar el dominio, rango y graficar la función f(x) definida por: f(x) =
(13)
|4-jr, si x<\
2 + .v2, si jc>1
Solución
El dominio se determina en la forma siguiente: Df = < -°°, l] u < 1,+°° >= R
Ahora calculamos el rango:
Six<l => y-4-x2 => x2-4-y
.v2 = - (y — 4) => V(0, 4) de acuerdo al criterio de la función cuadrática.
Parax>l => y-2 + x2, de donde y-2 = jc2
Ahora graneando se tiene:
V(0, 2)
Luego Rf = <-<x>,4] u<3,+°°> = R
Hallar el rango y graficar la función f definida por: f(x) ■
Solución
Calculando el rango de la función
1 49
Síxe[-4,6] => y = x2 -x-\2 = (x--Y - —
x2 -x-\2, si xe[-4,6]
x-2
x+l
si xe <6,+o°>
380
Eduardo Espinoza Ramos
xe [-4,6] => -4<x<6
9 1 11
<x < —
2 2 2
^ , U2 121
2 4
_49< _¿,2_f9 121 49
4 ~ * 2 4<4 4
49 , 1 2 49 ,„
<(x—y <18
4 2 4
49 49
=> <><18 => ve[—-,18>
4 4
Si x e < 6, + «>> => 3* = = 1 -
x+l x+l
x e <6, + °°> => 6 < x < +00 => 7 < x + 1 < + ■
^ o<J-<! => o<-^-<l
x+i 7 x+i 7
3 3 n 4 , 3 ,
— < <0 => —<1 <1
7 x+l 7 x + l
4 , 4 ,
=> —<V<1 => V6< —,1>
7 7
49 4
Luego el rango es: 7?^ =[ ,18>u< —,1>
49
.-. Rf=[ ,18>
1
l\
l\
l\
1
-4
¡
18
\ °
\y
8
_4/7_
l2' 4'
II
/l
l
6 X
Relaciones y Funciones
381
Hallar el dominio, rango y graficar la función: f(x) ■
Solución
jc3 + x2 +x + l
\x+l\
Calculando el dominio de la función f(x) es decir, f(x) está definida si x * -1
Luego el Df =R-{-l)
Ahora a la función expresaremos en la forma:
/(*) =
, como ¡x +1
{jc + 1, si x>-l
-x-l, si x<-l
\R, = <-oo,-2> vj [1 ,+«*>
x3 +x2 +x+l _ (x2 + 1)U + D
M ÑT
Por lo tanto la función f(x) es dada por:
Ix1 +1 si x>-\
— x~—\ si jc<—1
Ahora graneando se tiene:
Six>-1 => y = x2 +1 => y-l = x2. V(0,1)
x<-l => y = -x2-l => y + l = -x2 , V(0,-1)
Hallar el dominio, rango y graficar la función: f(x) = [| x |] + ^/x-ljxl]
Solución
La función f(x) está definida si x-[\ x |] > 0
De donde x > [| x \) es valida V x e R, luego Df =R
Si xe[0,l> => [|jc|] = 0 => f(x) = y[x
xe[1.2> => [|*|1 = 1 => /U) = l + >/Jn
xe[2,3> => [|jc|1 = 2 => f(x) = 2 + Jx~^2
382
Eduardo Espinoza Ramos
(16
x e [3,4 >
XE [-1.0 >
xe [-2,-l>
[|*|] = 3 => f(x) = 3 + yfx~^3
[| Jcll = -1=> /(x) = -l + >/í+^
[\x\] = -2=* /(*) = -2 + ^2+7
Y
Determinar el rango y graficar la función f(x) = | x2 -91
Solución
Aplicando la definición de valor absoluto a la función f(x) expresamos:
/(*H*2-9| =
\x2-9, si x2>9
9-jc\ si x2 <9
/(*) =
\x -9, si j:e<-<x>,-3]u[3,+oo>
(9-jc , si jcg<-3,3>
El rango de la función f(x) es R, - [0,+°°>
La gráfica es como se muestra en la figura
(l7j Construir la gráfica de la función f(x)
\x + [\x\]\ si [\x\] es par
\x + [\x-l\]\ si [\x\] es impar
Solución
Relaciones y Funciones
383
Sixe [0,1 > =>
xg [1,2 > =>
x e [2,3 > =>
x g [3,4 > =>
xe [-1,0> =>
xe [-2,-1 >=>
x e [-3,-2 > =>
x e [-4,-3 > =*
[| x \] = 0 es par => f(x) = | x | - x
[| x |] = 1 es impar => f(x) = | x | = x
[|jc|] = 2 es par => f(x) = | x + 2 | = x +2
[| x |] = 3 es impar => f(x) = |x + 2| = x + 2
[|x\] = -1 es impar => f(x) = |x-2| = 2-x
[| x \] = -2 es par => f(x) = | x - 2 | = -x + 2
[|x|] = -3 es impar => f(x) = |x-4| = -x + 4
[|x|] = -A es par => f(x) = | x-4 | = -x + 4
-3 -2 -1 0
12 3 4 x
D, = R, R, = [0,+«o>
Hallar la gráfica de f(x) = (x-[\ x |])2
Solución
xe[0,l> => [U|] = 0 => f(x) = x2
xe[l,2> => [I Jt |] = 1 => /U) = U-1)2
xg[2,3> => [|jc|] = 2 => f(x) = (x-2)2
xe[-l,0>=> [|jcÍJ = -1 => f(x) = (x + l)2
384
Eduardo Espinoza Ramos
xe[-2,-l>=> [|.v|] = -2 => /U) = (jc + 2)2
■Y
Df =R, Rf =[0,1 >
3 -2 -1 0 1 2 3 X
U9) Graficar la función f(x) = ^J\x\
Solución
, , í x, si x > 0
Por definición | x \ = < , luego la función f(x) queda expresado así:
[—x. si x<0
HX):
y¡X, SÍ X > 0
[v-jc, si x < 0
donde Df = R y /?y =[0,+ °° >
Hallar el rango y graficar la función f definida por: f(x) = | 2x - 1 | - x
Solución
1
7.x— 1 si x>
Por definición de valor absoluto ] 2jc — 11 = -
1 — 2 x si x< —
2
1
Sí *<- => |2x-l|=l-2x => f(x)= l-3x
x>- => |2x-l| = 2x-l => f(x) = x-l
Ahora la función dada se expresa así: f(x) =
\-3x si x< —
2
JC —1 Sí X> —
2
Relaciones y Funciones
385
calculando el rango de la función f(x)
1
SI A < -
SÍ A>-
y = 1 - 3x. despejando x
x = ^—^-<- r=> 2 2y<3
3 2
»■>■
y = x - 1, despejando x => a=v + 1>— => v> —
Por lo tanto R, = <—,+oc>v^f—,+oc> = f—,+*>. Su gráfica es:
' 2 2 2
(2l) Hallar el rango y graficar la función f[\) dado por:
x' , si .ve [1,2 >
/(*) = '[|*|] + V*-[I*I] • si xe[-U>
—J-x , si re[-4,-l>
Solución
x e [-1,0 > => [|jc|] = -1 => f(x) = -\ + yfx + \
xe[0,l> => [|*|] = 0 => J(x) = yfc
Ahora expresaremos a la función:
J(x) =
V^a , si x e [-4,-1 >
-lWx + 1, si xe[-l,0>
Y"
, si .v e [0,1 >
, si xe[l,2>
» R, =[-2,4>
Sistema de Números Reales
285
(5Í) [|a-2-2a-3|] = 0
Solución
[|jt-2jc-3|] = 0 <=> 0<a-2-2a—3<1
0<a-2-2a--3<1 <=> 0<a-2-2a--3 A *2-2r-3<l
(52)
(53)
ZV
<=> (a—3)(a + 1)>0 A (jc-1)z<5
_v +
A ->/5+1<a:<>/5+1
-1 3
<^> jre<-oo,-l] u[3,+o°> n jre<l--v/5,l + -v/5 >
1 ->/£"
o--
1 +>/5
--o
xe<l-yÍ5,-\]^i[3,\ + yÍ5>
íl-*ll
■<0
Solución
II -x\]
<0 « (a->0 A [|-jc|]<0) V (x<0 A [|-jcI) >0)
<=> (x>0 A x>0) V (x<0 A x<-l)
<=> (x>0 V x<-l)
<=> x e <-°o,-l] u <0,+<=o>
Se conoce que | x \
Solución
jr
-A'.
x>0
v<0
386
Eduardo Espinazo Ramos
Graneando cada parte de la función
Si f(x) = ax, Demostrar que f[x + y) = fíx) f(y)
Solución
Como /(v) = «2 => f(x + y) = ax+} =ay.a> = /(.y)../(v)
.-. f(x + y) = f(x).f(y)
La función f(x) es lineal, hallar dicha función sí f(-l) = 2 , f(2) = -3
Solución
Como f(x) es una función lineal entonces f(x) = ax + b
Ahora calculamos los valores de a y b
5
/(-I) = -a + ¿> = 2
/(2) = 2a + ¿ = -3
3 -5 y 1
, por lo tanto f(x) = + —
. 1 3 3
b = —
3
Dada la función f(x) = mx + b, V xeR, si se sabe que f(3) =11, f(-3) = 6.
Hallar m + b
Solución
Calculando los valores de m y b
f(-3) = -3m + b = 6
a 28
m + b = —
3
__5
"2_6 , , 5 51 56 28
, entonces: m+b = — + — = — = —
L 51 6 6 6 3
b = —
6
Dada la función f(x) = ax + b, xeR, donde a y b son constantes reales, si
f(x + y) = f(x) + f(y) V x, y e R , y sí f(-2) = -6. Hallar a y b
Solución
Relaciones y Funciones
387
Como f(\ + y) = f(x) + f(y)
a(x + y) + b = ax + b + ay + b
a(x + y) + b = a(x + y) + 2b => b = 0
Luego fl[x) = ax + b => f(x) = ax
fl[-2) = -2a = -6 => a = 3 /. a = 3. b = 0
Si f(x + 4) = .v2 + 3a- , Hallar f(a + 1)
Solución
Definiremos la función f(\) para esto se hace una sustitución z = x + 4 => \ = z-4
Ahora se sustituye en /"(.v+4) =.v2+3.v => f(z) = (:-4)2 +3(r-4)= -: -5r + 4
Luego la función f(x) es dado por: f(x) = x~ - 5.v + 4
Calculando f(a + 1) es decir: /"(a + l) = (a + l)2 -5(a + l) + 4 = a2 -3«-4
.-. f(a + \) = a2 -3a-4
Dado el polinomio P(x) = x +(a + l).v"+.r, se define la función f con dominio
{0,1,2,3,5}, por fi» = resto de la división de P(x) entre x + a , calcular f\2) + f(3)
Solución
Calculando el resto de la división de P(x) entre x + a
.v3 + (a + \)x2 + x | x + a Como f(a) = a2 -a
f(2) = 4 - 2 = 2
x —ax'
X^+X f(3) = 9-3 = 6
-.v" -ov
Luego fX2) + fX3) = 8
(l-a)x
-(1 -a)x-a(l -a)
a~ —a = resto
388
Eduardo Espinoza Ramos
4.15. EJERCICIOS PROPUESTOS,
M) Hallar el dominio de cada una de las funciones
a) /(a) = ^v2-4a- + 3 b) f(x) = Jl-\x
c) Av) =
e) /(*) = .
4-v¿
I2.v--.v-l
' v2+3.v
g)
i)
Irt
fí-e\-Jr2 tv 1 7 l
V3 + 2.V-A-2
/w-i^+iv^
1 4 r-3
d) /(v) =
0 A-v) =
h) /(.v) =
A'-l
.v" - 5.v + 6
(■v--4)(.v--9)
-a-4+17.v2-16
yl*-\x\
j) /(.v) = a/a^T + 2VT^ + n/a-2 +1
1) /(*>=,
Vr - 3.v -'
yfíl-yjx2 -4
V(A-+1)2 V + l
Rptas:
a) Dj = < -x,l] u [3,+oo >
c) Dr = < -oo,-2 > u [0.2 >
e) Df=< -oo,-3 >u[--,0>u [1. +* > f) £>,-=[-3,3>-{-1,±2}
b) Z>, =[-1,1]
d) Df =[1,2> u<3,oo>
g) £>, = <-!,!] u [2,3 >
i) £>/=0
k) [-* -1>U<-1.~]
3 4
h) D, =<*
j) £>/=»}
1) <-5,-2] u [4,5>
Relaciones y Funciones
389
\2) Halle el dominio de la función /(*)=—¡ ¡ Rpta. Df =< -°°,-4]u[4,+<» >
v-' Jtt| jr-f-41] —jc J
(D Hallar el dominio de la función f(x) = yj\x2-x-2\-\l-x2 \-\x + l\ + lfx
Rpta. Df =<-<*>, 1]
(?) Hallar el dominio de la función /U) = 4 {^Ü - * + 2' + >/7^7
^ \ I jr I +1 I jc I -1-3
Rpta. Df =[>/3-l,7]
(5) Hallar el dominio de la función f(x)yjx2sig(\x\+\)-1 +yJ4-x
Rpta. Dr =< -«>,-l > u < 1,4]
(ó) Dadas las funciones f(x) = x2 -5x+5, g(x) = -2x-\—, hallar el dominio de
F(x)=f {x)~4gix) Rpta. Df=R-{1,10}
f(x) + 3g(x)
©\x2 -9 si jc< 4
Determinar el dominio, rango y grafícar la función: f(x) - <
(5*-2 si x>4
Rpta. Df =R , Rf = [-9,+°° >
Qn Hallar el dominio de las funciones siguientes:
1 x 2x2
a) f(x)= \ b) f(x)= ' c) /(x) =
d) /U) = [|-|] e) /(jr) = [|-L-|] f) /<jr)=[|jr2|]
x x—3
390
Eduardo Espinoza Ramos
j) /U) = Vl->/4^7 k) f(x) = l-y]&-X2-2x
1) f(x) = $]x2 + 4jc-12 +-¡=J^
tjx+20-x2
\9j Determinar el dominio, rango y granear cada una de las funciones siguientes:
[3x-2 si -4< x<4
a) /(*) = <
\-x3 si x>l
b) g(x) =
si 4 < x < 6
\yJx-2 si x>2
c) /(*) = ,
[x~+2x-3 si .re<-l,l>
(jo) Hallar el dominio, rango y granear la función:
a) /(*) = -
| je -H 21 —jc si Jce<-4,0>
■j4-x si xe < 0,4 >
2.r-8 si Jce<4,oo>
d) /(*) =
\x -4 51 jr<3
2jc-1 5/ .r>3
b) f(x) =
5/ 4 < x < 7
íi jc < 4
c) /(*) = -
2[|jc|] + 2 si -5 < jc < 1
yfx SÍ l < X < 4
6 si -7 < x < -5
d) /(*) = <
ffl jc —11] si 4<*<7
[y]\x\ si x<4
e) f(x) = |x-l| + |x+l|
f) /(jc) = (a-2+4)[|2a- + 3|]
g) /(*) =
V4-jc2+2 si -2<*<2
[|jc|] jí jc<2
2 5/ jc<-2
h) /(*) =
[|2jc|] si *e[0,3]
2[|*|] si *e<3,5]
i) /(*) = •
2[| jc I] si Jce<-5,1]
yfx si x e < l, 4]
x2+3 si xe<-7,-5]
j) /(*) =
I jr + 31 si jr < 0
2(jc-1)2 51 *e[0,l>
2-|jc-4| si xe [2, +00 >
Relaciones y Funciones
391
ní) Hallar dominio, rango y granear cada una de las funciones siguientes.
a) f(x) = |x + l| + |x-l|-2|x| b) /(*) = [|jr|]-|jr|
c) f(x) = | x + 2 | + | 2x - 2 | + | -x + 5 |
e) f(x) = | x - 2 | + | x + 1 |
g) nx) = yJH\2x + 5\]-4[\x\]
d) f(x) = | x 11 x - 1 |
f) f(x) = |x + 2| + |x-2|-|x|-l
h) f(x)=>J\x-2la-[\x\¡
i) /U)=UHU|]
j) fí*) = <
|jr + 3|,jr<0
2(jc-1)2, xe[0,2>
2-|jr-4|,*e[2,<»>
k) f(x) = -x2
\x + \\-í
x+3
-3<x<4
1)
f(x) = -y¡2x-4x , sixe[l,9]
Determinar dominio, rango y gráficar cada una de las funciones siguientes.
a) /(jc) = 2[|*|]-2jc b) f{x) = j5-\x-3\ c) /(*)=[|2-3jr|]
d) f(x) =
g) /(*) =
[|2*|]
1
[|jc-3|]-[|jc|]
e) /(*) =
h) f{x) =
2-x
X-ylM
1*1
[|jc|]+l
f) /(*) =
1*1
i) f(x) =
[\x\] + l
l*HHl
yl2-[\x\]
j) f(x)=[\x\] + yl\x\-[\x\)
Construir la gráfica de las funciones siguientes.
a) f{x)=sig (\x2-l\-l)
b) f(x) = [\yl4-x2\]
d) f(x) = sig(- )
x + 4
c) f(x) = sig(x+l)-sig(x-1)
En cada una de las funciones dadas, hallar el dominio, rango y hacer su gráfica.
392
Eduardo Espinoza Ramos
(x + l)(x2 +3jt-10) L^ ti ^ jr2 -IOjc-1
a¡
c)
e)
g)
i)
X' +ÓJT + 5
f(x) =
2jc + 3
f(x) = [\x\)+\x \+x+2
f(x)- '*'
H) \x\-l
/«=, ?*n ,
b) /(*) = -
l\x2\]-2x-\
d) /(*) =
(x2 +3x-4)(x2-5x + 6)
{x2 -3x+2)(x-3)
x-[\x\]
h) /U) = 5ií(t|jr-l|l-|) + 5íg([|jr + l|]-l)
. , J) f(x) = sig( —)
|jc|-jc + 1 x + l
QlS) Grafícar las funciones siguientes.
a) /W = [|-*2|] b) /Oc) = [|-*2+l|]
c) f(x) = y¡\7\ d) f(x) = ^\xj]
4|2.r-l|]-2jr | jc-i- 11 —4
(ló) En cada función, hallar el dominio, rango y hacer la gráfica.
[|.r+l|] \xH\2x\]
C) /(jc)= _JL== d) /(*)- '*'
VI 2jc | -2[| jc |] [|*|]
e) Hx) = [\-^—\] f) /(jc) = (jc-[|jc|D2
1 + jr
g) /U) = jr-[||jr||] h) /W = [|jr|] + (jr-[|jr|])2
Relaciones y Funciones
393
©
®
®
®
Hallar el rango de la función f(x) = x - |x - 2|, x e R
Graficar la función f{x) = (x2 + 4)[| 2x+3|], Df = [-1,1]
Hallar el rango de f(x) = |x + 2|-2|3-x|, x e [-4,10> graficar la función f.
Sea /(*) = | x | +V-*-[ÑI. 0 < x < 2 Hallar el rango de f.
Hallar el rango de f(x) = - [|21 x +11|] (| x | -1) para x e <-5/2 , 2 > , graficar f.
Hallar el dominio, rango y graficar la función
a) f(x) =
|i^J-^| si -1<*<1
3-x
V*2 + 2x si 1 < x < 2
2
x + l
si -2 < x < -1
b) f(x) = x2 -2x-3
b) /(*) = •
5-x , jc e < -2,3 >
2
x +
l-x
. Jce[3,5]
c) /(jr)=>/rrí+>/i77
(23)
d) /(*) = -
l-x¿
h) /U)=|6 + *-*2|
Hallar dominio, rango y graficar la función
a) /(*) = •
1 ' si -\<x<8
x + 3
|16-;c2|
16*1
5i — 5 < x < — 3
e) /(jr) = >/t|*|] + l->/í=*
g) /U) = *2+|*|-* + l
b) /(*) =
(24) Hallar el dominio, rango y graficar la función: /(*) =
* +1
*2-2 , -3£*<0
jr— I jc — 21 , 0<*<8
2 + V*-4, 4<jc<8
, sí .r < 3
[| 1] +3x , ji 4<jc<6
jc2-1
t|3(jf 6)'-4|] , sí 8<*<9
394
Eduardo Espinoza Ramos
I 1 1 "2
Hallar el rango de /(jc) = '— sí x e [-2,4>
1+|jc-3|
*2[|~|] + 3*-l j
Hallar el rango de f(x) = sí x e < -2,—>
|5jt-1|-15 + 6|jc+2| 5
(27) Determinar dominio, rango y granear: f(x) = yJ9-x sig
^^ jc —1 jc + 3
@í|.r-[|jir|] | , si [| jc |] es par
Hallar el dominio, rango y graficar: /(jc) -<
[\x-[\x + l\]\, sí[|jc|] es impar
(29) Construir la gráfica y hallar el rango de:
,, , ([|*-2|] , si [\x\] es par
/(*) = 1, m xihl rl n ,Vxe[-3,4]
[3jc-[| jc + 1|]| , si [\x\] es impar
Rpta. Rf =[-7,-4] u [-3,0] u [1,4] u [5,8 >
®Sea f: [-2,4> -» R / /(jr) = I**1!-3 Hallar el rango de f. Rpta. Rf =[--,l]
1+|jc-3[ 5
(5y Dadas las funciones f(x) = -x2+3x + l, g(x) = 3x2 +2x + \ Hallar Rf s,Rg
r2 13,
Rpta. [-,—]
3 4
62) Hallar los valores de a y b para que cada uno de los conjuntos de pares ordenados sea una
función y determinar la función en cada caso.
/ = {(1,8), (2,-3), (1, a2 +b2U-l,a + b),(a2 + b,b),(b + a2,b))
g - {(4,3)(-5,-3)(4,a2 -b2),(-5,a + b),(a2 +b,á),{a2 +b2,b)}
Rpta: a) a = 2 , b = 2 b) a = -2 , b = -l
(33) Hallar el rango de la función f(x) = | x - 2 | + | x - 1 | + 1, si x e <1,3].
Rpta. Rf =[2,4>
Relaciones y Funciones
395
®Í2*-1, *e<l,2]
Hallar el rango de la función /(.v) = \ , Rpta. Rf =< 1,3] u < 5,50 >
[*-+1, jre<2,7>
®Sea f: R » R una función definida por: f(x) - \ , , ' _ , determine el
1 [|*|] . 1<*<2
rango de la función. Rpta. R, = {-1,1,2}
(36) Sí /(.v) = x2 [| -1] -44| -1], x e <0,6]. Hallar el rango y graficar
f\ x I x~ Ix II
(371 Hallar dominio, rango y graficar la función f(x) = -
| jc | -C| jc |]
(38) Determinar el rango y graficar la función: f(x)= \x2[\ 1]-4|, x e <1,3]
@ Sí/(jr) = a.r2+bjr+c, /(-l) + /(-) = —, f(-l) = 0 y f(l) = 8. Hallar f(5)
Rpta. a = 3 , b = 4 . c = 1, f(5) = 96
(40) Determinar las siguientes funciones lineales
a) f(l)=l y f(3) = 3 b) fíl) = 3 y f(3) = 1
c) f(7) = 0 y f(8) = 42
(41) Si f es una función real es de variable real tal que f(x+2) = x2 + x .
Calcular /(« + 3)-/(«-3) 3 6
2o-3 2
M2) Si f es una función real de variable real tal que /(x +1) = x~ + 3
Calcular /(0 + 1)~/(1),a^0 Rpta. a
a
(43) Sea f una función real de variable real definida por f(x) = mx + b tal que :
396
Eduardo Espinoza Ramos
2f(2) + f(4) = 21 y f(-3) - f(l) = -16 Hallar el valor de - /(l) Rpta. -
(44) Sea /Ot) = In( ), demostrar que: f(x) + f(y)-f( —)
v-x l-x l + xy
M5) Sea f(n) la suma de n miembros de una progresión aritmética, demostrar que:
f(n + 3) - 3f(n + 2) + 3f(n + 1) - f(n) = 0
Mó) Sea <p(x) = — (ax + a~x) y y/(x) = —(a-a~*)
Demostrar que: (p (x + y) = (p (x) cp (y) + y (x) y(y) y
y (x + y) = (p (x) y (y) + (p (y) i|/ (x)
(47) Demostrar que, si f(x) es una función exponencial, es decir f(x) = a*(a<0) y los
números xl,x2,xi constituyen una progresión aritmética, los números /(-*|),/(.*2) y
f(x}) forman una progresión geométrica.
(48) Hallar analíticamente el rango de la función f(x) = 4x-x2 -1, x e [0.10].
M9) Determinar el rango de la función f(x) = yj2x-y[x , sí xe [1,9]
(50) Determinar el dominio, rango y graficar la función f(x) = x2 + \x\-x + l.
(51) Hallar el dominio, rango y graficar las funciones dadas.
a) /U)=[|l-*2|] b) g(x) = y[x~Í4-yfx~^5
®í 1-2* , -1<at<0 , x ¡x2 , *<0
Sí f(x) = \ , . , g(x) = i
[t|3 + eosjc|] , *>0 [sen* , 0<jr<7T
Hallar dominio, rango y graficar f + g.
(S5) Halle el dominio, rango y dibujar la gráfica.
Relaciones y Funciones
397
(54)
(55}
a) fM-g1"
C) /(A) =
[|jc--16|]
x+\x\
b) /(a) =
y¡2x-\
[|1-at|]
IjcRIjcII
e) /(a) = [|a2-2a-3|]
d) f(Jc) = [||l-2jc||]
f) /W = >/tU|]-3jr
g) f<x) =
i) /U) =
Va:2-9 , *e<-5,-3]
|a + 3|-2 , Ae<-3,5]
a2-10a+26 , Ae<5,7]
5-a , xe<-2,3>
2
h) /(*) =
x2-2
*e[-3,0>
a-|a-2| , Ae[0,4>
2 + Va-4, *e[4,8>
x +
\-x
. Ae[3,5]
j) /(*) =
|*|+2 , Are [-7,-2]
1-|a + 1|
l 2a-1
, *e[2,5]
k) /(a) =
1) /(*)
Í[||a— 1|-2|]a2-2* , ag<-1,2>
[|a-4| , *e[2,9>
*|] si [|a|] es impar
_Í3a-[|1 + j
"t Il-'t
11) /(a)-.
25-a
7-a
si [|a|] es par V xe [-2,4]
• *eH>.-]
y¡\x-3\ , xe[-A>
Determinar una función polinómica de segundo grado f(x) tal que f(0)=-5,f(-l)=l, f(l)=-7
Hallar el rango de la función /(a) =
Hallar el rango de la función /(a) =
A' +A+2
[|1-a|] + [|a-1|]
2-VN-ÍÑ]
sí xe [-1,10]
, sí xe <0,1>
398
Eduardo Espinoza Ramos
©
Hallar el rango de la función /(*) = 8*[|^-^|] + jt[|^—^|] donde Df =<-l,l]
x—4 jr + 2 J
Hallar el rango de la función f(x) = '— sí x e <-3,5>
2|jt-2|+l
(59) Si /(jc) = y Df=[4.20], Hallar/?,
^-^ l + x2
(60) Hallar el rango de la función /(*) = — , sí x e [1,10]
©
(62)
4x¿+l
Dado
f(x) = 4-yj(x + 6)2-9 , xe <-°°,-ll>.
Hallar Rt
7-x,
Determinar le rango y graficar la función /(jt) = 14 - x [| 1] |
(63) Determinar él domino, rango y graficar la función /(jc) =
(<>4) Hallar el rango y graficar las funciones:
(65
1 -x, x>l
COS7T, -1<JC<1
x-x2, x<-l
a) f(x) = [\x2 ^ l\], xe[-l,3] b) f{x) = ^x\~[\ x\], x 6 [-2,1:
Calcular el rango y graficar las funciones dadas:
jc+5
a) /(*) =
x-2
, si | jc —21 > 3
>/jc2+4jc-1, si 0<jc<1 b) f(x) =
2+|2jc-5|, si 2<jc<3
y¡x2-9-2, -5<jt<-3
| jc -l- 21 —3, 0<jc<5
3jc-16
x-5
x>6
c) /(jc) =
|jc + 3|, si -4<jt<0
3-jt2, si 0<jc<4 d) f(x) =
-2, si | jc | > 4
-|a- + 4|, si -8<jc<2
jt2-4jc-2, sí 2<jc<5
-jc2+10jc-22, si 5<a<8
-3, si |jc|>8
Relaciones y Funciones
399
4.16. OPERACIONES CON FUNCIONES.-
Consideremos dos funciones reales de variable real, f,g: R
Entonces:
a) IGUALDAD DE FUNCIONES.-
Diremos que las funciones f y g son iguales sí y sólo sí
R si Df r\Dg *<¡>,
i)
¡i)
»f=Dg
f(x) = g(x) => VxeDf=Dg
Ejemplo.- Las funciones f(x) = x* -1, g(x) =x3 -1
Son iguales porque D¡ =Dg = R y f(x) = g(x).
Ejemplo.- Las funciones f(x) = yj(x-l)(x-6) y g{x) = -Jx-l-Jx-6 no son iguales
puesto que D¡ = < ~«>,1] u [6,+«> > y Dg = [6,+«> > de donde Df *■ Dg
Ejemplo.- Las funciones f(x) = 2x2 -Ix, x e <0,5] y g(x) - 2x2 -Ix, x e [1,9] no
son iguales a pesar de tener la misma regla de correspondencia, debido a que
sus dominios no coinciden.
b) SUMA DE FUNCIONES.-
Teniendo en cuenta que una función está definida cuando se indica su dominio y su
regla de correspondencia
DEFINICIÓN.- Si f y g son dos funciones con dominio Df y Dg
respectivamente, entonces a la suma de f y g denotado por
f + g se define:
i) Df+g=Dfr^Dg
«) (/ + g)(x) = /(*) + g(x) VxeDfn Dg
400
Eduardo Espinoza Ramos
Ejemplo- Hallar f+gsi: f={(-l,2),(0,0),(2.4),(3,-l),(4,3)}. g= {(2.0),(3.4).(4,7).(6.2)}
Solución
Primero calculamos el dominio de f y g.
Df = {-1,0,2,3,4} , Dg = {2,3,4,6}
Luego calculamos el dominio de la suma: Df+g = Df *Dg = {2,3,4}
ahora calculamos los pares ordenados que pertenecen a f + g.
'(/ + *X2) = /(2) + *(2) = 4 + 0 = 4 (2A)ef + g
(/ + *X3) = /(3) + *(3) = -l + 4 = 3 =* (3,3)6/ + *
(/ + *)(4) = /(4) + *(4) = 3 + 7 = 10 (4.10)e f + g
Luego la suma de f y g es: f + g = {(2,4),(3.3),(4,10)}
\2x + 1, si x> 1
[x2 -2, si jt<0
\3x + 1, si .v < 8
Ejemplo- Calcular (f + g)(x) sí: f(x) = \ , g(x) = i
~ " 2x , si x > 10
Solución
Primero calculamos el dominio de f y g
D/ = <-°°.0>u [l.+°°> , Dá=<-«»,8] u <10,+°°>
Luego calculamos el dominio de la suma f + g es: Df+g = D¡ r\Dg
< o o ► D,
10
O ►D,
D
D/+g =Df r\Dg = <-°°,0>u [1,8] u<10,+°°>
Ahora definimos la suma en cada intervalo
Six<0, (f + g)(x) = f(x) + g(x) = x2 -2 + 3x + l = x2 +3x-l
Si 1 < x < 8, (f + g)(x) = f(x) + g(x) = 2x + 1 + 3x + 1 = 5x + 2
Relaciones y Funciones
401
Six< 10. (f + g)(x) = f(x) + g(x) = 2x+\ + 2xi =2xi +2x + \
Luego la suma (f + g)(x) es: (/ + #)(*) =
c) DIFERENCIA DE FUNCIONES.
x + 3jt-l si x<0
5* + 2
si 1 < x < 8
2x3 + 2* + l si *>10
Si f y g son dos funciones con dominio Df y Dg respectivamente entonces a la
diferencia de f y g denotada por f - g se define:
i)
ü)
Df_g=DfnDg
(f- g)(x) = f(x) - g(x), V xeDfr^Dg
Ejemplo.- Hallarf-g síf = {(1,2),(2,5),(3,4).(4,1)} y g= {(0,2).(1,0).(2.1),(-1.3)}
Solución
Primeramente calculamos el dominio Dj y D : Df= {1,2,3,4}, D = {-1,0,1,2}
Ahora calculamos el dominio de la diferencia
Df.g=DfnDt=U,2)
Calculando los pares ordenados que pertenecen a f - g
Í(/-S)(D =/(!)-£(!) = 2-0 = 2
l(/-*X2) = /(2)-*(2) = 5-l = 4
(1.2)e/-*
(2A)ef-g
Luego la diferencia f - g es: f- g = {(1,2),(2,4)}
d) MULTIPLIC \CIÓN DE FUNCIONES.-
Si f y g son dos funciones con dominio D, y Dg respectivamente, entonces a la
multiplicación de f y g denotado por f.g se define:
i) Dfg=DfnDg
ii) (f.g)(x) = f(x).g(x), V xeDfnDg
402
Eduardo Espitwza Ramos
Ejemplo.- Hallar f.g si: f = {(1,4),(4,5)(2,3),(3.2)} y g= {(0,2),(1,2),(2,-1),(3,0),(5.2)}
Solución
Primeramente calculamos el dominio Df y Dg : Df ={1,2,3,4}, Dg ={0,1,2,3,5}
Ahora calculamos el dominio del producto: Df g = Df a Dg = {1,2,3}
Calculamos los pares ordenados que pertenecen a f.g
'(/■SXD = /O) + £(D = 4.2 = 8
(/•£)(2) = /(2) + g(2) = 3.(-l) = -3
(/•«)(3) = /(3) + g(3) = 2.(0) = 0
(1,8) e f.g
(2,-3) 6 f.g
(3,0) e f.g
Luego el producto f.g es: f.g = {(l,8),(2,-3),(3,0)}
Í2x + 1,jc>1 Í3jc + 1 , jc<8
Ejemplo.- Hallar (f.g)(x) donde: f(x) = \ , , g(x) = \ .
|*2-2,*<0 |2*3 ,jt>10
Solución
Primeramente calculamos los dominios de f y g:
Df = < -«»,0 > u [l,+oo > , Dg = < -°°,8] kj < 10,-H» >
Ahora calculamos el dominio del producto f.g
D, <
0
1
0
o
i
1
1
8
1
10
►
*Do
Dfg =DfnDg = <-~,0> u [1,8] u < 10,°°>
Ahora definimos el producto en cada intervalo
Six<0, (/.^)U) = /(jr).^U) = (jr2-2).(3jr + l) = 3jt3+Jc2-6j:-2
Si 1 < x < 8, (/.*)(*) = f(x).g(x) = (2x+ 1)(3* +1) = 6x2 + 5x +1
Six> 10, (f.g)(x) = f(x).g(.x) = (2x + l)2x:i = 4*4 +2x3
Relaciones y Funciones
405
A^
-*■ B
h = gof \
*♦
OBSERVACIÓN. Para que exista la composición de funciones g o f es necesario que:
RfnDg*<t>.
ILUSTRACIÓN GRÁFICA
Doof RfnDfl¿0
En esta representación gráfica se tiene:
R.
gof
i) D^zDjCA
¡i) Rgqf^Rg^C
Ejemplo.- Sean f = {(0,1).(1.2).(2,3),(4.3).(5,2)} y g= {(6,7),(5,4),(4,3),(2,4),(1.4),(0,7)}
Hallar Dgof , Dgof , así como f o g y gof.
Solución
i) Calculando Dgof
(-3.3) e f - g
(2.-3)e f - g
(7,6)e f - g
406
Eduardo Espinoza Ramos
Dfog = {xe Dg I xe Dg *g(x)e Df] por definición:
Dg={ 0, 1, 2, 4, 5, 6}
•X> >*■ •*■ •*■ ^ ^
g(0) g(l) g(2) g(4) g(5) g(6)
II II II II II II
veremos cuales pertenecen al D,
Se observa que el 4e D¡ entonces D¡og = {1,2,5}
Ahora veremos su regla de correspondencia.
(/0á?)(l) = /(áKl)) = /(4) = 3
(/os)(2) = /(£(2)) = /(4) = 3
Ufa*)(5) = /(s(5)) = /(4) = 3
(1,3) e fog
(2,3) efog
(5,3) e fog
-► B
.-. fog = {(l,3),(2,3),(5,3)}
ii) Calculando Dgo¡ ;
Dgo¡ =[xe Df /xe Df /\ f(x)e Dg} por definición.
Df={ 0, 1. 2, 4, 5}
f(0) f(l) f(2) f(4) f(5)
11 II II II II
12 3 3 2
-► C
Veremos cuáles de estos elementos pertenecen al Dg , entonces \e Dg, 2e Dg luego:
Dgof= {0,1,5}
Relaciones y Funciones
403
Luego el producto (f.g)(x) es: (f-g)(x) =
3x + x~ - 6x - 2, si x < 0
6x2 + 5x +1 , si 1 < x < 8
4x4+2jt3 , si x>10
e) COCIENTE DE FUNCIONES.-
Si f y g son dos funciones con dominios D¡ y Dg respectivamente entonces el
cociente de f y g denotado por f/g se define
i) Df/g=DfnDg-{xeDg/g(x) = 0}
H) (A(*) = ^T7 , V«D//g
g gW J g
Ejemplo.- Hallar f/g si:
f={(-2,3), (0,3), (4,0), (5,-3), (6,3)} y g ={(0,-2), (-2,5), (3,2), (5,0), (8,-2)}
Solución
Primeramente calculamos el dominio de f y g: Df ={-2,0,4,5.6}, Dg ={-2,0,3,5,8}
Ahora calculamos el dominio del cociente f/g
Dflg =Dfr^Dg -{xe Dg Ig(x) = 0}
= {-2,0,4,5,6}n{-2.0.3,5,8}-{5e Dg /g(5) = 0] = {-2,0,5} - {5} = {-2,0}
Calculando los pares ordenados que pertenecen a f/g
g g(~2) 5
f f(0) 3 3
(i)(0) = ^-^ = - =—
* S(0) 2 2
3 f
(0.-|,U
2 g
f / 3 3
Luego el cociente — es: — = {(-2, -), (0, —)}
g g 5 2
404
Eduardo Espinoza Ramos
c- i u n //« x * «x Í2jf + l,sixe[-3,0> /x x2+l. si xe[-2.2]
Ejemplo.- Hallar (—)(*) si: /(*) = { n .g(x) = i
g |* + 2,si xe[0,4] [x-4, si jce<2,5]
Solución
Calculando los dominios de f y g: Df = [-3,0 >u [0.4] , Dg =[-2,2] u < 2,5]
Ahora calculamos el conjunto {.ve Dg /g(.x) = 0)
a) Sixe[-2,2] => g(x) = x2 +1 = 0 => 2 x tal que g(x) = 0
b) Si x e <2,5] => g(x) = x-4 = 0 => x = 4 entonces: x e <2.4> u <4.5]
j l
J L
-3 -2
2
4 5
D//g = Df n Dg - {4} = [-2,0 > u < 0,2] u < 2,4] - {4} = [-2,0 > \j < 0,2] u < 2,4 >
2x + l r „ ~
^—, si xe[-2,0>
(-)(*) = ■{
x¿+l
x+2
x2+\
x+2
si xe<0,2]
x + 4
, si xe<2,4>
4.17. COMPOSICIÓN DE FUNCIONES.-
DEFINICIÓN.- Dadas dos funciones f y g, tales que: f: A > B ; g: B > C y que
Rj nD * 0 , entonces la función compuesta "g o f" es aquella función
definida por:
n
iVt
D¡¡fíf=\xlxeD} a/hieD,!
(gof)( x) = gi ti x n es la regla de correspondencia.
Relaciones y Funciones
407
Ahora veremos mi regla de conespondencia.
(vo/)(0) = í(/(0))=s(1) = 4
(gof)(l) = g(f{\)) = g(2) = 4
(f>o/)(5) = /(g(5)) = g(2) = 4
(0.4) e gof
(\A)egoJ
[(5,4) egqf
.-. gof={(0,4),(1.4).(5.4)}
Ejemplo.- Sean f. g: R >R tal que: f(x) = x2 +2.r + 3. g(x) = x-5
Hallar [<LS0fM + lf08X2Ufo8)G)-{gogK2) 2
(/o«)(2)
Solución
Calculando cada una de las operaciones
(gof)( 1) - (g(f( 1)) = g(6) =1 ; (fog)(2) = (f(g(2)) = f(-3) = 6
(fog)í3) = f(g(3)) = f(-2) = 3 : (gog)(2) = g(g(2) = g(-3) =-8
Ahora reemplazamos en la expresión dada:
Agof)(\) + (fog)(2).(fog)0)-(gog)a) 2 = l + (6)(3)-(-8) 2 = 27 2 = 9 2 = A_
(fog)(2) 6 (6 2 81
Ejemplo.- Sea #(*) = { Hallar -£-£ 2-z—
[jc-1 six<l (.gogK-D + g-W
Solución
Calculando cada operación se tiene:
(gogXl) = g{g(\)) = gi-2) = -3
(gogX-l) = g(g{-D) = g{-2) = -3
g(-l) = -2,g{l) = -2
, --„ (gogXD + 2g(-l) -3+2(-2) -3-4 _
Ahora reemplazamos en la expresión: — = t- = = - /
(gog)(-l) + g2(l) -3 + (-2r -3 + 4
408
Eduardo Espinoza Ramas
Ejemplo.- Si f(x) = x* encontrar dos funciones g para los cuales
(fog){x) - 4.r2 -12jc + 9
Solución
(fogKx) = f(.g(x)) = 4jc2 -12a + 9 = Í2.V-3)2
£2(a) = (2a-3)2 => g(x)=±(2x-3)
.-. £,(*) = 2a-3 , £,(a-) = -2a+3
Ejemplo.- Dadas las funciones f(x) = 3x - 2 sí x e < 0 .+£»> ; g(x) = x~ sí x e <-3.5>
a) Hallar fog (la función f composición g)
b) Hallar gof (la función g composición 0
Solución
a) 1 ro. calculamos el dominio de f o g: DJog =[xe Dg I x e Dg a #(*)e Df\
xe Dg Ag(*)e Ds
xe< -3.5 >a jc2e<0,o°> entonces x e <-3,5> A <-°°,0> u <0.°°>
x e <-3,0> u <0,5>
2do. Calculando la regla de correspondencia de f o g
(fog){x) = f(g(x)) = f(x2) = 3jt -2
Por lo tanto: (fog)(x) = 3a2 -2 para x e <-3,0> u <0,5>
b) 1ro. Calculamos el dominio de g o f: Dgef =[xe Df / xe Df * f{.x) e Dg }
xeDf*f(x)eDg
x e <0,°°> A 3x - 2 e <-3,5> entonces x e <0,°°> A -3 < 3x - 2 < 5
Relaciones y Funciones
409
1 7 7
x e <0,m> A -l<3x<7 entonces ag<0,oo>a — <jc<— => xe<0,— >
3 3 3
2do. Calculando la regla de correspondencia de g o f
<.gof)(x) = g(f(x)) = g(3x-2) = Ox-2)2 =9x2 -\2x + 4
Por lo tanto: (gof)(x) = 9x2 -12a + 4 , para: xe< 0,— >
Ejemplo.- Hallar fog si f(x) = 3x + 2, x e <-°°,3>, g(X)
Solución
_ Í2a sí a < 0
|-3jcsi x>\
¡gl(x) = 2x si x<0
g(x) = < , donde DC=DC uD. dominio de la función g
[gz(X)=-3X SÍ A>1 S SI «2
Ahora calculamos el dominio de f o g
Dfog = {xeDg/xeDg*g(x)eDf} ={xe Dg /xe Dg¡ uDg2 Ag(x)eDf]
= {jte Dg¡ Ag.w^lu^e Dg; *g2{x)e Df}=Dfog¡ vDfog2
hfogOW si xeDf
Luego: ífog)(x) = \ '
\{fog2){x) si xeDfog2
Ahora calculando Dfog¡ y Dfog^
x e <-m,0> A 2x e <-°°,3>
x e <-oo,0> A x e <-o°,3/2> entonces x e <-oo,0> por lo tanto Djog¡ - < -°°,0 >
Dfog2=txeDg2/xzDg2*g2(x)zDf]
xe ll,°°>A-3xe <-°°,3> entonces xe [1,»> A x e <-l,°°> entonces xe [1,°°>
410
Eduardo Espinoza Ramos
(/»* i X*) = /(* i (*)) = f{2x) = 3(2x) + 2 = 6* + 2
(/»* 2 )(jr) = f{g 2 (x)) = /(-3jc) = 3(-3x) + 2 = -9x + 2
6jt+2 sí Jte<-o°,0>
-•■ (fog)W =
\-9x + 2si jce[l,oo>
„ \x" si x<l \ — x six<2
Ejemplo.- Hallar(fog)(x)sí: f(x) = \ , g(x) = \tt
[-X3 si x>2 [2x si x>4
Solución
Veremos el caso cuando las funciones tienen dos reglas de correspondencia.
r/,(x) si xeDf íg(x) si A-eDgi
|/2(*) « *e D/2 |«2W si xe Dg2
el dominio de f o g se obtiene siguiendo el mismo criterio del ejemplo anterior, es decir:
x e <-°°,2> A -x e <-oo,i> entonces x e<-oo,2> A x e <-l,°°> de donde x e <-l,2>
ü) D/,»S2 = be Ds2 7 A e s2 A*2 W e /i)
x e [4,°°> A 2x e <-oo,l> entonces x e [4-°°> A x e <-°°,l/2> => x e <¡)
üi) D/!í|,=lx6D.l/"Di,A«iW6D/1l
x e <-oo,2> A -x e [2,°°> entonces x e <-oo,2> A e <-<»,-2> de donde x e <-°°,-2]
iv> Dhog2 ={xeDg2/xe Dg2 Ag2(jt)e Bfi}
xe[4,«>A2xe [2,«> entonces x e[4,°°> A x e [1,«> de donde xe[4.°°>
Luego de i), iii), iv), la regla de correspondencia es:
Relaciones y Funciones
411
(flOgl )W = /, (gl (A)) = /, (-X) = JC2
(f2°8i X*) = /2(*i (*)) = /2l-*> = *'
(/2og2)(jr) - /2 (g2 (*)) - /2(2.v) - -8jc3 , luego
UbgXx) =
(/iOg,)U) , 5i .ve<-l,2>
(f2ogi)(x) , si xe<-°°,-2] .". (fog)(x) = -
(.fiOgzXx) . si *e[4,«>
jc , si" jr e < -oo,-2]
jc2 , si jre<-l,2>
- 8.v3 , si" x e [4,00 >
4.18. PROPIEDADES DE LA COMPOSICIÓN DE FUNCIONES.
Consideremos las funciones f, g, h, I (identidad)
\lj f o g * g o f no es conmutativa \2J (fog) o h = fo(goh) asociativa
(?) (f + g)oh = (foh) + (goh) distributiva (4) (fg)oh =(foh).(goh)
© foI = f,Iof=f,Vf © rol'" =/"", n,meZ+
0 IUnor=r o /""=/, «6 z*. nimpar ® I" = LLLJ^
14.19. EJERCICIOS PESARROLLADOS.-
® Dada las funciones f = {(2,l),(-2,3),(l,5),(-3,4),(7,8)}; g = {(3,-2),(7,2),(-3,l),(2,4)}
Calcular f + g, f - g, f.g , f/g
Solución
Calculando el dominio de cada función: Dj ={-3,-2,1,2,7} ; Dg = {-3,2,3,7}
Como Df+g =Df_g = Df_g = DfnDg ={-3,2,7}
'(/ + *)(-3) = /(-3) + *(-3) = 4 + l = 5
(/ + *)(2) = /(2) + *(2) = l + 4 = 5
(/ + g)(7) = /(7) + g(7) = 8 + 2 = 10
(-3,5)e/ + g
(2,5)e/ + g
(7,10)e/ + g
.-. f+g={(-3,5),(2,5),(7,10)}
412
Eduardo Espinoza Ramos
(/-g)(-3) = /(-3)-g(-3) = 4-1 = 3
(/-g)(2) = /(2)-g(2) = l-4 = -3
(/-gX7) = /(7)-g(7) = 8-2 = 6
.-. f-g={(-3,3).(2,-3),(7,6)}
'(/•*X-3) = /(-3).g(-3) = 4(1) = 4
(/.g)(2) = /(2).g(2) = l(4) = 4
(/.g)(7) = /(7).g(7) = 8(2) = 16
(-3,3)e/-g
(2,-3)6/-g
(7,6)e/-g
f (-3,4)6/.*
(2,4) e/.*
(7.16)6 f.g
:. f.g={(-3,4),(2,4),(7,16)}
Calculando el dominio de f/g: D//g = DfnDg- [x/g(x) = 0} = {-3,2,7}
(</™-/!t)-T-«
£ «(-3) 1
g g(2) 4
. 8 g(7) 2
.-. ^- = {(-3.4). (2,1). (7.4)
# 4
(-3,4)6^
4 g
(7,4)6^
}
© Sean f = {(1,3),(3,5),(2,4),(4,6)}; g= {(4,1),(0,-3),(3,2),(1.0)}. Hallarf/g
Solución
Calculando el dominio de cada función: Df = {1.2,3.4} Dg = {0,1,3,4}
Calculando el dominio de f/g: Dflg =DfnDg -{x/g(.v) = 0} = {1,3,4} - {1}={3,4}
8 8(3) 2
(¿X4,-¿gUf-6
(3.f)^
2 g
(4.6)6
/
- = {(3A(4.6)}
* 2
Relaciones y Funciones
413
®Íjc + 4, jc<-1 Í-2jc, -4<jc<3
Sí ^(jt> = «i ,gW = \ . ^_ • Calculando f + g
[a-3, -1¿jc<4 [-4, x>3
Solución
Calculando el dominio de cada función:
Df = < -°°,-l > u [-1,4 >■; Dg = < -4,3 > u [3,~ >
Ahora interceptamos los dominios
—O
-4
O-
-1
Df+g = DfnDg = < -4,-1 > u [-1,3> u [3,4 >
Si x g <-4,-l>, f(x) + g(x) = x + 4-2x = -x + 4
x e [-1,3>, f(x) + g(x) = x-3-2x = -x-3
x e [3,4>. f(x) + g(x) = x-3-4 = x-7
de donde (/ + g )(.v) = ■
-jc + 4 si jtg<-4,-1>
— jc-3 si xe [—1.3 >
jr-7 s/jce[3,4>
(£) Hallar (f + g)(x) si f y g están definidas por:
n*-ii, «i*-i|si
[3jc , si I x -11> 1
[| JC |] , Si -3<A<1
-2 , si 1 <jc<2
1 —2jc , si x<2
D,
3 4
-O
-*D„
Solución
|x-l|<l => -1 <x- 1 < 1 => 0<x<2
|x-l|>l=> x-l>l Vx-1<-1 => x>2Vx<0
f|jc — 11 ji 0<jc<2
Ahora a la función f(x) expresamos así: /(a) :
3x si xe<-oo,0 > u< 2.+oo >
414
Eduardo Espinoza Ramos
Dibujando los dominios de cada función en una recta horizontal.
1
-3
1
0
1
1
I
2
©
Df+g =DfnDg= [-3,0 > u [0,1 > u [1,2] u < 2,°° >
Calculando la suma en cada intervalo
xe[-3,0> => /(jc) + g(jr) = 3jr + l|jc|]
xe[0,l> => fíx) + g(x) = \x-l\M\x\)
xe[l,2] => /(*) + *(*)= | Jt-11-2
x g <2,°°> => f(x) + g(x) = 3x + 1 - 2x = x + 1
NOTA.- Se efectúa la operación en sus propias reglas de correspondencia
(/ + g)(x) =
3jc + [|jc|] , si jce[-3,0>
|jc-1|+[|jc|], si xe[0,l>
|jc-1|-2 , si jce[l,2]
x + 1 , si xe<2,+°°>
Sí f(x) = | x - 2 | + | x + 2 | , g(x)
Í3x + 2, si x<0
~\l-x, six>0
y H(x) = f(x) + g(x) ,
DH - [-2.3 >. Hallar la gráfica y el rango de H.
Solución
Primero definiremos los valores absolutos
\x — 2 , si x>2
,„_,„. , , ,x+2 , si x>-2
U-2 = ; \x + 2 =
1 ' ^2-x , si x<2 \-x-2 , sí x<-2
\ r
+ V
~^ZL
Relaciones y Funciones
415
Ahora definiremos f(x) en cada intervalo
Six<-2 , f(x) = (2 - x) + (-x - 2) =-2x
-2<x<2 , f(x) = 2-x + x + 2 = 4
x>2 , f(x) = x-2 + x + 2 = 2x
por lo tanto f(x) =
— 2a , si x<— 2
4 , si -2<Jt<2
2x , si x>2
Ahora calculemos los dominios de cada función
o o
^2 0 2 3~~
J O .
o 1-
! in
DH = [-2.3 > = [-2.0 > u [0.2 > u [2.3 >
Definiremos a la función H(x) en cada intervalo
x e [-2,0> => H(x) = 4 + 3x + 2 = 3x + 6
x e [0,2> => H(x) = 4+l-x =5-x
x e [2.3> => H(x) = 2x+l-x =x+l
Por lo tanto la función H(x) queda definida por:
H(x) = -
3jc + 6 si - 2 < x < 0
5-x si 0<x<2
jc + 1 si 2<jc<3
Graficando la función H(x) se tiene:
RH = [0,6 >
416
Eduardo Espinoza Ramos
©
©
Si se tiene que f(x + 2) = x2 sí x e <-5,5] y g(x-\) = x2 si x e [-2,2]. Calcular f(x) y
g(x)
Solución
Calculando f(x), para esto x + 2 = y => x = y-2
Como x e <-5,5] =* y-2 e <-5,5] de donde -5< y- 2 < 5 =» -3<y<7=>ye <-3,7]
Luego f{x + 2) = x2 =*> /(v) = (v-2)2, ye<-3,7]
Ahora evaluamos en x: f(x) = (x-2)2, x e <-3,7]
Calculando g(x), para esto x-l=y =* x = y + l
Como xe [-2,2] =* y+le[-2,2] => -2<y+l<2=*-3<y<l =* ye [-3,1]
Luego g(x-l) = x2 =* g{y) = {y + \)2 ,ye [-3,1]
Ahora veremos en x: g(x) = (x+1)2, x e [-3.1]
je — 1, si ;c<0
x , si 0 < x < 2
a: + 5 , si a- > 2
Calcular (f+g)(x) y (f/g)(x), donde f(x) = I *' ; *(x) = <|
[v* , si ;c>4
Solución
Calculando el dominio de cada función
Df =< -~,1] u [4,+o° > , D^ = < -oo,0 > u [0,2] u < 2,+o° >
Ahora calculamos Df+g
■>D.
O
-o
1
-►D„
Df+g=DfnDg = <—o,0>u[0,l]u[4,4oo>
Relaciones y Funciones
417
Calculando f(x) + g(x) en cada intervalo
Sí x e <-oo,0> , /(*) + g(x) = Vl-x + x2 -1
xe[0,l], f(x) + g(x) = yn::x + x
X e [4,+oo> , f(x) + g(x) = yfx+X + 5
Vl-*+;c2-l , sí *<0
(/ + £)(*) = /(*) + £(*) = ■^/iT¿ + ;c , 5/ 0<*<1
Vjt+Jc + 5 , si x>4
Ahora calculamos Dflg es decir:
Dflg =Df nDg-[x/g(x) = 0} = <-oo,0>kj [0,1] v[4,+oo>- {0,-1}
= <-«v 1> vj <-l,0> u <0,1] u [4,+°°>
^
*2-l
Vi
, s/ xe<-o°,-l>u<-l,0>
, sí xe<0,l]
jc + 5
, 51 X > 4
(?) Calcular (f+g)(x) y (f/g)(x) donde
/(*) =
* -1 , si x<-2
•Jl-x , 5i -2<x<0 ; g(x) =
x , si 0 < * < 20
f jc2 — I , ji -10<*<2
yfx , SÍ X>2
Solución
Calculando el dominio de cada función
Df = < -oo,-2 > u [-2,0 > u [0,20 >, Dg = < -10,2 > u [2,-h*> >
418
Eduardo Espinoza Ramos
Ahora calculamos el D
f+g
-10
-2
•
0
2
o D,
20
*"D„
Df+g =DfnDg =< -10,-2 > u [-2,0 > u [0,2 > u [2,20 >
Calculando f(x) + g(x) en cada intervalo.
xe <-10,-2>, f(x) + g(x) = x2 -1+jc2 -\ = 2x2 -2
xe[-2.0>, f(x) + g(x) = y/í^x + x2-\
x e [0,2>, f(x) + g(x) = x + x2 -1
x 6 [2,20>, f(x) + g(x) = x + yfx
Luego se tiene: (/ + g)(x) = f(x) + g(x) = ■
Calculando (f/g)(x)
si -10<jc<2-{-1,1}
2*2-2
si -10<jc<-2
(-)(*) = •{
8
x2-\
x2-\
J\-x+x2-\ si -2<jc<0
x2+2x-\ si 0<*<2
x + Jx si 2<x<20
1 si -10<jc<-2
^x
x2-\
¿í-2<jc<0-{-1,1}
,/,
ósea (—)(a) =
* sí0<*<2-{-1.1} *
x¿-\
-jL si 2£*<20
.V*
x'-l
X
x2-]
si xe [-2,-1 >u<-1,0>
si *e[0,l>u<l,2>
-f= sí'jre[2.20>
\9j Dadas las funciones definidas por:
f={(0,0),(4,3),(2,4),(-3,2),(3,-l)} y g= {(6,2),(3,4),(2,0),(4,7)}. Calcular fog
Relaciones y Funciones
419
Solución
Calculando Dfog es decir: Dfog ={x/xe Dg Ag(x)e Df]
Dg = { 2, 3, 4, 6 }
-4r >*' -4r 4-
g(2) g(3) g(4) g(6)
II
0
II
4
Veremos cuales pertenecen al D¡
Se observa que: Oe Df , 4eDf, 2e Df entonces Dfog ={2,3,6}
Ahora calculamos los elementos de f o g
(/o*)(2) = /UK2)) = /(0) = 0
(/0£)(3) = /(£(3)) = /(4) = 3
(/o*)(6) = /0K6))=/(2) = 4
(2,0) e Dfog
(3,3)eD/og
[(6,4) € Dfog
.: fog={(2,0),(3,3),(6,4)}
_\x + 2 , x<\
\x-\ , *>! '
Sean las funciones reales de variable real f{x)
Hallar f o g
Solución
De acuerdo a los criterios establecidos se tiene:
/WJ/'Wb'+2'xS1.íwJ"Wb'1 • *<0
[f2(x) = x-l , x>l "" [g2(x) = l-x, x>0
Calculando Df¡ogi ={xe Dg¡ A gl(x)e Df¡}
xe< -o°,0 > A x2 < 1 desarrollando x e <-oo,0> A -1 < x £ 1
(/ioS,)(*) = /,(*,(*)) = /,(*2) = *2+2, xe [-1,0>
íW =
|xz , x<0
\l-x, x>0
X € [-1,0>
420
Eduardo Espinoza Ramos
Calculando Df¡ogz = [x/xe Dg2A g2(x)e Df¡)
x e [0,+t»> A 1 - x e <-«>.i] entonces x e [0,+°°> A 0 < x < <» => x e [0,+«>>
Calculando Dfi0gi = {x I x e Dg( A g, (x) e Df¡}
jce<-«>,0> A x2 e<l,+°° >
xe <-oo,0> Axe <-«vi> u<l,+«>> = <-oo,-i> =* x e <-«>,-i>
ihogx )U) = f2 (*, (*)) = f2 (x2) = x2 -1
Calculando D^ =[x/xe Dg2A g2(x)e Dfi}
x e [0,+£»> A 1 - x e <!,+«>> entonces x e [0,+«>> Axe <-£»,()> =* 0
(/o*)(*) =
;c2-l si ;c<-l
x2 +2 si xe [-1,0 >
3-jc 5i Are[0,+<»>
í x, xe<-«>,l]
» = i
(_-1, X e < l,+oo 3
Dadas las funciones: /(*) = i ''' g(x) = i
' ■> [l\x\] , x>0
Calcular (f o g)(x)
Solución
(/,(,) = ,«<-«,.] gix)J^x) = x2-Z si x<0
[/2W = -Ue<l,+-> s \g2(x) = [\x\] si x>0
DM =D/,<*, ^Df¡ogl ^DhoKl VDfi0g2
Dfl0t¡={x/xBDtiAgl{x)sDft)
x<0 A x2-8e<-<»,l] =* x<0 A -°o<x2 <9
=* i<0AH<x2Ax2<9) => x<0 A(RA-3<x<3)
Relaciones y Funciones
421
=* x<0A-3<x<3=*xe [-3,0>
(/iO£i) = /i(£iU)) = /iU2-8) = jc2-8
ifiOglXx) = x2-*, x€ [-3,0>
Df¡ogi ={xfxeDgiA g2(x)eDft]
x>0 A [|x|]e<-oo,l] =» x>0 A -oo<[|^|]<1
=* x>0A-oo<x<2=>xe [0,2>
(fiOgjXx) = /, (S2 W) = /i (ti * II) = ti * |]
í/iOí2K*) = [|*|]. xe [0,2>
D/2««, =ix/xeDgiA g{x)BDh]
x<0 A ^2-8e<l,+oo> => x<0 A 9<x2<oo
x < O A (9 < x2 A x2 < +0°) => x < O A (x < -3 V x > 3) => xe <-«>,-3>
(f2ogi )(x) = f2 (*, (x)) = f2(x2 -8) - -1
(/2og, Ka:) = -1, x e <-«>,-3>
Df20g2={x/xeDg2A g2{x)eDfi]
x>0 A [|jc|]e<l,+«o> =* *>0 A 1<[|jc|]<+oo
=* x>OA2<x<oo =>xe [2,+t»>
(f2og2) = f2(g2(x)) = f2a\x\]) = -l, xe [2,+oo>
(f2og2)(x) = -l, xe [2,+oo>
(fog)(x) =
jc2-8 si xe [-3,0 >
[|x|] si A-e[0,2>
-1 si' x e < -00,-3 > u[2,+oo >
422
Eduardo Espinoza Ramos
Si f(x) = x2 y (fog)(x) = 4x2 -\2x + 9 encontrar dos funciones g(x).
Solución
ifog\x) = f(g(x)) = 4x2 -12* + 9
£2(.v) = (2*-3)2 => g(x) =±(2x-3) .-. gl(x) = 2x-3, g2{x) = -2x + 3
Sí f(x-l) = x-2 y {gof)(x + 2) = 2x2 -x. Calcularg(x)
Solución
f(x-l) = x-2 =* f(x) = x-l
(gof)(x + 2) = 2x2-x =» {gof)(x) = 2(x-2)2-(x-2) =2a2-9a + 10
(go/)U) = 2a:2-9^ + 10 de donde g(f (x)) = 2x2-9x +10
g(x-l) = 2x2 -9x + l0 => £(jc) = 2U + 1)2-9U + 1) + 10 =2jc2 -5jc + 3
Si /(;c) = jc2+2 y g(x) = x + a. determinar el valor de a de modo que
(fog)(3) = (gof)(a-l).
Solución
(fog)0) = f(gQ)) = f(3 + a) = Q + a)2 +2 =a2 +6a + \l ... (1)
(gof)(a-l) = g(/(a-l)) = £((a-l)2 +2)
= g(a2 - 2a + 3) = a2 - 2a + 3 + a = a2 - a + 3 ... (2)
Igualando (1) y (2) se tiene: a2 +6a + \\=a2 -a + 3 =* a = —
Si H(x) = eos 2x y f(x) = sen x encuentre una función g tal que H(x) = (g o f)(x)
Solución
H(x) = (g o f)(x) = g(f(x)) = eos 2x
g(sen *) = eos2 jc-sen2 x =l-2sen2x .: g{x)-l-2x~
Relaciones y Funciones
423
4.20. EJERCICIOS PROPUESTOS.
© Calcular f± g , f.g . f/g , donde f = {(1,2),(3,4),(2,5),(4,1)}; g={(3,-l),(2,l),(l,0)(0,2)}
© Calcular f ± g . f.g , f/g , donde f = {(-3,2),(0,0),(2,4),(3,-1 ),(4,3)} .
g={(2,0),(3,4),(4,7),(6,2)}
© Sif={(l,3).(2,6),(4,8),(6,2)} y g= {(1,2),(2.-1),(0,1),(4,5),(7,0)}
Hallarf + g.f-g, f.g, f/g
® Si f={(l,4),(2,5).(3,6),(4,-6),(5,-5)} y g= {(0,8).(1.3),(2,0),(3,7).(4.0),(5,10)}
Calcular f + g , f - g , f.g , f/g
® Sean f = {(2.8),(8,4),(6,9),(4,7),(3.6),(1,5)} y g= {(7,1),(3,2).(5,5),(10,5),(1,3)}
Hallarf + g,f-g,f.g,f/g
© Sean f = {(4,1),(6,5),(5,4),(8,3),(9,2),} y g= {(8,-5),(2,2),(5,-4)}
Calcular f + g , f - g, f.g , f/g
(?) Calcular f + g , f.g . f/g de las funciones
a) /(*>=, 2
2jt+l,x>l
jc2-2,jc<0
*(*) =
Í3jc + 1,jc<8
Í7 ,*<10
b) /(*) = , >n
c) /(*) = «
d) /(*) =
x si x>l
\x-l\si x<\
3jc\jc>10
Í3JC-1 . |*-1|<1
[ x , x>3
y¡X + l , X>-1
íW =
*2-i
x2 si jce [-10,-7 >
2x si *e[-4,0> , g(x)
2jc2-2 si" xe<0,8>
, jc < —1
-x2+x , si jce<-8,-4]
-x + 3 , si *e<-4,0]
x2+2 , si *e<0,3]
424
Eduardo Espinoza Ramos
®
®
2jc-1 , Are [0,1 >
e) fíx) = \
[x2 , *e[2,5>
g(x):
Í3x , xe<-l,l]
[2at , jce<l,4]
f) /(*) =
g) /(*) =
\x\ , a:£ [-1,3>
-2x + 3 , Are [3,6]
jc2-1 , U|<2
x , x > 2
8(X):
-n/at-I , Are [1,4 >
íl*|]
g(x)
_\x-\ , 0<x<
~\x + \ , x<0
a:s [5,7 >
3
Hallar (f+g)(x) y (f / g)(x) sí: f{x) =
x<l
x>4
; gW =
x-l , x<0
x ,0<*<2
a: + 5 , a:>2
Hallar (f + g)(x), donde:
/(*) =
f[|*-l|] , jce<-4,-l]
[|jc|] + 1 , Are [0,2] , g(x) =
|jc — 21 +3 , Are<-l,0>u<2,3]
5 , Are<-3,-1 >
-2 , .ne<0,2>
-3 , Are[-l,0>u[2,3>
Dadas las funciones definidas por: f(x) = u
4at + [|at|] , Are<-3,0>
Jat2+1|-3 , A-e<l,6>
g(x)
[|-jc|]-5jc , Are<-4,-l]
|*-3| , xe<0,2]
Hallar (f + g)(x) y graficar
Hallar (f/g)(x) donde: f{x) =
\x\ , Are [-5,-1]
2a: , Are [1,4]
g(x) =
\[\x-2\] , xe[0,3>
I at2 , Are [3,6]
Hallar (f + g)(x) y graficar donde
/(*) =
[|jr-l|] , Are<-4,-l]
[|at|] + 1 , Are [0,2] , g(x) =
|at-2|+3 , Are<-l,0>u<2,3]
7 , Are [-3,-1 >
1 , Are [0,2 >
-2, at e [-1,0 > u[2,3]
g(x) , Are<-1,2>
Halle Df+gnRf si f(x) = \ , g(x)-
1 g J * U +2 , Are[2,oo>
12*-!,
jre<-°°,-l>
Are<2,+«o>
Rpta. <9,+t»>
Relaciones y Funciones
425
04
Dado las funciones f(x) = 2x-3, -l<x<3 ; g(x) = x-[\x\] , x e R, hallar (—)(x)
8
(Í5) Dadas las funciones: f(x) = •
r. 25-jc. x + 2 5
[|- 1] , -<0 a x<-
1—x x-4 2
,¡\x^3\ , í<x<4
g(x) = V" , ' . Hallar (f+g)(x) y graficar
x-4 ,2<x<9
ftó) Hallar (f + g)(x) y graficar donde
/(*) =
[|jr2|]+U2-l|-3 , «[-2,2]
2*-l
jc-1
xe<2,4>
. íW =
4-[\x2\] , x<2
-2 ,x>2
17
fl8l
fl«
Dada las funciones /(jc) = 2jc—[| 2x+[\ x |] |], - < x < 1
g(x) = ||x-2|-|x|| , |x|<l; Hallar(f + g)(x)
Hallar (f + g)(x), (f-g)(x), (f.g)(x) donde
\3x + \ , xb [-1,1 > Í2VÍ-1
|5jc , xe<l,6] U-2
Hallar (2f - 4g)(x), donde
fiH,PD «<-u> t H
l[|x-3|],jre[l,4>
l*2-4|
x + 2
xe[0,3>
xe<3,5]u[6,8>
xe<-2,l>
III1!!]-!!^!] . *e[1.10>
x ix + 5
(20) Calcular (f + g) (x), (f.g) (x), (f/g) (x) y graficar donde
Í2jc-1 , xe[0,2] r
a) fíx) = \ l,J ; *(*) = >£ , D,=[l,4]
[3 , xe[3,5]
426
Eduardo Espinoza Ramos
b) f(x) = <
X X <1
3jc, 1 < x < 3 ; g(x) =
eos jc , x> 3
- x , x < -2
11 . 2<jc<3
34 , x < 6
, „ ^ Í[W] [|V'2~411 ' X<3
c) /(*) = 4 i- , g(x)
Nx'-16 , jc>4
fx, x<2
[x-l , x>i
d) /W = ir, „ h . _ . 8(x) = \
[[|-4+cosx|] , x>0 sen x ,0<x<n
U + 3 si xe[-4,0] ) = J2jc_4 ' Jcet-3-2l
13jc+2 si:jce<0,5> ' \2-x , jce<2,8>
f) /(x) = «
f VI^2 , jce[2.4>
Ix2-14jc + 48 , jce[6,10>
, ííx) =
[| |] , xe[l,8>
J2jc-10|, jcg[8,12>
g) f(x)
J|x2-4|, xe[-6,0]
1 2 , te [1,6 >
*(*) =
: + 2 . x>-2
1 , jc<-2
^ o- „, ÍU-1|[|si^(3-a)|1 , *e[0,6] nx-2 , xe<-8,3>
h) Si /(x) = ^ , , #(x) = ^
[ a- , jce<6,10> |x|x-2| , xe<3,8]
., ,, , Ux2-2x si \x-\\>\ o |x-l|<3 . .
0 f{x) = \ ,g(x) =
[jc2-4jc-4 sig (|x|-3) , jee [0,2]
l\-f—\l » x<3
x +1
x2 + jc + 1
l x-l
, si xe [5,10 >
j) Sí /(x) = -
Vjc2+16 , jce<-4,-2>
[|x|]-2x , xe[-l,2
|x2+2| , jce<4,6>
[|x|]-2x , xe[-l,2> , g(x)=u
2jc + 4 , *e<-3,-l>
| jc2 -21 , jce[-l,5>
m) Determinar fog , cuando f = {(1,3U2,4),(3,5),(4.6)} y g = {(4,l),(l,2),(6,3),(0,-2)}
Relaciones y Funciones
427
(22) Determinar fog, gof, cuando: f = {(0,1),(1,2),(2.3),(4,3),(5.2)}
g = {(6.7).(5.4).(4.3).(2.4).(1.4),(0,7)}
@ Hallar gof sí: f = {(2.5),(3,4),(6,2),(5,0).(1,7)} y g = {(4,8),(5,3),(0,9),(2,2),(7,4)}
@ Hallar gof sí: f= {(2.5),(5.7),(3,3),(8,1)} y g= {(1,2),(2,3),(4,5),(6,7)}
®Í3jc-2 . *e[-4,4> ,
Sí/U)= ' : g(x) = x1+\. Hallar(fog)(x)
[x . xe [4,6]
(26) Consideremos las funciones reales de variable real
[x2 x<0 Íjc + 2 , jc< 1
g(x) = f ' ; f(x) = \ . Hallar fog
[l-x, x>0 [x-l , x>l
fon Sean las funciones f y g definidas por:
x2-5x , x<-2 , , \2x-4 , x>-2
|jc-2|-2jc , x>-2 [x2+3x , x<-2
Hallar: f(0) + g(0) . f(l) f(-3) , (fog)(-2) , ^"TT • (Bof)0) . (gog)(-3/2)
s(-i)
-jc + 1 , xe<-°o,-2>
2x , xe<6,°°>
2x , x<0
(3) Hallar fog sí f{x) = 2x2 +1 , x e <-2,20>, g(x) =
(S) Hallar fog sí f(x) = 3x + 2 , Df =< -°°,3 >, g(x) =
-3x, x>l
, , \2x-\ , x<-l \x , x<0
(30) Determinar gof si. f(x) = \ , g(x) = i
vy 'jc + 2,jc>2 [2x, x > 0
A ' jc<-1 ,
12 , jc<1
-1 , l<oc<2 , g(x) = \
1 , jc>4 L
ttl) Hallar fog sí, f(x) =
Í2jc-1 , jcg[0,2] r
Hallar fog y gof, donde, f(x) = { „ „ • gM = vx
[x .ve<3,5]
428
Eduardo Espinoza Ramos
(S) Sí H(x) = y¡x2-2x + 3 y (Hof)(x) = y¡[\x|] + 3 . Calcular f(x)
®f I jc2 — 11 , jc < 3 í
Calcular (f o g)(x), donde f(x) = \ . , g(x) = {.
\yjx2+l , x*3 U
|jT-1| , x<3 _ \x , jc>4
\x\-x , x<0
®\[\x\] , *<0 ,
Calcular f o g y granear sí: g(x) = < , , f(x) = ylx+l , -l<x<2
U -1 , xZO
®Í2jt-5 , x <2 \x2 -2x , x< 1
Calcular fog, donde, g(x) = \ , g(x) = \
\-x-2 , x ¡>2 [e* , *>i
(37) Sí /(jc) = V2jc-1 y g(jc) = y¡2x2-7 . Hallar la función h tal que f o h = g
(38) Dadas las funciones f(x) = 2x-[\2x + [\2x\]\], -<x<l
g(x) = |x + 2 |-|x|, |x|<l. Hallar fog, gof
(39) Sean f(x) - 2x2 -1, g(jc) = 4jc3 -3x , x e R , probar que f o g = g o f
(40) Sif(x + l) = 3x+l ,g(x) = 2x-3, hallar(fog)(x+l)
®\x2 , <1 f—jc ,x<2 m „
Seanf(x) = \ , *(x) = L . hallar gof
[-jc\ x>2 |2x. x>4
(42) Hallar fog y gof si existen, donde
/(*) =
1
jce<-l,l> ÍH*|] . xe[0,l>
x-\ , £(*) =
|jc2+1| , jce<l,2>
2,11 „^io^ IVJf2 — 1, xe[l,3>
(43) Hallar (f o g o h)(x) si f{x) = x2+ 2x + \ , g(x) = x - 2, h(x) = x - 3
(44) Seanf(x) = ax + 2 , g(x) = x-6, a#0, b#0 si fog = gof hallar b(a-l)
Relaciones y Funciones
429
(45
(46
47
Sean /W = P ' ~1<X~3 y gix)^^'1^ Ú ^<X*°
[a/2 , 4<a<6 [a- [|x-3|] + 2 , si 2<x<4
Hallar fog si existe
Dadas las funciones f y g definidas por: /(a) ■■
[|i^|] , xe<-l,l>
3—x
Va2 + 2a , ag[1,2>
g(x) = ■
x-l ' ^e[ ' l> ■ Calcular (fog)(x) y (gof)(x)
1-a , ag<0,6>
\x , *e [-3,0]
Determinar gof sí f(x) = { , g(x) = x - 15, x e <-10 , 9]
he2 , ae<0,5]
(48) Sean /(x) = [|x|] y g(x).
[|x-4|] , a>0
Hallar: h(x) =
\(fog)(x2) , *<0
x- , x<0 [(gcfX-Jx) , a>0
(49) Si F(x) = ctgx y g(x) = cosecx encontrar una función f tal que F(x) = (fog)(x)
(50) Si (go/)(x+2) = 2x2-A y f(x-l) = x-2 Calcularg(x).
@ Si (fog)(x-1) = xz -2x y g(x) = x + 3 Determinar f(x).
(52) Dadas las funciones f,g: R > R, definidas por:
f(2x + 3) = 4x + 1 y g(x) - x2 + 3. Determinar (f o g)(x) y (g o f)(x)
(53) Sí F(x) = (1 - cos2x) secx y f(x) = senx. Hallar una función g tal que F(x) = (gof)(x)
(54j
Si F(x) - eos x y /(a) = T, hallar una función g tal que F(x) = (fog)(x)
1 + A"
Si F(x) = sen 2x y g(x) = eos x , encontrar una función f tal que F(x) = (fog)(x)
0 , a<0
Determinar gof sí, f(x) = \x2, ae[0,1] , g(x)-
0 , a>1
1 , a< 0
2A , A£ [0,1]
1 , A>1
430
Eduardo Espinoza Ramos
(57) Si f(x) = 4x-x2 , 0<x<7, g(x) =
®
®
<60)
Í641
65
ffifl
jc2-4 , jc<0
jc+2
:>2
, hallar (gof)(x)
Si(gof)(x) = x + 2 , /(jc) = a-3 + 6jc2+12jc + 8, hallarg(x).
Dadas las funciones f(x)=\ x2 -1| y g(x) = y¡9-x2 . Determinar (gof)(x)
f[|jc-1|] , 0<jc<3 x + i
Si /(jc) = ^ , .— y g(x) = , detenninar gof
[VU-Jcl-2 , x>3 x-4
(61J Hallar fog , siendo f(x) =
2jc -1 , - 4 < jc < 4
[l\x\] , x>4
(62) Si g(2-x) = yfx^í y (gof)(x) = 2x - 1, hallarf(x)
g(x) = x3-2x
(63) Sí/(x) =
2x , si x es impar , g(x) - — . Hallar gof si es que existe.
2x+\ , si x es par
2.
0 . si x no es entero
Sean las funciones f y g definidas por:
/(*) =
|-i-1 , si x<-2
1 — jc
(jc + 2)2 , si xe[-2,-\]
í |*+6|
. «W =
, si jce<-4,-1>
| jc + 31 -3
>/5-x-2 , si jce<-l,5>
Hallar las funciones (fog)(x) y (gof)(x)
Sean las funciones f y g definidas en R, tales que:
/(*) =
[x + 2
, JC<1
8(x) =
■2 , jc>2
[0c-l)~+3 x>l \x-5 , jc<2
Hallar las funciones (fog)(x), (gof)(x)
' , x<\ \-x , jc<2
Sean las funciones /(jc) = < , #(*) = <
-jc, .í>2 [2jc , x>4
Hallar gof
Relaciones y Funciones
431
(67) Hallar gof, si f y g son funciones reales, tales que:
a" +1 , jc<1 Íjc-I , x<2
\-x2 , x>4 { 2 , x>4
[68) Sean las funciones f y g definidas por:
jc--3.!c sí x<3 fjc — 1, x<2
f(x) = \ y g(x) = { . Hallar fog y su rango
-JT+3 si x>3 1 2 . x>4
(69) Sean las funciones f y g definida por:
/(*) = •{ , y #(.*) = { Hallar fog
-jcz , jc>4
0 , *e<4,7>
(70) Dada las funciones f y g definidas por:
/(*) = •
:¿+l , x<l
■xz , x>4
y £« =
x2-4 , xe[0,4]
0 , *e<4,7>
(7l) Dadas las funciones f y g definidas en R por:
/(*) =
íi*(|*2-4|) si |x|£3
jf + 6
si xe<3,9> y g(x) = 3 , x e <-»,9>
x2+\0x + 2\ si |jc-3| >6
Í72
Construir la gráfica de f + g, indicando explícitamente su rango.
„„ c ■ j r, ^ W +1 ' X<>3 l ^ JV*2-2jC SI JC(*-2)>0
Hallar fog, siendo /(jc) = { y gU) = \ v
x , *> 3 I [1 jc|] si *(*-2)<0
, , . x si jce<-~,l] , x \x2-4 , *e[0,4]
(73) Hallar fog, siendo: f(x) = < y g(x) = <
|-1 sí jce<l,+°o> 0 , jce<4,7>
432
Eduardo Espinoza Ramos
2.r + l , -3<jc<-1
(74) Hallar fog siendo: f(x) = \ 1 , -1<jc<1 y g(x) =
Jjc -4 , jce[0.4]
0 , jcg<4,7>
(75) Dadas las funciones f(x) = y g(x) = 1 - x determinar los dominios de las
^•^ 1 + jr
composiciones fog y gof.
fié) Si g(2-x) = Jx^\ y (gof)(x) = 2x-l. Hallar la función f(x)
(77) Dadas las funciones f(x) y g(x) = 1 - x, determinar los dominios de las
1 — jc"
composiciones fog y gof y sus reglas correspondientes.
'2jc + 1, -3<jc<-1
(78) Hallar (fog)(x) sí: f(x) =
1. -1<jc<1 , g(x) =
i, ,2.
x
-1, x<0
3x + 2, x>0
© Si f(x) = Jx2-16 y g(x) = ^-, Hallar (fog)(x)
x + 2
®x" + 3x, si x<3 í3 — x, si x<\
Sean las funciones f y g definidas por: f(x) = < , g(x) = <
[-x2+3, si x>3 I5"*. « X>1
Hallar (fog)(x).
1
(811 Si/(jc) =
,jce<-2,2> f[|*-l|l. *e[0,l>
*-2 , g(x) = < 1 Hallar (fog)(x) si es que existe
|2*2+3Ue<2,3> IV*2-!, *e[1.3>
82
Si f(x) = x2+2x+ 2, hallar la función g(x) tal que (fog)(x) = x-4x + 5
(83) Hallar (fog)(x) sí f(x)-
x. xe<-°°,l] ¡x2-S, x<0
-1, jce<l,+°°>' 8X ~\[\x\], x>0
Relaciones y Funciones
433
®f[|jr-l|]. 0<jc<3 x + i
Si /W = i /n r-r „ y «W = 7. calcular (gof)(x)
y\l-x\-2. x>3 x-4
85
(86)
íl^-^|]. *e<-l.l>
Sean f y g dos funciones, tales que: f(.x) = < 3—x
yjx2 + 2x, xe[l,2>
*(*) =
-, xe[-2,-l>
jc-1 • Hallar fog, si es que existe.
| jc—11, jce<0,3>
Si H(x) = y]x2-2x + 3 y (HoF)(x) = J[\x\] + 3 calcular F(x)
®Íjc—1, jce[0,l] \x3 xef-lll
Dados f(x) = \ , , í(x) = ^ , .Hallar
[x'+l, xe<-oo,0>u<l,+o°> [2jc + [|jc|].jc-, jcg[3,4]
(fog)(x) si es que existe.
(88
Halle el complemento del dominio de (f o g)(x), donde f(x) = x2 -1, x e <6,13>;
? 13
g(x) = x -6jc + 6, xe<4,— >
13
Rpta. <-»,61u[—,-h»>
® Si f(x) = \ * ' X<E [5'9 > , g(x) = x + 5, x e [1.12]. Halle (f o g)(x).
U/jc , xe [10,16 >
Rpta. (fog)(x)
\{x + 5)2 , jce[l,4>
[jx + 5 , jce[5.11>
4.21. FUNCIONES: INYECTIVAS, SURYECTIVAS Y BIYECTIVAS.-
a) FUNCIÓN INYECTIVA.-
La función f: A —» B es inyectiva (univalente) si a cada elemento del rango le
corresponde un único elemento en el dominio, es decir, si existen dos elementos
jcj x2 e Df distintos xx * x2 cuyas imágenes son distintas /(je, ) * f(.x2) lo que
es equivalente a decir:
434
Fduardo Espinoza Ramos
Si xx,x2^Df : f(xl) = f(x2) => xx=x2 que es la forma más práctica para
determinar si una función es inyectiva
Ejemplo.-
a-
b-
c-
*-1
*-2
+ 3
b
f
2
fe *3
f función inyectiva f no es inyectiva
OBSERVACIÓN.- Si la función f(x) tiene varias reglas de correspondencia es decir:
/(*) =
/,(x) , xeDfi
/,U) , xeDf2
/,(*)
xe D
'/.
diremos que es inyectiva si y solo si cada función /,, /, fn deben ser inyectivas y
además Rf c\Rj =<¡> Vi*j
Ejemplo.- Determinar que la función f(x) = 5x + 3 es inyectiva
Solución
f es inyectiva sí f(x¡) = f(x2) => xx=x2
f(x}) = f(x2)=* 5xl+3 = 5x2+3 ^> xi=x2
.: f(x) = 5x + 3 es inyectiva
OBSERVACIÓN.- En forma gráfica se puede determinar si una función es inyectiva o
no, para esto tracemos una recta paralela al eje X, si dicha recta
corta a la gráfica en dos panes o más, entonces la función f no es inyectiva y si corta en
un sólo punto, entonces la función f es inyectiva.
Ejemplo.- Si f(x) = x2 y g(x) = Jx
Relaciones y Funciones
435
Yt
g(x) =v/x~^.
0
X
f no es función inyectiva
b) FUNCIÓN SURYECTIVA.-
g es inyectiva
La función f: A —» B, es suryectiva (o sobre) si y sólo si, V y e B, existe x e
A tal que y = f(x); esto quiere decir que todo elemento de B es imagen por lo menos
de un elemento de A es decir que f: A —» B es suryectiva si Rf = B
R,= B
Ejemplo.- La función f: [0,°°> —» [0,°°> tal que f(x) = -Jx es suryectiva puesto que
Rf =[0,°°>
Ejemplo.- Determinar si la función f(x) = 3x + 5 es suryectiva.
Solución
Comof:R -» R/f(x) = 3x + 5
v-5 y-5
y = 3x+5 despejamos x es decir x = -: Luego V y e R, 3x =
Tal que /(x) = f( ) = 3( ) + 5 = .y entonces f es suryectiva.
c) FUNCIÓN BIYECTIVA.-
La función f: A —> B se llama función biyectiva, si la función f es inyectiva y
suryectiva simultáneamente.
436
Eduardo Espinoza Ramos
Ejemplo.- Determinar si la función f: [0,2> —» <-oo,0] tal que f(x) es biyectiva.
x-2
Solución
i) Veremos si f es inyectiva, es decir: f(x) = f(x,) => x = x¡
x Aj -2x = xlx-2xl
x-2 xx-2
—2xx = — 2x2 => x{= x2 por lo tanto f es inyectiva.
ii) Ahora veremos si f es suryectiva, para esto es suficiente ver si el rango de f coincide
con el conjunto de llegada.
y = -?— => x = -^- e [0,2>=> 0<-^-<2
x-2 y-l y-l
0<-^-<2 <=> 0<-^-a-^-<2 <=> 0<^-a—^—<0
y —l y —l y — ] y —l y —1
\/ \ / \ /
± V : i¿ ± a - V ±
y e <-°°,0], luego R, —<—°°,0] entonces fes suryectiva.
Como f es inyectiva y suryectiva entonces f es biyectiva.
4.22. FUNCIONES CRECIENTES, DECRECIENTES Y MONÓTONAS.
a) FUNCIÓN CRECIENTE.-
La función f se llama creciente si para todo x,, x2 e Df se tiene:
a, <x2 => f(xl)<f(x2)
Relaciones y Funciones
437
b) FUNCIÓN DECRECIENTE.-
La función f se llama decreciente si para todo par xi, x2 e Df se tiene:
*i<*2 =» f(xl)>f(x2)
x___X y=fw
i
f(x,)
fíXg)
0
' Y
¡\y = f(x)
i '\
i ' \
i ' \
x, x2 ' Y
c) FUNCIÓN MONÓTONA.-
La función f se llama monótona si la función f es creciente o decreciente
d) TEOREMA.- Si una función f es creciente, entonces f es inyectiva (univalente).
Demostración
Sean x¡,x2e D* , tales que xt *■ x2 , de donde se tiene x, < x2 6 x2 < xl
Si jc, <x2 entonces f(xl)< f(x2) por ser f creciente
438
Eduardo Espinoza Ramos
Si x2 < xx entonces f(x2) < /(a, ) por ser f creciente
Por lo tanto en ambos casos se tiene f(xl) * f(x2) es decir, si x, * x2 entonces
/(x,) *■ f(x2) ■ Luego la función fes inyectiva.
e) TEOREMA.- Si una función es decreciente, entonces f es inyectiva (univalente).
Demostración
La demostración se hace en forma similar al teorema anterior.
4.23 CALCULO DE RANGOS DE FUNCIONES INVECTIVAS
MONÓTONAS.-
Cuando las funciones dadas son inyectivas su rango se encuentra en forma muy práctica
de la siguiente manera:
Sea la función inyectiva cuyo Df = [o, b] entonces se tiene:
Si f es creciente se tiene: Rf - [/(o), f(b)\; Fig (a)
Si f es decreciente se tiene: Rf = [/(fc), /(o)]; Fig(b)
i
f(b)
f(a)
'Y
_ — T-^m ^^^
\y = f(x)
1 '\
1 ' \
1 \ ^
a
b ^ x
Ejemplo.- Calcular el rango de f(x) = x para x e [-2,2].
Solución
fes inyectiva y creciente entonces Rf =[f(-2),f(2)] => ^=[-8,8]
Relaciones y Funciones
439
4.24 FUNCIÓN INVERSA.
a) DEFINICIÓN.- Consideremos la función: f = [(x, f(x))/xe. D,} con dominio
Dj y rango R, entonces diremos que existe la función inversa
de f. si y sólo si. f es inyectiva.
A la función inversa de f denotaremos por / * ó /_l, la cuál es definida en la forma
siguiente:
f* = {{f(x),x)/xeDf}
donde: Df, = Rf y R¡* = Df
Ejemplo.- Consideremos una función inyectiva f = {(1,3),(2,5),(4,7),(6,9),(8,11)}
entonces la función inversa de f es: /* = {(3,1), (5,2), (7,4), (9,6), (11,8)}
donde Df, = {3,5,7,9,11} = Rf y Rf* = {1,2,4,6,8} = Df
b) GRÁFICO DE LA FUNCIÓN INVERSA.-
Consideremos una función f y su inversa / *, el gráfico de la función inversa / *
es simétrica a la función f con respecto a la función identidad I(x) = x por tal motivo
dicho gráfico se obtiene por reflexión con respecto a la recta I(x) = x.
440
Eduardo Espinoza Ramos
"Y
f(x)
/ *
"T^wy
7¡ 7 V'W. */
/ 1 /'
/ \ / 1
/ 1 /I
/ i /I
X /
f(x) X
c) PROPIEDAD FUNDAMENTAL DE LAS FUNCIONES INVERSAS.-
Sí f: A—*B es una función inyectiva y / *: B—>A es la función inversa de f entonces:
/*(/(*)) = * , V*6D/
d) CÁLCULO DE LA FUNCIÓN INVERSA.-
Sea f: A—>B una función inyectiva, entonces a la función inversa /*: B —> A se
puede hallar resolviendo la ecuación
/(/*(*)) = * v f*(nx)) = x
Ejemplo.- Hallar la inversa de la función f(x) = 7x + 3
Solución
/(/•(*)) = * => 7f*(x) + 3 = x
.-. f*{x) =
jc-3
También la inversa de una función inyectiva se puede obtener en la forma siguiente:
Ejemplo.- Hallar la inversa de la función f(x) - 5x-3 sí x e [0,5]
Solución
Como y = f(x) => y = 5x - 3, x e [0,5]
Relaciones y Funciones
441
y+ 3
Primeramente se despeja x: x = , x e [0,5]
Luego se determina la variación de y
x = ^-e[0,5] => 0<,^-<,5 => 0<y + 3iS25
5 5
-3 < y <, 22 => ye [-3, 22]
y + 3
x = , y e [-3, 22]. ahora permutaremos x por y es decir:
x + 3 r „ „„, „ , ,„,, , x + 3 r „ „„,
y = , x e [-3, 22]. Por lo tanto f*(x) = , x e [-3, 22]
4.25. FUNCIÓN INVERSA DE UNA COMPOSICIÓN.-
Si dos funciones f y g son inyectivas y la función composición f o g existen entonces la
función f o g es inyectiva por lo tanto tiene inversa (f o g)* en este caso tiene la siguiente
propiedad, (f o g)* = g* o f*
4.26. EJERCICIOS DESARROLLADOS.-
Cíj Determinar si la función es inyectiva f(x)= l—— —
v^ \3xi/2+2xU2
Solución
Simplificado 3x3'2 + 2x112 = JxQx+2) de aquí se tiene que x>0 => | x | = x entonces
/(JC)._ ,2\x\+x+2 _ \ 3x+2 _ 1
\3xv2+2xul y¡4~xOx + 2) *Tx
debemos probar que f(a) = f(b) => a = b con lo cual se determina que es inyectiva.
f(a) = f(b) => —= = —= => a = b. Por lo tanto f es inyectiva.
442
Eduardo Espinoza Ramos
[2J Demostrar que f es inyectiva donde f(x) - 5" , V x e R.
Solución
Debemos probar que: f(a) = f(b) => a = b
f(a) = f(b) => 5° =5'' => a = b
Por lo tanto f es inyectiva.
\3J Dada la función f(x) = x+yjx2 + 7 , x e [-3,3], demostrar que fes inyectiva
Solución
Probaremos que f(a) = f(b) => a = b
f(a) = f(b) => a + y¡a2+l =b + y¡b2+l
a-b = \b2 + 7 - Vfl2 + 7 , elevando al cuadrado:
(«-tí)2 = (y]b2+7 - Ja^Tl)2
ab + 1 = \a2 + 7 v¿2 + 7 , elevando al cuadrado:
a2b2 +Uab + 49 = a2b2+7a2 +7b2 +49
a2 -2ab + b2 = 0 => (a-b)2 = 0 => a = b .-. fesinyectiva
(4) La función f: R -»[0,+°°> definida por f(x) = 5x2 . ¿Es f suryectiva?
Solución
Debemos de comprobar que: V y e [0,+°°> , 3 x e R tal que f(x) = y
pero como y = 5x2 => x = ± y/5 .entonces:
3x = ± y/5 , y e[0,°°>tal que f(x) = f(±yjy/5) = 5(±JyTx)2 = v
.-.f(x) = y => f es suryectiva.
Relaciones y Funciones
443
Qs) Determinar si la función f(x) = x + 1 -[| x |] , x e R es inyectiva.
Solución
Definimos el L| x |], V x e R
[|x|] = £ <=> k<x<k+l,keZ. Luego la función f(x) queda definida
/(*) =
x+3 . jte[-2,-l>
x + 2 , jte[-1.0>
x+1 , .xe[0,l>
Luego la función f(x) es la unión de una familia de funciones lineales donde cada una de
las cuales es inyectiva, es decir:
/(a-) = jc+1-[|jc|] => f(x) = x+l-k
Probaremos que si f(a) = f(b) => a = b
f(a) = f(b) => a + 1 - k = b + 1 - k => a = b
Por lo tanto cada función f(x) sea inyectiva falta ver que la intersección de los rangos de
dos en dos es el vacío.
fk(x) = x + l-k
xe [k. k+l> => k <x<k+l => k+l<x + l<k + 2 => l<x+l-k<2
1 < fk (x) < 2 .-.ye [1,2> => Rft = [1,2 >
f I fk (x) = [1,2 > * 0 . por lo tanto f(x) no es inyectiva.
444
Eduardo Espinoza Ramos
©
©
©
Determinar sí la función f: <-4,3] > [-9,13> definida por f(x) = -2x + 1 es biyectiva.
Solución
Veremos si fes inyectiva, es decir: f(xl) = f(x2) => x¡ =x2
/(x,) = -2*,+l
f(x2) = -2x2+l
-2xx +1 = -2x2 +1
*i = x2 . Por lo tanto f es inyectiva.
Ahora veremos si f es suryectiva, es decir: Rj = [-9,13 >
1-V
Comoy = -2x+l => x = —-e<-4,3]
2
1-y
-4 < —y- < 3 => -8<l-y56=>-9 5-yS5 => -5 < y < 9
/. Rj = [-5,9 >* [-9,13 >, por lo tanto f no es suryectiva.
Luego la función f no es biyectiva.
Determinar el dominio de la función /(a) = x2 -6x + 8 para que la función f sea
inyectiva.
Solución
El dominio de una función cuadrática
para que sea inyectiva se determina
completando cuadrado es decir:
f{x) = x2 -6jc + 8 = (jc-3)2-1 que es
una parábola con vértice en el punto
(3,-1) por lo tanto f es inyectiva si
Df - [3,+°° > o para Df = < -°°,3]
Si existe f o g, donde f y g son invectivas. Demostrar que f o g es inyectiva.
Demostración
\
0
-1
'Y
___
y = f(x) I
3 /
v ' y
X
Relaciones y Funciones
445
r f • ,- í/(*.) = /U2) U =
Como f y g son inyectivas, entonces: < => <
U(^) = /U4) 1*3 =
.t, = x, ... (1)
... (2)
Probaremos que f o g es inyectiva, es decir:
(fi>g)(xl) = (fog)(x2) => xl=x2
(fog)(xl) = (fog)(x2) => /(«(*, )) = /(*(x2))
=> g(.xl) = g(.x2), por ser f inyectiva.
=> x, = x2, por ser g inyectiva.
Como (fogXxj) = (fog)(x2) => jc, = jc2 , entonces f o g es también inyectiva.
{9j Si f: R > B es una función suryectiva. Tal que f(x) = |x - 3| - x, Hallar el conjunto B.
Solución
. „. fjc-3 , x>
Se conoce que |x-3| = <
[3-x , x<
>3
3
, -3 , x>3
Luego a la función f expresaremos así: f(x) = <
[3 - 2jc , x < 3
Donde D¡ = < -»,3 > u [3.+«> >, ahora calculamos el rango
3-v
Si x < 3 => y = f(x) = 3 - 2x => x = < 3 =* y > -3 => ye <-3,+oo>
Si x>3 => y = f(x) = -3 => y = -3
Rf = < -3,+°° > u {-3} = [-3,+°° >
Por lo tanto la función f es suryectiva cuando: B = [-3,+°°>
(lO) Si la función f es creciente en todo su dominio demostrar que f es inyectiva.
Solución
446
Eduardo Espinoza Ramos
Aplicaremos la definición siguiente de función inyectiva f es inyectiva, si x, * x2
implica que f(xl) * f(x2), V x,, x2 e Df
Como x, * x2 => x, < x2 V x2 < x, pero f es creciente entonces:
/(x\) < f(x2) ^ /(x2) < /(x!) de donde /(x,) * /(x2 ) por lo tanto f es inyectiva.
(íí) Demostrar que la función f es inyectiva, donde: /(x) = -
Solución
2
-¡p= , si xe<4,+°°>
Vx
-x2 , si x<0
2
Primero veremos si /, (x) = —j= y f2 (x) = —x2 son inyectivas.
Vx
2 2
Vx,,i2eD, => /i(x1) = /1(x2) => -7= = -7= => x,=x2
y¡Xl Jxt
Por lo tanto /, (x) es inyectiva.
Vx,,x2eD/2 => /2(x,) = /2(x2) => -x,2=-xf => x,=x2
Por lo tanto f2 (x) es inyectiva.
Ahora veremos que R * A R, =<¡>
r, 2 4
Para x e <4,+<=o> => y = —. => x = —-
Vx y
4 4 7
x = —7e<4,+oo> => ~~f>4 =* 3,<1 =» ye<0.1> => /?y = < 0,1 >
y" y
para x
<0 => y = -x2 => x = -N/-y<0 => ypy>0 => -y>0 => y <0
fl/2 = < -~>,0 >
Relaciones y Funciones
447
Rf a R^ = < 0,1 > a < -oo,0 > =<¡>
Por lo tanto es invectiva.
(l2) Determinar si es inyectiva la siguiente función f(x) - •
[ >Px* , x<0
i-5x2+7x-3 , x>0
Solución
La función /,(x) = < 0, es inyectiva.
La función f2 (x) = -5x2 + 7x- 3, x > 0 no es inyectiva. Por lo tanto la función no es
inyectiva.
®, Í2x + 1 , x<0
Hallar la inversa / (x) si existe, de la función f definida por: /(x) = < ,
[x" +1 , x>0
Solución
Graneando a la función f(x) se tiene: Si x < 0 => Rf =< -°°,l]
a y
T ' x > 0 => Rj = < l,+°° > además cada función /, (x)
y = f(x) y f2 (x) son inyectivas, y como Rf r\R^ =<¡>
entonces f(x) es inyectiva.
Por lo tanto existe la inversa de f(x). Ahora
Para esto: /,(/,* (x)) = x
"^ calculamos la inversa de f(x)
Si x<0, /,(x) = 2x + l
x-1
xe<-oo.l], 2/, (x) +1 = x, de donde /, (x) = , x<l
448
Eduardo Espinoza Ramos
14
Sí x>0, f2(x) = x2+l
para esto: f2 (f2 (■*)) -x, x e <1 ,+°°>
fl2 (*) +1 - x > de donde f2(x) = -Jx-\ , xe<l,+oo>
rx-l
por lo tanto: / (x) = ■
, jc51
¿
yjx-l , x>l
Probar que f(x) - 4vx -x para 0 < x < 1, posee inversa y hallar la función inversa si es
que existe.
Solución
Para que f(x) tenga inversa debe de ser inyectiva y para esto debe cumplir que:
4y[xx-xl=4jx2~-x2 => 4(yJx~l-yjx2~)-(x1-x2) = 0
=> 4(yfx^-yjx2~)-(y[x~í-yjx2~)(y[xí + yjx2~) = 0
=* (yfx~i-yfx2')(4-yl7l-X2) = 0
Como 0<X]<1 => 4-yfx^-yjx^ *0
Luego yfxi - y[x\ = 0 => x, = jr2 por lo tanto
f(x) es inyectiva entonces existe f*(x), ahora calculamos la inversa f*(x) para esto:
f(f*(x)) = x, x e [0,3]
despejando f*(x) se tiene: /*(x) = (2 + y¡4-x)2 , x e[0,3]
^S) Hallar f*(x) si existe donde f(x) =
-x[\l — |] si -2<*<0
|x2-l|-l si 0<*<1
Relaciones y Funciones
449
Solución
Primeramente definiremos el máximo entero [|l — |] y el valor absoluto |x"-l| en
cada intervalo [| 1--1] = 1+[| --|] = 1 + 0 = 1
Como -2 < x < 0
0 < -x <2
=> 0<--<l => t|--|] = 0
2 2
=> x -l = (x+l)(x-l)
Para 0 < x < 1 => |x2-l| = l-x2 por definición
\ /
+ m
0
-1
Por lo tanto la función f(x) queda en la forma:
f-x si -2<x<0
/(*) = •
-x2 si 0<x<l
_^ X
Como f(x) es inyectiva, entonces f*(x) existe:
Si -2 < x < 0 , /, (x) = -x, calculando su inversa
/,(/,"«) = *
x e < 0 , 2>, -/, (x) = x, de donde .-. /, (x) = -x , 0 < x < 2
Si 0 5 x < 1 , /2(x) = -x2, calculando su inversa /2*(x)
Se tiene: /2(/2*(*)) = * , -1 S x < 0, de donde - /22 (x) = x, -1 < x < 0
:.f2(x) = yf1^, -Kx <0
Por lo tanto la inversa de f(x) es
{-x si 0 < x < 2
V-x si -Kx<0
©Hallar f*(x) si existe donde /(x) = *, +,„
\3x3/2 + 2xI/2
450
Eduardo Espinoza Ramos
Solución
Calculando el dominio para definir | x |
3jc3/2 + 2x1/2=Vx(3x+2) deaquíx>0 => |x| = x
..c. J ,, N . 2|x|+x+2 3x + 2 1
Ahora simplificado se tiene: f(x) = ' - ' - -
3xi/2 + 2x1'2 \yfi{3x + 2) 4VÍ
Determinaremos si f(x) es inyectiva: f(a) = f(b) => a = b (f es inyectiva)
f(a) = f(b) => 4ñ = 4r => a = b
tía *¡b
Por lo tanto f(x) es inyectiva entonces f(x) tiene inversa. Ahora calculamos la inversa.
f(f*(x)) = x
, = x , de donde f*(x) = —-
Si f es la función definida por f(x) - vr +16 + 2x, x e [0,3] determinar si existe f*(x)
Solución
Para que exista f*(x) la función f(x) debe de ser inyectiva, es decir.
Sí f(a) = f(b) entonces a = b
yla2+l6+2a = y¡b2 +\6 + 2b entonces 2(a-b) = yjb2 +l6-yja2+16
para que sea f inyectiva debe cumplir a = b de donde
a-b = 0=> ylb2+l6-<Ja2+\6=0
4a2 + \b=Jb2+\(> => a2=b2 => |a|2=|¿|2
=> | a | = | b | =* a = b puesto que a , b e [0,3]
por lo tanto f(x) es inyectiva => 3 f*(x)
Relaciones y Funciones
451
Miora calculamos f*(x) mediante la ecuación: f(f*(x)) = x . x e [4,11]
yjf*(x))2+\6 + 2f*{x) = x => yj(f*(x)f+16 = \-2f*(x) elevado al cuadrado
(/*(x))2 +]6 = x2 -4x/*(x) + 4(/*(x))2 => 3(/*(x))2-4x/*(x) + x2-16 = 0
,,, , 4x±Vl6x2-12(x2-16) 4x±2%/x2+48
/*(v) = í => /*(*)=
6 6
,„, ^ 2x±Vx2+48 2xWx2+48 .....
/*(*) = .\/*(x) = ,xe[4.11]
k/x-3 x>3
Si /(x) = ^ Determinar si f*(x) si existe.
[x2+2x-3 , xe[-l,l>
Solución
Determinaremos si f(x) es inyectiva
Síx>3 => ft(x) = Jx-3 donde Rf¡ = [0,°°>
Si /, (x,) = /, (x2) => <Jx\-3 = jx2-3 elevando al cuadrado => x, = x2 => fx es inyectiva
Si -1 <x< 1 => /2(x) = x2+2x-3 = (x + l)2-4
Como-l<x<l =>0<x+l<2 => 0<(x + l)2<4
=> -4<(x + l)2-4<0 => «y, = [-4.0>
Si /2Ui) = /2(*2)=» (x,+l)2-4 = (x2+l)2-4
=> (x, +1)2 =(x2 + 1)2=> x, +l = x2 +1
==* x, =x2 puesto que x,,x2 e 1-1,1 > . Por lo tanto f2 es inyectiva.
Como Rf a Rf, = [0,o° > a 1-4,0 > = <p .
452
Eduardo Espinoza Ramos
Entonces f(x) es inyectiva y por lo tanto 3 f*(x)
Ahora calculando la inversa de cada función: /, (/,* (x)) -x ,xe [0,+°°>
V(/i*U))-3=x =* /,*(x) = x2+3, xe[0,+~>
/2 (/*«) = * ,xe [-4,0>
(/2*W)2+2/*U)-3 = a- => /2" (*) = >/* +4-1 ,xe [-4,0>
íx2+3 , x>0
[Vx + 4-1 , -4<x<0
(l9) Si fíx) = 2x - 3b , determinar el valor de b de manera que f(b +1) = 3/ * (b2)
Solución
Calculando la inversa de f(x): f(f*(x)) = x, xe Df*
2f*(x)-3b = x, xeD^,, de donde /*(x) = ——, xe Df*
como f(b +1) = 3/ * (b2), entonces 2(b +1) -3b = 3(—-—)
3¿2+llfc-4 = 0=> (3b-l)(b + 4) = 0, de donde b = - , b = -4
®íx2-8x + 7 si 4<x57 V -3<x<-l „ „ , , . .
Sea/(x)=^ . Hallar f*(x) si existe.
[V7-2x sí -1 < x < 3
Solución
Analizaremos sí /,(x) = x2 -8x + 7 , f2(x) = y]l -2x es inyectiva
Sí4<xS7 V-3<x<-l => /,(x) = x2-8x + 7
/,(x) = x2 -8x + 7 = (x-4)2 -9
Funciones y Relaciones
453
Sí x¡.x2e Df¡; /1(x1) = /,(x2) => x,=.v2
(.r1-4)2-9 = (.v2-4)2-9 => |x, -4|2=| x2 -4|;
=> | x, - 41 = | x2 - 41 => X| = x2, puesto que |x - 4| = x - 4
Sí 4 < x < 7, |x - 4| = 4 - x si -3 < x < -1. Luego /[ (x) es inyectiva
Sí-l<x<3 => f2{x) = yjl-2x
Sí x, . x2 e Df2; /, (x,) = /, (x2) => x, = x2
^7 - 2xl — yjl - 2x2 => 2x, = 2x2 => x, = x2. Luego /2 (x) es inyectiva.
Ahora calcularemos el rango de cada función.
Sí 4<x<7 V -3<x<-1 => 0<(x-4)2 <9 V -7<x-4<-5
-9<(x-4)2-9<0 V 16<(x-4)2-9<40, pro lo tanto Rf¡ =< -9.0] u < 16,40]
Sí-l<x<3 => -6<-2x<2 => l<7-2x<9 => l<V7-2x<3
Entonces 7?^ = < 1,3]
Como /?^ a /?, = <¡> entonces f es inyectiva en todo su dominio.
Ahora calculamos f*(x)
/i (/i* (*» = * . x e <-9,0] u <16,40]
(/,*(x))2 -8/,*(x) + 7-x = 0 , x e <-9,0] u<16,40]
f*(x) = 4±Jx~+9
,, U + Jx~+9 , xe<-9.0]
/,(*) = <
4-Vx + 9 , xe< 16,40]
454
Eduardo Espinoza Ramos
/2(/2*(x)) = x ,xe <1,3] => N/7-2/2*(x)=x,xe <1,3]
f¡{x) = ^(7-x2) ,xe<l,3]
Luego la función f *(x) queda en la forma: / * (x) = -
4 + A + 9 , xe<-9,0]
4-A + 9 , Jte<16,40]
l/2(7-x2) , xe<l,3]
14.27. EJERCICIOS PROPUESTOS.
(Y) Sea la función f: [1,4] -» [a,b], tal que /(jt) = x2 -2x + 3 , Demostrar que fes inyectiva
y hallar los valores de a y b para que f sea biyectiva. Rpta. a = 2 , b = 11
(l) ¿Es inyectiva la función real f(x) = — ? Rpta. No es inyectiva
^■^ x2 +1
(5) Sea f: A -» <1,10] dada por f(x) =
4-llx
4-2x
a) Determinar A Rpta. <-°°,0]u[4,°°>
b) Mostrar que f es inyectiva
10 + 3*
(4) Sea f: A -* <-4,1] definida por /(x) = -
10 -2x
a) Determinar A Rpta. <-°o,0] u <10,°o>
b) Mostrar que f es inyectiva
3 + 4x
(J) Sea f: A ->[-9,-l> dada por f{x) ■■
3-x
a) Determinar A Rpta. <0,°°>
b) Probar que f es inyectiva
c) ¿fes suryectiva? Rpta. no
Funciones y Relaciones
455
[6J Dadas las funciones reales siguientes:
x + 1
f(x) = 3x + 2| x |, g(x) = , x * 1 y h(x) = 3x + 7, p(x) = x + 2| x |
x-1
¿Cuál de estas funciones es inyectiva?
{7J Demostrar que las siguientes funciones son inyectivas
a) f(x) = 3x-2, x >0 b) f(x) = sen x, xe<—,—]
2 2
c) f(x) = (x-h)2+k ,x>h d) f(x) = 2-x3 , x e R
e) f(x) = yl9 + x2 ,x > 1. En forma analítica y gráfica
\S) Demostrar que la función f defínida por: f(x) = 1 - Vx2 -4x — 5 , x £ - 1 es inyectiva
\9J Demostrar que f(x) = , x * -2 es inyectiva
x+2
(lo) Sean f: A —»B, g: B —> c, demostrar que:
a) Si g o f es suryectiva entonces g es suryectiva
b) Si g o f es inyectiva entonces f es inyectiva.
Ul) La función f(x) = J .¿Es suryectiva?
(Í2j Sea f una función definida por: f(x) - — , x e < 0,2 > u < 2,°°>
^"^ x -4
Determinar si f es una función biyectiva Rpta. si es biyectiva
(J3) Determinar si la función f(x) = 6x-x2 -5 es f inyectiva, si no lo es, restringir su
dominio para que sea inyectiva. Rpta. No es inyectiva
456
Eduardo Espinoza Ramos
(Í4) Sea f una función definida por f(x) = -—¡— ,Df = R. Es f una función inyectiva? *
Rpta. f es inyectiva
®i> j 1 c -¿ r, ^ (* + 2)U2+6*-16)(jc-6) a, , . . r.
Dada la función f(x) = - Mostrar que f es inyectiva y granear
(*-2)(jc2-4.t-12)
lió) Sea f(x) = + --1 ,xe <1,2>. Demostrar que f es inyectiva (ó univalente)
^-^ *-l (x-lf
(l7) Si se sabe que f(-l) = 4 y f(3) = -2 , donde f es una función lineal, hallar la ecuación que
define f*(x) Rpta. / * (x) = -—+-
3 3
@ Sí f(x) = 2x+c y /(c) = 2/*(c2). Encontrar el valor de :
a) f(0). f*(0) Rpta. -8 b) -^- Rpta. - 4
(l?) Si f(x) = 3x + 2a, Determinar los valores de a de modo que f(a2) = f*(a + 2)
2
Rpta. a = -1 V a- —
9
(20) Hallar la inversa f *(x) si existe para la función. f(x) = jc2 + 4* -1 ,xg <-4,-3>
Rpta: f*(x) = -2-Jx+5 ,xe[-4,-l>
(21) Hallar la inversa f*(x) si existe de la función, f(x) = x2-2x-l ,x>2
Rpta. /*(jc) = 1 + í+2 ,x>-l
(22) Hallar la función f*(x) si existe, para la función, f(x) - (| x - 51 +1 + x)y¡5-x
1 ■>
Rpta. /*(*) =—(180-jc2) ,x£ [0,oo>
36
Funciones y Relaciones
457
(23) Sí/U):
\x2 + 2x + 2,x>\
U3+4,jc<1
. Hallar la función inversa de f(x) si existe
Rpta. /*(*) =
í-l + VJ^l, jc>5
'Vjc-4, jc<5
Sí la función f: <-l,l>—> R, definida por: /(jc) = —■—- Hallar la inversa de f(x) si existe
1-1*1
(25) Hallar f*(x) si existe de:
Rpta. /*(*) =
1+UI
a) f(x) =
-yfí^x, x<0
x2 + l, x>0
b) /(*) = •
Í— jc, jc < 0
-jc2,jc>0
, I jc — 61 +jc + >/J7^6 — TIjc — 4|"| jc + 6
c) f{x) = (\x-3\+xyJ¥^x d) /(*) = =J¿ ü
Vt=3
®
2jc+3 7 9
Dada la función /(*) = , xe<—,— >. Hallar f*(x) si existe.
jc-1 2 2
®f|2-jc|,jc>2
Sí f: R —> R tal que f(x) = < . Determinar la función inversa f*(x) si existe.
-jc2,jc<0
(28) Consideremos la función f definida por: /(jc) =
jc+3
, jc<-3
jcz+4jc-2, 0<jc<3
n -, x<n
4-x
Determinar si f es inyectiva, si lo es hallar f*(x).
(S) Sea f: R -» R tal que /(jc) = ¡—-, si f es inyectiva hallar f*(x)
^-^ -*-[|*|]
(30) Hallar la inversa f*(x) si existe de:
458
Eduardo Espinoza Ramos
a) f(x) =
2jc-1,jc<-1
4jc2,-Kjc<0
jc + 4,jc>0
b) /(*) =
—<J-x +1 , jc < 1
x-[x] , l<.v<2
4>
• x-[x] , i<x<:
[3.V-5 , .ve<2,^
c) /(*) = .
| -4x2 , jc < O
\yl4-x2 , Oá:
<2
d) /(*) = «
Í--\/9-jr2 , -3<jc<0
taje , 0<jc<4
(31) Dada la función f{x) =
|jc2-4| , 0<jc<2
+ jc-1 , x>2
4
Hallar f*(x) si existe.
Í2>/^( + 2, jc<0
Rpta: f*(x) = \
[■J4-X, 0<jc<4
fo2) Dada la función f{x) = -
2jc —1 , jc < —1
4jt 2, -1 < jc < 0, Hallar f*(x) si existe.
jc + 4, jc>0
Rpta: f*(x)-
JC+1
, jc < -3
-Í ■ 0:
<jc<4
x-4 , x>4
(33J Dada la función f(x) =
•V+2jc + 2 , jc< —1
-v/jr+l , jc>-1
, Hallar f*(x) si existe.
Rpta. /*(*) =
-l--Jx-\ , jc > 1
jc2-1 , jc<0
fá$) Dada la función f definida por: /(v);
yl-x2+x + 2+l , -1<jc<1/2
7
2 —
A + l
2<jt<4
Funciones y Relaciones
459
Hallar f*(x) si existe.
Rpta. /*(*) =
jc + 5
1 1
, —<x< —
3 5
i_I^9_4(jc_l) f l^jc^l
2 2 2
Hallar la inversa si existe para la función. f{x) =
U-ll-1
, xe <-2,0>u<0,l>
37
(38)
Rpta. f*{x) = ,x e <-oo,-5> u <1,°°>
JC + 1
uó) La función f definida por la regla de correspondencia
/(*) =
\4-y]x2+ftx + n , SÍ jc<-11
\x2+6x'+6 , si x>0
Demostrar que f es inyectiva y hallar f *(x)
Rpta. f*(x) = <
I-v/jc+3-3 , x>6
Sea la función f: R -»R, definida por: f(x) = [\ x |] + ^/jc-fl jc|] , hallar f*(x) si existe
Rpta. /*U) = Jk + (jt-Jk)2 ,xe[k,k+l>
Sea las funciones f y g definida por:
yJx2+4x-5 , 6<x<7
/(*) =
. g(x) = ■
[| jc|] , 9<*<10
|jc — 21 — 13-jc| , 3.5<*<7.5
(*-8)2-9 , 7.5<jc<9.5
x , 9.5 <*< 13.5
Hallar (f + g)* si existe
\39j Dadas las funciones f y g definidas por: /(je) =
0, x<0
x2,0<x<2 , g{x) =
n, x>2
2, x < 0
4x, 0 < x < 1.
-1,*>1
Hallar (f o g)(x), determinar si es inyectiva en caso afirmativo, calcular (f + g)* (x)
460
Eduardo Espinoza Ramos
(40) Dadas las funciones f(x) = , x < -2 y g(x) = ■
^~* x + 2
2jT-12je + 2 , -2<jc<3
2
3
m
x>3
Hallar f * o g
Rpta. (/*ogX*) =
4(je2-6je + 1)
-(2je2-12jí + 1)
, -2<je<3-VÍ7
l4x + 2
4x-~i-y[x+2
x> 3
(41) Sean las funciones /(je) = y g(x) = 3x - 1. Hallar la intersección del dominio
v-' jc + l
f* o g con el dominio de (f o g)(x).
Rpta. R-{0,2)
(42) Sí /(je) = 3x2 -2je+5 , D^ =< 1,4 > y g(x) = | x | + 3. Determinar el dominio de f*o g.
(43) Si /U-2) = . Hallar el valor de x que satisfaga (/*o/)(-^2.
^-^ JE + 3 JE
(44) Dada la función f definida por: /(je) =
Hallar f*(x) si existe.
I je - 51 +4je + >/je^5 - [| x \]x + 5
Rpta. /*« =
6je2+5
je2+1
®JE + 4
Si f* es una función biyectiva tal que / *( ) = D. Hallar el conjunto solución de la
3je
inecuación: /(c) >
3je
je + 4
Rpta. x e <-4,-l> u <0,2>
6ó) Sean /(jc) = je3+2, g{x) = ?—^ si g*(/*(«)) = -~ . Hallarg*(a + 5)
47
.v + 3
Rpta. —
2
Dada las funciones reales /(je) = —— , g(x) = —, x *■ 0. Hallar el dominio de f*og*
.v x
Rpta. <-l , 1> - {0} = <-l, 0> U <0, 1>
Funciones y Relaciones
461
(48) Sif y g son dos funciones donde f(x-l) = 3x+2, g(2x+3) = 4x+4 . Hallar (g* o g)(x)
Qx + 7)
Rpta.
(49
Analice la unívalencia de la función /(jc) = -J[\ jc|]-jc + 4jc + 4vjc2 -2x y halle la
función inversa.
Rpta. /*(*) =
8(*-4)
can
Sea /(*) =
jc2+8jc + 12, xe<-6,^l>
x/í+2
jc + 5
jce[-2,l> determine f*(x) si existe.
jcíe[1,4]
Rpta. f*{x) =
-4-Vjc + 4 , jce<-4,-l>
jc2+2 , jcg[0,>/3>
3jc-5 , jce[2,3]
(SI) Sea f: <-1,1 > -»R , tal que /(jc) =
i-U|
, analizar si f es inyectiva.
(52) Hallar f*(x) si existe, donde, /(jc) -
_ I Vi + V x2 +x , jc> 5
Ix
x<-\
jc+(jc2+1)1/2 , jc>1
®JC+^JC +1)
Analizar la inyectibilidad de la función, f(x) = < .
-V-Jc3+1 ,
, en caso
jc<-1
afirmativo hallar f *(x)
(54J Sea f y g dos funciones, tales que:
/(*) =
3-* :«(*) =
Vjc2+2jc , .ve'[l,2>
, jce[l,2>
x-l . Hallar f o g si es que existe.
I jc—11, jcg<0,1>
462
Eduardo Espinoza Ramos
(55) Hallar f*(x) si es que existe de la función, /(je) =
*~+2jt-2, -3<jc<-2
U + 3|
|*-2|-1
, —1 < jc < 1
®a,~+2je-1 , x<2
Analizar la inyectibilidad de tal función, /(je) = < , en caso
[ -x3 , x>2
afirmativo hallar f *(x)
(57) Hallar f*(x) si existe donde
a) /(*) = -
Ix2+4x-5 , jcg[-2,1>
x-5 , jce[5,+«>>
b) /(*) =
jcz+2jc + 2 , jc>1
x2+4 , x<l
c) /(jc) =
2jc —1 , jce<-°°,-l>
4x2 , Jce[-1,0]
x + 4 , jce<0,-H>°>
d) /(*) =
+ 1 , jce[-4,-2>
Vx + 2 , jc<=[-2.2]
e) /(*) =
jT-8jc + 7 , xs< -3,-1 >u< 4,7]
[yjl - 2x , .re[-l,3>
f) /(*) =
j jc2 +10JC+21 . *e[-7,-5>u[-2,-l>
[Vjc+T + 1 , jce<-l,3]
g) /(*) =
\x +2jc + 2 , jce<-«>,-l>
I—n/jc + 1 , jce[—1,
+oo>
h) /(*) =
-(jc +6at + 8) , jte<-°°,-4]
jc + 3
*e<0,3>
jcg[10,+°o>
i) /(*) =
-jcz-4jc-3 , jte<-«,-2]
3 + >/Jc
JCG[l,+oo>
Relaciones y Funciones
463
j) /« = ■
-x¿-2x
jce[-3,-l>
2 + -n/3 + 2x-ji:2 , xe[-l,l]
k) /(*) =
\4-yjx2+\2x +
\x2 +6jc + 6
27
*<-l
jc>0
jcz , xe[l,2>
1) f(x) = \[\x\] + y]x-[\x\] , jce[-l,l>
-yf^X , JCG[-9,-l>
11) /(*)=
-4-(x + 2)2 , Jce[-5,-2]
24|jc + 3|] , jcg<-2,-1>
2 + Jx + l , jcg<-1,3>
4 , jc = 1
(59)
U2_l X<_1 [2jc-1 , x<0
Dadas las funciones /(*) = < ' y g(jc) = s ,-
[jc + 1 , jc>-1 [yjx , x>0
Hallar si existe fog*
Analizar si las funciones reales f y g son inyectivas
/(*) =
-2jc + 10 , x<0
Va:2 +16 , 0<*<3
3
x2-A
x>3
-* -10x-21
g(x) = \\x-2\-l
{ \x + 3\
x e[-5,-l]
x e<l,2]
(¡60) Sí g: A —> B y f: B —> C, son funciones inyectivas, demostrar que fog: A -» C es
inyectiva.
(ól) Analizar la inyectividad de la función f(x) = \
W [Sx2 +
-x3 , x < 0
en caso
7jc-3 , x>0
afirmativo, hallar su inversa.
464
Eduardo Espinoza Ramos
(62) Si /(*) =
-jT , x < O
1 probar si es inyectiva, si lo es, hallar su inversa.
- , x>0
x
®¡2-x2 , n/3<*:S2 r—. ¡—
Dadas las funciones /(x) = < . , g(x) = vi x - 41 -3 , xe <-°°,-4]
[I-Va:2-4 , *:£-4
U<0,2] tal que f = h*og
i) Demostrar que f y g son funciones inyectivas.
ii) Hallar la función h.
©Dadas las funciones f(x) = -^—, xel0,4]-{2} y g(jc) = i(*_3) ' l^x<5
x-2 * ' [x + 3 . -6<Í*<1
Hallar f*og si es que existe.
x2-4 . x<-2
(ps) Determinar la inversa f*(x) si existe donde /(*) = - —Jx-2 , 2 < x < 6
-2jc + 10 , x>6
@ Sí /(*) =
Jx~^3
:>3
x2+2x-3 , *e[-l,l>
Determinar f *(x) si existe
®jc2-4 , si x<-2 _
Si /(*) = ■! . Determinar f*(x) si existe
HJt-2 , si x>2
(68) Hallar la inversa de f si existe donde /(*) =
\x2+2x-3 , x<.2
-x3 , x>2
®¡\x\, x<-\
Decir si f(x) es inyectiva, si es así hallar f*(x) donde f(x) = j 2
2-x\ x>\\
®¡2x, x<3
Dado f(x) = < _ , probar que f(x) es inyectiva y hallar f*(x).
\x2, 3<x<5
Relaciones y Funciones
465
(71
(72
Analizar si es inyectiva la función f(x) - x2 -3jc+2 , x e [0,+°°>, en caso que no sea,
determinar el dominio para que sea inyectiva y hallar su inversa.
Analizar si la función f(x) - xA - 2x2 - 3, x > 2 es inyectiva, en caso afirmativo, hallar
su inversa.
(73) Sea f(x) =
y¡X-3>, JC>4
-t¡3^x, x<2
mostrar que f es inyectiva y hallar f*(x).
(74) Si f(x)- + r-K x e <1,2>, analizar rigurosamente si f es inyectiva, en
v-' x-l (jc-1)2
caso afirmativo, hallar f*(x) y sus dominios.
uS) Encontrar f(x) y f*(x), si se sabe que:
i) g(x) = , (fog)(x) = 2x + 3
4jc + 1
ii) g(x) = 3x-2, (gof)(x) = 2x + 4
(7o) Sean f(x) = 2x2 -4jc-1, xe [l,+°°>, £(*) = — , xe R. Calcular (gof*)(x) si existe
^-^ x2+4
^7) Si f(x - 1) = 3x + 2, g(2x + 3) = 4x + 4, encontrar (g*of)(x)
(7¿) Calcular f*(x) si existe, donde: /(je) =
*2+4x-l, jre<^,-3]
\x + 4\
|*-1|-1
, jce<-2,0>u<0,l>
©Sean /(*)=- , x<-2 y $(*) =
2 + x
2x1-\2x+\ Jce<-2,3]
x+2
U-3
, jc>3
Calcular (f*og)(x), si existe
(80) Hallar f*(x) si existe donde /(*) =
x + 2, x<2
yj9x-2, jce<2,3>
(jc-3)2+5, x>3
466
Eduardo Espinazo. Ramos
4.28. APLICACIONES DE LAS FUNCIONES EN LA
ADMINISTRACIÓN Y ECONOMÍA.-
Se ha estudiado las funciones en forma general, ahora estudiaremos las aplicaciones de
estas funciones en administración y economía y para esto recordemos el concepto de
función en términos económicos.
a) MODELOS MATEMÁTICOS.- Al proceso de formular los problemas en el
lenguaje de las matemáticas se denomina
modelación matemática, por lo tanto un modelo matemático puede describir con
precisión el problema en cuestión.
Ejemplo.- El tamaño de un tumor canceroso se puede aproximar mediante el volumen
4nr2
de una esfera V = , donde r es el radio del tumor en centímetros, ahora
3
observemos las siguientes expresiones:
Un fabricante desea conocer la relación entre la ganancia de su compañía y su nivel
de producción.
Un biólogo se interesa en el cambio de tamaño de cierto cultivo de bacterias con el
paso del tiempo.
Un Químico le interesa la relación entre la velocidad inicial de una reacción química
y la cantidad de sustrato utilizado.
Ahora nos preguntamos ¿Cómo depende una cantidad de otra?
Esta dependencia entre dos cantidades se describe convenientemente en matemáticas
mediante una función; por lo tanto, una función es una regla que asigna a cada elemento
de un conjunto A uno sólo un elemento de un conjunto B y la notación que se tiene es:
f: A > B, donde Df = A y Rf = B .
Todo esto se puede pensar en una función f como en una máquina. El dominio es el
conjunto de entrada (la materia prima) para la máquina, la regla describe la forma de
procesar la entrada y los valores de la función son las salidas de la máquina.
Relaciones y Funciones
467
ENTRADA
x
I
t
I
I
I
/ J* N
f(x)
SALIDA
NOTACIÓN.- El símbolo f(x) se lee "f de x", la regla de correspondencia es dado por
una fórmula, como por ejemplo f(x) = \x2 +1, esta fórmula puede
considerarse como un conjunto de instrucciones .
nombre de
La función
número de entrada
'—■+ f(x) = Jx2+l
número de
salida
Ejemplo.-
instrucciones que indican, que hacer con la
* entrada x para producir la salida correspondiente;
esto es, elevar al cuadrado, sumarle 1 y sacar la
raíz cuadrada al resultado.
La electricidad se cobra a los consumidores a una tarifa de $ 10 por unidad
para las primeras 50 unidades y $ 3 por unidad para cantidades que exceden
las 50 unidades. Determine la función C(x) que dá el costo de usar x
unidades de electricidad.
Solución
468
Eduardo Espinoza Ramos
Si x < 10, cada unidad tiene un
costo de $ 10, el costo total de x
unidades es lOx ; C(x) = lOx
para x < 50
Para x = 50, obtenemos el total
de las 50 primeras unidades
C(50) = $ 500
Si x > 50, el costo total es igual
al de las 50 primeras unidades,
que es $ 500, más el costo del
resto de las unidades usadas
x - 50 y cuestan $ 3 cada una y
el costo total es $ 3(x - 50)
Luego para x > 50, es
C(x) = 500 + 3(x - 50)
C(x) = 3x + 350, x>50
C(x) =
ÍIOjc , x<
[3x + 350,
50
x>
50
b) FUNCIONES LINEALES DE COSTOS, INGRESOS Y GANANCIAS.-
La conducción de una empresa, debe mantener un registro constante de los costos de
operaciones, de los ingresos íesultantes de la venta de productos y servicios; tres
funciones ofrecen a los conductores de una empresa para tomar las mediadas de
estas cantidades: La función lineal de costos totales, la función de ingresos y la
función de ganancia.
i) FUNCIÓN LINEAL DE COSTO TOTAL (MODELO DE COSTO
LINEAL).-
En la producción de una empresa de cualquier bien, se tiene dos tipos de
costos, los costos fijos y los costos variables, a los costos fijos se le considera
sin importar la cantidad producida del artículo, es decir que no depende del
nivel de producción.
Ejemplo de costos fijos: son las rentas, interés sobre prestamos y salarios de
administración.
Relaciones y Funciones
469
Los costos variables dependen del nivel de producción, o sea de la cantidad de
artículos producidos.
Ejemplo de costos variables: son los costos de los materiales y de la mano de
obra.
Luego el costo total está dado por:
Costo Total = Costos Variables + Costos Fijos
Cuando el costo variable por unidad del artículo es constante, en este caso, los
costos variables totales son proporcionales a la cantidad de artículos
producidos.
Si m representa el costo variable por unidad, entonces los costos totales al
producir x unidades de artículos en mx $ y si los costos fijos son de b dólares,
se desprende que el costo total C(x) = yc (en dólares) de producir x unidades
está dado por:
Costo Total = Costos Totales Variables + Costos Fijos
C(x) = ye =?nx + b
(1)
La ecuación (1) es un ejemplo de un modelo de costo linea], la gráfica de la
ecuación (1) es una línea recta cuya pendiente representa el costo variable por
unidad y cuya ordenada al origen da los costos fijos.
NOTA.- m = pendiente de la recta L
Y'
0
P2(x2,y2);í/ L
/ ! y2" yi
P,(x1,y1)y<^.___riA
/ 1 A2 *1 |
A \ ! .
/ x, x2 X
m = tgd-
y2-y\
x2-x¡
m
_y2-yi
470
Eduardo Espinoza Ramos
OBSERVACIÓN.- En la función lineal de costo C(x) = mx + b. el costo fijo se
obtiene haciendo x = 0, es decir: C(0) = m(0) + b = b, así,
entonces, el costo fijo es la intersección de la función costo con el eje Y.
En economía, el costo marginal es la razón de cambio del costo, el costo marginal es
importante en la administración al tomar decisiones en áreas como control de costos,
fijación de precios y planeación de la producción. Si la función de costo es C(x)=mx
+ b, entonces su gráfica es una recta con pendiente m, como la pendiente representa
la razón de cambio promedio, el costo marginal es el número m.
Si C(x) es el costo total de fabricar x artículos, entonces el costo promedio por
artículo está dado por:
x
Ejemplo.- El costo variable de procesar un kilo de granos de café es de $ 0.5 y los
costos fijos por día son $ 300.
a) Dé la ecuación de costo lineal y dibujar su gráfica.
b) Determine el costo de procesar 1000 kilos de granos de café por un día.
Solución
a) Como C(x) = vr representa el costo de procesar x kilos de granos de cafe por
día, y como el modelo lineal es:
C(x)= yc =mx+b
en donde m representa el costo variable por unidad y b es el costo fijo y para
nuestro caso es m = 0.5, b = 300 por lo tanto C(x) = 0.5x + 300 ... (1)
para graficar la ecuación (1), primero ubicamos dos puntos sobre la gráfica (la
recta).
Relaciones y Funciones
471
Y-
400
200
0
.^(200,400)
(0,300) ¡
200
X
x = 0
x = 200
y = 300
y = 400
Observe que la porción de la gráfica está situada por completo en el primer
cuadrante, puesto que x y yc no pueden ser cantidades negativas.
b) Al sustituir x = 1000 en la ecuación (1) se obtiene:
yc = 0.5(1000) + 300 = 500 + 300 = 800
por lo tanto, el costo de procesar 1000 kilos de granos de café al día
será de $ 800.
ü)
iü)
FUNCIÓN LINEAL DE INGRESO.- Supóngase que una empresa tiene
costos fijos por b dólares y costo de
producción de m dólares por unidad y un precio de venta de a dólares por
unidad, entonces la función de ingreso R(x) está dado por:
R(x) = ax
Donde x es el número de unidades de un producto fabricados o vendidos.
FUNCIÓN LINEAL DE GANANCIA.- Si C(x) = mx + b, es la función
de costo y R(x) es la función de
ingreso, entonces la función de ganancia denotado por P(x) es dado por:
P(x) = R(x) - C(x) = ax - (mx + b)
P(x) = (a - m)x - b
Donde x representa la cantidad de unidades del artículo producidos y
vendidos.
472
Eduardo Espinoza Ramos
Ejemplo.- Puritrón, fabricantes de filtros para agua, tiene costos fijos por $ 20,000,
costos de producción de $ 20 por unidad y un precio de venta unitario
de $ 30. Determinar las funciones de costos, ingresos y ganancias para Puritrón.
Solución
Sea x = números de unidades producidas y vendidas
Luego la función de costo es: C(x) = 20x + 20,000
La función de Ingreso es: R(x) = 30x
Y la función de ganancia es: P(x) = R(x) - C(x)
P(x) = 30x - (20x + 20,000) = lOx - 20,000
c) APLICACIONES DE LAS FUNCIONES CUADRÁTICAS.-
Como el vértice de una función cuadrática y = f(x) = ax + bx + c, a * 0 es el punto
más alto o más bajo sobre la gráfica, se puede usar en las aplicaciones para encontrar
un valor máximo o un valor mínimo; es decir:
Qf) Cuando a > 0, la gráfica se abre hacia arriba y por lo tanto la función tiene un
mínimo.
\2j Cuando a < 0, la gráfica se abre hacia abajo y por lo tanto la función tiene un
máximo.
00 El vértice de la función cuadrática es V( , /( ))
^ 2a 2a
(4) El eje de simetría de la función cuadrática es x = .
v~' 2a
\5) La intersección con el eje X (si existe) se determina resolviendo f(x) = 0.
\6) La intersección con el eje Y es f(0) = c.
Relaciones y Funciones
473
Y4
f(-—)
v 2a'
V(-¿-f(-^
Si a > O y se tiene:
Df=R- R =[/(_A)i+00>
2a
_b_
"2a
Si a < O y se tiene:
Df=R; Rf=<
.,/(-->]
Ejemplo.- Juan López atiende y es el dueño de la pastelería Milagros, contrató un
consultor para analizar las operaciones del negocio. El consultor dice que
sus ganancias P(x) de la venta de x unidades de pasteles, están dadas por
P(x) = 120jc- x~ ¿Cuántos pasteles debe vender para maximizar las ganancias? ¿Cuál es
la ganancia máxima?
Solución
A la función ganancia dada expresamos en la forma P(x) = —x +120*
su gráfica es una parábola que se abre hacia abajo y su vértice es:
V( ,/( )) dondea = -l,b= 120yc = 0
2a 2a
_ A = _!^ = 60, /(—) = /(60) = 3600 , por lo tanto V(60,3600)
2a -2 2a
V(60,3600)
P(x) = 120x-x2
474
Eduardo Espinara Ramos
La coordenada x es el número de pasteles, la coordenadas y es la ganancia con ese
número de pasteles. Sólo la porción de la gráfica en el cuadrante I (donde ambas
coordenadas es positiva) es importante aquí, porque no puede vender un número negativo
de pasteles y no tiene interés en una ganancia negativa. La ganancia máxima ocurre en el
punto con la mayor coordenada "y", es decir, el vértice como en la figura: la ganancia
máxima de $ 3600 se obtiene cuando se vende 60 pasteles.
Ejemplo.- La ganancia trimestral de una tienda de calzado (en miles de dólares) está
x~
dada por: P(x) = — + 7jc + 30, (0<x<50) donde x (en miles de
dólares) es la cantidad de dinero que la tienda gasta en publicidad cada trimestre.
Determine la cantidad que la tienda debería invertir en publicidad para obtener una
ganancia trimestral máxima ¿Cuál es la máxima ganancia trimestral que puede lograr la
tienda?
Solución
Como la función ganancia P(x) es una función cuadrática, entonces su gráfica es una
x2 1
parábola P(x) = + 7x + 30 dedonde a-— , b = 7,c = 30
3 3
V\ V\ V\ *7 01
su vértice es V( ,/( )), de donde — = — = 10.5
2a la 2a o/__\ 2
( 3}
/( ) - /(10.5) = 66.75, por lo tanto el vértice de la parábola es V(10.5; 66.75) como
la
la parábola se abre hacia abajo, el vértice de la parábola es el punto más alto sobre la
parábola, luego la ordenada del vértice proporciona el valor máximo de P(x), esto
significa que la máxima ganancia trimestral de $ 66.750 se presenta cuando la tienda
gasta $ 10,500 por trimestre por concepto de publicidad.
Relaciones y Funciones
475
d) ANÁLISIS DE EQUILIBRIO.-
Sean C(x) la función de costo lineal; R(x) la función de ingresos, y P(x) la
función ganancia de una empresa donde C(x) = mx + b, R(x) = sx,
P(x) = R(x) - C(x) = (s - m)x - b, donde m denota el costo de producción por
unidad, s el precio de venta por unidad; b los costos fijos de la empresa, y x, el nivel
de producción y ventas.
El nivel de producción en que la empresa no tiene ganancias ni perdidas es el "nivel
operativo de equilibrio" y se puede determinar resolviendo las ecuaciones P = C(x) y
P = R(x) en forma simultanea.
El nivel de producir x0, la ganancia es cero, de modo que:
P(x0) = R(x0)-C(x0) = 0 por lo tanto R(x0) = C(x0)
El punto Íof-Vfl.j'o) que es la solución de las ecuaciones simultaneas P = R(x) y
P = C(x), se conoce como el "punto de equilibrio"; el número x0 y el número P0
son la cantidad de equilibrio y el ingreso de equilibrio respectivamente.
Geométricamente, el punto de equilibrio Po(x0,yo) es el punto de intersección de
las líneas rectas que representan las funciones de costos e ingresos, esto es así
porque P0(x0,y0) es la solución de las ecuaciones simultaneas P = R(x) y P = C(x)
y debe estar en ambas rectas al mismo tiempo.
476
Eduardo Espinazo Ramos
p >
0
1
^^
P = R(x)/
^o^o'yo'
X
Se observa que si x < x0 . entonces R(x) < C(x) de modo que P(x) = R(x) - C(x) < 0
y así la empresa tiene pérdidas en este nivel de producción, sin embargo si x > x0
entonces P(x) > 0 y la empresa opera con ganancia.
Ejemplo.- La compañía J.J. Servicios fabrica sus productos con un costo $ 4 por
unidad y los vende a $ 10 la unidad. Si los costos fijos de la empresa son de
$ 12000 al mes, determinar el punto de equilibrio de la empresa.
Solución
De los datos del problema, las funciones de costos, y de ingresos están dados por:
C(x) = 4x + 12000 y R(x) = lOx respectivamente al hacer R(x) = C(x), se obtiene:
lOx = 4x + 12000 => 6x = 12000 de donde x = 2000
Al reemplazar este valor de x = 2000 en R(x) = lOx se tiene
R(2000) = 10(2000) = 200000
Esto quiere decir que para una empresa de equilibrio, la empresa debe fabricar 2000
unidades de su producto, a fin de producir un ingreso de equilibrio de $ 20000.
_^
<5 £
~" CO
.*: cu
3 Cfl
o o>
o S
d) O
^E
P
30
?n
10
0
L
1 2
R(x) = 10x
„—^C(x) = 4x + 12000
3 4 X
unidades de millar
Relaciones y Funciones
477
Ejemplo.- Con los datos del ejemplo anterior, responder las siguientes preguntas.
a) ¿Cuál es la pérdida de la empresa si sólo se producen y venden 1500 unidades por
mes?
b) ¿Cuál es la ganancia si se producen y venden 3000 unidades por mes?
c) ¿Cuántas unidades debe producir y vender la empresa para obtener una ganancia
mensual mínima de $ 9000?
Solución
Como la función ganancia P(x) está dado por la regla
P(x) = R(x) - C(x) = lOx - (4x + 12000) = 6x - 12000
a) Si se producen y venden 1500 unidades por mes, se tiene
P(1500) = 6(1500) - 12000 = -3000 de modo que la empresa tendrá una pérdida de
$ 3000 por mes.
b) Si se producen y venden 3000 unidades por mes, se tiene
P(3000)=6(3000)- 12000 = 6000 es decir, se tiene una ganancia mensual de $ 6000.
c) Al reemplazar a P(x) por 9000 en la ecuación P(x) = 6x - 12000 se tiene
9000 = 6x - 12000 de donde 6x = 21000 entonces x = 3500 es decir, la empresa
debe producir al menos 3500 unidades para obtener una ganancia mensual mínima
de $ 9000.
14.29. EJERCICIOS DESARROLLADOS.-
(\j El costo marginal de producir un medicamento es de $ 10 por unidad, mientras que el
costo de producir 100 unidades es de $ 1500. Encuentre la función de costo C(x),
suponiendo que es lineal.
Solución
Como C(x) es lineal => C(x) = mx + b
El costo marginal es de S 10 por unidad, es decir que m = 10 entonces C(x) = lOx + b
478
Eduardo Espinoza Ramos
Ahora calculamos el valor b y para esto se tiene que el costo de producir 100 unidades del
medicamento es de $ 1500 es decir C(100) = 1,500 y como
C(x) = lOx + b =* C(100) = 10(100) + b
1,500= 1,000+ b =* b = 500
Luego la función de costo es C(x) = lOx + 500 donde el costo fijo es b = $ 500
\2j La compañía financiera de Alpamayo planea abrir dos sucursales dentro de dos años en
dos lugares: un complejo industrial y un centro comercial en la ciudad. Como resultado de
estos planes de ampliación, se espera que los depósitos totales de Alpamayo durante los
^/2x: + 20; si 0<*<2
próximos 5 años crezcan de acuerdo a la regla: f(x) = < i donde
-jr + 20; si 2<jc<5
12
y = f(x) proporciona la cantidad total de dinero (en millones de dólares) en depósitos con
Alpamayo en el año x (x = 0 corresponde al presente) trace la gráfica de f(x).
Solución
Se observa que el dominio de f(x) es [0,5], donde f(x) = -J2x + 20 para 0 < x < 2, los
valores de f(x) correspondiente a x = 0, 1 y 2 presentamos en la tabla
X
f(x) = Vlx + 20
0
20
1
21.4
2
22
Para f(x) = — + 20 para 2 < x < 5, los valores de f(x) correspondiente a x = 3, 4 y 5
aparecen en la tabla
X
x2
fM = — + 20
3
24.5
4
28
5
32.5
Relaciones y Funciones
479
(¿) La ganancia de la compañía de controles S.A. debe decidir entre dos procesos de
producción de su termostato electrónico modelo C. El costo mensual del primer proceso
está dado por C¡(x) = 20jc+1 0,000 dólares, donde x es la cantidad de termostato
producidos, y el costo mensual del segundo proceso está dado por C2(x) = 10*+30,000
dólares. Si las ventas proyectadas son de 800 termostatos a un precio unitario de $ 40
¿Cuál proceso debe elegir la gerencia para maximizar las ganancias de la compañía?
Solución
Veremos el nivel operativo de equilibrio con el primer proceso y que se obtiene
resolviendo la ecuación
40x = 20x + 10,000: de donde 20x = 10,000 entonces x = 500
lo que nos da como resultado 500 unidades, ahora veremos el nivel operativo de
equilibrio con el segundo proceso y que se obtiene resolviendo la ecuación:
40x = lOx + 30000, de donde 30x = 30,000 =» x = 1,000
lo que nos dá 1000 unidades como las ventas proyectadas son de 800 unidades , se
concluye que la gerencia debe elegir el primer proceso.
(4) Un fabricante tiene costos fijos mensuales de $ 60,000 y un costo de producción unitario
de $ 10. El producto se vende por $ 15 la unidad.
a) ¿Cuál es la función de costos?
480
Eduardo Espinoza Ramos
b) ¿Cuál es la función de Ingresos?
c) ¿Cuál es la función de ganancia?
d) Calcule la ganancia (o perdida) correspondiente a los niveles de producción de
10,000 y 14,000 unidades.
Solución
Sea x = el número de unidades producidas y vendidas
a) Como m = 10 y b = 60,000 costo fijo, entonces C(x)=mx + b => C(x = lOx + 60,000
b) Como cada producto se vende a $ 15 entonces la función ingreso es: R(x) = 15x
c) La función ganancia es: P(x) = R(x)-C(x)
P(x) = 15x - (lOx + 60,000) = 5x - 60,000
d) Cuando se produce x = 10,000 se tiene: P( 10,000) = 5(10,000) - 6,000 = -10,000
se tiene una perdida de $ 10,000 cuando se produce x = 140,00 se tiene:
P( 14,000) = 5(140,000) - 60,000 = 70,000 - 60,000 = 10,000
Es decir que se tiene una ganancia de $ 10,000
SJ La función de demanda para cierta marca de videocasetes está dada por
P = D(x) = -0,01jc2 -0,2x + 8 donde P es el precio unitario al mayoreo. en dólares, y x
es la cantidad demandada cada semana, en unidades de millar. Trace la curva de demanda
correspondiente ¿Arriba de cuál precio ya no habrá demanda? ¿Cuál es la cantidad
máxima demandada por semana?
Solución
La función demanda P =-0,0 Le2-0,2*+ 8 es cuadrática y su gráfica se puede trazar
por el método de completar cuadrados y calcular su vértice.
P-8 = -0.01(jc2+20jt) => P-8-1 = -0,01(jc2+20* + 100)
P-9 = -0,01(x + 10)2 => V(-10,9)
Relaciones y Funciones
481
P = -0,01x2-0,2x + 8
La intersección con el eje P que es 8, dá el precio unitario por el mayoreo arriba del cual
ya no habrá demanda, ahora para obtener la máxima cantidad demandada se hace P = 0
es decir: -O.OLv2 -0.2^ + 8 = 0 (multiplico por-100)
x2 + 20* - 800 = 0, factorizando
(x + 40)(x - 20) = 0, de donde se tiene: x = -40 y x = 20, como x es positiva entonces
nos quedamos con x = 20, luego él número máximo de videocasetes demandadas por
semana es 20000.
{6j La función de oferta para cierta marca de videocasetes está dado por
P - S(x) = O.Ol.v2 +0,1jc + 3 , donde P es el precio unitario al mayoreo, en dólares, y x
representa la cantidad que el proveedor pondrá en el mercado (medida en unidades de
millar). Trace la curva de oferta correspondiente ¿Cuál es el precio mínimo para el cual el
proveedor colocara los videocasetes en el mercado?
Solución
Como la función oferta P = S(x) = 0,OLv2 + 0, Ix + 3 es cuadrática y su gráfica se puede
trazar por el método de completación de cuadrados por determinar su vértice.
P = 0,01jc2 +0,Lv+3 = 0,01(jr + IQjc) + 3
P-3 + 0,25 = 0,0lU2+10jr+25)
P-2J5 = 0,0l(x + 5)2
V(-5;-2,75)
482
Eduardo Espinoza Ramos
\
\
\
\
\
\
1
1
1
-5
P»
]/
3
0
P = S(x)
X
La intersección con el eje P que es 3 dá el precio mínimo que el proveedor estaría
interesado en dejar los videocasetes en el mercado.
\TJ Cuándo una empresa vende x unidades de un producto, sus ganancias son
P(x) = -2x2 + 40jc + 280 encuentre:
a) El número de unidades que deben venderse para que la ganancia sea máxima.
b) Cual es la ganancia máxima.
Solución
Como la función ganancia es: P(x) = -2x2 + 40jc + 280 su gráfica es una parábola que se
abre hacia abajo y su vértice se determina por el método de completar cuadrados
•y = />(Jr) = -2jc2+40jr+280 => y-280 = -2(*2 -20*+ 100)+ 200
y-480 = -2(jr-10)2 => V(10.480)
a) Luego la coordenada x = 10 es el número de unidades producidas.
b) La coordenada y = $ 480 es la ganancia máxima que se obtiene al vender 10
unidades del producto
Relaciones y Funciones
483
P(x) = -x2 + 40x + 280
\SJ El costo total de producir 10 unidades de una calculadora es de $ 100. El costo marginal
por calculadora es $ 4. Encuentre la función de costo, C(x) si es lineal.
Solución
Como C(x) es lineal => C(x) = mx + b
Como el costo marginal por calculadora es $ 4 es decir m = 4
Luego C(x) = 4x + b, como la producción de 10 unidades es $ 100 es decir: C(10) = 100
entonces 100 = C(10) = 40+ b => b = 60 .-. C(x) = 4x + 60
4.30. EJERCICIOS PROPUESTOS.-
©
Suponga que la venta esperada (en miles de dólares) de una pequeña compañía para los
próximos diez años está aproximada por la función
S(x) = 0. 08jc4 - 0,04jt3 + x2 + 9x + 50 .
a) ¿Cuál es la venta esperada este año?
Rpta. a) $ 54,000
b) ¿Cuál será la venta en tres años?
b) $95,400
®
Un contratista estima que el costo total de construir x grupos de departamentos en un año
está aproximado por S(x) = x2 +80.X + 60, donde S(x) representa el costo en cientos de
miles de dólares. Encuentre el costo de construir.
a) 4 grupos
Rpta. a) $ 39'600,000
b) 10 grupos
b) $96'000,000
484
Eduardo Espinoza Ramos
(¿) En cierto estado, el impuesto T sobre la cantidad de artículos es de 6% sobre el valor de
los artículos adquiridos "x'\ donde T y x se miden en dólares.
a) Exprese T como función de x. b) Determine T(200) y T(5.65)
Rpta. a) T(x) = 0,06x b) $12; $0,34
\4j Según las fuentes de la industria, el ingreso correspondiente a la industria de ventas a
domicilio durante los años posteriores a su introducción se puede aproximar mediante la
c ■■ „, x í-0,03í3+0,25f2-0,12/ si 0</<3 _, _, „,, ._, , .
función /?(/) = < donde R(t) se mide el ingreso en
[0,57/-0,63 si 3</<ll
miles de millones de dólares y t se mide en años con t = 0 correspondiente al inicio de
1984 ¿Cuál fue el ingreso al inicio de 1850 y 1993?
Rpta. $ 0,1 mil millones; $ 4,5 mil millones
Q5) Puritrón, fabricante de filtros para agua, tiene costo fijos por $ 20,000; costos de
producción de $ 20 por unidad y un precio de venta unitario de $ 30. Determinar las
funciones de costos, ingresos y ganancia para puritrón.
Rpta. C(x) = 20x + 20,000 ; R(x) = 30x ; P(x) = lOx - 20,000
(ó) La electricidad se cobra a los consumidores a una tarifa de $ 10 por unidad para las
primeras 50 unidades y a $ 3 por unidad para cantidades que exceden las 50 unidades.
Determine la función C(x) que dá el costo de usar x unidades de electricidad.
flOjc ; jc<50
Rpta. C(x) = \
v [350 + 3* ; a>50
(7) Una empresa que fabrica radio - receptores tiene costos fijos de $ 3000 y el costo de la
mano de obra y del material es de $ 15 por radio. Determine la función de costo, es decir,
el costo total como una función del número de radio producidos. Si cada radio receptor se
vende por $ 25, encuentre la función ingresos y la función de utilidades.
Rpta. C(x) = 15x + 3,000 , R(x) = 25x , P(x) = lOx - 3,000
Un Un granjero tiene 200 yardas de cerca para delimitar un terreno rectangular. Exprese el
área A del terreno como una función de la longitud de uno de sus lados.
Rpta. A(x) = x( 100-x)
Relaciones y Funciones
485
(V) Se construye una cisterna de modo que su capacidad sea de 300 pies cúbicos de agua. La
cisterna tiene como base un cuadrado y cuatro casas verticales, todas hechas de concreto y
una tapa cuadrada de acero. Si el concreto tiene un costo de $ 1.50 por pie cuadrado y el
acero cuesta $ 4 por pie cuadrado, determine el costo total C como una función de la
longitud del lado de la base cuadrada. Rpta. C(x) = 5,5x2 +—
x
[Vn Un fabricante tiene gastos fijos mensuales de $ 40,000 y un costo unitario de producción
de $ 8. El producto se vende a $ 12 la unidad.
a) ¿Cuál es la función de costos?
b) ¿Cuál es la función de Ingresos?
c) ¿Cuál es la función de ganancia?
d) Calcule la ganancia (o pérdida) correspondiente a niveles de producción de 8,000 y
12,000 unidades.
Rpta. a) C(x) = 8x + 40,000 b) R(x)=12x
c) P(x) = 4x - 40,000 d) $8,000; $8,000
fn) Encuentre el punto de equilibrio para la empresa con función de costo C(x) = 5x + 1,000
y función de ingresos R(x) = 15x. Rpta. 1,000 unidades ; $ 15,000
(12) Encuentre el punto de equilibrio para la empresa con función de costos C(x) = 0,2x +120
y función de ingresos R(x) = 0,4x Rpta. 600 unidades; $ 240
(13) Encuentre el punto de equilibrio para la empresa con función de costos
C(x) = 150x + 2,000 y función de ingresos R(x) = 270x.
Rpta. 1000 unidades; $270,000
(14) El azúcar tiene un costo de $ 25 para cantidades hasta de 50 libras y de $ 20 por libra en
el caso de cantidades por encima de las 50 libras. Si C(x) denota el costo de x libras de
azúcar, exprese C(x) por medio de expresiones algebraicas apropiadas y graficar.
4
Í25.Í si jc<50
Rpta. C(x) = \
|20jc si ;c>50
486
Eduardo Espinoza Ramos
[1SJ Auto - time, fabricante de cronómetros, tiene gastos fijos mensuales de $ 48000 y un
costo unitario de producción de $ 8. Los cronómetros se venden a $ 14 cada uno
a) ¿Cuál es la función de costos?
b) ¿Cuál es la función de ingresos?
c) ¿Cuál es la función de ganancia?
d) Calcule la ganancia (o pérdida) correspondiente a niveles de producción de 4,000,
6,000 y 10,000 cronómetros, respectivamente.
Rpta. a) C(x) = 8x + 48,000 b) R(x) = 14x
c) P(x) = 6x - 48,000 d) $24,000; $ 12,000 ;$ 12,000
(ló) Los impuestos personales en Estados Unidos entre 1960 y 1990 son aproximados por:
Í7.9x + 50.4 de 1960 a 1975
f(x) = i trace la gráfica de la función si x = 0 representa
35.4-361.6 de 1975 a 1990
1960 ¿Qué sucedió a los impuestos personales en 1975?
[yjj El costo de cuidados de salud en Estados Unidos, como porcentaje del producto nacional
, .5 para 1960 a 1985
bruto entre 1960 y 1992, esta dado por: f(x) = < . Haga
r '""" ".75 para 1985 a 1992
_ Í0.22x + 5.í
'[0.29x + 3J
la gráfica de esta función si x = 0 representa 1960 ¿Qué sugiere la gráfica respecto al
costo de las ciudades por salud?
Rpta. Se elevaron más rápidamente de 1985 a 1992 que de 1960 a 1985
(18) Suponga que las ventas de una guitarra eléctrica satisface la relación S(x) = 300x + 2000,
donde S(x) representa el numero de guitarras vendidas en el año x, con x = 0
correspondiente al año 1987. Encuentre las ventas en cada uno de los siguientes años.
a) 1987 b) 1990 c) 1991
Rpta. a) 2000 b) 2900 c) 3200
Relaciones y Funciones
487
(19) La demanda mensual, x, de cierto artículo al precio de P dólares por unidad está dada por
la relación x = 1350 - 45p el costo de la mano de obra y del material con que se fabrica
este producto es de $ 5 por unidad y los costos fijos son de $ 2,000 al mes ¿Qué precio
por unidad P deberá al consumidor con objeto de obtener una utilidad máxima mensual?
Rpta. $5031.25 al mes
(20) El ingreso mensual por concepto de la venta de x unidades de cierto artículo está dado por
R(x) = 12jt-0,01jt" dólares. Determine el número de unidades que deben venderse cada
mes con el propósito a maximizar el ingreso ¿Cuál es el correspondiente ingreso máximo?
Rpta. 600 unidades, $3,600
(21) Una empresa tiene costos fijos mensuales de $ 2,000 y el costo variable por unidad de su
producto es de $ 25.
a) Determine la función de costo.
b) El ingreso R obtenido por vender x unidades está dado por R(x) = 60x-0.0lx2.
Determine el número de unidades que deben venderse al mes de modo maximicen el
ingreso ¿Cuál es este ingreso máximo?
c) ¿Cuántas unidades deben producirse y venderse al mes con el propósito de obtener
una utilidad máxima? ¿Cuál es esta utilidad máxima?
Rpta. a) C(x) = 25x + 2,000 b) 3,000; $90,000
c) 1,750; $28,625
(22) .El ingreso mensual R obtenido por vender zapatos modelo de lujo es una función de la
demanda x del mercado. Obsérvese que, como una función del precio P por par, el
ingreso mensual y la demandan son R = 300/? - 2p2 y x = 300 - 2p ¿Cómo depende R
dex? Rpta. R(x) = l50x-0,5x2
(23) La demanda x de cierto artículo está dada por x = 2000 - 15p, en donde p es el precio
por unidad del artículo. El ingreso mensual R obtenido de las ventas de este artículo esta
jc(2000-jc)
dado por R = 2000-I5p ¿Cómo depende R de x? Rpta. R(x) = -
15
488
Eduardo Espinoza Ramos
(24) El número "y" de unidades vendidas cada semana de cierto producto depende de la
cantidad x (en dólares) gastada en publicidad y está dado por v = 70 + 150jr-0,3jr2.
¿Cuánto deberían gastar a la semana en publicidad con el objeto de obtener un volumen
de ventas máximo? ¿Cuál es este volumen de ventas máximo?
Rpta. $ 250; 18,820 unidades
(25) Los costos fijos semanales de una empresa por su producto son de $ 200 y el costo
variable por unidad es de $ 0.70. La empresa puede vender x unidades a un precio de $ p
por unidad en donde 2p = 5 - O.Olx ¿Cuántas unidades deberán producirse y venderse a
la semana de modo que obtenga?
a) Ingresos máximos b) Utilidad máxima
Rpta. a) 250 unidades b) 180 unidades
(26) Lynbrook West, un complejo habitacional, tiene 100 departamentos de dos recamaras. La
ganancia mensual obtenida por la renta de x departamentos está dado por
P(x) = -I0x2 + 1,760a:.-50,000, dólares ¿Cuántas unidades deben rentarse para
maximizar la ganancia mensual? ¿Cuál es la máxima ganancia mensual que se puede
obtenerse? Rpta. 88 unidades ; $ 27,440
(27) La ganancia mensual estimada obtenida por la empresa cannon al producir y vender x
unidades de cámaras modelo MI es P(jc) =-0.04jc2 +240jc- 10,000 dólares. Encuentre
cuántas cámaras debe producirse cada mes para maximizar sus ganancias.
Rpta. 5,000 unidades ; $ 40,000
(28) La relación entre las ganancias trimestrales de cunningham, P(x), y la cantidad de dinero
x invertido en publicidad por trimestre queda descrita mediante la función
P(x) + Ix + 30 (0 < x < 50), donde P(x) y x se miden en miles de dólares.
8
a) Trace la gráfica de P
b) Determine la cantidad de dinero que debe invertir la compañía en publicidad por
trimestre para maximizar sus ganancias trimestrales.
Rpta. $ 28
Relaciones y Funciones 489
El ingreso mensual R (en cientos de dólares) obtenido por la venta de rasuradores
eléctricas Royal se relaciona con el precio unitario P (en dólares) mediante la ecuación
P2
R(P) = + 30P.
2
a) Trace la gráfica de R.
b) ¿Cuál precio unitario maximiza el ingreso mensual?
Rpta. b) $ 30
Una firma de confecciones, tiene costos fijos de $ 10,000 por año. Estos casos, como
arriendo, mantenimiento, etcétera, deben pagar independientemente de cuánto produzca la
compañía, para producir x unidades de un tipo de vestido, éste cuesta $ 20 por prenda
(unidad) además de los costos fijos. Es decir, los costos variables para producir x de estos
vestidos es 20x dólares.
Estos son los costos que se relacionan directamente con producción, como material,
salarios, combustibles, etcétera. Por tanto, el costo total C(x) de producir x vestidos en
una año está determinado por una función C:
C(x) = (costos variables) + (costos fijos) = 20x + 10,000
a) Representar gráficamente las funciones de costos variables, costos fijos y costos
totales.
b) ¿Cuál es el costo total de producir 100 vestidos? ¿400 vestidos?
c) ¿Cuánto más debe costar producir 400 vestidos, en vez de producir 100 unidades?
Rpta. b) $12,000; $18,000 c) $6,000
®
®
490
Eduardo Espinoza Ramos
CAPITULO V
INDUCCIÓN MATEMÁTICA
5.1. INTRODUCCIÓN.-
Un método de demostración muy útil en matemática es el llamado por inducción o
recurrencia que se fundamenta en la propiedad de los números naturales llamado el
principio del "buen orden"
También trataremos de la notación sigma "L" para la suma finita ya que es de gran
importancia en matemática y la notación de producto "n".
Para el estudio de inducción matemática daremos algunas notaciones de los números
naturales.
Al conjunto de los números naturales se simboliza por N, es decir:
N= (0,1,2,3,4,5,-).
Que se representa en la recta numérica
• • • • • • +■
0 12 3 4 5 » +oo
Al conjunto de los números naturales son el cero, se simboliza por N0, es decir:
N0= {1,2,3,4,5,...}
OBSERVACIÓN.- El cero "0" que significa "ausencia de elementos" se considera
como un numero natural para algunos autores y para otros no, en
el presente libro el cero "0" será considerado como un numero natural; considerar o no el
cero como un numero natural es una cuestión de convenio.
Inducción Matemática
491
5.2. CONJUNTOS ACOTADOS.-
a) DEFINICIÓN.- Llamaremos cota superior de un conjunto A c R a todo
número k e R tal que x < k, Vxe A, o sea que cualquier número
que sea mayor o igual que los elementos de A se llama "cota superior de A".
Cuando A tiene alguna cota superior, diremos que el conjunto A es acotado
superiormente.
Ejemplo.- Sea A = <-»,3> y la cota superior k = 5
cotas superiores de A
Observamos que cualquiera de los números reales mayores que 3 e incluso el 3 es cota
superior de A.
De todas estas cotas superiores de A, él número 3 es la menor. Luego daremos la
siguiente definición.
b) DEFINICIÓN.- A la menor de las cotas superiores de un conjunto A c R y
acotado superiormente, se le llama supremos de A o mínima cota
superior de A y se denota por Sup(A).
OBSERVACIÓN.-
(V) El supremo de A es también una cota superior de A.
(2) La menor cota superior k = Supremo de A = Sup A está caracterizada por las
condiciones siguientes que es equivalente a la definición.
K = Sup A«Vxe A y para toda cota superior k' de A, se tiene que x < k £ k'
(3) El supremo de un conjunto A, si existe, no es necesariamente un elemento de A,
como en el caso de A = <-»,3> cuyo supremo es 3 no pertenece al conjunto A.
La existencia del supremo para conjuntos acotados superiormente está dado por el
siguiente axioma.
492
Eduardo Espinoza Ramos
5.3. AXIOMA DEL SUPREMO O AXIOMA DE LA MÍNIMA COTA
SUPERIOR.-
Todo conjunto A de números reales, no vacío y acotado superiormente, tiene una menor
cota superior en R.
Ejemplo.- Demostrar que sí A = <-°°,3> entonces Sup A = 3
Solución
Probaremos esta afirmación por el absurdo.
Supongamos que 3 no es la menor cota superior de A, entonces se puede asegurar que
k+3
existe una cota superior k de A tal que k < 3 y puesto que k < < 3
it + 3
Tomamos k' = => k<k'<3 ...(1)
2
De donde k'e A = < -«°,3 >, pero siendo 1 cota superior de A debería tenerse k'< k
contradiciendo a (1).
La suposición es absurda por lo tanto Sup A = 3.
a) DEFINICIÓN.- Llamaremos cota inferior de un conjunto A c R a todo
número k e R tal que k <, x, V x e A. O sea que cualquier
número que sea menor o igual que los elementos de A se llama "cota inferior de A"
Cuando A tiene alguna cota inferior, diremos que el conjunto A es acotado
inferiormente.
Ejemplo.- Sea A = [-2,7> y la cota inferior k = -2.
cotas superiores de A
■■ A R
1 i • 1
-4 -3 -2 7
Se observa que cualquiera de los números reales menores que -2 e incluso el -2 es cota
inferior de A.
Inducción Matemática
493
De todas estas cotas inferiores de A el número -2 es la mayor. Luego daremos la
siguiente definición.
b) DEFINICIÓN.- A la mayor de las cotas inferiores de un conjunto A c R y
acotado inferiormente, se le llama ínfimo de A o máxima cota
inferior de A y se denota por inf (A).
OBSERVACIÓN.-
M^ El ínfimo de A es también una cota inferior de A.
(2) La mayor cota inferior k = inf(A) = ínfimo de A está caracterizada por la condición.
K = inf(A) <=> V x e A y para toda cota inferior k' de A se tiene k'<k<x.
^3) El ínfimo de un conjunto puede no ser elemento del conjunto dado.
Ejemplo.- El conjunto A = [-2,7> esta acotado superiormente por 8 e inferiormente por
-3, además la mayor cota inferior es -2 y la menor cota superior es 7 por lo
tanto: Sup(A) = 7 y Inf(A) = -2 de donde Sup(A) g A, Inf(A) e A
Cuando en un conjunto A se tiene que Sup(A) e A entonces el Sup(A) también se le
llama el máximo de A y si el Inf(A) e A entonces al ínfimo de A también se le llama el
mínimo de A.
c) DEFINICIÓN.- Un conjunto A se dice que es acotado, si es a la vez acotado
inferiormente y superiormente.
Ejemplo.- El conjunto A = <1,7> u [30,50] es acotado y Sup(A) = 50, Inf(A) = 1.
Ejemplo.- El conjunto A = <-°°.-5] u <l,+°o> no es acotado inferiormente ni
superiormente.
5.4. PRINCIPIO ARQUIMEDIANO.
Si x es un número real positivo entonces existe un número natural n0 tal que
0 < — < x (o equivalentemente tal que xn0 > 1)
494
Eduardo Espinoza Ramos
Demostración
Demostraremos por el absurdo. Suponiendo que nx < 1, V n e N
Por lo tanto el conjunto A= {nx / n e N) está acotado superiormente al menor por k = 1,
y por el axioma del supremo el conjunto A posee una menor cota superior k (Sup A) en R
que satisface la condición nx < k < 1, VneN pero siendo x>0 => k - x < k y por
lo tanto (k - x) no puede ser cota superior de A puesto que k es la menor de todas ellas.
Luego existe un elemento de A: mxx como ml e N tal que fc-jr<w1jr</c ...(1)
Pues si así no fuese, entonces se tendría que nx<k-x, VnxeA => k-x seria cota
superior de A lo cuál es falso.
Luego de (1) => /c<(m1+l)jc => k<mx, con m = (m1+l)eN
lo cuál es absurdo, pues siendo k = Sup A debería tenerse mx < k, de esta manera el
principio queda demostrado por el absurdo.
Ejemplo.- Probar que el conjunto A = {—I n e N) es acotado.
n
Solución
Ubiquemos los elementos de A en una recta para x = — , n e N.
n
n=5 n=3 n = 2 n=1 R
1 1 1 1 1 1
oiii i 1
n 5 3 2
Ahora encontraremos el supremo y el ínfimo de A como:
Vne N => n>l => 0<x = -<l ... (1)
n
Cuando n crece los elementos de A se acercan al cero (0) pero sin coincidir con el 0 para
n e N de esta observación se tiene:
Sup(A)= le A inf(A) = 0 eA
Inducción Matemática
495
Probaremos que inf(A) = 0, de (1) se vio que 0 es una cota inferior, si no fuese la mayor
existiría otra cota inferior k mayor que 0 y por principio Arquimediano se tiene que existe
un n0B N tal que 0 < — < k lo cual es absurdo pues — e A y siendo k cota inferior
"o "o
de A debería cumplirse que k < —, de manera que Inf A = 0.
"o
5.5. PRINCIPIO DEL BUEN ORDEN.-
Todo conjunto no vacío de enteros positivos tiene un elemento mínimo .
En general, un conjunto de números A es bien ordenado si todo subconjunto no vacío de
A posee elemento mínimo así por ejemplo, el conjunto de los números enteros positivos
es bien ordenado, por ejemplo el sub conjunto formado por todos los números enteros
positivos impares tiene elemento mínimo 1.
5.6. MENOR ELEMENTO Y MAYOR ELEMENTO DE A c R~
DEFINICIÓN.- "a" es menor elemento (o primer elemento) de A, sí y sólo si a e A y
"a"' es cota inferior de A.
DEFINICIÓN.- "b" es mayor elemento (o ultimo elemento) de A, sí y sólo si b e A y
"b" es cota superior de A.
NOTACIÓN.- a = Min(A) ; b = Máx(A)
Ejemplo.- Sea A = [0,2> entonces "0" es un menor elemento: 0 = Min (A)
2 no es mayor elemento, puesto que 2é A
Ejemplo.- Sea B = N, entonces 0 es menor elemento de B y no existe elemento
mayor de B.
Ejemplo.- Sea A = (-/neZ+) entonces % Min (A), 3 Max (A) =1
n
496
Eduardo Espinoza Ramos
OBSERVACIÓN.-
(lj Todo conjunto finito tiene mínimo y máximo.
f_J Todo intervalo cerrado tiene mínimo y máximo.
(3) Todo intervalo abierto no tiene mínimo ni máximo.
5.7. PROPOSICIÓN.-
Todo A cz Z+ , A 5t <¡) tiene menor elemento, acotado inferiormente.
Demostración
lro. Sea A c Z+ , A * <)> y acotado inferiormente (hipótesis)
2do. Entonces 3 a = inf (A) (por el axioma del ínfimo)
3ro. Luego ct < x, V x e A (definición de inf(A))
4to. Además a + 1 no es cota inferior de A (pues de lo contrario si fuera así a no seria
la mayor de las cotas inferiores)
A
x0 -1 a x0 a +1
5to. Si (VxeA, a + 1 < x) definición de cota inferior.
6to. 3 xQ e A tal que a + l> x0
7mo. Así x0 e [a,a +1 > (es decir a < x0 < a +1)
8vo. jc0 será el menor elemento de A (pues x0 e A por 6to) como A c Z entonces
todo entero menor que x0 no puede estar en A.
5.8. SUB CONJUNTOS INDUCTIVOS DE R.
DEFINICIÓN.- Diremos que A cz R es un conjunto inductivo sí y sólo si se cumple:
i)leA ii) xeA =í x+1eA
Inducción Matemática
497
NOTA.- Si no se cumple ninguno de los dos o alguna de ellas, no es conjunto inductivo.
Ejemplos.-
Ql) El conjunto A = Z+ es un conjunto inductivo.
En efecto: i) le Z*
ii) ieZ* =* x >0
=*x + 1>1>0=* Jt+leZ+
f2) El conjunto A = N es un conjunto inductivo.
En efecto: i) 1 e N
ii) x e N =* x > 0
=* x + 1 > 1 > 0 =* x + 1 e N
(3) El conjunto A = [-2,+°°> es un conjunto inductivo.
En efecto i) le [-2,°o>
ii) x e [-2,oo> =» x 2:2
=* x+l>-l>2 =* x + le[-2,°o>
(4) El conjunto A = N-{101] no es inductivo.
En efecto: i) leN-{101}
ii) xeA=>x + leA
100 e A ^ x + 1 = 100+1 = 101 e A
.'. no es inductivo
Qj) El conjunto A = [0,2>uN no es inductivo.
En efecto: i) 1 6 A
498
Eduardo Espinoza Ramos
ii) x-—eA => x+l = — eA
2 2
x = — eA =* Jt+1 = — eA
4 4
• • • • • • •
0 1 2 9^ 3 4 5
4
5.9. EL PRINCIPIO DE INDUCCIÓN MATEMÁTICA COMPLETA.-
Este principio establece que dado un subconjunto de enteros postivos S c N tal que:
i) El número 1 pertenece a S (1 e S)
ii) h e S entonces h + 1 e S entonces S coincide con el conjunto de los enteros
positivos, es decir S = N
Este es uno de los métodos que se utiliza generalmente para demostrar la validez de
proposiciones que incluyen todos los valores de n.
Ilustraremos este método mediante un ejemplo puramente intuitivo.
Supongamos que tenemos una escalera con un número indefinido de peldaños y queremos
demostrar que podemos subir hasta un determinado peldaño cualquiera, esto podemos
hacerlo si conocemos dos hechos:
a) Podemos subir el Io peldaño.
b) Si estamos en un peldaño cualquiera podemos subir al peldaño siguiente; de a)
sabemos que podemos subir al primer peldaño y de b) sabemos que podemos subir
al segundo peldaño, nuevamente de esto y de b) sabemos que podemos subir al 3o
peldaño, etc. con el propósito de generalizar este razonamiento a otras cosas
similares, veamos un ejemplo numérico, esto es:
1 = 1 = 12
l + 3 = 4 = 22
l + 3 + 5 = 9 = 32
Inducción Matemática
499
l+4 + 5 + 7 = 16 = 42
podemos demostrar por inducción completa que: V n e N es válida la proposición.
/>(/i) = l + 3 + 5 + ... + (2n-l) = /r
5.10. TEOREMA 1 (PRIMER PRINCIPIO DE INDUCCIÓN).-
Si S es un conjunto de todos los números naturales n que satisface la propiedad P(n) es
decir:
S = {n e N / P(n) es verdadera} si se cumple:
(l) 1 e S (5) Sí n e S entonces n + 1 e S
Demostración
Debemos demostrar que el conjunto S es igual al conjunto de todos los números naturales.
Sea T el conjunto de todos los números naturales que no están en S ahora veremos que T
es el conjunto nulo, para esto supongamos que T no es nulo, entonces por el principio del
buen orden, T tiene un elemento mínimo a e T, como 1 e T, entonces a * 1, a - 1
es menor que a, entonces a-líT =* a-leS, pero entonces por la parte2),
a = (a - 1) + 1 e S, lo cual contradice a que a e T de donde T es nula, concluyendo que S
es el conjunto de todos los números naturales.
5.11. TEOREMA 2 (SEGUNDO PRINCIPIO DE INDUCCIÓN).-
Sea P(n) una propiedad asociada a n, para cada entero n, si son verdaderos:
i) P(l) ii) P(h) => P(h+ 1), VhS: 1
entonces P(n) es verdadera para todo entero positivo n.
Demostración
Sea S el conjunto de todos los enteros positivos n, para los cuales P(n) es verdadera, S
satisface la hipótesis del teorema 1, por lo tanto S contienen a todos los enteros positivos,
es decir: P(n) es verdadero para todo entero positivo n.
500
Eduardo Espinoza Ramos
5.12. DEFINICIÓN.-
La suposición de que n e S o lo que es lo mismo la proposición P(n) es verdadera se
llama "hipótesis inductiva".
OBSERVACIÓN.- En la hipótesis (1) del teorema decimos 1 e S, equivalentemente
P(l) es verdadera, como S es un conjunto de números naturales o
enteros positivos, por el principio del buen orden, tiene un elemento mínimo,
naturalmente ese elemento no necesariamente es 1, puede ser cualquier otro n > 1.
EJEMPLOS DE DEMOSTRACIÓN POR INDUCCIÓN.-
(T) Probarque: l + 2 + 3 + ... + n = —,Vn>l
Solución
Vn>l se verifica P(n) = l + 2 + 3 + ...+n = "(" + 1)
2
i) Para n=l comprobaremos que se verifique: P(l) = 1 = = 1 es verdadero
híh 4-11
ii) Para n = h, P(h) = es verdadera por la hipótesis inductiva.
iii) ahora probaremos si P(h) es verdadera entonces P(h + 1) es verdadera.
En efecto tenemos:
P{h +1) = 1 + 2 + 3 +... + h + (h +1) = P(h) + (h +1)
% v ■*
hipótesis inductiva
= Wl±!)+(/i+1) a (*±!)(A+2) a(ft+iX(ft+i)+u
2 2 2
por lo tanto la proposición es válida V n > 1
l + 2 + 3 + ... + n = , vn>l
Inducción Matemática
501
©Probarque — + — + — + ... + = -2-, VneZ +
1.2 2.3 3.4 7j(n + l) n + 1
Solución
Como V ne Z+ se verifica P(n) =—+ — h +...+-
1.2 2.3 3.4 n(n+l) n + \
i) para n= 1, comprobaremos que se verifica: P{\) = — = = — = — se verifica
1.2 1 + 1 2 1.2
¡i) para n = h, P(h) = es verdadera por la hipótesis inductiva.
h + \
ii¡) ahora probaremos que si P(h) es verdadera entonces P(h + 1) es verdadero. En
efecto tenemos:
P{h + \) = — + — + — + ... + ! + í = P(h) + - l
1.2 2.3 3.4 ft(/i + l) (li + l)(li + 2) (A + l)(A + 2)
hipótesis inductiva
h 1 _ li(li + 2) + l _ h + \ _ h + \
h + \ (Ji + IX/i + 2) (li + l)(/i + 2) li + 2 [(/i + l) + l]
por lo tanto la proposición es válida para n = h + 1
{3} Probar que n3+2n es divisible por 3.
Solución
Sea P{n) = n3 +2n
i) Si n = 1, P(l) = 1+ 2 = 3 es divisible por 3.
ii) Para n = h, se supone que: P(h) = h3 +2h es divisible por 3 (o sea que P(h)
es verdadera por hipótesis inductiva).
iü) Para n = h + 1, se debe probar que P(h + 1) es divisible por 3.
502
Eduardo Espinoza Ramos
P(h + l) = (h + l)3 +2(/i + l) = (Ji3 + 2h) + 3(h2 +/i + l)
los dos sumandos es divisible por 3, el primero por la hipótesis inductiva y el
segundo por tener como factor a 3.
P{h +1) = 3m + 3(/i2 + h +1) = 3(iw + h 2 + h +1)
Luego P(h + 1) es divisible por 3.
Por lo tanto se concluye que: P(l) es V y P(h) es V entonces P(h + 1) es V
(4) Probar que: 52" + 7, es divisible por 8.
Solución
Sea P{ri) = {neN/52" +1 es divisible por 8}
i) Para n = l, P(\) = 52+7 = 25 + 7 = 32 = 8(4) es divisible por 8.
Luego P( 1) es verdadero.
ii) Para n = h se supone que P(h) = 52h +7 es divisible por 8, por la hipótesis
inductiva.
iii) Para n = h + 1, debemos de probar que P(h + 1) es divisible por 8.
P(A + l) = 52(*+,)+7=52.52*+7=5*+7 + 24.5* = (52A+7) + 8.(3.5*)
es divisible por 8 es divisible por 8
por la hipótesis por tener factor 8
inductiva
Luego P(h + 1) es divisible por 8.
Por lo tanto P(l) es V y P(h) es V entonces P(h + 1) es V.
(5) Probar por inducción que 2" > 8(n - 2), V n > 4
Solución
i) para n = 4, 24 > 8(4 - 2) -16 = 24 se verifica es verdadero.
Inducción Matemática
503
ii) para n = h, 2ft>8(/t-2) es verdadera por la hipótesis inductiva
iii) Ahora probaremos para n = h + 1.
2/.+i =22h >2.8(/i-2) = 8.2(Ji-2)>8[(h+l)-2]
puesto que para h > 4 =» h > 3
=» 2h-4>h-l =»2(h-2)>h-l
por lo tanto se concluye que: 2" > 8(w - 2), V n > 4
(é) Probar que: 11"+2 +122,,+1 tiene como factor a 133, V n> 1
Solución
Sea P(n) = {ne NIW*2 + 122n+1, tiene como factor a 133}
i) paran=l, />(1) = 11I+2+122+1 =113+123 =133(11 + 12)
Luego P( 1) tiene como factor a 133 se verifica es verdadero.
ii) para n = h, P(h) = llft+2 +12 l+1 tiene como factor a 133 por la hipótesis
inductiva es verdadero.
iii) ahora probaremos para n = h + 1.
P(h +l) = Ul,+3 +12a,+3=ll.ll*+2 +122.122"+1 +U.122M -11.122*-1
= ll.(ll',+2+122',+1) + (122-ll).122/,+1 =ll.(ll/,+2 +122/,*i)h-133.122/,+1
el primer término de la derecha tiene como factor a 133 por la hipótesis
inductiva y el segundo término tiene como factor a 133 con lo cual se concluye
que 11"+2 + 122n+1 tiene como factor a 133.
(?) Probar que: 10" + 3(4"+2) + 5 es divisible por 9.
Solución
504
Eduardo Espinoza Ramos
Sea P(n) = 103 + 3(4"+2) + 5 es divisible por 9.
i) Para n=l,P(l) = 10+3(43)+5=9(23)es divisible por9 Luego P(l) es verdadero
ii) Para n = h, P{h) = 10a + 3(4A+2) + 5 es verdadero por la hipótesis inductiva.
iii) Ahora probaremos para n = h + 1, es divisible P(h +1) por 9.
P(h + \) = mh+l + 3(4,I+2) + 5 = 10.10a +3.4/,+2.4 + 5
= 10,'+3(4,'+2) + 5 + 9(4h+2) + %\Qh) = PQi) + 9(4*+2 +lO*)
el primer término de la derecha P(h) es divisible por 9 por la hipótesis
inductiva y el segundo término es divisible por 9 por tener como factor a 9
por lo tanto P(h + 1) es divisible por 9.
Es decir P(l) verdadero y P(h) es verdadero entones P(h + 1) es verdadero
(5) Demostrar que 2" < n\. V n 5 4
Solución
Sea P(n) = {ne N12" <«!}
i) Para n = 4, P{1) = 24 < n!= 1.2.3.4 = 3.23 se verifica
ii) Para n = h, P(h) = 2h < h\ es verdadero por la hipótesis inductiva.
iii) Ahora probaremos para n = h + 1 que P(h + 1) es verdadero es decir:
P(h +1) = 2ft+1 < (h +1)! es verdadero, en electo,
Vh>4 => h+l>4, luego2.2h<22.2'' </i!(Ji + l)
Luego 2h+l <(li + l)! de donde P(/i+ 1) = 2h+1 <(/i + l)!
Es verdadero por lo tanto se concluye que: 2" <«!,Vn>4
Inducción Matemática
50<>
(?) Probar que: 32n+2 + 26,,+1 es múltiplo entero de 11.
Solución
Sea />(«) = {«e 7V/32n+2 +26"+1 es múltiplo entero de 11}
i) Para n = 1, P(l) = 34 + 27 = 11(19) es verdadero.
¡i) Para n = h, P(h) = 32h+2 + 26ft+1 es verdadero por la hipótesis inductiva
iii) Para n = h + 1, probaremos que P(h + 1) es un múltiplo entero de 11 es decir:
P(h + l) = 32lh+u+2 +26(/,+1)+1 =9.32/,+2 +64.26/,+1
= 9(32/,+2 + 26ft+1) +11(5(26',+I)) = 9P(h) +11[5(26,,+1)]
el primer término de la derecha es múltiplo entero de 11 por la hipótesis
inductiva y el segundo término es múltiplo entero de 11 por tener un factor 11.
Por lo tanto P(h + 1) es un múltiplo entero de 11 con que concluye que P(h + 1) es
verdadero.
(lO) Probar que para cualquier número real P > -1 y cualquier entero positivo n,
(1 + p)" >\ + np
Solución
Sea P(n) = {neZ+/(1 + p)" >l + np]
i) Para n=l,P(l)=l+p>l+p es verdadero se verifica.
ii) Para n = h, P(h) = (\ + p)1' >l + hp es verdadero por la hipótesis inductiva.
iii) Ahora probaremos que para n = h + 1; P(h + 1) es verdadero.
P(h + l) = (1 + p)h+l = (1 + p)ha + p) >(l + hp)(l+ p)
= 1 + p + hp + hp2 >l + (h + \)p
506
Eduardo Espinoza Ramos
Luego P(h +1) = (1 + p)h+x £ 1 + (h + \)p se verifica por lo tanto P(h+1) es verdadero
(ly Sea {xn/neN} un conjunto de números reales tales que xx - v60,
xn+\ ~ y]xn + 60 , V n £ 1, entero entonces probar por inducción matemática que
jc„<4,VneN.
Solución
i) Paran=l, xl - v60 < >/64 = 4 => xl < 4 se verifica.
ii) Para n = h, xh < 4 es verdadera por la hipótesis inductiva.
üi) Ahora probaremos para n = h +1, xh+l < 4 se cumple:
xh<4 =* ^+60<60 + 4 = 64 =* ^/jrh + 60 < ^64 = 4
^+1 = 3/I~T60<4 =* xh+¡ < 4 es verdadero
por lo tanto xn < 4, V n e N
12) Probar que x2n~l + y2n~l es divisible por x + y, V n > 1
Solución
Sea P(n) = (neiV/jf2""1+>'2""1 es divisible por x+y)
i) Para n = 1, P(l) = j:2-1 + y2~x = x+ y se verifica.
ii) Para n= h, P(h) = x2h~x + y2h~x es divisible por x+y por la hipótesis inductiva.
üi) Ahora probaremos para n = h +1, P(h + 1) es divisible por x + y, en efecto
tenemos:
P(fc + 1) = *2(*+1>-1 +>.2",+1)-1 = x2h+1+y2h+x =x2.x2h-i+y2.y2h-1
= x2.x2h~l -y2.x2"-1 +y2.y2h-l+y2.x2h-1
^y2(x2h-,+y2h^) + (x2-y2)x2'-i=y2P(h) + (x+y)(X-x)x21"1
Inducción Matemática
507
el primer término de la derecha es divisible por x + y por la hipótesis inductiva
el segundo término es divisible por x + y por tener como factor a x + y por lo
tanto P(h + I) es divisible por x + y.
5.13. EJERCICIOS PROPUESTOS.-
1. Ejercicios de Conjuntos Acotados.
(T) Si A * <|>, B * (}>, dos conjuntos acotados superiormente tales que AcB, probar
que Sup A < Sup B.
Q2J Si A * <(), B * <|> son dos conjuntos acotados inferiormente tales que AcB probar
que Inf(B)<Inf(A).
Hallar supremos y el ínfimo de A = { In e N], B = [ In e N)
3« + 4 3« + 8
Rpta. sup(A) = —, inf(A) = -2, sup(B) = 4, inf(B) = 0.2
(4) Determinar el supremo y el ínfimo si existen en cada uno de los ejercicios.
a) A = [xbR/x2 <9] Rpta. Sup A = 3, InfA = -3
b) A = {xeR/21 + 4x-x2 >0} Rpta. SupA = 7, InfA = -3
c) /1 = (—/«€ÍV| Rpta. Sup A = 5. InfA = -7
3 —2«
d) A = [xeR/x2-4x-l2<0) * Rpta. SupA = 6, InfA = -2
e) A = {jce /?/|jc||jc + 1| <2} Rpta. SupA=l, InfA = -2
f) A = {xeR/\6 + x-x2 | <6} Rpta. SupA = 4, lnfA = -3
(5) Encontrar el supremo y el ínfimo de A = { /ne N], B = { fne N)
v-' 2 + n 2-ln
508
Eduardo Espinoza Ramos
1 1 4
Rpta. sup(¿) = - , inf(A) =— , sup(B) = — , inf(fl) = -2
fó) Hallar el supremo y el ínfimo si existe de:
A = [xeR/x2-4x-12<0], B = {x2 -4*-12/*e<-°°,«>>}
Rpta. Sup (A) = 6, Inf (A) = -2, Sup (B) = 2, Inf (B) = -16
[JJ Dar un ejemplo de dos conjuntos A y B, mediante intervalos tales que
Inf (A nB)> Sup {Inf(A), Inf(B)}.
fin Determinar el supremo y el ínfimo si existe de los siguientes conjuntos.
a) A = {xeR/\4-x\>x} b) A = {xs R/\x2-4\ <16}
c) A = {xbR/\x + 6\ + \3-x\ =9} d) A = {xe R/\x2 +2x-4\<7)
e) ¿ = {*e/?/|*-8|-|4*2-l|<0}
II. Demostrar por inducción matemática.
(J) 1 + 3 + 5 + ... + (2n-l) = n2
©
_L _L _L 1 = n
1.3+ 3.5 5.7 "" (2«-l)(2« + l) 2n + l
2 02 o2 2 _ W(W + l)(2w +1)
(5) l2+22+32+... + «
^ 6
(4) 2 + 4 + 6 + ...+ 2n = n(n+l)
0 3 + 6 + 9 + ... + 3« = — (n + 1)
©
111 1
- + — + + ... + -
2.5 5.8 8.11 (3«-l)(3« + 2) 6n + 4
Inducción Matemática
509
©
l+3 + 32+... + 3"-'=^—!■
(S) 1.2+2.3 + 3.4 + ...+«(« + l) = -(« + l)(« +2)
©
111 1 «(« + 3)
+ + + ... + -
1.2.3 2.3.4 3.4.5 «(« + !)(« + 2) 4(/i + l)(/i + 2)
(lO) l.l2 +2.32 +3.52 +... + /i(2/i-l)2 = -(« + l)(6«2 -2/i + l)
^-^ 6
(jl) l3 +33 +53 +... + (2n-l)3 = «2(2«2 -1)
12) 2J+4J+6J+... + (2«)J =2«"(« + ir
(Í3) l2+32+52+... + (2«-l)2=-(4«2-l)
@ 1.3+2.4 + 3.5+ ... + /Kn + 2) = -(« + l)(2« + 7)
QÍ) 2.5 + 3.6 + 4.7 + ...+(« + lX« + 4) = -(«+4)(/i + 5)
/Q\ 111 1 n
(16) —+— + — + ... + -
1.2 2.3 3.4 /?(/i + l) /i + l
/T^ 1 1 1 1 /i(3/i + 5)
(17) — + — + — + ... + -
1.3 2.4 3.5 «(« + 2) 4(n + l)(« + 2)
(lS) 1.2 + 2.22+3.23+... + «.2" = («-l).2n+1+2
(19) 1.3 + 3.32 +5.33 +... + (2«-l).3" = («-l).3n+1 +3
(3) -L + -L + -L + ... + l = ^,Vn>2
^ 2.4 4.6 6.8 2n.(2n-l) 4n
(2Í) Pruébase que: síx>l y «eZT entonces a" >1
510
Eduardo Espinoza Ramos
<©
©
III.
©
©
©
©
©
©
®
©
®
®
©
©
©
@
(21)
Pruébase que: síx<0y nsZ* entonces x2" ' <0
Demuéstrese que:
a) (aJb)n =a"Jb\ \fneZ + b) (am)n =amn, VneZ +
VPeR,P>l y VneZ+, pruébase que: (1 + p)" >l + wp + "(W~1) p2
Probar por inducción matemática que:
5" 21 + 4«, Vn> 1
«!>2".Vn>4
4" >«4,Vn>5
4" -1 es divisible por 3, n > 1
22n +5 es divisible por 8, n > 1
® 3" >l + 2«, Vn>]
(4) 2" >«2. Vn>5
(?) 24" es divisible por 15. n > 1
(§) 32" + 7 es divisible por 8, V n>l
3« " +15« + 6 es divisible por 6, n > 1.
32n+3 + 2"+3 tiene un factor al número 7, V n > 1
n2+n es divisible por 2, V n > 1 (l3) n3 -n es divisible por 3, V n >1
h5 -n es divisible por 5, V n > 1
15) n1 -n es divisible por 7, V n >1
32n+2 - 2n+1 es divisible por 7, V n > 1
32„+3 + 2n+3 es divisibie por 7, V n > 1
22„+i +32«+i es divisible p0r 5, V n > 1
3.52n+I +23n+I es divisible por 17, V n > 1
32„+2 + 26«+i es un multiplo de ! 1
Demuéstrese que a + b es un factor de a2"'1 +b2"~l, para todo entero positivos n.
Inducción Matemática
511
5.14. SUMATORIAS,
A la suma de los n números ax,a2.—,an es decir: a{ +a2 +... + an, representaremos por
n
la notación N a,=ai +a2 +... + an, que se lee "sumatoria de los a¡ desde i=l hasta
í=i
i = n", a 1 se denomina limite inferior, a "n" se denomina limite superior y el símbolo X
se llama signo de sumación y es la letra Griega mayúscula del alfabeto Griego.
Por ejemplo a la suma de los 5 primeros números enteros positivos impares se puede
expresar así:
5 5
Ver,- = V(2í-1) = 1 + 3 + 5 + 7 + 9 = 25
i=i í=i
GENERALIZANDO.- Consideremos m y n dos números enteros de tal manera que
m < n y f una función definida para cada i e Z donde m < i < n.
M
Luego la notación N f(i), nos representa a la suma de los términos f(m), f(m + 1),
n
f(m + 2),..., f(n) es decir: V/(/) =/(w) +/(m +1) +/(m + 2) + ... + /(«)
Donde i es el índice o variable, m es el limite inferior y n es el limite superior.
6 6
o- r.: ' V r,; V ' 12 3 4 5 6
Ejemplo.- Si /(/)= .entonces: > /(«)= > -—r = - + T + T + T + 7 + ^
1 + / ¿^ x-¿\ + i 2 3 4 5 6 7
5.15. PROPIEDADES DE LA SUMATORIA.-
n
\lj ^ k = nk , k constante cualquiera.
i=i
Demostración
512
Eduardo Espinoza Ramos
i=l i=l
Demostración
n
£* /(i) = */(l) + */(2) + */(3) + ...+*/(n)
i=i
= k (f(l) + f(2) + f(3) + ... + f(n)) = *]T/(O
1=1
n+1 w
i=i i=i
Demostración
Aplicando la definición de sumatoria se tiene:
n+1 n
^T /(i) = /(l)+ /(2)+ ... + /(») + /(n +1) = ^T /(i) + /(« +1)
«=i f=i
® £[/(») ±s(0] = ]£/(i) ±]£s(i)
i=l i=l i=l
Demostración
La demostración se puede hacer por definición de sumatoria pero también se puede
demostrar por inducción.
i i i
i) Para n = 1, ^[/(0 ±S(0] =/(O ± ¿(0 = ^/(O ±^£(0 luego se verifica.
/=i i=i í=i
Por lo tanto es verdadero.
ii) Para n = h, ^ [/(i')±£(0]= V"/0)± V" g(0 es verdadero por la hipótesi
/=i i=i í=i
inductiva.
iii) Ahora probaremos para n = h + 1, en efecto:
Inducción Matemática
513
^[/(i)±S(/)] = ^[/(i)±S(/)] + [/(A + l)±S(A + l)]
1=1 <=i
h h
= ^f(i)±^g(i) + f(h + l)±g{h + l)
i=l i=l
h h
i=l
h+l /i+l
= y /(O ± N g(0 (por la propiedad 3).
i=i i=i
Con la cual queda demostrado.
b b+c
© X/(0=X/(/"c)
i'=o i=o+c
fc fc-c
© £/(«)= ]T/(' + c)
i=o i—a—c
n
© ^[/(0-/0'-l)] = /(n)-/(0) (Io regla telescópica).
¿=i
(?) ^V [/(0-/0-1)] = f(n)-f(k-l) (Io regla telescópica generalizada).
/=*
S X[/(' + ^ ~ /(' ~ 1)] = /(" + D + ^^ ~ /U) " /(0) (2° rCgla tdeSCÓPÍCa)-
í=l
100
X"1 1 1
Ejemplo.- Hallar el valor de > ( )
■*-^ í í' + l
i=i
Solución
Mediante la regla telescópica se tiene:
514
Eduardo Espinoza Ramos
f(i) = => /(/ -1) = -, entonces se tiene:
i +1 i
100 100
Y <■--t1:) = Y(t^-1) = -(/000)-/(0)) = -(-¿--1) = M
^ i í + i ¿^ i + i i 101 101
1=1 «=1
40
Ejemplo.- Hallar el valor de N (yÍ2i + l - y¡2i -1)
Solución
Aplicando la regla telescópica se tiene: /(/') = \¡2i +1 => /(i -1) = vi' -1 , dé donde
40
Y (V2/ +1 -y/2i-1) = /(40)-/(0) =>/8Í-VÍ = 9-l = 8
i=i
Ejemplo.- Hallar una fórmula para la sumatoria \ 5'
i=i
Solución
Aplicando la regla telescópica se tiene:
n n
^(5'+,-5«') = /(n)-/(0) =* ^(5.5'-5') = 5"+1-5
i=i
n n
4 Y 5' = 5(5" -1), de donde se tiene: Y 5' = - (5" -1)
i=i 1=1
Ejemplo.- Si p, q, a¡, b,: e R , probar para todo n e N que:
n n n
2pq^aib¡ < q2^af + P2^bf
i=l i=l i=l
Solución
Aplicaremos la propiedad j:2 + v2 > 2xy, V x, y e R
Inducción Matemática
515
I
i) para n= 1, 2pgVcr,fe, ^Ipqafa =2(ga,Up¿,) <(qax)2 +{pbij1
1=1
i=i i=i
/l /! /i
ii) Para n = h, Ipq} a¡b¡ ^q2/ aj+ Py bi~ es verdadero por la hipótesis
i=i i=i i=i
inductiva.
iii) Ahora probaremos para n = h + 1, en efecto:
/l+l /l
Ipq^afy = Ipq^afy +2pqah+1bh+¡
i=i i=i
h h
- (92Xa'2+^2X^)+(<?2fl*+i+p2bh*o
1=1 «=1
h h /i+l /i+l
= q2(2^af + a2M) + p2(^b2 + ¿j*+I) = q2 /a? + P2 /b? (por la propiedad 3).
i=i ¡=i í=i i=i
Con lo cual queda demostrada.
n n
Ejemplo.- Probar V n e N, V {a¡b¡? <(S\af){S\bf) (Desigualdad de CAUCHY
1=1 1=1 i=i
- SCHWARZ)
Solución
i) Paran=l, a\b\ < (a2)(b2) se verifica es verdadero.
h h h
ii) Para n = h, N (afy)2<(\ a?X/ b2) es verdadero por la hipótesis inductiva.
i=i /=i i=i
iii) Ahora probaremos para n = h + 1, en efecto:
/i+l h h h
(^«,A)2 =(^a,A + «/.+A+i)2 =(^fl,A)2 +2fl*+A+i-^fl,A + aLibL
.■=1 1=1 1=1 1=1
516
Eduardo Espinoza Ramos
n n n n
s(Xa'2)(S^)+(fcA2+iZo'2+o'+iS^)+a'+1^1
1=1 1=1 1=1 1=1
h h h h h
=Xfl'2iXfe'+^>)+°*+i(X^+^+,)=[Zfl2+fl*2*i«X^+6*+i1
1=1 1=1
/l+l /l-rl
=(Efl2)(zfc')
1=1 1=1
con lo cual queda probado la desigualdad
f=i
i=i
fc+i fc+i
í£°A)2 <i£a?^b-
=i ¿=i
5.16. FORMULAS DE LA SUMATORIA.-
© !•=
n(n + l)
® l'1"
.2 n(ii + l)(2n + l)
i=i
® !•' =
■3 «2(« + D2
/■Jv V1 -4 _ «(" + D(6n3 + 9n2 + n -1)
i=i
i=i
30
Demostración
Ql) Existen varias formas de hacer la demostración, una es mediante la inducción, otra
mediante la regla Telescópica y otra la que demostraremos en la forma.
n
y/ = l + 2+3 +... + (n-2) + (n-l) + M
" t t t t t t
„ i i i i i i
Vi' = n + (n-l) + (n-2) + ...+ 3 + 2 + 1
1=1
2^t = (« + !) + (« +!) + (« + !)+ - + (»+ !) + («+ !) + (« + !)
i=i n-veces (n+1)
Entonces se tiene: 2 >^ /' = n(n +1)
n(n + l)
1=1
í=l
Inducción Matemática
517
(¿) La fórmula (2) demostraremos aplicando la regla Telescópica.
n
y [(i +1)3 -í'3] = /(«)- /(O), de donde f(i) = (i +1)3 => /(í -1) = i3 entonces se tiene:
¿=i
Fl
/[(' +1)3 -1'3 ] = (n +1)3 -1, desarrollando se tiene:
i=i
fí n n n
V('3+3r+3/ + l-/3) = (/i + l)3-l => 3V'2+3Ví + Vl = (n + l)3-l
i=i í=i i=i i=i
n
,V -2 3«(n + l) , ,s3 ,
3> i +—^—-+n = (n + \y -1
2
i=i
3y/2=(/i + l)3-—(n + l)-(n + l) =(m + 1)[(/i + 1)2-—-1]
¿-¿2 2
i=i
3y,2=(n+i)(n2+2n-^)^(n+1)(2"+1) ,. yt2 = »(»+D(2n+i)
-¿^ 2 2 a-1 6
i=i f=i
NOTA.-Las fórmulas 3) y 4) se deja como ejercicio.
EJEMPLOS DESARROLLADOS.-
n
Ql) Hallar una fórmula para la sumatoria > ln(i)
/=i
Solución
Aplicando propiedad de logaritmo se tiene:
n
V ln(0 = ln(l) + ln(2) + ln(3) + ...+ln(«) = ln(1.2.3...n) = ln(n!)
;=1
n
.-. y ln(/) = ln(n!)
i=i
518
Eduardo Espinoza Ramos
n
(l) Hallar una fórmula para la sumatoria >
V^ ^(¿ + 1)0-1)!
1=1
Solución
Multiplicando numerador y denominador por i, es decir:
n n ti n n
y» 1 y i _yi i _y»¿+i-i_y» /+i 1
¿<f(i + l)(/-l)!~>^(i + l)i(!'-l)!~-2-f(i + l)! ~ 2-i(i + l)\ ~ 2-i (i + l)i (í + 1)!
1=1 1=1 1=1 1=1 1=1
^ i! (/ + !)! ¿-1 (i + 1)! i! (« + !)! (n + 1)
(zi + DM
1
1=1 1=1
1 (n + l)!-l
4-<(i + lXi-l)! (n + 1)!
1=1
(5) Hallar una fórmula para la sumatoria y 5'
1=1
Solución
n
Mediante la regla Telescópica se tiene: N (5,+I -5') = /(n)-/(0) donde /(/) = 5
fí n
V (5.5'' - 5') = 5"+1 - 5, simplificando 4Y 5' = 5(5" -1)
1=1
n
por lo tanto: > 5' =:
1=1 1=1
c, 5(5"-1)
4
1=1
(4) Hallar una fórmula para la sumatoria ^i i!
1=1
Solución
Inducción Matemática
519
n
Aplicando la regla telescópica se tiene: N [(/ + 1)!-*"!] = /(«)-/(0) de donde f(i)=(i+l)!
n n n
V[(i + l)i! -i!] = («+l)!-l => Vi!.(i + l-l) = (n + l)! -1 de donde Vii! = (n + 1)!-1
i=i i=i í=i
n
\5) Hallar una fórmula para la sumatoria N sen(úr)
i=i
Solución
Usando la identidad: coSi4 + cosB = -2sen( )sen( ) «.(1)
2 2
De donde haciendo la sustitución se tiene:
A + B .
= ix
ía+b = :
\a-b = :
2 j4 + B = 2ú
=* < resolviendo el sistema:
A-B \A-B = 2x
= x
l 2
A = (i+ l)x ; B = (i-l)x ...(2)
Reemplazando (2) en (1) se tiene: eos (i + l)x - eos (i - l)x = -2 sen ix . sen x
aplicando la sumatoria a ambos miembros:
n n
y [cos(i + l)jc-cos(/-l)jc] = -2senJcN sen(úr)
i=i 1=1
y mediante la segunda regla Telescópica se tiene:
n n
cos(n + l)jt + cos(mc)-cos.v-l = -2senjcN sen(¿c), despejando y sen(úr) se tiene:
i=i i=i
n
X~" ,- ^ 1 + cosx-cosiu: —cos(/i + 1)jc
> sen(í.c) =
^■^ 2sen*
í=i
520
Eduardo Espinoza Ramos
n
\6J Hallar una fórmula para la sumatoria N senh(9i.v)
/=!
Solución
Mediante la segunda Regla Telescópica se tiene:
n
2^ [cosh 9(i + l)x - cosh 9(i - l)x] - cosh 9(« + l)x + cosh 9nx - cosh 9 x -1
i=i
n
2 senh(9*) N senh(9iA) = cosh 9(n + 1)jc + cosh(9n*) - cosh 9x -1
i=i
V"1 , «. , cosh9(n + l)jt + cosh(9n*)-cosh9jc —1
> senh(9iJt) =
¿-i 2senh(9*)
1=1
5.17. NOTACIÓN DEL PRODUCTO DE n NUMEROS.-
Al producto de los n números «,,«2,«3,...,«n, es decir: ai.a2.a3....an representaremos
por la notación:
n
/=i
a¡ = al.a2.a3....a„
que se lee el producto de los a¡ desde i = 1 hasta i = n, donde a "1" se denomina limite
inferior, a "n" se denomina limite superior y al símbolo n se llama "Pi" y es la letra
mayúscula griega.
Ejemplo.- Hallar los 5 primeros números enteros positivos impares.
Solución
J 3
T~T a¡= T~T(2/-1) = 1.3.5.7.9 = 945
í=i ;=i
Inducción Matemática
521
GENERALIZAiNDO.- Si f es una función definida para i e Z, donde 1 < i < n, la
n
notación I I /(i) nos representa al producto de los términos
1=1
ff 1), f(2), t"(3) fin), es decir:
Y[fO)=fO).fa\fO)...f(n)
donde i es el índice o variable, n es el limite superior.
6 6
Ejemplo.- Si /(i') = .entonces: I |f(/)=| I = —.— .—.—.—.— = —
i + 1 11 llí + 1 2 3 4 5 6 7 7
_i 12 3 4 5 6 1
(=i i=i
OBSERVACIONES.- Si m y n son enteros tal que m < n y a¡ representa una
expresión en i. entonces:
n w—1 m
t—m i=m
n n
© J|«,-="«,-fl«.+i-«Ut2-fl» ® J~[í = 1-2.3.4...^ =«!
í=i
n n n
5.17.1. TEOREMA.- FTa.fc,^=T~[ai,T\b,
í=i i=i i=i
Demostración
La demostración es por inducción.
i i i
Si n = 1, entonces por definición se obtiene: I I o,fc, = a,i>| = I I a¡. I \b¡
í=i i=i i=i
h h h
Si n = h, II ap, = | I «¿-I I b¡ es verdadero por la hipótesis inductiva
i=i i=i
522
Eduardo Espinoza Ramos
Ahora probaremos para n - h + 1, en efecto:
h+\ h h h
i=l ;=1 i=l i=l
h h h+l h+\
=iYla')ja^-<Ylbi)JbM=HaTíbi
i=i i=i i=i i=i
por lo tanto, para todo entero positivo n.
n n
Uah-UaYlh
i=i i=i i=i
n
5.17.2. TEOREMA.- Si c es una constante, entonces I I c - c"
í=i
Demostración
n n
Sea c = c¡, para todo i, entonces I I c = I le,
1=1 1=1
i
Si n = 1, entonces por definición se tiene: I |cI=c,=c = c
/=i
h
Si n = h, I \c¡= ch es verdadero por la hipótesis inductiva
i=i
h+l h
Ahora probaremos para n = h + 1, en efecto: I I c, = (I I c¡)-ch+\ =ch.c = c'
.=i i=i
n
por lo tanto: I I c, = c", esto es, para todo entero positivo n.
i=i
n
n
1=1
Inducción Matemática
523
5.17.3. TEOREMA.- Si c es una constante, entonces:
n~,=<-íj>
1=1
i=i
Demostración
La demostración se deja como ejercicio para el lector.
5.18. EJERCICIOS PROPUESTOS.-
I. Hallar el valor de las siguientes sumatorias.
99
® I1"2'
i=i
100
© 5>7ÍÍ>
i=l
20
© 5>2 +
2)
Rpta. 4950 ln 2
Rpta. ln( )
102
Rpta. 133,560
i=i
© y*ü-\)
i=i
100
© y sen2,'(2jc)
i=i
Rpta. 10,400
200 :
Rpta. tg ' (2jc)(1 - sen zuu 2x)
© I*
Rpta.
63
25 -,
© 1t-
1=0
Rpta. 27(2-¿)
524
Eduardo Espinoza Ramos
40
360 „ , 7.560
© X-^- Rpta. ™
50
© V(2i2+i-l) Rpta. 85,359
®
II.
©
1=14
i=i
Escriba en forma explícita las siguientes sumas:
5 6
t=i *=i
2jr-32
Rpta. —
12
© I
7
© i>2í © i>2" © í>2+3*}
¡=2 *=1 k=\
5 5 5
k=\ k=\ *=1
5 n 8
© £(**-**_,) © 5/«-*+d4 © Z(*+2)4
«.=1 *=i *=i
III. Hallar la fórmula para cada una de las siguientes sumatorias.
© V í Rpta. -ü—
1=1
© V l- Rpta. -J2-
^ Z-r(3¿ + l)(3/-2) 3h + 1
© Y 1 Rpta. -5-
w Zw(2i-l)(2i + l) 2n + l
í=i
Inducción Matemática
525
©
©
©
©
©
©
®
©
©
©
y. 4
^(4z"-3)(4i + l)
i=i
n
^ln(i + l)
1=1
£,2«
1 = 1
n
2^2'
1=1
V> y¡T+\-y[i
y
^(i + l)(i2+5i + 6)
" .7
y
^-((2i + l)(2/-l)
i=i
« ln(l + !)'(l + i)
y '
^ln(¿')[ln(l + i),+']
R
V sen2í(2jt)
i=i
N cos(3iJt)
4n
Rpta.
Rpta.
Rpta.
Rpta.
Rnta.
4n + l
ln(n+ 1)!
(n-l)2"+l
2 2 + n
2"
Vn+1-1
Vn + 1
n2+3n + 3
2(n + 2)(/i + 3)
/i(n + l)
Rpta.
2(2n + l)
1
1
21n2 (/i + l)ln(n + l)
2n.
Rpta. tg~ x(l-sen (2x))
Rpta.
i=i
sen(3/i + 3)jc + sen(3n*) — sen 3x
2 sen*
n
© Xcos'
1=1
2x
Rpta.
senn+'(2jt)
2"+1senjc
526
Eduardo Espinoza Ramos
2'+i(i + l) „ , , 1 1
g) V^l Rpta. 1
_ v. ., 2n + 2 2n+1
i=i
IV. Pruébese cada una de las siguientes fórmulas por inducción matemática.
® y^_ = -£- (2) Y(3*2-3* + l) = n3
*=i *=i
n n
(?) \k.2k~* =l + (.n-l)2" (3) Vcos(2*-1)jc =
sen(2njr)
2sen;c
k=\ k=l
*=1 *=1
n
(Y) Pruébese que: \, sen(2fc - 1)jc =
l-cos(2n*)
2 sen*
/t=i
n „
0 Pruébese que: V ar1"1 = a{l~r }, r* 1
*=i
n n
(3) Pruébese que: sí aA ^£>*. k= 1,2,3 n; implica /a* ^ / ^
*=i *=i
n n
(4) Pruébese que: | \\ ak I - ]¿J a* I
*=i *=i
(?) Hallar el valor de n para que: }j(2+i2)=}j(l + i2)
¡=1 1=1
Inducción Matemática
527
Fl
Y* '
(ó) Si jc = — , demostrar que N (jc,-jc)2 = N a^-jcN jc,-
í=i i=i i=i
VI.
Qj Calcular los valores de las siguientes sumas:
©
a)
I3" « 2y
*=i *=i
Encontrar en términos de n el valor de:
a)
b)
c)
V< l i l l
¿Jk{k+\) 1.2 ' 2.3 h(h + 1)
V< 1 11 1
¿-t (fc + l)(fc + 2) 2.3 ' 3.4 (« + 1)(h + 2)
n
*=i
n
V 1
<> I
n
5
3*"'
*=1
fl
d) Y(2*_1+3*_l)
*=i
k=i ' " k=l
n
fa) Si I I a, = a,.a2-fl3■■•<!„.evaluar
i=i
a) JJ* b) ppi+1>
í=i í=i
o TT-Sl d) fía—l-
2>
i=i
528
Eduardo Espinoza Ramos
n
\4J Si I I a, = atja2-a3... an' pruébese que:
1=1
n n 2n+l
.) u^'f U'>2 -> ri(i-F,=íTí
í=l i=l *=2
n n «
¡=i i=i /=]
41
(5) Obtenga la suma de \ (3/3i-l -3/3/+ 2)
i=i
10 12
(?) Si V(A)t-B) = 22 y V (Ak-—B) = 62, Hallar A + B
*=0 *=3
(7) Sí V (i2----) = 72. Hallar el valor den
3 3
i=i
3 3
(?) Si V(ai + ¿) = 7 y V(ai+í>) = 20.Hallara-k. '
l=-l 1=1
(?) Determinar a y b sí: 2_. (ak+b) = l0 y V" (ai + b) = 14
*=o ¿=i
(jo) Sean A y B números enteros positivos tales que sí:
A B
V (i2- — --) = 1944 y V(2i-1) = 1024. Hallar A + B
i=i i=i
(ll) Demostrar los siguientes ejercicios:
n n n n
a) fJ[/(or=[fJ/(or b> f|c/(o=cn^J/(i)
i=i i=i i=i i=i
Inducción Matemática 529
n+1 n n n n
c) ]^[/(0 = /(n + l).p[/(í) d) fj/(0^(i) = fj/(ixf[*(0
¡=1 i=] í=l i=l i=l
■, - • - /(0>
i=i /=i
n n
g) £logfc/(/) = logfc(P[/(/))
5.19. DIVISIBILIDAD EN Z.-
5.19.1. NÚMEROS PRIMOS Y COMPUESTOS.-
Un número entero "a" es múltiplo de otro número entero "b" si existe un número
entero "c" tal que a = b.c, de donde se dice que b y c son factores o divisores de
"a" y que "a" e s múltiplo de b y c.
Ejemplo.- Como 3 x 5 = 15, el número 3 es un factor o divisor de 15 y el 15
es un múltiplo de 3.
También 5 s un factor o divisor de 15 y el 15 es un múltiplo de 5.
El número 15 también tiene otros factores o divisores, por ejemplo -3 y -5
puesto que (-3)(5) =15.
MOTACIÓN.- Usaremos el símbolo b\a para indicar que "b" es un factor o
divisor de "a".
Si b no es un factor de "a" escribiremos bjfa .
i) DEFINICIÓN.- Un número entero diferente de cero y de uno, es un
número primo si tiene únicamente dos divisores; la
unidad y al mismo número.
Ejemplos.-
flj 5 es número primo, porque sus únicos divisores son 1 y 5.
530
Eduardo Espinoza Ramos
{2J 11 es número primo, porque sus únicos divisores son 1 y 11.
ii) DEFINICIÓN.- Un número entero es compuesto si tiene más de dos
divisores.
Ejemplos.-
(V) 4 es un número compuesto, puesto que tiene como divisores a 1, 2 y 4.
(¿) 6 es un número compuesto, puesto que tiene como divisores a
1,2, 3 y 6.
{3J 8 es un número compuesto, puesto que tiene como divisores a
1,2, 4 y 8.
iii) DEFINICIÓN.- Sean a * 0. a e Z, el número a "divide" al número b y
escribiremos así:
a\b <=> 3ce Z/b = a.c
NOTA.- rí) a\b significa a*0, a divide a b.
(Q Caso contrario ajfb
\3J Si: a\b diremos "a número factor de b" o "a es un
divisor de b" o " b es divisible por a".
Ejemplo.- (Y) 31-12 puesto que existe c = -4e Z tal que -12 = (-4).3
(2) 5 I 15 puesto que existe c = 3 e Z tal que 15 = 5(3).
(^ 3/l 6 puesto que no existe c e Z tal que 16 = 3c
(3c = M*Z).
Ejemplos.- (T) 1 | a, VaeZ, puesto que existe c = a/a = a.l.
(2) a I a, V a * 0, a e Z, puesto que existe c = 1 / a = a. 1.
(3) a I a, V a * 0, a e Z, puesto que existe c = 0 / 0 = a.0.
Inducción Matemática
531
5.19.2. TEOREMA.-
mQ Si a I b y c e Z entonces a | be.
Demostración
lro. a | b
hipótesis
lro. y definición iii)
(propiedad en R)
(propiedad asociativa)
2do. 3 k e Z / b = ka
3ro. V c e Z / be = (ka) c
4to. be = a(kc), V c e Z
5to. Sea A, = kc e Z entonces be = Xa
6to. a | be Sto. definición iii)
^) a | b a b | c entonces a | c
Demostración
lro. a | b a a | c
2do. Btj.^eZ I b = ak¡ a c = ak2
3ro. b + c = akx + ak2 = a^ +k2)
b + c = ak
5to. a | b + c,
f3) a | b a a | c entonces a | bx + cy, V x,y e Z
Se deja como ejercicio.
Cí) a I b a b | a entonces a = ± b
Se deja como ejercicio.
CS) a,beZ+ a a|b entonces a<b
Se deja como ejercicio.
4to. Sea k = kx+k2e.Z
hipótesis
lro. y definición iii)
2do. propiedad distributiva
4to. definición iii)
532
Eduardo Espinoza Ramos
5.19.3. TEOREMA.- (ALGORITMO DE LA DIVISIÓN O TEOREMA
FUNDAMENTAL DE LA DIVISIÓN)
Dado a, b e Z, con b *■ 0 entonces 3 q, r e Z, tales que a = bq + r, con
0<r<|b|.
Demostración
lercaso: Si b>0
(Y) Sea A = {a-bx/xe Z a a-bx >0}, construcción.
(i) A * <¡>, pues si a > 0 a x = 0 de donde a - bx = a > 0 entonces a e A
Sia<0 => -a>0 y además b>0 por hipótesis
.*. 3jteZ+/-a<bx (propiedad Arquimediana)
=> 3 xeZ+/ a>-bx => a>b(-x)
entonces 3 jce Z+ / a-b(-x)>0 =» 3a-b(-x)e A =* A*0
(D Entonces AcN a A*ty de(l)y(2)
QQ 3 r = ler elemento de A (del 3) y propiedad del buen orden en N.
\SJ re A, luego r = a-bx0 para algún *0eA (definición de A)
fó) 3x0,reZ / a = bxQ + r, con r>0 (pues re AcN) falta demostrar
que r < b, por contradicción.
\TJ Supongamos que r > b (hipótesis auxiliar)
(D r = a-bx0>b de 5) y 7)
(9) r-b = a-bx0-b>0 (restandob)
(w) r-b = a-b(x0 + l)>0, luego r-be A (definición de A)
(ll) Pero r - b < r (pues b>0) a r-beA entonces r no es el ler
elemento de A =* II <= (4)
Inducción Matemática
533
ni) Luego debe cumplirse que r<b dell)y7)
13) Así dados a,beZ, b * 0, 3q = x0, reZ tal que a = bq + r con
0<r<b de 6) y 12)
2do. Caso.- Si b<0
(l4) Si b < 0 entonces -b > 0 (propiedad de números reales)
(is) 3q, re Z/a = (-b)q + r conO<r<-b (parte lercaso)
(íó) 3 -q, r e Z / a = b(-q) + r con 0 < r < | b |
17) Dados a, b e Z con b * 0, 3q, reZ/a-bq + r como 0 < r < | b | de
13) y 16) falta probar la unicidad de q y r.
18; Suponiendo que existen otros q1,rie Z tal que a=bqx+ r, con
0 < r, < | b | y además supongamos que rx>r (hipótesis auxiliar).
Entonces tenemos: a = bq + r = bqx + rx de 17) y de la hipótesis auxiliar
b{q -ql) = rl-r>0 (restando) => b | r, - r definición iii)
=* I b 11 r\ - r (propiedad de la división) => | b \ < r, - r ... (a)
de 18) => 0<r,-r<|fc|-r<|¿>| (pues r>0)
=> rx-r<\b\ ...(p) =>//<= (a)
debe ser r, = r, como b(q -ql) = rl-r = 0 => q = qx
OBSERVACIÓN.- Si en el teorema anterior r = 0, se tiene a = bq, en este
caso se dice que la división es exacta, y también se dice
que no hay residuo y además rminimo=l, rmiximo =b-\
NOTA.- (^ Si a = bq, si y solo si b | a si y solo si r = 0.
(2) S¡ r * 0, a = bq + r con 0 < r < b => b\a
534
Eduardo Espinoza Ramos
5.20. MÁXIMO COMÚN DIVISOR: M.C.D.-
Los divisores comunes de varios números son los números que dividen exactamente a
todos, es decir: un número n > 1 es divisor común de M y N si n divide a M y también n
divide a N.
Ejemplo.- Hallar los divisores de 28 y 36 por separado, es decir:
Número
28
36
Divisores
2,4,7,14,28
2,4,6,9,12,18,36
Los divisores comunes simultáneos son 2 y 4
Luego el máximo común divisor de 28 y 36 es 4, es decir que es el mayor de los divisores
comunes.
5.20.1. DEFINICIÓN.- Sean a, b e Z no nulos simultáneamente.
El número D > 0 se llama máximo común divisor (D = (ab)) si y solo si D
satisface las propiedades:
i) D|a a D|b
ii) d | a a d | b entonces d | D : d = algún número.
NOTA.- (I) (0,0) = 0
@) Si D existe =^ D es único es decir:
Si D = (a,b) y Dt=(a,b) entonces
(D\a y D\b =>D|D,
\Dx\a >>D,|í> => DX\D
entonces D, = ±D
D¡=D (pues D > 0)
NOTA.-
Ejemplo.
Máximo común divisor = M.C.D. de a y b = (a,b)
(8,12) = 4
Inducción Matemática
535
5.20.2. LEMA1.- (a,b) = (b,a)
Demostración
lro. Sean (a,b) = D y (b,á) = Dx (construcción)
2do. D | a a D | b de lro y definición de M.C.D.
3ro. D | b a D | a de 2do y tautología
4to. D | (b,a) es decir D \ £>, condición ii) de M.C.D.
5to. D,|í> a £>, | a de lro. definición M.C.D.
6to. Dl\a a D, | b de 5to y tautología.
7mo. Dj | (a,b) es decir D¡ \ D de 6to y condición ii) de M.C.D.
8vo. D = Dl de 4to. y 7mo.
5.20.3. LEMA 2.- (a,b) = (a,-b)
Demostración
La demostración es similar al lema 1, se deja como ejercicio.
5.20.4. TEOREMA.- Sean a, b en Z no ceros simultáneamente entonces Bn^/rioen
Z/ D = n0a+m0b; D = (a,b)
Demostración ,
lro. Sean a y b enteros positivos (por el lema anterior, siempre se puede tener
a y b enteros positivos).
2do. Sea A={an + bm/n, meZ a an + bm>0} (construcción)
3ro. A c N (de la definición de A en 2do)
4to. A ^ <{) hasta considerar a + b e A
5to. 3 D, =an0 +bmQ, 1er elemento de A de 3er y 4to y axioma del buen
orden.
536
Eduardo Espinoza Ramos
6to. D = (a,b) hipótesis
7mo. D | a a D | b 6 to definición de M.C.D.
8vo. D | an0 + bm^ 7mo y propiedad de la divisibilidad
9no. D | D, 5to y 8vo.
Probaremos que D, | D por contradicción
lOmo. Suponiendo que d\d (hipótesis auxiliar)
llvo. a = Dlq + r con 0<r<D, (teorema de la división)
12vo. r = a-D1q = a-(an0+bmQ)q 8voyllvo
13vo. r = a(l-qn0) + b(-qmQ) = an'+bm' 12vo
14vo. r € A (13vo y 4to y definición de A en 2do)
15vo. r>Di (D, es 1er elemento de A en 5to)
de donde =>//<= llvoyl5vo
16vo. Luego debe cumplirse D, \b de lOmo y 15vo
17vo. En la misma forma D, | b (repetir los pasos 11 vo al 16vo)
18vo. D, | (a,b) de 16vo y 17vo y condición ii) de M.C.D.
19mo. D,|D 18voy6to
20vo. D = D¡ es decir: D = an0 + bm^
COROLARIO 1.- D = el M.C.D. de a y b es el menor entero positivo de la
forma an + bm, con n,m € Z.
Demostración
Es inmediato del 5to paso del teorema anterior
Inducción Matemática
537
COROLARIO 2.- Si m > 0 entonces (ma,mb) = m(a,b)
Demostración
Aplicando el corolario (1) se tiene:
D - (ma, mb) -(ma )n0 + (mb)mQ = m(an0 + bm^)
= m(a,b) por el corolario 1
.\ (ma,mb) = m(a,b)
COROLARIO 3.- SiD>0AD|a a D I b entonces: (—,—) = — (a, b)
D D D
Demostración
lro. D | a a D | b (hipótesis)
2do. 3 x, yeZ/a = Dx; b = Dy lro y definición iii)
3ro. (a,b) = (Dx,Dy) = D(x,y) Corolario 2
4to. x = —, v = — de 2do.
D D
5to. ( jc, y) =—(a, b) de 3ro.
n V\ 1
6to. (—,—) =—(a,b) de 4to y 5to
D D D
5.20.5. DEFINICIÓN.- Sean a, b e Z no ceros simultáneamente: a y b son "primos
entre si" o "coprimos" si y solo si (a,b) = 1.
Ejemplo.- (4,15) = 1 entonces 4 y 15 son primos entre si, además 4 y 30 no
son primos entre si puesto que (4,30) * 1
5.20.6. DEFINICIÓN.- o,,o2 an e Z son primos entre sí, sí y sólo si
(fl1,fl2....,ÍJn) = l
538
Eduardo Espinoza Ramos
5.20.7. DEFINICIÓN.-
o,,fl2 a„ son primos entre si 2 a 2 si y solo si (a¡.aj) = 1.
Vi*j
Ejemplo.- 4, 10, 15 son primos entre si puesto que (4,10,15) = 1, pero 4, 10,
15 no son primos entre si 2 a 2 puesto que (4,10) *■ 1, (10,15) * 1
Ejemplo.- 4, 9, 5 y 77 son primos entre si 2 a 2.
5.21. LEMA.-
Si a = bq + r, entonces (a.b) = (b,r)
Demostración
lro. a = br + r
2do. Sean D = (a,b), D, = (b, r)
3ro. D|a a D|b
4to. D|b a D|r
5to. D | D,
6to. D, | b a D, | r
7mo. Dl\a a D, | b
8vo. D, | D
9no. D = DX
lOmo. Luego (a,b) = (b,r)
Ejemplo.- Calcular (1348,72)
hipótesis
notación
2do definición M.C.D.
(combinación a|b a a|c => a|bx + cy
de lro y teorema 5.20.4)
4to y 2do y definición M.C.D.
2do y definición M.C.D.
(igual que el 4to paso)
7mo y 2do definición M.C.D.
5to y 8vo puesto que D, D, e Z+
2do y 9no.
Solución
Inducción Matemática
539
1348
72
| 72
18
628
576
.-. 1348 = 72x18 + 52
(1348,72) = (72,52) = 4
52
5.22. MÍNIMO COMÚN MÚLTIPLO.-
5.22.1. DEFINICIÓN.- Sean a, b e Z no nulos, M > 0. M es el mínimo común
múltiplo de a y b denotado por M = [a,b] si y solo si
satisface las propiedades.
i) a | M y b | M ii) a|myb|m=>M|m
OBSERVACIÓN.- Si existe M = [a.b] => M es único.
En efecto: Si M = [a,b] y Mt=[a,b]
.j\M a b\M M.\M
Entonces < . . => . => M = M,
u
i\My a fc|A/, A/|M,
NOTACIÓN.-
(1) M = [a,b] = es el mínimo común múltiplo de a y b.
Q2¡) M = [o,,a2 an] es el mínimo común múltiplo de al,a2,—,an .
Ejemplo.- [8.12] = 24
5.22.2. TEOREMA.-
(Y) Si bes un múltiplo de ai,a2,. -,an , entonces [a1,a2,...,an]\b
(2) (a,b) [a.b] = | ab |, V a,b e Z
(5) [ka,kb] = k[a,b], Vfc€Z+
540
Eduardo Espinoza Ramos
a fc, 1
(4) Si D|a a D|b entonces [—,— ] = — [a,b], D>0.
Demostración
Queda como ejercicio.
5.23. REGLA PARA AVERIGUAR SI UN NUMERO DADO ES PRIMO.
La forma práctica para saber si un número es primo es la siguiente:
lro. Se extrae la raíz cuadrada del número dado, tomando solo la parte entera.
2do. Se divide el número dado entre todos los números primos menores o iguales a la
raíz entera.
3ro. Si todos los divisores efectuadas son inexactas, el número dado es primo.
Ejemplo.- Averiguar si los números dados son primos.
© 97
Solución
lro. Sacamos la raíz cuadrada v97 = 9
2do. Los números primos menores que 9 son: 2, 3, 5, 7 y dividimos:
97 12 97 13 97 15 97 17
17 48 7 32 , 47 19 , 27 13
112 6
3ro. Como todas las divisiones son inexactas entonces el número 97 es primo
© 149
Solución
lro. Sacamos la raíz cuadrada: >/94 = 12
2do. Los números primos menores que 12 son: 2, 3,5,7,11 y dividimos así:
Inducción Matemática
541
149 |2
1 74
149
29
2
|3
49
149 |5
49 29
4
149 |7
2 21
149
39
6
1 11
13
3ro. Como todas las divisiones son inexactas, entonces el número 149 es primo.
5.24. CRIBA DE ERASTOSTENES.-
Es una manera de formar la tabla de los números primos que no son mayores que 100.
En la tabla suprimimos el 1 porque no es primo.
Se toma el 2 el primer primo (porque es divisible por la unidad y por si mismo).
Se suprime en la tabla todos los múltiplos de 2 excepto el 2.
De los que no hemos suprimido, el primer número es 3 que es primo.
Suprimimos en la tabla todos los múltiplos de 3 excepto el mismo 3.
El primer número no suprimido es 5 que también es primo.
Suprimimos en la tabla todos los múltiplos de 5 excepto el mismo 5 y así
sucesivamente.
Todos los números no suprimidos serán primos.
542
Eduardo Espinoza Ramos
5.25. EJERCICIOS PROPUESTOS.-
(\\ Demostrar que si a y b son enteros positivos tales que a | b y b | a, entonces a = b.
\l) Si a. b e Z, Demostrar que: sia|byb|a => b = ±a
\3\ Demostrar que si a, b e Z, entonces a | bx + cy
(4) Si a 11 entonces a = ± 1
(5) Si a, b e Z, entonces si a | b <=> |a|||b|
(ó) Si a I b.c => a 11 b I c, para a, b, c e Z
(7) Si c I ab y (b,c) = 1, entonces c | a
QQ Si (a,m) = (b,m) = 1, entonces (ab,m) = 1
^n Demostrar que si ac | be entonces a | b
(10) Dado a I b y c | d. probar que ac | bd
(11) Demostrar que: Si b|c y (a,c) = l, entonces (a,b)=l.
(12) Dado que (a,4) = 2 y (b,4) = 2 probar que (a + b, 4) = 2.
Q3) Probar que si (b.c) = 1 y r | b entonces (r,c) = 1.
(14) Demostrar que: si b | c, entonces (a,b) = (a + c, b)
(i?) Demostrar que: si(a,c)=l, entonces (a,b) = (a, be)
(lé) Demostrar que: si a | c y b|c y (a,b)=l, entonces ab | c
(l?) Demostrar que: si (b,c)=l, entonces (a,bc) = (a,b).(a,c).
(l8) Demostrar que: si (a,bc) = 1 entonces (a,b) = 1 y (a,c) = 1.
(w Probar que (a2,b2) = c2 si (a,b) = c.
(w) Probar que: si (a,b) = (a,c), entonces {a2,b2) = (a2,c2)
Inducción Matemática
543
(21) Probar que: si (a.b) = (a,c) entonces (a.b) = (a,b,c)
(22) Probar que: si o3 | c3, entonces a | c
(23) Probar que: si b\a2-l, entonces fc|a4-l
(24) Probar que si a y b son enteros positivos que satisfacen (a,b) = [a,b], entonces a = b
(25) Encontrar los enteros positivos a y b que satisfacen simultáneamente las ecuaciones
(a,b) = 10 y [a.b] = 100, encontrar todas las soluciones.
5.26. LA FUNCIÓN FACTORIAL.-
a) DEFINICIÓN.- La función factorial es la aplicación /: N0 -» N definida por:
/(0) = 1
/(D = l
/(/i + 1) = (/i + 1)/(/i) si h>l
el símbolo característico de la función factorial es !, en lugar de f escribiremos h!
para indicar f(h) por lo tanto:
0!=1
1!=1
(h + l))=(h + l)Ji\
La expresión h! se lee "factorial de h" ó "h factorial".
La función factorial no es invectiva, puesto que: 0*1 y 0! = 1!
b) PROPIEDADES DEL FACTORIAL.-
n
(T) V n e N, n > 2, el factorial de n es dado por: n\ = 1.2.3...n = I I«
1=1
^) (n + 1)! = n! (n + 1) Propiedad degradativa
@ Sí a! = b! => a = b, a,b e N
544
Eduardo Espinoza Ramos
(4) Sí a! = 1 => a = 1 v a = O
© -5- = l L_,neN
^ (n + l)! n! (n + l)!
©
12 3 n , 1
+ —+ — + ...+ = 1 —
2! 3! 4! (n + l)! (n + l)!
n
V / 1
También se expresa: > = 1
Zw(i + 1)! (n + l)!
1=1
\7J Sean nü, n e N, entonces: nü = n(n - 2)!! Propiedad degradativa de los
semifactoriales.
^8) Producto de semifactoriales y el factorial:
a) (2n)!!=2"n!
b) (2n + l)!!=(2n + 1)!,ne N
2"(n)!
Ejemplo.- Verificar la igualdad:
1 1
(n + l)! n! (n + l)!
Solución
1
1
n + l
1
n + l
1
n + 1-1
n! (n + l)! n!(n + l) (n + l)! (n + l)! (n + l)! (n + l)! (n + l)!
1 1
n! (n + l)! (n + l)!
5.27. NÚMEROS COMBINATORIOS.-
a) DEFINICIÓN.- Consideremos n y k números enteros positivos tales que n > k,
llamaremos números combinatorios n sobre k, al símbolo
definido por:
Inducción Matemática
543
Los elementos de un número combinatorio se Llaman numerador y denominador.
fo\
Ejemplo.'
v5.
51.6.7.8.9 6.7.8.9
= 7.2.9=126
5!(9-5)! 5!.4! 1.2.3.4
b) CASOS ESPECIALES DE LOS NÚMEROS COMBINATORIOS.-
fn\
© <°
®
0!
0!
v°,
/^
0!(0-0!)! 0!.0!
= 1
V° J
0!(«-0)! n\
©
©
£)
V
n
\ i
n\ =(b-I)?ii
l!(n-l)! (»-!)!
■ = ■
= ^>1
n!.0! w!
©
r«+n
n
\ j
(n + l)\ (« + !)! «!(« + !)
= « + 1
n\
n!(n + l-n)! «!
c) PROPIEDADES DE LOS NÚMEROS COMBINATORIOS.-
Si dos números combinatorios de igual numerador son tales que b auna de aas
denominadores coinciden con aquel, se llama números combinatorios de ordenes
complementarios.
Ejemplos.- y son números combinatorios de ordenes cotnpkmmarvm
(V) Dos números combinatorios de ordenes complementarias son iguales.
m r n ^
n-k
En efecto:
fn^
ni
n\
m
n-k
k) k!(n-k)l («-*)!*!
(2) La suma de dos números combinatorios es en general un número combinatorio,
pero si tiene igual numerador y denominador consecutivos vale la fórmula
r«-r
k-\
V J
+
'/I-f
k
=
V
k
\ 1
En efecto:
546
Eduardo Espinoza Ramos
¿fc-1
fn-l
(«-D! + («-D!
(Jfc-1) !(«-*)! kl{n-l-k)\
k(n-l)l (n-k).(n-l)\ _ k.(n-l)\ (n-k).(n-iy.
(k-iy.k(n-ky kKn-k).(n-l-ky k\.(n-k)l *!.(«-*)!
(k + n-k).{n-l)l n.(n-l)\ n\
'n^
*!(«-*)! *!.(«-*:)! *!(«-*:)!
v*,
Ejemplo.* Si
'32^
x
\ i
( y¿ \
* + 18
, Hallar el valor de E =
/■v\
4 ,
v5,
'32 ^
x
\ i
32
jc+18
por lo tanto x = 7 entonces
7^1 (1^
Solución
de donde x + (x + 18) = 32
v5,
7! 7!
+ -
(7-4)!4! (7-5)!5!
l^ + ^L=5^Z+5^ =5.7 + ^ = 35 + 21 = 56
3!.4! 2!.5! 6 2.5! 2
5.28. PRINCIPALES PROPIEDADES DE LOS COEFICIENTES
BINOMIALES.-
fn^
\ )
® U='-neN ©
f5J Propiedad de los coeficientes binomiales complementarios:
= 0 sí n, k e N, n < k
= n, ne R
r„\
v*/
n-k
,n> k, n,ke N
Inducción Matemática
547
k + l
(n + l
k + l
, si k e N, n e R
mí) Suma de pares de coeficientes binomiales:
(jj Suma de los coeficientes binomiales de inferiores iguales y superiores decrecientes.
n
V )
+
+
rm-2y
n
K )
+ ...+
V
n
K )
=
'm + V
; ne N
QQ Suma equivalente en la versión de complemento:
' m ^
m — n
m-\ }
m-n-l
m-2 ^\
m-n-2
+ ...+
fn\ (m + \\
0,
n + l
ne N
®
®
m
0
V )
+
1
^ )
+
2
+ ...+
Z1,
= 2",meN
'i>T
1
V )
-
,3>
+
5
-
'i>T
7
k )
+ ...±
--!>
= 2m ', m e N, pares
+
,2,
+
4
+
6
+...+
r m >
w-1
>m-l
= 2 , me N, impares
'nC
2
\ )
+
m
3
-
4
^ )
+ ...±
'in
w Y «
= 0, me N
w Y M
w Y n
+ ...+
w Y «
' m + n^
{Pk°) {P-lkl) {P-2k2) {°kP)
Igualdad de coeficientes binomiales:
donde m. n, p e N
fa\ fn\
,b,
P
a — p a b=q , b,qeN
v
a = p a b + q=a = p, a,b,p,qe N
Propiedades degradatividad de los coeficientes binomiales:
, degraden el superior e inferior, n e R, k e N
rn\
v*/
n(n-\\
k\k-l
548
Eduardo Espinazo Ramos
'n^
v*,
k
n-k
fn\ n-(k-\)( n '
, degrada únicamente el superior, n e R, k e N
k-\
degrada únicamente el inferior, n e R, k e N
5.29. EL TRIANGULO DE BLAISE PASCAL O DE TARTAGLIA.-
1
1
1
9
10
11 55
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
16 15 20 15 6 1
7 21 35 35 21 7 1
8 28 56 70 56 28 8 1
36 84 126 126 84 36 9
45 120 210 252 210 120 45 10
165 330 462 462 330 165 55
11
Los elementos equidistantes de cada fila son iguales
5.30. POTENCIAS DE UN BINOMIO.-
a) BINOMIO DE NEWTON.- Una aplicación de los números combinatorios se
presenta en el desarrollo de la potencia de un binomio
con exponente natural que se conoce con el nombre de binomio de Newton que está
dado por:
(a + b)" =
[:}■"♦
i1)
n\"-2b2+...+
2
\ )
Cí-
mediante el símbolo de la sumatoria, se expresa:
El binomio de Newton se demuestra por inducción matemática:
Inducción Matemática
549
i) Para n = 1 se tiene: a + b= 2_\ Ia
k=0 ^ >
1 L.-v-í1 1
.o.
a +
al~lb = a + b
ü) Para n = h se tiene: (íJ + ¿>)n=Vj \ah~kbk , es verdadero por la hipótesis
inductiva.
iii)
Para n = h + 1, demostraremos que: (a + b)h+l = ^
/i + l
Uh*U-kbk
k=0 v /
En efecto se tiene:
(a + b)h+x=(a + b)\a + b) = (^r\¡''-kbk)(a + b)
■í:y-*íí:V"'*íí/.,)
i *=i
a b
*=i v. i
(u\
aM +
0
v /
0, + P
v ° ,
M
fl"+,+
h
\ i
ft*+'+^[|." 1+
\a b
k-\ v
k=í v ) v y
0 ,
„-+^+n
a b +
*=i v /
>+l
I. , 1 \
ah+[~kbk (propiedades de N° combinatorios)
i=o^ i
550
Eduardo Espinoza Ramos
OBSERVACIÓN.- En el desarrollo del binomio de Newton se tiene:
(a
0
V )
a" +
1
v /
a"-[b + ...+
\a"'kbk +...+
n
b" donde
se tiene:
0
v /
1 ,
KkJ
es el coeficiente del primer término
es el coeficiente del segundo término
es el coeficiente del k + 1, término
Tk+l =
(n)
a"-kbk
de donde él término que ocupa el lugar k + 1 es:
esta fórmula nos permite obtener un término cualquiera sin necesidad de conocer los
anteriores.
Ejemplo.-
Hallar el coeficiente del término independiente de x en el desarrollo de (x —-) ~
x
Solución
** ..96-12*
(A8
Él término independiente corresponde a 96 - 12k = 0 de donde k = 8 luego el
coeficiente es: (-1)
fl2\
= (-!)'
fX1\
,8 ,
12!
8!(12-8)!
= 495
\2) Hallar el desarrollo del binomio (x2y + —)5
Inducción Matemática
551
Solución
2 a
r5N
íx<v?+\%2yf¿) +
c^\
2
v i
(A2V)3(^ +
Í5
V
A
y
<*2y>2(-
A'
2 v)(-)4 +
X
)3+
'5N
,5,
r
= vlüy5 +10a-7 v4 + 40* V +80A72 +mx-2y + 32x~5
(¿) Encuéntrese él término que contiene xl2y2 en el desarrollo de: (x2y -)8
y
Solución
12 ..2
Suponiendo que k + 1 es él término que contiene a x y~ esto es:
^*+i -
x2y)"~k(-y~2)k para n = 8
**+i _
rjV2»M(-y-2)' =
'8^
pea*-*) y8-3* (_d*
Luego 2(8 - k) = 12 de donde k = 2
Por lo tanto *12>'2 es el tercer término y su valor es: ¡ \>c]2y2 = 2%xny~
5.31. EJERCICIOS PROPUESTOS.-
© » ^=5 +
(#i + 2)! _e . (#» + 12)!
(#i + ll)!'
para n e N, encontrar el valor de n.
®
_. . (#» + 2)! 72#»!
Resolver = 0
í/7-2)' (#7-2)!
552
Eduardo Espinazo Ramos
©
©
©
©
©
©
©
®
Demostrar que:
3n! n! _ 3
(n-3)! (n-2)! (n-1)!
Demostrar que: (n + l)[n.n! + (2n - l).(n - 1)! + (n - l).(n - 2)!] = (n + 2)!
„, (w + 1)! m\ (w-1)! r „•>.,,„ .
Si - + + - — = 6 y n = 2m~+l. Hallar el valor de
m\ (w-2)! (w-2)!
'n^
m
\ J
Sí
Si
Si
Si
Si
v1/
+ 14
2M3
+ 24
= 256 . Hallar el valor de n.
M + l
m + l
n + H
m
= 1 y
M + l
V m l
m + 1
m-\
= —, Hallar m.n
3
'n^
Kmj
'22^
.2/1,
m + l
y 4
m-\
m
v /
= 5
Hallar m + n
21 ^
2«-l
11
'wi + 3^
m + l\
2
2 , „2
= m + 2, Hallar el valor de m +n
'n\ _M
K5,
= 8
18 ^
n + 2
= 0, para m * 2. Hallar el valor de m + n
( 80 W80 1
3/^-4
(12) Si
Si n e N y
f 50 W 50 ^
2«-l
, Hallar el valor de A = n -5
JC--20
118-14a
Sean A =
n-2
r2n-n
n-l
Hallar el producto de todos los posibles valores enteros de x.
r2«-3^
M-l
(14) Sea x e N tal que
y B =
40 W 40 ^
f2#i-3^ A 132 „ „
tal que — = . Hallar n
M B 35
a~+15jc-10
5.v + 6
, entonces hallar el valor de A =
v3.
Inducción Matemática
553
MIS) Demostrar que:
n+l
A=0
'«+1^
V /
=1-1)
,1+1
( n ^
n + l
, V neZ*
16
Determinar el valor de "n" sí: ^ + l)!.(w + 9)! _ 2g,
(n + 10)!+(«+9)!
Rpta. n= 18
fl7^
®
r , , 2(2w + 10n + 12).(2n + 5)!(2w + 4)!
Calcular n en: — = 86!
(2« + 5)! -(2n + 4)!
íl20'+lV-5'" i.
Calcular a y b en ._..,." = (a!\)h
(120!-!)!
(Í9) Calcular m en 1!.22 + 2!.32+3!.42+... + 20L212 =/n!-2!
£5) Calcular n en: (^ + _íii_ + i^)L + ... + ü = 209
v~,/ «! (m-1)! («-2)! 1!
® Calcularn en: ("~3)!(/1~4)! =5040(/i2-8/1 + 15)
(«-3)! -(«-4)!
Rpta. n = 40
Rpta. a = 5, b = 2
Rpta. m = 23
Rpta. n = 19
Rpta. n= 13
(22) Calcular n y m en la relación:
12
m\n\
m\ +n\ n2-m2+3
sí m!.n = n!
©Resolver [| x |]!+-^- = 30, xeR-(O)
$) Calcular "n" en 3(3«2+10n + 8)(3« + 5)!(3,, + 4)! = 108!
^ (3« + 5)! -(3n + 4)!
Rpta. n = 34
\15) Simplificar
2"[(2/Q!]2
(4n)!!.(2n-l)ü
Rpta. n!
(2ó) Sí (x - 3)! = 1, cuáles son los posibles valores que puede tomar x. Rpta. x - 3 o x=4
(27) Si se cumple que (a - 2)! = 6 entonces el valor de a es.
Rpta. a = 5
554
Eduardo Espinoza Ramos
©Calcular el valor de "x" sí: (* 5)!(* 6>! =720(^-12^ + 35) Rpta. x = 14
(a-5)! -U-6)!
(29) Demostrar que: N
ír(Á + k\ (n + k+l\
k + l
para todo entero no negativo n y k.
I „„ /T„4 „x9
(30) Hallar el coeficiente de x~ en (2a: —x)
fol) Hallar el coeficiente de a-14 en (x3+—)'
(32) Hallar el coeficiente de y en (—-—^—)
7 _ ,_1 2r,i4
4y3 3
ft3J Demuéstrese que NI =2"
KM) Desarrolle, usando el teorema del binomio.
a) UV-)4
x y
c) (^-1+2>>-2)6
d) <.^-+y)5
2x
e) (jr-jt + 1)4
I) (^-f)6
3 2a:
h) (^_£_)4
a a:
0 (^f + -V)4
a:2 2c2
j) (3a-2+2)6
k) (^-2)5
1) (yfc-l[y?
Inducción Matemática
555
fas) Proporciónese el término que contiene a *8 en el desarrollo de (2v3 —=)5
V-v
(3<n Proporciónese el término que contiene y1 en el desarrollo de (x+y)u
(37) Proporciónese el término que contiene a x5 como factor en el desarrollo de (v2 -x)
Encuéntrese el término que contiene x ' v" en el desarrollo de (x'\ -)
y
[39) Determine él término que no tiene factor a x en el desarrollo de:
a) U2+i)9 b) Cr+-V)3" O (-U-)'2
x
(40) Sean x e y dos números reales positivos, tales que x + y = 3,
X "~
.2,
^
x y~ +
V3,
.2..3
x-y- =120.
Hallar x~ +y~.
^í) El sexto término de (^--2y2)" es 33o*V7 . Hallar (a + n)4
(42) Al desarrollar (x + ay)", en orden decreciente con respecto a las potencias de x, se tiene
el cuarto término igual a 672x6yi, hallar n - a.
Que término del desarrollo de ( ^r)15 est^ formado por potencias iguales a x e y.
y 3x4
M4J Que término del desarrollo de (—- y)18 tiene a x e y con el mismo exponente.
*1
•>
y xr
(4?) Si el quinto término del desarrollo de (2jT——)" es 2640jt18;y12, determinar el
coeficiente del término que contiene a xl .
556
Eduardo Espinoza Ramos
\4b) En el desarrollo del binomio (9.v2 —-)10. Hallar el coeficiente que contiene a x>2.
2*3 , / u2
(47) Hallar el término independiente de x e y en el desarrollo de (——+~^")1
^^ y 4x
Rpta. 495
Hallar el término independiente de x en el desarrollo de ( )9
Rpta. —
18
©Hallar el coeficiente del término central del desarrollo de ( r~—)" , si la parte literal
ya+l x"
de dicho término es x20 y24. Rpta. 70
Números Complejos
557
CAPITULO VI
NÚMEROS COMPLEJOS
6.1. ECUACIONES SIN SOLUCIÓN EN R.-
Consideremos una ecuación sin raíces reales: .v"+2 = 0, es decir:
[xs Rlx2 +2 = O} = 0, esto es debido a que: VxeR,jt2>0, luego
jt+2>0 ,V*e R..
GENERALIZANDO.- Consideremos la ecuación ax2 +bx + c = 0, a*0, con
coeficientes reales, no tiene solución en R. Sí el discriminante
es menor que cero, es decir: b~ -4ac<0 .
Luego para resolver la ecuación ax1 +bx+c = 0, ampliaremos a otro conjunto llamado
el conjunto de los " Números Complejos".
6.2. DEFINICIÓN.-
Llamaremos números complejos a todo par ordenado de números reales el cual
denotaremos por z = (a , b).
Al conjunto de los números complejos denotaremos por:
C = Rx R = l(a,b)/aeR a b eR }
6.3 DEFINICIÓN.-
La parte real de un número complejo es su primera componente y la parte imaginaria es
su segunda componente, luego tanto la parte real como la parte imaginaria de un número
complejo son números reales. Si z = (a,b) es un número complejo, entonces la parte
real de z = (a,b) denotaremos por: Re(z) = a, y la parte imaginaria de z = (a,b)
denotaremos por: Im(z) = b
558
Eduardo Espinoza Ramos
6.4. EL PLANO COMPLEJO.-
©
Entre los números complejos y los puntos del plano cartesiano, existe una
correspondencia biunivoca, de tal manera que todo número complejo z = (a.b) se puede
representar geométricamente por un segmento orientado (flecha), que tiene su origen, en
el origen de coordenadas y su extremo en el punto (a,b).
Z = (a,b)
6.5. DEFINICIÓN
Un número complejo es real, si y sólo si, su parte imaginaria es cero; un número complejo
es imaginario puro, si y sólo si, su parte real es cero. Es decinz = (a,b) un número
complejo es real <-> Im(z) = b = 0
z - (a.b) un número complejo es imaginario puro <-> Re(z) = a = 0
Ejemplo.- Determinar analíticamente y gráficamente los complejos z = (x,y), tal que
verifiquen:
© Re(z) = 5
(5) Re(z)+ Im(z) = 3
(2) Im(z) < 4
©
Solución
Sea z — (x,y) un número complejo, entonces
Re(z) = x. pero como Re(z) = 5, entonces
x = 5. es una recta paralela al eje de ordenadas
que pasa por el punto de abscisa x = 5
-l<Re(z)<l a -1 <Im(z)< 1
Yt
. Re(Z) = 5
Números Complejos
559
\l) Sea z = (x,y) un número complejo entonces
Im(z) = y, pero como Im(z) < 4 entonces
y < 4, que corresponde al semiplano que
contiene al origen , cuyo borde es la recta
de la ecuación y = 4 (ver gráfica ).
^3) Sea z = (x,y) un número complejo de
donde Re(z) = x a Im(z) = y, pero como
Re(z) + Im(z) = 3, entonces x + y = 3,
que nos representa la recta que pasa por
los puntos (3,0), (0,3).
(4) Sea z = (x,y) un número complejo, de
donde Re(z) = x a Im(z) = y pero como
-1 < Re(z) < 1 a -1 < Im(z) < 1 entonces
-1 ¿x <1 a -1< y <1
®
®
©
®
®
®
®
(S)
Y
_4
lm(z) < 4
Re(Z) + lm(z) = 3
6.6. EJERCICIOS PROPUESTOS.
-1
Y"
1
0
-1
1
X
Describir analíticamente y gráficamente las siguientes relaciones:
Re(z) = -3 (2) Im(z) = -2
Re(z) < 0 (£) Im(z) > 0
Re(z) + Im(z) = - 2 (ó) Re(z) - Im(z) = 4
Re(z) = Im(z) (?) 5 Re(z) - 3 Im(z) = 1
-2 < Re(z) < 2 @ -2 < Im(z) < 2
Re(z) + Im(z) < 0 (l2) Re(z) + Im(z) < 1
Re(z) + Im(z) > -2 (Í3) 4 Re(z) - 5 Im(z) < 1
-3 < Re(z) < 2 a -2 < Im(z) < 3
560
Eduardo Espinazo Ramos
(16) -2<Re(z)<2 a -2< Im(z)<2
(n) 2 < Re(z) < 4 a 2 < Im(z) < 4
(li) -6<Re(z)<-2 a -6<Im(z)<-2
(19) -3<Re(z)<5 a -5<Im(z)<-2
(20) -5<Re(z)<-3 a 2 <Im(z)<5
6.7. CERO Y OPUESTO DE UN NUMERO COMPLEJO.-
Un número complejo es cero; si, tanto su parte real, como su parte imaginaria es cero, es
decir: z = (a,b) es un número complejo cero <=>a = ÜA b = 0.
El opuesto de un número complejo z = (a,b) es definido por:
- z = - (a,b) = (-a, -b)
Z = (-a,-b)
Z = (a,b)
6.8. OPERACIONES EN COMPLEJOS.-
a) IGUALDAD DE NÚMEROS COMPLEJOS.-
Dos números complejos son iguales cuando tienen iguales su parte real y su parte
imaginaria, Es decir:
(a,b) = (c.d) <=>a = CAb = d
Ejemplo.- z,=(2,3) y ¿2=(2,3) son iguales (zl - z2)
Números Complejos
561
Ejemplo.- z,=(2.3) y z2 = (3,5) no son iguales (Z|#z2)
Luego: (a,b) *■ (c,d) <=> a * c y/o b * d
b) SUMA DE NÚMEROS COMPLEJOS.-
La suma de dos números complejos, es un número complejo, que tiene por parte real
a la suma de las partes reales de los sumandos y por parte imaginaría a la suma de
las partes imaginarias de las mismas, es decir:
Sí z, ={a,b) y z2 = (c,d) entonces la suma:
z1 + z2=(a + c,b + d)
Ejemplo.- Calcular la suma de (2,4) y (3,5) es decir:
(2,4) + (3,5) = (2 + 3,4 + 5) = (5,8)
c) REPRESENTACIÓN GEOMÉTRICA DE LA SUMA DE DOS NÚMEROS
COMPLEJOS.-
Sean z, =(a.b) y z2 = (c.d) dos números complejos, entonces se tiene:
zi+z2 = (a,b) + (c,d) = (a + c,b + d) = z3
Y'
0
/^^_—-/ Z, = (a,b)
X
d) PROPIEDADES DE LA SUMA DE NÚMEROS COMPLEJOS.-
Sean zl.z2,z3eC, entonces:
P,.- Propiedad de Clausura: zí+z2€lC
P2.- Propiedad Conmutativa: z, + z2 - z2 + Z\
P3 .- Propiedad Asociativa: (z, +z2) + z3 - z¡ +(z2 +z3)
562
Eduardo Espinoza Ramos
P4.- Propiedad de Existencia y Unidad del Neutro Aditivo:
Existe el elemento neutro w e C tal que:
z + w = z, VzeC
P5 .- Propiedad de Existencia del Inverso Aditivo, para cualquier z e C existe otro
elemento que denotaremos por -z, tal que z + (-z) = (0,0).
NOTA.- La demostración de estas propiedades se deja para el lector,
e) SUSTRACCIÓN DE NÚMEROS COMPLEJOS.-
Sean z, = (a, b) y z2 = (c, d) dos números complejos, definimos la diferencia de
z, y z2 por: z, - z2 = zx +(-z2), es decir;
zx -z2 =(a,b)-(c,d) = (a-c,b-d)
Ejemplos.- Efectuar las operaciones indicadas analíticamente y gráficamente.
© (3,4)+ (5,2)
Solución
(3,4) + (5,2) = (3 + 5, 4 + 2) = (8,6)
Y
0
(3,5)_____
__(8,7)
W(5,2)
1
X
© (4,-2) + (2,-4)
Solución
Números Complejos
563
(4.-2) + (2,-4) = (4 + 2, -2 - 4) = (6,-6)
© (6,-2)-(2,-5)
Y'
0
.
V\^-,(4,-1)
(2.-4)"--\¿
"* (6.-6)
X
Solución
(6,-2) - (2,-5) = (6,-2) + (-2,5) = (6 - 2, -2 + 5) = (4,3)
(-2,5) r^
0 (2.3) - (-4,5)
Solución
(2,3) - (-4,5) = (2.3) + (4,-5) = (2 + 4. 3 - 5) = (6,-2)
Y'
0
(2,3)
/ \
/ \
/ \
/ \
f \
\ ^^(6,-2)
\ /
(4,-5)
X
564
Eduardo Espinoza Ramos
f) MULTIPLICACIÓN DE NÚMEROS COMPLEJOS.-
Sean z, = (a,b) y z2 =(c,d) dos números complejos, al producto de z, y z2
definiremos por:
z¡.z2 ~(a,b).(c,d) = (ac-bd,ad +bc)
Ejemplo.- Sean z, = (2,3) y z2 = (1,5)
Luego zvz2 = (2,3).(1,5) = (2-15, 10+3) = (-13,13)
g) PROPIEDADES DE LA MULTIPLICACIÓN DE NÚMEROS COMPLEJOS.-
Sean Zi,z2,z3eC, números complejos, entonces:
P¡.- Propiedad de la Clausura: z, .z2 e C
P2.- Propiedad Conmutativa: Zy.z2 = z2.zx
P3 .- Propiedad Asociativa: (z,.z2).z3 = z¡ -(z2.Zj,)
P4.- Propiedad Distributiva: z, .(z2 + z3) = z{ .z2 + Zi -z3
P5 .- Propiedad de Existencia y unicidad del neutro multiplicativo. Existe un único
número complejo u tal que u.z = z, V z e C siendo u = (1.0)
P6.- Propiedad de Existencia y unicidad del inverso multiplicativo. Para cada
número complejo z* (0,0), 3 aeC tal que, z.a = u siendo a = z"1; u=(l,0)
P-,.- Para z e C, k e R, k.z = k.(a,b) = (ka, kb).
Demostraremos la propiedad Pb, las otras propiedades dejamos como ejercicio para
el lector.
Sea z = (a,b) *(0,0), suponiendo a = (x,y) tal que, z.a = u, siendo u = (1,0), es decir:
(a,b).(x,y) = (1,0). que al efectuar la operación se tiene:
(ax - by, ay + bx) = (1,0), por definición de igualdad tenemos
húmeros Complejos
565
ax —bv = \ a
resolviendo el sistema se tiene: x =
a\ + bx = 0
a2+b2 ' y a2+b2
Observamos que: (a,b) * (0,0) <=> a*0 y/o b*0, entonces a2+b2 *0
por lo tanto:
a = (x, y) = (
a2+b2' a2+b2
-i,3 5
Ejemplo.- Síz = (3,5) => z =(—,-—)
34 34
h) UNIDAD Y RECIPROCO.-
El elemento neutro multiplicativo es la unidad compleja y denotaremos por
u = (1,0) o también 1 = (1,0).
El inverso multiplicativo a de un número complejo z = (a,b) *■ (0,0) se llama
reciproco de z y denotaremos por:
-\ , a -b .
a +b a +b
Observación.- El número complejo (a,0) se identifica con el número real a, y
denotaremos como (a, 0) = a, en forma intercambiable.
i) DIVISIÓN DE DOS NÚMEROS COMPLEJOS.-
Sean z,, z2 e C, siendo z2 * (0,0), la división de z, y z2 definiremos por:
— = z, .z2' de esta definición obtenemos la regla para la división.
Z2
-1 C
Sí z, = (a, b) y z2 = (c,rf)* (0,0), entonces: z2 =(■
„2 . j2 ' „2 , j2;
c +d c +a
ÍL=Zl.z-'=(fli¿,).( c
d ac + bd bc-ad
) — ( í ~ • í ~)
2 , j2 ' 2 , .2; V„2,j2' 2, .2
Luego:
'! _ ac+bd bc—ad
\~í TT'-t 17'
<-2
\-2 , j2 ' 2 , .2'
r +a c +d
566
Eduardo Espinoza Ramos
6.9. UNIDAD IMAGINARIA.
El número complejo imaginario puro de segunda componente igual a 1, se llama unidad
imaginaria y denotamos por: i = (0,1).
OBSERVACIÓN.- La multiplicación de un número complejo real por la unidad
imaginaria permuta las componentes, es decir:
(í>.0).i=(í>,0).(0,l) = (0,í>)
6.10. FORMA STANDAR (RECTANGULAR O BINOMICA) DE LOS
NÚMFROS COMPLEJOS.-
Sea z = (a,b) un número complejo, por definición de suma tenemos :
z = (a,b) = (a,0) + (0,b) = a (1,0) + b (0,1) = a + bi
Luego z = a + bi es la forma estándar (rectangular o binómica) del número complejo z.
6.11. TEOREMA.-j Demostrar que: i2 =-1
Demostración
i2 =ii = (0,l).(0,l) = (-l,0) = -l por lo tanto i2=-l, como i2 =-1
entonces i = v—1
6.12. LA CONJUGACIÓN EN C,
a) DEFINICIÓN.- Llamaremos conjugado de z = a + bi al número complejo a - bi,
al cual representaremos por z = a-bí
b) DEFINICIÓN.- Dos números complejos son conjugados si difieren solamente en
sus partes imaginarias en los signos.
Los números complejos conjugados caracterizan puntos simétricos respecto al
eje real, asi: Si z = a + bi su conjugada es: z = a - bi
Números Complejos
567
Y
0
Z = a + bi
b /i
\ a¡ X
■b ^!z = a-b¡
PROPIEDADES: Sean z,, z2, e C, Entonces:
/>, .- Zi±Z2= Zi ±Z2
P2-" Zl-Z2=Zl-Z2
Pi.- Zl = Zl
/'a-- (iT)"1 =(z,"') , z, *(0.0)
P5.- (ÍL) = ^, z2*(0,0)
z2 z2
6.13. MÓDULO DE UN NÚMERO COMPLEJO.
El módulo de un número complejo z = a + bi es un número real positivo definido por:
Hz|hV«2+*>2
Geométricamente; el módulo de un número complejo z = a + bi, es la longitud del
segmento orientado que representa a z = a + bi
Ejemplo: Sí z = 3 + 4i => ||z|| ^^32+42 =5
a) PROPIEDADES DE LOS NÚMEROS COMPLEJOS
Sean z,, z2, z3 e C, entonces:
P,.- Sí z,* (0,0) =* ||z, ||>0
P2.- Sí || z, ||=0 =* z,=(0,0)
568
Eduardo Espinoza Ramos
P3- Sf || Zl ||=||—z, || = || z, || /»„.- Sí||Zl||2=Zl.Zl
z, „ II z,
Ps- Hz,+Z2llS||z1|| + ||z2|| Pt- H-H'F^. ^2^(0,0)
z2 II z2 II
P, ■- II Zi -z2 II = II Zi II ■ II z2 II P8 ■- Re(z) < II z ||, Im(z) < || z ||
Demostraremos la propiedad Ps, los demás dejamos para el lector:
II z, + z2 ll2 = (Zi + z2)-(Zi + z2) = (Zi +z2)-(zT + Z2)
= Zi-Zi +z,.z2 + z2.z, + z2.z2 =|| z, ||2 +z,.z2 + z7z2 +II z2 II2
= || z, ||2 +2Re(z,.z2)+||z2 ||2 < ||z, ||2 +2||z, ||.||z2 || + ||z2 ||3
-llz,ll2+2||z1||.||z2|| + ||z2||2=(||zI|| + ||z2||)2
Por lo tanto: || z,+z2 ||2<(|| z, || + || z2 ||)2
••• Hz,+Z2ll^l|Zlll + llz2ll
Il2
6.14. EJERCICIOS DESARROLLADOS.
Ql) Hallar los valores de x e y sí: (1 + 2i)x + (3 — 5i)y = 1 - 3/
Solución
Sean z, = l + 2i = (l,2)
z2= 3-5/= (3,-5)
z3=l-3i = (l,-3)
Como (1 + 2i)x + (3 - 5i)y = 1 - 3i, entonces
(l,2)jc + (3,-5)y = (l,-3)
(jc.2jc) + (3y.-5y) = (U-3)
Números Complejos
569
(x + 3y , 2*-5>0 = (l,-3) , por igualdad
Íjc + 3>' = 1 4 5
< resolviendo el sistema se tiene x = , y = —
l2jr-Sy = -3 11 ' 11
(¿) Determinar los números reales a y b sabiendo que: (-1 +/) a + (1 + 2/) b = \
Solución
Sean zx =-l + i = (-l,l)
z2= l + 2i = (l,2)
z3 = i = 1 + 0/ = (1,0)
Como (-l + i)a + (l + 2i)b = 1 , entonces: (-l,l)a + (1,2)¿> = (1,0)
(-a + b . a + 2b) = (1,0) , por igualdad
-a+b=\ . 2 1
, resolviendo el sistema a = — , b = —
a + 2¿>=0 3 3
^3) Expresar cada uno de los siguientes ejercicios como: 1,-1, i, -i
a) i3
Solución
i'3 = 12. / = -/ ,de donde i3 = -/
b) i7
Solución
i1 =(j2)3/ = (-1)3/ = -/ de donde i7 =-/
O i8
Solución
/8=(,-2)4=(-l)4=l , de donde i8 =1
570
Eduardo Espinoza Ramos
d) i14
Solución
i14 =(¿2)7 =(-l)7 =-1, de donde i14 =-1
e) i17
Solución
i" = (i2)8 ./ = (-1)8/ = i , de donde i" = i
(4J Efectuar las siguientes operaciones y el resultado expresar en la forma binómica
a) (5 + 7i) + (8 + 2i)
Solución
(5 + 7i) + (8 + 2i) = (5 + 8) + (7 + 2)i = 13 + 9/
b) (2 + a/3i).(5-6a/3í)
Solución
(2 + n/3i).(5 - 6>/3/) = (2, n/3).(5, -6&)
= (10 + 18.-12n/3 +5n/3) = (28,-7%/3) = 28-7>/3/
(2 + /).(3-2i).(l + 2i)
Solución
(l-O2
(2 + i).(3-2í).(1 + 2i) = (8-i)(1 + 2i) = 10+15i, además (1-i)2 =-2i, luego
(2 + i).(3-2f)-(l + 2i) _ 10 + 15/ _ (10 + 150.(0 _-15 + 10i_ 15
(1-02 -2' (-2i)i
¿4+í9+/16
o)
2-is+i,0-i15
Solución
í4+í9+i16 =l + i + l = 2 + i
Números Complejos
571
2-i5+i10-i15 =2-i-1 + i = 1
i4+/9+i16 2 + « „ .
LUCg0 2-í+/«'-,« ="T = 2 + I
, 3(1 +O2 2(1-O3
(l-i)2 (l + i)3
Solución
W = 3( l±i)2 = 2[ O + OO + O 2 = , 2i 2 = _3
(l-O2 l-« (1-00 + 0 2
^3
20^ = w 3 = OzOOzO 3 = 2(Z2/ 3 = 2/.
(l+O3 l+i 0 + 0(1-0 2
3(1 +O2 2(1-O3 „ „.
Luego se tiene: — = -3 - 2i
D l±i+_L
i 1 - i
(1-0Z 0 + 0J
Solución
l + i ¿ =(l + Q(-Q i(l + 0 _l-i / —1 _ 1 i
i l-i i(-i) (i-l)(l+1) 1 2 2 2
g) (1 + 0"+(l-0"
Solución
Si n es par entonces:
a) n = 4k. k e Z. Entonces (1 + i)" = (1 + O4* = (-4) *
(l-i)"=(l-i)4*=(-4)t
(1 + 0"+0-0" =(-4)*+(-4)* = 2(-4)*, ke Z
572
Eduardo Espinoza Ramos
b) n = 4k + 2,keZ entonces: (1 + j)" = (1 + i)4k+2 = (-4)*(+2/)
(l-i)n=(l-i)4*+2=Hl)*(-2i)
(1 + /)" +(l-i)" = 2í(-4)* -2i(-4)* =0
Si n es impar entonces:
a) n = 4k+l, keZ, entonces:
(l + i)" =(l + i)4t+l =M)* (1 + 0
(l-O^d-O4**1 =(-4)*0-í)
(l + i)"+(l-i)" = (-4)*(l + í) + (-4)*(l-i) = 2(-4)\ ke Z
b) n = 4k + 3, k e Z, entonces
(1 + /)" = (l + /)4t+3 =(-4)*(-2+2i)
(l-i)" = (l-i')4t+3 = (-4)*(-2-2i)
(l + i)"+(l-i)" = (-4)*(-2 + 2i) + (-4)*(-2-2i) =(^l)*+l
(¿) Calcular 1", donde n es un entero.
Solución
Si n es par entonces
a) n = 4k, ke Z, entonces: i" =i4* =1
b) n = 4k + 2, k e Z, entonces: i" = iAk+2 = i4* .í2 = -1
Si n es impar entonces:
a) n = 4k+l, keZ, entonces: i" = i'4*+1 = i4k.i = i
b) n = 4k + 3, k e Z entonces: 1" = i4*"1"3 = í4*i3 = -1
Números Complejos
573
Cú) Demostrar que: ——^-r = i"'(l-i)
Solución
(1+iT (í+o-'d+o ,i + /,„_.
■ = (f^)""'(i+¿)
(1-0 (l-i)" 1-»
i /(-/)
(Y) Probar que:
z + z
a) Re(z) = -
Solución
„ . , z + Z x + iy + x-iy 2x n , .
Seaz = x + y => z = x-iy, luego = - — = — = jc = Re(z)
2 2 2
Re(z) = ——
b) Im(z) = —-
2i
Solución
Sea z = x + iy => z = x-iy
1+l=x + iy-(x-iy) = 2iL= . Im(z) = izl
2 2i 2/ 2i
c) Im(iz) = Re(z)
Solución
Sea z = x + iy => iz = -y + ix => Im(iz) = x
además Re(z) = x entonces Re(z) = Im(iz)
574
Eduardo Espinoza Ramos
d) Im(z1.z2) = Re(z1).Im(z2) + Im(z1).Re(z2)
Solución
Por el ejercicio b) se tiene Im(z) =
2¿
T r , . Zi-Z2 — Z\Z-i ¿ZiZt ~ ¿ZiZo
Luego Im( z, .z,) = -1— — = —— —
2/ 4/
Im(7 7 ) = Z1Z2 Z1Z2 t Z1Z2 Zlz2 _ Zl + zl £2 5l + ^ Zj_ Z2 + Z2
1 2 4i 4/ 2 ' 2/ 2i ' 2
= Re(z!).Im(z2) + Im(z,).Re(z2)
(¿) Si z es un número complejo tal que: || z || = 1, calcular || 1 + z ||2 +1| 1 - z ||2
Solución
||l + z||2+||l-z||2-(l + z)(l+_z) + a-z)(l-"z)
= l + z + z+||z||2+l-z-z+||z||2=2 + 2||z||2=2 + 2 = 4
C9) Demostrar que: \\z — i || = — sí z = , donde a es un número real.
^-^ 4 4 l + 2fli
Solución
3 . i-a 3 . 2a + i
z—í =— 1 = -
4 l + 2ai 4 4 + 8af
3. 2a + i (2a + i)(4-8a/) 16a 4-16a2 .
z—1= = - - = =- + t-i
4 4 + 8ai (4 + 8ai)(4-8ai) 16 + 64o2 16 +64c2
3 . a l-4a2 ....
z — 1 = - + -í , de donde
4 l + 4a2 4 + 16a2
3 ll / a x2 . , l-4a2 ,2 ¡i 1
Números Complejos
575
®
Calcular z2 siendo Z = -||-l + ¿\\+y¡2i
Solución
||1-||| = >/Í+I = V2 => Z = -yf2 + yf2i
z2=(-yÍ2+j2i)2 = 2-4i-2 = -4i ;. z2 =-4í
Hallar el número complejo z tal que: || z || = 1 y Re(z) = 0
Solución
Sea z = x +iy => Re(z) = x = 0 => z = 0 + iy
Como || z ||=1 =* ||z|| = 7>^ = l => y2=l =* y = ±l
z = ±i
Describir y construir la gráfica del lugar representado para cada una de las ecuaciones
siguientes
a) ||z-i|| = 2
Como z = x + iy
Solución
Y
\^fJ
2/\
to.1) j
X
entonces || z -í || = yjx^+íy-1)2 = 2
de donde x2 +(y-l)2 =4, que es
una circunferencia de centro (0,1) y radio 2.
b) Re[z(z + 2)] = 3
Solución
Sea z = x + iy => z = x-iy
Como z(z + 2) = 3 => (x + iy)[x-iy + 2] = 3
T.
x2 +2x+y2 +2yi = 3 de donde x2 +2jc+>'2 =3 entonces (jc + 1)2+>-2 = 4 que
es una circunferencia de centro (-1,0) y radio 2.
576
Eduardo Espinoza Ramos
tY
■—*■
X
c) Im(z2) = 4
Solución
Seaz = x + iy => z2 = x2 -y2 +2xyi, dedonde
Im(z2) = 2jcy como Im(z2) = 4 entonces
2xy = 4 ^ xy = 2 que es la ecuación de una hipérbola, su gráfico es:
d) ||z|| = Re(z)+l
Solución
Sea z = x + iy => Re(z) = x
\\Z\\ = Jx2 + y2
Como || z || = Re(z) + 1, entonces
Se tiene -y/jt2 + y2 =x+l
x2+y2 = jc2 +2jc+1 de donde se tiene y2 =2* + l que es la ecuación de la
parábola
0 y
Números Complejos
577
e) ||z + 2i|| + ||z-2i|| = 6
Solución
Sea z = x + iy => z + 2i = x + (y + 2)i
\\z + 2i\\=yjx2+(y + 2)2
z-2i = x+(y-2)i
\\z-2i\\ = ylx2+{y-2)2
como || z + 2i II +1| z - 2/1| = 6, entonces:
^jc2 + (y + 2)2 + y]x2 + (y - 2)2 = 6, de donde al quitar el radical y simplificando
,2 =
se tiene: 9x +8y = 45 , que es la ecuación de una elipse.
(l3) Describir gráficamente la región representada por cada una de las siguientes
desigualdades.
a) || z || S 1
Solución
Sea z = x + iy => \\z\\ = Jx2 + y2
Como || z || S 1 => yjx2 + y2 < 1
De donde x2 + y2 < 1, su gráfico es:
b) ||z||>l
Solución
Sea z = x + iy => \\z\\ = Jx2 + y2
Como || z || > 1 => Jx2 + y2 > 1, de
Donde x;2 + y 2 > 1, su gráfico es:
z||*1
z
r
\L
rN.ll z 11*1
J x
578
Eduardo Espinoza Ramos
c) 1 <, || z + i || <, 2
Solución
Seaz = x + iy ^ z + i = x + (y+l)i
||z + i|| = >/Jt2+(y + I)2 como l£||z + i||£2
entonces 1£ ^x2 + (y +l)2 £ 2, de donde
l£jr2+(;y + l)2 £4
d) Re(z2)>l
1*112 + 111*2
Re(Z2) > 1
Solución
Seaz = x + iy =» z2 = x2 -y2 +2xyi
Luego Re(z2) = x2 - y 2 , como
Re(z2)>l =* A2-y2>l. Su gráfico es
e) ||z-l||s2||z+l||
Solución
Sea z = x + iy =» z - 1 = (x - 1) + iy
z + 1 = (x + 1) + iy
Además \\z-l\\ = y¡(x-l)2 + y2
\\z + l\\ryj(x + l)2 + y2
como || z - 1 || á 2 || z + 1 || => N/U-D2 + )'2 ^ 2N/(x + l)2+y2 , de donde
jt2-2x + l + ;y2 S4(*2+2jt+l + ;y2)
3*2 +3y2+10.v + 3£0 entonces (x+-)2+ >>2 > —
Números Complejos
579
Demostrar la identidad: || 1 - zw ||2 -1| z - w ||2 = (1-1| z ||2)(1-1| w ||2)
Demostración
Se conoce que || z ||2 = z.z, por lo tanto
\\l-zw\\2=(\-zw)0-zw)
II z - w ||2 = (z - w).U - w)
\\l-zw\\2 -\\z-w\\2=(l-zw)(l-zw)-(z-w)(z-w)
= (1 - ZW- ZW+ ZZ-WW) -(ZZ -WZ — ZW+ ww)
= l + z.z.w.w-z.z-w.w=l+||z||2||w||2-||z||2-||w||2
= (i-IUII2)-lk||2(i-|ui|2)=(i-||z||2)(i-||lv||2)
Sí || z || < 1 y || w || < 1. Demostrar que: | —=^- | < 1, z, w e C
l-zw
Demostración
Por hipótesis se tiene: || z || < 1 y || w || < 1 => || z \\2 < 1 y || w ||2 < 1
Luego 1-||Z||2>0 y 1-|| w||2>0, de donde (1-|| z||2).(l-|| w||2)>0 ... (1)
En el ejercicio 19) se tiene: (1-1| z ||2)-(1-1| w||2H|1-zh>||2 -|U-^||2 ...(2)
reemplazando(2) en(l) se tiene: ||l-zw||2 -||z-w||2>0
de donde ||z-w||2<||1-zh>||2=> ||*-HI<l|l-w|l => ||-^=2ÍL||<1
1-ZVf
z w
Si z,w e C, Demostrar que: Re( ) + Re( ) = 1
Z + W Z+W
Demostración
580
Eduardo Espinoza Ramos
Sean z = a + bi, w = c + di, entonces: z + w = (a + bi) + (c + di) = (a + c) + (b + d)i
z _ a + bi _ (a + bi).{(a + c)-(b + d)i)
z + w {a + c) + (b + d)i [(a + c) + (b + di)][(a + c)-(b + d)i]
_a(a + c) + b(b + d) a(b + d) + c(b + d)i
(a + c)2+(b + d)2 {a + c)2+(b + df
Re(_^)=^^Kb + d) (l)
z + w {a + cY +(b + d)~
w c + di (a + di)((a + c)-{b + d)i)
z+w (a + c) + (b + d)i [(a + c) + (b + d)i][(a + c)-(b + d)i]
c(a + c) + d(b + d) -c(b + d) + d(a + c),.
= 5 y + ( 5 5~)'
{a + cf +{b + df (a + c)2+(b + d)2
te^^cia + O + díb + d) ^{2)
z + w (a + c)~ +(b + d)
sumando (1) y (2) se tiene:
R _z_ Re(_vv_) = a(íJ + c) + ¿7(¿7 + í/) _ c(a + c) + d(b + d) _{a + c)2 +(Jb + df _,
z + w z + w (a + c)2+(b+d)2 (a + cf+(b+d)2 {a + c)2 + (b + d)2
Re(—^-) + Re(—^-) = 1
Z + W Z+W
•Jsenx + i-Jcosx -iJsenx-iyfcosx
Simplificar la expresión: , —,
Vsenx+i-Jcosx -/ Vsenx-iylcosx
Solución
Multiplicando por su conjugando se tiene:
Vsen x + i\lcos x -; Vsen x - ¿Veos x _ (Vsen x + ¿ycos x - ¿Vsen x - iylcosx)
Vsen x + jVcosT + i Vsen x - /Veos x sen x + «Veos x + sen x - ¿Veos x
Números Complejos
581
sen x + ívcosjc - 2/vsen2 x+eos x - sen x + i-J<
COSJC
2 sen*
_ 2i(>/cosx — Vsen jc+cosjc) _ ¿(Vcosjc—Vsen jc+cosjc)
2 sen* sen*
@ Probar que: ||Z| + ¿2 || + |U, -z2 II = 2(11*, ||2 +||*2 ||2)
Solución
II Zl +Z2 \\2=(Zi +Z2)(ZX +Z2) = ZlZl +Z2Z2 +ZXZ2 +Z2Zi
= IUlH2+IU2l|2+Zlz!+*2-Zl~ — (1)
IUl-Z2 II =(Zi-Z2)Ul-Z2) = ZiZl+Z2Z2-ZlZ2 ~Z2Zy
= \\Zyf +\\z2f -ZxZ2-Z2.z\ -(2)
Sumando (1) y (2) se tiene:
II 4 + Z2 ||2 +|U, ~Z2 |NU, II2 +11 22 H2 +*lí + *2*l + lk II2 + 11*2 II2 ~ZxZ~2 ~ ^1
= 2|U1||2+2|U2||2=2(|Ul||2+|U2||2)
••■ IU,+ ^2 ll2+IU.-^2 ll2=2(|U1 H2 +|U21|2)
gs¡) Hallar el módulo de 1 + cos0 + 'sen0 , o < 6 < n
^-^ l-cos0 + isen0
Solución
„ l+cos0+/sen0 (l+cos0 + /sen0).(l-cos0-i'sen0) sen20 sen0.cos0 .
Sea z = = = 1
l-cos0+/sen0 (l-cos0+/sen0).(l-cos0-isen0) l-cos0 l-cos0
■k
sen40 sen2 0 eos2 0 |sen20(sen20 + cos20)
COS0)2 (1-COS0)2 V (1-COS0)"
582
Eduardo Espinoza Ramos
2 Q
\ sen26 | l-cos20 /l+cosg 2cos ^ _ I T±_i 6_,
:Vd-cos0)2 VO-cos0)2 \l-cos0 ~\2sen2^~^CtS ^~ ^
• • IUII = ktg||
(ío) Hallar el módulo de: (2-30(3 + 40 6+4» ^ ^
^ (6 + 40(15-80 5 + i
Solución
_ (2-30(3 + 40 „ „ >/Í3.5 5
5 + í
(6 + 40(15-80 >/52.>/289 34
M±> - M-zS
5 + í
z3 = (a/3 -Ía/2)(3 + 40 => || z31| = >/5.5
Luego ||Zl.Z2.z3|| = IM.|U2||.|U3H =¿-2a/5.a/5.5=^
ll ll 125
•■ ll«i-«2-«i ll = -jy
w = . donde z = eos a + i sen a, hallar w.
l-z
Solución
Reemplazando z en w se tiene:
2cos — + 2isen—eos— 2cos— eos—+ isen —
l + z 1 + cosa + isena 2 2 2 2/2 2_-,
w = = = = ( —j
l-z 1-cosa-isena 2sen2^-2isen^.cos^ 2sen^ sen^-icos?
(eos — + isen—)(sen — + icos—) „
(Y *y 9 9 9 Of
= cíe—. — = ctg—(sena-i'cosa)
2 2CC 2« 2
sen — + eos —
2 2
Números Complejos
583
(22) Demostrar que: Sí Zi+z2 = z¡+z3, Entonces z2=Zj (Propiedad de cancelación
para la suma)
Solución
Como Z\tC => 3 -z, e C tal que z, + (-z,) = (0,0)
Luego z1+z2=zl+z3 => -z1+(zl+z2) = -zi+(Zi+z3)
=* (-zi+z1) + z2={-Zi+zi) + z3
=> 0 + z2=Q+z3
=» *2=*3
(23) Demostrar que: Sí z¡ *0 y sí zxz2 =2^3 Entonces z2 = z3 (Propiedad de cancelación
para la multiplicación)
Solución
Como z, * 0 =^ 3 z\l tal que z, .zj"' = 1
Luego zi.z2=zi.z3 => zi*.Ui-z2) = z[l.(zi.z3)
=> l.z2 = l.z3
=> z2=z3
(24) Sí z, .z2 = 0 entonces Zj =0 o z2 =0
Solución
Suponiendo que Zj # 0 => 3 zf1 tal que z, .zf1 = 1
Como z¡.z2 =0 => zj"1.(z1.z2) = zf1.0
=> (zr'.z,).z2=0
=> l.z2 =0 de donde z2=0
584
Eduardo Espinoza Ramos
en forma similar para z, = 0
Suponiendo que z2*0 => 3 z2l tal que z2-z2l =1
Como Zi.z2=0 => z2i.(Zi-z2) = z21.0
=> (zí'-ZjU, =0
^ l.Z[ =0 de donde z, =0
(25) Hallar dos números complejos z, y z2 cuya suma sea el número real x y cuya diferencia
sea el número imaginario iy.
Solución
[zx + z2=x (1)
Por condición del problema se tiene:
1*1-22='? (2)
x y
Sumando (1) y (2) se tiene: 2z\=x+iy de donde z, = —+—i
restando (1) y (2) se tiene: 2z2 = x - iy de donde Z2 = i
@ Demostrar que: ||z||2>2||Re(z)||.||Im(z)||
Solución
Sea z = x + iy => || z || = ^x2 + y2 , además Re(z) = x, Im(z) = y
Luego || z || = yJRe(z)2 + Im(z)2 => || z ||2= | Re(z) |2 +1 Im(z) |2 ... (1)
como (| Re(z) | -1 Im(z) |)2 > 0, de donde
Re2 (z) + Im(z)2 > 21 Re(z) |. | Im(z) | ... (2)
por lo tanto de (1) y (2) se tiene: || z \\2 > 21 Re(z) |. | Im(z) |
Números Complejos
585
Demostrar que: y¡2 || z ||2> | Re(z) | +1 Im(z) |
Solución
Como ||z||2>2|Re(z)|.|Im(z)| sumando ||z||2
2||z||2>||z||2+2|Re(z)|.|Im(z)|
21| z ||3 > | Re(z) |2 +1 Im(z) |2 +21 Re(z) |. | Im(z) |
2||z||2>(|Re(z)| + |Im(z)|)2 => 2 ||z|| > |Re(z)| + |lm(z)|
Probar que | Re^ + Im(¿> | < || z || < | Re(z) | +1 Im(z) |
Solución
Sea z = x + iy de donde Re(z) = x, Im(z) = y
Además || z || = Va2 + >'2 • Ia demostración del problema equivale probar que:
|^|S¿c2 + >2<M + |v|
como x,y e R entonces (x-y)2 >0, Vx,ye R
(a - y)2 > 0 => a-2 + v2 > 2xy
2x2 +2y2 >x2 +2xy + y2
2(x2 +y2)>(x+y)2
^2y¡x2+y2 >|A + y|
de donde |^|<^2 + y2
,Re(z) + lm(z). ., .. .
Luego | -j= \£\\z\\ ... (1)
586
Eduardo Espinoza Ramos
Como | x |.| y | > 0. V x, y e R, entonces
2|x|.|y|>0 =* |*|2+M2+2|*|.|y|>M2+|v|2>0
(\x\ + \y\)2>\x\2+\y\2>0
\x\ + \y\>ylx2 + y2
Re(z) + Im(z) > || z ||
Luego || z || < | Re(z) | + | Im(z) | ... (2)
de (1) y (2) se tiene: | Re(z)t-Im(z) \<\\z\\<\ Re(z) | +1 Im(z) |
V2
Hallar z tal que: || z || - z = 1 + 2i
Solución
Sea z = x + iy =* || z || = yjx2 + y2 , al reemplazar se tiene:
yjx2 + y2 - x - iy = 1 + 2í, por igualdad
_y_2 vjc +4 = 1 + jc => x = —
Luego z =— 2/
2
Sí z=cos 6 + isenG, z" =l.z*l y M =l + 2z + 3z2+... + n.z"~l. Hallar Re(M) y Im(M)
Solución
Como M =l + 2z + 3z2 +—+n.z"~i, multiplicando por z
zM = z + 2z2 +3z3 +... + n.z", ahora restando se tiene
M-zM=I + z + z2+...+ zn_1-«zn — (1)
Números Complejos
587
como z"=l => z"-l = 0 => (z-l)(zn_1+z''~z+...+ zz+z + l) = 0
comoz*l zn_1+z"~2+...+ z2 + z + l = 0 ...(2)
reemplazando (2) en (1) se tiene: M -zM =0-nz"
M(l-z) = -n.z" de donde M = puesto que z"=l
1-z
Como z = eos 8 + i sen 8, entonces
—n -n
M=-
l-cos0-/sen0 (l-cos0)-/sen0
-n -n
2sen 2isen —eos— 2sen —(sen «eos—)
2 2 2 2 2 2
—m sen —+ icos—) .
M=——2—-¿- — "-"culi
2sen* 2 2 2
2
de donde Re(M) = — y Im(M) = —ctg—
2 2 2
(31) Sí w = cos8 + isen6. Hallar (\ + w)n
Solución
f\ tí tí OO £}
1 + w = 1 + cos0 + /sen0 = 2cos2 — + 2sen—eos—/ = 2 eos—(eos—+¿sen—)
2 2 2 2 2 2
.n6
(1 + w)n = 2" eos" i(cos—+ /sen^) = 2" eos" ?-.e'^
2 2 2 2
(32) Simplificar (1 + w)", donde w = cos—+/sen—
Solución
588
Eduardo Espinoza Ramos
1 + w = 1 + eos— +1 sen — = 2cos —+2sen—eos—1
3 3 3 3 3
- 2 eos—(eos—+/sen—) = eos—+/sen—
3 3 3 3 3
(1 + w) =(cos—usen—) =cos—+isen— = e 3
3 3 3 3
Hallar la suma de sen x + sen z3jt+...+senz(2«-l)jt
Solución
Aplicando la identidad sen — =
2 2
sen2 jc + sen2 3x + sen2 5x + ... + sen2(2/J-l)x
1-cos2jc 1-cos6jc 1-cos10jc l-cos2(2n-l)
+ + + ... + ^
= (—+—+...+—)—(cos2jc+cos6jc + cosl0jf + ...+cos2(2«-l))
2 2 2 2
= (cos2jc+cos6jc + cosl0jc+...+cos2(2n-l)) ••• (1)
2 2
A = eos 2x + eos 6x + eos lOx + ... + eos 2(2n - l)x
B = sen 2x + sen 6x + sen lOx + ... + sen 2(2n - l)x
iB = i sen 2x + i sen 6x + i sen lOx + ... + i sen 2(2n - l)x
ahora sumando A y iB se tiene:
A+ iB = (eos 2x + i sen 2x) + (eos 6x + i sen 6x) +...+ (eos 2(2n - 1) + i sen 2(2n - 1))
donde z = eos x + i sen x => z" = eos nx + i sen nx
Números Complejos
589
A + ¿g = z2(l + zUz8+... + z4'"-1>)=2V + (^)") = zV-cos4m-|Sen4njc)
l + z l-cos4jc-isen4jr
->. 2 sen 2 2nx - 2i sen 2nx eos 2n r.
= z ( 5 )
2 sen 2jc - 2í sen 2jc.cos 2jc
~ , _ . ^ _ cos( —2m:)-/sen( —2nx)
, ._ 2 2sen2ru: sen2/ur-icos2nx ->sen2/urr 9 2 ,
A+/B = Z¿. ( ) =z~ [ ]
2senZv senZv-ícosZv senZx ^ *_Zv)_Isai( *-2x)
sen 2/ix
= (eos 2x + i sen 2x)[cos(-2n* + 2 r) +1 sen(2«x - .v)l
sen2jc
sen2/ur ,„ „ „ „ .„ _ „ , sen2n*r „ „ ,
= [cos(2jc-2nx-Zx)+ísen(2/u-Zv+2jf)j = [cos2/u-ísen2/n]
sen2jc sen 2.x
sen2«.v „ sen4wx „ sen2«jc „ sen2 2nx
A = cos2«jc = y B- sen2/iA =
sen2jc 2sen2x sen2jc sen2jc
6.15. EJERCICIOS PROPUESTOS.
fl) Hallar los números reales x e y tal que: 2x-3iy -2y-5-10i = (x+y-2)-(y-x+3)i
Rpta. x = 1 , y = -1
Qf) Que valores han de tomar x e y para satisfacer la ecuación
(2 - 5i)x + (1 + 3i)y - 8 + 9i = 0
Rpta. x = 3 , y = 2
®\{\ + i)x-iy = 2
Resolver el sistema de ecuaciones en C. <
\(2 + i)x + (2-i)y = 2i
= _2__W.
T> ♦ 13 13'
Rpta.
* 12 11.
y = +—i
13 13
(4) Hallar los valores de a y b sí (a + b) + (a - b)i = 7 + 2i
Rpta. a =4.5, b = 2.5
590
Eduardo Espinoza Ramos
(s) Hallar los valores de a y b sí: (a + b) + (a-b)i -(2 + 5i)2 +i(2-3i)
Rpta. a = 2 , b =-20
®3z 3z 4
Si z = x + iy, donde x,y e R, hallar los valores de x e y cuando + — =
l-i i 3-i
Rpta. x = 0.27, y = 0.53
(7J Efectuar las siguientes operaciones y el resultado expresar en la forma binómica.
a) Rpta. —i
(1-0(2-1)(3-í) 2
(3-0(2 + 0 D . , t
b) z = " Rpta. z = 1 - 7i
i 4 2
c) z = l+ Rpta. Z-—+—Í
l + _^_ 3 3
l + -i-
1 + /
.. 1 + 3/ 2 D . 22 75.
d) +- Rpta. 1
¿(4-50 i 41 41
. 5(7 + 20 .,. .., D t 17 66.
e) v /-t(4-60 Rpta. -— -—/
3-4i 5 25
0 Í^+Cf-Í)2 Rpta.-2 + 0i
l-i l+i
g) J_ + _L Rpta. l+0i
l+i 1-i
h) — í- Rpta. 0-i
1+í 1-i
.j 1 + ltga Rpta. cos 2a + i sen 2a
1-j'tga
Números Complejos
591
©
®
®
®
j)
k)
1)
(1 + 2i)2-(1-i)3
(3 + 203-(2 + i)2
(1-0-1
(l + i)5+l
0 + 0"
(l-O7
r> . . d + 0" j a
Calcular -, donde n es un entero positivo.
(1-i)"-2
Resolver el sistema de ecuaciones:
a)
(3 + i> + (4+2/)y = 2 + 6/
(4 + 2i)A--(2 + 3/);y = 5 + 4;
D . 44 5 .
Rpta. 1
318 318
d . 1 32.
Rpta. 1
25 25
Rpta. 2
Rpta. 2in_1
x = 1 +1
b)
c)
f(2+i)jr+(2-i
|(3+2i>+(3-
-i)y = 6
20> = 8
jc + /y-2z = 10
Z-y + 2/'z = 20
/j: + 3iy-(l + /)z = 30
Rpta.
Rpta.
Rpta.
y-
X-
y--
x =
y-
z =
= /■
= 2 + /
= 2-i
= 3-
= 3-
= 1-
-llí
-9j
7/
Demuestre que: a) Re(zw+zw) = zw+zw, z, w e C
b) Im(zu'-zvv) = zvv-zvv, z, w e C
Resolver el sistema de ecuaciones:
a)
b)
x+iy = 1
ix+y = l + i
(1-i)jc + 2iv = 3
4jc + (1-i)> = 2 + í
Rpta.
Rpta.
jc = 1- —
2
1
i 7
jc = —+ —
2 10
= J 9/_
y~io io
592
Eduardo Espinoza Ramos
(12) Si x e y son reales, resolver la ecuación: =
^s \ + iy x + 3 v
Rpta. jc = ±2 , y = ±-
(13) Si z = x + iy, probar que: | x \ +1 y \ < + iy\
(14) Probar que sí z1,z2eC' entonces: Refe^) = Re(z1)Re(z2)-Im(z1)Im(z2)
© Probar que: V zx,z2eC entonces || z, + z2 ||2 +1| z, -z2 ||2= 2(|| z, ||2 +1| z2 ||2)
(l6) Sí z, = 1 -1, z2 = -2 + 4f, Z3 = V3 - 2¿. Hallar el valor numérico de la expresión
z, + z2 +1 „
a) II
z,-z2 + l
Rpta.
Rpta.
RDta.
3
5
1
7
6x/3 + 4
b) I(JU3L)
2 z3 z3
c) Iiní-^-)
z3 7
d) Re(2z,3+3z2-5z32) Rpta. -35
(ir) Sí w = 3t"z - z2 y z = x + iy. Hallar || w ||2 en términos de x e y.
Rpta. xA +/ +2*2y2 -6jc2y-6>3 +9jc3 +9>2
u» Resolver las siguientes ecuaciones en z.
a) iz = 1 Rpta. z = -i
b) (l+iz)=l Rpta. Z=\~\
c) (2-i)z = i Rpta. z = ~+y
Números Complejos
593
d) — = / Rpta. z = -i
z
e) iz = (l+i)(l-i) Rpta. z = -2i
(l9J Si z = x + iy, siendo x e y reales. Demostrar que el lugar geométrico II II = 2 es
v~-^ z + 2
una circunferencia y determina un centro y radio.
(20) Describir geométricamente la región representada por cada una de las siguientes
desigualdades.
a) 1 < || z + 1 || < 2 b) || z + 3i || > 4
c) ||z + 2-3i|| + ||z-2 + 3i||<10 d) 2<||z||<4
e) 4<||z-l|| + ||z+l||<5 f) ||2z + 3||<l
g) ||z-i||<||z + i|| h) ||z||<||2z+l||
i) || z + 1 || > 2 j) -2 < Im(z) S3a1 <Re(z)<5
k) -0.5 < Re(z) < 0.5 a || z || =2 1) -2 < Im(z) < 2 a -2<Re(z)<2
(21) Qué lugar describe el punto z = x + iy, cuando satisface a las siguientes ecuaciones,
a) ||z-2|| + ||z||=4 b) ||z-2||-||z|| = l
c) ||z-2||-||z|| = -l d) ||z-i|| + ||z + i|| = 5
e) z + z = \ f) z + z=||z||2
g) ||z-i|| = ||z+l|| h) z~l+z = 0
i) z-z"'=0 j) z + z'leR
k) ||z + i|| = ||z + 2i|| 1) || z - 1 II = 5
H) || z-4 || = 3 m) ||^||=4
z-1
n) Im(z2) = 4
594
Eduardo Espinoza Ramos
(22) Sí z = 2 + 3i , w = 1 + 2i , v = 3 + i
Hallar a) Re(z-w) b) Im(—)
v
c) - + — d)
Z W V
(23) Demostrar que la elipse ||z + 3|| + ||z - 3|| = 10 se puede representar en forma rectangular
¿♦¿
25 16
x2 y2
—+^- = 1
(24) Describir cada uno de los siguientes lugares geométricos expresándolos en términos de
las coordenadas conjugadas z, z .
a) z.z = 16 b) z.z-2z-2z-3 = 0
c) z + z = 14 d) z = z + 6i
Rpta. a) x2+y2=l6 b) x2+y2-4x-Sy = W
c) x = 2 d) y = -3
(25) Mostrar que la ecuación de una recta es determinado por dos puntos z, y z2 que cumple
con la ecuación Im( —) = 0
Z2-Zi
(26) Determinar analíticamente y gráficamente los subconjuntos de C que verifican.
a) ||z+l|| + ||z-l|| = 3 Rpta. Ííl+^1 = 1
b) ||z + c||.||z-c||=c2 Rpta. (jt2 + y2)-2c2(.v2 -y2) = 0
@ Verificar la identidad, donde z,w e C. ||-^±^-(zw)2 || + ||i±^ + (zw)2 || = || z|| + || w\\
(28) Sí |a,|<l. A, >0, i=l,2,...,n
A,+A2+A3+...+A„ =1. Probarque \\ax + A2a2 +...+ A„an | <1
Números Complejos
595
SZ¡S „. rr (cos2a-isen2a)(cosfc-i'sen¿?) (cos2a + i'sen2a)(cos¿?-i"sen¿?)
cos(a + b) + i sen(a + b) cos(a + b)-i sen(a + b)
Rpta. 2cos (3a - b)
(30) Si z = x + iy, hallar:
131
a) Re(-)
z
d) Re(-U
Z2
g) Re(^-
Rpta. a)
d)
g)
Si 7.w <= C_
7)
1
X
x2 + y2
.*2+>2
U2 + V2)2
X
x2+{y-\j1
Demostrar nue:
b)
c)
Ir
Im(-)
z
Re(z2 + z)
b) _>
"'22
x +y
c) x2-y2+x
*
ni Z i+Imr W ^-0
c)
I)
Im(z3)
Re(-zz2)
c) jt3 -3xy2
0 2xy
62) Si z,w e C. Probar la desigualdad:
z + w z + w
HU+1U1I"Q 2||zw|
z + w z + zw
®Sea w = — , donde a,b,c,de R. Demostrar que: vv-w = , zeC
cz + rf |cz + í/|2
QÍ) Calcular ;2 siendo z=-||-l + í||+>/2z. Rpta. 4i
(35) Dado z = 1 + sen a + i eos a. Determinar || z2 - z ||
Rpta. [(sena - cos2a)2 + (3cosa - sen2a)2 ]1/2
596
Eduardo Espinoza Ramos
®„ . . (l-iV3).(cos0 + i'sen0) „ . y[lr .„_ /r. ._„ jr ,
Calcular - —— Rpta. [cos(20 ) + /sen(20 )]
2(l-i).(cos0-isen0) 2 2 2
(37) Demostrar que sí || z || < —, entonces |(1+/)Z3 +iZ\ < —
Q§) Sí z,=2 + /, z2 =3-2i. Hallar el valor numérico de:
a) l|3z1-4z2|| Rpta. VÍ57
b) ||^2 + Zl"^"'ll Rpta. 1
2z,-z2+3-i
(39) Si z y w son complejos y u = 4zw . Probar que: || z|| + || w|| = || "11 + 11 + "ll
Mü) Mostrar que una ecuación para una circunferencia que pasa por 3 puntos z,, z2, Z3 está
dadopor: (1ZÍ)/(Í3ZÍL) = (IZÍL)/(Í1ZÍL)
z-z2 z3-z2 z-z2 z3-z,
(41) Hallar z tal que || z || + z = 2 + i Rpta. z~~7 + i
(42) Hallar todos los z e C tales que Im(z+—) = 0
®Sea p>0 y p*l, probar que ||—^-|| =p representa a una circunferencia
1 + z
(44) Hallar todos los z que satisface la relación z(l + ai) = 1 - ai
(4?) Demostrar que: Re(z, .z2) =—(z, .z2 + Zi .z2)
©Demostrar que: lm(zi .z2) =—(Z) -z-> - zl .z2)
2¿
Números Complejos
597
(47) Hallar los z = x + iy que satisfacen la condición dada:
a) ||z-3i||-||z + 2i||<9 b) ||l + z2||<||2z||
c) ||z + 2||-||z-2||>5 d) ||z-3|| + ||z-4||<5
e) 11-^11 < 2 fj ||^||>2
z + 2 z+2
(48) Sean a, b y c tres constantes complejas, z una variable compleja. Probar que:
a + a + bz + bz + (c -c)z.z = 0 es la ecuación de una circunferencia.
[49j Sea a y b dos constantes complejas, si b * 0 probar que: a + a + bz+bz =0 es la
ecuación de una recta, donde z es una variable compleja.
@ Si ||z,||<l y || z2 || <1. Probar que: ||z,+z2 || < ||l + z,z2 ||
@ Si || z || * 0 . probar que ||-^--l || < | arg(z) |
w II z II
@ Si || z ||?t0. Demostrar que: || z-l||<||| z||-l | + || z||.|arg(z)|
@ Demostrar que: || z, + z2 || > i(|| z, + z2 ||) || -ÍL- + -Í2-1|
^-/ 2 || z, || || z21|
\5y Si || z, || < 1 y || z2 || < 1, probar que: || ' _2 || < 1. ¿En qué caso se cumple la igualdad?
l-z,z2
(§) Demostrarque: || z, || + || z2 || - ||il±Í2.-(Zl.z2)2 || + \\íi±ÍL + (Z].Z2f ||
Z] Z\
® Demostrarque: ||z0 +z, +...+ zn ||>||z0 ||-||z, ||-|| z2 ||-...-|| z„ ||
(57J Determinar el conjunto de puntos del plano que satisface a la relación: || z - 1 + i || = 2.
Rpta. (\-l)2+(v + l)2 =4
598
Eduardo Espinoza Ramos
®
Hallar los conjuntos de puntos del plano de la variable z que se determina por las
condiciones dadas.
a) ||^4||<1
c) 4<||z-l|| + ||z+l||<8
e) || z || - 3 Im(z) = 6
b) ||z2-l||>o2, a>0
d) ||z-i||-||z + i|| = 2
f) ||z-2|| = ||l-2z||
59) ¿Qué curva determina la ecuación |z + c| + |z -c| = 2a, donde ayce R+ , a > c?
feo) ¿Qué curva del plano XOY se determina por la ecuación z.z + i(z - z) - 2 = 0 ?
6.16. FORMA TRIGONOMÉTRICA O POLAR DE UN NUMERO
COMPLEJO.-
Sea z = a + bi, un número complejo distinto de cero, entonces el módulo de z es
r=||z||=Vfl2+l»2*0
Y'
Z = a + bi
Denotaremos por 9 el ángulo formado por el segmento orientado que representa al
número complejo z, con el eje X. en sentido antihorario.
Luego del gráfico se tiene:
n a
eos© = —
a b
sen© = —
, dé donde
{::
= rcos0
rsenfi
Números Complejos
599
Como z = a + bi. al reemplazar a y b se tiene:
z = r(cos 9 + i sen 9)
Que es llamado forma trigonométrica o forma polar del número complejo z.
Al ángulo 9 se le llama argumento de z y r = || z || es el módulo de z que denotaremos por:
9 = arg(z) , r= \\z\\ =Ja2+b2
por lo tanto: z = a + bi = r(cos 9 + i sen 9)
r=\\z\\ = Ja2+b2 y 0 = arctg(-)
Y
II
9 = 180°-a
ni °
9 = 180° +a
.
e
i
9 = a
IV X
= 360°- a
Ejemplo.- Expresar z = 1 + v3i en forma trigonométrica o polar.
Solución
Calculamos su módulo y su argumento
Y
n/3
0
»
sá
Z=1 +n/3í
I
I
I ,
1 X
r=||z||=VÍT3=2
6 = arctg(—) => tg0 = yf3 => 9 = 60°
z = l + \/3i' = r(cos0+/sen0)
z = 2(cos 60° + i sen 60°)
Ejemplo.- Expresar z = -3 + v3í en forma trigonométrica o polar
Solución
600
Eduardo Espinoza Ramos
Calculando su módulo y su argumento, r = || z || = 49 + í = 2^3 => r = | Z | = 2^3
6 = arctg(—) de donde 8 6 2do. cuadrante.
Es decir 8= 180°-a, donde tga =— => a = —
3 6
6=t: = — => 8= —
6 6 6
z = -3 + y¡3i = 2-\/3 (eos— +1 sen —)
6 6
6.17. MULTIPLICACIÓN Y DIVISIÓN EN FORMA POLAR.
Sean Z] = r,(cos0, + t"sen0,) y z2 =r2(cos82 + i'sen<?2)
Dos números complejos en su forma trigonométrica, entonces:
z1.z2 = rj(cos0i + í"sen0j)r2(cos2+isen02) -r]r2[cos^l +62)+isen(81+62)]
Sí z2 * (0.0) y r2 qt (0,0), entonces:
z2 r2(cos02 +isen02) r2
Ejemplo.- Sí z, =3(cos—+ i'sen—) y z2 =4(cos— + isen—)
6 6 3 3
Entonces Z, .Z2 = (3)(4)[cos(— + —) + / sen(— + —)] = 12(cos— + i sen —)
6 3 6 3 2 2
4(cos—+zsen—) .
z2 3 3 4r ff ns . ,n k„ 4. n, . tt
» £-=-[cos(----)+ísen(---)]--(cos-+ísen-)
*> 3(cos^+/Sen^) 3 3 6 3 6 3 6 6
Números Complejos
601
6.18. POTENCIAS Y RAICES DE NÚMEROS COMPLEJOS.-
TEOREMA (FORMULA DE MOIVRE)
Para todo z = a + bi y todo entero positivo n se cumple la siguiente relación.
(a + bi)n = r" (eos n6+ i sen n6)
Llamada fórmula de MOIVRE
Demostración
La demostración lo haremos por inducción
i) Para n = 1, a + bi = r(cos 8 + i sen 9)
ii) Para n = h, (a + bi)h = rh(cosh6+isenh0)
■oIeD
iii) Para n = h+l,
(a+bí)h+{ =(a+bi)h(a+bi) = rh(cosh6 + iseT)h6)r(cos6 + isen6)
= rh+1 (cos(h0 +9) +i sen(h0 +0)) = rh+l [cos(/j +1)6 + i seníhjr1)6]
Por lo tanto se cumple la fórmula para todo entero positivo n.
Ejemplo.- Calcular (1 + V3/)7
Solución
Z = l + y¡3i => r= \\z\\ =a/Í+3 = 2 y e=arctg — = —
(1 +V3i)7 = 27(cos— + /sen—) =128(cos—+isen—)
3 3 3 3
TEOREMA.- Si z = a + bi es un número complejo y n es un entero positivo. La raíz
n - ésima de z es z = r [eos + isen ] para
n n
valores de k = 0,l,...,n-1
Demostración
602
Eduardo Espinoza Ramos
Sea w = x + iy, la raíz n -ésima de z
Es decir: w" = z pero como z = r(cos 9 + i sen 9)
w = p(cos a + i sen a)
(x+iy)" =a + bi, reemplazando setiene: pn(cos«a + ¿senA7a) = r(cos0 + i'sen<?)
dedonde p" = r , an = 6 + 2kn, k = 0,l,2 n-1
t Un 6 + 1kK . _. , „ ,
Luego p = r , a = , k = 0,1,2,.., n-1
„ .... i/nr 6 + 2kn . e + 2kn.
Como w = p(cos a + i sen a) setiene: w = r [eos + /sen ]
como w es la raíz n - ésima de z, se tiene:
rrlln 1/nr 6+ 2k7t , . 6 + 2kjt^ -
Z =r [eos + ísen ] para k= 0,1,2,.., n-1
n n
Ejemplo.- Hallar las raices de (-4 + 4Í)1'5
Solución
Calculando su módulo y su argumento
z = -4 + 4i => r = || z || = 4>/2 , 6 = arctg(—) => 9 e 2do. cuadrante
-4
Luego 9 = 180° - a, donde tg a = 1 => a = 45°
Por lo tanto 9 = 180° - 45° => 9 = 135°
, a w/5 ,A /^si/Sr 135° + 2fcff , . 135°+ 2**,
(-4 + 4z) =(4v2) [eos + isen ]
/rr 135° + 2fc;r . l35° + 2kn1
= V 2 [eos + í sen ]
5 5
para k = 0, wl= %/2(cos 27° +1 sen 27°)
Números Complejos
603
k = 1, w2 = y¡2 (eos 99° + i sen 99°)
k = 2, w3=%/2(cosl7r + /senl71°)
k = 3, w4 = >/2(cos 243° +1 sen 243°)
k = 4, w5 = y¡2 (eos 315° + /sen 135°)
m l_
TEOREMA.- Sea z = a + bi, definimos z" = (z")'", para m y n enteros positivos,
donde m y n son primos entre sí, se cumple la relación siguiente:
m m
Z" =r"[cos,—(6 + 2kn) + isen—(6 + 2kn)] siendo r = y]a2+b2, 0=arctg(—)
n n a
Ejemplo.- Efectuar la operación (1 + V3í')5'6
Solución
Calculamos r = y¡a2 + b2 , 6 = arctg(—)
a
r = JÍ+3, e=arctg—= 60° = -
1 3
(l + ^i)5/6=25/6[cos-(- + 2^) + /sen-(-+2^)]
6 3 6 3
para k = 0 , w, = 25/6(cos50° + isen50°)
k=l , w2 = 25/6 (eos 350° +/sen 350°)
k = 2 , w3 = 25/6 (eos 290° + i sen 290°)
k = 3 , w4 = 25'6 (eos 230° +1 sen 230°)
k = 4 , w5 =25/6 (eos 170° +1 sen 170°)
k = 5 , w6=25/6(cosll0o + j'senll0o)
604
Eduardo Espinoza Ramos
6.19. EXPONENCIALES COMPLEJOS (FORMULA DE EULER).
Por el momento admitiremos la definición de la exponencial real.
que más adelante demostraremos, en dicha expresión observamos que:
e°=i, ex+y=ex£y
Definimos la exponencial compleja por: eix = eos x+i sen x (e: número de Euler)
que es llamado la fórmula de Euler.
Sí z = x + iy => ez = ex+,y =ex.e'y = ev(cos v + /sen y)
Cuando y = 0, ez =ex se obtiene la función exponencial real.
Cuando x = 0, e' = e'y = eos y + i sen v , se obtiene la fórmula de Euler.
PROPIEDADES.- Sean z, w 6 C
P,.~ e:
■ = e"
P3.- Si ez=l => z - 2nrci, n es un entero. P4.- (ez)n =e"z, n es un entero
Si en la fórmula de Euler sustituimos x por -x, es decir:
se obtiene: e_Lt = cos(—x) + i sen(—x) de donde
e =cosjc+ísen;c
e =cos jc-tsen x
Luego e" = eos x + i sen x
e =cosx-isenx
Sumando
e'x + e =2 eos x, ósea que:
cosjc = -
Números Complejos
605
analógicamente para el sen x
e = eos x +1 sen x
e " = eos x - i sen x, restando se tiene:
e - e = 2i sen x, de donde:
Por lo tanto:
senjc =
cosx =
e —e
2í
eu-e-Lx
2i
e"+e-"
2
Estas fórmulas sirven para el estudio de las funciones trigonométricas.
i6
Si z = r(cos 9 + i sen 9) entonces z = re' es la fórmula exponencial del complejo
donde r = || z || y 9 se denomina argumento de z que es denotado por 0 = arg (z)
Ejemplo.- Sí z = e'° => || z || = 1
Solución
Como z = e'e => z = eos 9 + i sen 9 de donde || z || = Veos2 8 + sen2 0=1 => || z || = 1
Ejemplo.- Probar que: e 2 = i
Solución
T K K „
el =cos —+ isen—= 0 + i =i
*2 =¡
6.20. LOGARITMO EN C-
La exponencial compleja z = re'e es un número complejo el valor de 9 se denomina
argumento principal de z, que denotaremos por: 9 = arg(z)
606
Eduardo Espinoza Ramos
Para todo complejo z*0, le corresponde solamente un valor de 8 con O<0< 2tc.
Sin embargo cualquier otro intervalo de longitud 2tc por ejemplo -tc < 9 < tc se puede
emplear.
El logaritmo complejo es la inversa de la exponencial compleja, es decir:
Si z = re' es un número complejo => 3 w e C único tal que r = || z || y 9 = arg(z)
Generalizando se tiene:
Lri z = w = ln r + i(9 + 2k7t)
El valor principal de ln z es el que se obtiene cuando k = 0 , es decir:
V.P. de ln z = ln r + i9
Ejemplo.- Hallar ln z, donde z = 1 - i
Solución
7
z=l-i => r=||z||=>/2. tg0=— => 0= —
1 4
ln z = ln(l - i) = ln r + i(9 + 2kn) = lny¡2 + í(— + 2kn) = lnyfí + (- + 2k)ni
4 4
y el V.P.de lnz = ln>/2+—i
4
6.21. EXPONENCIAL COMPLEJA GENERAL.
Sean z, y z2 donde zr *0, entonces consideremos la exponencial compleja w=z¡~
aplicando logaritmos en base natural se tiene:
ln w = ln z,J: = z2 ln Z], y por definición se tiene:
yV=e*-]nz>
Números Complejos
607
6.22. EJERCICIOS DESARROLLADOS.-
Ql) Obtener la forma polar o trigonométrica de los siguientes números complejos.
a) z = >fe + i
Solución
Sea z = x + iy = r (eos 9 + i sen 9)
Donde r=||z|| = 2y tg0=-!==> B= —
V3 6
z = v3 + /= 2(cos—+ i"sen—)
6 6
Y
0
2/
/k/6
Z = y/3 + i
X
b) z = -2-lSi
' = 11*11 = 4 y tg0
-2y¡3
-2
Solución
9 € 3er cuadrante
n
sea a / tga = -Js => a = —
3
n
Luego 6 = 180° + - = 240°
Como z = r (eos 9 + i sen 9)
z = 4(cos 240° + i sen 240°)
c) z = -l-i
z = -l-i => r=\\z\\ =&
Igd - — => 8e 3ercuadrante
Sea a/tga=l=> a = 45°
Luego 9 = 180° + 45° = 225°
Z = -2-2v/3¡
Solución
z = -1-¡
608
Eduardo Espinoza Ramos
z = r(cos 6 + i sen 6) entonces z = >/2(cos 225° + i sen 225°)
d) z = - 4i
Solución
r = ||z|| = 4
- 4
Yt
tge=-
o
6 = 270°
z = r(cos 0 + i sen 0)
z = 4(cos 270° + i sen 270°)
(2) Calcular las potencias indicadas
a) (l-/)5
Solución
Sea z = 1 - i => r = || z || = -Jl
tg6 =— => 0€ 4to cuadrante
1
Sea a/tga=l=> a =
Luego 6 = 2n — = —
4 4
n
Y"
V*
\o
-X. ' x
z=1 -i
35
35
(1-í)5 =r5(cos50 + ísen50) = 4-s/2(cos—/r + i'sen—n)
4 4
b) (x/3-i)6
Solución
Sea z = y¡3-i => r = ||z|| = 2
tg0=—= => 0€ 4to cuadrante
V3
Seaa/tga = —=r => a = —
>/3 6
Y
Y
\
-1
.
•^ *
\ ! x
Z=n/§"-¡
Números Complejos
609
Luego 6 = 2tt =
6 6 6
(>/3 - z')6 = r6 (eos 69 +1 sen 69) = 64(cos lln + i sen 11/r)
c) (-1 + JÍi)7
Solución
Sea z = -l + >/3/' => r = ||z|| = 2
tge =
-i
9e 2to cuadrante
Sea a/ tga = >/3
=* a =
/r
Luego 8=tc = —
6 3 3
(-l + >/3 í)7=128(cos—+/sen—)
3 3
QQ Efectuar las operaciones indicadas.
a) (-128 + 128>/308
Solución
Sea z = -128 + 128>/3/ => r = ||z|| = 256
128 /^
tg0 = => 0 € 2do. cuadrante
-128
Sea a/ tga = ^3
n
=» a = —
3
1 a n 2n
Luego 6 = K = —
5 3 3
(-128 + 12&J%)* = rg(eos6 + 2A7r + /sen0 + 2A7r) donde k =0,1,2,3,4,5.6,7
O O
610
Eduardo Espinoza Ramos
i i
(-128 + 128V308 =(256)8(cos—— + isen — )
2n + 6kn 2n + 6kn,
24
para k = 0 , w.=2(cos— + i'sen—)
F ' 12 12
k=l , w, =2(cos—i-isen—)
2 3 3
7/r . ,___ 7ttn
k = 2 , w-, =2(cos-— + /sen—)
3 12 12
, _ -. 5/r . 5/r.
k = 3 , w4=2(cos—r + isen-:-)
6 6
k = 4 , vv5 =2(cos-:^- + ísen-:-r-)
12
12
k = 5 , W6 = 2(COS —+ ISen—)
k = 6 , w7=2(cos + »sen )
7 12 12
11/T llTT.
k = 7 , wg =2(cos——+ isen——)
24
b) (4>/3-4i)1/3
Solución
Sea z = 4>/3-4i => r = ||z|| = 8
tg0 =
-4
4>/3
9 e 4to. Cuadrante
1 n
Sea a/ tga = —■=- => a = —
V3 6
Y'
V"
\0
k
\ i X
Z = 4n/3-4¡
Números Complejos
611
Luego 6 = 2n =
6 6
i i
ia R *<i i, 8 + 2kn . 6 + 2kn^
(4v3-4í)3 =r3(cos + isen )
3 3
,a R a-^ ->, \\n + \2kn lln + llkn.
(4V3-4j)3 =2(cos + jsen )
18 18
para k = 0 . w. = 2(cos +1 sen )
1 18 18
ii _, ll/r . 11/r.
k=l , w2 = 2(cos + /sen )
, -, -, 35/r 35tt.
k = 2 , w3 = 2(cos +1 sen )
18
18
©
Demostrar que: (1 + i)" = 2 2 (eos—+i sen —)
4 4
Solución
Sea z = 1 + i => r=\\z\\=yf2
tg0 = i = l =» 0=-
1 4
(1 + /)" = r" (eos n0 + / sen nG)
Y
0
/i
i
i
i
X
(1 + í) =22(cos— + /sen—)
4 4
(Y) Demostrar que: (•s/3 - /')" = 2" (eos í sen —)
^"^ 6 6
Solución
612
Eduardo Espinoza Ramos
Sea z = yfí-i => r = ||z|| = 2
tg0 =
£
9 € 4to. Cuadrante
o , 1 n
Seaa/tga = -;= => a = —
& 6
Luego 0 = 2tt = o 8 = —
5 6 6 6
iS-if = 2"(cos/i0+isen/i0) =2"[cos(-—)+isen(-—)] =2"[cos—-/sen—]
6 6 6 6
(ó) Calcular (l + cosa + isencO"
Solución
©
, - 2(x , -. a a „ a, a . a.
l + cosa + ísena = 2cos —h2«sen—eos— = 2cos—(eos—+ isen—)
2 2 2 2 2 2
(1+cosa+isena) =[2cos—(eos—+jsen—)] =2 eos —(eos—+isen—)
2 2 2 2 2 2
Demostrar que: Sí z +— = 2cos0 . Entonces z'" +— = 2cos(/n0)
z zm
Solución
i
► z = eos 9 + i sen 9
Sí z + - = 2cos0
z
— = cos0-/sen0
z
aplicando MOIVRE se tiene: zm = eos m6 + i sen m9
1
eos mQ — i sen m8 Sumando
z'" +— = 2cosw0
Números Complejos
613
Qy Usando la forrrtula de MOIVRE, demostrar las siguientes fórmulas:
a) sen 2x — 2 eos x sen x . eos2a- = eos2 a—sen2 x
1 Solución
(eos a + i sen a)2 — eos 2a + i sen 2a ... (1)
(eos x + i sen v)2 = eos 2 a + 2i eos x sen a - sen 2 x
= eos ' x - sen 2 a +1'(2 eos v sen a) ... (2)
de (1) y (2) se tiene: eos 2a +1 sen 2a = eos ~ x — sen a+ i( 2 eos a sen a)
De donde: sen 2x = 2 eos x sen x ; eos 2a = eos 2 x—sen 2 a
b) sen3A = 3cos2 a senA—sen3 a ; cos3a = cos3 A-3cosAsen2 a
Solución
(eos x + i sen a) = eos 3a +1 sen 3a ... (1)
(eos a + /sen a)3 =cos a + 3ícos a sen a —3 eos a sen x — /sen x
= cos3 A-3cosAsen2 a + (3cos2 Asen A-sen3 x)i ... (2)
de(l)y (2) se tiene:
eos 3a + í" sen 3a = eos3 x -3 eos x sen a+ (3 eos a sen a — sen x)i
de donde por igualdad se tiene: eos 3a = eos x—3 eos x sen * x
sen 3a = 3 eos2 x sen a - sen3 x
{9j Desarrollar eos3 6 en términos de sen 9 y eos 9 de múltiplos de 9.
Solución
z + - = 2cos6 => (z + -f =8cos30
614 / Eduardo Espinoza Ramos
„3fl_í. . K3_J , 1
8cbsJ0 = (z + -r = z +—+ 3(z+-) = 2cos30 + 6cos0
3rt cos30 + 3cos0
eos 8 =
Probar que: sen 0 eos 0 =—(sen 50 - sen 30-2 sen 0)
16
Solución
(2ísen0)3(2cos0)2=(z--)3-(z + -)2=(z5--'r)-(z3--V)-2(z--)
z z z z z
3 2¿ sen 3 0 eos 2 0 = 2i sen 50 - 2/ sen 30 - 4/ sen 0
,3fl„„02,~ !
sen 0 eos 6- (sen50-sen30-2sen0)
16
Demostrar que la raíz cuadrada de z = a + bi es el complejo x + iy, donde:
Solución
Si x+iy es la raíz cuadrada de z = a + bi => (jc + iy)2 = a+bi, aplicando módulos
|| x + iy \\2 - || a + bi || y por definición se tiene:
x2 + y2 =yja2+b2 es decir x2 + y2 = || z || ... (1)
Como (x + iy)2 =a + bi, desarrollando x2 - y 2 + 2xyi = a + bi, por igualdad
x2-y2-
2xy
i 2
x +y -
2 2
x¿-y ■■
~a
= b
= II ^ II
-a
=>
(2)
■ (3)'
W2
sumando
= IUH+«
= \\z\\-a'
y restando (1)
de donde x =
y (2)
■^
:||+*
2 '
. >' =
■*,r"
:||-
2
a
^T^
Aquí se obtiene cuatro pares de miembros reales, de los cuales seleccionamos dos de la
ecuación (3).
Si b > 0 => x, y se eligen con el mismo signo.
Si b < 0 => x, y se eligen con distinto signo.
(l2) Resolver la ecuación en C; z2 =2i
Solución
Resolver esta ecuación es equivalente a sacar la raíz cuadrada.
Luego a = 0, b = 2, || z || = 2
■v = ±.
como b > 0 => z = y¡2i = x + iy = ±(1 + i)
(131 Resolver la ecuación z2 = —3 — 4i"
Solución
Como ||z|| = ^9 + 16=5. a = -3 , b = -4
Como b<0, xey se eligen con signo distinto, es decir (1,-2), (-1,2)
Luego. z = V-3-4í'=±(1-2í")
(l4) Escribir las expresiones siguientes en la forma: a + bi
a) e 3
Solución
. t jt. rr
I+T' 7' r * ■ t, ,1 .V3,
e J =e.es =écos — + isen—\ =e(— + 1—)
3 3 2 2
í>16 Eduardo Espinoza Ramos
■\
b) e 4
Solución
, n. jt.
1—i —i ji /[
e 4 = e.e 4 =efcos( ) + isen( )]
4 4
= e[cos—-isen—] = e(——i—) = (1-í)
4 4 2 2 e
(l5) Si z = 6e3 , Hallar el valor numérico de \e'z \
Solución
jr.
Como z = 6e3 =6[cos—usen—] = 3 + 3v3i
3 3
=> iz = -3>/3 + 3¿, de donde eiz = e~~3 j3+3i = e'^ (eos 3 +1 sen 3)
ll^ll^-*6
(lé) Si z = x + iy, Hallar el lugar geométrico arg(z + l) = —
Solución
Se conoce arg(z) = 0 => arg(z) = arctg(—)
Síz = x + iy => z+l=x+l+iy
arg(z +1) = arctg(——) = —, de donde —^— = tg— = ■& => y = V3(* +1)
jc + 1 3 y + 1 3
[Y7J Si z = x + iy, halle la ecuación del lugar geométrico arg(z~) =
Solución
Números Complejos
617
Siz = x + iy => z" = x —y~ + 2xyi
2, , , 2xy n
arg(z ) = arctg(— =r) = -T
x~-y- 4
, " , =tg(--) = -l => >' =*-+2xv
jc" - v~ 4
sen(—-)A.sen(—)
(18) Demostrar que: senjc + sen2.í + ... + sen/u = —
sen(-)
9
Solución
T = sen x + sen 2x + ... + sen nx
Sv= eos x + eos 2x + ... + eos nx
X X
Sea a = cos—+ ísen —, luego
2 2
a ~ = eos x +1 sen x
a4 = eos 2x + i sen 2*
a" = eos wjc +1 sen nx, entonces
.-r 2 4 2« 2,a"n-K i „ (a"-a") n+! a"-a.
s + iT = a + a + ..:+a =a (—; ) = a a ¡— =a (
a2-l a(a-a ') a-a '
j j n+i ,n + l . n + 1
donde a =cos( jc) + isen( x)
2 2
„ n ■_ . n.v
a =cos — jc + jsen —
2 2
/tí
, sen —
-n n . nx . r -7- .« + K . .n + 1 . 2
a =cos—x-isen—, portanto S + iT-co%{ ) + /sen( x)
2 2 2 2 *
¿ ^ sen-
2
618
Eduardo Espinazo Ramos
sen(/7 + l) —sen —
senjt + sen2jc + ...+ sen/u = —
(19) Calcular
a) ln i '''2
x
sen —
2
Solución
Se conoce que: ln z = ln r + i(6 + 2kn) donde r = || z ||= 1 y 6 = arctg(z) => 6 - —
ln/^=-lni=-(lnl + i(- + 2*;r)) => lni^ =-(—+ 2Jtff)
2 2 2 2 2
b) ln (1 + i)
Solución
z = l + i => y = ||z||=>/2, 0=arctg(—) = 315°= —
1 4
ln(l + í) = ln 72 + /(— + 2kn)
6
(20) Resolver la ecuación x ' — 2x' +2 = 0
Solución
, 2±V4-8 2±2i ,_,_.... , ■ / , • / , ■
x— = = 1±í de donde se obtiene x =1 + 1 v x =1 —1
2 2
aplicando logaritmo se tiene: i ln x = ln(l + i) v i ln x = ln(l - i)
ilnjc = lnV2 + i(- + 2it7r) v iln* = ln>/2+¿(— + 2kn)
4 4
lnx = -2^-iln-s/2 v lnjc = — + 2kn-ilnj2
4 4
*_íln2 Zí-,,n2
x = e4 v x = e 4 donde k = 0.
Números Complejos
619
6.23. EJERCICIOS PROPUESTOS.-
(T) Calcular z4 siendo:
a
a) z = , a e R, 0 < a < 2n
sena—i sen a
b) z-í-^ + i)-1 c) z =
l + i
yfc-i
a* ., 1 .42 . 43 i
— b) + i— c)
sen4 a 32 32 2 2
(2) Sabiendo que n = 3k demostrar que: (— + i —)" + ( i—)" = 2
{3) Calcular 1+2 eos x + 2 eos 2x + ... + 2 eos nx, sug. eos kx -
e +e
(4) Si z = x + iy, hallar la ecuación del lugar geométrico definida por arg(z + 2) = —
„ x + 2
Rpta. y=~j~
Cs) Si z = x + iy, hallar las ecuaciones del lugar geométrico definido por:
a) arg(l±i) = £ Rpta. jc2+y2+2jc + 2;y = 0
2 4
b) arg(-^—í-) = - Rpta. x2 +y2 +jc-2 = 0
x-2 2
(ó) Si z = x + iy, demostrar que el lugar geométrico arg(——) = — es una circunferencia,
^-^ z —2 6
hallar su centro y radio.
(7) Demostrar que: arg(——^-) = — , entonces || z, || = || z2 II
Z! - Z2 2
620
Eduardo Espinoza Ramos
Demostrar que: ( £—) = —
1-í'tga l-/'tg«a
MH Efectuar las operaciones siguientes:
a) (-1 + /)6 b) Cy~)W c) (1 + ^)7
d) (2+2/)"1 e) (l + O-8
\W) Calcular las raíces siguientes:
a) 3/1^7 b) lP~i c) &/5 + Í
d) 3/8 e) #4 f) #í
h) y¡2-2y¡3i i) ^/3-¿
k) (1 + V305'6 1) (-2í)2/3
m)
©
g)
j)
11)
ñ)
q)
v¡
(-1)4/5
y 2+i
V1+1V3
(^ + 4i)1/5
Demostrar que:
a)
H~>
e2m=l
\ 1-í , 11+1
te n) te
o) (2a/3-2i)1/2 p) (,2+2-&i)m
r) (-16/)1'4 s) (02/3
b)
e)
e" =-1
eí+m=-e*
c)
f)
£2±3TO=_e2
(Í2) Sí z = reie => z = r<T''e
Números Complejos
621
U3) Hallar el módulo de los números complejos
a) e2+l b) e2~3i c) e3+4> d) e~^
Rpta. a) e2 b) e2 c) e3 d) £~3
(l4) Expresar en la forma binómica los números complejos.
a) e6 b) 2e 3 c) e4 +e 4
JT.
,2ro ~'
d) 2/e-iro e) 6c6 f)
U5) Hallar la solución de las ecuaciones en C. z2=-lS + 2i
l + e*'
\-e*'
Rpta. z = ±yJ2-j3+iy¡2 + yj3
rió) Simplificar las expresiones siguientes:
. _ l+cos0 + i'sen0 l + itg0 „ l-ictg0 n
a) Z. = b) z = ( ) + ( )
l-cos0+í'sen0 l-/'tg0 l + ictg0
O z = (Ll±lr+(rf^±ir
,-_! (-/)-'+1
(17) Resolver las siguientes ecuaciones:
a) e2^l=l b) ^=i±^í c) ,--=*'»"«■
d) lnc = 2 + — i e) cosz=l-i f) senZ = 2 + -
4 4
fíi) Dado c = -1| -1 + 2/1| +y¡2i, Hallar ln z Rpta. ln I = ln Jl + i(6 + 2kn)
622
Eduardo Espinoza Ramos
(19) Determinar los valores principales de las exponenciales sieuientes:
a) z = V2-i b) ; = (1-iS/3)'" c) z = Oi)2i
Rpta. a) , = ¿'-oi*^-" b)
(m) Calcular: a) [-¿T1-3']3
c) (l + i)-'
(2l) Calcular: a) ln(-i)
c) ln(l+i) d) \n(yj3-j3i)
(22J Obtener los siguientes complejos.
100 100
a) z = JV b) z = Y\'
11
= ¿,6-1" ln 2
b)
d)
b)
c)
(l-i)4'
4+f
2 2
ln/1/3
-—+3iln22
e -
i*
k=0 k=\
ion ino
Sugerencia: I |i'*=i'N
*=I k=\
@e'z-e~iz eiz-e~iz
Sí eos z = , sen z = ■ Demostrar que:
2 2¿
a) eos z = eos x . cosh y - i sen x . senh y
b) sen z = sen x . cosh y + i eos x . senh y
(24) Si z,.z2eC, Probar que: arg(z,z2) = arg(z,) + arg(z2) + 2*7r k=0,±l,±2,..
®n 2n 5n In 9n 1
Demostrar que: a) eos — + cos— + cos— + cos — + cos —- = —
H 11 11 11 11 11 2
Números Complejos
623
6.24. MISCELANIA DE EJERCICIOS.-
\1J Hallar las soluciones reales de las ecuaciones
a) (3x-i)(2 + i) + (x-iy)(l + 2i) = 5 + 6i Rpta. x = —, y = —
b) (x-iy)(a-bi) = i5, dondeayb son números reales |a|*|b|.
D * b °
Rpta. x= , , y = „
a"-* a"-b"
c) (4 + 2i)x + (5 - 3i)y = 13 + i Rpta. x = 2, y = 1
(¿) Si z = (a.b) y w = (c,d) resolver el sistema: iz + (l+i)w = 3 + i ; (l + i)z-(6-i")w = 4
(3) Demostrar que: . = i (x es real)
x — ijl+x2
M) Expresar x e y mediante u y v sí: + = 1, x,y,u,v son reales
^-s x + iy u + iv
2 2
„ u +v -u v
Rpta. * = -, y = - -
(1-m)2+v2 (1-m)2 + v2
(5) Comprobar que:
5 1 ., 1 + 2/ 2-i 2j
a) = — b) + =
(l-i)(2-i)(3-i) 2 3-4/ 5/ 5
(ó) Si z = x + iy demostrar que: z-z-x2 + y2
(7) Demostrar si 9 es un ángulo arbitrario, entonces: = eos 6 +1 sen 6
v~/ eos© ±1 sen0
^8) Demostrar que:
^ (2 + 0 ,
a) z + 3i = z-3i b) iz = -iz c) \ =1
3-4i
624
Eduardo Espinoza Ramos
\9J Si a y b son números reales, Demostrar que: || 1| = 1
b + ai
(lO) ¿Cuál es Re(z2 - 2z) e Im(z3 - 2;) de donde z = x + iy?
© Comprobar que si ||Z2||H|z3ll se cumple ||—3—1|<|| " z- ]J ||
Z2+-3 IIZ2II-IU3H
@ Demostrar que: \\ *' Z 2 ||<1, Z1+Z2*0
W l|Zlll + l|z2ll
(l3) Reducir las siguientes expresiones algebraicas a + bi
a) (l-02+(2 + 02 Rpta. 3 + 2i
b) !±£_!zí Rpta. 2i
l-i l+i
c) Rpta. 1
- 5 10
d) ——r Rpta. 1-i
e) ^ Rpta. |-^
l + i 2 2
f) i Rpta. -i
1
z + 2 „ „ r2 + y2 + 3jc + 2 iv
g) ^ Síz = x + iy Rpta. , % -. /
z + l x2 + y2+2x+l x2 + y2+2.v + l
h) (1+i)(2-i)(l-i) Rpta. 4-2i
i) 12±8/ + 52±13i Rpta. l-4i
2-3/ 13/
(3-
(2-
3 +
1 + /
-0(1-
l + i
+ 0(1 4
2/
0
-20
Números Complejos
625
j) Rpta. —+-i
(l-i)2 2 2
k) 'Re(Z)
lm(/Z)
Reducir las siguientes expresiones a la forma a + bi
a) [ 1 + Re(z) + i lm(z)] [ 1 - Re(z) -
b) [ 34 t
(1-4í)(5 + 3i)
c) (2 + 3i)(3 - 2i) + (2 - 3i)(3 + 2i)
... 4 + i 5-3/
d) +
2-¿ 3-í
. 1 1
e) +
l + 4¿ 4-/
(1+0(1 + 0 (1-0(3-/)
3-i 3+i
, (5 + 5¿)(->/3 + 3i)
8) -S-i
h) (-^ + 3/)6
i) (2v'3 + 2i)(3-3V3i)
... 8 + 8>/3i
i Im(z)]
Rpta. i
Rpta. [l-Re(z)]2+[Im(z)]2
Rpta. 2i
Rpta. 12 + 5i
_ , 16 3.
Rpta. —+—i
5 5
D * 5 3/
Rpta.
17 7
Rpta. -2i
Rpta. 5^3(1-/)
Rpta. 1728
Rpta. 12/3-12/
Rpta. 2>/3 + 2i"
4 + 4^f 2 R ^ + 4i
2 + 2/
(a + bif (a-biT (a2+b¿f
626
Eduardo Espinoza Ramos
115) Hallar el valor absoluto o módulo de:
(4-3í)¿ + i)4
a) —^ Rpta. l
(1-4/X-3+4Í)
4
b) (—)8 Rpta. 1
l-i
c) (3 + 4i)3(-l-i)
d) (3+4¿)(>/6 + /)(2->/3/) Rpta 35
(6 + 7ÍM4-2Q _j_
4 + 2/ 7 + 6¿
d OíOlc^+to Rpta. ^
®
4 + 6i
1
Ql6^ Si z= 1 + i, representar geométricamente los puntos z, —, z2, z 3
(J7) Si z, =l + i, z2 =2-/, representar geométricamente los puntos z,, z2 , Z!+z2. Z1Z2'
¿1
Si z
a)
d)
g)
= x + iy,
Re(±)
Re(-^)
Im(4iz2
hallar:
-6z + 8í)
b)
e)
lm(i)
z
Re(z2+z)
h)
Re(—-
Z
-0
c)
f)
Im(z3)
Re(-iz)
Números Complejos
627
U9) Demostrar que sí (eos a + i sen a)" = 1 entonces (eos a - i sen a)" = 1
(20) Siendo z un número complejo demuéstrese que:
a) ||z||>|Re(z)| _ b) || z || > |Im(z)|
c) ||z||2>2|Re(z)||lm(z)| d) Jl ||z||>|Re(z)| + | Im(z)|
(21) Si w=l(1~z). Demuestre que || z || < 1 implica Im(vv) > 0
\Xl) Indicar que líneas se determina por las siguientes ecuaciones:
a) Im(z2) = 2 Rpta. Hipérbola xy = 1
b) Re(z~2) = 1 Rpta. Hipérbola x2 - y2 = 1
c) Im(—) = — Rpta. Circunferencia x~+{y + \Y= —
Z 2. 4
d) Im(z2 - z) = 2-Im(z) Rpta. Hipérbola xy = -1
c) z2+z =1 Rpta. Hipérbola x2-y2- —
f) 2zz + (2 + /)z + (2-i)z = 2 Rpta. (x+1)2 +(>---)2 =-
2 4
x2 V2
g) ||z-i|| + ||z + i|| = 4 Rpta. Elipse ±- +i- = 1
3 4
(>- + -)2 2
h) || z || - 2 Im(z) = 6 Rpta. Hipérbola —-4 í— = 1
<f>2 <!>2
<*-f>2 y2
i) 3 || z || - Re(z) = 12 Rpta. Elipse —-^— + ' , = 1
(d)2 (3V2)~
2
628
Eduardo Espinoza Ramos
k) Re(z-i) = 2
H) ||z_/|| = ^£>
j) ||z-l+i||=l
1) ||z-i|| = ||z + i||
o) Re(z2-z) = 0 m) Re(l+z) = ||z
n) ||z + i|| = 2Im(z) ñ) Re(z-/) = 2
Determinar la región que describe la región siguiente:
a) ||z-l||<Re(z)
c) 0<arg(z)<^
e) ||z-2 + i||<l
g) 0<arg(z)<^
4
i) | Re(z) | < || z ||
k) || z || > 2 + Im(z)
II) -<Re(-) + lm(-)<-
4 z z 2
n) ||z-l||<||z-i||
Determinar la forma polar de
a) z =
b) 0 < Re(z) < Im(z)
d) 0<arg(-)<^
z 2
0 ||2z + 3||>4
h) ||z-4||>||z||
j) Re(i)<i
z 2
1) || z || - Re(z) < 0
m) 1 < || z + 2 + i || < 2
b) z=-
c) z = (>/3-i)6
l + Si ' " -2-2í
Usar la forma polar de un número complejo para demostrar que:
a) (l + 3¿)"I0=2-"(-l + í>/3) b) (-1 +1)7 =-8(1 + 0
Demostrar que si c es una constantCréaí positiva, entonces la ecuación representa un
círculo sí c * 1 y una recta sfc = 1.
Números Complejos
629
(27) Demostrar que z = a + bi es una solución de la ecuación:
z3 -4(a + bi)z2 +5(a2 -b2 + 2abi)z-2{a3 -3ab2 + i(3a2b-b3)) = 0
(28) Demostrar que si || z - 4i || + || z + 4i || = 10 es una elipse.
(29) Calcular las potencias indicadas.
a) (2-2;)7 Rpta. 2,0(l + i)
b) (V5-3/)6 Rpta. 1728
c) (112^)40 Rpta> -2*\l + iS)
1-i
d) (f4)8 Rpta. 1
l + i
e) ( 5 + 5i f Rpta. -í-
HH/3 + 10i 512
6 + 61 4 4
g) (
i^)4 h) (V2->/608
2
(30) Hallar las raíces indicadas: /
a) 3Jül b) &/5-1 c) $2 + 2-j3i
d) #=32 e) </l6-16>/3/ f) (4>p-4/)
g) (lóV^)1'5 • h) (1Ü)"6 i) «7=1
V2 1-'
j) íA k) ^8-573/
630
Eduardo Espinoza Ramos
1) s¡yf2(cos- + isen-)
V 6 6
U) [(24+24í)(24-24i)]i/9
(31) Resolver las siguientes ecuaciones:
a) z2+9 = 0 b) z2-2z + 2 = 0
c) z2+2z+5 = 0 d) z5+l = 0
c) z8+l = 0 f) z6-l = 0
g) z12-l = 0 h) Z8-l = 0
i) z,2 + l = 0 j) z6-l = 0
(32) Aplicando la fórmula de Movre expresar las potencias de sen 9 y eos 9 las siguientes
funciones de ángulos múltiples.
a) sen 49 Rpta. 4sen0.cos3 0-4sen3í?cos0
b) cos49 Rpta. eos4 0-6cos2 e.sen2 6 + sen4 6
c) sen 59 Rpta. 5sen6.cos4 0-lOcos2 e.sen3 0 + sen5 6
d) eos 59 Rpta. eos5 6-lOcos3 0.sen2 0 + 5cos0.sen4 6
\3ó) Si e'z = eos z + i sen z, demuéstrese que:
a) eos z = b) sen z =
ea -e~n
2 2í
[34) Verificar que:
a) senh iz = i sen z b) cosh iz = eos z
c) sen iz = i senh z d) eos iz = cosh z
c) itghz = tg(iz) f) ctg iz =-i ctgh z
Números Complejos
631
g>
8>
-i
Calcular a y b en: [e
Demuéstrese que:
a)
c)
e)
g)
i)
em=e-ie
a e^-e-*
sen0 =
2/
2 a 1 + COS20
eos 0 =
2
eos iz = eos iz
senh (z + i) = - senh z
™—¡=-
l->/=2
. - «i
] +a + bi = e2
„¡e . „-¡e
b) cosé? =
... 2 o 1-COS20
d) sen 6 = ■
f) eos3 6 =
2
cos30 + 3cos0
4
h) sen i z* sen iz
j) cos(z + iit) = - cosh z
(37) Efectuar las operaciones indicadas y expresar el resultado en la forma x + iy.
.K 3x 2x, 7jt
a
) 3e'3.2V2e4' b) 5e3'.4e6'
5jt. jt. 3jt. 5jt.
c) 2e6'.3e2' d) y¡2e *' .yfee *'
e) 2V2¿1 0 7e»
i, 3e,,r
3e2
[38) Determinar todas las raíces de las siguientes ecuaciones:
a) eos z = 2 b) sen z = cosh 4 c) cosh z = —
d) senh z = i c) cosh z = -2
69) Expresar en la forma compleja los siguientes ejercicios.
, >/3-/V5 D . 11 .VÍ5
a) -^-=—^-t= Rpta. 1
2>/3-«V5 17 17
632
Eduardo Espinoza Ramos
b)
c)
d)
e)
d + 02
4-i
V-7 + 24i
- 1 íl 3~4Í
l-W3-^1*3^1'
3-/
1-i 3-i 5-2/
3+i'7 + ¿'5 + 2i
f)
u * 10 6
Rpta. + —i
17 7
Rpta. ±(3 + 4i)
5 + 3/
1,/ 1"/
4-i+
3-»
MO) Determinar los z e C tales que Im(z+—) = 0
(41j Hallar todos los valores reales de x y los correspondientes de w que hacen que el número
complejo w — (x — i)[(x + 3) - 9i] sea imaginario puro.
Rpta. *=~3 + 3^3 , w = (12-15>/5)i
2
-3-3V5
w
= (12 + 15>/5)i
(42) Si z e C, Demostrar que (z)2 = z2
(43) Hallar el módulo de las siguientes expresiones.
(2-3Q(3 + 4Q 5_ (6 + 40(3-0 ^
(6 + 40(15-80 34 5 + í
® 1 + itgct „ 1+ttgna
Demostrar que: ( —) =
1-t'tgct 1-í'tgna
@ Calcular:
a) <^±Üf> b) (i^í)8 O (75-306
l-i" l + i
Números Complejos
633
d) (S + if e) (4^-)12 I) (- + -)16
V3+i 2 2
. (3 + 3i)"-3
g)
(3*-3i)n
•Mó) Hallar todos los valores de las raíces de las siguientes expresiones.
a) Ifi b) iT\ c) yj3 + 4i d) V21/-20
Expresar el siguiente número complejo en su forma polar
3-4/
(3 + >/3)-(l + 3>/3)!
z = 1-í'+ ^-^ ^ Rpta. z = 2.Seia donde <x = arctg(-0.416)
1->/3i
+ -
3-i
n . . 1 1
(48) Dado z = (5-i)4(l + i) probarque: — = 4arctg--arctg——
(S) Hallar a) Re(é>*2) b) Im(e,Z2)
Rpta. a) e~2"cos(,t2->2) b) e~2xy sen(>2 -x2)
feo) Hallar una fórmula reducida para:
a) 1 + eos x + eos 2x + ... + eos (n -l)x
b) sen x + sen 2x + ... + sen (n - 1 )x
c) eos x + eos 3x + ... + eos (2n - l)x
d) sen x + sen 3x+... + sen (2n-l)x
„ . .. l-cosjc-cosnx + cos(n-l)jc .„ sen(«-l)-jcsenn* + sen.x
Rpta. a) : b)
2(1- eos x) 2(1- eos x)
(Si) Hallar z, tal que || eiz || < 1
(52) Hallar a) Re(e'z") b) lm^"), neZ
634
Eduardo Espinoza Ramos
(56
f„\
Sea z — x + iy = re' , Demostrar que: a) r" eosn6 = x"
■7
V" J
x" -y +
v4y
^V+.
b) r"senn0 =
1
v j
rt-'y-
"~V+~
Calcular z siendo:
a) z = (->/3+7r'
l + i
b) z =
^7
„ . 1 «>/3
Rpta. + ——
32 32
2 2
(55) Determinar los valores principales de las expresiones siguientes:
b) »v = (3í)2'
a) w = (V2-/)1-'
Rpta. a) p = >/3
Obtener el valor principal de z en los siguientes casos
a) (l-i)z=l
c) w = {\-iSf
b) p = arctg(-^) c) vv = ^-)">^-)
b) (1^)-=,-
2
Rpta. a) z = 0
b) z = -
(57) Resolver las siguientes ecuaciones:
a) jc2,'-2jcív+2 = 0
(58
b) x2Si-xJli+\ = 0
^-¡ln2
Rpta. a) x = eA
b) jt = í- 4 '
Probar que z*0
a) Re(-)>0 <=> Re(z)>0
z
x = í>4
* = <? 9 '
b) Im(-)<0 <=> lm(z)>0
z
Teoría de Ecuaciones
635
CAPITULO VII
teoría de ecuaciones
7.1. DEFINICIÓN.-
Llamaremos polinomios de grado n en la variable x a la expresión algebraica definido en
la forma:
... (1)
P{x) = anx" +an_]x" + ...+ aix + a0
donde n > 0 es entero positivo y a0,a{,...,an son números arbitrarios llamados
coeficientes y además an *0 es llamado coeficiente principal.
Al coeficiente a0 le llamaremos término independiente; a cualquier número constante
diferente de cero le llamaremos polinomio de grado cero.
Él número cero es el único polinomio constante que su grado no está definido.
Cuando en un polinomio el coeficiente principal es (an = 1) le llamaremos polinomio
mónico.
Ejemplo.- El polinomio P(x) = x4 + 2x3 +4x + 5, es un polinomio mónico.
NOTACIÓN.-
QT) Con K, denotamos a uno de los conjunto Z, Q, R, ó C.
(^ A los polinomios denotaremos en la forma P(x), Q(x), R(x), H(x), etc.
(3) El conjunto de todos los polinomios en x, con coeficientes en K, denotaremos por
K[xl, es decir: K[x] = [P(x)/P(x) = anx" +an_lx-l + ... + alx + a0, n > 0, a, e K)
(4) Si el grado del polinomio P(x) es n denotaremos en la forma grad (P(x)) = n.
636
Eduardo Espinoza Ramos
En el conjunto K[x] definimos dos operaciones, una de suma (+) y la otra de producto (.)
es decir:
Sí P(x) = anxn +a„_lx'-1 +...+aíX+a0 y Q(x) = bmxm+b„^xm-1 +...+blX+b0
son dos polinomios en x, entonces:
P(x) + Q(x) = (a0+b0) + (al+bi)x + ... + (a¡+bi)xi +...
P(x).Q(x) = c0 +cíx + ... + cm+nxm+", donde
r c0 = a0b0
c, =a0¿, +axba
C2 =O0b2 +Ai¿| +^2^0
c_j =a0bj+albj_l+... + aJb0
, c,n+n = «A
Ejemplo.- Hallar la suma y el producto de los polinomios:
P(x) = 5 + 3x-x2 y £>(*) = 4+ 6x-10x4
Solución
a) />(*) + (2(*) = (5 + 3a-a2) + (4 + 6a-2-10a4)
= (5 + 4) + (3 + 0)a + (-1 + 6)a2+(0 + 0)a-3+(0-10)a-4 = 9 + 3a + 5a2-10x4
b) /'(a).G(a) = (5 + 3a--a2).(4 + 6a-2-10a4)
= 20+12a + 26a2 +18a3 -56a4 -30a5 +10a6
Teoría de Ecuaciones
637
7.2. ECUACIONES POLINOMICAS DE SEGUNDO GRADO.
Las ecuaciones polinómicas de segundo grado son de la forma:
ax2 +bx + c = 0, a*0
(1)
donde a,b.c e R
7.3. RAICES Y DISCRIMINANTES DE UNA ECUACIÓN
CUADRÁTICA.-
Para determinar la naturaleza de las raíces de una ecuación de segundo grado
ax" + bx + c = 0 ,a*0 completamos cuadrados, es decir:
9 0 l? C
ax +bx+c = 0 como a*0 entonces x h—x+— = 0
a a
, b .-> b -4ac
2a 4a-
^
sacando la raíz cuadrada x + — = +
2a 2a
4ac
de donde
x — -
-b±4l?
-4ac
2a
(2)
ahora denotaremos por A = fc* —4ac, al cuál le llamaremos discriminante.
Luego analizamos sus raíces.
Iro. Si h-b2 -4ac>0, entonces la ecuación ax2 +bx + c = 0. tiene dos raíces reales
distintas jr,, x2 dadas por la fórmula (2).
En este caso siempre es posible factorizar ax +bx+c como
ax +bx + c = a(x — Xi)(x — x2).
2do. Si A = ¿r-4ac = 0, entonces la ecuación ax2 +bx + c = 0, tiene una raíz real
f doble) jc, = xn = v = — .
638
Eduardo Espinazo Ramos
Luego en este caso la ecuación ax + bx: + c = 0 es un cuadrado perfecto.
ax + bx + c = a(x-\ )
2a
3ro. Si A = b" — 4ac < O, en este caso se tiene:
Si a > O, ax" +bx + c> O, V x e R, nunca se anula
Si a < O, ax" +bx + c< O , V x e R, nunca se anula
Por lo tanto la ecuación ax" +bx + c = O, no tiene soluciones reales.
7.4. RELACIÓN ENTRE RAICES Y COEFICIENTES DE UNA
ECUACIÓN CUADRÁTICA.-
Suponiendo que a, y x2 son las raíces de la ecuación x~ +bx + c — O, entonces:
x" +bx + c = (x-xi)(x-x2) = x -(\j +x2)x + xlx2
x" +bx + c = x~ — (a, +x2)x + xlx2
por el criterio de la identidad se tiene:
x, + x-, = -b
x,.x0 =c
l,.A2
por lo tanto:
a) La suma de la» raíces de una ecuación cuadrática es igual al coeficiente de x. con el
signo cambiado.
b) El producto de ambas raíces es igual al término independiente.
Ejemplo.- Hallar el valor de k para que la suma de las raíces de la ecuación
2fcr-(12A- + lU + 2 = 0 sea 7.
Solución
A la ecuación 2kx _-(12fc + l)v + 2 = 0. escribiremos así.
Teoría de Ecuaciones
639
2 12* + 1 1 _ - , .
x a + — = O, suponiendo que a, . x2 son las raices entonces:
12* -t-1 .1
x, + jc, —-b- = 7 => A: = —
1 2 2* 2
Ejemplo.- Hallar el valor de k para que el producto de las raíces de la ecuación
(Jt - 2)jc2 - x + 2k = 0 sea 6.
Solución
Suponiendo que a, , x2 sean las raíces, je, .x2 - c (c término independiente)
para esto a la ecuación (k - 2)x - 5x + 2k — 0 escribiremos en la forma:
2 5- + -M- = 0
*-2 *-2
2* ¿ / 3
x, .a, = c = = 6 ^ *: = —
12 Jt-2 2
7.5. ECUACIONES REDUCIBLES A CUADRÁTICAS.-
Como su nombre lo indica son aquellas ecuaciones que no son cuadráticas, pero que
mediante una sustitución adecuada se transforma en una ecuación cuadrática, ilustraremos
estos casos con los ejemplos siguientes:
(7) Resolver la ecuación (x + 9)(x - 3)(x - 7)(x + 5) = 385
Solución
Primeramente ordenaremos los factores.
[(x + 9)(x-7)][(x-3)(x + 5)] = 385 => (jc2 +2a—6)(a2 +2a-15) = 385
observamos que la sustitución adecuada es m = x +2x
(m-63)ím-15) = 385 => (m2 -78w+945>=385
m:-78w + 560 = 0 => (m-$)(m-70) = 0 dedonde m = 8 m = 70
640
Eduardo Espinoza Ramos
|a2+2a-8 = 0 *i=4 , x2=-2
|a2+2a-70 = 0 xi=-l + Jñ , x4 =-1-771
f2) Resolver la ecuación
-v--9 5x
x2-9
= 4
Solución
x2-9 5x
A la ecuación -1— = 4 , expresaremos así:
x x2-9
x2-9 5 . , , ....... JT-9
a2-9
: 4, observamos que la sustitución adecuada es - = m .
entonces m = 4,de donde /tj2-4/w-5 = 0 =* (m-5)(m+l)=0 =*m=5,m=-l
m
x2-9
Sím = 5 => = 5 => a~-5a-9 = 0
5±V25 + 36 5±Vóí . . . 5 + Vól 2 5-Vóí
a = = , de donde a, = , a =
a2-9 ,
Sí m = -l => - = -1 => a-2+a-9 = 0
-i±Vi+36 -i+yfy} , , . -i+yfyi -i-Jy?
— , de donde a, = , x, = ■—
7.6. ECUACIONES IRRACIONALES.-
Las ecuaciones irracionales son aquellas ecuaciones que contienen radicales. La solución
se obtiene por el método de eliminación de los radicales, luego se resuelve la ecuación
resultante por los métodos conocidos, sin embargo, al sustituir todas las raíces posibles en
la ecuación original puede resultar que algunas de estas raíces no sean solución de la
ecuación original debido a que el método de eliminación de radicales requiere elevar a
una determinada potencia a los dos miembros de una igualdad y en éste procedimiento
puede introducirse raíces que no corresponde a la ecuación original.
Teoría de Ecuaciones
641
Veremos algunos ejemplos.
Ejemplos.- Resolver las ecuaciones siguientes:
(l) yj2x-3+yfx:l = yl3x-2
Solución
El método consiste en elevar al cuadrado ambos miembros de la ecuación
(yllx-l+Jx^)2 =(V3x-2)2
2x-3 + x-1 + 2yj2x-3\lx-l = 3x-2 , simplificando
\l2x-3yjx-l = 1, elevando al cuadrado 2a 2 - 5a + 3 = 1 => 2a2 -5x + 2 = 0
(2x-l)(x-2) = 0 de donde a = —, x = 2, ahora comprobando se tiene:
1 fTI fi~* /3~T K ■ Jí ■ 1 p i
para x = , vl-3+J—1= —1 => ^2i + —¡=i^—¡= falso
2 \2 \2 ■& Jl
x = 2, yj4-3+y¡2:-Í = ^6-2 => 1 + 1 = 2 = 2 verifica
Luego el conjunto solución es {2}
(5) V2.r + 8 + >/7+5=7
Solución
Cuando en un miembro se encuentra dos radicales y en el otro miembro no hay
radical es más fácil, pasar un radical al otro miembro de elevar al cuadrado, es
decir:
J2x + &=l-yfx + 5 , elevando al cuadrado
2a + 8 = 49 -14yJx + 5 + a + 5, simplificando
+ 5 , elevando al cuadrado
v2-288a + 1 136 = 0 => (x - 284)(x - 4) = 0 de donde x = 4, x = 284
642
Eduardo Espinoza Ramos
ahora comprobaremos cual es la solución para x = 4, V8 + 8 + V4 + 5 =4 + 3 = 7
x = 284. V568 + 8 + V284 + 5 = 24 + 17*7 falso
por lo tanto la solución es {4}
7.7. ALGORITMO DE LA DIVISIÓN.-
Consideremos dos polinomios P(x) y Q(x) dados por
P(x) - 2a5 + 3a4 + 5jc3 + 6a2 -x: + 6 ; Q(x) = xi + Ix2 + 8a:-1 ahora efectuaremos la
división de P(x) entre Q(x), y para esto adecuamos cada polinomio en potencia
decreciente de x.
P(x) = 2x5 + 3a-4 + 5a-3 + 6a 2 - a- + 6 | x2 -3x + 2 = Q(x)
- 2a5 + 6a4 -4a3 2a3 + 9a2 + 28a + 72 = C(x)
9a-4+a3+6a-2-a- + 6
-9*4+27a3-18a2
28a-3 -12a2 -a- + 6
-28a3 + 84a2 -56a
72a2-57a+6
-72a2+216a + 144
159x-138 = R(x)
COMENTARIO.-
Primero se divide 2x5 entre a2 , que resulta 2a3 ; luego se multiplica 2a" por Q(x) y el
resultado con signo cambiado, se escribe debajo de P(x) y se efectúa la suma se repite este
proceso tomando P(x)-2xiQ(x) en lugar de P(x), hasta obtener el residuo R(x). en este
ejemplo, el cociente es C(a) = 2a3 + 9a2 + 28a + 72 y el residuo es R(x) = 159x - 138
Luego el resultado podemos indicar escribiendo:
2a-5 +3a4 +5a3 +6a2 -a + 6 = (a3 -3a + 2)(2a3 +9a2 + 28a+ 72) +159a—138 ósea
P(x) = Q(x).C(x) + R(x)
Con este ejemplo de ilustración mencionaremos el teorema del algoritmo de la división.
Teoría de Ecuaciones
643
7.8. TEOREMA (ALGORITMO DE LA DIVISIÓN PARA
POLINOMIOS).-
Dado dos polinomios P(x), Q(x) e K[x], donde n > 1 es el grado de P(x) y m es el grado
de Q(x) con 1 < m < n entonces existen dos polinomios de modo que:
P(x) = Q(x).C(x) + R(x) donde el grado de R(x) es menor que el grado de Q(x).
7.9. LA DIVISIÓN SINTÉTICA.-
La división sintética es un procedimiento práctico para encontrar el cociente y el resto de
la división de un polinomio P(x) entre x - r, a la división sintética también se le conoce
con el nombre de "Regla de Ruffini".
Supongamos que P(x) = anx" + an_lx"~l +... + o]x + a0 de grado n, dividiendo entre el
polinomio x - r. de grado 1, entonces por el teorema del algoritmo existe
Q(x)=bn_lx" ' + b„_2x"~2 + ... + b1 degradon- 1 y R(x) un polinomio constante tal que:
P(x) = Q(x).(x - r) + R(x) ... (1)
Ahora reemplazando el polinomio Q(x) y R(x) en (1)
a„x" +a„_lx"~l + ..+alx+a0 = {bn_lx"~i + bn_2x"~2 + ...+b2x + bl)(x-r) + R
= bn_xx" + (b_2-rb„_l)x"^ +(fc„_3 -rbn_2)x"~2 +... + (bl -rb^Jx + iR-rb^
por igualdad de polinomios se tiene:
Vi = an
b„_2 =a„_, +rfcnH
fc„_3 = fl«-2 + rbn-2
¿7, = o, + rb2
R = a0 + rb¡
an =bn-\
a„_l =bn,2 -rb_¡
an-2 =bn-3 ~ rt> n - 2
a | = b, — rb2
a (J = R — rb f
644
Eduardo Espinoza Ramos
estas relaciones nos permite expresar los coeficientes sucesivos de C(x) y R(x) en
términos de los coeficientes de P(x) y C(x), previamente determinado:
««
K-\ = an
««-1
V2
«2
rb3
b2
«1
rb2
*i
«0
rbx
R
r
Los números de la primera fila son los coeficientes de P(x) dispuestos en forma
decreciente a las potencias de x, como an - bn_l, ésta lo bajamos a la tercera fila y el
producto r¿>„_, se escribe como primer elemento de la segunda fila y bn_2 es la suma de
los elementos que están encima de el y así sucesivamente de la tercera fila de ésta tabla
escribiremos el cociente C(x) = bn_¡x"~l + bn_2x"~2 +... + bl y el resto R(x) = a0+ rb{.
OBSERVACIÓN.-
lro. Cuando el divisor es un polinomio de segundo grado factorizable de la forma
(x - a)(x - b), también es aplicable la división sintética.
Es decir: Si P(x) es el polinomio dividendo y (x - a) es el polinomio Divisor,
entonces por la división sintética podemos encontrar el cociente C'(x) y el resto
^talque P(x) = {x - a)C (x) + /?, —(1)
Ahora tomamos a C'(x) como polinomio dividendo y (x - b) como polinomio
divisor de donde encontramos el cociente C(x) y el resto R2 tal que:
C(x) = (x-b).C(x) + R2 ...(2)
Luego sustituyendo (2) en (1) se tiene: P(x) = (x-a)(x-b).C(x) + R2(x-a) + Rx
de donde se observa que C(x) es el cociente y el resto es R = R2 (x-a) + Rl
EJEMPLO DE APLICACIÓN.-
Por división sintética, hallar el cociente y resto de la división
P(\) = 2xA -7x3 +12x2 -1 Ix:- 7 entre 2x2 -3x - 2
Solución
Teoría de Ecuaciones
645
Factorizando 2x~ -3a-2 = (2a + 1)(a-2), ahora hallaremos sucesivamente C"(a) y
C(x) de la división de P(x) entre (x - 2)(2x + 1).
C'U)
C(x)
2
2
2
-7
4
-3
-1
-4
12
-6
6
2
8
-11
12
1
-4
-3
-7
2
-5
2
1
2
C(jc) = 2jT - 4a + 8, /?(*) = -3(a - 2) - 5 = 1 - 3x
2do. Cuando el divisor es un polinomio de segundo grado factorizable o no factorizable o
un polinomio de grado mayor que 2, también se aplica la división sintética y esto se
realiza por el método de "HORNER".
7.10. TEOREMA DEL RESTO.-
Si al polinomio P(x) se divide entre x - r, siendo R una constante arbitraria, hasta obtener
el cociente C(x) y su residuo R entonces P(r) = R, en efecto: por el algoritmo de la
división se tiene:
P(x)
R
x-r
C(x) entonces P(x) = C(x).(x - r) + R
Como ésta igualdad es válida para todo x, en particular es válida para x = r, de donde:
P(r) = (r-r).C(r) + R
= O.C(r) + R = R entonces P(r) = R
Ejemplo.- Hallar el residuo de la división de P(x) = a3 -3a2 -3a-3 entre x - 1
a
Solución
Por el teorema del Testo sejiene P(-l) = R
R = P(-I) = -1 -3 + 3-3 = -4 => R = -4
646
Eduardo Espinoza Ramos
7.11. TEOREMA DEL FACTOR.-
Si P(x) es un polinomio, entonces diremos que r es una raíz de P(x) si y sólo si x - r es un
factor de P(x).
Demostración
Por el teorema del algoritmo de la división se tiene: P(x) = (x - r).C(x) + R
Por el teorema del resto se tiene que R = P(r), pero como r es una raíz de P(x) (o un cero)
es decir: P(r) = (r - r).C(r) + R = R = 0 =* R = 0
Por lo tanto P(x) = (x - r).C(x)
Luego x - r es un factor de P(x) recíprocamente, si se tiene que x - r es un factor de
p(x) =* P(x) = C(x).(x - r), como el resto es R - P(r) = 0 entonces P(r) = C(r).(r - r) = 0,
esto quiere decir que r es una raíz de P(x).
7.12. RAICES DE UN POLINOMIO^
De acuerdo al teorema del factor se conoce que dado un polinomio P(x) con grado n > 1,
un número r se llama raíz o cero del polinomio P(x) sí P(r) = 0.
Ejemplo.-SeaP(jt) = x3, + 3x2 +3jc + 1 el número r=-l es raíz de P(x) puesto que P(-1)=0.
7.13. TEOREMA FUNDAMENTAL DEL ALGEBRA.-
Todo polinomio P(x) de grado n > 1, definido por
P(x) = anx" +an_ix"~l +... + alx + a0, con an *0 tiene por lo menos una raíz la cual
puede ser real o compleja.
Por ahora admitiremos válida la proposición, ya que no es posible dar una demostración
elemental de el.
Teoría de Ecuaciones
6A1
7.14. NÚMERO DE RAICES DE UNA ECUACIÓN POLINÓMICA.-
a) TEOREMA.- Todo polinomio de P(x) de grado n > 1 de la forma
P(x)-anxn +an_lx"~l +... + alx + a0, con an*0, tiene
exactamente n raíces.
Demostración
Mediante el teorema fundamental del álgebra se tiene: que el polinomio P(x) tiene al
menos una raíz r, y por el teorema del factor tenemos: P(x) = (x—rl).C¡(x)
donde C, (jc) es el cociente de la división de P(x) por x — r,.
En forma similar Cx (jc) tiene una raíz r2, de modo que al aplicar el teorema del
factor se tiene: Cl(x)-(x— r2).C2(x) porlotanto P(x) = (x-r]).(x — r2).C2(x)
ahora comentamos: Como cada nuevo cociente es de grado menor en una unidad al
del cociente anterior, podemos continuar el proceso hasta finalmente obtener:
P(jc) = (jt-r,XJC-r2)...(JC-rII) ...(1)
donde cada r¡ es una raíz o cero de P(x).
Si en la ecuación (1) hacemos x = r, donde r es un número arbitrariamente tenemos:
P(r) = (r-ri)Xr-r2)...(r-rn)
Si rí r¡, Vi ninguno de los factores (r-r¡) es cero, donde an *■ 0, P(r) stOyrno
es un cero de P(x), se concluye que hay exactamente n raíces con lo cual el teorema
queda demostrado.
7.15. DEFINICIÓN.-
A la raíz r de un polinomio P(x) diremos que es de multiplicidad m > 1 sí
P(x) = (x-r)'"C(x), donde C(x)*0.
648 Eduardo Espinoza Ramos
Ejemplo.- El polinomio P(jc) = (*+)(*-2) 4(jc-3)2 es de grado 7 y sus raíces
son-1,2,2,2,2,3,3, en donde r, =-1 es una raíz simple
r2 = 2 es una raíz de multiplicidad 4
r3 = 3 es una raíz de multiplicidad 3.
7.16. RAICES ENTERAS.-
Si en la ecuación polinomica P(x) = 0, tenemos raíces entera, entonces estas raíces son
divisores del término independiente.
Ejemplo.- Hallar las raíces enteras de P(x) = 2x3 - x2 - 4x+3
Solución
Las posibles raíces enteras son los divisores de 3 es decir, ±1, ±3, ahora comprobaremos
P(l) = 2-1-4+3 = 0 =* P(1) = 0 =* r=l
Es una raíz entera P(-l) = -2 - 1 + 4 + 3 = 4 * 0 no es raíz
P(3) = 54 - 9 - 12 + 3 = 36 * 0 no es una raíz
Ejemplo.- Hallar las raíces enteras de P(x) = jc4 + jc3 — x1 -Ix — 6
Solución
Las posibles raíces enteras son los divisores de 6, es decir:
±1, ±2, ±3, ±6, ahora probaremos:
P(l)=l + l-l-7-6)-12
P(-l)= 1-1-1+7-6 = 0
P(2)= 16 + 8-4-14-6 = 0
P(-2)= 16-8-4+14-6=12
P(3) = 81 + 27 - 9 - 21 - 6 = 62
Teoría de Ecuaciones
649
P(-3) = 81 - 27 - 9 + 21 - 6 = 60
P(6)= 1296 + 216-36-42-6=1428
P(-6) = 1296 - 216 - 36 + 42 - 6 = 1080
ComoP(-l) = 0 yP(2) = 0 entonces r=-l, r=2 son las raíces enteras.
7.17. FORMA FACTORIZADA DE UN POLINOMIO.-
TEOREMA.- Si el polinomio P(x) = anx" +an_lx"~l +...+ alx + a0 se anula para
r,,r2,r3,...,rn valores diferentes, entonces el polinomio P(x) puede
expresarse en la forma: P(x) — an(x — r,).(jc — r2)...(•* —rn)
Demostración
Sea P(x) = anx" +an_lx"~i +... + aix + a0
Si x = r, anula a P(x) entonces por el teorema del factor se tiene que x- r, es un factor
de P(x), por lo tanto
P(x) = (x-rl).C1(x)
Si x = r2 es una raíz de P(x) => P{r2) = (r2-ri).Cl(r2) => P(r2) = 0=> x-r2es un
factor de C, (x).
Luego P(x) = (x-rl)(x-r2)C2(x)
En forma similar para x = r3 se tiene:
P( x) = (x-r] )(.r - r2)(x - r3 )C3 (x)
P(x) = (x- r, X*- r2 )(x- r3 )...(x - rn )Cn (x)
donde an = Cn (jc) ; por lo tanto:
P(x) = an (x- r, Xx- r2 )...(x- rn )
650
Eduardo Espinoza Ramos
7.18. RELACIÓN ENTRE LOS COEFICIENTES Y LAS RAICES DE
UNA ECUACIÓN POLINÓMICA.-
Consideremos la ecuación polinómica P(x) = 0, de grado n,. es decir:
P(x) = anx" + an_ix"~i +... + aix + a0 =0,con a„ *0
como an *■ 0, a al ecuación podamos escribir en la forma:
jr»+füzL^-i+„.+fL,+f!e. = o
x" + bxxn~l +... + b„_lx + bn =0
(1)
por descomposición factorial se tiene: (x-rx)(x-r2)...(x-rn) = 0 .-(2)
donde rx, r2,..., rn son las raíces de la ecuación P(x), ahora efectuaremos el producto de la
ecuación (2) e igualando coeficientes con la ecuación (1).
n
/ ri:= r\ + r2 + — + rn ~ ~b\ • suma de raíces
i=i
n
\ r¡rj =r\r2+r2r3+... + rn_lrn =b2 , suma de los productos de las raíces de dos en dos.
n
/ r¡rjrh = r\r2r7>+ — + rn-2rn-\rn =~^3 suma de los productos de las raíces de tres en tres.
¡<j<h
rxr2r-i....rn = (-l)"bn, producto de todas las raíces, casos particulares:
para n = 2, ósea: P(x)-x2 +x + b = 0 ...(1)
P(x) = (x-r,)(x — r2) - 0, rx,r2 son raíces efectuando las operaciones.
P(x) = x2 -(r, +r2)x+rxr2 ...(2)
.——a
igualando coeficientes de (1) y (2) se tiene:
-b
\rxr2=í
Teoría de Ecuaciones
651
ahora veremos para n = 3, ósea P(x) = x3 +ax2 +bx + c ...(3)
si r,,r2,r3 son las raíces de (3) entonces: P(x) = (x-rl)(x-r2)(x- r3)
efectuando operaciones se tiene: P(x) = x3 ~(ri+r2+r3)x2 + (rlr2+r1r3+r2r3)x-r,r2r3
igualando los coeficientes con la ecuación (3)
ri + r2 + r3 = fl
• r,r2 + r2r3 + r,r3 =fc
.rlr2r3 =c
7.19. NATURALEZA DE LAS RAICES DE POLINOMIOS RALES.-
Mediante el teorema fundamental del álgebra, se conoce que todas las raíces de un
polinomio con coeficientes reales se encuentra C, en donde algunas de estas raíces son
reales y las otras complejas.
Veremos enseguida que las raíces, tanto complejas como irracionales, se presentan por
pares.
a) TEOREMA.- Consideremos un polinomio real no constante
P(x) = anx" +an_lxn~l +...+ ayX + aQ sí un número complejo
r = a + ip, p / 0. a, P e R, r es una raíz de P(x) = 0 entonces su conjugado
r = a-i¡5 también es raíz de P(x) = 0.
Demostración
Si r es una raíz entera de P(x) = 0, esto es:
a„(r)n +a„_,(r)""1 +...+a,(r) + «0 =0, como los a, son reales, tomando
conjugados se tiene: a„(r)" +a„_1(r)""1 +... + a¡(r) + a0 =0, lo cual demuestra
que r es una raíz de P(x) = 0.
b) COROLARIO.- Todo polinomio real P(x) con coeficientes reales y de grado
impar, tiene por lo menos una raíz real.
652
Eduardo Espinoza Ramos
Demostración
Sí n = 1 => P(x) = ax + b, a * 0, a,b e R
Entonces x = — es una raíz real de P(x)
a
Si n > 3 y r, = or + /J,, P * 0 es una raíz de P(x).
Luego por el teorema (2.19) a), r2 =a, -/V también es una raíz de P(x), por lo tanto
por el teorema del factor: P( x) - (x - r,)(x - r2 )Q( x) - (x 2 - 2ax + p2 +cc2 )Q(x)
donde el grado de Q(x) es n - 2 > 1, donde n - 2 es impar por ser n impar.
Razonando por inducción podemos afirmar que Q(x) tiene una raíz real que también es
raíz de P(x).
c) COROLARIO.- A todo polinomio real P(x) con coeficientes reales podemos
escribirlo como un producto de factores lineales y cuadrático
con coeficientes reales donde a cada factor lineal le corresponde un cero real y a
cada factor cuadrático le corresponde un par de ceros complejos conjugados.
d) TEOREMA.- Si un binomio irracional cuadrático a + yfb es raíz del polinomio
real: P(x)-a„x" +an_lx"~l +...+ a,jc + a0, con coeficientes
racionales entonces el binomio irracional cuadrático a- es también raíz de P(x)=0
Demostración
Como r = a + yjb es raíz de P(x) = anx" +an_ix"~1 +...+ a[Jc + a0 =0, entonces
se cumple: anrn +a„_lr"~l +... + alr + a0 =0
Ahora aplicamos conjugada se tiene:
a„(r)" +a„_i(r)"_1 +... + «,(r) + a0 =0, lo cual quiere decir que r = a- es
raíz de P(x) = 0.
Teoría de Ecuaciones
653
7.20. RAICES RACIONALES DE UN POLINOMIO.-
Consideremos un polinomio P{x) — a„x" +an_lx" ' +...+alx + aQ, con aQ *0, a„ *0,
cuyos coeficientes son enteros.
Si él número racional — es raíz de P(x) = 0 entonces P es divisor del término
independiente a0 y q es divisor exacto de an.
Ejemplo.- La ecuación polinómica P(x) = 9x* -42x3 + 13x2 + 84x + 36 = 0 tiene
cuatro raíces.
Las raíces enteras posibles son los divisores del término independiente 36; ±1, ±2, ±3,
±4, ±6, ±12, ±18, ±36 raíces fraccionarias posibles — donde p es divisor de 36; q es
<?
12 2 4 4
divisor de 9: ±1, ±3, ±9 entonces las raíces posibles son ±—, ±—, ±—, ±—, ±—.
3 3 9 3 9
7.21. TEOREMA DEL LIMITE SUPERIOR DE LAS RAICES REALES)
(LAGRANGE).-
Si en la ecuación P(x) = anx" +an_lx" ' +... + alx + a0 =0, de coeficientes reales, k
representa el número de términos positivos o nulos anteriores al 1er. término negativo y G
es el mayor valor absoluto de los coeficientes negativos, entonces toda raíz real de P(x)=0
es menor que 1 + tí— (an es el coeficiente de x" ) es decir que 1 + kl— es una cota
superior de las raíces positivas del polinomio.
Ejemplo.- Hallar la cota superior de las raíces
P(x)-3x5 +7x4 -ISx3 +5x2 -I2x+l = 0 de acuerdo al criterio la cota
superior es: L = 1 + */—, donde an = 3 , k = 2, G= |-18| = 18, reemplazando
L -1 +, /— = 1 + y¡6 = 4 cota superior.
V 3
654
Eduardo Espinuza Ramos
7.22. VARIACIÓN DE SIGNOS DE UN POLINOMIO.-
Si en un polinomio ordenado en forma descendiente dos ténninos difieren en signo, se
dice que dicho polinomio tiene una variación de signos.
Ejemplo.- P( x) = 8a4 + Ix3 - 2 v2 -3a + 5, 2 variaciones
PU^?*' + 8a2 + 7a-1, 1 variación
P(x) = lx~ +5.V + 8 , ninguna variación
7.23. REGLA DE LOS SIGNOS DE DESCARTES."
Si P(x) = 0 es una ecuación polinómica entera con coeficientes reales y con raíces reales,
entonces:
i) Él número de raíces positivas con coeficientes reales es igual al número de
variaciones de signos de dicho polinomio o es menor que este número en un número
entero positivo par.
ii) El número de raíces negativos es igual al número de raíces positivas de P(x).
Ejemplo.- P(a) = 8a5 -7.v4 +5x3 -2a2-a + 5 = 0 tiene 4 variaciones de signo.
P(-jc) = -8a5 - 7a4 -5 x - 2a2 + 3a + 5 tiene 1 variación de signos
4+ T
■ 2+ 1" 2 imaginarios
0 1~ 4 imaginarios
7.24. ECUACIONES BINÓMICAS.-
Una ecuación binómica es la que consta de dos ténninos de la forma
a"±o = 0
La solución de estas ecuaciones se encuentra por medio del teorema de MOIVRE o por
factorización.
Teoría de Ecuaciones
655
Ejemplo.- Resolver la ecuación jc3 +1 = 0
Solución
Resolviendo por factorización se tiene:
jc3+1 = U + 1)(jc2-a + 1) = 0 dedonde x+l=0 v jc2-jc + 1 = 0
x = -l v x = = —±—i, otra forma es por MOIVRE.
2 2 2
jc3+1 = 0 =» x = }J-V => z = -l+0i
r = ||z||=l, tg6»= —= 0 => e=180° = n
■t/T ii ir r 6 + 2kn 6 + 2kn, , . , „.,
x = yj-l = |UII [eos + isen ], donde k = 0,l,2.
k = 0, jc, =cos— + isen— = — +—£
1 3 3 2 2
k = 1, x2 = eos 3/r + /" sen 3n = -1 + 0¿ = -1
. - 7/r , . 7/r 1 y¡3 .
k = 2, x, =cos — + jsen— = f
3 3 2 2
7.25. ECUACIONES TRINÓMICAS BICUADRADAS.-
Estas ecuaciones son de la forma siguiente:
ax2"+bx"+c = 0
Estas ecuaciones se resuelven transformándolas en una ecuación cuadrática haciendo la
sustitución siguiente y = x" => y" = x""
Luego la ecuación transformada será:
ay~ +by + c = 0
Ejemplo.- Resolver la ecuación siguiente: x" "+6 = 5v
Solución
656
Eduardo Espinoza Ramos
La ecuación dada es: x2'" -5.x"" +6 = 0
sea y = xUn => y2 = x2'", reemplazando v2 -5v + 6 = 0 => (y - 2)(y - 3) = 0 de donde
[y = 2 = jr,/n jc,=2n
[v = 3 = jc"n ^ x, =3"
7.26. ECUACIONES RECIPROCAS,
A los polinomios que tienen la propiedad característica de tener los coeficientes extremos
y los equidistantes de los extremos iguales se denomina polinomios recíprocos, es decir:
P(x) = a„x" +a„_lx"~l + ...+ a„_2x2 +an_1x + a„
la ecuación P(x) - 0 se denomina ecuación recíproca, el nombre es debido a que el
cambio de x es por su recípro*
a un polinomio de 4to. grado.
cambio de x es por su recíproco , la ecuación no se altera como caso particular veremos
x
ax4 +bx3 +cx2 +bx + a-0
para resolver esta ecuación la transformamos al dividir por x~ , es decir:
ax2+bx + c+ + =0 => a(x2 +—) + ¿>(jc + — ) + c = 0
x x2 x2 x
Sea Z=x + - => Z2=x2+\ + 2 => Z2-2 = x2 +
x x2 '" ^ ~ '"" ' x2
Reemplazando se tiene: o(Z -2) + bZ + c = 0, de donde aZ +bZ+c-2a=0
Que es una ecuación de segundo grado.
Ejemplo.- Resolver la ecuación siguiente: x4 +x~ -4x + x +1 = 0
Solución
Teoría de Ecuaciones
657
Como la ecuación x4 +x3 —4x +x+l=0 es recíproca entonces lo dividimos entre x" ,
es decir:
x¿+x-4 + - + —- = 0 => (x¿+—-) + U + -)-4 = 0
X X XX
..(1)
Sea Z = x + - => Z2=*2+4r+2 => Z2-2 = x2+Ar
Reemplazando en la ecuación (1).
Z2-2 + Z-4 = 0 => Z2+Z-6 = 0 => (Z + 3)(Z-2) = 0 => Z = -3, Z =
como x + = Z entonces se tiene:
x
para Z = 2, x + - = 2 => x"2 -2x+l=0 => (jc-1) =0 => x=l de multiplicidad 2
x
■7-3 1 a ^ 2 o , n -3±>/9^4 -3±^
para Z = -3. jc + — = -3 => x +3.x + l = 0 => x = =
7.27. ECUACIONES POLINOMICAS DE TERCER ORDEN.-
Consideremos la ecuación polinómica de tercer grado
a3x +a2x +axx + aü=Q, a3*0
..(1)
como a3 * 0, entonces la ecuación (1) se transforma en la forma
x3 +bx2 +cx + d = 0
... (2)
La ecuación polinómica (2) lo transformamos en otra ecuación polinómica mediante la
sustitución
b
x=y--
es decir: (v—)3+Wv—)2+c( v—) + d =0
3 3 3
658
Eduardo Espinoza Ramos
desarrollando y simplificando se tiene: v3+(c —)v + d = 0
* 3 3 27
y +py+q-0
(3)
, . b . be b
donde p-c—., q-d
3 3 27
ahora hacemos y= A + B, de donde y3 = A3 + B3 + 3AB{A + B)=> y3 = A3 +B3 + 3ABy
y3-3ABy-{A3 + B3)
... (4)
comparando (3) y (4) se tiene: 3AB = -p , A3 + B3 = -q
3 3
como B = —I- => A3—?— = -q, de donde (A3)2+qA3—^- = 0
3A
27 A
27
resolviendo como una ecuación cuadrática en A se tiene:
en forma similar para B3, luego se tiene:
Sea a la raíz real y w, w1 las raíces imaginarias de la unidad.
A = ¡
B-i
-^l^f-
-,-^
a
a w
a w2
T p w
Fórmula de Cardano
Teoría de Ecuaciones
659
Luego y —
}\=cc+P
y2 =aw+ pw2
v3 -aw2 +pw
x\
x2
**
= a+p —
3
n 2 b
= aw+pw —
3
-aw +pw—
3
Como x = v —, la soluciones:
' 3
Ejemplo.- Resolver la ecuación de tercer grado: x3 -9x2 - 9jc -15 = 0
Solución
9
Sea x— v — (—)— v + 3, reemplazando en la ecuación:
3 '
(v + 3)3 -9(y + 3)2 -9(v + 3)-15 = 0, desarrollando y simplificando se tiene:
y3-36y-96 = 0, donde p = -36, q = -96
sea y = A + B siendo: A = \
-i
2 Y 2
= ^96 + V92l6Tn28 = ^96 + 8^7 = 3/^^
660
Eduardo Espinoza Ramos
como x=y —, la solución es: xl = ^4(12 + VÜT) + ^4(12 - ViW) + 3
x2 =^4(12 + vTn)+^4(12->/ri7) + 3
*,=^4(12 + VÍT7)h>2 + ^4(12->/FÍ7)h> + 3
7.28. ECUACIONES CUARTICAS.-
La ecuación de cuarto grado es de la forma:
Je4 +2px3 + qx2 + 2rx + s = Q
... (1)
para obtener la solución, a la ecuación (1) descomponemos en 2 ecuaciones de segundo
grado y estos se consigue de la siguiente manera:
Sumamos a cada miembro de la ecuación (1) (ax + b)
x4 +2px3 +{q + a2)x2 +2(r + ab)x + s + b2 =(ax + b)2
... (2)
donde a, b son cantidades por determinar de tal manera que el primer miembro sea un
cuadrado perfecto.
■y ^
Supongamos que el primer miembro de la ecuación (2) sea igual a (x + px+k) es
decir:
x* +2px3 +(p2 +2k)x2 +2pkx+k2 =(ax + b)2
(3)
comparando las ecuaciones (2) y (3) se tiene:
fp2 +2k = q + a2
pk = r + ab eliminando a y b de estas ecuaciones se tiene:
k2 =s + b2
\p2+2k = q + a2
\k2=s + b2
\a2 =p2+2k-q
\b2=k2-s
pk=r+ab=> pk-r = ab, elevando al cuadrado (pk-r)2 -a2b" =(p" +2k-q)(k~ -s)
Teoría de Ecuaciones
661
efectuando operaciones y agrupando se tiene
2k3-qk2 +2(pr-s)k-p2s + qs-r2 =0
de esta ecuación siempre se halla un valor real para k y con estos valores se hallan los
valores de a y b.
como (x~ +px + k)2 = {ax + b)2 , de donde
(x +px+k) — (ax + b)2 =0, por diferencia de cuadrados
[a-2 + (p + a)x + (k+b)][x2 +(p-a)x + (k-b)] = 0
Luego los valores de x se obtienen de las dos ecuaciones cuadráticas.
x +(p + a)x + k + b-Q
x2 +(p-a)x + k-b-0
Ejemplo.- Resolver la ecuación cuadrática a4 +2x3 -lx2 -8.x+ 12 = 0
Solución
Como la ecuación de cuarto grado es de la forma: x4 + 2px3 + qx2 + 2rx +5 = 0
entonces comparando con la ecuación dada se tiene:
p=l, q = -7, r = -4, s = 12, además se conoce que:
2¿t3 -qk2 +2(pr-s)k-p2s + qs-r2 =0
al reemplazar los valores de p,q,r y s, se tiene: 2k3 +7k2 -32k-112 = 0
Luego por Ruffini se tiene el valor de k.
2
2
7
8
15
ía2 =
-32 -112
60 112
28 0
p2 +2k-q
k = 4
a = A
como
\b2=k2-s
b = 2
662
Eduardo Espinoza Ramos
como las ecuaciones de cuarto grado se descompone
x2 + (p-a)x + k-b-0
x2 +(p + a)x + k+b-0
reemplazandop=l,a = 4, b = 2,k = 4
x2-3.x + 2 = 0 jc, = 1 , x2=2
x2+5;c + 6 = 0 x3=-2, x4 = -3
7.29. GRÁFICA DE UN POLINOMIO^"
Como un polinomio P(x) es una función continua, entonces las coordenadas de los puntos
de la gráfica de un polinomio se determina dando valores reales a la variable x, luego
calculamos dando valores reales a la variable x, los valores correspondientes a P(x) y por
lo tanto la gráfica del polinomio P(x) es el conjunto de puntos {(x,P(x)) / x e R}.
Ahora veremos algunos criterios que nos permita aproximar la gráfica de un polinomio
evitando de ésta manera la forma laboriosa de tabular los puntos (x, P(x)).
En primer lugar, los puntos de la gráfica que corresponde a los ceros o raíces reales de un
polinomio P(x) están sobre el eje X y son de la forma (x,0).
Io Si x = a es una raíz real simple de la ecuación P(x) = 0 la gráfica de P(x) corta al
eje X en el punto (a,0).
Y'
0
,
/(a.O) x
Teoría de Ecuaciones
663
2° Si x = a es una raíz de multiplicidad m par, la gráfica de P(x) es tangente al eje X en
el punto (a,0).
3o Si x = a es una raíz de multiplicidad m impar, la gráfica de P(x) es tangente y corta
al eje X en el punto (a,0) en este caso se dice que (a,0) es un punto de inflexión de la
gráfica de P(x).
(a,0)
Mediante el criterio de los puntos críticos se determina en que intervalos la gráfica
está sobre el eje X y en que intervalos está la gráfica debajo del eje X.
Ejemplo.- Granear el polinomio P(x) = x3 — Ix —6
Solución
Calculando las raíces de la ecuación P(x) = 0
1
1
1
0
-1
-1
_2
-3
3
-7
1
-6
6
0
-6
6
0
x = -l
x = -2
x = 3
1 0
664
Eduardo Espinoza Ramos
ahora ubicamos las raíces de P(x) = 0 en el eje X y luego aplicamos el criterio de los
puntos críticos.
Se puede determinar, los intervalos en los cuáles se encuentra las raices reales de la
ecuación P(x) = 0, mediante la siguiente regla.
7.30. REGLA,
Sean a y b dos enteros consecutivos con a < b.
i) Si P(a) y P(b) son de signos iguales, entonces entre a y b existe por lo menos un par
de raíces reales o ninguna raíz real de P(x) = 0.
Y'
ii) Si P(a) y P(b) son de signos contrarios entre a y b existe un número impar de raíces
reales de P(x) = 0.
Y
P(a)
0
P(b)
i
a 1 I
1 b
\ ' x
Teoría de Ecuaciones
665
Ejemplo.- Hallar el intervalo donde se encuentra las raíces de la ecuación
x2+3x-2 = 0.
Solución
Calculando la cota superior de las raíces de jc2 + 3.x - 2 = 0
L = 1 + k\— donde k = 2 es el número de términos anteriores al 1er. termino negativo.
G = 0 es el mayor valor absoluto de los coeficientes negativos
an = 1 es el coeficiente de x2 , reemplazando tenemos: L = 1 + 0 = 1
Sí />(*) = x2 + 3jc- 2 de donde:
|7>(0) = -2
< => existe una raíz real en (0,1)
[P{1) = 2
I>(-1) = 4
< =* en (-1 ,-2) no existe otra raíz
\P(-2) = -*
ÍP(-3) = 9-9-2 = -2
< => d otra raíz en (-4,-3)
|/>(-4) = 16-14 = 2
Ejemplo.- Determinar donde se encuentra las raíces de jc3-3x2 +3x + 2 = 0
Solución
Calculando la cota superior de las raíces.
L = 1 + k\— donde k = 1, G = 4, an = 1, reemplazando se tiene:
L = 1 +4 = 5 cota superior
P(x)- jc3 -4x2 +3jc+2 de donde
P(5) = 42
P(4)= 14
666
Eduardo Espinoza Ramos
P(3) = 2
P(2) = O es una raíz
P(l)=2
P(O) = 2 "I
\ => 3 una raíz real en (-1,0)
P(-D = -6j
P(-2) = -28
7.31. SOLUCIÓN NUMÉRICA DE ECUACIONES CON EL MÉTODO
DE NEWTON.-
Consideremos la ecuación de la forma: F(x) = 0 ... (1)
A las soluciones de la ecuación 1 se le llama raíces de la ecuación ó ceros de la función F
Si F es una función polinomial de grado menor que cinco, existen fórmulas para calcular
sus raíces, por ejemplo para el caso de la función lineal o la función cuadrática, para el
caso de una función polinómica de grado tres o cuatro, el método general de obtener las
raíces es complicado; además para obtener las raíces de una función polinómica de grado
cinco o mayor existe un teorema, que corresponde a "Niels Abel 1802 - 1829" el cuál
manifiesta que no puede haber fórmula general en términos de un número finito de
operaciones sobre los coeficientes, sin embargo existen procesos numéricos para
aproximar soluciones de ecuaciones y que debido al uso creciente de las computadoras y
calculadoras programables son de mayor importancia que antes, uno de estos métodos es
la aplicación de la derivada y que fue desarrollada por Sr. Isaac Newton en el siglo XVII
y que se conoce con el nombre de el Método de Newton.
El Método de Newton es un procedimiento que aproxima una raíz de la ecuación F(x)=0
es decir:
Un número r tal que F(r) = 0, para esto daremos una interpretación geométrica tomando
la gráfica de y = F(x).
Teoría de Ecuaciones
667
Y
0
y=F(x)\ T T
/PX.F^))
"^^ 3 / 2 1 *»
El número r es la intersección de la gráfica de F con el eje X, para obtener una primera
aproximación para r, se toma un número jc, observando la gráfica y se traza la recta
tangente 7, a la gráfica de F en el punto (jc, , F(jc,)) que intercepta al eje X en x2, ahora
x2 sirve como una segunda aproximación de r, nuevamente el proceso trazando la recta
tangente a la gráfica de F en el punto P2 (jc2, F(jc2 )) que intercepta al eje X en jc3 el cual
es una tercera aproximación, se continua el proceso hasta que se tenga el grado de
precisión requerido para obtener las aproximaciones sucesivas jc2,jc3,..., a partir de la
primera aproximación jc, se usan las ecuaciones de las rectas tangentes.
La recta tangente 7, en el punto Px (jc, , F(jc, )) tiene una pendiente F' (jc, ) y por lo tanto
su ecuación es: 7,: j-F(jc,) = F'(jc, )(jc-jc,)
La intersección de T¡ con el eje X es cuando jc = x2 , y = 0.
F(*,) „
0-F(jc,) = F'(jc,)(jc2-jc,) => x2=xl-
FU)
Sí F'(jc)*0
en jc = jc2 , la ecuación de la recta tangente T2 es: T2 : y — F(jc2) = F'(x2)(x — x2)
La intersección de T2 con el eje X es cuando jc = jc3 , y = 0
F(JC2)
0-F(x2) = F'(jc2)(jc3-x2) => jc3=jc2
F'(Jc2)
Sí F'(jc2)*0
668
Eduardo Espinoza Ramos
continuando de esta manera se obtiene la fórmula general para la aproximación xn+x en
términos de la aproximación anterior xn .
F(xn)
*„+, = *„ - _ , Sí F'{xH)*0
*n+l - "Si
FW
(2)
La fórmula (2) es la que se usa en una computadora o calculadora programable.
Ejemplo.- Utilice el método de Newton para calcular la raíz real de la ecuación
x —4x -2 = 0 con cuatro cifras decimales.
Solución
Sea F(x) = x3-4x2-2
> F'{x) = 3xí -%x
Los extremos relativos se encuentran cuando F'(x) = 0
o
3jc2-8jc = jc(3jc-8) = 0 =* x = 0, x = -
F(0) = -2, F(2) = -10, F(3) = -11, F(4) = -2, F(5) = 23
La raíz se encuentra entre 4 y 5.
Luego una primera aproximación seria x, = 4.5
n
1
2
3
4
5
*„
4.5
4.17
4.12
4.11
4.117
xl-4xt-2
n n
8.125
0.96
0.03
-0.13
-0.02
3*n2-8*„
24.85
18.81
17.96
17.8
17.91
*n3-4*;-2
3x2n-Sx„
0.33
0.05
0.0017
-0.007
-0.001
Xn+\
4.17
4.12
4.11
4.117
4.118
Teoría de Ecuaciones
669
7.32. EJERCICIOS PROPUESTOS.-
I. Problemas sobre ecuaciones de segundo grado
(i) Hallar el valor de k para que la suma de las raíces de la ecuación
2Jb:2-(12Jt + l).r + 12 = 0 sea7. Rpta. k=-
\2J Hallar el valor de k para que el producto de las raíces de la ecuación
(k-2)x2-5x + 2k = 0 sea6. Rpta. k = 3
(3j Hallar el valor de k en la ecuación x2 +(2k + 5)x + k=0 si una raíz excede a la otra en 3
unidades. Rpta. k = -2
\4j Determinar los valores de m para que la ecuación jc - 2(1 + 3m)x + 7(3 + 2m) = 0,
tenga una solución. Rpta. m = 2, m =
(5) Si a y P son las raíces de la ecuación ax1 + bx+c = 0, hallar el valor de:
2 02
a) —+— Rpta. b(3ac-b2)
P «
b) a"3+j3_3 Rpta. -^-(3ac-b2)
c
(ó) Hallar la suma de las raíces de la ecuación (2k + 2)x 2 + 4x - 4kx + k-2 = 0, sabiendo que
o ♦ 10
estas son inversas. Kpta. —
©Para que valores de m, la suma de las raíces de la ecuación = , es igual al
jc —jc _ m-1
4jc-5 m + l
duplo del producto de las raíces de dicha ecuación menos 1.
(5) Si r y s son las raíces de la ecuación wjc2 - 2(m - 1)jc + m = 0, con m constante y cumplen
r s
— + — = 4, Hallar la suma de todos los valores de m que satisfacen tal propiedad.
s r
Rpta. -4
670
Eduardo Espinoza Ramos
\9J Si {a,b) es el conjunto solución de la ecuación 3jc2 -2(w + 1)jc + (w-1) = 0 hallar m
para que se cumple 9ab2 +3o3 + 9a2b + 3b3 = 192 Rpta. m = 5
UO) Hallar m para que la suma de los cuadrados de las raíces de la ecuación
x2 - (m + 3)x + m + 2 = 0 sea igual a 2. Rpta. {-1,-3}
(ll) Determinar k en la ecuación x2 +kx + l2 = 0, de modo que entre las raíces r y s exista la
... 1 1 1 „ t 32
relación —1— = — Rpta.
r s 9 3
[íl) Hallar todos los valores no negativos de P para los cuáles las raíces de la ecuación
2 18
cuadrática (p-3)x -2px + 6p = 0 sean reales y positivos. Rpta. < 3, — >
(l3) Hallar la ecuación cuadrática cuyas raíces son la suma y el producto de las raíces de la
ecuación ax2 -{a2 +l)jc + a = 0, donde a*0. Rpta. ax2 -(a2 +a+)x + a2 +]-0
(j^ Si a y b son constantes en R, se tiene que las raíces de la ecuación x2 +ax + b = 0 son
los cuadrados de las raíces de 2x2 +jc-6 = 0. Hallar |4a + b|. Rpta. 16
Q5) Las raíces r y s de una ecuación cuadrática satisfacen 4r-16s = 7 y 8r + 4s = 5.
Hallar la ecuación cuadrática cuyas raíces son respectivamente las inversas de r y s.
Rpta. 3a2+8jc-16 = 0
(ló) Hallar el valor de k para que la ecuación 25jc2 +foc + l = 0 tenga sus dos raíces reales e
iguales. Rpta. ± 10
U?) Si las raíces de la ecuación mx2 + (m +1) = (2m + l)x se difieren en 0.5. Hallar las raíces.
Rpta. 1. - y 1,-
2 2
Teoría de Ecuaciones
671
(18) Si a y p son las raíces de x~ + px + q = 0 , fórmese la ecuación cuyas raíces son (a +)3)2
y(or-)3)2. Rpta. x2 + {2q-p2)x+p2{p2 -4<?) = 0
(19) Hallar el valor de k en la ecuación x2 + (2k + 5)x + k = 0, si una raíz excede a la otra en 3
unidades. Rpta. k = -2
(20) Si r y s son las raíces de la ecuación x2 - px + q = 0 , hallar
a) r2+s2 b) r3+í3
Rpta. a) p2-2q b) p{p2 -3q)
(21) Si a y p son soluciones de la ecuación x2 +bx + c = 0 y sí a - p = 2 y a3 - ¡53 = 26
Hallar |-|. Rpta. -
b 4
(22) Si r y s son las raíces de la ecuación v" -4jc +1 = 0 . Hallar la ecuación cuyas raíces sean
r2+-yí2+-. Rpta. jc2-18jc + 54 = 0
r s
(23) Si a y b son las raíces de la ecuación x2 +mx+2m2 = 0. Hallar el valor de a^b1 +a7b5.
Rpta. -96 w12
(24) En la ecuación 2x2-(m-l)x + (m + \)=0 ¿Qué valor positivo debe darse a "m" para
que sus raíces se diferencien en uno? Rpta. m = 11
(25¡) Sean a y P raíces de la ecuación cuadrática (m-2)x2 -2mx + 2m-3 = 0, sí
a~l + /T1 = — . Hallar el valor de | a - P | Rpta. -
\2ú) Hallar los valores de m para los que la ecuación cuadrática (m + 3)jc* — 2mx + 4 = 0 tienen
soluciones reales. Rpta. m e <-°o,-2] u [6,+°°> - {-3}
672
Eduardo Espinoza Ramos
(27) Sea P un número real fijo, si r y s son las raíces de x2 + px + 36 = 0 tales que — h— = — .
Hallar el valor de p2-2p + l. Rpta. 252
(28) Formar una ecuación cuadrática cuyas raíces sean la suma y el producto respectivamente
de las raíces de ax2 +bx+c = 0,a*0. Rpta. ax2 +a(b — c)x — bc = 0
II.
©
©
©
©
Resolver las siguientes ecuaciones:
(jc--)2-4jc + —= 12
X X
x(2x+l)(x-2)(2x-3) = 63
:+jc = 7-\/jc2+jc + 2-12
(£±L)2_£li_2 = 0
jc-3 jc —3
© *2"
72
jc + — = 18
x2-x
(4) (2jc-7)(jc2-9)(2a- + 5) = 91
© (jc2-3jc)2-2(jc2-3jc)-8 = 0
® 3(^±l)2-4-^- + l = 0
^ 2jc-1 2jc-1
(9) ^±2_3_4£z2=0
^ x-2 x+2
[10) -!±¿-5 + 4^i!- = 0
jc + 1 jc + 3
(H) 3£±2_i0 + 92£-1=()
^S 2-jc-I 3jc + 2
12) jc6+7jcj-8 = 0
(U) ÍJC + 1 + —)Cjc-1 + —) = 24
— x x
(14) jc8 -17jc4 +16 = 0
(16)
8 + 9yj{3x -1)(jc - 2) = 3jc2 - 7jc
U2 ~ 1,
Hallar la suma de las soluciones reales de la ecuación 2(jch—) - l{x+—) + 5 = 0
jc x
(17
a-z-3_2jc-2
Jc-l "jc2-3
-1
(18) 4jc2-3jc+ —- 6 = 0
4v2-3jc
Teoría de Ecuaciones
673
III. Hallar todas las raíces enteras y racioi
© 12jc3+7jc2-42jc-40 = 0
© 6jc3+7jc2-9jc + 2 = 0
© 108jc3-270jc2-42jc + 1=0
© jc3-6jc2 +15jc-14 = 0
© *4-2jc3-8jc2+13jc-24 = 0
@ jc5-7jc3-12x2+6jc + 36 = 0
@ 24jc5+10jc4-jc3-19jc2-5jc + 6 = 0
@ IOjc4 -13jc3 +15jc2 -18*-24 = 0
IV. Resolver las siguientes ecuaciones.
© V5*+9 = 2jc + 3
© >/3jc + 1+1 = >/4jc + 5
© >/jc+T + V3jc + 4 = >/5^ + 9
© Vjc2+jc-4=2
© yl2x-3 + Jx~^Í = j3x-2
de las ecuaciones.
© jc3-jc2-14jc + 24 = 0
© 24jc3-2jc2-5jc + 1 = 0
© 3jc4-40jc3+130jc2 -120^ + 27 = 0
® 6jc4-37jc3+79jc2-68jc + 20 = 0
(ÍO) 12jc4-67jc3-15jc2+484jc-480 = 0
@ 6jc4+19jc3-7jc2-26jc + 12 = 0
@ jc45-2jc4-4jc3+4*2-5jc + 6 = 0
@ jc4+2jc3-13jc2-38x-24 = 0
© >/5jc + 1=V2jc + 1+2
© V3jc + 12-1 = V5jc + 9
© yl3x + l+yl2x + 6=Jll-5x
© 4/jc2-2jc + 8=2
@ yjl2-yfx~+S=yj2-2x
674
Eduardo Espinoza Ramos
V. Resolver las siguientes ecuaciones
\\J Que valor debe tomar k para que el polinomio
P(jc) = x6 +2x5 +k\* -x3 + 2(8 +A')*2 + 6jc-18 sea divisible por jc3 +2x2 -3.
Rpta. k = -2
(¿) Dados los polinomios x4+ax2+b, jc2+2jc + 5, determinar a y b de modo que el
primero sea divisible por el segundo. Rpta. a = 6, b = 25
(¿) Encontrar valores para a y b de tal manera que 2x2 ~4lx + b sea divisible de
6jc3 -137jc2 +ax-91.
\4J Determinar p, q, r en xA + 3x3 + px2 +qx + r para que sea divisible exactamente por
(jc2-4)U + 1). Rpta. p = -2, q = -12, r=-8
(s) Determinar el valor de k de manera que:
a) P(jc) = 3jc3 + 7jc2 +kx-3 sea divisible por x + 3. Rpta. k = -7
b) P(x) = 2x4 -kx3 -x-6 sea divisible por x - 2. Rpta. k = 3
(é) Determinar "n" y "m" para que el polinomio jc4 +2jc3 -7jc2 +mx + n sea divisible por
jc2-3jc + 15. Rpta. m= 16, n= 15
\j) Si el polinomio P(x) = x* -3axi +a2jc2 +ma3x-na es divisible entre el polinomio
Q(x) = x2 -ax + 2a2. Hallar él valor de (m + n)(m2 -mn + n2). Rpta. 215
Qj) Que valor ha de tener X para que sea divisible el polinomio 2x4 -3x3 +hc2 -9x + 9
por x-3. Rpta. X = 7
(9) Que valores han de tener pyq para que sea divisible el polinomio 3.v3 + px' +<?v + 42
por(x-2)(x-3). Rpta. p = -8, q = -17
Teoría de Ecuaciones
675
(10) Qué valores han de tener a y b para que sea divisible el polinomio
x4 -ax3 +bx2 +bx + 9 por x2 -1.
(11) Hallar el valor de k para que el cual 3jc — 2x2 +kx—8 sea divisible entre x- 2.
Rpta. k = -4
(12) Si el polinomio P(x) = 2x4 -mx3 +x2 -nx + 2 es divisible por x-1 y x + 2, hallar el
valor de n-m. Rpta. 21
(13) Determinar "m" y "n" para que el polinomio jc4 + 2jc3 -lx2 +mx + n sea divisible por
jc2-3jc + 5. Rpta. m= 16, n= 15
(14) Determinar la relación que debe existir entre "p" y "q" para que el polinomio
x +px + q, sea divisible entre jc +mx-\. Rpta. p + q +1 = 0
Ql5) Si se sabe que el polinomio {a-b)x3 + (b-c)x2 +(b + c)x + a-b es divisible entre
x2+n2 calcular — Rpta. —
2 2 o
a +c 2
(ló) Sea P(x) = jc3 +ax2 +bx + c al dividir P(x) tanto por x + 2 como x + 3 el residuo
obtenido es cero, pero al dividir por x-1 el residuo es -12. Calcular
A=14a-5b + 3c
(l7) Determinar a, b, y c de modo que (x - 3)(x + l)(x - 1) sea un factor de
x5 -2jc4 -6a:3 +ax2 +¿jc + c.
VI.
(1) Hallar el valor de k en la ecuación jc3+fcc+16 = 0 sabiendo que tiene dos raíces iguales.
(2) Hallar el valor de k en la ecuación jc3 -3x2 -6x+k = 0 para que sus raíces estén en
progresión aritmética.
676
Eduardo Espinoza Ramos
(3J Hallar las raíces de la ecuación 2x3 +(k + 2)x2 + (2k - 2)x + 1 = 0. sabiendo que su suma
1
es
2
Q) Hallar las raíces de P(x) = xA + 2x2 + 25 conociendo la raíz r = yJ2 + y¡3i.
(SJ Hallar todas las raíces de P(x) = x3 +2x3 -4x2 -I4x-2l sabiendo que r = -l + y¡3i es
una raíz.
(ó) Hallar todas las raíces de P(x) = x4 +2x3 -4x2 -I4x-2l sabiendo que a = -1 + >/5i
es una raíz.
\7j Demostrar que la ecuación x1 —4x6 + 2x3 —9x2 —6 = 0 tiene por lo menos cuatro raíces
complejas y por lo menos una raíz positiva, pero ninguna raíz negativa.
Qn Hallar todas las raíces 4x4 -15x2 -3x + 7 = 0 sabiendo que r = — v2 es una de sus
raíces.
(?) Hallar todas las raíces de 3x5 -20x4 + 62x2 -51x + 10 = 0 sabiendo que r,=2->/3,
r2 = 1 - v6 son dos de sus raíces.
(10) Hallar todas las raíces del polinomio x4-10x3+53x2 -140jc + 196 = 0, sabiendo que
tiene dos raíces dobles.
(11) Hallar las raíces del polinomio 3x4 +8x3 +6x2 +24x-9 = 0 conociendo dos raíces r, y
r2 que satisface rlr2 =—1 .
^2) Resolver la ecuación x3 -lx2 + 14x-8 = 0 que tiene las raíces en progresión
geométrica.
(o) Resolver la ecuación x3 -\2x2 + 39*-28 = 0 que tiene las raíces en progresión
geométrica.
Teoría de Ecuaciones
611
(l4J Resolver la ecuación .v4 + 4x3 — 2x2 -12x + 9 = 0 que tiene dos pares de raíces iguales.
(ís) Hallar las raíces enteras de:
a) 3x3-37x2+93jc-27 = 0 b) x3-4x2-x+4 = 0
c) 2x3-x2-4x+3 = 0 d) x4+x3-x2-7x-6 = 0
(ló) Hallar los valores de a y b para los cuales -3 y 2 sean raíces de la ecuación
x4 +x3 +ax2+bx + 30 = 0
U7) Hallar las raíces de los polinomios siguientes conociendo las raíces que se indican.
a) x3+6x2 -24x + 160 = 0, r, = 2-2y¡3i
b) x3 -3x2 -6*-20 = 0, r, =-l + y¡3i
c) x4+2x2+25 = 0, rl=y/2+y¡3i
d) x4+2x3-4x2-Ux-2l = 0, r, =-l + y¡3i
e) x4 -4x2+Sx-4 = 0, r, =1 + /
f) x3-3x2-5x+l = 0, r, = 1-J%
g) x4-13;c2+4;c+2 = 0, r = 2->/2
h) 4x4-l5x2-3x + l = 0, r = --yÍ2
2
i) *4-2;c3-5;<:2-6;c + 2 = 0, r = 2-y¡3
j) ^4-3x2+10x-6 = 0, r = -l + >/3
VIL Resolver las siguientes ecuaciones:
© x4-2;c2+7 = 0 ® x4-10x2+9 = 0
© 4x4-5x2+l=0 © x4+2.í2+25 = 0
678
Eduardo Espinoza Ramos
©
©
VIII.
©
©
©
©
IX.
©
©
©
©
©
®
©
®
©
©
®
x3 + x3-l = 0
i
x-4x2 + 3 = 0
Resolver las siguientes ecuaciones
xA + 4x3 -3>x2 + 4x + \
x4-2x3-x2-2x + l =
xA +5x3 +6x2 + 5x + l
x4 -Wx3 +26x2 -Wx
= 0
0
= 0
+ 1 = 0
Encontrar todas las soluciones de las
y3-9y-12 = 0
y3-6y-6 = 0
y3-15y-30 = 0
y3+15y-20 = 0
x3-9x2-9x-15 = 0
x3-6x2-12x-8 = 0
x3+9x-6 = 0
x3-12x-34 = 0
x3+18;c-6 = 0
2x3-3x2+5 = 0
x3+6x2-36 = 0
®
6x2
©
©
©
siguientes ecuaciones
©
©
©
©
©
©
©
©
®
©
@
-lLc4-2 = 0
x4 -x3-4x2-x+l = 0
x4-&x3 +17x2-8x + ]
2x4+x3 -6x2+x+2 =
cúbicas.
y3+18y + 6 = 0
y3+21y-42 = 0
y3-18y-3 = 0
y3+12y + 12 = 0
x3-3x2 -18x-36 = 0
x3-6x2-6x-U = 0
x3-6x-6 = 0
x3+9x-6 = 0
2x3+6x + 3 = 0
3x3-6x2-2 = 0
x3+3x2+9x + 14 = 0
Teoría de Ecuaciones
679
(23) a3+6a2+6a + 5 = 0 (24) x3 -15a2 + 105a-245 = 0
(25) 8a3+12x2+102a-47=0 (ló) a3 + 3a2 + 9a + 14 = 0
(27) x3-6a2-12a-8 = 0 (28) a3 + 3a2 -3a-1 = 0
(29) a3+9x2+18a+28 = 0 (30) a3-6a2 + 57x-196 = 0
(3l) 2a3+3jc2+3a + 1=0 (32) *3 -15a2 -33a + 847 = 0
Í33) a3+6*2+6a + 5 = 0 (34) a3 -15a2 + 105x-245 = 0
(35) 8a3 + 12x2 + 102a-47 = 0 (36) a3 +6a2 -24a+160 = 0
6t) a3-3a2-6a-20 = 0 (38) a3+9a-6 = 0
(39) 2a3-6a2+3 = 0 Q»o) a3+12a-12 = 0
(4l) a3+18a-30 = 0 62) a3+21a + 342 = 0
(43) a3+4a-1 = 0 (44) a3-6a2-4 = 0
^5) a3-15a-30 = 0 Qló) 28a3-9a2+1 = 0
(Í7) a3-63a-316 = 0 (48) a3 +72a-1720 = 0
X. Encontrar las soluciones de las siguientes ecuaciones:
0 a4-2a2-8a-3 = 0 @ x4-a2+2a-1 = 0
0 a4-25a2+54a + 10 = 0 @ x4 -13a2 +36a-18 = 0
0 a4-3a2+18a-20 = 0 ® a4-6a2+20a-24 = 0
0 a4-11a2-6a + 10 = 0 0 x4-24a2+16a + 10 = 0
0 a4-28.v2+24a + 12 = 0 © x4-31x2+54a-14 = 0
© a4-25a2+12a + 18 = 0 @ a4 -3a2 -12a + 40 = 0
680
®
®
©
®
®
®
@
®
®
®
®
®
®
®
®
®
®
®
©
x4+10x2+12x + 40 = 0
x4-8x2-4x+3 = 0
x4+x3-5x2+2 = 0
x4-3x2+6x-2 = 0
x4+3x3-2x2-10x-12 = 0
x4 + 2x2+x + 2 = 0
2x4+x3+2x2-3x-2 = 0
x4-2x3-5x2-6x + 2 = 0
x4-2x3+2x2+4x-8 = 0
x4-2x3+4x -2x + 3 = 0
x4-8x3+17x2-8x + l = 0
x4-4x3+3x2+2*-l = 0
x4 - 6x3 + 6x2 + 27x - 56 = 0
x4+2x3-7x2-8x+12 = 0
x4-x3-3x2+5x-10 = 0
x4+5x3+6x2 +5x + l = 0
x4-9x3+12x2-80x-192 = 0
X
x4-2x3-8x2+13x-24 = 0
x4-13x2+4x + 2 = 0
®
®
®
©
®
®
®
@
®
®
®
®
®
®
®
®
®
®
®
Eduardo Espinoza Ramos
x4+llx2+10x + 50=0
x4-4x2+x+2 = 0
2x4+5x3-8x2-17x-6 = 0
x4-x2-2x-l = 0
x4+5x3+x2-13x + 6 = 0
x4+5x2+2x + 8 = 0
x4+x3+5x2+5x + 12 = 0
x4-2x3-x2-2x+l = 0
x4+2x3+8x2+2x + 7=0
x4-6x3+10.v2-2x-3 = 0
x4+2x3-2x2+6x-15=0
x4 -2x3 +4x2 + 2*-5 = 0
x4 + 2x3+9x2-8x-10 = 0
x4-2x3-12x2+10x + 3 = 0
x4-3x3+x2+4x-6 = 0
x4+2x3-4x2-14x-21 = 0
x4+2x3-13x2-38x-24 = 0
24x4 - 42x3 - 77x2 + 5x + 60 = 0
x4-3x2+10x-6 = 0
Teoría de Ecuaciones
681
[SÍ) .v4-4.v2+8x-4 = 0 (52) 3x4-40jc3+130x2-120^ + 27 = O
(53) 6x4+19x3-72-26x+12 = 0 (54) 10x4-13x3+15x2-18x-24 = 0
(s7) 6x4-37x3+79x2-68x+20 = 0 (ió) 12x4 -67x3 -15x2 +282^-280 = 0
XI. Utilizar el Método de Newton para calcular la raíz de la ecuación con cuatro cifras
decimales.
(T) 6.v3+9x + l = 0 (2) x3-4x-8 = 0
(5) x3-2x + 7=0 (4) x4-10x + 5 = 0
0 x4-10x + 5 = 0 (ó) 2*3+x-2 = 0
© 3x3-7x-2 = 0 ® x3-;c-3 = 0
® *3+x2-2;<:-2 = 0 © x3-4x2 -5*+20 = 0
@ *3+2;c2-8;c-16 = 0 @ *3+2;c2-3;c-6 = 0
6S2
Eduardo Espinoza Ramos
CAPITULO VIII
1 VECTORES BIDIMENSIONAL
8.1. CONCEPTOS BÁSICOS.-
a) INTRODUCCIÓN.- Los antiguos Griegos desarrollaron la Geometría elemental,
ellos crearon una forma sistemática de analizar las
propiedades de los puntos, las rectas, los triángulos, las circunferencias y otras
configuraciones.
Todos sus trabajos estaban sistematizados en "Los elementos de Euclides" que
fueron las bases de la geometría plana y del espacio hasta nuestros días, sin embargo
no se había conseguido avances importantes; pero en 1637. el filosofo y matemático
Francés Rene Descartes revolucionó la matemática de su época, al crear la geometría
analítica en la que introduce las coordenadas rectangulares, llamadas también en su
memoria, coordenadas cartesianas y de esta forma consigue algebrizar las ideas
geométricas de sus antecesores.
El propósito de este método consiste en introducir mediante un sistema de
coordenadas, los conceptos de relaciones geométricas a conceptos de relaciones
algebraicas y viceversa, por lo tanto en este capítulo estudiaremos el método
analítico y para esto nos familiarizaremos con el concepto de vector que es una
herramienta de gran importancia en la matemática moderna.
b) PAR ORDENADO.- Llamaremos par ordenado a dos objetos cualquiera "a" y "b";
que denotaremos por (a,b), donde "a" es llamado la primera
primera componente y "b" la segunda componente.
Ejemplo.- Son pares ordenados (2,5), (-1,3), (Pedro, María), (hombre, mujer).
Dos pares ordenados (a,b) y (c,d) son iguales, si sus primeras componentes son
iguales y las segundas también.
Vectores Bidimensional
683
En forma simbólica es:
(a,b) = (c,d) <=> a = CAb = d
c) PRODUCTO CARTESIANO DE CONJUNTOS.-
Consideremos dos conjuntos A y B, se llama producto cartesiano de A y B, al
conjunto de los pares ordenados (a,b) donde "a" pertenece al conjunto A, y "b"
pertenece al conjunto B y denotaremos por A x B, es decir:
A x B = {(a,b) / a G A a b G B}
Ejemplo.- Sean A = {1,2,3 J y B = {a,b}, el producto cartesiano de A y B es:
A x B - {(l,a), (l,b),(2,a),(2,b),(3,a),(3,b)}
Si A = B, denotaremos AxA = A2 y para nuestro caso tomaremos A = B = R, es
decir RxR = R~ ya sus elementos llamaremos pares ordenados de números reales.
Consideremos un sistema de coordenadas cartesianas de ejes X e Y, y a los
puntos de este sistema de coordenadas cartesianas, denotaremos por Px (x,, y,),
Pi^yz). P¡(x3, v3),..., etc.
Su representación gráfica es:
Y
y2
Vi
-t P¿W¿
tpi(xt'Vi)
d) DISTANCIA ENTRE DOS PUNTOS.- Consideremos dos puntos /JOc,,?,) y
P2(x2,y2), a la distancia de P¡ a P2
denotaremos por d(P¡,P2) y es dado por la fórmula:
d(Pl,P2) = yj(x2-x1)2+(y2-y1)7
684
Eduardo Espinazo Ramos
Es decir: En él APlAP2, por Pitágoras se tiene:
d(Pl,P2) = yj[d(Pl,A)]2 +[d(A,P2)]2
... (1)
además se tiene:
d(Px,A) = x2-xl
d{A,P2) = y2-y,
..(2)
Y'
V2
yi
0
i
J *2 ' X1
]pi(xi.yi)
xi >
y2-Vi
•Aí^y,)
<2 X
reemplazando (2) en (1) se tiene:
d{Px,P2) = yj(x2 -Xi)2+(y2- y,)2
e) SUMA DE ELEMENTOS EN RxR = R 2 .-
Dados dos puntos Pl{xl,yl) y Pj^,^) de i?2, la suma de elementos de R2 se
define del modo siguiente:
Pi(xí,yí)+P2(x2,y2)=Pi(x1+x2,y1+y2)
f) MULTIPLICACIÓN DE UN NÚMERO REAL POR UN ELEMENTO DE
Sean r e R y P(x,y) e R2, el producto de un escalar r por un par P(x,y), denotamos
por r.p(x,y) y se define como:
r.P(x,y) = P(rx,ry)eR¿
Dentro de las aplicaciones de la matemática a la física e ingeniería se usan
frecuentemente cantidades que poseen magnitud y dirección; por ejemplo, tenemos
la fuerza, velocidad, aceleración y desplazamiento, a estas cantidades se representan
geométricamente por un segmento de recta dirigido de P a Q que denotaremos por
PQ donde el punto P se llama punto inicial y el punto Q se llama punto terminal o
final. Luego el segmento dirigido PQ se llama vector de P a Q y denotaremos por:
Vectores Bidimensional
685
PQ = a
8.2. VECTORES BIDIMENSIONAL.-
8.2.1. DEFINICIÓN.- Un vector bidimensional es una pareja ordenada de números
reales (x,y), donde "x" se llama la primera componente y, "y"
se llama la segunda componente.
8.2.2. OBSERVACIONES.-
\\J A los vectores bidimensional se representan por una letra minúscula y en la
parte superior se le coloca un segmento de recta o una flecha, es decir:
a=(íj|,a2), b=(bí,b2), c=(q,c2), ...
Q¡) Al conjunto de los vectores bidimensional denotaremos por V2, tal que:
V2 =RxR = {& =(fl,,fl2)/oi e R a a2 e R}
(3) Al vector cero simbolizaremos por 0=(0,0).
\4J Si ae V2, entonces el opuesto del vector a =(a,,a2) quedará definido
—>
por: -a =(-a,,-a2)
y5) El vector fila, sus componentes se escriben una a continuación de la otra:
—»
a = («j, «2)
Qn El vector columna, sus componentes se escriben una debajo de la otra:
a =
donde a¡ es la primera componente.
a 2 es la segunda componente.
686
Eduardo Espinoza Ramos
8.2.3. REPRESENTACIÓN
BIDIMENSIONAL.-
GEOMETRICA
DE
UN
VECTOR
Un vector bidimensional a = (a,,a2) es representado mediante un segmento de
recta dirigido, cuyo punto inicial es cualquier punto P(x,y) del plano cartesiano y
el extremo final es el punto cuyas coordenadas son: Q(x + al, y + a2), tal como
se muestra en la figura.
Y'
y + a2
y
0
Qíx + a^y + aj)
*^ ai |
| p(x.y) i
x x + a1 x
8.2.4. VECTOR DE POSICIÓN O RADIO VECTOR.-
Al vector cuyo punto inicial se encuentra en el origen del sistema de coordenadas
y el extremo libre puede ubicarse en cualquier cuadrante del plano cartesiano, se
denomina vector de posición o radio vector, así como se muestra en la figura.
tY
A(ara2)
—>
OBSERVACIÓN.- Al vector 0 lo representaremos por cualquier punto
siendo su dirección indefinida.
Ejemplo.- Representar gráficamente al vector a , cuyo punto inicial es P(x,y), sabiendo
que su representación de posición es:
Vectores Bidimensional
687
© 7 = (3,4), P(2,1) (Ver figura 1)
® 7 = (4,0), P(2,6) (Ver figura 2)
© 7 = (-2,5), P(3,-4) (Ver figura 3)
Solución
Y
1
0
< Q(5,5)
T/ /a
-/-/P(2,1)
2 3 X
Y
0
a
P(2,6)
Q(6,6)
X
(figura N° 1)
(figura N° 2)
-4 JP(3,-4)
(figura N° 3)
8.3. OPERACIONES CON VECTORES.
8.3.1. IGUALDAD DE VECTORES.- Dos vectores a y b son iguales si y sólo si,
sus componentes correspondientes toman los
mismos valores; es decir:
Si a , b e V2, entonces a = (c,,c2), b =(bx,b2) y expresaremos así:
688
Eduardo Espinoza Ramos
a = b «=> al=b1 /\ a2=b2
Si a y b no son iguales, entonces escribiremos:
a *■ b <=> ai,* b{¡, para algún i = 1,2,3.
Ejemplo.- Calcular el valor M = 7x + 5y si a = b donde
—» -*
a = (5x + 3y, 4x-y-4), b=(4x+2y + 5. 3x+y + 7)
Solución
Aplicando el concepto de igualdad de vectores.
a = b <=> (5x + 3y, 4x - y - 4) = (4x + 2y + 5, 3x + y + 7)
Í5jt + 3;y = 4^ + 2^ + 5 \x = l
< de donde <
\4x-y-4 = 3x+y + 7 [3' = -2
M = 7x + 5y = 7(7) + 5(-2) = 49 - 10 = 39
M = 39
8.3.2. INTERPRETACIÓN GEOMÉTRICA DE LA IGUALDAD DE
VECTORES.-
VECTORES IGUALES.- Dos vectores son iguales si tienen la misma
dirección, el mismo sentido, el mismo tamaño,
—» -*
el mismo punto inicial y el mismo punto final y se denota por a = b .
punto inicial b
VECTORES EQUIVALENTES.- Dos vectores son equivalentes si
tienen la misma dirección, el mismo
sentido, el mismo tamaño pero diferente punto inicial y se denota por
—> —>
a = b.
Vectores Bidimensional
689
punto inicial punto inicial
8.3.3. PRODUCTO DE UN ESCALAR POR UN VECTOR.-
—>
Sea X un escalar (X e R) y sea a e V2 un vector bidimensional. entonces
—> —>
llamaremos producto de X por a denotado por A. a , al vector resultante cuyas
componentes deben ser multiplicados por X, es decir:
Si a e V2 entonces a =(a,.a2), luego
A a =k.{ax,02) = {Xax,hj2)
Xa / Xa
X>0 /X<0
Ejemplo.- Sea a = AB un vector donde:
(T) A(l,l,), B(4,3), X = ±2, graficar los vectores AB y XAB
Solución
a = AB =B-/\ = (4,3)-(l,l) = (3,2)
690
Eduardo Espinoza Ramos
A a =2(3,2) = (6,4)
A a =-2(3,2) = (-6,-4)
-5
4 7 X
(2) Si a =(2,3) graficar 3 a y -3 a
Solución
3^ = 3(2,3) = (6.9)
-3 T =-3(2,3) = (-6,-9)
Y"
9
3
-6
1 /
1 _"*■ /
■3a/
/
1 /
1 •
^
• 1
/ |
~7< !
•ir !
2 6
-9
x
8.3.4. PROPIEDADES DE LA MULTIPLICACIÓN DE UN ESCALAR POR UN
VECTOR.-
—» —»
Para todo escalar r.s e R y los vectores a, b e V2 - se verifican las siguientes
propiedades:
r. a es un vector.
©
\hj r{a+b) = ra + rb
(?) l.a = a
(4) r(s. a ) = (r.s) a
© 0.a =0
8.3.5. SUMA DE VECTORES BIDIMENSIONAL.-
—. -» —> —»
Dados los vectores a y b . el vector resultante suma a + b se obtiene sumando
sus correspondientes componentes, esto es:
Vectores Bidimensional
691
Si a,be V2 , entonces a =(«,,«,). b-{bx,b2)
—> —» ,
a+¿ =(flj +¿(,02 + ^2)
—» -»
Ejemplo.- Si a =(3,5) y b =(1,4), entonces:
a+£ = (3,5) + (l,4) = (3 + l, 5 + 4) = (4,9)
8.3.6. INTERPRETACIÓN GEOMÉTRICA DE LA SUMA DE VECTORES.-
En la interpretación geométrica de la suma de vectores consideramos los
métodos siguientes:
ler. MÉTODO DEL PARALELOGRAMO.-
—> —>
Se dibujan las representaciones de los vectores a y b desde el mismo punto (se
—* —»
hace coincidir los puntos terminal de a e inicial de b ) y se completa el
-» —>
paralelogramo. La diagonal trazada desde el punto común representa a + b .
2do. MÉTODO DEL TRIÁNGULO.-
—» —>
Los vectores a y b se grafican uno a continuación del otro, luego el vector
-> -» -»
resultante a+b se obtiene del punto inicial del vector a con el punto final del
—>
vector b .
692
Eduardo Espinoza Ramos
3er. MÉTODO DEL POLÍGONO VECTORIAL.-
La resultante de la suma de varios vectores se obtiene llevando los vectores una
continuación de otro haciendo coincidir el extremo de uno con el origen del otro,
para finalmente determinar la resultante uniendo el origen del primer vector con
el extremo del último vector.
a = 1+ 2+ 3 + ...+ n
8.3.7. PROPIEDADES DE LA SUMA DE VECTORES.-
Para todo vector a,b,c se verifican las siguientes propiedades:
(V) a+b es un vector. \2J a + b = b+ a conmutativa
—^. —>—*—> —> —» —*
\3j a + (b+c) = (a+b)+ c , asociativa
(4) V a vector, existe un único vector 0 , tal que a + 0 = a , neutro aditivo.
[Sj V a vector, existe un único vector - a , tal que a + (- a) - 0 , inverso
aditivo.
Vectores Bidimensional
693
8.3.8. DIFERENCIA DE VECTORES-
-* -»
Consideremos los vectores a, b ; a la diferencia de estos vectores se define de la
siguiente manera:
a-¿> = a + (-£>)
Si a,fceV2 => a=(a,,a2), ¿> = (fc]f¿>2), de donde:
a- b = {a^-bi,a¿-b2)
Ejemplo.- Sean a =(-1,3) y b =(4,8). Hallar 3.(¿?-2a ) + 6a-2¿
Solución
fc- 2 a = (4,8) - 2.(-L 3) = (4,8) - (-2,6) = (6,2)
6a-2¿?=6.(-l,3)-2(4,8) = (-6,18)-(8,l6) = (-14,2)
3(fc-2Í) + 6r-2fc=3.(6,2)+(-14,2) = (18,6) + (-14,2) = (4,8)
8.3.9. INTERPRETACIÓN GEOMÉTRICA DE LA DIFERENCIA DE
VECTORES.-
-* -* —>
A los vectores a, b lo representaremos por los segmentos dirigidos PQ y
PR con la condición de tener el origen común en el punto P, entonces la
-* —» —> -*
diferencia de a,¿» es decir: a— b quedará representado por el segmento
—> -*-*-* -*
dirigido QR , puesto que £>+(a-£>) = a (ver gráfico).
694
Eduardo Espinoza Ramos
Ejemplo.- Dado la representación de a y b dibuje a — b, usando la
definición de resta y la regla del triángulo para la suma.
Solución
Dibujando los vectores a = AB , b = AC, desde el mismo punto inicial A.
B,
Ahora dibujamos — b
y A
Empleando la regla del triángulo para la suma se dibuja a- b
8.4. LONGITUD O MÓDULO O NORMA DE UN VECTOR.
La longitud o módulo de un vector a es el numero real no negativo representado por
—»
|| a || y es definido por la raíz cuadrada de la suma de los cuadrado de sus componentes.
esto es:
Vectores Bidimensional
695
Si aeV, => a=(a,,a2) de donde:
|| a || = yjaf+a
cuya representación gráfica es:
Yt X -*
0
a1
X
Si a = (o, ,a2) es un vector de posición cuyo módulo y representación gráfica es:
Y'
0
i
'$7
»i
s
T= (ava2)
a2
X
Ejemplo.- Si a = (3,4) su módulo es: || a || = -\/32+42 = V9 + 16 = >/25 = 5
Ejemplo.- Si a =(2,4) y b =(3,5) entonces:
||2a-3fc || = ||2.(2,4)-3(3,5)|| = ||(4,8)-(9,15)|| =||(4-9,8-15)||=||(-5,-7)||
= -s/(-5)2 + (-7)2 = V25 + 49 = V74
696
Eduardo Espinoza Ramos
8.5. PROPIEDADES DEL MODULO DE UN VECTOR.-
Se verifican las siguientes propiedades:
© ||a||>0, v7 vector © ||^|| = 0 <=> 7=0
® ||r.a|| = |r|||a||. Va* vector, re R.
Q4} || a+ ¿ || < || a || + || ¿||, Va, b (desigualdad triangular)
Demostración
© Si a = C¿?,,í32)5t C0.0) => a, *0 v a2 *0
|| a || = ,/a,2 + a2 * 0, como ^/a2 + a2 ^ 0 entonces /. || a || > 0
© i) Si || a || = 0 =» 7=0
Si a=(fl,,fl2) => II a II = v^í2 + fl2 = 0 entonces
a2+a2=0 <=> fll =0 a «2=0. Por lo tanto a=(0,0)=0
En forma similar si a = (a,, a2»a3) entonces
ii) Si a = 0 => || a || = 0
Si a =(0,0) => ||a|| = Vo2+02=0 => ||a|| = 0
Si a* = (0,0,0) => ||7|| = V02+02+02=0 => || a || = 0
(3) Si a = (a,,a2), r e R entonces: r a = r(a,, a2) = (ra,, ra2) su módulo es:
Vectores Bidimensional
697
Por lo tanto: || r a || = | r | || a ||.
(4} La desigualdad triangular lo demostraremos posteriormente en base a la desigualdad
de CAUCHY-SCHWARZ.
8.6. VECTOR UNITARIO.-
Se llama vector unitario, al vector cuyo módulo es la unidad, es decir: a es un vector
—»
unitario si y solo si || a || = 1.
Ejemplo.- El vector a =(—,—) es unitario por que II a II = .1—H =J— = 1
F 5 5 \25 25 \25
8.7. TEOREMA.-
Dado un vector a * 0 , entonces el vector u = es un vector unitario.
Ha||
Demostración
-* —»
Sea a € V2 => a = (a, ,a2) * (0.0) entonces:
"* a , a, a-, . ..-*,. .
u= = (——,—^-) esunitanosi ||«|| = 1
lla|| ||a|| IUII
esdecir: i^.ri^aí'.L¿_+_á_-Jlit-i
Vil a || ||a|| Vil a II2 II a ||2 \||a||2
Por lo tanto como || u || = 1 entonces « es unitario.
Ejemplo.- Si 7 = (3.4) => || a || = >/9 + 16 = V25 =5
-* a 3 4
por lo tanto: u = = (—,—) es unitario.
Ha|| 5 5
698
Eduardo Espinoza Ramos
8.8. DIRECCIÓN DE UN VECTOR EN R2 .-
Cada vector no nulo a =(ax,a2) y su representación como radio vector le corresponde
—»
una dirección dada por la medida del ángulo 0 formado por el vector a y el eje X
positivo en sentido antihorario.
—» —» i
Si a=(fl,,fl2) => || a || = Vfl,2+o|
Y
0
L
\\Z\\/
/)Q
31
a = (a
32
X
sen 0 = —— " ^"^fl — —-
y cos0 =——, de donde se tiene:
Hall ||a||
a, =|| a ||cos0 ; a2 = || a ||sen0 ... (1)
además 0°<6<360o y de (1) se tiene:
a =(a,,fl2) = (||a ||cos0, || a ||sen0)=||a ||(cose,sen0)
por lo tanto, un vector queda determinado por su magnitud y su dirección.
—» —» -» -»
Si u = a es un vector unitario, es decir || u || = || a || = 1
—»
Luego si « es un vector unitario se puede expresar en función de 0 es decir:
u =(cos0,sen0)
y el ángulo 0 se denomina ángulo de inclinación o ángulo de dirección del vector a
OBSERVACIÓN.- La medida del ángulo 0 se obtiene de la forma siguiente:
Mediante un ángulo de referencia a y haciendo uso de una tabla de valores se halla el
valor de a con 0o < a < 90° para el cual tga - \ — |, a, * 0 .
Si a,>0, a-, >0 => 0e 1er. cuadrante:
0 = a
Vectores Bidimensional
699
a, <O, a2 >O => Ge 2do. cuadrante: 0 = 180°- a
a,<0, a2<0 => 0 e 3er. cuadrante: 0=180°+ a
«! > O, a2 < O => 0e 4to. Cuadrante: 0 = 360° - a
Y1
6 = 180°-a 6 = a
8 = 180° +a
6 = 360°- a
Ejemplo.- Hallar un vector a de longitud 6v3 y que tiene la misma dirección de un
vector que forma un ángulo de 30° con el sentido positivo del eje X.
Solución
~a=\\~a\\ (eos 30°, sen 30°) = 6^ (—, -) = (9,3^)
Y1
3\/3
0
i
x<30°
a - /O r>.
/I
I
1
1
1 ,
9 X
Ejemplo.- Expresar el vector a = (3,-3\/3) en términos de su magnitud y su ángulo de
inclinación o dirección.
Solución
Como a = || a || (cos0,sen0), de donde || a || = ^9 + 9(3) = 736 = 6
3>/3
Calculando 0 se tiene: tg 8 = —
a, 3
0 e 4to. Cuadrante 0 = 360° - a
700
Eduardo Espinoza Ramos
donde iga = = y¡3 => a = — = 60°
3 3
Luego 0 = 360° - a = 360° - 60° = 300°
Por lo tanto a = 6(cos0.sen0) = 6(cos300°,sen300°)
6 = 300°
8.9. PRODUCTO ESCALAR DE VECTORES.-
El producto escalar (o producto interno) de dos vectores ayo está dado por la suma
de los productos de sus componentes correspondientes, es decir:
—» —» -^ —>
Sí a,oeV2=> a=(fl,,a2)> b=(bl,b2)
a .o = {a^,a2).{bl,b2) = alJbl + a2Jb2
x + z
Ejemplo.- Si a=(x,3y) y o = (-2y,z), hallar el valor de de modo que
a+o=(8,-4) y a.ox=0.
Solución
a + b = (8,-4) = (x,3y) + (-2y, z) = (*- 2y,3y + z), de donde
í.x-2y = 8
(x - 2y, 3y + z) = (8,-4), por igualdad de vectores se tiene: < ... (1)
3v + z = —4
como o = (-2y, z) => o x= (-z,-2y) y como a . b L= 0
(x,3y).(-z,-2y) = 0 => -jrz-6yz=0
.6/
(2)
al reemplazar (2) en (1) se obtiene:
Vectores Bidimensional
701
jc-2y = 8 * = 2y + 8
>y x ^ * 2v + 8 y + 4
3y(y + 4)-3y =-4(>> + 4) => 16y = -16 => y = -l
como x = 2y + 8 entonces x = -2 + 8 = 6 => x = 6
6/ -6(-l)z x+z 6-1 _
como z = —— = = -1 => z = -l. Luego = = -5
x 6 y —1
OBSERVACIÓN.- El producto escalar de dos vectores es un número real
8.10. PROPIEDADES DEL PRODUCTO ESCALAR DE VECTORES.-
Consideremos tres vectores a,fc,ceV2 y reRun número real cualquiera; entonces:
a.b = b.a (2) (ra).fc=r.(a.h)
->
.a
©-»—»—» —» —» —» —» /»->^ —» /—» -
a.(fc+c)=a.fc+a.c (4} ||a||=Va.¡
(¿+c).a = fc.a+c.a (ó) ||a||2 = a.a
© |U+&|p=||a||2+2a.& + ||&||2 ® ||a-fc||2=||a||2-27.fc + ||fc||2
NOTA.- La prueba de estas propiedades son bastantes simples por lo tanto dejamos
para el lector.
Ejemplo.- Sí |M| = 7. || fe || = 3 y t.fo=-4. Hallar M -(11 a + 3¿>).(2 a + 7i>)
Solución
M=(lla + 3fc).(2a + 7¿>) =11 a.(2a + 7fc) + 3fc.(2a + 7fc)
702
Eduardo Espinoza Ramos
= 22a.a + 17a.b+6a.b+2lb.b =22 ||a ||2 +83a .b + 2l \\b\\2
= 22(49) + 83(-4) + 21(9) = 1078 - 332 + 189 = 1267 - 332 = 935
.-. M = 935
8.11. VECTORES PARALELOS Y ORTOGONALES.-
íi) Dos vectores a y b son paralelos (all b) si uno de ellos es igual al otro vector
multiplicado por un número real, es decir:
a// b <=> 3 r e R tal que a = r b
—» —> 3 -* —» —> —*
Ejemplo.- Sí a =(2,3), b =(1,—), entonces a/Ib <=> r = 2, tal que a=2.fc
—> —»
Ejemplo.- Los vectores a =(2,3) y b =(5,3) no son paralelos porque 3 r e R,
—» —>
tal que a = r.b .
—»
OBSERVACIÓN.- El vector nulo 0 es paralelo a todos los vectores, en efecto:
0 = 0.a , Va vector, 0 e R, entonces: a y 0 son paralelos.
CONSECUENCIAS.- Sean a, b e V2 => a = (a,, a,); fc = (¿j, b2), entonces
-* —» —» -»
a //fc <=> 3 X e R tal que a = Xb , es decir:
(a,, o2) = Aíí»,, £>2) ^e donde «, = Xb , a2= Xb2
Luego tenemos X = — = —, es decir: si a II b
¿>, b2
entonces existe proporcionalidad entre las componentes correspondientes.
-» -»
Ejemplo.- Determinar si los vectores a =(-6,4,10) y £> =(9,-6,-15) son paralelos.
Vectores Bidimensional
703
Solución
Si a // b => debe existir proporcionalidad entre los componentes correspondientes:
j 6 4 10 2 i "7!
A =— = — = —— = —. Luego ayo son paralelos.
9 6 15 3
8.12. CRITERIO DE COLINEALIDAD.
El conjunto de puntos A, B y C son colineales si y sólo si pertenecen a una misma recta.
• • • L
A€L B€L C€L
Por lo tanto, tomando de dos en dos se obtienen vectores paralelos, AB// AC .
Ejemplo.- Determinar si los puntos A(3,1), B(2,2) y C( 1,3) son colineales.
Solución
Los puntos A, B y C son colineales situados de dos en dos se generan vectores paralelos
AB = B-A = (2,2) -(3,1) = (-1.1)
AC = C- A = (1,3)-(3,1) = 2í-l,l)K-
BC = C-B = (1.3)-(2.2) = (-U)
Luego AC — 2AB => AC y AB son paralelos
BC = \AB => BC y AB son paralelos
por lo tanto los puntos A, B y C son colineales
5
(ü) Dos vectores ayo son ortogonales (alo) si se verifica la siguiente relación.
704
Eduardo Espinoza Ramos
|a+fc|| = ||a-fo|
así por ejemplo, los vectores a = (a,0) y b-(0,b) son ortogonales en efecto:
||a*+H| = ||(a,0) + (0.fc)|| = ||(a.fo)|| = VíT+fc-
... (1)
\\a-b\\ = \\(a.0)-(0,b)\\ = \\(a,-b)\\ = Ja2+(-b)2=Jaz+b2 .-Í2)
Comparando (1) y (2) se tiene: ||a+ b || = || a- b |
si los vectores a y fc son ortogonales, entonces denotaremos por a ± b , es decir:
a±¿> <=> II a+¿II = 11 a-¿I
8.13. INTERPRETACIÓN GEOMÉTRICA DE LA ORTOGONALIDAD
DE VECTORES.-
Como los vectores &+b y a—b son las
—»
diagonales del paralelogramos cuyos lados son a -*■
-» —» —>
y ¿ entonces si los vectores a y b son
ortogonales, esto significa que el paralelogramo
es un rectángulo, por lo tanto sus diagonales son
congruentes.
Otro modo de interpretar la ortogonalidad de los
—* —>
vectores a y b es:
a - b/
/
/
/
4
/
a + b
Vectores Bidimensional
705
8.14. TEOREMA.-
Los vectores a y b son ortogonales sí y sólo sí a . b = 0
Demostración
—» -» —» —>
i) Sí a X fc => a. fc = 0 (por demostrar)
por hipótesis se tiene que a y fe son ortogonales, entonces || a + b \\ = || a - b \
(por definición de ortogonalidad).
—» —» —» —>
Luego || a + fc ||2 = || a — ft ||2, desarrollando los cuadrados se tiene:
\\a>\\2 + 2li.b*+\\b\\2= \\a*\\2-2a.b*+\\b\\2 de donde 4^ = 0 => 7.^ = 0
-* —» —» —»
i¡) Si a. fc = 0 => a X b (por demostrar)
Como a.¿7=0 => 4 a. ¿> = || a + ¿ ||2 — || a — fc ||2 , de donde
|| a + b ||2 = || a - b ||2 =* || a + ¿71| = || a - ¿71|, esta relación nos indica que los
—» —»
vectores a y ¿7 son ortogonales (por definición de ortogonalidad)
Ejemplos.- Determinar cual de los pares de vectores dados son ortogonales.
(l) ^ = (2,1), £ = (-1,2), de donde
-» -» -* -»
a. ¿7 =(2,1).(-1,2) =-2 + 2 = 0 => a y b son ortogonales.
(5) a* = (2,3) y Ib = (-2,7), de donde
-» -» -» -»
a.¿7 = (2,3).(-2,7) = -4 + 21 = 17*0 => a y ¿7 no son ortogonales.
706
Eduardo Espinoza Ramos
8.15. TEOREMA.
* 9 9 T » 9
Los vectores a , b son ortogonales sí y sólo sí || a + b ||~ = || a ||~ +|| b ||~
La demostración de este teorema queda como ejercicio para el lector.
—» -»
OBSERVACIÓN.- Consideremos el vector a e V2 entonces a=(a,.a2) definiremos
—» -»
un vector ortogonal al vector a al cual denotaremos por a "L
cuyos componentes son (-a2,a,) y que es obtenido aplicando un giro de 90° sobre el
—>
vértice del vector a en sentido antihorario.
—* —>
El vector a x=(-a2,a,) así definido es ortogonal al vector a .
—* —>
En efecto: a.a ' = (a,,a2)(—a2,al) = -axa2 + a,a2 = 0
Luego a.a=0 => ala
a = (a1fa2)
Ejemplos.- Sea a =(-1,3) => su ortogonal es a =(-3,-1)
-» -».
Sea a =(2,3) => su ortogonal es a =(-3,2)
8.16. TEOREMA.-
Dados los vectores a=(a,,a2) y b=(bl,b2) diferentes de 0 , se tiene que a es
—» —» —»
ortogonal a b si y sólo si &±ll b .
Vectores Bidimensional
707
Demostración
—» —» —>
Como a * 0 , entonces por lo menos una de las componentes de a es diferente de cero,
supongamos que a, * 0 .
-»-»-»-» a b
&Lb <=> a . b = axbx + a2b2 = 0 <=> fc¡ =——
-* h -* —* —*
b=-^a => fc//ax
¿i
8.17. COLORARIO.-
Dados los vectores a y b no nulos, entonces a y fc no son paralelos si y sólo si
a.fc^O y a.fc *0.
Demostración
-» -» ' -»,
Del Teorema anterior es una equivalencia, entonces a y b no son paralelos <=> a no
-> -»i -* . . ~* -*j.
es ortogonal a fe y de igual manera que fc no es ortogonal a a si y solo si a.b * 0.
—*
Ejemplo.- Hallar todos los valores de x de tal manera que el vector a = (jc, 2x +1) sea
—»
paralelo al vector b = (2jc-1,jc + 2)
Solución
Aplicando el teorema 2.16. se tiene:
Si~a//~b => a^lfe => 7J-.fc=0
—> —>
Como a=(jc,2x+l) => a x= (—2jc — 1,x)
708
Eduardo Espinoza Ramos
a x. b = (-2jc-1,x).(2x-1,x + 2) = 0
-(4jc2-1) + jc(* + 2) = 0 => 3jc2-2jc-1=0 =» x=l, jc = —-
8.18. COMBINACIÓN LINEAL DE VECTORES.-
Sean a y b dos vectores no paralelos diferentes del vector 0 , se dice que el vector c
—> —»
es una combinación lineal de los vectores a y b si existen escalares r, s (r, s e R) tales
que:
Y4
Los vectores r a y s b geométricamente se puede construir del hecho que a y b no
—»
son paralelos de tal manera que la suma sea igual al vector c .
~* "* ~* ~*±
Analíticamente que a y b no sean paralelos es equivalente a decir que a.b /O y
—» —*
a ■"■. fc * 0 (corolario 1.27) y por lo tanto podemos calcular r y s de la siguiente manera.
Partimos de c =ra + sb
—»
Multiplicamos ambos miembros de (1) por a ±
—» —> —» —» —» —» —» —»
c.a±=ra.a±+sb.a, como a. a =0
c .a±=sb.a± =»
(1)
s =
-»
c
b
—>
a1
:-
Vectores ¡¡¡dimensional 709
multiplicamos ambos miembros de (1) por b L
c .bx= ra.b±+sb.b± , como b.b±=0
c .bL=ra.b
8.19. TEOREMA.-
Si los vectores a y b no nulos de R2, no son paralelos, entonces cualquier vector c de
R2 puede expresarse de manera única c = r a + s b donde los números r y s son
calculados en la forma anterior explicada, es decir:
c = ( ) a+( ) b
a.b± b.a±
Ejemplo.- Expresar al vector c = (2,3) en combinación lineal de los vectores
7 = (1,-1) y fc=(l,2).
Solución
Si c es combinación lineal de a y b entonces 3 r,s e R, tal que: c =ra + sb
-» -»±
Como r = — , donde fc=(l,2) => 'b±=(-2,l)
7.Z>
_c.bí ^ (2,3).(-2,l) _-4 + 3_\ = c.a1 (2,3).(1,1) _ 2 + 3 _ 5
a.b
(1,-1).(-2,1) -2-1 3
b.a
j. (1,2).(1,D 1 + 2 3
por lo tanto (2,3) = -(1,-1)+ -(1,2)
710
Eduardo Espinoza Ramos
8.20. TEOREMA.-
Consideremos dos vectores a y b no nulos. Si estos vectores no son paralelos, la
igualdad ra+sb = 0 , implica que r = s = 0.
Demostración
—»—»—» —» —»
Por hipótesis tenemos que: ra + sb = 0 y que a , b son vectores no paralelos
—> _ —» ->
suponiendo que r * 0 => an— fe = 0
r
~* s~* ~* s
Luego a = — b =kb , donde k = —
r r
—» —» —» —> -» -*
Como a = k b , esto significa que a y b son paralelos {all b) lo cual contradice a la
hipótesis, por lo tanto r = 0.
Y —* —* —* —* y — — »*
Suponiendo que s*0 se tiene — a+ b - 0 , de donde fc = — a = A a , donde A = —
s s s
Como b = A a , esto significa que a y b son paralelos lo cual contradice a la hipótesis,
por lo tanto s = 0.
8.21. DEPENDENCIA E INDEPENDENCIA LINEAL DE VECTORES EN
R2.-
Dos vectores a y b son '"linealmente independiente" si ra + sb = 0 entonces
—* —»
r=s = 0, en caso contrario se dice que los vectores a y b son "linealmente dependientes".
—* —♦
Ejemplo.- Determinar si los vectores a =(-1,1) y fc=(4,3) son linealmente
independiente o dependiente.
Solución
Vectores Bidimensional
711
ra + sb = 0 => r(-l,l) + s(4,3) = (0,0)
(-r,r) + (4s,3s) = (0,0) => (-r + 4s, r + 3s) = (0,0)
-r + 4j = 0 jr = 0
- + 3s = 0 ^ \s = 0
r = s = 0
por lo tanto a y b son linealmente independiente.
—* —»
Ejemplo.- Determinar si los vectores a =(-6,3) y fe =(2,-1) son linealmente
independiente o dependiente.
Solución
ra + sb = 0 => r(-6,3) + s(2,-l) = (0,0)
(-6r + 2s, 3r - s) = (0.0), de donde por igualdad
í-6r + 2s = 0 s = 3r J J L. .
< => , donde r es arbitrario
[3r-s = 0 s = 3r
—* . —*
entonces a y b son linealmente dependientes.
OBSERVACIÓN.- Tres vectores cualesquiera en R2 son linealmente dependientes
entre si.
OBSERVACIÓN.-
(1) Los vectores a.fc son linealmente dependiente cuando los vectores a y b son
colineales.
7 b*
►- >
(2) Los vectores a, b son linealmente independiente cuando los vectores a y i no
son colineales.
712
Eduardo Espinoza Ramos
8.22. VECTORES FUNDAMENTALES.-
Consideremos los vectores (1,0) y (0,1) en V2 al cual denotaremos así: i =(1,0),
—»
j-(0,\), estos vectores son unitarios y se representan a partir del origen de
coordenadas, situadas sobre los ejes coordenados en sentido positivo al de los ejes, a estos
vectores se les llama Vectores fundamentales.
-i =(0,1)
i =(0,1) *
Todo vector de V2 se puede expresar en combinación lineal de los vectores
-» —>
fundamentales i =(1,0), y =(0,1)
—> —* —»
Sea a e V2 => a=(a1,a2). pero al vector a expresamos así:
a=(a„a2) = (a,,0) + (0,a2) = al(l,0) + a2((U)
a =al i+Ü2 j
A los números ax,a2 se denominan componentes escalares de a y a los vectores a¡ i y
-> ->
a2 y se denominan componentes vectoriales del vector a .
Vectores Bidimensional
713
8.23. PROPIEDADES DE LOS VECTORES ORTOGONALES
UNITARIOS.-
En la combinación lineal de dos vectores se presenta un caso importante cuando estos
—* —»
vectores son unitarios y perpendiculares entre si como es el caso i = (1,0) y j = (0,1).
Si se considera un vector unitario u de i y el vector u en lugar de j , entonces el
-» -» -. -» -»
vector c =3u + 4u es una combinación lineal de los vectores unitarios u y u
4u
3u
Luego la longitud del vector c es || c ||= v32 +42 = 5 por la hipotenusa de un triángulo
rectángulo donde la medida de sus catetos son 3 y 4 respectivamente.
—»
OBSERVACIÓN.- Si u es un vector unitario se cumple las siguientes relaciones
Ejemplo.- Calcular la longitud de los vectores dados a=3«-4«"L,
b=35u + \2u±, c=5u + l2u±
Solución
714
Eduardo Espinoza Ramos
j&24. DEFINICIÓN,
Si dos vectores a y b son unitarios y ortogonales entre si, entonces los vectores a y
—»
b se denominan vectores ortonormales.
B§5. PROYECCIÓN ORTOGONAL Y COMPONENTE.-
Consideremos dos vectores a y b no nulos, construyamos un triángulo rectángulo cuya
—» —*
hipotenusa sea el vector a y su base sea el vector r. b (donde r e R) paralelo al vector
—* —>
b de modo que los lados del triángulo quedará representado así: hipotenusa el vector a
y por catetos los vectores r.b , c = a-r.b donde c ±b
rb
Como c J. b , lo cual es lo mismo expresar así:
(a-r.b)lb => (a-r.b).b = 0, de donde a.b-r \\ b ||2=0
entonces r = -
a.fc
II ¿II2
es el único número real.
como clfc, significa que el triángulo cuya hipotenusa es el vector a tendrá por catetos
-» -» -» -» -» -»
a.b -* ~* a.b . , a.b -? , ,
a los vectores: .b ; a . En consecuencia al vector .b que es paralelo
II ¿II2 II ¿II2 II ¿II2
-» -» -»
al vector b , llamaremos proyección ortogonal del vector a sobre el vector b .
Vectores Bidimensional
715
o i% —* r% ¡j —* ñ h h
Al vector —'-—.b expresaremos en la forma siguiente: —'■—.b = (—'■—). , donde
IIHP
IIMI2 II ¿ II 11*11
b , •-,,-•-., 7* i - a-¿>
es el vector unitario en la dirección del vector b , en tanto que el numero es
II MI II & II
—*
la longitud dirigida del vector proyección le llamaremos la componente del vector a en
-»
la dirección del vector b .
8.26. DEFINICIONES.
Qi_) Sean a y b dos vectores, donde b * 0 , definimos la proyección ortogonal del
—» —»
vector a sobre el vector b y los representaremos del modo siguiente:
» &-b t
proy^ =-^—.b
-> -» -» -» a .b
ü) Sean a y b dos vectores, donde b * 0, al número —'■— que es la longitud
II MI
-» —*
dirigida del vector proyt le llamaremos la componente del vector a en la
b
—»
dirección del vector b y denotaremos así:
comp^ =
b
a.b
II MI
Ejemplo.- Hallar la proyección del vector a = (7,12) sobre el vector b = (3,-4).
Solución
~* a.b ~*
Por definición se tiene: proyt — —-—• b
" II ¿II2
716
Eduardo Espinoza Ramos
: (7,12).(3,-4) „ ^ 21-48 27
PW^ = ||(3,-4) |P -(3,-4) = ^^0,-4) = —(3,-4)
proyi = --—(3,-4)
¿> 25
Ejemplo.- Dados los vectores a = (3,>/3) y fe = (>/3,-l). Hallar 2(proyt + proyt)
Solución
2(provH + prov») = 2(-^-. a+-^-.¿)
* Hall2 IMP
_ (3,>/3).(>/3,-l) g (3,>/3).(>/3,-l) /r
" ^ II(3,^)|P (3'^+ ||(^-1)||2 (^_1))
= 2[^(3,>/3)+^(73,-l)] =^(3,>/3) + >/3(>/3.-l)
= (^, 1) + (3, -y¡3) = (3 + >/3,1 - y¡3)
8.27. PROPIEDADES DEL VECTOR PROYECCIÓN Y
COMPONENTE.-
(Y) La proyección ortogonal de una suma de vectores en la dirección de algún vector no
nulo c es la suma de las proyecciones ortogonales.
(a+fc) a , b
proy\ = proy^ + proy^
_-v -» —»
\2) La proyección del vector t a en la dirección de b es igual a t veces el vector
—»
perpendicular de a .
proy^ = tproy-,
b b
Vectores Bidimensional
717
\3J La componente de una suma de vectores en la dirección de algún vector c es la
suma de los componentes.
(a+b) a b
comp\ ' = comp^> + comp„
Mj La componente del vector t a es igual a t veces la componente de a
comp(',*' = tcompt
8.28. RELACIÓN ENTRE PROYECCIÓN Y COMPONENTE.-
Consideremos dos vectores a y b , donde b *■ 0 por definición de proyección
ortogonal sabemos que:
-» -»
proy^ =—^—.b
" Wbf
al vector prov", expresaremos en la forma siguiente:
' b
7 a.b -» (a.fc) b 7 a.b
proy^ = . b = . , como comp_ - _^
b ii i. ||2 ii i. II n i. n b
IMf 11*11 II¿II
II MI
Entonces se tiene:
i) Si la compt > 0, la proyt y b tienen la misma dirección.
b b
718
Eduardo Espinoza Ramos
ii) Si la compt < O, la proyü, y b tienen direcciones opuestas.
b b
proy.t
üi) Si la compt = 0, quiere decir que ali
b
OBSERVACIÓN.- La diferencia entre proyección ortogonal y componente radica en
que la proyección ortogonal es un vector y la componente es un
número real.
8.29. ÁNGULO ENTRE DOS VECTORES.-
TEOREMA.- Demostrar que el ángulo formado entre dos vectores a y i no nulos
corresponden a la siguiente relación.
Demostración
Como a y b son dos vectores no nulos y 6 es el ángulo formado por estos dos vectores
—» —»
(6 = jC (a, b)), de modo que el campo de variabilidad está dado por 0 < 6 < n.
Vectores Bidimensional
719
Por definición de componente sabemos que:
~* a b ~* - -» -»
compt, = —'-— => || b || compt = a. b ... (1)
* 11*11
comp^, _ _j
del gráfico se sabe que cosí) = — de donde compt = || a || cosO ... (2)
Hall
reemplazando(2) en (1) se tiene: || a |||| b ||cosí) = a.b
o ab
coso =
lall ||b|
Ejemplo.- Dados los vectores a = (4,3), b = (1,-1). Hallar:
-» -»
a) La proyección de a sobre b
—» —»
b) La componente de a en la dirección de b
c) El ángulo entre los vectores propuestos.
Solución
, 7 a.fc 7> (4,3).(1,-1)„ 1 1 1
a) /voy_ =—-—.b = - -r-(l,-l) =-(1,-1) = (-,--)
b nt II a.-i) ii2 2 2 2
., t a. fe (4,3).(1,-1) 4-3 y¡2
b) comp^, =- — -
* || 61| l|(W)l1 ^ 2
c) cos# = '- = —j= => 0 = arccos(—j=)
IU IIII fe II W2 W2
720
Eduardo Espinoza Ramos
8.30. LA DESIGUALDAD DE CAUCHY - SCHWARZ.-
—> —?
TEOREMA.- Demostrar que: para todo vector a y b vectores se verifica la
-> -» -» -»
siguiente relación. | a. b | < || a ||. || b \\
Demostración
-» .->
Veremos primero para el caso en que a Jf b
► b
proy_t
b
del gráfico aplicando el teorema de Pitágoras se tiene:
-» —» -* —»
|| proyt ||2= || a ||2 -1| c || < || a ||2, lo que es lo mismo
b
-* —» -♦-♦—> -•
|| proyt || < || a ||, además a. b — \\ b \\ compt,
b b
\1Z\ = Íh\\.\\comp\\\ < Il7ll.ll 6 || porlotanto: | l.b \ <|| ^ || -1| b \\ ... (1)
b
ahora veremos el caso cuando a // b es decir:
Si a // b => 3 re R tal que a = r. b
|7.fc| = |(rfc).fc| = |r|.||fc||2=|r|||fc||.||fc|| = ||rfc||||fc||=|U||.||fc||
-> -> —> ->
porlotanto: | a.b \ = || a ||.|| b \\ ...(2)
—> -♦ —> -♦
Luego de (1) y (2) se tiene: .\ | a.fc | <|| a ||.|| b ||
Vectores Bidimensional
721
APLICACIÓN.- Como aplicación de este teorema, demostraremos la desigualdad
-> -» -» —»
triangular: || a+ b \\<\\ a || + || b \\
\a+b\\¿=\\ a \r+2a.b + \\b ||2<||a |P + 2|| a II.II 6 || + || b\
a+ 6 ||2< || a |p +21| a ||. || b \\ +1| b ||2, de donde
|| a+ fc ||2< (|| a || +1| b ||)2 por lo tanto: || a+ fc || < || a || +1| b ||
8.31. ÁREA DE: TRIÁNGULOS Y PARALELOGRAMOS.-
Consideremos un paralelogramo cuyos lados son los vectores a y b .
/
proy^.
b-1-
■"b1
l
a /
/i
i-*-
I C
i
h
/
/
/
/
/
►•
La altura del paralelogramo es // =|| c ||, de donde
h = II c II = II P^oyi II = II compt ||, además se conoce que:
b1 b'-
área del paralelogramos es: A = base x altura
A = ||H|.||co^||=||fc||l^-!
II¿XH
=|a.fex|
A = \a.bL\
En consecuencia el área del triángulo cuyos lados son los vectores a y b está dado por:
A = -\a.bL\
2
722
Eduardo Espinoza Ramos
Ejemplos.- Hallar el área del triángulo cuyos vértices son los puntos A(-3,2), B(3,-2),
C(4,5).
Solución
a= AB =B-A = (7,3)
b=~AC=C-A = (6,-4)
A(-3,2)
b=(6,-4) => bx=(4,6)
A = -|a.fc-L| = -|28 + 18| = 23
8.32. EJERCICIOS DESARROLLADOS.
(Yj Dados los vectores a =(-2,2), b=(3.-2) y c =(-1,1), resolver la ecuación:
3a-2[3(fe-2c) + 2a] + 3jc=2c+jc.
Solución
—> -* —> -*—*—»-*
3a-2[3(fc-2c)+2a] + 3jc = 2c+x , efectuarlas operaciones
—» —» -*-*-> -* —»
3a-6fc+12c-4a + 3jc = 2c+* , simplificando
-»-*-* -»
2* = a + 6fc-10c, reemplazando los vectores
2 jc = (-2,2) + 6(3, -2) -10(-1,1), efectuar las operaciones
2 x = (-2,2) + (18,-12)-(-10,10) = (-2+18 + 10,2-12-10)
2 jc =(26,-20) de donde jv =(13,10)
Vectores Bidimensional
723
\2) Sean P(c,d) y Q(c + a, b + d). Muestre que la magnitud de PQ es \a2 +b2 .
Solución
PQ = Q-P = (c + a,b + d)-(c,d) = (c + a-c,b + d-d) = (a,b)
\\~PQ\\=Ja2+b2
\3J Sí a=(x + l, 3jc-2) y b—(\ — x,x). Hallar x para que a+5b sea paralelo a
c=(l,-7)
Solución
-» -»
a+5fc=(x + l, 3x-2) + 5(l-x, jc) = (6-4jc, 8x-2)
como a+5b//c =» 3XeR tal que: a+5¿=Ac, dé donde:
(6 - 4x, 8x - 2) = X(l,-7) por igualdad se tiene:
6-4x = A. ; 8x-2 = -7A. => 8x-2 =-7(6-4x)
=> 20x = 40 de donde x = 2.
(4) Determinar para qué valores de a los vectores a+ab ; a-a fe son perpendiculares
—» —»
entre sí, sabiendo que || a || = 3, || b ||= 5.
Solución
Como a+afc-La-afc => (a+ab).(a-ab) = 0
de donde 7.7-a2 b.lb =0 => || a ||2 -a2 || fe ||=0
2 II a ||2 9 .3
a =-—— = — => a = ±—
II Mf
,2 25 5
724
Eduardo Espinazo Ramos
(?) Calcular || a- b || sabiendo que: || a ||= 13, || fc ||= 19 y || 1+ b \\ = 24
Solución
-* —»
Como || a + b \\ = 24, elevando al cuadrado tenemos:
a+ b ||2 = 242 =* || a ||2 +1| b ||2 +2 a.b = 576, de donde
169 + 361 + 2a. b=576 => 2a.fc=46
|| a*-fc ||2=|| a ||2 +|| fc ||2 -2^.6 =169 + 361-46 = 484
||a-fc||2=484 => || 7- b || = 7484 = 22
Qé) Los vectores a y b forman un ángulo a = 60°, se sabe ademas que: || a || = 5 y
|| b || =8. Determinar: ||a + fc|| y ||a-fc||.
Solución
-* -*
¿(7,b) = 60° => cos60° = ——— => 7.6=20
lia» || fe ||
||r+fc||2=||r||2+||fc||2+ 2^.6=25 + 64 + 40 = 129 .-. || 7+fc || = VÍ29
|| a-fc||2=|| a ||2 +|| aj2-2a.fc =25 + 64-40 = 49 .-. ||a-fc|| = 7
Í7j Los vectores a y fc forman entre sí un ángulo de 45° y el módulo de a es 3. Hallar el
módulo de b , de modo que (a— b) sea perpendicular al vector a
Solución
-» —» -»—»-*-* % Fy ~*
¿(a,fc) = 45° => a.fc=||a|IIIH|cos45° = —||fc|!
Vectores Bidimensional
725
a-fc_l_a=> (a- fc). a =0» de donde a.a-a.¿>=0 => || a ||2= a.fc =—^—¿>
9 = ^11*11 =» ||*|| = 3>/2
(8) Los vectores a y fe forman entre sí un ángulo de 45° y el módulo de a es 3. Hallar el
-» —» -» -»
módulo de fe para que a + fe forme con a un ángulo de 30°.
Solución
-> -» —»
Por datos tenemos: ¿(a,fe) = 45° y ||a|| = 3
—» -»-»-*
Determinaremos || fe ||. para que ¿(a,a+fe) = 30°
Como ¿(a,a+fe) = 45° => a.fe = || a |||| fe ||cos45° = -^-|| fe ||
¿(a,a+fe) = 30° =» a.(a*+fe) = ||a||||a + fe||cos30°
-»-»-»-* —» —» -»
a.a+a.fe=||a |||| a + fe ||cos30° , de donde
ll«ll2+4ll*ll=3|l"+*llT =* 9+^H*ll=^«"+*H
3 + 1| b ||= —1| a+ fe || elevando al cuadrado y simplificando
||fe||2-3>/21|fe||-9 = 0 =» ||fc||=|(>/6+^) = -
2 2senl5°
Sean a = cosí) 1+sen0 y y fe =cos(0+—) i + sen(0+—) y dos vectores. Demostrar
—» —»
que a y fe son ortogonales.
Solución
726
Eduardo Espinoza Ramos
alí ( a y b ortogonales) <=> a b = 0
a.b = (cosí?, sen f?).(cos(f?+— )).sen(6+—) = cosf?.cos(f?+— )+senf?.sen(f?+—)
2 2 2 2
= cosf?[cosf?.cos sen f?.sen—] + senf?[senf?.cos— +cosiesen—1
2 2 2 2
= eos 6 (0 - sen 6) + sen 6(0 + eos G) = - sen 6 eos 6 + sen 6 eos 6 = 0
—» —> —» —>
Como a . ¿ = 0 => a ± b
(10) Demostrar que a + b y a-b son ortogonales sí solo sí || a || = || b ||.
Solución
i) Si a+b L a-b => || a || = || b || por demostrar
como a+fc-La-¿ => (a+¿>).(a-¿>) = 0
||a||2-||¿||2=0 => ||a||2 = ||¿||2 dedonde ||a*|| = ll*ll
ii) Sí || a || = || b || => a + b ± a - b por demostrar
como || a || = || ¿|| => ||a||2=||¿||2 => II a ||2 -II b ||2=0
=> (a+fc).(a-¿) = 0 => a + ¿±a-¿ (ortogonales).
nllj Demostrar que: Si dos vectores son unitarios, entonces la suma es un vector unitario si y
sólo si el ángulo formado por dichos vectores es de 120°.
Solución
—» —»
i) Sean a , b vectores unitarios de modo que:
Vectores Bidimensional
727
a || = || ¿ || = || a+¿ || = 1 => 0=¿(a,¿) = 12O° pordemostrar
a+¿||2=l => ||a||2+||¿||2+2||a||.||¿||=l
a||2+t|M|2+2||a||.||¿||cos0 = l
l + l+2cos6=l => 2cos6 = -l => cos0 =— => 6=120°
¡i) Sí 0 = ¿(a,¿) = 12O° => ||a+¿|| = l
a+¿||2=||a||2+||M|2+2||a||.||¿||=l
= l|a||2+||¿||2+2||a||.||¿||cosl20°=l + l-2(i) = l =>||a + ¿|| = l
como || a+fe || = 1 => a+b es unitario.
[I2j Probar que la suma de vectores es conmutativa, es decir: a+ b = b+a
Solución
Se observa que: AD + DC = AC por definición
de suma de donde: a+b-c
AB + BC - AC por definición de
suma de donde: b+a — c ... (2)
comparando (1) y (2) se tiene: a + b = b + a
728
Eduardo Espinoza Ramos
(13) Demostrar que la suma de vectores es asociativa, es decir: (a+ b) + c = a + (fe+ c)
Solución
Se observa que: AB + BC - AC , por definición de suma de vectores, de donde:
a+b = AC
- (1)
BC + CD - BC , por definición de suma de vectores, de donde:
b+c= BD
... (2)
AB + BD = AD , por definición de suma de vectores, de donde:
a+(b+c) = d
(3)
AC + CD = AD , por definición de suma de vectores, de donde:
(a+¿)+ c =d
... (4)
comparando (3) y (4) se tiene: (a+ b)+ c = a+(¿+c)
(14) Demostrar que el segmento que une los puntos medios de dos lados de un triángulo es
paralelo al tercer lado e igual a la mitad de su longitud.
Vectores Bidimensional
729
Solución
Sea A ABC, de modo que:
AB=B-A, BC=C-B, AC =C-A M = A±C
2
MN=N-M =
B + C A + C B-A
como MN = — AB entonces: MN || AB , a continuación se debe comprobar
que el segmento que une los puntos medio de dos lados de un triángulo es igual a la mitad
de la longitud del tercer lado del triángulo, para ello sabemos que:
|A«V|| = ||-^B ||=-||^||, porlotanto: \\MN\\ = -\\ AB
Sean a y b dos vectores que tienen distinta dirección. Hallar la expresión de cualquier
—» —> —>
vector c del plano determinado por a y b .
Solución
Sabemos que el vector t b es paralelo al
—»
Vector b , V t e R, análogamente el vector
-» —»
s a es paralelo al vector a , V s e R, y
aplicando la regla del paralelogramo
—> —» —»
tenemos: c=sa + tb, V s, teR;quees
la expresión pedida.
sa
Demostrar que en un triángulo isósceles, la mediana es igual a la altura.
Solución
730
Eduardo Espinoza Ramos
Por hipótesis tenemos que: || a || = || b ||
—» -»
debemos demostrar que: h.c —0.
Según el gráfico sabemos que:
h.c —{a ).c
2
.-(I)
igualmente según el gráfico se tiene: c + b = a => c = a- b
(2)
reemplazando(2) en (1) tenemos: (a ).(_&-b)= h.c , de donde
/^.c=-(¡>+fc).(¡>-fc) = -(7.7-¿.¿) =-(||a||2 -||fc||2) = 0
entonces h.c =0 => h ± c
(l7) Demostrar que el triángulo inscrito en un semicírculo es un triángulo rectángulo.
Solución
Se observa que || a || = \\c || por ser radio de un circulo.
Por demostrar que: a+ c J. a- c
es decir que: ( a+ c ).( a- c ) = 0
a - c
Luego: ( a+ c ).( a- c )= a.a- c.c =|| a||~-||c|
perocomo ||a|| = ||c|| => (a+C).(a-c)= ||a||2HIcf = ||a|PH|a|p=0
En consecuencia ( a+c ).( a-c ) = 0 => a+c±a-c
Vectores Bidimensional
731
(18) Demostrar que si los vectores a y b no son paralelos la igualdad r a + s b = 0 , implica
que r = s = 0.
Solución
Por hipótesis tenemos que: r a + s b = 0 donde a, b son vectores no paralelos.
Suponiendo que r*0 => a + — b = 0. Luego a= — b=kb, donde fc = —¡corno
r r r
—» —* —» —» —» —»
a = fc fe , esto significa que a y ¿ son paralelos (a // b) lo cual contradice a la
hipótesis, por lo tanto r = 0. Suponiendo que s * 0 se tiene — a + b = 0 de donde
-» r-» -» r
¿ = — a = fc a , donde /r = — .
5 S
Como b —ka esto significa que a y b son paralelos lo cual contradice a la hipótesis,
por tanto s = 0.
[Í9j Demostrar que si a, b son dos vectores cuyas direcciones se cortan, entonces la igualdad
—» —» —» —»
vectorial o^ a+P¡ b =o^ a+/i> fe , implica que a, = a2; /^ = P2 ■
Solución
—• —» —•
Por hipótesis se tiene que los vectores a y b se cortan, entonces los vectores a
y b no son paralelos; como a, a + /J, ¿ = cc2 a + /J2 b . entonces:
—> —» —»
(a, -a2) a+(/J, ~P2)b = 0 (por el ejercicio 18). Se tiene: a, -a2 =0 y /J, -/J2 =0,
de donde se tiene: a, = a2; P¡ = P2 ■
(20) Demostrar que las diagonales de un paralelogramo se cortan en su punto medio.
Solución
732
Eduardo Espinoza Ramos
Consideremos el paralelogramo OABC
cuyas diagonales se cortan en el punto P, a
además en la gráfica se observa que:
D
i) a+ AC = b entonces AC=b-a y AP=r.AC o AP = r(b- a), r e R
puesto que AP y AC son paralelos.
ii) OB=a+b y OP=s.OB o OP=s(a+b), seR puesto que OP y
OB son paralelos.
iii) a = OP- AP reemplazando i), ii) en iii) se tiene:
—>—»—»—»—* —» —» —»
a -s(a+ b)-r{b-a),de donde a =(s + r)a + (s-r)b
—> —»
como a y b no son paralelos y de acuerdo al (ejercicio 19) se tiene que:
_±
s+r=\ ~2
entonces por lo tanto:
s-r=0 1
r — —
2
^p =sOB =-OB , AP =r.AC =-AC
2 2
con lo que se afirma que P es el punto medio de las diagonales.
(2l) En un triángulo cualquiera, demostrar que existe otro triángulo cuyos lados son iguales y
paralelos del primero.
Solución
Vectores Bidimensional
733
La condición para que tres vectores a, b, c formen un triángulo es: a+ b+ c = 0
Figura (1)
En la figura (2) se tiene: d -— (b+ c)
e =—(a+b)
2
Figura (2)
/=—(c+a) Sumando se tiene:
2
d+ e + f =— (a+¿+c)=a+¿+c = 0
2
Luego d+ e+ / = 0 cumple la condición de formar un triángulo.
Demostrar vectorialmente que: si el cuadrado de la longitud de un lado de un triángulo es
igual a la suma de los cuadrados de las longitudes de los otros dos lados entonces el
triángulo es un triángulo rectángulo.
Solución
Se sabe que: || a ||2 +|| b ||2=|| c ||2
Y como la trayectoria es cerrada entonces
—*->—»—> —* —> ->
a + ¿+c = 0.pero a+b=-c.
(a+£)(a+fc) = (-c)(-c)
734
Eduardo Espinoza Ramos
—♦ —* —t —9 —9 —* —» —* —* —» —*
II a ||" +|| ¿||2 +2a.fc=|l c ||2 de donde || c \\2 Yla.b =\\c ||2 entonces a.b =0 por lo
—» —» —» —»
tanto a ± í?; como a y b son ortogonales, por consiguiente el triángulo es un
triángulo rectángulo.
Demostrar vectorialmente que en un triángulo isósceles hay dos medianas de igual
medida.
Solución
—> —»
Sabemos por hipótesis que: || a || = || b || por ser triángulo isósceles:
además del gráfico se tiene: V = —v b
por definición de suma de vectores
u = a-i—, por definición de suma de vectores
Luego demostraremos que: || v || = || u \\
v||2=ll|+¿
,_l|a||2
+ a.6+ 11 fe ir, como I a | = \\b
■i ~* n2 51| a |r -7*
entonces: v = ——— + a. b
... (1)
,i2_„„. bu n-\l2 .rr.n*ir
«II =l|a + y|| = ||a||¿+a.¿+^-, como ||a|| = |l*l
"V 51 a ^ -7*
u \\ =—-——+ a.b
(2)
al comparar (1) y (2) se tiene: || v ||2=|| u ||- => || v || = || u ||
por lo tanto las dos mediana» de un triángulo isósceles sus medidas son iguales.
Vectores Bidimensional
735
(24) Demostrar que si las magnitudes de la suma y la diferencia de dos vectores son iguales,
entonces los vectores son perpendiculares.
Solución
—> —»
Consideremos dos vectores a y b , entonces por condición del problema se tiene:
—> —» —»
|| a + b || = || a - b ||, de donde se tiene:
a+ b ||2= || a- b ||2, desarrollando tenemos:
II a II2 + II b ||2 +2 a. ¿> = || a ||2 +1| ¿> ||2 -2 a. ¿>, simplificando
4a. ¿ = 0 => a.f?=0, esto indica que los vectores a y b son perpendiculares.
(25) Demostrar que si la suma y la diferencia de dos vectores son perpendiculares, entonces
los vectores tienen magnitudes iguales.
Solución
—> —>
Consideremos dos vectores a y b de tal manera que:
a+fc-La-¿ => (a+¿).(a-¿>) = 0, desarrollando el producto escalar se tiene:
||a||2-a.¿+fc.a-l|¿||2=0 => II a ||2=||¿||2 entonces II a II = 11 ¿II
(2¿) Sumar gráficamente y analíticamente los vectores A, B y C que se muestran en la figura
Y'
0
t \ 1
4K
"3X
-*■
3 'A
■b"
4
X
736
Eduardo Espinoza Ramos
Solución
Analíticamente: A = (3,0), £ = (0,4)
tgor= =1.73 => a = 53°
Cy= 12 sen 53° = 9.58
Cx =12cos(180°-53°) = -7.22
Como R = A+B+C = (-4.22,13.58)
|| R || = V(-4-22)2+(13.58)2 = 14.22
\Zn Sea u -2 i-3 j y v =- i + 2 j . Encuentre un vector unitario en la misma dirección
-» —»
que k+ v .
Solución
u =2 i-3 j =(2.-3) y v =- i + 2j =(-1.2)
« + ^ = (2,-3) + (-l,2) = (2-l,-3+2) = (l,-l)=*> => |U||=>/2
Sea m el vector unitario en la misma dirección que el vector k =(1,-1) es decir
m = -^- = J=(l,-l).
II MI V2
.-. m = (—,—=)
n/2 V2
(28) Si a, fe y a+fc son vectores unitarios, hallar la norma del vector a - b
Solución
Como a, b y a-fc son unitarios => || a ||=|| ¿> ||=|| a+fc ||=1
Vectores Bidimensional
131
Como ||a + ¿>||=l
I a + b ||2= l2, desarrollando
a ||2 +2a.b + \\b ||2=1 de donde l + 2a.¿>+l = l entonces 2a.fc=-l
a-¿||2=||a||2+||¿||2-2a.fc=l+l + l = 3
.-. l]a-*|j=>/3
En la figura adjunta determinar el vector v
Y*.
Solución
Como a es un vector de posición => a =(1,1) de donde ||a||=v2
a (1,1) , 1 1
II a II "* "* "* * * *
,g60° = HAJl = ^ => ||¿||=>/3|U||=>/3>/2=>/6
l|a||
b =|| 6 || « x= >/6(—U4=) = Í-^.V5)
V2 V2
7=a+fe=(l.l) + (->/5,>/5) = (l->/5,l + >/5)
"v=(l->/3,l + >/3)
738
Eduardo Espinoza Ramos
(30) En la figura adjunta determinar AC sabiendo que || AB ||= a/b , ||¿?C||=— VÍ3
Solución
—»
"*- v
Calculando el vector unitario u v = donde
II vR
||"v||=V42+62 =yJl6 + 36=y¡52=2-JÜ
v = (4,6)
v (4,6) . 2 3
m v = —— = —7= = (-
II v||
2>/Í3 x/¡3'n/Í3
V13 V13
KAB =
II as II
AB = ||AB||«^S=>/Í3(-^=~) = (2f3)
VI3 V13
H -=
II BC ||
BC'^:Hm-é-é"lí-3)
AC = AB+ BC = (2,3) + (--,3) = (--,6)
2 2
.-. AC = (~,6)
2
__ —»
Gl) En la figura adjunta determinar las componentes del vector v
Vectores Bidimensional
739
Como a es un vector de posición entonces a =(-1,2)
—»
Calculando el vector unitario en la dirección del vector a
-»- t (-1,2) 1 2 . _ -± . 2 1
«a = —= , =( í=.-¡=) => «-=( /=' /=)
M* ="
l|a||
—»
b
II 6 II
=> 6 =|| 6 II «* como lUIhH^lh^
"»± , 2 1
W -,= (-=r,-7=)
a V5 V5
2 1
por ser un triangulo isósceles se tiene: b = V5(-=-,-^) = (2,1)
V5 V5
v = a+fc=(-l,2) + (2,l) = (-l + 2,2 + l) = (l,3)
v=(1.3)
740
Eduardo Espinazo Ramos
(32) Demostrar que si G es el centro de gravedad del triángulo de vértices A, B y C, entonces
G = -{A + B + C).
3
Solución
Se conoce que el centro de gravedad de
un triángulo, es el punto de intersección
de sus medianas.
En este caso las medianas son: AA', BB' y CC (ver gráfico)
además mediante el ejercicio (14) se tiene: C'A' = —AC
2
..(1)
por otra parte AG = rGA' = r(GC+ C A) de donde AG =r(GC'+CA') ...(2)
ahora reemplazando (2) en (1) obteniéndose: AG - r(GC'+— AC) ... (3)
por otro lado: AG = AC + CG
... (4)
pero CG = t GC
(5)
reemplazando (5) en (4) se tiene:
AG = AC + tGC
... (6)
igualando (3) y (6) se tiene:
r{GC'+-AC)= AC + tGC
2
{r-t)GC+{—1) AC =0
pero como GC y AC son no nulos y ni paralelos, entonces por el ejercicio (19)
setiene: r-t = 0 y —r-l = 0 de donde r=t = 2.
2
Vectores Bidimensional
741
Luego AG=2GA => G-A = 2A-2G de donde 3G = A + 2A ...(7)
R 4- C
Como A' es un punto medio de B y C entonces A' = ... (8)
/? + C
ahora reemplazando (8) en (7) se tiene 3G = A + 2( )
G=-(A + B + C)
3
Si G es el centro de gravedad del triángulo de vértices A, B, C demostrar que:
GA+ GB+GC =0 .
Solución
Mediante el ejercicio (32) el centro de gravedad del AABC es:
G = -(A + B + C) dedonde 3G = A + B + C
3
(1)
GA+ GB+GC =A~G + B-G + C-G = A + B + C-3G
... (2)
ahora reemplazamos (1) en (2) y se obtiene: GA + GB + GC - 3G -3G = 0
GA + GB + GC = 0
(34) Dado un paralelogramo de vértices los punto A, B, C y D. Si M es el punto medio de
CD y P está en AM a — de la distancia de A a P, demostrar vectorialmente que:
BP =-BD
3
Solución
De las condiciones del problema se tiene:
~AP=-A~M, DM =-DC
3 2
de donde DM = — CD
2
742
Eduardo Espinoza Ramos
por demostrar BP = — BD , de donde:
3
~BP=~BA+~AP= ~CD + -A~M = CD + -(AD + DAÍ)
3 3
~BP = ^D + -(BC--CD) = CD + -BC-—
3 2 3 3
= -CD + -BC =-(BC + ^D) = -Td
3 3 3 3
por lo tanto: BP =-BD
Deducir la ley de los cósenos en un triángulo empleando producto escalar.
Solución
Se conoce que: || A || = A. A
c ||z = ||A+B||=(/V+fi).(/V+fi)
= A.A+ A.B+ B.A+ B.B =\\ A\\2 +2A.B+W B\\2
®
II c Ir =11^II +1| BII2+21| AHll fi||cosa, donde a = ¿(A,B)
Un automóvil recorre 5 km. hacia el norte, luego 8 km. hacia el noreste; representar
gráficamente y hallar la resultante del recorrido.
Solución
O A = a (representa el desplazamiento
de 5 km. hacia el norte).
AB = b (representa el desplazamiento
de 8 km. hacia el noreste).
Vectores Bidimensional
743
OB = c (representa a la resultante del recorrido, es decir: c = a + b .
En el triángulo OAB los lados son los vectores a, b y c cuyas longitudes son:
a|| = 5.||fe||=8.||c|| = ?
para determinar la longitud de c , aplicamos la ley del coseno, es decir:
c||2=||a||2+||M|2-2||a||||¿||cos0.
|| c ||2 = 89-80eos6 , de modo que G es el ángulo comprendido entre a, b cuyo valor es:
G + 90° + 45° => 6 = 135° (ver gráfico)
eos 6 = eos 135° = -—. Luego reemplazando se tiene: || c ||2=89 - 80(-—) = 89+40>/2
.-. |M|=V89 + 40V2 kms.
A qué distancia del punto de partida se encuentra una persona que recorrió 5 m. hacia el
sur-oeste, 10 m. hacia el norte y 8 m. hacia el este 30° norte.
Solución
Representaremos por:
OA = a el desplazamiento de 5 m.
—»
hacia el sur-oeste || a || = 5 m.
AB = b el desplazamiento de 10 m.
—♦
hacia el norte ||¿>||=10w.
744 Eduardo Espinoza Ramos
BC - c el desplazamiento de 8 mts. hacia el sur-oeste
Este 30° norte; || c ||= 8 m., OC = d el desplazamiento resultante, es decir:
d = a+ b + c , ahora determinaremos || d ||= ?
como || d || = || a+ b+ c II, entonces elevamos al cuadrado
l|d|r-H|a||2+|M|2+||c||2+2(a.fc+a.c+¿.c)
como G = ¿ (a,fc) = 135° entonces a.fc =|| a || || b ||cosl35° =-25yJl
también a = ¿ (b.c)-60° entonces
b.c =|| ¿Hile || eos 60° = 40
P = ¿ (a, c) = 45°+90° + 30° = 165°, entonces
a ■ c = || a || || c ||cosl65° = 40(-cosl5°)
a. c =-40cos
15° =^or2+>/6) = -10(>/2~ + >/6J
||d||2=25 + l00 + 64 + 2(-25N/2+40-10(N/2 + V6))=189-70>/2+80-20v/6
.-. || d || = V269-70>/2-20v/6
(38) En la figura propuesta, es un cuadrado de lado "a". Hallar el valor del ángulo 6, si P y T
son los puntos medio de los lados del cuadrado
Solución
Vectores Bidimensional
745
Sean OT y OP los vectores que forman el
ángulo G. como T, P son puntos medios de la
figura entonces: T(—,a) y P(a,—) de modo
a * a
que: OP =(a,—) y OT =(—,«), entonces:
Y"
T
a
0
1*^^
a
P
X
COS0 =-
OP .OT
OP II || OT
► > 2 2
pero OP .OT = — + — = a2
2 2
además || OP || = —a y || 07" || = —a, reemplazando en la relación
a a 4 a 4
COS0=—7= =— = — ^ COS0= —
yf5 yfE 5 5
—a.—a
2 2
0 = arccos(—)
Demostrar que el segmento de recta que une los puntos medios de los lados no paralelos
de un trapecio es paralelo a las bases, y su longitud es igual a la mitad de la suma de las
longitudes de las bases.
Solución
DA = 2 MA
2M = A+ D
A - D = 2A - 2M
A + D
M =-
..(1)
2 PB = DB => 2B - 2P = B - D
2P = B + D => P = -(B + D)
2
BC =2BN
C - B = 2N - 2B
N =
B + C
(3)
746
Eduardo Espinoza Ramos
pero MP =P-M = -(B+D)--(A + D) = -(B-A)=-AB
2 2 2 2
MP\\ = -\\AB
... (4)
PN =N-P = -(B + C)--(B + D) = -(C-D) = -DC
2 2 2 2
PN\\ = -\\DC
... (5)
sumando (4) y (5) se tiene:
.Mf»|| + ||/W|| = ±||AB||+±||DC
\\MN\\ = ±(\\AB\\ + \\DC\\)
Sean a y b dos vectores no nulos tales que || a || = || b || = m si el ángulo entre a y
n
b es de — radianes y la norma de su diferencia es 2 - m. Hallar m.
3 }
Solución
Como — = jC (a, b) entonces:
eos—= '■ como || a || = || ¿ || = m
3 IUIIII fe II
1 a.b -» 7 »r
— = —— => a.o= —
2 m2 2
... (1)
además II a-fc II = 2-»i
a-fc||2=(2-»i)2
l|a||2+||H|2-2a.fc-2a.fc=4-4»i + »i2, reemplazando || a ||=|| b ||= w
»i2 +»i2 -m2 =4-4m + m2 => 4-4m = 0 de donde m=l
Vectores Bidimensional
747
Mlj Un sólido de 100 N. de peso depende del centro de una cuerda (como se observa en la
figura).
100 k
Determinar la tensión T en la cuerda.
Solución
-» -»
Por hipótesis se tiene: || a || = || b || = T
-> -»
así mismo sabemos que: ||w||=||-w||=100 N.
-» -* -*
además a + b = — w
||a+fc||2=||-w||2=1002 => ||a||2+||fc||2+2||a||||fc||cosl20° = 1002
donde ¿(a,fe) = 120° entonces 7"2+72+2r2(--) = 1002
2
72=1002 => T=100N
Dados los vectores unitarios a, b y c que satisfacen a+b+c = 0, calcular
—» —» —» —» —» -♦
a.b+ b.c+ a.c
Solución
Por hipótesis se tiene: || a || = || b || = || c || = 1
Y además a+b+c = 0 => \\a+b+c II = 0, entonces:
748 Eduardo Espinoza Ramos
II a ||2 +1| b ||2 +1| c ||2 +2(a .b+ b. c + a. c) = O
v v y
3 + 2(a.fe+a.c+fe.c) = 0 de donde a.b+b.c+ a.c = —
2
(43) Los vectores a y b forman un ángulo a = —, además sabemos que: || a || = V3 .
|| b ||= 1, calcular el ángulo 0 formado por los vectores p= a+ b y q = a—b .
Solución
n
¿(a,fe) = or = -, y ¿{p,q) = 6
o
a.fc = |a||fe|cos30° = -
p = a + b
q = a - b
de donde a. b = —
2
—» -»
cos6 = J'\ .donde || ?|| = || T+ fe || y || J || = || 7-fe ||
II Hl II? II
IIH|2=Ha||2+||fe||2+2r.fe=3 + l + 2(|) = 4 + 3 = 7 => fp\\=fi
Nll2=l|a||2+||fe||2-2a.fc=3 + l-2(|) = 4-3 = l => ||J||=1
112 II u 112
co-g- P-g = (a+fe).(a-fe) = ||a||¿-|IH
II Hl II 9 II ||a+fe||||a-fe|| ||a+fe||||a-fe|
44 = 2- =* tareco**)
yflyfl yfl V7
Vectores Bidimensional
749
(44) Dado el vector a = (-3,4), encontrar otro vector b , tal que sea perpendicular al vector
—»
a y que su módulo sea 10.
Salarien
Sea b* = (x,y) => |ft| = Jjr2 + y'=iO => jc2+>>2=100
Por otro lado se tiene que a J. b entonces a. b = 0
(-3,4).(x.y) = 0 =» -3x + 4y = 0
¡x2 + y2=lO0 . . . , .
Luego < resolviendo el sistema se tiene x = ±8, y = ±0 entonces
[-3x + 4y-0
b = (±8,±6)
®-* -* 1 4 -* ■N/73 -»
Dados los vectores a=(at,a2), b =(—,—). Hallar a2-ar-si llall = y si a y
—♦
b tienen direcciones opuestas.
Solución
—» —»
Como a y fc tienen direcciones opuestas entonces 3 X < 0, tal que
a=Afc de donde: (a„a,) = A(—,—)='(—, ) => «■ = —, a-, =
2 3 2 3 2 3
,,-,. >/73 A2 16A2 73 . ..
como a = => —+ = — => K = ±2
3 4 9 9
—» —»
como a y b tienen direcciones opuestas => X = -2
-♦8 8
Luego a =(a,,a2) = (-l,-) => a,=-l, o2=-
8 11
Por lo tanto a-,-a, = — (-1) = —
2 1 3 3
750
Eduardo Espinoza Ramos
@ En la figura se tiene 11711 = 6, ||fc||= 8 Hallar a\i>
-a
Solución
El ángulo formado entre los vectores a y b es
-» -»
a. b
60
120° = ¿(a,fc) => cosl20° = -
a IIII¿I
Tf / 120°
b/
de donde: a. b = || a || || b || eos 120° = —(6)(8) = -24
(47) Determinar el ángulo formado por los vectores: a = (V12. 2). b=(-3,JS)
Sofacrén
Sea 6 = ¿(a,b) => cos# = -
a.fc
', de donde
eos© =
II a INI MI
-3>/Í2 + 2n/3 -6S + 2S -4>/5 1
Vl2+4.>/9 + 3 4VÍ2 8>/3 2
como cos# =—
2
6 = 120°
U8J Si A+£+C=0 y A=||A||=3, B=||B||=5r C=||C||= 7 . Determine el ángulo que
forma A y B
Solución
Sea a = ¿ (A, B) = 180° - 6 , ahora por la ley de los cósenos:
X
lkl|2=||A||2+||B||2-2||A||||B||cos»
a
9 A-
Vectores Bidimensional
751
49=34-30cose dedonde cos0 = — => 9=120°
2
Luego a = 180° - 9 = 180° - 120° = 60°
a = ¿ (A, B) = 60°
n
Los vectores ayo tienen igual longitud y forman un ángulo de — si la longitud de
-♦ —» —»
a+ b es 4 unidades mayor que la longitud que uno de ellos. Hallar || a ||.
Solución
Datos del problema: || a ||=|| b ||= x; ¿(a,o) = — ; ||a+o||=jt+4
Si ¿(a,o) = -
3
a.o=||a||||o||cos| = ^-
a.o=-
(1)
||a+o||2=(jt + 4)2 => ||a||2+||o||2+2a.o=.x2+8jt + 16
reemplazando (1) en (2) se tiene: jt2-4jt-8 = 0,de donde
x2 -4jc = 8 => (jc-2)2 = 12 => x-2 = ±2j3
jt = 2±2N/3 dedonde x = 2 + 2ji porlotanto || a ||=2 + 2-s/3
-» -* -* -»
En la figura: a+o=(-V3,3), si ||a|| = m y ||o||=n. Hallar m + n
(2)
Solución
752
Eduardo Espinoza Ramos
El vector a = (a,,a2) se expresa en la forma:
a = (|| T||eos60°. || a || sen60°) = (-,—)
de igual forma para el vector b = (fc,, b2)
fe=(-||6||cos30°. || fe || sen30°) = (-^.-)
~~* ~? ,m \13m , v3 n, rr „, , ,
como a+fc=(—, ) + ( n,~) = (-•\/3,3), de donde
2 2 2 2
2 2
V3m n _
+ — = 3
resolviendo el sistema se tiene: n = 3, m =
L 2 2
Luego: »i + n = 3 +
La presente figura es un hexágono regular de lado "a". Si s = a+ b+ c+d . Calcular
11*11-
Solución
Ubiquemos la figura en un sistema de coordenadas
Yt
Vectores Bidimensional
753
2 2 22 22 22
Calculando los vectores a.fc.cy d se tiene:
7=OD=D-0 = (^-,-^-a)
2 2
~b= OB =B-0 = (—,—a)
2 2
c= CB =B-C = (--,—a)
2 2
rf =7(9= O-A = (--,-—a)
2 2
í = a+fc+c+d=(2a,0) => ||s||=2a
Demostrar que si dos vectores tienen la misma magnitud M y hacen un ángulo 0, su suma
0 6
tiene una magnitud s = 2M cos(—) y su diferencia D = 2A/ sen(—).
Solución
Sean A y B dos vectores tal que:
A = ||A|| = ||B|| = Af y 6 = ¿<A.B)
S = A+B =* s = \\~S\\ = \j\\A\\2 +\\B\\2 +2A.B
'=VlMI|2+l|B||2+2||A||||B||cose-VA/2+A/2+2AÍ2cose
= j2Myll + cosG = J2M.Jicos- = 2M cos-
s = 2Mcos—
2
M/VTA /- 2 ^ 1 + COS0
NOTA.- Como eos — =
2 2
Vi
—a \r~o
+ cos0 = 2cos—
V 2
en forma similar para D = A-B
754
Eduardo Espinoza Ramos
O = ||D|| = N/||A||2+||B||2-2^.fi=>/||A||2+||fi||2-2|U||||fi||cos0
: yJM2+M2-2M2cose = yf2.M.y¡l-cos8 = y¡2My¡2sen-
2
a
D = 2M sen(-)
2
KIftT. i6 1-cosS r. n; 6
NOTA.- sen — = => vi - eos 6 = yJ2sen —
2 2 2
(53) Sea ABCD un rectángulo tal que 2 AB = AD y sean E y F puntos medios de los lados
BC y DC , respectivamente. Sí M = AE + AC + AF Hallar el valor de:
compM +comp2M .
AB
AD
Solución
De los datos del problema el gráfico es:
Como M = AE+ AC+ AF
(1)
Calculamos los vectores: AE. AC y AF
AE =(a,a), AC =(2a,a), AF =(2a,-)
2
(2)
Ahora reemplazamos (2) en (1) se tiene:
M = AE+ AC+ AF =(a,a) + (2a,a) + (2a,-) ={a + 2a + 2a,a + a + -) = {5a,—)
2 2 2
también calculamos AB , AD y 2 M
AB = (0,a); AD = (2a,0); 2 M = (10a,5a)
Vectores Bidimensional
755
¡¡ M.lB (0-a)-(5fl'f) 5a
comp = = =— = —
-* a 2
AB
AB
2m 2M.AD (2a,0).(10a,5a)
comp = = = 10a
"71? * 2a
*B II AD II
Ai 2AÍ 5fl 25
comp + comp¿M =— + 10a =—a
AB
AB
©
En la figura, calcular FD
Y
Solución
Del gráfico se tiene || FG ||= 4
|| GD ||=3 además FD = FG+GD
calculando FG :
P(12,5)
(1)
Y
~0
D
12
P(12,5)
5
X
—* ~* OP 12 5
como OP = (12,5) de donde U = = (—,—)
13 13
OP
OP
además FG y OP tienen la misma dirección y sentido
OP FG
~* 12 5
7o 13 13
756 Eduardo Espinoza Ramos
Luego FG =\ FG \U =4(—,—) = (—,—)
7^ 13 13 13 13
(2)
* ~* ~* 5 12
ahora calculamos GD : U =U' =( ,—)
—' —' 13 13
gd op lJ 1J
como GD = || GD || ¿7 =3(-—,—) = (-—,—)
-fi) 13 l3 13 13
... (3)
reemplazando (2), (3) en (1) se tiene:
~^ ~¿2 T^ ,48 20v , 15 36, ,33 56
FD = FG+GD =(—,—) + ( ,_) = (_,_)
13 13 13 13 13 13
13 13
(i?) Dado el gráfico ABC donde ¿ A = 120°, || AB ||= 4 y || AC || = 7 .
a) Graficar el triángulo ABC.
b) Hallar comp ABf y comp^
BC
BC
Solución
A II AC II = 7 C X
Las coordenadas de AB =(-|| AB ||cos60°, || AB || sen 60°) = (-2, lS) y AC =(7,0).
ÍC = AC-A5=(7,p)-(-2,2V3) = (9,-2^) => || BC ||=>/81 + 12=<s/§3
comp
. AB
AB.BC _(-2.2>/3).<9.-2>/3)_-18-12 _ 30 _ 10 ¡^
BC
BC
>/93
n/93 >/93 31
Vectores Bidimensional
757
"ic AC.BC (7,0).(9,-2>/3) 63-0 21 ¡-r
comp = = ?== = —;==-=—V93
BC
BC
>/93
M 31
(56) En la figura M es un punto, tal que el área del triángulo A es 3 veces d ¿rea del triángulo
B. Hallar ||p||.
Yt
0
Solución
Del gráfico dado se tiene: P,(-6,0) y P2(0JS)
Por condición del problema se tiene: área A = 3 área B entonces — = 3=r siendo r la
razón o relación entre las áreas; si M(x,y) es un punto que divide al segmento P, a P2
entonces se tiene:
_xl+rx2 _-6 + 3(0) __6__3_
l + r ~ 1 + 3 4~ 2
v_>'i+O'2_0-t-3(8)_24_6
l+r 1+3 4
3
x = —
2
y=6
Luego M(—.6)
p = OM =(-|,6)
KPII
=1
^+36=^
4 2
(S"n Hallar la proyección del vector a = (7,12) sobre el vector b = (3,-4).
Solución
Por definición se tiene pro\t = —-— - b
'" II* II2
758 Eduardo Espinoza Ramos
7 (7,12)^3.^4) #, ,x 21-48,, ., 27 ,_ _.
proyi = — .(3. -4) = (3. -4) = (3, -4)
* lltt^)||2 25 25'
27
proyl =-—(3,-4)
¿ 25
(58) Dados los puntos A(-l,3). B(5,6) y C(7,5); si P divide al segmento AB en la razón
AP : PB = 2, hallar la proyección del vector AP sobre el vector BC
Solución
AP — —
Sea P(x,y), si ^ = 2 => AP = 2PB
PB
' =3
fx+l = 10-2x (* = ;
b>-3 = 12-2y "* \y = i
(x+l,y-3) = 2(5-x,6-y) » , „ ,„ „
Luego P(3,5) => AP = /'-A = (3.5)-(-l,3) = (4,2)
BC = C-B = (7,5)-(5,6) = (2,-l)
_ w AP.BC ^ (4,2).(2,-l) „ 6.- n
Entonces proy!Z, = .BC = , .(2,-1) = —(2,-1)
BC «i "^ii2 (V4 + 1)2 5
proyí = £(2,-1)
6?) Los lados de un triángulo son a, b, a-fc si ||a||=6. ||fc||=2 y ||a-fc||=5.
calcular comp* —comp:
b a
b
Solución
a*-fc||2=52 => II7II2 + II fe |p-2 a. fe =25
Vectores Bidimensional
759
36 + 4-2 a. fc=25
a.fc = —
2
a* í a.fc a.fc 15 15 15 5 10 5
comp^ —comp_, = = = = — = —
b a" „?„„-*„ 4 12 4 4 4 2
II Hl ||a||
a* fc 5
comp-, — comp_ = —
(60) Encontrar el vector DE de la figura adjunta.
Sea u el vector unitario en la dirección del vector OB pero del gráfico se tiene B(-15 8)
y por ser OB un vector de posición entonces OB = (-15,8), luego el vector unitario.
uob =•
■ OB
\\ob}\
(-15,8) (-15.8) 15 _8_
V225+64 17 17*17
como uob ={-—.—) => «_=(-—,-—)
17 17 ob 17 17
por otra parte del triángulo DCE se tendría.
D£ = 8«ct + 6(-«L.) = 8(~,¿)-6(-A,_1|)
ob 17 17 17 17
760 Eduardo Espinoza Ramos
. 120 64, ,48 9, .-120 + 48 64 + 90, , 72 154,
= (-l7--n)+(n'n) = (-17-'-^-) =(-¡7'n"'
17 17
8.33. EJERCICIOS PROPUESTOS,
(^ Sea a =(2,1), fc=(3,-3) una flecha que representa al vector. 2a-4¿? tiene su punto
terminal en (5,5). Hallar el punto inicial. Rpta. (13,-5)'
{2) Sí a = (2x -3y, 4x-y), b = (2,-3). Hallar los valores de x e y para que a = 5 b .
Rpta. x = -1, y = -4
\3J Encontrar el valor de M = 5x - 8y sí a = b , donde -&M=(3.x-y + l, -2jc+>>) y
fc=(x-3y + 3, ;t + 5}>-l) Rpta. M = 31-
\4J Dados los vectores a=(3x-5, *-2;y + 2) y b = {x-y-2, 3-2;y). Hallar x e
-» -» 9
y de modo que 3a=4£>. Rpta. x = 5, y-.~±
(5) El vector a cuyo origen es el punto A y cuyo extremo es el punto B. Expresar al vector
a en la forma a = ax i + a2 j , sabiendo que las coordenadas de A,B se dan a
continuación.
i) A(-7,2) . B(3,4) ii) A(-.-j2~y , B(-7,5V2)
iii) A(0,0) B(3,-7) iv) A(0,5) , B(-6,-l)
Rpta. i) lo7+27 ü) -—7+4^2 7 ÜO 3 i - 7 7 ¡v) -6i-6j
Vectores Bidimensional
761
^—>^ —» —»—»—» —» —»
\6j El vector c =(2,-1) es expresado como c - a+ b , donde los vectores a y b son
—» —♦
paralelos & x = (3w,4w) e y = (-3n,-n) respectivamente, además m ^ 0, n ^ 0. Hallar
-» —» —» —» i
a-fc. Rpta. a-b=—(48,31)
\j) Desde el punto A(0,1) se ha trazado un segmento hasta el punto B(-4,3), hasta que punto
es necesario prolongarlo en la misma dirección para que se triplique su longitud.
Rpta. (-12,7)
f8) Hallar el vector x en las siguientes ecuaciones:
i) -3<U, + 2; = 5(0,-2, + 4; Rpte. ;.(-|.I,
ü) (15,-12) + 2 ;t+2(-6,5) = 4(1,-2) +x Rpta. x = (-,-2)
iü) 3(0,-2) + 2 jc-5(1,3) = (-3,-5) Rpta. jc = (1,-8)
iv) 3(a:-(8,-2)) = 6(7,0) Rpta. *=(22,2)
\9J Muestre analíticamente y. gráficamente que existen números r y s, que satisfacen
c = r a + s b , donde:
i) 1 = (5,1); 1 = (3,5); c - (5,4) ii) a = (2,1); 1 = (3,2); c = (5,2)
UO) Si a = (x, y) y b - -(2,-4) tienen direcciones opuestas y x1 + y2 = 25 . Hallar y - x.
Rpta. 3^5
(ll) Si a =(-2,1), fc=(3,-2) dos vectores no colineales (direcciones diferentes) y
r ~ 2 i - 4 j es otro vector. Hallar los escalares k y m de modo que r =k a + mb .
Rpta. k = 8, m = 6
762
Eduardo Espinoza Ramos
(l2) Se dan tres vectores a =(3,-1), ¿>=(l,-2), c = (-1.7). Determinar la descomposición
del vector p = a+ b+ c en la base a y b . Rpta. p = 2 a-3 b
(li) Dado tres vectores en el plano a =(3,-2), ¿>=(-2,l) y c=(7,-4). Determinar la
descomposición de cada uno de los vectores con relación a los otros dos.
-» -,_>_, j _, j _> -> _, _,
Rpta. a-2b+c, b= — a—c, c = a-2fc
2 2
(14) Si a=(4x, x-3) y fc=(2, jt + 3). Determinar los valores de x tales que a sea
perpendicular a fc Rpta. x = 1 o x = -9
(15) Si a y fc son vectores no paralelos tales que: c =(m + n-l)a + (m + n)b,
—> —> —» -» -»
d = (m-n) a + (2w — n + \)b . Hallar m y n tal que c =3d .
2 1
Rpta. m = —, n
3 12
®-»-» -»-» n -> ^^
Sean a = eos 1 +sen0 j y b = cos(6 +—) i +sen(0 h—) y dos vectores. Demostrar que
—» —»
a y b son ortogonales.
Q^ Dados los vértices consecutivos de un paralelogramo A(7.-l), B(-3,l) y C(-5,5).
Determinar el cuarto vértice D y la longitud de la diagonal BD .
Rpta. D(5,3) , -|| BD ||= 27Í7
^8) Dados los puntos A(2,l), B(3,2) y C(-4,-l). Hallar la longitud de BD sabiendo que el
punto D está definido por la relación DC = AB Rpta. || BD || = 10
ft9) Hallar un vector c cuya magnitud es igual a la del vector a = (4, -3) y cuya dirección es
la misma que la del vector b = (l,v3). Rpta. c = (—, )
2 2
Vectores Bidimensional 763
(20^ Dados los vectores a = (-5,2) y b — (3,-4). Hallar un vector unitario de sentido opuesto
al vector a - b . Rpta. «T-t =(—,—)
(21) Los vectores a, b y c de ■ V2 cumplen que: 2 a - 3 £> = c y 3a-2fe=5c siendo a
un vector unitario, calcular la norma de b— c . Rpta. ||fc-c||=—
13
y22J Sean a y b vectores de V2 tales que b es el opuesto de a . Si b tiene el mimo
-* 1 1 ~* _»_»_,
sentido que el vector c = (—,—) y la norma de a es 5. Hallar el vector x = 2 b+ a
3 4
Rpta. x=(4,-3)
(23) Sean a, fc y c vectores diferentes, mostrar con un ejemplo que si se cumple
a. b = a. c , no se puede afirmar que b =c.
(24J Hallar un vector que tenga la misma magnitud del vector que va de A(-2,3) a B(-5,4) y
que tenga el sentido opuesto al vector que va de S(9,-l) a T( 12,-7). Rpta. a = V2(-l, 2)
(25) Sean a = (2,-3), b = (-2,1) y c = (3,2). Hallar un vector unitario ortogonal al vector
-»-*-*-» -* 24 7
v =5a-3(fc+c). Rpta. «=(—,—)
25 25
(2é) Pruébese que: si c^Oysiayfe son paralelos al vector c , entonces a y b son
paralelos.
[2n Demostrar que si a + fc y a-fc son ortogonales sí y sólo sí || a || = || b ]|
(28) Si a y fc son vectores no nulos ni paralelos. Demostrar que a a + /J fc = 0 implica que
a = p = 0.
(29) Pruébese que sí: rf = b+ c y si b es paralelos a a entonces d es paralelo a a si y
—» —»
sólo si r es paralelo a a .
764
Eduardo Espinoza Ramos
(30) Hallar la longitud de la suma de los vectores unitarios u y v si u tiene la misma
~* -* -» 3 /—
dirección que a =(4,-3) y v tiene la dirección opuesta de ¿>=(-5,0). Rpta. —VIO
(31) Sí a = (-3,5), b = (2.-3) . Hallar la longitud del vector c sí:
i) c=(& + b*).(t-2b)lbL ii) 7 = U.¿).¿>-L-(a>-L.fc)t
Rpta. i) 29>/Í3 ii) 5>/259
fa¿) Hallar un vector v de longitud y que tiene la misma dirección de un vector que
forma un ángulo de 30° con el sentido positivo del eje X. Rpta. v = (9, ±3V3)
(33) Demostrar que el vector ¿>.(a.c)-c.(a.£>) es perpendicular al vector a .
—¥ —¥
®~~* a b ~* ~*
Demostrar que el vector b '■—.a es perpendicular al vector a .
II a ||2
®-» -* , -»-*-»-»
Demostrar que si a y b son vectores paralelos en R~ entonces | a. b \ = || a ||. || b ||.
(36) Si a y ¿> son vectores tal que a±+bJ~=a+b . Demuestre qué || a || = || fc ||.
®—> —» —> ■—» -» -► —»
Pruebe que c es paralelo al vector (b*~.c)a-{& .c)b
® -»-»-» ^ -» -» -» -» -»
Sea c -ta + sb ,hallarel valorde - sí c ±(&+b) donde a=(3,5) y fc=(2,2).
Rpta. - =
s 25
Q9) Dado el vector a = (3,-4), encontrar otro vector b , tal que sea perpendicular al vector
—» —»
a y que su modulo sea 10. Rpta. b — (±8. ±6)
Vectores Bidimenüonal
765
(40) Halle || u ||, || 2 u + 3 v ||; si || v ||= 6 y u Lv y los vectores («+ v) y (4 m-9 v) son
ortogonales. Rpta. 18\/2,9
Ul) Si el vector jc = (.1.18) es expresado como a = x+ y , donde x// b , yll c y sí
—» —» —» —»
¿7 = (-1.4), c = (2w,3/n). Hallar el vector x . Rpta. x = (-3,12)
(42) Los vectores a , fc y c de V2, cumplen que & + 2b = c y a-3fc = 2c . Siendo a un
4
vector unitario. Hallar la norma de b+ c
Rpta. ||fc+c||=:
U3) Sí a=(a,,a2). ||a|| = 2, -i- = 4 . Hallar a
Rpta. a =±-==(8,2)
VI7
(44) El vector a tiene longitud 5 y el punto de apoyo en (1,-1) encontrar el vector a si la
—♦
abscisa del punto terminal es 4. Rpta. a = (3, ±4)
(45) Dados los vectores u = (a.-b), v = {Ib, c), u + v = (1,1); si u/1 v , calcular
ab
Rpta. --
(46) En la figura adjunto, Si P es tal que el área
del triángulo APC es el doble del área del
triángulo CPB. Hallar || CP \\.
Rpta. -V73
B(2,10)
A(-4.2)
C(2.2)
(47) Si a=(m.2m), fc||a, a-b =(2m,p) y || a-fc ||**20 calcular || b || donde m*0
Rpta. ||fc||=10
766 Eduardo Espinoza Ramos
Se tiene los vectores a = r p , b =t q ,
c=(-3.2>/3) calcular || b || sí
c =r p + t q
Rpta. || é ||= 5
®
®
—-» —* —» —» —» —9
Encontrar los vectores a y fc tales que a+fa =(-1,5), a x+fc es ortogonal a (-5,3),
-> -» -» -» -» -»
a + fc es paralelo a (1,-1) y a.¿>+ll = 0. Rpta. a = (-3,4), b = (1, -2)
—»—*—*—»—* —» —» —» —» —* —*
Si a+b+c+d = 0 , calcular 2 c .d , sabiendo que || a+ é || = 6, ||c||=3, ||í/||=4
Rpta. —
—» —» —*
Dados los vectores a , b y p de V2, determinar los números r y s en términos de sus
—» —» —»
productos escalares de manera tal que el vector p -ra-sb sea perpendicular a los
—» —»
vectores a y é simultáneamente.
Pruebe que en cualquier paralelogramo la suma de los cuadrados de las longitudes de las
diagonales es igual al doble de la suma de los cuadrados de dos lados adyacentes.
Deducir la ley de los cosenos en un triángulo empleando el producto escalar.
Sí PC = 3 PA y PB = 2 PD . En que razón el punto O de intersección de las rectas
AB y CD divide a AB y CD ?.
Rpta. -2 y --
(55) En la figura ABCD es un paralelogramo:
AF=-AD, ED=5BE
3
Sí EF =m AD + n AB . Hallar m + n
Rpta
Vectores Bidimen$ional
767
Hallar las coordenadas del vector
AC de V2 del gráfico
Sí || AC ||=10, ||"Afl ||=6,
EF ||=15 y || Ffl||=8
(57) La figura PQRS es un rombo
tal que || PQ \\ = a
Demostrar que: PR . SQ = 0
Rpta. 7c=(-^.^)
F 17 17
(58
(59
Si ABCD es un cuadrilátero y M un punto medio de DC probar que AE --AM y
H>E=-1)B .
3
En la figura adjunta tenemos un cubo y "techo"
una pirámide regular, todas de arista x, sí:
1 = ~DE + ~BA+~KC + ~HC+ FG .
—»
Hallar la norma de s .
—»
Rpta. t| s ||= x
768
Eduardo Espinoza Ramos
(ód) Si ABCD es un paralelogramo y M es
punto medio del segmento AB, hallar
6m-9n si AM =m AC + nMD
Rpta. 6m - 9n = 5
En la figura: OC = -OB, AD = -AB, E
3 3
es punto medio de OA , probar que: OD y
BE se cortan en O y también:
OP = -OD, AP=-AC y BP = PE
4 4
Si ABCDEF, es un hexágono que se
muestra en la figura cuyo lado mide
"x" unidades, determinar:
1 » 2 »
\-AE + -CF
3 3
Rpta. -VÍ9
Dados los puntos P(l,2), Q(2,5), R(5,8), S(9,10) que forman un trapecio, encontrar dos
1>S-QR
puntos M y N sobre las diagonales, si se sabe que: MN — •
figura.
-, tal como en la
S ^ ..J09 180, XJ 164 235,
b Rpta. Af( , ),N( , )
v 33 33 33 33
Vectores Bidimensional
769
(64
O
En el triángulo ABC, se tiene
3 EC = AB , hallar s y t sí
EB =s BA+r BC .
2 4
Rpta. i = — , t = —
5 5
En el paralelogramo ABCD, M es punto medio de AB. Hallar s y t sí
AM =s AC + tDM
B„ „C
Rpta. s = t = -
Vg6/ En la figura ABCD es un paralelogramo sí
Hp=-Tc y sí ~BE=m~BC+n~AP .
3
Calcular mn
Rpta. mn =
16
(67) En el triángulo ABC se tiene AM =-MC
Sí BM =r BA+t BC . Hallarr-t
Rpta.
4 3
r=-, t=-
7 7
(68)
Si M y N son puntos de trisección del lado BC del triángulo ABC y
» ► ► 1 1
AN =m AC + n AB . Calcular
m n
770
Eduardo Espinoza Ramos
Rpta. -
2
(69) En la figura adjunta OABC es cuadrado, P,Q,R y
S son puntos medios de los lados OA, AB, BC
y CD respectivamente. Hallar || ST + BH \\ si T
es punto medio de PQ y H es punto medio de
~QR . Rpta. || ^T+ ~BH || = 2>/2
S c(4,0)
(70) En el triángulo MPQ, ME es la mediana del lado PQ, demostrar que:
||iMP||2+||AfG||2=2||M£||2+i||POl|2
(7l) En la figura consideremos: || OM ||= 12.
Sí ~ON =mXM + nOMi-. Hallarm + n
Rpta.
3 + S
@ En la figura 1p \ \ OX , || OP || = 8
Si OT =mOP + n OP1, calcular m y n
_ . V5 + 1 y¡3-l
Rpta. m = , n =
Vectores Bidimensional
771
(73) Encontrar el vector AB de la figura. y
Rpta. AB =—(429,460)
(74) En la figura, si P es un punto tal que el área del triángulo A es cinco veces el área del
triángulo B. Calcular || OP ||
Y
(-10,0)
(75) Dados los vectores a=(jc,-3v), b = (2v,-z). Hallar x + y + z para que a+¿>=(8,-4)
-» -*
y a // b . Rpta. x + y + z - 8
wó) Dados los vectores a = (x,3v) y b = (-2 y, z). Hallar x + z, de modo que a+ b = (8,4)
—» —>
y sea a // ¿ . Rpta. x + z = 5
67) En el hexágono regular ABCDEF, de lado "a",
—»
hallar la norma de s , sabiendo que:
-> 2 » 1 ► 1 »
5=-(AD + -D£) + - £fi .
3 2 2
Rpta. —a
3
F^ A
/ *
D^ C
B
772
Eduardo Espinoza Ramos
(78) En la figura, si q = a+ b+ c , determinar q sabiendo que la segunda componente de q
i r~
es cero (asumir sen 37° = —) y || b ||= 20, || a || = 10V2 y que la primera componente de
—»
c es igual a 20.
Se tiene los vectores a =r p , b =t q , c = (-3,2V3) calcular \\b\\ si c = r p+í q
q
fto) Sean los vectores a y b . tal que a = (x,2x), a-b = (2a.y), b II a y el módulo de
a-fc es >/Tl2 . Hallar \\b\\. Rpta. || b \\ = 2yff
Consideremos los vectores a = (x,-y), fc = (2y, z), a+ fc = (1,1) y a/Ib . Hallar .
Rpta. ±>=_1
z 2
®^ -» 1 4 "* >/73 "* ~*
Dados los vectores a=(x,3') y b-(—,—). Hallar y + x si ||a||= y si a y b
tienen direcciones opuestas.
Rpta. ,v + x = -
Vectores Bidimensional
773
© Dados || a || = 1, ||fc||=23, || a - b \\ = 30 . Calcular ||a+¿>||. Rpta. \\&+b*\\ = 20
(84; Los vectores a y b son perpendiculares entre sí y ||a|| = 5, ||¿|| = 12, calcular
|U + é||, ||í-fc||. Rpta. |U+é|| = |U-é|| = 13
© Si 7 = a-é, Hallar || 71|, sí ||a|| = 4, ||fa||=5 y a.é=11.5 Rpta. |k||=8
(86) Los lados de un triángulo son los vectores a, ¿ y a-¿> sí || a || = 2 , || £ ||=3 y
a*.*=--. Hallar ||a*-fc|| Rpta. ||a-¿|| = 4
(87) Si a = (m, 2m), b II a , a - £ = (2wi, /?) y || a - b || = 20 calcular el módulo de b .
Rpta. || ¿||= 10
(88) Sí a*+¿M-c = 0, ||a|| = 3, ||¿||=4 y || c ||= 6. Hallar el valor de a.(2¿>-a)
Rpta. 2
© Sean los vectores a,b y c tales que || a || = >/26 , \\b\\ = 3y¡2 y b.c =12 sí
a = ¿> - c . Hallar || c || Rpta. || c || = 4x/2
®—» —> —> —»—»—»—» -» /_ —» —»
Sean los vectores a,í> y c tales que a = ¿>+ c , || a || = 5, ||é|| = 2v5 y ¿>.c = 10.
Hallar || 71|. Rpta. ||c||=5
© Sí a+é-7=0 y ||a|| = 2, ||é|| = 4>/3, ||c||=8. Calcular a.7.
Rpta. a. c = 10
—-- -» -» -» -»-»-»-»
(92) Sabiendo que ||a|| = 3, ||*||=1, ||c||=4 y a + fc + c = 0 . Calcular la suma
-» -» -» —» -» -»
a.b+b.c+a.c. Rpta. -13
774
Eduardo Espinoza Ramos
(93) Si a+b+c+d= O, calcular 2 c .d , sabiendo que || a+b || = 6, ||c||=3, ||</||=4
11
Rpta. —
2
(94) Sí íh-¿h-7=0 y ||a|| = 2, ||¿>||=5, || 71|=6. Calcular a.é. Rpta. -
(95) Dados los vectores a =(8,6) y b = (-2,6). Hallar los vectores p y q tales que pLq,
qllb y a = p+q. Rpta. p = (l,-3), J = (9,3)
(%) En la figura se tiene: || a ||= 4, \\b ||= 6 . Hallar a. b .
120°
Rpta. a.¿>=12
197)
Calcular a. ¿> , siendo || a
—» -»
a y b . Y
1 = 4, ||¿>|| = 2>/3, donde en la figura aparece los vectores
Rpta. a . b = 4-S
98
Dos vectores a y b forman un ángulo agudo cuyo sen 9 = 0.75, averiguar el módulo del
—» —» —» —» —*
vector b , sabiendo que a—b es ortogonal a a y que el módulo de a es 27.
Rpta. ||fc||=^V7
(99) Los vectores a y fc forman un ángulo de 9 = 120°, sabiendo que || a || = 3 y || b ||= 5.
Determinar || a+é II, ||a-fc||. Rpta. ||a+fa|| = VÍ9: \\a-b\\ = l
Vectores Bidimensional
775
nlOOj Los vectores a y b forman un ángulo de 45° y el módulo de a es 3. Determinar el
—» -» -» —» —»
módulo de b de modo que a - b sea perpendicular a a . Rpta. || b || = 3V2
Uoi) Calcular || a + £ || sabiendo que a y b forman un ángulo de 150° y que || a || = V48 y
||é||=6. Rpta. \\a+b*\\ = lS
(102) Los vectores a y b forman un ángulo de 60°, sabiendo que ||a|| = 5, ||¿||=8,
—» —» —» —» .
determinar || a + b || y || a-b ||. Rpta. Vl29 y 7
f 103J Sean a, b y c vectores diferente de cero, y suponiendo que el ángulo entre a y c es
—> —> —»
igual al ángulo entre b y c ; para qué valor de t es el vector c perpendicular al vector
d = ||é||£H-ré Rpta. r = -|M|
(l04J Dados dos vectores a y b forman entre sí un ángulo de 60° y el módulo || a || = 6.
Hallar el módulo de b para que a-b forman con a un ángulo de 30°. Rpta. || b ||= 3
(l05j Si a, b son vectores unitarios y 9 es el ángulo entre ellos. Demostrar que:
i||7-é|| = |sen||
(l06/ Consideremos los vectores de la figura:
-» -» —»
Sí c =ma + na±, donde:
||7||=8. || a || = 2. Hallar m-yfen
Rpta. 2>/3->/6
776
Eduardo Espinoza Ramos
(107) En la figura adjunta se dan los vectores.
Si c =ma+nb , siendo:
a || = 3, || fe ||=2, || c ||=6
Hallar m + n Rpta.
5>/3
Í108) Se tiene los vectores de la figura:
Sí || a || = 2-fi . Hallar: m + n
donde b =ma+nb
Rpta. m + n = ■
YÍ
b* T
\45°
0
X60°
X
(Í09) Enlafigura: ||fc||=10, ||7||=20,
además a =(20,-3). Hallar a+b+2c
Rpta. (—,2 + 20>/3)
6
(llO) Calcular a. b, donde a y b son los
vectores de la figura adjunta para los
cuales || a || = 8 y \\b\\ = -Jll.
bV
Y
2rX
0
L
^Í8°
jra
X
Rpta. a.b=- 48
Vectores Bidimensional
111
[lllj Dados los vectores que se muestran en
la figura. Hallar m + sabiendo
que c =wa + «ai, siendo a un
—»
vector unitario y || c ||= 8 .
Rpta. 8>/3
(112) En la figura se tiene los vectores a, o y
—» —» _—»-*-*
c donde || a || = 2V3 sí c =ma + nb .
Hallar m - n.
Rpta. —
(ll3j En la figura: ~AB \\ ~OY y || "oT ||= 4.
Si OB =mOA+nOA1, Hallar el
valor de m - n.
Rpta. -(3->/3)
Y
^
30°X
0
>^ a
X
Í114J Los lados de un triángulo son los vectores a, o, a- o , sí || a ||=5 , || b ||=3, además
comp*, = —. Hallar || a- b \
b 2
Rpta. \\a-b\\=yj\9
\115J Sean ayo dos vectores tales qué a =(5,-2), compt =-58 y ||o||=29 Hallar
comp-,.
b
Rpta. -2V29
filó) Si a es un vector del mismo sentido que v = (1,2) tal que || a ||= 50 y || o ||= 29. Hallar
comp^
Rpta. -40
778
Eduardo Espinoza Ramos
ÍII7) Los lados de un triángulo son los vectores a, b y a+b sí ||a||=4, ||fc||=6 y
-• —» —» —» —»
comp* = 2. Hallar || a + o ||. Rpta. || a + o ||= V76
(118) Encontrar el vector proy-, si comp^ =-3 y si (1,-1) es un vector que tiene la misma
\-S b b
-» ~* 1
dirección que b. Rpta. proyt, =-7= (-3,3)
fc V2
U19) Los lados de un triángulo son los vectores a,b y a+b , tales que || a ||= 3, || b ||= 2V2
y || a+ b ||= %/53 . Calcular Icompl -comp{J+b).
b a
(120) Los vectores ayo son los lados de un paralelogramos si || a ||= 6, || a ||= 21| b || y
~* 10 ~* ~* "* ~*
compÜ, = —, determinar || a- b ||. Rpta. || a- o ||= 5
b 3
121) Dados los vectores a =(k + 2, 2k) y b =(-3, k + l), determinar los valores de k de
-» 3
manera que /vuyS y o están en direcciones opuestas. Rpta. £e<—,2>
¿> 2
(l22j Dado el triángulo de vértice A, B y C con ángulo en A igual a 45°; || AB ||= 6V2 ,
graficar y hallar || BC ||, comp AB^ -compAC^
BC BC
Í123J Los lados de un triángulo son a, b y a- o tales que || a ||= 10, || b ||= 6 y comp!!, = -5 .
—» —» -* —»
Hallar la longitud de a- 0 Rpta. || a- b ||= 14
124J Los lados de un triángulo son a b y a+¿ tales que ||a||=8, ||o||=6y
||T+ Ib ||= V68 . Hallar complJ*b) -3complJ'h) Rpta. 32
a 6
Vectores Bidimensional
779
(125) Sí || 7 - ~b ||= 4, || Ib ||= 3 y comp^h = —. Hallar la norma de T . Rpta. \\7\\=y¡69
b J
126) Sea || a |j= V65 , ||a+fc||=164 y compla + b) = -^=-. Hallar comp^K
Ha||
6
Rpta. comp^-*^ —
¿> 5
(127) Sabiendo que pro?!? fc) = (1,2) y proy^' = (-4,-8). Hallar proy(^'x' 4b~y)
a a a
(12J0 Si a y i son dos vectores no nulos tales que el módulo de || a || = || b || = k y el ángulo
-» -* 7T
entre a y fc es — y la norma de su diferencia es 2 - k. Hallar k Rpta. k = 1
@Sí proy* =(2,-5), proyl =(-3,2) y ¿=2^+7x. Hallar ||£|| Rpta. ||%||= 5>/2
™ Dados los vectores a = (3,>/3) y fc = (V3.-1). Hallar 2{proyi + proyt)
Rpta. (3 + >/3, l->/3)
(m) Dado el AABC en el cual ¿ A = 120° || ^AB ||= 4 y || ~AC ||= 7 , encontrar || ^BC || y
las proyecciones de AB y AC sobre BC .
(132) Dado el AABC con ¿ A = 45°, || ~AB ||= 8, || 7c ||= 6>/2 , encontrar || IbC || y las
proyecciones de AB y AC sobre BC .
(133) Dado el triángulo ABC con ||^B||=10, ||7c||=9, ||BC||=7, encontrar las
proyecciones de AC y BC sobre AB .
(134) Dado el AABC con || AB ||= 5, || AC ||= 7 , \\ BC ||= 9, encontrar las proyecciones de
AB y AC sobre CB .
780
Eduardo Espinoza Ramos
H35) Sí d = a+b+c, || a ||= p , ||fc|l=<7, ||c||=r, a .b = pq , a .c = pr y pro>^ =r .
—» -*
Hallar el módulo de d . Rpta. || d ||= p + q + r
U3<y Hallar el ángulo formado por los vectores a y proyt sí a = (1,2) y b = (1,3).
Rpta. 6 = arccos(-p)
Si proyt =(1,3) y proy_ =(3,1), calcular a+fc y el ángulo entre los vectores a y
-* -» ~* 20 20
fc. Rpta. a+b = (—,—)
3 3
Í138) Demuestre que: compíJ+c) =compt +comp%
(139) Demuestre que: Sí compt, _, - compt -, = 0 entonces || a || = || fc |
a+fc a+fc
(140) Sí a.b^O y a. c ^ 0. Demuéstrese: proyt = proyt <=> c—"kb
[141) Sean a,b,c,d vectores en V2 tal que a=fc+c+d. Demostrar que:
i) proy., + proyt + proy^ = a
a a a
ü) Si || b ||=|| c ||=|| rf || entonces proyt + proyt + proyt es paralelo a a
¿> c rf
(142) En el paralelogramo ABCD. ¿ (BAD) = 60°. B
|| AB ||= a, || AL> ||= 2a , donde a e R - {0}
Sí p = || pretil y q = \\proy^\\.
AD AB
9
Hallar p + q Rpta. p + q= — a
Vectores Bidimensional
781
143) En la figura, a, b y c son tres vectores de
-* —>
V-,. tales que b es unitario, c es ortogonal a
a y a . fc = — II a II ■ Hallar compt
2 r
Rpta. compt, =
>/3
144J En el rectángulo de la figura: H, P y Q son
puntos medios AB = 4 FB , || OC ||= 4a,
||7mJ=<3 Sí v = HF+ AP+^C .
Hallar: compv +compv
AB QB
Rpta. —(26>/5 + 53)fl
20
Dados tres puntos A, B y C, los cuales forman un triángulo, hallar la dirección de una
altura cualesquiera del triángulo, usando el vector proyección.
Rpta. La altura relativa al lado AB : PC = AC - proy
AC
AB
Consideremos el cuadrilátero ABCD tal que E(l,5) es el punto medio de AB , H(4,2) es
el punto medio de AD ; CE es paralelo al vector (2,3), DE es paralelo a (1,-2) y
CH
proy - (5,5) encontrar los vértices A, B, C y D.
AC
Rpta. A(3,7), B(-l,3), C(-3,-l) y D(5,-3)
(147) En el paralelogramo ABCD, ¿ (BAD) = 60°, || AB ||= 2, \\ AD ||= 4, sí
p =|| proy^ ||, q =\\ proy^ ||. Hallar p + q. Rpta. p + q = 9
AD
AB
782
Eduardo Espinoza Ramos
(148) Si a y b no son nulos y proyt + (pro\t)x =(a)x + b entonces probar que:
b ' a
ii r 11=» b ii y r±u-fc).
(149) Si a =-^--^— y compt =4. Hallar T1.^
II ¿II II ¿i
Í150) Sean P(2,3), Q(5,7), R(2,-3) y S(1.2) calcule proy.
5 Rpta. proy«í=Q^)
pq pq 25 25
(151) En la figura adjunta, determinar los
vectores AC, AB y BC, sabiendo
que: ||Afi||=3 y AC paralelo al
eje Y.
—* 9 12 —' 9 27
Rpta. AB = (-|,y), BC = {j,^),
AC = (0.—)
4
Í152) En la adjunta, determinar los vectores AB, OC, CB sabiendo que \\AC ||=VÍ3,
11^11=^3,11^11=^
—* 9 —* 9 —* 7 9
Rpta. AB = (-,3), OC = (-3.-), CB =(-,-)
Vectores Bidimensional
783
Í153J Un triangulo DEF se encuentra sobre un plano inclinado como se muestra en la figura
adjunta. Hallar el vector DF .
Rpta. £>F = (2,3)
[154) En el paralelogramos de la figura se
tiene: DE = EC, m ¿ (BAD) = 60°.
La altura relativa a la base AD es h. Si
M = AB+ AE- BD y P = proy.
hallar II PII en función de h.
M
» i
AD
Rpta. \\p\\=^-h
í 155) Si b y c son diferentes de 0 , demuestre que:
i) Si b y c son paralelos, entonces proyt - proy^
b c
ii) Si comp3^ = compt, si r>0 (b ^ 0)
rb b
iii) Si comp\ = —compt , si r<0 (b ^ 0)
rb b
784
Eduardo Espinoza Ramos
BIBLIOGRAFÍA
Qj Conjuntos y Estructuras por: Alvaro Pinzón.
(2) Teoría de Conjuntos y Temas Afines, por: SEYMOUR LIPSCHUTZ.
^H Lógica Matemática, por: Patrick Suppes.
(5) Introducción a la Lógica por: Alfredo TARSKI.
(7) Matemática Básica, por: JOHN C. PETERSON.
{6\ Análisis Matemático Vol. I por: Hasser - La Salle - Sulliva.
(Y) Análisis de una Variable Real, por: Miguel A. Sanz Alix.
(ü) Álgebra Superior por: Leithold LEVIS.
MM Cálculo y Geometría Analítica, por: Stein.
(jo) Cálculo y Geometría Analítica, por: Larzon - Hosttler
(ín Calculo y Geometría Analítica, por: Louis Leithold.
(l2) Elementos de Álgebra Superior por: Pablo Miguel y Merino.
Ui) Álgebra I, por: Armando Rojo.
@ Álgebra, por: PAULK REES.
(í?) Álgebra, por: Stanley A. SMITH.
(ló) Variable Compleja por: ARTHUR A. HAUSER.
(l7) Variable Compleja por: Willian R. Derrick.
@ Variable Compleja, por: DA VIS WUNSCH.
(19) Ejercicios y problemas de Análisis Matemática, por: B. Deminovich.
(20) Ejercicios y problemas de Análisis Matemático, por: G. N. Berman.
PEDIDOS AL POR MAYOR Y MENOR
AV. GERARDO UNGER N° 247 Of. 202
Urbanización Ingeniería (Frente a la UNÍ)
Teléfono: 388-8564 Fax: 382-4990
Celular: 9853-3465
email: edueduca@hotmaiI.com
LIMA-PERÚ
IMPRESO EN:
EDITORIAL SERVICIOS GRÁFICOS J.J.
Eduardo Espinoza Ramos
Graduado y Titulado en Matemática Pura.
Catedrático de las principales
Universidades de la Capital
OBRAS PUBLICADAS
► Solucionarlo de Análisis Matemático por Demidovich tomo III
► Solucionario de Análisis Matemático por GBerman, tomo I, II
► Solucionario de Leithold 2da. Parte.
► Geometría Vectorial en R2
► Geometría Vectoi ial en R3