УДК 373.167.1:514
ББК 22.151я.721
Г 36
Атанасян Л. С, Бутузов В. Ф., Кадомцев СБ., Юдина И. И.
Геометрия. 8 класс. — М.: ФИЗМАТЛИТ, 2005. — 240 с. —
ISBN 5-9221-0573-6.
Настоящее издание является второй частью учебно-методического пособия,
содержащего решения задач из учебника «Геометрия 7-9» Л. С. Атанасяна,
В. Ф. Бутузова, СБ. Кадомцева, Э. Г. Позняка, И. И. Юдиной (М.: Просвеще-
Просвещение, 1990 и последующие издания). Данный выпуск содержит решения задач,
относящихся к 8 классу.
© ФИЗМАТЛИТ, 2005
© Л. С. Атанасян, В. Ф. Бутузов,
ISBN 5-9221-0573-6	СБ. Кадомцев, И. И. Юдина, 2005

ОГЛАВЛЕНИЕ
Глава 1. Четырехугольники		5
§ 1. Многоугольники		5
§2. Параллелограмм и трапеция		7
§3. Прямоугольник, ромб, квадрат		19
Дополнительные задачи		28
Задачи повышенной трудности		36
Глава 2. Площадь		49
§ 1. Площадь многоугольника		49
§2. Площади параллелограмма, треугольника и трапеции		53
§3. Теорема Пифагора		61
Дополнительные задачи		68
Задачи повышенной трудности		85
Глава 3. Подобные треугольники		97
§ 1. Определение подобных треугольников		97
§2. Признаки подобия треугольников		102
§3. Применение подобия к доказательству теорем и решению задач. .	109
Задачи на построение		116
§4. Соотношения между сторонами и углами прямоугольного тре-
треугольника 		119
Дополнительные задачи		124
Задачи повышенной трудности		138
Глава 4. Окружность		161
§ 1. Касательная к окружности		161
§2. Центральные и вписанные углы		166
§3. Четыре замечательные точки треугольника		174
§4. Вписанная и описанная окружности		177
Дополнительные задачи		184
Задачи повышенной трудности		191

Оглавление
Глава 5. Векторы		209
§ 1. Понятие вектора		209
§2. Сложение и вычитание векторов		213
§3. Умножение вектора на число		221
Применение векторов к решению задач		225
Средняя линия трапеции		227
Дополнительные задачи		229
Задачи повышенной трудности		234

Глава 1
ЧЕТЫРЕХУГОЛЬНИКИ
§ 1. Многоугольники
364.	Найдите сумму углов выпуклого: а) пятиугольника; б) шестиуголь-
шестиугольника; в) десятиугольника.
Решение, a) S5 = 180° • E - 2) = 180° -3 = 540°;
б)	S6 = 180° • F - 2) - 180° • 4 = 720°;
в)	Sio = 180° • A0 - 2) = 180° • 8 = 1440°.
Ответ, а) 540°; б) 720°; в) 1440°.
365.	Сколько сторон имеет выпуклый многоугольник, каждый угол кото-
которого равен: а) 90°; б) 60°; в) 120°; г) 108°?
Решение. Пусть выпуклый многоугольник имеет п сторон и:
а)	каждый угол его равен 90°, тогда
180° -(п-2) =90° -п,
180° • п - 360° = 90° • п, 90° • п = 360°, п = 4;
б)	каждый угол его равен 60°, тогда
180°-(п-2)=60°-п,
180° • п - 60° • п = 360°, 120° • п = 360°, п = 3;
в)	каждый угол его равен 120°, тогда
180° '(п-2) = 120° -п,
180° • п - 360° = 120° • п, 60° • п = 360°, п = 6;
г)	каждый угол его равен 108°, тогда
180° '(п-2) = 108° -п,
72° -п = 360°, п = Ъ.
Ответ, а) 4; б) 3; в) 6; г) 5.
366.	Найдите стороны четырехугольника, если его периметр равен 8 см,
а одна сторона больше каждой из других соответственно на 3 мм, 4 мм и 5 мм.
Решение. Пусть большая сторона, например, АВ четырехуголь-
четырехугольника ABCD, равна х мм, тогда ВС = (х — 3) мм, CD = (х — 4) мм,
DA = (х — 5) мм.

Гл. 1. Четырехугольники
По условию периметр его равен 8 см = 80 мм, следовательно,
АВ + ВС + CD + DA = х + (х - 3) + (х - 4) + (х - 5) = 80,
4х - 12 = 80, 4х = 92, х = 23, т. е. АВ = 23 мм, ВС = 20 мм,
CD = 19 мм, DA= 18 мм.
Ответ. 23 мм, 20 мм, 19 мм, 18 мм.
367. Найдите стороны четырехугольника, если его периметр равен 66 см,
первая сторона больше второй на 8 см и на столько же меньше третьей
стороны, а четвертая — в три раза больше второй.
Решение. Пусть первая сторона четырехугольника равна х см,
тогда его вторая сторона (х — 8) см, третья сторона (х + 8) см,
а четвертая сторона равна 3 • (х — 8) см. По условию периметр этого
четырехугольника равен 66 см, следовательно,
х + (х - 8) + (х + 8) + 3(х - 8) = 66,
х + х - 8 + х + 8 + Зх - 24 = 66, 6х = 90, х = 15.
Ответ. 15 см, 7 см, 23 см, 21 см.
368. Найдите углы выпуклого четырехугольника, если они равны друг
другу.
Решение. Сумма углов выпуклого четырехугольника равна
360°, и так как все они равны друг другу, то каждый из них равен
360° :4 = 90°.
Ответ. 90°.
369. Найдите углы А, В и С выпуклого четырехугольника ABCD, если
ZA = ZB = ZC, a ZD= 135°.
Решение. Так как сумма углов выпуклого четырехугольника рав-
равна 360° и по условию ZD =135°, то ZA + ZB + ZC = 360° - 135° =
= 225°.
ZA = ZB = ZC по условию, а их сумма равна 225°, следовательно,
ZA = ZB = ZC = 225° : 3 = 75°.
Ответ. 75°.
370. Найдите углы выпуклого четырехугольника, если они пропорцио-
пропорциональны числам 1, 2, 4, 5.
Решение. Так как сумма углов выпуклого четырехугольника рав-
равна 360° и по условию они пропорциональны числам 1, 2, 4, 5, то Z\ =
= 360° : A+2 + 4 + 5)- 1 =30°,
/2 = 360° : 12-2 = 60°,
/3 = 360° : 12-4= 120°,
/4 = 360° : 12-5= 150°.
Ответ. 30°, 60°, 120°, 150°.

§ 2. Параллелограмм и трапеция
§ 2. Параллелограмм и трапеция
371.	Докажите, что выпуклый четырехугольник ABCD является парал-
параллелограммом, если: a) ABAC = ZACD и ABC А = ZDAC; б) АВ \\ CD,
ZA = АС.
Решение, а) Пусть в выпуклом четырехугольнике ABCD про-
проведена диагональ АС. Равные углы ВАС и ACD являются накрест
лежащими при пересечении прямых АВ и CD секущей АС, поэтому
АВ || CD, а равные углы ВС А и DAC являются накрест лежащими
при пересечении прямых ВС и AD секущей АС, поэтому ВС || AD.
Итак, противоположные стороны выпуклого четырехугольника
ABCD попарно параллельны, следовательно, по определению этот
четырехугольник — параллелограмм.
б) В выпуклом четырехугольнике ABCD углы А и D — односто-
односторонние при пересечении параллельных прямых АВ и CD секущей AD,
поэтому ZA + ZD = 180°, а так как по условию ZA = ZC, то ZC +
+ /-D = 180°. Углы С и D являются односторонними углами при
пересечении прямых ВС и AD секущей CD, и их сумма равна 180°,
поэтому ВС || AD.
Итак, в выпуклом четырехугольнике ABCD имеем АВ || DC
и ВС || AD, следовательно, четырехугольник ABCD — парал-
параллелограмм.
372.	Периметр параллелограмма равен 48 см. Найдите стороны параллело-
параллелограмма, если: а) одна сторона на 3 см больше другой; б) разность двух сторон
равна 7 см; в) одна из сторон в два раза больше другой.
Решение, а) Пусть сторона AD параллелограмма ABCD на 3 см
больше стороны АВ, тогда по условию
2(АВ + AD) = 48 см и AD = АВ + 3 см.
Имеем:
АВ + AD = 24 см, АВ + АВ + 3 см = 24 см,
2АВ = 21 см, АВ = 10,5 см, AD = 13,5 см.
б) Пусть разность сторон AD и АВ параллелограмма ABCD равна
7 см, тогда по условию имеем
2(АВ + AD) = 48 см и AD - ЛВ = 7 см.
Получаем:
ЛВ + AD = 24 см, AD = АВ + 7 см, откуда
2АВ + 7 см = 24 см, 2ЛВ = 17 см, АВ = 8,5 см, AD = 8,5 см +
+ 7 см = 15,5 см.
в) Пусть сторона AD параллелограмма ABCD в два раза больше
стороны АВ, тогда по условию имеем
2(АВ + AD) = 48 см и AD = 2AB.

Гл. 1. Четырехугольники
Получаем:
АВ + AD = 24 см, АВ + 2АВ = 24 см, ЗАВ = 24 см, АВ = 8 см,
AD = 16 см.
Ответ, а) 10,5 см, 13,5 см; б) 8,5 см, 15,5 см; в) 8 см, 16 см.
373.	Периметр параллелограмма ABCD равен 50 см, АС = 30°, а перпен-
перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма.
Решение. Пусть ВН — высота параллелограмма ABCD (рис. 1).
В прямоугольном треугольнике СВН АС = 30°, поэтому катет ВН,
лежащий против угла в 30°, равен половине гипотенузы и С В = 13 см.
Так как периметр параллелограмма равен 50 см, то СВ + CD = 25 см
и CD = 25 см - 13 см = 12 см.
Ответ. АВ = CD= 12 см, AD = ВС = 13 см.
374.	Биссектриса угла А параллелограмма ABCD пересекает сторону ВС
в точке К. Найдите периметр этого параллелограмма, если В К =15 см, КС =
= 9 см.
Решение. Обозначим углы ВАК, KAD и ВКА цифрами 1, 2, 3,
как показано на рисунке 2.
Zl = Z2, так как луч АК — биссектриса угла A, Z2 = Z3, так как
эти углы накрест лежащие при пересечении параллельных прямых ВС
и AD секущей АК, следовательно, Zl = Z3.
Треугольник АВК — равнобедренный, так как два его угла 1 и 3
равны, поэтому АВ = ВК = 15 см.
Так как точка К лежит на стороне ВС, то ВС = ВК + КС =
= 15 см + 9 см = 24 см.
Итак, Pabcd = 2(АВ + ВС) = 2A5 + 24) см = 78 см.
Ответ. 78 см.
375. Найдите периметр параллелограмма, если биссектриса одного из его
углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Решение. Возможны два случая.
а) Рассмотрим параллелограмм ABCD, в котором биссектриса угла
А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 14 см,
и обозначим углы ВАК, KAD и АКБ цифрами 1, 2, 3, как показано
на рисунке 2.
В
н
D
Рис. 1
Рис. 2

§ 2. Параллелограмм и трапеция
Z\ = Z2, так как луч АК — биссектриса угла A; Z2 = Z3, так
как эти углы — накрест лежащие при пересечении параллельных
прямых ВС и AD секущей АК. Следовательно, Zl = Z3 и треугольник
АВК — равнобедренный, поэтому АВ = ВК = 7 см.
Так как точка К лежит на стороне ВС и ВК = 7 см, КС =
= 14 см, то
ВС = ВК + КС = 7 см + 14 см = 21 см.
Итак, Pascd = 2G + 21) см = 56 см.
б) Пусть в параллелограмме ABCD биссектриса угла А пересекает
сторону ВС в точке К так, что ВК = 14 см, КС = 7 см. Треугольник
АВК — равнобедренный (см. п. а), поэтому
АВ = ВК = 14 см, ВС = 21 см.
Итак, Pabcd = 2A4 + 21) см = 70 см.
Ответ. 56 см или 70 см.
376. Найдите углы параллелограмма ABCD, если: a) ZA = 84°;
б) ZA- ZB = 55°; в) ZA + ZC = 142°; г) ZA = 2ZB; д) ZCAD = 16°,
ZACD = 37°.
Решение, а) Рассмотрим параллелограмм ABCD, в котором
ZA = 84°. Так как ZA и ZC — противоположные углы параллелограм-
параллелограмма ABCD, то ZC = ZA = 84°.
Углы А и В — односторонние углы при пересечении параллельных
прямых AD и ВС секущей АВ, поэтому ZA + ZB = 180°, откуда
ZB = 180° — 84° = 96°. Углы В и D — противоположные углы парал-
параллелограмма ABCD, поэтому они равны, т. е. ZB = ZD = 96°.
б)	ZA + ZB = 180° (см. п. а), а по условию ZA- ZB = 55°, следо-
следовательно, 2ZA = 235°, ZA = 117°30', ZB = 62°30х.
Противоположные углы параллелограмма равны, поэтому ZA =
= ZC = 117°30/, ZB = ZD = 62°30x.
в)	Так как ZA и ZC — противоположные углы параллелограмма
ABCD, то они равны, а так как по условию ZA + ZC = 142°, то ZA =
= ZC = 142° :2 = 71°.
ZA + ZB = 180° (см. п. а), следовательно, ZE = 180° - 71° = 109°.
Углы В и D — противоположные углы параллелограмма, поэтому
ZB = ZD= 109°.
г)	ZA + ZB = 180°, а так как ZA = 2 • ZB по условию, то 2 • ZE +
+ Z? = 180°, 3 • ZB = 180°, ZB = 60°, aZA= 120°.
Итак, ZA = ZC = 120°, ZB = ZD = 60°.
д)	Рассмотрим треугольник ADC. По условию в этом треугольнике
ZA = 16°, ZC = 37°, поэтому ZD = 180° - A6° + 37°) = 127°.
Углы D и В — противоположные углы параллелограмма ABCD,
поэтому ZB = ZD = 127°.
ZD + ZC= 180° (см. п. а), следовательно, ZC = 180° - 127° = 53°.

10
Гл. 1. Четырехугольники
Углы А и С — противоположные углы параллелограмма ABCD,
поэтому ZA = ZC = 53°.
Ответ, а) 84°, 96°, 84°, 96°; б) 117°30', 62°3(У, 117°30', 62° 30';
в) 71°, 109°, 71°, 109°; г) 120°, 60°, 120°, 60°; д) 53°, 127°, 53°, 127°.
377. В параллелограмме MNPQ проведен перпендикуляр NH к прямой
MQ, причем точка Н лежит на стороне MQ. Найдите стороны и углы парал-
параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ZMNH = 30°.
Решение. Точка Н лежит на отрезке MQ (рис.3), поэтому
МН + HQ = MQ = 8 см и NP = MQ = 8 см.
В прямоугольном треугольнике MHN ZMNH = 30°, следователь-
следовательно, ZM = 90° - 30° = 60°, а катет МН, лежащий против угла в 30°,
равен половине гипотенузы.
Итак, MN = PQ = 6 см.
Так как противоположные углы параллелограмма равны, то АР =
= ZM = 60°, ZN = 180° -ZM= 120°, ZQ = ZN = 120°.
Ответ. 6 см, 8 см, 6 см, 8 см; 60°, 120°, 60°, 120°.
379. Из вершин В и D параллелограмма ABCD, у которого АВ ф ВС
и ZA острый, проведены перпендикуляры ВК и DM к прямой АС. Докажите,
что четырехугольник BMDK — параллелограмм.
Решение. Пусть в параллелограмме ABCD углы ВАК, DCM,
ВКМ, DMK обозначены цифрами 1, 2, 3, 4 соответственно (рис.4).
Рассмотрим прямоугольные треугольники АКБ и CMD. Эти тре-
треугольники равны по гипотенузе и острому углу (АВ = DC по свойству
противоположных сторон параллелограмма, Z\ = Z2, так как эти уг-
углы — накрест лежащие при пересечении параллельных прямых АВ
и CD секущей АС), поэтому ВК = DM.
По условию Z3 = Z4 = 90°, и эти углы — накрест лежащие при
пересечении прямых ВК и DM секущей КМ, поэтому ВК || DM.
Итак, в четырехугольнике BMDK стороны ВК и DM рав-
равны и параллельны, поэтому четырехугольник BMDK — параллело-
параллелограмм (признак 1° параллелограмма, п. 43 учебника).
380. На сторонах АВ, ВС, CD и DA четырехугольника ABCD отмечены
соответственно точки М, N, Р и Q так, что AM = СР, BN = DQ, ВМ =
= DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы.
Рис. 4

§ 2. Параллелограмм и трапеция	11
Решение. 1) Рассмотрим четырехугольник ABCD (рис.5). Так
как АВ = AM + MB, DC = DP + PC и по условию AM = PC, MB =
= DP, то AB = DC. Аналогично можно доказать ВС = AD. Итак,
в четырехугольнике ABCD противоположные стороны попарно равны,
поэтому четырехугольник ABCD — параллелограмм (признак 2°, п. 43
учебника).
2) Треугольники MAQ и PCN равны по двум сторонам и углу
между ними (AM = СР, AQ = CN — по условию, углы А и С равны
как противоположные углы параллелограмма ABCD), следовательно,
MQ = PN. Аналогично можно доказать, что треугольники MBN
и PDQ равны и, следовательно, MN = PQ.
Итак, в четырехугольнике MNPQ противоположные стороны по-
попарно равны, поэтому MNPQ — параллелограмм.
381.	На рисунке 163 учебника изображены два одинаковых колеса теп-
тепловоза. Радиусы О\А и О2В равны. Стержень АВ, длина которого равна
расстоянию О\О2 между центрами колес, передает движение от одного колеса
к другому. Докажите, что отрезки АВ и О\О^ либо параллельны, либо лежат
на одной прямой.
Решение. Рассмотрим положение стержня АВ, показанное на ри-
рисунке 6. Четырехугольник О\АВО^ — параллелограмм, так как его
противоположные стороны равны: О\А = 0%В и О\О^ = АВ (по усло-
условию), поэтому АВ || O\C>2.
Так как ААО\О^ = /-ВО^В\, где угол ВО^В\ — смежный с углом
ВО^О\, то при повороте колеса на угол АО\О^ точка А совместится
с некоторой точкой А\ прямой О\О^, а точка В — с некоторой точкой
В\ этой прямой и, следовательно, отрезки АВ и О\О^ будут лежать
на одной прямой. Итак, отрезки АВ и О\О^ либо параллельны, либо
лежат на одной прямой.
382.	Диагонали параллелограмма ABCD пересекаются в точке О. Дока-
Докажите, что четырехугольник A\B\C\D\, вершинами которого являются середи-
середины отрезков О А, ОВ, ОС и OD, — параллелограмм.
Решение. Так как диагонали АС и BD параллелограмма ABCD
точкой пересечения делятся пополам, то ВО = OD, а так как точки
В\ и D\ — середины отрезков ВО и OD, то В\О = OD\. Аналогично
можно доказать, что А\О = ОС\. Таким образом, в четырехугольнике
В
Рис. 5	Рис. 6

12
Гл. 1. Четырехугольники
A\B\C\D\ диагонали А\С\ и B\D\ пересекаются в точке О и точкой
пересечения делятся пополам. Следовательно, этот четырехугольник —
параллелограмм (признак 3° параллелограмма, п. 43 учебника).
383. На диагонали BD параллелограмма ABCD отмечены две точки Р
и Q так, что РВ = QD. Докажите, что четырехугольник APCQ — паралле-
параллелограмм.
Решение. Возможны два случая.
1)	Точка Р лежит между точками В и Q (рис.7, а). Так как
АВ || CD, то ZABD = ZCDB и ААВР = ACDQ по двум сторонам
и углу между ними (АВ = CD, РВ = QD, ZABP = ZCDQ). Отсю-
Отсюда следует, что АР = CQ. Аналогично доказывается, что AADQ =
= АСВР и поэтому AQ = СР.
Итак, в четырехугольнике APCQ противоположные стороны по-
попарно равны (АР = CQ, AQ = СР), поэтому APCQ — параллело-
параллелограмм (признак 2°, п. 43 учебника).
2)	Точка Q лежит между точками В и Р (рис. 7, б).
В этом случае из равенства ВР = DQ получаем: PD = QB, после
чего доказательство утверждения, что четырехугольник APCQ — па-
параллелограмм, проводится так же, как в первом случае.
386. Докажите, что отрезок, соединяющий середины боковых сторон тра-
трапеции, параллелен основаниям трапеции.
Решение. Пусть точки М и N — середины боковых сторон АВ
и CD трапеции ABCD. Проведем через точку М прямую, параллель-
параллельную основаниям AD и ВС трапеции ABCD. Эта прямая по теореме
Фалеса (задача 385 учебника) пересечет отрезок CD в его середине,
т. е. пройдет через точку N. Таким образом, отрезок MN, соеди-
соединяющий середины боковых сторон трапеции, параллелен основаниям
трапеции.
387. Найдите углы В и D трапеции ABCD с основаниями AD и ВС,
если ZA = 36°, ZC= 117°.
Решение. В трапеции ABCD основания AD и ВС параллельны,
углы А и В, углы С и D — односторонние углы при пересечении
В
В
D

§ 2. Параллелограмм и трапеция	13
параллельных прямых AD и ВС секущими АВ и CD соответственно,
поэтому
АВ = 180° - АА = 180° - 36° = 144°,
AD = 180° -АС = 180° -117°= 63°.
Ответ. АВ = 144°, AD = 63°.
388.	Докажите, что в равнобедренной трапеции: а) углы при каждом
основании равны; б) диагонали равны.
Решение. Рассмотрим равнобедренную трапецию ABCD с осно-
основаниями AD и ВС. Пусть AD > ВС.
а)	Проведем прямую BE, параллельную прямой CD, E — точ-
точка на отрезке AD (рис.8, а). Так как BCDE — параллелограмм,
то CD = BE. Но CD = АВ (ABCD — равнобедренная трапеция),
поэтому АВ = BE, т. е. треугольник ABE равнобедренный и, значит,
АА = ABE А.
Так как BE \\ CD, то ABE A = AD, следовательно, АА = AD, т. е.
углы при основании AD равны.
Далее, АВ = 180° - АА, АС = 180° - AD, поэтому АВ = АС.
Итак, углы при каждом основании равнобедренной трапеции равны.
б)	Треугольники ABD и DC А равны по двум сторонам и углу меж-
между ними (АВ = CD, AD — общая сторона, АА = AD по доказанному
в п. а) (рис.8, б), следовательно, BD = АС.
389.	Докажите, что трапеция равнобедренная, если: а) углы при основа-
основании равны; б) диагонали трапеции равны.
Решение, а) Пусть в трапеции ABCD с основаниями AD и ВС
ВС < AD, АА = AD (рис. 9, а).
Проведем прямую СЕ, параллельную прямой АВ (точка Е лежит
на прямой AD). Тогда А\ и A3 — соответственные углы при пересече-
пересечении параллельных прямых АВ и СЕ секущей AD, поэтому A3 = А\.
По условию А\ = Z2, следовательно, А2 = A3 и поэтому треуголь-
треугольник ECD — равнобедренный: CD = СЕ.
Так как четырехугольник АВСЕ — параллелограмм, то СЕ =
= АВ, а так как СЕ = CD, то АВ = CD, т. е. трапеция ABCD -
равнобедренная.
ВС	В
EDA	D
а	б
Рис. 8

14
Гл. 1. Четырехугольники
Е
D
A	D	Е
а	б
Рис.9
б) Пусть в трапеции ABCD с основаниями AD и ВС диагонали
АС и BD равны (рис.9, б).
Через вершину С проведем прямую СЕ, параллельную диагонали
BD (точка Е лежит на прямой AID). Образовавшийся четырехугольник
BCED — параллелограмм (ВС \\ DE и BD \\ СЕ), поэтому СЕ =
= BD = АС и, следовательно, треугольник АСЕ — равнобедренный
с основанием АЕ, а значит, Zl = Z3.
Так как Z2 = Z3 (соответственные углы при пересечении парал-
параллельных прямых BD и СЕ секущей АЕ) и Zl = Z3, то Zl = Z2.
AACD = ADBA по двум сторонам и углу между ними (АС = DB
по условию, AD — общая сторона, Zl = Z2), следовательно, АВ =
= CD, т. е. трапеция ABCD — равнобедренная.
390. Один из углов равнобедренной трапеции равен 68°. Найдите осталь-
остальные углы трапеции.
Решение. Пусть в равнобедренной трапеции ABCD с основа-
основаниями AD и ВС А А = 68°. Так как углы при каждом основании
равнобедренной трапеции равны (задача 388, а), то AD = АА = 68°.
Углы А и В — односторонние углы при пересечении параллельных
прямых AD и ВС секущей АВ, поэтому
Z?= 180° -68° = 112°,
Ответ. 68°, 112°, 112°.
ZC = АВ= 112°
391. Докажите, что из одинаковых плиток, имеющих форму равнобедрен-
равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть
плоскости.
Решение. Рассмотрим две плитки — две равные равнобедренные
трапеции ABCD и A\B\C\D\ (АВ = CD = АХВХ = C\D\, AD =
= AXDX, ВС = ВХСХ, АА = ZL> = ZA{ = ZDU ZB = ZC = ZB{ =
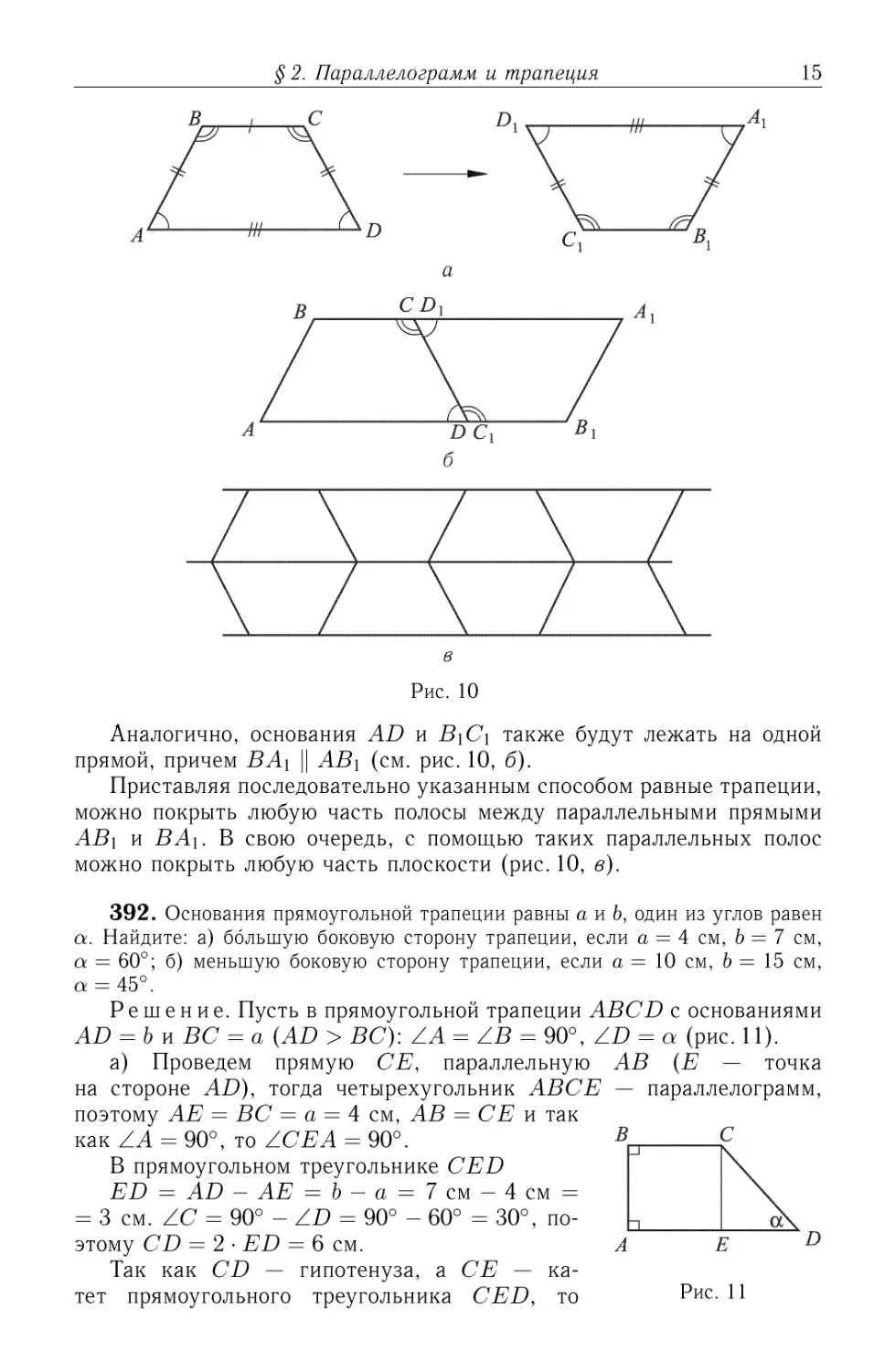
= ZCi (рис. 10, a)).
Приложим эти трапеции друг к другу так, чтобы совместились
их равные боковые стороны CD и C\D\, причем точка С совместилась
с Di, а точка D — с С\ (рис. 10, б). Тогда основания ВС и A\D\ будут
лежать на одной прямой, так как сумма углов С и D\ равна 180°.
Действительно, ZC + AD = 180°, a AD = ZD\, поэтому
= 180°.

§ 2. Параллелограмм и трапеция
15
В
CDX
DCX	Bi
Рис. 10
Аналогично, основания AD и В\С\ также будут лежать на одной
прямой, причем ВА\ || АВ\ (см. рис. 10, б).
Приставляя последовательно указанным способом равные трапеции,
можно покрыть любую часть полосы между параллельными прямыми
АВ\ и ВА\. В свою очередь, с помощью таких параллельных полос
можно покрыть любую часть плоскости (рис. 10, в).
392. Основания прямоугольной трапеции равны а и Ь, один из углов равен
а. Найдите: а) большую боковую сторону трапеции, если а = 4 см, Ь = 7 см,
а = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, 6=15 см,
а = 45°.
Решение. Пусть в прямоугольной трапеции ABCD с основаниями
AD = Ъ и ВС = a (AD > ВС): ZA = ZB = 90°, ZD = а (рис. 11).
а) Проведем прямую СЕ, параллельную АВ (Е — точка
на стороне AD), тогда четырехугольник АВСЕ — параллелограмм,
поэтому АЕ = ВС = а = 4 см, АВ = СЕ и так
как ZA = 90°, то АСЕ А = 90°.
В прямоугольном треугольнике СЕВ
ED = AD - АЕ = Ъ - а = 7 см - 4 см =
= 3 см. АС = 90° -ZD = 90° - 60° = 30°, по-
поэтому CD = 2 • ED = 6 см.
Так как CD — гипотенуза, а СЕ — ка-
катет прямоугольного треугольника CED, то
В
D
Рис. 11

16	Гл. 1. Четырехугольники
CD > СЕ = АВ, поэтому CD — большая боковая сторона трапеции
ABCD. Итак, большая боковая сторона трапеции равна 6 см.
б) В прямоугольном треугольнике CED
ED = AD - АЕ = Ъ - а = 15 см - 10 см = 5 см, ZD = а = 45°,
поэтому
ZC = 90° -ZD = 45°
и, значит, треугольник CED — равнобедренный: СЕ = ED = 5 см.
Следовательно, АВ = СЕ = 5 см, т. е. меньшая боковая сторона тра-
трапеции равна 5 см.
Ответ: а) 6 см; б) 5 см.
393.	Постройте параллелограмм: а) по двум смежным сторонам и углу
между ними; б) по двум диагоналям и углу между ними.
Решение, а) Пусть даны отрезки P\Q\ и P2Q2 и угол hk. Требу-
Требуется построить параллелограмм ABCD, у которого смежные стороны,
скажем, АВ и AD, равны соответственно отрезкам P\Q\ и P2Q2, a угол
BAD равен данному углу hk.
Сначала построим треугольник ABD по двум заданным сторонам
и углу между ними (п. 38, задача 1), а затем достроим его до паралле-
параллелограмма.
Описанный ход построения показывает, что при любых данных
отрезках P\Q\ и P2Q2 и неразвернутом угле hk задача имеет един-
единственное решение.
б) Пусть даны отрезки P\Q\ и P2Q2 и угол hk. Требуется постро-
построить параллелограмм ABCD, у которого диагонали АС и BD равны
соответственно данным отрезкам P\Q\ и P2Q2, угол между ними равен
углу hk.
Сначала построим угол АОВ, равный данному углу hk, а затем
на сторонах этого угла и их продолжениях отложим отрезки О А =
= ОС = ^ PiQi, ОВ = OD = ^ P2Q2. Четырехугольник ABCD и есть
искомый параллелограмм.
Описанный ход построения показывает, что при любых данных
отрезках P\Q\ и P2Q2 и неразвернутом угле hk задача имеет един-
единственное решение.
394.	Даны три точки А, В и С, не лежащие на одной прямой. Постройте
параллелограмм так, чтобы три его вершины совпали с данными точками.
Сколько таких параллелограммов можно построить?
Решение. Пусть А, В, С — данные точки, не лежащие на од-
одной прямой. Соединим попарно эти точки отрезками и через каждую
вершину треугольника ABC проведем прямую, параллельную проти-
противолежащей стороне (рис. 12) (задача 222). Четырехугольники А\ВАС,
С\АСВ, В\АВС — параллелограммы, так как их противоположные
стороны попарно параллельны. Каждый из них удовлетворяет усло-
условию задачи. Задача, очевидно, имеет только эти три решения, так

§ 2. Параллелограмм и трапеция	17
как не существует других прямых, проходящих через точки А, В, С
и параллельных прямым ВС, АС, АВ соответственно.
Ответ. Три.
395. Даны острый угол hk и два отрезка P\Q\ и PzQz- Постройте парал-
параллелограмм ABCD так, чтобы расстояние между параллельными прямыми АВ
и DC равнялось PXQX, АВ = P2Q2 и А А = Zhk.
Решение. Построим прямоугольный треугольник ADE по катету
DE = P\Q\ и противолежащему острому углу А, равному данному
углу hk (задача 314, б). На луче АЕ отложим отрезок АВ, равный
данному отрезку P2Q2 (рис. 13). Через точки В и D проведем прямые,
параллельные прямым AD и АВ соответственно. Они пересекаются
в некоторой точке С. Четырехугольник ABCD — по построению па-
параллелограмм, в котором АВ = P2Q2, ^A = ^hk, и так как DE JL АВ,
то DE — расстояние между параллельными прямыми АВ и CD,
причем DE = P\Q\.
Итак, построенный параллелограмм ABCD удовлетворяет всем
условиям задачи. Ясно, что если ZA < 180°, то задача имеет един-
единственное решение.
397. Постройте равнобедренную трапецию ABCD: а) по основанию AD,
углу А и боковой стороне АВ; б) по основанию ВС, боковой стороне АВ
и диагонали BD.
Решение, а) Пусть даны Zhk и отрезки MN и M\N\ (рис. 14, а).
Требуется построить трапецию ABCD такую, что
AD || ВС, АВ = CD, AD = MN, АВ = MXNX, ZA = Zhk.
Построение, а) Построим AABD так, чтобы AD = MTV, АВ =
= MiiVi, ZA = Zhk (cm. n.38, задача 1) (рис. 14, б).
Через точку В проведем прямую а, параллельную прямой AD.
Затем от луча DA отложим угол ADE, равный углу А (см. рис. 14, б).
Точку пересечения луча DE с прямой а обозначим буквой С. Четырех-
Четырехугольник ABCD и есть искомая трапеция. Действительно, по постро-
построению ВС || AD, а стороны АВ и CD не параллельны (если допустить,
D
Рис. 12	Рис. 13

18
Гл. 1. Четырехугольники
м,
м
fl
Рис. 14
D
0з
Рис. 15
что ЛВ || CD, то ZA + ZD = 180°, а так как ZA = ZD и ZA + ZL> =
= 180°, то ZA = ZD = 90°, но угол равнобедренной трапеции не может
быть прямым).
По построению AD = MN, АВ = M\N\, ZA = Zhk, а так как
ZD = ZA (по построению), то трапеция ABCD — равнобедренная (за-
(задача 389, а). Таким образом, трапеция ABCD удовлетворяет всем
условиям задачи.
Если угол hk — тупой, то задача имеет единственное решение.
Если же угол hk — острый, то задача имеет единственное решение,
если луч DE лежит во внешней области угла ADB, и не имеет
решения, если луч DE лежит внутри угла ABD или совпадает с лучом
DB.
б) Пусть даны отрезки MN, M\N\ и M2N2. Требуется построить
трапецию ABCD такую, что
AD || ВС, АВ = CD, ВС = MN, АВ = MXNU BD = M2N2.
Построение. Сначала построим треугольник BCD по трем сто-
сторонам так, чтобы ВС = MN, DC = M{NU BD = M2N2, а затем
достроим его до равнобедренной трапеции ABCD (см. п. а).
Задача не будет иметь решения, если какой-нибудь из данных
отрезков больше или равен сумме двух других отрезков.
398. Постройте прямоугольную трапецию ABCD по основаниям и боко-
боковой стороне AD, перпендикулярной к основаниям.
Решение. Пусть даны отрезки P\Q\, P2Q2, P3Q3 (рис. 15, а). Тре-
Требуется построить прямоугольную трапецию ABCD так, чтобы ее бо-

§3. Прямоугольник, ромб, квадрат	19
ковая сторона AD, перпендикулярная к основаниям, была равна P\Q\,
а основания DC и АВ были равны соответственно P2Q2 и P?>Q?>-
Проведем две взаимно перпендикулярные прямые а и Ъ, пересека-
пересекающиеся в точке А, и от точки А на прямой а отложим отрезок АВ,
равный данному отрезку Рз<2з> а на прямой Ъ — отрезок AD, равный
данному отрезку P\Q\ (рис. 15, б).
Через точку D проведем прямую, параллельную прямой АВ (зада-
(задача 222), и от точки D отложим на ней отрезок DC, равный данному
отрезку P2Q2 так> чтобы точка С лежала по ту же сторону от пря-
прямой AD, что и точка В. Соединив точки В и С отрезком, получим
трапецию ABCD. Построенная трапеция удовлетворяет всем условиям
задачи. Задача имеет единственное решение.
§ 3. Прямоугольник, ромб, квадрат
399.	Докажите, что параллелограмм, один из углов которого прямой,
является прямоугольником.
Решение. Пусть в параллелограмме ABCD ZA = 90°. Тогда
и ZC = 90°, так как противоположные углы параллелограмма равны.
ZB = 180° -ZA = 90°, ZD = ZB = 90°.
Итак, все углы параллелограмма ABCD прямые, поэтому этот
параллелограмм — прямоугольник (по определению).
400.	Докажите, что если в четырехугольнике все углы прямые, то четы-
четырехугольник является прямоугольником.
Решение. Пусть в четырехугольнике ABCD все углы прямые.
Так как ZA = ZB = 90°, то AD \\ ВС, а так как ZA = ZD = 90°,
то АВ || DC. Таким образом, противоположные стороны четырех-
четырехугольника ABCD попарно параллельны, поэтому четырехугольник
ABCD — параллелограмм, а так как все его углы прямые, то ABCD —
прямоугольник.
401.	Найдите периметр прямоугольника ABCD, если биссектриса угла А
делит: а) сторону ВС на отрезки 45,6 см и 7,85 см; б) сторону DC на отрезки
2,7 дм и 4,5 дм.
Решение, а) Возможны два случая.
1) Пусть биссектриса угла А пересекает сто-
сторону ВС в точке Е так, что BE = 45,6 см,
ЕС = 7,85 см (рис.16).
Так как AD \\ ВС, то Z2 = Z3, a Z2 = Z1 -
по условию, поэтому Zl = Z3. Следовательно,
ААВЕ — равнобедренный и поэтому АВ =
= BE = 45,6 см, ВС = ВЕ + ЕС = 45,6 см +	рис 16
+ 7,85 см = 53,45 см.
Pabcd = 2(АВ + AD) = 2D5,6 + 53,45) см = 2 • 99,05 см =
= 198,1 см.

20	Гл. 1. Четырехугольники
2) Пусть BE = 7,85 см, ЕС = 45,6 см, тогда АВ = BE = 7,85 см
и Pabcd = 2G,85 см + 53,45 см) = 2 • 61, 3 см = 122,6 см.
б) Возможны два случая.
1)	DE = 4,5 дм, СЕ = 2,7 дм
(рис. 17). Так как AADE равнобедрен-
равнобедренный (см. п. а), то AD = DE = 4,5 дм;
DC = 4,5 дм + 2,7 дм = 7,2 дм.
Pabcd = 2D,5 дм + 7,2 дм) = 2 х
х 11,7 дм = 23,4 дм.
2)	DE = 2,7 дм, СЕ = 4,5 дм.
В этом случае AD = DE = 2,7 дм,
РисЛ7	DC = 7,2 ям.
Pabcd = 2B,7 + 7,2) дм = 2 • 9,9 дм = 19,8 дм.
Ответ, а) 198,1 см или 122,6 см; б) 23,4 дм или 19,8 дм.
402.	Диагонали прямоугольника ABCD пересекаются в точке О. Дока-
Докажите, что треугольники AOD и АОВ равнобедренные.
Решение. Так как ABCD — прямоугольник, то его диагонали
равны, а так как прямоугольник является параллелограммом, то его
диагонали точкой пересечения делятся пополам, поэтому АО = OD
и АО = ОВ, т. е. треугольники AOD и АОВ — равнобедренные.
403.	В прямоугольнике ABCD диагонали пересекаются в точке О. Най-
Найдите периметр треугольника АОВ, если ZCAD = 30°, АС =12 см.
Решение. Так как ABCD — прямоугольник, то его диагонали
равны и точкой пересечения делятся пополам, поэтому ААОВ —
равнобедренный, боковая сторона которого равна 6 см.
AADC — прямоугольный с гипотенузой АС, равной 12 см, и ост-
острым углом А, равным 30°, поэтому катет CD = - АС = 6 см. АВ =
= CD = 6 см. Таким образом, ААОВ — равносторонний и Раов =
= 3 • 6 см = 18 см.
Ответ. 18 см.
404. Докажите, что медиана прямоугольного треугольника, проведенная
к гипотенузе, равна половине гипотенузы.
Решение. Пусть ВЫ — медиана прямоугольного треугольника
ABC, проведенная к гипотенузе АС. Докажем, что ВЫ = - АС.
Рассмотрим четырехугольник ABCD (рис. 18), в котором D —
точка, симметричная точке В относительно точки М.
В четырехугольнике ABCD ВЫ = MD (так как точки В
и D симметричны относительно точки М), AM = МС по усло-
условию, поэтому четырехугольник ABCD — параллелограмм (при-
(признак 3°, п.43).

§ 3. Прямоугольник, ромб, квадрат
21
Так как в параллелограмме ABCD угол В — прямой по условию,
то параллелограмм ABCD — прямоугольник (задача 399), а в прямо-
прямоугольнике диагонали равны.
Итак, ВЫ = - BD = - АС, что и требовалось доказать.
405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба;
б) углы, которые диагонали ромба образуют с его сторонами.
Решение. Пусть в ромбе ABCD диагональ BD равна его сто-
стороне (рис. 19).
а)	Треугольник ABD — равносторонний, поэтому все его углы
равны между собой и каждый равен 60°, в частности, ZA = 60°.
ZC = ZA = 60°; ZB = ZD = 180° - 60° = 120°.
б)	Zl = 60° (см. п. a), Z2 = Z\ = 60°; так как диагонали ромба
делят его углы пополам, то Z3 = Z4 = - ZA = - • 60° = 30°.
Итак, диагонали ромба составляют с его сторонами углы, равные
60° и 30°.
Ответ, а) 60° и 120°; б) 60° и 30°.
406. Найдите периметр ромба ABCD, если ZB = 60°, АС = 10,5 см.
Решение. В треугольнике ABC AB = ВС (так как стороны ромба
равны) и угол В равен 60°. Следовательно, этот треугольник — равно-
равносторонний, а так как АС = 10,5 см по условию, то и АВ = 10,5 см.
Pabcd = 4 • 10,5 см = 42 см.
Ответ. 42 см.
407. Найдите углы, которые образуют диагонали ромба с его сторонами,
если один из углов ромба равен 45°.
Решение. Пусть угол А ромба ABCD равен 45° (см. рис.19).
Тогда ZD = 180° - 45° = 135°.
Zl = Z2 и Z3 = Z4, так как диагонали ромба делят его углы
пополам. Поэтому Zl = Z2 = 67°30', Z3 = Z4 = 22°30'.
Ответ. 22°30' и 67°30'.
Рис. 18
Рис. 19

Гл. 1. Четырехугольники
408.	Докажите, что параллелограмм является ромбом, если: а) его диа-
диагонали взаимно перпендикулярны; б) диагональ параллелограмма является
биссектрисой его угла.
Решение, а) Пусть диагонали АС и BD параллелограмма ABCD
взаимно перпендикулярны, О — точка их пересечения (см. рис. 19).
Так как АО = ОС и ВО = OD, то прямоугольные треугольники АОВ
и ВОС, COD и DOA равны друг другу по двум катетам. Отсюда
следует, что равны их гипотенузы: АВ = ВС = CD = DA, т. е. парал-
параллелограмм ABCD является ромбом.
б) Пусть диагональ АС параллелограмма ABCD является биссек-
биссектрисой его угла А (см. рис. 19). Тогда в треугольнике ABD медиана
АО является биссектрисой и поэтому AABD — равнобедренный (за-
(задача 342), т. е. АВ = AD. Но АВ = CD, AD = ВС и, следовательно,
в параллелограмме ABCD все стороны равны, т. е. параллелограмм
ABCD - ромб.
409.	Докажите, что ромб, у которого один угол прямой, является квад-
квадратом.
Решение. Согласно задаче 399 ромб, у которого один угол пря-
прямой, является прямоугольником, а так как у этого прямоугольника все
стороны равны, то это квадрат.
410.	Является ли четырехугольник квадратом, если его диагонали: а) рав-
равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую
середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Решение, а) Нет. Например, в четырехугольнике ABCD на ри-
рисунке 20 диагонали АС и BD равны и взаимно перпендикулярны,
но точка их пересечения не является серединой
отрезка АС, и поэтому АВ ф ВС. Значит, четы-
четырехугольник ABCD не является квадратом.
б)	Нет. Например, диагонали ромба взаим-
взаимно перпендикулярны и имеют общую середину,
но ромб может не быть квадратом.
в)	Докажем, что в этом случае четырехуголь-
четырехугольник является квадратом.
Так как диагонали четырехугольника имеют
Рис 20	^
^	общую середину, т. е. пересекаются и точкой пе-
пересечения делятся пополам, то этот четырехуголь-
четырехугольник — параллелограмм, а параллелограмм, в котором диагонали рав-
равны, — прямоугольник. С другой стороны, параллелограмм, диагонали
которого взаимно перпендикулярны, — ромб (задача 408, а), т. е. все
его стороны равны.
Итак, в данном случае четырехугольник является прямоугольни-
прямоугольником, у которого все стороны равны, т. е. это квадрат.
Ответ: а) Нет; б) нет; в) да.

§ 3. Прямоугольник, ромб, квадрат
23
411.	В прямоугольном треугольнике проведена биссектриса прямого угла.
Через точку пересечения этой биссектрисы с гипотенузой проведены пря-
прямые, параллельные катетам. Докажите, что полученный четырехугольник —
квадрат.
Решение. Пусть в прямоугольном треугольнике ABC с гипотену-
гипотенузой АВ проведены биссектриса CD и прямые DE и DF, параллельные
катетам ВС и АС соответственно (рис.21).
Тогда четырехугольник CEDF — параллелограмм (DE \\ FC
и СЕ || FD), а так как АС = 90°, то параллелограмм CEDE —
прямоугольник (задача 399).
По условию А\ = Z2, т. е. диагональ CD делит угол С пополам.
Отсюда следует, что CEDE — ромб (задача 408, б).
Итак, четырехугольник CEDE является прямоугольником и ром-
ромбом, поэтому этот четырехугольник — квадрат.
412.	Даны равнобедренный прямоугольный треугольник ABC с прямым
углом С, катетом АС = 12 см и квадрат CDEF такой, что две его стороны
лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите
периметр квадрата.
Решение. Так как треугольник ABC равнобедренный и прямо-
прямоугольный (рис.22), то АА = АВ = - • 90° = 45°. В прямоугольном
треугольнике ADE АА = 45° и, следовательно, AD = DE. Но DE =
= DC (так как CDEF - квадрат), поэтому AD = DC = ^ АС =
= - • 12 см = 6 см; Pcdef = 6 см • 4 = 24 см.
Ответ. 24 см.
413. Постройте прямоугольник: а) по двум смежным сторонам; б) по
стороне и диагонали; в) по диагонали и углу между диагоналями.
Решение, а) Пусть даны отрезки P\Q\ и P2Q2 (рис.23, а).
Требуется построить прямоугольник ABCD так, чтобы АВ = P\Q\,
= P2Q2-

24	Гл. 1. Четырехугольники
Проведем прямую АЕ, а затем построим прямую AF, перпенди-
перпендикулярную к прямой АЕ (см. п. 23 учебника). На луче АЕ отложим
отрезок АВ, равный P\Q\, а на луче AF — отрезок AD, равный
P2Q2 (рис.23, б). Через точку В проведем прямую, параллельную AD,
а через точку D — прямую, параллельную АВ (задача 222). Прове-
Проведенные прямые пересекаются в некоторой точке С. Четырехугольник
ABCD — искомый прямоугольник.
В самом деле, по построению четырехугольник ABCD — паралле-
параллелограмм (ВС || AD и DC || АВ), а так как ZA = 90°, то ABCD - пря-
прямоугольник (задача 399), причем АВ = P\Q\, AD = P2Q2, т. е. постро-
построенный прямоугольник ABCD удовлетворяет всем условиям задачи.
б)	Пусть даны отрезки P\Q\ и P^Qi- Требуется построить прямо-
прямоугольник ABCD так, чтобы АВ = P\Q\ и BD = P^Qi-
Сначала построим прямоугольный треугольник ABD с прямым
углом А, в котором АВ = P\Q\, BD = P2Q2 (задача 314, в).
Затем через вершины В и D проведем прямые, параллельные пря-
прямым AD и АВ соответственно. Они пересекаются в некоторой точке С.
Полученный четырехугольник ABCD является искомым прямоуголь-
прямоугольником.
В самом деле, по построению ABCD — параллелограмм, у которого
угол А — прямой. Следовательно, ABCD — прямоугольник, причем
АВ = P\Q\, BD = P2Q2, т. е. прямоугольник ABCD удовлетворяет
всем условиям задачи.
в)	Задача решается так же, как задача 393, б, в случае, когда
диагонали равны.
414.	Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Решение, а) Задача решается так же, как задача 393, б, в случае,
когда угол между диагоналями — прямой.
б) Задача решается так же, как задача 393, а, в случае, когда
смежные стороны равны.
415.	Постройте квадрат: а) по стороне; б) по диагонали.
Решение, а) Задача решается так же, как задача 413, а, в случае,
когда смежные стороны равны.
б) Задача решается так же, как задача 414, а, в случае, когда
диагонали равны.
Л

§ 3. Прямоугольник, ромб, квадрат
25
416. Даны две точки А и В, симметричные относительно некоторой
прямой, и точка М. Постройте точку, симметричную точке М относительно
той же прямой.
Решение. Построим прямую а, проходящую через середину от-
отрезка АВ и перпендикулярную к нему (см. п. 23 учебника). Точки А
и В симметричны относительно прямой а (рис.24, а). Если точка М
лежит на прямой а, то она симметрична самой себе относительно этой
М
О , В
О-
1 //
о
мг в
ом = ом1
Рис. 24
прямой и поэтому является искомой точкой. Если же точка М не лежит
на прямой а, то через точку М проведем прямую, перпендикулярную
к прямой а (задача 153). Пусть эта прямая пересекается с прямой а
в точке О\ (рис.24, а). На продолжении луча О\М отложим отрезок
О\М\, равный О\М. Очевидно, точка М\ симметрична точке М отно-
относительно прямой а, т. е. М\ — искомая точка.
417.	Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Решение, а) Отрезок имеет две оси симметрии. Одной осью
симметрии отрезка АВ является прямая а, проходящая через середину
этого отрезка и перпендикулярная к нему (рис.24, б). В самом деле,
для любой точки М отрезка АВ симметричная ей относительно прямой
а точка М\ также принадлежит отрезку АВ (см. рис.24, б), а это
и означает, что прямая а — ось симметрии отрезка АВ. Другой осью
симметрии отрезка АВ является прямая АВ, так как каждая точка
этого отрезка симметрична самой себе относительно прямой АВ.
б)	Прямая имеет бесконечное множество осей симметрии. Любая
прямая, перпендикулярная к прямой а, и сама прямая а являются осями
симметрии прямой а. Это доказывается так же, как в п. а).
в)	Луч имеет одну ось симметрии. Осью симметрии луча ОА
является прямая О А, так как любая точка луча О А симметрична самой
себе относительно прямой О А.
Ответ, а) Две; б) бесконечно много; в) одну.
418.	Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F?
Решение. Одну ось симметрии имеют буквы А и Е (прямые а и Ъ
на рисунках 25 и 26). Две оси симметрии имеет буква О (прямые т
и и на рисунке 27).
Ответ. А, Е, О.

26
Гл. 1. Четырехугольники
Рис. 25
Рис. 26
Рис. 27
419.	Докажите, что прямая, проходящая через середины противополож-
противоположных сторон прямоугольника, является его осью симметрии.
Решение. Пусть прямая ЕЕ проходит через середины сторон ВС
и AD прямоугольника ABCD (рис.28). Докажем, что она является
осью симметрии этого прямоугольника.
Так как BE = AF и BE || AF, то четырехугольник BEFA —
параллелограмм, а так как в этом параллелограмме ZA = 90° (по усло-
условию), то четырехугольник BEFA — прямоугольник, откуда следует,
что ZE = ZF = 90°.
Итак, прямая ЕЕ перпендикулярна к сторонам ВС и AD и прохо-
проходит через их середины. Поэтому для любой точки М стороны ВС (и
также стороны AD) симметричная ей относительно прямой ЕЕ точка
М\ лежит на этой стороне (см. рис.28).
Возьмем теперь произвольную точку N на стороне АВ прямоуголь-
прямоугольника ABCD и на стороне DC отметим точку N\ так, что DN\ =
= AN. Так как AN \\ DNU AN = DNX и ZA = 90°, то ANNXD -
прямоугольник. Прямая EF, параллельная прямым АВ и CD, проходит
через середину отрезка AD и по теореме Фалеса делит отрезок NN\
пополам, т. е. NP = PN\. Кроме того, прямая EF, перпендикулярная
к прямой AD, перпендикулярна и к прямой NN\. Таким образом, точки
N и N\ симметричны относительно прямой ЕЕ.
Итак, для каждой точки N на стороне АВ прямоугольника ABCD
симметричная ей относительно прямой ЕЕ точка N\ лежит на стороне
DC этого прямоугольника. Точно так же для любой точки на стороне
DC симметричная ей относительно прямой ЕЕ точка лежит на стороне
АВ.
Мы доказали, что для каждой точки прямоугольника ABCD сим-
симметричная ей относительно прямой ЕЕ точка также принадлежит это-
этому прямоугольнику. Это и означает, что прямая ЕЕ — ось симметрии
прямоугольника ABCD.
420.	Докажите, что прямая, содержащая биссектрису равнобедренного
треугольника, проведенную к основанию, является осью симметрии треуголь-
треугольника.
Решение. Пусть ABC — данный равнобедренный треугольник
с основанием АС и BD — его биссектриса (рис.29).

§ 3. Прямоугольник, ромб, квадрат
27
Тогда отрезок BD является также высотой и медианой треуголь-
треугольника, т. е. BD _1_ АС и AD = DC. Следовательно, точки А и С
симметричны относительно прямой BD. Точка В симметрична самой
себе относительно прямой BD, так как лежит на этой прямой.
Возьмем произвольную точку М на основании АС. Пусть, напри-
например, точка М лежит между точками А и D (см. рис.29). Отметим
точку М\ между точками D и С так, что DM\ = DM. Очевидно, точка
М\ симметрична точке М относительно прямой BD.
Итак, для каждой точки на основании АС симметричная ей отно-
относительно BD точка также лежит на основании АС.
Возьмем теперь произвольную точку N на одной из боковых сторон
треугольника ABC, например, на стороне АВ. Отложим от вершины В
на луче ВС отрезок BN\, равный BN. Так как BN < АВ, то BN\ <
< ВС и точка N\ лежит на стороне ВС. Треугольник BNN\ —
равнобедренный, ВК — его биссектриса, следовательно, NN\ JL BK,
NK = N\K, и поэтому точки N и N\ симметричны относительно
прямой BD. Мы доказали, что для каждой точки треугольника ABC
точка, симметричная ей относительно прямой BD, также принадлежит
этому треугольнику. Это и означает, что прямая BD — ось симметрии
треугольника ABC.
422.	Имеет ли центр симметрии: а) отрезок; б) луч; в) пара пересекаю-
пересекающихся прямых; г) квадрат?
Решение, а) Середина отрезка является его центром симметрии.
б)	Луч не имеет центра симметрии.
в)	Центром симметрии двух пересекающихся прямых является
их точка пересечения.
г)	Точка пересечения диагоналей квадрата является его центром
симметрии.
Ответ, а) Да; б) нет; в) да; г) да.
423.	Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Решение. Центром симметрии буквы О является точка пересече-
пересечения двух ее осей симметрии (см. рис.27). Из остальных букв центр
симметрии имеет, очевидно, только буква X.
Ответ. О, X.
в
n\
м
Е Мг
Р
F
D
М D
Рис. 28
Рис. 29

28	Гл. 1. Четырехугольники
Дополнительные задачи
424.	Докажите, что если не все углы выпуклого четырехугольника равны
друг другу, то хотя бы один из них тупой.
Решение. Пусть не все углы выпуклого четырехугольника равны
друг другу. Если допустить, что среди них нет тупого угла, то их сумма
будет меньше 360°, чего не может быть. Следовательно, хотя бы один
из углов тупой.
425.	Периметр параллелограмма ABCD равен 46 см, АВ = 14 см. Какую
сторону параллелограмма пересекает биссектриса угла А} Найдите отрезки,
которые образуются при этом пересечении.
Решение. Так как в параллелограмме противоположные стороны
равны, то Pabcd = 2(АВ + AD) = 46 см, откуда АВ + AD = 23 см
и AD = 23 см - АВ = 23 см - 14 см = 9 см.
Пусть луч AF (биссектриса угла А) пересекает прямую DC в неко-
некоторой точке Е (рис.30), тогда AADE — равнобедренный (Zl = Z2
и Z2 = Z3, поэтому Zl = Z3), и, следовательно, DE = AD = 9 см.
Так как DE < DC (DE = 9 см, DC = АВ = 14 см), то точка Е
лежит на отрезке DC, т. е. биссектриса угла А пересекает сторону DC
и делит ее на отрезки DE = 9 см и ЕС = DC — DE = 14 см — 9 см =
= 5 см.
Ответ. Сторону DC; 9 см и 5 см.
426.	Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух
углов, прилежащих к большей стороне, делят противоположную сторону на три
отрезка. Найдите эти отрезки.
Решение. Пусть биссектрисы углов А и D, прилежащих к боль-
большей стороне AD параллелограмма ABCD, пересекают противополож-
противоположную сторону ВС в точках Е и F (рис.31) и тем самым делят ее на
три отрезка: BE, ЕЕ и FC.
Так как в параллелограмме противоположные стороны равны,
то ВС = AD = 10 см, АВ = DC = 3 см.
Треугольники ABE и DCF — равнобедренные (Zl = Z2, так как
луч АЕ — биссектриса угла A, Z2 = Z3, так как эти углы накрест
лежащие при пересечении параллельных прямых AD и ВС секущей
В	Е	F	С
5'4
Рис. 30	Рис. 31

Дополнительные задачи	29
АЕ, поэтому Zl = Z3. Аналогично Z4 = Z5 = Z6), тогда BE = Б А =
= 3 см и ЕС = CD = 3 см.
EF = ВС - (BE + FC) = 10 см - 6 см = 4 см.
Ответ. 3 см, 4 см, 3 см.
427.	Через произвольную точку основания равнобедренного треугольника
проведены прямые, параллельные боковым сторонам треугольника. Докажите,
что периметр получившегося четырехугольника равен сумме боковых сторон
данного треугольника.
Решение. Пусть прямые, проведенные через произвольную точку
М основания ВС равнобедренного треугольника ABC параллельно
боковым сторонам, пересекают эти стороны в точках D и Е (рис.32).
Так как DM \\ АС, то Zl = ZC, а так как ЕМ \\ АВ, то Z2 = ZB.
Но АВ = АС, поскольку ААВС — равнобедренный, поэтому Z1 = АВ
и Z2 = АС, а значит, треугольники BMD и МСЕ равнобедренные,
т. е. MD = DB и ME = EC.
Если Р — периметр четырехугольника ADME, то Р = AD +
+ DM + ME + ЕА = AD + DB + ЕС + ЕА = АВ + АС, что и требо-
требовалось доказать.
428.	В параллелограмме, смежные стороны которого не равны, проведены
биссектрисы углов. Докажите, что при пересечении образуется прямоугольник.
Решение. Пусть в параллелограмме ABCD биссектрисы углов А,
В, С и D при пересечении образуют четырехугольник PEFQ (рис.33).
Zl = Z2, так как луч АР — биссектриса угла A, Z2 = Z3, так как
эти углы — накрест лежащие при пересечении параллельных прямых
AD и ВС секущей AQ, а угол 2, в свою очередь, равен углу 4, так как
это половины равных углов параллелограмма, поэтому Zl = Z3 = Z4.
Равные углы 3 и 4 — соответственные углы при пересечении пря-
прямых AQ и СЕ секущей ВС, следовательно, AQ || СЕ. Аналогично
можно доказать, что BE || DQ.
Таким образом, PEFQ — параллелограмм.
Так как Zl = Z3, то ААВТ — равнобедренный. Отрезок ВР —
биссектриса, а значит, и высота этого треугольника, т. е. ВР _l_ AQ.
Итак, в параллелограмме PEFQ один угол прямой, поэтому он явля-
является прямоугольником (задача 399).
Рис. 32	Рис. 33

30
Гл. 1. Четырехугольники
429.	Докажите, что выпуклый четырехугольник является параллелограм-
параллелограммом, если сумма углов, прилежащих к каждой из двух смежных сторон,
равна 180°.
Решение. Пусть углы А и В, прилежащие к стороне АВ выпук-
выпуклого четырехугольника ABCD, в сумме составляют 180°, и углы А
и D, прилежащие к смежной стороне AD, также в сумме составляют
180°. Углы А и В — односторонние при пересечении прямых AD и ВС
секущей АВ, поэтому AD || ВС. Углы А и D — односторонние при
пересечении прямых АВ и DC секущей AD, поэтому АВ || DC.
Итак, в четырехугольнике ABCD противоположные стороны по-
попарно параллельны, следовательно, четырехугольник ABCD — парал-
параллелограмм.
430.	Докажите, что выпуклый четырехугольник является параллелограм-
параллелограммом, если его противоположные углы попарно равны.
Решение. Пусть в выпуклом четырехугольнике ABCD противо-
противоположные углы попарно равны, т. е. ZA = ZC и ZB = ZD. Сумма
углов выпуклого четырехугольника равна 360°, поэтому 2(ZA + ZB) =
= 360°, откуда ZA + ZB = 180°, и, следовательно, ZA + ZD = 180°.
Из двух последних равенств следует, что четырехугольник ABCD —
параллелограмм (см. задачу 429).
431.	Точка К — середина медианы AM треугольника ABC. Прямая В К
пересекает сторону АС в точке D. Докажите, что AD = - АС.
о
Решение. Проведем через середину стороны ВС (точку М) пря-
прямую MF, параллельную В К (рис.34). Тогда по теореме Фалеса (за-
(задача 385) AD = DF и CF = DF. Отсюда AD = DF = FC, поэтому
AD = \ АС.
о
432. Точки М и N — середины сторон AD и ВС параллелограмма
ABCD. Докажите, что прямые AN и МС делят диагональ BD на три равные
части.
Решение. Пусть прямые AN и СМ пересекают диагональ BD
параллелограмма ABCD в точках Р и Q соответственно (рис.35).
М
N
D F
Рис. 34

Дополнительные задачи
31
Четырехугольник ANCM — параллелограмм, так как две его про-
противоположные стороны NC и AM равны и параллельны, поэтому
AN || СМ.
В треугольнике BCQ через середину N стороны ВС проведена пря-
прямая NP, параллельная CQ, следовательно, ВР = PQ (см. задачу 384).
В треугольнике ADP через середину М стороны AD проведена
прямая MQ, параллельная АР, следовательно, PQ = QD.
Таким образом, ВР = PQ = QD, т. е. прямые AN и СМ делят
диагональ BD на три равные части.
433.	Из вершины В ромба ABCD проведены перпендикуляры ВК и ВМ
к прямым AD и DC. Докажите, что луч BD является биссектрисой угла
квм.
Решение. Так как диагональ BD ромба делит угол D пополам,
то Zl =Z2 (рис.36).
Прямоугольные треугольники BKD и BMD равны по гипотенузе
и острому углу (BD — общая гипотенуза, Zl = Z2). Отсюда следует,
что Z3 = Z4, т. е. луч BD — биссектриса угла КВМ.
434.	Докажите, что точка пересечения диагоналей ромба равноудалена
от его сторон.
Решение. Пусть О — точка пересечения диагоналей АС и BD
ромба ABCD (рис. 37) и пусть OF JL AD, OP JL ВС, OE JL AB,
OQ JL DC.
Диагональ АС ромба делится точкой О пополам (ОА = ОС) и,
в свою очередь, делит пополам равные углы ромба А и С, т. е. Z1 =
= Z2 = Z3 = Z4. Отсюда следует, что прямоугольные треугольники
АЕО, AFO, СРО и CQO равны друг другу по гипотенузе и острому
углу. Поэтому OE = OF = OP = OQ, т. е. точка О равноудалена
от сторон ромба.
435. Докажите, что середина отрезка, соединяющего вершину треуголь-
треугольника с любой точкой противоположной стороны, лежит на отрезке с концами
в серединах двух сторон.
Решение. Пусть D — произвольная точка стороны АС треуголь-
треугольника ABC и Р — середина отрезка BD (рис.38).
В
С

32
Гл. 1. Четырехугольники
Проведем через точку Р прямую, параллельную стороне DC. Она
пересекает стороны АВ и ВС в некоторых точках М и N. Согласно
задаче 384, ВЫ = МА и BN = NC, т. е. точка Р лежит на отрезке
MN, концы которого являются серединами сторон АВ и ВС, что
и требовалось доказать.
436. Диагональ АС квадрата ABCD равна 18,4 см.
Прямая, проходящая через точку А и перпендикулярная
к прямой АС, пересекает прямые ВС и CD соответ-
соответственно в точках М и N. Найдите MN.
Решение. Так как диагональ АС делит угол С
пополам, то Z1 =/2 = 45° (рис.39). Отсюда сле-
следует, что углы М и N в прямоугольных треуголь-
треугольниках САМ и CAN также равны 45°. Поэтому
эти треугольники равнобедренные и, следователь-
следовательно, AM = AC и AN = AC, а значит, MN = 2AC =
= 2- 18,4 см = 36,8 см.
Рис. 39
Ответ. 36,8 см.
437. На диагонали АС квадрата ABCD взята точка М так, что AM =
= АВ. Через точку М проведена прямая, перпендикулярная к прямой АС
и пересекающая ВС в точке Н. Докажите, что ВН = НМ = МС.
Решение. Прямоугольные треугольники
АВН и АМН (рис.40) равны по катету
и гипотенузе (АВ = AM по условию, АН —
общая гипотенуза), поэтому ВН = НМ.
Треугольник СМН — прямоугольный и равно-
равнобедренный (ZHCM = 45°, так как диагональ АС
делит угол С пополам, и ZCHM = 45°, так как
сумма острых углов прямоугольного треугольника
равна 90°), поэтому НМ = МС.
Итак, ВН = НМ = МС, что и требовалось
доказать.
Рис. 40
438. В трапеции ABCD с большим основанием AD диагональ АС пер-
перпендикулярна к боковой стороне CD, ZBAC = ZCAD. Найдите AD, если
периметр трапеции равен 20 см, a ZD = 60°.
Решение. В прямоугольном треугольнике ACD ZD = 60°
(рис.41), поэтому Z2 = 30°, а так как по условию Zl = Z2, то ZA =
= 2-Z2 = 60°, т. е. ZA = ZD.
Отсюда следует, что трапеция ABCD — равнобедренная (зада-
(задача 389, а), значит, АВ = CD.
Так как в прямоугольном треугольнике ACD угол 2 равен 30°,
то катет CD, лежащий против этого угла, равен половине гипотену-
гипотенузы, т. е.
CD = ^AD, или AD = 2CD = 2АВ.

Дополнительные задачи	33
Поскольку Zl = Z2 и Z2 = Z3, то Zl = Z3 и, значит, треугольник
ABC — равнобедренный, т. е. ВС = АВ.
Итак,
Pabcd =AB + BC + CD + AD = ЪАВ,
поэтому ЪАВ = 20 см, откуда АВ = 4 см, a AD = 2AB = 8 см.
Ответ. 8 см.
439* Сумма углов при одном из оснований трапеции равна 90°. До-
Докажите, что отрезок, соединяющий середины оснований трапеции, равен их
полуразности.
Решение. Пусть сумма углов А и D при основании AD трапеции
ABCD равна 90°, а точки М и N — середины ее оснований ВС и AD.
Проведем прямые МР и MQ, соответственно параллельные
боковым сторонам АВ и CD (рис.42). Тогда образовавшиеся
четырехугольники АВМР и DCMQ — параллелограммы, поэтому
ВЫ = АР, СМ = DQ, а так как по условию ВЫ = СМ, то АР = DQ.
Отсюда следует, что PN = NQ, т. е. точка N — середина отрезка PQ.
Кроме того,
PQ = AD- (АР + DQ) = AD- ВС.
Так как МР \\ АВ, то Zl = ZA, а так как MQ \\ CD, то Z2 = ZD.
Но ZA + ZD = 90° (по условию), поэтому Zl + Z2 = 90° и, значит,
треугольник MNP — прямоугольный с прямым углом М.
Отрезок MN — медиана этого треугольника, поэтому MN =
= - PQ (задача 404), т. е. MN = - (AD — ВС), что и требовалось
доказать.
440* На двух сторонах треугольника вне его построены квадраты. Дока-
Докажите, что отрезок, соединяющий концы сторон квадратов, выходящих из одной
вершины треугольника, в два раза больше медианы треугольника, выходящей
из той же вершины.
Решение. На сторонах АВ и АС треугольника ABC (вне тре-
треугольника) построены квадраты, отрезок EF соединяет концы сторон
этих квадратов, выходящих из вершины А, отрезок AM — медиана
треугольника ABC. Требуется доказать, что EF = 2AM.
Пусть точка D симметрична точке А относительно точки М. Дока-
Докажем, что треугольники ABD и EAF равны (рис.43).
Так как ABMD = АСМА (по двум сторонам и углу между ними),
то BD = АС и Zl = ZACB. Следовательно,
В М
D
Р	N	Q
Рис.41	Рис.42
2 Л. С. Атанасян и др.

34
Гл. 1. Четырехугольники
ZABD = ZABC + Z\ = ZABC + /АСБ = 180° -
С другой стороны, ZEAF = 180° - ZBAC, поэтому ААВВ =
= LEAF.
Треугольники ABD и EAF равны по двум сторонам и углу между
ними (АВ = АЕ, BD = АС = AF, ZABD = LEAF). Отсюда следует,
что EF = AD = 2AM.
441. Докажите, что прямые, содержащие диагонали ромба, являются его
осями симметрии.
Решение. Пусть О — точка пересечения диагоналей АС и BD
ромба ABCD (рис.44). Треугольник BAD — равнобедренный и АО —
В
Рис. 43
Рис. 44
его биссектриса, проведенная к основанию, поэтому прямая АО явля-
является осью симметрии треугольника BAD (задача 420). Также и прямая
СО является осью симметрии треугольника BCD. Так как АО и СО —
одна и та же прямая, то прямая АС — ось симметрии ромба ABCD.
Аналогично можно доказать, что прямая BD является осью симметрии
ромба ABCD. Итак, прямые, содержащие диагонали ромба, являются
его осями симметрии.
442. Докажите, что точка пересечения диагоналей параллелограмма явля-
является его центром симметрии.
Решение. Пусть О — точка пересечения диагоналей параллело-
параллелограмма ABCD, тогда О А = ОС, OB = OD и поэтому вершины А
и С (и также В и D) симметричны относительно точки О.
Рассмотрим теперь произвольную точку М, лежащую на од-
одной из сторон параллелограмма, например на стороне АВ (рис.45),
В	С и покажем, что точка, симметричная
точке М относительно точки О, ле-
лежит на стороне CD параллелограм-
параллелограмма ABCD.
Проведем прямую МО и обозна-
обозначим через М\ точку ее пересечения
со стороной CD. АВОМ = ADOM{
М
Рис. 45

м
\
н
|_
о
п
а
т
\ Ъ
Дополнительные задачи	35
по стороне и двум прилежащим к ней углам (см. рис.45), следователь-
следовательно, ОМ = ОМ\, и, значит, точки М и М\ симметричны относительно
точки О.
Итак, для каждой точки М параллелограмма симметричная ей от-
относительно точки О точка М\ также принадлежит параллелограмму.
Это и означает, что точка О пересечения диагоналей параллелограмма
является его центром симметрии.
443. Сколько центров симметрии имеет пара параллельных прямых?
Решение. Пусть а иЬ — данные параллельные прямые. Рассмот-
Рассмотрим прямую т, параллельную прямым а и Ъ и находящуюся на равных
расстояниях от этих прямых (рис.46). Докажем, что любая точка О
прямой т является центром симметрии па-
пары параллельных прямых а и Ъ.
Проведем через точку О прямую НН\,
перпендикулярную к прямым а и Ъ. Так
как прямая т находится на одинаковых
расстояниях от прямых а и Ь, то ОН =
= ОН\, т. е. точки Н и Н\ симметричны
относительно точки О.	Н\	Мх
Возьмем теперь произвольную точку М
на одной из данных прямых, например,	^ис- ^6
на прямой а, причем точка М отлична от Н. Проведем прямую ОМ
и обозначим через М\ точку пересечения прямых ОМ и Ь. Прямоуголь-
Прямоугольные треугольники MHO и М\Н\О равны по катету и прилежащему
острому углу (см. рис.46), поэтому ОМ = ОМ\, т. е. точки М и М\
симметричны относительно точки О.
Итак, для любой точки М одной из данных параллельных прямых
симметричная ей относительно точки О точка М\ лежит на другой
данной прямой. Это означает, что точка О — центр симметрии пары
параллельных прямых а и Ъ. Таким образом, любая точка прямой т
является центром симметрии прямых а и Ь, т. е. пара параллельных
прямых имеет бесконечное множество центров симметрии.
Ответ. Бесконечно много.
444* Докажите, что если фигура имеет две взаимно перпендикулярные
оси симметрии, то точка их пересечения является центром симметрии фигуры.
Решение. Пусть взаимно перпендикулярные прямые 1\ и 1% — оси
симметрии фигуры F. Докажем, что точка О пересечения прямых 1\
и /2 является центром симметрии этой фигуры.
Возьмем сначала произвольную точку А фигуры F, не лежащую
на прямых 1\ и /2- Построим точку А', симметричную точке А отно-
относительно 1\, а затем точку А\, симметричную точке А! относительно
/2 (рис.47, а). Так как 1\ и 1^ — оси симметрии фигуры F, то точки
А' и А\ принадлежат этой фигуре. Рассмотрим треугольник АА'А\.
Поскольку /2 -L ^1 и АА1 !_ 1\, то 1^ || АА', а так как 1^ проходит

36
Гл. 1. Четырехугольники
h Ai , О
Рис. 47
через середину стороны A\Af, то /2 пересекает сторону АА\ в ее
середине (задача 384). Аналогично можно доказать, что и прямая
1\ пересекает сторону АА\ в ее середине. Следовательно, середина
отрезка АА\ совпадает с точкой О, и, значит, точка А\ симметрична
точке А относительно точки О.
Тем самым мы доказали, что точка А\, симметричная точке А
фигуры F относительно точки О, также принадлежит этой фигуре.
При этом мы рассмотрели случай, когда точка А не лежит на прямых
1\ и I2. Если точка А фигуры F лежит на какой-то из этих прямых,
например, на прямой 1\ (рис.47, б), то симметричная ей относительно
точки О точка А\ является также симметричной точке А относительно
прямой /2 и, значит, точка А\ принадлежит фигуре F. Таким образом,
для любой точки А фигуры F симметричная ей относительно О точка
А\ также принадлежит этой фигуре. Это и означает, что точка О —
центр симметрии фигуры F.
Задачи повышенной трудности
811. Дан выпуклый шестиугольник A\A2AsA4A^Aq, все углы которого
равны. Докажите, что А\А2 — А\А^ = A$Aq — А2А3 = А3А^ — AqA\.
Решение. Пусть А\А2 = а\, А2А3 = п2, А^А\ = аз, А\А^ = а±,
А^А§ = с&5, AqA\ = clq. Продолжив стороны данного шестиугольника
так, как показано на рисунке 48, полу-
получим треугольник B\B2B%. Так как все углы
данного шестиугольника равны друг другу,
то каждый из них равен 120°, поэтому смеж-
смежные с ними углы равны 60°. Отсюда следует,
что треугольники А\А2В\
равносторонние, т. е.
В
В\В2 = В2В3 =
или
Рис. 48
а\
а\.

Задачи повышенной трудности	37
Из этих равенств получаем:
&i + ci2 = &4 + «5, аз + а4 = аб + а\,
или
ai — а4 = а5 — а2 = аз — аб,
т. е.
АХА2 - АААЪ = А5А6 - А2А3 = А3А4 - А6А{.
812. Положительные числа а\, а2, аз, «4, &5 и аб удовлетворяют условиям
п1 — аА = а5 — а2 = а3 — а6. Докажите, что существует выпуклый шестиуголь-
шестиугольник A\A2AsA4A^Aq, все углы которого равны, причем А\А2 = а\, А2А% = а2,
А3АА = а3, А4А5 = а4, А5А6 = а5, A6^i = «6-
Решение. По условию
ai — п4 = а5 — а2 = аз — аб,
поэтому
ai + а2 = а4 + а5, аз + а4 = аб + а\
и, следовательно,
ai + a2 + аз = аз + a4 + as = as + аб + аь A)
Построим равносторонний треугольник BxB^B^, сторона которого
равна а\ + а2 + аз (см. рис.48). На стороне B\B2 этого треугольника
отметим точки А2 и А3 так, что
5^2 = а\, А2А3 = а2, А^В^ = аз-
Далее, на стороне Б2Д3 отметим точки А4 и А5 так, что
Б2А4 = а3, А4А5 = а4, А5В3 = а5,
а на стороне В%В\ — точки Aq и А\ так, что
Б3Аб = a5, A6Ai = аб, А\В\ = а\.
В силу равенств A) такие точки существуют (см. рис.48).
Так как по построению А\В\ = В\А2, А^В2 = В2А4, A5B3 =
= В3А6 и /_В\ = ZB2 = АВЪ = 60°, то треугольники В\А\А2, В2А3А4,
B^A^Aq — равносторонние. Отсюда следует, что каждый угол шести-
шестиугольника А\А2АзА4А$А§ равен 120° (т. е. углы равны друг другу),
а стороны удовлетворяют условию: А\А2 = а\, А2А^ = а2, А^А4 = аз,
А4А$ = а4, A$Aq = a5, AqA\ = аб.
813. Докажите, что из одинаковых плиток, имеющих форму произвольного
выпуклого четырехугольника, можно сделать паркет, полностью покрывающий
любую часть плоскости.
Решение. Пусть плитки имеют форму выпуклого четырехугольни-
четырехугольника ABCD. Через вершины А и С проведем прямую а, а через вершины
В и D — прямые Ъ и с, параллельные прямой а (рис.49).

38
Гл. 1. Четырехугольники
Затем проведем прямые d и е, параллельные прямой а, так, что
расстояние между прямыми Ъ и d равно расстоянию между прямыми
а и с (обозначим его г\), а расстояние между прямыми сие равно
расстоянию между прямыми а и Ъ (обозначим его гг). Продолжая
этот процесс неограниченно, мы разобьем всю плоскость на полосы,
причем ширина полос (расстояние между соседними параллельными
прямыми) принимает попеременно значения г\ и т^. Четыре такие
полосы представлены на рисунке 49.
Разобьем полосу, заключенную между прямыми а и Ь, на треуголь-
треугольники, равные треугольнику ABC, так, как показано на рисунке 49,
а полосу между прямыми а и с — на треугольники, равные треуголь-
треугольнику ADC. То же самое сделаем и с другими полосами (см. рис.49).
В результате всю плоскость можно представить себе разбитой
на четырехугольники, причем каждый из них равен четырехугольни-
четырехугольнику ABCD. Докажем, например, что четырехугольник ECBF равен
четырехугольнику ABCD. Стороны этих четырехугольников соответ-
соответственно равны, и также углы соответственно равны (на рис.49 равные
углы отмечены одинаковыми цифрами).
Отсюда следует, что эти четырехугольники можно совместить на-
наложением, а это и означает, что они равны.
Таким образом, любую часть плоскости можно покрыть паркетом
из одинаковых плиток, равных четырехугольнику ABCD.
814. Докажите, что диагонали выпуклого четырехугольника пересе-
пересекаются.
Решение. Пусть ABCD — выпуклый четырехугольник. Докажем,
что его диагонали АС и BD пересекаются.
Так как четырехугольник ABCD выпуклый, то точка С лежит
по ту же сторону от прямой АВ, что и точка D, и по ту же сторону
от прямой AD, что и точка В. Поэтому точка С лежит внутри угла
BAD. Следовательно, луч АС проходит внутри этого угла и поэтому
пересекает любой отрезок с концами на сторонах угла, в частности,
пересекает отрезок BD. Аналогично можно доказать, что луч BD
Рис. 49

Задачи повышенной трудности
39
пересекает отрезок АС. Отсюда следует, что точка пересечения луча
АС и отрезка BD лежит на отрезке АС, т. е. отрезки АС и BD
пересекаются.
815. Докажите, что в любом четырехугольнике какие-то две противопо-
противоположные вершины лежат по разные стороны от прямой, проходящей через две
другие вершины.
Решение. Если данный четырехугольник выпуклый, то согласно
задаче 814 его диагонали пересекаются, поэтому любые две проти-
противоположные вершины четырехугольника лежат по разные стороны
от прямой, проходящей через две другие вершины.
Пусть ABCD — невыпуклый четырехугольник. Тогда одна из пря-
прямых, содержащих сторону четырехугольника, например прямая АВ,
пересекает сторону CD в некоторой точке М. Отрезки АВ и CD
не пересекаются, поэтому возможны два случая:
а)	Точка А лежит на отрезке ВЫ (рис.50, а). В этом случае
точки В и М лежат по разные стороны от прямой АС. Отрезок MD
не пересекается с прямой АС, поэтому точка D лежит по ту же сторону
от прямой АС, что и точка М. Итак, вершина В лежит по одну сторону
от прямой АС, а противоположная вершина D — по другую сторону
от этой прямой.
б)	Точка В лежит на отрезке AM (рис.50, б). Аналогично случаю
а) можно доказать, что противоположные вершины А и С лежат
по разные стороны от прямой BD.
816. В равнобедренном треугольнике ABC с основанием АС проведена
биссектриса AD. Прямая, проведенная через точку D перпендикулярно к AD,
пересекает прямую АС в точке Е. Точки М и К — основания перпендикуля-
перпендикуляров, проведенных из точек В и D к прямой АС. Найдите МК, если АЕ = а.
Решение. Пусть Р — точка пересечения прямых DE и АВ,
DO || АС, О G АВ, а N — точка пересечения прямых DO
и ВЫ (рис.51).
D
М
б
Рис. 50

40
Гл. 1. Четырехугольники
М К Е
Прямоугольные треугольники ADP и
ADE равны по катету и прилежащему
острому углу (AD — общий катет, Z1 =
= Z2 по условию), поэтому АР = АЕ = а
и PD = DE, т. е. точка D — середина
отрезка РЕ.
Рассмотрим прямую OD, параллель-
параллельную АС (см. рис.51). Эта прямая про-
проходит через середину стороны РЕ тре-
треугольника АРЕ и OD || АС, поэтому АО = ОР (задача 384) и, следо-
следовательно,
АО- АР - а
Так как OD \\ АС, то Z2 = Z3, а поскольку Zl = Z2, то Z1 =
= Z3, откуда следует, что AAOD — равнобедренный и, значит,
Рис. 51
Кроме того, так как OD \\ АС, то углы О и D треугольника OBD
равны соответственно углам А и С треугольника ABC. Но углы
А и С равны, поскольку ААВС — равнобедренный. Следовательно,
углы О и D треугольника OBD также равны, и поэтому AOBD —
равнобедренный с основанием OD.
Наконец, так как OD || АС и ВЫ JL АС, то BN _L OD (см. рис. 51),
т. е. отрезок BN — высота равнобедренного треугольника OBD,
проведенная к основанию, а значит, и медиана. Итак, ND = N0 =
Четырехугольник MNDK, очевидно, является прямоугольником,
поэтому МК = 7VL> = -.
Ответ. -.
4
817. Докажите, что в треугольнике сумма трех медиан меньше периметра,
но больше половины периметра.
Решение. Пусть в треугольнике ABC:
ВС = а, С А = Ъ, АВ = с, а медианы, проведен-
проведенные к сторонам ВС, С А и АВ, равны соответ-
соответственно та, тъ и тпс.
Достроим треугольник ABC до параллело-
параллелограмма ABDC так, как показано на рисун-
рисунке 52. Тогда в треугольнике ABD: BD = Ъ,
AD = 2тпа. Используя неравенство треугольни-
треугольника, получим
Рис. 52
AD < АВ + BD, или 2та < Ъ + с,
откуда ша < —А

Задачи повышенной трудности	41
Аналогичные неравенства имеют место для ть и тпс:
а + с	а + Ъ
гпъ < —?-, тс < —?-.
Сложив три последних неравенства, получим
TTIq ~\ TYbfo ~\ TTbB <~^ (Л ~\ О ~\ С,
т. е. сумма трех медиан треугольника меньше его периметра.
Напишем теперь неравенство треугольника для ААВМ и ААСМ,
учитывая, что ВЫ = СМ = -:
ml 	 ^> г>	7Т7 —I— 	 ^> Г)
а * су ^ ь» а * су ^ и'
Складывая эти неравенства, получим
2та + а > Ь + с,
откуда
о + с — а
та >	.
Аналогичные неравенства имеют место для ть и тс:
а + с — Ъ а + Ь — с
ть > 	~	, тпс >	.
Сложив три последних неравенства, приходим к неравенству
тпа + гпъ + ттгс > — (а + о + с),
2
т. е. сумма трех медиан треугольника больше половины его периметра.
818. Диагонали выпуклого четырехугольника разбивают его на четыре
треугольника, периметры которых равны. Докажите, что этот четырехуголь-
четырехугольник — ромб.
Решение. Пусть ABCD — данный выпуклый четырехугольник,
а О — точка пересечения его диагоналей. Докажем сначала, что АО =
= ОС, ВО = OD. Предположим, что это не так. Тогда возможны два
случая:
а) Точка О - середина одной из диагоналей и не является серединой
другой диагонали. Пусть для определенности АО = ОС, ВО < OD.
Отметим на отрезке OD точку В\ так, что ОВ\ = ОВ, и рассмотрим
треугольник ОВ\С (рис.53, а). Так как ААВО = АСВ\О (по двум
сторонам и углу между ними), то АВ = СВ\.
По условию Раво = Pcdo,
АВ + АО + ОВ = ОВХ + BXD + DC + CO.
Отсюда, учитывая равенства АО = ОС и ОБ = ОВ\, получаем
АВ = BXD + DC, или CBi = BXD +

42
Гл. 1. Четырехугольники
Рис. 53
Но в треугольнике CBXD: СВХ < BXD + DC. Мы пришли к проти-
противоречию и, значит, случай а) не может иметь места.
б) Точка О не является серединой ни одной из диагоналей. Пусть,
например, АО < ОС, ВО < OD.
Отметим точки Ах и В\ на отрезках ОС и OD так, что ОА\ =
= О А, ОВ\ = ОВ, и рассмотрим треугольник ОАХВХ (рис.53, б). Так
как ААОВ = ААХОВХ, то АВ = АХВХ.
По условию Раво = Pcdo,
ОВ = ОВХ + BiD
Отсюда, учитывая равенства ОА\ = О А и ОБ = ОВ\, получаем
АВ = BxD + DC + CAu или АХВХ =
Но в четырехугольнике AXBXDC АХВХ < BXD	i
Мы пришли к противоречию, и, значит, случай б) также не может
иметь места.
Итак, АО = ОС, ВО = OD, и поэтому ABCD — параллело-
параллелограмм (признак 3°, п.43). Но из условия Раов — Рсов следует, что
АВ = ВС, т. е. смежные стороны параллелограмма ABCD равны.
Следовательно, параллелограмм ABCD — ромб.
819. Найдите множество середин всех отрезков, соединяющих данную
точку со всеми точками данной прямой, не проходящей через эту точку.
Решение. Пусть А и а — данные точка и прямая, АН — пер-
перпендикуляр, проведенный из точки А к прямой а, точка В — середина
отрезка АН (рис.54). Через точку В проведем прямую р, параллель
ную прямой а, и докажем, что искомое мно-
множество точек есть прямая р.
Если X — произвольная точка прямой а,
то прямая р пересекает отрезок АХ в его
середине (см. задачу 384). Следовательно,
середины отрезков, соединяющих точку А
со всеми точками прямой а, лежат на пря-
прямой р.
Н
Рис. 54

Задачи повышенной трудности
43
Докажем теперь, что любая точка М прямой р является серединой
отрезка, соединяющего точку А с какой-то точкой прямой а. Пусть
прямая AM пересекает прямую а в точке Y (см. рис.54). Согласно
задаче 384 прямая р пересекает отрезок AY в его середине, т. е. точка
М — середина отрезка AY.
Итак, искомым множеством точек является прямая р.
Ответ. Прямая, параллельная данной прямой и проходящая через
середину перпендикуляра, проведенного из данной точки к данной
прямой.
D
/ „ з\
°2 С
7 \
А „ \
О, "
В
820. Докажите, что прямая, проходящая через середины оснований рав-
равнобедренной трапеции, перпендикулярна к основаниям. Сформулируйте и до-
докажите обратное утверждение.
Решение. Пусть О\О^ — прямая, проходящая через середины О\
и О2 оснований АВ и CD равнобедренной трапеции ABCD (рис.55).
Согласно задаче 388, а АА = /Б, поэто-
поэтому /\AO\D = АВО\С по двум сторонам
и углу между ними. Отсюда следует, что
O\D = О\С, т. е. AO\DC равнобедрен-
равнобедренный. Отрезок О\О^ — медиана этого тре-
треугольника, следовательно, О\О^ — высо-
высота, т. е. О\О^ -L CD, а так как прямые АВ
и CD параллельны, то О\О^ 1- АВ, что
и требовалось доказать.	Рис. 55
Обратное утверждение сформулируем так: если прямая, проходящая
через середины оснований трапеции, перпендикулярна к основаниям,
то трапеция — равнобедренная.
Докажем это утверждение. Воспользуемся рисунком 55, на котором
точки О\ и О2 — середины оснований АВ и CD трапеции ABCD
и ОХО2 У- АВ, ОХО2 -L CD. В треугольнике OXCD отрезок ОХО2 -
медиана и высота, поэтому этот треугольник равнобедренный, т. е.
O\D = О\С и, кроме того, Zl = Z2 (см. рис.55). Отсюда следует, что
Z3 = Z4, поэтому AAOxD = ABOxC по двум сторонам и углу между
ними. Следовательно AD = ВС, т. е. трапеция ABCD равнобедренная.
821. При пересечении биссектрис всех уг-
углов прямоугольника образовался четырехуголь-
четырехугольник. Докажите, что этот четырехугольник —
квадрат.
Решение. Пусть MNPQ — четы-
четырехугольник, образованный при пересе-
пересечении биссектрис углов прямоугольника
ABCD (рис.56).
Согласно задаче 428 четырехугольник
MNPQ — прямоугольник. Докажем, что
Рис. 56

44
Гл. 1. Четырехугольники
MTV = NP. Треугольник AND — равнобедренный, так как Z\ =
= Z2 = 45°, поэтому AN = DN. Ho AM = DP, так как A ABM =
= AD PC (по стороне и прилежащим к ней углам). Таким образом,
MN = AN- AM = DN - DP = NP.
Итак, в прямоугольнике MNPQ две смежные стороны равны, сле-
следовательно, MNPQ — квадрат.
822. На сторонах параллелограмма вне его построены квадраты. Дока-
Докажите, что точки пересечения диагоналей этих квадратов являются вершинами
квадрата.
Решение. Пусть О\, О2, О3, О\ — точки пересечения диагона-
диагоналей квадратов, построенных на сторонах параллелограмма ABCD вне
его (рис.57). Сначала докажем, что
ААО{О4 = АВОХО2 = АСО3О2 = ADO3OA.	A)
Сравним треугольники АО\О\ и ВО\О2. АО\ = ВО\ и АО\ = ВО2,
так как эти отрезки являются половинами диагоналей соответствую-
соответствующих квадратов; ZO\ АО а = 45° + а + 45° = 90° + а, где а = ZBAD;
так как ZOXBO2 = 90° + а, то ZOXAO4 =
= ZOXBO2.
Следовательно, ААО\О\ = АВО\О2
по двум сторонам и углу между ними.
Остальные равенства в A) доказываются
аналогично.
Из равенств A) следует, что
OiO4 = ОХО2 = О3О2 = О3О4,
т. е. четырехугольник О\О2О3О\ — ромб.
Из равенства треугольников АО\О\ и
ВО\О2 следует, что Zl = Z2, поэтому
угол О2О\О\ — прямой, а значит, ромб
Рис. 57	О\О2О3О\ является квадратом.
823. На стороне CD квадрата ABCD отмечена точка М. Биссектриса
угла ВАМ пересекает сторону ВС в точке К. Докажите, что AM = ВК +
+ DM.
Решение. На луче АВ отложим отрезок AN, равный отрезку
AM, проведем отрезок NM, а затем в треугольнике AMN проведем
высоту NS (рис. 58). Пусть ZMAK = ZNAK = а.
Прямоугольные треугольники ASN и MDA равны по гипотенузе
и острому углу (AN = AM по построению, ZNAS = 2а, ZAMD =
= 90° - ZDAM = 2а и, следовательно, ZNAS = ZAMD), поэтому
AS = DM, NS = AD.

Задачи повышенной трудности
45
Прямоугольные треугольники АВК и NSM равны по катету
и острому углу (NS = AD = АВ, ZBKA = 90° - a, ZAMN =
= 18° ~2а = 90° - а, поэтому АВК А = ZAMN). Отсюда следует,
что
ВК = SM.	B)
Из равенств A) и B) имеем:
AM = AS + SM = DM + ВК,
что и требовалось доказать.
824. На рисунке 59 (рис. 268 учебника) изображены три квадрата. Найди-
Найдите сумму ZBAE + ZCAE + ZDAE.
Решение. Пусть D\ — точка, симметричная точке D относительно
точки Е. Тогда DDX = 2 • DE = FC и поэтому AAFC = ACDD{
по двум катетам.
Отсюда следует, что АС = CD\ и Zl = Z2.
Так как Z2 + Z3 = 90°, то Zl + Z3 = 90°, следовательно, ZACD{ =
= 180° - (Zl + Z3) = 90° и, значит, ЛАСА — равнобедренный пря-
прямоугольный треугольник с основанием AD\. Поэтому ZCAD\ = 45°.
Так как ADAE = ADXAE (по двум катетам), то ZDAE = ZDXAE.
Итак,
ZBAE
Ответ. 90°
ZCAE + ZDAE = 45° + ZCAE + ZA Л? =
= 45° + ZCADX = 45° + 45° = 90°.
825. Внутри квадрата ABCD взята точка М такая, что ZMAB = 60°,
ZMCD = 15°. Найдите ZMBC.
Решение. На луче AM (рис.60) отложим отрезок АК, равный
АВ, и докажем, что точки К и М совпадают.
Так как АК = АВ и ZBAK = 60°, то треугольник АВК — равно-
равносторонний, т. е. ВК = АВ = АК.
В
D
Рис. 59

46
Гл. 1. Четырехугольники
Рис. 60
Ответ. 30°.
Так как АВ = ВС, то ВК = ВС,
и, значит, треугольник ВКС равнобедрен-
равнобедренный, а поскольку ZKBC = 90° - 60° =
180°-30°
= 30°, то ABC К =
= 75°. Отсю-
Отсюда следует, что ZDCK = 15°. Но по усло-
условию ZDCM =15°, следовательно, ZDCM =
= ZDCK. Это означает, что лучи СМ и СК
совпадают, поэтому совпадают точки М и К.
Итак,
ZMBC = ZKBC = 30°.
826. На сторонах треугольника ABC во внешнюю сторону построе-
построены квадраты BCDE, АСТМ, БАНК, а затем параллелограммы TCDQ
и ЕВКР. Докажите, что треугольник APQ — прямоугольный и равнобед-
равнобедренный.
Решение. На рисунке 61 изображена данная фигура. Сначала
докажем, что
АВКР = A ABC = ACQT.	A)
Треугольники ВКР и ABC равны
по двум сторонам и углу между ни-
ними {ВК = АВ, КР = ВЕ = ВС, АВКР =
= ААВС, так как АВКР = 180° - ZKBE
и ZABC = 180° - ZKBE, см. рис. 61).
Поэтому ВР = С А и ZKBP = ABAC.
Треугольники ABC и CQT также рав-
равны по двум сторонам и углу между ни-
ними (АС = СТ, ВС = CD = QT, ZACB =
= ZCTQ, так как ZCTQ = 180° - ZDCT
и ZACB = 180° - ZDCT, см. рис.61).
Поэтому АВ = CQ, ABAC = Z.TCQ.
Так как ZABP = 90° + ZKBP = 90° +
+ ABAC, ZACQ = 90° + ZTCQ = 90° +
+ ABAC, то ZABP = ZACQ. Отсюда
и из равенств ВР = С А, АВ = CQ сле-
следует, что ААВР = AQCA (по двум сторонам и углу между ни-
ними), поэтому Z\ = Z2 и АР = AQ, т. е. AAPQ — равнобед-
равнобедренный.
Далее, поскольку ZBAC = ZABP - 90°, то
ZPAQ = Z3 + ZBAC + Z2 =
= (Z3 + ZABP+ Z1)-90° = 180° -90° =90°.
Q
Рис. 61
Итак, AAPQ — равнобедренный и прямоугольный.

Задачи повышенной трудности	47
&
fi
Рис. 62
827.	Постройте равнобедренную трапецию по основаниям и диагоналям.
Решение. Пусть P\Q\, P2Q2, P3Q3 — данные отрезки (рис.62, а).
Требуется построить равнобедренную трапецию ABCD с основаниями
AD и ВС так, что AD = PXQX, ВС = P2Q2, АС = BD = P3Q3.
Анализ. Пусть ABCD — искомая трапеция (рис.62, б). На прямой
AD отложим отрезок DE, равный ВС, так, как показано на рисун-
рисунке 62, б. Так как DE = ВС и DE || ВС, то DECB — параллелограмм
и поэтому СЕ = BD = P3Q3. Таким образом, в треугольнике АСЕ
АС = СЕ = P3Q3, АЕ = AD + DE = PXQX + P2Q2.	A)
Формулы A) показывают, что по данным отрезкам P\Q\, P2Q2,
P3Q3 можно построить треугольник АСЕ. Это дает возможность по-
построить затем искомую трапецию ABCD.
Построение. Построим треугольник АСЕ, стороны которого вы-
выражаются формулами A). На стороне АЕ отметим точку D так, что
AD = P\Q\, и проведем через точку D прямую, параллельную СЕ,
а через точку С — прямую, параллельную АЕ. Эти прямые пересека-
пересекаются в некоторой точке В.
Трапеция ABCD — искомая.
Доказательство. По построению AD = P\Q\, DE = P2Q2, AC =
= P3Q3. Так как ВС \\ DE и BD \\ СЕ (по построению), то DECB -
параллелограмм, и поэтому ВС = DE = P2Q2, СЕ = BD = Рз^з-
Таким образом, трапеция ABCD удовлетворяет всем условиям
задачи.
828.	Докажите, что если треугольник имеет: а) ось симметрии, то он
равнобедренный; б) более чем одну ось симметрии, то он равносторонний.
Решение, а) Пусть прямая а — ось симметрии треугольника
ABC. Тогда прямая а имеет по крайней мере одну общую точку
с треугольником (объясните, почему). Более того, прямая а пересекает
хотя бы одну из сторон треугольника, так как в противном случае
точка, симметричная вершине треугольника, не лежащей на прямой а,
не может принадлежать треугольнику (рис.63, а).
Пусть, например, прямая а пересекает сторону ВС в точке М. Тогда
вершина А лежит на прямой а. В самом деле, если допустить, что
А (? а, то прямая а пересекает наряду со стороной ВС еще какую-то
сторону треугольника. Пусть, например, прямая а пересекает сторону

48
Гл. 1. Четырехугольники
в
а
С
ВА
М
"С
АВ в точке N (рис.63, б) и пусть точка В\ симметрична точке В
относительно прямой а. Тогда множеством точек, симметричных точ-
точкам отрезков ВЫ и BN относительно прямой а, будут отрезки В\М
и B\N. Но хотя бы один из этих отрезков не принадлежит треуголь-
треугольнику ABC. Следовательно, прямая а проходит через вершину А.
Рассмотрим снова точку В\, симметричную точке В относительно
прямой а (рис.63, в). Очевидно, АВ\ = АВ и точки, симметричные
точкам стороны АВ, лежат на отрезке АВ\. Поэтому отрезок АВ\
лежит на стороне АС и, следовательяо, АВ\ = АВ < АС. Аналогично,
если точка С\ симметрична точке С относительно прямой а, то отрезок
АС\ лежит на стороне АВ и АС\ = АС < АВ.
Отсюда следует, что АВ = АС, т. е. треугольник ABC — равнобед-
равнобедренный.
Отметим, что ось симметрии (прямая а) пересекает сторону ВС
в ее середине.
б) Пусть треугольник ABC имеет более чем одну ось симметрии.
Тогда согласно доказанному в п. а) каждая из осей симметрии проходит
через вершину треугольника и пересекает противоположную сторону
в ее середине. Пусть, например, одна ось симметрии проходит через
вершину А, а другая — через вершину В. Тогда АВ = АС и В А = ВС,
т. е. АВ = АС = ВС и, значит, треугольник ABC — равносторонний.

Глава 2
ПЛОЩАДЬ
§ 1. Площадь многоугольника
445. Вырежьте из бумаги два равных прямоугольных треугольника и со-
составьте из них: а) равнобедренный треугольник; б) прямоугольник; в) паралле-
параллелограмм, отличный от прямоугольника. Сравните площади полученных фигур.
Решение. Пусть площадь первого вырезанного прямоугольного
треугольника равна S, тогда по свойству 1° площадей многоугольни-
многоугольников площадь второго треугольника тоже равна S. Площадь каждой
полученной фигуры по свойству 2° площадей многоугольников равна
2S (рис.64).
Ответ. Площади фигур равны.
Рис. 64
446. Начертите квадрат и примите его за единицу измерения площадей.
Далее начертите: а) квадрат, площадь которого выражается числом 4; б) от-
отличный от квадрата прямоугольник, площадь которого выражается числом 4;
в) треугольник, площадь которого выражается числом 2.
Решение. Смотри рисунок 65.
1
\
\
Рис. 65

50
Гл. 2. Площадь
М
В,
О
Рис. 66
447. Начертите параллелограмм ABCD и отметьте точку М, симметрич-
симметричную точке D относительно точки С. Докажите, что Sabcd = Samd-
Решение. Пусть О — точка пересече-
пересечения отрезков AM и ВС (рис.66).
ААВО = АМСО по стороне и двум
прилежащим к ней углам (АВ = CD = CM,
Zl = Z2, Z3 = Z4, так как эти углы — на-
накрест лежащие при пересечении параллель-
параллельных прямых АВ и CD секущими AM и ВС
соответственно), поэтому Sabo = Smco-
По свойству 2° площадей многоуголь-
многоугольников
Saocd-
С
D
Sabcd = Sabo + Saocd, Sadm = Smoc
Итак, Sabcd = Sadm-
448. На стороне AD прямоугольника ABCD построен треугольник ADE
так, что его стороны АЕ и DE пересекают отрезок ВС в точках М и N,
причем точка М — середина отрезка АЕ. Докажите, что Sabcd = Sade.
Решение. Проведем перпендикуляр
EF к прямой ВС (рис.67).
ААВМ = AEFM по гипотенузе и
острому углу (AM = ME по условию,
ZAMB = ZEMF, так как эти углы верти-
вертикальные), поэтому Sabm = Sefm-
ADCN = AEFN по катету и остро-
острому углу (CD = АВ = i?F, так как тре-
треугольники АВМ и ?FM равны, ZCDN =
= ZFEN, так как эти углы — накрест ле-
лежащие при пересечении параллельных пря-
мых CD и ЕЕ секущей DE). Следователь-
Следовательно, Sdcn = Sefn-
Рис. 67
Sabcd = Sabm + Samnd
Saed = Sefm + Samnd + Sefn-
Так как Sabm = Sefm, Sdcn = Sefn, to
Sabcd = Saed-
449. Найдите площадь квадрата, если его сторона равна: а) 1,2 см;
о
б) — дм; в) Зл/2 м.
Решение. Так как площадь квадрата со стороной а равна а2, то:
а) 5= A,2 смJ = 1,44 см2;
^ч с /3 \2 9 2
6M= (-дм] ^дм2;

§ 1. Площадь многоугольника	51
в) 5' = Cv/2 мJ = 18 м2.
Ответ, а) 1,44 см2; б) — дм2; в) 18 м2.
450.	Найдите сторону квадрата, если его площадь равна: а) 16 см2;
б)	2,25 дм2; в) 12 м2.
Решение. Так как площадь S квадрата со стороной а равна а2,
то а = л/S: а) а = л/Тб см = 4 см; б) а = \/2,25 дм = 1,5 дм; в) а =
= л/12 м = 2л/3 м.
Ответ, а) 4 см; б) 1,5 дм; в) 2л/3 м.
451.	Площадь квадрата равна 24 см . Выразите площадь этого же квад-
квадрата: а) в квадратных миллиметрах; б) в квадратных дециметрах.
Решение, a) S = 24 см2 = 24- 100 мм2 =2400 мм2;
б) S = 24 см2 = 24 : 100 дм2 = 0,24 дм2.
Ответ, а) 2400 мм2; б) 0,24 дм2.
452.	Пусть а и Ь — смежные стороны прямоугольника, a S — его площадь.
Вычислите: a) S, если а = 8,5 см, Ъ = 3,2 см; б) S, если а = 2д/2 см, 6 = 3 см;
в)	6, если а = 32 см, S = 684,8 см2; г) а, если 6 = 4,5 см, S = 12,15 см2.
Решение. Площадь прямоугольника равна произведению его
смежных сторон, поэтому:
а)	5 = аЬ = 8,5 см • 3,2 см = 27,2 см2;
б)	S = 2л/2 см • 3 см = 6л/2 см2;
в)	684,8 см2 = 32 см • Ь, Ъ = 684,8 см2 : 32 см = 21,4 см;
г)	12,15 см2 = а • 4,5 см, а = 12,15 см2 : 4,5 см = 2,7 см.
Ответ, а) 27,2 см2; б) 6л/2 см2; в) 21,4 см; г) 2,7 см.
453.	Как изменится площадь прямоугольника, если: а) одну пару противо-
противоположных сторон увеличить в 2 раза; б) каждую сторону увеличить в 2 раза;
в) одну пару противоположных сторон увеличить в 2 раза, а другую уменьшить
в 2 раза?
Решение. Пусть а и Ъ — смежные стороны прямоугольника, a S —
его площадь, тогда S = аЬ.
а)	Sx = 2а • Ь = 2ab, т. е. S{ = 2S;
б)	52 = 2а • 2Ъ = Aab, т. е. S2 = 45;
в)	S3 = 2а • | = аЪ, т. е. S3 = S.
Ответ, а) Увеличится в 2 раза; б) увеличится в 4 раза; в) не
изменится.
454.	Найдите стороны прямоугольника, если: а) его площадь равна
250 см2, а одна сторона в 2,5 раза больше другой; б) его площадь равна 9 м2,
а периметр равен 12 м.
Решение. Пусть а и Ъ — смежные стороны прямоугольника, S —
его площадь, а Р — периметр.

52	Гл. 2. Площадь
а)	По условию а = 2,56, S = 250 см2, поэтому S = аЪ = 2,562, т. е.
250 см2 = 2,562, откуда
6 = 10 см, а = 2,5 • 10 см = 25 см.
б)	По условию 5 = аЪ = 9 м2, Р = 2(а + Ъ) = 12 м, т. е. аЪ = 9 м2,
а + 6 = 6 м. Из этих равенств находим а и Ь\
а = Ъ = 3 м.
Ответ, а) 25 см, 10 см; б) а = 6 = 3 м.
455.	Пол комнаты, имеющей форму прямоугольника со сторонами 5,5 м
и б м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки
паркета равна 30 см, а ширина — 5 см. Сколько потребуется таких дощечек
для покрытия пола?
Решение. Площадь пола равна 5,5 м • 6 м = 33 м2 = 330 000 см2.
Площадь одной дощечки паркета равна 30 см • 5 см = 150 см2.
Для покрытия пола нужно
330000 см2 : 150 см2 = 2200 (дощечек).
Ответ. 2200 дощечек.
456.	Сколько потребуется кафельных плиток квадратной формы со сто-
стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника
со сторонами 3 м и 2,7 м?
Решение. Площадь части стены равна
3 м-2,7 м = 8,1 м2 = 81000 см2.
Площадь одной кафельной плитки A5 смJ = 225 см2.
Для облицовки стены потребуется
81000 см2 : 225 см2 = 360 (плиток).
Ответ. 360 плиток.
457.	Найдите сторону квадрата, площадь которого равна площади прямо-
прямоугольника со сторонами 8 м и 18 м.
Решение. Площадь прямоугольника равна 8 м • 18 м = 144 м2,
поэтому и площадь квадрата равна 144 м2. Пусть сторона квадрата
равна а.
Тогда о? = 144 м2, откуда а = 12 м.
Ответ. 12 м.
458.	Два участка земли огорожены заборами оданаковой длины. Первый
участок имеет форму прямоугольника со сторонами 220 м и 160 м, а второй
имеет форму квадрата. Площадь какого участка больше и на сколько?
Решение. Пусть S — площадь участка, имеющего форму прямо-
прямоугольника, Р — его периметр, S\ — площадь участка, имеющего форму
квадрата, а — его сторона. Тогда S = 220 м • 160 м = 35 200 м2,

§ 2. Площади параллелограмма, треугольника и трапеции	53
Р = 2B20 + 160) м = 760 м, 4а = Р = 760 м, откуда а = 190 м,
a Si = а2 = 36100 м2.
Si-S = 36100 м2 - 35200 м2 = 900 м2.
Ответ. Площадь квадрата на 900 м2 больше площади прямоуголь-
прямоугольника.
§ 2. Площади параллелограмма, треугольника
и трапеции
459. Пусть а — основание, h — высота, a S — площадь параллелограмма.
Найдите: a) S, если а = 15 см, h = 12 см; б) а, если S = 34 см2, h = 8,5 см;
в) а, если S = 162 см, h = - а; г) /г, если h = За, 5 = 27.
Решение, a) S = ah = 15 см • 12 см = 180 см2;
б)	Так как S = ah, то а = S : h = 34 см2 : 8,5 см = 4 см;
в)	Так как S = 162 см2, h = - а, то 162 см2 = ah = a--a=-a2,
откуда а2 = 324 см2, а = 18 см;
г)	Так как S = 27, /г = За, то а = -h и 27 = ah = -h2, откуда
Л2 = 81, /i = 9.
Ответ, а) 180 см2; б) 4 см; в) 18 см; г) 9.
460. Диагональ параллелограмма, равная 13 см, перпендикулярна к сто-
стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
Решение. Пусть S — площадь параллелограмма. Так как по усло-
условию диагональ параллелограмма перпендикулярна к его стороне, то она
является его высотой (рис. 68) и, следовательно,
5= 12 см- 13 см = 156 см2.
Ответ. 156 см2.
461. Смежные стороны параллелограмма равны 12 и 14 см, а его острый
угол равен 30°. Найдите площадь параллелограмма.
Решение. Пусть в параллелограмме ABCD: АВ = 12 см, AD =
= 14 см, BE — высота, АА = 30° (рис.69). Треугольник ABE —
Рис. 68

54
Гл. 2. Площадь
прямоугольный с острым углом в 30°, поэтому BE = -АВ = 6 см (так
как катет, лежащий против угла в 30°, равен половине гипотенузы).
Sabcd = AD • BE = 14 см • 6 см = 84 см2.
Ответ. 84 см2.
462. Сторона ромба равна б см, а один из его углов равен 150°. Найдите
площадь ромба.
Решение. Пусть в ромбе ABCD АВ = 6 см, BE — высота, ZD =
= 150° (рис.70). Так как сумма углов, прилежащих к одной стороне
ромба, равна 180°, то ZA = 180° — ZD = 30°. Из прямоугольного
треугольника ABE с острым углом в 30° находим BE = - АВ = 3 см.
Sabcd = AD • BE = 6 см • 3 см = 18 см2.
Ответ. 18 см2.
463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см,
образует с ней угол в 30°. Найдите площадь параллелограмма.
Решение. Пусть в параллелограмме ABCD: AD = 8,1 см, АС =
= 14 см, ZCAD = 30° (рис. 71).
Проведем высоту СЕ к стороне AD и рассмотрим прямоугольный
треугольник АСЕ. Катет СЕ этого треугольника равен половине ги-
гипотенузы АС, т. е. СЕ = 7 см. Следовательно,
Sabcd = 8,1 см • 7 см = 56,7 см2.
Ответ. 56,7 см2.
464. Пусть а и Ь — смежные стороны параллелограмма, h\ и h% — его
высоты. Найдите: a) /i2, если а = 18 см, Ь = 30 см, h\ = б см, h^ > h\\ б) hi,
если а = 10 см, Ъ = 15 см, h% = б см, h% > h\\ в) h\ и /i2, если S = 54 см2,
а = 4,5 см, 6 = 6 см.
Решение. Площадь параллелограмма равна произведению сторо-
стороны на высоту, проведенную к этой стороне, поэтому высота, прове-
проведенная к большей стороне, меньше высоты, проведенной к меньшей
стороне.
Рис. 70
Рис. 71

§ 2. Площади параллелограмма, треугольника и трапеции
55
а) По условию h^> h\, a = 18 см, Ъ = 30 см, т. е. Ъ > а, следователь-
следовательно, h\ — высота, проведенная к стороне Ъ. Можно записать: ah^ = bh\,
l • О
а	18
б) Аналогично п. а) получаем:
_ ah2 _ 10 • б
1 ~ Т~ ~ 15
см = 10 см.
= bh\, откуда
см = 4 см.
в) п\ = — = —-р см = 12 см, ti2 = 1- = -pr см = 9 см.
a 4,5	6 о
Ответ, а) 10 см; б) 4 см; в) 12 см, 9 см.
465.	Острый угол параллелограмма равен 30°, а высоты, проведенные
из вершины тупого угла, равны 2 см и 3 см. Найдите площадь паралле-
параллелограмма.
Решение. Пусть в параллелограмме ABCD А А = 30°, BE
и BF — высоты, проведенные к сторонам AD и CD (рис. 72). По усло-
условию BE = 2 см, BF = 3 см.
В прямоугольном треугольнике ABE А А = 30°, поэтому АВ =
= 2ВЕ = 4 см.
АВ = CD = 4 см,
Sabcd = CD • BF = 4 см • 3 см = 12 см2.
Ответ. 12 см2.
466.	Диагональ параллелограмма равна его стороне. Найдите площадь
параллелограмма, если большая его сторона равна 15,2 см, а один из его углов
равен 45°.
Решение. Пусть в параллелограмме ABCD: BD = AD (рис.73).
Тогда угол А — острый, так как треугольник ABD — равнобедренный.
По условию А А = 45°, поэтому ZABD = 45°, ZADB = 90°.
В треугольнике ABD: АВ — гипотенуза, AD — катет, поэтому
АВ > AD, т. е. АВ — большая сторона параллелограмма.
По условию АВ = 15,2 см. Высота DK равнобедренного треуголь-
треугольника ADB является медианой, поэтому DK = - АВ = 7,6 см (см. за-
задачу 404).
Sabcd = АВ - DK = 15,2 см • 7,6 см = 115,52 см2.
Ответ. 115,52 см2.
Рис. 72
Рис. 73

56	Гл. 2. Площадь
467.	Квадрат и ромб, не являющийся квадратом, имеют одинаковые пери-
периметры. Сравните площади этих фигур.
Решение. Пусть S — площадь квадрата, S\ — площадь ромба.
Так как по условию квадрат и ромб имеют равные периметры, то их
стороны равны. Пусть сторона квадрата и сторона ромба равны а,
высота ромба равна /г. Тогда 5 = a2, S\ = ah.
Так как ромб не является квадратом, то h < а, поэтому S\ < 5.
Ответ. Площадь квадрата больше.
468.	Пусть а — основание, h — высота, a 5 — площадь треугольника.
Найдите: a) 5, если а = 7 см, h = 11 см; б) 5, если а = 2л/3 см, h = 5 см;
в) h, если S = 37,8 см2, а = 14 см; г) а, если 5=12 см2, h = Зл/2 см.
Решение.
а) 5 = - ah = - • 7 см • 11 см = 38,5 см2;
2.
б)	S = - • 2л/3 см • 5 см = 5л/3 см
в)	Так как S = - а/г, то
25 л о^ о 2
Л = — = 2 • 37,8 см^ : 14 см = 5,4 см;
а
г) Так как 5 = - а/г, то
а = ^ = 2 • 12 см2 : Зл/2 см = 4л/2 см.
h
Ответ, a) 38,5 см2; б) 5л/3 см2; в) 5,4 см; г) 4лД см.
469. Стороны АВ и ВС треугольника ABC равны соответственно 16 см
и 22 см, а высота, проведенная к стороне АВ, равна 11 см. Найдите высоту,
проведенную к стороне ВС.
Решение. Пусть CD и АЕ — высоты, проведенные к сторонам
АВ и ВС соответственно. Так как
Sabc = \aB-CDk SABC = \
то АВ - CD = ВС • АЕ, т. е. 16 см • 11 см = 22 см • АЕ, откуда
АЕ = 8 см.
Ответ. 8 см.
470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведен-
проведенная к большей стороне, равна 2,4 см. Найдите высоту, проведенную к меньшей
стороне.
Решение. Пусть высота, проведенная к меньшей из заданных
сторон, равна /г. Тогда
7,5 см • 2,4 см = 3,2 см • /г,

§ 2. Площади параллелограмма, треугольника и трапеции	Ъ7
откуда h = 7,5 • 2,4 см : 3,2 см = 5,625 см.
Ответ. 5,625 см.
471.	Найдите площадь прямоугольного треугольника, если катеты равны:
а) 4 см и 11 см; б) 1,2 дм и 3 дм.
Решение. Если а и Ь — катеты прямоугольного треугольника,
S — его площадь, то
S = \аЪ.
а)	5= i-4 см- 11 см = 22 см2;
б)	5 = i • 1,2 дм • 3 дм = 1,8 дм2.
Ответ, а) 22 см2; б) 1,8 дм2.
472.	Площадь прямоугольного треугольника равна 168 см2. Найдите ка-
7
теты, если отношение их длин равно —.
Решение. Пусть а и Ь — катеты прямоугольного треугольника,
S — его площадь. По условию - = —, поэтому а = —.
7	9Д
и так как S = 168 см2, то 168 см2 = — Ь2, откуда Ь2 = 168 см2 • —
= 576 см2, откуда Ъ = 24 см, а = — Ъ = — • 24 см = 14 см.
Ответ. 24 см, 14 см.
473. Через вершину С треугольника ABC проведена прямая т, парал-
параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой
m и основанием АВ имеют равные площади.
Решение. Пусть высота треугольника
ABC, проведенная к стороне АВ, равна h. То-
Тогда Sabc — 9 ^-^ ' ^- РассмотРим треугольник
АВМ, где М — произвольная точка прямой пг,
параллельной АВ и проходящей через точку
С (рис.74). Так как все точки прямой m рав-
равноудалены от прямой АВ (см. п. 37 учебника),
то высота, проведенная из точки М к прямой
АВ, равна h, и поэтому
Рис. 74
Sabm = к
• h = Sabc-
Итак, все треугольники с вершинами на прямой m и основанием
АВ имеют равные площади.

58
Гл. 2. Площадь
474.	Сравните площади двух треугольников, на которые разделяется дан-
данный треугольник его медианой.
Решение. Пусть в треугольнике ABC проведены медиана BD
и высота BE (рис. 75). Так как BD — медиана, то AD = DC. Отрезок
BE — высота треугольников ABD и CBD,
Sabd = \AD-BE=l-DC-BE = Scbd-
Итак, Sabd = Scbd-
Ответ. Площади треугольников равны.
475.	Начертите треугольник ABC. Через вершину А проведите две пря-
прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие
равные площади.
Решение. Разделим сторону ВС на три равные части: BE =
= ЕЕ = ЕС и проведем через вершину А прямые АЕ и AF (рис.76).
Они разделят треугольник ABC на три треугольника, имеющие равные
площади. Действительно, эти три треугольника имеют равные осно-
основания и одну и ту же высоту AD (см. рис.76), поэтому их площади
равны.
476. Докажите, что площадь ромба равна половине произведения его
диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм
и 14 см; б) 4,6 дм и 2 дм.
Решение. Пусть в ромбе ABCD диагонали АС и BD пересека-
пересекаются в точке О (рис.77). Так как диагонали ромба взаимно перпенди-
перпендикулярны, то
Sabc = \АС • ВО, Sadc = \
DO, и поэтому
Sabcd = Sabc + SADc = \АС • ВО + Х-АС • DO =
= 1-АС - (ВО + OD) = l-AC - BD.
Итак, Sabcd = ^ АС • BD, что и требовалось доказать,
а) 5 = ^ • 3,2 дм • 1,4 дм = 2,24 дм2 = 224 см2;
Е D
Рис. 75

§ 2. Площади параллелограмма, треугольника и трапеции
59
б) 5 = - • 4,6 дм • 2 дм = 4,6 дм2.
Ответ, а) 224 см2; б) 4,6 дм2.
477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой,
а площадь ромба равна 27 см.
Решение. Пусть S — площадь ромба. Согласно задаче 476 S =
= -d\ • с?2, где d\ и d,2 — диагонали ромба. По условию с?2 = l,Sd\,
a S = 27 см2, поэтому
1	О	Q
27 см2 = -d\ • -d\ = -(
откуда (d\f = 36 см2,
d\ = 6 см, а cfo = x • 6 см = 9 см.
Ответ. 6 см, 9 см.
478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны.
Докажите, что площадь четырехугольника равна половине произведения его
диагоналей.
Решение. Пусть ABCD — выпуклый четырехугольник, в кото-
котором AC JL BD, а О — точка пересечения диагоналей (рис.78). Тогда
отрезки ВО и DO — высоты треугольников ABC и ADC, поэтому
OD.
Sabc = \ЛС ВО, Sadc = \
Следовательно,
Sabcd = SABC + SADC = \
ВО +l-AC -OD =
= i AC(BO + OD) = \AC- BD.
Итак, SABcd = \а.С- BD.
479. Точки D и Е лежат на сторонах АВ и АС треугольника ABC.
Найдите: a) Sade, если АВ = 5 см, АС = б см, AD = 3 см, АЕ = 2 см,
Рис. 78

60	Гл. 2. Площадь
Sabc = 10 см2; б) AD, если АВ = 8 см, АС = 3 см, АЕ = 2 см,
= 10 см2, Sade = 2 см2.
Решение. Так как треугольники ADE и ABC имеют по равному
углу А (рис.79), то площади этих треугольников относятся как произ-
произведения сторон, заключающих этот угол, т. е.
Sade ¦ SABC = (AD ¦ АЕ) : (АВ ¦ AC).	A)
а)	SADE = SABC ¦ (AD ¦ АЕ) : (АВ ¦ AC) = 10 ¦ C ¦ 2) : E ¦ 6) =
= 2 см2.
б)	Из равенства A) следует, что
AD = SADE -АВ-АС-. {SABC • АЕ).
Поэтому AD = B • 8 • 3) : A0 • 2) = 2,4 см.
Ответ, а) 2 см2; б) 2,4 см.
480.	Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а)АВ = 21 см, CD = 17 см, высота ВН равна 7 см; б) ZD = 30°, АВ = 2 см,
CD = 10 см, DA = 8 см; в) ВС !_ АВ, ЛВ = 5 см, ВС = 8 см, CD = 13 см.
Решение, a) SUscd = ^ (АВ + CD) - ВН = i B1 см + 17 см) х
х 7 см = 133 см2.
б)	Проведем высоту АЕ трапеции и рассмотрим прямоугольный
треугольник ADE. Так как ZD = 30°, а гипотенуза AD = 8 см,
то АЕ = 4 см.
Sabcd = „ B см + 10 см) • 4 см = 24 см2.
в)	Так как ВС !_ АВ, то отрезок ВС является высотой трапеции,
и, следовательно,
Sabcd = \ (АВ + DC)BC = i E см + 13 см) • 8 см = 72 см2.
Ответ, а) 133 см2; б) 24 см2; в) 72 см2.
481.	Найдите площадь прямоугольной трапеции, у которой две меньшие
стороны равны б см, а больший угол равен 135°.
Решение. Пусть в прямоугольной трапеции ABCD с основаниями
AD и ВС: AD > ВС, ZA = ZB = 90°, ZC = 135° (рис. 80).
Проведем высоту СЕ к стороне AD. Тогда СЕ = АВ = ВС = 6 см.
В прямоугольном треугольнике CDE АС = 45°, поэтому AD =
= 90° - Z.C = 45° и, следовательно, ED = СЕ = 6 см.
АЕ = ВС = 6 см (так как АЕ и ВС — противоположные стороны
прямоугольника АВСЕ), поэтому AD = АЕ + BD = 12 см.
Sabcd = \ (ВС + AD)CE = i F см + 12 см) • 6 см = 54 см2.
Ответ. 54 см2.

§ 3. Теорема Пифагора
61
482. Тупой угол равнобедренной трапеции равен 135°, а высота, прове-
проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см
и 3,4 см. Найдите площадь трапеции.
Решение. Пусть в равнобедренной трапеции ABCD с основа-
основаниями AD и ВС ZB = 135°, BE — высота, АЕ = 1,4 см, ED =
= 3,4 см (рис.81).
В прямоугольном треугольнике ABE АВ = 45°, А А = 90° — АВ =
= 45°, поэтому BE = АЕ = 1,4 см.
Проведем высоту CF. Тогда CF = BE = 1,4 см.
Так как в равнобедренной трапеции углы при основании равны (за-
(задача 388, а), то ZD = ZA = 45°. Поэтому в прямоугольном треуголь-
треугольнике СЕВ АС = 90° -ZD = 45° и, следовательно, FD = CF=1,4 см;
ВС = EF = ED-FD = 3,4 см - 1,4 см = 2 см;
AD = АЕ + ED = 4,8 см;
Sabcd = \ (ВС + AD) • BE = i B + 4,8) см • 1,4 см = 4,76 см2.
Ответ. 4,76 см2.
§ 3. Теорема Пифагора
483. Найдите гипотенузу прямоугольного треугольника по данным кате-
катетам а и Ъ\ а) а = б, Ъ = 8; б) а = 5, Ъ = 6; в) а = -, Ъ = -; г) а = 8, Ъ = 8л/3.
Решение. Пусть с — гипотенуза прямоугольного треугольника
с катетами а и Ь, тогда по теореме Пифагора с2 = а2 + б2, откуда с =
а) с = л/36 + 64 = 10; б) с = л/25 + 36 = л/бТ; в) с = W-^- + ^ = ^;
г) с = л/64 + 3 • 64 = л/64 • 4 = 8 • 2 = 16.
Ответ, а) 10; б) л/бТ; в) ^; г) 16.
484. В прямоугольном треугольнике а и Ь — катеты, а с — гипотенуза.
Найдите Ь, если: а) а = 12, с = 13; б) а = 7, с = 9; в) а = 12, с = 26; г) а =
= 2\/3, с = 26; д) а = 36, с = 2\/1б.
Решение. По теореме Пифагора с2 = а2 + б2, откуда Ъ =
а) Ъ = л/169- 144 = 5.
/ 9	9
/с2 - а2 .
D А
Рис. 79
Рис. 80

62	Гл. 2. Площадь
б)	b = л/81 -49 = л/32 = 4л/2 .
в)	Так как с2 = а2 + б2, а = 12, с = 26, то 462 = 144 + б2, откуда
б2 = 48, Ъ = 4л/3.
г)	Так как с2 = а2 + б2, а = 2л/3, с = 2Ъ, то 462 = б2 + 12, откуда
Ъ2 = 4, Ъ = 2.
д)	Так как с2 = а2 + Ъ2, а = ЗЬ, с = 2л/Ш, то 40 = %2 + б2, откуда
Ъ2 = 4, 6 = 2.
Ответ, а) 5; б) 4л/2; в) 4л/3; г) 2; д) 2.
485. Найдите катет прямоугольного треугольника, лежащий против угла
60°, если гипотенуза равна с.
Решение. Если один острый угол прямоугольника равен 60°,
то другой острый угол равен 30°. Пусть катет, лежащий против угла
в 60°, равен а, а против угла в 30° — равен Ъ. Тогда Ъ = - с.
По теореме Пифагора с2 = а2 + Ъ2, откуда
Ответ.
486. В прямоугольнике ABC В найдите: а) АВ, если АВ = 5, АС = 13;
б) ВС, если СВ = 1,5, АС = 2,5; в) CD, если ВВ = 17, БС = 15.
Решение, а) Применим теорему Пифагора к прямоугольному тре-
треугольнику ACD:
АС2 = AD2 + CD2, отсюда AD = VAC2 - CD2.
Так как ABCD — прямоугольник, то CD = АВ = 5 и, следователь-
следовательно,
AD = л/169-25 = л/144 = 12.
б) ВС = VAC2 - АВ2, АВ = CD = 1,5, поэтому
ВС = л/6,25 - 2,25 =2.
в) CD = VBD2 - ВС2 = л/289 - 225 = 8.
Ответ, а) 12; б) 2; в) 8.
487. Боковая сторона равнобедренного треугольника равна 17 см, а осно-
основание равно 16 см. Найдите высоту, проведенную к основанию.
Решение. Пусть в равнобедренном треугольнике ABC с основа-
основанием АС проведена высота BE к основанию, тогда АЕ = ЕС = 8 см.
Из прямоугольного треугольника ABE, используя теорему Пифа-
Пифагора, находим:
BE = \/АВ2 - АЕ2 = л/289 - 64 = л/225 = 15 (см).
Ответ. 15 см.

§ 3. Теорема Пифагора	63
488. Найдите: а) высоту равностороннего треугольника, если его сторона
равна б см; б) сторону равностороннего треугольника, если его высота равна
4 см.
Решение. Пусть отрезок BD — высота равностороннего
треугольника ABC, тогда AD = - АС и по теореме Пифагора для
прямоугольного треугольника ABD имеем: АВ2 = AD2 + BD2.
а)	AD = i АС = 3 см, BD = л/АВ2 - AD2 = л/36^9 = Зл/3 (см).
1	/ 4R\2
б)	AD = i АВ, АВ2 = BL>2 + AD2 = BD2 + (^ J ; отсюда полу-
получаем:
- АВ2 = BD2 = 16 см2, АВ=^ф- см.
Ответ, а) Зл/3 см; б) ^ см.
489. Докажите, что площадь равностороннего треугольника вычисляется
по формуле S = —-—, где а — сторона треугольника. Найдите площадь
равностороннего треугольника, если его сторона равна: а) 5 см; б) 1,2 см;
в) 2д/2 дм.
Решение. Проведем высоту BD равностороннего треугольника
ABC, в котором АВ = а. Высота BD является медианой треугольника
ABC, поэтому AD = -.
Применив теорему Пифагора к треугольнику ABD, получим:
4 2 '
BD = VAB2 - AD2 = \ а2 -— =
2 25\/3 2
cmz = —-— см ,
cm
б)	S = (MY см2 = 0,36л/3 см2;
ч с B\/2J- уД 2 о /о 2
в)	Ь =	 дм = 1у 6 дм .
Ответ, а) Щ^- см2; б) 0,36л/3 см2; в) 2л/3 дм2.
490. Найдите боковую сторону и площадь равнобедренного треугольника,
если: а) основание равно 12 см, а высота, проведенная к основанию, равна 8 см;
б)	основание равно 18 см, а угол, противолежащий основанию, равен 120°;
в)	треугольник прямоугольный и высота, проведенная к гипотенузе, равна 7 см.
Решение. Пусть в равнобедренном треугольнике ABC с основа-
основанием ВС проведена высота AD;

64	Гл. 2. Площадь
а) ВС = 12 см, АВ = 8 см, поэтому
Sabc = \ ' ВС - AD = i • 12 см • 8 см = 48 см2;
BD = DC = - ВС = 6 см. Из прямоугольного треугольника ABD
с помощью теоремы Пифагора находим:
АВ = \/AD2 + Б?>2 = л/36 + 64 = 10 см.
б) Так как треугольник ABC — равнобедренный, то его высота AD
является и биссектрисой, поэтому ZBAD = 60°, ZB = 30°. Отсюда
следует, что АВ = 2 • АВ. По теореме Пифагора АВ2 = AD2 + ED2,
а так как BD = ^BC = 9 см, то 4AD2 = AD2 + 81 см2. Отсюда AD2 =
= 27 см2, AD = Зл/3 см, АС = 6л/3 см.
• 18 см • Зл/З см = 27л/3 см2
SABC = \ ВС • AD = 1- • 18 см • Зл/З см = 27л/3 см
в) Так как треугольник ABC — равнобедренный, то его высота AD
является и медианой, а потому согласно задаче 404 ВС = 2 • AD =
= 7 см • 2 = 14 см.
Sabc = \ ВС • AD = i • 14 см • 7 см = 49 см2.
Из равнобедренного прямоугольного треугольника ABD находим:
АВ = VAD2 + Б?>2 = л/т^ТТ2 = 7л/2 см.
Ответ, а) 10 см и 48 см2; б) 6л/3 см и 27л/3 см2; в) 7лД см
и 49 см2.
491. По данным катетам а и Ь прямоугольного треугольника найдите
высоту, проведенную к гипотенузе: а) а = 5, Ь = 12; б) а = 12, 6 = 16.
Решение. Пусть гипотенуза равна с, высота, проведенная к гипо-
гипотенузе, равна h, a S — площадь треугольника. Тогда S = -oh и S =
= -с/г, откуда получаем: аб = ch или /г = —. Но с = л/а2 + Ъ2 (по тео-
теореме Пифагора), поэтому h =
а)	h = 5 • 12 : л/25 + 144 = ^ = 4^.
1 QO
б)	ft = 12 ¦ 16 : ^144 +256 = -^ = 9,6.
Ответ, а) 4-|; б) 9,6.
1 О
492. Найдите высоты треугольника со сторонами 10 см, 10 см и 12 см.
Решение. Пусть в треугольнике ABC: АВ = АС = 10 см, ВС =
= 12 см, AD — высота, проведенная к основанию ВС.

§ 3. Теорема Пифагора	65
Так как АВ = АС, то высота AD является и медианой, поэтому
= )-BC = 6 см.
Из прямоугольного треугольника ABD находим:
AD = л/АВ2 - BD2 = л/ЮО-36 = 8 (см).
Следовательно,
Sabc = I ВС • AD = i • 12 см • 8 см = 48 см2.
Пусть высота, проведенная к стороне АВ, равна h. Тогда
Sabc = ~ АВ • h или 48 см2 = - • 10 см • h, откуда h = 9,6 см.
Так как АВ = АС, то высота, проведенная к стороне АС, также
равна 9,6 см.
Ответ. 8 см, 9,6 см, 9,6 см.
493. Найдите сторону и площадь ромба, если его диагонали равны 10 см
и 24 см.
Решение. Пусть диагонали ромба ABCD пересекаются в точке О.
1. Так как диагонали ромба взаимно перпендикулярны и точкой
пересечения делятся пополам, то треугольник АОВ — прямоугольный
с катетами 5 см и 12 см. По теореме Пифагора
АВ = л/144 + 25 = л/169 = 13 (см).
2. Согласно задаче 476
Sabcd = \АС • BD = i • 10 см • 24 см = 120 см2.
Ответ. 13 см и 120 см2.
494. Найдите диагональ и площадь ромба, если его сторона равна 10 см,
а другая диагональ 12 см.
Решение. Пусть О — точка пересечения диагоналей ромба
ABCD.
1. Треугольник АОВ — прямоугольный с гипотенузой АВ = 10 см
и катетом АО = 6 см, поэтому
ВО = л/Ю0 - 36 = 8 (см) и BD = 2 • ВО = 16 (см).
2. Sabcd = \АС • BD = i • 12 см • 16 см = 96 см2.
Ответ. 16 см и 96 см2.
495. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 10 см, ВС = DA = 13 см, CD = 20 см; б) ZC = ZD = 60°, АВ =
= ВС = 8 см; в) ZC = ZD = 45°, АВ = б см, ВС = 9лД см.
3 Л. С. Атанасян и др.

66
Гл. 2. Площадь
В
Рис. 82
Решение. В трапеции ABCD с осно-
основаниями АВ и CD проведем высоты BE и
AF (рис.82).
а) Так как по условию трапеция равнобед-
D ренная {ВС = DA), то СЕ = DF = 1 (CD -
-АВ) = 1B0- 10) = 5 (см).
Из прямоугольного треугольника ВЕС по
теореме Пифагора находим:
BE = \/BC2 - СЕ2 = л/169 - 25 = 12 (см).
Sabcd = \ (АВ + CD) - BE = 15 см • 12 см = 180 см2.
б) Согласно задаче 389 трапеция ABCD — равнобедренная, так
как по условию углы при основании равны (АС = /-D = 60°). Отсюда
следует, что DF = СЕ.
Треугольник ВЕС — прямоугольный с углом В, равным 30°, по-
поэтому СЕ = - ВС = 4 см и по теореме Пифагора находим:
BE = VBC2 - СЕ2 = л/64 - 16 = л/48 = 4л/3 (см).
DC = 2 • ЕС + EF = 2 • 4 см + 8 см = 16 см.
Sabcd = \(АВ + DC) • БЕ = 1(8 см + 16 см) • 4л/3 см = 48л/3 см2.
в) В прямоугольном треугольнике ВСЕ АЕ = 90°, АС = 45°, по-
поэтому АВ = 45° и, следовательно, БЕ = СЕ. По теореме Пифагора
BE2
¦ СЕ2 = ВС2, или 2 • БЕ2 = 2-81 см2,
откуда BE2 = 81 см2, BE = 9 см.
Трапеция ABCD — равнобедренная, так как АС = ZD = 45° (за-
(задача 389, а), поэтому DF = СЕ = 9 см, а так как ЕЕ = АВ = 6 см, то
DC = DF + F? + ЕС = 9 см + 6 см + 9 см = 24 см.
Sabcd = \(АВ + DC) • BE = 1F см + 24 см) • 9 см = 135 см2.
Ответ, а) 180 см2; б) 48л/3 см2; в) 135 см2.
496. Основание D высоты CD треугольника
ABC лежит на стороне АВ, причем AD = ВС.
Найдите АС, если АВ = 3, a CD = лД.
Решение. Пусть AD = ВС = х. Тогда
BD = 3 — х (рис. 83). По теореме Пифагора для
В треугольника BCD имеем:
ВС2 = BD2 + CD2, или х2 = C - хJ + (л/3 J,
откуда ж = 2. Итак, AD = 2.

§ 3. Теорема Пифагора
67
По теореме Пифагора из треугольника ACD находим:
АС = \J AD2 + CD2 = л/4 + 3 = л/7 .
Ответ, л/7.
497. Одна из диагоналей параллелограмма является его высотой. Найдите
эту диагональ, если периметр параллелограмма равен 50 см, а разность
смежных сторон равна 1 см.
Решение. Пусть диагональ
BD параллелограмма ABCD яв-
является его высотой (рис.84). Так
как треугольник ABD — пря-
прямоугольный с гипотенузой АВ,
то АВ > AD и по условию АВ —
-AD=\ см.
По теореме Пифагора для тре-	Рис. 84
угольника ABD имеем:
BD = V'АВ2 - AD2 =
AD)(AB-AD).
Ясно, что АВ + AD есть полупериметр параллелограмма ABCD,
т. е. AB + AD = 25 см.
Поэтому BD = л/25- 1 = 5 (см).
Ответ. 5 см.
498. Выясните, является ли треугольник прямоугольным, если его стороны
выражаются числами: а) б, 8, 10; б) 5, б, 7; в) 9, 12, 15; г) 10, 24, 26; д) 3, 4,
6; е) 11, 9, 13; ж) 15, 20, 25. В каждом случае ответ обоснуйте.
Решение, а) Так как 102 = б2 + 82, то по теореме, обратной
теореме Пифагора, этот треугольник прямоугольный.
б)	Если треугольник прямоугольный, то квадрат его большей сторо-
стороны (гипотенузы) равен сумме квадратов двух других сторон (катетов).
Но в данном случае 72 ф 52 + б2, поэтому этот треугольник не является
прямоугольным.
в)	Треугольник прямоугольный, так как
г)	Треугольник прямоугольный, так как
262 = 102 + 242.
д)	Треугольник не прямоугольный, так как
е) Треугольник не прямоугольный, так как

68
Гл. 2. Площадь
ж) Треугольник прямоугольный, так как
252 = 202 + 152.
Ответ, а) Да; б) нет; в) да; г) да; д) нет; е) нет; ж) да.
499. Найдите меньшую высоту треугольника, если его стороны равны:
а) 24 см, 25 см, 7 см; б) 15 см, 17 см, 8 см.
Решение, а) Так как 252 = 242 + 72, то по теореме, обратной
теореме Пифагора, данный треугольник является прямоугольным. Его
катеты а = 24 см и Ъ = 7 см, а гипотенуза с = 25 см. Две высоты
этого треугольника равны соответственно его катетам, а высоту h,
проведенную к гипотенузе, вычислим по формуле h = — (см. решение
задачи 491): h =
24-7
25
см = 6,72 см. Очевидно, эта высота треугольни-
треугольника является наименьшей.
б) Так как 172 = 152 + 82, то данный треугольник — прямоугольный
с катетами а = 15 см и Ъ = 8 см и гипотенузой с = 17 см. Как и в
п. а, меньшей высотой треугольника является высота h, проведенная
, аЪ и 15-8	„ 1
к гипотенузе: h = —, h =	см = 7— см.
Ответ, а) 6,72 см; б) 7— см.
Дополнительные задачи
500. Докажите, что площадь квадрата, построенного на катете равно-
равнобедренного прямоугольного треугольника, вдвое больше площади квадрата,
построенного на высоте, проведенной к гипотенузе.
Решение. На рисунке 85 треуголь-
треугольник ABC — равнобедренный прямоугольный,
АН — высота, проведенная к гипотенузе ВС,
ABDC — квадрат, построенный на катете АВ.
Высота АН является также медианой
треугольника ABC, поэтому ВН = НС =
= АН (см. задачу 404). Отсюда следует, что
точка С является вершиной квадрата, постро-
построенного на высоте АН.
Диагональ ВС квадрата ABDC разбивает
его на два равных треугольника, поэтому
Sabdc =
Рис. 85
Аналогично, Sahck — ^Sahc- Но высота АН разбивает треуголь-
треугольник ABC на два равных треугольника, поэтому Sabc = 2$анс и>
следовательно,
Sahck = Sabc-	B)

Дополнительные задачи	69
Из равенств A) и B) получаем:
Sab dc = 2Sahck,
что и требовалось доказать.
501.	Площадь земельного участка равна 27 га. Выразите площадь это-
этого же участка: а) в квадратных метрах; б) в квадратных километрах.
Решение, а) 27 га = 270000 м2, так как 1 га = A00 мJ =
= 10000 м2.
б) 27 га = 0,27 км2, так как 1 га = 0,01 км2.
Ответ, а) 270000 м2; б) 0,27 км2.
502.	Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см.
Найдите площадь параллелограмма.
Решение. Пусть смежные стороны параллелограмма равны а и Ъ,
а проведенные к ним высоты равны соответственно 5 см и 4 см.
Тогда 2(а + Ь) = 42 см и S = 5 • а = 4 • Ъ, где S — площадь парал-
4	/ 4 \
лелограмма. Отсюда получаем а = - Ъ, поэтому 2(Ь+-Ь) =42 см,
35
откуда Ь = — см и, следовательно,
S = 4 • — cmz = 46- см.
Ответ. 46- см2.
о
503. Найдите периметр параллелограмма, если его площадь равна 24 см2,
а точка пересечения диагоналей удалена от сторон на 2 см и 3 см.
Решение. Пусть в параллелограмме ABCD диагонали пересека-
пересекаются в точке О, ОМ — перпендикуляр к стороне АВ, ОМ = 2 см,
и пусть прямая ОМ пересекает сторону CD в точке N. Тогда MN —
высота параллелограмма, проведенная к противоположным сторонам
АВ и CD. Так как О — центр симметрии параллелограмма, то ON =
= ОМ и поэтому
MN = 2 • ОМ = 4 см.
Sabcd = АВ • MN, или 24 см2 = 4 см • АВ,
откуда АВ = 6 см.
Аналогично, от каждой из двух других противоположных сторон
параллелограмма (AD и ВС) точка О удалена на 3 см, поэтому высота
параллелограмма, проведенная к сторонам AD и ВС, равна 6 см.
Из равенства 24 см2 = 6 см • AD получаем AD = 4 см.
Pabcd = 2(АВ + AD) = 2F см + 4 см) = 20 см.
Ответ. 20 см.

70	Гл. 2. Площадь
504. Меньшая сторона параллелограмма равна 29 см. Перпендикуляр,
проведенный из точки пересечения диагоналей к большей стороне, делит ее на
отрезки, равные 33 см и 12 см. Найдите площадь параллелограмма.
Решение. Пусть в параллелограмме ABCD АВ < AD, AB =
= 29 см, ON — перпендикуляр, проведенный из точки О пересечения
диагоналей к стороне AD, AN = 33 см,
ND = 12 см (рис.86).
Проведем высоту ВЫ данного паралле-
параллелограмма. Так как ВО = OD и ВЫ || ON,
то MN = ND = 12 см (см. задачу 384) и,
следовательно,
Рис. 86	AM = AN - NM = 33 см - 12 см = 21 см.
Применив теорему Пифагора к треугольнику АВМ, найдем высо-
высоту ВЫ:
ВЫ = л/292-212 = л/8-50 = 20 (см).
Sabcd = AD • ВЫ = 45 см • 20 см = 900 см2.
Ответ. 900 см2.
505.	Докажите, что из всех треугольников, у которых одна сторона равна
а, а другая — Ь, наибольшую площадь имеет тот, у которого эти стороны
перпендикулярны.
Решение. Пусть в треугольнике ABC: ВС = а, АС = Ъ, AD = ha,
где AD — высота треугольника. Тогда Sabc = т;а' ha-
Если стороны АС и ВС не перпендикулярны, то AD < АС (пер-
(перпендикуляр меньше наклонной), т. е. ha < Ъ и поэтому Sabc < ^&Ъ.
Если же АС !_ ВС, то сторона АС совпадает с высотой AD, т. е. ha =
= Ъ. В этом случае
Sabc = ^ а^-
Таким образом, наибольшую площадь имеет тот треугольник, у ко-
которого стороны, равные а и Ь, перпендикулярны.
506.	Как провести две прямые через вершину квадрата, чтобы разделить
его на три фигуры, площади которых равны?
Решение. Искомые прямые не могут пересечь одну и ту же сторо-
сторону квадрата, так как в этом случае площадь одной из трех указанных
в задаче фигур (четырехугольник АВСМ на рисунке 87, а) больше
-S, где S — площадь квадрата. Поэтому искомые прямые, проведенные
через вершину А, пересекают стороны квадрата ABCD в точках М
и N так, что одна из этих точек, например, точка М, лежит на стороне
ВС, а другая — на стороне DC (рис.87, б).

Дополнительные задачи
71
N М
Рис. 87
Пусть АВ = а, ВЫ = х. По условию
о	1 о а	1	12
Ьавм = -Ь = —, т. е. -ах = -а ,
откуда х = - а.
о
Итак, ВЫ = \ ВС. Аналогично DN = \ DC.
о	о
507* Каждая сторона одного треугольника больше любой стороны другого
треугольника. Следует ли из этого, что площадь первого треугольника больше
площади второго треугольника?
Решение. Приведем пример, показывающий, что площадь перво-
первого треугольника может быть меньше площади второго треугольника.
Пусть в треугольнике ABC: АВ = ВС = 13, АС = 24, BD - вы-
высота, а треугольник А\В\С\ — равносторонний со стороной, равной
12 (рис. 88). Тогда AD = i AC = 12,
BD = л/АВ2 - AD2 = л/132 — 122 = 5,
Sabc = \АС - BD = i • 24 • 5 = 60,
122-^3
S
(задача 489), т. е.
= 36л/3 > 60 > SABC.
Итак, площадь треугольника ABC, каждая сторона которого боль-
больше любой стороны треугольника А\В\С\, меньше площади треуголь-
треугольника A\BiC\.
Ответ. Нет.
В
13.
D
\
1
24
V 13
\
12
12
Рис. .

72
Гл. 2. Площадь
508* Докажите, что сумма расстояний от точки на основании равнобед-
равнобедренного треугольника до боковых сторон не зависит от положения этой точки.
Решение. Пусть D — произвольная точка на основании АС
равнобедренного треугольника ABC, a DM и DN — перпендикуляры,
проведенные из этой точки к прямым АВ и CD (рис.89).
Sabc =	\^
Отсюда следует, что DM + DN =
не зависит от выбора точки D.
9 Я
—ттр">
т- е- сумма DM + DN
509. Докажите, что сумма расстояний от точки, лежащей внутри равно-
равностороннего треугольника, до его сторон не зависит от положения этой точки.
Решение. Пусть О — произвольная точка, лежащая внутри рав-
равностороннего треугольника ABC со стороной, равной а, а ОК, ОМ
и ON — перпендикуляры к прямым, содержащим стороны этого тре-
треугольника (рис.90). Тогда
Sabc = Saob + Sboc
= \(OK-AB
Отсюда получаем
+ SCOA =
+ OM-BC-
OK+OM+
f ОЛ
¦ON
T-AC) = a-{C
2Sabc
Ш + ОМ-
e. сумма
OK +
+ OM + 07V не зависит от выбора точки О.
510* Через точку D, лежащую на стороне ВС треугольника ABC, про-
проведены прямые, параллельные двум другим сторонам и пересекающие стороны
АВ и АС соответственно в точках Е и F. Докажите, что треугольники CDE
и BDF имеют равные площади.
Решение. Пусть ВМ — высота треугольника BDF, а С К —
высота треугольника CDE (рис.91). Заметим, что ВМ и СК равны
высотам параллелограмма AEDF, поэтому
Sbdf = n
Saedf,
и, следовательно, Sbdf = Scde-
Scde = n
Saedf,
м
к
Рис. 90

Дополнительные задачи
73
511. В трапеции ABCD с боковыми сторонами АВ и CD диагонали
пересекаются в точке О. а) Сравните площади треугольников ABD и ACD.
б) Сравните площади треугольников АВО и CDO. в) Докажите, что О А х
хОВ = ОС- OD.
Решение, а) Треугольники ABD и ACD имеют равные высоты
ВН = CZ (рис.92) и общее основание AD, следовательно, Sabd =
= Sacd •
б)	Sabd = Sabo + Saod, Sacd = Scdo + Saod- Но по доказан-
доказанному в п. a) Sabd = Sacd, поэтому Sabo — Scdo-
в)	Углы 1 и 2 равны, поэтому
Sabo : #cdo = (ОА • ОБ) : (ОС • OD).
По доказанному в п. б) Sabo = Scdo, следовательно,
ОА • ОБ = ОС • OD.
Ответ, а) Площади равны; б) площади равны.
512* Основания трапеции равны а и Ъ. Отре-
Отрезок с концами на боковых сторонах трапеции, па-
параллельный основаниям, разделяет трапецию на две
трапеции, площади которых равны. Найдите длину
этого отрезка.
Решение. Пусть ABCD — данная тра-
трапеция, AD = а, ВС = b, a EF — указанный
в условии задачи отрезок (рис.93). Высота BN
трапеции пересекает этот отрезок в точке М. Пусть EF = х, ВЫ = h\,
MN = h2.
По условию Sfcbe = Saefd, и, значит,
Sabcd = 2Sebcf-
Запишем эти равенства, используя формулу площади трапеции:
Ъ + х , а + х
С
Рис-
+ft2) = (Ь
/12,
¦X)-

74	Гл. 2. Площадь
Разделим оба эти уравнения на h\ и положим — =у. Получим систему
fti
двух уравнении с двумя неизвестными х и у.
+ х = (а + х)у,
Исключив из этих двух уравнений у, получим:
=2(Ъ + х).
Отсюда находим: х = w
Ответ.
513. Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба
и расстояние между параллельными сторонами.
Решение. 1) Пусть в ромбе ABCD диагонали АС и BD пересека-
пересекаются в точке О. Диагонали ромба взаимно перпендикулярны и точкой
пересечения делятся пополам, поэтому в прямоугольном треугольнике
АОВ АО = 90°, О А = 12 м, ОВ = 9 м, и по теореме Пифагора
находим:
АВ = \/ОА2 + ОБ2 = \/l22 + 92 м = 15 м.
Pabcd = 4 • АВ = 4 • 15 м = 60 м.
2) Расстояния между попарно параллельными сторонами ромба
равны высоте ft ромба. Так как Sabcd = АВ • ft, а с другой стороны
Sabcd = \АС • BD (задача 476), то АВ • ft = Х-АС • BD, откуда
AC-BD 24-18
Ответ. 60 м и 14,4 м.
514. Площадь ромба равна 540 см , а одна из его диагоналей равна 4,5 дм.
Найдите расстояние от точки пересечения диагоналей до стороны ромба.
Решение. Пусть в ромбе ABCD диагонали АС и BD пересека-
пересекаются в точке О, АС = 4,5 дм = 45 см.
Сначала найдем диагональ BD:
Sabcd = \АС ¦ BD,
откуда
~ АС ~ 45 СМ ~

Дополнительные задачи
Треугольник АОВ — прямоугольный, и его катеты ОВ и О А равны
12 см и 22,5 см, поэтому
АВ =
f 22,52 = V650,25 = 25,5 (см)
и P = 4 • 25,5 см = 102 см.
Расстояние от точки пересечения диагоналей до стороны ромба
равно половине высоты h ромба. Так как Sabcd = АВ • h, то
h = Sabcd = ^40 см = 2{3_ ^
Ответ. 10— см.
515.	Найдите площадь равнобедренного треугольника, если: а) боковая
сторона равна 20 см, а угол при основании равен 30°; б) высота, проведенная
к боковой стороне, равна б см и образует с основанием угол в 45°.
Решение, а) Пусть в равнобедренном треугольнике ABC: АВ =
= АС = 20 см, ZB = 30°, отрезок AD - высота. Тогда BD = DC =
= - ВС, и из прямоугольного треугольника ABD находим: AD =
= - АВ = 10 см (по свойству катета, лежащего против угла в 30°).
Поэтому BD = VAB2 - AD2 = л/400 - 100 = Юл/3 (см) (по теореме
Пифагора) и ВС = 2BD = 20л/3 см.
Sabc = \bc 'AD=\' 20^3 см • 10 см = 100л/3 см2.
б) Пусть в равнобедренном треугольнике ABC с основанием ВС
проведена высота BD к боковой стороне АС, тогда по условию BD =
= 6 см, ZDBC = 45°. Треугольник В DC — прямоугольный с углом
В, равным 45°, поэтому ZC = 45°. Так как треугольник ABC —
равнобедренный, то и ZABC = 45°, а это означает, что угол DBC
совпадает с углом ABC, т. е. треугольник ABC — прямоугольный
с катетами, равными 6 см. Следовательно,
^авс = х • 6 см • 6 см = 18 см2.
Ответ, а) 100л/3 см2; б) 18 см2.
516.	В треугольнике ABC: ВС = 34 см. Перпен-
Перпендикуляр MN, проведенный из середины ВС к пря-
прямой АС, делит сторону АС на отрезки AN = 25 см
и NC = 15 см. Найдите площадь треугольника ABC.
Решение. Проведем высоту BD данного
треугольника (рис.94). Так как точка М — се-
середина стороны ВС и MN || BD, то DN =
= NC (см. задачу 384).
Рис. 94

76
Гл. 2. Площадь
В треугольнике BCD: ВС = 34 см, DC = 2NC = 30 см, следова-
следовательно,
BD = л/342 - 302 см = л/64-4 см = 16 см.
Sabc = \АС - BD = ^
Ответ. 320 см2.
NC) • BD = i • 40 см • 16 см = 320 см2.
517. Найдите площадь четырехугольника ABCD, если АВ = 5 см, ВС =
= 13 см, CD = 9 см, DA = 15 см, АС = 12 см.
Решение. Стороны треугольника ABC (рис.95) выражаются чис-
числами 5, 12, 13, а так как 132 = 122 + 52, то по теореме, обратной
теореме Пифагора, треугольник ABC — прямоугольный, и поэтому
SABC = \ • 12 см • 5 см = 30 см2.
Аналогично, треугольник ACD — прямоугольный, так как 152 =
= 122 + 92, и поэтому
Sacd = х • 12 см • 9 см = 54 см2.
Заметим, что точки В и D лежат по разные стороны от прямой
АС (в противном случае отрезки AD и ВС пересекались бы), поэтому
Sabcd = Sabc + Sacd = 30 см2 + 54 см2 = 84 см2.
Ответ. 84 см2.
518. Найдите площадь равнобедренной трапеции, если: а) ее меньшее
основание равно 18 см, высота — 9 см и острый угол равен 45°; б) ее основания
равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
Решение, а) Пусть в равнобедренной трапеции ABCD: ВС —
меньшее основание, BF и СЕ — высоты (рис.96).
AABF — прямоугольный с острым углом в 45°, поэтому он равно-
равнобедренный и, значит, AF = BF = 9 см.
Рис. 95
Рис. 96

Дополнительные задачи	11
Так как трапеция равнобедренная, то ED = AF = 9 см, а так как
FE = ВС = 18 см, то
AD = 2AF + EF = 36 см.
Sabcd = \ {ВС + AD) - BF = i A8 + 36) • 9 см2 = 243 см2.
б) Пусть в равнобедренной трапеции
ABCD с основаниями AD = 30 см и ВС =
= 16 см диагонали АС и BD взаимно пер-
перпендикулярны и пересекаются в точке О,
MN — высота трапеции, проходящая через
точку О (рис.97).
AABD = ADCA по двум сторонам и углу
между ними (АВ = DC, AD — общая сто-
сторона, ZA = ZD), поэтому Zl = Z2. Так как
Z3 = Zl, Z4 = Z2 (вследствие параллельности
ВС и AD), то Z3 = Z4. Отсюда следует, что треугольники AOD
и ВОС — равнобедренные, а поскольку AC _L BD, то эти треугольни-
треугольники — прямоугольные. Высоты ON и ОМ являются также медианами
этих треугольников, а потому согласно задаче 404: ON = - AD, ОМ =
= - ВС. Следовательно,
MN= i (AD + ВС) =23 см.
SWd = ^ (AD + ВС) • MN = MN2 = B3 смJ = 529 см2.
Ответ, а) 243 см2; б) 529 см2.
519. Найдите площадь равнобедренной трапеции, у которой высота равна
h, а диагонали взаимно перпендикулярны.
Решение. Пусть в равнобедренной трапеции ABCD со взаимно
перпендикулярными диагоналями высота равна h.
Тогда - (AD + ВС) = h (см. решение задачи 518, б).
Поэтому SABcd = \ (AD + ВС) -h = h2.
Ответ, h2.
520. Диагонали равнобедренной трапеции взаимно перпендикулярны,
а сумма ее оснований равна 2а. Найдите площадь трапеции.
Решение. Пусть в равнобедренной трапеции ABCD со взаим-
взаимно перпендикулярными диагоналями AD + ВС = 2а, MN — высота

78
Гл. 2. Площадь
трапеции (см. рис.97). Тогда MN = - (AD + ВС) = а (см. решение
задачи 518, б). Поэтому
Sabcd = ±
CD) • MN = а2.
Ответ, а2.
521. Докажите, что если диагонали выпуклого четырехугольника ABCD
взаимно перпендикулярны, то
AD2 + BC2 = АВ2 + CD2.
Решение. Пусть О — точка пересечения диагоналей АС
и BD (рис.98).
Используя теорему Пифагора, получаем:
AD2 + ВС2 = DO2 + АО2 + ВО2 + СО2;
АВ2 + CD2 = АО2 + ВО2 + СО2 + DO2.
Следовательно,
AD2 + BC2 =
CD2.
522. В равнобедренной трапеции ABCD с основаниями AD = 17 см,
ВС = 5 см и боковой стороной АВ = 10 см через вершину В проведена пря-
прямая, делящая диагональ АС пополам и пересекающая основание AD в точке
М. Найдите площадь треугольника BDM.
Решение. Пусть ВК — высота данной трапеции ABCD, точка
О — середина диагонали АС (рис.99).
ААОМ = АСОВ по стороне (АО = СО) и двум прилежащим
углам, следовательно, AM = ВС = 5 см, и поэтому
MD = AD - AM = 17 см - 5 см = 12 см.
Так как трапеция ABCD равнобедренная, то
Аъг AD-ВС а
АК =	= 6 см.
Рис. 98

Дополнительные задачи
79
Из прямоугольного треугольника АВК находим:
ВК = л/АВ2 - АК2 = л/Ю2-62 = 8 (см).
Sbdm = \ MD • ВК = i • 12 см • 8 см = 48 см2.
Ответ. 48 см2.
а2
а = "о"-
Рис. 100
523. Два квадрата со стороной а имеют одну
общую вершину, причем сторона одного из них лежит
на диагонали другого. Найдите площадь общей части
этих квадратов.
Решение. Пусть ABCD и CKMN - дан-
данные квадраты, АВ = СК = а (рис. 100). Об-
Общей частью данных квадратов является четырех-
четырехугольник CKFD с искомой площадью S.
S = Sacd — Sakf,
1
ACD - ? (
Треугольник AKF — прямоугольный с углом А, равным 45°, по-
поэтому этот треугольник равнобедренный и KF = АК = АС — КС =
= ал/2 -а = (л/2 - 1)а.
Следовательно,
^	l^z?2 1 / /о i\2 2 3 — 2v 2 2
-А^ =-(V^-lJa =	-а.
_ о^ _ 3-2\/2
Ответ, (л/2 - 1)а2.
= (л/2 -
525. Расстояние от точки М, лежащей внутри треугольника ABC, до пря-
прямой АВ равно б см, а до прямой АС равно 2 см. Найдите расстояние от точки
М до прямой ВС, если АВ = 13 см, ВС = 14 см, АС = 15 см.
Решение. По формуле Герона (задача 524) находим:
SUsc = л/21 • 6 • 7 • 8 см2 = 84 см2.
Соединим точку М с вершинами треугольника ABC и проведем
высоты MD, MF и МР в образовавшихся треугольниках (рис. 101).
По условию MD = 6 см, MF = 2 см, а тре-
требуется найти МР. Имеем:
Samb + Samc + Sbmc =
+ -Uc • MF + -Uc • MP
Отсюда, используя условия задачи, по- Л
лучаем:
84 = iA3-6+ 15-2+ 14-МР).

80
Гл. 2. Площадь
Из этого равенства находим: МР = 4- см.
Ответ. 4- см.
526. В ромбе высота, равная
4\/2
см, со-
ставляет — большей диагонали. Найдите пло-
о
щадь ромба.
Решение. Пусть диагонали ромба
ABCD пересекаются в точке О, АС >
> BD, MN — высота ромба, проходящая
4л/2
через точку О, MN = —— см, MN =
= %АС (рис. 102). Тогда АС = \mN = ^ см, ОС = Х-АС = ^ см,
о	о	о	Z	о
ОМ = ^MN = ^ф- см.
Рассмотрим прямоугольный треугольник ВОС. По теореме Пифа-
Пифагора
ВС = VOB2 + ОС2 = Х/ОВ2 + А- см2
Так как
Sboc = \
и SBoc = \ом • ВС = ^
- см2 , то
или
2 9
- см^ .
Возведем обе части последнего равенства в квадрат:
р2 , 2 о>
9 • ОБ2 = 4 (ОБ2 + | см2) .
~	^D 2\/2
Отсюда находим: ОВ = —— см и, следовательно,
3\/5
= 2ОБ =
1 А
3\/5
см •
cm.
см =
см2.
П
Ответ.
2
см .

Дополнительные задачи
81
527. В равнобедренной трапеции диагональ
равна 10 см, а высота равна б см. Найдите
площадь трапеции.
Решение. Пусть ABCD — данная
равнобедренная трапеция с основаниями
AD и ВС, ВК и СН - ее высо-
высоты (рис. 103).
Из прямоугольного треугольника АСН
по теореме Пифагора находим:
АН = VAC2 -СН2 = л/Ю2-62 см = 8 см.
Так как АК = HD, ВС = КН, то
i {AD + ВС) = ^(КН + 2АК + КН) =
В
Поэтому
= АН.
= \(AD + ВС) • СЯ =
• СЯ = 8 см • 6 см = 48 см2
Ответ. 48 см2.
528. В трапеции ABCD диагонали пересекаются в точке О. Найдите
площадь треугольника АОВ, если боковая сторона CD трапеции равна 12 см,
а расстояние от точки О до прямой CD равно 5 см.
Решение. Пусть ОЕ — перпендикуляр, проведенный к прямой
CD (рис. 104).
Тогда ОЕ = 5 см (по условию), поэтому
Scod = t,CD • ОЕ = ^ • 12 см • 5 см = 30 см2.
Согласно задаче 511,6: Saob =
= 30 см2.
Ответ. 30 см2.
, следовательно, Saob =
529. Диагонали четырехугольника равны 16 см и 20 см и пересекаются
под углом в 30°. Найдите площадь этого четырехугольника.
Решение. Пусть ABCD — данный четырехугольник, диагонали
которого пересекаются в точке О, АЕ и CF — перпендикуляры к пря-
прямой BD (рис. 105).
Рис. 104
Рис. 105

82
Гл. 2. Площадь
Так как А АО В = ZCOD = 30°, то
АЕ = l-AO, CF=l-OC.
Следовательно,
Sabd = \BD • АЕ = l-BD • l-AO = l-BD • АО,
Sbcd = \BD • CF = l-BD • l-OC = l-BD • ОС.
Sabcd = SAbd + SBCD = \bD • АО + l-BD • ОС =
= \BD • (АО + ОС) = \BD • AC = 80 см2.
Ответ. 80 см2.
530. В равнобедренном треугольнике ABC с основанием ВС проведена
высота AD, равная 8 см. Найдите площадь треугольника ABC, если медиана
DM треугольника ADC равна 8 см.
Решение. AADC — прямоугольный, DM — его медиана, прове-
проведенная к гипотенузе (рис. 106), поэтому, согласно задаче 404, DM =
= i АС, откуда AC = i DM = 16 см.
Из треугольника ADC по теореме Пифагора находим:
Г\Т2 см = 8л/3 см.
DC = VAC2 - AD2 = V256 - 64 см =
Так как треугольник ABC — равнобедренный, то его высота AD
является также и медианой, поэтому
ВС = 2DC = 16л/3 см.
Sabc = \ВС • AD = 8л/3 см • 8 см = 64л/3 см2.
Ответ. 64л/3 см2.
531. Стороны АВ и ВС прямоугольника ABCD равны соответственно
б см и 8 см. Прямая, проходящая через вершину С и перпендикулярная
к прямой BD, пересекает сторону AD в точке М, а диагональ BD — в точке
К. Найдите площадь четырехугольника АВКМ.
Решение. Sabkm = Sabd ~ SKmd (рис. 107),
М

Дополнительные задачи
83
Sabd = \ АВ - AD = i • 6 см • 8 см = 24 см2.
Чтобы вычислить Skmd, найдем KD и КМ.
В прямоугольном треугольнике BCD отрезок СК — высота, про-
проведенная к гипотенузе, поэтому (см. решение задачи 491)
ВС -CD	6-8
СК =
л/ВС2 + CD2
По теореме Пифагора имеем:
см = 4,8 см.
KD = \/CD2 - С К2 = л/б2 - 4,82 см = 3,6 см.
Отрезок KD — высота прямоугольного треугольника CDM, прове-
проведенная к гипотенузе, поэтому
CD-
KD = _^^^^ или 3,6\/36 см2 + DM2 = 6DM.
VCD2 + DM2
Отсюда после возведения в квадрат находим DM = 4,5 см.
По теореме Пифагора
КМ = VDM2 - KD2 = л/4,52 - 3,62 см = 2,7 см.
Следовательно,
Skmd = \ КМ • KD = i • 2,7 см • 3,6 см = 4,86 см2.
Sabkm = SABD ~ SKMD = 24 см2 - 4,86 см2 = 19,14 см2.
Ответ. 19,14 см2.
532. В треугольнике ABC проведена высота ВН. Докажите, что: а) если
угол А — острый, то ВС2 = АВ2 + АС2 — 2АС • АН; б) если угол А — тупой,
то ВС2 = АВ2 + АС2 + 2АС • АН.
Решение, а) Так как в треугольнике ABC угол А — острый,
то точка Н может лежать на стороне АС (рис. 108, а), лежать
на продолжении стороны АС (рис. 108, б) или совпадать с точкой
С (рис. 108, в). В последнем случае АН = АС и поэтому нужно
доказать, что
В
н
Рис. 108

84	Гл. 2. Площадь
ВС2 = АВ2 + АС2 - 2АС2, т. е. ВС2 = АВ2 - АС2.
Это верно в силу теоремы Пифагора.
Рассмотрим случаи, представленные на рисунках 108, а и 108, б.
Из прямоугольного треугольника ВНС по теореме Пифагора имеем:
ВС2 = ВН2 + НС2,
а из прямоугольного треугольника АВН:
ВН2 = АВ2 - АН2.
Поэтому
JJC = AJd —АЛ. -\-НС .	[[)
HC = AC - АН (рис. 108, а), либо НС = АН - AC (рис. 108, б).
В любом случае
НС2 = АС2 - 2АС • АН + АН2.
Теперь равенство A) можно записать так:
ВС2 = АВ2 - АН2 + АС2 - 2АС • АН + АН2,
или
ВС2 = АН2 + АС2 - 2АС • АН,
что и требовалось доказать.
б) Так как в треугольнике в ABC угол А —
тупой, то точка Н лежит на продолжении сторо-
стороны АС (рис. 109).
Из прямоугольного треугольника ВНС
по теореме Пифагора имеем:
ВС2 =ВН2 + НС2,
а из прямоугольного треугольника АВН:
ВН2 = АВ2-АН2.
Поэтому
ВС2 = АВ2 - АН2 + НС2.	B)
Так как НС = АН + АС, то
НС2 = АН2 + 2АС • АН + АС2.
Теперь равенство B) можно записать так:
БС2 = АБ2 - АН2 + АН2 + 2АС • АН + АС2,
ВС2 = АВ2 + АС2 + 2АС • АН,
что и требовалось доказать.

Задачи повышенной трудности
85
Задачи повышенной трудности
829. Через точку М, лежащую внутри параллелограмма ABCD, прове-
проведены прямые, параллельные его сторонам и пересекающие стороны АВ, ВС,
CD и DA соответственно в точках Р, Q, R и Т. Докажите, что если точка
М лежит на диагонали АС, то площади параллелограммов MPBQ и MRDT
равны, и, обратно, если площади параллелограммов MPBQ и MRDT равны,
то точка М лежит на диагонали АС.
Решение. Сначала докажем прямое утверждение. Пусть точка
М лежит на диагонали АС (рис. ПО, а). Так как ААВС = AADC,
Рис. ПО
ААРМ = АМТА и AMQC = ACRM, то
Smpbq = Sabc — Sapm — Smqc =
= Sadc — Smta — Scrm = Smrdt-
Итак, Smpbq = SMrdt-
Пусть теперь точка М не лежит на отрезке АС. Обозначим через N
точку пересечения отрезков АС и QT, а через Р\ и R\ точки пересече-
пересечения прямой, проходящей через точку N параллельно AD, с отрезками
АВ и CD (рис. ПО, б). Согласно доказанному Snp{bq = Snr{dt- Если
точка М лежит между точками N и Т (рис.110, б), то Smpbq >
> SNP{bq, a Smrdt < SNr{DT, и поэтому Smpbq ф SMrdt- Если
точка М лежит между Q и N, то аналогично приходим к неравенству
Smpbq ф Smrdt- Следовательно, если Smpbq = SMrdt, то точка М
лежит на отрезке АС.
830. На сторонах АС и ВС треугольни-
треугольника ABC взяты соответственно точки М и К.
Отрезки АК и ВЫ пересекаются в точке О.
Найдите площадь треугольника СМК, если
площади треугольников ОМА, ОАВ и ОВК
равны соответственно S\, S2, S3.
Решение. На рисунке 111 изобра-
изображена данная фигура. Пусть Somk = #4,
Scmk = S. Так как площади треуголь-
М
Рис. 111
ников, имеющих равные высоты, относятся как основания (следствие 2,
п. 52), то
МО : ОВ = S4 : S3 = Sx : 52.

86	Гл. 2. Площадь
Отсюда находим: S\ = 1 3. Еще раз применяя следствие 2, п. 52,
получаем:	2
В К : КС = Sbmk • Scmk = Sbak • Scak,
или
Отсюда, используя выражения для S4, после соответствующих пре-
преобразований находим S:
S =	о	.
831. На сторонах АС и БС треугольника ABC взяты точки М и
^^	^^	МР тт о
а на отрезке Mil — точка г* так, что	= —— = . Найдите площадь
треугольника АБС, если площади треугольников AMP и ВКР равны Si и S2.
Решение. Введем обозначение:
AM С К МР
Сравнивая площади треугольников AMP и СМР, получаем
Samp AM
Scmp MC
= х,
откуда Scmp = - • S\.
Аналогично, сравнивая площади треугольников ВКР и СКР, на-
находим: Sckp = х • S2.
х Scmp МР	~ 'S{	3[S^
1ак как —	 = —— = х, то ^—— = ж, откуда х = Р/тг > и»
следовательно,
Scmp = - • S\ = JS\S^, Sckp = x • S2 = у
Sckm = ^ckp + Scmp = у S\S^ + у
Воспользуемся теперь теоремой об отношении площадей треуголь-
треугольников, имеющих по равному углу:
СК-СМ'
СБ-СА СК + КВ СМ + МА
Поэтому ^лбс = A + -) A

Задачи повышенной трудности
87
Подставляя в правую часть этого равенства выражения для
и Sckm, после несложных преобразований приходим к равенству
Ответ.
832. Точки Р, Q, R и Т — соответственно середины сторон АВ, ВС, CD
и DA параллелограмма ABCD. Докажите, что при пересечении прямых AQ,
BR, СТ и DP образуется параллелограмм, и найдите отношение его площади
к площади параллелограмма ABCD.
Решение. Данная фигура изображена на рисунке 113, где
MNKL — четырехугольник, образованный при пересечении прямых
AQ, BR, СТ и DP.
Так как AT || CQ и AT = CQ, то ATCQ — параллелограмм,
поэтому MN || LK. Аналогично, ML || NK, следовательно, MNKL —
параллелограмм.
Пусть S — площадь параллелограмма MNKL, BF J_ CT
(см. рис.113). Тогда BF J_ AQ и, следовательно, отрезок
BE — высота треугольника ABN, а отрезок EF равен вы-
высоте параллелограмма MNKL, проведенной к стороне MN.
Так как BQ = QC, то BE = EF (задача 384), а так как
АР = РВ, то AM = MN и поэтому AN = 2MN. Следова-
Следовательно,
5 = MN • EF = MN • BE,
SABN = \AN • BE = MN -BE = S.
Аналогично можно доказать, что площадь каждого из треугольни-
треугольников ADM, CDL и СВК также равна S. Поэтому
С	гп SmNKL
^ABCD = 00 И -—
Sab cd
5S
Ответ. -.
5
R F
M
Рис. 112
Рис. 113

Гл. 2. Площадь
833. Докажите, что площадь трапеции равна произведению одной из бо-
боковых сторон на перпендикуляр, проведенный из середины другой боковой
стороны к прямой, содержащей первую боковую сторону.
Решение. Пусть ABCD — данная трапеция, М — середина
боковой стороны CD, a МК — перпендикуляр, проведенный к прямой
АВ (рис.114).
Докажем, что S = АВ • МК, где S — площадь трапеции.
S = Sam в + Samd + Sbmc-
Проведем через точку М высоту PQ трапеции (см. рис. 114). Тогда
Так как ACMQ = ADMP (по гипотенузе и острому углу),
то MQ = МР и поэтому
S
amd
= \{AD + ВС) -МР=1-- AD + BC . PQ = i5.
Таким образом, S = Sam в + ^S, откуда S = 2Samb-
Ho Samb = n
' МК, следовательно,
S = AB • MK.
834. В трапеции ABCD с основаниями ВС и AD диагонали пересекаются
в точке О. Площади треугольников ВОС и AOD равны Si и $2. Найдите
площадь трапеции.
Решение. Согласно задаче 511,6 площади треугольников АО В
и COD равны. Обозначим эти площади буквой S (рис. 115).
Площади S\ и #2 относятся как произведения сторон, заключающих
- ГЛ <	О	?ОЧ	Si	OB -ОС
равные углы с вершиной О (теорема 2, п. 52), т. е. — =
тт Si ОС Si OB ,	11 r\
Но — = -—- и — = ——- (см. рис. 115), и, следовательно,
Ь J J\ Ь CJ-LJ
откуда S =
OA-OD'
Рис. 114
Рис. 115

Задачи повышенной трудности
89
Таким образом,
О	ОС I С I С	О Го О I С I С	/ /~О~ I / О \2
&ABCD — ^^ ~\- о\ -\- О2 — Zy о\О2 + Oi + 02 — (у о\ + уО2 J .
Ответ.
835. Через концы меньшего основания трапеции проведены две парал-
параллельные прямые, пересекающие большее основание. Диагонали трапеции и эти
прямые делят трапецию на семь треугольников и один пятиугольник. Дока-
Докажите, что площадь пятиугольника равна сумме площадей трех треугольников,
прилежащих к боковым сторонам и меньшему основанию трапеции.
Решение. Пусть О — точка пересечения диагоналей АС и BD
трапеции ABCD с основаниями ВС и AD, ВС < AD, ВЫ || CN,
прямые ВЫ и АС пересекаются в точке К, а прямые CN и BD —
в точке Р (рис. 116). Требуется доказать, что
Smkopn = Sab к + Sbco + Scdp-
Если h — высота трапеции, то
Sbmnc = ВС • h, Sabc = n
• h,
1
Sbcd = 2 ' ВС • h, поэтому Sbmnc = Sabc + Sbcd- Следова-
Следовательно,
Smkopn = Sbmnc — (Sbck + Scop) =
= Sabc + ^scd — Sbck — Scop =
= (Sabc - SBck) + (Sbcd - SCop) =
= Sabk + (Sbco + Scdp)-
Итак, Smkopn = ^лвк + #всо + Scdp-
836. Прямая, проходящая через середины диагоналей АС и ?>?> четырех-
четырехугольника ABCD, пересекает стороны АВ и CD в точках М и К. Докажите,
что площади треугольников DCM и АКБ равны.
Решение. Пусть точки О\ и О^ — середины диагоналей АС и BD
данного четырехугольника, AF !_ О\О^ и СЕ _L O1O2 (рис. 117).
Так как АО\ = О\С, то AAFO\ = ACEO\ (по гипотенузе и остро-
острому углу), поэтому AF = СЕ. Треугольники АКМ и СМ К имеют
М	N	D
Рис. 116
D
Рис. 117

90
Гл. 2. Площадь
общее основание МК и равные высоты AF и СЕ, поэтому Sakm =
= Scmk-
Аналогично доказывается, что Sbkm — Sdmk-
Следовательно,
Sakb = Sakm + Sbkm = Scmk + Sdmk = Sdcm-
Итак, SDcm = Sakb-
837. Сторона АВ параллелограмма ABCD продолжена за точку В на от-
отрезок BE, а сторона AD продолжена за точку D на отрезок DK. Прямые ED
и KB пересекаются в точке О. Докажите, что площади четырехугольников
ABOD и СЕОК равны.
Решение. На рисунке 118 изображена
данная фигура. Треугольники ABD и EDC
имеют равные основания АВ и CD и рав-
равные высоты h, поэтому Sabd = Sedc- Ана-
Аналогично, треугольники BDK и CDK име-
имеют общее основание DK и равные высоты,
поэтому Sbdk = Scdk- Из этого равен-
равенства следует, что Sbdf = Sckf, поэтому
Sbdo = Sckf — Sdof-
Следовательно,
Рис. 118
Sabod = ^asd + Sckf — Sdof =
Итак, Sabod = Sceok-
— Sdof
= Sceok-
838. Два непересекающихся отрезка делят каждую нз двух противопо-
противоположных сторон выпуклого четырехугольника на три равные части. Докажите,
что площадь той части четырехугольника, которая заключена между этими
отрезками, в три раза меньше площади самого четырехугольника.
Решение. Пусть ABCD — данный че-
четырехугольник, AM = MN = NB, СР =
= PQ = QD (рис. 119). Требуется доказать,
что Smnpq = т: Sabcd-
Проведем перпендикуляры СС\, РР\,
QQ\ к прямой АВ, а через точку Р
проведем прямую, перпендикулярную к СС\
и QQ\ (см. рис.119). Пусть СС\ = hx,
РРХ = h, QQX = h2. Так как АСРК =
= AQPL (по гипотенузе и острому углу),
то СК = LQ. HoCK = h-huLQ = h2-h,
J12 + hi
Рис. 119
поэтому h — h\ = /12 — h, т. е. h =

Задачи повышенной трудности
91
Samq = g -AM-h2,
Из этих равенств, учитывая, что AM = MN = NB, получаем:
Smnp = -^{Samq + Snbc)-
Аналогично доказывается равенство
bo
S,
Следовательно,
pqm = -^
Smnpq = Smnp
+
= л
Итак, Samqd + Snbcp = 2Smnpq, поэтому
Sabcd = SSmnpq, t. e. Smnpq = ^
D
м
Рис. 120
839. Середины К и М сторон АВ и DC
выпуклого четырехугольника ABCD соедине-
соединены отрезками KD, КС, МА и MB с вершина-
вершинами. Докажите, что площадь четырехугольника,
заключенного между этими отрезками, равна
сумме площадей двух треугольников, прилежа-
прилежащих к сторонам AD и ВС.
Решение. На рисунке 120 изображе-
изображена данная фигура, N и Р — точки пере-
пересечения отрезков DK и AM, КС и ВМ.
Требуется доказать, что
Smnkp = Sadn + Sbcp-
Проведем перпендикуляры СС\, ММ\ и DD\ к прямой АВ. Пусть
СС\ = h\, DD\ = /12, тогда ММ\ = —Цг—- (см. решение задачи 838).
Поэтому
Samb = т> ' Ав ' * 2 2>
Так как АК = БК = i АВ, то
Samb =
или
2, SBCK = \-BK-hx.

92
Гл. 2. Площадь
(обозначения площадей представлены на рис. 120). Отсюда следует, что
S = S\ + S4, т. е. Smnkp = Sadn + Sbcp-
840. Точка А лежит внутри угла, равного 60°. Расстояния от точки А
до сторон угла равны а и Ь. Найдите расстояние от точки А до вершины угла.
Решение. Пусть АВ и AD — перпендикуляры, проведенные к пря-
прямым, содержащим стороны данного угла О, равного 60°, а С — точка
пересечения прямых АВ и OD (рис. 121). По условию АВ = a, AD = Ь.
Требуется найти АО.
В прямоугольном треугольнике О ВС АО = 60°, поэтому АС = 30°.
Отсюда следует, что ОС = 2ОВ. В прямоугольном треугольнике CDA:
АС = 2AD = 2Ъ. Поэтому ВС = а + 26.
По теореме Пифагора
ОВ2 = ОС2 - ВС2, или ОВ2 = 40В2 - (а + 26J,
^ d2 (a + 26J
откуда ОБ^ = ^——-^-.
Из прямоугольного треугольника ЛВО по теореме Пифагора полу-
получаем:
АО =
Ответ. 2
а + аЪ + 6
841. Прямая, проходящая через вершину С параллелограмма ABCD,
пересекает прямые АВ и AD в точках К и М. Найдите площадь этого
параллелограмма, если площади треугольников К ВС и С DM равны Si и S2.
Решение. Пусть AD = а, АВ = Ъ, ВК = с, DM = d, С К = е,
СМ = /, Sabcd = S (рис. 122).
Так как треугольники ABC и ВКС имеют общую высоту, прове-
проведенную из вершины С, то -^—^— = -, а поскольку Sabc = о Sabcd =
1 о „„ 2ft с
a D d	M
Рис. 122

Задачи повышенной трудности
93
Аналогично, сравнивая треугольники ADC и DMC, получаем:
2S~2 = d'
Используя теорему об отношении площадей треугольников, имею-
имеющих по равному углу (п. 52 учебника), приходим к равенствам:
S\ ae S\ се
#2 df
n	S 2Si
Следовательно, —— = —=-.
2o2 *b
Отсюда находим: S = 2л/S\S2.
Ответ. 2y/S\S2.
ас
гт, откуда - = -.
bf	d b
842. Через точку пересечения диагоналей
четырехугольника ABCD проведена прямая, пе-
пересекающая отрезок АВ в точке М и отрезок
CD в точке К. Прямая, проведенная через точку
К параллельно АВ, пересекает BD в точке Т,
а прямая, проведенная через точку М параллель-
параллельно CD, пересекает АС в точке Е. Докажите, что
прямые BE и СТ параллельны.
Решение. На рисунке 123 изображена
данная фигура. Так как треугольники ВОС и EOT имеют равные углы
при вершине О, то
Ьвос _ ОБ-ОС	/.ч
Seot ~ ОТ-ОЕ'	^ )
Так как ME \\ СК, то углы К и М (и также углы С и Е)
в треугольниках СОК и ЕОМ равны. Поэтому
Scok С К -КО ОС- С К
Рис. 123
Seom ОМ - ME ОЕ - ME'
откуда следует, что
ОМ = ~ОЁ'
Аналогично, сравнивая треугольники КОТ и ВОМ, получаем:
Skot КТ -ОТ КО- КТ
B)
откуда следует, что
Sbom ВМ-ОВ ОМ-ВМ'
ОТ КО
C)
Поэтому, согласно равенству A), Sboc = Seot и, следовательно,
Sbtc = Setc (см. рис. 123).
О В ОМ'
Из равенств B) и C) получаем:
ОС ОТ

94
Гл. 2. Площадь
Итак, треугольники ВТС и ETC имеют общее основание ТС
и равные площади, поэтому их высоты, проведенные из вершин В и Е,
равны, т. е. точки В и Е равноудалены от прямой СТ, и поэтому
BE || СТ.
843. Сторона АВ треугольника ABC продолжена за точку А на отре-
отрезок AD, равный АС. На лучах ВА и ВС взяты точки К и М так, что
площади треугольников BDM и ВСК равны. Найдите угол ВКМ, если
ABAC = a.
Решение. На рисунке 124 изображена данная фигура. Отметим,
что точки М и К лежат по одну сторону от прямой CD (это следует
из равенства BD • ВЫ = ВС • ВК).
Так как
Sdcm = Sbdm — Sbcd, Sdck = Sbck — Sbcd
(или Sdcm = Sbcd — Sbdm, Sdck = Sbcd — Sbck при ином распо-
расположении точек М и К) и по условию Sbmd = Sbck, to
Sdcm = Sdck-
Треугольники DCM и DCK имеют общее основание DC и рав-
равные площади, поэтому высоты, проведенные из вершин М и К,
равны, а следовательно, МК || CD. Отсюда следует, что ZBKM =
= ZBDC. Но ZBDC = ZACD, так как AACD - равнобедренный,
и поэтому, согласно свойству внешнего угла треугольника, ZBDC =
= -а (см. рис. 124). Итак, ZBKM = -а.
Ответ. —.
844. Внутри прямоугольника ABCD взята точка М. Известно, что MB =
= а, МС = Ъ и MD = с. Найдите МА.
Решение. Через точку М проведем прямые, параллельные сто-
сторонам прямоугольника ABCD, и обозначим через m, n, p и q длины
отрезков на этих прямых так, как показано на рисунке 125, а через х
искомую длину отрезка МА. Воспользуемся теоремой Пифагора для
D
Рис. 124
Рис. 125

Задачи повышенной трудности	95
образовавшихся прямоугольных треугольников МРА, МРВ, MQC
и MQD.
x2 = m2 + q2, а2 = т2+р2, Ъ2=п2+р2, c2 = n2 + q2.
Из этих равенств следует, что х2 + Ъ2 = а2 + с2, поэтому
= лА2 + с2 -
Ответ. л/«2 + с2 — б2.
845.	В треугольнике ABC проведена высота BD. Отрезок К А перпенди-
перпендикулярен к АВ и равен DC, отрезок СМ перпендикулярен к ВС и равен AD.
Докажите, что отрезки MB и KB равны.
Решение. Пусть АВ = с, ВС = a, BD = h (рис. 126). Используя
теорему Пифагора, получаем:
KB2 = АК2 + с2 = ВС2-г с2 =а2- h2 + c2,
ВЫ2 = СМ2 + а2 = AD2 + a2=c2-h2 + a2.
Таким образом, KB2 = MB2, поэтому KB = MB.
846.	Внутри прямоугольного треугольника ABC с прямым углом С взята
точка О так, что Soab = Sobc = So ас- Докажите, что О А2 + О В2 = 5 • ОС2.
Решение. Проведем перпендикуляры ОМ и ON к прямым АС
и ВС (рис. 127). Пусть площадь треугольника ABC равна S.
По условию задачи
SAOC = У, или 1-ОМ - АС =1--1-. АС-ВС.
Отсюда следует, что ОМ = -ВС. Аналогично доказывается,что
о
ON = {АС.
О
Заметим, что CM = ON= Х-АС, поэтому AM = АС - СМ = \аС.
о	о
2
Аналогично, BN = -ВС.
о
А " D	С
Рис. 126

96	Гл. 2. Площадь
Применим теорему Пифагора к треугольникам АОМ, BON
и СОМ:
О А2 = ОМ2 + МА2 = 1-ВС2 + \АС2,
OB2 = ON2 + NB2 = Х-АС2 + ^ВС2,
ОС2 = ОМ2 + МС2 = 1-ВС2 + {-АС2.
Из этих равенств следует, что О А2 + О В2 = 5 • ОС2.

Глава 3
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
§ 1. Определение подобных треугольников
533.	Найдите отношение отрезков АВ и CD, если их длины равны
соответственно 15 см и 20 см. Изменится ли это отношение, если длины
отрезков выразить в миллиметрах?
~	АВ 15 см 3
Решение.—= — = -.
Отношение не изменится, если длины отрезков выразить в милли-
АВ 150 мм 3
MeTpaX!CD = 200W = 4-
Ответ. -; не изменится.
4
534.	Пропорциональны ли изображен-
изображенные на рисунке 128 (рис. 189 учебника) от- Л	ВС	D
резки: а) АС, CD и МХМ2, ММХ; б) АВ,
ВС, CD и ММ2, ММХ, МХМ2; в) АВ,
11111111
11111
BD и ММх, МхМ2?	Мг
Решен ие. Примем за единицу из-	ЬНН
мерения отрезков отрезок ММ\. То-	^i
гда ММХ = 1, ММ2 = 3, МХМ2 = 2,
АВ = 9, АС = 12, ВС = 3, BD = 9,	Рис- 128
CD = 6.
ч АС 12 а CD б а	AC	CD
а) тттт = -7Г = 6> тттг = т = 6> следовательно,
2	ММх 1	MiM2 MMi
т. е. отрезки АС и CD пропорциональны отрезкам М\М2 и ММ\.
б) Аналогично п. а) получаем:
АВ ВС	CD _ Q
— о,
ММ2 MMi MiM2
т. е. отрезки АВ, ВС и CD пропорциональны отрезкам ММ2, ММ\
и М\М2.
, АВ 9 BD 9	АВ , BD
в) л^т.^ = т> л^ л^ = т:» следовательно, л^л^ Ф ът ът , т. е. от-
MMi I MxM2 2	MMi Л/Г Л/Г
резки АБ и 5D не пропорциональны отрезкам ММ\ и М\М2.
Ответ, а) Да; б) да; в) нет.
4 Л. С. Атанасян и др.

98	Гл. 3. Подобные треугольники
536.	Отрезок BD является биссектрисой треугольника ABC. а) Найдите
АВ, если ВС = 9 см, AD = 7,5 см, DC = 4,5 см. б) Найдите DC, если АВ =
= 30, AD = 20, BD = 16 и ZBDC = ZC.
Решение, а) Так как DD — биссектриса треугольника
AD АВ
ABC (рис. 129), то -=— = -—- (см. задачу 535). Отсюда получаем:
.L/C	-dC
лп ADBC 7,5-9	,г
АВ=-^^ = —см=15см.
б) Так как ZBDC = ZC, то треугольник ВВС — равнобедрен-
равнобедренный (см. рис. 129), т. е. ВС = ВВ = 16.
ЛЛ	AD АВ
Из равенства —— = —— следует:
.L/C	_dC
_ AD-ВС _ 20-16 _ 2
DC ~ АВ ~ ~W~ ~ W3-
Ответ, а) 15 см; б) ю|.
537.	Отрезок AD является биссектрисой треугольника ABC. Найдите
BD и ВС, если АВ = 14 см, ВС = 20 см, АС = 21 см.
Решение. Пусть В В = х, тогда ВС = ВС - ВВ = 20 см-
— х (рис. 130).
D
Рис. 130
HD АН
Так как AD — биссектриса треугольника ABC, то -=— = ——-, или
х	14
20 см-ж 2Г
Отсюда следует:
2\х= 14B0 см-ж), 35ж = 280см, х = 8 см.
Итак, ВВ = 8 см, DC = 20 см - 8 см = 12 см.
Ответ. ВВ = 8 см, DC = 12 см.
538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки
и -BD, равные соответственно 4,5 см и 13,5 см. Найдите АВ и АС, если
периметр треугольника ABC равен 42 см.
Решение. ВС = ВВ + CD = 13,5 см+ 4,5 см = 18 см.

§ 1. Определение подобных треугольников
99
АВ + АС = 42 см - 18 см = 24 см;
АВ_ _ BD_ _ К^5 _ .
~АС ~ ~DC ~ Ж ~ '
откуда АВ = ЗАС.
Итак, ЗАС + АС = 24 см, поэтому
= 6 см, АВ = 18 см.
Ответ. АВ = 18 см, АС = 6 см.
539. В треугольник MNK вписан ромб
MDEF так, что вершины D, Е и F лежат соот-
соответственно на сторонах MN, NK и МК. Найди-
те отрезки NE и ЕК, если MN = 7 см, NK =
= б см, МК = 5 см.
Решение. Диагональ ME ромба делит
его углы пополам, поэтому отрезок ME —
биссектриса треугольника MNK (рис. 131).
Следовательно,
NE MN
ЕК МК'
или
NE
б см - NE
Отсюда находим:
Рис. 131
5 • NE = 42 см - 7 • NE, \2-NE = 42 см, NE = 3,5 см,
ЕК = 6 см - NE = 2,5 см.
О т в е т. NE = 3,5 см, ЕК = 2,5 см.
540. Периметр треугольника CDE равен 55 см. В этот треугольник
вписан ромб DMFN так, что вершины М, F и N лежат соответственно
на сторонах CD, СЕ и DE. Найдите стороны CD и DE, если СЕ = 8 см,
ЕЕ = 12 см.
Решение. Диагональ DF ромба является биссектрисой треуголь-
треугольника CDE, поэтому
CD CF 8 2
СЕ = CF + ЕЕ = 8 см + 12 см = 20 см;
CD + DE = 55 см - СЕ = 35 см,
т. е. \DE + DE = 35 см, откуда DE = 21 см.
CD = |-21 см= 14 см.
Ответ. CD = 14 см, DE = 21 см.

100	Гл. 3. Подобные треугольники
541. Подобны ли треугольники ABC и DEF, если ZA = 106°, ZB = 34°,
ZE = 106°, ZF = 40°, АС = 4,4 см, АВ = 5,2 см, ВС = 7,6 см, DE =
= 15,6 см, DF = 22,8 см, EF = 13,2 см?
Решение. ZA = ZE; ZC = 180° - (ZA + ZB) = 180° - 140° =
= 40°, т. е. ZC = ZF; ZD = 180° - (ZE + ZF) = 180° - 146° = 34°,
т. е. ZB = ZD.
Итак, углы треугольников ABC и DEF соответственно равны.
АВ_ _ _^2_ _ \_ АС_ _ А^ _1 ВС _ 7,6 _ 1
DE ~ 15,6 ~~ 3' ЖР ~~ 13,2 ~~ 3' IXF ~~ 22,8 ~~ 3'
о	АВ АС ВС
Отсюда следует, что —— = —— = -=-=, т. е. стороны треугольника
ABC пропорциональны сходственным сторонам треугольника DEF.
Следовательно, треугольники ABC и DEF подобны.
Ответ. Да.
542.	В подобных треугольниках ABC и KMN стороны АВ и КМ, ВС
и MN являются сходственными. Найдите стороны треугольника KMN, если:
АВ = 4 см, ВС = 5 см, С А = 7 см, ^- = 2,1.
Решение. КМ = 2,1 • АВ = 2,1 • 4 см = 8,4 см;
^=2,1, откуда MN = 2,1- ВС = 10,5 см;
^ =2,1, откуда KN = 2,\ • АС = 14,7 см.
Ответ. КМ = 8,4 см; MN = 10,5 см; KN = 14,7 см.
543.	Докажите, что отношение сходственных сторон подобных треуголь-
треугольников равно отношению высот, проведенных к этим сторонам.
Решение. Пусть ААВС ~ АА\В\С\, АВ : А\В\ = k, h и h\ —
высоты, проведенные к сходственным сторонам АВ и А\В\. Тогда
= к2, т. е. Т2	= к2.
Отсюда получаем
) (тг) =к > Ишк(тг) =к -
h\)	\h\)
Следовательно, — = к.
fix
лл	АВ h	.
Итак,	= —, что и требовалось доказать.
A\Jd\ h\

§ 1. Определение подобных треугольников	101
544.	Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна
из сторон второго треугольника равна 9 м. Найдите сходственную ей сторону
первого треугольника.
Решение. Пусть коэффициент подобия данных треугольников
равен к. Тогда —— = к2, откуда к2 = -, к = -. Искомая сторона
OUU	т:	Z
равна к • 9 м, т. е. 4,5 м.
Ответ. 4,5 м.
545.	Треугольники ABC и А\В\С\ подобны, и их сходственные стороны
относятся как б : 5. Площадь треугольника ABC больше площади треуголь-
треугольника А\В\С\ на 11 см2. Найдите площади треугольников.
Решение. Площади треугольников ABC и А\В\С\ обозначим
через S и S\.
т	п п	/6\	36	г^Зб^т-г	гу	гу
Тогда 5 : 5i = - = —, откуда S = — S\. По условию S — S\ =
\о/	Zd	Zd
= 11 см2, т. е. — S\ — S\ = 11 см2, или — S\ =11 см2, откуда 5^1 =
Zd	Zd
= 175 см2.
5 = ^1+77 см2 = 252 см2.
Ответ. SABC = 252 см2, SAxBxcx = 175 см2.
546.	План земельного участка имеет форму треугольника. Площадь изоб-
изображенного на плане треугольника равна 87,5 см. Найдите площадь земельного
участка, если план выполнен в масштабе 1 : 100000.
Решение. Пусть S — площадь земельного участка, выраженная
в квадратных сантиметрах. Тогда
87,5 /2	7	1
= к , где к =
S ""^'" 100000-
Отсюда 5 = A00000J • 87,5 см2 = 87,5 км2.
Ответ. 87,5 км2.
547. Докажите, что отношение периметров двух подобных треугольников
равно коэффициенту подобия.
Решение. Пусть A ABC ~ АА\В\С\, причем
АВ ВС С А _ к
ВхСх
(где к — коэффициент подобия). Тогда
АВ = к
ВС = к-Bid,

102
Гл. 3. Подобные треугольники
Складывая эти равенства, получаем:
АВ + ВС + С А = к - (AiBi + ВХСХ +
откуда
АВ + ВС + С А
что и требовалось доказать.
548. Треугольники АБС и А\В\С\ подобны. Сходственные стороны ВС
и BiCi соответственно равны 1,4 м и 56 см. Найдите отношение периметров
треугольников ABC и А\В\С\.
Решение. Отношение периметров подобных треугольников ABC
и А\В\С\ равно коэффициенту подобия, т. е. отношению сходственных
сторон ВС и В\С\\
ВС 140 см _ 2 5
ВхСх
56 см
Ответ. 2,5.
549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите
стороны треугольника, подобного данному, если его периметр равен 26 см.
Решение. Отношение периметров данного треугольника и тре-
треугольника, подобного данному, равно коэффициенту подобия к, т. е.
15 + 20 + 30
k~	26	~АЬ'
Стороны треугольника, подобного данному, в к раз меньше сторон
данного треугольника, т. е. искомые стороны равны 15 см : 2,5 = 6 см,
20 см : 2,5 = 8 см, 30 см : 2,5 = 12 см.
Ответ. 6 см, 8 см, 12 см.
§ 2. Признаки подобия треугольников
550. По данным рисунка 132 (рис. 193 учебника) найдите х и у.
Решение, а) На рисунке 132, а прямоугольные треугольники
подобны по первому признаку подобия треугольников (они имеют
12	6
а
20	8
Рис. 132

§ 2. Признаки подобия треугольников
103
по равному прямому углу и по равному острому углу а). Из подобия
треугольников следует пропорциональность сходственных сторон:
— = -, откуда х = 9.
б) На рисунке 132, б прямоугольные треугольники также подобны,
поэтому
У
V102-82
Ответ. х = 9, у = 21.
28	28-6 О1
= —, откуда у = —— = 21.
551. На стороне CD параллелограмма ABCD
отмечена точка Е. Прямые АЕ и ВС пересекаются
в точке F. Найдите: а) ЕЕ и FC, если DE = 8 см,
ЕС = 4 см, ВС = 7 см, АЕ = 10 см; б) DE и ЕС,
если АВ = 8 см, AD = 5 см, СЕ = 2 см.
Решение. Треугольники ADE и FCE на
рисунке 133 подобны по первому признаку по-
подобия треугольников (углы 1 и 2 равны как на-
накрест лежащие при пересечении параллельных
прямых AD и BF секущей AF, углы 3 и 4 равны
как вертикальные). Из подобия треугольников
СЛ6ДуеТ:	EF FC ЕС
В
D
Рис. 133
АЕ AD
а) Из этих равенств получаем:
DE'
EF =
FC =
АЕ-ЕС _ 10-4
DE
AD-EC
DE
8
7-4
см = 5 см,
см = 3,5 см.
б) Из тех же равенств следует:
ЕС FC 2
Так как DE + ЕС = DC = АВ = 8 см, то
Отсюда
DE = — см = 5- см;
= 8 см.
2
2 40	2
= ^ • ^ см = 2^ см.
О т в е т. a) EF = 5 см, FC = 3,5 см; б) DE = 5- см, ЕС = 2- см.
552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются
в точке О. Найдите: а) АВ, если ОВ = 4 см, OD = 10 см, DC = 25 см;

104	Гл. 3. Подобные треугольники
б) —— и 7ТК, если АВ = a, DC = Ъ; в) АО, если АВ = 9,6 дм, DC = 24 см,
С/О
АС= 15 см.
Решение. На рисунке 134 треугольники
АОВ и COD подобны по двум углам (углы 1
и 2 равны как накрест лежащие при пересе-
пересечении параллельных прямых АВ и DC секу-
секущей BD, углы 3 и 4 равны как вертикальные).
Из подобия треугольников следует:
D*	*С	АВ _ АО _ ВО
Рис.134	DC~ ОС " OD'
Отсюда получаем:
DC -ВО 25-4
10
АО _ ВО _ а.
ОС ~ OD ~ V
см = 10 см;
v АБ	АО	96	АО	~
В) DO = АС^Ад' ИЛИ 24 = 15 см-АО' °ТСЮДа НаХ°ДИМ!
4A5 см - АО) = АО, АО = 12 см.
Ответ, а) 10 см; б) -; в) 12 см.
о
553.	Подобны ли равнобедренные треугольники, если они имеют: а) по
равному острому углу; б) по равному тупому углу; в) по прямому углу? Ответ
обоснуйте.
Решение, а) Два равнобедренных треугольника, имеющие по рав-
равному острому углу, могут не быть подобными. Например, равнобед-
равнобедренный треугольник с углом в 50° при основании и равнобедренный
треугольник с углом в 50° между боковыми сторонами не подобны,
так как углы первого треугольника равны 50°, 50°, 80°, а второго
50°, 65°, 65°.
б), в) Если два равнобедренных треугольника имеют по равному
тупому углу (или по прямому углу), то эти равные углы лежат между
боковыми сторонами треугольника. Боковые стороны одного равно-
равнобедренного треугольника пропорциональны боковым сторонам другого
равнобедренного треугольника. Следовательно, указанные треугольни-
треугольники подобны по второму признаку подобия треугольников.
Ответ, а) Не всегда; б) да; в) да.
554.	Основания трапеции равны 5 см и 8 см. Боковые стороны, равные
3,6 см и 3,9 см, продолжены до пересечения в точке М. Найдите расстояния
от точки М до концов меньшего основания.
Решение. Пусть ABCD — данная трапеция с основаниями AD =
= 8 см, ВС = 5 см и боковыми сторонами АВ = 3,9 см, CD =
= 3,6 см (рис. 135). Требуется найти MB и МС.

§2. Признаки подобия треугольников	105
Треугольники AMD и ВМС подобны по двум углам (угол М —
общий; ZA = ZMBC, так как эти углы являются соответственными
при пересечении параллельных прямых AD и ВС секущей AM).
Из подобия треугольников следует:
MB ВС	MB	5
-, или
MA AD'	МБ+ 3,9 см 8'
Отсюда получаем:
8МБ = 5МБ + 19,5 см, MB = 6,5 см.
Аналогично:
МС__ВС_	МС _ 5
JW ~ ~AD' ИЛИ МС + 3,6 см ~ 8'
откуда находим: МС = 6 см.
Ответ. 6,5 см и 6 см.
555. Точки М, N и Р лежат соответственно на сторонах АВ, ВС
и С А треугольника ABC, причем MN || AC, NP \\ АВ. Найдите стороны
четырехугольника AMNP, если: а) АВ = 10 см, АС = 15 см, PN : MN =
= 2 : 3; б) AM = АР, АВ = а, АС = Ь.
Решение, а) Четырехугольник AMNP — параллелограмм
AM 2
(рис. 136), поэтому AM = PN, АР = MN и, следовательно, ——- = -.
М N о
ААВС - AMBN по двум углам (/Б - общий, ZA = ZBMN),
поэтому
АВМВ	10 10 см-AM
ИЛИ
AC MN'	15	MN '
Отсюда следует:
2	_ 10 см _ 2 4 _ 10 см
3	~ MN 3' 3 ~ MN '
MN = 7,5 см, AM = \MN = 5 см.
о
Итак, MN = АР = 7,5 см; AM = PN = 5 см.
М
-С
Рис. 135	Рис. 136

106
Гл. 3. Подобные треугольники
г>\ Т	АЪ/Г	ATI	AM
б) Так как AM = АР, то — =
1.
Из равенства
АВ MB
AC
a
b
MN
a- AM
MN
получаем:
а а
нлнъ =
Отсюда находим:
Итак,
MN =
аЪ
а + Ъ'
AM = MN = NP = AP =
_ab_
а + Ъ'
Ответ, а) 7,5 см, 5 см, 7,5 см, 5 см; б) все стороны равны
аЬ
а + Ъ'
В
Рис. 137
557. Стороны угла А пересечены параллель-
параллельными прямыми ВС и DE, причем точки В и D
лежат на одной стороне угла, а С и Е — на другой.
Найдите: а) АС, если СЕ = 10 см, AD = 22 см,
BD = 8 см; б) BD и DE, если АВ = 10 см, АС =
= 8 см, ВС = 4 см, С? = 4 см; в) ВС, если
АВ :BD = 2:1 и DE= 12 см.
Решение. Согласно задаче 556
a) AB = AD - BD = 14 см,
АВ _ BD
AC ~ CE
AB-CE
(рис. 137).
14- 10
б) BD =
АВ-СЕ 10-4
см = 17,5 см.
см = 5 см.
AC	8
AADE rsj AABC по двум углам (угол А — общий, АС = ZE),
DE AE
поэтому
ВС AC
AE-BC
, откуда
(AC + CE) • ВС
(8
4) • 4	а( ,
^ см = 6 (см).
в) Так как АВ : BD = 2 : 1, то АВ = 2 • BD. Поэтому
AD _ AB + BD _ 3BD _ 3
~АВ ~ АВ ~ 2BD ~ 2'
Из подобия треугольников ADE и ABC следует:
DE AD	12 см 3
		тттттт 	 — _
ВС 2'
12-2
откуда
ВС АВ
см = 8 см.
Ответ, а) 17,5 см; б) 5 см и 6 см; в) 8 см.

§ 2. Признаки подобия треугольников
107
558. Прямые а и Ь пересечены параллельными прямыми АА\, ВВ\, СС\,
причем точки А, В и С лежат на прямой а, а А\, В\ и С\ — на прямой Ь.
АВ AiBi
Докажите, что —— = ——.
Решение. Если а \\ Ь, то четырехугольники АВВ\А\ и ВСС\В\ —
параллелограммы (рис. 138, а), и поэтому АВ = А\В\ и ВС = В\С\,
А/ ,В1 ., /С
" /С,
А/ 'вг/с\/
откуда следует, что
Рис. 138
АВ_ _ АхВх
JDLy	Л>х Oi
Если прямые а и Ь не параллельны, то через точку А проведем пря-
прямую Ь\, параллельную прямой Ь (рис. 138, б). Она пересекает прямую
ВВ\ в некоторой точке В^, а прямую СС\ — в точке С^. Четырех-
Четырехугольники АВ^В\А\ и В^С^СхВх — параллелограммы и потому
АВ2 = AiBi и В2С2 = ВХСХ.
Согласно задаче 556 имеет место равенство
АВ _ ВС
Jb~2 ~ в2с2'
Отсюда, используя предыдущие равенства, получаем
АВ ВС
559. На одной из сторон данного угла А отложены отрезки АВ = 5 см
и АС = 16 см. На другой стороне этого же угла отложены отрезки АР =
= 8 см и AF = 10 см. Подобны ли треугольники АСР и AFB? Ответ
обоснуйте.
т-.	rj,	AC 16 8 АР 8
Решение. Так как =- = -и — =-,	Су
то	,,
АВ ~ 5'
AF
АР
АВ'
т. е. стороны АС и AD треугольника ACD про-
пропорциональны сторонам AF и АВ треугольника
AFB (рис. 139). Угол А — общий угол треуголь-
треугольников ACD и AFB, заключенный между сторона-
сторонами АС и AD треугольника ACD и также между
Д
D F
Рис. 139

108	Гл. 3. Подобные треугольники
сторонами AF и АВ треугольника AFB. Отсюда по второму признаку
подобия треугольников следует, что AACD ~ AAFB.
Ответ. Да.
560. Подобны ли треугольники ABC и А\В\С\, если: а) АВ = 3 см,
ВС = 5 см, С А = 7 см, AiBi = 4,5 см, В\С\ = 7,5 см, С\А\ = 10,5 см;
б) АВ = 1,7 см, ВС = 3 см, С А = 4,2 см, АХВХ = 34 дм, В\С\ = 60 дм,
С\А\ = 84 дм?
D	ЛТ	АВ 3 2
Решение, а) 1ак как	= —— = -,
А\В\ 4,5 о
БС _ 5 _ 2
СА _ _^_ _ 2
С\А\ ~ 10,5 ~ 3'
то ААВС ~ АА\В\С\ по третьему признаку подобия треугольников.
б) Так как ——- = —— = -—— = -—, то ААВС - Л^
по третьему признаку подобия треугольников.
Ответ, а) Да; б) да.
561. Докажите, что два равносторонних треугольника подобны.
Решение. Три стороны одного равностороннего треугольника про-
пропорциональны трем сторонам другого равностороннего треугольника.
Поэтому два равносторонних треугольника подобны по третьему при-
признаку подобия треугольников.
562. В треугольнике ABC сторона АВ рав-
равна а, а высота СН равна h. Найдите сторо-
сторону квадрата, вписанного в треугольник ABC
так, что две соседние вершины квадрата лежат
на стороне АВ, а две другие — соответственно
_ на сторонах АС и ВС.
мн Q	Решение. Пусть MNPQ — квадрат,
вписанный в треугольник ABC (рис. 140).
Рис- 140	Тогда NP || АВ, и поэтому если СН - вы-
высота треугольника ABC, то СК — высота треугольника NPC. Пусть
NP = х, тогда
С К = СН - КН = h-x.
Треугольники ABC и NPC подобны по двум углам (угол С —
общий; ZB = ZCPN, так как NP || АВ). Отсюда, согласно задаче 543,
следует, что	NP ск	х h_x
Из последнего равенства получаем: xh = a(h — х), откуда х =	г.
а + а
~	ah
Ответ. 	-.
a + h

§3. Применение подобия к доказательству теорем и решению задач 109
563. Через точку М, взятую на медиане AD треугольника ABC, и вер-
вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите
АК	Лг. AM 1
отношение jt^;, если: а) М — середина отрезка AD; б) ——- = -.
Решение. Пусть DE \\ ВК (рис. 141). То-
Тогда, согласно задаче 556, имеют место равенства
BD КЕ AM АК
Рис. 141
DC ~ ЁС' MD
а поскольку BD = DC, то КЕ = ЕС.
а)	Так как точка М — середина отрезка
AD, то AM = MD, и поэтому АК = КЕ. Итак,
АК = КЕ = ЕС, следовательно, КС = 2АК,
АК _ 1
~КС ~ 2'
^ч ~	AM 1	АК 1	„_, о л Т.
б)	Так как ——- = -, то —— = -, т. е. КЕ = 2АК, а поскольку
ми z кь z
КЕ = ЕС, то КС = 2КЕ = \АК. Поэтому
АК _ 1
КС ~ 4'
Ответ, а) -; б) -.
§ 3. Применение подобия к доказательству теорем
и решению задач
564. Дан треугольник, стороны которого равны 8 см, 5 см, 7 см. Найдите
периметр треугольника, вершинами которого являются середины сторон дан-
данного треугольника.
Решение. Сторонами треугольника с искомым периметром явля-
являются средние линии данного треугольника, каждая из которых равна
половине соответствующей стороны данного треугольника. Поэтому
искомый периметр равен
7) см = 10 см.
Ответ. 10 см.
565. Расстояние от точки пересечения диаго-
диагоналей прямоугольника до прямой, содержащей его
большую сторону, равно 2,5 см. Найдите меньшую
сторону прямоугольника.
Решение. Пусть ОМ — перпендикуляр,
проведенный из точки Опересечения диагона-
диагоналей прямоугольника ABCD к его большей сто-
стороне AD (рис. 142). Тогда ОМ || АВ и так как
точка О — середина отрезка BD, то ОМ —
В

по
Гл. 3. Подобные треугольники
средняя линия треугольника ABD. Поэтому АВ = 2ОМ, а так как
по условию ОМ = 2,5 см, то АВ = 5 см. Итак, меньшая сторона
прямоугольника равна 5 см.
Ответ. 5 см.
566.	Точки Р и Q — середины сторон АВ и АС треугольника ABC.
Найдите периметр треугольника ABC, если периметр треугольника APQ =
= 21 см.
Решение. Так как Р и Q — середины сторон АВ и АС, то АВ =
= 2АР, АС = 2AQ, а поскольку отрезок PQ — средняя линия тре-
треугольника ABC, то ВС = 2PQ. Следовательно,
АВ + ВС + С А = 2(АР + AQ + PQ) = 2 • 21 см = 42 см.
Ответ. 42 см.
567.	Докажите, что середины сторон произвольного четырехугольника
являются вершинами параллелограмма.
Решение. Пусть точки М, N, Р,
Q — середины сторон четырехугольника
ABCD (рис. 143). Тогда MN и PQ - средние
линии треугольников ABC и ADC; поэтому
В
Рис. 143
MN || АС,
PQ || АС,
MN = Х-АС и
PQ = \ас.
Отсюда следует, что MN || PQ и MN = PQ.
Следовательно, четырехугольник MNPQ — параллелограмм.
568. Докажите, что четырехугольник есть ромб, если его вершинами
являются середины сторон: а) прямоугольника; б) равнобедренной трапеции.
Решение, а) Пусть точки М, N, Р, Q — середины сторон прямо-
прямоугольника ABCD (рис. 144, а). Тогда четырехугольник MNPQ — па-
параллелограмм, причем MN = PQ = -AC, MQ = NP = -BD (см. ре-
Q
б
D
Рис. 144

§ 3. Применение подобия к доказательству теорем и решению задач 111
шение задачи 567). Но в прямоугольнике диагонали равны, т. е. АС =
= BD. Следовательно, MN = PQ = MQ = NP, т. е. MNPQ - ромб,
б) Пусть точки М, N, P, Q — середины сторон равнобедренной
трапеции ABCD (рис. 144, б). Тогда четырехугольник MNPQ — па-
параллелограмм, причем MN = PQ = -AC, MQ = NP = -BD (см. ре-
решение задачи 567). Но в равнобедренной трапеции диагонали равны,
т. е. АС = BD (см. задачу 388, б). Следовательно, MN = PQ = MQ =
= NP, т. е. MNPQ - ромб.
569.	Докажите, что отрезок, соединяющий середины диагоналей трапе-
трапеции, параллелен ее основаниям и равен полуразности оснований.
Решение. Пусть точки М и N — середины диагоналей АС
и BD трапеции ABCD с основаниями AD и ВС, причем AD >
> ВС (рис. 145). Проведем через точку М прямую ME, параллельную
AD. Тогда отрезок ME — средняя линия треугольника ACD, и значит,
точка Е — середина стороны CD и ME = ^AD.
Так как прямая ME проходит через середину стороны CD
и ME || ВС, то прямая ME пересекает диагональ BD в ее середине,
т. е. в точке N. Поэтому отрезок NE — средняя линия треугольника
DBC и, следовательно, NE = ^ВС.
MN = ME -NE = ^AD - ^ВС = ^(AD - ВС).
Итак, отрезок MN параллелен основаниям трапеции и равен их по-
полуразности, что и требовалось доказать.
570.	Диагональ АС параллелограмма ABCD равна 18 см. Середина М
стороны АВ соединена с вершиной D. Найдите отрезки, на которые делится
диагональ АС отрезком DM.
Решение. Пусть точка N — середина стороны CD, P и Q —
точки пересечения отрезков DM и BN с диагональю АС (рис. 146).
Так как MB = DN и MB \\ DN, то MBND — параллелограмм и,
следовательно, DM || BN. Поэтому МР || BQ и так как точка М —
середина АВ, то отрезок МР — средняя линия треугольника ABQ.
Значит, АР = PQ.
Аналогично рассматривая треугольник CPD, находим, что CQ =
= PQ.
в
Рис. 145	Рис. 146

112
Гл. 3. Подобные треугольники
Итак, АР = PQ = CQ.
Отсюда получаем, что АР = -АС = 6 см, PC = 12 см.
о
Ответ. 6 см и 12 см.
571.	В треугольнике ABC медианы АА\ и ВВ\ пересекаются в точке
О. Найдите площадь треугольника ABC, если площадь треугольника АВО
равна 5.
Решение. Так как ВО : ОВ\ = 2 : 1 и так как треугольни-
треугольники АОВ и АОВ\ имеют общую высоту, проведенную из вершины
А (рис. 147), то
Sao в • Saobx =2:1,
откуда следует, что
1	3
Saobx = 2^' Sabbx = Sao в + Saobx = 2^'
Так как медиана ВВ\ разделяет треугольник ABC на два треуголь-
треугольника с равными площадями, то
Sabc = 2SabBx = 35.
Ответ. 35.
В условиях задач 572-574 использованы следующие обозначения
для элементов прямоугольного треугольника ABC с прямым углом С
и высотой СН: ВС = а, АВ = с, АС = Ь, СН = ft, АН = Ъс, НВ =
= ас (рис. 148).
572.	Найдите: a) ft, а и Ь, если Ъс = 25, ас = 16; б) ft, а и Ь, если Ъс = 36,
ас = 64; в) а, с и ас, если Ъ = 12, Ъс = 6; г) Ь, с и Ьс, если а = 8, ас = 4; д) ft,
6, ас и Ьс, если а = б, с = 9.
Решение, a) ft= д/ас • 6С = л/25 • 16 = 20;
а = х/сГПГг = \Да
f^ = vT^^O^c = л/41 • 16 = 4л/4Т;
Ь = л/с7^ = л/41 -25 = 5л/4Т.
б) ft = л/36-64 = 48;
а = д/C6 + 64) • 64 = 80;
6 = л/ЮО • 36 = 60.
Рис. 147
Рис. 148

§3. Применение подобия к доказательству теорем и решению задач 113
в) Из равенства Ъ = ус • Ъс следует:
Ъ2 122
= 24; а = л/с2 - Ъ2 = л/242 - 122 = 12л/3.
Из равенства а = .у/с • ас следует:
a2
-
A2V3J
Ъ = Vc^^ = VW^? =SV3;bc=°- = ^1L = 12.
д) b = л/с2 - a2 = л/92 - б2 = Зл/5;
Ответ, а) 20, 4л/4Т и 5л/4Т; б) 48, 80 и 60; в) 12л/3, 24 и 18;
г) 8л/3, 16 и 12; д) 2л/5, Зл/5, 4 и 5.
573. Выразите ас и 6С через а, Ъ и с.
Решение. Из формул а = у/с • ас , 6 = \[сУЬс следует:
а , Ъ
ас = —,ос = —.
с	с
гл	а -, Ъ
Ответ. ас = —, Ъс = —.
с	с
574. Докажите, что: а) /г = —; б) — = —.
с ас ос
Решение, а) Для площади S прямоугольного треугольника спра-
справедливы равенства:
S = -oh и S = -с/г.
Отсюда получаем аб = с/г, или /г = —.
а2 Ь2	С а2
б) Из формул ас = — и Ьс = —	(см. задачу 573) следует: с = —
ее	ас
Ъ2
Следовательно, — = —.
ас Ъс
575. Катеты прямоугольного треугольника относятся как 3 : 4, а гипоте-
гипотенуза равна 50 мм. Найдите отрезки, на которые гипотенуза делится высотой,
проведенной из вершины прямого угла.

114	Гл. 3. Подобные треугольники
Решение. По условию Ъ : а = 3 : 4, с = 50 мм (см. рис. 148).
Используя равенства ас = —, Ьс = — (см. задачу 573), получаем:
с	с
— - — - (-\2 - — т е Ъ - —а
ас a2 U/ 16' ' ' с 16
g
Так как ас -\- Ьс = с, то ас + —- ас = 50 мм, откуда
1о
ас = 32 мм, Ъс = 18 мм.
Ответ. 32 мм и 18 мм.
576. Высота прямоугольного треугольника, проведенная из вершины пря-
прямого угла, делит гипотенузу на отрезки, один из которых на 11 см больше
другого. Найдите гипотенузу, если катеты треугольника относятся как б : 5.
Решение. Пусть ас = Ьс + 11 см (см. рис. 148). Так как ас > Ьс,
то у/с - ас > ус - Ъс, т. е. а > Ъ. Поэтому, согласно условию задачи,
7 п г тт а л/с • ас	&с	/ас б	ас
а : о = о : 5. Но т = у; = \ ~т~ и» значит, w ¦— = -, откуда — =
о л/с-Ьс У °с	у 6С 5	6С
36	36 ,
= 25'Т-е-ас=256с-
Следовательно, — Ьс = 6С + 11 см. Отсюда находим:
Zd
bc = 25 см,
ас = Ъс+ \\ см = 36 см,
с = ас + 6С = 61 см.
Ответ. 61 см.
577. В треугольнике, стороны которого равны 5 см, 12 см и 13 см,
проведена высота к большей стороне. Найдите отрезки, на которые высота
делит эту сторону.
Решение. Так как 52 + 122 = 132, то данный треугольник —
прямоугольный, причем гипотенуза равна 13 см. Пусть а = 12 см, Ъ =
= 5 см (см. рис. 148). Требуется найти ас и Ъс.
2	т2	2
Из равенства — = — (см. задачу 574, б) следует, что -^ = -j =
ас ос	ос Ь
144 144 ,
Так как ас + 6С = с = 13 см, то ~^-Ьс -\-Ьс = 13 см, откуда находим:
,25	.12	144	,.1
6с = ТЗСМ=113СМ' «0 = -^ см =11- см.
1	12
Ответ. 11 —— см и 1— см.
1 о	1 о

§3. Применение подобия к доказательству теорем и решению задач 115
579. Для определения высоты столба А\С\,
изображенного на рисунке 149 (рис. 199 учебни-
учебника), использован шест с вращающейся планкой.
Чему равна высота столба, если ВС\ = 6,3 м,
ВС = 3,4 м, АС = 1,7 м?
Решение. Треугольники ABC и
А\ВС\ подобны по двум углам (угол В —
общий, углы С и С\ — прямые), поэтому
АхСх Щ
АС
°ТКУДа
ВС '
Л Г
АС •
Q
1 7 fi
1,/ • о,о
Ответ. 3,15 м.
580. Длина тени дерева равна 10,2 м, а длина тени человека, рост которого
1,7 м, равна 2,5 м. Найдите высоту дерева.
Решение. Пусть А\С\ — высота дерева, АС — высота человека,
ВС\ — длина тени дерева, ВС — длина тени человека (см. рис. 149).
лп АС-ВСх 1,7-10,2
МС	М
Ответ. 6,936 м.
581. Для определения высоты дерева мож-
можно использовать зеркало так, как показано
на рисунке 150 (рис.203 учебника). Луч света
FD, отражаясь от зеркала в точке D, попадает
в глаз человека (точку В). Определите высоту
дерева, если АС = 165 см, ВС = 12 см, AD =
= 120 см, DE = 4,8 м, Zl = Z2.
Решение. Треугольники ABD и EFD
подобны по двум углам (Zl = Z2 по усло-
условию, углы с вершинами А и Е — прямые).
Поэтому
Е
Рис
АВ _ EF
AD ~ DE'
откуда EF = 612 см = 6,12 м.
Ответ. 6,12 м.
или
165- 12
120
EF
480 см'
582. Для определения расстояния от точки А до недоступной точки В
на местности выбрали точку С и измерили отрезок АС и углы ВАС и АСВ.
Затем построили на бумаге треугольник A\B\Ci, подобный треугольнику
ABC. Найдите АВ, если АС = 42 м, А\С\ = 6,3 см, АХВХ = 7,2 см.
Решение. Из подобия треугольников ABC и А\В\С\ следует, что
АВ АС

116
Гл. 3. Подобные треугольники
откуда АВ =
АхВх-АС 7,2-42
АХСХ
Ответ. 48 м.
6,3
м = 48 м.
Рис. 151
583. На рисунке 151 (рис.204 учебника) показано,
как можно определить ширину ВВх реки, рассматривая
два подобных треугольника ABC и АВхСх. Определите
ВВх, если АС = 100 м, АС\ = 32 м, АВХ = 34 м.
Решение. Из подобия треугольников ABC
и АВ\С\ следует, что
АВ АС	34 м + ВВх _ 100
~ 2"'
Ж
34м
Отсюда находим: ВВ\ = 72,25 м.
Ответ. 72,25 м.
Задачи на построение
585.	Начертите отрезок АВ и разделите его в отношении: а) 2 : 5; б) 3 : 7;
в) 4 : 3.
Решение, а) Проведем луч AM, не лежащий на прямой АВ.
От точки А на этом луче отложим 7 равных отрезков произвольной
длины: АА\, А\А2, ..., A§Aj. Проведем прямую AjB, а через точки
А\, А2, ..., Aq проведем прямые, параллельные прямой AjB (как
это сделать, описано в решении задачи 222). Эти прямые разделяют
отрезок АВ на 7 равных отрезков: АВ\, В\В2, ..., BqB. Очевидно, что
АВ2 : В2В = 2:5.
б), в) Построение выполняется аналогично.
586.	Постройте треугольник по двум углам и биссектрисе, проведенной
из вершины меньшего из данных углов.
Решение. Задачу нужно понимать так: даны два неравных угла
и отрезок (рис.152, а); требуется построить треугольник, у которого
два угла соответственно равны двум данным углам, а биссектриса
треугольника, проведенная из вершины меньшего из этих двух углов,
равна данному отрезку.
В, В\
Рис. 152

Задачи на построение	117
Сначала построим какой-нибудь треугольник, подобный искомому.
Для этого начертим произвольный отрезок АВ\ и построим треуголь-
треугольник АВ\С\, у которого углы А и В\ равны соответственно меньшему
и большему данным углам (рис. 152, б).
Далее построим биссектрису угла А и отложим на ней отрезок
AD, равный данному отрезку. Через точку D проведем прямую, парал-
параллельную В\С\. Она пересекает стороны угла А в некоторых точках В
и С (рис. 152, б).
Треугольник ABC — искомый. В самом деле, по построению угол
А треугольника ABC равен меньшему из данных углов, а так как
ВС || В\С\, то ZB = ZB\ и, следовательно, угол В равен другому
из данных углов. Наконец, по построению биссектриса AD треуголь-
треугольника ABC равна данному отрезку. Итак, треугольник ABC удовлетво-
удовлетворяет всем условиям задачи.
Очевидно, задача имеет единственное решение, если сумма двух
данных углов меньше 180°, и не имеет решений, если эта сумма
больше или равна 180°.
587.	Постройте треугольник по двум углам и высоте, проведенной из вер-
вершины третьего угла.
Решение. Сначала построим какой-нибудь треугольник АВ\С\,
у которого углы В\ и С\ равны соответственно двум данным углам.
Затем проведем высоту АН\ этого треугольника и отложим на луче
АН\ отрезок АН, равный данной высоте искомого треугольника.
Через точку Н проведем прямую, параллельную В\С\. Она пересе-
пересекает лучи АВ\ и АС\ в каких-то точках В и С.
Треугольник ABC — искомый. Это доказывается таким же образом,
как и в задаче 586.
Если сумма двух данных углов меньше 180°, то задача имеет
единственное решение, в противном случае решений нет.
588.	Постройте треугольник ABC по углу А и медиане AM, если извест-
известно, что АВ : АС = 2 : 3.
Решение. Задачу нужно понимать так: даны угол и отре-
отрезок (рис. 153, а); требуется построить треугольник ABC, у которого
угол А равен данному углу, медиана AM равна данному отрезку,
а отношение сторон АВ и АС равно 2 : 3.
Рис. 153

118
Гл. 3. Подобные треугольники
Построим угол XAY, равный данному углу. Затем возьмем какой-
нибудь отрезок PQ и на луче АХ отложим отрезок АВ\, равный 2PQ,
а на луче AY — отрезок АС\, равный 3PQ (рис. 153, б).
Проведем отрезок В\С\, построим его середину и обозначим ее бук-
буквой М\.
На луче АМ\ отложим отрезок AM, равный данному отрезку, и че-
через точку М проведем прямую, параллельную В\С\. Она пересекает
лучи АХ и AY в некоторых точках В и С (см. рис. 153, б).
Треугольник ABC — искомый. Действительно, угол А по построе-
ЪП II D П	АВ	АВ^	2 LJ
нию равен данному углу, а так как ВС \\ В\С\, то ——- = ——— = -. На-
Наконец, отрезок AM, равный по построению данному отрезку, является
медианой треугольника ABC. Доказательство этого факта содержится
в решении задачи 611 (см. ниже). Таким образом, треугольник ABC
удовлетворяет всем условиям задачи.
Если данный угол не является развернутым, то задача имеет един-
единственное решение.
589. Постройте треугольник ABC по углу А и стороне ВС, если известно,
что АВ: АС = 2:1.
Решение. На рисунке 154, а изображены данный угол и данный
отрезок. Построим угол XAY, равный данному углу. Затем возьмем
какой-нибудь отрезок PQ и отложим на луче АХ отрезок АВ\, равный
2PQ, а на луче AY — отрезок АС\, равный PQ (рис. 154, б).
На луче С\В\ отложим отрезок С\Въ, равный данному отрезку,
и через точку В^ проведем прямую, параллельную АС\. Она пересекает
луч АХ в некоторой точке В.
Через точку В проведем прямую, параллельную С\В\. Эта прямая
пересекает луч AY в некоторой точке С.
Треугольник ABC — искомый. В самом деле, угол А равен данному
углу по построению. Так как ВС || В^С\ и В^В || С\С, то четырех-
четырехугольник BCC\B<i — параллелограмм, и поэтому ВС = C\B<i, а значит,
сторона ВС треугольника ABC равна данному отрезку. Наконец, так
Q
В
X
Рис. 154

§ 4. Соотношения между сторонами и углами	119
Л TD	/I D	О
как ВС || В\С\, то -—^ = -—^- = -. Таким образом, треугольник ABC
J\.Lj J\.kj\ 1
удовлетворяет всем условиям задачи.
Если данный угол не является развернутым, то задача имеет един-
единственное решение.
590. Постройте прямоугольный треугольник по гипотенузе и отношению
катетов.
Решение. Задача решается таким же образом, как и задача 589,
при условии, что АА = 90°.
§ 4. Соотношения между сторонами и углами
прямоугольного треугольника
591. Найдите синус, косинус и тангенс углов А и В треугольника ABC
с прямым углом С, если: а) ВС = 8, АВ = 17; б) ВС = 21, АС = 20; в) ВС =
= 1, АС = 2; г) АС = 24, АВ = 25.
~	\ • л ВС 8	л /Г, . 2 л 15 , л
Решение, a) sin Л = —— = —; cos А = у \ — sin Л = —; tg A =
sinA 8	& ВС . , 8 . D	, 15 , D 15
=	 = —; cosB = —— = smi = —; sin В = cos A = —; tgB = —.
cosA 15	AB	17	17	8
6) AB = VBC2 + AC2 = л/212 + 202 = 29; sinA = cosE = |i;
20	21	20
cos A = sinB = —; tgA = —; tgB = —.
в) АВ = \/BC2 + AC2 = л/5; sin A = cosE = -b cos A = sinE =
V5
w];24
r) sinE = —— = —; cosE = y/\ - sin2 Б = —; tgB = —; cos A =
J\d	АО	АО	I
= sin В = —; sin A = cosB = —; tgA = —.
Q	1 С	Q
Ответ, a) sin A = cosB = —, cos A = sinB = —, tgA = —, tgB =
1 /	1 /	1 о
15 ^ч . „	„ 21	Л . „ 20 x . 21 x „
= y; 6) sin A = cosB = —, cosA = sin В = —, tgA = —, tgB =
20	1	2	1
= —; в) sin A = cos В = -^, cos A = sin В = —=, tgA = -, tgB = 2;
^1	V5	V5	^
7	24	7	24
r) sinA = cos В = —, cos A = sin В = —, tgA= —, tgB = —.
1	3
592. Постройте угол а, если: a) tga = -; 6) tga = -; в) cos a = 0,2;
2	1
r) cos a = —; д) sin a = —; e) sin a = 0,4.
о	Z

120	Гл. 3. Подобные треугольники
Решение, а) Возьмем какой-нибудь отрезок PQ и построим пря-
прямоугольный треугольник ABC, у которого катет ВС = PQ, а катет
НС1 1
АС = 2PQ. Тогда ZA = а, так как tgA= —^ = -.
б)	Аналогично п. а) построим прямоугольный треугольник ABC,
у которого отношение катетов —— = -. Тогда ZА = а.
в)	Возьмем какой-нибудь отрезок PQ и построим прямоугольный
треугольник ABC, у которого катет АС = PQ, а гипотенуза АВ =
= 5PQ. Тогда ZA = а, так как cos А = —— = 0,2.
г)	Аналогично п. в) построим прямоугольный треугольник ABC
АС 2
с прямым углом С, у которого -г-=- = -. Тогда ZA = а.
J\d о
д)	Возьмем какой-нибудь отрезок PQ и построим прямоугольный
треугольник ABC, у которого катет ВС = PQ, а гипотенуза АВ =
= 2PQ. Тогда ZA = а = 30°, так как sin A = -.
е)	Аналогично п. д) построим прямоугольный треугольник ABC
с прямым углом С, у которого ВС = 2, АБ = 5. Тогда ZA = а.
593. Найдите: a) sin а и tga, если cos а = -; б) sin а и tga, если cos a =
= -; в) cos а и tga, если sin а = -—; г) cos а и tga, если sin a = -
о	А	4
г>	ч .	гЛ	о— Л/3	sin а /к
Решение, a) sm a = v 1 — cosz a = —--, tg a =	= v 3 ;
'2	cos a
6)sina = yi-(jj = ^-,
в) cos a = v 1 — sin a = -, tga = л/3 ;
r)cosa=Jl-(\) =-?-, tga =
T5 15 "
^	ч . л/3 ,	П5 s\ •	V^ ^	V^ \
Ответ, а) sina—, tga = л/3 ; 6) sin a = -—-, tga = -—-; в) cos a =
= -, tga = л/3; г) cosa = —^-, tga = ^
594. В прямоугольном треугольнике один из катетов равен Ь, а противо-
противолежащий угол равен E. а) Выразите другой катет, противолежащий ему угол
и гипотенузу через Ъ и C. б) Найдите их значения, если Ъ = 10 см, /3 = 50°.
Решение, а) Пусть другой катет равен а, противолежащий ему
угол равен а, а гипотенуза равна с.
Тогда
-=tg/3, a+ /3 = 90°, -=sin/3,

§ 4. Соотношения между сторонами и углами	121
откуда
а=А. а = 9О°-/3, с = —*
sin/3'
б) Если Ъ = 10 см, /3 = 50°, то
а = ^-^ « 8,39 см, а = 90° -50° =40°, с = ^^ ^ 13,05 см.
tg 50	sin 50
Ответ, а) -^-, 90° -/3, -^-; б) ^8,39 см, 40°, « 13,05 см.
tg/?	sin/3
595. В прямоугольном треугольнике один из катетов равен Ь, а приле-
прилежащий к нему угол равен а. а) Выразите второй катет, прилежащий к нему
острый угол и гипотенузу через Ь и а. б) Найдите их значения, если 6 = 12 см,
а = 42°.
Решение, а) Пусть второй катет равен а, прилежащий к нему
угол равен /3, а гипотенуза равна с. Тогда
?=tga, a+ /3 = 90°, -=cosa,
6	с
откуда
/3 = 90°-а, с=^
cos a
б) Если Ъ = 12 см, a = 42°, то
а= 12 CM-tg42° « 11 см,
/3 = 90° -42° =48°,
12 см 1Л,
С= 	—о « 16 СМ.
cos 42
Ответ, a) btga, 90° -a, —^—; б) « 11 см, 48°, « 16 см.
cos a
596. В прямоугольном треугольнике гипотенуза равна с, а один из острых
углов равен а. Выразите второй острый угол и катеты через с и а и найдите
их значения, если с = 24 см, а a = 35°.
Решение. Пусть второй острый угол равен /3, а катеты равны а
и 6, причем катет, равный а, лежит против угла а. Тогда
/3 = 90° — а, а = с - sin a, b = с • cos a.
Если с = 24 см, а = 35°, то
/3 = 90° -35° = 55°,
a = 24 см-sin35° « 14 см,
6 = 24 см -cos35° ^20 см.
Ответ. 90° — а, с sin а, с cos а; 55°, « 14 см, « 20 см.

122
Гл. 3. Подобные треугольники
597. В прямоугольном треугольнике катеты равны а и Ь. Выразите через а
и Ь гипотенузу и острые углы треугольника и найдите их значения при а = 12,
Ъ= 15.
Решение. Пусть гипотенуза равна с, угол, лежащий против кате-
катета, равного а, равен а, а другой острый угол равен C.
Тогда
с = \Д2 + б2 , tga=^, tg/3=-.
Если а = 12, 6 = 15, то
с =
19,
15
=||, tg/3=||,
откуда а « 38°39', /3 « 51°21'.
Ответ, л/а2 + б2, tga = ^, tg/З = ^; 19, « 38°39Х,
598. Найдите площадь равнобедренного треугольника с углом а при
основании, если: а) боковая сторона равна Ь; б) основание равно а.
Решение, а) Высота /г треугольника равна b-sina, а основание
а треугольника равно 2Ь • cosa (рис.155). Поэтому для площади S
треугольника получаем выражение
5= ^ah =
' sin a cos a.
б) h = - tg а, поэтому S = -ah = — tg а.
2
Ответ, a) 62 sin a cos а; б) —tga.
599. Найдите площадь равнобедренной трапеции с основаниями 2 см
и б см, если угол при большем основании равен а.
Решение. Пусть в равнобедренной трапеции ABCD: ВС = 2 см,
AD = 6 см, ZA = а, ВН и CF - высоты (рис. 156).
Тогда ААВН = ADCF (по гипотенузе и катету), поэтому Аи" =
= FD, а так как HF = DC = 2 см, то
= UAD-HF) =2
см.
а)
Рис. 155
Рис. 156

§ 4. Соотношения между сторонами и углами
123
Из треугольника АВН находим:
ВН = АН -tga = 2tga см.
Следовательно,
\	BC)-BH = 8tga см2.
Ответ. Stga см2.
60 м „
600. Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Како-
Какова ширина насыпи в нижней ее части, если угол наклона откосов к горизонту
равен 60°, а высота насыпи равна 12 м (рис. 157, в учебнике рис.209)?
Решение. Если из концов верх-
верхнего основания трапеции, изображен-
изображенной на рисунке 157, провести высоты
к нижнему основанию (как на рисун-
рисунке 156), то они разобьют нижнее ос-
основание на три отрезка. Средний отре-
отрезок равен 60 м, а каждый из крайних
12	, 4V3
Рис. 157
отрезков равен
tg60°
м, т. е.
м.
Следовательно, нижнее основание трапеции (ширина насыпи в нижней
ее части) равно F0 + 8л/3) м « 74 м.
Ответ. « 74 м.
601. Найдите углы ромба, если его диагонали равны
Д и 2.
Решение. Диагонали ромба взаимно перпендику-
перпендикулярны и точкой пересечения делятся пополам, поэтому
они разделяют ромб на четыре равных прямоугольных
треугольника с катетами, равными л/3 и 1 (рис. 158).
Следовательно, tga = —— = л/3, откуда находим: а =
= 60° и, значит, /3 = 90° - 60° = 30° (см. рис. 158).
Углы ромба равны 2а, 2/3, 2а и 2/3, т. е. 120°, 60°,
120° и 60°.
Ответ. 120°, 60°, 120°, 60°.
Рис. 158
602. Стороны прямоугольника равны 3 см и л/3 см. Найдите углы,
которые образует диагональ со сторонами треугольника.
Решение. Пусть искомые углы равны а и /3 (рис. 159).
Тогда tga = ^-, откуда а = 30°, а /3 = 90° - а = 60°.
Ответ. 30° и 60°.

124
Гл. 3. Подобные треугольники
603. В параллелограмме ABCD сторона AD равна 12 см, а угол BAD
равен 47°5(У. Найдите площадь параллелограмма, если его диагональ BD
перпендикулярна к стороне АВ.
Решение. Из треугольника ABD находим (рис. 160):
АВ = AD • cos 47° 50х = 12 см • cos 47° 50х,
BD= 12 CM-sin47°50/.
Следовательно,
Sabcd = AB-BD= 122 cm2 • со847°50х • 8т47о50х « 72 см2.
Ответ. « 72 см2.
Дополнительные задачи
604. Треугольники ABC и АхВхСх подобны, АВ = б см, ВС = 9 см,
С А = 10 см. Наибольшая сторона треугольника АхВхСх равна 7,5 см. Найдите
две другие стороны треугольника АхВхСх.
Решение. По условию
АхВх ВхСх СхАх 7
АВ
ВС
СА
где к — коэффициент подобия треугольников А\В\С\ и ABC.
Так как в треугольнике ABC наибольшей стороной является С А,
то в треугольнике А\В\С\ наибольшей стороной будет сходственная
сторона С\А\. Поэтому
СхАх
СА
10
и, следовательно,
А\В\ = к • АВ = ± • 6 см = 4,5 см,
ВХСХ =к- ВС =- -9 см = 6,75 см.
Ответ. 4,5 см и 6,75 см.

Дополнительные задачи
125
605. Диагональ АС трапеции ABCD делит ее на два подобных треуголь-
треугольника. Докажите, что АС2 = аЪ, где а и Ъ — основания трапеции.
Решение. Пусть AD и ВС — основания трапеции ABCD
(рис. 161). По условию ААВС ~ AACD и, следовательно, углы этих
треугольников соответственно равны. Так как AD \\ ВС, то Zl = Z2,
а так как АВ и CD не параллельны, то Z3 ф ZACD. Значит, Z3 =
= Z4, ZB = ZACD. Приравнивая отношения сходственных сторон,
получаем:
АС
~AD
ВС
или
АС
откуда АС2 = аЪ.
606. Биссектрисы MD и NK треугольника MNP пересекаются в точке
О. Найдите отношение OK : ON, если MN = 5 см, NP = 3 см, МР = 7 см.
Решение. Пусть МК = х, тогда КР = 7 см — х (рис. 162). Со-
Согласно задаче 535
В Ъ С
Рис. 161
МК MN
КР
NP'
или
X
7 см — х
Рис. 162
_ 5
~ 3'
О О
откуда х = —-, т. е. МК = — см.
8	8
Так как МО — биссектриса треугольника MKN, то
ОК МК 35 г п о
ON MN
Ответ. 7 :
607. Основание равнобедренного треугольника относится к боковой сто-
стороне как 4 : 3, а высота, проведенная к основанию, равна 30 см. Найдите
отрезки, на которые эту высоту делит биссектриса
угла при основании.
Решение. Пусть в равнобедренном тре-
треугольнике ABC с основанием АС высота ВН
и биссектриса AD пересекаются в точке О
(рис. 163). По условию АС : АВ = 4:3, поэтому
АН : АВ = 2 : 3.
Так как АО — биссектриса треугольника
АВН, то
D
ОН:ОВ = АН '.АВ = 2:3
Рис. 163

126
Гл. 3. Подобные треугольники
(см. задачу 535). По условию ВН = 30 см, следовательно,
ОН =
-2=12 см, ОВ = ВН-ОН= 18 см.
Ответ. 12 см и 18 см.
608. На продолжении боковой стороны ОВ равнобедренного треугольника
АОВ с основанием АВ взята точка С так, что точка В лежит между точками
О и С. Отрезок АС пересекает биссектрису угла АОВ в точке М. Докажите,
что AM < МС.
Решение. Так как ОМ — биссектриса треугольника АОС
(рис. 164), то
AM _ ОА
МС ~ ОС
(см. задачу 535).
ОА
По условию О А = ОВ, поэтому О А < ОС и, следовательно, -— <
Л А/Г	ОС
< 1. Значит, и —— < 1, т. е. AM < МС, что и требовалось доказать.
609. На стороне ВС треугольника ABC взята точка D так, —-^ = ——7.
Докажите, что AD — биссектриса треугольника ABC.
п	лл	BD DC
Решение. Из равенства —— = ——- следует, что
BD
DC
АВ
AC
АВ
Но биссектриса угла А делит сторону ВС в том же отношении —— (за-
(задача 535), поэтому AD — биссектриса треугольника ABC.
610. Прямая, параллельная стороне АВ треугольника ABC, делит сторо-
сторону АС в отношении 2 : 7, считая от вершины А. Найдите стороны отсеченного
треугольника, если АВ = 10 см, ВС = 18 см, С А = 21,6 см.
Решение. Пусть ED \\ АВ, АЕ : ЕС = 2 : 7 (рис. 165). Положим
ЕС = х, тогда
21,6 см-ж _ 2
х	~ 7'
Рис. 164
Рис. 165

Дополнительные задачи
127
откуда находим
х = 16,8 см, т. е. ЕС = 16,8 см.
Так как ЕВ || АВ, то AEDC ~ ААВС (по двум углам), поэтому
ED DC EC	ED DC 16,8
АВ
ВС АС
10 см 18 см 21,6'
Отсюда получаем: ED = 7- см, DC = 14 см.
Ответ. 16,8 см, 7- см, 14 см.
611. Докажите, что медиана AM треугольника ABC делит пополам
любой отрезок, параллельный стороне ВС, концы которого лежат на сторонах
АВ и АС.
Решение. Пусть DE \\ ВС, DE и AM пересекаются в точке
N (рис. 166). Требуется доказать, что DN = NE.
Так как DE \\ ВС, то
AADN ~ ААВМ, AANE ~ ААМС, AADE ~ ААВС.
Отсюда следует:
DN
~ВМ
AD
~ ~АВ'
NE
Же
АЕ
~ ~АС'
AD
~АВ ~
АЕ
~АС
лл	DN NE и ъъ/г ъ/гп
Из этих равенств получаем: —— = ¦——^. Но ИМ = МС, так как
JdM М С
AM — медиана треугольника. Следовательно,
DN = NE.
612. Два шеста АВ и CD разной длины а и Ь установлены верти-
вертикально на некотором расстоянии друг от друга так, как показано на рисун-
рисунке 167 (рис. 210 учебника). Концы А и D, В и С соединены веревками, которые
пересекаются в точке О. По данным рисунка докажите, что:

128	Гл. 3. Подобные треугольники
Найдите х и докажите, что х не зависит от расстояния d между шестами АВ
и CD.
Решение, а) Пусть точка Р — основание перпендикуляра, прове-
проведенного из точки О к прямой АС. Тогда ААОР ~ AADC (по двум
углам), поэтому	Ар Qp
АС = DC> ИЛИ Ч = Ь-
Аналогично, из подобия треугольников СОР и СВА следует:
СР OP	n х
С А В A	d a
6) Складывая почленно равенства
х _ п	х _ т
ad	Ъ d'
доказанные в п. а), и учитывая, что т + п = d, получаем:
х , х п + т
а Ь	d
Из этого равенства находим х:
ab
«
х =
откуда видно, что х не зависит от d.
ab
Ответ.
Ъ'
613. Докажите, что треугольники ABC и А\В\С\ подобны, если:
ч АВ АС ВЫ
а)	=	=	, где БМ и BiMi — медианы треугольников;
А\В\ A\L>\ B\M\
АС^	TlT-f
б)	А А = ZA\,	=	, где БЯ и В\Н\ — высоты треугольников ABC
А\С\ В\Н\
и АхВхСх.
Решение, а) Так как АС = 2AM, АХСХ = 2АХМХ (рис.168),
AC AM XT
то . ^ = . , т . Учитывая условие задачи, получаем:
АБ AM БМ
AxBx АхМх ВхМх'
М

Дополнительные задачи	129
Следовательно, ААВМ ~ АА\В\М\ по третьему признаку подобия
треугольников. Отсюда следует, что ZA = ZA\, а значит, ААВС ~
~ АА\В\С\ по второму признаку подобия треугольников.
б) Так как ZA = ZA\, то ААВН ~ АА\В\Н\ (по двум углам).
~	АВ ВН
Отсюда следует, что	=	, а так как по условию
А\В\ В\П\
ВН АС	АВ АС
то
ВхНх АхСх' АхВх АХСХ'
Поэтому ААВС ~ АА\В\С\ (по второму признаку подобия треуголь-
треугольников).
614. Диагонали прямоугольной трапеции ABCD с прямым углом А вза-
взаимно перпендикулярны. Основание АВ равно б см, а боковая сторона AD
равна 4 см. Найдите DC, DB и СВ.
Решение. По теореме Пифагора
DB = \/АВ2 + AD2 = 2л/Тз см (рис. 169).
Так как Zl + Z2 = ZD = 90°, то Z1 = 90° - Z2, а так как
Z2 + Z3 = 90° (сумма острых углов прямоугольного треугольника),
то Z3 = 90° - Z2. Следовательно, Zl = Z3 и поэтому AADC ~ ABAD
по двум углам (ZD = ZA = 90°, Z3 = Z1).
Из подобия этих треугольников следует:
AD _ DC
~АВ ~ ~AD'
откуда
_ AD2 16	О2
DC= —= -см = 2-см.
Пусть Ci^ — высота трапеции (см. рис. 169). Тогда
СН = AD = 4 см,
ВН = АВ - АН = АВ - DC = 6 см - 2§ см = 3^ см.
о	о
По теореме Пифагора
ев
Ответ.
=
9
2з
у/с
СМ,
'Я2
2л
Чм2
/13 см и
= 1
2
зА
/*
/бГ
+ (;
см.
2
= |л/бТсм.
615. Отрезок с концами на боковых сторонах трапеции параллелен ее ос-
основаниям и проходит через точку пересечения диагоналей. Найдите длину
этого отрезка, если основания трапеции равны а и Ъ.
Решение. Пусть ABCD — данная трапеция, а отрезок MN про-
проходит через точку О пересечения диагоналей и параллелен основаниям
AD и ВС (рис. 170).
5 Л. С. Атанасян и др.

130
Гл. 3. Подобные треугольники
Так как АВОС ~ AAOD (по двум углам), то
ОС ВС а
Отсюда получаем:
ОС
О A AD Ъ'
ОС + ОА _ а + Ъ
ОА ~~ Ъ '
т. е.
АС а + Ъ
АО Ъ '
Так как МО II ВС, то ААМО ~ ААВС и, следовательно,
ВС _ АС_	_о_
Ш~Ад' или мо
Ъ '
откуда МО =
аЬ
а + Ъ'
Аналогично находим ON =
Таким образом,
аЪ
а + Ъ'
MN = МО + ON =
2аЪ
а + Ъ'
Ответ.
2аЪ
а + Ъ'
Q
Рис. 171
616. Докажите, что вершины треугольника
равноудалены от прямой, содержащей его сред-
среднюю линию.
Решение. Пусть отрезок MN — сред-
средняя линия треугольника ABC (рис. 171);
АО, ВР, CQ — перпендикуляры, проведен-
проведенные к прямой MN. Требуется доказать, что
АО = ВР = CQ.
ААОМ = АВРМ (по гипотенузе и
острому углу), поэтому АО = ВР. Анало-
Аналогично, из равенства треугольников BPN
и CQN следует, что BP = CQ.
Итак, АО = ВР = CQ.

Дополнительные задачи
131
617. Докажите, что середины сторон ромба яв-
являются вершинами прямоугольника.
Решение. Пусть точки М, N, Р, Q —
середины сторон ромба ABCD (рис. 172). То-
Тогда четырехугольник MNPQ — параллело-
параллелограмм (см. задачу 567).
Так как MN и MQ — средние линии
треугольников ABC и ABD, то MN || АС
и MQ || BD. Отсюда следует, что MSOR —
параллелограмм, а так как угол SOR пря-
прямой (диагонали ромба взаимно перпендикуляр-
перпендикулярны), то MSOR — прямоугольник (см. зада-
задачу 399). Следовательно, угол RMS — также
прямой, а значит, параллелограмм MNPQ яв-
является прямоугольником.
618. Точки М и N являются соответственно серединами сторон CD и ВС
параллелограмма ABCD. Докажите, что прямые AM и AN делят диагональ
BD на три равные части.
Решение. Пусть О — точка пересе-
пересечения диагоналей АС и BD, a P и Q —
точки пересечения отрезков AM и AN
с диагональю BD (рис. 173). Требуется до-
доказать, что BQ = QP = PD.
Так как отрезки AN и ВО — медианы
треугольника ABC, то BQ : QO = 2:1,
2
откуда следует, что BQ = -ВО, а посколь-
поскольку BO = OD = )-BD, то BQ = ]-BD.
2	о
В
Рис. 173
Аналогично доказывается, что PD = -ВВ. Следовательно,
о
QP = BD- (BQ + PD) =BD- %BD = \
о	о
Итак, BQ = QP = PD.
619. Биссектриса внешнего угла при вершине А треугольника ABC пере-
пересекает прямую ВС в точке D. Докажите, что
BD
АВ
DC
АС
Решение. Пусть точка В лежит между точками С и D (рис. 174).
Треугольники ABD и ACD имеют общую высоту, проведенную из вер-
вершины А, поэтому (см. следствие 2 в п. 52 учебника):
Sabd _ BD
Sacd DC
(i)

132
Гл. 3. Подобные треугольники
Пусть DK и DH — перпендикуляры к прямым АВ и АС. Так
как AADK = AADH (по гипотенузе и острому углу), то DK = DH,
т. е. высоты в треугольниках ABD и ACD, проведенные из вершины
D, равны. Поэтому, снова используя следствие 2 из п. 52 учебника,
получаем:
B)
Sabd
АВ
~АС'
Sacd
Из равенств A) и B) следует, что
BD _ АВ
DC ~ АС
BD DC
откуда имеем: — = —.
620. В треугольнике ABC (АВ ф АС) через середину стороны ВС про-
проведена прямая, параллельная биссектрисе угла А, которая пересекает прямые
АВ и АС соответственно в точках D и Е. Докажите, что BD = СЕ.
Решение. Пусть АВ < АС, отрезок АК — биссектриса треуголь-
треугольника ABC, точка М — середина стороны ВС, MD || АК (рис. 175).
Согласно задаче 535	Т,^ г,~
АВ = АС'
Так как MD \\ АК, то
ААВК - ADBM и АЕСМ - ААСК,
поэтому
KB
ВЫ СМ
и
КС
АВ BD СЕ АС
B)
ЛЛ	П\	/О\	ВМ	СМ ТТ
Из равенств A) и (z) следует, что ——— = -рттт- Числители в этих
BD СЕ
отношениях равны (ВМ = СМ по условию), следовательно, равны
и знаменатели, т. е. BD = СЕ, что и требовалось доказать.
621. В трапеции ABCD с основаниями AD и ВС сумма оснований равна
Ь, диагональ АС равна a, ZACB = а. Найдите площадь трапеции.
Решение. Так как AD || ВС, то ZCAD = ZACB = а (рис. 176;
на этом рисунке представлен случай, когда а < 90°). Из прямоуголь-

Дополнительные задачи
133
ного треугольника АСН получаем: СН = a sin а (это выражение для
высоты трапеции сохраняется и в том случае, когда а > 90°). Следова-
Следовательно,
SAbcd = \(AD + ВС) • СН = l-ahsma.
Ответ, -ah sin a.
622. На стороне AD параллелограмма ABCD отмечена точка К так,
что АК = jKD. Диагональ АС и отрезок ВК пересекаются в точке Р.
Найдите площадь параллелограмма ABCD, если площадь треугольника АРК
равна 1 см2.
Решение. АСРВ ~ ААРК по двум углам (рис.177), поэтому
ВР _ ВС
РК ~ АК'
Так как АК = jKD, то АК = -iD = -БС, откуда следует, что
4	0	0
ВС г	ВР -
— = 5, а значит, и — = 5.
Треугольники АРК и АРБ имеют общую высоту, проведенную
из вершины Д поэтому ^Ард = —— = 5 и, следовательно,
Ьарк РК
Sap в = 5 Sap к = 5 см2.
НС1
Коэффициент подобия треугольников СРВ и АРК равен —— = 5,
откуда следует, что
Scpb
= 25, т. е. Scpb =25 см2.
Sabc = Sap в + Scpb = 5 см2 + 25 см2 = 30 см2,
Sabcd — 2 • Sabc = 60 cm .
Ответ. 60 см2.
В	С
Рис. 177

134
Гл. 3. Подобные треугольники
623. В прямоугольной трапеции ABCD с основаниями AD и ВС АА =
= АВ = 90°, ZACD = 90°, ВС = 4 см, AD = 16 см. Найдите углы С и D
трапеции.
Решение. Пусть Ci^ — высота трапеции (рис. 178). Тогда
АН = ВС = 4 см, HD = AD-AH= 12 см.
Согласно утверждению 1° из п. 63
СН = VAH • HD = л/4- 12 см = 4л/3 см.
Из прямоугольного треугольника CHD имеем:
. п СН
Следовательно,
ZL> = 30°, а
Ответ. 30° и 150°.
= 180° - ZD = 150°
624. Докажите, что медианы треугольника разбивают его на шесть тре-
треугольников, площади которых попарно равны.
Решение. Пусть медианы АА\, ВВ\ и СС\ треугольника ABC
пересекаются в точке О (рис. 179). Тогда
Sabbx = Scbbx и Saobx =
(см. задачу 474). Отсюда следует, что Sao в = $вос- Аналогично
доказывается, что Бвос = $соа- Но
Saob =
поэтому
что и требовалось доказать.
= Scobx —
Рис. 179

Дополнительные задачи
135
625. Основание AD равнобедренной трапеции
ABCD в пять раз больше основания ВС. Высота
ВН пересекает диагональ АС в точке М, площадь
треугольника АМН равна 4 см2. Найдите площадь
трапеции ABCD.
Решение. По условию AD = ЪВС. Пусть
С К JL AD (рис. 180). Тогда
Рис. 180
НК = ВС, АН =
AD - НК ЪВС - ВС
2	2
А АМН rsj AC MB (по двум углам), поэтому
МН АН
= 2ВС,
АН
ВС
= 2.
MB ВС
= 2, т. е. МН = 2MB.
Отсюда следует, что ВН = ^М
По условию
= 4 см2,
а так как АН = 2ВС, то ВС • МН = 4 см2.
Sabcd = \(AD + ВС) - ВН = 1-(ЪВС + ВС) • \мн =
= 4,5 • ВС • МН = 4,5-4 см2 = 18 см2.
Ответ. 18 см2.
626* Докажите, что треугольники ABC и А\В\С\ подобны, если
AC AD
АВ
-, где AD и A\D\ — биссектрисы треугольников.
Решение. Пусть DE \\ АВ и DXEX \\ АХВХ (рис.181). Тогда, со-
гласно задаче 556,
СЕ _ CD
ЕА ~ DB
, а так как AD — биссектриса треуголь-
CD АС
ника, то -—— = —— (задача 535). Следовательно,
DB АВ
СЕ
ЕА
АС
АВ'
с в/
Рис. 181

136	Гл. 3. Подобные треугольники
Аналогично из треугольника А\В\С\ получаем:
АхСх
АхВх'
1Я	АС АхСх	СЕ СхЕх
Из условия задачи следует, что ——- =	, поэтому	—— =
АН ЛхНх	ЕА
Прибавив к обеим частям этого равенства 1, получим
'
ЕА '	ЕхАх ' '	?А
~	?А	АС	АС
Отсюда имеем:	=	, а так как по условию
.C/iAi АхСх
АР
-, то
EA AD
В треугольнике AED Z2 = Z3 (это следует из того, что Z1 =
= Z2, так как AD — биссектриса, и Zl = Z3, так как эти углы —
накрест лежащие при пересечении параллельных прямых АВ и DE
секущей AD), поэтому DE = ЕА. Аналогично получаем: DXEX = E\A\
и, следовательно, в силу равенства A) имеем:
РЕ _ ЕА _ АР
РхЕх ~ ЕхАх ~ АхРх'
Отсюда следует, что AAED ~ AA\E\D\, а значит, Z2 = Z4 и по-
поэтому ZA = АА\. Из равенств
АВ АС / л / л
следует, что A ABC ~ АА\В\С\ (по второму признаку подобия тре-
треугольников), что и требовалось доказать.
627.	Дан треугольник ABC. Постройте треугольник А\В\С\, подобный
треугольнику ABC, площадь которого в два раза больше площади треуголь-
треугольника ABC.
Решение. Так как „х х х = ——— = 2, то ——— = V2, т. е.
Sabc V АВ )	АВ
AiBi = л/2 АВ, и также ВХСХ = л/2 ВС, СХАХ = л/2 С А.
Построим квадрат со стороной АВ. Его диагональ равна у/2 АВ,
т. е. равна АХВХ. Аналогичным образом построим отрезки, равные
ВХСХ и СХАХ, а затем построим треугольник АХВХСХ по трем сторонам.
628.	Даны три отрезка, длины которых соответственно равны а, Ь и с.
Построите отрезок, длина которого равна —.
Решение. Построим неразвернутый угол А (рис.182). На одной
стороне угла отложим отрезки АС = с и CD = а, а на другой стороне
угла — отрезок АВ = Ъ. Проведем прямую ВС, а затем через точку D

Дополнительные задачи
137
проведем прямую, параллельную прямой ВС. Она пересекает луч АВ
в некоторой точке Е. Отрезок BE — искомый.
В самом деле, согласно задаче 556
BE
т. е. BE = —.
с
629.	Постройте треугольник, если даны середины его сторон.
Решение. Пусть точки К, М, N — данные середины сторон
искомого треугольника (рис. 183). Проведем прямые KM, MN, NK,
а затем через точки К, М, N проведем прямые, параллельные со-
соответственно прямым MN, NK, КМ. Точки А, В, С пересечения
проведенных прямых являются вершинами искомого треугольника.
В самом деле, докажем, что точка К — середина стороны АВ.
По построению четырехугольники AKMN и BMNK — параллело-
параллелограммы, поэтому АК = MN и MN = KB, откуда следует, что АК =
= KB, т. е. точка К — середина стороны АВ. Аналогично доказыва-
доказывается, что точки М и N — середины сторон ВС и С А.
630.	Постройте треугольник по стороне и медианам, проведенным к двум
другим сторонам.
Решение. Сначала построим треугольник АОВ, в котором АВ —
данная сторона, а отрезки АО и ВО составляют - данных меди-
медиан (рис. 184).
Затем на лучах АО и ВО отложим отрезки AM и BN, равные
соответствующим данным медианам, и проведем прямые AN и ВМ.
Они пересекаются в некоторой точке С. Треугольник ABC — искомый.
Докажем это. Нужно доказать, что отрезки AM и BN являются
медианами построенного треугольника, т. е. точки М и N — середины
сторон ВС и АС.
т,	АО ВО о ,	ч
Так как ——: = ——- = 2 (по построению) и углы с верши-
вершиной О в треугольниках АОВ и M0N равны как вертикальные,
то ААОВ ~ AM0N (по второму признаку подобия треугольников),
Л Н
причем коэффициент подобия равен 2. Поэтому	=2 и Z1 =
= Z2 (см. рис. 184). Отсюда следует, что MN = -АВ и MN \\ АВ.
а D
N
Рис. 182
Рис. 183
Рис. 184

138
Гл. 3. Подобные треугольники
Следовательно, отрезок MN — средняя линия треугольника ABC,
а значит, точки М и N — середины сторон ВС и АС.
Задачи повышенной трудности
847. На рисунке 185 (рис.269 учебника) изображен правильный пяти-
пятиугольник ABCDE, т. е. выпуклый пятиугольник, у которого все углы равны
и все стороны равны. Докажите, что: a) AAED ~ AAFE; б) -—- = ——-.
Решение, a) AAED = АВАЕ по двум сторонам и углу между
ними (АЕ — общая сторона, ED = АВ, ZAED = ZBAE), поэтому
Z1 = Z2. AAED rsj AAFE по двум углам (угол А — общий, Zl = Z2).
б) Из подобия треугольников AED и AFE следует, что
РА
~АЁ
АЕ
~AF
и AAFE = ZAED. Но ZAED =
18°° '^5
= 108°, поэтому
ZAFE = 108°, Z3 = 180° - 108° = 72°.
1 оло 	 / A J71 ~П 1
Так как Z1 = ——2	= ^
2	^	- 108°) = 36°, то Z4 = 180° -
- (Zl + Z3) = 180° - C6° + 72°) = 72°.
Таким образом, Z4 = Z3 и, следовательно, DF = DE, а так как
DE = АЕ, то АЕ = DF.
Из равенства A) получаем:
РА
PF
PF
AF'
что и требовалось доказать.
848. В треугольнике ABC (АВ ф АС) через середину М стороны ВС
проведена прямая, параллельная биссектрисе угла А, которая пересекает пря-
прямые АВ и АС соответственно в точках D и Е. Докажите, что BD = СЕ.
Решение. Пусть АВ < АС и АК — биссектриса треугольника
ABC (рис. 186). Согласно задаче 535, -^^ = ^^ и, следовательно,
АВ KB
В
К
м
Рис. 185
Рис. 186

Задачи повышенной трудности	139
КС > КВ. Поэтому точка М лежит между точками К и С, КС =
= КМ + МС = 2КМ + KB,
АС_ _ 2КМ + KB _ 2KM
АВ ~ KB ~ KB
ссс KM AD
Так как, согласно задаче 556, —— = ——, то
АВ АВ
откуда
АВ + AD = АС - AD, т. е. BD = АС - AD.
Из параллельности АК и DM следует, что Z3 = Zl, Z4 = Z2, а так
как Zl = Z2, то Z3 = Z4 и, следовательно, AD = АЕ. Поэтому
BD = АС - AD = АС - АЕ = СЕ,
что и требовалось доказать.
849.	Докажите, что отрезки, соединяющие основания высот остроуголь-
остроугольного треугольника, образуют треугольник, в котором эти высоты являются
биссектрисами.
Решение. Пусть АА\, ВВ\, СС\ — высо-
высоты остроугольного треугольника ABC (рис. 187).
Требуется доказать, что лучи А\А, В\В и С\С
являются биссектрисами углов А\, В\ и С\ тре-
треугольника А\В\С\.
Из прямоугольного треугольника АВВ\ полу-
получаем: АВ\ = АВ • cos А, а из прямоугольного тре-
треугольника АСС\ находим: АС\ = АС • cos А. Сле- А	Вг С
АВХ АСХ	ЛТ^ л„
довательно, — = —, т. е. стороны АВ\ и АС\	рис lg?
треугольника АВ\С\ пропорциональны сторонам
АВ и АС треугольника ABC. Поэтому ААВ\С\ ~ ААВС, откуда сле-
следует, что Z1 = /.С. Аналогично доказывается, что АВА\С\ ~ ABAC,
откуда следует, что Z2 = Z.C.
Таким образом, Z1 = Z2, а так как ААСХС = АВСХС = 90°,
то ZB\C\C = ZA\C\C, т. е. луч С\С — биссектриса угла С\ треуголь-
треугольника А\В\С\.
Аналогично доказывается, что лучи А\А и В\В — биссектрисы
углов А\ и В\ треугольника А\В\С\.
850.	Точки Е и F лежат на стороне АВ треугольника ABC, причем так,
что точка Е лежит на отрезке AF и АЕ = BF. Прямая, проведенная через
точку Е параллельно стороне АС, пересекает прямую, проведенную через
точку F параллельно стороне ВС, в точке К. Докажите, что точка К лежит
на медиане треугольника ABC, проведенной к стороне АВ.

140
Гл. 3. Подобные треугольники
Решение. Пусть луч С К пересекает сторону АВ в точке
М (рис. 188). Требуется доказать, что AM = MB.
Так как ЕК \\ АС, то AM AC ~ AMEK, откуда следует, что
МС AM	МС АЕ + ЕМ АЕ , ,
МК
Так как ЕК
МС
т. е.
ЕМ' х' "" МК
ВС, то АМВС ¦
MB
МК ME'
т. е.
МС
МК
ЕМ
AMFK, откуда следует, что
MF + ЕЕ ЕЕ
MF
MF
+ 1.
МС	АЕ
Приравнивая два выражения для отношения -т-р^, получаем: ——: =
мк	ьм
Н АЕ = BF по условию, поэтому ЕМ = MF и, значит,
ЕМ = MF + БЕ, т. е. AM = MB.
851. Гипотенуза прямоугольного треугольника является стороной квадра-
квадрата, не перекрывающегося с этим треугольником. Найдите расстояние от точки
пересечения диагоналей квадрата до вершины прямого угла треугольника, если
сумма катетов равна а.
Решение. Обозначим данный прямоугольный треугольник через
ABC, а точку пересечения диагоналей квадрата, построенного на ги-
гипотенузе ВС, — буквой D (рис. 189). Требуется найти AD.
Проведем луч DE так, что ZCDE = ZBDA. Тогда AABD =
= AECD по стороне и двум прилежащим углам BD = CD, так
как каждый из этих отрезков равен половине диагонали квадрата;
ZBDA = ZCDE по построению;
ZABD = /1+45°,
ZDCE = 180° - (Z2 + 45°) = 180° - (90° - Z1 + 45°) = Z1 + 45°
и, следовательно, ZABD = ZDCE.
Отсюда следует, что AD = DE и АВ = СЕ. Поэтому
АЕ = АС + СЕ = АС + АВ = а.
Рис. 188

Задачи повышенной трудности	141
Треугольник ADE — равнобедренный (AD = DE) и прямоуголь-
л (ZADE = ZCDE + ZADC = АВВА + ZADC = ZBDC = 90°).
ный
Поэтому
Ответ. —=.
1 ЯП°
852. В треугольнике ABC AA = ——— и
360° „	111	^
= —. Докажите, что — = — + —.	^>^ Е
Решение. Пусть АВ = с, ВС = а, АС = Ъ.
х *	1 1,1
1ребуется доказать, что - = - -\—.
а о с
\.
а о с	С D	Л
ZC = 180° - (ZA + ZB) = 7-^f, поэтому	рис т
ZC = 2 • ZB, а /Б = 2 • ZA. Проведем биссек-
биссектрисы BD и СЕ (рис. 190). Тогда ABDC - ЛАБС (по двум углам),
откуда следует, что
B
с	а Ъ
Отсюда получаем:
BD=°^, CD=a-.
о	о
Так как в треугольнике ABD АА = ZABD (см. рис. 190), то
ас	ас	а
= BD = —. Сложив равенства AD = — и CD = —, получим: 6 =
о	оо
ас . а	,2	i 2
= -—Ь -г, или о = ас-\- а , откуда
о о
(Ъ-а)(Ъ + а) =ас.	A)
А АСЕ ~ А АВС (по двум углам), откуда следует, что
СЕ _ АЕ _ Ь
а	Ь с
Отсюда получаем:
СЕ=^, АЕ=Ь-.
С	С
Так как в треугольнике ВСЕ /Б = ZBCE, то BE = СЕ = —.
аЪ а -л Ъ	ab , Ь	о
Сложив равенства ВЬ = — и АЬ = —, получим: с =	1	, или с =
с	с	ее
= ab + b2 = b(a + 6), откуда

142	Гл. 3. Подобные треугольники
Подставляя это выражение в равенство A), приходим к равенству
(Ъ-а)с2	,	, ,
-—г^— = ас, или ос = ас-\- ао.
о
Разделив последнее равенство на abc, получим
abc
что и требовалось доказать.
853.	Из точки М внутренней области угла АОВ проведены перпендику-
перпендикуляры МР и MQ к его сторонам О А и ОВ. Из точек Р и Q проведены перпен-
перпендикуляры PR и QS соответственно к ОВ и О А. Докажите, что RS JL ОМ.
Решение. Пусть прямая МР пересекается с лучом ОВ в точке
Е, а прямая MQ с лучом О А — в точке F (рис. 191).
Так как PR \\ FQ, то AORP ~ AOFQ,
OP OF Л
откуда следует, что —- = -—-. Аналогично
OR OCJ
из подобия треугольников OSQ и ОРЕ сле-
следует, что —— = —-^. Перемножая получен-
ные равенства, приходим к пропорции —— =
^^	OF
= ——, которая показывает, что AOEF ~
Рис. 191	О6
- AORS. Следовательно, ZOEF = ZORS
и поэтому EF || i?S\
Пусть луч ОМ пересекает отрезок EF в точке Н. Для доказатель-
доказательства того, что RS _1_ ОМ, достаточно доказать, что Oi^ J_ EF.
Прямоугольные треугольники MPF и ЕРО подобны, так как
имеют по равному острому углу (ZMFP = ZQFO = 90° - ZAOB
и ZOEP = 90° - ZAOB, поэтому ZMFP = ZOEP). Из подобия
МР ОР
этих треугольников следует, что —— = ——, т. е. катеты МР и ОР
г h г hi
треугольника ОМР пропорциональны катетам PF и РЕ треуголь-
треугольника PFE. Следовательно, АОМР ~ APFE, а значит, ZPOM =
= ZPEF или ZPOM = ZMEH, т. е. в треугольниках РОМ и НЕМ
углы с вершинами О и Е равны. Углы этих треугольников с вер-
вершинами в точке М равны как вертикальные. Поэтому AHEM ~
~ АРОМ (по двум углам) и, следовательно, ZEHM = ZOPM = 90°,
т. е. ОН ± EF.
854.	В равнобедренном треугольнике ABC из середины D основания АС
проведен перпендикуляр DH к стороне ВС. Пусть М — середина отрезка DH.
Докажите, что ВМ !_ АН.
Решение. Пусть АЕ — высота треугольника ABC (рис.192).
Тогда DH || АЕ и так как AD = DC, то ЕН = НС.

Задачи повышенной трудности
143
Так как прямоугольные треугольники АЕС и BDC (они имеют
общий острый угол С) и также прямоугольные треугольники BDC
и BHD (они имеют общий угол с вершиной В) подобны, то ААЕС ~
~ ABHD. Отрезки АН и ВЫ — сходственные медианы в этих подоб-
подобных треугольниках, поэтому ААЕН ~ АВМН, откуда следует, что
ZEAH = ZHBM.
Пусть отрезки АН и ВЫ пересекаются в точке К. Тогда ZBHK =
= ZEHA = 90° - ZEAH = 90° - ZHBM = 90° - ZHBK, откуда по-
получаем:
ZBHK + ZHBK = 90°
и, значит, ZBKH = 90°, т. е. ВЫ _L АН.
855. В прямоугольном треугольнике ABC из вершины прямого угла С
проведен перпендикуляр CD к гипотенузе, а из точки D — перпендикуляры
DE и DF к катетам АС и ВС. Докажите, что: a) CD3 = АВ • АЕ • Б^;
б) ЛБ2 + BF2 + 3CL>2 = АВ2; в) ^АЁ* + ^F2" = ^АВ2".
Решение, а) Из прямоугольных треугольников ABC, BDC
и АСБ (рис. 193) находим (см. задачи 573, 574):
AD2 = АС • АЕ, BD2 = ВС • BF,
CD2 = AD • BD, АС-ВС = АВ- CD.	A)
Перемножая первые два равенства и учитывая третье, получаем
CD4 = АС • ВС • АЕ • BF.
Заменяя АС • ВС на АВ • CD (четвертое равенство в A)) и разде-
разделив на CD, приходим к равенству
CD3 = AB-AE- BF.
б) АВ2 = (АВ + BDJ = AD2 + BD2 + 2-AD-BD =
B)
Из треугольников ADE и BDF по теореме Пифагора находим:
AD2 = АЕ2 + ED2, BD2 = BF2 + DF2,
А
В

144
Гл. 3. Подобные треугольники
откуда
AD2 + BD2 = АЕ2 + BF2 + (ED2 + DF2) = АЕ2 + BF2 + CD2.
Подставляя это выражение в равенство B), получаем
АВ2 = AE2 + BF2 + 3CD2,
что и требовалось доказать.
в) AADE rsj ААВС, поэтому —— = ——, а так как АС = —— (пер-
/1ЧЧ AD AB-AE
вое равенство в A)), то —^ =	-2—, откуда
AD= у/АВ • АЕ2.
Аналогично, используя подобие треугольников BDF и ВАС и вто-
второе равенство в A), получаем:
BD= у/АВ • BF2.
Отсюда следует:
= AB= VAB • АЕ2 + V АВ • BF2.
О j
Разделив на у АВ, приходим к равенству
что и требовалось доказать.
856. В выпуклом четырехугольнике ABCD диагонали пересекаются
в точке Р. Известно, что ZADP = )-APDC, ZADP = \aPAD и AD =
= BD = CD. а) Найдите все углы четырехугольника, б) Докажите, что АВ2 =
= ВР • BD.
Решение, а) Пусть ZADP = а. Тогда
ZPDC = 2а, ZPAD = = |а (рис. 194).
Треугольник ACD — равнобедренный (AD =
= CD), поэтому ZACD = -а. В треугольнике
ACD:
|а+|а + 3а= 180°,
D откуда имеем: а = 30° и, значит, ZD = За = 90°.
В равнобедренном треугольнике ABD
ZA = ZABD = 180°-а = 75°.
В
Рис. 194

Задачи повышенной трудности	145
В равнобедренном треугольнике BCD
ZC = ZCBD = т°-2а = 60°.
A ABC = ZABD + ZCBD = 75° + 60° = 135°.
Итак, в четырехугольнике ABCD ZA = 75°, ZB = 135°, ZC = 60°,
ZD = 90°.
б) ZBAP = ZBAD - ZPAD = 75° - 45° = 30°.
ААВР ~ AABD по двум углам (ZBAP = ZABD = 30°, ZB -
ООЩИИ), ПОЭТОМУ —— = -Т7Т» т- е-
= ВР • BD,
что и требовалось доказать.
Ответ, а) 75°, 135°, 60° и 90°.
857.	Точка М не лежит на прямых, содержащих стороны параллелограмма
ABCD. Докажите, что существуют точки N, Р и Q, расположенные так, что
А, В, С и D являются соответственно серединами отрезков MN, NP, PQ
и QM.
Решение. Пусть точка N симметрична точке М относительно
точки А, точка Р симметрична точке N относительно точки В, точка
Q симметрична точке Р относительно точки С (рис. 195).
Тогда точки А, В, С являются середи-
серединами отрезков MN, NP, PQ и остается
доказать, что точка D — середина отрез-
отрезка QM.
Обозначим середину отрезка QM через
D\. Согласно задаче 567 четырехугольник
ABCD\ — параллелограмм. Но по усло-
условию задачи ABCD — тоже параллело-
параллелограмм. Следовательно, точки D\ и D сов-
совпадают, т. е. D — середина отрезка QM.
858.	Докажите, что если противополож-
противоположные стороны выпуклого четырехугольника не параллельны, то их полусумма
больше отрезка, соединяющего середины двух других противоположных сто-
сторон.
Решение. Пусть ABCD — выпуклый четырехугольник, в котором
стороны АВ и DC не параллельны, точки М и N — середины сторон
AD и ВС (рис. 196). Требуется доказать, что
mn < Ьав + cd).
Отметим точку D\, симметричную точке D относительно точки N.
Треугольники NDC и ND\B равны по двум сторонам и углу между
ними (NC = NB, ND = NDU ZDNC = ZD{NB), поэтому BDX = DC

146	Гл. 3. Подобные треугольники
и ZDCN = ZD\BN. Из последнего равенства следует, что BD\ || DC
и, следовательно, точки А, В и D\ не лежат на одной прямой.
В треугольнике ABD\
ADX <AB + BDU т. е. ADX < АВ + CD.
Отрезок MN — средняя линия треугольника DAD\, поэтому
AD\ = 2MN. Таким образом,
2 • MN <АВ + CD, т. е. MN < ^(АВ +
859. Докажите, что если сумма расстояний между серединами противо-
противоположных сторон выпуклого четырехугольника равна половине его периметра,
то этот четырехугольник — параллелограмм.
Решение. Пусть ABCD — выпуклый четырехугольник, точки М,
Р, N, Q — середины его сторон (рис. 197). По условию
MN + PQ= 1-{AB + BC + CD + DA).	A)
Требуется доказать, что ABCD — параллелограмм.
Докажем, что АВ \\ CD и AD \\ ВС. Предположим, что это не так:
например, АВ и CD не параллельны. Тогда, согласно задаче 858,
MN < UaB + CD).	B)
С другой стороны,
l	C)
Знак равенства в C) имеет место в том случае, когда ВС || DA.
Складывая равенства B) и C), получаем:
MN + PQ < UAB + BC + CD + DA),
что противоречит равенству A). Следовательно, наше предположение
неверно и, значит,
АВ || CD и AD || ВС,
т. е. ABCD — параллелограмм.
В
В
п/..
N
D	Q	С
Рис. 197

Задачи повышенной трудности	147
860.	Докажите, что если отрезок, соединяющий середины двух противо-
противоположных сторон выпуклого четырехугольника, равен полусумме двух других
сторон, то этот четырехугольник — трапеция или параллелограмм.
Решение. Пусть ABCD — выпуклый четырехугольник, в котором
отрезок MN, соединяющий середины противоположных сторон AD
и ВС, равен полусумме сторон АВ и CD, т. е. MN = ^(АВ + CD).
Тогда АВ || CD. В самом деле, если предположить, что АВ и CD
не параллельны, то, согласно задаче 858,
MN < ^(AB + CD),
что противоречит условию.
Итак, АВ || CD, откуда следует, что четырехугольник ABCD —
трапеция или параллелограмм.
861.	Диагонали трапеции ABCD пересекаются в точке О. Треугольник
АВО, где АВ — меньшее основание трапеции, равносторонний. Докажите,
что треугольник, вершинами которого являются середины отрезков ОА, OD
и ВС, равносторонний.
Решение. Пусть точки Е, F и G — середи-
ны отрезков ОА, OD и ВС (рис. 198). Требуется
доказать, что треугольник EFG — равносторон-
равносторонний, т. е.
EF = FG = EG.
ACDO ~ ААВО по двум углам (углы COD
и АОВ равны, как вертикальные, углы ВАО
D
и DCO равны, так как АВ || DC). Отсюда сле-
следует, что треугольник CDO — равносторонний,	Рис. 198
в частности, OD = ОС.
AAOD = АВОС по двум сторонам и углу между ними (АО = ВО,
OD = ОС, ZAOD = АВОС), поэтому AD = ВС.
Отрезок EF — средняя линия треугольника AOD и, значит, EF =
= \ad = \вс.
Отрезок CF — медиана равностороннего треугольника CDO, по-
поэтому CF _l_ DO, т. е. ZCFB = 90°. Медиана FG прямоугольного
треугольника CFB равна половине гипотенузы (задача 404), т. е. FG =
= \вс.
Аналогично, отрезок BE — медиана равностороннего треугольника
АВО, поэтому BE _L АО, т. е. ZBEC = 90°. Медиана EG прямоуголь-
прямоугольного треугольника ВЕС равна половине гипотенузы: EG = ^ВС.
Итак, EF = FG = EG = ^BC, откуда следует, что треугольник
EFG — равносторонний.

148	Гл. 3. Подобные треугольники
862. Из вершины А треугольника ABC проведены перпендикуляры AM
и АК к биссектрисам внешних углов этого треугольника при вершинах В и С.
Докажите, что отрезок МК равен половине периметра треугольника ABC.
Решение. Обозначим точки пересече-
L	ния прямой ВС с прямыми AM и АК бук-
вами D и Е (рис. 199). В треугольнике ABD
М//\^^К	(р	) ру
/У ^чС^^-^ отрезок ВМ является биссектрисой и вы-
D в	С	Е сотой, поэтому треугольник ABD — рав-
равнобедренный: DB = АВ. Кроме того, ВМ
Рис- 199	является также медианой, т. е. точка М —
середина отрезка AD.
Аналогично, в треугольнике АСЕ отрезок СК является биссектри-
биссектрисой и высотой, поэтому СЕ = АС и точка К — середина отрезка АЕ.
Таким образом, отрезок МК — средняя линия треугольника ADE
и, значит,
МК = ^DE = ^(DB + ВС + СЕ) = ^(АВ + ВС +
т. е. отрезок МК равен половине периметра треугольника ABC.
863.	Отрезки АА\, ВВ\ и CCi соединяют вершины треугольника ABC
с внутренними точками противоположных сторон. Докажите, что середины
этих отрезков не лежат на одной прямой.
Решение. Пусть точки А2, В^ и С^ — середины сторон ВС,
АС и АВ треугольника ABC. Согласно задаче 435 середина отрезка
АА\ лежит на отрезке В^С^, причем не совпадает с точками В^ и С^,
т. е. является внутренней точкой отрезка В^С^. Аналогично, середины
отрезков ВВ\ и СС\ являются внутренними точками отрезков А^С^
и А2В2.
Таким образом, середины отрезков АА\, ВВ\ и СС\ лежат со-
соответственно на сторонах В2С2, А2С2 и А2В2 треугольника А2В2С2
и не совпадают с вершинами этого треугольника. Отсюда следует, что
середины отрезков АА\, ВВ\ и СС\ не лежат на одной прямой.
864.	Середины трех высот треугольника лежат на одной прямой. Докажи-
Докажите, что этот треугольник прямоугольный.
Решение. Если треугольник ABC — остроугольный, отрезки
АА\, ВВ\ и СС\ — его высоты, то точки А\, В\ и С\ являются
внутренними точками сторон ВС, С А и АВ и поэтому, согласно
задаче 863, середины высот не лежат на одной прямой.
Если треугольник ABC — тупоугольный с тупым углом
А (рис.200, а), то основание высоты АА\ (точка А\) лежит на стороне
ВС, а основания высот ВВ\ и СС\ (точки В\ и С\) лежат
на продолжениях сторон С А и АВ (см. задачу 300). При этом середина
О\ высоты АА\ лежит на средней линии RQ (задача 435), а середины
О2 и Оз — на продолжениях средних линий PR и PQ (см. рис.200, а).
Таким образом, точка О\ лежит на стороне RQ треугольника PQR,

Задачи повышенной трудности
149
В
а точки О2 и Оз — на продолжениях двух других сторон этого
треугольника. Поэтому точки 0\, 0% и Оз не лежат на одной прямой.
Если же треугольник ABC — прямоугольный с прямым углом
А (рис.200, б), то его высоты, проведенные из вершин В и С, сов-
совпадают с катетами В А и С А. Поэтому середины 0% и Оз этих высот
являются серединами катетов, а отрезок O2O3 — средней линией
треугольника ABC. Середина 0\ высоты, проведенной из вершины А,
лежит на средней линии O2O3 (см. задачу 435). Таким образом, сере-
середины 0\, О2 и Оз высот прямоугольного треугольника лежат на одной
прямой.
Итак, если середины трех высот треугольника лежат на одной
прямой, то этот треугольник — прямоугольный.
865. В треугольнике ABC, сторона АС
которого в два раза больше стороны ВС, про-
проведены биссектриса СМ и биссектриса внеш-
внешнего угла при вершине С, пересекающая пря-
прямую АВ в точке К. Докажите, что Sbcm =
lQ	lQ	lQ
= -^ОАСМ = Т^ОАВС = -7ОСМК-
Решение. Согласно задаче 535
MB	ВС	1 ,	ОА1Ч ^
— = — = - (рис.201). Отсюда сле-
В
м
Рис. 201
дует, что
МВ
1 п	ал(л
= -. Согласно задаче Ы9
о
г> ту' Т-\С^ 1	1
—— = —— = - и, следовательно, ВК = -АК = АВ, а так как MB =
АК АС 2	2
1 , „ Л/ГТЭ 1 ъ/гт,	MB 1
= -АВ, то MB = -МК, т. е. —— = -.
3	4	МК 4
Треугольники ВСМ, ACM, ABC, CMK имеют общую высоту,
проведенную из вершины С, поэтому
MB
MA
1
S
bcm
Sacm
Отсюда получаем:
MB
~АВ
1
3'
Sbcm _ MB
Scmk MK
Sbcm = -^

150
Гл. 3. Подобные треугольники
866. Стороны треугольника EFG соответственно равны медианам тре-
л ъгч тл	SeFG 3
угольника ABC. Докажите, что —	= -.
Ьавс 4
Решение. Пусть АА\, ВВ\, СС\ — медианы треугольника ABC,
О — точка пересечения медиан (рис.202). Проведем прямую AM,
параллельную медиане СС\, и пря-
прямую А\К, параллельную медиане
ВВ\ (см. рис.202). Тогда отрезок
СС\ — средняя линия треугольника
АВМ и поэтому AM = 2ССХ.
Пусть прямая ВВ\ пересекает от-
В А С	М резок AM в точке N. Так как
1	АО : ОАх = 2, то AN : NK = 2 (см. за-
Рис 202	дачу 556), т. е. AN = 2NK и, значит,
АК = ЗМК.
N
К
Поскольку ВС = СМ и ВА\ = АХС = ^
следовательно,
, то А\М : ВА\ = 3 и,
КМ : NK = 3, т. е. КМ = 3NK.
Таким образом, АК = КМ, а так как AM = 2СС\, то АК = СС\.
Отрезок В\К — средняя линия треугольника АСМ, поэтому
В\К || ВА\ и так как А\К || ВВ\, то ВВ\КА\ — параллелограмм.
Отсюда следует, что А\К = ВВ\.
Итак, в треугольнике АА\К
А{К = ВВ{, АК = СС{,
т. е. стороны треугольника АА\К соответственно равны медианам
треугольника ABC и, значит, треугольник АА\К равен треугольнику
о	о
EFG (см. условие задачи). Тем самым нужно доказать, что АА]К
S
1
АВС
Так как ВМ = 2ВС, ВАХ = -ВС, то БАвм = 2SAbc, SAbax =
и поэтому
3
Saaxm = Sabm — Sab Ax = -r
Треугольники АА\М и АА\К имеют общую высоту, проведенную
из вершины А\, и АК = -AM. Поэтому
1
Saaxk = -z
Отсюда получаем:
что и требовалось доказать.
Saa{k _ 3
Sabc ~ 4'

Задачи повышенной трудности
151
867. В треугольнике ABC прямая, проходящая через вершину А и деля-
делящая медиану ВМ в отношении 1 : 2, считая от вершины, пересекает сторону
ВС в точке К. Найдите отношение площадей треугольников АВК и ABC.
Решение. Обозначим буквой D точку пересечения отрезка АК
и медианы ВМ и проведем через точку М прямую, параллельную АК.
Она пересекает сторону ВС в точке Е (рис.203).
Так как BD : DM = 1 : 2, то ВК : КЕ =1:2 (см. задачу 556),
т. е. КЕ = 2ВК. Отрезок ME — средняя линия треугольника АКС,
поэтому ЕС = КЕ = 2ВК. Таким образом,
ВС = ВК + КЕ
ВК _ 1
Т' е' ~ВС ~ 5'
Треугольники АВК и ABC имеют общую высоту, проведенную
из вершины А, поэтому
Sabk _ ВК _ 1
Sabc ~ ~ВС~Ъ'
Ответ. 1 : 5.
868. Через вершину А параллелограмма ABCD проведена прямая, пересе-
пересекающая прямые BD, CD и ВС соответственно в точках М, N и Р. Докажите,
что отрезок AM является средним пропорциональным между MN и МР.
Решение. AAMD ~ АРМ В по двум углам (рис.204), поэтому
MD AM
MB МР'
Аналогично,
Приравнивая
ANMD ~ ААМВ,
MD
MB
два выражения для
AM
МР
поэтому
MN
AM'
отношения ——, получаем:
MN
AM'
откуда
AM2 = MN • МР,
AM = VMN • МР,
В
с
А	М	С
Рис. 203
Рис. 204

152
Гл. 3. Подобные треугольники
т. е. отрезок AM является средним пропорциональным между
MN и МР.
869. Постройте точку, принадлежащую большему основанию равнобед-
равнобедренной трапеции и отстоящую от данной боковой стороны в п раз дальше, чем
от другой (п = 2, 3,4).
Решение. Пусть ABCD — данная равнобедренная трапеция, X —
искомая точка, принадлежащая большему основанию AD и отстоящая
от данной боковой стороны АВ в п раз дальше, чем от CD, т. е.	=
= п, где ХМ и XN — перпендикуляры к прямым АВ и CD (рис. 205).
ААМХ rsj AD NX (по двум углам), поэтому
АХ ХМ
= п.
XD XN
Таким образом, задача сводится к построению точки X, которая
делит отрезок AD в заданном отношении, т. е. АХ : XD = п : 1.
Построение такой точки описано в решении задачи 585.
870. Точка С лежит на отрезке АВ. Постройте точку D прямой АВ,
ли	* AD АС и
не лежащую на отрезке АВ, так, чтобы —— = ——-. Всегда ли задача имеет
ив ев
решение?
Решение. Пусть АС > С В (рис. 206). Отметим точку М, не лежа-
лежащую на прямой АВ, и на луче AM отложим отрезок АС\, равный АС,
а затем на луче С\А отложим отрезок С\В\, равный СВ. Проведем
через точку С\ прямую, параллельную прямой В\В. Она пересекает
прямую АВ в искомой точке D.
Действительно, так как C\D || В\В, то
С\В\	АВ\ у	г т\
__ = _ (см. задачу 556).
Отсюда, используя свойства пропорций, получаем:
СхВх _ АВх+СхВх _ АС±
DB ~ AB + DB ~ AD'
Но С\В\ = СВ, АС\ = АС (по построению), поэтому
СВ AC	AC AD
СВ = DB'
В
м
X D
Рис. 205
А	С В D
Рис. 206

Задачи повышенной трудности
153
Тем самым доказано, что точка D — искомая.
Если АС < СВ, то построение искомой точки D проводится та-
таким же образом, как и в случае АС > СВ, но только теперь точка А
будет лежать между С\ и В\.
Наконец, если АС = СВ, то -—- = 1, а для любой точки D прямой
СВ
АВ, не лежащей на отрезке АВ,
случае построение точки D невозможно.
Ответ. Не всегда.
AD
DB
1. Таким образом, в этом
871. Постройте равнобедренный треугольник по углу между боковыми
сторонами и сумме основания и высоты, проведенной к основанию.
Решение. Пусть Zhk — данный угол, PQ — данный отре-
отрезок (рис.207, а). Требуется построить треугольник ABC, в котором
ZA = Zhk, АВ = АС, ВС + АН = PQ, где АН — высота треугольни-
треугольника ABC.
Анализ. Пусть ABC — искомый треугольник (рис.207, б). Прове-
Проведем какой-нибудь отрезок В\С\, параллельный стороне ВС. Получим
треугольник АВ\С\, подобный треугольнику ABC. Ясно, что равно-
равнобедренный треугольник АВ\С\ с заданным углом А между боковыми
сторонами построить нетрудно. Из подобия треугольников следует:
ВхСх
АН,
ВС
~АН'
Прибавив к обеим частям равенства 1, получим:
В\С\ 1 ВС 1
+ 1	+ 1
ВС + АН
AHx	AH
Но ВС + AH = PQ по условию, поэтому
BxCx+AHx _ PQ_
~ AH'
A)
АНх
Q
Рис. 207

154	Гл. 3. Подобные треугольники
откуда
PQ ¦ АЩ
Если треугольник АВ\С\ построен, то отрезки с длинами АН\
и (В\С\ + АН\) нам известны. Отрезок PQ задан условием задачи.
Используя формулу B), можно построить отрезок длины АН, что дает
возможность построить весь треугольник ABC.
Построение. Строим какой-нибудь равнобедренный треугольник
АВ\С\, в котором А А = Zhk, AB\ = АС\, и проводим высоту АН\
в этом треугольнике. По трем известным отрезкам с длинами PQ, АН\
и {В\С\ + АН\) строим отрезок, длина которого выражается форму-
формулой B) (см. задачу 623). Отложив этот отрезок на луче АН\ от точки
А, получим точку Н. Проводим через точку Н прямую, параллельную
В\С\, и получаем искомый треугольник ABC (рис.207, б).
Доказательство. По построению ZA = Zhk. Треугольники ABC
и АВ\С\ подобны, поэтому АВ = АС и выполняется равенство A),
откуда следует, что
ВС + АН = ВхС\+„АНх ¦ АН.	C)
АН\
Но отрезок АН строился по формуле B). Подставляя выражение B)
для АН в равенство C), получаем
ВС + АН = PQ.
Таким образом, построенный треугольник ABC удовлетворяет всем
условиям задачи.
Исследование. Из построения видно, что задача всегда имеет ре-
решение, если угол hk — не развернутый. Формула B) показывает,
что какой бы треугольник АВ\С\, подобный искомому, мы ни взяли,
величина АН будет иметь одно и то же значение. Это доказывает
единственность искомого треугольника.
872. Постройте треугольник по двум сторонам и биссектрисе угла между
ними.
Решение. Пусть даны отрезки P\Q\,
P2Q2, P?>Q?>- Требуется построить треугольник
ABC, у которого АВ = P{QU AC = P2Q2,
AD = P3Q3, где AD — биссектриса треуголь-
треугольника.
Анализ. Пусть ААВС — искомый тре-
треугольник (рис.208). Для краткости запи-
записи обозначим длины данных отрезков P\Q\,
Рис. 208	P2Q2 и P3Q3 через Ъ, с и а. Тогда АВ =
= Ъ, АС = с, AD = а. Проведем BE \\ АС.

Задачи повышенной трудности	155
Получим равнобедренный треугольник ABE (АВ = BE = b). Выразим
DE через а, Ь, с. Из подобия треугольников EDB и ABC (по двум
углам) имеем:	DE ВЕ	аЬ
AC> ОТКУДЗ DE = Т-
По данным отрезкам с длинами а, Ь, с можно построить отрезок
DE (задача 623). После этого можно построить треугольник ABE,
а затем искомый треугольник ABC.
Построение. Строим отрезок, длина которого равна —. Далее
строим треугольник ABE по трем сторонам: AB = BE = b, AE =
= а -\	. Затем через точку А проводим луч AM так, что ZMAE =
= ZEAB, и на этом луче откладываем отрезок АС = с. Треугольник
ABC — искомый.
Доказательство. По построению АВ = Ь, АС = с, луч АЕ —
биссектриса угла CAB. Пусть D — точка пересечения АЕ и ВС.
Из подобия треугольников ADC и EDB следует:
AD АС	ЛТЛ ^^ АС аЬ с
AD = DE' be = ~с ' ь = а>
т. е. биссектриса AD треугольника ABC равна а. Итак, треугольник
ABC удовлетворяет всем условиям задачи.
Исследование. Ясно, что треугольник ABC можно построить в том
и только в том случае, когда можно построить равнобедренный тре-
треугольник ABE, а для этого его стороны должны удовлетворять соот-
соотношению АЕ < АВ + BE = 2 • АВ, т. е. должно выполняться нера-
неравенство	7	2h
а + — < 26, или а <
с	6 + с
Возвращаясь к исходным отрезкам, запишем это неравенство в ви-
Если данные отрезки P\Q\, P2Q2, P3Q3 удовлетворяют условию A),
то задача имеет решение. В противном случае решения нет.
Если решение есть, то оно единственное. В самом деле, допустим,
что имеются два треугольника ABC и А\В\С\, удовлетворяющие усло-
условиям задачи. Для каждого из них выполним такое же построение,
как на рисунке 208. Тогда получим: A ABE = AA\B\E\ (по трем сто-
сторонам), поэтому ZDAB = AD\A\B\. Следовательно, в треугольниках
ABC и А\В\С\ углы А и А\ равны, а значит, равны и сами тре-
треугольники (по двум сторонам и углу между ними). Это и доказывает
единственность решения.
873. Постройте треугольник ABC, если даны A A, ZC и отрезок, равный
сумме стороны АС и высоты ВН.

156	Гл. 3. Подобные треугольники
Решение. Пусть Zh\k\ и Zh2k2 — данные
углы, PQ — данный отрезок. Требуется постро-
построить треугольник ABC, у которого ZA = Zh\k\,
ZC = Zh2k2, AC + ВН = PQ, где ВН - высота
треугольника.
Эта задача решается методом подобия ана-
аналогично задаче 871. Пусть ABC — искомый
треугольник, у которого ZA = Zh\k\, ZC =
Рис. 209	= zh2k2, АС + ВН = PQ (рис. 209). Проведем
какой-нибудь отрезок А\С\, параллельный сто-
стороне АС. Получим треугольник А\ВС\, подобный треугольнику ABC.
Из подобия этих треугольников следует соотношение, аналогичное
формуле B) (см. решение задачи 871):
PQ
Это соотношение указывает способ построения искомого треуголь-
треугольника ABC. Строим какой-нибудь треугольник А\В\С\, у которого
ZA\ = Zh\k\, ZC\ = Zh2k2, и проводим высоту ВН\ в этом тре-
треугольнике. Затем по трем известным отрезкам с длинами PQ, ВН\
и (А\С\ + ВН\) строим отрезок, длина которого выражается форму-
формулой D). Отложив этот отрезок на луче ВН\ от точки В, получим точку
Я. Проводим через точку Я прямую, параллельную А\С\, и получаем
искомый треугольник ABC.
В самом деле, так как АС || А\С\, то ZA = ZA\ = Zh\k\, ZC =
= ZC\ = Zh2k2. Кроме того, АС + ВН = PQ. Это равенство доказы-
доказывается так же, как аналогичное равенство в задаче 871.
Если Zh\k\ + Zh2k2 < 180°, то задача имеет решение, и, как и в
задаче 871, это решение единственное.
874. Постройте треугольник по трем высотам.
Решение. Пусть даны отрезки P\Q\, P2Q2, PsQs- Требуется по-
построить треугольник ABC, высоты которого, проведенные из вершин
А, В и С, соответственно равны P\Q\, P2Q2 и P^Qz-
Анализ. Обозначим через а, Ъ и с длины сторон искомого треуголь-
треугольника, противолежащих углам А, В и С, а через ha, hb и hc длины
отрезков P\Q\, P2Q2 и P^Qz- Воспользуемся равенствами aha = bhb =
= chc (каждое из произведений равно удвоенной площади треугольни-
\ 1л	а Ъ
ка). Из первого равенства получаем пропорцию — = —, а из второго
hb ha
равенства имеем
h	h
b = -г^ - с и поэтому
ha I hahb

Задачи повышенной трудности
157
Таким образом,
hahb
A)
Полученные равенства показывают, что искомый треугольник
со сторонами а, Ь, с подобен треугольнику со сторонами hb, ha, a Ъ
Этот факт дает ключ к решению задачи.
Построение. По данным отрезкам P\Q\,
P2Q2 и PsQs с длинами ha, hb и hc построим от-
hc
резок P4Q4, длина которого равна
hghb
hc
(см. за-
В Н
Рис. 210
дачу 623). Далее построим треугольник АВ\С\
по трем сторонам: АВ\ = P4Q4, B\C\ = P2Q2,
С\А = P\Q\ (рис.210). Этот треугольник, как
уже было отмечено, подобен искомому тре-
треугольнику. Проведем высоту АН\ треугольника
АВ\С\ и на луче АН\ отложим отрезок АН,
равный P\Q\. Через точку Н проведем прямую,
параллельную В\С\. Она пересекается с лучами АВ\ и АС\ в некото-
некоторых точках В и С. Треугольник ABC — искомый.
Доказательство. Построенный треугольник ABC подобен тре-
треугольнику АВ\С\ и, следовательно, подобен искомому треугольнику.
Высота АН в треугольнике ABC равна P\Q\, как и должно быть
в искомом треугольнике, т. е. сходственные высоты в треугольнике
ABC и искомом треугольнике равны. Значит, коэффициент подобия
этих треугольников равен 1 (см. задачу 543), а это и означает, что
треугольник ABC — искомый.
Исследование. Искомый треугольник ABC можно построить в том
и только в том случае, когда можно построить треугольник АВ\С\,
стороны которого равны P\Q\, P2Q2 и P4Q4 = V» ^ • В свою оче-
^зУз
редь, треугольник с такими сторонами можно построить тогда и только
тогда, когда каждый из отрезков P\Q\, P2Q2, P4Q4 меньше суммы двух
других отрезков, т. е.
PiQ
i 'P2Q2
P3Q3
B)
РзЯз
Последние два неравенства приводятся к виду, аналогичному B):
P2Q2
P1Q1
C)

158	Гл. 3. Подобные треугольники
Итак, если данные отрезки P\Q\, P2Q2, P3Q3 удовлетворяют усло-
условиям B) и C), то задача имеет решение. В противном случае решений
нет.
Если решение существует, то оно единственное. В самом деле,
пусть AKMN — произвольный треугольник, удовлетворяющий усло-
условию задачи, т. е. высоты этого треугольника равны данным отрезкам
P\Q\, P2Q2 и PsQs с длинами ha, hb и hc. Пусть высота, проведенная
из вершины К, равна ha, а высота, проведенная из вершины М, равна
hb. Тогда, согласно равенствам A), треугольник KMN подобен тре-
треугольнику K\M\N\, в котором MiTVi = hb, K\N\ = ha, K\M\ = -?-^.
hc
Высота h\ треугольника K\M\N\, проведенная из вершины К\, од-
однозначно выражается через стороны этого треугольника и, значит,
через величины ha, hb и hc. Эта высота является сходственной высоте
ha треугольника KMN, подобного треугольнику K\M\N\. Поэтому
коэффициент подобия треугольников KMN и K\M\N\, равный —-,
hi
имеет одно и то же значение для всех треугольников KMN, удовле-
удовлетворяющих условию задачи. Отсюда следует, что все треугольники,
удовлетворяющие условию задачи, подобны друг другу с коэффициен-
коэффициентом подобия, равным 1, т. е. они равны друг другу. Это и означает, что
задача имеет единственное решение.
875. Постройте трапецию по боковой стороне, большему основанию, углу
между ними и отношению двух других сторон.
Решение. Пусть даны отрезки P\Q\, P2Q2, M\N\, M2N2 и угол
hk. Требуется построить трапецию ABCD с основаниями ВС и AD
так, чтобы
4Б =
ВС
ВС:
= P\Q\,
<AD,
CD = 1
AD
ZA
= P2Q2,
= Zhk,
: M2N2.
Построение. Сначала построим треугольник ABD по двум
сторонам и углу между ними: АВ = P\Q\, AD = P2Q2, ^А —
= Zhk (рис.211, а). Затем через точку В проведем прямую р,
параллельную AD, и на этой прямой по ту же сторону от прямой АВ,
что и точка D, отложим отрезок ВС\, равный M\N\. Далее построим
окружность радиуса M2N2 с центром С\. Пусть эта окружность
пересекается с лучом BD в точке D\. Проведем через точку D прямую,
параллельную D\C\. Эта прямая пересекает прямую р в некоторой
точке С (см. рис.211, а). Если при этом окажется, что ВС < AD,
то трапеция ABCD — искомая.

Задачи повышенной трудности
159
С Р
D
в
Рис. 211
Доказательство. По построению АВ = P\Q\, AD = P2Q2, ^-А =
= /hk, а так как CD || C\D\, то
ВС_ _ ВСХ _ MxNx
CD ~ CxDx ~ M2N2'
Если, кроме того, ВС < AD, то трапеция ABCD удовлетворяет
всем условиям задачи.
Исследование. По заданным отрезкам P\Q\, P2Q2 и углу hk всегда
можно построить треугольник ABD, в котором АВ = P\Q\, AD =
— ^2^2» ^-А = /hk (если /hk < 180°), а затем можно провести
через точку В прямую р, параллельную AD, и отложить отрезок ВС\,
равный M\N\. Через точку С\ проведем перпендикуляр С\Н к прямой
BD (рис.211, б). Если M2N2 < С\Н, то окружность радиуса M2N2
с центром С\ не имеет общих точек с лучом BD. В этом случае задача
не имеет решений.
Если M2N2 = С\Н, то окружность радиуса М2Щ с центром С\
имеет одну общую точку с лучом BD (точку Н). В этом случае задача
имеет единственное решение, если окажется, что ВС < AD. Последнее
неравенство будет выполнено, если /BCD > /А, т. е. /ВС\Н >
> /hk (см. рис.211, б). Итак, в случае M2N2 = С\Н задача имеет
единственное решение, если /ВС\Н > /hk, и не имеет решений, если
/ВСХН < /hk.
Если С\Н < M2N2 < M\N\ = BC\, то окружность радиуса M2N2
с центром С\ имеет две общие точки с лучом BD (точки D\ и D[
на рис.211, в). Поэтому в этом случае задача имеет два решения (тра-
(трапеции ABCD и ABC D), если /BC\D[ > /hk; одно решение (трапе-
(трапеция ABCD), если /BC\D[ < /hk < /BC\D\\ и не имеет решений,
если /BCXDX < /hk.
Если М2Л/2 ^ M\N\ = BC\, то окружность радиуса M2N2 с цен-
центром С\ имеет одну общую точку с лучом BD (точку D\). В этом
случае задача имеет единственное решение, если /BC\D\ > /hk, и не
имеет решений в противном случае.

160	Гл. 3. Подобные треугольники
876. Постройте ромб, площадь которого равна площади данного квадрата,
если известно, что отношение диагоналей этого ромба равно отношению дан-
данных отрезков.
Решение. Пусть даны квадрат KLMN и отрезки P\Q\ и P^Qi-
Требуется построить ромб ABCD, у которого Sabcd = Sklmn =
= KL2, AC : BD = PXQX : P2Q2.
Из условий задачи получаем два уравнения относительно АС и BD:
АС _ PxQx
BD P2Q2'
Отсюда находим:
V2KL-PXQX BD=V2KL. P2Q2
A)
y/PiQx • P2Q2 '
Полученные формулы позволяют построить отрезки, равные диаго-
диагоналям искомого ромба, а затем построить и сам ромб.
Построение. Сначала построим отрезок PsQs = \/P\Q\ • P2Q2 (см-
задачу 669). Так как у/2 KL = КМ, где КМ — диагональ данного
квадрата, то формулу A) для АС можно записать так:
KM-PXQX
По известным отрезкам KM, P\Q\ и P3Q3 построим отрезок, рав-
о КМ-РХОХ ,	гооч _	,
ныи 		(см. задачу Ь26). 1ем самым будет построен отрезок,
РгЧг
равный диагонали АС искомого ромба ABCD. Аналогично построим
отрезок, равный диагонали BD, а затем по известным диагоналям
построим сам ромб ABCD (см. задачу 414, а).
Формулы A) показывают, что при любых данных квадрате KLMN
и отрезках P\Q\ и P2Q2 задача имеет единственное решение.

Глава 4
ОКРУЖНОСТЬ
§ 1. Касательная к окружности
631.	Пусть d — расстояние от центра окружности радиуса г до прямой
р. Каково взаимное расположение прямой р и окружности, если: а) г = 16 см,
d = 12 см; б) г = 5 см, d = 4,2 см; в) г = 7,2 дм, с? = 3,7 дм; г) г = 8 см,
с? = 1,2 дм; д) г = 5 см, с? = 50 мм?
Решение, a) d < г, поэтому прямая и окружность имеют две
общие точки;
б)	d < г, поэтому прямая и окружность имеют две общие точки;
в)	d < г, поэтому прямая и окружность имеют две общие точки;
г)	d > г, поэтому прямая и окружность не имеют общих точек;
д)	d = г, поэтому прямая и окружность имеют только одну общую
точку.
Ответ, а), б), в) Прямая пересекает окружность; г) прямая лежит
вне окружности; д) прямая касается окружности.
632.	Расстояние от точки А до центра окружности меньше радиуса окруж-
окружности. Докажите, что любая прямая, проходящая через точку А, является
секущей по отношению к данной окружности.
Решение. Пусть О — центр данной окружности, г — ее радиус.
По условию О А < г. Рассмотрим произвольную прямую р, проходящую
через точку А, и обозначим буквой d расстояние от точки О до прямой
р. Если р JL О А, то d = О А; если же отрезок О А является наклонной,
проведенной из точки О к прямой р, то d < О А. И в том, и в другом
случае d < г, поэтому прямая р и окружность имеют две общие точки.
633.	Даны квадрат ОАВС, сторона которого равна
б см, и окружность с центром в точке О радиуса 5 см.
Какие из прямых ОА, АВ, ВС и АС являются секущими
по отношению к этой окружности?
Решение. Прямая О А проходит через центр
окружности, поэтому эта прямая является секущей.	о
Прямые АВ и ВС находятся на расстояниях О А =
= 6 см > 5 см и ОС = 6 см > 5 см (рис.212), а зна-
значит, эти прямые секущими не являются. Расстояние	рис 212
от точки О до прямой АС равно половине диагонали
б Л. С. Атанасян и др.

162
Гл. 4. Окружность
данного квадрата, т. е. -—- • 6 см « 4,25 см. Таким образом, это рас-
расстояние меньше 5 см, поэтому прямая АС является секущей.
Ответ. О А и АС.
634.	Радиус ОМ окружности с центром О делит хорду АВ пополам.
Докажите, что касательная, проведенная через точку М, параллельна хорде
АВ.
Решение. Прямая ОМ содержит медиану равнобедренного тре-
треугольника АОВ (рис.213), поэтому АВ JL ОМ. Касательная р, прове-
проведенная через точку М, также перпендикулярна к ОМ. Следовательно,
прямые АВ и р параллельны.
635.	Через точку А окружности проведены касательная и хорда, равная
радиусу окружности. Найдите угол между ними.
Решение. Пусть О — центр окружности, АВ — данная хор-
хорда (рис.214). Треугольник ОАВ равносторонний, поэтому угол ОАВ
равен 60°. Следовательно, искомый угол равен 90° — 60° = 30°.
Ответ. 30°.
636.	Через концы хорды АВ, равной радиусу окружности, проведены две
касательные, пересекающиеся в точке С. Найдите угол АСВ.
Решение. Пусть О — центр данной окружности (рис.215).
Треугольник ОАВ равносторонний, поэтому угол ОАВ равен 60°.
Из четырехугольника О АСВ находим: ZACB = 360° - 90° - 90° -
-60° = 120°.
Ответ. 120°.
637.	Угол между диаметром АВ и хордой АС равен 30°. Через точку С
проведена касательная, пересекающая прямую АВ в точке D. Докажите, что
треугольник АСВ — равнобедренный.
Решение. Пусть О — центр данной окружности (рис.216).
Из условия задачи следует, что углы при основании равнобедренного
треугольника О АС равны 30°. Угол ВОС — внешний угол этого
треугольника, а значит, ZBOC = 30° + 30° = 60°. В прямоугольном
треугольнике OCD АО = 60°, поэтому AD = 30°. Таким образом,
в треугольнике ACD углы при основании AD равны и, следовательно,
этот треугольник — равнобедренный.
М
А \С
Рис. 213
Рис. 214
Рис. 215

§ 1. Касательная к окружности
163
638.	Прямая АВ касается окружности с центром О радиуса г в точке В.
Найдите АВ, если О А = 2 см, а г = 1,5 см.
Решение. Из условия задачи следует, что треугольник АОВ —
прямоугольный с прямым углом В (рис.217). По теореме Пифагора
ОА2 = АВ2 + ОВ2 = АВ2+г2,
лтэ	Гл 9	V7
откуда АВ = л/4 — - см = -— см.
Ответ. -— см.
639.	Прямая АВ касается окружности с центром О радиуса г в точке В.
Найдите АВ, если ZAOB = 60°, а г = 12 см.
Решение. Из условия задачи следует, что треугольник АОВ —
прямоугольный с прямым углом В (см. рис.217). Поэтому
АВ = OB tg60° = rtg60° = гл/З = 12л/3 см.
Ответ. 12л/3 см.
640.	Даны окружность с центром О радиуса 4,5 см и точка А такая, что
О А = 9 см. Через точку А проведены две касательные к данной окружности.
Найдите угол между ними.
Решение. Пусть АВ и АС — касательные, В и С — точки ка-
касания (рис.218). Тогда Zl = Z2 = 90°. В прямоугольном треугольнике
АОВ гипотенуза О А = 9 см в два раза больше катета ОВ = 4,5 см.
Следовательно, ZOAB = 30°. Аналогично ZOAC = 30°, а значит,
ABAC = 30° + 30° = 60°
Ответ. 60°
641. Отрезки АВ и АС являются отрезками касательных к окружности
с центром О, проведенными из точки А. Найдите угол ВАС, если середина
отрезка АО лежит на окружности.
Решение. Пусть В и С — точки касания (см. рис.218). Тогда
Zl = Z2 = 90°. В прямоугольном треугольнике АОВ гипотенуза О А
в два раза больше радиуса окружности, или, что то же самое, в два
Рис. 216
Рис. 217
Рис. 218

164	Гл. 4. Окружность
раза больше катета ОВ. Следовательно, ZOAB = 30°. Аналогично
ZOAC = 30°, а значит,
ZBAC = 30° +30° =60°.
Ответ. 60°.
642.	На рисунке 218 (рис. 213 учебника) ОВ = 3 см, О А = б см. Найдите
АВ, AC, Z3 и Z4.
Решение. В прямоугольном треугольнике АОВ гипотенуза О А =
= 6 см в два раза больше катета ОВ = 3 см. Следовательно, Z3 = 30°.
Аналогично Z4 = 30°. Далее,
АВ = АС = OAcos30° = ОА^- = Зл/З см.
Ответ. Зл/З см, Зл/З см, 30°, 30°.
643.	Прямые АВ и АС касаются окружности с центром О в точках В
и С. Найдите ВС, если ZOAB = 30°, АВ = 5 см.
Решение. Поскольку АВ = AC, ZOAB = ZOAC = 30°
(см. рис.218) и, следовательно, ZBAC = 60°, то треугольник ABC
равносторонний, а значит, ВС = АВ = 5 см.
Ответ. 5 см.
644.	Прямые МА и MB касаются окружности с центром О в точках А
и В. Точка С симметрична точке О относительно точки В. Докажите, что
ZAMC = 3ZBMC.
Решение. Прямоугольные треугольники ОМ В и С MB (рис.219)
равны по двум катетам, поэтому ZBMO = ZBMC. С другой стороны,
ZAMO = ZBMO, а значит,
ZAMC = 3ZBMC.
645.	Из концов диаметра АВ данной окружности проведены перпендику-
перпендикуляры АА\ и ВВ\ к касательной, которая не перпендикулярна к диаметру АВ.
Докажите, что точка касания является серединой отрезка А\В\.
Решение. Пусть М — точка касания, О — центр окружно-
окружности (рис.220). Прямые АА\, ВВ\ и ОМ перпендикулярны к каса-
касательной, поэтому они параллельны. С другой стороны, О А = ОВ.
Следовательно, по теореме Фалеса, МА\ = МВ\.
646.	В треугольнике ABC угол В прямой. Докажите, что: а) прямая ВС
является касательной к окружности с центром А радиуса АВ; б) прямая АВ
является касательной к окружности с центром С радиуса СВ; в) прямая АС
не является касательной к окружностям с центром В и радиусами В А и ВС.
Решение, а) Расстояние от прямой ВС до центра А окружности
равно АВ (рис.221), т. е. радиусу этой окружности. Поэтому прямая
ВС является касательной к данной окружности.

§ 1. Касательная к окружности
165
Рис. 219
Рис. 220
б)	Расстояние от прямой АВ до центра С окружности равно
СВ (см. рис.221), т. е. радиусу этой окружности. Поэтому прямая АВ
является касательной к данной окружности.
в)	Отрезки В А и ВС являются наклонными, проведенными из точ-
точки В к прямой АС (см. рис.221). Следовательно, расстояние от пря-
прямой АС до центра В окружностей меньше радиусов В А и ВС этих
окружностей. Поэтому прямая АС не является касательной к данным
окружностям.
647. Отрезок АН — перпендикуляр, проведенный из точки А к прямой,
проходящей через центр О окружности радиуса 3 см. Является ли прямая АН
касательной к окружности, если: а) О А = 5 см, АН = 4 см; б) ZHAO = 45°,
О А = 4 см; в) ZHAO = 30°, О А = б см?
Решение, а) Найдем расстояние ОН от центра окружности
до прямой АН (рис.222). Имеем:
ОН = VО А2 - АН2 = 3
см.
Таким образом, расстояние от прямой АН до центра окружности
равно радиусу этой окружности. Следовательно, прямая АН — каса-
касательная.
б) Найдем расстояние ОН от центра окружности до прямой
АН (см. рис.222). Имеем:
ОН = OAsin45° = 2л/2 см.
А
Рис. 221
Рис. 222

166
Гл. 4. Окружность
Таким образом, расстояние от прямой АН до центра окружности
не равно радиусу этой окружности. Следовательно, прямая АН каса-
касательной не является.
в) Найдем расстояние ОН от центра окружности до прямой
АН (см. рис.222). Имеем:
ОН = ОА sin 30° =3 см.
Таким образом, расстояние от прямой АН до центра окружности
равно радиусу этой окружности. Следовательно, прямая АН — каса-
касательная.
Ответ, а) Да; б) нет; в) да.
648. Постройте касательную к окружности: а) параллельную данной пря-
прямой; б) перпендикулярную к данной прямой.
Решение. Пусть О — центр данной окружности.
а) Проведем через точку О прямую, перпендикулярную к данной
прямой (рис.223, а), и обозначим буквами А и В точки пересечения
р /
1
V
q
l_
О
A
J
В
в
Рис. 223
этой прямой с данной окружностью. Через точки А и В проведем
прямые р и q, перпендикулярные к прямой АВ. Прямые р и q —
искомые касательные. Таким образом, задача имеет два решения.
б) Проведем через точку О прямую, параллельную данной пря-
прямой (рис.223, б), и обозначим буквами А и В точки пересечения этой
прямой с данной окружностью. Через точки А и В проведем прямые
р и q, перпендикулярные к прямой АВ. Прямые р и q — искомые
касательные. Таким образом, задача имеет два решения.
§ 2. Центральные и вписанные углы
649. Начертите окружность с центром О и отметьте на ней точку А.
Постройте хорду АВ так, чтобы: a) ZAOB = 60°; б) ZAOB = 90°; в) ZAOB =
= 120°; г) ZAOB= 180°.
Решение, а) Проведем окружность с центром А радиуса О А
и обозначим буквой В одну из точек пересечения этой окружности
с исходной окружностью. Хорда АВ — искомая.

§2. Центральные и вписанные углы	167
б)	Проведем через точку О прямую, перпендикулярную к прямой
АО, и обозначим буквой В одну из точек пересечения этой прямой
с окружностью. Хорда АВ — искомая.
в)	Продолжим отрезок АО за точку О до пересечения с окружно-
окружностью в точке С. Затем построим хорду СВ так, чтобы угол СОВ был
равен 60° (задача 649, а). Хорда АВ — искомая.
г)	Продолжим отрезок АО за точку О до пересечения с окружно-
окружностью в точке В. Хорда АВ — искомая.
650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если:
а) А АО В = 60°; б) А АО В = 90°; в) А АО В =180°.
Решение. Обозначим угол АОВ буквой а. Если а ф 180°,
то треугольник АОВ — равнобедренный, а значит, АВ = 20Asm— =
= 32 sin —. Имеем:
а)	AB = 32sin30° = 16;
б)	АВ = 32 sin 45° = 16л/2;
в)	отрезок АВ — диаметр окружности, поэтому АВ = 20А = 32.
Ответ, а) 16; б) \6лД; в) 32.
651. Хорды АВ и CD окружности с центром О равны, а) Докажите, что
две дуги с концами А и В соответственно равны двум дугам с концами С и D.
б) Найдите дуги с концами С и D, если ZAOB = 112°.
Решение, а) Если хорды АВ и CD — диаметры, то каждая
из стягиваемых ими дуг — полуокружность, а значит, эти дуги равны.
Если же данные хорды диаметрами не являются, то треугольники АВО
и CDO равны по трем сторонам, поэтому эти треугольники можно
совместить наложением так, что точки А, В и О совместятся с точками
С, D и О. При этом наложении дуга АВ, меньшая полуокружно-
полуокружности, совместится с дугой CD, меньшей полуокружности, а дуга АВ,
большая полуокружности, — с дугой CD, большей полуокружности.
Следовательно, две дуги с концами А и В соответственно равны двум
дугам с концами С и D.
б) Дуги с концами А и В равны 112° и 360° - 112° = 248°.
Следовательно (см. задачу 651, а), дуги с концами С и D также равны
112° и 248°.
Ответ, б) 112° и 248°.
652. На полуокружности АВ взяты точки С и D так, что ^ АС = 37°
BD = 23°. Найдите хорду CD, если радиус окружности равен 15 см.
Решение. Имеем:
- CD = 180°- - AC- ^BD= 180° - 37° - 23° = 120°,

168
Гл. 4. Окружность
а значит, ^ COD = 120° (О — центр окружности). Из равнобедренного
треугольника COD находим:
^- = 15л/3 см.
Ответ. 15л/3 см.
653.	Найдите вписанный угол ABC, если дуга АС, на которую он опира-
опирается, равна: а) 48°; б) 57°; в) 90°; г) 124°; д) 180°.
Решение. Вписанный угол ABC равен половине дуги АС, на ко-
которую он опирается. Поэтому:
а)	ZABC = ^ =24°;
б)	ZABC =^-= 28°30х;
90°
в)	ZABC = Ц- =45°;
г)	ZABC =^=62°;
д)	ZABC = ^- =90°.
Ответ, а) 24°; б) 28°3(У; в) 45°; г) 62°; д) 90°.
654.	По данным рисунка 224 (рис. 222 учебника) найдите х.
п ч 360°-80°-152° ало
Решение, а) х =	= 64°;
б)	х = 360° - 125° - 2 • 30° = 175°;
,	360°-180°-112° Q/|O
в)	х =	= 34°;
г)	х = 360° - 215° - 2 • 20° = 105°.
Ответ, а) 64°; б) 175°; в) 34°; г) 105°.
152
Рис. 224

§ 2. Центральные и вписанные углы
169
655.	Центральный угол АОВ на 30° больше вписанного угла, опирающе-
опирающегося на дугу АВ. Найдите каждый из этих углов.
Решение. Пусть х — градусная мера вписанного угла. Если этот
угол опирается на дугу, меньшую или равную полуокружности, то гра-
градусная мера центрального угла равна 2х. Если же он опирается на дугу,
большую полуокружности, то градусная мера центрального угла равна
360° — 2х. В первом случае получаем: 2х — х = 30°, откуда х = 30°,
а значит, вписанный угол равен 30°, а центральный 60°. Во втором
случае 360° — 2х — х = 30°, откуда х = 110°. Таким образом, в этом
случае вписанный угол равен 110°, а центральный 140°.
Ответ. 60° и 30° или 140° и 110°.
656.	Хорда АВ стягивает дугу, равную 115°, а хорда АС — дугу в 43°.
Найдите угол ВАС.
Решение. Если точка С лежит на дуге АВ, большей полуокруж-
полуокружности (рис.225, а), то угол ВАС опирается на дугу, равную 360° —
В
Рис. 225
- 115° -43° = 202°, а значит, угол ВАС равен 101°.
Если же точка С лежит на дуге АВ, меньшей полуокружно-
полуокружности (рис. 225, б), то угол ВАС опирается на дугу, равную 115° — 43° =
= 72°, а значит, угол ВАС равен 36°.
Ответ. 101° или 36°.
657. Точки А и В разделяют окружность на две
дуги, меньшая из которых равна 140°, а большая
точкой М делится в отношении б : 5, считая от точки
А. Найдите угол ВАМ.
Решение. Дуга АВ, большая полуокруж-
полуокружности, равна 360° - 140° = 220°.
Пусть - AM = 6х, - ВМ = Ъх (рис.226).
Тогда
°
откуда х = 20°, а значит, - ВМ =100°
Следовательно, ZBAM = 50°.
Ответ. 50°.
Рис. 226
658. Через точку А к данной окружности проведены касательная АВ (В —
точка касания) и секущая AD, проходящая через центр О (D — точка

170
Гл. 4. Окружность
на окружности, О лежит между А и D). Найдите ZBAD и ZADB, если
- BD= 110°20'.
Решение. Из условия задачи следует, что центральный угол BOD
равен 110°20/. Поскольку этот угол является внешним углом прямо-
прямоугольного треугольника ОАВ (рис.227), то
ZBAD = ZBOD - 90° = 20°20'.
С другой стороны, угол BOD является углом при вершине равно-
равнобедренного треугольника BOD, поэтому
ZADB =
Ответ. 20°2(У и 34°5(У.
180° ~
= 34°50'.
659.	Докажите, что градусные меры дуг окружности, заключенных между
параллельными хордами, равны.
Решение. Пусть АВ и CD — две параллельные хорды (рис.228).
Вписанные углы ADC и DAB равны как накрест лежащие углы,
образованные при пересечении параллельных прямых АВ и CD секу-
секущей AD. Следовательно, градусные меры дуг АС и BD, на которые
опираются эти углы, также равны.
660.	Через точку, лежащую вне окружности, проведены две секущие,
образующие угол в 32°. Большая дуга окружности, заключенная между сто-
сторонами этого угла, равна 100°. Найдите меньшую дугу.
Решение. Обратимся к рисунку 229. Вписанный угол С BE,
100°
равный —-— = 50°, является внешним углом треугольника ABE. Сле-
Следовательно, угол BE А равен 50° — ZA = 50° — 32° = 18°, а значит,
дуга BD, на которую он опирается, равна 36°.
Ответ. 36°.
661. Найдите острый угол, образованный двумя секущими, проведенными
из точки, лежащей вне окружности, если дуги, заключенные между секущими,
равны 140° и 52°.
Решение. Обратимся к рисунку 229. Вписанный угол С BE равен
140°	52°
—— = 70°, а вписанный угол BED равен -—- = 26°. При этом угол
В
Рис. 227
Рис. 228
Рис. 229

§ 2. Центральные и вписанные углы
171
СВЕ является внешним углом треугольника ABE. Следовательно,
угол
ВАЕ = 70° - ZBED = 70° - 26° = 44°.
Ответ. 44°.
662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол
ВЕС, если - AD = 54°, - ВС = 70°.
Решение. Угол ВЕС является внешним углом треугольника
АЕС (рис.230), поэтому он равен сумме углов А и С этого треуголь-
треугольника. Но ZA =^
Ответ. 62°
ВС
= 35°
AD
= 27°. Следовательно,
ZBEC = 35° + 27° =62°.
663.	Отрезок АС — диаметр окружности, АВ — хорда, МА — касатель-
касательная, угол МАВ острый. Докажите, что ZMAB = ZACB.
Решение. Вписанный угол ABC опирается на полуокруж-
полуокружность (рис.231), поэтому этот угол прямой. Угол MAC также прямой.
Тем самым углы АСВ и ВАС, равно как и углы МАВ и ВАС,
составляют в сумме 90°. Следовательно, ZMAB = ZACB.
664.	Прямая AM — касательная к окружности, АВ — хорда этой окруж-
окружности. Докажите, что угол МАВ измеряется половиной дуги АВ, расположен-
расположенной внутри угла МАВ.
Решение. Если хорда АВ — диаметр окружности, то дуга, рас-
расположенная внутри угла МАВ, равна 180°, а угол МАВ = 90° =
180° ,,	ЛТЭ
=	. Допустим, что хорда АВ не является диаметром. Проведем
диаметр АС. Если угол МАВ острый (см. рис.231), то, согласно
утверждению, сформулированному в задаче 663, ZMAB = ZACB,
а значит, угол МАВ, как и вписанный угол АСВ, измеряется по-
половиной дуги АВ, расположенной внутри угла МАВ. Если же угол
МАВ тупой (рис. 232), то ZMAB = 180° - ZACB = —	^	=
АСВ
В
Рис. 230
Рис. 231
Рис. 232

172
Гл. 4. Окружность
665.	Вершины треугольника ABC лежат на окружности. Докажите, что
если АВ — диаметр окружности, то АС > ZA и АС > АВ.
Решение. Угол С опирается на полуокружность, поэтому этот
угол прямой. Следовательно, углы А и В — острые, а значит, каждый
из них меньше угла С.
666.	Хорды АВ и CD пересекаются в точке Е. Найдите ED, если:
а) АЕ = 5, ВЕ = 2, СЕ = 2,5; б) АЕ = 16, BE = 9,CE = ED; в) АЕ = 0,2,
BE = 0,5, СЕ = 0,4.
Решение. По теореме о пересекающихся хордах
Имеем:
АЕ- BE = CE- ED, откуда ED =
б) ED = Щ?, откуда ED = 12;
Ы)
АЕ-ВЕ
СЕ '
Ы)
В) ED =
= 0,25.
Ответ, а) 4; б) 12; в) 0,25.
667. Диаметр АА\ окружности перпендикулярен к хорде ВВ\ и пересекает
ее в точке С. Найдите ВВ\, если АС = 4 см, СА\ = 8 см.
Решение. Пусть О — центр окружно-
окружности (рис.233). Отрезок ОС является высотой рав-
равнобедренного треугольника ОВВ\, а значит, и его
Д
медианой. Поэтому ВС = СВ\ =
о пересекающихся хордах
Ответ. 8л/2
. По теореме
САх = ВС - СВХ =
ВВ\
откуда
ВВХ = 2^АС • САх = 8л/2 см.
см.
668. Докажите, что перпендикуляр, проведенный из какой-нибудь точки
окружности к диаметру, есть среднее пропорциональное между отрезками,
на которые основание перпендикуляра делит диаметр.
Решение. Пусть ВС — перпендикуляр, проведенный из точки
В к диаметру ААх (см. рис.233), ВВх — хорда, содержащая этот
перпендикуляр. В ходе решения задачи 667 мы установили, что
ВВх
• С Ах

§ 2. Центральные и вписанные углы
173
669.	Пользуясь предыдущей задачей, постройте отрезок, средний пропор-
пропорциональный между данными отрезками.
Решение. На произвольной прямой отложим последовательно от-
отрезки АВ и ВС, равные данным отрезкам (рис.234). Затем, найдя
середину отрезка АС, построим окружность с диаметром АС и про-
проведем через точку В прямую, перпендикулярную к АС. Пусть D —
одна из точек пересечения этой прямой с окружностью. Тогда согласно
утверждению, сформулированному в задаче 668, отрезок BD — иско-
искомый.
670.	Через точку А проведены касательная АВ (В — точка касания)
и секущая, которая пересекает окружность в точках Р и Q. Докажите, что
АВ2 = АР • AQ.
Решение. Треугольники АВР и ABQ (рис.235) подобны,
поскольку угол А у них общий, а каждый из углов АВР и AQB
измеряется половиной дуги ВР (см. задачу 664). Следовательно,
АВ
AQ
АР
АВ
, откуда АВ2 = АР- AQ.
671.	Через точку А проведены касательная АВ (В — точка касания)
и секущая, которая пересекает окружность в точках С и D. Найдите CD,
если: а) АВ = 4 см, АС = 2 см; б) АВ = 5 см, AD = 10 см.
Решение. Согласно утверждению, сформулированному в зада-
задаче 670, АВ2 = АС • АВ. Поэтому:
а)	AD = ^ см = 8 см, откуда CD = AD - AC = 6 см;
б)	АС = ^ см = 2,5 см, откуда CD = AD - AC = 7,5 см.
Ответ, а) 6 см; б) 7,5 см.
672.	Через точку А, лежащую вне окружности, проведены две секущие,
одна из которых пересекает окружность в точках В\, С\, а другая — в точках
В2, С2. Докажите, что
АВХ • АСХ =АВ2-АС2.
Решение. Пусть AD — касательная (D — точка касания). Тогда
согласно утверждению, сформулированному в задаче 670,
AD2 = АВХ • АСХ = АВ2 • АС2.
D
Рис. 234
Рис. 235

174
Гл. 4. Окружность
§ 3. Четыре замечательные точки треугольника
674.	Из точки М биссектрисы неразвернутого угла О проведены перпен-
перпендикуляры МА и MB к сторонам этого угла. Докажите, что АВ JL ОМ.
Решение. Прямоугольные треугольники О AM и ОВМ (рис.236)
равны по гипотенузе и острому углу, поэтому О А = ОВ. Прямая ОМ
содержит биссектрису равнобедренного треугольника ОАВ, а значит,
содержит и его высоту. Следовательно, АВ JL ОМ.
675.	Стороны угла О касаются каждой из двух окружностей, имеющих
общую касательную в точке А. Докажите, что центры этих окружностей лежат
на прямой О А.
Решение. Пусть О\ и 0% — центры данных окружно-
окружностей (рис.237). Каждая из этих точек равноудалена от сторон угла
О и, следовательно, лежит на биссектрисе этого угла. Отрезки О\А
и 0%А перпендикулярны к общей касательной, поэтому точки О\, А
и О2 лежат на одной прямой.
Таким образом, все четыре точки: О, О\, А и О^ — лежат на одной
прямой.
676.	Стороны угла А касаются окружности с центром О радиуса г.
Найдите: а) О А, если г = 5 см, ZA = 60°; б) г, если О А = 14 дм, ZA = 90°.
Решение. Точка О равноудалена от сторон угла А (рис.238),
поэтому луч АО — биссектриса этого угла. Имеем:
а) ОА =
sin 30'
Ответ, а) 10 см; б) 7 у/2 дм.
= 10 см; б) г = OAsin45° = 7 у/2
ДМ.
677. Биссектрисы внешних углов при вершинах В и С треугольника ABC
пересекаются в точке О. Докажите, что точка О является центром окружности,
касающейся прямых АВ, ВС, АС.
Решение. Проведем из точки О перпендикуляры ОА\, ОВ\ и ОС\
к прямым ВС, С А и АВ (рис.239). Поскольку точка О лежит на бис-
биссектрисе угла А\ВС\, то она равноудалена от прямых АВ и ВС,
а значит, ОА\ = ОС\. Аналогично, ОА\ = ОВ\. Следовательно, окруж-
окружность радиуса ОА\ проходит через точки В\ и С\. Прямые ВС, С А
и АВ касаются этой окружности в точках А\, В\ и С\, так как они
перпендикулярны соответственно к радиусам ОА\, ОВ\ и ОС\.
О'
А
Рис. 236
Рис. 237
Рис. 238

§ 3. Четыре замечательные точки треугольника
175
678. Биссектрисы АА\ и ВВ\ треугольника ABC пересекаются в точке
М. Найдите углы АСЫ и ВСМ, если: a) ZAMB = 136°; б) ZAMB =111°.
Решение. Поскольку М — точка пересечения биссектрис углов А
и В треугольника ABC (рис.240), то луч СМ — биссектриса угла С
этого треугольника. Следовательно,
ZACM = ZBCM =
ZC
_ _ 180° -ZA-ZB _ о _ ZA
2 ~	2	2
ZB
2
= 90° - A80° - ZAMB) = ZAMB - 90°
Таким образом:
а)	ZACM = ZBCM = 136° - 90° = 46°;
б)	ZACM = ZBCM = 111° - 90° = 21°.
Ответ, а) 46° и 46°; б) 21° и 21°.
679. Серединный перпендикуляр к стороне ВС треугольника ABC пе-
пересекает сторону АС в точке D. Найдите: a) AD и CD, если BD = 5 см,
АС = 8,5 см; б) АС, если BD = 11,4 см, AD = 3,2 см.
Решение. Точка D равноудалена от концов отрезка С В (рис.241),
т. е. BD = CD. Поэтому:
а)	CD = BD = 5 см, AD = АС - CD = 8,5 см - 5 см = 3,5 см;
б)	АС = AD + CD = AD + BD = 3,2 см + 11,4 см = 14,6 см.
Ответ, а) 3,5 см и 5 см; б) 14,6 см.
680. Серединные перпендикуляры к сторонам АВ и АС треугольника
ABC пересекаются в точке D стороны ВС. Докажите, что: a) D — середина
стороны ВС; б) ZA = ZB + ZC.
Решение, а) Точка D лежит на серединном перпендикуляре
к стороне АВ (рис.242), поэтому AD = BD. Аналогично AD = CD.
Следовательно, BD = CD, а значит, точка D — середина отрезка ВС.
6) Поскольку AD = BD, то треугольник ABD — равнобедренный,
а значит, ZBAD = ZB. Аналогично ZCAD = ZC. Поэтому
ZA = ZBAD + ZCAD = ZB + ZC.
В
в
Рис. 239
А
Рис. 241

176
Гл. 4. Окружность
681.	Серединный перпендикуляр к стороне АВ равнобедренного тре-
треугольника ABC пересекает сторону ВС в точке Е. Найдите основание АС
треугольника, если периметр треугольника АЕС равен 27 см, а АВ =18 см.
Решение. Треугольник ABC — равнобедренный (рис.243),
поэтому ВС = АВ = 18 см. Точка Е лежит на серединном
перпендикуляре к стороне АВ, а значит, АЕ = BE. Имеем:
АС = (АС + АЕ + ЕС) - (АЕ + ЕС) =
= (АС + АЕ + ЕС) - (BE + ЕС) =
= (АС + АЕ + ЕС) - ВС = 27 см - 18 см = 9 см.
Ответ. 9 см.
682.	Равнобедренные треугольники ABC и ABD имеют общее основание
АВ. Докажите, что прямая CD проходит через середину отрезка АВ.
Решение. Поскольку треугольник ABC равнобедренный, то точка
С равноудалена от концов отрезка АВ, а значит, лежит на серединном
перпендикуляре к этому отрезку. Аналогично, точка D лежит на се-
серединном перпендикуляре к отрезку АВ. Следовательно, прямая CD
и есть указанный серединный перпендикуляр, поэтому прямая CD
проходит через середину отрезка АВ.
683.	Докажите, что если в треугольнике ABC стороны АВ и АС не рав-
равны, то медиана AM треугольника не является высотой.
Решение. Предположим, что медиана AM является высотой.
Тогда она является серединным перпендикуляром к отрезку ВС и,
следовательно, точка А равноудалена от концов отрезка ВС. Но по
условию задачи АВ ф АС. Поэтому медиана AM треугольника ABC
не может быть высотой.
684. Биссектрисы углов при основании АВ равнобедренного треугольника
ABC пересекаются в точке М. Докажите, что прямая СМ перпендикулярна
к прямой АВ.
Решение. Каждый из углов А и В треугольника АВМ равен
половине угла при основании треугольника ABC, а значит, эти уг-
углы равны. Следовательно, треугольник АВМ — также равнобедрен-
Рис. 242
Рис. 243

§ 4. Вписанная и описанная окружности	177
ный. Поэтому прямая СМ — серединный перпендикуляр к отрезку
АВ (см. решение задачи 682).
685. Высоты АА\ и ВВ\ равнобедренного треугольника ABC, проведен-
проведенные к боковым сторонам, пересекаются в точке М. Докажите, что прямая
МС — серединный перпендикуляр к отрезку АВ.
Решение. По теореме о пересечении высот треугольника прямая
МС — высота равнобедренного треугольника ABC, а значит, и его
медиана. Но это и означает, что прямая МС — серединный перпенди-
перпендикуляр к отрезку АВ.
687.	Даны прямая а и две точки А и В, лежащие по одну сторону
от прямой. На прямой а постройте точку М, равноудаленную от точек А и В.
Решение. Построим серединный перпендикуляр к отрезку
АВ (см. задачу 686) и отметим точку М пересечения этого
перпендикуляра с прямой а (рис.244). Точка М — искомая.
688.	Даны угол и отрезок. Постройте точку, лежащую внутри угла,
равноудаленную от его сторон и равноудаленную от концов данного отрезка.
Решение. Построим биссектрису данного угла (рис.245), сере-
серединный перпендикуляр к данному отрезку (см. задачу 686) и отметим
точку их пересечения. Эта точка — искомая.
§ 4. Вписанная и описанная окружности
689. В равнобедренном треугольнике основание равно 10 см, а боковая
сторона равна 13 см. Найдите радиус окружности, вписанной в этот треуголь-
треугольник.
Решение. Пусть ABC — данный треугольник, АС — его основа-
основание, О — центр вписанной окружности, А\, В\, С\ — точки, в которых
вписанная окружность касается сторон ВС, С А, АВ (рис.246). Луч
ВО — биссектриса угла, противолежащего основанию равнобедренного
треугольника, поэтому прямая ВО является серединным перпендику-
перпендикуляром к основанию АС. Отрезок ОВ\ перпендикулярен к стороне АС.
Рис. 244	Рис. 245

178
Гл. 4. Окружность
Следовательно, точка В\ лежит на прямой ОВ и является серединой
основания АС, а значит, АВ\ = 5 см. По теореме Пифагора
ВВ\ = л/169 — 25 см = 12 см.
Прямоугольные треугольники ВОС\ и ВАВ\ подобны, так как
имеют общий острый угол В. Поэтому
г 12 см — г	О1
-— = —	, откуда г = 3- см.
5 см	13 см	3
Ответ. 3- см.
о
690. Найдите основание равнобедренного тре-
треугольника, если центр вписанной в него окруж-
окружности делит высоту, проведенную к основанию,
в отношении 12:5, считая от вершины, а боковая
сторона равна 60 см.
Решение. Пусть ABC — данный тре-
треугольник, АС — его основание, О — центр
вписанной окружности, А\, В\, С\ — точ-
точки, в которых вписанная окружность касает-
касается сторон ВС, С А, АВ (см. рис.246). Если
отрезок ВО обозначить через \2х, то радиус
вписанной окружности окажется равным Ъх,
а высота треугольника ABC, проведенная к основанию, — равной Их.
Из подобия треугольников ВОС\ и ВАВ\ (см. решение задачи 689)
находим:
^гп	I Чгп
-, откуда АС = 50 см.
Рис. 246
Ъх
Ответ. 50 см.
691. Точка касания окружности, вписанной в равнобедренный треуголь-
треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см, считая
от основания. Найдите периметр треугольника.
Решение. Обратимся к рисунку 246. Из условия задачи следует,
что боковая сторона треугольника равна 3 см + 4 см = 7 см. Посколь-
Поскольку отрезки касательных, проведенных из вершины основания, равны,
то основание равно 3 см + 3 см = 6 см. Следовательно, периметр тре-
треугольника равен 7 см + 7 см + 6 см = 20 см.
Ответ. 20 см.
692. В треугольник ABC вписана окружность, которая касается сторон
АВ, ВС и АС в точках Р, Q и R. Найдите АР, РВ, BQ, QC, CR, RA, если
АВ = 10 см, ВС = 12 см, С А = 5 см.

§ 4. Вписанная и описанная окружности
179
Решение. Поскольку отрезки касательных, проведенных из одной
точки, равны, то
АР = RA, РВ = BQ, QC = CR (рис. 247).
Следовательно, АР + РВ = АВ = 10 см, ВР + QC = ВС = 12 см,
AP = CA = 5 см.
Из этих трех равенств находим:
АР =1,5 см,
= 8,5см, CR = 3,5 см,
а значит, RA = 1,5 см, BQ = 8,5 см, CR = 3,5 см.
Ответ. 1,5 см, 8,5 см, 8,5 см, 3,5 см, 3,5 см, 1,5 см.
693. В прямоугольный треугольник вписана окружность радиуса г. Найди-
Найдите периметр треугольника, если: а) гипотенуза равна 26 см, г = 4 см; б) точка
касания делит гипотенузу на отрезки, равные 5 см и 12 см.
Решение, а) Рассмотрим прямоугольный треугольник ABC с пря-
прямым углом А. Пусть О — центр вписанной окружности, А\, В\, С\ —
точки, в которых вписанная окружность касается сторон ВС, С А,
АВ (рис.248). Четырехугольник АВ\ОС\ — квадрат, поэтому АВ\ =
= АС\ = г = 4 см. Имеем:
АВ + ВС + С А = АСХ + СХВ + ВАХ + АХС + СВХ
i A
Поскольку отрезки касательных, проведенных из одной точки, рав-
равны, то С\В = ВА\ и СВ\ = AiC. Таким образом,
АВ + БС + СА = 2г + 2Б^1 + 2AiC = 2r + 2БС =
= 8 см + 52 см = 60 см.
б) Аналогично получаем:
АВ + ВС + СА = 10 см + 24 см + 2г.
По теореме Пифагора
(г + 5 смJ + (г + 12 смJ = E см + 12 смJ,
В

180	Гл. 4. Окружность
откуда находим: г = 3 см. Таким образом, периметр треугольника ABC
равен 40 см.
Ответ, а) 60 см; б) 40 см.
694.	Найдите диаметр окружности, вписанной в прямоугольный треуголь-
треугольник, если гипотенуза треугольника равна с, а сумма катетов т.
Решение. В ходе решения задачи 693, а было установлено, что
периметр данного треугольника равен сумме его удвоенной гипотену-
гипотенузы и диаметра вписанной окружности. Поэтому диаметр вписанной
окружности равен т — с.
Ответ, т — с.
695.	Сумма двух противоположных сторон описанного четырехугольника
равна 15 см. Найдите периметр этого четырехугольника.
Решение. В описанном четырехугольнике суммы противополож-
противоположных сторон равны, поэтому периметр данного четырехугольника равен
2- 15 см = 30 см.
Ответ. 30 см.
696.	Докажите, что если в параллелограмм можно вписать окружность,
то этот параллелограмм — ромб.
Решение. Если в параллелограмм со смежными сторонами а и Ъ
можно вписать окружность, то суммы его противоположных сторон
равны: 2а = 2Ь, откуда а = Ь. Следовательно, этот параллелограмм —
ромб.
697.	Докажите, что площадь описанного многоугольника равна половине
произведения его периметра на радиус вписанной окружности.
Решение. Соединим центр вписанной окружно-
окружности с вершинами многоугольника отрезками (рис.249).
В результате многоугольник окажется разделенным
на треугольники, в каждом из которых за основание
можно принять сторону многоугольника, а за высоту —
радиус г вписанной окружности. Площадь многоуголь-
многоугольника равна сумме площадей этих треугольников, т. е.
произведения общего множителя г на половину пери-
периметра многоугольника.
698.	Сумма двух противоположных сторон описанного четырехугольника
равна 12 см, а радиус вписанной в него окружности равен 5 см. Найдите
площадь четырехугольника.
Решение. В описанном четырехугольнике суммы противополож-
противоположных сторон равны, поэтому периметр данного четырехугольника равен
2 • 12 см = 24 см. Площадь описанного многоугольника равна половине

§ 4. Вписанная и описанная окружности
181
произведения его периметра на радиус вписанной окружности (см. за-
задачу 697). Следовательно, площадь четырехугольника равна 60 см2.
Ответ. 60 см2.
699.	Сумма двух противоположных сторон описанного четырехугольника
равна 10 см, а его площадь — 12 см. Найдите радиус окружности, вписанной
в этот четырехугольник.
Решение. В описанном четырехугольнике суммы противополож-
противоположных сторон равны, поэтому периметр данного четырехугольника ра-
равен 2 • 10 см = 20 см. Площадь описанного многоугольника равна
половине произведения его периметра на радиус вписанной окружно-
окружности (см. задачу 697). Следовательно, радиус вписанной окружности
равен — см = 1,2 см.
Ответ. 1,2 см.
700.	Докажите, что в любой ромб можно вписать окружность.
Решение. Диагонали ромба взаимно перпендикулярны и делятся
точкой пересечения пополам. Поэтому диагонали ромба разделяют его
на четыре прямоугольных треугольника, равных друг другу по двум ка-
катетам. Следовательно, высоты этих треугольни-
треугольников, проведенные из вершины О прямых углов,
также равны. Иными словами, если провести
окружность с центром О, проходящую через
основание одной из этих высот, то она пройдет
и через основания трех других высот (рис. 250).
Стороны ромба касаются этой окружности, так
как они соответственно перпендикулярны к ее
радиусам.
Рис. 250
701.	Начертите три треугольника: остроугольный, прямоугольный и тупо-
тупоугольный. В каждый из них впишите окружность.
Решение. Чтобы вписать окружность в данный треугольник, нуж-
нужно построить биссектрисы двух его углов и найти точку их пересече-
пересечения — центр вписанной окружности. Затем из этой точки следует про-
провести перпендикуляр к какой-нибудь стороне. Окружность с найден-
найденным центром, проходящая через основание этого перпендикуляра, —
искомая вписанная окружность.
702.	В окружность вписан треугольник ABC так, что АВ — диаметр
окружности. Найдите углы треугольника, если: а) ^ ВС = 134°; б) ^ АС =
= 70°.
Решение. Вписанный угол С опирается на полуокружность. Сле-
Следовательно, угол С — прямой. По теореме о вписанном угле:
а) А А =
= 67°, а значит, ZB = 90° - 67° = 23°

182	Гл. 4. Окружность
б) АВ = -^ = 35°, а значит, А А = 90° - 35° = 55°.
Ответ, а) 67°, 23° и 90°; б) 55°, 35° и 90°.
703.	В окружность вписан равнобедренный треугольник ABC с основа-
основанием ВС. Найдите углы треугольника, если ^ ВС = 102°.
102°
Решение. По теореме о вписанном угле ZA = ——- = 51° или
/Л 360°-102° 1ono /D /r, 180°-51° ^ооп/
АА =	 = 129 , а значит, /Б = АС =	 = 64°30
1 яо° — 1 9Q°
или /Б = ZC = 1йи 2 ^ = 25°30'.
Ответ. 51°, 64°30', 64°30х или 129°, 25°3(У, 25°30х.
704.	Окружность с центром О описана около прямоугольного треуголь-
треугольника, а) Докажите, что точка О — середина гипотенузы, б) Найдите стороны
треугольника, если диаметр окружности равен d, а один из острых углов
треугольника равен а.
Решение, а) Вписанный прямой угол опирается на полуокруж-
полуокружность. Поэтому гипотенуза треугольника является диаметром, а зна-
значит, точка О — середина гипотенузы.
б) Гипотенуза треугольника равна d, а значит, его катеты равны
dsina и dcosa.
Ответ, б) d, dsina, dcosa.
705.	Около прямоугольного треугольника ABC с прямым углом С описана
окружность. Найдите радиус этой окружности, если: а) АС = 8 см, ВС = б см;
б) АС = 18 см, ZB = 30°.
Решение. Радиус описанной окружности равен половине гипоте-
АВ
нузы (см. задачу 704), т. е. равен —-. Имеем:
д)АВ = л/64 + 36 см = 10 см, qp = 5 см;
б) АВ = 36 см, 4р = 18 см.
Ответ, а) 5 см; б) 18 см.
706.	Найдите сторону равностороннего треугольника, если радиус описан-
описанной около него окружности равен 10 см.
Решение. По теореме о пересечении медиан треугольника высота
3
данного равностороннего треугольника равна - • 10 см = 15 см, а зна-
значит, его сторона равна Юл/3 см.
Ответ. Юл/3 см.
707.	Угол, противолежащий основанию равнобедренного треугольника,
равен 120°, боковая сторона треугольника равна 8 см. Найдите диаметр окруж-
окружности, описанной около этого треугольника.

§ 4. Вписанная и описанная окружности	183
Решение. Пусть ABC — данный треугольник, АС — его осно-
основание, О — центр описанной окружности (рис.251). Поскольку углы
ОБА и ОВС равны, то каждый из них равен 60°. Таким образом,
в равнобедренном треугольнике ОАВ один из углов равен 60°, а зна-
значит, этот треугольник равносторонний. Поэтому радиус О А описанной
окружности равен 8 см, а ее диаметр — 16 см.
Ответ. 16 см.
708.	Докажите, что можно описать окружность: а) около любого прямо-
прямоугольника; б) около любой равнобедренной трапеции.
Решение, а) Диагонали прямоугольника равны и делятся точкой
пересечения пополам. Поэтому окружность с центром в точке пере-
пересечения диагоналей, проходящая через одну из его вершин, проходит
и через три другие вершины, т. е. является окружностью, описанной
около прямоугольника.
б) Пусть ABCD — данная трапеция с основаниями АВ и ВС,
О — точка пересечения серединных перпендикуляров ОМ и ON к ее
сторонам АВ и CD (рис.252). Тогда О А = ОВ и ОС = OD. Углы
при основании равнобедренной трапеции равны (см. задачу 388), а от-
отрезок MN параллелен основаниям (см. задачу 386). Следовательно,
ZAMN = ZDNM, а значит, ZOMN = ZONM, т. е. треугольник
0MN — равнобедренный. Прямоугольные треугольники ОВМ и OCN
равны по двум катетам, поэтому ОВ = ОС. Итак, О А = ОВ = ОС =
= OD. Поэтому окружность с центром в точке О, проходящая через
одну из вершин трапеции, проходит и через три другие ее вершины,
т. е. является окружностью, описанной около трапеции.
709.	Докажите, что если около параллелограмма можно описать окруж-
окружность, то этот параллелограмм — прямоугольник.
Решение. В любом вписанном четырехугольнике сумма проти-
противоположных углов равна 180°. В параллелограмме противоположные
углы равны. Следовательно, если около параллелограмма можно опи-
описать окружность, то все его углы равны 90°, а значит, этот параллело-
параллелограмм — прямоугольник.
710.	Докажите, что если около трапеции можно описать окружность,
то эта трапеция равнобедренная.
Рис. 251	Рис. 252

184
Гл. 4. Окружность
Решение. Если около трапеции можно описать окружность, то ду-
дуги, стягиваемые ее боковыми сторонами, равны (см. задачу 659). По-
Поэтому вписанные углы при основании трапеции опираются на равные
дуги и, следовательно, равны. Из этого следует, что трапеция равно-
равнобедренная (см. задачу 389).
711. Начертите три треугольника: тупоугольный, прямоугольный и равно-
равносторонний. Для каждого из них постройте описанную окружность.
Решение. Чтобы описать окружность около данного треуголь-
треугольника, нужно построить серединные перпендикуляры к двум сторо-
сторонам и найти точку их пересечения — центр описанной окружности.
Окружность с найденным центром, проходящая через одну из вершин
треугольника, проходит и через две другие его вершины, т. е. является
искомой описанной окружностью. В случае прямоугольного треуголь-
треугольника построение можно несколько сократить, если воспользоваться
утверждением, сформулированным в задаче 704, а.
Дополнительные задачи
712.	Докажите, что касательные, проведенные через концы хорды, не яв-
являющейся диаметром окружности, пересекаются.
Решение. Пусть АВ — данная хорда (рис.253). Эта хорда обра-
образует с каждой из касательных угол, равный половине дуги АВ (см. за-
задачу 664). Тем самым сумма односторонних углов, образованных при
пересечении касательных секущей АВ, равна дуге АВ. Но ^ АВ ф
Ф 180°, следовательно, касательные пересекаются.
713.	Прямые АВ и АС — касательные к окружности с центром О, В
и С — точки касания. Через произвольную точку X, взятую на дуге ВС,
проведена касательная к этой окружности, пересекающая отрезки АВ и АС
в точках М и N. Докажите, что периметр треугольника AMN и угол MON
не зависят от выбора точки X на дуге ВС.
Решение. Прямоугольные треугольники ОХМ и ОВМ (рис.254)
равны по гипотенузе и катету. Следовательно,
MX = MB и ZMOX = ZMOB.
Аналогично из равенства треугольников OXN и OCN находим:
XN = CN и ZNOX = ZNOC.
Рис. 253

Дополнительные задачи
185
Имеем:
AM + MN
= AM + MB
ZMON = ZMOX + ZNOX =
MX
AC;
ZBOC
Тем самым периметр треугольника AMN и угол MON не зависят
от выбора точки X на дуге ВС.
714*. Две окружности имеют общую точку М и общую касательную в этой
точке. Прямая АВ касается одной окружности в точке А, а другой — в точке
В. Докажите, что точка М лежит на окружности с диаметром АВ.
Решение. Проведем через точку М общую касательную и обозна-
обозначим буквой К точку ее пересечения с прямой АВ (рис.255). Поскольку
К А и КМ — отрезки касательных к окружности, проведенных из точ-
точки К, то К А = КМ. Аналогично KB = КМ. Следовательно, К А =
= KB = КМ. Но это и означает, что точка М лежит на окружности
с диаметром АВ.
715.	Диаметр АА\ окружности перпендикулярен к хорде ВВ\. Докажите,
что градусные меры дуг АВ и АВ\, меньших полуокружности, равны.
Решение. Пусть О — центр окружности (рис.256). Прямая АА\
содержит высоту равнобедренного треугольника ОВВ\, а значит, и его
биссектрису. Следовательно, центральные углы АОВ и АОВ\ равны,
а значит, равны и дуги, на которые опираются эти углы.
716.	Точки А, В, С и D лежат на окружности. Докажите, что если
- АВ =- CD, то АВ = CD.
Решение. Пусть О — центр окружности. Равнобедренные тре-
треугольники CAB и CCD равны по первому признаку равенства тре-
треугольников, поэтому АВ = CD.
1\1'. Отрезок АВ является диаметром окружности, а хорды ВС и AD
параллельны. Докажите, что хорда CD является диаметром.
Решение. Накрест лежащие углы, образованные при пересече-
пересечении параллельных прямых ВС и AD секущей АВ, равны (рис.257),
поэтому равны и дуги АС и BD, на которые опираются эти углы.
В
Рис. 255
Рис. 256
Рис. 257

186	Гл. 4. Окружность
Имеем:
- CD =- СБ+ - BD = (^ АВ- - АС)+ - BD =- АВ = 180°.
Следовательно, хорда CD — диаметр окружности.
719. Через точку, лежащую вне окружности,
проведены две секущие. Докажите, что угол между
ними измеряется полуразностью дуг, заключенных
внутри угла.
Решение. Рассмотрим две секущие, про-
проведенные из точки М и пересекающие окруж-
окружность в точках А и В, С и D соответствен-
соответственно (рис.258). Угол BAD — внешний угол тре-
Рис. 258	угольника ADM, поэтому
ZBAD = ZAMD + ZADM,
откуда
ZAMD = ZBAD - ZADM =- Щ?-- - ^ = ^ BD~^ АС,
720.	Может ли вершина разностороннего треугольника лежать на сере-
серединном перпендикуляре к какой-либо стороне? Ответ обоснуйте.
Решение. Ясно, что вершина треугольника не может лежать
на серединном перпендикуляре к той стороне, концом которой она
является. Если бы вершина разностороннего треугольника лежала
на серединном перпендикуляре к противолежащей стороне, то меди-
медиана, проведенная из этой вершины, была бы высотой, что невозмож-
невозможно (см. задачу 683).
Ответ. Нет.
721.	Докажите, что если в прямоугольник можно вписать окружность,
то этот прямоугольник — квадрат.
Решение. Если в прямоугольник со смежными сторонами а
и Ъ можно вписать окружность, то суммы его противоположных сто-
сторон равны: 2а = 2Ь, откуда а = Ь, а значит, этот прямоугольник —
квадрат.
722.	Четырехугольник ABCD описан около окружности радиуса г. Из-
Известно, что АВ : CD = 2:3, AD : ВС = 2:1. Найдите стороны четырехуголь-
четырехугольника, если его площадь равна S.
Решение. Площадь описанного многоугольника равна половине
произведения его периметра на радиус вписанной окружности (см. за-
2S
дачу 697). Поэтому периметр четырехугольника ABCD равен —.

Дополнительные задачи
187
Следовательно, АВ + CD = AD + ?>С = —. Отсюда находим:
?-, ВС=%,
or	or
2S S 3S 2S
or
or
723. Докажите, что если прямые, содержащие основания трапеции, каса-
касаются окружности и точки касания принадлежат основаниям, то средняя линия
трапеции проходит через центр окружности.
Решение. Пусть Р и Q — точки, в которых окружность касается
оснований ВС и AD трапеции ABCD, О — центр этой окружно-
окружности (рис.259). Прямая ОР перпендикулярна к прямой ВС. Следова-
Следовательно, она перпендикулярна и к прямой AD, а значит, проходит через
точку Q (иначе из точки О оказалось бы проведено два перпендику-
перпендикуляра к прямой AD, что невозможно). Иными словами, отрезок PQ —
диаметр окружности.
Напомним, что средней линией трапеции называется отрезок, со-
соединяющий середины М и N ее боковых сторон. Средняя линия
трапеции параллельна основаниям трапеции (см. задачу 386). Следо-
Следовательно, по теореме Фалеса (см. задачу 385), она пересекает отрезок
PQ в его середине, т. е. проходит через центр О окружности.
725. Найдите радиус окружности, вписанной в прямоугольную трапецию
с основаниями а и Ъ.
Решение. Пусть ABCD — трапеция с основаниями AD
и ВС (AD > ВС), АВ JL AD (рис.260), г — радиус вписанной в нее
окружности. Проведем высоту СН и, учитывая, что
СН = 2r, DH = а - b,CD = (а - г) + (Ъ - г) = а + Ъ - 2г,
применим теорему Пифагора к треугольнику CDH:
г Ъ-г

188	Гл. 4. Окружность
откуда
ab
г = 	=
~	аЪ
Ответ. 	г.
а + 6
726.	Центр описанной около треугольника окружности лежит на медиане.
Докажите, что этот треугольник либо равнобедренный, либо прямоугольный.
Решение. Рассмотрим серединный перпендикуляр к той стороне
треугольника, к которой проведена данная медиана. Из условия задачи
следует, что центр описанной окружности является общей точкой этого
серединного перпендикуляра и данной медианы. Возможны два случая.
1°. Рассматриваемый серединный перпендикуляр и данная медиана
совпадают. В этом случае вершина, из которой проведена медиана,
равноудалена от концов противолежащей стороны, а значит, данный
треугольник — равнобедренный.
2°. Рассматриваемый серединный перпендикуляр и данная медиана
не совпадают. В этом случае серединный перпендикуляр и медиана
имеют единственную общую точку — середину стороны, к которой
проведена медиана. Тем самым центр описанной окружности лежит
на середине стороны треугольника, а значит, этот треугольник —
прямоугольный (см. решение задачи 665).
727.	В равнобедренный треугольник вписана окружность с центром О\,
и около него описана окружность с центром 0%. Докажите, что точки О\ и О%
лежат на серединном перпендикуляре к основанию треугольника.
Решение. Центр вписанной окружности лежит на биссектрисе,
проведенной к основанию треугольника. Эта биссектриса является
медианой и высотой, т. е. серединным перпендикуляром к основанию
треугольника. Следовательно, обе точки О\ и 0% лежат на серединном
перпендикуляре к основанию треугольника.
728.	Докажите, что если около ромба можно описать окружность, то этот
ромб — квадрат.
Решение. Противоположные углы ромба равны. Если около ромба
можно описать окружность, то эти углы составляют в сумме 180°.
Следовательно, каждый из них равен 90°, а значит, этот ромб —
квадрат.
730. Через точки Aw В проведены прямые, перпендикулярные к сторонам
угла АОВ и пересекающиеся в точке С внутри угла. Докажите, что около
четырехугольника АСВО можно описать окружность.
Решение. Каждый из углов А и В четырехугольника АСВО
равен 90°, а значит, сумма этих углов равна 180°. Поэтому (см. зада-
задачу 729) около четырехугольника АСВО можно описать окружность.

Дополнительные задачи
189
731. Докажите, что около выпукло-
выпуклого четырехугольника ABCD, образованно-
образованного при пересечении биссектрис углов трапе-
трапеции, можно описать окружность.
Решение. Пусть A\B\C\D\ —
данная трапеция (рис.261). Угол А че-
четырехугольника ABCD равен 180° —
/\
Рис. 261
Т	2 ГД6 Х И Х ~
трапеции. Но /_А\ + ZB\ = 180°. Сле-
Следовательно, ZA = 90°. Аналогично, АС = 90°. Таким образом, в че-
четырехугольнике ABCD сумма противоположных углов А и С равна
180°. Поэтому (см. задачу 729) около четырехугольника ABCD можно
описать окружность.
732. В прямоугольном треугольнике ABC из точки
М стороны АС проведен перпендикуляр МН к гипоте-
гипотенузе АВ. Докажите, что углы МНС и МВС равны.
Решение. В четырехугольнике ВСМН про-
противоположные углы С и Н прямые (рис.262),
а значит, сумма этих углов равна 180°. Поэто-
Поэтому (см. задачу 729) около этого четырехугольника
можно описать окружность. Опишем ее. Тогда
окажется, что вписанные углы МНС и МВС
равны, так как они опираются на одну и ту же
дугу МС.
Рис. 262
733.	Найдите радиус вписанной в равносторон-
равносторонний треугольник окружности, если радиус описанной
окружности равен 10 см.
Решение. Центры указанных окружностей совпадают с точкой
пересечения медиан треугольника, причем радиус описанной окружно-
окружности равен расстоянию от этой точки до вершины, а радиус вписанной
окружности — расстоянию от этой точки до стороны. Из теоремы
о пересечении медиан треугольника следует, что радиус вписанной
окружности в два раза меньше радиуса описанной окружности, т. е.
равен 5 см.
Ответ. 5 см.
734.	Докажите, что если в параллелограмм можно вписать окружность
и можно описать около него окружность, то этот параллелограмм — квадрат.
Решение. Если около параллелограмма можно описать окруж-
окружность, то этот параллелограмм — прямоугольник (см. задачу 709).
Если же в прямоугольник можно вписать окружность, то этот прямо-
прямоугольник — квадрат (см. задачу 721).

190
Гл. 4. Окружность
735. В трапецию с основаниями а и Ь можно
вписать окружность и около этой трапеции мож-
можно описать окружность. Найдите радиус вписанной
окружности.
Решение. Рассмотрим трапецию ABCD
с основаниями AD = а и ВС = Ъ (рис.263).
Для определенности будем считать, что а >
> Ь. Поскольку около данной трапеции можно
Рис. 263	описать окружность, то эта трапеция равнобед-
равнобедренная (см. задачу 710), т. е. АВ = CD. С другой стороны, поскольку
в эту трапецию можно вписать окружность, то АВ + CD = 2AB = а +
+ Ь, откуда
АВ = а-±±.
Пусть ВВ\ и СС\ — перпендикуляры, проведенные из точек В и С
к основанию AD. Тогда, очевидно, ВВ\ = СС\ = 2г, где г — радиус
окружности, вписанной в трапецию. Следовательно, прямоугольные
треугольники АВВ\ и DCC\ равны по гипотенузе и катету. Поэтому
АВ\ = C\D, а поскольку В\С\ = ВС = Ь, то
АВу = ^.
Осталось применить теорему Пифагора к треугольнику АВВ\\
откуда
- ЪJ _ (а + ЪJ
~4 ~ 4
г =
Ответ.
736. Даны прямая а, точка А, лежащая на этой
прямой, и точка В, не лежащая на ней. Постройте
окружность, проходящую через точку В и касающуюся
прямой а в точке А.
Решение. Построим серединный перпендику-
перпендикуляр к отрезку АВ, прямую, проходящую через точ-
точку А и перпендикулярную к прямой а, и найдем
точку О их пересечения (рис.264). Окружность
с центром О радиуса О А — искомая.
737. Даны две параллельные прямые и точка, не лежащая ни на одной
из них. Постройте окружность, проходящую через данную точку и касающую-
касающуюся данных прямых.
Решение. Через произвольную точку А одной из прямых проведем
прямую, перпендикулярную к этой прямой. Пусть В — точка пересече-
пересечения проведенной прямой со второй из данных прямых (рис.265).

Задачи повышенной трудности
191
Найдем середину М отрезка АВ и проведем через нее прямую,
перпендикулярную ранее проведенной. Затем проведем окружность
АВ	„	.
радиуса -— с центром в данной точке и обо-
значим буквой О одну из точек пересечения
этой окружности с последней из проведенных
прямых. Окружность с центром О радиуса
АВ
— искомая.
Ясно, что если данная точка лежит между
данными прямыми, то задача имеет два ре-
решения; в противном случае задача не имеет
ни одного решения.
Рис. 265
В
Задачи повышенной трудности
877. Две окружности имеют единственную общую точку М. Через эту
точку проведены две секущие, пересекающие одну окружность в точках А
и А\, а другую — в точках В и В\. Докажите, что АА\ || ВВ\.
Решение. Пусть О\ и О^ — центры данных окружностей. Тогда
точка М лежит на прямой О\О^ (в противном случае точка, симмет-
симметричная точке М относительно прямой О\О^, была бы еще одной общей
точкой данных окружностей). Следовательно, прямая CD, проходящая
через точку М и перпендикулярная к прямой О\О2, является общей
касательной двух данных окружностей. Возможны два случая: данные
окружности лежат по одну сторону от общей касательной (рис.266, а);
данные окружности лежат по разные стороны от общей касатель-
касательной (рис.266, б). Идея доказательства в обоих случаях одна и та же.
Поэтому доказательство проведем для первого случая, а в скобках
укажем те изменения, которые следует внести в текст доказательства
во втором случае.
Поскольку угол между касательной и хордой, проходящей через
точку касания, измеряется половиной заключенной внутри угла ду-
дуги (см. задачу 664), то величины дуг МА\ и МВ\, заключенных внут-
D
М
D
Рис. 266

192
Гл. 4. Окружность
ри угла А\МС (внутри вертикальных углов А\МС и B\MD), равны.
Следовательно, равны и вписанные углы А\АМ, В\ВМ, опирающиеся
на эти дуги. Но эти углы являются соответственными (накрест лежа-
лежащими) углами, образованными при пересечении прямых АА\ и ВВ\
секущей АВ. Поэтому АА\ \\ ВВ\.
878. Прямая АС — касательная к окружности с центром О\, а прямая
BD — касательная к окружности с центром О^ (рис.267, рис.270 учебника).
Докажите, что: a) AD || ВС; б) АВ2 = AD • ВС; в) BD2 : АС2 = AD : ВС.
Решение, а) Каждый из углов ADB и ВАС измеряется половиной
дуги АВ окружности с центром О\ (см. задачу 664). Следовательно,
эти углы равны. По аналогичной причине ZABD = ZACB. Таким
образом, треугольники ABD и ABC подобны. Поэтому углы DAB
и ABC также равны. Но эти углы являются накрест лежащими угла-
углами, образованными при пересечении прямых AD и ВС секущей АВ.
Поэтому AD || ВС.
б)	Из подобия треугольников ABD и ABC (см. а) следует, что
АВ : ВС = AD : АВ, откуда АВ2 = AD • ВС.
в)	Из подобия треугольников ABD и ABC (см. а) следует, что
BD : АС = АВ : ВС и BD : АС = AD : АВ.
Следовательно,
BD2 : АС2 = (BD : AC)(BD : АС) =
= (АВ : BC)(AD : АВ) = AD : ВС.
879. Точки В\ и С\ — середины дуг АВ и АС (рис.268, рис.271 учебни-
учебника). Докажите, что AM = AN.
Решение. Поскольку угол между двумя пересекающимися хорда-
хордами окружности измеряется полусуммой дуг, заключенных между этими
хордами (см. задачу 718), то
ZAMC, = -^'+-Д5' = -CCI+^AB1 = ZANB]_
2	2
Таким образом, в треугольнике AMN углы М и N равны. Следо-
Следовательно, AM = AN.
В

Задачи повышенной трудности
193
880. Окружность отсекает на двух прямых, которые пересекаются в точке,
не лежащей на окружности, равные хорды. Докажите, что расстояния от точки
пересечения этих прямых до концов той и другой хорд соответственно равны
между собой.
Решение. Возможны два случая: точка пересечения данных пря-
прямых лежит внутри круга; точка пересечения данных прямых лежит
вне круга. Ход рассуждений для этих случаев в основном один и тот
же. Поэтому доказательство проведем для первого случая, а в скобках
укажем те изменения, которые следует внести в текст доказательства
во втором случае.
Пусть АВ = а и А\В\ = а — равные хорды, М — точка пересечения
прямых АВ и А\В\ (рис.269), МА = х, МА\ = у (х < ^, у < ^).
По теореме о пересекающихся хордах (согласно утверждению, сформу-
сформулированному в задаче 672)
Вл
Рис. 269
х(а - х) = у(а - у) (х(а + х) = у (а + у)),
откуда х = у, а значит, и
а — х = а — у (а + х = а + у).
881.
окружности величина
Докажите, что для
АВ2
всех хорд АВ данной
где AD — расстояние
в точке В, имеет одно
AD '
от точки А до касательной
и то же значение.
Решение. Пусть АС — диаметр данной
окружности (рис.270). Прямоугольные треуголь-
треугольники ABC и ABD подобны, поскольку каждый
из их острых углов С и В измеряется половиной
дуги АВ (см. задачу 664). Следовательно,
АС : АВ = АВ : AD, откуда
АВ2
AD
= АС.
D
Рис. 270
Тем самым для всех хорд АВ данной окружности величина
имеет одно и то же значение, равное диаметру этой окружности.
7 Л. С. Атанасян и др.
АВ2
AD

194
Гл. 4. Окружность
882.	Через точку А пересечения двух окружностей с центрами в точках
О\ и О2 проведена прямая, пересекающая одну из окружностей в точке В,
а другую — в точке С. Докажите, что отрезок ВС будет наибольшим тогда,
когда он параллелен прямой О\О^.
Решение. Проведем из точек О\ и 0% перпендикуляры О\Н\
и О2Н2 к прямой ВС (рис.271). Отрезки О\Н\ и О^Н^ — высоты
равнобедренных треугольников О\АВ и О2АС, а значит, их медианы.
Следовательно, ВС = 2 • R\R<i- Длина отрезка Я\Я^ равна расстоя-
расстоянию между параллельными прямыми О\Н\ и О2Н2, поэтому ВС =
= 2 • Н\Н2 < 2 • О\С>2, причем знак равенства возможен только в том
случае, когда прямые В.\В.2 и О\О2 параллельны.
883.	Отрезок АВ является диаметром окружности с центром О. На каж-
каждом радиусе ОМ окружности отложен от центра О отрезок, равный рассто-
расстоянию от конца М этого радиуса до прямой АВ. Найдите множество концов
построенных таким образом отрезков.
Решение. Проведем диаметр CD, перпендикулярный к диаметру
АВ (рис.272). Пусть, например, точки М и С лежат по одну сторону
от прямой АВ, МН — перпендикуляр, проведенный из точки М к пря-
прямой АВ, Р — точка искомого множества, лежащая на радиусе ОМ.
Треугольники ОМН и ОСР равны по первому признаку равенства
треугольников: ОМ = ОС, МН = ОР, углы ОМН и СОР равны, по-
поскольку они являются накрест лежащими углами, образованными при
пересечении параллельных прямых МН и ОС секущей ОМ. Следова-
Следовательно, угол ОРС — прямой, а значит, точка Р лежит на окружности
с диаметром ОС.
Итак, если точки М и С лежат по одну сторону от прямой АВ,
то точка Р лежит на окружности с диаметром ОС. Точка Р лежит
на указанной окружности и в тех случаях, когда точки М и С совпада-
совпадают или когда точка М лежит на прямой АВ (в этом случае расстояние
от точки М до прямой АВ считается равным нулю). Ясно также,
что все точки этой окружности принадлежат искомому множеству
точек. Аналогичные рассуждения приводят к выводу о том, что и все
точки окружности с диаметром OD принадлежат искомому множеству,
Рис. 271

Задачи повышенной трудности
195
причем каждая точка этого множества лежит на одной из указанных
окружностей. Таким образом, искомое множество состоит из двух
окружностей с диаметрами ОС и OD.
884. Внутри угла ABC равностороннего треугольника ABC взята точка
М так, что ZBMC = 30°, ZBMA =17°. Найдите углы ВАМ и ВСМ.
Решение. Проведем окружность с центром А радиуса
АВ (рис. 273) и на ее дуге ВС = 60° возьмем произвольную точку
N. Угол BNC опирается на дугу ВС, равную
360° - 60° = 300°, поэтому он равен 150°. Тем
самым в четырехугольнике BNCM сумма про-
противоположных углов М и N равна 180°. Следо-
Следовательно, около этого четырехугольника можно
описать окружность (см. задачу 729). Но через
точки В, N и С проходит только одна окруж-
окружность — окружность с центром А радиуса АВ.
Значит, точка М лежит на этой окружности.
Треугольник АВМ — равнобедренный, по-
поэтому ZABM = ZAMB =17°,
ZBAM = 180° - 17° - 17° = 146°
АВСМ равна 360°. Следовательно,
N
Рис. 273
а значит,
Сумма углов четырехугольника
ZBCM = 360° - 60° - 146° - 17° - 30° = 107°.
Ответ. 146° и 107°
885. Через каждую вершину треугольника ABC проведена прямая, пер-
перпендикулярная к биссектрисе угла треугольника при этой вершине. Прове-
Проведенные прямые, пересекаясь, образуют новый треугольник. Докажите, что
вершины этого треугольника лежат на прямых, содержащих биссектрисы тре-
треугольника ABC.
Решение. Пусть А\, В\ и С\ — верши-
вершины нового треугольника (рис.274). Докажем,
например, что точка А\ лежит на прямой,
содержащей биссектрису треугольника ABC,
проведенную из вершины А (для точек В\
и С\ доказательство аналогичное). Заметим
прежде всего, что прямые А\В\, В\С\ и С\А\
содержат биссектрисы внешних углов тре-
треугольника ABC (например, на рисунке Z\ =
= Z2 = 90° — а). Поскольку точка А\ лежит
на биссектрисе внешнего угла В треугольни-
треугольника ABC, то она равноудалена от прямых АВ
и ВС. По аналогичной причине она равно-
равноудалена от прямых АС и ВС. Следовательно,
Рис. 274

196
Гл. 4. Окружность
она равноудалена от прямых АВ и АС, а значит, лежит на биссектрисе
угла ВАС. Иными словами, она лежит на прямой, содержащей биссек-
биссектрису треугольника ABC, проведенную из вершины А.
886. Пусть Н — точка пересечения прямых, содержащих высоты тре-
треугольника ABC, А', В', С' — точки, симметричные точке Н относительно
прямых ВС, С А, АВ. Докажите, что точки А', В', С лежат на окружности,
описанной около треугольника ABC.
Решение. Докажем, например, что точка А' лежит на окруж-
окружности, описанной около треугольника ABC (для точек В' и С до-
доказательство аналогичное). Возможны три случая: 1° — угол В ост-
острый (рис.275, а); 2° — угол В прямой (рис.275, б); 3° — угол В
тупой (рис.275, в). Рассмотрим эти случаи отдельно.
1°. Поскольку точки Н и А! симметричны относительно прямой
ВС, то АСВА! = АСВН = 90° - АС. Следовательно, ААВА! = 90° -
- АС + АВ. Аналогично, ААСА! = 90° - АВ + АС. Таким образом,
сумма противоположных углов В и С четырехугольника ABA'С равна
180°. Следовательно, около этого четырехугольника можно описать
окружность (см. задачу 729). Но через точки А, В и С проходит только
одна окружность — окружность, описанная около треугольника ABC.
Значит, точка А! лежит на этой окружности.
2°. Утверждение очевидно, поскольку точки В, Н и А! совпадают.
3°. Поскольку точки Н и А' симметричны относительно прямой
ВС, то
ААА'В = 180° - АН А'В = 180° - АВНА'.
Но АВНА' = АВНА = 90° - АСАН = АС.
Таким образом, сумма противоположных углов А' и С четырех-
четырехугольника АА'ВС равна 180°. Следовательно, около этого четырех-
четырехугольника можно описать окружность (см. задачу 729). Но через точки
А, В и С проходит только одна окружность — окружность, описанная
около треугольника ABC. Значит, точка А' лежит на этой окружности.
ЖН,АГ)
Рис. 275

Задачи повышенной трудности
197
887. Отрезок BD — биссектриса треугольника ABC. Докажите, что
BD2 = АВ • ВС - AD • DC.
Решение. Пусть Е — точка пересечения луча BD с окружностью,
описанной около треугольника ABC (рис.276). Треугольники ABE
и BCD подобны, так как ZABE = ZBDC по условию, а вписанные
углы BE А и ВС А опираются на одну и ту же дугу АВ. Следовательно,
АВ :BD = (BD + DE) : ВС,
откуда
BD2 + BD • DE = АВ • ВС.
Но по теореме о пересекающихся хордах
BD • DE = AD • DC.
Следовательно,
BD2 = АВ • ВС - AD • DC.
888.	В треугольнике ABC из вершины В проведены высота ВН и бис-
биссектриса угла В, которая пересекает в точке Е описанную около треугольника
окружность с центром О. Докажите, что луч BE является биссектрисой угла
овн.
Решение. Поскольку луч BE — биссектриса угла В, то дуги
АЕ и ЕС, а значит, и хорды АЕ и ЕС, равны (рис.277). Поэтому
прямая СЕ — серединный перпендикуляр к отрезку АС. Углы ИВЕ
и ВЕС равны как накрест лежащие углы, образованные при пересече-
пересечении параллельных прямых ВН и СЕ секущей BE. Углы ВЕС и ОБЕ
равны, так как они являются углами при основании равнобедренного
треугольника ОБЕ. Следовательно, ZHBE = ZOBE, а значит, луч
BE — биссектриса угла ОВН.
889.	Произвольная точка X окружности, описанной около равносторонне-
равностороннего треугольника ABC, соединена отрезками с его вершинами. Докажите, что
один из отрезков АХ, ВХ и СХ равен сумме двух других.
Решение. Пусть, например, ХС > ХА и ХС > ХВ (рис.278).
Отложим на отрезке ХС отрезок XD, равный ХА. В равнобедренном
Рис. 278

198	Гл. 4. Окружность
треугольнике AXD угол AXD равен вписанному углу АХС, опираю-
опирающемуся на дугу АС, равную 120°. Следовательно, этот угол, а значит,
и угол ADX, равен 60°.
Рассмотрим теперь треугольники АВХ и ACD. В этих треуголь-
350° — 120°
никах ZX =	= 120° = ZD, ZB = ZC, поскольку эти углы
опираются на одну и ту же дугу ХА. Следовательно, и ZBAX =
= ZCAD. Кроме того, АВ = АС по условию. Следовательно, эти
треугольники равны по второму признаку равенства треугольников,
а значит, CD = ХВ. Тем самым
ХС = XD + CD = ХА + ХВ.
Замечание. Эту задачу можно решить значительно быстрее, если
воспользоваться теоремой Птолемея (см. задачу 893). В самом деле,
пусть а — сторона треугольника ABC. Поскольку четырехугольник
АХВС — вписанный, то по теореме Птолемея
а - ХС = а - ХА + а • ХВ,
откуда
ХС ХА + ХВ.
890.	Докажите, что если диагонали вписанного четырехугольника перпен-
перпендикулярны, то сумма квадратов противоположных сторон четырехугольника
равна квадрату диаметра описанной окружности.
Решение. Пусть ABCD — данный четырехугольник. Проведем
диаметр ВВ\ описанной окружности (рис.279). Имеем:
- АВХ = 2ZABBX = 2(90° - ZABXB) =
= 2 (90°- - 4^) = 2(90° - ZACB) = 2ZCBD =- CD.
Поэтому АВ\ = CD. Следовательно,
АВ2 + CD2 = АВ2 + AB\ = ВВ\.
891.	В четырехугольнике ABCD, вписанном в окружность, биссектрисы
углов А и В пересекаются в точке, лежащей на стороне CD. Докажите, что
CD = ВС + AD.
Решение. Проведем через точку М пересечения биссектрис углов
А и В прямую, параллельную АВ, и обозначим буквами Е и F
точки пересечения этой прямой с прямыми AD и ВС (рис.280).
Рассмотрим треугольники DEM и CFM. Поскольку четырехуголь-
четырехугольник ABCD — вписанный, то ZA + ZC = 180°. С другой стороны,
поскольку EF || АВ, то ZA + ZE = 180°. Следовательно, ZC = ZE.
Кроме того, углы при вершине М рассматриваемых треугольников
равны как вертикальные углы. Поэтому эти треугольники подобны.
Заметим теперь, что точка М, будучи точкой пересечения биссектрис

Задачи повышенной трудности
199
D
Рис. 279
Рис. 280
углов А и В, равноудалена от прямых АВ и AD, а также от прямых
АВ и ВС, а значит, она равноудалена и от прямых AD и ВС. Иными
словами, высоты рассматриваемых треугольников, проведенные из вер-
вершины М, равны. Из этого следует, что треугольники DEM и CFM
равны (см. задачу 543).
Углы АМЕ и ВАМ равны как накрест лежащие углы, образован-
образованные при пересечении параллельных прямых АВ и EF секущей AM.
Следовательно, в треугольнике АЕМ углы А и М равны, а значит,
АЕ = ЕМ. По аналогичной причине BF = FM. Имеем:
CD = DM + МС = FM + ЕМ = BF + АЕ = ВС + AD,
поскольку отрезки CF и E^D равны.
892. Докажите, что площадь прямоугольной трапеции, описанной около
окружности, равна произведению ее оснований.
Решение. Радиус окружности, вписанной в прямоугольную тра-
трапецию с основаниями а и Ъ, равен	 (см. задачу 725), а высота
трапеции равна диаметру этой окружности. Следовательно, площадь
трапеции равна
о аЪ а + Ъ ,
2 •	г • ——- = ао.
а + Ъ 2
893. Докажите, что в любом четырехугольнике,
вписанном в окружность, произведение диагоналей
равно сумме произведений противоположных сто-
сторон (теорема Птолемея).
Решение. Рассмотрим вписанный четы-
четырехугольник ABCD (рис.281) и на его диаго-
диагонали АС возьмем такую точку К, что ZABK =
= ZCBD. Треугольники АВК и DBC подоб-
подобны, поскольку углы АВК и CBD равны по по-
построению, а углы ВАС и BDC равны как впи-
вписанные углы, опирающиеся на одну и ту же
дугу ВС. Следовательно,
AB:BD = AK : CD,
Рис. 281

200
Гл. 4. Окружность
откуда
АВ • CD = АК • BD.
(*)
Треугольники ВСК и ABD также подобны, так как ZCBK =
= ZABD, а углы АСВ и ADB равны как вписанные углы, опирающи-
опирающиеся на одну и ту же дугу АВ. Поэтому
ВС :BD = KC : AD,
откуда
AD • ВС = КС • BD.
Сложив последнее равенство с равенством (*), получим:
АВ • CD + AD • ВС = BD(AK + КС) = BD • AC.
894. Докажите, что в любом треугольнике радиус R описанной окруж-
окружности, радиус г вписанной окружности и расстояние d между центрами этих
окружностей связаны равенством d2 = В2 — 2Rr (формула Эйлера).
Решение. Рассмотрим треугольник ABC, у которого точка О —
центр описанной окружности, а точка М — центр вписанной окружно-
окружности. Допустим сначала, что d ^ 0 (рис.282, а). Проведем через точку
М диаметр PQ описанной окружности, а также биссектрисы AM
и ВЫ углов А и В. По теореме о произведении отрезков пересекаю-
пересекающихся хорд
РМ • MQ = AM • МАХ
или
(Д-
¦d)(R-d) = AM -MAX.
Далее, поскольку АА\ и ВВ\ — биссектрисы углов А и В,
то ^ ВА\ =^ А\С и ^ СВ\ =^ В\А. Следовательно (см. задачу 718),
ВАХ+ - АВХ - А{С+ - СВХ
/_ВМАХ =
= ZMBA
Рис. 282

Задачи повышенной трудности	201
Это означает, что треугольник МА\В — равнобедренный. Поэтому
найденное нами соотношение можно переписать так:
(R + d)(R- d) = AM • ВАг.
Проведем теперь диаметр А\А2 описанной окружности. Пусть К —
точка касания вписанной окружности и стороны АВ. Прямоугольные
треугольники А\А^В и AM К имеют равные острые углы А и А^,
поэтому эти треугольники подобны. Следовательно,
МК : В Ах = AM : АХА2,
или
г : ВАх = AM : 2Д,
откуда AM - В Ах = 2Rr. Таким образом, наше соотношение принимает
вид:
(R-d)(R + d) = 2Rr,
d2 = R2 - 2Rr.
Если d = 0 (рис. 282, б), то каждая сторона треугольника ABC рав-
равна 2y/R? — г2 , а значит, этот треугольник — равносторонний. Поэтому
ABAC = 60°, /БАО = 30° и, следовательно, R = 2г, или 0 = R2 -
-2Rr.
895. Для неравностороннего треугольника ABC точка О является цен-
центром описанной окружности, Н — точка пересечения прямых, содержащих
высоты АА\, ВВ\, СС\, точки А%, В2, С^ — середины отрезков АН, ВН, СН,
а точки As, B3, С3 — середины сторон треугольника ABC. Докажите, что точ-
точки А\, В\, С\, Ач, В2, Сч, As, B3, С3 лежат на одной окружности (окружность
Эйлера).
Решение. Пусть точка М — середина
отрезка ОН, MN _L AC (рис.283). Посколь-
Поскольку прямые НВх, MN и ОВя, параллель-
параллельны, то по теореме Фалеса (см. задачу 385)
BxN = NB%. Поэтому прямоугольные тре-
треугольники BxMN и B^MN равны по двум
катетам, а значит, МВх = МВ%.
Пусть Б4 — точка, симметричная точке
Я относительно стороны АС. В треуголь-
треугольнике ОНВ4 отрезок МВх — средняя
линия, поэтому МВх = —^— • Но точка В\
лежит на окружности, описанной около	р 2qq
треугольника ABC (см. задачу 886).
Следовательно, отрезок МВх, а значит, и отрезок МВ$, равен —, где
R — радиус описанной окружности.

202
Гл. 4. Окружность
Отрезок МВ2, будучи средней линией треугольника ВОН, также
R т
равен —. Тем самым
МБ, =МВ9 = MB* = ^.
Аналогично доказывается, что
МАХ = МА2 = МА3 = | и
Это означает, что все точки: А\, В\, С\, А2, В2, С2, А%, Б3, С% —
Л,	R
лежат на одной окружности с центром М радиуса —.
896. Докажите, что основания перпендикуляров, проведенных из произ-
произвольной точки окружности, описанной около треугольника, к прямым, содер-
содержащим стороны этого треугольника, лежат на одной прямой (прямая Симпсо-
на).
Решение. Пусть D — произвольная точка окружности, описанной
около данного треугольника. Обозначим вершины треугольника буква-
буквами А, В и С, так, чтобы получился четырехугольник ABCD (рис.284).
В этом четырехугольнике А А + АС = 180°, поэтому либо А А = АС =
= 90°, и тогда прямой Симпсона будет прямая АС, либо один из этих
углов острый, а другой тупой. Для определенности будем считать,
что угол А острый. Рассмотрим два случая: 1) угол ACD, а значит,
и равный ему угол ABD острые; 2) указанные углы тупые (случай
прямых углов рассмотрите самостоятельно). В первом случае основа-
основание Н перпендикуляра, проведенного из точки D к прямой АВ, лежит
между А и В, основание К перпендикуляра к АС лежит между А и С,
а основание М перпендикуляра к ВС — вне отрезка ВС (рис.284, а).
Во втором случае все три основания перпендикуляров лежат вне сторон
треугольника ABC (рис. 284, б). Ход рассуждений в этих двух случаях
в основном один и тот же. Поэтому проведем доказательство для
D
Рис. 284

Задачи повышенной трудности
203
первого случая, отмечая в скобках те изменения, которые следует
внести в текст доказательства для второго случая.
Поскольку углы AHD и AKD прямые, то точки А, Н, К и D лежат
на окружности с диаметром AD (см. задачу 704, а). Следовательно,
углы АКН и ADH, вписанные в эту окружность и опирающиеся
на одну и ту же дугу АН, равны.
Углы CKD и CMD также прямые. Поэтому точки С, К, М
и D лежат на окружности с диаметром CD (см. задачу 704, а).
Следовательно, углы СКМ и CDM, вписанные в эту окружность
и опирающиеся на одну и ту же дугу СМ, равны (во втором случае
эти углы составляют в сумме 180°).
Но ZADH = 90° - ZBAD, a ZCDM = 90° - ZMCD = 90° -
- A80° - ZBCD) = 90° - ZBAD, поскольку ZBAD + ZBCD =180°.
Следовательно,
ZADH = ZCDM.
Итак, ZAKH = ZADH, ZCKM = ZCDM (во втором случае
ZCKM + ZCDM = 180°), ZADH = ZCDM. Поэтому ZAKH =
= ZCKM (во втором случае ZAKH + ZCKM = 180°). Это и означа-
означает, что точки Н, К и М лежат на одной прямой.
897. Постройте общую касательную к двум данным окружностям.
Решение. Рассмотрим две окружности с центрами О\ и 0%
радиусов ri и 7*2, каждая из которых лежит вне другой окружно-
окружности (рис.285). Если 7*1 = 7*2 (рис.285, а), то решение задачи очевидно.
В
О ) \О2
а
Пусть, например, г\ > 7*2. Если центры окружностей лежат по одну
сторону от общей касательной, то касательная называется внешней,
а если по разные стороны — внутренней.
Построим сначала внешнюю касательную. Проведем окружность
с центром О\ радиуса г\ — т^ и построим к ней касательную
О^М (рис.285, б) так, как это описано в решении задачи 673.
По свойству касательной О\М А. О^М. Проведем теперь через
точку М радиус О\А, а также радиус О^В _1_ О^М. Прямая
АВ — искомая касательная. В самом деле, в четырехугольнике
МАВО2 противоположные стороны МА и О^В равны по построению
и параллельны, так как обе перпендикулярны к прямой О^М.
Поэтому этот четырехугольник — параллелограмм. Поскольку угол

204
Гл. 4. Окружность
0% этого параллелограмма прямой, то и остальные его углы прямые.
Следовательно, прямая АВ — касательная к обеим окружностям.
Для построения внутренней касательной следует сначала провести
окружность с центром О\ радиуса г\ +Г2, а затем выполнить построе-
построение, аналогичное описанному (рис.285, в).
Замечание. Мы рассмотрели случай, когда каждая из данных
окружностей лежит вне другой. В этом случае окружности имеют
четыре общих касательных, две из которых внешние, а две другие —
внутренние (рис.286, а). Ясно, что если одна из окружностей целиком
Рис. 286
лежит внутри другой, то общих касательных у них нет (рис.286, б).
Если окружности имеют единственную общую точку, то общих каса-
касательных три (рис.286, в) или одна (рис.286, г). Наконец, если окруж-
окружности имеют две общие точки, то общих касательных две (рис.286, д).
В каждом из этих случаев общие касательные могут быть построены
одним из двух указанных методов. Впрочем, в ряде случаев касатель-
касательную можно построить и проще — подумайте, как это сделать.
898. Даны окружность с центром О, точка М и отрезки P\Q\ и
Постройте прямую р так, чтобы окружность отсекала на ней хорду, равную
P\Q\, и расстояние от точки М до прямой р равнялось P^Qi-
Решение. Отметим произвольную точку А данной окружности
и построим хорду АВ = P\Q\ (рис.287). Найдем середину С этой
хорды и проведем окружность с центром О радиуса ОС, а также
окружность с центром М радиуса P^Qi- Теперь построим общую каса-
касательную р к проведенным окружностям (см. задачу 897). Прямая р —
искомая. В самом деле, расстояние от точки М до прямой р равно P2Q2
по построению, а длина хорды DE, отсекаемой данной окружностью
на прямой р, равна
2л/О?>2 - ОС2 = 2л/ОА2 - ОС2 = АВ = Р}
\Ч\-

Задачи повышенной трудности
205
Рис. 287
899. Внутри окружности дана точка. Постройте хорду, проходящую через
эту точку так, чтобы она была наименьшей из всех хорд, проходящих через
эту точку.
Решение. Пусть М — данная точка, АВ — хорда, проходящая
через эту точку. Для удобства введем обозначения: AM = x, MB = у.
Из теоремы о произведении отрезков пересекающихся хорд следует,
что для всех хорд окружности, проходящих через точку М, величина
ху = с одна и та же. Из этого равенства находим: у = -. С другой
стороны,	х
АВ =
с
X
Эта величина принимает наименьшее значение
тогда, когда ( Jx — ^L ) = 0, т. е. тогда, когда
V	^)
х = -=у.
Итак, стоящая перед нами задача состоит
в том, чтобы построить хорду АВ с серединой М.
Чтобы решить эту задачу, достаточно провести
через точку М диаметр окружности (рис.288),
а затем через точку М провести хорду АВ, пер-
перпендикулярную к этому диаметру.
900. Постройте треугольник: а) по стороне, про-
противолежащему углу и высоте, проведенной к данной
стороне; б) по углу, высоте, проведенной из вершины
данного угла, и периметру.
Решение, а) На стороне данного угла с вер-
вершиной М возьмем какую-нибудь точку А и от-
отметим на другой его стороне точку В так, чтобы
отрезок АВ был равен данной стороне искомого
треугольника (рис.289). Опишем около треуголь-
треугольника АВМ окружность. Далее, проведем пря-
прямую, параллельную прямой АВ, находящуюся
Рис. 288
Рис. 289

206	Гл. 4. Окружность
от нее на расстоянии, равном данной высоте, и лежащую по ту же
сторону от прямой АВ, что и точка М. Пусть С — одна из общих
точек этой прямой и окружности. Треугольник ABC — искомый.
В самом деле, сторона АВ этого треугольника равна данной стороне
по построению; угол АСВ равен данному углу АМВ, так как эти углы
вписанные и опираются на одну и ту же дугу АВ; высота, проведенная
из вершины С, равна данной высоте по построению.
б) Проведем биссектрису данного угла а и построим угол 90° +
+ — (рис.290). Затем построим треугольник A{BB\, сторона А\В\
которого равна данному периметру, высота, проведенная из вершины
Б, равна данной высоте, а угол при вершине В равен построенному
углу (см. задачу 900, а). Наконец, проведем серединные перпендику-
перпендикуляры к отрезкам А\В и В\В (рис.291) и обозначим буквами А и С
точки их пересечения с прямой А\В\. Треугольник ABC — искомый.
В
В г
Рис. 290	Рис. 291
В самом деле, высота, проведенная из его вершины В, равна данной
высоте по построению. Далее, поскольку АА\ = АВ и СВ\ = СВ,
то периметр треугольника ABC равен данному периметру. Кроме того,
поскольку треугольники АА\В и СВ\В — равнобедренные, а углы А
и С треугольника ABC являются их внешними углами, то для угла В
этого треугольника находим:
2
откуда АВ = а.
901. Постройте треугольник, если дана описанная окружность и на ней
точки Н, В и М, через которые проходят прямые, содержащие высоту, биссек-
биссектрису и медиану треугольника, проведенные из одной вершины.
Решение. Пусть О — центр данной окружности. Через точку Н
проведем хорду РН, параллельную прямой О В (рис.292). Затем через
точку А пересечения прямых ОВ и РМ проведем хорду QR, перпен-
перпендикулярную к прямой ОВ. Треугольник PQR — искомый. В самом
деле, прямые РН и ОВ параллельны, поэтому РН _l_ QR, а значит,
прямая РН содержит высоту треугольника PQR. Далее, высота О А
равнобедренного треугольника OQR является медианой и биссектри-
биссектрисой. Следовательно, QA = AR, т. е. прямая РМ содержит медиану

Задачи повышенной трудности
207
РА треугольника PQR. Кроме того, из равенства углов AOQ и AOR
следует равенство дуг BQ и BR, а значит, и опирающихся на эти дуги
вписанных углов BPQ и BPR. Иными словами, прямая РВ содержит
биссектрису треугольника PQR.
902. Даны три точки, не лежащие на одной прямой. Постройте треуголь-
треугольник, для которого эти точки являются основаниями высот. Сколько решений
имеет задача?
Решение. Пусть А\, В\ и С\ — данные точки, Н — точ-
точка пересечения биссектрис треугольника АхВхСх. Построим сначала
остроугольный треугольник ABC, для которого отрезки ААх, ВВх
и Сбавляются высотами. Проведем через точки Ах, Вх и С\ прямые,
перпендикулярные соответственно к АхН, ВхН и СхН. Точки пересече-
пересечения этих прямых обозначим буквами А, В и С (рис.293). Треугольник
ABC — искомый. В самом деле, вершина А этого треугольника лежит
на прямой АхН (см. задачу 885), а значит, прямая ААх перпендику-
перпендикулярна к прямой ВС по построению. Иными словами, отрезок ААх —
высота треугольника ABC. Аналогично доказывается, что отрезки
ВВх и СС\ являются высотами этого треугольника. Осталось доказать,
что треугольник ABC — остроугольный. Докажем, например, что угол
А — острый. Имеем:
ZBxHCx = 180° - ZBl ZCl 10AO ZBl + /П'
= 180° -
Следовательно,
2
180°-
2
= 90'
= 180° -
>90°.
ZA = 360° - 90° - 90° - ZBXHCX < 90°.
Аналогично доказывается, что углы АхНСх и АхНВх — тупые,
а значит, углы В и С — острые.
Обратимся к рисунку 293. Нетрудно видеть, что в каждом из трех
тупоугольных треугольников АВН, ВСЕ. и АСЕ. точки Ах, Вх и С\
м в
Рис. 292

208
Гл. 4. Окружность
также являются основаниями высот. Таким образом, мы построили
четыре треугольника, удовлетворяющих условию задачи.
Имеет ли наша задача другие решения? Чтобы ответить на этот
вопрос, рассмотрим сначала остроугольный треугольник А2В2С2, для
которого точки А\, В\ и С\ являются основаниями высот (рис.294).
Пусть Н\ — точка пересечения высот этого треугольника. Тогда лу-
лучи А\Н\, В\Н\ и С\Н\ являются биссектрисами углов треугольника
А\В\С\ (см. задачу 849). Следовательно, точки Н\ и Н совпада-
совпадают, а значит, треугольник А2В2С2 совпадает с треугольником ABC.
Тем самым, других остроугольных треугольников, удовлетворяющих
условию задачи, нет. Рассмотрим теперь тупоугольный треугольник
А2В2Н\ с тупым углом Н\, для которого отрезки А2В\, В2А\ и Н\С\
являются высотами (рис.295). Пусть С2 — точка пересечения высот
этого треугольника. Поскольку треугольники А2В2В\ и В2А2А\ —
С,
Рис. 294
Рис. 295
^ — острые; угол
прямоугольные, то углы А^ и В^ треугольника
С<2 этого треугольника — также острый, поскольку
ZC2 = 180° -/А2-/Б2 =
= 180° - (90° - АА2В2НХ) - (90° - АВ2А2НХ) =
= ZA2B2HX + ZB2A2HX < 90°,
так как угол Н\ треугольника А2В2Н\ — тупой.
Таким образом, треугольник А2В2С2 — остроугольный, причем
точки А\, В\ и С\ — основания его высот. Значит, он совпадает
с треугольником ABC. Но тогда и треугольник А2В2Н\ совпадает
с треугольником ABB.. Следовательно, задача имеет четыре решения.
Ответ. Четыре решения.

Глава 5
ВЕКТОРЫ
§ 1. Понятие вектора
744.	Какие из следующих величин являются векторными: скорость, масса,
сила, время, температура, длина, площадь, работа?
Ответ. Из указанных в задаче векторными величинами являются
скорость и сила.
745.	В прямоугольнике ABCD АВ = 3 см, ВС = 4 см, М — середина
стороны АВ. Найдите длины векторов АВ, ВС, DC, MC, MA, CB, АС.
Решение. Так как АВ = 3 см, ВС = 4 см (рис.296), то \АВ\ =
= \DC\ = 3 см, \ВС\ = \СВ\ = 4 см.
\МС\ = VMB2 + ВС2 = д/1,52+42 см = л/ТД25 см.
\МА\ = ^ВА = 1,5 см, \АС\ = VAB2 + ВС2 = 5 см.
Ответ. 3 см, 4 см, 3 см, \ЛД25 см, 1,5 см, 4 см, 5 см.
746.	Основание AD прямоугольной трапеции ABCD с прямым углом А
равно 12 см, АВ = 5 см, ZD = 45°. Найдите длины векторов BD, CD и АС .
Решение. Пусть СН — высота данной трапеции ABCD
(рис.297).
BD\ = VAD2 + АВ2 = л/122 + 52 = 13 см.
В треугольнике CDH: СН = HD = 5 см, поэтому
\CD\ = VCH2 + HD2 = V25 + 25 =
см.
4 см
3 см
В
Рис. 296

210	Гл. 5. Векторы
Воспользуемся теоремой Пифагора для треугольника ABC:
\АС\ = VAB2 + BC2,
ВС = АН = AD - DH = 12 см - 5 см = 7 см,
поэтому
\АС\ = л/25 + 49 см = л/74 см.
Ответ. 13 см, 5л/2 см, л/74 см.
747. Выпишите пары коллинеарных векторов, которые определяются сто-
сторонами: а) параллелограмма MNPQ; б) трапеции ABCD с основаниями
AD и ВС; в) треугольника FGH. Укажите среди них пары сонаправленных
и противоположно направленных векторов.
Решение, a) MNPQ — данный параллелограмм (рис.298, а).
Коллинеарными являются векторы: MN и QP, MN и PQ, NM и PQ,
WM и QP, ~MQ и WP, ~MQ и Ш, QM и WP, QM и PAT.
Сонаправленные векторы: M7V Ц QP, 7VM Ц PQ, MQ Ц '
дм ttPiv.
Противоположно направленные векторы: MN || PQ, NM ||
мд II рлг, дм ц Wp.
б)	ABCD — данная трапеция (рис.298, б). Коллинеарными явля-
являются векторы: БС и AD, ~ВС и DA, СБ и DA, СБ и AD.
Сонаправленные векторы: ВС \\ AD, СВ \\ DA.
Противоположно направленные векторы: ВС \\ DA, СВ \\ AD.
в)	FGH — данный треугольник (рис.298, в). Коллинеарных векто-
векторов нет, а потому нет сонаправленных и противоположно направленных
векторов.
Ответ, а) Сонаправленные: M7V и QP, WM и ?q, lV[Q и Wp,
QM и PN; противоположно направленные: MN и PQ, NM и
AIQ и РЛГ, gM и 7VP; б) сонаправленные: ~ВС и AD, СБ и
противоположно направленные: БС и DA, СВ и АД в) коллинеарных
векторов нет.
ВС	G
A	D	F	Н
б	в
Рис. 298

§ 1. Понятие вектора	211
748.	В параллелограмме ABCD диагонали пересекаются в точке О. Равны
ли векторы: а) АВ и 1X7; б) ~ВС и DA; в) АО и ОС; г) АС и ~BD}
Ответ обоснуйте.
Решение. ABCD — данный параллелограмм (рис.299).
а)	Векторы АВ и DC равны, так как
\АВ\ = \DC\hAB]]DC;
б)	векторы ВС и DA не равны, так как
ВСЦ1ХА;
в)	векторы АО и ОС равны, так как
\АО\ = \ОС\ и АО]] ОС;
г)	векторы АС и BD не равны, так как они не коллинеарны.
Ответ, а) Да; б) нет; в) да; г) нет.
749.	Точки S и Т являются серединами боковых сторон MN и LK
равнобедренной трапеции MNLK. Равны ли векторы: a) NL и KL; б) MS
и SW; в) WN и WL; г) TS и Ю1?; д) Й и КГ?
Решение. MNKL — данная равнобедренная трапеция (рис.300),
точки S и Т — середины боковых сторон MN и LK.
а) Векторы NL и KL не коллинеарны, поэтому
б)	Векторы MS и SN равны, так как
\Ш\ = \SN\ и Ш ]] 57V.
в)	Векторы MN и KL не равны, так как они не коллинеарны.
г)	Векторы TS и КМ не равны, так как
\TS\^\KM\.
в	с
N
s/
У
L
V
A	D	ML
Рис. 299	Рис. 300

212	Гл. 5. Векторы
д) Векторы TL и КТ равны, так как
\TL\ = \КТ\ и TL^KT.
Ответ, а) Нет; б) да; в) нет; г) нет; д) да.
750.	Докажите, что если векторы АВ и CD равны, то середины отрезков
AD и ВС совпадают. Докажите обратное утверждение: если середины отрез-
отрезков AD и ВС совпадают, то АВ = CD.
Решение. Рассмотрим случай, когда векторы АВ и CD ненулевые
и АВ || CD.
Пусть АВ = CD. Тогда АВ Ц CD, поэтому точки В и D лежат
по одну сторону от прямой АС (рис.301). Так как АВ || CD, то точки
А и В лежат по одну сторону от прямой
CD, а точки С и D лежат по одну сторону
от прямой АВ. Отсюда следует, что ABDC —
четырехугольник. По условию АВ = CD
и АВ || CD, поэтому ABDC — параллело-
грамм A°, п.43). По свойству 2° п.43 диаго-
диагонали AD и ВС этого параллелограмма точкой
рис 301	О пересечения делятся пополам, следователь-
следовательно, середины отрезков AD и ВС совпадают.
Докажем обратное утверждение: пусть середины О отрезков AD
и ВС совпадают. Докажем, что АВ = CD. Точки В и D лежат по ту же
сторону от прямой АС, что и точка О.
Аналогично, точки С и D лежат по одну
сторону от прямой АВ, а точки АиВ —
по одну сторону от прямой CD. Отсюда
следует, что ABDC — четырехуголь-
четырехугольник. По свойству 3° п. 43 ABDC -
параллелограмм, поэтому АВ = CD.
Утверждение, сформулированное в
задаче, верно и в том случае, когда век-
векторы АВ и CD — нулевые, или ес-
Рис. 302	ли эти векторы лежат на одной пря-
прямой (рис.302, а, б, в).
751.	Определите вид четырехугольника ABCD, если: а) АВ = DC
и \АВ\ = |-ВС|; б) АВ Ц DC, а векторы AD и ВС не коллинеарны.
Решение, а) АВ = ГЮ (рис. 303, а), поэтому АВ || DC и АВ =
= DC. Следовательно, ABCD — параллелограмм. Так как \АВ\ =
= \ВС\, т. е. АВ = ВС, то ABCD - ромб.
А
В
А
А
/
В
С
о
о
в
1
с
D
С
D
D

§2. Сложение и вычитание векторов	213
А	В
а	б
Рис. 303
б) АВ Ц ВС, поэтому АВ \\ DC, т. е. ABCD — параллелограмм
или трапеция. По условию векторы AD и ВС не коллинеарны, поэтому
АВ\ВС (рис.303, б), т. е. ABCD - трапеция.
Ответ, а) Ромб; б) трапеция.
752.	Верно ли утверждение: а) если ~~а = Ъ , то ~~а ТТ b ; б) если "ё? =
= 6 , то ~а и 6 коллинеарны; в) если ~а = 6 , то "<? || Ь ; г) если "<? ТТ & ,
то "<? = Ь ; д) если "<?= 0 , то "о* ТТ 6?
Ответ, а) Верно; б) верно; в) неверно; г) неверно; д) верно.
§ 2. Сложение и вычитание векторов
753.	Турист прошел 20 км на восток из города А в город В, а потом
30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы
АВ и ~вб. Равны ли векторы АВ + БС и АС?
Ответ. Да.
754.	Начертите попарно неколлинеарные векторы ~х , ~if, ~z и постройте
векторы ~х + ~у , ~х + ~z , ~^ + ~у .
Решение. На рисунке 304

214
Гл. 5. Векторы
755. Начертите попарно неколлинеарные векторы ~а, Ъ , ~с, d, ~e и,
пользуясь правилом многоугольника, постройте вектор ~а + Ъ +~с + d +~e .
Решение. На рисунке 305
АВ = ~а +~b +~c +~d +~е.
756. Начертите попарно неколлинеарные векторы ~х , ~if, ~z и постройте
векторы ~х — ~у , ~^ — ~у , ~х — ~z , —lc, —^y, —~z.
Решение. На рисунке 306
Рис. 306
757. Начертите векторы ~х, ~у и ~z так, чтобы ~х
Постройте векторы ~х + V' ~У ~ ~% > ~% + ~^•
Решение. На рисунке 307
TI
z .
АВ =х

§ 2. Сложение и вычитание векторов
215
758. Начертите два ненулевых коллинеарных вектора ~а и & , l"^ ^ | & |.
Постройте векторы: а) ~а — Ь ; б) Ь — ~а\ в) — ~а + Ь . Выполните еще раз
построение для случая, когда \~а\ = \ b .
Решение. На рисунке 308, а: \~а
В
А	В	А	В
Рис. 308
а)	АВ = ~а - ~Ь; б) RA = ~Ь - ~а; в) RA = -~а + ~Ь .
759. Дав произвольный четырехугольник MNPQ. Докажите, что:
a) WN + NQ = WP + PQ; б) MTV + Wp = Mq + QP.
Решение, а) По правилу треугольника MTV + NQ = MQ
(рис. 309), МР + PQ = MQ. Следовательно, MTV + 7VQ = МР + PQ.
б)	Аналогично: МАГ + 7VP = ~МР (см. рис. 309), MQ + QP = ШР.
Следовательно,
MTV
760. Докажите, что для любых двух неколлинеарных векторов ~х и "^
справедливо неравенство |"x^ + VI < |"^| + IV •
Решение. Сложим векторы ~х и ~у по правилу треугольни-
треугольника (рис.310):
где АВ = ~х ,
АС = ~х
Так как векторы "а? и V не коллинеарны, то ABC — треугольник.
Согласно неравенству треугольника
АС < АВ + ВС.
N
М
Рис. 309
х +J С
Рис. 310

216
Гл. 5. Векторы
Но АС = \~х + ~у\, АВ =
l поэтому
761. Докажите, что если А, В, С и D — произвольные точки, то АВ
Решение. Пусть А, В, С, D — произвольные точки. По правилу
многоугольника
Но АА = 0 , следовательно,
762. Сторона равностороннего треугольника ABC равна а. Найдите:
а) |АВ + ВE\; б) |АВ + АС\; в) |АВ + ОВ|; г) \ВА - ВС\; д) \АВ - АС\.
Решение. По условию задачи АВ = ВС = С А = а.
а) Так как АВ + ВС = АС, то \АВ +
Рис. 311
б) АВ + АС = AD = 2А0, где О — середина
стороны ВС треугольника ABC (рис.311). По-
В	этому
\АВ + АС\=2\АО\=2- ^ф- = ал/3 .
в) Построим ромб ABDC и проведем его высоту СН (см. рис. 311).
Тогда АВ + С В = CD + С В = 2СН, поэтому
|ЛВ + СВ| =2\СН\ = 2--
r)RA-BC = CA, поэтому
\Ш1-ВС\ = \СА\ =а.
д) АВ - АС = СВ, поэтому
\АВ-АС\ = \СВ\ =а.
Ответ, а) а; б) ал/3; в) ал/3; г) а; д) а.

§ 2. Сложение и вычитание векторов
217
763. В треугольнике ABC: AB = 6, ВС = 8, АВ = 90°. Найдите:
а) \~ВА\ - \~ВС\ и \~ВА - ~ВС ; б) \АВ\ + \~ВС\ и |АВ + вб\; в) |IL4| + \~ВС\
и |яЗ + Ж?|; г) \АВ\ - \ВС и |АВ-БС|.
Решение. По условию задачи в данном треугольнике ABC: AB =
= 6, ВС = 8, /Б = 90° (рис. 312).
а)	|БА| - \ВС\ = В А - ВС = -2; БА -
- ВС = СА, поэтому \в1-ВС\ = \СА\ =
= л/36 + 64 = 10.
б)	|АВ| + \ВС\ = АВ +ВС =14; АВ +ВС =
= АС, поэтому |АВ + ВС\ = \АС\ = 10.
в)	\ВА\ + \ВС\ = ВА +ВС =14; RA + I3C =
= BD, \ВА + ВС\ = \BD\ = \АС\ = АС = 10.
г)	|АВ| - \ВС\ = АВ - ВС = -2; АВ -ВС = DC + CB = ~DB;
\АВ - ВС\ = \DB\ = \АС\ = 10.
Ответ, а) -2 и 10; б) 14 и 10; в) 14 и 10; г) -2 и 10.
Рис. 312
764. Пользуясь правилом многоугольника, упростите выражения:
а) (АВ + ВС- ~МС) + (MD - Ш5); б) (<?Б + АС + Ш5) - (Ж + Xl3).
= (АВ + ВС +
Решение, а) (АВ + ВС- МС) +
СМ) + (MZ) + DK) = IK.
б) (СВ + 1С + RD) - (Ж + ZD) = (АС + СБ + Б!))
КМ) = АД?.
Ответ, а) АК; б) AM.
765. Пусть X, Y и Z — произвольные точки. Докажите, что векторы
=XY + 25X + YZ, ~q = (XY - Yz) + YZ и У = (ZY - XY) - ~ZX
нулевые.
Решение. ^ = XY + IX + YZ = IX + XY + YZ = IZ = "о.
~q = (XY - ~XZ) +YZ = XY + YZ ^	~
~t = (ZY - XY) -~ZX = ZY + YX
766. На рисунке 313 (рис.259 учебника) изображены векторы ~а, Ь , ~~с,
d , XY. Представьте вектор XY в виде суммы остальных или им противопо-
противоположных векторов.

218	Гл. 5. Векторы
Решение. По правилу многоугольника име-
имеем:		> 	> 	> 	> 	>
XY = XA + AB + BC + CY.
С
'+ Так как
d	>	^
А
то		>	_^	_^
XY = -а + (- Ь ) + с + d.
Ответ. —7? + (— Ъ ) + "с" + d .
767.	Дан треугольник ABC. Выразите через векторы ~а = АВ и 6 = АС
вектор С В + БЛ
Решение. По правилу треугольника С В + Б А = СА, СА =—
—АС = — 6 , поэтому СБ + В А = — b .
Ответ. — Ъ .
768.	Точки М и 7V — середины сторон АВ и АС треугольника АБС.
Выразите векторы ВМ, NC, MN, BN через векторы ~~а = AM и 6 = A7V.
Решение. Точки М и N — середины сторон АВ и АС данного
треугольника ABC (рис. 314), ~а = AM и Ъ = AN; ВМ = МА = -~а;
NC = AN = Ъ ; MN = AN — AM = b — ~а. По правилу треугольника
= БМ + МЛГ = -~а + G - "а
Ответ. ?, 6, 6 — ?, — ~б? + ( 6 — ~а).
769. Отрезок ВВ\ — медиана треугольника ABC. Выразите векторы В\С,
ШЗ[, ВА, ~ВС через ~х = Ав[ и ~у = АВ.
Решение. ББ1 — медиана данного треугольника ABC (рис.315),
~х =АВ\, ~у =АВ.
В
У,
А I N	С	А '? ~Bi •
Рис. 314	Рис. 315

§2. Сложение и вычитание векторов	219
- АВ = -~х - ~у ,
RA = -АВ = -V; ВС = Шз\ + ?JC = (~х - У) + ~х .
Ответ. ~х , —~х — ~у , —if, (~х — V) + ~% •
770.	Дан параллелограмм ABCD. Выразите вектор АС через векторы ~а
и V, если: а) ~а = АВ, ~Ь = ~ВС; б) ~а = СВ, ~b = CD; в) ~а = АВ, ~Ь = Г>А.
Решение, а) "о" = АВ, ~t = BC, AC = AB+ I3C = ~а +~Ь .
б)	~а = СВ, Ъ = CD; по правилу параллелограмма С А = СВ +
+ CD = ~а + 6 , следовательно, АС = — СА = — (~а + Ь) = —~а — Ъ .
в)	~а = ЛВ, 6 = ?Ы; по правилу параллелограмма АС = ЛВ +
+ AD = АВ + (-dI) = ~a - V.
Ответ, а) АС = "^ + 7; б) АС = -~а - ~Ь ; в)АС = ~а-~Ь.
771.	В параллелограмме ABCD диагонали пересекаются в точке О.
Выразите через векторы ~а = АВ и Ь = AD следующие векторы: DC + СБ,
БО + ОС, № - ОС, ВА - 1>А.
Решение. \.DC + CB = llB = AB -AD, поэтому ~DC + CB =
= ~а -~b (рис.316).
2.	ВО + ОС = ВС = AD,
следовательно, ВО + ОС = Ъ .
3.	вб-ОС = вб^СО = вб^ОА = КА = -It.
Ответ. ~а — Ъ , Ь , —~а, —~а-\- Ь .
772. Дан параллелограмм ABCD. Докажите, что
Ya + хс = ~хв + Yd,
где X — произвольная точка плоскости.
Решение. По правилу вычитания векторов АВ = ХВ — ХА,
DC = ХС - XD. Так как АВ = DC (рис. 317), то ~ХВ - YA = ХС -
— XD. Отсюда следует, что

220
Гл. 5. Векторы
D
Рис. 316
773. Докажите, что для любых двух векторов ~х и ~у справедливо нера-
неравенство х — у
у |. В каком случае \х — у
у\
Решение. Пусть х = АВ, у = АС. Тогда
1с -^у =АВ-АС = СВ.
Возможны три случая.
а) Векторы ~х и ~у не коллинеарны (рис.318, а). Тогда ABC —
треугольник и по неравенству треугольника С В < АВ + АС. Но С В =
= \СВ\ = [х -
б) "а? ][
, АВ = \АВ\ =
~х - V|
. Ъ этом случае точка
, АС = \АС\ = |У|, поэтому
лежит на отрезке
ВС (рис. 318, б), поэтому ВС = В А + АС Но БС =
В А = \АВ\ = \1с\, АС = \АС\ = |У|, следовательно,
~х - ~у\ = [х\ + |V .
в) "а? ТТ V- Если хотя бы один из векторов ~х или
то ясно, что | х — у
= х
+ | У|. Если
то СВ < АС + АВ, поэтому
у
/ — нулевой,
(рис.318, в),
Итак, |"^ — VI ^ 1^1 +jV|5 в случаях, когда ~х || V или когда
хотя бы один из векторов х и V ~~ нулевой, |"^ — Vl = l^l + lVl-
Ответ. Равенство имеет место при ~х ][ V или в случае, когда
хотя бы один из векторов ~х и V ~~ нулевой.
В
б
Рис. 318
А У С J В
А х В У С

§ 3. Умножение вектора на число
221
Рис. 319
774. Парашютист спускался на землю со ско-
скоростью 3 м/с. Порывом ветра его начинает отно-
относить в сторону со скоростью Зл/З м/с. Под каким
углом к вертикали спускается парашютист?
Решение. Пусть АВ — вектор скорости
парашютиста до порыва ветра, АС — вектор
скорости ветра (рис.319), тогда \АВ\ = 3 м/с,
\АС\ = Зл/З м/с, a AD — вектор скорости
парашютиста при ветре. Так как ZBAC = 90°, то ABDC — прямо-
прямоугольник, а треугольник ABD — прямоугольный, BD = АС =
По теореме Пифагора
AD =
Отсюда следует, что ZADB = 30° и а = ZBAD = 60°.
Ответ. 60°.
§ 3. Умножение вектора на число
779. Дан вектор ~р = 3~а, где ~а ф 0 . Укажите, как направлен каждый
из векторов ~а, —~а, -~а, —2~а, 6~а по отношению к вектору ~р, и выразите
их длины через \~р .
Решение. По условию задачи ~р = 3~а . Так как 3 > 0, то ~р Ц ~а.
Далее, |^?| = |3| \~а\, откуда \~S
Аналогично получаем:
— а
1-> п -^ ,1^
= \а
'' 2
-Та Т| р", | -2"а| =2|"а
=6|~а*| = 2|
Ответ. Направления: Ц, ||, |Г,||, ТТ; длины: -1^1, t
о	о
о
780. Докажите, что для любого вектора ~а справедливы равенства:
а) 1 • ~а = ~а; б) (—1) • 7? = — ~а\

222
Гл. 5. Векторы
Решение, а) По определению 11 • 7?| =
> 0, то 1 • 7? Ц ~а . Таким образом,
1 • 7? = ~а.
~а\. Так как 1 >
б) Пусть (— 1) • 7? = ~р . По определению произведения вектора
на число р | =
а | = 1 • | а
= а
. Так как — 1 < 0, то
(—1) • 7?| || 7? при 7? ф О, т. е. ~р \\ ~а . Таким образом, в этом случае
~р = — 7?, т. е. (— 1) • 7? = — ~а. Если же ~а = 0 , то ~р = 0 , поэтому
и в этом случае
( 1) ~	~
(— 1) • а = — а .
781. Пусть ~х = т + 7?, ~у = т — 7?. Выразите через т и 7? векторы:
а) 2~я? — 2V; б) 2~я? + -V; в) —~х — -~у .
2	3
Решение. По условию ~х = га + 7?, 7? = га — 7?. Поэтому:
а)	2"^ - 27? = 2(~ж - V) = 2((га + 7?) - (га - 7?)) = 2B7?) = 47?.
б)	2"^ + ^у = 2(га + 7?) + ^(га - 7?) = 2га + 27? + ^га - ^7? =
в)	-1с - -~у = -{т + 1г) - -(т - ~п) = -т - 1г - -т + -п =
О	О	ОО
Ответ, а) 47?; б) -га + -7?; в) —-га — -7?.
А	А	о	о
В ^
Е	D
Рис. 320
782. В параллелограмме ABCD точка Е —
л середина стороны AD, точка G — середина стороны
ВС. Выразите векторы ЕС и AG через векторы
DC = ~а и СВ = ~Ь.
Решение. На рисунке 320 изображен дан-
данный параллелограмм. Точка Е — середина сто-
стороны AD, а точка G — середина стороны ВС,
DC = ~a, * ~*
ЕС =
~DC, ~ED = -AD = -ВС = ~~Ь, Г>С = ~а, поэтому
ЕС = а - ^ Ъ .
AG = АВ + BG =
KD = ~a - I
Ответ. ~~а — - b , 7? — - b .

§ 3. Умножение вектора на число
223
783. Точка М лежит на стороне ВС параллелограмма ABCD, причем
ВМ : МС = 3:1. Выразите векторы AM и MD через векторы ~а = AD
и 7 = АВ.
Решение. На рисунке 321 изображен данный параллелограмм.
AM = АВ + БМ; БМ = -ВС = -AD = -~a, AM = ~Ь + -"а .
4	4	4	4
1 	>•
	ВС ~\~
4
—> 1 —>
CJD —	AD ~\~
4
—>• 1	.
БА = - а
4
—>•
— Ъ .
—у 3	 1
Ответ. Ь + - а , -а —
4 4
784. В параллелограмме ABCD диагонали пересекаются в точке О,
а М — точка на стороне AD такая, что AM = -MD. Выразите через векторы
~х = AD и If =АВ следующие векторы: а) АС, АО, СО, 1Ю, AD + Ш5,
d,CO + OA;6) AM, Шс, ~ВМ, ОМ.
Решение. На рисунке 322 изображен данный параллелограмм.
У)-
-ad) = \Су - ^).
= -DO = 1-{~х - "у
= СА= -АС = -~х - ~у.
б) АМ= \~	\
о
~ВМ = RA + AM = -АВ + AM =\~x - У.
о
д , , м с
Рис. 322

224
Гл. 5. Векторы
ОМ = ОА + АМ = -^(
Ответ, а) ~х -\-~у , о(~^
6	2У'
- У)> -х-у; б)-х,-х + у,-х-у,--х--у.
785. Точки М и N — середины диагоналей АС и BD четырехугольника
ABCD. Докажите, что МЫ = -{AD + CJB).
Решение. На рисунке 323 изображен данный четырехугольник
ABCD, M и N — середины диагоналей АС и BD. По правилу
многоугольника сложения векторов имеем:
МЛГ = ~МА + AD + DAT, MTV = МС + СБ + Ж/V.
Складывая эти равенства почленно и учитывая, что МА + МС =
= 0 , ?W + БАГ = 0 , получаем:
2МЛГ = AD + CB, или
786. Отрезки AAi, ВВ\ и CCi — медианы треугольника ABC. Выразите
векторы АА\, ВВ\, СС\ через векторы ~а = АС и 6 = АВ.
Решение. Воспользуемся задачей 1 п. 84. Точка А\ — середина
отрезка ВС (рис.324), поэтому АА\ = -{~а + Ъ ). Аналогично,
= 1(^ - V - t) = i о" -
Ответ. ^
b), -~a — b , — ~
- b .
Рис. 323
Рис. 324

Применение векторов к решению задач	225
787. Точка О — середина медианы EG треугольника DEF. Выразите
вектор DO через векторы ~а = ED и Ь = ЕЕ.
Решение. Согласно задаче 1 п. 84 EG = -(~а + Ь) (рис.325),
поэтому ЁО = ^Ш = U~a + ~Ь);
Ответ, -о — - а .
4	4
Применение векторов к решению задач
789. На сторонах треугольника ABC построены параллелограммы
АВВ\А2, ВСС\В2, АСС2А\. Докажите, что существует треугольник, стороны
которого соответственно параллельны и равны отрезкам А\А2, В\В2, С\С2.
Решение. На рисунке 326 изображена данная фигура. По правилу
вычитания векторов имеем:
А\Аъ = АА2 — АА\,
В\?J = B±J2 — ВВ\,
С\ С2 = CC2 — СС\.
Складывая почленно эти равенства и учитывая, что ВВ\ = АА2,
СС\ = КВ1, AAl = СС?2, получаем:
А{А2 + ВХВ2 + С\С2 = АЛ2 - АА\ + ВВ2 ~ ВВ\ + ССч - Сс\ = 0 .
Таким образом, если мы построим сумму векторов А\А2 -\- В\В2 +
+ С1С2 по правилу многоугольника, то получим треугольник 0.
790. Докажите, что отрезок, соединяющий середины диагоналей трапе-
трапеции, параллелен ее основаниям и равен полуразности оснований.
Решение. Пусть ABCD — данная трапеция с основаниями AD
и ВС, где AD > ВС, а М и N — середины диагоналей АС и BD.
Согласно задаче 785
х) Отметим, что если отрезки А\А2, В\В2 и С\С2 параллельны друг другу,
то треугольник получится «вырожденным»: все его вершины будут лежать
на одной прямой.
8 Л. С. Атанасян и др.

226
Гл. 5. Векторы
Так как AD и СВ — коллинеарные векторы, то вектор MN колли-
неарен этим векторам, поэтому MN || AD и MN || СВ.
Докажем второе утверждение.
AD Ц СВ и AD > ВС,
поэтому \AD + CB\ = \AD\ — \СВ\. Следовательно,
\MN\ = l-\AD
- \СВ\),
или MN = ±(AD-CB).
М
N
791. Докажите, что отрезки, соединяющие середины противоположных
сторон произвольного четырехугольника, точкой пересечения делятся пополам.
Решение. Пусть М, N, Р и Q —
середины сторон данного четырехугольника
ABCD, а Е и F — середины отрезков МР
и NQ (рис.327). Докажем, что точки Е и F
совпадают.
Согласно задаче 1 п. 84 ОМ = -(ОА +
D
Рис. 327
+ ОВ), ОР = ^(ОС + OD), ОЕ = ±(
+ ОР) где О — произвольная точка плоско-
плоскости. Таким образом,
ОЕ=^
Аналогично получаем:
ОВ + ОС + OD).
OF = ±
ОВ + ОС + OD),

Средняя линия трапеции	227
поэтому ОЕ = OF. Отсюда следует, что точки Е и F совпадают, т. е.
отрезки МР и NQ пересекаются и каждый из них точкой пересечения
делится пополам.
792. Докажите теорему о средней линии треугольника.
Решение. Пусть ABC — данный треугольник, a MN — его
средняя линия (рис.328).
Ш\Г = AN- AM = ^АС - ^АВ = ^(АС - АВ) = ^
Отсюда следует, что
MN || ВС и |МЛГ| = \\ВС\, т. е. MN = 1-ВС.
Средняя линия трапеции
793.	Боковые стороны трапеции равны 13 см и 15 см, а периметр равен
48 см. Найдите среднюю линию трапеции.
Решение. Сумма оснований данной трапеции равна 48 см — A3 +
+ 15) см = 20 см, поэтому ее средняя линия равна 20 см : 2 = 10 см.
Ответ. 10 см.
794.	Сторона АВ треугольника ABC разделена на четыре равные части
и через точки деления проведены прямые, параллельные стороне ВС. Стороны
АВ и АС треугольника отсекают на этих параллельных прямых три отрезка,
наименьший из которых равен 3,4. Найдите два других отрезка.
Решение. Пусть С\, С^, Сз — точки на стороне АВ треугольника
ABC, которые делят эту сторону на четыре равные отрезка: АС\ =
= C\C<i = С2С3 = С$В, а С\В\, С2В2 и СзДз — прямые, параллельные
стороне ВС, причем точки В\, В^ и В?, лежат на стороне АС (рис. 329).
По условию задачи В\С\ = 3,4.
N
Рис. 328	Рис. 329
Отрезок В\С\ — средняя линия треугольника АВ2С2, поэтому
В2С2 = 2 • В\С\ = 6,8. Далее, отрезок В2С2 — средняя линия треуголь-
треугольника ABC, поэтому ВС = 2 • В2С2 = 13,6. Отрезок Д3С3 — средняя
линия трапеции ВСВ2С\ поэтому Д3С3 = ^(^2^2 + ВС) = 10,2.
Ответ. 6,8 и 10,2.

228	Гл. 5. Векторы
795. Найдите диаметр окружности, если его
концы удалены от некоторой касательной на 18 см
и 12 см.
Решение. Пусть CD — диаметр данной
окружности с центром О (рис.ЗЗО). Проведем
перпендикуляры СС\, DD\ и ОН к касательной.
Четырехугольник CDD\C\ — трапеция с осно-
основаниями СС\ и DD\. Так как ОН || СС\ и ОС =
рис ззо	= ^^' то С\Н = HD\, поэтому ОН — средняя
линия этой трапеции.
Так как по условию СС\ = 12 см, DD\ = 18 см, то ОН = -(СС\ +
+ DD\) = 15 см. Отрезок ОН — радиус окружности, поэтому CD =
= 30 см.
Ответ. 30 см.
796. Из концов диаметра CD данной окружности проведены перпенди-
перпендикуляры СС\ и DD\ к касательной, не перпендикулярной к диаметру CD.
Найдите DDU если СС\ = 11 см, CD = 27 см.
Решение. Так как СС\ JL C\D\ и DD\ JL CXDX, то СС\ \\ DDX
(см. рис.ЗЗО), поэтому CC\D\D — трапеция. Пусть ОН — отрезок,
соединяющий центр О окружности с точкой Н касания. Тогда ОН —
средняя линия трапеции CC\D\D (см. решение задачи 795) и ОН —
радиус окружности, т. е. ОН = -CD = 13,5 см. Так как ОН =
= \{ССХ + DDi), то DDX = 2 • ОН - ССХ = 27 см - 11 см = 16 см.
Ответ. 16 см.
797. Докажите, что средняя линия трапеции проходит через середины
диагоналей.
Решение. Пусть MN — средняя линия трапеции ABCD с основа-
основаниями AD и ВС, а Е и F — середины диагоналей АС и BD (рис. 331).
Так как ME — средняя линия треугольника ABC, то ME || ВС.
Но MN || ВС, поэтому прямые MN и ME совпадают, т. е. Е —
точка отрезка MN. Аналогично доказывается, что F — точка того же
отрезка.
798. Боковая сторона равнобедренной трапеции равна 48 см, а средняя
линия делится диагональю на два отрезка, равных 11 см и 35 см. Найдите
углы трапеции.
Решение. Пусть MN — средняя линия трапеции ABCD с осно-
основаниями AD и ВС, К — точка пересечения диагонали АС с отрезком
MN, МК = 11 см, KN = 35 см (рис. 332). Согласно задаче 797 точка

Дополнительные задачи
229
К — середина отрезка АС, т. е. МК — средняя линия треугольника
ABC, а значит, МК = ^ВС. Аналогично, KN = ^AD. Отсюда имеем:
ВС = 2 • МК = 22 см, AD = 2 • KN = 70 см.
Таким образом, стороны трапеции ABCD равны: АВ = CD =
= 48 см, ВС = 22 см, AD = 70 см. Пусть ВВХ и ССХ - высоты трапе-
трапеции (см. рис.332). Тогда в треугольнике АВВ\ имеем: АВ\ = ^(AD —
- ВС) = 24 см, АВ = 48 см. Отсюда следует, что ZABB{ = 30°,
поэтому ZBAD = 60°. Так как трапеция равнобедренная, то ZCDA =
= 60° и, следовательно, ZABC = ZDCB = 120°.
Ответ. 60°, 120°, 120°, 60°.
799. Дана равнобедренная трапеция ABCD. Перпендикуляр, проведенный
из вершины В к большему основанию AD, делит это основание на два отрезка,
больший из которых равен 7 см. Найдите среднюю линию трапеции.
Решение. Пусть MN — средняя линия трапеции ABCD, BB\ —
перпендикуляр, проведенный к прямой AD (см. рис.332). По условию
BXD = 7 см.
MN = l-(AD + ВС) = \(АВХ + ВхСх + CXD + ВС).
Так как АВ\ = CXD, ВС = ВХСХ, то
MN = 1B • CXD + 2 • ВХС{) = CXD + ВХСХ = BXD = 7 см.
Ответ. 7 см.
Дополнительные задачи
800. Докажите, что если векторы т и ~п сонаправлены, то \т +
= т\ + |Т?|, а если т и ~п противоположно направлены, причем \т\ \
то|?п+п| = |?п| — | п .
Решение. Если хотя бы один из данных векторов нулевой,
то утверждение задачи очевидно. Поэтому рассмотрим случай, ко-
В
Рис. 331

230
Гл. 5. Векторы
С
С п В
В
Рис. 333
гда Й/ 0 и г?/ 0. Пусть га = АВ, ~п = ВС, тогда га + 7? =
= АС (рис.333).
Если га Ц 7?, то точка В лежит на отрезке АС, поэтому АВ +
+ ВС = АС (рис. 333, а). Но |га
следовательно, |га + ~п>| = |га| + |~
Пусть теперь га || "г? и |га|
= ВС,
\m
= AC,
|. Если |га| > |Т?|, то точка С
лежит на отрезке АВ (рис.333, б). В этом случае АВ = АС + СВ,
или
(р, )
— ВС, т. е. |га + Т?| = |га
. Если же |га| =
то точки А и С совпадают (рис.333, в), поэтому АВ = ВС и вектор
(р
га + ~п нулевой, а значит, |га +
? = |га| — \~п\
=0. Поэтому и в этом случае |га +
801. Докажите, что для любых двух векторов ~х и ~у справедливы
неравенства
х -
У
У
У\
Решение. Если хотя бы один из векторов ~х или ~у нулевой,
то утверждение задачи очевидно. Поэтому рассмотрим случай, когда
~х т^ 0 и ~у т^ 0 . Пусть АВ = ^, ВС = "^, тогда |^| = АВ, [7у\ =
= ВС, |~а? + Vl = ^^- Возможны три случая.
1. Векторы ~х и V не коллинеарны. В этом случае точки А, В
и С не лежат на одной прямой и являются вершинами некоторого
треугольника. По неравенству треугольника
АС <АВ + ВС, АВ <АС + ВС, т. е. АС > АВ - ВС.
Из первого неравенства следует, что |~а? +
<
+
него, что | х + у > | х
у |. Итак, в этом случае
х\- У\<
У\<
12/
2. ~х ТТ V- Согласно задаче 800 \~х
что
<
— | # +
х
> следовательно,
3. "а? || V- Согласно задаче 800 \~х +
V ^ V ^ V
а из послед-
последОчевидно,
Но \1с
+ |VI >
— I у = I x + у \, следовательно,
V| = \~x + Vl < 1^1

Дополнительные задачи	231
802. На стороне ВС треугольника ABC отмечена
точка N так, что BN — 2NC. Выразите вектор AN через
векторы ~~а = В А и Ъ = ВС.
Решение. Данный треугольник ABC изобра-
изображен на рисунке 334:
AN = BN - ВА = \~ВС -ВА=1~Ь -~а.	Рис- 334
о	о
Ответ. - b —~a.
о
803. На сторонах MN и NP треугольника MNP отмечены соответствен-
соответственно точки X и Y так, что	= - и —— = -. Выразите векторы XY и МР
через ~а = ШЛ и V = 7VP .
	> 2	> 2^ 	^ 3	>
Решение. По условию задачи NX = -NM = - а , ЛГУ = -7VP =
0	0	О
= |7 (рис.335).
О
Поэтому ХУ = ЛГУ-ЛГХ = ^- |"^. Далее,
о	о
МР = WP- W ~
3^ 2^ ^ -^.
Ответ. -6—-а, Ь — а .
о	о
На стороне AD отмечена точка К такая, что АК = —AD. Выразите векторы
о
804. В трапеции ABCD основание AD в три раза больше основания ВС.
стороне AD отмечена точка К такая, что
СК, ~KD и ~ВС через векторы ~а = ВА и V =
Решение. Так как ^
грамм (рис.336). Поэтому
Решение. Так как АК = -AD = БС, то ABC К — параллело-
о
СК = ВА = ~а,
= CD-CK = ~b -
BC=l-KD=l-(b-7t
Ответ. ~а, Ь -~а, -(Ь —~а).

232	Гл. 5. Векторы
805. Три точки А, В и С расположены так, что ВС = -цАВ. Докажите,
что для любой точки О справедливо равенство
ОВ = -ОА+ -ОС.
Решение. По правилу треугольника ОВ = ОА + АВ (рис.337).
Но АВ = \~АС = \{ОС - ОА), поэтому
о	о
ОВ = ОА + |(ОС -ОА) = ^ОА + |^
806. Точка С делит отрезок АВ в отношении т : п, считая от точки А.
Докажите, что для любой точки О справедливо равенство
0ё0А+0В.
т + п	т-\-п
Решение. По условию задачи АС : С В = —, или АС = — СВ.
п	п
Но АС = ОС- ОА,СВ = ОВ- ОС, поэтому
ОС-ОА=-(ОВ-ОС).
п
Отсюда получаем:
п	п
или		^		^
т + п ^7ч п ' О А + т • ОВ
ОС =
п	п
откуда
ОС = —?— ОА + -^— ОВ.
т + п	т + п
807. Пусть АА\, ВВ\ и СС\ — медианы треугольника ABC, а О
произвольная точка. Докажите, что
ОА + ОВ + ОС = ОАх + ОВ[ + ОС\.
в г.	ев
м1-	^р	к	"	о
Рис. 335	Рис. 336	Рис. 337

Дополнительные задачи	233
Решение. Согласно задаче 1 п. 84
~ОАХ = ^(ОВ + ОС),
0С\ = ^(ОА + ОВ).
Сложив эти равенства, получим искомое равенство.
808* Точки А и С — середины противополож-
противоположных сторон произвольного четырехугольника, а точ-
точки В и D — середины двух других его сторон.
Докажите, что для любой точки О выполняется
равенство
ОА + ОС = OB + OD.
Решение. Пусть MNPQ — данный че-
четырехугольник, а А, В, С и D — соот-	Рис. 338
ветственно середины сторон MN, NP, PQ,
QM (рис.338).
Согласно задаче 1 п. 84
поэтому
ОА + ОС = ^(ОМ + ON + ОР + OQ).
Аналогично,
OB + OD = -(ОМ + ON + OP + OQ),
следовательно,
809. В прямоугольной трапеции один из углов равен 120°. Найдите
ее среднюю линию, если меньшая диагональ и большая боковая сторона
трапеции равны а.
Решение. Пусть ABCD — данная трапеция, ZA = 90°, ZBCD =
= 120°, MN - средняя линия и АС = CD (рис.339). Тогда ZD =
= 60°. Треугольник ACD равнобедренный, следовательно, ZCAD =
= 60°, ZACD = 60°, поэтому АС = CD = AD = a.

234	Гл. 5. Векторы
Далее, ABAC = 90° - 60° = 30°, поэтому
ВС = \АС = \а.
Таким образом,
MN = l-(AD + ВС) = \ (а + 1<х) = \а.
Ответ, -а.
4
810. Докажите, что вершина угла, образованного биссектрисами двух
углов трапеции, прилежащих к боковой стороне, лежит на прямой, содержащей
среднюю линию трапеции.
Решение. Пусть MN — средняя линия данной трапеции ABCD
с основаниями AD и ВС, а О — точка пересечения биссектрис углов
Аи В (рис.340).
Согласно первой теореме п.72 точка О равноудалена от прямых
ВС и АВ, а также от прямых AD и АВ, поэтому она равноудалена
от параллельных прямых AD и ВС. Через точку О проведем прямую
d, параллельную прямым AD и ВС. Прямая d равноудалена от прямых
ВС и AD, поэтому середины М и N боковых сторон трапеции ABCD
лежат на этой прямой (задача 282). Таким образом, прямая d содержит
среднюю линию MN трапеции, т. е. точка О лежит на прямой MN.
Задачи повышенной трудности
904. Даны четырехугольник MNPQ и точка О. Что представляет собой
данный четырехугольник, если
Реш
В
М
А
ение. Так
С
/
ON-O1
как
0N-
а ОР-
то А
V
\
D
\d = OP-
0М = М1
-OQ = Q-
In = qp.
м
А *
OQl
В С
А \..
Рис. 339	Рис. 340

Задачи повышенной трудности	235
Таким образом, в четырехугольнике MNPQ стороны MN и PQ па-
параллельны и равны, поэтому MNPQ — параллелограмм (см. 1° п. 43).
Ответ. Параллелограмм.
905. Даны четырехугольник ABCD и точка О. Точки Е, F, G и Н
симметричны точке О относительно соответственно середин сторон АВ, ВС,
CD и DA. Что представляет собой четырехугольник EFGH?
Решение. Пусть Е\ — середина стороны АВ четырехугольника
ABCD. Согласно задаче 1 п. 84
поэтому
ОЕ = ОА + ОВ.
Аналогично получаем:
следовательно,
Аналогично,
OG = OC + OD, ОН =
следовательно,
HG = OG-OH = OC^OD-OD-OA =
Таким образом, ЕЕ = HG.
Отсюда следует, что в четырехугольнике EFGH стороны
ЕЕ и GH параллельны и равны, поэтому EFGH — параллело-
параллелограмм (см. 1° п. 43).
Ответ. Параллелограмм.
АВ АС
906. Дан треугольник ABC. Докажите, что вектор ) + ) направ-
\АВ\ \АС\
АВ АС
лен вдоль биссектрисы угла А, а вектор -^=г	^=р — вдоль биссектрисы
\АВ\ \АС\
внешнего угла при вершине А.
	у д^ 	у ~АС 	>
Решение. Рассмотрим векторы АВ\ = > , АС\ = , . AM =
\АВ\	\АС\
= АВ\ + ACi (рис. 341). По правилу параллелограмма сложения векто-
векторов четырехугольник АС\МВ\ — параллелограмм, а так как векторы

236
Гл. 5. Векторы
В
Рис. 341
АВ\ и АС\ — единичные, то
АС\МВ\ — ромб. Из равенства
AM = АВ\ + АС\ следует, что век-
вектор AM направлен вдоль диагонали
этого ромба. Отсюда, учитывая, что
Ав\ |t АВ, АС[ |t AC, мы заключа-
заключаем, что вектор AM направлен вдоль
биссектрисы угла ВАС.
Вектор С\В\ = АВ\ — АС\ направлен вдоль другой диагонали ром-
ромба (см. рис.341). Так как диагонали ромба взаимно перпендикулярны,
то вектор АВ\ — АС\ направлен вдоль биссектрисы внешнего угла при
вершине А треугольника ABC.
907. Докажите следующее утверждение: три точки А, В и С лежат
на одной прямой тогда и только тогда, когда существуют числа к, I и т,
не равные одновременно нулю, такие, что к + I + т = 0 и для произвольной
точки О выполняется равенство
ЮА + ЮВ + тОС = ~0 .
Решение. Предположим, что точки А, В и С лежат на одной
прямой. Тогда векторы АВ и АС коллинеарны, т. е. существует число
п такое, что АВ = пАС, или ОВ — О А = п(ОС — О А). Отсюда имеем:
(п- 1)ОА+ 1 -ОВ-пОС = ~0. Пусть к = п-\,1=\,т = -п. Тогда
Н1 + ш = 0и WA + ЮВ + тОС = ~0 .
Обратно, пусть существуют числа к, I, т такие, что к + / + т = О,
хотя бы одно из них не равно нулю, например к ^ 0, и
ЮА + ЮВ + тОС = 0 .
Тогда т = —{к -\-1) и равенство A) можно записать так:
ЮА + ЮВ - (к + 1)ОС = "О ,
ИЛИ		у		у		у		у	_>.
к(ОА - ОС) + 1(ОВ -ОС)= 0 .
Но О4 - ОС = сЗ, ОБ - ОС = СВ, поэтому
к СА	~
откуда
~СА = -
гь
A)

Задачи повышенной трудности
237
Таким образом, векторы С А и СВ коллинеарны, и, следовательно,
точки А, В и С лежат на одной прямой.
908. Используя векторы, докажите, что середины диагоналей четырех-
четырехугольника и точка пересечения отрезков, соединяющих середины противопо-
противоположных сторон, лежат на одной прямой.
Решение. Пусть ABCD — произвольный
четырехугольник, Е и F — середины диагона-
диагоналей АС и BD, a G — точка пересечения отрез-
отрезков, соединяющих середины противоположных
сторон (рис. 342). Тогда если Р и Q — середины
сторон АВ и CD, то согласно задаче 791 точка
G — середина отрезка PQ.
Поэтому (см. задачу 1 п. 84): OG = )-(ОР
Рис. 342
OQ), ОЕ = ^(ОА + ОС), OF = ^
+ OD), ОР= UoA + OB), OQ= UOC + OD), где О -произвольная
точка плоскости. Отсюда получаем:
OG = i • ^(ОА + ОВ + ОС + OD) = ^(ОЕ + OF).
Таким образом,
2OG - ОЕ - OF = ~0 .
Согласно задаче 907 точки Е, F и G лежат на одной прямой.
909. Биссектрисы внешних углов треугольника ABC при вершинах А, В
и С пересекают прямые ВС, С А и АВ соответственно в точках А\, В\ и С\.
Используя векторы, докажите, что А\, В\ и С\ лежат на одной прямой.
Решение. Пусть АВ = с, ВС = а, С А = Ъ (рис.343). Согласно
задаче 619
ЬВАХ = сСАх, сСв\ = оАВх, аАСх = ЪВС[.
Эти три равенства можно записать так:
а(АС
= Ь(ВС + СС[),

238
Гл. 5. Векторы
или
(а - с)Св\ = аСА,
(а - Ь)СС[ = ЪВС + аСА.
Из последних трех равенств следует, что
(с - Ь)СА[ + (а - с)Св\ + (Ь - а)Сс\ = ~0 .
Согласно задаче 907 точки А\, В\ и С\ лежат на одной прямой.
910. Пусть Н — точка пересечения прямых, содержащих высоты неравно-
неравностороннего треугольника ABC, а О — центр описанной около этого треуголь-
треугольника окружности. Используя векторы, докажите, что точка G пересечения
медиан треугольника принадлежит отрезку НО и делит этот отрезок в отно-
отношении 2 : 1, т. е. -^-г = 2.
СгСу
Решение. Пусть А\, В\ и С\ — середины сторон ВС, С А и АВ
данного треугольника ABC (рис.344).
По правилу треугольника сложения векторов
По теореме о пересечении медиан треугольника
AG = -2MG,
следовательно,
= -2А7о - 2OG.
в.
Рис. 344

Задачи повышенной трудности	239
Векторы АН и А\О коллинеарны, поэтому существует число Л
такое, что А\О = ХАН. Отсюда и из равенства A) получаем:
WG + 2OG = -BЛ + 1)АН.
Аналогично,
где число /i определяется из равенства В\О = fiBH. Векторы Аи" и
не коллинеарны, поэтому из полученных равенств следует, что
WG + 2OG = "О , т. е. WG = -2OG,
или
Это означает, что точка G лежит на отрезке ОН и
HG =
GO

Учебное издание
АТАНАСЯН Левой Сергеевич
БУТУЗОВ Валентин Федорович
КАДОМЦЕВ Сергей Борисович
ЮДИНА Ирина Игоревна
ГЕОМЕТРИЯ. 8 КЛАСС
Редактор B.C. Аролович
Оригинал-макет: A.M. Садовский
Оформление переплета: А.А. Логунов
ЛР №071930 от 06.07.99. Подписано в печать 30.12.04.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 15. Уч.-изд. л. 16,5. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Ивановская областная типография»
153008, г. Иваново, ул. Типографская, 6
E-mail: 091-018@adminet.ivanovo.ru
ISBN 5-9221-0573-6
785922 105736