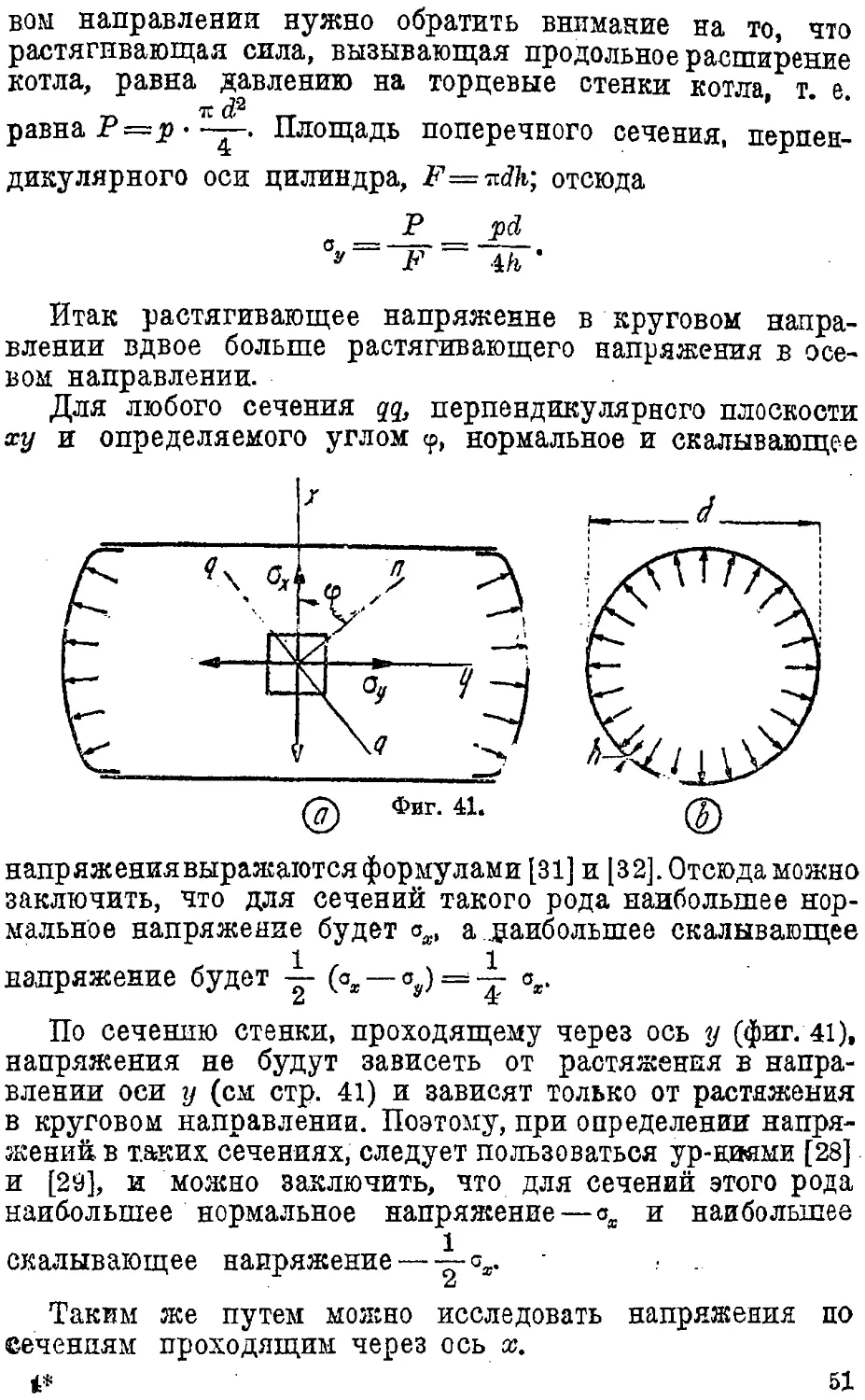
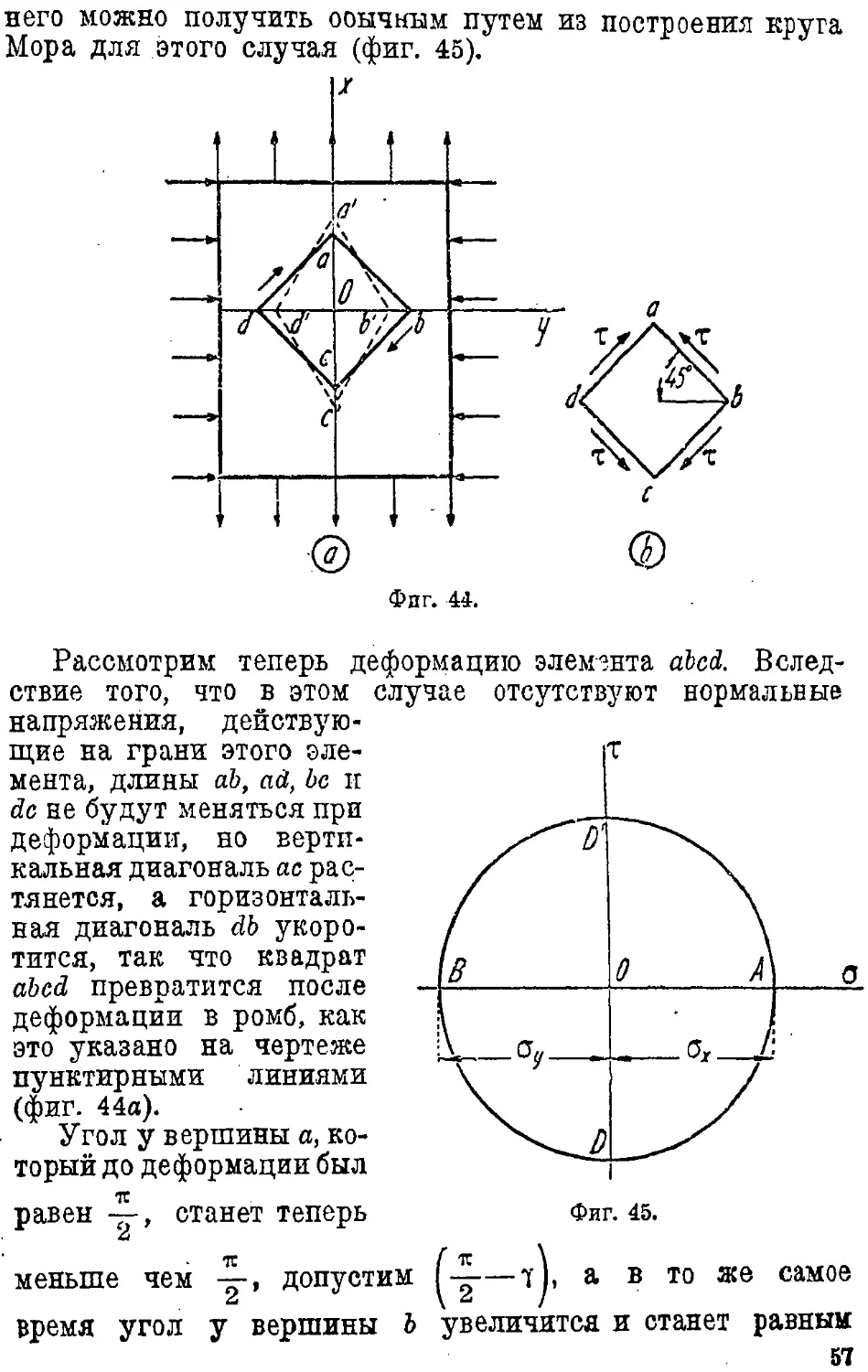
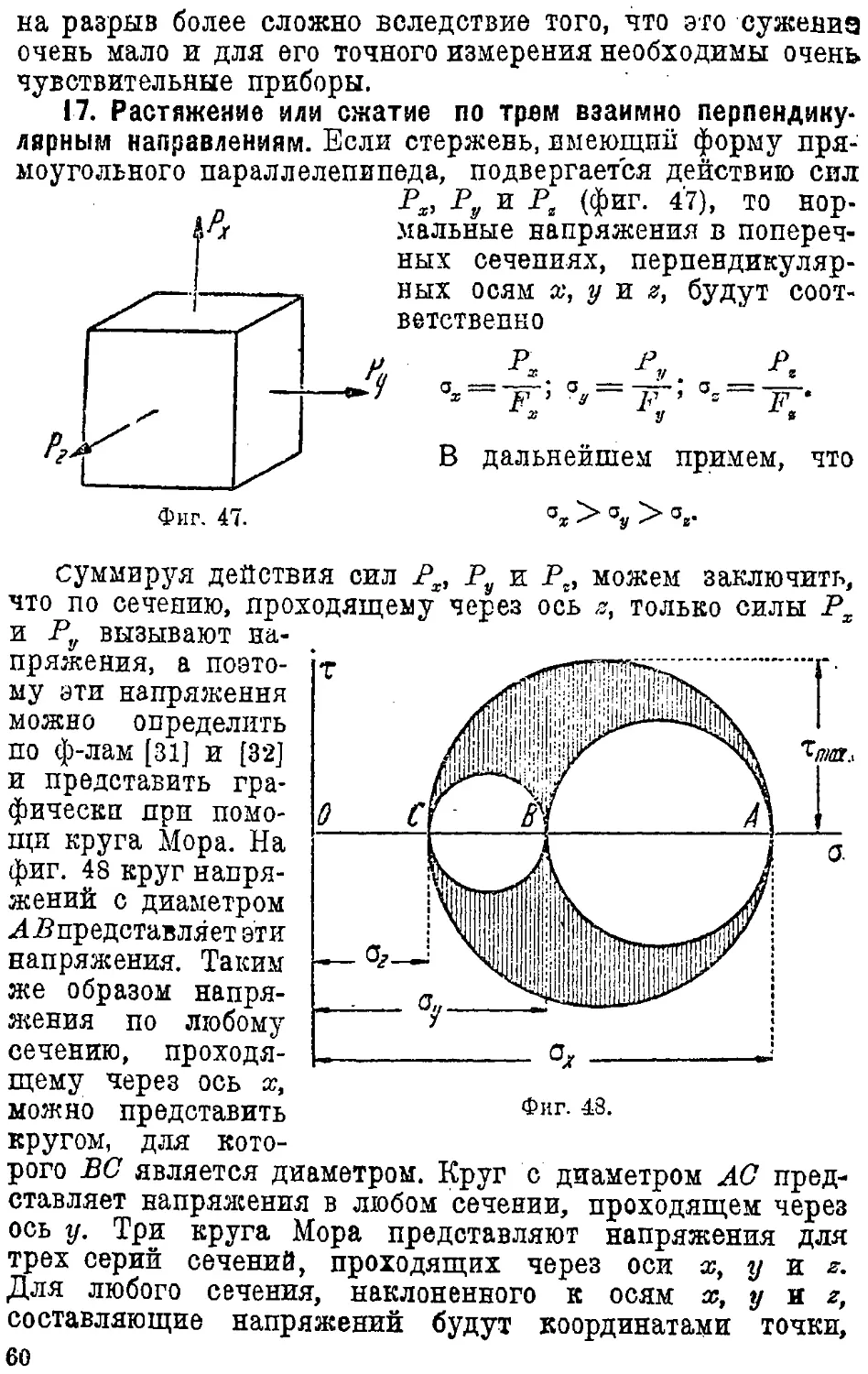
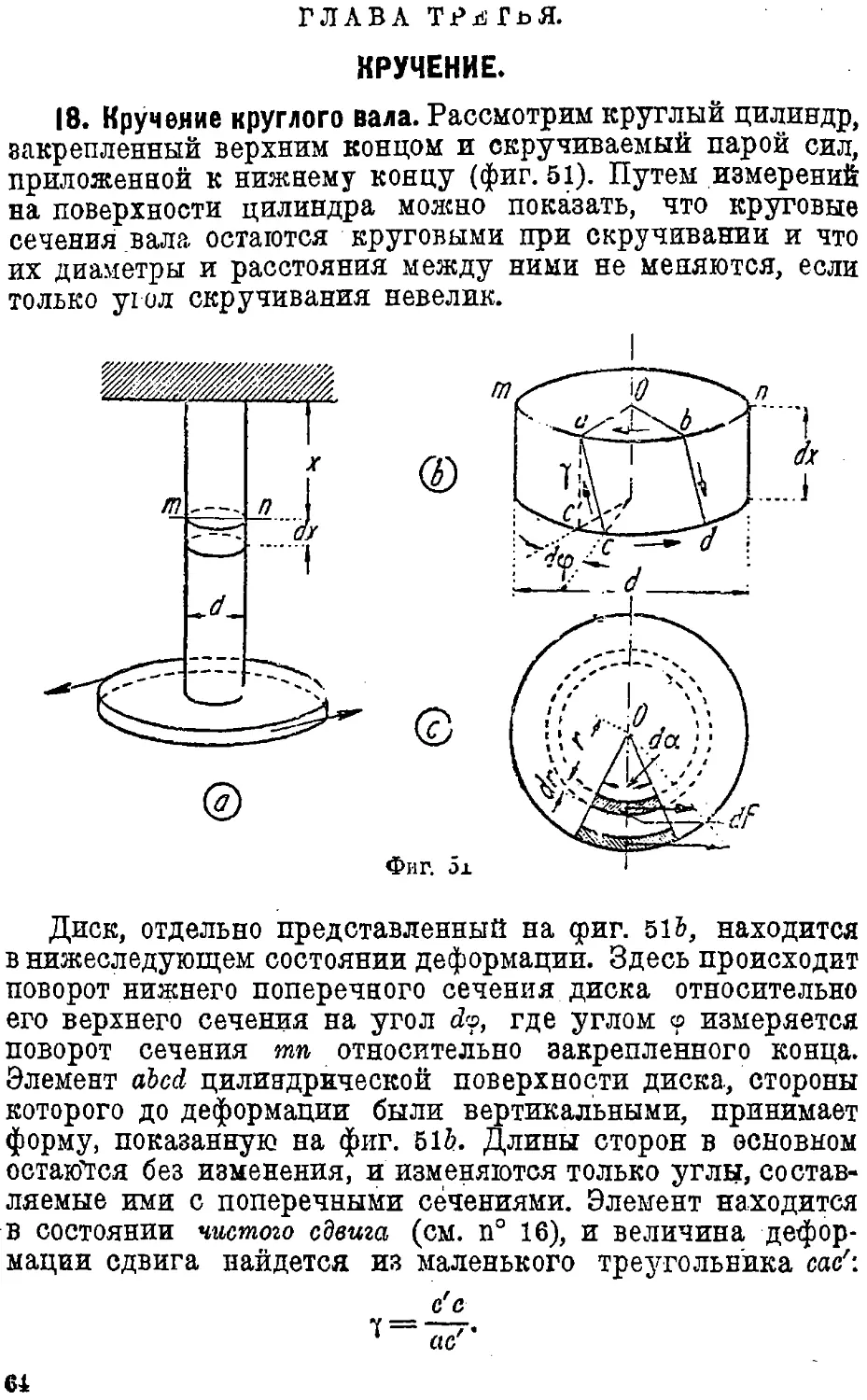
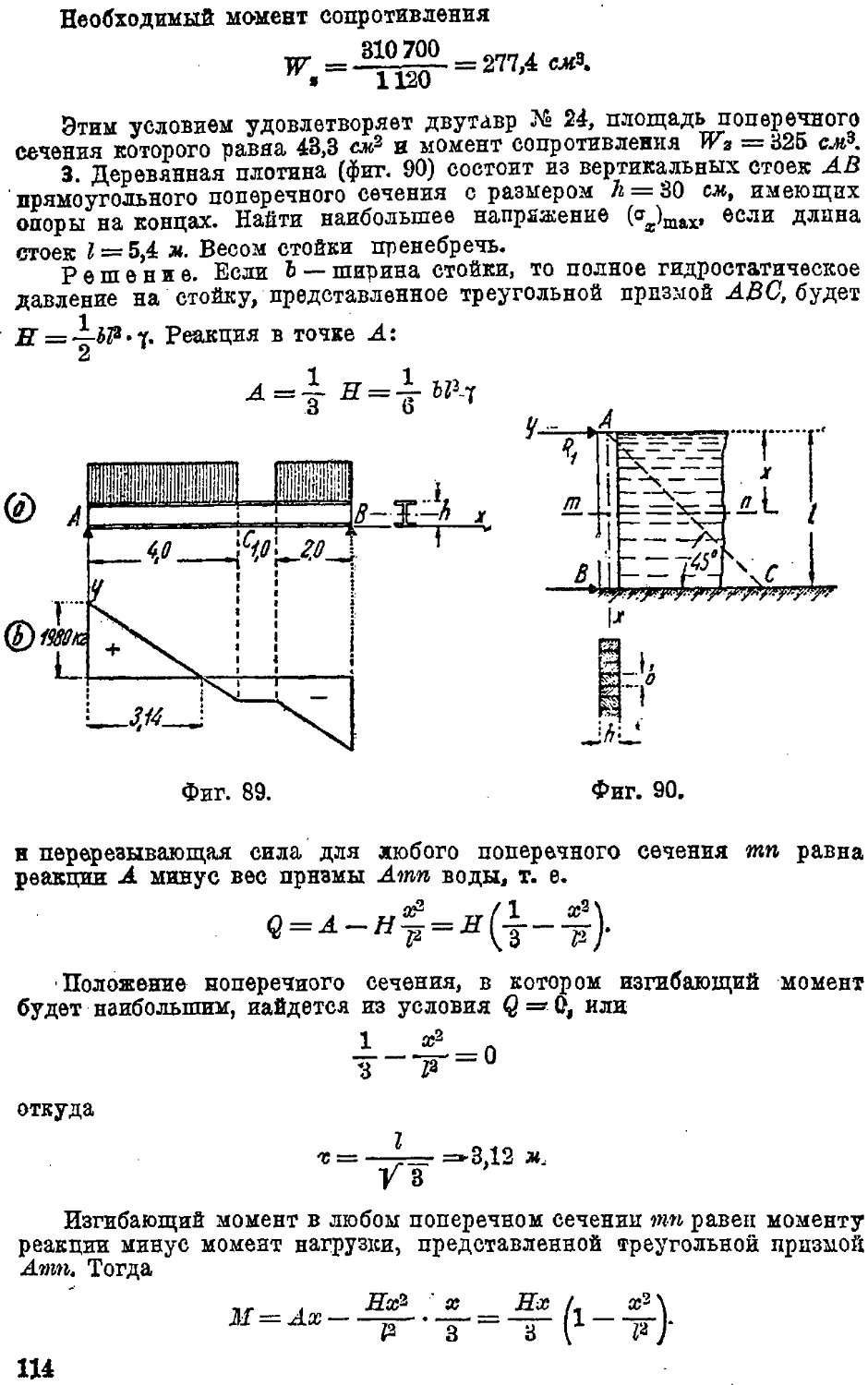
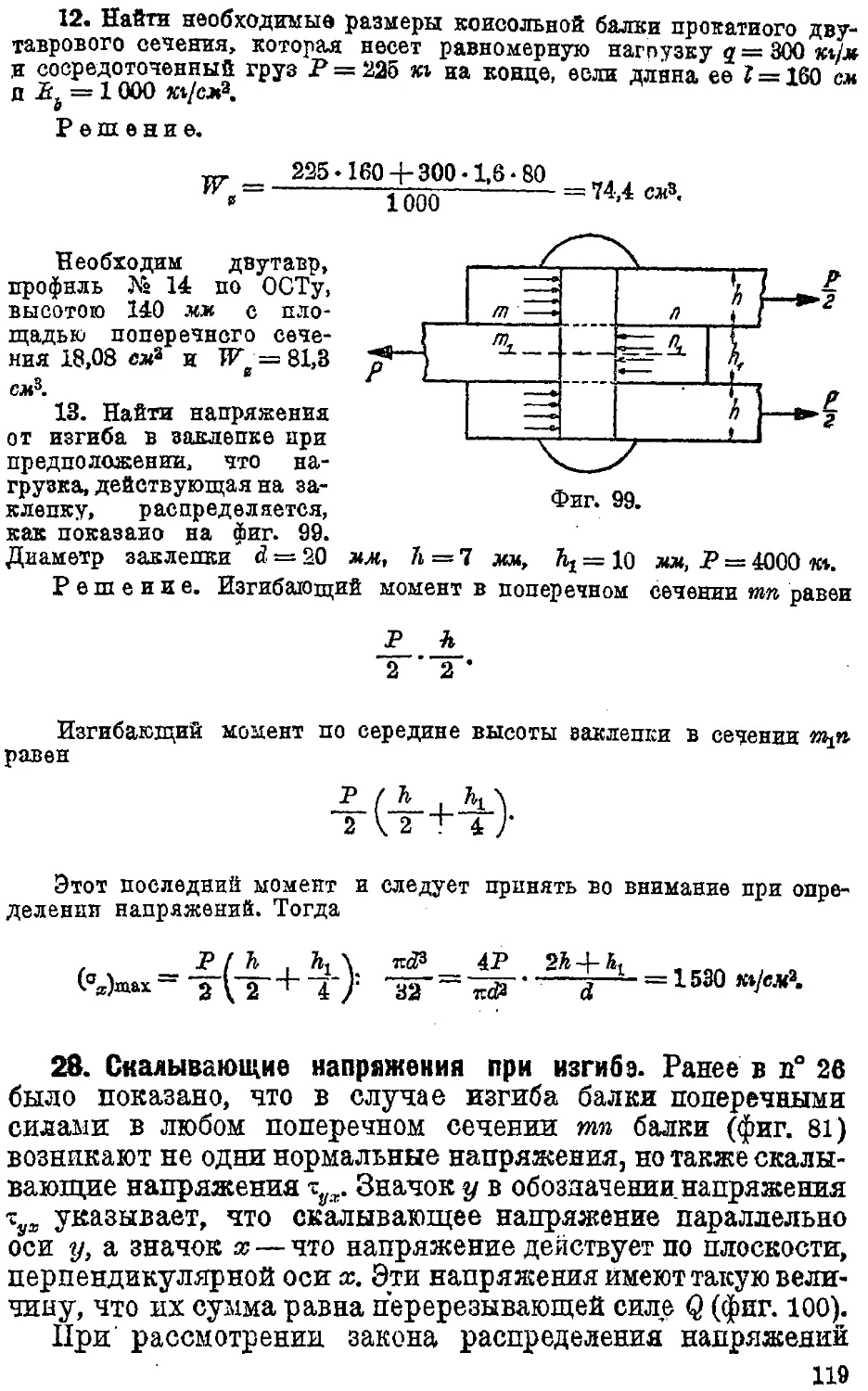
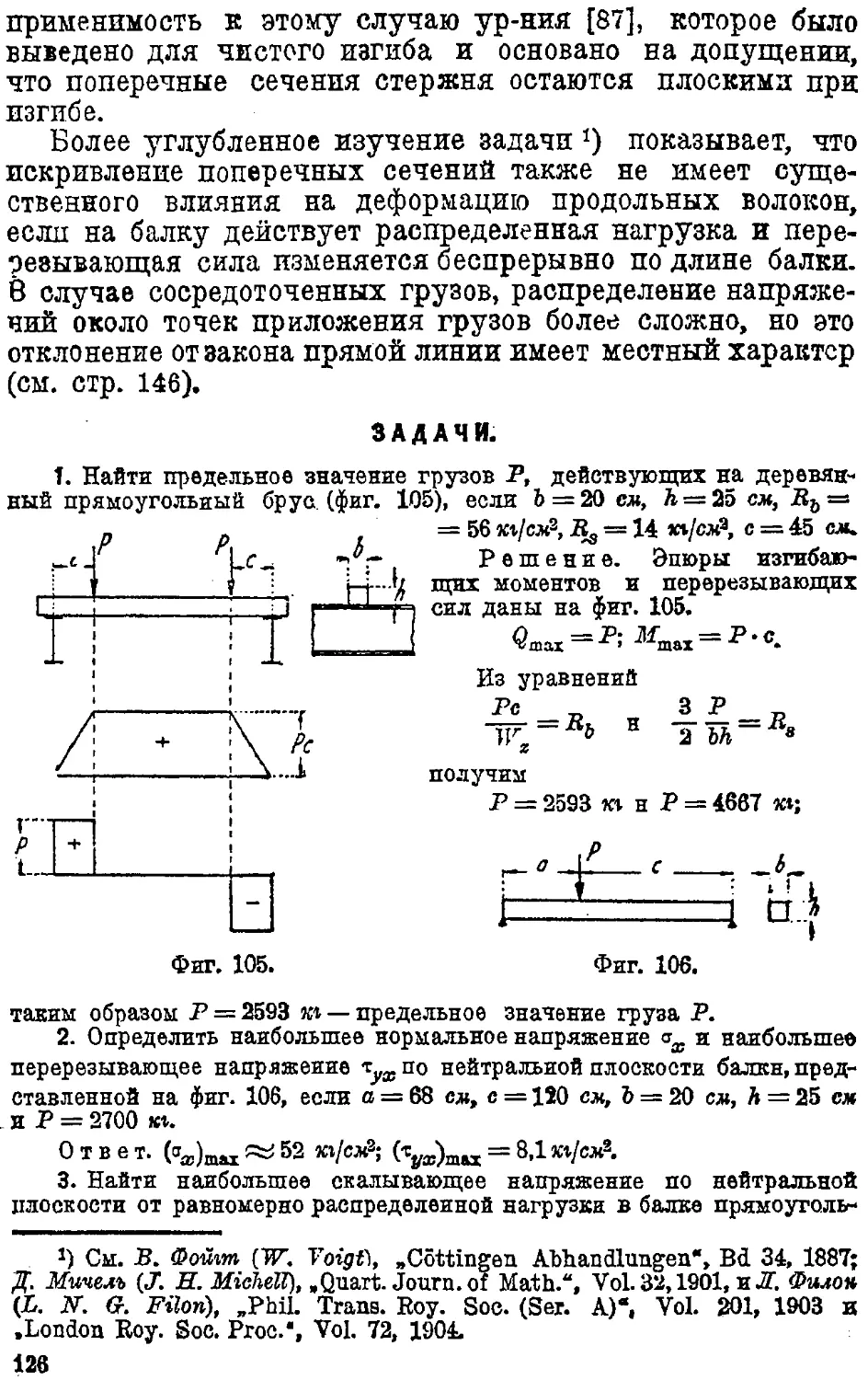
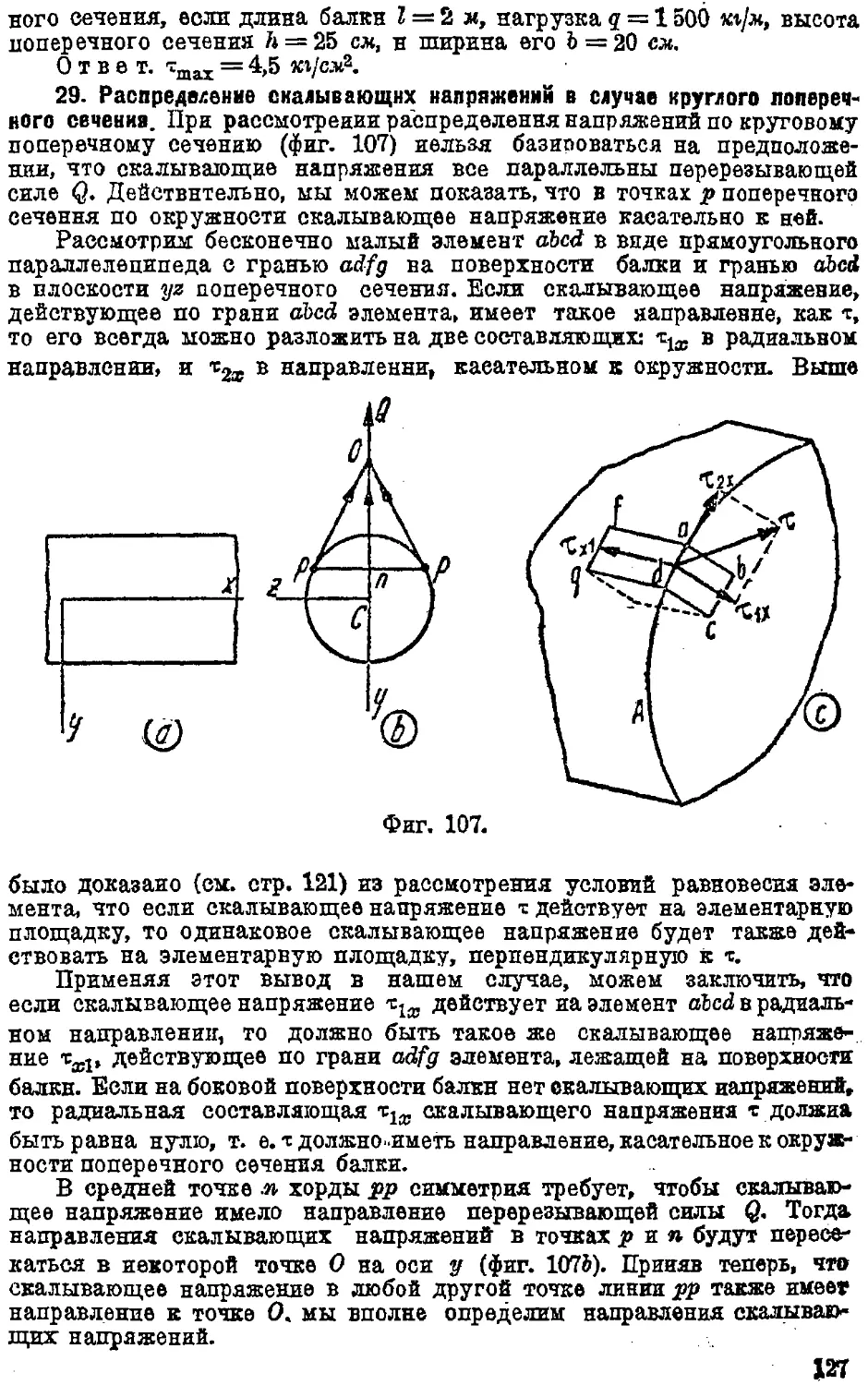
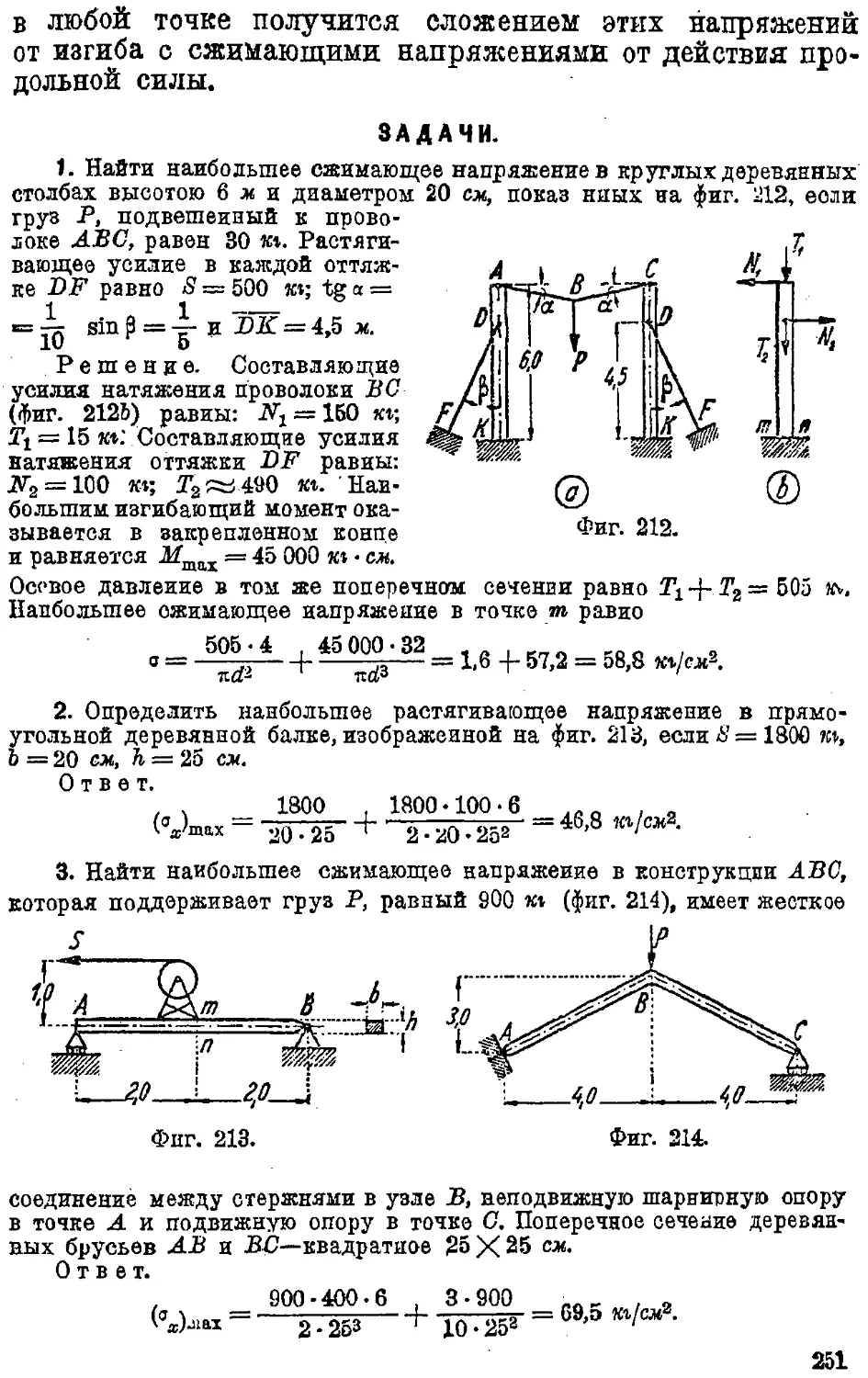
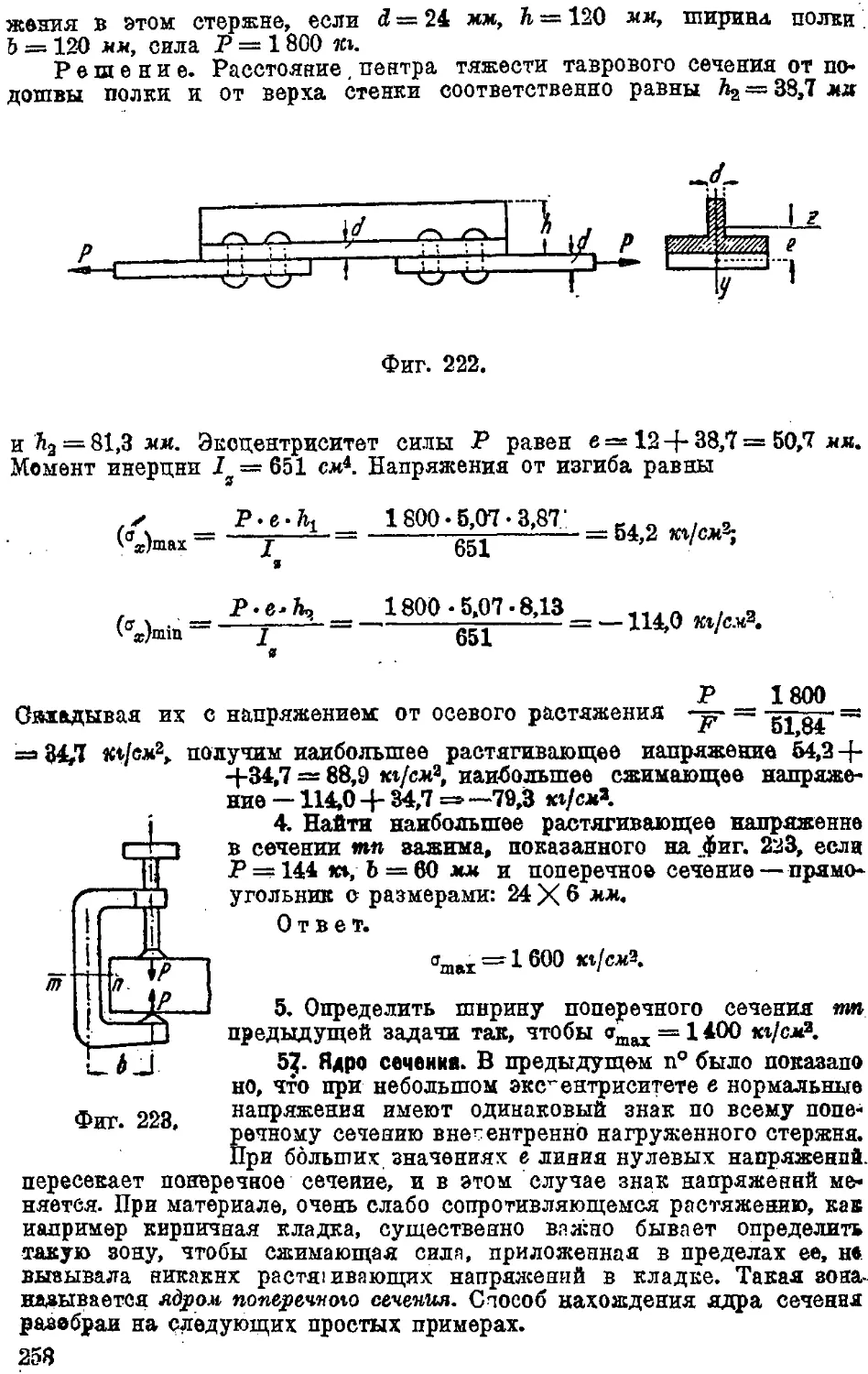
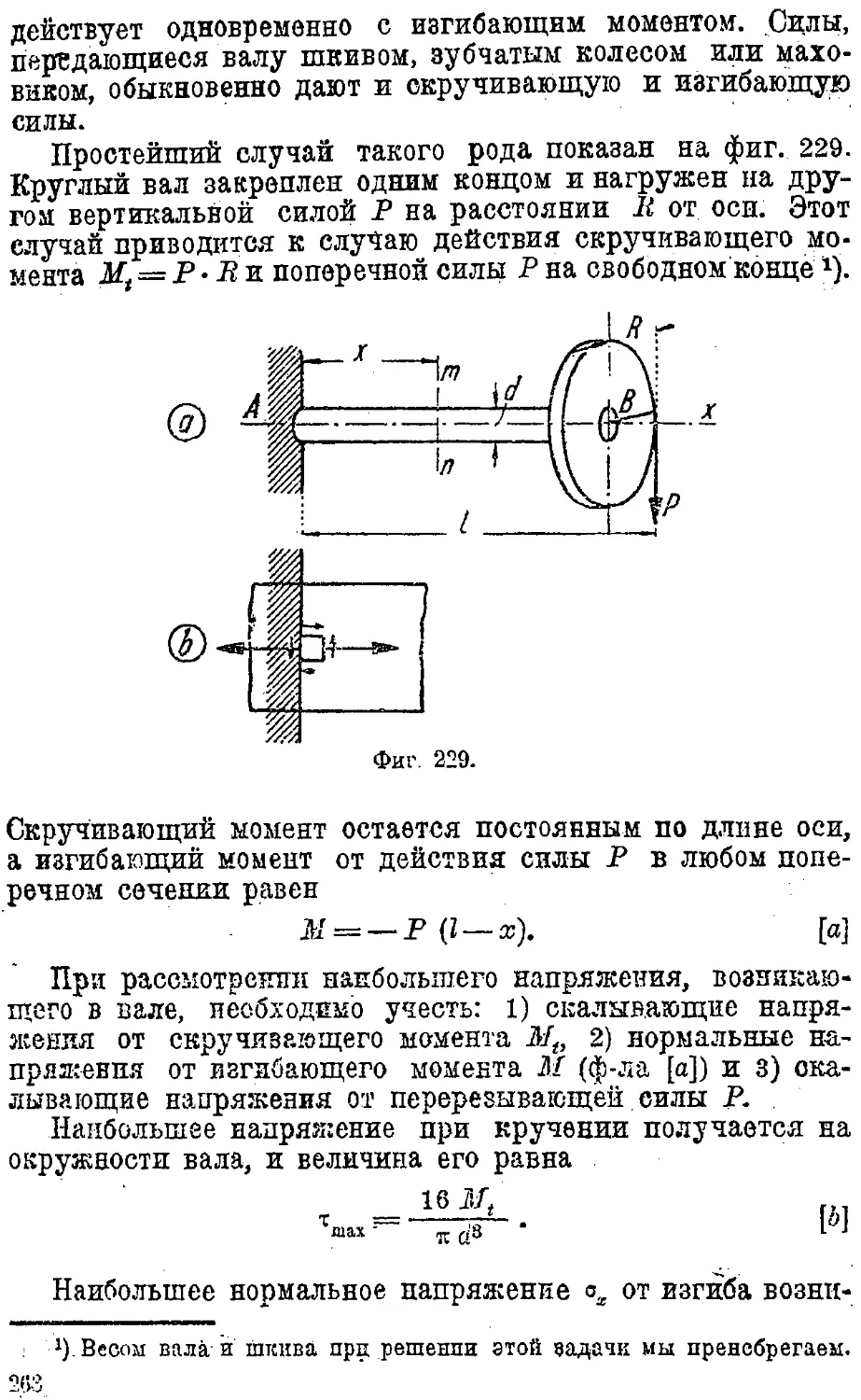
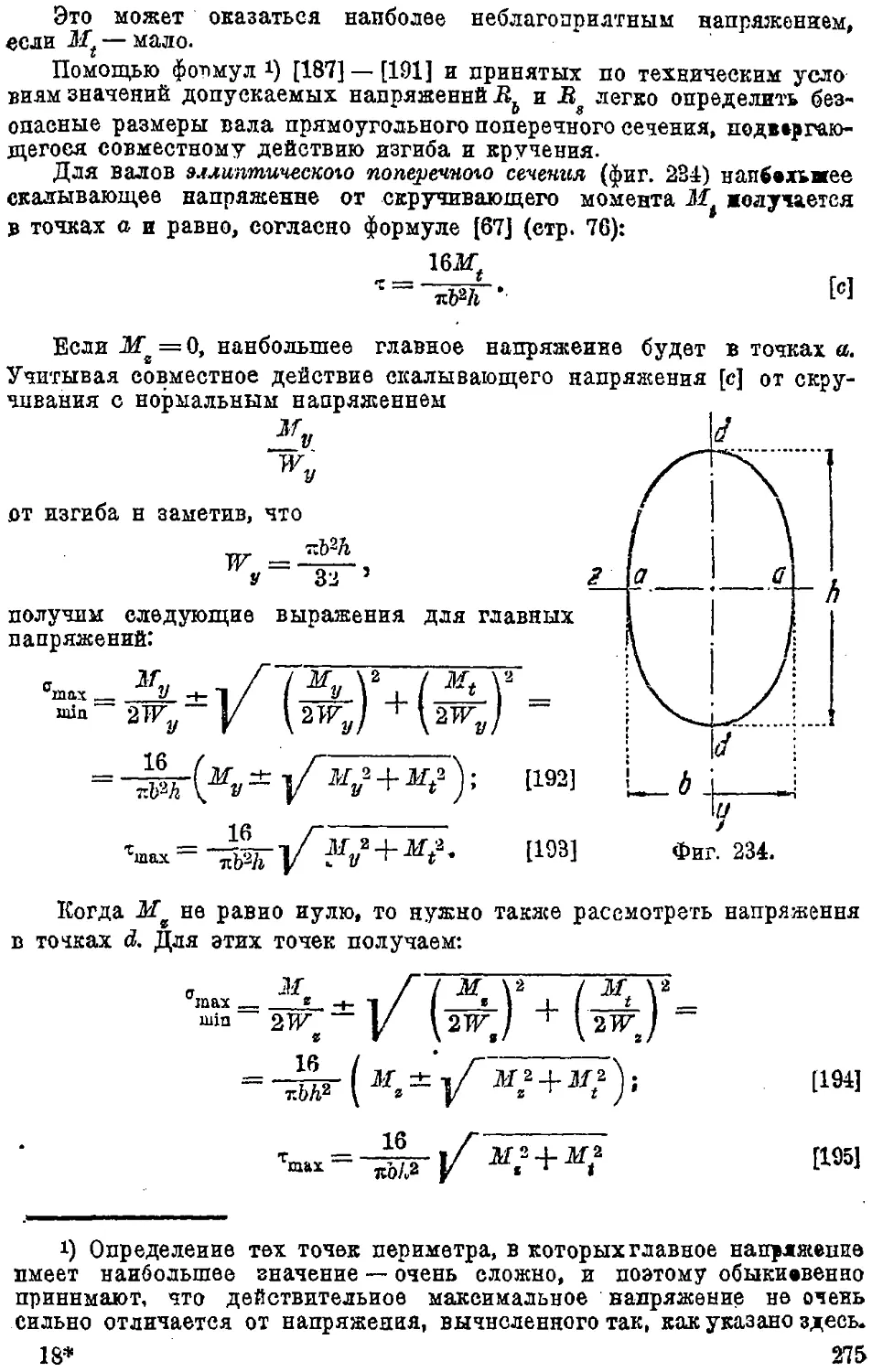
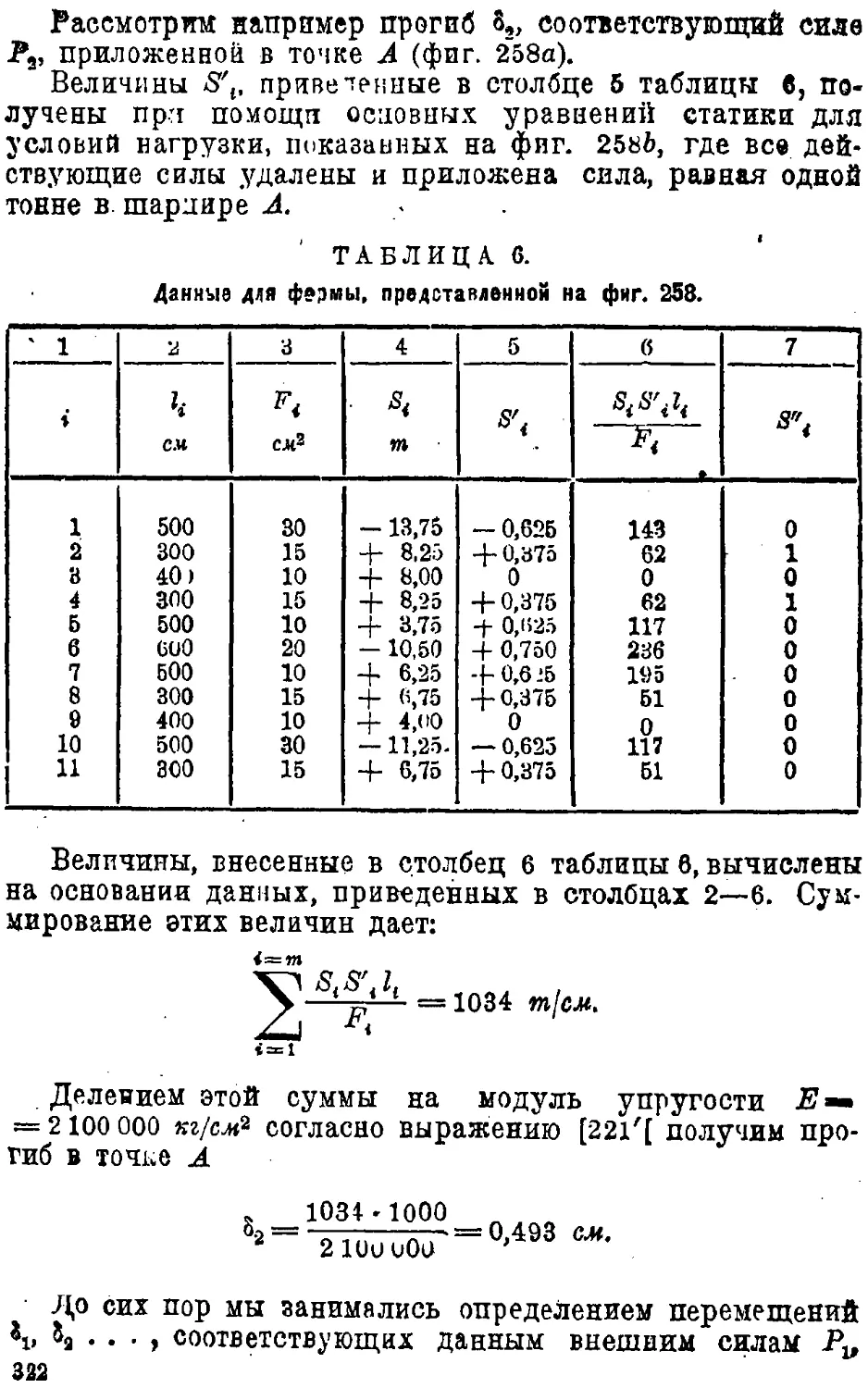
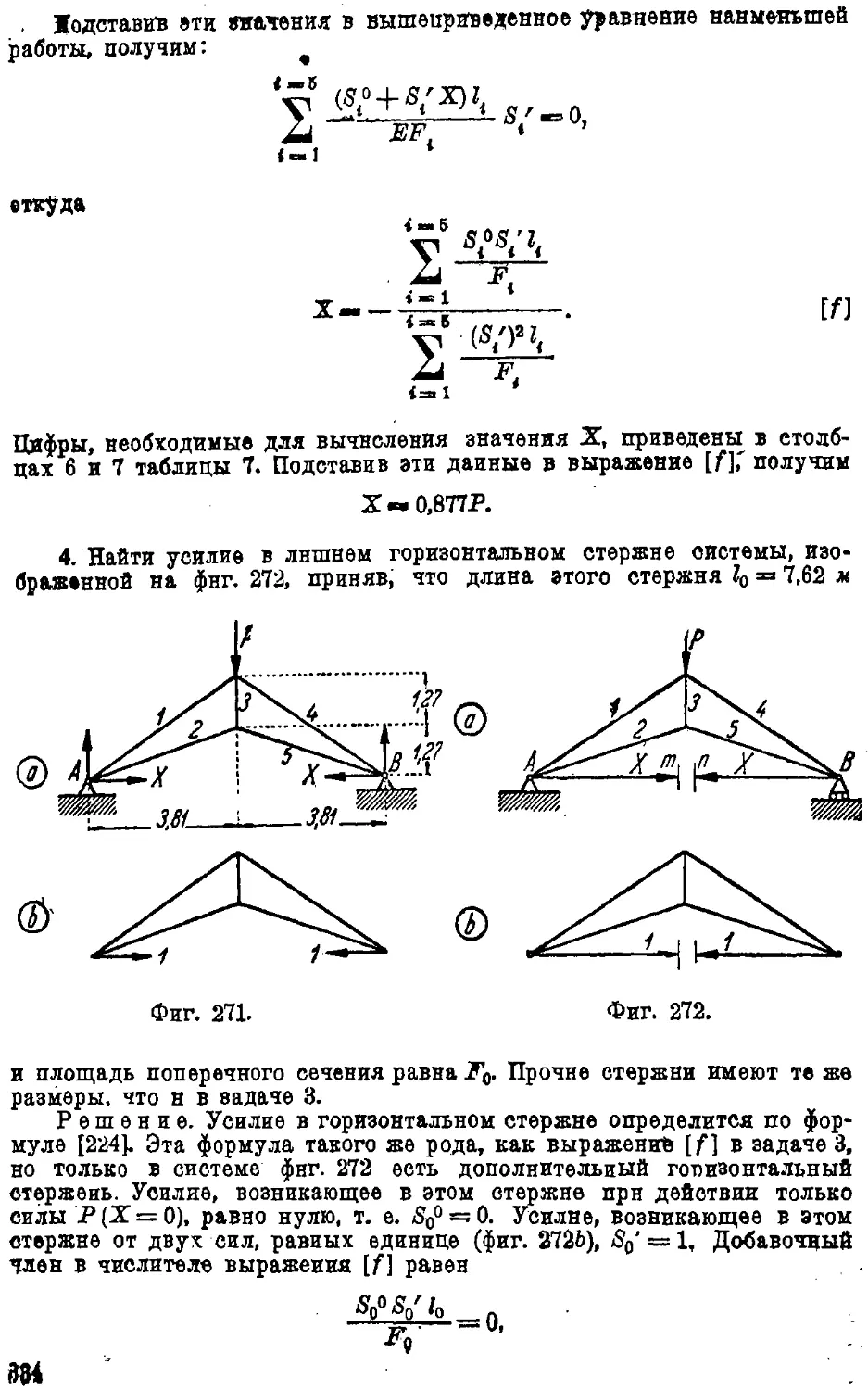
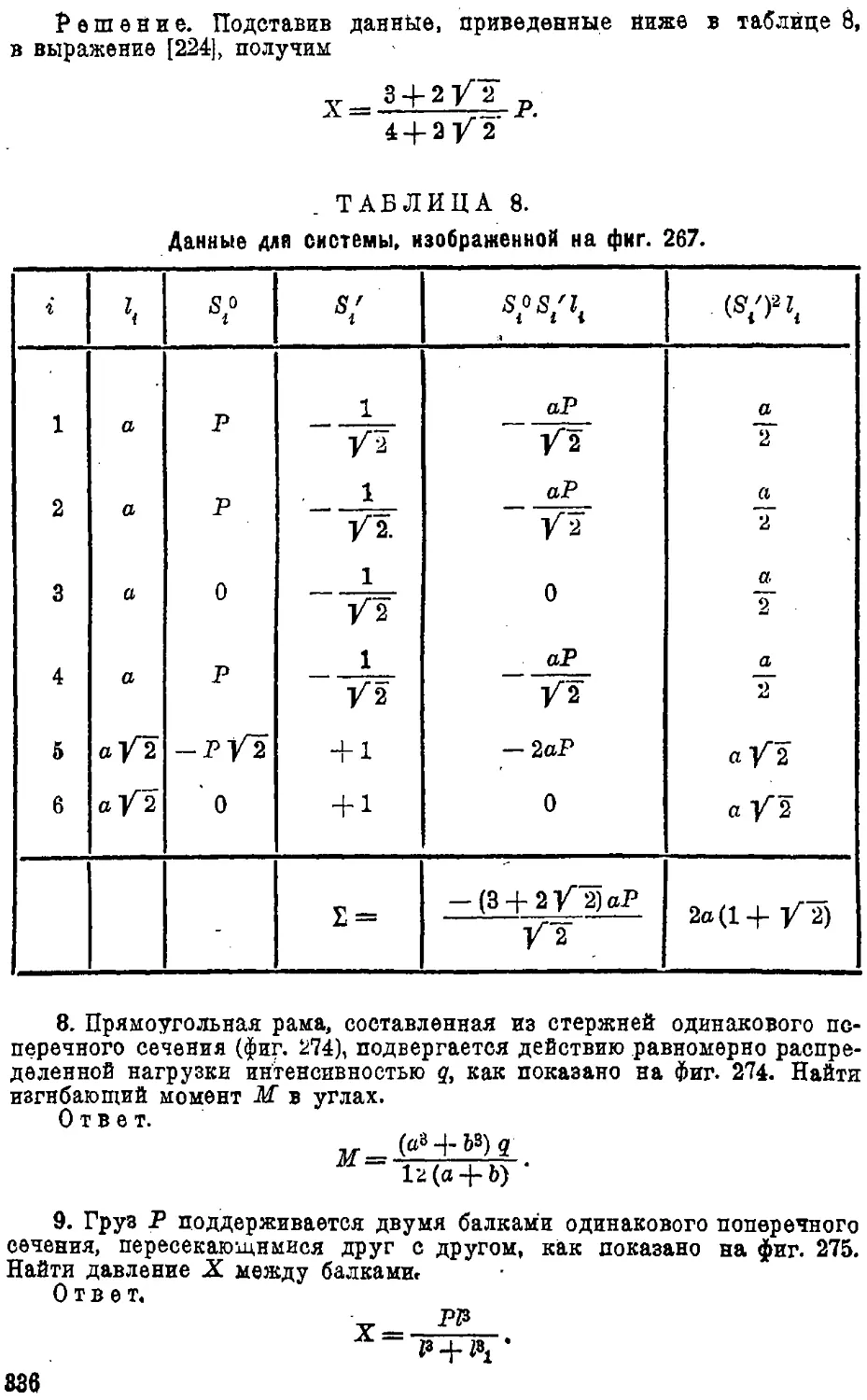
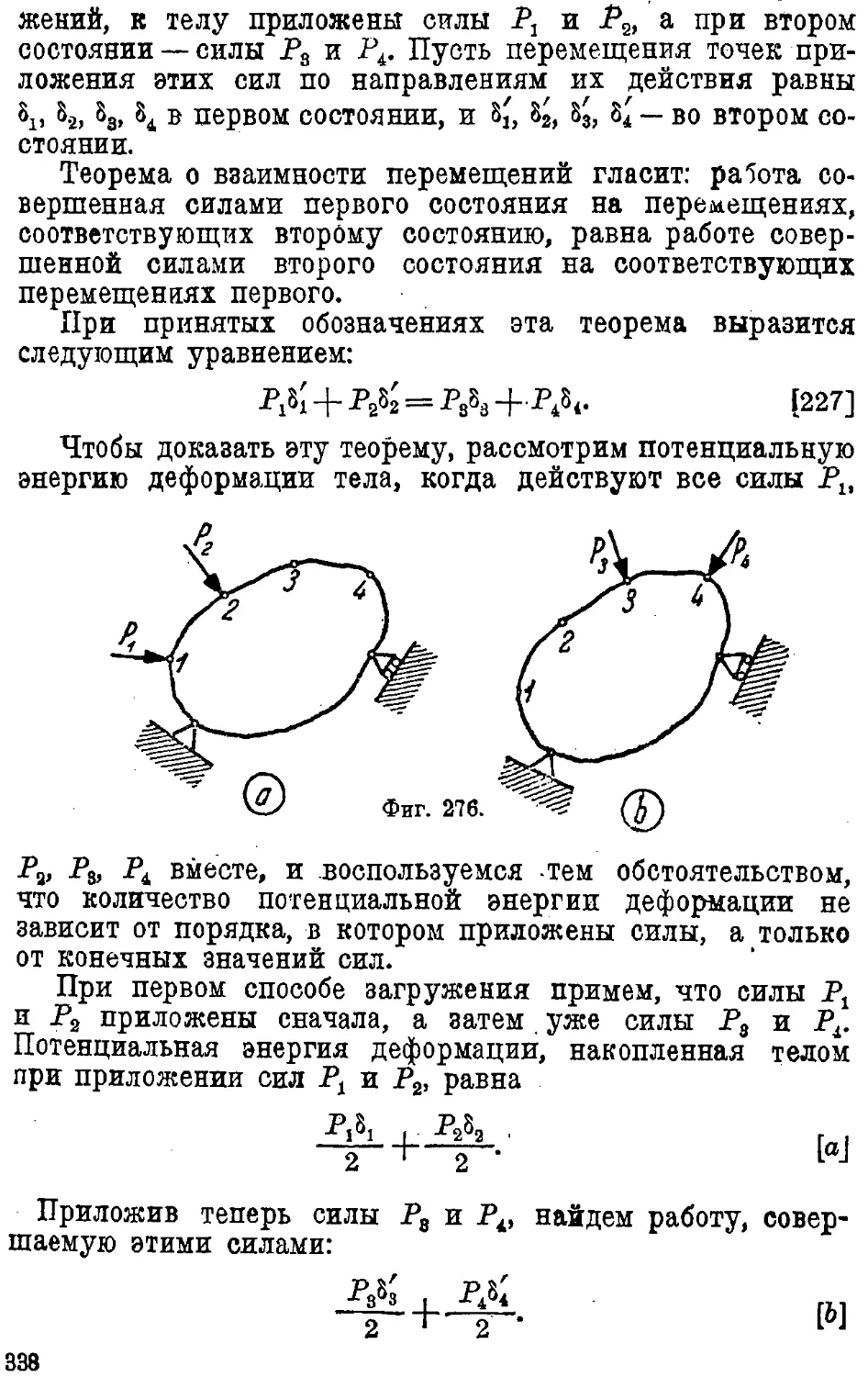
Text
С. Тимошенко
Сопротивление
материалов
Часть первая
Проф. О. П. ТИМОШЕНКО
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ЧАСТЬ ПЕРВАЯ
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ И ЗАДАЧИ
ПЕРЕВОД С АНГЛИЙСКОГО
ПРиФ. Н. А. Шошина
ВТОРОЕ ИЗДАНИЕ
ПЕРЕСМОТРЕННОЙ
II ИСПРАВЛЕННОЕ
Допущено в качестве учебного пособия к
переизданию в 19. 3 г. Комитетом по сысіие i\j
техническому образованию при ЦИК СССР
ГОСУДАРСТВЕННОЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ЛЕНИНГРАД • 1933 • МОСКВА
S. TIMOSHENKO
STRENGTH OF MATERIALS
NEW YORK
1930
Ответственны а редактор E. А. Шогиин. ТехяическяЙ редактор В. Д. Финиши,
Сдано в производство 17/VI 1938 г. Подписано к печати 29/IX 193S г.
Формат 82ХПОі/и ГТТИ № 258. Ткп.м. в 1 п. л. 41.360.
Леагорлит М 23644. Тяразс 50.000—284» л. Заказ W 1143.
2-я типография ОНТЙ имени Евг. Соколовой. Ленинград,- прочп. Красных Командиров, 23.
ПРЕДИСЛОВИЕ.
В настоящее время произошел коренной перелом во
взглядах инженеров, занятых проектированием", на вопрос
о применении аналитических методов к решению
инженерных задач. Расчет уже больше не основывается
преимущественно на эмпирических формулах. Важность
аналитических методов, в сочетании с лабораторными
исследованиями, при решении технических проблем стала
общепризнанной.
Типы машин и сооружений очень быстро меняются,
особенно в новых отраслях промышленности; нет обычно
времени для накопления необходимых эмпирических данных.
Размеры и стоимость сооружений непрерывно
увеличиваются, вследствие чего возникают жесткие требования
большей надежности сооружений. Экономический фактор
проектирования, в современных условиях, получает все
нарастающее значение. Конструкция должна быть
достаточно прочна и надежна и вместе с тем должна быть
спроектирована с наибольшей возможной экономией в
материале. При таких условиях задача проектирования
становится чрезвычайно трудной. Уменьшение веса влечет за
собой увеличение допускаемых напряжений, которое можно
безопасно допустить только на основе тщательного анализа
распределения напряжений в сооружении и -
экспериментального исследования механических свойств применяемых
материалов.
Цель этой книги — поставить вопросы сопротивления
материалов так, чтобы внимание студента было
сконцентрировано на практическом применении изучаемого. Если
это будет достигнуто и в результате в известной мере
укрепится связь между учением о сопротивлении
материалов и инженерным проектированием, то это будет
существенным шагом вперед.
Книга разделена на два тома. Первый том содержит
главным образом материал, который обычно проходится по
і* Ш
нормальным программам сопротивления материалов наших
(североамериканских) инженерных школ. Более
углубленные части теории представляют интерес главным образом
для окончивших и для инженеров-исследователей и
составляют второй том книги. Кроме того, в нем приводятся
новейшие практически важные достижения в области
сопротивления материалов.
При составлении первого тома сопротивления материалов
было обращено внимание на возможное упрощение выводов
с тем, чтобы студент с обычной подготовкой по математике
мог изучать предмет без затруднений. Например, при
выводе уравнений упругой линии широко применялся метод
фиктивной балки. Таким же путем было достигнуто
значительное упрощение при выводе прогибов балок для
различных нагрузок и условий опирания. При рассмотрении
статически неопределимых систем был применен метод па-
ложения, который оказался весьма полезным при
рассмотрении таких задач, как неразрезные балки и рамы. Для
объяснения совместных напряжений и вывода главных
напряжений был применен круг Мора, что значительно
упростило изложение этой части теории.
Благодаря этим приемам упрощения изложения, автору
удалось сжать материал и разобрать некоторые вопросы
более углубленного характера. Например, при
рассмотрении кручения, рассмотрено скручивание прямоугольных
стержней и прокатных профилей, таких как уголки,
корыта и двутавры. Деформация и напряжение в винтовых
пружинах рассмотрены детально. В теории изгиба рассмотрен
случай несимметричных поперечных сечений, определен и
пояснен центр скручивания и рассмотрено влияние
перерезывающей силы на прогиб балок. Изложена общая
теория изгиба балок для материалов, которые не следуют
закону Гука, и применена к изгибу балок за пределом
текучести. Рассмотрен изгиб железобетонных балок. При
рассмотрении совместного действия осевых и изгибающих сил,
учтено влияние прогибов на изгибающий момент, и
показаны пределы применимости метода наложения. При
изложении теории совместного ,изгиба и кручения разобраны
случаи прямоугольных и эллиптических поперечных
сечений, показано применение ее к расчету кривошипов.
Значительное место в книге отведено методам решения задач
теории упругости, основанным на рассмотрении
потенциальной энергии упругих тел. Эти методы применены к
решению статически неопределимых систем. Рассмотрены
также напряжения, возникающие при ударе. Все эти вопросы
IV
более углубленного характера напечатаны петитом и могут
быть опущены при первом ознакомленная с книгой.
В книге помещен ряд задач и приведены их решения.
Во многих случаях задачи выбраны так, чтобы расширить
круг представлений, охваченный текстом, или чтобы
иллюстрировать применение теории к решению вопросов
проектирования. Автор надеется, что эти задачи представят
интерес при преподавании и окажутся также полезными
проектирующим.
С, Тимошенко.
Анн Арбор, штат Мичиган, САСШ
1 мая 1930 г.
КО ВТОРОМУ РУССКОМУ ИЗДАНИЮ.
К этому изданию книга заново пересмотрена. Устранены
вкравшиеся в первое издание ошибки и опечатки как
английского оригинала, так и русского перевода.
Исправлены обнаруженные в рисунках недочеты. Проведен
полный пересчет ряда задач и уточнены числовые ответы.
Н. ШошШш
Ленинград
20 июня 1933 г.
ОГЛАВЛЕНИЕ
Стр.
Глава первая.
Растяжение и сжатие в пределах упругости.
1. Упругость ." 1
2. Закон Гука 2
3. Диаграмма растяжения 5
4. Допускаемое напряжение .... 7
б. Напряжение и деформация в стержне от собственного веса . 12
6. Стержень равного сопротивления на растяжение 16
7. Статически неопределимые задачи на растяжение и сжатие . 18
8. Начальные и температурные напряжения 24
9. Расширение кругового кольца ¦ 28
10. Напряжение в нити н в кабеле 32
Глава вторая.
Совместные напряжения.
11. Изменение напряжений при простом растяжении с изменением
положения поперечного сечения 4=0
12. Растяжение или сжатие по двум взаимно перпендикулярным
направлениям 44
13. Круг Мора 47
14. Деформация в случае простого растяжения 63
15. Дефопмация в случае растяжения или сжатия по двум взаимно
перпендикулярным направлениям 54
16. Чистый сдвиг • 55
17. Растяжение'или сжатие по трем взаимно перпендикулярным
направлениям 80
Глава третья.
Кручение.
18. Кручение круглого вала 64
19. Скручивание полого вала 70
20. Вал прямоугольного поперечного сечения или из прокатных
профилей . ._ ¦ 73
21. Другие виды поперечного сечения 76
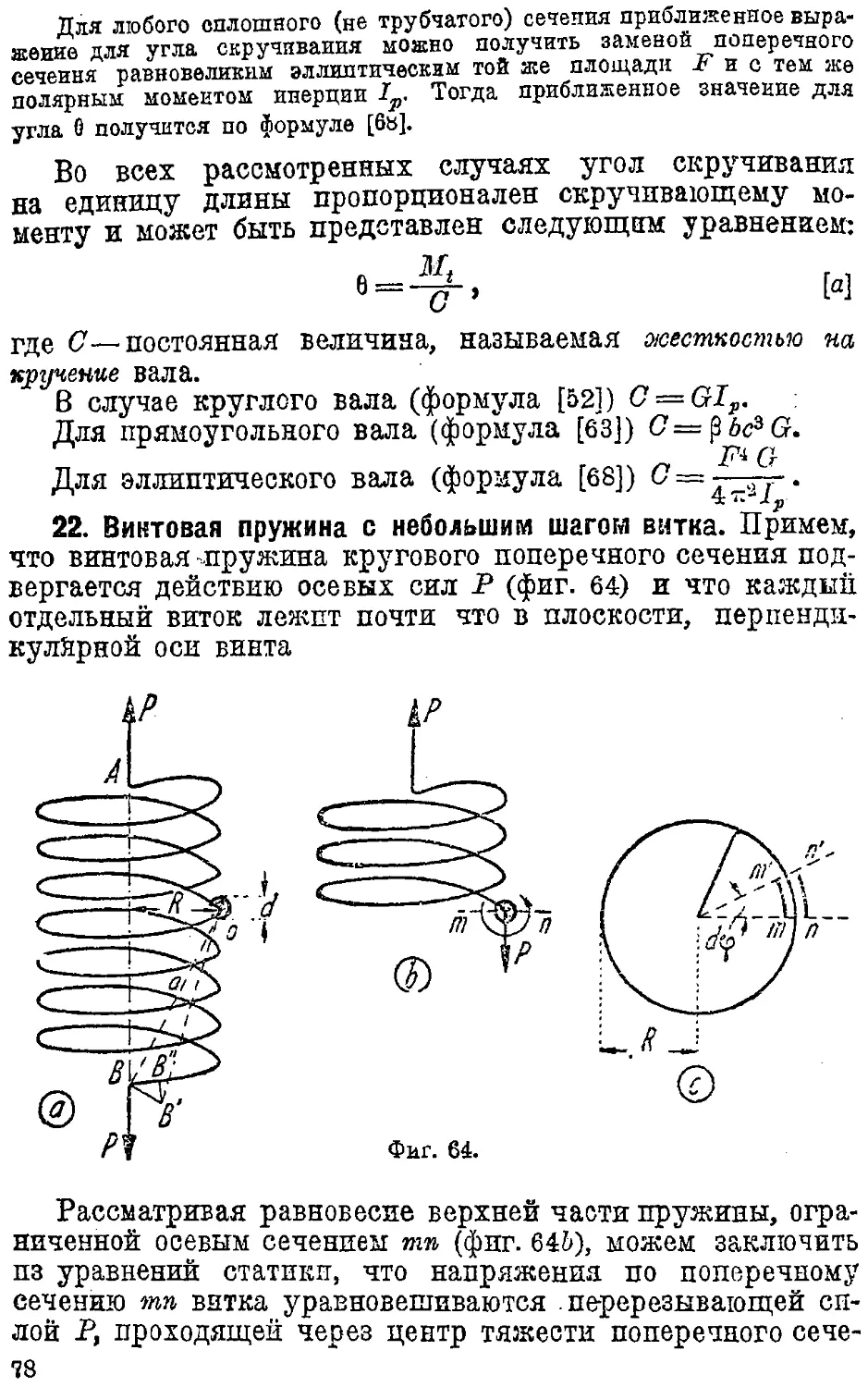
22. Винтовая пружина с небольшим шагом витка 78
23. Второстепенные напряжения при кручении 83
YI
Глава яетвер тая
Стр.
Напряжения при изгибе.
24. Чистый изгиб призматических стержней 87
25. Различные виды поперечных сечений балок 97
26. Изгиб балок поперечными силами 102
27. Эпюры изгибающих моментов и перерезывающих сил .... 105
28. Скалывающие напряжения при изгибе 119
29. Распределение скалывающих напряжений в случае круглого
поперечного сечения 12?
30. Распределение скалывающих напряжений в двутавровых
балках .* . L . . . 129
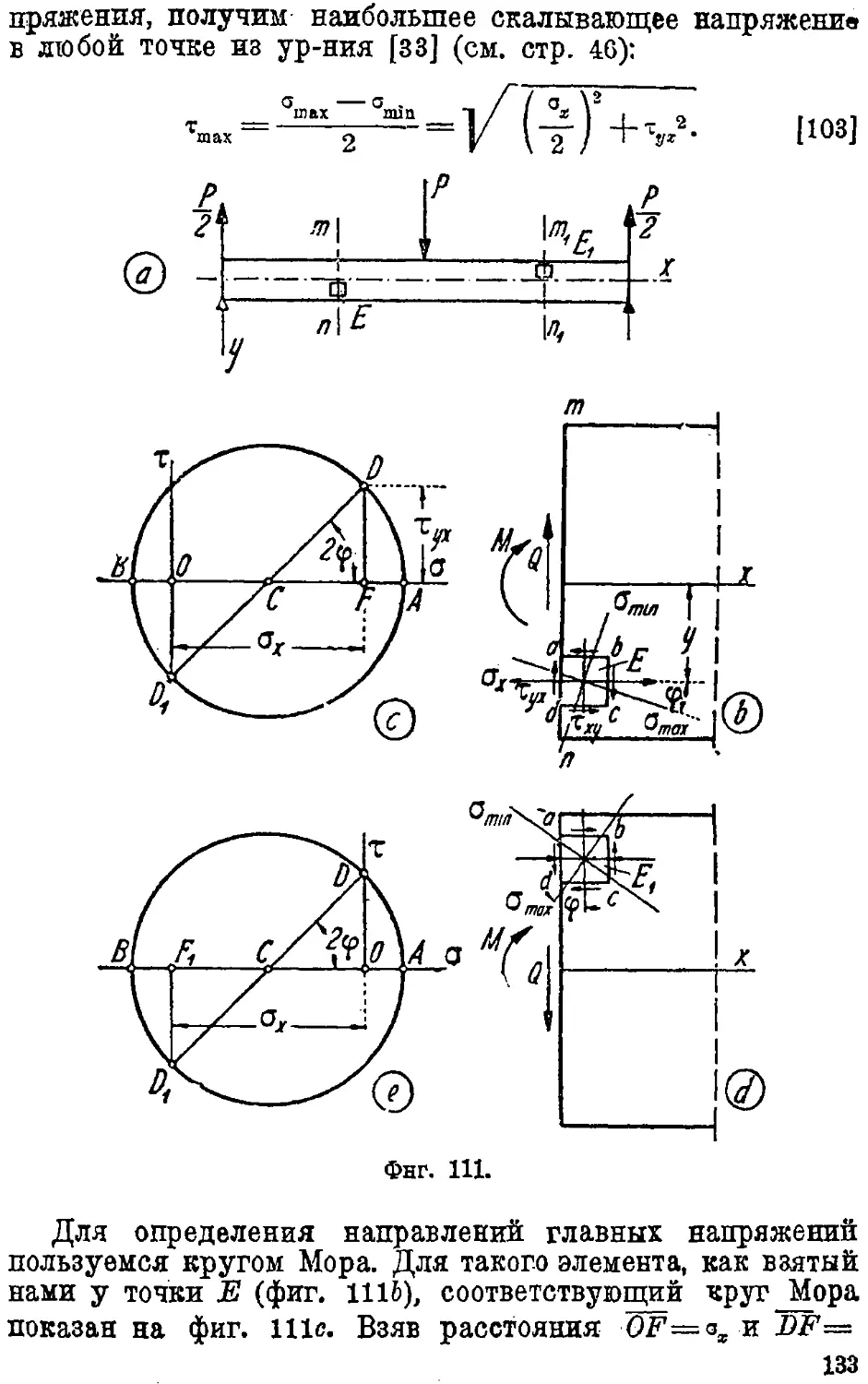
31. Главные напряжения при изгибе 13L
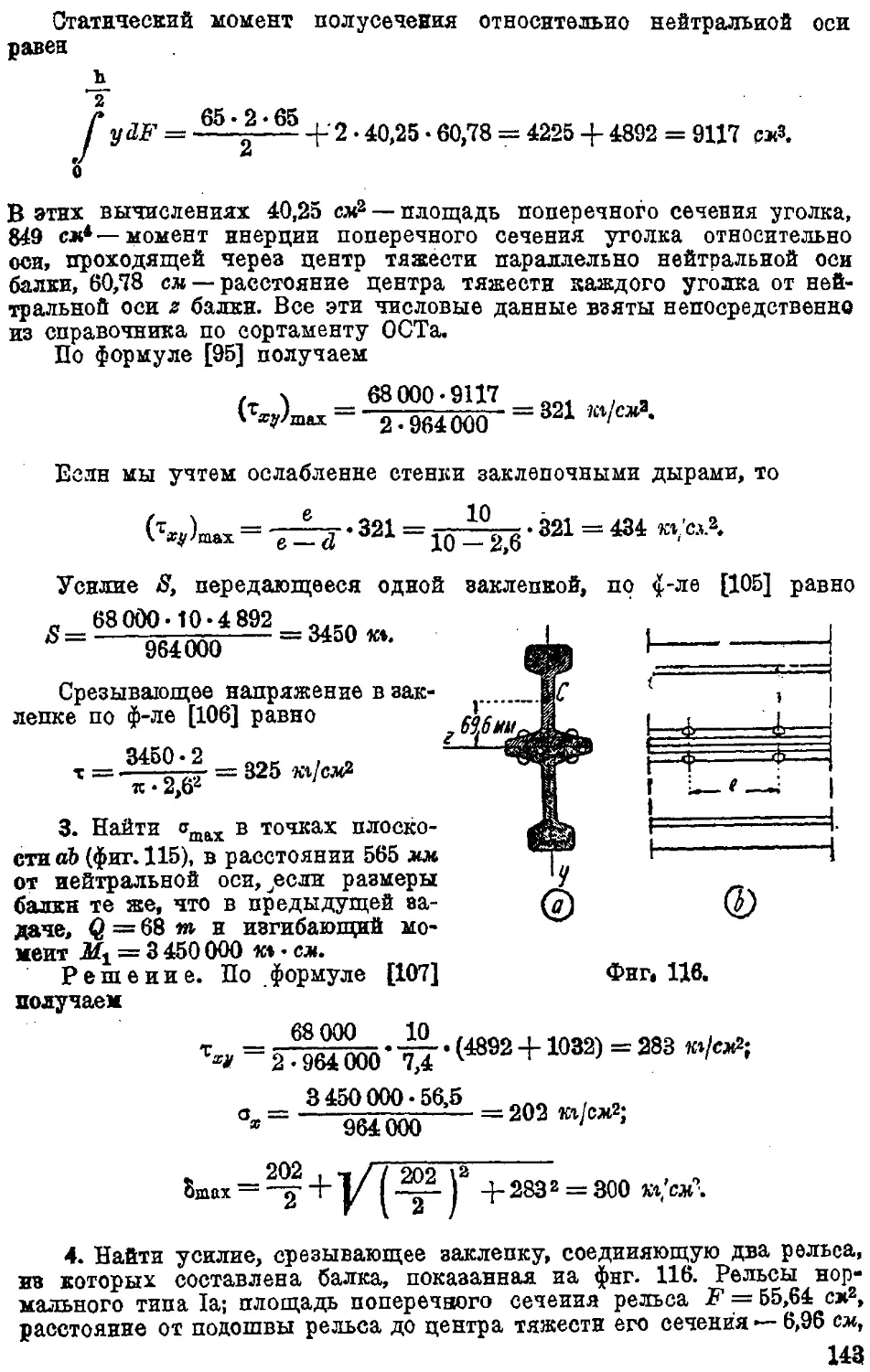
32. Напряжения в составных (клепаных) балках 137
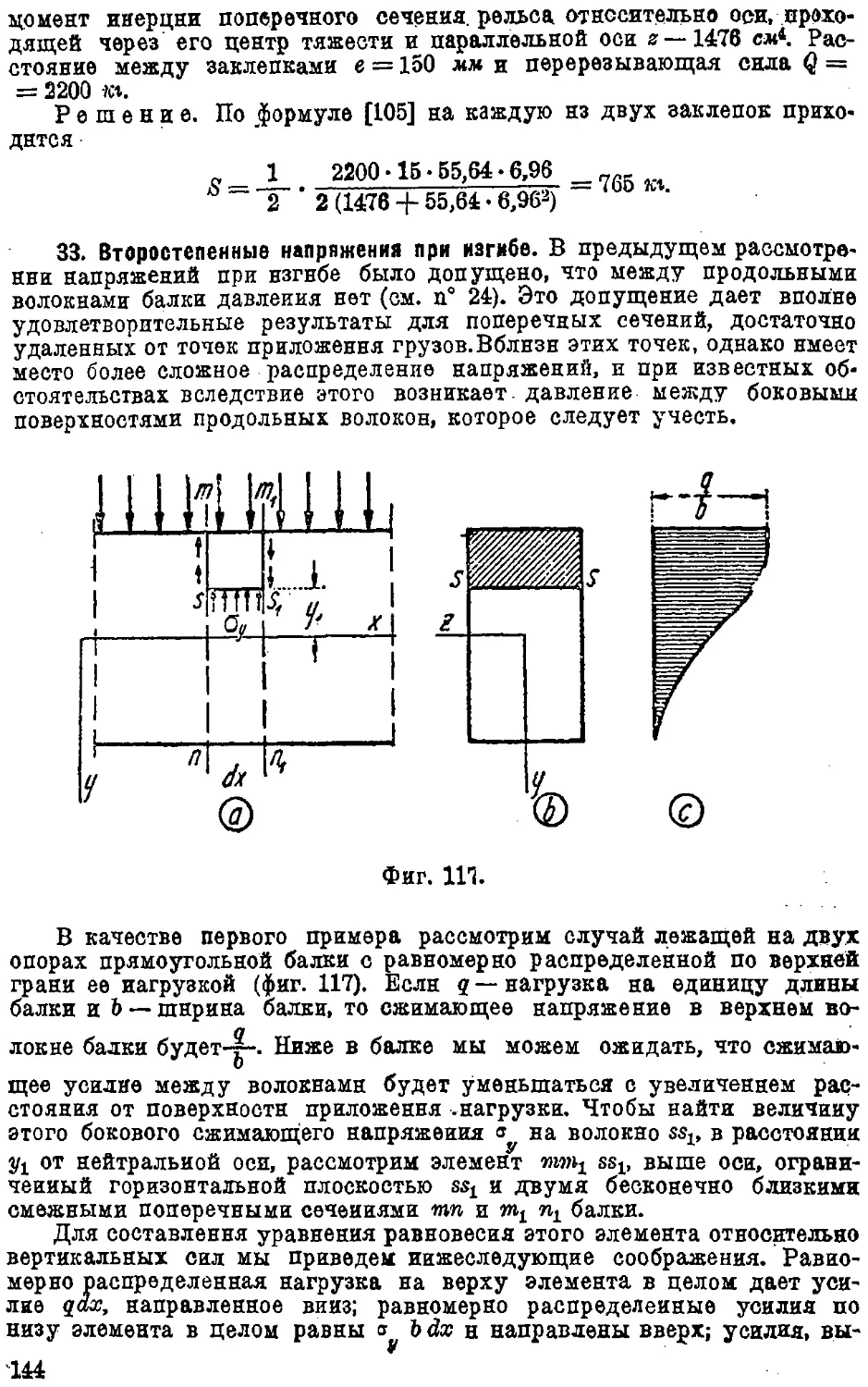
33. Второстепенные напряжения при изгибе 144
Глава пятая.
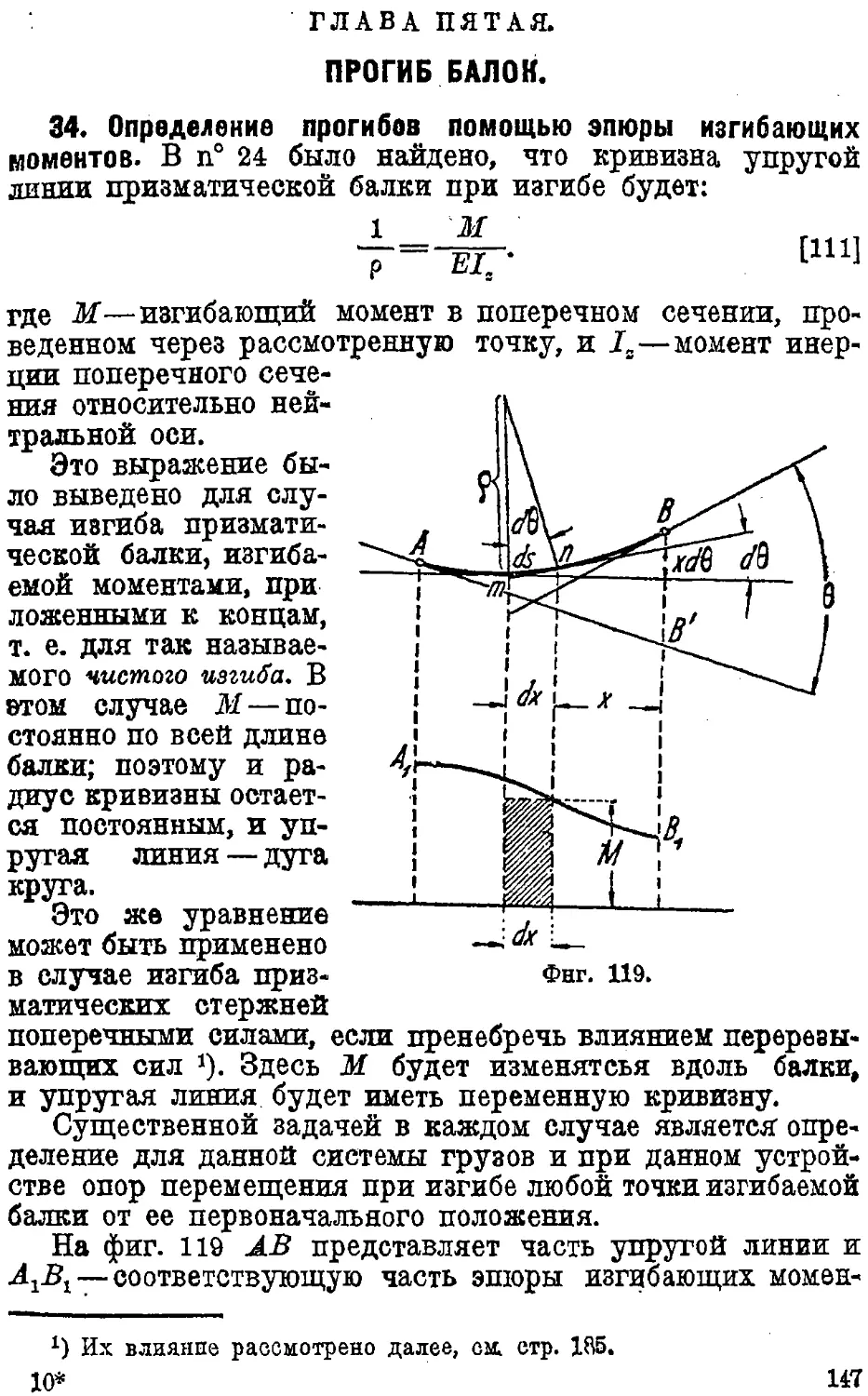
Прогиб балок.
34. Определение прогибов помощью эпюры изгибающих моментов Ш
35. Прогиб консоли 149
36. Прогиб балки опертой концами 157
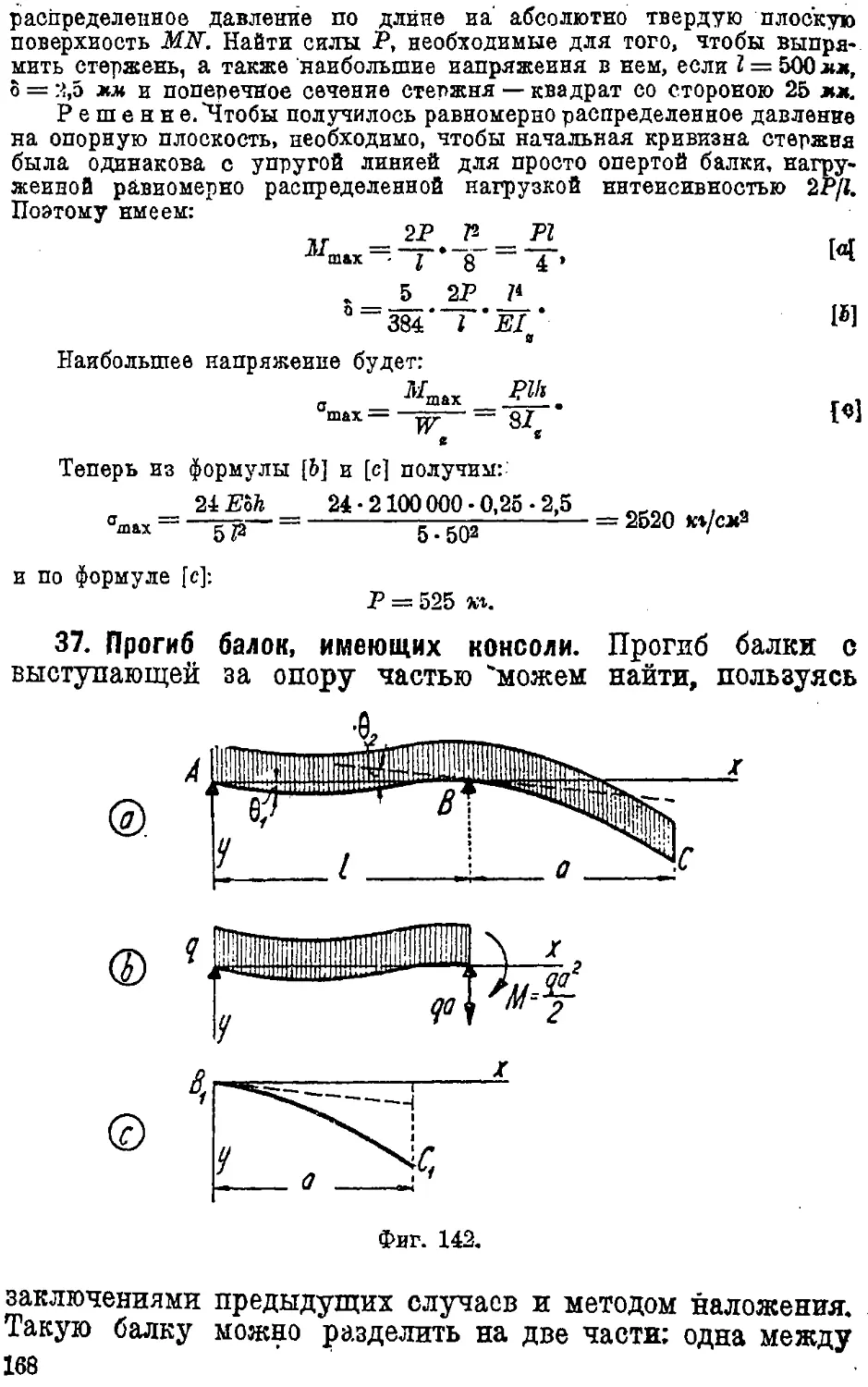
37. Прогиб балок, имеющих консоли 168
38. Балки переменного поперечного сечения ............ 172
39. Дифференциальное уравнение упругой линии . . • 180
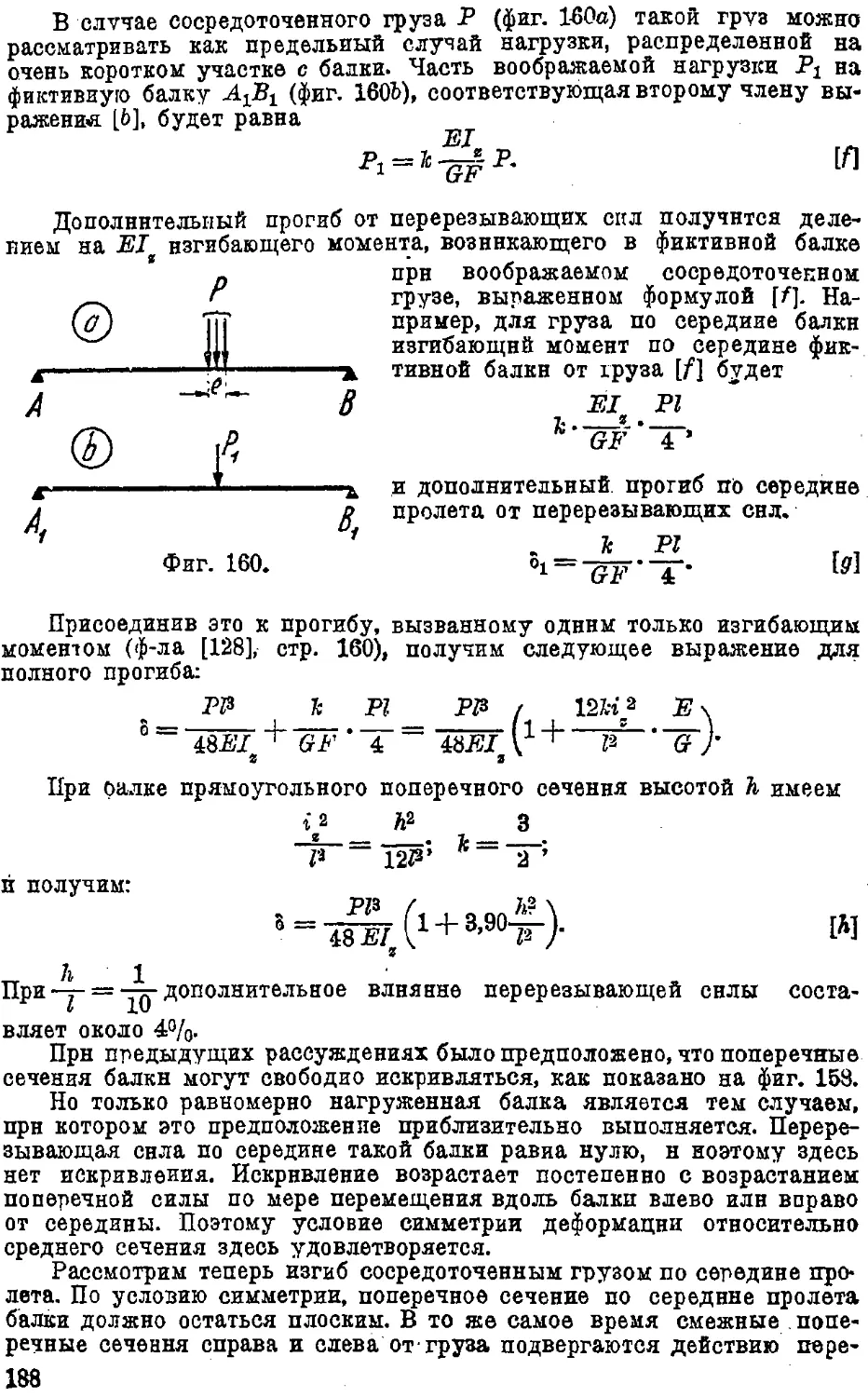
40. Влияние перерезывающей силы на прогиб балок 185
41. Изгиб балок* в главной плоскости, не являющейся плоскостью
симметрии . * .' . 190
42. Изгиб балок, когда силы непараллельны ни одной.из двух
главных плоскостей изгиба 194
Глава шестая.
Статически неопределимые задачи при изгибе.
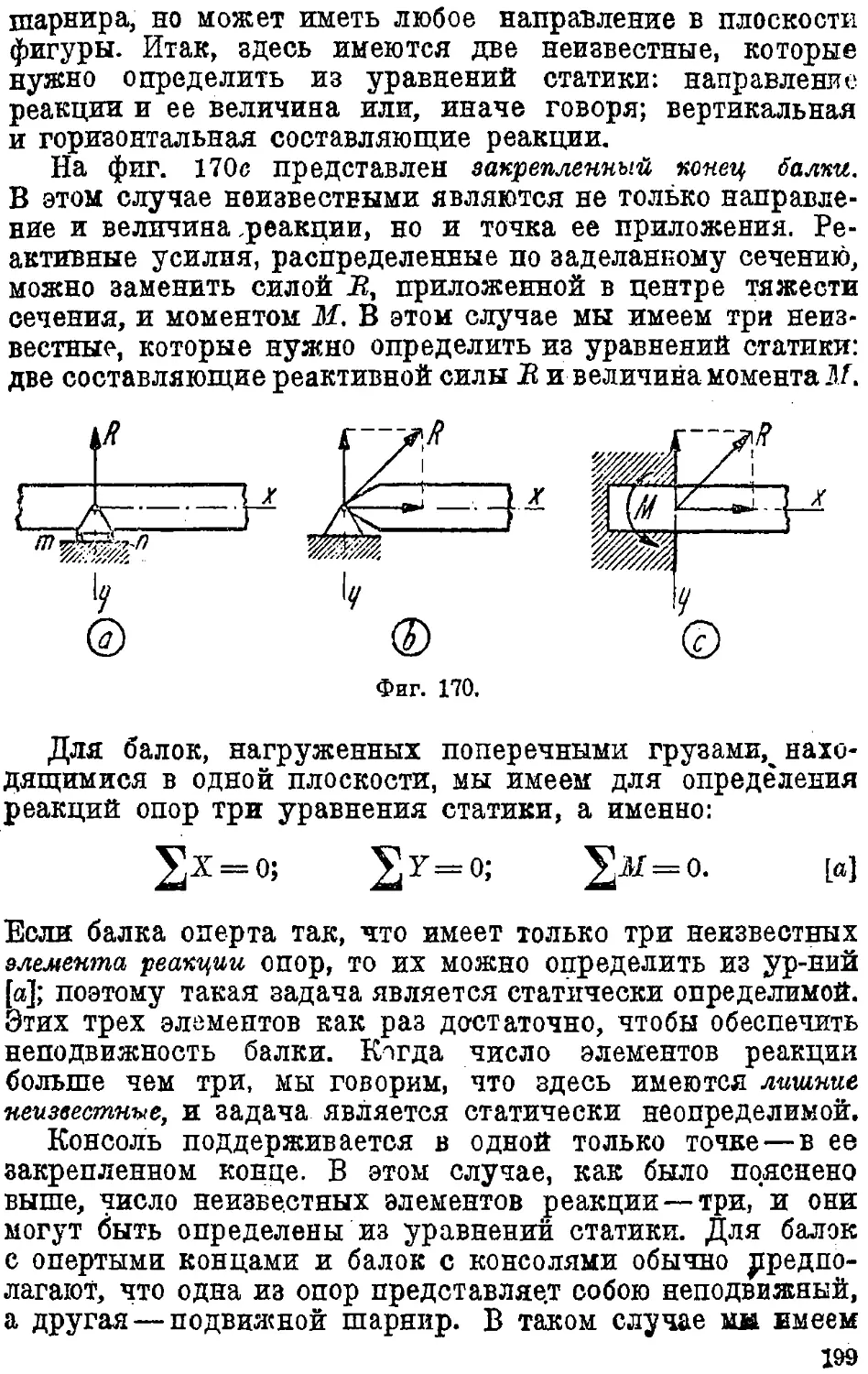
43. Лишние неизвестные 198
44. Балка, заделанная одним концом и опертая другим 201
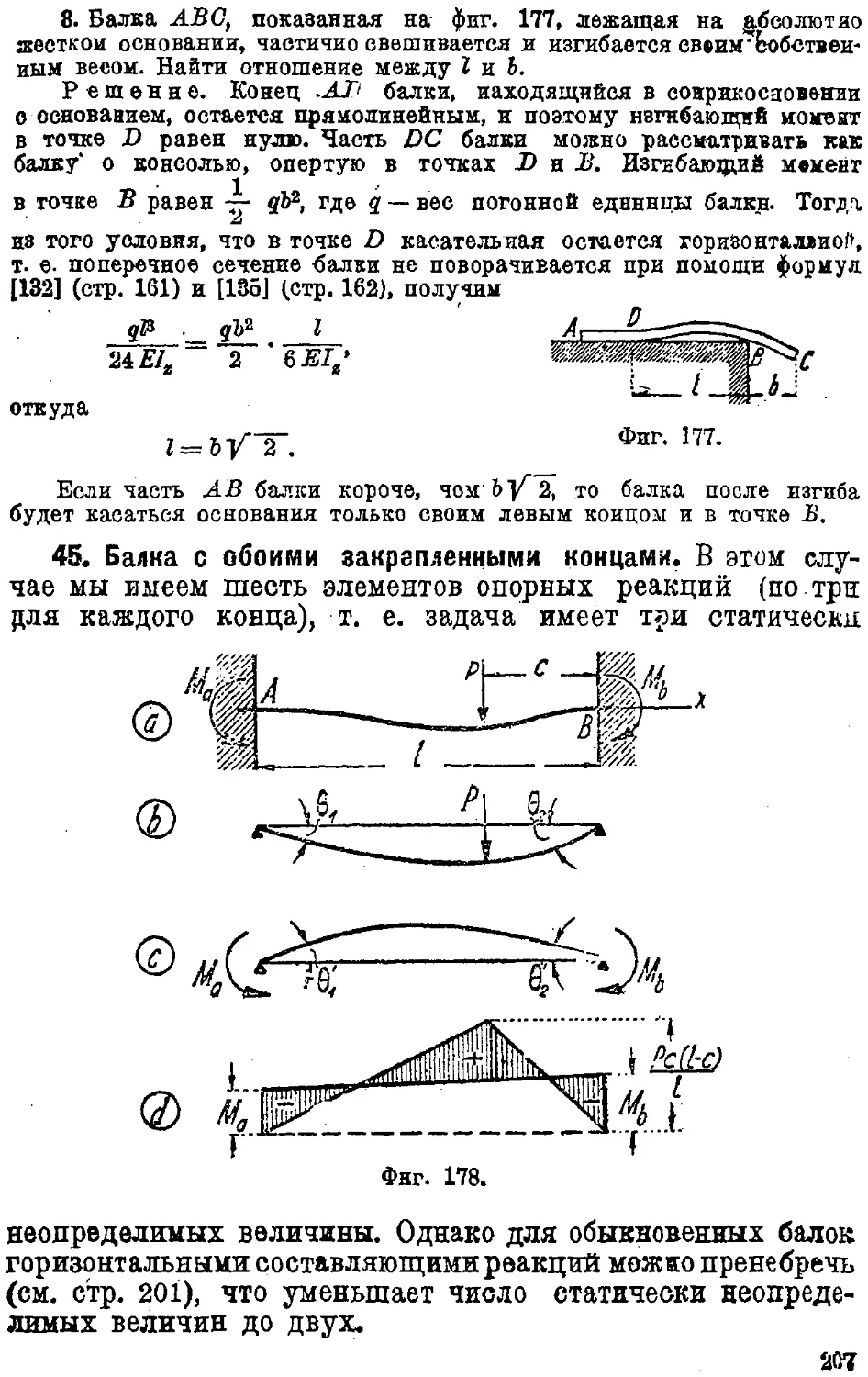
45. Балка с обоими закрепленными концами 207
46. Рамы • . . 212
47. Балки на трех опорах " 220
48. Неразрезвые многопролетные балки • . . 223
Глава седьмая.
Балки, материал которых не следует закону Гуна. Балки из двух
материалов.
49. Чистый изгиб, когда материал не следует закону Гука ... 230
50. Изгиб прямоугольного стального стержня за пределом
текучести • 234
61. Балки из материалов, имеющих различные модули упругости
при растяжении и сжатии 239
52. Балки из двух разных-материалов 241
58. Железобетонные балки . . . . . 244
64. Скалывающие напряжения в железобетонных балках ..... 248
VII
Глава восьмая.
Стр.
Напряжения от совместного действия осевых и изгибающих сил.
65. Изгиб и сжатие или растяжение 249
56, Внецентрениая нагрузка коротких стоек 253
57. Ядро сечения 257
68. Внецентрениая нагрузка длинной стойки, действующая
в главной плоскости 263
Глава девятая.
Совместное действие изгиба и кручения.
69. Совместный изгиб и кручение круглых валов '. . 267
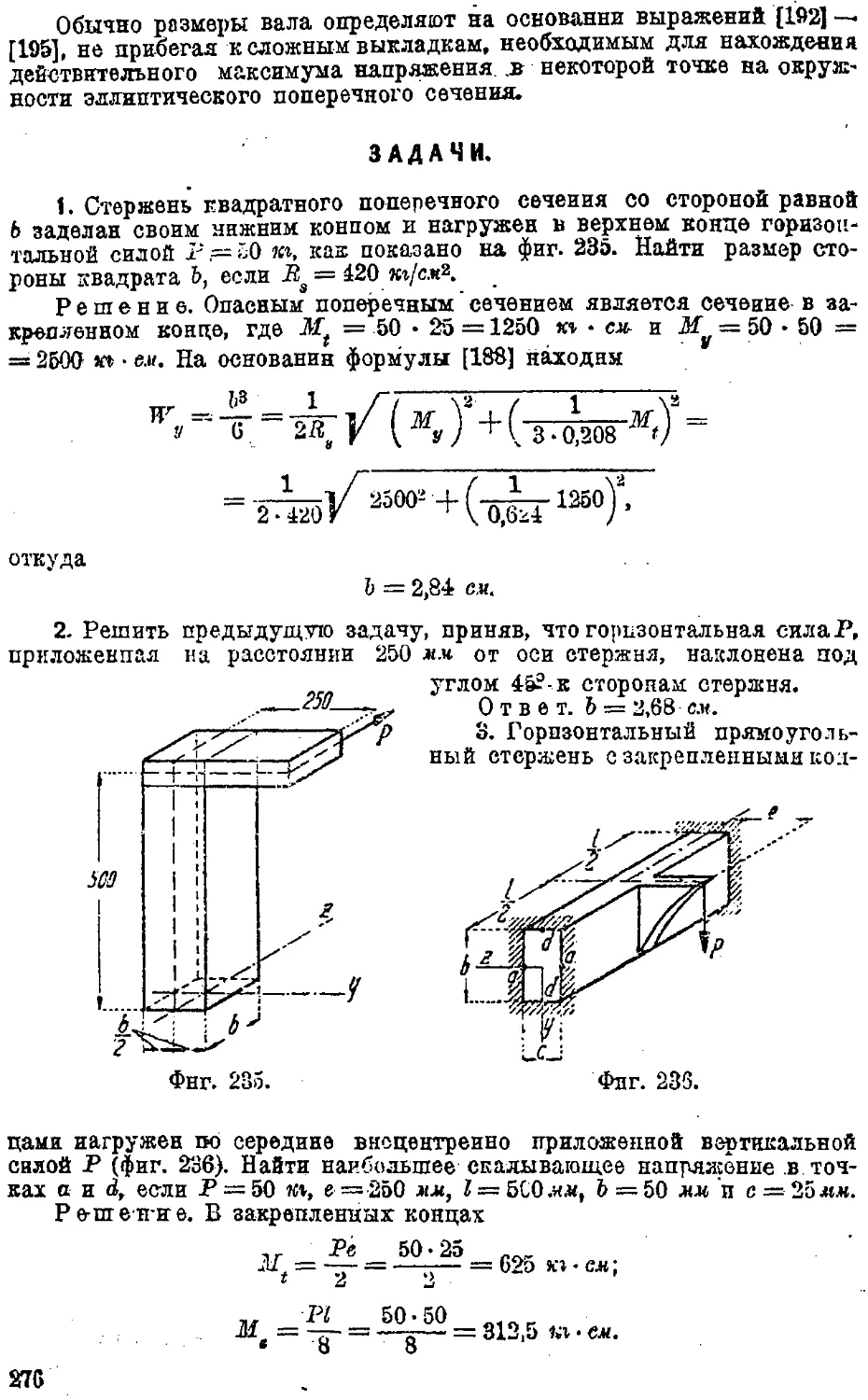
60. Совместный изгиб и кручение прямоугольных и
эллиптических валов 273
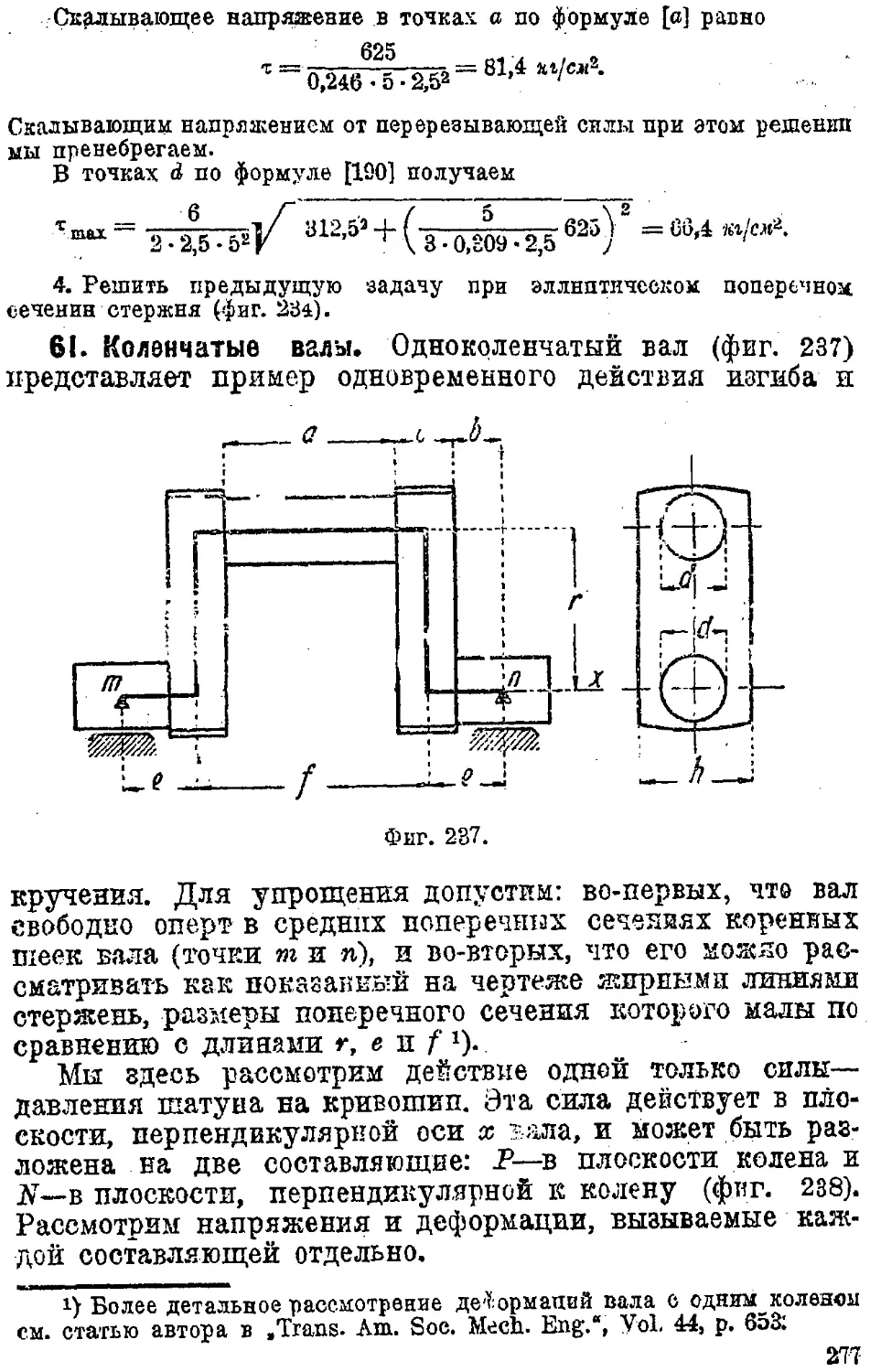
61. Коленчатые валы .... 277
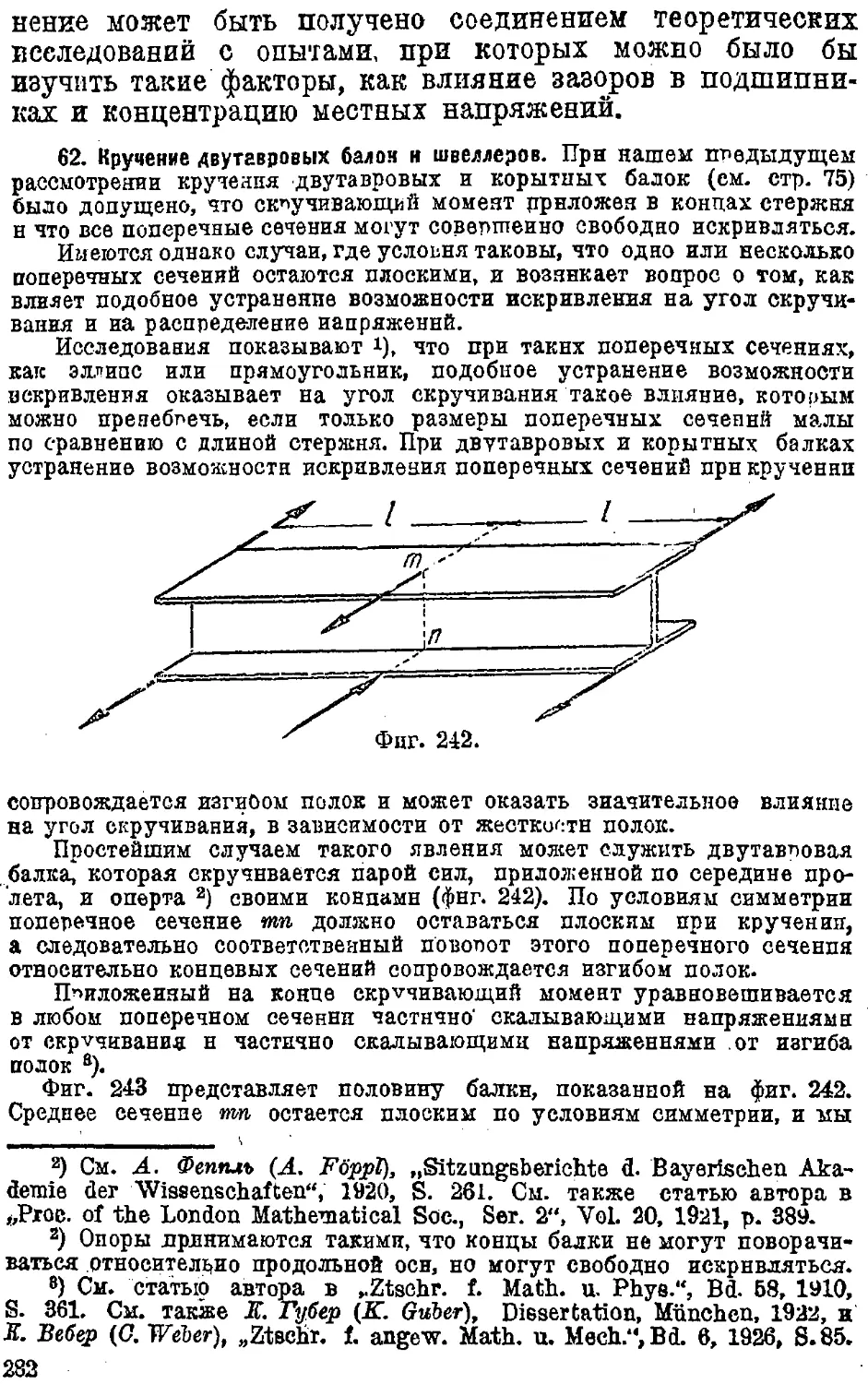
62. Кручение двутавровых балок и швеллерои 282
63. Винтовая пружина с большим шагом витка 288
Главадесятая.
Потенциальная энергия деформации.
64. Потенциальная энергия упругой деформации растяжения . . 2S9
65. Растяжение, вызванное ударом 293
66. Потенциальная энергия упругой деформации при сдвиге и
кручении 300
67. Потенциальная энергия упругой деформации изгиба 304
68. Изгиб при ударе 310
69. Общее выражение потенциальной энергии деформации .... 315
70. Теорема Кастильяно 317
71. Применение теоремы Кастильяно к решению статически
неопределимы • задач ¦ 327
7?. Теорема о взаимности перемещений 837
73. Напряжения от неточности сборки и температурные
напряжения в статически неопределимых системах 345
74. Исключительные случаи 847
ПРИЛОЖЕНИЕ.
Моменты инерции плоских фигур.
I. Момент инерции плоской фигуры относительно оси,
находящейся в ее плоскости 350
И. Полярный момент инерции плоской фигуры 353
III. Перенос оси . . 355
IV. Центробежный момент ине^ии, главные оси 356
, V. Поворот оси. Нахождение главных осей 35$
ОБОЗНАЧЕНИЯ.
Sgp Зу, 9Я — нормальные напряжения по площадкам перпендикуляр"
ньтм осям х, у и z\
ап — нормальное напряжение по площадке перпендикулярной
направлению щ
ст — предел текучести;
R, Еф Re —допускаемое нормальное напряжение вообще, при
растяжении и при сжатии;
Rb3Bbs,Bbd-~то же при изгибе вообще, при изгибе на растяжение и
на сжатие.
сз ~" временное сопротивление;
т — скалывающие касательные (V) напряжения;
тя*у» %уя* гяа> ~" скалывающие нааряжения параллельные осям х, у н s до
площадкам, перпендикулярным осям у, я и щ
&й — допускаемое напряжение на сдвиг;
Д,2,5— полное, абсолютное удлинение, полный прогиб;
s — относительное -удлинение;
*х> V ^ — относительные удлинения по направлению осей ее, у н <?;
Y — относительный сдвиг, вес единилы объема;
Е — модуль упругости при растяжении и сжатии;
G — модуль упругости при сдвиге;
Р- — Пуассоново отношение;
Д — увеличение объема;
К— модуль упругости объема;
М^—момент кручения;
ЛГ—изгибающий момент в балке;
Q — перерезывающая сила в балке;
F— площадь поперечного сечения;
/,., 2г—моменты инерции плоских фигур относительно осей у я*;
V г'в — радиусы инерции, соответствующие 1у н Iz\
/р — полярный момент инерции,
W—момент сопротивления;
? — уоилня в стержнях;
IX
С —жесткость при.кручений;
Z — длияа стержня, пролет балки;
Р, Q — сосредоточенные силы, грузы, в?о;
і — температура, толщина; ¦
а —коэффициент линейного расширения от температуры,
числовой коэффициент;
27— потенциальная энергия деформации;
а,.., аа — потенциальная энергия деформации, отнесенная к
единице объема, при растяжении и при сдвиге:
h — высота балки, толщина плиты;
q — равномерно распределенная нагрузка на единицу длины;
<Р, 0 — углы;
р — давление;
D, d! — диаметры;
Б, г —радиусы;
р — радиус кривизны.
УКАЗАТЕЛЬ ИМЕЙ.
Андре (Andree, W. L.) 21G.
Андрус (Andrews, E. S.) 319.
Арновлевпч (ArnovleviC, I.) 142.
Бах (Bach, С.) 234.
Бё'клей (Buckley) 83.
Берто (Bertot) 225.
Бетти (Betti, E.) 337.
Бнец?но (Biezeno, С. В.) 281.
Бредт (Bredt, R.) 72, 75.
Буссинеск (Boussinesq, I.) 208.
Давидеяков, Н. Н. 296.
Дрейер (Dreyer, G.) 261.
Журавский 120.
8аес (Sa«a, F.) 281.
Зеегар (Seegar, М.) 103.
Зеельман (Seelminn) 281.
Карман (Karman, Th.) 189.
Кастильяно (Castigliano, A.) 176,319,
323.
Кек (Keck, Z.) 261.
Кидвелл (Kidwell, E.) 139.
Клапейрон (Clapeyron) 31C.
Клейнлогель (Kleinlogel) 217.
Кокс (Сох, Н.) 29S, 312.
Навь? (NaTier) 298.
Парр (Parr, P. H.) 176.
Перри (Perry, J.) 266, 288.
Пвтерман (Petermann, J.) 234.
Пнявгиа 234.
Вагнер (Wagner, I) 135.
Валь (Wahl, A. M.) 80.
Вебер (Weber, C.) 77, 83, 193, 274,282.
Вейраух (Weyrauch, T.) 317.
Вельтер (Welter) 29G.
Вестергаард (Westergaard, H. M.) 1C9.
Вильсон (Wilson, C.) 146.
Вэкстэфф (Wagstaff, J. E. P.) -J99.
Гакштро (Hackstroh) 297,
Генкель (Henkel, 0.) 261.
Герберт (Herbert, H.) 231.
Г?сснер (Gessner, A.) 281.
Гриффиц (Griffith, A. A.) 75.
Грюнейзен (Griineisen) 7.
Грюнинг (Griinning, M.) 328.
Губер (Huber, K.) 282.
Гук (Hooke, R.) 2.
Ландау (Landau, D.) 176.
Леви (Levy, M.) 227.
Лове (Love, A. E. H.) 128.
Лоренц (Lorenz, Ы.) 72.
Льюис (Lewis F. M.) 281.
Ляме (LameV 316.
Майяр (Maillart, R.) 193.
Максвелл (Maxwell, C.) 324,337,
Марье (Marie, G.) 176.
Мейер (Meyer, E.) 231, 281.
Менабреа (Mcnabrea, F.) 327.
Мичелль (Michell) 126, 172.
Mop (Mohr, 0.) 50, 227, 328, 337.
Мур (Моог?, Н. P.) 142.
Мэрш (Morsch, E.) 227.
Мюллер-Бреслат (Miiller-Breslau
328, 337, 347.
XI
Пирсон (Pearson, К.) 193.
Поль (Pohl, К.) 261.
Прескотт (Prescott, Т.) 72.
Пуассон (Poisson) 53.
Рамзауер (Ramsauer, С.) 298.
Рейлей (Lord Rayleigh) 337.
Рёвер (Rover, V.) 80.
Риттер (Ritter, W.) 227,
Рочь (Ro§, M.) 313.
Сен-Венан (Saint-Venant) 73, 76, 77,
120. 128,288, 298, 313.
Сире (Sears, J. Е.) 298.
Годгёнтер и Пирсон (Todhunter and
Pearson) 73, 120, 176, 298.
Томпсон и Т»т (Thompson and Tait)
288.
Тшетш? (Tschetsclie) 313.
Тэйлор (Taylor, G. Y.) 75.
Ф'іппль, A. (Foppl, A.) 61,72,75,
282.
Феппль, Л. (Foppl, L.) 75.
Филлипс (Phillips, Б.) 176.
Филон (Filon, L. N. G.) 126, 189.
Фламан (Flamant) 145.
Фойгт (Voigt, W.) 126.
Ши^ер (Shearer, G. W.) 288.
Шюле (Schuele, W.) 234.
Эггеншвилер (Egge nschwyler, A.)
193.
Энгессер (Engesser, F.) 261, 328.
Бсдинг (.Esling, F. K.) 261.
i
ПРЕДМЕТНЫЙ
Балки, главы IV, V, VI, VII:
главные напряжения в, 131;
железобетонные, 244;
из двух различных материалов,
241; '
клепаные, 137;
консольные, 149;
материал, которых не следует
закону Гука, 230;
на трех опорах, 220;
неразрезные многопролетные,
2^3;
нормальные напрязкения в, 90;
переменного сечения, 172;
прогиб, глава V;
просто опертые концами, 167;
с заделанными концами, 207;
скалывающие напряжения в, 11S;
со свешивающимися консолями,
108;
составная, 137.
Безопасности коэффициент, 8.
Боковое сужение, 54»
Валы:
кругового сечения, 65;
некруглые, 73;
при действии изгиба ц кручения,
^67;
пустотелые, 70.
Взаимности теорема, 337
Виды поперечных сечений балок,
97.
Винтовые пружины:
с большим шагом витка, 28G;
о малым шагом витка, 78.
УКАЗАТЕЛЬ.
Внецентренная продольная
нагрузка, 253
Временное сопротивление, б, 7.
Второстепенные напряжения
при изгибе, 144;
при кручении, 83.
Главные:
напряжения, 4В;
напряжения в балках, 131; ¦
напряжения в валах, 289, 270,
273, 274, 275;
оси инерции, 356;
плоскости изгиба, 93, 190.
Гука закон, 2.
Давление на колонны, 263.
Деформация:
винтовых пружин
конических, 82;
с большим шагом витка. 2S8;
с малым шагом витка, 81;
остаточная. 2;
плоских пружин, 176;
при растяжении и сжатии, 4;
при сдвиге, 56.
Диф Ьеренциальное уравнение
упругой -линии, 180.
Допускаемое напряжение, 7.
Железобетонные балки, 244.
Жесткость:
на кручение, 78;
"при изгибе, 9L
Заклепок напряжение, 119,
Закрепление кондов, 199.
XIII
Изгиба, теория, главы IV, V, VI,
VII.
Изгибающий момент, 88, 103;
приведенная эпюра, 177;
эквивалентный, 269;
эпюра его, 105.
Изгиб:
в плоскости наклонной к главным
осям, 190;
эа пределом текучести, 234;
и кручение совместно, 267;
и осевые напряжения, 249;
коленчатых валов, 277;
неразрезных балок, 220, 223;
потенциальная энергия его, 304;
рам, 212;
составной из двух металлов
линейки, 242;
тавровой балки, 101;
чистый, 86.
Изменение объема, 61.
Изотропный материал, 53.
Инерции моменты 350.
Испытание на растяжение, 1;
диаграмма его, 5;
Кастильяно, теорема, 317;
определение прогибов ферм
помощью ее, 320;
решение статически
неопределимых задач помощью ее, 327.
Клапейрона уравнение трех
моментов, 225.
Клепаные балки, 137.
Клина изгиб, 172.
Коленчатый вал с одним коленом,
277.
Кольца круговые, 28;
вращающиеся, 29.
Конические пружины, 82.
Консоль, 149.
Кот?л цилиндрический, 50.
Кривизна балок, 89, 147, 180.
Критический груз, 265.
Круглый вал при кручен ни, 64.
XIV
Круговое кольцо, расширение ere,
28;
вращающееся, 29.
Коэффициент безопасности, 8.
Линейка из двух металлов, 242.
Линия влияния, 342.
Лишние неизвестные, 198.
Модуль упругости:
объемный, 62;
при растяжении и сжатии, 2;
при сдвиге, 59.
Момент:
изгибающий, 98;
инерции, 350;
сопротивления, 92, 262.
Мора круг, 47.
Наименьшей работы начало, 327.
Напряжения, 3;
главные, 46;
главные при изгибе, 131;
допускаемые, 7;
нормальные, 41;
от неточности оборки, 24, 345;
сжатия, растяжения, 4;
скалывающие при изгибе, 119;
скалывающие при растяжений,
41;
совместные, 44.
Начало наименьшей работы, 327.
Начальные напряжения:
при изгибе за пределом
текучести, 238;
при растяжении, 24.
Нейтральная ось, 89;
поверхность, 89.
Перазрезная балка, 220, 223;
с опорами н? на одном уровне,
226.
Нити, напряжения в них, 32;
температурные напряжения
них, 36.
Нормальные напряжения, 41.
Объемный модуль упругооти,
62.
Остаточная деформация, 2, 7,-
Остаточные напряжения при изгибе
за пределом текучести, 238.
Относительное удлинение, 4.
Параболический закон упругости,
233.
Переменное сечение.
балок, 172;
растянутых стержней, 15.
Перерезывающая сила при изгибе,
103;
влияние ее на прогиб, 185;
эпюра ее, 105.
Полярный момент инерции, 353.
Поперечное сечение балки,
различные виды, 97.
Потенциальная энергия
деформации, глава X, 289;
при изгибе, 304;
при кручении, 300;
при растяжении, 289;
при сдвиге, 300.
Предел пропорциональности, 5.
Предел текучести, G.
Приведенная масса, 297, 312.
Приведенный модуль упругости,
241.
Прогиб балок, глава V:
консоли, 149;
несимметричного поперечного
сечения, 190;
от удара, 310;
от перерезывающей силы, 185;
переменного сечения, 172;
просто опертых концами, 157;
под действием осевых
изгибающих сил, 263;
равномерно нагруженных, 151,
162, 168;
с закрепленными концами, 201,
207;
с консолями, 168.
Пружины винтовые с малым
шагом витка, 78;
с большим шагом витка, 286;
конические, 82;
плоские, 176.
Пуассоново отношение, 63.
Пустотелые валы, 70.
Равного сопротивления^ тело:.
на изгиб, 174;
на растяжение, 15.
Равное сопротивление
при изгибе, 174;
при растяжении, 15.
Радиус инерции, 352, 360.
Радиус кривизны, 89, 147, 180.
Рамы, 212.
Растяжение и сжатие, глава I;
потенциальная энергия его, 289;
при ударе 293.
Сдвиг чистый, 56;
в балках, 103, 119;
прогиб от него, 185.
Сжатие, 4;
внецентренное, 253;
деформация от него, 4;
напряжение от него, 4.
Скалывающие напряжения в бал*
ках, 119;
круглых, 127;
двутаврового сечения, 129;
железобетонных, 248;
при растяжении, 41;
прямоугольного сечения, 119.
Скручивающий момент, 66.
Скручивание корытных и
двутавровых балок, 74, 282;
круглых валов, 64;
некруглых валов, 73;
потенциальная энергия его, 300;
прокатного профильного сечения,
74;
прямоугольных валов, 73;
пустотелых валов, 70;
IV
еовместно с изгибом, глава IX,
тонких прямоугольных линеек, 85;
трубчатых сечений, 70.
Совместные напряжения, глава II,
40;
изображение их кругом Мора, 47.
Совместный изгпб и кручение,
глава IX, 26J.
Совместный изгиб и осевое
усилие, глава VIII, 249.
Сопротивление временное, 6.
Сопротивления момент, 92, 262,
Составные балки, 137.
Способ наложения при изгибе, 151.
Срезывание заклепок, 140.
Статически неопределимые
системы, 18, глава VI, 200, 3^6.
Стержень равного сопротивления,
15.
Стойки, 263;
короткие, внецентренно
нагруженные, 253.
Сужение боковое, 53.
Текучесть, 6.
Температурные напряжения:
в нитях, 3G;
при изгибе, 96,206, 345;
при растяжении и сжатии, 24, 29,
345.
Траектории напряжений, 134.
Трех моментов уравнение, 225.
Угол скручивания, 65, 68.
Удар пт>и изгибе, 310;
при кручения, 304;
при растяжении, 293.
Удлинение при простом
растяжении, 3;
при совместных напряжениях, 54,
60.
Упругой деформации
потенциальная энеттия, глава X, 289.
Упругая линия, ее
дифференциальное уравнение, 180;
построение ее при помощи
эпюры изгибающих моментов, 147.
Упругость 2.
Уравнение трех моментов, 225;
упругой линии, 180.
Фиктивная балка, фиктивная
нагрузка в теории изгиба, 158.
Центробежный момент инерции,
94, 356.
Центр скручивания, 192.
Цилиндрический котел, 50
Цилиндрические трубы,
температурные напряжения в них, 29.
Эллиптическое сечение вала, 76;
совместное кручение и изгиб
такого вала, і75.
Энергия деформации при изгибе
304;
при сдвиге, 300;
при растяжении, 289;
общее выражение, 315.
Эпюра изгибающих моментов, 107;
перерезывающей силы, 107Р
Ядро сечения, 258.
ГЛАВА ПЕРВАЯ.
РАСТЯЖЕНИЕ И СЖАТИЕ В ПРЕДЕЛАХ УПРУГОСТИ,
ш
ф
>-я
Г. Упругость. Мы предполагаем, что тело состоит из неболь*
ших частиц—молекул, между которыми действуют силы.
Эти молекулярные силы, сопротивляются изменению формы
тела, которое внешние силы
стремятся вызвать. Если такие
внешние силы приложены к телу,
то его частицы смещаются, и
их взаимные перемещения
продолжаются до тех пор, дока не
установится равновесие между
внешними и внутренними
силами. В таком случае говорят, что
тело находится в
деформированном состоянии. При деформации
внешние силы, действующие на
тело, совершают работу, и эта
работа целиком или частично
-превращается в потенциальную
энергию деформации. Примером
такого накопления
потенциальной энергии в деформированном
теле может служить часовая
пружина. Если силы, которые вызвали деформацию тела, бу
дут постепенно уменьшаться, то тело возвратится вполне
или отчасти к своей первоначальной форме, и при этой
•обратной деформации потенциальная внергии деформации,
накопленная в теле, может быть получена обратно в виде
внешней работы.
Возьмем например призматический стержень,
нагруженный на конце, как показано на фиг. 1. Под действием
этого груза произойдет некоторое удлинение стержня.
Точка приложения груза будет двигаться вниз, и во время
этого движения груз будет давать положительную работу.
Когда нагрузка уменьшается, то уменьшается также и
J Тийошенко — Сопротивлениематериалов, ч. I. 1
\Р
Фиг. 1.
удлинение стержня; нагруженный конец стержня
двигается вверх, и потенциальная энергия деформации
превращается в работу перемещения груза вверх.
Свойство тел принимать после разгрузки свою прежнюю
форму называется упругостью. Тело считается вполне упру-
ггш, если после разгрузки оно принимает полностью свою
первоначальную форму, и не вполне упругим, если
деформация, вызванная внешними силами, не исчезает вполне
после их удаления. В случае вполне упругого тела, работа,
совершенная внешними силами при деформации, целиком
превращается в потенциальную энергию деформации. В
случае не вполне упругого т$ла, часть работы, совершаемой
внешними силами при деформации, рассеивается в виде
тепла, которое развивается в теле при неупругой
деформации. Опыты показывают, что такие строительные
материалы, как сталь, дерево и камень, могут считаться вполне
упругими в известных пределах, которые зависят от свойств
материала.
Если допустить, что внешние силы, действующие на
сооружение, известны, то основной задачей для
проектирующего будет назначение таких размеров частям
сооружения, чтобы оно как можно больше приближалось к
состоянию вполне упругого тела при всех обстоятельствах
своей работы. Только при таких условиях мы будем иметь
постоянство надежной работы сооружения и отсутствие
остаточной деформации в его частях.
2, Закон Гуна. Непосредственным опытом с растяжением
призматических стержней (фиг. 1) установлено, что для
большинства строительных материалов в известных
пределах удлинение стержня пропорционально растягивающей
силе. Эта простая линейная зависимость между силой
и удлинением, которое она производит, была впервые
сформулирована английским ученым Робертом Гуком х)
в 1678 году, и носит его имя. Приняв обозначения: F—сила,
вызывающая растяжение стержня, I—длина стержня, F—
площадь поперечного сечения стержня, ЛI—полное
удлинение стержня, Е—упругая постоянная материала,
называемая модулем упругости, можем выразить основанный на
опыте закон Гука в виде следующего уравнения:
Удлинение стержня пропорционально растягивающей
і) liobert Лооке, De Potentia restitutiva, London, 1678,
2
силе и длине стержня к обратно пропорционально площади
поперечного сечения и модулю упругости. При испытаниях
на растяжение обыкновенно принимаются меры» чтобы
обеспечить центральность приложения растягивающей силы.
Таким образом предотвращается какой бы то ни было изгиб
стержня. Выключая из рассмотрения части стержня,
находящиеся в непосредственной близости к приложенным
силам *), можем принять, что при растяжении все продольные
волокна призматического стержня имеют одинаковое
удлинение, и поперечные сечения стержня, бывшие плоскими и
перпендикулярными к оси стержня, остаются таковыми и
после деформации.
Рассматривая величину, внутренних сил, представим
стержень разрезанным на две части поперечным
селением т? и рассмотрим условия равновесия нижней части
стержня (фиг. 16). К нижнему концу этой части приложена
растягивающая сила Р. На верхний конец действуют силы,
представляющие взаимодействие между частицами верхней
части растянутого стержня и частицами нижней его части.
Зти силы непрерывно распределены сплошь по всему
сечению. Хорошо известным примером такого непрерывного
распределения сил по поверхности является
гидростатическое давление или давление пара. При рассмотрении
подобных непрерывно распределенных сил существенно важно
знать гінтепсивиость силы, т. е, силу, действующую на
единицу площади. В нашем случае осевого растяжения, при
котором все волокна имеют одинаковое удлинение,
распределение сил по поперечному сечению тп будет
равномерным. Приняв во внимание, что сумма этих сил, из условия
равновесия (фиг. 1Ь), должна быть равна Р, и обозначив
силу, приходящуюся на единицу площади поперечного
сечения, через о, получим
°—Ж"" [2]
Эта сила, отнесенная к единице площади, называется
иапряжеигь&и, В дальнейшем сила измеряется в
килограммах и площадь в квадратных сантиметрах, так что
напряжение выражается в килограммах на квадратный сантиметр.
Удлинение стержня, отнесенное к единице длины его,
определяется выражением:
М
s
I
м
*) Распределение более сложных напряжений вблизи точек
приложения сил рассматривается далее в главе YI, части II.
1* і
и называется относительным удлинением. Пользуясь
уравнениями [2] и [3], можем представить закон Гука в
следующем виде:
Е
м
Относительное удлинение легко определить, если только
известны напряжение и модуль упругости материала.
Относительное удлинение е — отвлеченное число, являющееся
отношением между двумя длинами (см. ур-ние [3]); поэтому,
из ур-ния [4] можем заключить, что модуль упругости
измеряется в тех же единицах, что и напряжение о,
т. е. в килограммах на квадратный сантиметр. В таблице 1
(см. ниже) во втором столбце приведены средние значения
модуля Е для нескольких материалов х).
Ур-ниями [1] — [4] можно воспользоваться также в
случае сжатия призматических стержней. Тогда М будет
обозначать полное продольное укорочение, е —
относительное укорочение и <з— сжимающее напряжение. Модуль
упругости при сжатии для большинства строительных
материалов тот же, что и для растяжения. В дальнейших
выкладках будем считать растягивающее напряжение и
деформацию растяжения положительными, а сжимающее
напряжение и деформацию при сжатии — отрицательными.
ТАБЛИЦА 1.
Механические характеристики материалов.
Материи лы
Сталь лнтая 0,15—0,25% угле-
Никелевая сталь 3—3,5% ннкеля
Стекло . . . . . . . . . . . .
¦Е
иодуль
упругости
2100000
2000000
700000
1120000
700000
280000.
100000
предел
текучести
кг}сл*
2100-2800
2 300—3 500
2 450—3150
ев
временное
сопротивление
кг\слр
¦
3 850—4 550
5 450—7000
3780-4 550
2000-2 500
250
210
560-1400
і) Более, детально о механических свойствах материалов см. главу VII,
часть II. '
ЗАДАЧИ.
. 1. Определить полное удлинение стального стержня длиной СО см
если растягивающее напряжение — 1050 кг/ск2.
О т в е т. ДI = ? • I = —TqAqq • 60 = 0,03 см = 0,3 мм.
2. Определить силу, растягивающую цилиндрический стальной
стержень диаметром 25 мм, если относительное удлинение равно 0,0007.
Решение. Растягивающее напряжение в стержне по ур-ник> [4]
v = е. Е = 1 470 кг/сл2.
Растягивающая сила по ур-нию [2] равна:
Р = а . F » 1470 • ^-р^ = 7 220 кг.
3;:В каком отношении находятся модули упругости материалов двух
стержней одинаковых размеров, если под действием одинаковых
растягивающих сил относительное удлинение одного из стержней составляет
-g- относительного удлинения другого? Определить эти удлинения, если
одни из стержней стальной, а другой из меди, и растягивающее
напряжение равно 700 k\Jcm\
Решение. Модули упругости обратно пропорциональны
относительным удлинениям.
Для стали .
__ 700 _ 1
S 2100000 3000 '
Для меди
1 .
6 1600 *
3. Диаграмма раотяжениа. Пропорциональность между
растягивающей силой и удлинением сохраняется только до
известного предельного значения растягивающего
напряжения, называемого пределом пропорциональности, который
зависит от свойств материала. За этим пределом
соотношение между удлинением и растягивающим напряжением
становится более сложным. Для такого материала, как
литая сталь, пропорциональность между грузом и
удлинением остается в силе в широких границах, и предел
пропорциональности можно считать таким высоким, кг к
1-750 — 2100 кг/де*. Для такого материала, как чугун или
мягкая медь, предел пропорциональности очень низок, так
что уклонение от закона Гука можно отметить при
небольших растягивающих напряжениях. При исследовании
механических свойств материалов выше предела
пропорциональности, отношение между деформацией и
соответствующим напряжением обычно представляется гріа$йч;ес№'
5
диаграммой растяжения. Фиг. 2а представляет типичную
диаграмму для литой стали. Здесь удлинения отложены
по горизонтальной оси, а соответствующие напряжения даны
ординатами кривой OABCD. От О до Л напряжение и
деформация пропорциональны; за Л делается заметным
отклонение от закона Гука, почему напряжение в Л является
пределом пропорциональности. При нагрузке выше этого
предела удлинение
возрастает более быстро,
и диаграмма получает
вид кривой. В точке В
имеет место внезапное
удлинение стержня
без заметного
увеличения растягивающей
силы. Это явление,
называемое текучестью
металла, изображается
на диаграмме почти
горизонтальным
участком кривой.
Напряжение, соответствующее
точке В, называется
пределом текучести.
При дальнейшем
возрастании
напряжения стержня, к
металлу вновь
возвращаются его
первоначальные свойства, и,
как видно из
диаграммы, необходимая
растягивающая сила
возрастает вместе с
удлинением и далее до
точки С, в которой эта
сила достигает своего наибольшего значения.
Соответствующее напряжение называется временным
сопротивлением материала. За точкой С удлинение стержня
сопровождается уменьшением силы и наконец происходит
разрыв при грузе, отвечающем точке В диаграммы.
Следует отметить, что удлинение стержня сопрово*
ждается сокращением поперечных размеров; но, по
установившемуся обыкновению при определении предела
текучести и временного сопротивления, пользуются перво-
6
Фиг. 2.
начальной площадью поперечного сеіеняя Р. Этот вопроо
рассмотрен далее более детально (см. главу VII части II),
Фиг. 2Ъ представляет диаграмму растяжения для чугуна.
Этот материал имеет очень низкий предел
пропорциональности х) и у него нет определенного предела текучести.
Диаграммы, аналогичные таковым при растяжении/
можно получить также для сжатия различных материалов*
и для сжатия можно установить те же характерные точки:
предел пропорциональности, предел текучести—в случае'
стали, и временное сопротивление. Механические свойства
материалов при растяжении и сжатии рассмотрены более
подробно далее (см. главу VII части П).
4. Допускаемое напряжение. Диаграмма растяжения дает
очень ценное освещение механических свойств материала.
Зная предел пропорциональности, предел упругости и
временное сопротивление материала, возможно установить для
каждой частной задачи инженерного дела величину
напряжения^ которое можно рассматривать как безопаснее напряжение.
Это напряжение обычно называется допускаемым напряжением.
При выборе величины допускаемого напряжения длгг
стали следует принять во внимание, что при напряжениях
ниже предела пропорциональности этот материал можно
считать вполне упругим, а выше этого предела часть
деформации обычно остается после разгрузки стержня,
т. е. имеет место остаточная деформация. Чтобы сохранить
конструкцию в упругом состоянии и устранить возможность
остаточной деформации, обычно принято назначать
допускаемое напряжение значительно ниже предела
пропорциональности. При опытном установлении этого предела
необходимы чувствительные измерительные приборы (экстенсо-
метры), и положение этого предела зависит до некоторой
степени от точности, с которой произведены измерения.
Чтобы устранить это затруднение, обыкновенно берут за
основу для определения величины допускаемого напряжения
предел текучести или временное сопротивление материала.
Обозначив через В, ст и ов соответственно допускаемое
напряжение, предел текучести и временное сопротивление
материала, можем выразить величину допускаемого напряжения
одним из двух следующих уравнений.
Д = -^- или JB = -^-.- И
»———¦ т.II— 1.1 ИМ
*) Этот предел можно установить только пользуясь при измерении
удлинений очень чувствительными экстенсометрами. См. Грюнейзек
(trriineisen), Berichte d. deutsch. phys. Gesellschaft, 1906.
7
Здесь п и: гц—коэффициенты, обычно называемые коэф*
фициеитами безопасности (запас прочности) и определяющие
величину допускаемого напряжения. Для литой стали
логично принять предел текучести за основу для назначения
допускаемого напряжения, так как при напряжении выше
'этого предела может получиться значительная остаточная
деформация, которая недопустима в инженерных
сооружениях. Коэффициент безопасности п = 2 даст осторожную
величину для допускаемого напряжения в предположении, что
на сооружение действуют только постоянные нагрузки.
В случае внезапно приложенных сил, или переменных
нагрузок, что очень часто бывает в частях машин, —
становится необходимым больший коэффициент безопасности. Для
хрупких материалов, таких как чугун, бетон, различные
породы камня, и для таких материалов, как дерево, за базу
для назначения допускаемых напряжений обычно
принимают временное сопротивление.
Величина коэффициента безопасности зависит в
значительной мере от той точности, с которой определены
внешние силы, действующие на сооружение, от той
точности, о которой можно вычислить напряжения в частях
сооружения, а также от однородности применяемых'
материалов. Этот существенно важный вопрос о допускаемых
напряжениях будет рассмотрен более подробно далее (см.
главу VII части II). Здесь мы приводим несколько
простейших примеров назначения безопасных размеров
поперечного сечения стержней в предположении, что допускав
мое напряжение дано.
Фиг. 3.
8
ЗАДАЧИ*
1. Определить диаме.тр d стальных болтов JSf
пресса при наибольшем значении сжимающей
силы Р=45 000п (фиг. 3), если допускаемое
напряжение для стали в этом случае В = 100кг/см2.
Оиределить полное удлинение болтов при
наибольшей величине силы, если длина их между
гайками J — 120 см.
Решение. Необходимая площадь
поперечного сечения по ур-ншо [2] равна:
F =
г а1
Р
45 000
2 it 2-700
= 32,1 cjw2.
откуда
^j/ifEd^M
см
Полное удлинение получим по ур-ниям [3] и 14]:
А7 7 с1 700-120 ЛЛЛ
2. Конструкция, состоящая (фиг. 4) из двух одинаковых стальных
Стержней длиною 4,8 м с шарнирами в концах, находится под действием
вертикальной силы Р. Определить необходимую площадь поперечного
сечення .'стержней и прогиб среднего шарнира Р, когда Р = 2 240 к*,
дь=700 кі/сл2 и начальный угол
наклона стержней 6 = 30°.
Р еще н и е. Согласно фиг. 4Ь,
представляющей условие равновесия
гаарнира В, растягивающее усилие
в стержнях равно:
*= р
30е
при ?
Необходимая площадь
ного сечения:
S 2 240
2 sin 6'
?=Р = 2240 «і.
попер еч-
700
= 3,2 см2.
Фиг, 4.
Проги&.БВ} найдем из маленького прямоугольного треугольника
ВВВЬ в котором BD— дуга радиуса, равного длине стержня,
рассматривается как перпендикуляр, опущенный на линию АВЬ
представляющую положение стержня АВ после деформации
1 Удлинение стержня АВ
,і'
ч
а
и
BiD = z-l=*
R-l _ 700-450
В 2100000
= 0,16 см,
и прогиб
ВВ1 =
ВХВ
sin О
= 0,32 см = 3,2 жм.
г
і
Из этого ясно, что изменение угла вследствие прогиба ВВХ
очень невелико, и предыдущее определение усилия S,
основанное на допущении, что угол 6 остался равным 30°,
достаточно точно.
3. Определить полное удлинение стального стержня АВ
площадь поперечного сечения которого равна і*1 = б еле2 и
на который действуют силы (2 = 4620 м и Р = 2310 п
(фиг. б); 1Х = 4 = 25 см-
Решение. Растягивающая сила в верхней и нижней
части стержня равна Q, а в средней части равна Q — Р.
Полное удлинение поэтому будет:
(Q - Р) 12 _ л 4620-25 , 2310- 25
3
Фиг. 5.
дг=2і&+
до "2 2100000-5
= 0,022 + 0,0055 = 0,0275 "еда.
2100000. 5
4.' Определить размеры поперечного сечения деревянного бруса ВС
н стального стержня АВ конструкции ABC, несущей груз Р = 2700 %г
9
в В, если допускаемые напряжения для дерева -Вд —12 кг/см* и для
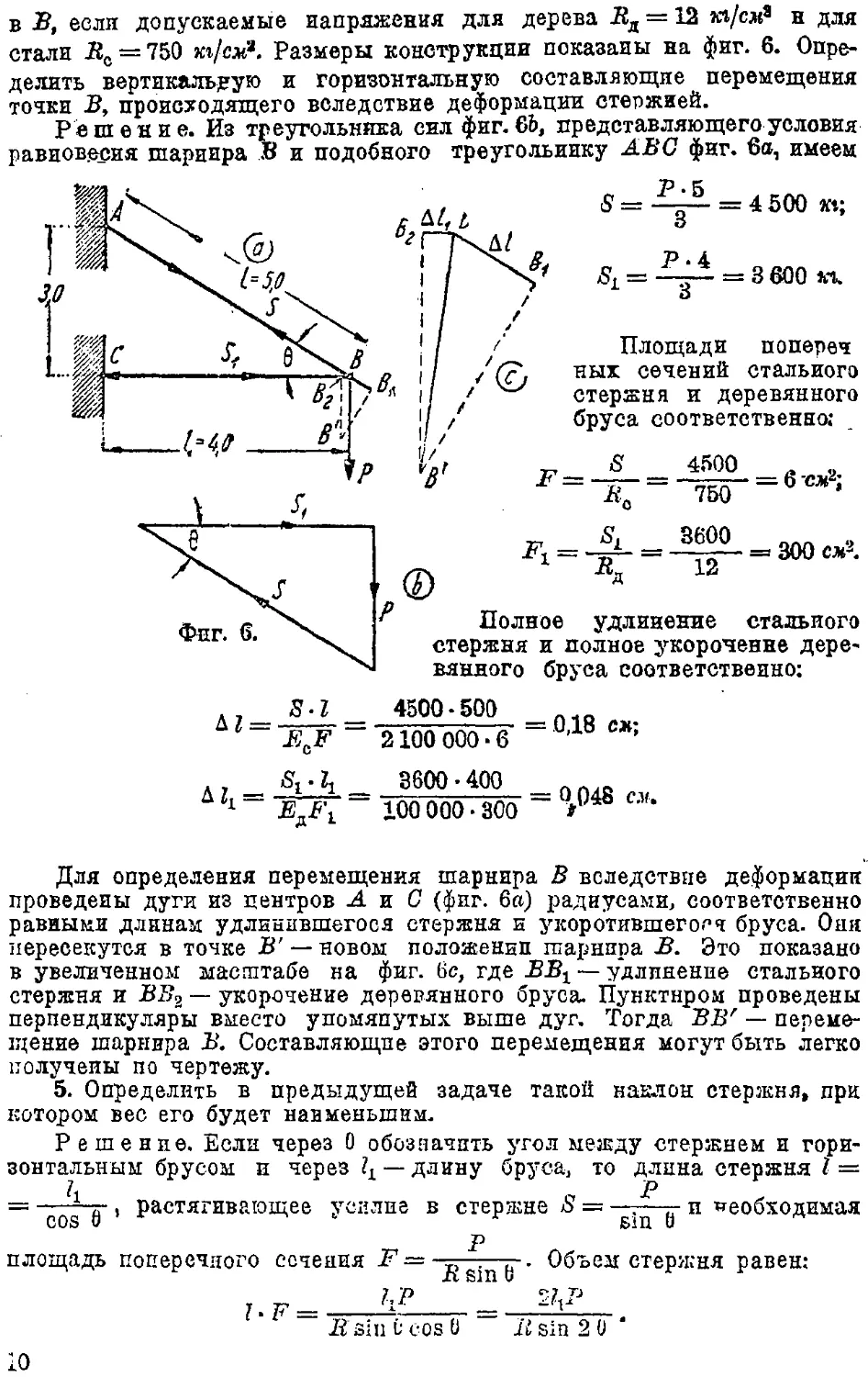
стали В0 — 750 кі/Ы*. Размеры конструкции показаны на фиг. 6.
Определить вертикальную и горизонтальную составляющие перемещения
тонки В, происходящего вследствие деформации стержней.
Решение. Из треугольника сил фиг. €Ь, представляющего условия
равновесия шарнира В и подобного треугольнику ЛВС фиг. 6а, имеем
Р-5
S = -^А = 4 500 т;
S,=
3
Р>4
3
= 3 600 т.
Площади поперек
ных сечений стального
стержня и деревянного
бруса соответственно;
, \
\е
Фнг.
6.
S,
J
'-¦h-
ф
*1=
А
д
4500
750
3600
12
= 6сл2;
= 300 с*3.
Полное удлинение стального
стержня и полное укорочение
деревянного бруса соответственно:
= 0,18 сщ
4500.500
2100 000 - 6
3600-400 ftn._
Тооооо-зоо = %т с*
Для определения перемещения шарнира В вследствие деформации
проведены дуги из центров А и С (фиг. 6а) радиусами, соответственно
равными длинам удлинившегося стержня и укоротившего.^ бруса. Они
пересекутся в точке В' — новом положении шарнира В. Это показано
в увеличенном масштабе на фиг. 6с, где ВВХ — удлинение стального
стержня и ВВ2 — укорочение деревянного бруса. Пунктиром проведены
перпендикулярны вместо упомянутых выше дуг. Тогда ВВ/ —
перемещение шарнира В. Составляющие этого перемещения могут быть легко
получены по чертежу.
5. Определить в предыдущей задаче такой наклон стержня» при
котором вес его будет наименьшим.
Решение. Если через 0 обозначить угол между стержнем и
горизонтальным брусом н через lL ¦— длину бруса, то длина стержня I =
— —?__- ( растягивающее усилие в стержне о =-гтги необходимая
Р
площадь поперечного сечения JF =
7,Р
jRsinb
hF =
sin Ь
Объем стержня равен;
о] TJ
Я sin 0 cos Ь
R sin 2 О
10
Из этого следует, что объем я вес стержня будут наименьшими при
sin 2 ? = 1 и ? = 45е.
6. Шарнирный квадрат ABCD (фиг. 7а) с диагональю из пяти
стальных стержней каждый площадью поперечного сечения в 6 сд*2,
находится под действием двух сил Р = 4200 кг, направленных по диагонали.
Определить изменение углов у точек Л и С вследствие деформации
конструкции. Определить изменение тех же углов, если силы
приложены, «как показано _
на фиг. 1Ъ. У.
Решение. В
случае, показанном на фиг.
1а, диагональ примет на
себя целиком нагрузку
Р. Допустив, что
шарнир D неподвижен и
направление диагонали не
меняется, получим, что
перемещение шарнира В
в направлении
диагонали будет равно
удлинению диагонали
Л 7 Ш
Фиг. 7.
Определенна нового положения С шарнира С указано на чертеже
пунктирными линиями. Из небольшого прямоугольного треугольника CCfi'
видно, что СС =-=г . Возникающий вследствие деформации конотрук-
. ции угол поворота стержня ВС равен
40 20
радиана,
Фиг. 8.
ссг _ м V 2 __±і і_
W у Y г ~* 1 ~зооо
и увеличение угла у точки С будет
2W~Wpa**afla'
ж
Фиг. 9.
Решение задачи, показанной на фиг. 76, предоставляется изучающему.
7. Найти такое положение груза Р на балке ABD, при котором
усилие в стержне ВС получается наибольшим. Определить угол 0, при
котором вес стержня ВС будет наименьшим (фиг. 8).
Ответ. Усилие в стержне ВС достигнет максимума, когда груз JP
займет свое крайнее правое положение в точке Ю. Объем и вес стержня
будет наименьшим при 6 = 45°.
8. Определить необходимую площадь поперечного сечения стального
стержня ВС (фиг. 9), если допускаемое напряжение В = 1050 кг/ом3
и равномерно по балке ЛВ распределенная вертикальная нагрузка
q = 1400 «г/л.
Ответ. F = 4 смК
11
9. Найти площади поперечных селений стержней ЛВ и ВС
конструкций, показанных на фиг. 10а и Ь, если В = Ц20 кг/см2.
Ответ. В случае
конструкции по фиг. 10а площадь
поперечного сечения стержня ЛВ
должна быть 14,9 см? и стержня
ВС — 11,9 см2. Для конструкции
по фиг, 10Ь площадь поперечного
сечения стержня ЛВ должна быть
11,9 см2 и стержня ВС — 10,7 емК
5. Напряжение и
деформация в стержне от
собственного веса. При
рассмотрении растяжения стержня
(фиг. 1) была принята во
внимание только сила Р,
приложенная в конце. Если
длина стержня велика, его
собственный вес может
вызвать 8начительное дополнительное напряжение, а потому
он должен быть учтен.. В этом случае наибольшее напря^
жение будет в верхнем заделанном поперечном сечении.
Обозначив через ^ вес единицы объема стержня, получим
полный вес flF, и наибольшее напряжение представится
в следующем виде:
~Л±іЩ р . 7
—F = ~р+Ч1
Фиг. 10.
max
Второй член правой части ур-ния [6] представляет
напряжение, вызванное весом стержня. Вес части стержня
ниже поперечного сечения на протяжении х от нижнего
конца {фнг. 1) — 4zFt и напряжение выразится следующей
формулой: J
И
Подставляя в ур-ние [6] вместо огаах допускаемое
напряжение Д получим выражение для определения безопасных
размеров площади поперечного сечения:
F-
л—тг
[3]
Интересно отметить, что с увеличением длины Z стержня,
собственный вес оказывает все большее и большее влияние,
знаменатель правой части ур-ння. [8] уменьшается, и необ-
и
юдимая площадь поперечного сечения F возрастает.
Когда il = R, т. е. когда напряжение от собственного веса
стержня становится равным само по себе допускаемому
напряжению, правая часть ур-ния [8] обращается в
бесконечность. При таких обстоятельствах невозможно
применять пневматический стержень, и приходится переходить
к стержню переменного сечения,
При определении полного удлинения призматического
стержня, подвергающегося действию растягивающей силы Р,
приложенной в нижнем его конце, и своего собственного
веса, рассмотрим сперва удлинение элемента длиною dx,
вырезанного из стержня двумя бесконечно близкими
поперечными сечениями (фиг. 1). Можно принять, что по всей
бесконечно малой 'длине dx растягивающее напряжение
остается постоянным и выражется формулой [7]. Тогда
удлинение kdx элемента будет
а —іГ~ Yf
Полное удлинение стержня получим суммированием
удлинений всех элементов. Тогда
о
Сравнивая это выражение с ур-нием [1], видим, что
полное удлинение, вызванное в стержне собственным весом,
представляет собой удлинение от сосредоточенного груза,
равного половине его веса и приложенного к концу стержня.
ЗАДАЧИ.
1. Определить площадь поперечного сечения вертикального
призматического стального стержня, несущего на своем нижнем конце груз
Р = 32 т, если длина стержня 220 м, допускаемое напряжение 700 кг/см2
и вес 1 л*3 стали 7,85 «t. Определить полное удлинение стержня.
Решение. Площадь поперечного сечения по ур-ншо Щ .
F = 8?000_ =
700 ~ 7,8° і осо ооо -
Полное удлинение по ур-нню [9]
А,я"ЙЙ(т^7'1,17)вМВ№
13
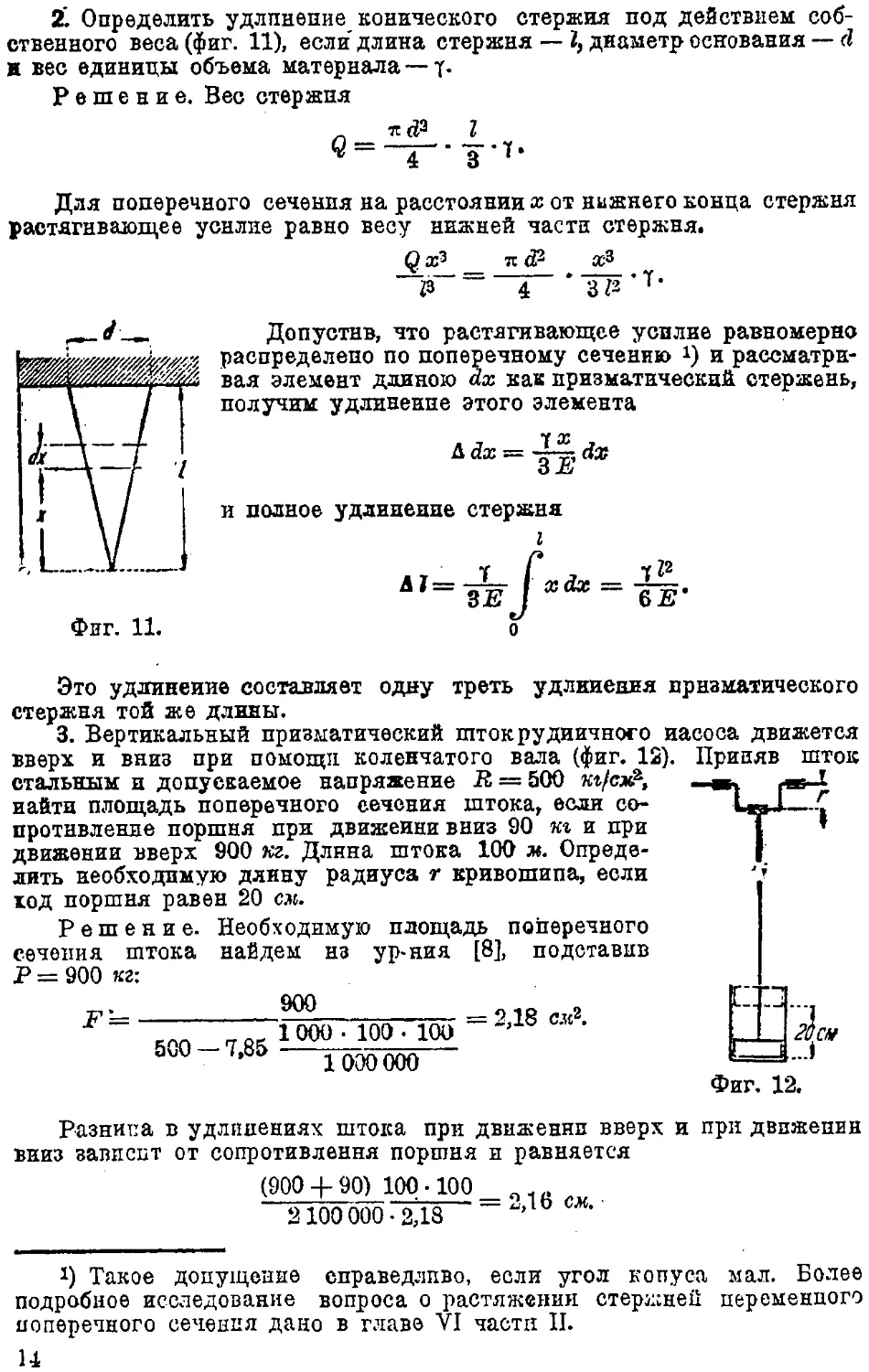
2. Определить удлинение конического стержня под действием
собственного веса (фиг. 11), если длина стержня — \ диаметр основания — d
к вес единицы объема материала — y-
Решение. Вес стержня
е-
T'T
Для поперечного сечения на расстоянии х от нижнего конца стержня
растягивающее усилие равно весу нижней части стержня.
Допустив, что растягивающее усилие равномерно
?тшм# распределено по поперечному сечению і) и рассматрн-
вая элемент длиною dx как призматический стержень,
получим удлинение этого элемента
&dx= ^™ dx
и полное удлинение стержня
і
А}
Фиг. 11.
= iwjxd* =
Это удлинение составляет одну треть удлинения призматического
стержня той же длины.
3. Вертикальный призматический шток рудничного насоса движется
вверх и вниз при помощи коленчатого вала (фиг. 12), Приняв шток
стальным и допускаемое напряжение В, = 500 «t/еж?,
найти площадь поперечного сечения штока, если
сопротивление поршня при движении вниз 90 кг и при
движении вверх 900 кг. Длина штока 100 м.
Определить необходимую длину радиуса г кривошипа, если
ход поршня равен 20 см.
Решение. Необходимую площадь поперечного
сечения штока найдем из ур-ния [8], подставив
Р = 900 кг:
F = ??L «^ ^ = 2Д8 «А
О
500 — 7,85
1 000 - 100 • 100
1000 000
Q
2Ш
Фиг, 12.
Разница в удлинениях штока при движении вверх и при движенви
вниз зависит от сопротивления поршня и равняется
(900 + 90) 1QQ -100
2100 000
2,18
= 2Л6 см.
*Jf
*) Такое допущение справедливо, если угол конуса мал. Более
подробное исследование вопроса о растяжении стержней переменного
поперечного сечения дано в главе VI части II.
U
Радиус крнвопшпа должен быть:
20 + 2Д6 „ Л0
г — ' = 11,03 см.
4. Длинные проволоки стальная и алюминиевая подвегпены
вертикально. Найти для каждой длину, при которой напряжение от
собственного веса проволоки будет равно временному сопротивлению, если для
стальной проволоки М = 21000 кг/см2 и y = 7850 кг/л3, а для
алюминиевой Е = 3 500 кг/сл2 и ¦/ = 2720 кг/ж3.
Ответ. Для стальной 2 = 26 800 м, для алюминиевой 2 = 12900 «.
5. В какой пропорции увеличится наибольшее напряжение,
возникающее в призматическом стержне от собственного веса, еела все
размеры стержня увеличатся в отношении я : 1?
6. Стержень равного сопротивления на растяжение. Из выкладок
предыдущего п° видно, что в случае вертикального призматического стераня,
подверженного действию собственного веса
и груза, приложенного на конце,
напряжение равно допускаемому только для
наиболее напряженного поперечного сечения.
Во всех остальных сечениях, как
видно из ур-ний [6] и [7], напряжение
будет меньше, чем допускаемое В,
Поэтому можно получить некоторую
экономию в материале при применении стержня
переменного поперечного сечения.
Наиболее благоприятное положение по
количеству потребного материала получим, когда
.площадь поперечного сечения будет
возрастать в той ж? пропорций, что и осевая
снла, так что в каждом поперечном
сечении напряжение как раз будет равно
допускаемому U. Форма стержня,
удовлетворяющая этому условию, называется
формой тела равного сопротивления.
Пусть фиг. 13 представляет такой
стержень. Тогда площадь поперечного сечения
F0 в нижнем конце стержня будет опреде-
р
ляться ур-нием FQ = -yj-. Пусть F обозначает площадь поперечного
сечения на некотором расстоянии ос от нижнего контта стержня. Эта площадь
будет некоторой функцией от х. Площадь смежного поперечного
сечения на расстоянии х -\- dx от нижнего конца стержня будет равна
/ dF '
F +
\ doc
( dF\
dx. В случае тела равного сопротивления увеличение пло-
dx должно быть как раз достаточным для того, чтобы
выдержать увеличение растягивающей силы, представляющее вес
заштрихованного элемента стержня. Получаем следующее уравнение.
Л —г- dx = V ¦#* dx,
dx '
откуда
dF
F
Y dx
lb
Интегрируя это ур-ане, имеем* •
InF:
ух
+ G.
где С — произвольная постоянная интегрирования — будет определена
далее. Площадь поперечного сечения получаем равной
rf + с
F = e =О0е
X
4-R
где е — основание натуральных логарифмов и С0 = е^.
Из того, что при х = О это ур-ние для F должно дать вяач?шг?
F = Fq, находим, что величина произвольной постоянной С0 должна
быть равна 2*'0. Тогда
F = Fne
X
[10]
При помощи этого ур-ния можно легко
определить площадь F для любого
значения х, если даны т и 1$. Площадь Fx
верхнего сечения получим подстановкой
»= 1 в ур-ние [10]. Тогда
Fi = Fn e
R
[И]
Так как растягивающая сила в верх'
нем конце стержня равна весу стержня Q
плюс сила Р, приложенная к конпіу, то
Q+P^B-Fj.
или
= рСт4"-і).
[12]
Полное удлинение стержня равного сопротивления легко
определить благодаря тому, что растягивающее напряжение всюду постоянно
и равняется R. Отсюда
лг = 4г* [1В]
Форма тела равного сопротивления иногда заменяется формой,
состоящей из нескольких призматических частей (фиг. 14) Ц. Пусть Ft,
F2, F&. . . и Iv l2t k> • • • обозначают площади поперечного сечения я
длины последовательных частей стержня Ль Л2, Л3, . . . Начав с
нижнего конца, определяем площадь Fv пользуясь ур-нием [8]:
_ Р .
!) Такая форма иногда применяется для длинных тросов в
глубоких шахтах,
1в
Тогда напряжение в верхнем сечении первой части равно; -В и сила»
действующая на нижний конец второй части, будет равна FtB. Бодста-
вив это в ур-ние [8] вместо Р, получим для определения Fl следующее
ур-ние:
_Fo =
FtB PR
Продолжая тем же путем рассуждения, получим общую формулу
для площади Fn n-ой части в следующем виде:
я Р-Вп^ fU1
В частном случае, когда \ = 7« = h = •«• = — > имеем:
F = — •- . 1161
я
(і._Лі-Г
Когда число частей бесконечно увеличивается, *» становится
бесконечностью., н Лы приходим к отержнюравного сопротивления. Отметив,
In
что — = х, имеем:
ш
или, пользуясь известным выражением
получаем:
('+й)"-"(,*)-
Подставляя в ур-ние [15], мы приходим к; ур-нию [10].
ЗАДАЧИ.
1. Стальной стержень, состоящий из пяти призматических частей
одинаковой длины, нагружен в нижнем конце грузом Р = 18000 «г.
Найти вес этого стержня, если его длина —150 м и допускаемое
напряжение равно 400 хл/смК
Решение. Площадь в верхнем конце по ур-ншо [15];
13000 _1 '„ 0 .
I1 1000 000-.5-400; /
Тогда вес стержня:
д. _ jr5. R — Р = 24 480 - 18 000 =6 480 ?л.
2 Тимошенко — Сопротивление материалов, ч. I, 11
2. Сравнить вес стержня предыдущей #. задачи с весом стержня,
имеющего форму тела равного сопротивления и предназначенного для
работы в тех условиях.
Решение. Площадь верхнего поперечного сечения.по ур-нию [11]
будет:
1 400
Вес стержня равного сопротивления
G = 60,4 • 400 —18 000 = G160 &.
Из этого видно, что форма равного сопротивления дает здесь
экономию в материале около 5%.
3. Опора моста, имеющая форму тела равного сопротивления,
подвергается действию сжимающей силы Р — 272 ш, приложенной к
верхнему сечению опоры. Найти объем кладки, если высота опоры 36 ж,
вес 1 м% кладки опоры 2400 кг и допускаемое напряжение R~ IQki/cmP.
Решение. При помощи ур-ния [12] получим следующее ур-ни?
для определения объема каменной кладки V:
155 лэ.
4. Найти полное укорочение этой опоры, если сжимающее
напряжение Я = 10 кг/ем2 и Е = 280 000 кг/см2.
Ответ: Д2 = 0,129 см.
5. Сравнить вес стержня задачи 1 с весом призматического стержня,
предназначенного для работы в тех же условиях.
Ответ. G = 7520 %г. Вес больше найденного в задаче 1 на 1040 к*.
Это показывает, что призматический стержень тяжелее на 16% стержня,
состоящего из пяти призматических частей.
7. Статически неопределимые задачи на растяжение и
сжатие. Сюда относятся случаи, где осевые усилия,
действующие в стержнях сооружения, не могут быть
определены помощью одних уравнении статики, и приходится
принимать во внимание деформацию сооружения. Такие
сооружения называются статически неопределимыми сише*
мами.
Простейший пример такой системы показан на фиг. 15.
Груз Р вызывает растяжение в стержнях OB, OG и OD,
находящихся в одной плоскости. Условия равновесия
шарнира О дают два уравнения статики, которых недостаточно
для того, чтобы определить три неизвестных растягивающих
усилия в стержнях. Для получения третьего уравнения
необходимо рассмотреть деформацию системы. Допустим
для простоты, что система симметрична относительно вер-
13
г
тикальной оси ОС. Вертикальный стержень — стальной
с площадью поперечного сечения F. при модуле
упругости материала Ес, а наклонные стержни —из меди с
площадью Fu и модулем упругости Ел, Длина вертикального
стержня — I, а наклонных — Z/cos а. Обозначив через X
растягивающее усилие в вертикальном стержней через Y—
усилия в наклонных
стержнях, получим
только одно ур-ние
равновесия для шарнира О;
X + 2rcosa = P. [a]
Чтобы вывести второе
уравнение для
определения неизвестных величин
X и Г, нужно
рассмотреть деформированное
состояние системы,
указанное на фигуре
пунктирными линиями. Пусть Ы—
полное удлинение
вертикального стержня при
действии груза Р; тогда
удлинение Ых наклонных
стержней найдем из
треугольника OFOv Допустив, что эти удлинения очень малы,
можем заменить дугу круга OF с центром В
перпендикуляром, и угол у точки Ох можем принять равным
первоначальному углу а; тогда
Л 1х = AI cos a.
Относительные удлинения и напряжения вертикального
и наклонных стержней будут соответственно:
A Z ЕЛ1 А г cos2 a
2
t
4 ""'
Фш\ 15.
И е =
' м
E^Ll COS2 a
Усилия в стержнях получим, помножив напряжение ыа
площади поперечных сечений;
FcEcAl
X = с F =
I
Y=o F
м и
F Д AZcos3a
I
Щ
откуда
2*
y=Xcos2a
F Е
М X
F Ещ
с о
19
Подставляя в ур-нке [а], получим:
Р
Х =
F Е
1 + 2с08за_і^
О О
[161
. Отсюда следует, что сила X зависит не только от угла
наклона а, но также от площадей поперечных сечений
и механических свойств материала стержней. В частном
случае, когда все стержни имеют одно и то же поперечное
сечение и тотже модуль упругости, получим изур-ния [16]:
X
l + 2cos3a'
Когда угол а приближается к нулю,
то соэа приближается к единице, а
усилие в вертикальном стержне.
приближается к Vs -Р- Когда угол а
приближается к 90°, наклонные стержни
становятся очень длинными и весь груз
воспринимается средним стержнем.
В качестве другбго примера
статически неопределимой системы
рассмотрим призматический стержень с
закрепленными концами, иесущий осевую
нагрузку в промежуточном поперечном
сечении тп (фиг. 16). Груз Р уравновесится
реакциями В sl Ві в концах стержня, и мы имеем ур-ние:
Чтобы получить второе уравнение для определения
реакций В и Ви нужно рассмотреть деформацию стержня.
Груз Р совместно с силой В вызывает укорочение нижней
¦части стержня, а совместно с силой В{ удлинение верхней
части. Полное укорочение одной части равно полному
удлинению другой. Поэтому, пользуясь ур-нием [і], получим:
отсюда
Вга
EF
Л
вь
EF'
а
щ
т. е. силы В и BL обратно пропорциональны расстояниям
20
точек их приложения от нагруженного поперечного
сечения шй. Далее из ур-ний [с] и [d] можно легко определить
величины этих сил и напряжения в стержне.
ЗАДАЧИ
1. Стальной цилиндр и. медная труба сжимаются между плитами
пресса (фиг. 17). Найти напряжения в стали л меди, а также
относительное укорочение, если Р = 45 т, d = 10 см и D — 20 см.
Решение. Здесь снова условий статики недостаточно, и при
выяснении, какая часть ' груза принимается" каждым из материалов,
следует рассмотреть деформацию цилиндра и трубы. Относительные
укорочения стали и меди должны быть одинаковы. Поэтому напряжения
каждого из материалов будут находиться в том же отношении как их
модули (ур-ни? [4], стр. 4), т. е. сжимающее напряжение в. стали
должно составлять тг сжимающего напряжения в меди. Тогда величину
о
напряжения меди можно найти из уравнения статики:
р-^-ть + ^-^ШШ
Подставив числовые
величины, получаем
см~Ш *і/сле3;
сс — V ** в 22° Kt/C*8' *L
Гт
Относительное укорочение
ев-~=104-10-в.
В
Фиг. 18.
2. Железобетонная колонна сжата силой Р = 27 т. Какая часть
этога груза воспринимается бетоном и какая часть приходится на
стальную арматуру, если площадь поперечного сечения стали
составляет jx поперечного сечения бетона?
Решение. Применяя тот метод рассуждений, что и в
предыдущей задаче, и принимая модуль упругости бетона равным =-^ модуля
упругости стали получаем, что груз, передающийся на "бетон, будет
равен 13,5 т.
3. Твердое тело ЛВ весом Q подвешено на трех вертикальных
проволоках, симметрично расположенных относительно центра тяжести
тела (фиг. 18). Найти растягивающие усилия в проволоках, еслн средняя
проволока—стальная, а две другие — медные. Площадь поперечного
сечения у всех проволок одинакова.
Указание. Воспользоваться методом, примененным для решения
задачи 1.
4. Найти усилия в четырех ножках квадратного стола (фиг, 1Я) от
груза Р, расположенного на одной из диагоналей. Верхняя доска стола
и пол предполагаются абсолютно 'жесткими, а ножки прикрепленными
к полу так, что они могут испытывать как растяжение, так и сжатие.
21
Решение. Есля допустить, что новое положение доски стола
таково, как указано пунктирной линией шг, то сжатие ножек 2 и 4
равно среднему арифметическому сжатий ножек 1 и 3, Следовательно
2Y=X4-Z,
а так как
то
2Y+X + Z = P,
2Г==Х + Л = уР.
[а]
Дополнительное уравнение для определения X я Z полупим, взяв
момент всех сил относительно горизонтальной оси 00, параллельной
оси з/ и находящейся в плоскости действия силы Р. Тогда
х(-|аУ*2+е)+ір.е = г(1аУ2-е).
М
Из ур-ииЕ [а] и [Ъ] получим*
\ 4, aW
Г =
4;'
Я
-*(*+^)-
При е > а — Y 2, X получается
отрицательным. Это указывает, что в этом случае
в ножке 1 возникает растяжение.
5. Определить
усилия в ножках
предыдущего стола, когда груз
приложен в точке с
координатами:
а? =
4
а:
У =
а.
Решение. При
решении этой задачи
следует отметить, что когда
точка приложения
груза -Р не находится на
диагонали стола, то груз
можно заменить двутія
Фиг. 19. грузами, статически эк- Фиг. 20.
Бивалентными грузу Р
и приложенными в точках, находящихся на двух диагоналях. Усилия,
вызванные в ножках каждым из этих двух грузов, найдем, как указано
выше. Суммируя действие двух составляющих грузов, можем найти
усилия в ножках при любом положении груза.
6. Шарнирный прямоугольник с диагоналями подвергается
действию сжимающих сил Р (фиг. 20). Найти усилия в стержнях, если они
все одинакового материала, площадь поперечного сечения стозк — F и
площадь остальных стержней — Р\.
Решение. Пусть X — сжимающее усилие в
У— сжимающее усилие в каждой диагонали, я;
22
каждой вертикали,
7* — растягивающее-
усилие в каждом горизонтальном стержне. Тогда из условия равновесия
одного из шарниров:
1 (Р-Х); Z= ycosa = (P— X)ctga. [о]
sine
Третье уравнение получим: из условия, что рама после деформации
остается в силу симметрии прямоугольной; поэтому:
аі+Ні-ткУ=Чі-М+аіі+ік)3''
отсюда, пренебрегая бесконечно малыми высшего порядка, имеем
"~ EF MFS
EF<
м
?П
И
Решая ур-ния [а] и [b\t получим следующую величину
усилия в диагонали:
Р
У =
а* + 1ь* F . a* F
А*
I
L
Усилия в прочих стержнях легко определим из ур-ний [а].
7. Решить предыдущую задачу, приняв: « = &, а = 45°, Фиг. 21.
F = 5Ft и j? = 25000 wi.
8» Какие напряжения возникают в стальном болте и медной трубе
(фиг. 21) при четверти поворота гайки, если длина болта I — 750 мм,
шаг нарезки болта 1г = 3 мм, площадь поперечного сечения болта
Fc = 6 см2, площадь поперечного сечения трубы Fu = 12 см2 ?
Решение. Обозначим через X неизвестное растягивающее усилие
в болте и сжимающее усилие в трубе. Величина X будет найдена из
того условия, что удлинение болта плюс укорочение трубы равно
перемещению гайки вдоль болта. В нашем случае, приняв длину болта рав«-
ной длине трубы, получим
XI
^О
XI __ 1
м
откуда
Х =
*JSeFe
« 1 +
0,3-2100000-6
7 15.іл\
^¦"V + stii,
J*
3 500 b,
Растягивающее напряжение в болте сс = -р-~1080 кг/сла.
X
Сжимающее напряжение в трубе ам = -^-?^540 жг/сж3.
9. Какое изменение в напряжениях, вычисленные для предыдущей
задачи, произойдет при приложении растягивающих сил Р к концам
болта? Р = 25 000 %г.
Решение. Пусть X обозначает увеличение растягивающей силы
23
в болте и У— уменьшение сжимающего усилия в трубе. Тогда из
условия равновесия:
X+Y=P. la]
Второе уравнение можем написать по тем соображениям, что
относительное удлинение болта и трубы при приложении сил Р должцо
быть одинаково, т. е.
X Y
И
Vc
Е F *
Из ур-ний [а] и [Ь] легко определить усилия X и Г, а затем и соотч
ветствующие напряжения.
10. Призматический стержень с заделанными концами несет осевую
нагрузку в двух промежуточных поперечных сечениях (фиг, 22) силами
Рх и Р2. Найти реакпии R и Вх.
Р е"ш е н и е. Если х и у — перемещения вниз поперечных сечений
щ щ и щ щ» вызванные грузами: Рг и Р2, а,.Ъ, с — длины трех частей,
на которые делится стержень поперечными сечениями тх nt и щ п^
и F —площадь поперечного сечения стержня, то"
напряжения в упомянутых частях стержня будут:'
Ех ш Е (у — х) ш Еу
—— «
о с
*
а
lOLi
J*JL
Г
в
4
jS
а
Ур-ния для определения ж и у
будут:
іЛ
Ех Е(у — х)
_ Л
а
Е(у — х)
+
Еу
F '
Р2
F '
Фиг. 22,
Реакции найдем из ур-ний:
в =
EFy
Фиг. 23.
11. Показать,. что тот же результат получим при помощи ур-йия [d]
(см. стр. 20), определяя реакции^ вызванные каждым грузом отдельно,
а затем суммируя эти реакцаи. Определить полные ракции при;
a=0,3Z; Ь = 0,3г и Р1 = 2Р2 = 450 кг.
12. Найти усилия в стержнях системы, показанной на фиг. 23;
ОЛ — ось симметрии.
Ответ. Растягивающее усилие в стержне 02 равно сжимающему
усилию в стержне ОС и равно — Р sin е. Усилие в горизонтальном стер-
жне равно нулю.
8. Начальные и температурные напряжения. В статически
неопределимой системе возможно наличие некоторых
начальных напряжений, получившихся при сборке и являющихся
следствием неточностей в. длинах стержней или цредна- ¦
ыеренных отклонений от правильных величина этих длин/
21 .
Эти напряжения будут существовать и в отсутствие
внешних сил и зависят только от геометрических размеров
системы, от механических свойств материалов и от величины
неточностей. Допустим, например, что система, предетавлен-
нйяна фиг. 15, имеет по ошибке длину вертикального стер-
эййя, вместо I, 1-\-а. Тогда после склепки стержней ВО ж
DO верикальный стержень можно будет поставить наместо
только после первоначального сжатия его; вследствие этого
появятся некоторые растягивающие усилия в наклонных
стержнях. Пусть X обозначает сжимающее усилие в
вертикальном стержне, которое получается после склепки.
Тогда соответствующие растягивающие усилия наклонных
стержней будут
X
2 cos а *
и перемещение шарнира О вследствие удлинения этих
стержней будет (см. ур-ние [Ъ], стр. 19)
Укорочение вертикального стержня будет:
К1==ігт- га
с о
На основании элементарных геометрических соображений
перемещение шарнира О вместе с укорочением
вертикального стержня должно равняться величине ошибки а в длине
вертикального стержня. Это дает следующее уравнение для
определения X:
XI . XV
2EuFucos**^ E0Fo
Отсюда найдем:
X = V^ г> [I?!
J[1~*rTEvF4COsSa)
после чего можно определить начальные напряжения во
всех стержнях-
Расширение стержней системы вследствие изменений
температуры может дать точно такой же эффект, как
неточности в-длинах. Возьмем стержень с закрепленными
25
концами. Если температура стержня поднимется от /0° до
f, а температурному расширению препятствуют реакции
заделанных концов, то в стержне возникнут сжимающие
напряжения, величину которых можно определить из уело-
вия, что длина стержня остается неизменной. Пусть а
означает коэфициент линейного расширения от температуры
и о—сжимающее напряжение, вызываемое реакциями
концов. Тогда ур-ние для определения а будет:
откуда
<, = «(* — tQ)E. [is]
В качестве второго примера рассмотрим систему,
представленную на фиг. 15, и положим, что вертикальный
стержень нагрет от температуры склепки і0° до новой
температуры f. Соответственное температурное удлинение частвч-
но будет * предотвращено сопротивлением двух других
стержней системы, и возникнут некоторые сжимающие
напряжения в вертикальном стержне и растягивающие
напряжения в наклонных стержнях. Величина сжимающего
усилия в вертикальном стержне определится ур-нием [17],
в которое вместо величины а — неточности длины — мы
подставим температурное удлинение al(t — tQ)
вертикального стержня.
ЗАДАЧИ.
1. Трамвайные рельсы сварены при 10° С» Какие напряжения
возникнут в этих рельсах при повышении температуры до 40° С, если
коэффициент линейного расширения стали — 0,000012?
' Решение. По ур-ниіо [16] а = 0,000012.30• 2100000 = 765 кг/см*.
2. Какое изменение напряжений вызовет в случае, представленном
на фиг. 21, повышение температуры от t0° до tQ, если коэффициент
расширения стали а0, а меди ам?
Решение. Вследствие того, что «м>ас, повышение температуры
вызовет сжатие в меди и растяжение в стали. Относительные
удлинения меди и стали должны быть одинаковы. Обозначив через X
увеличение растягивающего усилия в болте из-за изменения температуры,
долучим
X X
««(* - 'о) + -%-у = а« (* - *ь) - ЖТГ'
откуда
Y К - «J « - <о) Я0 *"«
EaF0
Е F
26
Изменение напряжений в болте и в трубе можно затем определить
обычным путем.
3. Полоска медн запаяна между двумя полосками стали (фиг. 24).
Какие напряжения возникнут в стали и в меди при подъеме
температуры полосок от t0° до і91
Указание. Нуэкно применить тот же метод, как и в предыдущей
задаче.
4. Какие напряжения возникнут в стержнях системы,
представленной на фиг. 15, если температура всех стержней поднимется от t0° до tQl
Решение. Пусть X обозначает растягивающее усилие,
возникающее в стальном стержне при повышении температуры. Тогда из
условия равновесия шарнира О можно видеть, что в медных стержнях
возникнут сжимающие усилия, равные •% ; следовательно, удлинение
стального стержня будет
•°о' ^ с
а удлинение медных стержней
/ XZ
Кроме того из предыдущих рассуждений (см, стр. 19) следует, что
Д1Х — ДI cos a.
Поэтому
XI I XI
'м* м
откуда
Х = _
«-^{¦^-"«У^ і
і+ l E°F°
2 cos3 a SMFM Фиг. 2*.
Напряжения в стали и в меди теперь получим из следующих
выражений :
X X
°с F,} °* 2 cos a F
м
5. Принять, что в случае, показанном на фиг. 17 (см. задачу 1,
стр. 21), постоянный груз Р = 45 от приложен при начальной
температуре t0°, и определить, при каком повышении температуры груз будет
целиком передаваться медной трубе, если ас = 0,000012 и «^ = 0,0000165.
Решение.
4Р
(*„ - «в)(* - « = п(1Р~д?)Ел>
откуда
t-tQ = 37,8°С
6. Найти напряжения, которые возникнут в системе,
представленной на фиг. 20 (см. задачу 6, стр. 22), если температура верхнего
горизонтального стержня поднимется с і0° до *°.
27
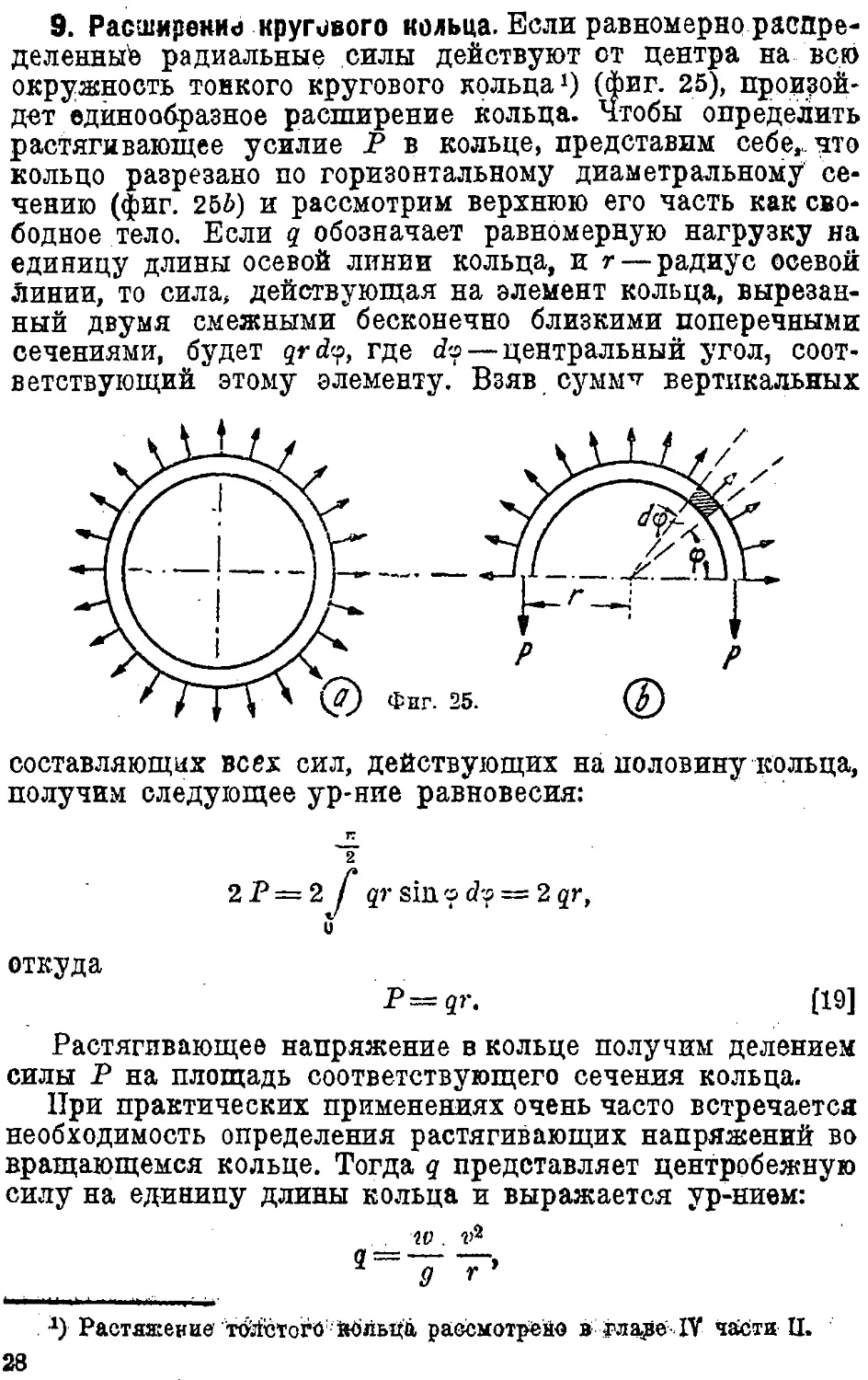
9. Расширение кругового кольца. Если равномерно
распределенный радиальные силы действуют от центра на всю
окружность тонкого кругового крльда1) (фиг. 25),
произойдет единообразное расширение кольца. Чтобы определить
растягивающее усилие Р в кольце, представим себе»., что
кольцо разрезано по горизонтальному диаметральному'
сечению (фиг. 2ЬЬ) и рассмотрим верхнюю его часть как
свободное тело. Если q обозначает равномерную нагрузку на
единицу длины осевой линии кольца, и г — радиус осевой
линии, то сила* действующая на элемент кольца,
вырезанный двумя смежными бесконечно близкими поперечными
сечениями, будет qrdy, где do — центральный угол,
соответствующий этому элементу. Взявсумм^ вертикальных
составляющих всех сил, действующих на половину кольца,
получим следующее ур-ние равновесия:
77
2Р=2 / gr sill<p c?-f = 2 gr,
и
откуда
P^qr. (19]
Растягивающее напряжение в кольце получим делением
силы Р на площадь соответствующего сечения кольца.
При практических применениях очень часто встречается
необходимость определения растягивающих напряжений во
вращающемся кольце. Тогда q представляет центробежную
силу на единицу длины кольца и выражается ур-нием:
'¦¦-¦¦••,'¦ ¦ ¦¦ ¦¦ ¦•¦¦ . • : ¦¦
. -1) Растяжение' '''тМЬхот^-ЫіШік рассмотрев в шъръ IY ча?ти II.
28
в котором w—вес кольца на единицу длины, г—радиус
его осевой линии, v — скорость движения частиц кольца,
лежащих на его осевой линии, -и д — ускорение силы
тяжести. Подставляя это выражение вместо g в ур-ние [19],
получим:
Р=
і«а
wo
и соответствующее растягивающее напряжение будет; -
Отсюда видно, что напряжение пропорционально
плотности — материала и квадрату скорости по наружной
поверхности. Для стального кольца, при скорости v = 30 л/сек.,
это напряжение равно 72,1 кг/сл2. Тогда для того же
материала при любой скорости vx напряжение будет равно
0,0801 V в %г\см*% если vx — в метрах в секунду.
ЗАДАЧИ.
I. Найти растягивающее напряжение в пидиндрической стенке
кресса, рассмотренного и задаче 1 (стр, 8) и изображенного на фиг. 3,
если внутренний диаметр — 25 см и толщина
стенки — 26 мм. •'^^^ Mm
Р е ш е н и е. Наибольшее гидростатическое дав- /у>~ ^vv- Г
ление-в цилиндре найдем из ур-ния:
jp ¦ 7 =45 000 кг,
откуда
р = 91,7 %%}см\
Фиг. 26.
Вырежем из цилиндра элементарное кольцо,
высотой 1 см, измеренной по направлению оси
цилиндра, и используем ур-ние [19], в котором в этом случае q—p = 91,7м*/с*а
и г = 12,5 см. Получаем
Р
F
91,7.12,5
2,5-1
= 183,4 к»/слА
2. Медная труба насажена на стальную трубу при высокой
температуре t (фиг. 26). Насаживание произведено так, что при
этой'температуре между трубами нет давления. Определить напряжения, которые
возникнут в медной и стальной трубах, когда температура понизится
до #0. Внешний диаметр стальной трубы — d, толщина стальной
трубы — Лс, а медной — Лм.
Решение. Вследствие раэницы между коэффиггйентами.лижейвога
расширения вси^при: с^лдвдении возникав^, ..давление.,между внеш-
2?
ней и внутренними трубами. Пусть х ооозкачает это давление на см2;
тогда растягивающее напряжение в медной труб? будет
__ xd
и сжимающее напряжение в стальной
xd
Давление х теперь найдем из условия, что при охлаждении обе
трубы имеют одно и то же сокращение размеров по окружности.
Поэтому
/, .ч %d и .ч , xd
а"(і~ад~1ЖХ"^ас(і~?о)+"2ЖТ"'
'М'М ""'С "С
откуда
Таким же путем можно определить напряжение и в стальной
трубе.
3. Какое дополнительное растягивающее напряжение возникнет
в труб? предыдущей задачи (фиг. 26), если подвергнуть ее
гидростатическому внутреннему давлению р — 7 къ/см2 ? Внутренний диаметр
d1 = 10 см, hQ = 2,5 мм и 7гм = — * 2,5 мм.
Решение. Вырежем из трубы элементарное кольцо высотой 1 ел;
полное растягивающее усилие в кольце будет
•Р = ??. = 85 к».
Вследствие того, что относительные удлинения цо окружности
в медной и в стальной трубках одни и те же, то напряжения в них
будут пропорциональны модулям упругости, т. е. напряжение в медной
трубке будет составлять -^- напряжения в стальной труб?. На пло
щадь поперечного сечения медной трубы составляет -jp стальной; по-
о
этому сила Р распределится поровну между обеими трубами, и растя*
гнвающее напряжение в медной трубе, вызванное гидростатическим
давлением:
Р 35
а = —— = — = 37,3 %х\сж\
2Лм 2.^-.0,25
Напряжение в стальной трубе
»в = -Т ** = *>«/**
4. Составное кольцо сделано из внутреннего медного кольца и
наружного стального. Внутренний диаметр стального кольца меньше чем
30
внешний диаметр медного кольца на величину 6, и на медное /сольдо
насажено стальное по предварительном нагревании последнего. При
охлаждении стальное кольцо сужаясь оказывает давление на медное
кольцо. Найти напряжение в стальном и в медном кольцах, после
сборки, если оба кольца имеют прямоугольное поперечное сечение с
размерами hc и Лк в радиальном направлении и размером, равным
единице в направлении, перпендикулярном плоскости кольца. Размеры
7?с и Лм можно рассматривать малыми сравнительно с диаметром d
поверхности соприкасания обоих колец.
Решение. Пусть х — равномерно распределенное давление на
квадратный сантиметр поверхности соприкасания колец; тогда
сжимающее напряжение в медном кольце и растягивающее—в стальном
найдем из ур-ний:
xd xd ¦
Уменьшение наружного диаметра медного кольца
Увеличение внутреннего диаметра стального кольца
сс даЗЭ
2 Е\ 2hcEc
Неизвестное давление х найдется из ур-ния:
откуда
х=~ с с
*(1+*А
кк
Напряжения вс и сгм получатся из ур-ний [а]:
5. Найти напряжения, возникающие в составном кольце предыдущей
задачи при вращении кольца с постоянной скоростью п оборотов
s минуту.
Решение. Вследствие того, что медь имеет большую плотность
и меньший модуль упрутосви, чем сталь, медное кольцо будет
нажимать на стальное при вращении. Обозначим через х давление на
квадратный сантиметр поверхности соприкасания между двумя кольцами.
Тогда соответствующие напряжения получим из ур-ний [а] предыдущей
задачи. В дополнение к этим напряжениям возникнут напряжения от
центробежных сил, которые также следует, учесть. Обозначив через
31
7в и ym веса единицы объема стали и меди и пользуясь уравнением [20],
получим:
Сложив эти напряжения с напряжениями от давления х и заметив,
что относительное удлинение обоих колец должно быть одинаковым»
получим следующее уравнение для определения х:
*.LT\ «О Д 2 j +2ЛС]-?М [ , ^ 60 ) [ 2 J 27у|'
откуда а; можно определить в каждом частном случае. Зная х, легко
можно найти полные напряжения в медном и стальном кольцах.
6. Найти предельную поверхностную скорость медного кольца, если
допускаемое напряжение Я = 210 кг/сяР н тм = 8 800 мг/А
Ответ, v = 48,3 ж/сек.
7. Для вадачи 2 (фиг. 26) найти напряжение в медной трубе при
температуре V, если t ~ *оI = 55°С, <хм — а0 = 0,0000045, Ас = Ам,
Ответ ам = 181 кг{см2.
8. Для вадачи б определить число оборотов п в минуту, при
котором напряжения в медном кольце становятся равными нулю, если
начальные напряжения при сборке этого кольца были сжимающими и
равными ffo» a hu = А0 и Ес = ЯЕМ.
Решение. Число оборотов w определится из ур-ния:
—&)'[К-^),+-К4*Л-
10. Напряжения в нити и кабеле. Положим, что
совершенно гибкая нить постоянного поперечного сечения
подвешена между точками А я В, которые лежат на одном и
том же уровне (фиг. 27). Под действием ее собственного
веса в нити возникнут растягивающие напряжения. При
определении этих напряжений обозначим через q — вес
единицы длины нити, I—пролет нити, f— стрелу провеса
нати, Л—растягивающее усилие в самой нижней точке О
нити. -Чтобы упростить задачу, примем, что' упругая
кривая нити очень полога; тогда не сделав существенной
ошибки, можем заменить равномерное распределение
нагрузки по длине кривой равномерным распределением по
длине пролета.
Рассмотрим равновесие одной половины пролета ннти и
заменим горизонтальной силой Л действие правой части
нити на левую часть (фиг. 276). Из условий ріавновесия
следует, что вертикальная составляющая реакции опоры А
равна половине веса нити, т. е. •— gJ, а горизонталь-
32
ная составляющая той же реакции равна Я, Величина силы
Я найдется из рассмотрения моментов всех сил вокруг
точки О;
B.f
л г
т-°-
откуда
Я=
Sf
ИЛИ
У~~8#'
[21]
Если вместо равномерного распределения нагрузки по
длине пролета взять равномерное распределение по длине
©
Фиг. 27.
кривой, то ур-ние [21] нужно заменить еледующпм ур-ниеи;
| cosh-^
(¦¦
[21']
а \ 2Я /
или, развернув гиперболический косинус в ряд, получим:
f==
II
q [ 2 \2Н
~ 1-2-3-
4 і2Д
)'+-]¦
[21"]
Взяв только первый член ряда, мы приходим к ур-нию [21]
г, f , 1
Более точными подсчетами можно показать, что при-у- < —
ошибка по ур-нию [21] меньше 1°/0. При -у =—.ошибка—
около 4%.
¦ 3 Тимошенко — Сопротивление материалов, ч. I. .?-3
Продолжая наше приближенное решение, получим
полную реакцию в точке А:
Реакция будет иметь направление по касательной к нити
в точке А и тангенс угла наклона реакции к горизонтали
будет равен -|U-- Если взять вместо точки А
какую-нибудь другую точку А' на расстоянии х от 0, то из
равновесия части О А4 нити можно заключить, что составляющие
растягивающего усилия в нити в точке Аг будут qx и J/,
и что касательная в этой точке образует с горизонталью
угол, определяемый ур-нием 1)\
ж^тг* га
• Длина L нити найдется из следующего уравнения:
2 2 :
і = 2 jV{dxY + (dyf = 2f d*yi + №J. M
о о
Подставляя выражение [Ъ] вместо -j- и интегрируя,
получим ур-ние для L. [Это уравнение, однако, получается
неудобным для числовых выкладок, поэтому
дадим'приближенное решение для L. Приняв во внимание, что в
случае пологой кривой величина (-р) мала по сравнению
с единицей, получим приближенно:
Подставив в ур-ние [с], имеем:
1) Это— уравнение параболы с вертикальной осью симметрии.
34
или, воспользовавшись ур-нием [21] для Я,.получим:
і"г(1+ій- [22]
Если точки опор не находятся в одном и том же уровне Сфнг. 28Л
го необходимо сперва определить расстояния а и Ь от низшей точки
О нити до вертикальных линий, проходящих через точки опор-
Допустив спять, что кривая — пологая, найдем, что веса частей АО и Oil
нити будут qa и дЬ соответственно, а реакции опор будут такими, как
показано на фигуре. Обозначив через f и f\ стрелки провесов частей
АО и ОБ нити от горизонталей, проведенных через соответствующие
Фиг. 28.
опорные точки, получим следующие два уравнения моментов сил
вокруг точки О;
14
Вычитая второе уравнение из первого и пользуясь обозначением
h = fx — f, получим:
а
Второе уравнение для определения а и Ъ будет
а + Ь = L
Тогда из ур-ний [е] и [/] получим: -
I ЬЕ
ь =
2 + &'
3*
И
И
35
Подставляя вьшеполученно? выражение для Ь в первое нэ
ур-ний [d]t получим следующее уравнение для определения Л:
откуда
[24]
Из ур-ний [2S] видно, что а и Ъ оба — положительны, и что точка
наибольшего провеса будет между опорами (фиг. 28), когда
<тг ЕЛИ #< J
, v. т дли *а \ тТгГ ¦
^ ^ 2 2ft
Это условие будет выполнено, если взять знак'минус перед корнем
в ур-нии [24]. Знак плюс перед корнем отвечает случаю, при котором
растягивающая сила настолько велика, что параболическая кривая,
ппедставляющая прогиб нити, имеет вершину слева от опоры At как
показано на фиг. 28 пунктирной линией, проходящей через точки А и В.
Рассмотрим теперь влияние перемены температуры. Вследствие
того, что напряжение в нити зависит от стрелки ее провеса, т. е. от ее
длины, любое изменение температуры, вызывая изменение- длины нити,
отразится таким образом на растягивающем напряжении. В случае нити,
подвешенной между точками А и В, которые находятся на одном
уровне (фиг. 27), примем, что начальная температура имеет некоторое
значение f0, начальная стрелка провеса — fo; тогда начальная
растягивающая сила в низшей точке
Я°= В/0
и длина нити
*»-'(1+т?)-
Если температура увеличится от *0 до ty и f обозначает провес при
этой новой температуре, то
Я~"87
— соответствующая растягивающая сила в низшей точке, и
— длина нити. Легко видеть, что изменение длины нити зависит не
только от изменения температуры, но также от изменения
растягивающего усилення в нити.
Рассматривая случай пологой кривой и пренебрегая бесконечно
малыми величинами высших порядков, можем принять при определении
температурного удлинения длину нити равной I (см. ур-ние [22], а
растягивающую силу можем рассматривать как постоянную по длине
нити и равную силе Н в низшей точке. Тогда удлинение нити
вследствие возрастания температуры будет al(t— tQ)f а уменьшение длины
вследствие уменьшения растягивающего усилия будет
ж
отсюда
L —i0 = a?(*-f0) +
Подставляя место Hy ff0, L и La их вышенайденные выражении
в величинах f, /0 н I, получим следующее кубическое уравнение для h
[25]
Из этого уравнения можно определить стрелу провеса нити при
новой температуре. Иногда оказывается полезным преобразовать выше-
написанное кубическое уравнение при помощи обозначений
Сп =
ffP
8*Гп
F
и
F
для начального напряжения и для веса единицы объема материала.
Тогда получим:
[26]
Ур-ния [25] и [26] имеют
следующий вид:
p=af+b,
где а и Ь известные числа.
Такое уравнение можем легко
решить графически, нанеся на
чертеж левую и правую части
как функции Л Тогда
действительный корень уравнения
получится на пересечении
кубической параболы у = /з с
прямой y = af-\-b (фиг. 29). Зная
f, найдем, пользуясь ур-ннем
[21], напряжение в нити при
новой температуре і.
ЗАДАЧИ.
Фиг. 29.
1. Однопролетный
висячий мост имеет длину I = 450 м,
ст.релу провеса f = 4» ль и постоянную нагрузку, равномерно
распределенную по длине пролета, равную q=--lQ т/м. Найти горизонтальную
составляющую Л растягивающего усилия в каждом из двух кабелей.
Решение. Из ур-ния [21]
-¦4
1 16-4503 .,лл
2 8-4о
f
2. При какой величине отношения -урастягивающееуснлиенаопор?
будет больше на 2% растягивающего усилия в середине нити (фиг. 27)?
'37
Решение. Из ур-ния [а] (стр.34) растягивающее усилие на опоре
«-»1МА)'.
0]2
или, подставив # = -?7-в подкоренное выражение, получим:
о/
-Y»№
Чтобы удовлетворить условию: -g-% =1,02, мы должны положить
1-|-/if. \3=lf(kfc, откуда (х") ==0>04 или "Т" =0,05. Из этих выкладок
можем заключить, что для небольших величин отношения —• можно
принять без существенной ошибки, что растягивающее напряжение
будет постоянным по длине нити.
3. Найти растягивающее напряжение в стальной проволоке,
подвешенной в точках Л -в Б (фиг. 28), если I = 90 м, Д = I2 *» f = 6 я и
Тс = 7 850 **/м*т
Решение. Пользуясь ур-нием [24[ и рассматривая случай, при
котором вершина расположена между опорами Л и В, получим
/к--^—У>і(/і-*)].
откуда
4. Какой начальный прогиб следует дать стальной проволоке при
температуре -j- 18°С, чтобы иметь напряжение с0 = 1540 кг/см2 при
температуре— 26°С, если I =45 ле, а0 = 0,000012 и тс = 7850 кг/*з?
Решение. Подставив в ур-ние [26] /0 == — 26, t = 18 и с0 —
= 1540 кфм?, можем вычислить стрелу прогиба.
5. Найти растягивающее напряжение в медной проволоке,
подвешенной между точками А ж В (фиг. 27), если начальная длина проволоки
в ненапряженном состоянии равна пролету 2 == 36 м.
Р еш е н и е. Пусть f— стрела провеса проволоки, тогда растягиваю-
гт Я?
щее усилие И = -%7 и соответствующее удлинение.
йЬ~ EF~~ bEf*
Это удлинение можно положить равным разности в длинах
параболически й кривой и пролета, т. е. L — L Тогда, пользуясь ур-нием [22],
получим
SEf~~ з г *
откуда
^= j/ 1Ш~ = ]/ 64-11200О0-104 те0»40*.
33
Соответствуют,^ иапряжеяае
Н ир 8 800 • 362
g д Т = "ВТ = 8 ¦ 0,4-100* ~ 35G т'сл*
6. Найти изменение стрелки нити, вызванное дополнительной
равномерно распределенной нагрузкой.
Решение. Пусть qQ и fQ обозначают начальную нагрузку на
единицу длины нити и начальную стрелку. Если д —конечное значение
нагрузки и f — стрелка после приложения дополнительной нагрузки,
то увеличение длины нити из ур-ния [22] будет Д? =-^ (Z"2 — f02). Это же
увеличение длины получим, рассматривая удлинение вследствие
увеличения растягивающей силы, в следующем виде:
Ді~ EF\Sf 8/оГ
Приравнивая оба выражения для удлинения М, получим следующее
уравнение для определения стрелки f:
21 {Т ' ° } EF \ Sf 8/о J
откуда:
*+(ЛЙ5-»)'-в?-*
Зная ft можем определить напряжение, вызванное в нити
дополнительной нагрузкой.
7. Вывести уравнение для определения изменения стрелки нити,
если совместно изменятся и температура и нагрузка на единипу длины.
Решение. Если fn, q0 и t0 — начальные значения стрелки, нагрузки
на единицу длины и температуры, аЛз'иі- значения тех же
величин после изменения нагрузки и температуры, то изменение длины
о
нити на основании ур-ния [22] будет: М = -г-г (/2 — f02). Это же
удлинение, рассматривая изменение температуры и растягивающей силы,
можем представить в следующем виде:
Тогда уравнение для определения / будет:
вли
"+[ній-1-"-«г!-'ф-нё=«-
Это уравнение очень удобно для определения стрелки провеса и
напряжения в кабелях линий электрических передач, которые
испытывают изменения температуры н подвергаются действию таких
дополнительных нагрузок, как лед и давление ветра.
8. Медная проволока, несущая собственный вес 0,36 «t/ж и
дополнительную нагрузку от льда, равную 0,70 кг/и, имеет при температуре
39
—4°С напряжение з = 1750 кг/с*2. Найти стрелку провеса той же ировологи
при + 28°С в отсутствии дополнительной нагрузки. Найти напряжение
при —40°С и отсутствии дополнительной нагрузки. Принять 2=180 *,
ам = 0,0000165, F = 0,387 см2.
Решение. Подставив в последнее ур-ние задачи 7:
Гп =
<2о
0,35 + 0,70 = 1,05 кг/я,
_ 1Ш_ __
105 • 180'
= 6,28 *,
8/<'а 8-1750-0,387
tQ s= — 4°; q = 0,35 ш/м и t — + 28° или t = — 40°,
получим два кубических ур-ния для определения f при ? = +28° и
2 = — 40°, откуда можно найти Л после чего найдем напряжения
по ур-нию [21].
ГЛАВА ВТОРАЯ.
СОВМЕСТНЫЕ НАПРЯЖЕНИЯ.
П. Изменение напряжений с изменением положения попе*
оечного сечения при простом растяжении. В призматдческом
стержне, подвергающемся
осевому растяжению силон
Р (фиг. 30а), мы
рассматривали только напряжения
по поперечным сечениям,
перпендикулярным к оси
стержня. Возьмем теперь
случаи, при которых
поперечное сечение pq, перпен-
.у дикулярное к плоскости
фигуры, наклонено к оси
стержня. Вследствие того,
что все продольные
волокна имеют одно и то же
удлинение (см. стр. 3), усилия,
представляющие действие
верхней части стержня на
нижнюю его часть, будут
равномерно распределены
по всему поперечному
сечению pq. Нижняя часть
стержня, отдельно
изображенная на фиг. 305, находятся в равновесии под действием
этих усилий и груза Р, приложенного внизу; из этого
следует, что равнодействующая этих усилий равна Р. Уси-
40
Фиг. 30.
лие,отнесенное на единицу площади поперечного сечения
pq, называется напряжением в этом поперечном сечении.
Обозначив через F площадь перпендикулярного к оси стержня
поперечного сечения й через <р-угол между осью стержня
и нормалью п к поперечному сечению^д, получим, что
площадь поперечного сечения ра будет равна и налря-
COS <р
жение о„ по этому поперечному сечению будех
Pcos <?
?
.?
F
о cos <р,
[27]
где а обозначает, как выше, напряжение в поперечном
сечении, перпендикулярном к оси стержня. Из этого
следует, что напряжение оф по любому
наклонному поперечному сечению стерж- -
ня меньше, чем напряжение - о в
поперечном сечении, перпендикулярном к
оси стержня, и что оно. уменьшается с
тс
увеличением угла <р. При ? = — сечение /
jP2—вертикально и напряжение о обра- т*\
щается в нуль: это указывает, что м?- ^
жду боковыми поверхностями
продольных волокон нет давления. Для любого
наклонного поперечного сечения
напряжение имеет направление силы Р и уже
не перпендикулярно к поперечному
сечению. Обычно его раскладывают на
два составляющих напряжения, как
показано на фиг. 31. Одно из
составляющих напряжений oftf перпендикулярное
поперечному сечению, называется
нормальным напряжением. Его величина:
Фиг. 3L
°п == ао cos ? = ° cos9 9
.9 СР =S О:
¦cos2<p
[28]
Тангенциальная составляющая т называется
касательным или скалывающим напряжением и равна
о sin 2?
т = °9 sine? = asm 9 cos cp = ?—Ч [29]
Чтобы наглядно представить деформацию, вызываемую
каждым из этих составляющих напряжений/' рассмотр&й
41
элемент, вырезанный из стержня двумя параллельными
наклонными сечеЕИями pq и p1gl (фиг. 32). Усилия,
действующие на такой элемент и представляющие действие
верхней и нижней частей стержня на элемент, показаны
на фиг. 32а. Фиг. 326 и с получены разложением этих
усилий на две составляющие, как объяснено выше, и
представляют отдельна действие каждой из этих составляющих.
Из этих фигур видно, что нормальные напряжения оп
вызывают растяжение элемента по направлению нормали п, а
©
©
Фиг. 32.
спалывающие напряжения вызывают сдвиг сечения pq
относительно сечения ptqim
Из ур?ния [2.8] впдно, что наибольшее нормальное
напряжение действует в поперечных сечениях,
перпендикулярных'оси стержня, и равно: (aw)max = a. Наибольшее
скалывающее напряжение, как видно из ур-ния [29], действует в
поперечных сечениях, наклоненных по углом 45° к оси стержня,
для которых sin 2 ер = і, и равно
шах 2
[30]
Хотя наибольшее скалывающее напряжение составляет
полов іну наибольшего нормального напряжения, однако
в го напряжение иногда имеет большое практическое значе-.
цие, так как существуют материалы, которые значительно
42
слабее сопротивляются сдвигу, чем растяжению. Например,
при испытании на растяжение стержня из мягкой егали
с отшлифованной поверхностью, текучесть металла видна
невооруженным глазом. Она начинается по наклонным
плоскостям, для которых скалывающее напряжение
достигает максимума 1)> Это явление имеет место при пределе
текучести (фиг. 2а).
Фиг. 33.
Для поперечного сечения тп, перпендикулярного
поперечному сечению pq, рассмотренному выше (фиг. 33)
напряжение будет равно о sin ?. Его можно получить
по формуле [27] подстановкой!-^—®\ вместо у. Помощью
такого же рассуждения, как раньше, найдем нормальное
напряжение оп и скалывающее напряжение т' для
поперечного сечения тк
' . 0 ,¦ a sin 2 в
о.. = а sm2 '¦? И % = --
п
2
>) См. фиг. 128, часть И.
43
Направления этих напряжений показаны на фигуре.
Сравнивая эти напряжения с напряжениями в поперечном
сечения pq9 выраженными ур-ниями [28] и [29], получим
следующие уравнения:
о -f- о' = о COS2 <р -f" а sin2 е? = а; т = т .
Сумма нормальных напряжений по двум взаимно
перпендикулярным сечениям остается постоянной и равна с.
Скалывающие напряжения по двум взаимно
перпендикулярным сечениям равны по абсолютной величине. Взяв
в дополнение к сечениям pq и тп (фиг. 33), два
параллельных сечения тхпг и pxqu указанные'на фигуре
пунктирными линиями, вырежем из стержня элемент abed,
показанный на фиг. 336. Напряжения, действующие по граням
етого элемента, изображены на этой фигуре. Легко убе-<
диться, что скалывающие напряжения по всем четырем
граням будут равны по абсолютной величине,
ЗАДАЧИ.
1. Осевая растягивающая сила Р = 4500 кг вызывает удлинений
стержня, имеющего площадь поперечного сечения F = 6 см2. Найти
наибольшее касательное напряжение в стержне.
Ответ, т = -?¦ = 375 къ{ох2.
2. Найти положение тех площадок, для которых нормальное и
касательное напряжения численно. р|ивны.
Решение. Из ур-ний [28]"и 129] получил следующее уравнение
. a cos2 f = ± —з sin 2 <р,
откуда:
tg <f> = ііі ср = —- или ср = —.
3. Найти напряжения, действующие по площадкам элемента abed
(фиг. 33), если а =350 кл/см2 и угол <р = 30°.
12. Растяжение или сжатие по двум взаимно
перпендикулярным направлениям. Рассмотрим случай совместного
напряжения стержня в виде прямоугольного параллелепипеда,
на который действуют растягивающие силы,
перпендикулярные к четырем граням, как показано на фиг. 34. Обозначив
через Fx и Fy площади противолежащих граней и через
Рх и Ру— растягивающие силы в направлении осей а: и у,
получим растягивающее напряжение по граням Fx и F,:
и
Рассмотрим теперь напряжение в произвольном
поперечном сечении pq, перпендикулярном плоскости фигуры,
нормаль к которому составляет угол 9 с осью х.
Напряжения, возникающие в этом сечении от действия
растягивающих сил Рх или Ру> можно легко определить помощью
формул предыдущего п°.
Равнодействующее
напряжение, возникающее
при одновременном
действии обеих сил Рх и Ру,
получим, геометрически
суммируя напряжения,
возникающие от каждой р
из этих сил отдельно. На
основании формул [28] и
[29] нормальное и
скалывающее напряжения,
вызванные силой Рх, будут
1
ах COS2 ср И
о sin 2 <?
ау Sin2 с? И — "-?- ау Sin 2 <?.
соответственно. Тем же
путем получим
напряжения, вызванные силой Ру\
' Л
2
Направления этих
составляющих показаны на
фиг. 34, и, суммируя их,
мы получим следующие
ур-ния для определения равнодействующего нормального и
равнодействующего скалывающего напряжений:
[31]
[32]
Если ох алгебраически большее из двух напряжений,
то из ур-ния [31] наибольшее нормальное напряжение
(°»)max = a* и получается при cos2cp = i и ?=0; наимень-
шее же (Ощіп^0? и получается при cos 2? = —1 и ?=¦?.
Из этого следует, что нормальное напряжение достигает
максимума или минимума по плоскостям, где скалывающие
45
напряжение равно к нулю. Эти максимальное и
минимальное нормальные напряжения называются главными
нормальными напряжениями.
Из ур-ния [32] наибольшее скалывающее напряжение
max
[зз]
ТС
и получается при sin2<p = l и ? = -j-* -Если аа такое же,
как выше, тшах будет иметь направление, показанное на фиг. 31.
Вышеприведенный анализ напряжений, выполненный
для растяжения по двум направлениям, может быть
применен также тогда, когда
одна или обе силы сжи^
мающие; необходимо
только поставить знав
минус для сжимающих
напряжений в формулах
[31] И [32].
Взяв две пары
взаимно перпендикулярных
плоскостей, вырежем
элемент из такого стержня,
подверженного
совместным напряжениям (фиг
35).
Пользуясь теми же
рассуждениями, что и
раньше, можем
определить нормальное и
скалывающее напряжения,
действующие на каждой
. из сторон элемента.
Скалывающие напряжения на всех четырех сторонах будут
равны по абсолютной величине, а направления скалывакк
щих напряжений будут таюие,. как показано на фиг. 35.
ЗАДАЧИ.
1. Найти напряжения сгп, ^ и т по фиг. 35, если ах = 700 кг/см2,
vy = — 350 кг/см2 и ср =,30°.
Ответ. сгя = 437,5 кг/ом2; % = — 87,5 кг/см2; т = 454,7 кг/см2.
2. Найти ап, о^ и т для предыдущей задачи, когда <р выбран так,
что х имеет наибольшее значение.
Фиг. 35,
Ответ. оп =* 175 кг/см2; о?, = 175 mfcx2; тш — 525 кг/см\
43
13. Круг Мора* Состояние напряжений для любой
плоскости, такой как плоскость $q на фиг. 34, можем легко
представить графически, построив диаграмму, в -которой
составляющие напряжения оп и г приняты за координаты
пекоторой точки. Пусть фиг. 36 представляет такую
диаграмму. Тогда для любого угла?; определяющего положение
поперечного сечения pqf можно получить точку с
координатами а и т. Начнем с сечений, перпендикулярных осям х
и у, и, вспомнив, что по этим плоскостям нет скалывающих
напряжении, получим, что точки, представляющие
напряжения, действующие по этим двум плоскостям, будут
лежать на оси о. Пусть
А и В эти две точки. т л
Тогда в известном
масштабе ОА — о^. и
Легко доказать,
что составляющие
напряжения для
любого поперечного
сечения pq,
наклоненного под углом
9 (фиг. 34),
представятся
координатами круга,
диаметр которого —
отрезок АВШ Это и есть
так называемый
О
Фиг. за
круг Мора для этого случая. Чтобы получить на этом круге
точку, соответствующую сечению pg, необходимо только
измерить от точки А в направлении движения часовой
стрелки дугу, отвечающую углу, равному 2?. Пусть D—
точка, полученная таким путем (флг. 36). Тогда, из чертежа:
OF^OC-^CF
+
у
+
х
cos 2 © = ох cos2 © -f oy sin2 ©;
DF = CD sin 2 с?
X
'2- sin 2 с?.
Сравнивая полученные выражения с формулами [31] и
[32], легко убедимся, что точка D представляет состояние
напряжений в плоскости jpg. По мере того, как сечение
Р2 вращается вокруг оси, перпендикулярной плоскости
фиг- 34, в направлении движения часовой стрелки, и угол ?
меняется от нуля до -?-, точка D перемещается от Л к Д
так что нижний полукруг определяет изменение
напряжения для всех значений <р в указанных пределах.
Продолжив радиус CD до точки Dv т. е. взяв угол
те + 2-э вместо 2ср, получим напряжения в поперечном сече-
а, О
Фиг. 37.
Фиг. 38.
нии, перпендикулярном плоскостиpq. Очевидно, что DXFX =
— OF, т. е. скалывающие напряжения по двум взаимно
перпендикулярным поперечным
сечениям равны по абсолютной
величине. Что касается
нормальных напряжений, то из
чертежа мы видим, что
OF1 + OF=20C,
тв е.
- 0» + а'« = а*+<У
Сумма нормальных напряже-
ФПГ. 39. ний по Двум взаимно
перпендикулярным поперечным
сечениям остается постоянной при изменении угла ю.
Когда одно или оба напряжения ох и а^ — сжимающие,
можно применить тот же графический прием; нужно только
отрезки, представляющие сжатие, откладывать в
отрицательном направлении оси о. На фиг. 37, например,
представлено графически кругом с диаметром АВ совместное
сжатие по двум взаимно перпендикулярным направлениям.
В случае простого растяжения о^. == а, off = 0, и круг
43
Мора будет таким, как показано на фиг. 38. Легко
убедиться, что координаты OF и DF точки D представляют
собою правые стороны формул [28] и [29] соответственно.
В случае простого сжатия в направлении оси х, круг
Мора будет расположен, как показано на фиг. 39.
Из этого видно, что при помощи рассмотренного
графического способа можно легко определить напряжения,
действующие по граням такого элемента, как представленный
на фиг. 35, при любых значениях напряжений ох и су.
Что касается знаков нормальных напряжений, то было
условлено считать растяжение положительным, а сжатие
отрицательным. Для
скалывающего
напряжения
направление, вообще говоря,
не имеет значения
и практический ин
терес представляет
только его величи
на. Но-есть случаи,
когда направление
также доляшо быть
принято во
внимание. Тогда
направление скалывающих
напряжений будем
рассматривать
положительным, когда
они дают пару сил,
действующую в направлении движения часовой стрелки,
как например для „сторон ad и Ъс элемента abed на фиг. 35.
Скалывающие напряжения противополояшого направления
будем считать отрицательными. Согласно этому правилу
положительные скалывающие напряжения будут
соответствовать верхней половине круга Мора, а отрицательные
скалывающие напряжения—нижней половине круга.
Кругом Мора можно воспользоваться также для решения
обратной задачи: по данным напряжениям оп, а\ и х (фиг. а5)
найти, под каким углом © был вырезан элемент из
параллелепипеда, подвергающегося действию совместных нааря-
¦жений ах и ауэ и каковы величины главных напряжений
ах и qv. Откладывая напряжения ой и a'nf получим точки
F и Fx на оси о (фиг. 40). Тогда, следуя вышеуказанному
правилу знаков для скалывающих напряжений и принимая
Фнг. 40.
4 Тимошенко — Сопротивление материалов, ч. I.
49
перпендикуляры FD и FJ)X равными напряжению т,
получим диаметр DDt круга Мора. На этом диаметре вычертим
яруг и найдем точки А и JB, которые определяют главные
напряжения ох и о& (°*>оу).
Из чертежа видно, что
2
Тогда главные напряжения будут;
о 4-о' А/ о — а' \2
c=0J3=0C — CD=&
4
[84]
Угол <р найдется из уравнения:
SP 2 т
tg2<? = -=^ = ;-, [36]
к которому следует применить вышеприведенное правило
знаков для скалывающего напряжения.
Как пример совместных напряжениий рассмотрим
нормальное и скалывающее напряжения в цилиндрических
стенках котла, подвергающегося внутреннему давлению р
кмісм*. Обозначив внутренний диаметр через d и толщину
стенок через Ь (фиг, 41), вырежем элемент из стенки двумя
продольными сеченнями и двумя круговыми сечениями.
Под действием внутреннего давления цилиндр будет
расширяться в круговом и в осевом направлениях.
Растягивающее напряжение ов в круговом направлении будет
определяться тем же путем, как в случае кругового кольца
(см. п° 9). Пользуясь ур-нием [19], получим;
а — Pd
При определении растягивающего напряжения о в осе-
50
вом направлении нужно обратить внимание на то, что
растягивающая сила, вызывающая продольное расширение
котла, равна давлению на торцевые стенки котла т. е.
равна Р=#- —. Площадь поперечного сечения,
перпендикулярного оси цилиндра, F=itdh; отсюда
Р pd
У
F
¦ik
Итак растягивающее напряжение в круговом
направлении вдвое больше растягивающего напряжения в
осевом направлении.
Для любого сечения qq3 перпендикулярного плоскости
ху и определяемого углом ср, нормальное и скалывающее
©
Фиг. 41.
напряжениявыражаются формулами [31] и [32]. Отсюда можно
заключить, что для сечений такого рода наибольшее
нормальное напряжение будет oxt а.наибольшее скалывающее
Еэлряжение будет — (ох—о&)==— ов.
По сечению стенки, проходящему через ось у (фиг. 41),
напряжения не будут зависеть от растяжения в
направлении оси у (см стр. 41) и зависят только от растяжения
в круговом направлении. Поэтому, при определении
напряжении в таких сечениях, следует пользоваться ур-квдми [28]
и [29], и можно заключить, что для сечении этого рода
наибольшее нормальное напряжение — ая и наибольшее
1
скалывающее напряжение——оя.
Таким же путем можно исследовать напряжения по
©еченпям проходящим через ось х.
4* 51
Из рассмотрения этих трех типов сечений мы получим,
что наибольшим нормальным напряжением является
найденное выше az> и наибольшее скалывающее напряжение
равно у ох.
Можно показать *), что для любого сечения, наклонного
по отношению к трем основным сечениям, рассмотренным
выше, наибольшее нормальное и наибольшее скалывай щее
напряжения будут меньше, чем найденные выше напряже-
1
НИЯ Qx И —
й
от соответственно.
ЗАДАЧИ.
1. Элемент подвергается действию напряжений ап = 350 кг/см2,
ст' = 210 кі\см2; -с = 70 кг/см2 (фиг. 42). Найти величины и направления
главных напряжений и и о,
У
Решение. По ф-лам [34] и [35] получим:
__ЗбО + 210_+-/Т
350 — 210
х 2 * V \ 2
= 280 + 99 = 379 кг/см2;
350 + 210 ~/"7~350 — 210 \з
= 280 — 99 = 181 ьт/слА
Из ур-ния [33] имеем;
)3 + 702 =
а2/ =
)ЧТ03 =
Фиг. 42.
2'™
tg2y=== 350-210
2 tp = 45°г
= 1;
<р = 22°30'.
Соответственные направления главных осей показаны на фиг. 42.
2. Найти направления главных осей для предыдущей задачи в
случае, когда ай = — 350 кг/см2.
Решение. Угол <р между внешней нормалью к площадке al\ на
которую действует напряжение aw и наибольшим главным
напряжением ах найдем следующим образом:
1
2 ср = 165°58';
3. Кайти положение сечения qq (фиг. 41) так, чтобы
Ч = Y(в» + ^
Ответ, ф = -гя.
4
9 = 82W.
і) Дальнейшее развитие этого вопроса — см. стр. Q0.
52
1. Найти круг Мора для случая действия двух одинаковых
растягивающих напряжений с^ = ау ц= а или для двух одинаковых
сжимающих напряжений а = с = — с
х у
Ответ. В этом случае круги обращаются в точки на оси а с абсцнс
сами + с и — а соответственно.
14. Деформация в случае простого растяжения. В п° 2 было
рассмотрено осевое удлинение стержня при растяжении.
Опыты показывают, что такое осевое удлинение обычпо
сопровождается боковым сужением стержня и что
отношение относительного бокового сужения к относительному
осевому удлинению — постоянно для данного стержня,
если предел упругости не превзойден. Это постоянное
отношение обозначается буквой р и известно под названием
Пуассонова отношения, по имени французского математика,
который установил это отношение аналитически, применив
молекулярную теорию строения тел. Для материалов,
которые нмеют одинаковые характеристики упругости по
всем направлениям, т. е. для так называемых изотропных
материалов, Пуассон нашел, что р = —. Опытные
исследования бокового сужения в металлах, употребляемых для
сооружений а), показали, что значение \l обычно не очень
сильно отличается от значения, найденного Пуассоном.
Например, для литой стали можно принять ц. равным 0,30.
Зная Пуассоново отношение для материала, можно
определить изменение объема стержня при растяжении. Длина
стержня увеличивается в отношении (1 -\- е) ;^.. БокоБые
размеры уменьшаются в отношении (1—ys):l. Поэтому
площадь поперечного сечения уменьшается в отношении
'(1 — уе)2:і. Тогда объем стержня изменяется в отношении
(1 + в) (і — н-е)2:1, которое получается равным (1 -f- е — 2jie): 1,
если мы, вспомнив, что е — небольшая величина,
пренебрежем квадратом ее/ Относительное увеличение объема
будет равно е (і — 2ц). Трудно представить себе, что какой-
либо материал уменьшается в объеме при растяжении;
поэтому ^ должно быть меньше 0,50. Для таких материалов,
как резина и парафин, ^ приближается к этому пределу;
и объем этих материалов при растяжении остается
приблизительно постоянным. С другой стороны, такой
материал, как бетон, имеет небольшую величину р ( ц. =
х) Эти материалы можно рассматривать изотропными (см. п° 4$,
часть II).
53
—_* L\ а для пробки p. можно принять равным
нулю.
Эти соображения о боковом сужении при растяжении
можно применить соответствующими видоизменениями и
в случае сжатия. Продольное сжатие будет сопровождаться
боковым расширением, и для определения этого
расширения применяется то же значение для у, как и в случае
растяжения,
ЗАДАЧИ.
1« Найти увеличение объема стержня равного сопротивления на
растяжение, рассмотренного в задаче 2, стр. 18.
Решение. Увеличение единицы объема:
. а - ад = і а - 2<л) = -^^ а - о,б) = 0,0000762.
Увеличение объема стержня
6160
7850
0,0000762 • 108 — 59,8 см*.
2. Найти увеличение объема стержня, растяжение которого вызвано
силой -Р, приложенной к его концу, и собственным весом стержня
(см. "п0 5, формула [9], стр. 12).
Ответ. Увеличение объема равно:
(1 - 2р.) IF
В
(4-+4>
15. Деформация в случае растяжения или сжатия по двум
взаимно перпендикулярным направлениям. Если стержень,
имеющий вид прямоугольного параллелепипеда,
подвергается действию растягивающих сил в двух взаимно
перпендикулярных направлениях х и у (фиг. 34), то
удлинение в одном из этих направлений зависит не только от
растягивающего напряжения в этом направлении, но также
от напряжения в перпендикулярном направлении.
Относительное удлинение в направлении оси х, вызванное
растягивающим напряжением св, будет -^-, Растягивающее
напряжение оу будет вызывать боковое сужение в направлении
оси х3 равное —~; тогда,. если оба напряжения ода и
54
а7/ действуют одновременно, относительное удлинение в
направлении оси х будет:
-—у.
х Е г Е *
Точно так же, для направления оси у, получик:
[37]
Е~~Р~Т-
[38]
В частном случае, при двух одинаковых растяжениях
ов = а =о ПОЛуЧЙМ;
?л; = еу==:-^г(1—Н-)-
[39]
На основании формул [37] и [38] ягожно выразить налря-
зкения ох и off в функциях, зависящих от относительных
деформаций ех и еэ, таким образом:
V
(««4ч»»)-Е ?
1 — 1^ *
1—f* *
t«]
ЗАДАЧИ.
1. Найти увеличение объема цилиндрического стального котла,
испытывающего внутреннее давление (фиг. 41), пренебрегая деформацией
концевых стенок и приняв о- ¦ = 420 кг/см*.
Решение. По предыдущему (см.
стр. 51) <j = — а^ = 210 %г/см2т По ф-лам
[37] и [38J получаем;
_ 420
?* 2100000
210
\ 2100 000
-0,3
-0,3
210
2100 000
420
= 1,7-10-*;
= 04.10-4«
Фиг. 43.
2100000
Объем котла увеличится в отношение
(1 + гх)2 (1 + «f): 1 = (1 + 2", + «г): 1 = 1,00038:1.
2. Бетонный кубпк сжимается по двум взаимно перпендикулярным
направлениям, помощью устройства, показанного на фиг. 43. Найти
уменьшение объема кубике, если ею сторона—10 см, сжимающее
напряжение равномеоно распределено по граням кубика, н- = 0Д и Р = 9 ?«.
53
Решение. Пренебрегая 'трением в шарнирах и рассматривая
равновесие каждою шарнира (фиг. 43Ь), можем доказать, что кубик
испытывает одинаковое сжатие по двум взаимно перпендикулярным
направлениям и что сжимающая сила равна Р у 2 = 12,7 т. Соответствующее
укорочение из ур-ния [30]. будет:
12 700 (1 - ОД) _
е, = \ = Г6^280000- = " °'О0М1-
В направлении, перпендикулярном плоскости фигуры, кубик будет
испытывать боковое уширение, равное:
*х ** 12 700
>iq-^T^ if = 2'°Д 10»-280000 - + °-QQQQ9-
Уменьшение единицы объема кубика будет:
гх -f е + ?г = — 2 - 0,00041 + 0,00009 = - 0,00073.
3.гНайти увеличение цилиндрической боковой поверхности котла,
рассмотренного выше в задаче 1.
Решение. Увеличение единицы площади боковой поверхности
равно;
% + «, = <1,7 + М) 10-* = 2,Ы0-4.
4. Найти относительное удлинение в направлении оси х стального
стержня, если напряженное состояние таково, как указано в задаче 1,
стр. 52.
Решение.
379 - 0,3 • 181 в
е* = —юоооо =lo5>1Q '
16, Чистый сдвиге Вернемся к частному случаю п° 12
растягивающего напряжения ох и сжимающего
напряжения—^ той же величины (фиг. 44). Соответствующий круг
Мора показан на фиг. 45. Точкаі) этого круга
представляет напряжение но поперечному сечению аЬ, нормаль
которого наклонена под углом 45° к оси х, и точка 1У
представляет напряжение в поперечном сечении,
перпендикулярном первому. Из рассмотрения этого круга следует,
что нормальное напряжение каждого из этих поперечных
сечений равно нулю и что скалывающее напряжение для
этих же сечений, представляемое радиусом круга, равно
х = ся = — аг Отсюда заключаем, что если такой элемент,
как abed (фиг. 44), рассматривать в отдельности, то он будет
находиться в равновесии под действием только
скалывающих напряжений (фиг. 44d). Такое напряженное состояние
называется чистым сдвигом.
Если поперечное сечение будет наклонено под углом
4,5° к оси я, то на ряду со скалывающим напряжением бу-
цёт существовать нормальное напряжение. Величину послед-
6(5
него можно получить ооычным путем из построения круга
Мора для этого случая (фиг. 45),
Фнг. 44.
Рассмотрим теперь деформацию элемента abed.
Вследствие того, что в этом случае отсутствуют нормальные
напряжения,
действующие на грани этого
элемента, длины ah, ad, be и
dc не будут меняться при
деформации, но
вертикальная диагональ ас
растянется, а
горизонтальная диагональ db
укоротится, так что квадрат
abed превратится после
деформации в ромб, как
это указано на чертеже
пунктирными линиями
(фиг. 44а).
Угол у вершины а,
который до деформации был
тс
равен
с» У
станет теперь
Фиг. 45.
тс
меньше чем —, допустим
время угол у вершины Ъ
а в то же самое
увеличится и станет равным
57
( —-f-тЬ Небольшой угол т определяет перекос элемента
abed и называется относительным сдвигом.
Эту величину можно наглядно представить следующим
образом. Повернем элемент abed (фиг. 44) на 45°, и пусть он
находится в положении, показанном на фиг. 46а; после
искажения, вызванного скалывающими напряжениями ?, этот
элемент займет положение, указанное пунктирными линиями.
Тогда относительный сдвиг, измеряемый величиной
небольшого угла т, может быть принят равным отношению, dd'/dc.
Это отношение равно сдвигу dd' стороны ad по отношению
к стороне Ьс> деленному на расстояние между этими двумя
сторонами (в виду того, что dJP/dc = tg ^ = т. так как угол т
очень мал). Следует заметить, что равномерность
приложения скалывающего напряжения к сторонам такого элемента,
как изображенный на фиг. 46а, очень трудно осуществить.
Практические расчеты на сдвиг таких элементов, как
заклепки и болты (фиг. 466), в которых обычно
предполагается равномерное распределение скалывающего
напряжения по поперечному сечению тщ являются только гру
бым приближением.
Чтобы установить соотношение между деформацией
сдвига и скалывающими напряжениями т, действующими
на стороны элемента abed, рассмотрим правый
треугольник оаЪ фиг. 44. Удлинение стороны ао и укорочение
стороны оЪ этого треугольника при деформации могут быть
найдены из ур-ний [37] и [38]. Отметив, что в этом случае
ох = —а =т,
получим:
е _ т(1 + Л>. т _ т(1 + 1*)
х Е ' у~ Ц * .
58
Тогда
оа'= оа Г1 + —Ц=^ ; оЬ' = оЬ
я я.з правого треугольника оа'й' получим:
Е
г *(1+У-)
,,, , I ' -я ч\ оЬ' Е
JE7
При малом угле т можно принять, что
Подставив это в ур-ние [а], получим
Т_'с(1+^)
И
или, .обозначив
Е
Е
имеем
2<1-М
= ff, [41]
[42]
Отсюда следует, что относительный сдвиг
пропорционален скалывающему напряжению т и обратно
пропорционален величине G, которая зависит от упругих свойств
материала и называется модулем упругости щи едете. Его можно
определить из ур-ния [41], если мы предварительно будем
знать Е и р.. Для стали например
„ 2100 000 ™л^л , о
а=2а+о^)~800000кг/^-
В следующей главе (см. стр. 67) будет показано, что
модуль упругости на сдвиг G можно определить опытным
путем при скручивании круглого вала. Тогда, определив Е-
из испытаний на растяжение, величину ^ можем вычислить
по ур-нию [41], Прямое определение Пуассонова
отношения у* путем измерения бокового сужения при испытаниях
59
на разрыв более сложно вследствие того, что это сужениэ
очень мало и для его точного измерения необходимы очень
чувствительные приборы.
17. Растяжение или сжатие по трем взаимно
перпендикулярным направлениям. Если стержень, имеющий форму
прямоугольного параллелепипеда, подвергается действию сил
Ря> Ру и Р2 {фиг. 47), то
нормальные напряжения в
поперечных сечениях,
перпендикулярных осям х, у я г, будут
соответственно
Р,
1
р,У
У
р
F
71 *
В дальнейшем примем, что
Фиг. 47.
ах > °у > °г-
t/7MT.x
суммируя действия сил Рх, Ру и Рг, можем заключить,
что по сечению, проходящему через ось ,?, только силы Рх
и Ру вызывают
напряжения, а
поэтому эти напряжения
можно определить
по ф-лам [31] и [32]
и представить
графически яри
помощи круга Мора. На
фиг. 48 круг
напряжений с диаметром
ЛВпредставляет эти
напряжения. Таким
же образом
напряжения по любому
сечению,
проходящему через ось я,
можно представить
кругом, для
которого ВС является диаметром. Круг с диаметром АС
представляет напряжения в любом сечении, проходящем через
ось у. Три круга Мора представляют напряжения для
трех серий сечений, проходящих через оси х> у и г.
Для любого сечения, наклоненного к осям х, у и г,
составляющие напряжений будут координатами точки,
60
Фиг. 48.
расположенной в пределах заштрихованной площади
фНГ. 48 *).
На основании этого можно заключить, что наибольшее
скалывающее напряжение будет представляться величиной
радиуса наибольшего из этих трех кругов и может быть
представлено формулой
max о
Оно будет действовать по сечению, проходящему через
ось у и делящему пополам угол между осями х и г?
Уравнение для определения относительных удлинений
в направлениях осей х, у и в можем получить, складывая
действия сил Рх, Ру и Ре тем же способом, что и при
рассмотрении сжатия и растяжения по двум взаимно
перпендикулярным направлениям (см. п° 15). Таким образом получим:
[43]
Объем стержня увеличится в отношении
(і-К) (1 + .,) (1 + 0:1,
или, -пренебрегая бесконечно малыми величинами высшего
порядка малости, имеем:
(l + ee + e, + e,):l,
а отсюда видно, что единичное объемное расширение равно
* = * + * + «¦• 'і**]
Соотношение между относительным объемным
расширением и напряжениями, действующими на боковые грани
стержня, получим, сложив вместе ур-ния [43]. Таким образом
Дв!іі^>(в.+ о,-К). 145]
і) Доказательство можно найти в книге А, ФЫпля {A. Fojppl), Tech-
Dische Meehanik, Bd 5, S. 18,1918.
В частном случае равномерного гидростатического
давления имеем
о, = а =0, = — р.
Тогда из ур-ний [43]
Р
в, = в» = *. = -4-^"2^
Е ИЗ ур-НИЯ [44]
Да_ 8(1-2,0
Е
или, прийяв обозначение
Е
получим
3(1— 2р)
д=
•=іт,
J>
*•
[46]
[47]
[48]
[49]
Относительное сжатие пропорционально сжимающему
напряжению р ж обратно пропорционально величине К,
которая называется объемным модулем ynpijwcmu,
ЗАДАЧИ
1. Найти уменьшение объема сплошного стального шара, диаметром
25 см, на который действует равномерное гидростатическое давление
ді р = 700 кх/ем2.
| Решение. По формуле [49]
*- Я- 2100000 U'WU4'
Уменьшение объема поэтому равно
0,0004
= 3,27 с*3.
2. Изображенный на фиг. 49 резиновый цилинд*
рик Л подвергается сжатию в стальном цилиндре В
силой Р. Найти давление между резиновым
цилиндриком и стальным, если Р = 450 кг, d = 5 cjk, Пуас-
соново отношение для резины [х = 0,45. Трением
между резиной и сталью пренебречь.
Решение. Обозначим через р — сжимающее
напряжение в каком-либо поперечном сечении,
перпендикулярном оси цилндра, и через q — давление между
резиновым цилиндриком и внутренней поверхностью
стального цилиндра. Сжимающее напряжение такой же величины будет
действовать между боковыми поверхностями продольных волокон
резинового цилиндрика, из которого мы выделим элемент в виде прямо-
62
Фиг. 49.
угольного параллелепипеда со сторонами, параллельными оси цилиндра
(фиг. 49). Этот элемент находится в равновесии под действием сжимаю
щих напряжений q по боковым граням элемента и осевого сжимающего
напряжения р. Приняв, что стальной цилиндр абсолютно жесток,
найдем, что боковое уширение резинового цилиндрика в направлении осей
х и у должно быть равно нулю, и по первой или второй формуле [43]
получим
0 =
Е
S-fe+d.
откуда
0,45
— Н3 _
3— 1-й- "" 1-0,45
450-4
= 18,8 Jfi/сл2.
3. Бетонная колонна заключена в стальную трубу (фиг. 50)- Найти
давление между сталью и бетоном н растягивающие напряжения по
окружности в трубе, приняв, что здесь нет трения
между бетоном и сталью и что все размеры и
продольное сжимающее напряжение в колонне известны
(фиг. 50),
Решение. Пусть: р обозначает продольное ид-
боковое сжимающие напряжения, &—внутренний диаметр
и h—толщину трубы, 2SC—модуль упругости стали, Е6—
и р6—модуль упругости и Пуассоново отношение для
бетона.
Уширение бетона в боковом направлении по третьей
нз формул [43] будет равно:
*, = -JL + -b-lP + q). [а]
Е,
б
Ел
Фиг. 60,
Это уширение ^должно быть равно уширению 'по окружности трубы
(см. формулу [19])
е =
2НЕ*
М
Приравнивая выражения [а] и [Ь], получим:
qd
2НЕЛ ~^~ Ел ' Е
ЕГ- + "ВТ- (Р + «),
откуда
g=jp
Н
d Ел
2А Е
+ 1-Н»
ь. О
Растягивающее напряжение по окружности трубы определите^
по формуле:
qd
а =
2Л*
4. Найти наибольшее скалывающее напряжение в бетонной колонне
предыдущей задачи, приняв, чтоі> = 70 «г/сле3, ^ = 0,10, й/2&==7,5.
Решение.
63
max
2
ГЛАВА ТРдЬ'ГъЯ.
КРУЧЕНИЕ.
18. Кручеяие круглого вала. Рассмотрим круглый цилиндр,
закрепленный верхним концом и скручиваемый парой сил,
приложенной к нижнему концу (фиг. 51). Путем измерений
на поверхности цилиндра можно показать, что круговые
сечения вала остаются круговыми при скручивании и что
их диаметры и расстояния между ними не меняются, если
только угол скручивания невелик.
Диск, отдельно представленный на <риг. 51Ъ, находится
в нижеследующем состоянии деформации. Здесь происходит
поворот нижнего поперечного сечения диска относительно
его верхнего сечения на угол d®, где углом <? измеряется
поворот сечения тп относительно закрепленного конца.
Элемент abed цилиндрической поверхности диска, стороны
которого до деформации были вертикальными, принимает
форму, показанную на фиг. 515. Длины сторон в основном
остаются без изменения, и изменяются только углы,
составляемые ими с поперечными сечениями. Элемент находится
в состоянии чистого сдвига (см. п° 16), и величина
деформации сдвига найдется из маленького треугольника сас':
с'с
U
-Так как егс — небольшая дуга радиуса¦—d, соответствуй
ющая разности Ар угла поворота двух смежных бесконечно
близких поперечных сечений, получаем;-
TeTdJA М
Для вала, скручиваемого крутящим моментом,
приложенным к ко'нцу, угол скручивания пропорционален длине,
и величина-—*имеет постоянное значение. Она
представляет угол скручивания на единицу длины вала; обозначим его
через ?. Тогда выражение [а] получает следующий вид:
Скалывающие напряжения, действующие на грани и
вызывающие этот сдвиг, имеют указанные на чертеже
направления. Величина каждого из напряжений, согласно
формуле [42]:
±-Gbd. [51]
т
Таково состояние напряжения элемента на поверхности
вала. Что касается элемента внутри вала, то сделаем
предположение, что не только окружности поперечных сечений
вала остаются неискаженными, но также и сами
поперечные сечения остаются плоскими и поворачиваются так, как
будто они абсолютно жестки, т. е. все диаметры
поперечного сечения остаются прямолинейными и поворачиваются
на один и тот же угол* Испытание круговых цилиндряче-
ских валов показало, что теория, основанная на этом
допущении, очень хорошо согласуется о результатами опытов.
В виду этого рассуждение, приведенное для элемента
abed на поверхности вала (фиг. 516), применимо также и.к
подобному же элементу на поверхности внутреннего
цилиндра, с заменой только—d радиусом г (фиг. 61с). Тол-
?л
щина элемента в радиальном направлении рассматривается
как бесконечно малая.
Такие элементы испытывают тоже чистый сдвиг, и
скалывающее напряжение на их гранях:
Это указывает, ч:то скалывающее напряжение прямо, про-
Ь Тпмошеико — Сопротивление материалов, ч. I, 65
.0
*и
Фиг. Б2.
порционально расстоянию г от оси вала. Фиг. 52 поясняет
это распределение напряжений. Наибольшее напряжение
будет на внешней поверхности вала.
Для материалов упругих явление текучести начинается
сперва на их поверхности. При материалах, которые
сопротивляются слабее продольному сдвигу, учем поперечному,
например в деревянном валу с волокнами, параллельными
оси, первые трещины возникают от скалывающих
напряжений, действующих в осевых
сечениях, и появляются на поверхности
вала в продольном направлении* В
случае материала, более слабо
сопротивляющегося растяжению, чем
сдвигу, как например в круглом валу
из чугуна или в цилиндрическом
куске мела, часто наблюдаются трещины
по винтовой линии, наклоненной под
углом 45° к оси вала (фиг. 53).
Объяснение—просто. Вспомним, тао состояние чистого
сдвига эквивалентно состоянию совместного растяжения
в одном направлении и одинакового по
величине сжатия в перпендикулярном направлении
(см. фиг. 44). Прямоугольный элемент,
вырезанный на внешней поверхности скручиваемого
вала со сторонами, наклоненными под углом 45°
к оси, подвергается таким напряжениям, как
изображено на фиг. 53. Показанные на ней
растягивающие напряжения вызывают упомянутую
винтовую трещину.
Найдем теперь соотношение между
приложенной скручивающей парой сил Mf и
напряжениями, которые она вызывает. Из
рассмотрения равновесия части вала между
нижним концом и воображаемым сечением т? мы
заключаем, что скалывающие напряжения, рас-
лределенные по поперечному сечению, будут
статически уравновешиваться парой сил, равной и прямо
противоположной скручивающему моменту Mt. Для каждого
элемента площади dF (фиг. 51с) перерезывающее усилив
равно \dF. Момент этого усилия относительно оси вала по
подстановке выражения [Ь].-
(xrdF)r = Gbr*dF.
Фиг. S3.
66
Полный момент Mt вокруг оси вала равен распростра-
ненной на всю площадь поперечного сечения сумме таких
моментов отдельных элементов, т. е.
Г 2 ХГ 2
ft= С Gbr^dF^Gbf r*aF=GbIpy [с]
где 1Р—полярный момент инерции кругового поперечного
сечения. Из приложения (стр. 369) для круга диаметра d
тогда
и
?
? 32 '
ltd*
Mt = Gtb
32
Mt 32 _ Mt
uj»
Мы видим, что 6—угол скручивания на единицу длины
вала изменяется прямо пропорционально приложенному
крутящему моменту и обратно пропорционально модулю
упругости на сдвиг G и четвертой степени диаметра.
Если длина вала—I, полный угод скручивания будет
Это уравнение пригодно для физической проверки этой
теории и оно подтверждается многочисленными опытами,
-которые оправдывают предположения, сделанные при
выводе теории. Следует отметить, что испытания на
скручивание обычно применяются для определения модуля
упругости материала на сдвиг. Если измерить угол
скручивания, возникший в данном вале под действием данного
крутящего момента, то величину G можно легко определить
из формулы [53].
Подставив ? по формуле [52] в ф-лу [51], получим
выражение для определения наибольшего скалывающего на*
пряжения при кручении круглого вала:
т,
Mtd 16 Мх
*ах 2ір ^Ф
м
5* 67
Таким образом это напряжение пропорционально
крутящему моменту Ж, и обратно пропорционально кубу дна-
метра вала.
При практических применениях приходится обычно
определять диаметр вала по мощности Я в лошадиных
силах, которую передаем вал. Зная Я, получим
скручивающий момент в кг-см из общеизвестного выражения:
Л/,--^ = 7500 Я, [55]
где п обозначает число оборотов вала в минуту. Взяв Mt
из ур-ния [55] и подставив его в ур-ние [54], получим
d в см:
" max
Приняв, например, величину допускаемого напряжения
на сдвиг д,= в30 т/см*, получим d в см:
»v$
d = 8
ЗАДАЧИ.
1. Найти диаметр вала машины мощностью в_200 л. с. при 120
оборотах в минуту; допускаемое напряжение Re = 210 кг/см2.
Ответ.
2. Найти мощность в лот. силах, передающуюся валом, если d ~^=
= 150 мм, п = 120 оборотам в минуту, # = 840000 кг/см2 и угол
скручивания, измеренный между двумя поперечивши сечениями,
отстоящими друг от друіа на 7,5 м, равен Vis радиана.
Решение. Из ур-ния [53]:
^ кй^ ?r a те - 15* 840 000
*"" ~82 Г" = 32 * 15 • 750 *
Могущая быть переданной мощность из ур-ния [55] получается
равной:
Mt*2nn те. 154 • 840 ООО • 2 те • 120
Я== 60-7500 = 3;М5.750.<>0.7500~~.622 Л' С'
3. Вал, диаметром Ъ = 90 мм, делает 45 об/мин. Найти мощность,
которую можно передать, если наибольшее скалывающее напряжение
равно 216 кгМ2-
G8
4. Стальной вал (# = 840000 кг/сн2) имеет такие размеры, что
наибольшее скалывающее напряжение равно 950 кг/сл*2 Прн угле
скручивания 90°. Определить отношение l:d.
Ответ. I: d = 6У4
5. Стальной вал е заделанными концами (фиг. 54) подвергается
действию крутящего момента Mt, приложенного в промежуточном
поперечном сечении тп. Найти угол скручивания, если допускаемое
напряжение В8 известно.
Решение, Для обеих частей вала углы скручивания одинаковы;
поэтому из ур-ния [53] скручивающие моменты обратно
пропорциональны длинам этих частей. Если а>&, больший скручивающий момент
будет в правой части вала и его величина равна:
М.
а
f
а + Ъ*
Подставляя в ур-ние [54] эту величину вместо крутящего момента
и Es вместо тшах, получим следующее выражение для d:
У \QaMt
Угол скручввания получим теперь при помощи выражения [53].
6. Мощность в 500 л. с. передается от шкива I: кОО л. с. — шкиву
II и 300 л. с. — шкиву Ш (фиг. 55). Найти такое отношение между диа-
/
1
ш
И~\т
v
Фиг. 54.
Р
#
ж
щ
Фиг. 53.
метрами dx и d%, которое дает одинаковое наибольшее напряжение
в обеих частях вала. Найти отношение между углами скручивания этих
двух частей. /
Решение. Скручивающие моменты в обеих частях вала находят-
ся в отношении 5:3. Чтобы получить одинаковые наибольшие
напряжения, необходимо согласно ур-нию [54] взять
3
2 У 3
Углы скручивания согласно ур-ниям [53]' и [54] должны находиться
в отношении:
з
- ?АГТ
7. Найти длину стального вала диаметром ЬО мм (G == 840 000 къ/см%
если наибольшее напряжение равно 950 кг/см2 при угле скручивания,
равном 6°. !
Ответ. I = 231 см.
G9
_. 8. Найти диаметр, начиная с которого угол скручивания вала, а н?
наибольшее напр :жение, является решающим фактором расчета, если
? = 840 000 к\/см°, #s = 210 кг/см2 и наибольший допускаемый угол
скручивания равен 0,25° на метр.
Решение. Исключив Mt из ур-ний:
1631,
U
&
= 210;
32 Ж,
0,25 тс
840 000 • it d* 180 • 100 '
получим 3 = 11,6 см; для Я < 11,5 см угол скручивания является ре*
шающим фактором расчета.
9. Найти скручивание каждой части вала, заделанного концами.
который скручивается моментами Mt и Mf t приложенного в двух
промежуточных сечениях (фиг. 56).
Решение. Найдя скручивание, возникающее в каждой части вала.
отдельно от каждого из моментов Mf и Mf (см. выше, задача 5) и
складывая эти моменты для каждой части, получим
4;
м:
т
1\Щ
I
ш
щ
'#¦¦'4
Щ
?
Фиг. 50.
I
М\ а.— жТ с
с Z
I 5
Ъі\ а + Mf {а + Ь)
г •
10, Найти диаметры и углы скручивания вала задачи G, если
п = 120 об./ыин., ттах = 210 кі/сл3, Z, = 2 м, Ц = 1,30 ж
19. Скручивание полого вала. Из предыдущего
рассмотрения скручивания сплошного вала видно (фиг. 52), что
только на внешней поверхности вала материал напрягается
до предела, принятого за допускаемое напряжение.
Материал внутри вала работает при меньшем напряжении, и в
тех случаях, где уменьшение веса имеет большое значение,
как например в вале пропеллера аэропланов,
целесообразно применять полые валы. Рассматривая кручение полых
валов, сделаем те же допущения, что и в случае
сплошных валов.
Общее выражение скалывающих напряжений будет
таким же, как выраженное ур-ннем [Ъ] предыдущего п°. При
определении момента скалывающих напряжений в этом
случае радиус ** изменяется в пределах от радиуса
внутренней поверхности, который обозначим череэ — dl9 до
внешнего радиуса вала, который, как выше, равен -|- '.
70
Тогда ур-йне М предыдущего п° должно быть заменено
следующим ур-нием:
-И
въ[ г*аЕ=м^аыр>
2 L
где J^ = —г- (d4 — с7^)—полярный момент инерции кольце-
Ой
вого сечения. Тогда
' . _ 32 Mt 2k_
и угол скручивания будет
., Mtl
ъ = п = -аГр' №
Подставляя выражение |_57] в формулу [51},. получим:
16 Ж, Mtd
Из выражений [58] и [59] мы видимх что, приняв напри-
мер $!——-d, получим, что угол скручивания и напболь-
іпее напряжение, по сравнению с теми же величинами для
сплошного вала диаметра d, увеличатся примерно на 6%,
тогда как вес вала уменьшится на 25°/0.
Если толщина К стенки полого вала очень мала
сравнительно с диаметром d, скалывающие .напряжения т могут
быть приняты распределенными равномерно по
поперечному сечению вала. Тогда момент, соответствующий
скалывающим усилиям," будет
d-\-d, 7 d~\-dA ,-
где "у 1—радиус осевой линии кольцевого сечения вала.
Обозначив через F площадь, заключенную внутрн этой
осевой линии, получим из ур-ния [а]:
71
Угол скручивания на единицу длины, из ур-ний [57] ц
[59], будет:
ft 2т<
ели, подставив вместо ттах среднее напряжение г и вместо
d — диаметр осевой линии —5—*¦, получим:
max
¦у I
? =
4"т
т«
(d + dOtf 2FG'
[61]
гдеа = ' "^~ ''—длина окружности осевой линии, a .F
имеет то же значение, что и выше.
Далее будет показано (см. п° 48, часть II), что формулы
[60] и [61] дают х и ? также для случая тонких трубчатых
валов и некруговых сечений, но с постоянной толщиной
стенок hl). Здесь опять F—площадь, заключенная внутри
осевой линии сечения. Формулой [60] можно пользоваться
также для тонких труб непостоянной толщины. В этом
случае напряжение каждой точки поперечного сечения будет
обратно пропорционально толщине стенки в этой точке.
В случае трубчатых сечений с острыми углами получается
значительное увеличение напряжений в углах. Эти местные
напряжения рассмотрены далее (см. п° 48, часть II).
ЗАДАЧИ.
1. Полый гребной вал судна передает 8000 лош. сил при 100об./ьша.
и допускаемом напряжении 315 кг/см2. Найти d, если d:dt = 2.
Решение.
Mt =
7 500 ¦ 8 000 - 60
2 я • 100
Ур-нне [59] дает
тпіах =
16 161Г
15
я^з
з г
откуда
т j v^
л«-п *7 я if 16-10.7500-8000-
ФВГ'57' d = V 16.tt.816.2tt.jL0C
Тогда dx = 23,1 с*.
60
= 46,2 см.
і) Первое исследование скручивания полых стержней было
выполнено Р. Бредтоп (В. Bredt)— „V. D. I.<\ Bd 40, 1896, S. 815. См. также
Г. Лоренц (Я. Lorcnz), Technische Elastizit'atslehre, 1913, S. 98; Г. Ирг-
скотт (Т. Ршсоіі) — „Phil. Mag.*, Vol. 60, 1920, и А. Фёпплъ (A. Foppl)
и X Фёпплъ (L. Foppl — Drang und Zwang, Bd 2, 1928, S. 84.
72
2. Найти среднее значение скалывающего напряжения по толщине
стенок прямоугольной трубы, поперечное сечение которой показано на
фиг. 67, если она скручивается парой сил, дающей момент М%,
Решение. Допустим, что толщина стенки мала по сравнению
с боковыми размерами трубы, и воспользуемся формулой [60]. Получаем г)
М.
И.
х =
2 F h 2 (m — hf h *
3. Найти толщину h и относительный угол скручивания на единицу
длины для трубы предыдущей задачи, если It = 4*J0 кг/см2, т = Ъ00мм
и М = 14 т • м.
Решение, h = 6,86 мм.
Угол скручивания на единицу длины по формуле [61]:
6 =
4 (т — К) Я
2 • 49,31 • 420
2 (ш — hf G 49,312 ¦ 840 000
= 0,0000203 радиана на см.
20. Вал прямоугольного поперечного сечения или из прокатных профилей.
Задача скручивания вала прямоугольного поперечного сечения сложнее
вследствие того, что при скручивании имеет место
искривление поперечного сечения. Это искривление
можно показать на опыте с прямоугольным
резиновым стержнем, на гранях которого нанесена сетка
небольших квадратов.
На фиг. 5S видно, что при скручивании линии
сетки, первоначально перпендикулярно к осп стержня,
искривляются.
Это указывает, что искажение упомянутых выше
мелких квадратов неодинаково вдоль сторон
поперечного сечения стержня: достигает наибольшего
значения посередине и сходит на-нет у ребер. Поэтому
мы можем предположить, что скалывающее
напряжение изменяется так же, как это искажение, а именно:
достигает максимума в середине сторон и равно нулю ?
в углах поперечного сечения. Исследование этой за
дачи 2) показывает, что наибольшее скалывающее
напряжение получается посередине длинных сторон
прямоугольного поперечного сечения и выражается
формулой:
М.
0 wSSE**!
ттах
а Ь С2
[62]
Фиг. 58.
где Ь — большая и с — меньшая стороны прямоугольного поперечного
сечения и а — числовой коэффициент, зависящий от отношения —. Не-
с
которые значения коэффициента а приведены ниже в таблице 2.
і) Местные напряжения во входящих углах сечения рассмотрены,
далее (см. п° 48, часть И).
2) Полное решение дано Сен-Веианом (Saint Venant), Mem. des savants
ctrangers, t. 14, 1855. Изложение этой работы можно найти в книге
Тодгёнтера и Пирсона {Todhuntcr and Pearson) — History of the Theory
of Elasticity, Vol. II, p. 312.
7J
Интересно отметить, что величина наибольшего напряжения может
быть определена с достаточной точностью из следующего
приближенного выражения:
'max
Ъ1.
ос3
e + W-g-
ТАБЛИЦА 2.
Коэффициенты при скручивания вала прямоугольного поперечного сечения.
ь
с
1,00
0,208
0,141
1,50
0,231
0,196
1,75
0,239
0,214
2,00
0,248
0,229
2,50
0,258
0,249
3,00
0,267
0,263
4,00
0,282
0,281
6
0,299
0,299
8
^
0,307
0,307
10
0,313
0*313
оо
0,3^.
ОМ'с
Угол скручивания на единицу длины в елучае прямоугольного
поперечного сечения выражается формулой:
0 =
м.
$Ъс*&
[63]
Значения числового коэффициента р даны в третьей строке
вышеприведенной таблицы 2.
Из этой таблицы видно, что, в случае очень узкого прямоугольного
поперечного сечения, например тонкой полосы листовой стали, а = р =
— _ д формулы для наибольшего скалывающего напряжения и угла
скручивания на единицу длины принимает вид:
шах
Б =
ЪФ?*
Г64]
№'1
Эти формулы имеют большое практическое значение, потому что
ими можно пользоваться не только для узкого прямоугольника, но
также для приближенных решений в тех случаях, где-ширина поперечного
сечения мала. Например, в случае поперечных сечений однообразной
толщины, показанных на фжг. Б9а и Ь, угол скручивания пояуча?тея
из ур-ння [64'] подстановкой в эту формулу вмеето Ъ длины
развернутой кривой осевой линии, а именно: Ь = tpr в случае сечения, представ
ленного фиг. 59а, и & = 2а-"-с в случае, представленном на фиг. 595.
Наибольшее напряжение для первого из этих двух сечений получится
по ф-ле [64]. Для уголкового сечения (фиг. ЪдЪ) наибольшее
напряжение имеет место во входящем углу. Это наибольшее напряжение
получим, умножал напряжение, полученное по ф-ле [64], на коэффициент,
больший единицы; величина этого коэффициента рассмотрена далее
(см. п° 48, часть И).
74
В случае корытного сечения (фиг. 59с), угол скручивания получки,
разделив поперечное сечение на три прямоугольника, как показано на
Фигуре, и подставив в формулу [64'] ^с^ + ^с^ вместо Ьс\ Тогда
0 =
3Jf.
(ЪьС? + ЪЬ2с?)0-
[Щ
Чтобы определить напряжение, которое получается посредине
сторон Ьо сечений полок, необходимо только, как усматривается из формул
[64] ifp&'J, помножить ? на с2 G; тогда
т =
3 Mt с2
ъ^р + ъъ^ы*
т
Эти приближенные выражения применимы также в случае
скручивания двутавровых балок *)•
Следует отметить здесь, что формула [05] выведена заменой
сплошного стержня тремя отдельными стержнями узкого прямоугольного
а
?
і
t
--•V
О
®
Фиг. 59.
©
сечения. На самом деле, вследствие жесткого соединения между этими
стержнями, угол скручивания имеет величины 2) несколько меньшие
чем получающиеся по формуле [66]•
ЗАДАЧИ»
1. Найти отношение между углами скручивания сплошной и
разорванной круглых гонких труб, одинаковых геометрических размеров
(фиг. 60), под действием одинаковых скручивающих моментов.
*) Наибольшее напряжение получается во входящих углах н будет
рассмотрено далее (см. п* 48, часть Н).
а) Зта задача впервые рассмотрена В. Вредтом (Е. Bredf}, см. „V. D. Lttt
Bd 40, 1896, S. 785; см. также А, Фёпплъ(А.ГбррТ)кЖ.Фёпплъ{Ъ.&дрр1) —
Drang und Zwang, 1928, Bd 2, S. TO. Относительно опытов скручивания
двутавровых стержней и стержней прочих прокатных профилей
см. А. Фёпплъ (A. FoppT) — «Sitzungsber. der Bayr. Akad. d. "Wisseosch.*,
1921, S. 295, и „Der Bauingenieur*. Bd 3, 1921, S. 42, а также А. Три-
фиц и Г. Тэйлор (А. A. Griffith and G. I.-Гау?ог) — ,Engineering"» Vol.
104, 1917, p. 652.
• 75
Решение. Из ур-ний [571 и [64'] получим для сплошной и для
разрезанной трубы соответственно:
32 Мл
*<2М 1
_ W \
G
3Mt
d — d0\3
а
Отношение между углами скручивания получается
8 _ 2 (d — rfn)2
ех ~~ з & + d0*2'
Для очень тонкие труб d2 + d02 = 2d2 и отношение углов
скручивания будет:
3
(-5-)'
2. Найти угол скручивания на погонный сантиметр швеллера
(фиг. 59с), если і^ = 23 000 кг-с», bt — 250 ж*, Ц = 90 жлг, ^ = 10 «*,
с2 = 15 мм, G = 840 000 кг/см*3.
Фиг. 60.
Решение. По формуле [65]
3-23 000
0 =
= 0,000953 радиана на см.
(25-13 +2-». 1,53)840 000
3. Найти отношение между наибольшими касательными
напряжениями в трубах, рассмотренных в задаче 1, если скручивающие
моменты одинаковы для обеих труб.
21. Другие виды поперечного сечения. Есть еще несколько других
видов поперечного сечения скручиваемого вала, для которых задача
распределения напряжений и установления угла скручивания решена.
В дальнейшем приведены только некоторые окончательные результаты,
которые имеют практический интерес.
Эллштичи-кое поперечное сечение Ц. Наибольшее скалывающее
напряжение получается на концах меньшей оси (фиг. 61) и равно:
шах
16 М%
ъ Ь'іь
т
*) См. Сеи-Вскап— выноска на стр. 73 выше.
70
Угол скручивания на единицу длины:
0 =
f* a
[68]
где
Ip^irW + M)
— полярный момент инерции поперечного сечения (см. приложение,
стр. 370) и
— площадь поперечного сечения.
Равносторонний треугольник і). Наибольшее скалывающее
напряжение-имеет место по середине сторон (точки ш на фиг. 62) н может быіь
определено из уравнения:
20 Mt
"max
ЬЗ
Угол скручивания на единицу длина:
0 =
АГ,
QAGI
р
46,2 Mt
[Щ
[70]
Цравильиый шестиугольник, 2). В этом случае
171]
max
е =
0,217 Fd '
if,.
Фиг. 62.
7*>1
0,133/'70*0 * L J
где d—диаметр вписанного круга zF—площадь
поперечного сечения.
Правильный восьмиугольник -). В этом случае:
РЗ]
^шах
0,223 Fd '
С
е =
м<
0,130 F&G
[74]
Фиг. СЬ.
F и d имеют те ж? значения, что выше.
Равнобедренная трапеция2), В случае равнобедренной трапеции
приближенное значение наибольшего напряжения и угла скручивания
получается заменой трапеции равновеликим прямоугольником, который
строится как показано на, фиг. 63. Из центра тяжести С трапеции
опущены перпендикуляры ВС и CD на боковые стороны и затем
проведены вертикали через точки В и В. К прямоугольному поперечному
сечению, таким образом полученному, применимы формулы [6^] и [63].
*) См. Сен-Вепан — выноска на стр. 73 выше.
2) См. Я. Вебер (С, Weber), Die Leare von der Dreaimgsfestigkeit^
Berlin, 1921.
77
Для любого сплошного (не трубчатого) сечения приближенное
выражение для угла скручивания можно получить заменой поперечного
сечения равновеликим эллиптическим той же площади F и с тем же
полярным моментом инерции 1р. Тогда приближенное значение для
угла G получится по формуле [6ь].
Во всех рассмотренных случаях угол скручивания
на единицу длины пропорционален скручивающему
моменту и может быть представлен следующим уравнением:
? =
О
М
Где с—постоянная величина, называемая жесткостью на
кручение вала.
В случае круглого вала (формула [52]) C = GIP.
Для прямоугольного вала (формула [63]) C=p6c3G.
F* G
Для эллиптического вала (формула [68]) 0= .
22, Винтовая пружина с небольшим шагом витка. Примем,
что винтовая -пружина кругового поперечного сечения
подвергается действию осевых сил Р (фиг. 64) ж что каждый
отдельный виток лежит почти что в плоскости, перпенди-
кулйрной оси винта
Фиг. 64.
Рассматривая равновесие верхней части пружины,
ограниченной осевым сечением тп (фиг. 646), можем заключить
пз уравнений статики, что напряжения по поперечному
сечению тп витка уравновешиваются .перерезывающей
силой Р, проходящей через центр тяжести поперечного сече-
78
ния, и парой сил, действующей в направлении,
противоположном движению часовой стрелки, в плоскости
поперечного сечения, и равной PR, где R—радиус
цилиндрической поверхности, на которой находится осевая линия
пружины.
Пара PR скручивает виток и вызывает наибольшее
скалывающее напряжение по формуле [54], которая здесь
принимает вид:
16 PR
где d—диаметр поперечного сечения т? витка.
К этому напряжению от скручивания следует
присоединить напряжение от перерезывающей силы Р. В грубом
приближении перерезывающая сила может быть принята
равномерно распределенной по поперечному сечению;
соответствующее скалывающее напряжение будет:
"В точке т направления тх и т2 совпадают, так что здесь
получается наибольшее скалывающее напряжение, имеющее
величину:
. 16 PR / . d \
W^+*--^i-( 1 + Tr) ' [75]
Легко видеть, что второй член в скобках, который
представляет действие перерезывающей силы, увеличивается
с увеличением отношения -^-. Он получает большое
практическое значение в мощных винтовых рессорах — таких,
какие применяются в железнодорожном подвижном составе.
Из-за этого члена точки т на внутренней стороне витка
находятся в менее благоприятных условиях, чем точки »
на внешней стороне. Опыт практики применения мощных
рессор показывает, что трещины обыкновенно появляются
с внутренней стороны витка.
Есть и другая причина ожидать более высоких
напряжений на внутренней стороне витка. При определении
напряжений от кручения мы воспользовались ур-нием, которое
выведено для цилиндрических стержней. В
действительности каждый элемент пружины находится в условиях
показанных на фиг. 65. Из нее видно, что, если поперечное
сечение bf поворачивается относительно сечения, ас из-за
скручивания, то перемещение точки Ъ относительно точки а
79
будет одинаково с перемещением точки f относительно
точки с. Вследствие того, что расстояние аЬ меньше, чщ
расстояние cf, деформация сдеига
на внутренней стороне аЬ будет
рп больше, чем таковая на внешней
С стороне, а потому скалывающие
j?r- напряжения, возникающие от
7 действия пары сил Ріі, будут
больше в точке Ь, чем в точке f.
фиг 65> Приняв это во внимание
совместно с действием
перерезывающей силы *), заменим формулу [75] следующим выражением
для определения наибольшего скалывающего напряжения:
_ 16РД Urn — 1 0,615 \
icd» \4fn —4"1" wi /' l J
где
d щ
Легко видеть, что поправочный коэффициент в скобках
увеличивается с уменьшением т; например, при т = 4
этот коэффициент приблизительно равен 1,40, а при т = 19
он равен 1,14.
При определении прогиба пружины обычно принимают
во внимание только действие скручивания витков.
Применяя для угла скручивания элемента, выделенного двумя
бесконечно близкими смежными поперечными сечениями
тп и wV (фиг. 64с), ф-лу [53], где вместо I подставлена
величина Ыа, получим:
P'JR-Rda
ф*=—т^—
Из-за этого скручивания нижняя часть пружины
поворачивается относительно точки 0—центра сечения тп
(фиг. 64а), и точка приложения В силы Р описывает
бесконечно малую дугу BB? = ad&. Вертикальная
составляющая этого перемещения равна
В'В» = ВВ' А^д^?= рЯ**а , [С]
г
) Такие исследования произведены Ф. Рёеером (V. Roever) „V. D, I.*,
Bd 57, 1»13, S. 190:;; см. также Л. Валъ {А. М. Wahl), „Trans. Am. Soc.
Mech. Eng.\ 1928. Последний установил также распределение
напряжений опытным путем, произведя измерения на повеі)хностя витка.
80
Полный прогиб пружины получим суммированием
прогибов В'В{\ возникающих в каждом элементе тпт'п' но
всей длине пружины. Тогда
2кп
Г Р№ _ 64: П PR*
о '
где п обозначает число витков.
Для пружины иного, чем круговое, поперечного
сечения можно применить этот же способ для определения
напряжений и прогибов, если вместо формул [53] и [5і] мы
возьмем соответствующие выражения для данного вида
поперечного сечения. Например, в случае прямоугольного
поперечного сечения следует воспользоваться выражениями
[62] и [83]с
ЗАДАЧИ.
1. Найти наибольшее напряжение и удлинение винтовой пружины
(фиг. 64), если Р = 110 кг, В = 100 мм, d — 20 мм, число витков равно 20
и ?=840000 кг/слА
Решение. По формуле [76], где т = 10, имеем
16-110-10 ЛЛА -ОЛ . 9
и по формуле [77]
. 64.20.110-103 1ЛК
°~ 2*-840 000 = 10'5сдс-
2. Решить предыдущую задачу, приняв, что поперечное селение
пружины—квадрат со стороной 20 мм.
Решение Приняв, что поправочный коэффициент для
перерезывающего напряжения и кривизны витка (см. ф-лу [76]) в этом случае
равен 1Д4, как выше, получим по формуле [62]
PR л.л 110-10 ,_ __.. , .
1,14 = AOAQ ,t„ * 1Д4 = 754 «г/6*2*
-max 0,20863 ~'*~ 0,203 -23
При определении удлинения в формуле [77] нужно под ставить 0,141 d*
(см. ф-лу [63]), вместо-^-; тогда, пользуясь значением удлинения,
полученным в предыдущей задаче, найдем
10,5-и _7Э
* " 32 - 0Д41 ~ VJ СМ'
3. Сравнить вес двух винтовых пружин, одной круглого, другой
квадратною поперечного сечения, предназначенных для условий, излож?я-
ньг: в задаче 1, и имеющих одинаковое наибольшее напряжение.
Возьмем поплавочный коэффициент в обоих случаях равным 1Д4. Сравнить
прогибы этих двух пружин.
6 Тимошенко — Сопротивление материалов, ч. Г. 81
Решение. Размер стороны квадратного поперечного сечения най-
дется из уравнения 4g- = 0,208 Ь3, откуда Ь= (?/0,944) d = 0,981 d.
Веса пружин будут находиться в том же
отношении, как площади поперечного сечения,
т. е. в отношении
гс<?
;0,9812^== 0,816.
Прогибы этих двух пружин находятся в
отношении
0,іа ?: 4? = 0,141 • 0,926: ~ = 1,33.
1=^^t
п
й^=з=!
Фиг. 60
Фиг. 67.
Фиг. 68.
4, Как будет распределяться груз Р между двумя концами винтовой
пружины, изображенной на фиг. 66, если число витков выше точки
приложения груза — 6, а ниже этой точки — 5?
Ответ. .Вх:22а. = 5:6.
5. Две винтовые пружины одинакового материала и одинакового
кругового поперечного сечения и длины, вложенные одна в другую,
как показано на фиг. 67, сжимаются между двумя параллельными
плоскостями. Определить наибольшее напряжение в каждой пружине, если
d = 12 мя и Р = 45 %ъ.
Решение. Из ур-ния [77] следует, что груз Р распределяется
между двумя пружинами обратно пропорционально кубу радиусов
пружин, т. е. сжимающие силы наружной и внутренней пружин находятся
в отношении 27:64. Наибольшие напряжения в этих пружинах будут
равны (по формуле [76]) 462 кг/см2 и 866 к%/см2, соответственно.
6. Какова предельная нагрузка для пружины задачи 1, если
допускаемое напряжение В3 = 1400 кг/см?! Каков будет прогиб пружины
при этой предельной нагрузке?
Ответ. 193 кг; 8 л= 18,4 см.
7. Коническая пружина (фиг. 6S) подвергается действию осевых
сил Р. Найти безопасную величину силы Р при допускаемом
напряжении iJs —3150 къ/см2; диаметр поперечного сечения d —25 км; радиус
конуса в вершине пружины 1^ = 50 мм, а в основании пружины
82
JR3 = 200 лис. Найти прогиб пружины, если число витков-—« и
горизонтальная проекция осевой линии пружины — спираль, уравнение
которой:
Решение. Для точки Л пружины, определяемой величиной угла а
расстояние от оси пружины равно
Л—** + 2^ ' М
и соответствующий крутящий момент
Наибольший скручивающий момент будет при а = %кп и расен
Р*і?2. Безопасный предел величины енлы Р по формуле [76]
получается равным
Прогиб пружины получим по формуле [с] (ем. стр. 80)
2 т: п
32Р
о =
О
/ [* + ^пЭД'* - w w+зд №+ч.
8. Найтп необходимую площадь поперечного сечения конической
пружины, работающей в тех же условиях, что п в предыдущей задаче,
но квадратной. Поправочный коэффициент принять равным lfij (см.
предыдущую задачу).
„ О т в е т. б2 = 6 с*3.
V 23. Второстепенные напряжения при кручении1). При рассмотрении
кручения круглого вала было принято, что расстояние между поперечными
сечениями остается неизменным. Продольные волокна в таком случае
должны удлиниться при кручении на легко определимую величину.
Сравнивая длины ас и ас'-на фиг, 51 Ь, из Д асе' имеем:
=--сі^-('+-Н=-[^т("Л--
и относительное удлинение волокон на наружной поверхности вала:
То- 5? 1 о d? і W2
Соответствующее растягивающее напряжение
Ex 2
а Р— !_тах_
°тах = етах •" 2 ?**
х) См. В'Шей (Buckley), The Bifilar Property of Twisted Strips, „?Ы1
Mag.", 1914, p. 778. См. также E. Вебер (К. Weber), Die Lehre der Ver-
drehungsfestigkeit, Berlin, 1921, и статью того лее автора в сборнике
к юбилею Л, Фёшил (Л. Fopgl), Berlin, 1924.
6* 83
Для люоого другого волокна на расстоянии г от оси вала
относительный сдвиг будет меньше в отношении г:—¦ &} и растягивающее
напряжение
2г\з 2r* 2?W2
Сделанное допущение, что расстояние между поперечными
сечениями остается неизменным при скрещивании, приводит нас к
заключению, что к валу, чтобы длина еі о осталась неизменной, должно быть
приложено продольное растягивающее усилие, соответствующее
распределению напряжений по ур-нию (Ъ*. Если такое усилие не будет
приложено, а будет только чистое кручение, то скручивание будет
сопровождаться некоторым укорочением вала. Пусть с0 — соответственное
относительное укорочение. Тогда вместо ур-ния |6], получим:
2г> Ятшах2
ff = ~^ G* е°К W
Величину е0 определим из того условия, что продольная сила,
соответствующая закону распределения напряжений по ур-нию [с], должна
быть равна нулю. Разделив поперечное сечение на элементарные
кольца, как показано на фиг. 51с, получим
? ?
2 " 2
/—>./?-^-*о
откуда
о
*"*'W_r)_0
*- 2
''ШАХ
iU*
и согласно ур-нию [о] получим закон распределения напряжений таким:
Наибольшее напряженке получается на внешней поверхности, где
r = -frdt и мы имеем:
Ex a
В пентре тяжести поперечного сечения мы получим сжимающее
напряжение той же величины.
Интересно отметить, что напряжение а пропорционально ^шах^
вследствие этого величина этого напряжения увеличивается с возрастанием
ттах' Т* е* с увеличением угла скручивания. /Тля таких материалов, как
сталь, тшах обыкновенно очень мало по сравнению с модулем
упругости на сдвиг (г, и величина <*тах поэтому мала сравнительно с ?шлжг
8і
Но для таких материалов, как резина, ттах может получиться того же
порядка, что и <?, и ашах уже не будет мало по сравнению е ^тах, а
потому должно быть принято во внимание.
Если, вместо кругового поперечного сечения, мы имеем узкое
прямоугольное сечение, то можно показать, что даже для таких
материалов, как сталь, напряжения а могут получиться того же порядка, как
величина *тюс Если длинная сторона поперечного сечения Ь велика по
сравнению с его короткой стороной с, наибольшее удлинение наиболее
удаленною волокиа, вызываемое одним только скручиванием,
получается из ур-ния [а] подстановкой Ъ вместо d\
Для волокна на расстоянии у от оси удлинение уменьшается в
отношении I ~ ) . Учитывая совместно это удлинение и продольное относи*
тельное сжатие е0, получим:
~твл ь) ?°--2—?°-
Соответствующее растягивающее напряжение
б21/2 \
-(
Постоянная е0 определяется, как выше, из того условия, что
растягивающая продольная сила равна нулю. Отсюда
2 Ч
У%5Й2/ = ^^(^-?о)йу=с^(^.-^~е0^=:0,
ь_ __ ъ_
откуда
3 62 1,2
2 * 12 '
и мы получим по формуле [d]
Наибольшее растягивающее напряжение для наиболее удаленного
волокна при у = — Ъ будет:
- ?_?2^! гл
amax it) -• L/J
Наибольшее сжимающее напряжение в центре при у = 0 будет:
'24
Га Ч- U" . ,
Для сравнения этих напряжений с тщах можно воспользоваться
85
формулами [62] и [63]. Для очень узкого прямоугольного сечения
а = р = ¦—-, и мы получим
max
w~ cG m
1/4
Подставляя это в выражения [f] и [д], имеем:
^ сшах и
шах 126г3 "' еа * I
¦ьтшах ^
аша— 24G2 с* *
•
[80]
Отсюда следует, что, когда Ъ: с велико, то напряжения ашах и <?щі11
могут и не быть малы сравнительно с ^тах* Распределение напряжений
(см. ур-ни? [е], показано на фиг. 6D. Эти напряжения имеют
направление продольных волокон скручиваемой полоски,
и наклонены к оси полосы под углом ? у. Их проекции
на плоскости, перпендикулярной оси стержня, равны:
а-Ьу =
Я 63
C'-f)-
Составляющая [к]
поперечного сечения
стержня, равный
(У3
напряжения а для элемента cdy
дает момент относительно оси
П }
cydy.
2 VJ 12
Общий скручивающий момент от напряжений е-будет
/
ж*
Ь-у \ , ЕсЪ*.,
Присоединяя этот скручивающий момент к моменту,
Фиг G9. возникающему- от скалывающих напряжений,
распределенных по. поперечному сечению, получим следующее
выражение для полного момента кручения:
»,-!м0.«+^Лй.»-1мвв (l+^f !¦")¦ [811
Отеюда можно заключить, что в случае очень узкого
прямоугольного жоперечного сечения и сравнительно значительных углов
скручивания, напряжения а могут составить значительную часть крутящего
момента, так как эта часть, представляемая вторым членом ур-ния [81],
изменяется пропорционально Ь3, тогда как часть, зависящая от
скалывающих напряжений т, изменяется пропорционально ?. Когда величина
крутящего момента дана, то соответствующий угол скручивания ?
найдется из ур-ния [81]» Наибольшее перерезывающее напряжение т:тах
86
определяется затем из ур-ния [h]t а напряжение сгтах и сгщій —по
формулам [80].
Возьмем например Ь = 100 мщ с = 1,2 мщ -^ = 2Д G = 800 ООО «і/сл3
Ъс2
и М = -s-. 1050 «г • ел = 50,4 кг - ем.
Если нормальными напряжениями о пренебречь, то по формуле [64]
а формула [64'] дает относительный угол скручивания на 1 см длины
? = -*«*L = 0,0109.
cG '
Учитывая нормальные напряжения а и пользуясь ур-ннем {"81],
получим:
0,0109 = ? (1 + 15040 83),
откуда ? = 0,0066*
тшах = б • С • (? = 634 7Сг/слі2;
Отсюда можно заключить, что для столь большого угла
скручивания тонкой металлической полоски нормальные напряжения в
получаются того ж©- порядка, как скалывающие напряжения хл и ими уасе
нельзя пренебрегать при определении угла скручивания*
ГЛАВА ЧЕТВЕРТАЯ.
НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ.
24. Чистый изгиб призматических стержней.
Призматические стержень, находящийся под действием равных и прямо-
«I
*
® і—*—\у
Фиг. 70.
против?н&лежяых пар сил, приложенных к его концам,
называется находящимся в состоянии чистого изгиба.
Средняя часть CD стержня ЛВ (фиг, 70) является примером
87
такого состояния. Величина Ра пары снл, которая вызывай?
изгиб, называется изгибающим моментом.
Из равновесия, по условию равенства нулю суммы
моментов, части стержня, скажем—влево от поперечного сечения
тпу можно заключить, что внутренние усилия, которые
распределены по поперечному сечению и представляют
действие удаленной правой части стержня на левую часть,
должны быть статически эквивалентны моменту М, равному
и прямопротивоположному изгибающему моменту Ра.
Чтобы найти распределение этих внутренних усилий
по поперечному сечению, необходимо рассмотреть
деформацию стержня.
Для простейшего случая стержня, имеющего продольную
плоскость симметрии и подвергающегося действию
внешних изгибающих пар сил, находящихся в этой плоскости
изгиб будет происходить в этой же плоскости. Если
стержень— прямоугольного поперечного сечения и на его гранях
нанесены две смежные вертикальные линии mm и gp, то
непосредственный опыт показывает, что эти линии остаются
при изгибе прямолинейными и поворачиваются так, что
остаются перпендикулярными продольным волокнам стержня
(фиг. 71).
Нижеследующая теория изгиба основана на допущении,
что не только такие линии, как ш, остаются
прямолинейными, но и все поперечное сечение стержня, первоначально
плоское, остается плоским и нормальным к продольным
волокнам стержня и после изгиба.
Опыт показывает, что теория, основанная на этом
допущении, дает очень точные результаты для прогиба стержней
и деформации продольных волокон.
Из этого допущения следует, что при изгибе попереч-
^8
ные сечения mm и рр поворачиваются относительно друг
друга вокруг осей, перпендикулярных плоскости изгиба,
таким образом, что продольные волокна на выпуклой
стороне испытывают растяжение, а волокна на вогнутой
стороне—сжатие.
Пусть линия ппх — пересечение поверхности, в которой
волокна не испытывают деформации при изгибе, с
продольной плоскостью симметрии стержня. Эта поверхность
называется нейтральной поверхностью, и ее пересечение с любым
поперечным сечением называется нейтральной осью сечения.
Удлинение ssx любого волокна, находящегося на
расстоянии у от нейтральной поверхности, получается
проведением линии nxsx параллельно mm (фиг. 71а). Обозначив
через р радиус кривизны изогнутой оси *} стержня и
пользуясь подобием треугольников пОпі и sxnxs, найдем, что
относительное удлинение волокна ss равно
2»L eJL. [82]
Из-этого следует, что деформации продольных волокон
пропорциональны расстоянию у от нейтральной
поверхности и обратно пропорциональны радиусу кривизны.
-Опыты показывают, что продольное удлинение волокон
выпуклой стороны стержня сопровождается боковым
сужением и продольное укорочение на вогнутой стороне —
боковым расширением, как в случае простого растяжения или
сжатия (см. п° 14). В силу этого изменяется вид всех
поперечных сечений, вертикальные стороны прямоугольного
сечения становятся наклонными одна по отношению к
другой, как это видно на фиг. 71Ь. Относительная деформация
в боковом направлении равна
г
где ^ — Пуаесоново отношение.
Вследствие такого искажения, все прямые линии
поперечного сечения, параллельные оси е, искривляются таким
образом, что остаются нормальными к боковым сторонам
сечения. Радиус кривизны этой кривой В будет больше
і) Ось стержня — линия, проходящая через центры тяжести его
поперечных сечений* Точка О обозначает центр кривизны.
89
чем р в таком же отношении, в каком % по абсолютной
величине больше чем ев (см. формулу [83], и мы получим
В = — р.
[84]
Этим деформациям продольных волокон отвечают, по
закону Гука (ур-ние [4], стр. 4), следующие напряжения:
Щ
а
[85]
Распределение этих напряжений показано на фиг. 72.
Напряжение в любом волокне пропорционально его
расстоянию от нейтральной оси пп. Положение нейтральной
оси и радиус кривизны р—две неизвестные в ур-нии [85] —
можно определить из того условия, что усилия,
распределенные по любому поперечному сечению стержня, должны
образовать пару сил, которая уравновешивает внешний
момент М (фиг. 706).
Пусть ^обозначает
элементарную площадку
поперечного сечения, отстоящую
на расстоянии у от ней
тральной оси (фиг, 72).
Усилие, действующее на эту
элементарную площадку,
является произведением
напряжения (ур-ние [&5])на ее
площадь dFy т. е. равняется
?
Фиг. 72. йз того, что все усилия,
распределенные по
поперечному сечению, представляют систему, эквивалентную паре
сил, равнодействующая всех усилий должна быть равна
нулю, и мы получим: *
/
*^dF=JLft,aF=o,
т. е. статический момент площади поперечного сечения
относительно нейтральной оси равен нулю; отсюда следует, что
нейтральная ось проходит через центр тяжести сечения.
20
Момент усилия, действующего на выделенный выше
элемент, относительно нейтральной оси равен
Суммируя такие моменты по всему поперечному
сечению и приравняв результат моменту М внешних стел,
получим следующее уравнение для определения радиуса
кривизны:
/
р р
или
1 И
р ш. >
где
1. — J V2dF
[86]
"2
— момент инерции поперечного сечения относительно
нейтральной оси s (см. приложение, стр. 336).
Из ур-ния [86] следует, что кривизна изменяется прямо
пропорционально изгибающему моменту и обратно
пропорционально величине Elz9 которая называется жесткостью
на изгиб стержня.
Исключение р из ур-ний [85] и [86] дает следующее
уравнение для определения напряжений:
«,--»-. от
При предшествующем рассуждении был взят случай
прямоугольного поперечного сечения. Оно останется также
в силе для стержня с поперечным сечением любого вида,
который имеет продольную плоскость симметрии и
изгибается концевыми моментами, действующими в этой
плоскости, так как и в втих случаях изгиб происходит тоже
в плоскости действия моментов, и плоскости поперечных
сечений остаются плоскими и нормальными продольным
волокнам после изгиба.
В ур-нии [87] Ж—положителен, когда он вызывает
прогиб стержня выпуклостью вниз, как на фиг. 71а; у—поло-
91
жительно при направлении вниз. Отрицательный знак при ол
указывает на сжимающее напряжение.
Наибольшие растягивающее и сжимающее напряжения
получаются в крайних волокнах и для прямоугольного
поперечного сеченвя (или для сечений другого вида, но
для которых центр тяжести находится посередине высоты h),
напряжения получаются наибольшими при у = ±— я
равными:
г \ -т
\°х)тъх о"/
И
( \ - Ш
\ х/аиа л т f
[88]
Для упрощения будем применять следующее
обозначение:
w*=nr* [89]
Тогда
(О
max
(c*)iatn —
м
ш *
[90]
W.
г
К
w.
Величина Wt называется моментом сопротивления. В
случае прямоугольного поперечного сечения (фиг. 716] имеем:
* 12 ' в 6 *
Для кругового поперечного сечения диаметром d:
7 = . • W =
Для различных сечений прокатных профилей, т. е. для
двутавров, швеллеров и т. п., значения величин 19 и W9
при различных размерах этих сечений приводятся в виде
таблиц б любых справочниках.
В том случае, когда центр тяжести поперечного сечения
не лежит по середине высоты, как например в случае
тавровой балки, обозначим через ht и h2—расстояния от
нейтральной - оси крайних верхнего и нижнего волокон
92
соответственно. Тогда., при полооштельном изгибающем
моменте, получим:
(^ - -
rc/min
где
ту ' =-
. Пря отрицательном изгибающем моменте имеем:
М ш ( . _ Ж
I.
Mhf
і.
IF/ '
AT
NY'
IF " — Ll
•4
[91]
ТУ' = — ' W" = ±± Г991
. ___ж_, , . _ м_ r .
z
Здесь T7B' и ТУ/ — также моменты сопротивления
поперечного сечения.
Предшествующие выкладки сделаны в предположении,
что стержень имеет продольную плоскость симметрии, в
которой действует изгибающий момент. Однако их можно
также применить и тогда, когда такой плоскости симметрии
пе существует, лишь бы только изгибающий момент
действовал в осевой плоскости, которая заключает в себе одну
из двух главных осей поперечного сечения (см. приложение,
стр. 372). Эти плоскости называются главными плоскостями
изгиба.
Когда имеется плоскость симметрии и изгибающий
момент действует в этой плоскости, прогиб происходит
именно в ней. Моменты внутренних усилий, показанных на
фиг. 72, относительно горизонтальной оси уравновешивают
внешний момент. Моменты этих усилий относительно
вертикальной оси взаимно уничтожаются, так как моменты
усилий с одной стороны этой оси как раз
уравновешиваются моментами соответствующих усилий, лежащих по
другую сторону оси.
Когда плоскости симметрии нет, но изгибающий момент
действует в осевой плоскости, проходящей через одну из
главных осей поперечного сечения (плоскость <су на фиг. 73),
распределение напряжений по ур-нию [86] будет все же
удовлетворять всем условиям равновесия. Такое
распределение напряжений дает такой момент внутренних усилий
относительно горизонтальной оси, который уравновешивает
за
внешний момент. Вокруг вертикальной оси у получается
следующий суммарный момент:
Этрт интеграл называется центробежным моментом инер*
ции поперечного сечения (см. приложение, стр. 357), и он
равен нулю, если у и з — главные оси сечения. Поэтому и
момент М9 равен нулю, и, так как составляющая внешнего
У
©
Фиг. 73.
момента приложенных к стержню сил, относительно оси у
также нуль, то услозяя равновесия удовлетворяются.
ЗАДАЧИ.
1. Найти наибольшее напряжение в паровозной оси (фиг. 74), если
с = 360 мм, диаметр d осп равен 250 мм и сила Р от действия ресеоры
на цапфу оси равна 12 т.
Решение. Изгибающий момент, действующий в средней части оси,
равен М=Р-с = 12-35 т-см. Наибольшее напряжение по ур-нию [90J
равно
гХ~~^. иі
Фиг. 74.
сшах jy
М _ 32. И
32-12 000-35
я • 253
= 274 къ/смК
2. Найти радиус кривизны р и прогибе
паровозной оси предыдущей задачи, если
материал — сталь п расстояние между центрами цапф —1500 хм.
Решение. Радиус кривизны р определяется из ур-ния [85]
подстановкой
<і
у = - = 125 мм, (дшх = 274 кі/слЛ
Тогда
&
Р =
Е & 2100 000-12,5
2
274
При определении прогиба В (фиг. 74) примем во внимание, что
упругая линия —дуга круга радиуса р и D^ —катет прямоугольного
треугольника DOB, где О—центр кривизны. Поэтому
DB* = р2 — (р — 5)2 = 2 р Ь — ЬК
Прогиб Ь очень мал по сравнению с радиусом р, а потому
величиной оа в предыдущем выражении можно пренебречь; тогда
$ =
2р
150'
8 • 95 800
= 0,0293 см.
3. Деревянная балка квадратного поперечного сечения 25 X 25 сді
оперта в точках Л а В (фиг. 74), и в концах балки приложены грузы Р.
Определить величину груза Р и прогиба Ь по середине пролета, если
АВ=* 210 см; с = 35 см; (<*я)тих = 70 за/с*2 н В = 100 000 ю/слА Весом
балки пренебречь.
Ответ.
Р = 5208 Kt;
В — 0,309 с*.
іШііі-
1М1
#
іг
/5_
Ж*
Фиг. 76.
4. Двутавровая балка №40
(по ОСТу) расположена на 2
опорах, как показано на фиг.75,
и нагружена на консолях
равномерно распределенной на-
ірузкой 10 т/м. Найти наибольшее напряжение в средней части балки
и прогиб посредине нролета балки, если момент инерции двутавра Л* 40
1^ = 26087 ел*. Весом балки пренебречь.
Решение. Изгибающий момент для средней части балки будет
М = 10-1,6* 0,8 т- м = 12,8 wi-» = 1280000 кг-ел;
, ч И 1280 000-20 лол , з
(**)«« = -таг" = *Г?^ = ^82 Kt/crf;
W
26 087
о = 0,598 см.
б. Найти наибольшее напряжение, возникающее в стальной
проволоке диаметром d = 0,8 мм, навернутой на круглый шкив диаметром
В = 500 мм.
Решение. Наибольшее удлиненно от изгиба по ур-ниіо [82] будет
и соответствующее растягивающее напряжение
(дя)тах = е " Е — °'0016 ' 210° 00° — 3 360 ^/СлА
6. Стальная линейка, имеющая поперечное сечение 0,8X^5 мм
и длину I = 250 мм, изгибается парами сил, приложенными в концах ее,
так, что она обращается в дугу круга с центральным углом, равным"00°.
Найти наибольшее напряжение и прогиб.
93
Решение. Радиус кривизны р определяется из уравнения:
откуда р = 23,86 ем, и наибольшее напряжение получается по yp-mnoi85j:
, , В-ОМ 2100 000-0,01 ОГОЛ , 0
<'Л«* = -ЩГ = 23,86"— = 3 520 кг/см,
Ппогнб вычисляемый как стрелка дугя круга, получается
о = р (1 — cos Ь0°) = 23,86 (1 — 0,8015) = ЗД9 с.ір.
7. Иа?тн наибольшее напряя;ение и величину пар сил, приложенных
по концам линейки предыдущей задачи, если наибольший прогиб по
середине равен 25 мм.
Ответ.
8. Найти искривление, возникающее в свободно опертой стальной
балке прямоугольного поперечного сечения от. неравномерного
нагревания по высоте h поперечного сечения. Температура t для тонки,
находящейся на расстоянии- у от средней плоскости ocs балки (фиг. 71),
определяется ур-нием:
~г h k •
где ti — температура низа балки, *0 — температура верха балки, it — /0 =
= 68° Цельсия и коэффициент линейного расширения а0 = 0,000012. Какие
напряжения возникнут, если концы балки защемлены?
Решение. Температура средней плоскости xs равна *"р ° •
Изменения температуры других волокон ппопорпиональиы расстоянию у
от этой плоскости. Соответствующие относительные удлинения от
повышения температуры будут также пропорциональны величине у, т, ?.
они будут следовать, тому же закону относительных удлинений, который
выражен ур-нием {&!]. В результате этого неодинакового удлинения
волокон произойдет изгиб балки, и радиус р крпвизны найдется
іол1 fti — to \ h
из ур-ния [82], если подставить ас (-^—) вместо ех и -$- вместо у.
Тогда
Р = -* п = 1326А.
acvi~~*o)
Если концы балки защемлены, то возникнут концевые опорные
моменты, величина которых уменьшается с уменьшением кривизны
от неравномерного назревания.
Отсюда
EI EI
1 р 12267* '
Подставив это в формулу [87], получим
с - ЕУ
* ~~ 1826А "
(.6
5к наибольшее напряженке будет;
Е
9. Решить задачи 6 и 7, если центральный угол дуги —10° н
линейка— медная.
10. Решить задачу 4, приняв, что балка — деревянная и нмеет
квадратное сечение 30 X 30 см, а интенсивность равномерно распределенной
нагрузки —1500 кг/л.
26. Различные виды поперечных сечений балок. Из
рассуждений предыдущего п° следует, что наибольшее
растягивающее нли сжимающее напряжение в стержне при
чистом изгибе пропорционально расстояниям наиболее
удаленных от нейтральной оси поперечного сечения
волокон. Поэтому, если материал оказывает одинаковое
сопротивление на растяжение и сжатие, логично выбирать
такие виды поперечного сечения, центр тяжести которых
находится-по середине высоты балки. Таким путем
получаем один и тот же sanac прочности (коэффициент
безопасности) для волокон, испытывающих растяжение, и для
волокон сжатых. Это — основной принцип при выборе
сечений, симметричных относительно нейтральной оси,
для таких материалов, как литая сталь, которая имеет
одинаковый предел текучести и при растяжении и при
сжатии. Если сечение несимметрично относительно ней-
е тральной осп, например сечение рельса, то материал
распределяется между головкой и подошвой рельса так,
что центр тяжести лежит все-таки на середине высоты
рельса.
Для материала, обладающего малым сопротивлением
на растяжение и большим на сжатие, например чугун
или бетон, целесообразно применить для балки поперечное
сечение» несимметричное относительно нейтральной оси
и такое, что расстояния \ и А2 от нейтральной оси до
наиболее удаленных волокон в растянутой и сжатой зоне
находятся" в том же.отношении, как сопротивления материала
на растяжение и на сжатие. Таким образом, получается
одинаковое сопротивление балки на растяжение и на
сжатие. Например, для таврового сечения центр тяжести может
быть взят в любом заранее намеченном положении по
высоте сечения соответствующим выбором размеров полки
и стенки.
При данном изгибающем моменте наибольшее
напряжение зависит от момента сопротивления, и интересно
отметить, что встречаются случаи, при которых -увеличение
площади не дает уменьшения напряжений.
7 Тимошенко — Сопротивление материалов, ч. I. 97
Например, стержень квадратного поперечного сечения,
изгибаемый парами сил, действующими в вертикальной
плоскости, проходящей через диагональ поперечного
сечения (фиг- 76), будет иметь меньшую величину наибольшего
напряжения, если заштрихованные на фигуре уголки будут
отрезаны.
Пусть и обозначает длину стороны квадратного
поперечного сечения. Момент инерции относительно оси в равен
\/> і2
(см. приложение), и
соответствующий момент
сопротивления получается:
W,=
а 12
Примем теперь что угод-*
ки отрезаны так, что й*р=а а,
где а—дробное число, под*
лежащее определению. Но*
вое поперечное сечение
состоит из квадрата тт1тті9
Фвг. 76. со сторонами а(1 — а), и
sa двух параллелограммов
ттхЩш Момент инерции такого поперечного сечения
относительно оси з равен
ц=
о*(1— а)4 , aaV 2
"Т"2* о—
12
Нт4]"-
а*(1— а)» ., , л .
= \2 (1 + За);
и соответствующий момент сопротивления
Теперь, если мы определим величину дробного числа а
так, чтобы получался наибольший момент сопротивления
этого сечения, то наідем а = —. Подставляя это значение а
в выражение момента сопротивления TF/, найдем, что срезка.
98
уголков уменьшает наибольшее изгибающее напряжение
примерно на 5%.
Этот результат вполне понятен, если принять во
внимание, что момент сопротивления есть частное от деления
момента инерции на половину высоты поперечного сечения.
Срезая уголки, мы уменьшаем момент инерции
поперечного сечения в меньшей мере, чем высоту; поэтому момент
сопротивления увеличивается, и {<*„)„>„, уменьшается.
Такое же явление можно отметить и в других случаях.
Момент сопротивления прямоугольника с узкими
выступающими по высоте частями (фиг. 77а) можем увеличить,
ори известных условиях, отрезав эти части. Момент
сопротивления кругового поперечного сечения (фиг. 77&) увели-
®
®
Фиг. 77.
чивается на 0,7% при срезке двух заштрихованных
сегментов, которые имеют высоту S = 0,Olld. В случает
треугольного сечения (фиг. 77с), момент сопротивления можно
увеличить срезкой вверху уголка.
При подборе сечений балок, находящихся под действием
чистого изгиба, необходимо не только удовлетворить
условиям прочного сопротивления, но и условию наибольшей
экономии в собственном весе балки. Из двух поперечных
сечений, имеющих одинаковый момент сопротивления, т. е.
удовлетворяющих условию сопротивления при одинаковом
запасе прочности, более экономным будет сечение с
меньшей площадью. Сравнивая различные виды поперечных
сечений, рассмотрим сперва прямоугольник высотой h и
шириной Ъ. Момент сопротивления
тхг Ъ№ 1 _
м
где F обозначает площадь поперечного сечения.
7* S9
Из этого видно, что прямоугольное поперечное сечение
становится все более и более экономным о увеличением
его высоты h. Однако есть известный предел такому
увеличению, и когда сечение становится все уже, возникает
вопрос об устойчивости балки. Разрушение балки очень
узкого прямоугольного сечения может произойти не из-за
превышения временного сопротивления материала, но от
бокового выпучивания (см. п° 45, часть II).
В случае кругового поперечного сечения имеем:
Сравнивая круговое и квадратное поперечные сечения
одинаковой площади, найдем, что сторона h квадрата
должна быть равна
2 г
и ур-ние [а] дает:
ТГ, = 0,ШЖ
Сравнение этого момента сопротивления с моментом
сопротивления круга [Ь] показывает, что квадратное
поперечное сечение более экономно, чем круговое.
Рассмотрение распределения напряжений по высоте
поперечного сечения (фиг. 72) приводит к заключению, что
для получения наибольшей экономии нужно поместить
возможно больше материала балки как можно дальше
от нейтральной оси. Наиболее благоприятный случай при
данной площади поперечного сечения F и высоте h
получился бы при расположении каждой половины площади
на расстоянии —Л от нейтральной оси. Тогда
* " I о I а >
2 / 4
Это—-предел, к которому можно приблизиться
практически, применяя двутавровое сечение с наибольшим
количеством материала в полках. Вследствие необходимости
уделить часть материала для стенки балки, предельное
условие [с] никогда не может быть получено, и для
прокатных двутавровых профилей мы имеем приближенно:
WattQ,ZQFh. [d]
100
. Сравнивая выражение [d] с [а], видим, что двутавровое
сечение более экономно, чем прямоугольное сечение той же
высоты. В то же самое время, благодаря ширине полок,
двутавровая балка будет более устойчива против бокового
выпучивания, чем балка прямоугольного сечения той же
высоты и с тем же моментом сопротивления.
ЗАДАЧИ.
f* Найтн ширину х полки чугунной балки таврового сечения,
показанного на фиг. 78, так чтобы наибольшее растягивающее напряжение
т
Г ьШ
Фиг. 78.
составляло */з наибольшего сжимающего напряжения. Высота балки
Л « 100 мм, толщина стенки н полки t = 25 мм.
Решение. Чтобы удовлетворить этим условиям, необходимо»
чтобы балка имела такие размеры, прн которых расстояние центра
Фиг. 79.
.*и
тяжести от подошвы основания равнялось с = — h. Теперь (см. фиг. 7Ь)
положение центра тяжести определим из ур-ния:
Сж ht + (x — t)t 4 "
г
-«Ьісу,
откуда
А2
= 2,6 +
102
*^і«\,
1 '—і -*п«\.
— 22,6 см.
1- I....J
^
LLdltl
г 2
Фиг* 80.
Л —2*" "'" ' 10—2.2,5
2. Найти отношение (^тлх: (<*х)іаш Для п*вел-
лера, показанного на фиг. 79, если ?='50 мм,
А «= 250 мм% Ь — 600 мм.
Ответ.
3. Найти условие, при котором уменьшение высоты сечения,
показанного на фиг. 80, сопровождается увеличением момента сопротивления;
Решение.
6АХ + б '
W
"Ж"
ЬАЗ
17
<Sfti
101
Условие увеличения момента сопротивления W% при уменьшении
высоты \ будет:
6ЛХ2 ^ 3
ИЛЕ
U ^ A3 '
4. Найти, какую часть надо отрезать от вершины равнобедренного
треугольника (фиг- 77с), чтобы получить наибольший момент
сопротивления Wg.
5. Найти отношение между весами трех балок одинаковой длины,
подвергающихся действию одинакового изгибающего момента М и
имеющих одинаковое наибольшее напряжение (?х)тЛх* если поперечное
сечение балок соответственно — круг, квадрат и прямоугольник с
соотношением сторон h = 2Ь.
Ответ. 1,12:1:0,793.
6. Каким должно быть отношение между сторонами Ь : Ь для
прямоугольной балки, изготовленной из круглого бревна данного диаметра &>
чтобы балка оказывала наибольшее сопротивление чистому изгибу?
Ответ.
26. Изгиб балок поперечными силами. Рассмотрим теперь
более общай случай изгиба, при котором балка, опертая
по концам, изгибается системой грузов, перпендикулярных
к ее оси (фиг. 81). Для упрощения предположим, что балка
имеет осевую плоскость симметрии, в которой действуют
грузы, так что изгиб происходит в этой плоскости. Более
общий случай будет рассмотрен далее (см. п° 41).
Напряжения, возникающие при изгибе, можно
исследовать тем же способом, как и раньше. Начало координат
берем в центре левого концевого сечения, ось х направим
вдоль оси балки вправо и ось у—вниз. Представим балку
разрезанной поперечным сечением тп на расстоянии х
от левой опоры А, правую часть балки удаленной, а ее
действие замененным усилиями, распределенными по
сечению тп.
Из условия равновесия левой части балки (фиг. 81Ь)
находим, что эти усилия приводятся к паре сил, которая
уравновешивает момент М сил Аг Рг и Р2 относительно
нейтральной оси поперечного сечения тп, и к силе, равной
и прямо противоположной алгебраической сумме Q сил А,
Рх и Р2. Тогда
Ж = Ах—Рх(х— сх)— Р2(х — с2),
Q = A-PX —P2.
Момент Ж всех сил, действующих на балку по одну сто-
102
рояу поперечного сечения тщ называется изгибающим
моментом в поперечном сечении тп, а алгебраическая сумма Q
тех же сил называется перерезывающей силой в поперечном
сеченигь тп.
Если вместо іевой части балки рассматривать правую,
то перерезывающая сила Q и момент М будут иметь ту же
величину, но прямо противоположное направление (фиг. 81с).
Это следует из того, что грузы Рх, Р2, Р& действующие
на балку, уравновешиваются реакциями А и В; поэтому
момент всех этих сил относительно любой точки, взятой
А
®
©
Фдг. 81.
в плоскости ху, так же как их алгебраическая сумма,
должен быть равен нулю. Тогда момент сил, действующих
на левую часть балки относительно сечения тп, должен
быть равен и прямо противоположен моменту относительно
того яде сечения сил, действующих на правую,часть балки.
Точно так же алгебраическая сумма сил, действующих на
левую часть балки, должна быть равна и прямо
противоположна алгебраической сумме сил, действующих на
правую часть.
В последующем изгибающий момент и перерезывающая
сила считаются положительными, если они имеют
направления, указанные на- фиг. 81Ь и с, т. е. изгибающий
момент—положителен, если он вызывает изгиб балки вогну-
іоа
тостыо вверх, я перерезывающая сила—положительна, если
правая часть балки стремится сдвинуться вниз до
отношению к левой.
Рассмотрим теперь элемент балки, вырезанный двумя
бесконечно близкими смежными поперечными сечениями
тп и m^nv которые отстоят друг от друга на расстоянии dx
(фиг. 82). Допустим, что в поперечном сечении тп
изгибающий момент и поперечная сила—положительны. Тогда
действие левой части балки на элемент представится силой Q
и моментом Ж, как указано на фиг. 82. Таким же образом,
приняв, что в сечении т1пі изгибающий момент и
перерезывающая сила—положительны, представим действие правой
части балки на элемент моментом и силой, показанными
на фиг. 82а. Когда между сечениями тп и тгпх нет внешних
сил действующих на балку, то перерезывающие силы
M+di
?
в этих двух сечениях будут одинаковы, если весом
элемента, балки можно пренебречь. Из условия равенотва нулю
моментов при равновесия элемента следует, что
увеличение dM изгибающего момента равно моменту пары,
представляющей две равные и прямо противоположные силы Q
с плечом dx, т. е.
dM = Qdx,
или
Отсюда для всех частей балки между грузами
перерезывающая сила равна производной от изгибающего
момента по х.
Когда вдоль балки распределена непрерывная нагрузка,
то ее величина на единицу длины балки называется
интенсивностью и обозначается величиной q, которая может быть
в частности и переменной,
1<м
В этом случае нагрузка между двумя бесконечно
близкими смежными поперечными сечениями тп и т^ (фиг, 826)
равна qdx. Считая g положительным, когда нагрузка
действует по направлению вниз, можем заключить из условия
равновесия элемента, что перерезывающая сила в
поперечном сечении «у»! меньше, чем перерезывающая сила
в сечении тщ и что
dQ = — qd%,
откуда
?— т
Взяв теперь момент всех сил, действующих на элемент,
получим:
dM=^Qdx— qdx • -—-.
Пренебрегая вторым членом правой части, как величиной
второй степени малости, мы придем снова к. ур-нию [93],
Если между бесконечно близкими смежными
поперечными сечениями тп и т^ (фиг. 82с) приложен
сосредоточенный груз Р, то в величине перерезывающей силы
произойдет внезапная перемена. Пусть Q обозначает
перерезывающую силу слева от тп и Qx—справа от «^ Тогда
из условия равновесия элемента тпт^ найдем
«!=« —Р.
Теперь из ур-ния [93] можно заключить, что в точке
приложения сосредоточенной силы имеет место внезапная
перемена величины производной -j—.
При рассмотрении напряжений, возникающих в
поперечных сечениях тп и тхпх, мы учтем отдельно напряжения,
вызываемые изгибающим моментом, и напряжения от
перерезывающих сил. Первые рассмотрены уже в п° 24, и их
величины и распределение выражены соответственно
уравнением [87] и фиг. 72. Напряжения от перерезывающей
силы Q, действующей в плоскости поперечного сечения,
будут рассмотрены в п° 28.
27. Эпюры изгибающих моментов и перерезывающих сил.
Из рассуждений предыдущего п° можно заключить, что
наибольшее нормальное напряжение ох будет иметь место
в том поперечном сечении, в котором изгифдощщ .-мо-тяш
достигаем максимума, а наибольіаде,,с^а?щваіощее-.:напря-
105
жение х—в поперечном сечении, в котором перерезн-
вающая сила достигает максимума. Для упрощения
исследования распределения напряжений в балке удобно
пользоваться графическим изображением изменений
изгибающего момента и перерезывающей силы вдоль оси балки.
Абсциссы указывают положение сечения, а ординаты —
величины соответственно изгибающего момента и
перерезывающей силы, которые действуют в этом сечении, поло-
©
©
V Ыш ЯЙЛУ
Фиг. 83,
жительные—вверх и отрицательные—вниз. Такие
графические изображения носят название эпюр изгибающего ло-
мента и перерезывающей силы.
Рассмотрим, например, балку, лежащую на двух опорах
и загруженную одним сосредоточенным грузом Р (фиг. 83).
Реакции в этом случае будут:
А =
Р-с
В=
I
Для любого поперечного сечения тп слева от силы Р
юз
можно заключить из условия равновесия части балки между
тп и Л, что
Ре
Изгибающий момент и перерезывающая сила имеет то же
направление, что показанные на фиг. 81, и потому они—
положительны. Из выражений [а] следует, что перерезы»
вающая сила остается постоянной для всех сечений слева
от груза и что изгибающий момент изменяется прямо
пропорционально расстоянию х. При # = 0 момент равен нулю,
а при х = 1— с, т. е. в поперечном сечении, где приложен
груз, момент равен
Рс(1—с)
__ .
Соответствующие эпюры изображены на фиг. 836 и с
прямыми линиями АС и А'С\
Для поперечного сечения справа от груза Р условия
равновесия левой части балки дают:
M=^x — P(x-{-c — l); Q^^—P. [Ь\
Изгибающий момент является линейной функцией' х
и при х = I равен нулю. Он всегда положителен, и его
изменение между Р и В представлено прямой линией BG.
Перерезывающая сила для этой части балки остается
постоянной и по знаку — отрицательна. На фиг. 83с эта
сила изображена прямой СВ\ параллельной оси х. Под
силой Р происходит внезапная перемена величины перере-
Рс
зывающеи силы от положительного значения -=- до отри-
Р(1 — с)
цательного значения ^—-,¦ и резко меняется утод
наклона линии эпюры изгибающего момента. Ломаные
линии АСВ на фиг. 836 и А/С/С,/Вг на фиг. 83с представляют
соответственно эпюры изгибающего момента и
перерезывающей силы по всей длине балки.
Если на балку действуют несколько поперечных сил
(фиг. 84), то то же самое рассуждение показывает, что на
протяжении каждой части балки между двумя грузами
изгибающий момент изменяется, следуя линейному закону,
а перерезывающая сила остается постоянной. Эпюра
изгибающего момента показана на фиг. 846 ломаной линией
107
ACDEB, а эпюра перерезывающих сил изображена на
фиг. 84с ломаной линией А'СГОЧУ&ШФК. Из них видцо,
что под каждым грузом перерезывающая сила и угол
наклона линии изгибающего момента резко меняются.
При практических приложениях существенно важно
найти такие сечения, в которых изгибающий момент
достигает своего максимального или минимального значения.
На этот вопрос легко можно ответить по эпюре
перерезывающих сил. Изгибающий момент достигает наибольшего
©
©
©
дли наименьшего значения в том поперечном сечении, в
котором перерезывающая сила меняет знак и вследствие этого
меняется также и знак производной -у— (см. ур-ние [93]),
Если, следуя вдоль оси, перерезывающая сила переходит
от положительного к отрицательному значению в
некотором поперечном сечении, то в этом сечений мы получим
наибольший изгибающий момент. Перемена Q от
отрицательного на положительное значение указывает на наименьшее
значение изгибающего момента. Вообще говоря, на эпюре
изгибающего момента по длине балки может быть несколько
вершин; тогда следует определить абсолютные величины
108
всех этих вершин, чтобы выяснить наибольший по
абсолютной величине изгибающий момент.
Рассмотрим теперь случай просто опертой балки с
равномерно распределенной нагрузкой интенсивности q (фиг. 85),
Реакции балки равны — ф. Взяв поперечное сечение тп на
расстоянии х от левой опоры и рассмотрев часть балки
©
х лт
ИМ
! 2
I
qx
LA 7 \ \Л
П
А\
і
1
Фиг. 85.
?
2
слева от сечения, найдем,- что силы, действующие на эту
часть, будут: реакция -j! и равномерно распределенная
нагрузка, которая при определении момента и
перерезывающей силы может быть заменена ее равнодействующей
qxt приложенной в расстоянии -^- от поперечного сечения
тп. Тогда
ql qx*
M=fX-
Q=i
q%.
103
Как видим, иэгибающий момент положителен для всех
поперечных сечений балки, равен нулю на концах, т. е. при
х — О и х — 1, и достигает наибольшей величины — ді2 по
о
средине пролета при х = ~ L Эпюр а изгибающего момента
изобразится параболой АС В с вертикальной осью симметрии
Фиг. 86.
яо середине пролета балки. Эпюра перерезывающей силы
изобразится наклонной прямой А!(УВГ.
Если равномерная нагрузка занимает только часть
пролета просто опертой балки (фиг. 86), то реакции балка
можно легко получить, заменяя непрерывную нагрузку ее
равнодействующей, приложенной по середине загруженной
части. Тогда
но
*-¦№+.•*
В=*\а+і
Изгибающий момент в любом поперечном сечения нена-
груженной части а балки равен
Здесь М изменяется пропорционально а:, и поэтому
соответственная часть эпюры изгибающего момента изобразится
наклонной прямой АС (фиг. 866). Эту прямую получим
точно таким же образом (см. ур-ние fa]), как для
сосредоточенной силы ф, приложенной в расстоянии c-f—от
правой опоры балки. Таким же образом получим часть ?D
эпюры изгибающего момента. Части эпюры перерезывающей
силы вдоль незагруженных частей балки представятся
прямыми А'С и 1УВ', параллельными оси х (фиг. 86с).
Для любого поперечного сечения тп в загруженной
части балки (фиг. 86 а), из условия равновесия части балки
слева от сечения, наводим:
M^Ax—q (ж~а)а; Q = A-q(x~a). Щ
Здесь изгибающий момент изобразится параболой с
вертикальной осью симметрии и касательной к прямым на
эпюре в точках С и А Изгибающий момент достигает
максимума в точке Д отвечающей точке Ш пересечения
прямой С'ТУ эшоры перерезывающей силы с осью х
(фиг. 86 с). Нрямая CfBr выражается ур-нием [d] для
перерезывающей силы Q и имеет в точках С и D' ординаты
соответственно А и JB.
Если на балку одновременно действуют и
сосредоточенные грузы и равномерно распределенная нагрузка, то
эпюры изгибающего момента или перерезывающей силы
для сосредоточенных грузов и для равномерно
распределенной нагрузки могут быть построены отдельно, а
суммарная эпюра получена алгебраическим сложением
соответственных ординат.
В случае консольной балки (фиг. 87) применяется тот
же метод для определения изгибающих моментов и
перерезывающих сил, как и для просто опертой балки. Для
любого поперечного сечения шп левой части балки (фиг. 87 а)
м=—рхх и <г=— pt*
Для любого сечения правой части балки
lf= — Рхх — Р%{х — а); Я=-Рг — Ръ
Hi
По правилу, установленному фиг. 81, и изгибающий
момент и перерезывающая сила будут в этом случав
отрицательными, т. е. соответствующие прямые АСВ
и ArOfC"Bf на фиг. 87 имеют отрицательные ординаты.
Мы видели, что наибольшие напряжения от изгиба
получаются в сечениях, где изгибающий момент достигает но
абсолютной величине максимума. Поэтому отыскать такие
сечения очень важно при практических применениях. Их
легче всего найти по
эпюре
перерезывающей силы для тех
значений х, при
которых
перерезывающая сила Q меняет
знак и,
следовательно меняет знак и
^ (см. ур-ние [93]).
Таково условие,
при котором М
достигает максимума
или минимума в
этой части балки, и
из всех таких
значений вдоль балки
нужно взять то,
которое дает
наибольшее по абсолютной
величине значение
М. На фиг. 83 точка С, на фиг. 84 точка D, на фнг. 85
точка С, на фиг. 86 точка -Б и на фиг. 87 точка В
определяют положение опасного сечения»
?
а
с
с
в'
Фиг. 87.
ЗАДАЧИ.
1. Построить эпюры изгибающих моментов и перерезывающих сил
для случаев, показанных на фиг. 88.
Решение. Эпюры построены на фигуре.
2. Найти необходимые размеры прокатной двутавровой балки по
ОСТу, поддерживающей равномерно распределенную нагрузку в 630 х*/л,
как показано на фиг. 89, если допускаемое напряжение Rb — 1120 wjctiK
Учесть только нормальные напряжения а , а весом балки пренебречь.
Решение. Для нахождения опасного сечения следует построить
эпюру перерезывающих сил (фиг. 896). Реакция левой опоры
^і.ею-б + а-ю-і ю1И0|Ск
11?
Перерезывающая "сила для любого поперечного сечения части AG
(5&лки
Q = А — qx — 1980 — 630*.
Ж
IP"
м
П
і— с -Лк
* 1
р
т
-5»
Al
ЦРП А «\ ~^мтШШ.Г!0т^
ш
I
Q
И 1
II 1
| 1Л
Пи Т
liii
іііШ^1^
II III 111
t
\
Pa
I
f
1L
? 'jllltlttlfltlltlfffFfTTTilT
I.
1
itttiftnttftttftttttTtH
Фиг. 88.
1 980
Эта сила равна нулю при х = = 3,14 ж. Для этого сёчеаия
изгибающий момент получает наибольшее значение:
мть.х = 1980 * 3,14 - 630 • -і-' 3Д4* - 3107 кх. л.
8 Тимошенко — Сопротивление материалов, ч. I, 113
Необходимый мо-мент сопротивления
310 700
*
1120
= 277,4 см\
Этим условием удовлетворяет двутавр № 24, площадь поперечного
сечения которого равна 43,3 см2 и момент сопротивления W3 = 325 с*А
3. Деревянная плотина (фиг. 90) состоит из вертикальных стоек ЛВ
прямоугольного поперечного сечения с размером А = 30 см, имеющих
опоры на концах. Найти наибольшее напряжение {<зх)тііУі, если длина
стоек I = 5,4 м. Весом етойки пренебречь*
Решение. Если Ь — ширина стойки, то полное гидростатическое
давление на стойку, представленное треугольной призмой ЛВС, будет
JBT = і^г8• Y- Реакция в точке А:
Л
1 и-1
л=~ д=-і-ьр-т
?,
Ш5 г
*i!fe^aiL
(- - -я
К
г90^%
VjpjbfpB^/fjypjfffip?
1
J*U
Фиг. 89.
Фиг. 90.
н перерезывающая сила для любого поперечного сечения тп равна
реакции А минус вес призмы Атп воды, х- е.
в-^-»т-я(т-т>
Положение поперечного сечения, в котором изгибающий момент
будет наибольшим, найдется из условия Q = 0, или
неоткуда
і-тг=°
Уз
Изгибающий момент в любом поперечном сечении тп равен моменту
реакции минус момент нагрузки, представленной треугольной призмой
Атп. Тогда
М=Ах
X
т
_ Лх L х*\
114
а* 1
Подставив -jj- = -g-, как получено выше, и % = 3,12 ж, получим
-^шах = -^- ЗД2 = ~ 1000 • 3,12 кг - *
і \ - *"» -***"»»_ 2 /М2 am» .
іУтах jyz — 5АЗ "" 3 \ Л J 10О00 ™
'5,4\2 3120
3 \ДЗ/
10 000
= 67,4 «t/сжз.
4. Найти величину изгибающего момента в балке, несущей нагрузку,
распределенную по закону треугольника ABB и равную -Р = 5,4 т,
если 1 = 4лий = 1л ($нг. 91).
Решение. Расстояние с от вертикали, проведенной через центр
тяжести треугольника О, до опоры В р
равно 1,77 ^^^\
Реакция опоры .А равна тогда ОТ ' і \ \ " , \
Р.с б'4*~Г f L. <?—J
-4—у—Г™**-. 1 / і
Перерезывающая сила в любом по- Фиг. 91.
перечном сечении тп равна пеакции
А минус вес нагрузки, представленной площадью Атп. Поскольку
нагрузка, изображенная площадью треугольника ADE, равна:
P(l-d)_ 3
г 4
получим
4 (I — d)a '
Положение сечения, имеющего наибольший изгибающий момент
ЗГшаі> найдем из условия:
L Р ?
4. у —d>s
^-4-РтНЧ^-0,
или
as2 4-4. __ 5
(I — и)» " ТТ ~ 9 '
откуда
х = У"Т = 2,24 лс.
Изгибающий момент в любом поперечном сечении тп равен моменту
реакции А минус момент нагрузки Атщ т. е.
115
Подставляя вышенайденное значение Mm&v получаем
Мтм = 3,360 т - м = 336 000 %% • ел*.
¦шах
U'
Фиг. 92.
5. Найти наибольший
изгибающий момент и наибольшую
перерезывающую силу для случая,
представленного на фиг. 92, если Р = &00 к\%
а = с = 120 См, Ъ = 240 см.
Ответ. Мтйх = 540 %х • ж'
<2шах = 4=50 «t.
6. Построить эпіоры
изгибающего момента и перерезывающей
?
?
силы для случая, показанного
на фиг. 93 а и найти номер
двутавровой балки по ОСТу,
если а = с~ —=1,8ж,Р=900«г|
q = 600 1с%1м, Вь = 1050 къ/сл?.
Весом балки можно
пренебречь.
Решение. На фиг. 93 Ъ
и с построены эпюры
изгибающего момента и
перерезывающей сили, возникающих от
действия показанной на фиг. 93а .
равномерно распределенной на- (?) V
грузки. К этому ивгибающему
моменту и перерезывающей
силе надо прибавить таковые,
вызванные силой Р.
Наибольший изгибающий момент будет
в середине пролета:
і
4
Т
Фиг. 93.
М =
ОД. 1,8*
шах
+ 0,9 • 1,8 = 2,692 m • ж.
Необходимый момент сопротивления
259 200
W
1050
= 257 см».
Двутавр № 22, высотой 22 см, с площадью поперечного сечения
37,38 см* и W = 258,5 с»& — ближайший профиль, удовлетворяющий
условиям работы балки.
7. Найти нанневыгоднейшее положение тележки подъемного крана,
которая перемещается по балке, показанной на фиг. 94. Найти -И"тах, если
давление на ось Р = 4,5 т% I = 8 м, d = 2 м. Весом балки пренебречь.
Решение. Если х — расстояние от левой оси до левой опоры
балки, то изгибающий момент под этой осью равен
%р( г_я_і d\
X
1X6
Этот момент достигает максимума, когда
2 d
Отсюда, чтобы подучить наибольший изгибающий момент под левой
осью, тележку следует сместить от ее среднего положения на расстоя-
d
•ние-j- в направлении к правой опоре. Туже величину изгибающего момента
Фиг. 94.
10 щ а = 4 м, d = 2 л, вес
крана б1 = 4,5 «г, груз
поднимаемый краном Р=г
= 900 мг. Грузы действуют
в средней плоскости между
двумя двутавровыми
балками и распределяются
между ними поровну. Весом
балок пренебречь.
Решение.
Наибольший изгибающий момент
будет под правой осью,
когда расстояние этой оси
от правой опоры будет
равно
наибольший изгибающий момент JkfmftI = 1261600 wt • еле. Деля этот
момент поровну между двумя балками, найдем необходимый момент
сопротивления
1261500
• 2-1050 ~ U V
Требуется двутавр № 32 с площадью поперечного сечения ¦ 71,25 еж2
и моментом сопротивления W = 706 смК
9. Круглое сосновое бревно оперто в точке С и прекрёплено к
фундаменту в точке Л (фиг. 96). На нем находится нагрузка д = 450 кг/»,
равномерно распределенная по длине части СВ балки. Построить эш?ру
изгибающих моментов и найти необходимый диаметр бревна d} если
М = 90 кг/см2, а = 1 м, Ь — 2. ле. ¦¦ ¦
мы получим также под правой осью при
d
смещении тележки на -— от ее среднего
положения в направлении к левой опоре.
8. Рельсы мостового крана (фиг. 95)
поддерживаются двуми прокатными
двутавровыми балками. Найти наиневыгодней-
mee положение крана, соответствующий
наибольший изгибающий момент Мт&х
и J6 двутавра, если R = 1050 %ъ/сз&, I =
Фиг. 95.
,117
Решение. Эпюра изгибающих моментов изображена на фиг. 96 Ьт
Наибольший по абсолютной величине изгибающий момент—над опорой С
и равен 90 000 %г • см; необходимый
диаметр бревна:
®
В
d
8_ Г 32 М
22 см.
Фиг. 96.
10. Консольная Салка с двумя,
равными консолями (фиг. 97) нагружена
равномерно распределенной нагрузкой. При дан-
^'ной длине I балки найти наиболее
выгодное расстояние d между опорами.
Решение. Наиболее выгодное
условие—равенство по абсолютной величине
изгибающего момента по середпне
изгибающим моментам над опорами. Тогда
1 ^ 2 = 0,5S6Z.
а =
і + Уа
7?
щуп
Кривая
ACBFB,состоящая из трех парабол,
имеющих вершины в точках At
Т> и В соответственно,
представит собою эпюру
изгибающих моментов.
11. Дер евянная
плотина, поддерживаемая
вертикальными стойками,
закрепленными их нижними
концами (фиг. 98), состоит
из горизонтальных досок. Найти размер квадратного поперечного
сечения стоек, если I = 2 м, d = 1 м,В>ь = 100 хъ/см?. Построить эпюры
изгибающих моментов и перерезывающих сил.
Решение. Полное боковое давление
на одну стойку Л представляет собою
вес треугольной призмы ABC воды:
В любом поперечном сечении тп
перерезывающая сила н изгибающий момент
равны:
Н-з# „ Но? х
Q = — ж === йг •'р
^frppfftyi'f^mw^
г*
р
Фиг. 98.
"б"
М,
max
При определении знаков Q и М
принято, что фиг. 98 повернута на 90° в
направлении, обратном движению часовой
стрелки, так что оси х и у приводятся
к совпадению с таковыми по фжг. 81.
Необходимый размер стороны Ь сечения
стойки найдем из уравнения:
1-^.1000-2.100
Я.
2-3-100
откуда Ь = 20 см. Построение эпюр предоставляется читателю.
118
12. НаЙтн необходимые размеры консольной балки прокатного
двутаврового сечения, которая несет равномерную нагоузку #=300 %\/м
я сосредоточенный груз Р = 225 къ на конце, если дайна ее ? = 160 си
я Ж = 1000 яі/<мА
Решение,
225-160 + 300.1,6.80 .
• 1000 -74,4 С»».
Необходим двутавр,
профиль № 14 по ОСТу,
высотою НО «ж с
площадью поперечного
сечения 18,08 с*з и TFe = 81,3
сл^ ¦
13. Найти напряжения
от изгиба в заклепке при
предположении, что
нагрузка, действующая на
заклепку, распределяется,
как показано на фиг. 99.
Диаметр заклепки d = 20
Фиг. 99.
мм, h = 7 леи, uj = 10 жд*, Р = 4000 «*.
Решение. Изгибающий момент в поперечном сечении тп равен
2
h_
2
Изгибающий момент по середине высоты ваил?пки в сечении щ?
равен
2
(т+*>
Этот последний момент и следует принять во внимание при
определении напряжений. Тогда
Р / Ь , \\ п& 4Р 2h+ht
28. Скалывающие напряжения при изгиба. Ранее в п° 26
было показано, что в случае изгиба балки поперечными
силами в любом поперечном сечении тп балки (фиг. 81)
возникают не одни нормальные напряэкения3 но также
скалывающие напряжения хух. Значок у в обозначении напряжения
х я указывает, что скалывающее напряжение параллельно
оси у, а значок а;—что напряжение действует по плоскости,
перпендикулярной оси х. Эти напряжения имеют такую
величину, что их сумма равна перерезывающей силе Q (фиг. 100).
При' рассмотрении закона распределения напряжений
119
ло площади поперечного сечения, мы начнем с
простейшего случая прямоугольного поперечного сечения. В этом
случае естественно предположить, что скалывающее
напряжение х в каждой точке поперечного сечения параллельно
перерезывающей силе Q> т. е. параллельно сторонам тп
поперечного
сечения. В качестве
второго допущения мы
примем, что скалы-
вающиенапряж?ния
распределены
равномерно по ширине
балки ссг.
Эти два
допущения дадут нам
возможность найти за-*
кон распределения
скалывающих на?
пряжений.
Более
углубленное исследование
задачипоказыва^т1),
что это
приближенное решение обегано
достаточно точно я
что для узкого прят
моугольника (А.
велико сравнительно
с Ь, фиг. 100) почти
совпадает с точным
решением.
Если вырезать из балки элемент двумя бесконечно
близкими смежными поперечными сечениями и двумя
бесконечно близкими смежными плоскостями,
параллельными нейтральной плоскости, как показано на фиг. 1006,
то в соответствии с нашим допущением скалывающие
Фиг. 100.
*) Точное решение этой задачи дано Сен-Венаком {Saint Tenant),
„Journal de math.*, Licnmlle, 1856. Содержание этого замечательного труда
€бн-Венава приводится в книге Тодгёнтгра и Лгіреона (Todhunter and
Pearson), History of tne Theory of Elasticity. Приближенное решение,
приведенное дальше, дано Журавским. Перевод на французский язык
этой его работы см. „Annales des ponts et chaussees", 1856.
Точная теория показывает, что, если высота балки мала
сравнительно! с шириной, расхождение между точным и приближенным ..регае-
ние"й Еймуча?тск'',зйачителькымі'
120
напряжения суду* равномерно распределены яо
вертикальной г#ани acctav Этн напряжения дают момент (х bdy)cb
относительно нижнего заднего ребра еех элемента, который
должен уравновешиваться с моментом (х^Ъ dx) dy от
скалывающих напряжений, распределенных по горизонтальной
грани с<Цсх элемента. Тогда
xyJ)dydx = х bdxdy
и
"у* — ^ху*
т. е. скалывающие напряжения, действующие по двум
взаимно перпендикулярным граням элемента, равны.
\Р
л
г ®
ч
L
Фиг. 101.
Такое же
заключение получено было
ранее, при простом
растяжении (см. стр.
44), а также при
растяжении или сжатии
по двум взаимно
перпендикулярным
направлениям (см, стр. 46).
Существование этіх
скалывающих
напряжений в плоскостях
параллельных
нейтральной плоскости, можно
доказать на простых
опытах.
Возьмем два
одинаковых прямоугольных
стержня, положенных
один на другой, на
двух опорах, как показано на фиг. 101, и изгибаемых
сосредоточенным грузом Р. Если между стержнями нет трения, изгиб
каждого стержня будет независимым от изгиба другого;
у каждого будут сжаты верхние и растянуты нижние
продольные волокна, и деформация будет такой, как показано на
фиг. 101&. Нижние продольные волокна верхнего стержня
сместятся относительно верхних волокон нижнего стержня.
В сплошном стержне толщиною 2Л (фиг. 101а) возникают
скалывающие напряжения по нейтральной плоокости я»
такой величины, что они предотвращают то смещение
верхней части относительно нижней, которое показано
на фиг. 101ft. Благодаря этому предотвращению смещения
131
дельный стержень толщиной 2ft значительно жестче ы
прочнее, чем два стержня, каждый высотою 7г.
На практике в составных деревянных балках часто
применяют, чтобы предотвратить смещение, шпонки а, Ь,
с,..., как показано на фиг. 102а.
Наблюдение за просветами около шпонок (фиг. 1026) дает
возможность определить в случае составной балки
направление смещения и тем самым направление скалывающих
Фиг. 102.
напряжений по нейтральной плоскости в случае сплошной
балки.
Вышеизложенное показывает, что скалывающее
напряжение -zyx в любой точке вертикального поперечного сечения
вертикально по направлению, а по абсолютной величине
равно горизонтальному скалывающему напряжению х 9
возникающему в горизонтальной плоскости, проходящей
через ту же точку.
dx
\M+dM
07
.— А
¦т
л
Шшж
Р LJ1 Ч'ц Л ^
Фиг. 103.
Г1 L
Это последнее напряжение можно легко определить
из условия равновесия элемента рр^п^ вырезанного из балки
др$"М* бесконечно близкими поперечными сечениями тп и
mfa ь горизонтальной плоскостью ррг (фиг. 103а и Ъ).
Единственными усилиями, действующими на этот элемент
по направлению оси <с, будут скалывающие напряжения хЯ9
по грани ррг и нормальные напряжения оя по граням рп ж
122
pxiiv Если изгибающие моменты в сечениях т? и тхпг
одинаковы, т. е. в случае чистого изгиба нормальные
напряжения оя по граням пр и пхрг будут одинаковы и будут
взаимно уравновешиваться. Тогда скалывающее
напряжение тву должно быть равным нулю.
Рассмотрим теперь более общий случай переменного
изгибающего момента, обозначив через М и M-^dM моменты
в поперечных сечениях тп и тхпх соответственно. Тогда
нормальное усилие, действующее на элементарную
площадку dF грани пр будет (см, ур-ние [87])
CffdF=^-dF
Сумма всех этих усилий, распространенная по всей
грани пр элемента, будет
2
Му dF. [a]
Г М
J *<
Ух
Таким же образом сумма нормальных усилий;
действующих по грани nj>19 будет:
3
{М+Ш)у №
Усилие, возникающее от скалывающих напряжений т ,
действующих по верхней грани ррх элемента, равно
Усилия [о], [Ь] и [с] должны взаимно уравновешиваться,
поэтому
A Jl
Ух Уі
откуда
Vi
123
или, пользуясь ур-нием [93], получим:
z
Vi
Интеграл в этом уравнении имеет очень простое
значение. Он представляет статический момент заштрихованной
части поперечного сечения (фиг- 1036) относительно
нейтральной оси е. Для рассматриваемого выше
прямоугольного сечения
и интеграл получается равным
А А
;**-|*[-±(?-,,). и
Уі Ук
Тот же результат можно получить умножением площади
ааштрихованной части Ъ (——уі }иа расстояние — |—j-j^j
ее центра тяжести от нейтральной оси.
Подставляя значение [d] интеграла в ур-ние [95],
получше для прямоугольного сечения:
wary V 21 \ 4 }
№
Отсюда следует, что скалывающие напряжения т в
не распределяются равномерно сверху до низу балки.
Наибольшее значение іух получается при ух = о, т. е. для
точек, лежащих на нейтральной оси, и оно из ур-ния [Щ
равно
8/,'
' bh»
или, так как !,=——,
Такшіс ббразом * наибольшее скалывающее напряжение
в, случае, прямоугольного поперечного сечения на 50%
124
больше среднего значения скалывающего напряжения,
полученного делением перерезывающей силы на площадь
поперечного сечения.
Внизу и вверху поперечного сечения
-4- К
и ур-ние [96] дает \х — 0.
Эпюра ур-ния [96] (фнг. 103 с) показывает, что
распределение скалывающих напряжений по высоте балки
следует параболическому закону. Заштрихованная площадь,
ограниченная параболой, умноженная на ширину Ъ балки,
2
дает — (чгДмхЬ&=в» как и следовало ожидать.
Естественным последствием таких скалывающих напряже
ний является деформация сдвига, которая вызывает
искривление
первоначально плоских
поперечных
сечений. Искривление
можно легко
продемонстрировать,
изгибая силой,
приложенной на конце,
прямоугольный
кусок резины (ф. 104),
на боковых гранях
которого нанесены
вертикальные
линии. Эти линии не
останутся прямыми,
как указано пунктиром, а получат искривление, так что
наибольшая деформация сдвига получится по нейтральной.
поверхности. В точках т\ тгг, ?\ п/ деформация сдвига:
равна нулю, так что кривые tn'/z' и т./»/- остаются нор--
мальными к верхней ж нижней поверхностям стержня и-
после изгиба. На нейтральной поверхности углы между
касательными кривых *»V и т/п/ и нормальными
сечениями тп И т^ равны Т==тг* (V)mai* Д° тех П0Р пока
перерезывающая сила остается по длине балки
постоянной, искривление всех поперечных сечений будет одинаково,
так что mm' = m1m1/f nnr = пхпх' и удлинение или
укорочение, вызываемое изгибающим моментом в продольных
волокнах, остается без изменения. Это обстоятельство объясняет
125
Фиг. 104.
применимость к этому случаю ур-ния [87], которое было
выведено для чистого изгиба и основано на допущении,
что поперечные сечения стержня остаются плоскими при
изгибе.
Более углубленное изучение задачи х) показывает, что
искривление поперечных сечений также не имеет
существенного влияния на деформацию продольных волокон,
если на балку действует распределенная нагрузка и
пережевывающая сила изменяется беспрерывно по длине балки.
8 случае сосредоточенных грузов, распределение
напряжений около точек приложения грузов более сложно, но это
отклонение отэакона прямой линии имеет местный характер
(см. стр. 146).
ЗАДАЧИ.
Т. Найти предельное значение грузов Р, действующих на
деревянный прямоугольный бруа (фиг. 105), если Ь = 20 ем, h = 25 см, Ль —
= 56 кфм2, Вз = 14 *і/<?л3, с = 45 см*
Решение. Эпюры
изгибающих моментов и перерезывающих
сил даны на фиг. 105.
d
Р
Vmax —х > ¦* max * v-
Из уравнений
Рс
W=B*
и
12-_л
2 bh~ *
получим
Р = 2593 к\ и Р = 4667 к%;
1
Фиг. 105.
Фиг. 106.
таким образом Р = 2593 кг — предельное значение груза Р.
2. Определить наибольшее нормальное напряжение ах я наибольшее
перерезывающее напряжение т по нейтральной плоскости балки,
представленной на фиг. 106, если а = 68 см, с = 120 сл«, о = 20 см, h = 25 ем
и Р = 2700 кг.
Ответ, (од,),^ « 52 кі/ел?; (^)max = 8,1 кг/с*3.
3. Найти наибольшее скалывающее напряжение по нейтральной
плоскости от равномерно распределенной нагрузки в балке прямоуголь-
J) См. Б. Фойгт {W. Voigt), „Cottingen Abnandlungen*, Bd 34, 1887;
Д. Мтель (J. Н. MichelT), „Quart. Journ.o? Math.*, Vol. 32,1901, и Л". Филон
(L. 1ST. a. Filon), „Phil. Trans. Roy. Soc. (Ser. A)*, Vol. 201, 1903 и
.London Eoy. Soc. Pxoc.% Vol. 72, 1904.
126
ного сечения, если длина балки 1 = 2 м, нагрузка q = 1500 «t/jn, высота
поперечного сечения h = 25 см, и ширина его о = 20 ел.
Ответ. тта1 = 4,5 кг/емК
29. Распределение скалывающих напряжений в случае круглого
поперечного сечения. При рассмотрении распределения напряжений по круговому
поперечному сечению (фиг- 107) нельзя базироваться на
предположении, что скалывающие напряжения все параллельны перерезывающей
силе Q. Действительно, мы можем показать, что в точках р поперечного
сечения по окружности скалывающее напряжение касательно к ней.
Рассмотрим бесконечно малый элемент abed в виде прямоугольного
параллелепипеда с гранью adfg на поверхности балки и гранью abed
в плоскости yz поперечного сечения. Если скалывающее напряжение,
действующее по грани abed элемента, имеет такое направление, как т:,
то его всегда можно разложить на две составляющих; т1а, в радиальном
направлении, н т2я в направлении, касательном к окружности- Выше
* ф
Фиг. 107.
было доказано (см. стр. 121) из рассмотрения условий равновесия
элемента, что если скалывающее напряжение т действует на элементарную
площадку, то одинаковое скалывающее напряжение будет также
действовать на элементарную площадку, перпендикулярную к т.
Применяя этот вывод в нашем случае, можем заключить, что
если скалывающее напряжение *с1гв действует на элемент abed в
радиальном направлении, то должно быть такое ж? скалывающее напряже*.
ние хх1> действующее по грани adfg элемента, лежащей на поверхности
балки. Если на боковой поверхности балки нет скалывающих напряжений*
то радиальная составляющая tla? скалывающего напряжения т должна
быть равна нулю, т. е. тдолжно-иметь направление, касательное к
окружности поперечного сечения балки.
В средней точке ? хорды рр симметрия требует, чтобы скалываю-'
щее напряжение имело направление перерезывающей силы Q. Тогда
направления скалывающих напряжений в точках р и п будут
пересекаться в некоторой точке О на оси у (фиг. 107&). Приняв теперь, что
скалывающее напряжение в любой другой точке линии рр также имеет
направление к точке О. мы вполне определим направления
скалывающих напряжений.
J27
В качестве второго допущения мы предположим, что вертикальные
составляющие скалывающих напряжений одинаковы для всех точек
линий до і). Так как это допущение вполне совпадает с допущением,
сделанным для случая прямоугольного поперечного сечения, то мы
можем воспользоваться ур-нием [У5] для определения этой
составляющей. Зная действительное направление скалывающего напряжения
н его вертикальную составляющую, можно легко определить его
величину в любой точке поперечного сечения.
Определим теперь скалывающие напряжения по линии рр попереч-'
ного сечения (фиг. 108). Применяя ур-ние [95] к определению
вертикальной составляющей tyW этих напряжений, мы должны найти статиче
ский момент площади круговою сегмента, лежащего ниже линии до,
относительно осп г. Элементарная площадкам» имеет длину 2У Я2 ~ у*
и ширину dy. Площадь элемента равна dF = dy • 2 V 2& — у*.
Статический момент этой волоски относительно G& будет ydF и полный момент
площади всего сегмента
(2 у -W^tf) ydy = -|(Й2 _ Уі2,т#
Подставляя это в ур-ние [95} и
взяв 2У В?—у{г вьеотоЬ, получим
усе
_0(&-±уЯ
ZL
№1
Фиг. 108.
и полное скалывающее напряжение
в точках р (фиг. 108) будет:
ух
V&-V1*
SL
Отсюда следует, что максимум т получается при уг = 0, т. е. для
нейтральной оси поперечного сечения. Тогда, подставляя Iz = ,
получим;
т =
4 Q
ти Зяй2
_4
а
?
№}
Таким образом в случае кругового поперечного сечения наибольшее
скалывающее напряжение на 33% больше, чем среднее эначение,
полученное делением перерезывающей силы на площадь поперечного сет
чения.
х) Приближенная теория, основанная на двух вышеприведенных
допущениях, дает удовлетворительную точность, в сравнении с точной
теорией показывает, что ошибка в величине наибольшего скалывающего
напряжения около 5%, что /невелико для практических применений.
См. Ссн-Венап, труд, упомянутый выше на стр. 120. См. также книгу
-А.. Лове (А. Е. И. Love), .^Mathematical Theory of Elasticity, 4 ecL 1Й27,
P* o4cD«
128
39. Распределение скалывающих напряжений в двутавровых
балках. При рассмотрении распределения скалывающих
напряжений по сечению стенки двутавровых балок (фигл09)
сделаем те же предположения, что были сделаны для
прямоугольного поперечного сечения, а именно, что
скалывающие напряжения параллельны перерезывающей силе Q
и равномерно распределены по толщине Ъг стенки. Тогда
можно воспользоваться для определения напряжений хух
ур-ннем- [95]. Для точек на линии рр в расстоянии уі от
нейтральной оси, где ширина поперечного сечения равна Ъи
статический момент заштрихованной части площади сечения
относительно нейтральной оси s будет:
— У?
Подставив это в ур-ние [95], получим:
Q
'ух
КіЛ
[100]
Таким образом напряжение изменяется по высоте балки,
следуя параболическому закону. Наибольшее и наименьшее
значения тв, в стенке балки полу-
h
чим, приравнивая уг = 0 и ух = •—¦ :
(О
Q
ул 'max
(т,
/min
8
8
Ф-h
Q I bfc» IKS
yjy/шш
hh
8
8
;[101]
[101']
Если Ъг очень мало по сравнению
6, то разница между (От(й и
с
(vXnin невелика, и распределение
скалывающих напряясений по
поперечному сечению стенки почти
равномерное
Хорошее приближение для (^)шах
получается делением полной перере- Фиг. 109.
зываюідей силы на площадь
поперечного сечения одной только стенки. Это следует из того, что
скалывающие напряжения, распределенные по поперечному
сечению стенки, дают усилие, которое почти равно Q. Это
значит, что стенка берет на себя почти всю перерезыва-
9 Тимошенко — Сопротивление материалов, ч. I. >¦ 129
ющую силу, а пояса играют только второстепенную роль
в передаче этой силы. Докажем это. Сумма напряжений
хух по всей стенке, которую мы назовем Qu будет
л,
;
VAd2A
h
2
Из ур-ния [100):
8 ГГі'т4)4(?-».')]*
и, после интегрирования:
Vl J, L 2 ' 2 2 "*" 12 J#
м
При малой толщине полок, т. е. когда \ приближается
к К, момент инерции Ig можно представить - с достаточной
точностью выражением:
• 2 * 8 ^ 12 ' L J
в котором первый член является произведением площади
поперечного сечения полок на квадрат расстояния —1—-5
их центров тяжести от оси #, что является приближенным
значением момента инерции поперечного сечения полок.
Второй член выражения [Ъ]—момент инерции поперечного
сечения стенки.
Сравнивая выражения [а] и [Ь], мы видим, что по мере
того, как kx приближается к h9 сила Qx приближается к Q,
т. е. перерезывающая сила воспринимается одной только
стенкой.
При рассмотрении распределения скалывающих
напряжений по поперечным сечениям полок, нельзя сделать
допущение, что по ширине сечения напряжения не
меняются. Например, на уровне ае (фиг. 109) по нижнему краю
верхней полки ас и de скалывающее напряжение т должно
быть равным нулю, так как соответственное равное ему
напряжение т^ на свободной нижней поверхности полки
130
равно нулю (см. стр. 121, а также фиг. 107с). В части ей
однако скалывающие напряжения неравны нулю, но имеют
величины, определенные выше для {іух)тіп в стенке.
Это указывает, что в месте соединения cd стенки и полки
распределение скалывающих напряжений подчиняется
более сложному закону, чем можно вывести при нашем
элементарном анализе. Чтобы избежать концентрации
напряжений в точках сий, резкие переломы обычно заменяются
закруглениями, как показано на фиг. 109 пунктиром. Более
детальное рассмотрение распределения скалывающих
напряжений в полках будет дано далее (см. п° 41).
ЗАДАЧИ.
1. Найти ¦ (Туа^тазс и (rt/x)min в стенке двутавровой балки (фиг. 109Х
если Ь = 125 мм, Ьі==12 лея, h — 300 мм, \ = 270 мм, ? = 13500».
Найти перерезывающую силу Qi, передающуюся
стенкой.
Ответ.
іг —959 см*; (туаг)тах~442кг/сле2;
(V)mm ^Шкг/см2; Qt = 0,958 Q.
2. Найти наибольшее скалывающее напряжение
в стенке тавровой балки (фиг. 110), если h = 200 мм,
\ =¦ 180 мм, Ъ = 100 мм, \ = 25 мм и Q = 450 кг.
Ответ. Применяя тот же метод, что и для
двутавровой балки, найдем С^х)таа ~ 12 кг/смК |л
31. Главные напряжения при изгибе,Помоіцъю Фиг. но.
ур-ний [89] и [95] можно легко определить
для любой точки поперечного сечения нормальное
напряжение ох и скалывающее напряжение ъух% если только
изгибающий момент М и перерезывающая сила Q для
этого поперечного сечения известны. Наибольшее по
абсолютной величине ах будет в наиболее удаленном от
нейтральной оси волокне, а наибольшее значение т?я.—
обыкновенно на нейтральной оси. Большей частью для
расчета достаточны только полученные таким путем
наибольшие значения ож иту„ и размеры поперечного
сечения балок подбираются такими, чтобы удовлетворить
условиям:
Здесь предполагается, что материал одинаково
сопротивляется растяжению и сжатию, и допускаемое
напряжение Вь и при растяжении и при сжатии одинаково. В
пробивном случае условия сопротивления на растяжение и
131
на сжатие должны быть удовлетворены каждое порознь
и мы получим:
KW < Щ» на растяжение;
(От** < Ad на сжатие.
Встречаются однако обстоятельства, при которых тре
буется более детальный анализ напряженного состояния.
Рассмотрим метод исследования, применяемый в этих случаях
для балки, лежащей на двух опорах и несущей груз по
середине пролета (фиг. ш). Для точки Е ниже
нейтральной оси поперечного сечения тп величины напряжений ох
и х9Я = хХ9 получаются из ур-ний [87] и [95]. На фиг. lllfc
эти напряжения показаны действующими на бесконечно
малый элемент, вырезанный из балки у точки Е;
направления их легко определить по направлениям действия
изгибающего момента М и перерезывающей силы Q. Для
такого бесконечно малого элемента можно пренебречь
изменениями напряжений ох и zyx для различных точек элемента
и допустить, что элемент находится в однородно-напряженном
состоянии, т. е. что величины ох и тух могут быть
рассматриваемы одинаковыми в любой точке элемента. Такое
состояние напряжения показано по отношению к элементу
конечных размеров на фиг. 35 (стр. 46).
Из предыдущего мы знаем (см. стр. 45), что напряжения
по граням элемента, вырезанного из напряженного тела,
меняются с изменением направления этих граней и что
возможно выбрать такое положение элемента, при котором
будут иметь место только нормальные напряжения (см.
стр. 50). Направления таких граней называются главными
направлениями и соответствующие напряжения главными
напряжениями. Величины этих напряжений можно найти
по формулам [34] и [85] подстановкой в эти выражения oft
вместо о/ и нуля вместо oft. Тогда получим
w=T+]/(ir)2-bv2- f10,2i
°;n = T- |/(-t)2 + V3- [102']
Следует заметить, что <*Шйх всегда растягивающее,
а атЫ всегда сжимающее напряжение. Зная главные, на-
пряжения, получим наибольшее скалывающее напряжение
в любой точке нз ур-ния [33] (см. стр. 46):
т =
шах
о — а .
max nun
/(*
7А
а) -
т
2 V \ 2 / ~ vz "
]Р Л.
{103J
Ж
•±
У
п\Е
\п,
L
,х^ш*—I
Фиг. 111.
Для определения направлений главных напряжений
пользуемся кругом Мора. Для такого элемента, как взятый
нами у точки Е (фиг. 1116), соответствующий круг Мора
показан на фиг. 111с Взяв расстояния OF~ox и DF==
133
=ха9 получим точку D, представляющую напряжения
на гранях Ъе и ad элемента. Расстояние OF взято в
направления положительных о, a DF в направлении вверх,
потому что ох—растягивающее напряжение, а скалывающие
напряжения * на гранях Ьс и ad дают пару ежг,
вращающуюся по направлению часовой стрелки (см. стр. 49).
Точка Dj представляет напряжение по граням ad и cd
элемента, для которых нормальные напряжения равны
нулю и скалывающие напряжения — отрицательны.
Круг, построенный на диаметре DDlf определяет <зтах=
О А и о.
шш
= — ОБ.
вление <*
шах
Фиг. 112.
Из того же построения определяется угол 2?, а напра-
на фиг. 1ИЪ получается откладыванием угла <р
от оси х в
направлении движения
часовой стрелки. Конеч-
- но ошіп перпендику-
-h-Z-r. лярно отах.
Взяв сечение «ijMj
справа от груза F
(фиг. 111а) и
рассматривая точку Ег
выше нейтральной оси
получим
направление напряжений,
действующих на
элемент abed в точке Ег такими, как указано на фиг. Hid.
Соответствующий круг Мора построен на фиг. 1Ш. Точка
В представляет напряжения по граням аЬ и dc элемента
abed, а точка В1 — напряжения по граням ad и Ьс. Угол ф,
определяющий направление отах, следует измерять в
направлении движения часовой стрелки от внешней нормали
к граням аЪ или ей, как показано на фиг. 1П#.
Бели мы возьмем точку на нейтральной поверхности,
то as получится равным нулю. Элемент в этой точке
будет находиться в состоянии чистого сдвига. Направления
главных напряжений здесь составляют с осями ее и у углы
В 45°.
Возможно построить две системы ортогональных
кривых, касательные к которым в каждой точке имеют
направления главных напряжений в этой точке. Такие
кривые называются траекториями напряжений.
Фиг. 112 изображает траектории напряжений для прямо--1
ш
угольной консольной балки, нагруженной на конце
сосредоточенным грузом. Все ?ти кривые пересекают
нейтральную поверхность под углом в 45° и имеют горизонтальные
или вертикальные касательные в точках, где скалывающее
напряжение %ух равно нулю, т. е. на верхней и на нижней
поверхностях балки. Траектории, изображающие
направления напряжений а^ (растяжения), показаны сплошными
линиями, а другая система траекторий, сжимающих
напряжений—пунктирными линиями.
На фиг. ИЗ показаны траектории и эпюры
распределения напряжений ах и хух для нескольких поперечных
сечений лежащей на двух опорах прямоугольной балки,
находящейся под действием
равномерно
распределенной нагрузки Очевидно,,
что <*х имеет наибольшее
значение по середине ql
пролета, где изгибаю- j
щий момент
М—наибольший, а хух имеет
наибольшее значение на —
опорах, где действует
наибольшая перерезы- ді
вающая сила *). y
Для расчета балок
интересно знать абсо- Фиг. из.
лютные величины
максимальных значений о. Из формулы [102]
усматривается, что для наиболее удаленных волокон в растя~
нутой зоне, где скалывающее напряжение равно нулю,
продольное нормальное напряжение <зх становится главным
напряжением, т. е. отах = (oJmax. Для волокон, лежаках
ближе к нейтральной оси, продольное напряжение сх
меньше чем для крайнего волокна; однако здесь имеется
также скалывающее напряжение хух> и напряжения ах и
^действующие совместно в этой точке, дают главное
напряжение по формуле [102], которое может по абсолютной
величине быть даже больше напряжения крайнего волокна.
В случае балок прямоугольного или круглого сечения,
где скалывающее напряжение хух изменяется непрерывно
по высоте балки, этого обычно не бывает, т. е. напряжение
*) Некоторые примеры построения траекторий напряжений
рассмотрены Ж. Вагнером {I, Wagmr), „Zeitschr. d. Osterr. Ing. u. Archit. Yer*"
Ш1, S.615.
135
(°*)max > определенное для наиболее удаленного волокна
в сечении, где изгибающий момент достигает максимума,
является наибольшим напряжением, возникающим в балке*
Однако в таких случаях, как двутавровая балка, где
в месте соединения полки и стенки резко меняется
величина скалывающего напряжения (см. стр. 131), наибольшее
главное напряжение, вычисленное для этого места по
формуле [102], может оказаться большим, чем
растягивающее напряжение (аД^ в наиболее удаленном волокне,
а потому при подборе сечения балки следует принять во
внимание это наибольшее главное напряжение.
•Для пояснения рассмотрим случай, представленный на
фиг. ilia. Двутавровая балка тех же размеров, что в за-
Фиг. 114.
даче 1, стр. 131, длиною 2 = 60 ем, несет нагрузку Р,
равную 27 т. Тогда ^mwc==405 000 кг • см; Qmax=13 500 кг.
По формуле [87] найдем растягивающее напряжение в
наиболее удаленном волокне:
К Х/т&Х
405 000-15
9 590
634 %г\см\
Для точки в месте сопряжения полки и стенки
получим следующие значения нормального и скалывающего
напряжений:
634-13,5 „_ , _ '
% = ^~- = 571 %г\смЦ
V=314 KtjcAfi.
Тогда по формуле [102] найдем главное напряжение
а-ци = 709 **/**"•
136
Итак главное напряжение стах в месте сопряжения
долки и стенки больше, чем растягивающее напряжение
для наиболее удаленного волокна, и поэтому при расчете
должно быть принято первое.
Изменения напряжений ах, тух, ошах и ашіп по высоте
двутавровой балки показаны на фиг. 114.
ЗАДАЧИ.
1. Найти сшах и amin в точке, лежащей на 5 см ниже нейтральной
оси в сечении, находящемся на 1 м от несущего нагрузку конца
консоли (фиг. 112), если балка прямоугольного поперечного сечения, высота
балки k = 20 ся, ширина Ъ = 10 см и Р = 900 кг. Найти угол,
составляемый направлением главного нормального напряжения в этой точке
с осью х.
Решение. (Сд,) = —67,6 кг/см2; (хух^ = 5Д хг/ся2; &тах = +-0Д кг/см2;
amin —~~ 67,9 кг/см2. Угол, составляемый ащах с осью ху измеренный по
направлению движения часовой стрелки, равен 85° 4А'.
2. Определить атах и с^п по нейтральной оси поперечного сечения,
отстоящего на 30 см от левой опоры, для равномерно загруженной
балки прямоугольного сечения, опертой сеоими концами (фиг. 113).
Размеры поперечного сечения те же, что в предыдущей задаче;
интенсивность q — 1 500 кг/м; I = 3,2 ж.
Ответ. атах = — ffmin = 14,6 кг/елЛ
3. Найти пролет двутавровой балки, рассмотренной на стр. 136*
если в месте сопряжения полки со стенкой (ff^)max' равно ащах.
Ответ. I = 93,9 см,
32. Напряжения в составных (клепаных) балках. В
инженерной практике часто применяются составные (клепаные)
балки, и напряжения в них обыкновенно определяются при
допущении, что их отдельные части жестко соединены
друг с другом. Расчет таких балок требует: 1) расчета их
как сплошной балки и 2) поверки расчетои и определения
расстояния между элементами, которые соединяют в одно
целое отдельные составные части балки. Для первого
пользуются формулами сплошных балок, учитывая ослабление
сечения заклепочными отверстиями, дырами для болтов,
врубками и т. п. соответственным уменьшением рабочей
площади поперечных сечений. Необходимые для поверки
соединения частей сечения в одно целое расчеты будут
рассмотрены на примерах.
Рассмотрим сперва составную деревянную балку,
изображенную на фиг. 102. Предполагается, что шпонки,
примененные для соединения двух частей балки, достаточно
прочны, чтобы. сопротивляться сдвигающим усилиям 8
(фиг. Ю2Ьі стр. 122). Тогда для определения ох можно вос-
• 137
пользоваться формулой [87]. Чтобы учесть ослабление се*
чения врубками для шпонок и дырами для болтов, следует
принять во внимание только заштрихованную часть
сечения, как показано на фиг, 102с*
Тогда
I, = ^[(2fc)3-(2C)*].
При определении сдвигающего усилия #, действующего
на каждую шпонку, допустим, что это усилие равно
перерезывающей силе, распределенной в сплошной балке по
площади е-Ъ нейтральной поверхности, где Ъ—ширина
балки и е—расстояние между средними точками шпонок
(см. фиг. 102а). Тогда, пользуясь формулой [97] и считая,
что высота балки в этом случае равна 2fe, получим
Размеры дшонок и расстояние е между ними должны
быть выбраны так, чтобы обеспечить достаточное
сопротивление шпонки на скалывание и на смятие по боковым
граням шпонки и брусьев по врубкам для шпонки.
При таких расчетах обычно делают грубое
предположение, что скалывающие напряжения равномерно
распределены по среднему сечению а • Ъ шпонки и что давление
на боковых гранях шпонок равномерно распределено по
площади с • Ь.
Тогда, обозначив через Bs допускаемое напряжение щ
скалывание шпонок и через R'd—допускаемое напряжение
на боковое смятие дерева шпонки или врубки, получщі
следующие выражения для расчета шпонок:
— <В- ~<ВГ
Необходимо также обеспечить достаточное
сопротивление на скалывание дерева балки вдоль волокон между
двумя шпонками. Скалывающее усилие равно тому же S,
а площадь сечения балки, сопротивляющаяся скалыванию,
равна Ъ - (е — а). Обозначив через Л/ допускаемое
напряжение на скалывание вдоль волокон материала балки, полу*
чям следующее условие прочного сопротивления;
, s <д'
138
В дополнение к шпонкам здесь применяются болты
(фиг. 102), соединяющие части балки. Натяжением их
создается трение между частями балки. Этик трением обычно
пренебрегают при вычислениях, и предполагают, что вся
скалывающая сила воспринимается шпонками. Опыты
показывают, что такая составная: деревянная балка слабее
сплошных балок тех ж? размеров поперечного сечения1).
При определении напряжения аЛ в клепаной
двутавровой балке влияние ослабления заклепочными дырами
обычно учитывается в предположения, что все дыры
находятся в одном и том же поперечном сечении балки (фиг.
М е M+dM
Фиг. 115.
115а) 2), путем вычета их диаметральных сечений при
вычислении для подстановки в формулу [87] момента
инерции Iz.
При определении наибольшего скалывающего
напряжения %ух на практике также принято учитывать влияние
ослабления заклепочными дырами. Легко видеть, что
площадь поперечного сечения стенки уменьшается при нали-
(e — d)
чии дыр в отношении -, где е—расстояние между
!) Опыты, произведенные проф. Э. Жидвело» (Е. Kidwell) в Мичиган
ском горном колледже, показали, что составные деревянные балки
обладают сопротивлением равным 75% такового сплошной балки тех
же размеров.
2) Дыры в вертикальной стенке находятся в сечениях, где к балке
приклепаны вертикальные уголки жесткости,
139
центрами дыр (шаг заклепок) и d—диаметр дыр. Поэтому
при определения tyx в стенке клепаных двутавровых балок
в правую часть формулы [ 95 ] обыкновенно вводится мно-
е
житель т зт-
{в — d)
Необходимо отметить, что такой способ учета влияния
ослабления заклепочными дырами является лишь грубым
приближением. Действительное распределение напряжений
около дыр очень сложно. Некоторые соображения о местных
напряжениях у краев дыр приведены далее (см. п° 46,
часть II).
При определений срезывающего усилия, действующего
на отдельную ваклепку, например на заклепку А (фиг*
115 6), рассмотрим два поперечных сечения тп и тхпл\
Вследствие разницы между изгибающими моментами
в этих двух поперечных сечениях, нормальные
напряжения в сечениях, тп и тхпх будут отличаться друг от'друга
и поэтому пояс балки, зачерненный на фиг. 115с, будет
стремиться сместиться вдоль стенки. Смещению
противодействуют силы трения и заклепка А, Пренебрегая
трением, получим, что сила, действующая на заклепку, равна
разности усилий, действующих по сечениям тп и тхпх
пояса. Усилие в поясе по поперечному сечению тп (см.
ур-ние [а], стр. 123) равно:
М
ы».
где интегрирование должно быть распространено на всю
зачерненную площадь поперечного сечения пояса. Таким
же образом для поперечного сечения т1и1 получим:
Тогда усилие передающееся через заклепку А от пояса
на стенку, будет:
S=±j^fUdF. [a]
Пользуясь ур-нием [93] и подставляя расстояние е
между заклепками вместо dx, получим:
ДЖ=<2 е, .-.
где Q — перерезывающая сила в.поперечном сечении балки,
проходящем через заклепку А.
140
Подставив в формулу [а], получим:
S^^CydF. [105J
Интеграл, входящий в состав этого выражения,
представляет статический момент зачерненного поперечного
сечения пояса (фиг. 115с) относительно нейтральной оси в.
Легко видеть, что для того чтобы могло произойти
смещение пояса вдоль стенки, заклепка должна быть срезана
по двум ее поперечным сечениям. Допустив, что усилие S
равномерно распределено по этим двум поперечным
сечениям, получаем срезывающее напряжение в заклепке
2 ^
4
Усилие #• иногда дает значительное скалывающее
напряжение в стенке балки по плоскости аЬ (фиг. 115&),
которое следует учесть. Допустив, что эти напряжения
равномерно распределены, получим скалывающее напряжение
в стенке, разделив усилие S на площадь Ъг(е—d);
bxIt # e — d
Кроме этого напряжения, вызванного усилиями S,
передающимися от поясов, здесь будут действовать, по той же
плоскости db, скалывающие напряжения т" от изгиба стенки.
Величина этих напряжений получится из того же ур-ния
[Ь] подстановкой вместо интеграла
/
ydF
статического момента относительно нейтральной оси части
прямоугольного поперечного сечения стенки выше
плоскости аЪ.
Таким образом мы придем к следующему выражению для
скалывающего напряжения тяу в стенке по плоскости аЪ:
где интеграл распространяется на зачерненную на
фиг. llbd часть площади поперечного сечения.
141
Зная ох и хх'у\ можем определить по ф-лам [102] и [102']
°шах Н атЬ ДЛЯ Т0Чек ПЛОСКОСТИ (#, Как ПОЯСНвНО быЛО
в предыдущем и0, а также определить направления главных
напряжений.
Из вышеприведенного видно, что при определении
напряжений в клепаной балке делаются некоторые
допущения для упрощения подсчетов. Это до некоторой степени
понижает точность определения напряженки и должно быть
принято во внимание при выборе допускаемых напряжений
для клепаных двутавровых балок1).
ЗАДАЧИ.
1. Составная деревянная балка (фиг. 102) состоит из двух брусьев
прямоугольного сечения, соединенных шпонками. Найти
перерезывающую силу, действующую на шпонку, скалывающее напряжение в шпонке
н давление на единицу' площади ее боковой грани, если груз Р = ? 200 кг
ширина балки Ъ —13 см, высота 2 h = 40 см, ширина шпонки а = 8 см,
высота шпонки 2 с = 6 см и расстояние между центрами шпонок
« = 28 см.
Ответ,
„ 3 2200-28 tiKK
8 = Т '-^40Г- = П55кг'
Скалывающее напряжение' в шпонке
Давление на единицу площади по боковой грани шпонки
2. Найти скалывающее напряжение по нейтральной оси клепаной
балки, вертикальная стенка которой имеет толщину 20 мм и высоту
1300 ммг пояса которой состоят из двух пар уголков 160 X150 Х1^ **»¦
если полная перерезывающая сила в сечении равна 68 т. Найти также
срезывающие напряжения в заклепках, соединяющих пояса со стенкой,
если диаметр этих заклепок 26 мм и шаг заклепок е = 100 мм (фиг. 115).
решение. При данных размерах имеем
1=2. -~^- + 4 f849 + 40,25 (65 - 4,22)21 = 964 000 с*К
х) Опыты показывают, что разрушение двутавровых балок обычно
происходит вследствие выпучивания сжатых поясов или стенки [см.
Т. Мур (Я. F. Moore), University of Illinois, Bulletin 68, 1913]. Вопрос
о выпучивании будет рассмотрен далее.
Влияние изгиба стержня заклепок на распределение напряжений
в двутавровых балках было рассмотрено И. Арповлевичем (/. Arnovle-
vic), „Zeitschr. f. Axchitekt. u. Ingenieurwesen", 1910, S. 56. Он нашел, что
вследствие этого изгибающие напряжения в балках при обычных
соотношениях размеров возрастают примерно на 6%.
№
Статический момент полусечения относительно нейтральной оси
равен
Л
2
65'^'65 +'2.40,25 • 60,78 = 4225 + 4892 = 9Ц7 см*.
Гу№=*
В этих вычислениях 40,25 ел*2 — площадь поперечного сечения уголка,
849 сх4—момент инерции поперечного сечения уголка относительно
оси, проходящей через центр тяжести параллельно нейтральной оси
балки, 60,78 си — расстояние центра тяжести каждого уголка от
нейтральной оси z балки. Все эти числовые данные взяты непосредственно
из справочника по сортаменту ОСТа.
По формуле [95] получаем
68000-9117
(Vmax = 2.964000 = 321 К%/СМ •
Если мы учтем ослабление стенки заклепочными дырами, то
в 10
(Т**)тах - -JZTd *321 - Ю-2,6
• 321 = 434 кі.'сдА
Усилие S, передающееся одной эаклепкой, по $-л? [105] равно
5 =
68000-10*4892
964000
= 3450 %\.
Срезывающее напряжение в зак- _Щс
г Цбж,
лепке по ф-ле [106] равно
3450-2
х =
= 325 «і/с«8
тс • 2,6?
3. Найти ашьх в точках
плоскости аЪ (фиг. 115), в расстоянии 665 мм
от нейтральной оеи,^если размеры
балки те же, что в предыдущей
задаче, Q = 68 т и изгибающий
момент Ifi = 3 450 000 к* - еж.
Решение. По формуле [107]
получаем
68 000 10
Т** "2-964000* 7,4
3450000-56,5
V
-г~
gfc
±
2Е
°х =
964000
Ф
Фиг. Ц6.
(4892 +1032) = 283 да/ел*;
= 202 кг/сж2;
Отах «Г п^
VW1
+ 283а = 300 «г/слЛ
4. Найти усилие, срезывающее заклепку, соединяющую два рельса,
нв которых составлена балка, показанная на фиг- 116. Рельсы
нормального типа 1а; площадь поперечного сечения рельса F = 55,64 еж2»
расстояние от подошвы рельса до центра тяжести его сечения — 6,96 см,
143
момент инерции поперечного сечения, рельса относительно оси,
проходящей через его центр тяжести и параллельной оси z —1476 емК
Расстояние между заклепками е —150 мм и перерезывающая сила Q =
= 2200 да.
Решение. По формуле [105] на каждую из двух заклепок
приходится
„ 1 2200-15.55,64.6,96 „.-
* = Т" * 2 (1476 + 55,64.6,96*) = 766 ^
33. Второстепенные напряжения при изгибе. В предыдущем
рассмотрении напряжений при изгибе было допущено, что между продольными
волокнами балки давления нет (см. п° 24). Это допущение дает вполне
удовлетворительные результаты для поперечных сечений, достаточно
удаленных от точек приложения грузов.Вблизи этих точек, однако имеет
место более сложное распределение напряжений, и при известных
обстоятельствах вследствие этого возникает- давление между боковыми
поверхностями продольных волокон, которое следует учесть.
Фиг. 1П.
В качестве первого примера рассмотрим случай лежащей на двух
опорах прямоугольной балки с равномерно распределенной по верхней
грани ее нагрузкой (фиг. 117). Если q — нагрузка на единицу длины
балки и Ь — ширина балки, то сжимающее напряжение в верхнем
волокне балки будет-—-. Ниже в балке мы можем ожидать, что
сжимающее усилие между волокнами будет уменьшаться с увеличением
расстояния от поверхности приложения .нагрузки. Чтобы найти величину
этого бокового сжимающего напряжения о на волокно ssx> в расстоянии
Ух от нейтральной оси, рассмотрим элемент тщ ssv выше оси,
ограниченный горизонтальной плоскостью sst и двумя бесконечно близкими
смежными поперечными сечениями тп а тх nL балки.
Для составления уравнения равновесия этого элемента относительно
вертикальных сил мы приведем нижеследующие соображения.
Равномерно распределенная нагрузка на верху элемента в целом дает
усилие qdx, направленное вниз; равномерно распределенные усилия по
низу элемента в целом равны в Ъ dx и направлены вверх; усилия, вы-
144
званные скалывающими напряжениями по грани ms, имеющие
равнодействующую, направленную вверх*-), получатся из ур-ния [Щ:
2
усилия, вызванные скалывающими напряжениями т по грани т^,
имеющие равнодействующую, направленную вниз, получатся таким
же путем:
(Q~-gdx)b { h* Д8уі Уіз \
Условие равновесия дает таким образом следующее уравнение:
, gb <Ы A» #Vt , ft» \ .
g^-^bto^LJ — -±+-l-Je0|
откуда боковое сжимающее напряжение между волокнами
A3 Afyx 2/Г
% 2 J
Подстановка Уі = -«- в это уравнение дает нам величину бокового
сжимающего напряжения по верхней поверхности о = •$-. Для
нейтральной оси Ух = 0 и «у = ~г. Для нижней поверхности балки yt =
= _4-и= =0.
2 - у
Отсюда следует, что по всей высоте балки имеются боковые
сжимающие напряжения между продольными волокнами. Изменение этого
напряжения по высоте балки представлено графически на фиг. 117с.
В случае сосредоточенного груза Р, приближенного к верхней
поверхности балки узкого прямоугольного поперечного сечения (фит. 118).
получается более сложное распределение напряжений. В
непосредственной близости от груза к обычным напряжениям от изгиба,
определенным выше, будут присоединяться местные напряжения. Это
местное напряжение для любой точки А является простым сжатием в
радиальном направлении. Бесконечно малый элемент, имеющий радиаль
но? направление, показанный на фиг. 118а и отстоящий на расстоянии
г от точки приложения груза, будет испытывать простое сжатие, и
величина этого напряжения2)
2Р cos 9
<j = т- • , [109]
1) Допущено, что перерезывающая сила в сечении тп —
положительна.
*) Это решение получено Фламапом (Flamant), nAnnates desponts ,-et
chaussees" 1893, Paris.
10 Тимошенко — Сопротивление материалов, ч. I. ' 145
где Ь — ширина поперечного сечения балки и ?—угол, составляемый
радиусом г с направлением действия груза.
Интересно отметить, что равнодействующая упомянутых
радиальных сжимающих напряжений по цилиндрической поверхности малого
радиуса (фиг. 118с) уравновешивается вертикальной силой Р и двумя
р «
равными и прямо противоположными горизонтальными силами -^- *).
%
h
Эти последние силы, приложенные примерно в расстоянии — от оси
і
1
г
j?
^8^
4»
Ч
р
'0
/
2
У
7
D
А
X
L
-Ь
1
h
®
PR
©
Фиг. 118.
балки, вызывают в поперечном сечении не только растягивающие
напряжения
и
Сложив напряжения о ' и e_f с напряжениями от изгиба по
формуле [87], получим окончательно растягивающее напряжение в
продольном волокне у точки п;
но
также
напряжения
от
X
изгиба,
%bk
равные
РА
2тс
і
У
I ?
Г \ ъ Pl 6
, р зр _гр / зг 2 |
¦*" яЬА яЬА ЪЛ\ 2А я j
[НО]
Отсюда следует, что вследствие влияния местных напряжений
в точке приложения груза, имеет место уменьшение наибольшего
напряжения в точке те, которое, для очень коротких балок, составляет
значительный процент этого напряжения. Результаты опытов2) дали
достаточно удовлетворительное совпадение с подсчетами по ф-л? [110].
і) С. Тимошенко (J5. Imoskenko), „Phil. Mag.", Vol. 44, p. 1014, 1912.
2) Первые опыты по проверке ур-ния [110] были выполнены Еарусом
Вильсоном (Cams Wilson), .Phil. Mag. (Ser. 5), Vol. 32, 1891.
146
ГЛАВА ПЯТАЯ.
ПРОГИБ БАЛОК.
34. Определение прогибов помощью эпюры изгибающих
моментов. В п° 24 было найдено, что кривизна упругой
линии призматической балки при изгибе будет:
1 И
Т=-Ш7' [1П]
где М—изгибающий момент в поперечном сечении,
проведенном через рассмотренную точку, и Itt—момент
инерции поперечного
сечения относительно
нейтральной оси.
Это выражение
было выведено для
случая ивгиба
призматической балки,
изгибаемой моментами, при
ложенными к концам,
т. е. для так
называемого чистого изгиба. В
©том случае Ж —
постоянно по всей длине
балки; поэтому и
радиус кривиэны
остается постоянным, и
упругая линия — дуга
круга.
Это же уравнение
может быть применено
в случае изгиба
призматических стержней
поперечными силами, если пренебречь влиянием
перерезывающих сил !). Здесь М будет изменятсья вдоль балки,
и упругая линия будет иметь переменную кривизну.
Существенной задачей в каждом случае является
определение для данной системы грузов и при данном
устройстве опор перемещения при изгибе любой точки изгибаемой
балки от ее первоначального положения.
На фиг. 119 АВ представляет часть упругой линии и
А1В1 — соответствующую часть эпюры изгибающих момен-
г) Их влияние рассмотрено далее, ел етр. 185.
10*
147
тов. Два смежных поперечных сечения балки на
расстоянии ds друг от друга пересекутся после изгиба, под углом
й?, и из ур-ния [111]: ¦
й ? = — as = -^y-ds.
р Ыг
Для балок, применяемых в сооружениях, кривизна
получается очень небольшой, и мы можем заменить d$ через
dx. Тогда
db = -—(Mdx). [a\
Графически эти означает, что элементарный угол <й
между двумя последовательными радиусами или между
двумя последовательными касательными к упругой линии
равен заштрихованному элементу площади Mdx эпюры
изгибающих моментов, разделенной на жесткость при
изгибе х). Так как -это применимо к каждому элементу, то
угол ? между касательными в точках А и В получим
суммированием элементов, подобных представленному
выражением [а]. Итак
в
?
в \-жШх> [112]
т. е. угол между касательными в двух точках А Ъ В
упругой линии равен площади эпюры изгибающих
моментов между соответствующими вертикальными линиями,
разделенной на жесткость балки при изгибе.
Рассмотрим теперь расстояние точки В от касательной
АВГ к упругой линии в точке А. Вспомнив, что упругая
линия—пологая кривая, можем измерить это расстояние
по вертикали ВВ\ Приращение, получаемое этим
расстоянием при изгибе элемента тп балки и заключающееся
между двумя последовательными касательными в точках т
и п, равно
Это представляет графически деленный на Ш9 момент
:) Что касается измерений, то угол db — в радианах; т. е.
отвлеченное число; Mdx — в килограммах, умноженных на сантиметр во второй
степени; Ш% — в килограммах на квадратный сантиметр, умноженных
на сантиметр в четвертой степени.
143
заштрихованной площади Mdx эпюры изгибающих
моментов относительно вертикали, проходящей через точку -В.
Интегрирование дает полный прогиб ВВ'\
в
~і Л
¦xMdx,
[113]
©
т* е. расстояние точки В от касательной в точке А равно
моменту относительно вертикали, проходящей через точку В
площади эпюры изгибающего момента между точками А и
В, деленной на жесткость при пзгибе ЕТВ. При помощи
ур-ний [112] и [113] можно легко определить угол наклона
касательной к упругой линии и величину прогиба в
любом поперечном сече-.
нии балки.
Рассмотрим теперь некоторые
примеры такого
определения.
35. Прогиб консоли.
В случае балки,
заделанной одним концом,
ссосредоточеннкмгру-
зом на свободном
конце (фиг. 120а), эпюра
изгибающих моментов
представится фиг. 120Ь.
Так как касательная
в закрепленном конце
остается неизменной,
то расстояния точек
упругой линии от этой касательной являются
действительными прогибами балки. Угол ?^, который составляет каса-
талъная к упругой линии в точке В с касательной в точке А,
называется углом * поворота сечения В относительно
сечения Л. Тогда из ур-ния [112] *)
®
Фиг. 120.
*»я-4
Р/2
EL
2EL
[114]
Прогиб 8 определится из ур-ния [113], как момент шіо-
і) Абсолютная величина угла поворота сечения вычисляется по
этой формуле. Направление поворота легко выясняется из условия-за-
іружения.
149
щади А'АгВх относительно вертикали, проходящей через
точку Ви деленный на Е1е. Тогда
г 9 1 Рі*
JEL
BEL
Для любого поперечного сечения тп поворот сечения
относительно закрепленного конца А представится
площадью т^А^А' (фиг. 1206), деленной на Шш.
Для пологих кривых, какими являются упругие линии
балок, угол поворота сечения можно принять равным
тангенс/ угла наклона касательной к кривой, и мы получим:
6
dx
РР
2EI.
{
(1-х
р
ОРТ
[ивЗ
Прогиб у в том же поперечном сечении равен йоменту
площади щт^А^ относительно тхп19 деленному на JET,
(см. уравнение [113])* Подразделив эту площадь на
прямоугольник и треугольник, указанные на фигуре 120&,
получаем:
У
El
г и
2
т.
г;-
[117]
®
Для консоли, несущей сосредоточенный груз Р в
поперечном сечении на расстоянии с от опоры (фиг. 121а), эпюра
/ изгибающих момен-
щ^ш — -t т^ представится
фиг. 1216. Угол
наклона касательной ж
прогиб для любого
сечения слева от
точки приложения
груза определятся
по ф-лам [116] и
[117] подстановкой с
вместо L
Для любого
поперечного сечения
вправо от груза
изгибающий момент
и кривизна равны
НО
©
t
Фиг. liil.
нулю. Эта часть балки остается прямолинейной. Угол
наклона ее постоянен и равен углу наклона касательной в
точке С, т. е. по формуле [114] равен
2Е19 ш
Прогиб в любом поперечном, сечении тп равен моменту
площади треугольника АхА'Сг относительно вертикальной
линии тхп1У деленному на EIZ, что дает
У =
Рс*
F1.
<-*>
[118]
©
?«J4
Если на консоль действует несколько грузов, то
изгибающий момент в любом поперечном сечении будет равен
сумме изгибающих
моментов, вызываемых
действием каждогогру-
за отдельно. Поэтому
прогиб в любой точке
можно получить как
сумму прогибов.в этой
точке, вызванных
отдельными грузами.
Этот способ получения
общего результата
путем сложения частных /т\
результатов называет- ^&/
ся способом наложения.
Он широко
применяется при исследовании
изгиба балок и будет
далее показан на ряде примеров *).
Для консоли с равномерно распределенной нагрузкой
интенсивности g (фиг. 122а) изгибающий момент в любом
поперечном сечении тп на расстоянии хх от закрепленного
конца
Флг. 122.
Угол наклона касательной к упругой линии в любом
*) Случаи, к которым этот способ неприменим, рассмотрены далее
(см. стр. 267).
151
поперечном сечении на расстоянии х от опоры согласно
ур-нию [112]
х
b--dT-mJ 2 dXl
о
f^-^2+^). [119*]
2Д
Тангенс угла наклона касательной на конце получим
подстановкой I вместо х в это уравнение, что дает:
(-Н- -лиг- ' '-і
Прогиб в сечении на расстоянии х от закрепленного
конца равен моменту площади АгАгсй относительно
вертикальной линии cd, деленному на Е1Ъ (фиг. 12"2Ь). Момент
заштрихованного на фиг, 122Ь элемента этой площади равен
и полный момент получится интегрированием этих
элементов по хг от хг — 0 до хг = х. Тогда
а?
О
Прогиб в сечении на расстоянии х от опоры получается
таким образом после интегрирования равным
а I fix* te» . а* \ , ,
»"2ш:ч-2—F+T2-J- ^
Для прогиба на конце при х — 1 получаем: .
Эту же задачу можно легко решить применением
метода наложения. Равномерно распределенная нагрузка
может быть рассматриваема как система бесконечно
малых грузов qdc, показанных заштрихованной площадкой
152
на фиг. 123. Прогиб, вызываемый в поперечном сечении тп
каждым элементарным грузом qdc влево от сечения, может
был найден по формуле [118] подстановкой qdc вместо Р.
Прогиб yt от всех грузов слева от тп равен сумме
прогибов, вызванных всеми такими элементарными грузами
при изменении с от о = 0 до с = х:
х
Уі
Ш. J 2 \
X
dc
Я.
2EL
2-.
4
Прогиб, вызванный в поперечном сечении тп
элементарным грузом qdcu находящимся вправо от сечения,
найдется по формуле [117]
подстановкой qdcx вместо — /
Р и ct вместо I. Прогиб
у2, вызываемый в
сечении тп всеми грузами,
лежащими вправо от
сечения, равен сумме
прогибов от всех таких
элементарных грузов при
изменении ct от сі — х до
Фиг. 123.
X
Тогда полный прогиб в сечении тп
хЧ* Ы
)¦
2EI.
\ 2 3 "* 12 /'
что совпадает с выражением [121], найденным раньше.
ЗАДАЧИ.
t. Найти прогиб и угол наклона касательной в конце консоли,
рассмотренной в задаче 12, стр. 119.
Решение. '
ЪЕі ' BEI '
Z Z
2. Определить прогиб верха стойки, представленной на фиг. 98
(задача 11, стр. 118).
Решение. Изгибающий момент в поперечном сечении тп на
расстоянии х от верха равен
м=-ЕхЬ
3Z2
153
у? 73 '
где Л = —— • 1000 кг — полное гидростатическое давление, передаю-
щееса на одну стойку {d и I в метрах). Пользуясь ур-нием [ИЗ],
получим прогиб верха стойки:
г
?Я_ /У&р„ Л?31_ 1-22-1000-2003«12 _0
Ш / ЗР — I5if/ 2-15-100 000-20*2 ' *"
О
3. Найти прогиб и тангенс угла наклона касательной в конце коп-
соли, изгибаемой моментом М (фиг. 124).
Ответ.
(y)tez =
Ж*
jr~
1
(&Л
2EI *
Ml
**'*=%
EI
Фиг. 124.
-.*-.
¦*+¦
X
і
/
Фиг. 125.
4. Две деревянные балки
прямоугольного сечения, скрепленные на
левом конце (фиг. 125), 'изгибаются
из-за стягивания болтом на правом
конце. Найти диаметр болта,
дающий для деревянных балок и для
стального болта одинаковые запасы
прочности. Длина изгибающейся
части балок I = 1 м, высота h = 20 см,
ширина Ь = 15 ел, допускаемое
напряжение для стали 840 кг/с*2,
для' дерева 84 кг/см2. Найти прогиб
балок, когда растягивающее напряжение в болте равно 840 кі/сх\
Решение. Если Р — усилие в болте,
то уравнение для определения его
диаметра d будет:
4Р . №
Ы3 : *&»
1
2
= 840:84 = 10,
Ж
Ж
ш
J
і
откуда <2=1ДЗ см и
4
Р =
840 = 840 кг.
ш
щ
ішііі
і
Фиг. 126.
нагрузки одинакова
По формуле [115], приняв Е = 100 QOQmfex-
получим прогиб Ь = 2,8 хм.
5. Каково отношение прогибов в кон-
пах консолей, показанных на фиг. 126,
если интенсивность равномерно распределенной
в обоих случаях:
Ответ. 7:41.
6. Каким должно быть уравнение оси стержня ЛБ до изгиба, если
груз Р, движущийся вдоль стержня, остается все- время на одном к
том же уровне (фиг. 127)?
Ответ.
РжЗ
у=-
ШЬ
154
7. Определить при заданном допускаемом напряжении Въ
безопасный прогиб балки, показанной на фиг. 124. Найти такой же прогиб и
для консоли, нагруженной на конце (фиг. 120).
Ответ.-
2 RP
} ? Eh *
8. Намагниченный круглый диск JV радиусом В (фиг. 128)
оказывает на тонкую стальную ленту, толщиною h, равномерно распределен^
нов притяжение q къ/смК Найти длину I свешивающегося конпа АС
ленты и наибольшее напряжение в ней, если h = 0,26 *ж, Е = 1Ь мм
ж 2 = 1 kiJcmZ.
Фиг. 127.
Фиг. 128.
Решение. Длина свешивающейся части ленты может быть
определена из условия, что в точке С кривизна, вызываемая равномерно
распределенной нагрузкой q, должна быть равна -^-. Поэтому
ф
е
В '
откуда
г
/
2Ш
г
дВ
= 0,854 еж.
Наибольшее напряжение определится из выражения
<W = -sir = 3 500 да/мА
2В
9. Определить соотношение между грузом JP и прогибом о в конце
етержня АВ, закрепленного другим конном А (фиг. 129), если при
изгибе стержень постепенно приходит в соприкосновение с абсолютно
жесткой поддерживающей поверхностью АС, имеющей постоянную кри-
1 л
визну-^-и горизонтальную касательную к точке А.
Решение. До jrex пор, пока кривизна оси стержня у точки А
которая равна
1 М Рі
~Е1
Еі '
Z
меньше, чем кривизна опорной поверхности-^-, стержень будет
касаться поверхности АС только в точке А, и прогиб стержня получится
до формуле [11б[:
165
Положив
~Е1
1
1і '
W
получим предельное значение груза Р, при котором стержень начнет
приходить в соприкосновение е" опорной поверхностью н за точкой А.
ш
1
с
t,-JX
I
Фиг. 129.
Фиг. 130
8
Р
Бели через Pt обозначить величину этого предельного груза, то из
ур-ния [Ь]
*і =
т
М
При Р>Рі часть АВ стержня будет опираться как показано на
фиг. 129 пунктирной линией. Длина х свешивающейся части найдется
из уравнения, подобного ур-нию [Ь]:
[А
а? —
~ВР
Полный прогиб в точке В таким образом составляется из трех
частей:
1) прогиб части ВВ стержня, как консоли:
Рх* (#1е)2 щ
*і== ЗЖГ=='ШРЗ*
2) прогиб, представляющий расстояние точки В от касательной
к опорной поверхности в точке А:
о3 =
АВ-
ад
О-*)* I еі9\* 1
ZR
ер т*
Ь) прогиб части ВВ вследствие наклонного положения стержня
в точке В:
о3 =
АВ (J —*)» / EI
х= -—— = 12 —
т
в
R
ВР / В*Р '
Тогда
72
1 JS№
5 = 5* + 52 + 5з==2іГ в~И*Р* '
Из этого можно видеть, что в этом случае прогиб не
пропорционален грузу и. что жесткость возрастает с. возрастанием груза.
10. Консоль АВ, нагруженная на конце В, поддерживается более
156
короткой консолью CD того же поперечного сечения, что и консоль ЛВ
(фиг. 130). Найти давление X между двумя балками в точке С.
Решение. Давление X найдется из того условия, что в точке С
обе консоли имеют один и тот же прогиб.
Пользуясь формулой [115] для.нижней консоли и ур-нием [117]
совместно с формулой [115] для верхней консоли, получим
хг\
1ЁГ =
z
откуда
(т-і)-
Из рассмотрения эпюр изгибающего момента для верхней и нижней
консолей можно заключить, что в точке С верхняя консоль имеет
больший угол поворота сечения, чем нижняя консоль. Это показывает, что
соприкосновение между двумя консолями будет только в точках D и С.
36. Прогиб балки с опертыми концами. Рассмотрим сперва
случай действия на балку одного сосредоточенного груза Р
(фиг- 131). "Эпюра изгибающего момента — треугольник
АгВхСг на фиг. 131&, Площадь его равна
Рс(1 — с)
и его центр тяжести расположен на расстоянии -r-(J + с)
о
от вертикали* проведенной через правую опору. Расстояние
Ъ' конца В от касательной в точке А получим из ур-ния [113].
1 РС(1-С) 1+С PC(Z2-C2)
Зная эту величину, получаем угол наклона касательной
для левого конца балки
Представим себе теперь балку АгВх (фиг. 1316), опертую
по концам и несущую нагрузку, закон распределения
которой представляется эпюрой изгибающего момента АХСХВХ.
Реакция Ах левой опоры от этой нагрузки
.Сравнение этого выражения с формулой [123] показываем,
157
что угол наклона касательной на опоре А действительной
балки можно получить делением на Е1Ш реакции опоры Аг
воображаемой балки Аг Ви которая оперта по концам, имеет
тот же пролет I, что и действительная балка, и несет
нагрузку, распределенную по закону, представленному эпюрой
изгибающего момента действительной балки. Для простоты
условимся называть такую балку фиктивной балкой.
Путем таких же рассуждений найдем, что абсолютная
величина угла наклона касательной на другой опоре В равна
Рс{1 — е) 21 —с 1 1
02 =
2
I EL
_ Рс(1 — с)(21 — с)
~ bUEL
[124]
Для определения угла наклона в любом поперечном
сечении тп балки нужно лишь (фиг. 131а) вычесть из
1-е _
ф
угла ?а на опоре А угол 0 между касательными в точке А
и в поперечном сечении ит *). Тогда при помощи ур-ний
[123] и [112] получаем
dy jgffl —с8) лл.-АА1щпі 1 {А А .
158
г) Всюду предполагается, ^то упругая линия — пологая кривая.
Первый член в скобках этого выражения—реакция
левой опоры фиктивной балки AXBV а второй — нагрузка
фиктивной балки слева от поперечного сечения %пг Таким
образом, полное выражение в скобках представляет
перерезывающую силу для поперечного сечения т^
фиктивной балки.
Следовательно, угол наклона касательной
действительной балки в любом поперечном сечении тп может быть
получен делением перерезывающей силы в
соответствующем сечении фиктивной балки т^ на Е1й.
Что касается прогиба у в любом поперечном сечении тп
балки слева от груза Р, то, как это усматривается из
чертежа,
у = ас — Ьс. [Ъ]
Из подобия треугольника Аас и ABIf первый член
правой части этого выражения, согласно формуле [а],
— Ъ'х Ахх Гл1
ас = -Г=Жг' [с]
где Ах—реакции левой опоры фиктивной балки. Второй
член правой части ,ур-ния [Ь] представляет расстояние
точки Ь от касательной Ас и получается из ур-ния [113]
Ы= -^- • пл. Д Ахт^ - — х. [d]
Подставляя выражения [с] и [#] в формулу [Ь], получим
У^-jtf-(Ах—пл.Д^п^. — х у И
Выражение в скобках имеет очень простое значение,
оно представляет изгибающий момент в сечение щ^
фиктивной балки. Отсюда прогиб в любой точке балки с
опертыми концами может быть получен делением изгибающего
момента фиктивной балки для того же поперечного сечения
на жесткость Е1г. Подставляя в [е] вместо Ах его значение
из ур-ния [123] и заметив, что
#2 Рсх*
ПЛ. Д Ахт&і = п_с™ • нл- А ЛСД = ~2Г».
159
получим
і_ГРс (?2—с2) * — Рсх* 1—
у~~~ тг [ бі 6? J
Из этого уравнения молено определить прогиб- в любом
сечении балки слева от груза Р.
Уравнение упругой линия для правой части балки
можно получить таким же путем. Мы его получим
подстановкой 1 — с вместо с, I—х вместо я в ур-ние [125], что
дает:
y==F{l^EI~X) [с(21-с)-(1-хП [126]
Для получения прогиба в точке приложения груза сле=ш
дует подставить х = 1—о в ур-ние [125] или в ур-ние [126]/
Тогда
РсЦі-с)*
»
Если груз приложен по середине пролета, то с = —
и прогиб по середине пролета
(^4=ііЬ [128]
Если с> —, то наибольший прогиб будет слева от
груза. Положение поперечного сечения, в котором у
достигает максимума, получится, если взять производную от у
относительно х в ур-нии [125] и приравнять ее нулю. Это
дает
гз—с2—зя2 = о,
откуда
« = —Lr/P — с2. [129]
V 3
Подставляя это значение х в ур-ние [125], получим
наибольший прогиб;
3
рс(р_с2)Т
«--«уп-и,- [1301
ісо
Гірогио по середине для этого случая получим
подстановкой я = —J в ур-ние [125]:
(у)«=4-
Рс
48Ж.
(3Z2--4c2).
[131]
®
Ур-ние [129] показывает, что точка наибольшего прогиба
всегда близка к середине пролета балки. Когда с = — lt
то оно будет по середине пролета, и в предельном положении,
когда с = О и груз Р находится над опорой, точка наибольшего
прогиба отстоит от середины пролета лишь на расстоянии;
-j= — ~ = 0,077?.
V В 2
Поэтому прогиб по середине пролета очень близок к
наибольшему прогибу. В наиболее неблагоприятном случае,
когда с приближается к нулю, разница между этими двумя
прогибами равна лишь
2j5°/0, как это
получается из выражений
[130] И [181].
Пользуясь методом
наложения, то же
самое заключение можно
получить и для случая
балки, нагруженной
несколькими
поперечными силами,
действующими в одном и
том же направлении-
В случае действия момента И на конец балки (фиг, 132),
эпюра изгибающего момента представится фвг. 132&.
Воображаемая нагрузка фиктивной балки будет изображаться
прямоугольным треугольником А^В^ площадь которого
равна */2 ML Реакции опор Ах и В1 фиктивной балки равны
1 Ж1 2 Ml _т
— -—и — -— соответственно; разделиз их на Ж8, полу-
^им абсолютные значения углов \ и 02:
в1=ш
©
Фиг. 132
?.
6EI,
т
BEL
11 Тяыошенко — Сопротивление материалов, ч. I.
[132]
[133]
161
Прогиб в любом поперечном сечении тп действительной
балки получим делением изгибающего момента для того же
сечения фиктивной балки на Е19 (фиг. 1326), что дает:
У
Mix Ml
EL
6
X
~3
¦)-
Mix
SET
ж2
[134]
Интересно отметить, что ф-лы [132], [133] и [134] можно
получить сразу же из ф-л [123], [124] и [125] подстановкой
в эти последние Рс = Ж и с = О.
Итак из решения для случая одиночного груза методом
наложения можно получить прогиб в любой точке балки
для любой системы грузов. Тот же метод применим также
к случаю распределенной нагрузки.
®
®
Фиг. 133.
В качестве примера возьмем случай балки, лежащей на
двух опорах и находящейся под действием равномерно
распределенной нагрузки (фиг. 133). Согласно ф-ле [123],
угол поворота на опоре А от действия элементарного груза
qdc, показанного на фиг. 133, равен
<йх =
qccU{P — с2)
6/. Г'
Полный угол поворота ?х равен сумме этих
элементарных углов при изменении с от О до /.
? = f qG dc № ~ °2) = ql*
1 J 61-Е1Я ~ 24Ш„
[135]
163
Тот зк? результат получим, определив реакцию опоры Ах
фиктивной балки АХВХ.
Прогиб по середине пролета можно определить из
ур-ния [131], которое было выведено в предположении, что
груз- находится справа от середины.
Если груз находится слева от середины, то можно
применить то же уравнение, но в этом случае с следует
рассматривать как расстояние груза от левой опоры. Любой
элементарный груз qde справа от середины (фиг. 133а)
вызывает прогиб по середине пролета, равный
т-т~ •?&(&--**)*
Суммируя прогибы, вызванные такими элементарными
грузами, находящимися справа от середины, и заметив, что
нагрузка на левой половине балки вызывает такой же
прогиб в середине пролета, как нагрузка в правой половине,
получим:
т
О
Тот же результат получается делением изгибающего
момента для середины пролета фиктивной балки (фиг. 133Ь)
на жесткость.
Воспользуемся способом фиктивной балки для
получения общего уравнения упругой линии. Площадь
параболического сегмента равна двум третям площади
прямоугольника, показанного на фиг. 1336 пунктирными линиями;
поэтому полная нагрузка фиктивной балки равна:
3 ' 8
9. л/а
Так как эта нагрузка делится поровну между опорами, то
реакции фиктивной балки равны
ql*
24 в
Тогда угол наклона касательной в точке А
ql*
«1 =
24JBI/
11*
163
Так как изгибающий момент для любого поперечного
сечения т? действительной балки
qlx qx*
то изгибающий момент в поперечном сечении тлпу
фиктивной балки
х
ql3X f(ql дяМ , ч 7
24 ./ \ 2
9
О
и прогиб в сечении мш действительной балки
О
Способ наложения можем также применить, если
распределенная нагрузка покрывает только часть пролета
балки, воспользовавшись
у уравнением, подобным
ур-нию [136] при преде-
Ш,
i ff i i—^—s лах интегрирования, от-
L / -i вечающих данному
случаю *). Если мы имеем,
Фиг. 134. например, нагрузку,
показанную на фиг. 134, то
прогиб в середине пролета, вызываемый этой нагрузкой
справа от середины, равен:
т
ъ
Нагрузка слева от середины дает прогиб;
а
J) Упругие линии для большого числа частных случаев балок
приведены в книге .Steel construction" Американского института стальных
конструкций, 1Уь8, р. 93.
164
Полный прогиб по середине пролета поэтому равен:
7/2 г/2
а
ЗАДАЧИ.
I. Определить углы наклона касательной на концах и прогнб под
грузами и по середине балки, изображенной на фиг. 135.
Решение. Нагрузка фиктивной балки представится трапецией
АгСхВхВь площадь которой равна Рс (1-е). Углы наклона касательных
на концах равны
0і=0а= ш g *
г
Прогнб под грузами равен
ы,»=е ш^ у 2 а " a J -Е/Д а ~ з j *
Прогиб по середине балки получим из ур-нпя [131]:
'I
Шііі
Фиг. 135.
Фиг. 136.
2. Найти наклон концов балки, показанной на фиг. 90 (стр. 114).
Ответ.
/ dy \ =J_J№
\dx-)x==0 180 EI;
( dy \ 8_ HP_
\ dx L. ~ 180 BI '
3. Найти прогиб по середине пролета балки ABt изображенной на
фиг. 136, если 1я — 3600 см*, q = 750 кг/л, г = 7,2 л, а = 3,6 м, Ъ = 2,4 -и,
JE = 2100000 кг/смК
Решение. Так как a = Z/2, прогиб, возникающий в сепедин? от
нагрузки, действующей на левую половину балки, получим по формуле [36]:
/ ч „I I JL
\У\)х=а\г — 2 * 384 EI *
Z
Прогиб по' середине пролета от нагрузки на правой половине балки
равен (Ь = і/зО-
ъ
/„ \ _ f W dc ,.,., - 2, _ 25 ql*
165
Полный прогиб равен:
+
_25 \jfiL— —
2 38± ' 48-162/Ж*
3,45 ок.
4. Найти прогиб по середине пролета балки, показанной на фиг. 94
(стр. 116), когда груз находится в положении, дающем наибольший
изгибающий момент.
Указание. Прогиб можно получить при помощи ур-ния [131] по ме-
l d
тоду наложения с подстановкой в это уравнение: с= — — для
I Ы
одного груза и с = — —
для другого.
5. Найтн упругую линию средней части балки, показанной на фиг. 92.
Решение. Полный прогиб получим как сумму прогибов, вызванных
каждым грузом отдельно. Дірогнбы, возникающие от силы Р,
приложенной справа от середины,
направлены вверх и вы-
ражаютсяформулой[125]«
д\ і ] v^_ \\^J х Прогибы, * вызываемые
@ 4^— чД-? f""^ грузом, приложенным
слева от с?р?дины,полу-
чатся по формуле [126]
подстановкой b-f-c
вместо с.
6. Найти углы ?х и
?2 и прогиб в
поперечном сечении тп балки,
свободно опертой на
концах и изгибаемой
парой сил Ре (фиг. 187).
Фиг. 137. Решение.
Нагрузка фиктивной балки
показана па фиг. 137Ь. Реакции в точких Ax-ts. Вх будут:
©
Ь>1 =
Следовательно
PccPf, . а
РсЪ'
21
2Ь~|
Pea? 2а РсЪ*[ Ъ
[1,-К«+|)].
2PEIz
Если а = Ъ = —, то получится
А й Рс1
Изгибающий момент в поперечном сечении тхпх фиктивной балки
равен
* Рса2 & х Per» Г «Л . а\ 21^1 РсхЗ
гі
#з аз Рсх Г „Л . а\ %Щ Pert
1€6
Поэтому уравнение упругой линии для левой части рассматриваемой
балки будет:
Рсх Г*. Л . а\ 2 „Л Рсэ&
2РЕЬ
К»+іН»]-
вгжь
7. Балка с опертыми концами изгибается двумя моментами Мг и
М& приложенными на концах (фиг, 138)» Найти углы поворота концов
н положение того поперечного
сечения, в котором прогиб до- М1
стихает максимума. /~**
Решение. ( Ь=
МЛ . MJL Ч
6, =-г-тЛ: \-
е,=
ZEIz
mJ
ВЕ1
+
Фиг. 138.
Уравнение упругой линии на
основании ур-ния [134] будет:
У
6JEZ
, ДГ2?р
"*" б Ж/
м;
г
+
1 г«/
Фиг. 139.
Место наибольшего прогиба можем найти из этого уравнения,
приравнивая первую производную нулю.
8. Балка изгибается двумя моментами, как изображено на фиг. 139.
Найти отношение Мх: М2} если точка перегиба находится на расстоянии
*/з* от левой опоры.
Ответ.
М2 = 2 №г.
9. Две доски разной толщины Лх и h.2t положенные друг на друга,
несут равномерно распределенную нагрузку, как показано на фиг. 140.
мшит
і
і V-
п
At
Фиг. НО.
Фиг. 141.
Найти отношение наибольших нормальных напряжений, возникающих
в каждой из них.
Решение. Обе доски имеют одинаковую упругую линию и кривизну.
Отсюда изгибающие их моменты находятся в том же соотношении, как
моменты инерции их поперечных сечений, т. е. в отношении 1ь? : Л^8.
Моменты сопротивления находятся в отношении йх2 : h2i поэтому
наибольшие нормальные напряжения находятся в отношении /ij : h%.
10. Стальной стержень АБ имеет такую начальную кривизну, что
выпрямленный от изгиба силами Р (фиг. 141) оказывает равномерно
1в7
распределенное давление по длине на абсолютно твердую плоскую
поверхность МК. Найти силы Р, необходимые для того, чтобы
выпрямить стержень, а также наибольшие напряжения в нем, если Z —500лж,
о = %Ь мм и поперечное сечение стержня — квадрат со стороною 25 мм.
Решение. *Чтобы получилось равномерно распределенное давление
на опорную плоскость, необходимо, чтобы начальная кривизна стержня
была одинакова с упругой линией для просто опертой балки,
нагруженной равномерно распределенной нагрузкой интенсивностью 2P/J.
Поэтому имеем:
2Р П Рі
•Цпах=-
I
о =
8
2Р
7*
384 і EI
Наибольшее напряжение будет:
^тах1^
тйх
W
рш
$1
М
14
М
Теперь из формулы [Ь] и [с] получим:'
24 Eoh 24 ¦ 2100 000 - 0,25 • 2,5
ffmax
5Р
и по формуле [с]:
5-502
Р = 525 «і.
= 2520 к\/см*
37. Прогиб балок, имеющих консоли. Прогиб балки с
выступающей за опору частью "можем найти, пользуясь
©.
аШШ
9
у
/
©
©
Фиг. 142.
заключениями предыдущих случаев и методом наложения.
Такую балку можно разделить на две части; одна между
168
опорами, которую можно рассматривать как балку, опертую
на концах, и вторая—свешивающаяся часть—консоль.
Для примера рассмотрим изгиб одно^онсольной балки
под действием равномерно распределенной нагрузки q
(фиг. 142). Балка делится на части АВ и ВС, и действие
консоли на часть балки между опорами заменяется
действием перерезывающей силы qa и момента М=Щ-. Мы вн>
дим, что перерезывающая сила непосредственно передается
на опору, а потому можно ограничиться рассмотрением
действия только момента 4/адА
^ Тогда прогиб балки в любом сечении между опорами
получим вычитанием прогиба, вызванного моментом Vzga2,
из прогиба междуоперной части от равномерно
распределенной нагрузки q (фиг* 1426).
Воспользовавшись ур-ниями [134] п [137], получим;
Угол поворота поперечного сечения над опорой В
получим по ф-лам [133] и [135], откуда, считая поворот
положительным в направлении движения часовой стрелки,
имеем
_ даЧ дР
"* — '6Еі9 24J?//
Прогиб в любом поперечном сечении консоли (фиг. 142с)
получим наложением прогиба самой консоли (ур-ние [121])
на прогиб
возникающий вследствие поворота поперечного сечения
над опорой В. Прогиб балок с консолями можно также
исследовать способом фиктивной балки г). В случае,
представленном на фиг. 143д, соответствующая фиктивная балка
несет действующую вверх нагрузку по треугольнику A1BlGv
Чтобы получпть прогибы и углы наклона касательных
действительной балки по изгибающим моментам и перере-
*) Способ фиктивной балки очень полезен и при многих других
случаях. Подробное рассмотрение этого метода можно найти в статье
Г. Вестерьарда (Н* М. Wesiergard) „Journal of the Western Society of
Engineers", Vol. 26, 1921, p. 869.
169
зывающим силам фиктивной балки, следует выяснить
способ опирания этой последней на основании заключений
предыдущего п°.
Конец С действительной балки имеет прогиб и угол
наклона касательной, отличный от нуля; отсюда на конец Сг
фиктивной балки должны действовать: некоторая реакция
Сх и некоторый опорный момент М. На конце А
действительной балки прогиб равен нулю, но угол наклона
касательной не нуль. Поэтому в конце Ах фиктивной балки
.должна быть реакция Ах и отсутствует опорный момент.
Итак у нас есть три величины Аи Сг и Мі9 подлежащие
определению и только два уравнения статики.
Дополнительное уравнение найдем из условия, что прогиб в точке В
действительной балки равен нулю. Поэтому изгибающий
момент в точке Вх фиктивной балки должен быть равен
также нулю. Это условие дает нам следующее уравнение
для определения Ах:
3#
Л 1 Ра1
Тогда два остальные величины Сх и М получим из
уравнений статики, а дальнейшее рассмотрение задачи пойдет
тем же путем, как и в случае балки с опертыми концами.
ЗАДАЧИ.
1. Определить ігоогнб н наклон касательной на конце С балки,
представленной на фиг. і4іі.
А ^ \Р х
Ответ. Прогнб
РФП-\-а)
Ф
о =
ЗЖ
наклон касательной
dj/ __ Ра (21 + За)
dx WEI
Фиг, U3.
2. Для балки,
показанной на фяг. 144,
определить прогнб на конце
С, а также для точки,
лежащей по середине
между опорами.
Решение. Часть балки между опорами находится в условиях балки,
на которую действуют сила Р и пары сил Рха и Р2Ь на опорах.
Пользуясь формулами [131] и [131] (стр. 161 и 162) ы методом наложения,
получим прогиб по середине
. Рс(ЗР —4с2) PjaP Р2ЬИ
О ~-
48 Ж
16 Ж 10 Ж
170
Угол поворота 6t на опоре Л получим по формулам [123], [L32I н
[133] (см. стр. 159 и 161):
>і —
Ы-Е1
Рха1
?Ё1
PJbl
Из ур-ния [115] получим
прогиб конца С:
Рха?
ZEJ
abv
3. Балка с консолью
изгибается в одном случае силой Р на
конце консоли (фиг. 145а), а в
другом: случае такой же силой,
приложенной по середине
пролета (фиг. 14.ЗД. Доказать, что
прогиб точки 1> в первом случае
равен прогибу конца С во втором
случае.
Ответ. В обоих случаях
прогиб равен
16 Ж *
Фиг. 145.
,р
8
¦*¦—¦
I
3
D
Р
4. Балка длиною I с двумя одинаковыми консолями нагружена
двумя одинаковыми силами Р на концах (фиг. 146). Найти такие
значения отношения х : I, при первом из которых
прогиб по середине равняется прогибу
любого конца, а при втором прогиб по середине
получает наибольшее значение.
Ответ: 1) # = 0,152 2; 2) or = і/67.
5. Деревянная балка круглого сечения,
опертая в точке (7, с концом, закрепленным
в точке А, несет равномерно
распределенную нагрузку q на консоли CJD (фиг. 147).
Определить диаметр поперечною сечения и
прогиб в точке і>, если 2 = 1 щ, а = 2 м>
2 = 4$Э к*/*> М§ = 84 *V<aA
Решение. Диаметр d найдется из
уравнения
2 * 32 -"¦"*
Фиг. 146.
ШШНЖЦд
Фиг- 147,
прогяб в конце D
* = -*?
даЧ
SEI
6Ш
Фигі 148.
6. Балка длиной 2 несет равномерно
распределенную нагрузку интенсивности g
(фиг. 148). Найти длину консолей, при
которой наибольший изгибающий момент будет
возможно малым. Определить прогиб по середине пролета для
случая.
такого
1»
Решение. По задаче 10 (стр. 118)
х = 0,2071;
прогиб по середине определится по формуле:
°~~384' MI 'WEI >
в котором первый член правой части представляет прогиб, вызванный
нагрузкой между опорами (ф-ла [136]), а второй—прогиб, вызванный
нагрузкой на консолях (ф-ла 134]).
33. Балки переменного поперечного сечения. В предыдущем
рассматривались балки, имеющие призматическую форму,
Фнг. 149.
Основные формулы для определения напряжений и
прогибов, полученные при таком предположении, обычно
применяются также к случаям балок переменного поперечного
сечения,
Чтобы составить представление о точности этого
способа определения, рассмотрим изгиб консоли, имеющей
форму клина (фиг. 149). Точное решение этой задачи
^'показывает, что напряжение в любой точке А балки имеет
направление АО и величину
7 Р cos 6
°г = *—л—• М
і) Си. Мичеллъ (Ш. MichelT), „Proceedings of the London Math. Soc",
Vol. 32, 1P00.
172
где г—расстояние ОА, 6—толщина клина, 6—угол между
радиусом АО и направлением силы Р, и
2
Тс
2 а — sin 2a
постоянная, зависящая от величины угла клина.
При помощи формул [28] и [29] (стр. 41) найдем нормаль*
*ные и касательные составляющие напряжения,
выраженного формулой [а], по плоскости, перпендикулярной к оси #:
_ My 4 tg3 а • sin* О
а*~~ 1д ' 3 (2а —Sin2a)'
_ Р. 16?/ tg3 а ¦ sin4 6
Х*в~ 6& " ft2 * 2а —sin2a '
где
/.--^ **=-**.
Для нейтральной плоскости клина в-=іс/2, и
нормальное и скалывающее напряжения равны нулю. Наибольшие
нормальное и скалывающее напряжения получаются при
е = ж/2 + *-
Их можяо определить из выражений: ?
Mh Р
где
й_ 4tg8a>C0Sia
Р~~ 3 (2a —sin2a)e
При а = 5°, 10°, 15°, 20°, р имеет величину 1,00; 0,97; 0,947;
0,906 соответственно.
Из этого видно, что наибольшее нормальное
напряжение <v приблизительна равно тому, что получается до
формуле [88] (стр* 92), если только угол а достаточно мал. При
увеличении угла а ошибка при применении формулы [88]
к клину возрастает. При a = 20°, эта ошибка, вычисленная
как разность между точным решением и решением по
формуле [88], составляет около іо°/о. Наибольшее
скалывающее напряжение приблизительно втрое больше среднего
Р
значения скалывающего напряжения -гт- и получается в точ-,
173
ках, наиболее удаленных от нейтральной оси* Необходимо
отметить, что это последнее обстоятельство находится в
прямом противоречии, с результатами, полученными для
призматических стержней. Во многих случаях касательными
напряжениями можно пренебречь и рассматривать только
нормальные напряжения.
- Из предыдущего легко усмотреть, что формулы [88],
выведенные для призматических стержней, можно применять
с достаточной точностью также к стержням переменного
•сечения, если только изменение сечения не слишком резко.
Случаи внезапной перемены поперечного сечения,где имеют.
место значительные местные напряжения, будут рассмотрены
далее (см. п° 50, часть II).
Если для приближенного' определения нормальных
напряжений пользоваться формулами [88], то для
приближенного определения кривизны балок переменного
поперечного сечения логично
применять формулу [111], так как это
последнее выражение выведено
из рассмотрения лишь
нормальных напряжений. На этом же
основании для приближенного
определения угла наклона
касательной и прогиба непризмати-
Фнг. 150. ческих балок можно применять
формулы [112] и [113).
Первым рассмотрим прогиб консольной балки равного
сопротивления, т. е. балки, в которой момент сопротивления
изменяется по длине балки в таком же отношении, как
изгибающий момент. Тогда, как это следует по формуле [90],
(?)шх остается постоянным вдоль балки и может быть взято
равным Rb. Такое положение благоприятно с точки зрения
вкономии материала, так как каждое поперечное сечение
будет иметь площадь только достаточную, чтобы
удовлетворить условиям прочного сопротивления.
Для консоли с грузом на конце (фиг. 150), изгибающий
момент в поперечном сечении на расстоянии х от груза
равен по абсолютной величине Рх. Чтобы получить балку
равного сопротивления, момент сопротивления должен быть
также пропорционален хт Это условие может быть
выполнено различными путями.
Первым примером возьмем случай прямоугольного
поперечного сечения с постоянной шириной Ъ и переменной
высотой К
т
Из самого определения балки равного сопротивления
следует, что
М _6Px _ GPI _
о
где h0—высота балки в закрепленном конце. Тогда
I
Отсюда видно, что в этом случае высота балки
изменяется, следуя параболическому закону. На загруженном
конце площадь поперечного сечения равна нулю. Этот
результат получился потому, что мы пренебрегли
скалывающими напряжениями при выводе формы бруса равного
сопротивления. При практических применениях эти
напряжения также следует учесть, чтобы путем некоторых
изменений в приведенной выше форме у загруженного конца
получить площадь поперечного сечения, достаточную для
передачи перерезывающей силы/ Прогиб балки на конце
найдется по формуле [113]:
Г12 Px*dx 12 РГЬ Л,/™, 2 РР
о о
где 10 = -—— представляет момент инерции поперечного
сечения в закрепленном конце. Сравнение с формулой [115]
показывает, что этот прогиб вдвое больше, чем прогвб
призматического стержня, имеющего жесткость на изгиб Ш0
и подвергающегося действию того же груза. Таким
образом, стержень имеет то же сопротивление, но не обладает
той же жесткостью, что призматический стержень.
Вторым примером рассмотрим консоль прямоугольного
поперечного сечения постоянной высоты h и переменной
ширины Ъ (фиг. 151а и Ь). Так как момент сопротивления
и момент инерции 1Ъ балки треугольной формы
увеличиваются с возрастанием х в том же отношении, как и
изгибающий момент, наибольшее напряжение (ojmeI и кривизна
(ф-ла [111]) остаются постоянными по длина балки, и
величина радиуса кривизны может быть определена из
следующего ур-вбя (см. формулу [85]):
175
Прогиб конца балки, как стрелку дуги круга, можно
принять равным при небольшой величине
2р~ 2ЕЦ
[139]
или согласно ур-нию [с]
V-
^Ыпах^
ъ
[U0]
Из этого выражения видно, что для этого типа консоли
равного сопротивления прогиб*„на конце изменяется прямо
пропорционально
квадрату длины и
обратно
пропорционально высоте.
Этими
результатами можно
воспользоваться для
приближенного
вычисления напряжений и
прогибов в листовых
Ь i рессорах.
Представим себе, что
рассмотренный выше
треугольный лист
разрезан на полоски,
собранные затем
вместе, как
показано на фиг. 151*Г'с
и d. Первоначальной
кривизной и трением
между полосками
можно пренебречь
и в первом
приближении примените
дающую
достаточную точность фор-
| Мулу [140] *).
Ч Это решение было получено Е. Филлипсон (E.Phillips), „Annales
des Mines", vol. 1, pp. 195—336, 1852. См. также Тодгёитер и Пирсон
(Todhunter and Pearson), History of Elasticity, Vol. 2, Part. 1, p. ЗЯ
и А. Еаетильяпо (A. Casiigliano), Theorie der Biegungs- und Torsions-Fe-
dern, Wien, 1888.
Влияние трения между полосками было рассмотрено Марье (G, Marie),
„-Ахшаіез des Mines",, vol. 7-9, 1905 и 1906 г. Д. Ландау и Л. Ларр
исследовали распределение груза между отдельными полосками рес-
176
©
©
I
Фиг- 151.
; 4
\ 1.
V
' 4
\ '
1,
Г
* і
•
'о J
вк
К определению прогиба балок переменного поперечного
сечения можно также применить способ фиктивной балки.
При ©том необходимо лишь помнить, что кривизна упругой
линии в любом сечении равна отношению jrHyp-ние [ill],
стр. 147). Поэтому увеличение жесткости на изгиб в дан*
ном сечении оказывает такое же самое влияние на прогиб,
как уменьшение в том же отношении изгибающего момента.
Следовательно, задача определения прогиба балок
переменного поперечного сечения может быть приведена к
задаче определения прогиба балок постоянного поперечного
сечения с помощью приведенной эпюры изгибающего
момента, в которой каждая ордината помножена на
отношение 10:1, где I—мо- р
мент инерции соот- / I \ I I
ветственного попе- "
речного сечения, и
10—постоянный
момент инерции
призматического
стержня, к прогибу
которого мы приводим
наш стержень
переменного сечения.
Например, задача А
определения
прогиба круглого вала
(фиг. 152), который
имеет части двух различных диаметров с моментами
инерции 10 я 1х я несет нагрузку Р, может быть приведена
к задаче для круглого вала с постоянным моментом
инерции поперечного сечения 10 нижеследующим образом.
При рассмотрении фиктивной балки ЛгВи вместо
треугольной нагрузки AiOxBu представляющей эшору
изгибающих моментов, мы воспользуемся нагрузкой,
представленной на фиг. 152 заштрихованной площадью. Эта площадь
получается уменьшением ординат эпюры для средней части
вала в отношении 10: 1Х. Определение прогибов и углов
наклона касательной может быть теперь выполнено как для
призматического стержня; величина прогиба и угол на-
Фнг. 152.
соры (D. Landau и Р. И. Parr, „Journ. of the Franklin Inst.", Vol. 185,
18t>, 187). Полная библиография по рессорам была у опубликована
Американским обществом инженеров-механиков (Amer. Soc. Mech. Eng.,
Шут York, 1927).
12
Тимошенко — Сопротивление материалов, ч. L
177
клона в любом поперечном сечении балки будут равны
изгибающему моменту и перерезывающей силе фиктивной
балки, деленным на JEIQ.
Следует отметить, что в случае, представленном на
фиг. 152, внезапная перемена размера диаметра вала,
имеющая место на расстоянии lU * от опор, вызывает местные
напряжения в этих точках. Эти напряжения не оказывают
существенного влияния на прогиб вала, если только
разница в диаметрах двух частей вала мала по сравнению
с длинами этих частей.
Метод, примененный к валу переменного поперечного
сечения, можно также применить к клепаным двутавровым
балкам переменного поперечного сечения.
Призером тайой двутавровой балки, лежащей на двух
опорах и равномерно нагруженной, может служить балка,
показанная на фиг. 153. Изгибающий момент уменьшается
от середины к концам балки, и вес балки может быть
понижен уменьшением числа листов .в поясах балки, как
показано схематически на фигуре.
Прогиб такой балки можем определить, взяв за основной
момент инерции среднего поперечного сечения. Нагрузка
на фиктивную балку вместо, того, чтобы быть простой
параболой, должна быть взята та$?й, как показано
заштрихованной эпюрой на фиг. 153. Каждое уменьшение
поперечного сечения должно быть уравновешено соответствующим
повышением ординат эпюры моментов в отношении 16р>: і.
ЗАДАЧИ.
1; Стальной лист формы, изображенной на фиг. 154, заделан одним
концом и нагружен силой Р на другом конце. Определить прогиб
конпг, если длина равна 21, а — ширина, h — толщина листа и Р — груз,
приложенный на конце.
178
Решение. Прогиб состоит из трех частей:
1) прогиб в точке В
2) прогиб в точке С яз-за наклона в точке В
айв
в
к 3) прогиб вследствие изгиба частя BG листа
Полный прогиб равее
17 PZ3
2 Опоеделить ширину d листовой вагонной рессоры (фиг- 151) и е?
прогиб, если Р-2700Ч-г, А =12 ** 2 = 600.**, 2^=4800»/»* и число
листов w — 10.
Решение. Рассматривая листы рессоры, как вырезанные из
треугольного листа (фиг. 1516), найдем наибольшее напряжение
_ 6Р1 р
откуда
* I
бК 6-2700-60 _log fM эшГ"""
d-«A»s- 10-4800-1,2* "' * Щ
? М,Л1, ^^
Прогиб определится по формуле- [MOJ. шуа
=У
72 602 Л ЛЛ Фиг. 154-
»- V Я - 4800 • 1^2100000в 6>86СЛ!-
3 Сравнить прогиб по середине пролета и наклон кондов вала,
изображенного на фиг. 152, с таковыми вала той же длины, но
постоянного поперечного сечения, момент инерции которого равен і0- Принять
Ik: Jo =.2.
Решение. Вследствие большей жесткости на изгиб по середине
наклоны концов вала, показанного на фиг. 152, будут меньше, чем
таковые концов цилиндрического вала, в отношении заштрихованной
площади к общей площади треугольника AXGXBX. Полная площадь —
фиктивная нагрузка для случая цилиндрического вала. Для заданных
значений это отношение равно-g-: 1. ' ~
Прогпбы по середине этих двух видов вала находятся в отношения
изгибающею момента, вызванного заштж-ованной площадью, к
изгибающему моменту, вызванному площадью треугольника л^щ. ото
9 ,
отношение равно ^т. 1.
*12
4. Балка, опертая на концах, нагружена, как показано на фиг. 155.
Как должна меняться высота h балки, чтобы получить форму балка
равного сопротивления, если ширина Ъ прямоугольного поперечного
сечения ее остается постоянной по длине белки?
Ответ. ft3 = v(l — 8 -|^Л .
5. Определить прогиб изображенного на фиг. 158 стального листа
толщиною 12 мм под действием груза Р = 9 кг, приложенного по
середине.
Решение. Приведем задачу к задаче определения прогиба листа
постоянной ширины, равной 100 мм. Приведенная площадь эпюры
изгибающих моментов для этого случая
представится трапецией AXDEBX,
и мы получим
о =
11
Рі*
F
4
8 4У Ш
450±j5iij5ii
Фиг. 156.
где I — момент инерции для сечения по середине' пролета. Величина
прогиба может быть теперь легко вычислена.
6. Определить наибольший прогиб листовой рессоры (фиг. 151),
если I — 900 мм, k = 12 мм, Е — 2100 000 к\[см*, Вь = 4200 кг/см*.
О т в е т. Ь = 13,5 см.
39. Дифференциальное уравнение упругой линии.
Встречаются случаи, когда необходимо знать дифференциальное
уравнение упругой линии изогнутой оси балки.
Для координатных осей; расположенных, как показано
на фиг. 157, тангенс угла Ь наклона в оси х касательной
к изогнутой оси балки в любой точке т упругой линии
равен
*--?•
Угол ? обыкновенно очень мал для Оалок, применяемых
в инженерных сооружениях, и с достаточным
приближением можно принять tg6 = 6 и ds = dx. Тогда
ах
180
и
ах2
[а]
По фиг. 157 имеем:
отсюда *)
р d ? = ds = dx\
db
dx
dx*
здесь вертикальные линейки показывают, что мы
рассматриваем только абсолютную величину. Другое значение
Фиг. 157,
для—выражено формулой fill]. Приравнивая эти оба
значения, получим:
№у^_ . М
dx*
+
в/.-
Знак в этом уравнении выбирается на основании
следующих соображений; изгибающий момент мы считали
положительным, когда балка изгибается вогнутостью вверх
!) Сравнение с общеизвестной точной формулой:
dx*
Ыі)Т
dy
dx
так как она
показывает, что мы пренебрегаем величиной
мала сравнительно с единицей. Это. согласуется с предположением»
dy й
4X0 "55" — ° ~ очень мало; поэтому квадратом последней величины
можем пренебречь.
¦181
(стр. 103); при таком изгибающем моменте вторая
производив/
ная ~7~2—отрицательна, если координатные оси надрав-
лены так, как показано на фнг. 157. Поэтому в
предыдущем уравнении следует взять знак минус:
Это уравнение имеет широкое применение в задачах
на изгиб. Для примера рассмотрим случай балки, опертой
концами и несущей равномерно распределенную нагрузку
(фиг. 138), При нагрузке интенсивности q на единицу
длины изгибающий момент в любом поперечном сечешщ
тп равен:
I х*
и ур-ние [141] получает вид:
Фу
dx*
III х*\
Умножая обе части уравнения на dx и интегрируя,
получим:
где С—постоянная интегрирования, которую следует так
подеірать, чтобы она удовлетворяла условиям задачи.
Вл сюшехрая угол наклона касательной по середине
-, дм I
пролета равея нулю. Положив -j^-= О при »=-о"» получим
24Ж/
и ур-ние [Ь] принимает вид:
dy 1 / qlx% qx* ql3
EIA
dx EIt \ 4 6 24 /
Вторичное интегрирование дает:
1 fqlafi qx* qPx\ ¦
Ш
Новая произвольная постоянная интегрирования Сх
определится из того условия, что прогиб на опоре равен нулю,
т. е. полагая в ур-нии [с] при х = о и у = о, находим, что
С1 = 0. Таким образом из ур-ния [с] получаем уравнение
упругой линии:
Это уравнение было получено ранее (стр. 164) при помощи
метода наложения.
Несколько других примеров применения ур-нжя [141]
будет рассмотрено ниже. Здесь мы только укажем, что
последовательно дифференцируя ур-ние [ш] д
воспользовавшись ур-ниями [98] и [94], получим:
и
da* EL
[143]
Этими уравнениями воспользуемся далее дяя
исследования изгаоа балок на упругом основании, оказывающем
равномерное реактивное противодействие.
ЗАДАЧИ.
1. Найти уравнение упругой лянни консоли, несущей груз на конце
(фиг. 120).
Ответ.
P/W jf
у~~ тж\2 (
2. Найти уравнение унрутои линии равнок&рдо нагруженной дон-
соли (фиг. 123).
Ответ.
_ q /fog Ы а*\
у ~~ 2Еів [г з + іа j
3. Найти прогиб в конце для консолж, изображенной на фиг. 124.
Решение. Ур-ние [141] в атом случае получает вид:
<% м
dx* El '
где Ж—постоянное. Первое интегрирование дает
dy _ Мх г
dx Ш "*" '
183
Тангена угла наклона касательной в закрепленном конце равен
нулю, т. е.
о*)-.-
отсюда С =г 0 н
dy _ Мх
9
Вторичное интегрирование дает:
Заметив, что (у)#—о = 0> найдем, что С?х = 0, и получим уравнение
упругой линии:
Прогиб свободного конца консоли
Мга
& =
2Я/ '
4. Найти уравнение упругой линии балки с опертыми концами и
нагруженной сосредоточенным грузом Р (фиг. 131).
Решение, Дифференциальное уравнение для левой части балки
будет
дРу __ 1 Рсх
Ж~~"ш ~Т~*
Интегрируя ато уравнение, получим:
где С и (^ — произвольные постоянные интегрирования, величину
которых нужно определить.
Дифференциальное уравнение для правой части балки:
*»- і r*»_p(e_,+eJj.
йаР Ж
г
Интегрирование этого уравнения дает:
dy__ 1_ ГРсдЗ р (х — г + с)2]
М
1 ГРсд* і>(а;_г + сЯ
где D и Dj —опять произвольные постоянные интегрирования.
Из условия непрерывности прогибов н наклонов касательных в точке
приложения груза следует, что ур-ния [с] и [dj должны совпадать
184
с ур-'ниями [aj и [Ь] при ее = 1-е, «Эти условия будут выполнены, когда
D = G и jDj = Ct. Из условия равенства нулю прогиба на опорах
получим: положив я = 0из/ = 0в ур-нии [Ь], ^ = 1^ = 0, а из ур-ния (й],
положив х = Z и у = 0.
откуда
Е1 \ &
d = c=
6
Рс
ы-еі
(1> - С*).
Подставив полученные значения С и Ct в ур-ни? [Ь], получим
уравнение упругой линии левой части балки
Тех
У —
6Z • Я/
(22 — С2 — Я*),
Уравнение упругой линии для правой части балки получим
подстановкой значений JD ж Вхъ ур-ни? Jd].
40. Влияние перерезывающей силы на прогиб балок. В предыдущем
(см. стр. 147) было рассмотрено влияние на величину прогиба только
изгибающего момента. Действие
перерезывающей силы вызывает дополнительную
деформацию в виде взаимного сдвига
смежных поперечных сечений одного относи*
тельно другого.
Вследствие неравномерного
распределения скалывающих напряжений
первоначально плоские поперечные сечения
искривляются, как изображено на фиг. 158,
которая показывает искривление,
вызываемое только сдвигом і). Элементы
поперечных сечений, лежащие около их пен-
тров тяжести, остаются вертикальными и
лишь смещаются один по отношению к
другому. Поэтому наклон упругой линии под действием только
перерезывающей силы в каждом поперечном сечении равен деформации сдвига
центра тяжести этого поперечного сечения. ,
Обозначив через ух прогибы от сдвига, получим для любого
поперечного сечения следующее выражение тангенса угла наклона касатель-
нрй к упругой линии:
дУі _ (ту )*/ = <>__ *^
сіх "" G лв" 1о]
Фиг. 158.
GF
Q
где -р—среднее значение скалывающего напряжения tyx1 ¦&•—модуль
упругости на сдвиг и к — числовой, коэффициент, на который нужно
помножить среднее значение скалывающего напряжения, чтобы
получить скалывающее напряжение для центра тяжести поперечных сечений.
При прямоугольном поперечном сечении Ъ — — {ф-ла [9?], стр. 124),
а
4
для кругового поперечного сечения Ь = — (ф-ла [99], стр. 128).
о
г) Деформация, вызываемая изгибающим моментом и состоящая
jao взаимном повороте смежных поперечных сечений, исключена из
рассмотрения.
185
При непрерывной нагрузке на балке перерезывающая сттда Q
является непрерывной функцией, которую можно дифференцировать
по ж. Кривизна, возникающая от одного только сдвига, равна тогда
dx* ~ GF их- ~ GF ъ
Сложив это с кривизной, вызываемой изгибающим моментом (см.
ур-ние [141]), имеем:
Фу . 1 / Ш1 \
_ = __rJM+_^2j. ГШ]
Это уравнение следует применять вместо ур-ния [141] для
определения прогибов во всех тех случаях, когда необходимо бывает принять во
внимание влияние перерезывающей силы. Выразив М и q в функциях
от х, можем без затруднений проинтегрировать ур-ние [144] тем же
путем, как это было показано в предыдущем п°.
®\ , =?
ч
Фиг, 159.
AG
В этом случае также можно применить с большим успехом способ
фиктивной балки (см. стр. 158), приняв за ординаты эпюры фиктивной
нагрузки вместо одного М
Рассмотрим, например, равномерно нагруженную балку с опертыми
концами (фиг. 159). Изгибающий момент в сечении х
Нагрузка фиктивной балки состоит из двух частей: 1) той, что
выражается первым членом выражения [Ь] и изображается параболической
эпюрой изгибающего момента (фиг. 169&), и 2) той, которая
представляется вторым членом выражения [Ь] и которая равна
FI
Так как интенсивность q — постоянная величина» то эта вторая часть —•
равномерно распределенная нагрузка, изображенная на фиг. 159о.
186
Дополнительный прогиб в любом сечении вследствие действия
перерезывающей силы равен изгибающему моменту для этого же сечения
фиктивной балки от указанной выше второй части нагрузки, деленному
на Ж. По середине балки дополнительный прогиб равен следовательно
Прибавив это к прогибу от изгибающего момента (см. ур-ние [136]
ётр- 163), получим полный прогиб
о =
ql* . Щі 5 ql* (л . Шк \2 Е
384 Ш l BGF 384 Ж V т 5 -2» ?
і яа-я ййд* иг г"г r * гг а )' f^l
где *я — у _js—радиус инерции поперечного сечения относительно
оси z.
f Для прямоугольного поперечного сечения высотой ft, і 2 = -^г &2,
fc = -S-. Положив — = 2 (1 + р.) = 2.6, получим пз ур-ния Щ
а 5 #Ч 1 а. ч ю Ш \
Отсюда заключаем, что при-т-~10 влияние перерезывающей силы на
I
прогиб оценивается примерно В%. При уменьшении отношения-^- это
влияние возрастает.
Для двутавровых балок коэффициент'1 fc обыкновенно получается
больше двух, и если балки коротки, то влияние перерезывающей силы
может получиться сравнительно большим. Пользуясь формулой [101] и
фиг. 109 (стр. 129) имеем:
откуда
Возьмем например двутавр J& 45 по ОСХу: ft = 45 ел; F=147 си?;
J *з 45 888 еде4; толщина стенки Ьг == 1,62 еле; ширина полки Ь = 17 еж;
AtB= 45 — 2 • 2,43 = 40,14 см; I = 6 ft = 270 ок. .Тогда ур-ние [е] дает
jfc = 2,38. Подставив в ур-ние [d], находим:
t б q* Л , 48-2,88 45888 \ б ^
384 EI К ^ б 147 - 2702 *»-; -*—- 384 Ж *
Дополнительный прогиб от сдвига в этом случае составляет 25,4%
от прогиба, возникающего под действием изгибающего момента, и
поэтому должен быть учтен.
187
В случае сосредоточенного груза Р (фиг. 1-бОа) такой груз можно
рассматривать как предельный случай нагрузки, распределенной на
очень коротком участке с балки. Часть воображаемой нагрузки Рх на
фиктивную балку AXBX (фиг. 160Ь), соответствующая второму члену
выражений [6], будет равна
Дополнительный прогиб от перерезывающих сил получится
делением на Ш изгибающего момента, возникающего в фиктивной балке
- при воображаемом сосредоточенном
®i грузе, выраженном формулой [f]. Ha-
Т7 пример, для груза по середине балки
1 ' изгибающий момент по середине фик-
X тивной балки от груза [f] будет
4 4
В ш pi
h GF 4»
и дополнительный прогиб по середине
пролета от перерезывающих сил.
Ь Рі
Фиг. 160. Bl=="5F""T' ^
Присоединив это к прогибу, вызванному одним только изгибающим
моменіом (ф-ла [128], стр. 160), получим следующее выражение для
полного прогиба:
PZ3 Ь Рі Р& / 12b'j> Яч
г z * '
При оалке прямоугольного поперечного сечения высотой h имеем
г 2 Ш 3
(і + 8>90^-). [А]
н получим:
*~ 4&EI
г
„ А ' 1
При —г- = —7г дополнительное влияние перерезывающей силы соста-
вляет около 4%.
При предыдущих рассуждениях было предположено, что поперечные
сечения балки могут свободно искривляться, как показано на фиг. 163.
Но только равномерно нагруженная балка является тем случаем,
при котором это предположение приблизительно выполняется.
Перерезывающая сила по середине такой балки равна нулю, и поэтому здесь
нет искривления. Искривление возрастает постепенно с возрастанием
поперечной силы по мере перемещения вдоль балки влево или вправо
от середины. Поэтому условие симметрии деформации относительно
среднего сечения здесь удовлетворяется.
Рассмотрим теперь изгиб сосредоточенным грузом по середине
пролета. По условию симметрии, поперечное сечение по середине пролета
балки должно остаться плоским. В то же самое время смежные .
поперечные сечения справа и слева от-груза подвергаются действию пере-
188
резываюідей силы, равной-^-; а стало быть должно иметь место
искривление поперечных сечений вследствие действия этих перерезывающих
еил.
По условию-непрерывности деформации однако здесь не может быть
внезапного перехода от плоского среднего сечения-к смежным
искривленным сечениям. Здесь должно быть непрерывное нарастание
искривления по мере перемещения вдоль балки в любом направлении от
середины.
И только на некотором расстоянии от груза искривление может
Р
стать таким, каким оно было бы под действием перерезывающей оси —
2
в условиях, дающих возможность свободно искривляться.
Из этого следует заключить, что в непосредственной близости от
среднего поперечного сечения распределение напряжений будет совеем
не то, что предусматривается элементарной теорией изгиба (см. стр. 145).
Искривление будет частично устранено, и дополнительный прогиб от
перерезывающих сил будет несколько меньше, чем найденный выше
(см. формулу [д\).
Более детальное исследование г) показывает, что прогиб по
середине поолета будет
PZ3
48 EI
1 + 2,95^-
0,02
А
г
№
Аналогичное положение получается также и в случае консоли. Если
закрепленное поперечное сечение может искривляться свободно, как
показано на фиг. 161а, о'бстоятель- п
ства прогиба будут теми же, ка *'
кими мы предположили их при
выводе формулы [h]. Прогнб
консоли прямоугольного поперечно- (
го сечения получится подстанов- *-
кой I вместо-тр и Р вместо -трв
эту формулу, что дает
ргз
BEI
1+0,98
г*
т
Фиг. 161.
Если в закрепленном
поперечном сечении полностью
устранена возможность искривления
(фиг. 161Ь), то условия прогиба будут такими яге, как было принято
при выводе формулы [к], а потому прогиб
^(1 + 0,744-0,01-4-) CJ
$*=
что меньше прогиба по формуле [Ц.
і) См. X Филон (L. Ж a. Filon), „Phil. Trans. Roy. Soc. (A)/ Vol.
201, p. 63, 1903, C. Tuxoiuewo (SSimoshenko), „Phil. Meg.", Vol.-47,.p.
1095, 1924. См. также Т. Жармс-н (ГА. v. Karman), „Scripta Universitatis
&tquQ Bibliotnecae Hierosolmitanarnm*, 1923*
189
41. Изгиб балон в главной плоскости, на являющейся плоскостью сини
метркн. Ранее при рассмотрении изгиба балок было показано, что в
случае чистого изгиба плоскость упругой линии совпадает с плоскостью
внешних моментов, если только эти моменты действуют в одной из
двух главных плоскостей изгиба (стр. 93).
Что касается изгиба поперечными силами, мы рассмотрели только
случаи, при которых изгиб происходил в плоскости симметрии балки.
На основании этой симметрии было выведено заключение, что
плоскость упругой линии совпадает с плоскостью действия сил.
При более общем случае пзгиба поперечными силами,
находящимися в одной плоскости, предположим, что плоскость этих сил
параллельна одной из двух главных-плоскостей изгиба, но уже не является
плоскостью симметрии балки.
Простейшими примерами являются такие случаи, при которых
поперечное сечение балки имеет одну ось симметрии (ось s) и силы
действуют в плоскости, перпендикулярной этой оси (фиг. 162а).
Рассмотрим случай, представленный на фиг. 162а, и определим
положение вертикальной плоскости, в которой должны действовать
поперечные силы, чтобы
происходил простой изъиб
балки в вертикальной
/'-**Л
п
Q
%
у —1_
У плоскости. Под простым
— изгибом мы понимаем
Ф
Lfca
?
Фиг. 162.
х
вдееь такое состояние,
при котором обе полка'
поперечного с е'ч е н и я
имеют одинаковый
прогиб в направлении оси #,
так что происходит изгиб
без поворота
поперечных сечений вокруг
продольной оси балки,
поперечного сечения совпадает
в любой точке поперечного се-
В этом случае нейтральная ось
с осью st и нормальное напряжение оя
чения пропорционально расстоянию у этой точки от нейтральной осн.,
Чтобы найти соответствующее положение плоскости действия
поперечных сил, необходимо рассмотреть распределение скалывающих
напряжений т по поперечному сечению.
Наши предыдущие рассуждения показывают (стр. 130), что
напряжения т не будут равномерно распределяться вдоль оси z\ кроме
того можно ожидать, что скалывающие напряжения * в стенке будут
малы и что в сущности вся перерезывающая сила будет
восприниматься одними только полками.
Если мы будем рассматривать полки как две отдельные балки»
попзречные сечения которых имеют моменты инерции соответственно
I и I то их кривизна и их прогиб при изгибе будут одинаковы, если
силы распределяются между ними в отношении I : Iv
Перерезывающие силы в этих полках будут также находиться
в том же отношении. Это условие может быть выполнено, если
поперечные силы будут действовать в вертикальной плоскости, проходящей
через такую точку О (фиг. 162а), что
190
h
Z
где Лі и 7ig — расстояния точки О от центров тяжести поперечных
сечений полок.
Таким образом мы находим, что в случае небольшой толщены
полок точка О смещается с центра тяжести С всего поперечного сечения
в целом по направлению к полке, поперечное сечение которой имеет
больший момент инерции.
При предельном случае, показанном на фиг. 162Ь, где одной из
полок нет вовсе, можно щшнять с достаточной точностью, что точка О
совпадает с центром тяжеоти полки, и для того, чтобы получился
простой изгиб, поперечные силы должны действовать в вертикальной
плоскости, проходящей через эту точку.
Рассмотрим теперь корытное сечение (фиг. 162с) чи найдем;
положение плоскости, в которой должны действовать вертикальные силы,
чтобы получилось явление простого изгиба с осью s в качестве
нейтральной оси. Для этого необходимо рассмотреть распределение
скалывающих напряжений по попереч-
N
ному сечению.
К определению
скалывающих напряжений т для
поперечного сечения стенки
применим тот же метод, как и для
случая двутавровой балки
(стр. 129). При этом можно
предположить с достаточной
точностью, что вертикальная
перерезывающая сила Q
воспринимается одной лишь
стенкой- В полках появятся
горизонтальные скалывающие
напряжения, которые будем
обозначать через т . .
. Чтобы найти величину
этих напряжений, рассмотрим
элемент, вырезанный из полки
двумя смежными
поперечными сечениями, отстоящими
друг от друга на расстоянии dxt
параллельной стенке (фиг. 163).
им.
ММ
Фиг. 163.
и вертикальной плоскостью тпт^
Если балка обращена выпуклостью
вниз, то верхняя полка "будет сжата, и сжимающие усилия JT и N^dlf,
действующие на выделенный элемент* будут1 по абсолютной величине
равны:
Ж
-ъ/~
н
JVT+&V =
*+•?*)
і ydF,
где интегрирование должно быть распространено на всю
заштрихованную часть поперечного сечения полки. Интеграл .представляет момент'
заштрихованной площади относительно оси s.
Разность между сжимающими усилиями N и 2T-\-dN должна
уравновешиваться суммой скалывающих напряжений тжш, действующих по
грани шпш^х элемента. Предположим, что эти напряжения равномерно
191
распределены по этой грани, и обозначим чепез t толщину- полки.
Тогда получаем следующее уравнение для определения т :
<LM dx
dx
%/yiF.
оікуда с помощью ур-ния [93] имеем:
М
R
О
Статический момент заштрихованной площади пропорционален
расстоянию и от края полки, а поэтому т^ пропорционально м.
Как мы показывали ранее (стр. 122), скалывающие напряжения .
равные напряжениям т^, должны действовать горизонтально в точках,
лежащих по линии ппх поперечного сечения полки. Следовательно,
напряжения т распределяются не равномерно по поперечному сечению
полки, а пропорционально расстоянию м.
В месте соединения полки со стенкой
распределение . скалывающих напряжений
является более сложным.
, При наших приближенных выкладках
Л % предположим, что формула fa] применима в
пределах от и = 0 до и = Ь. Тогда, обозначив
через h расстояние между центрами тяжести
полок и заметив, что статический момент
поперечного сечепия Ы полки относительно
оси z по абсолютной величине равен Ы- —
3~і
с
Q\
Ч
Фиг. 161.
R
получим-по формуле [а]
Qbh
2/
И
Равнодействующая В скалывающих напряжений т^ ,
распределенных по площади Ъі поперечного сечения полки, равна
- Qbh Ы Qb*ht
% е
Сумма скалывающих напряжений т в поперечном сеченпи нижней
полки будет, очевидно, равной и прямо противоположной усилию. Та*
ким образом, скалывающие напряжения в корытном сечении
приводятся к силам, показанным на фиг. 164, Эта система сил статически
уравновешивается силой Q, приложенной к точке О на расстоянии от
центра тяжести стенки
Eh Ъ?Ч
Q
U
Отсюда заключаем, что', для того чтобы получить простой изгиб
с осью s как нейтральной осью, вертикальная плоскость, в которой
действуют поперечные силы, должна проходить через точку О, которая
называется центром скручивания.
Прн любом другом положении этой плоскости изгиб балки будет
сопровождаться скручиванием, и напряжения уже не будут следовать
тому простому закону распределения их, по которому а пропорцио-
192
нально у и не зависит от координаты z. Такое скручивание балок
двутаврового или корытного сечения будет рассмотрено далее (стр. 282).
В случае уголкового сечения (фиг. 165) скалывающее напряжение т
в точках, лежащих на линии тп, будет иметь указанное на фигуре на-
ТТПЯПЛГАИПА ТТ ПЯТПТЛ 1\
правление и равно 1)
Q
t-J
fydF,
где интеграл представляет момент заштрихованной площади
относительно оси 2. Эти скалывающие напряжения дают равнодействующую Л
указанного направления равную:
Я
Qtbfi
Чтгг
Для нижней полки- уголка получим силу той же самой величины.
Равнодействующая этих двух сил равна Q и проходит через точку
пересечения средних линий
полок, которая поэтому и
является центром
вкручивания О.
Задача определения
центра скручивания в
общем случае
несимметричного профиля может быть
разрешена с достаточной
точностью, если только
толщина мала настолько, что
распределение по ней
скалывающих напряжений
может быть принято
равномерным 2).
Тогда силы,
параллельные главным плоскостям
и проходящие через центр
скручивания, будут
вызывать простой изгиб без скручивания. Когда все размеры поперечного
сечения — величины одного и того же порядка, задача определения центра
скручивания становится более сложной, и точное решение получено
только для небольшого числа случаев а).
Фиг. 165.
х) Для определения этих напряжений можно применить тот же
способ, который был применим для корытных сечений.
2) Задача определения центра скручивания была рассмотрена в
новейшей технической литературе несколькими авторами. Упомянем здесь
Р. Майяра (В. Maillart), „Schweiz. Bauz.\ Bd 77, S. 197; Bd 79, S. ^54;
Bd. 83, S. Ill, S. 176; К. Вебера (С. Weber), „Zeitschr. f. angew. Math.
•uhd MechanikVBd 4, S. 344, 1924; А. Эігепшвилера (A. EggenscJiwyler),
Proceedings of the Second International Congress for Applied Mechanics,
1927, p. 434.
8J Поперечное сечение в виде кругового сектора "рассмотрено М. Се-
іарол и Е. Пирсоном (М. Seegar and К. Pearson), „London Roy. Soc. Proe.
(Ser. A)K, Vol. 96, p. 211, 19^0. Случай, при котором сечение
представляет собою равнобедренный^ треугольник, рассмотрен С, Тимошежо
(S. TimoshenJco), .London Math. Soc.Proc. (Sen 2)", Vol. 20, p. 3i/S, 1922-
2Z Тимошенко — Сопротивление материалов, ч. I.
193
42. Прогиб балок под действием сил, непараллельных ни
одквй из двух главных плоскостей изгиба. Рассмотрим
сперва нростейший случай —консоль, поперечное сечение ко-
терой имеет две оси симметрии (фиг. 166). Груз Я,
приложенный в конце консоли, перпендикулярен к оси х балки
и составляет угол а с главной осью у поперечного
сечения консоли.
Применим для определения напряжений и прогиба этой
балки м^тод наложения. Груз Р разложим на две
составляющие: JPcosa и Psina по направлениям двух главных
осей поперечного сечения. Прогиб от каждой из этих
составляющих можно легко найти, применяя теорию изгиба
в. плоскости симметрии. Тогда общий прогиб получим
наложением.
Абсолютные значения двух составляющих изгибающего
момента для любого поперечного сечения тп консоли бу-
к дут: Jf, = P(Z—х) cosa
~.і
щ і;
El
X Z
pi
р
й
Г
I
относительно оси > z и
Мп = Р(1—jc)sina -отн<ь
сительно оси у. Из
направлений двух
составляющих и осей у ж з
у видно, что момент Мя
Фиг. 166. ' вызывает сжатие в
точках с положительными
у и Му — сжатие в точках с положительными z.
Тогда рогмальное напряжение ох в любой точке
поперечного сечения (у, z) получится путем сложения
напряжений, вызванных в отдельности моментами М% и Мг Та*
кям образом, мы приходим к выражению:
Р(1 — х) cos a • у P(l — х) sin я ¦ я
L
I.
v
= -Р{1-х)
«/cos д . #sina
L
L
М
Нейтральную ось найдем, взяв точки с такими
координатами, чтобы выражение в скобках в формуле [а]
равнялось нулю. Уравнение нейтральной оси таким образом:
f/COSa
+
я sin a
= 0,
ЕЧ
194
Это — ось, проходящая через центр тяжести поперечного
сечения- и составляющая с осью z угол р (см. фиг, 167),
тангенс которого согласно ур-нию [Ь] равен
tgP-
У
tgce
И
Отсюда видно, что в общем tg(3 не равен tga. Поэтому
нейтральная ось ?? не перпендикулярна плоскости
изгибающих сил, и плоскость упругой линии,
перпендикулярная пп9 не совпадает с плоскостью изгибающих сил. Эти
две последние плоскости совпадут только тогда, когда либо
tga = О или tga = со, либо 1% = 1Г
В первых двух случаях
плоскость ' изгибающих сил
совпадает с одной из главных
плоскостей изгиба. В последнем
случае эллипс инерции становится
кругом, так как оба главные
момента инерции равны, и любые
два взаимно перпендикулярные
направления можно взять за две
главные оси поперечного
сечения.
Если ---имеет большую вели-
чину, т. е. если жесткость
балки в плоскости.асу значительно
больше жесткости в плоскости хг,
то tg р становится большим по
сравнению с tga, и, если угол а не велик, то угол [3
приближается к 90°, а нейтральная ось приближается к
вертикальной оси. Прогиб будет происходить главным образом
в плоскости xzf т. е. здесь имеет место стремление к
прогибу в плоскости наибольшей гибкости.
4 Это можно продемонстрировать очень простым способом
на тонкой линейке. Малейшее отклонение изгибающей силы
из плоскости наибольшей жесткости влечет за собою изгиб
в перпендикулярном направлении. Это можно показать
также разложением силы Р (фиг. 166) на две составляющих
и определением прогибов от каждой из составляющих.
Если жесткость на изгиб консоли в горизонтальной
плоскости очень мала сравнительно с жесткостью в
вертикальной плоскости, то даже небольшая горизонтальная соста-
Фиг. 107.
13*
195
вляющая может вызвать горизонтальный прогиб значитель-і
но больший, чем прогиб в вертикальной плоскости;
поэтому общий прогиб будет главным образом в плоскости
наибольшей гибкости.
Интересно отметить, что нейтральная ось пп
параллельна касательной, проведенной к эллипсу инерции в точке
пересечения этого эллипса с направлением силы Р. Это
можно доказать следующим образом. Уравнение эллипса:
•2 ~ -2 х>
г г
Z
и уравнение касательной к эллипсу в точке D с
координатами г/о и ?о (ФЙГ- 1б7):
.2 I л — 1щ
г г
* У
Тангенс угла между осью г и этой касательной будет
2 т
- • -i—tga.-^tgp.
Когда направление нейтральной оси выяснено, то
точками с наибольшим нормальным напряжением будут точки,
наиболее удаленные от этой оси. В нашем случае
наибольшее растяжение будет в точке А, а наибольшее сжатие
в точке В. Подставляя в выражение [а]
h Ь
х = о; у = -; м = -,
получим:
, I feeds a fcsina \ г_
Сжимающие напряжения в точке В будут той же
величины.
Метод, поясненный выше на примере консоли с двумя
плоскостями симметрии, нагруженной силой на конце,
можно применить также к балкам с опертыми концами и
загруженным несколькими силами. Разложив каждую силу
на две составляющие, параллельные двум осям симметрии
поперечного сечения, сведем задачу к двум простым зада-,
чам изгиба балки в двух главных плоскостях. Суммарные
прогибы получим наложением этих двух прогибов в двух
главных плоскостях.
1?б
Чтобы иметь изгиб без скручивания в случае балки
поперечное сечепие которой имеет только одЬу ось S
метрии, или не имеет вовсе симметрии, силы должны бы?ь
приложены по линиям, параллельным'оси^6aS™pox0.
дящим через центр скачивания (стр. 192). Каждую силу
нужно разложить на две составляющие, параллельные гл2
вше плоскостям изгиба, и этим задача сводам ™i?SS.
му изгибу каждой, из этих двух плоскостей/ Р
ЗАДАЧИ.
іТУз^КрНі°180 к!7С^68Гш^.НаГрУ?еЕіа іа коаце вертикальным
грузом ^-іьи къ (фиг. 168). Найти наибольшее нормальное напряже-
ние % иг вертикальную и
горизонтальную составляющие прогиба
конца балки. Размеры даны на фигуре.
Угол а = 18°5.'. Главные моменты
инерции 1Ч .= 2764 с**; J^ = 160 см*.
Ответ. (^)шах = 49 кг/см2 в
точке В; вертикальный
прогиб — 0,452 см,
горизонтальный—0,864 см.
. 2. ронсоль
прямоугольного поперечного
сечения изгибается
силой Р.. приложенной на
ее конце. Какую кривую
опишет загруженный ко-
258L
Фиг. 168.
166) будет изменяться от нуля ^о IS" УГ°Л * (фнр-
Ответ. Кривая — эллипс с полуосями:
РР
ЪЕ1
и
РП
концах в положении, показанном на фиг. 169 Найти-иатгй^™^?
мальное напряжение и вертикальный п?огиб °по SJ^^SK есТи
Длина балки I = 3 ж, а = 320 «г/*, h = 20 еж, 6 = 15 см, tg а * J-.
Решение. Наибольший изгибающий момент будет цо середине:
М.
max
8
320 ¦ 3002
8-100
= 36 000 кг - см.
Составляющие вгибающего момента в главных плоскостях будут;
М9 = Мшк ' cOQ « = 36 000 • 0,94-9 = 34 200 кг. см;
М9 ^ Ч***.'sin а ^ 36 000 • 0,313 = 11400 кг. си.
197
Наибольшее напряакение в точке В будет
34 20О.6 , 11400-6 0
(в \ = — —Г" = 4:9,4 W.
^aJmax 15.202 ' 20 • 15а '
Прогибы по середине пролета в двух главных плоскостях:
* _ 5 $*costt * — JL jffsinа.
°*~3§Г Ml и °*~384' JS7/- '
Вертикальный прогиб по середине пролета равен
o = oyCOSa + os8ina = ^.Xj- Г COS2 а + -^~ ВШ2 a J =
= 0,387 -1,08 = 0,364 см.
4. Решить предыдущую задачу, если расстояние между опораыс
1,8 * и балка имеет две равных консоли, каждая длиною по 0,6 м.
ГЛАВА ШЕСТАЯ.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ ИЗГИБЕ.
43. Лишние неизвестные. До сих пор мы рассматривали
лишь три типа балок: 1) консоль с одним закрепленным и
другим свободным концом, 2) балку с опертыми концами,
свободно лежащую на двух опорах, и 4) такую же балку
с выступающими за опоры частями, т. е. консольную балку.
Во всех трех случаях опорные реакции можно было
определить из основных уравнений статики; поэтому эти зада-.
чи называются статически определимыми.
Теперь мы будем рассматривать задачи изгиба балок,
при которых уравнений статики недостаточно для
определения всех реактивных усилий опор, так что приходится
находить дополнительные уравнения, основанные на
рассмотрении прогиба балок. Такие задачи называются
статически неопределимыми.
Рассмотрим различные типы опор, которые может иметь
балка. Опора, представленная на фиг. 170а, называется
шарнирной подвижной опорой. Если пренебречь трением в
шарнире и в катках, то становится очевидным, что в этом
типе опор реакция должна проходить через центр шарнира
и быть перпендикулярной к лопасти тп, по которой могут
перемещаться катки. Следовательно мы знаем точку
приложения реакции и ее направление, и остается только-
одна неизвестная — величина реакции.
На фиг. 170& показана шарнирная неподвижная опора.
В этом случае реакция должна проходить через центр
198
шарнира, но может иметь любое направление в плоскости
фигуры. Итак, здесь имеются две неизвестные, которые
нужно определить из уравнений статики: направление
реакции и ее величина или, иначе говоря; вертикальная
и горизонтальная составляющие реакции.
На фиг. 170с представлен закрепленный конец балки.
В этом случае неизвестными являются не только
направление и величина .реакции, но и точка ее приложения.
Реактивные усилия, распределенные по заделанному сечению,
можно заменить силой Д приложенной в центре тяжести
сечения, и моментом М. В этом случае мы имеем три
неизвестные, которые нужно определить из уравнений статики:
две составляющие реактивной силы В и величина момента Л/.
© © ©
Фиг. 170.
Для балок, нагруженных поперечными грузами,^
находящимися в одной плоскости, мы имеем для определения
реакций опор три уравнения статики, а именно:
2* = 0; J Y = О; Jlf = 0. [а]
Если балка оперта так, что имеет только три неизвестных
элемента реакции опор, то их можно определить из ур-ний
[а]; поэтому такая задача является статически определимой.
Этих трех элементов как раз достаточно, чтобы обеспечить
неподвижность балки. Когда число элементов реакции
больше чем три, мы говорим, что здесь имеются лишние
неизвестные, и задача является статически неопределимой.
Консоль поддерживается в одной только точке — в ее
закрепленном конце. В этом случае, как было пояснено
выше, число неизвестных элементов реакции — три/и они
могут быть определены из уравнений статики. Для балок
с опертыми концами и балок с консолями обычно
предполагают, что одна из опор представляет собою неподвижный,
а другая — подвижной шарнир. В таком случае ьш вмеем
199
сйова трі неизвестных элемента опорных реакций, которые
можно определить из уравнений статики.
Если балка имеет неподвижные шарниры в обоих
концах (фиг. 171), то задача становится статически
неопределимой. В каждом конце у нас будут по два неизвестных
элемента — две составляющих соответственной реакции,—
и для определения этих четырех неизвестных мы имеем
только три уравнения. Таким образом здесь, имеется одна
лишняя: неизвестная, и становится необходимым для
определения реакций рассмотреть деформацию балки.
Вертикальные составляющие, реакций можно определиіь из
уравнений статики. В случае вертикальных грузов, из тех же
уравнений статики можно заключить, что горизонтальные
'составляющие Яравны, но противоположны по направлению.
Фиг. 171.
Чтобы найти величину Н, рассмотрим удлинение оси
балки при изгибе. Удовлетворительное приближенное
значение этого удлинения можно получить при предположении,
что упругая линия балки—парабола 1). Тогда разнипа
между длиной упругой линии и расстоянием I между
опорами представит полное осевое удлинение балки, и оно
будет равно (см. стр. 35)
8 В2
тт1
относительное удлинение, следовательно, равно
Зная это и обозначив через Е модуль упругости
материала балки и через F площадь ее поперечного сечения,
получим горизонтальную реакцию И из уравнения:
8 8е
H=±.—EF. [й]
Ц Точное выражение для упругой линии будет дано далее (см. п° 3,
часть II).
200
Интересно отметить, что для большинства балок,
применяемых в технике, прогиб S очень мал сравнительно
с длиной, и растягивающее напряжение
8 8з _
Т • "F * Е>
вызываемое силами Н, обычно мало сравнительно с
напряжениями от изгиба, поэтому этим напряжением можно
пренебречь. Это оправдывает обычный прием расчета балок
с опертыми концами, основанный на предположении, что
одна из двух опор — подвижной шарнир, хотя в
действительности особые меры для предоставления свободы
перемещения шарниру принимаются только в случае больших
пролетов, как например в мостах.
В случае изгиба гибких стержней или тонких
металлических полос, где прогиб 8 уже не очень мал
сравнительно с длиной I, растягивающими напряжениями,
возникающими от действия продольных сил, уже нельзя
пренебречь. Подобные вадачи будут рассмотрены далее (см.п°з,
часть II). При дальнейшем рассмотрении статически
неопределимых задач изгиба будем .применять метод
наложения и находить решения путем комбинирования стати-'
чески определимых случаев таким образом, чтобы
удовлетворить условиям на опорах.
44. Балка, заделанная одним концом и опертая другим.
Рассмотрим сперва случай нагрузки одним сосредоточенным
грузом Р (фиг. 172)х). В этом случае мы имеем три
неизвестные элемента реакции на левом конце и один—на
правом. Следовательно, задача статически неопределима,
и имеется одна лишняя неизвестная-
При решении этой задаче в качестве лишней
неизвестной будем рассматривать .ту, которая устраняет возможность
поворота левого конца Л балки при изгибе, т. е. опорный
момент Ма левой опоры.
Удалив эту неизвестную, мы получим статически
определимую задачу, как показано на фиг. 1726. Изгиб
вызываемый статически неопределимым моментом Ма, будем
рассматривать отдельно, как изображено на фиг 172с.
Очевидно, что изгиб балки, представленный на фиг. 172а,
можно получить • .сочетанием случаев Ъ ж с. Необходимо
х) Упругая линия и эшора изгибающих моментов начерчены • на
фиг. 1726 и с вместе.
201
только взять величину момента Ма на опоре такой, чтобы
удовлетворялось условие
6 = ?/. [а]
При выполнении этого условия поворот левого конца
балки под действием
* р\_с силы Р будет
уничтожаться
моментом Ма, и условие на
закрепленном конце
о равенстве нулю
угла касательной к
упругой линии
будет удовлетворено.
Чтобы найти ста-
* тическинеопредели-
"' мцй момент Мау
необходимо только
подставить в ур-ние [а]
известные уже
выражения [123] (стр.
157)и[133](стр.161).
Тогда
Рс(Р — &) Ма-1
откуда1)
= Рс(Р-<?)
2Й
Фиг. 172.
[145]
Теперь получим эпюру изгибающих моментов соединением
эпюр для случаев бис, как показано на фиг. 172d
заштрихованной площадью. Наибольший изгибающий момент
будет или в точке Л или в точке D.
Прогиб в любой точке можно легко получить, вычитая
ив прогиба в этой точке, вызванного грузом Р, прогиб от
момента Ма. Уравнения упругих линий для обоих этих
случаев уже получены: это ур-ния [125] и [126] (стр. 160)
и уу-ние [134] (стр/162).
*) Таким путем получается абсолютное значение момента Ма. Знак
момента—отрицательный, так как здесь происходит изгиб вогнутостью
вни»/
203
Возьмем, например, случай, когда с< —?, и определил
jdi ¦
прогиб по середине пролета. Из ур-ний [131] и [134];
или, пользуясь выражением [145], имеем:
В точке С, где изгибающий момент становится равным
нулю, кривизна упругой линии также равна нулю, и ьш
имеем точку перегиба, т. е. точку, где кривизна меняет
знак.
Из формулы [145] усматривается, что изгибающий
момент в закрепленном конце зависит от положения груза Р.
Если мы приравняем нулю производную выражения [145]
но с, то мы найдем, что момент Ма получает наибольшее
значение при с = —=і. Тогда
У в
т^в1^ = 0дв2 FL [Ш]
Изгибающий момент под грузом (фиг. 172d) равен
Рс(1 — с) с Рс(Р—<Р) Рс ,т Ч9,л7 . .
Бели взять производную от выражения [Ь] по с и
приравнять ее нулю, то мы найдем, что Мй достигнет
максимума при
с = -1(|/"з_і) = о,.366 I.
Подставив это значение в формулу [Ъ], получаем?
W)max = 0,174B.
Сравнивая последнее с выражением [146], найдем, 'что
в случае подвижного груза наибольшие нормальные
напряжения ох получатся в закрепленном сечении.
Имея решение для одного сосредоточенного груза и
применяя принцип наложения, можем решить задачу для
других видов поперечной нагрузки простым
распространением изложенных выше заключении,
?03
Возьмем для примера случай, представленный на фиг.
173. Момент на опоре, вызываемый любым элементом qdc
нагрузки, получится из выражения [145] подстановкой qdc
вместо Р. Полный опорный момент Мл будет равен:
М,
о
-/¦
gc(P — e*)de
2Z2
2V
J2(b2_a2) b* — a*
2
M
Фиг. 173,
Если нагрузка
распределена по всей
длине балки, то
подставляя в формулу
[с] а = 0 и Ъ = 1,
получим
шшшпшш
?
/
Эпюра изгибающих моментов получится вычетом
треугольной эпюры момента Ма (фиг. 174) из параболической
эпюры моментов от
равномерно
распределенной нагрузки.
Легко убедиться,что
наибольшие
напряжения от изгиба
будут в сечении на
закрепленном
конце. Прогиб любой
точки получим вы- Q\ дд
"чтением прогиба в ^ с
этой точке, вызван- \_Х.
ного моментом Ма
(см. ур-ние [134],
стр. 162), из прогиба
в той же точке от равномерно распределенной нагрузки
(см. ур-ние [137], стр. 164). Для середины пролета получим
f
Фяг. 174.
8 =
384
2*1
E'L
гЧ
192EI;
[148]
ЗАДАЧИ.
1. Найти наибольший прогиб для случая равномерно
распределенной нагрузки балки, изображенной на фнг. 174,
204
Решение. Соединяя в одно ур-ния [137] н [134], получим
следующее уравнение упругой линии:
у = -щт" (3/2а;2 ~~ ЪіхЪ + 2^'
[d]
dy
Приравняв производную -— нулю, найдем точку, где имеет место
наибольший прогиб; абсцисса этой точки х равна
х =• ~ (15 - УЩ = 0,579 /.
Подставив в ур-пие [d], получим
тах 185?Л
2. Найти реакцию правой опоры балки» изображенной на фиг. 174,
приняв эту реакцию за лишнюю неизвестную.
Решение. Устранив onopv В, получим прогиб этого конца балки,
рассматривая как консоль, по формуле [122J (стр. 152).
Реакция В правой опоры (фиг. 174а), должна быть взята такой,
чтобы этот прогиб был устранен. Тогда при помощи выражения [115]
(стр. 150) получим уравнение
Ф
в-$
гЕК
откуда
В=^ф
¦ 3. Балка несет нагрузку, пока-
ванную на фиг. 175. Найти момент
Ма и реакции А и В обеих опор.
Ответ.
Фиг. 175.
Мл =
ql<
VJ)
Яі&\
^ = ?9/ + іо^/;
п 3 . , 11 .
4. Найти реакцию В правой опоры от равномерно распределенной
нагрузки балки, показанной на фиг. 174, если опора В упруга, так что
действующая вниз сила к вызывает опускание опоры па единицу длины.
Решение. Пользуясь тем же методом, как и в задаче 2 выше,
получим уравнение для определения В:
ql*
8?А
В
к'
откуда
в=і*
і+
¦кР
?05
5. Построить эпюру изгибающего момента для балки, несущей
равномерно распределенную нагрузку и опертой в трех равно отстоящих
друг от друга точках.
Указание. По условию симметрии, среднее поперечное сечение
не может поворачиваться при изгибе, а потому каждая половина балки
будет находиться в положении балки, закрепленной на одном конце
и опертой другим.
6. Определить прогиб конда С балки, изображенной на фиг. 176.
Решение. Заменяя действие консоли парой сил Ра, получим
изгиб балки между опорами наложением случаев іи с Статически,
неопределимый момент Ма найдется из уравнения 0Х = ?/, т. е.
Pal
маі
ъеі-
откуда Л/а = -т-Ра. Прогиб в точке С будет:
-Sr+'ft
о =
Первый члеп правой части представляет прогиб консоли, а второй—
прогиб, вызванный поворотом поперечного сечения балки в точке Ь*.
7. Найти дополнительное
давление балки АВ на опору В (фиг. 172),
вызванное неравномерным
нагреванием балки, при условии, что
температура изменяется от tQ внизу
балки до t вверху, следуя
линейному закону.
Решение. Если устранить
опору В, то от неравномерного
нагревания упругая линия получит вид
дуги круга. Радиус этого круга
можно найти* из ур-ния
1 _ a{t-t0)
р- h >
Фиг. 176.
где Л— высота балки и а—коэффициент линейного расширения.
Соответствующий прогиб в точке В можно найти так зке> как в задаче 2
(стр. 94), и он равен
2р
•л
Этот прогиб должен быть устранен действием реакции опоры В.
Обозначив через Вь эту реакцию, получим:
3?Л
a(t-tQ)P
2Л '
откуда:
206
? =
« {і - <„).
8. Балка ABCt показанная на фиг. 177, лежащая на абсолютно
жесткой основании, частично свешивается и изгибаетея
сввим'собственным весом. Найти отношение между I и Ь.
Решение. Конец *АТ) балки, находящийся в соприкосновении
о основанием, остается прямолинейным, и поэтому изгибающий момент
в точке D равен нулю. Часть DC балки можно рассматривать как
балку* с консолью, опертую в точках J> и В. Изгибающий мснейг
в точке В равен — Ф2, где q — вес погонной единицы балки. Тогда
из того условия, что в точке D касательная остается горизонталвно^,
т. е. поперечное сечение балки не поворачивается при помощи формул
[132] (стр. 161) и [135] (стр. 162), получим
24 EL
«*V
откуда
1=ЪУ2.
Фш\ 177.
Если часть АВ балки короче, чомбУ"2, то балка после изгиба
будет касаться основания только своим левым концом и в точке В.
45. Балка с обоими закрепленными концами, В этом
случае мы имеем шесть элементов опорных реакций (по.три
для каждого конца), т. е. задача имеет три статически
Рс(і'С)
Фнг. 178.
неопределимых величины. Однако для обыкновенных балок
горизонтальными составляющими реакций можао пренебречь
(см. стр. 20і)3 что уменьшает число статически
неопределимых величин до двух.
207
Примем опорные моменты Мй и Мь за статически
неопределимые величины. Тогда в случае одного
сосредоточенного груза Р (фиг. 178а) решение можно получить
соединением вместе двух статически определимых задач,
изображенных на фиг. 178& и с. Очевидно, что условия на
закрепленных концах балки АВ будут удовлетворены, если
моменты Ма и Мь будут выбраны так, что
\ = V
и
во = Ь9\
и
Из этих двух уравнений получим два статически
неопределимых опорных момента. Пользуясь формулами [123]
и [124] при действии сосредоточенного груза и формулами
[13.2] и [133] при действии моментов, получим ур-ния [а]
в следующем виде:
рс(/»-с») Ма1 Мь1
Ы ¦• El. ?Е1. т ЪШ.'
Fc(l — c) (2l— с)
Ы ¦ EL
Ма1 Мъ1
GE1
ВШ.
откуда
J}1 а- ?2 '
Л/,
Рс (I — с)*
[1«]
Соединяя вместе іэпюры изгибающего момента для
случаев Ъ и с, получим эпюру изображенную на фиг. 178<2.
Наибольший положительный изгибающий момент будет
под грузом в точке С. Его величину можно найти по фиг.
178d и представить в следующем виде:
М.=
Рс {I — с) Afac Мъ (I — с) 2Рс3 (/ — с)2
/
I
I
гз
[150]
На фиг. HSd видно, что наибольший по абсолютной
величине изгибающий момент будет либо для точки О, либо
на ближайшей опоре.
Для движущегося- груза, т. е. когда с — переменно,
предположив с < — I, получим наибольшее значение момента
МЪ1 подставив во вторую из формул [149] с==--. Этот паи-
4
больший момент равен—PJ,
203
Изгибающий момент под грузом будет наибольшим, когда
<»*=—Z, и это наибольшее значение момента по ф-ле [150]
будет равно -$- PL Отсюда следует, что при подвижном
грузе наибольший момент будет на конце.
Пользуясь методом наложения, можем получить прогиб
в любой точке, алгебраически суммируя прогиб от груза
Р, с прргибом от моментов Ма и Мь.
Получив решение для одного сосредоточенного груза Р,
можем легко рассмотреть действие любого другого вида
поперечной нагрузки помощью метода наложения.
ЗАДАЧИ.
1. Построить эпюру изгибающего,момента_ для равномерно
нагруженной балки с закрепленными концами (!>иг. №)•
Решение. Момент на опоре А от отдельного элемента qdc на
грузки (фиг, 179а) равен согласно ф-ле [149]
q*dc'C2(t — с)
dMa =
V
Момент от нагрузки до всему'
пролету равен поэтому
г
Р " 12 *
*•-/
Фиг. 179..
Момент на опоре В получается
такой же величины.
Соединяя параболическую эпюру изгибающего момента от
равномерно распределенной нагрузки с эпюрой в виде прямоугольника от
двух равных моментов, приложенных по конпам получим эпюру,
показанную на Л>яг. 1796
заштрихованной площадью.
2. Найти опорные моменты балки
с закрепленными концами,
нагруженной по закону треугольника, как
показано на фиг. 180.
Решение. Интенсивность
нагрузки на расстоянии с от опоры В
равна
V
г
v/A
Фиг, 180.
и нагрузка, представленная заштрихованным наклонао элементом
равна
<1а'
сйс
14 Тимошенко — Сопротивление материалов, ч. I.
20Э
Моменты, действующие на конпах и вызванные этим элементарным
грузом по выражению [149], будут:
dMa^
did,
Поэтому
г
M.-J.
Qa&G — c)dc
qacS{l-c)dc_ qaP
~~ 20 ;
Р
М>
_ <1асЧ1-сУ<1с
г»
го
3. Определить опорные моменты Ма и Мъ балки с* закрепленными
конттами, изгибаемой парой сил Рс (фиг. 181).
Р е ш е н и е. IkuLb3vacb решением задачи б (стр. 166) и
выражениями [ізз] и [133], получим следующие уравнения:
«.-">--^[¦^--(•Ч-Н
откуда легко определяются моменты М и Мь*
4. Найти изгибающие моменты в \закрепленных конпах балки от
неравномерного ее нагревания, если
температура изменяется от і0 внизу
до * вверху балки, следуя
линейному закону.
Ответ.
М„ = iff,
а
Фаг. 181.
где а—коэффициент линейного
расширения и Л — высота балки.
. 5. Определить влияние на величину опорной реакции и опорного
момента на опоре А небольшого вертикального перемещения Ь
закрепленного конца Л балки АВ (фиг. 178).
Решение. Удалим опору А; тогда прогиб ох точки А и угол
наклона 6й в этой точке найдутся как для консоли, закрепленной в точке
В и нагруженной силой Р, т. е.
РсЗ jp#{l—c)
Ч~ТЩ,
6,=
2EL
210
Приложив в точке А действующую вверх реактивную силу X н
реактивный момент Y того же направления что и момент Мл, та оЗ
величины чтобы угол наклона ?х уничтожался, а прогиб становился
равным 8, получим
.следующие уравнения для определе-
¦ ни я неизвестных величин X
Ж Г:
2E1S
ХР
л
YP
2EJL
Рс*
2EL
= о« •— о.
'I A
ж
і—ТТШР
Ф
©
Фиг. 182.
6. Найти изгибающие
моменты на концах балки АВ,
изображенной на фиг. 182, с
закрепленными концами и
нагруженной грузом по
середине. Принять Ix : Jq= 2.
Р е ш е ни е. Решение
получается соединением вместе
двух простых случаев,
показанных на фиг. 1826 и с.
Ясно, что условия на закрепленных концах будут удовлетворены, если
углы наклона касательных на концах будут равны нулю, т. ?. если
реакции от фиктивной нагрузки (см. стр. 158), представленной
заштрихованными площадями на фнг. 1826 и с, равны. Поэтому уравнение для
определения И получается в таком виде:
Рі ±_$_
*4 * -J 8
».±-m.,-!LL.
откуда
*=5И-
7. Решить предыдущею задачу в предположении, что
приложено два равных груза Р в точках С is. В.
Ответ.
U-<7 —
8. Равномерно нагруженная
балка с заделанными концами,
изображенная на фиг. 183, поддерживается
Фиг 183 в сРедне^ своей части жестким
основанием, так что на длине этой
части прогиб 8 постоянен. БаЙгя
нагибающие моменты в закрепленных концах и длину а.
Предполагается, что:
^ 384 еі;
Решение. Часть балки CD, соприкасающаяся с»основанием,
остается прямолинейной, так что от точки С до точки D нет
изгибающих моментов, из чего следует, что здесь между точками С и Ъ должны
14* 211
возникнуть равномерно распределенные реактивные усилия и
возможно появление сосредоточенных реакций X в упомянутых точках."
Рассматривая часть балки ЛС как .консоль с равномерно
распределенной нагт>узкоЙ q и сосредоточенным rpvsoM X. на конце и заметив, что
поперечное сечение С не будет поворачиваться, получим из
выражений [116] и [120] (стр. 150 и 152)
да? __ Ха?'
6Шг ~~ 2Е1Я9
откуда
Другое уравнение получим из условия, что прогиб в точке С ра-
воа 5, а именно:
Из выражений [а] и [Ь] получим
Величина изгибающего момента на опоре А поэтому равна
46. Рамы. Способ, примененный выше к исследованию
статически неопределимых балок, можно применить также
к изучению рам.
Возьмем простейший пример — симметричную и
симметрично нагруженную раму (фиг. 184), имеющую
шарниры в точках С и D. Вид рамы после деформации
показан на фиг. 184а пунктирными линиями.
Пренебрегая изменениями длин стержней *) и
рассматривая только изгиб, можем полагать раму состоящей из
трех балок, как показано на фиг. 1846.
Очевидно, что на концах горизонтальной балки .4.В будут
действовать моменты М, которые препятствуют свободному
поворачиванию этих концов и представляют собою действие
вертикальных стержней на горизонтальную балку. Этот
момент М можно рассматривать как единственную
статически неопределимую величину в рассматриваемой раме.
Зная Ж, можем без каких-либо затруднений исследовать
изгиб всех трех стержней рамьь
Для определения И воспользуемся тем, что в точках
J и -В стержни жестко соединены друг с другом, так что
г) Одновременное действие изгиба и сжатия рассматривается далее
(п° 3, часть II).
аіа
доворот верхнего конца вертикального стержня АС должен
равняться повороту левого конца горизонтального стерэ&ня.
Отсюда получаем уравнение для определения- Ы:
?і = ?і'«
[а]
Угол ?х найдем из рассмотрения изгиба горизонтальной
балки AJB. Обозначив через I длину этой балки и через
Ш— ее жесткость на изгиб, получим, что поворот конца Л
вызванный грузом Р, по формуле [123] при с = 11%1 равен
Рі*
16 ЕГ
Моменты на концах противостоят этому изгибу--и
вывивают поворот в противоположном направлении; величина
©* *
_. U _\С
T""J\
®
wM>
его по формулам [132] и
[133] равна
Ml
2 EI
Полное значение угла .поворота конца А ригеля
рамы АВ
е ^ РР Ml
.! Г •
1 10 Ш 2Е1
Рассматривая вертикальный стержень АС как балку,
с опертыми концами, изгибаемую моментом М, п обозначив
через h — длину стержня и через Е1г— акестьостьг его на
изгиб, найдем по формуле [133] угол поворота вверху ноги
АС рамы
ft' m
3 Е.[{
213
Подставив полученные значения углов ?х и ?/ в .ур-ние [а],
получим
PV* Ml МП
откуда
16-01 2EI 8EIJ
М= 4г л ъ т» [151]
т
8
1
^ 3 1 іі
Зная Ж, можем построить,, как показано на фиг. 184с,
эпюру изгибающих моментов/
¦На фиг. 184а показаны опорные реакции в шарнирах С
и D. Вертикальные реакции получаются на основании
уравнений статики. Горизонтальные реакции
найдем,"применяя уравнения равновесия к выделенным из рамы
вертикальным стержням.
Эту же задачу можем решить и другим путем, приняв
за статически неопределимую величину вместо момента М
горизонтальную1 реакцию Н в шарнирах С и D (фиг. 185).
Статически неопределимая задача решится наложением
двух статически определимых задач, изображенных на
фиг. 1856 и с.
В случае Ъ> лишняя неизвестная, препятствующая
горизонтальному перемещению шарниров С и D, устранена.
Вертикальные стержни не .будут испытывать уже никакого
изгиба. Горизонтальный стержень АВ находится в
положения стержая с просто опертыми концами, углы поворота
которых равны
\ьТг
Горизонтальное перемещение каждого из шарниров С
и D равно поэтому
Р1?
16 ЕГ
В случае с рассматривается действие сил Я. Под
действием этих сил возникают изгибающие моменты на
концах горизонтального стержня АВ, равные Н • h, так
что углы поворота этих концов
~ 2ЕГ
214
Перемещение каждого из шарниров С и D состоит из
двух частей: перемещения от поворота верхнего конца
В'. Л
и прогиба
1?Ч
2EJ
ЦК*
зшг
и вертикальных стержней как
^Ц??~* консолей.
#м&ж -q действительности (фиг.
185а) шарниры С к D не мо-
Фпг. 185.
Фиг. 186.
гут иметь перемещений; отсюда следует, что горизонталь-
ные перемещения, вызываемые силой Р(фиг. і8бд), должны
быть устранены противодействием сил Н (фиг. 185с), т. е.
от г •" а А?
16Ж ~~ 2EI ^ ??1г'
откуда
Н=
8/і
2 ]і 1_*
215
Вспомним, что Hh = M, мы найдем, что этот результат
совпадает с ранее полученным выражением [151],
Этот последний .способ определения усилий в раме
особенно пригоден дЛя несимметричной нагрузки, .такой, как
показанная на фиг. 186 (см. стр. 215). Удалив лишнюю
неизвестную, препятствующую горизонтальному
перемещению шарниров С и .D, приходим к положению,
представленному на фиг. 186Ь.
Очевидно, что увеличение расстояния между
шарнирами G и D может быть получено умножением суммы углов
Ьг и ?2 на высоту ног рамы h. Пользуясь формулами [123]
и [124], находим, что увеличение этого расстояния равно
h
Рс(1*—с*) , Рс{1 — с)(2і — с)] _ Pe(l — c)h
Ы-Ш + 61-Ш } 2EI
Оно должно быть устранено противодействием
горизонтальных реакций .Н\(фиг. 185с). А потому, пользуясь
результатами, полученными при решении предыдущей,
задачи, мы приходим к следующему уравнению для
определения Л:
откуда
2 ( 2Ш ~*~ ?Е?Х }~ 2EI
Е^Рс(1~с)
2hl ч . 2 h J
1 + -втТ'Тх
[152]
Получив решение для одного сосредоточенного груза,
можем легко перейти к любому другому случаю загрузки
ригеля АВ рамы, пользуясь методом наложения.
Рассмотрим теперь раму с закрепленными концами ног и
несимметричной нагрузкой, показанной на фиг. 187. В этом случае имеем до
три элемента опорных реакций в каждой опоре и система имеет три
статически неопределимых величины.
При решении этой задачи применим способ, основанный на методе
наложения, при котором данная система нагрузки разбита на
отдельные части, так что для каждой частичной нагрузки можно найти
простое решение 1).
Задача, изображенная на фиг. 187а, может быть решена наложением
решений двух задач, показанных на фиг. 1S7& и 187с.
Случай-, изображенный' на фиг. 187Ь — случай симметричной
нагрузки и может быть рассмотрен таким же путем, как первый пример,
показанный на фиг. 18і.
і) Такрй метод широко применялся.В. Аидрэ (Ж. X. Andree), см. его
книгу Das B=U Vexfahren, Miinchen und Berlin, 1919.
218
: Изучение случая, представленного на #иг. х87с, показывает, что
точка перегиба О горизонтального стержня АВ расположена по середине
стержня. Это следует из того, что-грузы -%-Р расположены на
одинаковом расстоянии от вертикальной оси симметрии рамы и имеют прямо
противоположное направление.
Момент, прогиб и осевая сила, возникающие в средней точке О
Горизонтальной балки АВ от одного из грузов — Р, будут устраняться
. *
действием другого груза —-Р. Отсюда следует, что в точке О не будет
ни изгибающего момента, ни прогиба» ни осевой силы.
Величина перерезывающей силы X в этой же точке найдется из того
условия, что вертикальный прогиб точки О равен нулю (фиг. 187d).
Этот прогиб состоит Н8 двух частей: прогиба 5j от изгиба консоли ОВ
и прогиба 32 от поворота конца В вертикального стержня В1>? Поль-
?
і2
Р
С L JC
а о \г в
"'¦ -J-T"F---J'-'4
1-2
ж
X
О
\2 В
h
о
ш
®
©
©
@
Фиг. 1ST.
зуясь известными формулами для консоли (ур-нне [118], стр. 151"), и
обозначениями, указанными на фиг. 187, получим следующие значения
этих прогибов:
о, =
р_
2
зяг + а ' ъеі \2 с)
X
©'
ZEI
о.,
/ Ус XI \
v 2 2;
Ы
ZEL
Подставив эти прогибы в уравнение ^-(-og — S, может найти
величину X перерезывающей силы. Найдя X, можем определить изгибающий
момент в каждом поперечном сечении рамы для случая нагрузки по
фиг. 187с. Складывая их с изгибающими моментами для случая
симметричной нагрувкипо фиг. 187&, получим решение задачи для нагрузки
по фиг. 187а*).
г) Решение многих важнейших задач по рамам можно найти в книге
Жмйнлогеля (Kleinlogel)t Mehrstielige Eahmen, Berlin, 1927.
217
ЗАДАЧИ.
1. Определить изгибающие моменты в углах рамы, изображенной
на фиг. 188.
Решение. Рассматривая стержень АВ как балку, опертую по
концам (фиг. 188Ь) н обозначив через М моменты в углах, получим
угол ?і равным
р& мі
IV>EI 2EI *
Приравняв его углу б/ в концах вертикальных стержней от изгиба их
только моментами М9 получим следующее уравнение для М:
РР Ml Ш
откуда
10EI
8
2EI 2Е1і *
1
1 +
h
I ' Ix
2. Найти горизонтальные реакции И в случае, показанном на фиг. 189.
uL I®
Фиг. 188.
V
D
Фиг. 189.
Указание. Пользуясь формулой [152] и применял метод
наложения получим
q$ . 1
# =
247* . " 2 7* I
3. Пайти' изгибающие моменты в узлах рамы, указанной на фиг. 190.
Решение. Разрезав раму, как показано на фиг. 1905, получим
такие уравнения для определения моментов М и М$
?1 = ?/ и 63 = ?2'.
Подставляя в эти уравнения значения углов поворота:
- Рс$ —с)* ш . а / „ _Mh Mxh
Ші -.225/;
»і =
8/
)/ =
?Е1Х
Mh
gel
3/(7А ;
придем к двум уравнениям для определения М и Мь
218
4. Симметричная прямоугольная рама подвергается действию
горизонтальной силы Я, как изображено на фиг. 191. Найти изгибающие
моменты М н М-L в узлах.
Решение.»Рама в деформированном виде изображена на фиг. 191а-.
Разрезав раму, как представленб на фиг. 191Ь, для стержня СВ получаем
h
№1 \ 2
М
6#і"
[а]
Рассматривая теперь
вертикальный стержень АС как
консоль, закрепленную в конце G
под углом ?х, найдем угол
наклона касательной в конце А
, Я Л» Mh
Ъ^ + Т'-Щ—Ж' С]
Наконец, от изгиба стержня АВ
Тогда из ур-нпй [а], [Ь] и [с] получаем
Фиг. 190.
м—
h
2 ч1+т
В
1\ 1
¦ГJ -, , / , й А
2і
1<ч
Подставляя в формулу [а] полученное
выражение для момента М, найдем
изгибающий момент Afj.
Если нижний горизонтальный стержень
имеет очень большую жесткость, мы
приблизимся к положению рамы, показанной
на фиг. 187 и подвергающейся действию
іщщ (tf) боковой силы Я. Подставляя в формулу [d]
'"'*"* 7 = со, получим в этом случае
М =
Eh
х * 6
1_
h
h
М
Фиг. 191.
X
Для рамы с шарнирными опорами
такой, как показанная на фиг. 184, и
подвергающейся действию боковой силы,
приложенной в узле А, момент Ж может быть
получен также . из выражения [d\
подстановкой 1=0.
5. Найти распор Ш и моменты М
показанной на фиг. 192.
Ответ.
и М в узлах А и В рамы»'
Я =
Ж = М, =
Ь_ Xhn + 20
Ь ' 2W + 3 '
q№ 1т
'* GO 2w + 3'
219
где
*т
6. Рама состоит из двух жестко связанных в узле В стержней с
заделанными концами А и С (фиг. 193). Найти изгибающий момент М
в узле В и ежи мающе е усилие Р в
стойке АВ, если от повышения
температуры стержень АВ увеличился в длине
на ДI = а {і — і$) I
Ответ. Р и И можно найти из
уравнений:
і-Ы
~ 2EI
Щ.
= AL
Ml
Фит. 192.
2Ш EI 4Шш
*
?Ш
/
Г
/
Ш
47. Балки на трех опорах. В случае
балки на трех опорах (фиг. 194а)
имеется один статически
неопределимый элемент опорных реакций.
Пусть этим элементом будет
реакция промежуточной опоры. Тогда,
пользуясь методом наложения,
можем получить решение для случая
фиг. 194а соединением вместе
случаев, представленных на фиг. 1Mb
и 194с.
Реакция X промежуточной опоры найдется из того
условия, что прогиб 8, вызываемый в точке G грузом Р,
должен быть устранен действием реакции X. Пользуясь
формулами [125] и [127], мы придем к следующему
уравнению дЛя определения лишней неизвестной X:
А
Фиг. 193.
Pel, [fo-fga — c»--/,»] XW
6 (/, + /,) Ж.
3(/1ГТ-ЩЯ7,
откуда
X
-pfeKii+w9
с2
вд
<V]
[153]
Если сила Р действует в левом' пролете балки, можно
применить то же уравнение, но в этом случае
расстояние с следует измерять от опоры Л, а пролеты \ и 7а должны
220
быть взаимно заменены. TLpal1 = l1 = l, по формуле [153]
получим
Fe{ZP — с*)
X
21*
[154]
Получив решение при действии одиночного груза Р,
легко исследовать любое другое загружение методом
наложения.
Та же задача может быть решена и другим способом.
Представим балку разрезанной на две части над опорой О
А
mm
L
С
L
тШі
(фиг. I94d), и пусть
Ме обозначает
величину изгибающего @
момента для
первоначальной балки в
этом поперечном
сечении. Таким
образом задача
сводится к рассмотрению
двух просто
опертых балок,
показанных на фиг. 194й, (7)
которые являются
статически
определимыми.
Величина -Мв
определится из
условия непрерывности
упругой линии над
опорой С. Это
условие требует, чтобы
6 = ?/, откуда при
помощи формул [123], (стр. 167) и [133] (стр. 161) получим
Фиг. 194.
BEL
Рс (U
с*)
мл
СИ
61, • EL
ъш,
откуда
м.
Рс (?2Й — с*)
2h(h + h) '
[155]
Эпюра изгибающих моментов показана на фпг. 194Д
заштрихованной площадью.
221
ЗАДАЧИ.
1. Для вышеприведенного примера доказать, что величина
изгибающего момента М по формуле [155] та же, что получается помощью
выражения [153] для поперечного сечения над опорой С.
2. Балка на трех опорах (фиг. 194а) несет равномерно
распределенную нагрузку интенсивности q. Найти изгибающий момент на опоре С.
Решение, Помощью метода наложения, подставляя qdc вместо
груза Р в формулу [155] и интегрируя в пределах обоих пролетов,
получим
h. к
И
с
Г 9е ffa2 — с^ dc Г %с (гі3 — с2)dc _ g h* + h2
если \ = \ = ls то
qP
Mc~ 8
Направление этого момента будет такое, как показано на фиг. 194а*.
3. Найти наибольший по абсолютной величине изгибающий момент
балки АСВ (фиг. 1У5), если Р равняется 4,5 т.
О т в ? т. Мтъх = 8,54: т • ж.
4. Балка на трех равноотстоящих опорах несет равномерно
распределенную нагрузку интенсивности q. Какое влияние на реакцию средней
опоры окажет понижение ее на величину 5?
Решение. Пользуясь способом, указанным на фиг. 194Ь и 194«,
найдем реакцию средней опоры X из уравнения:
<? (ЭД* л Х(2*)« , .
384 Ж_ 48Ш
откуда
Х== — 2^2 —
6*Ж
с
Фиг. U5. В а 2»
б. Определить дополнительное давление балки АВ на опору G
(фиг. ^194а), возникающее под влиянием неравномерного нагревания
балки, если температура изменяется от t внизу до tt вверху балки,
следуя линейному закону, t > ^ и ?і = Ц =• I.
Решение. Если устранить опору 6', то от неравномерного
нагревания упругая ось балки обратится в дугу круга. Радиус этого круга
определяется уравнением:
т ~ Л '
где 1ь — высота балки и а —коэффициент линейного расширения.
Соответствующий прогиб для середины равен
и реакция X опоры С найдется из уравнения:
Х(203
4?Е1 °'
2
222
6. Найти эпюру изгибающего момента для балки ЛВС, опирающейся
на три понтона (фиг. 196), если площадь горизонтального поперечного
сечения каждого понтона равна F и вес единицы объема воды ?.
Решение. По устранении опоры в точке С, прогиб Ь,
возникающий в этой точке от действия груза Р, будет состоять из двух частей:
1) прогиб от изгиба балки и ^) прогиб от погружения понтона А я В
в воду. Из ур-ния [131] получим
Реакция X средней опоры уменьшает найденный прогиб иа
Х(21)3 . X
4AEI ' 2F-Y
И
Разность между
выражениями [а] и [Ь] представляет
величину погружения среднего
понтона; пользуясь этим,, получим
следующее уравнение для опре-
дел-ения X:
ТС го „м Arfi.JP Х$Ф Х - Х
4SEI L { } * Ji~ 2F4 4&EI г 2*'Т "'Ft
в
Зная реакцию X, без затруднений построим эпюру изгибаюнщх моментов.
43. Керазрезныв многопролетные балки. 5 случае
неразрезной балки на многих опорах (фиг, 197) одна из опор
обычно рассматривается как неподвижная шарнирная опора,
тогда как все другие опоры считаются имеющими шарниры
на катках. При таком устройстве каждая промежуточная
опора имеет один только неизвестный элемент опорной
реакции—величину вертикальной реакции; поэтому число
статически неопределимых величин равно числу
промежуточных опор. Например, в случае, показанном на фиг. 197а,
число статически неопределимых элементов—пять.
Здесь можно применить оба метода исследования,
показанные в предыдущем п°. Если число опор велико, то
второй способ, при котором за статически неопределимые
величины принимаются опорные изгибающие моменты,
оказывается более простым.
Пусть фиг. 1976 представляет два смежных пролета п
Hw-fl неразрезной балки,-разрезанные на опарах п—1, п
и п + 1. Пусть Mn_v Мп и Мп+і обозначают изгибающие
моменты на этих опорах. Направления этих^моментов
зависят от нагрузки балок. Допустим, что направления эти
таковы, как показано на фиг. 197b1).
й) Если в конечном результате мы получим отрицательные знаки
для некоторых моментов, то это укажет, что направления этих моментов
противоположны показанным на фиг. J97&.
223
Очевидно, что, если изгибающие моменты на опорах
известны, то задача определения усилий в неразрезной
балке сведется к задаче определения усилий в стольких
просто опертых балках, сколько пролетов имеет неразрезная
балка.
Для определения изгибающих моментов Mn_v Мп и Мп+і
применим условие непрерывности упругой линии на опорах,
^ М, М2 М3 М, Мь
Фнг. 197.
Для любой опоры п это условие непрерывности будет В№
полнено, если
е = —?\ од
Допустим, что углы поворота положительны, если
вращение имеет то же направление, что соответствующий
момент Мл (фиг. 1976).
Общие выражения для этих углов получим как опорный-,
реакции фиктивной балки, загруженной площадямл
соответствующих эпюр изгибающих моментов (фиг. 197с). *
Пусть для пролета п, рассматриваемого как просто,
опертая балка, Fn обозначает площадь эпюры изгибающих'
моментов, возникающих от действительной нагрузки этого
пролета. Пусть ап и Ьп представляют горизонтальные
расстояния центра тяжести Сп эпюрц моментов от опор п—і
224=
и п. Тогда при данном загружении угол поворота сечения
на опоре п будет:
^Ж
1»Ш\
Кроме этого прогиба от нагрузки, пролет п будет изга>
баться моментами Мп_г и МпУ и поворот поперечного
сечения на опоре щ вызываемый этими моментами, по
формулам [132] и [133] получится равным
Ml J\f Л
зш. ' ъеі
г
Полный угол поворота
ЗЖ2+ вЖ, '^ lnEIz ' l°J
Таким же образом для пролета «-f 1 получим
~ '«+і^. Ш"*1 бЖ"'
Подставив [*] и [с] в ур-ние [а], имеем.'
11 П 7J + 1 Л + 1
2 2
п п + 1
[156]
Это — общеизвестное уравнение трех моментов1).
Очевидно, что число таких уравнений равно числу
промежуточных опор, и опорные моменты определяются без
затруднений.
В-начале было допущено, что концы неразрезной балки
просто оперты. Если один или оба конца заделаны, то
число статически неопределимых величин будет больше
числа промежуточных опор, и представится необходимым
вывести дополнительные уравнения, выражающие условие,
что в закрепленных концах нет поворота сечения (см.
задачу 5 ниже).
*) Это уравнение дано Берто (Beriot); см. „Comptes rcndus de la
societe des* ingenieurs civils", 1855, p. 278; см. также Еяапейрон {Clap&y-
ron). „С. гЛ t. 46, 1867.
15 Тимошенко — Сопротивление материалов, ч. I. - 225
Зная опорные моменты, можем без труда определить
опорные реакции неразрезной балки. Возьмем, например,
два смежных пролета пж п-j-l (фиг. 1976) и рассмотрим
их как две просто опертые балки. Реакция Л/ опоры п
под действием нагрузок этих двух пролетов при таком
предположении определится без затруднений. В дополнение
к этой реакции здесь возникает еще реакция от моментов
Приняв направления этих моментов,
Ж
n — V
Мп * Jfn + 1.
как указано на фиг. 1976, получим, что дополнительное
давление на опоре ? будет равно
Мт < — М» —М„Л-Ъ1.Л
П — 1 72. ¦ Т П ' 11 4-1
I
п
I
Л+1
Прибавив эту реакцию к полученной выше реакции-4/,
получаем полную реакцию
А
п
л г ! Я — 1 П і П 1 П-j-i
I
п
I
157]
п+1
Общ?? уравнение непрерывности [а] можно также использовать для
тех случаев, когда при неправильной установке опоры не находятся
П-1
7--
/.
п
г—
/
М-
і
t
_ і
I
ч
Фиг. 198.
на одном и том же уровне (фиг. 198). Пусть §п и Рп^_і обозначают
углы наклона к горизонтали прямых линий, соединяющие точки опЗры
в ?г-ом и (w-j-I)-om пролетах. Угол поворота, представленный
выражениями [Ь] и [с], измеряется от линии, соединяющей центры шарниров;
поэтому угол ? между касательной в точке » и горизонтальной линией
будет для пролета п равен:
?
BEL
+
Mn-Xln
+
F a
J 7lU1l
p«*
Таким же образом для продета п + 1
-^«4-1*» + *
+ Р«
-fi-
22в
Подставляя в ур-ние [а], получим:
6іГ« ал
г
^я+iVm
я
'П-j-l
«^(Рп+і-в*).
[158}
Если АЛ+1, Ап и /?-w_! обозначают вертикальные отметки опор л+1»
« и » —1 относительно некоторой горизонтальной линии, то
Р« =
Ля-і-Ап
»
Рп+і =
^»"~ ^п +1
'й -f1
Подставив эти выражения в ур-ние [158], без затруднений найдем
опорные моменты, возникающие от расположения опор не на одном уровне.
В вышеприведенном изложении было допущено, что жесткость на
изгиб неразрезной балки постоянна по ее длине. Изложенный способ
можно однако применить и к случаю неразрезных балок переменного
поперечного сечения путем простого видоизменения эпюр изгибающих
моментов, как показано на стр. 177, при определении углов ? и А'
по выражениям [Ь] и [с].
Для определения опорных изгибающих моментов неразрезной балки
применяются также графические способы *).
ЗАДАЧИ.
1. Построить эпюры изгибающего момента и перерезывающей силы
для неразрезной балки с тремя равными пролетами, нагруженной
равномерно распределенной нагрузкой интенсивности 2 (фиг. 199).
Решение. Для ,3
просто, опертой балки U. [
при равномерно распре- лТТЯ^
деленной нагрузке, эпю- (о) Ш\Ь№^^:У V
ра изгибающего
момента — парабола с
наибольшей ординатой
- ql з
8 *
Площадь
параболического сегмента равна:
F = ~ с
ql 2
8
ql 3
12
Фиг. 199.
*) Эти способы разработаны главным образом Мором (0. МоЪт);
см. „Zeitschrift des Architekten- u. Ingenieur-Vereins zu Hannover",
1874: а также О. Mohr, Abhandlungen aus dem Getriete d. techn. Meeha-
nik. 3 AufL, Berlin 1928. См. также Б. Pummep (IF. Bitter). Die elastisehe
Lime und ihre Anwendung anf den continuirlichen Balken. Zurich 1883;
А- Мёрш (E. MOrsch). Der durchlanfende Trager, Stuttgart 1928 (русский
перевод: Э. Мёрш, Неразрезные балки, 2 изд. 1931); Ж. Жеви [Маигйе
Levy), La statigue graphique, Paris 1886.
16* 227
1166']
Центр тяжести находится посередине пролета, а потому <^-'=Ь "=
Подставляя в ур-иие [156], получим:
Vi^ + S^lUWO + ^+lWl^ 4 4 •
Применяя это уравнение к нашему случаю (фиг. 199) для первого
и второго пролетов п заметив, что на опоре 0 изгибающий момент
равен нулю, получим
4Mxl + MJ = -&. [d]
Из условий симметрии ясно, что MX = M2. Тогда из ур-ния [d]
*-~$. ¦
Эпюра изгибающих моментов показана на фиг. 199а заштрихованной
площадью. ¦,*»..,,
« Л j $ w 1 * 7
Реакция опоры О Л0 = — НЬ Г = Т(Г 2
Реакция опоры 1 ^і = ql -f-
10
L 11 ,
_ с
Эпюра перерезывающих сил показана на фиг. 1996.
Наибольший момент будет очевидно на расстоянии 4/іо от кондов
балки, где перерезывающая сила равна нулю. Наибольший по
абсолютной величине изгибающий момент — опорный момент средних опор.
2. Составить выражение
для правой части ур-ния [156],
когда на пролете п находится
сосредоточенный груз, а
пролет +1 ничем не нагружен
(фиг. 200).
1— Решение. В этом слу-
/7*/ чае F^ — площадь
треугольника . высотой.
F =
Фиг. 200.
г
п
и основанием 2 ; поэтому
м
И
а = I
н п
I
Подставляя в ур-ние [156], имеем:
М.
»-і К> + **п <^+Чп+1) + ЛГп+1 *п+1= -
I
3. Найти опорные моменты и реакции неразрезной балки,
показанной на фиг. 201 (см. стр. 229).
О т в е т. Мх ~ — 0,57 m • м; М2 — — 1,S7 m - м; М% = — 0,825 m • м. Реак-
228
дйЯ опор: ^0 = —0,386 т; ^ = 2,69 m; A2 = S,22 w; Л.3 = 3,75 tn; Al]t =
е-- 0,275 w. Сюрные моменты — отрицательны я вызывают изгиб
выпуклостью вверх.
4. Построить эпюры изгибающих моментов и перерезывающих сил
для неразрезной балки, изображенной на фиг. 202, если Р= ql c = lj^
Р е ш е н и е. В этом случае фиктивная нагрузка первого пролета равна
Fl~ 12 '
для второго пролета Ъ\ = 0, и для третьего пролета:
F* =
Ре (1-е) ш
«з
2?
3
Ьч =
1 + с
\8т
Подставив полученное в ур-нне [156], составим следующие
уравнения для определения изгибающих моментов Мх и М%.
AMJ + MJ^-^;
откуда
49 44:
je.
-a—f—z-
fftu iltf'L \3
3,o Jmm 2jLL.
1
ЗА
Фиг. 20L
Оба эти момента отрицательны, так что эпюра изгибающих
моментов получится такой, как показано на фиг. 202Ь,
Чтобы построить эпюру перерезывающих сил, необходимо найти
реакции опор отдельных пролетов (ур-ни? [157]). Давления на опоры О
и 1 первого продета балки
_j<Tl~ будут:
2
М,
і __
= 0,551 ql.
©«я
I ош
і.ілш»ніііпітт
Рс
I
М2
I
Фиг. 202.
0,296 ql
\ Давления на опоры 1 и 2
второго пролета балки:
ЧГ г
и на опоры 2 и 3 третьего
пролета:
и
Р(г-с) . лл
р^+^=ОЛ04^
Яа основании этих данных на фиг. 202с построена эпюра'перерезы
вающих сил.
229
5. Построить эяюру изгибающих моментов для случая,
изображенного на фиг. 203.
Решение. Ур-ни? [159] для этого случая получает вид
•
I
I
О
т
1 \2РС
Фиг. 203.
MqI + ^MJ + MzI^O.
р Здесь Ма = — Рс, в то время как
" условие на закрепленном конце
(опора 0) дает (по формулам [132] и [133]):
?еі "*¦ ьш и"
» 9
Из этих уравнений получаем:
Jf0 = —~Pc;
2
lft = + —Рс;
3fa = —Рс.
Эпюра изгибающих моментов показана на фиг. 203&.
6. Найти опорные моменты неразрезяой балки с семью равными
пролетами, когда нагружен равномерно распределенной нагрузкой д,
только один самый средний пролет.
Ответ.
ГЛАВА СЕДЬМАЯ.
БАЛКИ, МАТЕРИАЛ КОТОРЫХ НЕ СЛЕДУЕТ ЗАКОНУ ГУНА.
БАЛКИ ИЗ ДВУХ МАТЕРИАЛОВ.
49. Чистый изгиб, когда материал не следует закону Гуна-
Вышеизложенная теория чистого изгиба (см. стр. 87)
была основана на предположении, что плоские поперечные
сечения балки остаются плоскими и после изгиба, т. е. что
удлинения и укорочения продольных волокон
пропорциональны4 расстояниям от нейтральной поверхности. На
основании закона Гука было показано, что здесь имеет место
линейное изменение нормальных напряжений по высоте
балки.
Эта теория применима с достаточной точностью к
стальным балкам, когда деформации остаются в пределах упру-
230
гостя. Но при изгибе стальных балок за пределом текучести,
а также при изгибе стержней из таких, например,
материалов, как чугун или бетон, уже простой
пропорциональности между деформацией и напряжением нет, и
распределение напряжений !от изгиба по поперечному сечению
становится более сложным.
Опыты с такими балками показывают однако, что даже
для таких материалов, которые не следуют закону Гука,
деформация продольных волокон при изгибе может быть
принята пропорциональной расстоянию от нейтральной
поверхности. Поэтому ранее полученная зависимость
(СМ. СТр. 89)
р
[а]
применима также и в этом случае *).
Наибольшее удлинение ег и наибольшее укорочение еа
получатся подстановкой в формулу [а] у = \ и у = Ьр где
х d О
® Г.Л ©
Фиг. 204
h{ и й2 обозначают расстояния от нейтральной поверхности
наиболее удаленных волокон в зонах растяжения и сжатия
(фиг. 204). Тогда
1 Р
И
_*¦
[Ь]
Чтобы найти величину напряжений, необходимо знать
соотношение-между напряжением и деформацией для
случаев простого растяжения и сжатия. Эти соотношения
определяются опытным путем и обычно представляются
графически диаграммами испытаний на растяжение и
1) См. статью Евгения Мейера (Eitgen Meyer), „Physical, Zeitsehrif fc%
1907. См. также Г. Герберт {Л. Eerbsrt), Dissertation. Gottingea, 1909.
231
сжатие, как показано на фиг. 2046, по которым легко
найти напряжение о, когда деформация е известна.
Эта деформация может быть определена по формуле [а],
если положение нейтральной поверхности, а также радиус
кривизны р известны. Для определения этих двух
неизвестных воспользуемся двумя уравнениями статики:
nL
fo<?F=0; [с]
faydF=M. [d\
-ft»
Эти уравнения указывают, что внутренние усилия в лю-^
бом поперечном сечении балки составляют пару сил и
что момент этой пары равен изгибающему моменту.
В качестве простейшего примера рассмотрим случай
балки прямоугольного поперечного сечения шириною Ъ,
так что dF—bdy. Заметив, что по формуле [а]
d* = ^L,
р
получим dF=bdy = bpdz.
Подставляя это в ур-ние [с] и меняя соответственно
пределы интегрирования, получим:
н
—«а
ИЛИ
fcdz= fcde, [с']
о о
где о должно быть взято из диаграммы испытаний" на
растяжение и сжатие (фиг. 2ЫЪ).
Способ определения положения ¦ нейтральной оси будет
в этом случае таков. Допустим, что наибольшее удлинение
имеет некоторую величину ех и затем определим
наибольшее укороченне е2 из ур-ния [с']. Это уравнение указывает,
что на фиг. 2016 площадь Odf должна быть равновелика
площади Оас* Последнее может быть выполнено с
достаточной точностью графически. Здая же вх и е2, расстояния
232
\ и Л2 можем найти из следующих уравнений (см.
формулы Щ):
|L = iL; Л + Ч = *
'«'3 ^
Очевидно, что в общем случае положение нейтральной
оси будет зависеть не только от формы диаграммы на
растяжение и сжатие, но. также от величины ег я от
величины изгибающего момента.
Когда положение нейтральной оси определено, находим:
соответствующую величину изгибающего момента по
ур-нию [d]. Подставив в это уравнение у = рг и dy = pdz
по формуле [а], получим:
V
/06Й8+/
aeds
—t»
= М. [d'}
Выражение в скобках представляет статический момент
относительно вертикальной линии, проходящей через
точку О площадей, заштрихованных на фиг. 204Ь. Этот
момент можно легко вычислить или получить графически
для каждого частного значения величины ег
Величина радиуса кривизны получится по первому из
выражений [&]: р ——
еі
Таким образом, ур-ния [с'] и [d% вместе с диаграммой
фиг. 204b решают задачу распределения напряжений
в прямоугольных балках, материал которых не следует
закону Гука.
Если, вместо диаграммы, известна аналитическая зави
симость между а и е, то ур-ния [с'] и [й'\ можно также
решить аналитическим путем. Рассмотрим, например,
случай, для которого диаграммы зависимости напряжений от
деформаций и для растяжения и для сжатия имеют форму
параболы, выражаемой уравнением *):
где т и п — постоянные, определяющие вид диаграмм.
Будем рассматривать только те величины деформации
для которых 2»в < т, т. е. -т— > 0. В этом случае, еслі
as
1) Знак минус при растяжении, знак плюс при сжатии.
свойства упругости материала одинаковы при растяжении
и при сжатии, нейтральная ось будет проходить через
середину прямоугольника, и ур-ние ]d'] получит такой вид:
2 Ър2 / (те — пг2) eds = М.
И
Интегрируя и подставляя et = —-f получим:
ір
Когда материал следует закону Гука, то п = оу аяі=Д
и это уравнение приводится к ур-нию [ill] (см. стр. 147).
Уравнение [е] может быть также взято в таком виде:
—— е- Я! ( 1 —- } == Ж,
откуда можно легко пайти наибольшее удлинение вх и
тогда выразить согласно уравнению [/] наибольшее
напряжение в функции изгибающего момента Ж.
Задача определения закона распределения напряжений
при изгибе может быть решена и тогда, когда зависимость
между деформацией и напряжением представлена в виде
показательной функции
п
е = то •
Закон в виде такой функции был предложен Бахом
при исследовании им изгиба чугунных стержней, и при
гаком виде зависимости было получено очень
удовлетворительное совпадение этого закона с опытными данными 1).
50. Изгиб прямоугольного стального стержня за пределом
текучести. В случае стали с ясно выраженным пределом
текучести, удлинение материала при текучести
(горизонтальный участок диаграммы фиг. 2а у точки В) может быть
во много раз большим, чем упругое удлинение. Иногда оно
достигает от одного до полутора процентов, т. е. в 10—15 раз
больше, чем упругая деформация до предела текучести
для стали, имеющей а =2100 kzjcmK
-*9
і) Ж. Вах (С. Bach), „V. D. I.", Bd 32, 1838, S. 198. См. также его
книгу Elaetizitat und Festigkeit, 1905, S. 224. См. также В. ЛТюле
(W. Schuele), „Dingler's Pol. Journal", 1902, S. 149, Линегин (Pinegin), Mit-
tejlungen uber Forsclmngsarbeiten, n° 48; И. Летерман (L Petermann),
Dissertation, Berlin 1914.
234
В таком случае диаграмма на растяжение и сжатие
может быть представлена обычно с достаточной точностью
прямыми линиями ntm9 и тп и т,пи показанными на
фиг. 2056.
Предположив, что предел текучести от одинаков и при
растяжении и при сжатии, получим, что при изгибе за
пределом текучести прямоугольного стержня нейтральная
ось будет по середине высоты балки. Наибольшая
деформация растяжения вх и наибольшая деформация сжатия е2
будут равны.
Обозначив деформацию ^ через ет, получим, что
напряжения, которые возникают при изгибе, представятся
на фиг. 2056 заштрихованными площадями.
*— и7*-—і
0
0
IF
1/
ті Ш,
¦tar—
г: / т
—«,—і
L ©
Фиг. 205.
Взяв некоторое удлинение гх, т. е. некоторую кривизну
можем найти соответствующую величину изгибающего
момента из уравнения [cf]. Подставив в это уравнение
V8!
1 „ 2
-—о • е
3 т т
W
вместо статического момента заштрихованной площади
„ фиг. 20ЬЪ, получим уравнение для определения
изгибающего момента в таком-виде:
^.(¦г-т-О--*-
m
2В5
Если г1 велнко сравнительно с ет то мы можем
пренебречь членом — г\ до сравнению с е2, ж ур-ние Щ до-
лучит вид:
ЦЧ\о^М. [с]
¦ Распределение напряжений по поперечному сечению
балки представится тогда двумя прямоугольниками,
показанными на фиг. 205а, и соответствующий изгибающий
момент будет иметь величину
которую можно получить непосредственно из фиг. 205а, а
также из ур-ния [с] подстановкой в него
К
8,
Обозначив через Мт величину изгибающего момента, при
которой напряжение в наиболее удаленных волокнах
достигает предела текучести, мы получим
т.
и ур-ние [d] принимает вид:
При этом значении изгибающего момента, явление
текучести будет продолжаться без увеличения сопротивления
моменту до тех. пор, пока зависимость между деформацией
и напряжением будет отвечать диаграмме фиг. 20§Z>. Оно
прекратится только тогда, когда вследствие удлинения
произойдет затвердение материала. Сила сопротивления
материала тогда возрастет (см. п° 55, часть II).
Уравнение [6] может быть также применено для
определения кривизны при изгибе за пределом текучести. При
помощи ур-ний [с] и [d'\ ур-ние [Ь] может быть
представлено в следующей форме:
3
м,
m
откуда
s
еі рт V К
EI,
где рт = -уд*- есть радиус кривизны, при котором напря-
Т
женив в наиболее удаленных волокнах только подходит
к пределу текучести.
Тогда
Р = ^Р1/ 3-2 3/
1 Ж 1
р ЕГе Ж , /\ м
С/
V
м-.
т г х
Отсюда видно, что текучесть материала может быть
учтена подстановкой вместо жесткости на изгиб Е1г
уменьшенной величины жесткости, равной
*/-
m.^Li/ з — 2м
м.
Уменьшение зависит от отношения М:Мті и когда это
з
отношение приближается к—, жесткость на изгиб
приближается к нулю. Вследствие этого в балках, где
изгибающий момент изменяется вдоль балки и Л1т?Х приближается
з
к-—3f, наблюдается стремление изгиба сосредоточиться
в том месте, где изгибающий момент достигает максимума,
и упругая линия за пределами упругости получается иной
формы, чем та, которую овГа имеет ниже предела
упругости.
Например, при изгибе балки силой, приложенной по
середине, явление текучести происходит главным образом
у середины пролета, в результате чего получается
значительная кривизна, тогда как остальные части балки только
слегка изогнутся.
При изгибе за пределами текучести материал дает
некоторую остаточную деформацию, и получается остаточный
прогиб разгруженной балки. Так как некоторые из волокон
237
находятся в условиях упругости и стремятся после
удаления груза вернуться к своей первоначальной длине, а
другая часть волокон дает остаточную деформацию, в балке
после удаления нагрузки останется некоторая доля
напряжений.
Чтобы получить картину распределения таких
напряжений в поперечном сечении, рассмотрим простейший
случай прямоугольного стержня, когда распределение
напряжений при изгибе за пределом текучести может быть
представлено двумя прямоугольниками (фиг. 205а). Когда
материал подвергается растяжению за пределом текучести и
затем разгружается, то при разгружении материал следует
закону Гука, как показано на фиг. 2055 . пунктирной
линией х).
Вследствие этого напряжения от изгиба, которые
подлежат вычитанию, во время равгружения балки следуют
линейному закону, указанному' на фиг. 205а пунктирной
Лидией mxnv
Разность между площадями двух диаграмм
распределения напряжений, прямоугольной при загружении и
треугольной при разгружении, показанная на фиг. 205а
заштрихованными площадями, представляет напряжения,
которые остаются в балке после разгрузки. Эти напряжения
называются остаточными напряжениями.
Из условия, что обе диаграммы распределения
напряжений представляют один и тот же изгибающий момент,
следует, что статический момент треугольника тОтг
относительно оси Os должен быть равен статическому моменту
прямоугольника mlsO относительно той же оси.
Поэтому напряжение, представленное отрезком тт1у
должно быть равно 1,5 ат и наибольшее растяжение и
сжатие, которое остается в наиболее удаленных волокнах после
разгрузки балки будет равно 0,5 от. Остаточные
напряжения в волокнах у нейтральной поверхности будут
достигать величины ст.
Из этого видно, что распределение напряжений,
представленное заштрихованными площадями, приводится к двум
равным и прямо противоположным парам сил, дающим
момент
о .
т 27
и находящимся в равновесии.
,!) Подробйее по этому вопроеу ем. пь 55, часть It
238
Существование таких остаточных напряжений можем
доказать опытным путем, распилив стержень по
нейтральной плоскости; тогда каждая половина стержня получит
некоторый изгиб.
Если стержень с такими остаточными напряжениями,
как покааано на фиг. 20ба, изгибается снова моментами
той же величины и того же направления, как в
предыдущем опыте, то напряжения, вызываемые ?тими моментами,
представленные прямой линией тхпі9 будут накладываться
на остаточные напряжения, изображенные
заштрихованными площадями, так что диаграмма распределения
суммарных напряжений будет представляться
прямоугольниками Omls и Опк$г
Наибольшее напряжение будет а^ н при этом повторном
изгибе явление текучести не будет иметь места. Поэтому
остаточные напряжения, вызванные первоначальным
изгибом, будут такого свойства, что они увеличат изгибающий
момент, которому можно будет подвергнуть стержень в
пределах упругости, если только направление изгиба останется
тем же.
Такое явление улучшения упругих свойств сооружения
предварительным загружением и созданием соответствен-*
ных остаточных напряжений нередко применяется на
практике, и некоторые частные случаи этого применения
рассмотрены далее (см. п° 55, часть П).
51. Балки из материалов, имеющих различные модули
упругости при растяжении и сжатии. Рассмотрим теперь
материал, который следует закону Тука, но модули
упругости которого на растяжение и на сжатие различны.
Мы получим такой случай, например, при рассмотрении
выпучивания стержня,
подвергаемого
продольному сжатию (см.
п° 37, часть II).
Предположим снова, М
что поперечные сече- Г
ния остаются плоски- \^
ми при чистом изгибе,
получим диагр амму
распределения
напряжений в поперечном
сечении тп такой, как
изображено на фиг. 206. Если Ех и ^—модули упругости
на растяжение и на сжатие соответственно, а Ьх и йа"—
239
расстояния наиболее удаленных волокон от нейтральной;
плоскости, то наибольшее растягивающее и наибольшее
сжимающее напряжения будут:
Для прямоугольного поперечного сечения
растягивающие и сжимающие усилия N будут:
^в 2 = 2 ' М
где Ь обозначает ширину сечения.
Подставляя [а] в выражение [Ь], имеем:
я&\=в&\. [с]
Заметив также, что
получим, из выражений [$] и [Л]
Момент усилий N равен
2 а . bh, 2 о . Ъ№ УЖ
M = — kN= ша* * . — & = - ща* \_>
3 2 3 3(/л?1 + і/^
откуда
№
+/*)¦
в»« = -й5Г|і-М/ -#-]• t159l
Если JE?t равняется і?2, то это выражение совпадает
с полученным раньше выражением [90] (см. стр, 92).
Чтобы получить кривизну упругой лкяАш, подставим
в формулу [159] выражение для отах по формуле [о]. Тогда,
или, пользуясь первым из выражений [г], получим:
12
1 12 М {УЕг +1/^): Г ,
240
'1г—
h
Wy<
Это уравнение для материала с двумя различными
модулями упругости соответствует ур-нию [111] (стр. иг) для
материала с одним модулем упругости Д и оба уравнения
могут быть приведены к совпадению введением в
"уравнение [160] величины
Эта величина Е' называется приведенным модулем
упругости. Величина этого модуля зависит от отношения между
Bt и Е2.
При Ег — Е^ — Е получим по формуле [161] ЕГ = Е.
При Ег:Е2 = 0,5, Ш = 0,68Е2. При Ег: Е2 = 0,1, Е' = 0,23 Е2.
52. Балки из двух разных
материалов. На практике
встречаются случай применения
балок из двух или
нескольких различных материалов.
Фиг. 207 представляет
простейший случай деревянной
балки, усиленной стальнцм
листом, приболченным к бадке
снизу.
Предположив, что между
сталью и деревом при изгибе
пет смещения, здесь можем
применить теорию сплошных
балок. Согласно этой теории, удлинения и укорочения
продольных волокон пропорциональны расстоянию от
нейтральной оси.
Вследствие того, что модуль упругости дерева много
меньше, чем модуль упругости стали, деревянная часть
балки при изгибе будет эквивалентна гораздо более узкой
стальной стенке, как показано на фиг. 2076. Для того,
чтобы сохранить момент внутренних усилий неизменным
для данной кривизны, т. е. для данного удлинения и
укорочения, толщина Ъх этой стенки должна быть следующая:
С
h
X...J
!,
®
Фиг. 207.
ЪЕЪ
Е.
М
Таким образом, задача приводится к эадаче изгиба
стальной тавровой балки,' которая может быть решена на
основе вышеизложенной теории изгиба.
Рассмотрим, например, свободно опертую балку длиною
3 м и нагруженную по середине пролета грузом в 400 кг.
16 Тимошенко — Сопротивление материалов, ч. I. 211
Размеры поперечного сечения деревянной части балки;
ширина * = 10 см и высота Ъ= 15 см, а внизу она усилена
стальной полосой шириною в 20 мм и толщиной 10 мли
Приняв Е '-E=— и пользуясь ур-нием [а], получим
эквивалентное сечение со стенкой іъоу^ь мм и полкой
20 X10 мм- Расстояния крайних волокон от нейтральной
оси (фиг, 207$) будут: 7^ = 6,92 см и fc2 —9,08 см. Момент
инерции относительно нейтральной оси 1% = 230,3 см*,
вследствие чего напряжения в крайних волокнах (по
формулам [91], стр. 92):
М_
max
шах
w,
и.
шах
шп
W,
30 000 - 6,92
230,3
30 000 • 9,08
230,3
= 900 mjCM?;
= — 1180 кг/см*.
Чтобы получить наибольшее сжимающее напряжение
в дереве действительной балки, нужно полученное выше
напряжение оЫп для стали помножить на і?д: _#, = —; таким
образом наибольшее сжимающее напряжение в дереве
а = — 59 кг/см?.
Другим примером изгиба балки из двух разных материалов может
служить линейка (фиг. 208), составленная яз двух: одной из никеле-
<2к|
4
/а
п
D
и—., Сталь
%
т
®'<~?
Рг-Х
м2
л
V-",
©
щ
Ju 2
п
Ъ
%
Фиг. 208.
вой стали и другой из монель-сплава [сплав никеля (67,15%) и меди
(28,71%)].
Изгиб такой линейкя внешними силами можно рассмотреть таким
же путем, как в предыдущей задаче для дерева и стали. Необходимо
242
только знать отношение ЕА: Ес, где Еы и Е0 соответственные модули
упругости монель-еплава и никелевой стали.
Рассмотрим изгиб такой линейки» вызванный изменением
температуры. Коэффициент линейного расширения монель-еплава — больше, чем
коэффициент линейного расширения никелевой стали, и при повышении
температуры происходит изгиб вогнутостью со стороны стали- Этим
явлением изгиба линейки, составленной из двух металлов, при изменении
температур часто пользуются в различных автоматических приборах
для регулирования температуры х) (термостаты).
h
Пусть ~~ толщина линейки каждого металла, Ъ — ширина
линейки, t — увеличение температуры, г — радиус кривизны, сс0 и ам —
коэффициенты линейного расширения стали и монель-еплава
соответственно, ЕС1С — жесткость на изгиб стальной линейки, E^JU — жесткость
на изгиб линейки из монель-еплава.
При повышении температуры, линейка из монель-еплава, имеющая
больший коэффициент линейного расширения, будет подвергаться как
изгибу, так и сжатию, а стальная — изгибу и растяжению.
Рассматривая элемент линейки, вырезанный двумя смежными
поперечными сечениями тп и %% (фиг. 208с), найдем, что внешние усилия
в поперечном сечении стальной линейки могут быть приведены к
растягивающей силе Рх и к моменту Mv Тем же путем для линейки из монель-
еплава внешние усилия можно привести к сжимающей силе Р2 и к
моменту М2.
Внешние усилия в любом поперечном сечении балки должны
находиться в равновесии; поэтому
Е
РХ = Р2 = Р
Ph
2
= М1 + М2. [a]
По предыдущему
Мл = ; Мо = .
Р 2 ¦ Р
Тогда ур-ни? [а] получим в таком виде:
Ph Е01а ЯИ7И
"—+—• м
Другое уравнение для определения Р и р можно вывести из
условия, что по поверхности соприкасания с — с относительное удлинение
линейки из монель-еплава и стальной должно быть одно и то же.
Поэтому
д? | 2рі | *_д , 2р2 Ъ
или
EQbh ' 4р * E^bh 4p
2Р / 1 , 1 \ , . . Ь ..
Ы> \В* ЛЬ) v* °' 2Р
*) См. статью автора в „Journal of tfce Oprical Soc. of Amer.*, VoL
11, 1925, p. 2i*3
16* 243
и-
w
Из ур-ний [b] и [с] получим
-тег ад+ВД (-ж-+і) =(а» - *>' - I-
Подставив в эти уравнения:
'о=^м=|г И Я, = 1.15^,
получим следующее приближенное решение:
1 _ 3 (ам-ае)«
р ~~ 2 Л
Теперь из ур-ния [Ь] находим
и
3 (ам — а)* 3 (ам —а.)*
ifi = т • м ,/ ад,; ^2=т • м / я,л- (г)
По формулам [/] и Г^гі можно найти Р, Мх и Мг. Наибольшее
напряжение в стальной линейке получится присоединением к растягивающему
напряжению, вызванному силой Р, растягивающего напряжения от изгиба
1
с кривизною —:
2Р h Е0 4 / Ш \
Допустив, для примера, что оба металла имеіот одинаковые модула
упругости Е, получим
_ hE
или на основании решения [е] *)
ffflax^ у^К-^-
Прн Е = 1900 000 да/сла, ? = 200° С и <хм — л0 = 0,000004 найдем
Распределение напряжений, возникающих от повышения темпера,
туры," показано на фиг. 208с.
53. Железобетонные балки. Известно, что сопротивление
бетона на сжатие значительно больше, чем на растяжение
. Поэтому прямоугольная бетонная балка разрушится от растя
і) Это выражение применимо также при Еа = Fu.
244
гивающих напряжений на получившей от изгиба выпуклость
стороне балки. Сопротивление балки можно значительно
повысить введением в бетон стальных стержней на
выпуклой стороне, как показано на фиг. 209.
Так как бетон крепко схватывается со сталью, то здесь
не будет смещения стальных стержней относительно бетона
при изгибе, а потому здесь могут быть применены методы
определения напряжении от изгиба, изложенные в
предыдущем п°.
На практике площадь поперечного сечения стальных
стержней обычно такова, что сопротивление бетона на
растяжение на выпуклой стороне изогнутой балки преодолевается
раньше, чем появляется текучесть стали, и при больших
нагрузках в сущности только сталь воспринимает все
растяжение. Поэтому принято при подсчетах напряжений
/77
7
©
Фпг. 209.
от изгиба в железобетонных балках предполагать, что все
растяжение принимает на себя сталь, а все сжатие—бетон.
Заменив растягивающие усилия в стальных стержнях
их равнодействующей Д получим распределение
внутренних усилий в любом поперечном сечении тр таким, как
показано на фиг, 2096- Приняв как раньше, что
поперечные сечения остаются плоскими при изгибе и обозначив
через Ш расстояние нейтральной оси пп от верха балки *),
получим наибольшее продольное относительное укорочение
бетона еб и относительное удлинение осей стальных
стержней ео в следующем: виде;
Ш (1 — Ъ)Ъ
Бетон не следует закону Гука, и диаграмма испытания
на ся^атие этого материала имеет вид подобный диаграмме
х) 1с — отвлеченное число, меньше единицы.
245
для чугуна (см, фиг. 2Ь, стр, 6). По мере увеличения
сжимающего напряжения, наклон касательной к диаграмме
уменьшается, т. е. модуль упругости бетона понижается с
увеличением напряжений. При определении напряжений в
железобетонных балках обычно предполагают, что закон Гука имеет
силу и для бетона, а чтобы возместить переменность модуля
упругости, берут для этого модуля меньшее значение,
чем то, которое получается из диаграмм испытаний па
сжатие при небольших напряжениях. В технических условиях
по железобетону обычно принимается, что Е0:Еб — 1Ь.
Тогда на оснований формул [а] наибольшее сжижающее
напряжение в бетоне и растягивающее напряжение в стали1).
будут соответственно:
? v (1 —*)Л _
Найдем положение нейтральной оси из условия, что
нормальные усилия в поперечном сечении юр приводятся
к моменту, равному изгибающему моменту. Сумма
сжимающих усилии в бетоне должна быть равна растягивающему
усилию В в стальных стержнях, т. е.
ЪШ а,
где F0—полная площадь поперечного сечения стали.
Пользуясь обозначениями
Fc Ей
ж = п, и . -щ^п,
О
получим из выражений [с] и [Ь] следующее ур-ние для
определения к:
№ = 2(1—Jc)nnlt [d]
откуда: -
Тс = — ппх -f- !/".(»»!)*+2ппь [162]
После определения положения нейтральной оси по
выражению [162], отношение между наибольшим напряжением
в бетоне и напряжением в-стали получим, согласно
формулам [Ь]:
аб
°с (1—*К
[163]
і) Размеры площади поперечного сечения стальных стержней обычно
малы, ш вместо наибольшего напряжения пользуются средним значением
растягивающего напряжения. * ¦
246
Расстояние а между равнодействующими В сжимающих
и растягивающих усилий, действующих в данном
поперечной сечении балки (фиг. 209?), равно
а = АйЬ + (1—*)fr=(l —у)* [1в4]
и момент внутренних усилий, равный внешнему
изгибающему моменту, будет:
-г» тт йТЛТь ,,
откуда:
с
2 if
О
6 аШ'
[166]
По формулам от [162] до [166] напряжения при изгибе
в железобетонных балках определяются без затруднений.
ЗАДАЧИ.
1. При EQ: Еб = 16 п Fc = О,О08Ъ7* найти расстояние нейтральной оси
от верха балки (фиг. 209).
Решение. Подставив в формулу [162) те = 15 и пх == 0,008, получим:
7с = 0,384, и расстояние от верха балки будет Ш = 0,384&.
2. Найти характеризующее содержание стали число
п1 =
ЪК '
если наибольшее растягивающее напряжение стали равно 840 %\1см2*
наибольшее сжимающее напряжение в бетоне равно 44 кг/см? и
Ес:Еб = п = 1Ь.
Решение. По формуле [163] к = 0,446. Тогда по формуле [d]
3. Определить число пи если наибольшее сжимающее напряжение
в бетоне составляет одну двадцатую растягивающего напряжения стали.
О т в ? т. % = 0,0107.
4. При п = 15 и допускаемом напряжении на сжатие для бетона —
45 %г/см%, найти величину безопасного груза, поставленного по середине
пролета железобетонной балки длиною 3 м, опертой на концах и имеющей
Ъ = 25 см, h = 30 см, Fc = 7,5 см*.
2*7
Решение. По формуле [162]
16-7,5 , -./715-7,542 , 0 15-7,5 ЛАЛй
Тогда по формуле [166J 3fmax = 182 000 %\ • с*, и безопасный груз
равен
Р =
4Ж
шах
182000-4
Z
300
= 2430 кг.
54. Скалывающие напряженна в железобетонных балках.
Помощью того же метода, что и в п° 28, из рассмотрения
элемента т?щпх между дву-
мя смежными
поперечными сечениями тр и w^
(фиг. 210) можно заключить,
h что наибольшее скалываю-
' ' ~п ' Ж' а
й
I щее напряженке х^ воз-
-* никнет по нейтральной по-
La
А
Фиг. 210
верхности ппу.
Обозначив через dB
разницу между сжимающими
усилиями в бетоне по
поперечным сечениям тр и т^ри найдем скалывающее
напряжение т^ по нейтральной поверхности из следующего ур-ния;
v ссу/ха.ал *
откуда
(О:
ь
dB
dx'
;г#'т*х
Так как изгибающий момент
то формула [а] получается в таком виде:
1 dM Q
[а]
dx ab'
м
где Q — перерезывающая сила в рассматриваемом
поперечном сечении.
Пользуясь формулой [164], получаем предыдущее
уравнение для скалывающих напряжений в следующем виде:
(О
3Q
а^тах. ЬЬ^8<—70"
[167]
248
Для практических расчетов необходимо бывает звать
не только скалывающее напряжение по нейтральной
поверхности, но также скалывающие напряжения по поверхности
соприкасания между сталью и бетоном.
Из рассмотрения тех же двух смежных поперечных
сечений (фиг. 210) следует, что разность между растягивающими
усилиями в стальных стержнях для этих двух сеченнй
равна
Qdx
dJR =
а
Эта разность уравновешивается скалывающими
напряжениями, распределенными по поверхности стержней.Обозначив
через F—полную боковую поверхность всех стальных
стервеней на единицу длины балки, получим скалывающее
напряжение на поверхности стержней.
dR - Q *Q [168]
Fdx F-a (3—Jc)hF'
Это напряжение получается больше, чем напряжение
понейтральнойповерхности(формула[іб7]),?слиі^меныпе&.
Чтобы увеличить F и в то же время не менять площади
сечения арматуры, необходимо лишь взять большее число
стержней при соответственном уменьшении их диаметра.
ГЛАВА ВОСЬМАЯ.
НАПРЯЖЕНИЯ ОТ СОВМЕСТНОГО ДЕЙСТВИЯ ОСЕВЫХ
И ИЗГИБАЮЩИХ СИЛ.
55- Изгиб и сжатие или растяжение. Предположим, что
призматический стержень нагружен силами в одной вз
своих плоскостей симметрии, но, тогда как в предыдущих
случаях эти силы были всегда поперечными, здесь они
имеют составляющие, действующие и по оси стержня.
Простейший пример такого рода показан на фвг. 211,
которая представляет колонну, находящуюся под действием
наклонной силы Р. Разложим эту силу на поперечную
составляющую N и продольную Т и допустим, что колонна
сравнительно жестка, а деформации настолько малы, что
ими при рассмотрении напряжений, вызываемых силой Т,
можно пренебречь.
Тогда равнодействующая напряжений в любой точке
получится сложением сжимающих напряжений от силы Т с
напряжениями, возникающими от изгиба поперечной силой К
Гибкая колонна, давление на которую из-за отклонения
ее вследствие деформации от вертикали (фиг. 2116;
оказывает существенное влияние на ее изгиб, будет рассмотрена
далее (см. стр. 263).
Напряжение от силы Т постоянно для всех попереч-
Т
пых сечений колонны и равно -=-, где F—площадь
поперечного сечения. Напряжения от изгиба зависят от
величины изгибающего момента,
\х
который возрастает от нуля,
на вершине колонны до
максимального значения $ • I
в основании колонны.
Поэтому опасным
сечением является заделанный
конец колонны,' и
напряжение здесь для точки, взя-"
той на расстоянии у от оси
z этого сечения, будет равно
Т N-1-y
F
L
[а]
Фиг. 211.
Взяв, например,
поперечное сечение колонны
в виде прямоугольника Ъх\ со стороной h, параллельной
плоскости изгиба, мы имеем:
F=bh и '."НіР
Наибольшее сжимающее напряжение будет в точке п,
для которой
( \ _ 6Ш L \п
\ахШл ы,а 7,1. * і°і
Ь?*
ъ\?
Это напряжение является по абсолютной величине
наибольшим.
Для точки m получим
. QNI Т
(О:
ay тел
ък*
Ыьш
Когда сила Р не параллельна ни одной иэг двух
главных плоскостей изгиба, напряжения при изгибе,
возникающие от ее поперечной составляющей N, найдутся путем
разложения N на составляющие, гіараллельные этим
главным плоскостям (см. выше п° 42). Суммарное напряженно
в любой точке получится сложением этих напряжения
от изгиба с сжимающими напряжениями от действия
продольной силы.
ЗАДАЧИ.
1- Найти наибольшее сжимающее напряжение в круглых деревянных
столбах высотою 6 м я диаметром 20 см, показ иных на фиг. У12, если
груз Р, подвешенный в
проволоке ABC, равен 30 кг.
Растягивающее усилие в каждой
оттяжке DF равно S = 500 кг; tg в =
*=тк sin 8 = — и ВК = 4,5 м.
1\) о
Решение. Составляющие
усилия натяжения проволоки ВС
(фиг. 2126) равны: 2^ = 160 кг;
Тг = 15 к%*. Составляющие усилия
натяжения оттяжки DF равны:
іУ2 = 10О кг; Г2?=^490 кг.
Наибольшим: изгибающий момент
оказывается в закрепленном конце
и равняется Мтйх = 45 000 кг < см.
Осовое давление в том же поперечном сечении равно Гі+Т2 = 505 «v.
Наибольшее сжимающее напряжение в точке т равно
¦ШМ
%
т
\ ц
®
Фиг. 212.
о =
505-4 . 45000-32 к_0 ко 9
Н і^а— " I»6 т* 57,2 = 58,8 кг/см2.
псР
Ы3
2. Определить наибольшее растягивающее напряжение в
прямоугольной деревянной балке, изображенной на фиг. 213, если S = 1800 %\>
Ъ = 20 см, h = 25 см.
Ответ.
/ v 1800 . 1800-100.6 лпо . .
3. Найти наибольшее сжимающее напряжение в конструкции ABC,
которая поддерживает груз Р, равный 900 кг (фит. 214), имеет жесткое
14-Л
Фиг. 213.
Фиг. 214.
соединение между стержнями в узле Д неподвижную шарнирную опору
в точке А и подвижную опору в точке С. Поперечное сечение
деревянных брусьев АВ и ВС—квадратное 25X^5 см.
Ответ.
900-400-6 . 3-900 ._ . о
(°*)-х = 2.253 + -WW e G9'D КЧСМ '
251
4. Стенка из каменной кладки толщиной I м и высотой 5 м
испытывает давление от насыпанного за стенкой песка (фиг. 216). Найти
наибольшие растягивающее и сжимающее напряжения по подошве стенки,
если у—вес кубического метра ее равен 2 400 «і/ж3 и боковое
горизонтальное давление песка Е = 5 000 «г на погонный метт) стенкн.
Распределение давления песка по высоте стенки следует линейному вакону,
представленному на фиг, 215 прямой АВ.
Ответ. Напряжение в точке т
2400-5-2-1 5000-500.6
200 • 100
3-200»-100
= -1,20 - 1,25 = - 2,45 %%1ем\
Напряжение в точке п
2400-5-2.1 т 5000-500-6 10ЛМЛ. , лл_ , 0
" "ТОО -100 + ."3T2602T1CO- в ~~ 1,2° + !'2° ^ + °'°° %х'СМК
5. Найти такую толщину стенкн предыдущей задачи, при которой
напряжение в точке п равно нулю.
Ответ. 2,04 м. -
6. Круглый стержень АВ, имеющий шарнир в точке В и
опирающийся на гладкую вертикальную поверхность (трения нет) в точке А,
находится под действием' своего
собственного веса. Найти
положение такого поперечного сечения тл
А
ЫЛЪ
Фиг. 215.
Фиг. 21G.
(фиг. 216), в котором сжимающее напряжение достигает максимума.
Решение. Обозначим через I длину стержня, через q — его
погонный вес и через а —угол наклона к горизонту. Горизонтальная
реакция в точке А
В - -f- ctg«.
Сжимающее усилие в любом поперечном с?ченни тп, отстоящем от
точки А на расстоянии х, равно
, qI COS2 cz
gasme + -7: :—.
2 SHI а
Изгибающий момент в том же поперечном сечении
М = — cos a
2
Ч cos а „
252
Наибольшее сжимаалце? дапряжение равно
4 /™.rfr,„j_ $ cos2a\ . 32 / gZor о#з \
^^aJsina + _.ii_J + _r(^X- ««a-JL сов»)
где # —диаметр стержня.
Приравнивая производную этого напряжения по а нулю, получим
I \ d ^
7. Стержень изображенный на фиг. 21 la, имеет 1,8 м длины, и
диаметр его равен 30 си. Найти величину сил Р, если ее составляющие
N ж Т равны и наибольшее сжимающее напряжение в точке п равно
70 кг/слЗ,
Ответ. Р = 1427 кг.
8. Сила Р вызывает изгиб стержня ABC, закрепленного в точке Л
.(фиг. 217). Определить угол поворота свободного конца С при изгибе,
если изгибающие -моменты в точках A f -
и В равны по абсолютной величине. Шр- ' -> д
Решение. Из равенства изгибаю- %jm .. _г
щих моментов в точках А к В следует/ щШ ^Г\
что сила Р проходит через точку В, на- Щі ! X
годящуюся по середине стержня АВ* ^ 2~*
Тогда
* 2а *
Фиг. 217.
и можно будет найти составляющие Р^
н Р . Поворот поперечного сечения В от изгиба части АВ под
действием составляющей Р равен
У Р 22
у
2.EI
Z
н имеет направление по движению часовой стрелки. Поворот того же
поперечного сечения по действием составляющей Рх раве'н
Р аі
х
EJ
г
в'направлении, обратном движению часовой стрелки. Поворот
поперечного сечения С относительно поперечного сечения В от изгиба части ВО
стержня равен
Раз
2 Ж
г
в направлении против часовой стрелки. Общий угол поворота конца О
по часовой стрелке равеп
Р Р Р аі Р а? Р а*
у х х х
2 Ж Ж 2 Ж 2 Ж '
• 2 г г г
Б6. Вн?центренная нагрузка коротких стоек. Внецеитренная
нагрузка является частным случаем совместного действия
253
осевых сил и сил, вызывающих изгиб. Когда длина стержня
не очень велика по сравнению его с размерами его
поперечного сечения, то отклонение его от вертикали настолько
мало, что им можно пренебречь по сравнению с
первоначальным эксцентриситетом е. В силу этого здесь можно
воспользоваться методом наложения *).
Возьмем, например, случай сжатия продольной силы Р,
приложенной с эксцентриситетом е (фиг. 218) в точке,
лежащей на одной из двух
Главных осей поперечного
сечения. Тогда, если мы
приложим две равных и прямо
противоположных силы Р в
центре тяжести О поперечного
сечения, то положение не
изменится, так как приложенные
силы в сумме дают нуль, и
мы получим осевое сжатие
силой Р, вызывающее
простые сжимающие напряжение
Р
ЦТ *
Фиг. 218.
как показано на фиг. 2185,
и изгиб в одной из главных
плоскостей парой сил Р«е,
напряжение от которого равно
Реу
как показано на фиг. 218с. Общее напряжение равно
„__Р Реу
а
[а]
Эпюра распределения этих общих напряжений
изображена на фиг. 218&
- Если допустить, что наибольшее напряжение от изгиба
меньше, чем простое сжатие, то тогда получим только
сжимающее напряжение по всему поперечному сечению
стержня. Если наибольшее напряжение от изгиба больше,
чем осевое сжимающее напряжение, то получится линия
1 Случал вн?дентренной нагрузки длинных стержней рассмотрен
ниже (ом. стр. 263).
254
нулевых напряжений, параллельная оси е% делящая
поперечное сечение на две зоны с растягивающими
напряжениями слева и сжимающими напряжениями справа от нее.
При прямоугольном поперечном сечении со сторонами Ь
и Ъ (фиг. 218а) выражение [а] становится таким:
°*=—bh ьР~# [а]
Положив # = ——9 получаем
2
"Ък { bJfi ~ bh\ * l h
, , Р , вРе Р I ее х m
. к
а при у =+"2"
, v Р бРе Р / , . 6«\ * м
Отсюда следует, что, если е< —, то в поперечном
сечении не будет перемены знака напряжений; если е =
6 '
2Р
наибольшее сжимающее напряжение по формуле [с] равно-rrv
и напряжение на противоположной стороне прямоугольного
сечения равно нулю; еслие>—, то эдесь будет иметь
о
место перемена знака напряжения. Положение нулевой линии
определим, приравняв нулю общее выражение [а7] для
нормальных напряжений ол; это дает:
или, пользуясь обозначением ів для радиуса инерции
относительно оси ш (см, приложение, стр. 352), получим
У = -^ [Ив]
Отсюда видно, что расстояние нулевой линии от центра
тяжести О сечения уменьшается с увеличением
эксцентриситета е.
Подобное же рассуждение применимо также к случаю
внецентренной нагрузки, вызывающей растяжение.
255
Ур-яие [169] может быть также использовано и при
других видах поперечного сечения, если точка приложения
груза находится на одной из главных осей инерции,
л
Рассмотрим теперь случай, при котором Б — точка приложения вне-
дентренной сжимающей силы Р — не находится ни на одной из двух
главных осей поперечного сечения, принятых за оси у и г на фиг. 219.
Приняв т и п за координаты этой точки, получим моменты силы Р
относительно осей у ж z-.P-m и P*w, соответственно. Помощью
наложения получим напряжение для любой точки А поперечного сечения:
Р Рту Pns r ,
°х=—г—г—7-. м
в у
где первый член правой части представляет- напряжение от осевого
сжатия, а два других члена — напряжения от изгиба, возникающие под
действием моментов Р m и Р п
у2 соответственно. Отсюда видно,
что распределение напряжении
следует линейному закону.
Уравнение нулевой линии
. получим, приравнивая правую
часть выражения [е] нулю.
Пользуясь обозначениями
-?--:?
и
F
I
_у
F~
= »2,
у *
где г и г — радиусы инерции
относительно осей s и у, соот^
ветственно получаем
^+-+1 = 0.
z у
Подставляя в это уравнение сперва у = 0, а затем s — 0, получим
точки М и 2? пересечения нулевой линии с осями координат * и, у
(фиг. 219). Координаты этих точек s и г будут:
Фиг. 219.
s =
п
m
ш
Из этих выражений получаем:
п=- —
і 2
У
т== —
t'2
Эти формулы имеют тот же вид, что выражения \д] и отсюда можно
заключить, что когда груз приложен к точке Вг о координатами 5 и г,
соответствующей линией нулевых напряжений будет линия НИМ',
показанная на фиг. 219 пунктиром и дающая на осях у и s отрезки
длиною' w к п.
256
Есть и другая существенно важная зависимость между точкой
приложения В груза и положением соответствующей линии пулевых
напряжений, а именно: при перемещении точки В по какой-нибудь
липни BJB% (фиг. 220), соответствующая нулевая линия поворачивается
вокруг некоторой постоянной
точки В'.
Это доказывается
следующим образом. Разложим груз,
приложенный в точке В, на две
параллельные составляющие:
одну, приложенную в точке Ві9
а. другую — в точке В2-
Составляющая, приложенная в точке
Blt действует в главной
плоскости яз. Поэтому
соответствующая нулевая линия параллельна
оси у9 и ее пересечение с осью х
найдется по формуле подобной
формуле [169], а именно:
« =
у
М
Фиг. 220.
Подобная же линия нулевых напряжений для составляющей,
приложенной в точке Вь параллельна оси s, и ее расстояние от этой оси
равно
_JL_
т
При любом положении груза на линии BLB2, напряжения в точке В*
будут равны нулю. Поэтому при перемещении точки приложения груза
по прямой линии В^В2 соответствующая нулевая линия
поворачивается вокруг точки В', координаты которой опре-
ЩШШ' деляются выражениями [А] и [к].
і
В)
ъ
т
Фиг. 221.
ЗАДАЧИ.
1. Площадь поперечного сечения квадратного стержня
в сечении тп уменьшается в половину (фиг. 221). Найти
наибольшее растягивающее напряжение в этом поперечном
сечепии, возникающее под действием осевой силы А
Ответ,
'"Wmax
2Р , Р-а
а<
+
іі
Ф
RP
а2
предыдущую задачу, приняв, что стержень круглого
2. Решить
сечения.
3. Стержень таврового сечения нагружен виет?нтренно силами; Р
4фнг. 222). Определить наибольшие растягивающее и сжимающее напря-
17 Тимошенко—Сопротивление материалов, ч. 1. 257
ж?ния в этом стержне, если d = 24 мм, Ъ = 120 мму ширина, полки
Ь = 120 мм, сила Р = 1800 к*.
Решение, Расстояние, пентра тяжести таврового сечения от
подошвы полки и от верха стенки соответственно равны Ь^ = 38,7 яд
о ^>
-н-
VU
J?
^ гч
гп—с
\-> VJ/
1
j? '
-/-
Фиг. 222.
иЛ3 = 81,Зжж. Эксцентриситет силы Р равен е = 12 -f- 38,7 = 50,7 ля.
Момент инерции 1 = 651 см*. Напряжения от изгиба равны
(А - P'e'*i - 1600-8,07-8,87.: _б12 . з.
Р.е-Тц 1800-6,07.8,13 --.Л , в
Р 1800
Оязсадывая их с напряжением от осевого растяжения -=- = ,1jU'~
=э 34*7 «і/слі2> подучим наибольшее растягивающее напряжение 54,2 +
-^34,7 = 88,9 к\/см\ наибольшее сжимающее
напряжение —1140 4" W7 =» —79,3 xt/c*a.
4. Найти наибольшее растягивающее напряжение
в сечении тп важима, показанного на .фиг. 223, если
Р == 144 кц о = 60 мм и поперечное селение —
прямоугольник о размерами: 24 X 6 -и*.
Ответ.
<W = 1600 кі/с*э.
5, Определить ширину поперечного сечения тп
предыдущей задачи так, чтобы <Jmax = 1400 кфм2.
Щ. Ядро сечения* В предыдущем п° было показано
но, что при небольшом эксцентриситете е нормальные
Фиг 223 напряжения имеют одинаковый знак по всему
поперечному сечению внепентренно нагруженного стержня.
При больших, значениях е линия нулевых напряжений,
пересекает поперечное сечение, и в этом случае знак напряжений
меняется. При материале, очень слабо сопротивляющемся растяжению, как
например кирпичная кладка, существенно важно бывает определить
такую зону, чтобы сжимающая сила, приложенная в пределах ее, н*
вызывала никаких растяіивающих напряжений в кладке. Такая зона
называется ядром поперечною сечемил. Способ нахождения ядра сечення
разобран на следующих простых примерах.
258
В случав круговою поперечного сечения радиуса R мы можем
заключить по симметрии, что ядро сечения — круг. Радиус а этого круга
найдется из того условия, что, когда точка приложения груза находился
на граиип? ядра сечения, .соответствующая линия нулевых напряжений
должна касаться к окружности поперечного сечения. Вспомнив, "что
1
момент инертгии круга относительно люСого диаметра равен —т- я Й1
(см. приложение, стр. 353), а потому радиус инерции круга
пайдем по формуле [169] (стр. 255), подставив а вместо е и R вместо у,
4'
[ПО]
т. ?. радиус ядра сечения равен четверти радиуса поперечного сеч?ния.
В случае кругового кольцевого сечепия с внешним радиусом Я
и внутренним Rit имеем:
1 = ^.(^-21,4);
7С
т
;«=
о ' і
F 4
и радиус ядра сечения по формуле [169] получается равным
ГЗ .R2J-.R2
а~іГ™ 4-R
[171]
При Rt = 0,. выражение [171] совпадает с выражением [170]. При очень
узком кольце» когда Ві приближается к Во, радиус ядра сечения
приближается к величине
Л
2
*/\ 1 V7
В случае прямоугольного поперечного се-
чашя (фиг. 224), линия нулевых напряжений
совпадает со стороной сд, когда груз
приложен в точке А, находящейся в расстоянии
-трот центра тяжести (см. стр.~2б5). Точно так же
нулевая линия совпадает со стороной gft
когда груз будет приложен в точке В на
расстоянии -?- от центра тяжести. При
движении груза по линии АВ нейтральная ось
поворачивается вокруг точки д (см. стр. 257),
не пересекая сечения. Поэтому АВ является
одной из сторон ядра сечения. Другие
стороны получим из условий симметрии. Ядро
сечения является поэтому ромбом с диаго-
h Ь ^
налями ,равными — и -^-. До тех пор, пока
О О
точка приложения груза остается внутри этого ромба, нулевая линия
не пересекает сечепия, и не будет перемены знака напряжений.
17* 253
Фиг. 224.
При двутавровом сечении (фиг. 225), крайние положения нулевых
линий, при которых они не пересекают сечения, представятся
сторонами АВ и CD и пунктирными линиями ВС и BD. Соответствующие
положения точки приложения груза могут быть определены по
формуле [К59]. На основании симметрии можно заключить, что эти точки
будут вершинами ромба, заштрихованного на фиг. 225.
Если точка приложения вне-ентренной силы находится вне ядра
сечения, соответствующая нулевая линия напряжений пересекает сечение,
и груз'вызывает не только сжимающие, но также и растягивающие
напряжения. Если материал совсем не обладает способностью
сопротивляться растягивающим напряжениям, то часть поперечного сечения
останется не напряясенной, а остальная часть будет испытывать только
сжимающие напряжения. Возьмем, например, прямоугольное поперечное
Фиг. 225. Фиг. 226. Фиг. 227.
сечение .(фиг. 226) и точку А приложения груза на главной оси у на
-^ А
расстоянии с от края сечения. .Если с меньше, чем -т-, часть
поперечного сечения не будет работать. Рабочая часть сечения найдется из
того условия, что распределение сжимающих усилий по поперечному
сечению следует линейному закону, представленному на чертеже
линией ww, и что равнодействующая этих усилий равна силе Р. Так как
эта равнодействующая должна проходить через центр тяжести
треугольника urns, размер ms рабочей части поперечного сечения должен быть
равен Зс
В случае кругового поперечного сечения (фиг. 227), если
эксцентриситет С А груза больше, чем, —, а материал не может сопротивляться
растягивающим напряжениям, только часть поперечного сечения будет
работать. Пусть линия *ж, перпендикулярная к АС, является границей
этой части. Ее расстояние Ь от точки А может быть найдено из таких
условий: во-первых, сжимающие напряжения пропорциональны
расстоянию у от прямой пщ во-вторых, сумма ежнмающих усилий в рабочей
части сечения равна грузу 1, и в-третьих, момент этих усилий
относительно пи равен моменту РЬ груза Р относительно той же осн.
Обозначив наибольшее сжимающее напряжение через <Jmax> .получим
сжимающее напряжение на некотором расстоянии у от прямой пп
равным
С Ь + с
266
к уравнения для определения Ъ в следующем виде
f-%?-* = * f^tr-Pi,
откуда
I
1 «"
где
— момент инерции рабочей части поперечного сечоппя отноептельно
оси пп, и
—статический момент рабочей части поперечного сечения относительно
той же оси.
Пользуясь формулами [а], можем легко найти положение точен А
при любом положении линии ігп.
Это же уравнение можно также использовать и для других видов
поперечных сечений, если только точка Л находится на одной из
главных осей О- Если -?$уг не- лежит на главной оси, то задача
определения рабочей части сечения становится более сложной 2).
Пользуясь понятием об ядре сечения, можем значительно.упростить
определение наибольших напряжений при изгибе, происходящем не в
главной плоскости.
Пусть например на фиг. 224. тпъ—осевая плоскость балки, в
которой действует изгибающий момент М, и и»— соответствующая
нейтральная ось, которая составляет угол а с плоскостью mm- (см. стр. 1S4).
Обозначив через <гтаі наибольшее напряжение наиболее удаленной точки с
и черев.fe— ее расстояние от нейтральной оси юн, получим, что
напряжение в любой другой точке, находящейся в расстоянии w от пя-, равно
и момент всех усилий, распределенных цо нанесенному сечению,
относительно оси пп, равен
J к к »*'
*) Для случаев круговых поперечных сечений я круговых кольтгевых
сечений, которые имеют важное значение при ррсчете напряжений
в фабричных трубах, имеются таблицы, значительно упрощающие а-ти
расчеты. См* Еех (Keck), „Zeitschr. Hannover. Arok. u Ing. Ver." 1882,
S. 627; си. также „V. D, L" 1902, S* 1321 н статью Г. Дрейера (ф Dreyer)
в „Die Bautechnik", 1935.
2) Некоторые данные для прямоугольного поперечного сечения
можно иайтн в следующих статьях: Эмессери (Engesser), „Zentralblatt d.
Bauv.", 1918» S, 447; К* Поля (1С .РоМ). „Der Eisenbau*, 1918, S. Л1;-
0. Геюселя (О. Eenhzl), .Zentralbl. d. Bauv.", 1918, S. 44=7; Ф. Эслшмх.
(F*K. Eslvng), „Pxoc-of tde Institute of (Лт.. Eng Л 1905—1906, part &
161
где I —момент инериии поперечного сечения относительно оси «я»
Момент* внеттник сил относительно той же оси равенЖбіпа.
Приравнивая его выражению [Ъ\, имеем
JcM sin a
а.
max J
М
Эту формулу можем значительно упростить, пользуясь свойствами
ядра сечения.
Пусть 0 — точка пересечения плоскости mm с ядром сечения
и г — ее расстояние от центра тяжести сечения. Из свойства ядра
сечения следует, что сжимающая сила Р, приложенная в точке О,
вызовет нулевое напряжение в углу с. Следовательно растягивающее
напряжение, возникающее в точке с от изгибающего момента Р*г,
действующего в плоскости щ?, равно по абсолютной величине осевому
р
сжимающему напряжению -=г, или, подставив Р * г вместо Ж в формулу [с],
получим
Р _ Ъ Pr sin g •
nn
откуда
"к sin а 1 г 7,
пп
Подставив это в выражение [с], получим:
'шах = ^Г- [172]
Произведение Fr называется моментом сопротивления поперечного
сечения в плоскости тт. Это определение совпадает с определением,
которое мы доли выше (см. стр. 92), и при изгибе в главной плоскости Fr
становится равным W.
ЗАДАЧИ.
1. Найти ядро сечения нормальной двутавровой балки № 45 по ОСТу.
Высота ее 450 мм, площадь сечения F = 147 см, 1 = 458<s8 см*, г = 17,65 см,
J =1722 см*, г = 3,42'сл. Ширина полок о= 170 мм.
Ответ, Ядро сечения — ромб с диагоналями, равными 27,7 см и
2,75 еж.
2. Найти радиус ядра сечения кругового кольца, если В =* 250 мм
и Et = 200 хле. °
Ответ. Радиус ядра сечения 102,5 мм.
3. Определить ядро сечения равностороннего треугольника.
4. Определить ядро сечения квадратной тонкой трубы.
Решение. Если h — толщина трубы и Ъ — сторона квадратного
поперечного сечения, то
1=1.'яЛ ОД *я = |2я|.
* у 3 ' * у 6
262
Ядро сечения — квадрат с диагоналями
*2
<г=2
h
-b-
5. Найти положение такой точки приложения А внецентрежиого
груза (фиг. 227), когда работает только половина кругового сечения.
Решение. На основании формулы [а] (стр. 2<Ц)
пп
S
= 0,689 В.
пп
58. Вк?центренная нагрузка длинной стойки, действующая
в главной плоскости. В случае стойки, длина которой очень
велика сравнительно с размерами ее поперечного сечения,
например заделанной внизу стойки, показанной на фиг. 228а,
уже нельвя пренебречь отклонением 8 стойки от вертикали
по сравнению с эксцентриситетом е.
Изгибающий момент изменяется вдоль оси стержня. Его
величина в поперечном сечении тп будет Р (8 + « — #)•
Дифференциальное
уравнение упругой линии (ур-ние
[141], стр. 182), будет
следовательно таким х)і
El
Р(* + « —V). М
Пользуясь обозначением
Р
El
7.3
[173]
получим
a*y
{-**«/= #(8-}-в).
Решение этого
уравнения в общем виде:
у = А sinia?4--Bcosua5 +
¦ +« + «. И
®
Фиг. 228.
*) При направлении осей «иг/, принятом на фиг. 228а, вторая
производная -г~ положительна при прогибе, изображенном на фигуре,
и потому пе*ед моментом в правой части ур-ння {141] должен быть
положительный знак.
263
Чтобы удовлетворять условиям на закрепленном-конце:
произвольные постоянные этого общего решения должны
быть:
Л = 0; JB = —(d-f-e),
ir уравнение упругой линии получится таким:
у = (8 -]- е) (1 — cos Щ. ' [с]
Можно показать подстановкой, что это—решение
уравнения [а], удовлетворяющее условиям в закрепленном конце.
Подставив х = 1 в ур-ние [с], получим
(»)—, = *=?(*+•) (1-cosM),
откуда
/" ^W • Ь74>
Подстановкой этого значения в ур-ние [с] получим
следующее уравнение упругой линии:
е (1 — cos Ы)
" У- \oskl ' Г175*
В случае-короткой стойки, величина М—мала, и с
достаточной, точностью можно принять, что в числителе
ур-ния [174]
/ДО
cosM = l ,
а в знаменателе cosKZ = o. Это дает:
или, пользуясь выражением [173], получим:
8=іж- и
Это совпадает с выражением для прогиба консоли,
изгибаемой парой сил Ре, приложенной на свободном конце
(см. задачу 3, стр. 154). Если Ы не мало, деформация уже
264
не пропорциональна грузу Р и возрастает быстрее, чем Р,
как это. видно- на величин прогвба\- вычисленных по
ф-ле [174] и внесенных во вторую строку нижеприведенной
таблицы 3. Из этой таблицы можно видеть, что прогибы
возрастают все быстрее номере того, как величина Ы
приближается к значению —.
ТАБЛИЦА 3.
Деформации, возникающие,ври действии внецеитренной продольной силы.
1 ш
ь
прибл. зн. о
sec kl
Р
од
0,005 е
0,005 с
1,005
0,004
0,5
0Д39е
0,139 е
1Д40
0Д01
1,0
0,851 е
0,840 е
1,867
0,405
1,5
іЗДе
12,8 е
13,2
0,911
тс
т
1
со
со
со
1
При Ы = — получим по формуле [173]
EI ««
рвЖ.** = ^-, [170]
и деформация согласно выражения [174] становится
бесконечно большой.
Это показывает, что сжимающая сила такой величины
вызовет очень большую деформацию и что следует
ожидать напряжений, выходящих за предел текучести. Эта
величина груза Р называется кртттесним грузом (см. н° 36,
часть II) и впредь будет обозначаться Ркр. Тогда
а из ур-ния'[174] и вышеприведенной таблицы 3 видно,
что прогиб зависит главным образом от величины отноше-
Р
вия —р—. При небольших значениях этого отношения е. до
кр
статочной точностью можно применять формулу [d]. Щш
26S
больших значениях этого отношения можно воспользоваться
следующим приближенным выражением *):
Р
Первый множитель правой части представляет прогиб,
определенный по формуле [d] для консоли, %-. ?. когда мы
пренебрегаем влиянием деформаций на величину
изгибающего момента. Второй множитель представляет влияние
деформации на изгибающий момент. Обозначив
Pel* Р
можем написать формулу [178] в таком виде:
S = 30 . —і- . [179]
1 — а
Некоторые числовые величины, полученные по этой
формуле, приведены в третьей строке таблицы 3. Сравнивая
нх с точным решением, данным во второй строке той же
таблицы, убеждаемся в том, что приближенное значение [179]
дает достаточную точность и может быть применяемо на
практике 2).
Наибольший изгибающий момент — в закрепленном конце
стойки и может быть представлен в следующем виде:
ъ Г , е (1 — cosM) 1 _ т7 Г.ЛЛ1
= Р И оовИ ]--Г«вео W. [180]
Ряд значений sec Ы дан в четвертой строке таблицы 3.
Из нее видно, что Мтах возрастает беспредельно при 1\
приближающемся к Р^
Если, вместо точного значения для 8, подставить его
приближенное значение подформуле [179] в выражение [180],
то мы получим
і) Это приближенное решение было дано Дою. Леррп (J*. Perry),
си. „Engineer*, December 10 and 24, 1886.
2) Вывод этого приближенного выражения дан в п? 5, часть П.
268
откуда можно определить наибольший изгибающий момент
Р
при любом значении а=^—.
Существенно отметить, что в рассматриваемом случае
отсутствует пропорциональность между величиной
сжимающей силы и деформацией, которую она производит.
Поэтому метод наложения (стр. 151) нельзя здесь
применить. Любая осевая сила Р вызывает только сжатие стержня,
но когда эта же сила действует совместно с изгибающим
моментом Ре, она вызывает не только сжатие, но- также
дополнительный изгиб, так что общая деформация не
может быть получена простым наложением осевого сжатия
от силы Р на изгиб от момента Ре *).
Если стержень с шарнирными концами сжат двумя
силами Р, приложеннымиА с одинаковым эксцентриситетом е
(фиг. 228Ь), то упругая линия симметрична относительно
середины; касательная посередине высоты—вертикальна,
и каждая половина стержня находится в тех же условиях,
что и стержень на фиг. 228а. Поэтому для этого случая
деформация по середине высоты и критический груз-могут
быть получены из выражений [174] и [176] подстановкой
— I вместо I в эти выражения. Таким путем найдем:
л*
Л^-Peseo-y,. [180']
И
т _
*.~2?- И*!
Что касается подбора сечений для стержпей,
испытывающих внецентренное сжатие, см. п° 38, часть IL
ГЛАВА ДЕВЯТАЯ.
СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ.
59. Совместный изгиб и кручение круглых валов. Ранее
при рассмотрении кручения (см. стр. 64) было
предположено, что круглый вал находится в состоянии простого
скручивания. В технических применениях мы часто
встречаемся с такими случаями, где скручивающий момент
("¦""^-¦•••™^"^"
1) Вопрос о допускаемых напряжениях дрн таких условиях работы
стержней рассмотрен в п° Ь8, яасть И.
267
действует одновременно с изгибающим моментом. Силы,
передающиеся валу шкивом, зубчатым колесом или
маховиком, обыкновенно дают и окручивающую и изгибающую
силы.
Простейший случай такого рода показан на фиг. 229.
Круглый вал закреплен одним концом и нагружен на
другом вертикальной силой Р на расстоянии R от оси. Этот
случай приводится к случаю действия скручивающего
момента Mt == Р • В и поперечной силы Р на свободном конце1).
Скручивающий момент остается постоянным по длине оси,
а изгибающий момент от действия силы Р в любом
поперечном сечении равен
М^ — Р{1 — х). [а]
При рассмотрении наибольшего напряжения,
возникающего в вале, необходимо учесть: 1) скалывающие
напряжения от скручивающего момента Mt9 2) нормальные
напряжения от изгибающего момента И (ф-ла [а]) и 3)
скалывающие напряжения от перерезывающей силы Р. .
Наибольшее напряжение при кручении получается на
окружности вала, и величина его равна
_ 16 Mt .
Наибольшее нормальное напряжение ох от изгиба возни-
"-1). Весом вала и шкива прд .решении зтой задачи мы пренебрегаем.
кает в волокнах, наиболее удаленных ох нейтральной оси,
в закрепленном конце, где изгибающий момент по
абсолютной величине достигает максимума; оно равно:
Напряжение от перереэывающей силы обычно имеет
лишь второстепенное значение» Его наибольшее знамение
получается по нейтральной оси, где нормальное
напряжение от изгиба равно нулю.
Поэтому наибольшее сложное напряжение обыкновенно
получается для точки, где напряжения 1) и 2) достигают
максимума, — в данном случае для элементов, лежащих на
верхней и нижней поверхностях вала в закрепленном конце.
На фиг. 229? дан вид сверху части вала в
закрепленном конце и показана элементарная площадка и
напряжения, действующие на нее.
Главные напряжения, действующие на этот элемент
найдем по формуле [102] (стр. 132):.
max о I о г % t ^ »
или на основании выражений [Ь] и [с]
^ax = 2TF(^+V^+^) =^{М+УМ* + ИД. [182]
Таким же образом при помощи выражения [102']
получим:
*шіа = ^<Ж~УШ+Ш-^М-УЖ+М?). [183]
Следует отметить, что атах будет иметь ту же величину
как и в случае простого изгиба моментом, который
называется эквивалентным изгибающим моментом и равен;
Наибольшее скалывающее напряжение для того же
элемента (фиг. 2295) по формуле [33] (стр. Щ равно:
о —а . 16 Г
W= Тх2 М=^)ЛИЧ-*Л [184]
259
Иногда при рассмотрении условий прочности, т. е.
сопротивления разрушению х), принимают во внимание
наибольшую деформацию. Это дает по формуле [37] (стр. 55);
шах пца ,
ЯИЧ 2 2
Приняв [a = 0,30, полу таем эхо выражение в таком виде:
•«,=-Зж(0'35 м+°'65 ^Ж2+^ ti85i
Для ковких металлов, таких, какие употребляются при
изготовлении валов, теперь общепринято определение
безопасного диаметра валов вести по наибольшим
скалывающим напряжением.
Обозначив допускаемое напряжение при сдвиге М8я
подставив последнее вместо гтах в формулу [184], получим, что
диаметр вала должен быть равен
Это же рассуждение может быть применено и к случаю
пустотелого вала с наружным диаметром d и
внутренним с\. Тогда
*У'~ Ь2<1 ~ 32 [ \ d ) }>
а обозначив —^- = ?г, получаем формулы [182] и [183] для
пустотелого вала в таком виде:
^ = T^rr^^+VM^fW), [1821
°min= ^s(i6_w,) (M+VM* + *lfl. [183']
l) Рассмотрение различных теорий прочности будет дапо ниже
(см. п° 62, часть'И).
270
Наибольшее скалывающее напряжение равно
16
шах
iz№ (1 — П±)
уър+мг\
tie*']
и Л получается равным
Если на вал действует несколько параллельных ноае-
ретаых сил, то при определении необходимого диаметра
вала для каждого поперечного сечения следует взять при
пользовании формулами [186] или [186'] общий
изгибающий момент М и общий скручивающий момент Mt в ©том
месте.
Если поперечные силы, действующие на вал, не
параллельны-, то вызываемые ими изгибающие моменты должны
быть сложены геометрически для получения
равнодействующего изгибающего момента М. Пример такого опре*
деления рассмотрен в нижеприведенной задаче 3,
ЗАДАЧИ.
1. Круглый вал диаметром 60 мм несет шкив диаметром 750 мм
ж весом 240 кг (фиг. 230). Найти наибольшее скалывающее напряжение
в поперечном сечении тп, если горизонтальное натяжение верхней и
нижней ветвей ремня равны соответственно
840 кь и 120 **. W
Решение. Для поперечного сечения т? \ ; jC
jf -- (840 —120) • 37,5 = 27000 %% • см; ~
М = 15* У 2402 + 9бб2" = 14 820 «t * см.
т
ЯГ
¦арг
840м
120кг
Фиг. 230.
}240кг
Фиг. 23L
Тогда по формуле [184]
16 Yl± 8202 + 2700Q2 = 726 кг/см*.
тшах
и.б3
2. Вертикальная тр"уба, изображенная на фиг. 231, подвергается
действию горизонтальной силы Р, равной 100 т и приложенной на рае-
т
стоянии 1 л* от оси трубы. Найти crmax и тшах, еоли длина трубы I ~ 8.0 и
и момент сопротивления поперечного сечения W = 160 см\
F е ш ? н и ?. В закрепленном поперечном сечении мы получаем
lff = 100-100 = 10000 кг-см;
М = 100 • 800 — 80 000 кг; см.
По формуле [182']:
W~ 2-160
(80 000 + У"80 0002 +10 000^ = 502 *»/<аА
По формуле [184']:
*с =
У" 80 0002 +10 00G* = 252 %^см\
а*х 2 • 160
3. Определить необходимый диаметр цилиндрического вала (фиг. 232)*
несущего два одинаковых шкива диа-*
метром 760 мм и весом 240 ж*
каждый. Горизонтальные усилия в
ремне-* для одного шкива и
вертикальные для другого —показаны на,
чертеже. Допускаемое напряжение
Л =420 %%ЫК
S '
Решение. Опасными
сечениями будут сечения тп и т>іпькоторые
240кг подвергаются действию полногоекру-*
чивающего момента и наивысших
внач?ний изгибающего момента.
ф од*) Скручивающий момент в обоих
* ~" сечениях равен
M..JJS&1
%240кг 240нг \
Mt = (720 — 240) • 38 = 18 240 кг • см. ~
Изгибающий момент в сечении inn
(720 + 240 + 240) • 15 =18000 т • см.
Изгибающий момент в сечении %% в горизонтальной плоскости
(720 + 240) -76
4
18 240 АЧ. ел.
Изгибающий момент в том же поперечном сечении в вертикальной
плоскости
240 - 76 (720 + 240 + 240) .15-38
= — 4440 кг - см.
4 76
Полный изглбающий момент в поперечном сечении щп{
, : Величина его больше момента в поперечном сечении wm, и поэтому
в выражение [186] следует подставить эту величину вместе с paueV
определенным скручивающим моментом Ж * Отсюда, находим
d = 6,82 см.
если допу-
4. Определить диаметр вала, показанного на фиг. 230,
скаемое напряжение на сдвиг Яа = 420 жі/слА
5. Определить внешний диаметр пустотелого вала, если й = 420 кг/сла,
d± : d = 1: 3, а все- прочие размеры и действующие силы таковы, каа
доказано на фиг. 232.
60. Совместный изгиб н кручение прямоугольных и эллиптических валов.
В общем случае нагрузка вала может состоять из скручивающих мом?нтой
относительно оси вала и сил перпендикулярных этой ося, но не всегда
находящихся в одной и той же осевой плоскости.
Каждая сила может быть разложена на составляющие вдоль каждой
главной оси у и & (фит. 23d), и эти составляющие дадут соответственно
изгибающие моменты Ж% и Ж, которые
действуют в главных плоскостях ху и хг.
Тогда задача сведется к тому, чтобы
найти наибольшее по абсолютной величине
главное нормальное напряжение smax, о^
н наибольшее скалывающее напряжение ттах
которые возникают при совместном действии
этих изгибающих моментов и скручивающего .
момента Ж. Ц_.
В случае прямоугольного поперечного
сечения (фиг. 2оЗ) при Ъ^> с наибольшее
скалывающее напряжение от действия одного
только скручивающего момента получается
в средних точках а длинных сторон Ъ и равно
(формула [62], стр. 73)
М.
а. Ьс1
[а]
Фиг. 133.
где а — числовой коэффициент, зависящий от отношения Ь : с (см.
таблицу 2 на стр. 74).
Простейшим случаем определения наибольших главных напряжений
является случай» когда Ж = 0, т. е. изгиб происходит только в
плоскости sex. В этом случае наибольшее напряжение будет в точках о, где
наибольшее скалывающее напряжение- от скручивания (формула [а]у
налагается на наибольшее нормальное напряжение от изгиба:
Ж Ш
I tfjrnax W be3
Пользуясь формулами [102] и [102'], получаем:
2flf,
13 Тдагошелио — Сопротивление материалов, ч. I.
[1871
2іЗ
н
т =
шах
а — (т .
max mm
2 ~~
2ТГ
*, )•+(#)•
[188]
Если действует только изгибающий'момент в плоскости^ (If =0),
то напряжение, возникающее от скручивания в точках а, нужно сравнить
с главным напряжением в точках а. Напряжение от изгиба в этих
точках по абсолютной величине равно
М
—.-
W
6М
Скалывающее напряжение от скручивания в тех же точках равно
М.
-Ті =
а^Ьс
2 з
М
где ах — числовой коэффициент, зависящий от отношения Ъ : с.
Некоторые значения этого коэффициента приведены ниже, в таблице 4 х).
ТАБЛИЦА 4.
Значение коэффициента av
Ъ/с
«і
1
0,208
1,5
0^270
2
0,309
3
0,354
4
' 0,379
6
0,402
со
0,448
Главные напряжения и наибольшее скалывающее напряжение в
точке d по формулам [102] и [102'] равны:
сттах —
тіп
"шах
2FK
*-?(Ф№У
ТііУЬН
Зас
[139]
[190]
Если действуют оба изгибающие момента Ж н M%t то главные
напряжения и наибольшее скалывающее напряжение в точках а
получатся по формулам [187] и [188], а для точек d — по формулам [189] и
[190]. Напряжениями от перерезывающих сил при этом рассмотрении мы
пренебрегли.
В дополнение к напряжениям в этих точках обычно определяют
главное напряжение в углах сечения (см. стр, 194) по формуле:
К)
шах
[19Ц
*) См. Ж, Вебвр, см. выноску выше на стр. 77. См. также
справочную хснижку .Хютте", русский перевод с 25-го немецкого издания, т. I,
стр. 635.
274
Это может оказаться наиболее неблагоприятным напряжением,
если Ж — мало.
Помощью фопмул1) [187] —[191] и принятых по техническим уело
виям значений допускаемых напряжений Яъ ж В легко определить
безопасные размеры вала прямоугольного поперечного сечения,
подвигающегося совместному действию изгиба и кручения.
Для валов эллиптического поперечною сечения (фиг. 234) наибвльжее
скалывающее напряжение от скручивающего момента М жолучаетея
р точках а и равно, согласно формуле [67] (стр. 76):
М
Если Ж" =0, наибольшее главное напряжение будет в точках а.
Учитывая совместное действие скалывающего напряжения [с] от
скручивания с нормальным напряжением
М.
V
W.
от изгиба и заметив, что
у
W =
33
получим следующие выражения для главных
напряжений:
max __
лііп
.К
у
2TF,
у
3lY
+
I М, V
2W.
у
Фиг. 234.
Когда Ж^ не равно нулю, то нужно также рассмотреть напряжения
в точках й. Для этих точек получаем:
[194]
[W5]
!) Определение тех точек периметра, в которых главное напряжение
имеет наибольшее значение — очень сложно, и поэтому обыкновенно
принимают, что действительное максимальное напряжение не очень
сильно отличается от напряжения, вычисленного так, как указано здесь*
18* 275
Обычно размеры вала определяют на основании выражений [192] —.
[195], не прибегая к сложным выкладкам, необходимым для нахождения
действительного максимума напряжения, в некоторой точке на
окружности эллиптического поперечного сечения.
ЗАДАЧИ.
1. Стержень квадратного поперечного сечения со стороной равной
6 заделан своим нижним конпом и нагружен в верхнем конце
горизонтальной силой г.— 50 кг, как показано на фиг. 235. Найти размер
стороны квадрата Ь, если И9 = 420кі}сяР.
Решение. Опасным поперечным' сечением является сечение в
закрепленном конце, где М% = 50 • 25 =1250 к\ * см- и Ж = 50 • 50 =
= 2600 кг ¦ ем. На основании формулы [188] находим
W —
у
if.
G
¦^o/"25002+(w1250T'
откуда
Ь = 2,84 см.
2. Решить предыдущую задачу, приняв, что горизонтальная еилаР,
приложенная на расстоянии 250 мм от оси стержня, наклонена под
углом 45?-к сторонам стержня.
Ответ. Ъ = 2,68-см.
3. Горизонтальный
прямоугольный стержень с закрепленными ісои-
Фпг. 235.
цами нагружен по середине внсц?нтренно приложенной вертикальной
силой Р (фиг. 238). Найти наибольшее скалывающее напряжение .в
точках а и dt если Р = 50 их, е = 250 мм, 1 = Ы0мм, Ь = Ь0 мм п с —25*t«.
Ре-пген-ие. В закрепленных концах
,г Ре 50-25 .„
Mt = — = —— = 62о кг. ем;
,, Рі 50-50 О1ог
Mt = —- — —— = 312,5 %\ • см.
270
•:-Скрывающее напряжение в точках, о по формуле [а] равно
625
Скалывающим напряжением от перерезывающей силы при этом решенин
мы пренебрегаем.
В точках d по формуле [190] получаем
*¦»" = T^W 312'5'2 + (з.0,?09>2,5 625)2 = т>± */"*
4. Решить предыдущую задачу при эллиптическом поперечном,
сечении стержня (фиг. 234).
61. Коленчатые валы» Одноколенчатый вал (фиг, 237)
представляет нриыер одновременного действия изгиба и
Фиг. 237.
кручения. Для упрощения допустим: во-первых, что вал
свободно оперт в средних поперечных сечениях коренных
шеек вала (точки т и п), и во-вторых, что его моясяо
рассматривать как показанный на чертеже жирными линиям
стержень, размеры поперечного сечения которого малы по
сравнению с длинами г, е и f1).
Мы здесь рассмотрим действие одной только сшш—
давления шатуна на кривошип. Эта сила действует в
плоскости, перпендикулярной оси х Sana, и может быть
разложена на две составляющие: Р—в плоскости колена и
Лт—в плоскости, перпендикулярной к колену (фиг. 238).
Рассмотрим напряжения и деформации, вызываемые
каждой составляющей отдельно,
*¦) Более детальное рассмотрение деформаций вала с одним холеноы
см. статью автора в .Trans. Am. Soc. Mech. Eng.", Vol. 44, p. 653:
247
Сила Р вызывает изгиб во всех частях колена (фиг. 239а).
Эпюра изгибающих моментов для коренных шеек вала и
шейки кривошипа представится треугольником АгВхС^
полученным как для просто опертой балки длиной 2 =
= 2e-j-/i несущей нагрузку по середине пролета. По всей
длине щек вала нагибающий момент остается постоянным *),
Ре
и его величина представляется ординатой иг» = ш1«1 = —•
По изгибающим моментам могут быть вычислены
напряжения при помощи
обычных формул
изгиба балок 2). В щеках
* вала напряжения от
изгиба должны быть
г сложены с осевыми
напряжениями,
вызываемыми осевой силой
При определении
прогибов коленчатого
вала применим способ
фиктивной балки.
Допустив, что жесткость
на изгиб коренных
шеек вала и шейки
кривошипа одинакова
и равна EIt угол
наклона касательной и
прогиб для любого сечения от одного только изгиба
коренных шеек и шейки кривошипа получим делением на EI
перерезывающей силы и изгибающего момента в этом
сечении для фиктивной балки с нагрузкой A1C1BV
*) Влиянием осевой силы на изгибающий момент можно пренебречь»
2) Местные напряжения (концентрация напряжений) во входящих
углах и выточках рассмотрены в п° 60 часть II.
Фиг. 239.
278
Щеки вала испытывают постоянный изгибающий момент,
а потому они изгибаются по дуге круга. Угловое
перемещение одного конца щеки относительно другого равно
Per
2Е1г>
где Шг—жесткость на изгиб плеча в плоскости колена.
Добавочный прогиб колена вала от изгиба его щек получим
по изгибающим моментам, возникающим в фиктивной балке
от сосредоточенных грузов
как показано на фиг. 2396.
Поэтому для среднего сечения С шейки кривошипа
общий прогиб от действия силы Р равен
Р(2е+Л8 3W
~ 48 ?і + 2 Ёіі
Что касается составляющей N9 перпендикулярной
к плоскости колена, то ее действие на коленчатый вал
изображено схемой фиг. 240.
По симметрии реакция в каждом конце будет равна
Nr 1
скручивающему моменту Mt — -^- и силе — N. Эти силы,
2
/
С
Фиг. 240-
В X
//
2
очевидно, вызывают совместный изгиб и крученяе в шейках
и щеках вала. Скручивающий момент, действующий на
Nr „, Ne
шейку вала, равен Mt =
а на щеку М/ ="^-.
а
Изгибающий момент в каждой части колена может быть
определен обычным путем, а напряжения от совместного
изгиба и кручения могут быть затем найдены, как
показано в предыдущем п°.
Прогиб среднего сечения С в этом случае составится
из следующих четырех частей:
279
1) прогиба от изгиба коренных шеек и шеек кривошипа
2) прогиба от скручивания щек вала
й2
где
Ner
2$h<PG
—угол; скручивания щеки, которую мы предполагаем
прямоугольного поперечного сечения (см. ур-нке [63], стр. 74);
3) прогиба от изгиба щеки в плоскости параллельной
плоскости уз
о3 =
2 ' 3 EI*
где Е12—жесткость щеки на изгиб в этой плоскости;
4) прогиба от скручивания коренных шеек вала
Nr*e
о
4 2 gi;
где 1,—полярный момент инерции поперечного сечения
коренной шейки.
Полный прогиб средней точки С от действия силы N
равен поэтому:
°~ AHJEI ~r2$U*G ' QJiI2 + 2GlJ
Рассмотрим теперь скручивание колена под действием
скручивающего момента *Жі9 приложенного по середнне
коренных шеек вала в точках Л и -В (фиг. 241). Шейки вала
я шейка кривошипа будут в этом случае находиться в
условиях простого скручивания, а щеки—в условиях чистого
изгиба. Угол .скручивания конца JB относительно конца А
состоит из двух частей:
1) угла от скручивания коренных шеек вала и шейки
кривошипа; этот угол при предположении, что обе шейки
имеют одинаковый диаметр, равен
*--¦(*/,
280
2) угла от изгиба щек
_ 2 Mtr
*- Eh
Общий угол скручивания равен поэтому:
_{2e + f)Mt , 2Mtr
Определение этого угла скручивания имеет
существенное значение при исследовании колебаний кручения
коленчатых валов.
В предыдущем решении мы пренебрегли реакциями
подшипников (см. стр. 277), и поэтому оно представляет
только грубое приближение. Для более точного
определения угла скручивания обычно применяются формулы,
полученные непосредственно из испытаний валов *)•
/-г—'
Фиг. 34L
Соединяя вместе случаи, представленные-на фигурах 239,
240 и 241, получим общее выражение действия изгиба и
кручения на вал с одним коленом.
Для маогоколенчатого вала на нескольких подшипниках
задача определения напряжений становится очень сложной,
и решение может быть получено только путем некоторых
допущений относительно условий на опорах.
Например, приняв, что вал просто оперт посередине
подшипников, мы придем к задаче, подобной задаче
неразрезной балки й).
Решения, основанные на подобных допущениях,
представляют только грубые приближения, и дальнейшее уточ-
*) См. статью Ф, Льюиса (F. М. Lewis), „Trane. Soc. of Naval
Architects and Marine Engineers*, Vol. 33, 1925, p. 109, New York. См. также
Зеелъжш {Seehnann), #V. D. L*, Bd 69, 1925, S. 601; Ф. 3acfr(F. Sass\
„Maschinenbau", Bd. 4 1925, S. 1223; н Е. Метр (Ж Meyer), ,V. I>. 1%
Bd. 53, 1909, S. 295.
a) См. статью автора в ,Дт. Soc. Mech. Engineers Transactions",
Vol. 35,1923, p. 449. См. также К. Биецено {С. В. Внгепо). „De Ingeniextf\
1927 (Голландия), и А. Гессн&р (А« Gessner), Mefarfach gelagerte, abgesetzte
und gekropfte Kurbelwellen, Julias Springer, Berlin,
231
некие может быть получено соединенней теоретических
исследований с опытами, при которых можно было бы
изучить такие факторы, как влияние зазоров в
подшипниках и концентрацию местных напряжений.
62. Кручение двутавровых балон и швеллеров. При нашем предыдущем
рассмотрении кручения двутавровых и корытных балок (см. стр. 75)
было допущено, что скручивающий момент приложен в концах стержня
н что все поперечные сечения могут совершенно свободно искривляться
Имеются однако случаи, где условия таковы, что одно или несколько*
поперечных сечений остаются плоскими, и возникает вопрос о том как
влияет подобное устранение возможности искривления на угод
скручивания и на распределение напряжений.
Исследования показывают *), что при таких поперечных сечениях
кате эллипс или прямоугольник, подобное устранение возможности
искривления оказывает на угол скручивания такое влияние, которым
можно пренебречь, если только размеры поперечных сечепий малы
по сравнению с длиной стержня. При двутавровых и корытных балках
устранение возможности искривления поперечных сечений при кручении
' Фиг. 242.
сопровождается изгиоом полок и может оказать значительное влияние
на угол скручивания, в зависимости от жесткости полок.
Простейшим случаем такого явления может служить двутавровая
.балка, которая скручивается парой сил, приложенной по середине
пролета, и оперта 2) своими концами (фиг. 242). По условиям симметрии
поперечное сечение тп должно оставаться плоским при кручении
а следовательно соответственный поворот этого поперечного сечения
относительно концевых сечений сопровождается изгибом полок.
Приложенный на конце е^чивающий момент уравновешивается
в любом поперечном сечении частично' скалывающими напряжениями
от скручивания и частично скалывающими напряжениями ог изгиба
ПОЛОК J.
Фиг. 243 представляет половину балки, показанной на фиг. 242
Среднее сечение ть остается плоским по условиям симметрии, и мы
йаЛ Сі!?* 4- Феппл? $А' F6ppl)' «SitzimgBberichte d. Bayerisehen. Aka-
ь г< п е London Mathematical Soc, Ser. 2", Vol 20, 1921, p. 389
*a*,L ЛП°РЫ лРлнимаютея такими, что концы балки не могут поворачи-
ваться_относитель,но продольной оси, но могут свободно искривляться.
<5 Л ШТЬ1? aBJ°La в ,Zt8chr. L Math. u. РпувЛ Bd. 58, 1910,
I $L?Z'w*?*? %rfep(K. Guber), Dissertation, Mtochen, 1922, и
Л Вебер (G. Weber), „Ztschr. t angro. Math, *. Meeh/\Bd. 6, 1926, 8.8b
282
можем рассматривать, что балка закреплена по этому сечению, а
скручивающий момент приложен к другому конпу балки.
Пусть <р—угол скручивания для некоторого поперечного с?ч?ння
балки. Тогда
dp
dx
= 9
—угол скручивания на единитту длины балки. Та часть скручуающего
момента М^ которая уравновешивается скалывающими напряжениями;
возникающими от действия скручивающего момента» определится кв
формуле [65] (см. стр. 75):
Ж;=С6, [а]
где С—жесткость па кручение стержня (см. стр. 78).
Чтобы определить ту часть Mt скручивающего момента, которая
уравновешивается скалывающими усилиями, возникающими в волках
от изгиба, нам придется рассмотреть изгиб полок (фиг. 243с). Обозначав
§f.„,„„„„„„„„,„„,.,,„„„„% .e
/*'&ШШ
I
©
х
Фиг. 243.
чепез h расотояние^ между центрами тяжести полок (фиг. 243Ь), получим
прогиб в любом поперечном сечении верхней полки равным
Hi дифференцируя, находим:
"&~~ 2 * dai»
2
К_
2
dzb
м
Теперь, обозначив через В жесткость на изгиб одной полки в
плоскости хг и заметив, что ось s имеет положительное направление вверх
(фиг. 243с}, по формуле [142] (ств. 1&3) получим для перерезывающей
силы, появляющейся при изгибе в полках, следующее выражение:
Q
ш
dec
da?
Dh
2
<P0
dx2
Приняв направление Q положительным (фиг. 243c), мы пояучим
м
Ml = - Qh = —
dx*
И
¦w
S83
и полный скручивающий момент
В нашем случае момент М постоянен по длине I балки, и общее
решение ур-ния [f] полусна в таком виде:
ir I cosh—^—
\ cosh —
где
Так как жесткость на изгиб В и жесткость на кпучени? С — обо
измеряются одними и теми же единицами (кі-с*3), то выражение [к]
показывает, что а имеет линейную размерность и зависит от
соотношения размеров балки.
Зная 9, можем определить части Мгі и ^'полного скручивающею
момента М для любого поперечного сечения по формулам [а] и [с}.
Для закрепленного сечения х = 0 и угол ? = 0, и мы получим
щ> формуле-[а]
M't = (k
Итак в этой точке весь скручивающий момент уравновешивается
моментом скалывающих усилий, возникающих от изгиба полок силой Q,
к мы получаем
М
«--jiV
Для другого конца х ~ \ и по формуле [д]
Если длина балки велика по. сравнению с разменами иопв'печпог»
селения, то I—велико по сравнению с а, н второй член в скобках
формулы [Ц получается таким, что им можно пренебречь, а следова-
тельно 6 приближается к значению -^г, т. с полный скручивающий
момент Mf уравновешивается скалывающими напряжениями от
скручивания, и величина этих напряжений может быть определена по
формуле [66], стр. 75..
Выражение Щ дает перерезывающую силу в полках, и на основании
его получаем изгибающий момент в полках равным
ъ, Dh die
284
или, подставив выражение [д] вместо 0 н пользуясь обозначением Щ,
получим
М =
I)h
аС
sinh
I
х
а
sirih
cosh —
а
а 1Г
1—се
а
cosh
а
Для изгибающего момента в закрепленном конце находим
*ш*=-г мі № і -
w
Когда I в несколько раз больше чем а, то tgh
а
к единице, и мы можем принять:
V-»-
приближается
.«У .
Ашв
[OTJ
т. е. наибольший изгибающий момент в
полках тот же, что и для консоли длиною а,
М.
нагруженной на конце силой —~ *
Для очень короткой балки 2—мало по
сравнению с a, tgh — приближается в
300 -
а
•—, н мы получаем по формуле [Ц.
о
-*
ю
^шах =
М
J
/4;
1
Фиг. 244.
Возьмем, например, двутавровую балку >& 30 по ОСТу> с площадью
поперечного сечения 63,61 спК Заменяя поперечное сечение
равновеликим поперечным сечением, показанным на фиг. 244, состоящим из
трех прямоугольников, имеющих те же самые площади поперечных
сечений, как полки н стенки двутавра, и воспользовавшись формулой [65]
(стр, 75), получим:
С = 4-(27Д -1,053 + 2 • 12,1.1,45») G = 35,0 ?.
о
Величину D получим *), взяв половину момента инерции сечения
нормального профиля двутавра относительно вертикальной главной оси
н умножив ее на модуль упругости 23. Тогда I) — — ¦З?6і?==183і?,нпо
выражению [Л] найдем
¦='/?=» УЧЩг=^
М
Итак, если балка нагружена, как показано на фиг. 242, то
наибольший изгибающий момент в полках но выражению [т] приблизительно
*) Здесь мы пренебрегаем моментом инерции поперечного сечения
стенки.
285
в" 2,6 раза больше скручивающего момента Mt, если только балка
достаточно длинна, чтобы можно было принять tgh —— приблизительно pan-
О/
ным 1. Например, при— = 2,1 приближается к 5,2A, tgh—= 0,СЗ
и ошибка вышеприведенного определения составляет 4%-
Чтобы определить угол скручивания <р> воспользуемся формулой [д].
Вспомнив, что 0 = -=-*-, интегрируя ур-ние [д] и подобрав произвольную
постоянную интегрирования так, чтобы <р —О при # = 0, получим:
a smb.
9 ~ с1 ^ г a tgh "о" '* ^
V cosh.
Подставив х = Z в это уравнение, получим угол скручивания на кон да
Второй член в скобках представляет влияние изгиба полок на угол
скручивания.
Для длинных балок tgh — ?& 1, и выражение [д\ становится
равным:
(*)*=* «if (*-*>• И
Влияние изгиба полок на угол скручивания таким образом
эквивалентно уменьшению длины I на величину а.
Способ, изложенный выше, может быть применен также, когда
скручивающий момент меняется па длнн? балки при подстановке
в 7р-ни© If] вместо Ж" его выражения в функции от х.
Все полученные выше- для двутавровой балки формулы можно
применять также к балкам корытного сечения.
63. Винтовая пружина с большим шагом витка. Ранее нами были
рассмотрены винтовые пружины (см, стр. 78) при предположении, что угол a
между витком н плоскостью, перпендикулярной к оси винтовой линии.
очень мал. Пренебрегая этим углом, мы привели деформацию пружины
только к скручиванию проволоки пружины.
В пружинах с большим шагом витка угол а уже не мал, и
деформация, возникающая от действия осевых сил Р, состоит и кз скручу
ванкя и из изгиба (фиг. 246).
В ллобой точке А касательная к осевой винтовой линии пружины
не перпендикулярна к силе Р, и потому эта сила вызывает в
поперечном сечении Л проволоки изгибающий момент относительно оси nt
и скручивающий момент. Силу Р разложим на две составляющие:
Р cos а и Р sin a( соответственно перпендикулярную и параллельную
к касательной в точке Л.
В этом поперечном сечении составляющая Р cos a вызывает
скручивающий момент
М =РВ cos a, [a]
28G
где R—радн-vc винтовой лпниіг, а составляющая Р sin а вызывает
изгибающий момент
М = PR sin а. [Ь]
Наибольшее главное нормальное напряжение получим тогда но
формуле [182] (сер. 26У):
16 PR
amax re d?
(1-f Sin a),
[1ОД
где d — диаметр проволоки.
Наибольшее . скалывающее напряжение по
формуле [18і] равно:
16РЯ
max
ъФ
Из этого видно, что наибольшее
скалывающее напряжение такою же,
как и в случае туго скрученной
винтовой пружины (см. стр. fli).
Рассмотрим теперь деформацию
пружины при
предположении, что она закреплена
в верхнем конце и
нагружена осевым грузом* Р в
нижнем контте. Элемент ds
между двумя смежными
бесконечно близкими
сечениями у точки А
скручивается моментом Mt на угол
, PR cos а ,
Др = —о}—я*- М
toc&sct
Вследствие этого
скручивания нижняя часть
пружины поворачивается относнтель,нсг"»аса-
тельной в точке А как раз на этот зле
угол с(<р* Этот бесконечно малый поворот
представлен на фигуре вектором п,
направленном по касательной, и взят такого
направления, что между направденне и
вектора и направлением вращения
получается то же самое соотношение, как между
перемещением и вращением винта с
правой нарезкой.
Бесконечно малый поворот м может
быть разложен на две составляющие:
1) поворот п соз а относительно горизонтальной оси и 2) поворот п sin a
относительно вертикальной оси. Этот последний поворот не вызывает
никакого понижения конца В пружины, и поэтому нет необходимости
его здесь рассматривать.
Опускание конца В пружины вследствие поворота п cos а следует
тому же закону, что и для туго скрученной пружины (см- стр. ЬО),
Вследствие этого вращения точка В переместится в точку Вх (фиг. 24бс)
и мы имеем:
Фиг, 245.
JBBt = AB ncos о.
287
Вертикальная составляющая этого перемещения
В
В?* = BBt • ¦ = Вп cos cu ы\
лв т
Общее опускание конца В от скручивания равно сумме элемент-ар
ных деформаций, представленных формулой [d\t т, ?.
с
lL = / Вп cos a, [ej
В
где cvMiinpouanne берется по всей длине пружины от ее нижнего
конна В до верхнего закрепленного конпа С.
Деформация от изгиба может быть определена таким же порядком.
Угловая дефсрмация от изгиба элемента ds моментом Ж (см. формулу [Ь])
равна:
.. PR sin а _
*Рі = -ЩГ^8' ЛП
Cooтвeтcтвvюпшй поворот нижней части пружины представлен на
фигуре вектором %.
Таким же nvT6M, как выше, можно показать, что только его гори-*
зонталъная составляющая п^ sin а отражается на вертикальном
перемещении конца В и что величина этого перемещения равна:
с
$2 = / Впх віп а. \&\
В
Складывая прогибы \і\ н \д], получим полное опускание конца Ві
с
Ь = %і -f- $а = В / (« cos a -J- nA fiin а).
^одставляя выражение [с] «вместо п и выражение [/] вместо пь
полечим
;2 « оіт»2
или, заметив, что выражение в скобках—постоянная величина, и
обозначив длину проволоки пружины через I, имеем:
г==рвп
Формулы [196], [197] и [198] дают нам полное решение задачи для
винтовой пружины с большим шагом витка, находящейся под действием
осевой силы. Таким же образом Ц могут быть исследованы совместные
кручение и изгибы .винтовых пружин.
х) Теория винтовых пружин была изложена Сен-Венаном (Saint
Ymani\ ом. „Comptes xen&as..." vol. 17, 1843, т>. 1020. Ряд частных
случаев разобран Томсоном и Тетом (Thompson and Tait), Nat. Phil. 2 part,
p. 13;:.; Дою. JJteppu {J. Pern/), Applied Mechanics, New-York 1907, p. '613,
и Т. Шщ>ф (6\ W.lSctearsfy .Engineering", Vol. 913, 912, p. 206.
288
ГЛАВА ДЕСЯТАЯ.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ.
64. Потенциальная энергий упругой деформации растяжения.
При рассмотрении простого растяжения стержня (фиг. 1)
мы видели, что при удлинении под действием постепенно
.возрастающей силы стержень производит работу, и что эта
работа превращается либо частично, либо полностью в
потенциальную энергию деформации. Если деформация остается
в пределах упругости, совершенная внешними силами
работа будет полностью превращаться в потенциальную
энергию и может быть получена
обратно при постепенном
разгружении
деформированного стержня,
Если конечная величина
силы равна Р и
соответствующее удлинение равно
8, то диаграмма
растяжения будет такой, как
показано на фиг. 246, где
абсциссы представляют
удлинения, а
ординаты—соответствующие силы. Величина
Рг представляет
промежуточное значение силы, Ъг —
удлинение от ее действия. Приращение <іРг силы вызывает
приращение dbx удлинения. Работа, выполненная силой
при этом удлинении, равна Р^ЬХ и представлена на
чертеже заштрихованной площадью. Если принять во
внимание приращение силы Рг при удлинении, то выполненная
работа представится площадью трапеции abed.
Полная работа внешних сил при нарастании силы от О
до Р равна сумме таких элементарных площадок и
представится площадью треугольника О А В. Это представляет
полную энергию, накопленную стержнем при.,
деформации, — U. Поэтому
Фиг. 246.
/
и=
2
[199]
На основании выражения [1] (см. стр. 2) мы получим
19 Тимошенко — Сопротивление материалов, ч. I. 289
следующие два выражения для потенциальной энергии
призматического стержня:
¦ U=^-. [201]
Первое из них дает энергию деформации в зависимости
от силы Р, а второе — ту же энергию в зависимости от
удлинения 8. Для стержня определенных размеров из
материала, имеющего определенный модуль упругости,
потенциальная энергия деформации вполне определяется
величиной силы Р или величиной удлинения 8.
При практических применениях очень часто необходимо
бывает знать потенциальную энергию деформации,
отнесенную к единице объема, т. е. так называемую удельную
работу деформации. Она равна, в соответствии с
выражениями [200] И [201]:
ИЛИ
*. = 4-> [201']
где о = -^—растягивающее напряжение и е = — —
относительное удлинение.
Наибольшее значение потенциальной энергии на единицу
объема, которое может быть накоплено- в стержне без
остаточной деформации1), найдется подстановкой предела
упругости материала вместо о в формулу [200'].
Сталь, имеющая предел упругости равный 1100 т/см2 и
модуль упругости JS= 2100000 кг/&*а,дает а, = 1,05кг . см/см?;
разина с модулем упругости равным і?=і0,5 кг/см? и.пре-
/ 212
делом упругости—21 кг/алР, дает gl = ———-=21кг • см\см\
z 2 * 10,5 **
Иногда интересно знать наибольшую величину az
потенциальной энергии на единицу веса материала, которая
может быть накоплена без появления остаточной
деформации. Эта величина определяется по формуле [200']
подстановкой, предела упругости вместо а и делением ае на вес
і) Эта величина называется иногда модулем эластичности (modulus
of resilience).
290
единицы объема материала. Некоторые числовые
результаты, полученные таким путем, приведены в
нижеследующей таблице 5,
ТАБЛИЦА 5.
Значения потенциальной энергии деформации 'на единицу объема и на
единицу веса.
Материал
Литая сталь . .
Инструментальная сталь . . .
flv6
Резина ......
'•іі
Удельный
вес
7,8
7,8
8,5
1.0
0,93
Е
кг/сч2
2100000
2100 000
1120 000
100 000
10,5
I960
8 400
280
280
21
а
е
т • си
см$
0,915
16,8
0,035
0,392
21,0
а
%% • €.4
кг
117
2160
4Д
3S2
¦ 22600
Из таблицы 5 усматриваем, что величина потенциальной
энергии, которая может быть накоплена куском -резины
данного веса, примерно в десять раз больше, чем энергия
для куска инструментальной стали такого же веса, и
примерно в двести раз больше энергии, накапливаемой куском
такого же веса обыкновенной литой стали.
ЗАДАЧИ.
1. Призматический стальной стержень, длиною 250 мм и площадью
25 см\ сжимается силой Р равной 1800 кг. Найти наибольшее значение
потенциальной энергии деформации.
Ответ.
U = 0,76 кг. ем.
2. Определить величину потенпиальной энергии в предыдущей
задаче, если площадь поперечного сечения равна 12,5 см2 вместо 25 ем\
Ответ.
U = 1,52 кг • смт
3. Найти величину потенциальной энергии деформации
вертикального призматического стальною стержня испытывающего деформацию
под действием собственного веса, если длина стержня .-.0 м и площадь
его поперечного сечения 6,5 смК Вес стали принять равным 7850 кг/ж3.
Ответ.
J7=0,644 кг-еле.
4. Определить величину потенпиальной энергии в предыдущей
задаче, если, кпоме его собственною веса, на стержень действует осевая
сила А равная 450 кг и приложенная к концу стержня.
Ответ.
U = 30,5 кг ¦ см*
19* 291
5. Найти величину потенциальной энергии стального стержня,
имеющего #орму тела равного сопротивления, о котором шла речь
в»задаче 2, стр. 18. '
Решение. Потенциальная энергия на 1 с*3 равна, согласно
формуле 1200']:
4002 we*
W= 2.2100 0иО,==0>0381^Г-?
объем стержня равен
6160 = 0,7843 Л
7850
Отсюда
U =» 0,0381 • 0,7843 • 100» = 29 900 »і • с*.
6. Проверить решение задачи, показанной на фиг. 15 (стр. 19) для
случая, при котором все стержни имеют одинаковое поперечное сечение
и одинаковый модуль упругости, плиравняв потенциальную энергию
деформации системы работе, совершаемой силой Р.
Решение. Если X—усилие вертикального стержня, то его
удлинение равно:
EF
и работа, выполненная силой Р, равна:
2 EF
Приравняв ее потенциальной энергии деформации, получаем:
JLp Xl - 'ХЧ ? (Хсозад2?
2 EF 2EF + 2EFcosa '
откуда
1 + 2 COS3 а '
что совпадает о предыдущим решением.
7. Проверить задачу 2, стр. 9f показав, что работа внешней силы
равна потен і.иальной энергии деформапии обоих стержней.
8 Стальной стержень, длиной 750 мм и площадью сечения 6 см%
удлинился на 0,5 мм. Найти величину энергии деформации.
Ответ. По формуле [201]
гт 2100000-6-0,052 л "
V = гг-г^—- = 210 к* • ем,
2'7о
9- Сравнить величину потенциальной энергии в двух круглых
стержнях, показанных на фиг. 247а и Ь, в предположении равномерного
распределения напряжений по поперечным сечениям обоих стержней.
Решение. Потенциальная энергия деформации призматического
стержня равна
' ТЧ
2EF'
292
Энергия деформации стержня, имеющего выточку, равна
2.EF
2Я « AF
16
Р^
2JSJ?"
Поэтому
г/1;Тг = 7:16,
^_
/
®
При данном наибольшем нанря-
женин, количество потенциальной
энергии, накопленной стержнем,
имеющим выточку, меньше, чем
стержнем постоянной толщины. Чтобы
довести растягивающее напряжение
до опасного предела в стержне,
показанном на фиг. 24:7с, имеющем очень
узкую выточку и большой внешний
диаметр, потребуется очень небольшое количество работы, хотя бы
диаметр в наиболее ослабленном сечении и равнялся диаметру
цилиндрического стержня (фиг. 247с).
65. Растяжение, вызванное ударом. Простое
приспособление для получения растяжения от удара изображено на
фиг. 248. Груз Q падает с высоты h на выступ тп и при
ударе производит растяжение
вертикального стержня ЛВ, закрепленного своим
верхним концом. Если масса стержня и
выступа малы сравнительно с массой
падающего тела, то удовлетворительное
приближенное решение получится, если
пренебречь массой стержня и принять, что
здесь нет потерь энергии при ударе.
После удара о, выступ тп тело
продолжает двигаться вниз, вызывая растяжение
стержпя. Из-за сопротивления стержня
скорость движущегося тела уменьшается
до тех пор, пока не станет равной нулю.
В этот момент удлинение стержня и
соответствующие растягивающие напряжения достигают
максимума, и их величины определяются при допущении, что
вся работа, выполненная грузом Qy превратилась в энергию
деформации стержня 1).
Бели через Ь обозначить наибольшее удлинение, то
работа, совершенная грузом Q, будет равна Q (Ь +8)-
!) В действительности часть энергии рассеивается и
действительное удлинение будет всегда меньше, чем определенное при принятом
нами допущении.
29?
Потенциальная энергия деформации стержня получится по
формуле [2011- Т.огда уравнение для определения 8 будет:
Я&+Ъ) = ^-Ъ\ [а]
откуда
где
— статическое удлинение стержня от груза 6 и v =
= Y'2gii — скорость падающего тела в момент соприкасания
с выступом «і». Если высота Ь велика сравнительно с &ст, то
приближенно можно принять
Соответствующее растягивающее напряжение в стержне
будет:
ЪЕ Е f~K& /~~2Ё Qv*~
°-т-ту -"г-у ~w"^~' [203]
Подкоренная величина прямо пропорциональна
кинетической энергии падающего тела, модулю упругости
материала стержня и обратно пропорциональна объему IF
стержня. Поэтому напряжение можно уменьшить не только
увеличением площади поперечного сечения, но также
увеличением длины стержня, или уменьшением модуля
упругости К Это резко отличается от статического растяжения
стержня, где напряжение не зависит от длины I и модуля
упругости Е.
Подставляя вместо а в формулу [203] допускаемое
напряжение, получим следующее уравнение для назначения
размеров стержня, подвергающегося действию осевого
Удара:
7 _ 2Е Qv* , .
'•*втНг' [204]
294
т. е., чтобы получилось при данном материале одно и то зке
наибольшее напряжение, объем стержня должен быть
пропорционален кинетической энергии падающего тела.
Рассмотрим теперь другой крайний случай при k = 0,
т. е. когда тело Q внезапно положено на выступ т?
(фиг. 248), но не обладает начальной скоростью. Хотя в эт?м
случае в начале растяжения стержня кинетическая
энергия отсутствует, все же задача резко отличается от случая
статического загружения стержня.
В случае статического растяжения мы предполагаем
постепенное приложение груза, и соответственно этому все
время между действующим грузом и внутренними силами
упругости стержня существует равновесие. Вопрос о
кинетической энергии груза при таких условиях совершенно
выпадает ив рассмотрения.
В случае внезапного приложения груза удлинение
стержня и напряжение в нем вначале равны нулю, и
внезапно приложенный груз начинает падать под действием
своего собственного веса. При этом движении сила
сопротивления стержня постепенно нарастает до тех пор, пока
не станет равной грузу Q, когда вертикальное перемещение
груза будет равно 8СТ. Но в этот момент груз обладает
некоторой кинетической энергией, благодаря перемещению^,.
Поэтому груз продолжает свое движение вниз до тех пор,
пока его скорость не станет равной нулю из-за
противодействия возникающих в стержне внутренних усилий.
Наибольшее удлинение при таких условиях получится
по формуле [202] при « = 0, что дает
8=28„, [205]
т. е. внезапно приложенный груз, вследствие условий
динамики, вызывает деформацию, которая вдвое больше
деформации, полученной при постепенном приложении
груза.
Это можно показать графически так, как это сделано
на фиг, 249. Наклонная линия ОА представляет собою
диаграмму растяжения стержня, изображенного на фиг. 248.
Для любого удлинения ОС площадь АОС даст
соответствующую потенциальную энергию деформации стержня.
Проведем на расстоянии Q от оси удлинений 8
горизонтальную линию DB, тогда площадь ODBC представит
работу, совершенную грузом ф.при этом перемещении ОС.
295
Когда S равно 8ст, работа силы Q представится на
чертеже площадью прямоугольника ODAfi^ В то же время
потенциальная энергия, накопленная в стержне,
изобразится площадью треугольника ОАхСх, которая равна только
половине площади упомянутого выше прямоугольника.
Вторая половина работы, превратится в кинетическую
энергию движущегося тела.
Вследствие полученной скорости тело продолжает
-двигаться и приходит в состояние покоя только на
расстоянии 8 = 2 Зст от начала деформации. В этот, момент вся
работа, совершенная грузом Q, представленная
прямоугольником ODBC, сравняется с
величиной накопленной в стержне
потенциальной энергии,
изображенной треугольником ОАС?
Предыдущее рассмотрение
действия удара основано на
предположении, что напряжение в
стержне остаетсявпределах
упругости. За этим пределом задача
становится более сложной, так
как удлинение стержня уже не
будет пропорционально
растягивающей силе. ^Допустив, что
диаграмма растяжения не
зависит от скорости, с которой
совершается деформация стержня *),
получим, что удлинение за
пределом упругости при ударе
может быть найдено при помощи обыкновенной диаграммы
растяжения, показанной на фиг. 250.
При любом значении наибольшего удлинения 8
соответственная площадь OAJDF представит работу, необходимую
для того, чтобы произвести такое удлинение; она должна
быть равна работе Q(h-\-§), совершаемой грузом Q. Когда
6(* + 8) равно или больше всей ^площади О ABC
диаграммы растяжения, падающее тело вызовет разрушение
стержня.
Из этого следует, что любое изменение в форме стержня,
которое приводит к уменьшению полной площади ОАВС
А) Опыты с мягкой сталью показывают, что при- большой скорости
деформирования предел текучестн выше и величина работы,
необходимой для разрушения стержня, больше, чем при статическом испытании.
См. Я. Л. Даеидепков, „Известия Цолитехничеекого института",
С.-Петербург, 1913, а также Велгтер {Welter) „Ztschr. f. Metallkimde", 1924.
296
Фиг. S49.
диаграммы, уменьшает также силу сопротивления стержня
удару.
В стержнях с выточкой, изображенных на фиг. 247й и с
например, явление текучести металла будет
концентрироваться у выточки, и полное удлинение и работа,
необходимые для разрушения стержня, будут значительно
меньшими, чем в случае цилиндрического стержня, показанного
рядом на той же фигуре. Такие стержни с выточками
очень слабо сопротивляются удару; легкий толчок может
вызвать разрушение стержня, хотя бы материал сам по
себе и обладал упругостью. Элементы, имеющие
заклепочные отверстия или какие-либо резкие изменения сечений,
также слабо сопротивля- D
ккгся удару *).
До сих пор мы
пренебрегали массой стержня со
сравнению с массой падающего
тела U. Только благодаря
этому мы могли допустить,
что вся энергия падающего
тела превращается в
потенциальную энергию стержня.
Действительные условия п
удара более сложны, и если
стержень имеет массу,
которой нельзя пренебречь, часть
энергии теряется 'при ударе.
Хорошо известно, что когда
касса —, движущаяся со скоростью v, столкнется центрально с
неподвижной массой—1, и деформация в точке удара упруга, то конечная
общая скорость обоих тел va равна:
Фиг. 250.
v
U
а
U+Ut
v.
т
В случае стержня, изображенного на фиг. 248, условия еще
сложнее. При ударе веркшіа конед А находится в покоэ, тогда как ннжшій
конет; приобретает скорость движущеюся тела U*
Поэтому, чтобы определить конечную скорость va по формуле [J,
мы вместо действительной массы стержня, возьмем приведенную иасеу.
Приняв, что скорость стержня изменяется по линейному заколу вдоль
его длины, можем показать, что приведенная масса в этом случае
і) См. Гакштро (ЛасЫгоіъ), „Banmaterialenkimde", 1905, S. 321 и
Г. Циммерман (И. Zimmermann), „Zentralbl. <]. Bauverw.", 1SS9, S* 2t>5,
297
равна ©дной трети массы стержня3)- Для стержня весом q на единицу
длины ф-ла ]Ь] получает вид:
Q
Q + f
• Это — общая скорость груза Q и нижнего конца стержня, которая
устанавливается в первый момент удара.
Предположив, что на поверхности соприкасания между падающим
грузом и выступом гт фиг. 248 происходит упругпя де?юрмапия, так
что здесь не возникает вопроса об отдаче, получим соответствующую
кинетическую энергию равной
v а / ql \ W& 1
<3 +
Эту величину следует подставить вместо
Wv*
П
= Wh
в ур-ни? fa], чтобы учесть потерю энергии в первый момент удара.
Тогда вместо ф-лы [2(L] мы получим
* = *« + - / W +
ст і * / *ст і q л *
1+-J-
[202']
Описанный способ дает удовлетворительные результаты, пока масса
стержня мала сравнительно с массой подающего тела. В противном
случае становится необходимым рассмотрение продольных колебаний
стержня 2). Местные дейоршшии в точке касания при ударе
рассмотрены Дж. бирсом, 3) и Дж. Вэьстаффом 4).
ЗАДАЧИ.
1. Груз весом 5 %\, прикрепленный к стальной проволоке, диаметром
3 ми (фиг. 251), падает от точки Л с ускорением д. Няйти напряжеаив
в проволоке, когда ее верхний конец Л внезапно остановлен.
Пренебречь массой проволоки.
Ч Это решение было получено Г. Коксом (Я. Сох\ „Cambridge Phil.
Soo. Trans.*, 1349, p. 73. См. также Tod\mmep и Пирсон (Todlwnier and
Pearson), History, vol. I, p/895.
2) Продольные колебания призматического стержня при удар?
рассмотрены были Лавье (Wavier). Более общее решение изложено СЫ-
Вепаном; см. его перевод книги Елебша (Ktebsck), «Theorie <ier Elasticity
fester Korper", заметку к параграфу 6L См. также Я. Бусеинеск (J. Вои$-
sinesq), Application des potentiels, p. 5S0, и К. Рамзауер (С. Uamsauer)
„Ann. d. Phys.% Bd. 30, i90».
3) Дж. Cupc (J. E. Sears), „Trans. Cambridge Phil. Soc", Vol. 21,
190*, p. 49.
4) Дж. Вегстафф (J.EJP. Wagstaff), „London Eoyal Soc. Proc. (Ser. A)"
Vol. 105, 19з4, p. 514:.
293
Решение. Если ускорение груза Q равно д, го растягивающих
напряжений в проволоке не будет. Напряжение после внезапной
остановки проволоки в точке А получится по формуле 1203], в которой
статическим прогибом ост следует пренебречь. Подставив v% = яда и
S = h, получим:
,/ %?Q ,/" 2-210ОСС0.5-? „_._ . .
Отсюда следует, что напряжение не зависит от высоты h, с которой
Груз падает, так как кинетическая энергия тела увеличивается в
такой же мере, как и объем проволоки.
2. Груз Q весом 450 кг падает с высоты h'= 1 м 'на вертикальный
деревянный столб длиной б м, диаметром 30 см, закрепленный своим
нижним концом. Определить наибольшее сжимающее
напряжение в столбе, приняв, что для дерева ^==100000 к\/см2, л^А ,
и пренебрегая массой тела и величиной ост. -н*—-
Ответ, с = 145,5 кг/см2.
3. Груз Q весом 4,5 т, прикрепленный к копну
стального проволочного каната (фиг. :51), движется вниз с
постоянной скоростью v, равной 1 .и/сек. Какие напряжения
возникнут в тросе, когда его верхний конец внезапно
остановлен? Свободная длина троса в момент остановки равна
I = 18 л, площадь нетто поперечного его сечения F — 16 см2
и Е = 1 050 000 кг/см2.
Решение." Пренебрегая массой тросса и принимая, что
кинетическая энергия движущегося тела полностью
превращается в потен анальную энергию деформации троса» получим
уравнение для определения наибольшего удлинения о троса в таком виде:
ЕГЪ2 EFbJ Q
4* + <№-Ът), [d\
г
й
Фиг. 251.
21
21
2<7
Д? 5,
ст обозначает статическое удлинение троса. Заметив, что
8.
Q = EF~
ст
получим из ур-ния [d]
откуда:
EF
(»
*ст
I
.)2=
EFg
Следовательно, при внезапном прекращении движения
растягивающее напряжение в стержне возрастает в отношении
A-el+'/_SL=i
>ст *СТК EFa
V
-ст -EFg ' У*6СТ
По цифровым данным задачи вычисляем
QI 451 :Q. 1800
М
ст .
KF
10.0О0О-10
В 100
--1+
ст
У 0,482-«81
; = 0,482 см;
= 5,00.
299
Отсюда
=зБ.бо.-&»
F
6,60
4500
16
= 1675 HtfcMK
4. Решить предыдущую задачу, если между тросом и грузом
вставлена пружина, которая удлиняется на 12 мм под действием груза
в 450 кг.
•Решение.
5СТ = 0,482 + 1,2 • 10 = 12,482 см
Подставив это в выражение [е], получим:
= 1 + 0,92=1,92;
«1.92 -?- =
ст
1,92-3L = 540 кг/см?.
F
5. Для случая, представленного на фиг. 248, определить высоту ht
при которой наибольшее напряжение в стержне при ударе равно
2і00 kxjcmK Принять Q = 12 кг, I = 1,6 *, F = 3 с*2, В = 2100 U00 кг/смК
Массой стержня пренебречь.
Ответ. Л == 42 см.
66. Потенциальная энергия упругой деформации при сдвиге
и кручении. Энергия деформации, накопленная элементом,
испытывающим чистое
скалывающее напряжение (фиг. 252), может
быть определена способом,
примененным к случаю простого
растяжения. Если нижнюю грань ad
элемента принять закрепленной,
то нужно принять во внимание
только работу, совершаемую при
деформации силой Р в верхней
грани Ъс элемента.
Предположив, что материал
следует вакону Гука, получим, что
деформация едвигапропорцаональ-
на скалывающему напряжению, и
что диаграмма, показывающая зависимость между ними,
подобна диаграмме, изображенной на фиг. 246, Работа, ее-
вершенная силой Р и накапливаемая в виде
потенциальной энергии упругой деформации, равна в этом случае
(см. ф-лу [199])
U-.
РЬ
Г199']
Вспомнив, что
получим из ф-лы [199'] следующие два выражения;
U=~2GF> Р°Ч
Для потенциальной энергии сдвига, отнесенной к
единице объема, делением этих уравнений на объем IF тела
мы получим два выражения:
«. = ^> [207']
Р 8
где т = "ег—скалывающее напряжение и т = ~? дафор-
мация сдвига. Количество потенциальной энергии на
единицу объема, которое может быть накоплено телом
безостаточной деформации, получится подстановкой предела
упругости при сдвиге вместо х в выражение [206'].
Потенциальная энергия, накапливаемая в скручиваемом
круглом валу, легко определяется при помощи ф-лы [206'].
Если tmax — наибольшее скалывающее напряжение на
поверхности вала, то в любой точке на расстоянии г от оси
скалывающее напряжение .равно:
2г
Tmax ' d '
где d—диаметр вала. В этой точке согласно выражению
[206'} потенциальная энергия, отнесенная к единице объема,
равна:
2 т* -а
max
Потенциальная энергия, накопленная материалом,
заключенным между двумя цилиндрическими поверхностями
с радиусами г и r^\-dr, равна
2х2 г2
301
где /—длина вала. Тогда полное количество
потенциальной энергии, накопленной валом:
2
"2 т2 г* 1 тей2/ z*
max
max
2G
[208]
Это показывает, что полная потенциальная энергия
составляет лишь половину того, что должно было бы быть,
если бы все элементы вала были напряжены максимальным
скалывающим напряжением т .
Потенциальная энергия
кручения может быть определена из
диаграммы кручения (фиг. 253), в
которой скручивающие моменты
представлены ^ординатами, а углы скру-
чнвания-1-абсциссами. В пределах
упругости угол скручивания
пропорционален скручивающему мо-
<р менту, что изображается
наклонной прямой О А. Небольшая
площадь, заштрихованная на фигуре,
представляет .работу, совершаемую
скручивающим моментом при
увеличении угла скручивания <? на
ФИГ. Х?.
<Ь. Площадь ОЛИ, равная
представляет полную потенциальную энергию, накопленную
валом при кручении. Вспомнив, что
получим
или
?
ЕГ
GI/
Щ1_
2GL
21
[209]
В первом из этих двух выражений потенциальная
энергия выражена в функции скручивающего момента, во вто
ром—в функции угла скручивания.
302
В общем случае, для любого вида поперечного сечения
и для скручивающего момента, изменяющегося по длине
вала, угол скручивания между двумя смежными
поперечными сечениями выразится уравнением (см. стр. 78):
•г1 dx = —— dx.
dx С
Энергия деформации отдельного момента вала равна
п полная потенциальная энергия скручивания —
О
ЗАДАЧИ.
1. Найти зависимость между пределом упругости при сдвиге и
пределом упругости при растяжении, если количество потенциальной
энергии деформалии на кубический сантиметр, которое может быть
накоплено без остаточной деформации, одинаково и для растяжения и
для сдвига.
Решение. По формулам, [200'] и 206']
т2
2Е 2Q*
откуда
Для сталя
X=S9V Ж"0'621-
2. Определить деформацию винтовой пружины (фиг. 6і, стр. 78) при
помощи выражения для потенциальной энергии кручения.
Решение. Обозначаем через Р силу, действующую по
направлению оси винтовой линии (фиг. 64), через Й —радиус витка и через п —
число витков. Потенпиальная энергия кручения, накапливаемая
пружиной, по первому из выражений [209] равна:
тг (PRf2nEn
Приравняв это работе внешней силы
'4-
303
получим:
3. Вес стальной винтовой пружины равен б к\. Найти количество
потенпиальной энергии, которая может быть накоплена этой пружиной
бее появления остаточных деформаций, если предел упругости при
сдвиге равен 5200 %г/см\
Решение. Количество потенциальной энергии на кубический ел
по выражению [206'] равно
52005
2» 800-000
Потенциальная энергия на килограмм материала (см. стр. 292) равна
2160 кі • см. Тогда полная энергия кручения *), которая может быть
накоплена пружиной, равна >
~ .$ • 21G0 = 5400 кі. с*.
4. Сплошной круглый вал и тонкая труба одного и того же
материала и одного и того же веса подвергаются скручиванию. В каком
отношении находятся количества потенциальной энергии в вале н
в трубе, если наибольшие напряжения в обоих случаях равны?
О т в ? т. -т- : 1.
5. Круглый стальной вал с маховиком на одном конгте вращается
со скоростью 120 оборотов в минуту. Вал внезапно заторможен на
другом кон^е. Найти наибольшее напряжение в валу отг внезапной
остановки, если длина вала I = 1,5 м, диаметр d = 50 мм, вес маховика
Q — 45 кг и его радиус инерции г = 2о0 мм.
Решение. Наибольшее напряжение возникнет в валу тогда, когда
полная кинетическая энергия маховика превратиться в потенциальпую
энергию деформация скручиваемого вала. Кинетическая энергия
маховика равна
PA*» 45-25М4*)а оор. _
Подставив эту величину вместо V в выражение ]208], получим
_ fWGU .fib ¦ 800 000 ¦ 2 2'і"
Tmax-|/ %d4 У тс. б2-150
6. Два круглых стержня одинакового материала, одной и той же
длины, но с разными площадями поперечных сечений F и Fu
скручиваются одним и тем же скручивающим моментом. В каком отношении
находятся количества потенциальной энергии деформации, накопленной
в этих двух стержнях?
Ответ. Обратно пропорционально квадратам площадей
поперечных сечений. %
67. Потенциальная энергия упругой деформации изгиба.
Начнем с чистого изгиба. Для призматического стержня,
1) Распределение напряжений принято такЕш, какое имеет место
в скручиваемом круглом стержне.
304
закрепленного одним концом и изгибаемого внешним
моментом М, приложенным в другом конце (фиг. 254),
угловое перемещение свободного конца
Ml
Это перемещение пропорционально изгибающему
.моменту М. Пользуясь диаграммой, подобной представленной
на фиг* 253, мы можем заключить путем таких же
соображений, что работа, совершаемая
при деформация | изгибающим
моментом М9 а следовательно и
потенциальная энергия, накоп- j^fL
ляемая стержнем, равна V.
^=~у-- [Ь] У Фиг. 254.
Пользуясь выражением [а], можем представить эту
энергию в таких двух видах:
_ МП
U=^> [212]
Иногда представляется полезным выразить
потенциальную энергию в функции наибольшего ^нормального нааря-
жения*
м
ЩЙ.Х»
например, в случае прямоугольного стержня
_ 6М „'._ „ bh*'a
в_._ = -^- или Ж= -22-
и формула [211] получает следующий вид:
2
О
^ТШ~ЙР [21l'J
В этом случае полная потенциальная энергия составляет
очевидно только одну треть той энергии, которая была бя
накоплена, если бы все волокна были напряжены до о^.
20 Тимошенко — Сопротивление материалов, ч. I. **Оо
При рассмотрении изгиба поперечными силами мы
сначала пренебрежем потенциальной энергией сдвига.
Энергия, накопленная элементом балки длиной dz, по форму*
лам [211] и [212] равна;
,гг ffidx
2Е1Ш
ИЛИ
Здесь изгибающий момент Ж является переменной
относительно х величиной, и
dx
d*y
dx
(см. стр. 181). Полная потенциальная энергия, накопленная
балкой, следовательно:
г
U
чт ™
Z
О
или
О
Возьмем, например, консоль АВ (фиг. 255). Изгибающий
момент в любом поперечном сечении т? равен М = — Вх.
Подстановка его в формулу [213] дает:
г
Г Р*хЧх __ РФ
U~J 2Е19 ~6Шшш W
о
Для прямоугольного стержня
6PZ
°шах— № >
и выражение [с] получится в таком виде:
Это показывает, что количество потенциальной энергии,
которое может быть накоплено прямоугольной консолью,
нагруженной на конце, без появления остаточных дефор-
306 .
мацииг, составляет одну треть энергии при чистом изгибе
того же стержня и одну девятую энергии тога же стержня
при простом растяжении.
Это соображение существенно важно при
проектировании рессор, которые должны поглощать данное количе*
ство энергия без поломок и вместе с тем иметь возможно
меньший вес. Способность консоли поглощать энергию
может быть увеличена
приданием ей переменного
поперечного сечения.
Например, консоль,
представляющая тело равного
сопротивления с
прямоугольным поперечным сечением
постоянной высоты h (фиг.
151 стр. 176), при тех же
значениях Р, h и Gmax дает
прогиб, а потому и поглощает
количество энергии на 50%
больше призматического
стержня. В то ,же время
стержень равного
сопротивления весит в два раза
меньше призматического
стержня и таким образом
ца килограмм веса
материала может накопить в Фиг. 235.
три раза больше энергии.
Возвращаясь к выражению [с] и приравнивая
потенциальную энергию деформации работе внешней силы Р
при прогибе, получим
РЬ РЧ*
откуда прогиб на конце^
8 =
Ш.
Р1&
BEL
что совпадает с выражением [115] (см. стр. 150).
Дополнительный ппогиб от сдвига может быть определен также из
рассмотрения потенциальной энергии деформации. Для консоли,
показанной на фиг. 255, прямоугольного поперечного сечения скалывающее
напряжение на расстоянии у от нейтральной оси равно (сы. ф-лу [96],
стр. 124).
" Р fW
2/
Г
20*
307
Энергия сдвига, отнесенная е элементарному объему bdxily, равна
поэтому, согласно выражению [206'],
^ \~-y^dxdy9
??і\
и полная энергия сдвига
I ^ 2
С Г Р2 /А2 И\л л ?*№
Это должно быть прибавлено к правой стороне ур-ния [d],
приведенного выше Ц% "чтобы получить уравнение для определения полного
прогиба:
рв р^з ,. тк2
2 6EI ^ 20GJJ
l/'l
следовательно:
в *
Второй член в скобках представляет влияние скалывающих
напряжений на прогиб балки. Пользуясь методом, изложенным в п* -іО,
в предположении, что элемент поперечного сечения в центре тяжести
закрепленного конца остается вертикальным (фиг. 255b), получим, что
дополнительный наклон касательной к упругой линии, вызываемый
сдвигом,
'''max
Y" G
и дополнительный прогиб равен
3
2
поэтому
. Р/з 3 Ті
•Ш ' 2 JbhG
3 Р
~~ 2 ' bhG '
рі
bhG •
PZ3 / 3 Аз Е
~~ ЪМіі Л ' 8 Р G
)¦
19']
Из этого видно, что выражения [д] и [д'\ не совпадают. Это
различие объясняется следующим образом. Вывод п° 40 был основан на
допущении, что поперечные сечения балки могут свободно
искривляться под действием скалывающих напряжений. В таком случае поп?реч-
х) Такое прибавление энергии сдвига к энергии, возникающей от
нормальных напряжений, оправдывается тем, что скалывающие
напряжения» действующие на элемент, (фиг. 252), не вызывает изменений
в длинах сторон элемента, н если на эти стороны действуют
нормальные усилия, то они не совершают работы при деформации, сдвига
Поэтому скалывающие напряжения не изменяют количества энергии от
растяжения или сжатия, и оба рода энергии могут быть просто
сложёны друг с другом.
808
нов сечение в закрепленном конце примет вид криволинейной
поверхности топ (фиг. гЬЪЬ)л дифференциальное уравнение которой;
dx ттах^т _ 8 Р Р I Й2 \
dy \? 2 bhG 2?1ш [ ~ ~"у* /*
•Интегрирование дает уравнение кривой топ і):
„. рУ3
X =
№1
%
щ
Нормальные напряжения в закрепленном сечении:
__ My __ __ Ply
совершают работу при искривлении, и эта работа равна:
РЧ1&
^ 2
1 Г j?ys Ply-
806?! '
J^ • % *
2
Это должно быть прибавлено к работе внешней силы Р. Тогда
вместо ур-ния [/"], получим
рь рзда -PW , рчш
2
откуда
806е/ 6-ЁУ ' 2о0/'
* * «
еа= '.pz3 /- . з ш в\
ZEI
(1 + ±*-±)
Равнина между решениями [д] и \д'] тажим образом устраняется
если принять во внимание искривление закрепленного сечения.
Если возможность этого.искривления предотвращена, то
распределение скалывающих и нормальных напряжений в закрепленном
сечении будет отличаться от того, что было предположено в выше
приведенной теории. Влияние этих .отклонений** в распределении
напряжений на прогиб балки не может быть исследоваііо элементарными
методами, и в этом случае приходится обращаться к теории упругости 2).
ЗАДАЧИ.
1. Консоль, представляющая деревянный брус длиной 1,8 м,
прямоугольного поперечного сечения 20 X12 см> несет равномерно
распределенную нагрузку 2=300 кг/л. Определить количество накопленной
энергии деформации, если В — 100 000 «t/cx2.
Ответ:
U- № _ 3002 • 1,8^ • 18Q3.12 _ ff
u 4ujsf ~40-iooooo.au». 12-5<5Д4 Кг см-
ш
і) Начало координат взято здесь в центре тяжести закрепленного
сечения.
а) См. статьи, упомянутые выше в выноске па стр. 189.
309<
2. В каком отношении возрастет количество потенциальной энергии
деформации, определенной в предыдущей задаче, если высота балки
равна 12 си, а ширина 20 см?
Ответ. Энергия де^орматтии возрастет в отношении 52: За =^= 25:9.
3. Два одинаковых стержня, один просто опертый концами, другой
незакрепленным концами, изгибаются одинаковыми силами,
приложенными по середине, В каком отношении находятся количества
накопленной потенциальной энергии деформации?
Ответ: 4:1.
4. Решить предыдущую задачу при равномерно распределенной
нагрузке одинаковой интенсивности q для обоих стержней.
5. Найти отношение между количествами накопленной
потенциальной энергии в балках прямоугольного поперечного сечения, одинаково
нагруженных, имеющих одну и ту же длину и одинаковую ширину
поперечных сечений, но высоты которых находятся в отношения 2:1.
Решение.' При данной нагрузке энергия деформации
пропорциональна прогибу, а этот последний обратно пропорционален моменту
инерции поперечного сечения. Поэтому, птщ уменьшении высоты вдвое,
про.иб возрастает в восемь раз, и количество энергии деформации
увеличивается в такой же пропорции,
68. Изгиб при ударе. Динамический ирогиб.балки, о
которую ударяется падающее тело Q, можно определить мето-<
дом, примененным в случае уда-
іра, вызывающего растяжение
*_. (П° 65).
^ г х Возьмем для примера просто
#-~^^ I—^_1'^# N§ опертую балку, испытывающую
/
у t—1~ удар по середине пролета (фиг.
~ 256), и предположим, что
массой балки можно пренебречь
Фиг. 256, сравнительно е массой
падающего тела и чте балка на
напрягается выше предела текучести. При таких
обстоятельствах не будет потери энергии при ударе, и работа,
совершенная грузом Q при его падении, полностью превратится
в энергию деформации изгиба балки *)-
Пусть & обозначает наибольший прогиб балки при ударе.
Если мы предположим, что упругая линия при ударе имеет
тот же вид, что и при статическом прогибе, то сила,
которая вызвала бы такой прогиб, равна как это следует из
формулы [128] (см. стр. 160):
48EL
» *' [а]
г) При этих выкладках мы пренебрегаем местной деформацией на
поверхности соприкосновения и в грузе и в банке.
Полная энергия, накопленная балкой, равна работе,
совершенной внешней силой Р:
и=Л-=ы2АШ~
J8 •
Если h обозначает, как выше, высоту падения, то
уравнение для определения 8 получается в таком виде:
откуда
8«+і/>«+~^' М
где
* —
9
01s
К,= „„г ¦ И ^У^"
Выражение [215] точно такое же, как выражение [202]
для удара, вызывающего растяжение.
Следует отметить, что вид выражения прогиба остается
тем же самым и для любого другого случая удара, если
только прогиб точки удара пропорционален силе Р,
приложенной в этой точке. Если мы обозначим через а
коэффициент пропорциональности который зависит от
конструкции балки, то мы получим;
Р8 82
2а
Тогда
2а'
и так как b^=Q-af то это уравнение приводит к
вышеприведенному выражению [215].
Следует отметить также, что прогиб 8, определенный по
ф-ле [215], представляет собою верхний предел, к которому
приближается наибольший динамический прогиб, когда
отсутствуют потери энергии при ударе. Любая такая потеря
уменьшает динамический прогиб. Есла динамический
прогиб найден по ф-ле [215], то соответствующие напряжения
8
можно получпть умножением на-к—напряжений для слу-
ст
чая статического приложения груза Q.
811
Если Л—велико по сравнению с 5от, то выражение [215]
может быть дано в более простом виде:
-/?•
В случае балки, опертой по концам и удаляемой по
середине, это выражение дает
Наибольший изгибающий момент в этом случае будет;
м =—= — • —
max 4 j3 4*
3 _Мпа_Ъ.4ВЕ1. J_
При прямоугольном поперечном сечении, пользуяср
формулой [d], получим
а -1 f W 18Е п
ю&х V 2д * IF * [еі
Это показывает, что наибольшее напряжение зависит
от кинетической энергии падающего тела и от объема IF
балки.
При выяснения влияния массы балки на наибольший прогиб мы
предположим, что уптіугая линия при уда^?. имеет тот же вид, что и
при статическом прогибе. Тогда можно показать, что приведенная
масса балки *), опертой по концам, равна
17 ді
В5 д '
н общая скорость, которая установится в первый момент удара, будет:
...—і—..
Полная кинетическая энергия после установления общей скорости
равна
-аді в + ТГ*/—аГ"- i4.JL.jL '
і) См. статью Гомершама Еокса (Homerscham Сох)', упомянутую
выше в выноске на стр. 198.
312 •
Подставив это вместо
В
УР*
¦ние
W.
2$
получим формулу:
*=*сх + |/ t + -
— V
0
* f#
t?
1+
1
17
35
[2151
Которой учитывается влияние массы балки на прогиб Ь і).
Для консоли в случае если груз Q, ударяет по конпу балкиг
величина .приведенной массы балки равна
33 ql
140 , д
Когда балка просто оперта по концам и подвергается удару в точке,
расстояние котогой от опор равно соответственно а и Ь, то приведенная
масса балки составит
ЗАДАЧИ.
1. Лежащая на двух опорах прямоугольная деревянная балка
длиною 2,7 м испытьтвпет удар по середине грузом в 18 кг, падающим
с высоты 30 см. Определить необходимую площадь поперечною сечения,
если допускаемое напряжение Вь = 10 «г/с*2, Е= 100 000 щсл\
Решение. Применяя формулу [е] (стр. 315і)2), получаем
« «** 18 Е ^ 18-100 000 _-,.-
F 2Г'ТйТ- = 18"30, 270-702 =785^
2. В каком отношении изменится площадь сечения в предыдущей
задаче: 1) если пролет балки увеличится с 2,7 м, до 3,6 м; 2) если вес
rpysa Q увеличится на 50%?
Ответ. 1) Площадь сечения уменьшится в отношении 3:4 2)
Площадь сечения увеличится на 50%*
!) Некоторые примеры применения этой формулы можно найти
в статье проф* Тшетше {Tscheische), „Ztschr. d. Ver. cl lug.", 1894, S. 134.
Болеа точная теория поперечного удара балки основана на исследовании
бокового колебания балки с учетом местных деформаций в точке удара.
См. Сен-Венет (Saint 1 enant), вышеупомянутый труд, етр. 537,
заключительное примечание к параграфу 01, „Compt. Rend.", t. 45, 1857, p. 204.
См. также С. Тимошешо, „Ztschr. f. Math. u. РпузЛ Bd. 02, 1913, S. 198.
Опыты с балками, подвергающимися удару, были произведены в Швей-
парий и Дали удовлетворительное согласование с вышеизложенной
приближенной теорией; см. Teehn. Komm. d, Verband Schweiz. Bruckenbau-
und Eisenhochbau-fabriken, доклад M. Роча (Ж, Bo$)t март. 1922. г.
2) При этом определении мы пренебрегаем местными деформациями
на поверхностях соприкасания груза и балки,
313
3. Груэф весом 45 иг падает с высоты 30 си на середину просто
опертой двутавровой балки пролетом 3 .и. Найти безопасные размеры, еспи
_йь=2Ю0 кг/аи2.
Решение. Пренебрегая статическим прогибом ост по сравнению
с высотою падения А (см. ф-лу [с]\ получим отношение между
динамическим и статическим прогибами равным
= і/^7 = |/
2А
'ст у у "at у "от
Если упругая линия при ударе того же вида, что и при статическом
прогибе, то наибольшие напряжения от изгиба будут находиться в том
же самом отношении, что и прогибы. Поэтому
откуда
W QHQ h
с а 2 г *
о
где W — момент сопротивления сечения балки и с — расстояние от
нейтральной оси до наиболее удаленного волокна, которое в нашем
случае равно половине высоты балки.
Подставляя цифровые данные, получим:
W 6.2100000-45.30
г
21003-300
= 12,9 с*а.
Необходим двутавр высотой 16. ем (№ 16 по ОСТу), весом 17,5 кг/м.
4. Какое напряжение вывЛет в балке предыдущей задачи груз Q
весом 90 кг, падающий на середину балки с высоты 15 см?
О т в е т. ( *„)„„ =- 2000 «г/с*2.
5. Деревянная консоль длиною 1,8 м квадратного поперечного
сечения 30 X ЬОсн подвергается удару в свободный конец грузом Q = 45 «t,
падающим, с высоты А = 30 см. Определить наибольший прогиб, приняв
во внимание потерю энергии от массы самой балкн. Вес дерева 750 ісг/м9.
Решение. Пренебрегая ост по сравнению с А, получим
выражение, подобное формуле [215']:
-/¦
>«*
1 +
33 ql
140 Q
При ql = 750 • 0,32 • 1,8 = 121,6 кг.
ст л , зз ш,5 У a.id
1+М0*~і5~
Ь = / ъ_ 2-30 ,/ 45-1809-12
100000-30*
. 36,7 — 0,689 см.
314
6. Балка, обеими концами положенная на опоры, подвергается удяру
но середине грузом Q, падяющимсвысоты А. Пренебрегая ост до
сравнению с h, найти величину отношения ql : Q, при котором влияние массы
балки уменьшает динамический прогиб на 10vo*
Ответ. 2Z:Q = 0,483.
69. Общее выражение потенциальной энергии деформации»
При изложении задач на растяжение, вжатие, кручение и
изгиб мы показали, что энергия деформации может быть
представлена в каждом случае функцией второй степени
от внешних сил (ф-лы [200], [206] и [211]) или функцией
второй степени от перемещений (ф-лы [201], [207] и [212]).
Это также справедливо для более общей деформации
упругого тела при следующих предпосылках: 1) материал следует
закону Тука, 2) условия таковы, что небольшие перемещения
при деформации не оказывают
влияния на действие внешних
сил и ими можно пренебречь
при определении
напряжений *).
При этих двух
предпосылках, перемещения упругой
системы будут выражаться
линейными функциями внешних
сил; если эти силы возрас
тут в некоторой пропорции,
то все перемещения
возрастут в той же пропорции.
Рассмотрим- тело, подвергающееся действию внешних
сил Ри Р2, Р3(... (фиг, 257) и опертое таким образом,что
движение его как твердого тела невозможно и возможны Лишь
перемещения от упругих деформаций. Пусть 8,, 82, 83,.#1
обозначают перемещения точек приложения внешних сил»
причем каждое измеряется по направлению действия
соответствующей силы.
Если внешние силы нарастают постепенно, так что они
постоянно находятся в равновесии с внутренними силами
упругого сопротивления, то работа, совершаемая ими при
деформации, будет равна потенциальной энергии
деформации, накопленной в деформируемом теле. Количество этой
энергии не зависит от порядка, в котором приложены силы,
а всецело определяется их конечными величинами.
*) Такие задачи, кяк изгиб стержней боковыми силами с
одновременным осевым напряжением или сжатием, не удовлетворяют этим
условиям и исключаются из рассмотрения. Об этих исключительных
случаях см. п° 74:.
315
Фиг. 257.
Допустим теперь, что все внешние силы Рг, Р2, Р3і**.
возрастают одновременно в одном и том же отношении;
тогда зависимость между каждой силой и соответственным
ее перемещением может быть представлена диаграммой,
подобной показанной на фиг. 246, и работа, совершенная
всеми силами Ри Р2, Р8,..., будет равна потенциальной
энергии деформации, накопленной телом:
т. е. полная потенциальная энергия деформации равна
половине суммы произведений каждой внешней силы на
соответствующее ей перемещение 1).
На основании сделанных выше предположений,
перемещения 8„ 8g, 83,.,. являются линейными функциями сшг
Pv Р2, Р3,... Подстановка этих функций в выражение [216]
дает общее выражение потенциальной энергии деформации
в виде однородной функции' второй степени от внешних
сил. Если силы представить линейными функциями
перемещений и эти функции подставить в ф-лу [216], то
получим выражение потенциальной энергии деформации в виде
однородной функции второй степени от перемещений.
'В предыдущем рассмотрении нами пе принимались во
внимание реакции опор. Работа, совершаемая этими
реакциями при деформации, равна нулю, так как перемещение
неподвижной опоры, например опоры Л на фиг. 257, ріівно
нулю, а перемещение подвижной опоры, такой, как
опора В — перпендикулярно реакции, если пренебречь
трением в опорных частях. Следовательно, реакции ничего не
прибавляют к выражению [216] потенциальной энергии.
Как пример применения ф-лы [216] рассмотрим этергию,
накопляемую элементом в виде куба, подвергающимся равномерно
распределенному растяжению по трем взаимно перпендикулярным направлениям
(фиг. 47, стр. 60). Если ребро куба — едннита длины, то растягивающие
усилия по его граням численно равны о^, сг и о^ а соответствующие
удлинения — е , е и е. Тогда энергия дефотжаттии, накопленная одний
кубическим сантиметром, согласно выражению [216], равна:
о е ее а е
2 ^ 2 ^ 2
*) Это заключение было получено впервые Клапецрочом (С1ареуг?п\>
см. Жяме (Lame), Lecons sur la tbeorie mathematique de l'elasticite, 2'ed.,
1Ь65, р. 79.
316
Подставив вместо удлинений их значения по ф-лам [43] (стр. 61) *),
получаем:
а = —Кг^2 + ^г+^2)~-^г^ >+и|н). ' /217]
Этим выражением можно также воспользовптг-ся, когда некоторые
из нормальных'на пряжений окажутся сжимающими. В зтоы случае они
должны иметь отрицательны^ знак.
- Если, кроме нормальных напряжений, имеются скалывающие
напряжения, действующие по граням элемента,, то энешия сдвига должна
быть прибавлена к энеріии от растяжения или сжатия (см. стр. ЗОгі), и,
пользуясь формулой [2-)6'], получим полную величину потенциальной
энергии, накопленной одним кубическим сантиметром, равной
а =-Д-(а а-f a2_|,c2)— -?-(сгс -fj ff -fcc) +
Ч -5>-(т 2 + т 2 + т 2). [2181
Вторым примером рассмотрим балку, опертую по конттам,
нагруженную по середине пролета силой Р и изгибаемую моментом if,
приложенным к концу А. Прогиб по середине пролета равен, согласно
выражениям [128] и [134] (см. стр. 160 и 162):
. РР , М&
ж
Угол наклона касательной в конце А по формулам [123] .и [133]
(см. стр. 157 и 161) равен:
Тогда потенциальная энергия деформации балки, равная работе
внешней силы Р и момента М, будет:
2 + 2 ~ Жв { 96 + 6 + 16 )'
[с]
Это выражение является сіднородной функцией втогюй степени
от внешней силы и от внешнего момента. Решив ур-ния [а] и [Ъ]
относительно М и Р и подставив в формулу [с], получим выражение для
потенциальной- энергии в виде однородной функпии второй степени
от перемещений. Следует отметить, что, если на тело действуют
внешние моменты, соответствующими перемещениями являются угловые
перемещения траней элементов, на которые эти моменты действуют.
70. Теорема Кастильяно.— Помощью рассмотренных для
различных случаев выражений потенциальной энергии де-
*) .Здесь считаем, что изменения температуры вследствие дейор-
ма^ий не имеют .практического значения. Что касается дальнейшего
углубления вопроса, см. книгу Вейрауха (Т. Weyrauch), Theorie elasti-
echer Кбгрег, Leipzig, 1884, S. 163; См. также „21 f. Architektur- und
Ltgenieur-wesen", Bd. 54, 1908, SS. 91, 277.
V "SIT"
формации можно установить очень простой способ для
определения перемещения точек упругого тела при
деформации.
Например, в случае простого растяжения (фиг. 1), эпер-
гия деформации представится, по формуле [200], в виде:
РЧ
77====——
U 2EF*
Беря производную этого выражения относительно Р,
получим:
dU _ PI
dF ~~ JSF ~ '
т. е. производная потенциальной энергии деформации- по
силе дает перемещение, соответствующее этой силе, т. е.
перемещение точки приложения силы по направлению ее
действия.
В случае консоли, нагруженной на конце, энергия
деформации (формула [d], стр. 307) равна
77 —
еж/
Производная этого выражения по силе Р дает нам
известное уже выражение прогиба свободного конца:
Рів
8 =
ЗЖ/
При кручении круглого вала потбнциальная энергия
деформации (формула [209]) равна
Ы*1
2GJ,
Производная этого выражения по скручивающему моменту
дает:
dU Mtl _
dMt GI9
Этот угол скручивания вала и представляет перемещение
соответствующее скручивающему моменту.
Если Ъа упругое тело действует несколько грузов, можно
применить тот же метод определения перемещений.
Например, выражение [а] предыдущего п° дает энергию
деформации балки, изгибаемой силой Р, приложенной по. серег
дине пролета, и моментом Ж на конце балки. Частная
производная этого выражения по Р дает прогиб под грузом,
а частная производная по М дает угол поворота того конца
.балки, на которой действует момент М.
Теорема Кастильяно является общим выражением этих
заключений J). Если материал системы следует закону Гука
и условия таковы, что небольшими перемещениями вря
деформации можно пренебречь при рассмотрении действия
внешних сил, то потенциальная энергия деформации такой
системы может быть представлена однородной функцией
второй степени от действующих внешних сил (см. п° 69).
Тогда частная производная энергии деформации по любой
из таких сил дает перемещение, соответствующее этой силе
(исключительные случаи см. п° 74).
Термины сила и перемещение здесь имеют обобщенное
значение, л\ е. они включают понятия: момент пары сил
Н угловое перемещение соответственно.
Рассмотрим общий случай, представленный на фиг. 257.
Допустим, что энергия деформации выражается функцией
сил Ри Р2, Р3,, • ¦, так что:
U=f(Pv Р2, Р8,...). [а]
Если придать любой внешней силе Рл небольшое
приращение dPn, то энергия деформации возрастает также,
? ее новое значение будет:
u+^fapn. [ь]
UJ-n
Но величина потенциальной энергии деформации не
зависит от порядка, в котором прикладываются силы к телу,— ~
она зависит только от их конечных величин. Допустим,
что сначала приложена бесконечно малая сила dP^ а потом
силы Р„ Р2, Р3, Конечная величина энергии
деформации останется такой же, как представлено выражением [А].
Сила dPn, первоначально приложенная, вызовет только
бесконечно малое перемещение, так что соответствующей
работой силы, как бесконечно малой величиной второго
порядка, можно пренебречь. Приложив теперь силы Plf P2,
Р3,..., отметим, что их действие не изменится под влия-
*) См. статью Еастильяпо (СаНгдііапо), Nuova Teoria Intorno dell»
Equilibrio dei Sistemi Elastiei, „Atti della Academia delle scienze", Torino,
1876. См. также его Тііеогі? de ГёфіШЪге des systemes elastiques ..Turin.
Английский перевод работы Кастильяно см. Э. Андрус (Е* S. Andrews),
Лондон, 1910>
319.
нием силы dP„, предварительно приложенной *), и раббта,
совершенная этими силами, будет равна U (выражение [а]),
как ранее. При приложении этих сил однако сила dPn
получает некоторое перемещение 8П по направлению
действия силы Р0 и совершает работу (dPv) 8„. Эти два
выражения для работы силы должны быть равны. Поэтому
U+^~(dPtl)=U+(dPn)bn9 [с]
откуда
К = §-\. [219]
. Эта теорема особенно удобна для определения прогибов
решетчатых ферм.
В качестве примера рассмотрим ферму, изображенную
на фцг. 258. Все элементы фермы перенумерованы, и их
Йлины и площади поперечных сечений приведены, в таб?
лице 6 ниже.
Усилие 80 возникающее в любом стержне і системы при
действии сил Ри Р2, Ps, может быть определено просто из
уравнений статики. Эти усилия приведены в столбце
4 таблицы 6.
Потенциальная энергия деформации любого стержня г
согласно выражению [200] равна
л *
2ЕЬ\
Количество потенциальной энергии всей системы равно
Я=УШ-> [220]
где суммирование распространяется на все элементы
системы, число которых в нашем случае і» = іі.
Усилия St являются функциями внешних сил Р, и по-.
Ч Это следует из предпосылок, сделанных нами выше (стр. 316),
на основе которых потенциальная энергия деформации была получена
в виде однородной функции второй степени.
320
атому прогиб 8П под любой силой Рп согласно ф«ле [219]
равен
ЫТ ^Л Stlt dS{
dst
діТ ^Л Stlt
<=1
ЭР.
[221]
Производная «-—- представляет собой отношение
приращения усилия Si к приращению силы Рп. По абсолют-
ной величине она равна усилию, возникающему в стержне і
6
Pfllm - ?2*8m Pfim
Фиг. 258.
от единичной силы, приложенной к системе в том же
положении, как Рп, и этим обстоятельством мы воспользуемся
для нахождения этой производной. Эти производные
в дальнейшем будем обозначать: ?,'.
Уравнение для определения прогибов- получится тогда
Э следующем виде:
<==«»
$5'Л
" 2л EF*
91 Тимошенко — Сопротивление материалов, ч. I.
[221х}
Ш
Рассмотрим например прогиб 8,, соответствующий силе
Р2, приложенной в точке А (фиг. 258а).
Величины S\t приведенные в столбце б таблицы в,
получены прл помощи основных уравнений статики для
условий нагрузки, показанных на фиг. 2586, где все
действующие силы удалены и приложена сила, равная одной
тонне в.шарлире А.
ТАБЛИЦА 6.
Данные для фермы, представленной на фиг. 258.
v 1
і
1
2
В
4
5
6
7
8
9
10
11
и
см
500
300
40)
300
500
000
500
300
400
500
300
3
см3
30
15
10
15
10
20
10
15
10
30
15
4
• а4
-13,75
+ 8,25
+ 8,00
+ 8,25
+ 3,75
- 10,50
+ 6,25
+ «,76
+ 4,00
—11,25-
+ 6,75
5
*\
- 0,625
+ 0,375
0
+ 0,375
-f 0,1525
-|- 0,750
+ 0,6і5
+ 0,375
0
— 0,625
+ 0,375
(5
*4
143
62
0
62
117
236
195
51
0
117
51
7
8%
0
1
0
1
0
0
0
0
0
0
0
Величины, внесенные в столбец в таблицы 6, вычислены
на основании данных, приведенных в столбцах 2—6.
Суммирование этих величин дает:
ЩА- =- Ю34 «л/ел.
5
F<
Делением этой суммы на модуль упругости Е**
= 2100 000 кг/см2 согласно выражению [22і'[ получим
прогиб в точке А
% 1034*1000 лллл
h = -WTT.—^т = 0,498 см,
• До сих пор мы занимались определением перемещений
*і, \ . . . , соответствующих данным внешним силам Ри
322
Рь , • . . При исследовании деформаций упругой системы
может оказаться необходимым определение перемещения
точек, в которых не приложено никаких сил, или
перемещение точки приложения силы в направлении отличном от
направления силы.
Метод Кастильяно применим также и в этом случае.
Для этого нужно только приложить в этой точке
дополнительную воображаемую* силу Q в таком направлении, по
которому требуется найти перемещение.
Затем следует взять производную
д?
в ?той производной приравнять нулю добавленную силу
ф, и тогда мы получим искомое перемещение.
Например, пусть нам нужно набта горизонтальное
перемещение узла А фермы, показанной на фиг, 258а.
Приложим горизонтальную снлу Q в этой точке. Тогда
соответствующее горизонтальное перемещение будет:
<==от
izzl
[d\
где суммирование распространяется на все элементы
системы.
Усилия 8і в выражении [d] имеют то же самое значение,
что и раньше, так как приложенная дополнительно сила
Q равна нулю. Производные
получаются как усилия в стержнях фермы, возникающие
от нагрузки, показанной на фиг. 258с. Эти величины
приведены в столбце 7 таблицы 6.
Подставив эти усилия в выражение [d]t найдем, что
горизонтальное перемещение точки Л равно сумме
удлинений стержней 2 и 4, а именно:
(8,25-f 8,25)-300-1000
15- 210и 000
«*-0,1Б7 см.
в
При исследовании деформаций ферм иногда необходимо
бывает знать изменение расстояния между двумя узлами
системы. Это тоже может быть
получено на основании
теоремы Кастильяно.
Пусть нам, например,
требуется определить, какое
rpf уменьшение 8 расстояния
между узлами А ж В (фиг. 259а)
происходит при действии сил
Рц Р2, Р3- Приложим в этих
узлах две равные и прямо
противоположные
воображаемые силы Q, как указано на
чертеже пунктирными
линиями. Из теоремы
Кастильяно следует, что частная
производная
дает сумму перемещений
узлов А я В в направлении АВ,
возникающих при действии сил Р1У Р2, Р3. По формуле
[219] находим это перемещение 1):
і = т і—т
Ъ-(дЛ) - VAii. . M-VAi.f Г2221
J^\ « = 1
где S{—усилия, возникающие в стержнях системы от
действительных сил Pv JP& Р3; 8\ — величины, определяемые
для нагрузки, показанной на фиг. 2596, при которой все
действительные силы устранены и приложены две прямо
противоположные единичные силы в узлах А и В, и т —
число элементов.
ЗАДАЧИ
1. Система, состоящая из двух призматических стержней
одинаковой длины и одинакового' поперечного сечения (фиг. 260), нагружена
вертикальным грузом Р. Найти вертикальное-перемещени? шарнира А.
Решение. Растягивающее усилие в стержне АВ и сжимающее
усилие в стержне АС равны Р. Поэтому энергия деформации системы
17-а. т
Фиг. 2159.
2EF'
Щ Эта задача была впервые решена Дж. Максвэллом (J. С. Maxwell),
On the Calculation of the Equilibrium and Stiffness of Frames, „Phil. Mag/
(4), Vol. 27, 1864, p. 294, .Scientific Papers", Vol. 1, Cambridge,* 1890,
p. 698.
824
Вертикальное перемещение точки А
* = -:
dU 2Р1
дР EF ¦
2. Найти горизонтальное перемещение шарнира А в задаче 1.
Решение. Приложим воображаемую горизонтальную силу Qt как
показано на фиг. 260 пунктиром. Потенциальна а энергия этой системы
С/ =
(г+уИ'' ,('-??«)''
2EF
2EF
Производная этого выражения по Q при Q = 0 дает горизонтальное
перемещение
3. Определить угловое перемещение стержня .АБ под действием
груза Р (фиг. 261).
Решение. Приложим к системе воображаемую пару сил,
показанную на чертеже пунк-
fU тирными линиями. Пере-
/_ / мещение,
соответствующее этой паре сил будет
угловое перемещение ?
й
Фиг. 260.
V_ if/
в
wt.
ш
Фиг. 262.
стержня ЛВ от действия груза Р. Усилия Si в этом случае будут:
в стержне АВ Р-\- __і -у- и в стержне -4 С — Р р=
Потенциальная энергия деформации:
I
V 3 Г
Z7 =
откуда
_(dU\ _(РУТ ] 5Ж\ __РУТ
4. Найти прогиб и угол наклона касательной в конце консоли ЛВ
(фиг. 262) под действием силы Р и момента Ма,
Решение. Изгибающий момент в любом поперечном сечений ш»
равен И == — Рх — Ма, и.энергия деформации шь формуле [218]
і
-/¦
2 EI,
825
'Тогда прогиб и угол наклона касательной будут соответственно:
дР
о о
773 МЛ*
іт »
?Е1, ' 2Ш.
Й =
<ШЛ ~~ EL
к/мщdx=~щ/іРх+Ма) dx=
Р22
2 Ж
+
EL
5. Найти прогиб по середине пролета равномерно нагруженной балки
с просто опертыми концами (фиг. 133, стр. 162).
Решение. Приложим воображаемую силу Q до середине пролета.
Изгибающий момент слева от этого груза
*-(*+-*>-*
* и потенциальная энергия деформации
изгиба
U
Фиг. 263.
Прогиб посередине пролета
>л
М*йх
ъшящ
* / дСГ \ 2 лггп дМ
dx
%lj \ 2 2 J 2 384
Ж'
6. Какое горизонтальное перемещение опоры В рамы, показанной
на фиг. 263, вызовут горизонтальные силы if?
Ответ.
h 3 EIX + EI \
7. Найти вертикальное перемещение точки А и горизонтальное —
точки С стальной фермы, изображенной на фиг. 264, если Р равно 900 кг,
площади поперечных сечений сжатых стержней — по 30 см2, а прочих
стержней —12 смК
326
8- Определить приращение расстояния АВ, вызванное действием
сил Л (фиг. 265), если стержни АС и ВС имеют одинаковые размеры
Фиг. 264. Фиг. 266.
выечитывается только изгиб стержней. Допустить, что угол а не очень
мал, так что влиянием прогибов на величину изгибающего момента
можно пренебречь.
Ответ.
71. Применение теоремы Кастильяно к решению
статически неопределимых задач. Теоремой Кастильяно также
очень выгодно пользоваться при решении статически
неопределимых задач. Начнем с задач, в которых
статически неопределимыми величинами рассматриваются
реакции опор. Обозначив через X, Y, Z, . Г. статически
неопределимые реактивные силы, получим потенциальную
энергию деформации системы в функции этих сил. При
применении теоремы Кастильяно, частные производные
потенциальной энергии деформации по неизвестным
реактивным силам должны равняться нулю для неподвижных
опор и для тех опор, перемещение которых
перпендикулярно направлению реакций. Поэтому
йхв0; аг=0; а2~*; • ' [223]
Таким образом мы получим столько уравнений, сколько
у нас есть статически неопределимых реакций.
Можно показать, что ур-ния [223] представляют собой
условия, при которых функция U достигает минимума.
Отсюда следует, что величины статически неопределимых
реактивных сил должны быть таковы, чтобы
потенциальная энергия деформации системы получалась наименьшей.
Это и есть начало наименьшей работы в применении копре-
делению лишних неизвестных опорных реакций О-
*) Начало наименьшей работы было впервые установлено Ф. Же-,
набреа (F. Menabrea) в ею статье Nouveau principe виг la distribution
327
В качестве примера применения этого начала рассмотрим
равномерно нагруженную балку, закрепленную одним
концом и опертую другим (фиг. 266). Это —задача с одной
статически неопределимой опорной реакцией. Приняв
вертикальную реакцию X правой опоры за статически
неопределимую величину, мы найдем эту неизвестную силу из
уравнения:
Потенциальная энергия деформации балки, согласно
формуле [213], равна
J *Ш*1
о
где
Фиг. 266.
М=Хх —
qx<
щ
Подставнв в ур-ние [а], получим:
dU 1_ Г„ЛМ
dX ~' EI
о
М
dX
dx —
EI
x._tf).fc _'(x4-?)-^
откуда -
х=іф-
Вместо опорной реакции X за статически
неопределимую величину можно было бы взять опорный момент Маи
des tensions dans les systemes elastiques, Paris, „Compt. Rend*, vol. 46,
1858, p. 1056. См. также „Compt. Rend.", vol. 98, 1884, p. 714. Полное
доказательство начала наименьшей работы было дано Еасгтлъяно,
который положил этот принцип в основу метода решений статически
неопределимых систем. Применение .методов,- основанных на
рассмотрении пот?нпиальной энергии деформации, к инженерному делу было
изложено О. Мором (О. Mohr), см. его Abhandlungen aua dem Gebiete d.
teclmischen Mechanik, Г. Мюллер-Вреслау (Я. Miiller-Breslau) в его книге
Die п?и?г?п Methoden der Festigkeitslehre и Ф. Энгессерох (F. Bnges$er)t
Ueber die Berechming statisch unbestimmter Systeme, „Zentralbl. d. Bau-
verwalt*, 1907, S. 606. Очень полная библиография по этому вопросу
дана в статье Ж. Грюниніа (М. Griining), Encyklopadie d. Math. Wise.
Bd. IV, 2, U, S. 419.
328
левого конца балки. Потенциальная энергия деформации
будет теперь выражена в функции от опорного момента М
Выражение [Ь] и здесь имеет силу, но в нем теперь
изгибающий момент в любом поперечном сечении
^_J&-U-
йх*
Из того условия, что левый конец действительной балки
не может поворачиваться при изгибе балки, следует, что
производная потенциальной энергии деформации по М
должна быть равна нулю. Отсюда мы получим:
*ыа еі9 J
=-ж/[(4-^
о
Ж „, Лх ==
dM,
х
qx*
х
dx =
Mal
sM=o,
С X X 2 О
з
откуда
Ж.
8
При помощи теоремы Кастилья-
но можно также решать задачи;
при которых мы рассматриваем
статически неопределимыми
величинами усилия, действующие
в лишних элементах системы.
Возьмем для примера случай,
изображенный на фиг. 267. Здесь
реакции—статически определимы;
но когда мы попытаемся найти-
усилия в стержнях, то мы
обнаружим, что эта система имеет один
лишний элемент.
Будем рассматривать стержень GD этим лишним
элементом. Разрежем этот стержень в любом месте и приложим
к каждому концу F и Fx силу X, равную усилию в
разрезанном стержне. Таким образом мы придем к статически
Фиг. 267.
329
определимой системе, на которую действуют, кроме
известной внешней силы Р, еще и неизвестные силы X
Усилия в стержнях системы найдем в двух
предположениях: сперва усилия, вызываемые внешней силой Р и
обозначаемые через #{°, где значок і указывает номер
стержня, затем усилия, возникающие тогда, когда внешняя
сила Р устранена и вместо сил X действуют единичные
силы (фиг. 26 7?). Эти последние усилия обозначим через #/.
Тогда полное усилие в любом стержне, когда действуют
и сила Р и силы X, равно
%*=$* +S/X. [с]
Полная потенциальная энергия деформации системы
на основании выражения [220] будет равна
' и~ \ 8*1< - 'V ШМ*'Ф J, ш
U~ 2±2EF. = 2і Ш§ * W
где суммирование распространяется на все стержни системы
с включением стержня CD, который- мы разрезали.
Теперь применим теорему Кастильяно. Производная
потенциальной энергии U по X даст нам перемещение концов F
и Fx по направлению навстречу друг к другу. В
действительной системе стержень CD 'не разрезан, а потому это
перемещение равно нулю. Отсюда
dU r
!х=0> М
т. е. усилие X в лишнем стержне должно быть таково,
чтобы потенциальная энергия системы получала
минимальное значение. Из ур-ий [d] и [е] получаем
dX Zj 2ffi ~ ?± ~ Щ — °»
откуда
i=sm
Этот прием ііожно распространить и на систему, вторая ймвет
несколько лишних стержней. Разрезав эти стержни и приложив в
разрезах соответствующие усилия X, Y, Z, . . ,, мы придем к статически
определимой системе, нагруженной известными внешними силами -Р3,
Pg, Р& . .. и неизвестными усилиями X, У, Zt. > . Пусть 8 обозначает
усилие, возникающее от действия известных внешних сил в стержне г
этой системы, 8! — усилие от действия двух равных и прямо
противоположных единичных усилий, приложенных вместо усилий X, S" —
усилие от единичных усилий, которыми заменены усилия У, и так далее.
Полное усилие в стержне і равно
8Л = S? + S'X + S!' Y+ 8!nZ -\
Подставим это в выражение [220] для потенциальной энергии
деформации и применим теорему Кастильяно. Статически неопределимые
усилия получатся тогда из уравнений:
* = т (8* + 8/Х + 8"Т+8"'г-] )\
EF.
8{ - 0,
(S0 + S/X + S^Y+8^Z+ . • ¦ )*,
EF
В"
і
0,
[225]
Все эти уравнения — линейны относительно неизвестных X, YtZ,, . .
и этих уравнений столько же, сколько неизвестных.
Начало наименьшей работы можно применить также и
тогда, когда статически неопределимыми величинами
являются моменты. Вовьмем например равномерно нагру-
©
л
А",
I
4
в~
і
\С
ТМб Мь
Фиг. 268.
зкенную балку на трех опорах (фиг. 268). Если за
статически неопределимую величину принять изгибающий момент
над средней опорой и разрезать балку над опорой Б, то
мы получим две просто опертых балки (фиг. 2686), на
которые действуют, кроме известной равномерно распреде-
831
/
ленной нагрузки q, еще и неизвестные моменты Ма. Так
как в действительной системе (фиг. 268а) упругая линия
непрерывна, то над опорой В не может происходить
поворота вднца И относительно конца -В". Поэтому
dU
= 0/
{226]
Й в этом случае значение статически неопределимой
величины должно быть взято таким, чтобы потенциальная
энергия системы обращалась в минимум.
ЗАДАЧИ.
I. Вертикальная сила Р воспринимается вертикальным стержнем DB.
длиной I о площадью поперечного с?ч?ния F и двумя одинаковыми
наклонными стержнями длиною I с площадью поперечного сеч?яия Fx
(фиг. 269). Определить усилия в стержнях, а также такое отношение
$і: F, при котором усилия во всех стержнях буд^т одинаковы по
абсолютной величине.
Решение. Система — статически неопределима. Пусть X
—растягивающее усилие в вертикальном стержне- Сжимающие усилия в
наклонных стержнях равны
Р-Х
YH
и потенциальная энергия деформации системы
ХЧ . (Р — Х)32
U =
2EF
2EFt
Фиг. 269.
Начало наименьшей работы дает:
dU _ XI (P-X)Z
dX
я
откуда
EF
Х =
шг
= 0,
1+
F
Подставив это в уравнение:
Р-Х
Х =
VT
мы получим
Fx = FY 2.
2. Найти горизонтальную реакцию X системы, показанной ча
фиг. 270.
Решение. Неиэвеотная сила X войдет только в выражение, потен-
днальной энергии изгиба части АВ стержня. Для этой части Af ¦.
*=>Ра — Хх, и начало наименьшей работы дает:
аи
ах
, d Г №dx 1 Г 1Ж dM J
XP PaP
2
ь
откуда
T 3Pa
3. Найти горизонтальные составляющие' опорных реакций системы,
показанной на фиг. 271. Все размеры даны в таблице 7 (см. ниже).
Решение. На основании начала наименьшей работы имеем:
dU
$Х
d
dX
jU 2EFi — jU EFi dX
= 0.
Пусть &f° —усилие в стержне t, возникающее от действия известной
силы Р, ^' — усилие, возникающее в том же стержне от единичных
сил, которые заменяют силы X (фиг. 271Ь). Значения 8° и S'
определяются по уравнениям статики. Эти значения помещены в столбцах 4
и 5 таблицы 7. Полное усилие в любом стержне равно
8
t t ' і •*
ТАБЛИЦА 7.
Данные для сиотемы, показанной на фиг. 271.
і
1
2
3
4
б
см
457,5
401,2
127
457,5
401,2
F
і
еле2
30
; 18
12
30
18
So
— 1,803Р
+ 1.581Р
+ 1.000Р
— 1.803Р
+ 1,581Р
8!
1,202
— 2,108
—1,333
1,202
— 2Д08
Е~
- 33,0Р
- 74.3Р
- 14ДР
- 33,0Р
- 74,ЗР
- 228,7Р
22,0
. 99,0
18,8
22,0
99,0
260,8
883
Жодставиъ ети значения в вышеприведенное уравнение наименьшей
работы, получим: щ
*?\ W + S/XSL
2d ^F\й« и'
і-1 *
откуда
Х- —
<«1
s
(?/)Ч
ГЯ
Цифры, необходимые для вычисления значения X, приведены в
столбцах 6 и 7 таблицы 7. Подставив эти данные в выражение [/*],' получим
Х«0,877Р.
4. Найти усилие в лишнем горизонтальном стержне системы,
изображенной на фиг. 272, приняв, что длина этого стержня 10 =* 7,62 м
Фиг. 271.
Фиг. 272.
и площадь поперечного сечения равна F& Прочие стержни имеют те же
размеры, что и в задаче 3.
Решение. Усилие в горизонтальном стержне определится по
формуле [224]. Эта формула такого же рода, как выражение [f] в задаче 3,
но только в системе фиг. 272 есть дополнительный горизонтальный
стержень. Усилие, возникающее в этом стержне при действии только
силы Р(Х=0), равно нулю, т. е. S0Q=;0. Усилие, возникающее в этом
стержне от двух сил, равных единице (фиг. 2726), ?0' = 1, Добавочный
член в числителе выражения [f] равен
№
о,
Добавочный член в знаменателе будет;
Тогда пользуясь данными эадачи 3, получим
У 228,7Р
^ + 260,8
Взяв, например, ^о_= 64,6 ел*2, имеем:
Х =
228,7
11,8 + 260,8
= 0.839Р.
Это всего лишь на 4,3% меньше, чем значение, полученное в
задаче 3 при неподвижных опорах *).
Веяв площадь поперечного сечения FQ равной 6,46 см2, имеем:
228ДР в0,604Р.
Х =
762
6,45
+ 260,8
Фиг. 273.
Отсюда видно, что в статически
неопределимых системах усилия в стержнях зависят также
от площадей поперечных сечений стержней.
5. Найти усилия в стержнях систем,
изображенных на фигурах 15 (стр. 19) и 20 (стр. 22),
пользуясь началом наименьшей работы.
6. Определить усилия в стержнях системы,
изображенной на фиг. 273, приняв, что все стержни —
одного и того же размера и одинакового материала.
Решение. Если устранить один из стержней, то усилия в
остающихся стержнях можно определить из уравнений статики. Поэтому
система имеет один лишний стержень. Пусть 1 — этот стержень, и X —
усилие, действующее в нем. Тогда все боковые стержни,
шестиугольника будут иметь растягивающие усилия X, стержни 8, 9, 11 и 12 —-
сжимающие усилия X а стержни 7 и 10 — усилие Р — X.
Потенциальная энергия деформации системы
Ш . . (Р — Xfl
17=10
2EF
+ 2
2EF
Ш уравнения
dU
dX
0
получим:
*-f
7. Найти усилия в системе, показанной на фиг. 267, приняв, о
площади поперечных сечений всех стержней одинаковы, и взяв усилие
X в диагонали AD за статически неопределимую величину.
*)% Приняв F0*mco, мы получим то же, что при неподвижных
опорах.
836
Решение. Подставив данньг?, приведенные ниже в таблицей,
в выражение [224], получим
4 + 2/2
. ТАБЛИЦА 8.
Данные для системы» изображенной на фиг. 267.
г
1
2
3
4
5
6
h
а
а
а
а
аУ~2
аУ1
V
Р
Р
0
Р
-рУъ
0
-
8'
і
1
1
і
/2
1
У2
+ 1
+ 1
Е =
¦.»
аР
У2
аР
/а
0
аР
— 2аР
0
— (3 + 2У"2)аР
/У
¦ W,
а
У
а
У
У
а
У
аУ%
aY%
2а(1+УУ)
8. Прямоугольная рама, составленная из стержней одинакового
поперечного сечения (фиг. 274), подвергается действию равномерно
распределенной нагрузки интенсивностью qt как показано на фиг. 274. Найти
изгибающий момент М в углах.
Ответ.
(дЗ + ЬЗ)д
П(а + Ъ) '
9. Груз Р поддерживается двумя балками одинакового поперечного
сечения, пересекающимися друг с другом, как показано на фиг. 275.
Найти давление X. между балками*
Ответ,
Р2з
Х =
й +1\ в
10. Найти статически неопределимую величину распора #"-в раме,
доказанной на фиг. 186 (стр. 215), пользуяеь началом наименьшей работы.
Решение. Потенциальная энергия изгиба раакг.
ft
О 6
где М0 обозначает изгибающий момент для горизонтального стержня,
определенный как для балки просто опертой по концам.
Подставив это значение [д] потенциальной энергии в уравнение
найдем:
2# 7*з , Н№
Е1г 3 ' EI
= -шт]М(№'
m
Интеграл в правой части последнего уравнения представляет
площадь треугольной эпюры изгибающих моментов для балки, несущей
груз Р. Поэтому
I f И* = »*=*-. 1 Ш 1
Подставив это в ур-ние [fc], і 2 ііі ??
j ^ получим для Н то же выра- і—. .-рлт *~~' • і
" ¦ ¦ | , ¦ ¦ ¦¦ ¦ ¦ ~ жени?, что и выражение [152] i-'i LL—i.—J
¦ПШНіі (см. стр. 216). г1~Ч* 2
3>иг. 274. 11. Найти статически не- Фиг. 275.
определимые величины в
рамах, изображенных на фигурах 185,'" 188 и 190, пользуясь началом
наименьшей работы.
72. Теорема о взаимности перемещений *). 6 этой теореме
сопоставляются два различных напряженных состояния
упругой системы.
Возьмем тело, представленное на фиг. 276, и допустим,
что оно оперто таким образом, что перемещение его как,
твердого тела невозможно. При первом состоянии напря-
1) Частный случай этой теоремы был получен ДЫ& Максвэллом
(J. С. Maxwell) (см. его труд, указанный в выноске на стр. 323), Теорему
впервые высказал Э. Бетти (Е, Betti), „II nuovo Cimento", Ser. 2, Vol. 7
и 8,1872. В более общей форме теорема был"а дана Рейлеем (Lord Bay-
leigh\ „London Math. Soc. Proc.% Vol. 4, 1873, или „Scientific Papers",
Vol, 1, p. 179. Различные применения этой теоремы к решению
инженерных задач выполнены О. Моро», см. его труд в выноске выше на
стр. 328 и Г. Мюллер-Бреслауі см. выноску там же.
22 Тимошенко — Сопротивление материалов, ч. I. 337
жений, к телу приложены силы Рх и Р^ а при втором
состоянии —силы Р3 и Р& Пусть перемещения точек
приложения этих сил по направлениям их действия равны
*и h> h> К ъ нервом состоянии, и 8^ 82, 83, 84 — во втором
состоянии.
Теорема о взаимности перемещений гласит: работа
совершенная силами первого состояния на перемещениях,
соответствующих второму состоянию, равна работе
совершенной силами второго состояния на соответствующих
перемещениях первого.
При принятых обозначениях эта теорема выразится
следующим уравнением:
РА + Р& = Р&+Р?і- [227]
Чтобы доказать эту теорему, рассмотрим потенциальную
энергию деформации тела, когда действуют все силы Ри
Фиг. 276.
Р*> J?s» ^4 вместе, и воспользуемся -тем обстоятельством,
что количество потенциальной энергии деформации не
зависит от порядка, в котором приложены силы, а только
от конечных значений сил.
При первом способе загружения примем, что силы Рх
и Р2 приложены сначала, а затем, уже силы Р3 и Р4.
Потенциальная энергия деформации, накопленная телом
при приложении сил Рх и Р2, равна
РА
¦ -РА
[а]
Приложив теперь силы Р8 и Pv найдем работу,
совершаемую этими силами:
PsK , Р&
И
338
Следует отметить однако, что, при приложении сил
Р8 и Р4, точки приложения ранее приложенных сил
Рх и Р2 переместятся на Ь[ и 8* Тогда силы Рх и Р3
совершат работу г)
P& + PJ&. [с]
Поэтому полная потенциальная энергия деформации,
накопленная телом, равна сумме [а], [Ь] и [с];
г7=^ + -^ + -?-+-?- + рА'+і% и
При втором способе загружения сперва приложим силы
Р8 и Pv а затем Рх и Р3. Тогда, повторяя те же самые
рассуждения, что и раньше получим
U==lfflf + IA+M.JrPAJrPA. [в]
Приравняв выражение [d] и [е], получим уравнение [227].
Эту теорему можно доказать для любого числа сил,
а также для пар сил, или для сил и пар сил. В случае
приложения пары сил, за перемещение принимается
соответствующий угол поворота.
В частном случае, когда действует только одна сила Рг
в первом состоянии напряжений и одна только сила Р2 во
втором состоянии, получаем ур-ние [227] в следующем
виде 2):
РА' = РА- Г227'!
Если РХ = Р2, то следовательно 8^ = 8,, т. е.
перемещение точки приложения силы Р2 в направлении ее действия,
возникающее при действии силы Ри равно возникающему
при действии силы Р2 перемещению точки приложения-
силы Рг в направлении ее действия. Проверка этого
заключения в частном случае дана в эадаче 3 п° 37 (см.
СТр. 171).
Вторым примером рассмотрим изгиб просто опертой
балки. Пусть в первом состоянии происходит изгиб под
действием груза Р, приложенного по середине, и при
втором состоянии — изгиб под действием изгибающего момент
і) Эти выражения не поделены на 2, так как силы Рг и Р2
остается постоянными все время, когда точки их приложения испытывают
перемещения 1'г и о'3.
а) Это было доказано впервые Дж, Иашэлло?* (/. С. MaxwclT) i
часто называется теоремой Максбзлм*.
22* S88
та М, приложенного в конце балки. Груз Р дает на конце
угол наклона касательной;, равный
PZ-2
? =
ібж;
Момент Ж, приложенный в конце, вызывает прогиб по
середине пролета
ЛЯ»
«ж;
Уравнение [227'J получается в таком виде:
Ml2 №
1вЖ, ~м~ IQET/
Рассмотрим далее деформацию консоли, при первом
состоянии напряжений изгибаемой грузом; приложенным
в конце, и во втором состоянии
напряжений—скручиваемой моментом, приложенным в конце.
Для груза, приложенного в конце, соответствующим
перемещением является прогиб балки в точке приложения
¦груза в направлении его действия. Для момента
соответствующим перемещением явится угол скручивания. Если
труз приложен в центре скручивания (см. п° 41, стр. 190)
концевого поперечного сечения, то поворота конца при
изгибе не произойдет, т. е. здесь перемещения,
соответствующего скручивающему моменту, не будет. 'Тогда из
уравнения [227'] можно заключить, что скручивающий
момент, приложенный в конце консоли, не вызовет бокового
перемещения центра скручивания. Поворотц поперечных
сечений консоли при скручивании поэтому происходят)
вокруг продольной оси, проходящей через центр
скручивания.
Например, в случае стержня с уголковым сечением
(фиг. 165, стр. 193) поворот при скручивании будет иметь
место вокруг продольной оси, проходящей через точку
пересечения О средних линий цолок уголка.
Теоремой о взаимности перемещений очень удобно
пользоваться при решении задач о нахождении наиболее
неблагоприятного положения подвижных грузов для
статически неопределимых систем.
Пример, показанный на фиг. 277, представляет балку,
закрепленную одним концом и просто опертую другим,
несущую сосредоточенный груз Р. Нужно цайти изменение
345
в величине реакции X левой опоры при изменении
-расстояния груза от этой опоры. Рассмотрим действительное
состояние балки (фиг. 277а) как первое состояние
напряжений. Второе, фиктивное состояние показано на фиг. 2776.
Внешний груз и лишняя опора Л здесь устранены, и сила,
равная единице, направленная вверх, замещает
неизвестную реакцию X. Второе состояние напряжений —
статически определимо, и соответствующая упругая линия для
него известна (см. ур-ние [117], стр. 150). Если оси
координат взяты так, как показано на фиг. 27 7&, то
уравнение упругой линии будет:
Пусть Ь обозначает прогиб конца и у —прогиб на
расстоянии х от левой опоры. Тогда, применяя теорему о
взаимности перемеще-
нии, получим, что
работа, совершаемая
силами первого
состояния на
соответствующих перемещениях
втор бго со стояния,
равна:
ХЪ — Ру.
При определении
теперь работы,
совершаемой силами
второго состояния, мы имеем
только силу, равную
единице, на конце *),
точки А в первом
®
®
Фиг. 277.
а соответствующее перемещение
состоянии равно нулю. Следовательно,
эта работа равна нулю, и теорема взаимности дает
уравнение:
хь—pVt=o,
откуда
Х = Р
L
8
Ы
Из этого следует, что при изменении положения груза Р
реакция X изменяется пропорционально соответствующему
*) Реакции закрепленного конца не приняты во внимание ни в том,
ни в другом случае, так как соответствующие перемещения равны нулю.
значению прогиба у на фиг. 277&. Поэтому упругая линия
второго состояния (ур-ние [f]) дает полную картину того
порядка, в котором X изменяется с изменением х. Такая
кривая называется линией влияния реакции X.
Если одновременно действуют несколько грузов, то
применяя ур-ние \д] и пользуясь методом наложения, получим:
Т~ ^ *пУп>
где уп — прогиб, соответствующий грузу Рп, а
суммирование распространяется на все грузы
^
^4
L
fs
ЗАДАЧИ.
1. Построить линии влияния для реакций опор двухпролетнЪй
неразрезной балки (фиг. 278).
Решение. Чтобы получить линию влияния для реакции средней
опоры, за первое состояние напряжений примем действительное
состояние, показанное на фиг. 278а. Второе
состояние показано на фиг. 278&,
где груз Р устранен и реакция X
заменена силой, равной единице и
направленной вверх. Это второе
состояние напряжений статически
определимо, и упругая линия для него
известна (ур-ния [125] и [12ft], стр.
161); отсюда можно определить
прогибы Ь и у. Тогда работа,
совершенная силами первого состояния на
соответствующих перемещениях1
второго состояния, будет
ХЪ-Ру.
Фиг. 278. Работа сил второго состояния
(сила-единица) на соответствующих
перемещениях первого состояния (нулевой прогиб в точке С) равна
нулю; поэтому
©
©
Х8 — Ру = 0;
*-нь
Следовательно, упругая линия второго состояния является линией
влияния для реакции X. Для того, чтобы получить линию влияния
реакпии В, втопо? состояние напряжений следует взять таким, как
показано на фиг. 278с.
2. Пользуясь линией влияния предыдущей задачи, определить
р?акпию В, если груз Р находится на середине первого пролета
(я « 0,5У (фиг. ?78). '
Ответ. Реакция направлена вниз и равна-
*і
ВР
16 * jJ+Jft'
ш
3. Найти линию влияния для изгибающего момента на средней
опоре С балки, лежащей на трех опорах (фиг. 279). Пользуясь этой
линией, определить изгибающий момент М, когда груз Р находится по
середине второго пролета.
Решение, Первое состояние напряжений — действительное
состояние (фиг. 279а) с ивгибающим моментом М, действующим в попе-
речном сечении С. При втором состоянии напряжений груз Р устранен,
балка разрезана в точке С, и вместо М приложены два равных и прямо
противоположных единичных момента (фиг. 279Ь). Этот случай
статически определим.
Углы ?х и ?2 получатся по формуле [133] (см. стр. 161), а прогиб у
по формуле [134] (стр. 162). Сумма углов ?х и ?2 представит
перемещение при втором состоянии, соответствующее изгибающему моменту М
действующему в первом состоянии. Работа, совершаемая силами первого
состояния на соответствующих перемещениях второго состояния, равна *)
Работа, совершаемая силами второго состояния на перемещениях
первого состояния, равна нулю, так как в действительном случае у нас
нет разреза над опорой С и
перемещение, соответствующее двум Р. х
единичным моментам второго со- . М \ •
стояния, равно нулю. Поэтому Q\ А^ ¦ € 1—і^
Ж(?1 + ?3)-Р2/ = 0,
откуда
м =р у
4
4"-
Ч 1 jt
с' і i
Из этого видно, что при
изменении положения груза Р изгибающий
момент М изменяется таким же образом, как прогиб у. Следовательно
упругие линии второго состояния представляют линию влияния для К
Заметив, что
в
и что прогиб по середине второго пролета
получим, что изгибающий момент, когда груз Р находится на середине
второго пролета, по формуле [А] равен
з рі
И = 2
16 h+h
і) Принято, что изгибающий момент М0 дает упругую линию,
обращенную вогнутостью вниз.
т
4. Ёайть линию влияния для изгибающего момента в закрецленноы
конце В балки АВ, изображенной на фиг. 277, и определить этот
момент, если груз находится на расстоянии % = -у I от левой опоры.
Ответ
б. Построить линию влияния для горизонтальных реакций Н рамы,
показанной на фиг. 186а (стр. 215), если груз Р движется вдоль стержня АВ.
Ответ. Линия влияния имеет тот же вид, что и упругая линия
стержня АВ для условий загружения, показанных на фиг. 185с.
6. Построить линию влияния для усилия X в горизонтальном
стержне CD (фиг. 280а), если груз Р движется по балке АВ.
Определить X, когда груз находится на
середине пролета.
Перемещениями от удлинений и укорочений
стержней пренебречь и принять
во внимание только перемещение
от изгиба балки АВ,
Решение. Возьмем
действительное состояние (фиг. 280а)
за первое состояние напряжений.
При втором состоянии груз Р
устранен, и силы X заменены
силами, равными единице
(фигура 280а). Под действием этих сил,
направленные вверх вертикаль-
ные давления равные——
передаются балке АВ в точках F и
Н, и балка изгибается, как
показано пунктирной линией на
фиг. 280Ь. Если ?/ — прогиб балки
в точке, соответствующей точке
приложения груза Р, н о —
перемещение точек С и D навстречу друг другу при втором состоянии
напряжений, то теорема о взаимности перемещений даст нам:
©
®
._—Л- ..
в
©
Фиг. 280.
Хо — Ру = 0 и
х = рХ
о
и
Поэтому упругая линия балки АВ для второго состояния является
искомой линией влияния. Изгиб балки двумя симметрично
расположенными грузами рассмотрен в задаче 1 стр. 165. Подставив ——
с
вместо Р в формулы, полученные там, находим прогиб балки в точке F
и прогиб по середине пролета соответственно;
(У)х=с =
eh
6EI
(32 - 4с)
и
h
<^=0,5! =^r(3Z2-*C2)
Из рассмотрения поворота треугольника AFC (фиг. 280с) как твер*
дого тела находим, что горизонтальное перемещение трчки С равно
вертикальному перемещению точки F, умноженному на —; поэтому
с
Z
Подотавив это и прогиб по середине пролета в ур-ние [t], получим
8Л ' зг-4с '
7. Найти линию влияния для усилия в стержне CD системы,
изображенной на фиг. 281, причем перемещениями от укорочений и удлинений
пренебречь и рассматривать только изгиб балки АВ.
Ответ. Линия влияния будет такая же, как и для реакции
средней опоры двухпролетной н?разрезной балки (см. задачу 1, стр. 842).
Фиг. 281. Фиг. 282.
8. Построить линию влияния для стержня ВС, который поддержи
вает балку АВ, Найти усилие в нем, если груз Р приложен по
середине пролета АВ (фиг. 282).
Ответ. Пренебрегая перемещениями вследствие удлинения
стержня ВС и укорочения балки АВ, найдем, что усилие в стержне ВС
равно
5 Р
16 Sin а *
73. Напряжения от неточности сборни и температурные напряжения
в статически Неопределимых системах. При рассмотрении статически
неопределимых систем, работающих на растяжение (см. п°8), было
показано, что в таких системах могут возникнуть начальные напряжения
при сборке от неточности в длинах стержней. Могут также появиться
напряжения от температурного расширения. Теорема Кастильяно дает
общий метод определения таких напряжений.
Например предположим, что в ферме, показанной на фиг. 271,
расстояние между неподвижными опорами А и В оказалось меньше, чем
расстояния между соответствующими шарнирами фермы, на величину Ь.
Чтобы поместить, ферму на опоры, необходимо приложить некоторые
силы X, величина которых ' должна быть достаточна для того, чтобы
сократить расстояние между шарнирами А к В фетшы на величину* 5.
Обозначив, как обычно, через о"^ — величину усилия, возникающего
в стержне і от единичных сил, приложенных вместо сил X (фиг. 27Ш,
получим, что уоилне в стержне, возникающее при действии сил X,
845
равно Si = S/i 1Х. Потенциальная энергия деформации, накопленная
фермой при приложении сил X,
гт у3*2h _у(*/)2*Ч Гв1
U " U 2EF{ ~ Lk 2EF{ * laJ
Тогда, применяя теорему Кастилъяно. найдем необходимую величину
сил X из уравнения:
О =
dX JU EF{ '
откуда
__ ЬЕ
Х= - (8^1 ~~ ^ (?/)«1, * [2281
F
і — і
Например, если о = 2,5 мм, Е = 2100 000 «г/ом2 и цифровые данные
гаковы, как указано в таблице 7 на стр. 333, то мы получим
Зная X, легко определить усилия от сборки в любом стержне по
выражению 8 = 8{' X.
Следует отметить, что на практике опоры иногда нарочно
смещаются с их нормального положения, чтобы создать начальные
напряжения такими, которые бы в соединении с напряжениями от внешних
грузов давали более благоприятное распределение напряжений в
системе.
Например, в неразрезной равномерно нагруженной балке на трех
равно отстоящих опорах, наибольший изгибающий момент будет над
средней опорой. Соответствующим понижением этой опоры однако
можно уменьшить максимальный момент и получить более
благоприятное распределение напряжений.
Теорема Кастильяно применима также и тогда, когда начальные
напряжения в системе вызваны неточностями в размерах элементов.
Например, предположим, что в системе, показанной на фиг. 272,
горизонтальный стержень сделан короче расстояния между
шарнирами А и В на величину 8. Когда система будет собрана, то в элемен*
тах фермы появятся некоторые усилия ~ от сборки. Пусть X — такое
усилие в стержне АВ.
Если мы разрежем этот стержень, то тем самым мы устраним все
усилия от неточности сборки, но в то же самое время концы тк п его
(фиг. 272а) раздвинутся на расстояние о.
Усилие X найдем из того условия, что его величина должна быть
достаточной для того, чтобы соединить опять вместе концы тип.
Пользуясь теоремой Кастильяно и вышеприведенным выражением [а]
для потенциальной энергии, получим
*ТГ _у(8'?Х1€
dX~2i EFi '
откуда
-^ ЬЕ
F
і
346
s
Сумма в знаменателе ф-лы [228'] содержит одним членом больше
чем сумма в выражении [228], и этот член равен
и соответствует горизонтальному стержню АВ.
Взяв например
Ь « 2,5 лж, JP0 =* 64,5 см\ Z0 = 7,62 * и Е = 2100 000 %%jgm\
получим
„^025.2100000^^^
W + 260'8
Зная X, получим усилие от сборки в любом другом стержне по
формуле
Изложенный выше способ определения усилий от неточностей
в сборке можно применить также и к усилиям от изменений
температуры.
Возьмем опять в качестве примера ферму, показанную на фиг. 271а,
и предположим, что температура всех элементов увеличилась на і
градусов. Если одна из опот> — подвижная, то пролет фермы увеличится
на al0t, где Iq — расстояние между опорами А и В, и а — коэффициент
линейного расширения. Если опотш неподвижны, то такое расширение
будет устранена их горизонтальными реакциями Л, Эти реакции можно
получить из ур-ния [228] подстановкой al0t вместо 5 в это уравнение.
Если температура стержня і системы возрастет на t градусов, то его
длина возрастет при возможности свободного расширения на
величину а.1 t. В статически неопределимых системах такое свободное
расширение может встретить препятствия со стороны других стержней
или от опор, отчего в системе могут возникнуть температурные
напряжения. Величина этих напряжений — та же, что напряжений от
неточности сборки, которые возникли бы в системе, если бы стержень »
был длиннее, чем нужно, на Ь = a I t, и эту величину можно вычислить
по ур-нию [228'].
В предыдущем изложении были рассмотрены только примеры
с одним лишним элементом. Подобные же методы могут быть
применены и к более сложным системам с несколькими лишними стержнями 3)>
74. Исключительные случаи. При выводе и теоремы Кастильяно и
теоремы взаимности перемещений было предположено, что перемещения
при деформации пропорциональны силам, действующим на упругую
систему. Есть однако случаи, при которых перемещения не
пропорциональны силам, хотя бы материал тела и следовал закону Гука.
Это всегда получается, когда шш рассмотрении действия внешних
сил нужно бывает учитывать перемещения, возникающие от деформаций.
В таких случаях потенциальная энергия деформации уже не является
функцией второй степени, и теорема Кастильяно не имеет силы.
Чтобы пояонить это ограничение, рассмотрим простейший случай,
при котором на упругую систему действует одна только оида Р.
і) Примеры решения таких задач, даны в книге Г, Мюллера-Бреслау,
ом. выноску на стр. 328. См. также его Die Graphisohe Statik der Bau-
fconitruktionen, Stuttjart, 192?-1925,
8*7
Предположим сначала, что перемещение 5 пропорционально
соответствующей силе Р, что изображается прямой линией О А на фиг. 283а.
Тогда площадь треугольника ОАВ представит потенциальную энергию
деформации, накопленную системой при приложении силы Р.
Фиг. 283.
Бесконечно малому приращению do перемещения соответствуот
приращение потенциальной энергии деформации на величину, показанную
на чертеже заштрихованной площадью, и мы получаем, что
аи=раь. ' [в]
При линейной зависимости бесконечно малый треугольник ЛВС
подобен треугольнику ОАВ; поэтому
®
¦
г-
і
/*
?
®
•8
/
dF=p нли
d 8 б
Ш Подставляя
% [а], получаем
dU=P
db =
bdP
ГО
это в ур-ни?
'Ь dP
откуда в соответствии с теоре -
мой Кастильяно имеем
dU
dP
о.
М
Пример, к которому теорема
Кастильяно неприменима,
показан на фиг. 284. Два
одинаковых горизонтальных стержня АС и ВС, с шарнирами в точках А
В к С, подвергаются действию вертикальной хилы Р, приложенной
в шарнире С. Пусть (^ — положение шарнира С после деформации, и
а —угол наклона каждого из стержней в деформированном состоянии.
Относительное удлинение стержней, согласно фиг. 284<», равно
т
Если только рассматривать перемещения очень малыми, то угол а-
тоже мал, и приближенно
COS a \ 2
а2
Тогда из выражепия [d] имеем:
?=^--
Соответствующие усилия стержней
EFo&
T=SF.e = ^L. [e]
Из условия равновесия шарнира Сх (фиг. 284Ь)
Р = 2аТ, И
и пои Т, взятом по выражению [с], получаем
P = EFa*,
откуда
-V
8, р
3
М
о = а I = г • j/"-g^r. (229]
В этом случае ¦ перемещение не пропорционально' силе Р, хотя ма*
териал стержней и следует закону Гука.
Зависимость между о и Р изображена на фиг. 283Ь кривой ОА.
Заштрихованная площадь ОЛВ на этом чертеже представляет
потенциальную энергию деформации, накопленную в этой системе. Величина
энергия деформации равна
б
U
Q
Подставив по формуле [229]
= Гыь. щ
р = вРф И
получим
о
и
Это показывает, что энергия деформации уже не является функцией
второй степени от силы Р. Вместе с тем энергия деформации равна
уже не половине, а только четверти произведения Р8 (см. п° 69).
Теорема Кастильяно конечно здесь неприменима:
-1&8/Z]-I zi3/"X-l&
"" dP \ 4 V EF1 ~ 3 V EF 3
dU
dP
Подобные же результаты получим во всех случаях, где двреме-
щени:і не пропорциональны силам.
349
ПРИЛОЖЕНИЕ
МОМЕНТЫ ИНЕРЦИИ ПЛОСКИХ ФИГУР.
I. Момент икерции плоской фигуры относительно оси,
находящейся в ее плоскости. При рассмотрении изгиба балок
мы встречаем интегралы такого вида:
I2 = fy*dF,
F
[і]
где каждый элемент площади dF умножается на квадрат
его расстояния от оси z и интегрирование распростра-
ч
Щ'- ¦>
С
f
."/'¦'4 ¦¦¦'¦]
2
\
г
h
г
Z
'—J і
Ь _ J
Рис. 1.
Рис. 2.
Рис. а
няется по всей площади F поперечного сечения балки
(рис. 1).
Такой интеграл называется моментом инерции площади
F относительно оси е.
' В простейших случаях моменты инерции могут быть
легко определены аналитически. Возьмем, например,
прямоугольник (рис. 2). Для определения моментауинерции этого
прямоугольника относительно горизонтальной оси
симметрии г мы разделим прямоугольник на такие бесконечно
малые элементы, как показано на чертеже заштрихованной
площадкой. Тогда
L =
у? dy =
12
И
350
Таким же обрааом получим
угольника относительно оси у
момент инерции прямо-
-./¦
sfihds
12
Выражение [2] может быть также применено для
нахождения момента инерции 12 для параллелограмма,
показанного на рис. 3, так как этот
параллелограмм можно
получить из прямоугольника,
начерченного пунктирными
линиями, помощью перемещения
параллельно оси z таких
элементов, как отмеченный на
чертеже штриховкой.
Площади элементов и их
расстояния от оси z остаются
неизменными при таком
перемещении, а потому момент
инерции It тот же, что для прямоугольника
При определении момента инерции треугольника отцо-
сительно его основания (рис. 4); площадь такого элемента/
как показанный на чертеже штриховкой, равна
Рис. 4
dF=b Ъ^і dy,
и выражение [1] дает
h
УУ**у=Ш
12
Показанный на этих примерах способ определения
момента инерции может быть применен и к самому общему
случаю. Момент инерции получится делением фигуры на
бесконечно малые полоски, параллельные оси *,. и затем
интегрированием согласно выражению [1].
Отыскание момента инерции часто может быть
упрощено, если только фигуру можно поделить на такие части,
моменты инерции которых относительно данной оси
известны. В этом случае полный момент инерции равен сумме
моментов инерции всех частей. *
Из самого определения (см. выражение [1]) следует, что
момент инерции фигуры относительно любой оси имеет
351
размерность длины в четвертой степени; поэтому, разделив
момент инерции относительно некоторой оси на площадь
фигуры, получим квадрат некоторой длины. Эта последняя
длина называется радиусом инерции относительно рассматри*
ваемой оси. Для осей у ж z радиусы инерции будут:
Vе у тг; 1*=У ~F-
[з]
ЗАДАЧИ.
1. Найти момент инерции прямоугольника (рис. 2) относительно
основания.
Ответ. і и і = -^-.
у * 3
; 2. Найти момент инерции треугольника ЛВС относительно оси z*
(рис. 4).
Решение. Этот момент является разностью между моментой
инерции параллелограмма ABDC и треугольника ВВС, Отсюда
ЬА» Ъ№ Ыі*
'.'-
12
(7
7
г?
7
L.
іА
с
9.
4 '
t
к
С 2
і4
®
©
Рис. 5.
^ ff
#
е..
3. Определить і для фигур, показанных на рис. 5.
о
Ответ.
(а —2А)* т _ Ьа3 (Ь — Ах) (а - Щ*
12
а«
12
12
_ ЪФ
* 12
4. Найти момент инердии квадрата со сторонами а относительно
диагонали. •¦
Ответ. I = _—.
12
5. Найти * и t для прямоугольника, показанного на рис. 2.
• Ь . А ' .
Ответ, t н * = т^г; і и г = —-.
у г 2/3 » * 2^3
6. Найти * для фигур рис. б а и 5&,
852
II. Полярный момент инерции плоской фигуры. Момент
инерции плоской фигуры относительно оси,
перпендикулярной к плоскости фигуры, называется полярным
моментом ищрции относительно точки пересечения этой оси
с плоскостью фигуры (точка О на рис. 1). Он выражается
интегралом;
1,= fr*dF9 [4]
где каждая элементарная площадка dF умножается на
квадрат ее расстояния г от оси, и интегрирование
распространяется на всю площадь фигуры.
Возвращаясь снова к рис. і, имеем; га = уа-|-*3.и,
согласно выражению [4]:
1>= f (y* + **)dF=It + rvi [5]
го есть полярный момент инерции относительно точки О
равен сумме моментов инерции относительно двух взаимно
перпендикулярных осей у и в, проходящих через ту же
точку в плоскости фигуры.
Рис. 6. Рис. 7.
Рассмотрим пруговое сечение. Мы встречали полярный
момент инерции круга относительно его центра при
рассмотрении скручивания круглого вала (см. п° 18). Если
разделить площадь круга на тонкие элементарные кольца,
23 Твасошенко — Сопротивление материалов, ч. I. 368
как показано на рис. ?, то мы имеем dF=2wdr и,
согласно выражению [4]:
1,-2
uj r»<fr = —. [6]
о
Мы знаек из условий симметрии, что в этом случае
/tf = J2; поэтому из выражений [5] и [6] следует, что
Момент инерции эллипса относительно главной оси &
(рис. 7) можно получить сопоставлением эллипса с кругом,
показанным на чертеже пунктиром.
Высоту у такого элемента эллипса, как показанный
заштрихованным на чертеже, можно получить уменьшением
высоты yt соответствующего элемента круга в отношении
Ь: а. По формуле [2] моменты инерции этих двух элементов
относительно оси в находятся в отношении &3: а3. Моменты
инерции эллипса и круга очевидно должны находиться
в том же отношении; следовательно момент инерции
эллипса равен
*¦ = —64~ ^=~Т~~-' [8]
Таким же образом относительно вертикальной оси
получим
/ — , •
Ч — 4 '
полярный момент инерции эллипса равен поэтому, согласно
выражению [5]:
. ъа? тгаб3 каЪ ,
I# = ^ + Jr. = -l"H 4~ = -4-( Ь 3
ЗАДАЧИ.
, 1. Найти полярный момент инерции прямоугольника относительно
его центра тяжести (рис. 2).
Ответ.
* 12 ^ 12 12 k Ч-">
2. Найти полярные моменты инерции относительно центров тяжести
фигур, показанных на рис. б.
854
Рис. 8.
III. Перенос оси. Если момент инерция фигуры относя*
тельно оси 0, проходящей через ее центр тяжести (рис. 8)f
известен, то момент
инерции относительно любой
параллельной оси &' может
быть определен из
уравнения:
I.'= *• + *»>. [Ю]
где F— площадь фигуры
и d — расстояние между
осями. Это можно доказать
следующим образом.По
формуле [1]
Iz,= f(y + d)*dF= fy*dF-Jr2jtyddFJrfd*dF.
F F F F
Первый интеграл правой части этого выражения равен
1„ третий интеграл равен d2 • F, а второй интеграл
обращается в нуль вследствие того, что ось z проходит через
у центр тяжести; поэтому последнее
выражение приводится к выражению [10].
-z | Выражение [10] особенно пригодно для
определения моментов инерции
поперечных сечений клепаных балок (рис. 9).
Положение центров тяжести
стандартных профилей уголков и моменты инерции
их относительно осей, проходящих через
центры тяжести, даются в справочных
книжках.
Момент инерции такого клепаного
сечения относительно оси г легко опреде-
Рис, 9. ляется помощью переноса оси.
ЗАДАЧИ.
1. Помощью переноса оси определить момент инерции треугольника
(рис. 4) относительно оси, проходящей через его центр тяжести и
параллельной основанию.
Ответ:
С
tk:I
2 =
36
2. Определить момент инерпии I фигуры, показанной на рис. 9*
еоли h = 600 мм, Ь = 12 мм, и уголки имеют размеры 100 X ЮО X 12 мм.
Решение.
1,2 - 503
I =
12
+ 4 [206,4 + 22,73 (25 - 2*9)2] « 57 700 с**.
23*
856
3. Найти момент инерции относительно Нейтральной оси
поперечного сечення швеллера, показанного на фиг. 79 (стр. 101).
IV* Центробежный момент инерции, главные оси. Интеграл
где каждая элементарная площадка dF умножается на
произведение ее координат и интегрирование
распространяется по всей плещади плоской фигуры, называется
центробежным моментом инерг$ии фигуры.
Если фигура имеет ось симметрии
и последняя взята за ось у или z
(рис. 10), то центробежный момент
инерции равен нулю. Это следует из
того обстоятельства, что в этом случае
всякому элементу dF с
положительным в соответствует равный и
симметрично расположенный элемент dFr
с отрицательным %. Соответствующие
элементарные произведения yz • dF
взаимно, уничтожаются, а поэтому
интеграл [11] обращается в нуль.
В общем случае, для любой точки
любой плоской фигуры мы всегда можем найти такие две
взаимно перпендикулярные оси, что центробежный момент
инерции относительно этих осей будет равен нулю.
¦ Возьмем, например, оси у и 0 для
фигуры на рис. 11. Если оси
повергнуть вокруг точки О на 90° по
часовой стрелке, то новые положения
осей будут ?/ и а', как ^показано на
чертеже. Здесь имеется следующая
зависимость между старыми
координатами элемента dF и его новыми
координатами:
dF
ш
1
т
у/
г
Рис. 10.
у' =*;
*' =
у-
Поэтому центробежный момент инерции для новых
координатных осей
Iy>,. = fy'zrdF=~fyzdF=-Iyz.
Итак при повороте центробежный момент инерции
меняет свой знак. Так как центробежный момент инерции
356
изменяется непрерывно при изменении угла поворота осей,
то должны быть такие направления осей, для которых его
величина становится равной нулю. Оси, имеющие такое
направление, называются главными осями.
Обыкновенно началом координат берут центр тяжести,
и соответствующие главные оси тогда называются
центральными главными осями.
/W-' -I
ч
Если фигура имеет ось
симметрии, то эта ось и ось,
перпендикулярная к ней,
будут главными осями
фигуры, так как
центробежный момент инерции
относительно этих осей равен
нулю, как объяснено выше.
Если центробежный
момент инерции фигуры
известен для осей у и в
(рис. 12), проходящих через центр тяжести, то
центробежный момент относительно осей у' и z\ параллельных
упомянутым выше, можно найти из выражения:
Рио. 12.
If
JN
\
/-
/
h.
Т
Координаты любого элемента
dF для новых осей будут:
Уг — У + ъ*> *' = * + «.
Поэтому
f{y + b)(z+a)dF=
Рнс. 13.
"-1 V**
fy'0>dF=
-» fy*&F-\- JabdF+ j\ja dF+ jbz dF.
Ж F Ж F
Последние два интеграла обращаются в нуль, так как
С—центр тяжести, а потому это выражение приводится
к выражению [12].
ЗАДАЧИ.
1. Найти Jyrz, для прямоугольника (рис. 2).
Ответ.
857
2* Определить центробежный момент инерции уголкового еечвнн*
относительно осей у и *. Определить то же самое для осей yt в
г, (рис. 13).
Решение. Разделив фигуру на два прямоугольника и применяя
выражение [12] к каждому из этих прямоугольников, найдем
_ a?h* Л2(Д2 — Щ
Из условий симметрии Iytz, = 0.
3. Определить цетрооежный момент инерции 1уя фигур,
показанных на рис. 5, если точка С—центр тяжести.
Решение. Для фигур рис. 5а и 66 Iyz = 0 из условий симметрии.
Для фигуры по рис. 5с, разделив сечение на три прямоугольника и,
пользуясь выражением [12], найдем
V. Поворот оси. Нахождение главных осей. Предположим,
что моменты инерции
y*dF;
= fjfidF
[а]
и центробежный момент
инерции
I^fytdF [Ь]
РИС 14.
известны, и требуется
найти те же величины для новых осей уг и ег (рис. 14).
Для элементарной площадки dF новые координаты
согласно чертежу будут равны:
ег = z cos ? -f у sin 9; Ух = у cos 9—s sin <р, [с]
где (?—угол между осями z и ev Тогда
7*і ^ у1^2 dF== f(y cos ? ~8 sin ?)а йі?Тжв
? • f
«в fj/*cos*<?dF-{- f&®n*<fdF—2 [2 ум sin 9 cos 9 ЗУ.
Или, на основании выражений [я] и [6]
/, *™ I$ cos3 <? -f ^ sin* т — ^ вЬ 2 ».
[UJ
866
Уг*і
Таким же образом
Взяв сумму и разность выражений [13] и [13'], найдем:
2* - 4=(1* - Vcos 2 ? ~2 7*«sin 2 *¦ (15і
Эти уравнения удобны для определения 1Г1 и ItfI
Для определения I находим:
/ Уі ^і <?F= / (г/ cos © — 0 sin©) (з cos ? + у sin ©) dF~»
= f у* sin <? cos vdF— A2 sin ©cos© dF -f-
_l f yg (cos* </ — sin2©)dF,
или на основании выражений [а] и [Ь], имеем:
^-Л-^-^ + ^оовг?.- Tie]
Главные оси инерции будут те две взаимно
перпендикулярные оси, для которых центробежные момент инерции
равен нулю. Оси ух и гх на рис. 14 будут главными осямя,
если правая часть ур-ния [1G] обращается в нуль:
, г т ч sin 2 © .
что да#т:
tg2©=7%r. [17]
Пусть нам нужно определить, например, направления
главных осей прямоугольника, проходящих через один -из
углов его (рис. 2). В этом случае: ,
_іМ. г —J^L т — &9&*
следовательно:
*82*—ГПЗ лГ^дог#,а_^ W
21—_-^-\ 2(ЛЯ —А*)'
aw
При выводе выражения [17] угол ? считался положи*
гельным в направлении против часовой стрелки (рис. 14);
поэтому угол 9 должен быть отложен в том же
направлении, если он получился положительным. Уравнение [d]
дает два различных зна-
^ чения для угла <р,
отличающиеся друг от друга
на 90°. Эти два взаимно
перпендикулярных
направления будут
направлениями главных осей.
Зная направления глав*
ных осей, можно найти
соответствующие им
моменты 'инерции по
выражениям [14] л [15].
Радиусы инерции,
соответствующие главным
осям, называются
главными радиусами инерции.
инерции (рис. 15) и і и
Рис. 16.
Если у1 и гг — главные оси
і —главные
радиусы инерции, то эллипс с полуосями
показанной на чертеже, называется эллипсом
инерции. Имея этот эллипс, можно получить графически
радиус инерции іе для любой оси z проведением
касательной к эллипсу параллельно оси z. Расстояние от начала
координат О до этой касательной и будет длина, равная
if. Эллипс инерции дает картину того, как меняется
момент инерции при повороте оси г в плоскости фигуры
относительно точки 0, и показывает, что наибольший и
наименьший' моменты инерции будут главными моментами
инерции.
ЗАДАЧИ.
1. Определить Управление центральных главных осей зетового
зечсния (рис. 5е), если h = пх = 25 мм, Ь =1^5 мм, а = 250 мм.
2. Найти направление пентральных главных' осей и
соответствующие главные моменты инерции для уголка 160 X 80 X 12 мм.
3. Определить полуоси -эллипса инерции для эллиптического
поперечного сечения (рис. 7). -
Ответ. %в= 0,56; іу = 0,5?
4. При каких условиях эллипс инерции становится кругом?
Ответ. Когда моменты инерции относительно главных осей равны
ОТ*1 ДРУГУ-