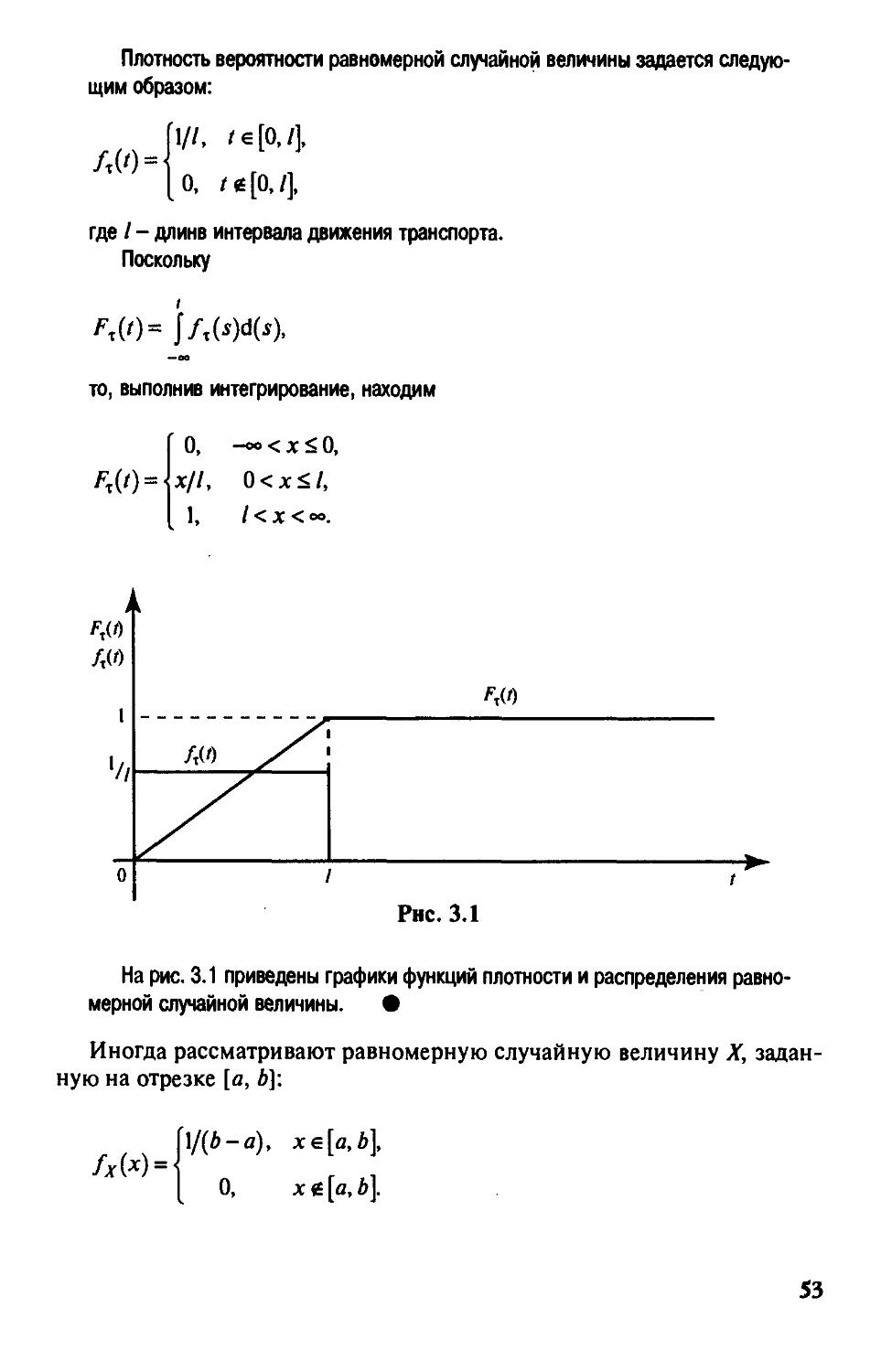
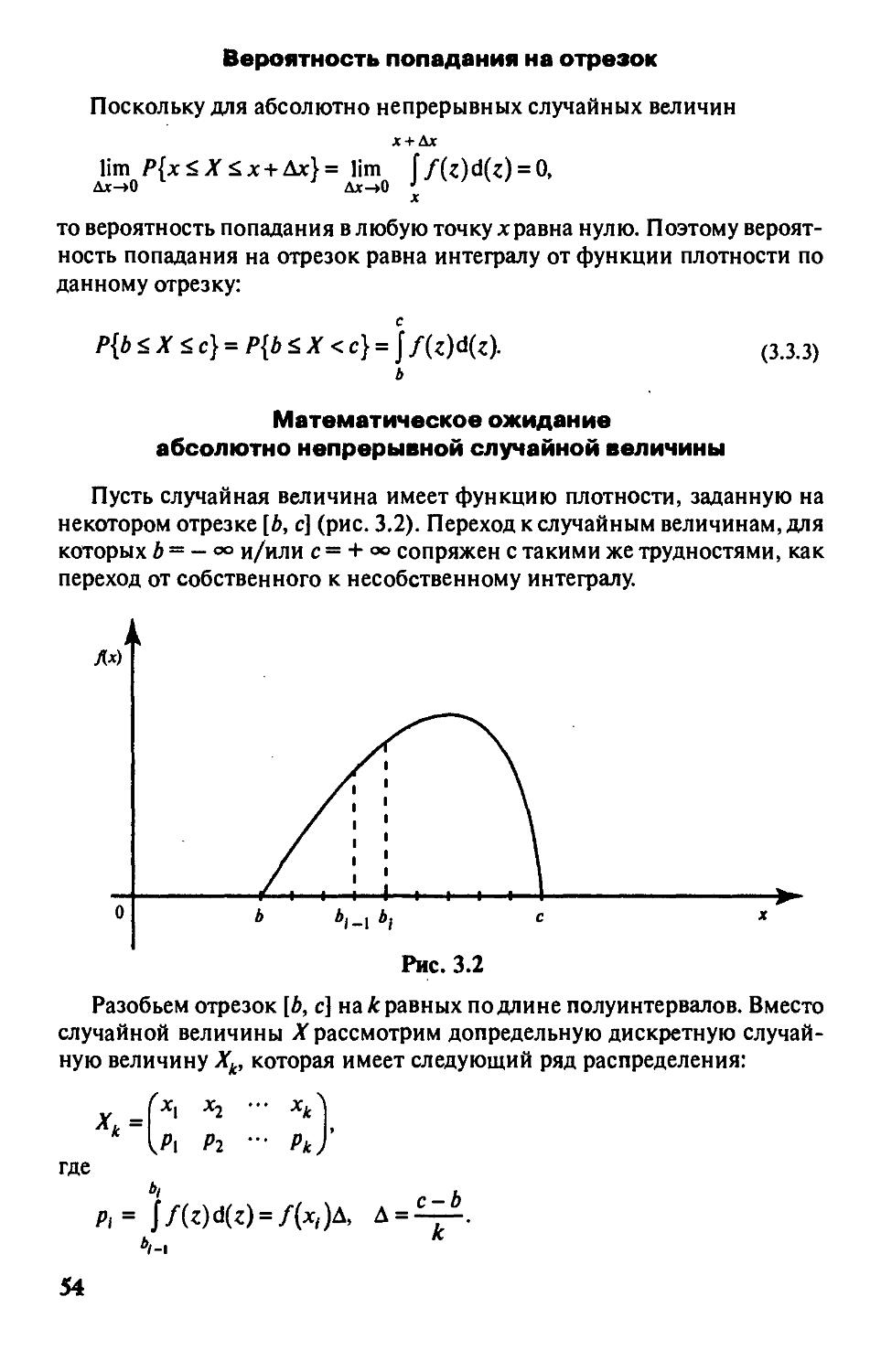
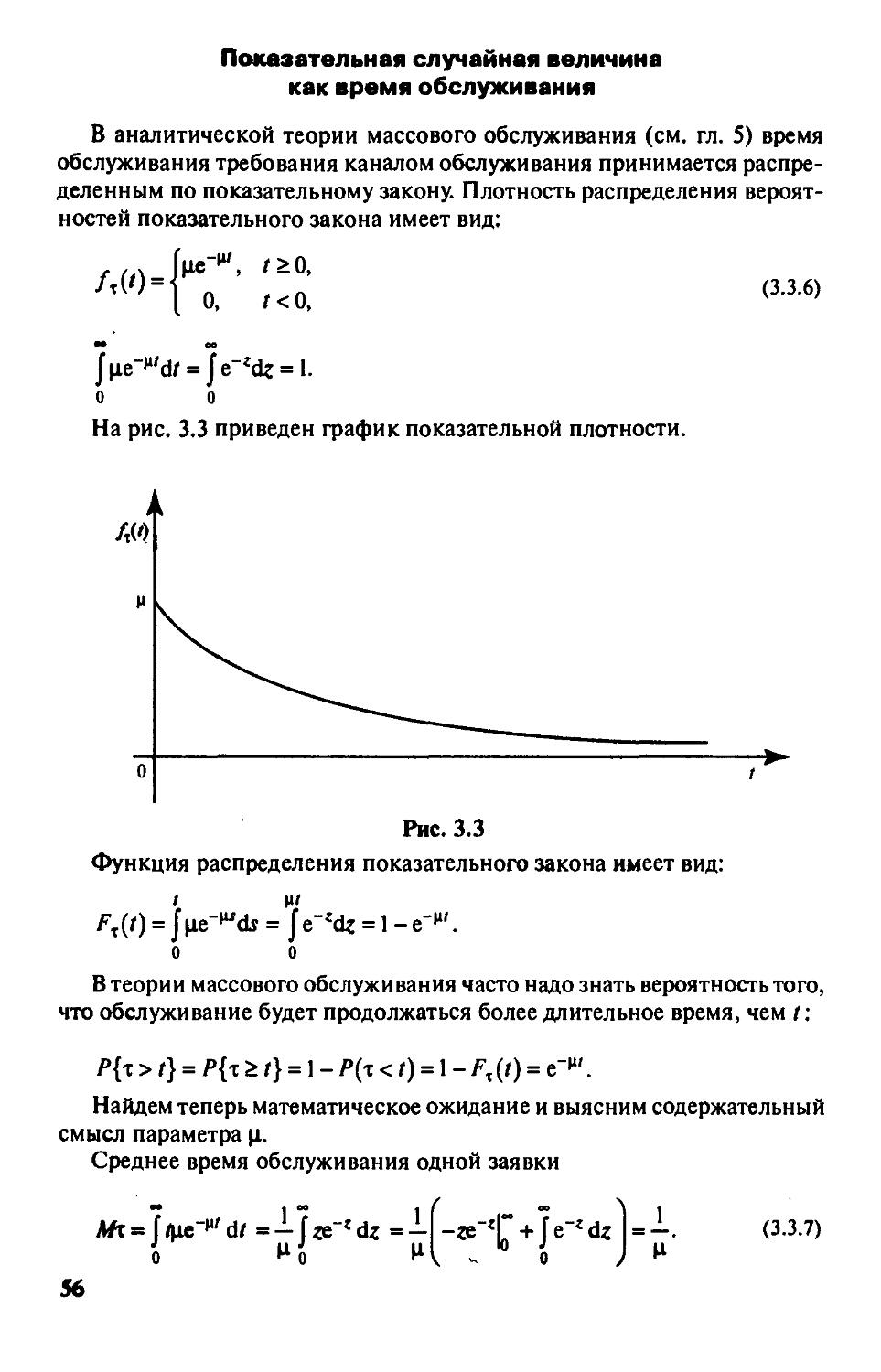
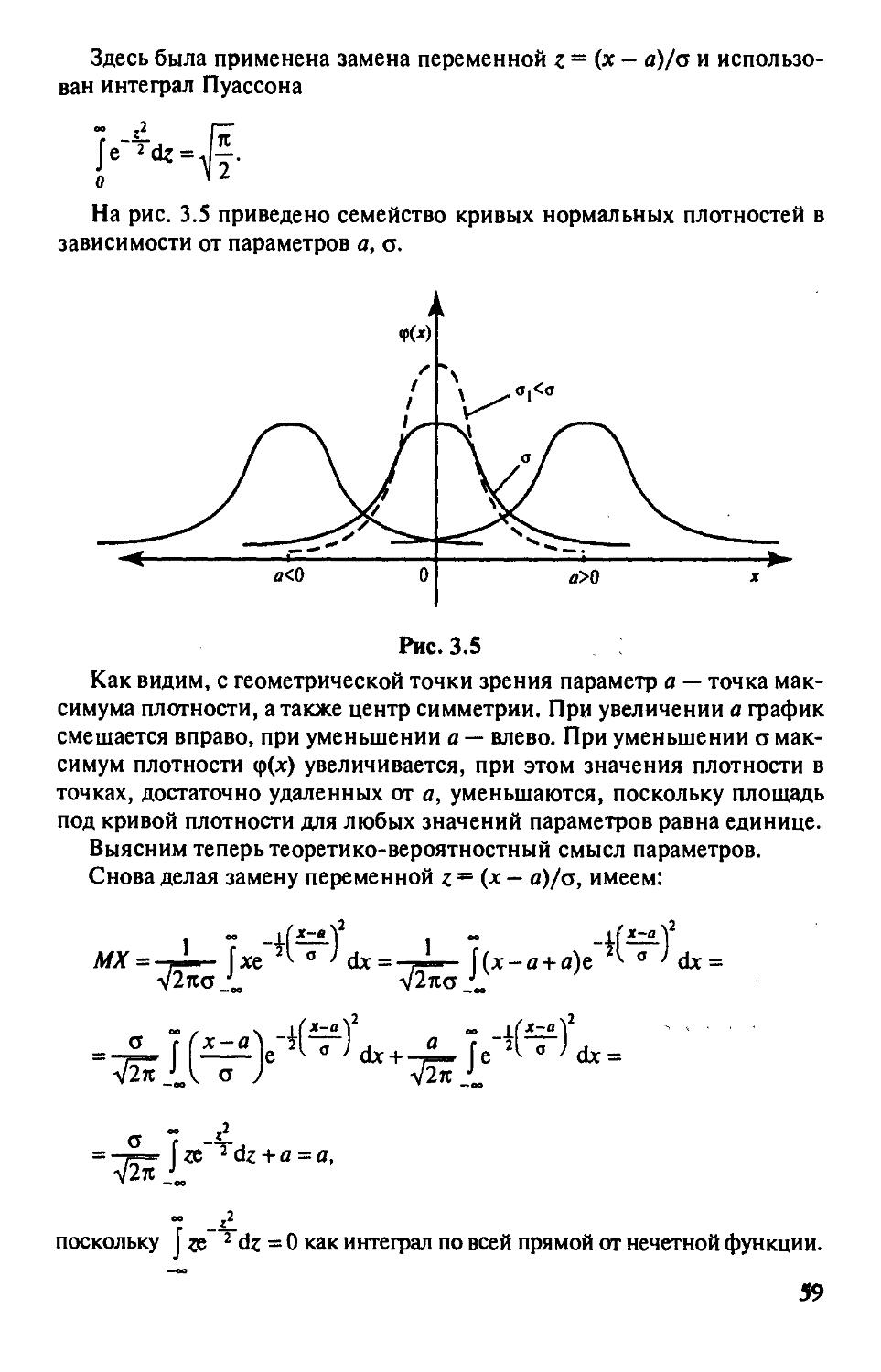
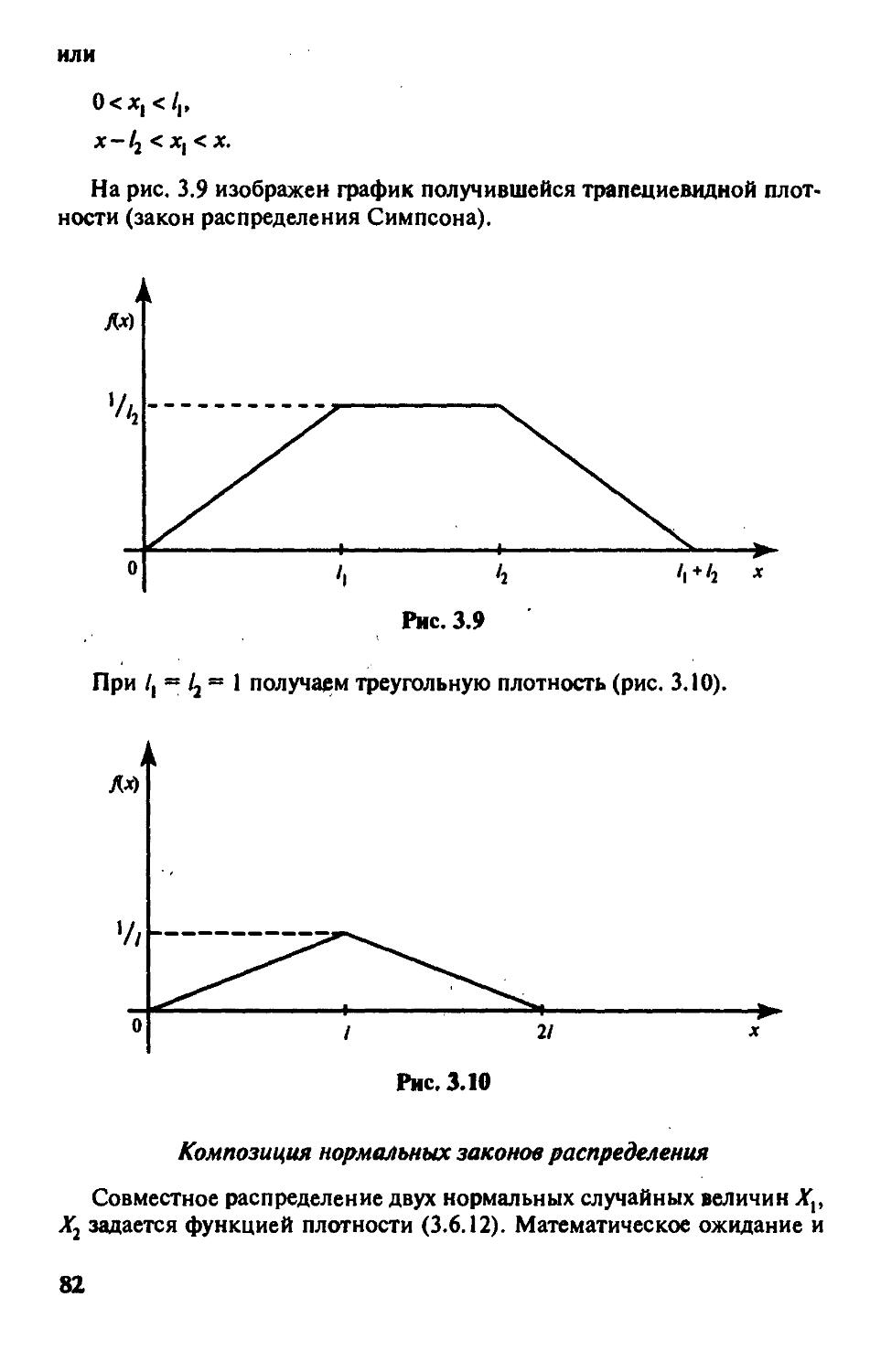
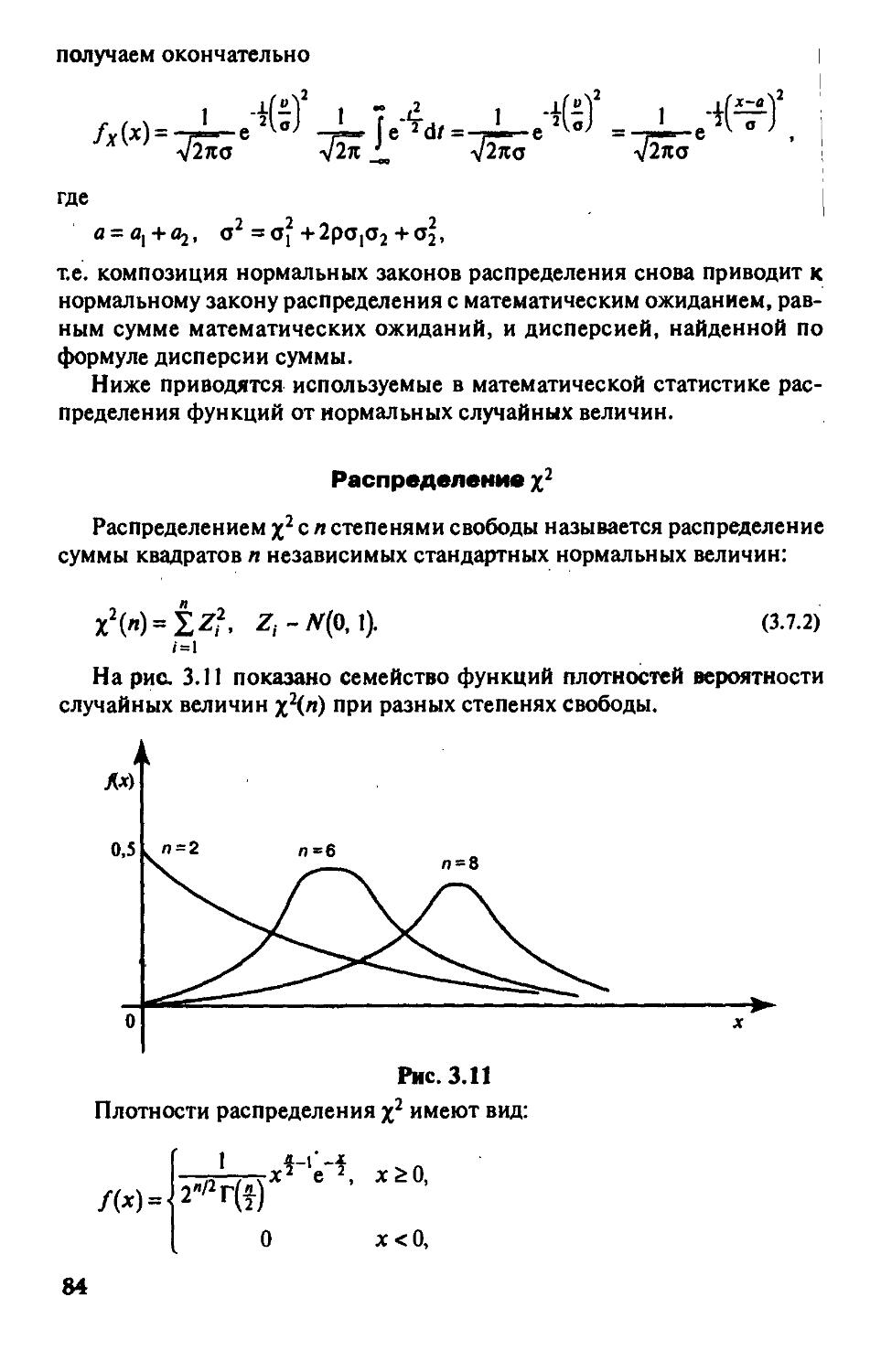
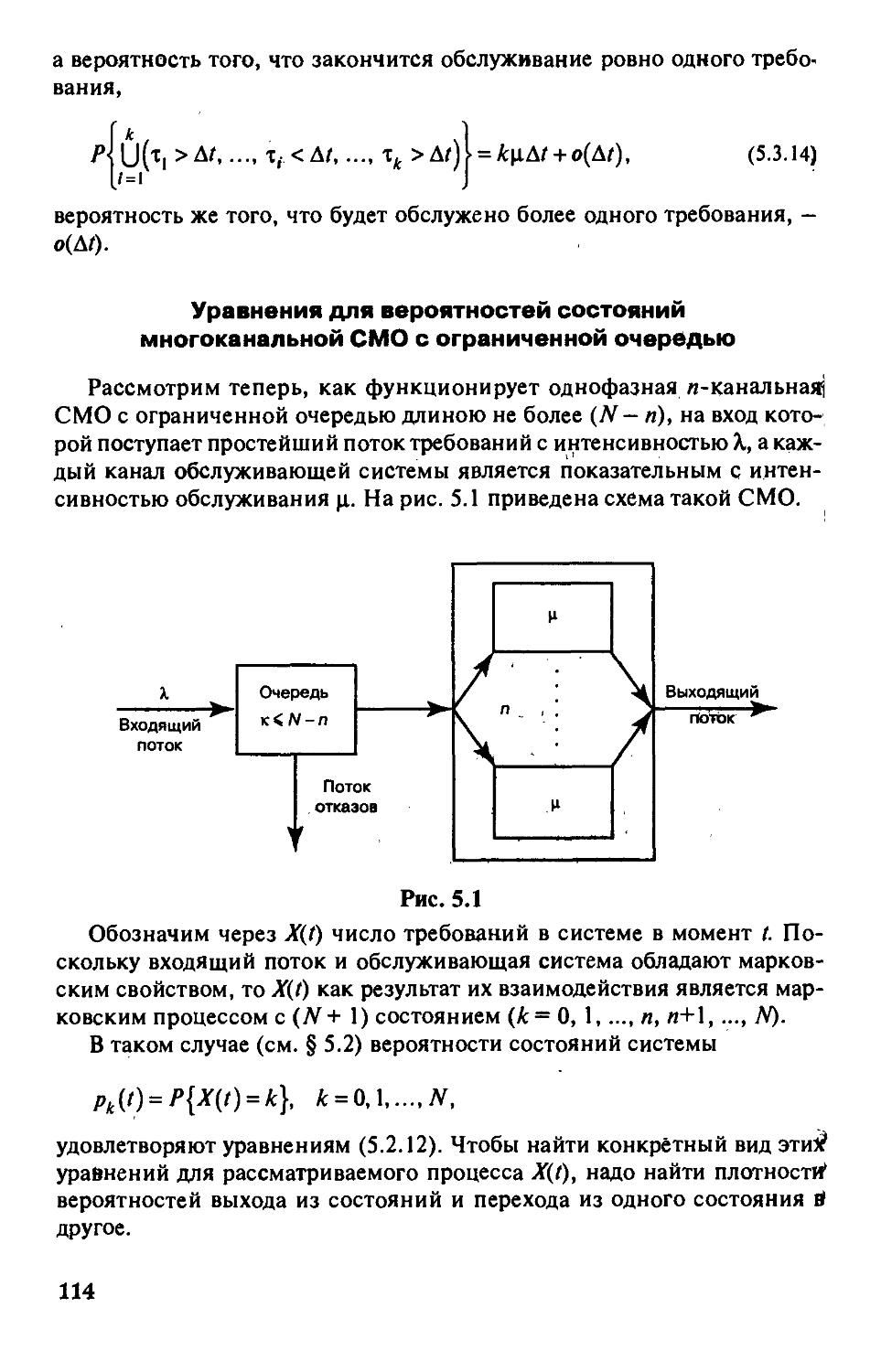
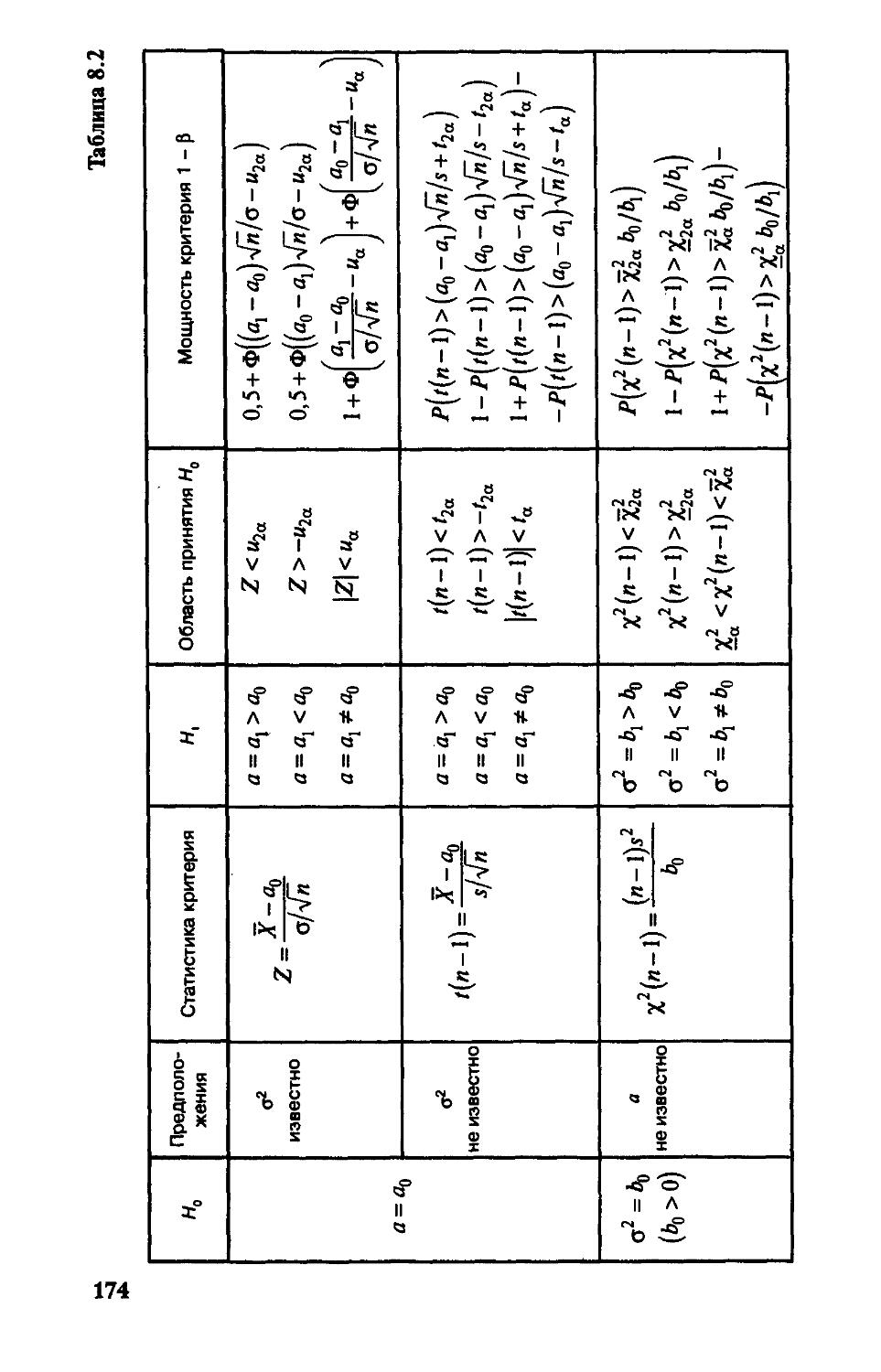
Author: Колемаев В.А. Калинина В.Н.
Tags: болезни животных (кроме болезней домашних животных) патология животных теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 5-86225-571-0
Year: 1997
i>
Серия «ВЫСШЕЕ ОБРАЗОВАНИЕ»
В.А. Колемаев, В.Н. Калинина
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
УЧЕБНИК
Под редакцией
проф. В.А. Колемаева
Рекомендовано Министерством общего
и профессионального образования
Российской Федерации в качестве учебника
для студентов высших учебных заведений,
обучающихся по направлению и специальности
«Менеджмент»
•щ. ж -ш*
Москва
ИНФРА-М
1997
УДК 591.21(075.8)
ББК22.17Я7
К 60
Авторы: В.А. Колемаев{гл. 1—6, 9—11, Приложения 1—3);
В.Н. Калинина (гл. 7 и 8, Приложение 4)
Рецензенты: кафедра статистики
Российской экономической академии им. Г.В. Плеханова
(зав. кафедрой —д-р экон. наук, проф. Б.И. Искаков)
и д-р экон. наук, проф. Ю.П. Лукашин
Колемаев В.А., Калинина В.Н.
К 60 Теория вероятностей и математическая статистика; Учебник /
Под ред. В.А. Колемаева. - М.: ИНФРА-М, 1997. - 302 с. -
(Серия «Высшее образование»).
ISBN 5-86225-571-0
Излагаются основы теории вероятностей, теории массового
обслуживания и математической статистики согласно соответствующему разделу
программы дисциплины «Математика» для специальности «Менеджмент».
Изложение сопровождается примерами и задачами из экономической практики.
Предназначен для студентов специальности «Менеджмент» и может быть
использован и для других экономических специальностей. Будет также
полезен аспирантам и слушателям факультета магистерской подготовки,
работающим в области экономики и управления.
ISBN 5-86225-571-0 ББК22.17я7
© В.А. Колемаев, В.Н. Калинина, 1997
©ИНФРА-М, 1997
Оглавление
Предисловие 6
Введение 8
Часть 1. Теория вероятностей 10
DiaBal. Вероятностные пространства 10
§ 1,1. Классическое определение вероятности 10
§ 1.2, Конечная схема с неравновозможными исходами 15
§ 1,3. Исчисление событий 19
§ 1.4, Аксиоматическое построение теории вероятностей 22
Вопросы и задачи 25
DiaBa 2. Условные вероятности.
Последовательности испытаний 27
§ 2,1. Условные вероятности 27
§ 2.2. Последовательности испытаний 30
Вопросы и задачи 35
DiaBa 3. Случайные величины и их числовые характеристики 37
§ 3.1. Определение случайной величины
и ее функция распределения 37
§ 3.2. Дискретные случайные величины
и их важнейшие числовые характеристики 42
§ 3.3. Непрерывные случайные величины
и их важнейшие числовые характеристики 51
§ 3.4. Нормальное распределение 58
§ 3.5. Производящая функция и числовые характеристики
случайной величины 62
§ 3.6. Многомерные случайные величины 69
§ 3,7, Функции от случайных величин 80
Вопросы и задачи 86
DiaBa4. Предельные теоремы теории вероятностей 89
§4.1, Законы больших чисел 89
§ 4.2, Центральная предельная теорема 93
Вопросы и задачи 98
Гпава 5. Введение в теорию случайных процессов
и теорию массового обслуживания 100
§ 5,1. Случайные процессы и их виды 100
§ 5.2. Марковские случайные процессы с непрерывным временем
и дискретным множеством состояний 103
§ 5,3, Введение в теорию массового обслуживания 109
Вопросы и задачи 122
Часть 2. Математическая статистика 124
Гпава 6. Основы выборочного метода 125
§ 6.1. Оценка числовых характеристик случайных величин 125
§ 6.2. Оценка функций распределения и плотности 137
Вопросы и задачи 139
Гпава 7. Точечные и интервальные оценки параметров распределений 141
§ 7.1. Метод моментов 141
§ 7.2. Метод максимального правдоподобия 146
§ 7.3. Понятие интервальной оценки. Интервальные оценки
параметров нормального распределения 151
§ 7.4. Асимптотический подход к интервальному оцениванию 158
Вопросы и задачи 163
ГпаваЗ. Проверка гипотез 166
§ 8.1. Основные понятия проверки гипотез.
Гипотезы о параметрах нормального распределения 166
§ 8.2. Гипотезы о равенстве средних и дисперсий
двух нормальных распределений 176
§ 8.3. Критерии согласия 179
§ 8.4. Введение в дисперсионный анализ 184
Вопросы и задачи 192
П1ава9. Корреляционный и регрессионный анализ 195
§9.1. Введение в корреляционный анализ 196
§ 9.2. Регрессионные модели как инструмент анализа
и прогнозирования экономических явлений 206
§ 9.3. Парная линейная рефессия 208
§ 9.4. Множественная линейная регрессия 221
§ 9.5. Особенности практического применения
рефессионных моделей 231
Вопросы и задачи 235
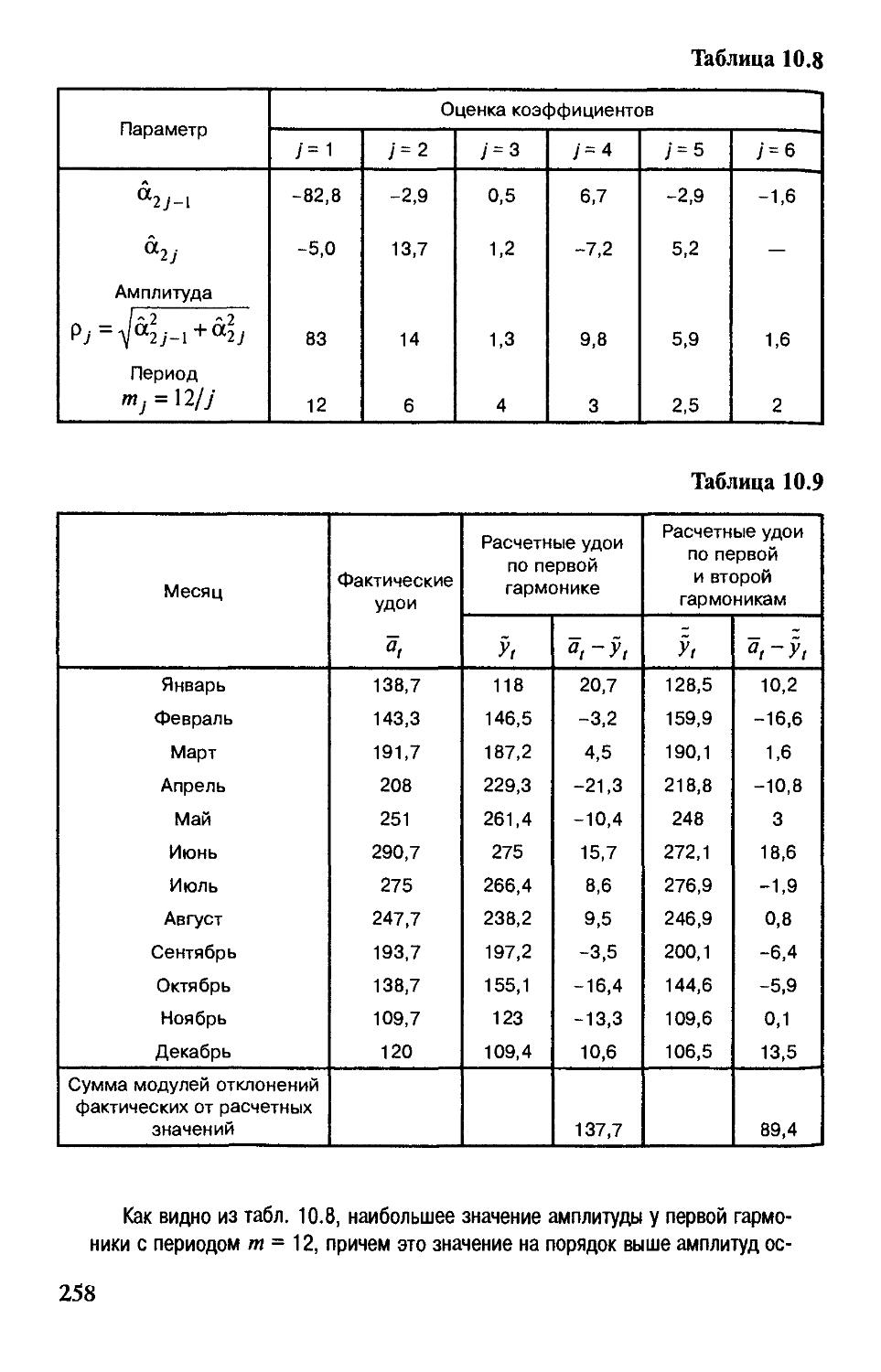
Diaea 10. Статистический анализ экономических временных рядов 237
§ 10.1.Трендовые модели 238
§ 10.2. Выявление тренда в динамических рядах
экономических показателей 242
§ 10.3. Нелинейные тренды 259
§ 10.4. Экспоненциальное сглаживание 262
Вопросы и задачи 268
DiaBa 11. Элементы многомерного статистического анализа 270
§ 11.1. Модель факторного анализа и метод главных компонент 271
§ 11.2. Понятие омногомерной классификации 278
Вопросы и задачи 280
Приложение 1. Доказательство сходимости вероятностей
состояний СМО к стационарным значениям 281
Приложение 2. Расчет сумм, содержащих
тригонометрические функции 286
Приложение 3. Обоснование сходимости метода Ньютона—Гаусса 289
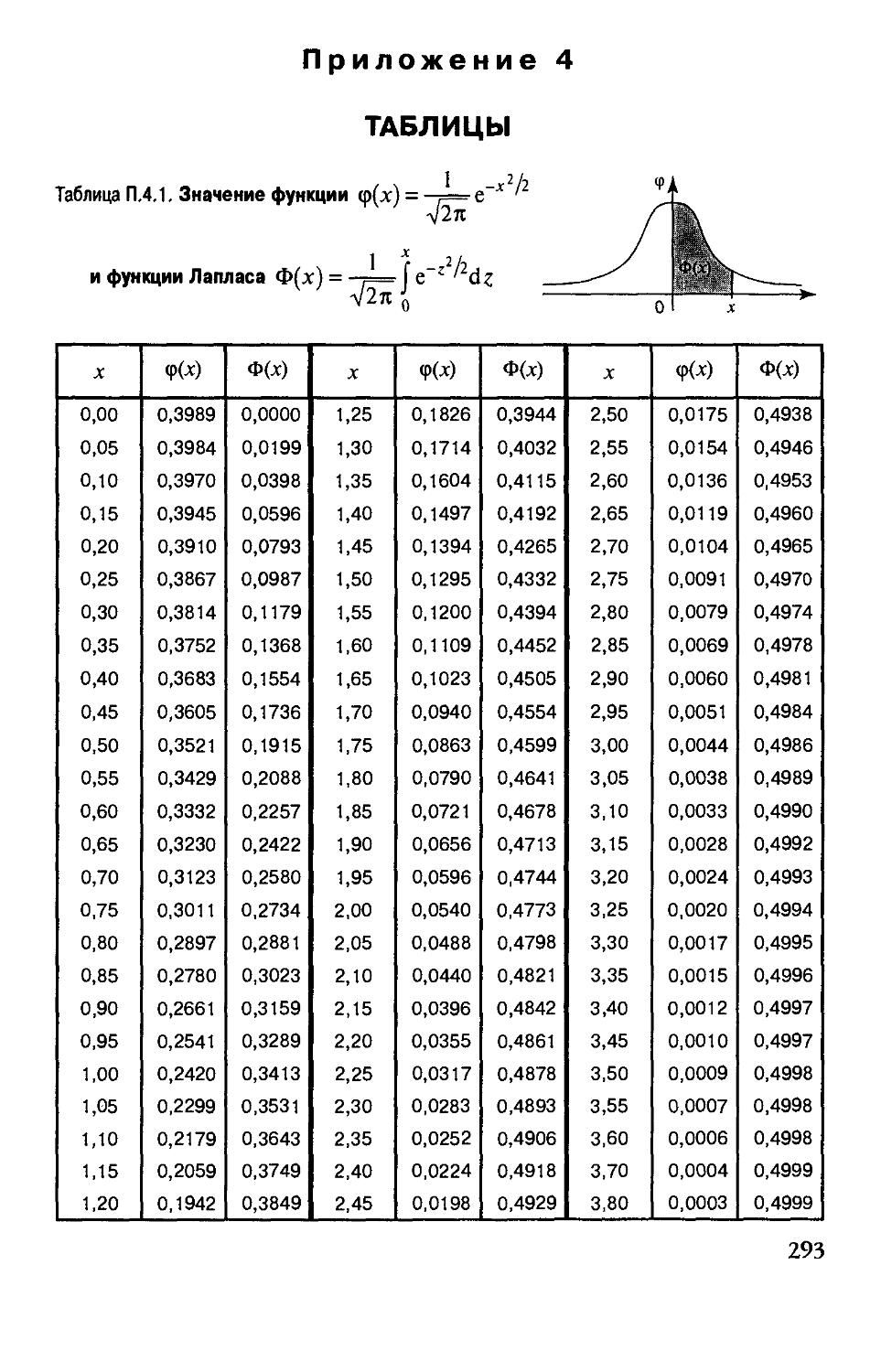
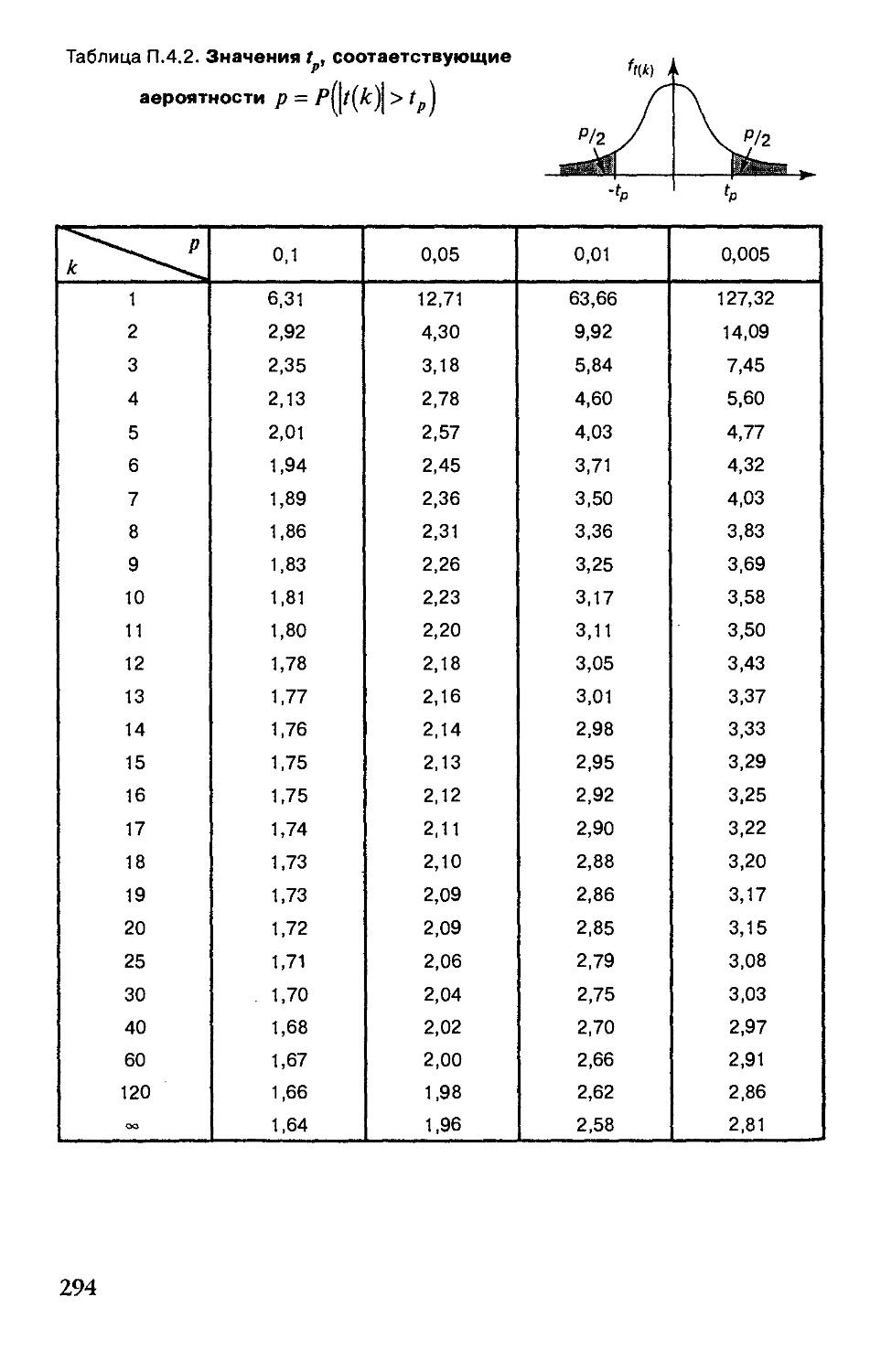
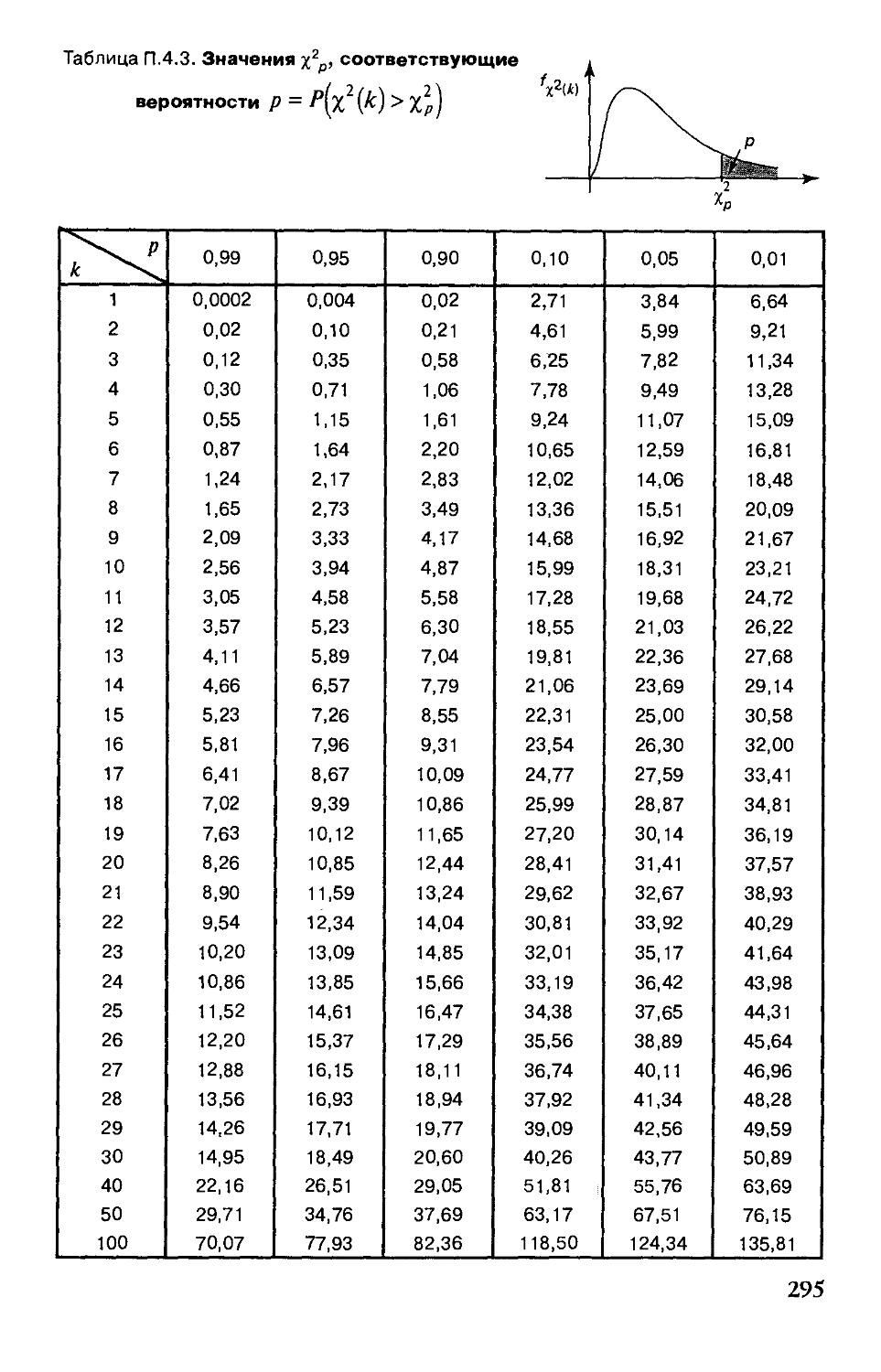
Приложение 4. Таблицы 293
Список литературы 299
ПРЕДИСЛОВИЕ
В основу книги положен многолетний опыт преподавания
дисциплины «Теория вероятностей и математическая статистика» кафедрой
Прикладной математики Государственной академии управления
им. С. Орджоникидзе (ГАУ) для студентов специальностей
«Менеджмент», «Менеджмент в социальной сфере», «Мировая экономика»,
«Национальная экономика», «Государственное и муниципальное
управление», «Маркетинг», «Бухгалтерский учет и аудит», «Социология» и
«Связи с общественностью».
При написании учебника авторы старались добиться максимальной
доступности изложения, сохраняя необходимый уровень строгости. Ведь
теория вероятностей и математическая статистика — математические
науки, построенные на аксиоматической основе. Пытаясь приблизить
материал к практическим нуждам экономики и управления, авторы
добавили соответствующие примеры и задачи.
Книга написана с учетом опыта издания учебников для
экономических и других специальностей. Наиболее тесная связь существует с
учебным пособием «Теория вероятностей и математическая статистика»,
изданным в 1991 году в издательстве «Высшая школа», членом авторского
коллектива и научным редактором которого был один из соавторов
настоящего учебника. Птавы, написанные научным редактором, вошли в
учебник с относительно небольшими изменениями. Другие главы
существенно отличаются от глав-аналогов учебного пособия, поскольку
заново написаны авторами в соответствии с профаммой «Математика» для
специальности «Менеджмент».
Предполагается, что читатель знает основы дифференциального и
интефзльного исчислений, дифференциальных уравнений,
матричного исчисления.
Книга состоит из двух частей: в первой части излагаются основы
теории вероятностей, во второй — математической статистики.
Формулы имеют трехступенчатую нумерацию: номер главы, номер
парафафа, номер формулы. Таблицы, примеры и рисунки
двухступенчатую: номер главы, номер таблицы или рисунка. Для удобства
читателей начало и конец выводов, доказательств и рассуждений, приводящих
к определенным результатам, отмечены соответственно пустым (неза-
черненным) и залитым квадратиками (Q и ■), начало и конец
примеров— соответственно пустым (Q) и залитым (•) кружками, а начало и
конец задач — треугольниками (V и Т).
Вопросы и задачи к главам намеренно расположены без
соответствия с порядком следования материала в главах.
Авторы выражают искреннюю признательность рецензентам: зав.
кафедрой статистики РЭА им. Г.В. Плеханова д-ру экон. наук, проф.
Б.И. Искакову, зав. сектором экономического моделирования ИМЭМО
д-ру экон. наук, проф. Ю.П.Лукашину
В подготовке рукописи учебника к изданию приняли участие
следующие сотрудники и студенты ГАУ: Гончарова Л.В., Сынкова А.В.,
Синельникова М.Н., Стружкин Н.П., Боярский Н., Осадчук Е.,
Петров Д., Путинцев е., Рыбаков И., Смирнов Р.
ВВЕДЕНИЕ
По форме проявления причинных связей законы природы и
общества делятся на два класса: детерминированные и статистические.
Например, на основании законов небесной механики по известному
в настоящем положению планет Солнечной системы может быть
практически однозначно предсказано их положение в любой наперед
заданный момент времени, в том числе очень точно могут быть предсказаны
солнечные и лунные затмения. Это пример детерминированных законов.
Вместе с тем не все явления макромира поддаются точному
предсказанию, несмотря на то что наши знания о нем непрерывно углубляются
и уточняются. Так, долговременные изменения климата,
кратковременные изменения погоды не являются объектами для успешного
прогнозирования. Еще менее детерминированы многие законы и
закономерности микромира. Например, с точки зрения теоретической физики
нельзя говорить о точном положении электрона в определенный момент
времени, но можно говорить о его распределенном положении в
пространстве («электронное облако»). Такого рода законы называются
статистическими. Согласно этим законам, будущее состояние системы
определяется не однозначно, а лишь с некоторой вероятностью,
являющейся объективной мерой возможности реализации заложенных в
прошлом тенденций изменения.
Теория вероятностей изучает свойства массовых случайных событий,
способных многократно повторяться при воспроизведении
определенного комплекса условий. Основное свойство любого случайного
события независимо от его природы — вероятность его осуществления.
Теория вероятностей — математическая наука. Из первоначально
заданной системы аксиом вытекают другие ее положения и теоремы.
Впервые законченную систему аксиом сформулировал в 1936 г советский
математик академик А.Н. Колмогоров в своей книге «Основные понятия
теории вероятностей».
Теория вероятностей вначале развивалась как прикладная
дисциплина. В связи с этим ее понятия и выводы имели окраску тех областей
знаний, в которых они были получены. Лишь постепенно
выкристаллизовалось то общее, что присуще вероятностным схемам независимо от
области их приложения: массовые случайные события, действия над ними
8
и их вероятности, случайные величины и их числовые характеристики.
Большой вклад в развитие теории вероятностей внесли русские ученые.
Практические приложения способствовали зарождению теории
вероятностей, они же питают ее развитие как науки, приводя к появлению все
новых ее ветвей и разделов.
На теорию вероятностей опирается математическая статистика,
задача которой состоит в том, чтобы по ограниченным данным (выборке)
восстановить с определенной степенью достоверности характеристики,
присущие генеральной совокупности, т.е. всему мыслимому набору
данных, описывающему изучаемое явление. За несколько последних
десятилетий от теории вероятностей «отпочковались» такие отрасли науки,
как теория случайных процессов, теория массового обслуживания,
теория информации, эконометрическое моделирование и др. Этот процесс
продолжается и теперь.
Одной из важнейших сфер приложения теории вероятностей
является экономика. В настоящее время трудно себе представить
исследование и прогнозирование экономических явлений без использования эко-
нометрического моделирования, регрессионного анализа, трендовых и
сглаживающей моделей и других методов, опирающихся на теорию
вероятностей.
Статистические закономерности присущи и централизованно
управляемой, и тем более децентрализованной экономике. Наличие таких
твердо устоявшихся в экономике понятий, как страховой запас,
резервные мощности, государственные резервы, финансовые риски и тп.,
свидетельствует об этом.
Необходимо также заметить, что без элементов случайности вообще
невозможно развитие. Без случайности были бы невозможны
возникновение жизни и совершенствование биологических видов, немыслимы
история человечества, творческая деятельность людей, развитие
социально-экономических систем. Таким образом, проявление случайности
в экономике следует рассматривать как отклонение от сложившегося
русла событий либо в положительную сторону (появление новых
научных открытий, технологий, способов ведения и организации
производства и т.п.), либо в отрицательную (стихийные бедствия, поломки
оборудования, болезни работников, конфликты людей и т.п.), что
впоследствии приводит к существенному изменению самого течения событий.
С развитием общества экономическая система все более
усложняется. Следовательно, по законам развития динамических систем должен
усиливаться статистический характер законов, описывающих
социально-экономические явления. Все это предопределяет необходимость
овладения методами теории вероятностей и математической статистики
как инструментом статистического анализа и прогнозирования
экономических явлений и процессов.
Часть 1
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Глава 1
ВЕРОЯТНОСТНЫЕ ПРОСТРАНСТВА
в настоящей главе в сжатом виде представлена эволюция теории
вероятностей от классической схемы с конечным числом равновозможных
исходов до аксиоматического построения. Вводятся важнейшие
понятия теории вероятностей: пространство элементарных событий,
случайные события и действия над ними, поле событий, вероятность,
вероятностное пространство.
§1.1. Классическое определение вероятности
Достоверным называют событие, которое обязательно произойдет
при осуществлении определенного комплекса условий. Так, например,
вода при нормальных атмосферных условиях и 0° С замерзает.
Соответственно, невозможным является событие, которое при заданном
комплексе условий никогда не произойдет. Случайным естественно назвать
такое событие, которое при заданном комплексе условий может как
произойти, так и не произойти. Мера возможности осуществления такого
события и есть его вероятность. Достоверное и невозможное события
могут рассматриваться как крайние частные случаи случайных событий.
Далее случайные события будем обозначать большими латинскими бук-
вамиу4, В, С,.... Достоверное событие обозначим буквой Q, невозможное —
символом 0. Введем теперь некоторые отношения между событиями.
Два события Ак В несовместны, если наступление одного из них
исключает наступление другого. Сумма событий А, В — это такое третье
событие С — А + В, которое происходит тогда, когда наступает либо со-
10
бытие А, либо событие В, либо они оба одновременно. Произведение
событий А, В — это такое событие С = АВ, которое наступает тогда, когда
происходят и событие А, и событие В. Событие А противоположно
событию А, если оно несовместно с событием А и вместе с ним образует
достоверное событие А+А = П.
Покажем, как могут быть построены математические модели
явлений с конечным числом исходов. Одной из таких моделей является
модель, известная под названием «классическая вероятностная схема».
В этой схеме определение вероятности основывается на равновозмож-
ности любого из конечного числа исходов, что характерно для первых
попыток исчисления шансов в азартных ифах.
Так, в случае с ифальной костью при однократном бросании равно-
возможно выпадение любой из шести граней, на которые нанесены
цифры 1, 2, 3, 4, 5, 6. Обозначим эти равновозможные исходы, или
элементарные события, через со,, cOj. ^з' ^4' ^5' ^б- Естественно, что шанс
осуществиться не одному исходу, а одному из двух, например или со,, или
(Oj, в 2 раза больше. Рассуждая таким образом, можно определить
шансы осуществления любого события, состоящего из нескольких
элементарных, так называемого составного события.
В общем случае, когда имеется п равновозможных элементарных
событий со,,..., (Од, вероятность любого составного события А, состоящего
из т элементарных событий {0/|, ..., со/^, определяется как отношение
числа элементарных событий, благоприятствующих событию А, к
общему числу элементарных событий, т.е.
р[А) = т/п. (I.I.I)
Например, в случае с ифальной костью вероятность события А,
состоящего в выпадении четного числа очков (т.е. А = {cOj, (о^, cOg}), равна
Р(А)=^/^—^/2, так как в событие А входят три элементарных события,
а общее число элементарных событий равно 6.
Из классического определения вероятности, в частности, вытекает,
что вероятность полного события Q, включающего все п элементарных
событий, равна единице:
/'(Q) = «/« = l.
Но ведь тогда полное событие Q, состоящее в появлении любого из
всего набора элементарных событий Q ={(0|, ..., (о„}, и является
достоверным событием, так как оно обязательно происходит. Поэтому
вероятность достоверного события равна единице.
Если события рассматривать как подмножества множества
элементарных событий, то отношения между событиями, введенные выше.
Можно интерпретировать как соотношения между множествами.
Несовместные события — это такие события, которые не содержат общих
11
элементов. Сумма (А+ В)» произведение событий АВ— это
соответственно их объединение AUB и пересечение Af)B, противоположное
событие А — дополнение А. Запись Ас: В означает, что в В содержатся все
элементарные события из А » могут содержаться элементарные
события, не входящие в А. Если А с В и В с: А, то А = В.
В случае классического определения вероятности справедлива
следующая теорема сложения вероятностей:
Теорема 1.1. Если два составных события А = {(0/|, ..., й>/^} и
В = {(й:, ..., шд} являются несовместными, то вероятность
объединенного события С = AUB равна сумме вероятностей этих двух событий.
□ Действительно, вероятности событий Aia В равны соответственно т/п и к/п,
а событие С = A\JB = {со/,..., со/^, ш^^,..., соу^} содержит т +
А:элементарных событий, так как по условию теоремы среди элементарных событий
{{0/|,..., со/^} нет ни одного, которое бы входило в набор {(Oj^,..., ау^},
поэтому, согласно классическому определению, его вероятность
т+к_т к
п п п
Из теоремы сложения вытекает, что
'W—^T^-'l^l-^in
р{а) = р{А)+р(А) = \,
поэтому
Р(а) = \-Р[а). (I.I.2)
Отсюда, в частности, следует, что вероятность невозможного
события, являющегося противоположным по отношению к достоверному
событию, равна нулю:
/'(0) = !-/'(«) = 0.
Урновая схема
Классическая схема, несмотря на всю свою офаниченность,
пригодна для решения ряда сугубо практических задач.
Рассмотрим, например, некоторую совокупность элементов
объема N. Это могут быть изделия, каждое из которых является годным или
бракованным; или семена, каждое из которых может быть всхожим или
нет; или избиратели, которые могут проголосовать за или против
кандидата, и тд. Подобного рода ситуации описываются урновой схемой:
в урне имеется Л'шаров, из них Л/белых w(N - М) черных.
12
Представим себе, что имеются только разрушающие средства
контроля каждого изделия на годность. Например, электролампа считается
годной, если до перегорания нити накаливания пройдет не менее чем
определенное число часов, а это можно определить только
непосредственным испытанием. В таком случае можно обследовать только часть
изделий, а не всю партию.
Итак, из урны, содержащей Л'шаров, в которой находится
неизвестное число Л/белых шаров, извлекается выборка объема п.
Требуется определить вероятность того, что в выборке будет
обнаружено т белых шаров. В частности, определить вероятность того, что т/п
близко к M/N, т.е. достоверно ли представление о генеральной
совокупности, полученное по выборке. Последняя из этих двух
сформулированных задач, как будет показано далее, является задачей математической
статистики.
Первая же задача — на применение классического определения
вероятности. В самом деле, в описанной ситуации каждая выборка не
имеет предпочтения по отношению к любой другой, т.е. все они равновоз-
можны. Подсчитаем число всех возможных выборок объема п из
Л'элементов. Как известно из комбинаторики, число способов, с помощью
которых можно выбрать п элементов из общего их числа Л', равно числу
Л"
сочетаний из Л'по л, т.е. С^ =—.—^—г-, где N1 = \-2-N. Таким образом,
«!(Л'-«]!
общее число исходов равно С^. Выясним, сколько исходов из общего
числа элементарных исходов благоприятствуют событию А, т.е. наличию
в выборке объема п белых шаров в количестве т. Число способов,
которыми можно из Л/белых шаров извлечь т штук, равно С^, а число
способов выбрать v\3(N— Af) черных шаров (л — т) штук равно С^Тд/-
Поэтому число исходов, благоприятных событию А, равно С^ C^Z^m ,
следовательно, вероятность события А, равная отношению числа
благоприятных исходов к их общему числу, такова:
О Пример 1.1. Пусть имеется партия, состоящая из 500 изделий, среди которых
два бракованных. Какова вероятность в выборке из 5 изделий не обнаружить ни
одного бракованного?
Воспользуемся формулой (1.1.3):
С^ С*
^498,50о(5. 5) = —3 = 0,98. ф
^-500
13
Какой вывод можно сделать о генеральной совокупности, не
обнаружив в выборке ни одного бракованного изделия? Кажется естественным
перенести этот вывод на всю генеральную совокупность. Таким образом,
по выборке, составляющей 1% от генеральной совокупности, мы
получили с вероятностью 0,98 абсолютно неправильный ответ: в
генеральной совокупности нет бракованных изделий. Этот вывод из очень
простой задачи должен не обескуражить, а, напротив, помочь правильно
построить статистические выводы по выборочным данным. В
рассматриваемом случае, очевидно, не следует пытаться оценивать долю
бракованных изделий {N — M)/N по их доле в выборке (л - т)/п, а, по-видимому,
целесообразно указывать интервал, который с определенной
надежностью должен накрыть неизвестную долю бракованных изделий {N— M)/N.
Этот интервал естественно задать в виде ±о, где ширина интервала
п
5(«, q) является функцией от объема выборки п и уровня надежности q.
Причем естественно ожидать (в чем мы и убедимся в дальнейшем),
что ширина интервала при прочих равных условиях уменьшается с
ростом объема выборки и увеличивается при возрастании уровня
надежности.
Как отмечалось выше, говорить о вероятности Р{А) как о мере
возможности осуществления случайного события А имеет смысл, только
если выполняется определенный комплекс условий. При изменении
условий изменится и вероятность. Так, если к комплексу условий, при
котором изучалась вероятность Р{А), добавить новое условие, состоящее в
появлении события В, то получим другое значение вероятности Р{А/В) —
условную вероятность события А при условии, что произошло событие В.
Вероятность Р{А) в отличие от условной будем называть безусловной.
Выведем теперь формулу условной вероятности. Пусть событиям А и
В благоприятствуют т v\ к элементарных исходов из п; тогда, согласно
формуле (1.1.1), их безусловные вероятности равны т/пи Л/л
соответственно. Пусть событию А при условии, что событие В произошло,
благоприятствуют г элементарных исходов, тогда, согласно формуле (1.1.1),
условная вероятность события А
Р(А/в) = г/к.
Разделив и числитель и знаменатель на п, получим формулу условной
вероятности:
П^/^)-^—^- (I.I.4)
поскольку событию у4П5соответствуют/-исходов и, следовательно, г/п —
его безусловная вероятность. Событие А называется независимым от В,
14
если его условная вероятность равна безусловной, т.е. Р(А/В) = Р{А), при
этом из формулы (1.1.4) получаем
р[АПВ) = р(а)р{в), (I.I.5)
те. свойство независимости взаимно и для независимых событий
вероятность их одновременного осуществления равна произведению их
вероятностей. Формула (1.1.4), записанная в виде
р(аПВ) = р(а)р(в/а), (I.I.6)
называется формулой умножения для зависимых событий, а
формула (1.1.5) — теоремой умножения для независимых событий.
Например, в опыте с игральной костью пусть событие А состоит в
выпадении числа очков, делящегося на три, т.е. А = {cOj. й>^}, а
событие В— в выпадении четного числа очков, т.е. В = {cOj, со^' ^бУ> тогда
АГ\В = (й^и по формуле условной вероятности (1.1.4) получаем:
но Р(А) = Ve ~ '/з> поэтому Р{А/В) = Р{А), т.е. события А v\ В
независимы.
§ 1.2. Конечная схема
с неравновозможными исходами
Ограниченность классического определения вероятности, в
частности, заложена в равновозможности исходов. Действительно, даже
небольшое усложнение практической ситуации немедленно войдет в
противоречие с равновозможностью, которая может рассматриваться
скорее как частный случай более общей ситуации.
Рассмотрим, например, стрельбу по круговой мишени.
Элементарными исходами здесь являются попадания в то или иное кольцо
круговой мишени. Попадание в малый внутренний круг оценивается в 10
очков, в окружающее его кольцо — 9 очков, в следующее — 8 и т.д.,
во внешнее кольцо — одно очко, непопадание в круговую мишень — нуль
очков. Итак, имеется одиннадцать элементарных событий (О,о, со,' •••' %•
Для каждого стрелка определенного класса имеются свои определенные
устойчивые шансы (вероятности) выбить за один выстрел то или иное
число очков/?,(,,..., Pq. Эти события, вообще говоря, неравновозможны.
Например, для мастеров спорта, по-видимому, исключено событие сОц,
Поэтому/?() = О, т.е. сразу исключается равновозможность.
15
Конечная схема с неравновозможными исходами определяется так.
Имеется конечный набор элементарных событий Q= {(О,,..., (0„}, и для
каждого элементарного события со^ задана его вероятность/?^, О < /?. < 1, причем
п
Y,Pi = 1- Вероятность любого составного события А = {co/i,..., со/^,} опре-
1=1
деляется как сумма вероятностей входящих в него элементарных
событий:
т
P(a)=1p, = 1p„. (1.2.1)
Эта схема является обобщением классической схемы. В самом деле,
если вернуться к случаю равновозможности и приписать каждому
элементарному событию вероятность '/„. то формула (1.2.1) приводит к
классическому определению вероятности.
В случае конечной схемы также верна теорема сложения.
Для двух несовместных событий АиВ, являющихся подмножествами Q,
p(aub)=p(a)+p[b).
□ В самом деле, пусть А = {{0/|,..., со/^}, В = {(Oj^,..., co^}. Согласно
формуле (1.2.1),
р(а)=1р,, P(B)=ipu.
1 = 1 К = |
Поскольку события А, В несовместны, они не имеют общих элементарных
событий и, следовательно, С = A[JB = {со/,, ..., со/^, (Oj^,..., соу^}.
На основании формулы (1.2.1) имеем:
p(c)=ip,^ipj^=p(A)^p(B). ■
Точно так же, как конечная схема с неравновозможными исходами
является обобщением классической конечной схемы с равновозможны-
ми исходами, дискретная схема с бесконечным числом неравновозмож-
ных событий, в свою очередь, является обобщением конечной схемы с
неравновозможными исходами.
В дискретной схеме множество Q = {со,,..., со^,...}, вообще говоря,
содержит счетное число элементарных событий. Для каждого
элементарного события задана его вероятность/?^ = Дсо^), О </?,< 1, причем Ха = 1-
/=1
Вероятность любого конечного либо счетного подмножества/4 с Q
множества элементарных событий Q равна сумме вероятностей
составляющих его элементарных событий, т.е. если A = \J(u, , то
16
Ф)=1Л = 1/'/,. (1.2.2)
т
если же /4 = U^/,> то имеет место равенство (1.2.1).
В конечной схеме, как и в классической, можно вывести формулу
условной вероятности.
Рассмотрим события А = {(0/|,..., щ,..., со/^}, B={(aj^,..., соу,,..., co^J,
такие, что{0/, = а)^|,..., {0/,=й)^р Km, к. Иными словами, /4 ni5= {щ^,..., щ}.
Тогда
/'И=1а,, p(B)=ipj^>o, p(Af]B)=ip,
Ц = 1 К = | Ц = |
Пусть событие В произошло, поэтому имеет место новая конечная
схема с к исходами, к < п, следовательно, сумма вероятностей полного
набора этих новых исходов должна быть равна единице, а она, согласно
первоначальной схеме, равна
к
1
к = 1
1р, = р(в).
Чтобы обеспечить равенство суммы вероятностей элементарных
событий единице, введем новые вероятности исходов:
-_^
в рамках новой схемы (т.е. при условии, что произошло событие В)
определяем вероятность события А:
Р{Л1В\-УЪ -1^-МШ
Таким образом, мы снова пришли к той же формуле условной
вероятности, что и в классической схеме [см. формулу (1.1.4)].
Независимость событий определяется аналогично классической схеме.
В качестве применения конечной схемы в следующей главе будет
исследована схема последовательных испытаний.
Рассмотрим простейшие 'Примеры схемы последовательных
испытаний как иллюстрацию конечной схемы с неравновозможными исходами.
О Пример 1.2. Система контроля изделий состоит из двух независимых
проверок, выполняемых одновременно. Изделие считается годным, если оно прошло
обе проверки. В результате каждой проверки бракованное изделие признается
годным с вероятностями а,, а^ соответственно. Найти вероятность того, что
бракованное изделие успешно пройдет обе проверки.
17
Если на вход системы контроля поступило бракованное изделие, то возможны
следующие четыре элементарных исхода: со, = {О, 0), coj = {О, 1), coj = {1, 0),
0)4 = {1, 1), где О означает, что изделие признано бракованным, 1 - годным.
Испытания независимы, поэтому получаем следующие значения вероятностей
элементарных исходов со = {/,, /j)-'
/,, = /,((0,) = />{/, = О, /, = 0} = (1 - а, )(1 - а,),
/^3=/'К) = «■('-«2)'
Сумма вероятностей элементарных событий должна быть равна единице.
Действительно,
4
Р{П)= Хл =(l-a,)(l-ct2) + (l-a,)a2+a,(l-a2) + a,a2 = 1.
Согласно условиям задачи и сформированной схеме, вероятность
пропустить бракованное изделие есть элементарное событие со^, состоящее в том, что
после первой проверки бракованное изделие будет признано годным и после
второй также, поэтому искомая вероятность р^ = ajUj. •
О Пример 1.3. В условиях примера 1.2 вероятности того, что в результате
первой и второй проверок будет отбраковано годное изделие, равны
соответственно р, и Pj. Найти вероятность отбраковки годного изделия.
Если на вход системы контроля поступило годное изделие, то возможны те
же самые четыре элементарных исхода, однако их вероятности будут другими.
Снова воспользуемся независимостью испытаний, тогда получим следующие
вероятности элементарных исходов:
^, =/?((0, )=/>{/,= О,/2=0} = р,Р2,
^2=/'К) = Р.(1-Р2).
^3=/'К) = (1-Р>)Р2.
^4=/'К) = (1-Р>)(1-Р2)-
Событие, состоящее в том, что отбраковано гбдное изделие, включает в себя
элементарные события ш,, Wj, Ш3, поэтому искомая вероятность равна
Л +Р2 +Рз =PlP2 +Pl(l -Р2) + (1-Р,)Р2 =Pl +Р2 -Р.Р2- •
18
§ 1.3. Исчисление событий
Одним из основных понятий теории вероятностей являются
пространство элементарных событий Q и события как некоторые
подмножества этого пространства. В общем случае пространство D. может быть
любой природы, как конечным, так и бесконечным, как дискретным,
так и непрерывным.
Рассмотрим, например, стрельбу по мишени. Если нас интересует
только сам факт попадания в мишень, то элементарными исходами
служат (О = 1 (попадание в мишень) и со = О (непопадание в мишень). Если
важно попадание в отдельные области мишени (области различаются с
точки зрения уязвимости реальной цели), то элементарными
событиями могут быть (0,0 = 10, (О, = 9, ..., со, = 1 (соответствуют числу очков,
приписанных попаданию в определенную область) и cOq = О
(непопадание в мишень). Наконец, если существенно важно, в какую именно
точку щита, на котором изображена мишень, произошло попадание, то
произвольный элементарный исход со = {х, у) представляет собой
координаты точки попадания, а пространство элементарных событий Q — это
множество точек щита.
Итак, пусть имеется пространство элементарных событий D. любой
природы. Будем рассматривать в качестве событий подмножества А, В,
С,... этого пространства. В таком случае действия над событиями
становятся действиями над подмножествами.
Событие А происходит тогда и только тогда, когда происходит одно
из элементарных событий со, из которых состоит А. Напомним
некоторые отношения между событиями, введенные ранее. События А и В
несовместны, если наступление одного из них исключает наступление
другого. Но ведь это означает, что Ан Вне имеют ни одного общего
элементарного события, т.е. не пересекаются.
Аналогично, событие А + В эквивалентно объединению A\JB,
т.е. множеству элементарных событий, которые входят или в А, или в В,
а событие АВ— пересечению АПВ, т.е. множеству элементарных
событий, которые являются общими для А и В. Операции объединения и
пересечения множеств симметричны, т.е.
A\JB = B\JA, Af]B = Bf]A.
Событие, которое включает все элементарные события, те. совпадает с
пространством элементарных событий Q, называется достоверным. Отсюда
Можно сделать вывод, что для любого события А ПЛ = А. Пустым
(невозможным) называется событие 0, которое не содержит ни одного элемента.
Отсюда два события Ан В несовместны, если АГ\В=0. Очевидно, A\J0 = A.
Напомним, что теоретико-множественной разностью двух событий А
и В называется такое событие А\В, которое содержит те элементарные
19
события, принадлежащие А, которые не входят в В. Отсюда событие А,
противоположное событию А, есть Л\А. В самом деле, Af]{D.\A) = 0 и
A\J(il\A) = Q, т. е., действительно, А =П\А. В частности, Q = 0, 0 = Q.
Иногда используется симметрическая разность событий С = А^В,
представляющая собой такое событие, в которое входят те
элементарные события, которые входят в А или В, но не входят в их пересечение
Af]B. Таким образом, эта операция может быть представлена с помощью
уже введенных операций следующим образом:
C = A^B = {A\B)\J{B\A).
Для лучшего понимания операций над событиями —
подмножествами — обычно используют условные графические изображения,
представляя достоверное событие Q как прямоугольник, а другие события — как
круги. Тогда введенные выше операции над событиями могут быть
представлены в виде диафамм Вьенна (рис. I. I), где результаты операций
изображены в виде затемненных фигур. Операция объединения изображена
на рис. \Л, а, пересечения — на рис. 1.1,^, разности — на рис. 1.1, в,
дополнения — на рис. 1.1, г, симметрической разности — на рис. 1.1, d
д)
А&В
А^ци^^
fp.'^'f ^
\ "if \
А
Т'Гх
^Фщ
^^K.«fw
в
Рис. 1.1
Действия над событиями, в частности операции объединения
(сложения) и пересечения (умножения), в определенном смысле
аналогичны сложению и умножению чисел. Так, выше отмечалось, что эти
операции симметричны; они также ассоциативны, т.е.
{AUB)\JC = A\J{B\JC), {АПВ)ПС = АП{ВПС).
20
Кроме того, эти операции, так же как и операции над числами,
обладают свойством дистрибутивности:
{A\JB)nC = {AnC)\J{BnC). (1.3.1)
Q Множество Z)=И и^ П С изображено в виде диаграммы Вьенна на рис. 1.1, е,
Как видно из этой диаграммы, пересечение множества С и объединения /4 U Я
состоит, вообще говоря, из объединения трех непересекающихся частей:
D = [{A\ В)ПС]и[{В \ А)ПС][\{АПВ)Г\С].
Так клкА = А \JA при любом А, то
D = [{A\ В)ПС]и[{В \ А)ПС]и[{АПВ)ПС]Ц{АПВ)ПС].
Используя теперь свойство симметричности операций объединения,
объединим первый и третий операнды, второй и четвертый:
[{А \ В)Г\С][\{АПВ)ПС] = АПС; [{В \ А)Г\С][\{АГ\В)Г\С] = ВПС,
откуда окончательно получаем D = [АГ\С)и{ВГ\С), т.е. свойство
дистрибутивности действительно выполняется. ■
Другое сходство с действиями над числами заключается в том, что для
операции пересечения роль, аналогичную роли единицы и нуля при
умножении чисел, выполняют соответственно множества Q и 0, так как
Clf]A = А, АГ\0. = Ак 0Г\А = АГ\0 = 0. Вместе с тем
теоретико-множественные равенства /4Ш = А, Af]A = А и им подобные показывают, что
полной аналогии нет.
Действия над событиями важны не сами по себе, а как средство
определения вероятностей одних событий через вероятности других
событий. Так, например, если верна теорема сложения вероятностей, то
вероятность события С, являющегося объединением несовместных событий А
и В, равна сумме вероятностей последних событий PiQ = Р{А)+ Р{В), что
позволяет найти вероятность одного из трех событий через известные
вероятности двух других. Точно так же, если для событий А, Ви C=Af]B
справедлива теорема умножения, можно выразить вероятность одного
события через вероятности двух других:
Р{С) = Р{А)Р{В).
В случае конечной или счетной теоретико-вероятностной схемы,
рассмотренной в предыдущем параграфе, в качестве события
рассматривалось любое подмножество конечного или счетного пространства
элементарных событий Q. и вероятность события определялась как сумма
вероятностей входящих в него элементарных событий. Если же пространст-
21
во Q непрерывно, то имеет место континуум элементарных исходов.
Попытка считать событием любое подмножество непрерывного
пространства Q. сопряжена с большими трудностями.
Поэтому в общем случае приходится иметь дело не со всеми
подмножествами пространства Q., а лишь с определенным классом, замкнутым
относительно операций объединения, пересечения, дополнения.
Класс подмножеств пространства Q., замкнутый относительно
операций объединения, дополнения и пересечения, а также содержащий
множества 0, С1, называется полем. Будем обозначать поле буквой S.
Минимальное поле Sq состоит из полного и пустого множеств S^ = {0,0]. В
самом деле, 0 и Q входят в этот класс, а результатами операций
объединения, дополнения и пересечения над этими множествами снова служат
данные множества: 0\JQ. = CI, 0ПЙ = 0, 0 = Q, Q = 0. Другим, более
содержательным примером поля событий служит класс из четырех
событий S= {0, А, А, О]. Действительно,
0\jA = A, 0\jA = A, 0un=n, A\jA=a, A\jci=a A\jci=a
0ПА = 0, 0Г\А=0, 0Г\С1 = 0, АПА=0, АПП = А, АПП = А,
0 = П, А = А, П = 0.
§ 1.4. Аксиоматическое построение
теории вероятностей
При аксиоматическом построении теории вероятностей исходным
«материалом» служит пространство элементарных событий Q. и выделенный в
нем класс подмножеств, образующий поле событий S. Строение
пространства Q. и класса 5определяется конкретной областью приложения.
Определение 1.1. Вероятностью называется числовая функция,
определенная на поле событий 5 и обладающая следующими свойствами:
Аксиома I. Вероятность любого события Ае S
0<Р(А)< 1.
Аксиома 2. Вероятность достоверного события равна единице:
Р(С1)=\.
Аксиома 3. Вероятность объединения двух несовместных событий
равна сумме вероятностей этих событий:
P{A\JB) = P{A) + P{B), Af)B = 0.
22
Проверим, например, что конечная схема удовлетворяет условиям
этих аксиом. Напомним, что конечная схема задается конечным
множеством элементарных событий Q = {со,,..., (аJ и вероятностями каждо-
ГО из них о < />,. < 1, причем Хл =' • Вероятность любого события А,
являющегося подмножеством С1, те. А = {щ^, ..., Ш/^}, определяется по
формуле:
т
Pi^)=lPi = lP>r (1.4.1)
Класс S всех подмножеств Q. образует поле. В самом деле, 0 и Q
являются подмножествами, поэтому принадлежат S; очевидно также, что
для любых событий А е S, В е 5 их объединение и пересечение также
являются подмножествами Q; А, В — также подмножества.
Теперь проверим, что конечная схема удовлетворяет требованию
аксиомы 1. Для этого выберем произвольное событие А, которое является
подмножеством Q, так какА = {(0/|,..., ш/^}, то, согласно конечной схеме,
т
поэтому
0^Р(А)<1,
т.е. условие аксиомы 1 выполняется.
Условие аксиомы 2 выполняется, поскольку Q. = {со,, ..., ш^} и на
основании формулы (1.4.1)
<=1
Условие аксиомы 3 также выполняется, так как оно представляет
собой содержание теоремы сложения для конечной схемы. Эта теорема
была доказана в § 1.2.
Итак, конечная схема является примером объекта, для которого
выполняется система аксиом теории вероятностей.
Простейшим частным случаем конечной схемы служит
вероятностное описание испытания, которое может закончиться успехом или
неудачей. В этом случае Q. = {Шц, со,} состоит из двух элементарных
событий: (0(, = 0— неуспех в испытании, со, = 1 — успех в испытании,
Дш,) = р, Р{ы^ = 1 -Pz4- Поле в данной ситуации состоит из четырех
событий: 0, А ={(0,}, А = {(Од}, Q. = {(Од, со,}.
В качестве примера вероятностей схемы с непрерывным
пространством элементарных событий рассмотрим схему с геометрическими
вероятностями. Пусть пространством элементарных событий служит множё-
23
ство точек некоторой области G, имеющей площадь на плоскости. В
качестве событий будем рассматривать имеющие площадь подмножества
Л, В, С,... этой области. Самостоятельно докажите, что класс таких
подмножеств образует поле. При этом вероятность любого события Л
(подмножества, имеющего площадь mes (Л)), можно задать следующим
образом:
mesi^
^ ' mes (С/)
Докажите (по аналогии с конечной схемой), что описанная схема
удовлетворяет аксиомам теории вероятностей. Аналогично можно
построить геометрические вероятности в любом конечномерном
пространстве.
Из аксиом теории вероятностей вытекает ряд следствий, которые
могут быть доказаны так же, как это было сделано для классической
схемы. Предлагаем самостоятельно доказать утверждения, содержащиеся в
задачах к настоящей главе.
Во многих случаях требуется расщиренный вариант аксиомы 3.
А именно, аксиома 3 постулирует сложение вероятностей для
конечного числа несовместных событий, в то время как в расщиренном
варианте речь идет о счетном числе несовместных событий.
Аксиома 3'. Если
A^eS, 1 = 12,..., Aif]Aj=0, i^j.
то
ил
'■ = ' у
1рМ
(=1
Аксиомы теории вероятностей лищь постулируют существование
вероятностей для всех событий, образующих поле S, и задают
определенные правила действия с вероятностями.
Экспериментальное же определение вероятности любого события
А 6 Сможет быть осуществлено в результате испытаний, выполняемых
при определенном одном и том же комплексе условий. Как будет
показано ниже, выборочная частость т/п появления события А при больщом
числе испытаний п является достаточно хорощей оценкой
теоретической вероятности р = Р{А), что означает сходимость в некотором смысле
т
— =»/)при л-» оо.
п
Например, если событие А представляет собой выпадение «герба» при
однократном бросании симметричной монеты, то, согласно
классическому определению вероятности, Р{А) = '/2> поэтому есть основание счи-
24
тать, что при многих испытаниях частость выпадения «герба» близка к
I/,. Действительно, в XVII в. Бюффон провел такие эксперименты. В
результате оказалось: при 4040 бросаниях монеты частота выпадения
«герба» составила 2048, что дает частость, равную 0,507. Английский
статистик К. Пирсон провел 24 000 таких опытов, частость оказалась равной
0,5005.
Итак, определенная теоретико-вероятностная схема задается тремя
компонентами {Q, S, Р}, те. конкретным пространством элементарных
событий, конкретным набором подмножеств Q, образующих поле S,
а также конкретным заданием вероятностей Р на множествах поля.
Набор этих трех компонент далее везде будем называть вероятностным
пространством. Вероятность Рна {С1, S\ называется распределением
вероятностей на Q.
Вопросы и задачи
1. Опираясь на аксиомы теории вероятностей, докажите следующие
утверждения: а) Р{А)= \ - Р{Ау, б) 1\0) = 0; в) Р{А) > Р{В) при A:dB;
г)Р(А)<\.
2. Покажите, что из аксиомы 3 вытекает следующее следствие:
и 4 =1 ^(4) при 4 П /1, = 0 для I * j.
( = 1
3. Докажите, что для любых событий А, В имеет место следующая
формула сложения:
P{A\JB) = Р{А) + Р{В)- P{AV[B).
4. /4,, А^,..., А^ — случайные события. Доказать для л = 3, 4 формулу:
( = 1 ) ( = 1 \Si<jSn lii<j<kSn
5. Партия изделий состоит из т изделий 1-го сорта и п изделий 2-го
сорта. Проверка первых к изделий, выбранных из партии наудачу,
показала, что все они 2-го сорта (к < п). Чему равна вероятность того, что
среди следующих двух наудачу выбранных из оставщихся изделий по
меньщей мере одно окажется 2-го сорта?
6. Двое договорились о встрече в течение определенного часа. При-
шедщий первым ждет 20 мин и уходит. Какова вероятность встречи?
25
Указан и е. Рассмотреть вероятность как отношение площадей
множества точек (исходов), благоприятствующих встрече, и множества
возможных исходов. _
7. Докажите, что из независимости А, Д вытекает независимость/4, В;
А, В', В, А.
Глава 2
УСЛОВНЫЕ ВЕРОЯТНОСТИ.
ПОСЛЕДОВАТЕЛЬНОСТИ ИСПЫТАНИЙ
Все теоремы и формулы теории вероятностей и математической
статистики выводятся из аксиом теории вероятностей. В этой главе дается
определение условной вероятности, доказываются наиболее часто
используемые теоремы и формулы, основанные на условных
вероятностях. Вводится понятие независимости событий, которое затем
используется в схеме последовательных испытаний.
§ 2.1. Условные вероятности
в § 1.1 формула условной вероятности была выведена для
классической схемы. В общем случае эта формула служит определением условной
вероятности события А при условии, что произошло событие В, Р{В) > 0.
Определение 2.1. Условная вероятность события А при условии В
^ ' ' Р{В)
Определение 2.2. Событие А не зависит от события В, если
Р[А1В) = Р{А).
Независимость событий взаимна, т.е. если событие А не зависит от В,
то и событие В не зависит т А.Ъ самом деле, используя определения 2.1
и 2.2, при Р{А) > О имеем:
Из определения 2.1 вытекает следующая формула умножения
вероятностей:
Р{А(\В)^Р{А)Р{В1А). (2.1.1)
27
Для независимых событий вероятность произведения событий равна
произведению их вероятностей:
Р{А[)В) = Р{А)Р{В). (2.1.2)
Определение 2.3. События/4,,/42, ...,/4^ образуют полную группу
событий, если они попарно несовместны и вместе образуют
достоверное событие, т.е.
Aif)Aj=0, 1Ф], иД="-
Имеет место следующая теорема о формуле полной вероятности.
Теорема 2.1. Если события A^,..., А^, /Х'4,)>0 образуют полную группу
событий, то вероятность события Д может быть представлена как сумма
произведений безусловных вероятностей событий полной группы на
условные вероятности события В:
P{B)=tp{A^)P{B/A^). (2.1.3)
Q События полной группы /4,,..., А^ попарно несовместны, поэтому попарно
несовместны и их произведения (пересечения) с событием В, т.е. события ВГ\ А.,
BHAj при i^^j несовместны. Так как событие В можно представить в виде
B=\j{Bf)A^),
1 = 1
то, применив к этому разложению события В аксиому сложения вероятностей,
имеем:
Р{В)=±Р{ВПА,).
Используя формулу умножения вероятностей (2.1.1) для каждого
слагаемого, окончательно получаем:
P{B)=tp{A,)p{B/A^). ■
Требование, состоящее в том, что события /4^. образуют полную
группу событий, может быть заменено более слабым: события попарно не
я
пересекаются, В с: U4 • Кроме того, на основе аксиомы счетной адди-
тивности теорему полной вероятности можно распространить и на счет-
28
ное множество попарно непересекающихся событий А^, Р(А^) > О,
( = 1
Р{В)=1^Р{А^)Р{В/А^). (2.1.4)
( = 1
Из формулы полной вероятности (2.1.3) легко получить формулу Бай-
еса: для события В с Р{В) > О и для системы попарно несовместных
событий/1,, Д'^,) > О, B<z\jAi,
( = 1
. . р(аЛр(в/аЛ
P{AJB)= ^\ ki \ I ki (2.1.5)
ЪР{А)Р[В1Л,)
( = 1
в самом деле, применив формулы условной вероятности и
умножения вероятностей, имеем:
теперь, заменив вероятность события В по формуле полной
вероятности, получаем формулу (2.1.5),
Вероятности Р{А) событий А. называют априорными вероятностями,
т.е. вероятностями событий до выполнения опыта, а условные
вероятности этих событий Р{А./В) — апостериорными, т.е. уточненными в
результате опыта, исходом которого послужило появление события В.
О Пример 2.1. На предприятии изготовляются изделия определенного вида на
трех поточных линиях. На первой линии производится 20% изделий от всего
объема их производства, на второй - 30%, на третьей - 50%. Каждая из линий
характеризуется соответственно следующими процентами годности изделий: 95,
98 и 97%, Требуется определить вероятность того, что наугад взятое изделие,
выпущенное предприятием, окажется бракованным, а также вероятности того,
что это бракованное изделие сделано на первой, второй и третьей линиях.
Решение, Обозначим через A^, А^, А^ события, состоящие в том, что
наугад взятое изделие произведено соответственно на первой, второй и третьей
линиях. Согласно условиям задачи P(A^) = 0,2; PiA^) = 0,3; Р(,А^) = 0,5
и эти события образуют полную группу событий, поскольку они попарно
несовместны, т.е. PiA^) + Р(А^) + Р(А^) = 1.
Обозначим через В событие, соаоящее в том, что наугад взятое изделие
оказалось бракованным. Согласно условиям задачи Р {В/А^) = 0,05; Р (В/А^) = 0,02;
Р(В/А^) = 0,03,
29
Используя формулу полной вероятноаи, получаем P{B)^P{B/A^)P{A^) +
+ Р{В/А^)Р{А^) + Р(В/А^)Р{А^) = 0,05 0,2 + 0,020,3 + 0,03-0,5 =
= 0,031, т.е. вероятность того, что наугад взятое изделие окажвгся
бракованным, равна 3,1%.
Априорные вероятности того, что наугад взятое изделив изготовлено на
первой, вгорой или третьей линии, равны соответственно 0,2; 0^3 и 0,5.
Допустим, что в результате опыта наугад взятое изделие оказалось
бракованным; определим теперь апостериорные вероятности того, что это изделие
изготовлено на первой, второй и третьей линиях. По формуле Байеса имеем:
^ '' ' 0,031 31 ^ ^' ' 0,031 31
ы J ,п\ 0,03.0,5 15
' " ' 0,031 31
Таким образом, вероятности того, что наугад взятое и оказавшееся
бракованным изделие изготовлено на первой, второй или третьей линии, равны
соответственно 0,322; 0,194; 0,484. •
Формула умножения вероятностей (2.1.1) может быть
распространена на случай произвольного конечного числа событий:
/'(/1,П/12П...П/1„) = /'(/1,И^2/Л)-'РК/ЛП/<2П...П/1„_,). (2.1.6)
Определение 2.4. События /4,, А^,..., А^ независимы в
совокупности, если для любого их подмножества
ф,, ПЛ, П...П4,) = /'КЖ.)-''К). к<п.
Если это условие выполнено только для А; = 2, то события попарно
независимы.
Из независимости событий в совокупности вытекает попарная
независимость, а из попарной независимости не следует независимость в
совокупности.
§ 2.2. Последовательности испытаний
Пусть прпвплится конечное число л последрвательных независимых
испытаний, в каждом из копгррых может п1Юизойтирг1ределенное
событие: либо успех, либо противоположное событие —, чеудача. Такая
последовательность испытаний называется, сх€^мой,£ернулли, если
вероятности положительного исхода в каждом испытании о/^инаковы.
30
в качестве таких испытаний можно рассматривать, например,
производство изделий на определенном оборудовании при постоянстве
технологических и организационных условий, в этом случае изготовление
годного изделия — успех, бракованного — неудача. Эта ситуация
соответствует схеме Бернулли, если считать, что процесс изготовления
одного изделия не зависит от того, были годными или бракованными
предыдущие изделия. Другим примером является стрельба по мишени.
Здесь попадание — успех, промах — неудача. Если же речь идет о
выборочном контроле качества конечной партии изделий объема N по
выборке объема п, то даже при независимости и случайности отбора
единиц совокупности отдельный акт отбора зависит от того, сколько на
предшествующих этапах было извлечено годных изделий и бракованных
изделий. Ниже будет показано, что при N-¥ оо эта гипергеометрическая
(урновая) схема, рассмотренная в § 1.1, переходит в схему Бернулли.
В схеме Бернулли одному испытанию соответствует множество
элементарных исходов, состоящее из двух элементарных событий: {Шц, со,},
(Од = О (неудача) и со, = Г (успех), при этом А = {со,}, А = {щ}. Множество
элементарных исходов для п испытаний состоит уже из 2" элементарных
событий (О = {/,, ..., /д}, каждое из которых соответствует конкретному
исходу испытаний, при этом набор /,,..., /^ представляет собой
конкретную последовательность нулей и единиц, соответствующую результатам
испытаний на каждом шаге.
Если заданы вероятности успеха и неудачи в отдельном испытании
Дш,) = р; Pioif)) = 1 - /> = ^, то можно определитъ вероятность любого
элементарного исхода в п испытаниях. Действительно, рассмотрим
любой элементарный исход (/,,..., /„), при этом (<,, ij,..., /„) — конкретная
последовательность нулей и единиц, соответствующая
последовательности неудач или успехов в каждом из п индивидуальных испытаний,
например (0 = (1, О,..., 1).
Тогда, поскольку результаты отдельных испытаний независимы друг
от друга, получаем:
P{(x>) = P{(x>^)p{(x>o)■■■P{^x>^)= ... =pq-p.
Таким образом, если общий элементарный исход включает т успехов
» п - т неудач, то его вероятность
Р{о)) = р'"д"-'", ' (2.2.1)
и, следовательно, по аксиоме сложения вероятностей может быть
определена вероятность любого события, состоящего из нескольких
элементарных событий.
В частности, если нас интересует вероятность Р^т) того, что в п
испытаниях произошло т успехов, то ее определяем как сумму
вероятностей элементарных событий, характеризующихся т успехами. Вероят-
31
ность такого элементарного исхода, согласно формуле (2.2.1), равна
р1"дп-т Следовательно, для нахождения вероятности Р„(.т) надо
определить число элементарных событий, характеризующихся т успехами,
т.е. установить, сколькими способами могут быть на п мест расставлены
т единиц (остальные п - т мест занимаются нулями). Но ведь это
аналогично тому, что из п элементов надо выбрать (пометить) т элементов.
Число таких выборок, как известно, равно числу сочетаний из п по т,
т.е. С". Окончательно получаем
P„{m) = C:'p'"q"-'". (2.2.2)
Сумма получившихся биномиальных вероятностей равна единице:
!/>„(/«)= tc:p'"q"-'"=ip + q)"=\"=l
т = 0 т = 0
В ряде задач представляет интерес наивероятнейшее число успехов,
те. такое число т* успехов, вероятность которого самая большая среди
всех вероятностей (2.2.2). Чтобы определить это число, рассмотрим
отношение
Р„{т + \)^{п-т)р
Р„{т) ('« + 1^'
Если последующая биномиальная вероятность PJ,m + 1) превышает
предыдущую P„{fn), то это отношение больше единицы; если же
Р^{т + 1) < Р„(т), то меньше единицы.
Для нахождения т* надо уловить тот момент, когда отношение,
бывшее больше единицы, станет меньше единицы. Отношение
Р„(т* + \) ^(п-т')р ^^
/>„(/«*) (т* + \)д~
имеет место при т* > пр - q, а отношение
Р„(т*) ^(n-m' + l)p ^^
Р„[т*-\) m'q
при т* <: пр + р; следовательно, окончательно получаем, что т* лежит в
интервале единичной длины:
np-q<m' <пр + р. (2.2.3)
Вернемся еще раз к урновой схеме, чтобы сравнить ее со схемой Бер-
нулли. В случае урновой схемы можно представить себе, что мы
осуществляем выборку объема п из урны не сразу, а последовательно шар за
32
шаром. В результате приходим к схеме последовательных испытаний,
однако в отличие от схемы Бернулли здесь результаты последующих
испытаний уже зависят от результатов предыдущих. Так, если вероятность
на первом шаге извлечь белый шар равна M/N, то условная вероятность
извлечь белый шар на втором шаге равна (А/- 1)/(УУ- 1), если на
первом шаге извлечен белый шар, и M/(N- 1), если на первом шаге
извлечен черный шар.
Однако в том случае, когда генеральная совокупность велика
(т е. УУ-»оо),урновую схему можно заменить схемой Бернулли. В самом
А/
деле, пусть N, М-¥оо таким образом, что -гг-* Р = const. Тогда форму-
N
лу урновой схемы (1.1.3) можно преобразовать следующим образом:
М\ {N-M)\
D ( \_^m^"n'-'m т\{М-т)\ {n-m)\{N-М-п + т)\ _
О/, yvl'"'") ps ^1
С
n\{N-n)\
M-{M-m + \){N-M)--{N-M-n + m + \)
N-{N-n + \)
Используя то, что в получившейся дроби и в числителе и в
знаменателе по п сомножителей, разделим и числитель и знаменатель на Л*" так,
что каждый сомножитель при этом разделится на Л'^:
Переходя к пределу при N, М-*°°, получаем
Jim PM.Nifrt,n) = C;;'p'"q"-'" = Р„{т),
те. при бесконечном объеме генеральной совокупности урновая схема
эквивалентна схеме Бернулли. На практике это означает, что при
объеме выборки, существенно меньшем объема генеральной совокупности,
можно вместо вероятностей урновой схемы приближенно использовать
Соответствующие вероятности схемы Бернулли, т.е. при п « N
Рм.Агг'<")-C:\jj-j [—j;^j ■ (2.2.4)
2—670 33
Схема Пуассона (закон редких событий)
Рассмотрим, как ведут себя биномиальные вероятности при л -»<»
р-*0, пр-¥Х. Поделим числитель и знаменатель на п", тогда
j(l-V„)...(l,(„,|)/„) (!_„,,„). у,^
/и! ^ ' О-Р)" '«'
Предельные вероятности называются пуассоновскими:
•хШ
Р(т) = — е"'^, /и =0,1,... (2.2.5)
т\
Полиномиальная схема
От схемы независимых последовательных испытаний с двумя
исходами (схема Бернулли, или биномиальная схёШГможноТтёрейти к
полиномиальной схеме, т.е. к схеме последовательных независимых
испытаний, в каждом из которых возможны к исходов, к>2,с вероятностями
к
/)|, Р2,..., P/i,0<Pj<\, ^Pj =\.В этом случае пространство элементар-
ных событий содержит к" таких событий, а вероят«ость того, что из п
испытаний /и, закончатся первым исходом, /Wj — вторым исходом, ...,
Ш/^— к-м исходом, равна
Схема с зависимыми испытаниями
На практике, как было показано на примере урновой схемы, далеко
не всегда имеют место схемы с последовательными независимыми
испытаниями. Рассмотрим схему с зависимыми испытаниями, в каждом
из которых возможны к исходов. Элементарное событие, как и в случае
полиномиальной схемы с независимыми испытаниями, тогда таково:
ft> - {'|. '2' •••' 'дЬ ""Д^ каждый индекс может принимать к значений,
i,= ],2,...,k.
34
Вероятности алементарных событий такой схемы задаются
следующим образом:
(2.2.7)
к
I
p{is/iv-''s-i)^^' I P(is/h'-<is-i)=^
Q Сумма определенных таким образом вероятностей элементарных событий по
всему их множеству должна быть равна единице. Докажем это:
1рН= 1 p{h)p{h/'\]-p('n/ii ';-i) =
к к
= 1 P{h)p{'2/'\]-p{'n-l/'l'-''n-2)lp{'n/h '«-l) =
'I 'я-|=' '« = '
= I P[h)p[hlh)-p[in-\lh'-'ir,-2)-
h '«-!='
в последнем равенстве было использовано условие (2.2.7) при ; = л. Еще и
еще раз повторяя эту процедуру, мы наконец придем к следующему равенству:
Последнее равенство также следует из выражения (2.2.7). ■
Последовательности испытаний, в которых условные вероятности
зависят только от исхода последнего из предшествующих испытаний
p[^.|^v■■■^^s-] = p[^.|^s-!)'
называются цепями Маркова.
Вопросы и задачи
1. События/Ip/ljj ...,/1^независимы, Р{А)=Рр /= 1, ...,к. Найти
вероятность:
а) появления хотя бы одного из этих событий;
б) непоявления всех этих событий;
в) появления точно одного (безразлично какого) события.
2. В партии yv изделий, занумерованных в порядке изготовления от 1
ДО Л', изделия извлекаются наудачу по одному (без возвращения). Чему
Равна вероятность того, что хотя бы при одном извлечении номер выну-
''^ого изделия совпадет с номером испытания?
2» 35
3. Рабочий обслуживает 12 однотипных станков. Вероятность того,
что станок потребует к себе внимания рабочего в течение промежутка
времени Г, равна '/з- Чему равна вероятность того, что:
а) 4 станка за время Г потребуют к себе внимания рабочего;
б) число потребовавших внимания станков находится в интервале
между 3-м и 6-м (включая фаницы).
4. В семье 10 детей. Считая вероятности рождений мальчика и
девочки равными '/j, найти вероятность того, что в семье:
а) 5 мальчиков и 5 девочек;
б) число мальчиков от 3 до 8.
5. В вузе обучаются 730 студентов. Вероятность того, что день
рождения наугад взятого студента приходится на определенный день года,
равна '/зб5 ^^ каждого из 365 дней. Найти:
а) наиболее вероятное число студентов, родившихся 1 января;
б) вероятность того, что найдутся три студента, имеющих один и тот
же день рождения.
Глава 3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Наряду со случайным событием и вероятностью понятие случайной
величины является важнейшим в теории вероятностей. Случайная
величина — это числовая функция, определенная на пространстве
элементарных событий. В настоящей главе представлены случайные
величины, наиболее часто встречающиеся в сфере экономики и управления,
а также определены и изучены их важнейшие характеристики: функции
распределения вероятностей и плотности вероятности, ряды
распределения, показатели центра фуппирования их значений, степени
вариации значений вокруг центра и другие числовые характеристики.
§ 3.1. Определение случайной величины
и ее функция распределения
Случайные величины встречаются нам повсюду в окружающей нас
действительности: курс доллара или температура воздуха в наугад
взятый день, цены товаров, время ожидания транспорта при поездке на
работу, прибыль или убытки фирмы, предприятия, организации, в
которой работаем, и т.п. Даже число дней в наугад взятом году является
случайной величиной: с вероятностью V4 это число равно 365, а с
вероятностью 'Д — 366.
Из последнего примера видно, что значение случайной величины
зависит от результата эксперимента: является ли наугад взятый год
високосным или обычным. Под результатом эксперимента здесь
понимается наступление конкретного элементарного события (исхода) (о^ из
всего множества (пространства) элементарных исходов €1. В нашем
примере это пространство может быть таким:
Q = {(D,,(02,(03,(04},
где (0|, (Oj, (О3 — первый, второй и третий обычные (невисокосные) годы;
(0^ — високосный год.
37
Тем самым число дней в году (случайная величина А') является
функцией от элементарных исходов:
ДГ((о,) = 365, ДГ((02) = 365, ДГ((Оз) = 365, X{(a^) = 366.
Иными словами, случайная величина как функция от (о
осуществляет отображение пространства элементарных событий Q, в некоторое
подмножество на числовой прямой. При этом каждому (о отвечает одно и
только одно число (в нашем случае X((i)^) = Х{и)2) = Х{и)^) = 365,
Д®4) ~ ^66)- Напротив, прообразов конкретного значения случайной
величины может быть много. Например, множество тех элементарных
событий, для которых Дса) = 365, состоит из трех элементарных событий:
{(о: Х{(а) = 365} = |(0,, (02, (Ojj.
Случайная величина, принимающая конечное или счетное число
значений на числовой прямой, называется дискретной. В нашем случае мы
имеем дело с дискретной случайной величиной, поскольку она
принимает два значения: 365, 366. Если же случайная величина принимает
непрерывное множество значений (например, значения на всей прямой,
на полупрямой, на отрезке), то такая величина называется непрерывной.
Для того чтобы работать со случайными величинами, надо знать в той
или иной форме вероятности тех или иных значений случайной
величины. Так, для дискретной случайной величины надо знать вероятности
отдельных ее значений. В нашем примере надо знать вероятности
событий
A^ = {(О: X{ai) = 365} = {(о,,щ,(а^}, /Ij = {®' ^i"^) = ^Щ = {®4}>
поскольку любой год из четырех равновозможен, то по классическому
определению вероятности
Для непрерывных случайных величин надо уметь подсчитывать
вероятность попадания на полупрямую, на полуинтервал и т.п., т.е.
вероятности событий
{(о: А"((d) < х}, {(о: х < Х{(л) < Xj}.
Поскольку при x^ < х^
{(о:X< А'((о)<Xj} = {(О: ^"((0)<х-^\{(О: А'((о)<xj.
то на самом деле достаточно уметь подсчитывать вероятности
попадания на полупрямую. Следовательно, надо, чтобы для любого х
множество {(О: Х((й) < х\ имело вероятность, т.е. принадлежало полю событий Sr.
38
{(о:А'((о)<х}е5.
Эти наводящие соображения делают понятным следующее строгое
(формальное) определение случайной величины.
Случайной величиной называется числовая функция Дса), заданная на
пространстве элементарных событий С1 и измеримая относительно поля
событий S. Под измеримостью в данном случае понимается следующее:
для любого —°о < х<оо
{(о: Х{(а) <x]eS.
(Далее случайные величины будут обозначаться прописными лат^1нски-
ми буквами (например, X, Y, Z) или строчными греческими буквами.)
Таким образом, чтобы знать все о случайной величине, надо для
любого —°° <х< °о знать вероятность
P{(i): А'((о) < х],
т.е. совокупность всех таких вероятностей концентрирует все знания о
распределении вероятностей по значениям случайной величины.
Поэтому функция распределения вероятностей, значение которой при
конкретном X и есть одна из таких вероятностей,
Гх{х) = Р{(о:Х{(а)<х}
содержит в себе все сведения о случайной величине.
Если речь идет об одной случайной величине, как в данном
контексте, то в обозначении функции распределения опускается индекс
случайной величины, т.е. употребляется просто f{x) (без индекса).
Как числовая функция от числового аргумента х, заданного на всей
прямой, функция распределения обладает следующими свойствами:
l)0<f(x)<l;
2) является неубывающей функцией, т.е. для Xj > x^
F{x,)>F{x,);
3) непрерывна слева, т.е.
F{x) = F{x-0)=]m F{x„);
х„<х
4) /-(-00) = о, /•(+оо)=1.
Первое свойство очевидно, поскольку значение функции
распределения — это вероятность.
39
01 Для доказательава второго свойства введем следующие обозначения:
>4, = {(о:А'((о)<х,|,
Ai=[<u:X{<u)<X2], \ (3.1.1)
В = {(о: X, ^ А'((о) < Х21,
тогда
Поскольку X, < д^, то >4,Су42, кроме того, А^ = >4, U Д причем, как видно из
обозначений, события A^viB несовместны, поэтому согласно аксиоме сложения
Р{А^) = Р[Л^)+Р{В). (3.1.2)
Следует заметить, что множества >4,, >42 и ^действительно являются
событиями, т.е. Л^^S, A.^<eS, BeS. В самом деле, принадлежность >4р >42 полю
событий 5 непосредотвенно вытекает из определения случайной величины.
Множество ^ является теоретико-множественной разностью событий >4, и А^,
которую можно заменить операциями пересечения и дополнения
B = A2\A^ = Air^A^,
а поскольку поле замкнуто относительно операций пересечения и дополнения,
то Be S. Далее будем использовать полученный здесь результат: поле замкнуто
относительно операции теоретико-множественной разности, а следовательно, и
симметрической разности.
Используя формулу (3.1.2), последнее соотношение перепииюм в
следующем виде:
F{x2) = f{x,) + PiB),
или
F{x2)-F{xi) = P{B). (3.1.3)
Поскольку вероятность любого события неотрицательна, тоР{В)>0\л,
следовательно, /I^Xj) > Дх,). Таким образом, второе свойство доказано. ■
Используя обозначения (3.1.1), запишем формулу (3.1.3) в следующем
виде:
/'{x,<A'<X2| = /'(x2)-f(x,), (3.1.4)
иными словами, вероятность попадания на полуинтервал х, < Х< Х2 равна
разности значений функции распределения на концах полуинтервала.
40
Q При доказательстве третьего свойства будем пользоваться расширенной
аксиомой сложения, а также следующими обозначениями:
В„={<и:х„йХ<х], (3.1.5)
JC| <JC2 < ... <JC„ < ... <JC, lim jc„ =JC,
т.е. jc„ - монотонная последовательность, сходящаяся к х.
Поскольку последовательность х^ монотонна, то В^ э Bj для / < / Кроме
того, так как 5„П5„+, =Л„^,,то
^«=Кпд„„)и(/?„п/?„„)=(д„пд„„)иКп^„,2)и(д„„пд„.2)=
=...= йКпд*„)ип5*.
*=я ^ ' *=я
т. е. может быть представлено в виде бесконечного объединения непересекаю-
щихся «колец» ^^^ n^^+i * несовместного с ними ядра fj^^^, поэтому на
основании расширенной аксиомы сложения
P{Bn)=iP[Bk^B,,,)^l{[\B\ (3.1.6)
Но из формулы (3.1.5) видно, что
оо
n^t ={co:jcSA'<jc} = 0,
Т. е. ядро - невозможное событие, поэтому
Следовательно, формула (3.1.6) примет вид:
p{b„)^Ip[b,V\b,^,\
к=п
но ряд
как видим, сходится, поэтому его остаток сходится к нулю:
1/КП/?,„)=/'(/?„)-.0. (3.1.7)
41
кжп
Используя обозначения (3.1.5), запишем формулу (3.1.7) в следующем виде:
Р{Вп) = {«: ^« ^ ^И < ^} = Пх) - F{x„) -^ 0.
Отсюда
limF{x„) = F{x-0) = Fix),
х„-*х
х„<х
что И требовалось доказать. ■
Четвертое свойство вытекает непосредственно из того, что
{со: ^(со) < -оо} = 0,
{со: А'(со) < -н»} = П,
поскольку Д0) = О, а Р{С1) = 1.
§ 3.2. Дискретные случайные величины
и их важнейшие числовые характеристики
Как было сказано выше, дискретная слунайдая величина принимает
конечное или счетное число значений. Поскольку переход от конечного
числа значении к счетному не представляет больших технических
трудностей, то основные характеристики дискретной случайной величины
будем рассматривать при конечном числе значений.
Итакгпусть случайная величина принимает конечное число к
значений jc, < JCj < ... < JC^. Тем самым все пространство элементарных событий
Q, отобразится случайной величиной Л(со) в А: этих значений,
прообразами которых служат события
Aj=[(u:X{(u) = Xi}, i=\,...,k,
образующие полную группу, поскольку эти события несовместны и
вместе составляют П.
Следует заметить, что множества /J^ действительно являются
событиями (т.е. А.& S), поскольку в нашем случае для х,. < jc < JC,+ ,
Aj = {to: ^(to) = x,} = {со: x, < ^(co) < x} e 5',
тем самым заданы их вероятности
Pi=P{Ai), 0</>, <1, / = 1,...,А:,
к
причем Х/'/ = 1> так как события А/ образуют полную фуппу
/• = 1
42
Итак, каждому значению дискретной случайной величины отвечает
его вероятность. Последовательность таких пар и образует ряд
распределения дискретной случайной величины
(Xi Х2 ... ХЛ
"'[р. Р2 к Р,} <""
о<л<1. ' = 1 k, !/»,='•
/=|
Например, альтернативная случайная величина, описывающая
результат единичного испытания в схеме Бернулли, задается двумя
значениями — О (неудача) и 1 (успех) и отвечающими им вероятностями
отрицательного и положительного исходов д= I — рнр, поэтому ряд
распределения примет форму:
x-J" '1
U р)
(3.2.2)
Ойрй\, р + д = \.
Ряд распределения биномиальной случайной величины (числа
положительных исходов в схеме Бернулли) имеет вид:
О \ ... т ... пЛ
[д" прд"-' ... СЦ'р^д"-'" ... р"J ^^"^-^^
0<рй1, р + д = \, iC/»'"9"-'"=(/» + 9)"=l.
Зная ряд распределения, можно найти функцию распределения. В
самом деле, имеем
-оокхйх^, {со:Л'(со)<jc} = 0,
JC, <JC<JC2, {co:A'(co)<Jc} = {co:A'(co) = jc,}= A^,
L
/ /
JC, <JC<JC,+,, {со: A'(co) < Jc} = и {ю: A'(co) = x,} = \j Aj,
/•=1 /=1
L
* к
x^ <jc<«>, {со:A'(co)<Jc} = и{ю:A'(co) = jc,} = иЛ =^'
/•=1 /=i
43
поэтому функция распределения примет вид:
О, -oo<JC<JC,,
p^, Xf<x<X2,
F{x):
ip,., х,<хйх,^,, <^-2-^)
/• = 1
1, JC^ < JC < oo.
Таким образом, функция распределения F{x) является ступенчатой
(кусочно-постоянной) со скачками в точках, координаты которых
равны значениям случайной величины, а значение функций равно сумме
вероятностей значений, не превосходящих данное. Напротив, зная
ступенчатую функцию распределения дискретной случайной величины,
можно найти ее ряд распределения. В самом деле, пусть
F{x) = q,, x,<x<x,^^, 1 = 0,...,к Ц = -«., jt^^i =+ooj,
тогда
Р{(л: Х{(£,) = X,} = Р{тх, < X{ia) <х,^] = f(x,^^- F{x,) = 9,^, -q,.
Таким образом, и функция распределения, и ряд распределения
являются эквивалентными обобщающими характеристиками дискретной
случайной величины. При определении важнейших числовых
характеристик дискретной случайной величины (математического ожидания и
дисперсии) будем использовать ряд распределения.
Математическое ожидание
Математическое ожидание, или генеральное среднее, является
наиболее употребител.ьной числовой характеристикой центра
группирования значений дискретной случайной величины. Обозначается
прописной латинской буквой Л/, поставленной перед обозначением случайной
величины MX — математическое ожидание случайной величины X.
Математическое ожидание — средневзвешенное значение случайной
величины с весами-вероятностями
к
МХ='^х,Р(. (3.2.5)
/•=1
Например, если заработная плата (в некоторых денежных единицах)
имеет следующий ряд распределения:
Г 80 100 120 "1
"1,0.25 0,5 0.25/
44
то средняя заработная плата (математическое ожидание)
Л/;1Г = 800,25 + 1000,5 + 1200,25 = 100.
Свойства математического ожидания
1. Математическое ожидание постоянной равно самой этой постоянной:
МС = СР{С = С} = С.
2. Константа выносится за знак математического ожидания:
М{СХ) = 1(Сх, )■/»,= С S JC,/»,. =СМХ.
/• = 1 /=1
3. Математическое ожидание суммы случайных величин равно сумме их
математических ожиданий:
M{X + Y) = MX + MY.
(3.2.6)
Ul Чтобы доказать зто свойаво, введем ряды распределений участвующих в нем
случайных величин
1р{х = х,,Г^уМ' "^ ||/,,|
;ir + K = ILr„ \^ J 1 . х = 1 ' , Y
УЛ
tp{x = x,, Y = yj} = p^, l,P{x = x^, Y = yj} = gj.
/ = 1 к, У = 1 т.
Вначале дсжажем, что
к
I
7=1 * ' /=1
В самом деле, поскольку события
A,=[oi:X{(u) = Xi}, 1 = 1..„к,
образуют полную группу точно так же, как и события
Bj^^(o:Y{()i) = yj], у = 1 /и,
то
1я{со:^(со) = дг„ Y{(o) = yj}= 1/'(/(,П/?у) =
7 = 1
= Р
7 = 1
= P{Ai)=P{m:X{m) = Xi} = Pi,
45
аналогично
к
1
/• = 1
^р{(й:Х{(й) = Х1, Y((o) = yj} = qj.
Используем теперь полученные выражения для сумм вероятностей при
доказательстве третьего свойства, имеем:
M{X + Y)=it (xi + уМх = Xi,Y = y.) =
= ix,tp(x = x,,r = yj)+tyiip(x = x,,Y = yj) =
i=\ 7=1 ;=l /=l
= lx,p, + tyjQj = MX + MY,
1=1 ]=\
т.е. свойство доказано. ■
4. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий:
MXY = MXMY. (3.2.7)
Две дискретные случайные величины Хн Кназываются
независимыми, если события А, = {to: A'(to) = xj}, Bj = {to: K(to) = yj\ независимы для
любых /= 1,.... k\J= 1,.... да. В § 3.6 будет дано более общее определение
независимости случайных величин, из которого как частный случай
будет вытекать данное определение.
Перейдем к доказательству, используя введенные обозначения и
независимость JT, Y:
MXY=i tx,yjP(x = x„ Y=yj)=itx,yjP[X = x,)p(Y=yj) =
i = \j=\ i=>\j=\
= txiPityjqj = MXMY,
/•=1 ;=i
что и требовалось доказать.
Найдем теперь математические ожидания дискретных случайных
величин, наиболее часто встречающихся в экономических приложениях.
Математическое ожидание альтернативной случайной величины.
Используя ряд распределения альтернативной случайной величины
[см. формулу (3.2.2)], получаем:
МХ = Од + \р = р, (3.2.8)
46
т.е. математическое ожидание альтернативной случайной величины
равно вероятности положительного исхода.
Математическое ожидание биномиальной случайной величины.
Биномиальную случайную величину Л" (число положительных исходов в п
испытаниях по схеме Бернулли) можно представить как сумму
альтернативных случайных величин, каждая из которых JQ описывает
результат /-ГО испытания в схеме Бернулли (число положительных исходов в
одном испытании):
л
^=Х^/- (3.2.9)
/' = 1
Опираясь на формулу (3.2.9) и на свойство 3, получаем:
м \ и
МХ = М
/•=1
те. математическое ожидание биномиальной случайной величины
равно произведению числа испытаний на вероятность положительного
исхода.
Математическое ожидание пуассоновской случайной величины. Закон
редких событий, вероятности которого были найдены в § 2.2 как
предельные значения биномиальных вероятностей при л -»«>,/»-» О,
пр -»"К, задается следующим рядом распределения:
X
(О 1 ... т ..Л
(3.2.10)
Поскольку пуассоновская случайная величина является в указанном
выше смысле предельной по отношению к биномиальной, то
математическое ожидание первой является пределом математического ожидания
последней, поэтому математическое ожидание пуассоновской
случайной величины
МХ = Х. (3.2.11)
Тот же результат получается прямым счетом:
МХ= I/и —е-^=ХХ/^^—^e-^ = Xsh-^ = k.
Математическое ожидание геометрической случайной величины.
Геометрическая случайная величина — число испытаний по схеме Бернулли до
первого положительного исхода, ее ряд распределения имеет вид:
47
^ (\ 2 ... m ...]
m«l /=0 '~9
Математическое ожидание находим прямым счетом:
МХ= impq'"-' = p±mq'"-' =р± (q"") ' =
т.е. математическое ожидание геометрической случайной величины
обратно пропорционально вероятности положительного исхода.
:-Ш:-
V^^~p' (^-^-'з)
Дисперсия
Дисперсия случайной величины является наиболее употребительной
числовой характеристикой степени вариации значений случайной
величины вокруг центра фуппирования. Обозначается прописной латинской
буквой D, поставленной перед значком случайной величины:
ОЛ"—дисперсия случайной величины X.
Дисперсия — это математическое ожидание квадрата отклонения
случайной величины от своего математического ожидания:
DX = M{X-MXf. (3.2.14)
Если раскрыть квадрат под знаком математического ожидания, то
получим вторую формулу дисперсии:
DX = M{X-MXf = М\х'^ -2X-MX + {MXf] =
= MX^-2{MXf +{MXf = МХ^ -{MXf,
т. е. DX = МХ^ -{Mxf. (3.2.15)
В формулах (3.2.14), (3.2.15) встретилась квадратичная функция
случайной величины. По определению, функцией от дискретной
случайной величины ф(Л') называется случайная величина, ряд распределения
которой имеет вид:
9W =
Р\ Рг ■•■ Рк )
48
т.е. значения этой случайной величины — функции от значений
случайной величины (аргумента), а вероятности те же самые, что у величины-
аргумента.
Для конкретной случайной величины, использованной для
демонстрации расчета математического ожидания, MX- 100 (см. с. 44, 45):
{Х-мху
поэтому
(80-1 oof (100-1 oof (120-1 oof
0,25 0,5 0,25
ОА'= Л/(;Г - Ла) = 20^ • 0,25 + О • 0,5 + 20^ • 0,25 = 200.
Свойства дисперсии
1. Дисперсия постоянной равна нулю:
DC = М{С - MCf = M{C-cf = 0.
2. Постоянная выносится за знак дисперсии с возведением в квадрат:
LUCXf = М[СХ - M{CX)f = М[С{Х - МХ)^ =
= M\c'^{X-MXf\ = C'^DX.
3. Дисперсия суммы независимых случайных величин равна сумме
дисперсий:
D{X + Y) = DX + DY.
В самом деле, используя четвертое свойство математического
ожидания, имеем:
D[X + К) = М[Х + Yf -[М[Х + Y)f = МХ'^ +2MXY + MY^ -
-{MXf -2МХ■ MY-{MYf = МХ'^ -{MXf + MY^ -[MYf +
+2{MXY -MXMY) = DX + DY.
4. Дисперсия произведения независимых случайных величин X, Y равна
разности произведения математических ожиданий квадратов случайных
величин и произведения квадратов математических ожиданий случайных
величин:
D{XY) = MX^MY^ -{MXf{MYf.
Подсчитаем теперь дисперсии случайных величин, математические
ожидания которых были найдены выше.
49
Дисперсия альтернативной случайной величины. Поскольку МХ=р, то
{х-мху =
{о-рУ {\-рУ
я р
поэтому
DX = М{Х - MXf = p^q + q^p = pq,
т.е. дисперсия альтернативной случайной величины равна произведению
вероятностей положительного и отрицательного исходов.
Дисперсия биномиальной случайной величины. Поскольку
биномиальная случайная величина Может быть представлена как сумма
независимых альтернативных величин, то
DX = D
Y,DXi= npq,
i = \
(3.2.16)
т.е. дисперсия биномиальной случайной величины равна произведению
числа испытаний на вероятности положительного и отрицательного
исходов.
Дисперсия пуассоновскдй случайной неличияы. По тем же
соображениям, что и при подсчете математического ожидания,
DX = lim npq = X.
я-»<»
р-»0
(3.2.17)
С другой стороны, прямым счетом приходим к Т4)му же результату:
ml
op л/и op лт op •\т-2
= е-^ I т{т-1)^+ X т^с-^ = с-^Х' I т'-/^
+ Х = }:+Х,
поэтому
DX = Ш^ -{MXf = А? + Я,-Х^ = Х.
Таким образом, дисперсия пуассоновской случайной величины
равна параметру X.
Дисперсия геометрической случайной величины. Используя ряд
распределения (3.2.12) и расчеты (3.2.13), находим
МХ^ = J,m^pq
т-1 _
= '^т{т-1 + \)рд
т-1 _
50
in = 2 m = \ in=0 '« />
Z' - ^
= pq
поэтому
1я
m
J
" 1
■\-- = pq
f
DX = MX^-{MXf=^ + --\ = \. (3.2.18)
Дисперсия суммы случайных величин. Если случайные величины X, Y
зависимы, то дисцерсия их суммы и разности записывается в
следующем виде (см. доказательство третьего свойства дисперсии):
D{X±Y) = DX+DY±2co\{X,Y), (3.2.19)
где со\{Х, Y) = М{X - MX){Y - MY) = MXY-MX-MY - коэффициент
ковариации (совместной вариации) случайных величин X, Y.
§ 3.3. Непрерывные случайные величины
и их важнейшие числовые характеристики
Как было сказано выше, непрерывная случайная величина принимаг
ет континуальное множество значений на прямой (на отрезке, на
полупрямой, на всей прямой и т.д.). Непрерывные случайные величины
делятся на два класса: абсолютно непрерывные (именно их далее для
краткости часто будем называть просто непрерывными) и смешанные,
обладающие свойствами как дискретных, так и непрерывных случайных
величин.
Случайная величина называется абсолютно непрерывной, если ее
функция распределения может быть представлена в виде:
fW=J/(z)d(z). (3.3.1)
такая функция распределения непрерывна, как функция от верхнего
предела интефирования. Напомним, что функция распределения
дискретной случайной величины — ступенчатая функция. Смешанные
случайные величины имеют кусочно-непрюрывную функцию
распределения с конечным или счетным множеством скачков.
Покажем теперь, что подынтефальная функция в формуле (3.3.1) —
это функш1Я плотности вероятности, т.е. вероятность, приходящаяся на
единицу длины в данной точке.
51
в самом деле,
P{xUX<x + Ax} = F{x + /^)-F{x) =
-во -во X
поэтому вероятность, приходящаяся на единицу длины в данной точке,
lim -^Р{х<Х<х + Ах}= lim -!- lf{z)d{z) = Az),
T.e./(jc)—действительно функция плотности вероятности. Если надо
отличать плотность одной случайной величины от другой, то употребляют
индекс случайной величины:/J(.(x).
Поскольку по определению
П+<^)= lnz)d{z), аЯ+со) = 1.
то
+ во
jnz)d{z) = l (3.3.2)
т.е. функция/(х) является функцией плотности только тогда, когда ин-
тефал от нее по всей числовой прямой равен единице.
Итак, зная функцию плотности/(х), получаем функцию
распределения:
F{x)=]nz)d{z),
—OQ
напротив, если известна функция распределения, то функция плотности
nx) = F'{x).
Таким образом, для абсолютно непрерывных случайных величин
функция плотности и функция распределения являются
эквивалентными обобщающими характеристиками случайной величины. Ввиду
удобства обычно используется функция плотности.
Q Пример 3.1. Рассмотрим равномерную случайную величину.
Равномерное распределение имеет время ожидания наугад взятым пассажиром
транспорта, курсирующего с фиксированным интервалом. Обозначим время
ожидания через т, а отдельные значения этой случайной величины через /.
52
Плотность вероятности равномерной случайной величины задается
следующим образом:
т=
fl//. /е[0./].
[о, /«[О,/],
где / - длинв интервала движения транспорта.
Поскольку
—во
то, выполнив интегрирование, находим
F.it)-
0, -оо< X 5 О,
х//, 0<х</,
1, /<Х<'».
>
F^(i)
1
V/
0
к
т X
т
t
Рис. 3.1
Ма рис. 3.1 приведены графики функций плотности и распределения
равномерной случайной величины. •
Иногда рассматривают равномерную случайную величину X,
заданную на отрезке [а, Ь\:
/vW =
\\1{Ь-а), хв[а,Ь\
[ О, х^[а,Ь\.
53
Вероятность попадания на отрезок
Поскольку для абсолютно непрерывных случайных величин
х + йл
\т Р{хйХйх + Ах}= Ym \fiz)d{z) = 0.
Дх^О
Дх^О
ТО вероятность попадания влюбую точку л; равна нулю. Поэтому
вероятность попадания на отрезок равна интефалу от функции плотности по
данному отрезку:
Р{Ь^Х^с} = Р{ЬйХ<с} = ]fizHz).
(3.3.3)
Математическое ожидание
абсолютно непрерывной случайной величины
Пусть случайная величина имеет функцию плотности, заданную на
некотором отрезке [Ь, с] (рис. 3.2). Переход к случайным величинам, для
которых 6 = - оо и/или с = + оо сопряжен с такими же трудностями, как
переход от собственного к несобственному интефалу.
Рис. 3.2
Разобьем отрезок [Ь, с] на А:равных подлине полуинтервалов. Вместо
случайной величины А'рассмотрим допредельную дискретную
случайную величину Х/^, которая имеет следующий ряд распределения:
х,=
^Р\ Рг
Рк)
где
Pi= \f{z)u{z) = f{x,)ii, Л =
c-b
54
Последнее равенство получено с помощью теоремы о среднем.
Тогда Хр, = J/(^)d? = 1, те. X— действительно дискретная случай-
'■ = ' *
пая величина.
Ее математическое ожидание
к к
/•=1 /=1
т.е. представляет собой интефальную сумму, которая при к-*оо
сходится к интефалу
]xfix)dx.
ь
Последний естественно принять за математическое ожидание
случайной величины X.
Таким образом, в общем случае математическое ожидание абсолютно
непрерывной случайной величины X
ее
MX = \xf{x)<ix. (3.3.4)
—OQ
По указанным выше наводящим соображениям сохраняются все
свойства математического ожидания, приведенные в § 3.2.
Далее всегда будем сокращенно обозначать математическое
ожидание буквой а, т.е. Л/А'= а.
Используя это обозначение и определение математического
ожидания для абсолютно непрерывной случайной величины, получаем
следующую формулу для ее дисперсии:
ее
DX = М{Х - MXf = J(x - af /(x)dbc. (3.3.5)
или
DX = МХ^ - (MXf = JxV(*)<bc - a^.
55
Показательная случайная величина
как время обслуживания
В аналитической теории массового обслуживания (см. гл. 5) время
обслуживания требования каналом обслуживания принимается
распределенным по показательному закону. Плотность распределения
вероятностей показательного закона имеет вид:
/х(0 =
_1це
■\и
0.
t>0,
t<0.
(3.3.6)
о о
На рис. 3.3 приведен фафик показательной плотности.
/tC)
о
Рис. 3.3
Функция распределения показательного закона имеет вид:
I М'
о о
в теории массового обслуживания часто надо знать вероятность того,
что обслуживание будет продолжаться более длительное время, чем t:
Р{х >t} = P{'c^t} = \-P{x<t) = \-F, (О = е-*".
Найдем теперь математическое ожидание и выясним содержательный
смысл параметра ц.
Среднее время обслуживания одной заявки
о ^^o ^"^4^- о ) ^
(3.3.7)
56
Таким образом;-среднее время обслуживания обратно
пропорционально ц. В свою очередь
^=1Г.'
(3.3.8)
т.е. ц — среднее число требований (заявок), обслуженных в единицу
времени, или интенсивность обслуживания.
Дисперсия показательной случайной величины имеет вид:
о Г Ц i Ц
Поскольку
ее ее
I zh-'dz = -zh-'\^ +2J ^-'dz = 2,
о о
то получаем окончательно
/)г = 1/ц^
(3.3.9)
Закон распределения Лапласа
Распределение Лапласа задается двycтopo^rнeй показательной
плотностью (соответствующим образом нормированной):
f{x) = ^t-^^\'K -оо<х<оо.
Таким образом, плотность симметрична относительно нуля и в этой
точке достигает максимума.
График функции плотности распределения Лапласа приведен на
рис. 3.4.
2
i
0
к
)
X
Рис. 3.4
57
Дисперсия в 2 раза больше дисперсии показательной случайной
величины
DX^MX^ =-Н: Jx^e-^'Wdx =ц|х2е-'"ск =4--
Среднее квадратичное отклонение
Поскольку дисперсия имеет квадратные единицы измерения, то для
перехода к линейным единицам извлекают из нее квадратный корень:
(S = 4dX, (3.3.10)
который и называют средним квадратичным^ или стандартным,
отклонением.
Ниже часто будем использовать однобуквенное обозначение
дисперсии, как обычно опуская индекс случайной величины, если речь идет об
одной такой величине:
a\=DX. (3.3.11)
§ 3.4. Нормальное распределение
Нормальное распределение (распределение Гаусса) занимает в теории
вероятностей в определенном смысле центральное место, поскольку
согласно центральной предельной теореме, которая будет рассмотрена
р главе 4, достаточно большая сумма сравнительно малых случайных
величин имеет распределение, близкое к нормальному
Нормальное распределение имеет следующую плотность:
фМ = ;^е '^^ ^ . (3.4.1)
То, что случайная величина А'имеет нормальное распределение с
параметрами а, о, записывается так: X~N{a, о).
Прежде всего убедимся в том, что это действительно функция
плотности:
58
Здесь была применена замена переменной z — (х- а)/а и
использован интефал Пуассона
]e-Va.=f
На рис. 3.S приведено семейство кривых нормальных плотностей в
зависимости от параметров а, о.
Рис. 3.5
Как видим, с геометрической точки зрения параметр а — точка
максимума плотности, а также центр симметрии. При увеличении а фафик
смещается вправо, при уменьшении а — влево. При уменьшении о
максимум плотности ф(д:) увеличивается, при этом значения плотности в
точках, достаточно удаленных от а, уменьшаются, поскольку площадь
под кривой плотности для любых значений параметров равна единице.
Выясним теперь теоретико-вероятностный смысл параметров.
Снова делая замену переменной г = (jc - а)/о, имеем:
MX
= -7== \^~^uz-\ra = a,
V27C _■".
поскольку J да ^dz = о как интефал по всей прямой от нечетной функции.
~" 39
Таким образом, параметр а — математическое ожидание.
Найдем теперь дисперсию нормальной случайной величины, снова
применяя замену z—(x- а)/а и интефируя по частям:
DX = M{X-MXy=-
jix-af
-i^1
ск =
"Ш.
-да 2
Je ^dz
= o
Таким образом, o^ — это дисперсия, а о — среднее квадратичное
отклонение.
Случайная величина называется центрированной, если ее
математическое ожидание равно нулю. Для того чтобы центрировать случайную
величину, надо вычесть из нее математическое ожидание:
М{Х- MX) = MX- МХ^ 0.
Случайная величина называется нормированной, если ее дисперсия
равна единице. Для того чтобы нормировать случайную величину, надо
ее поделить на среднее квадратичное отклонение:
Центрированная и нормированная случайная величина называется
стандартной. Для того чтобы стандартизировать случайную величину,
надо вычесть из нее математическое ожидание и поделить на среднее
квадратичное отклонение. Стандартные случайные величины
обозначаются большой латинской буквой Z:
Z =
Х-а
где а = MX, а^ = DX.
Поскольку только что мы доказали, что для нормального
распределения MX =^а, DX- o^ то
Z =
Х-а
N{0,1).
60
т.е. стандартная нормальная случайная величина имеет плотность
функция ф(х) — четная, ее значения для х > О приведены в табл. П. 4.1.
Вероятность попадания на отрезок
Большинство задач с использованием нормального распределения
(как и других законов распределения абсолютно непрерывных
случайных величин) сводится к определению вероятности попадания на
отрезок.
Поскольку интеграл от нормальной плотности не табличный, то
приходится пользоваться таблицами для интегралов от стандартной
нормальной плотности в форме функции Лапласа:
считая эту функцию определенной для любых —<» < х < <», при этом
Ф(-х) = -Ф(х),
те. функция Лапласа нечетна, ее значения для х > О приведены в табл. П. 4.1.
Итак, пусть X ~ N(a, а), найдем вероятность попадания на отрезок
[Ь,с]:
P{b<X<c} = p\^^<^^^<^^] = p\^^<Z<^^] =
la а а J I а а J
0 2 ^^2
1 Je-Vd, + ^ j ,-'г^=ф(Ez£yф(t:£.\ (3.4.4)
При решении конкретных практических задач можно заново
проделывать все выкладки (3.4.4) либо пользоваться окончательным
результатом:
P{b<X<c} = <t{^y<:{^]. (3.4.5)
Правило «трех сигм»
Теоретически нормальная плотность вероятности отлична от нуля в
любой, даже очень отдаленной от а точке х, однако практически почти
61
вся вероятность сосредоточена на отрезке а ±3а (отсюда и название).
В самом деле,
= Р{-3 uZu3} = 2Ф(3) = 0.9973.
Таким образом, вероятность попадания вне 3tqfo отрезка равна всего
0,0027.
§ 3.5. Производящая функция и числовые
характеристики случайной величины
в § 3.2, 3.3 были рассмотрены важнейшие Числовые характеристики
случайных величин: математическое ожидание как одна из числовых
характеристик центра группирования и дисперсия как одна из
характеристик вариации значений случайной величины. Однако эти две
характеристики хотя и являются самыми важными, но далеко не
исчерпывают всего набора употребляемых числовых характеристик случайной
величины. В этом параграфе будут последовательно рассмотрены
числовые характеристики случайной величины и установлена связь
некоторых из них с производящей функцией.
Начальные моменты
Начальным моментом к-го порядка, который обозначается как v^^,
называется математическое ожидание k-Hi степени случайной величины:
\^=МХ'', Л = 1,2 (3.5.1)
Например, первый начальный момент — это обычное математическое
ожидание:
V, = MX.
При небольших допущениях относительно случайной величины
можно доказать, что знание всех ее начальных моментов позволяет
восстановить ее функцию распределения как обобщающую характеристику
случайной величины.
Например, если известны математическое ожидание и дисперсия
нормальной случайной величины:
а = \..
2 2
62
то известна и ее функция плотности (а следовательно, и функция
распределения), поэтому нормальная случайная величина полностью
определяется первыми двумя начальными моментами.
Центральные моменты
Центральным моментом к-го порядка, который обозначается как р.^^,
называется математическое ожидание k-vi степени отклонения
случайной величины от своего математического ожидания:
\i^=M{X-MXf, (3.5.2)
Например, второй центральный момент — это дисперсия:
[i^=M{X-MXf=DX.
Любой центральный момент можно выразить через начальные.
Например, третий центральный момент
\у^ = М{Х - MXf = М[Х -v^)^ = М[Х^ -Ъv^X'^ +Ъ\]Х -\f^ =
= V3-3v,V2 +2\].
Производящая функция
Производящая функция случайной величины X— это функция от
параметра /(вообще говоря, комплексного), которая равна:
mx{t) = Mt"^. (3.5.3)
Если t = iu I / = V-l I, TO производящая функция переходит в
характеристическую, которая широко используется в фундаментальной теории
вероятностей и в теории меры.
Наиболее важным является то, что производящая функция т^(0
содержит в себе сведения о всех начальных моментах («производит»
моменты), а это означает, что по ней можно определить, как говорилось
выше, функцию распределения, содержащую все сведения о случайной
величине.;В это^1 смысле производящая функция и функция
распределения являются эквивалентными обобщающими характеристиками.
В самом деле (индекс случайной величины опустим),
т'(0) = Л/Ле''^| =МХ = \.
и вообще для любого к
ЬЪ
т.е. к-я производная от производящей функции при t=0 равна
начальному моменту к-го порядка.
В качестве примера кайдем производящую функцию нормальной
случайной величины Х~ N(a, а):
=-JL- J exp|—^(x^-2x(a+<T^/) + a42a(T*r-2aa^/+aV-aV)|ck =
■ «. _ifa-tVf) J2,2 -2,2 , - _ifia=ai) „2(2
= I e^ 'e ^ax = e * i n | e ^ -* ox = e ' ,
л/2ла _■'„ л/2ла J^
поскольку
, ~ -Llx-t-vb]
V27CO_i ,
как интеграл, от плотности нормальной случайной величины
X ~N(a + ah, а).
Итак, производящая функция нормальной случайной величины
Х~ N(a, а)
mxit) = t ^^. (3.5.4)
в частности, производящая функция стандартной нормальной
случайной величины Z~ Л^(0, 1)
Найдем с помощью производящей функции отношение ц^^о* для нс^)-
мальной случа1йной величины:
Ц=Ш^^=м(^' = мг\
где MZ* — четвертый начальный момент стандартной нормальной
величины.
64
Для того чтобы найти четвертый начальный момент стандартной
нормальной случайной величины, надо найти четвертую производную ее
4'^
производящей функции е'' при/=0:
1<' ■
е^
= /е2
V J
( \л\ I
V J
L2
= е^ +/^е2
( .,Л"'
е2
V J
i/^ , i,^
= 3/e2 +/V ,
0,2 v
P,2
i,^
i/^ . i/^
= 3e2 +6/^e2 +/"62
/=0
= 3,
/=0
поэтому для любой нормальной случайной величины
Ъ.-
= 3.
(3.5.6)
Свойства производящей функции
\. Производ/(ищц функция случайной величины, умноженной на константу,
tcx.
«*сх (О = Ме'^ =тх (О). (3,5.7)
■2. Производящая функция суммы независимых случайных величин равна
произведению производящих функций этих величин.
Пусть
тогда
mAt) = Mf^"' ^ =М Пе^" =ПЛ/е^" = П«;.,(0-
(3.5.8)
/=i
3—670
65
Медиана
В качестве показателя центра группирования наряду с
математическим ожиданием используется медиана. Для абсолютно непрерывных
случайных величин медиана — это граница, левее и правее которой
находятся значения случайной величины с вероятностями, равными 0,5,
Медиана случайной величины X обозначается МсХ. Для нормального
распределения МеЛ'= МХ= а.
Для дискретных случайных величин медиана находится на отрезке
[Хр х^^|], который определяется из условий:
ipi йО,5; Х/»,>0.5.
/=1 (=1
Точное положение медианы устанавливается следующим образом:
МеЛ' = а,х, + (1 -а,)х,^1,
где
«/=■
1
или
(=1 ^
МеХ = X, +
Рм
Мода
Для абсолютно непрерывных распределений модой называется точка
локального максимума функции плотности. Мода случайной величины
Л'обозначается МоА'. Для нормального распределения МоЛ'= МХ^а.
Распределения, имеющие одну моду, называются одномбдвльшми.
Встречаются и многомодальные распределения (смеси одномодальных
распределений).
Квартили
Для абсолютно непрерывных случайных величин квартили — это
такие границы, которые делят всю вероятность на четыре равные части.
Квартилей три: О, — левая, Oj ~ центральная, равная медиане, Оз —
правая. На рис. 3.6 показаны квартили равномерного распределения
Квартили могут быть определены и для дискретных случайных
величин подобно медиане.
66
Лх)
V,
0,25
0,25
0,25
Q\
02
0,25
Оз '
Рис. З.б
Разность правой и левой квартилей Oj ~ Q\ может быть
использована как показатель вариации.
Иногда используются децили, разделяющие всю вероятность на
десять равных частей.
Коэффициент асимметрии
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию:
^''Ф
(3.5.9)
Для симметричных распределений (Xj = О, поэтому коэффициент
асимметрии равен нулю. Для распределения скошенных влево Р < О
(большие отрицательные отклонения определяют знак Р), для
скошенных вправо р > 0. Например, показательное распределение скошено
вправо.
Коэффициент эксцесса
Коэффициент эксцесса характеризует островершинность
распределения по отношению к нормальному:
■ = ^-3.
(3.5.10)
Выше было показано, что для нормального распределения \i^O* = 3.
Для более островершинных распределений у > О, для менее
островершинных у < 0. Например, для равномерного распределения у < О, в то
время,как для распределения Лапласа у > 0.
3»
67
Критические границы
Понятие критических границ для абсолютно непрерывных
случайных величин широко используется в математической статистике при
построении доверительных интервалов и критериев проверки гипотез.
Различают левосторонние, правосторонние идвусторонние
критические границы.
Левосторонней критической границей, или квантилью, отвечающей
вероятности а, называется такая граница, левее которой вероятность
равна а (см. рис. 3.7). Квантиль обозначается К^, по определению
a = P{X<K^} = F{K^), (3.5.11)
т.е. квантиль является решением уравнения
Правосторонней критической границей, otвeчaюlцeй вероятности а,
называется такая граница, правее которой вероятность равна а.
Правосторонняя граница обозначается В^, по определению
a = P{X>B,} = \-F{B,),
т.е. правосторонняя граница является решением уравнения
f(e„) = l-a. (3.5.12)
Между левосторонней и правосторонней границами существует
следующее соотношение:
^а = *1-а- (3.5.13)
На рис. 3.7 показаны левосторонняя и правосторонняя границы.
68
Двусторонними критическими границами, отвечающими
вероятности а, называются такие границы e„, e„, внутрь которых случайная
величина попадает с вероятностью 1 — а, а вне — с вероятностью а,
причем Р{Х < в„} = Р{Х г В^] = а/2.
Таким образом, двусторонние границы являются решением
уравнений (см. рис. 3.7):
f(e„) = |. F(I„)=1-|. (3.5.14)
Между односторонними и двусторонними границами существуют
следующие соотношения:
^а =^а/2 =*1-а/2> *а = ^^1-0/2 ~ *а/2- (3.5.15)
Для стандартного нормального распределения двусторонние
границы симметричны и имеют специальные обозначения ±и^, т.е.
причем Иц является решением уравнения
Ф(и„) = (1-а)/2. (3.5.16)
§ 3.6. Многомерные случайные величины
Многомерная случайная величина Х= {X^,..., Х^ — это совокупность
случайных величин Хр заданных на одном и том же пространстве
элементарных событий П.
Закон распределения вероятностей многомерной случайной
величины Л'задается ее функцией распределения
Fx{x^ x„) = P{X^<x^ Х„<х„], (3.6.1)
которая является числовой функцией многих переменных и как
вероятность принимает значение на отрезке [О, 1].
Функция распределения многомерной случайной величины
Л'обладает следующими свойствами:
1) не убывает по каждому аргументу;
2) непрерывна слева по каждому аргументу;
3) I'x, ^.(^1 х„_,.-оо) = 0;
4) Fx^ xX^i x„_,. + oo)=/i-^_ ^^_jx, x„_,).
69
' Следует заметить* что путем перенумерации любой аргумент можно
сделать последним, поэтому в третьем и четвертом свойствах на самом
деле речь идет о любом аргументе.
Доказательство первого и второго свойств аналогично
доказательству второго и третьего свойств соответственно для одномерной
случайной величины (см. с. 40—42).
Докажем третье свойство:
Fx, ;^.(^| ^„-\'^) = Р{^\<^\ ^„_,<x„_,.Jr„<-o} =
f.
= Р
/1-1
П4П0 =/'(0)=о.
где
Ai={(O.Xi{(o)<Xi}, i = \ /7-1,
А„={<о:Х„{(о)<-^} = 0.
Докажем четвертое свойство:
f/i-i
=р\Г{А,т\=р\Г{л,\=р{х,<х, jr„_,<x„_,}=
1'"='
где
/<, ={(о:А',((о)<х,}, / = 1 л-1,
Л={со:^Г„(ш)<+оо} = П.
Распределение вероятностей дискретных случайных величин удобнее
задавать в форме рядов распределения
\^1 ^п)~
PyC^ =Хц Х„ =х^^|
(3.6.2)
У| — 1,...,Агр ...; j„—\,...,k„,
где kf — число значений /-й случайной величины,
70
Распределения вероятностей многомерных абсолютно непрерывных
случайных величин удобнее задавать в форме функций плотности
вероятности /^1 ^^(^1 z„), которые следующим образом связаны с
функцией распределения:
Fx, ^„(^1 ^^^)=\■■■\fx, ^„(^1 г„)с1г,...с1г„, (3.6.3)
для таких величин четвертое свойство принимает форму
J4 хА^х Z.Yz„ =fx, ^„.,(^1 Х„_,). (3.6.4)
Для многомерной случайной величины подобно одномерной могут
быть определены начальные и центральные смешанные моменты,
поскольку в их образовании участвуют, вообще говоря, несколько
случайных величин из совокупности. Ниже будут рассмотрены только
смешанные центральные моменты второго порядка — коэффициенты кова-
риации, которые в нормированном виде используются как меры связи
случайных величин.
Случайные величины X^, ..., Х^ называются независимыми в
совокупности, если
Fx, ^Л* ^п)=Рх,{хУРх^{х,). (3.6.5)
в частности, две случайные величины независимы, если
Рх,.Хг (*!• *2) = ''х, [xx)Fx, {^)- (3.6.6)
Для дискретных и абсолютно непрерывных случайных величин это
определение приобретает специфическую форму.
Независимость дискретных случайных величин
Пусть две дискретные случайные величины X, Узаданы своими
рядами распределения
кР\ •■• Рк) УЯх ■•• Ят
а двумерная величина {X, Y) — рядом
b^yjl
, py = P^X = x,,Y = yjj, /=?1 к, J = l...,m.
71
Используем обозначения, применявшиеся в § 3.2:
А,={(й:Х{(й)^х,}. i = l....,k,
Bj={(o:Y{(o) = yj], j = l,...,m.
Поскольку эти множества могут быть также представлены в форме
^,={о):х, <ЛГ(й))<х,^.,}, i = l,...,k, x^+j =«>,
Д^ ={©:>',. <r(o))<>',^,}, J = \ т, x^^i =ов,
то
P(Bj) = Fr(yj,r)-Myj)-
Согласно рис. 3.8 имеем на плоскости значений случайной величины
(X, У):
\{х<х,, Y<yJ}\[x,<X<x,^^. У <yj]\[x<х„ у, UY<yj^i],(3.6.7)
т.е. множество точек незаштрихованного полузамкнутого
прямоугольника получается путем теоретико-множественного вычитания из
незамкнутого квадранта с вершиной в точке (х^.^.,, yJ^^) трех
непересекающихся заштрихованных фигур.
Рис. 3.8
72
Поэтому по аксиоме сложения из формулы (3,6.7) вытекает:
p[(o:x,uX{(o)<x,^i, yjuY{(o)<yj^i] = Fx,Y(x,^i, yj^i)-Fx,Y{x,,yj)-
-Р[(о:X, <, Х{(й)<x,^^, Г(а))< yj]-Р[т: Х{т)<x,,yju Y{(o)<yj^i].
Поскольку (см. рис. 3.8)
Р[(а: X, й Х{(а) <х,^,, У{(а) < yj]= Fxj(x,^i, yj)-Fxj{x,, yj),
P[(a: X{(a)< x,, yj й У{(а)< yJ^^] = Fxj(x,, yj^i)-Fxj(x„ yj).
TO получаем окончательно
p[(o: X, й X{(o) < x,^i, у J <, y(a)) < y^^^ =
= ^x.r(x,^vyj^i)-^x.r(xi^vyj)-^x.Y(xt>yj^i)+^x.Y(xi,yj)- (3.6.8)
Используя формулу (3.6.8) и независимость случайных величин
(X, У), имеем:
P(A,nBj) = р[(о:X, <. Х{(0) <x,^i,yj<. У{(о) О-у^,} =
= f'x.rixi^v yj^i)-''x.Y(xuv yj)-^x.Y(xi>yj^i)+fxA^i^ yj) =
т.е. события A^ и Bj независимы для любых i= \,..., к, J= \,..., m.
Таким образом, для дискретных случайных величин X, У
независимость означает независимость событий, состоящих в том, что каждая из
двух случайных величин приняла одно из своих значений.
Независимость абсолютно непрерывных
случайных величин
Пусть теперь X, У ~ абсолютно непрерывные случайные величины,
поэтому
—«о —«о
fxA^'У)= i ifxAZ'u)dudz,
где fx{x), /у{у)у /х,г{^'У) ~ функции плотности вероятности
соответственно для одномерных и двумерной случайных величин.
73
Для абсолютно непрерывных случайных величин тождество (3.6.8)
при Xf = х, yj = у, Х/^,, = X +Ах, yj^, = у +Д>' примет вид:
Jt+Дх у + ^у
X у
= Fxy{x + bx, y + ^y)-Fx_Y{x + ^x, y)-Fxy{x, y + ^y)+Fxy{x,y).
Используем теперь независимость и представление функций
распределения для одномерных случайных величин:
Jt + Дх y-¥diy
1 \fx,Y{Z'U)^"^Z = Fx{x + ^x)FY{y + Ay)-Fx{x + Ax)Fy{y)-
X у
-Fxix)Fy{y + Ay) + Fxix)Fyiy) =
= [Fx{x + /^)-Fxix)lFyiy + Ay)-Fyiy)]= fMz)dz jfr{u)du,
X у
таким образом,
Jt+Дх у+Ау х+Ах У + Ау
1 l/v.)'U.«)d«dz= ffx{z)dz ffAu)du.
X у X у
Разделив теперь левую и правую части последнего равенства найхАу
и перейдя к пределу при Ах->0, Ау-^0, получаем
fxA^'y) = fxix)fY{y)-
Таким образом, для абсолютно непрерывных случайных величин
независимость означает, что совместная двумерная плотность
вероятности равна произведению одномерных плотностей.
Коэффициент корреляции
как мера связи случайных величин
Выше были рассмотрены различные формы независимости величин.
А как измерять меру зависимости случайных величин? В § 3.2 при
выводе формулы дисперсии суммы Х+ Кдвух зависимых случайных величин
был введен коэффициент ковариации (совместной вариации):
соу(ЛГ, Y) = М{Х - МХ){У - МУ) = MXY - MX ■ MY, (3.6.9)
причем
cov(^, X) = M{X-MXf =DX.
74
Этот коэффициент в известной мере является измерителем связи
случайных величин, поскольку обладает следующими свойствами:
1) для независимых случайных величин равен нулю, поскольку для
таких величин М(Х- МХ)(У- MY) = М(Х-МХуМ(У- Л/К) = 0;
2) для случайных величин X, Y, имеющих тенденцию колебаться в
одну сторону [т.е. с большей вероятностью signCA'- MX) = sign( Y- MY)],
положителен;
3) для случайных величин X, Y, имеющих тенденцию колебаться в
разные стороны [т.е. с большей вероятностьюsign(A'- МХ) = -sign( Y- MY)],
отрицателен.
Следует заметить, что по каждому аргументу коэффициент ковариа-
ции удовлетворяет второму и третьему свойствам математического
ожидания (см. с. 45), т. е.
соч{СХ, Y) = Cco\{X, Y), соу(ЛГ, CY) = С со\{Х, У); (3.6.10)
COV
1X„Y
= Хсоу(ЛГ,-, Y), COV X,^Yj = £cov[A', Yjj
1=1
J=i
J=i
Предлагаем доказать это читателю.
Однако этот коэффициент может принимать значения на всей
числовой прямой, поэтому не вполне пригоден для измерения степени
зависимости. В этом смысле более пригоден нормированный
коэффициент ковариации, или коэффициент корреляции,
p^X,Y)='-^^^^^^. (3.6.11)
Далее аргументы X, Кбудем опускать, если речь идет об одних и тех
же случайных величинах.
Q Коэффициент корреляции меняется от -1 до +1. 6 самом деле, рассмотрим
случайную величину {X + tY)^, где X, Y- уже центрированы, т.е. МХ= О,
MY= 0. Эта случайная величина неотрицательна, поэтому и ее
математическое ожидание неотрицательно:
М{Х + tYf = МХ'^ + ItMXY + t^MY^ ^ 0.
Для неотрицательности получившегося трехчлена относительно t
необходимо, чтобы его дискриминант был неположителен:
4iMXYf-4MX^MY^uO,
т.е.
__\МХУ1_^^^
{mx^^my^
75
но поскольку для центрированных случайных величин Л4Х¥= cov(A', У),
А/^2 = DX, МУ^ = DY.JO последнее неравенство принимает вид:
ОхОу
Т.е. |р|^1,
или-1^р^1. ■
Для независимых случайных величин р = О, поскольку для них
cov(;ir, Y) = 0.
Q Для линейно связанных случайных величин |р|= 1. В самом деле, пусть
тогда
cov(;ir, У) = cov(;ir, оА'+ р) = а cov(ЛГ, ЛГ) + р cov(ЛГ, 1) = а/)^,
DY = a}DX,
поэтому
соу(ДГ, К) aDX а
Таким образом,
Р =
, = !'• ">°'
[-1, а<0.
Итак, для независимых случайных величин р = О, для линей>^о
связанных |р| = 1, а в остальных случаях —1 < р < 1, р '^ 0. Чем ближе |р| к
единице, тем с большим основанием можцо считать, что Хи ^находятся
в линейной зависимости.
Если р = О, то это не всегда означает независимость случайных
величин. В этом случае говорят, что случайные величины
некоррелированны. Из независимости вытекает некоррелированность, но наоборот — не
всегда. Ниже будет показано, что для нормальных cny4af(tHMx величин
свойства независимости и некоррелированности эквивалентны.
Двумерная нормальная случайная величина
Двумерная нормальная случайная величина задается следующей
функцией плотности:
76
^(^'•^)=^;гё^Т^
(3.6.12)
С геометрической точки зрения фафик функции плотности
представляет собой «гору» с достаточно крутыми склонами, вершина
которой находится в точке (о,, Oj)- Линиями уровня служат эллипсы
\2
^1-^1
'I J
_2р^|-^.^2-^2 JjV3.| =c = const,
которые в случае р = О переходят в окружности.
Выясним теперь теоретико-вероятностный смысл параметров.
Q Прежде всего надо убедиться, что функция (3.6.12) - действительно плотность,
т.е. надо установить, что
1 |/(x,,X2)dx,dx2=l.
(3.6.13)
X, - а.
Вначале найдем внутренний интеграл, сделав замену Zj = -^—'-, ' = I, 2,
^1
и выделив полный квадрат в показателе экспоненты:
if{XvX2)dXi
2п
yi-p^a,a2
/ехр
Zi-2pZiZ2+Z2
1 Л
1 7
V2^<J2 ^2Jt(l-p2)i
exp
•a,d«,
2(,-р^)
сЦ,=
1 4 1 -i'
2 =
-<j2na.
(^f
это действительно так, поскольку
^н^
1"Р
(^|-P^2f
2(.-р^)
dz, = 1
как интеграл от одномерной плотности случайной величины
Z,-A^[pz2,VbV).
77
Поасольку согласно формуле (3.6.4) интеграл по одной переменной от
двумерной плотности является одномерной плотностью по другойпеременной, то
только что было доказано, что одномерная случайная величина Х^ ~ Ща^, с-^, т. е.
MX-i^Oi, 0X2= al,
поэтому и
МХ.=а., DX,=aU
I -"р
,2 „2
т.е. а,, ^2 - математические ожидания случгтных величин, а а,, Gj - дисперсии.
Кроме того, интефкфуя по второй переменной полученную нормальную
плотность, получаем единицу, т.е. равенство (3.6.13) действительно верно. ■
Осталось только выяснить смысл параметра р. Центрируем и
нормируем случайные величины X^, Ajt
тогда функция плотности для этих величин примет вид:
/Z|,Z2(^P^2)-
2л7Г
-ехр
Zi-2pZiZ2+Z2
2(,-р^)
поэтому (снова выделяем полный квадрат в показателе экспоненты)
p{^r,,^r2) = p(Z„Z2) = A/Z,Z2 =
2л^1-р^ -i-i
1 I Z1Z2 ехр
Zi-r-2pZiZ2+zi
2{,-р>)
dz,dz2 =
2л^1-р^ -i
|Z2«
_iL
|(z,-pz2+pZ2)exp-
(g|-Pg2)
2"1
2(,-p^)
dz,
dzi =
"Тгл'
/^.
.4
vkJ^vI'''""^'"^
(g|-Pg2)'
2(>-p^)
■d{Zi-pZ2) dz2 +
^vf^b^^^'^
d(z,-pz2)
dZ2=p.
78
в последнем равенстве были использованы значения следующих уже
ранее вычислявшихся интефалов:
V2n-(/l-p —
-- математическое ожидание центрированной нормальной случайной
величины;
^Je *• 'du = l, u = zi-pz2.
V^l-
p' —
— интеграл от плотности;
~ дисперсия стандартной нормальной величины.
Итак, параметр р — это коэффициент корреляции случайных
величин Л",, A'j.
Если две нормальные величины некоррелированны, т.е. р = О, то
согласно формуле (3.6.12) их совместная плотность
МЧ^)'
- • .-*М' -„.-^i^L
^ 157^^ "' =fx^{xi)fx,{xil
Ы2кc^ л/2ла2
т.е. является произведением плотностей одномерных случайных
величин ЛГ,, A'j, а это означает, по определению, что они независимы. Таким
образом, для нормальных случайных величин из некоррелированности
следует независимость.
Многомерное нормальное распределение
Многомерная нормальная случайная величина (ЛГ,, ..., Х^) задается
следующей функцией плотности:
79
где X — вектор-столбец переменных;
а — вектор-столбец математических ожиданий случайных величин;
В = ||соу(Л'|., Л^|| — ковариационная матрица случайных величин
\В\ — определитель матрицы В.
В частности, при /я = 2
(
В =
|^а,а2р
а,а2р
<^1 )
' 1 Р_
Д-' =
а?(1-р2) а,а2(1-р^)
Р 1
^ а,а2(1-р^) a^(l-p^) ^
(х-аМ-у-а)4^^-2р^'""'^""^-ь
^2-Д2
л^
поэтому приходим к изученной выше плотности для двумерной
нормальной случайной величины [см. формулу (3.6.12)].
Как видно из формулы (3.6.14), математические ожидания и ковари-
ационнай матрица случайных величин Л", Х^ полностью определяют
совместную функцию плотности.
§ 3.7. Функции от случайных величин
Рассмотрим наиболее употребительные (в том числе в
математической статистике) функции от случайных величин.
Композиция распределений
Композицией распределений называется алгоритм (формула), по
которому можно получить закон распределения суммы случайных величин
на основе совместного закона распределения случайных величин.
Следует заметить, что вид закона распределения суммы не совпадает,
вообще говоря, с законами распределения слагаемых (даже если они
одинаково распределены). Например, сумма двух одинаково распреде-
ао
денных независимых альтернативных случайных величин есть
биномиальная случайная величина (но не альтернативная!).
Найдем закон распределения для суммы Х~ X^+ Xj двух абсолютно
непрерывных случайных величин с совместной функцией плотности
Сделав замену z — x^+ Х2, jCj = г - х^ имеем:
FAx) = Р{Х^ +Х,<х]= JJ/(x,, x,)<ix^<ix, =
= jnf{x^,z-x^)(ix^\dz,
поэтому
во
fxix) = Fx{x)= jf{x^,x-x^)dx^ (З.7.1)
и есть плотность композиции распределений.
Композиция равномерных распределений
Пусть имеется две независимые равномерные случайные величины
X^, Xj с параметрами /р /j (например, время ожидания двух видов
транспорта), требуется найти закон распределения общего времени ожидания.
Совместная плотность распределения имеет вид:
/(Х,.Х2) =
—, х,б[0./,], Х2е[0,/2].
'l'2
О в противном случае.
Тогда, согласно формуле (3.7.1), плотность суммы равна (пусть /, < /j):
fx{x)= jf{Xl>x-x^)dx^ =
jr, OSx</„
V2
'l'2
/,/2
причем на каждом из трех участков область интефирования по х,
константы \/{1\1^ определяется из двух условий:
0<х, </,,
0<х-х, </2,
81
или
0<х, </,,
x-li <x^<x.
На рис. 3.9 изображен фафик получившейся трапециевидной
плотности (закон распределения Симпсона).
т
V/,
/i+/i
Рис. 3.9
При /| = /^ = 1 получадм треугольную плотность (рис. 3.10).
Рис. зло
Композиция нормальных законов распределения
Совместное распределение двух нормальных случайных величин Л',,
Х^ задается функцией плотности (3.6.12). Математическое ожидание и
82
дисперсию суммы А'= X^ + Х^ можно найти сразу, не дожидаясь
установления закона распределения:
а = МГ = МГ, + MA-j = а, + flj,
Cf^=DX = DX^ + Z)A'2 + 2 cov(Jr,, A'j) = a? + Gj + 2pa,a2.
Применим формулу композиции (3.7.1), используя формулу
двумерной нормальной плотности (3.6.12):
fx{^)=\f[xvx-x^)6x^ =
■щ\-
Р Ol02
Jexp
[ 2(i-P^)Li
flZfL
,pX,-aix,.fl, U-fl,
02
02
cU„
Сделаем теперь замену переменных
и = Х|-а,,. и = х-а, и-и = х-Х|-а2,
тогда числитель показателя экспоненты (без знака «минус») запишется
в следующей форме (помним, что о^ = <s\ +2рО|а2 +ci\):
I? ^ и V-U iv-u) 1 г 2_2 -. / 2\ 2_2l
\ иО^(р02+аЛУ и^0[(ра2+0^ 2„2
—гт
<J?<J2
ио-
tXT
(p<^2+qi)
•^С-р-)-
Подставляем полученное выражение в показатель степени экспоненты:
l2'
/^w=
1
2я7н
.-i(f г г
р^0,02
Jexp
ио,-
иО ^(р02 +0|)
2(1-р2)о?02'
du.
Сделав новую замену переменной
» Г«,-2Н1(ра2+о,)1. Л = —2^
OiOjVl-p L ^^ -I <^\<^2У^-[
83
получаем окончательно
\2
" Л
/xW = -7^e'^°^ "^'*'"'*^"V2^*'
■ .'»'■ е ^ '' I I I 1е
л/2ла л/2л jI,
1
(а"
<^]'
где
а = а,+«2. а^ =af+2ра,а2+а2,
т.е. композиция нормальных законов распределения снова приводит к
нормальному закону распределения с математическим ожиданием,
равным сумме математических ожиданий, и дисперсией, найденной по
формуле дисперсии суммы.
Ниже приводятся используемые в математической статистике
распределения функций от нормальных случайных величин.
Распределение х^
Распределением х^сп степенями свободы называется распределение
суммы квадратов п независимых стандартных нормальных величин:
x4n) = izf, z,-yv(o,i).
1=1
(3.7.2)
На рис. 3.11 показано семейство функций плотностей вероятности
случайных величин хЧп) при разных степенях свободы.
Рис. 3.11
Плотности распределения х^ имеют вид:
1
/W =
2«/2r^ij
х^ е ^, х^О,
О
х<0.
84
где
r(p)=J
t-'z'-^dz.
При построении доверительных интервалов и проверке гипотез
используются двусторонние критические фаницы распределения х^.
Поскольку двусторонние границы можно оп|»делить по односторонним
(см. § 3.5), то в табл. П. 4.3 приводятся только правосторонние
критические границы (для каждого значения степеней свободы).
Распределение Стьюдента
Закону распределения Стьюдента с л степенями свободы
удовлетворяет отношение
Кп) = -
где Z— стандартная нормальная величина, независимая от;^^.
Функция плотности распределения Стьюдента имеет вид:
(3.7.3)
/W-
iM
.л±1
2
ЩУ1ю1[ "*" п
(ЗЛА)
При л -^ <« эта плотность, как видно из формулы (3.7.4), сходится к
плотности стандартной нормальной случайной величины.
На рис. 3.12 приведены 1фивые плотности распределения Стьюдента
и стандартного нормального распределения, а также показаны двустО'
ронние критические гркшицы этих распределений.
-'а
-"о
■ 1
Ах)
0
к
"о
'о
X
Рис. 3.12
85
Как видим, двусторонние критические границы распределения Стью^
дента ± /ц шире соответствующих двусторонних критических границ
стандартного нормального распределения (/^ > uj. В табл. П. 4.2 привел
дены правые двусторонние границы 1^{п) для разных значений степеней
свободы.
Распределение Фишера
/"-распределением с от, л степенями свободы называется
распределение /"-отношения
F[m,n)= J . .
Как видим, /"-отношение — положительная случайная величина.
В табл. П. 4.4 приводятся правосторонние критические фаницы /^
этого распределения для разных значений степеней свободы:
Р(/">/"„) = а.
Вопросы и задачи
1. Магазин имеет два входа, потоки покупателей на этих входах
независимы и распределены по закону Пуассона. Через вход А проходит в
среднем 1,5 чел./мин, а через вход В— 0,5 чел./мин. Определить
вероятность того, что в наугад взятую минуту хотя бы один человек посетит
магазин.
2. Троллейбус имеет интервал движения 8 мин, поезд метро — 2 мин.
Определить закон распределения суммарного времени ожидания транс-*
порта наугад взятым пассажиром, пользующимся троллейбусом и метро
(без пересадок).
3. Время между прибытием двух машин к светофору распределено
экспоненциально со средним 0,25 мин. Определить вероятность того,
что время между прибытием двух машин составит от 0,2 до 0,3 мин.
4. Время изготовления детали — равномерно распределенная
случайная величина на отрезке [4, 8] мин. Изготовлено пять деталей. Какова
вероятность, что время изготовления каждой из четырех деталей
отклоняется от среднего не более чем на 0,5 мин.
5. Пусть число ошибок при вводе студентом в компьютер
символьной и цифровой информации имеет следующие ряды распределения:
Символьная Цифровая
0 12 3 0 12 3
0.1 0.1 0.7 0.1 0,2 0,6 0.1 0,1
86
Известно, что студент допустил три ошибки. Какова вероятность
^ого, что цифровых ошибок больше, чем символьных?
6. Манометр показывает давление в колонне. Давление колеблется от
10,0 до 10,2 атм., и в этих пределах любое давление равновозможно.
^следствие повреждения манометра его стрелка не отклоняется больше
цем на 10,16 атм. Какое давление в среднем показывает манометр?
7. Детали A^ ч Aj можно изготовлять параллельно. Сборку узла А^
можно начинать только при наличии деталей А^, Aj. Пусть время (в
минутах) выполнения каждой операции задается следующими рядами
распределения:
'1^0.1 0.8 0,lj '^[0.4 0.4 0.2J ^ [о,2 0,3 0.5
Какова вероятность того, что от начала обработки деталей A^, Aj до
завершения сборки узла А^ пройдет более 6 мин?
8. Определить вероятность того, что средняя масса пяти наудачу
взятых пакетов с расфасованным товаром будет отклоняться от нормы не
более чем на 2 г, если средняя масса одного пакета — 1 кг, а
отклонение — 1,5 г (распределение массы пакетов нормально).
9. Автомат заполняет банки кофе. Масса кофе и масса банки имеют
нормальное распределение со средними соответственно 500 г, 50 г й
стандартными отклонениями 10 г, 2 г. Какова вероятность того, что вес
готовой к продаже банки будет менее 540 г?
10. Найти коэффициент асимметрии показательного распределения.
11. Найти коэффициент эксцесса равномерного распределения.
12. Найти квартили показательного распределения.
13. Независимые случайные величины Хн Уимеютряды
распределения
-1 О М (-2 2
0,1 0,1 O.sJ' ~[0,3 0,7
Найти ряд распределения случайной величины Z = XY.
14. На железнодорожную станцию поступило 8 вагонов угля.
Проверка показала, что в трех вагонах зольность угля составляет 11%, в
четырех — 13%, в одном — 15%. Два из прибывших вагона поступило на
завод. Определить ряд распределения средней зольности угля,
поступившего на завод.
15. Инвестор может формировать портфель из различных видов
ценных бумаг, нормы прибыли по которым являются случайными
величинами X^, ...., Лд, MXj =а,, DX, =а], cov(A'p Xj\ = Q, i^J. Определить
л
Доли вложения капитала 0,, О < 0, < 1, 5^0, =1, в различные ценные
/=1
87
бумаги, обеспечивающие среднюю норму а = 10 и минимизирующм
я
дисперсию нормы прибыли портфеля X = Хв/^< "^ основе следующи!
/=1
данных:
/ 12 3 4 5 6
аД%) 11 10 9 8 7 6
оД%) 4 3 1 0,8 0,7 0,7
16. Доказать, что случайная величина —у %{Xf - а\ имеет распреде<
лениех^(л), если X^,..., Х^ независимые случайные величины, Xj- N{a, а).
Глава 4
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
в этой главе представлены основные сведения о законах больших
чисел и центральной предельной теореме. Законы больших чисел
утверждают, что среднее арифметическое большого числа независимых
случайных величин ведет себя как среднее арифметическое их
математических ожиданий.
Согласно центральной предельной теореме достаточно большая
сумма сравнительно малых случайных величин ведет себя приближенно как
нормальная случайная величина.
Эти утверждения имеют большое практическое значение, поскольку
состааляют теоретическую основу математической статистики, широко
применяющейся для анализа экономической информации с целью
выработки обоснованных упрааляющих решений.
§ 4.1. Законы больших чисел
Теоретическую основу законов больших чисел составляют понятие
сходимости случайных величин по вероятности и неравенство Чебышева.
Сходимость по вероятности
Последовательность случайных величин Jf,, Jfj ^„' — сходится по
вероятности к случайной величине X, если для любого е > О
л
или
limP{|;f„-;f|<e} = l, (4.1.1)
lim WlA-.-Л'|>е} = 0.
Сходимость по вероятности символически записывается так: Х^ =^ X.
В законах больших чисел будет использоваться сходимость
последовательности по вероятности к константе.
89
Неравенство Чебышева
Если случайная величина X имеет математическое ожидание и ducnefi
сию, то для любого е > О
Р{\Х-МХ\>г]й^^. (4.1.2J
е
Докажем это неравенство для абсолютно непрерывной случайно!
величин^!. Для дискретных случайных величин доказательство прово]
дится аналогично, только интегралы заменяются соответствующим1(
суммами.
Обозначив MX = а, имеем:
Р{\Х-а\>г]= J/WdJc. (4.1.3J
\x-a\tz
Область интефирования \х- а\>г можно записать в эквивалентно!
форме 2— ^ '' поэтому в этой области
|l/Wdx< I (fL^/(x)dx, (4.14
|Д1-0|^Е |Д1-0|^Е ^
последний интеграл с неотрицательной подынтефальной функцией
может только возрасти, если расширить область интегрирования до всей
прямой:
4 |(x-a)VW(bc<4-|(x-«)VWcbc = ^. (4.1.5)
^ \x-a\tz ^ ^ ^
Собирая последовательно равенство (4.1.3) и неравенства (4.1.4),
(4.1.5), получаем неравенство Чебышева.
Неравенство Маркова
Для положительных случайных величин, имеющих математическое
ожидание, справедливо следующее неравенство Маркова (е > 0):
P{X>t}<^. (4.1.6)
Докажем его для абсолютно непрерывных случайных величин:
P{X>€) = ]f{x)ux<>]-f{x)6xu-]xf{x)^ =—.
г^ ^0 ^
90
Это неравенство в первоначальной форме [см. формулу (4.1.6)] или в
форме
е
может быть применено для определения вероятностей относительно
положительных случайных величин с неизвестным законом
распределения.
Теорема Чебышева
Если независимые случайные величины X^, ..., Х^, ... имеют
математические ожидания MXj = а. и ограниченные в совокупности дисперсии DX^ —
= о^ < о^, то разность средних арифметических случайных величин и
средних арифметических их математических ожиданий сходится по
вероятности к нулю:
X„-a„=^Q.
Q В самом деле, применим неравенство Чебышева К случайной величине Х„-а„.
Поскольку
\П1 = 1 «/ = 1 ) «/=1
D(X„-a„) = DX„=DUtx] = ±-Y^DX^=^f^oU^^
« /=1
то
^' ' J е ле
Следовательно,
\тР{\Х„-а„\>г} = 0,
таким образом, действительно Х„-а„=^ 0.
Следствие из теоремы Чебышева
Если все члены последовательности независимых случайных величин
-V, Х„,... имеют одинаковые математические ожидания МХ^- а и
одинаковые дисперсии DXj — а^ (например, одинаково распределены), то
91
среднее арифметическое случайных величин сходится по вероятности к
математическому ожиданию:
Х„ =*й.
Поскольку условия теоремы Чебышева выполнены, то, согласно по
следнему положению ее доказательства (в условиях след'<^твия),
lim P{\X„-a\>t] = Q,
а это и означает, что Х„ =* а.
Теорема Бернулли
Частость ^/п сходится по вероятности к вероятности:
п
Теорема Бернулли является частным случаем приведенного выш«|
следствия, поскольку биномиальная случа1йная величина может бы'^
представлена как сумма альтернативных случайных величин (см. § 3.2)
ц=Х^,, МХ,=р,
(=1
тем самым в этой теореме речь идет о сходимости среднего
арифметического к математическому ожиданию ал ьтернативной случайной
величины, т.е. к вероятности положительного исхода.
Теорема Бернулли имеет исключительно важное теоретическое и
практическое значение. В первой аксиоме теории вероятностей
постулируется, что любое событие А имеет вероятность О < р = /* (у4) < 1, но не
говорится, как эту вероятность установить^ Теорема Бернулли дает
простой рецепт для этого случая: надо провести эксперимент из п
испытаний, в котором с вероятностью р= Р{А) может появиться данное
событие (успех, положительный исход), потом подсчитать частость (долю
положительных исходов), вот эта частость и будет «хорошим»
приближением к вероятности при больших я, поскольку она является
реализацией случайной величины, которая сходится по вероятности к Р{А).
Кроме обычных законов больших чисел доказаны также усиленные
законы больших чисел, в которых вместо сходимости по вероятности
используется сходимость с вероятностью 1:
Р{Х„-*Х} = 1.
92
Из сходимости с вероятностью 1 вытекает сходимость по
вероятности, напротив, из сходимости по вероятности, вообще говоря, не следует
сходимость с вероятностью 1.
§ 4.2. Центральная предельная теорема
Во введении к данной главе приведена не совсем строгая, но
содержательная формулировка центральной предельной теоремы. Ниже дана
ее строгая формулировка, в которой J,,..., Л,,,... — последовательность
независимых случайных величин, МХ^ = а,., DX^ = аД удовлетворяющих
прилюбомт>0 условию Линдеберга (приведем это условие для
абсолютно непрерывных случайных величин, для дискретных случайных
величин интефалы заменяются на соответствующие суммы):
I ]{x,-a,ffi{xi)'^i
lim'"''"-"^'"^*' = а (42.1)
/=1
в знаменателе выражения (4.2.1) стоит сумма дисперсий случайных
величин X^,..., Х^, а в числителе — сумма «хвостов» этих дисперсий.
Когда это условие выполняется, говорят, что «хвосты» дисперсий «легкие».
Теорема Ляпунова
Функция распределения центрированной и нормированной суммы
" I Г^ э
Z„ = Y^[Xf-af) \Y,^i независимыхслучайныхвеличинХ^,...,Х„,...,удов-
,=1 / ^/=1
летворяющих условию Линдеберга, сходится к функции распределения
стандартной нормальной случайной величины:
' _ii
F„ (х) = P{Z„ < х) -* -^ J е" 2 d^. (4.2.2)
На практике эта теорема наиболее часто используется в том случае,
Когда члены суммы имеют одинаковое распределение. Например, в
математической статистике выборочные случайные величины (см. гл. 6)
Имеют одинаковые распределения, поскольку получены на основе
одной и той же генеральной совокупности.
93
Следствие из теоремы Ляпунова
Если независимые случайные величины Х^, ..., Х^, ... имеют одинаково^
распределение с MX. — а, DX. — а^, то функция распределения их
центрированной и нормированной суммы Z„ = Х(^< -а) \р-М\ сходится к
функции распределения стандартной нормальной случайной величины:
F„{x) = P{Z„ <х)^-4- Je-Td^. (4.2.3У
* —ов
Для того чтобы доказать это следствие, опираясь на теорему Ляпунова,
надопрказать, тр в данной ситуации выполнено условие Линдеберга.
Q Доказательство провоем снова на примере абсолютно непрерывных случайных
величин. В условиях следствия суммы в числителе и знаменателе формулы
(4.2.1) будут состоять из одинаковых слагаемых. Причем слагаемое
знаменателя - а^, поэтому надо доказать, что слагаемое числителя стремится к нулю при
я-»«>:
j{x-aff{x)dx^O,
\x-a\>ta-Jn
НО ЭТО в самом деле так, поскольку интеграл в последнем выражении
представляет собой остаток
a-ta-Jn "
j{x-aff{x)dx+ jix-affix)<ix
-сю a+ta-Jii
схо11цщг(зся несобственного интеграла
]{х-а)'Пх)Чх = о\ ■
—ее
Рассмотренное следствие из теоремы Ляпунова имеет те же условия
(одинаковость распределения независимых случайных величин), что и
соответствующее следствие из теоремы Чебышева, поэтому сравнение
поведения соответствующих сумм имеет большое содержательное
значение. Как обычно, будем использовать следующее обозначение для
стандартизованных исходных случайных величин:
Z,={X,-a)/o.
94
1 "
Следствие из теоремы Чебышева имеет вид — Х^/ =* я.что эквива-
«/=.1
лентно - Х-^ = - X ^/=> 0.
' «/=.1 о Я/=1
В следствии из теоремы Ляпунова используется следующая сумма:
" Х- -а 1 "
X^^ = 4-IZ,. (4.2.4)
,=1 Ол/я л/я /=1
Таким образом, в первом случае сумма стандартизованных слагаемых,
деленная на я, сходится по вероятности к нулю (т.е. к неслучайной
величине), во втором случае та же самая сумма, деленная на л/я, сходится
(в смысле сходимости функции распределения!) к стандартной
нормальной величине Z~ Л^(0,1).
Сумма (4.2.4) в следствии из теоремы Ляпунова может быть
представлена в виде
Таким образом, сравнительно большая сумма (п велико) достаточно
малых случайных величин (дисперсии слагаемых D\ -4' = ~ — малы)
распределена приближенно как стандартная нормальная случайная величина.
Этим положением пользуются при решении практических задач: при
я-»оо распределение соответствующей суммы заменяют на
распределение стандартной нормальной случайной величины.
О Пример 4.1. Опредэлить вероятность того, что средняя продолжительность
100 производственных операций окажется в пределах от 46 до 49 с, если мвте-
магическое ожидание одной операции равно 47,4 с, а среднее квадратичное
отклонение - 4,9 с.
В этой задаче Х- продолжительность наугад взятой производственной опе-
рации, д = MY= 47,4с, о = л//)^ = 4,9с, ^ = -Х^/. я = 100-средняя
Я/al
продолжительность 100 наугад взятых производственных операций, причем
MX = 47,4 с, DX'^ о^/п =(4,9)2/100 с^.
Находим вероятность
Р{46йХй49}жР
1,4 ;ir-47.4 1.6
0,49 0,49 0,49
95
» />{-2,857^ Z S3,265} = Ф(3,265)+Ф(2,857) = 0,9984.
При решении задачи на основании следствия из теоремы Ляпунова
распределение центрированного и нормированного среднего (J-47,4^0,49 было ^
приближенно заменено на распределение стандартной нормальной случайной
величины Z~ N(Q, 1). •
Интегральная теорема Муавра—Лапласа
Функция распределения центрированной и нормированной биномнйльнт
случайной величины при п-*^ стремится к функции распределения стац
дартной нормальной случайной величины:
4iipi£<xL^fe-Td,.
ynpq j V2n_-L
Эта теорема является частным случаем следствия из теоремы Ляпу<
нова, поскольку биномиальная величина является суммой
альтернативных случайных величин:
л
^^=X^/• (4.2.5)
Доказательство следствия проводилось путем проверки справедливо^
сти Условия Линдеберга в непрерывной форме. Однако альтернативные
случайные велинцны — д»)скр|^тные. Поэтому для доказательства сфор^
мулирр^^аиной тво|)вмы надо установить выполнение условия Л индебера{
га для альтернативных случайных величин-
Q Имеем для казной альтернативной величины Хр аходящей в сумму (4.2.5),
р я
\я р
поэтому
MXi = р, DX, =p^q + q^p = pq. (4.2.6)
Каждое из одинаковых слагаемых знаменателя условия Линдеберга - pq,
каждое иаодитковых слагаемых числителя
^{x-pfp„ (4.2.7)
\x-|\>■ч>q^!n
гдехпринимаетзначенияОи1, причем при х= о р^ = q,zvf>nx-\ Р^^р-
96
^
Полная дисперсия pq альтернативной случайной величины (слагаемое
знаменателя) состоит из двух слагаемых p^q и q^p, первое из них отвечает х = О и
войдет в сумму (4.2.7), если р > ipq^n \\ > т^-Уя), второе отвечаетх = 1 и
войдет в сумму (4.2.7), если q > xpq^fn {\ > xp^fnj. Поэтому при я >
первое слагаемое не войдет в сумму (4.2.7), а при я > , , - второе слагае-
т р
мое, т.е. при я > «0. «о = ^Щ ^^•"ТТ - ^ сумме (4.2.7) не останется ни
ух q X р )
одного слагаемого. Таким образом, допредельная величина в условии Линде-
берга будет равна нулю, тем самым и предел равен нулю, т.е. условие Линде-
берга выполняется. ■
Приведенное доказательство основывалось на теореме Ляпунова,
которая была дана без доказательства ввиду сложности последнего.
Между тем учебный материал предыдущих глав вполне достаточен для
прямого доказательства интефальной теоремы Муавра—Лапласа.
Прямое доказательство
интегральной теоремы Муавра—Лапласа
Q Доказательство будет проведено в терминах производящих функций, т.е. будет
доказано, что
4
где
_\1-пр
е ^ - производя1дая функция стандартной нормальной случайной величины
Z-A'CO, 1)(см. §3.5).
Стандартную биномиальную величину (4.2.8) представим в виде суммы
центрированных альтернативных величин:
Z = HZ^ = 1; X, -пр = -1= %[Xi -р). (4.2.9)
V«M inpq i^i ^npq ыС ^^ ■'•'''
Поскольку
Y (~P ^'
{l p
97
то
т
_М) = Мс^^'~''^' = с-'"д + с'"р.
Xi-p
Используя представление производящей функции суммы независимых
случайных величин в виде произведения производящих функций слагаемых,
получаем
'"-,, (0 = П'«;г,-,(0 = (е-'"9 + е"р)".
(=1
Применяя теперь выражение для производящей функции случайной величи-
" 1
ны У (Х - р), умноженной на константу С = г— , найдем
,=1 ' ^ПРЯ
( р>
mzAt) =
41 У
де
>w + neV"w
V
J
(4.2.10)
Разложим в ряд экспоненты, представленные в выражении (4.2.10):
■^npq 2npq \п)
■^npq Inpq \п)
После сложения получаем
9е^+ре^ = 1 + —+ 0 - .
2л \п)
где о — - бесконечно малая, стремя1дая к нулю быстрее, чем —.
\п) п
Подставим выражение (4.2.11) в равенство (4.2.10), окончательно получаем
(4.2.11)
'"z„(0 =
1 + — + о -
2я 1л
е^ =m^{t).
Вопросы и задачи
1. Закон распределения случайной величины, принимающей только
положительные значения, неизвестен. Определить вероятность того, что
98
случайная величина примет значение, не превышающее 10, если ее
математическое ожидание равно 5.
2. Средний стаж работы ассистента до защиты кандидатской
диссертации равен 7,9 года. Определить вероятность того, что стаж наугад
взятого ассистента не превышает 10 лет.
3. Определить вероятность того, что средняя арифметическая 50
случайных величин отклонится от средней арифметической их
математических ожиданий не более чем на 0,15, если дисперсия каждой
случайной величины не превышает 0,45.
4. Из большой партии деталей было отобрано 100 деталей.
Определить вероятность того, что отклонение средней прочности отобранных
деталей от средней прочности партии не превышает 0,3, если дисперсия
прочности наугад взятой детали равна 2,25.
5. Вероятность брака при изготовлении кинескопов равна 0,1.
Определить вероятность того, что при проверке 500 кинескопов будрг
забраковано не более 54.
6. Вероятность выхода из строя конденсатора за время Т равна 0,2.
Определить вероятность того, что за время Гиз 100 конденсаторов
выйдет из строя менее 25.
7. При штамповке изделий из пластмассы на каждые 6 изделий
приходится одно дефектное. Определить вероятность того, что из 80
изготовленных изделий число стандартных изделий будет находиться в
пределах от 60 до 75.
8. Инвестор покупает ценные бумаги за счет займа, взятого с
процентной ставкой г под залог недвижимости. Процентная ставка на ценные
бумаги X— случайная величина с MX = а,а> г, DX= а^. Какова
вероятность того, что инвестор не сможет вернуть долг и лишится своей
недвижимости?
Указание. Оценить с помощью неравенства Чебышева вероятность
события {Х< г).
4*
Глава 5
ВВЕДЕНИЕ В ТЕОРИЮ СЛУЧАЙНЫХ ПРОЦЕССОВ
И ТЕОРИЮ МАССОВОГО ОБСЛУЖИВАНИЯ
В данной главе приведены основные сведения о случайных
процессах. Дано определение случайного процесса, приведены основные виды
случайных процессов. Более подробно изучены марковские процессы с
непрерывным временем и дискретным множеством значений, которые
состаапяют основу аналитической теории массового обслуживания.
Описаны состав и виды систем массового обслуживания, выведены
дифференциальные уравнения для вероятностей состояний системы,
найдены вероятности состояний в установившемся режиме и по ним
определены важнейшие операционные характеристики систем
массового обслуживания с офаниченной очередью.
Операционные характеристики систем с неограниченной очередью
и с отказами могут быть получены как частные случаи соответствующих
характеристик систем с ограниченной очередью.
§ 5.1. Случайные процессы и их виды
Случайным процессом называется семейство случайных величин
X{t, ш), заданных на одном и том же пространстве элементарных
событий £1 и зависящих от параметра /б Т. В большинстве практических
приложений параметр /трактуется как время. Далее будем придерживаться
именно такой трактовки.
При фиксированном /= /,, ХО^, ш) представляет собой обычную
случайную величину (сечение процесса в момент /q), при
фиксированном (О X{t, ш) яапяется траекторией случайного процесса.
Математическим ожиданием случайного процесса называется
траектория математических ожиданий составляющих этот процесс случайных
величин
a{t)=MX{t,(si). (5.1.1)
Дисперсией случайного процесса называется траектория дисперсий
состаапяющих этот процесс случайных величин
100
<S^{t) = DX{t,fu). (5.1.2)
Ковариационной (автоковариационной) функцией случайного
процесса называется функция двух переменных ^ ; € Т, значения которой
представляют собой коэффициенты ковариации сечений процесса в
соответствующие моменты времени:
B{t, s) = cov[^(/, ©), X{s, oo)]. (5.1.3)
Далее аргумент oo опустим, но он будет подразумеваться по
умолчанию.
Конечномерным распределением случайного процесса в моменты
/|,..., t^ называется распределение многомерной случайной величины,
составленной из сечений в моменты /,,..., t^.
F,, /.(*!• •••'*«)=^W'l)<*l>--^('«)<*«}- (5.1.4)
Процесс называется регулярным, если его поведение полностью
определяется конечномерными распределениями и они согласованы. Под
согласованностью понимается следующее: любые два распределения в
^/|,.... t^, /д^^,,.... /„j и Up .... tf^, /^^,,.... t„\
моменты \t\,.... Гд, t^^\,.... f„j и I г,,.... r^, t^^^,.... t„ i приводят к
одному и тому же распределению в моменты (/,,..., t^). Здесь /,,..., /^^ для
удобства записи выбраны следующими подряд, однако имеется в виду, что
они могутлюбым способом чередоваться с ?), tj.
Процесс называется процессом с непрерывным (дискретным) временем,
если множество ^непрерывно (дискретно). Как правило, в первом
случае рассматривают 7== [О, <»), во втором — Т= О, 1, 2,... . Далее будем
считать, что имеет место один из этих случаев.
Процесс называется процессом с непрерывными (дискретными)
значениями, если составляющие его случайные величины принимают
непрерывные (дискретные) значения.
Процесс является процессом с независимыми значениями, если Х(() не
зависит от X(s) при t* s,t,se Т.
Процесс называется стационарным в широком смысле, если его
математическое ожидание и дисперсия не зависят от времени, а
ковариационная функция зависит только от разности моментов времени:
B{t,t + s) = B{s). (5.1.5)
Процесс называется стационарным в узком смысле, если его
конечномерные распределения инвариантны относительно сдвига по времени /t > 0:
^/,+А /«+*(*!• •••• *я) = ^'| /«(*!• ■••• *л)- (5.1.6)
101
Из стационарности в узком смысле следует стационарность в
широком смысле, но не наоборот
Q В самом деле, с одной стороны, из условия (5.1.6) вытекает одинаковость
одномерных распределений в разные моменты времени, а из этого следует, что
математические ожкздания и дисперсии одни и те же в разные моменты времени,
с другой стороны, условие (5.1.6) для двумерных распределений можно
записать так:
^l.t+s -(*!> ^l)- ^.j(*l> *2)>
ЧТО означает, что двумерные распределения одинаковы в моменты времени,
разность между которыми одинакова, а отсюда и следует, что ковариационная
функция зависит только от разности моментов врамени. ■
Процесс называется гауссовским, если все его многомерные
распределения являются нормальными (см. § 3.6).
Л J*) = -
1
где
Г^Л
х =
м
\^nj
(2яГ#1
М
expj-jC
х-а) В-\х-а)\,
(5.1.7)
а =
B = \B(t>.tj)\, /. У = 1...../».
Q Для гауссовских процессов из стационарности в широком смысле следует
стационарность в узком смысле. Это в самом деле так, поскольку плотность
конечномерного распраделения (5.1.7) целиком определяется первыми двумя
моментами: при a{t) = 0(1 = const вектор а всегда будет постоянным, а
ковариационная матрица инвариантна относительно сдвига по времени, так как ее
компоненты зависят только от разности моментов времени:
B(ti+h,tj+h) = B(tj-t,) = B(t,,tj\
тем самым
//|+А /,+А (*) - //| 1„ (*)•
а это и есть стационарность в узком смысле. ■
В главе 10 будут изучаться экономические временные ряды. В общем
случае их случайная составляющая является стационарной случайной
последовательностью.
102
Среди случайных процессов особое место занимают марковские
случайные процессы. Марковские процессы обладают следующим важным
свойством: при известном настоящем их будущее не зависит от
прошлого {t^ < t^ <...< t„<s< t):
p[X{t)<xlX{t^)<Xy,...,X[t„)<x„,X{s)<y] = P{X{t)<xlX{s)<y],(5A.%)
т.е. будущее поведение системы, описываемой марковским процессом,
целиком определяется ее состоянием в последний из известных
моментов времени.
§ 5.2. Марковские случайные процессы
с непрерывным временем
и дискретным множеством состояний
Марковский процесс с непрерывным временем и дискретным
множеством состояний составляет теоретическую основу для исследования
реальных систем массового обслуживания. Под состоянием системы
массового обслуживания понимается число требований (заявок) на
обслуживание, находящихся в системе. Поэтому далее изучается
марковский случайный процесс с непрерывным временем, который принимает
значения / = 0,1,..., N, где N— максимальное число требований, которое
может находиться в системе.
Для таких процессов марковское условие (5.1.8) запишется в
следующей форме:
p{x{t) = jlX{t,) = i,,...,X{t„) = i„,X{s) = i} =
= P{X{t) = JlX{s) = i]. (5.2.1)
Вероятности в правой части (5.2.1) называются переходными
вероятностями и обозначаются следующим образом:
p,j{s,t)=P{X{t)==JlX{s) = i}, (5.2.2)
ipij{s,t) = \.
Если переходные вероятности зависят только от разности моментов
Времени (т.е. только от длины интервала)
/'Л*. О = /»«('-■у).
То такой марковский процесс называется однородным по времени. Ниже
Рассматриваются только однородные марковские процессы.
103
Кроме того, исходя из поведения реальной системы массового
обслуживания, будем считать, что на конечном интервале процесс может
менять свое состояние не более чем счетное число раз, такие процессы
называются сепарабельными. Таким образом, траектории изучаемых
процессов являются кусочно-постоянными (ступенчатыми).
По этим же соображениям будем рассматривать только
стохастически непрерывные марковские случайные процессы, для которых при 5 -»О
X{t + s)=^X{t), (5.2.3)
т.е. для любого е
lim/'{|;!r(/ + 5)-;!f(/)|>e} = 0,
j-»0
откуда следует:
\m^P{X{t^s)*X{s)} = 0. (5.2.4)
Из условия (5.2.4) и, следовательно, из условия стохастической
непрерывности вытекает, что при s-^0» i*j
/'(/•('+*) = /'(/■(')- /»(/■(*)-> 0. (5.2.5)
Переходные вероятности удовлетворяют следующим уравнениям
Колмогорова—Чепмена:
/'^(' + 5)=1Л*('К(4 (5.2.6)
которые выводятся аналогично теореме полной вероятности (см. § 2.1).
Матрица, составленная из переходных вероятностей, называется
стохастической:
^(')=|К(0||. /.у=о.1.....ж.
в матричном виде уравнения (5.2.6) выглядят так:
P{t + s) = P{t)P{s).
Стохастически непрерывные сепарабельные марковские процессы
удовлетворяют следующим предельным соотношениям:
Нт-Ь.^5^ = Х,., l-p,;.{At) = XiAt + o{At), (5.2.7)
104
Постоянные X^ называют плотностями вероятности выхода из
состояния, а Я,^ — плотностями вероятности перехода из состояния в
состояние.
Q При доказательаве будем использовать следующее обозначение:
л, (О = Р{Х{и) = i,Ouu< t/X{0) = /}
- вероятность того, что процесс на всем полуинтервале [О, t) будет находиться
в состоянии /, не выходя из него. Пользуясь свойствами однородности и
марковости, имеем:
п, {t + s) = Р{Х{и) = i,Ouu<t + s/X{0) = /} =
= Р{Х{и) = i,Ouu<t/X{Q) = i}P{X{u) = /, t^u<s/X{Q) = /, X{t) = /} =
= it{t)P{X{u) = i, 0 ^ и < 5Д(0) = /} = л(0л(5). (5.2.8)
Поскольку О < л, (1) < 1, то эту вероятность можно записать в форме
л,.(1) = е-^',гдеХ, = -1пл,.(1).
Из соотношения (5.2.8) вытекает: лД 1)
Л, -
„-Ху In
= е "
.точно так же
"'(й°К;
Но поскольку любое t > О можно как угодно точно приблизить
рациональными дробями, то
л,(0 = е-^.
Обозначив tr =rt/n, имеем (выражение для вероятности справа
охватывает не все возможности перехода из состояния / в состояние у, / *j):
/'<у(О^^^'^Д^К{^]^('-^.0^|о«"''''''^*'й*
-Xj,
-Xj, (t\\-^'' ^ -Xj, r/V-e"*"'
-Xjt
■ = e ■'
l-e-^''^4n
X, tin
105
поэтому
Ру,(Л > е ^ ;; lim •' .
"^ ' Х,- 8-»о 5
Поделив левую и правую части последнего неравенства на / и переходя к
пределу при t -» О, получаем
т.е. существует плотность вероятности перехода
/-»о t "
Если Q<tQ<t^<...<t„<t,^o вероятность/»,.;(О можно представить в виде
л-1
/'//(0 = ЛД0+ X lni{tr)Pij{tr^l-tr)Pji{t-tr^l)-
Пусть теперь f -» О, тогда согласно только что доказанному угвередению
Pij{fr.i -fr)=hA.i-fr)+40. pjiit-',.,)=ьС-'г+i)+40.
поэтому р..{() = л,(/) + о{(), следовательно,
/-»0 / /-»0 / /^0 /
Уравнения Колмогорова
Пользуясь соотношениями (5.2.7) для плотностей вероятности
выхода из состояния и перехода из одного состояния в другое состояние,
можно вывести дифференциальные уравнения для переходных
вероятностей и для вероятностей состояний.
Прямая система уравнений Колмогорова
Пользуясь уравнениями Колмогорова—Чепмена [см. формулу (5.2.6)]
и соотношениями (5.2.7), имеем:
Puit + At)= I PiAOPkji^t) =
= (l - ljAt)py{t) + I Pik (t^At + o{At), (5.2.9)
k*J
106
поэтому
-^^ =-VHO+1^ р^ЛОК^-Л-
k*J
Переходя к пределу при Д/ -> О, окончательно получаем прямую
систему уравнений Колмогорова:
-7Г=^ PikK' K=-h' '.у = 0,1,...,ж. (5.2.10)
а' *=о
Обратная система уравнений Колмогорова
Если уравнения Колмогорова—Чепмена для переходных
вероятностей записать в следующей форме [сравните с уравнением (5.2.9)]:
р^(/ + Д0=1 Pu,iAt)p^{t),
*=о
то аналогичным образом может быть получена обратная система
уравнений Колмогорова
^Рц ^ у
-^=L^4Pkj- ' (5.2.11)
Уравнения Колмогорова для вероятностей состояний
Если задано начальное распределение вероятностей q = {д^, 9,,..., ^дг),
гяе q,=P{X{Q) = i}, S^, = l, то
Pjit) = P{Xit) = j}=ig,pyit).
1=0
Умножая каждое из прямых уравнений Колмогорова (5.2.10) на д. и
складывая их, получим следующую систему уравнений для
вероятностей состояний:
^Pj ^
— =1^Р,Я.^, (5.2.12)
107
или в матричной форме:
^ = М. Р{0) = д,
где р — {ро, Рр •••. Pj\f) — вектор-строка вероятностей состояний.
Система уравнений (5.2.12) имеет стационарную точку, в которое
—- = О; в стационарной точке дифференциальные уравнения переходят
at
в линейные алгебраические:
М = 0. (5.2.13)
Определитель этой системы равен нулю, поскольку сумма его
столбцов равна нулю. В самом деле, для любого At
1^^0 = 1.
у=о
или
J^p^j{At) = \-p,{At).
Поделив выражение на Д/и перейдя к пределу, получим
или (напомним, Х,,у=-Х,,)
^\ij=Q, i = OJ,...,N:
у=о
т.е. действительно сумма столбцов Л равна нулю. Поэтому одно из
уравнений системы (например, последнее) является следствием других. За-
N
менив это уравнение на естественное X Р* = '> получим следующую
систему линейных алгебраических уравнений для стационарных
вероятностей:
S РкК=0' y = o,i,...,/v-i,
V „ -1 (5.2.14)
*=о
108
§ 5.3. Введение
в теорию массового обслуживания
Предмет теории массового обслуживания — вероятностные модели
реальных систем массового обслуживания (СМО). Состояние СМО
описывает марковский процесс с непрерывным временем и дискретным
1У1НОжеством состояний.
Любая реально функционирующая СМО (автозаправочная станция,
парикмахерская, столовая и т.п.) соединяет в себе по крайней мере три
составляющие:
1) входящий поток требований (заявок) на обслуживание;
2) обслуживающую систему;
3) выходящий поток обслуженных заявок и поток заявок,
получивших отказ.
Любая реальная СМО может быть представлена как простая или
сложная система из многих таких составляющих.
Под входящим потоком понимается последовательность
случайных моментов времени /,, /j.--- поступления заявок в систему
Интенсивностью входящего потока называется среднее число требований,
поступающих в систему в единицу времени.
Если при занятой обслуживающей системе вновь пришедшая заявка
получает отказ, то такая СМО называется системой с отказами, в
противном случае — системой с очередью. Различают системы с
неограниченной очередью и ограниченной очередью, в последнем случае заявка
теряется, если очередь уже достигла предельной длины.
Под организацией очереди понимается порядок обслуживания
поступивших требований: если некоторые заявки имеют преимущества в
постановке на обслуживание, то такая СМО называется системой с
приоритетами.
Ниже будут рассматриваться системы без приоритетов и с Офаничен-
ной очередью. Системы с отказами и с неограниченной очередью
являются особыми частными случаями систем с ограниченной очередью.
Максимальное число требований, которые могут находиться в такой
системе, будет обозначаться через N.
Обслуживающая система состоит из обслуживающих каналов.
Каждый канал может осуществлять лишь один вид обслуживания и
единовременно обслуживать лишь одно требование. Если система включает в
себя каналы, которые могут выполнять много видов обслуживания, то
такая система называется многофазной.
Наличие нескольких каналов (многоканальная СМО) позволяет
увеличить интенсивность обслуживания однофазной системы, поскольку
Параллельно могут обслуживаться несколько требований. Далее будут
Изучаться многоканальные однофазные СМО. Число каналов в такой
системе будет обозначаться буквой п.
109
Интенсивностью обслуживания (каналом или всей обслуживающей
системой) называется среднее число требований, обслуженных в
единицу в|}емени.
Изучение выходящего потока особенно актуально тогда, когда
требования, прошедшие один вид обслуживания, поступают на следующий
вид обслуживания (на следующую фазу), те. выходящий поток стано-^
вится входящим потоком для другой фазы.
Простейший входящий поток
Входящий поток требований называется простейшим, если этот
поток обладает свойствами стационарности, отсутствия последействия и
ординарности.
Обозначим через X{t) число требований, поступивших во входящем
потоке к моменту времени t, полагая при этом, что Л'(О) = 0.
Вероятность того, что за время t придет конкретное число требований к,
зависит от того, где находится интервал длиною t:
P{X{t + s)-X{s) = k} = p^{s,t). (5.3.1)
Входящий поток требований называется стационарным, если
вероятности (5.3.1) не зависят от расположения интервала, но зависят только
от его длины:
P{X{t + s)- X{s) = к} = P{X{t) - X{Q) = k} = p^ (t). (5.3.2)
Таким образом, pj,t) — вероятность того, что за время t поступит к
требований.
Входящий поток требований называется потоком с отсутствием
последействия, если будущее поступление заявок не зависит от того, как
они поступали в прошлом, иными словами, если t^ < t^ <...< t^<s< t, то
p{X{t)-X{s)=k/X{t,)={,,...,X{t„)=i„,X{s)=i}=P{Xit)-X{s)=k}.(533)
Из отсутствия последействия вытекает условие марковости [см.
формулу (5.2.1)] процесса X{t):
P{X{t) = j/x{t^)=i,,...,X{t„) = i„, X{s) = i} =
= p{X{t)-X{s) = j-i/X{t^) = i^,...,X{t„) = i„, X{s) = i} =
= P{Xit) - Xis) = J - i/Xis) = /} = P{X{t) = j/X{s) = /•}.
Условие стационарности означает однородность марковского
процесса Л'(/) — числа заявок, поступивших за время t.
110
Входящий поток называется ординарным, если за малый промежуток
времени приход двух или более требований маловероятен (вероятность
такого события равна бесконечно малой величине более высокого
порядка по сравнению с ht):
p^{At) = o{At), к = 2,3,.... (5.3.4)
Q Докажем теперь, что простейший поток требований является пуассоновским, т.е.
все его конечномерные распределения - пуассоновские.
Начнем с вероятности/^„(О, т. е. вероятности того, что за время /в систему
не поступит ни одного требования. Поскольку О < />„( 1) < 1, то эту вероятность
можно записать в виде
Ро{^) = ^~^' где Х = -1п/>о(1)>0.
Пользуясь условиями стационарности и отсутствия последействия, имеем:
Po\Z
■■Ро{\) = е
-\
поэтому />о| - = е ^". Далее, поскольку />о — | =
Р.\'-
то
I ~ J ~ ' ^ отсюда уже с непреложностью вытекает [см. аналогичное
доказательство формулы (5.2.8)]
Ро(0 = е-^.
Подключая теперь условие ординарности, получаем следующее
дифференциальное соотношение для любой вероятности состояния при А: > 1 [приход
двух требований и более за время Л/имеет вероятность o(At)]:
p^it + At) = p^it)poiAt) + p^_^it)p^iAt) + oiAt).
Поскольку
PoiAt) = е"^' = \-XAt + o{At),
Pt(At) = \-poiAt)-p2{At)-... = XAt + o{At), ^^-^-^^
TO
p^{t + At)-p^it) = -\p^it)At + \p^_^it)At + oiAt).
После деления на At и перехода к пределу при At-^Q окончательно получаем
-^ = -'>^k+^k-v /'*(0) = 0- к = 12,..., (5.3.6)
111
при этом для А: > о /»^(0) = О, поскольку Р{Х(0) == 0} = 1.
Для решения уравнений (5.3.6) сделаем замену:
р^^ч'^и^, Ui^ = c^p^, А: = 0, 1, 2,...,
(в частности, при А: = О Иц = 1, поскольку p^ij) = е"*''), тогда
^ = 4-1. «*(0) = 0> к = \,2,.... (5.3.7)'
Решим сначала первое уравнение системы (5.3.7):
^ = Х. «,(0) = 0.
тогда u^ = 'Kt,
затем второе уравнение
^--kh, «,(о)=о.
тогда «2= — .
Наконец, для любого А: > О получаем
,*
* к\
Возвращаясь к вероятностям, окончательно имеем:
p^{t)=P{X{t)^k] = ^^i-^, Л = 0,1,:.., (5.3.8)
т.е. одномерные распределения являются пуассоновскими. ■
Используя формулу (5.3.8), найдем среднее число требований,
поступающих в систему за время /(см. § 3.2):
MX{t) = i Л^^е-^' = Xt. (5.3.9)
*=о *!
Из уравнения (5.3.9) находим
х-Шй. ,5.з.,о,
Таким образом, X, — среднее число требований, поступающих в
систему в единицу времени, или интенсивность входящего потока требований.
112
Система обслуживания сакспомемциальмыми каналами
В аналитической теории массового обслуживания предполагается,
что время обслуживания х одного требования каналом распределено по
показательному закону, функция плотности вероятности которого
имеет вид:
Ш-[ ^ ^^^ (5.3.11)
Поскольку
Мг=^, ji =—,
ц '^ Л/х
поэтому |д, — интенсивность обслуживания.
Поскольку
F,{t) = P{x<t} = \-t-^',
то
Р{х>(} = е~'^. (5.3.12)
В частности, при малом At >
Р{х > М} = е"!^' = 1 - цД/ + o(A/>t ''
P{i <At} = \- е"*^ = цД/ + о(Д/).
!
Показательное распределение как распределение времени
обслуживания обладает следующим свойством: длитв;1ьность предстоящего
обслуживания не зависит от того, сколько обслуживание уже
продолжалось:
Df W л P{^>s + t,x>l} P{x>s + t}
P{x>s + t/x>t} = —^'—~z —^ = —Ь г^'
^ ' ' Р{х>(} Р^Х}
= ^-r^ = t-^=P{x>s}. (5.3.13)
е ^
Если в обслуживающей системе в каждый момент / находится А:
требований, А:< л,то вероятность того, что за малое время Д/не закончится
обслуживание ни одного требования (х,— время обслуживания
требования /-М каналом):
к
P{xi > Д/ X;t > Д/} = П Р{'^1 > Д4 = е"**^' = 1 - *цД/ + о(Д/),
(=1
113
a вероятность того, что закончится обслуживание ровно одного
требования,
/'|и(х, > А/ X,- < Д/ х^ >Д/)1 = А:цД/ + о(Д/),
(5.3.14)
вероятность же того, что будет обслужено более одного требования, —
о(Д/).
Уравнения для вероятностей состояний
многоканальной СМО с ограниченной очередью
Рассмотрим теперь, как функционирует однофазная л-канальная|
СМО с ограниченной очередью длиною не более (N— п), на вход
которой поступает простейший поток требований с интенсивностью \, а
каждый канал обслуживающей системы является показательным с
интенсивностью обслуживания ц. На рис. 5.1 приведена схема такой СМО.
X
Входящий
поток
Очередь
к<А/-п
'
Поток
отказов
>
^^
<■: >
^
м
Выходящий
Поток '
Рис. 5.1
Обозначим через Х(() число требований в системе в момент /.
Поскольку входящий поток и обслуживающая система обладают
марковским свойством, то X(t) как результат их взаимодействия является
марковским процессом с (^+ 1) состоянием (к= О, 1 п, п+\,..., N).
В таком случае (см. § 5.2) вероятности состояний системы
р,{1) = Р{Х{1) = к}, А: = 0.1 N,
удовлетворяют уравнениям (5.2.12). Чтобы найти конкретный вид этих
уравнений для рассматриваемого процесса Х((), надо найти плотности'
вероятностей выхода из состояний и перехода из одного состояния й
другое.
114
Поскольку из-за ординарности входящего потока приход двух
требований и более за малое время Л/ имеет вероятность о(Л/), а
экспоненциальная обслуживающая система может за время Л/ закончить
обслуживание двух требований и более также с вероятностью о(Д/)> то отличны
от нуля только плотности вероятности перехода в соседние состояния.
Используя уравнения (5.3.5) и (5.3.14), получаем:
вероятность того, что за время А/ пришло новое требование во
входящем потоке,
p,^J^^^{At) = \^t + o{At), А: = 0,1 Л^-1,
а вероятность того, что за время Л/ обслуживающая система закончила
обслуживание одного требования.
Pk.k-ii^) =
ЛцД/, к = \,...,п,
йцД/, к = п + \
N.
Поэтому
ч.*+|
= К к = 0,\ N-\,
Поскольку
к = \ п,
к = п + \ N.
p^{At) =
\-XAt + o{At),
к = 0.
\-p^,^_i{At)-p^,^^^{At) + o{At), k = \,...,N-\,
\-п\1А1 + о{А(), k = N,
то
Xj. = lim
^-P^i^t)
At
К, k = 0,
'K + k\i, k = \ n,
Х + йц, k = n+\ ^-1,
1Ц1, k = N.
Соответственно
^kk -'
\ =
-K k = 0,
-{X+k\i), k = \ n,
-(Х + йц), k = n + \ ^-1,
-ЙЦ, k = N.
115
Тем самым матрица Л в нашем случае примет вид:
ц -(Х + ц)
Л =
О
2ц -(Х + 2ц)
О
О
О
О
о о
о о
о о
о ^
о
о
й|Д, -(X + йц) X,
о п\х. -п\1)
таким образом, полностью заполнены диагональ, а также верхняя и
нижняя подциагонали.
Расписывая матричную запись/>Л == О по уравнениям, получаем
следующую систему алгебраических уравнений для стационарных
вероятностей состояний:
Xp,^_^-{X + n\l)P|^+n\liP|^^^ =0, к = п,..., N-\,
Xpf/_i-n\ipff=0, k = N.
(5.3.15)
Поскольку определитель системы (5.3.15) равен нулю, то одно из ее
уравнений является следствием других. Поэтому, заменив последнее урав-
N
нение системы на естественное J)/?^ =1, окончательно получаем систе-
му из (Л^ + 1) уравнения для {N + 1)-й стационарной вероятности:
- Vo + Ц/>| = О, к = О,
V*-|-(^ + «^K+«Ц/'*+1 =0, к = п N -\,
Po+Pi+-+Pn=^-
(5.3.16)
Вначале выразим все вероятности через р^, а затем найдем р^ из
последнего уравнения, в результате получим
к = \,...,п.
Рк=\
Р*
, !,_„ Ро' k = n + \,...,N,
(5.3.17)
116
Pq =
tt'o*! л! 1-р/л
N+\
Нетрудно проверить, что вероятность
р^
найденная как решение уравнений (5.3.15) (без последнего уравнения),
удовлетворяет последнему из уравнений (5.3.15), т.е. это уравнение
действительно есть следствие остальных уравнений системы (5.3.15).
Далее через А'будем обозначать случайную величину — число
требований в системе в установившемся режиме.
Функционирование СМО различно для трех стадий (режимов):
1. Заполнение системы после начала ее работы, вероятности
состояний зависят от времени и определяются Как решение системы
дифференциальных уравнений.
2. Функционирование системы в установившемся режиме,
вероятности состояний не зависят от времени [см. выражение (5.3.17)].
3. Прекращение приема новых заявок на обслуживание и
освобождение системы от оставшихся заявок путем их обслуживания; вероятности
зависят от времени и являются решением дифференциальных
уравнений.
В нашем случае это следующие линейные неоднородные
дифференциальные уравнения (;'уу = 1 —Pq-Pi -——Ps-\) с начальными условиями
/'о(0) = 1, /'*(0) = 0, *= 1, ..., yV-1:
-^ = Хр^.,-(Х+Лц)/,^+(Л+1)ц/,^^,, А:=1,...,я-1,
<^Pn-i
d/
= -nii.Po-...-rniPf,.3+{K-n\i)Pf/.2-i'>^+2n\i)pf/_i+n\i, k = N-\.
В Приложении 1 найдено решение этой системы при л = 1, Л^= 2 и
любом начальном условии Pq{0) = д^, ^,(0) = g^. Это решение имеет вид:
Pi(/) = Pi+ B^.e-''^^ + В^^еГ"^', v„ Vj > О, т. е.
lim/),(/) = /),, / = 0,1,
117
поэтому при / -> оо решение стремится к стационарному. В общем слу<1
чае имеет место то же самое. Таким образом, после завершения переход^
ного процесса система переходит в установившийся режим, описывае<^
мый стационарным распределением вероятностей. Хотя чисто теорети»
чески переходный процесс продолжается бесконечно долго, практичес*
ки он занимает относительно небольшую долю общего времени
функционирования системы, наибольшая доля приходится на
установившийся (стационарный) режим. Поэтому средние характеристики,
описывающие качество и экономичность обслуживания, надо определять на баз|
стационарного распределения. Такие характеристики называются оле-
рационными.
Операционные характеристики многоканальной СМО
с ограниченной очередью
Наиболее важными, с точки зрения клиентов, характеристиками
СМО являются средняя длина очереди, среднее время ожидания в очере-^
ди, вероятность отказа и веррятность того, что прцдется стоять в очереди]
Обозначим через к — текущее число требований в очереди, х — BpeMjd
ожидания в очереди наугад взятой заявки.
Имеем (штрихом обозначена производная):
й!й ,=| UJp/„ n\n ,-=0 \n)
Pop
Л + 1
p/n
nln
\N-n+\
1-(P/")
N-n+l
l-p/«
p/n
_ РоРГ' \-{N-n+ \){p/ny-"+{N-n){p/n)
n\n {\-plnf
Сравнивая с выкладками для к , аналогично находим
к=п
к=пП\п'^~" ЙЦ
п\п\х i^; \п) п\п\1 -Ti U;
_РоР"^' 1-(ЛГ-«-И)(р/«)^-"-н(УУ-«)(р/«)^-"^'
п\пК i^-p/nf
118
j
о
II
I
=Hii
Q. s:
Л •**
+
s:
II
+
II
о
""c^l-^
o.
о
^
s:
I
I
lU] It
s:
I
+
s:
I
o.
I
+
s:
Q. s:
+
In!
II
'«^И^
X
с
I
+
+
I
I
a:
o.
I
^
И"
I
s
I
o.
I
1^*
VI
S
I
i VI
s
119
Заявка получает отказ тогда, когда в системе уже находится пределы(
но допустимое число требований Л^, поэтому вероятность отказа
Вероятность того, что заявка будет ждать, определяем следующие
образом:
к=п П\ ,=0 \П) л! 1-р/й
с точки зрения управляющего или владельца СМО, важное значение
имеют «холостой ход» (доля времени простоя обслуживающей системы!
и среднее число занятых каналов.
Первая (из названных) характеристика — вероятность того, что в син
стеме нет требований
Рй =
y'pi+piizM.
ttoA:! п\ 1-р/й
N+\
Вторую характеристику — среднее число занятых каналов — находил^
следующим образом (v — число занятых каналов):
я-1 N
t=l k=n
"£ P* , P
I-(P/")
N-n+l
k%ik-\)\ (й-1)! 1-р/й
Соответствующие характеристики для СМО с неограниченной
очередью получаем из приведенных выше путем перехода к пределу при
N-¥oo, при ЭТОМ должно быть р < 1, или я, < ц, а для СМО с отказами —
путем подстановки Л^=л. Все полученные результаты сведены в табл. 5.1.
Понятие об имитации функционирования СМО
Как только не выполняется одно из предположений, сделанных вышв|
для обеспечения аналитического исследования системы вплоть до по-!
лучения формул для важнейших операционных характеристик, так при-"
веденные формулы становятся, вообще говоря, неправильными.
Повторим эти предположения:
1) входящий поток требований — простейший, при таком потоке
время между приходом двух требований имеет показательный закон
распределения с параметром Я.;
120
2) все каналы обслуживающей системы — показательные с
параметром ^l;
3) система без приоритетов, те. все поступающие заявки обслужива-
,отся в порядке очереди;
4) система однофазная, т.е. производится один вид обслуживания;
5) система разомкнутая.
Имеющиеся имитационные пакеты прикладных профамм
моделируют:
длительность обслуживания с любым законом распределения;
время между приходом заявок также с любым законом распределения;
процесс функционирования СМО при строго формализованном
алгоритме такого функционирования.
Для имитации на ПЭВМ функционирования изучаемой СМО
необходимо:
1) составить блок-схему и алгоритм функционирования СМО;
2) установить законы (с точным указанием параметров
распределения) для промежутков времени между поступлением заявок во всех
входящих потоках и для времени обслуживания каждого канала;
3) подобрать пакет прикладных программ, пригодный для имитации
изучаемой системы;
4) описать на языке пользователя функционирование изучаемой
системы;
5) ввести указанные сведения в профаммную систему и провести иа
ПЭВМ имитацию функционирования СМО, в результате чего будут
получены оценки операционных характеристик, тем более точные, чем
больше заявок во входящих потоках будет разыфано.
В качестве примера на рис. 5.2 приведена блок-схема
функционирования трехфазной СМО, осуществляющей человеко-машинный процесс
доения коров:
фаза 1 — подготовка животного к машинному доению
(осуществляется оператором);
фаза 2 — доение (осуществляется доильной установкой);
Рис. 5.2
121
фаза 3 — освобождение животного от доильного аппарата
(осуществляется оператором).
На этом рисунке: TJ, — время между поступлением животных; Г. — время
/-ГО вида обслуживания, / = 1, 2, 3.
Законы распределения в такой ситуации могут быть нормальными с
примерно следующими средними: МТ^ = MT^ = МТ^ = 1 мин, МТ^-б мин.
Первую и третью фазы может осуществлять один оператор либо на
каждую из них может быть выделен отдельный оператор.
Вопросы и задачи
1. Автозаправочная станция имеет 4 бензоколонки. Среднее время
заправки — 2 мин. Входящий поток автомащин — простейщий с
интенсивностью 1,5 авт./мин. При всех занятых колонках требование
теряется. Определить вероятность отказа и среднее число занятых колонок.
2. Покупатели магазина образуют простейщий поток требований с
интенсивностью 150 чел./ч. Определить наименьщее число продавцов,
при которых среднее число покупателей, ожидающих обслуживания, не
превысит 3.
3. В нефтеналивном порту 4 причала для заправки танкеров, которые
приходят в среднем через 18 ч, а время загрузки составляет в среднем
двое суток. В очереди могут стоять не более 2 танкеров. Определить
пропускную способность и холостой ход порта.
4. Определить закон распределения промежутка времени между
приходом двух требований в простейщем потоке требований
интенсивностью X.
5. Поток желающих оформить вызов врача на дом — простейщий.
В среднем абоненты звонят через каждые 10 с. Время приема вызова
распределено по показательному закону со средним значением 12 с.
Определить наименьщее число телефонов в регистратуре, при котором вызов
принимается не менее чем от 90% абонентов. Считается, что в случае
неудачи абонент не предпринимает больще попыток дозвониться.
6. Доказать, что выходящий из показательного канала (на входе
которого всегда имеются заявки) поток является простейщим.
7. Автоматическая мойка может принять на обслуживание
одновременно 4 автомащины. В среднем мащины прибываютчерез2мин, а
средняя продолжительность мойки — 10 мин. В очереди могут находиться не
более 6 мащин. Определить вероятность того, что в системе находится хотя
бы одна машина, и загруженность одной установки для мойки мащин.
8. В магазине имеется 3 справочных телефона. В среднем обращаются за
справками 40 чел./ч. Средняя продолжительность справочного разговора
3 мин. Издержки, связанные с работой одного телефона, — аруб./мин.
Определить минимальную стоимость одной минуты разговора по телефону,
при которой система неубыточна.
122
9. Каким условиям должны отвечать случайные величины X, Кдля
того, чтобы случайный процесс Z{t) = A'cos со/ + Ksin со/ был
стационарном в широком смысле?
10. Платная стоянка для легковых автомашин имеет 7 мест. Найти
вероятность того, что прибывающая машина найдет свободное место,
если машины в среднем прибывают через 10 мин, а занимают место на
стоянке в среднем 1 ч.
11. Поток деталей, сходящих с конвейера, простейший с
интенсивностью 2 дет./мин. Время проверки детали контролером имеет
показательный закон распределения со средним 2 мин/дет. Определить долю
непроверенных деталей.
12. Город обслуживают 4 машины скорой помощи. Вызовы
поступают в среднем через 4 ч. Вероятность того, что хотя бы одна машина
занята, равна 0,25. Определить среднее число занятых машин и среднюю
долю простоя машин.
13. В парикмахерской работают два мастера. Время обслуживания
распределено по показательному закону со средним 12 мин. Ожидать
обслуживание могут не более трех человек. Поток клиентов —
простейший с интенсивностью Юклиентов/ч. Найти важнейшие операционные
характеристики этой системы.
14. Система автоматической посадки самолетов одновременно может
хранить данные только о шести самолетах, находящихся в воздухе.
Самолеты, подлетающие к аэродрому, образуют простейший поток с
интенсивностью 6 самолетов/ч. Если в момент запроса посадки система
заполнена, то самолет улетает к запасному аэродрому. Аэродром имеет
3 посадочные полосы, самолет занимает полосу в среднем 20 мин.
Найти пропускную способность СМО, загруженность одной полосы,
среднее число занятых полос, среднее время ожидания начала посадки
после запроса.
15. Система обслуживания изменяет свои состояния в дискретные
моменты времени /= О, 1,..., имеет два состояния: О(свободно), 1
(занято). Матрица переходных вероятностей (за один шаг) имеет вид:
j,J\-a а
У b \-b
Где а — вероятность поступления требования, b — вероятность
окончания обслуживания. Найти стационарное распределение вероятностей.
Часть 2
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Математическая статистика — раздел математики, посвященный
анализу данных. Основная задача математической статистики — оценить
характеристики генеральной совокупности по выборочным данным.
Под генеральной совокупностью понимается весь мыслимый набор
данных, описывающих какое-либо явление. Более строго: генеральная
совокупность — это случайная величина Дш), заданная на пространстве
элементарных событий Q с выделенным в нем полем событий S, для
которых указаны их вероятности Р. Или коротко: генеральная
совокупность — это генеральная случайная величина Дш) и связанное с ней
вероятностное пространство (Q, S, Р).
Выборка объема п — это совокупный результат п независимых
наблюдений за генеральной случайной величиной. Конкретная выборка
Хр ..., Хд — это конечная последовательность чисел — реализации
случайной величины Х{(й). Случайная выборка — это весь мыслимый наб^ор
конкретных выоорок, или, более строго: случайная выборка — это
последовательность А',, ..., Х^ независимых одинаково распределенных
случайных величин, распределение каждой из которых совпадает с
распределением генеральной случайной величины. Случайная выборка имее1Г
следующее распределение:
fx, ^„(x,....,x„) = /'{^,<x„...,^„<x„} = n^{^/<^/} = n/='.v,(^/)-
в разделе книги, посвященном математической статистике,
рассматриваются: методы получения и качество точечных и интервальных
оценок параметров и числовых характеристик случайных величин; основные
понятия проверки гипотез по выборочным данным и наиболее
употребительные в экономической практике виды гипотез; рефессионный анализ
как инструмент анализа и прогноза экономических явлений;
статистический анализ экономических временных рядов; основные понятия и
области применения в экономике многомерного статистического анализа.
124
Глава 6
ОСНОВЫ ВЫБОРОЧНОГО МЕТОДА
в настоящей главе разбираются вопросы построения оценок общих
и числовых характеристик случайных величин по выборочным данным
и показатели качества этих оценок.
§ 6.1. Оценка числовых характеристик
случайных величин
в результате осуществления п независимых наблюдений за
генеральной случайной величиной получена конкретная выборках,,..., х„,
представляющая собой последовательность из п чисел.
Кроме этих результатов наблюдений за случайной величиной,
ничего другого о ней не известно, за исключением, быть может, самых общих
представлений о форме закона распределения.
Каждое выборочное наблюдение х, в конкретной выборке не имеет
никаких преимуществ перед другими, т.е. они полностью равноправны
иравновозможны. Если выборочные наблюдения в конкретной
выборке переставить в порядке возрастания, то получим вариационный ряд.
Далее будем считать, что именно в таком порядке уже расставлены
выборочные наблюдения.
Все это дает нам основания для построения на базе конкретной
выборки ряда распределения обобщенной выборочной случайной
величины X:
Х =
Ч L X, ^
- L -
\п п J
(6.1.1)
Если все выборочные значения различны, то формула (6.1.1)
действительно задает ряд распределения: все значения случайной величины
Различны и расставлены в порядке возрастания, сумма вероятностей
зтих значений равна 1.
125
Если же некоторые значения совпадают (а это наверняка может
случиться для дискретных случайных величин, принимающих меньшее
число значений чем л), то следует каждое такое значение рассматривать
один раз и с вероятностью, кратной числу значений. Тогда получим
настоящую выборочную случайную величину:
Х =
( ^
т.
\ п
п
п )
(6.1.2)
%т^=п, 1<п.
Если по рядам распределения X и X найти любой начальный
момент А:-го порядка, то получатся одинаковые результаты:
1
/и,
Таким образом, с точки зрения расчета начальных моментов (а
следовательно, и центральных) обобщенный ряд распределения (6.1.1) и
обычный ряд распределения (6.1.2) полностью эквивалентны.
Поскольку все сведения о генеральной случайной величине
А'сосредоточены в конкретной выборке (х,,..., х„), а последняя представлена в
форме обобщенной выборочной случайной величины X, то естественно
оценки числовых характеристик генеральной случайной величины (далее все
оценки будем помечать символом '") получать в форме соответствующих
характеристик обобщенной выборочной случайной величины. Приведем
оценки наиболее употребительных числовых характеристик — моментов:
(6.1.3)
iLi^ = M{x-MX) =-I(x,.-x)*, 3c = -I;c,.
AI,=
/=I
Например, оценки математического ожидания и дисперсии,
согласно формулам (6.1.3), примут вид:
1 " _
a = v, =-Хх,. =х,
«/=1
О =l^2=-l{Xi-x) .
(6.1.4)
126
Оценкой числовой характеристики или параметра 0 случайной
величины называется функция от выборочных значений в{x^,..., х^), которая в
определенном смысле «близка» к истлнлому значению 0.
Например, в выражении (6.1.4) в качестве оценки математического
ожидания выступает линейная функция от выборочных значений с
равными коэффициентами 1/л, а в качестве оценки дисперсии —
квадратичная функция от выборочных значений и т.п.
Как измерить «близость» оценки 0 к истинному значению 0 или как
определить качество оценки?
Качество оценки определяется не по одной конкретной выборке,
а по всему мыслимому набору конкретных выборок, т.е. по случайной
выборке. Поэтому для установления качества полученных нами
оценок моментов [см. формулы (6.1.3), (6.1.4)] следует в этих формулах
заменить конкретные выборочные значения х- на случайные выборочные
значения X..
Качество оценки устанавливают проверяя, выполняются ли
следующие три свойства.
Состоятельность
Оценка 0 называется состоятельной, если она сходится по
вероятности к истинному значению (индекс п обычно опускается, но
подразумевается по умолчанию):
0„ => 0. (6.1.5)
Свойство состоятельности является обязательным для оценки;
несостоятельные оценки не используются.
Несмещенность
Оценка 0 называется несмещенной, если ее математическое
ожидание равно истинному значению:
Л/0 = 0. (6.1.6)
Это свойство желательно, но не обязательно. Часто полученная
оценка бывает смещенной, но ее можно поправить так, чтобы она стала
несмещенной. Иногда оценка бывает смещенной, но асимптотически
несмещенной, что означает стремление математического ожидания
Оценки к истинному значению:
Мв„^в. (6.1.7)
127
Эффективность
Оценка 0 называется э0д&ек/иывиоы в определенном классе оценок 0, если
она самая точная среди оценок этого класса, те. имеет минимальную
дисперсию:
Ов =minZ)e.
вб0
(6.1.8);
Ниже рассмотрим, какими из этих свойств обладают полученные
выше оценки числовых характеристик.
Среднее арифметическое выборочных значений
как оценка математического ожидания
Для случайной выборки оценка математического ожидания [см. фор;
мулу (6.1.4)] примет вид:
1 " -
Согласно следствию из закона больших чисел (см. § 4.1) средне
арифметическое независимых одинаково распределенных случайных ве
личин, имеющих дисперсию а^, сходится по вероятности кматематиче
скому ожиданию
X =i>a,
а это и означает, что а = X состоятельна.
Несмещенность устанавливаем прямой проверкой;
Ма = М
1 "
«/=1 ;
I л I л
Теперь докажем, что а эффективна в классе линейных несмещенны;|
оценок.
В самом деле, линейная оценка имеет вид:
й = Хс,.ДГ;, (6.1.9)
'=1
линейная несмещенная оценка должна удовлетворять условию Ма = а
поэтому '
/
Ма = М
/=1
/=1 /=1
128
т.е. для ее несмещенности необходимо ^с, = 1.
Найдем дисперсию
Da = D
/=1
^ п ^
/=1
/=1 /=1
(6.1.10)
Поэтому для определения наиболее эффективной оценки в классе
линейных несмещенных оценок надо минимизировать дисперсию
[см. формулу (6.1.10)] при выполнении условия несмещенности (а^ —
константа):
min Х^/ •
(6.1.11)
("
1с,
и=1
N
-1
/
Задача (6.1.11) — задача на условный экстремум, которая, как любая
такая задача, сводится к задаче на безусловный экстремум:
L{c^,...,c„,X)=lCl -X
/=1
Для определения точки экстремума находим производные и
приравниваем их к нулю:
-—= 2с;-Х = 0, / = 1, ...,л,
Подставляя значения с. = "k/l, полученные из первых уравнений, в
последнее уравнение, получаем
XI XI
— = -, или С;= —= -.
Итак, при с,= 1/л, /= 1,..., л, оценка (6.1.9) имеет минимальную
дисперсию, т.е. а = X является эффективной в классе линейных
несмещенных оценок.
В частности, р = ji/л (ji — биномиальная случайная величина)
является несмещенной, состоятельной и эффективной в классе линейных
несмещенных оценок оценкой вероятности.
5—670
129
Оценка математического ожидания
по неравноточным наблюдениям
Пусть имеются результаты п наблюдений за определенным
показателем а, выполненные с разной точностью:
или в случайной форме:
X^,...,X„, МХ. = а, DX. = a}, i=\,...,n. (6.1.12)
Требуется таким образом воспользоваться информацией,
содержащейся в конкретном ряде наблюдений х,, ..., х^, чтобы полученная по
этому ряду оценка была самой точной с точки зрения всех мыслимых
значений такого ряда.
Описанная ситуация не укладывается в схему случайной выборки,
поскольку выборочные случайные величины имеют одинаковые
дисперсии, а здесь дисперсии разные. Вместе с тем такая задача имеет большое
практическое значение и обобщает решенную выше задачу поиска
наиболее эффективной оценки в классе линейных несмещенных оценок.
В самом деле, в данной ситуации линейная оценка имеет следующую
дисперсию:
Da = D
/=1
1^/^/ =lcfaU
/=1
и задача поиска наиболее эффективной оценки в классе линейных
несмещенных оценок примет вид:
min J^cjol
Снова строим функцию Лагранжа:
(6.1.13)
/ \ 2 2
L[c^,..., с„,Я,) = Хс,а/ -X
/=1
1^/
l'=l
^
-1
J
и приравниваем ее производные к нулю:
| = 2,^-Я.О. с-.Л,
/ = 1,..., п.
ЭХ
/=1
= 0,
130
откуда находим
(6.1.14)
1
"'^
" 1
Таким образом, в этом случае наблюдения входят в самую точную
оценку обратно пропорционально своей дисперсии: более точные
наблюдения входят с большим весом, более грубые наблюдения — с
меньшим весом.
Свойства оценок начальных моментов
Выше было показано, что оценка а = X первого начального момента
является состоятельной, несмещенной и эффективной (в классе
линейных несмещенных оценок) оценкой момента v,, если генеральная
случайная величина имеет дисперсию а^.
Начальный момент и его оценка как функция от случайной выборки
имеют вид (А: > 1):
v^=A«r*, v^ = A/i*=-?-ixf=Z (6.1.15)
"/=1
Если ввести случайную величину t/ = А'*, то для нее
рассматриваемый момент будет моментом первого порядка:
v^ = MX'' = ми,
поэтому оценка v^ как оценка математического ожидания t/обладает
следующими свойствами: состоятельна, не смещена и эффективна в
классе линейных относительно ы,. (или к-х степеней х,*) оценок, если
существует дисперсия
DU = Ми'^ -{MUf =v^^-vl,
т.е. если существует у генеральной случайной величины А'наряду с
моментом v^, который оценивается, и момент Vj^.
Наличие этих свойств у оценок начальных моментов служит
теоретическим основанием метода моментов (см. гл. 7).
Свойства оценки дисперсии
Для случайной выборки оценка дисперсии [см. формулу (6.1.4)]
примет вид:
S» 131
a^=^Y.(Xi-X)\ (6.1.16)
Изучение свойств этой оценки начнем с проверки на несмещенность^
Раскрыв квадрат под знаком суммы в уравнении (6.1.16), имеем:
1 ^
Ма^ =-j;^(MXf-2M{XiX) + MX^. (6.1.17)
Найдем теперь каждое из слагаемых в скобках под знаком суммы:
MXf = DXi + {МХ^ f =а^+а^.
M[XiX) = М
1 "
. "7 = 1 ,
MX}+ % MX, MX J
j*i
a 2
— + a ,
n
MX^=M
1 " 1 " 11
i,MXf+ X MX, MX J
1=1 i.j=\
a 2
n
Подставив найденные выражения в (6.1.17), имеем:
Л/а^=а^-^
И-1 2
•а ,
п п
откуда видно, что оценка а^ имеет систематическое смещение (-aV"),
т. е. эта оценка занижает в среднем истинное значение дисперсии на а^/п.
Правда, это смещение сходит на нет при и —> оо, т.е. оценка
асимптотически не смещена.
С целью устранения смещения скорректируем оценку следующим
образом:
п-\ n-\f:^ ' I
(6.1.18)
в самом деле,
/1-1
т.е. скорректированная оценка действительно не смещена.
Теперь перейдем к доказательству состоятельности 5^. Для этого
понадобится утверждение: для состоятельности несмещенной оценки 9
достаточно, чтобы /)0 -> 0. В самом деле, применим неравенство Чебы-
шева к этой оценке, тогда для любого е > О
132
ф-е|.44-
Поскольку большая правая величина стремится к нулю, то левая
(меньшая) вероятность также стремится к нулю, а это и означает, что
0=>0, т. е. оценка 0 состоятельна.
Таким образом, для доказательства состоятельности достаточно
показать, что Ds^ -> 0.
Q Имеем:
(6.1.19)
Ms*=M
-\2
(и-1Г'.Г=.
J^(X,-X)(Xj-X)
X [MXfXJ -IMXfXjX + MXfX^ -IMXiXJX +
(и-l)^.r=.^
+4MX,XjX^ - 2MX,X^ + MX]X'^ - IMXjP + Л/Л"*).
Найдем теперь каждое из девяти математических ожиданий в скобках под
знаком суммы (считая, что все Л'; уже ц е н т р и р о в а н ы, т.е. Л/A^ = 0. Это
всегда_можно сделать, поскольку в выражении (6.1.19) используются разности
A^ - X, которые преобразуются в радности центрированных величин Х,- Х =
= Х.- Х + а-а={Х.-а)-{Х-а)).
Итак,
2v2
мх;х; =
MXt = \i„ i = j,
MXfXJ=a\ i^j.
MXfXjX = - f^MXfXjX, =
^i4
n
' = y.
a
n
Mxfx'=-L iMxfx,x, = -LiMxfx^=^J-^
" r.p=l
W /- = 1
MXiXJX =
n
_4
-. ' = y.
-, I^J,
133
_1_ «
2
MX,XjX'^ = -у I MX.,XjX,Xp =
^i4 3(/i-l)a''
-T-+- г
/I n
" /■./>.?=i "
n n
MXjP=-^[\i,+2{n-])a^],
MX' = -V tMX.X^X^X, = -l-[n4 +3(/2- Oa-»].
" r.p,q,l = l n ^ ^
Подставив полученные выражения в правую часть (6.1.19), получаем
(отдельно выписаны результаты суммирования по каждому из девяти математических
ожиданий):
Ms' = —^—^[гц1^+п{п-\)а' -2\1^-2{п-\)а' +\1^+{п-1)а'-
(/1-1)
2 б(/1-1) 4 ^l4 3(/1-1) 4
п п п п
и /i(/i-l)^ '
Теперь окончательно получаем выражение для дисперсии:
п п{п-\у ' п\Г' /1-1 )
которая действительно стремится к нулю при /i -> •», если существует ц^.
Итак, оценка а ^ состоятельна, если существует четвертый центральный
момент. ■
134
Соотношение между предельной ошибкой выборки,
риском и объемом выборки
Предельной ошибкой выборки А называется максимально допустимое
по модулю отклонение эмпирической характеристики от теоретической.
Риском* а называется вероятность того, что модуль отклонения
эмпирической характеристики от теоретической превысит предельную
ошибку
/'{|ё-е|>д| = а, (6.1.20)
тем самым вероятность противоположного события
/'{|ё-е|<А| = 1-а. (6.1.21)
Ниже под теоретической характеристикой будет подразумеваться
математическое ожидание а или вероятность р, а под эмпирической
характеристикой — оценка математического ожидания или вероятности.
В первом случае
/'{|л'-а|<д} = 1-а, (6.1.22)
поскольку МХ = а, то под знаком модуля стоит уже центрированная
случайная величина, но поскольку дисперсия среднего арифметического
и независимых одинаково распределенных случайных величин в п раз
меньше дисперсии одного слагаемого:
(л г, \ л п ^2
DX = D
1"'='
1 " а'-
W / = 1 П
то для нормирования левой части делим обе части неравенства на cil4n:
aj^
= 1-а.
Согласно следствию из центральной предельной теоремы
распределение центрированной и нормированной суммы независимых
одинаково распределенных случайных величин при и -»со стремится к
распределению стандартной нормальной величины, следовательно, при
достаточно больших п стандартную случайную величину под знаком модуля
можно приближенно заменить стандартной нормальной величиной
Если риск а пренебрежимо, мал (например, а = 0,05), то его в этом случае
называют уровнем значимости (см. гл. 8 «Проверка гипотез»).
135
Сравнив последнее выражение с определением двусторонних
критических фаниц стандартного нормального распределения
P{\Z\<u^} = l-a, или Ф(ы„) = (1-а)/2, (6.1.23)
находим
Ал/л
и„= , (6.1.24)
G
ЭТО И есть искомое выражение.
Во втором случае оценкой вероятности является частость ц/я, или
среднее арифметическое альтернативных случайных величин, поскольку
п
биномиальная величина Ц = Х^/ (число положительных исходов в п ис-
/=1
пытаниях) раашагается на сумму альтернативных, каждая из которых
представляет число положительных исходов в одном испытании (те. О или 1).
Поэтому при оценке вероятности формула (6.1.22) принимает вид:
^-р<А[ = 1-а, (6.1.25)
а вытекающее из этой формулы соотношение получается из формулы (6.1.24)
путем замены а на ^p{i- р), поскольку последнее и есть стандартное
отклонение альтернативной случайной величины:
Ал/л
(6.1.26)
При использовании формул (6.1.24) и (6.1.26) необходимо принимать
во внимание следующие два обстоятельства:
1) объем выборки п должен быть достаточно большим, по крайней
мере несколько десятков, но лучше л > 100;
2) стандартное отклонение а (или ■\[р{\-р)) должно быть хотя бы
приближенно известно.
Q Пример 6.1. Определить объем выборки для установления с точностью ±0,03
доли стандартных изделий в большой партии при допустимом риске 5%.
Предполагаемая доля стандартных изделий - 0,9.
При а = 0,05 находим по табл. П. 4.1 критическую границу стандартного
нормального распределения и^ = 1,96. Теперь непосредственно по
формуле (6.1.26) находим
а' (0,03)' •
136
§ 6.2. Оценка функций
распределения и плотности
Оценка функции распределения
Оценку функции распределения вероятностей получаем по тому же
принципу, который был применен при оценивании числовых
характеристик: оценкой функции распределения генеральной случайной
величины А'служит функция распределения выборочной случайной
величины X [см. формулу (6.1.2)]:
О,
^<xйx^,
т
Fx{x) = F.{x) = \Y^^-, х^<х<х^^,, А: = 1,..../-1,
/ = 1 П
1,
(6.2.1)
Х# < X < оо.
Эмпирическую выборочную функцию распределения (6.2.1) можно
представить также в следующей форме:
Fx{x) = m{x)ln, (6.2.2)
где т{х) — число значений конкретной выборки x^, ..., х^, меньших х
На рис. 6.1 приведен пример эмпирической функции распределения.
'"/-1
^
п
"И
Рис. 6.1
При больших п выборочная функция распределения fxi^) близка к
теоретической. Более точно это можно сформулировать так:
выборочная функция распределения Fxi^) в каждой точкех, —°° <х < °°,
рассматриваемая как функция случайной выборки, сходится по
вероятности к теоретической функции распределения в этой точке:
Fxix)=>Fxix).
(6.2.3)
137
Q В самом деле, обозначим
P = Fxix) = P{X<x},
тогда случайная выборках,,..., х„ порождает схему Бернулли, на каждом шаге
которой может произойти событие {А', < х}, / = 1,.... и, или случиться
противоположное {Xf > х}, причем прямое событие на каждом шаге происходит с
одинаковыми вероятностями
р = Р{Х,<х},
поскольку выборочные случайные величины Л', распределены как генеральная
случайная величина.
Тогда значение эмпирической функции распределения в любой точке х для
конкретной выборки х,, ■.-, х^ является отношением числа положительных
исходов (т.е. исходов, для которых Л', < х) к общему числу исходов п, а при
переходе к случайной выборке X^, ■■., Х^ становится случайной величиной \i{x)/n,
где \i(x) - биномиальная случайная величина.
Согласно теореме Бернулли (см. гл. 4), частость ц/п сходится по
вероятности к вероятности, поэтому
Fxix) = ^=^P = P{X<x} = F,ix),
п
т.е. Fx {х) =* Fx {х), что и требовалось доказать. ■
Оценка функции плотности
Функция плотности оценивается с помощью гистрофаммы. Под ги-
стофаммой понимается столбчатая фигура, построенная следующим
образом. Вся числовая прямая разбивается на / непересекающихся
полуинтервалов Д^ = [Ь.^, Ь), /■ = 1, ..., /, Ьд = —°°, Ь, = °°, по конкретной
выборке X,, ..., х„ подсчитывается число наблюдений т^, /= 1, ..., /,
попавших в каждый интервал. Затем над каждым полуинтервалом
строится прямоугольник, площадь которого пропорциональна /п,.
Точно так же, как и выше, можно доказать, что частости попадания
на полуинтервалы сходятся по вероятности к соответствующим
вероятностям
ь,
^^ \ГАх)йх = р[ь,_,йХ<Ь.].
При подходящем подборе полуинтервалов гистограмма будет
напоминать график функции плотности/J^x).
138
Если известно, что плотность отлична от нуля только на некотором
отрезке, то полуинтервалы можно, и желательно, выбирать одинаковой
длины Л, а площади прямоугольников — равными частостям m.Jn,
поэтому вся площадь под гистограммой будет равна единице. На рис. 6.2
показан пример именно такой гистофаммы.
л л л л л
Рис. 6.2
Вопросы и задачи
1. Для установления срока службы испытано на продолжительность
непрерывной работы 125 изделий. При этом средний срок службы
оказался равным 19,5 месяца, а дисперсия равна 2,25;
а) с вероятностью 0,683 определить, в каких пределах находится
теоретический средний срок службы изделий;
б) с какой вероятностью можно утверждать, что модуль отклонения
эмпирического среднего не превысит 0,3 месяца?
в) сколько нужно провести испытаний, чтобы модуль отклонения не
превысил 0,5 месяца с вероятностью 0,9973?
2. Сколько нужно провести испытаний, чтобы частость отличалась
от вероятности, равной 0,7, не более чем на 0,05 при риске 0,008?
3. При измерении диаметра детали одним прибором установлен
средний диаметр х^ = \^ мк, и, = 8, при измерении другим равноточным
прибором — Xj = 12 мк, /12= 16. Определить наиболее точную оценку
диаметра по измерениям двух приборов.
4. Рост десяти наугад отобранных студентов-юношей оказался
следующим (в см): 156,162, 170, 177, 180, 181, 183, 196, 199, 201. Найти
несмещенные оценки математического ожидания и дисперсии.
5. Как оценить по выборке медиану?
6. Сколько нужно опросить респондентов, чтобы средняя доля тех,
кто положительно ответил на поставленный вопрос, отличалась по
модулю от соответствующей доли не более чем на 0,03 при риске 0,05, если
Экспертная оценка указанной доли равна 0,7?
139
7. Для определения средней заработной платы работников
определенной отрасли было обследовано 100 чел. Результаты представлены в
следующей таблице (данные условные):
Зарплата в долларах
190-192
192-194
194-196
196-198
198—200
Число человек
1
5
9
22
28
Зарплата в долларах
200-202
202—204
204—206
206—208
Число человек
19
11
4
1
Построить гистофамму и фафик эмпирической функции
распределения, найти оценки математического ожидания и дисперсии зарплаты
наугад взятого работника.
8. Докажите, что в случае нормального распределения величины X
дисперсии оценокдисперсии/>Л'таковы: Da =
.2_2а>-Д
,aDs^ =
2а'
/1-1
Глава 7
ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ
Имеется два подхода к оцениванию неизвестных параметров
распределений по наблюдениям: точечный и интервальный. Точечный
указывает лишь точку, около которой находится оцениваемый параметр; при
интервальном находят интервал, который с некоторой, как правило,
большой, вероятностью, задаваемой исследователем, накрывает неизвестное
числовое значение параметра. В главе рассматриваются методы
точечного оценивания параметров; строятся интервальные оценки параметров
нормального распределения, обсуждается общий подход к
интервальному оцениванию параметров распределений, отличных от нормального.
§ 7.1. Метод моментов
Метод моментов является одним из методов точечного оценивания
параметров распределений.
Пусть закон распределения случайной величины Л'известен с
точностью до числовых значений его параметров в,, Bj, ..., 6^^. Это означает,
что известен вид функции плотностиУ^(х, 0), где 0 = (в,, Q^,..., Q^), если
А" непрерывна (известен вид функции вероятности Р(Х= х, 0), если X
дискретна), но числовые значения к параметров не известны. Найдем
оценку 0 = (в,,§2,...,6^1 параметра 0, располагая выборкой Xj.Xj, ■■■,х^.
Допустим, что существует к начальных моментов, каждый из
которых можно выразить через 0 (без ограничения общности можно
рассматривать только начальные моменты, так как центральные моменты
являются функциями начальных). Пусть такими моментами будут первый,
второй,..., k-Pi: V[, Vj,..., v^ (что вовсе не обязательно). Выразим каждый
из них через 0:
V,„=^m(0) =
Y,x'"P{X =х, 0), если А"дискретна,
4" /и = 1,2,...Д. (7.1.1)
\x'"fx{x,Q)dx, если А"непрерывна.
141
Заметим, что в системе
v„=«„(e,.e2,...,ej, m = l,2,...,k, (7.1.2)
число уравнений должно быть равным числу к оцениваемых
параметров. Найдем решение системы (7.1.2). Выразив казкдый параметр в^
через V,, Vj,..., v^, получим:
9/я=Л„(у,, Vj,..., v^), m = l,2,...,k. (7.1.3)
Свойство состоятельности выборочных начальных моментов
(см. § 6.1) является основанием для замены в уравнениях (7.1.3)
теоретических моментов V|, Vj, ..., v^^ на вычисленные при большом п
выборочные моменты V,, Vj,.... v^.
Оценками метода моментов параметров в,, Gj,..., 6^^ называются оценки
eL*'^=A«(v,.V2....,v,), /и = 1,2,....Аг, (7.1.4)
где Vy = 2*/ /«• У = 1, 2,...» к.
/=|
Вопрос о том, какие начальные моменты включать в систему (7.1.2),
следует решать, руководствуясь конкретными целями исследования и
сравнительной простотой форм зависимостей моментов от параметров.
В статистической практике дело редко Доходит даже до четвертых
моментов.
Q Пример 7.1. Случайная величина Х~ N(a, а), при этом числовые значения
параметров в и (^ не известны. Найдем оценки метода моментов для этих
параметров.
Используя формулу (7.1.1), выразим моменты v, и Vj через в и а^:
= f*"-j=^=e 2^"'d*, /и = 1, 2;
re ^* "
::. V2ico'
(v, = e)n(v2 = e^ +o^)- таков ВЩ системы (7.1.2) в данном примере. Ре-
итв ее относительно а и а^, получим: в = v,, а^ = V; - v,^. Отсюда оценки
метода моментов:
flC*^) = V, = - X jf, = Зс - это оценка математического ожидэния а;
ст^^**) =V2-v]=-txf- {xf =-t{xi-xf=a^-ш оценка дис-
Персии о^.Ф
142
Отмеченная ранее некоторая неопределенность выбора начальных
моментов может привести к получению раапичных оценок одного и того
же параметра.
Q Пример 7.2. Случайная величина X имеет распределение Пуассона:
■ух
Р(Х = х) =—e"^,jf = 0,1, 2,...; А,>О.Найде«#оценкупараметраХдпядвух
х1
вариантов:
а) в качестве начального момента возьмем v,; получим:
Vi =
-? X' _1 , , ггм! ^ I ^
= 1л:—е-^нХ; X = v,; Х^^) =v, =-Х;с,. =Jc;
б) в качестве начального момента возьмем Vj,* получим:
х% XI 2
4Д
I ' i + -lxf-l I =
Оценки - разные. Конечно, предпочтительнее первая: А, = Зс как более
простая и соответствующая смыслу параметре пуассоновского распределения:
Х- MX, поэтому за А, естественно принять х - хорошую точечную оценку
математического ожидания (см. § 6.1). •
Однако не все получаемые методом моментов оценки обладают
свойствами «хорошей оценки». Так, полученная в примере 7.1 оценка
о^ = — YIx, - Х) дисперсии о^ не обладает свойством несмещенности
(см. § 6.1); а^ является асимптотически несмещенной оценкой:
lim Mai - •>"> ^^ = ^^' '■".е. при больших п можно считать, что с^
не смещена относительно а^.
Приведем без доказательства теорему о функциях от моментов, из
которой вытекают определенные свойства оценок метода моментов.
Предположим, что 6„ является функцией двух выборочных
моментов v^ и v„: e„=/i(v^,v„), не содержащей явно п. Обозначим
9 = A(v^,v„), где \^ =Л/У^, а v„ =М\„ (последние два равенства вер-
143
ны в силу свойства несмещенности выборочных начальных моментов),
>Л- =•
ЭА
Теорема утверждает: если в некоторой окрестности точки (v^,v„)
функция h непрерывна со своими первыми и вторыми производными, то при
больших п распределение случайной величины 9„ = A(v^ , v„) близко к
нормальному (Q^ имеет асимптотически нормальное распределение) с
математическим ожиданием, равным в, и дисперсией, равной
D{y,,)hl +2cov(v,,v„)A,A„ +D{y>„)hi =С\ф, (7.1.5)
где С^(9) — некоторая постоянная, зависящая от в. (Теорему можно
распространить на любое количество моментов — аргументов функции h.)
Из теоремы вытекает, что при выполнении достаточно общих
условий оценка метода моментов ej,**' при больших и удовлетворяет
следующим соотношениям:
л/в|,**^ = е, (7.1.6)
т.е. оценка метода моментов является асимптотически несмещенной,
1)ё1*')=С2(6)//1. (7.1.7)
Убедимся в том, что Ь\ ' обладает свойством состоятельности.
Действительно, неравенство Чебышева для величины Qy' при больших и,
сучетом формул (7.1.6) и (7.1.7), примет вид:
»й(М)
<ГЧ")^4^'^.
отсюда получим, что при я -»<» р{ By' - в < е ] -»I.
Введем понятие эффективности и асимптотической эффективности
несмещенной оценки скалярного параметра 6.
Эффективностью ^(e„] несмещенной оценки 6^ параметра в
называют отношение n\mDQ„ — минимально возможного значения диспер-
сии оценки в классе S всех несмещенных оценок параметра О к
дисперсии DQ„ рассматриваемой оценки. При выполнении функцией плотно-
144
CT»fx(x, В) [функцией вероятности Р(Х= х, 0)] достаточно общих условий
регулярности: дифференцируемости по 0, независимости области
определения от в и т.д. — имеет место неравенство Рао—Крамера—Фреше:
^^п^-77^=т^^Ов„, (7.1.8)
где /(в) — количество информации о параметре в, содержащееся в
единичном наблюдении, определяется соотношением
^_Jd\nfAx,B)^
[ йв )
(/(в) — некоторая постоянная, за^висящая, от в). Поэтому
е{в„] = —;г-ттОв.= г-^1; (7.1.10)
если е(ё„ j = 1, то в„ — эффективная оценка параметра в в классе S всех
его несмещенных оценок.
Асимптотической эффективностью оценки e„ называют величину
eo(e„) = Jime(e„)^l; (7.1.11)
если eole„j = l, то в„ — асимптотически эффективная оценка
(очевидно, что эффективная оценка будет и асимптотически эффективной).
Найдем выражение для асимптртической эффективности оценки
в^^^\ Так как при больших и оцен!^ ej,**' можно считать несмещенной,
то с учетом формул (7.1.11), (7,1.10) и (7.1.7) получим
efiT^U lim e(ei'^))= lim ' =-»
1 1
(в)'
О Пример 7.3. Убедимся »том, что найденная методом мбмеитов по случайной
выборке из генеральной совокупности Х~ N (а, а) оценка X параметра а
является эффективной в классе несмещенных оценок, af оценка а^ параметра
а^ является, после исключения смещения, асимптотически эффективной.
Оценка JT - несмещенная, и DX = a^/n. Предположив, что а^ известна,
и используя формулу (7.1.10), в которой, с учетом нормальности распределе-
, /(о) = л/[ £lllZjc(fi£l I = 1 , получим, что е(х) = 1. Следователь-
ния
но, X - эффективная оцегаса.
145
Оценка а^ - смещенная; исключив смещение, получим оценку
s^ = = — , дисперсия которой Ds^ = (см.39дачу8гл.6).
л-1 л-1 л-1
Предположив, что а известно, и используя выражение (7.1.10), в котором.
'dln/^.(;c,a^)
1
2о^'
с учетом нормальности распределения, /[а^ ] = Л/
получим, что эффективность e[s^\ = < I, а асимптотическая эффектив-
^ ' п
ность eJs^\= lim eis^ j = I. Следовательно, ^ - асимптотически
эффективная оценка.
Замечание. Несмещенной и эффективной оценкой дисперсии является
используемая при известном значении параметра а оценка s^-'^[Х/ -а) п,
1=1 I
так как ш1 = о^, Dsl = 2оV" и e(jo) = 1.
При выполнении достаточно общих условий все три оценки: a^,s^ и sq
состоятельны. •
В приведенном примере оценки метода моментов X н а^ являются
соответственно эффективной и асимптотически эффективной. Однако
подобные примеры скорее исключение: гораздо чаще оценки метода
моментов с точки зрения эффективности не являются наилучшими из воз-
MOXHJiJX даже при больших п. Р. Фишер показал, что асимптотическая
эффективность этих оценок часто значительно меньше единицы.
Асимптотически эффективные оценки могут быть получены методом
максимального правдоподобия.
§ 7.2. Метод максимального правдоподобия
В основе метода максимального правдоподобия лежит понятие функции
правдоподобия. Пусть Х= (X^, Х^,..., Х^ — случайная, а дг = (дг,, д^,..., х^ —
конкретная выборки из генеральной совокупности X. Напомним,
случайной называют выборку, удовлетворяющую следующим условиям:
случайные величины X^, JTj,..., Х^ независимы, т.е.
Р
146
Г п
/=1
I {Xi = Jf,) = П P{Xi = Jf,), если ^дискретна; (7.2.1)
J
1=1
л,. Хг x„{^v^l -^/1)= П/а-Д-^.). если .ЧГнепрерывна; (7.2.2)
(=1
распределение каждой из величин Л^ совпадает с распределением
величины X, т.е. при /=1,2,..., п
P{Xi =х) = Р{Х = X, 0), если .Гдискретна; (7.2.3)
fxi W - fx{^' ®)' если Л'непрерывна. (7.2.4)
Функция правдоподобия — это функция L (х, 0), значение которой в
точке X определяется соотношением:
L{x.Q)=-
П I (^/ =*/) = П ^(^/ =*/) = П ^(^=*/. 0). если ^дискретна,
fx..X:, хМ'^2 ^») = ПЛ,(^,) = ПЛ(^с,. 0). если ^непрерывна.
1=1 1=1
Из определения следует: чем вероятнее (чем правдоподобнее) при
фиксированном 0 набор х, тем больше значение функции
правдоподобия L (х, 0), отсюда и ее название.
Итак,
L{x, 0)=
tlP{X=Xi, 0), если А'дискретна,
(=1
Y\fx{Xi,&), если А^непрерывна.
'"' (7.2.5)
1=1
Согласно методу максимального правдоподобия оценка максимального
правдоподобия 0^") =(§!"), 9^") в[")) параметра 0 = (в,,в2 ej,
при заданном наборе х определяется из условия:
l{x, ©("))= max L{x, 0), (7.2.6)
где {0} — область допустимых значений для 0.
Естественность такого подхода к определению оценки 0^"^ вытекает
из смысла функции L: при фиксированном 0 функция L {х, 0) — мера
правдоподобия набора х; поэтому, изменяя 0, можно проследить, при
каких его значениях набор х является более правдоподобным, а при
каких — менее, и выбрать такое значение 0^"^ при котором имеющийся
Набор X будет наиболее правдоподобным.
147
в ряде случаев 0^ ' удобнее определять из условия:
\п11\,эЩ=тал\п1(х,Э),
(7.2.7)
идентичного условию (7.2.6): если вместо функции L взять In L, точка
максимума не изменится. Функцию In L {х, 0) назыълют
логарифмической функцией правдоподобия.
Согласно формуле (7.2.7), для нахождения
0(П)
следует:
найти решения системы уравнений максимального правдоподобия
ЪХпйхМ
^ ^ = 0. У = 1,2 к.
(7.2.8)
при этом решением считается лишь такой набор 0* = (9,*, 9^..., 9^^), удов^
летворяющий (7.2.8), в котором каждое 9^* действительно зависит отх;
среди решений, лежащих внутри области {0}, выделить точки
максимума;
если система (7.2.S) не определена, не разрешима или если среди ее
решений нет тячк^ максимума внутри {0}, то точку максимума следуем
искать на фанице области {0}.
О Пример 7.4. Найдем методом максимального правдоподобия оценки
параметров ей 6 = а^ нормального распределения.
Согласно формуле (7.2.5), функций правдоподобия
^^'•''•*^=й:^ехр
{-,-«)'
2Ь
— I ехр
yjlnb)
логарифмическая функция правдоподобия
lnL(x.e,A) = -^ln(27c)-^lnA-ife:li-.
Частные производные:
d\nL _^Xi-a 9lnL_ n Д (jf/ -of
da ~^i b ' ЪЬ ~~2b ^i Ib^ '
Система (7.2.8) примет вид:
l(x,-e) = 0
П
/le=ljf,
или
/=1
№i-aflb = n.
1=1
t{x,-aflb = n.
/=i
148
& решение:
а* =х^ ** = Х(-^/-^) /n = ci^.
Проверим достато<:|ные Условия максимума функции In Lb точке (а*, о).
Найдем:
d'inL
^ дЬ^
п a^inL
/ . ..\ с^' дадЬ
— Q
Г. »
\,U') 2{b*)' h (^7 2а
2cr
так как д > О, a у4< О, то точка [а* =х,Ь* =а^] является точкой максимума,
функции In L. Поэтому оценки максимального правдоподобия в^") =х, о^^") =а^
СХ(енки совпали с оценками метода моментов. •
Q Пример 7.5. Найдем методом максимального правдоподобия оценки
параметров амЬ рав»^ерного на отрезке |в, Ь] распроделения.
Соглаою формуле (7.2.5), функция працдоподоби»!
^^/ д ^ч |l/(A-e)". если jf, е[в,А], / = 1,2 п
\'' О, если хотя бы одно значение X, (Е [в, 6].
При первом условии система (7.2.8) не разрешима, при втором - не опре^
делена. Оценки а^^^ и Ь^^^ следует искать на границе облаоти допустимых
значений для в и £:
где jf/,j =min(x,,jf2 ^п), а Jf(„) =*max(jf,, jtj,...,дг„). Тогда ус)ювйе
(7.2.6) примет вид: ,
1 I
max'
Таккакфункция L{a,b) = l/{b-a)" убывает при возрастании 6и убыван|^и в,
то ее максимум на области {0} достигается в точке f «^ -•*(!)• * "^(п))-
149
Это и будут оценки максимального праад)П0|Др6ия параметров в 11Ь pai^^
на отрезке [а, Ь] распределения (эти оценки отличаются от оценок
а = х- a^l2, Ь = х + a^l2 , которые можно получить методом моментов при
использовании первого и второго начальных моментов). •
Q Пример 7.6. Случайная величина Х- число успехов в единичном испытании:
Р{Х = х) = р'(1 - р)"', jf = 0,1; р - вероятность успеха в единичном
испытании. Найдем оценку максимального правдоподобия р("), располагая
выборкой x^, jCj,..., х^, где х^ - число успехов в ;-м испытании.
„ LXI п- Ixj
Согласноформуле(7.2.5), Цл:,р)=П/>(^Г=;с,,р)=р'"' (1-р) '=' ;
\nL{x,p)= Xjc,lnp+ п- Xjf,- In(l-p). Решив уравнение —— = 0,
/ = 1
^
/=i:J ' ' "^ Эр
• 1 " Э^In L
найдем р =—£х,,атаккак
я/=.' Ър'
< О, то оценка р^ > =-J.x, =—,
где т - число успехов в п испытаниях Бернулли (такую же оценку можно
получить и методом моментов). Эта оценка состоятельная, несмещенная и, в чем
нетрудно убедиться, эффективная. •
Отмеченная выше естественность определения оценок
максимального правдоподобия из условия (7.2.6) подкрепляется их хорошими
свойствами. Если функция плотности /д. (х, 6) (функция вероятности
Р {Х= X, 9), если ^дискретна) удовлетворяет достаточно общим услови-i
ям регулярности, оценка максимального правдоподобия Q„' имеет при!
больших п распределение, близкое к нормальному с математическим'
ожиданием, равным 6, и дисперсией, равной l/[/i/(6)], где /(6)
определяется соотношением (7.1.9), является состоятельной, асимптотически
несмещенной и асимптотически эффективной; более того, если
существует эффективная оценка параметра, она будет единственным
решением уравнения максимального правдоподобия.
Кроме описанных методов оценивания параметров существует ряд
других, например метод наименьших квадратов, согласно которому
оценка 6 параметра 6 находится из условия:
i (xi - of = min i (jf,. - 9)^. (7.2.9)
150
Обратим внимание на то, что при оценивании математического
ожидания нормального распределения с известным значением дисперсии
условие (7.2.9) идентично условию метода максимального
правдоподобия (7.2.6).
В последние годы развиваются так называемые робастные, или
устойчивые, методы оценивания, позволяющие находить оценки, хотя и
не являющиеся наилучшими в рамках предполагаемого закона
распределения, но обладающие достаточно устойчивыми свойствами при
отклонении реального закона от предполагаемого.
§ 7.3. Понятие интервальной оценки.
Интервальные оценки
параметров нормального распределения
Вычисленная на основе выборки оценка 6 является лишь
приближением к неизвестному значению параметра 6 даже в том случае, когда эта
оценка состоятельная, несмещенная и эффективная. Возникает вопрос:
нельзя ли указать такое А, для которого с заранее заданной близкой к
единице вероятностью 1 — а гарантировалось бы выполнение
неравенства: 9- 9 < Д, или иначе, для которого
p{Q-A<Q<Q + AJ = \-a. (7.3.1)
Если такое А существует, то интервал 19 - А, 9 + Д j называют
интервальной оценкой параметра 9, или доверительным интервалом; 9 - А, 9 + А —
нижней и верхней доверительными границами; А — ошибкой оценки 9,
1 — а — надежностью интервальной оценки, или доверительной
вероятностью. Выбор доверительной вероятности определяется конкретными
условиями; обычно используются значения 1 - а, равные 0,90; 0,95; 0,99.
Оценка О, будучи функцией случайной выборки, является
случайной величиной, А также случайна: ее значение зависит от вероятности
1 - а и, как правило, от выборки. Поэтому доверительный интервал
случаен и выражение (7.3.1) следует читать так: «Интервал (9-А,9 +AJ
накроет параметр 9 с вероятностью 1 — а», а не так: «Параметр 9 попадет в
Интервал (9-А, 9 + AJ с вероятностью 1 - а».
В формуле (7.3.1) фаницы доверительного интервала симмет1Ьичны
относительно точечной оценки. Однако не всегда удается построить
Интервал, обладающий таким свойством. Для получения доверительно-
151
го интервала наименьшей длины при заданном объеме выборки п и
заданной доверительной вероятности 1 - а в качестве оценки 6
параметра 6 следует брать эффективную или асимптотически эффективную
оценку.
Существует два подхода к построению доверительных интервалов.
Первый подход, если его удается реализовать, позволяет строить
доверительные интервалы при каждом конечном объеме выборки п. Он
основан на подборе такой функции у16, б), называемой в дальнейшем
статистикой, чтобы:
ее закон распределения был известен и не зависел от 6;
функция у(В, б) была непрерывной и строго монотонной по 6.
Задавшись доверительной вероятностью 1 - а, находят двусторонние
критические фаницы V„ и у„, отвечающие вероятности а. Тогда с
вероятностью 1 — а выполняется неравенство
V^<v(e.e)<v„. (7.3.2)
Решив это неравенство относительно 6, находят фаницы
доверительного интервала для 0. Если плотность распределения статистики Щ&, в]
симметрична относительно оси Оу, то доверительный интервал
симметричен относительно 0.
Второй подход, получивший название асимптотического подхода,
более универсален; однако он использует асимптотические свойства точ
чечных оценок и поэтому пригоден лишь при достаточно больших
объемах выборки.
Рассмотрим первый подход на примерах доверительного оценивания
параметров нормального распределения.
Интервальная оценка математического ожидания при известной
дисперсии. Итак, X ~ N {а, а), причем значение параметра а не известно»
а значение дисперсии а^ известно. _
При Х~ N{a, а) эффективной оценкой параметра а является X, при
этом X ~ N{a,<sl4n\- Статистика Z= , ^ имеет распределение
^ ' а/уп
N(0; 1) независимо от значения параметра а и как функция параметра а
непрерывна и строго монотонна. Следовательно, с учетом неравенства
(7.3.2) и симметричности двусторонних критических фаниц
распределения Л^ (0; 1) будем иметь:
/»(-«„ <7<и„) = 1-а.
152
„ X -a
Решая неравенство -и„ < —7-7= < **п относительно а, получим, что с
fsMn
вероятностью 1 — а выполняется неравенство
X -u^csl^ <а<Х + u^csl4n, (7.3.3)
при этом
А = и^а/^, (7.3.4)
что соответствует результату (6.1.23); число и^ находят по табл. П. 4.1 из
условия Ф(и„) = (1-а)/2.
Замечание. Если п велико, оценку (7.3.3) можно использовать и
при отсутствии нормального распределения величины X, так как в силу
следствия из центральной предельной теоремы при случайной выборке
большого объема п
Х-а^^
а/у/п
В частности, если Х= ц, где ц — случайное число успехов в большом
числе л испытаний Бернулли, то
—■ =* Z
и с вероятностью « 1 - а для вероятности р успеха в единичном
испытании выполняется неравенство
ц/л - и„ ^pq/n <p<n/n + Ua ^Jpq/n. (7.3.5)
Заменяя значения р и ^ = 1 - р в левой и правой частях
неравенства (7.3.5) их оценками р = ц/л и q = l-p, что допустимо при большом л,
получим приближенный доверительный интервал для вероятности р:
Р - "ал1РЧ/" <Р<Р + Ua^Pq/n. (7.3.6)
V Задача 7.1. Фирма коммунального хозяйства желает на основе выборки
оценить среднюю квартплату за квартиры определенного типа с надежностью не
менее 99% и погрешностью, меньшей 10 д.е. Предполагая, что квартплата
имеет нормальное распределение со средним квадратичным отклонением, не
превышающим 35 д.е., найдите минимальный объем выборки.
Решение. По условию требуется найти такое л, при котором
Р\\Х - а1 < 10) ^ 0,99, где а и Х- генеральная и выборочная средние.
153
Приравняв 1 - а = 0,99, по табл. П. 4.1 найдем число и^, при котором
Ф(и„) = (1 - а)/2 = 0,495; Идд,, = 2,6. При Д=10 и а = 35 из формулы (7.3.4)
2 2
''о 01"
получим л = —=-2— = 82,81. Но так как с ростом 1 - а и уменьшением Д
растет л, то л > 82,81 и л^,„ = 83 (конечно, при уменьшении верхней фзницы
для а будет уменьшаться и л^jJ,). ▼
Интервальная оценка математического ожидания при неизвестной дис
Персии. Итак, Х~ N{a, а), причем числовые значения ни а, ни а^ не из;
вестны. По случайной выборке найдем эффективную оценку парамет-
ра а: Л" и оценку s^ = Х(А', - Л") параметра а^.
Построение интервальной оценки для а основано на статистик<|
Х-а ^
/(л-1)= ■ ^, которая при случайной выборке из генеральной сово
s/^Jn
купности Х~ N{a; а) имеет распределение Стьюдента с (л - 1) степень
свободы независимо от значения параметра а и как функция парамет
ра а непрерывна и строго монотонна.
С учетом неравенства (7.3.2) и симметричности двусторонних крит^
ческих границ распределения Стьюдента будем иметь:
/>(-/„</(л-l)</J = l-a.
Х-а
Решая неравенство -/„ <—r-j=</„относительно а, получим, что
л/л/л
вероятностью 1 - а выполняется неравенство
X-t^ s/^ <a<X + t^ VVfl (7.3.7
и ошибка оценки X при неизвестном значении параметра а^
A = t^s/^, (7.3.8J
где число /ц находят по табл. П. 4.2 при А:=л-1ир = а.
Замечание. ПриА: = л— 1 > 30 случайная величина/(А:) имеет paOlj
пределение, близкое к Л'(0; 1), поэтому с вероятностью = 1 — а
Х-и^ s/^ <а<Х + ы^ s/-/n, (7.3.9!
гдеФ(и„) = (1-а)/2.
V Задача 7.2. Для отрасли, включающей 1200 фирм, составлена случайная
выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают
154
77,5 человек при ередеем квадратичном отклонении 5 =25 чеж>век.
Пользуясь 95%-ным доверительным интервалом, оцените среднее число работакмцих
в фирме по всей отрасли и общее число работающих в отрасли.
Предполагается, что количество работников фирмы имеет нормальное распредаление.
Решение. ПриА:=л-1 = 18и/» = а= 1-0,95 = 0,05 найдем в
табл. П. 4.2 /ggj=2,10. ДоверительньЛ) интервал (7.3.7) примет вид: (65,5; 89,5).
С вероятностью 95% можно ухввржр/пь, что этот интервал накроет среднее
число работающих в фирме по всей отрасли. Тогда доверительный интервал для
чист работающих в отрасли в целом таков: (1200-65,5; 1200-89,5). ir
Интервальная оценка дисперсии (среднего квадратичного отклонения)
при известном математическом ожидании. Эффективной оценкой
дисперсии в этом случае является sl= — %{X^-a) .
"1=1
Используются два варианта интервальной оценки для а^ (а).
1. Основу первого варианта составляет статистика
x4n) = nsl/a\ (7.3.10)
которая имеет распределение х^ с л степенями свободы независимо от
значения параметра а^ и как функция параметра а^ > О непрерывна и
строго монотонна.
Следовательно, с учетом неравенства (7.3.2) будем иметь:
^(Й<х'(«)<хУ = 1-а.
2—2 t
где Хд и Ха — двусторонние критические границы X -распределения с л
степенями свободы.
_ 2 "-% —2 ■>
Решая неравенство Х„ < т *" Ха относительно а^, получим, что с ве-
. —" с
роятностью 1 - а выполняется неравенство
■=5~<*^ <7^ (7.3.11)
Ла Лц
и с такой же версмтностью выполняется неравенство
^lnso/xl<<y<^nsl/xl. (7.3.12)
Числа Ха •* Ха находят по табл. п. 4.3 при А: = л и соответственно при
р = а/2 и р = 1 - а/2. Интервальнай оценка (7.3.12) не симметрична
относительно 5q.
155
2. Второй вариант предполагает нахождение интервальной оценки
для а при заданной ншежности 1 -^ а » виде
5отах(0; l-5a)<o<5o(l+5a)- (7.3.13)
При 5, < 1 фаницы этой оценки симметричны относительно Sq и
ошибка оценки s^, гарантируемая с вероятностью 1 - а,
Л = 5о5а.^ (7.3.14)
Как найти 5а? Решая неравенство (7J.13) относительно ns^/a^,
получим, что с вероятностью 1 - а выполняется неравенство
" '^< ", ^ .. (7.3.15)'
Г тах^(0;1-5„)
или, учитывая формулу (7.3.10) и заменив л на А:, а а на р,
'~^- (7.3.16)
{1 + Ь^^~а^^тахЦ0;\-Ь^У
f ' \
(1 + 5 J max^{0;l-5^,)^
Значения 5^, удовлетворяющие равенству (7.3.16) при различных р ^
к, приведены в табл. П. 4.6.
Итак,
/>(5^тах2(0; l-5„)<a^<5^(l + 5„f) = l-a, (7-3.17)
где 5ц — число, найденное в табл. П. 4.6 при к'^пнр'^а.
Интервальная оценка дисперсии (среднего квадратичного отклонения) прц
неизвестном математическом ожидании. Наилучшей точечной оценкой
дисперсии в этом случае является s^ = Е f А", - Л") , и построение ин-
тервальной оценки для а^ основано на статистике х^ (л -1) = (л - О^^/ст^
которая при случайной выборке из генеральной совокупнЬсти Х~ Ы_{а; а)
имеет распределение yi} с{п— 1) степенью свободы.
Проделав выкладки для величины х^ (л - 1)> подобные выкладкам прН
известном математическом ожидании, получим два Мутанта йнтерваль^
ной оценки для а^ (а):
1. Р
—;:j-—<а < j-y^
l-a, (7.3.18J
156
/>(V(/»-l>7Xa<a<V(«-iyAi) = l-«' <7.3.19)
—2 2
где числа Xa и X^ находят по табл. П. 4.3 при А: = л - 1 и соответственно
при р = а/2 и р = 1 - а/2.
2. />(52тах2(0;1-5„)<а^<5^(1 + 5„Я = 1-а, (7.3.20)
/>(5тах(0; 1-5„)<а<5(1 + 5„)) = 1-а, (7.3.21)
при этом ошибка оценки s, гарантируемая с вероятностью 1 - а,
Д = 55„; (7.3.22)
число 5ц находят по табл. П. 4.6 при А:=л-1ир = а.
Замечание. При А:= л - 1 > 30 случайная величина хЧ^) имеет
распределение, близкое к N^Uk-l/^, i/^], поэтому с вероятностью = 1 -а
2(л-1У 2 2(л-1У
где Ф(ц,) = (1-а)/2.
V Задача 7.3. Вариация ежесуточного дохода случайно выбранных 10 киосков
некоторой фирмы, измеренная величиной s = Ё (-*',• -^) , где Л'^-
доход /-Г0 киоска, оказалась равной 100 д. е. Найдите такое А, при котором с
надежностью 90% можно гарантировать, что вариация дохода по всем киоскам
фирмы не выйдет за пределы 100 т А. Предполагается, что доход - нормально
распределеннвя величина.
Решение. Так как средний доход киоска по всей фирме не известе)1 и
интервал для а должен быть симметричным относительно s, дня расчета
ошибки оценки £ при 1 - а = 0,9 воспользуемся формулой (7.3.22).
ПриА: = 9ир = а = 0,1по табл. П. 4.6 найдем б^, = 0,476; тогда Л = 47,6.
С надежностью 90% можно упержд/пъ, что генеральная вариация дохода
киоска не выйдет за пределы 100 т 47,6. Т
V Задача 7.4. Пользуясь 90%-ным доверительным интервалом, оцените в
условиях задачи 7.2 вариацию работающих в фирме ло всей отрасли.
Решение. По условию л = 19,5 = 25,1 - а = 0,9. Найдем два варианта
доверительного интервала:
157
1. Согласно формуле (7.3.19),
—2
а так как при А: = Л - 1 = 18 верхняя доверительная граница Xo.i=28,87, а
нижняя Xq , = 9,39 (см. табл. П. 4.3), то 19,740 < а < 34,613 - эта оценка не
симметрична относительно s.
2. Согласно уравнению (7.3.21),
р{25тах{0; 1 -S^,) < а < 25(l + 5о,)) = 0,9,
атаккакприА:=л-1 = 18 5д,=0,297(см.табл.П.4.6),то17,575<а<32,425-
эта оценка симметрична относительно s. Она, как и следовало ожидать,
отличается от предыдущей интервальной оценки, однако /'(17,575 < а < 32,425) =
=/'(19,740< а < 34,613) = 0,9. Т
§ 7.4. Асимптотический подход
к интервальному оцениванию
с примерами интервальных оценок, имеющих место только при
больших объемах выборок, мы уже сталкивались. Так, если
распределение случайной величины Л* отлично от нормального, но п велико, то с
вероятностью => 1 - а интервальная оценка для MX = а имеет вид
неравенства (7.3.3); с вероятностью = 1 - а интервальная оценка для р при
больших л имеет вид неравенства (7.3.6) и т.д. [см. неравенства (7.3.9),
(7.3.23)].
Рассмотрим асимптотический подход в общем случае.
В § 7.1 и § 7.2 было установлено, что при выполнении достаточно
широких условий оценка 0„ параметра 0, полученная или методом
моментов или методом максимального правдоподобия, имеет в самом общем
случае асимптотически нормальное распределение и является
асимптотически несмещенной, т.е. при больших л оценка 9„ - Л'! Q,-^DQ„ 1.
Однако в отличие от ситуации, рассмотренной на с. 152, где дисперсия DX
оценки X ~ N\a,yDX = а/л/л) предполагалась известной, в общем слу-
чае дисперсия DQ„ оценки 6„ зависит от оцениваемого неизвестного
параметра 6:
/)ё„=с2(е)/л. (7.4.1)
158
Поэтому напрямую первый подход к доверительному оцениванию
неприемлем.
Поставим вопрос так: нельзя ли преобразовать оценку 0 в f = g\Q] и
неизвестный параметр дв g = g{Q) так, чтобы дисперсия Dg не
зависела от 6. Изложим схему подбора такого преобразования, а затем
объясним, как, используя его, найти интервальную оценку для 6.
Пусть 0 — оценка метода моментов: 0, а следовательно, и ^ = glo)
являются функциями выборочных моментов. Тогда, согласно теореме о
свойствах функций выборочных моментов (см. § 7.1), распределение оценки
g = gV^] при больших л близко к нормальному, Mg = Мgyd) = g{Q) = g н,
с учетом выражений (7.1.5) и (7.4.1),
Z)| = Z)g(0) = Z)0[g'(0)f =c2(0)/«[g'(0)f =[c(0)g'(9)]7«
(аналогичные выражения получаются и для оценок максимального
правдоподобия в регулярном случае). Но так как дисперсия Dg не должна
зависеть от 0, то выражение c(0)g'(0) должно быть постоянным,
например, c{Q)g'{Q) = 1. Тргда g'(0) = 1/с(0) и
8i^) = j
d0
при этом произвольная постоянная в неопределенном интефале
выбирается из соображений простоты окончательных выражений.
Итак, при больших л распределение оценки g = gld] близко к
нормальному, при этом Mg = g{e), а Dg = 1/л и, следовательно,
g-Mg g(Q)-g(Q) „
1 = 7—7= == Z.
лЩ \l4n
Поэтому при больших л для g(0) с вероятностью = 1 - а имеет место
неравенство, подобное неравенству (7.3.3);
^(ё) -uj^< g{Q) < f (ё) + и„/л/я. (7.4.3)
гдеФ(«„) = (1-а)/2.
Применив ко всем частям неравенства (7.4.3) преобразование^',
которое является обратной функцией к функции g, получим интервальную
оценкудля0.
159
Q Пример 7.7. Построим доверительный интервал для параметра распределе-
нияПуассона:/>(^ = х) = — е~^, х = 0,1,...; ^>0.
х!
В примере 7.2 была найдена оценка метода моментов X. = х параметра
Х = MX; \, будучи оценкой метода моментов, имеет асимптотически
нормальное распределение (это свойство оценки X. = х вытекает также и из
центральной предельной теоремы), при этом X. - несмещенная оценка, так как МХ =
= MX = MX = X, а дисперсия оценки X зависит от параметра X:
Di = DX = DX/n = \/n.
Сопоставив выражение для Z)X с выражением (7.4.1), получим с(Х) = -Д^
и, согласно равенству (7.4.2),
с учетом вида функции g{\) неравенство (7.4.3) примет вид:
2"A-a„/V«<2Vx^<2"A + «oi/V«. (7.4.4)
Для функции у = g{x) = 2Vx при х > О и у > О обратная функция
* = S~\y) = {yftf ■ Поэтому, если в неравенстве (7.4.4)
то, применив ко всем его частям преобразование g~\ получим неравенство
которое выполняется при больших п с вероятностью == 1 - а. •
О Пример 7.8. Построим доверительный интервал для р - вероятности успеха в
единичном испытании.
В примере 7.6 методом максимального правдоподобия для р была найдена
оценка р = \i/n, где ц - случайное число успехов в п испытаниях Бернулли;
р имеет асимптотически нормальное распределение, при этом Мр = р,
а Dp = р{1 - р)/п - дисперсия зависит от параметра р.
Сопоставив выражение для Dp с выражением (7.4.1), получим
с(р) = д/р(1-р) и, согласно формуле (7.4.2),
160
с учетом вида функции g[p) неравенство (7.4.3) примет вид:
2arcsin-\/^ -Мц/л/и <2arcsin-\/^< 2arcsin-\/J + M„/V/i. (7.4.6)
Для функции у = g{x) = 2 arcsin л/х^ при О < л/х^ < 1 обратная функция
X = g~\y) = sin^(;'/2), где О < з' < 7с. Поэтому, если в неравенстве (7.4.6)
(2arcsin-\/J-Wa/Vw) > О и (2arcsinл[^ + Ug^/^fn] < тс, то, применив ко
всем его частям преобразование g "^ получим неравенство
sin
arcsin-^р-Мц—т= </?<sin arcsin-^/? + м„—т= 1, (7.4.7)
V 2л/яу V 2л/яу
которое выполняется при больших п с вероятностью » 1 - а. •
V Задача 7.5. В случайной выборке из 30 аспирантов, специализирующихся по
управлению предприятиями, составленной по нескольким основным
университетам, 18 человек оказались сыновьями бизнесменов и специалистов с высшим
образованием. Оцените долю аспирантов в обследованных университетах, отцы
которых являются бизнесменами и специалистами с высшим образованием, и число
таких аспирантов среди 2000 аспирантов при 90%-ных доверительных границах.
Решение. По табл. П. 4.1 найдем число и^, при котором Ф(мц) =
= (1 - а)/2 = 0,45; "о i ~ ^ >^^- Д"" генеральной доли р интересующих нас
аспирантов получим, согласно неравенству (7.4.7), неравенство
sin
arcsin л/о. 6 -1,65—?=• < о <sin arcsin л/О, 6 + 1,65—р= ,
I ^ 2V30J I- [ ^ 2л130)
или неравенство 0,451 <р< 0,741, которое выполняется с вероятностью » 0,9,
и тогда доверительный интервал для числа таких аспирантов среди 2000
человек-(902; 1482).
Если воспользоваться неравенством (7.3.6), интервал для р, отвечающий
надежности » 0,9, будет таким: (0,452; 0,748).
Точный же 90%-ный доверительный интервал для р, который можно
построить, используя биномиальное распределение случайной величины ц. (а не
аппроксимацию этого распределения нормальным, имеющую место только при
достаточно больших и) такой: (0,434; 0,750) (см. [5, с.107]).
В условиях задачи нижние границы первых двух интервальных оценок для р
практически одинаковы, но далеки от точной нижней границы (в задаче п = 30,
6—670 161
a это не так много), верхняя же граница второй оценки гораздо ближе к точной,
чем верхняя граница первой оценки. Т
Q Пример 7.9. Построим доверительный интервал для коэффициента
корреляции р - одного из параметров двумерного нормального распределения,
располагая результатами независимых, проведенных в одинаковых с вероятностной
точки зрения условиях наблюдений [X^, Y^), (A'j,)'2). • • ■. {Х„,У„)-
Оценкой метода моментов для р является выборочный коэффициент корреляции
g соу(;Г.Г)
где co\{X,Y) = — ^{^Xi -X'jlVi -У) - выборочный второй смешанный
«/=1
1 ^
центральный момент величин X \л Y; \i2{X) = — ^(Xi-X) =а^,
] л . _.2
А2(^) = ~Х(^ ~У) =^г ~ выборочные вторые центральные моменты
"/=1
соответственно величины Х1л величины Y.
Распределение оценки р при больших п близко к нормальному, при этом
Л/р = р и Z)pe(l-p^j /п. Сопоставив выражение для дисперсии Dp с
выражением (7.4.1), заключаем, что с(р) = 1 - р^ и, согласно формуле (7.4.2),
,(p) = J^ = l,„l±P.
■' 1 - р 2 1 - р
Преобразование zip) = -In-—- носит название г-преобразования Фи-
2 1-р
шера. Функция г(р) - нечетная; ее значения при О < р < 0,99 приведены в
твбл. П. 4.5.
Исследования точности приближения распределения случайной величины
г(р) к нормальному показали, что z{p) ~ N z{p) + ■ , l/л/и-З даже
I 2(/1-1) )
для сравнительно малых и, а потому, пренебрегая величиной -г-^—г, полу-
2(/1-1)
чим, что для z{p) с вероятностью » 1 - а имеет место неравенство,
аналогичное неравенству (7.4.3):
г(р)-Ua/^Jn-3< z{p) < z{p) + UaHn-3.
162
Поскольку функция z{^) возраааощая, то после применения ко всем частям этого
неравенства преобразования г~' получим:
Z~\z{p)-uJ^fJГ^)<p<Z~\z{p)+uJ^fJГ^), (7.4.8)
где z~\z) = -т; функция, обратная к функции z{p) =—In—^•
е +1 2 1-р
При достаточно больших п (оставляем только линейную часть разложения в
ряд Тейлора) z-\z{p)±uJ4^r3) = z-\z{p))±^(z{p))uJ^f^^ =
= р ± (l - р^ j м„ /л/я-З, поэтому доверительный интервал примет вид,
приводимый в большинстве книг по математической статистике (поскольку п
большое, то (и - 3) заменено на и):
р-(1-р^)и„/л/я<р<р + (1-р^)и„/л/я.
V Задача 7.6. Коэффициент корреляции между производительностью труда и
себестоимостью продукции, вычисленный по 20 отделениям фирмы, оказался
равным -0,35. Постройте 95%-ный доверительный интервал для генерального
коэффициента корреляции.
Решение. Согласно неравенству (7.4.8):
по табл. П. 4.1 найдем число m„, при котором Ф(иц) = (1-а)/2 =0,475,
«0,05 =1'35;
по табл. П. 4.5 при р = - 0,35 найдем z {- 0,35) = - 0,3654,
вычислим г, = г(р)- 1,95/Vl7 = -0,3654 -0,4729 = -0,8383,
e2 = e(p) + l,95/Vl7 = 0,1075;
по табл. П. 4.5 при г = г, и г = ^2 найдем р, * - 0,68, pj» 0,11.
Таким образом, с вероятностью » 0,95 для генерального коэффициента
корреляции выполняется неравенство - 0,68 < р < 0,11. Т
Вопросы и задачи
1. Что означает словосочетание «хорошая оценка»? Какому из
методов оценивания параметров вы отдаете предпочтение и почему?
2. Найдите методами моментов и максимального правдоподобия
оценки параметров известных вам распределений. Яапяется ли
выборочная средняя (выборочная доля) хорошей оценкой математического ожи-
163
Дания (вероятности)? Какие точечные оценки дисперсии вам извесгаы
н какой из них вы отдадите предпочтение?
3. Вам нужно найти пять человек, пользующихся услугами
некоторой фирмы. При опросе на улице случайных прохожих оказалось, что
11, 14, 20, 22 и 30-й прохожие пользуются услугами фирмы. Методами
моментов и максимального правдоподобия оцените вероятность того,
что случайный прохожий пользуется услугами фирмы; найдите для этой
вероятности 90%-ные доверительные фаницы.
4. По выборке объемом л == 42 из нормальной генеральной
совокупности найдена средняя х = 608. Предположив, что а = 15, определите:
а) среднее квадратичное отклонение средней; каков содержательный
смысл этого отклонения?
б) 95%-ный доверительный интервал для математического ожидания а;
в) вероятность того, что интервал (0,9923с; 1,0083с) накроет а;
г) вероятность того, что ошибка средней не превзййдет q:4,5;
д) объем выборки, при котором с надежностью 95% ошибка средней
не превзойдет т4,5.
5. Для отрасли, включающей 1200 фирм, была составлена случайная
выборка из 45 фирм. По выборочным данным оказалось, что в фирме
работают в среднем 77,5 человек при средйем квадратичном отклонении
20 человек;
а) пользуясь 95%-ным доверительным интервалом, оцените среднее
число работающих в фирме по всей отрасли и общее число работающих
в отрасли;
б) пользуясь 90%-ным доверительным интервалом, оцените
вариацию работающих в фирме по всей отрасли.
Результаты сравните с результатами решения задач 7.2 и 7.4.
6. Фирма с целью установления известности ее продукции опросила
на каждой из пяти улиц по 40 человек. Количество знакомых с
продукцией фирмы оказалось таким: 20, 10, 30, 10, 15. Задания:
а) методами моментов и максимального правдоподобия оцените
степень известности продукции фирмы;
б) постройте 90%-ный и 95%-ный доверительные интервалы для
степени известности продукции. Какой из интервалов шире и почему?
в) пользуясь 95%-ным доверительным интервалом, оцените число
жителей среди 2000, знакомых с продукцией фирмы.
7. Распределение 200 погибших от несчастных случаев по возрасту
таково:
Возраст
Число погибших
16-21
133
21-26
45
26-31
15
31-36
4
36-41
2
41-46
1
164
Предположив, что продолжительность жизни имеет показательный
закон распределения, найдите точечную и 90%-ную интервальную
оценки для среднего числа погибших за год.
8. Из 200 работников банка случайным образом отобрано 20 человек,
средняя зарплата которых составила 600 тыс. руб., а среднее
квадратичное отклонение 100 тыс. руб. Предположив, что зарплата распределена
по нормальному закону, определите с 95%-ной надежностью среднюю
зарплату в банке и суммарны^ затраты банка на зарплату в месяц.
9. При проверке двух предприятий 903ни<^ной торговли ревизор
установил, что в одном магазине'для случайной выборки л = 10 счетов
среднее сальдо счета равно 54 дол., а в другом, при таком же объеме
выборки, 45 дол. Используя 95%-ные доверительные фаницы, оцените
разность средних сальдо счетоь для двух магазинов, если среднее
квадратичное отклонение сальдо для Первого магазина 0', == 3 дол., а для второго
Gj >=* 2дол. Предполагается нормальное распределение сальдо счета.
10. С какой вероятностью можно ожидать, что:
а) ошибка от замены вариации а ежесуточного дохода киосков
некоторой фирмы вариацией s, вычисленной для 13 киосков этой фирмы, не
превзойдет 0,388»«.--.
б) отношение i^/oi- где f^ щкжг вычиет|«иа по^результатам
обследования 13 киосков,.будет за1(лю,чено^ иитероале (0,297^ 0,436).
11. Из двух генеральных совокупностей X ~ N[ax,o) и Y ~ М[ау,о)
извлечены случайные независимые выборки соответственно объемом n^
и /ij и найдены оценки s^ и sj дисперсии а^. Каков закон
распределения отношения s^/s2 ? Пусть я, = 13, а /ij = 7. Какова верхняя граница
отношения s^/s2, которую можно гарантировать с вероятностью 0,95?
Какова при той же вероятности нижняя фаница?
12. Для того чтобы определить отношение избирателей к предложению
админисфации области относительно выпуска облигаций, проводится
опрос 100 человек в каждом из двух районов. В <!i)ihom районе это
предложение поддержали 60 человек, а в другом ^ 50. Пользуясь 95%-ньшй
доверительными границами, оцените разность процентных долей лиц,
поддерживающих предложение администрации области в обследованных
районах.
13. Постройте 95%-ную интервальную оценку генерального
коэффициента корреляции:
а) по выборке (1; 5), (2; 4), (3; 1), (4; 1), (5; 2);
б) если л = 12, а р = 0,36;
в) если л = 12, а р = — 0,36.
165
Глава 8
ПРОВЕРКА ГИПОТЕЗ
На практике часто приходится на основе выборочных наблюдений
проверять различные предположения относительно генеральной
совокупности. Процедура сопоставления выдвинутых гипотезе выборкой м
вынесения решения относительно приемлемости этих гипотез получила
название проверки гипотез.
§ 8.1. Основные понятия проверки гипотез.
Гипотезы о параметрах
нормального распределения
Статистическая гипотеза — это некоторое предположение относи'''
тельно генеральной совокупности, проверяемое по выборочным данным;
Примеры статистических гипотез:
а) нормально распределенная случайная величина А'имеет генераль*
ную среднюю а, равную а^;
б) нормально распределенная случайная величина А'имеет
дисперсию, равную Од;
в) выборка X = (х,, Х2 х„) взята из нормально распределенной ге»
неральной совокупности. >
Гипотеза называется параметрической, если в ней содержится неко*
торое утверждение о значении параметра распределения известногв
вида. В непараметрической гипотезе заключается утверждение обо всем
распределении. Параметрическая гипотеза называется простой, если щ
ней речь идет ровно об одном значении параметра (одномерного или
многомерного). В противном случае имеют дело со сложной гипотезой!
Обычно выделяют некоторую основную, или нулевую, гипотезу Н^.
Например, простая гипотеза «а» запишется так: Н^: а = а^. Наряду с Яд
рассматривают конкурирующую, альтернативную гипотезу H^,
являющуюся логическим отрицанием Яц. Альтернативной к гипотезе «а» может,
например, быть гипотеза Я,: о = о, (о, — число, не равное а^) или
гипотеза Н^. а^ fl(,, или Я,: о < Oq и т.д.
166
Правило, по которому решают: принять или отклонить Яц
(соответственно отклонить или принять H^), — называют критерием. В общем,
схема построения критерия такова: все выборочное пространство
делится на две взаимодополняющие области — область 5" отклонения
основной гипотезы Яд и область S принятия этой гипотезы (область
отклонения основной гипотезы называется критической); если выборочная
точка X попала в S, то основная гипотеза Щ отклоняется и принимается
альтернативная гипотеза Я,; если же точка х попала в ^, то
принимается Яд, а Я, отклоняется.
При этом может иметь место ошибка двух родов:
будет принята гипотеза Я,, тогда как на самом деле верной является Яц—
это ошибка первого рода, ее вероятность обозначают а:
а=Р{хв8/Щ) = Р{Щ/Щ),
где Р{Н^/Н^ — вероятность того, что будет принята гипотеза Я,, если на
самом деле в генеральной совокупности верна гипотеза Н^, а называют
уровнем значимости и обычно для а используют некоторые стандартные
значения: 0,05; 0,01; 0,005; 0,001;
будет принята гипотеза Яд, тогда как на самом деле верной является
Я, — это ошибка второго рода, ее вероятность обозначают Р:
Р = /'(лсб^/Я,) = /'(Яо/Я,).
Правильное решение также может быть двух родов:
будет принята гипотеза Яц, тогда как и на самом деле в генеральной
совокупности верна Hq, вероятность такого решения 1- а = Р[х е S/NqJ =
= /'(Яо/Яо);
будет принята гипотеза Я,, тогда как и на самом деле в генеральной
совокупности верна Я,; вероятность такого решения 1 - Р = Р[хе SjH^ =
= P[H^|H^ называют мощностью критерия (табл. 8.1).
Таблица 8.1
Гипотеза
«0
Верна
Не верна
(верна Н|)
Условные вероятности того, что гипотеза Н„ будет
отклонена (будет принята Н,)
а = /'(Я,/Яо) = /'(лсб^/Яо)
(ошибка первого рода)
1-Р = /'(Я,/Я,) = /'(лсб^/Я,)
(правильное решение)
принята
\-oi = P{HJHo) = P(xeS/Ho)
(правильное решение)
Р = /'(Яо/Я,) = /'(лсб?/Я,)
(ошибка второго рода)
1А7
Критерий называется наиболее мощным, если из'всех возможных
критериев с заданным уровнем значимости а он обладает наибольшей
мощностью, т.е. если его критическая область S' является такой, что
p(xeSyH^ = maxP{xeS/H^), (8.1.1)
где максимум берется по тем S, для которых
Р{хе5/Но) = а. (8.1.2)
Так как мощность критерия равна 1 - Р, то использование наиболее
мощного критерия гарантирует при заданной вероятности а ошибки
первого рода наименьшую, по сравнению с другими критериями,
вероятность Р ошибки второго рода.
Задача построения наиболее мощного критерия (критической
области S') решается для простых гипотез с помощью леммы Неймана —
Пирсона. Поясним ее смысл, предположив, что случайная величина Л*
непрерывна.
При выполнении простой гипотезы Я^ плотностьу{)(л) величины
^'определяется однозначно, а потому и функция правдоподобия [см.
формулу (7.2,5)] также определяется однозначно, т е. в точке х
A)W = /o(*l)/o(*2)-/o{*«)-
Аналогично при выполнении простой гипотезы Я, однозначно
определяются плотность/,(х) и функция правдоподобия в трчке х
о правдоподобии выборки х в отношении гипотез Я, и Н^ будем
судить по отношению правдоподобия Li/L^ (конечно, при Lq =^ 0): чем
правдоподобнее выборка в условиях гипотезы Я,, тем больше L^ (по
сравнению с Lq), тем больше отношение Z,,/Z^.
Согласно лемме Неймана—Пирсона, существует такая константа С,
зависящая только от а, что критическая область 5* наиболее мощного
критерия
S^=Ll^{x) = 0[J^>CnpiiLo{x)^o\, (8.1.3)
при этом константа С является решением уравнения
ГГ1,{х)
Ых)^^.
ffn\ = 0" (8.1.4)
Метод построения критической области, использующий отношение
правдоподобия, называют методом отношения правдоподобия.
168
Q Пример 8.1. Случайная величина Х- N{a, а), причем числовое значение
математического ожидания а не известно, а числовое значение дисперсии о^
известно. Пусть основная гипотеза Я^: о = Оц, а альтернативная гипотеза
Нуа-а^>а^ (о, - число, большее а^).
Если верна гипотеза Яд, т.е. Х- N(а^, а), то функция правдоподобия в
точке jc=(jc,,j£^,...,xj
'«^'^ = '^'*'''Р
2а /=1
(8.1.5)
если же верна гипотеза Я,, т.е. Х- N(a^, а), то
AW =
-uT
1 V/ \2
7= I exp
oV2n^
Тогда отношение правдоподобия таково:
= exp-
2oS^
i[2x,(flo-fl,) + flf -flo^]i = exp{—5-(fl, -floX2?-fl, -flo)«
Uo'
Так как при a, > Oq это отношение является монотонно возрастающей
функцией от Зс и так как в примере Z.q(jc) * О, то неравенство Z./£g > С
равносильно неравенству Зс>С,гдеСи С - некоторые константы. Поэтому
соотношения (8.1.3) и (8.1.4) примут вид:
5'*={xjc>c}; (8.1.6)
7»((^>с)/Яо) = а. (8.1.7)
Известно, если Х~ N{a, а), то А" ~ nU, o/V«). а потому при
выполнении гипотезы HqI а = а^ получаем X ~ N^a^, o/V«); тогда
а = ,^(Х>с)/я.)Л.ф[£^\
Гг-
Отсюда Ф
С-Ор |_1-2а C-flp _
с = <% +«20, о/л/я.
(8.1.8)
169
Итак, наиболее мощный критерий проверки гипотезы Яд: а = uq при
альтернативной гипотезе Н{.а-а^>а^ такой:
если хка^ + и^а o/^fn, то Н^ принимают (Я, отклоняют); 1
> (8.1.9)
если Зс > Oq + i^„ a/V« до Яц отклоняют (Я, принимают). J
При использовании этого критерия вероятность ошибки первого рода равна числу
а, а вероятность ошибки второго рода, с учетом соотношений (8.1.6) и (8.1.8):
Р = /'(Яо/Я.) = Р(х е S'/H^) = Р((Х < С)/Х ~ N{a^,o/^fii)) =
4-
Г/=. . \
С-а
^i_^^(%+jha^N^ZA]r.
yCs/^fnj 2 [ a/^fn J
= --ф({a^-ao)^fii/o-U2^). (8.1.10)
Из выражения (8.1.10) видно, что:
с ростом вероятности а ошибки первого рода вероятность Р ошибки
второго рода уменьшается, если п константа;
с ростом объема п выборки вероятность р ошибки второго рода
уменьшается, если а константа.
Заметим, справедливость этих выводов не ограничивается рамками
рассмотренного примера.
Из выражения (8.1.10) нетрудно получить, что при заданном а риск ошибки
второго рода, меньший р, обеспечивается объемом выборки
^("2а+"2р) <J^
"^—( (г-' (8.1.11)
гдеФ(м2„) = (1-2а)/2. •
Итак, для Х~ N(a, а), где а не известно, а а известна, наиболее
мощный критерий проверки гипотезы Яд: о = flg "Ри альтернативной
гипотезе Я,: о = о, > flg имеет вид (8.1.9).
Нетрудно убедиться в том, что наиболее мощный критерий проверки
гипотезы Hq-. а = а^.
при Ну а = a^ < а^ будет таким:
если Зс > Oq - «2„ о/4п, то Н^ принимают;
,^ [ (8.1.12)
если X < Oq -«2„ о/V«. то //q отклоняют,
при Ну а= а^* Qf^ будет таким:
170
если flg ~«awV« <)X <Oq +«ao/л[п, TO Яд принимают; ->
если (3c <flo-«a V"^)U(3f >flo+"a<^/"^)'T° ^0°''"'^°"^'°''"- I
Проведем параллель между критерием (8.1.13) и интервальной
оценкой (7.3.3) параметра а при известной дисперсии а^. Решив первое
неравенство в (8.1.13) отиосительно Oq, получим такую формулировку
критерия проверки гипотезы Яд: а = а^ при альтернативной гипотезе
Я,: а = a^=^ а^: если для предполагаемого в основной гипотезе Щ
значения Oq параметра а выполняется неравенство
x-u^olyfnKaQKx + u^olyfn, (8.1.14)
то Яд принимают, в противном случае гипотезу Яц отклоняют. Сравнив
неравенства (7.3.3) и (8.1.14), заключаем: если предполагаемое в
основной гипотезе числовое значение неизвестного параметра попадает в
интервальную оценку этого параметра, отвечающую надежности 1 - а, где
а — заданный уровень значимости, то гипотезу Н^. а = а^ принимают;
в противном случае ее отклоняют в пользу Я,; а=а^* Oq. Такая
формулировка наиболее мощного критерия имеет место не только в данном
случае, но и при проверке гипотезы Н^. в = вц о числовом значении
любого параметра нормального или асимптотически нормального
распределения, если альтернативная гипотеза Я,; 6=6,'* 6q.
Приведем еще одну формулировку критерия (8.1.13) проверки
гипотезы Яц: о = flg "Ри ^1- о = О]'' Oq- Введем статистику критерия
csl4n '
в терминах этой статистики область принятия гипотезы Яц: о = Oq
задается неравенством -m„ < Z< и^ или неравенством
|Z|<«„, (8.1.15)
а область отклонения будет такой:
7б{-«',-и„)и{Иа,+«').
Если значение —-г-г^ статистики Z удовлетворяет неравенству
(8.1.15), гипотезу Щ. а^ а^ принимают; в противном случае отклоняют
в пользу гипотезы Я,: 0=0,9* а^. При такой формулировке критерия
область отклонения гипотезы Яц имеет вид {-«>,-Wa)U{«a.+°°) и ее
называют двусторонней критической областью значений статистики Z.
171
При использовании статистики 7тя проверки гипотезы Яц; в *= Оц
при альтернативной гипотезе Я,: а = a^> а^ область принятия Я^
задается неравенством
Z<M2a
И Критическая область значений статистики 7будет/|равосто/юн№«: (и^а, +<*>)■
При использовании статистики 7для проверки гипотезы Н^: а = а^
при альтернативной гипотезе Я,: а = af< а^ область принятия Я^
задается неравенством
И Критическая область значений статистики Z6yjiisT левосторонней: (-««, - «j„).
Критерии проверки гипотез о числовых значениях параметров
нормального распределения, коэффициента корреляции и вероятности
успеха в единичном испытании приведены в табл. 8.2.
В заключение отметим: принятие основной гипотезы Яд вовсе не
означает, что Яц является единственно подходящей, просто
предположение Яд не противоречит выборочным данным, однако таким же
свойствам могут наряду с Яд обладать и другие гипотезы.
V Задача 8.1. Крупная торговая фирма желает открыть в новом районе города
филиал. Известно, что фирма будет работать прибыльно, если еженедельный
средний доход жителей района превышает 400 марок. Также известно, что
дисперсия дохода о^ = 400.
а) Определите правило принятия решения, с помощью которого,
основываясь на выборке л = 100 и уровне значимости а = 0,05, можно установить, что
филиал будет работать прибыльно.
б) Рассчитайте вероятность того, что при применении правила принятия
решения, полученного при ответе на вопрос пункта «а», будет совершена ошибка
второго рода, если в действительности средний доход за неделю достигает 406 марок.
в) Считая альтернативное значение генерального среднего дохода равным
430 марок, рассчитайте объем выборки, при котором риск ошибки первого рода
не правысит 0,025, а риск ошибки второго рода не превысит 0,05.
Решение, а) Фирма не откроет филиал, если средний доход жителей не
превысит 400 марок. Поэтому будем считать, что Я^: а = 400, а Ну а> 400.
Значение дисперсии о^ дохода известно: в этом случае Я, принимают, если
—7-^>«2n- По условию о» = 400, Ищ = 1,65. Поэтому Я, принимают и,
а/л/л U U.I
следовательно, филиал открывают, если недельный среднедушевой доход 100
жителей х > 400 + 2 • 1,65 = 403,3.
б) Альтернативное значение среднего дохода равно: а, = 406 и гипотеза
Я,: а = 406 > йд. В этом случае вероятность ошибки второго рода
172
р = 0,5-ф{(о,-Оо)>/^/а-и2а} = 0,5-Ф{610/20-1,65} = 0,09.
в) При гипотезах Щ а - а^, [а^ = 400), и Я,: о = о, > о^, (о, = 430), объем
выборки рассчитаем по формуле (8.1.11), в которой а=0,025, а Р=0,05. Получим:
Kos + "o.i) -400 (1.95 + 1.65)^ -400
30^ ~ 900
V Задача 8.2. Торговец утверждает, что он получает заказы в среднем по
крайней мере от 30% предполагаемых клиентов. Можно ли при 5%-ном уровне
значимости считать это утверждение неверным, если торгов^ получил заказы от
20 из 100 случайно отобранных потенциальных клиентов.
Решение. Будем считать, что гипотеза Щ. р = 0,3 (т. е. число р^ = 0,3),
аНуР< 0,3; и = 100, /i/>Q > 5, и{1 - />q) > 5, поэтому для проверки гипотезы
Яд используем статистику Z= . i° числовое значение которой
при ^=20/100 = 0,2 равно - 2,18. Так как при а = 0,05 - 2,18 < -и^^ = -1,65,
то гипотезу Яд отклоняем: с утверждением торговца не согласимся. Т
V Задача 8.3. Поданным обследования 20 однотипных фермерских хозяйств
вычислен коэффициент корреляции р = - 0,47 между средней урожайноаыо и
средней себестоимоаью моркови. Поаройте 95%-ный доверительный
интервал для генерального коэффициента корреляции. Можно ли при 5%-ном уровне
значимости считать выборочный коэффициент статистически значимым?
Решение. Втабл.П.4.1 найдем«^д5=1,95,автабл.П.4.5г(-0,47)=-0,5101
и тогда, согласно (7.4.8), mnftm /'(^"'(-0,9830) < р < ^"'(-0,0372))« 0,95,
или Р{-0,76 < р < -0,04) = 0,95.
Коэффициент р называют статистически значимъш при заданном
уровне значимоаи а, если при этом а гипотезу Яд: р = О отклоняет в пользу
гипотезы Н^: р * 0. Используя соответствующий этой ситуации критерий
(см. табл.8.2),найдем z(-0,47)-Vl7 =-2,103,итаккак|-2,103|>«^^,5=1'95.
то гипотезу ^: р = О отклоняем, т.е. считаем р = - 0,47 статиаически значимым.
Замечание. Приведенный в табл. 8.2 критерий проверки гипотезы
Яд: р = рд при Я,: р ^ рд идентичен выяснению, накроет ли построенный с
надежностью 1 - а доверительный интервал для р число рд. Если это произойдет,
гипотезу^принимакя, в противном случае-ве отклоняют. В задаче 1 -а = 0,95,
а = 0,05 и рд = О « (-0,76; -0,04) - гипотезу Яд: р = О отклоняем. Т
173
ax
1
r-
a
s
a.
g
s
a
(5
8
1
о
af
5
E
X
s
a
с
i^
О
о
af
к
s
a
Ф
a
s
s
d
^
1
1
о
5 a
5 ®
gx
с
af
_^ ^ ^ ^
e e
a a
1 1
О о
^ a-
1 1
^5&^ ^®^
+ +
Ю Ю
o" o"
a
V л
N N
^ ^
л V
о* a"
II II
a a
1
1^
^
о
II
N
о
z
1-
~ о
о ф
flO
n
s
1
1
^
+
1
1
a"
^
О
e
+
V
^
^
Ц.
a"
II
a
«
1
, , 1
» 1 +
<» a a
'■':: 1 1
cf л л
Д 7 7
1 ■**» ■**»
^W
— 1 +
«V, J, Z
-T" 1 -J*
V л V
1 1 I
1 1 1
с с с
■^ '^ '^
^ <r ^
л V И.
сГ о" о"
II II II
а а а
1
1^
^
ч
1
1
с
Чок
о
Z
РТ
Ъ S
S
ф
X
?
i
■J»
1
!>
о"
1
а
л
1
'lok
«,
1
■«г "^ ^
'^ -^ ^ "^
„^ гч гч гч в -^
?<| 1?< г^ а
^-з Л Л ?<1
'^ 1=- СГ Л
Д 1 1 -^^^
' сч сч ^*-_
"ч^ «V, «V, viS
V л i "г
<>| в
|?< ?<| ^~,
Д Д 7
3 >S ^
сч сч V
сч о
?<i
rf? rf? -^
л V и.
.^ .^ .^
11 и 11
гч гч гч
0 о о
гч
1
^
^
II
1
с
о
X
гт
S
Ф
Z
^ о^
II л
174
/^ N/' N
0
0
it
e e
zS* :£*
1 1
^
1
к -
fti
b- "*•
с
5*
^
•^ j\^ J
+
~N
<§
0
0< _
eC
1
0
1
1
cT
1 "^
5?
L^
0 e 4 С
+ +
o" o"
e
a 1
V л
N N
О о
ts. ts.
Л V
«с аГ
II II
ts. ts.
о
tt.
1
1
'-'
II
«С
1
<tt.
CI
0 •>
tt. к
~^ ^
II „
X
со S flo
^50
2 0 » ^
= » a: S.
о
II
tt.
+
e
a
V
.0
tt.
Ц.
йГ
II
tt.
VI
л
1
"к'
5?
_5^
5*
eC
a
a
eC
1
0
oT
у
e
+
1
e
a 1
V л
N N
о о
о. О.
Л V
CL CL
о
^
►V
1
<оГ
►V
m
1
"^
II
N
о
л
с
о
о.
II
О.
а"
V
N.
о
о.
ц.
о.
*
о
II
^
о.
m
1
С
S ^?
= S
i J'
« N
ф
со
1
в
'«ч
V
-^:^
1
С
о
ц.
о.
«а.
,**-^
О)
1
с
^^;:i;
ск
1
~
1
оГ
1
S:
1
о
II
о.
175
§ 8.2. Гипотезы о равенстве средних и дисперсий
двух нормальных распределений
гипотеза о равенстве средних при известных дисперсиях. Итак,
случайные величины А'<') - Л^(о,, а,), а Х^^^ ~ N {а^, с^, при этом о, и 02 не
известны, а а, и 02 известны. Построим критерий проверки гипотезы
Я^: о, = 02. если Я,: а, > 02> предварительно заметив, что для случайной
величины Х= Jf^') — Х^^^ математическое ожидание МХ= о, — 02 ~ о-
Пусть A'f'), A'j'),..., 4|') и Л'р), Л'р),..., 4J) - независимые случайные
выборки из соответствующих нормальных генеральных совокупностей.
Напомним: вычисленные по этим выборкам средние имеют нормальные
распределения, а именно: Х^ > ~ N\a^,oJ^[nA, й Х^ ' ~ N[02,02!4^]•
Тогда, с учетом независимости случайных величин Х^^> и Х^^',
вытекающей из независимости случайных выборок, получим:
Jf = JfW-Jf(^)~A^
Г
(8.2.1)
Далее, гипотеза Я^: о, = 02 при Я,: о, > 02 равносильна гипотезе
Яо: о = Oq при Я^': о > Оо> "Р" этом а^ = О, критерий проверки которой
приведен в табл. 8.2. С учетом выражения (8.2.1) он формулируется так:
х-а. jc(')-jc(^)
если --2- = <Mj^, принимают Н^: а=0(или Я^: а, — а.^,
в противном случае принимают Н[:а>а (или Я,: о, > 02)-
Этот критерий, а также критерии проверки гипотезы Я^: о, = 02 ДЛЯ
случаев, когда Я,: о, < Oj и ^р Oi ** "г» приведены в табл. 8.3. i
Замечание. Если гипотезу Яд: а, = 02 принимают, то говорят, что раз^
личие выборочных средних jf''^ и х^^^ статистически не значимо
погнул общего математического ожидания такова: \х Ц +л^ 'п^ 1Ди, +«2).
Гипотеза о равенстве средних при неизвестных дисперсиях. Критерий
проверки такой гипотезы довольно прост, если известно, что неизвест-i
ные дисперсии о\ и Oj равны, — он использует распределение Стью-<
дента (см. табл. 8.3 и табл. П. 4.2). Если же заранее не известно, чтЬ
0^=02, то, прежде чем проверять гипотезу Я^: о, = 02. проверяют
гипотезу Н^:а\ =о\ (см. с. 178). И в случае приемлемости Я© приступают^
176
об
5
g
ii
a
с
siT
a
s
a
a
я
M
1-
5
1
о
с; a
ii
&?
e
V л V
NN Is
^ ^T «T
л V -H.
«Г a" a"
'
l^hbk
slvk
II
N
2
1
«
e
ГЧ 1 О
V Л V
1 1 1
«Г «Г ;Г
+ + +
^T «T cT
л V Ц.
сГ о" «Г
<^<ч
ч
f ч
1
1
+
ГЧ ^
ч
1
1
с
+
sT
н
п
ф
Lb
fS
1^
1
1^
'-1«г
+
ink
II
'гГ
1
£*
. +
^
'«ч
3 3
Г
г
в „
IbCllif
V V
1 1
1 7
к" sT
^"ь
л ц.
СЧ —'СЧ —'
0 b
<■—*^
г..^
л
«^ м
ч
II
1
f
7
ь^
■J
II
ц
Тг5
1 1- к
-х-^
1
сч ■—
1
1
и-
^ ,
1
1
sT
И-
II
Г4
ф
9
.4
1
1
1
1
И
1
1
1
^
m
+
II
.••-»■
1
>
>
л of
« 7'
1? ":
О II
в
V Л V
NN N
»С^ ^ ^Г"
ts, ts, ts,
л V и.
еС аГ еС
сч
S
+
£*
+
II
<tt.
п
-
+
-Ik-
V -y
1
<^
"^^^
<«?
1
-iS
II
N
^ 2 1 о
II
«с
e
a 1 a
V л V
N N Ng^
ГЧ ГЧ ГЧ
Q. Q. Q.
Л V Ц.
qT qT dT
v^
m
1
+
1.
■?$^
<Qj,
1
1
II
N
о 2
Л1 Л!
«Г «Г
Q.
II
оГ
177
с некоторой осторожностью (ведь принятие Яд, так же как и ее
непринятие, вовсе не означает, что и на самом деле а] = 02), к проверке
гипотезы Яд: д, = «2-
Гипотеза о равенстве дисперсий при неизвестных средних. Схема
проверки гипотезы Яд: о] = al приведена й табл. 8.3. При проверке Я^
используется табл. П. 4.4 — таблица критических точек распределения
Фишера.
Замечание. Если гипотезу Н^: aj = al принимают, то говорят^ что
различие выборочных дисперсий s^ и si статистически не значимо и
оценка общей дисперсии такова: [*?(«, -^) + ^1{п2 -1)|Ди, +«2-2).
В табл. 8.3 приведен критерий Бартлетта проверки гипотезы о
равенстве дисперсий более чем двух нормальных распределений; он основан
на х^-распределении (см. табл. П. 4.3) и будет использован в § 8.4.
В табл. 8.3 также даны критерий проверки гипотезы о равенстве дщх
вероятностей p^ и /?2 [для случая больших чисел и, и «2 испытаний Бернулли, когда
можно считать, что ^, ~ ^\р^,^р^{\-р^1щ 1и Рг ~ N\Pl>-lPl{}-Pl)|^h]] и
критерий проверки гипотезы о равенстве двух коэффициентов
корреляции.
V Задача 8.4. Расход сырья на одно изделие случаен. Результаты наблкздений
таковы:
Предположив, что расход сырья как при старой, так и при новой технологии
Старая технология Новая технология
Расход сырья 304 307 308 303 304 306 308
Число изделий ,14 4 2 6 4 1
имеет нормальное распредеяение, выясните, влияет ли текнология на средний
расход сырья на одно изделие. Примите а = 0,05.
Решение. Нападем выборочные средние: х^'^ = (304 + 307 • 4 + 308 • 4)/Э =
= 307,11 и х(^> = (303 • 2 + 304 • 6 + 306• 4 + 308)/13 = 304,77 и выборочные
дисперсии s\ = 2,378 w s\ = \ ,685. По условию генеральные дисперсии не
известны и неизвестно, равны ли они. Поэтому, прежде чем сравнивать
генеральные средние, проверим гипотезу Яд : а^ = 02, приняв в качестве
альтернативной Н[: а^ > 02. Согласно F-критерию (см. табл. 8.3), вычислим
178
F» 2,378/1,685=1,41,азагемпотабл.П.4.4приЛ,=И1--1=8и/(^=Л2'*1='12
найдем ^2 0.05 = 'o.os = 2,85. Так как 1,41 < 2,85, гипотезу о равенстве
генеральных дисперсий принимаем.
Теперь проверим гипотезу Я^: a^ - а^, приняв в каЦестве альтернативной
Ну а, > а^. Согласно Г-критерию (см. табл. 8.3) вычислим сначала
5^ = (8 • 2,378 +12-1,685)/20 = 1,9622, потом t = 3,852. Далее по табл. П. 4.2
при Л = и, + Л2 - 2 = 20 найдем ^„ = t^^ = 1,72.Так как3,852 > 1,72,
принимаем гипотезу Я,: а, > а^^, т.е. считаем, что применение новой технологии
снижает средние затраты сырья на одно изделие. Т
§ 8.3. Критерии согласия
Не всегда есть основания высказать альтернативную гипотезу в
явном виде. Часто в качестве такой гипотезы имеется в виду просто
невыполнение основной, и в этом случае проверка основной гипотезы
состоит в выяснении, согласуется ли высказанное в ней предположение с
выборочными наблюдениями х,, х^,..., х^ — соответствующие критерии
получили название критериев согласия.
Критерий согласи4| х^
относительно закона распределения
1. Яд.' выборка извлечена из совокупности, имеющей распределение с
функцией Ff^{x, 0), значения параметров (в,, Bj, ..., 6^) = 0 которой известны.
Процедура проверки этой гипотезы состоит из следующих эт^апов:
а) весь диапазон значений случайной величины ДГразбивают на
интервалы (фуппы) Ар Aj,..., \ без общих точек и подсчитывают число /я,
V
наблюдений, попавщих в каждый из интервалов; Х"»/ =";
1=1
б) предположив справедливость гипотезы Яд, подсчитывают вероят-
V
ности/?,. =/>(Л'€А,), / = 1,2 V, Z/'/=l;
'■='
в) подсчитывают ожидаемые частоты лр,, при этом если для
некоторых из интервалов пр^ < 5, то их объединяют с соседними так, чтобы в
итоге для каждого интервала ожидаемая частота была больще 5; новое
число интервалов обозначим v*;
г) за меру расхождения выборки с гипотетическим распределением
Fq(x, ©) принимают
2 *; (т,-пр,) ^ /я?
Х=1— ^^Х-^-и. (8.3.1)
/=1 пр, (=1 пр,
179
при выполнении гипотезы Яд выборочным распределением
величины f} будет х^-распределение с (v* - 1) степенью свободы. И если
Х^ <Х2а = Ха> •'Д^ Ха ~" ЧИСЛО, нэйденное при Л = у*-1и/? = апо
табл. п. 4.3, гапотезу Яд принимают, конечно, не считая ее при этом
абсолютно истинной; в противном случае Яд забраковывают, по крайней
мере до пскпучения дополнительных данных.
2. Щ, выборка извлечена из совокупности, имеющей распределение Ff^{x, 0)
с некоторыми заранее не известными значениями I {I К к) параметров
6,, 02,..., 6^ Так как значения / параметров не известны, то и вероятности
" т}
р, =Р(Л'€А(),/ = 1,2, ...,v, и y^^ = Y^—!--n будут не числами, а
некоторыми функциями неизвестных параметров. Естественно за оценки этих
параметров принять такие числа (в*, ^\,.... в*| = 0*, при которых
расхождение ¥в = ¥о(в*) между выборкой и F(,(jc, 0) будет минимальным
(заметим, что эти оценки не всегда совпадают с оценками,
приведенными в § 7.1 и § 7.2). Найденными оценками в* заменяют неизвестные
параметры в функции Fq{x, 0), а затем выполняют этапы *б» — *г»
процедуры пункта 1 с той лишь разницей, что в данной ситуации выборочным
распределением величины (8.3; 1) будет х^-распределение с (v* - /- 1)
степенью свободы, и если х^<Ха> •'Д* Ха ^ число, найденное по
табл. П. 4.3 при k-v' - I- 1 и/? = а, гипотезу Щ принимают.
Рассм(дрим некоторые этапы использования критерия согласия х^ на
примерах пуассоновского и нормального распределений.
О Пример 8.2. Гипотетическим является распределение Пувсоона:
ух
Р{Х = х) = — е"^, X = о, 1,.... с неизвестным А,, {/ = Л = 1).
Предположим, что по выборке x^, Xj,..., х^ получили:
т наблюдений с х < 9'>
/Я( наблюдений с х = /, где / = ^ + 1, ^ + 2,.... ^ + v - 2;
"*» + V-1 наблюдений с х > ^ + v - 1.
Тогда соответствующие вероятности будут такими:
p,^P{X = 0) + P{X = \) + ... + P{X = q);
р. =P{X = f), rasi = q + lq + 2,...,q + v-2;
оценка параметра \ будет такой: А, = — Ух,, а число степеней свободы вы-
«/=1
боронного распределения величины (8.3.1) будет равно (v* - 2). •
180
о Прммр 8.3. Гипотетическим является нормальное распределение N (а, а)
с пяотностыо ф(х) с неизвестными ^ и о.
Выборку x^, Xj, ..I, х^ разбивают на v интервалов длиной h: А, = (а,_, =
= i^, - 0,5Л; а, = ^1 + 0,5Л), /=1,2, ..., v; ^, — центр интервала. Пусть
V
интервал Л,, содержит /п, наблюдент), X '"л = "• Соответствующие вероятно-
(=1
сти будут такими:
Pi = 1Ф)<^х\
р, * 1ф)йх, / = 2,3 V-1;
ву-1
a оценки параметров о и а^ будут такими: а' = — Х^/'^{ ~ федняя выбор-
; И<=1
IV Э li^
ки,аруппированиойпоv интервалам, {а^У= — YLL -^а*] т,--—-дис-
^ ' Л/Гг ' 12
персижЫруппйроеанной выборки, скоррактирошкнНай на поправку Шеппарда.
Число степеней свободы выборочного расп^еления величины {8:3.1 )pвiнo^
(v*-3). •
V Задача 8.5. По данным ^ад^ 7 гл: в'выясМиТб, тш ли на уровне значимо-
сти.а ^ 0,05 считать» нормальным раофвделение ср^ей заработной платы.
Решение. Найдем оценки неизвестных параметров нормального распре-
делеН1й:
= 39594,44 - 39585,081 - 0,3(3) '= 9,0257 , а' = 3,00.
Результаты расчетов величины (8.3.1) приведены в табл. 8.4; в этой таблице
Ff/{aj) = '~+^ -^— , / = 1,2,...,8, и А соответствии с алгоритмом
f^y(ao) = 0,aF^y(a,) = l.
181
Таблица 8.4
i
1
2
3
4
5
6
7
8
9
Всего
«,-i -«,
190-192
192-194
194-196
196-198
198-200
200-202
202-204
204-206
206-208
—
т.
1
1
5
9
15
22
28
19
11
4
1
16
100
I'M.,)
0,0000
0,0107
0,0495
0,1587
0,3821
0,6368
0,8413
0,9554
0,9906
—
^//«.)
0,0107
0,0495
0,1587
0,3821
0,6368
0,8413
0,9554
0,9906
1,0000
—
0,0107
0,0388
0,1092
0,2234
0,2547
0,2045
0,1141
0,0352
0,0094
1,0000
"Pi
1,07
3,88
10,92
15,87
22,34
25,47
20,45
11,41
3,52
0,94
15,87
—
(т.-прУ
"Р,
0,048
0,005
0,251
0,103
0,001
0,408
Итак, х^ = 0,408. По табл. П. 4.3приА^ = у*-3 = 5-3 = 2 и /> = а = 0,05
найдем Хо.оз ~ ^'^^- ^^ *^ Х^ ~ 0i^8 < 5,99, гипотезу о нормальном распра-
делении зарплаты принимаем. ▼
Критерий однородности
Пусть имеются/независимых выборок, объемом «,каждая,/= 1, 2,..., /;
X«/ = и. Проверяется гипотеза Н^. выборки извлечены из одной и той
/=1
же совокупности, или иначе, выборки однородны.
Процедура проверки гипотезы Н^ состоит из следующих этапов:
а) Данные каждой выборки группируют в v одинаковых групп
(интервалов) и подсчитывают число т^ наблюдений из /-й выборки,
попавших ву-ю группу:
/V V /
б) Предположив справедливость гипотезы Щ, подсчитывают
вероятности Pj принадлежности отдельного результата к каждой из групп:
Pj = и.у/и. а затем ожидаемые частоты т*- = и,-,Ру = n^.n^jln.
182
в) Вычисляют величину
\2
/ V
{'"и-'"1)
1=1 ;=1 W
(8.3.2)
выборочным распределением которой, при справедливости
предположения Яц и при т*. > 5, будетх^-распределение с (/- l)(v - 1) степенями
свободы. И если х^ < xla - Ха- гипотезу Hq принимают.
V Задача 8.6. Предполагается, что применение новой технологии приведет к
увеличению выхода годной продукции. Результаты контроля двух партий
продукции, изготовленных по старой и новой технологии, таковы:
Технология
Старая
Новая
Всего
Изделия
годные
т,, = 140
Wj, = 185
"., = 325
негодные
ОТ|2= 10
'"22=15
".2=25
Всего
л, = Л|. = 150
«2 = «J. = 200
л = 350
Подтверждают ли эти результаты предположение об увеличении выхода
годной продукции? Примите а = 0,01.
Решение. В задаче требуется проверить гипотезу об однородности двух
выборок (/= 2), извлеченных из продукции, изготовленной по старой и по новой
технологии, причем каждая из этих выборок разбита на v = 2 группы. Иначе,
требуется проверить гипотезу Щ: Рц= Рц^^Рц^ Рц' ""Д^ Р\ \ ^гО -
вероятность изготовления годного изделия при старой (новой) технологии, ар,2 {Р22) -
вероятность изготовления брака при старой (новой) технологии. Так как
Pi2~ 1 ~Pii'^P22~ ' -/'21'™<^Ф<'Р'*У^^'Р0ванная гипотеза равносильна
гипотезе Я(,:р,, =Р21-
Проверим ее двумя способами:
1. С помощью критерия х^- Если гипотеза Щ: р,, =^2, верна, то
ожидаемые частоты будут такими:
'"и = «iAi/и = 150-325/350 = 139,3, т'2 = «..и.г/и = 150-25/350= 10,7,
т2,=Я2.и.,/и = 200-325/350= 185,7, /«2*2 =«2.«.2/« = 200-25/350= 14,3.
Все ожидаемые частоты больше т*- > 5. Вычислим
2 . (140-139.3)^ ^ (10-10.7)^ (185-185,7^ (15-14.3)^
^ 139,3 10,7 185,7 14,3 ' "
183
Потабл. п.4.3при)k= (/-l)(v - 1) = (2 - 1)(2- 1) = 1 ир = a = 0,01
найдем Xooi = 6,64; так как у} = 0,086 < 6,64, то гипотезу Я^ принимаем:
считаем, что приведенные данные не подтверждают предположение об
увеличении выхода годной продукции при применении новой технологии.
2. С помощью Z-критерия (см. табл. 8.3). Итак, Щ: p^^ = р^у Примем
за альтернативную гипотезу H^•.p^^<p■^y Если гипотеза Н^ верна, оценка
вероятности изготовления годного изделия будет такой:
)/(и, + «2) = (140 +185)/(150 + 200) = 0,929.
Оценки вероятностей /',,'^^21 ''^овы:
P\\=f"\\l»\ = 140/150 = 0,933, а p^i = '"2,/«2 =185/200 = 0,925.
Тогда
Далее, при а = 0,01 по табл. П. 4.1 найдем число и^^, при котором
*(«2а) = (1 - 2а)/2 = 0,49; Ща = 2.35. Так как 0,288 > -2,35, гипотезу Щ
принимаем. ▼
§ 8.4. Введение в дисперсионный анализ
Дисперсионный анализ используется для выявления влияния На
изучаемый показатель некоторых факторов, обычно не поддающихся
количественному измерению. Суть метода состоит в разложении общей
вариации изучаемого показателя на части, соответствующие раздельно-^
му и совместному влиянию факторов, и статистическом изучении эти)(
частей с целью выяснения приемлемости гипотез о существовании эти5^
влияний. Модели дисперсионного анализа в зависимости от числа фак-i
торов классифицируются на однофакторные, двухфакторные и т.д. П<)|
цели исследования выделяют следующие модели: детерминированная^
(Ml) — здесь уровни всех факторов заранее фиксированы и проверяют
именно их влияние, случайная (М2) — здесь уровни каждого фактора
получены как случайная выборка из генеральной совокупности уровней
фактора, и смешанная (МЗ) — здесь уровни одних факторов заранее
фиксированы, а уровни других — случайная выборка.
184
Однофакторный дисперсионный анализ
В основе однофакторного дисперсионного анализа лежит следующая
вероятностная модель:
YJI^ = MY + Q^'Ke^\ (8.4.1)
где У^^ — значение случайной величины Y, принимаемое при уровне А^'^,
/=1,2,..., V, фактора А в А:-м наблюдении, к= 1,2,..., и,., в^'^ — эффект
влияния на Yf^'^ уровня А^'^; еу — независимые случайные величины,
отражающие влияние на YjI' неконтролируемых остаточных факторов,
причем все е^'' ~ N[Q,Cf().
При этом в модели Ml все 9^'^ —детерминированные величины, а не
случайные, и 2^ "( = 0; а в модели М2 все 9^'^ и е^'' — независимые
1 = 1
случайные величины и предполагается, что 9^'' ~ Л^(0,ав).
По наблюдениям вычислим общую вариацию S^ результативного
признака У и две ее составляющие — S^ и 5\, отражающие
соответственно влияние фактора А и влияние остаточных факторов:
S^ = i i(yi''^ -ff, где f = £ irJ'V" - общая средняя;
/ = lt = P ' / = 1* = !
Sl = £(f ^'^ -y] "i, где f ('^ = £/1'7«- - групповая средняя;
•^bi £И'^-?^'^)^1«,в?. где a? = i(yi')-f(')}7«,- груп-^
новая дисперсия.
Нетрудно убедиться в том, что S^ =S^+S\. Разделив все части этого
равенства на и, получим:
^ = ^ + ^,тнс1= а?,,,) + af (8.4.2)
п п п ^
— это правило читается так: «Общая дисперсия наблюдений равна
сумме межгрупповой дисперсии (это дисперсия ci\,) групповых средних) и
внутригрупповой дисперсии (это средняя а? из групповых дисперсий)».
Для выяснения того, влияет ли фактор А на результативный признак:
в модели М1 проверяют гипотезу Hq. 0<') = 9<^^ = ... = 0<^) = О (если она
будет принята, то для всех / и к математическое ожидание Л/У^'^ = MY
185
[см. формулу (8.4.1)], а это означает, что при переходе от одного уровня
фактора к другому генеральная средняя не изменяется, т. е. фактор А не
влияет на У;
в модели М2 проверяют гипотезу Hq:cI=0 (ее принятие будет
означать, что эффект 6 постоянен, он не зависит от того, какие уровни
фактора А попали в случайную выборку, т. е. А не влияет на Y).
Критерии проверки этих и других гипотез, а также оценки
параметров модели (8.4.1) приведены в табл. 8.5.
V Задача 8.7. Исследователь хочет выяснить, отличаются ли четыре способа
рекламирования товара по влиянию на объем его продажи. Для этого в каждом из
случайно отобранных четырех однотипных городов (в них использовались
различные способы рекламы) были собраны сведения об объемах продажи товара
(в денежных единицах) в четырех магазинах и вычислены соответствующие
выборочные характеристики:
Способ рекламы
Объем продаж
п.
1
уо
1
1
140
144
142
145
4
142,75
4,92
2
150
149
152
150
4
150,25
1,58
3
148
149
146
147
4
147,5
1,67
4 = v
150
155
154
152
4
152,75
4,92
Можно ли на 5%-ном уровне значимости считать влияние доказанным?
Решение. Здесь факгором А является способ рекламы; зафиксированы
четыре его уровня, и выясняется, различаются ли по своему влиянию именно
эти уровни, - это модель Ml однофакторного анализа.
Обсудим, можно ли считать выполненными допущения модели (8.4.1), а именно:
y1^'^ = MY + 0^''^ + £^\ /, А: = 1,...,4, (8.4.3)
где е^'^ независимы и е^'^ ~ М{0,Сц).
Так как Л/Ки все 0^'^ - постоянные величины, то при выполнении (8.4.3)
наблюдения у['^ независимы и все
Yl>^~N(ai = MY + Q^'\cj=c\).
(8.4.4)
186
Допустим, что независимость наблюдений гарантируется организацией
эксперимента; условие же ^8.4.4) означает, что объем продаж при /-м способе
рекламы имеет нормальный закон распределения с математическим ожиданием
а, = UY -ь 9^'' и с дисперсией, одинаковой для всех способов. Допустим, что
нормальное распределение имеет место. Используя критерий Бартлетта
(см. табл. 8.3), убедимся, что результаты испытаний позволяют принять
гипотезу Н'^:af =... = а4. Вычислим
135^ ЗХ1п(з.27Д?)
1 +
3-3V3 3-4,
по табл. П. 4.3 при А: = V - 1 = 3 и /7 = а = 0,05 найдем xL = Ха = 7>82; так
как 1,538 < 7,82, гипотезу Н'^ принимаем.
Теперь проверим ключевую гипотезу дисперсионного анализа Яц: 9^'^ =... =
= 9^=0:
ВЫЧИСЛИМ S\ = 220,19, S\ = 39,27, S^ = 259,46;
убедившись в справедливости равенства (8.4.2), найдем оценку (8.4.5)
s\ = ЪЭ,П1\2 = Ъ,27 дисперсии о\;
проверим, выполняется ли неравенство (8.4.6):
потабл.П.4.4приА:, = 3,А:2=12и/7='а = 0,05найдем ^2„ = F„ = 3,49. Так
как 22,43 > 3,49, неравенство (8.4.6) не выполняется. Поэтому гипотезу
Hq-. 9^'' =... = 9^^' = О отклоняем: считаем, не все четыре способа
рекламирования продукции одинаково эффективны; при этом влиянием способа рекламирова-
ния объясняется ц^^^ ■ \ 00% = -у • 100% = 84,9% вариации объема продаж.
Далее, используя условие (8.4.8), можно выяснить, сравнимы ли по
эффективности любые два из предложенных четырех способов рекламы.
Изменим условие задачи. Предположим, что способы рекламирования
товара не заранее фиксированы, а выбраны случайным образом из всего набора
способов. Тогда выяснение вопроса о том, сравнимы ли по эффективности все
способы рекламирования (именно все, а не только те четыре, которые попали в
выборку), сводится к проверке гипотезы Яд: Ge = О модели М2. Критерий ее
187
проверки такой же, как и в модели Ml. Так как усломю (8.4.6) принятия
гипотезы Яд: Ge = О не .выполняется, гипотезу забраковываем, по крайней мере до
получения дополнительных данных: считаем, что способы рекламирования
товаров (во всем наборе этих способов) отличаются по эффективности. ▼
IMmimuiS.S
Ml
М2
9^'', /■ = 1 + V,— детерминированные
V ,.,
величины, при этом 5^в^''л,=0
/=1
9^') ~ N{0,Cq), 1= 1 + V, — случайные
валичины, независимые между собой и
с еу.кя^Х + П/
MY = Y
S/( = S/(/{n-v) — несмещенная оценка дисперсии а
е(') = у(')_у/ = i^v
R
.2^\ ^А -г) Чу-о
«=*
■-S
(8.4.5)
— несме-
щенная оценка дисперсии Cq
Яо:в^' =...= 9^^' =0 принимают, если
Яд: CTg =0 принимают, если
^'^-'•"-^)=Ш'^-.
(8.4.6)
Если условие (8.4.6) не выполняется, гипотезу Н^ не принимают и вычисляют
(оэффициент детерминации
^1/a=S'a/S' (8.4.7)1
— долю вариации наблюдаемых «игреков», объясняемую влиянием фактора А.
Яо:9(')=9(^), приЯ,:9('>9*9(^),
принимают, если
у(1) _ yU)
k(«-v)|=
л, л
'"у
<L
(8.4.g)
Nq'. my = Oq, при Я,: MY ;* fl(), принимают, если
\У-Оо\
4sll{n-v)l^
|/(v-l)|= , 1^ H, .</„
188
Двухфакторный дисперсионный анализ
(с одинаковым числом т > 1 наблюдений
при различных сочетаниях уровней факторов)
В основе двухфакторного дисперсионного анализа лежит следующая
вероятностная модель:
К/'-^) = A/K+eJ) +ву) +ei;^4ef-^l (8.4.9)
где У^' — значение случайной величины Y, принимаемое при уровне
A^'',i= 1,2,..., v^, факторау4и уровне B^^',j= 1,2,..., v^, фактора 5вА:-м
наблюдении, к = \,2,...,т; Q^^'^^f'^^AB^ ~ эффекты влияния на У^'"'''
соответственно уровней Af'^, Bf^^ и взаимодействия А^'"^ и BfJ>; е[''^' —
независимые случайные величины, отражающие влияние на Y^ '■'' некой*
тролируемых остаточных факторов, причем е[''-'^ ~ N[0, а^).
По наблюдениям вычисляют общую вариацию 5^ признака Ки ее че-*
тыре составляющие — S^,S\,S^g, 5\, отражающие влияние
соответственно факторов А, В, их взаимодействия и остаточных факторов:
S' = li lW'-^)-K .где У = 1 I iKf^V". « = v.v,m;
S'a = v,m2 (Fi')-y)\ где Fj') = I tri'-^Viv,n,);
Si = v,m 2 (n^) - y)\ где yO) = 2 i k/'-^)/(v,.);
^^,-2 2(Fii^)-Fi')-Fy)-ьF)^гдe fii^)=iKMA;
Нетрудно убедится в том, что S^ =Sl+Sl+ S^ + Sl.
Оценки параметров всех трех типов модели (8.4.9): Ml, М2 и МЗ,
проверяемые гипотезы и критерии их проверки приведены в табл. 8.6.
В моделях М2 и МЗ предполагается, что все случайные эффекты
независимы как между собой, так и с е[''^'.
189
Ml
' = 1 + V^, J = \->-Vg,
— детерминированные величины .
ei;) = fi')-f. ,/ = Uv,
ey) = fi^)-F. y^i*v.
6(Y).yM_fW_704F
Я.:в^ = ... = в(^^) = 0
принимают, если
^2 _
^.:в^=...=в(;')=о
принимают, если
^2
Я^:в!;.') = ... = в^-^')=0
При непринятии какой-либо из гипотез
показывающий долю вариации наблюдг
М2
Q^2~n{o,c,^), е^~лг(аав,).
^^'J^~n(o,c,J,
» = 1 + V^, J = \+Vg
о2
ifv - у. т^ - '^я
я-v^v.
4^=(*^--5У/Н*)
*в, =(4--5^*)/Н.«)
*в^=(*^д-4)/'"
Я^:<=0
принимают, если
Hg:al^=0
принимают, если
•^у4Д
ffAB-<yl,s=^
принимают, если
Н^, Hg, Hj^g вычисляют соответствующий
1емых «игреков», объясняемую влиянием
Примечание. Используются такие обозначения:
190
Таблица 8.6
мз
e!i^ '■=i-v,.
— детерминированные величины;
еу) ~лг(о. GeJ. y=uv^,.
e!li^ ~ ЛГ(0. Ge^ J
2
— несмещенная оценка дисперсии G/;
e5)=fi')-f. /=i.v,.
4s=(4-4)/{'f^A)
*e,, =K-4)/'"
Я,:в(') = ... = вЬ)=о
принимают, если
Нв:с1^=0
принимают, если
^2
ffAB-^O^B ^^
вУ\ J = \^y>B'
— детерминированные величины;
e!;)-Ar(O.GeJ. / = l-v,.
e!;y^~MO'%.)
ey^ = fi'^-f. y = l^v^,.
*в^=(*^-4)/(»^д)
4^={'\b-'\)I'"
Я,:ва)=... = 9Ь)=0
принимают, если
^AB
Я,:а§,-0
принимают, если
s^ -
F(v^-l.n-V^V^) = -f<Fj„
^R
ffAB-<^l^=^
^R
коэффициент детерминации: Цу/л ~ ^A1 ^ •
фактора A, фактора ^ и их взаимодействия.
Лу/Д -^в/^ ' ^r/AB -^Ав/^ '
^b^VK-1). 4='У1/К-1). s'AB=Sy[{v^-\bB-i)]-
191
Вопросы и задачи
1. Приведите примеры статистических гипотез (основной и
альтернативной) из области коммерческой или биржевой деятельности. j
2. Основную гипотезу отклоняют, если значение статистики
критерия попадает в критическую область. Почему?
3. Прогноз задолженности квартплаты по РЭУ таков: средняя
задолженность равна 120 000 руб. Среднее квадратичное отклонение
задолженности а = 20 000 руб. Выборочные подсчеты по девяти РЭУ дали среднюю
задолженность 135 000 руб. Принимается ли прогноз или отвергается при
а - 0,05? Какова вероятность того, что вывод будет ошибочным?
4. Что такое мощность критерия? Какой критерий называется
наиболее мощным? Докажите справедливость выражений для мощности
критериев, приведенных в табл. 8.2.
5. Партия изделий принимается, если дисперсия контролируемого
размера не превышает 0,2. По выборке л = 40 изделий вычислена
f = 0,25. Можно ли принять партию при а = 0,05?
6. Статистика по страховому обществу утверждает, что только 3 из
каждых 10 визитов страхового агента заканчиваются заключением
договора о страховании. Однако агент Иванов в результате 100 визитов за
месяц заключил 40 договоров. Если Вы — начальник Иванова, что Вы
решите: случайны его результаты или они свидетельствуют о его высокой
квалификации?
7. Поставщик ламп накаливания утверждает, что средний срок
службы лампы равен 2500 ч. Для выборки из 37 ламп средний срок службы
равен 2325 ч при среднем квадратичном отклонении 600 ч. Проверьте
справедливость утверждения поставщика при а = 0,05. Вычислите
мощность критерия, если Я,: а = 2390.
8. Средненедельный объем продаж для 15 торговцев района/1 составил
3000 дол. при среднем квадратичном отклонении 500 дол., а для 10 торгов^
цен района В — 2600 дол. при среднем квадратичном отклонении 600 дол.
Значимо ли различие средненедельных объемов продаж в районах Ан В
при 5%-ном уровне значимости? Значимо ли превышение средненедель-
ного объема продаж в районе А по сравнению с районом В при 5%-ном
уровне значимости? Чем отличается этот вопрос от предыдущего?
9. Сторонники строительства крупной ГЭС утверждают, что по
крайней мере 50% населения поддерживают данное строительство. Из 200
опрошенных 40% высказались заданный проект, а 30% — за
строительство малых ГЭС. При 5%-ном уровне значимости проверьте
справедливость утверждения сторонников крупной ГЭС; сравните количество сто-?
ройников крупной и малых ГЭС.
10. На протяжении месяца в произвольно отобранных районах Лн В
фирма проводила Новые мероприятия по расширению торговли, а в двух
других произвольно отобранных районах С и £) торговля велась тради*
192
ционными методами. Объемы продаж за текущий и за предыдущий
месяцы по четырем районам таковы:
А
75
115
В
45
75
С
30
40
D
150
170
Объем продаж за предыдущий месяц
Объем продаж за текущий месяц
По-видимому, в районах, где фирма проводила специальные
мероприятия, она добилась больших успехов, чем в остальных районах.
а) Определите ожидаемый объем продаж по каждому району за
текущий месяц (для вычисления доли суммарного объема продаж,
ожидаемой для каждого района в текущем месяце, используйте данные о
продажах в предыдущем месяце).
б) Значима ли при 5%-ном уровне значимости разность между
распределениями наблюдаемых и ожидаемых частот для текущего месяца?
11. Проверьте гипотезу о законе распределения, который
определяется двумя параметрами, причем значение одного из них известно,
по следующим данным:
/И;
nPi
2
1
5
3
15
11
14
15
15
18
21
24
12. Сравните при 1%-ном уровне значимости четыре фирмы по
качественному составу годной продукции, классифицированной по сортам,
по следующим выборочным данным:
Сорт
1
2
3
1
147
109
39
Фирма
2 3
184 120
113 192
57 33
4
282
139
49
13. Фирма с целью установления известности ее продукции опросила
в каждом из 100 населенных пунктов по 20 человек. Распределение
числа X, незнакомых с продукцией фирмы таково:
X,.
Число пунктов
0
65
1
20
2
10
3
3
4
1
5
1
Можно ли при 5%-ном уровне значимости считать, что число
незнакомых с продукцией фирмы подчиняется закону Пуассона?
14. По данным задачи 7 (см. гл. 7) выясните, можно ли считать, что
продолжительность жизни имеет показательный закон распределения?
Примите а = 0,01; 0,05.
15. Приведите примеры экономических задач, требующих
использования дисперсионного анализа (моделей Ml, М2, МЗ).
7—670
193
16. Найдите дисперсию каждой из следующих фупп:
I
II
13
28
11
26
10
25
9
24
7
22
Будет ли дисперсия 10 значений, полученных путем объединения
этих групп, меньше, больше или равна фупповой дисперсии?
17. В трех магазинах, продающих товары одного вида, данные
товарооборота (в д.е.) за 8 месяцев работы таковы:
Магазин
1
2
3
1
19
20
16
2
23
20
15
3
26
32
18
Месяц
4
18
27
26
5
20
40
19
6
20
24
17
7
18
22
19
8
35
18
18
Допустив, что условия дисперсионного анализа выполняются,
проверьте гипотезу о равенстве средних товарооборотов магазинов.
Оцените параметры соответствующей модели дисперсионного анализа. Если
гипотеза отклоняется, оцените долю вариации товарооборота,
объясняемую влиянием «магазина», проведите попарное сравнение средних.
Примите а = 0,01.
Измените условие задачи: предположите, что три магазина случайно
отобраны из всей совокупности магазинов, продающих товары одного
вида. Влияет ли «магазин» на средний товарооборот? Оцените
параметры соответствующей модели дисперсионного анализа.
18. Из совокупности экспертов извлечена случайная выборка в 10
человек. Каждый эксперт оценивал случайно выбранные 20 студенческих
работ по пятибалльной шкале. Общая вариация оценок 5^ =1831,6,
вариация оценок, обусловленная различиями экспертов, S^ = 94,32. Кто
в среднем отличается больше: эксперты или студенческие работы,
которые оценивает один и тот же эксперт?
19. Считая уровни факторов/1 и ^фиксированными величинами,
проведите двухфакторный дисперсионный анализ по следующим данным:
^(1)
лт
лт
6,3
6,5
7,9
В(1)
6,3
6,8
7,9
6,4
6,9
8,0
7,2
7,9
9,0
В(2)
7,3
7,9
8,9
7,5
8,0
8,9
20. Проведите полное исследование различных моделей двухфакторно-
го дисперсионного анализа по следующим данным: v^ = 3, Уд = 5, /и = 2,
194
Глава 9
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
Корреляционный анализ и рефессионный анализ являются
смежными разделами математической статистики и предназначены для
изучения по выборочным данным статистической зависимости ряда величин,
некоторые из них являются случайными. При статистической
зависимости величины не связаны функционально, но как случайные
величины заданы совместным распределением вероятностей. Исследование
взаимозависимости случайных величин приводит к теории корреляции
как разделу теории вероятностей и корреляционному анализу как
разделу математической статистики. Исследование зависимости случайной
величины от ряда неслучайных и случайных величин приводит к
моделям регрессии и рефессионному анализу на базе выборочных данных.
Теория вероятностей и математическая статистика представляют лишь
инструмент для изучения статистической зависимости, но не ставят
своей целью установление причинной связи. Представление и гипотезы о
причинной связи должны быть привнесены из некоторой другой теории,
которая позволяет содержательно объяснить изучаемое явление.
Формально корреляционная модель взаимосвязи системы случайных
величин А"' = (А',, А'г,..., ДГ^.) может быть представлена в следующем виде:
X = f{X,Z),
где Z— набор внешних случайных величин, оказывающих влияние на
изучаемые случайные величины.
Примером корреляционной связи является статистическая
взаимозависимость между отдельными частями человеческого тела.
В случае же одномерной (парной и множественной) рефессии одна
случайная величина (зависимая переменная Y) зависит от ряда
неслучайных факторов, которые представлены независимыми переменными
х' = {x^,X2,...,X|^), и от набора случайных величин Z:
Y = f{x,Z).
7* 195
Примером регрессионной зависимости служит зависимость между
урожайностью определенной сельскохозяйственной культуры и
влияющими на нее природными и экономическими факторами.
Первый параграф настоящей главы посвящен корреляционному
анализу как инструменту исследования статистической
взаимозависимости на основе выборочных данных. В остальных парафафах приводятся
сведения по исследованию зависимости результирующих
экономических показателей от детерминированных природно-экономических
факторов с помощью регрессионного анализа.
§ 9.1. Введение в корреляционный анализ
Парная корреляция
Корреляционная зависимость двух случайных величин задается
моделью
X = X{Y,Z), Y = Y{X,Z), '
где Z— набор внешних случайных факторов.
Парная корреляция занимается изучением характеристик взаимосвя«
зи двух случайных величин. Основой получения этих характеристик слу}
жит совместное распределение случайных величин i
F{x,y) = P{X<x,Y<y}. 1
Коэффициент корреляции уже был рассмотрен в § 3.6: ^
i
Линиями рефессии упохнхпоу называются линии условных
математических ожиданий:
y{x) = M{YIX = x), x{y) = M{XIY=y). (9.1.2J
Линии условных дисперсий характеризуют, насколько точно лини!
регрессии передают изменение одной случайной величины при измену
НИИ другой:
1
a\ix = D{YIX = х) = Л/{[У -У(х)]7^ = х}. (9.1.^
^xiY =D{XIY =у) = м1^Х -x{y)f Iy =у\
196
Средние из условных дисперсий характеризуют точность прогноза
одной случайной величины с помощью другой на всем диапазоне
изменения последней:
4д=Л/[Г-Я^)]', (9.1.4)
Точные (или приближенные) прямолинейные рефессии
задаются следующими коэффициентами:
Pi-zr-P—• Р2-ТГ-Р—'
Ох Ох Оу Оу
a^=MY-^^MX, Ог =Л/А'-р2Л/>'.
Если случайные величины А" и ^независимы, то р = О, все условные
математические ожидания и дисперсии не зависят от фиксированного
значения другой случайной величины и совпадают с безусловными:
y{x) = MY, х{у) = МХ, о\/х=а1, Ох/г=<^\-
В случае нелинейных рефессии степень концентрации
распределения вблизи линии рефессии показывает корреляционное отношение
Лкд =^M[y{X)-AfYf=\-^. (9.1.5)
Оу Оу
Как видно, корреляционное отношение меняется в пределах от О до 1,
оно равно единице тогда и только тогда, когда о\/х = О, т.е. все
распределение сосредоточено на кривой рефессии (имеет место
функциональная зависимость). Это отношение равно нулю тогда и только тогда,
когда линия рефессии упох представляет собой горизонтальную прямую
линию, проходящую через центр распределения, т.е. если Yh ДГнекорре-
лируемы. Можко доказать, что во всех случаях р^ ^ Л^/к> Р^ ^Лкд-
Множественная корреляция
При изучении корреляционной зависимости между более чем двумя
случайными величинами А",, ^fj» —. Ajj. с заданным совместным
распределением используют множественные и частные коэффициенты
корреляции и корреляционные отношения.
197
Применение обычных коэффициентов па)рной корреляции при
множественной корреляции для изучения связи двух случайных величин
может привести к неправильным выводам. Если коэффициент парной
корреляции между двумя случайными величинами уменьшается или
становится близким к нулю при других фиксированных случайных
величинах, то можно сказать, что взаимозависимость этих случайных величин
в значительной мере (или определяющим образом) имеет место
благодаря третьим факторам. Если же при фиксации третьих факторов
степень взаимозависимости двух случайных величин возрастает, то это
означает, что эти факторы «маскировали» истинную взаимозависимость
двух случайных величин.
Частный коэффициент корреляции — это мера линейной зависимости
между двумя случайными величинами из некоторой совокупности
случайных величин X^, A'j,..., А](., когда исключено влияние остальных
случайных величин:
_M[Y^-MY^){Y^-MY^)
Р..2.=Р..2.(з .)= ^ • ^'Г ^ —^ (91-6)
где yj - А", - А",, Y2-X2-X2, лX^-X^^^^ t)'^2-^2»(3 *) ~ "^""
лучшие линейные приближения величин А",, Х2 случайными величинами
Xj,..., Х/^, коэффициенты которых определяются из таких соотношений:
Г Ir \ ( к
min Л/
А-.-ао-ХаД,
1=3
min Л/
^2-«о-1«/^/
Частный коэффициент выражается через элементы корреляционной
матрицы R = ||р^.[|, составленной из коэффициентов парной корреляции:
р'-^-(^ *)""V^' ^'-'-^^
Здесь R.^ — алгебриическое дополнение элемента р,у в
корреляционной матрице.
Выше было показано, как по различию между обычным и частным
коэффициентами корреляции можно судить о зависимости X^, Х2 между
собой и от других случайных величин. Если случайные величины
X^, A'j,,.,, Xf^ попарно некоррелируемы, т, е, р^ = О при i '^J, то и все
частные коэффициенты корреляции равны нулю.
Множественный коэффициент корреляции служит мерой линейной
зависимости между случайной величиной X^ и некоторым другим
набором случайных величин Jfj. •••> ^^ Множественный коэффициент корре-
198
ляции р, /J ^ч определяется как обычный коэффициент парной
корреляции между А", и X*, где X* — наилучшее линейное приближение А",
случайными величинами Х2, ..., Х/^, коэффициенты которого
определяются из соотношения
Г 1г
min Л/
X^-щ- Y^^iXi
При к= 2 множественный коэффициент корреляции совпадает с
обычным коэффициентом корреляции.
Множественный коэффициент корреляции выражается через
элементы корреляционной матрицы следующил} образом:
л,,
где det R — определитель матрицы R; R^^ — алгебраическое дополнение
элемента р,,.
Если pj, = 1, то величина X^ с вероятностью, равной единице, равна
линейной комбинации случайных величин ^fj. •••> ^t- С другой стороны,
р, = О тогда и только тогда, когда X^ не коррелирована ни с одной из
случайных величин ^fj...., А](., т.е. р,2 =... = рц. =0.
Для вычисления множественного коэффициента корреляции можно
также использовать следующую формулу, которую легче
интерпретировать, чем формулу (9.1.8):
2 , ^?.(2 к) , Dx;
Р"=Р"(2 *) = ' ^ = '-ЛУГ ('■'■')
Именно это выражение оправдывает назначение коэффициента
множественной корреляции как показателя тесноты линейной связи. В
самом деле, чем лучше приближается случайная величина X^ линейными
комбинациями случайных величин Х2, ..., Х^ тем ближе модуль этого
коэффициента к единице; чем хуже линейное приближение, тем этот
коэффициент ближе к нулю.
Совокупность методов оценки корреляционных характеристик и
проверка статистических гипотез о них по выборочным данным
называется корреляционным анализом. В корреляционном анализе
используются следующие основные приемы:
1) построение корреляционного поля (двумерных и трехмерных
сечений пространства, если речь идет о многомерном пространстве значений
случайных величин А",, A'j,..., Х^) и составление корреляционной таблицы;
199
2) построение выборочных коэффициентов корреляции и
корреляционных отношений;
3) проверку статистических гипотез о значимости связи.
Некоторые из этих приемов уже были рассмотрены в гл, 8, поэтому
приведем лишь основные результаты, касающиеся методов и приемов
корреляционного анализа.
Анализ парной корреляции
При изучении по выборке (х,, j',), {х^,У2),..., {х„,у„) корреляционной
зависимости двух случайных величин общую картину их взаимной
изменчивости можно получить, изобразив на координатной плоскости все
выборочные точки. Это изображение называется корреляционным полем.
На рис, 9.1 приведено корреляционное поле, отражающее зависимость
между ростом и весом человека.
„'
у
70-
60-
50-
0
к
•
•
•
'^'Z^ •
150 160
%у/^
%i
%/
/ •
170
%f
• /yl^
II
180
• ^/^
•
X
Рис. 9.1
Если выборка небольшая, как это имеет место в примере 9.1
(см. рис, 9.1), то оценки корреляционных характеристик вычисляют
непосредственно по выборочным данным с помощью следующих формул:
оценки первых моментов
_ 1 Л - \ ^
x=-LXj, y=-l,yj,
«y=i rij=i
оценки вторых моментов
(9.1.10)
Ai.i = cov {X, У) = - 2(xj -x\yj -у).
(9.1.11)
200
По этим оценкам, в свою очередь, определяются оценки
коэффициента парной корреляции и приближенных линейных регрессий:
bxCSy
ai=y-^ix, p, =p
_ * ^Y
(9.1.12)
(9.1.13)
а2=х-р2У, p2=P-
B качестве примера рассмотрим расчет корреляционных
характеристик парной зависимости между ростом и весом наугад взятого студента-
первокурсника.
Q Пример 9.1. Исходные данные приведены в табл. 9.1. Для расчета
корреляционных характеристик воспользуемся формулами (9.1.10) - (9.1.12)
Таблица 9.1
Номер
наблюдения
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Е
Рост, см
^
165
171
182
165
1ВЗ
1В0
183
166
173
1В4
16В
164
170
174
172
2620
х^-х
-9,7
-3,7
7,3
-9,7
8.3
5,3
в,з
-В,7
-1,7
9.3
-6,7
9,3
-4,7
-0,7
-2,7
—
Вес, кг
У!
72,9
48,4
6в,3
64,1
62,7
76,0
72,В
50,6
52,3
68,6
52,6
72.8
61,6
66, В
56,5
945
У,-У
9.9
-14,6
3,6
1,1
-0,3
13
9,В
-12,4
-10,7
5,6
-10,4
9, В
-1,4
3,В
-6,5
—
201
Используя табл. 9.1, прежде всего находим средние арифметические выбо*
рочных значений:
_ 1 ^ 2620 ,_. _
"=Т1,?,">=—= '''''■'
y = ±i„. =215=63,0.
Вычислив отклонения от средних, одноименные отклонения возведем в
квадрат, разноименные - перемножим. Суммируя, имеем:
1(х,.-х)^= 747,35; ik--у)'=1153;
15
1(х,-ф,-у) = 482.
Используя приведенные выше суммы, получаем:
А2
= -^i(xy-xf =^ = 49,82; д;, =7.06;
a^r=^lb-7f =-4^ = 76,87; а,=8,77;
Теперь можно определить эмпирический коэффи1^ент корреляции и оценки
коэффициентов приближенной прямолинейной регрессии:
._ hi _ 32,12
Р = ^А!- = ,::';\ =0,519;
ОхОу 7,06-8,77
Р,=р-?^ = 0,645; а,=7-р,х = ^9,7;
^х <
р2=р5х = 0,418; а,=х-р,7 = 148,4;
Соответствующие пряйолинейные линии регрессии изображвны HS
рис. 9.1. •
202
Если выборочных данных много, то их объединяют в
корреляционную таблицу, в каждой клетке которой указывают число попавших в нее
выборочных данных я^^. Клетке таблицы соответствует на
корреляционном поле прямоугольник с координатами центра:
х^ =Хо+(*-!)Ах, к = \,...,п^,
при этом
т=\
к=\
где «j(, Пу — число paBHiMx интервалов длины Ах, Ау, на которые разбиты
области выборочных значений случайных величин X, Y.
При использовании данных корреляционной таблицы формулы
($.1.10) и (9.1.11) принимают следующий вид (они отлйчаютря от
предыдущих на пофешность округления, возникшую в результате замены
{(оординат каждой выборочной точки координатами центра
прямоугольника, в который эта точк«а попала):
1 "'
У=- I«m>'m.
1 "х
-\2
1 "у
^^=-1 "ki^k -х) . о^г = - I "п,{Ук -у) .
(9.1.14)
По данным корреляционной таблицы можно построить
эмпирические линии репрессии:
1 1i
"1с 1я=4*
%т) = —i**"^. m = l,-.,«r
(9.1.15)
Если линии эмпирической рвфессии заметно отклоняются от
линейной формы, то в качестве меры связи необходимо использовать
выборочные корреляционные отношения:
203
'^r/x=jYty{4)-yfnJoy,
Па-/)- = J- i [x{ym)-xfn„ bx-
(9.1.16)
Величину Цу1Х ~P используют в качестве индикатора отклонения
регрессии от линейной.
Проверка гипотезы о значимости связи основывается на
распределениях выборочных корреляционных характеристик. В том случае, если
совместное распределение случайных величин X, У нормальное,
выборочный коэффициент корреляции значимо отличается от нуля, если
Р^>, , \,/2' (9.1.17)
\ + {n-2)ltl
где f„ =?„(а1-2) — критическое значение распределения Стьюдента с
AJ — 2 степенями свободы, соответствующее уровню значимости а.
Если связь значима, то для истинного коэффициента корреляции
имеет место следующий приближенный доверительный интервал (при
больших выборках, см. также гл. 8):
1-р2 . 1-р2
р-н„-^<р<р + н„-7^, (9.1.18)
где и^ — критическая граница для нормального распределения,
соответствующая уровню значимости а.
Анализ множественной корреляции
В случае множественной корреляции основой статистического
анализа служит матрица выборочных значений А'=рсу, ; у' = 1,...,и,
г= 1, ..., к; п — объем выборки, к — число рассматриваемых случайных
величин. Для анализа парной зависимости могут быть использованы
формулы, приведенные выше для анализа парных корреляций. Однако
парная зависимость осложнена влиянием других случайных величин.
Поэтому наряду с корреляционной матрицей, состоящей из
коэффициентов парных корреляций, и с другими характеристиками парной
корреляции необходимо использовать и выборочные характеристики
множественной корреляции — частные и множественные коэффициенты
корреляции.
204
Выборочную оценку коэффициента частной корреляции случайных
величин Л*,, Aj, если исключено алияние остальных случайных величии
V .... Xf^, можно получить с помощью следующего выражения [аналога
рьфажения (9.1.7)]:
о
Pl,2.=Pu.(3 *)=Т1б • ('•'•''>
где R-ij — алгебраическое дополнение элемента Р^, выборочной
корреляционной матрицы к.
Сравнивая выборочные обычный и частный коэффициенты парной
корреляции р^ и р,у., можно делать выводы о том, насколько взаимоза^
0исимость между величинами X., Xj вызвана их собственной
взаимосвязью и зависимостью каждой из них от других случайных величин
(различные варианты таких выводов были даны в начале настоящего пара-
фафа).
В качестве выборочной оценки коэффициента множественной
корреляции используют выражение
1 " г 1^
где 0| =— X Р^л ~^1 ~ полная выборочная дисперсия случайной ве-
Личины Л",;
где Ху| — наилучшие линейные приближения выборочных значений x^.j
№1борочными значениями х„,..., х^, т.е.
/«2
Здесь ао,0(2,...,6(^ определены методом наименьших квадратов:
»( к Л
]Л /»2
2
>min.
Подробнее определение оценок коэффициентов линейной регрессии
Ч их свойства рассмотрены в последующих параграфах настоящей главы.
205
Чем ближе значение выборочного коэффициента множественной
корреляции к единице, тем лучше приближение случайной величины
линейными комбинациями случайных величин Х^, ..., Л'^^.
§ 9.2. Регрессионные модели
как инструмент анализа и прогнозирования
экономических явлений
Для описания, анализа и прогнозирования явлений и процессов в
экономике применяют математические модели в форме уравнений
или функций. Модель экономического объекта (или
производственного процесса), отражая основные его свойства и абстрагируясь от
второстепенных, позволяет судить о его поведении в определенных
условиях.
В случае применения регрессионных моделей результат действия
экономической системы или объекта в виде одного или нескольких
выходных показателей представляется как функция влияющих на него
факторов. Некоторые из этих факторов оказывают существенное влияние на
результат, другие — весьма незначительное. Как правило, существенных
факторов немного, в то время как несущественных достаточно большое
число, поэтому последними полностью пренебрегать нельзя. Как
известно из политэкономии, источником любого богатства является труд
(прошлый или настоящий). Поэтому к числу основных факторов при
изучении экономического объекта относят обычно настоящий труд (или
трудовые ресурсы в той или иной мере) и прошлый труд (энергия,
сырье, материалы, оборудование, здания, сооружения и т.д.) Вместе с тем
труд прилагается при определенном состоянии внешней среды, т.е. при
определенных экономических и природных условиях, поэтому
соответствующие факторы также должны найти отражение в модели.
В процессе производства и распределения продукции имеют место
массовые многократно повторяющиеся события, например
многократное изготовление одинаковых деталей, узлов, машин в крупносерийном
производстве, многократно повторяющиеся акты продажи в
продовольственных и промтоварных магазинах. Несмотря на развитие экономики
и ее отдельных частей, на протяжении относительно небольших
временных периодов и в пределах отдельных экономических подсистем имеет
место стабильность в условиях совершения массовых событий. По
крайней мере (особенно при прогнозировании), подразумевается
возможность многократного повторения производственной ситуации, быть
может, при других значениях существенных и несущественных
факторов, однако при относительно стабильном комплексе внешних
условий.
206
Таким образом, приходим к следующей теоретико-вероятностной
схеме. Результирующий показатель у яаляется функцией существенных
(Хр ..., х^ и несущественных (е,,..., е^) факторов:
>' = F(x,,...,x^,ep...,e„).
Исходя из предположения эволюторности* поведения
экономической системы на относительно небольшом временном интервале и при
сравнительно малых изменениях переменных, с помощью разложения в
ряд Тейлора получаем:
к п
/■ = 1 v=l
а =—М г" е" еМ / = 1 к
в =—М г" е" еМ v = l я
Hv -V l"*! ' •••• -^t' ''I > •••> ''л I' V — J,..., «,
Дх, = X, - xf, ДЕу = Ey - Ey, Л/Еу = 0,
Дх = тах(|Дх,| \l^\^-< ^^ - тах(|ДЕ,|,..., |Дел|),
где о(Д) — бесконечно малая величина большего порядка малости,
чем Д; Хр-.-.х^^.Е^ е" — набор значений факторов, в окрестностях
которого изучается поведение экономического объекта.
В случае независимости случайных факторов, их относительной
малости (в смысле алияния на результат) и достаточно большом числе,
согласно центральной предельной теореме теории вероятностей,
получаем, что случайная состааляющая
л
v=l
распределена по закону, близкому к нормальному с параметрами Мг = О,
Dt = а^. Если эти предположения нарушаются, то возможно
образование другого распределения.
Несмотря на инерционность поведения экономических систем (особенно
больших), возможны и резкие изменения в связи с достижениями научно-технического
прогресса (например, появление новой технологии); в новых условиях надо
рассматривать другую функцию.
207
Детерминированная составляющая регрессионной модели
F[x^, ..., х^, е,,..., е„) = ао + ^а,- Дх,- +о{Ах)
/'=1
при небольших изменениях независимых переменных (значений
существенных детерминированных факторов) является линейной функцией.
Если интервалы изменения независимых переменных увеличиваются, то
в случае существенной нелинейности функции следует рассмотреть ес
разложение в ряд Тейлора более высокого порядка:
/(Дх,,...,Ах^) = ао + |;а, Дх;+ Х а^. Дх,ЛХу+ o[(Axf |,
а,, =
^ ЭХ.ЭХ;
/""у
/• = 1 /•,У=1
, (Дх) =тах1Дх,ДХу
Введя новые переменные Zy = Дх,Дх^, вновь получим линейную
детерминированную состааляющую рефессионной модели:
к к
/(Дхр..., Дх^, г,,,, г,,2, -, г*.*) = «о + ia,. Дх,. + i а^ Zy +o\{Axf].
В принципе с помощью полиномов можно с высокой степенью
приближения описать любую достаточно «гладкую» (эволюторную)
функцию, однако это связано с пояалением большого числа коэффициентов,
которые можно определять на основании гораздо большего объема
исходных данных. Поэтому в случае невозможности линеаризиробаТ1{
функцию (разлагая в ряд или преобразуя) при небольшом числе
коэффициентов используют методы нелинейного оценивания (см. § 10.3).
§ 9.3. Парная линейная регрессия
в случае парной линейной рефессии имеется только один
детерминированный фактор X и линейная рефессионная модель записывается
следующим образом:
у = у{х) + г, Я^) = ао+«1^. (9-З.Ц
или
Ядг) = а"+а,(х-Хо), а" =у(-«о) = ао+«1^о> (9-3-2)
208
где у{х) — детерминированная состааляющая; е — случайная
составляющая с независимыми значениями Me = О, Dt = а^; а" =у{хо) —
значение детерминированной составляющей в стандартной точке; а, —
теоретический коэффициент регрессии, показывающий, насколько в
среднем изменится детерминированная составляющая, если фактор изме^
нится на единицу.
Оценка параметров регрессимад, а, в условиях конкретной ситуации
проводится по статистической совокупности, которая рассматривается
в качестве выборки:
[yp^l\ У = !.•••.«.
где я -^ число единиц совокупности (наблюдений), или объем выборки.
Как будет показано далее, удобнее всего в качестве стандартной
точки выбирать среднее арифметическое выборочных значений Хд =3с.
В этом случае
Ях) = а"+о,(х-Зс), а"=Ях). (9-3-3)
Я^)=Яг) = «" + «1г. Z=x-x, (9.3.4)
при этом
я я . \ "
I^y = I Х- -Х] = J^Xj -ПХ=0.
у = 1 У=Р у = 1
Для того чтобы определить два коэффициента регрессии по
правилам детерминированной математики, необходимы два уравнения,
однако в условиях вероятностной ситуации этого недостаточно, так как
требуются дополнительные уравнения для определения главных
характеристик случайной состааляющей. В данном случае имеется я уравнений
(я>2):
Уу =ао+а,х + еу, у = 1 я, (9.3.5)
где е.— реализация случайной составляющей, или те у^е я уравнений, но
записанных в другой форме:
УJ=a^'+a^ZJ+eJ, у = 1,...,я, (9.3.6)
Статистические оценки ао,а, параметров рефессии осц, а,
выбираются таким образом, чтобы эмпирические значения детерминированной
составляющей yj =ао +а,Ху как можно ближе находились к
фактическим значениям результирующего признака у» В качестве меры^ близости
209
обычно выбирают сумму квадратов отклонений, реже — сумму модулей
отклонений. Выбор той или иной формы меры близости определяется
статистическими свойствами случайной состааляющей. Так, если
случайная состааляющая имеет нормальное распределение, то оценки, об
ладающие наилучшими свойствами, получают с поКющЪю метода
наименьших квадратов (МНК).
Можно показать, что при распределении случайной составляющей па
закон/Лапласа* следует использовать метод минимальных отклонений,
а в случае равномерно1Ч) распределения — критерий минимизации мак"
симальных отклонений.
Наиболее прост и в определенном смысле наиболее универсален
метод наименьших квадратов, который и используется ниже для расчетов.|
Прежде всего составим сумму квадратов отклонений как функцию bq^^
можных, но не известных параметров Од, а,:
б(ао.а,)=Х(з';-ао-а,х^) .
(9.3.7)
Для минимизации функции необходимо приравнять^ нулю частные
производные по параметрам:
Эб
Эап
Эб
21(з'у-ао-а,х^) = 0,
оо=оо
У=|
^ =-2l(yj-&o-&iXj)xj=0.
I а, =а. J '
а,=а,
Получаем следующую систему из двух уравнений, которая называем
ся системой нормальных уравнении:.
\J=\ ) J=\
(п ^ (п Л
\J=\ J \J=l J J=l
(9.3.8J
Из первого уравнения получаем
ао=у-о,х.
(9.3.9J
Случайная величинах имеет р^пределение Лапласа, если ее плотность равНШ
—е""'*""', где а, \i — парамет^зы.
210
Подставляя это значение во второе уравнение, определяем оценку
другого коэффициента (при этом используем соотношения
lyj(xj -х)= t(yj -y){xj -х)= l,(yj -y)xj,
так как
«1=-?
i=V J=l '
(9.3.10)
Перейдя к стандартным обозначениям, имеем:
л л
lyjij l^yjZj
^'=У' ^^=^^^ = Цг—^ ^J=^j-^' ^yj=yj-y- (9-3-11)
j=\ j=\
Эмпирическая линия рефессии имеет уравнение
y{x)=y■\■a^{x-x), (9.3.12)
т.е. проходит через точку с координатами (Зс, у).
Полученные с помощью метода иаименьшихквадрато»оцеики
параметров регрессии являются несмещенными и состоятельными. В самом
деле, представим каждую из этих оценок в виде суммы
детерминированной и случайной составляющих:
а»=аЧё.
а, = а,+^^^^ • (9.3.13)
Так как А/еу= О, то А/а" = а", А/а, = а,, т. е. оценки не смещены. Эти
оценки имеют сле^^ющие дисперсии и ковариацию:
211
Da, = D
>i
ЬШ
y=i
1^]
Iz]
/'_ л Л
:0.
Iz]
(9.3.14)
cov (a", a,) = Л/(a" - a'')(a, - a,) = Л/
Следовательно, первая оценка всегда состоятельна, а вторая
состоятельна в том случае, когда Х^> ~^ °° "Р^^ "
—> <^о.
У=1
Можно также показать, что рассматриваемые оценки являются
эффективными (т.е. имеющими минимальную дисперсию) в классе
линейных несмещенных оценок.
Построим теперь несмещенную оценку дисперсии случайной
составляющей. Оценками реализаций случайной составляющей е, служат
отклонения фактических значений у. от выравненных yj-, обозначим эти
отклонения через е.:
eJ=УJ-yJ=a° + a^zJ + гJ-a^-a^zJ=(a^-oP) + {al-a^)zJ + гJ.
Оценки коэффициентов регрессии не смещены и Mtj = О, поэтому
Mej = 0. Представляется естественным строить оценку дисперсии на базе
л
суммы квадратов отклонений 5^ej .
Определим теперь коэффициент при этой сумме, при котором оценка
дисперсии является несмещенной. Согласно уравнениям (9.3.13),
л
/=1
ej=Zj-z-Zj „
Izj
1=1
поэтому [Mcj = о, co\(zj,еЛ = 0, j^I, co\(zj,гЛ = Dzj = а^j
212
Mej=Dej =DZj^Dl^D
"•J n
1=1
■2cov(ey,e)-2cov(a,2y,ey) + 2cov(a'',a,2y)-
■■<s + — + -;—--2 2cov
n
1=1
n
n
/=1
"■] n
Izf
1=1
a zj
Izf
1=1
и окончательно
Л/
V^^
=1
:lA/ej=a^(/i-2).
Таким образом, получена следующая несмещенная оценка дисперсии
случайной составляющей:
6'
1
/1-2
1^?
1
- \2
/1-2 у
(9.3.15)
При проверке гипотез и построении доверительных интервалов для
параметров регрессии и всего уравнения в целом необходимо знать
распределения соответствующих величин. Если случайные составляющие е.
распределены нормально, то оценки параметров регрессии и
детерминированной составляющей, являющиеся линейными функциями е^,
J= 1,..., /I, также распределены нормально*. При этом сумма квадратов от-
клонений —г XlJ'/ -У/1 распределена по закону х^ с {п- 2) степенями
свободы. Поэтому при построении доверительных интервалов следует
воспользоваться распределением Стьюдента с (/i - 2) степенями свободы.
Используя уравнения (9.3.13), получаем следующие доверительные
интервалы для параметров регрессии:
y-tp-Y'<a'^<y + tp-T''
4п
4п'
(9.3.16)
в общем случае при достаточно слабых ограничениях на е и x,,j= 1 я,
МНК-оценки параметров регрессии и детерминированной составляющей
являются асимптотически нормальными и эффективными.
213
где t — критическая граница распределения Стьюдента с (л — 2)
степенями свободы, соответствующая уровню значимости р.
В действительности может оказаться, что фактор х не влияет на
результирующий признак, что эквивалентно а^ = О, однако при этом
выборочный коэффициент а,, вообще говоря, отличен от нуля. Для
проверки существенности отклонения а, от нуля служит критерий
значимости. Рассматриваются гипотеза Н^: Oj = О и конкурирующая гипотеза
Ну Oj ^ 0. Затем рассчитывается эмпирическая значимость
'W=^
а, а,
Izjyj
\j^
% М o/iz]
(9.3.17)
которая сравнивается с теоретической значимостью t. Если k(«i) < t,
то с вероятностью ошибки р принимается гипотеза Я^, в противном
случае, т.е. при U(«i) > t, принимается гипотеза Я,. В случае принятия
гипотезы Яц фактор х исключается из модели и тем самым принимается,
что наилучшее описание системы наблюдений — с помощью среднего
арифметического у = у.
В качестве меры того, насколько хорошо регрессия описывает
данную систему наблюдений, служит коэффициент детерминации, при этом
за базу сравнения принято описание с помощью среднего
арифметического. Составляются следующие суммы квадратов отклонений:
S =Yt[yj-y] —фактических значений от их среднего арифметического;
^ -2lf\yj~yj — выравненных значений от среднего арифметического
■'"' фактических значений;
2 ■ir' I •> \
Sjf = Zjiyj ~yj) ~ фактических от выравненных значений;
У=1
214
s^ = I.(yj-y) =i(yj-yj+yj-y) =
при этом имеет место равенство
S^=S^+Sl, (9.3.18)
поскольку
= pj -yjf -tjyj -yf ^2pj -yjpj-y),
a последняя сумма равна нулю lyj =y+&fZj)-
tj,yj-yj){yj-y)=tj,yj-y-^iZj)^zj =
=^itjyj -y-^iZjh=^\ijyj -yh-ij^yj -yhM-
Коэффициент детерминации есть отношение объясненной части
вариации ко всей вариации в целом, поэтому из равенства (9.3.18) имеем:
J _ -^ _ -^ ^ -1 '^
Таким образом, чем «ближе» этот коэффициент к единице, тем лучше
описание, разумеется, если при этом модель методически правильна.
Расчеты и проверка достоверности полученных оценок
коэффициентов регрессии не являются самоцелью, это лишь необходимый
промежуточный этап. Основное — это использование модели для анализа и
прогноза поведения изучаемого экономического явления. Прогноз
осуществляется подстановкой значения фактора х в оценку
детерминированной составляющей:
Ях) = 7+а,(х-х). (9.3.19)
Это точечная оценка детерминированной составляющей у{х) в
точке X. Можно показать, что выражение (9.3.19) — наиболее точный в
среднеквадратичном прогноз. Чтобы измерить точность этой оценки и
построить доверительный интервал для з'(х), необходимо найти
дисперсию точечной оценки у{х):
Dy{x) = Dy + 1>(а,(х - х))+2 cov [у, а,(х - х)) =
215
о , _ч2
: +(Х-Х)
п
>=1
1 [x-xf
" и
(9.3.20)
Последнее равенство верно, поскольку
со\[у,а^{х-х)] = {х-х)со\(у,а^) = {х-х)со\(а'^,а^\ = 0.
Окончательно получаем следующий доверительный интервал для
прогностического значения y{x) = aQ + a^x детерминированной
составляющей:
У{х)-
tpO
1 {x-xf
—+
п
>=1
<y{x)<y{x) + tpC
^\2
1 , (^-^)
(9.3.21)
Рассмотрим конкретный пример расчета параметров парной
регрессии и прогноза по полученному уравнению эмпирической регрессии.
Q Пример 9.2. Исследуем зависимость розничного товарооборота (млрд. руб.)
магазинов от среднесписочного числа работников. Товарооборот как
результирующий признак обозначим через у, а среднесписочное число работников (чел.)
как независимую переменную (фактор) - через х. На объем товарооборота
влияют такие факторы, как объем основных фондов, их структура, площади
торговых залов и подсобных помещений, расположение магазинов по отношению к
потокам покупателей и др. Предположим, что в исследуемой группе магазинов
значения этих последних факторов примерно одинаковы, поэтому влияние
различия их значений на изменении объема товарооборота сказывается
незначительно. В табл. 9.2 во втором и третьем столбцах приведены значения
соответственно объемов розничного товарооборота и среднесписочного числа
работников, а в следующих столбцах - значения расчетных величин, необходимых
для определения оценок коэффициентов регрессии и дисперсии случайной
составляющей [zj =Xj-x, Ay J = у J - у, Cj =yj- Уу).
Найдя по итогам второй и третьей колонок средние х = 904/8 = 113,
У = 9,6/8 = 1,2, последовательно заполняем 4-8-й столбцы и подводим
итоги по этим столбцам. Теперь можно определять эмпирические коэффициенты
регрессии. По формулам (9.3.9), (9.3.10) находим следующие точечные оценки
коэффициентов регрессии:
216
Таблица 9.2
Порядковый
номер
магазина
1
1
2
3
4
5
6
7
8
Итого
X
2
73
85
102
115
122
126
134
147
904
У
3
0,5
0,7
0,9
1,1
1,4
1,4
1,7
1,9
9,6
Z
4
-40
-28
-11
2
9
13
21
34
0
Ау
5
-0,7
-0,5
-0,3
-0,1
0,2
0,2
0,5
0,7
0
е
6
1600
784
121
4
81
169
441
1156
4356
Ayz
7
28
14
3,3
-0,2
1,8
2,6
10,5
23.8
83,8
{АуУ
8
0,49
0,25
0,09
0,01
0,04
0,04
0,25
0,49
1,66
У
9
0,43
0,661
0,998
1,239
1,373
1,45
1,604
1,854
1,199
е
10
0,07
0,039
-0,088
-0,139
0,027
-0,05
0,096
0.046
0,001
е"
11
0,0049
0,0015
0,0077
0,0193
0,0007
0,0025
0,0092
0,0021
0,0479
а" = j7 = l,2; а, = J^AyjZj / I г} =83,8/4356 = 0,01924;
do =у-а,х = 1,2-0,01924-113 = -0,974.
. Рис. 9.2
217
Значение нулевого коэффициента а" представляет собой ординату
эмпирической линии рвфессии в точке х = х = 113, а коэффициент регрессии
а, = 0,019 - угловой коэффициент этой прямой линии. На рис. 9.2
изображены система соединенных штриховой линией точек наблюдений v\ прямая
эмпирической регрессии. Если не учитывать, что мы имеем не теоретическую, а
эмпирическую линию регрессии (которая действительно является приближением
теоретической линии регрессии), то коэффициент а, =0,01924 показывает,
что увеличение среднесписочной численности на одного человека приводит к
увеличению объема товарооборота в среднем на 19,24 млн. руб. Это своего рода
эмпирический норматив приростной эффективности использования работников
данной группы магазинов. Если увеличение численности на одного работника
приводит к меньшему росту объема товарооборота, то прием его на работу
необоснован.
Теперь можно вычислить выравненные значения (значения ординат
эмпирической линии регрессии)
yj=y+^Zj = l2 + 0M924zj
и заполнить 9,10и11-й столбцы табл. 9.2. Итог 11 -го столбца, в свою очередь,
позволяет получить оценку дисперсии случайной составляющей:
с^=-ЬЬ]=М47 ==0.008.
Знание дисперсии случайной составляющей позволяет проверить
статистические гипотезы о параметрах регрессии и уравнении в целом, а также строить
интервальные оценки параметров регрессии и прогнозного значения
детерминированной составляющей.
Для проверки гипотезы о том, значимо ли отличается от нуля выборочный
коэффициент а,, находим, согласно равенству (9.3.17), эмпирическую
значимость коэффициента
/(а,) =
которую теперь надо сравнить с теоретическим значением tin - 2), найденным
из таблицы распределения Стьюдента (см. табл. П. 4.2). Выбираем уровень
значимости равным 5% (т.е. с вероятностью 0,05 мы допускаем отклонение
гипотезы а, = О, когда она на самом деле верна), тогда по табл. П. 4.2 находим
/'pQ5(6) = 2,447. Эмпирическая значимость (14,198) существенно больше
теоретической (2,447), поэтому а, значимо отличается от нуля, т.е. принимаем
гипотезу а, * 0.
218
Этот же вывод подтверждается и высоким значением коэффициента
детерминации:
S ^д^2 1,66
который показывает, что в исследуемой ситуации 97,1% общей вариабельности
розничного товарооборота объясняется изменениями числа работников, в то
время как на все остальные факторы приходится лишь 2,9% вариабельности.
Этот статистический вывод не абсолютен. Допустим, что в магазинах
исследуемого типа стало больше работников, при этом предельная эффективность
работника упадет, а на первый план выйдет влияние других факторов.
По-видимому, это прежде всего доля дефицитных товаров в ассортименте и комплекс
всех факторов, который характеризует культуру обслуживания.
Построим интервальные оценки параметров регрессии а°, а, в форме
а ±/^0.0, a.^±tpa^ . Здесь середины интервалов являются точечными
оценками коэффициентов регрессии, которые уже рассчитаны: а" =У = 1,2;
а, = 0,01924. При выборе уровня значимости 5% получаем ^o.osl^) - 2,447.
Остается только найти стандартные ошибки коэффициентов регрессии.
Согласно формулам (9.3.14),
заменяя а на а, получаем:
а.о =a/V«= л/О. 008/л/8= 0,032,
Ой, =о/ tz] =V0,008/V4356= 0,0014.
Отсюда окончательно получаем, что с вероятностью 0,95 истинные значения
параметров лежат в пределах:
1,122 <а''< 1,278,
0,01581 < а, < 0,02267.
Найденные отклонения фактических значений от выравненных (столбец 10)
позволяют провести сравнительный анализ работы различных магазинов
рассматриваемой группы. Прежде всего необходимо обратить внимание на магази-
219
ны с отрицательным отклонением (3, 4, 6-й). Особенно велико отклонение у
4-го магазина. В реальной ситуации необходимо внимательно обследовать эти
магазины и установить причины отклонения фактического значения
товарооборота от выравненного («нормативного» значения). В данной ситуации это может
быть расположение магазина в стороне от основных потоков покупателей,
плохое снабжение товарами повышенного спроса, устаревшее оборудование,
неудовлетворительный кадровый состав и т.п. При чисто статистическом анализе
при сделанных выше предположениях и на основе имеющихся данных приходим
к выводу, что в этих магазинах, по-видимому, имеются резервы в организации
труда работников. Напротив, в магазинах 1, 2, 5, 7 и 8 работники используются
эффективнее статистического норматива, но может оказаться, что эти магазины
объективно находятся в лучших условиях.
Полученное уравнение регрессии может быть использовано для прогноза.
В частности, пусть намечается открытие магазина такого же типа с
численностью работников X =140 чел., тогда достаточно обоснованный объем
товарооборота следует установить по уравнению регрессии
y(x) = J; + a,(x-x) = 1,2 + 0,01924(140-113) = 1,72 млрд. руб.
С точки зрения принятой теоретической схемы полученный прогноз у{х)
является лишь точечной оценкой истинной детерминированной составляющей
у(х), а сама эта составляющая лежит внутри доверительного интервала
y{x)±tp^,^Y в котором, согласно формуле (9.3.20),
^у(х) = л/^Я^ = ^
1 (х - xf
1 1^'
ИЛИ
^уМ=^
U (£11^ ^VoM.Jl + MllH)! =0,039,
п Д,2 ^ ^8 4356
1 f-
поэтому получаем следующий доверительный интервал для теоретического
значения прогноза:
1,72-2,447-0,039 <у(х)< 1,72 +2,447-0,039,
или
1,625 <j;(x)< 1,815. •
220
§ 9.4. Множественная линейная регрессия
в случае линейной множественной регрессии модель имеет
следующий вид:
у = у{х) + е, Я^) = «о + 1«/^,-.
(=1
или
у{х) = а" + I а, (х, -xf), а« = ао + I а^х^
1=1 (=1
(9.4.1)
(9.4.2)
где у{х) — детерминированная составляющая, зависящая от факторов
х =
/„ ^
м
а =уух j — значение детерминированной составляющей в
стандартной точке jc":
^1
м
а,— коэффициент регрессии при /'-м факторе, показывающий,
насколько изменится детерминированная составляющая, если /-й фактор
изменится на единицу; е — случайная составляющая с независимыми
значениями, Мг = 0, De = а^.
Оценка параметров регрессии а^, а,,..., а^ осуществляется по
выборочным значениям результирующего признака и факторов yj, х^,,..., Хд,
у'= 1,..., п, п> к + 1. При наличии конкретной выборки целесообразно,
как было показано в § 9.3, в качестве стандартной выбирать точку,
координатами которой служат средние арифметические выборочных
значений факторов xf =Xj, при этом
j;(x) = а" + X а,- (^, - ^/) = « + Z «/ ^/'
Zi^Xj-Xj, а° = у{х).
(9.4.3)
221
При изучении множественной регрессии используется тот же подход
что и при изучении парной рефессии. Прежде всего определим оценки
метода наименьших квадратов:
dQ
дао
dQ
да
= -2l
--6. j=^
п
а=а J~^
yj-^o-l^iXj
= 0,
/
/ = 1 у
yj-^o-l^iXji
о, / = 1,...,A;.
Таким образом, для определения {к + 1)-й оценки параметров
регрессии получена система нз{к+ 1) нормального уравнения:
««0 + 1
(=1
и=1 ; v=i
txjiXji ai = %yjXj,, l=\,...,k.
(9.4.4)
Если выразить a^ из первого уравнения
_ * _
(=1
и подставить в другие нормальные уравнения, то для определения
оценок остальных к параметров получим следующую систему из к
уравнений:
I
/=1
l(xji-Xi)(xj,-x,)ai = 'lyj(xj,-x,), 1 = 1..„к, (9.4.5)
У=1 7=1
ИЛИ [в обозначениях формулы (9.4.3)]
I
(=1
IZjiZji a; = '^yjZji, / = 1,...Д.
(9.4.6)
V^=
У=1
Все дальнейшие расчеты и построения удобнее выполнять в матриЧ'
ной форме. Введем следующие матричные обозначения (слева от
обозначения матрицы указаны ее размеры):
222
(nxl)
'y^^
{ynj
вектор-столбец выборочных значений результирующего признака;
[лх(А; + 1)] Х =
1 x^^ Х|2
1 ^21 ^22
V ' ^п1 ^п2
^2к
'■nkj
— матрица значений факторов, включая единичный столбец,
отвечающий свободному члену;
[лх(А; + 1)] Z =
1 ^11 Zxi
1 Zi\ Z22
V' ^й1 ^й2
^2к
^nkj
— матрица центрированных значений факторов;
[(А;+1)х(А; + 1)] A=-Z'Z
— матрица нормальных уравнений в центрированной форме;
Г 1
[{к + \)х{к + \)] С = А'^ =
О О
о С|| С|2
V" ^к\ ^к2
^-кк)
матрица, обратная к матрице нормальных уравнений;
[(А; + 1)х1] а =
а,
V«*7
вектор-столбец всех параметров регрессии;
223
[(fc + l)xl]
^««^
a.
V«U
вектор-столбец параметров регрессии с начальным параметром а";
(и XI)
е =
р
вектор-столбец отклонений фактических от выравненных значений;
(и XI)
(f.\
\^nj
— вектор-столбец выборочных реализаций случайной составляющей с
ковариационной матрицей В^ = Мгг' = а^Е„, где Е^ — единичная
диагональная матрица (л х л), а штрих здесь и далее означает
транспонирование.
В матричном виде модель в форме (9.4.1) записывается так:
система нормальных уравнений имеет вид:
{X'X)a = X'Y, a = {X'Xy^X'Y,
а в форме (9.4.2) —
Y = Za + z
и система нормальных уравнений такова:
(9.4.7)
(9.4.8)
(9.4.9)
{Z'Z)a = Z'Y. (9.4.10)
Из выражения (9.4.10) получаем решение нормальных уравнений в
форме
a^{Z'ZY^Z'Y = CZ'Y,
ВТОМ числе а" =у.
224
(9.4.11)
Используя уравнение (9.4.9), разложим оценки на
детерминированную и случайную составляющие:
-I -7-/
a = {Z'Z) Z'Y = {Z'Zy'Z'{Za + z) = a + CZ'z,
(9.4.12)
-О - 1 ^
в том числе о. =у = — 2^
Л
a" + Sa/^y/+ey
■ а" + е,
в последнем равенстве воспользовались тем свойством, что
jlzji=0, i = \,...,k.
Как видно из уравнения (9.4.12), оценки параметров регрессии
являются несмещенными. Кроме того, оценка а" статистически не зависит
от любой из оценок а^, так как
/ п - \ Г_ * "
COV а", аЛ = М еХ HchZji^j
] п к п \0^* "
-II 1c,zj,m(e,ej) = — X с, Хг,-, = о,
] п к п
-112
' v = l/=l 7 = 1
поскольку
(9.4.13)
lZji=0.
Оценка а" имеет дисперсию
(9.4.14)
и поэтому состоятельна.
Найдем теперь ковариационную матрицу оценок остальных
параметров регрессии:
В. =М{а- а\а -а)=М {Z'Z)~^ Z'e\{Z'Z)~^ Z'e] '=
= {Z'Zy^ Z'M ее' Z{Z'zy^ = a^C.
Из выражения (9.4.15), в частности, вытекает, что
Dai=a^Cjj, cov(a,,а,) = а^с„,
*-~б70
(9.4.15)
(9.4.16)
225
и, следовательно, оценка состоятельна при е.. —> О, л —> «о. В частности,
если наблюдения факторов расположены таким образом, что матрица
l/v 2
нормальных уравнении диагональна, то с„ = 1/ 2.Zy, и, следовательно,
]=\
с,. -> О при X 2у; ~^ ""' " -^ °°-
7 = 1
Рассмотрим теперь сумму квадратов отклонений е^ =yj -yj
фактических значений от выравненных значений. Имеем в форме (9.4.1),
используя уравнения (9.4.8),
е = Y -Y = Ха + г-Ха. = Ха + г-Х{Х'ХУ'^Х'{Ха + г) =
^г-Х[Х'Х)'^Х'г = Нг,
где Н = Е„-Х[Х'Х)''^Х'.
Матрица Я симметрична и обладает следующим свойством
Е„-Х{Х'Х)'''Х' £'„-А'(А"А')"'А" =
= Е„- IXiX'Xy^X' + Х{Х'Х)'^Х'Х{Х'ХУ^Х' =
= Е„-Х{Х'ХУ^Х' = Н,
поэтому получаем:
MY.[yj - у if = MY.e] = Me'e = Мг'Н'Нг = Л/е'Я^е = Мг'Нг.
Так как Л/е^ = а^ и MzjZ^ - О при v ^^у, то
y,v = l 7 = 1
где tr (Я) — сумма диагональных элементов матрицы Я.
Так как
Гг(Я)=1г(£'„)-Гг А'(А"А') X' =и[Е„)-Хх [Х'ХУ'Х'Х
^Xx{E„)-ix(E,^,) = n-k-\,
то окончательно получаем:
Mt(yj-yj)^=^\n-k-\),
у = г
226
[J тем самым
1
^ =^ГТЛ^У^-^.) (9.4.17)
является несмещенной оценкой дисперсии случайной составляющей,
1 « , ч2
а величина —^ХГУ "J' > ^^^^ случайная составляющая нормальна,
распределена по закону х^ с (п — к — 1) степенью свободы.
Последний факт и соотношения (9.4.16) позволяют проверять
гипотезы о значимости выборочных коэффициентов регрессии. Если
расчетная значимость коэффициента а
ОС; ОС;
меньше по модулю теоретической значимости t^, то теоретический
коэффициент регрессии принимается равным нулю (а^ = 0) с
вероятностью ошибки, равной р. Теоретическая значимость — критическая
граница распределения Стьюдента с {п — к — 1) степенью свободы. Если
выборочный коэффициент а оказался незначимым, то
соответствующий фактор выводится из модели.
В ряде работающих программных систем на ЭВМ принят следующий
алгоритм последовательного исключения факторов из модели. На
каждом этапе рассчитываются эмпирические значимости всех
коэффициентов регрессии t., /= 1,..., к. Эти значимости ранжируются по
значениям их модулей, и если минимальное значение меньше теоретической
значимости, то соответствующий фактор выводится из модели и
расчеты повторяются. Как только все факторы оказались значимыми,
расчеты завершаются.
Качество всей модели в целом определяется по критерию Фишера:
если
'=Sl/in-k-r'^^'' "-'-')' (^•^•'«>
ч 7=1 У=1
^о уравнение в целом незначимо, в противном случае — значимо. Здесь
^р{к, п-к-]) — критическая граница распределения Фишера с
\^^,n-k-\) степенью свободы, соответствующая уровню значимости/?.
S»
227
Аналогично парной регрессии коэффициент детерминации може*
быть рассчитан как доля объясненной вариации в общей вариации:
Л2 о2
rf = ^ = l-£f. (9.4.19)
Знание распределений и дисперсий оценок параметров регрессии
позволяет построить доверительные интервалы для их теоретических
значений:
а о - о
а,- - tpC^Cji < а,- < а, + tpC^c^^. (9.4.20)
Наибольший интерес представляет использование модели регрессии
для прогнозирования. Точечный прогноз получаем подстановкой
прогностических значений факторов в уравнение эмпирической регрессии
y{x) = y + 'Zai{xi-Xi).
(=1
Чтобы получить доверительный интервал для теоретической
детерминированной составляющей, необходимо найти дисперсию точечного
прогноза:
^Ji,)=Dy{x) = Dy + D
к
( = 1
^2 к
= —+ <J l{Xi-Xih,{x,-Xi).
- (9.4.21)
" /,/=1
Здесь МЫ использовали формулы (9.4.13), (9.4.16).
Из выражения (9.4.11) получаем следующий доверительный
интервал для детерминированной составляющей:
к к
У + Xа,(х,. - X,.) -/ра?(^) < Я^) < У + Xа,, (х,. - X,.) +/ра^(^).
В матричной форме легко получить оценки параметров регрессии и в
том случае, когда значения случайной составляющей являются
зависимыми, те. Мгг' = В^. Введя новые переменные
y = b:^^y, х = в:^^х, г = в-^^г.
228
сводим задачу к предыдущей, поэтому
в^=(х%'ху\
В частности, в случае пространственно-временной выборки
случайную составляющую естественно представить как сумму двух компонент:
>J ~
У-1,...,и; t = \,...,T,
Dl,j=cl D5j,=a\
первая из которых характеризует случайные отличия единиц
статистической совокупности, а вторая является остаточным членом. Даже в
случае предположения о независимости обеих компонент друг от друга и
независимости их отдельных значений приходим к следующей форме
ковариационной матрицы размера {пТх пТ)\
В =
(В,
0
, 0
0
S,
0
0^
0
в„
в г
с 1 1
V ^0
<^1
<^1
а Л
о1
а +а,
о У
Обратная матрица также имеет блочно-диагональную структуру:
С'=11к,.
^J.i.J .1 Г
""lU-J-
o'HT-\)al
а^ + Tel
■ j = j\ t = t'
^0
О,
]*]'
119
Метод максимального правдоподобия (ММП) приводит к следу|о^
щим оценкам:
i=0\j.l.l'
пТ
l^j.f.i^j.tj.r^j.r.i «/= 1 yj.f^j.t.j.r^j.r.i' / = 0,1,...,А:,
J.I.C
„2 1
j.t ' ' J.I.I'
ol
>^T{T-^)u.i
S ^j.i^j.r
где
ejj=yjj-J.^i^j,i.i-
;=0
Если выборочные значения факторов приближенно ортогональны,
то можно вывести следующие формулы для дисперсии оценок метода
наименьших квадратов и ММП:
Да,=—^—(a^+7>,ag).
■^ ^j.i.i
J.I
Da, =
J.I
аЧ
где
Л
S '^^j.i.i
Р,=-р '
^14л/
*v J''
0<р.<\, qr^-P,
откуда видно, что оценка ММП, учитывающая структуру
ковариационной матрицы, более эффективна, чем оценка метода наименьших
квадратов. В целом обе эти оценки асимптотически эффективны. Можно
также показать, что оценки, полученные по пространственной выборке
осреднением данных по времени, менее точны, чем приведенные выше,
поэтому использование пространственно-временных выборок расширь'
ет возможности пространственных выборок.
230
§ 9.5. Особенности практического применения
регрессионных моделей
Регрессионная модель, как и всякая другая математическая модель,
отражая основные свойства изучаемого экономического явления или
объекта, не в состоянии полностью воспроизвести его поведение. Но
даже то, что исследователь наметил отразить, трудно сделать в условиях
реальной экономической ситуации. Все дело в том, что в распоряжении
исследователя имеются данные о фактической траектории
экономического объекта либо совокупности участков траекторий ряда сходных
объектов. При этом значения факторов не расположены так, чтобы оценки
параметров регрессии оказались самыми точными и чтобы
исследователь получил ответ на вопросы о влиянии на результирующий признак
всех интересующих его факторов отдельно и во взаимодействии.
Последнего можно добиться только в условиях контролируемого
(планируемого) эксперимента, когда значения факторов можно выбирать по
усмотрению исследователя, но при этом, разумеется, нельзя полностью
воспроизвести условия реальной экономической ситуации.
Например, при изучении влияния минеральных удобрений на
урожайность по фактическим значениям урожайности конкретной
сельскохозяйственной культуры и фактическим дозам внесения минеральных
удобрений под эту культуру на единицу площади в рамках определенной
совокупности сходных хозяйств может оказаться, что коэффициент
регрессии по этому фактору незначим, а это при прямолинейной
трактовке служит основанием для вывода: минеральные удобрения не влияют
на урожайность. На самом деле это, конечно, совсем не так. Более
тщательное изучение всех условий, формирующих результирующий
показатель и значения факторов, поможет выяснить обстоятельства
неправильного вывода. Так, может оказаться, что во всех этих хозяйствах внесение
минеральных удобрений находится примерно на одинаковом уровне и
практически не сказывается на вариабельности результирующего
признака. Могут быть и другие особенности, например с увеличением
внесения удобрений на единицу площади в меньшей степени соблюдаются
агротехнические условия внесения и т.п.
Итак, необходимо, чтобы в условиях конкретной выборки каждый из
введенных в модель факторов обладал достаточной вариабельностью (в смысле
влияния на результат). Это можно выяснить, исключая данный фактор из
модели и сравнивая полученные до и после исключения коэффициенты
детерминации и /"-отношения (на забывая при этом о возможном
взаимодействии исключенного фактора с другими). Существенность влияния
фактора в конкретных условиях определяется также его значимостью.
Следующим осложняющим обстоятельством является мультиколли-
неарность факторов, т.е. такое расположение их выборочных значений,
231
при котором последние близко прилегают к некоторой гиперплоскости
в пространстве факторов. Применительно к нормальным уравнениям
это означает, что их определитель близок к нулю и поэтому уравнения
практически нельзя решить. Наиболее распространены в таких случаях
следующие приемы: исключение одного из двух сильно связанных
факторов, переход от первоначальных факторов к их главным компонентам,
число которых может быть меньше, затем возвращение к
первоначальным факторам. Другим приемом является так называемая гребневая
регрессия с получением ридж-оценок. Суть приема состоит в усилении
обусловленности матрицы нормальных уравнений добавлением
неотрицательных чисел к ее диагональным элементам:
а(в) = (^'^ + в£„)"'^Т, (9.5.1)
при этом, естественно, оценки получают смещение, однако появляется
возможность более устойчивого их определения.
Особым случаем мультиколлинеарности при использовании
временных выборок является наличие в составе переменных линейных или
нелинейных трендов. В этом случае теория рекомендует сначала выделить
и исключить тренды, а затем определить параметры регрессии по
остаткам, при этом используется следующая теоретико-вероятностная схема:
x„=Xi{t) + i„i, i = ],...,к, (9.5.2)
В этой схеме y(t), x.(f) — регулярные функции времени, те. тренды
зависимой и независимых переменных, а г\,,Ь,ц — отклонения от
трендов. В условиях прогноза по тренду приходится считать эти отклонения
выборочными значениями случайных величин, однако при
рассмотрении регрессии в остатках отклонения от трендов независимых
переменных как детерминированные, а отклонение от тренда зависимой
переменной расчленяется на детерминированную (регрессию по остаткам
независимых переменных) и случайную составляющие.
Игнорируя наличие трендов в зависимой и независимой переменных,
мы завышаем степень влияния независимых переменных на
результирующий признак, что получило название ложной корреляции. В качестве
примера явно выделим ложную корреляцию в случае парной регрессии
по динамическим рядам зависимой и независимой переменных,
содержащих тренды:
^.x,=^..'-x,..+4,5,VQ^'' (9-5-3)
232
где Гу^,1^,г^ ^^ —эмпирические коэффициенты корреляции
первоначальных переменных и их отклонений от трендов; Гу ,,г^ , —эмпирические
коэффициенты корреляции переменных по времени; Qj,, .0? —доли
вариации остатков в общей вариации зависимой и независимой переменных.
Как видно из формулы (9.5.3), эмпирический коэффициент
корреляции переменных распадается на произведение эмпирических
коэффициентов корреляции переменных по времени (ложная корреляция) и на
часть, обусловленную истинной корреляцией в форме эмпирического
коэффициента корреляции остатков.
Наиболее часто в практических исследованиях возникает вопрос:
сколько надо наблюдений для надежного определения параметров
регрессии? Однозначного ответа на этот вопрос нет. Выше было показано,
что очень многое зависит от расположения выборочных значений
факторов. Далее в этом параграфе подробнее будут рассмотрены
осложняющие обстоятельства, связанные со случайной составляющей. Будем
предполагать, что случайная составляющая удовлетворяет стандартным
условиям, сформулированным в § 9.4, а матрица нормальных уравнений
достаточно обусловлена. Последнее означает, что можно перейти от
первоначальных к ортогональным факторам, например к главным
компонентам в том же количестве. Далее будем считать, что это уже сделано.
Выбор числа наблюдений зависит от требований к точности и
надежности оценок параметров, что определяется в конечном счете размером
доверительного интервала прогноза. Таким образом, из требований к
точности прогноза и вытекает требование определенного числа
наблюдений. Обозначим требуемый размер половины доверительного
интервала через Аа, где а^ — оценка дисперсии случайной составляющей.
Достижение этой желаемой точности определяется как объемом выборки,
так и расположением прогностических значений факторов. Чем более
разнесены последние отсреднихвыборочныхзначений, тем меньше
точность прогноза. Выберем определенные уровни отклонения,
пропорциональные отклонениям выборочных факторов:
-, [Х: - Х]
flf=:A_! '— 7 .. = Х.—Х /=1 к
и -^ -"
При указанных условиях необходимый объем выборки, согласно
формуле (9.4.21), при ортогональности выборочных значений факторов
определяется из следующего соотношения:
233
или
t
2 /" t ^
2
i + ie;
=A^
л
откуда
(=1
(9.5.4)
Из формулы (9.5.4), в частности, вытекает, что при А = I, 9^ = |,
/'=1,..., fc, и с = 2 на каждый фактор должно приходиться почетыре
наблюдения, а при сохранении тех же требований к точности прогноза, но
при увеличении в 2 раза отклонений прогностических значений от
среднего арифметического фактических значений факторов, т.е. при 9^ = 2,
/= 1,.... fc, — по 16 наблюдений.
Самым большим препятствием к применению регрессии является
ограниченность исходной информации, при этом наряду с указанными
выше затрудняющими обстоятельствами (мультиколлинеарность,
зависимость остатков, небольшой объем выборки и т.п.) ценность
информации может снижаться за счет ее «засоренности», т.е. проявления новых
обстоятельств, которые ранее не были учтены.
Резко отклоняющиеся наблюдения могут быть результатом действия
большого числа сравнительно малых случайных факторов, которые в
достаточно редких случаях приводят к большим отклонениям, либо это
действительно случайные один или несколько выбросов, которые
можно исключить как аномальные. Однако при наличии не менее трех
аномальных отклонений на несколько десятков наблюдений мы склонны
приписать это влиянию одного или нескольких неучтенных факторов,
которые проявляются только для аномальных наблюдений.
В таком случае приходим к следующей теоретико-вероятностной
схеме:
^У=^У+^;+^;' У = 1. •••.«.
где ^у — случайная составляющая, отражающая влияние неучтенных
факторов, которые проявляются только для аномальных отклонений,
Mt^j =0, Wi^j =<5\\ г J — обычная случайная составляющая, Mtj =0,
Согласно такой схеме имеет место система неравноточных
наблюдений, при использовании которой каждое наблюдение должно входить
в расчет обратно пропорционально своей дисперсии, т.е. аномальные
отклонения войдут с меньшим весом, обычные — с существенно
большим.
234
Перенумеруем наблюдения таким образом, чтобы первые n^ из них
были обычными: yj~yj> У = 1,..., и,, а последние «2 =
и-и,—аномальными: У" = У„.+]'> y = l,...,«2; «1 >> «2' '^ обозначим через
... .-2
б =
;_"2 <J
И, а^+Оо
Тогда «взвешенные» средние выражаются через средние обычных и
аномальных наблюдений так:
i-t 5" 2 2 2
y=ia;. а' &^<5^^
X, = (1-8)^4 8х,".
Коэффициенты нормальных уравнений и их правые части имеют вид:
а„=(1-8)а;, + 8а;;. Ь,^{\-Ь)Ц^ЬЬ''.
Следовательно, средние и коэффициенты регрессии таким образом
выражаются через соответствующие величины, рассчитанные по
обычным наблюдениям, при этом учитываются поправки, отвечающие
аномальным наблюдениям:
У = Г + 8(Г'-Г)' 0.^0.' + ЬА-\Ь"- \А-^Ь'\
Например, согласно этому правилу, два сильно отклоняющихся
аномальных наблюдения с приблизительно равными значениями
независимых переменных следует заменить одним наблюдением с теми же
значениями независимых переменных и значением зависимой переменной,
равным полусумме соответствующих значений объединяемых
наблюдений.
Подробную же процедуру реализует робастное оценивание, при
котором наблюдения с меньшими отклонениями берутся с большим
весом, с большими отклонениями — с меньшим.
Вопросы и задачи
I. Имеются следующие ряды оценок по тестам чтения и арифметики:
Чтение 43 58 45 53 37 58 55 61 46 64 46 62 60 56
Арифметика 32 25 28 30 22 25 22 20 20 30 21 28 34 28
235
Вычислите коэффициент корреляции.
2. Ниже приводятся данные об индексе розничных цен на пищевые
товары и об индексе промышленного производства:
Год 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958
Индекс цен 100 101 ИЗ 115 ИЗ ИЗ 111 112 115 120
Индекс производства 64 75 81 84 91 85 96 99 100 93
Обозначив через х индекс цен и через ;; индекс производства,
определите:
а) формулу для прогноза у по х;
б) значения у{х) для х= 100, ИЗ, 199;
в) долю вариабельности ;;, которая объясняется вариабельностью х.
3. Предскажите время реакции полуторамесячного ребенка по
следующим данным:
Возраст (мес.) Время реакции (с)
1 1,5
2 0,8
3 0,5
4 0,4
Глава 10
СТАТИСТИЧЕСКИЙ АНАЛИЗ
ЭКОНОМИЧЕСКИХ ВРЕМЕННЫХ РЯДОВ
в общем случае временной ряд содержит как детерминированную,
так и случайную составляющие; для простоты далее будем считать их
адцитивными:
y,=f{t,x,) + e,, t = \,...,T,
где )>! — значения временного ряда;/(^ х^ — детерминированная
составляющая; Xi — значения детерминированных факторов, влияющих на
детерминированную составляющую в момент t; е, — случайная
составляющая, Л/е, = 0; Т— длина ряда.
Математическая статистика занимается анализом и прогнозом
временных рядов, содержащих случайную составляющую.
В экономике роль детерминированной составляющей играет,
например, результирующий показатель, представляющий собой объем
производства, обусловленный общей тенденцией экономического роста,
научно-техническим прогрессом и затратами экономических ресурсов. На
этот результат кроме экономических факторов могут оказывать
долговременное влияние, поддающееся предсказанию, и некоторые
природные факторы. Например, солнечная активность оказывает влияние на
урожайность сельскохозяйственных культур с периодичностью 11,2 года.
Случайная же составляющая аккумулирует влияние множества не
включенных в детерминированную составляющую факторов, каждый из
которых отдельно оказывает незначительное воздействие на результат.
Основная задача анализа временных рядов состоит в выделении на
основе знания отрезка временного ряда {;;^,/= 1,..., 7}
детерминированной и случайной составляющих, а также в оценке их характеристик.
Получив оценки детерминированной и случайной составляющих, можно
решать задачи прогноза будущих значений как самого временного ряда,
так и его составляющих.
237
§ 10.1. Трендовые модели
Под трендом (в узком смысле) понимается детерминированная
составляющая, зависящая только от времени. Тогда временной ряд
представляется следующей теоретико-вероятностной схемой:
yt=f{f)+4,
(10.1.1)
где/(О — тренд; е, — случайная составляющая, Л/е, = 0.
Если тренд линеен относительно своих параметров, а случайная
составляющая имеет известную матрицу ковариаций, то задача сводится к
задаче множественной регрессии, описанной в гл. 9. В самом деле, в
таком случае соотношение (10.1.1) принимает следующую форму:
у, =ао + Ха,Ф/(0 + ем t = \,...,T,
(10.1.2)
где ф,(?) — полностью известные функции времени.
Например, в случае полиномиального тренда соотношение (10.1.2)
имеет вид:
Д'г =«о + Х«,''+£(. t = \,...,T.
Обозначив ф,(/) через X,., придем к обычной модели множественной
регрессии, линейной относительно параметров:
или в матричной форме
где
м
f 1 ^
м
y^lk)
1
^21
v^l
а =
«1
М
42
С22
\.j2
L
L
L
L
e =
M
K^T )
L
^Tk)
(10.1.3)
(10.1.4)
238
Приведем общее решение, исходя из теории регрессионного
анализа, содержащейся в гл. 9. Форма решения зависит от статистических
характеристик случайной составляющей.
Значения случайной составляющей независимы
Ковариационная матрица случайной составляющей с независимыми
значениями имеет вид:
наилучшие оценки коэффициентов тренда получаются по методу
наименьших квадратов и имеют следующий вид:
1) оценка коэффициентов тренда
a = {X'Xy^X'Y, Ма = а,
В^ = ||cov(a/, а,.)|| = а^ {Х'Х)'^ =а^С; (10.1.5)
2) оценка дисперсии случайной составляющей
^ ^ Т-к-\ ^^^'~^'-' ' СО'б)
где
к к
у, = х;а = а^ + Ха,.х„. = а^ + Ха,.ф,.(0-
Точечный прогноз детерминированной составляющей на глубину т
выполняется по формуле:
Отметим, что
Mf{T + x) = f{T + x) = a, + ia^ip^{T + x),
;=1
Df{T + x) = G'x'r,,Cx.,.,^,
Где
xf,,=[l, ф,(Г + т), ..., ф,(Г + т)].
239
Интервальный прогноз для детерминированной составляющей на
глубину т задается следующей формулой (в предположении, что
случайная составляющая имеет нормальное распределение либо
рассматривается достаточно длинный отрезок ряда):
/(Г + т)-/,а-,^ .</(Г + т)</(Г + т) + /,е,
(10.1.8)
где С = С (Т- к- \) — критическая граница распределения Стьюдентас
(Г— к— \) степенью свободы, соответствующая уровню значимости/?;
Рассмотрим более подробно случай линейного тренда:
/(0 = «0 + «l'' ^ = '. %{() = (■
Формулы (10.1.5) — (10.1.8) принимают следующий вид:
1) оценка коэффициентов линейного тренда
aQ=y-a.J, а^=^
-n2
t =
\ + Т
(10.1.9)
1=1
2) оценка дисперсии случайной составляющей
ч2
6' =
1 ^ 2
(10.1.10)
где
у, =a.f^ + a^t = y + a^{t-t);
3) точечный прогноз детерминированной составляющей
/(Г + т) = у + а,(Г + т-Г),
Df{T + x)^a'
1 , JT^r-jf
(=1
(10.1.11)
(10.1.12)
240
4) интервальный прогноз детерминированной составляющей
ао + й,(Г + х)-t,b.^^^^^ </(Г + х)<ао + а,(Г + х) + ?,а^^^^^,(10.1.13)
1 [T + x-tf
Априорные предположения о форме тренда могут быть
сформулированы в виде рабочей гипотезы. Например, в случае рабочей гипотезы о
постоянстве годовых абсолютных приростов/(/+ 1) —/(О = а, = const
приходим к линейному тренду Если же имеет место гипотеза
постоянства темпов роста/(/+ 1) //(О = а, = const, то получаем экспонентный
тренд /{1) = а^а\, который в логарифмах сводится к линейному. Так как
не всегда удается иметь дело с трендом, линейным относительно своих
коэффициентов или сводимым к такому виду, то приходится
использовать нелинейные методы оценивания, понятие о которых дано в § 10.3.
Значения случайной составляющей зависимы,
матрица ковариаций известна
В случае если значения случайной составляющей зависимы и задана
известная ковариационная матрица случайной составляющей В - Л/ее' =
= ||cov(e,, е^) , t,s=\,... ,Т, наилучшие несмещенные точечные оценки
коэффициентов тренда определяются методом максимального
правдоподобия. В матричной форме эти оценки определяются следующими
выражениями:
Л/а = а, 5^=||cov(a„a,.)|| = (A"5-'A')"'. (10.1.14)
Точечный прогноз детерминированной составляющей на глубину х
осуществляется по следующей формуле:
/(Г + х) = 6:о + 1:а,.ф,(Г + х), (10.1.15)
при этом
Л//(Г + х) = /(Г + х)-ао + Ха,Ф,(Г + х),
9—670 241
Df{T + x) = x'r^,(x'B-'x)''xr^,
где
4+т = ['. 9i(^ + 4 ■■•. Ф*(^ + ^)]-
Проверка гипотез о значимости оценок коэффициентов тренда и
всего уравнения тренда в целом может быть выполнена по формулам,
приведенным в гл. 9.
Значения случайной составляющей зависимы,
матрица ковариаций неизвестна
Если ковариационная матрица неизвестна, но имеет специальную
структуру, определяемую некоторым числом параметров, то для оценки
конечного числа параметров (коэффициенты тренда и параметры
ковариационной матрицы) можно применять метод максимального
правдоподобия.
В общем случае, когда о структуре ковариационной матрицы ничего
не известно, теория рекомендует применять итерационную, по крайней
мере двухшаговую, процедуру: на первом шаге с помощью метода наиг
меньших квадратов определяют оценки коэффициентов тренда а и
оценку ковариационной матрицы В по отклонениям, на втором шаге
находят уточненные оценки коэффициентов тренда по формулам
(10.1.14), в которые вместо матрицы 5 подставлена ее оценка В, что
позволяет получить прогноз детерминированной составляющей на глубину
X по формуле (10.1.15).
§ 10.2. Выявление тренда в динамических рядах
экономических показателей
При исследовании динамических рядов экономических показателей
обычно выделяют следующие четыре основные составляющие:
долговременную эволюторно изменяющуюся составляющую*;
долговременные циклические колебания; кратковременные циклические колебания
(сезонная составляющая); случайную составляющую. В нашем
понимании первые три составляющие представляют собой тренд, т.е.
детерминированную составляющую.
Случайная составляющая образована в результате суперпозиции
большого числа внешних факторов, не участвующих в формировании детер-
Многие исследователи именно эту составляющую называют трендом.
242
минированной составляющей и оказывающих каждый отдельно
незначительное влияние на изменение значений показателя. В целом
влияние этих факторов на изучаемый экономический показатель
проявляется в изменении во времени его значений.
Долговременная эволюторно изменяющаяся составляющая является
результатом действия факторов, которые приводят к постепенному
изменению данного экономического показателя. Так, в результате
научно-технического прогресса, совершенствования организации и
управления производством относительные показатели результативности и
эффективности производства растут, а удельные расходы ресурсов на
единицу полезного эффекта снижаются.
Долговременная циклическая составляющая проявляется на
протяжении длительного времени в результате действия факторов, обладающих
большим последействием либо циклически изменяющихся во времени.
Примером такого рода явлений служат кризисы перепроизводства и
структурные кризисы. Другой пример связан с природным фактором —
солнечной активностью. Так, с большой степенью достоверности
доказано, что изменение солнечной активности с периодичностью 11,2 года
оказывает существенное влияние на развитие биологических объектов.
Исследованиедлинных рядов урожайности сельскохозяйственных
культур в районах устойчивого земледелия позволяет выявить
долговременную циклическую составляющую с 11-летним периодом и амплитудой
5—7% от среднегодовой урожайности.
Сезонная циклическая составляющая легко просматривается в
колебаниях продуктивности сельскохозяйственных животных в зависимости от
времени года, а также в колебаниях розничного товарооборота по
временам года.
Эволюторно изменяющуюся долговременную составляющую можно
достаточно хорошо представить отрезком ряда Тейлора; следовательно,
эта составляющая во многих практических случаях может
рассматриваться как полиномиальный тренд.
Что касается долговременной и сезонной циклических
составляющих, то обе они являются периодическими функциями, которые
достаточно хорошо могут быть представлены отрезками ряда Фурье;
следовательно, эти составляющие могут рассматриваться как
тригонометрический тренд.
Ниже на простых примерах демонстрируется техника расчета оценок
Коэффициентов полиномиального и тригонометрического трендов и их
Чспользования для прогнозирования будущих значений
детерминированной составляющей. Оценка коэффициентов одновременно присут-
^^Твующих эволюторной и циклической составляющих — несколько бо-
^ее сложная задача, но она полностью укладывается в схему расчетов,
•Приведенную в § 10.1. Если амплитуда циклической составляющей
эволюторно изменяется, т.е. имеет место мультипликативное представле-
'>* 243
ние детерминированной составляющей в форме произведения эволю-
торной функции на периодическую, то для анализа и прогнозирования
можно воспользоваться методом сезонного экспоненциального
сглаживания, который рассмотрен в § 10.4.
Полиномиальный тренд
Схема расчетов, приведенная в § 10.1 для тренда, представляющего
собой линейную комбинацию некоторого набора функций Фо(/),
ф|(/), ...,ф^(/), в случае полиномиального тренда выглядит следующим
образом. Роль функций ф,(/) играют степени времени, т.е. ф,(/) = /',
Фо(0 = 1. поэтому
/(/,а) = ао + 1а,/', / = 1,...,Г.
; = 1
Исходную модель временного ряда [сравните с обозначениями
формул (10.1.3), (10.1.4)]
можно записать в матричной форме:
где в качестве А'используется матрица, столбцами которой служат
значения времени в различной степени:
Х =
1 2 2^ •■• 2*
у\ Т Т^ ... т" J
Остальные обозначения совпадают с обозначениями
формулы (10.1.4).
Матрица коэффициентов нормальных уравнений имеет вид:
А = Х'Х = \^('Щ, /,/ = 0,1,...,А;,
11'=' 11
т.е. ее элементы являются суммами натуральных чисел в целой степени»
которые могут быть заранее рассчитаны, протабулированы и использО'
244
ваны для любого исходного ряда. Правые части нормальных уравнений
необходимо подсчитывать для каждого ряда
^'>'= 1>'/''| / = 0,1,...Д,
причем для оценки свободного члена используется формула
_ * —
/=1
в которой коэффициенты при оценках а,
— ] т .
также могут быть заранее протабулированы.
Прогноз на глубину! осуществляется по формуле
/ = 1
Доверительный интервал для детерминированной составляющей
записывается в следующей форме:
где
Ъ(т.г)=^1р/Т^^^)'''' С = {Х'ХГ\
2 1 ^.. -^2
^ =?гг:тр'-^')
Q Пример 10.1. В качестве примера исследуем динамический ряд
среднегодовых удоев молока (кг) от одной коровы на сельскохозяйственных предприятиях
за 1961-1985 гг. (длина ряда - 25 лет). Для расчетов используем формулы
полиномиального тренда при jk = 1, т.е. примем гипотезу линейного тренда,
состоящую в примерном постоянстве по годам среднегодовых приростов удоев
молока от одной коровы [см. формулы для линейного тренда (10.1.9) -
(10.1.13)]. Пример расчетов по аналогичным формулам парной регрессии был
рассмотрен в § 9.3, поэтому аналогичные расчеты проведены менее подробно.
Исходные и расчетные данные представлены в табл. 10.1.
245
Таблица lO.i
Год
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1985
Итого
Фактический
удой
У,, кг
2532
2317
2341
2513
2968
2956
3041
3182
3177
3181
3201
3192
3156
3364
3489
3587
3648
3475
3475
3579
3473
3385
3701
3854
3966
80 753
ty,
2 532
4 634
7 023
10 052
14 840
17 736
21 287
25 456
28 593
31 810
35 211
38 304
41 028
47 096
52 335
57 392
62 016
62 550
66 025
71 580
72 993
74 470
81 523
92 496
99 150
1 121 733
Выравненный
удой
л
У,
2565
2621
2676
2731
2787
2842
2898
2953
3008
3064
3119
3174
3230
3285
3341
3396
3451
3507
3562
3617
3673
3728
3784
3839
3894
Отклонения
л
у-у.
-33
-304
335
-218
181
114
143
229
169
117
2
18
-74
79
148
191
197
-32
-87
-38
-200
-343
-83
15
72
Квадрат
отклонений
(y-y,f
1 089
92 416
112 225
47 524
32 761
12 996
20 449
52 441
28 561
13 689
4
324
5 476
6 241
21 904
36 481
38 809
1 024
7 569
1 444
40 000
117 649
6 889
225
5 184
643 793
Прежде всего по формуле (10.1.9) находим оценки коэффициентов
линейного тренда, используя исходные данные табл. 10.1:
_ 1 ^ 80753
J ,=1 г:>
■■ 3230,
- 1 ^
1 t = \
\ + т
= 13;
246
r^ 7-(7Ч-1Х27Ч-1)_ 25^26-51 _^д,д.
S' 6 6
, Ь-Я' £/>,-Ь ,|„„з-3230.25.,3 „„
i(/-/t i/^-r(Ff 5525-25.13^
«0 =y-a,/=3230-720 = 2510.
Теперь рассчитываем выравненные значения у, =а.^ + а,/ (с точностью до
1 кг) и заполняем столбцы у,, у,-у,, [у, - у,) табл. 10.1.
т
По найденной сумме квадратов отклонений Sl = "^(^у, -у,) = 643 792
/=1
теперь можно получить оценку дисперсии случайной составляющей
6'=^1(>',-Л)'=27 991, откуда 6 = 167,3.
Найдем расчетную значимость коэффициента линейного тренда:
,,.^-.«L/i(,_,Y.^^^37Vi300
' а-_ a^,t,^ '' 167,3
которая существенно превышает табличную значимость ^gos^^^) ~ ^■''^^ "Р^'
5%-ном уровне значимости (5%-ном риске), т. е. коэффициент линейного
тренда существенно отличается от нуля, и, следовательно, тренд действительно
имеет место.
Теперь можно найти прогностические значения тренда среднегодовых удоев
молока от одной коровы на 1986-1990 гг.:
>;^^, =ао + а,(Г + 1) = 3949 (1986 г.);
i;r^2=«o+«i(^ + 2) = 3995 (1987 г.);
Уг^^ =ао + а,(Г + 3) = 4050 (1988 г.) ;
i)r^4=«o+«i(^ + 4) = 4105 (1989г.);
i'7-+5=«o+«i(^ + 5) = 4161 (1990 г.).
247
Построим доверительный интервал для теоретического тренда удойности за
1987 г., т.е. при прогнозе на два года вперед:
>'7-+2-'о,05(23)а^^^2<ао + а,(Г + 2)<>)г^2+'о,05(23%^2.
Так как tQQ^{23) = 2,069,
УТ+2
1 (7- + 2-(Т
1
—+
т
т 1
К'-О
/=1
= 167,3
1 W
1Ъ 1300
= 72,9,
то окончательно получаем доверительный интервал
3844<ао + а,(Г + 2)<414б,
размах которого равен 302, т.е. достаточно велик и составляет 7,5% по
отношению к значению середины интервала. Вместе с тем размах вполне приемлем
для практических прогнозов значений долговременной тенденции удойности на
несколько лет вперед.
Более углубленный анализ динамического ряда удойности совместно с
динамическими рядами экономических факторов, оказывающих на удойность
решающее влияние, показывает, что колеблемость удойности вокруг тренда
главным образом обусловлена колеблемостью урожайности кормовых культур. И это
полностью соответствует действительности, поскольку именно обеспеченность
кормами оказывает решающее воздействие на продуктивность животных.
Практически синхронная колеблемость вокруг своих трендов рядов динамики удой-
Рис. 10.1
248
ности и урожайности зерновых хорошо видна на рис. 10.1, на котором точки
отсчета и масштаб выбраны таким образом, чтобы тренды исходили из одной
точки, а размахи рядов были примерно одинаковы. Фактические и выравненные
значения ряда урожайности зерновых показаны штриховой линией, а ряда
удойности коров - сплошными линиями.
Синхронное изменение значений двух рядов, обусловленное решающей
зависимостью продуктивности коров от обеспеченности кормами, приводит к
мысли о возможности прогнозирования отклонений удойности от тренда по
отклонениям урожайности от своего тренда (см. также § 9.3). Это имело бы
большое практическое значение для более достоверного предвидения производства
животноводческой продукции, если бы существовали надежные методы
прогнозирования отклонений значений урожайности от тренда в зависимости от
вариации погодных условий. Однако к настоящему времени надежных методов
прогноза урожайности сельскохозяйственных культур в зависимости от
метеорологических условий и их прогноза на длительный срок пока нет. Существующие
методы дают недостаточно достоверные прогнозы урожайности. Поэтому для
прогноза удойности пока наиболее практически доступным является метод
выделения тренда, прогноз остатков станет осуществим в будущем.
Что касается выявления тренда урожайности зерновых (ц/га), то результаты
соответствующих расчетов приводятся ниже и представлены в табл. 10.2 и 10.3:
an
14,6; а, =0,56; 5^=393;
а^=17,1; а = 4,13.
Таблица 10.2
Год
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
Значение урожайности
фактическое
13,3
12,2
12,4
12,4
16,4
22,0
17,2
21,8
22,4
24, В
21,3
26,7
17,9
выравненное
11,67
13,36
14,6
15,62
16,53
17,34
18,1
18,В1
19,49
20,13
20,76
21,36
21,95
Отклонение
1,63
-1,16
-2,2
-3,22
-0,13
4,66
-0,9
2,99
2,91
4,67
0,54
5,34
-5,05
Год
1973
1974
1975
1976
1977
1978
1979
19В0
1981
19В2
19ВЗ
1984
19В5
Значение урожайности
фактическое
19,5
30,1
26,7
31,0
28,4
20,0
24,7
26,9
21,3
28,6
27,7
30,0
22,9
выравненное
22,52
23,08
23,63
24,17
24,71
25,24
25,76
26,27
26,79
27,3
27,8
2В,3
28,8
Отклонение
-3,02
7,02
3,07
6,83
3,69
-5,24
-1,06
0,63
-5,49
1,3
-0,1
1,7
-5,9
249
Таблица 10.3
Год
1986
1987
1988
1989
1990
Прогноз
29,8
30,4
31,0
31,5
32,1
Стандартная ошибка
прогноза
1,69
1,32
1,9
2,02
2,11
Итак, стандартные ошибки достаточно высоки, поэтому размахи
доверительного интервала прогноза по тренду составят ± 3,4;...; ± 4,3, что весьма
значительно. Тем не менее эти прогнозы можно использовать на практике, если
предположить, что сохранится сложившаяся долговременная тенденция изменения
значений данного показателя. Если тенденция изменится под влиянием определенного
фактора, то отклонение от прогноза по тенденции можно будет рассматривать как
суперпозицию результата влияния нового фактора и случайной составляющей.
Таблица 10.4
Формула тренда
А+ Bt
Ле"
А+ B/t
1/СЛ + Bt)
А+ ВШ
qA.BI
Экспоненциальное
сглаживание
Уг^,= 29,68 +0,6427т
Значение коэффициента
А
14,6
14,5
24,9
0,069
9,27
3,2
29,68
8
0,56
0,029
-18,3
-0,0015
5,5
-0,97
0,6427
Остаточная сумма
квадратов отклонений
392
448
512
581
328
463
439
В табл. 10.4 приведены результаты расчетов по различным трендам,
линейным относительно двух параметров. Как видим, наименьшая из рассмотренных
сумм квадратов отклонений у логарифмического тренда, который
характеризуется постепенным падением абсолютных приростов, что отвечает
сформулированной выше гипотезе:
f{t + \)-f{t)^A + B\n{t + \)-A-B\nt = B\n{\+}).
250
Этот тренд дает более осторожный прогноз по сравнению с прогнозом по
линейному тренду, что видно из табл. 10.5.
Таблица 10.5
Год
1986
1987
1988
1989
1990
Прогноз по тренду
линейному
29,8
30,4
31,0
31,5
32,1
логарифмическому
27,4
27,6
27,8
28,0
28,1
Экспоненциальное
сглаживание
30,3
31,0
31,6
32,3
32,9
В табл. 10.4, 10.5 приводятся козффициенты прогнозирующего полинома и
прогнозы тенденции зтого же ряда на те же годы, полученные методом
экспоненциального сглаживания (см. § 10.4). •
Тригонометрическая регрессия
Снова рассмотрим модель, содержащую детерминированную и
случайную составляющие:
y,=f{t,a) + e,, t = \,...,T,
гдеЛ/е,=0, D£,=a^, cov(e,,е^) = О при /^^5,
/(/,а)—периодическая функция с известным периодом т, нацело делящим Т, т. е. Т= hm.
Далее т, а следовательно, и Гбудем считать четными.
При рассмотрении тренда только в наблюдаемые моменты времени
его можно точно выразить через Глинейно независимых
тригонометрических функций. Если же период тренда равен т< Т,то все его первые т
значений затем повторяются еще (Т/т — 1) раз, т. е. всего h раз, поэтому
в точное разложение функции в точках / = 1, ..., Т достаточно
включить т членов, которые дают точное представление функции в точках
/= 1, ..., т, а все остальные значения повторяют первые т значений.
Функции cos
(?')'Ч?')
т
имеют период —, поскольку
У
cos
sin
2 л/'
т
'inj
т
ч J)
т ) Km
т J К т
251
причем этот период укладывается в общей длине ряда Tj/m = hj раз,
т. е. целое число раз, еслиу — целое. Теперь подберем т таких функций с
наименьшими периодами. Прежде всего в разложение необходимо
включить константу, т.е. в число функций времени войдет Фо(0 = 1-
Затем последовательно будем включать пары тригонометрических функ-
27С/ . 27С/ . , ^
ции cos /, sin—-t приу = 1, 2,
т т
причем каждому у соответствует
пара функций с периодом m/j. Следовательно, остановившись на
т
У = —- -1, мы включим т — 1 функцию. Таким образом, осталось вклю-
т
чить еще одну функцию су =/я/2, имеющую период -^^^ = 2. В качестве
/я/2
такой функции выберем 9„_i(O = (~0'-
Окончательно получаем следующее представление периодического
тренда:
(m/2)-l
7 = 1
«27-1 COSi
{^/]+a2,sin[^/]] + a„_,(-l)'.(.0.2..)
Например, при рассмотрении ежемесячных данных, имеющих
сезонный характер (т.е. период /я = 12), достаточно включить в разложение
12 членов, т. е.
Фо(0=1.
V /я
92,.(0 = sinf^A У = 1,2,3,4, 5,
Ф,.(0 = (-!)'.
и разложение принимает вид:
«2,-.':os[^/]+a2;sin[^/]j + a„(-l)'. (10.2.2)
/(/, а) = tto + I
7 = 1 L
Теперь воспользуемся методом наименьших квадратов для оценки
параметров а,- получившейся теоретико-вероятностной схемы:
(m/2)-l
7 = 1
(Inj
«2,-.C0S^-^
/ l+ttjySinl
г 2 л/
V tn
+
+«m-lH)'+e" t = \,...,T.
(10.2.3)
252
Нормальные уравнения в терминах функций времени фД/)
запишутся следующим образом:
т-1
I
/=0
1ф,(0ф/(0
1=1
1=1
.,т-\,
(10.2.4)
— И в данном случае распадутся на т отдельных уравнений, содержащих
только одно неизвестное, что вытекает из ортогональности
тригонометрических функций.
Рассмотрим оценку для свободного члена
«о=У- 1«/Ф/(0-
/ = 1
Согласно Приложению 2,
Ф,,-,(о4ЬЧ^']4,1Ч
flKjh
t\ = 0,
ф„-,(0=71Н)'=о,
' 1=]
поэтому
Рассмотрим внедиагональные члены матрицы нормальных
уравнений (10.2.4). Только что было показано, что
1ф/(Офо(0=1ф/(0=о.
1=1 1=1
При условии, что о < / < /< /я - 1, внедиагональные коэффициенты
обращаются в нуль; действительно, согласно Приложению 2,
1 = 1 t = \ \ tn J \ т J
^ (2njh\ flnkh
= Ir^os _ / |cos| -
t=l
V T
V T
t\ = 0, i = 2J-\, l = 2k-\,
253
t=i i=\ \ m ) \ m )
i9/(09„-,(0=icosf^/l(-l)'=0, / = 2у-1,
i9/(09„-,(0=isinf^/l(-l)'=0, i = 2j.
Коэффициенты при единственном неизвестном в каждом из
нормальных уравнений также определяются по формулам, найденным в
Приложении 2:
i9/(o = icos^f^/l=icos2f
^ - t =—, i = 2j-\<m-\.
Т ) 2
I 2гл l-2f2nj\ l.2f2njh\ Т . ,.
r=i r=i V /я ; ,=, У т J 2
1=\ 1=1
Окончательно получаем:
a,j_,=^iy,cosl^^ty у = 1,...,^-1, (10.2.5)
2 Z, . f2nj Л . , т ,
1 ^ г
am-,=7^I(-')>'r-
' 1=1
254
Таким образом, точечные оценки тренда определяются выражением
(m/2)-l
7 = 1
2 л/
а,,._I cosi —^t +а2: sin
•' ^ т J ^ у т
Inj
+ ««,-!(-')'. ('0-2-6)
а оценка дисперсии случайной составляющей
6^ =
1
■Пу,-у.)
(10.2.7)
Построение доверительных интервалов для параметров не вызывает
затруднений, поскольку легко находятся дисперсии их точечных оценок:
Da^ = Dy = a'lT,
Da^j_, = Da^j=2a^lT, у = l,...,:|-l,
Вследствие некоррелируемости оценок параметров легко
определяется дисперсия точечной оценки тренда:
Dy, = Ощ +
7 = 1 L
cos^(^,j,,u,,_,.sin^(^.]z)a,,
+ ^««,-1 =
о^ 2о^ fm
■ + ■
2 2 2
_ 1 I _ - ^" ^
Т \2~ rY~~ h
Q Пример 10.2. Используем формулы тригонометрического тренда для
выделения тренда в динамическом ряде помесячных удоев от одной коровы. Для
примера выбраны данные только за те годы, которые характеризуются практически
одинаковым среднегодовым удоем; это означает, что отсутствует смещение,
отличающее один год от другого, и имеют место только сезонные циклические
колебания. В табл. 10.6 (и далее) используется обозначение:
1 2
«, =Т-1>', + ,2/. t = \,...M.
i 1=4
Используя данные табл. 10.6, получаем
йо =7 = 192,2.
255
Таблица 10.6
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Итого
Среднее
Удои (кг)
1975
140
147
196
210
259
288
271
244
190
136
104
116
2301
191,8
1978
143
148
196
208
240
290
278
245
195
136
110
120
2309
192,4
1983
133
135
183
203
254
294
276
264
196
144
115
124
2311
192,6
Всего
416
430
575
624
753
872
825
743
681
416
329
360
6921
576,8
Среднее
138,7
143,3
191,7
208
251
290,7
275
247,7
193,7
138,7
109,7
120
2307
192,2
Легко также найти
Остальные коэффициенты найдем следующим образом:
27Г/
1 ^-
л/
Исходные данные для расчета приведены в табл. 10.7.
На основе данных табл. 10.7 получаем значения оценок остальных
коэффициентов, которые помещаем в табл. 10.8.
256
J
■♦*»
с
ел
■♦*»
ел
0
О
■♦*»
&
с
*сл
■♦*»
сЬ
ел
0
О
■♦*»
К| CN
С
ел
■♦*»
К|гч
ел
0
о
С
*сл
■♦*»
К|гп
ел
0
о
С
'ел
K|vo
ел
0
о
|в"
**
ю
о
ю
ю
ю
о
1
ю
о
ю
о
1
1-
о
ю
о
ю
о
ю
о
ю
ю
о
m
-
(О
ю
со
о
1
ю
о
ю
о
1
ю
о
1
о
1
ю
о
ю
о
1
(0
ю
о
ю
о
со"
t
CJ
-
о
о
■^
1
о
о
Т
г-
о
Г-,
5
m
ю
ю
ю
о
1
ю
о
1
ю
о
ю
о
1
о
f-
ю
о
1
ю
о
1
ю
ю
о
ю
о
1
ю
о
CJ
t
ю
о
ю
ю
о
ю
о
i
1Л
о
1
т-
о
ю
о
1
ю
о
ю
о
ю
ю
ю
о
1
ю
CJ
ю
о
т
о
■^
о
1
о
"^
о
т
г-
о
05
CJ
ю
ю
о
1
ю
ю
о
ю
ю
о
1Л
о
1
т
о
ю
о
ю
о
ю
о
1
ю
ю
ю
о"
1
ю
CJ
г-
ю
ю
о
ю
о
1
ю
о
1
ю
о
1
о
f-
ю
о
1Л
о
1
ю
ю
ю
о
1
ю
о
1
г-
t
CJ
ю
т
о
о
■^
ч-
о
о
1
т
о
со"
05
05
ю
ю
о'
ю
о
ю
о
ю
о
1
о
1
ю
о
1
ю
о
1
ю
ю
о
1
ю
о
m
о
ю
о
1
ю
ю
"Я.
о
1
ю
ю
о
1
ю
о
t
т
о
ю
ю
о
1
10
о
ю
о
1
ю
ю
о
г-
О)"
о
-
о
-
о
■^
о
f-
о
^^
о
г-
о
CJ
05
о
m
т
1
ю
о'
t
r-
m
Ю
1
10
m
Г-"
T
10
о
m
1
10
05
1
/-^
■♦*»
-Hii
257
Таблица 10.8
Параметр
«27-1
«2У
Амплитуда
Период
mj = \2lj
Оценка коэффициентов
У=1
-82,8
-5,0
83
12
У=2
-2,9
13,7
14
6
у = з
0,5
1,2
1,3
4
У=4
6,7
-7,2
9,8
3
У=5
-2,9
5,2
5,9
2,5
У=6
-1,6
1,6
2
Таблица 10.9
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Сумма модулей отклонений
фактических от расчетных
значений
Фактические
удои
«г
138,7
143,3
191,7
208
251
290,7
275
247,7
193,7
138,7
109,7
120
Расчетные удои
по первой
гармонике
У!
118
146,5
187,2
229,3
261,4
275
266,4
238,2
197,2
155,1
123
109,4
^1-У1
20,7
-3,2
4,5
-21,3
-10,4
15,7
8,6
9,5
-3,5
-16,4
-13,3
10,6
137,7
Расчетные удои
по первой
и второй
гармоникам
h
128,5
159,9
190,1
218,8
248
272,1
276,9
246,9
200,1
144,6
109,6
106,5
а,-У,
10,2
-16,6
1,6
-10,8
3
18,6
-1,9
0,8
-6,4
-5,9
0,1
13,5
89,4
Как видно из табл. 10.8, наибольшее значение амплитуды у первой
гармоники с периодом m = 12, причем это значение на порядок выше амплитуд ос-
258
тальных гармоник, поэтому в практических случаях можно ограничиться одной
гармоникой:
j), =192,2-82,8 cosf^ Л-5,0sinf|^A
или двумя гармониками:
^, = 192,2-82,8 cosf^/l-5,0sinf^/l-2,9cosf—/l+13,7sinC—/'
Более точные результаты получаются при включении всех шести гармоник:
>;, =192,2-82,8 cosf^/l-5,0sinf—/]-2,9cosf—Л+
+13,7sinf^/] + 0,5cosf^/l + l,2sinf^/l + 6,7cosf^/]-
7 0 • |'8лЛ о о пол
-7,2sin|—/1-2,9 cosi —
/] + 5,2sin[i^/]-l,6(-l)'.
В табл. 10.9 приведены фактические значения ряда и их оценка по первой
гармонике, а также по первой и второй гармоникам. Добавление всех остальных
гармоник весьма незначительно улучшает результат. •
§ 10.3. Нелинейные тренды
в том случае, когда тренд нелинеен относительно коэффициентов и
его невозможно линеаризовать, применяют нелинейные методы
оценки коэффициентов, основанные на итерационных процедурах, на
каждом шаге которых используются алгоритмы получения линейных
оценок. В настоящем параграфе дано общее представление о нелинейном
оценивании на примере метода Ньютона — Гаусса.
В случае тренда, нелинейного относительно параметров, имеет
место следующая теоретико-вероятностная схема:
y,=f{t,a) + t„ t = l...,T, (10.3.1)
где /(/, а) — тренд, нелинейный относительно вектора параметров а,
а' = (а,,...,а^); е,— случайная составляющая с Л/е, =0, De,=G^,
причем для простоты будем предполагать, что ее значения независимы.
259
Рассмотрим сумму квадратов отклонений известного отрезка ряда к,
/= 1,..., Т, от тренда:
т
1
1=1
Q{o^)=l[y,-f{t,a)f
Для минимизации суммы квадратов отклонений необходимо
приравнять к нулю производные по параметрам:
^ = -21[>',-/(^а)]^ = 0, / = 1,...Д. (10.3.2)
Если -^ линейно независимы как функции времени, то матрица X
Эа,.
имеет ранг к:
Х = \ШЛ1 ( = 1 т i = \ к
II Эа; II
Для исследования движения к точке экстремума необходимо
рассмотреть и вторые производные:
Исследование проведем при следующих предположениях, которые
сознательно сформулированы не очень строго (чтобы можно было
только изложить суть метода):
1) нелинейный тренд имеет относительно невысокий порядок
нелинейности, иными словами, вторые производные имеют не очень
большие по модулю значения;
2) точка а}',с которой начато исследование, находится вблизи
точки минимума а* =arginf Q(a), т. е. разность (а'"'-а*] мала.
Исходя из этих предположений, рассмотрим разложение тренда в
окрестности некоторой точки а''^
/=1 За,-
(О
/ 1.\ -^ Э/(/, aW)
/(/, а) = /(/, aW)+X ^^^ ^(а, -а|") + о(Д), (Ю.З.З)
а, -а
Д = тах
причем вследствие сделанных нами предположений вторые
производные в разложении отсутствуют.
260
Последовательность точек а^'', /= О, 1, 2,..., будем строить таким
образом, чтобы она сходилась к а*. Введем следующие обозначения:
У =
h.^
КУт]
, /(«) =
7(1.«)
е =
Г Р. Л
\^TJ
Х,=
э/(л «(^))
Эа,
, t = ] Т, / = 1 к.
Тогда
У = /(а) + е = /(а(')) + Х,(а-а(')) + ё, (10.3.4)
где величина ё вобрала в себя и остаточные члены разложения каждой
временной компоненты/(а), при этом по-прежнему считаем, чтоЛ/ё= 0.
Если предыдущая точка а^'^ уже каким-то образом определена, то
будем искать последующую точку а^'^ ' с помощью метода наименьших
квадратов, рассматривая в качестве исходной модели (в матричном виде)
преобразованное в такой вид выражение (10.3.4):
y-/(aW) = X,(a-a(')) + e, Мг = 0. (10.3.5)
Выражение (10.3.5) представляет собой модель тренда, линейного
относительно коэффициентов а, -а.]'', причем наблюдаемыми
значениями ряда являются у, -fit, ее ], а значениями функций времени при
Э/(Л aW)
параметрах регрессии
Эа,.
Применяя метод наименьших
квадратов к оценке параметров линейной модели (10.3.5), получаем
обозначив полученную оценку а через а''^'', имеем:
261
в результате, начиная с некоторой точки а^^^ получаем
рекуррентную последовательность точек а^^^ а*'', а'^^... таким образом, что
каждая последующая точка получается из предыдущей с помощью метода
наименьших квадратов для линейного отнорительно коэффициентов
тренда. В Приложении 3 доказано, что данная последовательность при
ранее указанных предположениях сходится к точке минимума
а^'^ ^ а* = arginf Q(a).
§ 10.4. Экспоненциальное сглаживание
в случае линейных и нелинейных временных трендов,
рассмотренных в § 10.1, 10.3, необходимо было постулировать форму тренда с
точностью до параметров перед началом экспериментального исследования
на основе известного отрезкад»,, / = I,..., Т, временного ряда. Метод
экспоненциального сглаживания позволяет анализировать временной ряд
и получать прогноз без предварительного задания формы тренда.
Требуется лишь, чтобы в области исследования тренд изменялся достаточно
постепенно, эволюторно.
В основе экспоненциального сглаживания лежит следующая
теоретико-вероятностная схема:
>-, =/(/) + е,. Л/е, =0, Ог,=а^. (10.4.1)
Для простоты далее будем предполагать, что значения случайной
составляющей в разные моменты времени некоррелированны, т.е.
cov(e,, е^) = 0, t*s.
Из первоначального временного ряда >», сглаженный ряд Sfy) можно
получить с помощью следующего линейного оператора сглаживания:
S,{y) = ay,-^-{\-a)S,_,{y), (10.4.2)
гдеа—константа сглаживания, О <а<1. Если применить оператор
сглаживания последовательно ко всем значениям отрезка ряда, то получим
•Уг (Я = «>'г + (I - «)'Уг-1(>') = «>'г + С - «)[«>'г-1 + С -«)'^г-2 (>')] =
= ... = а>'у-+а(1-а)>'у,_[+а(1-а)^>'у-_2 +...+
+ a(l-af"V2+(l-ar>'i. (10-4.3)
262
при этом в последнем равенстве сглаженное значение S^{y) заменили на
первое известное значение ряда. Таким образом, в случае
экспоненциального сглаживания наблюдения входят в обработку не с
одинаковыми, а с экспоненциально убывающими весами, т.е. настоящие
наблюдения как бы воспринимаются с большим доверием, чем прошлые.
Напомним, что и в методе скользящих средних имеет место неравенство весов:
наблюдения, попавшие в отрезок осреднения, входят с равными
весами, а остальные наблюдения — с нулевыми весами.
Так как веса экспоненциально убывают, то при достаточно большой
длине ряда его прошлые значения входят с быстро стремящимися к нулю
(по мере удаления) весами, поэтому условно ряд можно считать
бесконечным, расширив за пределы самых удаленных значений. В этом
случае оператор сглаживания запишется в следующем виде:
My) = Oil{l-a.yy,-s- О0.4.4)
Оператор сглаживания как в первоначальной, так и в
унифицированной форме линеен, поэтому, применяя его к отдельным составным
частям теоретико-вероятностной схемы, можно после сложения получить
результат сглаживания всего исходного ряда.
Применим оператор к случайной составляющей, тогда
^г(е) = а£(1-аГе,_,.
Найдем теперь дисперсию сглаженных значений случайной
составляющей, воспользовавшись независимостью ее значений в различные
моменты времени:
DS,{e) = M
.,2„2
2
2
= а^ 1(1-а) Л/е,_,е,_, =
s,r=0
Отсюда следует, что в результате сглаживания дисперсия случайной
составляющей, вообще говоря, уменьшается, поскольку < 1, так
2-а
как а < 2 — а, т.е. действительно имеет место сглаживание.
«Выступающие» значения детерминированной составляющей также сглаживаются,
т.е. сглаживанию действительно подвергается временной ряд в целом.
263
Оператор сглаживания можно вновь применить к уже сглаженным
значениям; в результате получим оператор сглаживания второго
порядка, последующее сглаживание дает оператор третьего порядка и т. д.:
sl'^=ay,+{\-a)sj%{y), (10.4.5)
sr=aSr4y)H^-)^Siy)-
Применяя несколько раз оператор сглаживания, а также подбирая
соответствующим образом константу сглаживания, можно практически
полностью исключить случайную составляющую. В результате
останется только преобразованная детерминированная составляющая.
Возникает вопрос: как же все-таки построить прогноз? Из
изложенного выше следует, что пока имеет место такая же ситуация, как и в
случае метода скользящих средних: можно аналитически выделить в
преобразованном виде детерминированную составляющую, однако нет
аналитической формулы для получения ее прогностических значений.
В случае экспоненциального сглаживания (в отличие от метода
скользящих средних) имеются аналитические выражения для прогноза.
Теорема Брауна, являющаяся фундаментальной в методе
экспоненциального сглаживания, утверждает, что коэффициенты полиномов, по
которым производится прогнозирование, определяются с помощью
дисконтированного метода наименьших квадратов и аналитически
выражаются через сглаженные значения ряда.
Введем следующие обозначения для прогнозирующего полинома
степени N, построенного в предположении, что значение ряда в момент t
является последним:
I
Л.х=4" + 1^^'- (10.4.6)
Таким образом, по этому полиному можно получать прогноз в точках
{t + т). Коэффициенты полинома должны быть определены так, чтобы
прогноз был наиболее точным.
Теорема Брауна. Коэффициенты прогнозирующих полиномов,
определенные по дисконтированному методу наименьших квадратов
Г
j=0
y<-s-l^i-sy
->min, (10.4.7)
264
линейно выражаются через сглаженные значения ряда
Sl^ky), ..., Sr\y), ^(^-)(^).
□ Доказательство теоремы сопряжено с громоздкими выкладками, поэтому
приведем его только для случая yV= 1:
Найдем оценки двух параметров прогнозирующего полинома с помощью
дисконтированного метода наименьших квадратов (индекс t опущен, введено
обозначение р = 1 - а). Получаем
s=0
(10.4.8)
Точку минимума, как обычно, находим из условия равенства нулю
производных:
2af^s^'^y,_^-aQ + a^s) = 0,
откуда получаем следующие уравнения:
Г / „ \
1Р^
«0-
\
1^Р
Так как
«0-
1^Р^
2 р.
Is'Г
s=0
j=0
«1 = I^PV.
j=0
TO
265
поэтому окончательно имеем:
(10.4.9)
2f"=^
1-а
'Sl4y)-Sj^\y)
В случае наиболее часто используемого квадратичного
прогнозирующего полинома
можно аналогично получить следующие выражения для оценок его
коэффициентов:
(10.4.10)
а
(0_.
2(1 - а) L
.,2
av =
а
(6 - 5а)^;') (у) - 2(5 - 4a)sP{y) + (4 - 3a)sl\)
2 ~7, \2
(1-а) L
Для расчетов на ЭВМ применяют следующие рекуррентные
формулы, эквивалентные формулам (10.4.10):
ai'^=y,+{l-af{y,-y,),
а{') = 2!'-П4'-')-|а^(2-а)(Л->',),
а(') = 4'-')-а^(Л->',).
где
у,-% +a^ +—02
Из этих формул видно, что при появлении нового наблюдения не
обязательно хранить весь предыдущий отрезок временного ряда, надо
лишь знать коэффициенты прогнозирующего полинома, найденные по
этому отрезку
Для прогнозирования на глубину х за пределы известного отрезка ряда
используют прогнозирующий полином, найденный на основе всего ряда:
,=0 '!
(10.4.11)
266
в том случае, когда в окрестности точки Гдетерминированная
составляющая близка к постоянной, применяют аппарат однократного
экспоненциального сглаживания и прогноз определяется по формуле
Так как
DsPiy) = DsPie) = ^,
то получаем следующий доверительный интервал прогноза:
4''(>')±'ра^а/(2-а), 1^ = 1^{Т-\).
Если в окрестности точки Гдетерминированная составляющая
линейная, то применяют двойное экспоненциальное сглаживание и точечный
прогноз осуществляют по формуле:
Ут+х-"о +^1 ^•
в результате подсчетов можем получить
2
[2 а)
поэтому имеем следующий доверительный интервал для прогноза:
a^Kal'^^x±tpaJla\\+4{\-a) + 5{\-af +2a{4-3a)x + 2a4^/{2-af
Если детерминированная составляющая нелинейная в окрестности Т,
то применяют тройное экспоненциальное сглаживание и точечный
прогноз определяется формулой:
в том случае, если детерминированная составляющая кроме роста
испытывает еще и периодические колебания, т. е. в окрестности t может
быть описана формулой:
f{t^x) = {A,^B,x)F{t^x),
где F{t) — периодическая функция с известным периодом М, может быть
применено сезонное экспоненциальное сглаживание, которое
реализовано в ряде пакетов прикладных программ. Программная система по
267
заданному периоду инициализации М производит первоначальную
оценку периодической функции (кМ— число наблюдений):
nt)=y,
м + \ .,„
t = {i-])M + J, t<kM, J = \,...,M, i = \,...,k;
B,=
{k-\)M
\ кМ ] Л/
хж 2^ Уз 77 2^Уз
^(') = т^' Pj^T^hJ + iM), tJ = h...,M.
В дальнейшем производится взаимосвязанное сглаживание
периодической функции и коэффициентов тренда по формулам:
Я=а^^^ + (1-а)(Л,_1 + ^,_1),приКЛ/, F,_m = F,,
/■,=p4+(i-p)F,_^, t>M,
А=у(Я-1-Я)+(1-у)^,_,-
Прогноз временного ряда на т шагов вперед осуществляется по
формуле
yj^^=(Aj^-BjX^F{T^-x-M), Т = кМ.
Оптимальные значения констант сглаживания а, р, у выбирают по
минимуму суммы квадратов отклонений прогнозов (на один шаг) от
действительных значений ряда.
Вопросы и задачи
1. Определите вид и параметры тренда в динамическом ряде
выплавки стали с 1960 по 1979 гг (см. таблицу).
268
Год
1960
1961
1962
1963
1964
1965
1966
1967
1968
Выплавка стали, млн. т
65.3
70,8
76,3
80,2
85,0
91,0
96,9
102,2
106,5
Годы
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
Выплавка стали, млн. т
110,3
115,9
120,7
125,6
131,5
136,2
141,3
144,8
146.7
151,5
2. Имеются следующие данные о числе ошибок лиц, обучающихся
машинописи:
Число месяцев работы
на пишущей машинке
1
2
3
4
Среднее число ошибок
на страницу
25
10
5
2
Найти прогноз среднего числа ошибок для лиц с полуторамесячным
стажем.
3. Пусть у, =af) + a^t + £|, Л/е, =0, Dt,=(5^, со\{г,,г^) = ^, s =^ t,
t=\ Т.
При какомвоценка d, =0 ^^ \У1+\ ~Уп является несмещенной? Най-
1=1
ти дисперсию этой оценки.
Глава 11
ЭЛЕМЕНТЫ МНОГОМЕРНОГО
СТАТИСТИЧЕСКОГО АНАЛИЗА
Многомерный статистический анализ в экономике занимается
выявлением «скрытых» факторов, определяющих изменение системы
экономических показателей, а также классификацией совокупности
экономических объектов — носителей системы показателей.
В первом случае система показателей трактуется как многомерная
случайная величина, между компонентами которой существует
стохастическая связь, а «скрытые» факторы — как система центрированных
некоррелированных случайных величин. Выявлением этих «скрытых»
факторов занимается факторный анализ, в том числе метод главных
компонент.
Во втором случае совокупность экономических объектов трактуется
как совокупность носителей многомерных выборочныхзначений,
образующих выборку наблюдений за многомерной случайной величиной.
Каждое многомерное наблюдение — реализация многомерной
случайной величины — описывает конкретный объект изучаемой
совокупности и может быть отнесено (наблюдение и, следовательно, объект) к
одному из классов. Такая классификация осуществляется с помощью
методов дискриминантного анализа и распознавания образов. При этом
необходимо иметь априорную информацию о типе распределения
многомерной случайной величины. Если же такой априорной информации
нет, то классы выделяют по степени «близости» объектов; объекты
внутри класса «близки» между собой, но далеки от объектов других классов.
Расстояние между объектами определяется, например, как обычное
евклидово расстояние в я-мерном пространстве.
В главе рассматривается сквозной пример, связанный с
определением и эффективностью использования экономического потенциала.
Рассмотренные в предыдущих главах методы математической статистики
могут быть, по крайней мере в простейших случаях, реализованы
вручную. Так, для того чтобы лучше разобраться с алгоритмом
регрессионного анализа, следует решить вручную простейшую задачу парной
регрессии, после чего переходить к компьютерному решению сложных
задач множественной регрессии.
270
Реализация же процедур многомерного статистического анализа
немыслима без применения ЭВМ. Многомерный статистический анализ
представлен во многих лицензионных программных системах. Как одну
из лучших возможно рекомендовать программную статистическую
систему Statistical Analysis System (SAS). В системе SAS широко
представлены методы теории вероятностей, математической статистики и
математического программирования, имеются профаммные средства ведения
баз данных, графического и табличного отображения данных.
§ 11.1. Модель факторного анализа
и метод главных компонент
При индивидуальном пошиве одежды измеряют много параметров,
характеризующих фигуру данного человека, в то время как при
промышленном изготовлении одежды во внимание принимаются только три:
размер, рост, полнота.
Эта ситуация наглядно демонстрирует основную задачу факторного
анализа: перейти от первоначальной системы большого числа
взаимосвязанных показателей Х^ Х^ к относительно небольшому числу
«скрытых» факторов F^,..., Fj^, к< т, изменение которых в значительной
мере предопределяет изменение первоначальных показателей.
В экономике возникает множество как частных, так и общих задач
такого рода. Например, задача поиска одного или нескольких
обобщающих показателей эффективности использования ресурсов по многим
частным показателям эффективности (производительность труда,
фондоотдача, материалоотдача). Казалось бы, в скобках перечислено всего
три частных показателя эффективности. Но если вспомнить о разных
видах труда, фондов и расходуемых материалов, то станет ясно, что
таких показателей достаточно много.
Модель факторного анализа
Модель факторного анализа записывается в следующей форме:
к
Xi^ai + ^ayFj+VjEi, / = !,...,/я, к<т, (11.1.1)
где MX. = а.;
Fj, j= \,..., к, — общие («скрытые») факторы;
a.j— нагрузки первоначальных показателей на общие факторы;
Ej, /= 1 т, — характерные факторы;
V. — нагрузки показателей на характерные факторы.
271
Общие и характерные факторы центрированы {MF- = 0,у = 1, ..., к,
Л/е; = 0,(=1,...,/я),нормированы(M/i'j = 1, j = \,...,k, Mt] = 1, i=\,...,m)
и некоррелированны {MFjFj.=Q, j*j', Л/е,е,, =0, i*i', MFjt^=0,
j,j'= ],..., к, i,i' = \,...,m).
В матричной форме модель факторного анализа (11.1.1) примет вид:
X = a + AF + Ve,
где
Х =
м
а =
М
v"m;
(11.1.2)
— векторы-столбцы первоначальных показателей и
их математических ожиданий;
F =
fF,^
М
е =
м
V^my
— векторы-столбцы общих и характерных факторов;
А =
^«..
«21
L
k«ml
«12
«22
L
а -,
L
L
L
L
«iH
«2*
L
">«к^
, v =
(V,
0
L
.0
0
V2
L
0
L
L
L
L
Q\
0
L
t^my
матрицы нагрузок на
общие и характерные
факторы.
Согласно модели (11.1.2) многомерный показатель А'разлагается на
три некоррелируемые составляющие:
1) неслучайную составляющую а (математическое ожидание);
2) случайную составляющую AF, определяемую общими факторами;
3) случайную составляющую Ке, определяемую характерными
факторами.
Для того чтобы реализовать модель факторного анализа, по крайней
мере надо найти по.выборочным данным оценки математических
ожиданий а (это несложно и изложено в гл. 6), оценки факторных нагрузок
и сами общие факторы F, тогда последняя составляющая определяется
как остаток.
Имеются методы (центроидный и др.), которые позволяют это делать,
однако эти методы определяют факторы неоднозначно, поэтому в
большинстве практических исследований по применению многомерного
анализа используется метод главных компонент
272
Метод главных компонент
В отличие от общих факторов, которые исчерпывали большую часть
(но не всю!) вариации первоначальных факторов, главные компоненты
объясняют всю вариацию и определяются однозначно.
Модель главных компонент имеет вид:
т
Xi=a^ + Y,ayFj, i = ],...,m, (11.1.3)
или в матричной форме:
X = a + AF.
Как видим, в этой модели отсутствуют характерные факторы,
поскольку главные компоненты /^полностью исчерпывают всю вариацию
первоначальных показателей. Главные компоненты, как и факторы,
центрированы, нормированы и некоррелированны. Иногда рассматривают
и ненормированные главные компоненты.
Обозначим центрированные первоначальные показатели через
Y.^ = X.- йр ('= 1 т, тогда модель (11.1.3) запишется в форме
Y = AF. (11-1.4)
С целью определения матрицы нагрузок/1 найдем собственные
числа Х и собственные векторы / ковариационной матрицы
первоначальных показателей
(/я X /я) В= cov(A',. ,Xj) = cov(y,., Yj)
= MYY'.
Напомним: собственные числа и собственные векторы матрицы
определяются из уравнения
Bl = Xh или {В-ХЕ„)1 = 0, (11.1.5)
т.е. для таких векторов умножение на матрицу эквивалентно умножению
на собственное число. В уравнении (11.1.5) Е^ — единичная матрица.
Однородная система уравнений (11.1.5) имеет ненулевое решение,
если ее определитель равен нулю:
\В-ХЕ\ = 0. (11.1.6)
Характеристическое уравнение (11.1.6) является уравнением т-й
степени относительно X, поэтому имеет т решений X^, ..., А,^ —
собственных чисел матрицы В.
10-670 273
Каждому собственному числу отвечает целое направление
собственных векторов, так как уравнение (11.1.5) остается справедливым и для
любого С/, если оно верно для /. Поэтому из всех собственных векторов,
отвечающих собственному числу А,., выберем нормированный, т.е. такой,
длина которого равна единице:
1^ = 1-
Собственные векторы, отвечающие разным собственным числам,
ортогональны, поэтому матрица
L = {l,,...,!,),
составленная из нормированных собственных векторов, ортогональна.
Ортогональные матрицы задают поворот осей координат. Обратная к
ортогональной матрица также ортогональна, поскольку она задает
поворот с возвратом в первоначальное состояние. Для ортогональных
матриц обратная матрица равна транспонированной.
Поэтомулинейное преобразование центрированных первоначальных
показателей с помощью ортогональной матрицы L' означает поворот
осей:
f = L'Y, Y = Lf.
(11.1.7)
Покажем, что получившиеся новые показатели некоррелированны.
В самом деле, эти показатели согласно формуле (11.1.7) центрированы,
поэтому
||cov(/, ,fj.)= Mff = ML'YY'L = L' MYY'L = L'BL = \щ\ =
^1 0 L 0 ^
=i|/;v;i=
0 X.
0
L L L L
0 0 L A,
mj
таким образом, cov(/,. - /у) = О, i Ф j, и Df^ = cov(/,-, /у) = ^/ •
Поскольку ортогональное преобразование сохраняет расстояние, то
/•=1 /=1
274
Поэтому вся вариация первоначальных показателей равна вариации
ненормированных главных компонент:
/•=1
/•=1
= м
I//
/=1
/•=1 /=1
(11.1.8)
а последняя равна сумме собственных значений, тем самым полная
вариация равна сумме собственных значений. Главные компоненты
перенумеровывают в порядке убывания собственных значений
А,| ^ А,^ ^ ... ^ К^ .
На практике из всех ненормированных главных компонент
оставляют несколько первых, которые аккумулируют существенно большую
часть полной вариации, остальные отбрасывают.
Нормированные компоненты получаем делением компонент на свои
стандартные отклонения:
или в матричном виде:
О
L
О
где Л"'^ =
0
1x7
ч 1
L
0
L
L
L
L
0
0
L
У^т
откуда f = A^F, поэтому
т. е. матрица нагрузок на стандартизованные компоненты имеет
следующий вид:
/^ = Lл^^
(11.1.9)
где
К^' =
Ж.
О
L
О
о
■у/«2
L
О
т J
10*
275
На самом деле все эти расчеты выполняются не по теоретическим
математическим ожиданиям а и ковариационной матрице В, а по их
оценкам а, В, найденным по выборке.
Q Пример 11.1. Рассмотрим задачу определения агроресурсного потенциала
субъектов РФ. На объем выпуска сельскохозяйственной продукции при прочих
равных условиях долговременное решающее воздействие оказывают следующие
факторы (показатели): площадь и качество сельхозугодий, среднегодовая
температура, осадки за год, число занятых, основные производственные фонды,
дороги, минеральные удобрения, покупные концентрированные корма. Как
видим, первые три показателя относятся к природно-климатическим, а
последние - к экономическим.
Если все экономические показатели привести в расчете на гектар
сельхозугодий некоторого стандартного, базового качества (приведенный гектар
сельхозугодий), то получим окончательно следующий перечень показателей:
A'l - среднегодовая температура (°С),
Х^ - осадки (мм),
А'з - число занятых (чел./га),
Х^ - основные производственные фонды (тыс. руб./га),
Х^ - дороги с твердым покрытием (км/га),
A'g - внесение минеральных удобрений (т/га),
X-J - покупные концентрированные корма (т/га),
т.е. т = 1.
Носителями указанных показателей служат субъекты РФ - республики,
области и края, всего 77 субъектов, т.е. объем выборки равен п = 77. Расчеты
выполнялись с помощью программной системы SAS. В результате были
оценены математические ожидания первоначальных показателей а, их
ковариационная матрица В и найдены ее собственные числа:
А,, =4,22; А,2=1,30; X^=0J1\ А,4=0,36;
А,5 = 0,22; ^,^ = 0,12; А,7=0,05.
Таким образом, сумма первых двух собственных значений составляет 78,5%
общей суммы, т.е. вариация двух компонент объясняет (определяет) 78,5%
общей вариации.
Центрированные первоначальные показатели оказались следующими
линейными комбинациями ненормированных главных компонент:
Г, =0-/, + 0,69/2. Г5 =0,89/, -0,04/2,
Г2 = -0,09/, + 0,51/2, Г, = 0,76/, + 0,25/2 -
Гз = 0,94/, + 0,03/2, ^7 = 0,95/, + О, О2/2.
Г4=0,97/,+0-/2,
276
Как видим, экономические показатели (3-7) имеют достаточно высокие
нагрузки на первую компоненту, а климатические (1-2) - на вторую. Таким
образом, первую компоненту можно интерпретировать как «скрытый» обобщенный
экономический фактор, а вторую - как «скрытый» обобщенный климатический
фактор. •
Регрессия на главных компонентах
Модель множественной регрессии на главных компонентах имеет
вид:
где F— нормированные главные компоненты.
Будем считать, что модель регрессии и компоненты определяются по
одной и той же совокупности из п экономических объектов.
Так как главные компоненты, найденные по выборке, центрирова-
1 я . _ 1 "
ны, то — У F:: = О, следовательно, о.^=у =—Y,y ■., поэтому модель мож-
но представить в следующей измененной форме:
я
/•=1
Тогда теория множественной регрессии дает следующие оценки
коэффициентов регрессии:
a = {F'F)~^F^Y,
где F =
Fji F22 L Fji,
y/'ni I'm L F„i^j
a F^i — значение г'-й компоненты дляу-го наблюдения;
а =
Г«.1
м
л.
, ^Y =
(у,-уЛ
м
Jn -у,
вектор-столбец отклонений значений
результирующего показателя от своего
среднего.
277
To, что главные компоненты нормированы и центрированы для
выборочных значений, записывается в следующей форме:
поэтому в нашем случае матрица нормальных уравнении примет вид:
F'F =
l''ji''jr\\ =
;=1
fn О h 0^
О я L О
L L L L
О О h п)
тем самым каждое нормальное уравнение будет содержать только одну
переменную
я _
т. е. решение записывается в явном виде:
1 ^
-\ 1 ^
а,- = - I /";,- (yj-y) = -l Fflyj. так как X Fji = О •
§ 11.2. Понятие о многомерной классификации
Исходные экономические объекты (предприятия, организации,
регионы и т.п.) описываются системой из т показателей, тем самым
каждый такойу-й объект задается как точка в /я-мерном пространстве:
ICyi,..., Xji^, J — I, ..., П,
(11.2.1)
где Xij — значение г'-го показателя уу-го объекта; п — число изучаемых
объектов.
Совокупность всех наблюдений (11.2.1) можно трактовать как
выборку объема п из многомерной генеральной совокупности X^,..., Х^. Тогда
надо располагать априорной информацией о характере распределения
генеральной совокупности. Во многих практических случаях такой
информации не имеется. Поэтому применяются методы кластер-анализа,
основанные на «близости» наблюдений внутри класса и их
«удаленности» от наблюдений других классов.
278
Понятие о кластер-анализе
Примерный машинный алгоритм кластер-анализа выглядит
следующим образом.
1. Первоначальная система показателей, представленная п
выборочными наблюдениями (11.2.1), заменяется на систему п наблюдений над
первыми Л главными компонентами (часто к= 2):
Fji,...,Fji^, J = \ я, к<т,
тем самым каждый объект — точка в ^-мерном пространстве первых к
компонент (часто на плоскости).
2. Осуществляется собственно кластер-а нал из, состоящий в
разделении п объектов на заданное пользователем число классов г.
В свою очередь процедура собственно кластер-анализа, например,
может быть выполнена в два этапа:
1) выделяются первоначальные центры г классов, как система г
точек, наиболее удаленных друг от друга;
2) последовательно с каждой из оставшихся (п — г) точек проводятся
следующие операции:
а) определяется класс, к центру которого ближе всего расположена
данная точка;
б) точка включается в класс, после чего находится новый центр
класса как среднее арифметическое точек, входящих в класс.
Вернемся к примеру 11.1. Напомним, что из семи главных компонент
были отобраны две: первая получила интерпретацию как обобщенный
экономический показатель, а вторая — как обобщенный климатический.
На плоскости первых двух компонент было выполнено разбиение 77
субъектов РФ на 5 классов (разумеется, были варианты с разбиением на
другое число классов).
Полученные классы были расположены в порядке уменьшения
оснащения приведенного гектара экономическими ресурсами: первый
класс — самый высокооснащенный, последний класс — самый низко-
оснащенный. Когда на карте РФ республики, области и края были
размечены по принадлежности к классам, то выяснилось, что на самом деле
классы выстроены в порядке улучшения природно-климатических
условий: первый класс с самыми худшими природно-климатическими
условиями (в основном самые северные области), последний — с
наилучшими природно-климатическими условиями (в основном самые южные
области). Тем самым многие десятилетия худшие
природно-климатические условия компенсировались большей ресурсооснащенностью.
279
Понятие о дискриминантном анализе
В случае дискриминантного анализа предполагается, что каждая
выборочная точка х-
м
\^mj
может принадлежать одной из г генеральных
совокупностей, законы распределения которых известны. Пусть каждый
из этих законов имеет плотность
/,W, l=\,...,r.
Выборочная точка л; принимается принадлежащей генеральной
совокупности /q, если
" 1=1,...,г
В большинстве практических случаев распределения генеральных
совокупностей предполагаются нормальными. Кроме того, так же как в
случае кластер-анализа, первоначальные показатели предварительно
заменяются на новые некоррелированные в меньшем числе, тогда
каждую многомерную плотность можно представить как произведение
одномерных.
Вопросы и задачи
1. Найти собственные значения ковариационной матрицы при я = 2.
2. Исследовать при п = 2, как меняется доля первой главной
компоненты в общей вариации при изменении коэффициента корреляции р
от О до 1.
3. При я = 2 найти ортогональную матрицу, которая переводит
коррелированные центрированные случайные величины F,, Yj в
некоррелированные главные компоненты/,, ^.
Приложение 1
ДОКАЗАТЕЛЬСТВО
СХОДИМОСТИ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ СМО
К СТАЦИОНАРНЫМ ЗНАЧЕНИЯМ
В § 5.3 использовалось утверждение, что СМО с ограниченной
очередью после завершения переходного процесса входит в стационарный
режим, в котором вероятности состояний системы задаются
стационарным решением системы дифференциальных уравнений для
вероятностей состояний в переходном режиме. Эти стационарные вероятности
состояний не зависят от начального состояния СМО.
Докажем это утверждение для одноканальной СМО (л = 1) с
ограниченной очередью при N=2, т.е. в очереди не может быть более одного
требования.
Дифференциальные уравнения для вероятностей состояний системы
в переходном режиме имеют следующий вид (см. формулу (5.2.12) с
матрицей Л, определяемой из формулы (5.3.15) при л = 1, Л'^= 2):
<^Ро _
= -^Р0 + ^Р['
-^ = ^о-(?и-ц)/>, + ц/>2, (П.1.1)
d/
= Хр^-^Р2.
Эта система уравнений имеет стационарное решение, определяемое
системой линейных однородных алгебраических уравнений:
-Хро + р.р^=0,
Хро -{Х + ц)./>, + ц/>2 =0, (П. 1.2)
?1/>,-Ц/>2=0,
которая имеет ненулевое решение, поскольку ее определитель равен
нулю (последнее уравнение является суммой первых двух).
281
Заменяя последнее уравнение на естественное соотношение
/>о + />j + /?2 = 1, получаем невырожденную систему линейных
неоднородных уравнений:
-ХРо + щ=0,
Po + Pi+ Pi =1-
которая имеет решение, совпадающее с (5.3.17) прил= \,N=2,
Ро=-, Г'
1 + р + р
1+р + р''
р^ X
Р2=-Г-^ 2' Р = --
1+р+р ц
В свою очередь, из естественного соотношения Pq + Pi+ Р2= ^
вытекает —^ + —L + —^ = 0, поэтому последнее уравнение (П. 1.1) являет-
d/ d/ d/
ся суммой первых двух. Отбрасывая его и заменяя/JjCO = 1 — P^it) —p^{t),
получаем следующую систему дифференциальных уравнений для />о(0>
P,{ty.
^Рй _
= -ХРо + \хр^,
^* (П. 1.4)
-^ = (?1 - ц>о - (?1 + 2ц)/>, + ц.
Система (П. 1.4) имеет стационарное решение:
дО- ^ „0^___Р__
"о 1 1 ' Р\ л 2 '
1 + Р + р'^ 1+Р + Р
которое, конечно, совпадаете (П. 1.3).
Эта система неоднородна, поэтому сначала найдем решение для
однородной системы, которое, как предписывает теория, будем искать в
виде:
/>о = 4е", Pi = A^t".
Подставляя выражение для />q и/>, в (П. 1.4), получаем:
282
|'/4е"=-Х4е"+ц/1,е",
или
(П.1.5)
тем самым константа / должна удовлетворять следующему
характеристическому уравнению (чтобы получить нетривиальное решение
относительно Aq, /4,):
-Х-1 ц
= 0,
(П. 1.6)
или 1^ +2{Х + \х)1 + %} +^Х + ^^ =0,
откуда
/,2=-(?^+ц)±7й^.
Кроме того, из первого уравнения (П.1.5) (второе при /= /,, /j
является следствием первого) получаем
■{'■) _
X + L
'■) ,-^1
А"=^^^4>' ' = 1.2,
поэтому решение однородной системы примет вид (С,- = А^ , / = 1,2):
(П.1.7)
/,,(/) = C,(-l + Vp)e'''+C2(-l-Vp)e'^'=C,/,J')(/) + C2/»P(/),
где {X + /,. )/ц = (-Ц ± 7^)/ц = -1 ± Vp .
Решение первоначальной системы (П. 1.4) найдем методом вариации
постоянных С, =С,.(/), / = 1, 2. Подставляем выражение (П.1.7) в
систему (П. 1.4):
283
Поскольку ipo ,Pi )' i~ 1. 2, являются решениями однородных
уравнений, то для C^(t), C^it) получаем систему:
Приводим ее к стандартному виду (путем решения как обычной ал-
гебраическои системы относительно —!- —^):
d/ d/
dC,
i.-iL.e-V
d/ 2Vp
dq
2V?
d/
l___M_e-'2'.
При этом, как видим, получилось два отдельных уравнения с
разделяющимися переменными, которые имеют следующие решения:
2VP/i
C2{t) = ,r^^-''' + B,.
Итак, общее решение системы (П. 1.4) примет вид:
_1 1
+ 5,е'''+52е'^'.
l-^P 1 + Vp
V h
Ч )
+ 5,(-l + Vp)e^'-52(l + VpK''.
где 5j, ^2 ~ постоянные, определяемые из начальных условий.
Поскольку /, = -(ц + ^) + -^jIX^ < о, /2 = -(ц + ^) - -^jlx^ < О, то при t^°°
члены, содержащие В^, В^, стремятся к нулю, поэтому
lim pQ{t)
_ Ц
2J^l
2^|p {n + xf-^X 1 + р + р
' t-pI
284
lim/>,(/) =
__М_
-i+yp
+ -
'+Ур
2^1р\^\х + Х~л1\1х \x + X + ^|\xX
_p.[2^-2^{Vi + X)]_
27р(ц^+Ц^ + А?] 1+р + р
2 ~ Pi-
Таким образом, действительно по завершении переходного процесса
система входит в стационарный режим, вероятности которого являются
стационарным решением системы (П. 1.4):
\impi{t) = pf, / = 0,1,2,
при ЭТОМ
/'2(0 = 1-МО-Л(0. p',=\-p',-pf
Приложение 2
РАСЧЕТ СУММ, СОДЕРЖАЩИХ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
В § 10.2 при расчете коэффициентов тригонометрической рефессии
были использованы выражения сумм, содержащих тригонометрические функ-
f2nj Л . (2nj Л т . , т , „,
ции cos —^/ , sin —^/ , имеющие период—, / = ],..., 1, т = 21.
\ т J \ т J j 2
Ниже определяются эти выражения. Прежде всего найдем суммы
Z, / ч Х / S 2nj . , т ,
Xcos(9/), Х«1п(фО''"^^'•'^ ' ./ = '.■■•, —-1.
1=1 1=1 "^ ^
Используя формулу Эйлера
cos9 + ;sin9 = е"*", / = V-1,
и формулу суммы геометрической прогрессии, имеем:
т т т e''"Pfl-e'"P^)
Icos(9/) + /Ssin(9/)= Se'-f' =—i-—-i =
f=i 1=1 1=1 1-e^
(cos9-cos[9(7' + l)]+/jsin9-sin[9(7' + l)]i\[(l-cos9)+/sin9]
[(l-cos9)-/sin9][(l-cos9)+/sin9]
2 1—{cos9-cos[9(7'+l)]}(l-cos9)-sin9(sin9-sin[9(r+l)]}+
(l-cos9) +sin ф^^ L jj i L jj
+/(sin 9|cos Ф - cos[9(7' +1)]} + (1 - cos9)|sin ф - sin[9(7' + 1)Ш =
4sin(fjsin(^9)cos(^9J + /-4sin(-|)sin(^9)sin(^9)
286
<i)
отсюда
т sin(fr)cos[(r + l)f)
1 = 1 Sin +
X С08(ф/) = —^-^—^—тТГ^ '-^' S sin (ф/)
1 = 1
Поскольку ф = 2nj/m, h = Г/т — целое, то
^^_sin(fr)sin[(r+l)f]
sin(f)
sinfr^j = sinf r^^l = sin(n//i) = о,
m
поэтому
1=1 к m J ,^i К m J
Далее
,=i Km) ,=1
1 2 2
2,=i \ m J 2
1=1 \m ) ,=, 2 2 2,=i \ m ) 2
Поскольку при у '^ A: (используем формулу косинуса суммы и
разности)
^ (2nj Л (2пкЛ т (2п{1 + кУ] г Г2п]Л.(2пк
2,cos / COS / = 2.C0S —^ — + 2.sin —-t sin
1=1 у m J \ m J ,^i { m ) ,^i У m ) у m
T . (2nj Л . (2жк ^
= 2.sin / sin /
,=1 \ m ) \ m
Xcos —^t COS / = у COS — '- у sin -^t sinl ■
,=i \m ) ym ) ,=i у m J ,^i у m J у m
^ . f2nj^ . (2nk^
= -2.sin / sin / ,
,=i У m J У m J
sin / =
287
поэтому
I (iKJ л (Ink л т (2Ttj Л . [Ink
Xcos —^t COS / =±ysin -^t sin /
1=1 \ m J { m ) 1^1 [^ m J { m
следовательно,
^ (2nj Л (Ink Л ^ L . (2nj Л . (Ink
Xcos —^/ COS / =0, у sin —^/ sin -
1=1 \ m J { m j ,=i [^ m J {
t =0.
m
Точно так же, используя формулу синуса суммы и разности,
устанавливаем:
I (2п;Л . (2жкЛ „
Xcos —^/ sin / =0.
,=1 У т ) \ т )
Приложение 3
ОБОСНОВАНИЕ СХОДИМОСТИ
МЕТОДА НЬЮТОНА-ГАУССА
В § 10.3 в общих чертах был описан итерационный метод Ньютона-
Гаусса нахождения точки минимума функции
ОИ^ХЬ,-^")]'. а =
1=1
м
где/(/, а) — тренд, нелинейный относительно своих параметров.
Необходимым условием локального экстремума функции многих
переменных является равенство нулю ее первых производных:
= 0, i = \,...,k,
однако при этом неясно, является ли точка а , в которой все
производные обращаются в нуль, точкой максимума или минимума либо вовсе
не является точкой экстремума. Для выяснения того, какой же случай
действительно имеет место, следует рассмотреть вторые производные
функции Q{a).
Согласно предположениям, сделанным в § 10.3 при изложении
метода Ньютона—Гаусса, начальная точка а^"^ находится в достаточно
близкой окрестности точки локального минимума (условие 2), а функция
/(/, а) не слишком «нелинейна» относительно параметров а (условие 1),
точнее это выражается в том, что поведение матрицы Гессе, т.е. матрицы
вторых производных функции Q
j^J Э^е 11-21 ^-^ ^^ 2Т\у fit,а)] ^'^
Эа^Эау
289
2£,э/ э/
,=1Эа,. Эа^.
-^?,^'-л'•<^)lэS
Эа^Эау
= Н,+Н^,
определяется первым слагаемым Я, = Х'Х, где
v^r = Х{а) =
Э/(1,а) Э/(1,а) ^ Э/(1,а)
Эа,
За,
Эа^
Э/(/.(х) Э/(/, а) ^ Э/(/,а)
Э/(Г. а) Э/(Г,а) Э/(Г, а)
Эа,
За,
За
* J
Для доказательства сходимости метода Ньютона—Гаусса
понадобятся следующие две теоремы.
Теорема 1. Если столбцы матрицы Л'линейно независимы, то
матрица А = Х'Х положительно определена.
□ Доказательство. Линейная независимость столбцов матрицы А" означает,
что ни один из них не может быть представлен в виде линейной комбинации
других с хотя бы одним ненулевым коэффициентом, т.е. det А^О. Матрица А,
как и всякая другая, некоторым ортогональным преобразованием f/приводится
к главным осям, т.е.
U'AU = A =
^?l, О L О ^
о ^2 L о
L L L L
О о L ?1^у
Из невырожденности А вытекает, что все Х^ "^ О, поскольку
det Л = ^,^2 L ^^. = (det uf det А.
Теперь осталось только показать, что все ^^ > 0. Дейавительно, K = U'AU =
= U'X'XU = (XU) XU = В'В =
, В = Хи, и, следовательно.
^/ = Z*,/ > О, но ^, 9!: О, поэтому Xi > О, что и требовалось доказать.
1=1
290
Теорема 2. Если матрица А положительно определена, то и матрица А '
положительно определена.
□ Доказательство. Поскольку А положительно определена, то найдется
такое ортогональное преобразование U, что
а, О L 0^
U'AU=A =
О ^2 L
О
L L L L
О О L X
*;
где все Х^ > 0.
Тогда
л-' =
О L
Г,' L
О .2
L L L
О О L
О
о
L
= [U'AU) = и-^А'\и'У^ = U'A'V
поскольку для ортогональных матриц U' = U '.Так как Х/ > О для всех /, то
из последнего равенства следует положительная определенность /1~', что и
требовалось доказать. ■
Итак, условие 1 и доказанная теорема 1 обеспечивают положительную
определенность матрицы Гессе функции Q (а) в окрестности точки а.
Теперь докажем, что последовательность точек а'-'^, определенная в
§ 10.3, сходится к точке локального минимума а' функции
Q(«)=i[j,-/(/,a)f.
1=1
□ Прежде всего покажем, что на последовательности а^'' функция Q (а) арого
монотонно убывает, т.е. Q (а^' '*'''>)< Q (а^^).
В самом деле, имеем
[Mt) = f(t,a^'^), Х, = х(а^'^), f;={m,...,f,{T)[
Q{o.^'%i[y,-f,{t)f={Y-f,)\Y-f,),
'='
Q[a^>^'y[Y-f,--X,{X',X,)-'x',{Y-f,)\[Y-f,~X,{X',X,)-'x',{Y-f,)Y
291
={Y-f,)'{Y-f,)-2{Y-f,)'x,{x;x,)-'x;{Y-f,)+
+{Y-f,)'x,{x;x,)-'x;x,{x;x,)-'x;{Y-f,) =
= 0(а(')) - (К - f,)'x,{x;X,)-'x;{Y -/,) = о(а(')) - z'AjU -
где z = X'i(Y -fi)- вектор-столбец размером kxX, поэтому z'AJ^ -
дратичная форма с матрицей AJ^ размера (к х к).
Выше было доказано, что матрица А/ = А'/Л', положительно определена,
поэтому и матрица Af^ также положительно определена (см. теорему 2), так
что квадратичная форма ^'/1,~'^ > О для любых значений z- Поэтому дейави-
тельно 0(а'''^'М<о[а^'^), т.е. последовательноаь значений Qicc п аро-
го монотонно убывает. Вмеае с тем она ограничена снизу > О,
поэтому существует предел ОшЩ^О*. Из непрерывности Q (а) следует
а''' -> а*, Q(a*] = Q*, что и требовалось доказать. ■
ква-
Приложение 4
ТАБЛИЦЫ
1 -2/2
Таблица П,4,1. Значение функции ф(д:) = -т=е ^ '
-\/27t
и функции Лапласа Ф{х) = .— |е~^ '^d^
X
0,00
0.05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
(р(х)
0.3989
0,3984
0,3970
0,3945
0,3910
0,3867
0,3814
0,3752
0,3683
0,3605
0,3521
0,3429
0,3332
0,3230
0,3123
0,3011
0,2897
0,2780
0,2661
0,2541
0,2420
0,2299
0,2179
0,2059
0,1942
Ф(х)
0,0000
0,0199
0,0398
0,0596
0,0793
0,0987
0,1179
0,1368
0,1554
0,1736
0,1915
0,2088
0,2257
0,2422
0,2580
0,2734
0,2881
0,3023
0,3159
0,3289
0,3413
0,3531
0,3643
0,3749
0,3849
X
1,25
1,30
1,35
1,40
1.45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
(р(х)
0,1826
0,1714
0,1604
0,1497
0,1394
0,1295
0,1200
0,1109
0,1023
0,0940
0,0863
0,0790
0,0721
0,0656
0,0596
0,0540
0,0488
0,0440
0,0396
0,0355
0,0317
0,0283
0,0252
0,0224
0,0198
Ф«
0,3944
0,4032
0,4115
0,4192
0,4265
0,4332
0,4394
0,4452
0,4505
0,4554
0,4599
0,4641
0,4678
0,4713
0,4744
0,4773
0,4798
0,4821
0,4842
0,4861
0,4878
0,4893
0,4906
0,4918
0,4929
X
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
3,05
3,10
3,15
3,20
3,25
3,30
3,35
3,40
3,45
3,50
3,55
3,60
3,70
3,80
(р(х)
0,0175
0,0154
0,0136
0,0119
0,0104
0,0091
0,0079
0,0069
0,0060
0,0051
0,0044
0,0038
0,0033
0,0028
0,0024
0,0020
0,0017
0,0015
0,0012
0,0010
0,0009
0,0007
0,0006
0,0004
0,0003
Ф«
0,4938
0,4946
0,4953
0,4960
0,4965
0,4970
0,4974
0,4978
0,4981
0,4984
0,4986
0,4989
0,4990
0,4992
0,4993
0,4994
0,4995
0,4996
0,4997
0,4997
0,4998
0,4998
0,4998
0,4999
0,4999
293
Таблица П.4.2. Значения t, соотаетствующие
аероятности
Р = 4^{4>^р)
Чк) п
г^-^
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
40
60
120
оо
0,1
6,31
2,92
2,35
2,13
2,01
1,94
1,89
1,86
1,83
1,81
1,80
1,78
1,77
1,76
1,75
1,75
1,74
1,73
1,73
1,72
1,71
1.70
1,68
1,67
1,66
1,64
0,05
12,71
4.30
3,18
2,78
2,57
2,45
2.36
2,31
2,26
2,23
2,20
2.18
2,16
2,14
2,13
2,12
2,11
2,10
2,09
2,09
2,06
2,04
2,02
2,00
1,98
1,96
0,01
63,66
9,92
5,84
4,60
4,03
3,71
3,50
3,36
3,25
3,17
3,11
3,05
3,01
2,98
2,95
2,92
2,90
2,88
2,86
2,85
2,79
2,75
2,70
2,66
2,62
2,58
0,005
127,32
14,09
7,45
5,60
4,77
4,32
4,03
3,83
3,69
3,58
3,50
3,43
3,37
3,33
3,29
3,25
3,22
3,20
3,17
3,15
3,08
3,03
2,97
2,91
2,86
2,81
294
Таблица П.4.3. Значения у^^, соответствующие
вероятности
к ^\
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
50
100
0,99
0,0002
0,02
0,12
0,30
0,55
0,87
1,24
1,65
2,09
2,56
3,05
3,57
4,11
4,66
5.23
5,81
6,41
7,02
7,63
8,26
8,90
9,54
10,20
10,86
11,52
12,20
12,88
13,56
14,26
14,95
22,16
29,71
70,07
0,95
0,004
0,10
0,35
0,71
1,15
1,64
2,17
2,73
3,33
3,94
4,58
5,23
5,89
6,57
7,26
7,96
8,67
9,39
10,12
10,85
11,59
12,34
13,09
13,85
14,61
15,37
16,15
16,93
17,71
18,49
26,51
34,76
77,93
0,90
0,02
0,21
0,58
1,06
1,61
2,20
2,83
3,49
4,17
4,87
5,58
6,30
7,04
7,79
8,55
9,31
10.09
10,86
11,65
12,44
13,24
14,04
14,85
15,66
16,47
17,29
18,11
18,94
19,77
20,60
29,05
37,69
82,36
0,10
2,71
4,61
6,25
7,78
9,24
10,65
12,02
13.36
14.68
15,99
17,28
18,55
19.81
21,06
22,31
23,54
24,77
25,99
27,20
28,41
29,62
30,81
32,01
33,19
34,38
35,56
36,74
37,92
39,09
40,26
51.81
63,17
118,50
0,05
3,84
5,99
7,82
9,49
11.07
12,59
14,06
15.51
16.92
18,31
19,68
21,03
22,36
23,69
25,00
26,30
27,59
28.87
30,14
31,41
32,67
33,92
35,17
36,42
37,65
38,89
40,11
41,34
42,56
43,77
55,76
67,51
124,34
0,01
6,64
9,21
11,34
13,28
15,09
16,81
18,48
20,09
21,67
23,21
24,72
26,22
27,68
29,14
30,58
32,00
33,41
34,81
36,19
37,57
38,93
40,29
41,64
43,98
44,31
45,64
46,96
48,28
49,59
50,89
63,69
76,15
135,81
295
Таблица П.4.4. Значения F , соответствующие
вероятности р = Р[р{к^,к2)> Fр\
при/? = 0,05
'F{k^, к^
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
40
60
120
СО
1
161,45
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,84
4,75
4,67
4,60
4,54
4,49
4,45
4,41
4,38
4,35
4,24
4,17
4,08
4,00
3,92
3,84
2
199,50
19,00
9,55
6,94
5,79
5,14
4,74
4,46
4,26
4,10
3,98
3,88
3,80
3,74
3,68
3,63
3,59
3,55
3,52
3,49
3,38
3,32
3,23
3,15
3,07
2,99
3
215,71
19,16
9,28
6,59
5,41
4,76
4,35
4,07
3,86
3,71
3,59
3,49
3,41
3,34
3,29
3,24
3,20
3,16
3,13
3,10
2,99
2,92
2,84
2,76
2,68
2,60
4
224,58
19,25
9,12
6,39
5,19
4,53
4,12
3,84
3,63
3,48
3,36
3,26
3,18
3,11
3,06
3,01
2,96
2,93
2,90
2,87
2,76
2,69
2,61
2,52
2,45
2,37
5
230,16
19,30
9,01
6,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
3,11
3,02
2,96
2,90
2,85
2,81
2.77
2,74
2,71
2,60
2,53
2,45
2,37
2,29
2,21
6
233,99
19,33
8,94
6,16
4,95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,92
2,85
2,79
2,74
2,70
2,66
2,63
2,60
2,49
2,42
2,34
2,25
2,17
2,09
8
238,88
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,23
3,07
2,95
2,85
2,77
2,70
2,64
2,59
2,55
2,51
2,48
2,45
2,34
2,27
2,18
2,10
2,02
1,94
12
243,91
19,41
8,74
5,91
4,68
4,00
3,57
3,28
3,07
2,91
2,79
2,69
2,60
2,53
2,48
2,42
2,38
2,34
2,31
2,28
2,16
2,09
2,00
1,92
1,83
1,75
24
249,05
19,45
8,64
5,77
4,53
3,84
3,41
3,12
2,90
2,74
2,61
2,50
2,42
2,35
2,29
2,24
2,19
2.15
2,11
2,08
1,96
1,89
1,79
1,70
1,61
1,52
оо
254,32
19,50
8,53
5,63
4,36
3,67
3,23
2,93
2,71
2,54
2,40
2,30
2,21
2,13
2,07
2,01
1,96
1,92
1,88
1,84
1,71
1,62
1,51
1,39
1,25
1,00
296
Таблица П.4.5. ^-преобразование Фишера
г = 0,51п
1±£
i-pj
р
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0
0,0000
0,1003
0,2027
0,3095
0,4236
0,5493
0,6931
0,8673
1,0986
1,4722
1
0,0100
0,1105
0,2132
0,3206
0,4356
0,5627
0,7089
0,8872
1,1270
1,5275
2
0,0200
0,1206
0,2237
0,3317
0,4477
0,5763
0,7250
0,9076
1,1568
1,5890
3
0,0300
0,1308
0,2342
0,3428
0,4599
0,5901
0,7414
0,9287
1,1881
1,6584
4
0,0400
0,1409
0,2448
0,3541
0,4722
0,6042
0,7582
0,9505
1,2212
1,7380
5
0,0501
0,1511
0,2554
0,3654
0,4847
0,6184
0,7753
0,9730
1,2562
1,8318
6
0,0601
0,1614
0,2661
0,3769
0,4973
0,6328
0,7928
0,9962
1,2933
1,9459
7
0,0701
0,1717
0,2769
0,3884
0,5101
0,6475
0,8107
1,0203
1,3331
2,0923
8
0,0802
0,1820
0,2877
0,4001
0,5230
0,6625
0,8291
1,0454
1,3758
2,2976
9
0,0902
0,1923
0,2986
0,4118
0,5361
0,6777
0,8480
1,0714
1,4219
2,6467
Таблица П.4.6. Значения 5„, определяемые
уравнением
с-^г
:z'W<-
тах^{\-Ьр; О)
= ^~Р
'к/{^+Ь/ /t/max^d-SpiO)
1
2
3
4
5
6
7
8
9
10
12
14
16
18
20
25
30
35
40
45
50
60
100
1000
0,1
6,923
2,086
1,270
0,941
0,738
0,623
0,576
0,516
0,476
0,442
0,388
0,357
0,325
0,297
0,282
0,247
0,226
0,207
0,193
0,184
0,174
0,155
0,125
0,044
0,05
3,400
1,932
1,382
1,104
0,918
0,800
0,713
0,650
0,596
0,527
0,468
0,422
0,390
0,370
0,317
0,281
0,261
0,242
0,228
0,212
0,193
0,146
0,047
0,02
5,857
3,000
2,056
1,594
1,306
1,143
0,986
0,889
0,814
0,700
0,620
0,564
0.500
0,480
0,408
0,369
0,347
0,312
0,288
0,270
0,242
0,184
0.056
0,01
8,500
4,200
2,700
2,000
1,650
1,393
1,225
1,094
0,980
0,840
0,740
0,671
0,600
0,567
0,485
0,425
0,400
0,375
0,350
0,311
0,283
0,200
0,059
0,001
9,00
5,00
3,80
3,00
2,50
2,05
1,75
1,50
1,30
1,14
1,02
0.92
0,85
0,70
0,60
0,56
0,52
0,48
0,45
0,40
0,30
0,08
список ЛИТЕРАТУРЫ
1. Айвазян С.А., Бежаева З.И., Староверов О.В. Классификация
многомерных наблюдений. — М.: Статистика, 1974.
2. Айвазян С.А., Енюков И.С, МешалкинЛ.Д. Прикладная статистика.
Основы моделирования и первичная обработка данных. — М.: Финансы
и статистика, 1983.
3. Андерсон Т. Статистический анализ временных рядов. — М.: Мир,
1976.
4. БоксДж.,Дженкинс Г. Анализ временных рядов. Прогноз и
управление. — Вып. 1,2. — М.: Мир, 1974.
5. Большее Л.Н., Смирнов Н.В. Таблицы математической
статистики.— М.: Наука, 1983.
6. Боровков А.А. Теория вероятностей. — М.: Наука, 1986.
7. Ван дер Варден Б.Л. Математическая статистика. — М.: ИЛ, 1960.
8. Валтер Я. Стохастические модели в экономике. — М.: Статистика,
1976.
9. Венсель В.В. Интегральная регрессия и корреляция.
Статистическое моделирование рядов динамики. — М.: Финансы и статистика, 1983.
10. Гнеденко Б.В. Курс теории вероятностей. — М.: ГИТТЛ, 1954.
\\. Демиденко Е.З. Линейная и нелинейная регрессия. — М.:
Финансы и статистика, 1981.
12. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. — М.:
Статистика, 1973.
ХЗ.ДубДж. Л. Вероятностные процессы. — М.: ИЛ, 1956.
14. ЗаксЛ. Статистическое оценивание. — М.: Статистика, 1976.
15. Иберла К. Факторный анализ. — М.: Статистика, 1980.
16. ИтоК. Вероятностные процессы. — М.: ИЛ, 1960, 1963. — Вып. 1, 2.
17. Казмер Л. Методы статистического анализа в экономике. — М.:
Статистика, 1972.
18. Кемени Дж., Снелл Дж. Конечные цепи Маркова. — М.: Наука,
1970.
19. Кендэл М. Временные ряды. — М.: Финансы и статистика, 1981.
20. Кендэл М., Стюарт А. Статистические выводы и связи. — М.:
Наука, 1974.
21. Кендэл М., Стюарт А. Теория распределения. — М.: Наука, 1966.
299
22. Кильдишев Г.С, Френкель А.А. Анализ временных рядов и
прогнозирование. — М.: Статистика, 1973.
23. Колемаев В.А. О математическом обеспечении
экономико-статистических исследований и разработок: Ученые записки по статистике. —
М.: Статистика, 1980. Т. 36.
24. Колемаев В.А., Калинина В.Н. и др. Теория вероятностей в
экономике. - М.: МИУ, 1989.
25. Колемаев В.А., Калинина В.Н. и др. Математическая статистика в
экономике. — М.: МИУ, 1990.
26. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория
вероятностей и математическая статистика. — М.: Высшая школа, 1991.
27. Колемаев В.А., Калинина В.Н. и др. Теория вероятностей в
примерах и задачах. — М.: ГАУ, 1993.
28. Колмогоров А. Н. Основные понятия теории вероятностей. — М.:
ОНТИ, 1936.
29. Крамер Г. Математические методы статистики. — М.: Мир, 1975.
30. Леман Э. Проверка статистических гипотез. — М.: Наука, 1964.
31. ЛоулиД., Максвелл А. Факторный анализ как статистический
метод. — М.: Мир, 1967.
32. Лукашин Ю.П. Адаптивные методы краткосрочного
прогнозирования. — М.: Статистика, 1979.
33. Льюис КД. Методы прогнозирования экономических
показателей. — М.: Финансы и статистика, 1986.
34. Моленво Э. Статистические методы эконометрии. — М.:
Статистика, 1976.
35. Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. — М.: Наука,
1987.
36. Пугачев В. С. Теория вероятностей и математическая статистика. —
М.: Наука, 1979.
37. Рао СР. Линейные статистические методы и их применения. —
М.: Наука, 1968.
38. Розанов Ю.А. Случайные процессы. — М.: Наука, 1971.
39. СеберДж. Линейный и регрессионный анализ. — М.: Мир, 1980.
40. Смирнов Н.В., Дунин-Барковский И.В. Краткий курс
математической статистики для технических приложений. — М.: Физматгиз, 1959.
41. Тейл Г. Прикладное экономическое прогнозирование. — М.:
Прогресс, 1970.
42. Уилкс С. Математическая статистика. — М.: Наука, 1967.
43. Феллер В. Введение в теорию вероятностей и ее приложения. —
М.: Мир, 1967.
44. Фишер РА. Статистические методы для исследователей. — М.:
Госстатиздат, 1958.
45. Харман Г. Современный факторный анализ. — М.: Статистика,
1972.
300
46. Хеннан Э. Анализ временных рядов. — М.: Наука, 1964.
47. Химмельблау Д. Анализ процессов статистическими методами. —
М,: Мир, 1973.
48. Четыркин Е.М. Статистические методы прогнозирования. — М.:
Статистика, 1977.
49. Четыркин Е.М., Калихман И.Л. Вероятность и статистика. — М.:
Финансы и статистика, 1982.
50. Чистяков В.П. Курс теории вероятностей. М.; Наука, 1982.
51. Шеффе Г. Дисперсионный анализ. — М.: Физматгиз, 1963.
52. ЮлДж. Э., Кендэл М.Дж. Теория статистики. — М.: Госстатиздат,
1960.
Учебное издание
Колемаев Владимир Алексеевич
Калинина Вера Николаевна
Теория вероятностей и математическая статистика
Учебник
Редактор И.В. Мартынова
Корректор Г.Л/. Короткова
Художественное оформление «Ин-Арт»
Компьютерный дизайн — А.А. Маркин
ЛР № 070824 от 21.01.93 г.
Подписано в печать 28.08.97. Формат 60Х 90/16.
Гарнитура «NewtonC». Печать офсетная. Усл. печ. л. 19,0.
Тираж 25 000 экз. (1-й завод — 6000 экз.). Заказ № 670.
Издательский Дом «ИНФРА-М»
127214, Москва, Дмитровское ш., 107.
Тел.: (095) 485-74-00, 485-70-63.
Отпечатано с готовых диапозитивов
в ОАО «Ярославский полиграфкомбинат».
150049, Ярославль, ул. Свободы, 97.