Антенны сверхвысоких частот - Фрадин А.З.

Author: Фрадин А.З.

Tags: радиотехника антенны

Year: 1957

Similar

Устройства сверхвысоких частот и антенны

Ферриты на сверхвысоких частотах

Генераторы высоких и сверхвысоких частот

Измерение параметров антенно-фидерных устройств

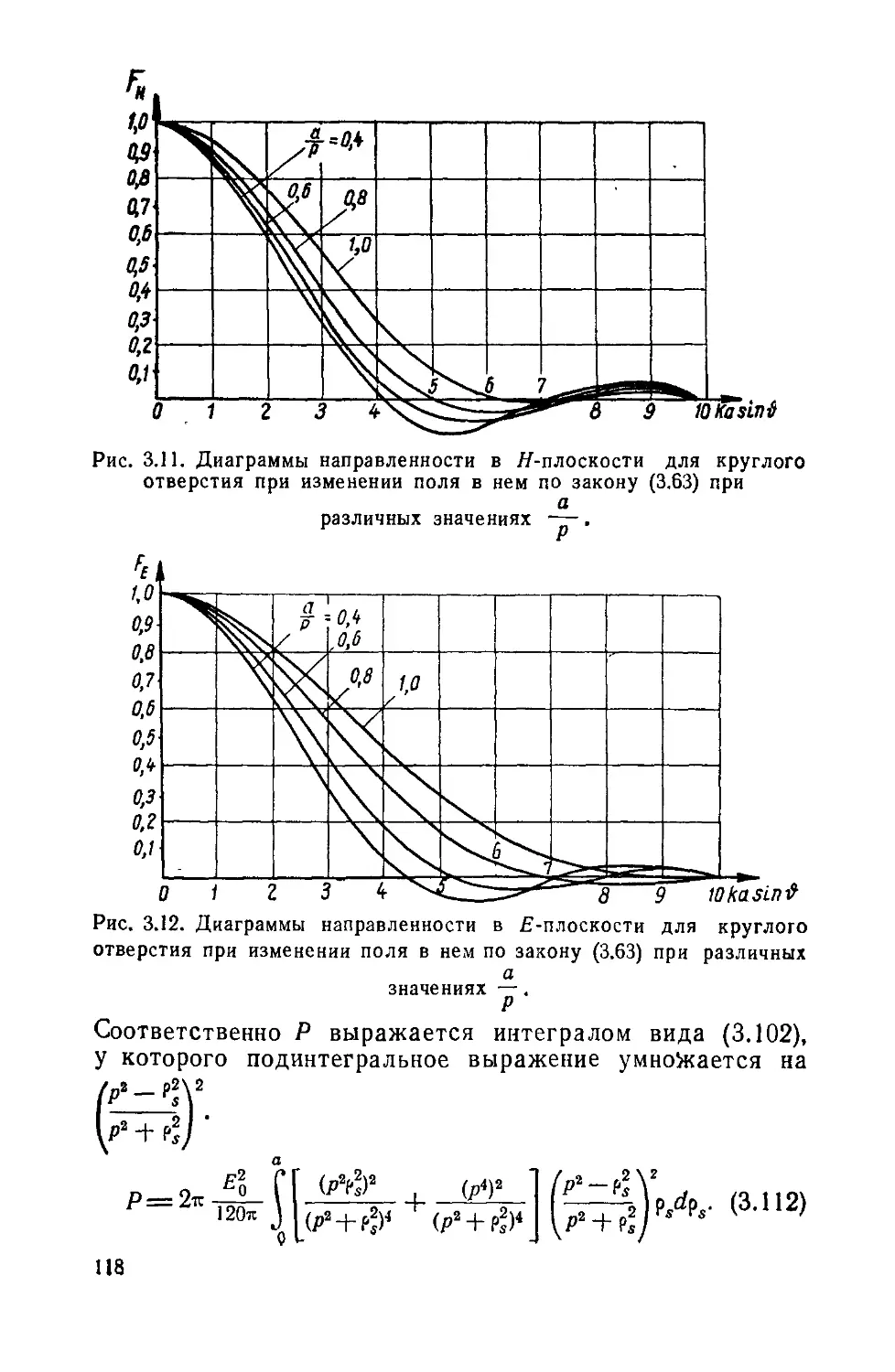
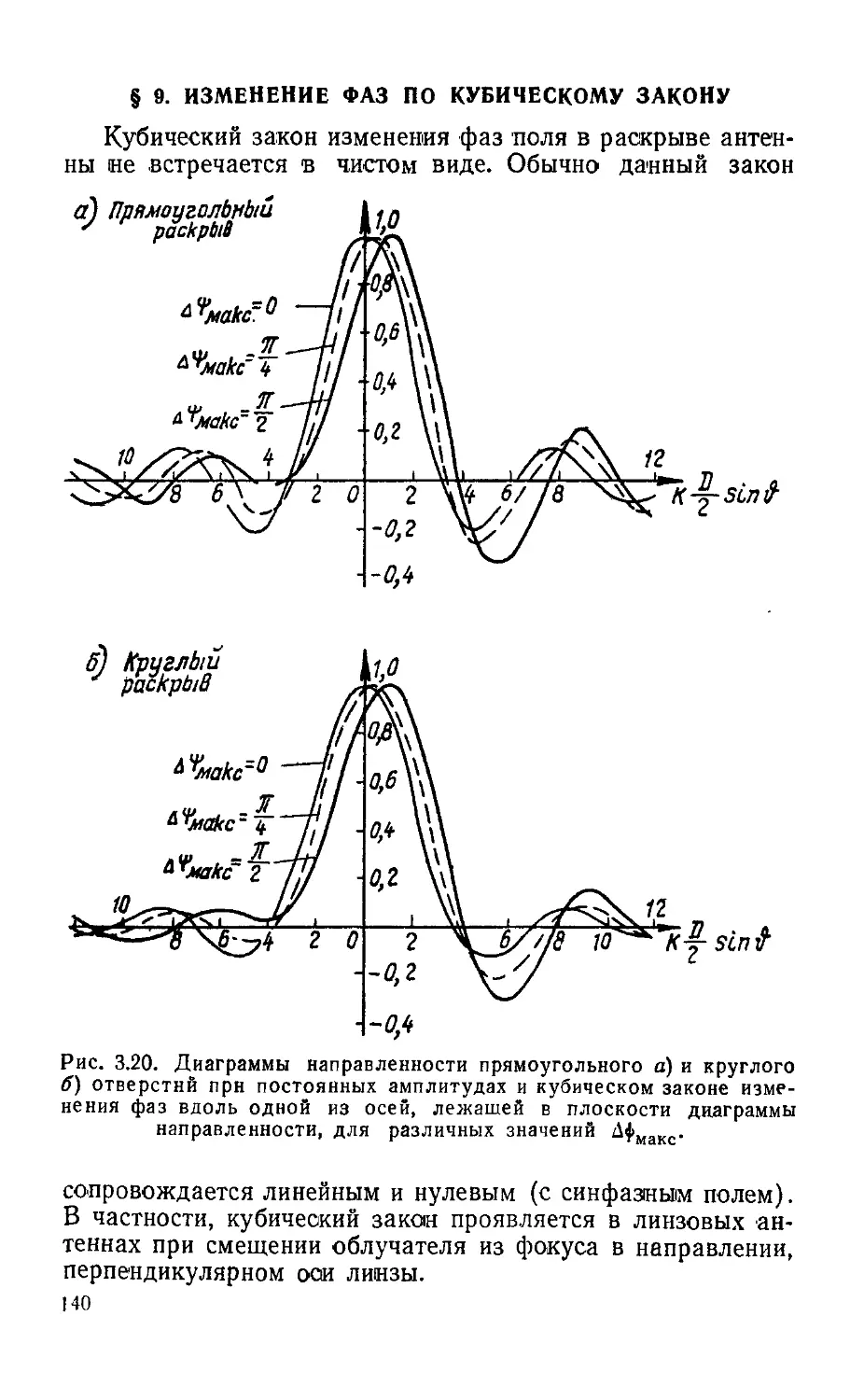
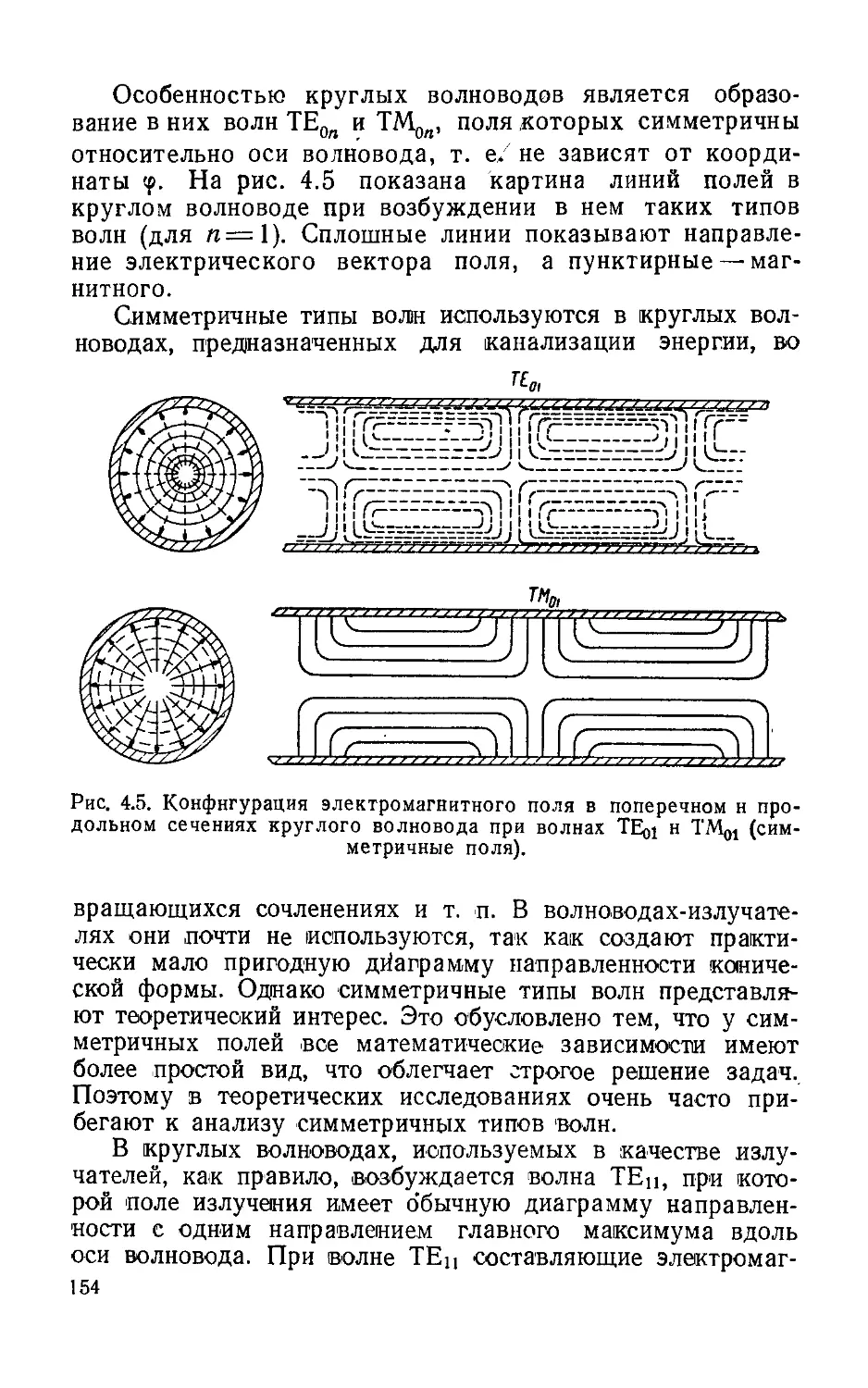
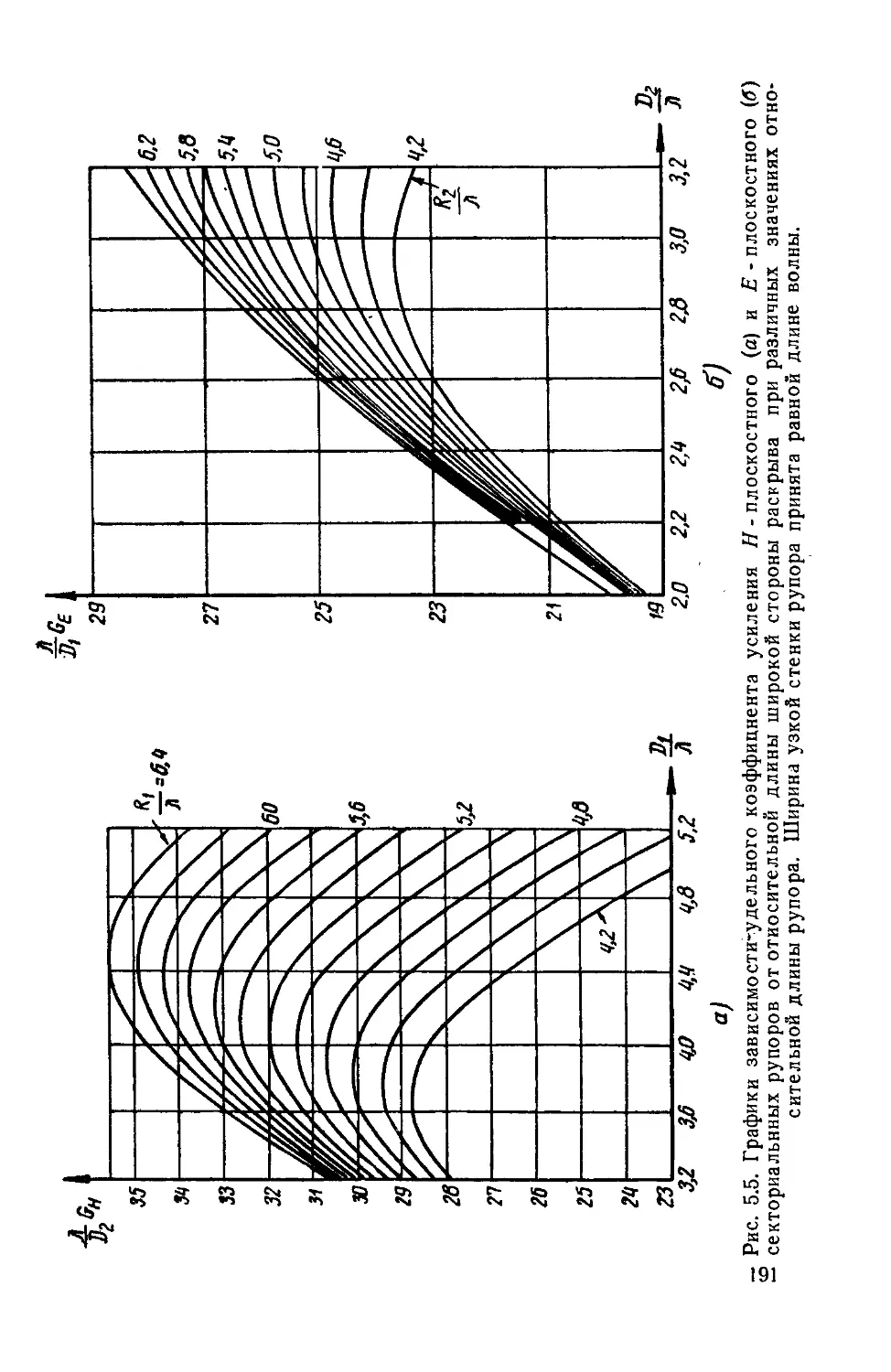
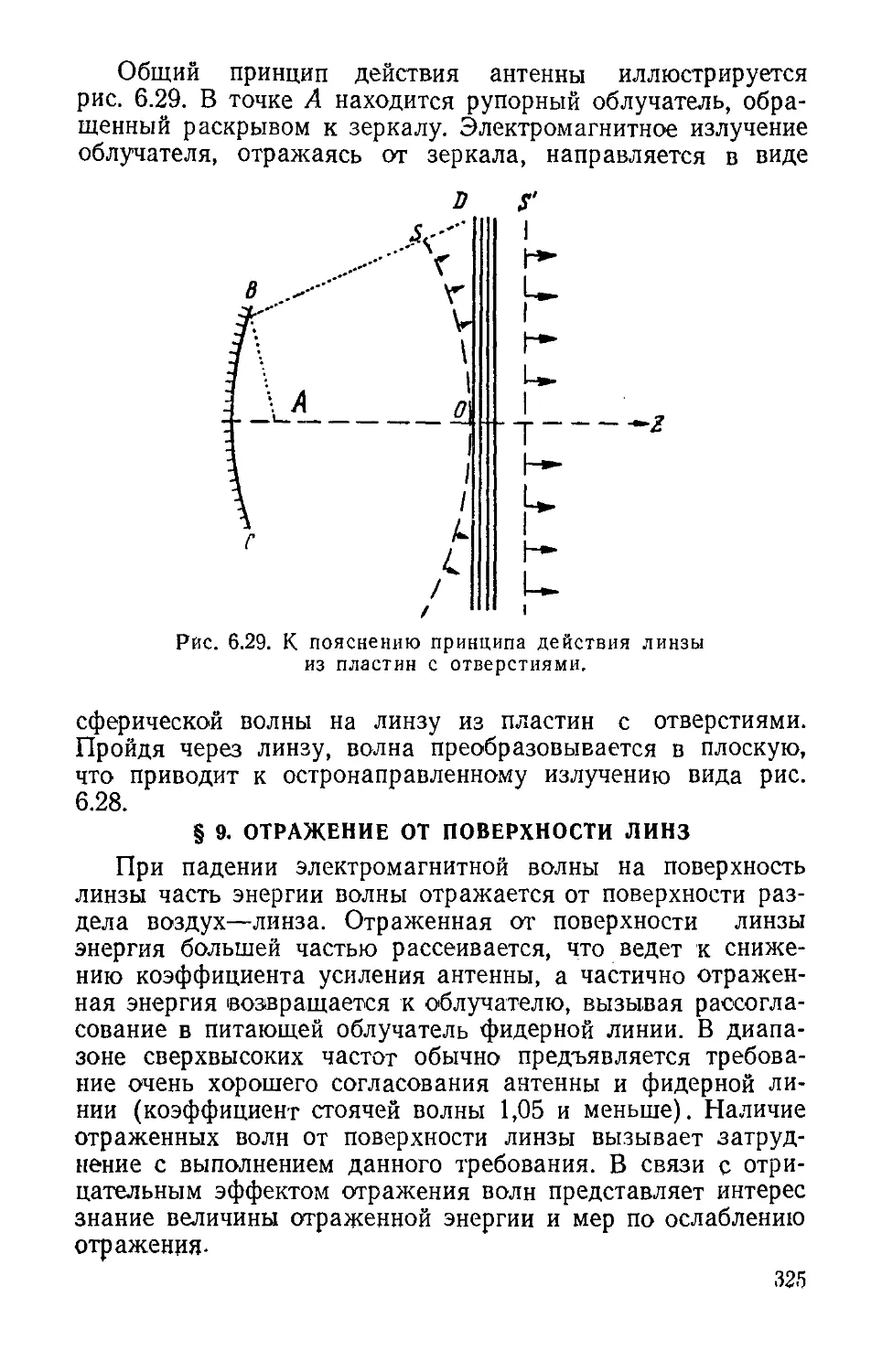
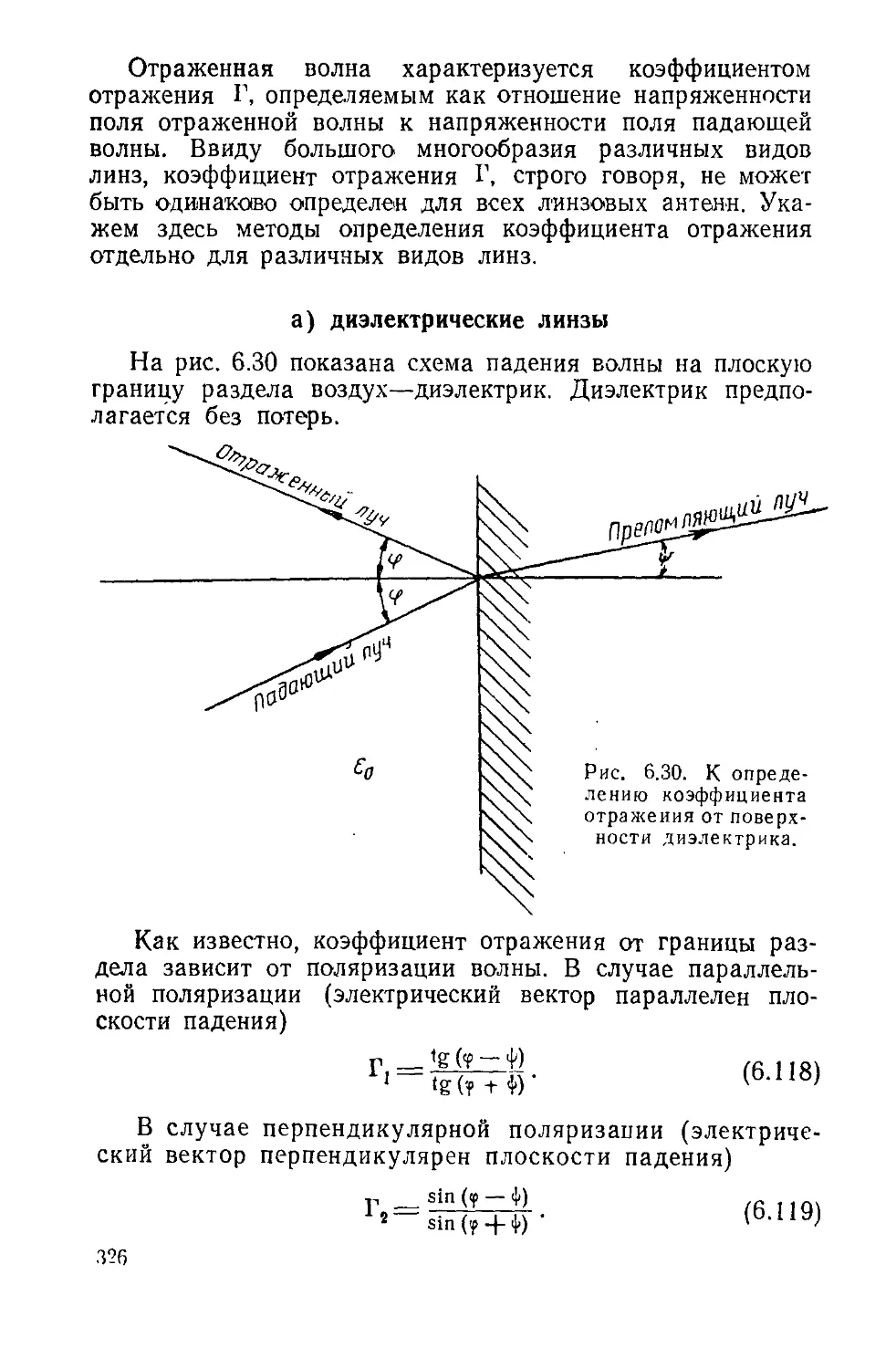
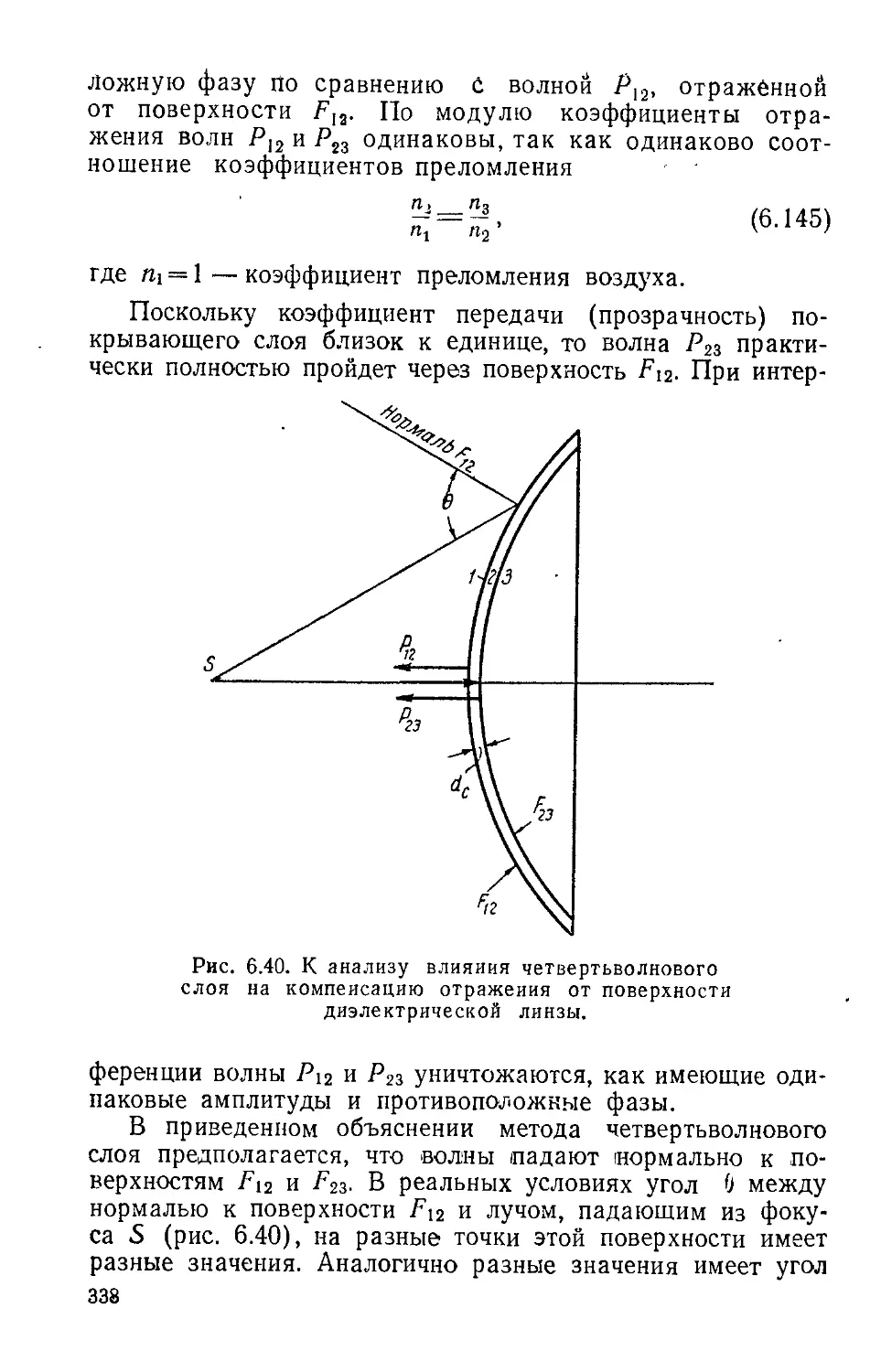
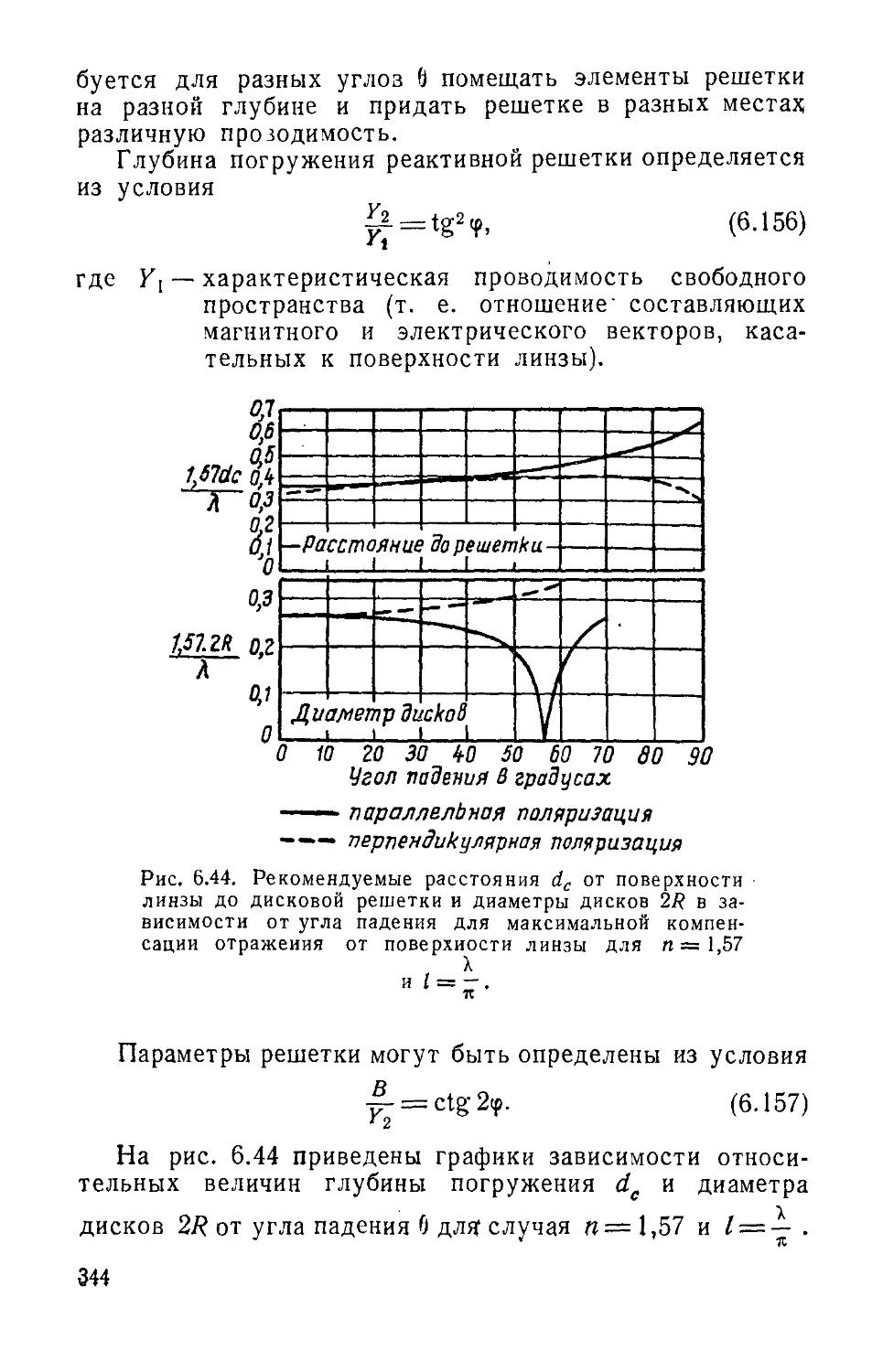
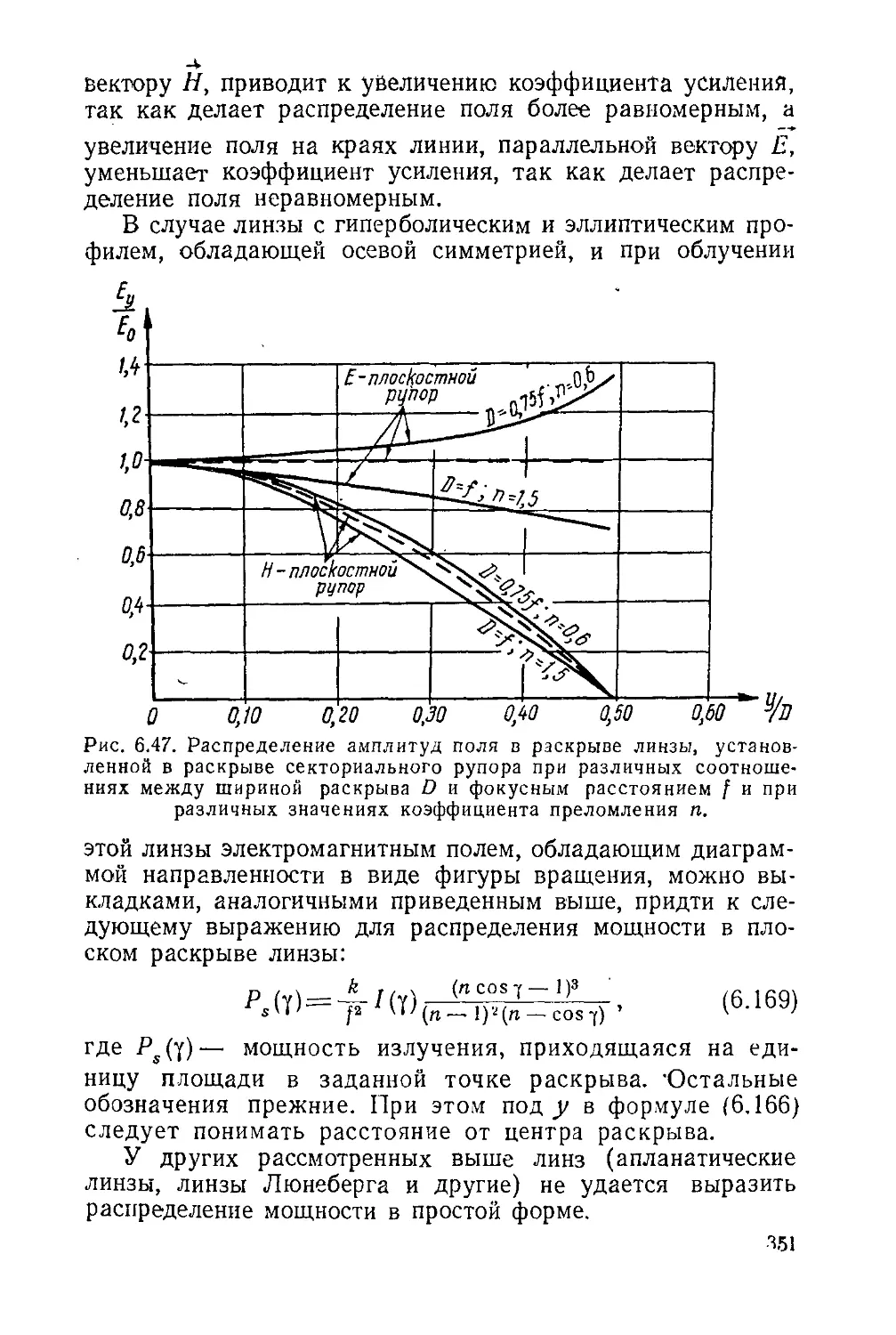
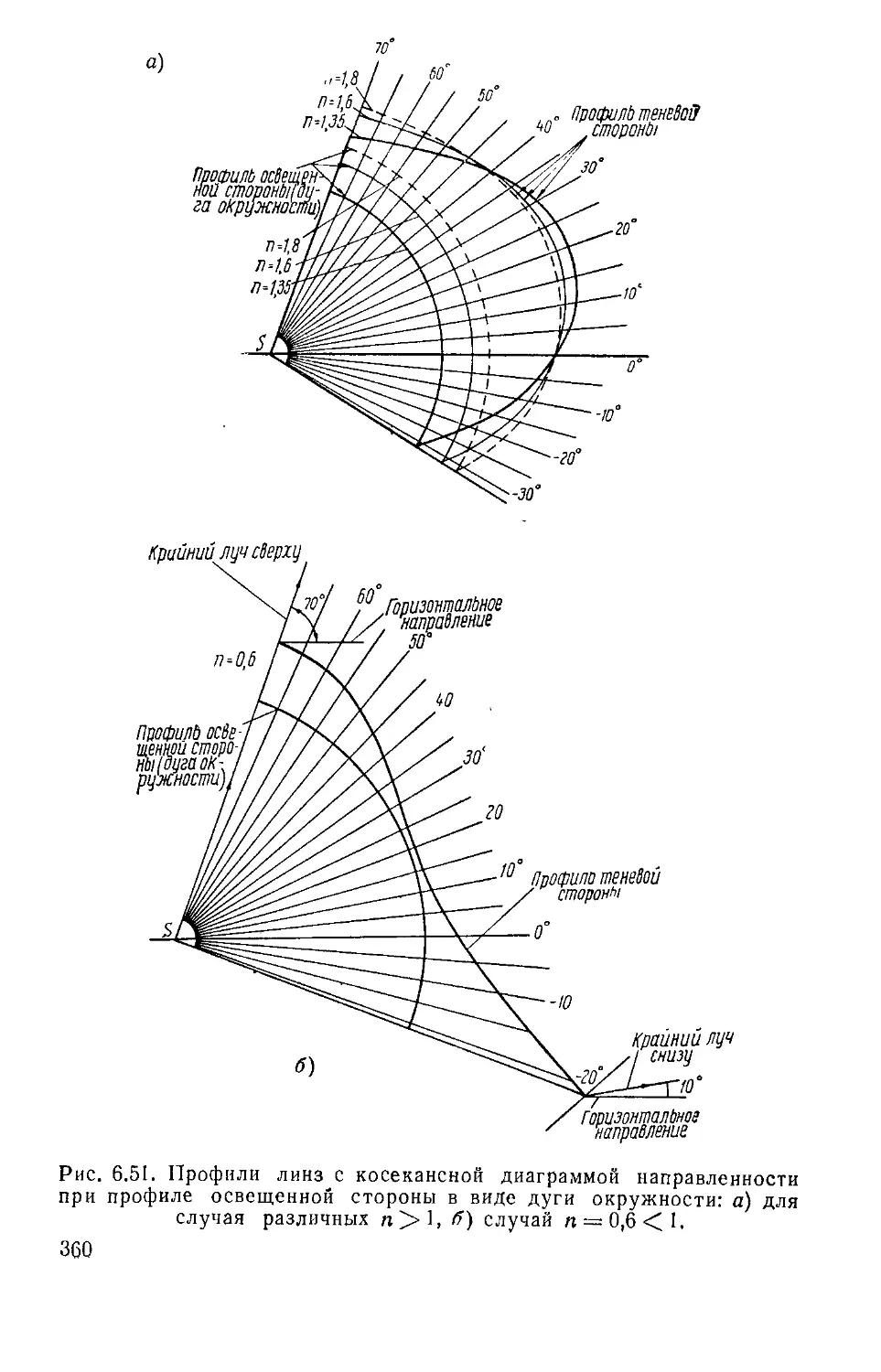
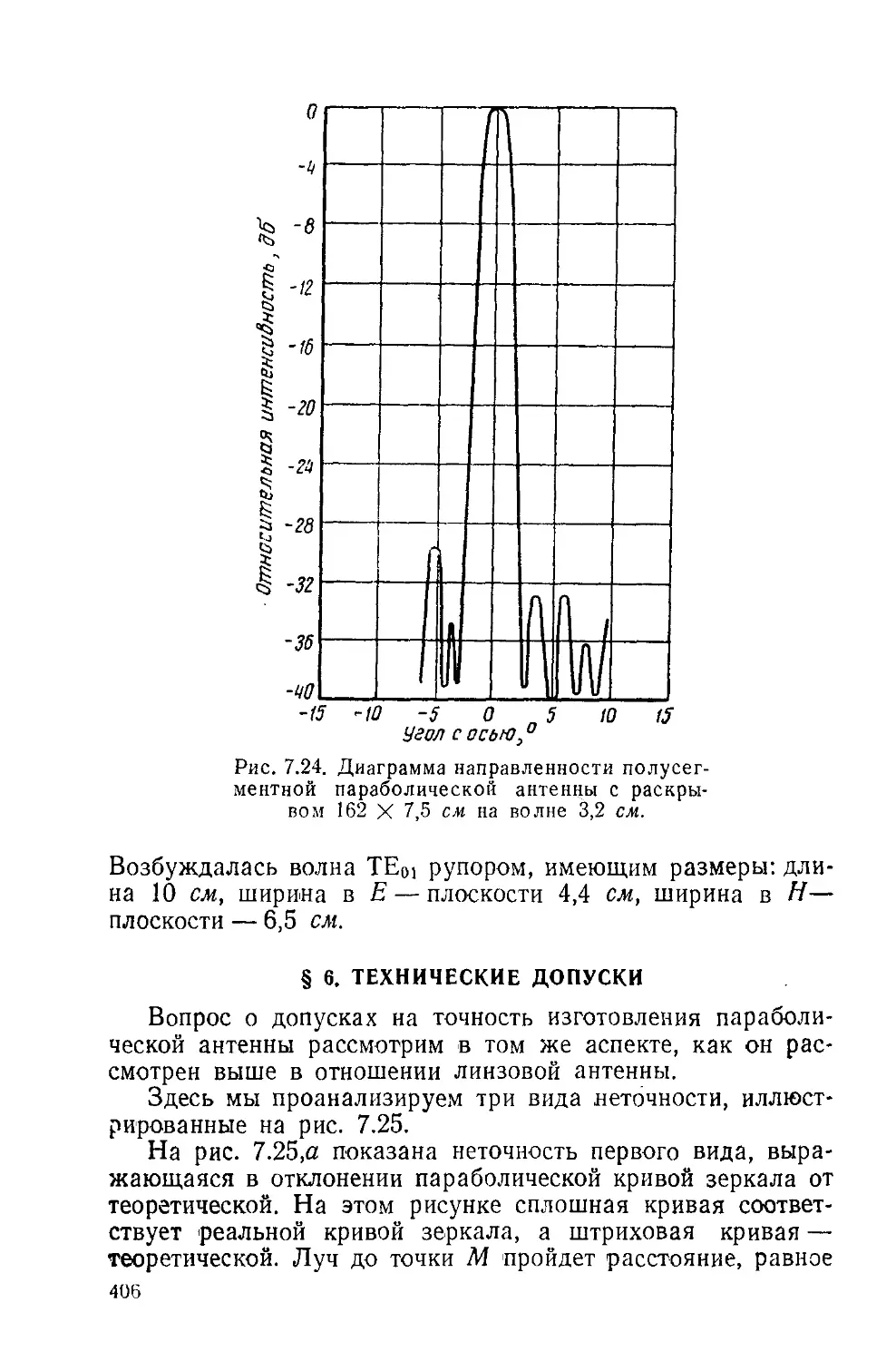
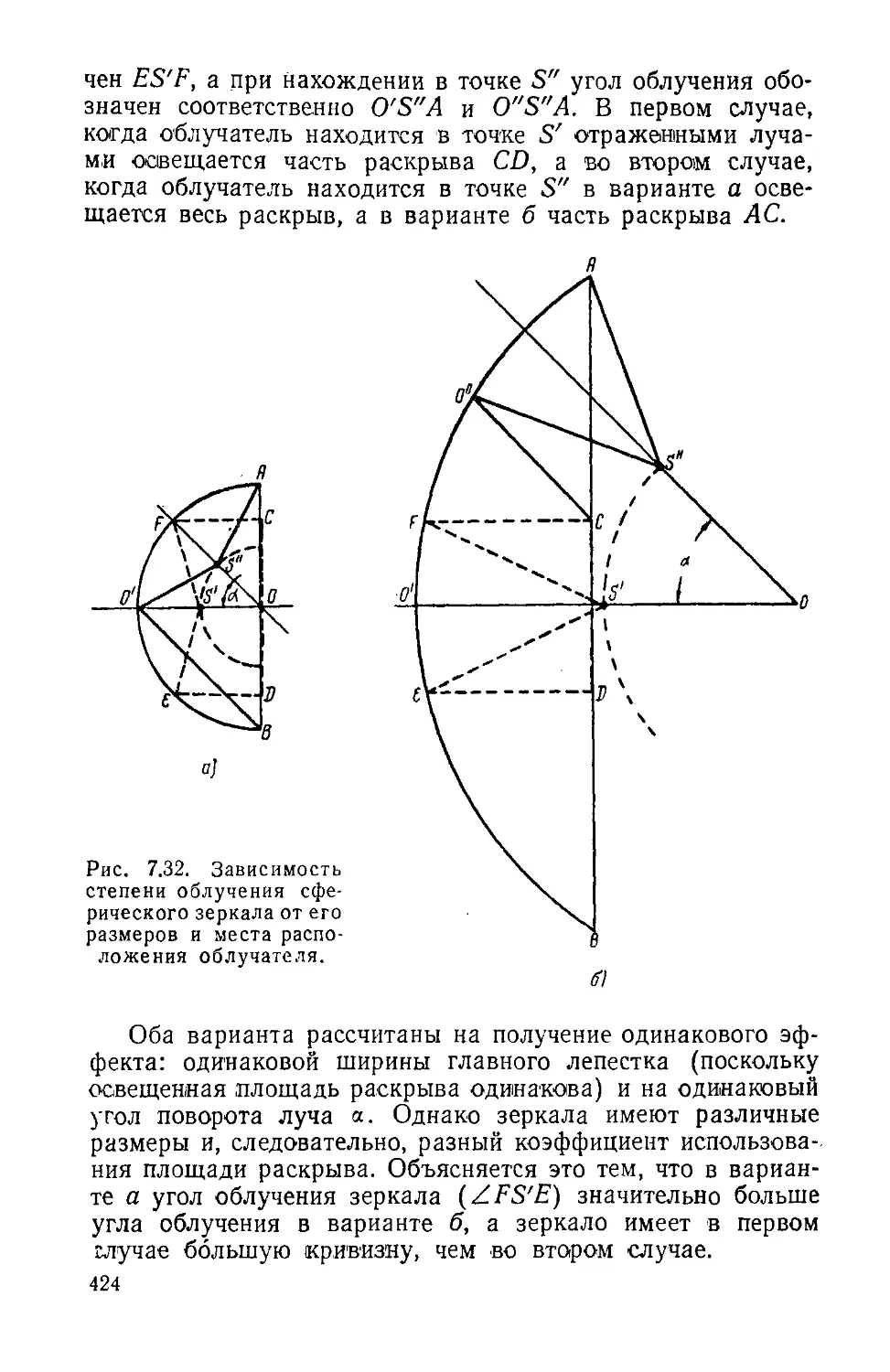
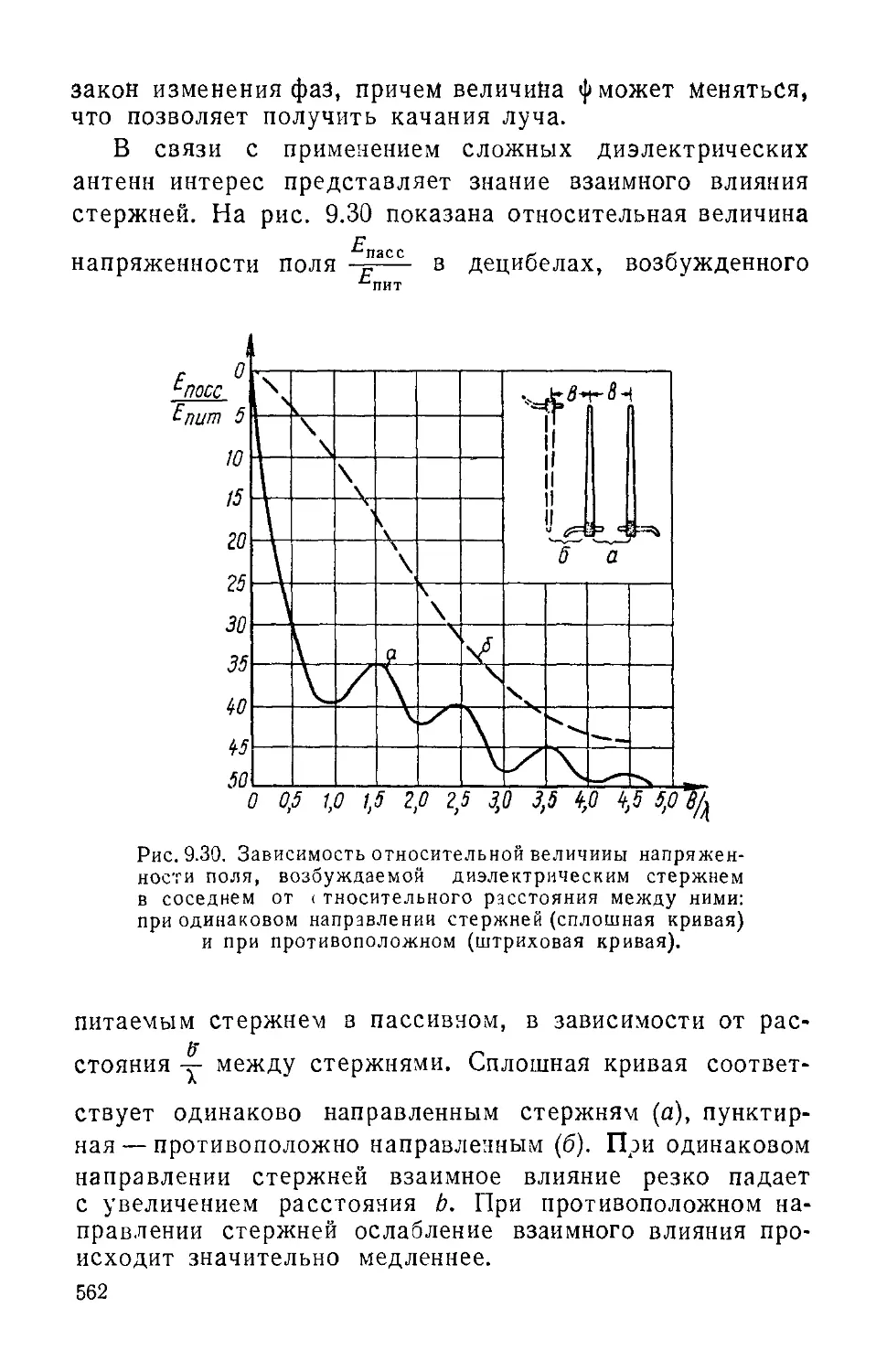
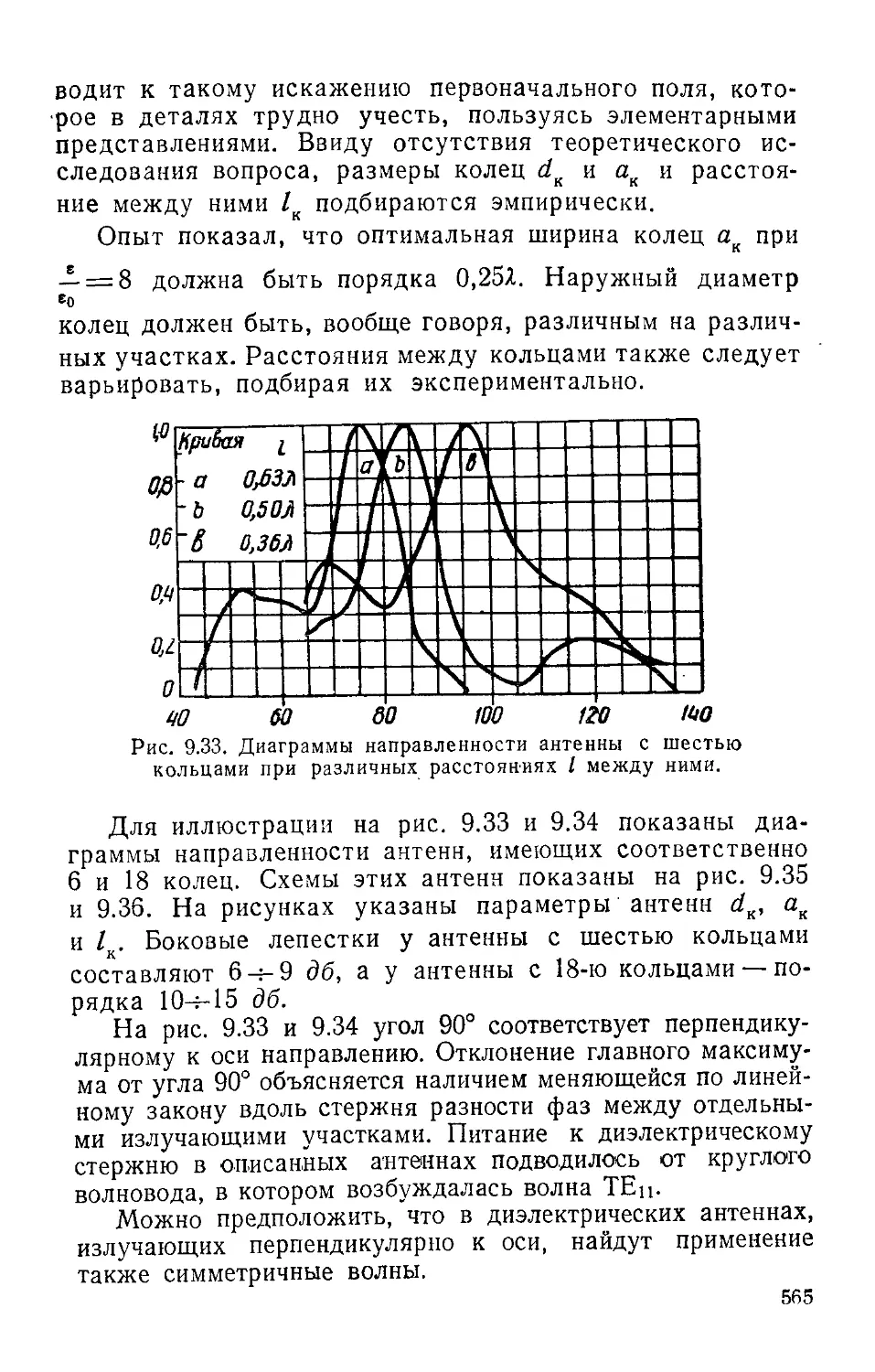
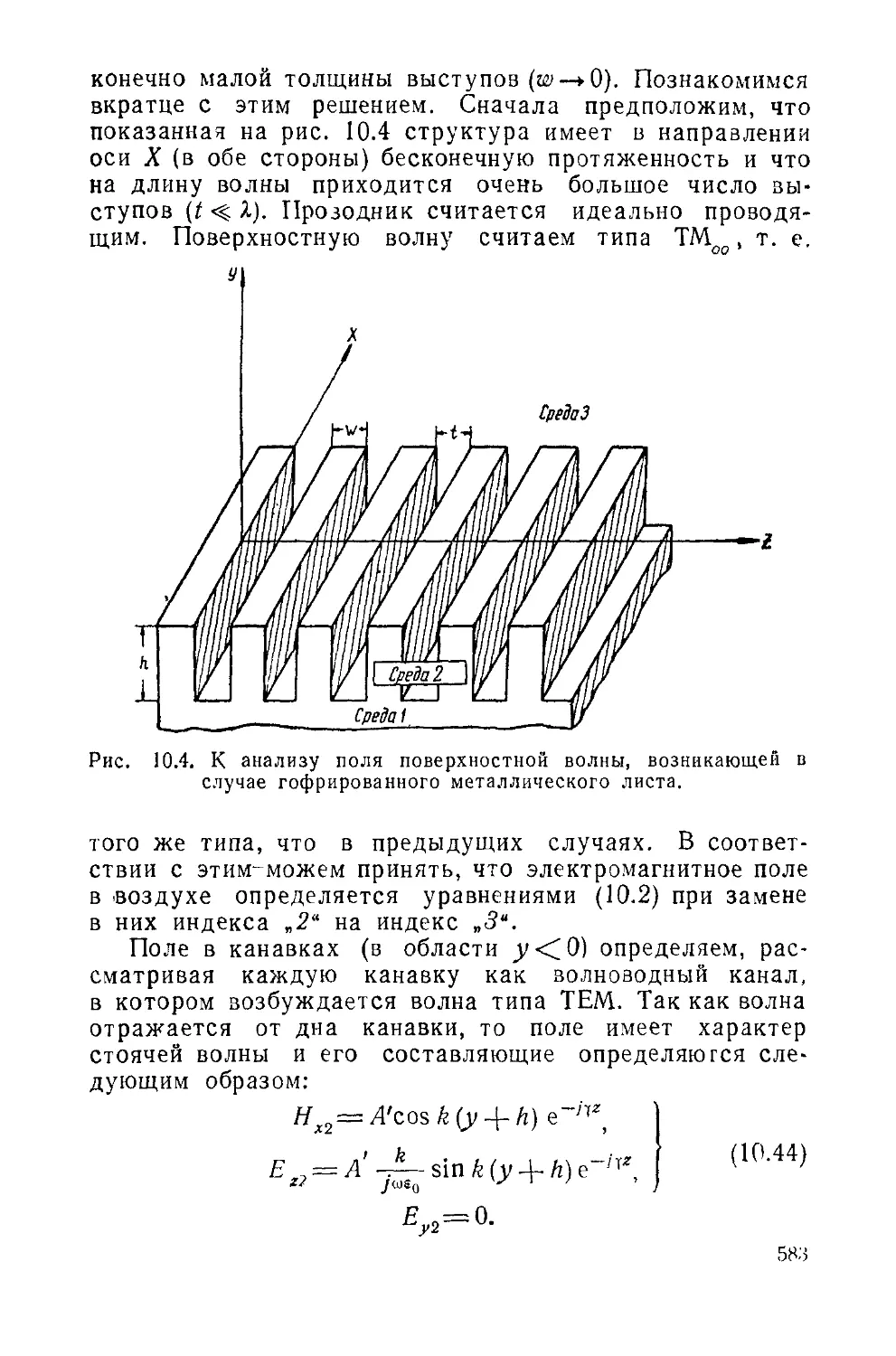
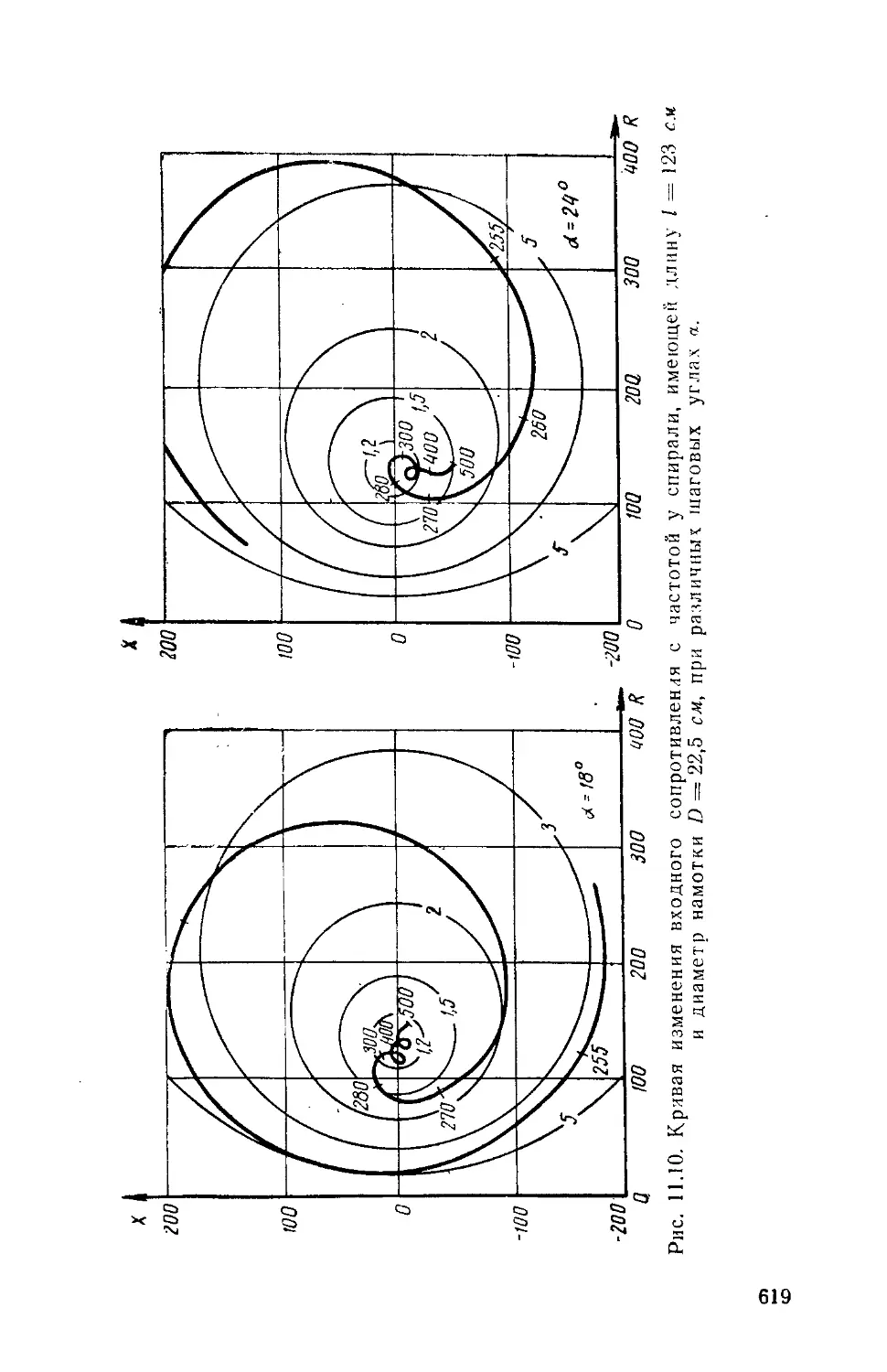
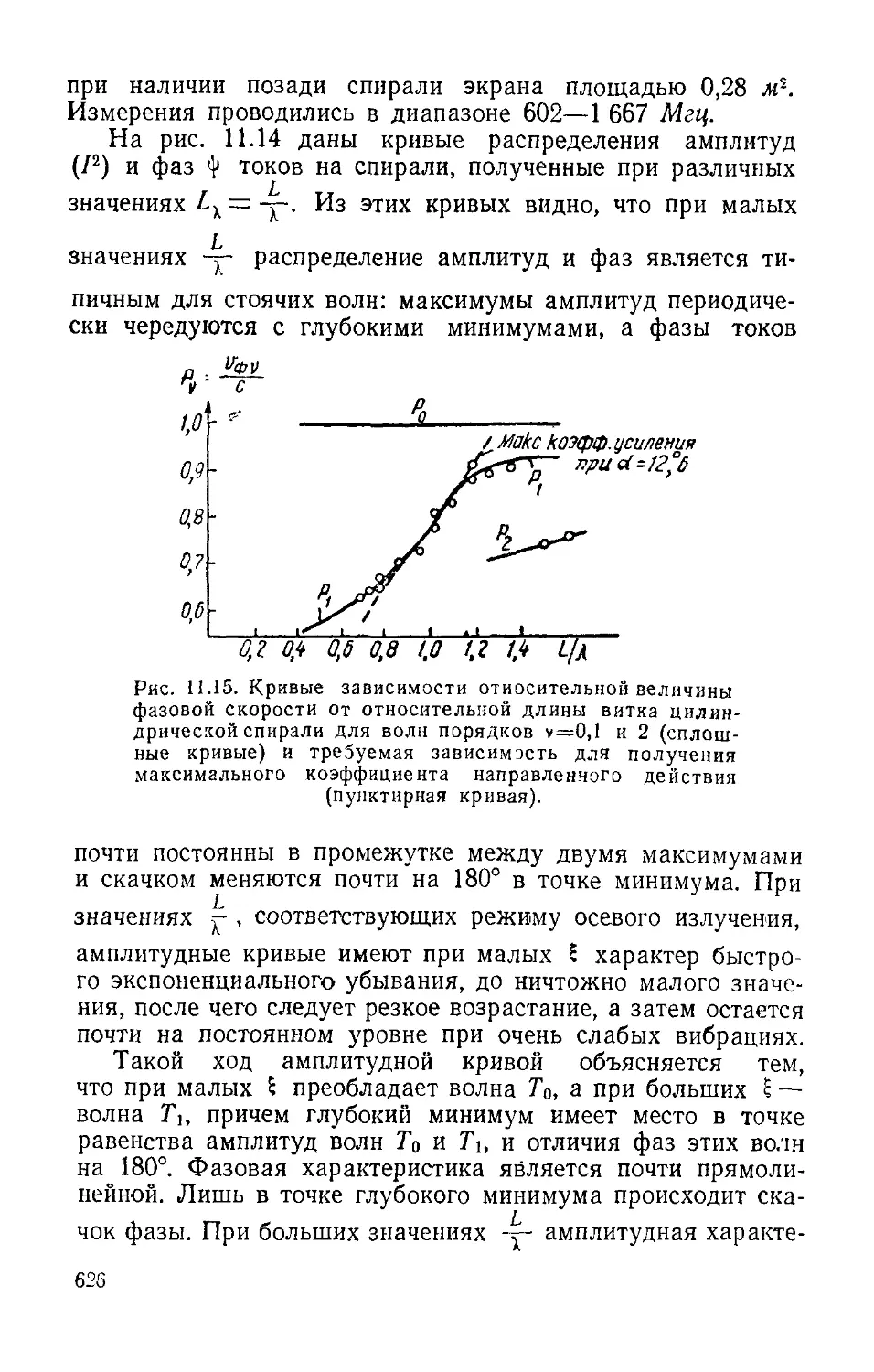
Text

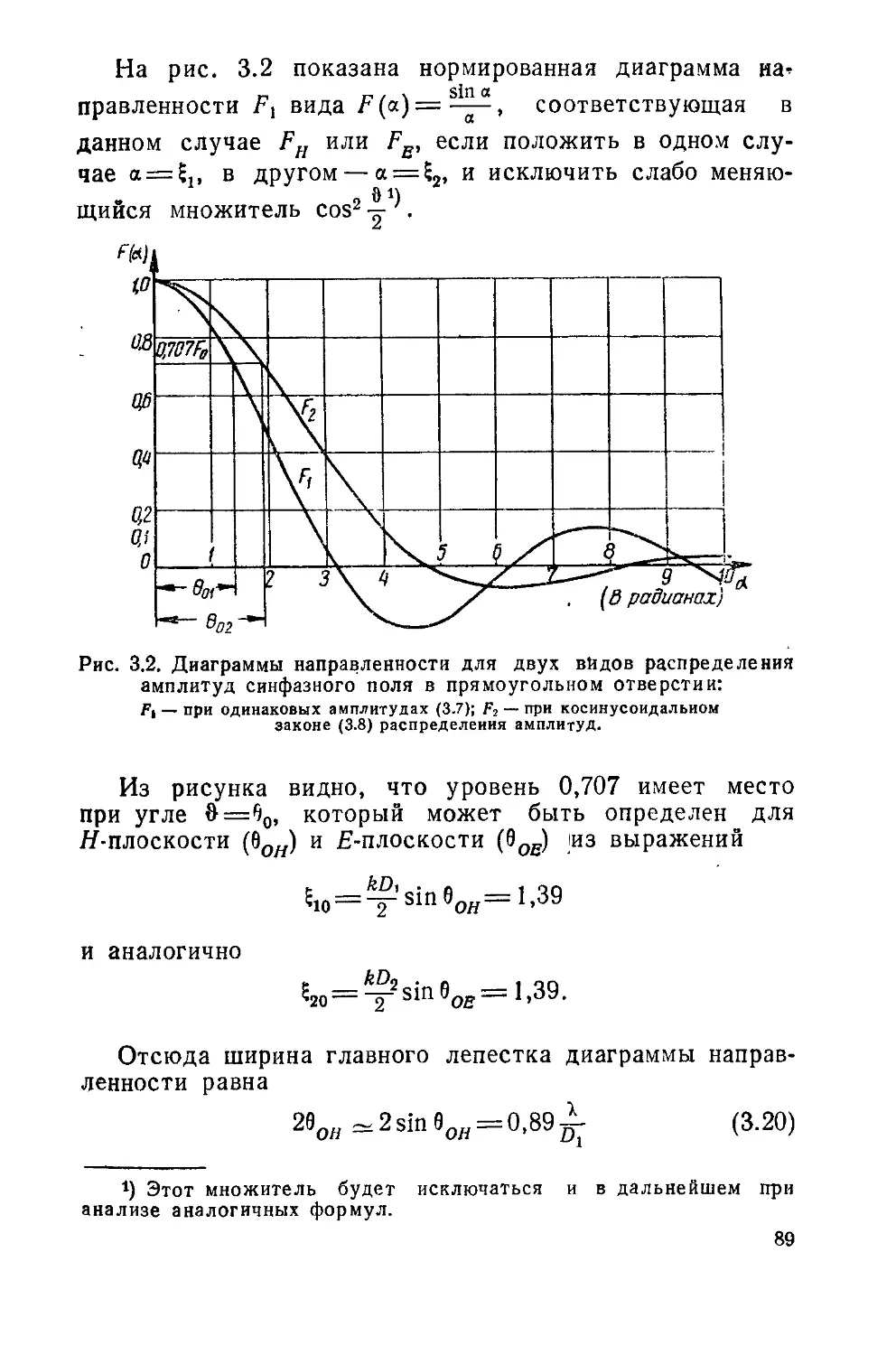
A. 3. ФРАДИН
АНТЕННЫ
СВЕРХВЫСОКИХ
ЧАСТОТ
ИЗДАТЕЛЬСТВО „СОВЕТСКОЕ РАДИО"
МОСКВА — 1957
A. 3. ФРАДИН
АНТЕННЫ
СВЕРХВЫСОКИХ ЧАСТОТ
В книге изложены теория излу-
чения антенн сверхвысоких частот,
сведения о всех существующих ви-
дах антенн этого диапазона, физи-
ческие принципы их действия и ме-
тоды инженерного расчета харак-
теристик.
Книга предназначена для радио-
специалистов и может служить
учебным пособием для студентов
и преподавателей вузов.
ПРЕДИСЛОВИЕ
В директивах XX съезда КПСС по шестому пятилетне-
му плану развития народного хозяйства СССР на 1956—
1960 гг. предусмотрено бурное развитие радиорелейной свя-
зи, радионавигации и других видов радиотехнических соо-
ружений, использующих технику сверхвысоких частот. Од-
ним из важнейших элементов таких сооружений являются
антенные устройства.
Антенны сверхвысоких частот (СВЧ антенны) образуют
в настоящее время самостоятельную весьма обширную от-
расль радиотехники, имеющую свою теоретическую базу,
свои методы расчета и специфические конструктивные ре-
шения. Однако сейчас не существует работы, которая до-
статочно полно и удовлетворительно освещала бы вопросы
современной теории и техники СВЧ антенн.
Известные книги по СВЧ антеннам представляют собой
либо монографии по очень узким вопросам, либо работы,
излагающие технику сороковых годов и не отражающие
достижения последних лет.
Предлагаемая вниманию читателя книга является по-
пыткой восполнить указанный пробел. Она представляет
собой новое значительно дополненное и переработанное из-
дание книги автора, вышедшей в 1950 г.
В первой главе книги вводится классификация СВЧ
антенн и дается описание их устройства и принципа дейст-
вия.
Во второй главе приводятся исходные положения тео-
рии СВЧ антенн и излагаются строгие и приближенные ме-
тоды их анализа.
Третья глава посвящена решению ряда математических
задач о диффракции на отверстии в плоском экране, к ко-
торым для большинства СВЧ антенн сводится определение
приближенными методами характеристик излучения. Выде-
з
ление этого материала в отдельную главу, с одной стороны,
дает возможность упростить изложение в разделах, посвя-
щенных конкретно отдельным типам антенн, а с другой сто-
роны, позволяет сделать обобщающие выводы о связи меж-
ду законом распределения амплитуд и фаз поля в раскры-
ве и характеристиками излучения.
В остальных главах подробно рассматриваются отдель-
ные типы СВЧ антенн. По каждому из типов анализиру-
ются различные разновидности, конкретизируются вопросы
устройства и освещается современное состояние теории.
Кроме того, приводятся расчетные формулы и графики, свя-
зывающие конструктивные параметры с электрическими
характеристиками антенн, и дается понятие о порядке рас-
чета.
Наряду с данными об антеннах, всесторонне исследован-
ных и используемых на практике, в книге содержатся све-
дения о получивших известность в периодической литера-
туре новых разработках и идеях, могущих служить основой
для дальнейшего исследования.
Книга, естественно, не может претендовать на исчер-
пывающе полное изложение всего теоретического и экспе-
риментального материала по СВЧ антеннам, накопленного
к настоящему времени. Приводимая библиография долж-
на помочь читателю найти в случае надобности дополни-
тельные сведения по излагаемым в книге вопросам.
Считаю своим приятным долгом выразить свою глубо-
кую благодарность редактору В. А. Хацкелевичу за боль-
шую помощь, оказанную в процессе подготовки рукописи
к печати, а также Б. В. Брауде и А. И. Потехину за цен-
ные замечания и советы, которые автор учел при перера-
ботке рукописи.
Автор
ГЛАВА ПЕРВАЯ
АНТЕННЫ СВЕРХВЫСОКИХ ЧАСТОТ,
ИХ КЛАССИФИКАЦИЯ, УСТРОЙСТВО
И ПРИНЦИП ДЕЙСТВИЯ
§ 1. ПРЕДМЕТ ИЗУЧЕНИЯ
Под сверхвысокими частотами (сокращенно СВЧ) по-
нимают ту часть радиотехнического спектра, которая охва-
тывает дециметровые и сантиметровые волны.
В технике диапазона сверхвысоких частот встречаются
проволочные антенны, применяющиеся и на более низких
частотах (например, антенны типа «волновой канал», син-
фазные вибраторные антенны, спиральные антенны и т. п.).
Однако наиболее широкое применение на СВЧ имеют так
называемые диффракционные антенны, многие из которых
аналогичны оптическим системам (зеркала, линзы и т. п.).
В данной работе под термином «Антенны СВЧ» пони-
маются только диффракционные антенны. Объяснение по-
нятия диффракционные антенны будет дано ниже (§ 9)
после описания устройства и принципа действия. Наряду
с диффракционными антеннами, которым уделяется основ-
ное внимание, здесь приводятся краткие сведения о про-
волочных спиральных антеннах, поскольку они применя-
ются главным образом на сверхвысоких частотах и в обыч-
ных учебниках не излагаются.
На сверхвысоких частотах нет специфических приемных
антенн, как это имеет место на длинных и коротких вол-
нах. Одинаковые антенны применяются как для передачи,
так и для приема. В некоторых практических случаях, на-
пример, в радиолокации, часто одна и та же антенна ис-
пользуется для обоих видов работы. Так как основные ха-
рактеристики антенн, согласно теореме взаимности, не за-
5
висят от вида работы, то антенны могут рассматриваться
при изучении либо как передающие, либо как приемные.
С методической точки зрения более удобным является
рассмотрение антенн как передающих. Поэтому ниже СВЧ
антенны везде рассматриваются как излучающие системы.
Предметом изучения СВЧ антенн могут быть следую-
щие вопросы:
1. Теория излучения.
2. Теория связи антенны и питающей линии.
3. Конструктивные особенности, специфичные для раз-
личных областей применения.
В настоящей работе основное внимание уделяется пер-
вому вопросу, т. е. теории излучения СВЧ антенн, включаю-
щей в себя:
а) исходные физические принципы,
б) строгие математические методы решения задач об
излучении,
в) формулы и приемы приближенного расчета харак-
теристик излучения: диаграммы направленности, коэффи-
циента усиления и др.
Остальные из указаных вопросов излагаются в той ме-
ре, в какой они служат конкретизации теории и способст-
вуют усвоению и правильному пониманию основного воп-
роса.
§ 2. КЛАССИФИКАЦИЯ СВЧ АНТЕНН
В настоящее время насчитывается много десятков раз-
нообразных СВЧ антенн. Однако, как будет показано ни-
же, по принципу действия они однородны и существенно
отличаются от антенн более низких частот. Поэтому мы их
будем рассматривать как особый класс антенн. Различия
между отдельными СВЧ антеннами проявляются в конст-
руктивных особенностях, способе питания и т. п.
В настоящее время можно выделить шесть типов СВЧ
антенн:
1. рупорные, 2. линзовые, 3. щелевые, 4. диэлектриче-
ские, 5. рефлекторные (зеркала), 6. поверхностных волн.
Каждый из указанных типов делится далее на несколь-
ко разновидностей, многие из которых, в свою очередь,
встречаются в большом числе вариантов.
Указанная классификация СВЧ антенн иллюстрируется
схемой рис. 1.1. На этом рисунке представлены лишь важ-
нейшие варианты, нашедшие практическое применение и
теоретически исследованные. При дальнейшем рассмотре-
нии будет указано и на ряд других вариантов представляю-
б
Рис. 1.1. Схема классификации антенн СВЧ.
щих интерес. Кроме того, следует иметь в виду, что на
практике встречаются комбинированные антенны, представ-
ляющие собой сочетание нескольких из указанных здесь
типов (например, рупор и зеркало, рупор и линза, зеркало
и щелевая антенна и т. п.). Во избежание излишнего за-
громождения схемы классификации эти антенны в нее не
включены. В тексте же в соответствующих местах они бу-
дут рассмотрены.
Ниже приводится описание устройства и принципа дей-
ствия отдельных типов и разновидностей антенн СВЧ.
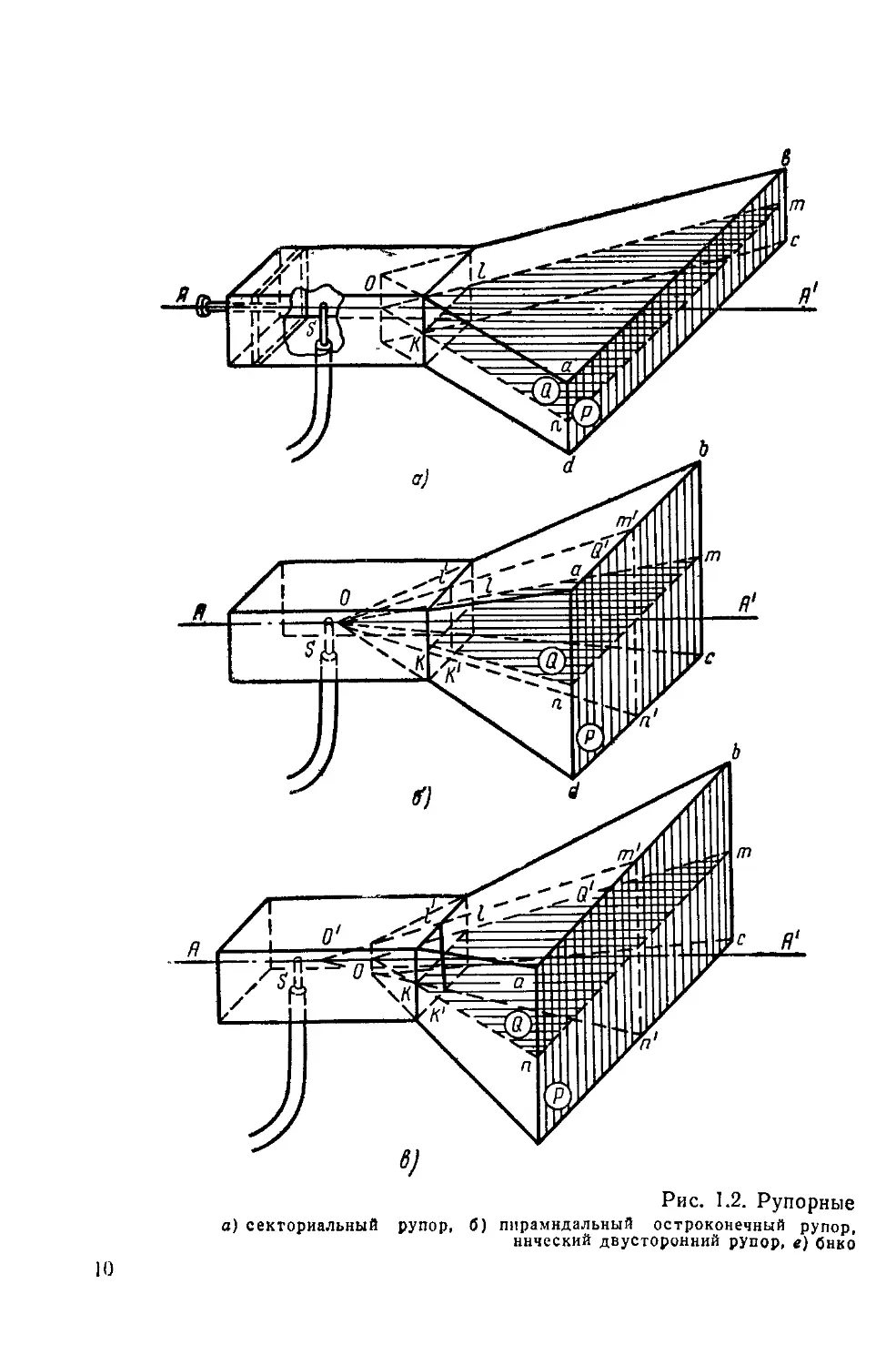
§ 3. РУПОРНЫЕ АНТЕННЫ
На рис. 1.2 показаны основные разновидности рупорных
антенн:
а) секториальный; б) пирамидальный остроконечный;
в) пирамидальный клинообразный; г) конический; д) би-
конический двусторонний и е) биконический односторонний
рупоры.
Из них первые четыре (рис. 1.2,а, б> в, г) представляют
собой систему из обычного радиоволновода и непосредст-
венно присоединенного к нему рупора. По существу послед-
ний является также волноводом, но переменного попереч-
ного сечения. У этих антенн обычные волноводы постоян-
ного поперечного сечения служат в качестве питающих ли-
ний, переносящих энергию от источника S к рупорам. Ис-
точником S или иначе возбудителем волновода является,
как известно, симметричный или несимметричный вибратор.
На рис. 1.2 он показан везде в виде открытого конца внут-
реннего провода коаксиального кабеля.
Биконические рупоры (рис. 1.2,5 и е) представляют со-
бой два усеченных конуса, имеющих общую ось АА' и об-
щую вершину О и расположенных по одну сторону
(рис. 1.2,е) или по разные стороны (рис. 1.2,5) от верши-
ныа). Оба конуса биконического рупора имеют одинаковую
длину образующих. Конусы являются усеченными. Малые
основания этих конусов, размеры которых значительно
меньше размеров больших оснований, расположены близко
друг к другу, закрыты металлическими дисками и между
1) Биконический симметричный вибратор, по существу, также
может рассматриваться как биконический рупор.
2) В промежуточном случае, когда один из конусов превра-
щается в плоскость (диск), получаем известную диск-коническую
антенну или конический штырь (см. гл. V).
8
ними помещается излучатель S в виде перпендикулярного
к ним вибратора.
При рассмотрении рупорных антенн будем пользоваться
следующими обозначениями и терминологией: назовем по-
верхностью раскрыва (сокращенно «раскрывом») поверх-
ность Р, проходящую через края рупора (рис. 1.2). Прин-
ципиально в качестве раскрыва может быть взята поверх-
ность любой формы, ограниченная краями рупоров. Но из
соображений удобства берут обычно ту из них, которая
имеет наименьшую площадь, а именно—у рупоров рис. 1.2,а,
б, в и г — плоскость, у рупора рис. 1.2,5 — цилиндр, а у ру-
пора рис. 1.2,е — усеченный конус.
Сечение рупора поверхностью, параллельной раскрыву,
будем называть поперечным сечением, а сечение плоско-
стью, проходящей через ось АА' и перпендикулярной стен-
кам рупора, будем называть продольным сечением. У ру-
поров рис. 1.2,а бив имеются две такие плоскости. Обе
они образуют разные продольные сечения. У рупоров
рис. 1.2,г, д и е, ввиду их круговой симметрии, таких пло-
скостей бесчисленное количество, но все они образуют
одинаковые продольные сечения. Учитывая, что у рупора
рис. 1.2,ai одно из продольных сечений является прямо-
угольником и тождественно таковому в обычных волново-
дах, будем считать характерным для него сечение klmn
(выделенное штриховкой). Для рупоров рис. 1.2,6 и в ха-
рактерными являются оба сечения klmn (заштрихованное)
и k'l'm'n' (обведенное пунктирной линией без штриховки).
У рупоров рис. 1.2,<5 и е продольное сечение состоит из двух
раздельных частей, представляющих собой зеркальное изо-
бражение одна другой, т. е. принципиально не отличаю-
щихся друг от друга. Поэтому рассматривать мы будем
только одно из них klmn (заштрихованное).
Во всех случаях продольные сечения представляют со-
бой равнобедренные трапеции, весьма близкие к треуголь-
никам. Поэтому, продолжив наклонные стороны трапеции
до их взаимного пересечения, будем считать, что продоль-
ными сечениями рупоров являются равнобедренные тре-
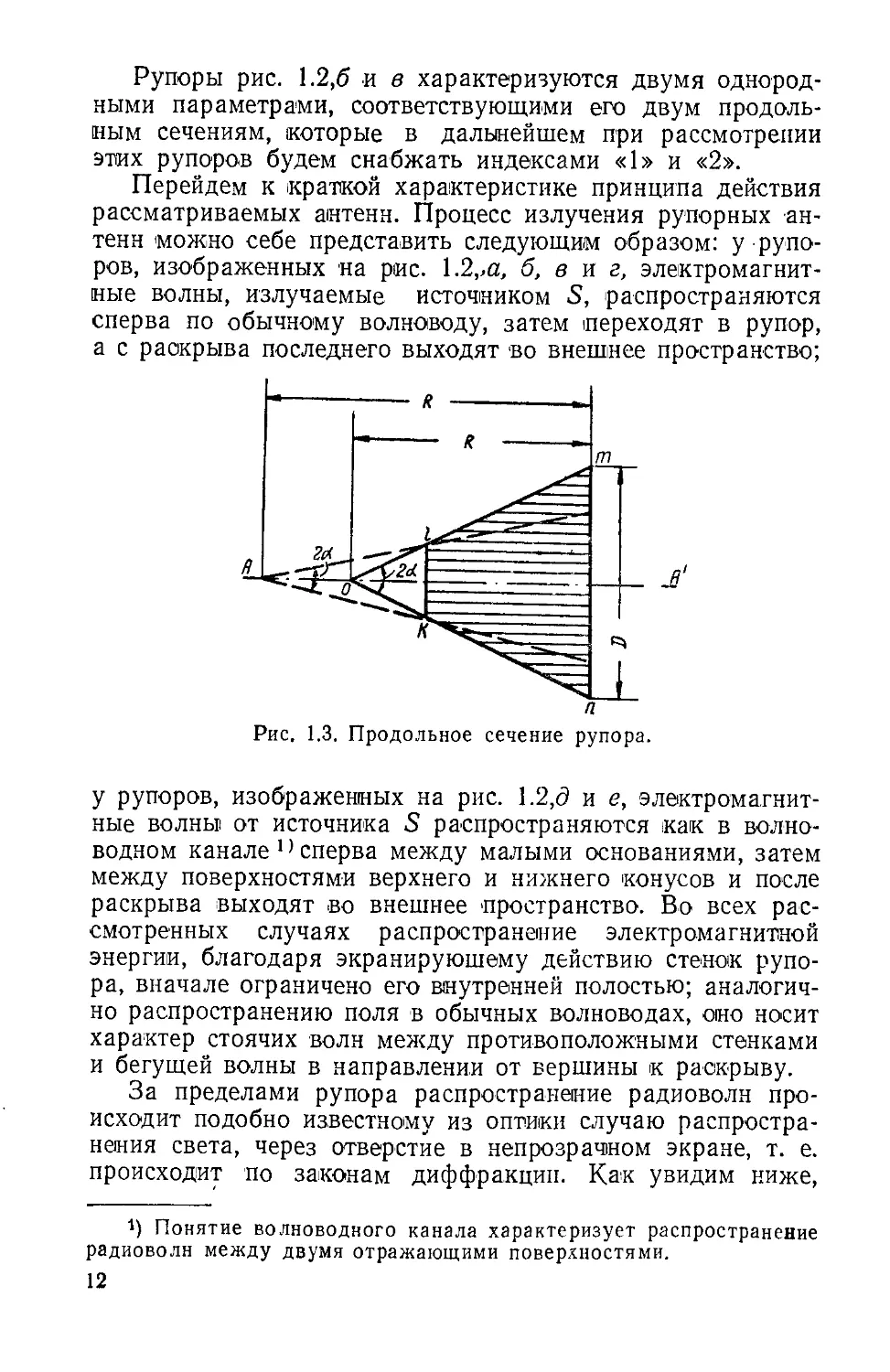
угольники. На рис. 1.3 отдельно показано продольное сече-
ние рупора в виде треугольника.
Параметры продольного сечения (рис. 1.3) — высота R,
Длина основания D, точка вершины О и угол при верши-
не 2а будем рассматривать как параметры рупора и на-
зывать соответственно: длина рупора R, ширина раскры-
ва О, угол раствора 2 а ц вершина рупора О.
9
8
Рис. 1.2. Рупорные
а) секториальный рупор, б) пирамидальный остроконечный рупор,
ннческий двусторонний рупор, е) бнко
10
е)
антенны;
«> пирамидальный клинообразный рупор, г) конический рупор, д) бико-
нический односторонний рупор.
11
Рупоры рис. 1.2,6 и в характеризуются двумя однород-
ными параметрами, соответствующими его двум продоль-
ным сечениям, которые в дальнейшем при рассмотрении
этих рупоров будем снабжать индексами «1» и «2».
Перейдем к краткой характеристике принципа действия
рассматриваемых антенн. Процесс излучения рупорных ан-
тенн можно себе представить следующим образом: у рупо-
ров, изображенных на рис. 1.2,,а, б, в и г, электромагнит-
ные волны, излучаемые источником S, распространяются
сперва по обычному волноводу, затем переходят в рупор,
а с раскрыва последнего выходят во внешнее пространство;
Рис. 1.3. Продольное сечение рупора.
у рупоров, изображенных на рис. 1.2,6 и е, электромагнит-
ные волны от источника S распространяются как в волно-
водном канале сперва между малыми основаниями, затем
между поверхностями верхнего и нижнего конусов и после
раскрыва выходят во внешнее пространство. Во всех рас-
смотренных случаях распространение электромагнитной
энергии, благодаря экранируюшему действию стенок рупо-
ра, вначале ограничено его внутренней полостью; аналогич-
но распространению поля в обычных волноводах, оно носит
характер стоячих волн между противоположными стенками
и бегущей волны в направлении от вершины к раскрыву.
За пределами рупора распространение радиоволн про-
исходит подобно известному из оптики случаю распростра-
нения света, через отверстие в непрозрачном экране, т. е.
происходит по законам диффракцип. Как увидим ниже,
*) Понятие волноводного канала характеризует распространение
радиоволн между двумя отражающими поверхностями.
12
характеристики поля излучения (диаграмма направленно-
сти коэффициент усиления и т. п.) рупорной антенны опре-
деляются размерами параметров рупора: длиной /?, шири-
ной раскрыва D и углом раствора 2 а. Рупор, следователь-
но, является главной частью антенны и поэтому часто отож-
дествляют рупор и рупорную антенну.
Итак, рупор представляет собой открытый волновод
или волноводный канал переменного поперечного сечения,
у которого продольное сечение имеет форму равнобедрен-
ного треугольника и излучение которого образуется в ре-
зультате диффракционного распространения радиоволн, вы-
шедших наружу через раскрыв.
Различие между отдельными разновидностями рупорных
антенн заключается в различии формы поперечного сечения
рупоров, определяющей картину стоячих волн между стен-
ками.
Обычный открытый волновод постоянного поперечного
сечения, равного kl, является предельным случаем рупор-
ной антенны, когда угол раствора 2а = О и длина R = ею.
Понятия «поперечное сечение», «продольное сечение», «рас-,
крыв» аналогичны таковым у рупора.
§ 4. ЛИНЗОВЫЕ АНТЕННЫ
Линзовые антенны характерны тем, что отдельные их
разновидности весьма существенно отличаются друг от
друга по своему устройству. Поэтому нам удобнее будет
начать их рассмотрение с описания принципа действия, ко-
торый является общим для всех линзовых антенн. Описа-
ние же устройства отдельных разновидностей приведем за-
тем в порядке иллюстрации различных методов осущест-
вления общего принципа действия.
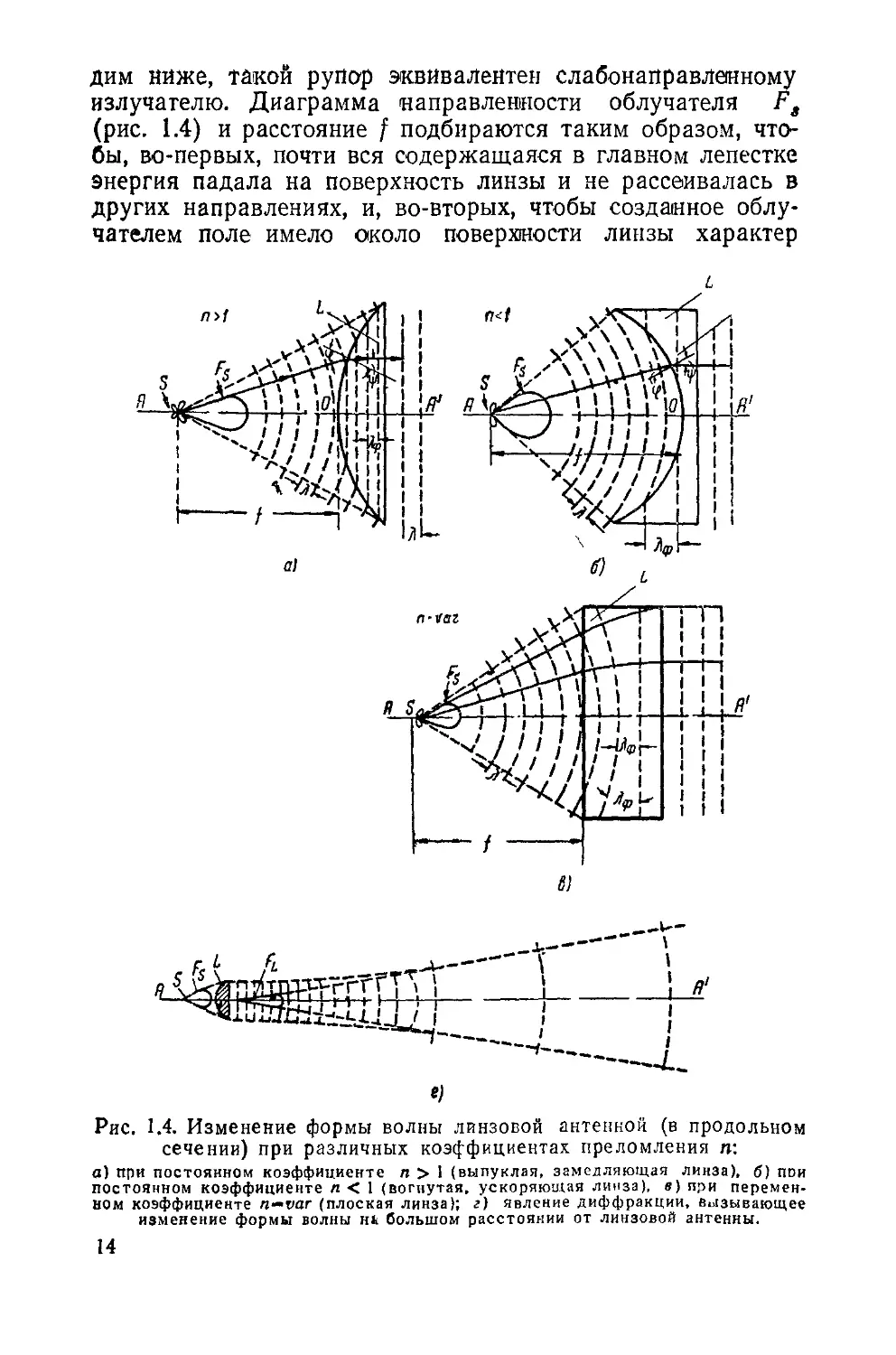
Обратимся к рис. 1.4, на котором схематически изобра-
жены три вида линзовых антенн. Они, как показано, со-
стоят из двух самостоятельных частей — облучателя S и
линзы L.
Облучатель представляет собой слабонаправленную ан-
тенну, помещенную на некотором расстоянии f от линзы.
Это расстояние обычно совпадает с так называемым фокус-
ным расстоянием линзы.
В качестве облучателей линзовых антенн могут приме-
няться: вибратор с пассивным рефлектором, открытый ко-
нец волновода и т. п. Часто линза устанавливается в рас-
крыве рупора, если у последнего размеры раскрыва D (в
единицах длины волны) велики, а длина R мала. Как уви-
13
дим ниже, такой рупор эквивалентен слабонаправленному
излучателю. Диаграмма направленности облучателя Fg
(рис. 1.4) и расстояние f подбираются таким образом, что-
бы, во-первых, почти вся содержащаяся в главном лепестке
энергия падала на поверхность линзы и не рассеивалась в
других направлениях, и, во-вторых, чтобы созданное облу-
чателем поле имело около поверхности линзы характер
t)
Рис. 1.4. Изменение формы волны линзовой антенной (в продольном
сечении) при различных коэффициентах преломления п:
а) при постоянном коэффициенте п > 1 (выпуклая, замедляющая линза), б) пои
постоянном коэффициенте п < 1 (вогнутая, ускоряющая линза), в) при перемен-
ном коэффициенте n—var (плоская линза); г) явление диффракции, вызывающее
изменение формы волны на большом расстоянии от линзовой антенны.
14
сферической волны1К Первое условие при пренебрежении
Излучением боковых лепестков означает, что практически
®ся энергия излучения облучателя направляется на линзу.
Второе условие позволяет рассматривать облучатель как
точечный источник, помещенный в центре сферической вол-
ны, совпадающем с фокусом линзы.
Для анализа линзовых антенн введем следующие обоз-
начения и терминологию. Назовем поверхность линзы, об-
ращенную к облучателю, освещенной стороной, а противо-
положную «теневую» раскрывом линзы Р (см. рис. 1.5).
Почти во всех практических случаях раскрыв линзы дела-
ется плоским, а освещенная сторона, как правило,— криво-
линейной. Встречаются также линзы с плоской освещенной
Стороной. На рис. 1.5 приведено шесть линз. Из них две
выпуклые (а) и (в), две вогнутые (б) и (г) и две с пло-
ской освещенной стороной (б) и (е). Как выпуклые и вог-
нутые, так и плоские линзы могут иметь раскрыв в виде
круга (а), (б) и (б) или в виде прямоугольника (в),
(г), (а). Прямую АА', перпендикулярную плоскости рас-
крыва и проходящую через его центр, назовем осью лин-
зовой антенны, а точку О пересечения оси с освещенной
стороной — вершиной линзы. Обычно облучатель распола-
гается на оси линзы. В этом случае фокусное расстояние f
представляет собой расстояние между облучателем и вер-
шиной О. Линия ВОС пересечения освещенной стороны лин-
зы продольной осевой плоскостью (последняя на ряс. 1.5
выделена штриховкой) называется профилем линзы. В слу-
чае круглого раскрыва обозначим его диаметр через D, а
в случае прямоугольного раскрыва длины сторон — через
£>i и D2.
Линза представляет собой тело определенной геометри-
ческой формы», прозрачное для радиоволн, т. е. пропускаю-
щее сквозь себя электромагнитное излучение диапазона ра-
диочастот, с фазовой скоростью Уф, отличающейся от фа-
зовой скорости в воздухе (с = 3 • 108 м/сек). Иначе говоря,
линзу можно представить себе как прозрачное тело, обла-
дающее коэффициентом преломления
-=^1. (1.1)
ф
9 Под сферической, плоской или цилиндрической волной в дан-
ной работе условно понимаются волны, у которых точки одинако-
вой фазы лежат соответственно на сфере, плоскости или на цилинд-
рической поверхности.
15
a) Packpbfi круглЬш
п>1
0 Pacj(pbiB круглей
Рис. 1.5. Линзовые антенны:
а) выпуклая с круглым раскрывом, б) вогнутая с круглым раскрывом, в) выпук*
лая с прямоугольным раскрывом, г) вогнутая с прямоугольным раскрывом,
д) плоская с круглым раскрывом,
е) плоская с прямоугольным раскрывом.
Ввиду различия коэффициентов преломления у линзы
и у воздуха сферическая волна, приходящая от облучателя,
достигнув поверхности линзы, изменяет свою форму, пре-
вращаясь внутри линзы при соответствующем подборе ко-
эффициента преломления и формы поверхности последней,
как правило, ,в плоскую волну.
16
Так как преломление волн на границе двух сред проис-
ходит по закону
sin у
sin Ф ’
(1.2)
где <р — угол падения волны, ф —угол преломления,
то, как видно из рис 1.4, а. и б, для получения плоской
волны внутри линзы, обладающей во всех точках одина-
ковым коэффициентом преломления, линза при должна
иметь обращенной к облучателю выпуклую поверхность
(рис 1.4, а), а при/г<4—вогнутую (рис. 1.4,6). Это также
легко видеть из условия, что в первом случае Лф«<к
(длина волны внутри линзы меньше длины волны в воз-
духе), а во втором случае наоборот ЛфД>2.
В случае переменного коэффициента преломления
n=var «профиль линзы может иметь различную форму
в зависимости
возрастание) и
пендикулярное
от характера изменения п (убывание или
dn
от градиента , где .у — направление, пер-
оси АА'. На рис. 1.4в иллюстрируется
пример линзы с плоской освещенной стороной и плоским
раскрывом. Так- как линза имеет разный коэффициент
преломления в разных точках, то и длина волны Хф раз-
лична в разных точках. Лучи претерпевают преломление
при переходе из воздуха в линзу и продолжают искрив-
ляться внутри линзы вследствие плавного изменения п.
Фронт волны постепенно выпрямляется внутри линзы.
Волна становится плоской лишь у раскрыва линзы. Для
получения плоской волны в раскрыве линзы, имеющей
обе (освещенную и теневую) плоские поверхности, должно
быть -"<0.
Полученная внутри или на выходе линзы плоская вол-
на, выйдя со стороны раскрыва во внешнее пространство,
вновь принимает благодаря лиффракпии на сравнительно
больших, расстояниях. характер сферической волны,
(рис. 1.4,г). Однако”диаграмма направленности линзовой1
антенны FL при этом существенно изменяется по сравне-
нию с первичной диаграммой облучателя Fs, становясь
обычно значительно более остронаправленной.
Помимо указанного случая формирования внутри линзы
плоской волны и получения в результате этого остронаправ-
2—1503
17
ленной диаграммы, Иногда встречается случай формирова-
ния внутри линзы волны, отличной от плоской, с целью
получения специальной диаграммы (например, косеканс-
ной) .
Поскольку главным назначением СВЧ антенн является
создание определенной диаграммы направленности, то мож-
но утверждать, что основным элементом у линзовых антенн,
выполняющим эту роль, является линза. Что касается об-
лучателя, то его роль, как видим, заключается в излучении
электромагнитных волн и канализации энергии к линзе че-
рез промежуточное пространство и аналогична роли обыч-
ных волноводов у рупорных антенн. Поэтому различие
между отдельными линзовыми антеннами определяем по
различию между линзами, хотя можно указать также на
значительное число разнообразных облучателей.
В принятой нами классификации (рис. 1.1) мы делим
линзовые антенны на разновидности по наиболее сущест-
венному признаку, а именно по методу получения тела с
коэффициентом преломления п Ф 1. ЛТожно указать на три
таких метода, определяющих три разновидности линз: ди-
электрические, металлические и металло-диэлектрические.
Перейдем теперь к описанию отдельных разновидностей
линзовых антенн.
а) диэлектрические линзы
Простейшими являются диэлектрические линзы. Это
просто диэлектрик (электроизоляционный материал), за-
полняющий весь объем линзы. У диэлектрика, как извест-
но, фазовая скорость равна
(1-3)
и коэффициент преломления равен
(1.3а)
где е и е0 — диэлектрические проницаемости соответст-
венно диэлектрика и воздуха (пустоты).
Так как е>е0, то в данном случае и диэлектри-
ческие линзы в соответствии со сказанным выше должны
быть выпуклыми.
18
Уместно будет заметить, что рассматриваемые диэлек-
трические линзы во всех отношениях идентичны оптическим
линзам и отличаются от последних лишь определением ус-
ловий прозрачности. На радиочастотах прозрачность опре-
деляется макроскопическими параметрами, а в области оп-
тического спектра частот — микроструктурой.
б) металлические линзы
Металлические линзы собираются из параллельных ме-
таллических пластин. Последние могут быть либо сплош-
ными (рис. 1.6,а, б, в), либо с отверстиями (рис. 1.6,г),
причем сплошные пластины могут быть плоскими
(рис. 1.6,а, б) или фигурными (рис. 1.6,s). Электромагнит-
ная волна распространяется в промежутках между пласти-
нами, причем электрический вектор поля волны может быть
либо параллелен поверхности пластин (рис. 1.6,а), либо
перпендикулярен к ней (см. рис. 1.6,6 и в соответственно
для плоских и фигурных пластин).
В первом случае пространство между двумя такими пла-
стинами с расстоянием d между ними образует волновод-
ный канал, в котором фазовая скорость распространения
волны, как известно, равна
Мысленно соединим края всех пластин огибающей по-
верхностью и назовем ее поверхностью линзы, а внутрен-
ний объем будем считать заполненным непрерывной средой
с коэффициентом преломления
С
П = —
&ф
(1-5)
Так как у этйх линз то мы будем называть
их металлическими ускоряющими линзами из сплошных
пластин. Эти линзы, как видно из (1.5), характеризуются
коэффициентом преломления п<Я и имеют поэтому вог-
нутую освещенную поверхность.
Различные варианты металлических ускоряющих линз
отличаются друг от друга, во-первых, как и линзы других
разновидностей, формой раскрыва (круглая или прямо-
угольная), во-вторых, характером профиля. У металличе-
2* 19
Рис. 1.6. Металлические линзы:
а) с плоскими металлическими пластинами, параллельными вектору Е,
б) с плоскими металлическими пластинами, перпендикулярными вектору Е,
в) с фигурными пластинами, перпендикулярными вектору £*,
г) с плоскими металлическими пластинами с отверстиями.
20
ских ускоряющих линз профиль может быть гладким
(рис. 1.7,а) или ступенчатым (рис. 1.7,6) ’). В последнем
случае профиль выполнен в виде небольших вогнутых уча-
стков, смещенных примерно на расстояние Друг отно-
сительно друга в направлении, параллельном оси линзы.
В случае линз, показанных на рис. 1.6,6 и в, в кото-
рых электрический вектор поля волны перпендикулярен
к пластинам, пространство между двумя пластинами
образует волноводный канал, где фазо шя скорость рас-
пространения равна скорости с в свободном пространстве.
В этих линзах путь лучей удлиняется в результате на-
клонного расположения пластин пэ отношению к оси
линзы АА' (рис. 1.6,6) или фигурного их выполнения
(рис. 1.6, в). Эти линзы будем называть замедляющими
металлическими линзами. Коэффициент преломления у них
больше единицы и равен у линз с наклонными пла-
стинами (где у —угол между пластинами и плоскостью
раскрыва) или отношению длины волнистого пути к длине
прямолинейного пути—у линз с фигурными пластинами.
В металлической линзе из пластин с отверстиями
(рис. 1.6,г) пластины устанавливаются перпендикулярно
направлению распространения, и электромагнитные колеба-
ния распространяются в результате прохождения через
отверстия. Отверстия делаются, как правило, круглыми,
хотя возможны отверстия и другой формы. При соответ-
ствующем выборе размеров отверстий пластины становятся
прозрачными для радиоволн. При прохождении волны че-
рез отверстия в металлической пластине меняется фаза
поля волны, причем изменение фазы происходит в сторону
опережения. Поэтому система из параллельных пластин
с отверстиями эквивалентна ускоряющей линзе.
Получающееся опережение фазы при прохождении вол-
ны через отверстия зависит от размеров последних. Про-
сверливая в разных местах пластин отверстия разных раз-
меров, можно получить в разных точках линзы различное
опережение фазы, т. е. можно получить систему, эквива-
лентную линзе, с переменным коэффициентом преломления.
Линза же с переменным коэффициентом преломления мо-
жет иметь, как указано выше, профиль различной формы,
!) Профиль линз схематически показан на рис. 1.7 справа от
соответствующей фотографии,
21
a)
б)
Рис. 1.7. Металлические линзы:
а) с гладким профилем, б) со ступенчатым профилем
22
в том чивле прямолинейный. Поскольку пластины устанав-
ливаются перпендикулярно направлению распространения,
наиболее удобной в данном случае и является линза с пло-
ским раскрывом и плоской освещенной стороной.
в) металло-диэлектрические линзы
Идея металло-диэлектрических линз заключается в сле-
дующем. Известно, что причиной отличия диэлектрической
проницаемости изоляторов г от диэлектрической проницае-
мости пустого пространства г0 является поляризуемость их
молекул под влиянием электрического вектора поля, при-
чем поляризация молекул заключается в появлении у них
электрического момента, имеющего направление, обратное
первичному электрическому полю, и величину, пропорцио-
нальную ему. Если же в электрическое поле поместить ме-
таллическое тело, то свободные электроны этого тела сме-
стятся, что также приведет к появлению электрического
момента, подобного моменту у молекул диэлектрика.
..Следовательно, если в каком-нибудь объеме в опреде-
ленном порядке разместить металлические тела небольшого
размера (частицы), изолированные друг от друга воздуш-
ными промежутками, то этот объем будет эквивалентен ди-
электрику. Металло-диэлектрические линзы и представляют
собой такого рода конгломерат из металлических частиц и
воздушных прослоек, эквивалентный диэлектрику. В этом
искусственном диэлектрике роль поляризующихся молекул
играют металлические частицы. Для механического крепле-
ния металлических частиц применяются твердые изолято-
ры; последние представляют собой либо пенистый полисти-
рол, обладающий диэлектрической проницаемостью
е = (1,05 ч- 1,10) е0 = гп, либо тонкие изоляционные пленки
или стержни, разделенные воздушным зазором. Во всех
случаях практически можно считать, что металлические ча-
стицы разделены воздушными промежутками.
Идея искусственного диэлектрика была впервые выска-
зана Н. А. Капцовым [1] в 1920 г. Результаты исследований
такого диэлектрика впоследствии (в 1922—1923 гг.) были
им опубликованы. В этих работах Н. А. Купцов сформули-
ровал основные положения, которыми руководствуются в
настоящее время при конструировании металло-диэлектри-
ческих линз, а именно:
1) расстояние между частицами должно быть меньше
рабочей волны;
23

2) размер частиц должен быть мал по сравнению с ра-
бочей волной.
В 1936 г. М. А. Бонч-Бруевич показал возможность ис-
пользования линз и призм из искусственного диэлектрика
для получения остронаправленного излучения.
Подобно диэлектрическим металло-диэлектрические
линзы характеризуются коэффициентом преломления п > 1
и имеют поэтому выпуклую освещенную поверхность. Раз-
личные варианты металло-диэлектрических линз, указанные
в схеме рис. 1.1, отличаются друг от друга геометрической
формой металлических частиц, составляющих линзу. Эти
частицы могут иметь форму шариков, дисков, пластинок,
лент и др.
На рис. 1.8 показано устройство металло-диэлектриче-
ских линз. Мы видим здесь:
а) шариковую линзу, у которой шарики крепятся с по-
мощью изоляционных стержней; для большей ясности здесь
показана схема линзы (наверху) и ее фотография (внизу);
б) шариковую линзу в виде шариков, заделанных слоя-
ми в пенистый полистирол;
в) дисковую линзу, у которой крепление дисков из
фольги осуществляется с помощью сравнительно тонких ли-
стов из пенистого полистирола;
г) пластинчатую линзу в виде квадратных пленок из
проводящей краски, нанесенных через трафарет на пласти-
ны из пенистого полистирола;
д) ленточную линзу, собранную из пенисто-полистиро-
ловых пластин с пазами, в которые вложены ленты из ме-
таллической фольги; здесь показано продольное осевое се-
чение линзы (наверху) и общий вид (внизу).
§ 5. ЩЕЛЕВЫЕ АНТЕННЫ
Идея щелевых антенн принадлежит М. А. Бонч-Бруе-
вичу [2] и М. С. Нейману [3]. Первым предложена остро-
направленная антенна в виде короткозамкнутого концентри-
ческого фидера или закрытого волновода, в стенке которого
вырезаны вдоль всей длины прямоугольные отверстия ма-
лого сравнителыно с волной размера, расположенные на
расстоянии I' друг от друга, где Аф— длина волны в фи-
дере или волноводе. Вторым предложена слабонаправлен-
ная антенна, представляющая собой эндовибратор с оди-
ночным круглым или прямоугольным отверстием. В обоих
случаях в качестве антенны предлагается замкнутая метал-
лическая поверхность с небольшими отверстиями, внутри
25
которой каким-либо способом возбуждается электромагнит-
ное поле. При этом предполагается, что последнее прони-
кает через указанные отверстия наружу, вследствие чего
создается излучение электромагнитной энергии во внешнее
пространство.
Впоследствии, в результате ряда работ А. А. Пистоль-
корса [4], в которых впервые дана правильная формулиров-
ка теории излучения таких антенн, в первоначальные идеи
Бонч-Бруевича и Неймана внесены соответствующие усо-
вершенствования, заключающиеся в основном в замене
прямоугольных и круглых отверстий небольшого сравни-
тельно с волной размера так называемыми полуволновыми
линейными щелями (т. е. достаточно узкими щелями дли-
нои порядка где х. —длина волны в пустом простран-
стве) .
Обозначив ширину щели через d и длину через /, можем
написать соотношение
(1.6)
Эти антенны названы щелевыми, поскольку излучателя-
ми у них являются полуволновые щели.
Из сказанного выше следует, что возможны три модифи-
кации щелевых антенн: волноводные, фидерные и эндови-
браторные, в зависимости от того, что применяется в каче-
стве тела антенны — волновод, экранированный фидер или
полый резонатор. Однако отличие между указанными моди-
фикациями заключается лишь в способе питания антенны,
т. е. в способе возбуждения щели. С точки зрения поля из-
лучения между ними нет принципиальной разницы.
Благодаря принципиальной идентичности волноводов,
фидеров, и эндовибраторов можно, во избежание повторе-
ния, не останавливаться на рассмотрении всех трех моди-
фикаций щелевых антенн, а ограничиться рассмотрением
одной из них.
Из соображений удобства ограничимся в дальнейшем
рассмотрением главным образом волноводных щелевых ан-
тенн, которые и изображены на рис. 1.9. Однако в соответ-
ствующих местах укажем на некоторые интересные электри-
ческие и конструктивные особенности двух других моди-
фикаций.
Как будет показано ниже, характер внешнего электро-
магнитного поля, т. е. поля излучения щелевых антенн, за-
26
висит от формы и размеров внешней поверхности волново-
да. По указанным признакам мы и проводим классифика-
цию щелевых антенн. На рис. 1.9 слева показаны антенны
Рис. 1.9. Волноводные однощелевые антенны с использованием
прямоугольного и круглого волноводов:
а) и е) продольная щель, б) и лс) поперечная щель, в) торцовая щель, г) и з)
петлевая щель, д) гантельная щель, и) П-образная щель, к) Н-образная щель,
л) антенна обратного излучения.
27
со щелями на стенках прямоугольного волновода. В соот-
ветствии с формой щели и расположением последней мы
различаем следующие варианты щелей: а) продольная,
б) поперечная, в) торцовая, г) петлевая, д) гантельная.
Оправа на рис. 1.9 показаны антенны со щелями на бо-
ковой поверхности круглого волновода. Здесь приведены
следующие варианты: е) продольная, ж) поперечная,
з) петлевая, и) 77-образная, к) 77-образная.
В самом низу (л) приведена так называемая антенна
обратного излучения, представляющая собой открытый вол-
новод, суживающийся к концу и снабженный у последнего
насадкой в виде буквы 77, образующей как бы разветвление
волновода на две ветви, обращенные открытыми концами
к началу волновода.
Приведенные на рис. 1.9 однощелевые антенны обла-
дают весьма слабой направленностью. Для получения
остронаправленного излучения делаются многощелевые ан-
тенны, представляющие собой волновод с одинаковыми ще-
лями, выполненными по одному из способов, иллюстриро-
ванных на рис. 1.9 и расположенных на одинаковом рас-
стоянии друг от друга, причем расстояние обычно выби-
рается таким образом, чтобы получить синфазное излучение
всех и:слей. Устройство многошелевых антенн подробно
рассматривается ниже в гл. VIII. Из рис. 1.9 видно, что
щелевые антенны состоят из трех элементов: источника,
волновода и щели1). Электромагнитные волны, излучаемые
источником, распространяются по волноводу, а достигнув
щелей, проникают в наружное пространство и дальше рас-
пространяются по законам диффракции.
§ 6. ДИЭЛЕКТРИЧЕСКИЕ АНТЕННЫ
Диэлектрические антенны, подобно щелевым и рупор-
ным, состоят из трех элементов. Этими элементами
(рис. 1.10) являются:
1) диэлектрический стержень Д,
2) металлический патрон 77, надеваемый на один из кон-
цов стержня и являющийся отрезком волновода, заполнен-
ного диэлектриком;
3) первичный источник электромагнитного излучения
S, вставляемый в экранированную патроном часть стерж-
ня (рис. 1.10в) или возбуждающий полый волновод
(рис. 1.10,г).
1) На рисунке источник показан в виде выступающей внутренней
жилы питающего кабеля,
28
Мы будем называть началом диэлектрического стержня
то место, где он выступает из патрона, и концом — проти-
воположный торец.
Диэлектрические стержни бывают двух видов — сплош-
ные (10,а) и полые (10,6). Полые стержни называются так-
Рис. 1.10. Простые диэлектрические антенны:
а) сплошная, б) полая (трубчатая), в) питание антенны с помощью коаксиаль-
ного кабеля, г) возбуждение антенны посредством волновода.
29
Жё диэлектрическими трубами. Толщина стенок последних
обычно делается по длине одинаковой. Форма поперечного
сечения стержней, как сплошных, так и полых может быть
различной: круглой, квадратной, прямоугольной. Форма по-
перечного сечения стержней характеризуется боковой их
проекцией, показанной на рис. 1.10 слева от соответствую-
щего им всем одинакового продольного сечения. Сплошные
диэлектрические стержни часто делаются суживающимися
к концу. Диэлектрические трубы, как правило, бывают по-
стоянного поперечного сечения.
Внутренняя поверхность патрона имеет ту же форму, что
и наружная поверхность стержня, поэтому металлический
патрон надевается на диэлектрический стержень вплотную
без зазоров.
Источник S (рис. 1.10,а и б) в виде перпендикулярного
к оси стержня симметричного (в случае труб) или несим-
метричного (в случае сплошных стержней) вибратора воз-
буждает в патроне волну типа Н(ТЕ).
На рис. 1.10,в показано питание сплошных диэлектриче-
ских антенн с помощью коаксиального кабеля. Свободный
конец внутреннего провода кабеля проходит в поперечном
направлении сквозь тело стержня внутри патрона, причем
выступающий по другую сторону конец провода входит
в настраивающуюся полость, которая служит для обеспече-
ния требуемого возбуждения стержня. При волноводном
питании (рис. 1.10,г) волна типа Н(ТЕ) возбуждается сна-
чала в полом волноводе, а затем переходит в патрон, за-
полненный диэлектриком. При отсутствии диэлектрического
стержня возбужденная в патроне волна вышла бы с его
открытого конца во внешнее пространство и, распростра-
няясь далее по законам диффракции, сформировала бы
диаграмму направленности, аналогичную диаграмме обыч-
ного открытого волновода. Наличие же диэлектрического
стержня заставляет волну, возбужденную в патроне, рас-
пространяться далее по диэлектрику или по внутреннему
пространству трубы, как по волноводу, являющемуся про-
должением патрона. Однако в отличие от обычного волно-
вода, металлические стенки которого полностью экранируют
внутреннее поле от внешнего пространства, волна, распро-
страняющаяся по диэлектрическому стержню, лишь частич-
но отражается от границы раздела диэлектрика и внешней
среды (воздуха), а частично во всех точках поверхности
выходит наружу. В результате таких условий образования
внешнего электромагнитного поля диаграмма направленно-
го
СДИ Диэлектрической антейны отличается от таковой для
открытого волновода, являясь более остронаправленной.
Как увидим ниже, диаграмма направленности диэлек-
трических антенн из сплошного стержня зависит от пло-
щади поперечного сечения тела диэлектрика в начале <3j
Рис. 1.11. Схема питания сложной (четырехстержневой)
диэлектрической антенны посредством коаксиального кабеля.
и в конце о2, от длины открытой части стержня I и от
диэлектрической проницаемости материала стержня е.
Диаграмма направленности диэлектрических труб за-
висит от площади поперечного сечения а, длины I, от
толщины стенок трубы Д и от диэлектрической проницае-
мс/сти материала е.
31
в)
Рис. 1.12. Сложная (42-стержневая) диэлектрическая
антенна с питанием посредством волноводов:
а) узел разветвления волновода для питания трехстержневой
группы, б) внешний вид спереди, в) внешний вид сзади со
снятой крепежной сеткой.
32
Наряду с описанными здесь простыми диэлектрическими
антеннами применяются сложные диэлектрические антенны,
состоящие из нескольких простых, первичные источники
которых соединены между собой общей фидерной системой.
На рис. 1.11 показана схема питания коаксиальным кабе-
лем. На рис. 1.12 показана сложная диэлектрическая антен-
на, в которой применяется волноводное питание. Она со-
стоит из 14 групп по 3 стержня в каждой. На рис. 4.12,а
показано разветвление волновода, питающего одну группу.
§ 7. РЕФЛЕКТОРНЫЕ АНТЕННЫ (ЗЕРКАЛА)
Из рефлекторных антенн наиболее широко применяются
параболические. С них мы и начнем рассмотрение. Парабо-
лические рефлекторные антенны состоят из двух элементов:
облучателя и собственно зеркала (рис. 1.13). Зеркало пред-
ставляет собой проводящую поверхность параболической
а) б)
Рис. 1.13. Рефлекторные антенны с зеркалами в виде:
а) параболоида вращения, б) параболического цилиндра.
формы, изготовленную из медных или алюминиевых листов.
Часто для уменьшения парусности поверхность зеркала де-
лается не сплошной, а решетчатой. Встречаются параболи-
ческие зеркала двух .видов: параболоиды вращения (а) и
параболические цилиндры (б).
Параболоид вращения, как известно, есть поверхность,
описываемая параболой при ее вращении вокруг своей оси.
Поскольку ось параболы проходит через ее фокус, то фокус
параболоида вращения является также точкой. Параболи-
ческий цилиндр тоже описывается параболой, но при ее пе-
ремещении параллельно самой себе вдоль прямой линии,
перпендикулярной к плоскости параболы. При таком пере-
мещении фокус параболы также перемещается по прямой
3—1503 зз
ВВ', которая (называется фокальной линией параболическо-
го цилиндра.
В случае параболоида вращения в качестве облучателя
применяется точечный источник, помещенный в фокусе и,
подобно облучателям линзовых антенн, представляющий
собой слабонаправленную антенну (с главным максимумом,
направленным в сторону зеркала), создающую электромаг-
нитное поле излучения в виде сферической волны. В случае
параболического цилиндра в качестве облучателя приме-
няется линейный источник, расположенный вдоль фокаль-
ной линии и представляющий собой антенну, создающую
электромагнитное поле излучения в виде цилиндрической
Рис. 1.14. Излучение рефлекторной антенны.
волны. Длина линейного облучателя равна примерно длине
образующей цилиндра, и расположен он симметрично отно-
сительно торцовых краев цилиндра.
Электромагнитная волна, излученная облучателем,
в обоих случаях, достигнув поверхности зеркала, отражает-
ся от нее и направляется обратно к выходу зеркала в виде
плоской волны. Выйдя наружу во внешнее пространство,
отраженная плоская волна принимает в соответствии с за-
конами диффракции на сравнительно больших расстояниях
от антенны характер сферической волны, имея при этом
значительно более острую направленность FR, чем перво-
начальное излучение облучателя F, (рис. 1.14).
Легко видеть, что рефлекторные и линзовые антенны
имеют общие черты. И те и другие состоят из двух элемен-
тов, из которых один (облучатель) создает сравнительно
слабо направленное излучение, а второй (линза или реф-
лектор) преобразует первичное излучение в значительно
более остронаправленное. Их отличие в принципе заклю-
чается в том, что у линзовых антенн указанное преобразо-
34
Вание осуществляется в результате прохождения первично-
го излучения сквозь линзу, а у рефлекторных антенн —
в результате обратного отражения энергии от поверхности
зеркала.
В дальнейшем будем пользоваться следующей термино-
логией и обозначениями.
Мы будем называть плоскость Р, проходящую через
края зеркала (рис. 1.13), раскрывом. У параболоидов вра-
щения раскрыв имеет, вообще говоря, форму круга диамет-
ром D, а у параболических цилиндров — форму прямо-
угольника со сторонами D\ и D2.
В ряде практических случаев применяются различные
варианты усечения параболоидов вращения. В этих случаях
раскрыв может принять форму прямоугольника или круга
с вырезанными сегментами.
Назовем осью зеркала прямую АА', перпендикулярную
плоскости раскрыва и проходящую через центр последнего.
Точку О пересечения оси с поверхностью параболоида на-
зовем его вершиной. Расстояние f между вершиной и фоку-
сом, как известно, называется фокусным расстоянием, а
удвоенное значение фокусного расстояния
P = 2f (1.7)
— параметром параболоида.
Сечение параболоида плоскостью Q, проходящей через
его ось, назовем продольным сечением. У параболоида вра-
щения все такие сечения одинаковы и в качестве продоль-
ного сечения может быть взято любое из них. У параболи-
ческого цилиндра сечения различны. Интерес для нас пред-
ставляет сечение, перпендикулярное фокальной линии ВВ'.
Параболические цилиндры будем называть горизонталь-
ными или вертикальными в соответствии с горизонтальным
или вертикальным расположением их фокальных ли-
ний ВВ'.
В технике сверхвысоких частот находят также примене-
ние рефлекторные антенны с зеркалами непараболической
формы. Работа этих антенн происходит по такому же прин-
ципу, но при этом отраженная волна не является плоской.
Выбор формы поверхности зеркала и соответствующей
ей формы поверхности фронта отраженной волны зависит
от требований к диаграмме направленности антенны. Этот
вопрос более подробно освещается ниже.
3* 35
§ 8. АНТЕННЫ ПОВЕРХНОСТНЫХ ВОЛН
Антенны поверхностных волн состоят из двух элементов:
возбудителя и направителя. Схема устройства направителя
приводится на рис. 1.15. По виду направителя различают
плоскостные и цилиндрические антенны поверхностных
волн.
<77
Рис. 1.15. Антенны поверхностных волн:
а) плоскостная антенна с плоским направителем прямоугольной формы в виде
диэлектрического слоя, б) то же круглой формы, в/ плоскостная антенна с
гофрированным направителем круглой формы, г) то же прямоугольной формы,
д) цилиндрическая антенна.
У плоскостных антенн направителем служит хорошо
проводящий металлический плоский лист, покрытый диэлек-
трическим слоем определенной толщины (рис. 1.15,а,б)
или гофрированный (рис. 1.15,в, г), а у цилиндрических
антенн направителем служит прямолинейный хорошо про-
водящий металлический стержень с насаженными на него
дисками (рис. 11.15,(9). Направители плоскостных антенн мо-
36
гут быть прямоугольными, как показано на рис. 1.15,а, г,
или круглыми (рис. 1.15Д в).
На рис. 1,16 показано несколько вариантов возбуждения
плоскостных антенн поверхностных волн. Направитель во
всех случаях показан здесь в виде гофрированного листа;
аналогично может возбуждаться металлический лист с ди-
электрическим слоем.
Возбудителями плоскостных антенн могут служить:
1) ряд гантельных щелей, питаемых от волновода пря-
моугольного сечения (рис. 1.16,а);
2) раскрыв рупора (рис. 1.16,6);
3) раскрыв волновода (рис. 1.16,б);
4) прямолинейный провод, протянутый на некоторой вы-
соте над направителем параллельно его плоскости и сим-
метрично относительно краев (рис. 1.16,г);
5) штыревая антенна (рис. 1.16,6).
Возбудителем цилиндрических антенн поверхностных
волн обычно служит раскрыв волновода круглого сечения,
в котором распространяется волна Нц(ТЕц) (см. рис. 1.17).
Антенны поверхностных волн по принципу действия род-
ственны диэлектрическим антеннам.
Действительно, направитель с диэлектрическим слоем
(например, рис. 1.15,а) можно рассматривать как диэлек-
трический стержень прямоугольного сечения, расположен-
ный на проводящей плоскости. У направителя с гофриро-
ванной поверхностью (рис. 1.15,г) выступы аналогичны
лентам в ленточной металло-диэлектрической линзе и поэто-
му гофрированную поверхность можно рассматривать как
слой из искусственного диэлектрика, т. е. как стержень
прямоугольного сечения из искусственного диэлектрика,
расположенный на проводящей плоскости. Аналогично на-
правитель цилиндрической антенны (рис. 1.15,6) представ-
ляет собой искусственный диэлектрик, составленный из ди-
сков и эквивалентен стержню круглого сечения из искусст-
венного диэлектрика.
У антенн поверхностных волн, так же как и у диэлектри-
ческих, электромагнитная волна, излучаемая возбудителем,
распространяется в виде плоской волны вдоль направителя.
Эти плоские волны, направляемые гофрированными или ди-
электрическими поверхностями, а также стержнями из есте-
ственного или искусственного диэлектрика, получили назва-
ние поверхностных волн, а антенны, использующие поверх-
ностные волны, получили название антенн поверхностных
волн.
37
Сл>
00
Волновод со вставкой из л юс шла
в)
Рнс. 1.16. Схемы возбуждения плоскостных антенн поверхностных волн.
Возбудители: а) гантельные щели в прямоугольном волногоде, б) раскрыв рупора, в) раскрыв прямоугольного волновода,
г) прямолинейный провод, д) штыревая антенна.
Превращение электромагнитного излучения возбудителя
в поверхностную волну способствует увеличению направлен-
ности излучения по сравнению с направленностью одного
возбудителя. Направленность излучения зависит от длины
волны и параметров этих антенн (рис. 1.15), а именно:
а) в случае диэлектрического слоя—от его длины I, ши-
рины Ь, толщины h и диэлектрической проницаемости е;
Рис. 1.17. Схема возбуждения цилиндричес-
кой аитениы поверхностных волн с помощью
раскрыва круглого волновода.
б) в случае гофрированной поверхности — от ее длины I,
ширины Ь, высоты выступов h, их ширины w и расстояния
между выступами I;
в) в случае цилиндрической антенны — от ее длины I,
диаметра дисков d, диаметра стержня Л, расстояния между
дисками t.
§ 9. ОБЩАЯ ХАРАКТЕРИСТИКА СВЧ АНТЕНН
Познакомившись с устройством и принципом действия
СВЧ антенн, можем теперь точнее определить их отличи-
тельные черты.
Вспомним, что задачей всякой антенны является, во-
первых, преобразование подводимой энергии токов высокой
частоты в энергию электромагнитного излучения и, во-вто-
рых, формирование определенной диаграммы направлен-
ности.
Первая часть задачи — преобразование подводимой
энергии в энергию излучения — производится у СВЧ
антенн, так же как и обычных, с помощью симметричных
или несимметричных вибраторов. Такого рода вибраторами
у рупорных, щелевых, диэлектрических и у части антенн
поверхностных волн являются возбудители волноводов, а
у линзовых, рефлекторных и другой части антенн поверх-
ностных волн вибраторы входят в состав облучателей.
39
Отличие СВЧ антенн от обычных антенн заключается
в способе выполнения второй части задачи, а именно, в спо-
собе формирования заданной диаграммы направленности.
У обычных антенн диаграмма направленности форми-
руется в результате интерференции на больших расстоя-
ниях излучения отдельных вибраторов. Для получения за-
данной диаграммы направленности у обычных антенн необ-
ходимо излучающие вибраторы расположить соответствую-
щим образом и возбуждать в них токи определенной ампли-
туды и фазы. Так, например, у синфазной антенны вибра-
торы располагаются в одной плоскости на одинаковом
расстоянии друг от друга и питаются токами, одинаковыми
по амплитуде и фазе. В результате у синфазных антенн
получается диаграмма направленности, имеющая острый
максимум в направлении, перпендикулярном плоскости
антенны. У антенны «волновой канал» вибраторы распола-
гаются вдоль прямой линии, вообще говоря, на разных рас-
стояниях и возбуждаются токами разной амплитуды и раз-
ной фазы. Диаграмма направленности системы «волновой
канал» имеет сравнительно тупой максимум вдоль линии
расположения вибраторов. Для получения требуемой диа-
граммы соответствующим образом располагаются и пита-
ются вибраторы и у других антенн.
Таким образом, у обычных антенн те же элементы, кото-
рые преобразуют подводимую энергию токов высокой ча-
стоты в энергию излучения (вибраторы) выполняют и вто-
рую часть задачи — формируют диаграмму направленности.
У антенн СВЧ функции между отдельными элементами
антенны разделяются. В то время как один из элементов
этих антенн (облучатель, возбудитель или первичный источ-
ник) выполняет первую часть задачи — преобразование
подводимой энергии токов высокой частоты в энергию элек-
тромагнитного излучения, другой элемент — рупор, линза,
зеркало, щель, диэлектрический стержень (труба) или на-
правитель, выполняют другую часть задачи — формирова-
ние заданной диаграммы направленности ".
Процесс формирования диаграммы направленности у
СВЧ антенн происходит следующим образом.
Зеркала и линзы придают электромагнитному излучению
облучателя форму плоской волны и направляют практиче-
*) Во многих случаях >у СВЧ антенн, как мы видели, имеется
еще третий элемент—волновод, канализирующий энергию от первого
элемента ко второму. Но роль этого элемента не принципиальна и
носит вспомогательный характер.
40
ски всю энергию излучения через раскрыв во внешнее про-
странство. В рупорах, как можно показать, электромагнит-
ное излучение .возбудителя принимает форму цилиндриче-
ской или сферической волны (в зависимости от вида
рупора) и вся энергия направляется во внешнее простран-
ство опять таки через раскрыв. У этих трех типов СВЧ
антенн диаграмма направленности формируется в результа-
те диффракции электромагнитной волны от плоского рас-
крыва. Мы имеем здесь случай, аналогичный известному из
оптики случаю диффракции света от отверстия в плоском
экране.
В случае щелевых антенн также имеет место диффрак-
ция электромагнитной волны от отверстия, хотя этот случай
отличается от указанного случая из оптики в связи с малы-
ми (по сравнению с длиной волны) размерами щели и в
связи с влиянием проводящей поверхности волновода на
поле во внешнем пространстве.
У диэлектрических и поверхностных антенн электромаг-
нитное излучение возбудителя принимает форму плоской
волны, распространяющейся вдоль оси диэлектрического
стержня (трубы) или вдоль направителя. При этом энергия
непрерывно рассеивается с поверхности этих антенн. Иначе
говоря, в данном случае имеет место диффракция электро-
магнитной волны от поверхности диэлектрического стержня
(трубы) или от поверхности направителя.
Итак, антенны СВЧ, помимо проволочного элемента,
имеют диффракционный элемент, формирующий диаграмму
направленности в процессе диффракции электромагнитной
волны от какой-либо части поверхности этого элемента.
ГЛАВА ВТОРАЯ
ОСНОВНАЯ ЗАДАЧА ТЕОРИИ СВЧ АНТЕНН
И МЕТОДЫ ЕЕ РЕШЕНИЯ
§ 1. ПОСТАНОВКА ЗАДАЧИ
Основной задачей теории СВЧ антенн является опреде-
ление электромагнитного поля излучения этих антенн. Одна-
ко поле излучения, т. е. поле на сравнительно больших рас-
стояниях от антенны непосредственно связано с полем
вблизи антенны. Следовательно, теория СВЧ антенн не мо-
жет ограничиться определением только поля излучения, а
должна заниматься нахождением электромагнитного поля,
созданного первичными излучателями — вибраторами как
внутри, так и вне этих антенн. Нахождение всего поля внут-
ри и вне СВЧ антенн представляет собой задачу электро-
динамики.
Мы видели выше, что СВЧ антенны можно считать со-
стоящими из двух основных элементов, выполняющих каж-
дый свою функцию. Один служит для преобразования энер-
гии токов высокой частоты в энергию электромагнитного
излучения, второй — для создания требуемой направленно-
сти. Во многих случаях СВЧ антенны содержат также тре-
тий вспомогательный элемент, например, волновод, связы-
вающий между собой первые два. С точки зрения электро-
динамики такое деление является условным. В строгой
постановке задачи все элементы антенны должны рассмат-
риваться во взаимосвязи друг с другом и с внешним про-
странством.
Определение поля СВЧ антенны сводится, вообще го-
воря, к следующей задаче электродинамики.
В неограниченном пространстве, заполненном возду-
хом (г=г0, р.=р-0, а=0), имеется незамкнутая поверхность 5,,
обладающая бесконечной проводимостью (рис. 2.1). До-
42
полним ее воображаемой поверхностью S2 с нулевой про-
водимостью так, чтобы 5, и 52 совместно образовали
замкнутую поверхность S. Конечная часть пространства
внутри S] и 32 может быть заполнена диэлектриком
с диэлектрической проницаемостью е., отличной от е0.
На сравнительно небольших расстояниях от Si имеются
возбуждающие токи, распределенные по заданному закону
в некотором объеме (в частности, возбуждение может про-
изводиться вибратором, как это изображено на рис. 2.1).
Требуется найти векторы электромагнитного Поля Е
и Н, удовлетворяющие уравнениям Максвелла во всем
неограниченном пространстве (за исключением точек, при-
варужнар
сторона Sf
Уа
$1
6"г-0
Рис. 2.1. К строгой постановке задачи по определению
электромагнитного поля антенн СВЧ.
fem
внутренняя
сторона
надлежащих поверхностям раздела двух сред), причем
такие, чтобы касательная составляющая Е обращалась
в нуль на Sj и чтобы при переходе через границу раз-
дела диэлектрик—воздух касательные составляющие Е
и Н оставались непрерывными. Помимо этого на искомые
решения накладывается условие бесконечности (так на-
зываемое условие излучения), которое в конечном счете
сводится к требованию, чтобы на больших расстояниях
от рассматриваемой системы поле имело характер ухо-
дящих от антенны сферических волн.
43
В настоящее время известно строгое решение некоторых
задач электродинамики, имеющих приложение в теории
СВЧ антенн.
Например, Я. Н. Фельд [5] разработал общую строгую
теорию щелевых антенн, Л. А. Вайнштейном [6] строгими
методами решена задача об излучении с открытого конца
волновода, Г. Т. Марковым [7] получено, в частности, стро-
гое решение задачи об излучении вибраторных и щелевых
излучателей вблизи круглой цилиндрической поверхности
или вблизи сферы и т. д.
Но, к сожалению, в большинстве случаев в точной поста-
новке задача оказывается неразрешенной, и мы вынуждены
прибегать к приближенным приемам. В качестве одного из
таких приемов, часто используемых при исследовании ан-
тенн СВЧ, можно указать на следующий.
Неограниченное ‘Пространство-условно Еразбивают на
две области, рассматривая антенну как одну из таких об-
ластей (внутреннюю), а внешнее пространство как другую
область (внешнюю). Антенна в этом случае соответствует
объему V. (рис. 2.1), замкнутому поверхностью 5, состоя-
щей из S, и S2. Через поверхность S2 внутренний объем V,
связан с внешним пространством Va.
Внутри объема V. находятся известные сторонние токи
/ст (вибратор), а средой, заполняющей этот объем, яв-
ляется диэлектрик, имеющий в общем случае кусочно-
постоянное значение диэлектрической проницаемости е..
Например, рупорные антенны можно в этом случае рас-
сматривать как объем, ограниченный поверхностями обыч-
ного волновода, рупора и раскрыва последнего. Первые две
поверхности образуют Si, а раскрыв соответствует S2. Внут-
ри этого объема в волноводной части находится вибратор.
Средой является воздух, имеющий диэлектрическую прони-
цаемость
____10-»#
е° 36л м
Аналогично можно рассматривать диэлектрические
антенны как объем, занятый диэлектрическим стержнем.
Этот объем частично экранирован патроном, поверхность
которого соответствует S,. Открытая часть поверхности
диэлектрического стержня соответствует S2. В экрани-
рованной части помещен вибратор. В случае сплошного
стержня средой, заполняющей объем V., является диэлек-
4.4
трик с sj>so, а в случае диэлектрических труб средой
язляется частично воздух с е=е0, а частично диэлектрик
с e>so-
В таком же аспекте могут быть представлены и дру-
гие типы СВЧ антенн.
В соответствии со сказанным, разделим условно нашу
задачу на две—внутреннюю и внешнюю, понимая под
перзой определение внутреннего поля, т. е. поля в объеме Vz
(рис. 2.1), а под второй — определение внешнего поля,
т. е. поля в пространстве Va. Оба поля взаимно связаны
и эта связь выражается в приведенных выше граничных
условиях.
Сущность приближенного метода решения задачи за-
ключается в том, что, несмотря на связь между полем
в области У(. и полем в области Va, внутреннюю задачу
решают независимо от внешней и полученные из этого
решения значения поля на поверхности S2 используют
для решения внешней ^задачи.
Внутреннее электромагнитное поле вызывается сторон-
ними токами /ст и зависит от формы, размеров и располо-
жения проводников, по которым текут сторонние токи, от
формы размеров и параметров внутренней среды, а также
от формы и размеров St и 5г- При приближенном решении
внутренней задачи обычно условия идеализируются. Так,
например, в случае рупорных или диэлектрических антенн
электромагнитное поле в рупоре или диэлектрическом
стержне определяется в предположении бесконечной длины
рупора или стержня; в случае линзовой антенны задача ре-
шается в предположении непрерывности среды линзы,
в случае щелевой антенны электромагнитное поле в щели
определяется в предположении, что щель вырезана в неог-
раниченно большой бесконечно тонкой проводящей плоско-
сти и т. п. Полученное решение для идеальных условий по-
лагается затем приближенно правильным для реальных
условий: рупора или диэлектрического стержня конечной
длины, линзы, состоящей из дискретных элементов, для по-
верхности тела щелевой антенны конечных размеров и лю-
бой формы.
Идеализируя условия внутренней задачи, мы тем самым
превращаем ее в самостоятельную задачу, не связанную
с внешней задачей.
Внешнее электромагнитное поле, ввиду отсутствия
сторонних токов в пространстве Va, является следствием
45
только Электромагнитных явлений в объеме V.. Но для
определения электромагнитного поля во внешнем прост-
ранстве Уа нет надобности входить в детали электро-
магнитного поля внутри Vz. Для этого достаточно лишь
знать электромагнитное поле на поверхности S. Следова-
тельно, электромагнитное поле на поверхности S в из-
вестном смысле играет для объема Va роль сторонних
токов. Отсюда внешняя задача может быть определена
как задача нахождения внешнего электромагнитного поля
по полю на поверхности S. В целях упрощения внешней
задачи делается следующее допущение: ^полагается, что
на внешней стороне S] (рис. 2.1) электромагнитное поле
равно нулю, что там отсутствуют заряды и токи, т. е.,
что роль указанных эквивалентных токов играет лишь
открытая часть поверхности антенны S3, причем под S,
понимают у рупорных, линзовых и рефлекторных антенн
соответственно раскрыв рупора, линзы или зеркала, у ще-
левых антенн—позерхность щели, у диэлектрических
антенн—открытую часть поверхности стержня, а у антенн
поверхностных волн—плоскость или цилиндрическую по-
верхность напразителя.
В действительности при отсутствии внешних сторонних
токов заряды и токи на поверхности Si отсутствуют лишь
при условии полностью замкнутой проводящей поверхно-
сти, т. е. при S2 = 0. Но в этом случае во всем внешнем про-
странстве поле равно нулю. При наличии же на проводящей
поверхности щелей и отверстий возникает поле во внешнем
пространстве, но одновременно возбуждаются также заряды
и токи на наружной стороне поверхности Sb Следователь-
но, приближенный метод вносит всегда ошибку, связанную
с тем, что при этом не учитываются токи и заряды на на-
ружной стороне проводящей поверхности. Однако во мно-
гих практических случаях, когда интересуются излучением
в пределах главного лепестка диаграммы направленности
СВЧ антенн, роль наружной стороны Si относительно не-
велика и поэтому ее влиянием пренебрегают (преимуще-
ство решения задачи в строгой постановке в том и заклю-
чается, что при таком решении удается более детально вы-
яснить направленные свойства антенн).
Таким образом, внешняя задача в упрощенном виде мо-
жет быть сформулирована так: задано значение электро-
магнитного поля на открытой части СВЧ антенны (на по-
верхности S2). Требуется найти поле излучения.
46
Так как поле на открытой части СВЧ антенн образуется
в результате прихода туда электромагнитной волны от пер-
вичного источника, то внешняя задача аналогична диф-
фракционной задаче волновой оптики Ч в которой рассмат-
ривается световое поле, полученное в результате прохожде-
ния света через отверстие в непрозрачном экране. Поэтому
при решении внешней задачи в теории СВЧ антенн приме-
няется метод волновой оптики.
Основная задача теории СВЧ антенн, как отмечалось
выше, заключается в определении поля излучения, а для
определения последнего требуется знать значение поля
лишь на S2, поэтому внутренняя задача может быть огра-
ничена определением поля только на открытой части поверх-
ности антенны S2. Однако практический интерес имеет зна-
ние всего внутреннего поля, в особенности поля вблизи ви-
братора, так как с этим связан вопрос о согласовании пи-
тающей линии и антенны. При строгом решении задачи нам
требовалось бы в соответствии с методом определить поле
во Всех частях антенны. Но при использовании приближен-
ных методов часто удается выделить вопрос о поле у ви-
братора и о согласовании в самостоятельную задачу. Осо-
бенно удобно это сделать в случае волноводного питания,
так как применяющиеся в технике СВЧ методы отфильтро-
вания высших типов волн в волноводах делают практически
независимыми поля около вибратора и на другом конце
волновода, присоединенном к рупору, облучающем зеркало
и т. п.
Внутренняя задача в смысле определения поля на S2
решается приближенными методами, различными для раз-
ных типов СВЧ антенн. Исходные положения, приемы и
результаты решения внутренней задачи будут рассмотрены
ниже в главах, посвященных отдельным типам СВЧ антенн.
В настоящей главе мы изложим метод волновой оптики,
являющийся в приближенной постановке общим методом
решения внешней задачи.
Кратко резюмируем оказанное. В настоящее время
в строгой постановке решены лишь некоторые частные за-
дачи теории СВЧ антенн. В большинстве случаев для ре-
шения задачи теории СВЧ антенн применяются приближен-
ные методы, заключающиеся в делении задачи условно на
две — внутреннюю и внешнюю. В первой разными для раз-
личных антенн методами находится поле внутри антенны и
*) При достаточно короткой волне.
47
на открытой части ее поверхности, во второй — общим поч-
ти для всех СВЧ антенн методом волновой оптики опреде-
ляется поле излучения.
§ 2. ИСХОДНЫЕ УРАВНЕНИЯ
Как указывалось выше, задача теории СВЧ антенн
заключается в определении векторов поля Е и Н, удовлет-
воряющих уравнениям Максвелла, граничным условиям
и условию излучения.
Уравнения Максвелла в практической системе единиц
при гармонических колебаниях, имеющих зависимость от
времени вида е'ю< пишутся следующим образом
rot Н—Jwz'E -|- J3
rot Е = — j^H — JM
(2.J)
гдег' = е — /—, и — круговая частота, е, у., а—парамет-
ры среды (диэлектрическая проницаемость, магнитная
проницаемость, проводимость), J3 и JM — векторы плот-
ности сторонних токов соответственно электрических и
магнитных.
Обычно под электрическими токами понимается движе-
ние электрических зарядов. Магнитных токов в смысле дви-
жения магнитных зарядов не существует.
Однако в теории Максвелла понятие электрических то-
ков трактуется в более широком смысле, чем только дви-
жение электрических зарядов. Как известно, в этой теории
рассматриваются, например, как эквивалентные друг другу
токи проводимости и токи смещения, т. е. токи в виде дви-
жущихся зарядов и токи в виде переменного электрического
поля [с соответствующим коэффициентом пропорционально-
сти (см. 2.1)]. Следует заметить в этой связи, что вектор J3
(2.1) также может содержать как сторонние токи проводи-
мости, так и сторонние токи смещения.
Уравнения Максвелла (2.1) симметричны относительно
вектороз Е и И. Следовательно, по аналогии с электри-
ческими токами в виде переменного электрического поля
можно ввести понятие магнитных токов в виде перемен-
48
ного магнитного поля. В этом смысле и введен в урав-
нение (2.1) вектор JM.
В электромагнитном поле векторы ЕиН связаны ме-
жду собой определенным соотношением. В наиболее общем
виде эта связь выражена в (2.1). Наличие связи между
£и Н принципиально позволяет в каждом частном слу-
чае выразить Е через Н и наоборот. Это, в свою очередь,
ддет возможность математически выразить /э и JM как
через Е, так и через Н. В (2.1) электрический ток J9 вы-
ражается через электрическое поле Е, а магнитный
ток JM— через магнитное поле Н.
Как увидим ниже, в задачах теории антенн сторонние
токи задаются не в виде объемных токов, как в уравне-
нии (2.1), а в виде поверхностных токов. В последнем
случае проще всего выразить электрические и магнитные
токи через касательные составляющие Е и Н к поверхно-
сти, причем электрические токи выражаются через каса-
тельную составляющую Н, а магнитные токи — через
касательную составляющую Е.
Условие излучения в дифференциальной форме пишется
так:
lim =0; lira 47^) =0, (2.2)
г-»оо г-»оо
, и> 2п
где г — расстояние от источников излучения, « = — = -у- ,
k2=a>2e0?0, с — скорость света в свободном' пространстве,
Л —длина волны в свободном пространстве.
Это означает, что напряженность электрического и
магнитного полей на бесконечно больших расстояниях от
источников равны:
4—1503
49
где е0 — орт, имеющий направление электрического век-
тора,
г0~ орт, имеющий направление радиуса-вектора, про-
веденного через точки излучения в точку наблю-
дения,
С — постоянная, не зависящая от г.
Как известно, уравнения Максвелла (2.1) справедливы
для среды с постоянными или меняющимися непрерывно
параметрами е, р, а. При нарушении этого условия, т. е.
при наличии нескольких сред с разными параметрами,
на границе двух сред 1 и 2 выполняются следующие
условия:
(;(£,-£Л=0,
На поверхности идеального проводника будет
[nEJ^O, |
} (2.5)
[пНг] = --С J,
где п — орт нормали к поверхности раздела,
4в-вектор поверхностной плотности тока, текущего
по поверхности раздела.
Ниже рассматриваются два наиболее часто используе-
мых метода строгого решения задач теории СВЧ антенн:
метод вспомогательных источников и метод векторного
потенциала.
§ 3. МЕТОД ВСПОМОГАТЕЛЬНЫХ ИСТОЧНИКОВ
Я. Н. Фельд [5] и ряд других авторов 18, 9] разработали
предложенный А. И. Мандельштамом и М. П. Свешнико-
вой метод вспомогательных источников для строгого реше-
ния задач электродинамики. Прежде, чем приступить к из-
ложению метода, приведем вывод леммы Лоренца, на ко-
торой основывается метод.
50
Предположим, что нам известно два электромагнитных
поля: £, Н и £|, Н\. Оба поля удовлетворяют уравнениям
(2.1), что позволяв» писать
rot Н = /шг'£ -j- f,
rot£= —
rotZ/j = yW Et 4- Jf,
rot £t = — jupHi—J?.
(2.6)
Умножим правые и левые части уравнения (2.6) соот-
ветственно на £ь Hh Е, Н, а затем сложим порознь пра-
вые и левые части всех четырех уравнений, причем у дзух
последних поменяем знаки на обратные. Тогда получим:
{Ех rot И) + (Н. rot £) — (£rot — (Н rot £0=
= (£1J9) -(hJ м) - (£~J3) + (HJ Г). (2.7)
Учитывая известное из векторного анализа соотношение
div [ab] = (b rot a) —(a rot b),
получаем лемму Лоренца
(2.8)
div [£^] 4- div [H£J = (£t>) — — (EJ3) + (HJT). (2.9)
Уравнение (2.9) используется для решения задач элек-
тродинамики следующим образом. Одно из рассматривае-
мых полей принимается за искомое, а другое — за вспомо-
гательное. В качестве вспомогательного поля может быть
взято любое поле, удовлетворяющее уравнениям (2.1). Про-
извольность вспомогательного поля позволяет выбрать его
таким, чтобы исключить из (2.9) максимальное число чле-
нов и тем самым упростить его. Далее правая и левая ча-
сти (2.9) интегрируются по объему, содержащему все ис-
точники электромагнитного поля и точки, в которых опре-
деляется поле.
Воспользуемся методом вспомогательных источников
для вывода ряда важных соотношений, широко применяе-
мых в теории антенн сверхвысоких частот. Одновременно
эти выкладки послужат иллюстрацией метода.
4* 51
Обратимся к рис. 2.2. Имеем объем V., окруженный
замкнутой поверхностью S. Эта поверхность, вообще
говоря, произвольна и к ней предъявляется лишь требо-
вание регулярности Вне этой поверхности в объеме Va
заданы источники — токи плотностью J3 и/*. Токи долж-
Рис. 2.2. К выводу основных уравнений теории антенн
СВЧ методом вспомогательных источников.
ны быть конечны в рассматриваемом объеме. Внешней
средой (Va) является воздух с соответствующими пара-
метрами (s = s0, р. = р.о, <j = 0). Требуется определить поле
£л, Нм в точке М, созданное источниками J3 и JM, если
известны значения поля на поверхности S. Введение
в рассмотрение поверхности S связано с тем, что внутри
*) Под регулярной понимается здесь поверхность, имеющая во
всех точках определенную касательную плоскость.
52
поверхности также имеются токи Ja и Ju. Однако они
неизвестны. Известными являются значения поля на по-
верхности S.
Окружим точку М двумя сферами большого R и ма-
лого р радиусов с центром в этой точке. Поверхность
первой сферы обозначим через аь а поверхность второй сфе-
ры — через а2. Объем внутри последней обозначим через Vo.
Далее поместим в точке М вспомогательный источ-
ник сначала в виде электрического диполя с моментом р,
ток которого обозначим через J’(J“=O).
Поле вспомогательного источника Elt Н\ и ток свя-
заны с искомым полем Е, Н и токами J3, JM соотноше-
нием (2.9) Проинтегрируем правую и левую части урав-
нения (2.9) по объему Va —• Vo. Поскольку из объема
интегрирования исключен объем Vo, то в оставшейся
части ./э = 0. Учитывая теорему Гаусса—Остроградского,
получаем:
- J {(п[е//пШ«[#А])}^ = J [№)-
-(JuH,)]dV, (2.9а)
где п — внутренняя нормаль по отношению объема
~ Vo-
Поверхностный интеграл по а1 при стремлении ра-
диуса R сферы к бесконечности равен нулю в силу (2.3).
Действительно, обозначив Е = Еей и Ех = Е\в, полу-
чим
-* -* -* -» е-/л(г+п) ' -* -*
[£ Н} ] + [//£,] = С {[е0 [г0 ео ]] - [е0 [гоео]]} =
е-/А(г4-г,) , -->• -> ,
= С —-----{Г о (е0 е0) — е0 (еог „)- г0 (е, е0) +е0 (е0 г0)} = 0,
(2.10)
поскольку (еовд)= (е'е0), а (еого) = О и (е'го) = О, как ска-
лярные произведения перпендикулярных векторов.
Поверхностный интеграл по а2 найдем следующим
путем. Проинтегрируем правую и левую части уравне-
53
ния (2.9) по объему Vo. Так как в этом объеме J9 = 0 и
JM = 0, то получим:
[£#!])+(« [ЯEi])HS==- \(J3E)dV. (2.11)
»» V»
В левой части (2.11) взят положительный знак, так
как п означает нормаль, внешнюю к объему Vo.
Стягивая объем Vo в точку, можем считать Е под ин-
тегралом в правой части (2.11) постоянной величиной
и равной £м, что дает
\(jiE)dV^^EM)=J^CpEMy (2-12)
Vo
где /’ — момент тока,
р —электрический момент диполя.
Стягивание объема Vo в точку позволяет распростра-
нить интеграл в правой части (2.9а) на весь объем V
поскольку J3 и JM в точке М не имеют особенностей по
условию.
Подставив (2.10), (2.11) и (2.12) в (2.9), получаем
после простых преобразований
(Р j {(«[ЕНХ]) + (n [Н Ej])} dS +
s
+jr J[(>£1)-(JMH})]dV. (2.13)
Va '
Как известно, векторы поля Е и Н электрического
диполя выражаются через его электрический момент р
следующим образом:
(Р ~~г) = rot rot (Р?)
= fc rotV’ —) = й ral (Pf)
где г — расстояние от точки М до точки интегрирования,
e~ikr
а <р = —•
54
Подставим Ej и Hj из (2.14) в отдельные слагаемые (2.13). При
этом будем иметь в виду, что вектор р — постоянная величина. Под-
становка приводит к следующей цепи преобразований:
a) j(« [£tfj) dS = J~ J {(n [£ rot (p?)]) dS =
s s
= J (« [grad <j>p]]) dS = (p [[«£] grad <p]) dS.
s s
6) jwtffij) dS= ~ J (n[tfrot rot (p<f)]) dS =
s s
=4^ [ l)rfS+ j (n [# gfad (P grad ?)1) dS =
S 5
£2 p 1 p -> -> ->•
= 4^7j + ] (nrot//) (pgrad®)dS —
s s
- 4^~ J (« rot {# (P grad ?)}) dS = ~ j (p [n H]) <p dS -j-
s s
+ 4^ j {(n/“£o E) + (n /э)} (P grad cp) dS —
s
— 4^- $ (Hdl) (p grad ?) dS.
г
Интеграл б) может быть иначе преобразован к следующему
виду:
J (п [И EJ])dS = ^^ (р [п Щ) <fdS -I- j (n [Н (р v) grad ?]) dS =
s s s
= 4^7 j (p i« H] yds + J ([n Я] (pv) grad ?) dS,
s s
где q) — контурный интеграл по границе Г [поверхностей St н S2
rd (рис. 2.2)],
V — так называемый оператор „набла".
.55
’ a
dV = ^T0 \(Р^^ +
Поскольку поверхность S принята замкнутой, контурный интег-
рал «= 0. При незамкнутой поверхности его необходимо будет учи-
г
тывать.
в) J (/ э£у) dV = 4^7 J 9 rot rot dV ~
Va Va
= 4^7 J (Р ^dV + 4^ grad (р grad dV =
Va Va
= 4^- j (P 7Э) fdV — 4^ [ (P grad <p) div/W +
va
+ 4^ j div V 3 (P grad
Va
+-4^f (pgrad tp) dV - ~4^Р7э) (p grad T) dS.
Va Va
Интеграл в) также может быть приведен к другому виду
[ (7Э£;) dV = J (р 7Э) If dV + 4^ j (7Э Jv) grad f) dV.
Va ' Va Va
г) = f(7Mrot(7f))^ =
Va Va
У (/M Igrad ?•/>]) dV = — ~ (p [ grad <f]) dV.
va Va
Через рэ выше обозначена объемная плотность электрического
заряда, связанная с /э соотношением
div J3 — — ywp9.
Подставив преобразованные выражения в (2.13) и ис-
ключив в правой и левой частях общий множитель р, по-
лучаем
К = i f[ln §rad dS + i Ь £rad VdS ~
s
s
56
grad <p(£dZ) 4-1 f[JMgrad<p]d\7 —
Г va
4-l- J p3 grad <₽ dV - f JVV, (2.15)
° va va
либо
f[[n^J grades 4-4^;]*([«#] v)grad<?dS —
s s
-^J[n^?dS4-lJ[JMgrad<P]61V4-
S Va
+ ^\v'^^dS~j^^dV. (2.16)
Va Va
Ес’ли теперь в качестве вспомогательного источника
в точке М взять магнитный диполь, задавшись его мо-
ментом или током, и произвести аналогичные выкладки,
то получим для магнитного поля в точке М следующее
выражение:
grades
s
+i.V"^grad <?dS +
s
+ gradual)- (2.17)
s г
- i f l>grad ,] dV - 4- f p"grad fdV - J J":fdV,
Va Va Va
либо
= i f [[« H] grad <p] dS ~ - J([n E] v) grad grad T] dV +
S Va
+ 4-4sf(?r)gradf<rt'-4? J
va va
(2.18)
57
Здесь под рм понимаются магнитные заряды, вводи-
мые в рассмотрение по тем же соображениям, по каким
вводятся магнитные токи JM и связанные с последними
соотношением
divJM=—/шрм.
Таким образом, методом вспомогательного источника
мы получили для произзольной точки М точные значе-
—1>
ния векторов Ем и Нм, выраженные через объемное рас-
пределение электрических и магнитных токов и зарядов
J9, JM, рэ, рм и через векторы поля Е и Н на выделен-
ной поверхности S.
Формулы (2.15) и (2.17) как непосредственно, так и
преобразованные широко используются ниже для расчета
полей излучения. Формулы (2.16) и (2.18) отличаются
тем, что в них поле в точке М выражено только через
касательные составляющие электрического и магнитного
векторов на поверхности S и только через токи J3 и
JM, в то время как в (2.15) и (2.17) входят, наряду с ними,
нормальные составляющие поля и заряды.
Если в объеме Va отсутствуют токи J3 и JM и внеш-
нее по отношению к S поле Ем, Нм определяется значе-
нием поля на S, то (2.15) и (2.17) сводятся соответ-
ственно к
i Jgfad dS + i Ь grad vdS —
s s
- J .ftn Щ ,dS - § grad , (Ж7),
s г
H = f[[n H) grad <p] dS j- f(n H) grad ydS -f-
s s
S г
(2.19)
58
В свою очередь (2.16) и (2.18) приводятся соответ-
ственно к виду
V=SpE] grades + j4-.]((» Й] V) grades-
s s
-
s
HM= J[[« H] grad <₽] dS - 4-^ j([n E] v)grad<pdS +
s s
(2.20)
+ /J° J[nE]^S.
s
Рассматривая замкнутую поверхность, можно поло-
жить контурные интегралы в (2.19) равными нулю.
Тогда получим:
Ем= & [Srad ds + i £rad VdS —
s s
s
HM= J[[n #1 &rad v]dS + i J(«#) grad <pdS+
s
+ J^\[nE]4dS.
s
В том случае, когда Ем, Нм определяются лишь
ними токами, они равны согласно (2.15) и (2.17)
i f [^м srad <?ldV—4^г f p3srad ?dV—
° Va
Va
g^d<₽]dV-£— [ P“ grad4dV~
Va Va
-ZipVV'
Va
(2.21)
внеш-
(2.22)
59
или, согласно (2.16) и (2.18)
£.=rj [7"gradT]dV4
Va
Va
J 4n.J T
(2.23)
P3grad<?W
(A)gra<MV-
Va
В случае хорошо проводящих металлических по-
верхностей токи и заряды сосредоточены в чрезвычайно
тонком поверхностном слое. В теоретических исследова-
ниях обычно принято считать этот слой бесконечно тон-
ким. Это позволяет перевести интегралы (2.22) и (2.23)
из объемных в поверхностные, и мы получаем:
f Йов grad ф] dS - 4^7 J Рпов £rad <fdS ~
8 S
Я — —1 I
М 4л )
S
-/^Упов^.
S
Йов gfad - 4^7 J Рпов grad <?dS -
s
J 4л J пов * ’
(2.24)
где ^ов - ЛМов - Рпов > Рпов - поверхностная плотность токов
и зарядов.
60
Или иначе
МЙов g^d ср] dS + j(7’0B v) grad <₽dS- '
s s
s
s
V) 8'ad ~J% Р». Vts-
s
(2.25)
Полученные формулы (2.19)-e(2.25) используются для
расчета электромагнитного поля в объме Va .
§ 4. МЕТОД ВЕКТОРНОГО ПОТЕНЦИАЛА
Часто для решения уравнения (2.1) применяется
метод векторного потенциала. Вводятся вспомогатель-
ные векторные функции Аэ и ЛМ1), связанные с векторами
поля Е и Н следующими соотношениями:
Е = — /сор. АЭЦ- grad div Аэ — rot Ам,
Й = ^graddiv АМ + ГО*ЛЭ. (2.26)
Подстановка (2.26) в (2.1) приводит к следующим
дифференциальным уравнениям для Аэ и Ам:
ДАэ4-62 АЭ=-7Э,
AAm + FA“ = -7m,
(2.27)
J) Наряду с вектор-потенциалом некоторыми авторами исполь-
зуется вектор Герца П, связанный с А соотношением
А = П.
61
где
АЛ == graddiv А — rot rotX. (2.28)
Как известно, неоднородные волновые уравнения
(2.27) имеют решения, удовлетворяющие условию излу-
чения, такого вида
V
AM = ^JM<fdV. (2.29)
v
Обозначения здесь те же, что и раньше.
Подставив (2.29) в (2.26), получаем
‘ graddiv pfdV -
V V
— ^rot
V
я=-/£ ( '"W + i г™'1 div J
V V
+ irotpMV. (2.30)
v
В задачах, в которых токи рассматриваются как по-
верхностные, можно писать
E = —j [j3 <fdS + т—г— grad div f J3 <fdS —
J 4n J пов» i 4к/а>е ° J пов"
S 5
s
= -/S.f ^noB 4dS + 4^r Srad diV J A”ob Vis-
's s
— j- rot f J3 ydS.
4k J повT
(2.31)
В задачах теории СВЧ антенн, как правило, точные
значения J3 и JM неизвестны. Поэтому в большинстве
62
блуйаев заДаются их приближенными зкйчениймй, ййтуй*-
тивно определенными или найденными опытным путем.
В небольшом числе простейших случаев, скажем, в слу-
чае металлических поверхностей простой геометрической
формы точное значение токов может быть получено
в результате строгого решения задачи. Для этого по-
ступают следующим образом. Ищут значения поля на
самой поверхности, по которой протекают токи. На этой
поверхности, поскольку она рассматривается как иде-
ально проводящая, касательная составляющая электри-
ческого вектора поля равна нулю. Найдя по (2.30) каса-
тельную составляющую Д и приравняв ее нулю, приво-
дим задачу о нахождении искомого тока к интегро-диф-
ференциальному уравнению для функций токов J3 и 7м
вида
~ 7з^РгповИ5 + т-т-gfad div -
J 4тс J т пов ‘ 1 4к/сй5 ° т J пов т
~4rotj7nMOB <fds = o, (2.32)
s
где т — индекс касательной составляющей вектора.
В частном случае (это имеет место, когда ток во
всех точках параллелен одной из ортогональных коор-
динатных осей), когда
7“ов = 0 и grad, div 75 = 0, (2.33)
s
получаем интегральное уравнение
<fdS = O.
(2.33)
В более сложных случаях строгая постановка задачи
может привести не к одному, а к системе интегро-диф-
ференциальных уравнений
- J S’ f <пов gradXi div J 7пэов yds -
s s
— rot f 7" <?dS = 0,
4k J ПОВ *
S
(2.34a)
63
- j‘i j grad,, div j 7;„ -
s s
-irol.J^.^s=0- <2-346)
s
где Т[ и т2 — индексы двух взаимно перпендикулярных
касательных составляющих векторов.
Сложность строгого решения заставляет ограничиваться
теми простейшими случаями, при которых рассматриваемая
поверхность совпадает с одной из координатных поверхно-
стей в какой-либо ортогональной системе координат (пря-
моугольной, цилиндрической, сферической и т. п.). Кроме
того, приходится учитывать возможность привести (2.33)
или (2.34) к такому виду, который известен из математи-
ческого анализа.
При определении поля по приближенным заданным зна-
чениям тока интересуются обычно полем вне поверхности
интегрирования. В этом случае можно ввести операторы
дифференцирования в (2.31) под знак интеграла. Это по-
зволяет провести следующие преобразования:
rot j JydS = J rot (J<f) dS = — j [./grad dS,
s s s
grad div J JydS — Jgrad div (J«p) dS =
s s
= Jgrad (/grad v)dS = J (J v) grades.
s s
Подставив (2.35) и (2.36) в (2.31), получаем
В= £ р:„ tdS + v) grad +
s s
+ ifc.SradT]</S.
s
H = — j^- [ J" ydS + ^4— f(J” v) grad <fdS —
' 4it J n0B ‘ 1 Jv n0B ° •
s s
S
(2.35)
(2.36)
(2.37)
64
Формулы (2.37) тождественны формулам (2.25), полу-
ченным методом вспомогательных источников. Это указы-
вает на принципиальную тождественность обоих методов.
Пользование тем или иным из них определяется в каждом
конкретном случае большей или меньшей простотой мате-
матических выкладок.
§ 5. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
Выше выведен ряд формул, служащих для расчета элек-
тромагнитного поля заданных источников. Кратко охарак-
теризуем эти формулы.
Наиболее общими являются уравнения (2.16) ч- (2.19).
Для расчета по ним необходимо знать объемное распре-
деление токов / и Г и зарядов р9 и рм, а также значе-
ние напряженности поля на выделенной поверхности 5,
окружающей неизвестные токи и заряды. Однако урав-
нения (2.16) ч-(2.19), как правило, не используются для
расчетов, так как требуют большого числа разнообразных
исходных данных, предварительное получение которых край-
не сложно. Обычно в теории антенн приходится вычислять
электромагнитное поле либо по заданным токам и зарядам,
либо по заданному полю на выделенной поверхности.
В первом случае могут быть использованы формулы (2.22)
и (2.23), являющиеся следствием (2.16) ч- (2.19) при 5=0.
Во втором случае используются формулы (2.20) и (2.21),
к которым приводятся (2.16)ч- (2.19) при V9=0, JM = 0,
рэ = 0, рм = 0.
Известно, что в хорошо проводящих металлах электри-
ческие токи проводимости и электрические заряды на сверх-
высоких частотах сосредоточены в чрезвычайно тонком по-
верхностном слое. При математическом анализе проводи-
мость а металлов обычно принимается равной бесконечно-
сти и, как следствие, толщина 6 слоя, в котором сосредо-
точены электрические токи и заряды, полагается равной
нулю. Таким образом, вводится понятие о поверхностных
электрических токах и зарядах.
Приняв, существование поверхностных электрических
токов и зарядов и вводя в рассмотрение по аналогии с ними
магнитные поверхностные токи и заряды, заменяем в урав-
нениях (2.22) и (2.23) объемные интегралы поверхностными
и получаем соответственно (2.24) и (2.25).
5—1503 «5
Сопоставив уравнения (2.20) и (2.21) с уравнениями
(2.24) и (2.25), легко видеть, что они соответственно анало-
гичны. В том и другом случаях выражения для электромаг-
нитного поля одинаковы как по числу интегралов, так и по
виду соответственных подинтегральных выражений. Отли-
чие заключается лишь в том, что в одном случае в подин-
тегральных выражениях содержатся токи и заряды, а в
другом случае касательные и нормальные составляющие
векторов Е и Н.
Итак, электромагнитное поле заданных источников рас-
считывается по одинаковым формулам как в том случае,
когда источники заданы в виде поверхностных токов и за-
рядов, так и в том случае, когда источники заданы в виде
электромагнитного поля на выделенной поверхности. Ска-
занное является основой так называемого принципа эквива-
лентности, который гласит: «По отношению к создаваемому
источниками электромагнитному полю между собой экви-
валентны поверхностные токи и заряды, с одной стороны,
касательные и нормальные составляющие векторов поля Е
и Н на поверхности, с другой стороны.»
Математически принцип эквивалентности выражается
следующим образом:
(п«]=-7;ов.„,
(/2 Е) ^Рпов.экв.’
(2.38)
(п^) = — 1р“овэкв
Г*
Как легко видеть из граничных условий (2.5), урав-
нения (2.38) соответствуют связи между электромагнит-
ным полем Е, Н, с одной стороны, и током /вов и за-
рядом рвов на поверхности идеального проводника (а = оо,
8 = 0),1) с другой.
1) В силу [п £] = 0, (пЯ) = 0 на поверхности идеального провод-
ника^пов“0- Рпов = °-
66
По принципу эквивалентности аналогичная связь пред-
полагается и в том случае, когда выделенная поверхность
проходит по диэлектрической среде, в частности, по возду-
ху. Однако в этом случае, наряду с эквивалентными элек-
трическими поверхностными токами и зарядами, должны
учитываться эквивалентные магнитные поверхностные то-
ки и заряды, определяемые по (2.38).
Как показал Б. В. Брауде [10], исключение из рассмот-
рения поверхностных магнитных токов в задачах теории
антенн может привести к серьезным ошибкам.
§ 6. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ВНЕШНЕЙ ЗАДАЧИ
ТЕОРИИ СВЧ АНТЕНН
Строгое решение задач теории СВЧ антенн, как указы-
валось выше, встречает большие математические трудности.
Поэтому к настоящему времени строгими методами решены
лишь очень немногие из них. В большинстве случаев поль-
зуются приближенными методами, заключающимися, как
указывалось, в делении задачи на две условно независи-
мые: внешнюю и внутреннюю, причем внутренняя задача
сводится к нахождению приближенного значения поля на
открытой части поверхности антенны (в раскрыве), а внеш-
няя заключается в определении поля излучения на большом
расстоянии от антенны по заданному полю в ее раскрыве.
Остановимся здесь на рассмотрении внешней задачи теории
СВЧ антенн.
Внешняя задача формулируется следующим образом.
Имеем замкнутую поверхность S (рис. 2.3), на одной части
которой Si векторы электромагнитного поля Е и Н равны
нулю, а на другой части S2 — имеют заданное значение, не
равное нулю. Поле на S2 образуется в результате прихода
электромагнитной волны от первичного источника /ст, на-
ходящегося внутри поверхности S.
Требуется определить поле во внешнем пространстве на
больших расстояниях от поверхности S. Внешней средой
является воздух с диэлектрической проницаемостью е0, маг-
нитной ^проницаемостью у0 и проводимостью з = 0.
В такой постановке неточность выражается, во-первых,
в том, что в известном смысле произвольно задано поле на
поверхности S2, во-вторых, в предположении равенства ну-
лю поля на наружной стороне поверхности Si.
5* 67
Исходными при решении данной задачи являются фор-
мулы (2.19) -ь (2.21) предыдущего параграфа. Сами эти
формулы, как мы видели, являются точными.
Учитывая принцип эквивалентности, расчет может быть
произведен также по формулам (2.24) и (2.25). Для даль-
Рис. 2.3. К приближенному решению внешней задачи
антенн СВЧ.
нейших выкладок наиболее удобным будет исходить именно
из этих формул.
На больших расстояниях от антенньГ указанные фор-
мулы могут быть значительно упрощены. При расстояниях,
значительно превышающих длину и линейные размеры
антенны (объема V{), можно положить
grad,----(л+1)±-±.;(1=<_/4т- (2.39)
(/v) grad = (/у) [ — ( Jk + —j— r0 ] =
= (^ro) ^- [— ( jk + y) ~~ r0 ] ~ k2<f (J r0) r0, (2.40)
где r0 — орт, имеющий направление радиуса-вектора, про-
веденного из точки интегрирования в точку наблюдения.
68
Подставив (2.39) и (2.40) в (2.25) и учитывая, что
средой является воздух, получаем:
С £>2 Г •* *♦
£«=- tds - 4^ j (/„• л) r^s-
s s
f fa *.l tdS=-/? (h [ 0.1] yds -
s s
-7s.ffa*olT«. (2.41)
Аналогично для магнитного вектора поля имеем
Н. --/ЙJhfajdltds tdS. (2.42)
s s
В соответствии с принципом эквивалентности фор-
мулы (2.41) и (2.42) могут быть использованы также для
расчета поля излучения по заданному полю на выделенной
поверхности. Для этого /пэов и /пвв заменяются эквива-
лентными значениями по формулам (2.38). Сделав соот-
ветствующие замены, получаем
£м = /Т/[г0[[«Я] ZoMS-
s
s
s
(2.43)
$ 7. ФОРМУЛА КИРХГОФА. СРАВНЕНИЕ С ВЕКТОРНОЙ
ФОРМУЛОЙ
Поле излучения по заданному полю в раскрыве ан-
тенны (на поверхности S2) нередко рассчитывается по
формуле Кирхгофа, имеющей вид
69
где ф —скалярная функция, характеризующая электро-
магнитное поле волны. Индекс М указывает на значение
функции в точке М, для которой определяется функция,
а индекс S — значение функции на поверхности интегри-
рования. Как увидим ниже, эта функция соответствует
одной из прямоугольных составляющих векторов Е и Н.
Как известно, прямоугольные составляющие Е и Н
удовлетворяют волновому уравнению. Для функций, удов-
летворяющих волновому уравнению, формула (2.44) может
быть легко получена с помощью скалярной теоремы Грина.
Для установления связи между (2.44) и полученными
выше векторными формулами, а также для определения
пределов применимости формулы (2.44) выведем послед-
нюю путекГ преобразования фурмул (2.19), учитывая, что
они соответствуют J3 = 0 и Ум = 0 во внешней среде V .
Начнем с первой из формул (2.19). Согласно (2.1) при
J” = 0 можем подставить в (2.19) равенство
JwpH = — rot Е.
В свою очередь векторное произведение [nrot£] с учетом
того, что п есть — орт, можно представить в следующем
виде:
[n rot £] = grad (£п)—-^-. (2.45)
Далее,
[[/г £] grad = — n (£ grad tp) -j- Е {п grad <р) =
= n(£grad<p) . (2.46)
Подставив (2.45) и (2.46) в первое уравнение систе-
мы (2.19), получаем
= -4^7 $ Srad(? (^0 Srad
Г Si
+ ^f<?grad(£n)dS. (2.47)
70
Используя далее тождество
(Е п) grad <р <р grad (Е п) = grad {<р (Е п)}
и объединив второй интеграл уразнения (2.47) с двумя
последними, приходим к выражению .
в, = - 4^7 f t ')+S f £ ж - T #)ds -
г s,
— f {п (Еgrad (р) — grad (<р (Е n))} dS. (2.48)
ft
Можно показать, что
{n (Egrad<р) — grad(?(En))} dS = 1 -р [Е</7]. (2.49)
ft г
Для доказательства (2.49) предположим, что S2 —
плоский прямоугольник. Взедем прямоугольную систему
координат с осью Z, направленной перпендикулярно к пло-
скости прямоугольника, и с осями X и У, параллельными
граничному контуру (рис. 2.4). Обозначим подинтеграль-
—►
ное выражение в левой части (2.49) через К,. Тогда
I2-5’)
<2S1>
^~^ + В^ + Еу^+Е.^
= -Т^+£,й+£Лт (2-S2>
Так как
.. р л &ЕХ [ ,п
divE=0=-57 + -^-4-1?, (2.53)
то
rz ..дЕ^ Г _ дЕу , С д<? , п д? _д(?Ех) ( д (•?£„)
Ч дх У ду *дх +Еу ду дх ' ду
(2.54)
71
Таким образом,
J (n (Еgrad?) —grad {?(En)})dS«=
$>
Г/ - d(fEz) •* dfrEJ -* (д^Ел)
*.1 \ГХ° ~di------Уо~ду~~ +Z° НГ-+ ~~d)H) dS'
* (2.55)
где x0, y0, z0 — орты, параллельные соответствующим
координатным осям.
Рассмотрим теперь интеграл, стоящий в правой
части (2.49). Направление интегрирования по контуру
ABCD на рис. 2.4 показано стрелками.
У к <
д
Рис. 2.4. Поверхность раскрыва S2 в виде
прямоугольника.
Учитывая свойства векторного произведения и под*
ставив его в виде суммы трех векторов, параллельных
осям координат X, У, Z, получаем
$ ? [Еd7] =[? [Ed7] 4- [ ? [Ed~l] -j- [? [Edl]4-
Г AB BC CD
4- j ? [E </ 7] = J? (y0Egdx — zaEydx) 4-
DA AB
+ f ? (— x0Ezdy 4- z0Ex dy) 4- j ? (-+ ^Eydx) +
Bt CD
4- dy — ZqE^ dy). (2.56)
DA
72
Уменьшим стороны прямоугольника ABCD до беско-
нечно малой величины. Тогда сторона CD приблизится
к стороне АВ и функции <р£г и <(Еу на стороне CD бу-
дут отличаться на бесконечно малую величину от этих
функций на стороне АВ, т. е.
WJcd = (^)ав + <*У>
„Л, (2.57)
WylcD = + —df- dy-
Аналогично имеем:
д (vEA
№z)BC=W,)DA + -^-dX,
д (vE ) (2.58)
(<?Ex)BC = (<?Ex)DA + -^LdX.
Одновременно при уменьшении сторон прямоугольника
до бесконечно малой величины интеграл (2.56) будет
равен подинтегральному выражению. Подставив туда
(2.57) и (2.58) и выполнив требуемые сокращения, полу-
чаем при ABCD-+0 следующее уравнение:

+ z0
р(?Ех)
L дх
Wy) 1Ъ rl
—j/ dxdy-
(2.59)
Легко видеть, что правая часть (2.59) совпадает
с подинтегральным выражением правой части (2.49), При-
менив обычный прием деления любой формы поверхности
на бесконечно малые прямоугольные площадки, можно
привести (2.59) к виду
г
(/ v и
Д 0 дх У° ду
St
ду )Г^’
(2.60)
что является доказательством (2.49).
Аналогичные преобразования могут быть проведены и
ео второй формулой системы (2.19).
78
Таким образом, выражения (2.19) приводятся к виду
К = ~ 4^Г0 $ g^d <р (Hdl) - 1 $ <? lEdl] +
г г
+ k\CB^-tK}dS.
Si
Н.=^$&^(ЕМ)-Ц\нй\ +
Если поверхность интегрирования S2 является замкну-
той, то контурные интегралы равны нулю и вместо (2.61)
получим
Si
(н^-^dS.
м .) \ дп т дп
st
(2.62)
Таким образом, формулы (2.62) являются точными лишь
в случае замкнутой поверхности S%. В случае же поверхно-
сти незамкнутой, они справедливы с точностью до слагае-
мых, содержащих контурные интегралы.
Перейдя от векторных выражений к прямоугольным
р-1'kr
составляющим и подстазив вместо <р его значение —-—
согласно примечанию к (2.14), получаем:
(2.63)
гм 4к J [ г дп \ г / г дп J
S,
74
Уравнения (2.63) имеют вид приведенного выше урав-
нения (2.44). Они получаются из (2.44) при поочередной
подстановке в него вместо функции ф прямоугольных со-
ставляющих электрического и магнитного векторов.
В (2.44) функция Ф — скалярная; в (2.63) прямоугольные
составляющие поля являются также скалярными.
Уравнения (2.63) обладают той особенностью, что от-
дельные составляющие поля в удаленной точке М опреде-
ляются через те же составляющие поля на поверхности 32.
При приближенном решении задачи, когда нам точно неиз-
вестно значение поля на S2, отмеченная особенность (2.63)
может привести к противоречию с основными положениями
электродинамики.
Покажем это на примере. Предположим, что S2 пред-
ставляет собой плоскость, а электромагнитное поле создает-
ся в результате падения на нее плоской линейно-поляризо-
ванной волны, имеющей направление векторов поля, пока-
занное на рис. 2.5. В случае, когда истинное поле на S2
неизвестно, предполагается, что поле соответствует невоз-
мущенной волне, т. е. в данном случае, что вектор Е па-
раллелен оси У, а вектор Н — оси X.
Итак, мы принимаем, что поле на 32 определяется сле-
дующими соотношениями:
Е = Еу, Н = — Нх,
E=E=Q, Ну = Н=0,
дЕ, дЕ. дН v дН,
—- =—- = 0 ——=—— = 0
дп дп ' дп дп '
75
Приняв эти исходные данные и определяя внешнее
поле по (2.63), придем к выводу, что во всем внешнем
пространстве единственными составляющими поля, не
разными нулю, являются Е и Нхм. Остальные состав-
ляющие получатся равными нулю. Но это противоречит
известным фактам. В действительности, например, в точ-
ке Л), лежащей в плоскости YZ на прямой ОМ, образую-
щей угол &>0 с осью Z, вектор электрического поля
будет направлен под углом & к оси У, т. е. будет иметь
составляющие, не равные нулю как по оси Y, так и по
оси Z.
Отмеченная особенность полученных формул объясняет-
ся следующим. Направление векторов Е и Н электромаг-
нитной волны в свободном пространстве перпендикулярно
к направлению распространения, как следствие уравнений
Максвелла. Можно показать, что уравнения (2.61) удовлет-
воряют системе уравнений Максвелла. Уравнения же (2.62)
и (2.63) в случае незамкнутой поверхности уравнениям
Максвелла не удовлетворяют.
Кстати, при и —♦ 0, как легко видеть, электрический век-
тор поля в точке М и в самом деле будет иметь направле-
ние, почти параллельное оси У, поскольку вектор г в этом
случае почти совпадает с осью Z.
Таким образом, в связи с приближенным определением
исходных данных расчет по формуле (2.63) оказывается не-
достаточным для правильного определения внешнего элек-
тромагнитного поля.
Сказанное является следствием того, что интегрирование
распространяется не на замкнутую поверхность и что при
этом не учитываются контурные интегралы уравне-
ний (2.61).
Рассмотрим применительно к только что разобранному
примеру значение контурных интегралов. Первый контур-
ный интеграл имеет в подинтегральном выражении множи-
тель grad <р, указывающий на то, что это слагаемое имеет
-►
направление, параллельное радиус-вектору г, соединяюще-
му точки поверхности S2 с точкой М. Второй контурный
интеграл дает слагаемое, перпендикулярное к первичному
полю и к контуру Г (в данном случае к сторонам прямо-
угольника, ограничивающего площадку S2). Если векторы
поля касательны к поверхности S2, как в нашем примере,
то второй контурный интеграл будет иметь осевое направ-
76
ление, т. е. направление, параллельное оси Z и перпенди-
кулярное к поверхности S2 (см. рис. 2.5).
Следовательно, контурные интегралы дают слагаемые
поля излучения такого направления, какого не хватает в ре-
шении, получаемом по формуле (2.63). Эти слагаемые при
соответствующей величине приводят к правильному направ-
лению суммарного вектора поля, которое перпендикулярно
к направлению распространения.
Заметим, что в точках, лежащих в области, близкой
к оси Z, контурные интегралы в рассматриваемом примере,
вследствие противоположного направления на противопо-
ложных сторонах контура дадут значение, близкое к нулю,
и результат, получаемый по формуле (2.61), мало будет
отличаться от такового, получаемого по (2.63).
Весьма большое число СВЧ антенн характеризуется
чрезвычайно острой направленностью с максимумом излу-
чения вдоль оси Z или под небольшим углом & к ней. Этот
случай соответствует плоской поверхности S2 и падению на
нее плоской волны перпендикулярно или под небольшим
углом к ее нормали. Практический интерес в таких случаях
обычно представляет знание поля в области небольшого
телесного угла вблизи максимума излучения, т. е. вблизи
оси Z. В таких случаях расчет может быть выполнен со-
гласно сказанному с достаточной точностью по системе
уравнений (2.63).
Покажем теперь, что формулы (2.43) приводят к пра-
вильному направлению векторов поля излучения. Посколь-
ку формулы (2.43) тождественны формулам (2.61), то этим
будет доказано, что контурные интегралы в (2.61) дают
как раз такие слагаемые поля (как по направлению, так и
по величине), которых не хватает в формулах (2.63).
Обратимся к рассмотренному выше примеру падения
плоской волны на плоское отверстие (рис. 2.5). Определим
с помощью формулы (2.43) поле в точке Л4, лежащей в пло-
скости YZ. На рис. 2.6 показано направление отдельных
векторных произведений, входящих в подинтегральные вы-
ражения формул (2.43). Учитывая данные рис. 2.6,а и б,
получаем:
Ем = — J ТГ % | Hscos&—— dS — j | Es -j—dS,
-* шел ** C p—ikr t, + p p—ibr
x0\Et-^-dS + J±x0J H,cos&-^— dS.
Si Sa
(2.64)
77

Для точек плоскости YZ х0 = — <р0. В сферической си-
стеме координат г0, Оо и <?0 показаны на рис. 2.6,в.
Выражения (2.Ь4) соответствуют точкам, лежащим
в плоскости YZ. Как и следозало ожидать, электриче-
ский вектор имеет напразление, параллельное координат-
ной оси 0, а магнитный вектор — направление, парал-
лельное оси X.
Можно аналогично показать, что в точках, лежащих
в плоскости XZ
-* k -» С р—1'hr -» f p—lkr
= -/ 4-^0 j Es с os 0 dS - j ^у0 j Hs dS,
Sa S2
Я 0 fp cosO-^dS-yAe [H,^-dS.
л J 4п о J s r J 4л о j s r
S, S,
(2.65)
Для точек плоскости XZ у0 = <?0.
В общем случае произвольной точки
-* k С -* + p—!kr
EM=~J— j£s(&psin? + ?oC°s&cos<p)—7— dS —
s,
cojin Г -> + £~ikr
— j"4л Jcousin? + ?0cos<p)——dS,
St
= — I 5s(?0sin? + ®0 cos & cos cp)y— dS —
Si
Jfe C "* a~l^r
яД°0СО8? + ?0 cos&sin<p) -y-dS.
Sa
(2.66)
Сопоставляя векторные формулы (2.64), (2.65) и (2.66)
со скалярной формулой Кирхгофа (2.44) мы видим, что
перзые не являются более сложными и отражают более
правильно картину электромагнитного поля на больших
расстояниях от антенны (в зоне излучения). Поэтому
в дальнейшем изложении будем основываться на вектор-
ных формулах (2.64), (2.65) и (2.66). Если принять, что
Es и Hs связаны между собой соотношением
(2.66а)
79
где р — постоянный множитель, не зависящий от
динат, то получим для точек плоскости KZ:
Ч (> + Tc°se)£- ^dS-
5*2
Н. = -/ГЛ» f <? + c°s'*)н.-^dS'
S,
для точек плоскости XZ:
-> k * Г / 1 Л е~^г
= (т+«»»)
S3
"«=-/sM(I+₽cos8X-£?‘'s’
- S.
а в общем случае
-* k с г / 1 V
Em = ~J^)Es[ ( Sin ? + Г COS & Sin <р 1 »0 +
Sa
/ J X-> 1 e— jkr
4~ (^cos & cos 
-* e—ikr
+ Oo (1 P c°s 0) cos <p ] —-— dS.
коор-
(2.67)
(2.68)
(2.69)
Формулы (2.64) -=- (2.69) получены в предположении,
что вектор Е в отверстии параллелен оси У, а вектор Н
параллелен оси X. Однако эти формулы могут быть легко
обобщены на случай произвольного направления векто-
ров Е н Н относительно плоскости отверстия.
§ 8. МЕТОД СТАЦИОНАРНОЙ ФАЗЫ
Мы видели, что на больших расстояних от антенны
электромагнитное поле излучения вычисляется с помощью
интеграла вида:
\F(q)^-dq, (2.70)
где через q условно обозначены координаты точек ин-
тегрирования, а через dq — элемент интегрирования:
объемный, поверхностный или линейный.
80
В связи с тем, что на сверх ;ысоких частотах токи
сосредоточены в чрезвычайно тонком поверхностном слое,
задача определения поля решается всегда с помощью по-
верхностного интеграла, который, как правило, приво-
дится к линейному интегралу от одной из координат
какой-либо ортогональной координатной системы. Обо-
значим эту координату через $. Расстояние г является
функцией Обычно линейные размеры антенны ничтожно
малы по сравнению с расстоянием г. Поэтому г мало
меняется с изменением 5. Мы обозначим kr через
kr^^=PU
\'о /
(2.71)
где
п— — е
р — Х/2тс ’ 1 ““ ’
(2.72)
г0— расстояние от некоторой точки антенны, принимае-
мой за начальную (точка £ = 0, т] = 0) до точки наблю-
дения.
На сверхвысоких частотах линейные размеры антенны
во много раз превышают длину волны. И если расстоя-
ние г значительно превосходит линейные размеры ан-
тенны, то еще во много раз больше г превосходит длину
волны Z, а тем более величину . Из сказанного ясно,
во-первых, что р — весьма велико, во-вторых, что U (•»]) —
безразмерная величина порядка единицы, которая явля-
ется функцией безразмерной величины iq.
Функция F (q) в (2.70), принимающая в рассматривае-
мом случае вид F (;), обычно слабо меняется в пределах
интегрирования. Объединим эту функцию с величиной у
и выразим объединенную функцию, как функцию
^ = Vh) = Af(^ (2.73)
где А — Уо(^) — значение функции V(r|) в начальной точке
антенны, f(iq) — также безразмерная функция порядка
единицы.
Таким образом, интеграл (2.70) после исключения по-
стоянных множителей может быть приведен к виду

(2.74)
6—1503
81
В интегральном выражении f (nq) — медленно меняю-
щаяся функция, a e~ipV(Tt)—быстро осциллирующая функ-
ция, поскольку она имеет повторяющиеся значения при
каждом изменении абсолютной величины показателя сте-
пени на 2тс, а р, как показано выше, — очень большая ве-
личина.
Вычисление интеграла. (2.74) упрощается, если функ-
ция U (т]) имеет точку экстремума в пределах интегри-
рования, так как в этом случае можно прибегнуть к при-
ближенному расчету по методу стационарной фазы, сущ-
ность которого выяснится ниже.
Предположим, что точкой экстремума является т]0.
В этой точке производная
^'Ы = 0. (2.75)
Следуя [11], введем новую переменную
Р = р (2.76)
<W=o.
Согласно (2.76)
2tdt==pdU =pU'd-f\, (2.77)
pU(^ = t2 + pU^ (2.78)
Подставив (2.77) и (2.78) в (2.74), получаем
р (71) • (2-79)
Разложим знаменатель подинтегрального выраже-
ния (2.79) в ряд по t около точки 7| = т]0 (/ = 0), учтя при
этом (2.75)
U'W \ t\d £/'h) ,
Ш Г01) \dt f(v)
d2 U'^j) _ I d U'W di] |
dt* Ш ---------------------Ь Ш dt |^o
(2.80)
Производную можно найти из (2.77)
2^-
d-ц I _.. I 2t _.. dq 2
~PU"M
dt
(2.81)
82
Из (2.81) следует
<2-82)
Подставив (2.80) и (2.82) в (2.79), получаем после
сокращения числителя и знаменателя на t
(т|) е~,г>и^(1ц =
Г c-^dt „ R„.
V —2— J + f У 2^0ь) [?' '(По) f (Чо) J + • ••
1
Знаменатель (2.83) представляет собой ряд по возра-
стающим степеням t, причем множителем у t, наряду с
другими, является -£=. Пренебрегая величиной —L= по
гр г Р
срав^ени1р с единицей, можно положить с точностью от-
брасываемых слагаемых
f f h) е-lpU (’1) dri = У f (Чо) е"ipU (J е~ “г dt. (2.84)
Множитель f (т]0) е есть прдинтегральное выраже-
ние (2.74) в точке экстремума, а
$е- «• Л = y/i [с (/I,) —jS (/Iх) ] . (2.85)
о
где С и S -г- так называемые функции Френеля.
Следовательно, сущность метода стационарной фазы
заключается в том, что при большом значении р интеграл
вида (2.74) определяется в основном значением подинтег-
ральной функции в точке ее экстремума.
В точке экстремума фаза под интегрального выражения
стационарна. Затем она быстро меняется. При изменении
фазы на гс подинтегральное выражение приобретает проти-
воположный знак. Частое периодическое чередование знака
подинтегрального выражения при медленно меняющейся
абсолютной его величине приводит к взаимному уничтоже-
нию областей интегрирования, удаленных от точки экстре-
мума, благодаря чему особое значение приобретает область
вблизи экстремума.
6
ГЛАВА ТРЕТЬЯ
ДИФФРАКЦИЯ ОТ ОТВЕРСТИЯ В ПЛОСКОМ ЭКРАНЕ
§ 1. ВВЕДЕНИЕ
В предыдущей главе было показано, что точное решение
задач теории СВЧ антенн строгими методами получить
очень трудно. В связи с этим широкое применение находят
приближенные методы, по которым многие задачи приво-
дятся к задаче диффракции от отверстия в плоском экране,
решаемой с помощью формул (2.67) -ь (2.69).
Разнообразные встречающиеся случаи разделим на
группы по характеру изменения фаз в отверстии и рассмот-
рим их в такой последовательности: сначала исследуем не-
которые примеры синфазного поля при различных законах
изменения амплитуд, затем перейдем к полям - с линейно
меняющимися фазами от одного края отверстия к другому,
после чего рассмотрим случаи изменения фаз по квадратич-
ному закону от центра отверстия к краям. Приведем также
краткие сведения о случае кубического закона изменения
фаз. Внутри каждой группы отдельно остановимся на слу-
чаях прямоугольного и круглого отверстий.
Нас будет интересовать напряженность поля излучения,
диаграмма направленности, ширина главного лепестка диа-
граммы направленности, относительная величина побочных
лепестков, коэффициент направленного действия и коэффи-
циент использования площади раскрыва антенны (опреде-
ление дано ниже — § 2, формула (3.26,а).
§ 2. СИНФАЗНОЕ ПОЛЕ В ПРЯМОУГОЛЬНОМ ОТВЕРСТИИ
На рис. 3.1 показано прямоугольное отверстие в плоском
экране и принятая система координат.
Электромагнитное поле будем считать линейно поляри-
зованным с электрическим вектором, параллельным оси У,
84
и магнитным, параллельным оси X. Это соответствует паде-
>нию на экран плоской волны типа ТЕМ с направления, пер-
пендикулярного плоскости экрана. При волне ТЕМ коэффиг
циент, р в (2.66,а) равен единице. При этом общие выра-
жения для Ем одинаковы, как видно из (2.67) и (2.68), для
плоскостей XZ и YZ.
Рис. 3.1. К расчету поля в удаленной точке при
наличии синфазного поля в прямоугольном отвер-
стии, вырезанном в плоском экране.
При расчете поля излучения, т. е. поля на больших
расстояниях от антенны, достаточно определить только
электрический вектор Е, так как магнитный вектор Н
связан с Е согласно (2.3) простым соотношением:
Н 120л Г°Е ’
(3.1)
где г0— единичный вектор, имеющий направление ра-
диус— вектора, проведенного из центра площадки в дан-
ную точку зоны излучения.
Пользуясь формулами (2.67) и (2.68), мы будем под-
ставлять в них
Es = Eys. (3.2)
Здесь индекс s означает принадлежность соответствую-
щей величины к точкам отверстия.
85
Обозначим прямоугольные Координаты точки М, в ко-
торой мы определяем поле излучения через х, у, г, а
координаты точек площадки отверстия через xs, ysi 0.
Расстояние rtM между произвольндй точкой на отверстии
и точкой М получится тогда равным
rsu = У (х - xs)2 + (у — js)2 + г’. (3.3)
Обозначим угол между прямой ОМ и осью Z через в,
а угол между отрезком ОМ, являющимся проекцией ОМ
на отверстие, и осью X через <р.
Легко видеть из рисунка 3.1, что
z = г cos &
j/ = rsindsin^
х = rsin&cos
(3.4)
где r, f>, <₽ — являются сферическими координатами точ-
ки М, причем г представляет собой длину прямой ОМ и
равно ____________
г — Р2 + г2-
Из (3.3) и (3.4) и из условия, что точка М находится на
расстоянии, значительно превышающем линейные разме-
XS . У* .
ры площадки, д. е. в предположении — 1 и < 1,
можно получить
rSM — + z2 - 2xxs ~ 2yys -j- x2 +Л2 =
= у r2 — 2xs r sin & cos <f — 2ys r sin & sin г e~lkr
E"=J^—X
X (1 + COS 3) J eM *{n e eoe ’ + *9ln *ein * dxs dys. (3.6)
Для расчета E по формуле (3.6) нужно знать зависи-
1) В формуле (З.б) и в дальнейшем индекс м у поля излучения
опускается.
86
мость Es от координат xs и ys. Как увидим ниже, при
прямоугольном отверстии интерес представляют случаи,
когда Es зависит только от xs и определяется одним из
следующих выражений:
а) — const = Е0, (3.7)
б) = Ео cos -д- , (3.8)
в) Е — F Р V р2 + (3.9)
г) р —р — (3.10)
В формулах (3.9) и (3.10)р является постоянным ли-
нейным параметром.
Начнем расчет с определения диаграмм направленно-
сти, т. е. с нахождения зависимости' поля излучения от
углов & и ср. Обычно эта зависимость определяется не
в самом общем виде, а для точек, лежащих в характер-
ных плоскостях. Вычислим диаграммы направленности в
двух взаимно перпендикулярных плоскостях XZ и YZ,
являющихся в нашем случае наиболее характерными.
Так как плоскость XZ параллельна магнитному век-
тору, а плоскость YZ— электрическому вектору, то
плоскость XZ принято называть //-плоскостью, а пло-
скость YZ — f-плоскостью. Соответственно этому будем
обозначать поле в перзой плоскости через Ен, а поле во
второй плоскости — через Е£. Аналогично обозначим диа-
граммы направленности через FH и FE.
Все точки плоскости XZ имеют сферическую коорди-
нату ср = 0 (sin<р = 0 и cos<₽=l), а точки плоскости YZ
имеют координату <p = -^-(sin<p= 1 и cos<p = 0). Подставляя
эти данные в (3.6), получим:
EH=J^(4-^s^^Eselkx^l^dxsdys, (3.11)
s2
+ ™s^Eselk*°sla*dxsdys. (3.12)
87
Для упрощения записи обозначим в дальнейших вы-
кладках
Р— /*г ft
X=/^-£0coS2|, (3.13)
где Ео — постоянный множитель, входящий в Es ,[см.
(3.7) —(3.10)].
Вычислим по отдельности значения Ен и Ее, соответ-
ствующие различным зависимостям Es от xs.
a) Es = const = Ео.
Амплитуды поля одинаковы во всех точках отвер-
стия. В антенной технике такой случай не встречается.
Он рассматривается как идеальный, и с ним сравнива-
ются встречающиеся на практике случаи для оценки их
качества. При этом
Da D\
2 2
ЕИ^А J dys J e'^8,n’dxs = ASn^l, (3.14)
_ О, _Di
2 2
О, О,
2 2
Ее = А $ dxs J e/VsS,n9d>s = ASn^, (3.15)
________Di ___Dz
2 2
где Sn = D]£>2 обозначает площадь прямоугольного отвер-
стия, а
$1 = ^sin&, (3.16)
52 = ^2sin&. (3.17)
Согласно (3.13)-=-(3.17) диаграммы направленности
имеют вид:
/feDi \
. Sin ( -р- sin в
?Н= cos2 ~2 kD{ ’ (3.18)
•у sin О
(3.19)
88
На рис. 3.2 показана нормированная диаграмма на*
правленности вида Е(а)=-^—, соответствующая в
данном случае FH или FB, если положить в одном слу-
чае a = (j., в другом — а = и исключить слабо меняю-
„ 9 в1)
щиися множитель cos2 -к .
Рис. 3.2. Диаграммы направленности для двух вйдов распределения
амплитуд синфазного поля в прямоугольном отверстии:
Fj — при одинаковых амплитудах (3.7); Г2 — при косинусоидальном
законе (3.8) распределения амплитуд.
Из рисунка видно, что уровень 0,707 имеет место
при угле &=90, который может быть определен для
Я-плоскости (90я) и Е-плоскости (9ог) 1из выражений
В10 = ф sin 9ОЯ= 1,39
и аналогично
^=^sin«OT=l,39.
Отсюда ширина главного лепестка диаграммы направ-
ленности равна
29ОЙ ~ 2 sin 90Н = 0,89^- (3.20)
0 Этот множитель будет исключаться и в дальнейшем при
анализе аналогичных формул.
89
и аналогично
26О£.-2 sin Oog = 0,89^.
(3.21)
Коэффициент направленного действия определяем по
формуле
ГЗ Е2 4яг2Е2
z> ' ^макс ^макс
Sa
(3.22)
где £макс—значение Е в направлении главного максимума
излучения; Р—мощность электромагнитного потока, про-
ходящего через отверстие, равная
Т20тс dxs йУв- (3.23)
За
В случае одинаковых амплитуд поля во всем отвер-
стии, т. е. при Es = Eq,
р2
Р=^ (3-24)
а
Е2 S2
r2<aKC = ^S>-^. (3.25)
Подставив (3.24) и (3.25) в (3.22), получаем
G
X2
(3.26)
Как увидим ниже, у всех антенн коэффициент направ-
ленного действия может быть выражен формулой, анало-
гичной (3.26), а именно
где S — площадь раскрыва антенны (площадь отверстия
в экране).
Величину
v = (3.26а)
"Зу-
мы будем называть коэффициентом использования пло-
щади раскрыва антенны.
90
В случае Ее = const v = 1
б) Es = Ео cos -р— ,
Косинусоидальный закон распределения амплитуд (по
осй X). Такой закон встречается в раскрыве волновода
прямоугольного сечения при возбуждении волны ТЕ01.
При этом
D. Й1
2 2
£„ = Л J f
2 2
о,
2
f 2
= 2 AD* I cos cos (kx, sin в) dx — — XS
J ^2 ' S * 7t n
0
(3.27)
Ds
2 2
£Г=Л j cos-^-dx, j =
__D\____________________________ Dt
2 2
Таким образом,
/Wi \
cosi-g-sina)
= cos2 -g 2 kD^ Г2, (3.29)
1 — (----s~ sin Э )
\ К £. 1
IkD. \
sin I -д' sin Э )
------ <3-30>
-HsinO
На рис. 3.2 показана диаграмма направленности вида
(3.31)
соответствующая Ён (3.29) при а=$,.
91
Из рисунка видно, что уровень 0,707 имеет место при
sin 0ОЯ= 1,86.
Отсюда следует, что ширина главного лепестка диа-
граммы направленности в Я-плрскости равна
2»O»=1.IS£- (3.32)
Форма диаграммы направленности и ширина главного
лепестка в ^-плоскости остается такой же, как и в пре-
дыдущем случае.
Коэффициент направленного действия определяем по
формуле (3.22). В данном случае
2
J cos2-^-dxs = . (3.33)
_Dj
2
Согласно (3.28) и (3.13)
= (3-34)
Откуда получаем коэффициент направленного действия
= (3.35)
Коэффициент использования
v = 0,81. (3.35а)
Такая зависимость напряженности поля от коорди-
наты xs получается при приближенном решений задачи
об облучении параболического цилиндра прямолинейным
нитевидным током, расположенным вдоль фокальной ли-
нии. Параметр р представляет собой в данном случае па-
раметр параболы, равный ее двойному фокусному рас-
стоянию.
92
Подставив выраженйе для Es в (З.И), получаем
Ен =ApD2
eikxs sin » dxs
о,
2
= 2ApD2
1‘ cos (ftxs.sin 9)
------------- — - dx .
I P3 + *s2
0
(3.36)
Интеграл в (3.36) разлагается в ряд по бесселевым
функциям. Для этого преобразуем множитель — -—
V Р2+ *з
следующим образом
(Р2+ х2 )~Т = [р® + (^)8]"Т (1 - fi)- Т =
= [р8+ (т)ТТ(1 + 4 ?+{ ?2 + г6^ + • • Л (3-37>
где
(3.38)
Подставив (3.37) в (3.36), получаем
Pi
2
О
+ |р2 + ^34-..Л cos(kxssmb)dxs. (3.39)
98
Таким образом, выражение содержит сумму интегра*
лов вида:
Si
2
§ Р" cos (kxssin b)dxs —
о
ii = k^sinb, (3.16)
J . (?,) — бесселева функция от пЦ-4‘г0 порядка,
л+Т 2
г(п+4) j
Л G1)= ----------;--J , (£,)— лямбда-функция
"+т (51)"+т Я+-*
порядка, Г (а) — гамма-функция от а.
В приложении 1 приведены таблицы функций Л .
для некоторых значений п.
Учитывая (3.40), приводим выражение для Ен к виду
00
(3.42)
94
Подставив значение Es из (3.9) в (3.12), получаем вы-
ражение для Ее
= 2Ар In
(3.43)
Согласно (3.42) диаграмма направленности в //-пло-
скости имеет вид:
FH — cos2 2 |л j ($])-!-J-Л з ($1)4_..._|_ JL—д Л .
1 ~2 Т 2n+1 J
(3.44)
В /^-плоскости диаграмма направленности выражается
формулой (3.19) и, следовательно, будет иметь вид кри-
вой F] на рис. 3.2.
Рис. 3.3. Диаграммы направленности прямоугольного отверстия при
изменении амплитуд поля в нем по закону (3.9) для различных
Графики нормированных диаграмм направленности FH
для двух значений отношения^, равных 1 и 5, изобра-
жены на рис. 3.3.
95
В таблице 3.1 приведены значения 5]0 и ширины глав-
ного лепестка 29ОЯ, соответствующие указанным выше
значениям . Ширина главного лепестка растет (хотя и
мало) с увеличением Величина 29ОЯ пропорциональ-
на Коэффициент пропорциональности здесь и в даль-
нейшем обозначен через хя.
Таблица 3.1
D, 2р 20оя = хя 57
1 1,40 0,925^- 0,98
5 1,60 1,02^ 1
Для определения коэффициента направленного дейст-
вия по формуле (3.22) находим
р2
2
₽ = ® рЛ . .
£>2 Р\
2 2
р,
2
Г (З-45)
r2 F2 ________
* '“'макс V'

2
. (3.46)
Откуда

2 D-
In
c, — 4nv 2Р
Р
£>1
arctg^>
(3.47)
и
1 {ln[&+ri +
ь
arctg b
(3.48)
к Dl
где b= -1.
На рис. 3.4 приведен график зависимости коэффи-
Z)l rr
циента использования v от Из рисунка видно, что
v —> 1 при —>0. Это следовало ожидать, так как при
У1—>0 данный случай переходит в случай Es = const.
С увеличением увеличивается неравномерность поля в
отверстии и v уменьшается.
Побочные лепестки диа-
граммы направленности
уменьшаются с увеличе-
нием^-1. Это связано с тем,
2D
D, к
что с увеличением бы-
стрее убывают амплитуды
поля с удалением от сере-
дины к краям отверстия.
р (pt —
r) <з-49)
Данная зависимость со-
ответствует приближенному
значению поля в раскрыве
параболического цилиндра,
облучаемого прямолиней-
ным нитевидным током, рас-
положенным вдоль фокальной линии, при наличии за
нитью, с противоположной от зеркала стороны, плоского
контррефлектора.
Ру
2
V
V>.
Ofi
Об
HI
02
О 2 Ч б в to Dt
Рис. 3.4. График зависимости ко-
эффициента использования ч от
для прямоугольного отвер-
стия при изменении амплитуд
поля в нем по закону (3.9).
Рг— ikxs sin»
------„ е dx —
(р’4-^)л
2
D.
2 .2
Г Р2 —
= 2ApD2\ cos(^xssind)—-—-^-^dx^ (3.50)
о Р s

Интеграл (3.50) также разлагается в ряд по бесселе-
вым функциям. Это следует из возможности представ-
7—1503 97
ления знаменателя подинтегрального выражения в сле-
дующем виде:
(р2+^Г’/2=(р2 + ^ (1-РГ’/2 =
д2 1~ ’/а
=- [р2 +^г] (! + 4 ? + т • • •) (3-51)
и из формулы (3.40). Обозначения здесь прежние.
Таким путем приводим выражение для Ен к виду
Л 1
п+г
Аналогично для Ее получаем
(3.52)
sin Е2
?2
(3.53)
Из (3.52) и (3.53) следует, что в f-плоскости диа-
грамма направленности выражается формулой (3.19) и
кривой А] на рис. 3.2, а в /У-плоскости формулой
(3.54)
98
На рис. 3.5 изображены диаграммы направленности в Н-
о D*
плоскости для некоторых значении .
В табл. 3.2 приведены значения 510 и величина 20оя ,
соответствующие нескольким значениям В данном
случае ширина главного лепестка также увеличивается
Рис. 3.5. Диаграммы направленности прямоугольного отверстия при
изменении амплитуд поля по закону (3.10) для различных
D1
2р •
значений
Для расчета коэффициента направленного действия
по (3.22) определяем
7*
Р

D,
120,1 Р 2 J (?2 + ^)3
(3.55)
99
и
(3.56)
Таблица 3.2
D1 2р 29он *
0.4 1.55 0,98^- 0.95
0,6 1,70 1,08 » 0,85
0,8 1,86 1.18 , 0,69
1.0 2,01 1.27 . 0,54
Рис. 3.6. График зависимости коэффициента использования э от
для прямоугольного отверстия при изменении амплитуд
поля в нем по закону (3.10).
100
откуда следует
(3.57)
На рис. 3.6 показана зависимость коэффициента ис-
пользования v от В данном случае имеют место те
же закономерности, которые характеризуют предыдущий
случай и которые отмечены выше.
§ 3. СИНФАЗНОЕ ПОЛЕ В КРУГЛОМ ОТВЕРСТИИ
На рис. 3.7 показано круглое отверстие и принятая
система координат. В случае круглого отверстия часто
л м(х,у,г)
X
Рис. 3.7. К расчету поля в удаленной точке
при наличии синфазного поля в круглом от-
верстии, вырезанном в плоском экране.
более удобным является проводить интегрирование по
полярным координатам и ср,.
Диаграммы направленности попрежнему будем опре-
делять в двух взаимно перпендикулярных плоскостях,
101
которые будем именовать, как прежде, /7-плоскостью и
Е-плоскостью. Напряженность поля в этих плоскостях
можно находить по формулам (3.11) и (3.12).
После перевода в полярные координаты получим
_ . е—^kr ,, , лчСГг. ikfs COS <Р, Sin ft
Ен =J (1 + cos &) j J Ese р/рД ’
St
(3.58)
f D MPs sln 4>S sln 9 . .
J £se
St
ЕЕ—J
e~Ikr
\r
В общем
вектор поля
щие Ех и Еу (или Ef и Е^).
Рассмотрим следующие зависимости
и V
случае будем считать, что
имеет в плоскости отверстия
(3.59)
электрический
обе составляю-
E, и E
от Ps
6)
Exs = ^
Eys — wasX==E0.
(3.60)
EXS=EO
a-------
Ps
s’
(3.61)
a——
Ps
J
£,s = £0
где Ji — бесселева функция первого порядка,
— производная бесселевой функции по аргументу
а
а
3 — первый корень уравнения ^-ps^=0 при
Ps=a, который получается 8 = 1,841,
а — радиус отверстия.
в)
„ m /’*₽ssin2lPs
XS= ° (P’ + Ps)1 ’
__ P8(P2 + Pscos2;Ps)
° (p2 + p?)2
(3.62)
102
г)
„ _р Р8р1 (Р3 — рЬ sln 2УД
0 (/ + р!)3 ’
Р — F & cos 2?J ~
ys~ ° (р2 + ?2)3
(3.63)
В последних формулах р есть постоянный линейный
Параметр, имеющий тот же смысл, что и в формулах
(3.9) и (3.10) (см. выше).
Легко видеть, что во всех намеченных к рассмотрению
случаях, исключая (3.60), Exs определяется нечетной функци-
ей от <ps, в то время как Eys — четной. В соответствии с этим
расположим Е-плоскость параллельно оси Y (<ps = 90°), а Н-
плоскость — параллельно оси X(?s = 0). В этих двух пло-
скостях Ех = 0, и электрический вектор поля в точке М
определяется только через Е .
а) £« = °> = const = Е0.
Как и в случае прямоугольного отверстия, зависи-
мость (3.60) (постоянные амплитуды поля в раскрыве)
не встречается в антенной технике и рассматривается
здесь как идеальный случай. Здесь имеем:
и ZTC ,, . о €*
л л Jkps cos?s Siriv л
Ен — A j ?d?s j е .d<fs =А j 2V0 (k?s sin 8) P/Pj =
0 0 0
= A7ra2?^JL = ASAAi(B>
(3.64)
И
А л /Лрс sin <p, sin $
Ee=AfPsdp,Je d^AS^E), (3.65)
о 0
где
E= ka sin 8,
Sk — площадь отверстия.
Диаграммы направленности в обеих плоскостях оди-
наковы и имёют вид
Гн = (1-}-cos&) А, (Е), (3.66)
Fe = (1 + cos 8) АДЕ), (3.67)
103
где
Л"(Х)=1ЛУ7“(Х)'
\2/
(3.68)
На рис. 3.8 изображена диаграмма направленности
(кривая Fi), соответствующая (3.66) без учета медленно
меняющегося множителя (l + cos&). Уровень 0,707 имеет
место при ?0=1,62.
Ширина главного лепестка
2»о» = 2’ог=
Далее
Р-S
120л ’
р2 с2
„2р2 ____
Г ^макс — X?
Коэффициент направленного действия
G = ~Sk.
х« k
Коэффициент использования
V=1
б) Еxs = Ео [£ Л ] cos Ъ sin <р,
Eys=Е° к 71 (^)sin2 cos2
(3.61)
Поле, определяемое уравнением (3.61), имеет место
в круглом волноводе при возбуждении в нем волны ТЕН.
При приближенных расчетах считают, что такое поле
сохраняется и в раскрыве.
Заменив в последнем выражении sin2 <рЛ и cos2^ через
cos2tp4, получим
г Ео Г (х)
'У^ 2 [ х
4-/(x) + ^(x)-^-)cos2?s], (3.69)
где х= •
104
Рис. 3.8. Диаграмма направленности круглого отверстия для двух видов распределения амплитуд
I синфазного поля в нем:
Fi—в Н-к Е-плоскостях при одинаковых амплитудах во всех точках отверстия (3.60) и в /(-плоскости при измене-
нии амплитуд поля по закону Fj—в Я-плоскости при изменении амплитуд поля по закону (3.61).
Подставив (3.69) в (3.58), получаем
£н=4- f pa/J [Аг^+л' w+
о о
+ (/ (,)_4й.)С0ЙГ.]
=^jl[A^-+/w]jocv)-
-[Х«-^]ЛМ)рА. (3.7Щ
где у = kps sin ft.
Подставив в (3.70)
A^+X(x) = J0W> (3-71)
(x) = J2(x),
получаем
£я = кА j* [Jo (х) Jo (у) -|- J2 (х) J2 (у)] Psrfps- (3.72)
В дальнейших выкладках воспользуемся формулой
Ломмеля [13]
JxJ„(ax)J„(₽x)dx =
= а-Г^р [Л («) 4г Jn (М - А (М 4г 4 (**)] • (3-73>
Применив эту формулу к уравнению (3.70), получим
£я = па^А [4- [ J’o (8) Jo (В) + (§) Л(0 ] -
- 4- [уо (S) 4 (8) + А ® 4 (8)]} . (3.74)
где попрежнему £=£asin&.
106
Подставив в (3.74) выражения
•4(8) = /(8)+ 4 Л (8),
Л(8) = -/(«) + 4-71(8)>
4(0=Х (04-pi
л(?)=-/(^)+471(?)-
и учитывая, что
Х(8) = 0,
после несложных преобразований приходим
щему выражению для Ея:
к
EH = 2ASK
(3.75)
(3.76)
следую-
(3.77)
«v0(8)./; (6)
где SK = тга2— площадь отверстия, соответствующая пло-
щади поперечного сечения волновода.
Перейдем к определению поля в Е-плоскости.
а 2п
о о
+ ( А (х) - ita’jeos 2 т,] е" ’* d<t. =
= чЛ f [7„(х)70(у) —(3.78)
О
Повторив все преобразования, которые проведены
с аналогичным уравнением (3.72), приходим к выраже-
£B=SeAJ0(8)Al(5). (3.79)
Соответственйо (3.77) и (3.79) диаграммы направлен-
ности выражаются следующим образом:
r„=(l + cos9)^, (3.80)
FB=(14-cos&)A1($). (3.81)
107
На рис. 3.8 .изображена диаграмма направленности FH
(кривая F2) для данного случая. Множитель l-|-cds&,
как медленно меняющийся, не учтен.
Уровень 0,707 имеет место при Воя==2.
Следовательно, ширина главного лепестка опреде-
ляется по формуле
29ОЯ=1,27А-,
где D = 2a.
Для FE получается такая же функция, как при по-
стоянных амплитудах (см. рис. 3.8, кривая Г]).
Для определения коэффициента направленного дей-
ствия вычислим1)

А
120л
2п
PsdPs Jsin2?/<p,4-
о
4- j (X W2 Psdps cos2
о
р2
_2_
120к
(3.82) .
Преобразуем (3.82), используя соотношения
4 (у; (х))2=( / (х) у 4- 2 у; (х) =
=[Л(*)]2+4
1) В (3.82) положено Е2 = E2xs-\- E2ys.
108
Эти преобразования позволяют написать
Р— 4.
120
а а
j(Л(*Я2рА + j4 гНЛ(»Я2р/р.=
.0 0
= w {4 КА <8»2 - 4 (8) 4 («Я+414 (S)l’} (3.83)
4Д- М. (*))’ (3.84)
(3.85)
Отсюда следует, что коэффициент направленного дей-
ствия равен
0 = 4xS^__________________[/0(8)]»______________
~2~ lz2(®)]2 — ~2~zi (®) zs (®)“Ь И1 (®)]2
а коэффициент использования
v==____________-_.Izo0)]8____(з.8б)
4- l;2 (S)]2 - 4 Л (°') Z3 (5) + -4 1Z1 (8>12
После подстановки сюда числовых значений, получим
v = 0,835. •
в) р — р ^Sin2?s
° (р2+р2)а
F _р
ys ° (Р2-^)2
Данный случай соответствует параболоиду враще-
ния, облучаемому элементарным электрическим диполем.
Напряженность поля в //-плоскости равна
а 2п
Г f Р2(р2 + ₽«СО8 2^) /йр sin» cos <fs
" = ЛГА] (8-+й- -е d,- =
о о
о . 2 С p2Zo(.y)-p/2W . Q7A
= 2пАр21-----------f------------р do . (3.87)
J (P2 + Ps)2
о
где Jo и J2 —бесселевы функции нулевого и второго по-
рядков.
109
Преобразуем числитель интеграла (3.87)
„ п! _
рЧ (у) - р, Л (у) = -Ц22- Ч Су)+Л О)) +
+W-АО’))=-т^ Ч О') +
+ 21S.. (3.88)
Z
Подставив (3.88) в (3.87), получаем
Ен = 2пАр2
А (У)
Р2 + ?з
PsdPs +
Рг~£ Л (У)
(р2 + Рз)2 ‘ У
РА.
(3.89)
Подставив в первый интеграл
X О) ^=та^[7> 0)1
и решая этот интеграл по частям, придем к следующему
выражению для Ен
Ен = Лр^,^а, 2;'<5> (МО)
Перейдем к определению поля Ее. Аналогично (3.87)
имеем
Р л Г л p2(P2 + P^c°s2b) MPsslnesinTs
= A J ?sd?s j —(~ + ^)2---e d<?s. (3.91)
о о
Вводим новую переменную
К
a==___?s.
Тогда
d<?s = ~da, sin<ps = cosa, cos 2<ps — — cos 2a.
110
Подставляя это в уравнение (3.91), имеем
а
Е£ = А Jpsdps
о
р2(ра—fhos2a)
(р2+^)2
/Лр- sin 9 cosa ,
е * da. (3.92)
Интеграл в (3.92) отличается от интеграла в (3.87)
знаком второго слагаемого числителя. Поэтому, учиты-
вая (3.90), можем написать
д О Л 2 С Р2/0 (Д') + Ps Z2 (Д') ,
EF = 2itAp2 I --------5----о dp =
J (P2 +P2S)2 s s
0
S„ P a2 J (y)
= Ap2-o—-A^ + 'UAp2 , РЛ.-
r рг -f- eft 1 ' ' 1 r I (p3 + fy2 Г Г
о
Рассмотрим интеграл вида
(3.93)
р.(У) ц,.+*)-- (3-94>
Подставив сюда известное равенство
Л О')=уг1 Л+1 О')+4н О')
и беря по частям слагаемое, содержащее производную,
получаем
f J (у} pmd? — -, + 1 fj (у) pw~lrfp I
J v (рг -f- p2)n k Sin 9 J ’+1 ¥’ (р* + р’)л
1 йт
_1_____!_______р_____j _
’ fcsin» (р2-гРТ п+1
_ 1 f j ( \ Г р,п 1 —
k sin & J ’+1 '-У) dp С (P2 + P2)n J
1 ?m
k sin & (p3 4- p2)n ,'pl ~'~
k Sin & J ^»+l ^) (p2 _j_ р2)Я
t 2n rpw+v,+1 W л
k sin 9 J _|_ p2)«+l P‘
(3.95)
ill
Если применить формулу (3.95) к уравнению (3.93),
то в первую очередь нужно подставить v=2; m=3; п=2.
Тогда v-|- l—m = Q и мы получаем
pgAW . _ 1 . pgAW
(P2 + pg)2 Ps Ps *sln* (P2 + P>
, 4 Г pg AW .
fe sin & j ^pi р2)з P®
(3.96)
Выполненное преобразование (3.96) показывает, что
интеграл, стоящий в правой части уравнения (3.93), мо-
жет быть представлен в виде слагаемого, содержащего
бесселеву функцию без интеграла и интеграл того же
вида, но с подинтегральным выражением более высокого
порядка. Повторяя дальше аналогичные операции, можем
разложить интеграл в правой части (3.93) в ряд по бес--
селевым функциям. Заменяя затем бесселевы функции А-
функциями, согласно (3.67), получим
^=^^{^(9+ ^4^ Wsin»»X
п=-3
Диаграммы направленности определяются следующими
выражениями:
F„=cos2-5-A1(S), (3.98а)
Гг=соа4{л1(У + -^^х
X J] г(„1,)„ Л.• О-98»)
л-3
На рис. 3.9 приведена серия диаграмм FE, соответ-
fl
ствующих различным значениям — .
Диаграмма направленности в Я-плоскости имеет та-
кой же вид, как в случае постоянных амплитуд.
По диаграммам рис. 3.9 определены величины $□, соот-
ветствующие уровню 0,707, и значения ширины главного
лепестка 2в0Е. Эти данные приведены в таблице 3.3.
112
Рис. 3.9. Диаграммы направленности в Д-плоскости для круглого
отверстия при изменении поля в нем по закону (3.62) при
а
различных значениях —— .
Таблица 3.3
ala. ^0 V
0,4 1,71 1,08^- 0,98
0,6 1,86 1,18 „ 0,94
0,8 2,01 1,27 „ 0,86
1,0 2,27 1,43 , 0,74
1,2 2,52 1,59 „ 0,64
1,4 2,86 1,81 . 0,54
Коэффициент аналогичен по смыслу коэффициенту 7.н.
Перейдем к определению коэффициента направленного
действия.
Учитывая, что Л (0) = 1, получаем
^2 j
г2/?2 __ 0 к Р (3 99)
Гамаке— (?2_|_а2)2 > '
а 2л
(з,1оо)
о
о
8—1503
113
Согласно (3.62)
3=^.+4.=
Р4'Р^ ,
(Р2 4 Р2)4 Ж
, 2P6PsCos2b „2
(р24Р2)4 °
(3.101)
При интегрировании слагаемое в (3.101), содержащее
cos 2<ps, дает нуль. Следовательно,
рА=
о
__ Ео па2р2 [Зр№ 4 Зр2а* 4 2ав]
12(4 За2(р24а2)3 '
P = 2,^_fp_£«r + _g4_
120, I 0>Ч-й< +Р=)<
получается
Отсюда коэффициент направленного действия
равным
(3.103)
Коэффициент использования равен
(3.104)
а
На рис. 3.10 приведена зависимость > от
—>0 v=l. Это и следовало ожидать, поскольку со-
гласно (3.62) при -у —>0 Exs—>0, a Eys —>Ео = const
P2Ps (Р2 — Р2) sin 2-fs
(Р2 + Р2)3
Рг (Р2 — Р2) (Р2 + Ps cos 2Vs)
(р2+р2)3
г) ЕХ.=ЕО
Такая зависимость амплитуд поля в отверстии от
координат последнего ps, <ps получается в раскрыве па-
114
раболОида вращения при облучении его элементарным
электрическим диполем с плоским контррефлектором.
а
для круглого отверстия при изменении поля в нем по
закону (3.62).
Аналогично (3.87) и (3.93) получим в данном случае
Р 0 , 2 f [P5W)-P&CH](P2-P*) ,
Ен = ^Ар*J ------------------------Psrfps. (ЗЛ05)
о
Ее=2к Ар * ------------------------?sd?s. (3.106)
о
Заменим в (3.105)
р2-р>р2 + р2-2Р2.
разбив числитель на два слагаемых. В слагаемом с мно-
жителем— 2р^ заменим
8*
115
Это позволит, после приведения подобных членов, по-
лучить
£я = 2тгДр2
С 4- Ps J2 (У)
J (/>2 $2
О
, Л (У) з
Р У Ps d?S
(p2 + p2s)3
(3.107)
Первый интеграл в (3.107) тождественен выражению
для Ее предыдущего случая см. (3.93). Второй интеграл
(3.107) имеет вид (3.94) и может быть разложен в ряд
по Л-функциям примененным выше приемом.
Таким образом получаем

Ля(?) +
^2(p2-j-a2) 2(n —l)n [jfi + a?) An (?)} • (3.108)
n=3
Произведя в (3.106) замены, аналогичные предыдущим
можно его представить в виде
ЕЕ = 2пАр2
Т Z>4(y)-P2Z2(y)
J (Р24-Р*)2
о
(3.109)

Первый интеграл (3.109) тождественен выражению
(3.87) для Ен предыдущего случая. Второй интеграл (3.109)
при одном первом слагаемом тождественен второму ин-
тегралу выражения (3.107). Второй интеграл (3.109) при
116
одном втором слагаемом имеет вид (3.94) и отличается
от второго интеграла (3.93) лишь степенью знаменателя.
Учитывая все сказанное, можем писать
Ее — ASK а2 J Л j (?) 2(рз + а?)2 X
OQ
L/ а2 \п-2
\ р*+а? ) Лл (&) +
л=2
+ * Е 2 („-Li,.-,- * л . <о). (3.110)
л=3
Из (3.108) и (3.110) легко составить выражения для
диаграмм направленности FH и FE аналогично предыду-
щим случаям.
На рис. 3.11 и 3.12 изображены диаграммы направ-
ленности, вычисленные для нескольких значений отно-
а т-т
шения — . По этим диаграммам определены значения
%, соответствующие уровню 0,707, и ширина глазного
лепестка. Эти данные приведены в таблице 3.4.
Таблица 3.4
а Р 'СОН 20оя “ хя “g- iOE 20ое“ V
0,4 1,67 X 1,06 1,73 1,10 0,98
0,6 1,73 1,10 . 1,95 1,24 0,84
0,8 1,90 1,21 . 2,27 1,44 0,66
1,0 2,17 1,38 ; 2,63 1,67 0,47
Перейдем к расчету коэффициента
действия. Так как ЛЛ(0)= 1, то
направленного
ч2 ч
г2/72 --- к р2 Р
' Смакс >2 0 (р2 О2)4 '
(3.111)
Р будем вычислять по формуле (3.100). Очевидно, что
Es выражается той же формулой (3.101), что в преды-
Р2— Р?
дущем случае, при умножении ее на множитель —---2.
Рис. 3.11. Диаграммы направленности в //-плоскости для круглого
отверстия при изменении поля в нем по закону (3.63) при
а
отверстия при изменении поля в нем по закону (3.63) при различных
а
значениях —.
Р
Соответственно Р выражается интегралом вида (3.102),
у которого подинтегральное выражение умножается на
У-р^\2
p2-t-py ‘
р= 2тс ([ <Р2&2 . (Р4)2
12°Я •() + (р2 + р?)4
-^2 РА- 0-112)
118
Заменяя, как прежде,
(Р2-р2)МР2+р2)2-4р=р2,
Получаем
а
₽=2'4j
о
(3.113)
РА- (3.114)
P4Ps+p8 Чр^+р*)&рг
(Р2 + Р^4± (Ра + Р?)в
Рис. 3.13, График зависимости коэффициента использования ч от —
для круглого отверстия прн изменении поля в ием по закону (3.63)
Первое слагаемое (3.114) тождественно (3.102). Второе
слагаемое представляет собой табличные интегралы вида
(* xdx
J (p2 + x)m.‘
Простые выкладки дают:
р__On: —1 [2Р2 (а1° ~ pW> । Р2 Ср8 ~ а8)
120гс [ 5(р2 + а2)5 । 2(р2+а2)4
р2(дб—р«) р2!
6(/>24-а2)3 15 J •
(3.115)
Коэффициент направленного действия равен
G = TV’
119
где коэффициент использования
На рис. 3.13 приведена зависимость v от В данном
случае коэффициент использования v также стремится
к единице при ——>0 по той же причине, что в преды-
дущем случае.
§ 4. ОБЩИЕ ОСОБЕННОСТИ НАПРАВЛЕННОСТИ ИЗЛУЧЕНИЯ
ПЛОСКИХ СИНФАЗНЫХ АНТЕНН
Приведенные в предыдущих двух параграфах данные
о поле излучения антенн, имеющих плоский раскрыв, а в
раскрыве — синфазное поле, позволяют сделать ряд важ-
ных выводов.
Синфазные плоские антенны имеют главный максимум
излучения в направлении нормали к раскрыву (при 8=0).
Коэффициент использования площади раскрыва
антенны
имеет наибольшее значение, равное единице, при одинако-
вых амплитудах поля во всех точках раскрыва. На практи-
ке коэффициент использования всегда меньше единицы, так
как идеальный случай точно одинаковых амплитуд в рас-
крыве не встречается. Имеет место та или иная степень
приближения к идеальному случаю.
Коэффициент использования площади антенны тем мень-
ше, чем больше неоднородность поля в раскрыве (при моно-
тонном убывании амплитуд от середины раскрыва к краям,
что соответствует рассмотренным выше зависимостям, v
тем меньше, чем больше отличается поле на краях от -поля
в середине).
Ширина главного лепестка диаграммы направленности
в //-плоскости (в нашем случае соответствует плоскости XZ,
120
(рис. 3.1) пропорциональна отношению длины волны к про-
тяженности антенны в направлении, параллельном оои X:
* он н Dy
при прямоугольном раскрыве или
2D ==х —
* он н d
при круглом раскрыве.
Аналогично ширина главного лепестка в ^-плоскости
(соответствует плоскости YZ на рис. 3.1) пропорциональна
Рис. 3.14. К анализу зависимости формы диаграммы направленности
от распределения амплитуд синфазного поля в отверстии:
а — прямоугольное отверстие; б — круглое отверстие.
отношению длины волны к протяженности антенны в на-
правлении, параллельном оси Y
on __у _2l
4 ОЕ ,Е D2
или
где хя или х£ —коэффициенты пропорциональности, ука-
занные в таблицах 3.1ч-3.4.
С точки зрения диаграммы направленности в какой-либо
плоскости всякая антенна может рассматриваться как ли-
нейная.
121
Если антенна плоскостная, то она может быть разделе-
на на полосы, перпендикулярные плоскости, в которой опре-
деляется диаграмма направленности, как показано на
рис. 3.14. Поле излучения отдельных полос, согласно (3.12)
и (3.13), равно

(3.117)
Поле излучения приводится к виду (3.117), когда
— и F=0; если же Er„^Q, то оно приводится
к указанному виду, когда Exs несимметрично относи-
тельно координат xs и ys.
Уменьшая ширину полос до бесконечно
чины, получим
dEH=±>x°^dxs {-Edy,
Л £ Q S I S * S
dEE=/eik^s'^dys [E dx .
c Cq S I 8 S
малой вели-
(3.117, a)
Из (3.117, a) следует, что таким путем плоскостная
антенна приводится к линейной с амплитудами поля,
пропорциональными ^Esdys или §Esdxs.
Коэффициенты хя и х.£, связывающие ширину главного
лепестка с размерами антенны, зависят от степени изме-
нения указанных интегралоз вдоль оси X или оси Y,
т. е. от степени неравномерности амплитуд поля на
эквивалентной линейной антенне.
На рис. 3.15 показаны кривые изменения величин ампли-
туд поля на эквивалентных линейных антеннах, соответ-
ствующих некоторым из рассмотренных выше случаев пря-
моугольной и круглой площадок.
Сопоставляя данные рис. 3.15 с полученными выше
значениями . коэффициентов хя и tE (см. табл. 3.1-=-3.4),
мы видим, что чем быстрее убывают эквивалентные
амплитуды от середины антенны к краям, тем больше
коэффициенты хя и х£> т. е. тем больше ширина главного
лепестка диаграммы направленности.
122
4/2
Рис. 3.15. Кривые изменения величин амплитуд поля вдоль длины эквивалентной линейной антенны,
соответствующей следующим случаям: 1 — одинаковые амплитуды в прямоугольном отверстии; 2—
распределение амплитуд по закону (3.9) при р —1 в прямоугольном отверстии; 3—одинаковые ампли-
туды в круглом отверстии; 4 — распределение амплитуд по косинусоидальному закону (3.8) в прямо-
угольном отверстии; 5 — распределение амплитуд по закону (3.10) при р= 1 в прямоугольном отверстии.
От неравномерности эквивалентных амплитуд на линей-
ной антенне зависит также относительная величина побоч-
ных лепестков диаграммы направленности. Из анализа при-
веденных выше диаграмм направленности легко заключить,
что чем быстрее убывают амплитуды от середины к краям,
тем меньше относительная величина побочных лепестков
диаграммы направленности. Можно показать, что при на-
личии возрастания амплитуд ог середины антенны к краям,
побочные лепестки увеличиваются по сравнению со случаем
одинаковых амплитуд.
§ 5. ПАРАЗИТНАЯ ПОЛЯРИЗАЦИЯ
В некоторых из рассмотренных выше случаев круг-
лого отверстия (формулы 3.61, 3.62, 3.63) электрический
вектор поля (а следовательно и магнитный) имеет в от-
верстии экрана как _у-овую (Еу), так и х-озую (Ех)
составляющие. При этом Еу выражается четной функ-
цией угла и имеет одинаковый знак во всем отверстии,
а Ех является нечетной функцией угла и имеет разный
знак в соседних квадрантах. В результате электромаг-
нитное поле в основных плоскостях (Е и Я-плоскостях),
а также в направлении глазного максимума определяется
лишь через составляющую Е . Наличие в отверстии не
равной нулю составляющей Ех, противофазной в соседних
квадрантах, обусловливает излучение электромагнитной
энергии вне основных плоскостей с четырьмя глазными
максимумами в промежутках между этими плоскостями.
Практически это излучение не используется и является
в этом смысле напрасной тратой энергии излучения,
приводящей к снижению коэффициента усиления антенны.
В силу сказанного составляющую электрического
вектора поля Ех (и соответствующую ей составляющую
магнитного вектора Ну) в отверстии, не участвующую в
образовании поля излучения в главном направлении и в
основных плоскостях, а приводящую лишь к излучению
вне основных плоскостей, принято называть паразитной
поляризацией.
§ 6. ИЗМЕНЕНИЕ ФАЗ ПО ЛИНЕЙНОМУ ЗАКОНУ
Изменение фаз поля в площадке отверстия в плоском
экране по линейному закону получается при падении на
этот экран плоской волны С направления, образующего
124
с нормалью некоторый угол, не равный нулю, как пока-
зано на рис. 3.16.
Обозначим угол падения через а. Как легко видеть
из рисунка, в точку xs фронт волны придет позже, чем
в. среднюю точку О, так как до точки xs путь длиннее
на отрезок x^sina. Благодаря этому фаза поля в точке
xs отстает на величину
* 2т:
-у- xs sin а = kxs sin а (3.118)
от фазы поля в точке О.
Если обозначить поле в точке О через Ео, то поле в
точке xs будет равно
Es(\. s,)r'*"’'"‘. (3-И9)
где f(xs, ys) — функция распределения амплитуд поля в
отверстии.
Обозначим
k sin а = у, (3.120)
тогда

(3.121)
В дальнейшем, для линеино-меняющихся фаз вдоль
оси X будем пользоваться как
формулой (3.121).
Когда а = 0 (у = 0), т. е.
когда волна падает с перпен-
дикулярного к зеркалу-направ-
ления, разность фаз равна ну-
лю, и поле в отверстии будет
синфазным. Следовательно,
синфазное поле может рас-
сматриваться при теоретичес-
ком исследовании лишь как
частный случай линейного за-
кона изменения фаз, являю-
щегося более общим.
В антенной технике изме-
формулой (3.119), так и
Рис. 3.16. Линейное изменение
фаз при наклонном падении
волны на отверстие в плоском
экране.
нение фаз по линейному зако-
ну осуществляется, как правило, в направлении какой-либо
одной оси, являющейся осью симметрии поля, при сохра-
нении синфазного поля в направлении другой оси.
125
Линейное изменение фаз поля в отверстии Может
иметь место при всех исследованных выше видах ампли-
тудных изменений, рассмотренных при условии синфаз-
ного поля.
Таким образом, множитель f (xs, ys) в уравнении (3.119)
будет одной из функций в формулах (3.7) (3.10) пр'и
прямоугольном раскрыве антенны или в формулах
(3.60) — (3.63) для Eys при круглом раскрыве. Что касается
составляющей Exs, то будучи нечетной функцией или
равной нулю, она не сказывается на величине поля в
Н-п Е-плоскостях.
Напряженность поля согласно (3.11) и (3.12) может
быть вычислена по формулам
=А jdvJ1 (х- *’>'“ dx‘=
= Л J Л/, j f К у,) г (3.122)
yjdy,, (3.123)
где
Из (3.122) видно, что при изменении фаз по линей-
ному закону выражение для поля излучения в Я-плоскости
имеет такой же вид, как при синфазном поле, но в этом
выражении следует заменить sinft на sinft—sina,
где
sin a = 4-.
k
Это указывает на то, что при линейном изменении фаз
в раскрыве форма диаграммы направленности (ширина
главного лепестка, относительная величина побочных
максимумов) сохраняется такой же, как у синфазной
антенны, при том же законе изменения амплитуд, но
направление главного максимума излучения смещается
на угол а от направления, перпендикулярного к раскрыву.
Несколько сложнее сказывается линейное изменение
фаз на диаграмме направленности в Е-плоскости.
Предположим сначала, что f(xs, ys) является постоян-
ной величиной, как в (3.7) и (3.6Э), или является функ-
126
цией только одной координаты xs, как в (3.8) -=-(3.10).
В этом случае можно написать
Ее= A' j f (х5) t~iVCsdxs J e/Aj,iS1" *dys. (3.124)
Из (3.124) следует, что при линейном изменении фаз
в раскрыве зависимость напряженности поля в Е-пло-
скости от угла &, т. е. диаграмма направленности будет
в точности такой же, как при синфазном поле, однако
величина поля Ее существенно изменится, так как инте-
грал у е f(xs)dxs существенно отличается от интеграла
Изменение величины поля в Е-плоскости связано с
отклонением направления главного максимума излучения
в //-плоскости на угол а от нормали к раскрыву. Это
обусловлено тем, что Е-плоскость проходит через нормаль,
а последняя при отклоненном главном максимуме может
проходить не только в области главного лепестка, но
также в области ’побочных лепестков и даже в направ-
лении нулевого излучения, что зависит от размера угла
а, ширины главного лепестка в //-плоскости, ширины
побочных лепестков и относительной величины побочных
максимумов.
В рассматриваемом случае отклоненного главного
максимума практический интерес имеет диаграмма на-
правленности не в Е-плоскости, как прежде, а в Е'-
плоскост’и (см. рис. 3.17), проходящей через главный
максимум, излучения; Е'-плоскость, очевидно, образует
угол а с Е-плоскостью.
В Е'-плоскости диаграмма направленности будет функ-
цией угла (см. рис. 3.17). Математическое выражение
для диаграммы направленности в Е'-плоскости Е£, может
быть получено, если воспользоваться формулой (3.6).
Легко видеть, что, подставив в эту формулу Es из
(3.121), получим:
f'e (»') = Fe (sin & sin ?) FH (sin & cos <₽ - -£-) ,
(3.125),
где Fe и Fh (без штрихов) функции диаграмм направлен-
ности синфазной антенны, имеющей данную амплитудную
127
зависимость поля в раскрыве, но у которых в аргументе
shift заменяется соответственно на sin ft sin» и sin ft cos <р —
----g-. При этом <p и ft могут быть определены через S'
и а по формулам:
cos ft = cos ft' cos a; sin ft sin f = shift'. (3.126)
В общем случае, когда Es является функцией обеих
координат xs, ys или pf, <ps, не удается выразить поле
излучения в £'-плоскости в простых математических
Рис. 3.17. Расположение нормальной к экрану плоскости Е и плоско-
сти Е', в которой находится главный максимум диаграммы направ-
ленности при линейном законе изменения фаз в прямоугольном и
круглом отверстиях.
выражениях. Однако можно указать, что при малых
углах а диаграмма направленности в Е'-плоскости как
функция &' при линейно меняющихся фазах будет при-
мерно такой же, как диаграмма направленности синфаз-
ной антенны в Е-плоскости как функция ft. Имеется в
виду, что в обоих случаях амплитудная зависимость поля,
в раскрыве одинакова.
§ 7. ИЗМЕНЕНИЕ ФАЗ ПОЛЯ ПО КВАДРАТИЧНОМУ ЗАКОНУ
В ПРЯМОУГОЛЬНОМ ОТВЕРСТИИ
Квадратичный закон изменения фаз в отверстии в
плоском экране приближенно получается при падении на
экран сферической или цилиндрической волны, что соот-
128
ветствует освещению экрана точечным или нитевидным
источником, находящимся на некотором расстоянии от
экрана.
Во всех рассматриваемых в этом параграфе случаях
примем прямоугольное отверстие и

Мы рассмотрим следующие зависимости Е от коор-
динат площадки отверстия
a) Eys = E0cos^e~!T1\ (3.127)
6) £^ = £oc°s^-e х,?2, (3,128)
в) £jzs = E0cos^-e“JTfc + «?), (3.129)
где/?! и /?2 — расстояния от соответствующих центров
фронта волны или от источников излучения до отвер-
стия (до раскрыва антенны).
Зависимости (3.127) и (3.128) получаются при падении
на экран цилиндрической волны. Зависимость (3.129) в
случае Rt = R2 получается при падении на экран сфери-
ческой волны, а в случае R}=^R2— при падении волны
двойной кривизны. Первые две зависимости соответствуют
полю в раскрыве секториального рупора, а третья—полю
в раскрыве пирамидального рупора. Причем в случае
RJ = Ra это соответствует остроконечному рупору, а в
случае Ry-^R^—клинообразному (подробно см. гл. VI).
В математическом отношении (3.127) и (3.128) явля-
ются частными случаями (3.129) при R2—>оо или Rt—>оо.
Поэтому рассмотрим все три случая одновременно.
В общем случае (3.129) напряженность поля в Я-пло-
скости определяется формулой
9—1ВОЗ
d2

о,
2
\ cos е
2
к
(3.130)
129
а в £-плоскости
5 £i
2 , « 2
. (' ~’‘"x~ib MJ's*111® , Г *xs
Ee=A \ e R> e dys \ cos-^-
_£j _£i
2 2
. к s
e * Ri dx .
s
(3.131)
В (3.130) и (3.131) содержится четыре интеграла. Рас-
смотрим. каждый из них в отдельности.
D3 D2
~2 ~ Т
==2y^[C(w)-jS(w)], (3.132)
где
и=А’ (3-132а)
а функции C(w) и S (w) — так называемые 'интегралы
Френеля [14], определяемые по формулам
130
Произведя следующую замену в показателях степени
(3.134)
ГЛХз Mi
X/?! Dj 2 Я1У2/ 2Df .
^_ । J- fM2 I ^iY Mi
>R1 ' Dj 2 + / 2D*
получаем
T _,л! r-
j cos^e XR1Jx = e 401 {[С (и) - C (0)] -
_£l
- j[S(u) —S(v)]J, (3.135)
где
u = jJ^ + -^} 1
/2 °1 J ’ «
' _ n / } (3.136)
1 fVlR, _D^\
V2\ D, V^J- J
Два рассмотренных интеграла в а) и б) представляют
собой постоянную величину, не зависящую от угла 0.
Остальные' интегралы являются функцией угла & и опре-
деляют диаграмму направленности.
2
— 2 ^-2
2 к У‘ 2 ж J’s
j * e'*'*“"X+ f е"'Т * ^',М 'лу.- (3-137)
О о
9*
131
Интегралы в правой части (3.137) имеют вид, подоб-
ный (3.134), и приводятся аналогичным путем к выраже-
нию
2
2. , «
Г Т rT <кУз sln а j
\ е Кг е dy==
Рг
2
/« sin* •
{[C-W-C^J-ZlSW-S^JJe 4 , (3.138)
^=^(^*81па+Йг)’ I
У2 ' yw [. (3.139)
В = ( УЩ k sin & —
У 2 V /W ’
2
г , " *
р их —' Т ikx*sln & <
г) I cos-р— е R1 е s dxs=
_о,_
2
%-
*2 / vxs KXS \ к S
= 2. Г (e'-A+ e*'^) Т^Х(.
(3.140)
После раскрытия скобок в (3.140) этот интеграл также
приводится к интегралам вида (3.134). После преобразо-
ваний, аналогичных сделанным выше, получаем:
где
х2
2 . те s
Р 1tX_ —1 у ~Б~ jkx, sin 9 ,
I cos-^e x R1 e s dx =
J Di
_£i_
2
= м {[С (о,) - C (v2)] -j [S (01) - 5 (v2)]J +
+ ^{[C(^3)-C(^4)]-У•[5(^3)-S(^4)]}, (3.141)
те . / 1 , 2 sin
'TXR-z>T + —
M = e v
132
N = q
J____2 sin 9\1
O, X )
1 F 2 F / 1 , 2 sin 9 ’
V2 L/M?1 ' < 1 . 2 sin S 1 X j
/2 I v'~' fT Г । i/) p ( i s^n e Г A i/itT ! 1 2 sin 9' v Ri Fa >• ,
Зная значения отдельных интегралов, нетрудно получить
общее выражение для Ен и Ее.
Выражение (3.138) является диаграммой направленно-
сти в f-плоскости, а выражение (3.141) дает диаграмму
направленности в //-плоскости при распределении поля в
раскрыве антенны, определяемсм формулой (3.129).
При распределении поля в раскрыве антенны по форму-
ле (3.127) диаграмма направленности в //-плоскости опре-
деляется выражением (3.141), а в Е-плоскости диаграмма
направленности имеет такой же вид, как у синфазной ан-
тенны при постоянных амплитудах (3.19). Если же поле
в раскрыве антенны определяется по формуле (3.128), то
диаграмма направленности в //-плоскости имеет такой вид,
как у синфазной антенны при косинусоидальном распреде-
лении амплитуд (3.29), а в ^-плоскости определяется выра-
жением (3.138).
На рис. 3.18 приведено несколько диаграмм направлен-
ности, вычисленных по (3.138) для различных значений
максимального отставания фазы. Согласно (3.128) фаза
поля в отверстии (раскрыве) определяется по формуле
* X Я8 '
Максимальное отставание фазы имеет место на краю
отверстия (раскрыва) при ys=~-. В этой точке
D2
ф = ---А
‘макс X 4/?2
133
Следовательно, диаграммы направленности рис. 3.18
вычислены при значениях R2, равных соответственно
2те£)|
<50, — ,
О2 D2
к и<2 я и2
2 Т И *8 Г*
2л£>2 ( __ я \
При R2 = —^— (тмакс—~8~ 1 диаграмма направленности
почти не отличается от диаграммы направленности син-
Рис. 3.18, Диаграммы направленности прямоугольного отверстия при
одинаковых амплитудах и квадратичном изменении фаз для различ-
ных значений максимального отставания фазы
* 4 такс
л Di I, те \
При /?2 — ~ U макс= Т) диаграмма направленности
имеет такую же ширину главного лепестка на уровне
0,707, как у синфазной антенны, но более широкий глав-
134
ньгй лепесток на уровне 0,2—0,3, за счет слияния с пер-
вым боковым лепестком,
При R2 = -^- -г-(Ф„а„ = 21г) главный лепесток имеет
прозал и почти вдвое большую ширину.
Перейдем к расчету коэффициента направленного
действия
S,
Р имеет одинаковую величину во всех трех случаях
f3.127)-г-(3.129) и такую же, как при синфазном поле и
косинусоидальном законе изменения амплитуд (см. 3.33),
т. е.
120л 2 •
Напряженность поля излучения в главном направлении
будет разная для различных случаев (3.127)-=-(3.129).
Выражение г2£2акс Для этих случаев имеет соответственно
следующую величину:
«) I I=т тг № W- С WJ!+Is (") - S (»)]=).
(3.142)
б) k2CJ=£o^Mc W + Is W}’ <3-143>
«) I Г24акс 1 = £0 № {[С («) ~ G (П)]2 + [$(«) - S (П)Р) X
x{[C(w)]2-h[S(^)]2}. (3.144)
Подставив (3.142)-г-(3.144) в выражение для коэффи-
циента направленного действия (3.22), получаем:
°) °н= <[с (и) “ с (и)]2 + [S {и) ~ 5 (У)?} ’ (3,145)
б) G£=64f^{[CWF + [SW]2}, (3.146)
в) О=3^ {[C(u)-C(o)]24-[5(u)-5(o)]2}x
X {[C(w)]2 + [S(w)]2}. (3.147)
135

Рис, 3.19. Графики зависимости удельного коэффициента усиления от длины сторон прямоугольного отверстия
Z£>1
I у или — 1для различных значении расстояний у и у;
а) при изменении амплитуд и фаз поля в отверстии по закону (3.127); б) то же по закону (3.128).
Индексы Н и Е при G указывает на то, что квадратич-
ное изменение фазы имеет место вдоль одной оси, парал-
лельной соответственно магнитному или электрическому
полю. Отсутствие индекса при G указывает на общий слу-
чай квадратичного изменения фазы радиально от центра
отверстия к краям.
Легко видеть, что между полученными величинами ко-
эффициента направленности для разных случаев существует
связь
G =
«Е / А \ / А
32 )\7\ иЕ
(3.148)
На рис. 3.19 приведены графики зависимости удельной
величины коэффициента усиления Он и ^(7£соответ-
D\ Dt v Rt Ro
ственно от -у- и -у1- для различных значении и .
А А А А
Мы видим, что при каждом заданном значении -у- или
Di Do
существует оптимальная величина или-^, при
А ДА
которой удельный коэффициент направленности макси-
мален. Через точки оптимальных значении -у- и -у- на
рисунке проведена пунктирная кривая.
§ 8. ИЗМЕНЕНИЕ ФАЗ ПОЛЯ ПО КВАДРАТИЧНОМУ ЗАКОНУ
В КРУГЛОМ ОТВЕРСТИИ
Мы остановимся здесь подробно на случае постоянных
амплитуд поля в отверстии, т. е. на предположении, что
Еу==Еое ‘XR. (3.149)
Здесь R — постоянный параметр, указывающий расстояние
до экрана от центра падающей на экран сферической вол-
ны. Приближенно формула (3.149) отражает зависимость
поля в раскрыве конического рупора от координат точек
раскрыва.
При одинаковых амплитудах напряженность поля и диа-
граммы направленности в И- и Е-плоскостях будут одина-
137
ковы. Поэтому дадим здесь вывод формулы только для то-
чек //-плоскости.
£ 2
2тс 2 „
р — Л С /TrAcos’ss"18 j .
Ен=А\ е е р/рА=
о о
т
= 2кЛ1е х л /О(//)РЖ (3.150)
о
Здесь введено обозначение y = £pssin&. Приведем (3.150)
к виду
~ k sin &
ЕН = А> J e-^’j0(y)yrfy, (3.151)
о
где
А'=—2~Л • R —
Д3 sin2 & ’ /?X*2sin2& •
Используя примененный выше метод, содержащий
преобразования (3.93)-i-(3.97), получим:
stD2 оо
Е —A'S е 7102 \ № Л m
ьн — 7Д4/?х) nl
(3.151а)
где попрежнему через S6 обозначена площадь раскрыва
антенны, а
5=^-^-sin&.
В направлении главного максимума
'^с= е; я21 (cos - 1)' + sin’ §] =
= 2Ej’R! (1 -cos§-)=4E2 S’sin’^.
(3.152)
(3.153)
138
Таким образом, коэффициент направленного действия
равен
X2 \ Sfe ) Sin ZkR • (3.154)
sk
Из (3.154) видно, что при малых значениях , когда
синус можно заменить его аргументом,
С увеличением Sk при постоянном R коэффициент исполь-
зования уменьшается, но G растет. В точке, где ^-=0,
согласно (3.154), имеем
& 21R 2\R
ИЛИ
£. = 2,34 2/?; -^-^3. (3.155)
* Л/\
Последнее выражение показывает соотношение пара-
метров, при котором коэффициент направленного действия
имеет максимальное значение. При дальнейшем увеличе-
нии Sk оба коэффициента G и v уменьшаются.
Более точно поле в раскрыве конического рупора
выражается следующей формулой:
£«=£ое/' R Pif4p>)~8^(4p')]cos^sin'f’^’
L / \ /J .
Р2 z /_£ \
Eys = Еое 1 Х R а----sin2 ^4- 8/j <2- Рcos2<ps .
(3.156)
Обозначения соответствуют таковым, принятым в (3.61).
Использование (3.156) вместо (3.149) для расчета
характеристик излучения чрезвычайно усложняет мате-
матические выкладки, а результат в обоих случаях прак-
тически почти одинаков. Поэтому мы здесь этих выкладок
не приводим.
139
§ 9. ИЗМЕНЕНИЕ ФАЗ ПО КУБИЧЕСКОМУ ЗАКОНУ
Кубический закон изменения фаз поля в раскрыве антен-
ны не встречается в чистом виде. Обычно данный закон
-34
Рис. 3.20. Диаграммы направленности прямоугольного а) и круглого
б) отверстий прн постоянных амплитудах и кубическом законе изме-
нения фаз вдоль одной из осей, лежашей в плоскости диаграммы
направленности, для различных значений Дфкакс.
сопровождается линейным и нулевым (с синфазным полем).
В частности, кубический закон проявляется в линзовых ан-
теннах при смещении облучателя из фокуса в направлении,
перпендикулярном оси линзы.
140
Следовательно, подробный анализ кубического закона
представлял бы практический интерес при его рассмотрении
совместно с синфазным полем и линейным законом. Ввиду
громоздкости решения данной задачи мы ограничиваемся
краткими введениями, позволяющими получить представле-
ние об общих закономерностях.
На рис. 3.20 приведены диаграммы направленности
антенны с прямоугольным (3.20,а) и круглым (3.20,6) рас-
крывом при постоянных амплитудах и чисто кубическом за-
коне изменения фаз. На рисунке величина дФмакс обо-
значает разность фаз между крайней и центральной точка-
ми отверстия. Из этих диаграмм видно, что при кубиче-
ском законе изменения фаз, как и при линейном, главный
максимум диаграммы направленности смешается относи-
тельно перпендикулярного к раскрыву направления. Но, в
отличие от линейного закона, здесь одновременно имеет ме-
сто искажение формы диаграммы направленности, выра-
жающееся в том, что по сравнению с синфазным случаем
побочные лепестки возрастают с одной стороны от главного
максимума и уменьшаются с другой стороны от него. Диа-
грамма направленности становится асимметричной.
§ 10. ВЛИЯНИЕ ПЕРИОДИЧЕСКОГО ИЗМЕНЕНИЯ АМПЛИТУД
НА ДИАГРАММУ НАПРАВЛЕННОСТИ СИНФАЗНЫХ АНТЕНН
Рассмотренные выше зависимости амплитуд поля от ко-
ординат точек раскрыва характеризуются, в общем, нали-
чием максимума в средней точке раскрыва и плавным моно-
тонным убыванием амплитуд к краям. Наряду с такими за-
висимостями в антенной технике (у линзовых антенн)
встречается многократное периодическое изменение ампли-
туд. Посмотрим, как сказывается такое изменение амплитуд
на диаграмму направленности.
Предположим, что поле в раскрыве антенны определяет-
ся по формулам
Exs = 0; )
г 2хх,1 • (3.157)
Eys = £0 f (WJ + ?2 cos J
где и q2 — постоянные величины.
Следует заметить, что в общем случае здесь не обя-
зательно приравнивание Exs нулю. Достаточным является
Предположение о нечетности функции Exs относительно
координат xs и ys.
141
Формула (3.157) указывает на то, что периодичность
имеет место лишь в одном направлении, параллельном
оси X.
Сделаем замену
2kxs ?kxs
cos^=z2T_+_V.d , (3.158)
тогда
е'^+^-е"' d j. (3.158,а)
Из (3.158) следует, что при периодически меняющихся
амплитудах поле в раскрыве может рассматриваться
как результат сложения трех полей: одного синфазного
с относительной амплитудой, равной q}, и двух полей
с линейно меняющимися фазами и относительной ампли-
тудой причем у последних направление убывания
фаз противоположно.
Аналогично и поле излучения может рассматриваться
как результат сложения трех полей — поля синфазной ан-
тенны и двух полей антенн с линейно меняющимися фазами.
Из сказанного выше следует, что, имея одинаковую ампли-
тудную зависимость, все три поля излучения характеризуют-
ся одинаковыми по форме диаграммами направленности,
но одна из них (соответствующая синфазному полю) будет
иметь главный максимум по перпендикуляру к раскрыву, а
две другие (соответствующие линейно меняющимся фазам)
будут иметь главные максимумы, смещенные относительно
перпендикуляра на угол а, определяемый согласно данным
§ 6 по формуле
sin« = ±A=^ = ^, (3.159)
где d согласно (3.157) есть длина участка, на котором
укладывается полный период изменения амплитуды.
Если где D — ширина раскрыва антенны в на-
правлении оси X, то а меньше 90 — половины ширины
главного лепестка диаграммы направленности синфазной
антенны, т. е. главные максимумы отклоненных диаграмм
будут находиться в пределах главного лепестка диаграммы
синфазной антенны, недалеко от главного максимума по-
следней. В результате наличие второго слагаемого в скоб-
142
ках выражения (3.157) приведет здесь к некоторому рас-
ширению главного лепестка диаграммы направленности.
Если d < Д-, но Л<1, то отклоненные диаграммы
будут смещены относительно синфазной диаграммы на
значительный угол. Следовательно, здесь наличие вто-
рого слагаемого в скобках выражения (3.157) не изме-
няет диаграммы направленности синфазной антенны в об-
ласти главного лепестка, но вызывает появление боль-
ших побочных лепестков ^с относительной величиной
далеко отстоящих от глазного. Одновременно увеличи-
вается и общее количество побочных лепестков.
При -У>1 не удовлетворяется условие (3.159). В дан-
ном случае диаграмма направленности синфазной антенны
существенно не изменяется. Лишь в области $ = 90°
несколько увеличиваются побочные лепестки.
На рис. 3.21 иллюстрируются сформулированные выше
положения. Слева на рисунках показаны диаграммы на-
правленности, а в верхнем правом углу — кривая измене-
ния напряжения в раскрыве. Здесь анализировалась диа-
грамма направленности в //-плоскости. В Е-плоскости диа-
грамма направленности сохранится такой же, как у синфаз-
ной антенны.
Мы рассмотрели периодический закон, определяемый
косинусоидальной функцией. В более общем случае перио-
дическая функция может быть разложена в ряд Фурье и
приведена к сумме косинусоидальных функций (имеется
в виду симметрия поля относительно средней линии рас-
Рис. 3.21. Графики, поясняющие влияние периодического закона изме-
нения амплитуд поля на диаграмму направленности синфазных антенн.
ГЛАВА ЧЕТВЕРТАЯ
ВОЛНОВОДНЫЕ ИЗЛУЧАТЕЛИ
§ 1. ПОЛЕ В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ
Волноводам, в частности, прямоугольным .волноводам
посвящена обширная литература. Достаточно полное осве-
щение теории волноводов можно найти в книгах Б. А. Вве-
денского и А. Г. Аренберга [15], Г. В. Кисунько [16],
В. И. Юзвинского [17] и др. [18—20]. Здесь вкратце напом-
ним некоторые сведения из теории регулярных волноводов.
Как известно, в теории регулярных волноводов находят-
ся и исследуются отдельные частные решения однородных
уравнений Максвелла, т. е. уравнений (2.1) при Ja =0 и
7м =0, полученные для внутренней области бесконечного
волновода при условии равенства нулю касательной состав-
ляющей электрического вектора поля на стенках волно-
вода.
Эти частные решения делятся на две группы:
а) так называемые Н-волны или поперечные электри-
ческие волны (Нтп или ТЕОТЛ), у которых отсутствует
составляющая электрического вектора вдоль оси волно-
вода,
б) так называемые Е-волны или поперечные магнит-
ные волны (Em/I или TMmJ, у которых отсутствует со.
ставляющая магнитного вектора вдоль оси волновода.
В каждой группе отдельные частные решения отличают-
ся друг от друга значением индексов тип, являющихся
целыми числами и указывающих на число полуволн между
противоположными стенками волновода. В зависимости от
размеров поперечного сечения волновода и способа его воз-
буждения в нем может возникнуть электромагнитное поле,
соответствующее определенному частному решению. На
144
практике, как известно, в волноводах прямоугольного сече-
ния обычно возбуждается волна TEOi, соответствующая
/п=0, л=1.
Рассмотрим волны ТЕ0Л, не конкретизируя вначале
индекс и. На рис. 4.1 показан прямоугольный волновод
и система координат, которой мы будем пользоваться
Рис. 4.1. Прямоугольный волновод и расположение
системы координат для его анализа.
при его рассмотрении. Известно, что волны ТЕ0Л, дви-
жущиеся в сторону положительного направления оси Z,
при выбранной нами системе координат (рис. 4.1) и при
зависимости от времени вида е^ш/ описываются уравне-
ниями:
£,=£,=<>, Я,=0, (4.1)
пп Е()
Di j<^a
я,=-
COS
(4.2)
где Ео — постоянный множитель, характеризующий интен-
сивность поля,
(4.2а)
18—1503
145
D\ — ширина стенки, перпендикулярной электриче-
скому вектору,
D2—ширина стенки, параллельной электрическому
вектору поля,
с — 3-108 м]сек — скорость света в свободном про-
странстве,
>1 —длина волны'в свободном пространстве,
, <о 2л
k =---= .
С Л
При п=1 волна ТЕ01 в прямоугольном волноводе
имеет следующие составляющие поля:
г' ('т^Х \ —/7^
Ey = E0cos е
Н
----— cos () е ц ,
“^о \ /
гг л Еа . / ЛХ \ —jyz
Н = -=г- -г-*- sin ( н- ) е п .
г Di j^a \Dt J
(4-3)
(4.3a)
На рис. 4.2 показана конфигурация электромагнитного
поля в различных сечениях , волновода, соответствующая
уравнениям (4.3). Сплошные линии указывают направле-
ние электрического вектора, а штриховые — направление
магнитного вектора.
Формулы (4.1)-i-(4.3) и рис. 4.2 указывают на следую-
щие особенности электромагнитных волн ТЕ в волново-
дах прямоугольного сечения:
1. Электрический вектор поля Е параллелен оси Y,
а магнитный Я — перпендикулярен к этой оси.
2. Величина векторов Е и Н не зависит от коорди-
наты у.
3. Еу и Нх меняются как функции координаты х при
четных п по синусоидальному закону, а при нечетных —
по косинусоидальному закону, образуя узлы поля на
стенках волновода и п—1 узлов в пространстве между
стенками.
4. Нг, наоборот, меняется как функция координаты х
при четных п по косинусоидальному закону, а при не-
146
четных п — по синусоидальному закону, имея п узлов
между стенками волновода, а на самих стенках — пуч-
ности.
5. В направлении оси волновода электромагнитное
поле имеет характер бегущей волны, распространяющейся
с фазовой скоростью
<0
v.=—
Ф 7
с
(4-4)
т-г
которая зависит от отношения у и от индекса п. При
фазовая скорость становится мнимои величиной,
что указывает на затухающий характер поля вдоль вол-
новода. Длина волны
X = -^,
«Р п ’
как известно, называется критической волной, так как
при этой волне скачком меняется характер распростра-
aj
Рис. 4.2. Конфигурация элек-
тромагнитного поля при волне
ТЕ01 в различных сечениях пря-
моугольного волновода:
а) в поперечном сечении,
б) в продольном сечении в
плоскости FZ; в) в продоль-
ном сечении в плоскости XZ.
Я
8)
нения волн в волноводе. При волновод пропускает
электромагнитные волны, а при 2>2кр не пропускает.
Через критическую волну Я.кр фазовая скорость в вол-
новоде определяется по формуле
10*
(4.5)
147
В прямоугольном волноводе на практике почти всегда
возбуждается волна ТЕ01. Учитывая сказанное о крити-
ческой волне Zkp, достаточным для возбуждения волны
ТЕ01 является выбор размеров поперечного сечения вол-
новода согласно -условиям
2
D
(4-6)
_х
2
Dt<^.
Широкое распространение имеют волноводы, у которых
Di = 0,71 Л;
D2 = 0,32Z.
При этом вибратор, возбуждающий волновод, должен быть
расположен перпендикуляр но. широкой стенке, как показано
на рис. 1.2,а, б, в. Если размеры поперечного сечения вол-
новода определяются условиями (4.6), то уже на расстоя-
нии нескольких длин волн от возбуждающего вибратора
интенсивность волн высших порядков настолько ничтожна,
что можно считать существующей в волноводе в чистом ви-
де волну ТЕоь У волновода конечной длины с открытым
концом электромагнитное поле у конца (у раскрыва) будет
практически таким же, как у полубесконечного волновода,
т. е. таким же, как если бы волна набегала на этот конец
из бесконечности.
§ 2. ИЗЛУЧЕНИЕ ИЗ РАСКРЫВА ПРЯМОУГОЛЬНОГО
ВОЛНОВОДА
Данная задача не имеет в настоящее время строгого ре-
шения. Наиболее простое решение можно получить, исходя
из условия, что поле в раскрыве равно невозмущенному
полю в волноводе. Некоторое уточнение результата может
быть достигнуто, если учесть, что от открытого конца волно-
вода имеет место отражение и поле в раскрыве определяет-
ся суперпозицией прямой и обратной волн. Ограничиваясь
практически наиболее важным случаем возбуждения в вол-
новоде волны TEoi, примем в качестве исходных формулы
(4.3). Обозначив коэффициент отражения, являющийся ком-
плексной величиной, через Г, будем иметь
148
£/,=(I+r)^cos^e-ft", j
»„ = -(!} (4.7)
Коэффициент отражения Г обычно определяется экспе-
риментально, причем получают при этом его модуль. Зна-
ние модуля коэффициента отражения достаточно для опре-
деления ряда важных характеристик электромагнитного
поля в волноводе: коэффициента бегущей волны, энергети-
ческого баланса, т. е. соотношения энергии падающей и от-
раженной волн и т. п. Для точного же определения поля
излучения необходимо знать точную величину поля в рас-
крыве волновода, которая определяется как амплитудой,
так и фазой отраженной волны. Но поскольку точное зна-
чение поля в раскрыве волновода нам неизвестно, так как
не учитываются волны высших порядков, то в расчетах ис-
ходят из предположения, что аргумент Г в (4.7) равен ну-
лю. При этом, как оказывается, полученные результаты
достаточно хорошо согласуются с опытными данными.
Модуль коэффициента отражения может быть легко оп-
ределен опытным путем. Точное теоретическое его значе-
ние дается ниже. Приближенно он может быть вычислен по
формуле
1-1
Г =------• (4.8)
4-4
Не следует забывать, что (4.7) также дает приближен-
ное значение поля, так как в нем учитывается лишь отра-
женная волна основного типа и игнорируются возбуждаю-
щиеся-волны высших порядков.
Расчет излучения по заданному полю в раскрыве может
быть выполнен по формулам (2.64) и (2.65).
Учитывая, что согласно (4.7) касательные составляю-
щие поля (Е =\Е I и Н =|Я„J) связаны между собой
соотношением
<4:9)
149
получаем в 77-плоскости
[c”s" + r+T-r]J£>^'iS <4|0>
и в Е-плоскости
+ г 7* Г 1 — Г „ 1 С е~/*г
[1 + TFrCos&jj E^^r-dS. (4.11)
В общем случае, когда точка Af, для которой вычисля-
ется поле излучения, произвольно расположена в прост-
ранстве, векторное выражение поля определяется форму-
лой (2.66). Отдельные составляющие поля по угловым ко-
.ординатным осям & и <f имеют следующие выражения:
(sin<? +1T+F cosSsin<? )ЦЕуз ~-y—dS, (4.12)
(cos&costp + -J- coscp) JEys-^—dS. (4.13)
Выражения (4.10) и (4.11) отличаются соответственно
от (3.27) и (3.28) лишь множителем перед интегралом.
Следовательно, и диаграмма направленности в данном
случае будет отличаться от (3.29) и (3.30) этим множите-
лем, т. е. у прямоугольного волновода, в котором распро-
страняется волна TEoi, диаграммы направленности излуче-
ния с открытого конца имеют вид:
в 77-плоскости
/АО.
COS f -g- Sin ft
(4.14)
в Е-плоскости —
(4-15)
На р::с. 4.3 приведены диаграммы направленности по
мощности в 77- и Е-плоскостях Ч Сплошные кривые соответ-
ствуют расчету при Г = 0, пунктирная — расчету прц Г,
определяемом (4.8), а кружочки — измеренным значениям.
4) Эти диаграммы взяты из [21].
150
Все данные относятся к прямоугольному волноводу, у ко-
торого стороны равны Z?i=0,71, £>2=0,32-i. .
Мы видим, что при сравнительно малых углах откло-
нения от главного направления обе теоретические кривые
почти сливаются, а экспериментальные точки хорошо ук-
ладываются на кривых. При больших углах отклонения от
б)
Рис. 4.3. Диаграммы направленности в Е- и Я-плоскостях (по
мощности) прямоугольного волновода при волне ТЕ01 в нем. Сплош-
ные кривые соответствуют расчету при коэффициенте отражения
Г = 0, пунктирные—расчету при величине Г, вычисленной по формуле
(4.8), а кружки — измеренным значениям поля
151
главного направления имеются значительные расхождения
между теоретическими и экспериментальными данными.
Для нахождения объемной диаграммы направленности
надо сначала вычислить Ей и по формулам (4.12) и
(4.13). Подставив в них значение Eys из (4.7), получаем
/ kDt \
COS ( -X- Sin О COS f
/ *7 1 _ р \ \ 2 ‘ /
£ft = Bsin<p (1 + TF+FCOS&)---TTkD.--------V х
v ' 1 — (— —sin$ cos f 1
/ kD% \
sin ( —2~ sin $ sin (4.17)
—g- sin ft sin ?
где
/S_ e—Jkro
5=^О + Г)Во^->
r0 — расстояние от центра раскрыва волновода до
точки наблюдения М,
Sn— площадь поперечного сечения прямоугольного
волновода.
Зная составляющие £9 и £?, можно определить пол-
ное поле £= j/£94-£^. Множитель этого корня, являю-
щийся функцией 0 и <р, будет представлять собой выра-
жение для объемной диаграммы напрайленности £0б. Со-
гласно (4.16) и (4.17)

1 —г 7 ft
T+7TC0S&
cos? ср sin2 & X
[ \ / kDn \
cos I —2~ sin 9 cos <p) sin I —sin 9 sin ?)
X / 2 kDt : V ^2 ' 18)
1 — I ——2~ sin 9 cos ? ) —g- sin 9 sin ?
152
При определен^ коэффициента направленного дейст-
вия можем воспользоваться данными § 2 предыдущей
главы случай б). Учитывая отличие (4.10) от (3.27) вместо
(3.34), проделав аналогичные преобразования, получим
С другой стороны, поскольку здесь Es связано с Hs
соотношением (4.9), то
^=(i+г)2 I <4-2°)
Таким образом коэффициент направленного действия
равен
0= 1.Л_Г k ' о,81 . (4.21)
1—Гу Р '
14-г k
§ 3. ПОЛЕ В КРУГЛОМ ВОЛНОВОДЕ
Сказанное в § 1 о характере отдельных частных реше-
ний однородных уравнений Максвелла для области внутри
регулярного прямоуголь-
ного волновода, в частно-
сти, о делении волн, соот-
ветствующих отдельным
частным решениям на по-
перечные электрические и
поперечные магнитные от-
носится также к волново-
дам круглого сечения.
В случае круглого вол-
новода удобнее выразить
решения уравнений Макс-
велла в цилиндрических
координатах. На рис. 4.4
показан круглый волновод
диаметра D и принятая
система цилиндрических
координат z, р, <р . Для
сравнения там также при-
ведена прямоугольная си-
стема координат.
Рнс. 4.4. Круглый волновод н распо-
ложение систем координат для его
анализа,
153
Особенностью круглых волноводов является образо-
вание в них волн ТЕОп и ТМ0„, поля которых симметричны
относительно оси волновода, т. е/ не зависят от коорди-
наты <р. На рис. 4.5 показана картина линий полей в
круглом волноводе при возбуждении в нем таких типов
волн (для п=1). Сплошные линии показывают направле-
ние электрического вектора поля, а пунктирные — маг-
нитного.
Симметричные типы волн используются в круглых вол-
новодах, предназначенных для канализации энергии, во
Рис. 4.5. Конфигурация электромагнитного поля в поперечном н про-
дольном сечениях круглого волновода при волнах TEqi н ТМо1 (сим-
метричные поля).
вращающихся сочленениях и т. п. В волноводах-излучате-
лях они почти не используются, так как создают практи-
чески мало пригодную диаграмму направленности кониче-
ской формы. Однако симметричные типы волн представля-
ют теоретический интерес. Это обусловлено тем, что у сим-
метричных полей все математические зависимости имеют
более простой вид, что облегчает строгое решение задач.
Поэтому в теоретических исследованиях очень часто при-
бегают к анализу симметричных типов волн.
В круглых волноводах, используемых в качестве излу-
чателей, как правило, возбуждается волна ТЕп, при кото-
рой поле излучения имеет о’бычную диаграмму направлен-
ности с одним направлением главного максимума вдоль
оси волновода. При волне ТЕц составляющие электромаг-
154
нитного поля по координатам г, р, <р, выражаются следую-
щим образом:
(2^)е Лг-
Еч = Т Ео cos <? ) e~IV'
^=-i4£ocoS?j;^;e-^
Viv£«sia?/i^)e4K’
(4.22)
где J( и J,— соответственно бесселева функция и ее
производная по аргументу,
8 — первый корень уравнения
Л'(8)=0.
На рис. 4.6 изображена картина электрических и маг-
нитных линий поля в поперечном и продольном сечениях
круглого волновода при возбуждении в последнем волны
ТЕП.
§ 4. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ ОБ ИЗЛУЧЕНИИ
ИЗ РАСКРЫВА КРУГЛОГО ВОЛНОВОДА
Рассмотрим здесь приближенное решение задачи об из-
лучении из раскрыва круглого волновода, используя метод,
примененный в § 2 для прямоугольного волновода.
155
Полагаем поле в раскрыве равным суперпозиции набе-
гающей и отраженной волн типа ТЕп. Коэффициент отра-
жения обозначаем через Г, причем в дальнейших выклад-
ках будем учитывать лишь его модуль Г. С учетом коэф-
фициента отражения составляющие векторов поля будут
выражаться формулой (4.22) при умножении составляю-
щих электрического вектора на множитель 1+Г, а состав-
ляющих магнитного вектора — на множитель 1 — Г.
Легко видеть, что между поперечной составляющей
электрического вектора, касательной к поверхности ра-
скрыва,
и поперечной составляющей магнитного вектора
имеет место соотношение, аналогичное (4.9), а именно
Е- = — 1/ Н. (4.23)
Если, далее, учесть, что между составляющими век-
торов по цилиндрическим и прямоугольным координатам
имеют место соотношения
Е = Е cos <р — Е„ sin <р,
Ej, = Ер sin ср 4* Е? cos ср, (4.24)
то приходим к выражениям для поля в раскрыве круг-
лого волновода Exs и Е равным (3.61) при умножении
правых частей последних на 1 Г.
Учитывая (4.23), а также множитель 1-J- Г, придем
к выражению для поля излучения в интегральной форме
вида (4.10) и (4.11), а подставив значение Е^, получим
следующие выражения для диаграмм направленности:
в /7-плоскости
FH = ^с os & + -р ,, / D \ _г + г k) fkD \2 ’ (4-25) 7 ’-(25sln9J
156
H-rmockocmh 6-плоскость
Рис. 4.7. Диаграммы направленности в Н- и Д-плоскостях круг-
лого волновода при волне TElt в нем. Сплошные кривые — теорети-
ческие, пунктирные — экспериментальные.
В Е-ПЛОСКОСТИ
РЕ=
'!+£
1 —г
+ -£-cos&) A!
(4.26)
Здесь А[ — лямбда функция [см. (3.68)].
Объемная диаграмма направленности может быть
определена из общего выражения для составляющих
поля излучения
£.=г>(‘+1 И7» <8>х
X^sin^P^), (4.27)
Е, == 2Т £° ^7“’(1 * * * * + Г) (cos & + T+F 1) (§) Т cos * Х
, (kD \
/j ( sin 0 1
X ~kD ' (4.28)
1 — ('25 sln®)
157
На рис. 4.7 приведены диаграммы направленности в Н- и
f-плоскостях для волновода круглого сечения Ч Расчетная
кривая . (сплошная) получена в предположении Г =0.
Экспериментальная кривая (пунктирная) снята на волне
Х = 3,2 см. Размер диаметра волновода D = 0,75X. Легко
видеть, что диаграммы направленности почти одинаковы
в /7-и ^-плоскостях.
Коэффициент направленного действия может быть
вычислен по формуле
1-г Т
1 4-г k
(4.29)
где Sk — площадь поперечного сечения волновода.
§ 5. СТРОГАЯ ПОСТАНОВКА ЗАДАЧИ
О ВОЛНОВОДНЫХ ИЗЛУЧАТЕЛЯХ
Для некоторых задач теории волноводных излучате-
лей найдено строгое решение [5], с которым вкратце
познакомимся здесь. Рассмотрим сначала плоский вол-
новодный канал, а затем круглый волновод при возбуж-
дении в последнем симметричных и несимметричных
волн.
а) Плоский волноводный канал
Имеем две идеально проводящие параллельные полу-
бесконечные пластины (плоский волноводный канал). Их
сечение и принятая система координат показаны на
рис. 4.8,а. Толщину пластин считаем бесконечно малой.
Ось X перпендикулярна к плоскости чертежа. В направ-
лении оси Z рассматриваемые пластины имеют протяжен-
ность от 0 до оо, а в направлении оси X от — оо до -f-oo-
Поле считаем независимым от координаты х, т. е. рас-
сматриваем случай распространения между пластинами
плоских волн. При этом возможна поляризация поля
двоякого рода: либо электрический вектор параллелен
оси X (поперечные электрические волны ТЕОл), либо маг-
нитный вектор параллелен оси X (поперечные магнитные
волны ТМ0/г).
!) Взяты из [21].
158
Наибольший интерес представляет случай, когда поле в
волноводном канале создается в результате набегания -на
края волновода волн типа ТМ00 = ТЕМ или ТЕОь Картина
линий поля набегающей волны этих типов показана на
рис. 4.8,6, в.
у.
РнС. 4.8. Плоский волноводный канал: а) расположение системы
координат для анализа; б) конфигурация электромагнитного поля
набегающей волны в поперечном и продольном сечениях при волне
ТМ00 = ТЕМ; в) то же при волне TEoi.
Решая задачу методом векторного потенциала, считаем
искомой величиной поверхностную плотность электрическо-
го тока J на верхней и нижней пластинах. Ток будет как
на внутренней, так и на наружной сторонах пластин. Под
суммарным током J понимается сумма этих токов. Зная
суммарный ток, можно будет найти и внутреннее и внеш-
нее электромагнитное поле. Определив отдельно внутрен-
нее и внешнее поля, можно будет затем определить отдель-
но ток на внутренней и на внешней сторонах пластин.
159
, Векторный потенциал А выражается через ток J сле-
дующим образом (см. (2.29)] *).
СО
-> Г* | р /Аг Г* ->
4кЛ=И J*_—ds=\J£)cK.
о
4-00 ______________
Г &-lk Пх-ер+^-^-Нг-С)’
J V(х-е)w-4)2+(2-c)a
—00
(4.30)
где x, у, z — координаты точки, в которой определяется
->
вектор А,
5, т), С — координаты точек интегрирования (точек
пластин).
Как известно,
+оо ____________
Г е-м /Д’ +-Е»
\ dt. = Jn Я<2) (kD),
J у £)2 _|_ £2 J 0 ' '
(4.31)
где Яд2’—ганкелева функция второго рода нулевого по-
рядка.
При интегрировании (4.30) следует учесть, что токи
протекают только по пластинам, имеющим координату
т\ = ±а (см. рис. 4.8,а). Поэтому (4.30) можно переписать
в следующем виде:
СО
4кЛ J 7(C) {Я2 (АУ^-.а^-Нг-С)2)4-
О
+ H[2\k Г(,у4-а)2 + (г - С)2)} < (4.32)
Вектор-потенциал А параллелен J. Направление J за-
висит от типа волны. У волн ТЕОл ток имеет направле-
ние, параллельное оси X, а у волн ТМОл—параллельное
оси Z. В этом легко убедиться из рис. 4.8, на котором
показаны поля этих волн при п = 0 (ТМ^) и л=1, (ТЕ0/),
учитывая, что направление тока перпендикулярно линиям
магнитного поля2. Следовательно, при волнах ТЕОл
Индексы »э* и „пов* здесь для сокращения опущены.
«) У = [пЯ]
160
A = Ax = J/e(Q {(kV(y~ a)2 + (z - Q2) +
0
± H™ (k /(j + a)2 + (z-Q2)} dC, (4.33)
где fE(')— искомая функция тока при волнах ТЕОл, а при
волнах
СО
А = 4 = 4-JГм(Q {Н™(k /(^-a)2+-(z-C)2) ±
О
± Я<2) (k /(_y+a)2 + (2_Q2)) л, (4.34)
где /Ы(С)— искомая функция тока при волнах ТМОп.
В обоих случаях положительный знак у второго сла-
гаемого под интегралом ставится при нечетных п, а от-
рицательный—при четных п, так как в первом случае
ток имеет одинаковое направление на верхней и нижней
пластинах, а во втором—противоположное.
Составляющие векторов поля определяются согласно
(2.26) через составляющие А, учитывая независимость
А от координаты х, а также то, что Лм = 0, следую-
щим образом:
при волнах ТВ„
1 ип
E=-J^A- Н=~д-^- Е=Е=0-,
нх — 0, (4.35)
при волнах ТМ„
„ 1 d*Az 1 ( д2Аг
р —______L р — 1 <____£ _1_ Ь2 л J.
у j^dydz ’ г >е0\ *)’
дАг <4-36>
^=-37: ^=0; яу=яг=о.
В качестве граничных условий принимается здесь ра-
венство нулю касательной составляющей электрического
вектора на пластинах, т. е. при j = и z>0. Эти
условия приводят к следующим уравнениям:
при волнах ТЕОл
00
= 0=Тf fB (Q { ^2)(Ф - С|) ± н <2) (^D2+(z-C)2)} Л
o’ (4.37)
H-I503 161
при волнах ТМОя
£.=°==;(£+
z о
±^2)(^/D2 + (z-C)2 )} dC, (4.38)
где D — 2a — расстояние между пластинами.
При волнах ТМол должно быть также выполнено усло-
вие fM(0) = 0, так как на краю пластин ток должен быть
равен нулю.
В (4.38) нельзя вносить оператор дифференцирования
под знак интеграла, так как линия интегрирования про-
ходит через точку М с координатой г, по которой осу-
ществляется дифференцирование.
Таким образом в строгой постановке задача о пло-
ском волноводном канале, как излучателе сводится либо
к интегральному уравнению вида
р(г-С)ПС)Л=0, (4.39)
О
либо к интегро-дифференциальному уравнению вида
00
(S + *2) J1 Л=о, (4.40)
где функция
/(г-0=4{я<2,(^|г-с1)±://02,(^ГР24-(г-С)2)}.
(4-41)
Нахождение f(C) из (4.39) и (4.40) позволит затем по
известному значению тока на плоскостях найти поле как
внутри волноводного канала, так и во внешнем простран-
стве.
б) Круглый волновод с симметричными волнами
На рис. 4.9 показан круглый волновод и принятая си-
стема цилиндрических координат г, р, <р. Ввиду симмет-
рии поля выбор начала отсчета угла tp не имеет значе-
ния. Поэтому направляем координатные оси так, чтобы
точка М, в которой определяется поле, имела коорди-
нату <р-= 0.
162
В данном случае будем также различать волны ТЕОп
и ТМОл. Картина линий поля волн ТЕОл и ТМОл для п=1
была показана на рис. 4.5.
Рис. 4.9. Круглый волновод, расположение систем координат
для его диализа и координаты точек.
Для решения задачи воспользуемся методом вектор-
ного потенциала. Вектор-потенциал, как указывалось
выше, связан с плотностью поверхностного тока соотно-
шением [см. (2.29)]
iff-* e~!kr
A=-^\)]Jt-rdS. (4.42)
Попрежнему через J обозначаем суммарный электри-
ческий ток на внутренней и внешней сторонах поверхности
волновода.
В данном случае
dS — adZdy,
г = У (z — С)2 4* (р — a cos <р)2 + a2 sin2 <₽ =
= У (z — С)2 4* р2 — 2а,э cos 4-fl2,
где а — радиус волновода.
Как видно из рис. 4.51), в случае волн ТЕОп ток будет
1) Учитывая, что J = —[nffj.
11*
163
иметь только одну составляющую по оси <р, а в случае
волн ТМОл — только составляющую по оси Z. Поэтому
можем писать
для волн ТЕОя
Со 2п ____________________
(* Р р—/Л У С)’Н- р*— 2ар cos
4iM = а | f (С) Л I _ ----- _ cos <pd<p,
т J J У (г — ?)а -f- ра— 2ар cos ® -f- а3
о о
(4-43)
для волн ТМОп
оо 2тс ____________________
Г С «—/Л Иг—С)’+ps—2ар cos <р + а*
4кЛ, = a \f (С) Л I /е______________= =•_-= = d<₽.
J J/(z — «)2 + р2~ 2apcos e-f-а2 T
о о
(4.44)
Как известно
e~jk V{z — C^+p’— 2op cos <p -f-a’
/(z-«)a + Pa — 2ap cos ® -|-aa
T J #o2’ (|/'(^2-w2) (p2 — 2aP cos <₽ + а2) е/а) (г “ Q'dw, (4.45)
—CO
причем, в свою очередь,
Я„2) ((/(k2 — w)2 (р2 — 2ар cos <р + а2)) =
т=-©о
Jm (Р/^2 — ®2 ) (а^k2 — w2 )
Jn (a\Tk2-w2)H^\p Уk2-w2)
(4.46)
здесь и ниже верхняя строчка соответствует г<Га, ниж-
няя—r>a.
Подставив (4.45) и (4.46) в (4.43) и (4.44) и выполнив
интегрирование по <р, получим:
для волн ТЕОя
00 -{~оо
4^=7^ jf(C)t/C j х
О —©о
Л (a Vk2 — w2) Н\2) (Р /F — w2) j
164
для волн ТМОя
00 -{-СО
faAt=jna (QdC j X
0 -—co
Jo (p Гk2 - w2) H™(a Vk2- w2) (г_^
Jo(a Vk2 — to2)//'2)(p ^2—to2)
(4.48)
Векторы поля через вектор-потенциалы выражаются
следующим образом:
при волнах ТЕОя
е, = -ЛМ,; и, = А (рлт); н = - | (4 w)
Е =Е =0; Н = 0, I
при волнах TMOrt
1 , \ 1 ам,
г |/ые0 \ dz2 + г / ’ р У“е0 дгд? ’
дА (4-50>
н = —Е =0, H=H=Q.
<р -dp ’ <р ’ z р
Поскольку на поверхности волновода, т. е. при г = а,
имеем в первом случае £^ = 0, а во втором Ez = 0, то
приходим к уравнениям для тока, аналогичным (4.39) и
(4.40), т. е.
при волнах ТЕОя
p(z-C)f(C)d; = O,
о
(4.51)
где
-{-СО
/(z — С) = ira j Ji (a Yk2—w2)Н\2\а f k2 w2) e'w (z~C)dw,
(4.52)
при волнах ТМОя
(<& + k2) J1 ~ <) f Ю = °’ (4’53>
165
где
Z (z — С) = тга j Jo (а /F — и>2) Я<2,(а V k2 — w2) ^z~^dw.
(4.54)
Таким образом, в случае симметричных волн в круг-
лых волноводах задача сводится к таким же уравнениям,
как в случае плоского волноводного канала. Отличие за-
ключается в разном виде функции l(z — С).
в) круглый волновод с несимметричными волнами
У несимметричных волн векторы электромагнитного
поля являются функциями угла <р. Требование однознач-
ности приводит к тому, что функции от имеют вид
sin (ту + ?о) или cos (тЧ + ?о),
где т — целое число (в данном случае отличное от нуля),
соответствующее порядковому номеру типа
волны,
<р0 — постоянный угол между плоскостью <р = 0 и
плоскостью узлов или пучностей векторов поля.
В случае несимметричных волн TMmn (поперечные
магнитные) электрические токи на поверхности волновода
имеют направление, параллельное оси Z (перпендикуляр-
ное магнитным линиям тока). Поэтому в данном случае
вектор-потенциал А имеет только одну составляющую Az,
В случае несимметричных волн ТЕтя (поперечные элек-
трические) токи на поверхности волновода имеют состав-
ляющие как по оси Z, так и по <р. Соответственно век-
тор-потенциал А также имеет составляющие Az и А^.
Следуя указанному выше приему приведения задачи
к интегральному или интегро-дифференциальному уравне-
нию, мы должны выразить Аг и А через соответствую-
щие составляющие тока (являющиеся искомыми) на по-
верхности волновода, затем, пользуясь полученными
таким путем выражениями для Az и А , должны вывести
выражения для составляющих поля, а к последним при'
менять граничные условия
£,=0 и £ =0
- Т
г—а г—а.
166
Легко видеть, что, идя по этому пути, мы придем
в данном случае к системе весьма сложных интегро-диф-
ферейциальных уравнений.
Следует еще учесть, что в случае несимметричных
волн в круглых волноводах необходимо рассматривать
совместно волны ТЕтл и ТМтл, так как у открытого конца
волновода происходит трансформация одних в другие.
Л. А. Вайнштейн [6], давший строгое решение задач
о волноводных излучателях при исследозании несиммет-
ричных волн в круглом волноводе, пошел по несколько
иному пути, который мы и рассмотрим.
Волны типа ТМтл будем характеризовать электриче-
ским вектор-потенциалом А3 , который имеет, как пока-
зано, только одну составляющую А3 = А3. Аналогично
волны типа ТЕтл можно характеризовать магнитным век-
тор-потенциалом Л", имеющим также одну составляющую
ЛМ = Л". Составляющие Е и Н по цилиндрическим коор-
динатам связаны с составляющими Лэ и Лм соотноше-
ниями
1
р У<о|*о д^дг ~ р д<е
В пространстве внутри и вне волновода, исключая
стенки, рассматриваемые как бесконечно тонкие, функ-
ции Лэ и Лм согласно (2.27) и (2.28) удовлетворяют вол-
новому уравнению, имеющему в цилиндрических коорди-
натах следующий вид:
1 л ( дА, \ , д*А, 1 д*Аг
т+?•#+кА^- (466)
Волновое уравнение имеет частные решения
71z = F(w)sin(p<p+<p0)e' н , (4.57)
где F (w)— коэффициент, независящий от пространствен-
ных координат и являющийся функцией от w,
w— постоянная разделения переменных, опреде-
ляющая фазовую скорость распространения
данной волны, v = \7k2— w2,
р — целое число,
J—функция Бесселя р-го порядка, справедливая
для области внутри волнозода,
Н—функция Ганкеля 2-го рода, р-порядка, спра-
ведливая для области вне волновода.
Общее решение для Аэ и Дм ищем в виде
Д’=вт(р<р + <ро) р/и’г
С

F{w)dw, (4.58)
Л“ =/cos(p<₽-|~ То) е>г
Jp(v?)H^(va)
Jp(ya)H^(v9)
G(w)dw,
(4.59)
где введенные функции F(w) и О (го) являются искомыми
функциями задачи. Верхняя функция в фигурных скобках
относится к области внутри волновода, а нижняя—к об-
ласти вне волновода.
Интегрирование проводится по контуру С в плоскости
комплексного переменного w.
Выбирается путь интегрирования вдоль вещественной
оси с огибанием снизу точек, соответствующих волновым
числам набегающих волн.
Функции от (р в (4.58) и (4.59) выбраны таким образом,
чтобы в выражениях (4.55) для составляющих Е и Н они
были одинаковыми у обоих слагаемых. Функции от р выб-
168
раны таким образом, чтобы при г = а и z<0, т. е. на
продолжении волновода Е^, Ег и Н(, были непрерывны.
Непрерывность остальных составляющих поля, а также
требование равенства
£р = £т = 0 (4.59а)
на поверхности волновода (р = а, z>0) обеспечиваются
следующим образом.
Напишем выражение для составляющих тока на по-
верхности волнозода, выражая их через соответствующие
составляющие магнитного вектора на поверхности
= — //z= cos(p<p4-(Po)( ^wzO(w)dw, (4.60)
Р—а—0 р—a-f-0 J
= H ~ /7 =sin(p-!• р р р-\ jkx ' '
где х — аргумент бесселевых и ганкелевых функций/
И Ч2).
Для обеспечения непрерывности составляющих магнит-
ного поля полагаем, что при г = аи z<0 составляющие
тока, определяемые уравнениями (4.60) и (4.61), равны
нулю
причем условие /г = 0 будет иметь место также и при
z = 0. Откуда получаем:
^e'azO(w)dw — 0 при z<0, (4.63)
+ G (tw)l е'a'zdw при z<0. (4.64)
169
Далее условие (4.59а) приводит к уравнениям
(wa)F(w) e!w2:dw = Q при z>0, (4.65)
( + Л = 0 пр» 2>0,
(4.66)
где
(wa) = 1ыаН’рт(ya) j'p (va), (4.67)
tp2(wa) = itvaH™ (va) Jp(va). (4.68)
Таким образом в результате выполнения сформулиро-
ванных выше условий получена система интегральных
уравнений (4.63) -г-(4.66). Из этой системы интегральных
уравнений должны быть определены искомые функции
F(w) и G(w). Зная эти функции, можем найти вектор-
потенциалы А и Л , а затем составляющие поля как
на внутренней, так ина наружной поверхностях волновода.
§ 6. РЕЗУЛЬТАТЫ СТРОГОГО РЕШЕНИЯ ЗАДАЧ
О ВОЛНОВОДНЫХ ИЗЛУЧАТЕЛЯХ
Не останавливаясь на деталях решения интегральных
и интегро-дифференциальных уравнений, полученных в пре-
дыдущем параграфе, с чем читатель может познакомиться
в цитированной работе [6], приводим ниже основные ре-
зультаты решения.
Рассматриваемые здесь задачи могут быть разбиты на
две группы:
а) в которых ток на поверхности волновода имеет толь-
ко одну составляющую по какой-либо из координатных
осей и является функцией только одной координаты z и
б) в которых ток имеет две составляющие по коорди-
натным осям и является функцией обеих координат.
К перзой группе относится плоский волноводный канал
при наличии в нем волн типов ТЕОя или ТМОя и круглый
волновод с симметричными волнами, а ко второй группе—
круглый волновод с несимметричными волнами.
Ввиду указанного различия исходных условий в зада-
чах этих двух групп имеет место некоторое различие в ха-
рактере получаемого решения.
170
В задачах первой группы искомая функция тока на по-
верхности волновода имеет следующий вид:
00
f (г) = В {e~lh‘ +2 Г,т + Q,(z)}. (4.69)
m=l
Здесь В —постоянный коэффициент пропорциональности,
h — волновое число волны, набегающей на край вол-
новода,
wm—волновые числа отраженных волн,
I — порядковое число набегающей волны (напри-
мер, wt = h),
т — порядковое число отраженных волн,
Q (z) — функция токов на наружной поверхности вол-
новода.
Коэффициенты Г/от под знаком суммы во втором сла-
гаемом выражения (4.69) означают при одинаковых ин-
дексах (Га) коэффициент отражения по току основной
(набегающей) волны, а при разных индексах — коэффи-
циент трансформации по току основной волны в волны
других порядков. Особенностью электромагнитных колеба-
ний, соответствующих первой группе задач, является то,
что тип колебаний (поперечное электрическое или попереч-
ное магнитное поле и соответствующее каждому из них
направление токов на поверхности) сохраняется в волно
воде таким, как у основной волны. На краю волновода,
наряду с обратной, основной волной, возбуждаются волны
других порядков, но того же типа, что и основная волна.
При электромагнитных колебаниях в волноводе, соот-
ветствующих второй группе 'задач, на краю волновода
возбуждаются обратная основная волна и волны других
порядков, а также волны другого типа. В частном слу-
чае, когда основная волна [является волной типа ТЕ//,
строгое решение задачи приводит к следующим выраже-
ниям для составляющих тока j и Jz\
00
4 = cos (<р + ?0) В {e-/ft* + £ Г, те'^г + Q,f (z)} , (4.70)
m-l
J,=sin (? + ?,) В {/1 —£ e-'“ + V -S Г, +
L °l “, °m
m-l
+ 5л.^'" + <3.й1. (4-71>
m-l
171
где 8 —корень т-ого порядка уравнения J;'(8) = 0,
Коэффициенты Г11п во втором слагаемом выражений
(4.70) и (4.71) имеют то же значение, что и выше, т. е.
они представляют собой в данном случае коэффициенты
Рис. 4.10. графики зависимостей от ка модулей коэффициента отра-
жения Ги волны ТЕП и коэффициентов трансформации Г12, Тп, Т]2
этой волны соответственно в волны ТЕ12, ТМП и ТМ12.
отражения или трансформации по току волны ТЕП в со-
ответствующие волны ТЕ;т. Коэффициенты Т 1т представ-
ляют собой коэффициенты трансформации по току волны
ТЕЯ в соответствующие волны типа ТМ/ОТ.
На рис. 4.10 приведены графики модулей коэффициен-
тов Г„, Г/2, Т„ и Т/2, а на рис. 4.11—графики фаз в;/
172
коэффициента отражения волны ТЕН и 9;2 — коэффициента
трансформации волны ТЕ;/ в волну ТЕ;2. На последнем
рисунке дан также график-^— так называемой поправ-
ки „на открытый конец", показывающей смещение узла
или пучности тока относительно края волновода.
Рис. 4.11. График зависимости от ка фазы 9И коэф-
фициента отражения волны ТЕц и фазы 9ц коэф-
фициента трансформации волны ТЕц в волну ТЕц
и поправки »на открытый конец .
Ток на наружной поверхности волновода не имеет
непосредственного практического интереса. Поэтому, не
вдаваясь в детали вопроса, ограничимся здесь замеча-
нием, что функции Qz и Q? убывают с удалением от
края волновода, причем на большом расстоянии от края
убывание происходит пропорционально некоторой сте-
пени z.
Точные выражения для диаграмм направленности (по
мощности, т. е. для Е2) открытого круглого волновода
при набегании волны ТЕ/7 имеют следующий вид:
173
в Е-плоскости
2 Zj(feasin9) ex(T/)4-x(ftasinO)
Fe ~ sin®9 | H\ (ka sin 9)| cos2 9 —cos2 9; X
I „ ода cos 9 —cos 9, 2 ,,
X j 1 — COS & 4- j_|_A2 j ^_cos9 > (4-7 )
В //-ПЛОСКОСТИ
r.2 Jifia sin 9) x(T/) + x(*asin»)
^(&)=sin®9|tf/(fea6iK9)|e • <473)
Последнее выражение должно быть еще умножено на
cos 9 — cos 9;
cos 9 -|- cos 9;
при размерах волновода, позволяющих прохождение волны
ТЕ;2, т. е. при
1,841 <£а< 3,832.
В формулах (4.72) и (4.73) использованы обозначения:
ka cos ft, = 8; = 1,841,
Ь = /(МЧ.
1 фл
A=nT--T- при р — 1,
2ka r г
+Аа
, . 1 f R (/ fe2— w2) ,
4г;) = т- I -------
J w — —L
—ka О
-[-ka sin 9 r____
i Г R^k2-i-w2 .
* (£a sin &)=-jr I ------.--T-rx- aw,
' ' Г J w — «sin 9
—ka sin ft
N, (x)
/?(x) = arctg7n7),
— функция Неймана,
J; — функция^Бесселя.
На рис. 4.12 сплошными линиями показаны точные диаг-
раммы направленности по мощности открытого круглого
волновода при возбуждении в нем волны ТЕц для ka = 2
174
Рис. 4.12. Диаграммы направленности в Е-и Я-плоскостях
(по мощности) круглого волновода при волне ТЕП в нем,
вычисленные точным методом (сплошные кривые) и при-
ближенным (пунктирные): а) прн ка = 2, б) при ка = 4.

(рис. 4.12,а) и ka = 4 (рис. 4.12,6). Пунктирными линиями
на этих рисунках показаны диаграммы направленности та-
кого же волновода, вычисленные приближенным методом
по формуле Кирхгофа (2.44) при условии, что в раскрыве
поле остается таким же, как у набегающей волны, а поле
на наружной поверхности волновода равно нулю. На диаг-
раммах учтен абсолютный уровень, получаемый в том и
другом случае.
Из диаграммы рис. 4Л2 видно, нто наибольшее расхож-
дение между точными и приближенными диаграммами име-
ет место при частотах, близких к критическим при ka = 2
(на критической частоте j«a|Kp = 1,841).
При диффракции от больших отверстий совпадение точ-
ной и приближенной диаграмм улучшается. Хорошее сов-
падение на каждой из диаграмм имеет место в передаем
полупространстве (при &> 120°). Следует помнить, что
на рис. 4.12 приведены квадратичные диаграммы. На ли-
нейных диаграммах различие увеличивается. При больших
углах с нормалью к раскрыву, а также в заднем полупро-
странстве приближенный метод, как мы видели выше, не
может дать правильного результата, что видно также из
приведенных здесь данных.
ГЛАВА ПЯТАЯ
РУПОРНЫЕ АНТЕННЫ
§ 1. ВВЕДЕНИЕ
Рупорные антенны не имеют в настоящее время доста-
точно строгой теории. Их исследование в основном прово-
дится указанным выше (см. гл. II, § 1) методом деления
задачи на две: внутреннюю и внешнюю.
Внутренняя задача у рупорных антенн решается сле-
дующим образом.
Рупор предполагается бесконечно длинным, а его
стенки—идеально проводящими. Находятся частные ре-
шения однородных уразнений Максвелла, соответствую-
щих J® =0 и JK = Q для такого рупора. Условия
J9—0 и 7м = 0 означают, что источники возбуждения
электромагнитного поля находятся вне рупора. Считается,
что из всех частных решений в соответствии со способом
возбуждения определяющее значение имеет решение, соот-
ветствующее волне низшего порядка. Далее предполагает-
ся, что при конечной длине рупора внутреннее поле в ру-
поре и в его раскрыве сохраняется таким, каким оно полу-
чается для бесконечно длинного рупора (невозмущенным).
Определив таким образом поле в раскрыве рупора, пе-
реходят к внешней задаче — вычислению электромагнитно-
го поля излучения,— которая решается методом диффрак-
ции на отверстии в плоском экране.
Следует заметить, что даже в такой упрощенной поста-
новке не удается провести исследования для всех разновид-
ностей рупорных антенн. При этом для облегчения решения
задачи заменяют реальную форму рупора другой, пример-
но ей эквивалентной, но более удобной для анализа. Напри-
12—1503 177
мер, в случае практически очень важного вида рупора —
пирамидального—прибегают к замене этой формы рупора
другой (названной здесь квазипирамидальной), правда,
очень близкой к исходной. Исследование квазипирамидаль-
ного рупора проводится обычным путем.
Характеристики излучения рупорных антенн, вычислен-
ные указанным здесь методом, подробно исследованы экс-
периментально и нашли достаточно хорошее подтвержде-
ние.
По рупорным антеннам известны некоторые теоретиче-
ские исследования, посвященные вопросу возбуждения
электромагнитного поля в рупорах. Ввиду математической
сложности вопроса эта область теории рупорных антенн
еще недостаточно развита. Однако выполненные работы
представляют интерес, особенно с точки зрения методики
исследования.
Рупорные антенны, характеризуются той особенностью,
что у них в раскрыве фазы поля не одинаковы и меняются
от середины к краям по квадратичному закону. На прак-
тике нашли применение некоторые методы коррекции фаз
в раскрыве рупорных антенн.
Ниже излагается решение внутренней и внешней задач
теории рупорных антенн, приводятся расчетные графики
характеристик излучения, излагаются некоторые методы
решения задач о возбуждении электромагнитного поля в
рупорах и описываются системы коррекции фаз в раскрыве
рупора.
§ 2. СЕКТОРИАЛЬНЫЙ РУПОР
У секториального рупора две противоположные стен'ки
являются параллельными плоскостями, а две другие расхо-
дящимися (см. рис. 1.2,а). Расстояние между параллель-
ными сторонами примерно равно расстоянию между соот-
ветствующими сторонами питающего волновода. Поэтому
одна из сторон разрыва, имеющего форму прямоугольни-
ка, сравнительно мала, а другая, наоборот, велика.
Полагая при анализе секториальный рупор бесконечно
длинным, нам будет удобно при исследовании внутрен-
него поля пользоваться цилиндрической системой коор-
динат у. р, (рис. 5.1). В исследуемом пространстве
внутри рупора (среда—воздух) электрические и магнит-
ные токи (У9 и /') равны нулю. Уравнения Максвелла
178
(2.1) при J9 = 0 и Vм = 0 для составляющих поля в цилинд-
рических координатах выражаются следующим образом:
1 д(рН ) 1 дН '
Т~дГ-7^-=^Еу'
1 дНу дН*_. „
~Р~д^----ду —/ffleo£p>
дн? дНу Р
— -^r=^s<A’
1 <^Р • о (5.1)
дЕ,„
дЕ„
ду
1
Р др
1 дЕу
Р
дЕР_______.
ду др

Исследуем частные решения уравнений (5.1), разделив
их, как в теории волнозодоз, на две группы, соответст-
вующие поперечным электрическим волнам ТЕтл и по-
перечным магнитным волнам ТМтл. В данном случае под
волнами ТЕтя понимаются такие, у которых равна нулю
радиальная составляющая электрического вектора (Е =
= 0), а под волнами ТМОТЯ — такие, у которых нулю равна
радиальная составляющая магнитного вектора (Яр = 0).
Поскольку в секториальных рупорах, как и в волноводах
прямоугольного сечения, на практике возбуждаются пре-
имущественно волны ТЕтя, то ими и ограничим здесь
исследование.
12* 179
Из волн ТЕтп рассмотрим здесь те из них, у которых
один из индексов (т ичи п) равен нулю, что соответст-
вует, помимо £р = 0, равенство нулю еще одной из со-
ставляющих электрического вектора (Еф = 0, либо Еу =
= 0). Волнам ТЕОл соответствует электромагнитное поле,
у которого электрический вектор имеет только одну со-
ставляющую Е , а волнам ТЕ;п0—поле, у которого элек-
трический вектор имеет только одну составляющую Е .
Секториальный рупор, в котором возбуждается поле
с электрическим вектором, параллельным большим пло-
скостям, показанным горизонтальными на рис. 5.1 (Е —
= Е ), называется Е-плоскостным рупором, а рупор, в
котором электрический вектор перпендикулярен большим
плоскостям (Е=Е ) называется /7-плоскостным. Рассмот-
рим отдельно оба вида рупоров.
а) Н-плоскостной рупор
В //-плоскостном секториально^ рупоре
Е = Е =0, Н =0.
р ° ’ у
Подставив (5.2) в (5.1), получим
с 1 д i и \ 1 дн?
J^aEy = 7 -(рТ/р---^,
• w 1 дЕУ
• и дЕУ I
/^0^ = -^- [
(5-3)
Уравнения (5.3) позволяют выразить Я и Н? через
Е . Следовательно, определиз Еу, можно будет найти и
^ртальные составляющие поля. Для Еу же, после под-
становки в первое уразнение (5.3) значений и из
остальных двух, получаем следующее дифференциальное
уравнение:
1 д / дЕ
—'s- Р —;—
Р др у др
1 д*Еу
р2 др2
(5.4)
где попрежнему & = шрСг0[х0=-^-.
180
Интеграл уравнения (5.4) ищем в виде произведения
двух функций, из которых одна 7?(р) зависит только от
р, а вторая Ф(<р) зависит только от <р.
^ = /?(Р)Ф(?). (5.5)
Подставив (5.5) в (5.4), получаем:
Ф (?) dr dR (р) I _R (?) dz<t> (?)
р dp [_Р dp ] р2 d?2
Разделим полученное уравнение на произведение /?(р)Ф(<р)
1 £ d Г dR (р) 1____________1____1_ d20 (?)
R(p) Р dp [Р dp ] Ф (?) р2 d?2
или
Ь2О2 I_____Р____d Г/^)
Р ' R (р) dp Р dp
1 d20 (?)
Ф (?) d?2
(5-6)
Левая часть уравнения (5.6) зазисит только от р, а
правая — только от ср. Они могут быть равны друг другу
лишь в том случае, если оба будут равны постоянной
величине. Обозначим эту постоянную через р2 и перепи-
шем (5.6) следующим образом:
£2р2 _1--Р_ А р АА ] — р2
К Р R (р) dp [Р dp J Р ’
_________1 d20(.)_ 2
Ф (?) d?2 р
Или, иначе,
+ (k2~ 4-} 7?(р) = 0 (5.7)
dp2 1 р dp 1 у Р2 / ' 7 ' '
^ + Р2Ф(?)-О. (5.8)
Интеграл уравнения (5.7) можно написать как линей-
ную комбинацию функций Ганкеля первого и второгорода
р-го порядка
R (р) = С}Н(" (^р) + С2^2) (£р), (5.7а)
а интеграл уравнения (5.8) — в виде тригонометрической
функции
Ф(<р) = 8т(р<р4-’?)- (5.8а)
Отсюда получаем:
= sin (р<р 4-Ф) [C^tk?) + C2H{p2\k?). (5.9)
181
Постоянные интегрирования Ch С2, р и ф определяются
из граничных и начальных условий. Граничным условием
является равенство нулю касательной составляющей
электрического вектора поля на стенках рупора, т. е.
£j, = 0 при tf> = rta. (5.10)
Согласно (5.10) имеют место равенства:
sin(pa + <p) = O. | 5П
sin(— ра + ф) = 0. J
Откуда, в свою очередь, получаем:
ра ф = /я,
— ра-\-$ = тк
или
ф = (5.12)
где i и т — любые целые числа. Так как вычитание из
ф целого числа л не изменит результата, то можем на-
писать
. i -+- т i — т
ф= к — ttln = —g— я.
Таким образом, окончательно получаем:
I X
ф = п 2 •
(5.13)
Постоянные С( и С2 определяем из следующих сооб-
ражений. Известно, что при больших значениях k? функ-
ции Ганкеля имеют асимптотические выражения
(5.14)
и
(5.15)
182
Так как зависимость от времени у нас принята в виде
(см. § 2, гл. II), то функция (&р) характеризует
на больших расстояниях от вершины рупора волну, бегу-
щую по направлению к вершине, а Н'у (£р) — соответст-
венно волну, бегущую от вершины в направлении увели-
чивающихся р. Если считать, как мы услозились, рупор
излучающим устройством, т. е. если ограничиться рас-
смотрением поля, волн, бегущих только в направлении
от вершины к раскрыву, то нужно положить С| = 0.
Что касается множителя С2, то он характеризует интен-
сивность поля.
Опуская индекс у множителя С2, окончательно полу-
чаем:
Еу = С sin ГЛк^+1у| С (йр),
L 4 ' J 2а
= “ С 777 ¥*cos ["к И + ^)] (йр)-
4 J 2а
(5.16)
В практически наиболее интересном частном случае
при п=1, волна ТЕ0| в секториальном рупоре имеет сле-
дующие составляющие поля:
^ = CcoSk£W^>(£p),
' 7 2а
Я = С -Л- cos \ Н™ (&р),
' 1 2а
Н = С -J— Sin (Z \ (йр).
Р уа>(*0 2ра ( 2а ) " ' г/
(5.17)
На рис. 5.2 показана конфигурация электромагнитного
поля в поперечном и обоих продольных сечениях рупора
при п=1, соответствующая уравнениям (5.17). Здесь и
ниже сплошные линии указывают направление электри-
ческого вектора, а штриховые — магнитного.
Из сравнения рис. 5.2 и рис. 4.2 видно, что картина
электромагнитного поля волн TEa„ в секториальном рупо-
ре подобна картине поля таких волн в волноводе прямо-
угольного сечения, только несколько деформирована по
183
сравнению с последней в соответствии с изменением формы
волновода, т. е. в соответствии с переходом от волновода
постоянного поперечного сечения к волноводу переменного
поперечного сечения, каким является рупор.
Для более детального анализа поля в секториальном
рупоре обратимся к формулам (5.16) и (5.17) и сравним
их с формулами (4.2) и (4.3). Из этого сравнения также
легко заключить о подобии волн ТЕОл в секториальном ру-
Рис. 5.2. Конфигурация электромагнитного поля волны ТЕМ в по-
перечном (а) и обоих продольных (б и в) сечениях Н-плоскостно-
го секториального рупора.
поре и волноводе прямоугольного сечения. Установим чер-
ты сходства.
Во-первых, в обоих случаях имеется только три состав-
ляющие поля, не равные нулю, из которых электрический
вектор параллелен, а магнитный перпендикулярен оси У.
Во-вторых, в обоих случаях составляющие поля имеют
сходную зависимость от координат. Действительно, со-
ставляющие поля Еу и у секториального рупора
меняются в зависимости от координаты <р при четных п
по синусоидальному закону; точно также у волновода
составляющие Еу и Нх меняются в зависимости от х.
Аналогично Hf у секториального рупора выражается
такой же функцией от <р, как Н2 у волновода от х.
184
В обоих случаях электромагнитное поле не зависит
от координаты у. Зависимость поля от координаты р в
секториальных рупорах- определяется ганкелевой функ-
цией, имеющей асимптотическое выражение (5.15), подоб-
ное множителю e~/iz, выражающему у волноводов зави-
симость поля от координаты г.
В-третьих, индекс п у секториальных рупоров, как
и у волноводов, характеризует количество стоячих полу-
волн между стенками, параллельными электрическому
вектору поля.
Таким образом, если .учесть, что цилиндрическим ко-
ординатам в секториальном рупоре <р, у, р соответствуют
в волноводе прямоугольные координаты х, у, г, а состав-
ляющим поля в рупоре Еу, и Н соответствуют в
волноводе составляющие поля Е , Нх и Нг, то подобие
электромагнитного поля в секториальном рупоре и вол-
новоде прямоугольного сечения проявляется в одинаковом
направлении векторов поля1), одинаковой зависимости
векторов поля от соответствующих координат и в одина-
ковой картине стоячих волн.
Наряду с указанными чертами сходства полей в ру-
поре и волноводе следует отметить также некоторые их
отличия.
Во-первых, в секториальном рупоре электромагнитное
поле имеет характер цилиндрической волны в отличие
от простого волновода, где оно имеет характер плоской
волны. В секториальном рупоре точки одинаковой фазы
лежат на цилиндрической поверхности р = const, по-
скольку переменным фазовым множителем является
(&р), а в волноводе — на плоскости z = const, так как
Тл
аналогичным фазовым множителем является е~пг.
Во-вторых, на больших расстояниях от вершины ру-
пора электромагнитное поле становится чисто попереч-
ной волной, распространяющейся со скоростью света
с=3-1С8^., так как на таких расстояниях можно пренеб-
речь составляющей поля Н по сравнению с Н^, а ган-
келеву функцию можно заменить ее асимптотическим вы-
’) По отношению к существующим координатным осям.
185
ряжением. Действительно, критерием больших расстоя-
ний, как видно , нз сравнения Hf и , является неравен-
ство
, . ПК
или
йр>^. (5.18)
В левой части неравенства (5.18) имеется аргумент ган-
келевой функции, а в правой ее порядок. Как известно, не-
равенство (5.18) является также условием, позволяющим
заменить ганкелеву функцию ее асимптотическим выраже-
нием (5.15).
Учитывая оказанное, можно при выполнении (5.18) за-
менить (5.16) следующими формулами для составляющих
поля:
Н^Ну = 0- Е=Е =0.
В-третьих, фазовая скорость в рупоре не постоянна.
Она имеет в областях более близких к вершине, большую
величину, а с удалением от вершины — уменьшается,
приближаясь к с = 3-108. Математически это выте-
CCfC
кает из характера ганкелевой функции, имею-
щей комплексное значение, аргумент (фазовый угол)
которого непрерывно меняется при изменении kp следую-
щим образом. При малых kp, как видно из рис. 5.3,
фазовый угол меняется медленно, имея на большом уча-
стке величину, равную 90° (что соответствует зоне ин-
дукции, находящейся вблизи вершины рупора); затем при
сравнительно больших значениях kp фазовый угол непре-
рывно меняется по прямой (что соответствует зоне оф==
— с), а между малыми и большими значениями kp нахо-
дится переходный участок (зона плавного изменения иф).
Физически это явление объясняется тем, что фазовая
скорость зависит от расстояния между стенками, ,парал-
лельными электрическому вектору поля. Так как в ру-
поре это расстояние меняется, то меняется и фазовая
скорость.
186
В-четвертых, в рупоре, в отличие от волноводов, нет
критической длины волны 2кр. Это означает, что принци-
пиально в рупоре могут распространяться волны любого
порядка с любым индексом п. Объясняется эта особенность
тем, что наше исследование относится к бесконечно длин-
ному рупору, у которого при любом конечном значении п
Рис. 5.3. Зависимость фазового угла ганкелевой функции от ее не-
зависимой переменной.
может быть найдено значение р, удовлетворяющее нера-
венству (5.18).
Следует отметить, что мы здесь определяли возможные
частные решения уравнений Максвелла (2.1), отвлекаясь
от вопроса о методе возбуждения электромагнитного поля
в рупоре. Поэтому, придя к выводу о принципиальной воз-
можности, из-за отсутствия критической частоты, возбуж-
дения в рупоре волн ТЕо„ любого порядка (с любым ин-
дексом п), мы не получаем из данного исследования от-
вета на вопрос об условиях возбуждения волн того или
иного порядка.
На практике Я-плоскостной секториальный рупор воз-
буждается волноводом прямоугольного сечения, в котором
187
распространяется волна TEot- В секториальном рупоре в
основном сохраняется волна того же порядка, которая име-
ется в возбуждающем волноводе.
Итак, электромагнитное поле волн ТЕОл в //-плоско-
стном секториальном рупоре с точки зрения направления
векторов поля, их зависимости от координат и картины
стоячих волн подобно полю того же порядка в волноводе
прямоугольного сеченйя. Однако пэ ряду существенных
признаков поле волн ТЕ0/г в /f-плоскостном рупоре отли-
чается от поля в волноводе. Основные из них следую-
щие:
а) фазовая скорость является переменной величиной;
б) отсутствует критическая длина волны Лкр;
в) фронт волны образует цилиндрическую поверхность
с осью на линии пересечения боковых стенок рупора;
г) поле на больших расстояниях от вершины принимает
характер чисто поперечной волны, распространяющейся со
скоростью света.
Мы рассмотрели поле внутри //-плоскостного рупора.
Теперь перейдем к анализу поля излучения этого рупора.
Как мы видели в предыдущей главе, при расчете поля
излучения из открытого конца волновода в переднем полу-
пространстве можно принять, при относительно больших
размерах поперечного сечения, что поле в раскрыве оста-
ется невозмущенным, т. е. равно полю набегающей волны.
Эго положение справедливо в отношении применяемых на
практике //-плоскостных секториальных рупоров.
Как указывалось выше (гл. I), раскрыв рупора явля-
ется плоским (см. рис. 1.2), а его продольное сечение име-
ет форму треугольника (рис. 1.3). Поскольку фазовый
фронт волны образует цилиндрическую поверхность, в рас-
крыве рупора фазы поля будут различны в разных точках.
Для расчета фаз на рис. 5.4 воспроизведено продолыное
сечение рупора. Пунктирная линия В'С' есть линия по-
стоянных фаз поля в этом сечении.
Примем фазу поля в точке О' равной нулю. В точке М,
находящейся на расстоянии х от точки О', фаза поля от-
станет на величину
__ 2” Г 1 х2 1 х4 , 1
— х I 2 у? 8 /?з + •••] (5.20)
188
Обычно у рупоров ширина раскрыва D значительно
меньше длины рупора R. Поэтому можно в (5,20) поло-
жить x<^.R. Тогда получим
Согласно обозначениям рис. 5.4
Рис. 5.4. К расчету фаз в раскрыве
секториального рупора.
Подставив (5.22) в уравнения (5.19), учтя (5.20) и (5.21)
и полагая равенство нулю фазы поля в точке О’, т. е.
(5.23)
получим для составляющих поля в раскрыве ff-плоско-
стного секториального рупора следующие выражения:
£ = Еп cos fir -у-) е
Е
S 120- ’ /
где
(5.24)
Учитывая, что х < R, обычно при расчетах
лучения полагают в (5.24)
-2L^i,l
} R2TX‘
<f X
27 " 1) ’
я S-Я
ф '
поля из-
(5.25)
189
где — касательная к кривой В'О’С', а Нх — параллель-
ная к прямой ВО'С.
Подставив (5.25) в (5.24), получаем:
. ГС X*
Ey = E0cos •^-'je х Л , I
Е (5-26)
Н = —
X 120TV )
Уравнения (5.26), за исключением некоторых обовначе-
ний, тождественны уравнениям (3.127).
Таким образом, задача об излучении из раскрыва Н-
плоскостного рупора приводится к задаче о диффракции от
прямоугольного отверстия в плоском экране при квадратич-
ном законе изменения фаз, рассмотренной в главе III.
Плоский раскрыв секториального рупора имеет форму
прямоугольника со сторонами Д и D2. Обозначим через Di
сторону, перпендикулярную вектору электрического поля,
а через D% — сторону, параллельную ему. Длину //-плос-
костного рупора обозначим через Ri.
На рис. 5.5а и 3.19,а приведены графики зазисимости
удельного коэффициента усиления Я-плоскостного сек-
ториального рупора от -у- . Отдельные кривые соответ-
D
ствуют различным значениям-^-. Размер раскрыва D2 =
= 1, При D2^=X приведенные значения GH на рис. 5.5,а
следует умножить на ~. Кривые вычислены по фор-
муле (3.145). Из кривых видно, что для каждой заданной
R,
длины рупора -у сущестзует определенная ширина рас-
крыла , при которой коэффициент усиления имеет
максимальное значение.
Рупоры, у которых размеры соответствуют точкам мак-
симума кривых коэффициента усиления, называются опти-
мальными. На рис. 3.19,а пунктирная кривая показывает
коэффициент усиления оптимальных рупоров.
1) Коэффициент полезного действия рупорных антенн практи-
чески равен единице. Поэтому у них коэффициент усиления и ко-
эффициент направленного действия совпадают.
190
a)
— Рис. 5.5. Графики зависимости-удельного коэффициента усиления //-плоскостного (а) и Е- плоскостного (б)
— секториальнных рупоров от относительной длины широкой стороны раскрыва при различных значениях отно-
сительной длины рупора. Ширина узкой стенки рупора принята равной длине волны.
Кривые рис. 5.6,а показывают зависимость от
угла &, соответствующего различным относительным
уровням в диаграмме направленности //-плоскостного
секториального рупора в //-плоскости. Эти кривые могут
быть использованы для вычерчивания главного лепестка
диаграммы направленности.
Г).
Рис. 5.6. а) зависимость от — угла О, соответствующего различным
относительным уровням (по амплитуде) диаграммы направленности
//-плоскостного секториального рупора в //-плоскости; ff) то же,
г-»
соответственно, от —£ для h-плоскостного секториального рупора в
X
^-плоскости.
Ввиду малых размеров стороны D2 фазы поля вдоль оси,
параллельной этой стороне, могут считаться постоянными и
диаграмма направленности этого рупора в £-плоскости мо-
жет быть рассчитана по формуле (3.18) или, точнее, по
формуле (4.15) с учетом того, что у = к и подстановки со-
ответствующего рупору коэффициента отражения Г.
192
б) Ё-плоскостной секториальный рупор
В f-плоскостном секториальном рупоре
Е = £„ = 0, Н = 0.
ру Т
Подставив (5.20) в (5.1), получим
__ дн9 дну
JweoE<p — ду др ’
-/^^=7-^-’
• W дЕ°
(5.27)
(5.28)
Выразим Н и Нf через Е* и их значения подставим
в первое уравнение (5.28). Это приведет к следующему
дифференциальному уравнению для :
, =_б_ г 1 а(Р£т)|
'? др L р др J "Т- ду*
(5.29)
Уравнение (5.29) решаем указанным выше методом
разделения переменных.
Полагаем:
E,=W)Y(y). (5.30)
Подставив (5.30) в (5.29), разделив переменные и при-
равняв обе части постоянной величине, получаем:
Ё!Ш) + р2Г(?)=0 (5.31)
?ВД + 1^(Р)+^2_Р2_ iWp) =0.. (5.32)
Интегралами уразнений (5.31) и (5.32) являются
y(y) = sin(p_y-f-<p), (5.33)
R(?) = CH\2\PVk^). (5.34)
В формуле (5.34) уже учтено, что электромагнитная
волна распространяется от вершины рупора к раскрыву.
13.^1503 193
Постоянные интегрирования определяем из услози i
£ф = 0 при =
откуда получаем:
тп . тк
P = D^
(5.35)
Подставив (5.33) н-(5.35) в (5.30), а полученное выра-
жение в (5.28), приходим к следующим выражениям для
соответствующих составляющих поля:
= С sin [т- (^ + 4) ] н\2) (YP)>
ну=~ чsin Н (4+^)] я°2) ш
Т^- тг cos Г ms (— -|- 4 s)] Н™ (ур),
/, , /тк\2
k W ’
(5.36)
При волна TE10 в Е-плоскостном секториаль-
ном рупоре имеет следующие составляющие поля:
Е ^Ccos^tf^Crp),
Н = —~ у cos Я<2) (yp),
Н =- — — sin7^ E(2)Yyp)
р j^oDi ьи Dj 1 НРА
(5.37)
На рис. 5.7 показана конфигурация электромагнитного
поля волны ТЕ|0 в поперечном и обоих продольных сече-
ниях Е-плоскостного секториального рупора, соответст-
вующая уравнениям (5.37).
Из сравнения рис. 5.7 с рис. 4.2 видно, что картина
электромагнитного поля волны ТЕ/0 в Е-плоскостном
секториальном рупоре подобна картине поля волн ТЕ/0
в волноводе прямоугольного сечения 1), но несколько де-
’) В волноводах прямоугольного сечения волны ТЕто и ТЕ0Л
при т = п идентичны.
194
формирована по сравнению с последней. Из анализа же
формул (5.36) и (5.37) можно заключить, что волны в Е-
плоскостном секториальном рупоре имеют еще больше
В)
Рис. 5.7. Конфигурация электромагнитного поля волны ТЕ10 в попе-
речном (а) и обоих продольных (б и в) сечениях" Е’-плоскостного
секториального рупора.
черт сходства с аналогичными волнами в волноводе, чем
волны в //-плоскостном секториальном рупоре. Действи-
тельно, ганкелевы функции в (5.36) и (5.37) имеют сле-
дующие асимптотические выражения:
(5.38)
Формулы (5.38) показывают, что в данном случае
фазовая скорость уфна больших расстояниях от вершины
13* 195
не равна с = 3-108 Mjcex, а имеет такую же величину,
как в волноводе
где X—рабочая длина волны,
Лк —критическая длина волны.
В соответствии с этим волны в ^-плоскостном секто-
риальном рупоре характеризуются критической волной
Л =—-L и, строго говоря, не становятся чисто попереч-
ными так же,, как аналогичные волны в волноводе.
Практически поперечные волны в ^-плоскостном ру-
поре имеют место при выполнении условия
2Di k^>~. (5.40)
При этом условии
у—V,—и //<//.
I 1 ф р <р
Фронт волны — поверхность одинаковых фаз поля в Е-
плоскостном секториальном рупоре представляет собой ци-
линдрическую поверхность, как и в //-плоскостном рупоре.
Указанная выше деформация поля в Е-плоскостном ру-
поре по сравнению с полем в волноводе выражается в том,
что электрический вектор поля направлен по дуге окруж-
ности с центром в вершине рупора, идущей от одной боко-
вой наклонной стороны рупора к другой. Кроме того, векто-
ры поля сохраняют постоянное значение вдоль этой дуги,
а не вдоль’ прямой, параллельной оси У, как в волноводе.
Перейдем к определению электромагнитного поля излу-
чения Е-плоскостного секториального рупора. Будем его
вычислять, исходя из условий сохранения в раскрыве не-
возмущенного поля падающей волны и выполнения нера-
венства (5.40). При этих условиях фазы поля в раскрыве
определяются по формуле (5.21), а амплитуды поля опре-
деляются из соотношений
|£?l = E0cos^ ,
где Ео — амплитуда поля на оси рупора (_у = 0),
Н (5.41)
120л
196
При малых углах раствора рупора 2а можно положить
Е ~Е
т
где ось X—’Одна из прямоугольных координат, парал-
лельная большой стороне плоскости раскрыва.
Таким образом, в случае ^-плоскостного рупора состав-
ляющие поля в раскрыве имеют приближенно следую-
щие значения:
Е =E0cos£p е
Ег
Н х
У 120л1
(5-42)
Выражения (5.42), кроме взаимозамены обозначений
координат х и у, ничем не отличаются от (3.128).
Характеристики f-плоскостного секториальаого рупора
могут быть определены по графикам рис. 5.5,6, 5.6,6 и
3,19,6. На рис. 5.5,6 и 3.19,6 приведены кривые зависи-
мости удельного коэффициента усиления Е-плоскостного
секториального рупора от относительной ширины его
о,
раскрыва -у- для различных относительных длин рупора
у- при ширине второй стенки рупора = При
приведенные значения коэффициента усиления на
рис. 5.5,6 и 3.19,6 следует умножать нау-.
Как видно из рисунка, Е-плоскостные рупоры также
характеризуются оптимальными параметрами — и .
Пунктирная линия на рис. 3.19,6 соответствует рупорам
с оптимальными параметрами.
Рис. 5.6,6 может быть использован для расчета главного
лепестка диаграммы направленности Е-плоскостных рупо-
ров в Е-плоскости. Цифры на кривых указывают уровень
поля по отношению к полю на осевом направлении.
Ввиду малых размеров стороны Dt фазы поля вдоль оси,
параллельной этой стороне, могут считаться постянными и
диаграмма направленности этого рупора в Е-плоскости мо-
жет быть рассчитана по формуле (4.14) при подстановке
соответствующего рупору коэффициента отражения Г.
197
§ 3. ПИРАМИДАЛЬНЫЙ РУПОР
Пирамидальный рупор показан на рис. 1.2,6 и в. Элек-
тромагнитное поле в таком рупоре теоретически не исследо-
вано. Трудности теоретического исследования поля пирами-
дального рупора связаны с тем, что его стенки не являются
поверхностями с постоянным значением какой-либо коорди-
наты в ортогональной системе координат. В данной задаче
это обстоятельство затрудняет определение постоянных ин-
тегрирования дифференциальных уравнений поля из гра-
ничных условий.
Некоторое представление о характере поля в пирами-
дальном рупоре можно получить, обобщая данные анализа
поля в секториальном рупоре, приведенные в § 2, и данные
приведенного ниже в § 5 анализа рупора, близкого по фор-
ме к пирамидальному.
По этим данным, а также по результатам эксперимен-
тального исследования коэффициента усиления и диаграмм
направленности можно заключить следующее.
Обычно пирамидальный рупор питается волноводом,
в котором формируется волна TEOi. Этот тип волны сохра-
няется и в рупоре. Но в пирамидальном рупоре волна TEoi
отличается от волны ТЕ0) в волноводе. Во-первых, фронт
волны (поверхность одинаковых фаз поля) в пирамидаль-
ном рупоре является сферой с центром в вершине рупора
в случае остроконечного рупора, либо несколько искаженной
криволинейной поверхностью, близкой к сфере, в случае
клинообразного рупора. Во-вторых, на больших расстояниях
от вершины электромагнитное поле практически мало от-
личается от чисто поперечного поля, т. е. на больших’рас-
стояниях от вершины очень мала и может быть принята
равной нулю продольная — радиальная составляющая век-
торов Е и Н, сами же векторы могут считаться касатель-
ными к поверхности фронта волны.
Электромагнитное поле излучения пирамидальных ру-
порных антенн рассчитывается методом диффракции от
прямоугольного отверстия в плоском экране, рассмотрен-
ном в главе III. Исходным при расчете по этому методу
является значение поля в раскрыве рупора.
Амплитуды поля в раскрыве рупора при малых углах
раствора (см. рис. 1.3) можно считать меняющимися в зави-
симости от координат точек раскрыва по тем же законам,
по которым меняется поле в поперечном сечении питающего
волновода. Если направить оси координат, как показано та
198
рис. 5.8, то амплитуды поля в раскрыве будут меняться
лишь в зависимости от координаты х (при волне TEoi—по
косинусоидальному закону) и не будут зависеть от коорди-
наты у. Направление векторов поля будет следующее: век-
тор Е параллелен оси Y, а вектор Н — оси X.
Фазы поля в раскрыве рупора можно определить ана-
логично- тому, как определились фазы поля в случае
//-плоскостного секториального рупора.
У
Рис. 5.8. К анализу пирамидального рупора.
Найдем разность длин отрезков ОМ и ОО1 (рис. 5.8).
Обе точки М и О’ лежат в плоскости раскрыва. Первая —
произвольная точка, вторая — центр раскрыва. Искомая
разность будет равна
(5.43)
где через R обозначен отрезок ОО', т. е. длина рупора.
Если принять фазу поля в центре раскрыва О' рав-
ной нулю, то в точке М фаза поля с точностью до вели-
чин второго порядка малости будет равна
Ф I П
Чл \\R ' R J
(5.44)
Формула (5.44) соответствует остроконечному рупору.
В случае клинообразного пирамидального рупора, имеюще-
го промежуточную форму между секториальным и остроко-
199
печным пирамидальными рупорами, можно считать с при-
нятой точностью
, а,
м X у R j /
(5.45)
где и /?2 — расстояния от центра раскрыва до линий
пересечения соответствующих противолежащих пар сторон
рупора.
Учитывая сказанное, можно вести расчет поля излучения,
пользуясь следующими выражениями для составляющих
векторов поля в раскрыве пирамидального рупора:
Еу EQ cos е- / т (£' +
Н s- Еу .
х 120 л ’
Е^ЕХ^О-, H^Hy^Q.
(5.46)
Электромагнитное поле, определяемое формулами (5.46),
тождественно полю, определяемому уравнением (3.129).
Как отмечалось в главе III при анализе такого поля и как
это следует также из сопоставления формул (5.46) с фор-
мулами (5.26) и (5.42), распределение амплитуд и фаз по-
ля в раскрыве векториального рупора является частным
случаем распределения поля в раскрыве пирамидального
рупора. В соответствии с этим диаграмма направленности
//-плоскостного секториального рупора в //-плоскости полу-
чается такой же, как у пирамидального рупора в //-плос-
кости, а диаграмма направленности ^-плоскостного секто-
риального рупора в /J-плоскости — как у пирамидального
рупора в f-плоскости. То же можно сказать и о других ха-
рактеристиках излучения: коэффициенте усиления и т. п.
Поэтому приведенные выше графики рис. 5.5 и 5.6 могут
служить для определения соответствующих характеристик
пирамидального рупора.
Коэффициент усиления пирамидальных рупоров G мо-
жет быть определен с помощью графиков рис. 5.5 и 3.19,
причем коэффициент усиления пирамидального рупора свя-
зан с соответствующими коэффициентами усиления секто-
риальных рупоров GH и G£ по формуле (3.148).
~ 32 (pf ' (/57 1
200
Подобно секториальный рупорам пирамидальные ру-
поры также характеризуются оптимальными размерами
— ’ Т’ Т и Т'
Графики рис. 5. 6 могут служить для определения глав-
ного лепестка диаграммы направленности оптимального пи-
рамидального рупора в И- и f-плоскостях.
Рис. 5.9. Зависимость оптимальных значений длины и размеров
раскрыва пирамидального рупора от коэффициента усиления.
На рис. 5.9 приведены графики зависимости оптималь-
ных размеров остроконечного пирамидального рупора от ве-
личины коэффициента усиления G.
Рис. 5.10 иллюстрирует диаграмму направленности
одного из оптимальных пирамидальных рупоров, имею-
щего Di — 11,52, D2 = 9,4l, R — 41X. Коэффициент усиле-
ния этого рупора равен Ges900 (28 дб)>
201
Как видно из рис. 5.10, диаграмма направленности
в ^-плоскости аналогична приведенной на рис. 3.18, рас-
считанной для постоянных амплитуд при фмакс = -|- • Диа-
грамма направленности в Д-плоскости характеризуется
малым уровнем побочных лепестков, что является след-
ствием косинусоидального закона изменения амплитуд
поля в направлении, параллельном магнитному вектору
поля.
Мы до сих пор рассматривали прямоугольные рупоры
(векториальные и пирамидальные), возбужденные линейно-
Рис. 5.10. Диаграммы направленности оптимального остроконечного
пирамидального рупора с размерами Oj = ll,5X, D2 = 9.4Х, R ~ 41 X в
//-плоскости (левая пунктирная кривая) в //-плоскости- (правая
сплошная кривая).
поляризованной волной (TEOi или ТЕю), которая получается
при питании рупора непосредственно от стандартного вол-
новода прямоугольного сеченния со сторонами £>i : D2=2 : 1.
В ряде практических случаев применяются рупоры, воз-
бужденные волной с круговой поляризацией. Такое возбуж-
дение осуществляется следующим образом. Стандартный
волновод плавным переходом переводится в волновод квад-
ратного или почти квадратного сечения, причем так, что
широкая стенка стандартного волновода остается парал-
лельной диагонали сечения квадратного волновода. При
этих условиях в квадратном волноводе возбуждаются как
волна ТЕ01, так и волна ТЕю, обе линейно поляризованные,
по с электрическими векторами, повернутыми на 90° друг
относительно друга. Для получения круговой поляризации
необходимо, чтобы амплитуды полей обеих волн были оди-
202
наковы, а фазы сдвинуты на 90°. Равенство амплитуд обес-
печивается соответствующим устройством плавного перехо-
да, а сдвиг фаз — различием фазовых скоростей волн TEOi
и ТЕю и выбором соответствующей длины квадратного вол-
новода от плавного перехода до рупора. В свою очередь раз-
личие фазовых скоростей обеспечивается либо помещением
в квадратном волноводе диэлектрической пластинки парал-
лельно одной из стенок волновода, либо небольшим расхож-
дением в ширине сторон «квадратного» волновода.
Получить точно круговую поляризацию — чрезвычайно
трудная задача. Обычно получается поляризация эллипти-
ческая с соотношением осей эллипса, близким к единице.
В случае эллиптической поляризации электромагнитного
поля характеристики излучения антенны могут рассчиты-
ваться по приведенным выше формулам и графикам для
каждой линейной составляющей поля.
§ 4. БИКОНИЧЕСКИЙ РУПОР
Биконический рупор представляет собой, как отмечалось,
волноводный канал переменного сечения. Прежде, чем при-
ступить к изложению теории биконического рупора, рас-
Рис. 5.11. Простой волноводный канал посто-
янного сечения (с параллельными проводя-
щими плоскостями).
смотрим для сравнения характер электромагнитного поля
в простом волноводном канале постоянного сечения, т. е.
между двумя параллельными плоскостями (рис. 5.11).
Введем цилиндрическую систему координат у, р, ср.
Ограничимся рассмотрением случая круговой симметрии
203
поля относительно оси К, т. е. случая волн ТЕОл и ТМОл,
характеризуемых соотношением
= 0; ^ = 0. (5.47)
d<f cty ' '
Волны ТЕОл, кроме того, определяются еще и сле-
дующим условием:
£=Е =0; Я=0. (5.48)
Условие (5.48) полностью совпадает с (5.27) и поэтому
для составляющих поля волн ТЕОл действительны фор-
мулы (5.36).
У волн ТМОп вместо (5.48) имеют место равенства
^=о; Wp=^=o. (5.49)
Ввиду симметричности уравнений Масквелла относи-
тельно электрического и магнитного векторов поля и
подобия условий (5.48) и (5.49) мы получим в случае
волн ТМОл для составляющих векторов поля выражения,
аналогичные (5.36), но с перестановкой электрического и
магнитного векторов, а именно:
НЧ = С cos + 4) ] (М
Ev — у cos [пк (-£ I -//<2)(ур),
У \ D 1 2 j J о
Е — -Я- sin Гпк (£ + 4-Л -Я(2) (ур),
р juzt.:D L 2/J 1 У,Г/
(5.50)
где D — расстояние между плоскостями (см. рис. 5.11).
При П — 0 волна ТМОл переходит в чисто поперечную
волну ТМ00 (ТЕМ), которая имеет только одну поперечную
составляющую электрического вектора Еу и одну попе-
речную составляющую магнитного вектора Н^. Эти со-
ставляющие равны
H4 = CH*\kP),
E=cJ-H™(kP). (5.51)
У jcoe0 о ' ' •
204
При п=1 волна ТМ01 в простом волноводном канале
имеет следующие составляющие поля:
(М
(YP)> (5.52)
На рис. 5.12 показана конфигурация электромагнит-
ного поля в простом волноводном канале для волн ТЕМ,
ТМ01 и ТЕ01, соответствующая формулам (5.43), (5.51)
и (5.52). Обозначения прежние. Волна ТЕМ в данном слу-
чае идентична с волной ТЕ01 в Н-плоскостном сектори-
альном рупоре, имеющем угол раствора 2а = 360°. Ана-
логично волна ТМ01 идентична с волной ТЕи в Н-пло-
скостном секториальном рупоре, а волна ТЕЭ1 с волной ТЕ)0
в Е-плоскостном секториальном рупоре.
Перейдем к рассмотрению электромагнитного поля
в биконическом рупоре. Рупор считаем двухсторонним
с конусами, симметрично расположенными относительно
оси (см. рис. 5.13а). Вводим сферическую систему коор-
динат г, &, <р. Уравнения Максвелла (2.1) для составляю-
щих поля в сферических координатах при Z = 0, JM = 0
выражаются следующим образом:
1 Г д dH&l
-4-5- (sin &н ) - -4 = Ё»е0Е ,
г sin & t' df } J ° r
1 Г 1 dfIr d . „ .1 . д.
T [sM 17 ~ oT (rHv) J
1 r<J(r^) .
r[ dr <59 J — 7Ш£оДр-
1 Г д дЕ^-]
(sin ~ 17 J = ~J^oHr’
т [ет di ~ =—/“Л’
1 [^_^]=_>Ион .
— L dr dft J J ro т
(5.53)
В данном случае также ограничимся рассмотрением
полей, имеющих осевую симметрию, т. е. волн ТЕОл
и ТМОл.
205
в)
Рис. 5.12. Конфигурация электромагнитного поля в простом волно-
водном канале для волн ТЕМ, ТМ01, ТЕ01.
У волн ТЕ0 имеют место соотношения
£г=£#=0; Я =0.
Подставив (5.54) в (5.53), получим
1 p(rtf8) дНД )
г | tir с*0 J <р’ I
1 4 (sin &Е ) = —j^oH
г sin 9 от' Г J и г’
(5.54)
1 d(rEv) и
(5.55)
206
Из (5.55) следует
„ 1 д <sln 0£<?)
Лг== jwpoTsinO
_ 1 д(гЕ„)
9 j^r dr
(5.56)
Подставив значения Нг и из (5.56) в первое урав-
нение (5.55), получим
J_ а Гд (г£<р) 1 , 1 д_ Г
г dr L dr J ~' г2 <?0 L
1 ^Sinag«?) 1 _ _ k2F
sin О d® J <? •
(5.57)
Подобно предыдущему положим
(5.58)
Рис. 5.13а. К анализу биконического рупора.

Рис. 5.136. Кривая зависимости
между углом раствора а и посто-
янной /j в биконическом рупоре
для волн ТЕ01 и'ТМ01.
207
Тогда (5.57) примет следующий вид:
[4(^)1 + 44 Г~4^&-0)] = -тЭ. (5.59)
г dr [dr ' ' ] ’г2 dO ] sin & do ' ’ J ' '
Разделив переменные в уравнении (5.59) и приравняв
обе части уравнения произвольной постоянной р2, полу-
чим
у 4 [4 И+- 44 Г+4 <sin 9-0)]=*>•
(5.60)
Иначе уравнение (5.60) может быть написано в виде
двух уравнений следующим образом:
rg-2(r/?) + (^r2-p2)7? = 0 (5.61)
и
4 [^4-4(sin&-0)l+P20 = O. (5.62)
d9 pin е d9 v /j । г \ /
После раскрытия скобок под знаком производной
в уравнениях (5.61) и (5.62) и подстановки
cos & = х (5.63)
в уравнение (5.62), получим
7т+44+(42“4)'?=0' <5'64>
(х=-1)^ + 2х£_(р!__Т^е = о. (5.65)
Чтобы разложить интеграл уравнения (5.65) по при-
соединенным функциям Лежандра, как обычно делается,
примем:
р2 = /(/+1). (5.66)
Тогда получим
R(r) = r~^H™(kr), (5.67)
о
0 (*) = £} (х),
(5.68)
208
здесь Я 2 j_ (kr) — ганкелева функция второго рода,
I — вещественное число, определяющее по-
рядок волны, функция
Z)(x) = ^P/1(x) + BQj(x), (5.69)
где Pz(x) — присоединенная функция Лежандра первого
рода,
Q)(x)— присоединенная функция Лежандра второго
рода.
Подставив (5.67) и (5.68) в (5.58), а затем полученное
значение Е в (5.56), после преобразования получим
E^ = L\(x)r 2H^±(kr),
— А
-7^-Z!(x) lr
J"l*0 I v '

(5.70)
Здесь функция
Lt(x) = /lPz(x)4-BQz(x), (5.69a)
где P^x) и Qz(x) — функции Лежандра первого и второго
рода.
Соотношение между постоянными интегрирования А
и В, входящими в выражение (5.69) и (5.69,а) для Zj(x)
и Zz(x), а также постоянная разделения I определяются
из условия Е? = 0 при & — у±а, где 2а — угол раствора
рупора, т. е. из условия
Zz1(xo) = O,
где
x0 = H=sin а.
14-1503
(5.71)
209
Иначе (5.71) представляется в виде
АР\ (sin а) BQ* (sin а) = О,
АР\ (— sin а) 4- BQ1, (— sin а) =± О
или
Р' (sin a).Qj (— sin а) — pj (— sin a) Q*(sin а) = 0. (5.716)
(5.71a)
Уравнение (5.71,6) служит для определения I. Имеется
бесчисленное количество дискретных корней этого урав-
нения, которые мы будем обозначать через 1п, где п — по-
рядковой номер корня, соответствующий порядку волны
в рупоре. На рис. 5.13,6 приведена кривая зависимости
между постоянной 1Х и углом раствора а для и=1. По-
стоянная li увеличивается с уменьшением а. При п—1
получим для волн ТЕ01 в биконическом рупоре следую-
щие значения составляющих поля:
E, = L\(x)r 2Н{2\i (kr),
т 1 ‘1 "I—2~
Hr=—-^-L.(x)-2r~~2H(2) 1 (kr),
r fan 'Р ’ /, + у
1Е= — ^-Ь\(х) г
а 1Р ’
3_ __1_ "I
2 Z/(2) 1 (kr)- kr 2 И™ 1 (kr)
l'+-2 Z1-T J
(5.72)
Для составляющих векторов поля волн ТМОп получим
выражения, аналогичные уравнению (5.54) и (5.70),
а именно
E^~L\(x) lr
£?=о, н==н. = о,
_ 1
Я=^(х)г 2H^±(kr),
Г 2
_ 3
3 __1_
2 Н(2> _1_ (kr) — kr 2 Н(2)_ _1_ (kr) .
1 + 2 2
(5.73)
210
В данном случае соотношение постоянных А и В и
постоянная интегрирования I должны быть определены
из условия
Ег—0 при d = yzta, т. е. из условия
/(/+1) £,(хо) = О (5.74)
при x0 = z^sin а.
Одним из корней уравнения (5.74) является / = 0.
Остальные корни уравнения (5.74) представляют собой
бесконечный ряд чисел, который мы обозначим через 1п,
где п — порядковый номер корня, также соответствующий
порядку волны в рупоре. Индекс п, соответствующий
Z = 0, будем считать равным нулю. На рис. 5.13,6 пока-
зана кривая зависимости между и углом а раствора
рупора.
При /1 = 0 в рассматриваемом случае получаем чисто
поперечную волну ТЕМ, у которой составляющие поля
равны
(5.75)
В общем случае /г/0 электромагнитное поле прибли-
жается к чисто поперечной волне ТЕМ лишь на больших
расстояниях ют вершины, определяемых из неравенства
kr>ln(ln-V О- (5-76)
При п=1 у волн-ТМ01 составляющие векторов поля
имеют следующие значения:
1 ’’’ 2
Er = L (х) ~ н&) {kr}
r J^O ' V 7 /< +-у V 7
[__3^ __1_ 1
г,г !и®+л(м-4г
2 1 2 J
(5-77)
14* 211
На рис. 5.14 показана конфигурация электромагнит-
ного-поля волн ТЕМ, ТМ01 ТЕ01, в биконическом рупоре,
соответствующая уравнениям (5.72), (5.75) и (5.77).
Сравнивая рис. 5.14 с рис. 5.12, легко заключить, что
электромагнитное поле волн ТЕ0П и ТМОп в биконическом
В)
Рис. 5.14. Конфигурация электромагнитного поля в биконическом
рупоре для волн ТЕМ, ТМС1, ТЕ01.
рупоре сходно с электромагнитным полем аналогичных
волн в простом волноводном канале ( в пространстве между
двумя параллельными плоскостями) и деформировано по
сравнению с последним в такой же степени, как поле в сек-
ториальном рупоре по сравнению с полем в простом волно-
воде прямоугольного сечения. Особенность биконического
рупора заключается в том, что в нем электромагнитное по-
ле имеет сферический фронт волны, т. е. точки одинаковой
фазы лежат на сфере радиуса г — const. Остальные особен-
212
ности рупорных антенн, подробно сформулированнные в пре-
дыдущем параграфе, как-то:
а) отсутствие критической длины волны,
б) переменная фазовая скорость,
в) превращение электромагнитного поля на больших
расстояниях от вершины в чисто поперечную волну (ТЕМ),
распространяющуюся со скоростью света, полностью при-
ложимы и к биконическим
рупорам.
Для двух практически
наиболее важных случаев:
волны типа ТЕМ, возбуж-
даемой штырем (как показа-
но на рис. 1,25), и волны ти-
па ТЕоь возбуждаемой вит-
ком тока (магнитным дипо-
лем, параллельным оси рис.
5.15), на рис. 5.16,а, б при-
водятся кривые зависимости
коэффициента усиления от
параметров рупора. Эти кри-
вые подобны аналогичным
кривым для других разно-
видностей рупорных антенн.
Низкий уровень коэффи-
циента усиления объясняет-
ся симметрией поля относи-
тельно оси (круговой диа-
граммой в плоскости, пер-
пендикулярной оси).
Рис. 5.15. Возбуждение в бикони-
ческом рупоре витком тока (маг-
нитным диполем, параллельным
оси) волны ТЕ01.
На рис. 5.16,в показана зависимость оптимальных па-
раметров и биконического рупора от требуемого
значения усиления.
Среди различных вариантов биконических рупоров ши-
рокое применение на практике нашли указанные в главе I
симметричный биконичеокий вибратор, диск-коническая ан-
тенна и конический штырь, схематически изображенные на
рис. 5.17.
Конический штырь и диск-коническая антенна питаются
несимметричным коаксиальным кабелем, а биконический
вибратор —симметричным кабелем.
Штырь и диск-коническая антенна отличаются друг от
друга по схеме питания тем, что у первого к конусу присое-
213
диняется внутренняя жила, а у второй—наружная оболочка
кабеля, в то время как внутренняя жила присоединяется
к диску. По устройству они отличаются тем, что штырь
нуждается в большой металлической плоской поверхности
Усиление,дб
Рис. 5.16. а) Графики за-
висимости коэффициен-
та усиления от парамет-
ров биконического рупо-
ра для волны ТЕМ,
б) то же для волны ТЕ0,;
в) графики зависимости
оптимальных парамет-
ров биконического рупо-
ра R и D от требуемого
коэффициента усиления.
в)
для экранировки наружной оболочки коаксиального кабеля,
а у диок-конической антенны можно ограничиться сравни-
тельно малыми размерами диска, так как оболочка кабеля
хорошо экранируется конусом (диаметр диска делается при-
мерно в 1,5 раза меньше длины образующей конуса).
Конусы биконического вибратора и конического штыря
214
to
сл
a) D)
Рис. 5.17. а) биконический вибратор; ff) диск-коническая антенна; в) конический штырь.
Рис. 5.18. Графики зависимости коэффициента стоячей волны в питающем фидере соответственно от частоты
или от r/Х для: а) биконического вибратора, «У) диск-конической антенны, в) конического штыря.
закрываются сферическим или коническим колпаком. На
рис. 5.17 у штыря для примера показан сферический кол-
пак, а у вибратора — конический.
Угол 2 7 у рассматриваемых антенн берется порядка 60°.
Как отмечалось выше, при анализе рупорных антенн, по-
следние характеризуются тем, что при больших по сравне-
нию с длиной волны размерах раскрыва и достаточно боль-
шой длине рупора электромагнитное поле вблизи раскрыва
становится практически поперечным с фазовой скоростью,
примерно равной скорости света в пустоте. Ввиду этого от-
ражение волн у раскрыва рупоров почти отсутствует.
Это свойство рупорных антенн присуще также рассмат-
риваемым антеннам, показанным на рис. 5.17. У последних
это свойство выражается в том, что при достаточной длине
конусов почти отсутствует отражение волны от их краев
(больших основанний). Это приводит к тому, что входное
сопротивление этих антенн оказывается почти чисто актив-
ным и постоянным в широком диапазоне частот, что позво-
ляет получить в этом диапазоне хорошее согласование ан-
тенны с питающим фидером.
Указанные свойства иллюстрируются на рис. 5.18. Здесь
приведены кривые изменения коэффициента стоячей волны
на питающей линии, имеющей волновое сопротивление, рав-
ное 50 ом (штырь и диск-конус) и 100 ом (вибратор).
§ 5. квазипира'мидальный рупор
В связи с отмеченными выше трудностями теоретическо-
го исследования пирамидального рупора рядом авторов [22]
предложено при математическом анализе заменить пирами-
дальный рупор сектором биконического рупора, ограничен-
ным двумя плоскими стенками, как показано на рис. 5.19.
Мы будем этот рупор называть квазипирамидальным. При
малых углах раствора 2 а (см. рис. 5.19) такой рупор по
форме мало отличается от пирамидального.
Интерес представляет изучение квазипирамидального
рупора при распространении в нем волн, аналогичных
используемым в пирамидальном рупоре, т. е. волн ТЕОп и
ТЕт0. В квазипирамидальном рупоре первые характери-
зуются отсутствием стоячих волн между плоскими стен-
ками, а вторые — отсутствием стоячих волн между кони-
ческими стенками.
Задача о распространении волн ТЕОл ничем не отли-
чается от аналогичной задачи для биконического рупора,
216
поскольку при E = £j. (условие 5.54) добавление плоских
стенок, перпендикулярных электрическому вектору, не
меняет граничных условий.
Следовательно, волнам ТЕОп соответствует электро-
магнитное поле, составляющие Е ,
деляются уразнениями (5.70) в
общем случае или (5.72) при
п = 1. Остальные составляющие
поля равны нулю
Е=Е, = 0- Я =0. (5.78)
Задача о распространении
волн ТЕт0 является несколько
более сложной. Дело в том, что
при волнах ТЕш0 только одна со-
ставляющая Ег = 0. Все осталь-
ные составляющие векторов Е
и Я не равны нулю.
Для определения составляю-
щих электромагнитного поля об-
ратимся к уравнениям (5.53), до-
полнив их известным равенством
div£ = 0. В сферических коор-
динатах
div Е = (г2 sin $ЕГ) -|-
+ ж ('sin + 1 ('£,)=°-
(5.79)
Н и Нй которого опре-
зипирамидального рупора
нз бикон'нческого.
Так как £г = 0, то согласно (5.79) можно положить
г sin &Еа = д- ,
ди
(5.80)
дЪ ’
где и— вспомогательная скалярная потенциальная функ-
ция,
217
Выразим также составляющие магнитного вектора
через и, воспользовавшись (5.80) и (5.53)
. ГТ 1 дги
—/шИоГ2 sin ЬН = - fsin » ~ (-Лг 4е")
J ги ' д9 да J d?\ sin 9 dyj
(5-81)
Далее, выразив в каком-либо из уравнений (5.53) со-
ставляющие Е и Н через и, получим;
<?2u I 1 д t' • л ди \ । 1 д2и . гп л ... ог>\
’dr2' + г2 sin 9 Ж (Sltl^d» J + г2 sin2 9'др' + “ — °- (5-82)
Подставив и в виде произведения трех функций
и = R (г) в (9)Ф(<р), (5.83)
и разделив переменные, получим
ы = Д cos (у<р + ф) Г (cos &) /г Н(2) . (kr), (5.84)
' + т
где А — коэффициент пропорциональности, v — число сто-
ячих волн вдоль центральной окружности, перпендикуляр-
ной оси АА', ф — угол между направлением tp = O и направ-
лением максимума функции и. Функции L^} и Н1 i пояс-
йены на стр. 181 и 209. Остальные обозначения прежние.
Применим граничные условия
а) £'9 = 0 при <р = 0 и при <р = <р0 (см. рис. 5.19),
б) Д, = 0 при & = у±а,
получаем из уравнений (5.84) и (5.80)
и
4£;<со^)|,.л„=0’
(5.85)
где ftisO, 1, 2, 3 ... и указывает порядок волны ТЕт0,
218
В результате получаем для составляющих поля сле-
дующие выражения:
E=Q,
Е* sin ср) (cos&) г 2 Я<2> Jfer),
_ 1
Е = -- A cos (— фЛ L] (cos &) г 2 Н{2) . (kr),
Т . \ <Ро J 0" 1 ' I -L 1 '
Z 2
Н = ~ -Л- COS (— <р\ . Ц (COS&)X
г }ш^а \Чо / 1
__ 3
XZ(/+I)r 2/7(2\(М
1 + Т
— А
г 1 А (tTiTz .Л \ d г v / л\ 2
Н,. = ~-—cos —? -т^-Z. (cos&)r х
\ tf>0 ) d& I V >
(5.86)
X krH{2} , (kr)-lH^ , I
mn
H„ = — -Д- sin (— (f>) £’ (c
? Sin и \ fo / 1 v
X\krH{2) . (kr)~lH(2) .
L ‘-T 1 + t
2
При m = Q (5.86) переходит в (5.70), т. e. при этом
Е. = Н =0, ^ = 0; ?^ = 0.
о т ’ d-f ’ d<f
При tn^zQ сохраняются все составляющие электромаг-
нитного поля, кроме Ег. Составляющие поля являются
функциями всех трех координат г, &, ср.
Зависимость от г выражается функцией Ганкеляот^г,
_ t_ _ з '
умноженной на г 2 или kr 2. При больших значениях
kr функция Ганкеля может быть заменена асимптотиче-
ским выражением вида (5.15), что указывает на образо-
вание сферической волны, распространяющейся со ско-
ростью света с = 3-108^-. Продольная составляющая
Нг при больших величинах kr значительно меньше цопереч-
219
ных составляющих Н и Н^. Следовательно, на больших
расстояниях от вершины электромагнитное поле стано-
вится поперечным полем типа ТЕМ.
Зависимость от $ определяется комбинацией присое-
диненных функций Лежандра, входящих в функцию
Z.j(cos&), либо в ее производную по 8, а у некоторых
1
составляющих — еще множителем —г—» . Постоянные I и
sin V
А'
g определяются из уравнения (5.85), которое выполняется
либо при L] (cos &) = const, либо при условии, что в точке
8 = -|±а эта функция имеет экстремум. Условие
Ц (cos &) = const требует
£т = Яа = 0,
(5.87)
d£__<W_n
да — да — и’
что не согласуется с уравнениями Максвелла (в чем можно
убедиться непосредственной подстановкой). Следователь-
но, функция Zj(cos&) имеет экстремум на конической
поверхности & = При отсутствии стоячих волн
между коническими поверхностями (рассматриваемый слу-
чай волн ТЕт0) функция Z)(cos&), невидимому, будет
иметь слабо выраженный максимум. Подробно (5.85) не
исследовалось. Мы не располагаем также данными о зна-
чениях I, являющихся корнями (5.85). Некоторое сужде-
ние о величине можно получить из полученного Зелкиным
неравенства [22]
(1 \ 2 Q
Z + 4) <*2 + 2v + -i. (5.88)
Зависимость составляющих поля от <р выражается
через sin или cos . В средней области ру-
пора-, т. е. вблизи =
/ тп X .. . / тп X
cos (17 7 <<с (17 7 • (5-89)
220
Так как, кроме того, синусоидальная функция умно-
жается на -у—>1, то в средней ^.области -рупора элек-
трический вектор практически имеет только одну состав-
ляющую^^. Вблизи & = 90° и ф = 0 или <р1=1_<р0 преобла-
тс/0
Рис. 5.20. Конфигурация электромагнитного
поли; в' поперечном сечении квазипирами-
дального рупора для волны ТЕ10.
дает составляющая Е^. Чем меньше <pd, тем больше
область, в которой Е^ЕЬ.
Картина линий поля в поперечном сечении квазипира-
мидального рупора при т=1 (волна ТЕ10) будет иметь
вид, показанный на рис. 5.20.
§ 6. КОНИЧЕСКИЙ РУПОР
Ограничимся здесь рассмотрением волны ТЕтл.
Общее решение задачи может быть выражено, как
в предыдущем параграфе, с помощью вспомогательной
функции и, определяемой по формуле (5.84), причем
составляющие векторов поля связаны с и соотношением
(5.80) и (5.81). Данная задача от предыдующей отличается
граничными условиями. В данном случае будут следую-
щие граничные условия:
1. Функция от ф однозначна, т. е. и(у) — и(пк -j-<p),
где п — целое число,
2. Е9 —конечно при & = 0,
3. Е9 = 0 при & —а.
Эти условия требуют:
1. v = m = 0, 1, 2„ 3 ...
221
2. L) (cos&) = P^ (cos&), где P™ (cos &)— присоедийей-
ная функция Лежандра первого рода. Присоединенная
функция Лежандра второго рода равна бесконечности
при 9 = 0 и поэтому коэффициент при ней полагается
равным нулю.
3. P™(cos&) = 0 при & = а. (5.90)
Таким образом
_ 1
n = Xsin m<pP7(cos8)r 2 Н{2) . (kr). (5.91)
z+t
В свою очередь, составляющие электромагнитного
поля равны
Е = 0
Е^ = А cos Р™ (cos &) г 2 Н(2) , (kr),
z +Т
_ i
= — A sin ~ Р™ (cos &)r 2 /У(2) ± (kr),
Hr= — А sin т?рГ (cos &) X
_ з
х 1(1+1) г 2Н(2) t(kr),
z + t
_ з
Н« =—А -Д— sinnup^- Р™ (cos&)r 2х
X\krH(2) , (kr) — 1Н{2) , (kr)V
l~~2 Z + T J
_ 2.
// =Л-7^------Дг-СОЭ/ЩрР™ (cos ft) r 2X
'P sin& T 1 v '
x \krH{2) . (kr) — IH{2} . (kr) .
i___________ i + _
2 2
(5.92)
Наибольший практический интерес имеет волна ТЕ]|,
которой соответствует т—1 и I — первый корень урав-
222
Пения (5.90). При m=l (5.90) может быть переписано
следующим образом:
щГ Л (cos 1&.я == О* (5.93)
На рис. 5.21 приведен график зависимости между I и углом
а соответствующий первому корню уравнения (5.93).
Не останавливаясь на подробном анализе формул (5.92),
заметим, что они указывают на подобие волн в коническом
223
Рис. 5.22. а) диаграмма направленности оптимального конического
рупора с размерами /? = 3,5>, /Э = 3,4 X в //-плоскости (левая пунк-
тирная кривая) и в //-плоскости (правая сплошная кривая); б) зави-
D
симость от у угла 9, соответствующего различным относительным
уровням диаграммы направленности конического рупора в //-плоско-
сти; в) то же в //-плоскости.
224
рупоре и волноводе круглого сечения. Аналогия и отличие
носят такой же характер, как у других разновидностей ру-
поров 'И им подобных волноводов.
При расчете поля излучения конических рупоров, поль-
зуясь при этом методом диффракции на круглом отверстии
в плоском экране, можно принять, что амплитуды состав-
ляющих поля в отверстии имеют такую же зависимость от
координат отверстия, как в случае волновода круглого се-
чения, а фазы меняются по квадратичному закону.
Рис. 5.23. а) график зависимости коэффициента усиления от пара-
метров конического рупора для волны ТЕц.
15—1503
225
к>
о
Рис. 5.23^) графики зави-
симости оптимальных
параметров конического
рупора от требуемого
коэффициента усиления.
С)
Расчет характеристик излучения конического рупора,
возбуждаемого волной ТЕц, может производиться по гра-
фикам рис. 5.22 и 5.23, аналогичным рисункам 5.5, 5.6
и т. п.
§ 7. СТРОГОЕ РЕШЕНИЕ ЗАДАЧИ О ВОЗБУЖДЕНИИ
КОНИЧЕСКОГО РУПОРА
Выше при рассмотрении рупоров мы определяли отдель-
ные частные решения уравнений Максвелла и сравнивали
их с аналогичными частными решениями для волновода и
простого волнового канала.
Обратим теперь внимание на зависимость электромаг-
нитного поля от условий возбуждения. Этот вопрос рас-
смотрим на примере конического рупора. Определим элек-
тромагнитное поле в коническом рупоре при возбуждении
его кольцевым электрическим током, помещенным внутри
рупора симметрично относительно оси (рис. 5.24).
Обозначим радиус кольца через р, а ток в кольце через I. Вве-
дем сферическую систему координат г, fl, ? с началом в вершине
рупора. Координаты точек кольца обозначим через г’, О', <р', причем
г’ и fl' являются постоянными для всех точек и связаны с радиусом
кольца соотношением
р = г' cos О', (5.94)
а координаты <р' различны для разных точек кольца.
Ввиду симметрии возбуждения электромагнитное поле в рупоре
получится симметричным относительно оси, т. е. не будет зависеть
от координаты <р, что позволяет произвольно выбирать начало от-
счета этой координаты.
Примем, что в точке наблюдения М (рис. 5.24) <р = 0, т. е. что эта
точка имеет координаты г, 0, 0. Расстояние R между точкой А и
какой-либо заданной точкой Q на кольце, имеющей координаты г,
в', ср' равно
R = У г2 -j- r'2—2rr' cos 0, (5.95)
где 6 — угол между прямыми г и г'1), связанный с углами В, р и fl', <р',
согласно известной из сферической тригонометрии теореме косину-
сов соотношением
cos 0 = cos Э cos 9' + sin 0 sin 0' cos (<p — <p'). (5.96)
Для определения электромагнитного поля в рупоре вычислим
—►
сначала вектор-потенциал Аэ, соответствующий кольцевому току-
в свободном пространстве, затем учтем изменение этого вектора,
вызываемое наличием идеально проводящей поверхности рупора и
И Точнее, угол между прямыми, соединяющими рассматриваемую
точку и точку на кольце с началом координат.
15* 227
наконец, найдя окончательное значение вектора А3, вычислим Век-
—>
торы электромагнитного поля по формулам (2.26); приняв 7м = О
£ = — Лво Мэ -f- та-grad div Дэ],1
(5-97)
~Н = rot Дэ. )
В дальнейших выкладках опустим индекс ,э*.
Вектор А при прямолинейном токе имеет направление, парал-
лельное току. В нашем случае кругового тока, очевидно, вектор А
будет параллелен касательной к окружностям, коаксиальным с то-
ковым кольцом, т. е. Д будет иметь только одну составляющую Д
Рис. 5.24. К анализу возбуждения конического рупора
кольцевым током.
не равную нулю. По величине (амплитуде) вектор А пропорционален
моменту тока, поскольку источником является линейный ток, и об-
ратно пропорционален первой степени расстояния £ от тока до точки
наблюдения' М, а фаза определяется обычным» фазовым множителем
е—Таким образом, вектор dA, созданный элементом кольца дли-
ной pdf', равен
-> 7pd®' е—
= (5.98)
а его <р-ая составляющая
= (5’99)
228
Полный вектор Ар созданный всем токовым кольцом, имеет сле-
дующую величину:
Р/fe~>w
Л1 (Г, 0) = ЛТ1 (г, 9, 0) = j — cos <p'dT'. (5.100)
о
Соответственно составляющие векторов электромагнитного поля
-» ->
Е и Н в нашем случае осевой симметрии равны:
1 <3
> (sinW-
Яа__±±(гЛх [. (5.101)
нь~ г dr
E? = —J^OAV.
e~ikR
Известно, что множитель!--- при R, определяемом нз (5.95)
R
может быть представлен в виде ряда
е-Лй V,
— = (2« + 1) ?л ’ &r) ф„ (kr') Рп (cos 9), (5.102)
п=0
где « — целое положительное число;
2_
/ л \2
(kr),
V / п+-
j —ганкелева функция второго рода,
1
/ л V
fn,L{kr'}'
где I , (kr') — бесселева функция,
л+Г
Pn(cos9)— полином Лежандра.
Ряд (5.102) абсолютно сходится для всех значений г>г'. Для
значений г<г' он будет абсолютно сходящимся при перемене ме-
стами г и г'.
Преобразуем ряд (5.102) в контурный интеграл. Предварительно
напомним некоторые сведения из математического анализа.
Из теории функций комплексного переменного известно, что
функция f (г)— аналитическая в некоторой замкнутой области,
229
может быть выражена через интеграл по контуру С, ограничиваю-
щему эту область, следующим образом:
1 Г f (s) ds
(5-ЮЗ)
С
где г — какая-либо точка внутри контура.
В то же время
jf(5)ds = 0. (5.104)
С
Известно далее, что
л=оо
где п — целые числа 1, 2, 3 . .., а штрих у знака суммы указывает
на отсутствие члена п = 0.
Рис. 5.25. Контур интегрирования (5.106).
Рассмотрим интеграл
(5-Ю6)
c
взятый по контуру с бесконечной протяженностью С, показанному
1 3 5
на рис. 5.25, включающему в себя точки s — , -у ,...
Согласно (5.105) и (5.106)
л=оо
£'(- 1)я+1х
* С $ 2 п=—со
230
2n+l
2
Так как внутри контура находятся особые точки 5 = '2'1 ~2"*
., то
00 п — оо
w=- f (4)+S <- +1 f +4)=S (- (л+4) •
п-1 п-0
(5.108)
Вернемся к ряду (5.102). Заменим в нем
Рп (cos 9) =(— 1 )пРп(— cos 9). (5.109)
Если теперь в (5.106) подставить
f(s) = 2j'M(2) (М’Ф । (kr’)P ](—cosfi) (5.110)
s-r s-r
то получим, согласно (5.108)
N=k fs(2) (fer)| j (kr')P ] (— cos&)^^- =
C s~2- S 2 s 2
= jk (2n + 1) ^\kr) ф„ (fer') Pn (cos 9) = (5.111)
n—0
Подставив (5.111) в (5.100), получим
2"
Ap, M>°) = cos f'df'X
0
X f 5(2) ! (kr) ф 1 (kr')P 1 (—cos9)^^-. (5.112)
В выражении (5.112) можем переменить порядок интегрирования
и написать
kpl С . sds
Л?1(гЛ0) = £ Ь(2>, (МФ 1 (^)—-X
V S--- S— О
С 2 2
Р ] (— cos 9) cos if'rf'f'.
(5.113)
S 2
231
Пользуясь теоремой сложения шаровых функций, можно найти
интеграл по у' в формуле (5,113). Он равен
2тс
J Р ] (— cos 9) cos = — 2it X
0 2
X P"1] (— cos 9) P~11 (cos S') cos ®. (5.114)
S~2~ S~2~
Уравнение (5.114) справедливо, согласно теореме сложения, при
9 >9'. В противном случае нужно поменять местами 9 и 9'.
Подставив (5.114) в (5.113) и учитывая, что у=Ов точке М, по-
лучим
Лф1(г, 9,0)=-^ffc(2>t (йг)-ф ( (йг')-Р-1! (-cosO)?
с S~T s~2- S *
s(s*-*г)
ХР-1. <cos»')-^---------d- (5115)
л,_ v \J О
В формуле (5.102), поскольку там п — целое число, функция
Рп (cos 9) представляет собой полином Лежандра В (5.110) и после-
дующих формулах, поскольку s непрерывно меняется по контуру С
и принимает различные комплексные значения, функция Р ^cosS)
ST
и аналогичные ей представляют собой функцию Лежандра. Лишь
1 3
в точках s = ... эта функция переходит в полином Лежандра.
—►
Формула (5.115) дает значение вектора Л, соответствующее коль-
цевому току в неограниченном пустом пространстве. Будучи поме-
щенным внутри рупора, кольцевой ток вызовет токи на стенках ру-
пора, которые также будут кольцевыми и коаксиальными ввиду
симметрии к возбуждающему току. Очевидно, что вектор Л2(г,9.0)
в точке М, соответствующий токам на стенках рупора, будет выра-
жаться через функцию, подобную (5.115). Различие между ними
должно заключаться главным образом в т м, что все точки на по-
верхности рупора имеют угловую ко> рдинату 9' = а, по отношению
к которой внутренние точки имеют угловые координаты 9<9’ = а.
Поэтому в соответствующем выражении для ЛТ2(г,й,О) следует по-
менять местами 9 н 9' по сравнению с выражением (5.115).
Итак, полагаем
Лф2(г,9,0) = -^ (\<2) , (М-Ф 1 (fer')-B (s)P—(cos 9) X
C S 2 s 2 s 2
I . 1 \
S (s2 — V)
X P711_ (~ C0S9,) " cos KS----ds' (5-116)
232
где В (s) — множитель, который подлежит определению из гранич-
ных условий
^(г,а,0) = 0. (5.117)
Как видно из (5.101), пропорционально А?, поэтому гранич-
ным условием будет также
Аа = А„ 4- = 0. (5.118)
<р <fl I ф2 V !
Подставив в (5.118) значение Af из (5.115) н А из (5.116), по-
лучим
Р~1 । (— cos а) Р~1 j (cos Э')
S-2"
В(5) =---п-----------=1-------------• (5.119)
Р ] (cosa)P [(—cos®')
*-2- S~2
Итак, суммарное значение составляющей вектора Аа равно
Л? = Л?1 + Л?2 =—у (>! (йг)4 ,(М)Х
£ s~2
_i / 1 \
Р I (cos &') S I S2— у
с____ \ ** /
Р 1 ] (cos a) COS КЗ
где
f J (®, а) =Р ~*| (cos а) Р~1 ] (— COS 9) — В""1] (— COS а) Р~1 ] (COS б).
S~ 2 s~ Г ,f ~ 2 2
(5.121)
Выражение (5.120) путем приведения к сумме интегралов вида
(5.ЮЗ) может быть опять преобразовано в ряд. Однако при этом сле-
13 5
дует иметь в виду, что точки з = -у,’ -у, у н т- Д- Уже не будут
особыми точками, так как в этих точках одновременно функция
f ,(в, а) = о.
j——
Подинтегральное выражение будет иметь особые точки лишь
там, где
Р~(cosa) = 0. (5.122)
3— —
Угол раствора 2a является величиной постоянной. Следовательно,
уравнение (5.122) может быть выполнено лишь при определенных
значениях Обозда^.им те значения з—у, которые при заданном
233
а удовлетворяют уравнению (5.122) через чп, где индекс п означает
номер корня. В принятых обозначениях имеем:
P“1(cosa) = 0, (5.123)
4 = _p~n1(~cos“),p^1(cose)- (5Л24)
В свою очередь, как можно показать,
2 sin(v) _______________________________1_________
•PVfi‘(-cosa)== v-?.no Vfi(v„ + l)PVn(cosa) • (5.125)
Подставив (5.122)-4-(5.125) в (5.120) и выполнив интегрирование,
получим согласно (5.101)
00
=- “но У cv A’ (fer) р~' (cos»)-
т ГС th п
М — 1
со
Яг=-^Ус e<2>(fer)P (cosfi), ]
ГС ГС ГС
11 = 1
00
= - Л Г с (т £ Wl| Л p“>os 9)1
Ml Л С*Л п ) ГС
п—1
(5.126)
где
п 2k?I / 1\ Р~п (cos9')
Sin a 2 Г OP-1 (cos а)'
P (cosa)-^j L
(5.126a)
В формулах (5.126) r^>r’, O^flsga. При г < г' следует поменять
местами ?(2) и .
'л vn
Формулы (5.126) показывают, что в коническом рупоре при воз-
буждении его кольцевым током возникает бесконечное число раз-
личных частичных волн, отличающихся друг от друга математиче-
ским индексом vn, подобно тому, как в секториальном, квазипира-
мидальном и биконнческом рупоре возникает бесконечное число
волн, отличающихся друг от друга индексом п или I. Зависимость
векторов поля в коническом рупоре от координаты г (расстояние
от вершины) выражается, как в предыдущих случах, с помощью ган-
келевой функции, умноженной на г 2 , а зависимость от коорди-
наты О с помощью функций Лежандра. Как и в предыдущих случаях,
индексы чн не образуют непрерывного ряда целых чисел (1,2, 3, 4 ...),
а представляют собой ряд, вообще говоря, иррациональных чисел v„,
234
Рис. 5.26. График зависимости корней чп от угла а
для различных значений п.
удовлетворяющих уравнению (5.123). На рис. 5.26 приведены графики
зависимости чисел чп от угла а для различных п. Из этого рисунка
видно, что чем меньше угол раствора рупора 2а, тем больше раз-
ность между двумя рядом стоящими значениями ~>п.
Например,
при а = 180° 41 = 1 = 2 v3 = 3 и т. д.
„ а=120° м1 = 1,3 v3 = 2,7 м3=4,1 и т. д.
, а = 60° 4j = 3 v2 = 6 м3 == 9 и т. д.
, а = 40° Vj = 5 у3 = 10 v3 = 15 и т. д.
Как увидим ниже, характер чередования индексов определяет
соотношение амплитуд отдельных частичных волн.
235
Из формулы (5.126а) видно, что амплитуды колеба-
ний отдельных частичных волн различны и опреде-
ляются выражением
(cos Э’)
(cos а)
дРч 1 (cos а)
д'»
Р„

Приведенное выражение позволяет судить об угле
раствора рупора 2а, размерах кольпа тока и его положе-
нии, при которых та или иная частичная волна будет
иметь наибольшую амплитуду. В этом выражении приме-
Рис. 5.27. Графики зависимости бесселевых
функций постоянного аргумента от их порядка.
чательно поведение функции ^n(kr'). На рис. 5.27 при-
ведены графики зависимости бесселевой функции /(£/') =
= |/"(kr') от v для различных заданных значений
kr'. Из этих графиков видно, что при каждом заданном
значении kr' существует небольшая полоса малых значе-
ний v, при которых J4(kr') сравнительно велико. После
этой полосы значений v величина быстро спадает до
нуля. Эта полоса тем шире, чем больше kr'. Из сказан-
ного вытекает, что хотя в рупоре возбуждается бесконечное
число частичных волн, но лишь некоторые из них с малым
индексом v ( волны низших порядков) будут иметь значи-
тельные амплитуды колебаний, а остальные — практически
236
будут отсутствовать. При этом, чем больше kH, т. е. чём
дальше от вершины находится возбуждающее кольцо тока
и чем чаще чередуются отдельные >, т. е. чем больше угол
раствора рупора (см. таблицу на стр. 235), тем больше
количество частичных волн возможно в рупоре с большими
амплитудами колебаний. При малом угле раствора и срав-
нительно близком к вершине расположении возбудителя все
частичные волны будут иметь малые амплитуды, что подоб-
но режиму затухания в волноводе, имеющем размеры мень-
ше критических. Соответствующим подбором угла раствора
и положения возбудителя можно, как в волноводах, от-
фильтровать одну волну от остальных. При возбуждении
рупора обычным волноводом, рассчитанным на волну низ-
шего порядка, в рупоре будет преобладать также волна низ-
шего порядка.
Мы рассмотрели случай возбуждения рупора кольцевым
электрическим током, эквивалентным магнитному диполю,
расположенному на оси. Аналогичным путем могут быть
легко получены выражения для векторов поля в рупоре при
его возбуждении электрическим диполем, т. е. линейным
током, расположенным на оси рупора. Так как последний
случай принципиально не отличается от рассмотренного, то
останавливаться на нем не будем.
§ 8. ПЕРЕХОД ОТ ВОЛНОВОДА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
К СЕКТОРИАЛЬНОМУ ИЛИ ПИРАМИДАЛЬНОМУ РУПОРУ
Большой интерес вызывает задача о возбуждении рупо-
ров волноводами. Решение этой задачи, во-первых, позволит
получить более ясное представление о характере электро-
магнитного поля в рупорах в практически важных случаях,
во-вторых, даст возможность определить отраженные волны
от места перехода волновода в рупор и выбрать необходи-
мые элементы согласования.
К настоящему времени данная задача частично решена
для перехода от прямоугольного волновода к секториаль-
иому или пирамидальному рупорам.
Разными авторами [23 и 24] применено два метода реше-
ния задачи: так называемый метод «сшивания» и метод
эквивалентной замены. Познакомимся подробнее с этими
методами.
а) Метод сшивания
Метод «сшивания» часто применяется для решения элек-
тродинамических задач. По этому методу сначала находят-
237
ся общие решений уравнений Максвелла для отдельных раз-
породных областей пространства, а затем определяются по-
стоянные интегрирования, используя граничные условия на
поверхностях сочленения рассматриваемых областей.
В задаче о питании рупора волноводом решение зада-
чи в общем виде встречает значительные математические
трудности. Поэтому ограничиваются приближенным реше-
нием, заключающимся в замене общих решений частными,
соответствующими основной волне (волне низшего порядка).
Рис. 5.28. Продольное сечение секториального рупора,
присоединенного к волноводу.
В связи с таким решением исключается возможность полу-
чения более или менее точных данных о поле в рупоре.
Удается лишь приближенно определить коэффициент отра-
жения в рупоре.
На рис. 5.28 показано продольное сечение секториаль-
ного рупора, присоединенного к волноводу. Длина рупора
равна Д = р0Д-Л. Через а обозначена половина угла ра-
створа рупора. Ось Y перпендикулярна плоскости рисунка.
Ширина волновода вдоль оси Y равна D.
Если рис. 5.28 относится к Д-плоскостному рупору,
то поле основной волны в волноводе имеет составляю-
щие:
= (е пг + Г£епг) cos ,
Н „ = J- (е~^ - Г„е"г) cos ,
(5.127)
где
2тс / X \2 -]/. / X \2
X Г ^2£)1/ г \2£>1/ ’
238
(5.128)
В (5.127) множитель e-;i* характеризует набегающую
волну, а множитель е*7* —отраженную. Множитель Г£—
коэффициент отражения от Е-плоскостного секториаль-
ного рупора. Индекс Е указывает на принадлежность
величины к задаче о Е-плоскостном секториальном рупоре.
В Е-плоскостном секториальном рупоре составляю-
щие поля основной волны [согласно (5.37)] выражаются
следующим образом:
Е<р= - T^cos^
Граничными условиями задачи является равенство
между собой — Е^ из (5.128) и Ех из (5.127), а также Ну из
(5.127) и (5.128) в точках того же поперечного сечения
волновода, которым он сочленяется с рупором.
Как указывалось, точное решение задачи может быть
получено лишь при приравнивании полей, являющихся об-
щими решениями уравнений Максвелла. Общее решение со-
ставляется как сумма частных решений с произвольными
коэффициентами. В рассматриваемой задаче базирование
на общем решении означает учет волн высших типов. Огра-
ничиваясь одним основным типом волны, мы не сможем
получить равенства полей, выражаемых (5.127) и (5.128) во
всех точках граничного поперечного сечения. Поэтому при-
бегают к такому приему: приравнивают (5.127) и (5.128)
в одной точке этого сечения на оси системы, т. е. в точке
2 = 0, _у = 0 (прямоугольные координаты),
р = ро,_у = 0 (цилиндрические координаты).
При малых углах раствора рупора приравнивание поля
в этой точке обеспечит с достаточной точностью их равен-
ство и в других точках граничного поперечного сечения.
Постановка этих значений координат соответственно
в (5.127) и (5.128) и приравнивание полей дает:
1-^=/М(о2,(ТРо)-j
239
Из (5.120) получаем коэффициент отражения в волно-
воде при нагрузке его на ^-плоскостной секториальный,
рупор
г W(i2)(7Po)-J^2,(7Po)
(5J30)
Знание коэффициента отражения Г£ позволит изве-
стными методами определить необходимый элемент согла-
сования.
Если рис. 5.28 изображает продольное сечение //-плос-
костного рупора, то мы получим вместо (5.127) и (5.128)
следующие уравнения:
для области волновода
Еу = 4. 1\епг) cos _g. >
Я = - -Д- (е~/тг - Г„еЛг) cos ,
X уыц0 ' н > D2 ' >
(5.131)
где

Г — коэффициент отражения от //-плоскостного
секториального рупора;
для области рупора:
^ = ^cos
2а (5.132)
Я = - Тн-J- cos (п Н™’ (k?).
<Р п 2а J п х г/
4 ' 2а
Штрих у ганкелевой функции означает производную по
аргументу.
Аналогично предыдущему, подставив в (5.131) 2 = 0,
х —0, а в (5.132) — р = р0, ср = 0, получаем
2а
2а
(5.133)
240
Откуда коэффициент отражения от //-плоскостного сек-
ториального рупора
тд . 2а 2а
н “ н^Мо)+j А (k?0) ‘ ( 1 4)
2а 7 2а
При решении аналогичной задачи для пирамидального
рупора последний заменяется квазипирамидальным. Пусть
рис. 5.28 изображает среднее меридиональное сечение ква-
зипирамидального рупора. Сохраним" обозначения, приня-
тые в § 5 (при этом следует на рисунке заменить пере-
менный угол <р через 90° — &).
Рассматривая в квазипирамидальном рупоре волну
ТЕ01, получим
для области волновода:
£A. = (e-^4-rehz) cosAA,
Н = -Д- (е-/1г — Ге'1*) cos ,
(5.135)
где Г — без индекса — коэффициент отражения от квази-
пирамидального рупора; для области рупора составляю-
щие поля основной волны определяются из уравнений
(5.86), которые в случае волны ТЕ01 переходят в (5.72)
Е =А' (х)Р 2//(2) , (Лр),
г‘+т
_ 1
= —2 х
( 1//(2) , (/гр)-^/7(2) , (£р)],
(5.136)
где Ц определяется по графику рис. 5.13,6 как функция
угла а£. Индекс „Е“ указывает здесь на то, что имеется
в виду угол раскрыва между стенками, параллельными
электрическому вектору.
Приравнивая составляющие поля в рупоре при & — у ,
р=р0 и составляющие поля в волноводе при z = 0, _у = 0,
16—1503 241
получаем:
;Я(2) , (ад
ptr ------------. (5.137)
Г ±Я<2> ! (k?0)-kH™ , (А,о)
Ро /.+ т Ц-т
Откуда определяем коэффициент отражения от квазипи-
рамидального рупора
, (ад-±н(2> J (ад + ^<2) , (ад
г = т Ре 1+т !'~т (5 138)
V/<2) J (ад + 2_//<2) 1 (kPo)-kff<2> , (ад
Zi+t Ро !‘^Т 1‘~Т
б) метод эквивалентной замены
Метод эквивалентной замены заключается в замене дан-
ной геометрической фигуры другой, близкой к ней по форме,
но более удобной для математического анализа поля в ней.
Данный метод нами уже применялся выше при замене пи-
рамидального рупора квазипирамидальным.
- При решении задачи об электромагнитном поле для си-
стемы волновод — рупор приходится, как мы видели, нахо-
дить сначала интегралы уравнений Максвелла отдельно для
волновода и отдельно для рупора , а затем «сшивать» эти
решения в месте сочленения. Такой путь решения диктуется
тем, что стенки волновода совпадают с координатными по-
верхностями декартовой системы координат (в случае пря-
моугольного волновода), в то время как поверхности рупо-
ра совпадают с координатными поверхностями цилиндриче-
ской (секториальный рупор) или сферической (конический,
биконичеокий, квазипирамидальный рупор) систем коорди-
нат.
По методу эквивалентной замены система волновод —
рупор заменяется такой системой, которая по форме очень
близка к системе волновод — рупор и у которой вся поверх-
ность (и эквивалентная волноводу, и эквивалентная рупору)
может быть представлена как единая координатная поверх-
ность в какой-либо ортогональной системе координат.
Этим методом решена задача для двух расходящйхся
пластин, которые будем называть плоским рупором, присо-
единенным к двум параллельным пластинам (волновод-
ному каналу) [24]. Полученный результат обобщен на слу-
чай секториального рупора. В качестве эквивалентной си-
242
стемы взята область между двумя эквипотенциальными по-
верхностями полубесконечного плоского конденсатора.
Поясним выбор эквивалентной системы.
На рис. 5.29 показаны края пластины плоского конден-
сатора и образующиеся около них в электростатическом
поле эквипотенциальные линии (тонкие сплошные) и сило-
вые линии (пунктирные). Эти линии взаимно ортогональны.
Как видно из рис. 5.29, внутри конденсатора эквипотен-
циальные линии являются параллельными прямыми, прохо-
Рис. 5.29. Электростатическое поле у краев пластин
плоскогоХконденсатора.
дящими параллельно пластинам, а вне конденсатора — рас-
ходящимися прямыми. Практически на небольшом участке
у краев пластин конденсатора происходит плавный криволи-
нейный переход от внешних расходящихся прямых к внут-
ренним параллельным прямым.
Методом конформного преобразования найдены функ-
ции, выражающие эквипотенциальные и силовые линии
плоского конденсатора. Эти линии являются координат-
ными линиями системы координат ср, ф, -q, связанной
с декартовой системой координат следующими соотно-
шениями:
z = А (<р-Ье? созф), '
х = А (ф + ет sin ф),
(5.139)
У = Ат],
где А — коэффициент, имеющий размерность длины, а <р,
ф, »] — безразмерные координаты.
16* 243
Из (5.139) следует, что при ф —> — до
z= А<р
х = Лф
а при <р —> 4- оо
р=]/г2Ц-х2 = Ле'р, a = arctgy—>ф.
(5.140)
(5.141)
Линии ty=const—эквипотенциальные линии, a <p=const—
силовые линии. Уравнения (5.140) и (5.141) находятся
в согласии с тем, что сказано выше о форме эквипотен-
циальных линий внутри и вне конденсатора.
Из сказанного ясно, что продольное сечение рассмат-
риваемой системы плоский волноводный канал — плоский
рупор может быть приближенно заменено частью пло-
скости, расположенной между двумя линиями ф= const.
В частности, при ф = у эта область на рис. 5.29 пока-
зана штриховкой.
Выразим уравнения Максвелла в координатах <р, ф, tq,
причем будем считать поле независимым от ц (соответ-
ствует независимости поля от z). Заметим предваритель-
но, что так называемые коэффициенты Ламе А2, Л3
равны в нашем случае:
А1==А2 = А= A |/l + 2e¥cosФ + е2?, I (5 И2)
' /г3 = А.
дЕ
В криволинейных координатах <р, ф, -q при условии -^=0
дН
и -S-
жаются
= 0 уравнения Максвелла с учетом (5.142) выра-
следующим образом:
1 № . „
1
—тт= fov-oH ,
h <?4» J “u <Р
(5.143)
LdJh.
h d<f
1 dHv
T ~лГ’ = JmeOE '
h di/ J 0 v

244
Простые преобразования (5.143) приводят к
уравнениям
следующим
+ =0,
<?ср2 I Дф2 1 т] >
1 ЫЕ
£ _____ 1________1
Ф Уше(Л d<f ’
1
jai^h дф *
д2Е
=0,
дф2 1
1 дЕ-
Н =______!_____1
Ф д<? ’
н =---------
V /шр0Л дф
/5.144)
д<р2
(5.145)

При условии Н =0 остается лишь система уравнений
(5.145), которая соответствует волнам ТЕ, а при условии
Е^ = 0 остается система уравнений (5.144), соответствую-
щая волнам ТМ.
В обоих случаях первые уравнения каждой системы
являются определяющими и приводятся к дифференциаль-
ному уравнению вида:
+ kW [ 1 + 2е” cos ф + ] и = 0, (5.146)
где и = Е^ при волнах ТЕ, или и = Н^ при волнах ТМ.
Граничные условия имеют следующий вид:
для волн ТЕ
и —0 при ф = ф1 и ф = ф2, (5.147)
для волн ТМ
|^ = 0 при ф = ф1 и ф = ф2, (5.148)
где Ф1 и ф2 — граничные значения ф.
В общем случае, когда ось рупора повернута на угол [3
относительно оси волновода, как показано на рис. 5.30,
а угол раствора рупора равен 2а,
Ф1 = р — а, ф2 = р4-а.
245
Коэффициент А в (5.139) и последующих уравнениях
определяется из условия
л(ф2 — Ф1) = а,
(5.149)
где а —расстояние между
Рис. 5.30. Переход волновода
в рупор при наличии угла меж-
ду их осями по методу экви-
валентной замены.
плоскостями волноводного ка-
нала; иначе
А = ~. (5.149а)
При малых углах а коор-
дината ф меняется в неболь-
ших границах. Это позволяет
ПОЛОЖИТЬ В (5.146) СО8ф=СО8₽,
что, в свою очередь, дает воз-
можность разделить перемен-
ные.
Подставив и в виде
получаем
ц = Ф(<р) ф (ф),
^»+^W) = 0,
+ {kW [ 1 + е? cos р + е2' ] - И Ф (<₽) = 0,
где р.2 — постоянная разделения.
Первое из уравнений (5.150) имеет решение
,ф (ф) = sin (р.ф 4~ Фо)-
(5.150)
(5.151)
Второе из уравнений (5.150) после подстановки
il = 2fi = 2jkA^, '
Ф1(М==^Ф(5), .
(5.152)
приводится к уравнению Уиттекера [25]
^Ф1 (
1
7

Ф1 = 0,
(5.153)
246
где
v = —/^-cos₽,
= (j?)2-!*2’
(5.154)
n = 0, 1, 2... для волн TM0/i и n=l, 2, 3. .. для волн TEOn.
Для случая возбуждения рупора волноводом1’ реше-
нием (5.153) является
__i_
9
UZ_v т(-2/е), (5.155)
где 1Г_У т —функция Уиттекера, которое при S—>0, <р—►—ею
имеет асимптотическое выражение
Ф ($)= С'ГЛ 4 D'lh= С 4- De'™ , (5.156)
а при £—+ос, <р—>ос
. ak .
РД -'T«cos?
Ф($)=^=е ’ (5.157)
Q
Отношение коэффициентов равно коэффициенту от-
ражения в волноводном канале. Модуль коэффициента
отражения равен
В случае совпадения осей волноводного канала и ру-
пора (Р = 0)
*) Рупор рассматривается как передающая антенна.
(5.159)
247
Аналогично решается задача для секториального ру-
пора. Коэффициент отражения и в данном случае выра-
жается формулой (5.158) или (5.159), но у должно опре-
деляться здесь вместо (5.154) следующим образом
(5.160)
а вместо множителя при cosp в (5.158) следует писать
-=2Т|/ *- (S)’. <516»
где Dj — расстояние между параллельными стенками ру-
пора.
§ 9. ОСОБЕННОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
В РАСКРЫВЕ РУПОРНЫХ АНТЕНН. КОРРЕКЦИЯ ФАЗ
Приведенный выше анализ электромагнитного поля
в секториальных, пирамидальных, конических и бикониче-
ских рупорах позволяет сделать ряд выводов^ о характере
электромагнитного поля в рупорных антеннах.
На практике рупорные антенны почти всегда делаются
в виде продолжения волновода или простого волноводного
канала, как показано на рис. 1.2. Электромагнитное поле
в рупорах может быть представлено в виде совокупности
волн ТЕт/1 и ТМт;г, аналогичных волнам в волноводах.
В волноводах, а также в простых волноводных каналах
питающих рупоры, обычно формируется волна наиболее
низкого порядка (соответственно ТЕщИлиТЕМ). Ввиду по-
казанного выше сходства волн в рупорах и волноводах,
в первых, вследствие плавного увеличения поперечного се-
чения, сохраняется в основном волна того же порядка, какая
была сформирована в питающих волноводах. Волны более
высоких порядков, если и возникают в рупорах, то имеют,
как правило, ничтожно малые амплитуды.
Картину электромагнитного поля в рупорных антеннах
можно трактовать следующим образом. Представим себе
электромагнитное поле в волноводе как движущуюся со
скоростью = —- —с — совокупность тончайших пло-
V 1_йз)
ских слоев, заполненных электрическими и магнитными ли-
248
ниями, например, как на рис. 4.2,6 (здесь, естественно, по-
казаны лишь поперечные составляющие векторов поля).
При переходе волновода в рупор эти слои, во-первых, про-
должают свое движение со скоростью, постепенно убываю-
щей до величины с=3- 10 м/сек., во-вторых, они деформи-
руются, приняв форму цилиндрической (у секториального
рупора) или сферической (у остальных разновидностей)
поверхности и растягиваясь последовательно до стенок
рупора. Деформация слоев рупора сопровождается ослаб-
лением радиальной составляющей векторов поля, так что
вскоре электрический и магнитный векторы поля становят-
ся практически касательными к слоям. Поверхность ука-
занных слоев представляет собой то, что обычно принято
называть фронтом волны (поверхностью одинаковых фаз
электромагнитного поля).
Итак, электромагнитное поле в рупоре, будучи сходно
с электромагнитным полем в волноводе, характеризуется
следующими отличительными чертами:
а) геометрическое место точек одинаковой фазы поля
(фронт волны) образует поверхность цилиндрической или
сферической формы;
б) фазовая скорость распространения практически рав-
на скорости света;
в) электрический и магнитный векторы поля касательны
к фронту волны.
Нас интересует в конечном счете электромагнитное поле
в раскрыве рупора, являющемся поверхностью (плоскостью)
поперечного сечения. Очевидно, что в поверхности раскрыва
фазы электромагнитного поля различны в разных точках,
а электрический и магнитный векторы поля не параллель-
ны раскрыву.
Однако при небольшом угле раствора рупора 2 а можно
считать с достаточной для практики точностью, что векторы
поля параллельны поверхности раскрыва и направлены так,
как соответствующие поперечные составляющие векторов1
в волноводе- Вообще вся картина электромагнитного поля
в раскрыве рупора (направление векторов поля и их зави-
симость от координат) при малом угле а может считаться
идентичной, в увеличенном масштабе, картине поля в попе-
речном сечении волновода. Это означает, что при питании
рупоров волноводом (как показано на рис. 1. 2.) имеем:
а) у секториального и пирамидального рупоров1 элект-
рический вектор параллелен стенкам Ьс и cd (рис. 1.2),
249
а напряженность поля имеет постоянную амплитуду в
направлении, параллельном электрическому вектору, и ме-
няется по косинусоидальному закону в перпендикулярном
направлении;
б) у биконических рупоров при возбуждении волны ТЕМ
электрический вектор параллелен образующей цилиндра Р
(рис. 1.2,5) или образующей конуса Р (рис. 1.2,г). Напря-
женность поля имеет во всех точках раскрыва постянную
амплитуду.
При возбуждении волны ТЕ0/ электрический вектор про-
ходит по касательной к кругу поперечного сечения, имеет
во всех точках круга одинаковую амплитуду и меняется
в направлении, параллельном оси рупора по лежандровым
функциям, имея максимальное значение в> середине раскрыва
и нулевые на краях;
в) в раскрыве конического рупора можно считать поле
таким же, как в круглом волноводе.
Фазы электромагнитного поля в раскрыве рупора ме-
няются пропорционально квадрату расстояния x2-|-j/2 от
центра раскрыва, причем коэффициент пропорциональ-
ности равен 2L, где R— расстояние от вершины рупора
до центра раскрыва. Наибольшее отставание фазы имеет
место в точках х = ^~ и У = ~^~ (на краю раскрыва). Сле-
довательно, максимальное отставание фазы равно
= MD2 + D22) °
“макс 41.R
Отсутствие синфазного поля в раскрыве рупора яв-
ляется существенным недостатком рупорных антенн, так
как это приводит к уменьшению коэффициента использо-
вания v антенны (и уменьшению ее эффективной площади),
а при большой величине фмакс (больше тс) также к значи-
тельным искажениям диаграмм направленности (росту
боковых лепестков, расширению или даже раздвоению
главного лепестка и т. д.). Однако следует иметь в виду,
что у других типов СВЧ антенн (зеркала, линзы), хотя
принципиально возможно получение синфазного поля в
раскрыве, но практически мы этого не имеем в силу раз-
i) В приведенном виде формула относится к пирамидальному
рупору. В остальных случаях, вместо следует писать £>2
(где D соответствует обозначению рис. 1.3).
250
ных технических причин. Поэтому всегда ограничиваются
определенными допусками. Считается допустимой макси-
мальная разность фаз между отдельными точками рас-
крыва порядка фмакс = ^ • При таком допуске коэффи-
циент- использования v уменьшается, примерно до 80%
От значения, соответствующего идеально синфазному
полю, а искажения диаграммы направленности мало су-
щественны.
Приняв указанный допуск фмакс^?г для рупорных ан-
тенн, получим согласно (5.162)
4KR ‘ 2
Отсюда следует
+
К" 2\
(5.163)
(5.164)
- Уравнение (5.164) связывает между собой параметры
рупорных антенн R, и D2, которые, в свою очередь,
связаны с а] и а2 следующими уравнениями
°Ч = arctg ± ,
а2 = arctg 2^- •
(5.165)
Достаточно задаться одним из параметров, чтобы с по-
мощью формул (5.164) и (5.165) определить все остальные.
При проектировании антенн обычно в'технических за-
даниях указывается рабочая длина волны X и ширина
главного лепестка диаграммы направленности 23О£ и 24он.
Зная Л, 2в0£. и 26ОЯ, можно определить Dr и D2 по приве-
денным выше графикам.
Определив таким путем и D2, находим затем /? и а.
В случае пирамидального рупора, вообще говоря, получа-
ется два значения </?. Чтобы фазовые отклонения не превы-
шали допускаемых выбирается наибольшее значение R.
9 Некоторые авторы [21] принимают меньшую величину допуска
Фмакс> что соответствует более жестким требованиям к равномер-
ности фаз поля в раскрыве.
251
ляется ширина раскрыва
определяется длина R и,
Плоские отражатели
Рис. 5.31. Конструкция верти-
кально расположенных пира-
мидальных рупоров, снабжен-
ных плоскими отражателями
для перевода излучения в го-
рияонтальное направление.
Итак, расчет параметров рупорных антенн проводится
по следующему плану: первоначально по приведенным
выше графикам и заданным значениям 2 и 26О опреде-
D, затем по формуле (5.164)
наконец, по формуле (5.165)
угол раствора 2а.
Среди современных СВЧ
антенн часто встречаются
чрезвычайно остронаправлен-
ные, имеющие ширину главно-
го лепестка порядка 290=2°-г
1° и даже меньше. У этих ан-
тенн ширина раскрыва D рав-
на, как легко видеть из ука-
занных графиков, £) = 30н-602
и больше. При таком D длина
рупора R должна быть, соглас-
но (5.164), не меньше /? =
= 500 -г- 2 0002. Даже на вол-
не 2 =3 см (одной из самых
коротких из широко используе-
мых в настоящее время) это со-
ставляет /?= 15 л-4-'60 м. Ан-
тенны с раскрывом 1 -= 2 м и
длиной 15-4-60 м найдут, воз-
можно, применение в стацио-
нарных установках. На рис.
5.31 показаны сравнительно
длинные пирамидальные рупо-
ры, установленные вертикаль-
но и прикрепленные к башне1.
Для перевода главного макси-
мума излучения в1 горизонтальное направление вверху
помещены плоские отражатели, образующие с осью рупора
угол 45°.
В передвижных станциях, а также во многих стационар-
ных устройствах применение длинного рупора нецелесооб-
разно. Таким образом, хотя принципиально и возможно
получение остронаправленной рупорной антенны, но это за
счет такой большой длины, которая во многих случаях яв-
ляется неприемлемой. Отсюда возникает проблема уменьше-
ния длины рупора у остронаправленных рупорных антенн.
1) Такие рупоры нашли применение в качестве приемных и
передающих антенн в радиорелейных линиях связи.
252
Имеется несколько Методов решения данной проблемы.
Одним из методов является применение многорупорной
антенны (рис. 5.32). У многорупорной антенны, состоящей
из п рупоров, расположенных на прямой линии, ширина
раскрыва D каждого рупора должна быть, примерно, в п
раз меньше, чем у однорупорной, а длина 'R, согласно (5.164)
уменьшается в п2 раз. Следовательно, достаточно сделать
антенну из двух параллельных рупоров, чтобы получить
возможность уменьшить ее длину в 4 раза, а при четырех
Рис. 5.32. Схема многорупорной антенны и ее питания.
рупорах длина антенны может быть уменьшена в 16 раз и
принять вполне приемлемую величину.
Другим методом уменьшения длины рупора является
помещение линзы в его раскрыве (рис.5.33). При данном
методе длина рупора может быть принципиально любой.
Подбирается она в соответствии с оптимальными парамет-
рами линзы. Расчет такого рупора, в основном, сводится
к расчету линзы, который рассматривается в следующей
главе.
Третий метод заключается в присоединении к рупору сек-
тора параболоида вращения, как показано на рис. 5-34.
Разработан ряд методов выравнивания фаз, относящихся
только к секториальному рупору. Сущность этих методов
заключается в замене плоских параллельных стенок секто-
риального рупора фигурными, но также параллельными
друг другу, причем форма этих стенок выбирается такой,
чтобы электромагнитная волна, движушаяся в радиальном
253
направлении, прошла одинаковый путь от вершины до любой
точки раскрыва. Раскрыв рупора сохраняется попрежнему
плоским. Расстояние между стенками должно быть везде
меньше половины длины волны, чтобы везде сохранялась
волна TEoi, скорость распространения которой равна
с=3-108 м,]сек, и не было отражений.
Рис. 5.33. Рупорная антенна с линзой,
помещенной в раскрыве рупора.
Рис. 5.34, Рупорная антенна
с добавлением сектора па-
раболоида вращения.
Один из таких методов показан на рис. 5-35. Мы видим
здесь обычный секторный рупор, имеющий вблизи раскрыва
углубление, выполненное следующим образом. На каждой
х
а)
Рис, 5.35. Выравнивание фаз поля в раскрыве секториального рупора
с помощью параболического углубления в стенках рупора.

из плоских стенок рупора сделан вырез в промежутке между
двумя пересекающимися параболами. В месте выреза к
каждой из пластин припаяна поверхность в виде полупара-
болоида вращения. Если бы выреза не было в стенке рупо-
ра, то фаза поля в точке М с координатой х была бы равна
254
Сделав вырез и припаяв полупараболоид вращения,
МЫ заставляем волну огибать поверхность полупарабо-
Лоида, т. е. заставляем волну отставать по фазе на ве-
личину
где dx — ширина выреза в месте, соответствующем точ-
ке х.
В среднем положении, соответствующем точке ра-
скрыва х = 0, отставание фазы, вызванное огибанием
полупараболоида, равно
= (5-166)
Чтобы во всех точках раскрыва фазы были равны,
очевидно должно быть выполнено условие
(5-167’
Из (5.167) следует
do~<5J68)
. Формула (5.168) является уравнением кривой, по кото-
рой делается вырез на стенке рупора. Легко видеть, что это
уравнение параболы.
В заключение заметим, что сказанное является изложе-
нием принципиальной стороны данного метода. При прак-
тическом осуществлении необходимо избегать острых углов
в месте спая полупараболоидов и плоских стенок рупора
в точках (а'Ь' и а"Ь"). Может оказаться также целесообраз-
ным делать нижний и верхний полупараболоиды различной
ширины do- В таком случае формулу (5.168) следует отнести
к средней кривой ab.
Рис. 5.36 иллюстрирует другой метод выравнивания фаз
в секториальном рупоре. Здесь показан согнутый секториаль-
ный рупор, у которого в месте сгиба стенки растянуты по
дуге. Уравнение кривой этой дуги определяется из условия
?2</0=21^+^. (5.169)
откуда получаем уравнение параболы
у2
<*<>-<*,= Ьг (5-170)
255
Еще один метод (так называемая система «R—2R»)
показан на рис.5.37. Здесь каждая из стенок рупора выпол-
нена из двух частей: 1) из пластины, представляющей часть
Рис. 5.36. Выравнивание фаз поля в раскрыве секториального рупора
путем сгиба рупора с параболической выпуклостью.
Рис. 5.37. Выравнивание фаз поля в раскрыве секториального рупора
посредством добавления колена, припаянного 'по дуге окружности
(система ,7?— 2R‘).
круга О'А'В' радиуса R и 2) пластины, ограниченной с од-
ной стороны прямой АВ, а с другой — дугой А"В" окруж-
ности радиуса 2R.
Обе пластины припаиваются друг к другу по дугам без
растяжения и при сохранении прямолинейности на линии АВ.
256
Это достигается за счет соответствующей деформации по-
верхностей пластин.
Легко видеть, что длина пути лучей от точки О до лю-
бой точки прямой СС' равна 27? = 00", т.е. постоянной вели-
чине. В самом деле
OA’ = OE=2Rcosa,
поскольку 00’ = ОА" = 2R. С другой стороны,
Д"С = £О"=27?(1 — cos а).
Следовательно,
ОЛ"4- A"C = 2R,
что и требовалось доказать.
Следует заметить, что методы выравнивания фаз в рас-
крыве секториального рупора часто используются для
осуществления электромеханического качания главного
Рис. 5.38. Электромеханический способ качания главного лепестка
диаграммы направленности путем перемещения питающего волновода
по дуге на входе секториального рупора.
лепестка диаграммы направленности. Для этого вход
рупора (место соединения с питающим волноводом) делает-
ся закругленным и значительно более широким, чем волно-
вод (см. рис. 5.38). Перемещая питающий волновод по дуге
А'В', мы тем самым будем поворачивать фазовый фронт
относительно раскрыва рупора АВ и будем также повора-
чивать направление главного лепестка диаграммы направ-
ленности. На рис. 5.38 показано три положения питающего
17—1503 257
волновода и соответствующие им направления фазового
фронта ф и главного лепестка F.
У систем с качающимся главным лепестком секториаль-
ный рупор делается без боковых стенок и представляет со-
бой по существу простой волноводный канал. В последнем
возбуждается с помощью волновода волна ТЕ0Ь которая
имеет вблизи точки возбуждения фазовую скорость = с =
=3 • 10® м[сек.
ГЛАВА ШЕСТАЯ
ЛИНЗОВЫЕ АНТЕННЫ
§ 1. ОДНОРОДНЫЕ ЛИНЗЫ С ПЛОСКОЙ ВОЛНОЙ В РАСКРЫВЕ
Электромагнитное поле в линзе и в раскрыве последней
определяется методами геометрической оптики, т. е. на
основе элементарных представлений о падающей и прелом-
ленной волне, изложенных в первой главе при описании
линзовых антенн. Линза рассматривается при этом как
сплошное абсолютно прозрачное тело, обладающее коэффи-
циентом преломления а
облучатель как точечный или
линейный источник, от которо-
го излучение в виде сфериче-
ской или цилиндрической вол-
ны падает на освещенную сто-
рону линзы и проникает во
внутрь по закону (1,1) —(1,2).
Мы будем в дальнейшем
различать два вида поляриза-
ции волны: параллельную и
перпендикулярную. На рис. 6.1
эти виды поляризации иллю-
стрируются на примере пло-
ско-выпуклой линзы. Под па-
раллельно-поляризованной по-
нимается волна, у которой элек-
трический вектор параллелен
плоскости падения, т. е. пло-
скости, проходящей через на-
правление распространения па-
дающей волны и через нор-
маль к поверхности линзы, а
под перпендикуллрно-поляри-
Рис. 6.1. Направление векто-
ров поля Ей И при волне по-
ляризованной: а) параллельно,
б) перпендикулярно.
17*
259
Рис. 6.2. К выводу формулы профиля
линзы: а) при п>1, б) при п<1.
26(1
зованной понимается волна, у которой электрический век-
тор перпендикулярен плоскости падения.
Зная поляризацию поля излучения и диаграмму направ-
ленности облучателя, а также форму поверхности и раз-
меры линзы, можно методом геометрической оптики легко
.определить поле в раскрыве линзы (его поляризацию и за-
кон изменения амплитуд и фаз). По известным значениям
гполя в раскрыве может быть вычислено электромагнитное
поле излучения методами, изложенными в гл. III.
Обычно линза имеет плоский раскрыв и ее задачей яв-
ляется создание в раскрыве синфазного поля или поля с ли-
нейно меняющимися фазами, т. е. задача преобразования
падающей сферической или цилиндрической волны в пло-
скую. Расчет линзовых антенн, имеющих плоский раскрыв,
в значительной мере состоит из расчета профиля освещен-
ной стороны линзы, обеспечивающего получение плоской
волны в линзе при заданных значениях коэффициента пре-
ломления среды п и фокусного расстояния f.
Обратимся к рис. 6.2. На этом рисунке схематически
показаны две линзовые антенны, у одной из которых (рис.
6.2,а) п>1 (соответствует диэлектрическим и металло-ди-
электрическим линзам), а у другой (рис. 6.2,6) п<1 (соот-
ветствует ускоряющим металлическим линзам). Профиль
линз показан соответственно в виде кривых ВОВ' и СОС'.
Облучатель в обоих случаях помещен в точке S1, находя-
щейся на расстоянии / от вершины линзы О. В обоих слу-
чаях применяется прямоугольная система координат XY
с началом в точке О и с направлением оси X вдоль оси
линзы АА'.
Найдем формулу для расчета профиля линзы (кривых
ВОВ' и СОС'), обеспечивающего плоскую волну в линзе.
Плоская же волна в линзе означает, во-первых, что любой
из лучей, исходящих от облучателя, достигнув поверхности
линзы, распространяется дальше параллельно оси X и, во-
вторых, что время прохождения луча по такому ломаному
пути от облучателя до раскрыва одинаково для всех лучей
(как принято говорить, одинакова оптическая длина путей).
В соответствии с приведенными на рис. 6.2 обозначениями
и указанными двумя характеристиками плоской волны мож-
но писать:
для случая п>1
L д_ * + ,6П
с "1" с ’ ' • >
261
для n< 1
f (f - W + У2 , x
с с ' Оф-
(6-2)
Умножив обе части уравнения (6.1) и (6.2) на с, заме-
нив — через коэффициент преломления п и освободив-
°Ф
шись от радикала, получим:
для случая п>> 1
x2(n2—1)-{-2/х(п —1)—>2 = 0, (6.3)
для случая п < 1
х2(1—п2) —2fx(l—п)+>2 = 0. (6.4)
Из уравнений (6.3) и (6.4) видно, что при про-
филь линзы имеет гиперболическую форму, а при п<1 —
эллиптическую. Облучатель устанавливается в удаленном
от поверхности линзы фокусе эллипса или гиперболы.
Обозначим координаты точки В через d' и у (рис. 6.2,а),
а координаты точки С через d" и (рис. 6.2,6). Легко
видеть, что D' и D” равны ширине раскрыва линзы соот-
ветственно при п>1 и я<1, ad'H а1' — максимальной
толщине линзы в том и другом случае. Из уравнений
(6.3) и (6.4) получаем следующие расчетные формулы для
толщины линзы (максимальной):
Из уравнений (6.5) и (6.6) видно, что d' всегда веще-
ственно, d" вещественно лишь при
у (* 4~п)
Это означает, что при п>1 для любого размера раС’
крыва D и любого фокусного расстояния f может быть най-
262
дена такая толщина линзы, при которой сферическая волна
будет преобразована в плоскую, в то время как при и<1
сферическая волна может быть преобразована в плоскую
лишь при сравнительно больших фокусных расстояниях,
определяемых неравенством (6.7).
На рис. 6.3 приведены графики зависимости отноше-
/ d' d"\
ния толщины линзы к ширине раскрыва ( // и ) от
коэффициента преломления п для различных значений фо-
кусного расстояния, вычисленные по формулам (6.5) и
(6.6). Эти графики показывают, что при заданной ширине
раскрыва, толщина линзы тем меньше, чем больше значе-
ние f и чем больше коэффициент преломления отличается
от единицы. Очевидно, что с конструктивной точки зрения
выгоднее иметь линзу возможно более тонкую. Однако уве-
личивать для этого фокусное расстояние и коэффициент
преломления мы можем лишь в определенных пределах,
тйк как увеличение фокусного расстояния связано с увели-
чением размеров антенны, а увеличение коэффициента пре-
ломления — с увеличением отражения энергии от освещен-
ной стороны линзы. Наиболее практичными по указанным
соображениям являются линзы, имеющие коэффициент соот-
ветственно 1,3 -5-1,6 и 0,5-5-0,7 и фокусное расстояние
f = D. Согласно кривым рис. 6.3 толщина линзы составляет
при этом несколько десятков процентов от размеров рас-
крыва (в случае n<Z 1 линза значительно толще, чем в слу-
чае п>1). В целях уменьшения толщины применяются
ступенчатые (зональные) линзы.
Дело в том, что для получения плоской волны в линзе
условия (6.1) и (6.2) не являются единственными. Вместо
равенства времени прохождения различными лучами своего
пути от облучателя до раскрыва, можно допустить также
различие времени на целое число периодов. Тогда вместо
(6.1) и (6.2) получим соответственно:
для случая 1
L+ л=0+2+2. (6.8а)
ИЛИ
f + ПХ = Г(/-М‘‘+>2 - рТс == K(f + x)2+>2 - pl, (6.86)
где р—целое число, равное О, 1, 2, 3...,
Т — период колебаний.
263
at 0,1 Q3 О,к 0,5 Ц5 п
б)
Рис. 6.3. Графики зависимости относительной толщины линзы
d d
D7 и 25" от коэффициента преломления п при различных относитель-
D’ D"
ных значениях соответственно у и ~г : а] при л>1, ff) при п<1.
264
После освобождения от радикала и приведения подоб-
ных членов получаем:
(* + А)2(«2- 1)+
+ 2(/-л-Тп) (* + = (6-8в>
Для случая п<1 получаем аналогично
L = tV-*)a+ У? + ±_рТ (6.9а)
с с1 аф н ’
или
f = V(f — х)2+у2+пх — pl, (6.96)
и после освобождения от радикала и приведения подоб-
ных членов

X
x(i-«)+j/2=o.
(6.9в)
Рис. 6.4,а, б иллюстрирует методику вычерчивания про-
филя ступенчатой линзы. Первоначально вычерчивается
ряд гипербол (при п>1) или эллипсов (при п<1), соответ-
ствующих (6.8в) или (6.9в) при поочередной подстановке
р = 0,1, 2,3... Из точек пересечения гипербол с осью У про-
водятся прямые, параллельные оси X до пересечения с со-
седними гиперболами (рис. 6.4,а). Из точек же пересечения
эллипсов с осью У проводятся прямые к облучателю
(рис. 6.4,6). Ломаные линии, образованные отрезками гипер-
бол или эллипсов и отрезками указанных прямых, образуют
профиль ступенчатой линзы (жирная ломаная линия).
Следует заметить, что при р = 0 формулы (6.8в) и
(6.9в) переходят соответственно в (6.3) и (6.4), т. е.
являются уравнением профиля гладкой линзы. При р = 1,
2, 3, 4 и т. д. получаются уравнения аналогичных кри-
вых, но смещенных друг относительно друга по оси X
на отрезок в сторону облучателя при или на
отрезок р—- в обратную от облучателя сторону при
п< 1.
На рис. 6.4,в, г также показан ход лучей в ступенчатых
линзах. Легко видеть, что в линзе, соответствующей п>1
265
Рис. 6.4. Ступенчатые (зональные) линзы: а) построение ступеней при
л>1, ff) то же при п<^1, в) образование вредных зон при л>1,
г) то же при л< 1, д) построение ступеней у линзы, не имеющей
вредных зон при л>1, е) то же при л<1.
266
(рис. 6.4,в), не все лучи попадают на гиперболическую фо-
кусирующую поверхность: часть попадает на ступеньки и
рассеивается. В линзе же, соответствующей п<1 (рис. 6.4,г),
с точки зрения геометрической оптики должны образоваться
бколо ступенек «пустые» (незаполненные излучением) зоны
(которые будем называть вредными зонами). В действи-
тельности вследствие диффракции электромагнитное поле
возникает и в указанных вредных зонах. Однако это связа-
но, во-первых, с некоторой деформацией плоской волны в
линзе, а во-вторых, с увеличением рассеяния (отражения
от поверхности линзы).
Таким образом, ступенчатые линзы как при п>1, так
И при п<1 имеют, вообще говоря, меньшую эффективную
площадь, чем гладкая линза при одинаковых размерах рас-
крыва. В тех случаях, когда вредные зоны невелики срав-
нительно с нормальными зонами облучения, можно их влия-
нием пренебречь. В случае широких вредных зон приходит-
ся считаться с их влиянием. Легко видеть, что вредные зоны
невелики вблизи оси линзы и увеличиваются к ее краям.
Далее, вредные зоны тем меньше, чем больше фокусное рас-
стояние и чем больше отличие коэффициента преломления
от единицы.
Во избежание появления вредных зон следует делать
профиль ступенчатой линзы таким, как показано на
рис. 6.4,д, е. Здесь поверхность освещенной стороны линзы
образована дугами концентрических окружностей с цент-
ром в точке S (где помещен облучатель). Радиусы окруж-
ностей отличаются друг от друга на д2.j (ПРИ
.или (при п<1).
При таком выполнении освещенной стороны лучи не бу-
дут претерпевать преломления при переходе из воздуха
в линзу, поскольку они падают перпендикулярно к поверх-
ности линзы и поэтому сохраняют сферический фронт вол-
ны. Из линзы они выходят в среду с коэффициентом пре-
ломления п0= 1. Поэтому, чтобы при выходе из линзы полу-
чить плоскую волну, необходимо теневую сторону линзы
сделать в первом случае (n > 1) в виде эллипса и рассчи-
тывать по формуле, аналогичной (6.4), а во втором случае
(п<1)—в виде гиперболы и рассчитывать по формуле,
аналогичной (6.3). Эти формулы имеют следующий вид:
при п>1
х2 <6J°)
267
где
f’ — f + nd1',
при n< 1
(6J1)
где
f'f=f + nd".
В заключение заметим, что диэлектрические, замедляю-
щие металлические и металло-диэлектрические линзы, как
увидим ниже, при гладком профиле являются широкодиапа-
зонными, что является чрезвычайно важным их достоин-
ством. Устройство же ступенчатого профиля делает их чрез-
вычайно узкодиапазониыми. Поэтому линзы с п>1, т. е.
диэлектрические, замедляющие металлические и металло-ди-
электрические, как правило, делаются с гладким профилем,
хотя не исключена возможность применения в некоторых
случаях таких линз со ступенчатым профилем, особенно
диэлектрических, в целях уменьшения веса. Ускоряющие
металлические линзы являются принципиально узко диапа-
зонными и поэтому они делаются ступенчатыми. Как уви-
дим ниже, ступенчатые ускоряющие линзы имеют даже не-
сколько более широкую полосу пропускания, чем гладкие.
§ 2. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ И КОЭФФИЦИЕНТ
ПРЕЛОМЛЕНИЯ МЕТАЛЛО-ДИЭЛЕКТРИЧЕСКИХ ЛИНЗ
Для расчета профиля линзы необходимо знать ее коэф-
фициент преломления п. У диэлектрических линз п зависит
от диэлектрической проницаемости е материала, из кото-
рого сделана линза, и может меняться лишь в’ соответствии
с ассортиментом материалов, имеющих различное значе-
ние s. Металлические и металло-диэлектрические линзы
являются искусственными и поэтому их коэффициент пре-
ломления может быть предварительно рассчитан и подобран
по нашему усмотрению. Коэффициент преломления уско-
ряющих металлических линз зависит от расстояния b между
пластинами, образующими линзу, и длины волны £ и рас-
считывается по простой формуле (1.5). Коэффициент пре-
ломления замедляющих металлических линз также рассчи-
тывается весьма просто (стр. 21). Что касается металло-
диэлектрических линз, то их коэффициент преломления за-
висит от нескольких параметров металлических частиц, из
которых сделана линза, как-то: их формы, размеров и рас-
положения. В настоящем параграфе излагаются общие
268
принципы, лежащие в основе определения диэлектрической
проницаемости и связанного с ней коэффициента прелом-
ления металло-диэлектрических линз, и частные прибли-
женные расчетные формулы, соответствующие отдельным
разновидностям.
Общие принципы теории металло-диэлектрических линз
рснованы на предположении об эквивалентности металло-
диэлектрических линз с диэлектрическими, т. е. о воз-
можности рассматривать металло-диэлектрические линзы
Эак непрерывную диэлектрическую среду, имеющую ди-
электрическую проницаемость е. Тогда коэффициент пре-
ломления этой среды п равен корню квадратному из отно-
шения этой диэлектрической проницаемости е к диэлек-
трической проницаемости пустого пространства е0, т. е.
п= V -. Более того, само определение понятия диэлек-
’ е0
трической проницаемости заимствуется здесь из теории
обычных диэлектриков.
Известно, что у обычных изотропных диэлектриков е
представляет собой коэффициент, связывающий электри-
—►
Ческий вектор поля Е в диэлектрике с вектором смеще-
ния D по формуле
Ъ = еЕ. (6.12)
С другой стороны, вектор смещения может быть вы-
ражен через вектор поляризации Р следующим образом:
D = e0£4-P. (6.13)
Вектор Р, как известно, разен суммарному дипольному
моменту единицы объема. Полагая количество поляризо-
ванных частиц (диполей) в единице объема равным IV, а
средний дипольный момент каждой частицы т пропорцио-
нальным электрическому вектору поля Е, т. е.
'p = Ntn, (6.14)
**
m = a£
получим
D=^E+tia.E. (6.15)
269
Коэффициент а называется средней поляризуемостью
частицы диэлектрика. Сразнивая (6.15) с (6.12), получим
L==i + ^ (6.16)
и соответственно
n = (6.17)
Формула (6.17), выведенная для обычных диэлектриков,
полагается также справедливой для расчета коэффициента
преломления металло-диэлектрических линз. В приложении
к последним под 7V понимается количество металлических
частиц в единице объема, а под а — отношение электриче-
ского дипольного момента одиночной частицы т, возникаю-
щего у нее в постоянном однородном электрическом поле
(в электростатическом поле), к напряженности этого поля
* = (6.18)
Исследозание проводящих тел различной формы в по-
стоянном однородном электрическом поле дает следую-
щие значения поляризуемости а и коэффициента прелом-
ления п:
а) шар радиуса
а = 4-гс#3е0 (6.19)
и
n = V\ (6.20)
б) эллипсоид вращения, имеющий полуоси а и b и полу-
ченный в результате вращения эллипса вокруг большой
полуоси а, при направлении электрического вектора поля
параллельно этой полуоси
а — 4-ab2eQ (6-21)
и
п = V1 4- 4п№#2; (6.22)
в) тонкий круглый диск радиуса 7? при электрическом
векторе, параллельном плоскости диска
« = (6.23)
и
n = ]/1 +^NR3.
(6.24)
270
г) тонкая прямоугольная лента шириной w и сравни-
тельно большой длины а (полагая а > к) при электриче-
ском векторе, параллельном узкой стороне
и _________
«=/i+T^> <6-26)
где а' — поляризуемость единицы длины ленты, N— ко-
личество лент на единицу площади продольного сечения
линзы (рис. 1.8,д).
Полученные здесь значения п нуждаются в некоторых
коррективах. Во-первых, значения а в приведенных выше
формулах получены в предположении нахождения в одно-
родном электрическом поле одиночной металлической ча-
стицы, в то время как линза представляет собой совокуп-
ность большого числа таких частиц, сравнительно близко
расположенных, и поэтому правильное значение п должно
учитывать их взаимное влияние. Во-вторых, коэффициент
преломления линз определен на основе решения задачи
о металлических частицах в электростатическом поле, в то
время как в действительности они используются в перемен-
ном электромагнитном поле сверхвысоких частот.
В переменном поле электромагнитной волны появляются
токи на поверхности металлических частиц, которые в неко-
торых случаях приводят к значительному искажению кар-
тины магнитных линий поля, что эквивалентно наличию
у среды магнитной проницаемости, отличной от пустого
пространства. В последнем случае подкоренное выражение
в (6.17) должно быть умножено на относительную магнит-
ную проницаемость среды —.
Но
Таким образом, приведенные выше формулы для коэф-
фициента преломления должны быть исправлены с учетом,
во-первых, взаимного влияния частиц, во-вторых, изменения
эквивалентной магнитной проницаемости под влиянием по-
верхностных токов.
Посмотрим характер требуемых исправлений. Начнем с вопроса
о взаимодействии частиц.
Здесь этот вопрос излагается применительно к шариковым лин-
зам, содержащим объемные частицы. Для других линз из плоскост-
ных частиц— лент, дисков и т. п. вопрос о влиянии взаимодействия
частиц на коэффициент преломления в электростатической поста-
новке задачи не исследован, ввиду математической сложности.
271
В электродинамической постановке анализ сводится к задаче о не-
однородностях в волноводе. В § 9 излагается методика определе-
ния параметров ленточной линзы, основывающаяся на' решений за-
дачи в такой постановке с использованием современной теории
волноводов. Параметры определяются с учетом взаимовлияния лент.
Развитая методика может быть обобщена на другие виды линзовых
антенн из плоских частиц.
Исследование взаимного влияния частиц в электростатическом
поле у шариковой линзы [26] приводит к следующей известной фор-
муле, связывающей диэлектрическую проницаемость * с поляризуе-
мостью а и концентрацией частиц N:
-----1
е0 Na
е Зе0 ’
-4-2 0
ео ~
Из (6.27) следует:
2 а
. 1 + з Л'., |+г„
О &0
где
(6.27)
(6.28)
(6.29)
Сравнивая формулы (6.23) и (6.16), приходим к выводу, что учет
взаимного влияния частиц сводится к умножению значения диэлек-
трической проницаемости, получаемой по формуле (6.16) на попра-
вочный множитель
1 1-4-2» 1 + 2о
П = 1 _|_ за ’ 1 _ 0 = i _|_ 2о — Зо« • (6‘30)
а
У сферических частиц отношение
согласно (6.19) равно объе-
а
му отдельной частицы (сферы), a о —JVs—, поскольку ЛГ—число
O6q
частиц в единице объема, представляет отношение той части объема
линзы, которую занимают металлические частицы, к полному объему
линзы, т. е. коэффициент заполнения. Легко видеть из (6.30), что в
случае малого коэффициента заполнения и < 1 (что соответствует
большим расстояниям между частицами) 1 н формула (6.28) пере-
е
ходит в (6.16). Опыт показывает, что при—= 1,5 нли v =0,17 фор-
мула (6.16) дает достаточно точный результат. В случае же боль-
шого коэффициента заполнения (о -> 1), что соответствует сближе-
нию частиц до касания, когда линза превращается просто в метал-
S
лическое тело, т]->оо и поэтому
со. На рис. 6.5 даны кривые
t
зависимости т) и — от V, иллюстрирующие характер исправлений,
*0
которые требуется вводить в формулу (6.16), при учете взаимного
влияния частиц.
При других вариантах металло-диэлектрических линз, очевидно,
общий характер будет таким же, особенно это относится к крайним
случаям v <? 1 и»->1. Следовательно, и при других вариантах линз
формула (6.30) может служить для приближенного определения по-
правочного множителя, тем более, что на практике обычно исполь-
Рис. 6.5. Графики зависимости относительной величины диэлектри-
ческой проницаемости среды
е
— и поправочного множителя -п, учиты-
ео
тывающего взаимовлияние частиц, от коэффициента их заполнения и
в металлрдиэлектрической линзе.
зуются линзы, имеющие сравнительно небольшую диэлектрическую
проницаемость । = 2 4- 2,5) . при которой г, еще довольно близко
• ео /
к единице.
Перейдем к рассмотрению второго вопроса о влиянии поверх-
ностных токов на величину коэффициента преломления. Этот вопрос
также излагается здесь применительно к шариковым линзам.
[ На рис. 6.6 показана картина магнитных линий поля плоской
волны вблизи металлического диска и шара. У первого из них по-
верхностные токи, как видно, не приводят к искажению магнитных
линий поля, у второго эти линии искажаются. Очевидно, что у эл-
липтических частиц, ввиду их объемного характера, магнитные линии
поля также искажаются, а у ленточных, как у плоских, остаются
неискаженными. Из сказанного ясно, что влияние поверхностных
токов на коэффициент преломления имеет место лишь у линз, обра-
зованных объемными частица ли (шариками, эллипсоидами и т. д.).
18—1503
273
Исследование шариковых линз показало, что искажение магнит-
ного поля поверхностными токами соответствует появлению у среды
линзы магнитной проницаемости:
(.= 1*0(1-27^8), (6.31)
Следовательно, если учесть влияние поверхностных токов на
величину коэффициента преломления, формула (6.20) должна быть
заменена следующей:
п = /(1 -j- (1 — 2t:W). (6.32)
Из (6.32) следует, во-первых, что шариковая линза не может
иметь коэффициент преломления больше
«макс = |/1=1.06 (6.33)
= —и, во-вторых, что при сравнительно большой концен-
/ 1 1 \
трации частиц I 2-nNRs> у илн коэффициент преломления
может принять значения меньше единицы. Оба вывода из (6.32) не
Рис. 6.6. Магнитное поле плоской волны вблизи металлического диска
(слева) и шара (справа).
соответствуют действительности, так как не учитывают взаимного
влияния частиц. В действительности, благодаря взаимному влиянию
частиц диэлектрическая проницаемость линзы растет значительно
быстрее, чем по закону
е
ео
= 1 -f- 4тсЛГ/?з, а при большой концентрации
частиц, при которой они близки к касанию,
с
— -> со. В соответствии
е0
с этим, коэффициент преломления шариковых линз также всегда
2 74
имеет значение большее, чем это следует из формулы (6.32) и при
большой концентрации частиц также стремится к бесконечности.
Формула (6.32) совместно с рис. 6.6 может служить лишь для об-
щей качественной характеристики влияния поверхностных токов.
На практике применяются главным образом дисковые и ленточ-
ные лннзы, из соображений малого веса и простоты устройства.
Эти линзы имеют также преимущество в связи с отсутствием у них
отрицательного эффекта поверхностных токов. Шариковые линзы
представляют преимущественно теоретический интерес. Их рассмо-
Ш|ние оказалось полезным для выяснения ряда закономерностей,
^Становление которых на примере других вариантов линз является
%еёьма затруднительным.
f- ' Известным практическим достоинством шариковых линз может
оказаться их изотропность, выражающаяся в том, что у них коэф-
фициент преломления п не зависит от поляризации падающей волны,
В то время как у дисковых линз коэффициент преломления зависит
, —>
ot угла, образованного направлением электрического вектора Е
с плоскостью дисков, а у ленточных — от угла между Е и узкой
стороной ленты. Однако анизотропность дисковых и ленточных линз
может проявиться лишь при расположении облучателя далеко в сто-
роне от оси линзы и наличии при этом параллельно поляризованной
волны, у которой электрический вектор поля параллелен плоскости
распространения, т. е. плоскости, образованной направлением рас-
пространения и осью линзы. В современной практике такой случай
почти не встречается и поэтому практические преимущества диско-
вых н ленточных линз бесспорны.
§ 3. ЧАСТОТНЫЕ СВОЙСТВА ЛИНЗОВЫХ АНТЕНН
Частотные свойства линзовых антенн в основном опре-
деляются частотной зависимостью коэффициента прелом-
ления.
У диэлектрических линз коэффициент преломления прак-
тически постоянен в пределах всего диапазона сверхвысо-
ких частот. Поэтому диэлектрические линзовые антенны
с гладким профилем являются неограниченно диапазон-
ными,
У металло-диэлектрических линз в связи с тем, ЧТО' раз-
меры частиц соизмеримы с длиной волны Д имеет место
зависимость коэффициента преломления от частоты. Харак-
тер этой зависимости в самых общих чертах иллюстрируется
рис. 6.7. На этом рисунке через f обозначена рабочая часто-
та, а через /о — собственная (резонансная) частота отдель-
ной частицы линзы. Мы видим, что вблизи резонанса имеют
место резкие изменения коэффициента преломления. Далеко
же от резонанса в области более низких частот коэффициент
преломления остается практически постоянным. Для количе-
ственной ориентировки в данном вопросе может служить
18* 275
Известная формула зависимости от частоты диэлектрической
проницаемости среды, состоящей из элементов, резонирую-
щих под действием электромагнитного поля высокой ча-
стоты:
(6.34)
f20-f2
и соответственно
л=/'+-^4' <б-35>
10 — 1
где k — коэффициент пропорциональности.
Формула (6.35) предполагает знание собственной ча-
стоты f0.
Как известно, собственная частота зависит от разме-
ров и формы частиц, а при близком расположении по-
Рис. 6.7. Графики зависимости коэффициента пре-
ломления от частоты у диэлектрических и металло-
диэлектрических линз.
следних—также от расстояния между ними. Однако при
проектировании можно в качестве исходной величины
принять, что резонанс у частиц наступает, когда макси-
мальный линейный их размер D в направлении, параллель-
1 т~т
ном электрическому вектору поля, равен g-. При таком
предположении выражение (6.35) можно преобразовать
следующим образом:
где k' — новый коэффициент пропорциональности.
276
В порядке иллюстрации рассмотрим следующий при-
мер. Предположим, что п —1,5 при £)<2. Тогда, согласно
(6.36) £'=1,25. Подставив в (6.36) это значение £' и
D=-^ или D=g, получим соответственно п = 1,63 или
П=1,53. Следовательно, при п=1,5 можно получить
динзу, у которой коэффициент преломления остается по-
стоянным с точностью до 10% для всех частот, для ко-
торых D<Z~^, или с точностью до 2% для всех частот,
г-1 Чшн ,
для которых О<—б—, где 2 — минимальная волна диа-
пазона. Очевидно, что подбором размеров частиц прин-
ципиально возможно получить металло-диэлектрическую
линзу с любым другим коэффициентом преломления для
любого диапазона частот.
Следует заметить, что в связи с возможностью резони-
рования частиц ленточные линзы пригодны лишь для ли-
нейно-поляризованной волны с электрическим вектором,
параллельным узкой стороне лент, в то время как шари-
ковые, дисковые или пластинчатые, ввиду круглой или
квадратной формы, могут применяться как при линейной,
так и при круглой поляризации поля.
У замедляющих металлических линз коэффициент пре-
ломления не зависит от частоты. В тех пределах, в каких
расстояние между пластинами у этих линз остается меньше
половины длины волны, они являются диапазонными.
У ускоряющих линз, при практически пригодных значе-
ниях коэффициента преломления (п=0,5ч- 0,7), последний
весьма резко меняется с изменением частоты. Металличе-
ские линзы являются принципиально узкодиапазонными и
могут применяться лишь в пределах весьма узкой полосы
частот.
Для расчета полосы пропускания металлической литы
определим фазовые искажения поля в раскрыве линзы,
возникающие на волне 2, отличающейся от частотной вол-
ны 20.
Введем обозначения:
/?0= 1/ 1 — —коэффициент преломления на волне20,
п—у 1 — (ЗА2— коэффициент преломления на волне 2,
277
b — расстояние между пластинами, образующими
линзу,
Уфо — фазовая скорость на волне 20,
Уф — фазовая скорость на волне 2,
Дфгл— максимальные фазовые искажения у гладкой
линзы,
Дфст— максимальные фазовые искажения у ступенча-
той линзы,
d' —толщина гладкой линзы,
d2—толщина ступенчатой линзы,
D'1 — ширина раскрыва,
f — фокусное расстояние.
а) Гладкая линза б) Ступенчатая линза
Рис. 6.8. К выводу формулы полосы пропускания линз: гладкой (а)
и ступенчатой (б).
Будем считать, что D'' и f одинаковы у гладкой и
ступенчатой линзы (О"= D”=D").
Очевидно, что на волне 2 наибольшая разность фаз
имеет место между полем в крайней точке М раскрыва
и полем в средней точке О (рис. 6.8). Следовательно,
(6.37)
(6.38)
278
На расчетной же волне Ло справедливы равенства (6.2.
и 6.9,а), из которых следует:
f = y^ (f — rf'i')2+ (т/ + МГ> (6.39)
f = }^(f~^)2+^)2 + n^2-P^ (6.40)
где р — число ступенек у линзы.
Подставив значение f из (6.39) и (6.40) в (6.37) и (6.38),
а затем умножив и разделив полученное выражение на
п0-1~п, получим:
2л и 2тЩ, X2 — Лл
Н,. = ^ (« — „о) d{ = , (6.41)
, , 2л . . ,п q Хг, 2л</2 X2 Ху
^ст — т (п — /Zo) d2 — 2тгр у- — —у- (Ив + и) (26)2 —
— (6.42)
У ступенчатых линз d? — сравнительно малая величина.
Поэтому в (6.42) преобладает слагаемое, пропорциональ-
ное р. Это слагаемое равно примерно величине Дфг1](6.41).
Так как другое слагаемое в (6.42) имеет противополож-
ный знак, то Д'рст <Дфгл.
Из выражений (6.41) и (6.42) с учетом сказанного сле-
дует, что фазовые искажения пропорциональны у гладкой
линзы ее толщине, а у ступенчатой—числу ступенек.
При помощи формул (6.41) и (6.42) вычислена зависи-
мость ширины полосы гладкой линзы от ее толщины, а
ступенчатой линзы от числа ступенек при п = 0,5 и до-
пустимом максимальном значении Д<{/ = ^-. Результаты
расчета графически изображены на рис. 6.9. Сплошная
кривая соответствует гладкой линзе, а штриховая—сту-
пенчатой. По оси ординат отложена полоса пропускания
в процентном отношении к средней частоте полосы, по
d\’
оси абсцисс---у- (верхний ряд цифр) и число ступенек
(нижний ряд цифр).
Толщина гладкой линзы, а также количество ступе-
нек у ступенчатой линзы зависит от размеров раскрыва,
фокусного расстояния и коэффициента преломления.
279
Размеры раскрыва определяются заданными в техни-
ческих требованиях характеристиками излучения (коэф-
фициентом усиления G и шириной главного лепестка 2%).
Поскольку в плоском раскрыве линзы получается син-
фазное поле, то, как показано в гл. Ill, С? = у-^~, где S —
площадь раскрыва, а 20о=х^, где D — диаметр ра-
скрыва.
Фокусное расстояние ограничено габаритными требо-
ваниями. Как указывалось выше, f=D.
Рис. 6.9. Графики зависимости относительной величины полосы про-
я"
пускания -г соответственно от относительной толщины линзы "L
' X
у гладкой линзы и от числа ступеней р у ступенчатой линзы.
Таким образом, нельзя изменением размеров раскрыва
или фокусного расстояния регулировать толщину линзы или
число ступенек, т. е. нельзя регулировать полосу пропуска-
ния металлической линзы.
Что касается коэффициента преломления п, то возмож-
ность его уменьшения в целях уменьшения d" и р также
ограничена. Дело в том, что малые значения п получаются
при расстояниях Ь между пластинами, близких к критиче-
ским, при которых резко возрастает рассеяние энергии по-
2?0
верхностью линзы и, кроме того, ее работа становится не-
устойчивой Поэтому обычно ограничиваются значением
п=0,5 л- 0,7.
Ввиду практической невозможности каким-либо спосо-
бом значительно снизить фазовые искажения в раскрыве
металлической линзы, ее следует рассматривать как узко-
полосную.
§ 4. ТЕХНИЧЕСКИЕ ДОПУСКИ
Расчет фазовых искажений в раскрыве линзы, вызывае-
мый отклонением частоты от расчетной, позволил опреде-
лить полосу пропускания линзы. Вычислим теперь фазовые
искажения, вызываемые неточностями изготовления антен-
ны, для определения технических допусков.
Рассмотрим следующие виды неточностей изготовления
антенны.
1. Кривая профиля отличается от расчетной (рис. 6.10,а),
причем облучатель находится точно в фокусе.
2. Облучатель смещен относительно фокуса в направ-
лении оси линзы (рис. 6.10,6), а профиль линзы точно соот-
ветствует расчетному.
3. Облучатель смещен относительно фокуса в направ-
лении, перпендикулярном оси, а профиль линзы соответ-
ствует расчетному (рис. 10,в).
4. Неточность установки пластин в ускоряющей метал-
лической линзе (рис. 10,6).
Анализ фазовых искажений, вызываемых указанными
неточностями изготовления, проведем на примере линзы
с коэффициентом преломления и>1, а затем обобщим полу-
ченный результат на случай линзы с п<1.
При неточности первого вида максимальные фазовые
искажения, т. е разность фаз поля между средней точкой
раскрыва О" и крайней точкой М, как легко видеть из
рис. 6.10,а, равны
Дф, = [(50' + пО'О") — 5Л4] =
= ?[(/ + «) + » — nd')] = 2£ а (п - 1). (6.43)
Из (6.43) можно получить величину допустимой неточ-
цости, если задаться значением Дф;. Как и прежде, по-
ложим Дф|Макс=£-- Тогда получим значение допуска
С1 макс на неточность в кривой профиля линзы:
ai макс 4(п —|)
(6.44)
281
Рис. 6.10. К расчету допусков на неточность выполнения линзовой
антенны: а) неточность выполнения профиля линзы, ff) смещение облу-
чателя из фокуса вдоль оси, в) то же в перпендикулярном к оси
направлении, г) смещение двух половин линзы на четверть волны
для ослабления отражения от поверхности линзы, д) неточная уста-
новка пластин в ускоряющей металлической линзе.
282
Так как отступление от теоретической кривой в раз-
ных точках может иметь разный знак, то в качестве до-
пуска следует принять
а1 макс
~“2

(6.44,а)
При неточности второго вида, т. е. при помещении
облучателя не в фокусе S, а в точке 5' (рис. 6.10,6),
максимальные фазовые искажения равны
Дф3 = ^[$'М — (5'0ф пОО')]. (6.45)
Так как согласно рис. 6.10,6
S’O = f — а,
S'M = SM — SP = f + nd — a cos а,
ОО' = d',
то
Д^2=уП(1—cosa). (6.46)
Положив Дф2 макс — , получим следующее значение
допустимого смещения облучателя из фокуса вдоль оси
линзы
^2 макс 4(1—cos а) ‘ (®-47)
В связи с возможностью такого сравнительно боль-
шого допуска, какой следует из формулы (6.47), часто
в целях ослабления поля отраженной волны от поверх-
ности линзы, последнюю делают из двух половинок, сме-
X
щенных друг относительно друга на как показано на
рис. 6.10,г. В этом случае каждая из половин получается
смещенной относительно фокуса на g-, что не приводит
к заметным фазовым искажением. Отраженные же от
поверхностей половинок волны имеют в направлении на
облучатель противоположные фазы и не вызывают его
рассогласования.
Фазовые искажения при неточностях первого и второго
вида имеют симметричный характер относительно оси лин-
зы, т. е. являются четной (квадратичной) функцией от коор-
динаты у, что, как мы видели в гл. III, приводит к иска-
283
жениям формы диаграммы направленности (рис. 3.18) при
сохранении нормального направления главного максимума.
Поэтому и необходимо в данных случаях ввести ограниче-
ния на неточность, определяемые формулами (6.44) и
(6.47). При неточности же третьего вида (рис. 6.10,в), вы-
ражающейся в смещении облучателя из фокуса в перпен-
дикулярном к оси направлении, изменения фаз в раскрыве
имеют монотонный характер и являются нечетной функ-
цией координаты у.
При линейном законе, как мы видели (гл. III § 6), это
приводит к отклонению главного максимума диаграммы
направленности на некоторый угол а от нормального на-
правления (перпендикулярного к плоскости раскрыва) при
сохранении общей формы диаграммы направленности такой,
какой она получается при строго синфазном поле. В некото-
рых практических случаях, такое отклонение главного ма-
ксимума является положительным фактором и, как изве-
стно, используется для получения вращающейся диаграммы
направленности (путем вращения смещенного облучателя
вокруг оси линзы). В тех случаях, когда отклонение глав-
ного максимума не используется для специальных целей,
оно также не приводит к серьезным отрицательным явле-
ниям, если не сопровождается искажениями формы диа-
граммы направленности, поскольку направление главного
максимума может быть определено опытным путем. По-
этому при третьем виде неточности будем определять до-
пуски не непосредственно по фазовым искажениям Д ф3, а
по отклонениям последних от линейного закона, так как
только такие отклонения вызывают искажение формы диа-
граммы направленности.
Так как фазозые искажения Д<р3 являются в данном
случае нечетной функцией от координаты у, то можно
их представить в виде следующего ряда:
00
д<р3 = £ САгУт+!=Сйу + С,^ + с„у+ ..., (6.48)
т=0
где коэффициенты Ст являются функциями смещения а,
фокусного расстояния f и толщины линзы d',
tn ~: 1, 2, 3 ...
Очевидно, при малых значениях у преобладает первое
слагаемое, т. е. Д практически является линейной функ-
цией координаты у, а при возрастании у начинает сказы-
284
ваться роль сначала кубического члена, затем члена пятой
степени и т. д. Так как мы ограничиваем фазовые искаже-
ния небольшой величиной, то они обычно определяются
лишь первыми двумя слагаемыми, из которых искажение
формы диаграммы направленности вызывается лишь куби-
ческим членом. На рис. 3.19 приведены диаграммы направ-
ленности антенны с прямоугольным (3.19,а) и круглым
(3.19,6) раскрывом при постоянных амплитудах и кубиче-
ском законе изменения фаз. Из этих диаграмм видно, что
наличие кубического члена в выражении (6.48) приводит
к дополнительному смещению главного максимума при
одинаковых знаках коэффициентов С] и С2 или к умень-
шению угла отклонения главного максимума при разных
знаках этих коэффициентов. Относительная величина боко-
вых лепестков с одной стороны от главного максимума воз-
растает, а с другой стороны от него уменьшается. Диаграм-
ма направленности становится асимметричной относительно
главного максимума.
При величине кубического члена на краю линзы
искажения формы диаграммы направленности не выходят
за пределы допустимого. Следует при этом учесть, что, как
правило, амплитуды поля в раскрыве линзовой антенны,
вследствие наличия некоторых направленных свойств облу-
чателя и перераспределения мощности из-за преломления
лучей (см. ниже § 11), не являются постоянными, а убы-
вают в направлении от центра к краям и что поэтому боко-
вые лепестки имеют меньшую величину, чем на рис. 3.19.
Перейдем к расчету фазовых искажений и определению
допуска на неточность третьего вида.
Если бы облучатель находился в фокусе (в точке S
рис. 6.10,в), то луч, падающий на точку N профиля, про-
1
шел бы до раскрыва путь SNM. Выйдя же из точки 5',
луч пройдет путь S'NM’. При сравнительно небольшой
толщине линзы у < 1 и при небольшом смещении у
разность путей Д/ приближенно равна отрезку S'p:
Д/ = SNM — S'NM'— S'p = a sin у — а = а . (6.49)
285
Соответственно фаза поля в различных точках раскрыва
будет определяться формулой
Ф3 = v (SNM— S'NM') s a sin 7 s 4-у. (6.50)
Л л л I
Из формулы (6.50) видно, что линейный закон изме-
нения фазы сохранится приближенно в тех пределах,
в которых справедливо равенство
sinY = -^-. (6.51)
Если бы закон (6.50) удовлетворялся на протяжении
всего раскрыва линзы, то в крайней точке L (рис. 6.10,в)
фаза поля фЗЛ равнялась бы
?зл х f 2 ' (6.52)
В действительности фаза поля ф £ равна
. 2л 2 г. a D’
Фзг — Та sin Y — т f + nd' ~2 ‘ (6-53)
Таким образом, максимальная величина отклонения от
линейного закона составит
Дфз = Фз! - Фзд = Т T FFW7) • (6-54)
Полагая, что допустимы отклонения Дф3 = у , полу-
чаем значение допустимого максимального смещения
азмакс облучателя из фокуса в перпендикулярном к оси
направлении
X р f-4-nd п
а3макс =Dr f 2nd’ ‘ (6.55)
Из (6.55) следует
а3макс _ X f -j-nd'
f ~ 1У~ '2nd’ ’ ' ’ ’
В свою очередь
^P-=tg»0MaKCSft0MaKc- (6.56а)
где &Омакс представляет собой максимальный угол между
прямой S'O и осью линзы, при котором еще сохраняется
линейный закон изменения фаз в раскрыве линзы. При
286
Слешеййи облучателя в точку S' фазовый фронт волны
Поворачивается относительно раскрыва линзы на угол &0
(рис. 6.10). Следовательно, угол &Омакс, определяемый фор-
мулами (6.56) и (6.56а), есть максимальный угол отклоне-
ния глазного максимума диаграммы направленности от
Нормального направления, без заметного искажения формы
яйаграммы направленности, которое может быть полу-
иено у линзовой антенны
фокуса. В этой формуле
^^7- представляет собою
при смещении облучателя из
равно примерно ширине глаз-
ного лепестка диаграммы направленности антенны, а
функцию параметров линзы,
равную в практических случаях 1,5-т— 2. Следовательно,
максимальный угол отклонения глазного максимума из-
лучения от нормального направления в 1,5-4-2 раза больше
ширины главного лепестка диаграммы направленности.
На рис. 6.11 приведено 6 серий кривых зависимости
разности хода Д/ лучей, идущих из фокуса S и из сме-
щенной точки 5'[см. формула (6.49)] от координаты раск-
рыва у . Каждая серия кривых соответствует определен-
ным значениям п и -j-. По оси ординат отложены значе-
У4 Д/ Д63 /, 2г. \
ния ^2" ’ а 110 оси абсцисс — значения у j .
Во всех случаях фаза в средней точке раскрыва принята
равной нулю, а облучатель предполагается смещенным
в сторону положительных (рис. 6.10,в). В каждой серии
отдельные кривые
а
НИям — .
йрямая-,
закону,
Для
ственно
относятся к определенным значе-
Около каждой кривой тонкой линией показана
соответствующая гипотетическому линейному
определяемому уравнением (6.50).
большей точности кривые вычислялись непосред-
по формуле
Д/ = (S'N -ф пШГ — f — nd'),
где (рис. 6.10,в)
S’N = —а ц-х)2 +У2,
NM' = NM sec о = (d' — х) sec 6,
ys=y — (d' — x)tg%.
(6.57)
287
' А/ У £>
Рис. 6.11,а. Кривые зависимости между и рД-; у = 1, 0, п = 1,35 и 1,8.
КОЗ I
Д/ У D
Рис. 6. И, б. Кривые зависимости межну— и — ;— =0,75. п = 1,35, 1,8.
£>/2 -£>/2 f
' М V D
Рис. 6. 11, в. Кривые зависимости между ------- и — ;— =0,5, п= 1,35 и 1,8.
f
Рис. 6. 11, г. Кривые зависимости междуи = 1,0, п = 1,6.
^/г ^/2 f
Рис. 6. 11, д. Кривые зависимости между и ; — = 0,75, п = 1,6.
Dlt ^/2 f
Рис. 6. 11, е. Кривые зависимости
Д/ D
между и -2- ; — = 0,5, п = 1,6.
^/2 ^/а f
Точки на рис. 6.11 соответствуют линзам особого
профиля, рассмотрению которых посвящен следующий
параграф.
Заметим, что формулы (6.44а), (6.47) и (6.55) для расчета
допусков справедливы также для линз с и<1 (ускоряющих
металлических). Но очевидно, что в формуле (6.44) нужно
заменить п — 1 на 1 — п.
У ускоряющих металлических линз, кроме отмеченных
выше, имеет место еще один вид неточности, а именно:
неточность установки пластин в линзе. Обратимся к
рис. 6.10,д.
На этом рисунке обозначены:
b—расчетное расстояние между пластинами,
Ь-\-а — действительное расстояние.
Вследствие изменения расстояния между пластинами
коэффициент преломления примет значение, отличное от
расчетного. Расчетное значение коэффициента преломле-
ния п0 очевидно равно
’-(i)2’ - <6’58)
а действительное равно
”1== Г 1— [ 2 (б-j- а) ] • (6-59)
Фаза поля в точке О (рис. 6.10,0) будет отличаться
от фазы поля в точке М на величину
2 9
2 тс л R(\
Дф4 = d" (nt - n0) = 2Т d” . (6.60)
Так как*при малой величине неточности ко-
эффициент п мало отличается от п0, то можно положить
«1 + «о = 2п0. (6.61)
В результате получим
А<11 _2itd" rto 2тс 1 />2 \ r.\d" 2а
— у а — ;ц6+а)а)^~п^ 4бз"
(6.62)
294
и соответственно, если считать наибольшее значение Дф4
равным ~
(6-63)
Из формулы (6.63) видно, что при заданной длине
волны допуск а4макс тем больше, чем больше b и п0 и чем
меньше толщина линзы d". Так как зависимость от b носит
кубический характер и так как коэффициент преломле-
ния п0 меняется в ту же сторону, что и b (п0 растет с
увеличением b и убы :ает с уменьшением Ь), то, следоза-
тельно, а4макс резко зависит от п0 и имеет тем большее
значение, чем больше п0.
Зависимость а4макс от d" говорит о том, что у сту-
пенчатой линзы, имеющей малую величину d", допуск
а4л)ожс больше, чем у гладкой с теми же параметрами (п0,
D, В-
§ 5. АПЛАНАТИЧЕСКИЕ ЛИНЗЫ
Мы до сих пор анализировали характеристики и осо-
бенности либо плоско-выпуклых линз, имеющих плоский
раскрыв и гиперболический профиль (п>1), либо плоско-
вогнутых с плоским раскрывом и эллиптическим профилем
(п<1). Параметры этих линз и их профиль, как мы видели,
рассчитываются по весьма простым формулам. Такие про-
фили и помещение облучателя в фокусе или вблизи фокуса
линзы обеспечивают получение плоской волны в раскрыве,
а следовательно, требуемые характеристики излучения.
В ряде практических случаев требуется обеспечить с по-
мощью линзовой антенны качание главного лепестка диа-
граммы направленности в пределах большого угла. Это
возможно осуществить при смещении облучателя из фокуса
на значительные расстояния в перпендикулярном к оси на-
правлении. Однако при обычных линзах, как показано
выше, значительные смещения облучателя из фокуса вызы-
вают, наряду с отклонением главного лепестка от нормаль-
ного направления, искажение формы диаграммы направ-
ленности. Чтобы при больших смещениях облучателя сохра-
нить форму диаграммы направленности, применяются линзы
специального профиля, которые по аналогии с оптиче-
скими линзами такого рода мы будем называть апланати-
ческими.
Линзы, как отмечалось (гл. 1), имеют две поверхности:
«освещенную» и «теневую» — раскрыв. Если на форму по-
29т
верхности линзы налагается только одно условие, например
условие получения плоской волны в раскрыве при помеще-
нии облучателя в фокусе, то одна из поверхностей может
быть выбрана произвольно. Из соображений удобства одна
поверхность делается плоской, а другая определяется уже
из указанного условия при заданной форме первой поверх-
ности. Если на форму поверхности линзы наложить еще
второе условие, то обе поверхности («освещенная» и «тене-
вая») определяются однозначно из заданных двух условий.
Мы видели, что плоская волна в раскрыве линзы со-
храняется приближенно до тех пор, пока справедливо ра-
венство (6.51) (рис. 6.10,в):
sinx = -j-, (6.51)
которое для краткости мы будем называть законом сину-
сов.
Апланатические линзы характеризуются той особен-
ностью, что на их поверхности налагаются следующие два
условия:
1) профиль освещенной стороны линзы должен удовле-
творять условию (6.51) (закон синусов);
2) раскрыв линзы должен удовлетворять условию полу-
чения синфазного поля при нахождении облучателя в фоку-
се (условие синфазности).
На рис. 6.12 показана двояковыпуклая линза и два луча
SPQP и SAB, исходящие из фокуса. Обозначения видны
из рисунка. Указанные выше два условия математически
выражаются следующим образом:
]. JL=sjny, (6.64)
2. г + ns-\-q = r0-lr nd, (6.65)
где f — пока не определенная постоянная, называемая
фокусом линзы, а п — коэффициент преломления.
Из рис. 6.13 видно далее, что между отрезками г, s,
q, r0, d существуют соотношения:
г cos у 4- s cos (у — P 4- ₽') + q = rQ + d, (6.66)
rsinY4- ssin(Y~04- (6.67)
9 = £ — (6.68)
-~ = tgp. (6.69)
296
Подставиз значение q из (6.65) в (6.66) и у из (6.64)
в (6.67) и учтя (6.68), получим
s[n — cos (у — 0)] = (n — l)d — r(l — cosy), (6.70)
ssin(y — 6) = (f — r)siny. (6.71)
А исключив из (6.70) и (6.71) параметр s, получим далее
sln (7-6) __ (f - г) sin f fi
n — cos(7 — в) (n—1) rf — r (1 — cos у) ’ ( -lz>
Рис. 6.12. К выводу формулы для профиля
апланатической линзы.
Учитывая закон преломления
sin р = rising (6.73)
и уравнение (6.68), можно (6.69) преобразовать к следую-
щему виду:
1 dr sin 0 /с „
Если учесть (6.72), то (6.74) можно рассматривать как
дифференциальное уравнение, связывающее г и у и пред-
ставляющее собой уравнение профиля освещенной стороны
линзы. Интеграл этого уравнения часто определяется чис-
ленным интегрированием в соответствии с условиями за-
дачи. Так как интеграл уравнения (6.74) должен содержать
297
s'
o'
27
S*
Рис. 6.13. Профиль линзы, удов-
летворяющий закону синусов
и условию синфазности при
п = 1,6.
произвольную постоянную, то отсюда следует, что задача
не имеет вполне определенного решения. В результате, на-
хождение профиля апланатической линзы указанным путем
в самом общей виде является задачей чрезвычайно труд-
ной.
Однако, как оказывается,
для практически наиболее важ-
ного случая (я = 1,6) может
быть найден весьма простым
способом профиль линзы, до-
статочно хорошо удовлетворяю-
щий сформулированным выше
- двум условиям: закону синусов
и условию синфазности. Такая
линза показана на рис. 6.13.
Она также является плоско-
выпуклой, но, в отличие от
обычных линз с гиперболиче-
ским профилем, у нее освещен-
ная сторона плоская, а раскрыв
криволинейный. Поскольку од-
на поверхность линзы нами за-
дана, то для определения вто-
рой поверхности можно приме-
нить только одно условие, а
именно, условие синфазности.
Найдем сейчас из условия син-
S'O'S", характеризующей фор-
фазности уравнение кривой
му поверхности раскрыва линзы, и покажем, что одновре-
менно линза удовлетворяет закону синусов.
Условие синфазности в обозначениях рис. 6.13 может
быть написано следующим образом:
r0 sec у + ns -f- (d — s cos £') = r0 -ф nd\ (6.75)
с другой стороны,
J = ''otgY4- ssin^'.
(6.76)
Подставляя значение s из (6.75) в (6.76), получим
v_ „ ts?у I sin Т (n-l)rf-ro(sec-r—1)
z о & I Т п п _ cos ji'
(6.77)
ИЛИ
J, = SinT[,0see7-! <" X-ЛоЛУ ~- <6-78)
298
При малых значениях у, cosps] и secy— Is0, сле-
довательно, в этом случае
? = siny + (6-79)
т. е. фокусное расстояние f в этой линзе в смысле (6.64)
равно
f=M- 4- <6-8°)
Для луча, проходящего через крайнюю точку S°, можем
написать
r0 sec a -\-d = г0 ф nd. (6.81)
Подставив r0-{-nd из (6.81) в (6.78), получим
, = 51пф0зесТ+\<—У]. (6.82)
Введем в квадратную скобку выражения (6.82) значе-
ние фокусного расстояния из (6.80)
> = sin, [f - г,-Л + r„sec 1 + ~:у>] . (6.83)
Учитывая, что согласно (6.81)
^='-0^4 (6-84)
уравнение (6.83) можно преобразовать к следующему виду:
V — sin-r ГГ-1-r П'~П~'(5СС7 11 rp(seca—secy) (1—cos g')l
J — siny|y-|-r0 n-1 (secy i) n(n-l)(n-cosfl') ]•
(6.85)
Выражение (6.85) состоит из трех слагаемых. Чтобы
оно удовлетворяло закону синусов, второе и третье сла-
гаемые должны равняться нулю. Для равенства нулю
второго слагаемого достаточно, чтобы
n2_n__i=o, (6.86)
откуда получаем nsl,6.
Что касается третьего слагаемого, то оно равно нулю
при у = 01) и при у = а, т. е. оно равно нулю для средней
*) Поскольку Р' = 0 при 7 = 0.
299
точки линзы О и для ее крайних точек 5' и S". Вслед-
ствие этого оно имеет небольшие значения и в проме-
жуточных точках между О и S', а также между О и S".
Таким образом, при коэффициенте преломления п=1,6
апланатическая линза может быть сделана плоско выпук-
лой с плоской освещенной стороной и профилем раск-
рыва, вычисляемым по формуле
у = Sin Г Г f - f9(se7r sec7)(l-c°^'). 1 . (6 87)
’ L' «(я—1)(л —cosji') J v '
Если закон синусов выполняется достаточно точно,
то криволинейная сторона линзы представляет собой дугу
окружности. Расчет профиля по формуле (6.87) для линз,
D . 3 1
у которых отношение параметров у = 1, и — пока-
зало, что значение координат профиля отличается от зна-
чения координат дуги окружности на небольшую долю
процента, т. е. практически профиль не отличается от
дуги окружности. Так как окружность может быть про-
ведена через три известные точки, то получается простой
способ определения профиля такой линзы: по заданной
ширине главного лепестка диаграммы направленности
определяется ширина раскрыва D, т. е. определяются
две крайние точки профиля, а для определения третьей
точки необходимо вычислить толщину линзы d. Толщина
же линзы, как легко видеть, может быть вычислена по
формуле
Действительно, из (6.80) и (6.84) с учетом (6.86) сле-
дует, что
f = roseca==SS'. (6.89)
Следовательно, вместо (68.1) можно писать
f-\-(r0 + d — f cos a) = r0 +nd (6.90)
или
f(l — cosa) = (n—l)d. (6.91)
В свою очередь *
cosa = ]/l —(6.92)
300
Подставив (6.92) и (6.91), можно получить после неко-
торых преобразований (6.88).
Точки на рис. 6.11 получены для соответствующих апла-
натических плоско-выпуклых линз, имеющих те же пара-
метры п, f, а и D, что обычные линзы с гиперболическим
профилем У этих апланатических линз освещенная сторона
представляет собой плоскость, а профиль раскрыва пред-
ставляет собой дугу окружности, опирающейся на хорду
длиной D, отстоящую от средней точки дуги на расстоя-
нии d, определяемом формулой (6.88). У таких линз, как
видно из рис. 6.11, отклонения фаз в раскрыве от линейного
закона ничтожны даже при весьма значительных смещениях
облучателя из фокуса.
§ 6. МЕТАЛЛИЧЕСКАЯ ЛИНЗА С ШИРОКИМ УГЛОМ КАЧАНИЯ
ЛУЧА
Выше при выводе формул для профиля освещенной сто-
роны линз мы располагали облучатель, как правило, на
оси линзы и налагали требование получения на выходе
линзы плоской волны с фазовым фронтом, перпендикуляр-
ным оси линзы.
Рассмотрим сейчас такую задачу. Имеем цилиндриче-
скую металлическую линзу (рис. 6.14,а), облучаемую ли-
нейным источником, т. е. цилиндрической волной. Для боль-
шей общности считаем криволинейными как освещенную
сторону, так и теневую (раскрыв). Облучатель смещен отно-
сительно оси линзы и находится на прямой OF0 (рис. 6.14,6),
образующей угол а с осью. Требуется найти профиль лин-
зы при условии, что на выходе должна получиться плоская
волна с фронтом, повернутым относительно оси на угол а.
Для решения задачи вводим систему координат х,у
(рис. 6.14,6). Толщину линзы обозначаем через d, при-
чем d — переменная величина, являющаяся функцией коор-
динаты у. На оси линзы толщина ее равна do. Расстояние
от облучателя до вершины линзы обозначаем через /о, а до
произвольной точки с координатами х, у через f. Очевидно,
что
f = j/a0cosa + x)2 + a0sina+>)2. (6.93)
На рис. 6.14,6 показано требуемое направление лучей.
В данном случае направление лучей внутри линзы не опре-
деляется законом преломления. Они вунуждены проходить
параллельно пластинам. Сформулированное выше требо-
вание выполняется при условии, что оптическая длина пути
301
Рис. 6.14. К анализу металлической линзы с широким углом качания
луча: а) схема преобразования цилиндрической волны в плоскую;
б) прохождение через линзу лучей, исходящих из точки О (сплошные
линии) и из точек О" и О'" (пунктирные линии).
луча OFM, падающего на точку F, имеющую координату х,
у, отличается от оптической длины луча OFoM0N, падаю-
щего на вершину линзы Fo, на целое число т волн, т. е.
если выполняется равенство
[ 4- nd — f0 — nadQ — s = mi,
(6.94)
302
где
s = (d— d0-j-*) cos а+_у sin а. (6.95)
Подставив значения f и s в (6.94) и освободившись
от радикала, получаем
{ml— [(и — cos a) d — (nQ — cos а) d0])2 +
4- 2 (f0 ( х cos a -f-j/sina) X
X {[mZ— [(n— cos a) a?—d0(n0—cos a)]} =
= x2sin2 a -\-y2 cos2 a — 2xy sin a cos a. (6.96)
Если линза симметрична относительно оси X, то на вы-
ходе линзы получится плоская волна также при нахожде-
нии облучателя В' симметричной точке О' (рис. 6.14,6).
Фронт плоской волны на выходе линзы при этом будет по-
вернут относительно оси X на угол а в другую сторону.
Очевидно, что когда облучатель помещен в точке О', требо-
вание получения плоской волны на выходе линзы удовле-
творяется уравнением вида (6.96), но при замене в нем зна-
ка у слагаемого, содержащего у, на противоположный.
Таким образом, получается два уравнения вида (6.96),
но с разными знаками у слагаемого у первой степени. По-
членное вычитание, а затем сложение этих уравнений при-
водит к следующим двум уравнениям:
х2 + у2 cos2 a 2 cos a-fgx = 0 (6.97)
и
ml — [(п — cosa)rf — (п0 — cos a)rf0] = — x cos a. (6.98)
Уравнение (6.97), связывающее между собой х и у, яв-
ляется уравнением профиля освещенной стороны линзы.
Легко видеть, что это есть уравнение эллипса с фокусами
в точках О и О'.
Из уравнения (6.98) следует, что его левая часть, содер-
жащая коэффициент преломления п и толщину d, является
функцией х. Одна из этих величин (п или d) однозначно
определяется из (6.98), а другая величина может быть вы-
брана произвольно. Ниже приводятся данные для следую-
щих вариантов выбора второй величины:
1) коэффициент преломления п постоянен,
2) толщина линзы d постоянна,
3) толщина линзы выбрана так, чтобы раскрыв был
плоский,
4) п и d являются такими функциями координат, кото-
рые обеспечивают получение плоской волны на выходе лин-
303
зы, при нахождении облучателя в какой-либо третьей точке,
кроме О и О'. Эта точка выбирается на оси X.
Рассматриваемая линза, благодаря обеспечению плоско-
го фазового фронта волны при нахождении облучателя
в двух выбранных точках, смещенных относительно оси (или
кроме того еще в третьей точке на оси), обладает малыми
фазовыми искажениями в промежуточных точках, лежащих
между выбранными. Это обеспечивает возможность качания
главного лепестка диаграммы направленности антенны без
особых искажений формы диаграммы направленности при
перемещении облучателя между выбранными точками.
Определим фазовые искажения, возникающие при сме-
щении облучателя в точку О" (рис. 6.14,6), находящуюся
на дуге окружности радиуса f0 с центром в вершине лин-
зы Fo (она называется фокальной дугой). Разность опти-
ческих длин В путей равна
t = f'-\-nd— f0—nbd0—s', (6.99)
где
f'=V(f0cos6 + x)2+(f0sin6 h^)2, (6.100)
s' — (d —+ x) cos6+jsin6. (6.101)
Учитывая уравнения (6.97), можно преобразовать f
к виду
f =fof/ 1 H---~р~У +2 (cos 9 — cos а) J- .
(6.102)
Подставив в (6.99) s' из (6.101) и f из (6.102) и учи-
тывая (6.98), можно написать
8—mZ = f0 1 4- j,-j- s-~-y2 4- 2 (cos 9 — cos а) £ —
— f0 — (cos 6 — cos a)(x4"^ — 4>) —У sin 6. (6.103)
Разложив радикал в ряд по возрастающим степеням у
(ряд сходится, когда подкоренное выражение меньше 2),
получим
8 — щХ = Ау2 -ф- Бу3 4- Су4 4-. . . — (cos 0 — cos a) (d — d0),
(6.104)
304
где
А = U- (sin2 а — sin2 9),
*/0
В = [(cos2 а — cos2 9) -[- cos а (cos 6 — cos а)],
2fo
С=—{(5sin2 0 — sin2 а) [(cos2 а — cos29)-j~
8fo
+ cos a (cos 9 — cos a)] cos 9 cos a (cos 0 — cos a)2}.
При малых углах a и 9 можно, заменив тригонометри-
ческие функции углами, привести 8 к виду
?,_/nXS±(a2_62)^_(t/_6?o)j + M(62_a2).
(6.105)
Из (6.105) видно, что кубические ошибки пропорцио-
нальны углу 9 и равны нулю при 9 = 0, т. е. на оси
линзы. Зависимость d от у в случае переменной толщины
должна выражаться четной функцией, поскольку линза
симметрична относительно оси X. Поэтому выбором функ-
ции d от у (формы профиля теневой стороны) можно
скомпенсировать квадратичные ошибки, но нельзя ком-
пенсировать кубические ошибки.
Для компенсации квадратичных ошибок разность d—dQ
должна быть пропорциональна у2, т. е. расти по квад-
ратичному закону от середины линзы к краям. Следо-
вательно, линза рассматриваемого вида, не имеющая
квадратичных ошибок, должна быть двояковогнутой.
Мы рассматривали смещение облучателя по фокаль-
ной дуге. Посмотрим, каковы ошибки при смещении об-
лучателя в радиальном направлении, т. е. в точку О'"
(рис. 6.14,6). Отрезок О”О'" обозначим через ef0, а рас-
стояние от О’" до F через f". Внутри линзы и по выходе
из линзы направление лучей сохраняется. Поэтому до-
полнительная ошибка, которую обозначим через Д8, равна
Д8 = р — sf0 — f". (6.106)
Можно показать, что приближенно
Д8 = — cos2 0 4- + s cos 9 sin 9 f cos 9 — 4- ...,
2 fo \ 2 / fo
(6.107)
а при малых углах 9
д5^_|Л + |9^. (6.Ю8)
20—1508
305
Сопоставляя (6.108) и (6.105), мы видим, что дополни-
тельная ошибка, получаемая при смещении облучателя с фо-
кальной дуги, имеет противоположный знак по сравнению
с основной ошибкой, получаемой при смещении облучателя
из фокуса. Это позволяет выбрать траекторию качания
облучателя таким образом, чтобы ошибка от смещения
Рис. 6.15. Профили металлических линз с широким углом качания
луча, удовлетворяющих различным условиям: а) плоский профиль те-
невой стороны, б) коррекция квадратичной фазовой ошибки, в) посто-
янная толщина линзы, г) постоянный коэффициент преломления.
облучателя из фокуса частично компенсировалась за счет
смещения облучателя с фокальной дуги.
На рис. 6.15 показаны четыре линзы, имеющие одина-
ковый профиль освещенной стороны, но с различными дру-
гими параметрами:
а) плоский профиль теневой стороны,
б) коррекция квадратичной фазовой ошибки,
в) постоянная толщина линзы,
г) постоянный коэффициент преломления.
Жирная кривая показывает оптимальную кривую кача-
ния луча.
30G
Вид линзы Дополнительное условие
Линза постоянной толщины
Линза с плоской внешней поверхностью d = d0 — х
Линза без квадратичных фазовых ошибок Линза с полной коррек- цией для трех положений облучателя Линза с постоянным коэффициентом прелом- ления у2 sin2 а d~d^+ 2f0(l—cosa) Третье положение облу- чателя соответствует полной коррекции на оси линзы п = п0 — const
Таблица 6.1
d = d (у) n = n O')
d = d(j X cos a ml rt-no+ d. a0
d = d,} - x d,> ml « = «оХГ + 'd~
yi sin2 a d~do + 2f0(l— cos a) d0 ml a0 z n:=n^ d + d + d X X {d — d0 + x)
. A d = d§ — x — fo-^ (fo + *)2 + >'2 1 — cos a do_ '. "Л , Qp n-n^d + d + dX X (d — d0-\- x)
m\ -+- x cos a d = d „ 4- ° ' n0 — cos a n = n0
о
оо
Вид лиизы фазовая
Облучатель перемещается по фокальной дуге
Линза постоянной толщины У2 бу3 ^(*2-62)-77,(*2-92) 4о 4ft
Линза с плоской внешней поверхностью у2 бу3 4г («2-б2)--^^ 2-62) 4о 4ft
Линза без квадратичных фазовых ошибок бу3
Линза с полной коррек- цией для трех положений облучателя бу3
Линза с постоянным коэффициентом прелом- ления ^(а?_62)_^(а2_02) + z/o */о д2 — 02 |"cos2a^2 1 +2 («о-COS a) [ 2ft m)'J
Продолжение
ошибка Величина смещения облучателя е/0
Облучатель смещается с фокальной дуги
— 9у3 (a2-92)f0
Пренебрежимо мала 4-(a2-e2)f<>
— 6 уз Пренебрежимо мала
бу3 -4| <-»> Пренебрежимо мала
— 9 У3 1 (а2 — 92) Рр °2) + 2 „0-cos, X Г у2cos2о 1 X 1 2^0 1 (a2-92)f0
В табл. 6.1 приведены основные характеристики металли-
ческих линз рассматриваемого типа, рассчитанных на полу-
чение широкого угла качания луча.
§ 7. СФЕРИЧЕСКИЕ И КРУГЛЫЕ ЦИЛИНДРИЧЕСКИЕ
НЕОДНОРОДНЫЕ ЛИНЗЫ
Из теоретической оптики известно два варианта сфери-
ческих линз с переменным коэффициентом преломления.
В оптике такие линзы не нашли применения из-за труд-
ности получения среды, прозрачной для света и имеющей
переменный коэффициент преломления, меняющийся по за-
данному закону. На сверхвысоких частотах имеется воз-
можность получения среды, прозрачной для радиоволн,
с переменным коэффициентом преломления, в связи с чем
такие линзы приобретают практический интерес.
Еще в 1865 г. Максвелл показал, что сферическая лин-
за, в которой коэффициент преломления п меняется в ра-
диальном направлении по закону
(6.109)
где г — расстояние от центра, a R — радиус сферы, обра-
зует изображение точки на поверхности в диаметрально
противоположной точке. На рис. 6.16 показан ход лучей
в такой линзе. Если использовать полусферу с такими
свойствами и поместить облучатель, как показано на рис.
6.16, то на выходе линзы (в плоскости сечения) получится
плоский фронт волны. Такая линза требует достаточно точ-
ного помещения облучателя в середине полусферической
поверхности. Смещение облучателя относительно этой точки
приводит к нелинейным фазовым ошибкам, вызывающим
искажение диаграммы направленности. Эта линза не может
быть использована для качания луча.
Другой вид неоднородной сферической линзы предло-
жен Люнебергом. У линзы Люнеберга коэффициент прелом-
ления меняется по закону
п = п> ="" / 4 (т)“- <6-1'°)
где nR и п0—коэффициенты преломления соответственно
при r = R и при г = 0.
309
Отличие зависимостей (6.109) и (6.110) заключается в
том, что в первом случае п уменьшается в два раза от
центра до периферии, а во втором случае — в J/2 раз.
Чтобы не было отражений и преломлений на выходе из
линзы выбирается п^ = 1. Ход лучей в линзе Люнеберга
показан на рис. 6.17.
Мы видим, что на выходе линзы получается параллель-
ный пучок лучей. Данная линза позволяет качать луч в пре-
делах 360° без искажений диаграммы направленности при
перемещении облучателя по поверхности сферы.
Ход лучей
Облуча '
телЬ
Изобра-
жение
Плоскость,пер-
пендикулярная
к лучам
Рис. 6.16. Траектории лучей
в сферической линзе Максвелла.
Рис. 6.17. Траекторий лучей
в линзе Люнеберга.
Такая линза была изготовлена (27] из пенистого полисти-
рола, имеющего^ как известно, малые потери. Общий вид
линзы показан на рис. 6.18,а. Изменение коэффициента пре-
ломления получалось путем изменения плотности материа-
ла. Применялась следующая технология изготовления.
Линза была разделена на 186 идентичных сферических
клиньев, получаемых при сечении сферы плоскостями, про-
ходящими через условную ось север—юг. Для получения
таких клиньев изготовлялись сегменты из обычного пени-
стого полистирола, которые затем прессовались — в цен-
тральных точках в большей мере, а в периферийных в мень-
шей мере — до требуемой плотности. Предварительно была
экспериментально определена зависимость коэффициента
преломления от степени спрессования материала. Для полу-
чения совершенно идентичных клиньев применялась панто-
граф-машина.
На рис. 6.18,6 показана, диаграмма направленности опи-
санной шаровой линзы, облучаемой рупорным облучателем,
в Я-плоскости при диаметре шара 27? = 30 см и 2. =3,2 см.
310
Зависимости (6.109) и (6.110) справедливы не только
для сферической линзы, но также для цилиндрической,
круглого сечения. В случае цилиндрической линзы в фор-
мулах (6.109) и (6.110) следует понимать под г расстояние
от оси цилиндра, а под 7? — радиус цилиндра.
Рис. 6.1В. Шаровая линза Люнеберга, изготовлен-
ная из пенистого полистирола: а) фотография лин-
зы, облучаемой коническим рупором, (У)диаграмма
направленности линзы, имеющей диаметр 2/?=30 см
в //-плоскости на волне 1 = 3,2 см.
Технология изготовления цилиндрической линзы с за-
данной зависимостью коэффициента преломления от рас-
стояния г от оси сравнительно проста. Цилиндрическая
линза изготовляется из двух круглых металлических пла-
стин, образующих волноводный канал. Пространство между
пластинами заполняется диэлектриком. При возбуждении
линзы волной с электрическим вектором, параллельным
311
пластинам, регулировка коэффициента преломления произ-
водится изменением расстояния между пластинами при
одновременном изменении толщины диэлектрика. На рис.
6.19 показано продольное сечение линзы, удовлетворяющей
условию (6.110). Диэлектрик показан штриховкой. Вплот-
ную к диэлектрику примыкают металлические пластины.
Размеры в миллиметрах соответствуют образцу, который
Рис. 6.19. Продольное сечение цилиндрической линзы
Люнеберга.
был подвергнут испытанию на волне 3,2 см. Для большей
наглядности расстояние между пластинами и кривизна по-
верхности пластин на рисунке показаны в большем масшта-
бе, чем длина.
Расстояние между пластинами b является функцией
от г и определяется, исходя из условия (6.110) с учетом,
что фазовая скорость волны ТЕ/0 в пространстве между
параллельными пластинами, заполненном диэлектриком
с диэлектрической проницаемостью е, равна
и
Отсюда следует
Приняв (6.112) и (6.110), получим
(6.111)
(6.112)
(6.113)
312
В целях предотвращения отражения и преломления
Молн на выходе линзы nR делается равным 1. Тогда
Имеем
Ь =---- -2 (6.114)
/ г г2
2 И ^-2 + ^
Так как из-за малого расстояния между пластинами
диаграмма направленности в //-плоскости имеет сравни-
тельно широкий главный лепесток, то к краям линзы при-
соединяется конический раструб.
пластины
Рис. 6.20. Волноводный облучатель цилиндри-
ческой линзы Люнеберга, показанный
на рис. 6.19.
На рис. 6.20 показано сечение питающего волновода, ис-
пользованного для питания линзы, показанной на рис. 6.19.
В качестве облучателя используется волновод, широкие
стенки которого сужаются до размера расстояния между
пластинами на входе линзы (13,2 мм), а узкие стенки рас-
ширяются для получения требуемого распределения ампли-
туд в раскрыве линзы
Расширение узких стенок волновода диктуется тем, что,
как видно из рис. 6.17, лучи сгущаются к краям линзы.
Поэтому следует ожидать, что при слабо направленном
облучателе, у которого интенсивность излучения мало ме-
няется в пределах ±90°, амплитуды поля будут на краях
зщ
линзы значительно превосходить амплитуды поля в сере-
дине линзы. При таком распределении поля в раскрыве
антенна имела бы большие побочные максимумы. Для
уменьшения подобных максимумов необходимо снизить
амплитуда поля на краях линзы. Это достигается путем
Рис. 6.21. а) Измеренная диаграм-
ма направленности в Л-плоско-
сти облучателя, показанного на
рис. 6.20 (кривая 1), распределе-
ние амплитуд поля в раскрыве
линзы, показанной на рис. 6.19
при таком облучателе (кривая 2)
и аппроксимированная диаграмма
направленности облучателя, ис-
пользуемая для расчета характе-
ристик линзовой антенн (кри-
вая 3);
б) обозначения углов р н ф и их
связь с координатой у.
увеличения направленности облучателя в Е-плоскости, для
чего, в свою очередь, увеличивается размер раскрыва пи-
тающего волновода в направлении, параллельном электри-
ческому вектору.
На рис. 6.21,а кривая 1 показывает диаграмму направ-
ленности в Е-плоскости облучателя, показанного на рис. 6.20,
кривая 2 — распределение амплитуд поля в раскрыве лин-
зы при таком облучателе, а кривая 3 — аппроксимацию диа-
да
граммы направленности облучателя, принятую для расчета
линзовой антенны.
На рис. 6.21,6 показаны обозначения углов ₽ и ф и
связь координаты у точек раскрыва с этими углами.
В связи с сужением широкой стенки волновода в рас-
крыве последнего помещена диэлектрическая пластина, так
как в противном случае размер волновода стал бы меньше
критического. В раскрыве волновода перпендикулярно ли-
ниям электрического вектора вставлены две металлические
пластины для предотвращения поворота поляризации, т. е.
возбуждения волны ТЕт с электрическим вектором, пер-
пендикулярным пластинам линзы.
Особенность цилиндрической линзы рассматриваемого
типа заключается в том, что у нее раскрыв не плоский, а
занимает половину цилиндрического пояса, противополож-
ную точке облучения. Фазы поля в раскрыве не одинаковы.
Соотношение фаз таково, что при дальнейшем распростра-
нении волны в воздухе образуется плоский фазовый фронт
в плоскости, касательной к середине раскрыва. В связи
с этим диаграмма направленности такой антенны в Е-пло-
скости подобна диаграмме направленности синфазной
антенны с шириной раскрыва 2/?, а в //-плоскости — диа-
грамме направленности антенны бегущей волны длиной R.
В соответствии с этим ширина главного лепестка в Е-пло-
скости определяется примерно по формуле
2вм = 58,8"^,
а в //-плоскости — по формуле
20„ = 200° 1/Z.
он V 2R
Для увеличения остроты направленности антенны в
//-плоскости к краям пластин линзы присоединяется рас-
труб, увеличивающий размер раскрыва в параллельном
вектору Н направлении.
На рис. 6.22 приведены экспериментальная (сплошная)
и теоретическая (пунктирная кривая) диаграммы направ-
ленности в Е-плоскости линзовой антенны, изображенной
схематически на рис. 6.19. На рис. 6.23 сплошная кривая
показывает диаграмму направленности в //-плоскости этой
антенны без раструба, а пунктирная кривая — диаграмму
направленности антенны с раструбом.
Рассмотренные сферическая и цилиндрическая неодно-
родные линзы с коэффициентом преломления, меняющимся
315
Относительная мощность .06
направленности в Е-плоскости линзовой антенны, изображенной на рис. 6.19.
По формуле (6.110), имеют тот недостаток, что при качании
луча приходится перемещать облучатель по окружности
большого радиуса (радиуса линзы). В связи с этим встает
вопрос о возможности подбора такого закона изменения
коэффициента преломления, как функции расстояния от
центра, при котором можно было бы получить на выходе
Я:
о
2_
4
6
8
-к
'и-
И-
'W-
а-
И;

iliiiiillliiiiiiiiiiHiliiiiiiiihiiilin'i______________________________
lllllllllllllllllllllllllUIIIШIllIIIHIHIIllllllllllnlllllll
llllllllIIIIIUIIllllllllllГЛIIIIIllll1lllllllllllilllllllllllllll
1!1!1Ш!111111111111111!1111гп..|1|>л-'1Н||||||||1||||||||Ш|||||ц||
lllllllllllllllllllllllll^<lllllllllllь llllilllllllllllllllllllllHI
IIIIIIIIIIIIIIIIIIIIIIIIIMIJIIIIIIIIIIIIII,VIIIIIIIIIIIIIIIIIIII|I||||
IIH'IIIIIIHUIIIIIIIIIIIII
llllllllllllllllllll'JlllllllHlllllllllllhlmмlllllllllllllllHllll
!И111111||||||||||1Г.Н111Н111111|||Ц|||||||||||ЬЧ|КИ111111ИИИИ
llllllllllllllllll>JIIIIVl||lllllllllllll|l|IMllll>IIПIIIIIIIIIllll
1Ш111111|1|||111Ш1|11111111111|||||||||||||||||||||Ш||||||||||||||||
11111ИП1111№!Ш1111Ш111111111И11111НН1 >Н1П1№Ч1111П|1111П1
iiiiiiiiiiiiirjiliiiiiiiiMiiiiiiiiiiiiiiiHiiiiiiiiiiiiiiiiiiiiiiiiiiiii
11111111111|Г.11111|11Ш1Л111111|||||||||11111111111>111||'|111111||||||
iiiiiiiiiiir.miiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiMiMiiihiiiiiiiiliu
11111П1НГЛН111НШ11Ч11111П11|11111ПШ11ГН1П1Н1№--------------------------
72 36 О 36 72
Угол диаграммы направленности, град.
£
I
1
Е

Рис. 6.23. Диаграмма направленности антенны, изобра-
женной на рис. 6.19 в //-плоскости без раструба (сплош-
ная кривая) и с раструбом (пунктирная кривая).
линзы плоскую волну при нахождении облучателя в какой-
либо внутренней точке сферы или цилиндра.
Исследование вопроса [28] и [29] показало, что можно
поместить облучатель внутри линзы на расстоянии f от
центра, если коэффициент преломления п меняется по фор-
муле
П=1//?2 + }2 — Г\
Если сделать линзу по типу предыдущей из двух
пластин, между которыми помещен диэлектрик, то рас-
стояние между пластинами b должно меняться по закону
21/ — )2_рг2_/^2_)2
Г е0
317
Из уравнения для п видно, что при f = R линза ста-
новится обычной линзой Люнеберга, Линза, у которой
f<ZR, названа модифицированной линзой Люнеберга.
Траектории лучей в модифицированной линзе Люне-
берга определяются уравнением
/ \
х2 — 2х_у ctg а + у2 (ctg2 а + — f2’= 0.
Это есть уравнение семейства эллипсов. Параметр а
показывает угол между направлением луча при выходе из
фокуса и осью линзы. Для иллюстрации на рис. 6.24 пока-
Рис. 6.24. Траектории
лучей в модифицирован-
ной лннзе Люнеберга
при различных значе-
ниях отношения рассто-
яния f облучателя до
центра сферы к ее ра-
диусу R.
зано прохождение лучей (сплошные кривые) в1 модифици-
рованной линзе Люнеберга при различных положениях
облучателя для углов а , меняющихся через 10° в преде-
лах от 0 до 90°. Пунктирные кривые на рис. 6.24 дополняют
часть траектории луча, проходящую внутри линзы, до пол-
ного эллипса. Легко видеть, что в выходящей из линзы пло-
ской волне лучи сгущаются на краях, что соответствует
усилению поля на краях. Для получения равномерного поля
в плоской волне необходимо применять облучатель, у кото-
рого поле убывает с увеличением угла а .
318
На рис. 6.25 показано устройство модифицированной ци-
линдрической линзы Люнеберга. Принцип устройства тот
же, что у линзы, изображенной на рис. 6.19. В качестве ди-
электрика взят поли-2,5-дихлорстирен, заполненный на 60%
окисью титаната с диэлектрической проницаемостью
е
= 9,36
Рис. 6.25. Устройство модифицированной цилиндрической линзы Лю-
неберга.
при тангенсе угла потерь tg8 =0,0013. Детали устройства
видны из рис. 6.25. Зазор между вращающейся и непо-
движной частями заполняется жидкостью —• метилалкого-
лем, имеющим - = 8,9. Рупорный облучатель вращается
с0
вместе с внутренней частью линзы.
§ 8. ЛИНЗА ИЗ МЕТАЛЛИЧЕСКИХ ПЛАСТИН С ОТВЕРСТИЯМИ
Наряду с описанными выше видами линзовых антенн
практическое применение нашли линзы, выполненные из
параллельных металлических пластин с отверстиями (30]. •
На рис. 6.26 показан общий вид антенны с такой линзой (а)
и схема ее продольного сечения (б).
Антенна состоит из трех элементов: металлического зер-
кала 3, рупорного облучателя Р и линзы Л. У вершины зер-
кала установлена пластина для компенсации обратной реак-
ции зеркала на рупор. Принцип действия зеркала и назна-
чение компенсационной пластины у его вершины излагается
319
ь следующей главе. Здесь рассмотрим принцип действия
линзы.
При падении электромагнитной волны на сплошную
идеально проводящую плоскость (экран) она полностью
отражается обратно. Если же в экране имеются отверстия,
Рнс. 6.26. а) Общий
вид антенны из ме-
таллических пластин
с отверстиями, уста-
новленной в раскрыве
пирамидального ру-
пора. б) Схема про-
дольного сечения ан-
тенны.
то часть энергии волны отражается, а часть проникает через
отверстия в другое полупространство. Если отверстия рас-
пределены по всему экрану, образуя периодическую струк-
туру (отверстия одинаковы и находятся на одинаковом рас-
стоянии), то при падении плоской волны на экран плоскими
будут как отраженная волна, так и проникшая через отвер-
стия. Отношение напряженности поля волны, прошедшей
320
через отверстия, к напряженности поля падающей волны
носит название коэффициента передачи и обозначается бук-
вой Т. Отношение напряженности поля отраженной волны
к напряженности поля падающей волны называется ко-
эффициентом отражения и обозначается буквой Г. Коэффи-
циенты Г и t являются комплексными величинами. Так как
между Г и t существуют соотношения
1 -}-/'=Т (согласно граничным условиям),
и
j (из условия энергетического баланса),
то можно их выразить в комплексной форме следующим
образом:
Г = — cosUe~‘u,
f =jsinUe~iU'.
При очень малых отверстиях, очевидно, |Т|—>0,
а I-П—При очень больших отверстиях, наоборот,
|Г|—»0, а |Г|—*1. Отсюда следует, что U меняется
от 0 при малых отверстиях до у при больших отвер-
стиях.
Значение U зависит также от расстояния между от-
верстиями. На рис. 6.27, а и б показаны кривые зави-
г г ф d it 2а
симости и и Т от у- для различных значении у, где
d — диаметр отверстия, а 2а— расстояние между двумя
соседними отверстиями. Данные соответствуют падению
волны в направлении нормали к.плоскости экрана.
Пользуясь представлениями геометрической оптики,
можно было бы определить коэффициент передачи как ко-
рень квадратный из отношения общей площади отверстий
к площади экрана. В этом случае коэффициент отражения
определялся бы по формуле
На рис. 6,27,в приведен график зависимости отношения
коэффициента передачи Т, полученного экспериментальным
путем, к коэффициенту передачи, вычисленному по фор-
муле (6.115):
r = ^ = 5/|sin|t/|. (6J16)
21—1503 321
Рис. 6.27. а) График зависимости вспомогательной функции U, опре-
деляющей коэффициенты отражения и передачи волны через отвер-
стия в металлической пластине, от относительной величины диамет-
d
ра отверстий -у при различных относительных величинах расстоя-
2а
ния между пластинами —,
б) то же для коэффициента передачи Т, полученного эксперимен-
тально,
в) то же для коэффициента передачи Т', полученного как отношение
экспериментального Т к теоретическому То, определенному по за-
конам геометрической оптики.
322
Из рис. 6.27 видно, что при ~ <0,3 волна прак-
тически не проникает через отверстия в экране, а при
— < 0,43 коэффициент передачи меньше, чем это следует
из представлений геометрической оптики. Значительные
величины Т (близкие к 1) получаются при0,6. Бэтой
области ^>0,6^ аргумент (фаза)? слабо меняется с из-
d
менением у.
В случае системы из нескольких одинаковых парал-
лельных пластин коэффициент передачи зависит от расстоя-
ния между ними. Расстояние между пластинами х выби-
рается из условия максимума общего коэффициента пере-
дачи, который получается при соблюдении соотношения
2™ = k'v — \U\, (6.117)
где k'= 1, 2, 3...
Система из нескольких пластин образует область про-
странства, в которой эквивалентная фазовая скорость рас-
пространения волны больше скорости света, так как при
прохождении через каждую пластину волна получает до-
полнительную опережающую фазу. Таким образом, про-
странство между пластинами эквивалентно линзе или приз-
ме с коэффициентом преломления п<1.
Приведенные выше данные относятся к нормальному
падению волны на пластины. В случае наклонного падения
имеет место явление, аналогичное явлению двойного луче-
преломления в кристаллах, приводящее к тому, что при про-
хождении через линзу линейно поляризованная волна пре-
вращается в эллиптически поляризованную из-за различ-
ного коэффициента передачи (по амплитуде и по фазе)
параллельно поляризованной и перпендикулярно поляризо-
ванной волн. Кроме того, следует иметь в виду, что при
больших углах наклона падающей волны резко снижается
коэффициент передачи.
Изложенное выше можно резюмировать следующим
образом.
В качестве линзы могут быть использованы параллель-
ные металлические пластины с отверстиями. Пластины уста-
навливаются перпендикулярно направлению распростране-
ния. При падении сферической волны (большой радиус кри-
21* 323
визны) необходимо пластины несколько изогнуть, приблизив
их форму к форме фронта волны. Диаметр отверстий и
расстояние между ними определяются по графикам рис. 6.27,
учитывая при этом необходимость получения достаточно
большого коэффициента передачи и плоского фронта волны
на выходе линзы. При параллельных пластинах (линза по-
стоянной толщины) преобразование сферической волны
в плоскую осуществляется благодаря большей фазовой ско-
рости на краях линзы, чем в середине. Это требует приме-
Рис. 6.28. Диаграмма направленности антенны, изобра-
женной на рис. 6.26а.
нения на краях линзы отверстий меньшего диаметра, чем
в середине. Расстояние между пластинами ориентировочно
определяется по формуле (6.117).
На рис. 6.28 показана диаграмма направленности по
напряженности поля антенны, изображенной на рис. 6.26,а
при следующих размерах ее элементов: диаметр раскрыва
зеркала—150 см, сторона квадрата раскрыва линзы —
300 см, расстояние между линзой и зеркалом — 300 смг чи-
сло пластин — 7, расстояние между центрами отверстий
в пластине — 6,5 см, диаметр отверстий меняется от 6,1 см
в середине до 4,2 см на краях, толщина листов — 2 мм,
длина волны Л~7,5 см.
324
Общий принцип действия антенны иллюстрируется
рис. 6.29. В точке А находится рупорный облучатель, обра-
щенный раскрывом к зеркалу. Электромагнитное излучение
облучателя, отражаясь от зеркала, направляется в виде
Рйс. 6.29. К пояснению принципа действия линзы
из пластин с отверстиями.
сферической волны на линзу из пластин с отверстиями.
Пройдя через линзу, волна преобразовывается в плоскую,
что приводит к остронаправленному излучению вида рис.
6.28.
§ 9. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ ЛИНЗ
При падении электромагнитной волны на поверхность
линзы часть энергии волны отражается от поверхности раз-
дела воздух—линза. Отраженная от поверхности линзы
энергия большей частью рассеивается, что ведет к сниже-
нию коэффициента усиления антенны, а частично отражен-
ная энергия возвращается к облучателю, вызывая рассогла-
сование в питающей облучатель фидерной линии. В диапа-
зоне сверхвысоких частот обычно предъявляется требова-
ние очень хорошего согласования антенны и фидерной ли-
нии (коэффициент стоячей волны 1,05 и меньше). Наличие
отраженных волн от поверхности линзы вызывает затруд-
нение с выполнением данного требования. В связи с отри-
цательным эффектом отражения волн представляет интерес
знание величины отраженной энергии и мер по ослаблению
отражения-
325
Отраженная волна характеризуется коэффициентом
отражения Г, определяемым как отношение напряженности
поля отраженной волны к напряженности поля падающей
волны. Ввиду большого многообразия различных видов
линз, коэффициент отражения Г, строго говоря, не может
быть одинаково определен для всех линзовых антенн. Ука-
жем здесь методы определения коэффициента отражения
отдельно для различных видов линз.
а) диэлектрические линзы
На рис. 6.30 показана схема падения волны на плоскую
границу раздела воздух—диэлектрик. Диэлектрик предпо-
лагается без потерь.
Как известно, коэффициент отражения от границы раз-
дела зависит от поляризации волны. В случае параллель-
ной поляризации (электрический вектор параллелен пло-
скости падения)
Г —(<р Ф) /с 1|о\
В случае перпендикулярной поляризации (электриче-
ский вектор перпендикулярен плоскости падения)
г sin^-jo
2 sin (if> + Ф) • (о.НУ)
326
Учитывая, что ^^ = /4— коэффициенту
получаем
j, __ n2 cos ср— V п2—sin2!
1 п2 со s <о У п2 — sin2 ср
г____—cos ® 4- Кп2— sin2 <о
•1 2 - -----------— ~ •
cos <р —|- г п2 — sin2 ср
преломления,
(6.120)
(6.121)
В предельном случае нормального падения волны
(tp = 0) оба выражения стремятся к одинаковому зна-
чению
г = 2—! .
л —1
Как видно из (6.118) Г, = 0 при <р 4- ф = . Угол <р,
при котором Г] = 0 носит наззание угла Брюстера. При
перпендикулярно поляризованной волне всегда Г2^=0.
Мы рассматривали отражение от одной поверхности раз-
дела двух сред. Линза имеет две преломляющие поверх-
ности: освещенную и теневую (раскрыв). Отражение имеет
место от обеих поверхностей. Отражение от теневой поверх-
ности может быть вычислено по приведенным выше форму-
лам с подстановкой 1/п, вместо п.
Отраженная от теневой стороны волна возвращается
к освещенной стороне и проникает через нее с коэффициен-
том передачи Т, близким к единице. Поле этой волны на-
кладывается на поле волны, отраженной от освещенной
поверхности, и, в зависимости от соотношения фаз между
ними, усиливает его или ослабляет. В обеих плоских по-
верхностях, т. е. в задаче о плоской пластине постоянной
толщины d при нормальном падении волны суммарный
коэффициент отражения от обеих плоскостей пластины
равен _________________
2Г2 ^1 + cos 4тс
1+2Г2со84к^+г/ rO^WW2^^’
* (6.122)
где
р__п — 1
1 ~п-|- 1 ’
'лф / 2Г sin yd
^ф —длина волны внутри диэлектрика,
2 г
327
Из (6.122) видно, что Г' меняется в пределах от О
2Г
до • При криволинейных поверхностях линзы ра-
счет усложняется. У диэлектрических линз, имеющих
гиперболической формы освещенную сторону и плоский
раскрыв, отражение от освещенной стороны носит более
или менее рассеянный характер, в то время как волна,
отраженная от теневой стороны, концентрируется в фо-
кусе, т. е. около облучателя. Следовательно, в данном
случае преобладающее влияние на облучатель будет ока-
зывать волна, отраженная от теневой стороны.
б) металлические линзы
Вопросу отражения от
линзы посвящено большое
[31]-*-[32]. В этих работах
металлической ускоряющей
число теоретических работ
решается задача о падении
Рис. 6.31. К определению коэффициента отражения от системы па-
раллельных металлических пластин.
плоской электромагнитной волны типа ТЕМ на систему
параллельных идеально проводящих бесконечно тонких
пластин. Электрический вектор падающей волны направ-
лен параллельно пластинам. Расстояние между пласти-
нами одинаково. Мы его обозначим через Ь, причем раз-
мер b удовлетворяет условию 0,5< 1, где Z —длина
волны в свободном пространстве. Остальные размеры и
обозначения показаны на рис. 6.31.
328
При падении волны типа ТЕМ отраженная волна
также является волной типа ТЕМ. Однако при соответ-
ствующих параметрах а, <р, а могут возникнуть, наряду
с основной волной ТЕМ, волны высших порядков ТЕОл.
На рис. 6.32 даны графики зависимости коэффициента
передачи Lno мощности Т2 и коэффициентов отражения
-90 - 60 -30 0 +30 + 60 + 90-90 -60 -30 0 +30 + 60 + 90
Угол падения, /
--------коэффициент передачи по мощности Г?
--------коэффициент отражения основной болид! Го2
--------коэффициент отражения болид: 1- порядка Г,
коэффициент отражения болид/ 2-порядка Г?г
Рис. 6.32. Графики зависимости от угла падения у коэффициента пе
редачи по мощности Т2 и коэффициентов отражения по мощности
Гц, Гр г| соответственно для основной волны ТЕМ и волн первого
и второго порядков ТЕ01 и ТЕп2 при различных углах а (см. рис. 6.31)
для металлической лиизы с коэффициентом преломления п = 0,6.
Т12 т?2 о
по мощности Го, Г|, Г2 соответственно основной волны
ТЕМ и волн первого и второго порядков ТЕ0, и ТЕ02 от
угла падения <р при различных углах а для линзы с коэф-
фициентом преломления п = 0,6. Из графиков видно, что
в сравнительно большом диапазоне углов и а един-
ственной отраженной волной является волна ТЕМ, при-
чем величина коэффициента отражения сравнительно не-
велика.
32?
Коэффициент отражения основной волны ТЕМ
дулю равен
Г—1/" cos (у — а) — 71 cos (?+«) — 71
V [6 cos (® — а) 71 Р cos (?+“) + 71 '
, 2г.
где k = у,
l = k ]/1“ (й)2-
При <р = 0
, р | _k COS а — 7
I ' k COS a -f- 7 ’
а при <x = 0, <p = 0
• p I_£ — 7__1 — n
' I k -47 1 -f-n ’
ПЭ MO-
(6.123)
(6.124)
(6.125)
Рис. 6.33. График зависимости фазы отраженной волны ф от отно-
26
сительной величины расстояния между пластинами-у- для метал-
лической ускоряющей линзы при нормальном падении на плоскую
поверхность линзы и при расположении пластин нормально к этой
плоскости (<р = 0, а = 0, — рис. 6.31).
330
Для случая ср = а = 0 найдено [33] следующее выра-
жение для суммарного коэффициента отражения Г' от
обеих плоскостей линзы (освещенной и теневой), если
обе поверхности параллельны, т. е. если линза имеет
постоянную толщину d:
Г' = 2Г .....sin(]> + 7d)--- (6.126)
/(1— Г2)2-К 4Г2 Sin (ф Ч-fd) '
где ф— изменение фазы при отражении определяется по
графику рис. 6.33 как функция у.
Коэффициент отражения в данном случае (6.126) отли-
чается от коэффициента отражения от диэлектрической
пластины (6.122) слагаемым ф в аргументе синуса.
Вопрос об отражении от металлических замедляющих
линз вида, изображенного на рис. 1.6,а и 1.6,6 не ис-
следован и рассматризаться здесь не будет.
в) металло-диэлектрические линзы
В первом приближении отражение от поверхности
металло-диэлектрических линз может рассчитываться по
приведенным выше формулам для диэлектрических линз.
В этих формулах коэффициент отражения является функ-
цией угла падения <р и коэффициента преломления п,
причем п==1/ —. Следует при этом иметь в виду, что
диэлектрическая проницаемость е металло-диэлектриче-
ских линз в § 2 определена методами электростатики,
и приведенные там выражения для г достаточно точны
на низких частотах (/—» 0). На сверхвысоких частотах
эти данные нуждаются в уточнении. Более точные дан-
ные могут быть получены при исследовании металло-
диэлектрической линзы в поле сверхвысоких частот.
В такой постановке сравнительно подробно исследована
ленточная линза. Имеются также некоторые данные
о дискозой линзе. Познакомимся вкратце с результа-
тами этих исследований. Начнем с ленточной линзы [34].
На рис. 6.34 показано некоторое количество тонких ме-
таллических лент шириной w и длиной а, образующих пе-
риодическую структуру с расстоянием I в направлении, пер-
пендикулярном плоскости лент, и расстоянием b в парал-
лельном направлении. На эту группу лент падает электро-
магнитная волна, поляризованная, как показано на рис. 6.34.
331
Перпендикулярно лентам в> плоскостях, показанных на рис.
6.34 пунктиром, поместим бесконечно тонкие идеально про-
водящие пластины. Так как электрический вектор Е пер-
пендикулярен пластинам, то последние не вызовут новых
граничных условий и не внесут изменений в процесс распро-
странения электромагнитных волн в среде, содержащей
металлические ленты. Пространство между указанными
пластинами имеет вид, показанный на рис. 6.35.
1_____
iv | | I l |—
1
Рис. 6.34. Расположение системы металлических лент, являющихся
частью ленточной металло-диэлектрической линзы.
Если аналогично поместить пластины перпендикулярно
лентам в остальных рядах, то совокупность лент можно бу-
дет представить в виде наложенных друг на друга ячеек
вида рис. 6.35. Каждая же ячейка представляет собой
плоский волноводный канал с периодически включенными
емкостными диафрагмами.
Как известно, методика расчета распространения элек-
тромагнитных волн в волноводном канале с диафрагмами
сводится к замене этой системы эквивалентной схемой рис.
6.36 в- виде длинной линии с относительным волновым со-
противлением z0=l, в которую через промежутки длиной I
включены реактивные (емкостные) утечки, нормированная
величина проводимости которых В равна для случая I > Ь
[34]
Л. A -w hf “]
B = yln cosec^ . (6.127)
332
Рис. 6.35. Плоский волноводный канал с периодически включенными
емкостными диафрагмами, эквивалентный области пространства
между двумя параллельными плоскостями, проведенными через
средние линии соседних рядов лент в ленточной металло-диэлектри-
ческой линзе (эти плоскости на рис. 6.34 обозначены пунктирными
линиями).
Рис. 6.36. Эквивалентная схема металло-диэлектрической линзы при
большом расстоянии I между слоями металлических частиц.
Постоянная распространения k в волноводном канале
рис. 6.36, содержащем диафрагмы, определяется по фор-
муле [35]
arccos Г cos kl — — sin kl\ , (6.128)
so I I Z I
если средой в канале является воздух или
kg = -у arccos Г cos kl —--sin kl\, (6.129)
если средой является
ломления п'о, где
диэлектрик с коэффициентом пре-
k =
2л
Т •
333
Коэффициент преломления п металло-диэлектрической
линзы из лент, определяемый по формуле (1.1)
ф
равен
п = arccos Г cos kl — sin kl 1 .
2~1 I 2
(6.131)
Эквивалентная проводимость схемы рис. 6.36 равна
j/14-Bctg kl~~B2.
(6.132)
Коэффициент отражения может быть вычислен по фор-
муле
(6.133)
Приведенные выше формулы относятся, как указыва-
лось, к случаю 1>Ь. При 1<^Ь имеет место взаимосвязь
Рис. 6.37. Эквивалентная схема металло-диэлектрической
линзы при малом расстоянии I между слоями металли-
ческих частиц.
между лентами и волноводный канал рис. 6.35 должен
быть заменен эквивалентной схемой рис. 6.37. Для этой
эквивалентной схемы
Y=y/~B0Bk, (6.134)
л = Д- arctg 1/
тЛ ' Вк'
(6.135)
Здесь Во и Bk — нормированные проводимости соответ-
ственно холостого хода и короткого замыкания полусек-
ции, равные:
334
а) при большой толщине d лент (</>/>')
= + -0,045] +
sin2 птЛ
п (пкИ)2 ’

(6.136)
sin2 п-д
п (пкб)2 ’
б) при малой толщине d лент (с?<6г)
В, ~1 , 2&, Tto .
0 = tg у + у In cosec у +
nitl \ i
— F I
. sin2 птл
~F 1 п (nnff)2 ’
Л-1
n , тЛ 2Ь, ,
Вк = - ctg у + у In cosec у +
/яЩ \
cth ( -г- Г)
\ ° J . sin2 пт.8
F ] п (rntfi)2 ’
где
(6.137)
(6.138)
(6.139)
(6.140)
с /г\ VI sin2mtc
S«(S)=
n-l
Изложенная здесь методика исследования ленточных
линз может быть распространена на другие виды металло-
диэлектрических линз. При этом у Других видов линз при
замене системы металлических частиц ячейками из волно-
водных каналов с неоднородностями последние вместо поло-
335
сок, показанных на рис. 6.35, будут иметь соответственно
иную форму.
На рис. 6.38 изображена система дисков, являющаяся
частью дисковой линзы. Пересекая эту систему дисков дву-
мя идеально проводящими плоскостями в месте, показан-
Рис. 6.38. Расположение системы металлических
дисков, являющихся частью дисковой металло-
диэлектрической лиизы.
Рис. 6.39. Плоский волноводный канал с включенными неоднородно-
стями в виде полудисков, эквивалентный области пространства, за-
ключенного между двумя параллельными плоскостями, проведенны-
ми через центры соседних рядов в дисковой металло-диэлектриче-
ской линзе (эти плоскости на рис. 6.38 показаны пунктиром).
нем пунктирной линией, пространство между этими плоско-
стями образует волноводный канал вида рис. 6.39. Заменим
такой волноводный канал эквивалентной длинной линией
с включенными реактивностями, как на рис. 6.36. В случае
системы дисков нормированная проводимость В равна (36]
для 1>Ь (рис. 6.38 и рис. 6.39).
32гс/?з 1
3 V 3JM* ЛсА2 ’
1-и /
(6.141)
336
где
ltl=i^r. (6.142)
R — радиус диска,
b—расстояние между центрами дисков.
Пользуясь приведенными в формуле (6.141) значениями,
можно определить коэффициенты преломления и отраже-
ния, а также другие характеристики по формулам (6.128)
-5- (6.133).
Для дисковых линз не исследован случай 1<Ь, при ко-
тором необходимо учесть взаимодействие дисков.
§ 10. МЕТОДЫ ИСКЛЮЧЕНИЯ ОТРАЖЕНИЯ
ОТ ПОВЕРХНОСТИ ЛИНЗ
В связи с тем, что отражение от поверхности линзы ска-
зывается отрицательно на коэффициенте усиления антенны
и на согласовании облучателя с питающей линией, в лин-
зовых антеннах тем или иным способом обычно добиваются
исключения или значительного ослабления отражения.
Одним из методов исключения отражения является ме-
тод четвертьволнового согласующего слоя, применяемый
в диэлектрических линзах и заключающийся в покрытии
поверхности линзы слоем диэлектрика, имеющим толщину
в четверть волны в этом слое и коэффициент преломления,
равный корню квадратному из коэффициента преломления
линзы. Этот метод иллюстрируется рис. 6.40. На этом ри-
сунке воздух обозначен цифрой 1, покрывающий слой —
цифрой 2, а линза — цифрой 3. Через Fi2 и F23 обозначены
границы сред. В обозначениях рис. 6.40
г?2 ф л3, (6.143)
< = (6-144)
где п2 и п3 — коэффициенты преломления соответственно
второй и третьей среды.
Принцип действия четвертьволнового слоя следующий.
У линзы с покрытием отражение имеет место как у по-
верхности Fiz, так и у поверхности F23. При dc = ^ от-
раженная от поверхности F23 волна Р23 пройдет внутри
слоя (2) четверть периода в прямом и четверть перио-
да в обратном направлениях и будет иметь противопо-
22—1503 337
Ложную фазу Но сравнению С волной Р12, отражённой
от поверхности А1а. По модулю коэффициенты отра-
жения волн Р12 и Р23 одинаковы, так как одинаково соот-
ношение коэффициентов преломления - •
«2___«3
"1 «2 ’
(6.145)
где «1 = 1 — коэффициент преломления воздуха.
Поскольку коэффициент передачи (прозрачность) по-
крывающего слоя близок к единице, то волна Р23 практи-
чески полностью пройдет через поверхность Fi2. При интер-
Рис. 6.40. К анализу влияния четвертьволнового
слоя на компенсацию отражения от поверхности
диэлектрической линзы.
ференции волны Р\2 и Р23 уничтожаются, как имеющие оди-
наковые амплитуды и противоположные фазы.
В приведенном объяснении метода четвертьволнового
слоя предполагается, что волны падают нормально к по-
верхностям F12 и А23. В реальных условиях угол 0 между
нормалью к поверхности А12 и лучом, падающим из фоку-
са S (рис. 6.40), на разные точки этой поверхности имеет
разные значения. Аналогично разные значения имеет угол
338
Между лучом и нормалью к поверхности F23- В связи с этим
в разных точках поверхности линзы по-разному будет ска-
зываться влияние четвертьволнового слоя на ослабление
отражения.
Рис. 6.41. Графики зависимости коэффициента отра-
жения от угла падения при наличии четвертьвол-
нового слоя (сплошные кривые) и отсутствии чет-
вертьволнового слоя (пунктирные кривые).
Суммарный коэффициент отражения от линзы при на-
личии четвертьволнового согласующего слоя определяется
по формуле
р__Г;з)2 • 4Г12Г2з sin2 у ,z. .
— И (1 + Г12Г23)2 + 4Г,21\3 sin2 ? ’
где __________
«2 — sin^S, (6.147)
О—угол падения волны в области 1,
Г12 и Г23 — коэффициенты отражения соответственно от
поверхностей F12 и Л23.
На рис. 6.41 сплошные кривые показывают вычислен-
ную по формуле (6.146) зависимость суммарного коэф-
фициента отражения по мощности от угла падения 0
у линзы, покрытой диэлектрическим слоем толщиной
в направлении, перпендикулярном к поверх-
22*
339
ности. Коэффициент преломления в расчете принят равг
ным и3 = 1,57 и n2 = yi,57. Пунктирные кривые пока-
зывают значения коэффициента отражения у линзы, не
имеющей согласующего слоя. Из сравнения соответ-
ствующих сплошных и пунктирных кривых видно, что
при перпендикулярной поляризации наличие четверть-
волнового слоя снижает коэффициент отражения при
всех углах падения, а при параллельной поляризации
это имеет место лишь при 9 <51°; при 0>51° наличие
слоя увеличивает коэффициент отражения.
Рис. 6.42. Реактивные решетки, используемые для компенсации от-
ражения от поверхности линзы: а) индуктивная проволочная (или
ленточная) сетка, б) емкостная решетка из дисков.
Так как амплитуды поля падающей от облучателя вол-
ны имеют вблизи оси линзы, где угол 0 мал, большую ве-
личину, а далеко от оси линзы, где угол в сравнительно
велик, малую величину, применение четвертьволнового со-
гласующего слоя приводит к значительному ослаблению
отражения от поверхности линзы.
Эффект, аналогичный четвертьволновому слою, полу-
чается, если на поверхности линзы сделать чередующиеся
через равные промежутки углубления — пазы глубиной
в четверть волны в линзе, причем ширина пазов должна
равняться ширине промежутков.
Разработаны, кроме того, методы ослабления отра-
жения с помощью так называемой реактивной решетки.
Этот метод заключается в помещении внутри линзы на
глубине у решетки из узких лент вида рис. 6.42а, об-
ладающей индуктивным сопротивлением или на глубине
340
-g-Л решетки из дисков вида, изображенного на рис. 6.42,6
(представляющего собой один слой системы, приведен-
ной на рис. 6.38), обладающей емкостным сопротивле-
нием. Технология выполнения реактивного слоя такова:
на поверхность линзы печатанием наносится решетка
из узких лент или дисков, а на них наклеивается слой
диэлектрика соответствующей толщины или .
Сохраним для данного случая обозначения, приведен-
ные на рис. 6.40, понимая под средой 2 наклеенный
слой диэлектрика, а под средой 3 основную часть линзы.
Под поверхностью F23 понимается поверхность решетки.
Суммарный коэффициент отражения от поверхностей
Ft2 и F23 в данном случае определяется по формуле
г [ г?2 + 2ГП («23 cos 2? + ^3sin 2f) + «23 + &23 /С 1ЛЯ\
1 — 1/ —------------------------й---й---й-т , (0.140)
V 1 + 2Г12 (a23 cos 2? -t- &23sin 2<р) + Г?2 (а2гз + Ь23)
где
<р —-у-}//г2 — sin29, (6.149)
«„+/*г,= Г!3=-у^. (6.150)
г23 — коэффициент отражения от поверхности F23,
У2 — характеристическая проводимость диэлектрика,
п — коэффициент преломления диэлектрика,
В—реактивная проводимость реактивного слоя.
В случае индуктивной решетки проводимость В опре-
деляется:
для параллельно-поляризованной волны
в = 1—~
г— cos 0
АФ
(6.151)
для перпендикулярно-поляризованной волны
п________
ь — I г, / / Г
^-C°s0 In-^ + F' ^0,т
(6.152)
где — длина волны в диэлектрике,
и f®’т) — небольшие корректирующие сла-
' / \ / гаемые.
341
6 — угол падения — угол между направлением распро-
странения и нормалью к поверхности решетки.
В случае емкостной решетки из дисков проводимость
определяется:
для параллельно-поляризованной волны
В_У2
32 л/?3 cos 0
3 /ЗХ&2
(6.153)
для перпендикулярно-поляризованной волны
&__у 32л/?3 1 sin2 0
2 зКзхбзсо8 0 (М2 Г Мс2.21
l‘-W Ч'-Ы!
(6.154)
где 41— критическая длина волны при колебаниях
типа ТЕ,] в круглом волноводе, имеющем ра-
диус, равный радиусу диска R, определяется
по формуле (6.142),
4г — критическая длина волны при колебаниях типа
TEyz в тех же условиях, определяется по
формуле
(6.155)
На рис. 6.43 даны графики (сплошные кривые) зависи-
мости от угла падения 6 коэффициентов отражения от по-
верхности линзы по мощности Г2, согласованной с по-
мощью индуктивной решетки (а) и с помощью емкостной
решетки и дисков (б). Расчет выполнен по приведенным
выше формулам для индуктивной решетки, имеющей
расстояние / = 0,45Х между лентами и для емкостной
, *
решетки при расстоянии между центрами дисков Ь = -^ .
Коэффициент преломления диэлектрика принят равным
«=1,57. Там же на рис. 6.43 приведены (пунктирные
линии) графики зависимости коэффициента отражения
от угла 6 у несогласованной линзы. Легко видеть, что и
в данном случае, аналогично методу четвертьволнового
слоя, реактивная решетка при перпендикулярной поляри-
зации снижает коэффициент отражения при всех углах
падения 6, а при параллельной поляризации — лишь при
6 С 42° = 45°.
Чтобы получить большое ослабление отражения при
любых углах падения 0 и при любой поляризации, тре-
342
---------- линза согласованная индуктив-
ной решеткой
----------линза,несогласованная
Рис. 6.43. Графики зави-
симости коэффициента
отражения от угла паде-
ния при согласовании с
линза согласованная, емкост-
ной решеткой из дисков
линза несогласованная
помощью индуктивной
решетки (а) и емкост-
ной решетки (б).
<9
343
буется для разных углов 6 помещать элементы решетки
на разной глубине и придать решетке в разных местах
различную проводимость.
Глубина погружения реактивной решетки определяется
из условия
^ = tg2<P, (6.156)
где У1 — характеристическая проводимость свободного
пространства (т. е. отношение' составляющих
магнитного и электрического векторов, каса-
тельных к поверхности линзы).
О 10 20 30 40 50 60 70 8 0 90
Угол падения В градусах
.....параллельная поляризация
— перпендикулярная поляризация
Рис. 6.44. Рекомендуемые расстояния dc от поверхности
линзы до дисковой решетки и диаметры дисков 2R в за-
висимости от угла падения для максимальной компен-
сации отражения от поверхности линзы для п=1,57
X
и I = — .
Л
Параметры решетки могут быть определены из условия
£ = ctg2<p. (6.157)
г 2
На рис. 6.44 приведены графики зависимости относи-
тельных величин глубины погружения dc и диаметра
дисков 2R от угла падения 6 длят случая п = 1,57 и 1 — ^-.
344
У металло-диэлектрических линз отражение от поверх-
ности линз может быть ослаблено подбором их пара-
метров. Действительно, согласно (6.133)Г = 0 при _у=1.
В свою очередь, как видно из (6.132),
при
В = 4 ctg£Z. (6.158)
Подбирая параметры линзы таким образом, чтобы их
проводимость определялась по формуле (6.158), можно
принципиально свести отражение к нулю.
Рис. 6.45. Ленточная линза в раскрыве пирами-
дального рупора, разделенная на две равные части,
которые смещены на расстояние друг относи-
тельно друга.
Помимо решения общей задачи об устранении или
ослаблении отражения от поверхности линзы, нередко огра-
ничиваются решением частных задач.
В ряде практических случаев главной задачей является
устранение влияния отраженной волны на облучатель. Эта
задача решается несколькими способами. Одним из спосо-
бов является деление линзы на две равные части и смеще-
ние этих частей на четверть волны друг относительно друга,
как показано на рис. 6.10,г. В этом случае лучи, отражен-
345
ные от обеих половин линзы, в точке фокуса будут Иметь
противоположные фазы.
Другой способ заключается в смещении облучателя из
фокуса, как показано на рис. 6.10,в. При небольшом смеще-
нии облучателя фазовый фронт волны на выходе линзы со-
хранится плоским, но будет наклонен к нормали к раскрыву.
Наклон фазового фронта может быть учтен в работе. Отра-
женные же от поверхности динзы лучи будут фокусировать-
ся с обратной стороны оси линзы и не окажут существен-
ного влияния на согласование облучателя и фидерной линии.
Таким образом, не устраняя полностью отражения от
поверхности линзы, мы можем значительно ослабить влия-
ние отраженной волны на облучатель.
Как отмечалось выше, широкое применение, в частно-
сти, в радиорелейных линиях, нашли рупорно-линзовые
антенны, представляющие собой рупор с помещенной в его
раскрыве линзой. В такой антенне рассеяние энергии, полу-
чающееся при отражении волн от поверхности линзы, устра-
няется тем, что система экранируется металлическими стен-
ками рупора. Влияние же отраженной волны на облучатель
существенно ослабляется, во-первых, делением линзы на
X
две смещенные на половины, во-вторых, небольшим на-
клоном линзы относительно оси рупора, что эквивалентно
вынесению точечного облучателя из фокуса. Рупорно-лин-
зовая антенна, состоящая из двух смещенных на ча-
стей, показана на рис. 6.45.
§ 11. РАСПРЕДЕЛЕНИЕ АМПЛИТУД ПОЛЯ В РАСКРЫВЕ
ЛИНЗЫ
Выше, анализируя прохождение радиоволн через линзы,
мы уделяли внимание только распределению фаз в рас-
крыве и определяли условия, при которых на выходе линзы
образуется плоский фазовый фронт волны, что, в частности,
при плоском раскрыве соответствует линейному закону рас-
пределения фаз поля.
Распределение амплитуд, как указывалось выше, опре-
деляется в основном диаграммой направленности облуча-
теля. При расположении линзы в раскрыве пирамидального
рупора, как, например, на рис. 6.45, амплитуды почти по-
стоянны в направлении вектора Е и меняются примерно по
косинусоидальному закону в направлении вектора Н, т. е.
амплитудное распределение сохраняется почти таким, каким
34В
оно было бы в рупоре без линзы. Аналогично получается и
при других облучателях. Однако сохраняя общий характер
распределения амплитуд таким, какой диктуется облучате-
лем, линза вносит некоторые изменения в это распределе-
ние.
Выше было показано влияние круглой цилиндрической
линзы типа Люнеберга на распределение амплитуд. Два
других примера приведены на рис. 6.46,а и б. Здесь пока-
зана линза, имеющая п>1, с выпуклой освещенной сторо-
ной (рис. 6.46,а) и линза, имеющая п<Д, с вогнутой осве-
щенной стороной (рис. 6,46,6). Мы видим, что в первом
случае электромагнитный поток сгущается в середине лин-
зы, а во втором случае, наоборот, (сгущается на краях лин-
зы. Таким образом, в зависимости от коэффициента пре-
ломления линзы и от формы поверхности, может произойти
усиление поля в середине раскрыва линзы или на краях.
Для определения количественных соотношений восполь-
зуемся выведенной выше (6.74) формулой освещенной сто-
роны профиля линзы. Пользуясь обозначениями рис. 6.46,в,
приведем выражение (6.74) к виду
(6.159)
cos(T— а) — —
где а = у— 9 является функцией у.
Интегрирование дает
(6.160)
COsfr — a(T)] — —
Для получения профиля линз в явном виде необходимо
знать функцию а (у). У линз, рассмотренных в § 1, у ко-
торых образуется плоская волна внутри линзы и которые
имеют плоский раскрыв а(у) = 0, уо = О и p0 = f-
Следовательно, для этих линз имеем
(6.161)
cos7-- COS7--
или
(6.162)
cosT_-
347
Если заменить р и cosy прямоугольными координатами
по формулам;
p = |/x2+j/2
cosy — ?+ х-
' р
(6.162а)
то придем к уравнениям (6.3) и (6.4).
Для определения закона изменения амплитуд поля
в раскрыве продлим лучи BE и CD до их пересечения
в точке S' (рис. 6.46,в). Угол между лучами BE и CD
обозначаем через da. Ограничимся здесь случаем цилин-
дрической линзы с гиперболическим или эллиптическим
профилем и плоским раскрывом. В этом случае задача
является двухмерной, а математический анализ сравни-
тельно простым. Обозначим диаграмму направленности
облучателя по мощности через /(у). Мощность излуче-
ния Р(у), приходящаяся на угол dy, пропорциональна
произведению I^dy. Эта мощность Р(у) распределится
по участку ED с линейной плотностью
Рг(а) = ^-^Г> <6Л63)
где k — коэффициент пропорциональности.
Если обозначить отрезок S'D через р', то
ED~p'da
и
piW=kL$£- (6.164;
Для нахождения РДа) необходимо знать зависимость
а от у. В разных конкретных случаях эта зависимость
определяется различно. В простейших случаях, рассмот-
ренных в § 1, когда раскрыв плоский и в линзе образуется
плоская волна, лучи CD и BE параллельны оси линзы
и а = 0, a р' = оо. В этом случае выразим РДа) непосред-
ственно как функцию у, а произведение p'da. через dy.
Следовательно,

(6.165)
348
Линза
для распределения амплитуд поля в
• °}
ОСИ
Рис. 6.46.
лучей у <
п.}
на
п <
Qcb линзЬн
Линза
Ocb линзЬ/
Сгущение
линзы при
1 Д) Сгущение лучей
краях льнзы при
1, в) К выводу выражения
раскрыве линзы.
349
Так как
—psin-f,
(6.166)
то
dy = d (psin у) Ц-р cos ycZy = pcfy fcos 7 4- sin -Л . (6.167)
X P^I /
Подставив dy из (6.167) с учетом значения — из (6.161)
и p из (6.162), получим после простых преобразований
= <6ЛМ)
Учитывая, что между р иу существует зависимость,
определяемая уравнением (6.162), можно, воспользовав-
шись соотношением (6.166), представить РДу) как функ-
цию у. Таким образом, Pz(y) можно рассматривать как
функцию распределения значений квадрата амплитуд поля
в раскрыве линзы.
На рис. 6.47 приведены вычисленные по формуле (6.168)
£ / р у
кривые зависимости отношения ъЧт от п> гДе
у I и
Еу — напряженность поля в точке у раскрыва линзы,
а £0 — напряженность поля в центре раскрыва линзы для
случая нахождения линзы в раскрыве секториального
рупора. Пунктирные кривые показывают амплитудное
распределение без учета влияния линзы. Верхние кривые
показывают соответствующие амплитудные зависимости
в f-плоскостном рупоре, а нижние кривые в //-плоско-
стном рупоре. Линзы во всех случаях взяты толщиной
d' = 0,2£>. Коэффициент преломления соответствует обычно
применяемым (л =1,5 и и = 0,55).
Рис. 6.47 находится в согласии с отмеченными выше за-
кономерностями. Он показывает наличие некоторого ослаб-
ления поля на краях линзы при л>1 и некоторое усиление
поля на краях при п<1. Ослабление поля на краях линзы,
как отмечалось выше, приводит к некоторому снижению
коэффициента усиления, к расширению главного лепестка и
уменьшению относительной величины побочных максиму-
мов. Увеличение поля на краях приводит к сужению глав-
ного лепестка и увеличению побочных лепестков. Что ка-
сается влияния на коэффициент усиления увеличения поля
на краях линзы, то здесь имеет место следующая законо-
мерность: увеличение поля на краях линии, параллельной
350
—V
вектору Н, приводит к увеличению коэффициента усиления,
так как делает распределение поля более равномерным, а
увеличение поля на краях линии, параллельной вектору Е,
уменьшав!' коэффициент усиления, так как делает распре-
деление поля неравномерным.
В случае линзы с гиперболическим и эллиптическим про-
филем, обладающей осевой симметрией, и при облучении
Рис. 6.47. Распределение амплитуд поля в раскрыве линзы, установ-
ленной в раскрыве секториального рупора при различных соотноше-
ниях между шириной раскрыва D и фокусным расстоянием f и при
различных значениях коэффициента преломления п.
этой линзы электромагнитным полем, обладающим диаграм-
мой направленности в виде фигуры вращения, можно вы-
кладками, аналогичными приведенным выше, придти к сле-
дующему выражению для распределения мощности в пло-
ском раскрыве линзы:
(6.169)
где РДу)— мощность излучения, приходящаяся на еди-
ницу площади в заданной точке раскрыва. ‘Остальные
обозначения прежние. При этом под у в формуле (6.166)
следует понимать расстояние от центра раскрыва.
У других рассмотренных выше линз (апланатические
линзы, линзы Люнеберга и другие) не удается выразить
распределение мощности в простой форме.
351
§ 12. РАСЧЕТ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
ЛИНЗОВЫХ АНТЕНН
Как показано выше, для определения электромагнитного
поля излучения и его характеристик (диаграммы направ-
ленности, коэффициента направленного действия и т. п.)
необходимо знать распределение амплитуд и фаз поля в рас-
крыве антенны.
У линзовых антенн распределение амплитуд может быть
найдено методом, изложенным в предыдущем параграфе.
При определении фаз поля у всех рассмотренных выше лин-
зовых антенн следует руководствоваться тем, что они рас-
считаны на получение плоской волны на выходе линзы. Зная
положение фазового фронта и траектории лучей, которые
определяются методами геометрической оптики, можно
найти по длине участка траектории от раскрыва до фазо-
вого фронта фазы поля в раскрыве линзы. Пользуясь полу-
ченными таким образом данными о распределении ампли-
туд и фаз поля в. раскрыве линзы, можно с помощью фор-
мул (3.6), (3.22) и т. п. получить достаточно точные
значения характеристик излучения линзовых антенн.
Однако расчет по этим данным встречает значительные
математические трудности из-за сложности выражений,
определяющих закон распределения амплитуд и фаз поля в
раскрыве линзы. Поэтому в целях упрощения задачи при-
бегают к аппроксимации этих выражений более простыми.
Рассмотрим вопрос о возможных аппроксимациях для
некоторых категорий линзовых антенн.
а) цилиндрические линзы с гиперболическим или
эллиптическим профилем и прямоугольным плоским
раскрывом, облучаемые линейным источником
У таких линз (рис. 6.48) фазовый фронт волны совпа-
падает с плоскостью раскрыва. Следовательно, фазы поля
в раскрыве одинаковы.
Амплитуды поля в направлении, параллельном облуча-
телю (т. е. вдоль образующей цилиндра) определяются рас-
пределением амплитуд поля вдоль облучателя и, как пра-
вило, бывают либо одинаковыми, либо меняющимися по
косинусоидальному закону [формулы (3.7) или (3.8)].
В перпендикулярном направлении распределение амплитуд
определяется формулой (6.168).
Для определения характеристик данной антенны можно
заменить распределение амплитуд поля вида (6.168) близ-
352
ким к нему распределением вида (3.9) или (3.10), подобрав
значение параметра р (точнее — отношение где D —
ширина раскрыва линзы), при котором кривые, вычерчен-
6)
[ Рис. 6.48. Иллюстрация цилиндрической лиизы с : а)
эллиптическим профилем и б) гиперболическим профилем.
ные по формулам (6.168) и (3.9) или (3.10), дают наилуч-
шее совпадение.
Если вдоль облучателя амплитуды поля одинаковы, то
все характеристики этой антенны определяются непосред-
ственно по данным гл. III § 2, разделы в или г, причем пло-
23—1503 353
скости, проходящей через образующую цилиндра соответ-
ствует в гл. III Е-плоскость, а плоскости, перпендикулярной
к образующей цилиндра, //-плоскость.
Если вдоль облучателя амплитуды поля меняются по ко-
синусоидальному закону, то в указанные данные гл. III
должны быть внесены следующие коррективы: диаграмма
направленности в плоскости, проходящей через образую-
щую цилиндра, будет определяться по формуле (3.29),
а коэффициент направленного действия будет равен коэф-
фициенту, определяемому формулами (3.47) или (3.57),
при их умножении на 0,81.
б) линзы, обладающие осевой симметрией
с гиперболическим или эллиптическим профилем и плоским
круглым раскрывом, облучаемые точечным источником
с диаграммой направленности в виде фигуры вращения
У этих линз (рис. 1.5,а или 1.5,6) фазы поля в раскры-
ве также одинаковы. Амплитуды поля меняются от центра
раскрыва к краям по формуле (6.169).
В данном случае можно аппроксимировать распреде-
ление поля в раскрыве линзы формулой (3.63), подобрав
соответствующее значение отношения — , где D — диаметр
раскрыва.
Как мы видели, при распределении амплитуд поля
по формуле (3.69), во-первых, поле излучения в основных
плоскостях (Е- и //-плоскостях) определяется только со-
ставляющей Е , во-вторых, распределение амплитуд раз-
лично в направлении = 0 и <р = у. Поэтому при подборе
2р
отношения — следует исходить из выражения для Е ,
причем в качестве исходной кривой следует принять кри-
вую, проходящую посередине между кривыми, для <р= 0
и ? =
2о
Определив отношение ~ , при котором распределение
амплитуд, выражаемое формулой (6.169), достаточно
хорошо аппроксимируется формулой (3.63), можно рас-
считать характеристики излучения по данным гл. III § 3,
раздел г.
354
в) усеченные линзы того же вида, что п. 2, имеющие
прямоугольный раскрыв
Как и в предыдущем случае, фазы поля в раскрыве
одинаковы, а амплитуды меняются по формуле (6.169) в
радиальных направлениях от центра к краям (рис. 1.5,о
или 1.5,а).
Удобная аппроксимация в данном случае может быть
найдена следующим образом.
Сначала определяются по формуле(6.169)кривые рас-
пределения амплитуд на главных направлениях, парал-
лельных сторонам прямоугольника раскрыва. Обозначим
размеры этих сторон прямоугольника через £>j и D2. Кри-
вые распределения на главных направлениях могут отли-
чаться друг от друга из-за различия диаграмм направлен-
ности облучателя в основных плоскостях. Например, при
нахождении такой линзы в раскрыве пирамидального ру-
пора, последний создает в одном главном направлении оди-
наковые амплитуды, а во втором — косинусоидальное рас-
пределение. Это первичное распределение корректируется
по формуле (6.169).
Полученные кривые распределения на главных направле-
ниях аппроксимируются формулами (3.9) или (3.10), как
в п. 1, причем та из кривых, которая характеризуется более
медленным спаданием амплитуд от центра к краю, приво-
дится к эквивалентно равномерному распределению (к
одинаковым амплитудам). Для определенности предполо-
жим, что более медленное спадание имеет место в направ-
лении, параллельном стороне D2. Для приведения имеюще-
гося распределения к эквивалентному равномерному, пред-
варительно определяется ширина главного лепестка диаг-
раммы направленности 2%, соответствующая исходному
распределению при размере раскрыва £>2, а затем по фор-
муле
20о=:О,89-А-
^ЭКВ
определяется эквивалентный размер раскрыва £)экв, соот-
ветствующий ширине главного лепестка 2% при одина-
ковых амплитудах.
Таким образом, рассматриваемый случай приводится
к задаче о прямоугольном отверстии со сторонами D,
и D9kb, причем вдоль стороны D3KB амплитуды поля одина-
23* 35/
ковы, а вдоль стороны D, меняются по формуле (3.9)
или (3.10). Расчет характеристик излучения может произ-
водиться по данным гл. III § 2, разделы в или г.
г) цилиндрические линзы Люнеберга
Как указывалось выше, у этой системы ширина глаз-
ного лепестка диаграммы направленности определяется
по формуле:
в //-плоскости
2^ =200»/
В Е-плсгскости
29^=58,8»^.
Зная ширину главного лепестка диаграммы направлен-
ности, можно этот случай аппроксимировать эквивалент-
ным плоским прямоугольным отверстием с синфазным по-
лем при равномерном распределении амплитуд вдоль широ-
кой стенки и по косинусоидальному закону вдоль узкой
стенки. При этом размер широкой стенки равен 2/?, а уз-
кой — определяется по формуле
'узк.экв — !>18 20о// •
д) сферические линзы Люнеберга
Сферические линзы Люнеберга аппроксимируются син-
фазным круглым плоским отверстием радиуса /?, равного
радиусу сферы.
Распределение амплитуд в эквивалентном отверстии
близко к равномерному. Расчет характеристик может про-
изводиться по данным гл. III § 3, разд. а.
§ 13. ПОЛУЧЕНИЕ КОСЕКАНСНОЙ ДИАГРАММЫ
НАПРАВЛЕННОСТИ С ПОМОЩЬЮ ЛИНЗЫ
В технике сверхвысоких частот нередко требуются
антенны, имеющие диаграмму направленности вида F (а) =
= cosec2а по мощности. Будем называть ее косекансной
диаграммой направленности.
Функция F (а) = cosec2 а меняется от 1 при а = у ДО оо
при а = 0. Так как при конечной величине излучаемой
356
мощности невозможно получить бесконечно большую
интенсивность излучения в каком-либо направлении,
то диаграмму направленности вида cosec2 а принципиально
получить нельзя. Поэтому считается достаточным полу-
чение диаграммы направленности, которая менялась бы
по закону cosec2а в определенном секторе. Этот сектор,
как правило, равен 60°. На рис. 6.49 показана форма
диаграммы направленности вида cosec2 а. Согласно этой
диаграмме интенсивность излучения меняется по закону
cosec2 а в секторе 10°—-70°, а при а = 0 и а = 90’
А(а)=0.
Косекансная форма диаграммы направленности обычно
требуется в одной плоскости (вертикальной) в то время как
Рис. 6.49. Диаграмма направленности вида cosec2 а.
в другой плоскости (горизонтальной) требуется диаграмма
направленности типа синфазной антенны с очень узким
главным лепестком. Антенну с такими диаграммами направ-
ленности можно получить как с помощью цилиндрической
линзы, имеющей линейный облучатель, так и с помощью
линзы двоякой кривизны, имеющей точечный облучатель.
Мы рассмотрим здесь цилиндрическую косекансную линзу,
поскольку ее анализ отличается большей простотой. Задача
в этом случае является плоской (двухмерной).
Пример цилиндрической косекансной линзы показан
на рис. 6.50.
Получение косекансной диаграммы направленности воз-
можно подбором соответствующего профиля линзы. По-
скольку в задаче ставится лишь одно условие — получение
косекансной диаграммы направленности, то это условие мо-
жет быть выполнено путем соответствующего подбора одной
из сторон линзы при произвольном выборе второй стороны.
Ниже приводятся данные расчета теневой стороны при
произвольном задании освещенной стороны. Рассматривают-
ся три случая.
1. Освещенная сторона — круглый цилиндр, на оси кото-
рого расположен облучатель. В этом случае лучи не прелом-
357
ляются на освещенной стороне, и внутри линзы образуется
цилиндрическая волна.
2. Профиль освещенной стороны обеспечивает внутри
линзы плоскую волну.
3. Освещенная сторона — плоскость.
Рис. 6.50. Общий вид цилиндрической линзы
с косекансной диаграммой направленности.
Расчет основывается на применении интегрального
уравнения профиля линзы (6.143), в котором — заменяется
на п, так как в данной задаче рассматривается переход
из среды в среду с п=1.
Итак основой расчета является уравнение
т
] п р __ f sin 1т —а (тг)1
Ро J cos [? — я(т)] — п
7о
В (6.169) обозначения те же, что в (6.162). Связь между
а и 7 попрежнему выражается формулой (6.164).
Выше мы применяли метод геометрической оптики (по-
нятие о лучах и об их преломлении) для определения
амплитуд и фаз поля в линзе и в ее раскрыве, т. е. ограни-
чивали применение метода внутренней областью линзы.
При расчете антенн с косекансными диаграммами на-
правленности предполагается, что метод геометрической
оптики может быть использован также и для определения
поля излучения. Это означает, что отрезки S'D и S'E на
рис. 6.46 продлеваются на очень большие расстояния (до
точки приема). Поскольку точки пересечения преломлен-
ных лучей находятся вблизи линзы (за исключением случая
358
(6.170)
(6.171)
(6.172)
параллельных лучей, который здесь исключается), а точка
приема на неизмеримо больших расстояниях, то можно по-
ложить ® (6.164) р' = const и учесть его в постоянном мно-
жителе k. Отсюда следует, что в рассматриваемой задаче
следует положить
Рг(а) da. = kl
При принятом методе решения
(а) — cosec2 а.
Следовательно, согласно (6.170)
“2 Т2
cosec2 ada—k J I (у) cZy
и
или
ъ
ctga, — ctg7 = /e j/(y)dy,
и
где ct । и a2— углы, в пределах которых диаграмма направ-
ленности должна иметь вид F (а) = cosec2 а,
Y1 и Ъ— углы между осью линзы и прямыми, прове-
денными из фокуса к крайним точкам
профиля линзы (рис. 6.47),
/г — (6.173)
J I (7) d'(
Система уравнений (6.169) и (6.172) дает выраженную
в квадратурах зависимость р от у для профиля линзы, обес-
печивающего приблизительно косекансную диаграмму на-
правленности. Приближенность решения определяется тем,
что оно получено методом геометрической оптики.
Как известно, метод геометрической оптики дает точное
решение задачи при 2 —»0. Следовательно, получений ре-
зультат тем точнее, чем больше размеры линзы в единицах
длины волны. Достаточно хороший результат получается
уже при ширине раскрыва порядка 15—20 2.
Следует заметить, что интеграл в правой части (6.169)
не приводится к известным функциям и вычисляется прибли-
женными методами.
359
Рис. 6.51. Профили линз с косекансной диаграммой направленности
при профиле освещенной стороны в виде дуги окружности: а) для
случая различных п>1, б) случай п==0,6<1.
360
Рис. 6.52. Профиль линзы с косекансной диаграм-
мой направленности при профиле освещенной сто-
роны в виде гиперболы.
361
Профили линз, создающих косекансную диаграмму на-
правленности, показаны на рис. 6.51, 6.52 и 6.53, причем
рис. 6.51 соответствует линзе, у которой внутри имеется
Рис. 6.53. Профиль линзы с косекансной диаграммой на-
правленности при профиле освещенной стороны в виде
прямой линии.
цилиндрическая волна, рис. 6.52 — наличию внутри линзы
плоской волны, а рис. 6.53 — линзе с плоской освещенной
стороной.
Функция I (у) в расчетах принималась равной cosy.
ГЛАВА СЕДЬМАЯ
ЗЕРКАЛА
§ 1. ДВА МЕТОДА РАСЧЕТА ЗЕРКАЛ
Расчет электромагнитного поля излучения антенн,
использующих отражающие поверхности (зеркала), может
быть выполнен двумя методами.
По первому методу [37] первоначально вычисляются
токи, возбужденные электромагнитным полем облучателя
на поверхности зеркала. При этом исходят из предположе-
ния, что поверхностная плотность электрических токов
равна
> = —2[^пад], (7.1)
где Япад — магнитный вектор падающей волны,
и — орт нормали к поверхности.
Равенство (7.1) является точным лишь в случае идеаль-
но проводящей бесконечно плоской отражающей поверхно-
сти. Если поверхность является, как у параболоидов, криво-
линейной, определение токов по формуле (7.1) перестает
быть точным. Однако при больших радиусах кривизны по-
верхности зеркала ошибка, вносимая формулой (7.1),
является вполне допустимой.
Определив по формуле (7.1) поверхностную плотность
токов на зеркале, затем вычисляется электромагнитное
поле излучения с помощью формул (2.41) и (2.42), пола-
гая в них JM = 0.
Как правило, вместо двойной операции — первоначаль-
ного расчета токов на поверхности зеркала по электро-
магнитному полю облучателя и последующего расчета поля
излучения по заданным токам на поверхности зеркала —
363
рассчитывают поле излучения непосредственно по значе-
ниям поля облучателя у поверхности зеркала. Для этого
могут быть использованы, например, формулы (2.43)- при
подстановке [п £] = 0.
По второму методу первоначально по законам геометри-
ческой оптики, т. е. на основе представлений о падающем
луче и луче, отраженном по закону равенства угла падения
углу отражения, вычисляется поле в раскрыве зеркала,
а затем методом волновой оптики, т. е. решая задачу о диф-
фракции на отверстии в плоском экране с использованием
формулы (2.43), вычисляется поле излучения.
Второй способ также является приближенным, посколь-
ку используемые законы отражения, строго говоря, также
точны при падении электромагнитной волны на бесконечно
большую идеально проводящую плоскость. Однако и здесь
при достаточно большом радиусе кривизны зеркала отра-
жение от криволинейной поверхности может с достаточной
точностью считаться равным отражению от плоскости [38].
Таким образом, расчет электромагнитного поля излуче-
ния по обоим методам производится с помощью одной и той
же формулы (2.43). Отличие методов заключается в том,
что по одному из них за исходное берется поле у зеркала,
а по другому поле в раскрыве. Исходные поля в обоих слу-
чаях определяются приближенно. Из-за отсутствия строгого
решения задачи не. удается теоретически оценить погреш-
ность расчета ни в том, ни в другом случае.
Учитывая, что оба указанных метода расчета зеркал
приводят к одинаковым значениям поля излучения в области
главного лепестка диаграммы направленности и ближайших
к нему побочных лепестков, а также к одинаковым значе-
ниям коэффициента усиления антенны, оба метода исполь-
зуются в теории антенн как равноценные.
Следует заметить, что на характеристики излучения
зеркал, как увидим ниже, оказывают существенное влияние
некоторые факторы, которые не могут быть практически
учтены в расчете, например, неточности изготовления фор-
мы зеркала, смещение облучателя относительно требуемого
положения, так называемый «теневой эффект» облучателя
и т. п. Ввиду этого неизбежны расхождения между расчет-
ными и экспериментальными данными исследования зеркал.
Эти расхождения невелики в области главного лепестка диа-
граммы направленности, но значительны в области побоч-
ных лепестков. Ошибки, вносимые этими не поддающимися
364
учету факторами, находятся на уровне ошибок, вносимых
неточностью указанных методов расчета зеркал.
Приводимые ниже выкладки основываются главным
образом на использовании второго метода, получившего на-
звание апертурного (от английского слова «апертура» —
раскрыв).
Рассмотрим подробнее апертурный метод. Как указыва-
лось выше, этот метод базируется на законе отражения от
бесконечного плоского зеркала. Поэтому сначала отметим
закономерности, определяющие отражение электромагнит-
ных волн от идеально проводящей плоскости.
Рис. 7.1. Падающий и отраженный от плоского зеркала
лучи: а) при параллельной поляризации; б) при перпен-
дикулярной поляризации.
Зная амплитуду, фазу и поляризацию поля волны, па-
дающей на плоское зеркало, можно точно определить
амплитуду, фазу и поляризацию поля отраженной волны.
Соотношение фаз и поляризации падающей и отраженной
волн иллюстрируется рис. 7.1. На рис. 7.1,а показан случай
так называемой параллельной поляризации, при которой
электрический вектор Е лежит в плоскости распростране-
ния Q, а на рис. 7.1,6 показан случай так называемой пер-
пендикулярной поляризации, при которой электрический
вектор перпендикулярен плоскости распространения. Из
рис. 7.1,а видно, что при параллельной поляризации направ-
ление электрического вектора поворачивается в точке отра-
жения на тот же угол (180° — 2 <р), на который поворачи-
вается отраженный луч относительно падающего, магнит-
ный же вектор сохраняет свое направление. Из рис. 7.1,6
в свою очередь следует, что при перпендикулярной поляри-
зации электрический вектор меняет свое направление в точ-
ке отражения на 180°, а магнитный вектор поворачивается
365
на угол 2 <р. Это означает, что при параллельной 'поляриза-
ции (рис. 7.1,а) отражающая плоскость приводит лишь к из-
менению направления распространения волны (и, естествен-
но, к соответствующему повороту векторов поля), а при
перпендикулярной поляризации (рис. 7.1,6) отражающая
плоскость, наряду с изменением направления распростране-
ния, вызывает поворот фазы поля на 180°.
Таковы закономерности, определяющие в случае плоско-
го зеркала соотношение фаз и поляризации поля падающей
и отраженной волны. Что касается соотношения амплитуд,
то они определяются на основе следующей закономерности:
при отражении от плоского зеркала форма волны сохра-
няется. Иначе говоря, при падении на плоское зеркало
плоской волны, отраженная волна также является плоской,
а при падении цилиндрической или сферической волны,
отраженная волна является также соответственно цилиндри-
ческой или сферической. Как известно, плоская волна ха-
рактеризуется постоянством амплитуды векторов поля вдоль
всего пути следования волны, цилиндрическая волна харак-
теризуется убыванием векторов поля пропорционально
половинной степени расстояния от источника, а сферическая
волна — убыванием амплитуды пропорционально первой сте-
пени расстояния. При отражении от плоского зеркала ука-
занная зависимость амплитуды векторов поля от расстоя-
ния данной точки до источника сохраняется, причем отра-
женный луч является непосредственным продолжением
падающего луча, т. е. для определения амплитуды поля
в точке М (рис. 7.1) должна учитываться вся длина лома-
ной линии SOM.
Из зеркал наибольшее распространение в технике сверх-
высоких частот получили параболические зеркала.
Параболические зеркала представляют собой криволи-
нейную отражающую поверхность. Закономерности, опре-
деляющие отражение электромагнитных волн от таких по-
верхностей в строгой постановке не исследованы. В совре-
менном состоянии теория параболических зеркал базируется
на предположении о возможности распространения, в не-
сколько измененной форме, законов, присущих плоским
зеркалам на зеркала криволинейные. Основы этой теории
могут быть сформулированы в виде следующих двух поло-
жений.
1. При определении фазы и поляризации векторов поля
волны, отраженной от криволинейной поверхности, могут
быть применены без изменения указанные выше правила,
366
определяющие фазу и поляризацию поля волны, отражен-
ной от плоского зеркала.
2. При определении амплитуды поля отраженной волны
должна учитываться различная форма падающей и отра-
женной волн. Например, излучение первичного источника
(облучателя) имеет, как указывалось выше (глава I), ха-
рактер сферической волны у параболоида вращения или
цилиндрической волны у параболических цилиндров в то
время, как отраженная волна в обоих случаях имеет харак-
тер плоской волны. В соответствии с этим амплитуды поля
падающего луча при расчете полагаются убывающими про-
порционально первой или половинной степени расстояния от
облучателя, а амплитуды поля отраженного луча полагают-
ся постоянными на всем пути распространения и такой же
величины, как у поверхности зеркала.
Ниже приводится, анализ поля в раскрыве и поля излу-
чения параболических зеркал, базирующийся на этих двух
положениях. Этот анализ, позволяя выяснить основные ха-
рактеристики параболических зеркал, одновременно может
служить иллюстрацией применения указанных положений
к решению конкретных задач.
§ 2. РАСЧЕТ ПАРАБОЛОИДА ВРАЩЕНИЯ АПЕРТУРНЫМ
МЕТОДОМ
Прежде чем перейти к анализу электромагнитного поля
в параболическом зеркале, отметим некоторые особенности
и математические соотношения, характеризующие параболи-
ческую кривую, которые нам потребуются в дальнейшем.
Как известно, парабола является геометрическим местом
точек, равноудаленных от заданной точки, называемой фо-
кусом параболы и от заданной прямой, называемой дирек-
триссой. На рис. 7.2 кривая KON изображает параболу, точ-
ка S — ее фокус и прямая K’O’N' — директриссу. Из опре-
деления следует
SO = 00' ’
SN = NN’
SK = KK'
(7.2)
Проведем прямую K"O"N", параллельную директриссе
(перпендикулярную к оси параболы О'ОО") и продлим пря-
мые ОО', NN' и КК' до пересечения с этой прямой. В силу
367
параллельности прямых K'O’N' и K"O”N" справедливо ра-
венство
N'N" = O'O''=K'K". (7.2а)
Учитывая же (7.2), можно из уравнения (7.2,а) полу-
чить
SW4-NN" = SK + KK" = SO±OO" = 2f + z = p ±z, (7.3)
где f — фокусное расстояние (см. рис. 7.2),
p — 2f—параметр параболы.
I
Рис. 7.2. К анализу свойств параболы.
Парабола обладает еще той особенностью, что касатель-
ная, проведенная к любой ее точке, образует одинаковые
углы с прямой, параллельной оси и с прямой, проведенной
в данную точку из фокуса. На рис. 7.2 эти равные углы
обозначены соответственно через а' и а".
Предположим теперь, что рис. 7.2 изображает продоль-
ное сечение параболоида, совпадающее с плоскостью рас-
368
пространения лучей SN, SK, SO и др. Тогда, согласно отме-
ченной только что особенности, луч, идущий от облучателя,
помещенного в фокусе, по направлению SN отразится в на-
правлении NN", а луч, идущий по направлению SK, отразит-
ся в направлении КК"- Аналогично любой луч, вышедший
из фокуса, отразится в направлении, параллельном оси
параболы. Согласно (7.3) все лучи, вышедшие из фокуса,
пройдут до прямой K"O"N" одинаковое расстояние.
Сказанное характеризует образование плоской волны из
лучей, отраженных от поверхности параболоида. Фаза век-
торов поля этой волны, как следует из первого положения,
определяется расстоянием р z, а их амплитуда, согласно
второму положению, убыванием на отрезках SO, SK, SN
и т. д. и постоянством на остальном пути 00", NN", КК"
й т. д.
Для удобства дальнейшего анализа выразим расстояние
от фокуса до параболы (длину отрезка SO, SK, SN и т. д.),
а также длину пути р -4- z через р и р0 (см. рис. 7.2).
Последние могут рассматриваться применительно к пара-
болоиду соответственно как текущая координата и как ра-
диус раскрыва зеркала.
Из рис. 7.2 легко видеть, что
SA4 NS' = p;=SN(l -|-cos&')| = | sun) (7.4)
Совместное решение уравнений (7.4) дает
„ р2 — р2 COS О = \ , 4 + р2 (7-5)
SN = P-±L2. 2р (7-6)
Из рисунка 7.2 следует далее
Ро = V(Р + 2)2 - г2 =/р2 + 2рг . (7.7)
Откуда имеем Р о~Р2 —6 или . Р2 + Ро ? + г- 2р • (7-8)
24—1503
3G9
Перейдем к определению электромагнитного поля в рас-
крыве параболоида и поля излучения. В качестве примера
рассмотрим случай, когда облучателем является диполь
Рис. 7.3. Поляризация поля лучей различным обра-
зом поляризованных относительно оси излучате-
ля— диполя Герца.
Герца. Прежде всего напомним основные особенности поля
излучения диполя Герца в свободном пространстве. Ампли-
туда и фаза электрического вектора поля определяется из
формулы
£=—y^^-cosO'e-7^, (7.9)
где
2к

2— длина волны электромагнитных колебаний,
q — Il— момент тока диполя,
I — ток в диполе,
I — длина диполя.
Остальные обозначения видны на рис. 7.3. Здесь же по-
казана поляризация поля излучения. Из рис. 7.3 видно, что
на экваториальной плоскости в каждый момент времени на
одинаковом расстоянии от диполя электрический вектор
поля Е имеет одинаковое направление, параллельное оси
диполя, в то время, как на более высоких широтах электри-
ческий вектор во всех точках, лежащих на одной параллели,
наклоняется на одинаковый угол к оси диполя. Магнитный
вектор Н везде перпендикулярен электрическому вектору Е
и вектору распространения Р.
370
Поместим дйполь в фокус параболоида вращения и про-
следим ход лучей, исходящих от него. На рис. 7.4 показан
ход лучей и направление электрического вектора поля у па-
дающего и отраженного лучей для трех случаев ориентации
диполя относительно вертикальной плоскости. На рис. 7.4,а
диполь параллелен вертикальной плоскости, являющейся
продольным сечением параболоида, на рис. 7.4,6 — перпен-
дикулярен к ней, а на рис. 7.4,в образует с ней угол я.
Очевидно, что плоскостью распространения любого из лучей
будет продольное сечение параболоида. Во всех случаях она
считается расположенной вертикально.
При общем анализе будем пользоваться прямоуголь-
ной системой координат x,y,z, а точки заданного попе-
речного сечения будем определять, кроме того, с помощью
координат р и <р = 90° —а (см. рис. 7.4,а), где р и <р свя-
заны с х и у соотношениями
р = |/х2Ц-_у2; х — Р COS ср,
<p = arctg~, _y = psin'f.
(7.Ю)
Третий случай (рис. 7.4, в) является более общим
и может быть представлен как совокупность первых
двух. Для этого разложим в данном случае момент тока
диполя q на две составляющие
= ? + (7.11)
причем
<7' = <7sin<p,
<7" = </cos ср ' ’ ’
и будем считать, что имеем два диполя, из которых один (q'}
параллелен плоскости распространения, а другой (<?") пер-
пендикулярен к ней. Вычислим напряженность поля в точ-
ке М (рис. 7.4,в) для третьего случая.
В свободном пространстве поле, созданное диполем, опре-
деляется уравнением (7.9). Эта формула, с учетом сказан-
ного выше о методике определения амплитуды, фазы и по-
ляризации поля отраженной волны может служить также
для расчета электромагнитного поля в параболическом
зеркале. Заметим, что строго говоря, в каждой точке внутри
зеркала имеются два поля: от прямого (падающего) луча
и от луча, отраженного от зеркала. Мы будем учитывать
24* 371

Рис. 7.4. Ход лучей
и направление элек-
трического вектора
поля у падающего и
отраженного от пара-
болоида лучей при
% различной ориента-
ции расположенного
в фокусе облучающе-
го диполя относи-
тельно вертикальной
плоскости продоль-
ного сечения парабо-
лоида: а) диполь па-
раллелен плоскости;
б) диполь перпенди-
кулярен плоскости;
в) диполь образует
с плоскостью угол СС.
здесь лишь электромагнитное поле, созданное отраженными
лучами, так как поле падающих лучей играет лишь роль
возбудителя токов на поверхности зеркала, а излучение
антенны определяется токами, которым эквивалентно поле
отраженных лучей.
Из рис. 7.4, в видно, что ось диполя q’ образует угол О'
с лучом SN, а ось диполя q"— угол, равный 90°. Сле-
довательно, поле En, созданное диполем q' в точке У,
равно
Е' = —j~^r~ cos&'e~ikr = cos S' sin <p e~ikr, (7.13)
N j kr J ir T '
а поле E", созданное диполем q" в той же точке У,
равно
где согласно (7.6) и (7.5)
м2 [ ..2 г. 2
г — SN — р ; cos 9' = ----------1L.
2р
В точке М амплитуда поля сохранится такой же, как
и в точке N, фаза же определится из того условия, что
в фазовый множитель е~'кг, имеющийся в (7.13) и (7.14),
необходимо подставить
Р2 + Ро
(7.8)
Р 1 2р
' Следовательно, в точке М напряженность поля, создан-
ная диполями q' и q", соответственно равна
Л, sincp-e 2р ,
р' ; 60л? 2р
Л J рЧ
(7.15)

2 + 2 C0S®-e ~р
м J * р2 + р2
Нас будут интересовать в дальнейшем проекции элек-
трического вектора на оси координат X и Y. Эти сос-
тавляющие выражаются, как легко видеть из рис. 7.4,в,
через Е'м и Е” следующим образом
Е =Е' cos Ф — Е ' sin ср,
— Ev= Е' sin ®-4-Е ' cos».
✓ М • 1 Лг •
(7.16)
373
Подставив Е'м и Е* из (7.15) в (7.16), получим
А ^_+p2co_s2?
J' (р2+р2)2 у1-11)
и
£,= -P-'S)
где
,к *а+?о~
Д =у60я£_ >2^ е 2р (7J9)
Если параболоид рис. 7.4,в повернуть на угол а таким
образом, чтобы ось Ё, а также ось диполя приняли вер-
тикальное направление, тогда точка М будет произволь-
ной точкой поперечного сечения, имеющей координаты
р и <р. Таким образом, уравнения (7.17)-н (7.19) определя-
ют составляющие Ех и Еу электрического вектора вер-
тикального диполя (случай рис. 7.4,а) в любой точке
внутри зеркала через ее координаты z, р, и при замене в
р- +
фазовом множителе р -ф z через —.
Соотношение между Ех и Е позволяет определить
направление электрического вектора поля, а следова-
тельно, также и направление магнитного вектора, пос-
кольку направления обоих векторов взаимно перпендику-
лярны (см. рис. 7.3).
Изобразим, как обычно, картину электромагнитного
поля в зеркале с помощью электрических и магнитных
линий поля. Уравнением электрических линий поля явля-
ется интеграл дифференциального уравнения
ФУ _ _ р2-|-р2 cos 2<р п 9пч
dx Ех р2 sin 2'f ’ И' U'
Аналогично уравнением магнитных линий поля явля-
ется интеграл дифференциального уравнения
__ Р2 sin2<р
dx Еу ~’ р’ф- р2 cos 2<р '
Подставив в (7.20) и (7.21) значения р sin ср и pcoscp из (7.10),
получим, после несложных преобразований и применения
374
метода разделения переменных, следующие формулы
для электрических линий поля
(7.22)
и для магнитных линий поля
__ Со 1 f Сп
У = р2 ~~ х~ >
(7.23)
где С, и С2 — постоянные интегрирования, определяемые
из граничных условий и имеющие разное значение для
каждой отдельной линии поля.
Подставив в уравнения (7.22) или (7.23) координаты
х и у какой-либо точки, получим значение С; или С2,
соответствующее электрической или магнитной линии,
проходящей через данную точку.
Мы будем в дальнейшем различать зеркала: мелкие
(рис. 7.5,а), средние (рис. 7,5,6) и глубокие (рис. 7.5,в). У
мелких зеркал фокус 5 находится вне зеркала, у сред-
них— в раскрыве зеркала, а у глубоких — внутри зерка-
ла. Легко показать, что у первых У вторых —
---^-=1, а у третьих — -^-)>1.
На рис. 7.5,2 показана конфигурация электромагнитного
поля отраженных волн в раскрыве глубокого зеркала
^-^-=1,4^. Электрические линии показаны сплошными,
а магнитные—пунктирными. На этом рисунке приведены
концентрические окружности, соответствующие различ-
ным значениям ~ . Картина линий поля внутри каждой из
этих окружностей соответствует картине поля в раскры-
ве зеркала, характеризующегося отношением^-, равным
приведенному на рисунке значению-^-. Таким образом,
рис. 7.5,г может служить также характеристикой поля в
раскрыве средних и мелких зеркал.
Уравнения (7.17)-н (7.19) и рис. 7.5 позволяют сделать
следующие выводы о характере электромагнитного поля
отраженных волн в параболоиде вращения, облучаемом
диполем Герца, помещенным в фокусе.
375
Зеркало
Зеркало j
Зеркало.
—Раскрыв
.5
jPo
Раскрыв
а)
б) В)
Рис. 7.5. Различные • виды параболических зеркал и конфигурация
электромагнитного ноля в их раскрыве: а) мелкое зеркало, б) сред-
нее зеркало, в) глубокое зеркало, ;) картина линий поля электри-
ческого (сплошные кривые) и магнитного (пунктирные кривые) в
„ /₽0
раскрыве глуоокого зеркала —=1,4
376
1. Во всех точках раскрыва зеркала фазы электро-
магнитного поля одинаковы.
'2. В раскрыве мелкого зеркала (р0 < р) амплитуды
поля почти одинаковы во всех точках, причем электри-
ческий вектор поля имеет практически только одну сос-
тавляющую Еу(Ех<^ Еу), а магнитный — только состав-
ляющую
3. В раскрыве глубокого или среднего зеркала (рп>р)
электромагнитное поле имеет полюсы (точки, в которых
поле равно нулю). Полюсы находятся на прямой, прохо-
дящей через центр параллельно оси диполя, в точке, от-
стоящей от центра на расстоянии р = р.
4. В центре раскрыва" векторы электромагнитного по-
ля имеют максимальное значение. С приближением к по-
люсам амплитуда поля убывает. Одновременно направ-
ление векторов поля изменяется, что выражается в воз-
растании составляющих Ех и Ну и соответствующем
уменьшении составляющих Еу и Нх. За полюсами ампли-
туда векторов поля вновь начинает расти с дальнейшим
удалением от центра, а направления векторов поворачи-
ваются на обратные.
5. На линии, соответствующей условию
Р / cos 2?
(7.24)
6. Чем глубже зеркало Гчем больше-^-
(эта линия на рис.7.5,г показана двойной штриховой ли-
нией) составляющие поля Еу и Нх равны нулю.
По разные стороны от этой линии эти составляющие
поля Еу и Нх имеют противоположные направления. Часть
поперечного сечения, лежащая за этой линией в проти-
воположную от центра сторону, называется вредной
зоной.
, тем больше
в нем вредные зоны.
Причиной образования полюсов является отсутствие
излучения вдоль оси диполя. Действительно, если ампли-
туда поля падающего луча SE (рис. 7.4,а) равна нулю, то
нулю равна также амплитуда поля у отраженного луча
EF.
Образование вредных зон иллюстрируется на рис. 7.4,а.
Оно является следствием особенностей, во-первых, элек-
тромагнитного поля диполя (рис. 7.2), а, во-вторых, поля
377
отраженного луча (рис. 7.1). Вследствие того, что у обо-
их лучей SE' и SE", лежащих по разные стороны от оси
диполя, согласно особенности поля излучения диполя,
электрический вектор направлен в сторону оси диполя,
он оказывается в разных случаях по-разному ориенти-
рован относительно нормали к поверхности параболоида.
У луча SE' электрический вектор направлен в сторону
нормали Е'К', а у луча SE''—-в обратную от нормали
Е"К" сторону. В результате, у отраженного луча E'L'
электрический вектор направлен к оси параболоида, а у
отраженного луча в обратную сторону. Граница
вредной зоны характерна тем, что при переходе через эту
границу _у-овая составляющая вектора Е проходит че-
рез нуль и меняет свое направление.
Наличие, полюсов и вредных зон приводит к уменьшению
коэффициента использования площади раскрыва парабо-
лоида. По этой причине на практике обычно применяются
зеркала, имеющие радиус раскрыва р<р. Более точные
количественные отношения получим в результате анализа
характеристик излучения.
Приведенная на рис. 7.5,а картина электрических и маг-
нитных линий поля может служить характеристикой карти-
ны токов на поверхности параболоида. При этом следует
иметь в виду, что электрические линии в раскрыве совпа-
дают с проекцией на плоскость раскрыва линий токов,
текущих по поверхности параболоида, а магнитные линии
в раскрыве являются проекцией на плоскость раскрыва
магнитных линий у поверхности параболоида.
Как отмечалось выше, применяя апертурный метод,
мы приводим задачу об излучении параболоида вращения
к задаче о диффракции на отверстии в плоском экране.
При облучении параболического зеркала диполем Герца
электромагнйтное поле в раскрыве имеет зависимость
от координат р и <р вида (7.17) и (7.18), тождествен-
ную (3.62). Следовательно, диаграммы направленности
в рассматриваемом случае в //-плоскости могут опре-
деляться по формуле (3.98а), либо по графикам рис. 3.8
(кривая F^) или рис. 3.9 ^кривая у=0^, а диаграммы на-
правленности в Е-плоскости— по формуле (3.986) или
по графикам рис. 3.9, составленным для различных зна-
чений — (см. цифры у кривых) Здесь р0 соответствует
обозначению а в главе III.
378
Из рис. 3.9 видно, что с увеличением отношения —
увеличивается ширина главного лепестка диаграммы на-
правленности в Е-плоскостн (численные данные ширины
главного лепестка приведены в табл. 3.3) и уменьшается
относительная величина побочных лепестков. В /7-пло-
скости диаграмма направленности при облучателе в виде
диполя Герца не зависит от отношения —.
В главе III определены также значения коэффициента
направленного действия такой антенны (см. формулу 3.103)
и коэффициента использования v (см. рис. 3.10). Однако
там расчет проводился в предположении, что подводимая
к антеннам мощность равна мощности, проникающей через
отверстие. В данном случае мощность подводится к облуча-
телю (диполю Герца) и лишь часть излучения последнего
падает на поверхность зеркала и концентрируется, а осталь-
ная часть рассеивается в пространстве.
Введем понятие коэффициента полезного действия пара-
болической антенны t)j , понимая под этим отношение
мощности, падающей на поверхность зеркала, к полной мощ-
ности, излученной облучателем.
Пользуясь сферическими угловыми координатами &'
и <р', ведя отсчет углов &' от оси зеркала, как показано
на рис. 7.2, можно выразить диаграмму направленности
облучателя F'oGti в виде
F'oGi (&', ср') = 1 — sin29' sin2 <р', (7.25)
а коэффициент полезного действия •ц1 антенны следующим
образом
% 2г.
J J (1—sin2 8' sin* <р') sill Q'M'd <с'
__,oo ________________
к 2-
У j1 (1—sin3 8' sin2 <p') sin 9' M'dy'
о b
= 1-jcos»;-lcos3&;, (7.26)
где ф’—угол облучения зеркала, т. е. угол между осью
зеркала и прямой, соединяющей фокус и край зеркала.
379
Согласно (7. )
COS&q
Р2 + Ро ’
На рис. 7.6 приведен график зависимости коэффициента
полезного действия тц от отношения радиуса раскрыва
к параметру параболы у-. На рис. 7.7 дан график зависи-
мости полного коэффициента использования v, от у, при-
чем V[ определяется следующим образом
^ = ^'6 (7.27)
где v без индекса — коэффициент использования, вычи-
сленный как в гл. III без учета коэффициента полезного
Рис. 7.6. Графики зависимости коэффициента полезного действия
параболоида от относительного размера его раскрыва
Ро
Р
при раз-
ных облучателях: гц —простой диполь Герца; т)2 — диполь Герца1 с
плоским проводящим экраном; г3— система диполей Герца с кар-
диоидной диаграммой направленности.
действия. Индекс у коэффициентов указывает на их отно-
шение к параболоиду вращения, облучаемому диполем
Герца.
Из приведенных данных видно, что из-за низкого коэф-
фициента полезного действия антенны (большого рассеяния
380
энергии облучателя) коэффициент использования vj имеет
малую величину (максимальная величина макс=0,37),
Рис. 7.7. Графики зависимости полного коэффициента использова-
ния параболической антенны от относительного размера раскрыва
/р0\
параболоида (— при разных облучателях (обозначения индексов —
\Р / см. рис. 7.6).
Рассмотрим случай облучателя, обеспечивающего более
высокий коэффициент полезного действия антенны. В каче-
стве облучателя примем диполь
Герца с плоским идеально проводя-
щим экраном, как .показано на
рис. 7.8.
Диаграмма направленности та-
кого облучателя будет, как извест-
но, равна произведению диаграммы
направленности диполя Герца, умно-
женной на множитель
sin(£d cos &'),
т. е. равна
Fo6A^’ Ф') =
Рис. 7.8. Облучение па-
раболоида диполем Гер-
ца с плоским проводя-
щим экраном.
==\f 1 — sin2 &' sin2 tp'sin (kd cos &').
(7.28)
381
При этом Поле равно нулю в Полупространстве j > 90°.
Полагая d < X, можно в (7.28) заменить sin(£d cosO-')
его аргументом, т. е. положить
/\,бл(&', — sin2&'sin2 ср' kd cos (7.28а)
Коэффициент полезного действия т)2 антенны опреде-
ляется следующим образом
(1 — sin2 9'sin2 у') cos2 9' sin B'dO'd?'
2 я
J j (1 — sin2 0' sin2 /) cos2 9' sin 8'db'd<f'
о о
= |cos3&;_|cos5&;. (7.29)
На рис. 7.6 показана кривая зависимости т]2 от .
Поле в раскрыве параболоида будет отличаться
от (7.17) и (7.18) множителем cos&', т. е. с учетом (7.5)
будет определяться уравнениями:
F ——Л (Р3 — P2cOs2?) (р2 —р2)
у (р* + Р2)3
А sin 2?
(Р2 + Р2)3
(7.30)
Картина электрических и магнитных линий поля полу-
чается в данном случае в основном такой же, как в преды-
дущем случае (см. рис. 7.5). Отличие заключается в том,
что на линии р0 = р и за ней поле равно нулю, так как
облучатель не излучает при | &' | > 90°.
Легко видеть, что (7.30) отличается от (3.63) лишь
постоянным множителем.
Следовательно, диаграмма направленности параболоида
вращения облучаемого диполем с плоским экраном, вычи-
сляется по формулам (3.108) и (3.109) соответственно
для //-плоскости и Е-плоскости.
Для расчета диаграммы направленности могут быть
также использованы графики рис. 3.11 и рис. 3.12.
Рл
Мы видим, что и в данном случае увеличение — приводит
к расширению главного лепестка и уменьшению побочных
максимумов.
382
Коэффициент использованияv2с учётом коэффициента Т)2
полезного действия определяется как функция у- по гра-
фику рис. 7.7. Коэффициент использования v2 имеет
максимальное значение при -у = 0,6, что соответствует
cos =0,470, или Sq =62°. При 9^ = 62° диаграмма
направленности диполя Герца с плоским экраном
<?') = °,47 при </ = 0 и К''л(9', ср') = 0,23 при
ср’ = 90°.
В табл. 3.4 приведены значения ширины главного
лепестка 26О// и 20ое диаграммы направленности для ряда
« Ро
значении —.
р
Аналогично предыдущему могут быть вычислены
характеристики параболоида вращения, у которого облу-
чателем является система из диполей Герца, имеющих
совместно, кардиоидную диаграмму направленности вида
<б>, <{>') = У 1—sin2 9'sin2!/ cos2 . (7.31)
Такую диаграмму направленности, имеет, например,
система Эдкока (два противофазных вибратора) совместно
с одиночным вибратором, питаемым со сдвигом фаз 90°
по отношению к системе Эдкока. Как увидим ниже, ряд
других облучателей имеет диаграмму направленности,
близкую к (7.31).
Коэффициент полезного действия т)3, коэффициент
использования v3 и диаграммы направленности FH и FE
параболоида вращения, облучаемого кардиоидным излуча-
телем, выражаются следующим образом
11 , ,2 , 1 , 1
3 -эд — cos Ио — cos2 00 — у cos3 &0 — у cos4 00 — у cos5 90
^З— ТГ ’
3 15 (7.32)
,2 / г2 \
)
р« \ + 2»2;
= Ъ\ ---------- (7.33)
Ро Ро
7 (, , Ро Y 1+F Ро 1 + F
30 + р2 ) ~ [ р2 \ Юр2 30
5V+A/
383
где
Fe = p2Fx -|- £2p2 sin2 &Л2!,
Fh = P2Fi~ *2Po sin2 ^F2>
(7.34)
На рис. 7.6 изображена кривая зависимости коэффи-
циента полезного действия iq3, а на рис. 7.7 — зависимость
коэффициента использования площади раскрыва v3 пара-
болоида вращения с облучателем, имеющим кардиоидную
диаграмму направленности от отношения —.
Картина электрических и магнитных линий поля в рас-
крыве параболоида, облучаемого излучателем с кардиоидной
диаграммой направленности получается такой же, как при
одиночном диполе Герца (рис. 7.5).
§ 3. ОБЛУЧАТЕЛИ ПАРАБОЛОИДОВ ВРАЩЕНИЯ
Выше рассмотрены характеристики параболоида вра-
щения при трех различных видах облучателей. Для упроще-
ния анализа взяты идеальные облучатели, у которых диа-
грамма направленности выражается наиболее простой функ-
цией от углов, а именно: а) одиночный диполь Герца;,
б) диполь Герца, расположенный вблизи плоского идеально
проводящего экрана и в) система диполей Герца, имеющая
кардиоидную диаграмму направленности. При анализе облу-
чатель рассматривался как точечный, т. е. как создающий
около поверхности зеркала сферический фронт волны
с центром в фокусе зеркала.
Здесь мы познакомились с реальными облучателями,
нашедшими применение в антенной технике. Прежде чем
перейти к их описанию, кратко охарактеризуем отличие
реальных условий работы параболоидов вращения от при-
нятых в предыдущем параграфе идеальных условий.
Во-первых, на характеристики параболоидов вращения
сказывается неточность изготовления антенны (отличие фор-
мы зеркала от идеального параболоида, неровности поверх-
384
ности, неточность установки облучателя и т. п.). Во-вторых,
у реальных облучателей диаграмма направленности отлича-
ется от диаграммы направленности рассмотренных выше
идеальных излучателей, в особенности это относится к ин-
тенсивности побочного и обратного излучения. В-третьих,
в реальных условиях сказывается так называемый «теневой
эффект» облучателя, не учтенный в приведенном выше
анализе.
Влияние указанных факторов на характеристики излуче-
ния антенны не поддается точному учету. Качественно оно
может быть оценено следующим образом.
Неточности изготовления антенны вызывают нарушение
синфазности поля в раскрыве, что в свою очередь приводит
к снижению коэффициента усиления антенны и к некоторым
изменениям в диаграмме направленности, например, частич-
ному заполнению промежутков между лепестками, т. е. к
слиянию лепестков.
Отличие диаграммы направленности реального облучате-
ля от диаграммы направленности идеального облучателя по
главному лепестку может быть учтено при выборе парамет-
ров зеркала р0 и р. Последние должны быть выбраны таким
образом, чтобы в обоих случаях было одинаково отношение
интенсивности облучения краев зеркала к интенсивности
облучения середины зеркала. При таком условии в обоих
случаях диаграммы направленности антенны будут одина-
ковы. '
Наличие у облучателей значительного излучения в боко-
вых и обратном направлениях приводит к снижению коэф-
фициента полезного действия антенны в указанном в преды-
дущем параграфе смысле, а следовательно, к снижению
коэффициента усиления. При наличии в диаграмме на-
правленности облучателя боковых лепестков они должны
оставаться вне области освещения зеркала, так как в про-
тивном случае это приведёт к образованию полюсов и вред-
ных зон. Влияние обратного излучения и боковых лепестков
облучателя проявляется не только в снижении коэффициен-
та полезного действия. Поле обратного излучения и боковых
лепестков облучателя складывается с полем излучения зер-
кала и может внести существенные изменения в диаграмму
направленности антенны, вызывая увеличение боковых ле-
пестков, в особенности, в случае сравнительно небольших
размеров зеркала. При наличии значительного обратного
излучения обычно облучатель располагается таким образом,
чтобы поля излучения зеркала и облучателя складывались
25—1503 385
в фазе в направлении главного максимума антенны. Это
дает некоторое увеличение коэффициента усиления и частич-
но компенсирует эффект от снижения коэффициента полез-
ного действия.
Облучатель параболоида вращения, находясь на пути
распространения плоской волны, отраженной от зеркала,
подобно приемной антенне поглощает, в соответствии со
своей эффективной площадью, некоторую часть энергии вол-
ны. Некоторая часть энергии волны обратно отражается
облучателем и приспособлениями, применяемыми для его
механического крепления. Отраженная часть энергии обра-
зует стоячие волны между облучателем и зеркалом, вызывая
нарушение амплитудных и фазовых соотношений поля
в раскрыве зеркала.
Явление поглощения и отражения облучателем плоской
волны, идущей от зеркала к раскрыву, носит название «те-
невого эффекта». Это явление приводит к некоторому рас-
ширению главного лепестка диаграммы направленности и
увеличению боковых лепестков, а также, естественно, к сни-
жению коэффициента усиления антенны.
В результате совместного действия всех перечисленных
факторов (неточность изготовления, отличие диаграмм на-
правленности реальных и идеальных. облучателей, теневой
эффект облучателя) реальные характеристики параболои-
дов вращения отличаются от соответствующих теоретиче-
ских характеристик, найденных в предыдущем параграфе
для идеальных условий, следующими данными.
Коэффициент усиления обычно находится на уровне 75—
80% от соответствующего теоретического значения. Относи-
тельная величина боковых максимумов больше теоретиче-
ской величины. Промежутки между лепестками частично
заполнены. Отсутствуют нулевые значения в диаграмме
направленности.
В пределах главного лепестка до уровня примерно 0,1
по мощности теоретические данные довольно хорошо согла-
суются с экспериментальными.
Перейдем к описанию отдельных видов облучателей.
а) вибраторные облучатели
На рис. 7.9 и 7.10 показано несколько вариантов вибра-
торных облучателей. Они могут быть разделены на две
группы.
Облучатели первой группы (рис. 7.9) состоят из двух
вибраторов, из которых один, более близкий к зеркалу,
386
имеет длину, несколько большую половины волны (настроен
как пассивный вибратор-рефлектор). Вибраторные облуча-
тели первой группы отличаются друг от друга способом пи-
тания. Питание возможно от коаксиального кабеля (а) и от
волновода (б) прямоугольного сечения с волной ТЕоь В пер-
вом случае (а) одно плечо' вибратора присоединяется к
внутренней жиле кабеля, для чего делается отверстие на
К зеркалу
К зеркалу
Ч Я
Рис. 7.9. Вибраторные облучатели из двух вибраторов: а) с пита-
нием от коаксиального кабеля; б) с питанием от волновода.
Рис. 7.10. Вибраторные облучатели, состоящие из одного вибратора
и круглого плоского диска: а) с питанием от коаксиального кабе-
ля; б) с питанием от волновода; в) с щелевым возбудителем
(общий вид), г) то же, в разрезе.
25*
387
оболочке кабеля, а второе плечо вибратора присоединяется
непосредственно к наружной оболочке. Во втором случае (б)
вибраторы крепятся к тонкой металлической пластине, уста-
новленной параллельно широким стенкам открытого волно-
вода на средней линии.
Облучатели второй группы (рис. 7.10) состоят из ви-
братора и круглого плоского диска, расположенного на рас-
стоянии около y от вибратора. Способы питания здесь те
же, что у облучателей первой группы (а и б). В случае при-
менения коаксиальной фидерной линии возможно возбужде-
ние вибраторов щелью (в). Для этого на наружной оболоч-
ке кабеля вырезаются две продольные щели длиной у, рас-
положенные диаметрально противоположно. Оба плеча ви-
братора прикреплены к оболочке кабеля посередине между
щелями. На продолжении одного из плеч вибратора жила
кабеля внутри замыкается с оболочкой тонкой радиальной
перемычкой. Благодаря перемычке внутри кабеля появляют-
ся затухающие волны высших порядков, имеющие продоль-
ную составляющую магнитного поля, что способствует воз-
буждению поля в щелях и возбуждению токов в плечах
вибратора.
Следует заметить, что питание вибратора способом, по-
казанным на рис. 7.9,а и 7.10,а, приводит к несимметрич-
ному возбуждению плеч вибратора и несимметричной диа-
грамме направленности облучателя, а также всей антенны
в целом в f-плоскости (максимум смещен на некоторый
угол относительно оси зеркала) в то время, как при воз-
буждении щелью, как показано на рис. 7.10,в, оба плеча
возбуждаются одинаково.
Выше указаны ориентировочные габариты облучателей.
Более точно они определяются экспериментально таким
образом, чтобы, во-первых, получить диаграмму направлен-
ности с минимальным обратным излучением, во-вторых,
обеспечить хорошее согласование антенны и питающей
линии.
Вибраторные облучатели образуют у поверхности пара-
болоида сферическую волну с центром сферы в промежутке
между вибраторами (двухвибраторные) или между вибра-
тором и диском.
Облучатели, состоящие из вибратора и диска, имеют диа-
грамму направленности, близкую к диаграмме направлен-
ности диполя Герца с плоским экраном, а облучатели,
388
состоящие из двух вибраторов, имеют диаграмму на-
правленности, близкую к кардиоидной. Двухвибраторные
облучатели характеризуются значительным обратным
излучением. Для определения характеристики излучения
параболоида вращения с ви-
браторными облучателями
можно воспользоваться соот-
ветствующими данными,
приведенными в предыду-
щем параграфе, учитывая
при этом необходимость вне-
сения корректив, указанных
выше на побочное и обрат-
Рис. 7.11. Вибраторный облуча-
тель, состоящий из двух пар
вибраторов, питаемых волново-
дом.
ное излучение и т. п.
Наряду с двухвибраторными облучателями применяется
облучатель, показанный на рис. 7.11, состоящий из двух пар
вибраторов вида, изображенного на рис. 7.9,6. Меняя рас-
стояние между парами вибраторов, можно менять диаграм-
му направленности облучателя (как и всей антенны) в Н-
плоскостп, выравнивая главный лепесток в этой плоскости
с главным лепестком в f-плоскости.
б) волноводные облучатели
В качестве облучателей параболоидов вращения исполь-
зуются также волноводные излучатели, как прямоугольного
сечения с волной TEOi, так и круглого сечения с волной ТЕц.
На рис. 7.12 показано два варианта расположения волново-
да около зеркала.
Волновод круглого поперечного сечения имеет преиму-
щество перед волноводом прямоугольного сечения при облу-
чении параболоидов вращения. Преимущество заключается
в том, что волновод круглого сечения создает более рав-
номерное облучение зеркала, так как диаграмма направлен-
ности такого волновода имеет почти форму фигуры враще-
ния (согласно рис. 4.7 ширина главного лепестка почти
одинакова в Е- и //-плоскостях), в результате чего парабо-
лоид вращения также имеет диаграмму направленности в
виде фигуры вращения. У волновода прямоугольного сече-
ния ширина главного лепестка различна в Е- и //-плоскос-
тях, что затрудняет равномерное облучение зеркала при
Рл
оптимальном соотношении —.
Р
Далее электромагнитное поле параболоида вращения при
Облучении линейно поляризованной волной имеет паразит-
389
ную поляризацию. Поле излучения волновода круглого се-
чения также обладает паразитной поляризацией, причем по
направлению паразитная составляющая поля волновода
круглого сечения противоположна паразитной составляющей
поля параболоида вращения (рис. 4.6 и 7.5). В результате
при облучателе в виде волновода круглого сечения в значи-
тельной степени ликвидируется паразитная поляризация
поля параболоида вращения. Кроме того, (рис. 4.3 и 4.7)
у стандартного круглого волновода (2а=0,75 3.) побочное и
обратное излучение значительно меньше, чем у стандартно-
го волновода прямоугольного сечения f-p =0,71; 2 = 0,32\
Параболоид Параболоид
облучатель
а) б)
Рис. 7.12. Волноводные облучатели: а) волно-
вод проходит сквозь параболоид; б) волновод про-
ходит сбоку от параболоида.
В результате более равномерного облучения зеркала, ликви-
дации паразитной поляризации, а также в связи с меньшей
величиной побочного и обратного излучений, волновод круг-
лого сечения обеспечивает более высокий коэффициент
использования v, чем прямоугольный волновод.
Электромагнитное поле волноводных облучателей у по-
верхности зеркала имеет характер сферической волны с
центром сферы в центре раскрыва волновода.
При ориентировочном определении характеристики излу-
чения параболоида вращения с волноводным облучателем
можно считать волновод круглого сечения эквивалентным
диполю Герца с плоским экраном, а волновод прямоуголь-
ного сечения — облучателю с кардиоидной диаграммой на-
правленности. При этом должны быть соблюдены условия
облучения краев зеркала, указанные выше.
390
Волноводные облучатели могут заканчиваться рупорами
(рис. 7.12) небольшого размера. При этом следует учесть,
что центром фазового фронта будет не точка в раскрыве
рупора, а вершина последнего. В случае клинообразного пи-
рамидального рупора центры фазового фронта в £- и //-плос-
костях не совпадают, что приводит к фазовым искажениям
а)
Рис. 7.13. Коробчатые облучатели: а) при непосредствен-
ной связи с питающим волноводом; б) при связи посред-
ством секториального перехода.
Рис. 7.14. Сложение полей волн ТЕМ и ТЁ03
в раскрыве коробчатого облучателя.
поля в раскрыве зеркала и ухудшению характеристик излу-
чения антенны. Следовательно, при переводе волновода пря-
моугольного сечения в рупор, последний должен быть пира-
мидальным остроконечным. При переводе волновода кругло-
го сечения в рупор применяется естественно конический
рупор.
В случае необходимости получения различной ширины
главных лепестков в Е- и //-плоскостях находят применение
в качестве облучателей так называемые коробчатые облуча-
391
тели, показанные в двух вариантах на рис. 7.13. У волновода
прямоугольного сечения, возбуждаемого волной ТЕщ скач-
ком или через небольшой секториальный переход меняется
сечение на значительно более широкое, такое, чтобы в нем
могла распространяться волна ТЕоз (при соблюдении сим-
метрии системы волна ТЕ02 не возбуждается). Подбором
размеров коробчатого излучателя можно регулировать со-
отношение амплитуд и фаз полей волны TEoi и ТЕоз- Фазы
полей подбираются такими, чтобы они были противополож-
ны в средней части излучателя и одинаковыми на краях,
а амплитуды подбираются такими, чтобы получить возмож-
но более равномерное поле в раскрыве коробчатого излуча-
теля. На рис. 7.14 показано сложение полей волн TEoi и
ТЕоз и получение суммарного равномерного поля.
Рис. 7.15. Облучатель Катлера (двухщелевая антенна
обратного излучения).
Фазовый фронт волны коробчатого излучателя является
сферическим. Центр сферы совпадает с центром раскрыва.
392
в) Облучатель Катлера
На рис 7.15 показано применение двухщелевой антенны
обратного излучения, известного под названием облучателя
Катлера. Схема устройства облучателя показана на рис.
1.9, л.
При таком облучателе антенная система получается ком-
пактной в конструктивном отношении. Облучатель имеет
меньший теневой эффект, чем другие облучатели.
Диаграмма направленности такого облучателя зависит
от длины и ширины щелей и от расстояния щелей от стенки
волновода, следовательно, она может быть регулируема и
подобрана оптимальной в соответствии с требованиями.
Регулировка осуществляется экспериментально.
Фазовый фронт волны, излучаемой этим облучателем,
является почти сферическим. Фазовые искажения, имеющие
место из-за отражения от стенок волновода, не превыша-
ют 30°.
Характеристики излучения параболоида вращения с об-
лучателем Катлера приближенно могут быть определены
по приведенным выше данным для кардиоидного облучателя.
§ 4. ВОЗДЕЙСТВИЕ НА ОБЛУЧАТЕЛЬ ВОЛНЫ,
ОТРАЖЕННОЙ ОТ ЗЕРКАЛА
Мы отмечали выше «теневой эффект» облучателя, выра-
жающийся в поглощении, а также обратном отражении не-
которой доли энергии плоской электромагнитной волны,
идущей от зеркала к раскрыву. В предыдущем параграфе
главное внимание было обращено на возмущение поля в рас-
крыве параболоида, и изменение характеристик излучения
антенны, вызываемое волной, обратно отраженной облуча-
телем. Здесь рассмотрим влияние поглощенной энергии на
режим работы облучателя. Это влияние принято характери-
зовать вносимым сопротивлением или в согласованной ан-
тенно-фидерной системе — степенью рассогласования, т. е.
коэффициентом отражения на фидерной линии, питающей
облучатель. Приближенно эти характеристики могут быть
определены следующим образом.
а) вибраторные облучатели
В случае вибраторных облучателей в соответствии с тео-
рией проволочных антенн удобнее рассчитывать вносимое
сопротивление.
393
Обозначим через / ток в питаемом вибраторе в точке
пучности. Ток в пассивном вибраторе в точке пучности
обозначим через ае/+/м, где а — отношение амплитуд токов
в пассивном и питаемом вибраторах, а ф— разность фаз
этих токов.
В случае плоского диска можно принять а=1, ф = к.
Электрическое поле облучателя у вершины зеркала
равно
60(1 4-a ,Ьг
E'=-—j —------------L е~‘кг, (7.35)
где г — расстояние от питаемого вибратора до вершины
зеркала (практически г = f, f — фокусное расстоя-
ние зеркала),
d — расстояние между вибраторами в случае рефлек-
тора в виде пассивного вибратора или расстояние
между вибратором и зеркальным изображением
в случае рефлектора в виде плоского диска.
Электрическое поле Е отраженной от зеркала волны
в месте нахождения питаемого вибратора по амплитуде
равно полю у вершины, а по фазе имеет отставание
на величину kr, т. е.
,60/м(1 4-ае/+-/м) е/ш
Вносимое сопротивление равно
вн /2 I
‘м “
В рассматриваемом случае
Таким образом
7 - 120(1+g е'Ф-^)2 „-2/АГ
ВН— J kr
(7.36)
(7.37)
(7.38)
(7.39)
Влияние вносимого сопротивления ZBH на режим бегу-
щей волны на фидерной линии определяется обычным
путем. Для этого определяется полное сопротивление
облучателя как сумма собственного сопротивления и вно-
симого.
394
Зная полное сопротивление, легко найти коэффициент
бегущей волны на фидерной линии.
Заметим, что вносимое сопротивление Сравнительно
~ . 120(1+а)2 19(1 +а)2
невелико. Оно по модулю не больше —7 ,
9 то время как собственное сопротивление составляет
70 — 100 ом.
б) волноводные облучатели
В случае волноводных облучателей удобнее рассчиты-
вать коэффициент отражения в волноводе.
Предположим, что предварительно до помещения
в зеркало, облучатель был согласован с волноводом.
Обозначим мощность излучения волновода через Р.
Тогда вектор Умова — Пойнтинга П у вершины зеркала
по абсолютной величине равен
(7.40)
где G — коэффициент усиления облучателя,
f— фокусное расстояние зеркала.
Такой же величины должен быть вектор Умова — Пойн-
тинга отраженной плоской волны у раскрыва волновода.
Мощность, поглощаемая волноводом Р’, равна
'>'=^г-5,фф. <7.41)
где 5эфф — эффективная площадь.облучателя. Учитывая
соотношение между эффективной площадью облучателя
и его коэффициентом, усиления, получаем
П = -^,
4nf2 ’
Коэффициент отражения в волноводе по модулю равен
I Г1 = • <7ЛЗ>
Полученное выражение для коэффициента отражения
(7.43) справедливо также для других типов облучателей при
условии их согласования с фидерной линией. Можно пока-
зать, что (7.39) также приводится к выражению (7.43) при
условии предварительного согласования вибратора и фидер-
ной линии.
395
Из изложенного видно, что, меняя расстояние между об-
лучателем и вершиной зеркала, можно менять фазу вноси-
мого сопротивления или фазу коэффициента отражения. По-
скольку при предварительной настройке облучателя идеаль-
ного согласования получить не удается, то имеется, вообще
говоря, возможность подбором расстояния между облучате-
лем и зеркалом добиться улучшения согласования облуча-
теля и питающей линии. Однако реализовать эту возмож-
Рис.7.16. Установка кор-
ректирующей пластины
в виде диска у вершины
параболоида.
ность, как правило, не удается. Де-
ло в том, что перемещение облучате-
ля означает еще смещение относи-
тельно фокуса, что, как увидим ни-
же, допустимо в очень ограниченных
пределах.
Рассогласование, вносимое отра-
женной от зеркала плоской волной
обычно ликвидируется путем под-
стройки линии питания облучателя
или другими мерами, например, с
помощью пластины, установленной
в вершине зеркала, путем поворота
поляризации поля отраженной вол-
ны, применением усеченных зеркал,
облучаемых сбоку и др.
Подстройка линии питания, по-
мимо неудобств, связанных с вы-
полнением этой операции, имеет еще
и тот недостаток, что при
стройке не может быть обеспечено
под-
согласование в достаточно широком диапазоне частот.
Предпочтением пользуются другие методы.
Одним из этих методов является установка корректирую-
щей пластины у вершины зеркала.
Идея метода заключается в следующем.
На рис. 7.16 показано сечение параболоида, имеющего
около вершины пластину в виде диска. При малых разме-
рах пластины и сравнительно большом фокусном расстоя-
нии поле облучателя будет иметь почти одинаковые фазы
во всех точках пластины. Поэтому отраженная от пластины
волна, вызванная токами на пластине, будет представлять
собой излучение круглой почти синфазной антенны диамет-
ра D, т. е. будет концентрированным в направлении на фо-
кус. Отраженная же от зеркала волна распределяется по
всему раскрыву. Поэтому имеется возможность подбором
396
размеров и местоположения пластины получить от нее около
облучателя поле по амплитуде такое же, как от зеркала,
а по фазе — противоположное.
Расчет пластины может быть произведен следующим об-
разом. Обозначим амплитуду поля излучения облучателя
у вершины зеркала через Ео. Примем, что у пластины поле
по амплитуде также равно Ео, так как расстояние от пла-
стины до вершины зеркала очень мало сравнительно с фо-
кусным расстоянием.
Тогда мощность, отраженная пластиной, равна
р _______ Eq ~[)2
Готр 2.120л’ 4
(7-44)
Поле £отр отраженной от пластины волны у облучателя
равно
р ____l/^отр'^ П ________if 4п /тс£)*\_________ £„ тс£>2
сотр— у 4пр •^•1^077 —4яр • хг Д 4 у- /л‘‘4
(7-45)
В (7.45) G — коэффициент усиления пластины как
антенны, равный
G = ~ = ~- (7.46)
Так как пластина, как указывалось, имеет сравни-
тельно малые размеры, то можно принять, что она не
нарушит работу параболического зеркала и что поле,
создаваемое отражением от поверхности параболоида,
будет около облучателя почти таким же, как при отсут-
ствии пластины,' т. е. будет равно £0.
Приравнивая
^отр Д),
получаем
D = j/|2f. (7.47)
Для обеспечения противофазности полей волн, отра-
женных от пластины и от зеркала, надо сместить пластину
на нечетное число четвертей волны от вершины.. Расстоя-
ние t (см. рис. 7.16) равно
^1(2и+ l)_2L = |(2n+ 1)-^ . (7.48)
397
Приведенные выражения для D и t являются прибли-
женными и уточняются обычно эмпирически.
Пластина обычно делается толщиной t и имеет электри-
ческий контакт с поверхностью параболоида. Этим создают-
ся непрерывные линии токов на пластине и зеркале, и рас-
пределение токов сохраняется соответственно полю падаю-
щей волны.
Недостатком корректирующей пластины является нару-
шение фазовых соотношений в раскрыве, приводящее
к уменьшению коэффициента направленного действия, рас-
Металличесхая
поверхность
Рис. 7.17. Устройство пластинчатого
параболоида для поворота поляри-
зации отраженной волны.
Рис. 7.18. Усеченный пара-
болоид, облучаемый рупо-
ром.
ширению главного лепестка и увеличению побочных макси-
мумов.
Другим методом ликвидации влияния отраженной от
зеркала волны на облучатель является поворот ее поляри-
зации. Осуществляется это мероприятие следующим обра-
зом. Поверхность параболоида выполняется из тонких па-
X
раллельных металлических пластин шириною , установ-
ленных «на ребро» под углом 45° к Е-плоскости (рис. 7.17).
Позади пластин перпендикулярно к ним помещается сплош-
ная металлическая поверхность. Расстояние между пласти-
нами выбирается равным $= g- -s-yg. Падающую на систему
пластин волну можно представить состоящей из двух ча-
стей, из которых одна часть имеет электрический вектор,
перпендикулярный к пластинам, а другая часть — электри-
ческий вектор, параллельный пластинам. Первая часть
пройдет через пластины и отразится от находящейся позади
них поверхности, а вторая часть отразится непосредственно
398
от пластин. В результате сложения этих двух частей после
их отражения электрический вектор отраженной волны бу-
дет повернут на 90° по сравнению с электрическим векто-
ром падающей волны. Волна другой поляризации не будет
оказывать влияния на облучатель.
На рис. 7.18 показано усеченное параболическое зерка-
ло, облучаемое сбоку рупором. Направление главного ма-
ксимума излучения рупорного облучателя показано стрел-
кой. Края зеркала облучаются значительно слабее. Так как
на рупор падает волна, отраженная от края зеркала, то ее
воздействие на облучатель будет сравнительно невелико, по-
скольку согласно (7.43) коэффициент отражения в питаю-
щей линии пропорционален коэффициенту усиления, т. е.
квадрату напряженности поля.
§ 5. ПАРАБОЛИЧЕСКИЙ ЦИЛИНДР.
СЕГМЕНТНО-ПАРАБОЛИЧЕСКАЯ АНТЕННА
Основные положения, которыми руководствуются при
определении поля внутри параболических зеркал, изложе-
ны в первом параграфе. Во втором параграфе эти положе-
ния применены к расчету поля в параболоиде вращения.
Перейдя к расчету поля в параболическом цилиндре, необ-
ходимо сделать некоторые дополнительные пояснения.
Вспомним, что при расчете поля в параболоиде враще-
ния мы исходили из значения поля излучения облучателя
в свободном пространстве (7.9), т. е. поля в дальней зоне
облучателя. Основанием для этого служило то, что у пара-
болоидов вращения расстояние от облучателя до поверхно-
сти зеркала весьма велико сравнительно с размерами облу-
чателя и с длиной волны. У параболического цилиндра дли-
на облучателя, как указывалось, равна длине образующей
цилиндра и сравнима с фокусным расстоянием, а часто даже
больше последнего.
Отсюда следует, что в случае параболического цилиндра
мы не можем пользоваться обычным выражением для
поля излучения облучателя, которое имеет зависимость
e~lkr
от расстояния г вида ---- (сферическая волна) и в ко-
торое множителем входит диаграмма направленности,
поскольку это выражение справедливо лишь на больших
расстояниях от облучателя. На таких расстояниях от об-
лучателя, на каких находятся точки поверхности парабо-
лического цилиндра, можно считать, что электромаг-
нитное поле облучателя имеет характер цилиндрической
399
Электромагнитное поле в раскрыве будем
волны и меняется в зависимости от расстояния р по
е—/*р
закону
считать образовавшимся в результате прихода туда пло-
ской волны, полученной после отражения от поверхности
зеркала цилиндрической волны, излучаемой облучателем.
В данном случае не будем определять абсолютного зна-
чения поля внутри зеркала и в его раскрыве через ток в об-
лучателе и параметры последнего, подобно тому, как это мы
делали в случае параболоида вращения.
Исходным положением в рассматриваемой задаче будем
считать предположение о том, что электромагнитное поле
облучателя носит характер цилиндрической волны. Не уточ-
няя амплитуды волны, мы сможем тем не менее определить,
пользуясь сформулированными выше положениями о соот-
ношении падающего и отраженного лучей, закон изменения
амплитуд поля в раскрыве. Зная этот закон, можно найти
диаграммы направленности и коэффициент направленного
действия методом диффракции на отверстии в плоском
экране (см. гл. III). Коэффициент же усиления мы найдем
как произведение коэффициента направленного действия и
коэффициента полезного действия, условно понимая под
последним отношение мощности излучения облучателя в сто-
рону поверхности зеркала, т. е. в угле 2&q (рис. 7.19,6) к его
полной мощности излучения. Потери в зеркале считаем
равными нулю. Длину облучателя считаем равной длине
образующей цилиндра.
Итак, в дальнейшем анализе предположим, что электро-
магнитное поле от облучателя распространяется к поверх-
ности зеркала в виде цилиндрической волны и отражается
от зеркала в виде плоской волны.
Рассмотрим два случая:
1) облучатель с круговой диаграммой направленности,
2) однонаправленный облучатель.
У первого из них мы будем считать напряженность поля,
не зависящей от угла &' (рис. 7.19,а), а у второго примем
напряженность поля пропорциональной cos&' в полупро-
странстве, обращенном к зеркалу и равной нулю в другом
полупространстве. В соответствии с этим коэффициент по-
лезного действия параболического цилиндра равен в первом
случае
400
а во втором случае
J cos2 O'dD'
о
’12= 7-----------
2
С cos2&'dD'
% Н~ 2 sln
гс/2
(7.50)
о
Согласно (7.5) при &' = ао , что соответствует
= -j~, имеем
Р=Л=
cos^'M-
и ,.о I ,,2
sin О' -
Р* + Уо
sin 2а; = 2^^.
2 ° (Рг+У20Г
а; = arc sin .
° Р2 + У2
Подставив (7.51) в (7.49) и (7.50), получим
т]] == — arc sin—- ,
Р2+у1
2рУ<Ар2 — Ун)
7+^)2
2
Т12= “Г
(7.52)
arcsin —
Р2 + ^о
На рис. 7.20 показаны зависимости ти и т]2 от
у0— половина ширины раскрыва (см. рис. 7.19), p = 2f-~
параметр параболы.
Поле Es в раскрыве будет функцией от координат х
и у:
(7.53)
7- где
Es = O(x, Л
Мы будем считать, что она представляет собой произ-
ведение двух функций, из которых одна зависит только
от х, а другая только от у.
Ф(х, у)=Х(х)Г(Л
26—1503
(7.54)
401
Рис. 7.19. К анализу параболического цилиндра: а) косоугольная
проекция; б) продольное сечение.
причем Х(х) определяется как зависимость амплитуды
тока в облучателе от координаты х, а Y (у) в случае
облучателя с круговой диаграммой направленности имеет
вид _
Г'«=^=-4'ТЙ^' (7'55)
а в случае однонаправленного облучателя — вид
(7-56)
где S^ — расстояние между облучателем и образующей
цилиндра, имеющей координату у (рис. 7.19); А, и Л2 —
коэффициенты пропорциональности.
Положив
(7.57)
и
Х(х) = Е0, (7.58)
402
Рис. 7.20.|Трафики зависимости условного коэффициента полезного действия Параболического
цилиндра['от относительного
размера его раскрыва
при разных
облучателях: —облучатель
с круговой диаграммой направленности; т)2 — однонаправленный облучатель.
мы приведем выражение для поля соответственно к виду
(3.9) и (3.10).
На рис. 3.3 и 3.5 приведены диаграммы направлен-
ности, соответствующие зависимостям (3.9) и (3.10), а
также (7.55) и (7.56) при выполнении (7.57) и (7.58). На
рис. 7.21 приведены кривые зависимости полного коэф-
фициента использования V] и *к2 от — с учетом т], и i)2.
Рис. 7.21. Графики зависимости полного коэффициента использова-
ния параболического цилиндра от относительного размера его рас-
крыва при разных облучателях (обозначения индексов—см.
рис. 7. 20).
Рис. 7.22. Сегментная параболическая антенна.
Разновидностью параболического цилиндра является
сегментная параболическая антенна, изображенная на
рис. 7.22. Она представляет собой короткий параболиче-
ский цилиндр (длина образующей значительно меньше
фокусного расстояния), закрытый двумя параллельными
плоскими металлическими пластинами. Пластины в дан-
ном случае необходимы потому, что из-за малой длины
404
облучателя (длина облучателя, как указывалось, равна
длине образующей цилиндра) его электромагнитное поле
излучения у поверхности параболоида без пластин имело
бы характер сферической волны, а не цилиндрической.
Облучается сегментно-параболическая антенна волново-
дом или рупором. Между пластинами могут возбуж-
даться волны ТЕМ, ТЕо1 и волны более высоких порядков,
в зависимости от расстояния между пластинами и типа
волны в облучателе. При возбуждении волны ТЕМ фазо-
вая скорость волны равна оф = с = 3• 108 Mjcex, а при
возбуждении волн высших порядков фазовая скорость
больше скорости света и определяется как в волноводах
по формуле пф= с
2 •
Наряду с полными сегментными антеннами, применяют-
ся полусегментные антенны (рис. 7.23). Последние облу-
чаются таким образом, чтобы максимум излучения облуча-
теля был направлен на середину цилиндрической поверх-
ности. Края
слабо.
У полных
облучаются
Рис. 7.23. Полусегментная пара-
болическая антенна.
сегментных
антенн облучатель находит-
ся в середине раскрыва, где
поле максимально, а у полу-
сегментных антенн облуча-
тель находится на краю рас-
крыва, где поле очень слабо.
Поэтому у первых сказывается теневой эффект облучателя,
а у вторых он почти не проявляется. Соответственно и обрат-
ное воздействие отраженной волны на облучатель у полу-
сегментных антенн исключается.
Некоторым недостатком полусегментной антенны являет-
ся несимметрия диаграммы направленности относительно
главного максимума, вызванная несимметричностью распре-
деления амплитуд поля относительно середины раскрыва.
Однако эта асимметрия практически ,не имеет значения, так
как она невелика и имеет место главным образом в области
низких уровней. Для иллюстрации на рис. 7.24 приведена
диаграмма направленности полусегментной антенны, имею-
щей раскрыв размером 162 смХ7,5 см, снятая на волне
3,2 см. Боковые лепестки находятся на уровне ниже 30 дб.
405
Рис. 7.24. Диаграмма направленности полусег-
ментной параболической антенны с раскры-
вом 162 X 7,5 см на волне 3,2 см.
Возбуждалась волна TEoi рупором, имеющим размеры: дли-
на 10 см, ширина в Е — плоскости 4,4 см, ширина в И—
плоскости — 6,5 см.
§ 6. ТЕХНИЧЕСКИЕ ДОПУСКИ
Вопрос о допусках на точность изготовления параболи-
ческой антенны рассмотрим в том же аспекте, как он рас-
смотрен выше в отношении линзовой антенны.
Здесь мы проанализируем три вида неточности, иллюст-
рированные на рис. 7.25.
На рис. 7.25,а показана неточность первого вида, выра-
жающаяся в отклонении параболической кривой зеркала от
теоретической. На этом рисунке сплошная кривая соответ-
ствует реальной кривой зеркала, а штриховая кривая —
теоретической. Луч до точки М пройдет расстояние, равное
406
Рис. 7.25. К расчету тех-
нических допусков на
точность изготовления
параболической антен-
ны: а) отклонение фор-
мы параболической кри-
вой от расчетной; ff) сме-
щение облучателя из фо-
куса вдоль оси парабо-
лоида: в) то же, но пер-
пендикулярно к оси па-
раболоида.
в)
SM=SO"+O"O', поскольку в идеальном случае все лучи
до раскрыва проходят одинаковые расстояния. До точки же
О' отраженный луч пройдет расстояние SO + OO' = SM + 2ai.
Легко видеть, что разность фаз поля в точках О' и М равна
(7.59)
Из (7.59) следует, что при Дф, макс = -^-
“,..„=7- <7-60>
407
Учитывая, что отклонения кривой от теоретической могут
иметь в разных точках разный знак, необходимо принять за
допуск на точность изготовления поверхности зеркала вели-
чину вдвое меньшую, чем (7.60)
(7.61)
1 ДОП 2 16 ' 7
Сравнивая (7.61) с (6.44,а) и учитывая, что у линз прак-
тически коэффициент преломления п=1,5—1,6, легко ви-
деть, что поверхность параболического зеркала должна вы-
полняться со значительно большей точностью, чем поверх-
ность линз.
На рис. 7.25,6 показана неточность второго вида — сме-
щение облучателя из фокуса вдоль оси параболоида.
Аналогично линзовым антеннам мы получим в данном
случае
Д'Ь=~у_(а2 — a2cosa), (7.62)
откуда следует
02 макс = ~4(1 — COS а) ’ (7.63)
Формула (7.63) совпадает с (6.47). Допуск на смещение
облучателя из фокуса в направлении оси зеркала одинаков
у параболических и линзовых антенн.
Рис. 7.25,в иллюстрирует третий вид неточности — сме-
щение облучателя из фокуса в направлении, перпендику-
лярном оси. Подобно линзовым антеннам такое смещение
используется в некоторых практических случаях для враще-
ния или качания диаграммы направленности относительно
нормального направления, соответствующего нахождению
облучателя в фокусе. Смещение облучателя из фокуса в пер-
пендикулярном направлении приводит к асимметричным фа-
зовым сдвигам (к монотонному изменению фаз) в раскры-
ве. . При сравнительно небольших смещениях облучателя
фазы в раскрыве имеют линейную зависимость от коорди-
наты (см. рис. 7.25в), что не вызывает искажений формы
диаграммы направленности, а приводит лишь к смещению
главного максимума на некоторый угол от нормального на-
правления. При значительных смещениях облучателя начи-
нают сказываться кубические и более высокого порядка сла-
гаемые, вследствие чего появляются искажения формы диа-
граммы направленности (см. рис. 3.19). Допуск на третий
вид неточности будем рассчитывать, как и в случае линзо-
408
вых антенн, исходя из отклонения фазовых искажений от
линейного закона ф = сг/,, причем коэффициент с опреде-
ляем, исходя из следующих предпосылок.
Предположим, что х0 f или р0<р (мелкое зеркало).
Примем за нуль фазу поля в раскрыве, получающуюся
при нахождении облучателя в фокусе. Тогда при смещен-
ном облучателе и р0 р получим в точке М', имеющей
координату ys=y, фазу фД], (см. рис. 7.25,в), определяе-
мую уравнением
Ър = -Г 55 sini£Tfl3f • (7-64)
Очевидно, что закон (7.64) изменения фаз в раскрыве
оправдывается с большей точностью в средних точках
раскрыва (близких к 0) и с меньшей точностью в край-
них точках, близких к М. Если этот закон принять для
всех точек раскрыва, то фаза поля в точке М", имею-
щей координату _у^ = р0, должна быть равна
(7-65)
В действительности фаза поля в этой точке равна
V' = т £Z3sinTo= у- аз = т аз-р2 WV • (7.66)
Отклонение от линейного закона (7.65) составляет
.2
Ч макс = Фаш - С = 1 2а3р0 . (7.67)
Р(Р — f-o)
Приравняв Дф3ыакС=-^-, получим
где
f = -f- и О=2р0.
Отношение -у- (рис. 7.25,в) равно углу отклонения
главного максимума от нормального направления. Следо-
вательно, максимальный угол отклонения главного мак-
симума в параболических зеркалах, который может быть
409
достигнут без заметных искажений диаграммы направ-
ленности, равен
2 2
а «3 макс X Р Ро I—
Г макс = ---7~ = --- • (7‘69)
1 го
При обычно принятых на практике параметрах зеркала
У =°’5 Угол 90макс равен
ч \
• (7.69,а)
Из сравнения (7.69,а) с данными о ширине главного
лепестка, приведенными в главе III, легко видеть, что угол
&омакс параболических зеркал равен примерно ширине глав-
ного лепестка диаграммы направленности этих антенн.
§ 7. ПАРАБОЛОИДЫ С РЕШЕТЧАТЫМИ
И ПЕРФОРИРОВАННЫМИ ПОВЕРХНОСТЯМИ
В целях уменьшения веса и парусности параболических
зеркал их поверхности делаются часто из решеток или пер-
форируются. На рис. 7.26 показан усеченный параболоид
вращения с решетчатой поверхностью, облучаемый волно-
водом (а) и параболический цилиндр с перфорированной
поверхностью, облучаемый системой синфазных вибрато-
ров (б).
Элементами решетчатой поверхности могут быть метал-
лические пластины или цилиндрические провода (см.
рис. 7.27). При применении решетчатой поверхности долж-
ны быть соблюдены следующие условия:
а) электрический вектор поля должен быть параллелен
элементам решетки;
б) зазор между элементами должен быть меньше поло-
вины длины волны.
При этих условиях каждый зазор между двумя соседни-
ми элементами представляют собой волноводный канал,
имеющий размеры меньше критических, и электромагнит-
ное поле в зазоре носит характер затухающей волны. Зату-
хание тем больше, чем меньше зазор и чем шире элементы.
Коэффициент передачи по мощности определяется как от-
ношение квадрата напряженности поля на теневой стороне
решетки к квадрату напряженности поля на освещенной сто-
роне и может быть найден по затуханию в таком волновод-
ном канале.
410
а) б)
Рис. 7.26. Внешний вид параболических антенн с решетчатой поверхностью:
а) усеченный параболоид вращения с пластинчатой поверхностью, облучаемый
волноводом; б) параболический цилиндр с перфорированной поверхностью,
облучаемый системой синфазных вибраторов.
Представление об экранирующем действии решеток из
пластин дают кривые рис. 7.28,а, заимствованные из [21].
Отдельные кривые рис. 7.28,а соответствуют определенному
коэффициенту передачи по мощности в процентах (см. циф-
ры у кривых) к мощности падающей волны. Толщина пла-
стин равна во всех случаях w=0,0175 X. Остальные обозна-
чения видны из рис. 7.27.
Рис. 7.27. Элементы решетчатой поверхности.
Коэффициент передачи решетки сравнительно тонких
проводов при падении волны нормально к плоскости ре-
шетки и при электрическом векторе, параллельном прово-
дам, определяется по следующей формуле:
Т’о = 11-------------—----------------- 2 (7.70)
В формуле (7.70) Я(02,(х)—Ганкелева функция второго
рода нулевого порядка, связанная с функцией Бесселя
70(х) и функцией Неймана N0(x) соотношением
C(x) = 70(.r)-/W0(x).
При расчете коэффициента передачи То по формуле
(7.70) можно воспользоваться приведенными в приложе-
нии 2 значениями рядов функций Бесселя и Неймана.
Обозначения параметров решетки соответствуют
рис. 7.27.
На рис. 7.28,6 даны графики зависимости коэффи-
циента передачи по мощности 72 решетки проводов от
отношения — для различных значении отношения ,
вычисленные по формуле (7.70).
412
Рис. 7.28. а) зависимость Z/Х от s/X при различных значениях коэф-
фициента передачи для пластинчатой решетки; б) зависимость коэф-
фициента передачи по мощности от относительных размеров элемен-
тов решетки (см. рис. 7.27) для проволочной решетки.
413
При падении волны наклонно На решетки из проводов
или из пластин коэффициент передачи будет меньше, чем
при нормальном падении.
Перфорированная поверхность представляет собою обыч-
ную поверхность из тонкого металлического листа с круг-
лыми или овальными отверстиями. К ним предъявляется
требование, чтобы размер отверстия, параллельный элек-
трическому вектору поля, был значительно меньше длины
волны.
Вопрос о коэффициенте передачи металлического листа
с отверстиями рассмотрен выше (гл. VI). Однако содержа-
щиеся там данные относятся к отверстиям с диаметром по-
рядка половины длины волны и больше. В данном случае
речь идет об отверстиях малого размера.
Исследование прохождения через малые отверстия в ме-
таллических листах дано Б. Е. Кинбером [39]. В этой рабо-
те исследуется коэффициент передачи плоского идеально
проводящего листа с круглыми отверстиями радиуса R < X.
Взаимодействием отверстий пренебрегается.
Расчет основывается на принципе двойственности. В со-
ответствии с этим принципом задача о прохождении через
металлический лист с отверстиями заменяется задачей о вто-
ричном излучении изоляционного листа с металлическими
плоскими дисками, подобного применяемым в дисковой ме-
таллодиэлектрической линзе Диски должны быть того же
радиуса R и расположены с той же плотностью, как отвер-
стия. При — < 1 задача может рассматриваться как квази-
статическая.
Согласно (6.14) и (6.23) в каждом диске в электриче-
ском поле возбуждается электрический момент
/n = -^-^3£oCOS({)i (7.71)
где Ео — амплитуда поля падающей волны,
<р — угол между нормалью к листу и направлением
распространения падающей волны.
Каждый отдельный диск, ввиду его малых размеров,
можно рассматривать как диполь Герца, электромагнитное
9 Принцип двойственности подробно рассматривается в сле-
дующей главе.
414
поле излучения Е которого связано с моментом т соотно-
шением
£=£^/1 — si^&'sin2^', (7.72)
где &' — угол между нормалью к диску, принимаемой за
полярную ось и направлением распространения
излученной диском волны,
tp' — вторая угловая координата, отсчитываемая от
Я-плоскости.
Подставив (7..71) в (7.72), получаем
£ = £0 cos <р У1—sin2 &' sin2 ср', (7.73)
При наличии на листе N отверстий, суммарное их
поле равно
£ = ^£0cos?£(0', <р'), (7.74)
где £(&’, tp') — диаграмма направленности системы N ди-
сков, как вторичных излучателей.
В случае возбуждения системы дисков плоской вол-
ной, падающей перпендикулярно на лист, поле в направ-
лении й' = 0 равно
р-75>
Выражение (7.75) определяет также поле соответствую-
щего металлического листа с отверстиями при нормальном
падении плоской волны с напряженностью поля Ео. При
малых размерах отверстий почти вся энергия падающей
волны отразится от металлического листа. Для расчета поля
отраженной волны можно воспользоваться методом отвер-
стия в непрозрачном экране, рассматривая этот лист как
отверстие в плоском экране площадью S, в котором поле
Е=Е0 (постоянно по амплитуде и фазе). Поле излучения
такого отверстия в направлении &' =0 согласно (3.14) и
(3.13) равно
£ = . (7.76)
макс '
415
Коэффициент передачи Т* в указанных условиях па-
дения плоской волны на пноский перфорированный лист
Е'2
можно определить как отношение , т. е.
^макс
~2__ /16 R Nr.R2 >2_/16 R S' \2 ,у
s ) ’ О-11)
где S' — N^R2 — общая площадь всех отверстий в перфо-
рированном листе,
S — площадь листа.
Не следует забывать, что (7.77) относится к случаю
большого расстояния между отверстиями, когда можно пре-
небречь их взаимовлиянием.
Зная коэффициент передачи /^плоского перфорирован-
ного листа или решетки при падении плоской волны нор-
мально к его поверхности, можно найти приближенную ве-
личину коэффициента передачи перфорированных и решет-
чатых параболических зеркал, понимая под этим отношение
интенсивности излучения зеркал в обратном направлении
к интенсивности прямого излучения (в направлении глав-
ного максимума).
На рис. 7.29 кривая NOM изображает продольное сече-
ние параболоида. В точке О' находится облучатель. Поверх-
ность параболоида перфорирована или выполнена из ре-
шетки, в результате чего будет создаваться поле за зерка-
лом. Определим напряженность поля излучения за зерка-
лом в точке О", находящейся на оси зеркала на очень боль-
шом расстоянии г от вершины О (г > D).
Вводим систему координат XYZ (ось Z перпендикуляр-
на плоскости чертежа).
Каждый элементарный участок ds поверхности , парабо-
лоида можно рассматривать как вторичный излучатель. При
большой величине г можно считать, что лучи будут итти от
поверхности зеркала до точки О" параллельно оси О'О".
Разность хода лучей 1 и 2 равна
О'А + АВ-0'0 = 2АВ = ^- , (7.78)
поскольку
BC = f- AO,= AC = f+AB\ АВ = ^ .
Если принять, что фаза ф0 поля, создаваемого в точ-
ке О" (x = r, у = 0, z = 0) элементом поверхности у вер-
416
шины зеркала О (x=Q, у=£, z = 0) равна нулю, то фазы
фуз полей, создаваемых в точке О'' другими элементами
поверхности зеркала, имеющими координаты у, z, равны:
в случае параболического цилиндра
(7.79)
в случае параболоида вращения
(7-8°)
Рис 7.29. К расчету коэффициента передачи перфорированных парабо-
лических антенн.
Амплитуды полей, создаваемых отдельными элемен-
тами поверхности зеркала в точке О" имеют, вообще го-
воря, сложную зависимость от координат поверхности.
Будем считать ее равной T^-F^y) для цилиндрического
параболоида и TaF2(y, z) для параболоида вращения.
27—1503 417
Функции Fify) и F2(y, г) характеризуют поле излучения
элементов поверхности зеркала в сторону раскрыва и за-
висят от параметров зеркала и от вида облучателя.
Они могут быть легко определены в каждом конкретном
случае.
Суммарное поле излучения всей поверхности зеркала
равно в случае параболического цилиндра
D' D
2 2 _jk
Et = T0 j dz ^(у)*1 2f dy,
D> D
2 2
(7-81)
а в случае параболоида вращения
Согласно методу стационарной фазы можно прибли-
женно выразить Е\ и £2 следующим образом (см. гл. II § 6)
£, 2fT0D'£x (0) /^2 = VKWFi (0), (7.83)
£2 T^F2 (0,0) = lfT0F2 (0,0). (7.84)
где £](0) и £2(0,0) функции, соответствующие области
стационарной фазы. В нашем случае эта область нахо-
дится у вершины зеркала. Обозначим через £1макс и £2макс
поля, создаваемые в направлении главного максимума
излучения антенны единицей площади зеркал в области
их вершин, соответственно у параболического цилиндра
и параболоида вращения.
Поскольку у вершины волна от облучателя падает
нормально к поверхности зеркала, то можно положить
^(0)-^МаКе
£2 (0,0) — Е„
* х ' / £ макс
(7.85)
(7.86)
418
Полное поле излучения рассматриваемых параболоидов
в направлении главного максимума разно
£sl = D'D7^1MaKC, (7.87)
= <7 А макс, (7.88)
где q{ и q2— коэффициенты неравномерности поля соот-
ветственно параболического цилиндра и параболоида вра-
щения, равные
D
(7-87а)
и .) С1 мэкс
О
(7-88а)
и JJ ^2 макс
$
Изложенное приводит к следующим приближенным
выражениям для коэффициентов передачи параболиче-
ского цилиндра 7] и параболоида вращения Т2 , имеющих
перфорированную или решетчатую поверхность
>2______/ \ % а 1
2 _ I 02^27'2 16
' 0
(7.89)
(7.90)
В(7.89) и (7.90) Топриближенно определяется по форму-
лам (7.70), (7.77) или соответственно по графикам
рис. 7.28.
Из сравнения (7.89) и (7.90), учитывая, что f^D, а
Л < D, видно, что перфорированный параболический ци-
линдр характеризуется значительно большим обратным
излучением, чем параболоид вращения при тех же разме-
рах раскрыва. У перфорированных или решетчатых пара-
болоидов вращения излучение в заднем полупространстве
является равномерным, а у параболических цилиндров —
направленным. Обратное излучение параболоидов умень-
шается с увеличением отношения у (у параболических
цилиндров пропорционально первой степени, а у парабо-
лоидов вращения — второй степени).
27* 419
§ 8. СФЕРИЧЕСКОЕ ЗЕРКАЛО
Большой интерес на сверхвысоких частотах проявляется
к сферическому зеркалу. Объясняется это тем, что благода-
ря своей симметричности, оно обеспечивает возможность,
у при перемещении облу-
Рис. 7.30. К анализу сферического
зеркала.
ИЛИ
_у2 = 2/?х fl
чателя по концентриче-
ской кривой, качания
луча в пределах широ-
кого угла без искаже-
ний диаграммы на-
правленности. Однако
В' случае сферического
зеркала имеются за-
труднения с получением
плоской отраженной
х волны. Исследуем этот
вопрос подробнее.
На рис. 7.30 кривая
CO"D изображает ду-
гу окружности радиу-
са R с центром в точ-
ке О. При принятой на
рис. 7.30 системе коор-
динат уравнение кри-
вой CO"D имеет вид
(x-7?)2+j/2 = /?2(7.9i)
(7-92)
Из (7.92) видно, что при малых значениях х (когда
2^-< 1) можно рассматривать дугу окружности, как
часть параболы и соответственно сферическую поверх-
ность, как параболоид вращения с фокусным расстоянием
f
<ЭКВ 2
(7.93)
Поместим точечный облучатель в точку О' (рис. 7.30),
находящуюся на расстоянии -у- от центра О. Прямую АВ
будем считать лежащей в раскрыве зеркала. Из сказан-
ного следует, что на некотором участке прямой АВ около
420
точки О’ поле отраженной от зеркала волны имеет оди-
наковые фазы, но в точках, удаленных от точки О' на
сравнительно большое расстояние, фазы поля будут зна-
чительно отличаться от фаз поля в точке О’. Определим
размеры той области около точки О', в пределах кото-
рой можно считать фазы одинаковыми.
Очевидно, что разность фаз между полями в точках
N и О' равна
ф = + MN ~ 2 00'). (7.94)
При этом
2-00' = /?,
(7.95)
Учитывая (7.92), можно привести выражение для О'М
к виду _______
O'M = yf (7.96)
Выразим MN через О'М.
Легко видеть, что ^MNO' = 90° у— ср, a ^_MO’N =
= 90°—у—Согласно теореме синусов можем написать
MN = МО' -^££3"^ = МО' j ~tg , (7.97)
sin (90 + 7 — ср) 1 -f- tg 7 tg р ’ V '
Следовательно,
2л / /"от ' 2 \
Из рис. 7.30 следует
= = (7.99)
В результате применения теоремы синусов к треуголь-
нику ОМО' можно получить после ряда простых преоб-
разований
= (7.100)
Подставив (7.99) и (7.100) в (7.93), получаем
R2 -+ 4Rx
2R.X — X2
+- /р2 _х2
(7.101)
421
Разложив выражение (7.101) в ряд по возрастающим
степеням ~ и отбрасывая члены высших порядков, по-
лучаем приближенно
(7-102)
А £\
Таким образом, фазы в раскрыве меняются пропорцио-
нально х2. Обозначим координаты точек прямой АВ че-
рез ys. В тех пределах, в каких сферическую поверхность
можно рассматривать как параболическую ys=y, а у2^
= 2Rx. Это позволяет написать
2к У*
X 4£3 •
(7.103)
Примем, что допускается отклонение фазы на краях
раскрыва по сравнению с центром раскрыва фмакс = ~у" •
Это дает следующее граничное значение _ys макс области
раскрыва, в которой фазы поля можно считать одинако-
выми:
* X Т"
Лмакс = ^/4- (7Л04)
На рис. 7.31 показано изменение фазы поля в пределах
области, условно принятой за синфазную. Мы видим, что-
в пределах половины этой области различие фаз не превы-
шает 5°, в пределах 75% области различие фаз составляет
меньше 30°, и что резкое возрастание фаз имеет место на
краях области. Применяя направленный облучатель, можно
значительно ослабить действие краев областей и получить
диаграмму направленности антенны, близкую к диаграмме
направленности синфазной антенны при аналогичном ампли-
тудном распределении в раскрыве.
Современные антенны сверхвысоких частот (исключая
радиоастрономические антенны) имеют диаметр раскрыва
при круглой его форме порядка D = (20--е 40) 2. Если при-
менить для таких антенн сферическое зеркало, то у него
Л макс = (10-4-20)2. Подставив это значение ^макс в фор-
мулу (7.104), получим, что зеркало должно иметь ра-
диус
/?зЦ21ч-54)2.
(7.105)
422
Фокусное расстояние такого зеркала равно
/,кв=4(10’5^27’0)2- <7-106)
Полученные числовые значения размеров имеют тот же
порядок величины, какой имеют аналогичные размеры па-
раболического зеркала. В данном случае отношение фокус-
ного расстояния к диаметру раскрыва получается несколь-
ко больше, чем у параболического зеркала, но не намного.
Рис. 7.31. График изменения фазы поля сферичес-
кого зеркала в пределах области, условно приня-
той за синфазную.
У сферического зеркала должна облучаться только та
часть поверхности (та область), которая обеспечивает в пре-
делах указанных выше допусков почти постоянные фазы
в раскрыве зеркала. В связи с применением качания луча
поверхность зеркала должна быть больше указанной облу-
чаемой ее части. При этом площадь раскрыва зеркала осве-
щается лишь частично, и такая антенна характеризуется ма-
лым коэффициентом использования площади раскрыва.
Сказанное иллюстрируется рисунком 7.32. На этом ри-
сунке показано два варианта сферического зеркала. В каж-
дом варианте показано два положения облучателя S' и S",
смещенных по дуге окружности на угол а. При нахожде-
нии 1в точке S' угол облучения в обоих случаях обозна-
423
чен ES'F, а при нахождении в точке S" угол облучения обо-
значен соответственно O'S"A и O"S"A. В первом случае,
когда облучатель находится в точке S' отраженными луча-
ми освещается часть раскрыва CD, а во втором случае,
когда облучатель находится в точке S" в варианте а осве-
щается весь раскрыв, а в варианте б часть раскрыва АС.
Рис. 7.32. Зависимость
степени облучения сфе-
рического зеркала от его
размеров и места распо-
ложения облучателя.
Оба варианта рассчитаны на получение одинакового эф-
фекта: одинаковой ширины главного лепестка (поскольку
освещенная площадь раскрыва одинакова) и на одинаковый
угол поворота луча а. Однако зеркала имеют различные
размеры и, следовательно, разный коэффициент использова-
ния площади раскрыва. Объясняется это тем, что в вариан-
те а угол облучения зеркала (Z.FS'E) значительно больше
угла облучения в варианте б, а зеркало имеет в первом
случае большую кривизну, чем во втором случае.
424
Вариант а имеет очевидные конструктивные преимуще-
ства. Однако- может оказаться, что при соответствующей
ему кривизне поверхности зеркала не будет выполнено усло-
вие (7.104).
Итак, сферическое зеркало с точечным облучателем мо-
жет обеспечить необходимую диаграмму направленности и
качание луча в широком угле. Но при большой остроте на-
правленности такое зеркало имеет малый коэффициент ис-
пользования площади раскрыва, так как согласно (7.117)
радиус кривизны растет быстрее, чем радиус раскрыва.
Работа сферического зер-
кала может быть улучшена,
если ввести коррекцию фаз
в раскрыве.
Идея коррекции фаз за-
ключается в следующем.
Предположим, что на сфе- •
рическое зеркало падает О
плоская волна. На рис. 7.33 t
прямая АР изображает один рис. 733. пояснению принципа
из лучей падающей волны, коррекции фаз сферического зер-
После отражения от зеркала, кала.
луч АР попадает в точку/7'.
Местоположение точки F' зависит от угла падения ф. Чем
меньше угол ф, тем ближе точка F' к точке F, находя-
р
щейся на расстоянии - от центра С сферы. При ф = 0
луч СО попадает в точку F. Очевидно, что фаза поля от-
раженной волны в точке F' отличается от фазы поля
в точке F.
Итак, плоская волна, падающая на сферическое зеркало,
концентрируется на центральной линии на участке F'F,
создавая поле переменной фазы. Отсюда следует, что если,
наоборот, расположить вдоль отрезка F'F линейный излу-
чатель, отдельные участки которого имеют соответствующие
фазы колебаний и излучают в соответствующих направле-
ниях, то после отражения от зеркала образуется плоская
волна.
Для определения соотношения фаз на отрезке F'F вы-
числим разность хода лучей 8 до прямой СО.
8 = (ДР + PF') — (СО -ф- OF) = R cos ф 4- sec ф — Р — £=
= Р(созф-1)4-у(эесф-1). (7.107)
425
п
Обозначим отрезок F'F через z, а — через f. Легко
видеть из рис. 7.33, что
z = f(sectp—1). (7.108)
Из (7.106) в свою очередь можно получить
/?(собФ—1) = — (7.109)
Подставив (7.108) и (7.109) в (7.107), получаем
8 = _z^. (7.110)
При
z<f, 8~ — z.
Экспериментальная проверка [40] изложенного метода
коррекции фаз проводилась при трех видах линейных облу-
чателей.
Первый облучатель представлял собой многощелевую
антенну, выполненную в виде стандартного трехсантиметро-
вого волновода с наклонными щелями на узкой стенке.
Второй облучатель представлял собой многовибраторную
антенну, у которой вибраторы питались от волновода прямо-
угольного сечения.
Третий облучатель представлял собой прямоугольный
волновод с удаленной узкой стенкой.
Соотношение фаз регулировалось изменением ширины
волновода или диэлектрическими вставками.
Следует отметить не вполне ^.четкое осуществление^
поставленном эксперименте изложенной здесь идеи. Дело
в том, что каждый из элементов линейной антенны из-
лучает не только в требуемом направлении, но и в дру-
гих направлениях. Кроме того, опыт проводился с зерка-
лом сравнительно небольшой кривизны (/? = 24Л) при не-
большой области освещения поверхности зеркала (в на-
ших обозначениях j/^lOk). При указанных размерах
достаточно хороший результат получался и при обычных
облучателях. Например, при облучении с открытого конца
волновода ширина главного лепестка равнялась 290 = 3,5°,
£
а боковые лепестки были на уровне -^- = —14 дб\ при
^ГЛ
облучении рупором ширина главного лепестка равнялась
426
260 = 3°, а боковые лепестки были на уровне -^-=—
^ГЛ
— 24 дб. При указанных же выше линейных облучателях
получались данные, соответствующие таблице 7.1.
Таблица 7.1
Вид облучателя
2в0- дб
градусы £гл
Первый ........
Второй ........
Третий ........
2 —17
2,8 —18
2,5 —22
Из сопоставления приведенных данных видно, что ли-
нейные облучатели давали известное улучшение характери-
стик излучения в результате предусмотренной коррекции
фаз.
§ 9. ПОСТРОЕНИЕ ЗЕРКАЛА ПО ЗАДАННОМУ
РАСПРЕДЕЛЕНИЮ ФАЗ ПОЛЯ В РАСКРЫВЕ
Мы видели выше (гл. III), что существует определенная
связь между формой диаграммы направленности и распре-
делением амплитуд и фаз поля в раскрыв антенны. Зная
эту зависимость, можно поставить перед собой задачу по-
лучения в раскрыве антенны заданного распределения ам-
плитуд и фаз поля, обеспечивающую требуемую диаграмму
направленности.
В предыдущей главе рассмотрено несколько примеров
решения аналогичной задачи с помощью линз. У линз для
решения этой задачи имеется три варьируемых параметра:
профиль освещенной стороны, толщина, коэффициент пре-
ломления. В случае зеркальных антенн имеется только один
варьируемый параметр — форма поверхности зеркала. По-
этому возможности у зеркал более ограничены. Оказывает-
ся, что подбором формы поверхности зеркала можно создать
либо заданное распределение фаз, либо заданное распре-
деление амплитуд поля в раскрыве Распределение ампли-
туд может в значительной мере регулироваться подбором
диаграммы направленности облучателя.
*) В [41] рекомендуется применение двухзеркальной системы
для одновременной регулировки и амплитуд и фаз поля в раскрыве
антенны.
427
Рассмотрим здесь методику определения формы поверх-
ности зеркала, обеспечивающей заданное распределение
фаз. Задачу считаем двухмерной, что соответствует цилин-
дрическому зеркалу или зеркалу с осевой симметрией.
Предположим, что раскрыв зеркала совпадает с осью У
(рис. 7.34), а источник электромагнитного излучения нахо-
дится на оси X в точке х0. Требуется найти форму зеркала,
при которой в раскрыве фазы меняются по формуле:
Ф = 'р(Л) + 'Ро, (7.111)
где <р0 — постоянная величина, не зависящая от ys,
ys — координаты точек раскрыва, соответствующие
х = 0.
Чтобы фазы менялись по формуле (7.111), луч должен
пройти из фокуса расстояние
(7.112)
428
Условию (7.112) удовлетворяет эллиптическая поверх-
ность с большой осью равной г и с фокусами, находящи-
мися в точках (0,^) и (х0, 0). Действительно, эллипс
есть геометрическое место точек, сумма расстояний от
которых до фокусов есть величина постоянная. Кроме
того, лучи, проведенные из фокусов в любую точку эл-
липса обрадуют одинаковые углы с касательной в данной
точке.
Искомая поверхность является огибающей семейства
эллипсов, имеющих фокусами точку (х0,0) и соответ-
ствующие точки (0,_ys) и большие оси, равные
2а = г(Л). (7.113)
При этом малые оси равны
2Ь=\/ г2-х20-у2. (7.114)
Центры эллипсов находятся в точках .
Уравнение эллипсов имеет вид
(у - Я
/ги.>'.Л) = ₽+к-3—-1=0. (7.115)
где х' и у' согласно рис. 7.14 связаны с х и
шениями
и — Л(х~хо)+^о
у СООТНО-
СИ 16)
ууд-х0(х —х0)
V +
Уравнение огибающей эллипсов, определяемых урав-
нением (7.115), может быть найдено, если из системы
уравнений F(.x,y,ys) — 0, (7.117) dF(x,y, Л) Q (7 П8) dys v ’
исключить параметр ys.
В качестве иллюстрации метода рассмотрим случай
нахождения излучателя в начале координат, т. е. хо = О
429
и требование получения синфазного поля в раскрыве,
т. е. требование г (ys) = r0 = const. При этих условиях
х' — х, у’=у, а = ~, Ь^У г2-у2 и уравнение (7.115)
приводится к виду
fy-лу
= + (тпэ)
'О Zs 'О
Можно легко найти, что уравнение
dF(x,y,ys)
dys
имеет решение
У,=У- (7.120)
Подставив (7.120) в (7.119), получаем уравнение оги-
бающей
у2 4)2 1
т=0. (7.121)
Уравнение (7.121) имеет два решения
1) y^ = 2r/x + riy
2) у^2г0[^-ху (7.122)
Оба решения представляют собой параболы, имеющие
фокус в точке х = 0 и фокусное расстояние f = y • Одна
парабода проходит с правой стороны от начала коорди-
нат, а вторая — с левой стороны.
Аналогично можно, задавшись другим видом функции
r(ys) найти ys как функцию х и у из (7.118) и подстанов-
кой этого значения в (7.117) исключить из последнегоys .
§ 10. ЗЕРКАЛА, ИМЕЮЩИЕ КОСЕКАНСНУЮ ДИАГРАММУ
НАПРАВЛЕННОСТИ
t
В предыдущей главе рассмотрена методика получения
косекансной диаграммы направленности с помощью линз.
Такая диаграмма направленности может быть получена так-
430
же с помощью зеркал. Методика расчета формы поверхно-
сти зеркала во многом сходна с методикой расчета профиля
линзы. Задачу будем считать плоской, что соответствует ци-
линдрическому зеркалу.
Сначала найдем интегральное уравнение поверхности
зеркала.
Рис. 7.35. К анализу зеркала, дающего косекансную диаграмму
направленности.
Обратимся к рис. 7.35. Кривая ЛОВ —сечение зер-
кала. Источник электроматнитного излучения находится
в точке F. Расстояние OF обозначаем через р0, а рассто-
яния от точки F до других точек кривой АВ— перемен-
ной величиной р.
Кривую АОВ можно построить, проведя из точки F
прямые линии под различными углами ф к оси OF и от-
кладывая на этих линиях соответствующие каждому
углу ф отрезки р, исходя из зависимости р от ф. Таким
431
образом для построения кривой АОВ надо знать указан-
ную функцию р от ф. Найдем эту функцию.
Проведем из точки F (рис. 7.35) два отрезка одина-
ковой длины CF и DF, образующие между собой угол йф.
Прямая соединяющая эти точки, может рассматриваться
как дуга окружности радиуса р и равна pt/ф. В свою оче-
редь прямая DE равна dp. Из треугольника CDE видно,
что ^ = tg{3, где р = <ОС£. Так как DCA.CF, а ЕС±.СС",
о в — Ф гл
то Р = —2 ’ ОтсюДа следует, что
<7-12з>
или
ф
1пД=Jfge_fcJ^. (7.124)
о
Уравнение (7.124) есть интегральное уравнение по-
верхности зеркала. Интеграл в правой части уравнения
(7.124) может быть вычислен, если конкретизировать
функцию 6(ф). Эта задача решается так же, как подоб-
ная задача решалась для линзовых антенн.
Считаем, что представления геометрической оптики
о падающем и отраженном лучах можно применить в
данной задаче не только для определения поля в рас-
крыве антенны, но также для определения поля в уда-
ленной точке, где осуществляется прием. Полагая, что
точки пересечения отраженных лучей находятся где-то
вблизи зеркала, а точка приема находится на очень боль-
шом расстоянии от зеркала, можем считать, что внутри
угла di распространяется мощность, пропорциональная
/(ф)с(ф, где I (ф) — диаграмма направленности облучателя
по мощности. Мощность, приходящаяся на одинаковые
углы di, лежащие в разных направлениях 0, различна.
Обозначим через Р(0) диаграмму направленности всей
антенны в целом. Очевидно, что должно выполнять-
ся равенство
Р(0)с(9 = ^'/(ф)с?ф, (7.125)
где k'—коэффициент пропорциональности.
По условию задано
£(6) = cosec®0.
(7.126)
432
Подставив (7.126) в (7.125) и проинтегрировав обе
части в соответствующих пределах, получаем
где
ctg 9
ctg е2 — ctg et
J I (Ф)
Ф1
(7.127)
(7.128)
Рис. 7.36. Графики зависимости угла 0, и относительной
р
величины радиуса — вектора — от угла ф, у зеркала с
Ро
косекансной диаграммой направленности при облучателе
с диаграммой направленности вида I (ф) = cos2
ся уравнением формы поверхности зеркала, обеспечи-
вающего косекансную диаграмму направленности.
Как отмечалось выше, диаграмма направленности,
близкая к виду cosec29, получается в ограниченном угле
(от 9] = 10э до 9г = 70°), причем реальная диаграмма
направленности тем ближе к теоретической, чем больше
28—1503 433
размеры зеркала. Вполне удовлетворительное совпадение
имеет место при размерах
Рис. 7.37. Форма поверхности
зеркала с косекансной диа-
граммой направленности, соот-
ветствующая диаграмме на-
правленности облучателя (по
мощности) I (А) = cos2 ф
раскрыва порядка (15 -е- 20) А.
Интеграл в (7.124) не бе-
рется в обычных функциях и
находится приближенно мето-
дом численного интегрирова-
ния. Выполненный расчет по-
казал, что форма профиля зер-
кала почти одинакова для
облучателей с диаграммами
направленности вида:
/(ф) = cosip, cos2 ф и cos2 у.
На рис. 7.36 дана зависи-
мость луча 6, определяющего
направление отраженного от
зеркала луча, от угла ф, опре-
деляющего направление па-
дающего луча (рис. 7.35), а
также зависимость от ф отно-
сительной длины радиуса —
вектора , проведенного из
точки F, где находите а облу-
чатель, до профиля зеркала,
имеющего косекансную диа-
грамму направленности.
На рис. 7.37 показана фор-
ма поверхности зеркала, соот-
ветствующая /(ф)=СОЭ2ф и
р (6) = cosec2 9.
§ 11. плоские зеркала
В технике сверхвысоких частот, наряду с описанными
выше криволинейными зеркалами, находят применение пло-
ские зеркала.
Как отмечалось выше (см. § 1), при отражении от пло-
ского зеркала форма волны не изменяется. Поэтому плоские
зеркала не могут быть использованы для получения острой
'направленности или для формирования диаграммы направ-
ленности специального вида. Они используются для поворо-
434
та главного лепестка диаграммы направленности другой
остронаправленной антенны. Применение плоских зеркал ил-
люстрируется рис. 7.38. Здесь схематически показаны две
линии связи. На одной из них (рис. 7.38,а) остронаправлен-
ные антенны помещены непосредственно на вершине башни.
На второй линии (рис. 7.38,6) остронаправленные антенны
установлены у поверхности земли и имеют главный макси-
мум соответственно излучения и приема, направленный вер-
тикально вверх, а на вершине башни помещены плоские
зеркала, которые поворачивают в горизонтальное направле-
ние главный максимум диаграмм направленности антенн.
Для определенности остронаправленные антенны изобра-
жены на рис. 7.38 в виде параболоидов, хотя они могут
быть любого другого типа.
Расчет плоского зеркала может быть произведен одним
из методов, изложенных в § 1. Здесь применяется апертур-
ный метод.
Обратимся к рис. 7.39,а, на котором показана система
из плоского зеркала и остронаправленной антенны, установ-
ленная на приемном пункте. На плоское зеркало падает
плоская волна с напряженностью поля Дь Проекция зерка-
ла на горизонтальную плоскость рассматривается как его
раскрыв (рис. 7.39,а). Очевидно, что во всех точках раскры-
ва плоского зеркала поле отраженной волны имеет одина-
ковые амплитуды (Et) и одинаковые фавы. По известному
полю в раскрыве зеркала можно найти поле в раскрыве
приемной остронаправленной антенны, а затем мощность Рг,
выделяемую во входном контуре приемника.
На рис. 7.39,6 показана та же остронаправленная антен-
на, установленная на той же высоте, что и плоское зеркало
в предыдущем случае, и непосредственно принимающая
энергию падающей плоской волны. В этом случае во всех
точках раскрыва плоской волны поле будет равно Е{. Обо-
значим через Pi мощность, выделяемую во входном контуре
приемника. Отношение
Я’=й.
показывающее изменение коэффициента усиления антенны,
вызванное применением плоского зеркала, будем называть
его эффективностью.
Эффективность плоского зеркала зависит от формы его
контура, размеров, расстояния между ним и остронаправ-
ленной антенной, типа и размеров антенны и т. п. Расчет
28* 435
Рис. 7.38. Схемы линий связи: а) без плоского зеркала, б) с плоским зеркалом.
эффективности проведем на примере плоского зеркала,
имеющего раскрыв в виде круга радиуса (т. е. зеркала,
контур которого имеет форму эллипса) при остронаправлен-
ной антенне типа параболоида вращения с радиусом рас-
крыва /?2- Расстояние между раскрывами плоского
зеркала и параболоида вращения обозначим через г0 (см.
рис. 7.39,а).
Плоское
зеркало
i Раскрыб плоского
1 зеркала

Облучатель
Е, / РаскрыВ
—— /'параболоида
^2
Приемная
антенна
линия
Рис. 7.39. а)Приемный
параболоид,работающий
совместно с плоским
зеркалом, б) то же без
плоского зеркала.
а)
Для расчета эффективности плоского зеркала необхо-
димо предварительно определить поле, созданное плоским
зеркалом в раскрыве параболоида вращения.
На рис. 7.40 раскрывы обоих зеркал изображены в виде
двух плоских параллельных кругов, перпендикулярных
оси Z, причем их центры лежат на этой оси. Оси X и У по-
мещены в плоскости раскрыва плоского зеркала. Поле Е?
в раскрыве параболоида вращения определяем по формуле
(2.69), положив в ней Р=1. Учитывая, что
г >/?! + /?,, (7.129)
можно положить в формуле (2.69) cosOs 1. Тогда выра-
жение для Е2 приводится к виду
= (7.130)
5
где________________________________________
^ = /'-о + (^-^2 + (У2~У1)2 (7-131)
437
Индексы 1 и 2 относятся к параметрам раскрыва со-
ответственно плоского зеркала и параболоида враще-
ния.
Рис. 7.40. К определению поля в раскрыве приемного параболоида
работающего совместно с плоским зеркалом.
Заменив,согласно обозначениям рис. 7.40,х и у через
р и <р и учитывая неравенство (7.129), получим
г го 4“ Pi Рэ 2?i?2cos (fa 'Fl) = ro +
. Р? + Р9 —2р Pocosb, —<Р1) (7.132)
+ - 2г о
Таким образом,
2 . р2 Е f 2р /А !— COS (®2—<р,) е 2г° P1dPl j е d^. 0 (7.133)
Если ввести обозначения
ьр2
f = ^,5=^0ffl = -, (7.134)
то получим
.. , ml1 i тР
-lkra-j — ‘ — -►
E2=jmEy& J0(m$/)e tdt=^E^‘ 'аg$),
(7.135)
где /0 — бесселева функция нулевого порядка.
438
Зная f2, можно найти мощность Р2, выделяемую во
входном контуре приемника. Можно показать [42], что .
1 |j(£2£nep)^r
’ 120 л:
пер
(7.136)
где £пер— напряженность поля, создаваемого в> раскрыве
остронаправленной антенны (в нашем случае — параболи-
ческого зеркала) при ее работе в качестве передающей
антенны и подведении к ней мощности, равной Рпер.
Аналогично можно показать, что при непосредствен-
ном приеме на параболоид вращения без плоского зер-
кала, как показано на рис. 7.39,6, мощность, выделя-
емая во входном контуре приемника, равна

1
120тс
^пер) ds
~Р
пер
(7.137)
Из (7.136) и (7.137) следует, что эффективность пло-
ского зеркала равна
D'
J (ЯЯерИ* 2
J (^l^nep)
(7.138)
Как мы видели, в случае параболоида вращения, яв-
— <[1, где р —параметр
параболы), вектор Е можно считать параллельным
векторам Е\ и Е2 и независимым от координаты <?2- В этом
случае скалярные произведения в подинтегральных вы-
ражениях (7.130) равны алгебраическим произведениям
величин векторов, а поверхностное интегрирование при-
водится к линейному.
Обозначив
Eaep = Eoh®< (7-139)
439
получаем
D' =
(7.140)
i
о
где / = ^—отношение радиусов раскрывов параболоида
«ч
вращения и плоского зеркала.
На рис. 7.41 приведены графики зависимости эффек-
тивности D' от относительной величины расстояния
между зеркалами ~ для различных значений , вы-
численные в предположении, что
7!($)= 1 -0,684^.
(7.141)
Рис. 7.41. Графики зависимости эффективности плоского
зеркала от относительного расстояния между ним и па-
раболоидом вращения при разных соотношениях размеров
плоского зеркала и параболоида.
440
Аппроксимация распределения поля, выраженная урав-
нением (7.141), соответствует плавному уменьшению поля
в радиальном направлении от центра к краям до относи-
тельного уровня 0,316. Как мы видели выше, оптимальным
условием при однонаправленном облучателе является спа-
дание величины поля до 0,47 в одном направлении и до 0,23
в другом, что примерно соответствует принятой здесь сред-
ней величине 0,316.
Таким образом, графики рис. 7.41 соответствуют пара-
болоидам вращения, наиболее часто встречающимся на
практике. При пользовании этими графиками не следует
забывать, что они получены при выполнении неравенства
(7.129).
Из графиков рис. 7.41 видно, что принципиально воз-
можно получить с помощью плоского зеркала увеличение
усиления антенны в 4 раза. Однако условием для получения
такого увеличения является, во-первых, очень большие раз-
меры плоского зеркала (7 = 0), во-вторых, расположение ан-
тенны и плоского зеркала на близком расстоянии друг от
друга.
В практических условиях эффективность плоского зер-
кала равна примерно единице, т. е. коэффициент усиления
системы из остронаправленной антенны и плоского зеркала
сохраняется примерно таким, как у антенны без плоского
зеркала.
ГЛАВА ВОСЬМАЯ
ЩЕЛЕВЫЕ АНТЕННЫ
§ 1. ПРИНЦИП ДВОЙСТВЕННОСТИ ПИСТОЛЬКОРСА
И ЕГО ПРИМЕНЕНИЕ К ЩЕЛЕВЫМ АНТЕННАМ
Задача об излучении щелевой антенны характеризуется
рядом особенностей, отличающих ее от аналогичных задач
для других типов СВЧ антенн. Так, например, суждение
о законе изменения амплитуд и фаз поля в раскрыве ру-
пора, линзы, параболоида мы получили, анализируя элек-
тромагнитное поле внутри антенны. Иначе обстоит дело
в случае щелевой антенны. Закон изменения амплитуд и фаз
поля в щели в практически интересных случаях, как прави-
ло, не зависит от внутреннего поля в волноводе, на стенке
которого вырезана щель.
При расчете излучения рупоров, параболоидов и т. п. мы
исходили только из значения поля в раскрыве, полагая токи
на наружной металлической поверхности антенны равными
нулю.1 У щелевых же антенн токи на наружной* металличе-
ской поверхности весьма существенно влияют на характери-
стики излучения и должны учитываться в расчетах.
В связи с указанными особенностями метод решения за-
дачи об излучении щелевых антенн получается отличным от
метода решения аналогичных задач для других типов СВЧ
антенн.
Как показал в 1944 г. А. А. Пистолькорс [4], к щелевой
антенне может быть применен принцип, названный им прин-
ципом двойственности, который весьма наглядно объясняет
1) При отсутствии токов иа металлической поверхности на по-
следней равны нулю все составляющие электромагнитного поля. Прн
наличии токов не равны нулю на этой поверхности касательная со-
ставляющая магнитного вектора и нормальная составляющая элек-
трического вектора,
442
физическую сторону явлений и значительно облегчает полу-
чение требуемых расчетных формул.
Принцип двойственности является вполне точным приме-
нительно к идеальному случаю — щели на неограниченной
идеально проводящей плоскости (такую антенну мы будем
в дальнейшем называть идеальной щелевой антенной).
Однако этим принципом можно пользоваться и в большин-
стве других встречающихся на практике случаев.
Содержание принципа двойственности сводится к сле-
дующему.
Если к идеальной щелевой антенне приложить от какого-
либо источника электродвижущую силу частоты f, то век-
торы электромагнитного поля Е и Н в щели и в окружаю-
щем щель пространстве будут иметь такое же направление
и являться такими же функциями пространственных коор-
динат, какое направление имеют и какими функциями явля-
ются соответственно векторы Н и Е электромагнитного поля
вибратора в виде идеально проводящей бесконечно тонкой
пластинки, находящейся в свободном пространстве и имею-
щей такую же форму и размеры, как щель, при приложении
к пластинке электродвижущей силы той же частоты f в ана-
логичных точках.
Обозначим векторы электромагнитного поля идеальной
щелевой антенны через Eit И,, а векторы электромагнитно-
го поля эквивалентного ей вибратора (имеющего ту же фор-
му и размеры и питаемого электродвижущей силой той же
частоты)—через Е2, Нг. Согласно принципу двойственности,
с точностью до постоянного множителя, не зависящего от
координат, Е\ равно Н2, а Н{ равно Е2.
Справедливость принципа двойственности может быть
доказана следующим образом.
Допустим, что в некотором объеме V, окруженном
поверхностью S, возбуждено электромагнитное поле,
Причем в этом объеме отсутствуют сторонние токи и
сторонние э. д. с., а среда обладает магнитной прони-
цаемостью ц = "0 и диэлектрической проницаемостью
е = е0. Это электромагнитное поле удовлетворяет урав-
нениям Максвелла
rot Н =j<DS0E,
rot£ = —
(8.1)
443
Введем в уравнения (8.1) новые вспомогательные пере-
менные Ев и Нв, связанные с Е и Н соотношениями
£B=/o,f0£',
Тогда получим
rotH8 =/«>/—во(лоЕ8,
rotEB=> )/-souo^b.
(8-2)
(8.3)
Уравнения (8.3) полностью симметричны относительно
Ев и Нв. Следовательно, интеграл уравнения (8.3) в об-
щем виде будет совершенно одинаковым для Ев и Нв.
В каждом частном случае интеграл зависит от значе-
ния постоянных интегрирования, которые определяются
из граничных условий.
Как известно, решения уравнений (8.3) определяются
единственным образом, если на поверхности 5 задана
касательная составляющая электрического вектора Ев
(1-я граничная задача электродинамики) или магнит-
ного вектора Нв (2-я граничная задача электродинамики),
либо если заданы на одной части поверхности касатель-
ная составляющая Ев электрического вектора, а на дру-
—>
гой части — касательная составляющая Нв магнитного
вектора (смешанная граничная задача электродинамики).
Два электродинамических процесса, характеризуемых
точно одинаковыми граничными условиями на поверхно-
сти S’, имеют точно одинаковое решение. Если же у одно-
го электродинамического процесса граничные условия
на S выражаются через Ев точно таким же образом, как
1) Ев и Нв, отличаясь от Е и Н, кйк видно из (8.2), постоянным
множителем, также представляют собой соответственно электри-
ческий н магнитный векторы поля, ио выраженные в другой си-
стеме единиц.
444
У другого они выражаются через Нв, то, вслед-
ствие симметричности уравнения (8.3) относительно £в
и Нв, и во всем остальном пространстве величина Ев
—►
одного процесса в точности равна величине Н другого
процесса и наоборот.
Покажем теперь, что у идеальной щелевой антенны
и у эквивалентного ей вибратора в свободном простран-
стве граничные условия одинаковы, если выразить их в
одном случае через касательную составляющую £_в элек-
трического вектора, а в другом случае — через касатель-
ную составляющую Н,в магнитного вектора.-
На рис. 8.1 показана конфигурация электромагнитного
поля в случае идеальной щелевой антенны, а на рис. 8.2—
в случае вибратора в виде металлической пластины, нахо-
дящейся в свободном пространстве. На обоих рисунках
сплошные линии указывают направление электрического
вектора, а штриховые — направление магнитного вектора.
Примем в качестве объема V полупространство, огра-
ниченное в первом случае идеально проводящей плоскостью,
на которой вырезана щель, а во втором случае—плос-
костью, являющейся продолжением металлической пластин-
ки — вибратора. Указанную ограничивающую плоскость
примем в качестве поверхности S.
В первом случае (рис. 8.1) на всей проводящей пло-
скости, за исключением щели, касательная составляю-
щая электрического вектора £*** равна нулю. В щели же
равна нулю касательная составляющая магнитного век-
тора Н[1), поскольку магнитные линии, образуя замкнутые
кривые вокруг электрических линий,везде проходят пер-
пендикулярно к плоскости щели (рис. 8.1, б). Во втором
случае (рис. 8.2), наоборот, почти на всей воображаемой
ограничивающей плоскости, проходящей через излучающую
пластинку, равна нулю касательная составляющая
магнитного вектора, а на самой металлической пластинке
равна нулю касательная составляющая £*2) электриче-
ского вектора.
Уместно заметить, что в теории проволочных антенн при-
нято определять электромагнитное поле антенны через ток
на ее поверхности или, что то же самое, через касательную
445
В)
Рис. 8.1. Конфигурация электромагнитного
поля идеальной щелевой антенны.
Рис. 8.2. Конфигурация электромагнитного
поля вибратора в виде металлической пласти-
ны, находящейся в свободном пространстве.
446
составляющую магнитного вектора.на поверхности провод-
ника. То же самое значение поля в пространстве можно
получить, если в основу расчета положить касательную со-
ставляющую электрического вектора на дополняющей ви-
братор бесконечной плоскости. Аналогично и в случае щеле-
вой антенны поле может быть определено либо через каса-
тельную составляющую электрического вектора в щели, либо
через ток на проводящей плоскости.
Таким образом, мы показали идентичность -граничных
условий у идеальной щелевой антенны и у эквивалентного
вибратора при условии взаимозамены электрического и маг-
нитного векторов. Следовательно, функции, выражающие
зависимость величины векторов поля от координат простран-
ства V, также должны быть одинаковыми у идеальной щеле-
вой антенны и у эквивалентного вибратора при условии
взаимозамены векторов поля Ев и Нв. Это и требовалось
доказать.
Покажем теперь применение принципа двойственности
к расчету щелевой антенны. В этих выкладках обозначим
поля, относящиеся к щелевой антенне, индексом «7», а поля,
относящиеся к вибратору,— индексом «2».
Известно, что векторы электромагнитного поля излу-
чения вибратора связа ш с его параметрами и с про-
странственными координатами г, & и ср следующим со-
отношением:
Е&= 120тг//2(? = ~j^~ Е (0) е“kr, (8.4)
где h— действующая высота вибратора,
/ — амплитуда тока в точке, по отношению к кото-
рой вычислена действующая высота,
F (&) — нормированная диаграмма направленности.
Направление координатных осей относительно оси ви-
братора показано на рис. 7.3.
Так как вибратор представляет собой бесконечно тонкую
пластинку, то периметр его поперечного сечения равен 2d.
Следовательно, ток на вибраторе может быть выражен через
касательную составляющую магнитного вектора //_2 в точ-
ке пучности следующим образом:
I = 2H^d. (8.5)
447
Подставив (8.5) в (8.4), поЛуЧиМ
3Qkh.2H.9d „ lbr .
=-J—F Wе (8-6)
Перейдем в формуле (8.6) от обычных значений век-
торов поля Е2 и Н2 к вспомогательным векторам Ев2 и
—
Нв2 в соответствии с (8.2). Получим
Я-2
ЗОйй 2
= - ]______V—n F (9)
У “‘О г
(8.7)
Формула (8.7), справедливая для вибратора в свобод-
ном пространстве, справедлива также для идеалыой
щелевой антенны, имеющей те же размеры, при условии
взаимозамены электрического и магнитного векторов.
Выполнив операцию
вместо индекса „2“,
взаимозамены и введя индекс
получим
Ет1
30kh 2-------
’ ~ "Но
/.-------J ~I
V ыг0 г
Перейдя обратно от вспомогательных значений £в( и
Нв1 к обычный выражениям для векторов поля £f и Hi
и выполнив соответствующие преобразования, получим
30£йд2£н -d
Я1{> =J------7-^ F е~‘кГ- W
Учитывая, что
»£li? = —120тг/71а
и что
е0 __ 1
НО (12071)2’
кроме того, обозначив
£^ = [/„ (8.10)
получим
£(, = - 120кЯ1а = -у± £ (&) е-;*\ (8.11)
448
В формуле (8.11) величина представляет собой
амплитуду напряжения в точке, по отношению к которой
вычислялась действующая высота Лд.
Из (8.11) видно, что идеальная щелевая антенна имеет
такую же диаграмму направленности, как эквивалентный ей
вибратор. Как известно, характерными особенностями этой
диаграммы направленности является нулевое излучение
вдоль оси и равномерное излучение в плоскости, перпенди-
кулярной оси.
Сравнивая (8.11) с (8.4), легко также видеть, что напря-
женность поля излучения идеальной щелевой антенны отли-
чается от напряженности поля излучения вибратора, в основ-
ном, лишь в обозначениях. Действительно, из соображений
удобства в случае вибратора напряженность поля излуче-
ния выражена через ток I, а в случае щелевой антенны —
через напряжение Uit деленное на переводной множитель
Д_
р0 60л ’
где _
Ро = = 120тс-
Величину р0 иногда называют волновым сопротивле-
нием свободного пространства.
Отсюда следует, что если мощность излучения Р12
вибратора, полученная как интеграл от вектора Умова-
Пойнтинга по сфере, окружающей вибратор, равна
PS2=4AR£, (8.12)
где — сопротивление излучения вибратора, то мощ-
ность излучения Р£1 щелевой антенны, вычисленная та-
ким же образом, будет равна
^£1 = -2^1 7^7» = 7 (60Sp (8‘13>
Согласно (8.13) активная проводимость (проводимость
излучения) gx идеальной щелевой антенны в пренебреже-
нии омическими потерями равна
__2РЪ __ /О 1Д\
^1— — ро 2— (60л)’ ’ '• '
29—1503
449
В формуле (8.14) равно сопротивлению излучения
эквивалентного вибратора. Проводимость, определяемая
по формуле (8.14), относится к точке, аналогичной той,
для которой определено у вибратора, т. е. к средней
точке щели.
Аналогичным путем может быть получено выражение
для реактивной составляющей проводимости идеальной
щелевой антенны.
Прежде чем приступить к математическим выйладкам,
заметим, что эквивалентность электромагнитного поля
идеальной щелевой антенны и вибратора относится не
только к зоне излучения, но также к зоне, непосред-
ственно примыкающей к щели и соответственно к вибратору.
Кроме того, поскольку электрический и магнитный век-
торы связаны с током и напряжением простыми соотно-
шениями (8.5) и (8.10), то из этого следует, что измене-
ние напряжения вдоль идеальной щели происходит по
такому же закону, как изменение тока по длине вибра-
тора, т. е. в первом приближении при узких щелях—в
соответствии с телеграфными уравнениями. Связь между
проводимостью щели и сопротивлением вибратора, опре-
деляемая соотношением (8.14) в виде переводного множи-
теля р-1 , относится не только к активным составляю-
(оОк)2
щим этих величин (/?х и £•]), но также к реактивным
(X и Ь{).
В соответствии со сказанным значение реактивной
составляющей проводимости щелевой антенны Ь\ может
быть получено следующим образом.
Известно, что реактивная составляющая сопротивле-
ния X вибратора в первом приближении равна
X — — pctg&y, (8.15)
где
р=120 (1п^ —0,69^ , (8.16)
I — длина вибратора,
г — эквивалентный радиус, равный в случае тонкой пла-
стинки
г = {-; (8.17)
d — ширина вибратора.
450
Реактивная мощность PRe2-s вибраторе равна
/2 I
Ри1-----p4rc»SS*4-- (8->8)
Учитывая указанную выше эквивалентность между
током в вибраторе и напряжением в щели, получаем для
реактивной мощности PReV возбужденной в щели, выра-
жение
(7? i
PRe\ — ~р 2 (60г.)2 k ~2 • (8-19)
Из (8.19) следует, что реактивная проводимость Ьу
щелевой антенны равна
2PRg Р , I
= ~ (60л)2 ctS 2 > (8.20)
ui
где р — волновое сопротивление эквивалентного вибратора,
определяемое из выражения (8.16).
Итак, полная проводимость Y идеальной щелевой ан-
тенны равна
а входное сопротивление равно
<8-2М)
Из (8.20), (8.21) и (8.21, а) видно, что реактивная со-
ставляющая проводимости Y имеет при kl<Zr- ин-
дуктивный характер и при 2т>/?/>тс — емкост-
ной характер. При Ы—~
-п-, реактивная составляющая
2 /
проводимости щели равна нулю. Следовательно, полувол-
новая щель является резонансной щелевой антенной.
Следует заметить, что в действительности резонанс
наступает не точно при l = ^t а при несколько меньшей
длине. Укорочение щели соответствует укорочению экви-
валентного вибратора.
29*
4Б1
На рис. 8.3 приведены экспериментальные кривые вход-
ного сопротивления (на рис. 8.3,а — активная составляю-
щая, на рис. 8.3,6 — реактивная составляющая) щели на
плосксм экране большого размера (снятые вблизи точки
резонанса). Длина щели равнялась 1=70 см, ширина щели d
равнялась соответственно 2 см, 4 см, 6 см, 8 см. В верхнем
правом углу на рис. 8.3 приведены для сравнения кривые
проводимости тонкого проволочного вибратора.
Из рис. 8.3 видно, во-первых, что точка резонанса сме-
щается в сторону более низких частот с увеличением шири-
ны щели, во-вторых, что кривые входного сопротивления
щели аналогичны кривым проводимости проволочного ви-
братора, в-третьих, что у узких резонансных щелей входное
сопротивление равно примерно
^ = ^ = 500 ом. (8.21,6)
На рис. 8.4 приведены экспериментальные кривые вход-
ного сопротивления (а — активная составляющая, б — реак-
тивная составляющая) гантельной щелевой антенны дли-
ной 1 = 70 см, шириной d=2 см. Остальные размеры видны
из рис. 8.4.
У гантельной щелевой антенны точка резонанса сме-
щается в сторону низких частот с увеличением диаметра D
закруглений на краях. В резонансной точке активное сопро-
тивление одинаково для всех случаев и равно примерно
500 ом.
Помимо щелей такого вида, как на рис. 1.9 (а, б, в,
Ж, и, к), которые сдмы будем называть разомкнутыми,
встречаются также щели замкнутые, как на рис. 1.9
(г, з). По аналогии с вибратором незамкнутая щель имеет
резонанс при длине I, равной целому числу полуволн
^1=п^, а замкнутые щели при длине Z, равной целому
числу волн (Z = nZ).
До сих пор мы считали щелевую антенну излучающей
и сравнивали ее с эквивалентным излучающим вибратором.
Отметим в заключение одно важное следствие из принципа
двойственности, относящееся к щелевой антенне, работаю-
щей на прием. Это следствие получим из сравнения щеле-
вой антенны с приемным вибратором.
452
*7
Рис. 8.3. Экспериментальные кривые входного сопротивления шели
на плоском экране большого размера при длине щели 70 см и раз-
личных значениях ширины I) 2 см, 2) 4 см, 3) R см, 4) 8 см.
т
Рис. 8.4. Экспериментальные кривые входного сопротивления гантель-
ной щелевой антенны: а) активная составляющая, б) реактивная
составляющая.
454
Известно, что электродвижущая сила $2, возбужденная
в приемном вибраторе равна
<f2 = £V<H <8-22)
где Е— амплитуда электрического вектора падающей
волны,
& — угол между электрическим вектором и осью ви-
братора,
F(Я) — нормированная диаграмма направленности вибра-
тора.
В целях получения максимального значения <82 прием-
ный вибратор обычно располагают параллельно электриче-
скому вектору поля.
В соответствии с принципом двойственности можно по-
казать, что э. д. с. в приемной щелевой антенне может быть
выражена через магнитодвижущую силу равную
= (8.23)
где Н — амплитуда магнитного вектора падающей волны,
& — угол между магнитным вектором поля и осью
щели.
В целях получения максимального значения следует
располагать щель параллельно магнитному вектору падаю-
щей волны.
Сделанные здесь на базе принципа двойственности вы-
воды о характере электромагнитного поля идеальной щеле-
вой антенны приближенно справедливы также для большин-
ства реальных щелевых антенн.
§ 2. ЩЕЛИ НА МЕТАЛЛИЧЕСКИХ ПЛАСТИНАХ
КОНЕЧНЫХ РАЗМЕРОВ
Как указывалось выше, в качестве излучателей исполь-
зуются щели, вырезанные на стенках прямоугольного вол-
новода. Очевидно, что характеристики излучения таких ще-
левых антенн должны отличаться от характеристик излуче-
ния идеальной щелевой антенны, поскольку размеры стенок
волновода сравнительно невелики (ширина стенок состав-
ляет примерно 0,3—0,7 2). Представление о характеристиках
излучения щели на стенке прямоугольного волновода можно
получить, исследуя излучение щели на металлической пла-
стине конечного размера.
455
На рис 8,5, а показана металлическая пластина с полу-
волновой щелью 1 = ~2 • Там же приведены обозначения
размеров и принятая система координат. Ось Z направ-
лена перпендикулярно чертежу. Требуется найти выраже-
ние для диаграмм направленности щели в основных пло-
скостях: уг (Е-плоскость) и xz (Я-плоскость).
Эта задача не решена строгими методами. Известно два
метода приближенного решения задачи: метод последова-
тельных приближений и метод, основывающийся на решении
задачи о диффракции плоской волны на эллиптическом ци-
линдре с последующим применением теоремы взаимности.
Начнем с метода последовательных приближений.
По этому методу в первом приближении предпола-
гается, что щель на пластине конечного размера создает
в пространстве такое же поле, как идеальная щелевая
антенна. Поскольку щель имеет длину 1 — ^, то в соот-
ветствии с принципом двойственности составляющая маг-
нитного вектора Нх на близких расстояниях равна
/ а~-jkRl а~~1‘
+ (8.24)
где и R2 —расстояния от точки наблюдения М (рис. 8, 5, а)
до концов щели,
U — напряжение в щели.
Составляющей поля Нх соответствует составляющая
плотности тока I на каждой стороне поверхности пла-
стины, причем
1у = Нх. (8.25)
Составляющая плотности тока 1Х не будет создавать поля
в главных плоскостях и в приводимом ниже расчете не
учитывается.
Как отмечалось выше, электромагнитное поле щелевой
антенны может быть однозначно определено либо через ка-
сательную составляющую электрического вектора в щели,
либо через токи на металлической поверхности, на которой
зырезана щель. В случае бесконечной плоскости оба спо-
соба определения поля приводят к одинаковому результату.
При приближенном расчете поля излучения щели на
плоской металлической пластине конечных размеров пред-
полагается, что составляющая тока 1у на пластине конеч-
456
a)
Рис. 8.5. а) Металлическая пластина
со щелью, б) то же при наличии
экранирующей полости с одной сто-
роны пластины.
в)
457
них размеров определяется по формулам (8.24) — (8.25),
полученным согласно первому приближению, хотя на самом
деле эти соотношения справедливы при неограниченно боль-
шой пластине. Далее, в качестве второго приближения при-
нимается, что электромагнитное поле в пространстве опре-
деляется токами на пластине конечных размеров, опреде-
ленными по (8.24) — (8.25).
Определив электромагнитное поле в пространстве по то-
кам на пластине, можно найти электрический вектор поля
в щели и на части плоскости, являющейся продолжением
пластины. В качестве третьего приближения можно опреде-
лить токи на пластине через новое значение поля в щели
и через значение поля на продолжении пластины, а затем
электромагнитное поле излучения через новое значение I
на пластине.
Аналогично может быть найдено четвертое, пятое и дру-
гие приближения. Сопоставление с экспериментальными дан-
ными показывает, что достаточно точное значение поля из-
лучения щели на плоской пластине конечных размеров мо-
жет быть найдено на основе приближенных формул (8.24)
и (8.25), т. е. на основе второго приближения.
Электромагнитное поле в основных плоскостях опре-
деляется по формулам (2.64) и (2.65) при подстановке
Es=0 и Hs — 2HX (множитель 2 при Нх учитывает токи
на обеих сторонах пластины). Итак,
£С=--2'Ш,[Н-с'в1>£Т“'г*' (8-26)
(8-27>
Интегрирование проводится по поверхности пластины.
г — расстояние от удаленной точки наблюдения до точек
пластины.
Аналогично предыдущему [см. (3.11) и (3.12)] можно
представить (8.26) и (8.27) в виде
Ее = ~ e~‘kPa j J cos C°S & dxdy' <8-28)
EH=~ e~‘kR° J j Ик eikX C°S 9dxd^ (8.29)
где /?0—расстояние от центра щели до точки, в которой
определяется поле излучения.
458
Интегралы в (8.28) и (8.29) не приводятся к простым
функциям. Для облегчения расчета можно аппроксимиро-
вать Нх более простым выражением, чем (8.24). В [43]
показано графическим построением, что приближенно
можно положить
—0,025у
—---------Iky
(8.30)
Подставив (8.30) в (8.28) и выполнив интегрирование,
получаем следующее выражение для диаграммы направ-
ленности в Е-плоскости:
fE = cos Я
-0.025Z
— ------jkL (1—sin ft)
e x — 1
— 0.025L
---------— jkL (1—sin S)
-0.025Z
---------JkL (1 -f-sin ft)
e k — 1
—0.025L
---------—jkL (1 Ц-sin 6)
(8.31)
На рис. 8.6 показана диаграмма направленности
в Е-плоскости щели, вырезанной на металлической пла-
стине прямоугольной формы размером 1,02X1,0^. Сплош-
ная кризая соответствует расчету, а пунктирная—экспе-
рименту. Совпадение кривых очень хорошее.
Мы видим, что диаграмма направленности имеет вид
восьмерки, в то время как идеальная щелевая антенна
имеет в Е-плоскости круговую диаграмму направленности.
Выражение (8.31) получено в предположении двухсто-
роннего излучения щели. Если с одной из сторон пластины
экранировать (закрыть) щель какой-нибудь металлической
поверхностью (полостью), как показано на рис. 8.5,6, то из-
лучение будет односторонним. Для определения электромаг-
нитного поля излучения в этом случае необходимо распро-
странить интегралы в (8.23) и (8,29) как на поверхность
основной плоской пластины, так и на дополнительную экра-
нирующую поверхность. Очевидно, что точное решение
в данном случае еще сложнее, чем при двустороннем излу-
чении.
В качестве основы для приближенного решения можно
принять, что токи будут отсутствовать на той стороне пла-
4 54
стины, где щель закрыта, а также на наружной стороне
экранирующей поверхности и что излучение определяется,
во-первых, токами на той стороне пластины, на которой
щель открыта и токами на внутренней стороне экранирую-
щей поверхности (внутри экранирующей полости). Далее
можно принять, что на соответствующей стороне пластины
токи сохраняются такими, как при двустороннем излучении,
т. е. определяются (8.24) — (8.25), а излучение токов на
внутренней стороне экранирующей поверхности может быть
Рис. 8.6. Диаграмма направленности в Д-плоскости
щели в металлической пластине прямоугольной
формы размером 1,0 X X 1,0 X, сплошная кривая —
расчетная, пунктирная —экспериментальная.
заменено излучением поля на открытой части поверхности,
т. е. поля в щели, которое равно полю идеальной щелевой
антенны.
Таким образом, при одностороннем излучении металли-
ческой пластины с полуволновой щелью электромагнитное
поле излучения складывается из поля токов на пластине,
меняющегося по диаграмме рис. 8.6, и поля излучения щели,
имеющего в f-плоскости круговую диаграмму направлен-
ности.
При'^расчете в-'этом^ случае также>используются фор-
мулы (2.64) и (2.65), но Es уже не полагается равным
нулю, как при получении формул (8.26) и (8.27), а'счи-
тается равным полю в щели. Если выполнить интегриро-
вание при указанных 'условиях, то получается следующее
460
выражение для диаграммы направленности в £-плоско-
сти:
—0,025^- —/*£-( 1—sin 0)
М»)= ----------z----------— +
— 0,025 у— jkL(l — sin в)
Здесь’
-0,025 —jkl (1+slnO)
e A —1
Г
—0,025 у— jkL(l + sinO)
cos &e /'Po kS — j
(8.32)
(8.33)
где Ф — интеграл 'вероятности.
На рис. 8.7 приведены диаграммы направленности, вы-
численные по формуле (8.32) (сплошные линии) и экспе-
риментально снятые (пунктирные линии) для нескольких
различных размеров L- и 77-пластины (см. рис. 8.5). И в дан-
ном случае экспериментальные и теоретические кривые хо-
рошо совпадают.
Пользуясь изложенным выше приемом, можно найти
также диаграммы направленности в //-плоскости. Посколь-
ку они более подробно исследованы вторым методом, то ни-
же приводится изложение основ этого метода.
Перейдем ко второму методу приближенного расчета
электромагнитного поля излучения щели на металлической
пластине конечных размеров. В отличие от предыдущего
метода здесь рассматривается пластина бесконечно боль-
шой длины, но конечной ширины.
По этому методу пластина представляется в виде бес-
конечно длинного эллиптического цилиндра, у которого от-
ношение большой оси к малой есть очень большая вели-
чина, и решается задача о диффракции плоской электромаг-
нитной волны на таком эллиптическом цилиндре, причем
падающая плоская волна предполагается образованной из-
лучением далеко удаленной щелевой антенны. Решая эту
задачу, мы находим поле, созданное щелевой антенной у по-
верхности пластины. На основании теоремы взаимности
можно утверждать, что, поместив щелевую антенну на по-
верхности эллиптического цилиндра, поле в далеко удален-
ной точке, где раньше находилась щелевая антенна, полу-
чается таким же, как в указанной задаче о диффракции.
461
Рис. 8.7. Диаграмма направленности в Д-плоскости щели в метал-
лической пластине прямоугольной формы для различных размеров
пластины: сплошные кривые — расчетные, пунктирные—эксперимен-
тальные.
462
Поскольку в обоих случаях речь идет об определении
поля в какой-либо точке, то щелевой излучатель должен
быть точечным, т. е. иметь размеры, в пределах которых
поле мало меняется. Если щель имеет длину I— у, то ее
можно разделить на большое число малых участков, а за-
тем обычным путем вычислить интегральный эффект от всех
участков.
Не останавливаясь здесь на подробном изложении весь-
ма громоздких выкладок, с которыми связано решение за-
дачи о диффракции электромагнитной волны на эллиптиче-
ском цилиндре и с которыми читатель может познакомиться
в оригинальных работах [44], приведем здесь окончательные
выражения, найденные по второму методу для диаграмм на-
правленности полуволновой щели на бесконечно длинной
пластине ширины а в плоскости, перпендикулярной оси пла-
стины.
При расположении щели параллельно оси пластины ука-
занная плоскость (перпендикулярная оси пластины), в ко-
торой определяется диаграмма направленности, соответ-
ствует Е-плоскости, а при расположении щели перпендику-
лярно оси — //-плоскости.
Согласно [44] диаграмма направленности щели длиною I
на пластинах конечных размеров может рассчитываться по
формулам:
а) щель параллельна оси пластины
00
гс=1 + <8-34)
п=0
в) щель перпендикулярна оси пластины
cos (k у cos — cos k-^
sin В
2
(8.35)
463
порядка,
Здесь
5Лп+^ка, cos &) —нечетная функция Матье 2n-f-l-ого по-
рядка [45],
С^Д/га, cos &) —четная функция .Матье 2п-ого
n _
2Л W<22U^,0)Ce2„(fea,0)’
(8.36)
/М“+1
^Й!г+1 °)
(8.37)
где Н{22п (ka, Е)— четная функция Матье—Ганкеля 2п-ого
порядка,
^s2n-f-i — нечетная функция Матье—Ганкеля 2п+
4-1-ого порядка.
Штрих у последних означает производную по Е.
и Bj"+1 — коэффициенты первых членов разложения со-
ответственно функции Се2п по cos iS и 5е2л+1 по sin/&.
В [45] приведены таблицы численных значений А20п и В2л+1
так же как таблицы функций Матье.
Из (8.34) и (8.35) видно, что диаграмма направленно-
сти имеет два слагаемых, из которых одно представляет
собой соответствующую диаграмму направленности идеаль-
ной щелевой антенны, а второе — диаграмму направленно-
сти токов на поверхности пластины.
Как мы видели выше, такую же структуру (в ином ма-
тематическом выражении) имеет диаграмма направленно-
сти, полученная первым методом. Диаграммы направленно-
сти, вычисленные для ряда конкретных случаев по тому и
другому методу, сравнительно хорошо совпадают.
Следовательно, оба метода можно считать равноцен-
ными.
На рис. 8.8 приведена серия диаграмм направленности
полуволновой щели в //-плоскости (щель перпендикулярна
оси пластины), вычисленных по формулам (8.34) — (8.35).
Из рис. 8.6—8.8 видно, что диаграмма направленности
щели на металлической пластине ограниченных размеров
в //-плоскости мало отличается от соответствующей диа-
граммы направленности идеальной щелевой антенны,
а в f-плоскости отличие между ними весьма заметно.
464
О о
Рис. 8.8. Диаграмма направленности в //-плоскости полуволновой
/ * \
щели U==2' в бесконечно длинной металлической пластине шири-
ной а (щель перпендикулярна оси пластины) для различных
а
значений у.
§ 3. ЩЕЛИ НА СТЕНКАХ ПРЯМОУГОЛЬНОГО ВОЛНОВОДА
Рассмотрим щелевые антенны в виде щелей на стенках
прямоугольного волновода при возбуждении в последнем
волны типа ТЕоь Условно будем их называть параллелепи-
педными щелевыми антеннами. Сами щели будем считать
резонансными полуволновыми (основной резонанс), так как
именно такие в основном и встречаются на практике.
Как показывает эксперимент, полуволновая резонансная
щель на стенке прямоугольного волновода имеет длину I,
30—1503 466
близкую (несколько меньшую) к половине длины волны,
а напряжение в щели меняется примерно по синусоидально-
му закону, имея нулевое значение на краях и максимум
в середине. Иными словами,. резонансная щель на стенке
прямоугольного волновода по основным признакам иден-
тична идеальной щелевой антенне. Как увидим ниже, эта
эквивалентность сохраняется и по ряду других признаков.
Сказанное позволяет положить в основу теории параллеле-
пипедной щелевой антенны принцип двойственности.
Следует, однако, заметить, что щель на стенке прямо-
угольного волновода в некоторых отношениях отличается
от идеальной щелевой антенны. Можно в этом отношении
указать следующие три основные особенности параллеле-
пипедной щелевой антенны:
1. Щель у рассматриваемой антенны вырезана не на не-
ограниченно большой плоскости, а на плоской стенке ко-
нечных размеров.
2. Щель в указанном выше (§ 2) смысле односторонне
излучает во внешнее пространство, в то время как идеаль-
ная щелевая антенна предполагалась излучающей по обе
стороны от проводящей плоскости.
3. Независимо от того, является ли антенна передаю-
щей или приемной, щель работает и на излучение и на
прием. Действительно, у передающих щелевых антенн щель
является по отношению к внешнему пространству передаю-
щей, а по отношению к внутреннему полю в волноводе —
приемной. У приемных щелевых антенн, наоборот, щель
является приемной по отношению к внешнему электромаг-
нитному полю и передающей по отношению к плоскости
волновода.
Можно, кроме того, отметить, что у реальной щелевой
антенны, в отличие от идеальной, стенки имеют конечную
проводимость и конечную толщину. Однако проводимость
стенок настолько велика, а их толщина настолько мала, что
эти параметры можно считать практически соответствующи-
ми идеальному случаю. Посмотрим, к каким отступлениям
от принципа двойственности приводят отмеченные выше три
особенности параллелепипедной щелевой антенны.
1. Поскольку в рассматриваемом случае щель сделана
на стенке конечных размеров, вполне естественно ожидать,
что форма ее диаграммы направленности будет отличаться
от формы диаграммы направленности идеальной щелевой
антенны.
Представление о диаграмме направленности щели на
466
стенке прямоугольного волновода можно получить из дан-
ных предыдущего параграфа. Однако из-за влияния трех
стенок, не имеющих щелей, эти данные должны быть не-
сколько прокорректированы.
Обобщая теоретические и экспериментальные данные,
можно представить себе диаграммы направленности парал-
лелепипедной щелевой антенны в виде рис. 8.9 (сплошная
кривая). Пунктирные кривые на этом рисунке соответ-
ствуют диаграммам направленности идеальной щелевой
антенны.
Отличие диаграмм направленности параллелепипедной и
идеальной щелевых антенн имеет место главным образом
Рис. 8.9. Диаграмма направленности в-£- и*//-плоскостях продоль-
ной щелевой антенны: сплошные кривые — параллелепипедной, пунк-
тирные — идеальной.
в Е-плоскости. Однако это отличие, важное с точки зрения
направленных свойств, мало сказывается на общем энерге-
тическом балансе антенны, т. е. на зависимости полной
мощности излучения от поля в щели.
2. В связи с тем, что щель имеет одностороннее излуче-
ние при вычислении мощности излучения интеграл от век-
тора Умова — Пойнтинга может быть взят лишь по одной
полусфере, так как интеграл, взятый по второй полусфере,
имеет очень малую величину и может считаться равным
нулю.
Приближенно можно принять, что зависимость векто-
ров Е и Н поля излучения от напряжения U в щели и
от полярных координат г и & определяется по формуле
(8.11), соответствующей идеальной щелевой антенне. По-
этому в данном случае для мощности излучения Ps,
30*
467
вследствие уменьшения пределов интегрирования, получим
в два раза меньшее значение, чем мощность излучения Pt]
идеальной щелевой антенны (8.13), а именно
= T = Z (60л)2’ (8.38)
Отсюда и для проводимости gz параллелепипедной
щелевой антенны получается величина в два раза мень-
шая, чем в случае идеальной щелевой антенны
2Р,.
— = 2 (60л)2' (8.39)
В приведенных формулах (8.38) и (8.39)
Rz = 73,1 ом
представляет собой сопротивление излучения эквивалент-
ного полуволнового вибратора.
3. Вследствие указанной выше одновременной работы
щели и на излучение, и на прием, вопрос о проводимости
щели не._.может быть решен так просто, как в случае иде-
альной щелевой антенны. Соотношение (8.39) в данном слу-
чае характеризует связь между напряжением в щели в точ-
ке пучности и мощностью излучения.
Для определения проводимости щели должна быть най-
дена также зависимость между напряжением в щели и
мощностью излучения в волновод. Для этого мы должны
обратиться к теории возбуждения волновода щелью.
Задача о возбуждении волновода щелью может быть
решена методом вспомогательных источников, который,
как мы видели выше, основывается на применении леммы
Лоренца (2.9, а). В нашем случае внутри волновода от-
сутствуют возбуждающие (сторонние) токи /эи/м. Поэто-
му (2,9а) приводится к виду
J[(n [£Я|]) + (л [Я£,])}^ = 0, (8.40)
где п — орт нормали, направленный внутрь объема, замк-
нутого поверхностью S.
На рис. 8.10 показан волновод прямоугольного сече-
ния со щелью. Размеры поперечного сечения D, и D2 со-
ответствуют условию (4.6), так что волновод пропускает
только волну ТЕ0|.
468
Применим уравнение (8.40) к участку волновода, огра-
-> —>
ничейному сечениями 5, и Snn. считая, что ЕН — поле,
* ЛсВ Прав ' >
—► ->
возбужденное щелью, а ЕХНХ — поле вспомогательных ис-
точников. Как следует из вывода леммы Лоренца (см. гл. II),
к полюЕ,#) предъявляется лишь единственное требова-
ние, чтобы оно удовлетворяло уравнениям Максвелла.
В остальном оно может быть произвольным. В данном
Рис. 8.10. Прямоугольный волновод со щелью (к анализу возбужде-
ния волновода щелью).
случае удобно принять в качестве ЕХН\ поле основной
волны ТЕ01, т. е. поле, определяемое уравнениями (4.3)
при распространении волны в направлении положитель-
ных значений z или аналогичными уравнениями с соот-
ветствующей заменой знаков при распространении волны
в направлении отрицательных значений z. Амплитуду
электрического вектора поля ЕХНХ в середине волновода
(х=0) считаем равной единице.
Итак, составляющие поля ЕХН} по декартовым коор-
динатам равны:
469
а) при распространении в направлении положительных z
„ /ТСХ\ ~П*
cos е
.. 7 /лх\ ~Пг
Н.=--------'-cos К- е
1Х \ • 1 /
тт к 1 /лх\ —Л*
fa) е ’
£х = £г = 0, ^ = 0.
(8.41)
б) при распространении в направлении отрицательных z
„ /ях\ h*
£v=C0S(s;)e •
Я, ^J-cosfS'le'1',
lx
к 1 /лх\ /т?
o?>MS1I1(oJe 1
£, = £,=0. Н,=0.
(8.42)
Интеграл в (8.40) распространяется на поверхность,
замыкающую рассматриваемый участок волновода между
S и S„„. . Так как на стенках волновода касательная
лев прав
—►
составляющая Е\ согласно (8.41) и (8.42) равна нулю во
всех точках, а касательная составляющая Е по условиям
задачи—во всех точках, кроме точек щели, то приходим
к следующему равенству:
’^лев'Ь’^прав
= — j (п [ЕНfids. (8.43)
щель
Предположим, что волновод имеет неограниченную
длину как в сторону положительных z, так и в сторону
отрицательных z. При этом условии излучение щели будет
распространяться в виде бегущей волны вправо и глево от
щели. Расположим сечения 5лев и 5прав (рис. 8.10) на тахом
расстоянии от щели, чтобы можно было считать, что
около этих сечений поле определяется только основной
470
волной ТЕ0[. В этом случае можно считать, что состав-
ляющие поля ЕН по декартовым координатам определя-
ются следующим образом:
а) в сечении 5лев
~ . /ях\ h*
Ey=Acos^e '
Н =А -Lcos е/тг,
х “!хо /
.. . т. 1 h*
Ех = Ег = 0, Ну = 0,
б) в сечении S
' прав
В, = Вс<»^е .
И =_BJ-costeV'’'
X Ш|Л0 у
* О] /Ш[10 \^1/
(8.44)
(8.45)
£х = ^ = 0, Ну=0.
Задача заключается в определении коэффициентов А
и В. Определим сначала коэффициент А. Для этого при-
мем, что ЕХНХ представляет собой поле волны, распро-
страняющейся в сторону положительных г, т. е. состав-
ляющие Е,//| определяются уравнениями (8.41). Подинте-
гральное выражение в левой части (8.43) приводится
к виду
(п [£//,]) + (п ]) = ± (Е1уНх - ЕуН1х), (8.46)
причем знак плюс перед скобкой соответствует плоско-
сти 5лев, а знак минус—SnpaB.
Подставив в (8.46) Е1у и Н[х из (8.41) и Еу и Нх из
(8.44), получим для точек сечения 5лев
(п [£Я,])4- (п [НЕХ |)= 2А cos2 (g) . (8.47)
'1'
471
Подставив в (8.46) Е]у и Н}х из (8.41) и Еу и Нх из
(8.45), получим для точек сечения 5прав
(п[£^1]) + (л[^£1])=0. (8.48)
Подставив, далее, (8.47) и (8.48) в (8.43), получаем
j (n[EHx})ds, (8.49)
щель
причем в (8.49) определяется соответственно (8.41).
Здесь 5n = D1D2— площадь поперечного сечения вол-
новода.
Аналогично, предположив, что Е{НУ—поле волны, рас-
пространяющейся в сторону отрицательных z, получаем
I sn J
щель
(8.50)
причем в (8.50) Нх определяется соответственно (8.42).
Интегралы в (8.49) и (8.50) зависят от расположения
щели, ее размеров и распределения поля в ней. Рассмот-
рим несколько наиболее характерных случаев располо-
жения щели (рис. 8.11), причем длину щели считаем во
всех случаях равной примерно половине волны в воз-
духе (резонансная щель), а распределение поля в щели
полагаем синусоидальным.
1. Продольная щель в узкой стенке волновода
Электрический вектор £ в щели (рис. 8.11,а) паралле-
лен оси Y. Нормаль к плоскости щели параллельна оси X.
Поэтому для подинтегральных величин в (8.49) и (8.50)
получаем
£ = £'J, = 7sin^/e^ — |z|^ , (8.51)
(n [ЕН']) = - ЕуН1г + ЕгН1у = - jsin [k -1 z Н1г,
(8.52)
где U — напряжение в центре щели,
d — ширина щели.
479
Рис. 8.11. Различные виды расположения щелей в стенках
прямоугольного волновода: а) продольная щель в узкой
стенке волновода, 6) наклонная щель в узкой стенке волно-
вода, в) продольная щель в широкой стенке волновода,
г) поперечная щель в широкой стейке волновода, д) то же,
но смещенная относительно средней линии стенки, е) на-
клонная щель в широкой стенке волновода.
473
Подставив (8.51) и (8.52) в (8.49) и (8.50) и учитывая
соответственно (8.41) и (8.42) при х=^~, получаем
(* т\
А=- V (n[Etf ])ds=l--------------------к—Z- =
1 J ' 1 ш J klDiSn _ /jf_\2
щель 1 I k I
8itD<U /лт\ /n
— 7^js7cos \2kj ’ (8-53)
B = A. (8.54)
2. Наклонная щель в узкой стенке волновода
Вводим новую систему координат У, Z', направив
ось Z' параллельно щели. В этой системе координат для
точек щели (рис. 8.11,6) имеем
E=Ely= rsin [* (т“ и)] . (8.55)
(п [ЕН4)=- EiyHiz, + Ez,Hly, = -4 sin [£ (I - J l)] •
(8.56)
Так как
/7]г, = cos О,
то
2
4
А =7^Г U f Sin (д - и)] е"Лг’C0S ^dz' =
~ Г
2л cos 6
(8.57)
В = А.
(8.58)
474
3. Продольная щель в широкой стенке волновода
Электрический вектор поля в щели параллелен оси X.
Нормаль к плоскости щели (рис. 8.11,в) параллельна
оси Y. Следовательно,
E = Ex = ^sm\k(^~\z\\], (8.59)
(« [ЕН,]) = - ВДх + ЕхН1г = sin [Hl -1 г |)] Н,г.
(8.60)
Подставив (8.59) и (8.60) в (8.49) с учетом (8.41), по-
лучаем
, d X
х‘+-2 *4
. 1 It 117 Г . JCX . Г ь ! | I \ 1 ~!1г J
Л =-----гтг-гт— -у I sin-H-ax I sin & Н— 2 е dz.
j Di tsn d J Dt j L \4 1 7J
___*
1 2 4
(8.61)
Так как d<^x, то можно положить
f . fnXtX
J slnVM
dx = dsin .
(8.62)
Второй интеграл в (8.61) тождественен интегралу в (8.53).
Следовательно
й = <8-63)
В = А. (8.63а)
4. Поперечная щель в широкой стенке волновода
с центром на средней линии (рис. 8.11,а)
Повторяя предыдущие рассуждения, приходим к сле-
дующим математическим выкладкам:
E = Ez = ysin[z> 0- — |x|)j, (8.64)
(n [ЕН,]) = -Е2Н1х + ЕХН12 = - у sin [ k (1 -1 х |)] н,x,
(8.65)
475
В (8.66) положено sU, поскольку yt/<l.
Аналогично получаем для поперечной щели на широ-
кой стенке волновода, смещенной относительно средней
линии (рис. 8.11, д)
В = — А.
(8.68)
(8.68а)
5. Наклонная щель в широкой стенке волновода
с центром на средней линии (рис. 8.11,е)
Вводим систему координат X', Z'. В этой системе ко-
ординат
E = Ex,=^sm[k (8.69)
(п [Ен\])= - Ег,Н1х, + Е,,Н1г> = у sin [б (4 - I |)] -Н1г„
(8.70)
Я1г, = //гсозб —tf^sinO. (8.71)
Если подставить в (8.71) значения Нг и Нх из (8.41),
то получим
гг я 1 . litx\ п —/уг у /лх \ . п —Лг ,Л
^rz' = 7T77rsln 7Г cos0e + — cos(n- Sin бе . 8.72)
u Dt juui, J 1 \DiJ v '
476
Вводим замены
х==х' sin 6,
z = z'cosG, •
ПХ КХ
. ях е D‘ — е D>
S1I4=-------2}----
.ПХ . ПХ
тгх е °’ + е °*
C0SD?=------2-----
Воспользовавшись (8.73) и (8.72), получаем
А = [Л1 sin О Ц- N cos 6],
где
1Z
COS -к COS^T-q
М=,—
1 — V 1 — V
я
COS у COS у *1
ЕЩ? 1 —
?=lcos9__J.sin0I
(8.73)
(8-74)
(8.75)
(8.76)
(8.77)
i)= 1 cos 9+^ sin 0, (8.78)
В = — А. (8.79)
Мы рассмотрели задачу о возбуждении волновода
шелью.
Рассмотрим обратную задачу. Предположим, что в не-
ограниченном волноводе из области z->—оовнаправле-
лении положительных значений z распространяется волна
типа ТЕ01. В волноводе прорезана щель, центр которой
имеет координату z=0. Требуется найти поле в щели.
Поскольку поле в щели^- связано простыми соотно-
шениями (8.53), (8.57) и т. п. с коэффициентом А, то за-
дача сводится к определению А.
Задача может быть решена с помощью уравнения
энергетического баланса.
Под влиянием электромагнитной волны в волноводе
в щели возбудится поле, которое приведет к излучению во
♦77
внешнее пространство и к обратному излучению в волновод.
Пользуясь приведенными выше обозначениями и учитывая,
что под влиянием щели поле внутри волновода будет созда-
ваться в результате суперпозиции поля первичной волны
и поля излучения щели в волновод, можно написать сле-
дующее уравнение энергетического баланса (связь между
мощностью и полем см. 4.20; при раздельном рассмотрении
падающей и отраженной волн для каждой из них коэффи-
циент отражения Г =0).
i^o т _______ А2 т Sn
120л k 2 120л k 2
, ± «5 2 _23Д_
+ 120л k 2 2-(60л)2'
Из (8.80) следует
и2 k 73,1 2 _ /. . В2 . 2ВЕп\
А2 т 60л Sn— ' А2 + А‘* J
(8.80)
(8.81)
(72
Мы видели выше, что В=±А. Отношение -г-„ для каж-
дого конкретного случая легко найти описанным выше
методом. ^Следовательно, уравнение (8.81) позволяет
А
наити -=г и поэтому является решением задачи.
•Со
Коэффициент А определяет амплитуду поля волны,
излученной щелью в сторону отрицательных значений г.
Отношение поэтому является коэффициентом отраже-
^-0
ния Г. Это позволит представить (8.81) в виде
U2 k 73,1 1 __ о А 1 \
Д2 ' 7 30л Sn— 1 (/ — Г/’
(8.82)
Из (8.82) можно найти коэффициент отражения Г в вол-
новоде, вызываемый резонансной щелью, вырезанной на
его стенках.
В теории волноводов для характеристики неоднородно-
стей, какими в частности являются щели, часто прибегают
к аналогиям с длинными линиями. Воспользуемся этим ме-
тодом аналогии для определения проводимости щели.
Рассматриваемый бесконечный волновод эквивалентен
длинной линии, нагруженной в конце на активное сопротив-
ление, равное волновому р. Предположим, что в какой-либо
точке эта согласованная линия шунтирована проводи-
478
мостью g. Как известно из теории длинных линий, между
коэффициентом отражения Г и нормированной проводи-
мостью £()=£? существует связь
г = (8.83)
или
£о =------(8-84)
1 +7"
Сопоставляя (8.84) и (8.82), приходим к выводу, что,
во-первых, щель в волноводе при В= + А эквивалентна
шунтирующей проводимости
120я с 7 A2 ,Q
73,1 (8.85)
во-вторых, что при В = — А щель не может быть пред-
ставлена в виде шунтирующей проводимости. При А=— В
щель эквивалентна сопротивлению г, включенному по-
следовательно в согласованную линию. Как известно,
коэффициент отражения в этом случае связан с норми-
рованным сопротивлением г0 = — соотношением
или
г0 = —Ц-. (8.87)
1 — Т”
Сопоставляя (8.87) и (8.82), заключаем, что при А —
— — В щель эквивалентна нормированному сопротивле-
нию
_ 120 л о dl
° 73,1 " k U2 '
(8.88)
Л2
Зная связь между или г0 и не представляет
труда с помощью формул (8.53), (8.63), (8.68) и (8.74)
найти соответствующие различным видам щелей значе-
ния g? или г0.
Объяснение того факта, что в одних случаях щель экви-
валентна шунтирующей проводимости, а в других последова-
тельному сопротивлению, можно видеть в том, что на поле
479
первичной волны накладывается поле, которое по разные
стороны от середины щели в направлении оси Z при А —
— +В имеет магнитное поле противоположного знака, а при
А = — В — электрическое поле разного знака. Поэтому в пер-
вом случае около щели имеет место разрыв непрерывности
магнитного вектора поля, что эквивалентно утечке тока, а во
втором случае имеет место разрыв непрерывности электри-
ческого вектора поля, что эквивалентно потере напряже-
ния на сопротивлении.
Мы до сих пор рассматривали бесконечный волновод.
Полученные данные могут быть обобщены на случай полу-
бесконечного волновода.
Предположим, что на расстоянии z0 от центра щели спра-
ва волновод закрыт поршнем. В этом случае уравнение
энергетического баланса будет выглядеть следующим об-
разом:
£’= |.А - (В + Ео) е-'2^Г + А AAL. (8.89)
Иначе
Е* = А2 + (В 4- Е0)2 - 2А (В + Ео) cos 2Tz0 Ц- A -A AjI .
7 Од
(8.90)
Подставив В = ±А, мы приходим к следующим
ствам:
£0sin2Y20=-------,
'+i
r0COS’TZ0 =--------S- .
1 ——
А
Из (8.91) находим
при В —А
А __ go Sin2 f z0
Ea 1 + go sin2 f z0 ’
при B—~ A
A r0cos2fz0
£0 1 -f- r0 cos'2 -fz0
равен-
(8.91)
(8.82)
(8.93)
Коэффициент отражения в волноводе равен
Г = А /л2 + (В + Е0)2 - 2А"(В + Ео) cos 2р0 =
У Un2~ M/coS27z0' }
480
Положительный знак под корнем в (8.94) и множитель
sin2yz0 соответствуют В = А, а отрицательный знак и
множитель cos2yz0 соответствуют В = — А.
Из (8.94) с учетом (8.92) и (8.93) следует, что при
вещественном значении Г = 0 имеет место в полубес-
конечном волноводе при одновременном выполнении двух
условий:
sin2ps0 |
cos2 уг0 J ’
1
''о/
(8.95)
2)
(8.96)
При бесконечном волноводе условием согласования,
согласно (8.84) и (8.87) является gQ — 0 или г = 0, т. е.
отсутствие щелей. Поскольку волновод согласован без
щелей, то щели всегда вносят расстройку.
Помимо однощелевых антенн, являющихся слабо на-
правленными, применяются многощелевые антенны, создаю-
щие остронаправленное излучение. Многощелевые антенны
представляют собой волновод, в какой-либо стенке которо-
го вырезан ряд щелей на одинаковом расстоянии друг от
друга, причем расстояние между ними выбирается с таким
расчетом, чтобы излучение всех щелей было синфазным.
Рассмотрим вопрос о наиболее целесообразном расположе-
нии щелей у многощелевой параллелепипедной антенны.
Обратимся к рис. 8.12,а, на котором показана картина
магнитных линий поля на внутренней поверхности стенок
волновода до образования щелей. Мы видим, что на узкой
стенке волновода магнитные линии везде параллельны оси
волновода, т. е. магнитный вектор поля имеет только про-
дольную составляющую. На широкой стенке волновода маг-
нитные линии поля образуют замкнутые кривые. Среднюю
линию АА широкой стенки эти кривые проходят перпенди-
кулярно, т. е. на этой линии магнитный вектор имеет только
поперечную составляющую. В других точках широкой стен-
ки магнитный вектор имеет как поперечную, так и продоль-
ную составляющую.
Указанные данные о направлении магнитного вектора
поля в различных точках на стенках волновода являются
исходными для определения ориентации щелей. Из сказан-
ного очевидно, например, что продольные щели, прорезан-
ные на средней линии широкой стенки волновода, и попе-
31—1503 481
речные щели на узкой стенке
г?
Рис. 8.12. Прямоугольный волно-
вод, возбуждающий щели: а) маг-
нитные линии поля на внутрен-
ней поверкчости стенок волно-
вода без щелей, б) расположение
продольных щелей на узкой стен-
ке волновода, в) расположение
поперечных щелей на широкой
стенке волновода, г) расположе-
ние продольных щелей на широ-
кой стенке волновода.
не излучают, как щели, рас^
положенные перпендикуляр-
но магнитным линиям поля.
На узкой стенке волновода
лучше всего излучают про-
дольные щели, а на широ-
кой стенке — поперечные.
Излучение продольных ще-
лей на широкой стенке вол-
новода зависит от расстоя-
ния Xi от средней линии
(рис. 8.11,6). Чем дальше
расположены эти щели от
средней линии, тем они луч-
ше возбуждаются и, следо-
вательно, тем больше интен-
сивность их излучения.
Итак, у параллелепипед-
ной щелевой антенны щели
целесообразно делать про-
дольными на узкой стенке и
поперечными или продоль-
ными на широкой стенке,
причем последние должны
быть смещены относительно
средней линии АА.
В сложной синфазной ан-
тенне, помимо вопроса об
ориентации щелей, важным
является также вопрос о вы-
боре расстояния между ще-
лями. Из рис. 8.12, а видно,
что продольные щели на уз-
кой стенке и поперечные ще-
ли на широкой стенке долж-
ны располагаться на рас-
стоянии 2Ф друг от друга (см.
соответственно рис. 8.12,6
и 8.12, в), так как на таком
расстоянии находятся точки
одинаковой фазы соответ-
ствующих составляющих
магнитного вектора поля.
Продольные же щели на
482
Широкой Стенке волйовода Могут располагаться в шаХМаТ-
л.
ном порядке на расстоянии друг от друга, как показано
на рис. 8.12, г, поскольку продольная составляющая магнит-
ного вектора поля на широкой стенке меняет фазу на
обратную при переходе средней линии АА в поперечном
направлении.
Расположение щелей в многощелевой синфазной ан-
тенне на расстоянии 2ф друг от друга должно привести
к значительным боковым лепесткам в диаграмме направ-
ленности, между тем как при расстоянии —диаграмма
направленности должна получиться такой же, как обыч-
но у синфазных антенн. По этой причине следует счи-
тать наиболее целесообразной многощелевую антенну
вида, показанного на рис. 8.12, г с продольными щелями
на широкой стенке ^олнозода.
Следует заметить, что применение продольных щелей на
широкой стенке волновода удобно также с точки зрения со-
гласования. Так как внутренняя проводимость этих щелей
зависит [как видно из (8.63) и (8.92)] от расстояния хх меж-
ду осью щелей и линией АА, то она может быть подобрана
так, чтобы удовлетворить условию согласования.
Если для однощелевэй антенны условием согласова-
ния является разенство (8.96), то для многощелевой ан-
тенны, у которой щели
или -j- друг от друга-,
соответственно
расположены на расстоянии 2ф
условием согласования является
п^о=1,
пг0= 1,
(8.97)
можно располагать также наклон-
где п — число щелей.
На расстоянии -у-
ные щели на узкой стенке волновода. Принцип действия ил-
люстрируется рис. 8.13,а. Вертикальные стрелки на рисунке
показывают направление токов. Так как ширина узкой
л
стенки меньше %, то Шель занимает всю ширину стенки
и продолжается еще на широкой стенке до резонансной дли-
ны (рис. 8.13,6).
Недостатком наклонных щелей является наличие пара-
зитной поляризации. В целях ее уменьшения требуется при-
31* 483
Менять большие углы G между осью щели и осью волново-
да (G>75°), при которых мощность, теряемая на паразит-
ную поляризацию составляет меньше 1%. Однако это огра-
ничивает возможность регулировки эквивалентной проводи-
мости g0 и условий согласования.
Помимо непосредственного возбуждения щелей от поля
в волноводе, применяется возбуждение с помощью реактив-
Рис. 8.13. Расположение наклонных щелей в узкой
стенке прямоугольного волновода.
Рис. 8.Н. Возбуждение щелей в прямоугольном волноводе
с помощью штырей.
ных штырей (рис. 8.14) или диафрагм. В этом случае щели
располагаются так, что они сами не возбуждаются от поля
в волноводе, т. е. они располагаются вдоль оси волновода
на широкой стенке или перпендикулярно оси на узкой стен-
ке. Сами щели при этом имеют длину, отличную от резо-
нансной, и настраиваются указанными реактивными эле-
ментами. Расстояние между щелями может быть равно —
при чередующемся расположении реактивных элементов по
разные стороны щели.
434
Щелевые антенны могут применяться совместно с ру-
порами (рис. 8.15, а) или сегментно-параболическими ан-
а)
Рис. 8.15. Возбуждение с помощью щелей: а) систе-
мы рупоров, ff) системы параболических сегментов.
теннами (рис. 8.15,6). В этом случае расстояние между
щелями может быть сделано больше .
§ 4. ЩЕЛИ НА КРУГЛЫХ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЯХ
Здесь мы рассмотрим щелевые антенны в виде щелей на
круглых металлических трубах, которые мы будем называть
цилиндрическими щелевыми антеннами.
Цилиндрические щелевые антенны еще в большей степе-
ни отличаются от идеальной щелевой антенны чем паралле-
лепипедные.
Во-перзых, у цилиндрических щелевых антенн щели
вырезаны не в плоской, а в криволинейной поверхности,
во-вторых, нередко в качестве тела такой антенны ис-
пользуются металлические трубки сравнительно малого
диаметра d(d<^X). Известна, например, щелевая антенна,
485
III КоаксиалЬнЬш
HI Оадер
Рис. 8.16. Цилиндри-
ческая щелевая ан-
тенна малого диа-
метра.
изображенная на рис 8.16, представляющая собой круг-
лую металлическую трубу диаметром а = у с рядом про-
дольных щелей, питаемых с помощью фидерной линии,
проходящей внутри этой трубы. Длина щелей у этой ан-
тенны равна / = ширина—а — ^- Расположены щели
на расстоянии 2 друг от друга.
Указанные две особенности цилин-
дрических щелевых антенн приводят,
во-первых, к образозанию значитель-
ного заднего излучения и, во-вторых,
к резонансной длине щелей, отличной
X г>
от-£. Рассмотрим эти вопросы по-
дробнее. Начнем с особенностей диа-
грамм направленности цилиндричес-
ких щелевых антенн.
Теоретическое решение задачи об
излучении цилиндрической щелевой
антенны (рис. 8.16) по заданному по-
лю в щели получено А. А. Пистолькор-
сом [46], а затем М. Л. Левиным (47).
Ими исследованы как продольные, так
и поперечные щели. Но поскольку прак-
тический интерес имеют главным обра-
зом продольные щелевые антенны, поз-
воляющие получить горизонтально по-
ляризованное излучение с круговой ди-
аграммой направленности, какая тре-
буется для телевидения, частотной мо-
дуляции и других областей УКВ радио-
техники и поскольку, кроме того, ре-
зультаты исследования продольных
большей полнотой и ясностью, мы здесь
эти щелевые антенны.
В отношении цилиндрических щелевых антенн с продоль-
ными щелями удобна будет следующая терминология:
плоскость, проходящую через щель и через ось цилиндра,
будем называть меридиональной плоскостью, а плоскость,
перпендикулярную к щели и к оси цилиндра, — азимуталь-
ной плоскостью. Составляющие поля, касательные к мери-
диональным и азимутальным линиям, будем называть мери-
диональной и азимутальной составляющими поля,
486
щелей характерны
оассмотоим только
У рассматриваемой щелевой антенны, очевидно, мери-
диональная составляющая электрического вектора Fs = 0.
Для азимутальной составляющей электрического векто-
ра одиночной продольной щели в металтическом ци-
линдре диаметра D на большом расстоянии R от ци-
линдра А. А. Пистолькорс [46] дает следующую фор-
мулу:
. _ __ 2U_ fn (ft) e~/kR 1
ч> r.W cos ft R. / D \
Яр ( 2 cos 9 )
к
0° ip ~x~
V] e z cos
(8.98)
где U — максимальное напряжение в щели,
&—меридиональный угол (относительно оси ци-
линдра),
tp — азимутальный угол (относительно нормали к щели),
f0(&)— диаграмма направленности такого же размера
идеальной щелевой антенны,
Д((2)— ганкелева функция второго рода первого по-
рядка,
Д',2’’— первая производная по аргументу от ганкелевой
функции второго рода первого порядка,
D — диаметр цилиндра.
Ряд в формуле (8.98) сходится тем быстрее, чем меньше
радиус цилиндра. При kD = 2^, т. е. при 0 = 1 достаточно
семь членов для расчета с точностью до 1%. При меньших
диаметрах можно ограничиться еше меньшим числом чле-
нов. Эта формула имеет наибольший интерес при малых
диаметрах цилиндра D, так как при значительных величи-
нах D излучение продольной щели в круглой трубе мало
отличается от излучения параллелепипедной щелевой ан-
тенны. Таким образом, как раз в тех случаях, когда фор-
мула (8.98) представляет практический интерес (£><!),
«расчет по ней значительно упрощается вследствие быстрой
сходимости ряда.
На рис. 8.17 приведены диаграммы направленности в
азимутальной плоскости,, вычисленные по формуле (8.98)
487
Рис. 8.17. Диаграммы направленности в азимутальной плоскости про-
дольной щели на цилиндрической поверхности при различных отно-
шениях -j-.
488
для ряда различных значений отношения у. На рис. 8.17,а
показана принятая система отсчета координат <р.
Из рис. 8.17 видно, что при малых диаметрах цилиндра
(D 0,1) диаграмма направленности в азимутальной плос-
кости имеет форму почти круга. С увеличением диаметра ци-
линдра растет интенсивность излучения впереди щели (<р =
= 0) и ослабляется заднее излучение (при <р —180°). При
диаметрах цилиндра порядка длины волны диаграмма направ-
ленности принимает вид кардиоиды, т. е. сходна с диаграм-
мой направленности параллелепипедной щелевой антенны.
Рис. 8.18. Кривая экранирующего действия цилиндра
у цилиндрической щелевой антенны.
На рис 8.18 приведена кривая экранирующего дейст-
вия цилиндра, т. е. кривая зависимости отношения на-
пряженности поля в направлении <₽ = 0 к напряженности
поля в направлении щ=180° от kD.
На рис. 8.19,а показана измеренная диаграмма направ-
ленности одиночной продольной щели на цилиндрической
поверхности в азимутальной плоскости для двух различных
отношений -у-:: 0,21 (сплошная кривая) и 0,125 (пунктир-
ная кривая). Характер этих диаграмм направленности нахо-
дится в согласии с теоретическими данными. На рис. 8.19,6
сплошная кривая показывает измеренную диаграмму на-
правленности такой щели в меридиональной плоскости.
Пунктирная кривая на рис. 8.19,6 соответствует теоретиче-
ской диаграмме направленности идеальной щелевой антен-
ны. Легко видеть, что в меридиональной плоскости измерен-
489
ная диаграмма направленности по форме не отличается от
теоретической. Имеющееся отличие выражается в проявле-
нии экранирующего действия цилиндра.
Рис. 8.19. а) Экспериментальная диаграмма направленности в азиму-
тальной плоскости продольной щели на цилиндрической поверхности
при различных £); <Т) то же в меридиональной плоскости при D — 0.21Х.
Рис. 8.20. Графики зависимости фазы поля от ази-
мутального угла для цилиндрических щелевых
антенн при различных значениях
D
у =0,0318л, п — целое число
DJ
X (
Интересно отметить, что электромагнитное поле излуче-
ния цилиндрической щелевой антенны имеет различные фа-
зы в точках, лежащих на одинаковом расстоянии от оси
цилиндра,, но под различными азимутальными углами. На
490
рис. 8.20 приведены кривые зависимости фазы поля от ази-
мутального угла (₽ для цилиндрических щелевых антенн,
D
имеющих различное значение -у-.
Знание фазы поля представляет интерес при устройстве
антенны, имеющей ряд щелей, расположенных по окружно-
сти цилиндра на одинаковой высоте. Такое расположение
щелей на цилиндре применяется для формирования опре-
деленной диаграммы направленности в азимутальной плос-
кости.
На рис. 8.21 приведены теоретические диаграммы на-
правленности в азимутальной плоскости цилиндрической
двухщелевой антенны (кружочки соответствуют измеренным
значениям). Диаметр цилиндра равен .0 = 0,5 2. Рис. 8.21,а
соответствует диаметрально противоположному расположе-
нию щелей, питаемых синфазно напряжением с одинаковы-
ми амплитудами; рис. 8.21,6 — диаметрально противополож-
ному расположению щелей, питаемых в противофазе, и
рис. 8.21,в — двум щелям, расположенным, как показано
на рис. 8.21,г, и питаемым со сдвигом фаз 90° при отноше-
нии амплитуд 1 :2. Из рис. 8.21 видно, что подбором ампли-
туд и фаз питания щелей, а также соответствующим их
расположением можно в значительных пределах видоизме-
нять диаграмму направленности в азимутальной плоскости.
Таковы основные особенности в диаграмме направлен-
ности цилиндрической щелевой антенны.
Перейдем теперь к вопросу о резонансной Длине щели.
У цилиндрических щелевых антенн резонансная длина
щели, соответствующая первому (основному) резонансу,
больше полуволны и зависит от диаметра цилиндра. Чем
меньше диаметр цилиндра, тем больше резонансная длина
щели. При больших диаметра цилиндра резонансная длина
равна примерно у.
Это явление может быть объяснено следующим обра-
зом. Щель в известном смысле эквивалентна двухпровод-
ной линии. Однако в отличие от обычной двухпроводной
линии, здесь ее провода замыкаются через проводящую
поверхность цилиндра, которая при малых диаметрах по-
следнего может рассматриваться как непрерывно распре-
деленная шунтирующая индуктивность. Длинная линия
же, шунтированная индуктивностью, характеризуется фа-
зовой скоростью Следует отметить, что при боль-
щой проводимости шунтирующих индуктивностей может
491
вообще не иметь места распространение волны по линии.
И действительно, цилиндрическая щелевая антенна ха-
рактеризуется критической длиной волны 2кр> являющейся
для данных щелей предельно большой. Более длинные
волны в данной щели не возбуждаются. Критическая
Рис. 8.21. Диаграммы направленности в азимутальной плоскости
цилиндрической двухщелевой антенны, имеющей при раз-
личном расположении и питании щелей: а) диаметрально противопо-
ложное расположение щелей, иитаемых синфазно с равными ампли-
тудами; б) то же, но при противофазном питании щелей; в) щели
сдвинуты одна относительно другой на 90° по азимуту, как показано
на рис. г), и питаются со сдвигом фаз 90° при отношении амплитуд 1:2;
г) размещение щелей у двухщелевой антенны с диаграммой направ-
ленности, показанной на рис. в).
длина волны зависит, во-первых, от ширины щели и от
толщины стенок цилиндра, поскольку от этих параметров
зависит погонная емкость щели, во-вторых, от диаметра
цилиндра, поскольку от этого зависит величина погонной
492
Шунтирующей индуктивности. От этих параметров зави-
сит также фазовая скорость va в щели. Количественно
эти зависимости пока подробно не исследованы. Некото-
рое представление об этом можно получить из приведен.
ного на рис. 8.22 графика зависимости отношения
от -^-для щелей шириной d — 0,0620, при толщине стенок
/> = 0,0150.
В заключение кратко остановимся на вопросе питания
цилиндрических щелевых антенн.
Рис. 8.22. График зависимости от-
носительной величины фазовой
скорости в щели от относитель-
ной величины диаметра волно-
вода при ширине щели —0,062 D
и толщине стенок волновода
b — 0,015 D.
нитного поля в волноводе. П
При достаточно большом
диаметре цилиндра, послед-
ний может быть использо-
ван в качестве волновода.
В этом случае щель может
возбуждаться от электромаг-
и малых диаметрах цилиндра
внутри последнего проводится коаксиальная или двухпровод-
ная линия, которая приключается к кромкам щели (обычно
в средней точке).
В случае волноводного питания щели для настройки ан-
тенны волновод обычно закрывается передвижным поршнем,
т. е. является согласно принятой здесь терминологии полу-
493
бескйнеиньш. Решение задачи о согласовании й нолубеско-
нечном волноводе круглого сечения может быть выполнено
тем же методом, каким выше решена задача о согласова-
Рис. 8.24. Экспериментальные графики зависимости активной (сплош-
ные .кривые) и реактивной (пунктирные кривые) составляющих вход-
I
ного сопротивления щелей от относительном длины щели -^-при
ширине щели d = 0,062 D и при различных значениях D.
нии в волноводе прямоугольного сечения, т. е. с помощью
уравнений (8.95) и (8.96).
В случае продольной щели на волноводе круглого сече-
ния, при условии, что в волноводе может распространяться
только волна ТЕц ,и при условии, что щель вырезана в ме-
сте, где продольная составляющая магнитного вектора ма-
494
ксимальНа, Нормированная эквивалентная проводимость Ще-
ли равна
где а —отношение внешней проводимости щели к поло-
вине проводимости идеальной щелевой антенны и может
быть определено по графику рис. 8.23, заимствованному из
[47].
В случае фидерного питания щелей для определения
условий согласования и подбора параметров фидера могут
быть полезны экспериментальные кривые изменения актив-
ной (сплошные кривые) и реактивной составляющей
(пунктирные кривые) входного сопротивления щелей в за-
висимости от отношения у, приведенные на рис. 8.24.
Кривые рис. 8.24 получены для щели шириной d = 0,0620
„ D
для различных значении у.
ГЛАВА ДЕВЯТАЯ
ДИЭЛЕКТРИЧЕСКИЕ АНТЕННЫ
§ 1. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В СПЛОШНОМ
ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ КРУГЛОГО СЕЧЕНИЯ
У диэлектрической антенны электромагнитное поле воз-
буждается, как сказано выше (гл. I, § 6), источником S'
(рис. 1.10) в той части диэлектрического стержня, которая
закрыта патроном, и там распространяется как по волново-
ду. Достигнув же границы патрона, оно продолжает распро-
страняться по диэлектрическому стержню, проникая одно-
временно через открытую часть поверхности последнего во
внешнее пространство (воздух). Для определения излуче-
ния такого стержня необходимо найти значение электро-
магнитного поля как внутри стержня, так и вне его.
Эта задача решена в настоящее время для идеализиро-
ванного случая стержня бесконечной длины и постоянного
круглого поперечного сечения. Приведем здесь это решение
и рассмотрим возможность обобщения его на случай реаль-
ных стержней, используемых в качестве диэлектрических
антенн.
На рис. 9.1 показана часть стержня и цилиндрическая
система координат z, р, ср. При исследовании электромаг-
нитного поля в стержне будем различать, как и в теории
обычных волнозэдоз, волны ТЕ и ТМ. Диэлектрические
потери в стержне будем считать разными нулю.
Первоначально рассмотрим случай осевой симметрии
поля
#- = 0, -^- = 0. (9.1)
dp ’ dp ' '
В этом случае у волн ТЕол
£р==£г = 0, Дс = 0. (9.2)
496
Условие (9.2) полностью совпадает с (5.27). Поэтому
для Е получим дифференциальное уравнение, совпадаю-
щее с (5.29), а именно:
, = _d_[_L d{?EJ I
'т д? L р dp ' dz2 ’
где
. 2л 1 / е
К = у- 1/ -
Л Г
(9.3)
(9.4)
В отличие от случая, рассмотренного в V-й главе,
в диэлектрическом стержне распространение происходит
Рис. 9.1. К анализу электромагнитного поля
в бесконечном диэлектрическом стержне.
вдоль оси Z. Поэтому в предположении отсутствия по-
глощения в стержне зависимость от координаты z будет
определяться множителем е-л2.
Следовательно,
д^Е
= (9-5)
Подставив (9.5) в (9.3), получим
<9-6>
Интегралом уравнения (9.6) является цилиндрическая
функция первого порядка Z, (р У k2 — у2). В результате
£9 = Л^(РГ^=?)е"/тг, (9.7)
где А — постоянная, независящая от координат г, р, (р.
Внутри стержня при р = 0 функция (9.7) должна быть
конечна и поэтому для внутренней области Zx представ-
ляет собой бесселеву функцию первого рода J\:
<9-S)
32—1503
497
Здесь индекс i показывает, чТо параметры относятся
к области внутри стержня.
Во внешнем пространстве координата р меняется в пре-
делах от р — г до р—>оо. Поэтому в качестве Z, может
быть принята сумма ганкелевых функций первого и вто-
рого рода с соответствующими коэффициентами. Как
известно, ганкелевы функции первого и второго рода,
имея асимптотическое представление вида (5.14) и (5.15),
выражают при вещественном аргументе: перзая — волну,
движущуюся в направлении убывающих значений р, вто-
рая— волну, движущуюся в направлении возрастающих р.
Мы же исследуем случай волны, движущейся лишь в на-
правлении оси Z, т. е. случай отсутствия радиального
излучения. Поэтому естественно искать решение задачи
для внешнего пространства в виде ганкелевой функции
от мнимого аргумента, которая соответствует убыванию
поля с возрастанием р.
Полагаем

Учитывая (9.7)-5-(9.9), а также (5.28), получим для со-
ставляющих векторов Е и Н электромагнитного поля
волн ТЕ0Л при осевой симметрии следующие выражения:
внутри стержня (р<г)
(9.Ю)
Н» = - 7^ (р/Т^) •
во внешнем пространстве (р>г)
н„=- i «I1 ’
498
(9.11)
На границе раздела диэлектрик—воздух при р = г усло-
вие непрерывности гласит:
£,i=^Ta’
Н,Г=Н;а-
(9.12)
Применив условия (9.12) к (9.10) и (9.11), получим
ДЛ(¥^7)е-^=лЛ,1,,(лКЙ^)е_''“’. '
^гЛ(г/^?)=-Л- =
= 1(9.13)
=(л /тХО-Х
Так как уравнения (7.13) справедливы при любом г,
то L=7a = Y. (9.14)
т. е. постоянная распространения в стержне у. равна по-
стоянной распространения во внешней среде у .
Учитывая (9.14), получаем после деления третьего
уравнения системы (9.13) на второе и умножения правой
и левой частей частных на г:
, 1/72-^ Z° (f - ,1/7СГЗ
' л^)ЛЧ--72) а я*!0 (;r J/V — *1)
(9.15)
Вводим обозначения
Х/ = Г^ ~ у2 1. (9.16)
*а='-1А2-*2
В этих обозначениях (9.15) принимает следующий вид:
h(xt)
и*а)
(9.17)
32»
499
На рис. 9.2 приведены кривые зависимости функции
П (х/)
rz =х/-ууу-от xz (сплошные линии) (9.17а)
и функции
//(О / г* \
Fa= а от (штриховая наклонная линия). (9.176)
Как видно из этого рисунка, функция Fa выражается
в виде одной кривой, в то время как функция F. в виде
нескольких (строго говоря, в виде бесчисленнного коли-
Рис. 9.2. Кривые зависимости функций Ft и Ра характеристического
уравнения (9.17) соответственно от параметров х; и ха для волн
низших порядков: п = 0 и п—1. Иллюстрация метода графического
определения корней уравнения (9.17).
чества) кривых. Это связано с тем, что во внешней среде
напряженность пол?/ во всех случаях непрерывно убывает
с координатой р, в то время как внутри стержня поле,
подобно полю в волноводах, имеет 'характер стоячих
волн и поэтому в разных случаях может отличаться ко-
личеством п стоячих полуволн между осью стержня и
наружной границей его.
500
Каждому значению п соответствует своя кривая на
рис. 9.2. Там приведены две кривые для п —0 и п=1.
Электромагнитное поле в стержне в первом случае на-
зывается волной ТЕ00, а во втором случае — волной TF01.
Кривые могут быть использованы для расчета парамет-
ров диэлектрического стержня (у,г,s). Для этого задаемся
определенным значением ха и находим по графикам
рис. 9.2 сначала соответствующее заданному значение
функции Fa, затем на кривых Ft— точки, имеющие орди-
наты F.=Fa и, наконец, значения хр соответствующие точ-
кам, найденным на кривых F. (см. ломаную пунктирную
линию со стрелками на рис. 9.2). Зная ха и соответству-
ющее ему определяем для каждого заданного значе-
ния е с помощью формул (9.16) величины параметров
у = —и г. Повторив эту операцию несколько раз для
Ф
различных исходных значений хд и найдя таким путем
ряд значений у и соответствующих им значений г, вычер-
чиваем кривую зависимости у от г. Так как обычно при-
нято характеризовать сечение стержня диаметром d=2r,
а волну—фазовой скоростью иф = -у-, то приводим здесь
кривые зависимости цф от d (см. рис. 9.3), причем для
общности и те и другие выражены в относительных еди-
ницах f^*_= -L 2L и _£=г_Е!_Л.
\ с f с \ к)
Проанализируем полученные данные.
Из рис. 9.3 видно, что фазовая скорость рф меняется
d с
в зависимости от-г-в пределах от с до -т= , причем
Л У е/го
при малых значениях -у- фазовая скорость цф = с, а при
больших значениях фазовая скорость цф = р^=.
Из формулы (9.16), как легко видеть, также следует
Y>Y>^a
или
с
с > р. > ,
*
ибо х и xq вещественны и > k .
501
Обратимся теперь к рис. 9.2. Из этого рисунка видно,
что Fa имеет при любом *а отрицательное значение, при-
чем при ха = 0 также Fa==0. Что касается Ft, то оно
имеет как положительные, так и отрицательные значе-
ния. Так например, при хр лежащих в пределах 0<х. <
<2,405 или 3,83 <*г<5,52, функция Ft имеет поло-
жительные значения, а при хр лежащих в пределах
Рис. 9.3. Кривые зависимости относительной величины фазовой скоро-
сти от относительной величины диаметра стержня для волн ТЕ00
(п = 0) и ТЕ01 (п — 1) при различных значениях относительной ди-
е
электрической проницаемости —.
®о
2,405<х/<3,83 или 5,52<х,<7,015, функция Ft имеет отри-
цательные значения. Различие знаков у Ft и Fa указыва-
ет на отсутствие вещественных корней уравнения (9.17),
т. е. на отсутствие в стержне такого поля (ТЕ0Л), какое
предполагалось вначале. Точки х.кр = 2,405 или х.кр = 5,52
назовем критическими точками, так как это начальные
точки, при которых условие (9.17) удовлетворяется. В
этих точках <=0 и Fa = 0. Но поскольку, как отмеча-
502
лось, при Fa=Q, также хо = 0тов этих точках соглас-
но (9.16) f = ka=^- и
аф = с. (9.18)
В свою очередь х, в этих точках равно
(9.19)
Из (9.19) получаем
(9.20)
Очевидно, что при г<гкр или при ^^>^крв стержне
не возбуждается электромагнитное поле типа TEOzj . Зна-
чение гкр соответствует минимальному радиусу стержня,
а значение Лкр — максимальной длине волны, при кото-
рой еще возможно возбуждение волн типа ТЕОп в диэлек-
трических стержнях.
Интересно отметить также, что при Л, близком к Дкр,
значение близко к нулю, что указывает на весьма
медленное убывание поля во внешней среде в радиаль-
ном направлении, т. е. на весьма большую относитель-
ную величину энергии, переносимой полем во внешней
среде, и соответственно малую относительную величину,
энергии, переносимой полем внутри стержня.
Перейдем теперь к рассмотрению симметричных
волн типа ТМОп. В данном случае
н =Н==0, Е=0.
р Ж ’ ?
(9-21)
Ввиду симметричности уравнений Максвелла относи-
тельно Е и Н и подобия (9.21) и (9.6), получим в данном
случае:
603
внутри стержня (р<>)
^=Bn~J^V
E^~Bi ^-kj~~ yo (p/^~Y?)e-/TZ
вне стержня (p>r)
£, = в.7=Г«"’(Л/7Г?)«-',г,
£.= -sX177“ "l"«> >e-'”
(9.22)
(9.23)
Из граничных условий получаем в данном случае,
во-первых, равенство постоянных распространения в диэ-
лектрике и в воздухе (у. = уа = у) и, во-вторых, связь
между х. и ха, определяемую соотношением, аналогич-
ным (9.18), а именно:
W _ е . Н^ЦХа)
Л(хг) ео J*a (Jxa)
(9.24)
Расчет параметров диэлектрического стержня в слу-
чае волн ТМол может быть также произведен с помощью
рис. 9.2 и изложенной выше методики пользования ими
при умножении значения Fa на . На рис. 9.4 показаны
v, d
вычисленные таким путем кривые зависимости____Фот-^-.
с *
Сплошные кривые соответствуют волне ТМад (п = 0),
а штриховые — волне ТМ01 (п=1).
Очевидно, что и в данном случае существует крити-
ческая длина волны Лкр и критический радиус стержня
гкр, определяемые уравнением (9.20). Справедливо т.акже
в данном случае сказанное выше о большой относитель-
ной величине мощности, переносимой внешней средой в
точках, близких к критической, и малой относительной
величине мощности, переносимой полем внутри стержня.
504
Из (9.10) и (9.22) следует, что картина электромаг-
нитного поля (картина линий поля) волн ТЕОп и ТМ0„ в
диэлектрических стержнях аналогична картине поля этих
волн в обычных волноводах круглого сечения за тем ис-
ключением, что в волноводах на поверхности касатель-
ная составляющая электрического вектора равна нулю,
а у диэлектрических стержней она имеет отличное от
нуля значение и удовлетворяет условию непрерывности
Рис. 9.4. То же, что на рис. 9.3, для волн ТМоо(п = О) и TMOi(n = l).
Волны ТЕОп и TMOzj, как правило, не используются в*
диэлектрических антеннах,' поскольку они привели бы к
нулевому излучению вдоль оси стержня, в то время как
обычно требуется иметь в этом направлении максималь-
ное излучение. Возбуждаются диэлектрические антенны,
как показано на рис. 1.10, что приводит к образованию
в них несимметричных волн типа ТЕ|Л и к максимуму
излучения вдоль оси стержня. Как увидим ниже, в диэ-
лектрических стержнях при несимметричном возбуждении
появляются одновременно как волны ТЕ, так и волны
ТМ, хотя возможно создать преобладание одного типа
над другим. Поэтому рассмотрим здесь несимметричные
волны обоих типов.
Обратимся к уравнениям Максвелла в цилиндричес-
ких координатах (5.1), заменив в последних координату
505
у на г и диэлектрическую проницаемость е0 на е. При-
няв зависимость от г в виде е-77*, получим:
1 1 дН9
--v-----= /шел ,
р ар р ар J г
\ дНг > . и
777+л^ =j™Et,
дН,
-лЕ,~=^
1 д(?Е) 1 дЕ? .
---у-эг=-/шЛ.
1 д^,
Т~д^+ЛЕ^~^Не
дЕ,
~ЛЕ9-~дГ = ~П^-
(9.25)
Система уравнений (9.25) позволяет выразить все со-
ставляющие поля через Ег и Нг следующим образом:
(^_72)Я=^^-/У^,
(^-Г2)Я?=/ше^--А^
дЕ,
(^2-у2) е =—
' । / <р р а?
р d<f ’
topn^z
J ? <?? ’
р ду ~i -^ш’хо др
(9.26)
В свою очередь, для Ег и Нг получаются дифферен-
циальные уравнения:
1 л t дЕ, \ I д2Е,
+ + (927
J_ + _L^.+^2_Y2)H=0.|
р Эр \* др / р* др* 1 ' • ' г
Разделяя все решения на группы ТЕ-волн (Ег = 0)
и ТМ-волн (Яг = 0), получаем согласно (9.26) для каждой
из групп:
506
для ТЕ-волн:
для ТМ-волн:
(*’-т!>я,=-Л^.
Интегралом уравнения (9.27) является функция вида
Azm (Р Vk2 — I2)sin (mtP + Ф)«
где Zm — цилиндрическая функция т-ого порядка.
Рассуждая так же, как и в случае симметричного воз-
буждения, т. е. учитывая, что электромагнитное поле
внутри стержня должно быть конечным и что должно
отсутствовать радиальное распространение волны во
внешнем пространстве, придем к выводу о том, что
внутри стержня в качестве цилиндрической функции
должна быть взята функция Бесселя первого рода, а во
внешней среде — функция Ганкеля первого рода от мни-
мого аргумента. Постоянная .ф зависит от выбора началь-
ного направления отсчета углов <? и в этом смысле
является произвольной. Положим ф=-^-. В соответ-
ствии с (9.28) и со сказанным здесь о характере цилинд-
рической функции и о величине ф, получим:
Для волн ТЕтп
в н у т р.и стержня (р<7):
Нг = AiJm (р V % — Ъ ) cos e-7TZ * ,
н,=А "—, J. ) cos
у — ъ
= Ai - (^2 ~2j Jrn (Р Кk2 - у2) sin msin ’
Е=А, Ут (Р ) cos т? c~h‘ ,
у ki - ti
£г = 0,
вне стержня (р>г):
",=4^’(/Р COS m?
= 4 н'" ('р > “st
и яа~1а
н<= Аа (7Р ) sin e-/TaZ.
£р л« Т^--?) — k2a) sin tnff e~haZ,
= A“ H'n cos
' Ra~ la
E=0.
Для волн TM
tnn
внутри стержня (p<г):
£. = -ВЛ.(₽/*!-7?)sm».? о-"",
4 = 4(РVк} — Г?)si"""te~'vZ,
£’~— )cosm<t e~‘n',
H, = B, p-^% 4 (P /^f) cos mlf o’'”1,
//’ = ®li^Tj4(p K^risin^e-'’",
йг = 0.
508
(9.29а)
(9.296)
(9.30a)
вне стержня (р>г):
£, = S44i’C/pKrl — i‘)sinm?e ,
в,=s« н""(Л sin mf е~"‘'
V ka~ Та
= Ва ~£-т ,2. Нт (/Р У Т2а~ kl ) C0S ’
Р У^а 1а >
Ч. = В. н" (Jr ]ЛУГ1Г) cos m, е-'- ,
Г\ка \а )
(9.306)
Н = В ——^Я- Н'™ (/р уГу2 — k2) sin /ntp е Па
<р а I/ д2 2 т * г • а а ' *
У ^а~ Та
н=о.
Применив, как и в случае симметричных волн, усло-
вие непрерывности отдельно к волнам ТЕ и к волнам ТМ,
получим, во-первых, равенство уг = уа = у и, во-вторых,
еще три независимых уравнения (не имеющих совмест-
ного решения) для определения двух величин: у и отно-
А, / В, \ п
шения д— / или g- 1. Этот результат является следствием
предположения о самостоятельном существовании волн
ТЕОТ„ и ТМ .
тп тп
В действительности в диэлектрических стержнях
волны ТЕтп существуют совместно с ТМтл. В зависи-
мости от способа возбуждения и параметров стержня
(е и d) лишь преобладает тот или иной тип. Совместное
существование волн ТЕОТЛ и ТМтл может быть объяснено
следующим образом. В обычных волноводах с проводя-
щими стенками имеют место поверхностные токи прово-
димости. Поскольку в диэлектриках отсутствуют токи
проводимости, то при возбуждении в них волн такого же
типа, как в обычных волноводах, возникают эквивалент-
ные токи смещения. Например, при возбуждении волн ТЕтл,
вместо продольных токов, возникает продольная состав-
ляющая Ег, т. е. возникают волны TMm/J.
Таким образом, с учетом обозначения (9.16), а также
очевидного равенства уг = уа = у, позволяющего опустить
множитель е~пг, составляющие электромагнитного поля
несимметричной волны выражаются следующим образом:
509
поле внутри стержня (р<г):
поле вне стержня (р>г):
Hz = АаНт ( A. v) C0S
(9.32)
° г
510
H=a —L_rJizi
a
V 12
- v) ] Sin m(₽>
rr(l) / • _P_'
p m a r
Jxa ~
E = A 1
P V^-72
-T-JVW (j
£*=‘4“F^=i[-
A„ JT . p Пт
“ J7'a ~~
Применив условие непрерывности при
ляющим поля Hz и Ez, получим:
Ai _ Bi
Аа Ва~ Jm(Xi)
Из (9.33) следует:
= —.
Аа
Применив условие непрерывности к Е?
> r f J ^’04)
=k Jnrik
Jxa m
B, . m ,
p = r
Ba
a

и Я,
(9.32)
к состав-
(9.33)
(9.34)
получим:
(9.35)

™ u(l)
1 2 m
W >
511
откуда следует!
Bi
аг
^в'^(Ла)
Ла
1 ’ 7х
пт Ла
J^n

В^(Ла)
(9.36)
Л
х'
Уравнение (9.36) определяет, во-первых, соотношение
между обоими типами волн ! -^-1, во-вторых, значение
постоянной распространения у или связанную с ней ве-
личину фазовой скорости рф. Расчет последней по фор-
Рис. 9.5. То же, что на рис. 9.3, для несим-
метричной волны.
муле (9.36) является весьма громоздким и производится
путем многократных графических построений. На рис. 9.5
d
приведены кривые зависимости -у от отношения -у , вы-
численные по формуле (9.36) для ряда значений —идля
£о
волны первого порядка (т=\, п = 0). Кривые рис. 9.5
асимптотически стремятся в верхней части к значению
уф . „ иФ 1Г е0
— =1 и в нижнеи части — к значению — = I/ — При-
С с У е ’ г
512
чем точно достигают они этих крайних значений соот-
ветственно при ~ = 0 и -^- = ео. Таким образом, в
случае несимметричных волн первого порядка (т=1)
при п = 0, строго говоря, не существует критической
волны 1кр, подобной таковой у симметричных волн, т. е.
вдоль бесконечного диэлектрического стержня возможно
распространение несимметричных волн при любых низких
частотах.
Специально вопросу распространения электромагнит-
ных волн вдоль бесконечных диэлектрических цилиндров
при низких частотах посвящена работа Б. 3. Каценелен-
баума [48]. В этой работе, в частности, показано,
во-первых, существование несимметричных волн при
низких частотах, во-вторых, наличие одновременно волн
ТЕ и ТМ и, в-третьих, что фазовая скорость волн при
низких частотах близка к с = 3.108-^-.
сек
Из рис. 9.5 также легко видеть, что, начиная с не-
d иФ 1
которого конечного значения -у, практически -у — I.
Обратимся к рис. 9.6, на котором показаны кривые
W,
зависимости отношения (W. — энергия, переносимая
стержнем, a Wa — энергия, переносимая внешним про-
странством) от для двух значений —. Из этих
Л Ео
W;
кривых видно, что отношение становится практически
"а
равным нулю не при-Я = ео, а при некоторой конечной
длине волны, определяемой из соотношения -^-=0,1н-0,2.
„ Г,
Равенство же нулю указывает на отсутствие волны
"а
в стержне.
Таким образом и при несимметричных волнах в диэлек-
трических стержнях можно указать волну, которая по
/и* wi \
основным признакам I-у-= 1 и jp-sOl практически не
отличается от критической.
На рис. 9.7 показана конфигурация электромагнитного
поля в поперечном (а) и продольном (б) сечениях диэлек-
трического стержня при возбуждении последнего излу-
33—1503 513
чателгм, расположи iw\i перпендикулярно оси (основная
волна —ТЕ10)’. На рис. 9.7 сплошные линии показывают
направление электрических линий поля, а штриховые —
магнитных линий поля. На рис. 9.7, а окружность, а на
рис. 9.7, б две горизонтальные линии указывают границы
диэлектрик — воздух.
Легко видеть, что электромагнитное поле в круглом
диэлектрическом стержне при указанном способе возбуж-
0,00! 0,000 0,010,020,00 0,1 0,2 0,0 1,0 2,0 0,0 10 20 00 100 Щ
Рис. 9.6. Кривые зависимости от диаметра стержня отношения мощ-
ности, переносимой стержнем к мощности, переносимой внешней
е
средой, для —=2,5 и 10.
ео
дения аналогично полю волны типа ТЕН в волноводе
круглого сечения за тем исключением, что электрические
линии не перпендикулярны к границе диэлектрик — воз-
дух, а магнитные не касательны к этой границе. Отличие
!) Второй индекс (л) в обозначении типа волны указывает, как
отмечалось выше, число стоячих полуволн между осью стержня и
границей раздела диэлектрик—воздух. В обычных волноводах это
число всегда целое. В диэлектрических стержнях целое число по-
луволн укладывается в этом промежутке лишь в критическом слу-
чае. Обозначение п — 0 соответствует отсутствию полной полу-
волны, п=1 соответствует наличию одной полной полуволны н
участка с неполной полуволной и т. д. Поэтому при сравнении
аналогичных полей в диэлектрическом стержне и в обычном
волноводе последнему будут соответствовать индексы л, бдльшие
на 1. индексов, соответствующих днэлектрнческнм стержням.
514
заключается в том, что в случае диэлектрического
стержня существует наружное поле за пределами
стержня.
Приведенный выше анализ позволяет сделать следую-
щие выводы об особенностях электромагнитного поля
симметричных и несимметричных волн в диэлектрических
стержнях:
1. Постоянная распространения у и фазовая скорость
одинаковы в стержне и во внешней среде.
Рис. 9.7. Конфигурация электромагнитного поля в попе-
речном (а) и продольном (<7) сечениях диэлектрического
стержня при возбуждении несимметричных волн.
2. Фазовая скорость распространения уф лежит между
фазовой скоростью —с-==. в неограниченной диэлектри-
V-
т ‘О
ческой среде, имеющей проницаемость г, и скоростью
света с в свободном пространстве.
3. При сравнительно малых диаметрах стержня иф=с,
начиная с некоторого диаметра, дальнейшее его увели-
чение приводит к быстрому уменьшению фазовой скорости,
с
которая вскоре достигает величины иф=- f, после
Vi
чего опять почти не меняется.
4. Чем меньше диэлектрическая проницаемость г, тем
более пологой является кривая изменения -у- от у- и тем
зз* 515
/ d \
позже (при больших значениях -у-1 начинается переход
от v.=c к v. _________
Ф * / е
V
£ У<Ь
5. При каждом заданном значении — кривая — имеет
е0 С
более пологий характер вблизи иф= с_____и более крутой
Vi
вблизи V.=c.
ф
6. При и. = с почти все излучение переносится внешним
„ с
пространством 1^=0 • При пф= " почти все излу-
Г ео
чение переносится стержнем оо .
\ а )
7. Картина электромагнитного поля в диэлектрическом
стержне аналогична картине поля в волноводе при возбуж-
дении в том и другом случае соответственно одинаковых
типов волн. На границе диэлектрик — воздух соблюдается
закон непрерывности касательных составляющих поля
в отличие от волноводов, где касательная составляющая
электрического вектора, вследствие появления поверхно-
стных токов, равна нулю.
8. При несимметричном возбуждении принципиально не-
возможно отделить волны типа ТЕ от волн типа ТМ, суще-
ствующих совместно. Подбором способа возбуждения можно
сделать тот или иной тип преобладающим. При возбужде-
нии перпендикулярным к оси излучателем преобладает
тип ТЕ.
§ 2. ЗАТУХАНИЕ ВОЛН В ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ
В предыдущем параграфе задача о распространении
электромагнитных волн по диэлектрическому стержню ре-
шалась при условии отсутствия потерь на излучение и на
нагревание диэлектрика вследствие конечной проводимости
материала. Излучение было исключено при постановке зада-
чи введением условий о бесконечной длине стержня, о рас-
пространении волны в направлении оси Z и отсутствии рас-
пространения во внешней среде в радиальном направлении.
Отсутствие потерь на нагревание диэлектрика было обуслов-
516
лено предположением о вещественном характере диэлектри-
ческой проницаемости среды е и магнитной проницае-
мости = р.о.
Введем здесь условие о комплексном характере
диэлектрической проницаемости, сохранив остальные из
указанных условий прежними. Будем обозначать комп-
лексные параметры штрихом, а аналогичные веществен-
ные— теми же буквами без штриха. В этих обозначениях
е' = е(1—jtg 8). (9.37)
Согласно (9.4) и (9.37) в полученных в предыдущем
параграфе формулах следует теперь писать вместо
k'.= k.Vl — /tgS.
(9.38)
Вследствие затухания волны комплексными
теперь также величины:
Подставив (9.38) ч-(9.40) в (9.16), получим:
(\ +Д)2 = [^ (1 ~JtgS) + (? +/«)2]г2, ’
-(xa+/V=[O(H>)2]'-2-
будут
(9.39)
(9.40)
(9.41)
Приравнивая мнимые составляющие в правых и левых
частях (9.41), получаем:
2«?—A?tg« |
V=------27---- r2’
(9.42)
Так как tg В обычно очень малая величина, то очень
малы также р по сравнению с а, т;. по сравнению с х. и
т]а по сравнению с ха>
Для определения аир нужно подставить в характе-
ристические уравнения (9.17), (9.24) и (9.36) комплексные
величины х', х^ и другие, а затем разделить веществен-
ные и мнимые составляющие, получив вместо одного
два уравнения.
5!"
Обозначим в уравнениях (9.17), (9.24) и (9.36) правые
части через F , а левые — через FneB. Это позволяет
писать их в следующем виде:
при tg 8 = О
при tg 8 О
F' (.L *'\=р' (21 / (9.43,6)
пр I ’ <’ а лев I Ь(] ’ И а I \ '
В области, где F и FLn являются аналитическими
’ пр лев
функциями (производные всех порядков конечны), они
могут быть разложены в ряд Тейлора. Разложение в ряд
дает:
д?пр
^пр
(\ / дР
*а) +/(~ tg 8 +
3F дР X
. и лев , .’1ев\ . 1)
+ + • • (9-44>
Ограничимся приведенными двумя членами разложе-
ния. Приравнивая вещественные слагаемые (9.44), мы
приходим к уравнению (9.43,а) для случая tg 8 = 0. Это
указывает на то, что при обычных значениях tg 8 по-
стоянная распространения а, фазовая скорость и соот-
ношение энергий, переносимых внешним пространством
Г,
и стержнем ==-, сохраняются в стержне с потерями с
точностью до величин порядка (tg З)2 такими же, как в
стержне без потерь.
Приравнивая мнимые слагаемые (9.44), получим третье
уравнение, которое совместно с двумя уравнениями (9.42)
позволяет определить р.
>) входит в Апр и Алев не
ха, но и в явном виде.
только в качестве аргумента х. и
518
а) симметричные волны TEOfl
Согласно (9.17) Глев является функцией только х., а
Гпр—только ха. В явном виде они не зависят от
е0
Приравнивая мнимые слагаемые (9.44), имеем в данном
случае:
^пр (^Пр Лиев)
_ д*д _ ______ <4 _d*i
ria дРлев _ д (Гпр-Глев) dxa •
cbt; dx(-
(9.45)
Образуя аналогичное отношение — путем деления
первого из уравнений (9.42) на второе и приравняв это
отношение уравнению (9.45), получим после некоторых
преобразований:
kj tg д 1
2а
1 + жа d,'a
(9.46)
Поскольку х. и ха определяются так же,
отсутствии потерь, можно писать
х^(^-а2)г2 = 4к2/А^_ПЛ
\ ф /
\ аф 7
как при
(9.47)
где X — длина волны при свободном распространении в
вакууме,
2ф— длина волны при распространении по диэлектри-
ческому стержню,
г — радиус стержня^
Из (9.47) следует:
хз
х dx = 8~2
a a
d\ d\
1» d\
(9.48)
519
После подстановки (9.48) в (9.46) с учетом
мости и а от Z и Яф, получаем:
е
tg3
9— £0
X е.
— — 1
«о
Производная может быть определена из
рис. 9.5, изображающих зависимость отношения
-у. Обозначим эту зависимость через
имеем
' * \2<*Ч Ч'
Ч ) X
зависи-
(9.49)
кривых
от
Тогда
~Ф
к
Я = Zf
Ф 1 \ к / »
-гг=Цт)~т (9.50)
dx.
Согласно (9.50) в выражение для производной
входят следующие данные кривых рис. 9.5.
(2г \
—) — ордината рассматриваемой точки кривой,
2г -
-г--абсцисса этой точки,
/'(—)—тангенс угла между касательной к кривой
' ' в данной точке и осью абсцисс.
Из (9.50) видно, что при малых и больших значениях
2г / 2г \ /2Г \
у производная f ( —1 = 0. Функция же Н у- J
1
первом случае единице, а во втором случае —
равна в
=. Учи-
2г
X
тывая, что г— равно единице при малых значениях у
-I Г 8 л
и равно у — при больших значениях у , легко зак-
лючить, что квадратная скобка в (9.49) равна нулю в
L — 1
первом случае и - во втором.
-о
:о
Равенство нулю коэффициента затухания [J при ма-
лых у объясняется тем, что при этом энергия в основ-
ном распространяется вне диэлектрика.
Множитель
соответствует коэффициенту затухания коаксиального
кабеля, заполненного диэлектриком. Следовательно, при
Рис. 9.8. Графики зависимости относительной величины коэффициента
затухания в диэлектрическом стержне от относительной величины
диаметра стержня при различных значениях относительной диэлектри-
ческой проницаемости для волны ТЕОл.
больших значениях у затухание в диэлектрическом
стержне равно затуханию в коаксиальном кабеле.
На рис. 9.8 приведены графики зависимости от
для нескольких значении — .
6П
521
б) симметричные волны ТЛ10л
Согласно (9.24) Гл’ев является функцией только
а Гпр — функцией хо и . Приравнивая мнимые слагае*
мне (9.44), получаем:
dF dF
/^ = -tg8Fnn. (9.51)
•> дх; а дха » пр ' '
Учитывая преобразования, сделанные в (9.45), можем
переписать (9.51) в следующем виде:
дрлев ( _ ^7/
dx;. I Ч d*a ,
а подставив »). и т]о из (9.42), приходим к следующему
равенству:
- у k2i tg *
(9.52)
пр’
г2
х<
лев
(9.53)

После
простых преобразований получаем:
где
k{
tg8 ±
1 пр
г2 дРлев
ди.
xdx,
1
Л_ /2 дРлев
е0 ( X J dxt
d = 2r,
F —
лев *г Л (*/) ’
F
"р
(9.54)
(9.55)
(9.56)
(9.57)
а
522
Выражение для р в данном случае отличается от та-
кового в предыдущем случае множителем N. Этот мно-
житель при больших диаметрах стержня стремится к еди-
нице, поскольку второе слагаемое, имеющее в знаменателе
более высокую степень d, стремится к нулю. При малых диа-
метрах стержня множитель N также стремится к еди-
нице, поскольку при этом >-ф ха —>0 и второе сла-
гаемое опять стремится к нулю. В промежуточных точках
множитель N несколько меньше единицы.
Таким образом, зависимость коэффициента затухания р
d ..
от -у- имеет примерно такой же характер, как в преды-
дущем случае.
На рис. 9.9 показана зависимость -f- от 4- для не-
h *
скольких значений (попрежнему —-коэффициент за-
тухания коаксиального кабеля).
523
в) несимметричные волны
Для несимметричных волн характеристическим урав-
нением является (9.36). Здесь обе части являются функ-
циями vjj и vja. Функцией в явном виде является лишь
левая часть. Однако для общности будем считать обе
части функциями всех переменных. Введем функцию
F = F — F . (9.58)
лев пр ' '
Тогда получим:
Подставив значения т>. и т]а из (9.42) в (9.59), получаем
после ряда преобразований, аналогичных предыдущим
где
(9.60)
(9.61)
Функцию F после простых преобразований можно при-
вести к виду
f=L Л(,)(;ха)1 р . я//;(|)(ал .
L ° ‘Я/'ДД,) j [V ° у1(хр '//(''(Ла)
(9.62)
524
На рис. 9.10 даны графики зависимости 4- от v Д;1Я
„ е
нескольких, значении -.
£о
Чтобы получить представление о величине затухания,
рассмотрим пример. Пусть стержень имеет диаметр d —
= 0,5, длину Z = 52, - = 2,5; tg 8 = 10"3.
ьо
Рис. 9.10. То же, что на рис. 9.8 для несимметричной волны.
Затухание равно
₽.5Х = ^-гс
Ра
5Х ]/ь-
—y-^tg8 = 0,7.K.51/ --IO-3.
Л г to
Таким образом, затухание, вызванное токами проводи-
мости в диэлектрическом стержне, незначительно у диэлек-
триков с указанными параметрами. Легко видеть из рис. 9.8,
9.9 и 9.10, что в случае несимметричных волн затухание бу-
дет еще меньше.
525
§ 3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ДИЭЛЕКТРИЧЕСКОЙ
АНТЕННЕ ИЗ СПЛОШНОГО КРУГЛОГО СТЕРЖНЯ
Как указывалось выше (см. гл. I, § 6), диэлектрические
антенны могут иметь разную форму поперечного сечения:
круглую, квадратную, прямоугольную и т. п. Наиболее рас-
пространенными антеннами из сплошного стержня являются
антенны круглого поперечного сечения. Среди них встре-
чаются антенны цилиндрические (с постоянным размером
поперечного сечения) и конические (с линейно меняющи-
мися размерами поперечного сечения). В том и другом слу-
чае возбуждение антенн осуществляется перпендикулярным
к оси током или прямоугольным волноводом (см. рис. 1.10).
Такие антенны подробно исследованы экспериментально.
Однако достаточно обоснованной их теории мы не имеем.
В современном состоянии теория круглых диэлектрических
антенн базируется, помимо опытных данных, с одной сторо-
ны, на обобщении результатов приведенного в предыдущих
параграфах анализа идеализированного случая (бесконечно
длинного стержня постоянного поперечного сечения) на слу-
чай реальной антенны, с другой стороны, на излагаемом ни-
же так называемом втором принципе эквивалентности.
Первое позволяет создать представление о характере элек-
тромагнитного поля в стержне, второе — о характере элек-
тромагнитного поля излучения.
Обобщение результатов анализа идеализированного слу-
чая на случай реальной антенны заключается в предполо-
жении, что для последней справедливы формулы (9.31) -е-
(9.36), а также вытекающие из них графики рис. 9.5 и 9.6,
полученные для бесконечно длинного стержня постоянного
сечения. Однако при этом следует учесть, что при выводе
формул (9.31) -г- (9.36) исходными были положения:
а) о распространении волны в одном направлении (в на-
правлении возрастающих значений z);
б) о независимости постоянной распространения " от
координаты z и
в) об отсутствии радиального излучения.
В действительности же как у цилиндрических, так и
у конических стержней должно иметь место отражение
от конца, приводящее к появлению обратной волны.
Кроме того, у конических стержней следует ожидать,
во-первых, наличия радиального излучения вследствие
изменения отношения энергии W(, переносимой стержнем,
к энергии )Га, переносимой внешним пространством, как
526
функции диаметра стержня, а во-вторых, зависимости у
от z вследствие изменения фазовой скорости с измене-
нием диаметра стержня.
Из сказанного следует, что использование формул
(9.31)-ь (9.36) для определения электромагнитного поля
в диэлектрической антенне из круглого стержня возможно
при внесении в эти формулы соответствующих корректив.
Рассмотрим этот вопрос подробнее. Обратимся к фор-
мулам (9.31) и (9.32). Как видно из этих формул, состав-
ляющие векторов поля являются функциями от цилиндри-
ческих координат z, р и <р (см. рис. 9.1). При этом зави-
симость от координаты <р выражается в виде синусо-
идальной или косинусоидальной функции от п<р, где п —
целое число, определяющее порядок волны, возбужденной
в стержне. Зависимость от z выражается в виде гармо-
нической функции от произведения yz, где у — постоянная
распространения. Зависимость от р выражается в виде
суммы с соответствующими коэффициентами пропорцио-
At Аа ,
нальности -в- или в- цилиндрических функции и их про-
Di ° а
изводных от или х —, где -4 и указывают со-
1 Г а Г Da J
отношение между волной типа ТЕ и волной типа ТМ,
А{
•т- характеризует соотношение амплитуд поля в стержне
Дд
и внешнем пространстве, а х и ха являются функциями у
и радиуса стержня г и определяются уравнением (9.16).
Порядок п возбужденной волны практически не зави-
сит от радиуса стержня и равен, как правило, п=1.
Следовательно, зависимость от координаты <р носит вполне
определенный характер, независимый от радиуса стержня.
Постоянная распространения у, коэффициенты пропорцио-
А; Аа Ai
нальности д'’ и , а также параметры х. и ха явля-
ются функциями радиуса стержня г и определяются
уравнением (9.36). В последнем уравнении у, х., хо выра-
жены в функции г в неявной форме.
Не имея точного решения задачи об электромагнитном
поле в диэлектрической антенне, можно принять, что
оно может быть определено с помощью уравнений (9.31)-т-
(9.32), причем в случае цилиндрических стержней пара-
метры у, х; и ха, а также коэффициенты Аа, Bt и Ва,
определяемые по формулам (9.16), (9.33), (9.34) и (9.35),
627
постоянны, в случае же конических стержней эти пара-
метры представляют собой функции z и также определя-
ются по указанным формулам, но отдельно для каждого
сечения стержня.
Теоретическим обоснованием этого предположения
могут в известном смысле служить, во-первых, соответ-
ствующие выводы из теории волноводов, во-вторых, сде-
ланные в V-й главе на базе математического анализа
выводы о характере поля в рупорах, имеющих переменное
поперечное сечение и у которых поле в каждом заданном
сечении эквивалентно полю в волноводе такого же раз-
мера сечения. Основанием для сделанного предположения
Рис. 9.11. Экспериментальная кривая изменения относительной вели-
чины фазовой скорости по длине круглого стержня переменного
сечения, имеющего в начале диаметр dMaKC= 0,5 X, в середине
dMHH = 0,3 X и постоянный диаметр, равный dMHH, на всей остальной
половине стержня.
могут служить также некоторые опытные данные, в ча-
стности, приведенная на рис. 9.11 экспериментальная
иФ z
кривая изменения отношения — от у у круглого стерж-
ня, суживающегося до половинной длины и имеющего
во второй половине постоянный диаметр, причем началь-
ный диаметр стержня равен 0,5Л, а конечный — 0,ЗЛ. Ди-
электрическая проницаемость равна — = 2,5. Легко ви-
е0
а.
деть, что значения , приведенные на рис. 9.11, хорошо
совпадают с соответствующими теоретическими значе-
ниями, приведенными на рис. 9.5 и вычисленными по
формуле (9.96).
Итак, в случае цилиндрических стержней формулы
(9.31) -г- (9.32) могут быть использованы непосредственно,
528
а в случае конических стержней должны быть применены
к каждому отдельному сечению стержня.
Сказанное до сих пор относилось к прямой волне, рас-
пространяющейся от начала к концу стержня. Обратная
волна, получающаяся в результате отражения от конца
стержня, определяется коэффициентом отражения Г, рав-
ным отношению напряженности поля отраженной волны
к напряженности поля падающей волны. Рядом авторов (49]
принято считать, что
Г= 1 — —
20’
где Z—так называемое волновое сопротивление стержня,
a Zo = 120тс = 377 ом — волновое сопротивление свобод-
ного пространства.
Волновое сопротивление стержня определяется как отно-
шение поперечной составляющей электрического вектора
к поперечной составляющей магнитного вектора
7._— ' '
Как видно из (9.31), в случае несимметричных волн
сопротивление Z (9.63) не является постоянной величиной
для всех точек данного поперечного сечения, а является
функцией р и <р. Поэтому оно в данном случае вычис-
ляется как усредненное значение по формуле
[[ Pz-Z (р, ?) ds
Z = ^-r-------- , (9.64)
где Pz — значение вектора Умова—Пойнтинга в данной
точке поперечного сечения, Z (р, <р) — соответствующее
данной точке значение волнового сопротивления, опреде-
ляемое по формуле (9.63). Интегрирование в (9.64) про-
водится по всему поперечному сечению стержня.
На рис. 9.12 показан график зависимости отношения
— от y , вычисленный для = 2,5 по формуле (9.64) с
учетом (9.31) и (9.63). Из сравнения рис. 9.12 с рис. 9.5
легко видеть, что кривая аналогична кривой —Дей-
др с
34—1503 520
ствительно, при - = 2,5 точкам — =1 соответствуют (ПРИ
d \ Z , «/”ь
том же г-) точки — = 1, а точкам — = 1/ — соответст-
* ) 20 с Г
Z - /\ т-г •> Z 1
вуют значения — = у Переход от значении 1
Zo to Zq
Z I / t „ „
к значению •=-= |/ - происходит по кривой, аналогичной
Zq г t0
„ %
кривой -у- .
Таким образом, коэффициент отражения может быть
также определен приближенно из соотношения
Г=1—^-.
с
Последнее соотношение может оказаться более
р.
чем предыдущее, так как для зависимости —
считаны более подробные графики.
удобным,
ОТ
d
г-раС-
Рис. 9.12. График зависимости относительной вели-
чины волнового с противления стержня от относи-
тельной величины диаметра стержня.
На практике диэлектрические антенны обычно дела-
ются из стержней, имеющих при - = 2,5; максимальный
ь0
диаметр d..e„„=O,5X и минимальный d , = 0,ЗА. Из
1 МЯКС МИН ’
d 7.
рис. 9.12 видно, что при v =0,5 отношение ^ = 0,85, а
A Zo
530
при 7- = 0,3 отношение = 1. Следовательно, у обычных
А Z()
диэлектрических антенн можно ожидать коэффициент
отражения порядка не более 0,15, т. е. весьма небольшой
величины.
Из сказанного следует, что при малом коэффициенте
отражения от конца стержня электромагнитное поле
в диэлектрической антенне может быть определено по
формуле (9.31) — (9.32). Картина линий поля соответствует
v В7.
рис. 9.7, а параметры —, и — могут быть найдены
С W а
по графикам рис. 9.5, 9.6 и 9.12.
Принимая за исходное сформулированные сейчас по-
ложения, в целях дальнейшего облегчения решения за-
дачи, обычно вводятся дополнительные упрощения.
Во-первых, предполагается, что распространение волны
происходит только в направлении оси Z, т. е. пренебре-
гается влиянием на фазу поля радиального распростра-
нения, связанного с излучением, во-вторых, предпола-
гается, что распространение происходит как у цилин-
дрических, так и у конических стержней с постоянной
фазовой скоростью, равной усредненному значению фазо-
вой скорости по всей длине стержня; в-третьих, прини-
мается какой-либо простой закон изменения амплитуды
поля в функции координаты (постоянные амплитуды или
экспоненциально убывающие). При определении фазовой
скорости и закона изменения амплитуды сообразуются
с указанными выше особенностями электромагнитного
иФ п
поля в стержне, в частности, с кривыми -у-, . Одна-
ко выбор практически делается на глаз и, естественно,
различными авторами по-разному.
§ 4. ВТОРОЙ ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
Задавшись приближенным значением электромагнитного
поля в стержне, можно перейти к расчету поля излучения.
Сначала определим методику расчета.
Как мы видели в главе II, расчет поля излучения систе-
мы электрических и магнитных токов может производиться
либо непосредственно по токам с помощью соответствующих
объемных интегралов, либо по полю на поверхности, окру-
34* 531
жающей заданные токи, с помощью соответствующих по-
верхностных интегралов (с помощью так называемых
диффракционных формул).
Применение диффракционных формул, выведенных
в гл. III для определения поля излучения по заданному
полю на выделенной поверхности и использованных для
расчета излучения рупоров, линз и зеркал, в данном случае
нецелесообразно. Диффракционные формулы дают правиль-
ный результат при точном значении поля на поверхности
антенны. Мы же пользуемся весьма приближенными дан-
ными.
Кроме того, как мы уже видели выше, достаточно хоро-
шую точность могут дать приближенные диффракционные
методы при диффракции на больших отверстиях, причем
лишь в области сравнительно небольших углов с нормалью
к плоской поверхности. В рассматриваемом случае диэлек-
трических антенн излучение определяется в основном ци-
линдрической или конической поверхностью с максимумом
в. направлении оси стержня, т. е. в направлении больших
углов с поверхностью. Роль торцовой поверхности сравни-
тельно невелика.
Все сказанное приводит к тому, что определение элек-
тромагнитного поля излучения оказывается более удобным
производить с помощью полученных в гл. II объемных
интегралов через распределенные по объему токи. При этом
пользуемся принципом, который мы будем называть вторым
принципом эквивалентности. По методу, основывающемуся
на втором принципе эквивалентности, в качестве исходного
берут значение поля внутри диэлектрического стержня, а не
на поверхности и эти значения поля заменяют эквивалент-
ными токами. Сущность этого принципа согласно М. И. Кон-
торовичу (50] заключается в эквивалентности токов смеще-
ния в диэлектрике токам проводимости в металлах.
Математическое выражение второго принципа эквива-
лентности получим из следующих выкладок.
Имеем пространство, заполненное средой с диэлектри-
ческой проницаемостью г, являющейся, вообще говоря,
функцией координат z, р, <р точек пространства
e = e(z, р, <р).
Магнитную проницаемость среды р. положим равной р.=
= р.о = 4л10-9 гн]м.
532
Напишем систему уравнений электродинамики для
этого пространства, полагая, что существуют электри-
ческие токи /’)• а магнитные равны нулю
rot£=— Hojf,
-> -* дЕ
rot /У = J~j~ £ »
->
div (e£) = p,
divtf = 0,
div J—
ot
(9.65)
Введем новые величины:
(9.66)
которые назовем соответственно суммарной плотностью
тока и суммарной i "
плотностью заряда. В уравнениях (9.66)
_____1
=0 Збтс
1СГ9-^.
м
системы
Исключив из
мощью (9.66) получим:
уравнений (9.65) J и р, с по-
rotE=
дН
rot ТУ — J* Ц- е0 ,
(9.67)
div /У== О,
,. t. др*
div j = — .
dt
*) индекс ,э* опускаем.
53S
Легко видеть из сравнения (9.67) и (9.65), что система
уравнений (9.67) соответствует среде с диэлектрической
проницаемостью е0, т. е. свободному пространству, но
в которой имеется плотность токов J* и плотность заря-
дов р‘, определяемые уравнениями (9.66).
При отсутствии токов проводимости и электрических
зарядов (/=0, р = о) можно диэлектрик с проницаемо-
стью е, в котором возбуждается электромагнитное поле Е,
условно рассматривать как среду с проницаемостью е0
(вакуум), в которой возбуждены токи и заряды с экви-
валентной плотностью
Акв = (s — ео) =J“> (s — ео) Е ,
P9KB = -'diV [(®— '-о)£] •
(9.68)
В случае однородной изотропной среды (г — const) и
отсутствия в ней токов проводимости и зарядов, как
известно,
divf= 0.
Следовательно, в такой среде рэкн =0.
Таким образом, согласно принципу эквивалентности,
диэлектрический стержень антенны, являющийся одно-
родной изотропной средой с диэлектрической проницае-
мостью е, в котором возбуждается электромагнитное
поле с электрическим вектором Е, может рассматри-
ваться как среда с диэлектрической проницаемостью е0,
но с возбужденными в ней электрическими токами плот-
ности /экв, имеющими величину, определяемую (9.68).
Поскольку же внешняя среда также обладает диэлек-
трической проницаемостью е = е0, то задача об излуче-
нии диэлектрической антенны может быть сведена
к задаче об электромагнитном поле в однородной»среде
с е==е0, в которой в месте нахождения диэлектрического
стержня возбуждены токи с плотностью /эка.
534
§ 5. ДИАГРАММА НАПРАВЛЕННОСТИ ДИЭЛЕКТРИЧЕСКОЙ
АНТЕННЫ
После того, как задача об излучении диэлектриче-
ского стержня приведена к задаче об излучении объем-
ных токов, можно для определения поля излучения вос-
пользоваться уравнениями (2.37). Положив в соответ-
ствии с условиями JM = 0 и применив к этим уравнениям
преобразования (2.39) и (2.40), получим для поля излу-
чения на больших расстояниях
-> f [-> г-> -Hie-'*'™
Е = ~№k J Ио UKBroJJ -^7" dV,
Л = (9.69)
Подставив в (9.69) значение /экв из (9.68) и выразив
элемент объема dV в цилиндрических координатах г,
р, <р, приходим к следующим выражениям для напряжен-
ности поля, создаваемого диэлектрической антенной со-
ответственно в Е- и Я-плоскостях
Е£ (е — М cos & f С ^Eye^ikrsM pd pdydz, )
„ 30fea> (e — e0) f ffp -M . , . I (9-70)
EH —------у---- И i Ey e rSM pd pd <pdz, )
где E— проекция электрического вектора внутри стержня
на напразление E'F' (см. рис. 9 7),
г — расстояние от точки наблюдения до начальной
точки на оси стержня,
г1и— расстояние от точки наблюдения до произволь-
ной точки внутри стержня,
& — угол между осью стержня и направлением от
точки наблюдения до начальной точки на оси
стержня.
. Мы учитываем здесь только составляющую Еу, по-
скольку составляющие Ех и Е* имеют противоположное
направление в точках, расположенных симметрично отно-
сительно линий EF и E'F' (рис. 9.7).
Для rsM может быть легко получено следующее выра-
жение, аналогичное (3.5), связывающее его с г, г, р и &,
rsM = r — a cos &— р sin (9-71)
535
В свою очередь, согласно вводимым упрощениям (по-
стоянство фазовой скорости и распространение волны
лишь в направлении Z) Еу может быть представлено в
виде
Ey = A(z)f(p^)& hI
где A(z) — амплитудный множитель, указывающий зави-
симость напряженности поля от координаты z,
f(P, ?) — функция, определяющая изменение поля в пре-
делах заданного поперечного сечения,
1 = у----постоянная распространения.
Как видно из (9.70) Ен отличается от Ее лишь мно-
жителем cos&. Поэтому, во избежание повторений, мы
в дальнейшем будем приводить лишь значение Ее.
Подставив (9.71) и (9.72) в (9.70), получим
d
I % 2я
=3-°-^-(t-~?(,-cos & f Л (z) е~ /TZe/ftz С09 9
(9.72)
e'ftf sln \d
(9.73)
, d
где / — длина стержня, у —средний радиус стержня.
Как уже отмечалось, картина поля в поперечном се-
чении диэлектрического стержня подобна картине поля
в раскрыве волновода круглого сечения. Поэтому
с достаточной точностью положить
d
2 2п
можно
о о
Тогда
eMpsm6p(ftps BAj ysin&y
(9.74)
где
С cos &А, sin О) J A (z) е'*г s,n adz,
О
(9.75)
Q 30feco (в — e0) д
г
(9.76)
Г
о
о о
Легко видеть, что формула (9.75) соответствует ко-
ротковолновой антенне бегущей волны с переменными
536
амплитудами колебаний в вибраторах и с непрерывным
расположением вибраторов.
Теперь конкретизируем множитель A(z). Примем
A(z) = Xoe~fz, (9.77)
где р — коэффициент, подлежащий определению из опыт-
ных данных.
Выбор функции (9.77) объясняется, во-первых, тем, что
эта функция в зависимости от величины и знака [} может
выражать различный характер изменения амплитуд (воз-
растание при ₽<.О, убывание при 0 и постоянные ам-
плитуды при р=0) и, во-вторых, тем, что при этой функ-
ции интеграл в выражении (9.75) приобретает сравнительно
простой вид. Так как излучение связано с потерей энер-
гии. то естественно ожидать ₽>0.
Подставиз (9.77) в (9.75), получим:
ге/ , / . 1
ч sh cosV)
Ее~ АоС cos &Л[ (k sin & . • е—------------------- X
' “ утjkg (5 — cos&)
—3 4- —/* 4- (Е - cos 9)
Хе , (9.78)
где
<9-79>
Нормированная диаграмма направленности F£(&) ди-
электрической антенны, согласно (9.78), может быть вы-
ражена следующим образом
F£.= cos&-Ai
k у sin &
(9.80)
где
a =z k -4 (? — COS&),
а0 = Ц(5-1)
(9.80,а)
(9.80,6)
587
Выражение для диаграммы направленности в £-пло-
екости является произведением трех функций от угла
F2 = A1^sin&J, (9.82)
F3 = cos&. (9.83)
Проанализируем эти множители. Начнем с Fv
На рис. 9.13 показаны кривые зависимости F} от а для
различных значений вычисленные по формуле 9.81.
Из этого рисунка видно, что чем больше р (чем бы-
стрее убывают амплитуды поля от начала антенны
к концу), тем шире главный лепесток диаграммы направ-
ленности и больше боковые максимумы. Однако расшире-
ние главного лепестка и увеличение боковых максимумов
незначительно. Основная особенность диаграммы напра-
вленности при ₽}>0 заключается в отсутствии нулевых
значений поля, т. е. в слиянии главного и боковых ле-
пестков в кривую со слабо выраженными точками
экстремумов. При этом чем больше р, тем слабее выражены
экстремальные точки. Боковые максимумы непрерывно
убывают с возрастанием а.
Кривые рис. 9.13 вычерчены для значений а от О
до 4лг. Меняется же а согласно (9.80а) от минимального
значения
“„.“‘Й-1). (9-84)
соответствующего углу & = 0, до максимального значения
•«“‘(но. (9.85)
соответствующего углу &=ш180°. Поэтому в каждом кон-
кретном случае в зависимости от параметров диэлектри-
ческого стержня^, 5 и I используется участок кривой
рис. 9.13 от значения амин до амакс. На рис. 9.14 приве-
дено несколько серий кривых зависимости Fy от &, по-
S38
Рис. 9.13. Кривые зависимости множителя Flt входящего в выражение для диаграммы направлен-
3/
ности диэлектрической антенны, от параметра а при значениях параметра -у = 0; 0,5; 1,0.
строенных для различных значений указанных парамет-
ров путем воспроизведения соответствующих участков
кривых рис. 9.13. Например, рис. 9.14,а, воспроизводит
после нормировки (приведения максимального значения
к единице) кривые рис. 9.13 на участке от о,о = ^Х
X (1,1 — 1,0) = 72° до «80«=й~(1,1 — cos80°) = 65°. Ана-
логично построены остальные серии кривых рис. 9.14.
Кривые на этих рисунках обрываются при & = 80н-90°.
При увеличении угла 0 продолжается периодическое че-
редование максимумов и минимумов, но при все более
убывающих уровнях.
Анализ кривых рис. 9.14 показывает, что при сравни-
тельно малых значениях %ин(амин <80°), определяемых
по формуле (9.84), кривые У7, имеют большой максимум
при 0 = 0, в несколько раз превосходящий боковые мак-
симумы. При сравнительно больших значениях %ин(амин >
>130°) максимум, получаемый при 0 = 0, незначительно
превосходит боковые максимумы. Иллюстрацией послед-
него могут служить кривая $ = 1,2 на рис 9.14,в или кри-
вая / = 82. на рис. 9.14,г, соответствующие одинаковым
значениям амин=130°. Заметим, что хотя указанные кри-
вые, ввиду одинакового значения а имеют примерно
одинаковый относительный уровень боковых лепестков,
однако ширина главного лепестка получается меньшей
при большей длине стержня I. Очевидно, что при боль-
шей длине стержня будет больше общее количество ле-
пестков. Легко видеть из кривых рис. 9.13, что при не-
которых значениях амин, например, амин=180° возможно
получение боковых максимумов большей величины, чем
главный (при 0 = 0).
Перейдем к анализу двух других множителей, входя-
щих в формулу (9.80).
На рис. 9.15 приведены графики зависимости F2 от &
v d
для различных значении у, а также кривая зависимости
F3 от &.
Легко видеть, что при малых диаметрах стержня
0- =и0,3-г-0,5^ функция F2 мало меняется с изменением
& в пределах от 0 до 90°. Следовательно, при таких диа-
метрах стержня множитель F2 может рассматриваться
как почти постоянный. При значительных диаметрах
540
tf-90 -60 -30 О 30 60 90&°
Рис. 9.14. Зависимость Л, (см. рис. 9.13.) от О
В/
при различных значениях параметров , 5, I.
841
стержня функция F2 резко меняется с измене-
нием &. Отсюда следует, что при множитель F2
может оказаться определяющим в диаграмме направлен-
ности диэлектрической антенны.
Рис. 9.15. Кривые зависимости от угла в множителей, входящих
в выражение для диаграммы направленности
a) при различных значениях диаметра стержня,
б) Fa = cosD.
542
Что касается множителя F3, то он относится, как по-
казано выше, только к плоскости Е. Этот множитель
примерно от & = 0 до & = 40-г-45° мало меняется. Более
быстрое убывание функции Ея с увеличением угла & на-
чинается после & = 45н-5Э°. Таким образом, наличие мно-
жителя F3 в выражении для FE (9.80) мало сказывается
на форме диаграммы направленности. Диаграмма направ-
ленности диэлектрических антенн малого диаметра опре-
деляется в основном функцией F} а большого диаметра—
произведением функций F} и F2.
§ 6. АНАЛИЗ ДАННЫХ ЭКСПЕРИМЕНТАЛЬНОГО
ИССЛЕДОВАНИЯ ДИЭЛЕКТРИЧЕСКИХ АНТЕНН ИЗ
СПЛОШНОГО СТЕРЖНЯ
На практике, как правило, используются диэлектриче-
ские антенны из стержней малого диаметра ^-=0,3=0,5j,
изготовленные из материала (полистирол, люсит и т. п.),
обладающего диэлектрической проницаемостью - =
= 2,5-т-2,6. Такие антенны подробно исследованы экспе-
риментально. Наряду с. этим опубликованы [51] данные
исследования диэлектрических антенн большого диаметра
(до - = 2,4). Так как изложенная выше теория диэлек-
\ е0 /
трических антенн основывается, как мы видели, на ряде
аппроксимаций, то интересно сопоставить теоретические
данные с экспериментальными.
Начнем с диэлектрических антенн малого диаметра.
Воспользуемся приведенными в [49] тремя сериями экспе-
риментально снятых диаграмм направленности диэлек-
трических антенн, соответствующих следующим усло-
виям: 1
1. Цилиндрические стержни различной длины при оди-
наковых диаметрах поперечного сечения ^=0,46 и оди-
наковой длине волны 2 = 3,2 см.
. 2. Конические стержни различной длины при одина-
ковых диаметрах начального сечения -у^ = 0,46 и конеч-
ного —=— = 0,3 и одинаковой длине волны 2 = 3,2 см.
К
143
3. Один конический стержень длиной I — 20 см, у ко-
торого диаметры поперечного сечения равны <^иакс=4,6 см
и = 3 см, на разных волнах.
Во всех случаях материал стержней имел диэлектри-
ческую проницаемость — = 2,5.
е0
На рис. 9.16 сплошные линии изображают эксперимен-
тальные диаграммы направленности первой серии изме-
Рис. 9.16. Диаграммы направленности диэлектрических стержней
цилиндрической формы диаметра d = 0,46 X и различной длины —
экспериментальные (сплошные кривые) и теоретические (штриховые
кривые).
рений, относящиеся к четырем цилиндрическим стерж-
ням, имеющим различную длину.
Примечательно, что во всех случаях обратное излу-
чение ничтожно мало. Это указывает на малую величину
отраженной волны от конца стержня при d = 0,462, что
согласуется со сказанным выше (§ 3).
Далее во всех случаях лепестки не спадают до нуля,
а имеют минимум, равный примерно половине максимума.
Следовательно, даже при постоянном сечении стержня
необходимо предположить наличие затухания амплитуды.
Предполагая экспоненциальным закон затухания (9.77) и
544
учитывая, что отношение боковых максимумов к миниму-
мам равно 2, следует принять р^- = 0,5.
Из рис. 9.5 находим, что в нашем случае (при !_ = 2,5
\ ef>
и у= 0,46 j$= 1,15. Поэтому на рис. 9.16 в целях срав-
нения нанесены диаграммы направленности (см. штрихо-
вую кривую), вычисленные по формуле (9.81) в предпо-
ложении $=1,15, = 0,5 и длине I, равной реальной
длине открытой части диэлектрического стержня. Учи-
тывая приближенный характер формулы (9.81), следует
признать сравнительно хорошее совпадение теоретических
кривых с экспериментальными >>.
Данные, приведенные на рис. 9.16, показывают, что
из-за большого значения $ при оГ = 0,46Л, />2Л и |- = 2,5
нецелесообразно применять цилиндрические стержни.
На рис. 9.17 сплошные кривые изображают экспери-
ментальные диаграммы направленности второй серии из-
мерений для шебти конических стержней различной длины.
Для конических стержней характерным являются ма-
лые размеры боковых лепестков даже при сравнительно
длинных стержнях. Штриховые кривые на этом рисунке
изображают диаграммы направленности, вычисленные по
формуле (9.81) в предположении, что во всех случаях
$=1,1, длина I равна реальной длине открытой части
стержня. Из рис. 9.17 видно, что при /=42 и / = 52 из-
меренные кривые хорошо совпадают с расчетными; при
более коротких стержнях или при более длинных расчетные
кривые заметно отличаются от экспериментальных, причем
при / = 22 и / = 32 главный лепесток получается в дей-
ствительности более узким, чем по расчету, а при /=62
и / = 82 более широким, чем по расчету. Кроме того, при
/ = 62 и Z = 82 боковые лепестки в действительности не-
измеримо меньше, чем по расчету. Если бы мы предпо-
ложили, что во всех случаях $>1,1, то получили бы луч-
шее совпадение при более коротких стержнях, но зато еще
большее расхождение при более длинных. Предположение
$<1,1 во всех случаях привело бы к обратному резуль-
9 В пунктирных (расчетных) кривых рис. 9.16, а также следую-
щего рис. 9.17 не учтены множители F2 и F3 как мало существен-
ные.
35—1503 545
ej l -5л
3) l-6л
e) l-вл
Рис. 9.17. Диаграммы на-
правленности диэлектри-
ческих стержней кони-
ческой формы различной
длины при dMaKC = 0,46 X
и ймин = 0.3Х: экспери-
ментальные (сплошные
кривые)и теоретические
(штриховые кривые).
Кривые зависимости
*эфф и ?опт от относи-
тельной длины стерж-
ня (ж).
546
Тату. Это заставляет предположить, что £эфф должно за-
висеть от длины стержня, имея большее значение у более
коротких стержней и меньшее значение—у более длинных
стержней. Действительно, как показывают расчеты, до-
статочно хорошее совпадение теоретических и экспери-
ментальных данных получается, если выполнить расчет
в предположении, что 0 -^ = 0,5 и 5эфф равно соответ-
ственно^ 1,17, L ..= 1,15, $ .. = 1,12,5 .. = 1,Ю
5, = 1,08 и А — 1,05.
иэфф ’ еэфф ’
Рис. 9.18. Экспериментальные диаграммы направленности диэлектри-
ческого стержня конической формы, имеющего длину I = 20 см
и диаметры = 4,6 см и =3 см на разных волнах X.
4 МйЛС мин 1
На рис. 9.17,ж дана кривая (сплошная) зависимости
5эффот I у конических стержней рассматриваемого вида
(d = 0,462, d =0,32, - = 2,5\
На рис. 9.18 приведены диаграммы направленности,
относящиеся к третьей серии измерений, снятые на раз-
личных волнах 2.
Легко видеть, что в пределах указанного полуторакрат-
ного диапазона ширина главного лепестка диаграммы
направленности меняется почти в два раза. Это следует
признать очень резким изменением. Действительно, у
антенн типа синфазных, излучающих в перпендикулярном
направлении к раскрыву (зеркала, линзы, рупоры), как
мы видели, ширина главного лепестка 20о пропорцио-
нальна длине волны 2, а у антенн типа бегущей волны,
35* 547
излучающих вдоль оси при фазовой скорости о =с($=1),
как можно показать, ширина главного лепестка 20о про-
порциональна корню квадратному из длины волны 2. Более
резкое изменение 290 у диэлектрических антенн объяс-
няется тем, что, наряду с изменением относительной
длины стержня, происходит изменение фазовой ско-
t С 1г
или параметра ? = — , причем изменение г и $
рости Цф
одинаково: либо оба увеличиваются (при укорочении волны),
либо оба уменьшаются (при удлинении волны).
Действительно, при </ = 4,6 см на волне \,ин = 8Дсл
параметр £макс = 1>2 и относительная длина стержня
4 = 2,36, а на волне 2 =13 см, ? =1,05 и -=1,54.
Аналогично при d=. 3,0 см на волне Амин = 8,5 см пара-
МеТР 5макс=1>05’ Э НЭ В0ЛНе 2макс=13 ™ А,ин=1М
Из приведенных цифр следует, что на волне 2=13 см
£ меняется от 1,05 до 1,00, т. е. — почти равно единице.
/К
и д.
Как отмечалось выше, условие — совпадает с условием
Г,
—- = 0. Это означает, что при \—13см излучение должно
происходить, как в условиях отсутствия диэлектриче-
ского стержня. И в действительности при 2= 13 с .и диа-
грамма направленности, как видно из рис. 9.18,д, близка
к диаграмме направленности открытого конца волновода.
Заметим, что на волне Хмин = 8,5 см диаграмма на-
правленности имеет значительные боковые лепестки;
оптимальная диаграмма направленности получается на
волне 2 = 10 см:
0,46; ^с = 0,з1
X /
Данные рис. 9.18 относятся к сравнительно короткому
стержню. Очевидно, что при увеличении длины стержня
будет иметь место еще более резкое изменение диа-
граммы направленности с изменением длины.
Изложенные выше данные относятся к широко рас-
пространенным стержневым диэлектрическим антеннам
сравнительно малого диаметра (</ = 0,46=0,32). Перей-
дем к анализу данных экспериментального исследования
548
диэлектрических стержневых антенн большого диаметра
[51].
На рис. 9.19 показаны диаграммы направленности в Н-
плоскости цилиндрической стержневой антенны из поли-
стирола ^|- = 2,5j длиной / = 6Х. Измерения проводились
на волне 2 = 3,2 см. По оси абсцисс отложены углы от-
носительно осевого направ-
ления, а по оси ординат—
относительный уровень по-
ля в дб. Питание стержней
производилось от волновода
круглого сечения, в кото-
ром возбуждалась волна
ТЕ,,.
На рис. 9.20 приведены
огибающие диаграмм на-
правленности этих стержней
в Е-плоскости. На этих ри-
сунках указаны соответст-
вующие отдельным кривым
значения относительных ве-
личин диаметров стержней.
На рис. 9.21 дан график
зависимости коэффициента
усиления антенн от относи-
тельного диаметра стержня
у при длине / = 62.
Из приведенных данных
видно, что при достаточно
большом диаметре
О 20 W6080100
Рис. 9.19. Экспериментальные диа-
граммы направленности в Н-
плоскости диэлектрических
стержней цилиндрической формы
длиной I = 6,0 X при различных
значениях диаметра d.
стержня ((/ = 2,02)
цилиндрического
возможно получить узкую диаграмму направленности
с малыми боковыми лепестками, а также сравнительно
большой коэффициент усиления. Характерно при этом,
что общее количество лепестков (рис. 9.19) остается
одинаковым независимо от диаметра d стержня и опре-
деляется, повидимому, относительной длиной стержня
соотношение же между максимумами зависит сущест-
венным образом от Объясняется это тем, что дна-
А
грамма направленности антенны определяется в Я-плоскости
произведением F\ • Е2, причем число экстремальных точек
549
зависит главным образом от функции F} (9.81), а соотноше-
ние максимумов при больших диаметрах зависит главным
образом от функции (9.82).
Практическое применение диэлектрических, антенн из
стержней большого диаметра неизвестно и, невидимому,
нецелесообразно, так как такие антенны очень громоздки,
имеют большой вес, а по характеристикам излучения не
Рис. 9.20. Огибающие эксперимен-
тальных ^диаграмм'; направленности
в Я-плоскости стержней, указан-
ных на рис. 9.19.
перед диэлектрическими
а)
Рис. 9.21.. График за-
висимости коэффици-
ента усиления цилин-
дрического стержня
от его относитель-
ного диаметра при
длине I — 6,0 X.
антеннами из тонких стержней, ни перед плоскостными
антеннами (волноводными, рупорными и т. п.), площадь
раскрыва которых равна площади поперечного сечения
стержня. Исследование стержней большого диаметра имеет
интерес главным образом с точки зрения проверки изло-
женных выше теоретических положений. Результаты экспе-
риментального исследования, как легко видеть, находятся
в согласии с теоретическими положениями.
§ 7. РАСЧЕТ ДИЭЛЕКТРИЧЕСКИХ АНТЕНН
ИЗ СПЛОШНЫХ СТЕРЖНЕЙ
Как указывалось выше, диэлектрические антенны из
сплошных стержней применяются цилиндрической и кони-
ческой формы. Цилиндрические стержни малого диаметра
целесообразны при небольшой их длине {К2 Л), так как
при большой длине стержня в диаграмме направленности
появляются большие побочные лепестки, т. е. ухудшается
направленность (см. рис. 9.16).
Цилиндрические антенны большого диаметра, как ука-
зывалось выше, имеют существенные конструктивные не-
550
достатки и, повидимому, практического значения не имеют.
Основным видом диэлектрических антенн из сплошных
стержней следует считать стержни конической формы мало-
го поперечного сечения.
Конические стержни имеют в начале (у патрона) боль-
ший диаметр, а у конца меньший. Срезание на конус может
производиться либо на всей длине стержня, либо на участке
от начала до середины стержня при сохранении диаметра
постоянным на остальной половине стержня. По характери-
стикам излучения оба вида конических стержней практиче-
ски равноценны.
Необходимость применения конических стержней мо-
жет быть объяснена следующим образом. У патрона
диаметр стержня должен быть достаточным для того,
чтобы энергия в основном направлялась по стержню, а не
излучалась непосредственно с раскрыва патрона, как
с раскрыва волновода, т. е. диаметр должен быть таким,
Г,
при котором отношение согласно рис. 9.6 было бы не
w а
малым. Судя по опытным данным, это отношение должно
быть не меньше 1. Однако при диаметре стержня, удов-
летворяющем указанному условию, сравнительно мала
фазовая скорость рф волны на стержне (велико значение
параметра $). Для увеличения пф (уменьшения $) стержень
срезается на конус до диаметра, при котором фазовая
скорость почти равна скорости света.
Исходя из указанных соображений и учитывая данные
эксперимента; диаметры конического стержня определяются
из следующих соотношений:
максимальный диаметр
d s - —
макс / /
1/ it | — — I
' Vo
(9.86)
минимальный
d
МИН
X
(9.87)
Диаграмма направленности диэлектрических антенн
как цилиндрических, так и конических рассчитывается
в Е-плоскости по формуле (9.80), а в //-плоскости по
такой же формуле, но без множителя cosft. При этом
551
для обоих видов антенн можно принять у = 0,5. Пара-
метр $ у цилиндрических антенн вычисляется по фор-
муле (9.79), причем определяется по графикам рис. 9.5,
У конических стержней, у которых dMaKC и dMHH вычислены
соответственно по формулам (9.86) и (9.87), параметр $
может быть определен по графику рис. 9.17,ж. Множи-
тель F2 определяется для среднего диаметра, равного
^^макс "Г ^мин
ср= ------2-----•
При определении коэффициента направленного дей-
ствия диэлектрических антенн можно воспользоваться
известной приближенной формулой, связывающей D с ши-
риной главного лепестка 29О£ и 29О// в Е- и Я-плоско-.
стях [52]
21600
2®ОВ2
Коэффициент направленного действия диэлектрических
антенн из конических стержней' можно, кроме того, при-
ближенно определять по формуле [53]
0 = 4X4 -
Л
(9.88)
(9.89)
где А — множитель, зависящий от а0 (9.80,6).
Зависимость А от а0 графически изображена на рис. 9.22
для различных значений относительной длины антенны
I
Р = т.
Формула (9.89) и соответствующие ей графики рис. 9.22
получены теоретически для антенны бегущей волны, со-
стоящей из диполей Герца, расположенных непрерывно
вдоль прямой линии длиной I при одинаковых амплитудах
тока во всех диполях. Диаграмма направленности такой
антенны также определяется формулой (9.80), но при под-
становке у = 0 (постоянные амплитуды^) и d = 0 (малые
размеры излучателей). Как видно из рис. 9.13 кривые
4=0 и у = 0,5, соответствующие диэлектрической ан-
тенне, мало отличаются друг от друга. Имеющееся не-
большое отличие кривых компенсируется функцией Г2,
552
играющей некоторую роль в образовании диаграмм на-
правленности диэлектрических антенн.
Из кривых рис. 9.22 видно, что максимальный коэф-
фициент направленного действия имеет место при а0 =
Я 1) гл f
— — Jto условие определяет оптимальное значение ?
или оптимальное значение
фазовой скорости кото-
рые равны
и=ч4' <м°)
°Ф=-£Т- (9-9‘)
1 “К 2Z
На рис. 9.17,ж пунктир-
ная кривая соответствует
зависимости $опт от у. Лег-
ко видеть, что эта кривая
почти повсюду, исключая
значения -т-^2, совпадает
Л
А
20
16
12
Ofi
0,0
О
-Об -0,11 -0,2 0 0,2 0,0 0,6 <*о
Рис. 9.22. График зависимости
множителя А, входящего в фор-
мулу для коэффициента направ-
ленного действия, от параметра
скривой?Эфф. Таким образом,
конические стержни, диа-
метры которых определяются уравнениями (9.86) и (9.87),
представляют собой антенны типа бегущей волны с опти-
мальными параметрами. Их коэффициент направленности,
следовательно, равен
D = (7^8)|.
Коэффициент усиления О диэлектрических антенн из
такого материала, как полистирол, обладающий малыми
потерями, равен коэффициенту направленного действия D.
§ 8. ДИЭЛЕКТРИЧЕСКИЕ ТРУБЫ
Как указывалось выше (см. гл. I, § 6), наряду с антенна-
ми из сплошных диэлектрических стержней находят приме-
нение антенны из диэлектрических труб.
1) а0 =-д- получается, когда разность фаз полей, создаваемых
крайними излучающими элементами антенны бегущей волны, равна л.
553
Теоретическое исследование диэлектрических труб мож-
но вести тем же путем, каким было проведено исследова-
ние сплошных диэлектрических стержней, а именно, считая
трубы бесконечно длинными, можно найти частные решения
уравнений Максвелла для отдельных областей, а затем,
применяя граничные условия, найти постоянные интегриро-
вания. Особенность диэлектрических труб заключается
в том, что у них имеются три среды и две границы раздела
сред, в то время как у сплошных стержней имеются две
среды и лишь одна граница диэлектрик—воздух.
Поэтому при определении постоянных интегрирования
мы должны прийти для практически наиболее интересного
случая несимметричных волн в диэлектрических трубах к ха-
рактеристическому уравнению значительно более сложному,
чем (9.36), которое получено для сплошных стержней.
Найти из такого уравнения описанным выше графическим
способом фазовую скорость или отношение мощностей,
переносимых внутри диэлектрика и во внешнем простран-
стве, как функцию —у- (где d — диаметр стержня) пред-
ставит неимоверно громоздкую операцию. До настоящего
времени такая работа не выполнена, и мы не располагаем
теоретически вычисленными характеристиками поля в ди-
электрических трубах.
Диэлектрические трубы исследованы лишь эксперимен-
тально. Опубликованные данные [54] представляют собой
результаты нескольких серий измерений. Данные исследо-
вания относятся к цилиндрическим трубам круглого се-
чения.
Для труб использован материал (прессованная фибра),
имеющий диэлектрическую проницаемость — = 6.
Одна серия измерений посвящена исследованию влия-
ния толщины стенок трубы Д на характеристики поля
около антенны, а также на характеристики излучения.
На рис. 9.23 представлены кривые распределения поля
вдоль диэлектрической трубы с внешней стороны (сплош-
ные кривые) и с внутренней стороны (штриховые кривые)
стенки трубы. Длина волны во всех случаях равнялась
Л = 3,110 см. На рисунке через -у- обозначена толщина
d
стенки в единицах длины волны, а через -у — диаметр
трубы в единицах длины волны. По оси абсцисс отло-
554

to
1 у!
4^77 Л 7

—
6
г
г
2
О_____
О 2
И б <5 Ю сгГ
V
Рис. 9.23. Кривые распределения квадрата амплитуд поля
вдоль диэлектрической трубы с внешней (сплошные кривые)
и внутренней (штриховые кривые) сторон стенки трубы,
снятые на волне к = 3,1 см при различной относительной
Д
толщине -у- стенки трубы.
555
жены координаты z (ось Z параллельна оси трубы), а по
оси ординат относительная мощность (величина, пропор-
циональная квадрату напряженности поля).
Мы видим, что при толстых стенках напряженность поля
с наружной стороны трубы значительно меньше напряжен-
ности поля с внутренней стороны трубы. При тонких стен-
V
Рис. 9.24. То же, что на рис. 9.23 в режиме
стоячих волн.
Интересно, что, начиная с расстояния примерно в одну
длину волны амплитуда поля вдоль трубы остается по-
стоянной.
На рис. 9.24 показаны кривые распределения поля вдоль
трубы при закрытии последней металлическим диском
с целью образования стоячих волн. Обозначения такие же,
как на предыдущем рисунке. Длина волны Х== 3,110 см.
Кривая рис. 9.24,а, соответствующая тонкостенной
трубе, представляет собой картину стоячих волн с рас-
556
стоянием между максимумами или минимумами, рав-
ным у, где Л — длина волны в вакууме. Это указывает на
то, что при тонких стенках фазовая скорость волны в трубе
равна скорости света с = 3-108— . Кривая рис. 9.24,6,
соответствующая толстостенной трубе, также указывает
на существование стоячих волн, хотя и не с такой по-
следовательностью как кривая рис. 9.24,а. Однако рас-
д Рис. 9.25. Диаграммы направленности
~^=Ц<26 диэлектрических труб длиной I =6Х
различной толщины А и различного
d] диаметра d.
стояние между максимумами или минимумами значительно
меньше — . Это показывает, что в толстостенных трубах
фазовая скорость намного меньше скорости света с =
= 3. Ю8—.
сек
На рис. 9.25 изображены две диграммы направленности
двух диэлектрических труб одинаковой длины / = 6Л, но
с разной толщиной стенок. Из этого рисунка ясно видно
преимущество тонкостенной трубы. Что касается причины
плохой диаграммы направленности толстостенной трубы,
то надо думать, что она кроется в том, что фазовая
скорость волны в этом случае значительно отличается
от с = 3-108 —.
сек
557
Согласно данным эксперимента рекомендуется приме-
нять трубы с толщиной стенок As 0,031 в случае — =6
ео
или вычислять по формуле:
Д — 10-г
------. (9.92)
— — 1
Ео
Следующая серия измерений посвящена исследованию
влияния диаметра трубы d на диаграмму направленности
антенны.
На рис. 9.26 приведена кривая зависимости ширины
главного лепестка диаграммы
кривая), определенной по уров-
ню половинного значения на-
пряженности поля от диаметра
трубы. Длина трубы в опыте
была равна / = 61 при 1 =
==3,21 см, толщина стенок
А = 0,031. Некоторые из сня-
тых в данной серии измерений
диаграмм направленности по-
казаны на рис. 9.27 (сплошные
линии).
Из приведенных данных
видно, что увеличение диамет-
ра трубы приводит к увели-
чению направленности антенны
(к сужению главного лепестка
при сохранении побочных ле-
пестков почти неизменными).
направленности (сплошная
fl
0). ^--^7
Рис. 9.27. Диаграммы направлен-
ности экспериментальные (сплош-
ные кривые) и теоретические
(штриховые кривые) диэлектричес-
кой трубы, имеющей I — 6,0 X и
Д = 0,03 X при различных диаме-
трах d.
Рис. 9.26. Кривые зависимости
ширины главного лепестка диа-
граммы направленности от отно-
сительного диаметра диэлектри-
ческой трубы, имеющей I = 6,0 X
и А = 0,03 К. Сняты на волне
X = 3,21 см.
558
Третья серия измерений посвящена исследованию влия-
ния длины стержня I на диаграмму направленности.
На рис. 9.28 приведена кривая зависимости ширины
главного лепестка диаграммы направленности, опреде-
ленной по уровню половинного значения напряженности
поля от длины стержня, а на рис. 9.29 — некоторые из
снятых в данной серии измерений диаграммы направлен-
ности. В этих измерениях.-^- = 0,03; -^=1,16; 2=3,21 см.
Особенностью приведенных выше диаграмм направ-
Рис. 9.28. Экспериментальная (сплошная) и теоре-
тическая (штриховая) кривые зависимости ширины
главного лепестка диаграммы направленности ди-
электрической трубы от относительной длины.
ленности является малый уровень побочных лепестков
у цилиндрических излучателей и независимость этого
I
уровня от относительной длины антенны у, что также
характерно для антенн типа бегущей волны с постоян-
ными амплитудами и _^*_=1.
С
Основываясь на всей совокупности изложенных здесь
данных, предлагается [54] рассчитывать диаграммы на-
правленности диэлектрических трубчатых антенн по фор-
муле
(1 — cos ft)
kl
(1 — cos ft)
F =
/fed . o\
COS I у sin V j .
(9.93)
Пунктирные кривые на рис. 9.26 = 9.29 соответствуют
расчету по формуле (9.93). Из перечисленных рисунков
559
видно, что измеренные диаграммы направленности при
имеют более узкий главный лепесток, чем можно
ожидать согласно формуле (9.93). Для совпадения рас-
четных и экспериментальных диаграмм следует подстав-
лять в (9.93) /эфф несколько большее действительного I.
Широкий главный лепесток у диаграммы направлен-
ности при у = 2,0 (рис. 9.29,г) объясняется, повидимому,
тем, что в этом случае сказывается убывание амплитуд
Рис. 9.29. -Диаграммы направленности экспериментальные (сплошные
кривые) и теоретические (штриховые кривые) диэлектрической трубы,
имеющей Д = 0,03 1, d = 1,16 X при различной длине I.
поля, имеющее место на участке от металлического пат-
рона до расстояния примерно в одну длину волны (см.
рис. 9.21). У более длинных антенн этот участок отно-
сительно мал и его влияние незаметно. У более коротких
антенн (2«5 2л) влияние этого участка существенно.
Диаграмма направленности в f-плоскости практически
не отличается от диаграммы направленности в //-пло-
скости.
§ 9. СЛОЖНЫЕ ДИЭЛЕКТРИЧЕСКИЕ АНТЕННЫ
Антенна из одиночного диэлектрического стержня или
одиночной диэлектрической трубы, как мы видели, имеет
при / = 8Л ширину главного лепестка порядка 29о = 2О°.
560
При дальнейшем увеличении длины (если это возможно
с точки зрения сохранения достаточно малой величины
боковых лепестков, что не исследовано) ширина глав-
ного лепестка должна изменяться как у антенн бегущей
волны обратно пропорционально корню квадрат-
ному из длины стержня (трубы). Так как применение
чрезмерно длинных и тонких стержней (труб) нецелесооб-
разно из конструктивных соображений, то при требова-
нии 29О < 20° применяются сложные антенны, состоящие
из п одинаковых стержней (труб), расположенных на
расстоянии b друг от друга (см. рис. 1.11 и 1.12).
Диаграмма направленности сложной антенны опреде-
ляется по формуле:
F = FaFn, (9-94)
где Fq — диаграмма направленности одиночного стержня,
Fn — диаграмма направленности системы п ненаправлен-
ных излучателей, взаимно расположенных и питаемых
так, как стержни (трубы) в диэлектрической антенне.
Множитель Fn (9.94) зависит от соотношения ампли-
туд и фаз колебаний, возбуждаемых в отдельных стерж-
нях (трубах). Как правило, амплитуды колебаний у них
одинаковы. Соотношение же фаз бывает двух видов:
либо одинаковые фазы во всех стержнях (трубах), либо
монотонное линейное изменение фаз. При одинаковых фа-
зах колебаний
/ ь \
sin ( nk sin 0 )
Fn=—^-b--------V’ (9'95)
п sin ( sin ® )
где & — угол между осью стержня (трубы) и заданным
направлением в плоскости расположения стержней (труб).
При монотонно линейном законе изменения фаз
п sin
F =
/ b
( k -% sin Э — <|»
6
fe-g" sin 0 — ф
(9.96)
где ф—разность фаз между колебаниями двух соседних
стержней.
В системе питания антенны, рис. 1.12, предусмотрены
волноводные фазовращатели, обеспечивающие линейный
36—1503 561
закон изменения фаз, причем величина ф может меняться,
что позволяет получить качания луча.
В связи с применением сложных диэлектрических
антенн интерес представляет знание взаимного влияния
стержней. На рис. 9.30 показана относительная величина
Е
напряженности поля ”асс в децибелах, возбужденного
£пит
Рис. 9.30. Зависимость относительной величины напряжен-
ности поля, возбуждаемой диэлектрическим стержнем
в соседнем от < тносительного расстояния между ними:
при одинаковом направлении стержней (сплошная кривая)
и при противоположном (штриховая кривая).
питаемым стержнем в пассивном, в зависимости от рас-
стояния у между стержнями. Сплошная кривая соответ-
ствует одинаково направленным стержням (а), пунктир-
ная — противоположно направленным (б). При одинаковом
направлении стержней взаимное влияние резко падает
с увеличением расстояния Ь. При противоположном на-
правлении стержней ослабление взаимного влияния про-
исходит значительно медленнее.
562
§ 10. ДИЭЛЕКТРИЧЕСКАЯ СТЕРЖНЕВАЯ АНТЕННА,
ИЗЛУЧАЮЩАЯ ПЕРПЕНДИКУЛЯРНО ОСИ.
АНТЕННА С ШИРОКОУГОЛЬНОЙ ДИАГРАММОЙ
НАПРАВЛЕННОСТИ
Обычные диэлектрические антенны, рассмотренные в § 3
и § 4, имеют главный максимум излучения вдоль оси. Это
объясняется тем, что электромагнитные колебания в них,
как мы видели, носят характер бегущей волны, распростра-
няющейся со скоростью, близкой к скорости света в на-
правлении оси. Обычные антенны имеют очень слабое излу-
чение в перпендикулярном к оси направлении (практически
оно отсутствует). Можно, однако, видоизменить эти антен-
Рис. 9.31. к пояснению принципа действия диэлек-
трической антенны, имеющей главный максимум
в направлении, перпендикулярном оси.
ны таким образом, чтобы получить главный лепесток излу-
чения в направлении, перпендикулярном оси, и слабое излу-
чение вдоль оси.
Принцип действия такой антенны можно объяснить сле-
дующим образом.
Мысленно разделим антенну на участки длиной ,
где — длина волны в антенне (см. рис. 9.31). Вдоль
каждого из участков фаза поля непрерывно меняется
в пределах 180°. Каждые два смежных участка являются
противофазными в том смысле, что каждому элементу
данного участка соответствует такой же элемент на со-
седнем участке с противоположной фазой электромагнит-
ного поля. Участки через один (оба четные или оба нечет-
ные) являются в этом смысле синфазными. При одинаковых
амплитудах поля вдоль всей антенны поля излучения двух
соседних участков имеют в перпендикулярном к оси направ-
лении противоположные фазы и при интерференции уничто-
жаются. При наличии затухания волны вдоль стержня поле
излучения в перпендикулярном к оси направлении хотя и не
равно нулю, но очень слабое.
36* 563
Представим себе, что мы каким-либо путем добились
уничтожения излучения четных участков. Тогда останется
излучение только нечетных участков, являющихся синфаз-
ными. В этом случае будет иметь место интенсивное излу-
чение в перпендикулярном к оси направлении. Если на
оставшихся участках сохранились прежние фазы поля, то
будет иметь место также интенсивное излучение вдоль оси.
Если же одновременно с уничтожением излучения четных
, участков нарушить прежние соотношения фаз
на нечетных участках, например, уменьшив фа-
зовую скорость распространения волны вдоль
«У | туГ антенны, то будет иметь место интенсивное
I IE излучение в перпендикулярном к оси направ-
Е лении и резко ослабится излучение вдоль оси
Е антенны.
ТГ По этой идее построена диэлектрическая
Д антенна, схема которой изображена на
К рис. 9.32. Она представляет собой диэлектри-
К ческий стержень цилиндрической формы диа-
JL-Л метром около 0,52 из полистирола (—=2,6)
/ и \ на который насажены через определенные
Рис 9 32 промежутки диэлектрические кольца из ди-
Устройство электрика с проницаемостью — = 8. На'ри-
диЭлектри- ео
ческой ан- сунке приняты обозначения: наружный диа-
тенны.^излу- метр колец dK (внутренний диаметр равен
пендТкуляр- диаметру стержня), их ширина ак и расстОя-
но оси. ние меЖду ними ZR.
Как мы видели выше, при больших диаметрах стержня
напряженность поля на его поверхности очень слаба,
очень мала мощность Wa, переносимая внешним прост-
ранством, что соответствует весьма слабому излучению.
Поэтому участки стержня, где насажены кольца, прак-
тически не излучают. Одновременно на этих участках
, с
фазовая скорость резко спадает до величины уф = -у—,
У е0
что нарушает необходимое соотношение фаз для получе-
ния осевого излучения. В результате получается антенна,
имеющая главный максимум излучения в перпендикуляр-
ном к оси направлении и слабое излучение вдоль оси.
Надевание колец на диэлектрический стержень при-
564
водит к такому искажению первоначального поля, кото-
рое в деталях трудно учесть, пользуясь элементарными
представлениями. Ввиду отсутствия теоретического ис-
следования вопроса, размеры колец dK и ак и расстоя-
ние между ними /к подбираются эмпирически.
Опыт показал, что оптимальная ширина колец ак при
^- = 8 должна быть порядка 0,252. Наружный диаметр
колец должен быть, вообще говоря, различным на различ-
ных участках. Расстояния между кольцами также следует
варьировать, подбирая их экспериментально.
Рис. 9.33. Диаграммы направленности антенны с шестью
кольцами при различных расстояниях I между ними.
Для иллюстрации на рис. 9.33 и 9.34 показаны диа-
граммы направленности антенн, имеющих соответственно
6 и 18 колец. Схемы этих антенн показаны на рис. 9.35
и 9.36. На рисунках указаны параметры антенн dK, ак
и / Боковые лепестки у антенны с шестью кольцами
составляют 6 -н 9 дб, а у антенны с 18-ю кольцами — по-
рядка 10^-15 дб.
На рис. 9.33 и 9.34 угол 90° соответствует перпендику-
лярному к оси направлению. Отклонение главного максиму-
ма от угла 90° объясняется наличием меняющейся по линей-
ному закону вдоль стержня разности фаз между отдельны-
ми излучающими участками. Питание к диэлектрическому
стержню в описанных антеннах подводилось от круглого
волновода, в котором возбуждалась волна ТЕц.
Можно предположить, что в диэлектрических антеннах,
излучающих перпендикулярно к оси, найдут применение
также симметричные волны.
565
В описанных антеннах использовались диэлектрические
стержни. Не исключена возможность устройства такой
антенны из диэлектрических труб.
Имеются сведения [55] о построении диэлектрической
антенны с шириной лепестка в пределах 180°<] 2% < 360°,
названной излучателем с широкоугольной диаграммой
направленности.
Рис. 9.34. Диаграммы направленности антенны с 18-ю
кольцами при различных параметрах /ц I,, 13.
0,5/ 0,6л 0,7 Л О.дл
Рис. 9.35. Схема диэлектрической
антенны с 6-ю кольцами.
0,5л 0,55л 0,6л 0,65л
€
Рис. 9.36. Схема диэлектрической антенны
с 18-ю кольцами.
566
0,25л
На рис. 9.37 схематически изображена такая антенна.
Она представляет собой два круглых диэлектрических
стержня, вставленных в прямоугольный волновод, причем
наружная часть стержней имеет цилиндрическую форму,
Рис. 9.37. Антенны с широкоугольной диа-
граммой направленности, состоящие из двух
диэлектрических стержней, вставленных в
волновод: а) круглые стержни, б) с дополни-
тельными клинообразными выступами.
Рис. 9.38. Оптимальные размеры элементов диэлек-
трической антенны с широкоугольной диаграммой
направленности.
567
а внутренняя (в волноводе)—коническую (рис. 9.37,а). С на-
ружной стороны к стержням добавлены клинья из диэлек-
трика (рис. 9.37,6). Размеры стержней и клиньев подби-
раются экспериментально. На рис. 9.38 показаны оптималь-
Рис. 9.39. Диаграмма направленности антенны,
показанной на рис. 9.38.
ные размеры отдельных элементов этой антенны, соответ-
ствующие длине волны I — 3,2 см.
На рис. 9.39 показана диаграмма направленности рас-
сматриваемой антенны в Я-плоскости. Аналогичным обра-
зом можно построить антенну с широким главным лепесткбм
в Е-плоскости.
ГЛАВА ДЕСЯТАЯ
АНТЕННЫ ПОВЕРХНОСТНЫХ ВОЛН
§ 1. ПОВЕРХНОСТНЫЕ ВОЛНЫ
Выше (гл. I, § 8) дано краткое описание устройства и
принципа действия антенн поверхностных волн. Здесь по-
знакомимся подробнее с особенностями и характеристиками
этих антенн. Прежде всего выясним, что представляют со-
бой поверхностные радиоволны, возбуждаемые у этих антенн
и определяющие их особенности
Образование поверхностных волн связано с наличием
поверхности раздела двух сред с различными параметра-
ми е, (х, а. По форме поверхности мы будем различать вол-
ны, связанные с круглой цилиндрической и с плоской по-
верхностью.
а) круглая цилиндрическая поверхность раздела
Примером поверхностных волн, связанных с круглыми
цилиндрическими поверхностями, могут служить рассмотрен-
ные в предыдущей главе волны, образующиеся внутри и
вокруг бесконечно длинного круглого диэлектрического
стержня. Как мы видели, электромагнитное поле, образую-
щееся в диэлектрическом стержне и пространстве, окружаю-
щем стержень, представляет собой слабо затухающую пло-
скую волну, распространяющуюся вдоль оси стержня с фа-
зовой скоростью, меньшей скорости света с. В радиальном
направлении поле убывает, причем вне стержня на значи-
тельных расстояниях от оси убывание происходит по экспо-
ненциальному закону.
В ряде работ [56,57] доказана возможность образо-
вания аналогичных волн вокруг одиночного тонкого круг-
лого металлического провода, находящегося в воздухе.
В данном случае практический интерес имеет только
569
поперечно-магнитная волна „основного типа0 ТМоо, ха-
рактеризующаяся тем, что скорость ее распространения в
осевом направлении близка к скорости света. Картина
линий поля волны ТМоо у металлического провода по-
казана на рис. 10.1. Эта волна является симметричной
относительно оси провода, т. е. векторы поля Е и Н не
зависят от угловой цилиндрической координаты <р. Амп-
литуды поля этой волны сравнительно быстро затухают
в радиальном направлении (по оси р) и очень слабо за-
В ид с too к у Вид с конца
Рис. 10.1. Конфигурация электромагнитного поля
поверхностной волны ТМ0(1, возникающей вокруг
круглого металлического провода.
тухают в осевом направлении (по оси Z). Все остальные
типы волн, возникающие вокруг металлического провода,
как поперечно-магнитные ТМт;1 более высоких порядков,
так и поперечно-электрические ТЕтл всех порядков, очень
быстро затухают и в радиальном и в осевом направле-
нии и поэтому практического значения не имеют.
Металлический провод с поперечно-магнитной волной
«основного типа» находит применение в качестве линии пе-
редачи (фидерной линии), имея по величине осевого зату-
хания некоторое преимущество перед коаксиальным кабелем
и перед волноводом. Вполне очевидно также его преимуще-
ство в конструктивном отношении. В качестве антенны та-
кой провод не используется, так как при волне «основного
типа», как симметричной, диаграмма направленности прово-
да будет конической формы, которая не находит практи-
ческого применения. Поскольку поверхностные волны, обра-
зующиеся вокруг металлического провода, непосредственно
в излучающих системах не используются, мы подробно рас-
сматривать их здесь не будем.
570
б) плоская поверхность раздела
Поверхностные волны, связанные с плоскими поверхно-
стями раздела, возбуждаются в плоскостных антеннах по-
верхностных волн (см. гл. I, § 8). Эти волны рассмотрим
более подробно.
У
Рис. 10.2. Конфигурация электромагнитного поля поверх-
ностной волны ТМ0Р, возникающей в случае плоской по-
верхности раздела двух сред: а) плоская волна (волна
Ценнека), б) цилиндрическая волна.
При плоской поверхности раздела встречаются волны
плоские (рис. 10.2,а )и цилиндрические (рис. 10.2,6). Пло-
ские волны иначе называют волнами Ценнека [58,59] по
имени ученого, впервые исследовавшего их. Соответст-
венно форме волны при анализе будем пользоваться в
571
случае плоской волны прямоугольной системой коорди-
нат XYZ, а в случае цилиндрической волны—цилиндри-
ческой j'p'p. В обоих случаях считаем, что среда 1 ха-
рактеризуется параметрами еь Ц], аь а среда 2 — воздух-
параметрами е2 = е0, р2 = р.о, с2 = 0.
Так же, как в случае металлического провода, практиче-
ский интерес имеет здесь поперечно-магнитная волна. На-
правление электрических и магнитных линий поля иллюстри-
руется на рис. 10.2.
Ищем решение уравнений Максвелла, которое удовлетво-
ряет следующим условиям:
1. Электромагнитное поле не зависит от координаты х
в случае плоских волн или от координаты <р в случае ци-
линдрических волн.
2. Зависимость поля от координат у и z или соответ-
ственно от у и р имеет характер экспоненциальной функции.
Кроме того, поле должно естественно удовлетворять
граничным условиям (2.4) и (2.5), а также равенству нулю
при у—»оо.
Решением уравнений Максвелла при указанной зависи-
——*
мости векторов поля Е и Н от координат являются приво-
димые ниже выражения для составляющих поля по коорди-
натным осям.
В случае плоской волны получаем:
для поля в среде 1
Ег.= — А .
Pij'-Л*
e
(Ю.1)
для поля в среде 2
Hx2 = Ae-^y41z,
Ez2=A-ke-
ZZ
г? _ Д 7 /V
ЕУ2-~А^й 6
(10.2)
572
Аналогично в случае цилиндрической волны имеем:
для поля в среде 1
В =-Л—еиН‘‘<
f1 Oj 4- /wej 1 '1 f
E , — A —Д— еР1У H<2) (yp),
J'l 31 “t" /ше1 О ' I
для поля в среде 2
(уР),
£,2=ЛДе“’'Х’(»>'
(10.3)
(Ю.4)
В этих уравнениях постоянная А характеризует амп-
литуду волны и зависит от мощности излучения. По-
стоянные распространения р2, у могут быть найдены
следующим образом.
Подставив выражения для составляющих поля из
(10.1)-г-(10.4) в уравнения Максвелла (2.1), получаем:
I2~Hi = — /u>pi (oj +/mei) (10.5)
и
- Г + й = % = - F = - (10.6)
В свою очередь, из условия непрерывности следует
Ь—= —Э-. (10.7)
®1------------------------------jcoe0
Уравнения (10.5)—е-(10.7) позволяют выразить fl2, у
через параметры сред.
Рассмотрим частные случаи, когда среда 1 является:
а) идеальным диэлектриком (<4 — 0),
б) хорошим проводником (а^ш®!, а^шеД
в) идеальным проводником (а,—юо)1).
1) Очевидно, что случай полупроводника, когда oj имеет тот
же порядок величины, что «еь является промежуточным между
первыми двумя.
573
Во всех случаях положим p.j = р.о.
При указанных здесь значениях параметров среды 1
решение системы уравнений (10.5)-г-( 10.7) приводит к
следующим значениям для постоянных распространения
в отдельных случаях
а)
(10.8)
V ^e°dh>-
б)
(10.9)
в)
(10.10)
7 = Ш /|хое0-
Уравнения (10.5)--г (10.10) справедливы как при пло-
ской волне (рис. 10.2,а), так и при цилиндрической волне
(рис. 10.2,6). Сначала воспользуемся этими уравнениями
для анализа поля плоской волны.
Из уравнений (10.8) следует, что в случае идеального
диэлектрика поле, определяемое уравнениями (10.1)-н
(10.2), представляет собой плоскую волну, распространяю-
щуюся в направлении, образующем с осью Y (т. е. с
нормалью к плоскости раздела) в среде 2 угол <р, опре-
деляемый соотношением
, (ю.н)
Г е0
а в среде 1 угол ф, определяемый соотношением
tg<p=j/ • (Ю.12)
Угол <р, соответствующий уравнению (10.11), известен
под названием угла Брюстера. При таком угле падения,
574
кйк известно, отсутствует отражение от поверхности
раздела. Легко показать, что углы у и ф, определяемые
уравнениями (10.11) и (10.12), связаны между собой сле-
дующим образом
4^ = /^. (10.13)
Sin ф Г е0 v ’
Соотношение (10.13) известно как закон преломления.
Фазовая скорость распространения вдоль поверхности
раздела равна
Таким образом, когда среда 1 является идеальным
диэлектриком, поверхностная волна представляет собой
в воздухе плоскую волну, падающую на плоскую по-
верхность раздела под углом Брюстера, а в диэлектрике
эту же волну, прошедшую через границу раздела по
известному закону преломления.
Из уравнений (10.9) видно, что в случае хорошего
проводника постоянные распространения [},, р2, у комп-
лексны. При этом у р! и р2 вещественная и мнимая части
равны, у у вещественная часть очень
НИЮ С МНИМОЙ. По модулю I р| | > | у |,
зывает на то, что в воздухе волна
почти параллельно границе раздела,
почти перпендикулярно ей. В воздухе
тухает как в направлении оси Y, так и в направлении
оси Z, причем затухание в направлении оси Z происходит
значительно медленнее, чем в направлении оси У. Сле-
довательно, электромагнитное поле в воздухе имеет
характер неоднородной плоской волны, у которой пло- -
скость одинаковых фаз поля почти перпендикулярна оси
Z, а плоскость одинаковых амплитуд почти перпенди-
кулярна оси У. В проводнике затухание происходит
очедаь быстро в направлении оси У. Толщина поверхно-
стного слоя Д (так называемого скин-слоя), в пределах
которого убывание поля в проводнике составляет один
непер, равна
велика по сравне-
| [321 < у. Это ука-
распространяется
а в проводнике —
поле медленно за-
(10.15)
Фазовая скорость распространения волны вдоль границы
раздела равна с.
Итак, в случае хорошего проводника поверхностная вол-
на представляет собой неоднородную плоскую волну, падаю-
575
Шую на поверхность раздела (имея в виду направление пе-
ремещения фазового фронта) под углом к нормали, близким
к 90°, проникающую в проводник без отражения и очень
быстро затухающую в нем.
Отсутствие отражения от поверхности проводника, по
аналогии с предыдущим случаем идеального диэлектрика,
принято трактовать как падение под углом Брюстера. Одна-
ко в отличие от предыдущего случая этот угол считается
комплексным и равным
<l0J6>
Введение понятия о комплексном угле Брюстера сле-
дует понимать в том смысле, что при падении неодно-
родной волны на поверхность проводника она может
пройти в проводник без отражения, но при обязательном
условии, что углы <ра и <рф наклона плоскостей соответ-
ственно одинаковых амплитуд и одинаковых фаз опреде-
ляются из условий:
(10.18)
В случае, когда средой 1 является идеальный про-
водник, поле поверхностной волны, как это следует из
(10.3), (10.4) и (10.10), в направлении оси Y в воздухе не
меняется, а в проводнике имеет бесконечно быстрое
убывание (Д—>0). По оси Z волна распространяется без
затухания. Составляющая поля Ег в воздухе равна нулю,
т. е. поле имеет только две составляющие Е„ и Н .
У ?
Следовательно, в случае идеального проводника поверх-
ностная волна представляет собой чисто поперечную пло-.
скую волну типа ТЕМ, распространяющуюся над проводни-
ком параллельно его поверхности.
Выше мы анализировали плоскую поверхностную волну
вида рис. 10.2,а. Отмеченные особенности в общих чертах
справедливы также для цилиндрической поверхностной вол-
ны вида рис. 10.2,6, поскольку уравнения (10.8) -ч- (10.10),
связывающие постоянные распространения с параметрами
сред, являются общими для плоской и цилиндрической волн,
а уравнения для составляющих поля цилиндрической волны
(10.3) -г-(10.4) аналогичны уравнениям для составляющих
576
поля плоской волны (10.1) и-(10.2). Действительно, ганке-
левы функции, входящие в уравнения (10.3) и (10.4) на
сравнительно небольших расстояниях от оси р = 0, опреде-
ляемых из условия
1тр1>1.
могут быть заменены асимптотическими выражениями,
являющимися экспоненциальными функциями от ур. При
такой замене вид выражений (10.1) и (10.2) не отличается
от вида выражений (10.3) и (10.4).
Отличие цилиндрической волны от плоской заклю-
чается, во-первых, в различном направлении составляю-
щих поля (Дф вместо Нх и Е вместо Ez, во-вторых, в
осевой симметрии поля, в-третьих, в наличии радиального
распространения, в-четвертых, в образовании около оси
р = 0 небольшой зоны, где электромагнитное поле ана-
логично полю ближней зоны нитевого тока и отличается
от поля распространяющейся волны.
Итак, поверхностные волны это волны, распростране-
ние которых направляется какой-либо поверхностью раз-
дела сред с различными параметрами е, ц, а. В случае
плоской направляющей поверхности фазовая скорость
распространения вдоль границы раздела меняется в пре-
делах от с ПРИ идеальном диэлектрике до с
при идеальном проводнике. Как увидим ниже, покрытие
металлической поверхности слоем диэлектрика или гофри-
рование металлической поверхности существенно влияет
на фазовую скорость и другие характеристики поля по-
верхностной волны.
§ 2. ПОВЕРХНОСТНОЕ СОПРОТИВЛЕНИЕ
Поверхностную волну принято характеризовать так
называемым поверхностным сопротивлением Zs, под ко-
торым понимается отношение касательных составляющих
к поверхности раздела электрического и магнитного век-
торов поля в воздухе. В случае плоской волны
Е
(io.i9)
в случае цилиндрической волны
Е
Zs = --^. (10.20)
37—1503
577
В обоих случаях согласно (10.2) и (10.4)
7 — __ -
« ““ >е0 •
(10.21)
Обозначим
Р2 = а2— jb2,
(10.22)
(10.23)
Тогда получим
п ___
X =
s и£о
часть поверхностного сопротивления
Вещественная
характеризует фазовую скорость распространения волн в на-
правлении нормали к поверхности раздела, а мнимая
часть — степень убывания поля в этом направлении.
В антенных устройствах, использующих сравнительно мало-
го размера направляющие поверхности, желательно иметь
поверхность, характеризующуся отсутствием распростране-
ния в направлении нормали к поверхности раздела и нали-
чием быстрого затухания волны в этом направлении, так
как при этом энергия будет сконцентрирована у поверхно-
сти раздела и волна будет распространяться только вдоль
этой поверхности. В противном случае должно иметь место
непосредственное излучение в пространство от возбудителя
поверхностной волны. Следовательно, в антенных устрой-
ствах желательно иметь поверхность с чисто реактивным
поверхностным сопротивлением.
Требование реактивного поверхностного сопротивления
диктуется еще следующими соображениями. Антенны по-
верхностных волн являются антеннами типа бегущей волны.
У последних, как отмечалось выше,
циент усиления получается (см. рис.
? = — > 1,
наибольший коэффи-
9.22), когда
(10.24)
т. е. когда фазовая скорость v^<Z.c. Из (10.6) видно,
что Рф = -у- будет меньше скорости света с, когда р2
вещественно или когда Zs чисто мнимо.
578
Из (10.8)-г-(10.10) видно, что при идеальном диэлектри-
ке поверхностное сопротивление чисто активно и равно
Z.=R-=V^,- <1о-25>
при идеальном проводнике ZS = Q, а при хорошем про-
воднике, но с конечной проводимостью а1
Z =1/ ^(1 + j)
s г 2с4 4 ' J ’
(10.26),
т. е. является комплексным, причем величина веществен-
ной и мнимой частей одинаковы. Такие значения Zs не
удовлетворяют указанным выше требованиям. Поэтому
поверхностные волны, образующиеся непосредственно на
плоской границе воздух—диэлектрик или воздух-металл,
не нашли применения в антенной технике.
§ 3. МЕТАЛЛИЧЕСКАЯ ПОВЕРХНОСТЬ,
ПОКРЫТАЯ ДИЭЛЕКТРИЧЕСКИМ СЛОЕМ
На рис. 10.3 показан диэлектрический слой (среда 2)
постоянной толщины h, находящийся между проводником
(среда /) и воздухом (среда 3). Исследуем характеристику
поверхностной волны в этом случае. Ограничимся рассмот-
рением только плоской волны.
В средах 1 и 3 выражения для составляющих векторов
поля имеют соответственно вид (10.1) и (10.2). Что касается
Среда 3 (iojdyx,б-0)
Среда / (металл-£1,р0,<э1)
Рис. 10.3. К анализу поля поверхностной вол-
ны, возникающей в случае металлического
листа, покрытого тонким слоем диэлектрика.
37
579
среды 2, то из-за наличия отражений от границ диэлек-
трик—воздух и диэлектрик—металл там образуются стоя-
чие волны. Таким образом, в рассматриваемом случае имеем
в среде 1
Ях1 = Л'ем“Лг .
JlO&j
(10.27)
р------д> ,&У—Ьг
У'~~ 01 + JOSj е
В среде 2
Hx2 = B'Q-^y4^
£ = В' Л е- — В" ?2 e?2j/-/TZ
Z2 Jwc3 J"e2
E „„ = — B'-L e~ м~'тг — В" J- e?2j"/TZ.
У* a>l3 <«£4
В среде 3
Hx3 = A"e-^-* ,
£ _Ди1з_е-^-Лг)
z3 J4D-0
E =—A"-1- q-^у-^ .
yb COSq
Условия непрерывности дают:
при _у = 0
Л' = В' + В",
— А' —Л— = Д- (В' — В"),
°1 + Уш61 v
при y = h
Д»е_?’й=В'е_м-|- В"ем ,
Л" Д- е-м = Д- (В'е-М — В"е^Л
/^е0 '
(10.28)
(10.29)
(10.30)
(10.31)
Исключение коэффициентов А', А", В', В" из системы
уравнений (10.30) и (10.31) приводит к следующему ра-
венству:
j . ?lEo
РзЧ °1 + /ШЕ1
tgM^ —

?1 1л-0
(10.32)
L °i + 7^1
580
Уравнение (10-32) сомвестно с уравнениями
— Y2 -Hi =УшРоа1 — “21’оеь 1
— 124-{>2= —ш2Ное2- | (10.33)
— Т2 j Й = —ш%ео- I
позволит выразить постоянные распространения у, р2
и р3 через параметры сред eb е2, е0, [i0, at. Следует при
этом учесть, что толщина h слоя диэлектрического по-
крытия берется очень малой, благодаря чему можно за-
менить tgf2/isp2/i. Примем далее, что среда I является
хорошим проводником и поэтому можно пренебречь сла-
гаемым o'Sj, по сравнению с at.
Все это позволяет привести (10.32) к следующему виду
1 —• (Ю.34)
₽3Е2 ’1 01 е3 V ’
Из второго и третьего уравнений (10.33) получаем
(10.35)
Подставив (10.35) в (10.34), получаем
22. о h _. <->аМо6з — и.)_А Jo _1_ в и == — 1 — Ь . (10.36)
нз Рз s2 п J =i н ei ₽з v 7
В уравнении (10.36) можно пренебречь слагаемым
-^-р3/г по сравнению с единицей и слагаемым по
сравнению со слагаемым у-, так какрз/г<1. Пренеб-
регая указанными величинами, приводим (10.36) к виду
= (10.37)
Постоянную распространения можно выразить в
данном случае так же, как в (10.9) Учитывая это полу-
чим следующее выражение для р3
₽3 - »Ч<« {Л + 4 ] - /1]}=“з - А. <10.38)
где Д —толщина скин-слоя, определяемая уравнением
(10.15).
581
Из (10.38) получаем следующее выражение для по-
верхностного сопротивления
А=«. +Лн + А).
(10.39)
Из (10.39) видно, что в случае идеального провод-
ника, у которого Д = 0, покрытого тонким слоем идеаль-
ного диэлектрика, можно получить чисто мнимую вели-
чину поверхностного сопротивления. В реальных усло-
виях хорошего проводника получается значительное
преобладание реактивной составляющей над активной.
Зная рз, можно из третьего уравнения системы (10.33)
найти постоянную распространения у. Легко видеть, что
(10.40)
Учитывая, что kh < 1 из-за малого размера h — тол-
щины слоя диэлектрического покрытия, можно положить’
Из (10.41) получаем следующие выражения для фазо-
вой скорости волны в направлении, параллельном по-
верхностям раздела и постоянную затухания 3 в этом
направлении:

1 + 2
^2 — 6» A
е0 h
(10.42)
(10.43)
§ 4. ГОФРИРОВАННАЯ МЕТАЛЛИЧЕСКАЯ ПОВЕРХНОСТЬ
На рис. 10.4 показана гофрирозанная металлическая
поверхность, принятая при этом система координат и
обозначения. Для такой поверхности задача о распро-
странении поверхностных волн решена при условии бес-
582
конечно малой толщины выступов (©—♦0). Познакомимся
вкратце с этим решением. Сначала предположим, что
показанная на рис. 10.4 структура имеет в направлении
оси X (в обе стороны) бесконечную протяженность и что
на длину волны приходится очень большое число вы-
ступов (t << Z). Проводник считается идеально проводя-
щим. Поверхностную волну считаем типа ТМоо, т. е.
Рис. 10.4. К анализу поля поверхностной волны, возникающей в
случае гофрированного металлического листа.
того же типа, что в предыдущих случаях. В соответ-
ствии с этим-можем принять, что электромагнитное поле
в воздухе определяется уравнениями (10.2) при замене
в них индекса „2“ на индекс „5“.
Поле в канавках (в области _у<0) определяем, рас-
сматривая каждую канавку как волноводный канал,
в котором возбуждается волна типа ТЕМ. Так как волна
отражается от дна канавки, то поле имеет характер
стоячей волны и его составляющие определяются сле-
дующим образом:
ЯЛ2= Д'соэ k (у Ц- Л) е ,
Е. = а'sink (у
z? VI/ >
(10.44)
583
Из условия непрерывности касательных
щих поля на плоскости _у = 0 находим
Д'соз kh^=A,
А' -Л- sin kh = Д Д-.
/ше0
Из (10.45) следует
ctg kh=Y
Рз
составляю-
(10.45)
(10.46)
В свою очередь fi3 и k согласно (10.6) связаны между
собой соотношением
— 72 + р2__ (10.47)
Система уравнений (10.46) и (10.47) позволяют выра-
зить у и рз через £ = у и глубину канавок h. Согласно
(10.46) рз — величина вещественная. Поэтому и фа-
зовая скорость, равная
СО
п — —
Ф f
будет меньше скорости света
Из условия равенства нулю поля на бесконечности
следует, что р3 должно быть положительным. Это ука-
зывает на экспоненциальное убывание поля в перпенди-
кулярном к плоскости у = 0 направлении.
Полученные данные, как указывалось, справедливы при
наличии большого количества выступов на одну длину
волны, т. е. при условии у -*0. Точное решение задачи
[60], учитывающее конечную величину расстояния между
выступами дает значения фазовой скорости цф, которые
могут быть определены по графикам рис. 10.5. Точки
, t
обрыва кривых внизу соответствуют значениям -у и
h
у, при которых поверхностная волна существовать не
может. Кривая у = 0 соответствует расчету по форму-
лам (10.46) и (10.47).
584
Как отмечалось, приведенные выше данные относятся
к случаю бесконечно тонких выступов (®—+0). Ввиду отсут-
ствия точного решения рекомендуется [61 ] учитывать конеч-
ную ширину w выступов следующим образом. При со-
ставлении уравнений непрерывности следует приравни-
вать на плоскости у = 0 касательные составляющие поля
в воздухе не непосредственно значениям этих состав-
Уф
Рис. 10.5. Графики зависимости относительной
величины фазовой скорости поверхностной волны
от относительной глубины канавок в гофрирован-
ном металлическом листе при разных относитель-
ных значениях расстояния между выступами.
ляющих поля в волноводных каналах, как в (10.45),
а их усредненным значениям по всей плоскости _у = 0.
Так как касательная составляющая электрического век-
тора равна нулю на самых ступеньках, то усреднение
означает умножение выражения для £г] в (10.44), а
также левой части второго уравнения (10.45) на множи-
t
тель т-1—
В итоге мы получим, вместо (10.46), следую-
щее равенство
ctg kh = -7-^—
О f _4— w, FL
(10.48)
При w^t достаточно хороший результат дает фор-
мула (10.46). В случае, когда w и t величины одного
порядка, следует определить и у по системе уравне-
ний (10.47) и (10.48). При этом необходимо иметь в виду,
585
Рис. 10.6. Гофрированный металлический лист с канавками конечной
ширины 1>.

Рис. 10.7. К определению фазовой скорости поверхностной волны в
случае гофрированного листа с канавками конечной ширины. Кривые
соответствуют: 1. кЬ = оо; 2. «6 = 18,0; 3. кЬ = 9,0; 4. кЬ = 6,0;
5. кЬ — 4,0.
586
?то как (10.46), так и (10.48) получены в предположении
большого количества выступоз на единицу длины волны
И должны быть прокорректированы по кривым рис. 10.5.
В том случае, когда гофрирозаннач область в направ-
лении оси X ограничена шириной Ь, как показано на
рис. 10.6, расчет постоянных распространения может
производиться по графикам рис. 10.7, на котором для
различных значений kb дан график функции
где = ~j/~k2 — . Кривые рис. 10.7 вычислены в пред-
положении, что в пространстве между выступами суще-
ствует волна ТЕ01. Это всегда справедливо, когда
и может быть также обеспечено при b
если применен соответствующий способ возбуждения,
исключающий возможность возникновения волн высших
порядков.
§ 5. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ПЛОСКОСТНЫХ АНТЕНН,
ИСПОЛЬЗУЮЩИХ ПЛОСКУЮ ПОВЕРХНОСТНУЮ ВОЛНУ
Выше изложены особенности поверхностных волн, воз-
никающих в разных частных случаях на плоской границе
раздела сред с различными параметрами е, у., а. Перейдем
к рассмотрению характеристик излучения антенн, использую-
щих такие поверхностные волны. Начнем с плоских волн,
у которых закономерности наиболее просты и наглядны.
Из рассмотренных выше различных случаев в антенной
технике используются лишь поверхностные волны, образую-
щиеся над плоским металлическим листом, либо покрытым
тонким слоем диэлектрика, либо гофрированным. Как мы
видели, в обоих случаях плоская поверхностная волна
распространяется параллельно (вдоль) поверхности металли-
ческого листа (по обозначениям рис. 10.3 и 10.4 в направле-
нии оси Z) с фазовой скоростью несколько меньшей скоро-
сти света в пустоте. В воздухе, в направлении, перпендику-
лярном к поверхности металлического листа (в направлении
оси У) амплитуды поля быстро убывают по экспоненциаль-
ному закону.
Сопоставляя эти особенности плоских поверхностных
волн с особенностями поля в диэлектрическом стержне
(см. гл. IX § 1), легко видеть, что характер изменения поля
587
вдоль антенны поверхностных волн и в перпендикулярном
к ее поверхности направлении аналогичен характеру изме-
нения поля вдоль диэлектрической антенны и в перпендику-
лярном к ее поверхности направлении. В соответствии с этим
и по характеристикам излучения антенны поверхностных
волн аналогичны диэлектрическим антеннам.
В случае металлического листа, покрытого диэлектриче-
ским слоем, этот слой, согласно второму принципу эквива-
лентности (см. гл. IX § 4), может рассматриваться как
Рис. 10.8. Металлический лист, покрытый слоем диэлектрика
конечной ширины Ь.
объем, в котором имеются токи. Плотность этих токов Уэкв
определяется по формуле (9.68) через поле в диэлектриче-
ском слое.
Расчет электромагнитного поля излучения по известным
значениям Лкв может производиться по формулам (9.69).
Для электромагнитного поля в диэлектрическом слое
выше получены формулы (10.28). Однако при их выводе
допускалась идеализация условий, в связи с чем они нуж-
даются в некоторых коррективах.
При выводе формул (10.28), в связи с предположением
о неограниченной протяженности поверхности в направле-
нии оси X, ранее было принято, что поле от х не зависит.
В реальных же условиях, когда ширина b диэлектрического
слоя конечна (рис. 10.8), амплитуды поля будут зависеть
588
от координаты х. Кроме того, фазовая скорость в на-
правлении оси Z также будет отличаться от величины, опре-
деляемой формулой (10.42).
Следует заметить, что желательно иметь на краях
диэлектрического слоя (при х = — у и х= у! поле,
весьма слабое или равное нулю. В противном случае,
при больших значениях поля на краях диэлектрического
слоя, будут возбуждены значительные поля и вне его
(при х<—и ХУ> у) > гДе условия распространения
отличаются от условий распространения в слое. Это
приведет к нарушению картины поля и искажению ха-
рактеристик излучения. При условии слабого или нуле-
вого поля на краях диэлектрического слоя фазовую ско-
рость можно приближенно определять по формуле (10.42).
Требуемая зависимость амплитуд поля от координаты х
в основном задается возбудителем поверхностных волн.
Такие возбудители, как рупор, волновод, ряд щелей
и другие (см. рис. 1.16), имеют максимальное поле
в середине раскрыва или щели и нулевое на краях.
Очевидно, что в диэлектрическом слое они возбуждают
максимальное поле в средней части (х = 0) и очень сла-
бое на краях.
Учитывая, что поле в раскрывах рупора и волновода,
а также вдоль щели имеет синусоидальное распределе-
ние, примем, что в диэлектрическом слое зависимость
поля от координаты х аналогична, т. е. определяется
функцией cos у.
Толщина диэлектрического слоя h, как отмечалось
выше, очень мала. Так как координата у в слое ме-
няется в пределах от 0 до h, то можно принять, что
множитель в (10.28) равен единице или что поле не
зависит от у.
В связи с тем, что распространение волны в диэлек-
трическом слое происходит в направлении оси Z,|£ |>
>£z, т. е. электрический вектор поля практически имеет
только одну составляющую Еу . Это позволяет привести
(9.69) для дачного случая, как и для диэлектрической
антенны, к (9.70), причем здесь
Ey = AvK™e~* (10.49)
589
Подставив значение Еу из (10.49) и rsu ил
(9.71) в (9.70), учитывая при этом, что в ^-пло-
скости р =_у, а в /7-плоскости р = х, получим после
исключения постоянных множителей, не зависящих от
угла &, следующие выражения для нормированных диа-
грамм направленности рассматриваемой антенны:
sin у ($ — cos 0)
— cos & —А---------------- ,
Е М ’
у (5 — cos 6)
/А& _\ ГА/
cosi-s-sinS sin -у (5 — cos 0)
р =-------2_______<_____L____________
н . fkb 2 kl
1 — ( —sin&l *2^ — cosO)
(10.50)
где В= Д = ------отношение скорости света в пустоте
Ф к фазовой скорости распространения
волны в диэлектрическом слое в на-
правлении оси Z,
Я — угол между осью Z и направлением на
заданную точку в пространстве.
При малой ширине b диэлектрического слоя первые
множители в обоих выражениях (10.50) имеют очень
близкие кривые зависимости от угла &. Множитель же
cos &, как показало выше (гл. IX § 5), значительно
влияет на форму диаграммы направленности, которая
в основном определяется вторым множителем, одинако-
вым в обоих выражениях. Таким образом, объемная
диаграмма направленности антенны поверхностных волн,
выполненной в виде металлического листа, покрытого
тонким узким слоем диэлектрика является почти фигурой
вращения вокруг оси Z и определяется формулой
F(&)
sin 2" (5 — cos 9)
(10.51)
(5 — cos »)
Диграмма направленности вида (10.51) характерна
для антенны типа бегущей волны. Коэффициент направ-
ленного действия такой антенны рассчитывается по
формуле (9.89). Входящий в эту формулу множитель А,
как указывалось выше, является функцией L Фазовая
590
скорость Уф и параметр $ зависят от толщины /г диэлек-
трического слоя и его диэлектрической проницаемости г.
Они могут быть выбраны такими, чтобы $ было опти-
мальным, соответствующим максимальному значению
коэффициента направленного действия
D = (7 ч-8)4--
макс \ } \
В случае гофрированного металлического листа
(рис. 10.6; в предположении неограниченной его протя-
женности канавки рассматривались выше как волновод-
ные каналы, и это привело к уравнениям поля в них
вида (10.44). При конечной ширине канавок они должны
рассматриваться как прямоугольные волноводы и поле
в них будет определяться следующим образом:
Hxl = X'cos cos k(y + h)e nz,
E . = cos sin k (v -4- h) ,
(10.52)
Определяя электромагнитное поле излучения, можем
рассматривать края канавок при _у = 0 как щелевые из-
лучатели, амплитуда электрического поля в которых
определяется по формуле
Е. = С cos е /v,
zi b *
(10.53)
k
где С = А'-------постоянный множитель.
/сого
Так как канавки расположены близко друг к другу, то
можно принять, что на поверхности антенны (у = 0) поле
распределено непрерывно и меняется по формуле (10.53).
Сравнивая (10.53) и (10.49), легко видеть, что распределе-
ние амплитуд и фаз поля в случае гофрированной металли-
ческой поверхности получается примерно таким же, как
в случае металлического листа, покрытого диэлектрическим
слоем. Следовательно, диаграммы направленности в обоих
случаях одинаковы и определяются по формулам (10.50),
а при небольшой ширине b — приближенно по формуле
(10.51). Одинаков также в обоих случаях коэффициент на-
правленного действия. Он определяется по формуле (9.89).
591
На рис. 10.9 и 10.10 приведены расчетные по формуле
(10.51) и экспериментальные диаграммы направленности
антенны поверхностных волн, изготовленной из гофрирован-
ного металлического листа вида рис. 10.6 при различных
видах возбудителя, указанных в гл. I, § 8. Из этих рисунков
видно, что при некоторых видах возбудителей, например,
Рис. 10.9. Теоретическая диаграмма направленности
антенны из гофрированного металлического листа
(/) и экспериментальные диаграммы при различных
видах облучателей: рупорном (2), в виде подвешен-
ного провода (3) и штыревой антенны (4). Пара-
метры гофрированной поверхности: I = 60 см, Ь —
= 17,5 см, 1 = 3 мм, w = 3 мм, h — 12,5 мм. Длина
волны X = 10 см.
при волноводном возбудителе или при возбудителях в виде
провода, подвешенного параллельно плоскости и в виде ряда
гантельных щелей, совпадение расчетных и эксперименталь-
ных диаграмм направленности весьма хорошее. В случае
рупорного возбудителя или возбудителя в виде штыревой
антенны имеется заметное расхождение расчетных и экспе-
риментальных кривых, которое объясняется наличием непо-
средственного излучения возбудителя, т. е. слабой эффектив-
ностью возбуждения поверхностной волны.
592
Для более подробного ознакомления с проблемой эффек-
тивности возбуждения поверхностной волны, т. е. с вопросом
о зависимости от вида возбудителя соотношения мощности,
направляемой вдоль поверхности, и мощности, непосред-
е)
Рис. 10.10. Экспериментальные (сплошные кривые) и теоретические
(штриховые) диаграммы направленности (по мощности) антенны из
гофрированной поверхности при возбудителях в виде: а) ряда из 6 ган-
тельных щелей при длине антенны Н6.73Х, б) волновода при длине 7,ЗЗХ.
Остальные параметры гофрированной поверхности одинаковы в обоих
Случаях и равны: 6 = 6 см; h = 3 мм; / = 0,8 мм; w =1,5 мм. Длина
волны X = 3 см.
38—1503 593
§ 6. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ПЛОСКОСТНЫХ АНТЕНН,
ИСПОЛЬЗУЮЩИХ ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТНУЮ
волну
Цилиндрическая поверхностная волна возникает в круг-
лом диэлектрическом диске, находящемся на плоском ме-
таллическом листе или в гофрированном круглыми цилин-
дрическими канавками плоском металлическом листе при
помещении излучателя в виде штыревой антенны в центре
соответственно диска или системы канавок. На рис. 10.11
показана схема возбуждения цилиндрической поверхностной
волны в диэлектрическом слое0.
Рис. 10.11. К анализу антенны, использующей цилиндрическую
поверхностную волну.
Общие особенности цилиндрической поверхностной вол-
ны, как показано выше, аналогичны особенностям плоской
поверхностной волны. В частности, постоянная распростра-
нения и фазовая скорость цилиндрической волны в радиаль-
ном направлении приближенно определяется в зависимости
от толщины диэлектрического слоя и его диэлектрической
проницаемости или от глубины и ширины канавок теми же
формулами и графиками, которыми они определяются для
плоской волны в направлении оси Z.
В случае цилиндрической волны электромагнитное поле
симметрично относительно оси У и не зависит от координа-
ты <р (рис. 10.11). Соответственно этому пространственная
диаграмма направленности является фигурой вращения во-
круг оси У.
1) Диск показан на рисунке срезанным на конус в соответствии
с требованиями снижения уровня побочных лепестков (см. ниже).
594
Выведем формулу для диаграммы направленности
антенны в виде металлическою листа, покрытого ди-
электрическим слоем радиуса р0 и малой толщины h.
Последнее (й < Я) обусловливает возможность принять,
во-первых, что поле в слое не зависит от координаты у,
во-вторых, что Еу > Ег, т. е. что согласно (10.3) можно
положить
Е^Еу^СН^г), (10.54)
где С — постоянный множитель, не зависящий от коор-
динат р, <р, у,
Y — постоянная распространения, определяемая при-
ближенно по формуле (10 41).
Применив, как и в случае плоской волны,
принцип эквивалентности, получаем согласно
(10.54)
р° 2? к 1
£'5=CIsindj//'2)(Tp)prfp Je 1 r‘M j
a 0 j
Eu = const ‘
n
второй
(9.70) и
(10.55)
где Ci —постоянный множитель, не зависящий от угла &,
rSM — расстояние между точкой на поверхности ди-
электрического слоя, который можем считать
бесконечно тонким, и точкой М, в которой оп-
ределяется поле (рис. 10.11),
а — радиус возбуждающей штыревой антенны.
Второе равенство в .(10.55) является следствием сим-
метрии поля относительно оси Y.
Подставив в (10.55)
rSK = r — р sin & cos (<р — tpj, (10.56)
получаем после интегрирования и исключения постоян-
ных множителей следующее выражение для диаграммы
направленности в .Е-плоскости
FjB=[F(Po) —F(a)]sin&, (10.57)
где
. .___7Р(/о (&pr,sin 0) //^2)(7Р0) — йр0 sin OJj (/гр.-.sin ft) //^2) (тр0)
Ь 'Р°) 72 — £2sin2» ’
(10.58)
7aZn (ka sin 0) (7a) — ka sin Wj (ka sin 0) (7a)
f W ~ 72 —Й2 sin2» ‘
(10.59)
38* 595
Аналогичным образом, выводится выражение для диа-
граммы направленности антенны из гофрированного ме-
таллического листа с кольцеобразными канавками. Рас-
сматривая последние как кольцевые щелевые излуча-
тели и суммируя излучение этих кольцевых щелей, мы
приходим к выражению для диаграммы направленности
антенны в f-плоскости вида
Fe=F(Po)-F(a),
(10.60)
т. е. к выражению, отличающемуся от (10.57) лишь мно-
жителем sinft.
Теоретическое исследование диаграммы направлен-
ности вида (10.60) показало, что она отличается боль-
Рис. 10.12. График зависимости меж-
ду относительной толщиной диэлек-
трического слоя и относительной ве-
личиной постоянной распростране-
шим количеством побоч-
ных лепестков, имеющих
большой относительный
уровень. Эксперимен-
тальное исследование ан-
тенны как при диэлек-
трическом слое, так и
при гофрированной по-
верхности подтвердило
этот вывод теории. При
этом опыты с диэлектри-
ческим слоем показали,
что наибольший коэффи-
циент усиления и мини-
мальные боковые лепест-
ки получаются при дис-
ния.
ках, у которых толщина
линейно уменьшается от
максимальной в середине до нулевой на краях, как пока-
зано на рис. 10.11.
Рис. 10.12, показывая связь между относительной
величиной постоянной распространения (4- ——- ) и от-
\ я иф /
„ „ 2~d
носительнои толщиной слоя у, характеризует изме-
нение фазовой скорости на диске переменной толщины.
Рис. 10.13 показывает экспериментальную диаграмму
направленности антенны поверхностных волн, выполнен-
ной из полистиролового диска (-^- = 2,6), помещенного,
на металлическом листе и имеющего диаметр 2ро = ЗО,5сл«
596
и максимальную толщину hMaKC = 0,64 см. Измерения про-
водились на волне Л = 3,53 см. Коэффициент направлен-
Рис. 10.13. Диаграммы направленности антенны, показанной
на рис. 10.11.
ного действия получился D=10. Для сравнения на
рис. 10.13 приведена диаграмма направленности штыревой
антенны.
§ 7. ЦИЛИНДРИЧЕСКАЯ АНТЕННА ПОВЕРХНОСТНЫХ ВОЛН
Помимо рассмотренных выше плоскостных антенн по-
верхностных волн, использующих в качестве направителя
металлический плоский лист, у которого часть поверхности
покрыта тонким диэлектрическим слоем или гофрирована,
разработана [63] так называемая цилиндрическая антенна
поверхностных волн, использующая в качестве направителя
круглый металлический стержень с насаженными на него
металлическими дисками (рис. 1.17). Возбудителем у этих
антенн служит волновод круглого сечения, в котором воз-
буждается волна ТЕн.
Принцип действия этой антенны следующий. Система
металлических дисков, так же как в линзах, представ-
ляет собой искусственный диэлектрик. В отличие от линз,
гд^эти диски размещаются в определенном объеме, здесь
они располагаются в ряд по прямой. Такой ряд дисков
эквивалентен диэлектрической антенне из сплошного
стержня, имея аналогичные с последним характеристики
излучения. Фазовая скорость распространения волны по
системе дисков, как и в диэлектрической антенне, меньше
597
скорости света и зависит от расстояния между дисками t
и разности d—8 диаметра дисков и диаметра металличе-
ского стержнт, на который насажены диски. Представ-
ление об этой зависимости дает рис. 10.14. Из кривых
рис. 10.14 видно, что с увеличением d — 8 фазовая ско-
рость убывает, причем изменение имеет монотонный
fl.
характер. Зависимость же от t более сложна. При
Рис. 10.14. Графики зависимости относительной
фазовой скорости распространения волны в цилин-
дрической антенне поверхностных волн от относи-
тельной величины разности диаметров дисков и
стержня, на который они насажены, при различных
относительных величинах расстояния между дис-
ками.
t 1 ,
Y = j кривая зависимости фазовой скорости от расстоя-
ния между дисками проходит через максимум. Меняя
расстояние между дисками при постоянном их диаметре
или меняя диаметр при постоянном расстоянии, можно
найти параметры антенны, соответствующие максималь-
ному коэффициенту направленности.
Авторам разработки [63] удалось построить антенны
описанного типа очень большой длины (до 80^1 и получить
весьма большие значения усиления (до 28 дб), сравнимые
с теми, которые обычно получаются от антенн, излучающих
с плоского раскрыва при синфазном поле в нем (от антенн
типа синфазных—зеркал, линз). Некоторые данные о ре-
зультатах их опытов приведены на рис. 10.15-4-10.17.
Из рис. 10.15 видно, что коэффициент усиления рассмат-
риваемых антенн пропорционален отношению длины антен-
598
ны к длине волны, а ширина главного лепестка обратно
пропорциональна корню квадратному из этого отношения.
Эти характеристики излучения могут быть выражены фор-
мулами:
Cz = ^5 4-lg4) дб'
29(| = j , радиан.
(10.61)
(10.62)
Соотношения (10.61) и (10.62) обычны для антенн типа
бегущей волны.
При устройстве такой антенны большой длины рекомен-
дуется разделять ее на ряд последовательных секций дли-
Рис. 10.15. Зависимость коэф-
ф ициента усиления в дб цн-
линдрической антенны поверх-
ностных волн от относитель-
ной длины антенны. Точки со-
ответствуют измеренным зна-
чениям.
Рис. 10.16. Зависимость обратной ве-
личины ширины главного лепестка
диаграммы направленности цилин-
дрической антенны поверхностных
волн от корня квадратн го из отно-
сительной длины антенны. Точки со-
ответствуют измеренным значениям.
ной в несколько длин волны каждая. Отдельные секции при
этом следует делать из дисков, расположенных на одина-
ковом расстоянии, но разного диаметра, причем в начале
и конце секции следует иметь диски меньшего диаметра так,
чтобы огибающая поверхность имела форму сигары.
В антенне такие секции — «сигары», естественно, должны
быть расположены вершинами друг к другу. В каждой сек-
ции параметры подбираются из условия получения макси-
599

Рис. 10.17. Диаграммы направленности цилиндричес-
кой антенны поверхностных волн: а) I = 4 X
б) 1 = 20 X, в) /=80 X.
600
мального коэффициента усиления для данной секции. При
этом создается определенное соотношение фаз между эле-
ментами секции. Оптимальное соотношение фаз внутри сек-
ции не соответствует оптимальному соотношению фаз
в антенне в целом.
Для обеспечения оптимального соотношения фаз в антен-
не можно включать между секциями фазирующие участки
из дисков одинакового диаметра, выбрав соответствующим
образом расстояния между ними.
ГЛАВА ОДИННАДЦАТАЯ
СПИРАЛЬНЫЕ АНТЕННЫ
§ 1. УСТРОЙСТВО. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
На сверхвысоких частотах находят применение так на-
зываемые спиральные антенны [64]. Спиральные антенны
могут быть цилиндрическими и коническими. Устройство
спиральных антенн показано на рис. 11.1. Они представляют
собой проволочную спираль из хорошо проводящего метал-
ла постоянного (у цилиндрической а, б, в, г) или переменно-
го (у конического е, ж) диаметра намотки. Один конец
спирали присоединяется к внутренней жиле коаксиального
кабеля. Второй конец спирали в большинстве случаев
остается свободным (а, б, е, ж). Однако он может быть
присоединен к наружной оболочке коаксиального кабеля
(в, г). К наружной оболочке кабеля, как правило, присоеди-
няется в качестве противовеса плоский, металлический экран
(а, г, е, ж) круглой или прямоугольной формы. Возможно
присоединение коаксиального конуса (б) в качестве проти-
вовеса или использование антенны без противовеса (в).
Наряду с одиночными спиралями применяются сложные
спиральные антенны, состоящие из нескольких синфазно
питаемых спиралей. На рис. 11.2 показана антенна, состоя-
щая из четырех цилиндрических спиралей, питаемых
коаксиальным кабелем. Там указаны размеры, при которых
данная антенна испытывалась. Позади спиралей установлен
общий плоский металлический экран — противовес.
Спиральные антенны применяются, кроме того, в каче-
стве возбудителей колебаний в рупорах, а также в качестве
облучателей зеркал, линз и т. п. (см. рис. 11.3).
Параметры цилиндрической спирали будем обозначать
следующим образом (рис. 11.1в, ж):
,602
/ — осевая длина спирали, D — диаметр намотки спирали,
D
а= -g----радиус спирали, $ — расстояние между витками
(шаг), L — длина одного витка (см. развертку на рис. 11,1 ,<?),
а — шаговый угол, п — число витков, d — диаметр про-
вода спирали.
Г---- г -------
°)
Рис. 11.1. Виды спиральных антенн: а) цилиндрическая с плоским
противовесом и свободным концом, б) то же с коническим противо-
весом, в) цилиндрическая без противовеса с концом, замкнутым на
оболочку кабеля, г) то же с плоским противовесом, <б) развертка
витка цилиндрической спирали, е) коническая спираль с увеличиваю-
щимся шагом, ж) то же с уменьшающимся шагом.
603
Между указанными параметрами цилиндрической спи-
рали существуют соотношения
Z2 = (kD)2^_s2>
a = arctg^, <11-1)
l = ns.
У конических спиралей сохраним в основном приведен-
ные выше обозначения параметров. Однако следует учесть,
вид спереди
линия
Рис. 11.2. Антенны из четырех синфазных спиралей.
Рис. 11.3. Спиральные излучатели: а) в качестве
возбудителя колебаний в рупоре, б) в качестве
облучателя параболического зеркала.
что радиус спирали а (расстояние точек спирали от ее оси),
расстояние между витками s и длина витка L переменны,
(а остается постоянным) и поэтому a, s, L не считаются
параметрами конической спирали. Вместо них в качестве
604
параметров принимаются начальный радиус а0 и быстрота
изменения радиуса, характеризуемая величиной р.
В цилиндрической системе координат координаты точек
спирали (z, a, ? ) определяются приближенно следующими
соотношениями:
а = а0(1±р?), (11.2)
dz = atg<idq, (П.З)
9
Z = J a0(l±:p<p)tg<xd. (11.4)
о
Положительный знак у р Соответствует спирали вида
рис. 11,1,е, а отрицательный знак — спирали вида
рис. 11,1,ж.
Из (11.2) ясен смысл параметра р.
Легко видеть из третьего уравнения (Н.4), что длина
спирали связана с числом витков п углом а и парамет-
ром р соотношением
Z = aotga(l ±пртс)2шг. (11.5)
Известные типы проволочных антенн: штыревая и ра-
мочная являются предельными частными случаями спи-
ральных антенн. Рамке (круглой) соответствует спираль,
имеющая малый по сравнению с длиной волны диаметр D
и шаговый угол а—>0, а штырю соответствует спираль,
у которой a = 90°.
Как известно, рамочная и штыревая антенны имеют ма-
ксимум излучения в направлении, перпендикулярном к оси,
и нулевое излучение (у рамочной почти нулевое) в направ-
лении оси (в осевом направлении). Спиральная антенна,
близкая по своим параметрам к штырю или рамке, также
имеет максимум излучения в перпендикулярном к оси на-
правлении, а ввиду осевой симметрии, — ненаправленное
излучение в плоскости, перпендикулярной оси. Однако су-
ществуют такие значения а и D, при которых спираль имеет
максимум излучения в осевом направлении и очень слабое
излучение в перпендикулярном к оси направлении. Режим
работы спирали в первом случае называется режимом не-
направленного излучения, во втором случае — режимом осе-
вого излучения.
В антенной технике наибольший практический интерес
имеет режим осевого излучения.
605
§ 2. РЕЖИМ ОСЕВОГО ИЗЛУЧЕНИЯ
Режим осевого излучения отличается рядом замечатель-
ных особенностей. К таким особенностям, помимо наличия
максимума излучения вдоль оси, относятся: образование
бегущей волны на проводах спирали, круговая поляризация
поля излучения, активное входное сопротивление, диапазон-
ность и т. п.
Рассмотрим подробнее эти особенности режима осевого
излучения.
а) максимум излучения в направлении оси спирали
Для пояснения условий образования максимума излуче-
ния вдоль оси спирали рассмотрим одиночный виток, причем
сначала будем считать его плоским (а = 0).
Рис. 11.4. К пояснению осе-
вого излучения одиночного
плоского витка тока.
Введем системы координат
Z, X, Y и г, 9, » (см. рис. 11.4)
с осью Z, совпадающей с осью
витка.
Предположим, что на витке
установилась стоячая волна с
пучностью тока в средней точке
x=i—а. Для двух различных
отношений длины витка L к дли-
не волны < 1 и у-= 1^на рис.
11.5 стрелками показано направ-
ление тока / и его составляю-
щих 1х и I в четырех точках
А, В, С, D, расположенных по-
парно симметрично относительно осей X и Y. Там же
даны кривые распределения амплитуд тока на витке (виг).
Векторы токов будем в дальнейшем снабжать индексами
А, В, С, D соответственно тому, к какой точке они от-
носятся.
Из рис. 11.5 видно, что как при -^-<1, так й при у=1
хА = хС '
хВ = Ло •
(Н-6)
Уравнение вида (11.6) справедливо для любых двух
точек, расположенных симметрично относительно оси X.
Отсюда следует, что электромагнитное поле излучения
606
в осевом направлении (в направлении оси Z) не будет
содержать составляющей Ех, т. е. поле витка при ука-
занных условиях (режим стоячей волны с пучностью в
средней точке) имеет линейную поляризацию с электри-
ческим вектором, параллельным оси Y. Можно показать,
что в режиме стоячей волны излучение в осевом направ-
Рис. 11.5. Распределение тока на круглом плоском витке: а) направ-
ление вектора тока при L < X, б) то же при L = X, в) кривая ампли-
туд тока на развернутом витке при L < X, г) то же при L = X .
лении имеет линейную поляризацию и в том случае,
когда пучность тока смещена относительно середины витка.
Поле излучения в плоскости витка также является
линейно поляризованным, однако в зависимости от на-
правления преобладает Ех или Е .
Из рис. 11.5 видно, что при < 1 IуЛ и / с имеют
знак, противоположный знаку 1уВ и /yD , а при = 1
все составляющие токов по оси Y имеют одинаковый знак.
Поэтому излучение в осевом направлении, в котором
длина лучей от отдельных участков витка одинакова,
должно быть при-^-< 1 менее интенсивным') , а при у=1
1) Излучение в осевом направлении не равно нулю, как обычно
предполагается у рамочных антенн, так как I А ф 1 и lyc^Iyp,
т. е. из-за наличия косинусоидального изменения амплитуд тока
вдоль витка.
607
более интенсивным, чем в направлениях, лежащих в пло-
скости витка.
Относительная интенсивность излучения в осевом на-
правлении растет с увеличением у в промежутке 1
и убывает с увеличением у- в промежутке 1 <у <2. При
-у- = 1 интенсивность излучения в осевом направлении
максимальна.
Эти общие закономерности уточним количественно.
Выведем формулы для электромагнитного поля излучения
витка в осевом и нормальных к оси (лежащих в плоскости
витка) направлениях и сравним их между собой.
Поле излучения в осевом направлении равно
« , зоа/л —ikz п С
Ey = —J—^e -2 l cosma'p«cos<p-(Mf 1 — (ka)2 ' '
где /0 — ток в пучности,
а— радиус витка.
При -у-< 1 {ka < 1) можно приближенно считать
чт« Д^т
(11.8)
При -у- = 1 {ka=l) имеем
= (11.9)
Амплитуда поля излучения в нормальных к оси на-
правлениях при -у- < 1 почти не зависит от угла <р. Пред-
ставление о поле излучения в этих направлениях при
< 1 можно получить, вычислив его для любого <р.
608
Для <р = 90° и -у- < 1 (ka 1)
Еу = — у 32^Л> &~lkr2J J cos kay -sin (&asin ®)-sin(p-d(a-.p)=
о
s^e~Mr(^a)2-^- . (11.10)
Сравнивая (11.10) и (11.8), мы видим, что при
-у- < 1 (ka < 1) излучение в нормальных направлениях в
4- раз больше, чем в осевом.
При у~=1 амплитуда поля излучения в нормальных
направлениях существенно меняется с изменением <р.
Вычислим его для двух крайних значений: ад = 90° и ср = 0.
При <р = 90° и -^- = 1 (ka=i)
Еу = ^-~- e~ikr J cos ад • sin (sin ад) sin cprfp = 0. (11.11)
о
При <р — 0 и у' = 1 (&а=1)
С» 60/п —i kr С . . ,
Ех — —-е 1 cos'f •cos(cos<p)-cos?ap —
о
= [Jo(1)-J2(1)] = 6-^- *-ikr.^ 0,65, (11.12)
где Jo и J2 — бесселевы функции.
Сравнивая (11.9) с (11.11) и (11.12) видим, что в случае
-у = 1 интенсивность излучения в осевом направлении
превосходит интенсивность излучения в нормальных к оси
направлениях.
Из изложенного следует, что для получения режима
осевого излучения должны применяться спирали, у кото-
рых YS1.
Следует, однако, заметить, что в случае одиночного
витка даже при1 не обеспечивается большое пре-
39—1503 609
обладание осевого излучения над излучением в нормаль»
ных направлениях.
В целях значительного ослабления излучения в нор-
мальных направлениях и усиления осевого излучения
применяется плоский противовес, как показано на
рис. 11.1 (а, г, е). Кроме того, ослабление нормального
излучения и усиление осевого получаются в многовитковой
спирали, т. е. в случае системы коаксиальных витков
при фазировке питания витков аналогично фазировке
питания элементов в антенне типа бегущей волны.
В приведенном выше анализе полагалось а = 0. В слу-
чае а^О ток на спирали имеет не только составляющие
1Х и 1 , но также состав,,
ляющую Iz.
При < 1 цилиндричес-
кая спираль может быть
представлена в виде ряда
питаемых синфазно коак-
сиальных плоских витков,
соединенных между собой
прямолинейными отрезками,
как на рис. 11.6,а. Как вит-
ки, так и прямолинейные
отрезки имеют максимум
излучения в нормальных к оси направлениях.
При -у=1 не удается достаточно точно представить
спираль по какой-либо простой схеме.
По характеру поля излучения цилиндрическая спираль
эквивалентна ряду коаксиальных плоских витков и несколь-
ким рядам диполей, расположенных по образующим ци-
линдра, как на рис. 11.6,6, причем как витки, так и диполи
питаются, токами, соотношение фаз которых соответствует
соотношению фаз в вибраторах антенны бегущей волны.
Соотношение интенсивности излучения в осевом и нормаль-
ных направлениях для ряда плоских витков с — = 1 нами
рассмотрено выше. Что касается ряда диполей, то он подоб-
но нити с бегущей волной, имеет максимум излучения под
небольшим углом к оси спирали, а в осевом направлении —
нулевое излучение и очень слабое излучение в нормальных
направлениях.
610
°) i*'
Рис. 11.6. Эквивалентная замена
спирали системой круглых плос-
ких витков и прямолинейных от-
резков: а) при L <Х, б) при L=K.
Ток на проводе конической спирали также может быть
представлен в виде составляющих, параллельных и перпен-
дикулярных оси спирали, причем соотношение интенсивно-
стей в осевом и нормальных направлениях определяется
преимущественно перпендикулярными к оси составляющими
тока.
Таким образом, наличие составляющих тока Ц не вно-
сит существенных изменений в соотношение интенсивностей
излучения в осевом и нормальных направлениях по сравне-
нию с соотношением, имеющим место при/а <-0(7—- 0), т. е.
данные приведенного выше анализа для случая «==0 могут
быть обобщены на случай а =# 0.
Итак, оптимальными условиями получения максимума
излучения в осевом направлении являются:
2. Применение плоского противовеса.
3. Наличие многих витков при фазировке их питания как
в антенне бегущей волны.
б) бегущая волна на проводах спирали.
Круговая поляризация
При выполнении условия = 1 (режим осевого излу-
чения) на проводах спирали из нескольких витков, как пра-
вило, устанавливается почти бегущая волна 1
В режиме бегущей волны кривую распределения тока на
проводах спирали можно себе представить в таком же виде,
как при стоячей волне, т. е. как показано на рис. 11.5,г.
Однако, если при стоячей волне кривая рис. 11.5 показывает
постоянное соотношение величин токов в различных точках
витка, то при бегущей волне эта кривая соответствует рас-
пределению токов в какой-либо момент времени. Иначе го-
воря, если при стоячей волне точки нуля и максимума тока,
а также точки других уровней фиксированы, то в случае
бегущей волны эти точки непрерывно перемещаются вдоль
витка со скоростью, равной фазовой скорости распростране-
ния волны по проводу.
В связи с перемещением точек различных уровней по
спирали непрерывно поворачивается (смещается вокруг
оси Z) в режиме бегущей волны вся картина электромагнит-
i) Более подробные данные о распределении тока на спирали
приводятся ниже.
39* 611
ного поля, в том числе поворачивается (вращается) направ-
ление электрического и магнитного векторов поля. Таким
образом, в режиме бегущей волны, который совпадает с ре-
жимом осевого излучения, в осевом направлении создается
электромагнитное поле с вращающимися векторами Е и Н,
т. е. поле круговой поляризации.
Приведенный анализ относится к случаю системы плос-
ких витков (а = 0). У спирали с а б указанные соотно-
Рис. 11.7. К пояснению круговой поляризации
и коэффициента равномерности.
шения несколько усложняются. В частности, поле излучения
имеет, вообще говоря, не круговую, а эллиптическую поля-
ризацию, в особенности в направлениях, отличных от осево-
го, т. е. при 6 -т^О (см. рис. 11.7). На рис. 11.7 ось Z совпа-
дает с осью спирали.
Эллиптичность поляризации измеряется так называе-
fg Е
мым коэффициентом равномерности или (в числи-
ло
теле ставится большая из величин), где Е6 и £— проек-
ции электрического вектора Е на сферические координаты
Ед
9 и ср (см. рис. 11.7). При круговой поляризации £-= 1-
В режиме осевого излучения это соотношение весьма
хорошо выполняется в осевом направлении. В других
направлениях оно отличается от единицы.
512
При бегущей волне на спирали фаза тока меняется
вдоль витка и от витка к витку. Разметь фаз тока двух
соседних витков в соответственных точках равна
где — фазовая скорость волны вдоль витка,
с — скорость света в свободном пространстве.
Чтобы излучение соответственных участкоз всех вит-
ков складывалось в осевом направлении в фазе, должно
выполняться условие
= + 5). (11.14)
Сравнивая (11.14) и (11.13), получаем
и, т
^=4^- о1-15)
Можно легко показать, что при целом числе витков
и при бегущей волне на спирали условие (11.15) соот-
ветствует —— — 1 в осевом направлении.
Как мы видели выше (гл. IX, § 7), максимум коэффи-
циента направленного действия антенны типа бегущей вол-
ны имеет место в том случае, когда разность фаз полей,
создаваемых крайними излучающими элементами (в случае
спирали — крайними витками) в направлении главного ма-
ксимума равна примерно *. Это означает, что максималь-
ная направленность получается у спиральной антенны в том
случае, когда падение фазы вдоль длины одного витка
равна
= + + (11.16)
Сравнивая (11.16) и (11.13), приходим к следующему
условию получения максимального коэффициента направ-
ленного действия спирали в осэвом направлении
=(11.17)
s + k + 27Г
При большом количестве витков (11.17) мало отличает-
ся от (11.15).
613
в) диапазонность цилиндрических спиралей
Одной из важнейших особенностей режима осевого излу-
чения является его диапазонность, заключающаяся в том,
что диаграмма направленности осевого вида (с главным
максимумом вдоль оси) имеет место у спирали в широком
диапазоне частот. Ширина диапазона* осевого излучения раз-
лична у цилиндрических и конических спиралей. У ци-
линдрических спиралей ширина диапазона несколько боль-
ше половины октавы. У некоторых типов конических спира-
лей ширина диапазона составляет полторы-две октавы и
больше. Цилиндрические спирали исследованы более по-
дробно, а связь диапазонных свойств с параметрами спира-
ли проявляется у них в более простой форме, чем у кони-
ческих спиралей. Поэтому здесь мы уделим внимание лишь
цилиндрическим спиралям. Диапазонные свойства кониче-
ских спиралей рассматриваются ниже в § 5.
На рис. 11.8 приведены нормированные полярные ди-
аграммы направленности цилиндрической спирали, сделан-
ной из медной трубки диаметром d — 12,25 мм. Параметры
спирали следующие:
общая длина Z = 118 см,
шаговый угол а=14°,
число витков п = 6,
длина провода одного витка Z = 78 см.
Применялся плоский круговой экран диаметром 60 см. Для
уменьшения парусности экран был сделан в виде сетки из
16 радиальных проводов и четырех концентрических колец
из того же провода.
У кривых рис. 11.8 указаны частоты, при которых сни-
мались диаграммы направленности. Сплошные кривые со-
ответствуют Ец, а пунктирные — Ег..
На рис. 11.9 дана кривая зависимости равномерности от
частоты для поля излучения в направлении вдоль оси спи-
рали. ,
Из рисунков 11.8 и 11.9 видно, что спиральная антенна
имеет в широком диапазоне (от 290 до 500 Мгц) диа-
грамму направленности осевого типа п, причем во всем этом
диапазоне коэффициент равномерности близок к единице,
т. е. поле излучения в осевом направлении имеет почти кру-
говую поляризацию. В пределах главного лепестка диаграм-
1) Наличие значительного о5ратного излучения объясняется,
повидимому, сравнительно малыми размерами экрана.
614
мы направленности коэффициент равномерности меняется,
однако не очень значительно.
Как отмечалось выше, в режиме осевого излучения на
проводах спирали устанавливается бегущая волна. Подроб-
ное изучение вопроса показало, что бегущая волна на спи-
Рис. 11.8. Изменение формы диаграммы направленности
с частотой у цилиндрической спирали из шести витков
с длиной витка L = 78 см.
рали имеет место во всем указанном диапазоне частот осе-
вого излучения.
Заметим, что на средней частоте диапазона ([ =
= 400 Мгц, Л, =75 см) -^-=1. В пределах диапазона
ср
частот 290 — 500 Мгц отношение -р меняется примерно
от 0,75 до 1,30. Получение диаграммы направленности
615
осевого типа при столь значительном отличии от 1
объясняется изменением фазовой скорости распространения
волны вдоль провода спирали с изменением частоты. При-
мечательно, что фазовая скорость в диапазоне осевого излу-
чения меняется почти линейно с частотой и таким образом,
Частота, Мгц
Рис. 11.9. Кривая зависимости коэффициента
равномерности от частоты у цилиндрической
спирали, имеющей п = 6, L = 78 см.
что на всех частотах выполняется условие (11.16), соответ-
ствующее максимальному значению коэффициента направ-
ленного действия.
Спираль с указанными здесь параметрами имеет коэф-
фициенты направленного действия: И на частоте 300 Мгц
и 25 на частоте 500 Мгц.
г) входное сопротивление цилиндрической спирали
в диапазоне частот в режиме осевого излучения
При наличи бегущей волны на проводах спирали, что
имеет место в режиме осевого излучения, ее входное сопро-
тивление является активным. Величина этого сопротивления
зависит от параметров спирали. Наиболее полно эта зави-
симость исследована у цилиндрических спиралей.
Данные измерений входного сопротивления цилиндриче-
ских спиралей приведены на рис. 11.10 и 11.11 (см. жирные
кривые). Числа у кривых указывают частоты, при которых
определялись значения сопротивлений, отмеченные попереч-
ной к кривым черточкой. Окружности из тонких линий на
этих рисунках соответствуют точкам постоянного значения
коэффициента стоячей волны (величина к. с. в. показана
числами у окружностей), рассчитанного для линии с волно-
вым сопротивлением р = 125 ом.
616
Спирали, данные о входном сопротивлении которых при-
ведены на рис. 11.10 и 11.11, были сделаны из медной трубки
диаметром €/=1,26 см. Диаметр намотки спирали D =
= 22,5 см. Применялся плоский квадратный экран размером
1,5 X 1.5 м2.
Рис. 11.10 иллюстрирует влияние шагового угла а на
форму кривой входного сопротивления. В опыте осевая дли-
на спирали сохранялась постоянной /—123 см; менялось
количество витков п и шаговый угол а. Отдельные из кри-
вых рис. 11.10 соответствуют углам а =6°, 12°, 18° и 24°
или числу витков п = 15, 8, 5 и 3, 9.
Из кривых рис. 11.10 видно, что в сравнительно широ-
ком диапазоне частот (при разных а этот диапазон раз-
ный) входное сопротивление очень мало меняется, имея
активную составляющую порядка 120—140 ом и очень ма-
лую реактивную составляющую. При а =12° = 24° этот
диапазон равен примерно 300—500 Мгц, при а. =6° он не-
сколько меньше (350—450 Мгц).
Рис. 11.11 иллюстрирует влияние количества витков на
форму кривой входного сопротивления спирали. В данном
опыте шаговый угол сохранялся постоянным, равным а =
= 12°. Менялось число витков. Отдельные кривые относятся
к значениям и =1,4,10.
Из этой серии кривых видно, что при одном витке вход-
ное сопротивление имеет малую реактивную составляющую
в сравнительно узком диапазоне; при числе витков, равном
4 и больше, входное сопротивление остается в большом диа-
пазоне почти постоянным и с малой реактивной составляю-
щей, причем форма кривой почти не меняется с изменением
числа витков при п)>4.
д) эмпирические формулы для характеристик
цилиндрической спирали в режиме осевого излучения
В результате многочисленных измерений характеристик
спиральных антенн в,режиме осевого излучения установле-
ны следующие приближенные зависимости для спиралей
с шаговым углом а = 12° = 16°.
Средняя ширина главного лепестка диаграммы направ-
ленности:
а) по половинной мощности
2%= , 52z-= градусов, (11.18)
L 1/ nS
/. К /.
617
О
ОС
Рис. 11.10. Кривая изменения входного сопротивления с частотой у спирали, имеющей длину 1= 123 см
и диаметр намотки D = 22,5 см, при различных и аговых узлах а..
619
Рис. 11.10. Кривая изменения входного сопротивления с частотой у спирали, имеющей длину 1 = 123 см
и диаметр намотки 0 = 22,5 см, при различных шаговых углах а.
Рис. 11.11. Кривые изменения входного сопротивления с частотой у спирали, имеющей D ~ 22,5 см
и а =12° при различном числе витков п.
б) между первыми нулями
оо' И5
290 = ----7= градусов.
L — / Л-о
т V v
Коэффициент усиления
п 1cf L\2 S
О = 15 -г- ) -п -г-.
\ К j к
Входное сопротивление
Вл Вл Д
(11.19)
(11.20)
(11.21)
Зависимость ширины главного лепестка диаграммы на-
правленности и коэффициента усиления от отношения дли-
ны антенны к длине волны являются здесь примерно такими
же, как у других антенн типа бегущей волны.
При изменении шагового угла а между 12° и 16° не-
большие изменения характеристик проявляются в том, что
с уменьшением а уменьшается уровень боковых лепестков,
а с увеличением а делается более постоянным входное со-
противление.
§ 3. РЕЖИМ НЕНАПРАВЛЕННОГО ИЗЛУЧЕНИЯ
Как мы видели выше, режим ненаправленного излу-
чения имеет место у одновитковой спирали при -у-< 1-
В случае многовитковой спирали режиму ненаправленного
nL , <
излучения соответствует условие у-<1, где п — число
витков. Для режима ненаправленного излучения харак-
терным является также стоячая волна на проводах спи-
х nL _ .
ради, которая всегда ооразуется при у-< 1.
Каждый из витков спирали, ввиду малых его размеров,
может быть представлен в виде суммы плоского витка и
аксиального линейного отрезка, как паказано на
рис. 11.6,а. Длина этого линейного отрезка равна расстоя-
нию между витками.
Поле излучения такого отрезка в нормальных к оси
направлениях, т. е. при 6 = 90° (см. рис. 11.7) имеет
только одну составляющую электрического вектора Е0 ,
равную
£в==_у-(11.22)
621
Плоский виток создает поле, имеющее одну состав-
ляющую £tt, равную согласно (11.10)
£9=^£-(^а)2е-^г, (11.23)
D
где п = “2-радиус спирали.
Из (11.22) и (11.23) видно, что поле излучения спирали
в нормальных направлениях при режиме ненаправленного
излучения имеет две составляющие £0 и Еа, сдвинутые
по фазе на 90°, т. е. поле в этих направлениях, вообще
говоря, поляризовано эллиптически. При
|£е|=1-М (П-24)
поле излучения имеет круговую поляризацию. Из (11.24)
с учетом (11.22) и (11.23) получаем после простых пре-
Рис. 11.13. К пояснению принципа
действия антенны, показанной на
рис. 11.12.
Рис. 11.12. Четырехвибратор-
ная антенна, излучающая поле
круговой поляризации.
образований следующее
поля излучения спирали
режиме ненаправленного
условие круговой поляризации
в нормальных направлениях при
излучения:
или
/252
, kD
tga= —
(11.25)
(11.26)
Характеристики, аналогичные спиральной антенне, в ре-
жиме ненаправленного излучения имеет вибраторная антен-
на, изображенная на рис. 11.12. Эта антенна состоит из
Ь22
четырех питаемых вибраторов, средние точки которых рас-
положены по углам квадрата. Оси вибраторов наклонены
к плоскости квадрата, образуя с ней угол а. Стороны квад-
рата очень малы по сравнению с длиной волны.
На рис. 11.13 дана схема этой антенны. Круглая пунктир-
ная линия изображает окружность, описанную вокруг
квадрата, в углах которого помещены вибраторы. Наклонен-
ные к плоскости круга стрелки показывают направление
вектора тока. Вектор тока в каждой точке разложен на две
составляющие: параллельную плоскости круга (г) и перпен-
дикулярную плоскости круга (в). Параллельные составляю-
щие (г) совместно образуют систему, аналогичную рамке,
а перпендикулярные — аналогичную штыревой антенне.
Условием получения круговой поляризации является уравне-
ние (11.26), справедливое также для спиральной антенны.
§ 4. РАСПРЕДЕЛЕНИЕ АМПЛИТУД И ФАЗ ТОКА
НА ЦИЛИНДРИЧЕСКОЙ СПИРАЛИ
Выше было отмечено, что режим осевого излучения ха-
рактеризуется наличием бегущей волны на проводе спирали.
В действительности, как показало подробное исследование
вопроса [65], на спирали одновременно существует несколько
бегущих волн различных порядков, обозначаемых через Т
где v — целое число, указывающее порядок волны.
Если обозначить через ; координату точки провода спи-
рали, отсчитываемую от экрана по линии спирали, то ток
волны v-oro порядка определится по формуле
I = L e~M=fc/M , (11.27)
где /Ov— амплитуда тока v-ой волны в начале спирали,
ov — постоянная затухания,
— постоянная распространения.
Знак минус в показателе соответствует волне, рас-
пространяющейся в направлении положительных $, а знак
плюс — отраженной волне.
Через фазовая скорость волны определяется по
формуле
щ = -£- • (И.28)
фч R ' '
В зависимости от величин параметров спирали на ней
преобладает волна того или иного порядка.
623
В режиме осевого излучения на цилиндрической спи-
рали возникают волны То и T’I(v = O и >=1).
Волна То имеет фазовую скорость пф0
а
амплитуда волны экспоненциально убывает от начала к
концу спирали. Волна То отражается от конца. Отражен-
ная волна, которую обозначим через 7'дТр, распространя-
ется от конца к началу с той же фазовой скоростью
цф0 = с, а амплитуда также убывает экспоненциально.
Отраженная волна 7'°тр в режиме осевого излучения при-
ходит к началу спирали с очень малой амплитудой.
Волна Т[ имеет фазовую скорость пф1, меньшую ско-
рости света, причем уф| является функцией у и меняется
примерно по формуле (11.12)1’. Амплитуда волны посто-
янна на всей спирали (Sj = O). Отраженная волна Т°тр
имеет в диапазоне режима осевого излучения весьма
малую амплитуду.
Ввиду быстрого затухания волны То в режиме осевого
излучения преобладающее влияние имеет волна 7\.
При частотах более низких, чем частоты диапазона осе-
вого излучения, на цилиндрической спирали, преобладает
волна То. Коэффициент затухания % на этих частотах очень
мал, и практически амплитуда волны То может считаться
постоянной. Волна Т^р имеет на низких частотах почти та-
кую же амплитуду, как волна То, что приводит к образова-
нию стоячих волн. Волна Л имеет весьма малую амплиту-
ду и слабо проявляется.
На частотах более высоких, чем частоты диапазона осе-
вого излучения на цилиндрической спирали возникают вол-
ны Т2, Т3 и т. д. При этом на частотах, примыкающих к диа-
пазону режима осевого излучения со стороны более высоких
частот, волна Т} становится затухающей, в то время как
волна Та имеет постоянную амплитуду. Фазовая скорость
на этих частотах оф2 < оф1 причем цф2 меняется с из-
L
менением — .
Л
’) Фазовые скорости пф| меняются таким образом, что на спи-
рали автоматически обеспечивается максимальный коэффициент на-
правленного действия во всем диапазоне осевого излучения.
624
О 40 80 f20 160 lai
О 40 80 120 160 [,с/ч
Рис. 11.14. Кривые распределения квадрата амплитуд т 'ка (Л) и
фаз'ХФ^вдоль провода спирали, имеющей £> = 8,61 см, а= 12,6°, п—6.
Возникновение на спирали волн различных порядков и
их особенности иллюстрируются приводимыми здесь дан-
ными измерений распределения тока на спирали, имеющей
параметры
D = 8,61 см,
а= 12,6°,
п = 6,
40—1503
625
при наличии позади спирали экрана площадью 0,28 м2.
Измерения проводились в диапазоне 602—1 667 Мгц.
На рис. 11.14 даны кривые распределения амплитуд
(/2) и фаз токов на спирали, полученные при различных
значениях = —. Из этих кривых видно, что при малых
L
значениях — распределение амплитуд и фаз является ти-
пичным для стоячих волн: максимумы амплитуд периодиче-
ски чередуются с глубокими минимумами, а фазы токов
Рис. 11.15. Кривые зависимости относительной величины
фазовой скорости от относительной длины витка цилин-
дрической спирали для волн порядков v=0,1 и 2 (сплош-
ные кривые) и требуемая зависимость для получения
максимального коэффициента направленного действия
(пунктирная кривая).
почти постоянны в промежутке между двумя максимумами
и скачком меняются почти на 180° в точке минимума. При
значениях , соответствующих режиму осевого излучения,
амплитудные кривые имеют при малых $ характер быстро-
го экспоненциального убывания, до ничтожно малого значе-
ния, после чего следует резкое возрастание, а затем остается
почти на постоянном уровне при очень слабых вибрациях.
Такой ход амплитудной кривой объясняется тем,
что при малых £ преобладает волна То, а при больших ? —
волна Гь причем глубокий минимум имеет место в точке
равенства амплитуд волн То и Ti, и отличия фаз этих волн
на 180°. Фазовая характеристика является почти прямоли-
нейной. Лишь в точке глубокого минимума происходит ска-
чок фазы. При больших значениях -у- амплитудная характе-
62G
ристика имеет несколько глубоких минимумов, возникаю-
щих в результате интерференции волн То, Т\ и Тг.
Анализ кривых рис. 11.14 позволяет выделить в от-
дельности составляющие токов, соответствующие волнам
Рис. 11.16. График зависимости коэффициента затухания волны от
относительной длины витка.
На рис. 11.15 для сравнения нанесена пунктиром кривая
изменения фазовой скорости, соответствующая максимуму
коэффициента усиления (формула 11.12), имеющая хорошее
совпадение с кривой = в диапазоне осевого излу-
чения.
Кривая рис. 11.16 показывает быстрое возрастание по-
стоянной затухания 30 волны То при приближении к диапа-
зону осевого излучения и сохранение г0 почти на одинако-
вом уровне в пределах этого диапазона.
§ 5. ХАРАКТЕРИСТИКИ КОНИЧЕСКИХ СПИРАЛЬНЫХ АНТЕНН
Имеющиеся в настоящее время данные по коническим
спиральным антеннам представляют собой несколько серий
диаграмм направленности спиралей с различными парамет-
рами и отрывочные данные о входном сопротивлении и рас-
40* 627
пределении тока. Несмотря на ограниченность этих данных,
они позволяют сделать ряд важных выводов о принципе
действия этих антенн и о практическом их использовании.
Одна серия измерений (66] проводилась со спиралью,
имеющей следующие параметры
п = 10,25,
а =17°,
2а0 = 25,5 мм,
2а „„„ — 76 мм,
мзкс *
р=0,03,
I = 1 000 мм,
где р — параметр конической спирали (см. уравнение (11.2),
амакс — максимальный радиус,
а0 — начальный радиус.
Измерения проводились в диапазоне частот 1 000—
3 400 Мгц. Исследовалось распределение фаз тока на спи-
рали, диаграммы направленности и входное сопротивление.
Результаты измерений соотношения фаз на проводе спи-
рали схематически изображены на рис. 11.17. На рисунке
условно принято, что на отрезке от знака до знака —
фаза меняется на '180°.
Из рис. 11.17 видно, что на всех частотах от 1000
до 3 000 Мгц на спирали имеется группа витков (3,5—4 вит-
ка), на каждом из которых укладывается одна волна. Это
группа витков, длина которых меняется примерно в преде-
лах 0,8—1,3 А, где Л —длина волны в вакууме. Эти витки
работают в режиме, аналогичном режиму осевого излуче-
ния цилиндрической спирали. Фазовая скорость в различных
точках этой группы витков различна, и она автоматически
устанавливается такой, чтобы получить максимальный коэф-
фициент направленного действия. На этой группе витков
преобладает волна Т\. На более низких частотах диапазона
эти витки находятся в области максимальных значений а,
на более высоких частотах — в области минимальных зна-
чений а, на средних частотах — в средней части спирали.
На витках, радиус которых меньше требуемого для ре-
жима осевого излучения, преобладает волна То, а на витках,
имеющих большой радиус (2^а= L > 1,3), преобладают
волны Т2, и высших порядков.
628
Таким образом, одной из особенностей конических спи-
ралей является возбуждение на разных витках одной и той
же спирали волн разных порядков.
При волне То одна длина волны (изменение фазы тока
в пределах 360°) укладывается на протяжении нескольких
витков. При этом токи на отдельных витках имеют разные
фазы. В свою очередь каждый из витков эквивалентен рам-
ке. В результате всего этого участок спирали, на котором
существует волна То, слабо излучает по сравнению с группой
витков, возбужденных волной Ту.
ЮООМгц , 15QOM2U - £000Мгц 250QMZU, ЗОООМгц
" t
Рис. 11.17. Схема распределения фаз тока на конической спирали
при разных частотах.
При волне Т2 и волнах более высоких порядков, которые
формируются на некоторых витках, имеющих достаточно
большой диаметр, на них укладывается больше одной вол-
ны (больше 360°). Поэтому на каждом из таких витков
имеются противофазные участки, излучение которых
взаимоослабляется. Кроме того, из-за разнообразной фази-
ровки отдельных витков еще больше ослабляется их излуче-
ние. Таким образом, интенсивность излучения витков, воз-
бужденных волной Т2 и волнами более высоких порядков,
также мала по сравнению с интенсивностью излучения
группы витков, возбужденных волной Ту.
Итак, у конических спиральных антенн излучает глав-
ным образом группа витков, работающих в режиме осевого
излучения.
629
У конической спирали диаграмма направленности осево-
го типа образуется во всем диапазоне частот, в пределах
которого существует группа витков, на которой возбуждает-
ся волна Г], т. е. группа витков, у которых длина L лежит
между 0,8 X и 1,3 Я..
Из сказанного следует также, что острота направленно-
сти у конических спиралей определяется не общим числом
^7
ЮООМги.
34
МО Мгц
Е? £в
гооомги
2/00Мгц
Kpi,s:i
Рис. 11.18. Изменение формы диаграммы направленности конической
спирали с изменением частоты. Параметры спирали I — 1 м; п = 10,25;
а =а 17°; 2а0 = 2,55; 2амакс = 7,6 см. У кривых указана величина коэф-
фициента равномерности (кр).
ЗЬООМгц
Кр5-.1
витков или полной длиной спирали, а лишь числом витков
в группе с волной 7\ и длиной этого участка спирали. Хотя
излучение остальных витков не является решающим, но оно
также накладывает некоторый отпечаток на форму диаграм-
мы направленности.
На рис. 11.18 даны диаграммы направленности рассмат-
риваемой спирали на разных частотах диапазона 1 000—
3 400 Мгц. Отдельно приведены диаграммы направленности
для £0 и £?. На рисунке указано также значение коэффи-
циента равномерности (кр) в осевом направлении.
630
На рис. 11.19 показан ход кривой изменения входного
сопротивления спирали в диапазоне 900—3 200 Мгц. Сопро-
тивления даны в относительных единицах п. Окружности из
тонких линий соответствуют постоянному значению коэффи-
циента стоячей волны.
Из приведенных данных видно, что рассматриваемая ко-
ническая спираль обладает почти трехкратной диапазон*
х
ностью. В пределах этого диапазона спираль имеет диа-
грамму направленности осевого типа, поле излучения имеет
почти круговую поляризацию, входное сопротивление слабо
меняется с частотой и обладает сравнительно большой
активной составляющей при сравнительно малой реактив-
ной составляющей.
1) Нормированных относительно волнового сопротивления р из-
мерительной линии.
631
Другая серия измерений [67] проведена с четырьмя оди-
наковыми спиралями со следующими параметрами:
п =10, а = 6°, 2ао = 2О см, 2амакс — 60 см, р = 0,03,
/ = 112 см, d = 4 mmi
Главным отличием этих данных от предыдущих является
значение а = 6°. Применялся плоский круглый экран-про-
тивовес диаметром 100 см. Измерения проводились в диапа-
зоне 120—450 Мгц.
Рис. 11.20. Различные схемы расположения
и питания конических спиралей.
Исследованные спирали отличались друг от друга своим
расположением относительно экрана и выбором точки пи-
тания. Расположение спиралей и система питания показаны
на рис. 11.20. Две спирали были обращены к экрану боль-
шими основаниями (а, б), две—малыми основаниями (в, а).
В каждой из этих пар спиралей в одном случае питание
подводилось к нижней точке (к точке спирали у экрана),
в другом случае питание подводилось к верхней, точке.
В результате данной серии измерений выяснилось, что
диаграмма направленности осевого типа получается у спи-
ралей с указанными параметрами лишь в том случае, когда
63S
Рис. 11.21. Диаграммы направленности конической спирали, показан-
ной на рис. 11.20, а, на разных частотах.
Рис. 11.22. Диаграммы направленности спирали, показанной на рис.
11.20, б, на разных частотах.
633
спираль расположена большими основаниями у экрана
(а,б), причем при питании снизу (а) такая диаграмма на-
правленности (осевого типа) получалась в диапазоне, не-
сколько большем двукратного, а при питании сверху
(б) — в трехкратном диапазоне.
Рис. 11, 23. Диаграммы
направленности коничес-
кой спирали с малым
шаговым углом а= 2,5°.

Диаграммы направленности этих спиралей в диапазоне
осевого излучения показаны на рис. 11.21 и рис. 11.22.
Спирали вида (в) и (г) при указанных выше параметрах
не имеют диаграммы направленности осевого типа.
Третья серия измерений проводилась с конической спи-
ралью, имеющей следующие параметры:
/1 = 6, а = 2,5°, 2ао=1Осл/, 2амакс=130 см,
р = — = 0,32, / = 60 см, d = 4 мм.
' те ’
Экран имел форму квадрата со стороной 183 см и был
выполнен из густой медной проволочной сетки, имеющей
634
40 ячеек на 2,5 см длины. Измерения проводились в диапа-
зоне частот 100—500 Мгц.
Спираль была поднята над экраном-противовесом на
высоту 17,5 см.
Данная спираль, как видно из приведенных данных,
имеет малый шаговый угол (2,5°) и сравнительно большой
параметр р, число же витков невелико. При этих условиях
не обеспечивается образование группы витков, возбужден-
ных волной Гь Получение диаграммы направленности осе-
вого типа основывается в данном случае главным образом
на влиянии экрана-противовеса.
Так как витки почти параллельны экрану, а размеры
экрана сравнительно велики, то диаграмма направленности
имеет максимум в перпендикулярном к экрану направлении
и почти нулевое излучение в плоскости экрана. Параметры
спирали и ее положение относительно экрана подобраны та-
ким образом, что обеспечивается диаграмма направленности
осевого типа в пятикратном диапазоне. Полученные диа-
граммы направленности на разных частотах диапазона при-
ведены на рис. 11.23.
Как и другие спиральные антенны, данная антенна соз-
дает поле почти круговой поляризации и имеет входное со-
противление, сравнительно мало меняющееся с изменением
частоты.
§ 6. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ИЗЛУЧЕНИЯ
ЦИЛИНДРИЧЕСКИХ СПИРАЛЬНЫХ АНТЕНН
Выяснив основные особенности спиральных антенн, в частности,
закон распределения тока на спирали, можно аналитически полу-
чить выражение для поля излучения антенны и для диаграммы на-
правленности.
Рассмотрим только цилиндрическую спираль, для которой во-
прос о распределении тока достаточно ясен. Обратимся к рис. 11.24,
на котором спираль изображена в виде винтовой линии на цилиндре
радиуса а. Координатные системы выбраны таким образом, что ось
спирали является осью Z в прямоугольной системе координат или
полярной осью в сферических координатах. Начало координат,
вообще говоря, выбирается в произвольной точке на оси спирали.
Удобнее всего поместить начало координат в середине спирали.
Точку наблюдения М помещаем в плоскости YZ. Координаты точек
спирали и точки наблюдения равны соответственно.
zs = atga-(p, '
xs = a cos <р,
— a sin <р,
(11.29)
635
и
zM — г cos "
хм = °’
Ум = r sin 9- ,
(11.30)
После простых выкладок, аналогичных тем, которые привели к
формуле (3.5), получаем в данном случае
rs = г — (a tg a cos 0) <р — a sin 4 sin <р.
(11.31)
Обозначения приведены на рис. 11.24.
Для расчета электромагнитного поля излучения воспользуемся
формулой (2.41). Учитывая, что диаметр провода спирали очень мал
Рис. 11.24. К выводу формулы для диаграммы направленности цилин-
дрической спирали.
по сравнению с длиной волны, можно исключить из (2.41) интеграл,
содержащий магнитные токи, и привести второй поверхностный ин-
теграл к линейному, взятому по линии спирали. Таким образом, в
рассматриваемом случае электрический вектор поля излучения Е
равен
-> -+ -> —!krs
Е = [ r° [!s , r0]] - de. (11.32)
nL
636
где Is — вектор тока, протекающего по всему сечению спирали в
точке s (рис. 11.24),
d%—линейный элемент провода,
г0 — орт, имеющий направление радиуса-вектора rs.
Как указывалось выше, нас интересуют в отдельности две со-
ставляющие вектора поля и Для их нахождения разлагаем
вектор Is иа составляющие, параллельные £0, Е^, которые обозна-
чаем соответственно через /0 и Как легко видно из рис. 11.24,
J = Is cos a sin с,
(cos а cos 9 cos ip — sin a sin 9).
(11.33)
Через I® и /е составляющие поля £? и £8 выражаются следу-
ющим образом
Р —ikrs
nL
л
/<01Хп г е
-4^- \ Is (cos a cos 9 cos <р — sin a sin 9) —------------ds,
nL
(11.34)
(* —ikrs . —jkr^
nL nL
Теперь необходимо конкретизировать выражение для Is. Мы
видели выше, что ток иа проводе спирали может быть выражен как
сумма функций вида (11.27). В режиме осевого излучения, который
представляет для нас наибольший интерес, преобладающее значе-
ние для излучения имеет волна Ту характеризующаяся постоян-
ством амплитуды тока. Ввиду громоздкости полного выражения для
тока, мы будем учитывать в дальнейших выкладках только волну
Ту т_ е. положим
Is=I0le4?'\ (11.35)
где /0] — амплитуда тока волны 7\.
Подставив в (11.34) значение Is из (11.35), rs из (11.31), а также
а
£ COS а
а
d; =--------- d<c,
* cos а
(11.36)
637
получим
o /*>ДО J e~'kr C
^9- — ”47" 'oi—~
(cos 9 cos у — tg a sin в) X
9i
ika
„ a, \
a COS v— -------- I ®
k cos a I T
7
-•b ?2
p Z~‘kr C
(11.37)
jka si n f> sin <f 4- I tg a cos i>—
X Sin tp e L '
rft?.
Угол <pt соответствует нижнему концу спирали, а —верхнему
концу.
Для упрощения выражений (11.37) введем обозначения
>Роа , e~iltr г.
~ХГ Ан —— = £о.
t = ka sin ft,
v = ka tg a cos 9 — -—— .
° COS а
(11.38)
(11.39)
(11.40)
В этих обозначениях f9 и Еа выражаются следующим образом:
92
|
cos <f — tga sin 9) e^sln 7 e^®d?,
<?2
( sin?e//sin7 e/v7 <*<?•
(И.41)
71
Как известно, экспоненциальная функция e,7sin? разлагается в
ряд Фурье с коэффициентами в виде бесселевых функций, а именно
е;7 sin 9 = (— l)mZm (0 е''"?,
т——оо
(11.42)
где m — целое число,
Im (t) — функция Бесселя m-ого порядка.
В свою очередь
cos ? =-X-
зш?=__----
(11.43)
® j
E*
638
Подставив (11.42) и (11.43) в (11.41), получаем
О»
£e = -£0 У] (-l)m/m(o{4 Jcosfre''"’*1^ +
/и——оо <Pj
! ¥*2
4-4 J cos 8 (,л—</<р — tga sin 8 J
?i <Pi
(11.44)
Из (11.44) видно, что значения £9 и Е^ зависят от величин уг-
лов <р( и <р2, т. е. зависят от положения плоскости YZ (рис. 11.24),
в которой находится точка наблюдения относительно концов спи-
рали. Следовательно, спираль имеет различную диаграмму направ-
ленности в разных плоскостях и разный коэффициент равномерно-
Ео
сти -7Г. В частном случае симметричного расположения плоскости
YZ относительно концов спирали, когда — tpj = ср2 = То
е Е- V / n»ir /а) чГ Sint(m+1 4-4?о1 .
Ео = - Ео <- ’) Jm (0 jcos 9 [ -------m '4-T-Fv----+
sin [(m — 1 4- v) <p0 I . sin[(m + 4»d)
-r OT-14-4 j К rn + vj (11.45)
„ , (sin [(m -4-1 -I- v) ifP]
E. = - P (~ П V) ( - ~
_ sin [(m — 1 4-v)yn] 1
m — 1 -f- ч j ‘
Из (11.45) видно, что E$ и E„ смещены no фазе на 90°, но по
амплитуде они, вообще говоря, различны.
Формулы (11.45) упрощаются, когда спираль состоит из целого
числа витков. В этом случае
<fo= niz,
sin (m 4-1 4-4 ?0 = (- 1)(ш+1)я sin (vTo),
sin (m 4- 4 ®o = (— O'"" sin O'f’o)»
639
и
оо
£9 = -£о J) 4(f) [(-l)(m+1)/,+mcos9X
т——оо
л sinvrtTt sinvrtTt'l
X 2 (v Ч- tn) ,-----&----Г + (— 1) ( + +1 2 tg a sin Э —,—
v ' ' (v -f- ту2—1 1 ' 1 ь т 4- v ]
(11.46)
00
E^jE0 £
п ——00
При практических расчетах можно ограничиться несколькими
или даже одним слагаемым из рядов (11.46). Лело в том, что у
спиралей, работающих в режиме осевого излучения
t — -yj- sin 0 — (0,8 4- 1,3) sin в.
(пл;
Бесселевы же функции малого аргумента t (t не больше 1,3) очень
быстро убывают с увеличением их порядка т.
В направлении 0 = 0 (вдоль оси)
sin 0=0, cos О = 1, t = 0, ’
Jo (0=1,
4 (0 = о при т о
7
Тогда
_ sinvnnrt
4 = -£0(-I)'l2v0-^->
>о — 1
„ 2 sin 4nmt
E^JE0(-ir 44^-,
v0 1
где
v0=featga-^?7.
(11.48)
(11.49)
(11.50)
Из (11.49) видно, что круговая поляризация (Е^ = Еа) имеет
место при v0=l. При учете (11.1) это означает выполнение условия
(11.15).
ПРИЛОЖЕНИЕ № 1
Таблица A-функций п го порядка
X Л'/2 Л’/2 Лг/2 Лт/ / 2 л"/2 Л1,/2 А|’/г
0 1 1 1 1 1 1 1
1 0,8413 0,9933 0,9301 0,9457 0,9555 0,9635 0,9730
2 0,4546 0,6530 0,7437 0,7973 0,8309 0,7979 0,8626
3 0,0470 0,3456 0,4974 0,5912 0,6549 0,7010 0,7363
4 —0,1891 0,0871 0,2589 0,3761 0,4609 0,5252 0,5760
5 —0,1918 —0,0571 0,0808 0,1930 0,2326 0,3551 0,4147
6 —0,0465 —0,0838 —0,0155 0,0664 0,1435 0,2117 0,2715
7 0,0942 —0,0494 —0,0411 —0,0004935 0,05218 0,1064 0,1583
8 0,1237 0,0126 —0,0260 —0,02114 0,004809 0,04012 0,07891
9 0,0458 0,0354 —0,0919 —0,01614 —0,01117 0,006266 0,03521
10 —0,0544 0,0235 0,0117 —0,004147 —0,009975 —0,005769 0,006013
ПРИЛОЖЕНИЕ № 2
Таблица рядов функций Бесселя и Неймана
X OQ « = 1 X © "а СО Л'о (пх) п~\
0,3 2,8333 1,0047 7,2 0,2078 0,2595
0,6 1,1667 0,7828 7,5 0,1220 0,2407
0,9 0,6111 0,6515 7,8 0,0909 0,2219
0,2 0,3333 0,5568 8,1 0,0147 0,2и22
1,5 0,1667 0,4815 8,4 —0,0223 0,1843
1,8 0,0556 0,4183 8,7 —0,0527 0,1639
2,1 —0,0238 0,3627 9,0 —0,0485 0,1435
2,4 —0,0833 0,3124 9,3 —0,1008 0,1222
2,7 —0,1296 0,2655 9,6 —0,1202 0,0998
3,0 —0,1667 0,2207 9,9 —0,1376 0,0756
3,3 —0,1970 0,1769 10,2 —0,1531 0,0494
3,6 —0,2222 0,1331 Ю,5 —0, 1671 0,0201
3,9 —0,2436 0,0880 Ю,8 —0,1797 —0,0132
4,2 —0,2619 0,0401 И,1 —0,1913 —0,0533
4,5 —0,2778 —0,0125 И,4 —0,2021 —0,1039
4,8 —0,2917 —0,0729 11,7 —0,2119 —0,1739
5,1 —0,3039 —0,1466 12,0 —0,2211 —0,2851
5,4 —0,3148 —0,2456 12,3 —0,2296 —0,5380
5,7 —0,3246 —0,4004 12,6 1,9249 0,2272
6,0 —0,3333 —0,7356 12,9 0,4413 0,2152
6,3 4,0029 0,3164 13,2 0,2431 0,2030
6,6 0,6416 0,2973 13,5 0,1470 0,1907
6,9 0,3462 0,2782
41—1503
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1. Н. А. Концов. Annalen der Physik IV, В. 69, S 112—124. См.
также „Труды III съезда Российской ассоциации физиков в Нижнем
Новгороде, стр. 23. Издательство Нижегородской Радио лаборатории,
1923 г.
2. А. 3. Фр а дин и Б. С. Мудрогин. ИЭСТ № 2, 1941 г.,
стр. 40.
3. М. С. Нейман. ИЭСТ Ns 6, 1940 г., стр. 1.
4. А. А. Пистолькорс. Ж. Т. Ф., т. XIV, вып. 12, 1944 г.,
стр. 693; ЖТФ, т. XVI, вып. 1, 1946 г., стр. 3.
5. Я. Н. Фе ль д. „Основы теории щелевых антенн”, изд. „Совет-
ское радио”, Москва, 1948 г.
6. Л. А. Вайнштейн. „Диффракция электромагнитных и зву-
ковых волн на открытом конце волновода”, изд. „Советское радио”,
Москва, 1953 г.
7. Г. Т. Марков. ЖТФ, 1952 г., вып. 5, стр. 747—753 и 1953 г.,
вып. 5, стр. 638—648.
8. М. Л. Л е в и н. Изв. Акад, иаук СССР, сер. физ., Ns 3, 1943 г.
9. М. Б. 3 а к с о н. Д. А. Н. СССР, т. 66, Ns 4, 1949 г.
10. Б. В. Брауде. ЖТФ, 1955 г., вып. 10, стр. 1819 — 1824.
11. Я. Л. А л ь п е р т, В. Л. Гинзбург и Е. Л. Фейнберг.
Распространение радиоволн”. Госиздат Технико-теорет. литературы,
1953 г., стр. 46.
12. П о д р е д. М. И. К о н т о р о в и ч а. „Антенные устройства”,
вып. 3, стр. 71, изд. ВКАС, Ленинград, 1947 г.
13. Е. Янке и Ф. Эм де. „Таблицы специальных функций”,
стр. 237, Гостехиздат, 1948 г.
14. Там же, стр. 125.
15. Б. А. ВведенскийиА. Г. Аренберг. „Радиоволноводы”,
ч. 1, ТТИ, 1946 г.
16. Г. В. К и сунь ко. „Электродинамика полых систем”. ВКАС,
Ленинград, 1949 г.
17. В. И. Ю з в и и с к и й. „Питание антенн сверхвысоких частот”.
„Антенные измерения”. ВКАС, Ленинград. 1951 г.
18. Под редакцией А. И. Шпунтов а. „Теория линий
передачи сантиметровых волн”, изд. „Советское радио”, 1951 г.
19. Под редакцией Г. А. Ремеза. „Линии передачи санти-
метровых волн”, изд. „Советское радио”, 1951 г.
20. Под редакцией Я. Н. Фельда. „Справочник по волно-
водам”, изд. „Советское радио”, 1952 г.
21. Под редакцией Я. Н. Фе ль да. „Антенны сантиметро-
вых ьолн”, изд. „Советское радио”, 1951 г., чч. I и П.
642
22. Е. Г. 3 е л к и н. ЖТФ, т. 21, № 10, стр. 1228—39, 1951 г.
23. Л. Левин. «Современная теория волноводов", стр. 137.
Издательство иностранной литературы, 1954 г.
24. Б. П. Рождественский. ДАЙ СССР, 1951 г., стр. 77, № 2.
25. Е. Г. Уиттекер и Ватсон. «Курс современного анализа",
ГТТИ, 1934 г., стр. 139.
26. И. Е. Тамм. «Основы теории электричества". Гостехиздат,
1946 г., стр. 135.
27. G1 е и Р. Robinson. Tele-Tech [Electronic Industries,
november 1954, стр. 73.
28. Гутман. «Вопросы радиолокационной техники", № 1 (25),
1955 г., стр. 91—96.
29. A. Gutman. J. Appl. Phys. 25, №7, July 1954 г., стр. 855—859.
30. J. С. Simon Ann, de Radioel. 1951 г., т. VI, № 25, Juillet,
стр. 205—243.
31. 1. F. Can Ison and Heins. Quarterly of Appl. Mathematics,
vol. IV, January 1947 r.
32. B. A. Whitehead. PJEE, PHI V., 98, № 52, 1951 r.
стр. 133—140.
33. Gerhard Piefke. Archiv der Elektrischen Ubertragung
Marz, 1954 г., B.8 H—3, стр. 101—110.
34. S. B. Cohn. Appl. Phys.,.vol. 20, III, 1949 г., p. 257—62.
35. A. M. M о де л ь. Радиотехника, № 6, 1955 г., стр. 52—57.
36. Е. М. Т. Jones and S. В. Cohn. Appl. Phys. vol. 26, 4,
1955 r., p. 452—457.
37. У з к о в А. И. Вестник НИИ, МИСС, № 7, 1950 г.
38. М. И. К о н т о р о в и ч и Ю. К. Муравьев. Ж. Т. Ф., 1952 г.
39. В. К и н б е р. Вестник НИИ МИСС СССР, 1952 г., № 1 (24),
стр. 3—12.
40. Спенсер Слетте н—У о л ж. «Вопросы радиолокационной
техники", 1953 г., № 3 (15).
41. Б. Е. К и и б е р. Вестник НИИ МИСС СССР, № 6 (51), 1954 г.,
стр. 33.
42. W. С. Ja ke s. PJRE № 2, 1953 г., № 41, стр. 272—274.
43. Г. А. К о ч е р ж е в с к и й. .Радиотехника", № 3, 1953 г.
стр. 49.
44. А. М. Модель. „Радиотехника", № 5, 1952 г.
45. М. Д. О. Стретт. «Функции Ляме, Матье и родственные
им в физике и технике. Гос. научно-техническое издательство
Украины, 1935 г.
46. А. А. Пистоль коре. ЖТФ, № 3, 1947 г., стр. 365 — 76.
ДАН СССР, 1946 г., т. 52, № 2.
47. М. Л. Л е в и н. ЖТФ, № 7, 1951 г., up. 772.
48. Б. 3. К а ц е н е л е н б а у м. «Доклады Академии наук СССР",
т. № 7, 1947 г., стр. 1317.
49. D. F. Holliday and D. G. К i е 1 у. J. J. E. E. vol 94, part 1ПА,
p. 610, 1947 r.
5'J . M. И. К о н т о p о в и 4. «Труды ВКАС им. Буденного", № 6.
51. С. W. Horton and С. Мс. К i w п а у. Appl. Phys., oct. 1951г.,
vol. 22, № 10, стр. 1241—49.
52. W i г е 1 le s s E n g i n. № 4, 1948 г., стр. 110—117.
53. Дж. К. Саусворт. «Принципы и применения волноводной
передачи, «Советское радио", 1955 г., стр. 418.
54. D. G. Kiely. PJEE. 1950, № 49, сентябрь, стр. 311—320.
55. D. G. Kiely. Wirelless Engirt. XXVI, июнь 1951 г., стр. 177—178.
41* 643
56. A. Sommerfeld. Ann. der Phys, und Chemie 1899, 67
стр. 233.
57. G. Goubau Journ, of Appl. Phys. 1950. 21, стр. 1119.
58. Zenneck J. Ann. der Phys. 1907, 23, стр. 846.
59. H. M. Barlow and Cullen. 1953 г., № 68, 100 ноябрь,
стр. 329.
60. Л. А. Вайнштейн. Журнал Технической физики, т. XXVI,
вып. 2, февраль 1956 г., стр. 385—397.
61. Рейнольдс Д. и Лак У. „Вопросы радиолокационной
техники", вып. 5, 1953 г., стр. 36—45.
62. G. J. Rich. PJEE рВ 1955, № 2, March, стр. 237—246.
63. J. С. S i m о n a t. V Biggi L’onde Electrigue Nov 1954 г.
64. Под редакцией Я. Н. Фе льда „Техника сверхвысоких
частот", 1. Изд. „Советское радио", Москва, 1952 г.
65. James A. March. PJRE V 39. № 6, 1951 г„ стр. 668—675
66. J. S. Chatterjee. Appl. Phys. V 24, № 5, 1953 г., стр. 550—559.
67. J. S. Chatterjee. Appl. Phys, V 26, № 5, 1955 г., стр. 331—335.
ОГЛАВЛЕНИЕ
Предисловие............................................... 3
Г лава первая. Антенны сверхвысоких частот, их классифи-
кация, устройство и принцип действия.......................
§ 1. Предает изучения ................................ 5
§ 2. Классификация СВЧ антенн......................... 6
§ 3. Рупорные антенны................................ 8
§ 4. Линзовые антенны................................ 13
§’5. Щелевые антенны . . .’......................... 25
§ 6. Диэлектрические антенны..........’.............. 28
§ 7. Рефлекторные антенны (зеркала).................. 33
§ 8. Антенны поверхностных волн...................... 36
§ 9. Общая характеристика СВЧ антенн................. 39
Глава вторая. Основная задача теории СВЧ антенн и ме-
тоды ее решения......................................
§ 1. Постановка задачи............................... 42
§ 2. Исходные уравнения.............................. 48
§ 3. Метод вспомогательных источников................ 50
§ 4. Метод векторного потенциала..................... 61
§ 5. Принцип эквивалентности......................... 65
§ 6. Приближенное решение внешней задачи теории СВЧ
антенн................................................ 67
§ 7. Формула Кирхгофа. Сравнение с векторной формулой . 69
§ 8. Метод стационарной фазы......................... 80
Глава третья. Диффракция от отверстия в плоском
экране ..............................................
§ 1. Введение....................................... 84
§ 2. Синфазное поле в прямоугольном отверстии....... 84
§ 3. Синфазное поле в круглом отверстии.............101
§ 4. Общие особенности направленности излучения пло-
ских синфазных антенн.................................120
§ 5. Паразитная поляризация.........................124
§ 6. Изменение фаз по линейному закону..............124
§ 7. Изменение фаз поля по квадратичному закону в прямо-
угольном отверстии ...................................128
§ 8. Изменение фаз поля по квадратичному закону в круг-
лом отверстии.........................................137
645
§ 9. Изменение фаз по кубическому закону...........140
§ 10. Влияние периодического изменения амплитуд на ди-
аграмму направленности синфазных антенн..............141
Глава четвертая. Волноводные излучатели...................
§ 1. Поле в прямоугольном волноводе..................144
§ 2. Излучение из раскрыва прямоугольного волновода . . 148
§ 3. Поле в круглом волноводе........................153
§ 4. Приближенное решение задачи об излучении из раскры-
ва круглого волновода ............................ 155
§ 5. Строгая постановка задачи о волноводных излучате-
лях .................................................158
§ 6. Результаты строгого решения задач о волноводных из-
лучателях ...........................................170
Глава пятая. Рупорные антенны.............................
§ 1. Введение........................................ 177
§ 2. Секториальный рупор..............................178
§ 3. Пирамидальный рупор..............................198
§ 4. Биконический рупор...............................203
§ 5. Квазипирамидальиый рупор.........................216
§ .6 . Конический рупор...............................221
§ 7. Строгое решение задач о возбуждении конического
рупора..................................... ' . : . 227
§ 8. Переход от волновода прямоугольного сечения к век-
ториальному или пирамидальному рупору................237
§ 9. Особенности электромагнитного поля в раскрыве ру-
порных антенн. Коррекция фаз.........................248
Г лава шестая. Линзовые антенны...........................
§ 1. Однородные лиизы с плоской волной в раскрыве . . 259
§ 2. Диэлектрическая проницаемость и коэффициент пре-
ломления металло-диэлектрических линз..............268
§ 3. Частотные свойства линзовых антенн............275
§ 4. Технические допуски...........................281
§ 5. Апланатические линзы..........................295
§ 6. Металлическая линза с широким углом качания луча 301
§ 7. Сферические и круглые цилиндрические неоднород-
ные линзы............................................309
§ 8. Линза из металлических пластин с отверстиями . . . 319
§ 9. Отражение от поверхности линз . ..............375
§ 10. Методу исключения отражения от поверхности линз. 337
§ 11. I аспределение амплитуд поля в раскрыве линзы . . 346
§ 12. Расчет характеристик излучения линзовых антенн . . 352
§ 13. Получение косекансной диаграммы направленности
с помощью линзы......................................356
Г лава седьмая. Зеркала...................................
§ 1. Два метода расчета зеркал................... . . 363
§ 2. Расчет параболоида вращения апертурным методом. 367
§ 3. Облучатели параболоидов вращения...............384
§ 4. Воздействие на облучатель волны, отраженной от
зеркала ......................................... 393
§ 5. Параболический цилиндр. Сегментно-параболическая
антенна .............................................399
§ 6. Технические допуски............................406
646
§ 7. Параболоиды с решетчатыми и перфорированными
поверхностями...........................................410
§ 8. Сферическое зеркало.................... . . 420
§ 9. Построение зеркала по заданному распределению
фаз поля в раскрыве.....................................427
§ 10. Зеркала, имеющие косекансную диаграмму направ-
ленности ...............................................430
§ 11. Плоские зеркала .............................. 434
Глава восьмая. Щелевые антенны............................
§ 1. Принцип двойственности Пистолькорса и его приме-
нение к щелевым антеннам .............. . ..............442
§ 2. Щели на металлических пластинах конечных размеров. 455
§ 3. Щели на стенках прямоугольного волновода........465
§ 4. Щели на круглых цилиндрических поверхностях . . . 485
Г лава девятая. Диэлектрические антенны...................
§ 1. Электромагнитное поле в сплошном диэлектрическом
стержне круглого сечения................................496
§ 2. Затухание волн в диэлектрическом стержне.......516
§ 3. Электромагнитное поле в диэлектрической антенне
из сплошного круглого стержня...........................526
§ 4. Второй принцип эквивалентности.................531
§ 5. Диаграмма направленности диэлектрической антенны. 535
§ 6. Анализ данных экспериментального исследования ди-
электр ических антенн из сплошного стержня..............543
§ 7. Расчет диэлектрических антенн из сплошных стер-
жней ...................................................550
§ 8. Диэлектрические трубы..........................553
§ 9. Сложные диэлектрические антенны................560
§ 10. Диэлектрическая стержневая антенна, излучающая
перпендикулярно оси. Антенна с широкоугольной диаг-
раммой направленности...................................563
Глава десятая. Антенны поверхностных волн.................
§ 1. Поверхностные волны.............................569
§ 2. Поверхностное сопротивление......................577
§ 3. Металлическая поверхность, покрытая диэлектричес-
ким слоем..........................................579
§ 4. Гофрированная металлическая поверхность......582
§ 5. Характеристики излучения плоскостных антенн, ис-
пользующих плоскую поверхностную волну.............587
§ 6. Характеристики излучения плоскостных антенн, ис-
пользующих цилиндрическую поверхностную волну . . . 594
§ 7. Цилиндрическая антенна поверхностных волн .... 597
Глава одиннадцатая. Спиральные антенны............
§ 1. Устройство. Основные определения.................602
§ 2. Режим осевого излучения..........................606
§ 3. Режим ненаправленного излучения..................621
§ 4. Распределение амплитуд и фаз тока на цилиндричес-
кой спирали.............................................623
§ 5. Характеристики конических спиральных антенн . . . 627
§ 6. Электромагнитное поле излучения йилиндрических
спиральных антенн.....................................635
Афроим Зеликович Фрадин
АНТЕННЫ
СВЕРХВЫСОКИХ ЧАСТОТ
Редактор В. Г. Машарова
Техн, редактор И. Н. Корузев
Обложка художн. В. В. Волкова
Сдано в набор 4/V11I 1956 г. подписано
к печати 14/11 1957 г. Формат 84X108/32.
Печ. л. 33,21. Бум. л. 10,125. Уч.-изд. л. 32,11.
Г-32063. Заказ 1503.
Цена в переплете № 5 17 р.
в переплете № 7 17 р. 5.» к.
Типография Госзнергоиздата.
Москва, Шлюзовая наб., 10.
ОПЕЧАТКИ
к книге А. 3. Фрадина .Антенны сверхвысоких частот
Стра- ница Строка Напечатано Должно быть По чьей вине
80 10 сверху 1 у sin <Р 1 усов ? автора
е-/*г е-/*г
86 5 снизу /“7- J 2Хг ” ”'ж
94 1 снизу 9^ oh, zT + с t с*о + • п
Е2 Г £0 I е1 г
108 5 снизу — 120л [ ••• ~ 120 [ •• •
а2 жа2
ПО 8 снизу Aj}' р2 + а2 Ар~ р2 + а2
112 авА2 sin2 8 1 - V а4А2 sin2 9
2(р2 + а2)2 74 ‘ 2(р2 + а2)2 х •
116 10 сверху а2р2 «’Р2 —
117 4 сверху 2(р*-|-а2)2 х ' (рг 4- а2)2 i
Стра-
ница
120
126
132
132
132
139
146
155
155
174
Строка Напечатано
2 / a® V
4 сверху + 15 v +А/ je~lkr »
18 сверху А— cos® 2 /n^ft«sin>9
5 сверху 7 сверху 8 сверху е YkA’jfe sin 0
8 снизу 1 1 1 а | ©?
12 сверху 7 Нх = — cos.. х шИ0
7 сверху £ц ‘о |<м II
9 сверху 7 3 Н~ 2 -f-йа stn 9
7 снизу -Я —ka sin &
Продолжение
Должно быть По чьей вине
Ь4 ° . 1 Х-—X в о, ы я , в|ч % 1 о + о N |2 '« + "| ч автора ~"г»
ЛР, *• , ,,, / — sin* S 4 те е _ ——
V hRt •— sin 9 те —»—
«о | <3 «|с£
^=-i£ocos---
Е^ЪЕ0 • ” ~
Но=- — й£0 Р Ш[<0 u 4*ч sin # 1 —»~~
К 1 • • •
~ka sln
Здра- вица Строка Напечатано
-j-ka
174 8 снизу -г J •••
—ka
193 4 сверху (5.20)
210 9 снизу LZt(x)2r-s/i
221 6 снизу и—(ПК 4- ?)
2л
283 14 сверху ~ 2 •"
327 5 снизу- 2Г sin yd
К(1-Г»)‘ 4-4Г* sin* -fd
Г 1/ — 4Г12Га3 sin1 sin 7) + ...
350 5 сверху dp
(6.167) с учетом значении
из (6.161)
358 9 сверху (6.143)
Продолжение
Должно быть По чьей вине
4-Ас
1 С
я J ' * автора
—ka
(5.27)
Lt, (zjGGi+l)^* а “
и (2ля -f- р) г ' "
2я
— к >
2Г sin 4- j
|/ (! _r««4-4fsin>^d 4-Jj »
Г -« 1/ g3-t S1 П1 <р (14" ГцГм)* — 4Г1*Гза sins 9 —ж
dy = sin 7</р + • • • ~~а
(6.167) в (6.165) с учетом значения "' а
dp из (6.159)
(6.160) a J1''
Стра- аица Строка Напечатано
470 9 сверху яи"= —р? •••
472 11 сверху в= 7 ...
474 3 сверху -Я -
щель
474 10 сверху 14 II 14 ч II
474 11 сверху в — E\yH\z> + Ez'H iy> =
и гм „\1 = —~d sin [А(“г—1г| И
480 17 сверху 120тсЛ 2 73,1
+ Т Sn 2(б0п)2
510 1 снизу Ва + А7 ₽ «а г
511 1 снизу
— уХд iJ^^a —
524 9 сверху dF wlia
581 12 снизу “%(ч—»t)A «0 , , “»2 0 1
h b+J м-
Продолжение
Должно быть По чь$Й вине
тс Ht<> ~ • • автора
1
. <Д|*о 1 С А~'~ т $„ J
щель Е=Еу,=
— Ey'Hiz' "i~ = *»п '"г
= - ‘Г stn [* ("Г - lz'i) ] 120тсЛ 2 73, It/2 t
+ 7 5П 2(60^’
Ва jawi
ь А . ₽ а
“ J*a ~ - jxa .»
dF •
х . Ео , . ь>е0 - V Хе2+'г1М- а~