Б. П. ДЕМИДОВИЧ и И. А. МАРОН
ОСНОВЫ
ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ
ИЗДАНИЕ ТРЕТЬЕ,
ИСПРАВЛЕННОЕ
Допущено Министерством
высшего и среднего специального образования РСФСР
в качестве учебного пособия
для высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
MOCK В А 19 66

518
Д 30
УДК 518. 0
АННОТАЦИЯ
Книга посвящена изложению
важнейших методов и приемов вычислительной
математики на базе общего втузовского
курса высшей математики. Основная часть
книги является учебным пособием по курсу
приближенных вычислений для втузов.
Книга может быть полезна также для
лиц, работающих в области прикладной
математики.
Борис Павлович Демадозич и Исаак Абрамович Марон
Основы вычислительной математики
М., 1366 р. 664 стр. о илл.
Редакторы М. Af. Горячая и В. М. Гринберг
Теки, редактор К. Ф. Брудно Корректор С. Д. Кайсер
Сдано в набор 30/Ш 1966 р. Подписано к печати 28/VI 1966 р. Бумага 60x90/16
Физ. печ. л. 41,5 Условн. печ. л. 41>5 Уч.-изд. л. 41,06
Тираж 75 000 экз. Т-08270. Цена книги 1 р. 54 к. Заказ № 339.
Издательство «Наука»
Главная редакция
Физико-математической литературы
Москва, В-71, Ленинский проспект, 15
Первая Образцовая типография имени А. А. Жданова
Главполиграфпрома Комитета по печати при Совете Министров СССР
Москва» Ж-54, Валовая, 28
2-2-3
4-66

ОГЛАВЛЕНИЕ
Предисловие к первому изданию 9
Предисловие ко второму изданию 12
Предисловие к третьему изданию 12
В ведение. Общие правила вычислительной работы 13
Глава I. Приближенные числа 17
§ 1. Абсолютная и относительная погрешности . . . . 0 17
§ 2. Основные источники погрешностей . 20
§ 3. Десятичная запись приближенных чисел. Значащая цифра.
Число верных знаков . . « 21
§ 4. Округление чисел 24
§ 5. Связь относительной погрешности приближенного числа с
количеством верных знаков этого числа 25
§ 6. Таблицы для определения предельной относительной
погрешности по числу верных знаков и наоборот 28
§ 7. Погрешность суммы 31
§ 8. Погрешность разности 33
§ 9. Погрешность произведения 35
§ 10. Число верных знаков произведения 37
§ 11. Погрешность частного 38
§ 12. Число верных знаков частного 39
§ 13. Относительная погрешность степени 39
§ 14. Относительная погрешность корня 39
§ 15. Вычисления без точного учета погрешностей 40
§ 16. Общая формула для погрешности 41
§ 17. Обратная задача теории погрешностей 43
§ 18. Точность определения аргумента для функции, заданной
таблицей 46
§ 19. Способ границ 48
§ 20*. Понятие о вероятностной оценке погрешности 51
Литература к первой главе 52
Глава П. Некоторые сведения из теории цепных дробей 53
§ 1. Определение цепной дроби 53
§ 2. Обращение цепной дроби в обыкновенную и обратно 54
§ 3. Подходящие дроби 56
§ 4. Бесконечные цепные дроби 64
§ 5. Разложение функций в цепные дроби 70
Литература ко второй главе 73
Глава 111. Вычисление значений функций 74
§ 1. Вычисление значений полинома. Схема Горнера 74
§ 2. Обобщенная схема Горнера 77
§ 3. Вычисление значений рациональных дробей 79
1*

4 ОГЛАВЛЕНИЕ
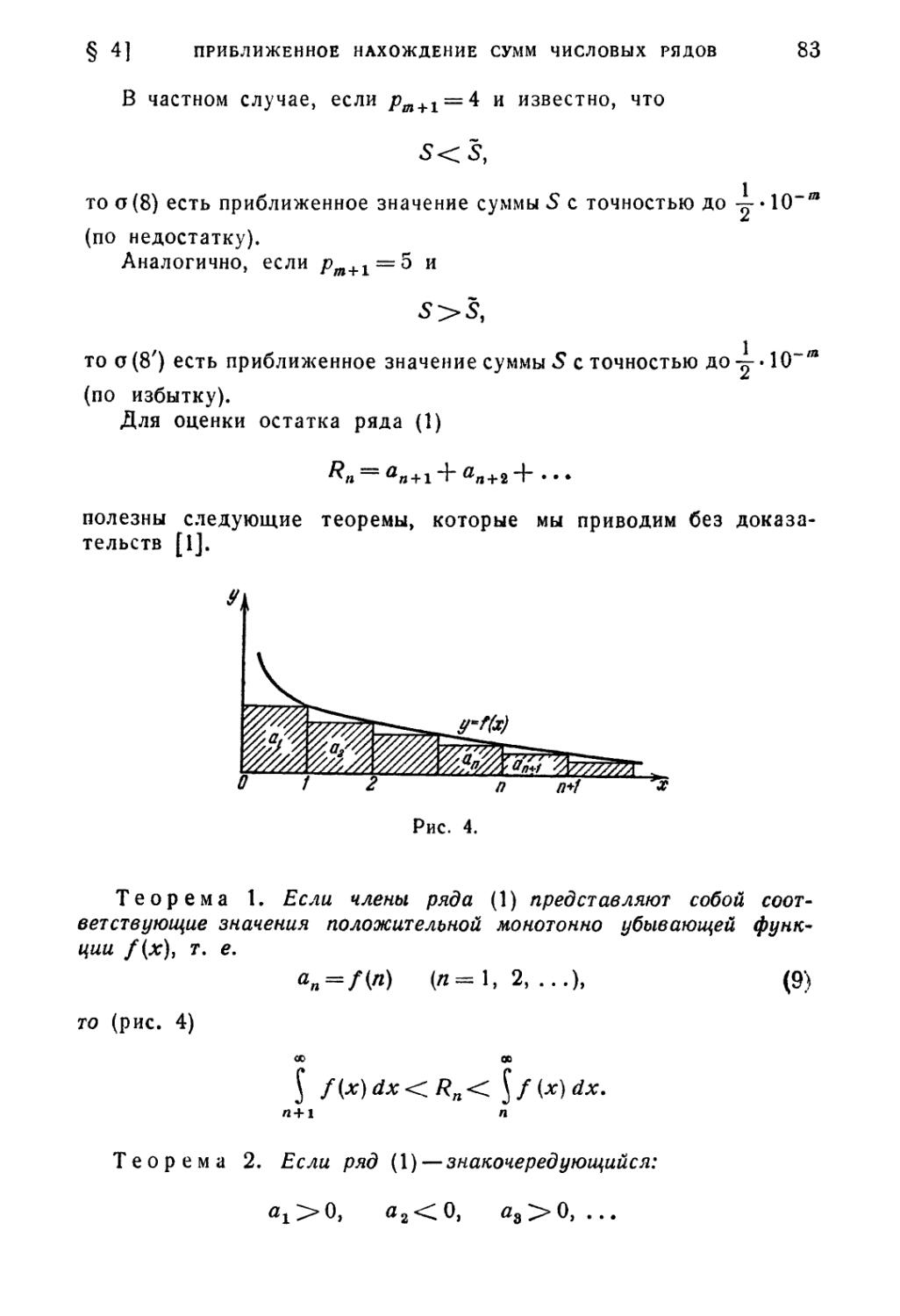
§ 4. Приближенное нахождение сумм числовых рядов 80
§ 5. Вычисление значений аналитической функции 86
§ 6. Вычисление значений показательной функции 88
§ 7. Вычисление значений логарифмической функции 92
§ 8. Вычисление значений тригонометрических функций 95
§ 9. Вычисление значений гиперболических функций 98
§ 10. Применение метода итерации для приближенного вычисления
значений функции • . . . 100
§11. Вычисление обратной величины 101
§ 12. Вычисление квадратного корня 104
§ 13. Вычисление обратной величины квадратного корня 108
§ 14. Вычисление кубического корня 108
Литература к третьей главе 111
Глава IV. Приближенное решение алгебраических и
трансцендентных уравнений 112
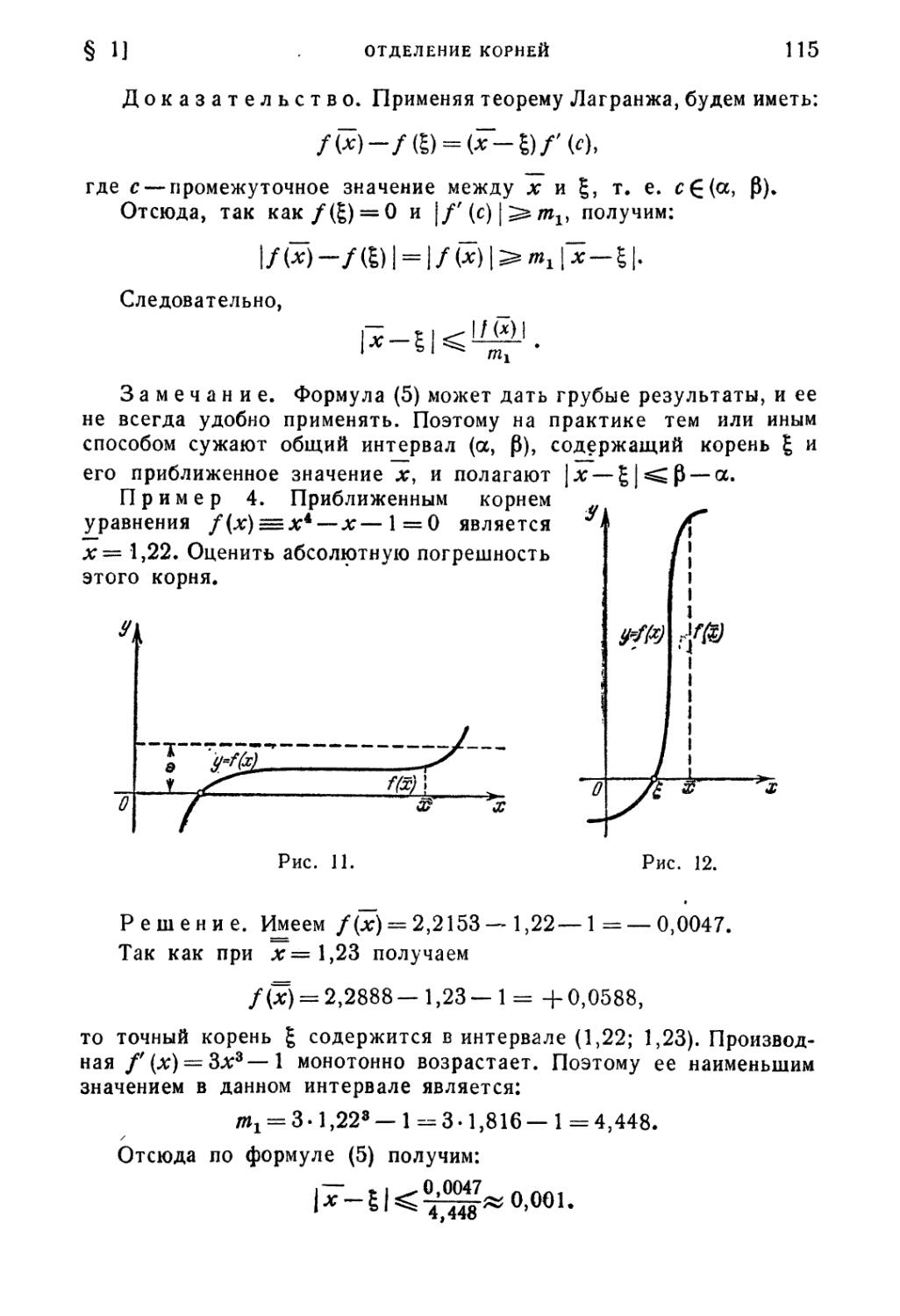
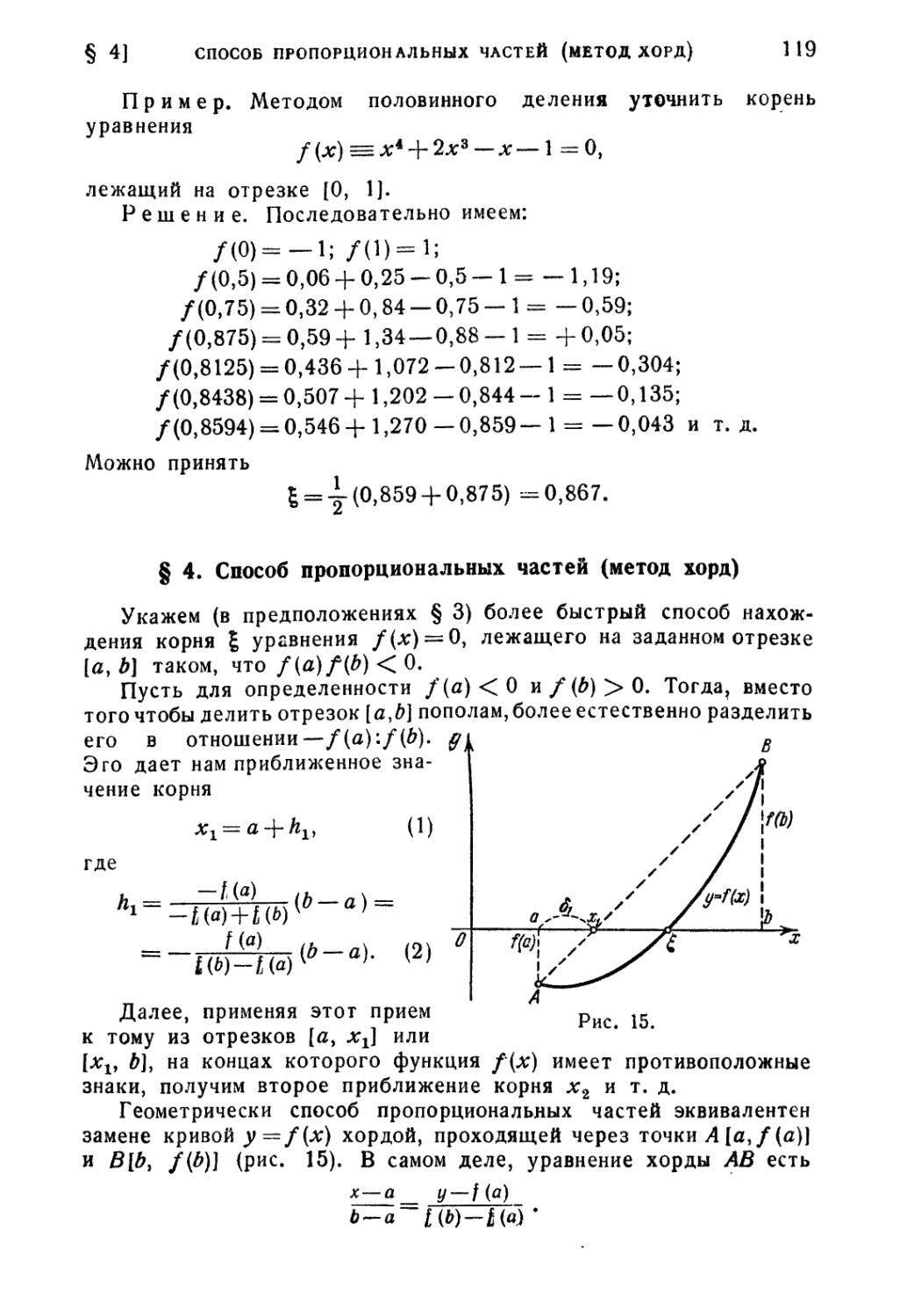
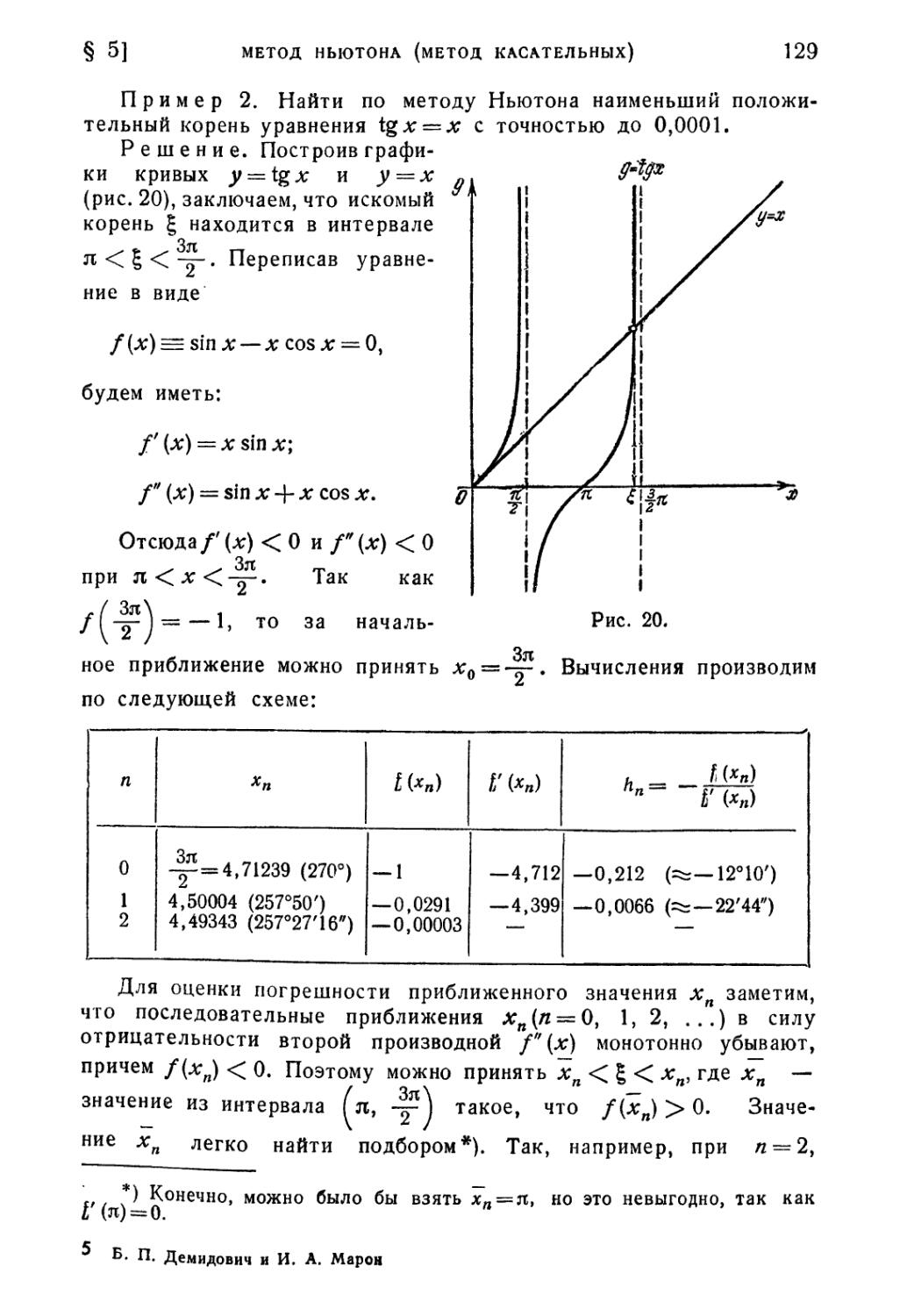
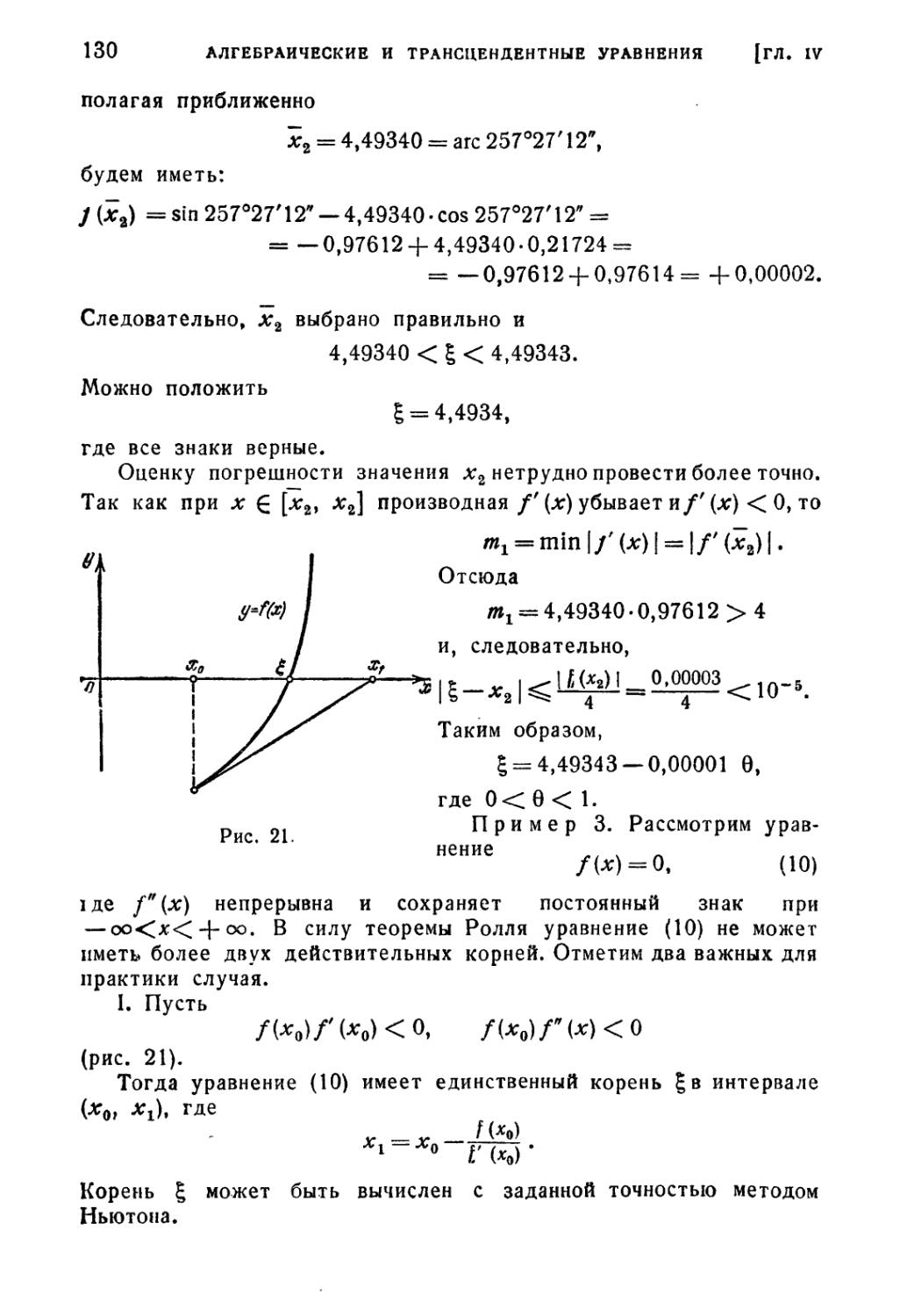
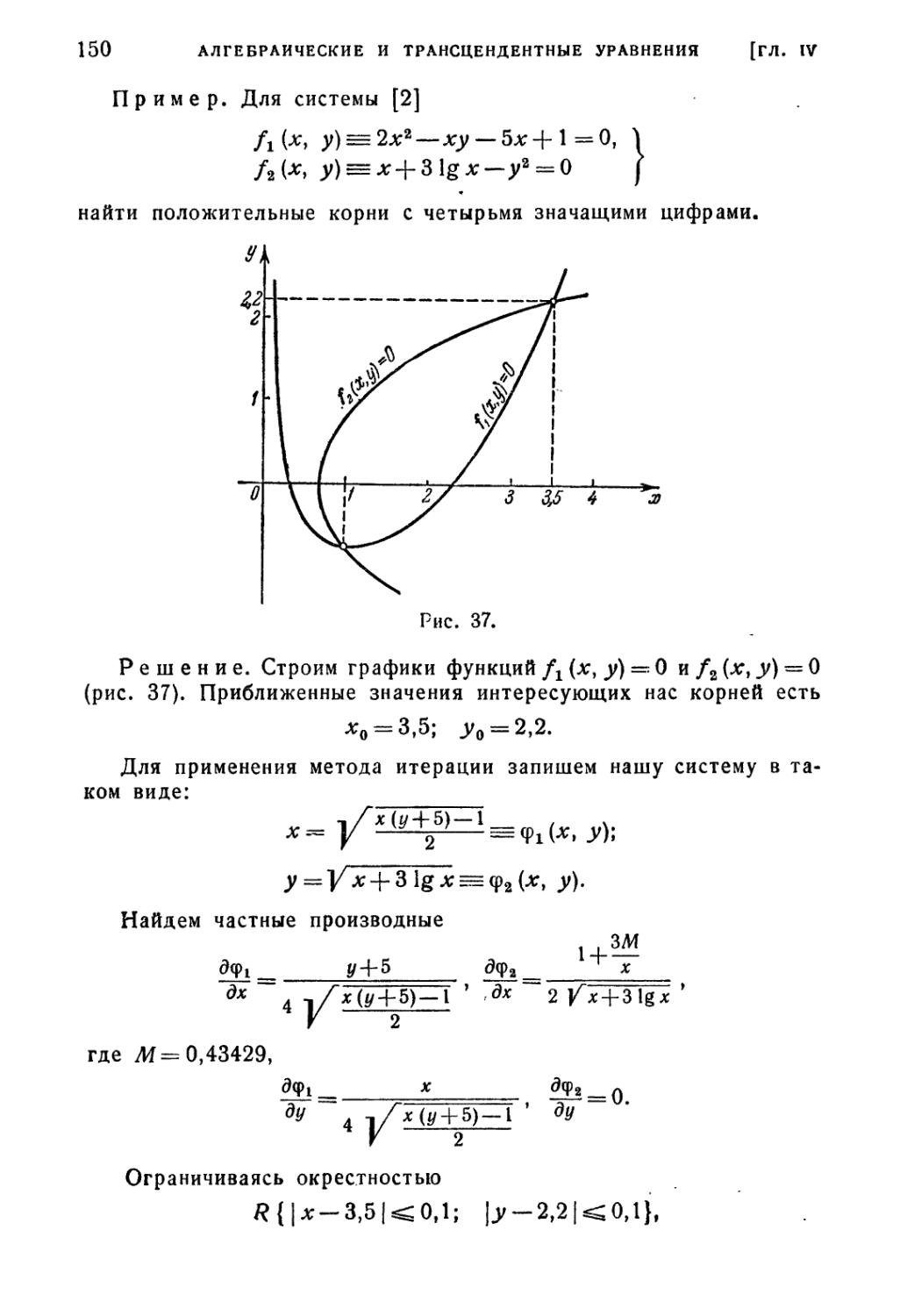
§ 1. Отделение корней 112
§ 2. Графическое решение уравнений 116
§ 3. Метод половинного деления 118
§ 4. Способ пропорциональных частей (метод хорд) 119
§ 5. Метод Ньютона (метод касательных) 123
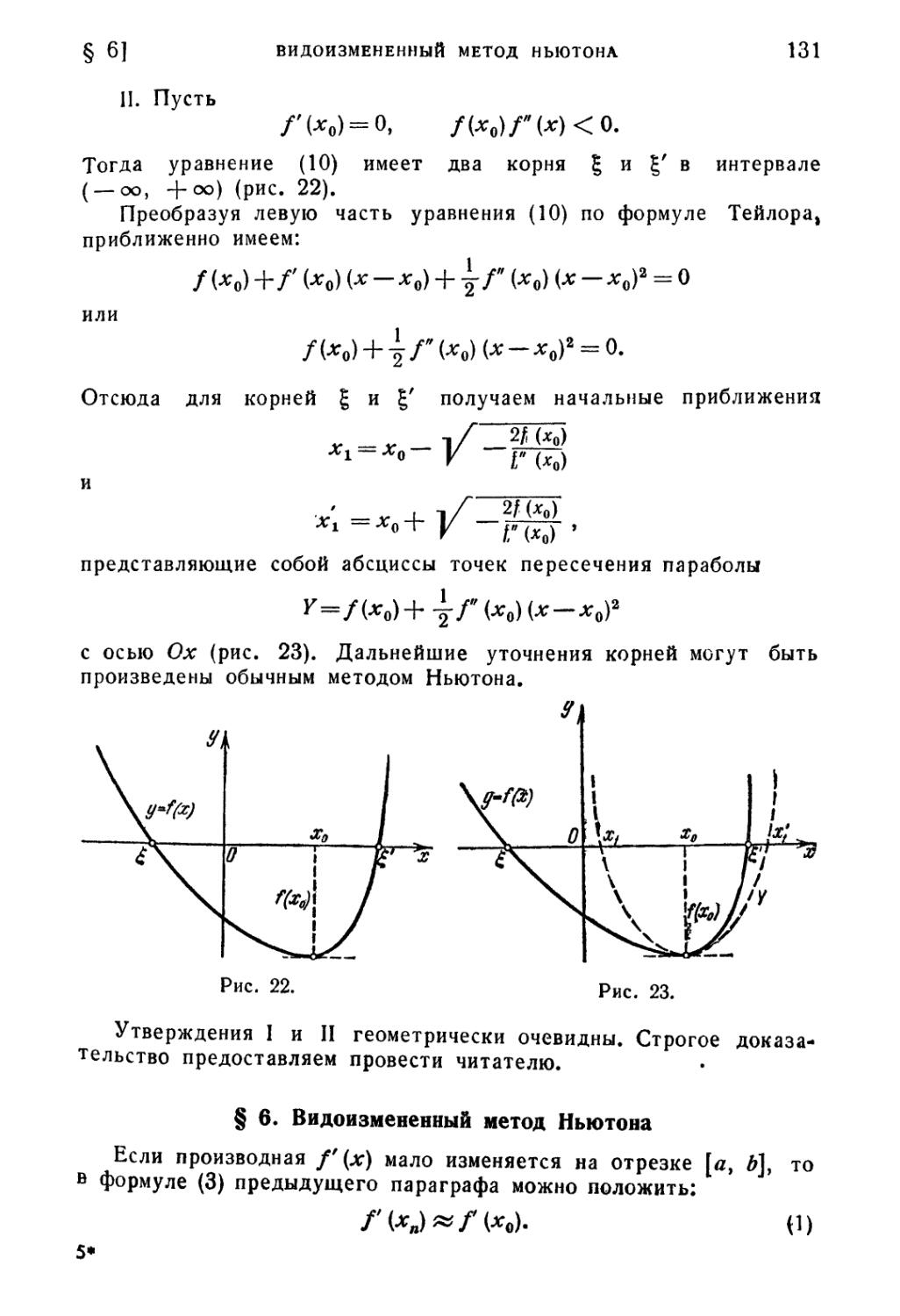
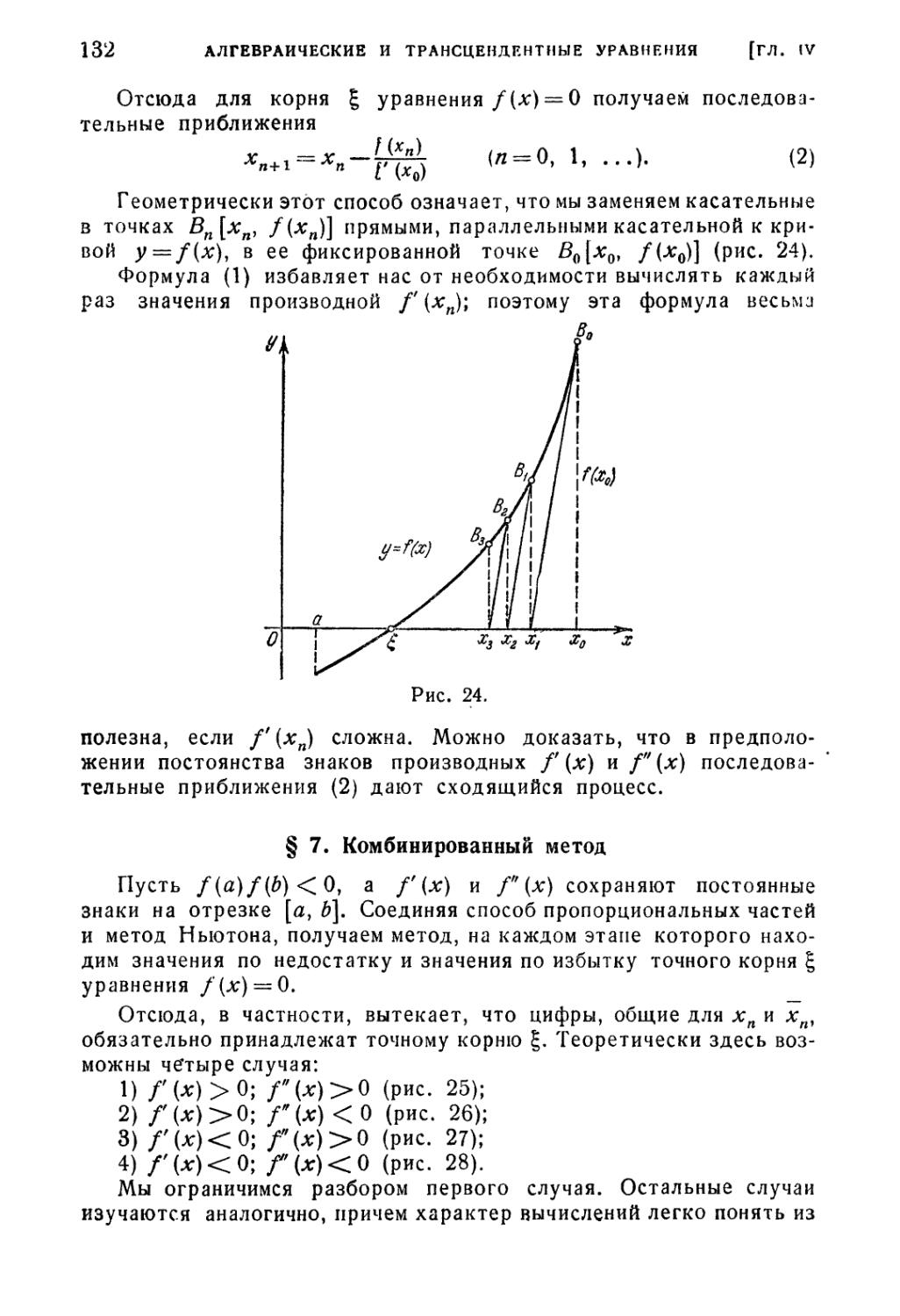
§ 6. Видоизмененный метод Ньютона 131
§ 7. Комбинированный метод 132
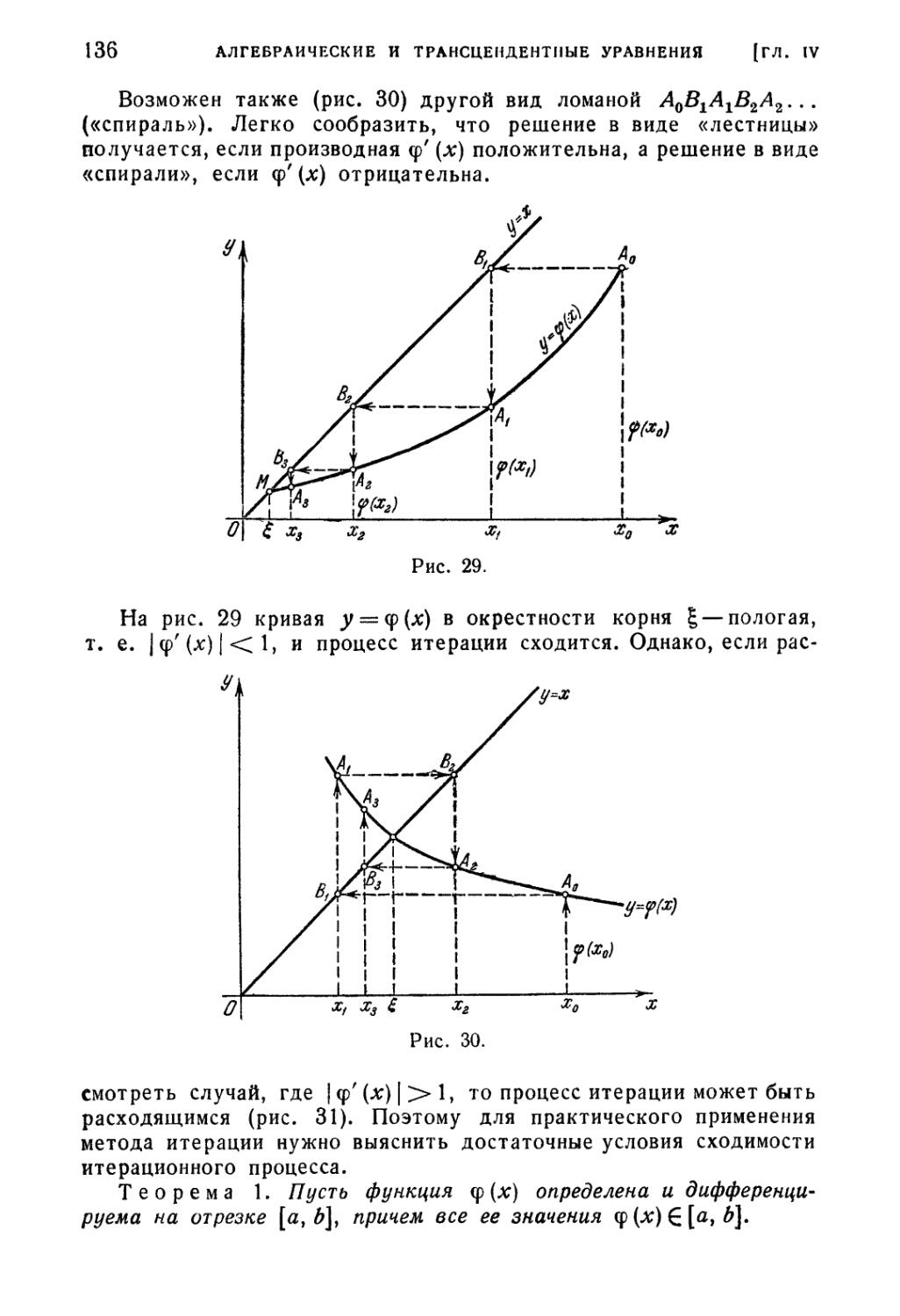
§ 8. Метод итерации 135
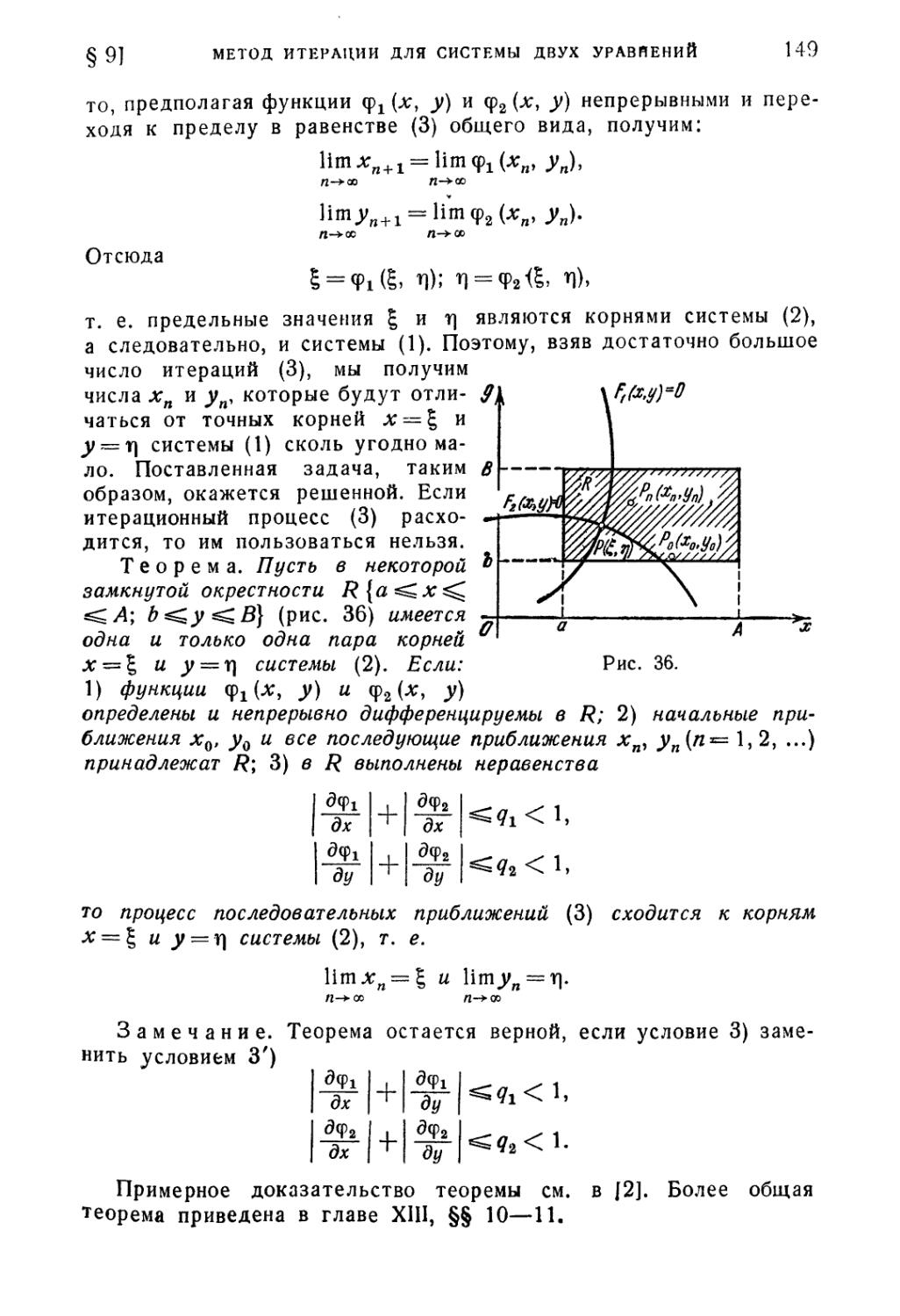
§ 9. Метод итерации для системы двух уравнений 148
§ 10. Метод Ньютона для системы двух уравнений 152
§ 11. Метод Ньютона для случая комплексных корней 153
Литература к четвертой главе 157
Глава V. Специальные приемы для приближенного решения
алгебраических уравнений 158
§ 1. Общие свойства алгебраических уравнений 158
§ 2. Границы действительных корней алгебраических уравнений . 163
§ 3. Метод знакопеременных сумм 165
§ 4. Метод Ньютона 167
§ 5. Число действительных корней полинома 169
§ 6. Теорема Бюдана — Фурье 171
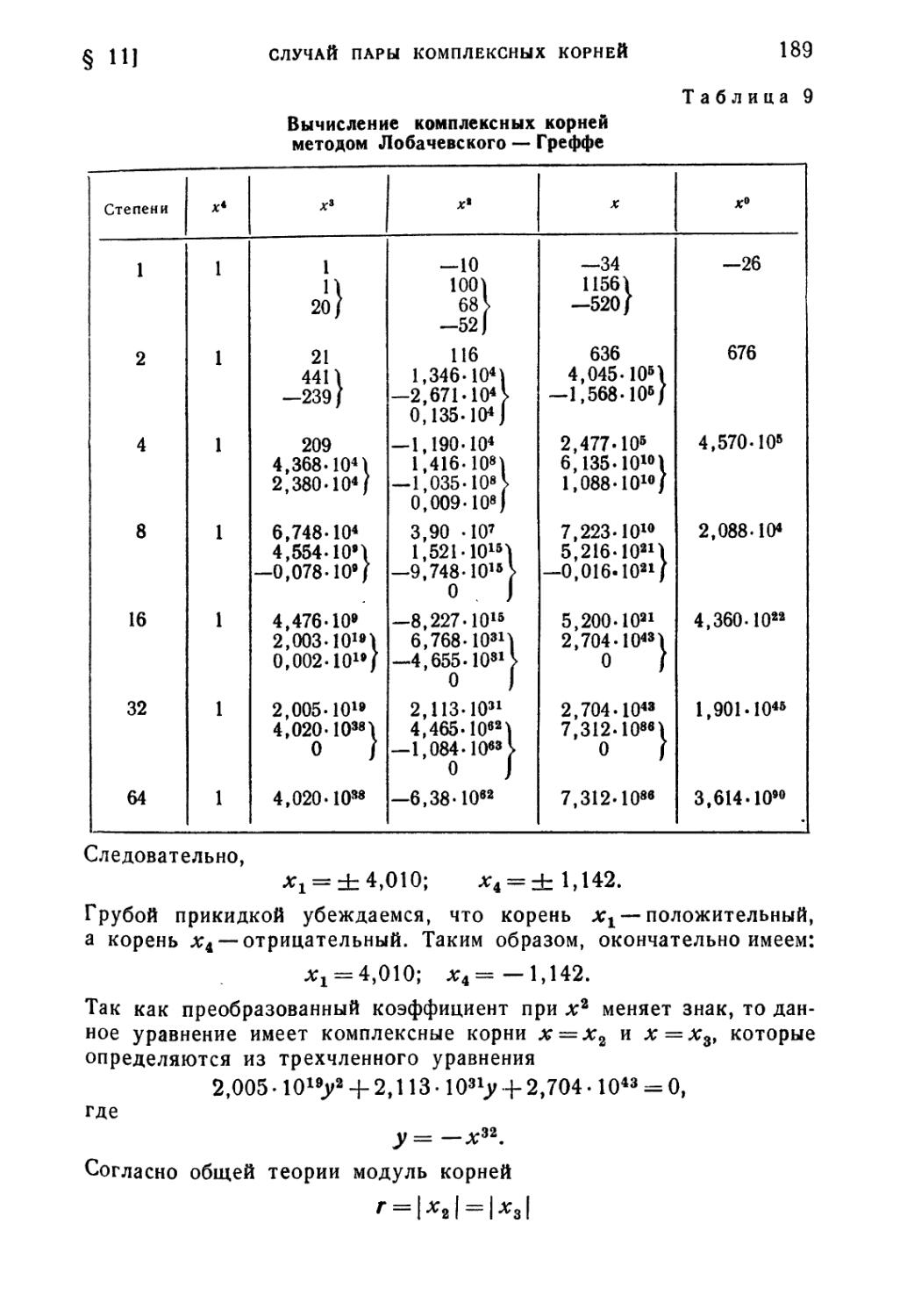
§ 7. Идея метода Лобачевского—Греффе 176
§ 8. Процесс квадрирования корней 178
§ 9. Метод Лобачевского — Греффе для случая действительных
различных корней 180
§ 10. Метод Лобачевского — Греффе для случая комплексных корней 183
§ 11. Случай пары комплексных корней 186
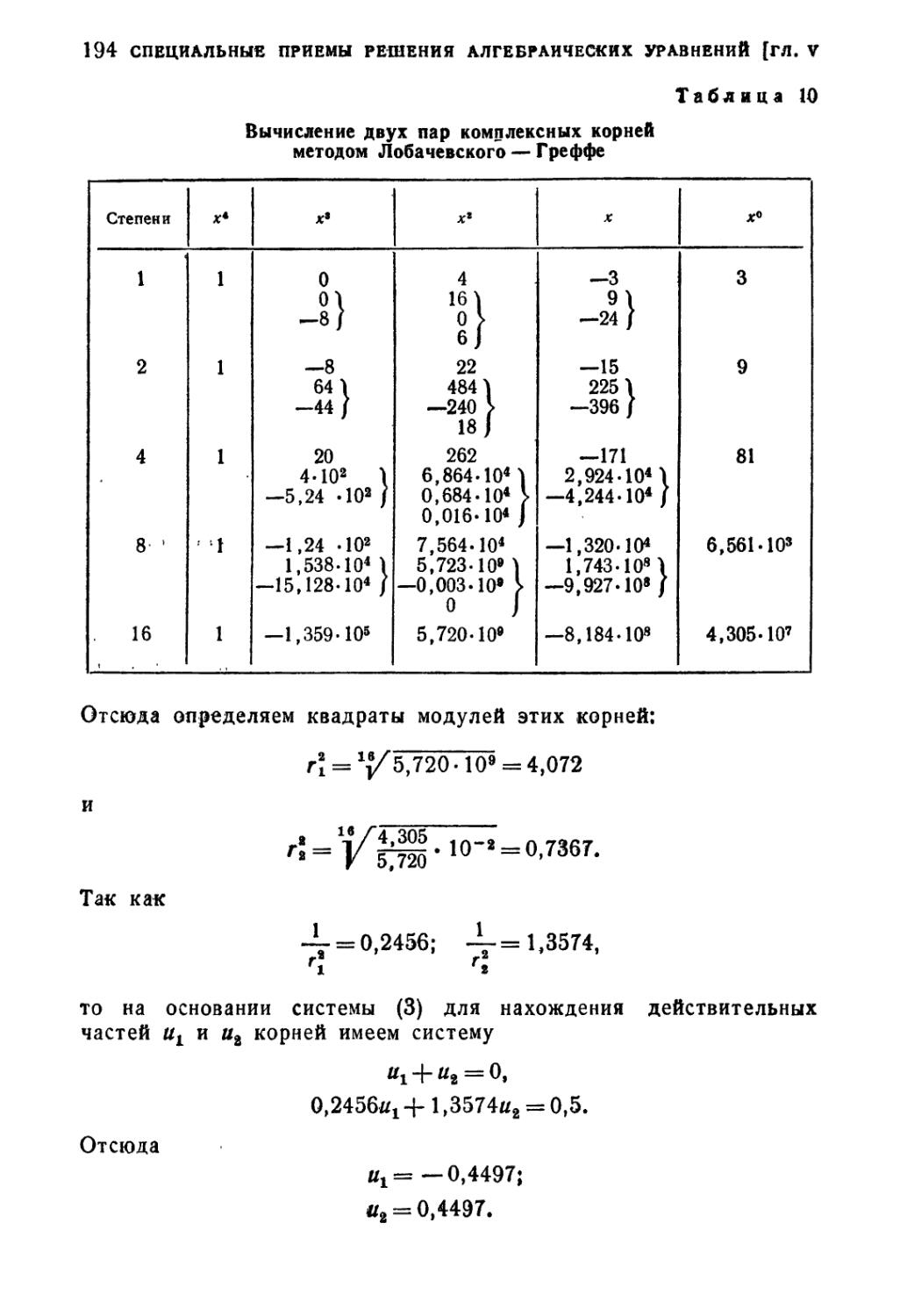
§ 12. Случай двух пар комплексных корней 190
§ 13. Метод Бернулли 195
Литература к пятой главе 198
Глава VI. Улучшение сходимости рядов 199
§ 1. Улучшение сходимости числовых рядов 199
§ 2. Улучшение сходимости степенных рядов методом Эйлера —
Абеля .. 205
§ 3. Оценки коэффициентов Фурье 210
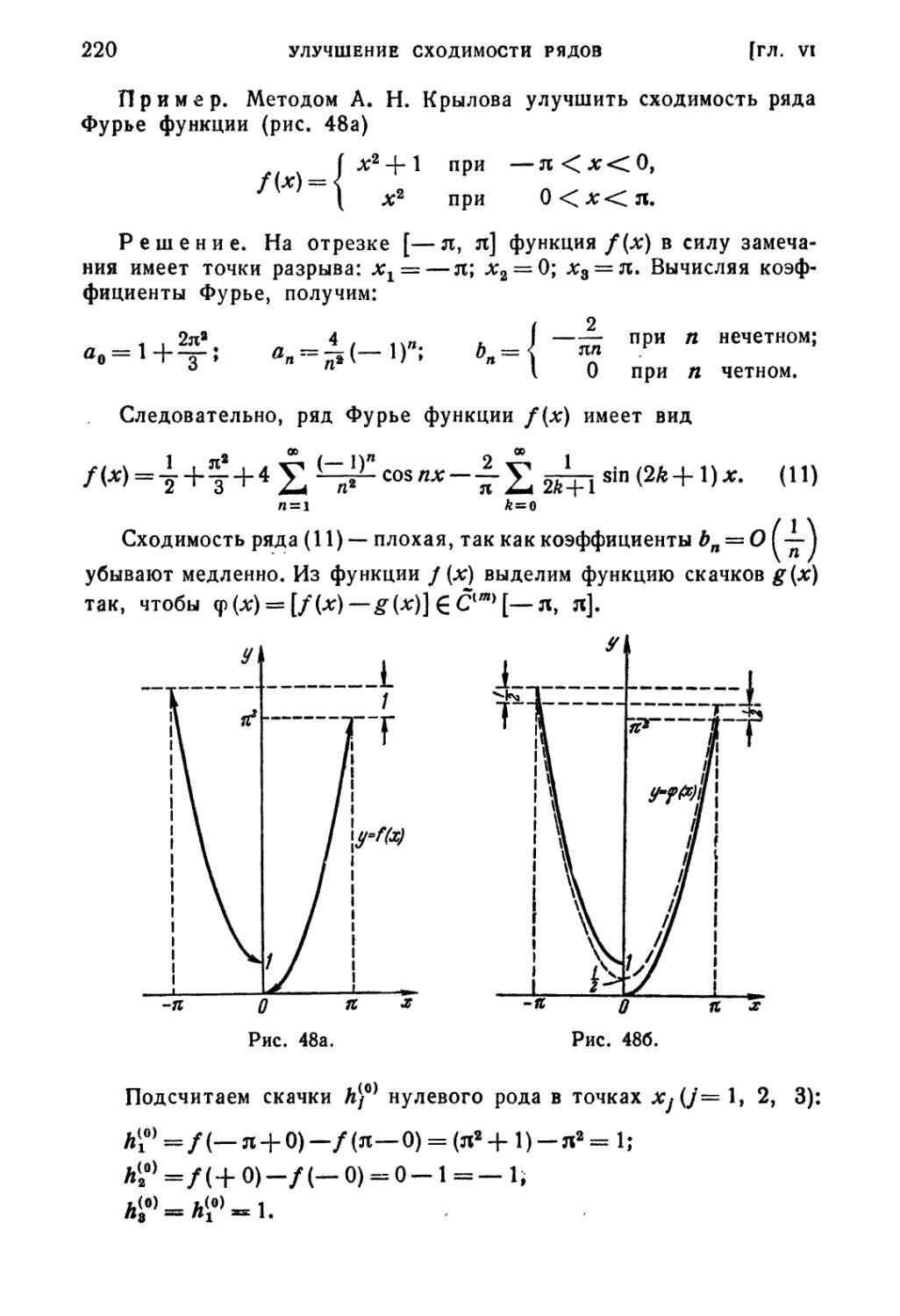
§ 4. Улучшение сходимости тригонометрических рядов Фурье
методом А. Н. Крылова 213
§ 5. Приближенное суммирование тригонометрических рядов . . . 222
Литература к шестой главе 224

ОГЛАВЛЕНИЕ 5
Глава VII. Алгебра матриц * . . 225
§ 1. Основные определения 225
§ 2. Действия с матрицами 226
§ 3. Транспонированная матрица 230
§ 4. Обратная матрица 231
§ 5. Степени матрицы „ 236
§ 6. Рациональные функции матрицы 237
§ 7. Абсолютная величина и норма матрицы 238
§ 8. Ранг матрицы 244
§ 9. Предел матрицы 245
§ 10. Матричные ряды ¦ 247
§11. Клеточные матрицы 252
§ 12. Обращение матриц при помощи разбиения на клетки . . . . 255
§ 13. Треугольные матрицы 260
§ 14. Элементарные преобразования матриц 263
§ 15. Вычисление определителей 264
Литература к седьмой главе 267
Глава VIII. Решение систем линейных уравнений 268
§ 1. Общая характеристика методов решения систем линейных
уравнений 268
§ 2. Решение систем с помощью обратной матрицы. Формулы
Крамера . . . . 268
§ 3. Метод Гаусса 272
§ 4. Уточнение корней 279
§ 5. Метод главных элементов 281
§ 6. Применение метода Гаусса для вычисления определителей . . 283
§ 7. Вычисление обратной матрицы методом Гаусса 285
§ 8. Метод квадратных корней 287
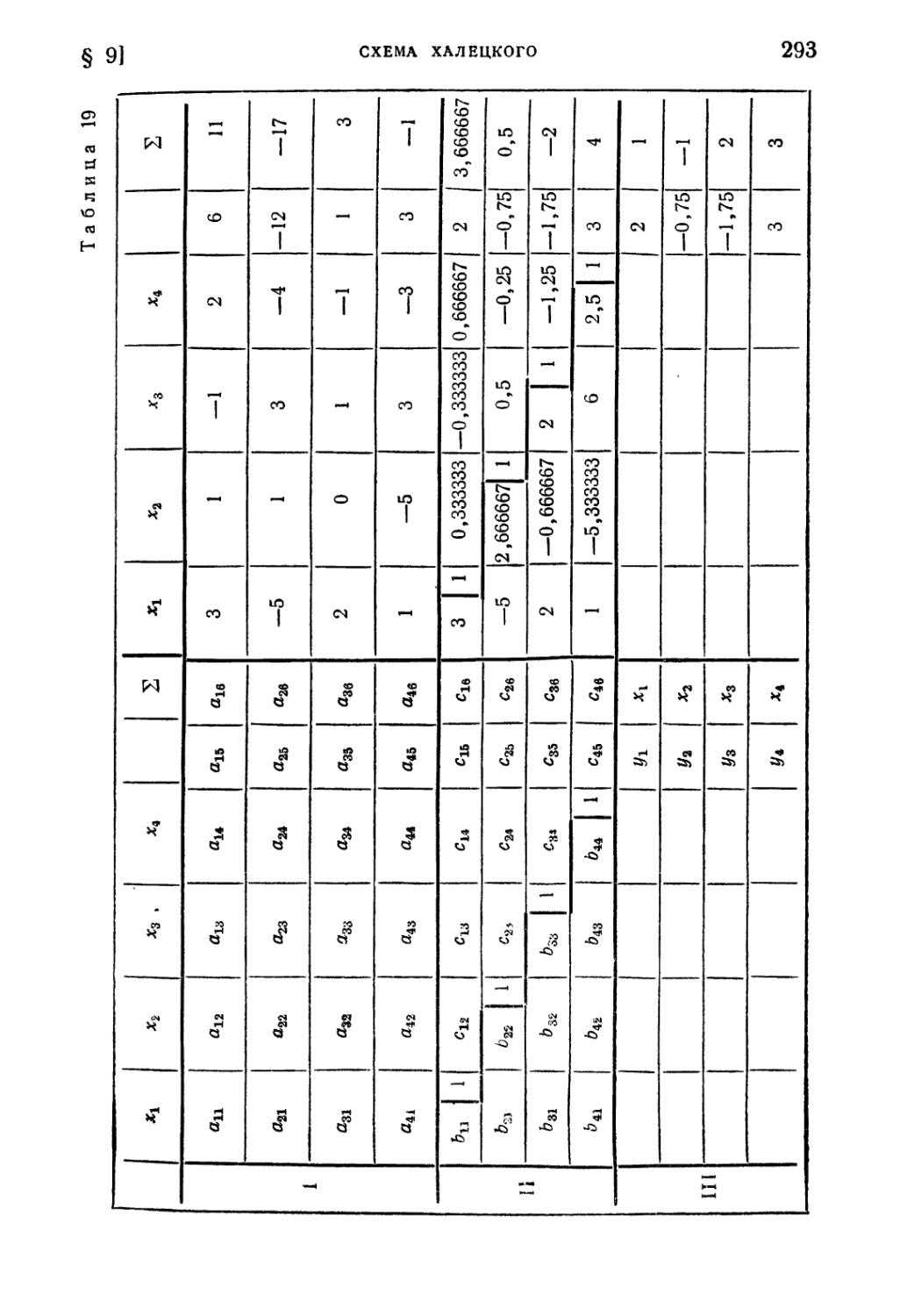
§ 9. Схема Халецкого 290
§ 10. Метод итерации 294
§11. Приведение линейной системы к виду, удобному для итерации 301
§ 12. Метод Зейделя 303
§ 13. Случай нормальной системы 305
§ 14. Метод релаксации 307
§ 15. Исправление элементов приближенной обратной матрицы ... 310
Литература к восьмой главе 314
Глава IX*. Сходимость итерационных процессов для систем
линейных уравнений 315
§ 1. Достаточные условия сходимости процесса итерации 315
§ 2. Оценка погрешности приближений процесса итерации .... 317
§ 3. Первое достаточное условие сходимости процесса Зейделя . . 320
§ 4. Оценка погрешности приближений процесса Зейделя по
m-норме 322
§ 5. Второе достаточное условие сходимости процесса Зейделя . . 323
§ 6. Оценка погрешности приближений процесса Зейделя по
/-норме 325
§ 7. Третье достаточное условие сходимости процесса Зейделя . . 326
Литература к девятой главе 328
Глава X. Основные сведения из теории линейных векторных
пространств 329
§ 1. Понятие линейного векторного пространства 329
§ 2. Линейная зависимость векторов 330

О ОГЛАВЛЕНИЕ
§ 3. Скалярное произведение векторов 335
§ 4. Ортогональные системы векторов 338
§ 5. Преобразования координат вектора при изменениях базиса . . 340
§ 6. Ортогональные матрицы 342
§ 7. Ортогонализация матриц 343
§ 8. Применение методов ортогонализации к решению систем
линейных уравнений 351
§ 9. Пространство решений однородной системы 356
§ 10. Линейные преобразования переменных 359
§ 11. Обратное преобразование 365
§ 12. Собственные векторы и собственные значения матрицы .... 367
§ 13. Подобные матрицы 372
§ 14. Билинейная форма матрицы 375
§ 15. Свойства симметрических матриц 376
§ 16*. Свойства матриц с действительными элементами 381
Литература к десятой главе 385
Глава XI*. Дополнительные сведения о сходимости итерационных
процессов для систем линейных уравнений 386
§ 1. Сходимость матричных степенных рядов 386
§ 2. Тождество Гамильтона — Кели 389
§ 3. Необходимые и достаточные условия сходимости процесса
итерации для системы линейных уравнений 390
§ 4. Необходимые и достаточные условия сходимости процесса Зей-
деля для системы линейных уравнений 392
§ 5. Сходимость процесса Зейделя для нормальной системы . . , 395
§ 6. Способы эффективной проверки условий сходимости ..... 397
Литература к одиннадцатой главе 401
Глава XII. Нахождение собственных значений и собственных
векторов матрицы 402
§ 1. Вводные замечания , • • . 402
§ 2. Развертывание вековых определителей 402
§ 3. Метод А. М. Данилевского 404
§ 4. Исключительные случаи в методе А. М. Данилевского . . . 410
§ 5. Вычисление собственных векторов по методу А. М.
Данилевского 411
§ 6. Метод А. Н. Крылова 412
§ 7. Вычисление собственных векторов по методу А. Н. Крылова 416
§ 8. Метод Леверрье 417
§ 9. Понятие о методе неопределенных коэффицентов 419
§ 10. Сравнение различных методов развертывания векового
определителя ; 421
§11. Нахождение наибольшего по модулю собственного значения
матрицы и соответствующего собственного вектора 421
§ 12. Метод скалярных произведений для нахождения первого
собственного значения действительной матрицы 428
§ 13. Нахождение второго собственного значения матрицы и
второго собственного вектора 431
§ 14. Метод исчерпывания 434
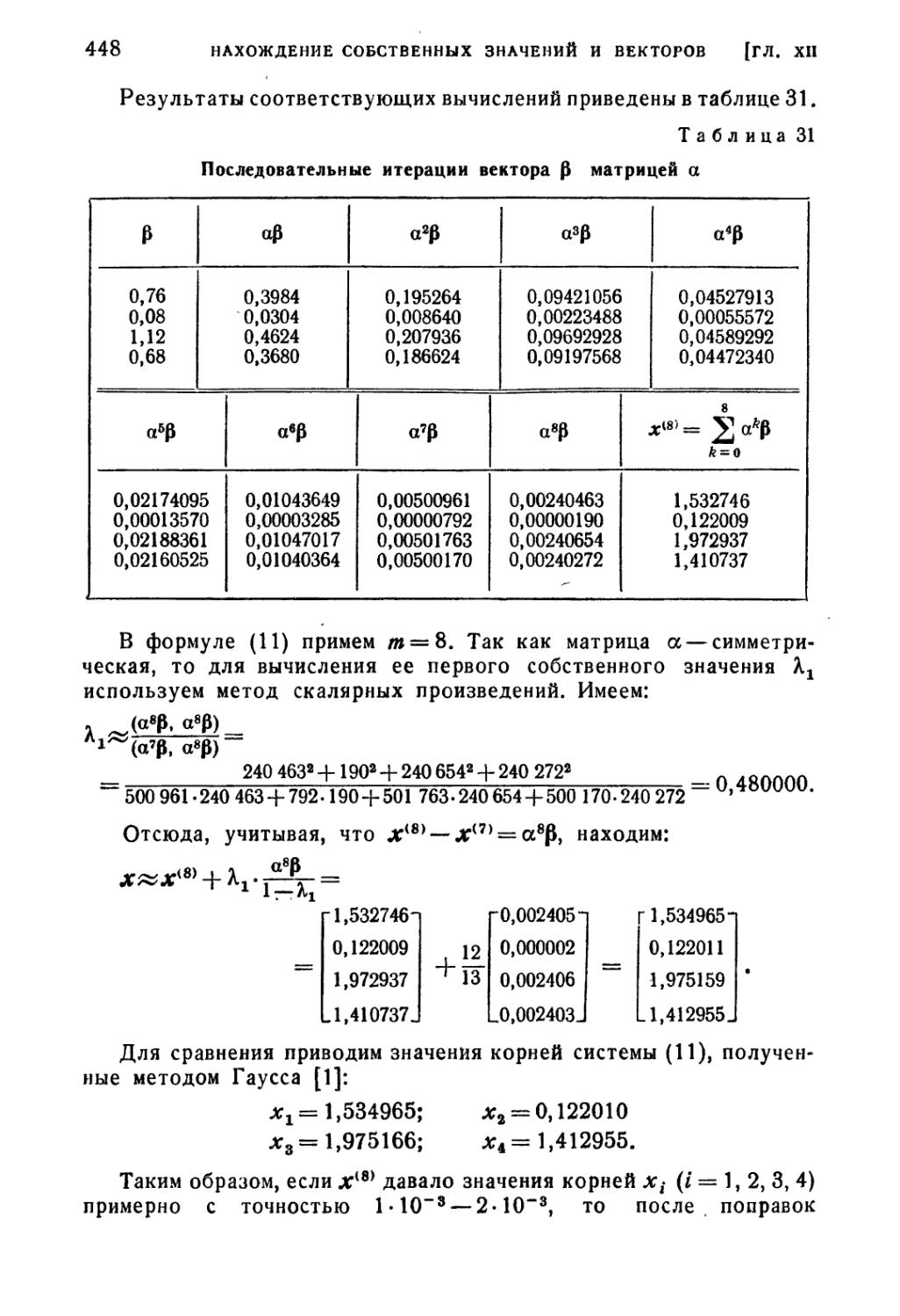
§ 15. Нахождение собственных элементов положительно
определенной симметрической матрицы 437
§ 16. Использование коэффициентов характеристического полинома
матрицы для ее обращения 442
§ 17. Метод Л. А. Люстерника улучшения сходимости процесса
итерации для решения системы линейных уравнений 444
Литература к двенадцатой главе , 449

ОГЛАВЛЕНИЕ 7
Глава XIII. Приближенное решение систем нелинейных
уравнений 450
§ 1. Метод Ньютона 450
$ 2. Общие замечания о сходимости процесса Ньютона 456
§ 3*. Существование корней системы и сходимость процесса
Ньютона 460
§ 4*. Быстрота сходимости процесса Ньютона 465
§ 5*. Единственность решения 466
§ 6*. Устойчивость сходимости процесса Ньютона при
варьировании начального приближения 469
§ 7. Модифицированный метод Ньютона ...••.. 471
§ 8. Метод итерации 474
9*. Понятие о сжимающем отображении 477
§ 10*. Первое достаточное условие сходимости процесса
итерации 481
§ 31*. Второе достаточное условие сходимости процесса итерации 483
§ 12. Метод скорейшего спуска (метод градиента) 485
§ 13. Метод скорейшего спуска для случая системы линейных
уравнений 490
§ 14*. Метод степенных рядов 494
Литература к тринадцатой главе 496
Глава XIV. Интерполирование функций 497
§ 1. Конечные разности различных порядков 497
§ 2. Таблица разностей 500
§ 3. Обобщенная степень 505
§ 4. Постановка задачи интерполирования 507
§ 5. Первая интерполяционная формула Ньютона 508
§ 6. Вторая интерполяционная формула Ньютона 514
§ 7. Таблица центральных разностей 518
§ 8. Интерполяционные формулы Гаусса 539
§ 9. Интерполяционная формула Стирлинга 521
§ 10. Интерполяционная формула Бесселя 521
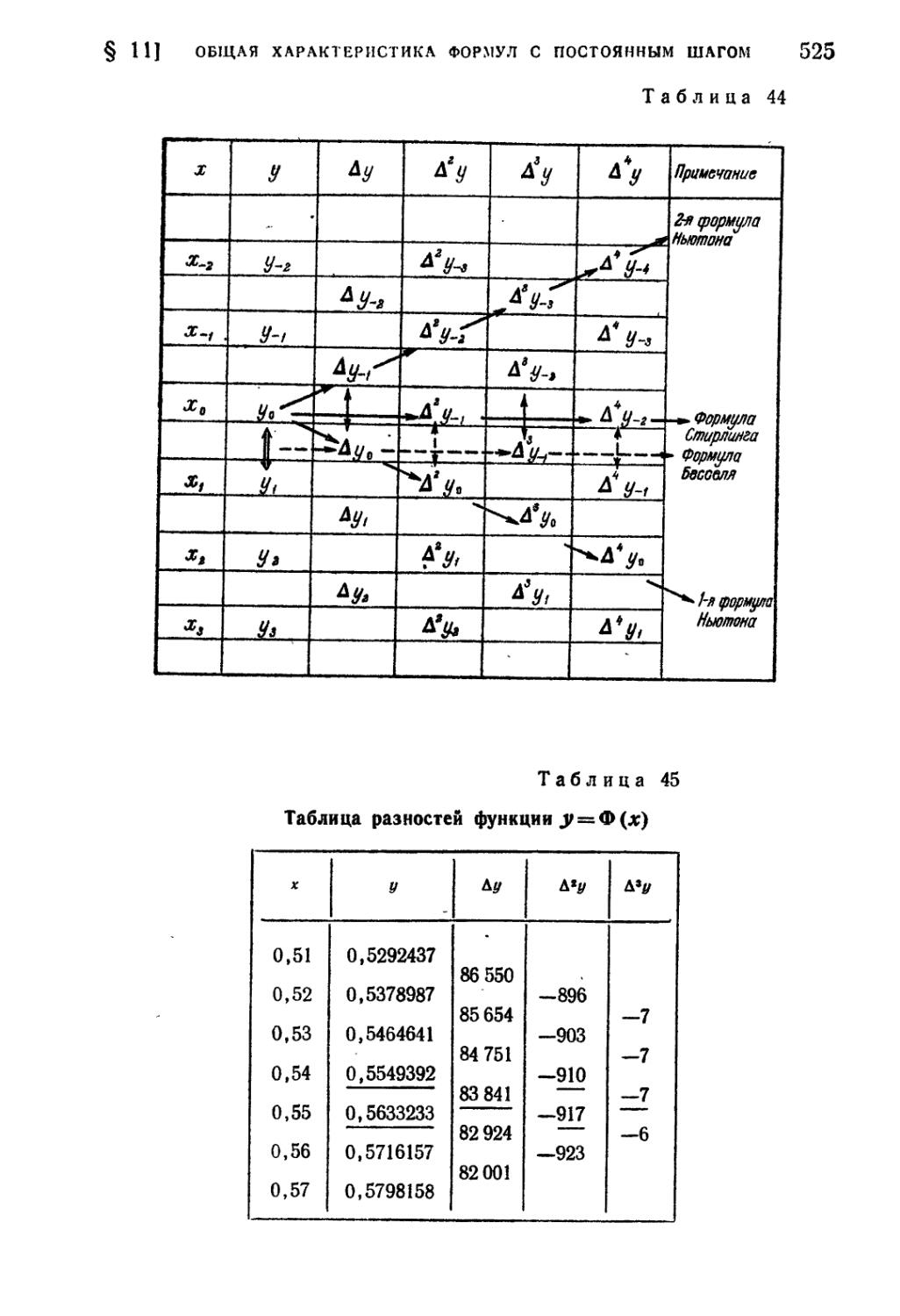
§ 11. Общая характеристика интерполяционных формул с
постоянным шагом 524
§ 12. Интерполяционная формула Лагранжа 527
§ 13*. Вычисление лагранжевых коэффициентов 531
§ 14. Оценка погрешности интерполяционной формулы Лагранжа 535
§ 15. Оценки погрешностей интерполяционных формул Ньютона 537
$ 16. Оценки погрешностей центральных интерполяционных формул 539
§ 17. О наилучшем выборе узлов интерполирования 540
§ 18. Разделенные разности 542
§ 19. Интерполяционная формула Ньютона для неравноотстоящих
значений аргумента 544
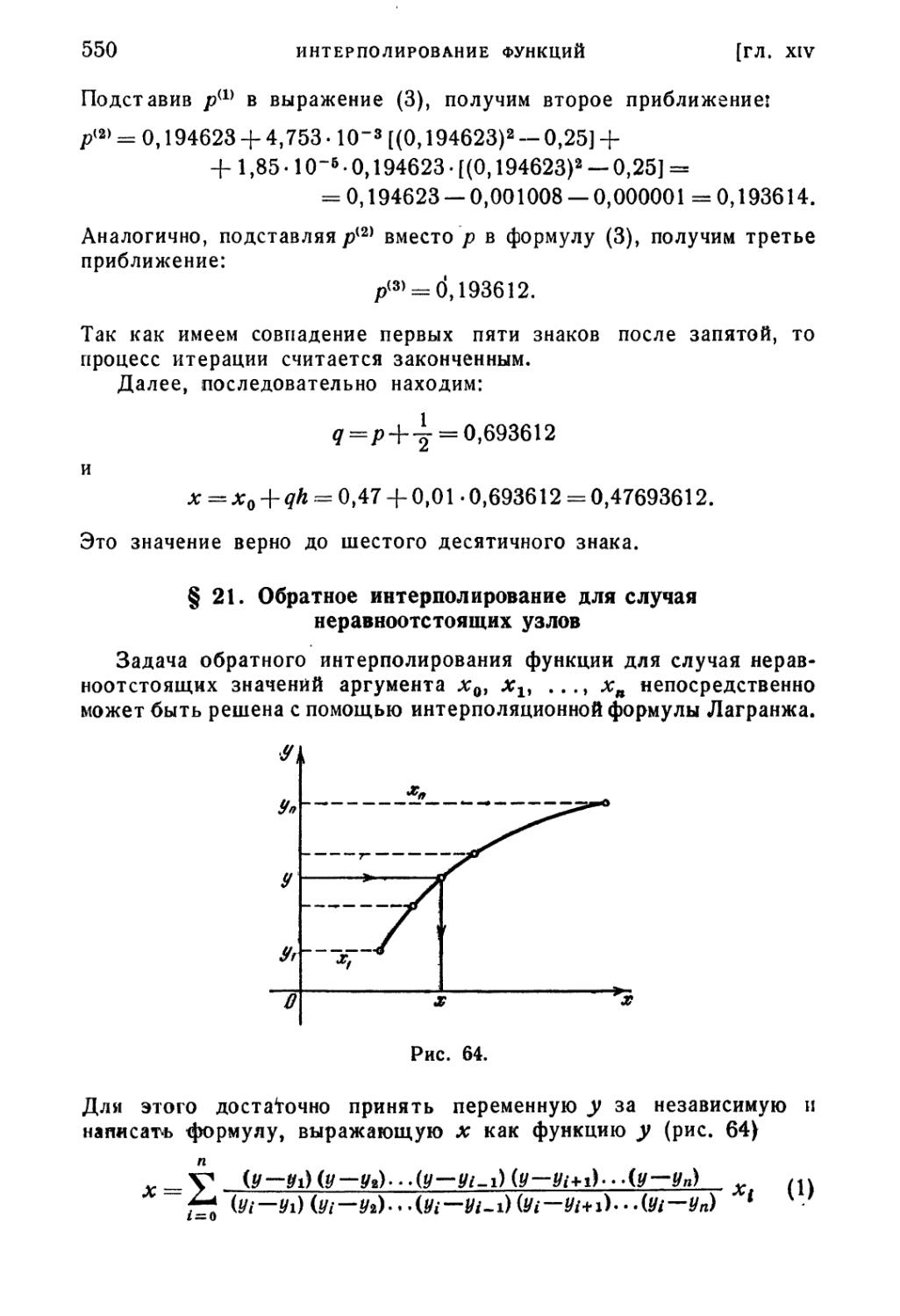
§ 20. Обратное интерполирование для случая равноотстоящих узлов 547
§ 21. Обратное интерполирование для случая неравноотстоящих
узлов , . . 550
§ 22. Нахождение корней уравнения методом обратного
интерполирования 551
§ 23. Метод интерполяции для развертывания векового
определителя . . 553
§ 24*. Интерполирование функций двух переменных 555
§ 25*. Двойные разности высших порядков 557
§ 26*. Интерполяционная формула Ньютона для функции двух
переменных 558
Литература к четырнадцатой главе 661

О ОГЛАВЛЕНИЕ
Глава XV. Приближенное дифференцирование 562
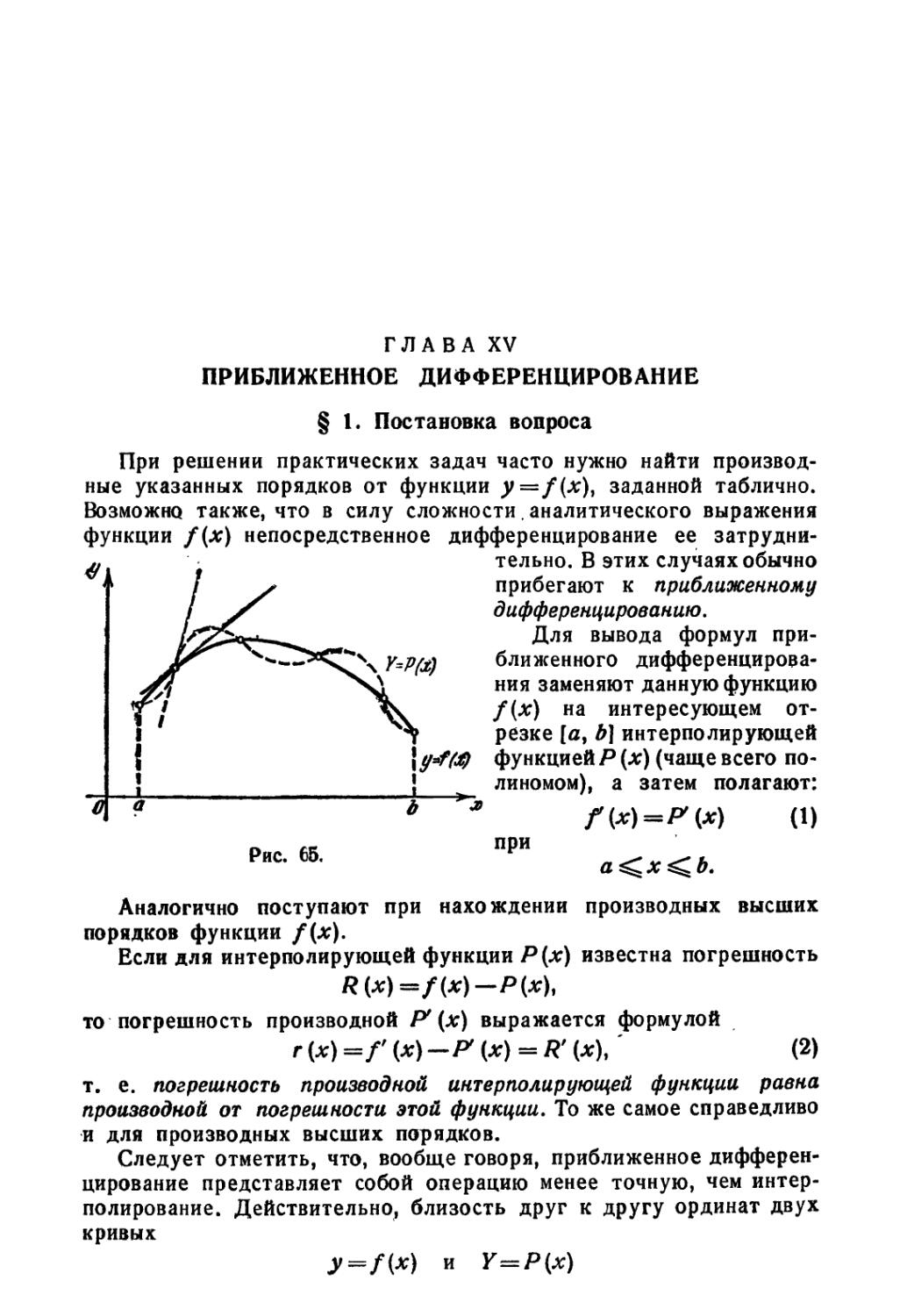
§ 1. Постановка вопроса .... 562
§ 2. Формулы приближенного дифференцирования, основанные на
первой интерполяционной формуле Ньютона 563
§ 3. Формулы приближенного дифференцирования, основанные на
формуле Стирлинга 567
§ 4. Формулы численного дифференцирования для равноотстоящих
точек, выраженные через значения функции в этих точках . . 571
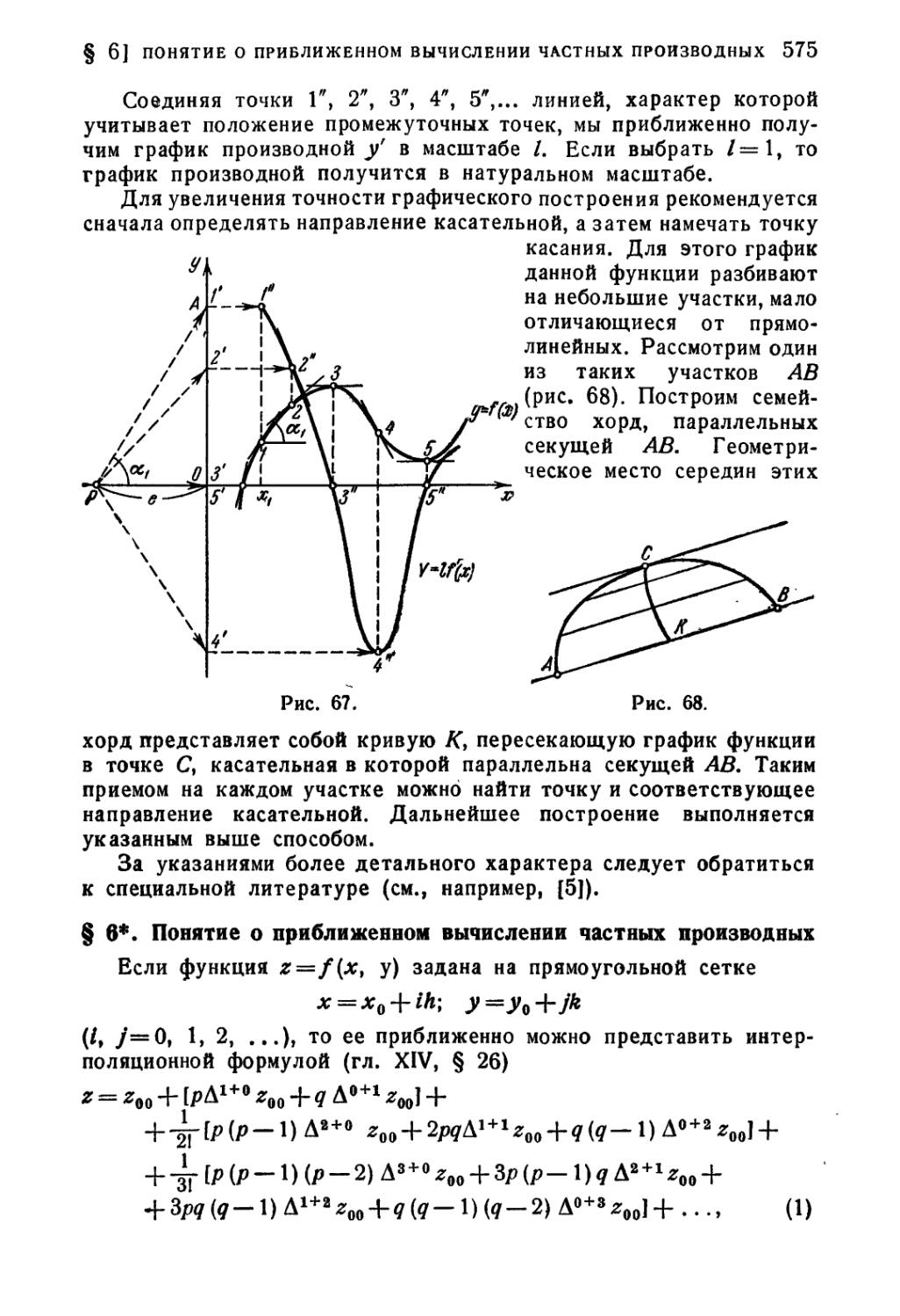
§ 5. Графическое дифференцирование 574
§ 6*. Понятие о приближенном вычислении частных производных 575
Литература к пятнадцатой главе • 576
Глава XVI. Приближенное интегрирование функций 577
§ 1. Общие замечания 577
§ 2. Квадратурные формулы Ньютона — Котеса 580
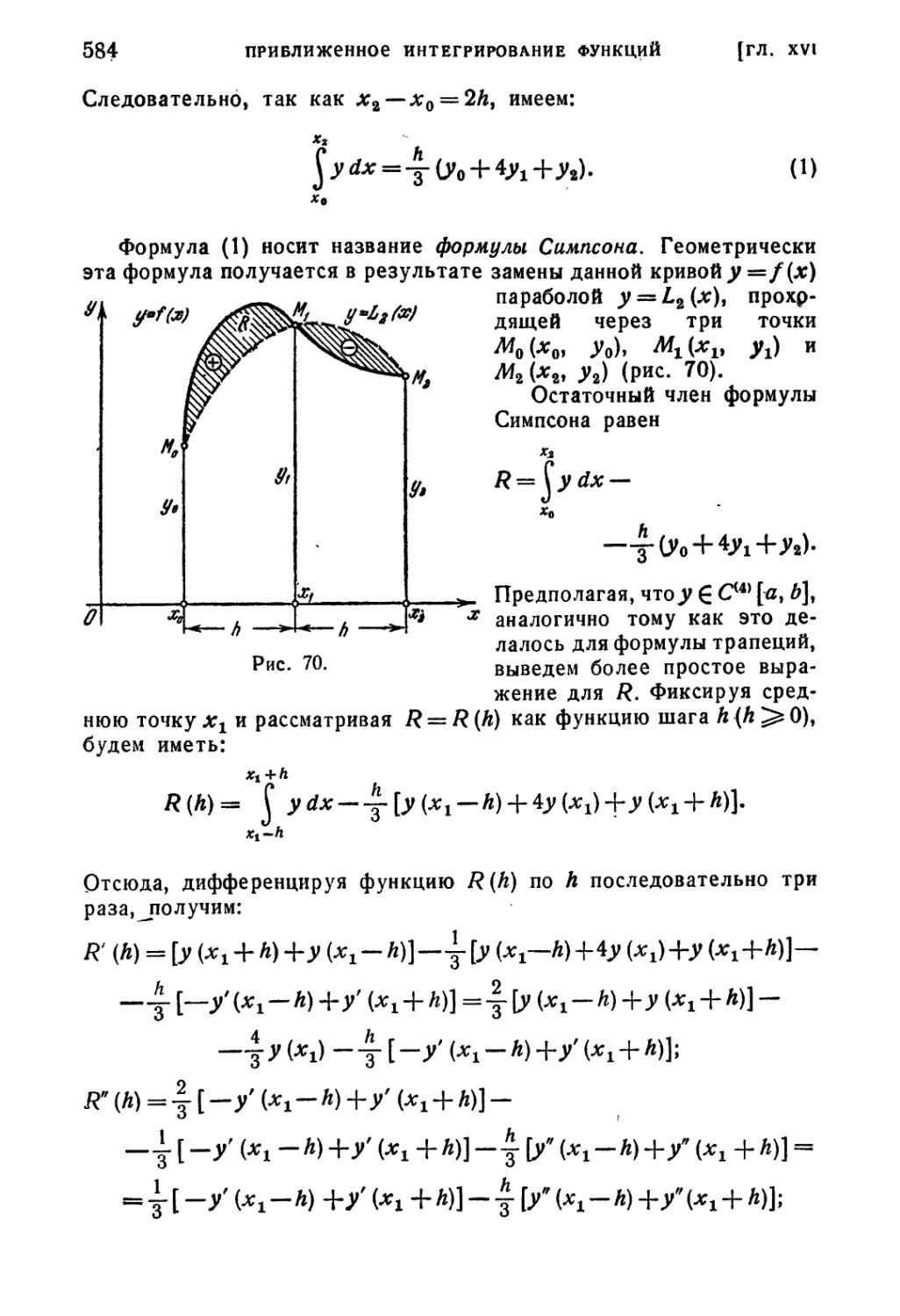
§ 3. Формула трапеций и ее остаточный член 582
§ 4. Формула Симпсона и ее остаточный член 583
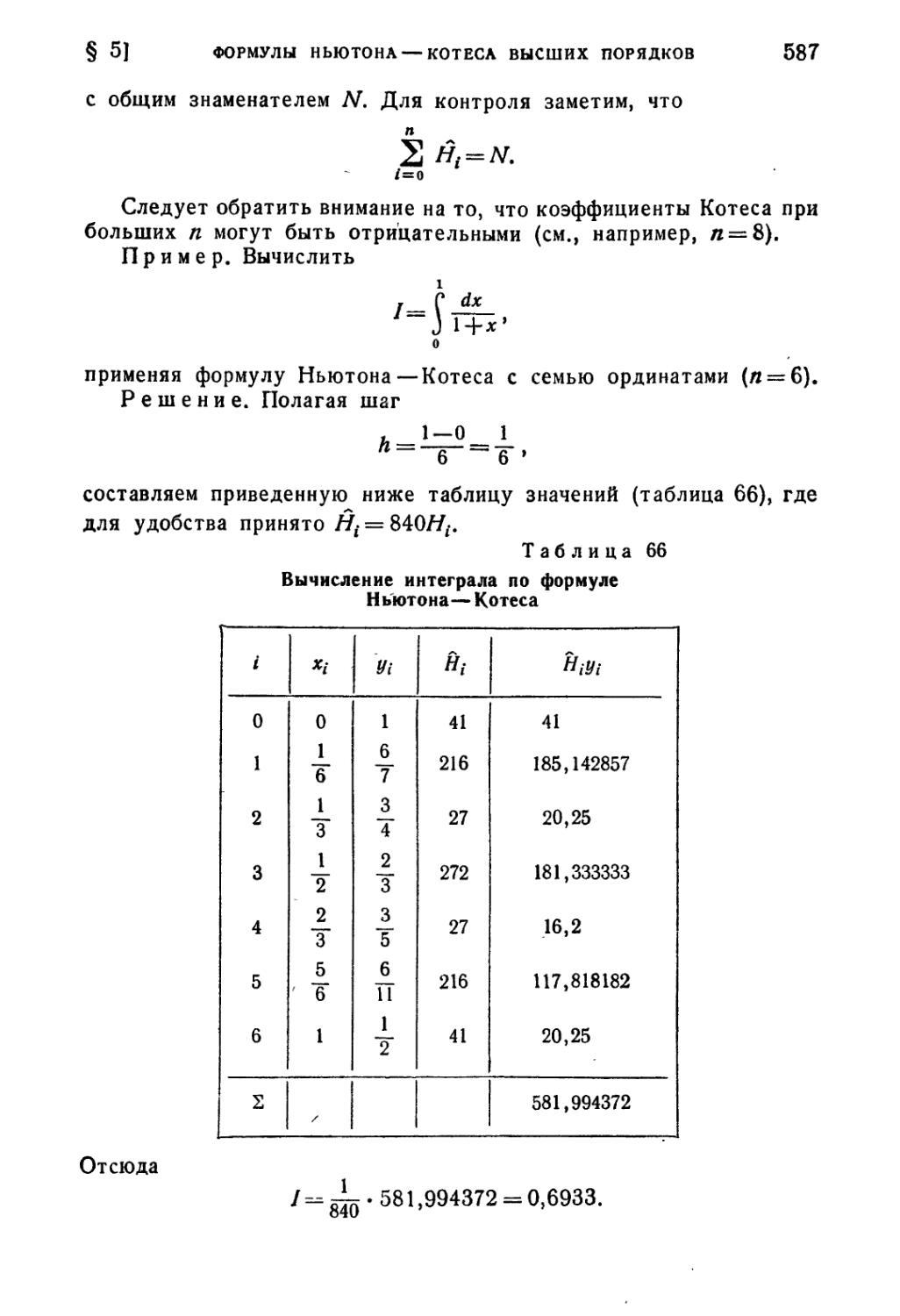
§ 5. Формулы Ньютона — Котеса высших порядков 586
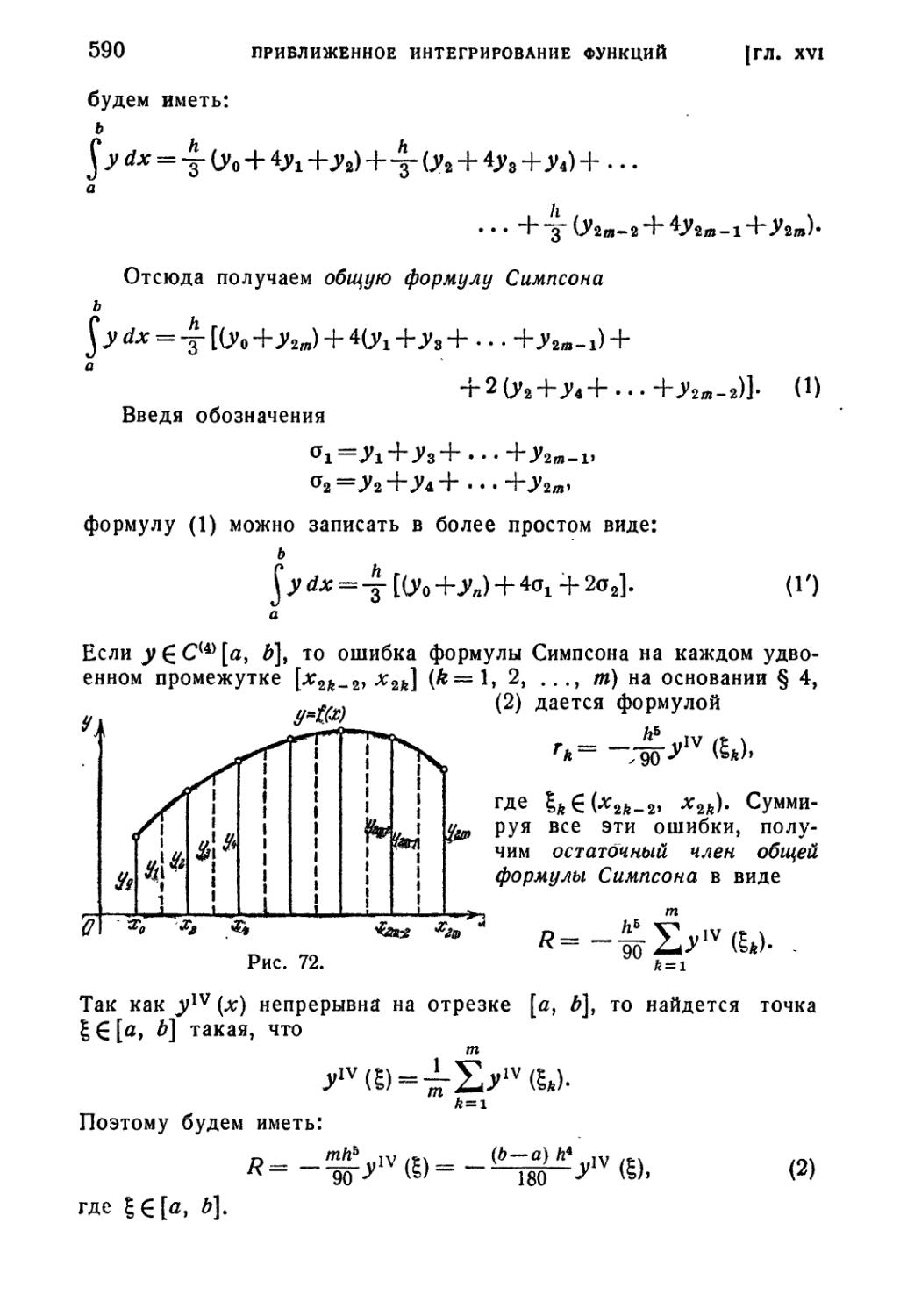
§ 6. Общая формула трапеций (правило трапеций) 588
§ 7. Общая формула Симпсона (параболическая формула) .... 589
§ 8. Понятие о квадратурной формуле Чебышева 593
§ 9. Квадратурная формула Гаусса 597
§ 10. Некоторые замечания о точности квадратурных формул . . . 604
§11*. Экстраполяция по Ричардсону 607
§ 12*. Числа Бернулли 611
§ 13*. Формула Эйлера—Маклорена 613
§ 14. Приближенное вычисление несобственных интегралов .... 618
§ 15. Метод Л. В. Канторовича выделения особенностей 621
§ 16. Графическое интегрирование 624
§ 17*. Понятие о кубатурных формулах 627
§ 18*. Кубатурная формула типа Симпсона 629
Литература к шестнадцатой главе 633
Глава XVII. Метод Монте-Карло 634
§ 1. Идея метода Монте-Карло 634
§ 2. Случайные числа 635
§ 3, Способы получения случайных чисел 638
§ 4. Вычисление кратных интегралов методом Монте-Карло .... 641
§ 5*. Решение систем линейных алгебраических уравнений методом
Монте-Карло 650
Литература к семнадцатой главе 658
Предметный указатель 659

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Бурное развитие новейшей техники и все большее внедрение
современных разделов математики в инженерные исследования
неизмеримо повысили требования к математической подготовке
инженеров и научных работников, занимающихся прикладными вопросами.
Математическое образование инженера-исследователя в
настоящее время не может ограничиться традиционными разделами так
называемого «классического анализа», сложившегося, в основных
своих направлениях, к началу нашего века. От инженера,
работающего в научно-исследовательском институте, требуется теперь
знание многих разделов современной математики и в первую
очередь основательное владение методами и приемами вычислительной
математики, так как решение почти каждой инженерной задачи
должно быть доведено до численного результата.
Вычислительная техника наших дней представляет новые мощные
средства для фактического выполнения счетной работы. Благодаря
этому во многих случаях стало возможным отказаться от
приближенной трактовки прикладных вопросов и перейти к решению задач
в точной постановке. Это предполагает использование более
глубоких специальных разделов математики (нелинейные
дифференциальные уравнения, функциональный анализ,
теоретико-вероятностные методы и др.).
Разумное использование современной вычислительной техники
не мыслимо без умелого применения методов приближенного и
численного анализа. Этим и объясняется чрезвычайно возросший как
у нас, так и за рубежом интерес к методам вычислительной
математики.
В нашей стране было издано несколько оригинальных и
переводных книг, посвященных приближенным и численным методам.
Однако это не удовлетворяет в полной мере потребности
читателей, так как многие из этих книг стали библиографической
редкостью, а часть из них устарела или носит слишком специальный
характер.
Основное назначение настоящей книги — дать в известной мере
систематическое и современное изложение важнейших методов и
приемов вычислительной математики на базе общего втузовского

10 ПРЕДИСЛОВИЕ
курса высшей математики. Книга составлена так, что основная часть
ее представляет собой учебное пособие по первому концентру
приближенных вычислений для высших технических учебных заведений.
Многие институты нашей страны приступили к подготовке
специалистов для работы в вычислительных центрах. Большие разделы
приближенного и численного анализа включены в программу
аспирантской подготовки по ряду специальностей и в программы
различных курсов усовершенствования инженеров. Поэтому в книгу
включен дополнительный материал, выходящий за рамки обычного
втузовского курса. Это обстоятельство не затруднит пользование
книгой: читатель без ущерба для понимания выберет нужные ему
разделы и опустит лишние. Для удобства пользования книгой главы и
параграфы, необязательные при первом чтении, отмечены звездочкой.
В книге широко используются основы матричного исчисления.
Понятие вектора, матрицы, обратной матрицы, собственного
значения и собственного вектора матрицы и т. п. являются рабочими.
Применение матриц дает ряд преимуществ при изложении, так
как, пользуясь ими, легче удается выяснить закономерность многих
расчетов. Особенно выигрышным в этом смысле является
проведение доказательств теорем сходимости различных численных
процессов. Кроме того, современные быстродействующие вычислительные
машины легко осуществляют основные матричные операции.
Для полного понимания содержания книги от читателя требуется
известный минимум сведений по линейной алгебре и теории
линейных векторных пространств. Чтобы облегчить усвоение этого
минимума и избежать отсылки к многим источникам, в книге
приведен весь необходимый дополнительный материал.
Соответствующие главы независимы от основного текста и могут быть опущены
подготовленным читателем.
Вкратце остановимся на содержании книги. Книга в основном
посвящена следующим вопросам: действия с приближенными
числами, вычисление значений функций при помощи рядов и
итеративных процессов, приближенное и численное решение
алгебраических и трансцендентных уравнений, вычислительные методы
линейной алгебры, интерполирование функций, численное
дифференцирование и интегрирование функций, метод Монте-Карло.
Большое внимание обращено на удобные способы оценки
погрешностей. Почти для всех процессов даются доказательства
теорем сходимости, причем изложение построено так, что при
желании можно их опустить и ограничиться лишь технической
стороной дела. В отдельных случаях, в целях наглядности изложения
и устранения излишней громоздкости, вычислительные приемы
сообщаются рецептурно.
Основные методы доведены до численных приложений — даны
расчетные схемы и приведены числовые примеры с подробным
ходом решения. В целях лучшего понимания сути дела большинство

ПРЕДИСЛОВИЕ 1 1
приведенных примеров рассматривается в упрощенной трактовке
и носит иллюстративный характер. Использованная и
дополнительная литература указана по главам.
Настоящая книга излагает избранные методы вычислительной
математики, и в нее не включен материал, связанный с
эмпирическими формулами, квадратичным аппроксимированием функций,
приближенным решением дифференциальных уравнений и др. Аз-
торы намерены посвятить этим вопросам отдельную книгу.
В книгу также не включены сведения о программировании и
технике решения математических задач на счетных машинах; по этому
вопросу следует обратиться к специальным руководствам.
Авторы приносят благодарность коллективу кафедры высшей
математики Артиллерийской инженерной академии им. Ф. Э.
Дзержинского, принимавшему участие в обсуждении рукописи книги.
Особую признательность выражаем Л. А. Люстернику, Г. П. Тол-
стову и Н. П. Бусленко, сделавшим ряд замечаний общего
характера, Э. 3. Шуваловой, представившей некоторые письменные
материалы, Д. М. Гробману за ценные практические советы и
А. А. Юшкевичу, прорецензировавшему главу XVII.
Авторы благодарны также проф. X. Л. Смолицкому и доц.
С. В. Фролову и Р. Я. Шостаку, рецензии которых позволили
улучшить качество рукописи.
Считаем своим долгом отметить компетентную работу редактора
Г. И. Бирюк,
Москва, 1959 г. Авторы

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Второе издание книги печатается с незначительными изменениями
по сравнению с первым. Внесены исправления замеченных ошибок.
В конце некоторых глав добавлены отдельные фрагменты. Так,
в введении даны дополнительные указания к общим правилам
вычислительной работы. Сделаны также некоторые замечания к методу
Бернулли и др.
В 1962 г. Физматгизом была выпущена книга Б. П. Демидович,
И. А. Марон, Э. 3. Шувалова «Численные методы анализа»,
посвященная приближению функций и дифференциальным уравнениям и
являющаяся естественным продолжением настоящей книги. Обе эти
книги вместе составляют двухтомное учебное пособие по
вычислительной математике, охватывающее основные методы численного
решения важнейших математических задач. Это учебное пособие
содержит материал, достаточный для большого курса приближенных
вычислений во втузах, и может быть использовано также студентами
физико-математических факультетов, специализирующихся в области
вычислительной математики.
Москва, 1963 г. Авторы
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Третье издание отличается от второго лишь тем, что
исправлены замеченные опечатки.
Авторы считают приятным долгом выразить свою благодарность
Л. Я. Цлафу за ряд ценных указаний.
Москва, 1965 г. Авторы

ВВЕДЕНИЕ
Общие правила вычислительной работы
При выполнении массовых вычислений важно придерживаться
определенных простых правил, выработанных практикой, соблюдение
которых экономит труд вычислителя и позволяет рационально
использовать имеющуюся вычислительную технику и вспомогательные
средства.
Прежде всего вычислитель должен разработать подробную
вычислительную схему, точно указывающую порядок действий и
дающую возможность получить искомый результат наиболее простым
и быстрым путем. Это особенно необходимо при однотипных
вычислениях, так как такая схема, автоматизируя вычисления, позволяет
выполнять их более быстро и надежно, что с пользой окунает время,
затраченное на составление схемы. Кроме того, имея детальную
вычислительную схему для решения задачи, можно использовать
труд менее квалифицированных вычислителей.
Составление вычислительной схемы проиллюстрируем на
следующем примере. Пусть требуется вычислить значения данной
аналитической функции
для заданных значений аргумента x = xv х21 ..., хп. Если число
этих значений велико, то неразумно вычислять отдельно сначала
значение /(хг), затем значение f(x2) и т. д., каждый раз выполняя
всю совокупность операций, указанных символом /. Гораздо
целесообразнее, расчленив функцию / на элементарные операции
(действия)
/(*)=/» (-..(Л (Л (*)))...).
вычисления производить однотипными операциями:
ui —fi (xi) (' = 11 2, ..., n);
«*=/«(«/) (/ = l- 2, ...,«);
У=/ш(Щ) (' = !. 2- ••••«).

14
ВВЕДЕНИЕ
выполняя одну и ту же операцию /у(у=1, 2, ..., т) для всех
рассматриваемых значений аргумента. При этом широко могут быть
использованы соответствующие таблицы функций и
специализированные счетные машины. Запись результатов вычислений следует
производить на особых вычислительных бланках или формулярах,
представляющих собой специальным образом разграфленные и
размеченные листы бумаги (применительно к выбранной вычислительной
схеме!). На этих бланках, в строго определенных местах, заносятся
промежуточные результаты по мере их получения, а также
окончательные результаты.
Вычислительные бланки обычно строятся таким образом, чтобы
результаты каждой серии однотипных операций заносились в один
столбец или в одну строку, причем расположение записей
промежуточных результатов должно быть удобным для производства
последующих вычислений.
Например, для составления таблицы значений функции
A)
можно рекомендовать вычислительный бланк, приведенный в
таблице 1.
Таблица 1
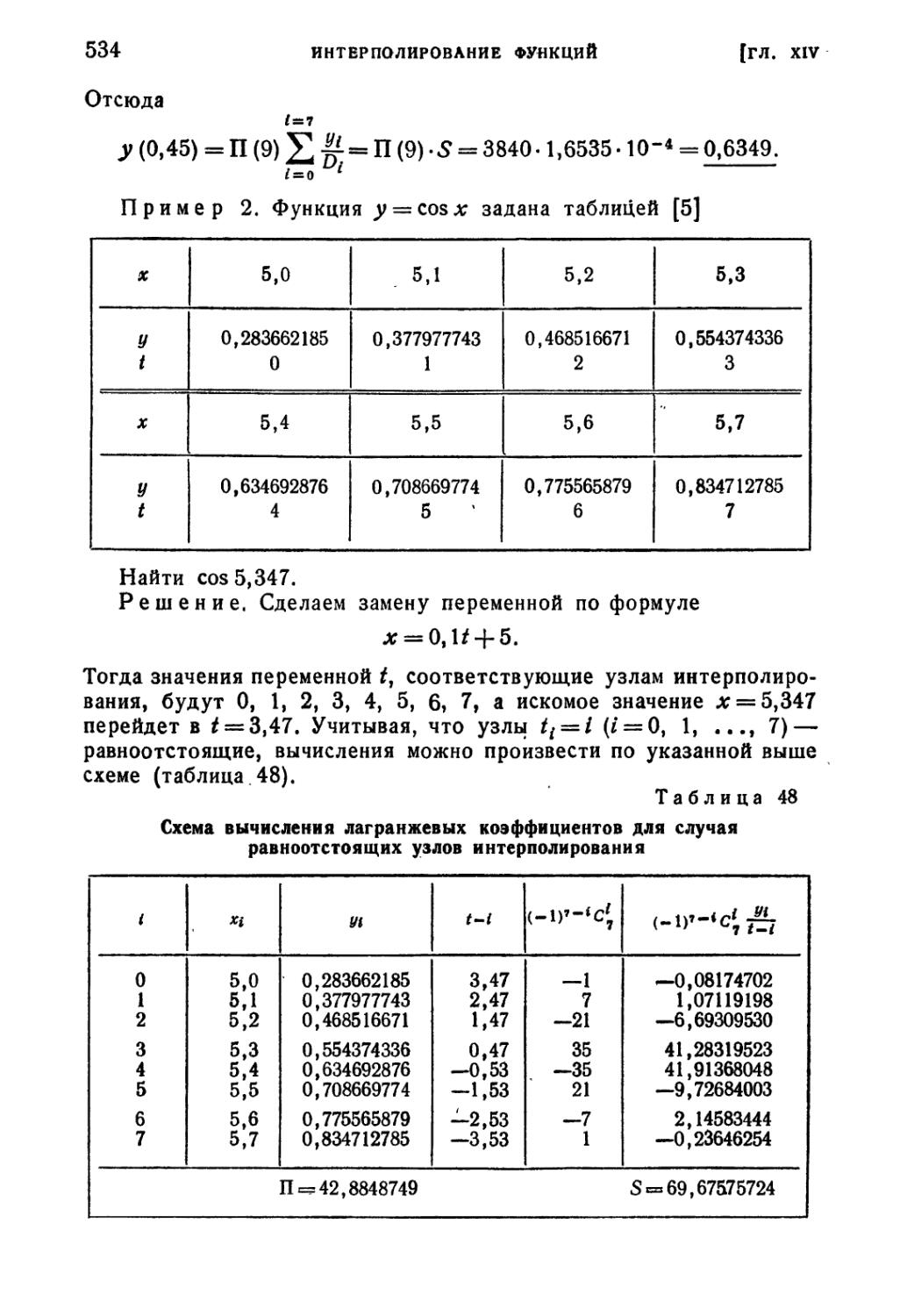
X
1
ОJ
2
ех
3
sin х
4
Вычислительный бланк для
COS X
5
er+cos x
6
(D + B)
**+cos л;
1+х*
8
функции A)
sin2*
DJ
9
1+sin2*
(D + (9)
10
V 1+sin2 x
11
У
(8) +
12
Вычисления ведутся по столбцам, причем характер выполняемых
однотипных операций ясен из самого вычислительного бланка.
Сначала в столбец A) записываются данные значения аргумента х.
Затем все числа столбца A) возводятся в квадрат и заносятся в
столбец B). Далее по таблицам определяются для каждого числа столбца A)
последовательно значения е*9 sin л;, cos л; и заполняются
соответственно столбцы C), D), E).
В дальнейших столбцах указаны результаты промежуточных
операций. Например, столбец F) содержит значения сумм е*-\-со&х
(схематически C) + E)) и т. д. В последнем столбце A2) приводятся

ОБЩИЕ ПРАВИЛА ВЫЧИСЛИТЕЛЬНОЙ РАБОТЫ 15
значения искомой функции у. При правильно составленном бланке
вычислитель в процессе вычисления уже фактически не пользуется
формулой, по которой ведется расчет, его внимание сосредоточено
исключительно на последовательном заполнении столбцов.
Заметим, что расчетная схема и форма бланка существенно зависят
от используемой техники вычислений и вспомогательных таблиц. Так,
например, в некоторых случаях отдельные промежуточные результаты
хранятся в памяти машины и в бланк не заносятся. Иногда
стандартные совокупности операций удобно рассматривать как отдельное
действие. Например, при использовании логарифмической линейки
численное значение выражения вида
ab
с
можно вычислять сразу, не фиксируя промежуточный результат,
и поэтому нет необходимости расчленять его на простейшие операции
умножения и деления. Аналогично при работе на электрических
счетных машинах процесс отыскания суммы парных произведений
2 «А
является единым действием. Во многих случаях выгодно
преобразовывать данные выражения к специальному искусственному виду
(например, заменять деление умножением на обратную величину, или
приводить выражение к виду, удобному для логарифмирования^ т.п.).
Второе, на что нужно обратить серьезное внимание, — это кон~
троль вычислений. Без проверки вычисление не может считаться
законченным. Контроль разделяется на текущий и заключительный.
При текущем контроле, производя добавочные действия, мы с
большей или меньшей степенью достоверности убеждаемся, что
полученные промежуточные результаты правильны. В противном случае
производится пересчет соответствующего этапа. При заключительном
контролепроверяется лишь окончательный результат.Например,если
вычисляется корень уравнения, то найденное значение можно
подставить в уравнение и таким образом узнать, правильно или нет
решена задача. По здравому смыслу ясно, что если вычисление очень
большое, то рискованно ставить под угрозу всю вычислительную
работу, дожидаясь проверки окончательного результата. Поэтому
целесообразно проверять правильность расчетов по этапам. В
ответственных случаях расчеты контролируются путем независимого
выполнения расчетов двумя различными вычислителями, или же задача
решается одним и тем же вычислителем двумя различными способами.
Третий важный момент — оценка точности. В большинстве
случаев вычисления производятся с приближенными числами и притом
приближенно. Поэтому даже для точного метода решения задачи
на каждом этапе вычислений возникают погрешности действий и

16 ВВЕДЕНИЕ
погрешности округлений. Если сам метод —приближенный, то к этим
двум погрешностям присоединяется погрешность метода. При
неблагоприятных обстоятельствах суммарная погрешность может быть
столь велика, что полученный результат будет иметь лишь
иллюзорное значение. В соответствующих главах книги указаны методы
оценки погрешностей для основных вычислений.
В вычислительном бланке полезно предусмотреть столбцы для
табличных разностей (см. гл. XIV, § 2), которые можно использовать
для контроля вычислений. А именно, если правильность таблицы
разностей нарушается на отдельном участке, то следует пересчитать
соответствующие элементы таблицы (либо выявить причину
нарушения).
Нужно обратить внимание также на аккуратность и четкость
записи в вычислительных бланках. Практика показывает, что нечеткая
запись цифр часто приводит к ошибкам и может погубить хорошо
организованное вычисление. Особенно опасны ошибки в записи чисел,
содержащих большое число нулей. Такие числа следует записывать
в нормальной форме, выделяя целую степень десяти, например
0,00000345 = 3,45- 1(Гв
и т. п.
Дальнейшая часть книги посвящена главным образом методам
вычислений. Приводимые числовые примеры во многих случаях
упрощены, причем промежуточные выкладки часто опускаются.

ГЛАВА I
ПРИБЛИЖЕННЫЕ ЧИСЛА
§ 1. Абсолютная и относительная погрешности
Приближенным числом а называется число, незначительно
отличающееся от точного А и заменяющее последнее в вычислениях.
Если известно, что а < Л, то а называется приближенным значением
числа А по недостатку, если же а>Л, то — по избытку.
Например, для У2 число 1,41 будет приближенным значением по
недостатку, а 1,42 — по избытку, так как 1,41 < У 2 < 1,42. Если а
есть приближенное значение числа Л, то пишут а« А.
Под ошибкой или погрешностью Да приближенного числа а
обычно понимается разность между соответствующим точным
числом А и данным приближенным, т. е.
Да = Л —а*).
Если А > а, то ошибка положительна: Да > 0; если же А < а,
то ошибка отрицательна: Да<0. Чтобы получить точное число Л,
нужно к приближенному числу а прибавить его ошибку Да, т. е.
Таким образом, точное число можно рассматривать как
приближенное с ошибкой, равной нулю.
Во многих случаях знак ошибки неизвестен. Тогда целесообразно
пользоваться абсолютной погрешностью приближенного числа
Определение 1. Абсолютной погрешностью Д
приближенного числа а называется абсолютная величина разности между
соответствующим точным числом Л и числом а, т. е.
Д-|Л —а|. A)
Здесь следует различать два случая:
1) число Л нам известно, тогда абсолютная погрешность Д легко
определяется по формуле A):
*) Иногда ошибкой называют разность а — Л

18 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
2) число А нам не известно, что практически бывает чаще всего,
и, следовательно, мы не можем определить и абсолютную
погрешность Д по формуле A).
В этом случае полезно вместо неизвестной теоретической
абсолютной погрешности Д ввести ее оценку сверху, так называемую
предельную абсолютную погрешность.
Определение 2. Под предельной абсолютной погрешностью
приближенного числа понимается всякое число, не меньшее
абсолютной погрешности этого числа.
Таким образом, если Дв— предельная абсолютная погрешность
приближенного числа а, заменяющего точное Л, то
Д = |Л-а|<Да. ' B)
Отсюда следует, что точное число Л заключено в границах
C)
Следовательно, а — Дл есть приближение числа Л по недостатку,
а я + Дл— приближение числа Л по избытку.
В этом случае для краткости пользуются записью
Л = а±Да.
Пример 1. Определить предельную абсолютную погрешность
числа а = 3,14, заменяющего число я.
Решение. Так как имеет место неравенство
3,14<я<3,15, то [а —к | < 0,01
и, следовательно, можно принять дл = 0,01.
Если учесть, что
3,14 <я<3,142,
то будем иметь лучшую оценку: Дд = 0,002.
Заметим, что сформулированное выше понятие предельной
абсолютной погрешности является весьма широким, а именно: под
предельной абсолютной погрешностью приближенного числа а
понимается любой представитель бесконечного множества неотрицательных
чисел Да, удовлетворяющих неравенству B). Отсюда логически
вытекает, что всякое число, большее предельной абсолютной
погрешности данного приближенного числа, также может быть названо
предельной абсолютной погрешностью этого числа. Практически
удобно в качестве Дл выбирать возможно меньшее при данных
обстоятельствах число, удовлетворяющее неравенству B).
В записи приближенного числа, полученного в результате
измерения, обычно отмечают его предельную абсолютную погрешность.
Например, если длина отрезка / = 214 см с точностью до 0,5 ел*,
то пишут / = 214 см± 0,5 см. Здесь предельная абсолютная
погрешность Д, = 0,5сл*, а точная величина длины / отрезка
заключена в границах 213,5 см ^/ < 214,5 см.

§ 1] АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ 19
Абсолютная погрешность (или предельная абсолютная
погрешность) не достаточна для характеристики точности измерения или
вычисления. Так, например, если при измерении длин двух
стержней получены результаты 1Х= 100,8 см ± 0,1 ежи /2 = 5,2 сж±0,1 см,
то, несмотря на совпадение предельных абсолютных погрешностей,
качество первого измерения выше, чем второго. Для точности
данных измерений существенна абсолютная погрешность, приходящаяся
на единицу длины, которая носит название относительной
погрешности.
Определение 3. Относительной погрешностью 6
приближенного числа а называется отношение абсолютной погрешности Д
этого числа к модулю соответствующего точного числа А(А^0),
•-от- D)
Отсюда Д = |Л|о.
Так же как и для абсолютной погрешности, введем понятие
предельной относительной погрешности.
Определение 4, Предельной относительной погрешностью 6а
данного приближенного числа а называется всякое число, не меньшее
относительной погрешности этого числа. По определению имеем:
а, E)
т. е. гту^Од, отсюда Д«^|Л|6а.
Таким образом, за предельную абсолютную погрешность числа а
можно принять:
Так как на практике А & а, то вместо формулы F) часто
пользуются формулой
Дв = !*!*•¦ F')
Отсюда, зная предельную относительную погрешность бй, получают
границы для точного числа. То обстоятельство, что точное число
лежит между аA — 6а) и аA + бй), условно записывают так:
Пусть а— приближенное число, заменяющее точное Л, и Да —
предельная абсолютная погрешность числа а. Положим для
определенности, что Л>0, а>0 и Дл < а. Тогда
Ь А <_*«-
и = т" ^5 ;;— •
Л а—Да
Следовательно, в качестве предельной относительной погрешности
числа а можно принять число

20 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Аналогично получаем Д -~= Аб ^ (а+ Д) 6а; отсюда
Если, как обычно бывает, ka<^ta и ба<^1 (знак <^ обозначает
«значительно меньше»), то приближенно можно принять:
а
Пример 2. Вес 1 дж3 воды при 0°С р = 999,847 Г±0,001 Г.
Определить предельную относительную погрешность результата
взвешивания.
Решение. Очевидно, что Дя = 0,001 Г и /?< 999,846 Г.
Следовательно,
. __ 0,001 ^1О-4о/
Пример 3. При определении газовой постоянной для воздуха
получили R = 29,25. Зная, что относительная погрешность этого
значения равна 1°/00, найти пределы, в которых заключается R.
Решение. Имеем 6^ = 0,001, тогда kR — RdR«0,03.
Следовательно, 29,22 </?< 29,28.
§ 2. Основные источники погрешностей
Погрешности, встречающиеся в математических задачах, могут
быть в основном разбиты на пять групп.
1. Погрешности, связанные с самой постановкой математической
задачи. Математические формулировки редко точно отображают
реальные явления: обычно они дают лишь более или менее
идеализированные модели. Как правило, при изучении тех или иных явлений
природы мы вынуждены принять некоторые, упрощающие задачу,
условия, что вызывает ряд погрешностей (погрешности задачи).
Иногда бывает и так, что решить задачу в точной постановке
трудно или даже невозможно. Тогда ее заменяют близкой по
результатам приближенной задачей. При этом возникает погрешность,
которую можно назвать погрешностью метода.
2. Погрешности, связанные с наличием бесконечных процессов
в математическом анализе. Функции, фигурирующие в
математических формулах, часто задаются в виде бесконечных последователь-
/ хв х& \
ностей или рядов (например, sinA; = Ar — 3T + 5I+ • • • г Более того»
многие математические уравнения можно решить, лишь описав
бесконечные процессы, пределы которых и являются искомыми решениями.

§ 3] ДЕСЯТИЧНАЯ ЗАПИСЬ. ЗНАЧАЩАЯ ЦИФРА. ЧИСЛО ВЕРНЫХ ЗНАКОВ 21
Так как бесконечный процесс, вообще говоря, не может быть
завершен в конечное число шагов, то мы вынуждены остановиться на
некотором члене последовательности, считая его приближением
к искомому решению. Понятно, что такой обрыв процесса вызывает
погрешность, называемую обычно остаточной погрешностью.
3. Погрешности, связанные с наличием в математических
формулах числовых параметров, значения которых могут быть
определены лишь приближенно. Таковы, например, все физические
константы. Условно назовем эту погрешность начальной.
4. Погрешности, связанные с системой счисления. При
изображении даже рациональных чисел в десятичной системе или другой
позиционной системе справа от запятой может быть бесконечное
число цифр (например, может получиться бесконечная десятичная
периодическая дробь). При вычислениях, очевидно, можно
использовать лишь конечное число этих цифр. Так возникает погрешность
округления. Например, полагая -^- = 0,333, получаем погрешность
о
д = 4'10. Приходится так же округлять и конечные числа,
имеющие большое количество знаков.
5. Погрешности, связанные с действиями над приближенными
числами (погрешности действий). Понятно, что, производя
вычисления с приближенными числами, погрешности исходных данных
в какой-то мере мы переносим в результат вычислений. В этом
отношении погрешности действий являются неустранимыми.
Само собой разумеется, что при решении конкретной задачи те
или иные погрешности иногда отсутствуют, или влияние их
ничтожно. Но, вообще говоря, для полного анализа погрешностей
следует учитывать все их виды. В дальнейшем мы ограничимся
в основном исчислением погрешностей действий и погрешностей
методов.
§ 3. Десятичная запись приближенных чисел.
Значащая цифра. Число верных знаков
Известно, что всякое положительное число а может быть
представлено в виде конечной или бесконечной десятичной дроби
B+il0-"+1+..., О)
где а,- —цифры числа а @^ = 0, 1,2, ..., 9), причем старшая цифра
а^^О, а т — некоторое целое число (старший десятичный разряд
числа а). Например,
3141,59.., = 3103 + МО2 + 4-101+ Ы0° +

22 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. С
Каждая единица, стоящая на определенном месте в числе а,
написанном в виде десятичной дроби A), имеет свое значение.
Единица, стоящая на первом месте, равна \0т, на втором—10я1,
на П'М — \0m~n+l и т. д.
На практике преимущественно приходится иметь дело с
приближенными числами, представляющими собой конечные
десятичные дроби
ft = Pffl10* + pm_110"-i+... + P/B_n+110m-n+i (Рж=?0). B)
Все сохраняемые десятичные знаки р/(/==т, т— 1, ...,/» — п +1)
называются значащими цифрами приближенного числа Ь, причем
возможно, что некоторые из них равны нулю (за исключением jJm).
При позиционном изображении числа Ъ в десятичной системе
счисления иногда приходится вводить лишние нули в начале или
в конце числа. Например,
или
Такие нули (в приведенных примерах они подчеркнуты) не считаются
значащими цифрами.
Определение 1. Значащей цифрой приближенного числа
называются всякая цифра в его десятичном изображении, отличная
от нуля, и нуль, если он содержится между значащими цифрами
или является представителем сохраненного десятичного разряда.
Все остальные нули, входящие в состав приближенного числа и
служащие лишь для обозначения десятичных разрядов его, не
причисляются к значащим цифрам.
Например, в числе 0,002 080 первые три нуля не являются
значащими цифрами, так как они служат только для установления
десятичных разрядов других цифр. Остальные два нуля являются
значащими цифрами, так как первый из них находится между
значащими цифрами 2 и в, а второй, как это отражено в записи,
указывает, что в приближенном числе сохранен десятичный
разряд 10~в. В случае, если в данном числе 0,002 080 последняя цифра
не является значащей, то это число должно быть записано в виде
0,002 08. С этой точки зрения числа 0,002 080 и 0,002 08
неравноценны, так как первое из них содержит четыре значащих цифры,
а второе — лишь три значащих цифры.
При написании больших чисел нули справа могут служить как
для обозначения значащих цифр, так и для определения разрядов
остальных цифр. Поэтому при обычной записи, чисел могут
возникнуть неясности. Например, рассматривая число 689 000, мы не имеем
возможности по его виду судить о том, сколько в нем значащих
цифр, хотя можно утверждать, что их не меньше трех» Этой
неопределенности можно избежать, выявив десятичный порядок числа

§ 3] ДЕСЯТИЧНАЯ ЗАПИСЬ. ЗНАЧАЩАЯ ЦИФРА. ЧИСЛО ВЕРНЫХ ЗНАКОВ 23
и записав его в виде 6,89-105, если оно имеет три значащих цифры;
или 6,8900-105, если число имеет пять значащих цифр, и т. п.
Вообще, такого рода запись удобна для чисел, содержащих большое
количество незначащих нулей, например 0,000 000 120 = 1,20-10~7
и т. п.
Введем понятие о верных десятичных знаках приближенного
числа.
Определение 2. Говорят, что п первых значащих цифр
(десятичных знаков) приближенного числа являются верными, если
абсолютная погрешность этого числа не превышает половины единицы
разряда, выражаемого п-Pl значащей цифрой, считая слева направо.
Таким образом, если для приближенного числа а A),
заменяющего точное число Д известно, что
то, по определению, первые п цифр ай, <%m-v ..., <xm-n+i этого
числа являются верными.
Например, для точного числа А = 35,97 число а = 36,00
является приближением с тремя верными знаками, так как \А — а\ =
-0,03 <—0,1.
Заметим, что в математических таблицах все помещенные
значащие цифры являются верными. Так, например, в пятизначных
таблицах логарифмов гарантировано, что абсолютная погрешность
мантиссы не превосходит -^--Ю и т. п.
Термин «л верных знаков» не следует понимать буквально, т. е.
так, что в данном приближенном числе а, имеющем п верных
знаков, п первых значащих цифр его совпадают с соответствующими
цифрами точного числа Л. Например, приближенное число а = 9,995,
заменяющее точное А =10, имеет три верных знака, причем все
цифры этих чисел различны. Однако во многих случаях дело обстоит
именно так, что верные знаки приближенного числа одинаковы
с соответствующими цифрами точного числа.
Замечание. В некоторых случаях удобно говорить, что
число а является приближением точного числа А с п верными
знаками в широком смысле, понимая под этим, что абсолютная
погрешность Д = |Л— а\ не превышает единицы десятичного разряда,
выражаемого /z-й значащей цифрой приближенного числа.
Например, для точного числа А = 412,3567 число а = 412,356
является приближением с шестью верными знаками в широком
смысле, так как Д = 0,0007 < ЫО.
В дальнейшем верные знаки приближенного числа мы будем
понимать в смысле определения 2 (т. е. в узком смысле), если явно не
оговорено противное.

24 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
§ 4. Округление чисел
Рассмотрим некоторое приближенное или точное число а,
записанное в десятичной нумерации. Часто бывает надобность в
округлении этого числа, т. е. в замене его числом аг с меньшим
количеством значащих цифр. Число а± выбирают так, чтобы погрешность
округления \al — a\ была минимальной.
Правило округления (по дополнению). Чтобы округлить число
до п значащих цифр, отбрасывают все цифры его, стоящие справа от
#-й значащей цифры, или, если это нужно для сохранения разрядов,
заменяют их нулями. При этом:
1) если первая из отброшенных цифр меньше 5, то оставшиеся
десятичные знаки сохраняются без изменения;
2) если первая из отброшенных цифр больше 5, то к
последней оставшейся цифре прибавляется единица;
3) если первая из отброшенных цифр равна 5 и среди
остальных отброшенных цифр имеются ненулевые, то последняя оставшаяся
цифра увеличивается на единицу;
За) если же первая из отброшенных цифр равна 5 и все
остальные отброшенные цифры являются нулями, то последняя оставшаяся
цифра сохраняется неизменной, если она четная, и увеличивается на
единицу, если она нечетная (правило четной цифры).
Иными словами, если при округлении числа отбрасывается
меньше половины единицы последнего сохраняемого десятичного
разряда, то цифры всех сохраненных разрядов остаются неизменными;
если же отброшенная часть числа составляет больше половины
единицы последнего сохраненного десятичного разряда, то цифра
этого разряда увеличивается на единицу. В исключительном случае,
когда отброшенная часть в точности равна половине единицы
последнего сохраненного десятичного разряда, то для компенсации
знаков ошибок округления используется правило четной цифры.
Очевидно, что при применении правила округления погрешность
округления не превосходит у единицы десятичного разряда,
определяемого последней оставленной значащей цифрой.
Пример 1. Округляя число
я = 3,14159 26535 ...
до пяти, четырех и трех значащих цифр, получим приближенные
числа 3,1416; 3,142; 3,14 с абсолютными погрешностями, меньшими
1.10-*; 1 -Ю-* и I.10-2.
Пример 2. Округляя число 1,2500 до двух значащих цифр,
получим приближенное число 1,2 с абсолютной погрешностью,
равной j- 10" ' = 0,05.

§ 5] ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ И ЧИСЛО ВЕРНЫХ ЗНАКОВ (АЪ
Точность приближенного числа зависит не от количества
значащих цифр, а от количества верных значащих цифр [1], [2].
В тех случаях, когда приближенное число содержит излишнее
количество неверных значащих цифр, прибегают к округлению.
Обычно руководствуются следующим практическим
правилом: при выполнении приближенных вычислений число значащих
цифр промежуточных результатов не должно превышать числа
верных цифр более чем на одну или две единицы. Окончательный
результат может содержать не более чем одну излишнюю
значащую цифру, по сравнению с верными. Если при этом абсолютная
погрешность результата не превышает двух единиц последнего
сохраненного десятичного разряда, то излишняя цифра называется
сомнительной.
Приведенное правило позволяет без ущерба точности
вычислений избегать написания лишних цифр и значительно экономит время
вычислений. Сохранение запасных знаков имеет тот смысл, что
обычно оценка погрешностей результатов производится для
наихудших вариантов, и фактическая погрешность может оказаться
значительно меньше максимальной теоретической. Таким образом, во
многих случаях те значащие цифры, которые считаются неверными,
на самом деле являются верными.
Приходится также округлять точные числа, содержащие
слишком много или бесконечное количество значащих цифр, сообразуясь
с общей точностью вычислений.
Заметим, что если точное число А округлить по правилу
дополнения до п значащих цифр, то полученное таким образом
приближенное число а будет иметь п верных цифр (в узком смысле).
Если же приближенное число а, имеющее п верных цифр,
округлить до п значащих цифр, то полученное новое
приближенное число av вообще говоря, будет иметь п верных цифр в
широком смысле. Действительно, в силу неравенства
И — «if^M—
предельная абсолютная погрешность числа ах складывается из
абсолютной погрешности числа а и погрешности округления.
§ 5. Связь относительной погрешности приближенного числа
с количеством верных знаков этого числа
Докажем теорему, которая связывает величину относительной
погрешности приближенного числа с количеством верных знаков
этого числа [3], [4].
Теорема. Если положительное приближенное число а имеет п
верных десятичных знаков в узком смысле, то относительная
погрешность Ь этого числа не превосходит \тЛ , деленную на первую

26 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ.
значащую цифру данного числа, г. е.
еде ат — первая значащая цифра числа а.
Доказательство. Пусть число
является приближенным значением точного числа Л и имеет п
верных знаков. Тогда по определению имеем:
отсюда
Последнее неравенство еще более усилится, если число а
заменим заведомо меньшим числом ад10й,
A)
Правая часть неравенства A) достигает наименьшего значения при
л= L Поэтому
Л > 1.10-Bав--1), B)
или, так как
то
^ " да *
Следовательно,
1 т_п
л А ^-" + *
2 т
Итак,
6<^(~] . C)
Теорема доказана.
Замечание 1. Пользуясь неравенством B), можно получить
более точную оценку относительной погрешности 6.

§ 5] ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ И ЧИСЛО ВЕРНЫХ ЗНАКОВ 27
Следствие 1. За предельную относительную погрешность
числа а можно принять:
?(АГ-
где ат — первая значащая цифра числа а.
Следствие 2. Если число а имеет больше двух верных
знаков, т. е. п^*2, то практически справедлива формула
Действительно, при п^2 числом тщ^т в неравенстве A) можно
пренебречь. Тогда
отсюда
"-Л"* ая10-
Следовательно,
* = 2о^ V 10
Замечание 2. Если приближенное число а имеет п верных
десятичных знаков в широком смысле, то оценки D) и E) следует
увеличить в два раза.
Пример 1. Какова предельная относительная погрешность,
если вместо числа я взять число а = 3,14?
Решение. В нашем случае аот = 3 и # = 3. Следовательно,
~~600~~ 6 /0#
Пример 2. Со сколькими десятичными знаками надо взять
|/г20, чтобы погрешность не превышала 0,1%?
Решение. Так как первая цифра 4, то агп = 41 причем
6 = 0,001. Имеем 4>IqW-1 <0,001, отсюда 10*-г^250 и я>4.
Приведенная теорема дает возможность по числу верных знаков
приближенного числа
1\0'»-i+... F)
определить его относительную погрешность б.

28 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Для решения обратной задачи — определения количества п
верных знаков числа F), если известна его относительная
погрешность б, обычно пользуются приближенной формулой
6 = А(а>0),
где А — абсолютная погрешность числа а. Отсюда
Д = дд. G)
Учитывая старший десятичный разряд числа А, легко установить
количество верных знаков данного приближенного числа а. В
частности, если
то из формул F) и G) имеем:
д < (ат + 1) \от. Ю-" < 10/л-п+1,
т. е. число а заведомо имеет п верных десятичных знаков в
широком смысле. Аналогично, если
в< 2Л65"'
то число а имеет п верных знаков в узком смысле.
Пример 3. Приближенное число а = 24253 имеет
относительную точность 1 %. Сколько в нем верных знаков?
Решение. Имеем:
А = 24 253.0,01л; 243 = 2,43 • 102.
Следовательно, число а имеет верными лишь первые две цифры
(п = 2); цифра сотен является сомнительной. Согласно
приведенному выше правилу число а предпочтительнее записать в виде
а = 2,43-104.
Замечание. Указанный способ определения числа верных
знаков является приближенным. При точном подсчете верных цифр
числа а следует исходить из неравенств
§ 6. Таблицы для определения предельной относительной
погрешности по числу верных знаков и наоборот
Если приближенное число написано с указанными верными
десятичными знаками, то можно легко подсчитать его предельную
относительную погрешность. Практически с таким подсчетом
приходится сталкиваться часто и поэтому желательно рационализиро-

§ 61
ТАБЛИЦЫ
29
вать эту операцию. Таблица 2 [5] указывает относительную
погрешность в процентах приближенного' числа в зависимости от
количества верных в широком смысле десятичных знаков его и от
первых двух значащих цифр числа, считая слева направо.
Таблица 2
Относительная погрешность (в %) чисел с п
верными знаками
Первые две
значащие цифры
10—11
12—13
14, ..., 16
17,
20,
23,
26,
30,
35,
40,
45,
50,
60,
70, .
80, .
. • •
•..
t
f t
• •»
90, ...,
, 19
, 22
, 25
, 29
, 34
, 39
, 44
49
59
69
79
89
99
2
10
8,3
7,1
5,9
5
4,3
3,8
3,3
2,9
2,5
2,2
2
1,7
1,4
1.2
1,1
n
3
1
0,83
0,71
0,59
0,5
0,43
0,38
0,33
0,29
0,25
0,22
0,2
0,17
0,14
0,12
0,11
4
0,1
0,083
0,071
0,059
0,05
0,043
, 0,038
0,033
0,029
0,025
0,022
0,02
0,017
0,014
0,012
0,011
Пусть, например, имеем приближенное число 0,00354 с тремя
верными десятичными знаками. Так как здесь п = 3 и число 35
содержится в промежутке 35, ..., 39, то по таблице 2 находим
6 = 0,29%.
Если известна только первая цифра числа, например 4, то
берем, конечно, большее из чисел 2,5 и 2,2, соответствующих
возможным вариантам 40, ..., 44 и 45, ...,49 (при п = 2). Если и
первая цифра неизвестна, то берем числа из первой строки A0 °/0;
1 %; 0,1 %), как наибольшие. Из этой таблицы мы видим, что три
верных знака обеспечивают относительную точность (не менее 1 °/0),
достаточную для большинства технических расчетов. Заметим,
что если приближенное число имеет два, три или четыре верных
знака в узком смысле, то все числа таблицы нужно уменьшить
вдвое.
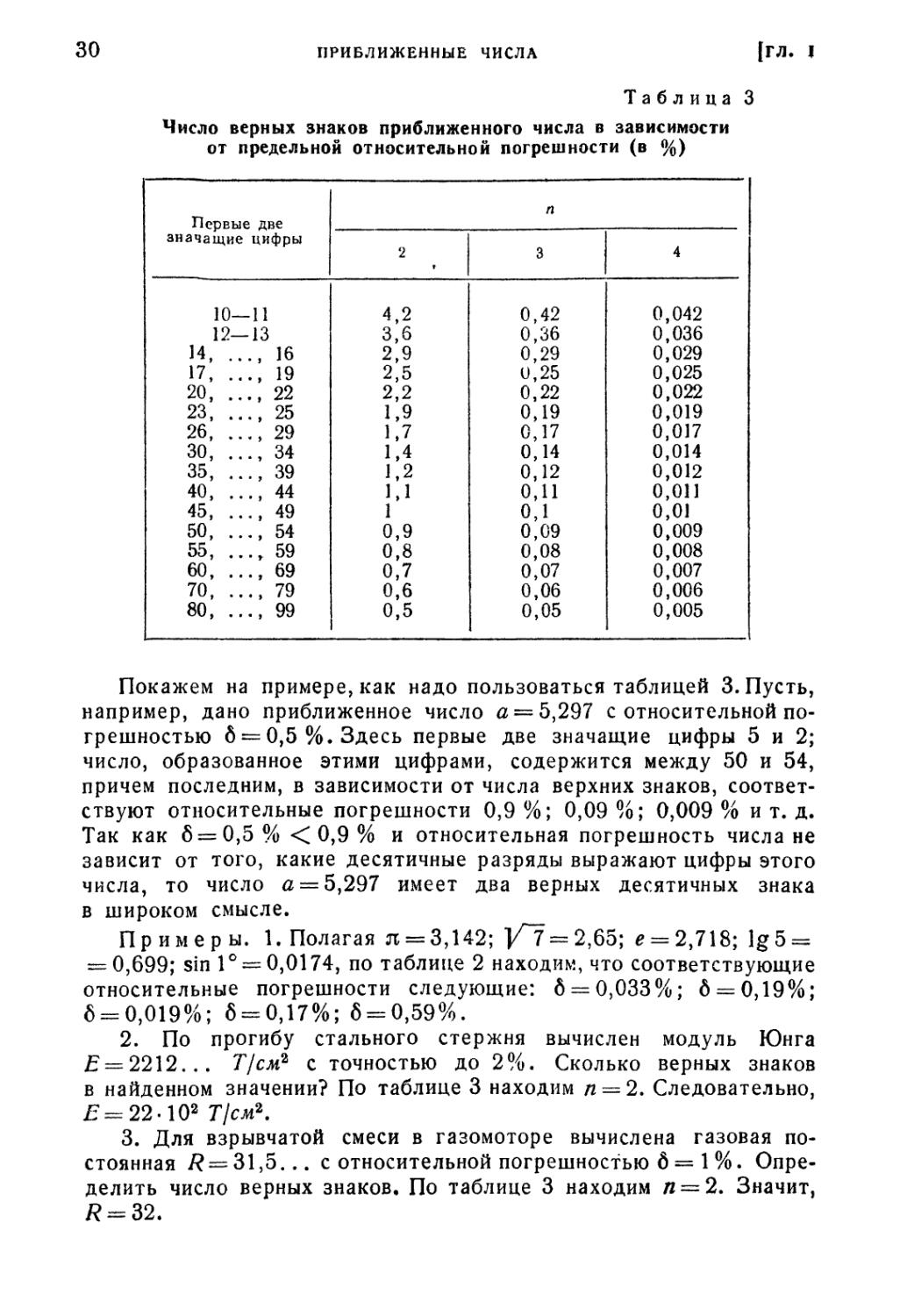
В таблице 3 [5] приведены верхние границы для
относительных погрешностей (в процентах), обеспечивающих данному
приближенному значению то или другое число верных знаков в широком
смысле в зависимости от его первых двух цифр.

30
ПРИБЛИЖЕННЫЕ ЧИСЛА
[гл.
Таблица 3
Число верных знаков приближенного числа в зависимости
от предельной относительной погрешности (в %)
Первые
две
значащие цифры
10—11
12—13
14, ...
17, ...
20, ...
23, ...
26, ...
30, ...
35, ...
40, ...
45, ...
50, ...
55, ...
60, ...
70, ...
80, ...
16
19
22
25
29
34
39
44
49
54
h 59
69
79
99
п
2
4,2
3,6
2,9
2,5
2,2
1,9
1,7
1,4
1,2
1,1
0,9
0,8
0,7
0,6
0,5
3
0,42
0,36
0,29
0,25
0,22
0,19
0,17
0,14
0,12
0,П
0,1
0,09
0,08
0,07
0,06
0,05
4
0,042
0,036
0,029
0,025
0,022
0,019
0,017
0,014
0,012
0,011
0,01
0,009
0,008
0,007
0,006
0,005
Покажем на примере, как надо пользоваться таблицей 3. Пусть,
например, дано приближенное число а = 5,297 с относительной
погрешностью 6 = 0,5%. Здесь первые две значащие цифры 5 и 2;
число, образованное этими цифрами, содержится между 50 и 54,
причем последним, в зависимости от числа верхних знаков,
соответствуют относительные погрешности 0,9 %; 0,09 %; 0,009 % и т. д.
Так как 6 = 0,5 % < 0,9 % и относительная погрешность числа не
зависит от того, какие десятичные разряды выражают цифры этого
числа, то число а = 5,297 имеет два верных десятичных знака
в широком смысле.
Примеры. 1. Полагая я = 3,142; 1/7=2,65; * = 2,718; Ig5 =
= 0,699; sin 1° = 0,0174, по таблице 2 находим, что соответствующие
относительные погрешности следующие: 6 = 0,033%; 6 — 0,19%;
6 = 0,019%; 6 = 0,17%; 6 = 0,59%.
2. По прогибу стального стержня вычислен модуль Юнга
? = 2212... Т/см2 с точностью до 2%. Сколько верных знаков
в найденном значении? По таблице 3 находим п = 2. Следовательно,
? = 22-102 Т/см\
3. Для взрывчатой смеси в газомоторе вычислена газовая
постоянная /? = 31,5... с относительной погрешностью 6 = 1 %.
Определить число верных знаков. По таблице 3 находим л = 2. Значит,
# = 32.

§ 7] ПОГРЕШНОСТЬ СУММЫ 31
§ 7. Погрешность суммы
Теорема 1. Абсолютная погрешность алгебраической суммы
нескольких приближенных чисел не превышает суммы абсолютных
погрешностей этих чисел.
Доказательство. Пусть xv лг2, ..., хп — данные
приближенные числа. Рассмотрим их алгебраическую сумму
Очевидно, что
Аи = ± A#i ± Л#2 ±. •. ± АлгЛ
и, следовательно,
|Ди|<|Д*1| + |Д*а|+...+|Д*и|. A)
Следствие. За предельную абсолютную погрешность
алгебраической суммы можно принять сумму предельных абсолютных
погрешностей слагаемых
. B)
Из формулы B) следует, что предельная абсолютная
погрешность суммы не может быть меньше предельной абсолютной
погрешности наименее точного (в смысле абсолютной погрешности) из
слагаемых, т. е. слагаемого, имеющего максимальную абсолютную
погрешность. Следовательно, с какой бы степенью точности ни были
определены остальные слагаемые, мы не можем за их счет
увеличить точность суммы. Поэтому не имеет смысла сохранять излишние
знаки и в более точных слагаемых. Отсюда вытекает следующее,
обычно применяемое, практическое правило для сложения
приближенных чисел.
Правило. Чтобы сложить числа различной абсолютной
точности, следует:
1) выделить числа, десятичная запись которых обрывается ранее
других, и оставить их без изменения;
2) остальные числа округлить по образцу выделенных, сохраняя
один или два запасных десятичных знака;
3) произвести сложение данных чисел, учитывая все сохраненные
знаки;
4) полученный результат округлить на один знак.
При округлении по правилу дополнения слагаемых суммы
до m-го десятичного разряда погрешность округления суммы с
самом неблагоприятном случае не превышает величины
Локр<я.-1- 10*. C)

32 ПРИБЛИЖЕННЫЕ ЧИСЛА \ТД. I
Можно получить более точный расчет погрешности округления
суммы, если учесть знаки ошибок округления слагаемых.
Пример. Найти сумму приближенных чисел: 0,348; 0,1834;
345,4; 235,2; 11,75; 9,27; 0,0849; 0,0214; 0,000354, каждое из
которых имеет все верные значащие цифры (в широком смысле).
Решение. Выделяем числа наименьшей точности 345,4 и 235,2,
абсолютная погрешность которых может достигать 0,1. Округляя
остальные числа с точностью до 0,01, получим:
345,4
235,2
11,75
9,27
0,35
0,18
0,08
0,02
0,00
602,25
Округляя результат до 0,1 по правилу четной цифры, получим
приближенное значение суммы 602,2.
Полная погрешность Д результата складывается из трех
слагаемых:
1) суммы предельных погрешностей исходных данных
Д1== Ю+ 10+ 10"x+ КГ1^- 10-2+ 10~2+ 10 +
+ 10+ 10~e = 0,221 301 < 0,222;
2) абсолютной величины суммы ошибок (с учетом их знаков)
округления слагаемых
Д2 == | — 0,002 + 0,0034 + 0,0049 + 0,0014 + 0,000 354 | =
- 0,008054 < 0,009;
3) заключительной погрешности округления результата
Д3 = 0,050.
Следовательно,
Д = Дх + А2 + Аз < °>222 + °>°°9 + 0,050 = 0,281 < 0,3;
и, таким образом, искомая сумма есть 602,2 ± 0,3.
Теорема 2. Если слагаемые — одного и того же знака, то
предельная относительная погрешность их суммы не превышает
наибольшей из предельных относительных погрешностей
слагаемых.
Доказательство. Пусть и = х1-{-х2~\- . . . -\-хп> где, для
определенности, xt > 0 (/ = 1, 2, ..., п).

§ 8] ПОГРЕШНОСТЬ РАЗНОСТИ 33
Обозначим через A((At > 0; /= 1, 2, .. ,,п) точные величины сла-
гаемыхлг,., а через А = Л1 + Л2+ ... + Д,— точное значение суммы и.
Тогда за предельную относительную погрешность суммы можно
принять:
2+...+Ап • W
Так как
то
А*? = ^в^ D')
Подставляя это выражение в формулу D), получим:
Л1
Пусть б является наибольшей из относительных погрешностей Ьхр
т. е. 6*{<6. Тогда
Следовательно, 8и ^ б, т. е.
6И < max (8Xl, 6Xi> ..., 6Хп).
§ 8. Погрешность разности
Рассмотрим разность двух приближенных чисел и = хг — дг2.
По формуле B) § 7 предельная абсолютная погрешность Ди
разности
т. е. предельная абсолютная погрешность разности равна сумме
предельных абсолютных погрешностей уменьшаемого и
вычитаемого.
Отсюда предельная относительная погрешность разности
ь^ЩЬ,, A)
где А — точное значение абсолютной величины разности чисел хх и дг2.
Замечание о потере точности при вычитании
близких чисел. Если приближенные числа хх и х2 достаточно
близки друг к другу и имеют малые абсолютные погрешности, то
число А мало. Из формулы A) вытекает, что предельная
относительная погрешность в этом случае может быть весьма большой, в то
2 Б. П. Демидович и И. А. Марон

34 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
время как относительные погрешности уменьшаемого и вычитаемого
остаются малыми, т. е. здесь происходит потеря точности.
Вычислим, например, разность двух чисел: ^ = 47,132 и д:2 =
= 47,111, каждое из которых имеет пять верных знаков. Вычитая,
получим и = 47,132 — 47,111=0,021.
Таким образом, разность и имеет лишь две значащие цифры, из
которых последняя сомнительна, так как предельная абсолютная
погрешность разности
Да = 0,0005+ 0,0005 = 0,001.
Предельные относительные погрешности вычитаемого,
уменьшаемого и разности соответственно
« 0,00001;
6,-^0,05.
Предельная относительная погрешность разности здесь примерно
в 5000 раз больше предельных относительных погрешностей
исходных данных.
Поэтому при приближенных вычислениях полезно
преобразовывать выражения, вычисление числовых значений которых приводит
к вычитанию близких чисел.
Пример. Найти разность
с тремя верными знаками.
Решение. Так как
B)
1 = 1,4177 4469...
и
1^2=1,41421356 ...,
то искомый результат есть
и = 0,00353 = 3,53- Ю-3.
Этот результат можно получить, если записать выражение B)
в виде
и °'01
^2,01 + V 2
и взять корни ]/2,01 и \^2 лишь с тремя верными знаками.
Действительно,

§ 9] ПОГРЕШНОСТЬ ПРОИЗВЕДЕНИЯ 35
Исходя из вышесказанного, получаем следующее практическое
правило: при приближенных вычислениях следует по возможности
избегать вычитания двух почти равных приближенных чисел; если
же в силу необходимости приходится вычитать такие числа, то
следует уменьшаемое и вычитаемое брать с достаточным числом
запасных верных знаков (если такая возможность имеется). Например,
если известно, что при вычитании чисел хх и х2 первые т значащих
цифр их пропадут, а результат необходимо иметь с п верными
значащими цифрами, то следует взять хх и х2 с т + п верными
значащими цифрами.
§ 9. Погрешность произведения
Теорема. Относительная погрешность произведения нескольких
приближенных чисел, отличных от нуля, не превышает суммы
относительных погрешностей этих чисел.
Доказательство. Пусть и = ххх2...хп.
Предполагая для простоты, что приближенные числа xv x2i ..., хп
положительны, будем иметь:
In и = In хг + In х2 + ... + In хп-
Отсюда, используя приближенную формулу д1плг«йИп*
находим:
Оценивая последнее выражение по абсолютной величине, получим:
Если At (i = l, 2, ..., л) —точные значения сомножителей х{ и
I A#f |, как это бывает обычно, малы по сравнению с х^ то
приближенно можно положить:
где б,- — относительные погрешности сомножителей^ (/ = 1,2, ... ,я)
и S — относительная погрешность произведения.
Следовательно,
О)
Формула A), очевидно, остается верной также, если
сомножители ДГ| (* = 1, 2, ..., п) имеют различные знаки.
2*

36 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Следствие. Предельная относительная погрешность
произведения равна сумме предельных относительных погрешностей
сомножителей, т. е,
B)
Если все множители произведения и весьма точны, за
исключением одного, то из формулы B) следует, что предельная
относительная погрешность произведения в этом случае будет практически
совпадать с предельной относительной погрешностью множителя,
обладающего наименьшей точностью. В частном случае, если
приближенным является лишь множитель xv то имеем просто
Зная предельную относительную погрешность 6и произведения и,
можно определить его предельную абсолютную погрешность Дй
по формуле
Пример 1. Определить произведение и приближенных чисел
^=12,2 и лс2 = 73,56 и число верных знаков в нем, если все
написанные цифры сомножителей верные.
Решение. Имеем Д^ = 0,05 и Д^я = 0,005. Отсюда
Так как произведение и = 897,432, то Да = и8а = 897-0,004 = 3,6
(приблизительно).
Отсюда и имеет лишь два верных знака и результат следует
записать так:
и = 897 ± 4.
Отметим частный случай
U — kXy
где k — точный множитель, отличный от нуля. Имеем:
т. е. при умножении приближенного числа на точный множитель k
относительная предельная погрешность не изменяется, а абсолютная
предельная погрешность увеличивается в \ k \ раз.
Пример 2. При наведении ракеты на цель предельная угловая
ошибка е = Г. Каково возможное отклонение Дц ракеты от цели
4SL дальности х = 2000 км при отсутствии корректирования ошибки?

§ 10] ЧИСЛО ВЕРНЫХ ЗНАКОВ ПРОИЗВЕДЕНИЯ 37
Решение. Здесь
^2000 580 м.
Очевидно, что относительная погрешность произведения не может
быть меньше, чем относительная погрешность наименее точного из
сомножителей. Поэтому здесь, как и в случае сложения, не имеет
смысла сохранять в более точных сомножителях излишнее
количество значащих цифр.
Полезно руководствоваться следующим правилом: чтобы найти
произведение нескольких приближенных чисел с различным числом
верных значащих цифр, достаточно:
1) округлить их так, чтобы каждое из них содержало на одну
(или две) значащую цифру больше, чем число верных цифр в
наименее точном из сомножителей;
2) в результате умножения сохранить столько значащих цифр,
сколько верных цифр имеется в наименее точном из сомножителей
(или удержать еще одну запасную цифру).
Пример 3. Найти произведение приближенных чисел ^ = 2,5
и х2 — 72,397, верных в написанных знаках.
Решение. Применяя правило, после округления имеем х^ = 2,5
и лг2 = 72,4. Отсюда ^^ = 2,5-72,4= 181 « 1,8-102.
§ 10. Число верных знаков произведения
Пусть имеем произведение л сомножителей (ж: 10) и^=ххх2.. .лги
каждый из которых имеет по крайней мере /я(/я > 1) верных цифр.
Пусть, далее, а1? а2, ..., ап—первые значащие цифры в десятичной
записи множителей:
+... (/=1, 2, 3, ..., п).
Тогда по формуле E) § 5 будем иметь:
и, следовательно,
?) «.)
<•>
Так как 1 + 1+...+1«Ю, ,ов,<4 (й)""'-
Следовательно, в самом неблагоприятном случае произведение и
имеет т~~ 2 верных знака.
Правило. Если все сомножители имеют т верных десятичных
знаков и число их не больше 10, то число верных (в широком
смысле) знаков произведения на одну или на две единицы меньше /».

38 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Следовательно, если нужно обеспечить в произведении т верных
десятичных знаков, то сомножители следует брать с одним или
двумя запасными знаками.
Если сомножители обладают различной точностью, то под т
следует понимать число верных знаков в наименее точном из
сомножителей. Таким образом, число верных знаков произведения
небольшого числа сомножителей (порядка десяти) может быть на одну
или две единицы меньше числа верных знаков в наименее точном
из этих сомножителей.
Пример 1. Определить относительную погрешность и
количество верных цифр произведения и = 93,87«9,236.
Решение. По формуле A) имеем:
55=4-10~3<Т-10~3'
Следовательно, произведение и имеет по меньшей мере три
верные цифры (см. § 5).
Пример 2. Определить относительную погрешность и число
верных цифр произведения и= 17,63-14,285.
Решение. _.
Следовательно, в произведении будут по крайней мере три верные
цифры (в широком смысле).
§ 11. Погрешность частного
Если й = —, то 1пи = 1плг — lnv
Отсюда
Ли
и
X
У
Из последней формулы вытекает, что теорема § 9 верна и для
частного.
Теорема. Относительная погрешность частного не превышает
суммы относительных погрешностей делимого и делителя.
Следствие. Если и-~ —, то 6tt = 6X + б .
Пример. Найти число верных знаков частного и = 25,7:3,6,
если все написанные знаки делимого и делителя верны.
Решение. Имеем:
6« -|^ + |f = 0,002 + 0,014 = 0,016.

§ 14] ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ КОРНЯ 39
Так как и = 7,14, то Дц = 0,016-7,14==0,11. Поэтому частное и
имеет два верных знака в широком смысле, т. е. # = 7,1 или,
более точно,
н = 7,14±0,И.
§ 12. Число верных знаков частного
Пусть делимое х и делитель у имеют по меньшей мере т верных
цифр. Если а и Р—их первые значащие цифры, то за предельную
относительную погрешность частного и может быть принята величина
1
Отсюда получаем правило: 1) если а^2 и р^2, то частное и
имеет по меньшей мере т—1 верных знаков; 2) если а=1 или
Р=1, то частное и заведомо имеет т — 2 верных знака.
§ 13. Относительная погрешность степени
Пусть и = хт(т — натуральное число), тогда In и = т\пх и,
следовательно,
Ни
Отсюда
бв = 7»бх, A)
т. е. предельная относительная погрешность т-й степени числа
в m раз больше предельной относительной погрешности самого
числа.
§ 14. Относительная погрешность корня
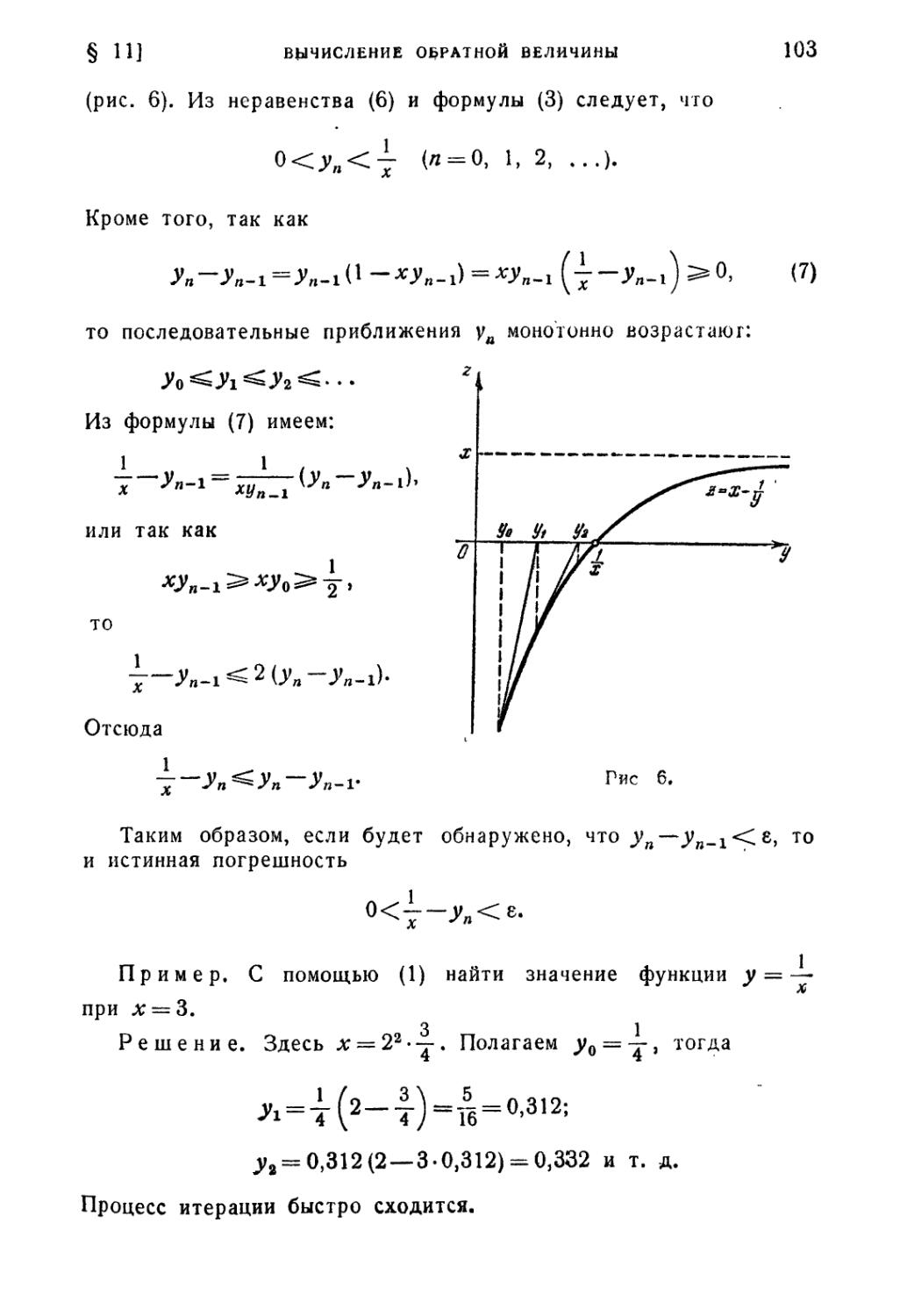
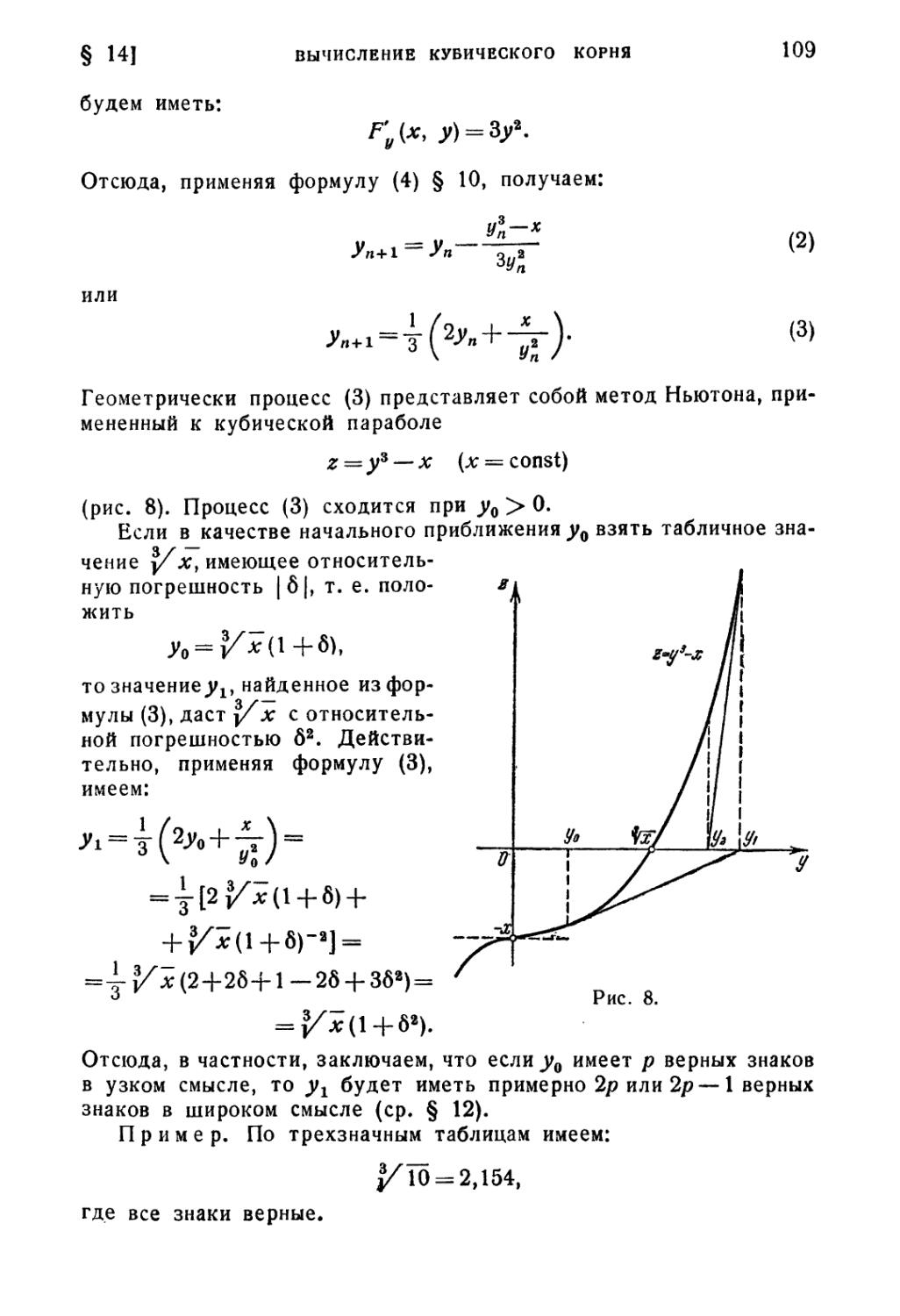
Пусть теперь и^у^х, тогда ил = дг. Отсюда
4
т. е. предельная относительная погрешность корня m-й степени
в m раз меньше предельной относительной погрешности
подкоренного числа.
Пример. Определить, с какой относительной погрешностью
и со сколькими верными цифрами можно найти сторону а квадрата,
если его площадь s= 12,34 (с точностью до 0,01).
Решение. Имеем a =]/~7= 3,5128... Так как

40 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
то бл = -j 6^ = 0,0004. Поэтому
Да = 3,5128.0,0004=1,4.10-3.
Отсюда число а будет иметь примерно четыре верных знака
(в широком смысле) и, следовательно, а = 3,513.
§ 15. Вычисления без точного учета погрешностей
В предыдущих параграфах мы указали способы оценки
предельной абсолютной погрешности действий. При этом предполагалось, что
абсолютные погрешности компонент усиливают друг друга, что
практически бывает сравнительно редко.
При массовых вычислениях, когда не учитывают погрешность
каждого отдельного результата, рекомендуется пользоваться
следующими правилами подсчета цифр [6].
1. При сложении и вычитании приближенных чисел младший
сохраненный десятичный разряд результата должен являться наиболь -
шим среди десятичных разрядов, выражаемых последними верными
значащими цифрами исходных данных.
2. При умножении и делении приближенных чисел в результате
следует сохранять столько значащих цифр, сколько их имеет
приближенное данное с наименьшим числом верных значащих цифр.
3. При возведении в квадрат или куб приближенного числа
в результате нужно сохранять столько значащих цифр, сколько
верных значащих цифр имеет основание степени.
4. При извлечении квадратного и кубического корней из
приближенного числа в результате следует брать столько значащих цифр,
сколько верных цифр имеет подкоренное число.
5. Во всех промежуточных результатах следует сохранять на одну
цифру больше, чем рекомендуют предыдущие правила. В
окончательном результате эта «запасная цифра» отбрасывается.
6. При вычислениях с помощью логарифмов рекомендуется под-л
считать число верных значащих цифр в приближенном числе, имеющем
наименьшее число верных значащих цифр, и воспользоваться таблицей
логарифмов с числом десятичных знаков, на единицу ббльшим. В
окончательном результате последняя значащая цифра отбрасывается.
7. Если данные можно брать с произвольной точностью, то для
получения результата с k верными цифрами исходные данные следует
брать с таким числом цифр, которые согласно предыдущим правилам
обеспечивают &+1 верную цифру в результате.
Если некоторые данные имеют излишние младшие десятичные
разряды (при сложении и вычитании) или больше значащих цифр,
чем другие (при умножении, делении, возведении в степень,
извлечении корня), то их предварительно нужно округлить, сохраняя одну
запасную цифру.

§ 161
ОБЩАЯ ФОРМУЛА ДЛЯ ПОГРЕШНОСТИ
41
§ 16. Общая формула для погрешности
Основная задача теории погрешности заключается в следующем:
известны погрешности некоторой системы величин, требуется
определить погрешность данной функции от этих величин.
Пусть задана дифференцируемая функция
и =
2> •.•> хп)
и пусть |д.#. |(/=1, 2, ..., л) —абсолютные погрешности
аргументов функции. Тогда абсолютная погрешность функции
Обычно на практике |Дл;;|— малые величины, произведениями,
квадратами и высшими степенями которых можно пренебречь. Поэтому
можно положить:
\Au\&\df(xv
Итак,
3.
A)
Отсюда, обозначая через Д^(/=1, 2, .... л) предельные
абсолютные погрешности аргументов xt и через Дв — предельную
погрешность функции и, для малых Длгг получим:
ди
i = 1
А*.
B)
Разделив обе части неравенства A) на и, будем иметь оценку
для относительной погрешности функции и
C)
Следовательно, за предельную относительную погрешность
функции и можно принять:
v-Z
In
D)
Пример 1. Найти предельные абсолютную и относительную
грешности об
±0,05 см, а я
погрешности объема шара Vse-g-m/8, если диаметр d — S,7 см±

42 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Решение. Рассматривая п и d как переменные величины,
вычисляем частные производные
dd 2
В силу формулы B) предельная абсолютная погрешность объема
дУ
дп
Дя|
dV
1 = 8,44.0,0016 + 21,5.0,05 =
= 0,013+1,075=1,088 см3 «1,1 еж3.
Поэтому
l/=lm/3»27,4 еж3 ±1,1 см*. E)
Отсюда предельная относительная погрешность объема
Пример 2. Для определения модуля Юнга Е по прогибу стержня
прямоугольного сечения применяется формула
4 * a?bs J
где / — длина стержня, а и b — измерения поперечного сечения
стержня, s — стрела прогиба, р — нагрузка.
Вычислить предельную относительную погрешность при
определении модуля Юнга ?, если р = 20 кГ\ Ьр =0,1%; а = 3 мм; бл = 1%;
? = 44 лш; 6Ь=\%; /=50 еж; б,= 1%; $ = 2,5 см; 6,= 1°/о.
Решение. ln?" = 31n/ + lnp — 31п а — Inb—Ins — In 4.
Отсюда, заменяя приращения дифференциалами, будем иметь:
Д?_о А/, Др о La ДЬ As
Следовательно,
| / = 3-0,01 +0,001 + 3-0,01 +
+ 0,01+0,01 =0,081.
Таким образом, предельная относительная погрешность
составляет 0,081, т. е. примерно 8% от измеряемой величины.
Произведя численные расчеты, имеем:

ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОГРЕШНОСТЕЙ
43
§ 17. Обратная задача теорий погрешностей
На практике важна также обратная задача: каковы должны быть
абсолютные погрешности аргументов функции, чтобы абсолютная
погрешность функции не превышала заданной величины.
Эта задача математически неопределенна, так как заданную
предельную погрешность Дй функции u=f(xv лг2) ...,#п) можно
обеспечить, устанавливая по-разному предельные абсолютные
погрешности Д*. ее аргументов.
Простейшее решение обратной задачи дается так называемым
принципом равных влияний. Согласно этому принципу
предполагается, что все частные дифференциалы
зт- A-tff (/=1, 2, ..., п)
одинаково влияют на образование общей абсолютной погрешности Да
функции u=f{x1% х2, ..., ха).
Пусть величина предельной абсолютной погрешности Да задана.
Тогда на основании формулы B) § 16
ди
A)
Предполагая, что все слагаемые равны между собой, будем иметь
ди
ди
дх2
Д.,
ди .
дхп
Отсюда
ди
дХ:
(/=1, 2, ..., п).
B)
Пример 1. Радиус основания цилиндра R « 2 м; высота цилиндра
И « 3 м. С какими абсолютными погрешностями нужно определить R
и //, чтобы его объем V можно было вычислить с точностью до 0,1 м3?
Решение. Имеем V~nR2H и Ду = 0,1 м3.
Полагая /? = 2 м; Н=3 м; п = 3,14; приближенно получим:
dV
dV
дН'

44 ПРИБЛИЖЕННЫЕ ЧИСЛА (ГЛ. I
Отсюда, так как л = 3, то на основании формулы B) будем иметь:
Пример 2. Требуется найти значение функции
и = 6л:2 (lg х — sin 2j/)
с точностью до двух десятичных знаков (после запятой), причем
приближенные значения х и у равны соответственно 15,2 и 57°.
Найти допустимую абсолютную погрешность этих величин.
Решение. Здесь
;лг — sin 2^) = 6 A5,2J (lg 15,2 —sin 114°) = 371,9;
^= 12л; (lg x — sin 2-у) + 6л:Ж=88,54,
где М = 0,43429 — модуль перехода;
|J=— 12л:2 008 2^-1127,7.
Для того чтобы результат был верен до двух десятичных знаков,
нужно выполнение равенства Аа = 0,005. Тогда по принципу
равных влияний имеем:
0j005= 0,000028;
2.88,54
Нередко при решении обратной задачи по принципу равных
влияний мы можем столкнуться с таким случаем, когда найденные по
формуле B) предельные абсолютные погрешности отдельных
независимых переменных окажутся настолько малыми, что добиться
соответствующей точности при измерении этих величин практически
невозможно. В таких случаях следует отступить от принципа равных
влияний и за счет разумного уменьшения погрешностей одной части
переменных добиться увеличения погрешностей другой части
переменных.
Пример 3. С какой точностью надо измерить радиус круга
/? = 30,5 см и со сколькими знаками взять я, чтобы площадь круга
была известна с точностью до 0,1°/0?

§ 17] ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОГРЕШНОСТЕЙ 45
Решение. Имеем s = nR* и In 5= Inn+ 2 In/?. Отсюда
По принципу равных влияний следует положить:
^ = 0,0005; ?^? = 0,0005.
Отсюда Дтс< 0,0016 и Д^< 0,00025/? = 0,0076 см.
Таким образом, следовало бы взять я = 3,14 и измерять /? с
точностью до тысячных долей сантиметра. Ясно, что такая точность
измерения практически трудно осуществима. Поэтому выгоднее
поступить следующим образом: взять я= 3,142; отсюда -^ = 0,00013;
тогда ^= 0,001 —0,00013 = 0,0087 и Д^<0,13 см. Такая
точность достигается сравнительно легко.
Иногда допускают, что предельная абсолютная погрешность всех
аргументов xi(i = \1 2, ..., п) одна и та же. Тогда, полагая
из формулы A) будем иметь:
А„= я К (/-1, 2, ..., я).
Наконец, можно предположить, что точность измерения всех
аргументов xt (/ = 1, 2, ..., п) одинакова, т. е. предельные
относительные погрешности 6^ (/ = 1, 2, ..., п) аргументов равны между собой:
Отсюда получим:
где k — общее значение отношений.
Следовательно,
и I y I // 19 tt\
Подставляя эти значения в формулу A), находим:
п
ди

46 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. I
Таким образом, окончательно имеем:
— 1 xi 1 ^я // __ 1 о п\
Можно также использовать и другие варианты.
Аналогично решается вторая обратная задача теории
погрешности, когда задана предельная относительная погрешность
функции и ищутся предельные абсолютные или относительные
погрешности аргумента.
Иногда в самой постановке задачи имеются условия, не
позволяющие использовать принцип равных влияний.
Пример 4. Стороны прямоугольника а &5 м и 6«200 м.
Какова допустимая предельная абсолютная погрешность при
измерении этих сторон, одинаковая для обеих сторон, чтобы площадь S
прямоугольника можно было определить с предельной
абсолютной погрешностью А5=1 ж2?
Решение. Так как
S = ab,
то
ASttbA a + aAb
Согласно условию задачи
поэтому
л - AlL-±
§ 18. Точность определения аргумента для функции,
заданной таблицей
В вычислительной практике часто возникает необходимость
определить аргумент по значению функции, заданной таблицей. Например,
постоянно встречается необходимость определить число по его
табличному логарифму или угол по табличному значению какой-
либо тригонометрической функции и т. п. Понятно, что
погрешность функции вызывает погрешность в определении аргумента.

§ 18J ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ АРГУМЕНТА ДЛЯ ФУНКЦИИ 47
Пусть имеем таблицу с одним входом для функции у*=/(
Если функция f(x) дифференцируема, то для достаточно малых
значений |Длг| имеем:
Отсюда
lAfi — JL^lL
или
Применим формулу A) к некоторым наиболее
распространенным табулированным функциям.
А. Логарифмы
Пусть у = \пх, тогда у' = ~.
Отсюда
ДХ = *ДГ B)
Если же y = lgAr, то/ = — , где М~ 0,43429;
Отсюда, в частности, получаем бж = 2,30Ду, т. е. предельная
относительная погрешность числа в таблице десятичных логарифмов
равна примерно 2у-кратной предельной абсолютной погрешности
логарифма этого числа.
Б. Тригонометрические функции
у)» то У = cos x и, следовательно,
рад. C)
1.
2.
имеем
и
Если
Для
y = $it\
функции
AJC = Aycos2A: pad. D)
3. Если y = \g(sinx)(o<x<j\ то
и AJP = 2,30tgArAy po^. E)

48 ПРИБЛИЖЕННЫЕ ЧИСЛА \ГЛ. I
4. Положим y = lg(tgx) (о<х<.y ), тогда
и &x-hl5sin2xAy рад. F)
Так как, очевидно, S1" х < tg х при 0 < х < у , то из
формул E) и F) следует, что угол х по таблице логарифмов тангенсов
определяется точнее, чем по таблице логарифмов синусов.
В. Показательная функция
Если y~e*t то у* — ех и
А -^ G)
* ~~ ех
ИЛИ
д =±
* У '
Примерь С какой точностью можно определить число лс«5000,
пользуясь четырехзначной таблицей десятичных логарифмов?
Решение. По формуле B') получаем:
т. ei число х имеет примерно четыре верные цифры.
Пример 2. Найти погрешность в определении угла дг
а) по пятизначной таблице логарифмов синусов,
б) по пятизначной таблице логарифмов тангенсов.
Решение. Для первого случая по формуле E) имеем:
л ~10 рад = 0,00002
Во втором случае по формуле F) получаем:
Дж= 1.15.1^3. у. 10 рш?«0,000005 рад&\\
т. е. погрешность в четыре раза меньше.
§ 19. Способ границ
Обычно применяемая оценка погрешности функции (§ 16,
формула B)) является приближенной, так как эта оценка основана на
пренебрежении произведениями ошибок. В некоторых случаях
требуется иметь точные границы для искомого значения функции
если известны границы изменения ее аргументов. Проще всего,

§ 19] СПОСОБ ГРАНИЦ 49
этого можно добиться, используя способ двойных вычислений,
иначе называемый способом границ.
Пусть
u=/(xv лг2, ..., хп)
— непрерывно дифференцируемая функция, монотонная по каждому
аргументу X;(i = 1,2, ..., л). Для этого достаточно предположить,
что производные •—- (/==1, 2, ..., л) сохраняют постоянный знак
в рассматриваемой области со изменения аргументов. Допустим, что
*/<*/<*"/ (/=1, 2, ..., л), A)
причем параллелепипед A) целиком принадлежит области о).
Положим, что Xj = xi} лг1- = лг1-, если функция
/—возрастающая по переменному х0 и х{ = л:/, xt = xiy если функция
/—убывающая по переменному xt.
Тогда, очевидно,
и< и<и, B)
где
Заметим, что переменные х{ (/=1, 2, ..., л) и результат
действий / над ними можно округлять лишь в сторону уменьшения
величины и, а переменные х{ (/=1, 2, ..., л) и результат действий/
над ними можно округлять лишь в сторону увеличения величины и.
При этих обстоятельствах будет гарантировано строгое выполнение
неравенства B). В частном случае, если функция /—монотонно
возрастающая по каждому аргументу х( (/=1, 2, •.., л), то имеем
просто
f[xvx%9 ..., xn)<u<f(xv х2, ..., *„). C)
Пример. Алюминиевый цилиндр с диаметром основания
d = 2 cjk±O,O1 см и высотой й=11 сл*±0,02 см весит /? = 93,4/"±
±0,001 Г. Определить удельный вес у алюминия и оценить его
предельную абсолютную погрешность.
Решение. Объем цилиндра равен
nd2 h
отсюда

50 ПРИБЛИЖЕННЫЕ ЧИСЛА [ГЛ. t
Из формулы D) вытекает, что в области р>0, */>0, й>0
функция у — возрастающая по аргументу р и убывающая по аргументам
d и к. Согласно условию задачи имеем:
1,99 сл*<</<2,01 см;
10,98 сл«< А < 11,02 см;
93,399 Г <р< 93,401 Г.
Кроме того,
3,14159 < я < 3,1416.
Поэтому
4-93,399 _дв71Г
Х-~~ 3,1416.2,01*.11,02 ' см*
(с недостатком) и
~ 4-93,401
Y
Y "" 3,14159- 1,99а. 10,98 ~"z> ' ом»
(с избытком). Взяв среднее арифметическое, получим:
у- 2,703^0,027^, E)
или после округления
Для сравнения приведем приближенную оценку погрешности.
Используя средние значения аргументов, получим:
Логарифмируя формулу D), имеем:
In у == In 4 + In p — In я — 2 In d — In A;
отсюда, взяв полный дифференциал, получим:
Ау__Др An 2 Ad АЛ
Y р я d h
Следовательно,
°»001 1 0,00001 . 2-0,01 . 0,02
= 1,07-10-5 + 3,18-Ю-в+10~2+ 1,82-Ю-8 =1,183-10.
Далее, находим:
Дт = бт-у = 1,183-10~а.2,703 = 3,2-Ю-2^-,-.

§ 20] ПОНЯТИЕ О ВЕРОЯТНОСТНОЙ ОЦЕНКЕ ПОГРЕШНОСТИ 51
Таким образом, приближенно имеем:
Y = 2,708 ?±0,082 ?„
что очень близко совпадает с точной оценкой E).
§ 20*. Понятие о вероятностной оценке погрешности
Пусть имеем сумму п слагаемых
и = х± + х2 + ... +хп.
Тогда предельная абсолютная погрешность суммы, как известно,
равна
Aa = AXi + AX2+...+AXn. A)
Отсюда в случае, когда предельные абсолютные погрешности
слагаемых одинаковы,
А*! = АХ2 = ... = АХп = А,
будем иметь:
Ав = лА. (Г)
Формула A) дает максимальное возможное значение абсо-
лютнойпогрешности суммы. Эта предельная погрешность достигается
лишь тогда, когда ошибки всех слагаемых: 1) наибольшие из
возможных и 2) имеют одинаковые знаки. При большом количестве
слагаемых такое неблагоприятное стечение обстоятельств является
маловероятным. Фактически ошибки отдельных слагаемых, как
правило, имеют различные знаки и, следовательно, частично
компенсируют друг друга. Поэтому наряду с теоретической предельной
погрешностью суммы Аа вводят практическую предельную
погрешность А*, реализуемую с некоторой мерой достоверности.
Ограничимся рассмотрением простейшего случая. Пусть
абсолютные погрешности Ал:,- (/=1, 2, ..., п) слагаемых суммы A)
независимы и подчиняются нормальному закону с одной и той же
мерой точности. Положим, что с вероятностью, превышающей
число у> абсолютные погрешности слагаемых не превышают числа А,
При этом условии в теории вероятностей доказывается, что
с той же мерой достоверности абсолютная погрешность суммы и
будет удовлетворять неравенству | Аи\ ^ А ]^я, где п — число
слагаемых.
Таким образом, за предельную абсолютную погрешность суммы
можно принять число
;' B)

52 ПРИБЛИЖЕНИЕ ЧИСЛА [ГЛ. I
Например, складывая 100 чисел с абсолютной погрешностью
0,1, мы получим теоретическую предельную ошибку суммы Ац =
= 0,1 • 100 = 10. Фактически же можно ожидать, что эта ошибка
не превзойдет величины 0,1-10=1.
В частности, рассмотрим среднее арифметическое п чисел
Согласно строгой теории предельная абсолютная ошибка
тогда как с ббльшей степенью достоверности можно утверждать,
что практически
А ¦ А У"п Д
т. е. практически достоверно, что среднее арифметическое
приближенных чисел имеет повышенную точность по сравнению с этими
числами, причем
Д$ -> 0 при п-+ оо.
Аналогично для случая умножения л сомножителей с одинаковой
относительной предельной погрешностью 6 можно доказать, что
практическая предельная относительная погрешность произведения
определяется формулой
6*=6]Лг. . C)
Литература к первой главе
1. А. Н. К р ы л о в, Лекции о приближенных вычислениях, Изд. 2, АН СССР,
Л., 1933, гл. I
2. Д. А. В е нтцел ь, Е. С. Вентцель, Элементы теории
приближенных вычислений, Изд. ВВИА им. Н. Е. Жуковского, М., 1949, гл. I.
3. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
1934, гл. I.
4. Я. С. Б е з и к о в и ч, Приближенные вычисления, Гостехиздат, 1949,
гл. I и II.
5. F. М. Фихтенгольц, Математика для инженеров, ГТТИ, 1933, ч. 1,
гл. I.
6. В. М. Брадис, Устный и письменный счет. Вспомогательные средства
вычислений. Энциклопедия элементарной математики, кн. 1, Учпедгиз,
1951.

ГЛАВА II
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ
§ 1. Определение цепной дроби
Выражение вида
называется цепной или непрерывной дробью. Для цепной дроби A)
употребляется также сокращенная запись
В общем случае элементы цепной дроби я0, ak, bk (k = 1,2, ...) —
вещественные или комплексные числа, или функции одной или
нескольких переменных. Дроби ао = у, — (&=1, 2, ...) называются
звеньями цепной дроби A) (соответственно нулевым, первым и т. д.),
а числа или функции ak и bk (k^\) — членами ft-ro звена
(частными знаменателями или числителями). Мы будем предполагать, что
akz^0. Заметим, что в сокращенной записи A) звенья— сокращать
нельзя.
Если цепная дробь A) содержит конечное число звеньев
(например, л, не считая нулевого), то она называется конечной пппп-звен-
ной и сокращенно обозначается следующим образом:
J B)
Конечная цепная дробь отождествляется с соответствующей
обыкновенной, полученной в результате выполнения указанных
действий. Цепная дробь A), имеющая бесконечное множество звеньев,

54 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. II
называется бесконечной, причем употребляется обозначение
Цепная дробь
у которой все частные числители равны 1, называется
обыкновенной или стандартной цепной дробью. Знаменатели звеньев
называются неполными частными. Заметим, что в теории чисел
неполными частными обычно являются натуральные числа, т. е. целые
положительные,
§ 2. Обращение цепной дроби в обыкновенную и обратно
Всякую конечную цепную дробь можно обратить в
обыкновенную. Для этого достаточно произвести все действия, указанные
в изображении цепной дробив
Пример 1. Обратить цепную дробь
i
3+Г~Г
в обыкновенную.
Решение. Последовательно выполняя указанные действия,
находим:
1'lt4"' ' 1' 5 — 19 '
2). = 4-4; ?|
Следовательно,
 • Т' T
Обратно всякое положительное рациональное число можно
обратить в цепную дробь с натуральными элементами. Пусть,
например, дана дробь —. Исключив из нее целую часть а0, будем иметь:
Я Я
где г0 —остаток (если — — правильная дробь, то яо = О и го=

§ 2] ОБРАЩЕНИЕ ЦЕПНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБРАТНО 55
Разделив теперь числитель и знаменатель дроби — на г0,
получим:
L '
где а1 — целое частное, г1 — остаток от деления q на г0.
Разделив числитель и знаменатель дроби — на гх, получим:
го го:гг
где а2 — целое частное, г2 — остаток от деления г0 на гг.
Аналогично можно продолжить процесс дальше.
Таккак ^>го>г1>г2>г8> ... и г, (/= 0, 1, 2,
...)—целые положительные числа, то в конце концов мы будем иметь
остаток гя = 0, т. е.
ri
Подставляя выражение дробей , будем иметь:
= я
^0
62
Пример 2. Обратить jq в цепную дробь.
Решение. Последовательно имеем:
62 „5 - . 1 о, 1
3+ 3 + 3 +
з+-5
4
Таким образом, ^= Гз; -1, |-, —1.
Аналогично преобразуются общие цепные дроби.

56 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. U
Пример 3. Обратить цепную дробь
' 1 f 3
в обыкновенную.
Решение. Имеем:
П i *2 __i Sx2 _ 15 — 6jc2 щ
' о *2 ~ 15—л-2 ~~ 15—д;2 ;
6 5~
х2 __ 15л:2 — х4 15 —
2) 1~Г5=6^2— ^ — 15—
15—л:2
Таким образом,
х*_ — х% —л:2 ] __15 — 21л
I » 3 ' 5 J~ 15—
; 1
§ 3. Подходящие дроби
Пусть дана конечная или бесконечная цепная дробь
w а:-
Обыкновенную дробь
, , ....
(k=l, 2, ...), где А^л, называют k-R подходящей дробью
цепной дроби A). Следуя Эйлеру, обычно полагают:
причем для определенности считают, что
Р = а О — 1 B*
и
При работе на электронной цифровой машине подходящие
цепные дроби

§ 3] ПОДХОДЯЩИЕ ДРОБИ 57
удобно находить с помощью схемы Горнера (см. гл. III) для
деления
-^1
Указанная последовательность действий легко программируется.
Теорема 1. (Закон составления подходящих
дробей). Числа Pki Qk(k=— I, 0, 1, 2, ...)> определяемые из соот-.
ношений
являются соответственно числителями и знаменателями подходящих
р
дробей -?j* цепной дроби A)*).
Доказательство. Пусть Rk (k = 1, 2, ...) —
последовательные подходящие дроби цепной дроби A). Нужно доказать, что
**=?; <*=!. 2,...).
Доказательство будем проводить методом математической
индукции.
При fc=l для подходящей дроби Rt имеем:
С другой стороны, из соотношений C) и C'), учитывая D),
находим:
р
Следовательно, R± = {-г- и для k = 1 утверждение теоремы
справедливо.
*) Такие подходящие дроби будем называть каноническими.

58 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ.П
Пусть теперь теорема верна для всех натуральных чисел,
непревышающих k. Покажем, что теорема справедлива также для
очередного натурального числа /г+1. Из соотношений C) и C') получаем:
Согласно индукционному предположению имеем:
По способу составления цепной дроби A), подходящая дробь /?ft+1
получается из подходящей дроби Rk путем замены члена ак на сумму
ак + ?*±±. Поэтому
что и требовалось доказать.
Замечание. Так как члены подходящих дробей определяются
неоднозначно, то в общем случае нельзя утверждать, что числитель
и знаменатель подходящих дробей неканонического вида
удовлетворяют уравнениям C) и C'). В дальнейшем мы будем предполагать,
что рассматриваемые подходящие дроби являются каноническими.
Следствие. Для обыкновенной цепной дроби
числители и знаменатели ее подходящих дробей^ (&=1, 2, ...)
могут быть определены из соотношений
где положено ро=0о, р^х— 1 и #0= 1, ^м1 = 0.

§ 3]
ПОДХОДЯЩИЕ ДРОБИ
59
Замечание. Для нахождения по формулам C) и C') членов
последовательных подходящих дробей удобно применять следующую
схему:
к
bk
я*
Pk
Qk
— l
l
0
0
1
*0
а0
1
1
Ьг
«1
Pi
Qi
2
Ьг
<*2
Р*
Q2
3
Ьз
р*
...
...
...
...
• • .
Для обыкновенной цепной дроби, где bk=\ (&=1, 2,
имеют место формулы C"), в схеме опускают строку bk.
Пример 1. Для цепной дроби
163 _ о _i !
9* ~г±~ 1
..) и
3+-
вычислить все подходящие дроби.
Решение. Используя схему, получим:
Pk
Як
2
2
1
1
3
1
3
11
4
4
47
17
1
58
21
2
163
59
Таким образом,
<7о
Яг
. ?l —И.
f Яг~ 4 '
Яг
Пример 2. Найти все подходящие дроби для общей цепной
ДР°би Го-1 3 1 П
[ ' 2 ' 4 ' 8 ' 16J *

60 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ
Решение. Применяя указанную выше схему, имеем:
[гл. и
к
ьк
Ч
Pk
Qk
— 1
i
0
0
1
0
0
1
1
1
2
1
2
2
3
4
4
11
3
5
8
37
98
4
7
16
620
1645
Отсюда
Q«
_i. ?з — 5Z. ^4_ 62Q
11 ; Q3""~98; Q4~1645'
Теорема 2. Для двух соседних подходящих дробей
и -тг цепной дроби (\) справедлива формула
k-i
v к ^ Л—» *
Доказательство. Имеем:
Р* Рк-г
D')
E)
где
Pk Pk-i
Qk Qk-i
Используя соотношения C) и C'), в силу известных свойств
определителя получаем:
akQk.i+bkQk_a Qft_x =** Qft_2
Отсюда последовательно будем иметь:
где
Ро Р-1
0
1 0
==— 1.
Таким образом,
и, следовательно, на основании формулы E) выводим:

§ 3]
ПОДХОДЯЩИЕ ДРОБИ
61
Р Р
Следствие 1. Если ~^ и -^(k> 1) — две соседние подхо-
дящие дроби цепной дроби A), то
Следствие 2. Для соседних подходящих дробей
1) обыкновенной цепной дроби справедливо равенство
Pk_ Pk^l = (— I)*
Як
Теорема 3. Для двух одинаковой четности соседних
подходящих дробей Aft- и -рг* (k^2) цепной дроби A) справедливо
Q/5-2 Qk
соотношение
Доказательство. Имеем:
Р* Pk_t _ Dk
Qk Qk-i~Qk-»Qk'
G)
где
Pk-,
Отсюда на основании закона составления подходящих дробей и
элементарных свойств определителя получаем:
где Д^ — определитель, рассмотренный в теореме 2. Согласно
следствию 1 теоремы 1 имеем:
откуда
Следовательно, используя соотношение G), получаем формулу F).
Следствие. Если ^^ и ——две соседние подходящие дроби
Як—2 Як
одинаковой четности для обыкновенной цепной дроби
то имеет место соотношение
F')

62 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. II
Теорема 4. Если все элементы конечной цепной дроби
положительны, то ее подходящие дроби четного порядка образуют
монотонно возрастающую последовательность, а подходящие
дроби нечетного порядка образуют монотонно убывающую
последовательность. При этом каждая подходящая дробь четного
порядка меньше любой подходящей дроби нечетного порядка.
Само же число а, выражаемое цепной дробью, содержится
между двумя соседними подходящими дробями.
Доказательство. Пусть имеем цепную дробь
• bl Ь-±
с положительными элементами ak и bk и пусть -~ (k = 0,1, ..., п) —
ее последовательные канонические подходящие дроби. Очевидно, что
Рк>0 и Qk>6.
Рассмотрим два случая.
1. Пусть & = 2/я— четное число. Тогда из соотношения F),
учитывая, что ak>0 и bt>0 (/ = 1, ..., ?), получаем:
Следовательно,
> d
(/»=!, 2, ...)
,-Р%»
Qim-t Qtn
или
2. Пусть А = 2/я + 1—нечетное число. Следовательно, k—1
будет четным числом. Тогда из того же соотношения F) будем иметь:
или
п п г»
(Ю)
Таким образом, доказанв, что четные подходящие дроби
образуют монотонно возрастающую последовательность, а нечетные —
монотонно убывающую (рис. 1).
Далее, если в соотношении D') положить k = 2m) то получим:
(И)

§ 3] ПОДХОДЯЩИЕ ДРОБИ 63
т. е. всякая подходящая дробь нечетного порядка больше
соседней подходящей дроби четного порядка. Отсюда заключаем, что любая
подходящая дробь нечетного порядка больше любой подходящей
, & I t -
Рис. 1.
дроби четного порядка. Действительно, пусть -д*3 — какая-нибудь
нечетная подходящая дробь. Если s^m, то
если же s > /я, то
Следовательно, при любых sum имеем:
fe>ft;- A2)
Наконец, из способа образования цепной дроби
имеем очевидные соотношения
*>?*, о
и т. д. Следовательно,
если к — четное число, и
если к — нечетное число. Очевидно, что для последней подходящей
дроби вместо строгих неравенств A3) и A3') мы будем иметь справа
равенство.
Следствие 1. Если элементы цепной дроби (8) положительны
г Pk
и д-2 — ее подходящие дроби, то справедлива оценка

64
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ
[гл. и
Действительно, так как согласно доказанному имеем:
Pk+i *
Qk+i Q
то на основании формулы D') получим оценку A4).
Следствие 2. Если цепная дробь а с положительными
элементами — обыкновенная и &—ее последовательные подходящие
Як
дроби, то
ос — Ph\^ l .
Як I ^~ ЯкЯк+i '
Замечание. Если элементы обыкновенной цепной дроби —
натуральные, то можно показать [1], что подходящая дробь— является
наилучшим приближением числа а, т. е. все остальные дроби —
со знаменателем
отклоняются от числа а больше, чем дробь ~ .
Як
• СО
Пример 3. Для дроби -^ предпоследней подходящей дробью
являлась 2| (см- пример 1). Поэтому
1
163
59"
58
1
< 0,001,
Пусть
§ 4. Бесконечные цепные дроби
A)
—бесконечная цепная дробь. Рассмотрим ее отрезок, т.е. конечную
цепную дробь
h ?. & .... y-g; («=1.2, з, ...).
B)
Определение. Бесконечная цепная дробь A) называется
сходящейся, если существует конечный предел
а=Нш
C)
причем число а принимается за значение этой дроби. Если же
предел C) не существует, то цепная дробь A) называется расходящейся
и ей не приписывается никакого числового значения.

§ 4] БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОби 65
Согласно критерию Крши [3] для сходимости последовательности
Р
-~*(л=1, 2, 3, ...) необходимо и достаточно, чтобы для каждого
8>0 существовало число N—N(z) такое, что
Р р
гп+тп г п
<гп<8
при п > N и любом m > 0.
Если Qk=^z0t то, очевидно, имеем:
р* - *± 4- Y (?1*—ilAzd \ D\
> v^ fPu Ри Л
Отсюда
т. е. сходимость цепной дроби A) эквивалентна сходимости ряда D').
Если цепная дробь A) сходится:
то в силу формул D) и D') имеем оценку-
Pk Pk-i
Qk Qk-i
< S
Теорема 1. Если все элементы ak> dk(k~O, 1, .,.) цепной
дроби A) положительны, причем
то цепная дробь A) — сходящаяся.
Док аз ательство. При доказательстве первой части теоремы 4
предыдущего параграфа не было использовано свойство конечности
цепной дроби. Поэтому, повторяя это доказательство, устанавливаем,
что если элементы цепной дроби A) положительны, то ее четные
Р
подходящие дроби -^(k — 0, 1, 2, ...) образуют монотонно воз-
V2fe
растающую последовательность, ограниченную сверху (например,
Р \
числом -~). Отсюда в силу известной теоремы заключаем, что
VI/
существует
Ь — йо ^ 2 h
3 Б. П. Демидович и И. А. Марон

66 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. II
Аналогично в условиях нашей теоремы нечетные подходящие дроби
*fe+1 (fe«=0, 1,2, ...) цепной дроби A) образуют монотонно убываю-
1 ( М
щую последовательность, ограниченную снизу! например, числом ^-l.
Следовательно, существует также
Ига
причем Р^а. Кроме того, для любого k^O имеем:
42k Q2k+1
поэтому, используя теорему 2 § 3, получим:
ath, F)
Покажем, что r\k—>О при k—*оо. В самом деле, на основании
эакона составления подходящих дробей при k^2 имеем:
Отсюда в силу условия E) теоремы выводим:
Следовательно,
2. G)
Из неравенства G) последовательно получаем:
О
так как Q1 = a1^A1. Перемножая неравенства (8) и (9), находим
и, значит,
Таким образом, r\k—*0 при k

§ 4] БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ 67
Поэтому, переходя к пределу при k—»оо в неравенстве F),
будем иметь О^р — а<:0, т. е.
а=р= lim ?*,
и, следовательно, цепная дробь A) сходится.
Замечание. Для сходящейся дроби A) с положительными
элементами ее значение а заключено между двумя последовательными
Р Р
подходящими дробями -"-1 и тг • Следовательно,
vh_i Чп
n
Следствие. Обыкновенная цепная дробь с натуральными
элементами всегда сходится.
Можно доказать [1] также следующую теорему.
Теорема 2. Каждое положительное число а можно разло~>
жить в обыкновенную сходящуюся цепную дробь с натуральными
элементами, причем это разложение единственно. Полученная
цепная дробь конечна, если а — рациональное число, и бесконечна,
если а—иррациональное число.
Пример. Разложить в цепную дробь число УТГ и найти его
приближенное значение.
Решение. Так как наибольшее целое число, заключающееся
в 1^41, есть 6, то имеем:
Отсюда
.6+J^4T
5
Наибольшее целое число, заключающееся в av есть 2, поэтому
A2)
Отсюда
5 _4+)/4Т о , 1
Аналогично
^Г2-УШ^ б —-г^" A3)
3*

68
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ
[гл. и
Мы замечаем, что а^ — а^ поэтому элементы цепной дроби будут
повторяться, т. е. цепная дробь получится периодической.
Производя последовательную подстановку в равенство A1) выражений A2),
A3), A4), A5) и т. д., получим:
/41 = 6 + Ц
12
Таким образом, иррациональное число У^Х выразилось
бесконечной периодической цепной дробью:
V *1 ^о; 2 , 2 , 12, 2 , 2 ' 12Э 2 ' 2 ' 12 • '"/'
Подходящие дроби ^(? = 0, 1, 2, ...) находим, пользуясь еле-
Як
дующей схемой:
Pk
Як
p-i-1
^-1 = 0
6
ро=6
2
13
2
2
32.
5
12 |
397
• 1
2
826
129
2
2049
320
12
...
...
Ограничиваясь, например, пятой подходящей дробью, мы будем
у ,— 2049
иметь приближенное значение к 41 по избытку: ]/41 = —--=
= 6,403125 с абсолютной погрешностью меньшей, чем
1 1
" 320 B-320+ 129) "" 320-769
<5.10~в.
Теорема 3 (Принсгейма). Если для бесконечной цепной
дроби
A6)
Г Ь± Ь^ Ь„ Л
выполнены неравенства
(л = 1, 2, ...),
A7)
го эта дробь — сходящаяся, причем абсолютное значение ее не
превышает единицы [4].

§ 4] БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ 69
р
Доказательство. Пусть ^ (&=1, 2, ...) —подходящие
дроби цепной дроби A6).
Так как
то
Отсюда, используя неравенство A7), получаем:
ИЛИ
IQ*|-|Q*-il>IM(|Q*-il-IQ*-tl). 08)
Последовательно применяя неравенство A8) и учитывая, что Q0=l
и Q_1==0, будем иметь:
Из неравенства A9) вытекает, что |QJ монотонно возрастает при
возрастании &, причем \Qk\ ^|Q0|=: 1.
Сходимость цепной дроби A6) эквивалентна сходимости ряда
Qk Qb
Рассмотрим ряд модулей
А \Ьг\\Ь%\ .,.
На основании неравенства A9) имеем:
Таким образом, частные суммы ряда B1) ограничены и,
следовательно, этот ряд сходится, причем
М1М >¦¦ \Ьк\ _ у
Но тогда, в силу признака сравнения, также сходится, и притом
абсолютно, ряд B0), т. е. существует

70 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. II
Кроме того, учитывая неравенство B2), имеем:
Замечание 1. Для сходимости цепной дроби A6) достаточно,
чтобы неравенство A7) имело место при п^т, причем Qk^=0
при k^m.
Замечание 2. В условиях теоремы 3 для значения цепной
дроби а имеем следующую оценку:
о;
В частности, если \Q
Pk
h\
\Q
\Q»
p,
f-l
Qk-i
. . .
*-x|IQ»
k
Z
a
\bk
(n
X3 I
Qn
¦<
1
2ft-
ipn
00
z
li 1
1
I Qn 1
1QH-
1
Qk\)
* CXD, TO
•
\Qk-i
\\Qk\
1
\Qn\
!_
, Urn l
11111 1 П
§ 5. Разложение функций в цепные дроби
Цепные дроби являются удобным аппаратом для представления
и вычисления функций. Подробности по этому вопросу изложены
в специальной литературе (см., например, [2]), а мы ограничимся
лишь рассмотрением отдельных примеров.
Заметим, что если функция f(x) с помощью какого-нибудь
приема разлагается в бесконечную цепную дробь, то в общем случае
нужно доказать сходимость этой дроби и убедиться, что
предельное значение цепной дроби равно функции f(x).
А. Разложение рациональной функции
в цепную дробь
Если
f(x) =
то в общем случае, производя элементарные преобразования, будем
иметь:
.1 ___ g10
Cqq -
Clo

§ 5]
где
РАЗЛОЖЕНИЕ ФУНКЦИЙ В ЦЕПНЫЕ ДРОБИ
71
Аналогично
где
= 0, 1, ...)
и т. д.
Таким образом
?20*
Гл. сю С2р* ^чо^
L сео сю с*е
причем легко убедиться, что цепная дробь A) получится конечной.
Коэффициенты разложений^ удобно последовательно вычислять
по формуле
С =—
/-1, О
где
у
Заметим, что в некоторых случаях коэффициенты Cjk могут
оказаться равными нулю. Тогда в разложение A) нужно внести
соответствующие изменения [2].
Пример 1. Разложить в цепную дробь функцию
Решение. Выписываем коэффициенты c/ft в следующую схему:
0
2
3
4
0
1
1
—4
—2
— 12
1
—5
—1
6
0
0
2
6
0
0
0
0

72 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕПНЫХ ДРОБЕЙ [ГЛ. II
Следовательно,
1
4*
— 4 + бд;
Б. Разложение е* в цепную дробь
Для е* Эйлер получил разложение [2]
1 ох х2 х2
Л. _f_ ^л _^ л
' 1 ' 5Т^' 6 ' 10 ' •" *
сходящееся для любого значения лс, действительного или
комплексного [2].
Отсюда получаем подходящие дроби:
Q. ~ 2—ж •
Р4_ 120 + 60л: + 1 2-у2
Q4~ 120—бОх+12*2—л;»
И Т. Д.
Полагая, в частности, #=1 и ограничиваясь четвертой
подходящей дробью, имеем
Для достижения той же точности нужно в разложении Маклорена
взять не менее восьми членов.
В. Разложение tgлг в цепную дробь
Для tg лг Ламбертом получено разложение
Гл х — х2 — х2 -х2 1
tg х = \0; т i -3"' ~5~*» * ' • > ъГ+Т »•••!» C)
сходящееся во всех точках непрерывности функции.
Пример 2. Найти приближенно tgl.
Решение. Полагая в формуле C) х = 1, будем иметь:

ЛИТЕРАТУРА КО ВТОРОЙ ГЛАВЕ
73
На основании формулы C) из § 3 составим следующую схему
для членов подходящих дробей:
k
Ok
Рк
-1 | 0 | 1
1
0
1 1 х
0
0
1
1
1
1
2
— 1
3
3
3
—1
5
14
9
4
1
7
95
61
Ограничиваясь четвертой подходящей дробью, будем иметь:
tgl «2^=1,557377
(по таблицам tg 1 = 1,557396).
Литература ко второй главе
1. А. Я. X и н ч и н, Цепные дроби, Гостехиздат, 1949, гл. I.
2. А. Н. Хованский, Приложение цепных дробей и их обобщений
к вопросам приближенного анализа, Гостехиздат, 1956, гл. I и II.
3. Г. М. Ф и х т е н г о л ь ц, Основы математического анализа, Гостехиздат,
1955, т. 1, гл. III.
4. О. Perron, Die Lehre von den Kettenbrtichen, Teubner, 1913, гл. VII»

ГЛАВА III
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ
При вычислении с помощью счетных машин значений функций,
заданных формулами, далеко не безразлично, в каком виде записана
соответствующая формула. Математически эквивалентные выражения
часто оказываются неравноценными с точки зрения приближенных
вычислений. Поэтому возникает практически важная задача о
нахождении для элементарных функций наиболее удобных аналитических
выражений. Вычисление значений функций обычно сводится к
последовательности элементарных арифметических действий.
Учитывая ограниченность объема памяти машины, желательно эти
операции разбивать на повторяющиеся циклы. Ниже мы рассмотрим
некоторые типовые приемы вычислений.
§ 1. Вычисление значений полинома. Схема Горнера
Пусть дан полином /z-й степени
Р(х) = аохп + а1х*~1 + . . Н-*„-!* + *„ 0)
с действительными коэффициентами ak(k = 0, 1, . . ., п). Положим,
что требуется найти значение этого полинома при лг = |:
B)
Вычисление числа P(Q удобнее всего производить следующим
образом. Представим формулу B) в виде
Отсюда, последовательно вычисляя числа
Ьг = ах + Ь0Ъ,
C)
находим

§ 1]
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ПОЛИНОМА. СХЕМА ГОРНЕРА
75
Покажем, что числа Ь0 = а0, Ь1У ... , Ьп_1 являются
коэффициентами полинома Q{x), полученного в качестве частного при делении
данного полинома Р(х) на двучлен х — |. В самом деле, пусть
i D)
E)
причем на основании теоремы Безу остаток от деления PW =
Из формул D) и E) получим:
или, раскрыв скобки и сделав приведение подобных членов, будем
иметь:
Сравнивая коэффициенты при одинаковых степенях переменной х
в левой и правой частях последнего равенства, получим:
Отсюда
Ро = ао =
что и требовалось доказать.
Таким образом, формулы C) позволяют, не производя деления,
определять коэффициенты частного Q(x), а также остаток Р(?).
Практически вычисления осуществляются по следующей схеме,
называемой схемой Горнера:

76 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ill
Пример 1. Вычислить значение полинома
Р(х) = Зх* + 2х2 — 5х + 7 при аг = 3.
Решение. Составляем схему Горнера:
,32—57 13
"г 9 33 84 '—
3 11 28 91 = РC)
Замечание. Пользуясь схемой Горнера, можно получить
границы действительных корней данного полинома Р(х).
Положим, что при лг=р (Р>0) все коэффициенты Ь{ в схеме
Горнера неотрицательны, причем первый коэффициент положителен,
т. е.
?0==а0>0 и Ь;^0 (/ = 1, 2,..., п). F)
Тогда можно утверждать, что все действительные корни xk
(*= 1, 2, ...,/»; ms^n) полинома Р(х) расположены не правее р,
т. е. лг?<Р(? = 1, 2, ...,/») (рис. 2).
В самом деле, так как
то при любом х> р в силу условия F) будем иметь Р{х) >0, т. е.
любое число, большее р, заведомо не является корнем полинома Р(х).
Таким образом, имеем верхнюю оценку для действительных корней xk
полинома.
Для получения нижней оценки корней xk составляем полином
(— \)п Р(— х) = аохп- а1хя'1+ ...+(—\)пап.
Для этого нового полинома находим такое число лг = а(а>0),
чтобы все коэффициенты в соответствующей схеме Горнера были
неотрицательны, за исключением пер-
.—i ^L но—--Й ¦> вого, который, очевидно, будет по-
~а V Р х ложительным. Тогда согласно преды-
рЙС 2. дущим рассуждениям для
действительных корней полинома (—\)п Р(—х),
очевидно, равных —xk{k=\y 2, ...,/»), имеем неравенство
k
Следовательно, xk^—а (&=1, 2, ... , т). Таким образом, мы
получили нижнюю границу—а действительных корней полинома Р(х).
Отсюда следует, что все действительные корни полинома Р(х)
расположены на отрезке [—а, Р].
Пример 2. Найти границы действительных корней полинома
Р (х) = *4 —

§ 2] ОБОБЩЕННАЯ СХЕМА ГОРНЕРА 77
Решение. Подсчитаем значение полинома Р(лг), например,
при х = 2. Пользуясь схемой Горнера, получим:
1-234-1
2 0 6 20
1 0 3 10 19
|9
Так как все коэффициенты bt ^ 0, то действительные корни хк
полинома Р(х) (если они существуют) удовлетворяют неравенству
xk<2. Верхняя граница действительных корней найдена. Перейдем
к оценке нижней границы. Составим новый полином:
Q(x) = (— 1LЯ(— х) = *4 + 2а:3 + Злг2 — 4*— 1.
Подсчитывая значение полинома Q (лг), например, при х = 1, имеем:
1 2 3—4—1
13 6 2
13 6 2 1
м
L1
Все коэффициенты bt>0, значит, —*л<1, т. е. xk>—1.
Итак, все действительные корни данного полинома находятся
внутри отрезка [—1, 2].
§ 2. Обобщенная схема Горнера
Пусть в данном полиноме
Р(х) = аохп + а1хп-1+ ... + ап A)
по каким-.то соображениям требуется произвести замену
переменной х по формуле
B)
где ?—фиксированное число и у—новая переменная.
Подставив выражение B) в полином A) и произведя указанные
действия, после приведения подобных членов получим новый
полином относительно переменной у:
Р{у + 1) = Аоуп + А,уп-1+...+Ап. C)
Так как полином C) можно рассматривать как разложение
Тейлора по степеням у функции Р(у-\-%), то коэффициенты At
(i~0, I, ... , п) могут быть вычислены по формуле
Л, = -
Укажем более удобный на практике способ отыскания
коэффициентов i4;(/ = 0, 1, 2, ... ,я) с помощью схемы Горнера. Положим
сначала у~0 в выражении C). Тогда будем иметь i4rt = P(|).

78 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Разделив полином A) на двучлен х—?, получим:
P(x) = (x-l)P1(x) + P(l)i D)
где
Далее, если в выражение C) вместо j> подставить его значение
у — х—\, то будем иметь:
. E)
Сопоставляя формулы D) и E), заключаем, что
Р1{х) = А0{х-1)-1 + А1{х-1)-*+...+Аи_1. F)
Отсюда
Аналогично, разделив полином Рх{х) на двучлен х—|, можем
положить:
1), (8)
где Рг {х) = c/"s + с^"-8 + ... + с„_2.
Кроме того, из формул F) и G) имеем:
Сопоставляя формулы (8) и (9), заключаем, что
Отсюда Ап_г = Рг&).
Продолжая этот процесс далее, мы последовательно выразим все
коэффициенты /4((/ = 0, 1, ... , л) через значения соответствующих
полиномов Р0(х) = Р(х) и Рг{х), ... ,Рп(х)==а0 при * = |:
Ла -=Р F);
Ло =Ра{1),
где полиномы Pk+l{x), исходя из полиномов Pk(x), строятся по формуле
(А = 0, I,..., я).

§ 3] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ РАЦИОНАЛЬНЫХ ДРОБЕЙ 79
Для вычисления значений Р(|), ^iE)> ^2 (Е)» ••• пользуемся
обобщенной схемой Горнера:
aQ ах a2 az ... ап_1 ап |?
Пример. Чтобы уничтожить в полиноме
Р (х) = х* — Sx3 + 5х2 + 2х — 7
член, содержащий третью степень неизвестной, полагают
Найти преобразованный полином.
Решение. Применяем обобщенную схему Горнера:
1
1
1
1
1
—8
2
-6
2
—4
2
to to
5
-12
— 7
— 8
—15
4
— 19
2
—14
—12
—30
—42
— 7
-24
—31
Следовательно,
в — 42у —31.
§ 3. Вычисление значений рациональных дробей
Всякую рациональную дробь R{x) можно представить в виде
отношения двух полиномов, т. е.
где
Q (л;) =

80 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. III
Пусть нам требуется определить значение R(x) в точке # = ?:
Числитель РA) и знаменатель Q(Q дроби B) можно найти,
пользуясь схемой Горнера. Отсюда получаем простой способ
вычисления числа /?(?).
Другой способ вычисления состоит в преобразовании функции
R (х) в цепную дробь. Для этого можно воспользоваться способом,
указанным в главе II, § 3.
§ 4. Приближенное нахождение сумм числовых рядов
Определение. Числовой ряд
Я1 + я2+ ...+<*„+... A)
называется сходящимся, если существует предел последовательности
его частных сумм
S = limSnJ B)
Л-> 00
где
Sn=at + at+...+an.
Число 5 называется суммой ряда.
Таким образом, сходимость ряда A) эквивалентна сходимости
последовательности его частных сумм. Согласно критерию Коши [1]
эта последовательность сходится тогда и только тогда, когда для
любого е>0 существует N = N(e) такое, что
при n>N и произвольном /?>0.
Из формулы B) получаем:
S = Sn + Rn, C)
где Rn—остаток ряда, причем Rn—>0 при п—> оо.
Для нахождения суммы S сходящегося ряда A) с заданной
точностью е нужно выбрать число слагаемых п столь большим,
чтобы имело место неравенство
|Я„1<е- D)
Тогда частная сумма Sn приближенно может быть принята за
точную сумму 5 ряда A).
Заметим, что на практике слагаемые av a2, ... также
определяются приближенно. Кроме того, сумма Sn обычно округляется
до заданного числа десятичных знаков. Чтобы учесть все эти
погрешности и обеспечить нужную точность, можно применить
следующую методику: выберем, в общем случае, три положительных
числа ev e2 и е3 такие, что

§ 4] ПРИБЛИЖЕННОЕ НАХОЖДЕНИЕ СУММ ЧИСЛОВЫХ РЯДОВ 81
Возьмем число п членов ряда столь большим, чтобы остаточная
погрешность \Rn\ удовлетворяла неравенству
|Я«1<в1- E)
Каждое из слагаемых ak(k=\, 2, ... , п) вычислим с предельной
абсолютной погрешностью, не превышающей —, и пусть ак
(k= 1, 2, ... , п) — соответствующие приближенные значения членов
ряда A), т. е.
Тогда для суммы
погрешность действий (суммирования) удовлетворяет неравенству
|3.-5.|<в,. _ F)
Наконец, полученный приближенный результат Sn округлим до более
простого числа Sn с таким расчетом, чтобы погрешность
округления была
|5й-5„|<е8. G)
В таком случае число Sn является приближенным значением
суммы S ряда A) с заданной точностью 8. Действительно, из
неравенств E) —G) имеем:
Разбиение числа е на положительные слагаемые е^ е2 и е3
следует производить, сообразуясь с потребным объемом работы для
получения искомого результата. Если е — 10~w и результат должен
содержать m верных десятичных f 2 Н
знаков после запятой, то чаще ~jgm ^m ~щяг
всего принимают: 0* '—> « »—« «-J—' ^
8 8 8
ei = T» 82 = Т' Ьь^Т* Рис« 3*
Если заключительное округление отсутствует, то обычно полагают:
8 8 л
e e е °
Задача усложняется, если нужно найти сумму ряда с точностью
до m верных десятичных знаков после запятой в узком смысле
слова. Геометрически это значит, что требуется найти элемент
k
множества r^ (k — целое), ближайший к числу «S (рис. 3).

82 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Пусть для определенности сумма S положительна и
{pk — целые неотрицательные числа, п^т) — рациональное
приближение такое, что
I5 $\ ^
Допустим, что
^4 И
Тогда, округляя число 5, получнм искомый результат:
S3, (8)
или
^^] (8')
Действительно, в первом случае, при округлении по недостатку
мы имеем:
^ 10л + 1 ' Ют+г ' ' * '. Юл 10/
Во втором случае, при округлении по избытку, получим:
Поэтому в обоих случаях имеем:
iSoK 4
и, следовательно,
Таким образом,
Если рст+1г=4 или pm+i = 5, то следует увеличить точность
вычислений приближенной суммы S, привлекая очередной десятичный
разряд.

§ 4] ПРИБЛИЖЕННОЕ НАХОЖДЕНИЕ СУММ ЧИСЛОВЫХ РЯДОВ
В частном случае, если /?я+1 = 4 и известно, что
S<Sy
то о (8) есть приближенное значение суммы 5 с точностью до -^
(по недостатку).
Аналогично, если рт+1==5 и
83
то о (8') есть приближенное значение суммы 5 с точностью до у • \0~
(по избытку).
Для оценки остатка ряда A)
полезны следующие теоремы, которые мы приводим без
доказательств [I].
Теорема 1. Если члены ряда A) представляют собой
соответствующие значения положительной монотонно убывающей
функции /(#), т. е.
an=f{n) (л=1, 2, ...), (9)
то (рис. 4)
J f(x)dx<Rn< \f(x)dx.
Теорема 2. Если ряд A)—знакочередующийся:
<*! > О, Я2<0, Яд>0, ...

84 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ill
и модули его членов монотонно убывают, то
Пример. Найти сумму ряда
с точностью до 0,001.
Решение. Примем остаточную погрешность
6l_ 4 iu -4000.
Члены ряда A0) представляют собой соответствующие значения
монотонно убывающей функции
Поэтому для п-то остатка ряда
00
имеем оценку
Решая неравенство
2л2 "^ 4000 J
получим:
п ^Т/2000 ^44,7.
Примем п = 45.
Предельную погрешность суммирования выберем равной
отсюда допустимая предельная абсолютная погрешность слагаемых
частной суммы ?45 ряда A0) есть:
т # 10~3 к
п ^ 45 "" 9 lU '
Rn, т. е. sgn Rn = + \, если /?„>0;
sgn
*) sgn Rn обозначает знак числа Rn, т. е. sgi
/?я = —I, если #„<0; sgn/?w = 0, если #й=0.

§ 4] ПРИБЛИЖЕННОЕ НАХОЖДЕНИЕ СУММ ЧИСЛОВЫХ РЯДОВ 85
Положим
п
т. е. члены ряда A0) будем вычислять с пятью верными, в узком
смысле, десятичными знаками после запятой. Ниже выписаны
соответствующие значения слагаемых и результаты частичного
суммирования:
1,00000
0,12500
0,03704
0,01562
0,00800
0,00463
0,00292
0,00195
0,00137
0,00100
0,00075
0,00058
0,00046
0,00036
0,00030
0,00024
0,00020
0,00017
0,00014
0,00012
0,00011
0,00009
0,00008
0,00007
0,00006
0,00006
0,00005
0,00004
0,00004
0,00004
0,00003
0,00003
0,00003
0,00003
0,00002
0,00002
0,00002
0,00002
0,00002
0,00002
0,00001
0,00001
0,00001
0,00001
0,00001
1,19998 0,00151 0,00029
Следовательно,
S45 = 1,19998 + 0,00151 + 0,00029 = 1,20178.
Округляя это значение до тысячных, получим приближенное
значение суммы
5 «1,202.
Так как погрешность округления
83 = 0,00022 <^-. 10~3,
то суммарная погрешность найденного результата не превышает
е<-| • 10 + -р 10-3 + 1. ю-8<|.. ю-з.
Таким образом,
5= 1,202 ±0,001.
Оценку можно провести точнее, если учесть знаки округлений. Для
сравнения приводим значение суммы 5 с точностью до -^ • 10[2]:
5=1,202057.

86 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Замечание. Так как расчет суммарной погрешности
представляет собой весьма трудоемкую операцию, то на практике для
обеспечения заданной точности 8 = 10"™ все промежуточные вычисления
производят с одним или двумя запасными знаками. При этом не
вполне строго предполагают, что допущенные погрешности не
повлияют на десятичные знаки w-ro разряда искомого результата.
Заметим, что при решении этого примера приходилось находить
сумму сравнительно большого числа слагаемых. На практике данный
ряд стараются предварительно преобразовать так, чтобы для
достижения искомого результата можно было ограничиться малым
количеством членов. Такого рода преобразование называется улучшением
сходимости ряда и во многих случаях значительно экономит время
вычислений. Этот вопрос рассмотрен в главе VI.
§ 5. Вычисление значений аналитической функции
Действительная функция f(x) называется аналитической в точке !-,
если в некоторой окрестности |лг — ?|<С# этой точки функция
разлагается в степенной ряд (ряд Тейлора):
f(x)=f(l)+f(l)(x-t) + Q^(x--tJ+...
При % = 0 получаем ряд Маклорена
Разность
называется остаточным членом и представляет собой ошибку при
замене функции f(x) полиномом Тейлора
Как известно [1],
где 0<9<1. В частности, для ряда Маклорена B) имеем [1]:
„+1 D)
где 0<9-<1. Имеются также другие формы остаточных членов.

§ 5] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 87
Разложение функции в ряд Тейлора во многих случаях является
удобным способом вычисления значений этой функции.
Если /(?) известно и требуется найти значение /(? + А), где
h — «малая поправка», то формулу A) выгодно записывать в виде
^h*+...+^p-hn+Rn(h), E)
где
Пример. Приближенно найти J/T6.
Решение. Имеем:
(). F)
Полагая
последовательно получим:
дг) = 1
ь
Отсюда, приняв ? = 0, А = -к- и учитывая, что
в силу формулы E) находим:
а _ J_ J^ L. JL4-J ? I-/? —
= 1 + 0,05556 —0,00154+ 0,00009+ /?з = 1,05411+/?31 G)
где
24 16 V ^ 9 J 6561 ~"
10
1680 616

88 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Очевидно,
Из формул F) и G) получаем:
/ГО = 3,16233 + Е, (8)
где
|fi|<3~. Ю-6 + 3-6- Ю-8 = 3,3- Ю-5.
Округляя найденное значение до четырех знаков после запятой,
окончательно будем иметь:
/Т0==3,1623±6'10-5.
Для сравнения приводим табличное значение
VT0 = 3,1622777 ...
§ в. Вычисление значений показательной функции
Для экспоненциальной функции ех справедливо разложение [I]
**=1+* + ?+... + ?+..., A)
интервал сходимости которого —оо< лг<С + оо. Остаточный член
ряда A) имеет вид
RW x"+1 B
При больших по модулю значениях х ряд (I) мало пригоден для
вычислений. Поэтому обычно поступают следующим образом: пусть
где Е(х) — целая часть числа х и 0^#<1—дробная часть его.
Имеем:
е — е • ?". {о)
Первый множитель произведения C) может быть найден с помощью
умножения:
Е {х) раз
еЕ(Х)__ее ^ если В{Х)^0,
или
-Е_{х) Раз
^w=:i.i .., I, если Е(х)<0,
6 6 6

§ 6] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ 89
где
^ = 2,71828 18284 59045...
и
-!-=0,36787 94411 71442 ...,
в
причем е или —, для обеспечения заданной точности, следует взять
с достаточно большим числом десятичных знаков (в настоящее время
число е определено свыше чем с 250 десятичными знаками).
Что касается второго множителя eq произведения C), то для
вычисления его пользуются приведенным выше разложением
e<?=2-ir> D)
n — o
которое при 0s^#< 1 образует быстро сходящийся ряд, так как
на основании формулы B) для остаточного члена Rn(q) имеем оценку
Выведем более точную формулу для оценки остатка Rn{q) при
0 < q < 1. Имеем:
И + 1 Пп+% /7«+3
fT1 , q
^ (t+l)!
Отсюда, суммируя геометрическую прогрессию, стоящую в
квадратных скобках, получим:
или при О<0<1, учитывая, что
п+1^ п
окончательно будем иметь:
т. е.
где ип==~—последний сохраненный член.

90 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Если остаточная погрешность е задана, то необходимое число
членов п можно найти подбором, решая неравенство
п\ п ^ -
Приближенное вычисление ех по формуле A) для малых х удобно
производить по схеме
где
ио=1, «А = ——^ (*= 1, 2, ..., л). (8)
На счетных машинах вычисления удобно вести по схеме
X
x
где 0ф=1, 5в1 = 0, 50=1. Число ?л = ^-гг приближенно дает
искомый результат е*.
Если е — заданная допустимая остаточная погрешность и п^
^2|л:|>0, то процесс суммирования следует прекратить, как
только будет выполнено неравенство
1
п+2
т. е. если
|«nWI<e. (9)
Иными словами, процесс суммирования прекращается, если
последний выработанный член ип по модулю не превышает е, при этом
Для расчета суммарной погрешности следует пользоваться
общей схемой (§ 4). __
Пример 1. Найти Ye с точностью до 10~6.
Решение. Принимаем остаточную погрешность

§ 6!
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
91
Так как тогда число слагаемых в сумме G), по грубой прикидке,
порядка десяти, то слагаемые подсчитываем с точностью до у • 10~7,
т. е. с двумя запасными десятичными знаками.
Полагая
последовательно имеем:
1
и1 = у = 0,5000000
и3 = ^ = 0,0208333
а4 = ^ = 0,0026042
й5 = ^ = 0,0002604
г/6 = ^ = 0,0000217
И7 = т^ = <
1,6487212
Округляя сумму до пяти десятичных знаков после запятой, получим:
/7=1,64872, (Ю)
с суммарной погрешностью
е<" l,6-10~e + 5'-rr» 10~7+1,2-10~в = 3,05» 10~6 <! -тг • Ю,
т. е. все знаки результата A0) верные в узком смысле.
Для вычисления ех можно использовать также разложение в
цепную дробь [4]
(И)
е "I I ' 2 + ~х' Т> ТО •••'
сходящуюся для любого значения х (действительного или
комплексного).
Пример 2. Найти Vе, пользуясь формулой A1).

92
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ
[ГЛ. III
Решение. Полагая в формуле A1) х = у, составляем таблицу
подходящих дробей для соответствующей цепной дроби.
к
ak
Pk
Qk
— l
l
l
0
0
0
1
0
1
1
1
1
1
1
2
—1
5
2
5
2
3
2
3
1
4
6
61
4
37
4
4
1
4
10
1225
8
743
8
5
1
4
14
34 361
16
20 841
16
Останавливаясь на 5-й подходящей дроби, имеем:
1/Т~Р» 34361.20841 34361 fi4R791
У е да07 = -Тб-:-Тб 20841=1,648721
С ТОЧНОСТЬЮ ДО -J • 10~в.
Для вычисления значений общей показательной функции а* (а> 0)
можно использовать формулу
§ 7. Вычисление значений логарифмической функции
Для натуральных логарифмов чисел, близких к единице,
справедливо разложение [1]
In
ЛГ "О "t~ Q A \ ' * *
& О *г
A)
Формула A) малопригодна для вычислений, так как диапазон чисел
0<1+лг^2 невелик и, кроме того, при | х |, близком к единице,
ряд A) сходится медленно.
Введем более удобную формулу для вычислений натуральных
логарифмов чисел. Заменяя х в формуле A) на —лг, будем иметь:

§ 7] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ 93
Вычитая почленно из формулы A) формулу B), находим:
Полагая
1-х
получим:
и, следовательно,
при
Пусть х — положительное число. Представим его в виде
где т — целое число и -tr^z<il. Тогда, полагая
где
о<5< f
и применяя формулу C), будем иметь:
1 п х = 1 п 2 лг =т 1 п 2 +1 п z =
где
t2rt+8
При 0<?^-^-имеем:
2 9
1 —ga —= 4
и поэтому
q p2t
°<*.<т
или, более грубо,

94 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. III
Введя обозначение
?2fc~l
получим:
2^ + ^+...+*/„)-/?„, E)
где
1п2 = 0,69314718 ...
Процесс суммирования прекращается, как только
и» < 4е>
где е—допустимая остаточная погрешность, так как тогда в силу
формулы D) имеем:
Предельную погрешность суммы 2ил можно оценить^ задавшись
определенным количеством десятичных знаков слагаемых и
установив на основании формулы D) примерное число слагаемых п*
Пример. Найти In 3 с точностью до 10~6.
Решение. Вычисления будем производить с двумя запасными
знаками. Положим
Отсюда z = 0,75 и
&
Имеем:
±-0 1428571
7 -^14^0/1.
иг = ^ = 0,1428571
и3 = -у- = 0,0000119
и4 = -^- = 0,0000002
0,1438410
Используя формулу E), получаем:
In 3 = 2-0,69314718 —2.0,1438410=1,09861.
Замечание. Можно также вычислять натуральные логарифмы
чисел, исходя из представления
х = epz,
где р—целое число и — <С«г^1 (см. {5]).

§ 8]
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
95
Для вычисления десятичных логарифмов используется формула
= М\п АГ,
где
=\ge = 0,43429 44819 03252 ...
§ 8. Вычисление значений тригонометрических функций
А. Вычисление значений синуса и косинуса
С помощью формул приведения аргумент х можно заключить
в отрезок
-у. Если 0
4 '
Bл+ 1)!'
то имеем:
A)
если же -j- ^ х ^-^-, то полагают
B)
где ^==~ л; и
-~.
Сумму ряда A) удобно вычислять процессом суммирования
sinx = u1 + u2+ ...+un + Rn, C)
где слагаемые uk(k — \, 2, ..., п) последовательно находятся с
помощью рекуррентного соотношения
Так как ряд A) знакочередующийся с монотонно убывающими,
по модулю, членами, то для остаточного члена Rn справедлива
оценка
Поэтому процесс суммирования можно прекратить, как только
будет обнаружено, что
где е —заданная остаточная погрешность.

96 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Аналогично
где
и
= K+il> sgn/?w = sgnt>n
Пример. Найти sin20°30' с точностью до 10".
Решение. Имеем:
х = arc 20°30' = ~- + ~g = 0,349066 + 0,008727 = 0,357793,
Применяя формулу C), получим:
Ul = x= 0,357793 '
иг = ^ = — 0,007634
и8 = |^-2= +0,000049
И4 = ^-3=—0,000000
— 0,350208
Отсюда
sin 20°30'=: 0,35021.
Аналогично вычисляются значения cosat.
Б. Вычисление тангенса
Можно считать, что 0<лг^^~. Для tgx при 1лг|<:-5- спра-
ведливо разложение [6]
*» , 2а:5 , 17л:7 62л:»
+ + + +
Коэффициенты разложения выражаются через числа Бернулли
(см. гл. XVI, § 12).
Значение тангенса просто вычисляется с помощью цепных
дробей. Полагая
Х
в силу формулы Ламберта (гл. II, § 6) будем иметь;
_ Г1 -*а -а:2 -х* 1
У-[1; "Г"» Т~} •••' 2/1 + г •"]•

§ 8] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 97
Для вычисления у с точностью до 10~10 достаточно принять
п = 7. Тогда
у=\ -х2:C — Jt2:E — x2:G — х2:(9 —
— л:2: A1 — х2; A3 — л:2:15)))))). D)
Вычисление у обычно производится с помощью схемы Горнера
для деления (начиная с конца):
^=13 — д;2:15,
= 7-х2-Уз,
Отсюда tgx = —,
Пример. Найти tg40°.
Решение. Имеем:
х = arc 40° = 0,698132
Отсюда
^ig388 12,967508;
о 0,487388 9СШ
•^«~ d~4,929928 = 2|9;
„_« - 1 °-487388 Л8Ч9ПП1
У-У1- г-2,901137 = °'832001
й, следовательно,
В полученном результате все знаки верные.
4 Б- п- Демидович и И. А. Марой

98 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
§ 9. Вычисление значений гиперболических функций
А. Вычисление значений гиперболического синуса
Как известно,
причем
sh (—х)= — sh*.
Для гиперболического синуса справедливо разложение
$hx = x-\-^+~+... (-оо<л;<+оо).
Предполагая, что лг>0, вычисления удобно производить процессом
суммирования
sh х = их + щ + ...+ип + Rrr
где
и х ^ ^ (kh 2 Л1)
и /?rt — остаточный член. При п^х> 0 имеем:
<
Bп+\)\
х2л + 1 1 4 х*п+х 4
< <
Так как, очевидно,
tf«+1 — 2л Bя +
ТО
Б. Вычислениезиаченийгиперболическогокосинуса
Как известно,
ch х = g »
причем
ch (— лг) = ch лг.
• Для* гиперболического косинуса справедливо разложение
Вычисления удобно производить процессом суммирования
chх = v1 + v2+ ... +vn + Rn,

§ 9] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ 99
где
и /?„ — остаточный член. При /z^|je|>0 имеем:
Х2П
_
" Bл)!
U
Х2П Г
Bл) 1 L
j
Bn)l
V2« 1 A ir2W A
^ Л 1 ^^, « Л ТЕ
]^Bn+l) B/1 + 2)
Так как при л^1 справедливо неравенство
х2 <LV
то
В. Вычисление гиперболического тангенса
Имеем:
chx e^ + e
где
При малых |л:| для вычисления значений гиперболического
тангенса можно использовать разложение
При любом х значение гиперболического тангенса выражается
цепной дробью
«1*=Г0;4-. ?- i, ....
2/1-1
причем так как при лс>0 элементы этой дроби положительны,
то \hx при х>0 заключен между двумя соседними подходящими
дробями.
Если х > 0 велико, то i\\x удобно вычислять, применяя формулу
4*

100 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. III
§ 10. Применение метода итерации для приближенного
вычисления значений функции
Пусть требуется вычислить значение непрерывной функции
У=/(х) A)
для заданного значения аргумента х. Если функция A) достаточно
сложна и нужно подсчитать большое количество ее значений, то
вычисления обычно производятся на счетных машинах. Может
случиться, что в силу конструктивных особенностей машины
непосредственное вычисление значений функции по формуле A) будет
затруднительным. При этом самые простые действия могут оказаться
«сложными» и даже невыполнимыми. Так, например, существуют
счетные машины «без деления». Тогда во многих случаях оказывается
полезным следующий прием. Запишем функцию A) в неявном виде
) = 0. B)
Предположим, что F(x, у) непрерывна и имеет непрерывную
частную производную Fy(x, y)^0.
Пустьуп—приближенное значение у. Применяя теорему Лагранжа,
будем иметь:
F(x, yn) = ()
где уп — некоторое промежуточное значение между уп и у. Отсюда
Значение уп нам не известно. Полагая упжупу для вычисления
значения у получим итеративный процесс [7]
(« = о, 1. 2, ...). W
У«р7Г7\
г у \х* Уп)
Формула C) имеет простой геометрический смысл. Зафиксируем
значение х и рассмотрим график функции
z = F(x, у). D')
Из формулы D) вытекает, что наш процесс представляет собой
метод Ньютона (см. гл. IV, § 5), примененный к функции D),
т. е. последовательные приближения уп+г получаются как абсциссы
точки пересечения с осью Оу касательной к кривой D),
проведенной при у =уп(п~0, 1, 2, ...) (рис. 5). Сходимость процесса
будет обеспечена, если
Fy{x} у) и F*yy(xyy)

§ 11]
ВЫЧИСЛЕНИЕ ОБРАТНОЙ ВЕЛИЧИНЫ
101
сохраняют постоянные знаки в рассматриваемом интервале,
содержащем корень у.
Начальное значение у0, вообще говоря, произвольно и выбирается
по возможности близким к искомому значению у. Процесс
итерации продолжается до тех пор, пока
в пределах заданной точности е два z
последовательных значения^ъуп-х не
совпадут между собой: \уп_г—Уп\< е*
При этом, строго говоря, не
гарантируется, что
\у-У*\<*> E)
поэтому в каждом конкретном случае
требуется дополнительное
исследование.
Достоинством итеративных процес-
сов является однообразие операций и
вследствие этого сравнительно легкая
программируемое^. рис 5,
Заметим, что представление
F(x,y) = 0 для заданной функции A)
можно реализовать бесчисленным множеством способов. Этим следует
воспользоваться, чтобы получить быстро сходящийся итерационный
процесс. В следующих параграфах приведены типы основных
процессов.
Пусть у =
§11. Вычисление обратной величины
1
Для определенности будем считать, что х^>0. Положим
1
тогда
Применяя формулу D) § 10, будем иметь:
1
п + 1
=Уп
X
Уп
1
или
т. е. мы получили итерационный процесс, не содержащий деления.
Начальное значение у0 выбирается следующим образом. Пусть

102 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ill
аргумент х записан в двоичной системе:
х = 2тх1, где т — целое число иу<^<1,
Тогда полагают
Выясним условия сходимости процесса A). Из формулы A) имеем:
отсюда
Для сходимости процесса D) необходимо и достаточно, чтобы было
выполнено неравенство
или
-1<1 -хуо< 1.
Таким образом, окончательно получаем следующий результат: если
0<лгу0<2, E)
то
Л-* С» Л
Заметим, что при нашем выборе ^0B) имеем:
поэтому
F)
и, значит, условие E) выполнено. Кроме того, из формулы C)
выводим:
1 / 1
дс V 2
т. е. сходимость итерационного процесса чрезвычайно быстрая.
Выведем другую оценку ошибки значения уп1 иногда практически
более удобную. Прежде всего, заметим, что последовательные
приближения уо~ yv y2 ... в данном случае получаются по методу
Ньютона, примененному к гиперболе
Z = х (А? = Const)

§ 11] ВЫЧИСЛЕНИЕ ОБРАТНОЙ ВЕЛИЧИНЫ 103
(рис. 6). Из неравенства F) и формулы C) следует, что
""" — (п = 0 1 2 ).
G)
Кроме того, так как
то последовательные приближения уй монотонно возрастают:
^ г
Из формулы G) имеем:
~х Уп-!^ хУп 2 (-У»
или так как
то
Отсюда
1
Рис 6.
Таким образом, если будет обнаружено, что ^„—*
и истинная погрешность
c, то
Пример. С помощью A) найти значение функции у = —
при л: = 3.
3 1
Решение. Здесь х = 22~. Полагаем j/0 = -j-, тогда
j;a = 0,312B—3-0,312) = 0,332 и т. д.
Процесс итерации быстро сходится.

104
Пусть
Положим
тогда
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ
§ 12. Вычисление квадратного корня
у =
(X > 0).
[гл. ш
A)
F(x, y)E=zy2-x =
Применяя формулу D) § 10, имеем:
ИЛИ
B)
= 0, 1, 2, ...)—процесс Герона.
Последовательные приближения у0, у1% у21 ..., очевидно,
получаются по методу Ньютона,
примененному к параболе
z=y2—х (х = const)
(рис. 7).
Заметим, что если за у0
принять табличное значение,
дающее Ух с относительной
погрешностью | б |, тоjflf опре-
деленное по формуле B),
даст значение Ух
приблизительно с относительной по-
1 А2
грешностью -д-о .
Действительно, полагая
и пренебрегая степенями б, выше 3-Й, будем иметь:
Отсюда получаем важный вывод: при применении процесса Герона
число верных цифр примерно удваивается на каждом этапе по
сравнению с первоначальным количеством.

§ 12] ВЫЧИСЛЕНИЕ КВАДРАТНОГО КОРНЯ 105
Пример 1. Лдяу = ]/Г2 приближенно имеем:
Уточняя это значение, получаем:
Л = 1 A,4 + ^) =0,7 + 0,714= 1,414.
Еще раз повторяя процесс, будем иметь:
причем восемь или семь десятичных знаков являются верными.
Действительно,
j/*2== 1,41421356...
Выясним условия сходимости процесса Герона. Из формулы B),
заменяя п+\ на п> при >>0=7^0 имеем:
Отсюда
Следовательно,
j?-K, D)
где
Из формулы D) вытекает, что процесс Герона сходится при
МО.
т. е. если
В этом случае, очевидно, имеем:
причем
П (л=1, 2, ...).

106 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Заметим, что
4(^) %^>о- F)
поэтому приближения уп при п^\ образуют монотонно убывающую
последовательность
Ух ^У2 ^ • • • >Л-1 > Л > > V^*).
При работе на счетной машине число лс удобно записывать
в двоичной системе
x = 2mxXi где /я—целое число и ^^хг < 1.
Тогда за нулевое приближение обычно принимают:
е(-)
J>e = 2 K*\ G)
где ?Dг)—целая часть числа -^-.
Пример 2. Найти |/5".
Решение. Здесь лг = 5 = 23-^-. Поэтому
По формуле B) последовательно находим:
у2 = i- B,25 + 2^5) = j B,25 + 2,2222) = 2,2361
и т. д. По таблицам квадратных корней имеем:
1/5 = 2,236068...
Оценим величину \д\, выражаемую формулой E), исходя из
значения у0, определяемого формулой G).
Если т — 2р есть число четное, то имеем:
и, следовательно,
1+1/4-
¦) Знак равенства может иметь место только при 1/0 =

§ 12J ВЫЧИСЛЕНИЕ КВАДРАТНОГО КОРНЯ 107
Аналогично, если т = 2р-\-\ есть число нечетное, то
р(—\
Поэтому
_У2^-\_. 2 2
Таким образом, всегда имеем:
Отсюда на основании формулы D) получим:
при
где
Отсюда
Из формулы (8) легко можно определить число итераций # =
достаточное для обеспечения заданной точности.
Приведем еще одну формулу для оценки погрешности значения
Уп(п^*2). Так как
У п —1
то, учитывая формулу F), имеем:
Следовательно,
Таким образом, если 0^.уп^г—уп < е (п ^ 2), то гарантировано,
что 0^j/w — |/*лг < е.
Укажем еще один способ вычисления квадратного корня,
оказывающийся иногда полезным. Заменим функцию A) эквивалентным
соотношением
«)==* 1=0.

108 ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Тогда
Применяя формулу D) § 10, получим:
У3п
ИЛИ
/ у2\
Выяснение условий сходимости итеративного процесса A0) и
оценку погрешности мы оставляем без рассмотрения.
§ 13. Вычисление обратной величины квадратного корня
Положим
у = 1= (*>0).
Записав функцию в виде
из формулы A0) предыдущего параграфа получим итеративный
процесс «без деления»
Уп+1 = УлC—Ху*п) (л = 0, 1, 2, ...). A)
Если x — 2mxv где -о-^л;1<1, то за у0 выбирается значение
Заметим, что, пользуясь очевидным равенством
в силу формулы A) извлечение квадратного корня из числа можно
производить также «без деления».
§ 14. Вычисление кубического корня
Если
у = Ух (*>0), A)
то, положив
F(x, j;)=>r3 —лг = О,

§ 14J ВЫЧИСЛЕНИЕ КУБИЧЕСКОГО КОРНЯ
будем иметь:
У
Отсюда, применяя формулу D) § 10, получаем:
109
ИЛИ
B)
C)
Геометрически процесс C) представляет собой метод Ньютона,
примененный к кубической параболе
? = у5 — х (х = const)
(рис. 8). Процесс C) сходится при у0 > 0.
Если в качестве начального приближения^ взять табличное
значение \/х, имеющее
относительную погрешность |б|, т. е.
положить
то значение^, найденное из
формулы C), даст у/х с
относительной погрешностью б2.
Действительно, применяя формулу C),
имеем:
* B+28+1— 26 + 362)=
Рис. 8.
Отсюда, в частности, заключаем, что если у0 имеет р верных знаков
в узком смысле, то уг будет иметь примерно 2р или 2р—1 верных
знаков в широком смысле (ср. § 12).
Пример. По трехзначным таблицам имеем:
10 = 2,154,
где все знаки верные.

ПО ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ [ГЛ. Ш
Применяя формулу C), получаем:
1 (^) ==у B-2,154 + 2,155304)==: 2,154435.
^Т0 = ()
Для сравнения приводим значение из таблиц Барлоу
10 -2,1544347...
целое ч
ное значение у0 обычно выбирают
Если х = 2тх1У где т — целое число и у < хг < 1, то за
начальл 0. D)
Так как
rt— I
ТО
Л^^^ ПРИ л^1. E)
Кроме того, из формулы B), заменяя я+1 на л, имеем:
Уп-г-Уп-%^1 F)
поэтому
Отсюда вытекает, что существует
lim иУд=ву>0.
/г -> оо
Переходя к пределу при п—^оо в равенстве C), будем иметь:
т. е. уг = х и, следовательно, у — \/х. Таким образом,
Если начальное приближение у0 выбирается на основании фор-
мулы D), то можно доказать, что
при п ^ 2.

ЛИТЕРАТУРА К ТРЕТЬЕЙ ГЛАВЕ 111
Литература к третьей главе
1. В. И. С м и р н о в, Курс высшей математики, т. I, изд. 17, Гостехиздат,
М., 1957, гл. IV.
2. А. Марков, Исчисление конечных разностей, изд. 2, Матезис, 1911,
гл. III.
3. Г. П. Толсто в, Курс математического анализа, т. II, Гостехиздат, М.,
1957, гл. XXIV.
4. А. Н. Хованский, Приложение цепных дробей и их обобщений к
вопросам приближенного анализа, Гостехиздат, 1956, гл. II.
б. Б. М. Каган и Т. М. Т е р-М и к а э л я н, Решение инженерных задач
на автоматических цифровых вычислительных машинах, Госэнергоиз-
дат, М.— Л., 1958, гл. III.
6. Г. М. Фихтенг о л ь ц, Курс дифференциального и интегрального
исчисления, ОГИЗ, М.— Л., 1948,"т. II, гл. XII.
7. Л. А. Люстерник, А. А. Абрамов, В. И. Шестаков, М. Р. Шура-
Бура, Решение математических задач на автоматических цифровых
машинах, Изд. АН СССР, 1952.

ГЛАВА IV
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ
И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
§ 1. Отделение корней
Если уравнение алгебраическое или трансцендентное достаточно
сложно, то его корни сравнительно редко удается найти точно.
Кроме того, в некоторых случаях уравнение содержит
коэффициенты, известные лишь приблизительно, и, следовательно, сама задача
о точном определении корней уравнения теряет смысл. Поэтому
важное значение приобретают способы приближенного нахождения
корней уравнения и оценки степени их точности.
Пусть дано уравнение
0, A)
где функция f(x) определена и непрерывна в некотором конечном
или бесконечном интервале а < х < Ь.
В дальнейшем в некоторых случаях нам понадобится
существование и непрерывность первой производной /' (х) или даже второй
производной /"(#), что будет оговорено в соответствующих местах.
Всякое значение ?, обращающее функцию f(x) в нуль, т. е.
такое, что
называется корнем уравнения A) или нулем функции f{x).
Мы будем предполагать, что уравнение A) имеет лишь
изолированные корни, т. е. для каждого корня уравнения A) существует
окрестность, не содержащая других корней этого уравнения.
Приближенное нахождение изолированных действительных корней
уравнения A) обычно складывается из двух этапов:
1) отделение корней, т.е. установление возможно тесных
промежутков [a, |J], в которых содержится один и только один
корень уравнения A);
2) уточнение приближенных корней, т. е.
доведение их до заданной степени точности.
Для отделения корней полезна известная теорема из
математического анализа ([5], гл. IV).

§ 1]
ОТДЕЛЕНИЕ КОРНЕЙ
113
Теорема 1. Если непрерывная функция f(x) принимает
значения разных знаков на концах отрезка [а, C], т. е. /(а)/(р)<0,
то внутри этого отрезка
содержится по меньшей мере один
корень уравнения f(x) = 0, т. е.
найдется хотя бы одно число
6 6 (а, Р)*) такое, что /(g) = 0
(рис. 9).
Корень | заведомо будет
единственным, если производная
f'(x) существует и сохраняет
постоянный знак внутри
интервала (а, р), т. е. если /'(#)>О
(или /'(*)<0) при а<дг<р
(рис. 10).
Процесс отделения корней
О
Рис. 9.
х — а и х = Ь области ее суще-
начинается с установления знаков
функции f(x) в граничных точках
ствования.
Затем определяются знаки функции f(x) в ряде промежуточных
точек x =
a2>
Рис.
выбор которых учитывает особенности
функции f(x). Если окажется, что
/(ал)/(ал+1)<0, то в силу
теоремы 1 в интервале (<xft, ccft+i)
имеется корень уравнения/(дг)—0.
Нужно тем или иным способом
убедиться, является ли этот
корень единственным. Дляотделения
корней практически часто бывает
достаточно провести процесс
половинного деления,
приближенно деля данный интервал
(а, р) на две, четыре, восемь и т. д.
равных частей (до некоторого
шага) и определяя знаки функции
f(x) в точках делений. Полезно помнить, что алгебраическое
уравнение п-й степени
имеет не более п действительных корней. Поэтому если для такого
уравнения мы получили п-\-\ перемену знаков, то все корни его
отделены.
Пример 1. Отделить корни уравнения
0. B)
*) Запись ? g (a,P) обозначает, что точка 6 принадлежит интервалу (а,Р).

114 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Решение. Составляем приблизительную схему:
X
— 00
--3
— 1
0
f (х)
+
+
X
1
3
+ 00
fix)
4
+
Следовательно, уравнение B) имеет три действительных корня,
лежащих в интервалах (—3, —1), (О, 1) и A, 3).
Если существует непрерывная производная f'(x) и корни
уравнения
/'(*)--о
легко вычисляются, то процесс отделения корней уравнения A) можно
упорядочить. Для этого, очевидно, достаточно подсчитать лишь знаки
функции f(x), в точках нулей ее производной и в граничных точках
х = а и х — Ь.
Пример 2. Отделить корни уравнения
= x* — 4х — 1=0. C)
Решение. Здесь /' (х) = 4 (х3 — 1), поэтому /' (х) = 0 при
х= 1.
Имеем/(-оо)>0( + );/A)<0(-); /(+оо)>0(+).
Следовательно, уравнение C) имеет только два действительных корня, из
которых один лежит в интервале (— оо, 1), а другой — в интервале
A, +00).
Пример 3. Определить число действительных корней уравнения
f(x)=x + e* = 0. D)
Решение. Так как /' (х)= 1 +е* > 0 и /( — оо)=—оо,
/(+оо)= +оо, то уравнение D) имеет только один действительный
корень.
Дадим теперь оценку погрешности приближенного корня.
Теорема 2. Пусть ? — точный, а х — приближенный корна
урцвнения f(x) = 0, находящиеся на одном и том же отрезке
[а, ($], причем \f (лг) [^ ш1 > 0 при а^лг^Р*).
В таком случае справедлива оценка
!/(*)!
E)
*) В частности, за тг можно взять наименьшее значение \f'(x)\ ПРИ

§ 1] . ОТДЕЛЕНИЕ КОРНЕЙ 115
Доказательство. Применяя теорему Лагранжа, будем иметь:
где с — промежуточное значение между х и ?, т. е. с?(а,
Отсюда, так как/(?) = 0 и \f (c)\^mv получим:
Следовательно,
\х-Ъ\<
I/WI
Замечание. Формула E) может дать грубые результаты, и ее
не всегда удобно применять. Поэтому на практике тем или иным
способом сужают общий интервал (а, р), содержащий корень ? и
его приближенное значение х, и полагают \х — ?|^Р —ос.
Пример 4. Приближенным корнем
уравнения /(лг)=злг4-дг— 1 =0 является
х= 1,22. Оценить абсолютную погрешность
этого корня.
fffi \
х
/Г
Рис. 11.
7? «"
Рис. 12.
Решение. Имеем /(х) = 2,2153 — 1,22— 1 = — 0,0047.
Так как при лг = 1,23 получаем
= 2,2888— 1,23— 1= +0,0588,
то точный корень ? содержится в интервале A,22; 1,23).
Производная f'(x) = 3x3—1 монотонно возрастает. Поэтому ее наименьшим
значением в данном интервале является:
m1 = 3.1,228 —1=3.1,816—1=4,448.
Отсюда по формуле E) получим:

116 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Замечание. Иногда на практике точность приближенного
корня дг оценивают по тому, насколько хорошо он удовлетворяет
данному уравнению f(x) = О, т. е. если число |/(#)| малое, то считают,
что х является хорошим приближением точного корня ?; если же
\/{х)\ велико, то х полагают грубым значением точного корня ?.
Такой подход, как показывают рис. 11 и 12, является неправильным.
Не следует также забывать, что если уравнение f{x) = О умножить
на произвольное число Af=^O, то получается равносильное уравнение
Nf(x) = 0, причем число \Nf(x)\ можно сделать сколь угодно
большим или сколь угодно малым за счет выбора множителя N.
§ 2. Графическое решение уравнений
Действительные корни уравнения
/(х) = 0 A)
приближенно можно определить как абсциссы точек пересечения
графика функции y~f(x) с осью Ох (рис. 9). Если уравнение A)
не имеет близких между собой корней, то этим способом его корни
легко отделяются. На практике часто бывает выгодно уравнение A)
заменить равносильным ему уравнением*)
ф (х) — г|э (а:), B)
где функции у(х) и ip (л;) — более простые, чем функция f(x).
Тогда, построив графики функций у~у(х) и y = ty(x)y искомые
корни получим как абсциссы
У
Рис. 13.
точек пересечения этих
графиков.
П р и м е р 1. Графически
решить уравнение
x\gx=l. C)
Решение. Запишем
уравнение C) в виде
равенства
1в*
Отсюда ясно, что корни уравнения C) могут быть найдены как
абсциссы точек пересечения логарифмической кривой y~\gx и
гиперболы ^ = —. Построив эти кривые (рис. 13) на координатной
*) Два уравнения называются равносильными, если они имеют
одинаковые корни.

§ 2]
ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
117
бумаге, приближенно найдем единственный корень ?»2,5
уравнения C).
Нахождение корней уравнения B) упрощается, если одна из
функций <р(х) или г|) (х) линейная, т. е., например, ф (х) = ах + b. В этом
случае корни уравнения B) находятся как абсциссы точек
пересечения кривой у = ^(х) и прямой у = ах-\-Ь. Особенно выгодным
оказывается этот прием при
решении ряда однотипных
уравнений, отличающихся
только коэффициентами а
и b линейной функции. Здесь
графическое построение
сводится к нахождению
точек пересечения
фиксированного графика y = ty(x)
различными прямыми. К
указанному типу, очевидно,
относятся трехчленные
уравнения
Рис. 14.
Пример 2. Решить ку-
бические уравнения
л;3— 1,75*+ 0,75 = О
Xs + 2х + 7,8-0.
Решение. Построим
кубическую параболуву=л:3.
Искомые корни находятся
как абсциссы точек пересечения этой параболы прямыми (рис. 14)
у=\,75х—0,75 и у——2х — 7,8. По чертежу ясно, что первое
уравнение имеет три действительных корня: хг =—1,5; л;2 = 0,5;
лг3 = 1, а второе уравнение —лишь один действительный корень
^ = —1,65.
Отметим, что хотя графические методы решения уравнений
весьма удобны и сравнительно просты, но они, как правило, применимы
лишь для грубого определения корней. Особенно неблагоприятным
в смысле потери точности является случай, когда линии
пересекаются под очень острым углом и практически сливаются по
некоторой дуге.
Разновидностью графических методов решения уравнений
являются номографические методы, для ознакомления с которыми
следует обратиться к специальным руководствам.

118 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
§ 3. Метод половинного деления
Пусть дано уравнение
/(*) = (>, 0)
где функция f(x) непрерывна на [а, Ь] и /(#)/(#) <0.
Для нахождения корня уравнения A), принадлежащего отрезку
[а, Ь], делим этот отрезок пополам. Если /(""о/— ^» то ^^
является корнем уравнения. Если /(^-~— ] =^=0» то
= 4-- является корнем уравнения. Если /(]
раем ту из половин а, ~4— или —у-» И > на концах которой
функция f{x) имеет противоположные знаки. Новый суженный
отрезок [dv bx] снова делим пополам и проводим то же рассмотрение
и т. д. В результате получаем на каком-то этапе или точный корень
уравнения A), или же бесконечную последовательность вложенных
друг в друга отрезков [av bx]y [a2, b2], .. ., [ая, bn]f ... таких, что
/(«„)/(*„)< 0 (л=1, 2, ...) B)
и
Ьп-аа = ±(Ь-а). C)
Так как левые концы av а2, . . ., ап, .. . образуют монотонную
неубывающую ограниченную последовательность, а правые концы
bv Ьг, ..., Ьп} ...—монотонную невозрастающую ограниченную
последовательность, то в силу равенства C) существует общий
предел
Переходя к пределу при п—> оо в неравенстве B), в силу
непрерывности функции /(х) получим [/(?I2<0. Отсюда /(g) = 0,
т. е. ^ является корнем уравнения A), причем, очевидно,
0<|-а„<1(?--а). D)
Если корни уравнения A) не отделены на отрезке [а, А], то
таким способом можно найти один из корней уравнения A).
Метод половинного деления практически удобно применять для
грубого нахождения корня данного уравнения, так как при
увеличении точности значительно возрастает объем вычислительной работы.
Заметим, что метод половинного деления легко реализуется на
электронных счетных машинах. Программа вычисления составляется
так, чтобы машина находила Значение правой части уравнения A)
в середине каждого из отрезков [а^ Ьп] (/2=1, 2, ...) и
выбирала соответствующую половину его.

§ 4]
СПОСОБ ПРОПОРЦИОНАЛЬНЫХ ЧАСТЕЙ (МЕТОД ХОРД)
119
Пример. Методом половинного деления уточнить корень
уравнения
/ (х) = х* + 2*3 — х— 1 = О,
лежащий на отрезке [0, 1].
Решение. Последовательно имеем:
,25 —0,5 —1 = —1,19;
/@,75) = 0,32 + 0,84 — 0,75 — 1 = — 0,59;
/@,875) = 0,59 + 1,34 — 0,88 — 1 = + 0,05;
/@,8125) = 0,436+ 1,072 —0,812—1 = -0,304;
/@,8438) = 0,507+1,202—0,844—1 = — 0,135;
/@,8594) = 0,546+1,270— 0,859— 1 = —0,043 и т.д.
Можно принять
?=1@,859+0,875)^0,867.
§ 4. Способ пропорциональных частей (метод хорд)
Укажем (в предположениях § 3) более быстрый способ
нахождения корня ? уравнения f(x)~0, лежащего на заданном отрезке
[а, Ь) таком, что f(a)f(b) < 0.
Пусть для определенности f(a) < 0 и/(?)>0. Тогда, вместо
того чтобы делить отрезок [а,Ь] пополам, более естественно разделить
его в отношении—f(a)*f(b).
Это дает нам приближенное
значение корня
где
Далее, применяя этот прием р
к тому из отрезков [а, хг] или
[xv b), на концах которого функция f(x) имеет противоположные
знаки, получим второе приближение корня х2 и т. д.
Геометрически способ пропорциональных частей эквивалентен
замене кривой y=f(x) хордой, проходящей через точки A [a, f(a)]
и В№> /(*)] (Рис- 15). В самом деле, уравнение хорды АВ есть
дс-fl у-Ца)

120 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
Отсюда, полагая х = хх и у = 0, получим: . .
г. /«\
ЛЬ-а).
[ГЛ. IV
Формула (Г) полностью эквивалентна формулам A) и B).
Для доказательства сходимости процесса предположим, чтокорень
отделен и вторая производная f" (х) сохраняет постоянный знак
на отрезке [a, b].
Пусть для определенности /" (х) > 0 при а^х^Ь (случай
/" (х) < 0 сводится к нашему, если записать уравнение в виде
Рис. 17.
—/(аг) = О). Тогда кривая у=/(х) будет выпукла вниз и,
следовательно, расположена ниже своей хорды АВ. Возможны два
случая: 1) f(a)>0 (рис. 16) и 2) /(а)<0 (рис. 17).
В первом случае конец а неподвижен и последовательные
приближения: лго = #;
X „ _|_ 1 -—* X л* —*""* ——-—-———————-- I jQ I Д I \П —— V. 1 • А| •••/ l^F
И"ГА fl Г I V 1 Г l/ll > П 'х ' * * ' х'
образуют ограниченную монотонно убывающую последовательность,
причем
а < I < ... < хп+1 <хп<...<х1<х0.
Во втором случае неподвижен конец bt а последовательные
приближения: х0 = а;
i- __ г Нхп) /1 Y \ 1Л\
образуют ограниченную монотонно возрастающую
последовательность, причем
п+1
< ...

§ 4J СПОСОБ ПРОПОРЦИОНАЛЬНЫХ ЧАСТЕЙ (МЕТОД ХОРД) 121
Обобщая эти результаты, заключаем: 1) неподвижен тот конец,
для которого знак функции f(x) совпадает со знаком ее второй
производной f(x)\ 2) последовательные приближения хп лежат
по ту сторону корня ?, где функция f(x) имеет знак,
противоположный знаку ее второй производной /" (лг). В обоих случаях
каждое следующее приближение хп+1 ближе к корню ?, чем
предшествующее хп. Пусть
Ъ^Шхп (a<J<d)
(предел существует, так как последовательность {хп} ограничена
и монотонна). Переходя к пределу в равенстве C), для первого
случая будем иметь:
отсюда /(|) = 0. Так как по предположению уравнение /(лг) = О
имеет единственный корень ? на интервале (а, Ь)} то,
следовательно, ? = |, что и требовалось доказать.
Совершенно так же переходом к пределу в равенстве D)
доказывается, что ? = ? для второго случая.
Для оценки точности приближения можно воспользоваться
формулой (б) § 1
где I/' (х)\^т1 при
Приведем еще формулу, позволяющую оценивать абсолютную
погрешность приближенного значения лгл, если известны два
последовательных приближения хп_х и хп.
Будем предполагать, что производная /' (х) непрерывна на
отрезке [а, Ь]у содержащем все приближения, и сохраняет
постоянный знак, причем
О < mt < |/' (х) | <МХ < + оо. E)
Примем для определенности, что последовательные приближения хп
точного корня ? вырабатываются по формуле C) (рассмотрение
формулы D) аналогично)
JfJf-(*""a)
(л=в1, 2, ...), где конец а является неподвижным. Отсюда,
учитывая, что /(|) = 0, будем иметь:
f(Y \ __fi(xn-i) — fi(a) (г г \

122 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Применяя теорему Лагранжа о конечном приращении функции,
получим:
?»-i €(¦*„-1> I) и хп_1^(а, xn_j). Следовательно,
Так как /'(л:) сохраняет постоянный знак на отрезке [а, Ь]> причем
**-i€la> *1 и &n-i €1^> *1> то, очевидно, имеем:
Поэтому из формулы F) выводим:
где за /их и Мх могут быть взяты соответственно наименьшее и
наибольшее значения модуля производной /' (х) на отрезке [а, Ь]. Если
отрезок [а, Ь] столь узок, что имеет место неравенство
то из формулы G) получаем:
1Б-^Я|<|^Я-^П.1|.
Таким образом, в этом случае, как только будет обнаружено, что
l*»-*,,-il<e.
где е — заданная предельная абсолютная погрешность, то
гарантировано, что
|6-*„|<е.
Пример. Найти положительный корень уравнения
/(*)=== *3 — 0,2л:2 — О32лг — 1,2 = 0
с точностью до 0,002.
Решение. Прежде всего отделяем корень. Так как
/A)=-0,6<0 и /B) = 5,6>0,
то искомый корень \ лежит в интервале A, 2). Полученный
интервал велик, поэтому разделим его пополам. Так как
/A,5) = 1,425, то 1< К 1,5.

§ 5] МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ) 123
Последовательно применяя формулы A) и B), будем иметь:
11 "'" /1С 1\ 1ГЛ1ГГ 11 ?.
/(*!)=-0,173;
лга = 1,15+1 ^S+0 Q73 A,5 —1,15) = 1,15 + 0,040= 1,190;
/(^а)= —0,036;
Х3= 1,190+ { 42ь°11 036A|5--1,190) = 1,190+ 0,008 =1,198;
f(xs)= —0,0072.
Так как /' (х) = Зх2 — 0,4лг — 0,2 и при лг3<лг<1,5 имеем
/(л:)>3.1,1982—0,4-1,5 —0,2 = 3.1,43—0,8 = 3,49,
то можно принять:
Таким образом, 5=1,198 + 0,0029, где 0<9<1.
Заметим, что точный корень уравнения E) есть 6 = 1,2.
§ 5. Метод Ньютона (метод касательных)
Пусть корень 5 уравнения
/(*)=0 A)
отделен на отрезке [а, Ь], причем f'(x) и f(x) непрерывны и
сохраняют определенные знаки при а<:х^Ь. Найдя какое-нибудь
/z-e приближенное значение корня хп « | (а^лгп^^), мы можем
уточнить его по методу Ньютона следующим образом. Положим
B)
где hn считаем малой величиной. Отсюда, применяя формулу
Тейлора, получим:
Следовательно,
и _ Ы*п)
Внеся эту поправку в формулу B), найдем следующее (по
порядку) приближение корня
Хп+1~ Хп ;' и \ (Л = 0, 1, 2, ...). C)

124
АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ, IV
Геометрически метод Ньютона эквивалентен замене.небольшой
дуги кривой y=f(x) касательной, проведенной в некоторой точке
кривой. В самом деле, положим для определенности, что f (х) > О
при я<Ж# и /F)>0 (рис. 18).
Выберем, например, хо = Ь, для которого f{xo)f"(xo) > 0.
Проведем касательную к кривой y=f(x) в точке BQ [х0, f(xQ)].
О
Рис. 18.
В качестве первого приближения хг корня g возьмем абсциссу точки
пересечения этой касательной с осью Ох. Через точку B1[xvf(x1)]
снова проведем касательную, абсцисса точки пересечения которой
даст нам второе приближение х2 корня ? и т. д. (рис. 18).
Очевидно, что уравнение касательной в точке Вп [хп,/(хп)] (я = 0, 1,2, ...)
есть
Полагая у — О, x=*xn+v получим формулу C)
Заметим, что если в нашем случае положить xQ = а и,
следовательно, f(xo)f" (х0) < 0, то, проведя касательную к кривой у = /(х)
в точке А[а, /(#)], мы получили бы точку лг, (рис. 18), лежащую
вне отрезка [at b]y т. е. при этом выборе начального значения
метод Ньютона оказывается непрактичным. Таким образом, в данном
случае «хорошим» начальным приближением х0 является то, для
которого выполнено неравенство
^о)>О. D)
Докажем, что это правило является общим.
Теорема. Если f(a)f(b)<Oy причем /' (х) и/"(х) отличны
от нуля и сохраняют определенные знаки при а ^ х ^ Ь, то,

§ 5] МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ) 125
исходя из начального приближения х0 ? [a, b]y удовлетворяющего
неравенству D), можно вычислить методом Ньютона (формула C))
единственный корень | уравнения A) с любой степенью точности.
Доказательство. Пусть, например, /(а) < 0, /(#)>0,
/'(.*;)> О, /"(л;)>0 при а^.х^Ь (остальные случаи
рассматриваются аналогично). Согласно неравенству D) имеем f(x0) >0
(например, можно принять хо = Ь).
Методом математической индукции докажем, что все
приближения #„>?(# —О, 1, 2, ...) и, следовательно, f(xn) > 0. В самом
деле, прежде всего, х0 > ?.
Пусть теперь хп > \. Положим
Применяя формулу Тейлора, получим:
0 = /(|) =/(*,) +/' (х„) (| -хп) + у/" (с„) (|-хп)\ E)
где 1 < с„ < j?B.
Так как /"(х)>0, то имеем:
и, следовательно,
*. у. /i \хп) n. t
что и требовалось доказать.
Из формулы C), учитывая знаки f(xn) и /'(лгя), имеем
лгп+1 < агп(л = О, 1, ...), т. е. последовательные приближения
хо,хи ..., л:„, ... образуют ограниченную монотонно убывающую
последовательность. Следовательно, существует ^~
Переходя к пределу в равенстве C), будем иметь:
т. е. /(g) = 0. Отсюда g = g, что и требовалось доказать.
Поэтому, применяя метод Ньютона, следует руководствоваться
следующим правилом: в качестве исходной точки х0 выбирается
тот конец интервала (а, Ь), которому отвечает ордината того же
знака, что и знак f" (x).
Замечание 1. Если: 1) функция f(x) определена и
непрерывна при — оо<лг< + оо; 2) /(<*)/(*)< 0; 3) /'(х)фО при
а^.х^Ь; 4) f (х) существует всюду и сохраняет постоянный
знак, то при применении метода Ньютона для нахождения корня
уравнения /(лг) = О, лежащего в интервале (а, Ь), за начальное

126 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
приближение лг0 можно принять любое значение с ? [«,?]¦ В
частности, можно взять хо = а или хо = Ь.
Действительно, пусть, например, /' (л:) > 0 при a^ix^b,
/" (х) > 0 и хо = с, где а < с < Ь.
Если /(с) = 0, то корень ? = с и задача, таким образом, решена.
Если f(c) > 0, то справедливо приведенное выше рассуждение
и процесс Ньютона с начальным значением с сходится к корню
I € (а, *).
Наконец, если /(с) < 0, то находим значение
Xl~Xo i'W~ t'(c)
Применяя формулу Тейлора, будем иметь:
где с —некоторое промежуточное значение между с и хх.
Таким образом,
Кроме того, из условия /*(#)> О вытекает, что f (х)—
возрастающая функция и, значит, /' (х) > /' (а) > 0 при х>а.
Следовательно, хг можно принять за начальное значение для процесса
Ньютона, сходящегося к некоторому корню | функции f(x) такому,
что |>с^а. Так как в силу положительности производной /' (х)
при х > а функция f(x) имеет единственный корень на интервале
(а, +оо), то
! = ?€(*, *)•
Аналогичное рассмотрение можно провести для других комбинаций
знаков производных /' (х) и /" (х).
Замечание 2. Из формулы C) видно, что чем больше численное
значение производной /' (х) в окрестности данного корня, тем
меньше поправка, которую нужно прибавить к /г-му приближению,
чтобы получить (п-\-\)~е приближение. Поэтому метод Ньютона
особенно удобно применять тогда, когда в окрестности данного
корня график функции имеет большую крутизну. Но если
численное значение производной /' (х) близ корня мало, то поправки
будут велики, и вычисление корня по этому методу может оказаться
очень долгим, а иногда и вовсе невозможным. Следовательно, если
кривая y=f(x) вблизи точки пересечения с осью Ох почти
горизонтальна, то применять метод Ньютона для решения
уравнения f(x) = 0 не рекомендуется.

§ 51
МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ)
127
Для оценки погрешности я-го приближения хп можно
воспользоваться общей формулой E) § 1
где mt — наименьшее значение | /*' (at) | на отрезке [а, Ь].
Выведем еще одну формулу для оценки точности приближения хп.
Применяя формулу Тейлора, имеем:
/(*„) =/[*„-!+ (¦*»-*»-!)] =
где |я-1
имеем
„_1> лгя). Так как в силу определения приближения хп
то из G) находим:
I/W К ^ л, (*„-*„_!)«,
где Ж2—наибольшее значение
\f" {х)\ на отрезке [а, Ь].
Следовательно, на основании формулы F)
окончательно получаем:
* Если процесс Ньютона сходится,
то xn — xn-i—*0 при п—юо.
Поэтому при п ^N имеем:
|5-*я К | *„-*„_! I,
Рис. 19.
т. е. «установившиеся» начальные десятичные знаки приближений
л:„_1 и хп, начиная с некоторого приближения, являются верными.
Заметим, что в общем случае совпадение с точностью до е двух
последовательных приближений хп_г и хп вовсе не гарантирует, что
с той же точностью совпадает значение хп и точный
корень I (рис. 19).
Установим также формулу, связывающую абсолютные погрешности
двух последовательных приближений хп и лгя+1. Из формулы E)
получаем:
1Ы1 Г
где сп ^ (лг„, 5)- Отсюда, учитывая формулу C), будем иметь:
—Х 1 . I" (Cn) /t у 42

128 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
и, следовательно,
\-хп)\ (9)
Формула (9) обеспечивает быструю сходимость процесса Ньютона,
если начальное приближение х0 таково, что
В частности, если
то из формулы (9) получаем:
I % y
I ь x
и 1&-
|
т. е. в этом случае, если приближение хп имело /и верных
десятичных знаков после запятой, то следующее приближение хп+1 будет
иметь по меньшей мере 2т верных знаков; иными словами, еслиц, ^ 1,
то с помощью метода Ньютона число верных знаков после запятой
искомого корня ? удваивается на каждом шаге.
Пример 1. Вычислить методом Ньютона отрицательный
ко* 2
рень уравнения
ными знаками.
Решение.
— 100, ...,
р
f(x) = x* — Зх2 + 1Ьх— 10 000 = 0 с пятью
верПолагая в левой части уравнения je = O, —10,
получим /@)=—10 000, /(— 10)= — 1050,
8
Следовательно, искомый корень ? находится в интервале
—100<|< —10. Сузим найденный интервал. Так как /(—11) =
= 3453, то — 11 < \ < — 10. В этом последнем интервале /' (х) < 0
и.Г(*)>0. Так как /( — П)>0 и/"( —11)>0, то можем
принять за начальное приближение х0——11. Последовательные
приближения хп(п=\, 2, ...) вычисляем по следующей схеме:
п
0
1
2
3
— 11
— 10,3
— 10,27
— 10,261
3453
134,3
37,8
0,2
f (х \
— 5183
— 4234
— 4196
0,7
0,03
0,009
—
Останавливаясь на я = 3, проверяем знак значения
/(*„ +0,001) =/(— 10,260). Так как /(— 10,260) < 0, то
— 10,261 < ? < — 10,260, и любое из этих чисел дает искомое
приближение.

§ 5]
МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ)
129
Пример 2. Найти по методу Ньютона наименьший
положительный корень уравнения tg.x: = .*; с точностью до 0,0001.
Решение. Построив
графики кривых y = tgx и у=х
(рис. 20), заключаем, что искомый
корень ? находится в интервале
я<?<-2~. Переписав
уравнение в виде
f(x) = sin x — х cos x = 0,
будем иметь:
f(x) = xsinx;
f" (x) = sin x + х cos x.
Отсюда/ (х) < 0 и /"(#) < 0
при я<лг<-^. Так как
) —1> то за
началь\ f
Рис. 20.
ное приближение можно принять лго =
по следующей схеме:
Зя
Y • Вычисления производим
п
0
1
2
-^=4,71239 B70°)
4,50004 B57°50')
4,49343 B57°27/16")
t(xn)
— 1
—0,0291
— 0,00003
—4,712
—4,399
и 1(хп)
Ь' (хп)
—0,212 (=5s—12°10')
—0,0066 (=5:—22'44Ж)
Для оценки погрешности приближенного значения a:w заметим,
что последовательные приближения хп(п = 0, 1, 2, ...)в силу
отрицательности второй производной f"(x) монотонно убывают,
причем f(xn) < 0. Поэтому можно принять хп < ? < лгп, где д;п —
значение из интервала f я, -~) такое, что /(хй) > 0.
Значение лгп легко найти подбором*). Так, например, при п — 2,
VI V ^онечно' можно было бы взять хп = п, но это невыгодно, так как
L \Jt>) = 0.
5 Б. П. Демидович и И. А. Марон

130 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
полагая приближенно
х2 = 4,49340 = arc 257°27'12",
будем иметь:
J (#2) = sin 257°27'12"-4,49340*cos 257°27'12" =
= —0,97612 + 4,49340-0,21724==
= —0,97612 + 0,97614= +0,00002.
Следовательно, х2 выбрано правильно и
4,49340 < I < 4,49343.
Можно положить
1 = 4,4934,
где все знаки верные.
Оценку погрешности значения х2 нетрудно провести более точно.
Так как при х ? [лг2, х2] производная f'(x) убывает и/' (х) < 0, то
т1 = min |/' (лг) | = |/' (лг2) |.
Отсюда
^ = 4,49340.0,97612 > 4
и, следовательно,
Рис, 21.
Таким образом,
5 = 4,49343 — 0,00001 9,
где О<0< 1.
Пример 3. Рассмотрим
уравнение , v
f(x) = 09 A0)
1де f"(x) непрерывна и сохраняет постоянный знак при
— oo<#< + oo. В силу теоремы Ролля уравнение A0) не может
иметь более двух действительных корней. Отметим два важных для
практики случая.
I. Пусть
(рис. 21).
Тогда уравнение A0) имеет единственный корень ?в интервале
(х0, хг), где
Корень ^ может быть вычислен с заданной точностью методом
Ньютона.

§ 6]
ВИДОИЗМЕНЕННЫЙ МЕТОД НЬЮТОНА
131
II. Пусть
/'(*о) = О, f(xo)f"(x)<O.
Тогда уравнение A0) имеет два корня g и ?' в интервале
( —оо, +оо) (рис. 22).
Преобразуя левую часть уравнения A0) по формуле Тейлора,
приближенно имеем:
или
Г
Отсюда для корней ? и ?' получаем начальные приближения
— if 2А
± — Xq у г„
(*о)
xt = .
представляющие собой абсциссы точек пересечения параболы
с осью Ох (рис. 23). Дальнейшие уточнения корней могут быть
произведены обычным методом Ньютона.
Рис. 22.
Рис. 23.
Утверждения I и II геометрически очевидны. Строгое
доказательство предоставляем провести читателю.
§ в. Видоизмененный метод Ньютона
Если производная f'(x) мало изменяется на отрезке [а, А], то
в формуле C) предыдущего параграфа можно положить:

132
АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Отсюда для корня
тельные приближения
уравнения /(х)=0 получаем последова-
^п+1
= 0, 1, ...).
B)
Геометрически этот способ означает, что мы заменяем касательные
в точках Вп [хп, f(xn)] прямыми, параллельными касательной к
кривой y = f(x)y в ее фиксированной точке В0[х0У f(x0)] (рис. 24).
Формула A) избавляет нас от необходимости вычислять каждый
раз значения производной /' (хп); поэтому эта формула весьма
п *•
</=№
х3 х2 xf
Рис. 24.
полезна, если f'(xn) сложна. Можно доказать, что в
предположении постоянства знаков производных /' (х) и f"(x)
последовательные приближения B) дают сходящийся процесс.
§ 7. Комбинированный метод
Пусть /(я)/F)<0, а /'(х) и f"(x) сохраняют постоянные
знаки на отрезке [а, Ь]. Соединяя способ пропорциональных частей
и метод Ньютона, получаем метод, на каждом этапе которого
находим значения по недостатку и значения по избытку точного корня ?
уравнения f(x) — Q.
Отсюда, в частности, вытекает, что цифры, общие для хп и хп,
обязательно принадлежат точному корню ?. Теоретически здесь
возможны четыре случая:
1)/'М>0; f"(x)>0 (рис. 25);
2) f(x)>0; /"(*)< 0 (рис. 26);
3) /'(*)<0; f(x)>0 (рис. 27);
4) /'(*)<0; f"(x)<0 (рис. 28).
Мы ограничимся разбором первого случая. Остальные случаи
изучаются аналогично, причем характер вычислений легко понять из

§ 7]
КОМБИНИРОВАННЫЙ МЕТОД
133
соответствующих чертежей. Заметим, что эти случаи можно свести
к первому, если заменить рассматриваемое уравнение f(x) = 0
В
П
Рис. 25.
Рис. 26.
Рис. 27.
Рис. 28.
равносильными ему уравнениями: —f(x) = 0 или ±/(— z) — 0,
где z — — х.
Итак,_пусть /'(д:)>0 и /"(лг)>0 при а^х^Ь. Полагаем
*0= с; хо = Ь и
f{Xn)
l(Xn)-fi*n)
(хп-хп)*);
I' (*»)
(л = 0, 1, 2, ...)*).
A)
A')
Из доказанного выше (§§ 5 и 6) следует, что
*) На каждом шаге метод хорд применяется к новому отрезку [хп> хп\.

134 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
И
<><?-*„<*„-*,,. B)
Если допустимая абсолютная погрешность приближенного
корня хп задана заранее и равна е, то процесс сближения
прекращается в тот момент, когда будет обнаружено, что хп— хп<С?>.
По окончании процесса за значение корня ? лучше всего взять
среднее арифметическое полученных последних значений:
1Г= у (*„ + *„).
Пример. Вычислить с точностью до 0,0005 единственный
положительный корень уравнения
f{x) = xb—x — 0,2 = 0.
Решение. Так как /A)<0 и/A,1)>0, то корень
содержится в интервале A; 1,1). Имеем:
/'(*) = 5л;4-1 к
В выбранном нами интервале f'(x)>0; f"(x)>0y т. e. знаки
производных сохраняются.
Применим комбинированный метод, полагая хо=\ и лг0 —1,1.
Так как
/(*в) =/0) = — °>2; ЯЛ) =/0,1) = 0,3105;
/'(*<,)=/' 0.1) = 6,3205,
то формулы A) и (Г) дают:
xi==zl +0,51051 ^ 1'039; ^1= !'1 ~ 6,3205' ^ 1H51#
Ввиду того, что хх—хх — 0,012, то точность недостаточная.
Находим следующую пару приближений:
д, = 1,039 +°'0^282^ 1,04469;
Здесь х2 — х2 = 0,00018, т. е. нужная степень точности достигнута.
Можно положить
| = у A,04469+ 1,04487) = 1,04478 «1,045
с абсолютной погрешностью, меньшей
у * 0,00018 + 0,00022 = 0,00031 < у • \0~\

§ 8] МЕТОД ИТЕРАЦИИ 135
§ 8. Метод итерации
Одним из наиболее важных способов численного решения
уравнений является метод итерации*). Сущность этого метода
заключается в следующем. Пусть дано уравнение
0, A5)
где /(д:) —непрерывная функция, и требуется определить его
вещественные корни. Заменим уравнение A) равносильным уравнением
* = <р(*). B)
Выберем каким-либо способом грубо приближенное значение
корня х0 и подставим его в правую часть уравнения B). Тогда
получим некоторое число
х1 = ф (х0). C)
Подставляя теперь в правую часть равенства C) вместо х0
число xv получим новое число лг2 = ф(лг1). Повторяя этот процесс,
будем иметь последовательность чисел
Если эта последовательность — сходящаяся, т. е. существует
предел ? = Нтдги, то, переходя к пределу в равенстве D) и пред-
П -*¦ оо
полагая функцию ф (х) непрерывной, найдем:
lim xn = (f
ИЛИ
Б = Ф<Е). E)
Таким образом, предел ? является корнем уравнения B) и может
быть вычислен по формуле D) с любой степенью точности.
Геометрически способ итерации может быть пояснен следующим
образом. Построим на плоскости хОу графики функций у = х
и«У = ф(#). Каждый действительный корень ? уравнения B) является
абсциссой точки пересечения М кривой у = (р(х) с прямой
у = х (рис. 29).
Отправляясь от некоторой точки Л0[лг0; ф(лг0)], строим ломаную
линию Л0Б1Л1Б2.42... («лестница»), звенья которой попеременно
параллельны оси Ох и оси Оу, вершины Ао, Av А2, ... лежат на
кривой у = Ц)(х), а вершины Bv B2, BSi ...—на прямой^ = лг.
Общие абсциссы точек Ах и В1У А2 и В2, ..., очевидно,
представляют собой соответственно последовательные приближения х1У
*2> • • • корня g.
*) Часто метод итерации называют методом последовательных
приближений.

136
АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Возможен также (рис. 30) другой вид ломаной А0ВхАгВ2А2...
(«спираль»). Легко сообразить, что решение в виде «лестницы»
получается, если производная ф' (х) положительна, а решение в виде
«спирали», если ф' (я) отрицательна.
Рис. 29.
На рис. 29 кривая д; = ф(д:) в окрестности корня g — пологая,
т. е. |ф'(л:)|<:1> и процесс итерации сходится. Однако, если рас-
'у-х
х, х3 ? хг
Рис. 30.
смотреть случай, где |ф'(лг)|>1, то процесс итерации может быть
расходящимся (рис. 31). Поэтому для практического применения
метода итерации нужно выяснить достаточные условия сходимости
итерационного процесса.
Теорема 1. Пусть функция ф (х) определена и
дифференцируема на отрезке [а, ?], причем все ее значения ф(лг)?[а, Ь].

§ 8] МЕТОД ИТЕРАЦИИ 137
Тогда, если существует правильная дробь q такая *), что
G)
при a<ix<b, то: 1) процесс итерации
сходится независимо от начального значения хо?[а, Ь]; 2)
предельное значение
П -> ОО I
является единственным корнем урав- *-
нения . . /о.
х = у(х) (8)
на отрезке [а, Ь].
Доказательство. Рассмотрим
два последовательных приближения
(которые в силу условий теоремы
заведомо имеют смысл). Отсюда
Применяя теорему Лагранжа, будем
иметь:
где хп? (хп_1У хп). Следовательно, на основании условия F) получим:
ln-*,,-i|. (9)
Отсюда, давая значения л=1, 2, 3, ..., последовательно
выводим:
I у- д- I «-^ дП | у y I " /1 С\\
Рассмотрим ряд
—хп_1)+..., A1)
для которого наши последовательные приближения хп являются
(яМ) частными суммами, т. е.
*) За число q можно принять наименьшее значение или нижнюю грань
модуля производной |<р'(х)| ПРИ аЬ

138 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
В силу неравенства A0) члены ряда A1) по абсолютной
величине меньше соответствующих членов геометрической прогрессии
со знаменателем #< 1, поэтому ряд A1) сходится и притом
абсолютно. Следовательно, существует
lim Sn+1= lim *л=?,
Л-> 00 П -+ 00
причем, очевидно, ??[я, b].
Переходя к пределу в равенстве G), в силу непрерывности
функции ф(лг) получаем:
Б = Ф(Б). A2)
Таким образом, ? есть корень уравнения (8). Другого корня
на отрезке [а, Ь] уравнение (8) не имеет. Действительно, если
Б = ф(Б), A3)
то из равенств A2) и A3) получим:
Б-Б = ф(Б)-ф(Б>
и, следовательно,
ф'(*)] = о, A4)
где с ? [?, ?]. Так как выражение в квадратной скобке в
равенстве A4) не равно нулю, то Е = Е» т« е« корень ?—единственный.
Замечание 1. Теорема остается верной, если функция ф(лг)
определена и дифференцируема в бесконечном интервале — оо <
< х < + оо, причем при х ? (— оо, -f- оо) выполнено неравенство F).
Замечание 2. В условиях теоремы 1 метод итерации
сходится при любом выборе начального значения х0 из [а, Ь].
Благодаря этому он является самоисправляющимся, т. е. отдельная
ошибка в вычислениях, не выводящая за пределы отрезка [а, Ь]у не
повлияет на конечный результат, так как ошибочное значение
можно рассматривать как новое начальное значение лг0. Возможно,
возрастет лишь объем работы. Свойство самоисправления делает
метод итерации одним из надежнейших методов вычислений. Само
собой разумеется, что систематические ошибки при применении
этого метода могут помешать получению нужного результата.
Оценка приближения. Из формулы A0) имеем:
Хп I ^ I Хп+р Хп+р-1 I ~Ь I хп+р-1
Просуммировав геометрическую прегрессию, получим:
I Х«+Р ~ хп I

§ 8]
МЕТОД ИТЕРАЦИИ
13Э
Устремляя число р к бесконечности и учитывая, что \imxn+ =1,
р -»¦ оо
находим окончательно:
IE-*J<tzi;I*i-*oI- A5>
Отсюда ясно, что сходимость процесса итерации будет тем
быстрее, чем меньше число q.
Для оценки приближения можно также дать другую формулу,
полезную в некоторых случаях. Пусть
f(x) =лг—ф(лг).
Очевидно, что /' (лг) = 1 — ф' (дг) ^ 1— <7« Отсюда, учитывая, что
= 0, получим:
где хп?{хп} g), и, следовательно, у
Iхп — si ^ 1 JL » ' 1")
т. е.
Y
1. A6')
Используя формулу (9), имеем также:
откуда, в частности, следует, что
если q ^ у, то
т. е. в этом случае из неравенства \хп —
венство
Рис. 32.
n_il <C 8 вытекает
нераЗамечание. Существует распространенное мнение, что если при
применении метода итерации два последовательных приближения
xn-i и хп совпадают между собой с заданной точностью е
(например, для этих приближений установились т первых десятичных
знаков), то с той же точностью справедливо равенство ? «хп (т.е.,
в частности, в приведенном примере т знаков приближенного числа
хп являются верными!). В общем случае, как наглядно показывает
рис. 32, это утверждение ошибочно. Более того, легко показать, что
если ф' (лг) близка к 1, то величина |?—хп\ может быть большой,
хотя величина \хп—хп_г\ весьма мала.

140 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Формула A6") дает возможность оценить погрешность
приближенного значения хп по расхождению двух последовательных
приближений хп_т1 и хп.
Процесс итерации следует продолжать до тех пор, пока для
двух последовательных приближений хп_г и хп не будет обеспечено
выполнение неравенства
\х —х К —^е
\Хп Хп-1\^ q е>
где 8 — заданная предельная абсолютная погрешность корня ? и
|ф'(лг)|^#. Тогда в силу формулы A6") будет иметь место
неравенство
т. е.
Заметим, что если
то
-*я-1| (*«-i €(*„-!. В).
т. е.
Таким образом, при сходящемся итеративном процессе погрешность
|?—хп\ стремится к нулю монотонно, т. е. каждое следующее
значение хп является более точным, чем предшествующее значение хп_^.
Конечно, при всех этих выводах игнорируются погрешности
округлений, т. е. предполагается, что последовательные
приближения находятся точно.
На практике обычно бывает так, что грубым приемом
устанавливается существование корня ? уравнения B) и методом итерации
требуется получить достаточно точное приближенное значение корня,
причем неравенство F) выполняется лишь в некоторой окрестности
(а, Ь) этого корня. Здесь при неудачном выборе начального
значения ^последовательные приближения хп = (р(хп_т1) (л=1, 2,...)
могут покинуть интервал (а, Ь) или даже потерять смысл. Поэтому
полезна другая формулировка теоремы 1.
Теорема 2. Пусть функция ф (х) определена и
дифференцируема на некотором отрезке [а, Ь], причем уравнение
* = <р(*) A7)

§ 8J МЕТОД ИТЕРАЦИИ 141
имеет корень ?, лежащий в более узком отрезке [а, Р], где а =
= а +j(*-a) а р = ?—у(*-в) (рис. 33).
Рис. 33.
Тогда, если: а) |ф'(*)К?<1 приа<х<Ь; б) начальное
приближение х0 ? [a, Р], то:
1) все последовательные приближения содержатся в интервале
(я, *):
*Я = Ф (*„_!)€ (а, *) (л=Ь 2, ...),
2) процесс последовательных приближений — сходящийся, т. е.
существует
причем ^ — единственный корень на отрезке [а, Ь] уравнения A7), и
3) справедлива оценка A5).
Доказательство. 1) Действительно, пусть
Тогда равенство
очевидно, имеет смысл. Используя равенство
на основании теоремы Лагранжа получаем:
отсюда
Вообще, если ^^ g (а, Ь) (л=1, 2, ...) и | аг„_х — ||< ^,
то
имеет смысл и
Следовательно, хп?(а, Ь), где п=\, 2, 3, ...
Что касается утверждений 2) и 3), то доказательство их вполне
аналогично доказательству теоремы 1.

142 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Замечание. Пусть в некоторой окрестности (а, Ь) корня g
уравнения A7) производная ф' (лг) сохраняет постоянный знак и
выполнено неравенство
Тогда» если производная ф' (л;) положительна, то последователь-
ные приближения
xn = (f(xn^1) (я=1, 2, ...). лго€(л. *)
сходятся к корню ? монотонно.
Если же производная ф' (#) отрицательна, то последовательные
приближения колеблются около корня ?.
1) В самом деле, пусть 0«^ф'(#) ^С<7 < 1 и, например,
Тогда
где g1€(^0» ?)»
Следовательно,
аг0 < ^i < ?•
Применяя метод математической индукции, получаем:
*0 < *1 < Х2 < • • < I
(рис. 34а).
Аналогичный результат получается при х0 > ?.
Таким образом, в случае положительной производной ф'(лг)
достаточно выбрать лишь начальное приближение аг0, принадлежащее
Рис. 34а.
окрестности (а, ^) интересующего нас корня |; все остальные
приближения хп(п= 1, 2, ...) автоматически будут содержаться в этой
окрестности и с увеличением номера п монотонно будут стремиться
к корню ?.
2) Пусть —1<—-?<ф'(*Х0 и, например, лг0 < g, причем
*1 = <Р(*о)
Имеем:
т. е. лгх> g и I*! —

§ 8J
МЕТОД ИТЕРАЦИИ
143
Повторяя эти рассуждения для приближений xv лг2, . •.,
получаем:
Х2
Х3
XV
т. е. последовательные приближения будут то меньше, то больше
корня g (рис. 346).
Таким образом, в случае отрицательной производной ф' {х), если
два приближения х0 и хх принадлежат окрестности (а, Ь) корня g,
Рис. 346.
то все остальные приближения хп(п~21 3, ...) также принадлежат
этой окрестности, причем последовательность {хп} «обертывает»
корень g.
Заметим, что, очевидно,
т. е. в этом случае установившиеся
знаки приближения хп обязательно
принадлежат точному корню g.
Пример 1. Найти
действительные корни уравнения х — sin дг ==
= 0,25 с точностью до трех знача-
щих цифр.
Решение. Представим данное
уравнение в виде
рис< 35.
Графическим способом устанавливаем, что уравнение имеет в
отрезке [1,1; 1,3] один вещественный корень g, приближенно равный
лго=1,2 (рис. 35).
Придерживаясь обозначений теоремы 2, примем:
а=1,1 и 8=1,3;
отсюда
и
Так как
и
а = а — ф — а) = 0,9 « arc 52°
Ь = р + (р - а) = 1,5 « arc 86°.
Ф (х) = sin лг + 0,25
ф' (д:) = cos ЛГ,
то при 0,9<лг<1,5 имеем:
| ф' (х) | < cos 52° « 0,62 = q.

144 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Если мы выберем лго?A,1; 1,3), то все условия теоремы 2
будут полностью соблюдены и, следовательно, гарантировано, что
последовательные приближения
*„ = sin*„_! +0,25 (л=1, 2, ...)
1) содержатся в интервале @,9; 1,5) и 2) хп—> ? при п—юо.
Выбирая лго= 1,2 и задаваясь, согласно условию задачи,
предельной абсолютной погрешностью
строим последовательные приближения хп(п= 1, 2, ...) до тех пор,
пока два соседних приближения хПтт1 и хп не совпадут друг с
другом в пределах точности, равной
Ь^е==о,51 .1. Ю-2 «0,0025.
Имеем:
хх = sin 1,2 + 0,25 = 0,932 + 0,25 = 1,182;
A:a = sin 1,182 + 0,25 = 0,925 + 0,25= 1,175;
*, = sin 1,175 + 0,25 = 0,923 + 0,25 = 1,173;
лг4 = sin 1,173 + 0,25 = 0,922 + 0,25 =1,172;
хь = sin 1,172 + 0,25 = 0,922 + 0,25 = 1,172.
Четвертое и пятое приближения совпали с точностью до четырех
значащих цифр. Поэтому (см. A6"))
Так как предельная абсолютная погрешность приближенного корняд:5,
включая погрешность округления, не превышает
?=0,0016 + 0,002 < 1. Ю-2,
то можно принять:
5 = 1,17 ±0,005.
Замечание. Данное уравнение
/(*) = 0 A8)
можно записать в виде равенства
выбирая различным образом функцию ср(лг).
Способ записи A8') отнюдь не безразличен: в одних случаях
|ф'(лг)| окажется малой в окрестности искомого корня |, в других —

§ 8} МЕТОД ИТЕРАЦИИ 145
большой. Для метода итераций выгодно то представление A8'), при
котором выполнено неравенство
|ф'(*I<?<1, 09)
причем, чем меньше число q, тем быстрее, вообще говоря,
последовательные приближения сходятся к корню |.
Укажем один достаточно общий прием приведения уравнения A8)
к виду A8'), для которого обеспечено выполнение неравенства A9).
Пусть искомый корень ? уравнения лежит на отрезке [a, ft], причем
0</»1<//И<Л*1 B0)
при а ^лг <!?*). В частности, за тг можно взять наименьшее
значение производной f'(x) на отрезке [д, ?], которое должно быть
положительным, а за Мг— наибольшее значение f'(x) на отрезке
[я, Ь]. Заменим уравнение A8) эквивалентным ему уравнением
Можно положить ф(лг)=лг — /)
Подберем параметр А, таким образом, чтобы в данной
окрестности [а, Ь] корня | было выполнено неравенство
1. B1)
Отсюда на основании выражения B0) получаем:
1 — КМг ^ 1 — Km±
Следовательно, можно выбрать:
* 1
Таким образом, неравенство B1) выполнено.
Пример 2. Найти наибольший положительный корень ?
уравнения
л:3 + лг=1000 B2)
с точностью до 10~4.
Решение. Грубой прикидкой получаем приближенное значение
корня лго=1О, причем, очевидно, |< лг0.
*) Если производная f (х) отрицательна, то вместо уравнения
рассматриваем уравнение —j5(H

146 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
Уравнение B2) можно записать в виде
#=1000— л;3,
ИЛИ
ИЛИ
1000 1
= У 1000 —лг,
[ГЛ. IV
B2')
B2")
B2'")
и т. п. Наиболее выгодным из приведенных вариантов оказывается
вариант B2'"), так как, взяв
Таблица 4 за основной интервал (9,10) и
- ПОЛОЖИВ
Значения последовательных
приближений хп цуп <р (*) = уЛ
будем иметь
п
0
1
2
3
10
9
9
9
,96655
,96666
,96667
990
990
990
Уп
,03345
,03334
"з?/A000—хJ'
Отсюда
IФ' (
Вычисляем последовательные приближения хп с одним запасным
знаком по формулам
^=1000-*,,;
Найденные значения помещены в таблице 4.
Так как 1— #«1, то с точностью до 10"* можно положить
g = 9,9667.
Метод итерации можно применять также для вычисления корней
уравнений, заданных в виде степенных рядов.
Пример 3. Найти действительный корень уравнения [2]
* 3 + 10 42 "+" 216 1320"*"
...=0,4431135.
Решение. Имеем лг = ф(лг), где
х* х* , х7 х9

§ 8] МЕТОД ИТЕРАЦИИ 147
Отбрасывая все степени х выше первой, определяем приближен»
ное значение корня л:0 = 0,44. Далее,
*! = 9@,44) «0,47;
*2 = ф @,47) «0,476;
х3 = ф @,476) « 0,4767;
д;4 = ф @,4767) «0,47689;
хь = ф @,47689);« 0,476927;
дгв = ф @,476927) « 0,476934;
лг7 = ф @,476934) « 0,476936.
Следовательно, ? = 0,47693.
Укажем еще один прием улучшения сходимости процесса
итерации, который может оказаться полезным в некоторых случаях [7].
Пусть имеем уравнение
х = ф (л:)
такое, что в окрестности искомого корня ? выполнено неравенство
Тогда процесс итерации для этого уравнения расходится. Однако,
если данное уравнение заменить эквивалентным уравнением
где г|) (х) = ф (х) — обратная функция, то мы получим уравнение,
для которого процесс итерации сходится, тЯк как
Пример 4. Уравнение
f(x) = ** — x —1-0 B3)
имеет корень ??A,2), так как /A) = — 1 <0 и /B) = 5> 0.
Уравнение B3) можно записать в виде
др = лр8 — 1. B4)
Здесь
Ф (х) = xz — 1 и ф' (*) = Зл:2;
поэтому
' при 1<лг<2
и, следовательно, условия сходимости процесса итерации не
выполнены.

148 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Если записать уравнение B3) в виде
X^YT+Y7 B5)
то будем иметь:
Отсюда 0 <\|/ (х)<. —з/^" <Т при * ^х^^ и> значит> процесс
3 |/ 4 ^
итерации для уравнения B5) быстро сойдется.
§ 9. Метод итерации для системы.двух уравнений
Пусть даны два уравнения с двумя неизвестными
A)
действительные корми которых требуется найти с заданной степенью
точности.
Мы предположим, что система A) допускает лишь
изолированные корни. Число этих корней и их грубо приближенные значения
можно установить, построив кривые ^(л;, J>) = 0; F2 (лг, у) = 0 и
определив координаты их точек пересечения.
Пусть x — xQ\ У—Уо—приближенные значения корней системы
A), полученные графически или каким-нибудь другим способом
(например, грубой прикидкой).
Дадим итерационный процесс, позволяющий при известных
условиях уточнить данные приближенные значения корней. Для этого
представим систему A) в виде
*» у)Л
р. у) I
и построим последовательные приближения по следующим
формулам:
C)
Если итерационный процесс C) сходится, т. е. существуют
пределы
И Т) = ]

§9]
МЕТОД ИТЕРАЦИИ ДЛЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ
149
то, предполагая функции фх (лг, у) и <р2 (л?, У) непрерывными и
переходя к пределу в равенстве C) общего вида, получим:
1 = Итф1(^111 уп),
Отсюда
Ф1
qJ(xn, yn).
= ф2<Е» л).
т. е. предельные значения ? и т] являются корнями системы B),
а следовательно, и системы A). Поэтому, взяв достаточно большое
число итераций C), мы получим
числа хп и уп, которые будут
отличаться от точных корней х — \ и
ут=ц системы A) сколь угодно
мало. Поставленная задача, таким в
образом, окажется решенной. Если
итерационный процесс C)
расходится, то им пользоваться нельзя.
Теорема. Пусть в некоторой
замкнутой окрестности R{a^x*
^Л; Ь^у^В} (рис. 36) имеется
одна и только одна пара корней
лг = ? и у = ц системы B). Если:
1) функции ф^лг, у) и ф2(лг, у)
определены и непрерывно дифференцируемы в R; 2) начальные
приближения х0, у0 и все последующие приближения хп, уп(п*=\,2у ...)
принадлежат R; 3) в R выполнены неравенства
Рис. 36.
дх
то процесс последовательных приближений C) сходится к корням
¦*г==? и У~Ц системы B), т. е.
Нтлги = 5 и
/1->-СО
Замечание. Теорема остается верной, если условие 3)
заменить условием 3')
~~дх~
Примерное доказательство теоремы см. в J2]. Более общая
теорема приведена в главе XIII, §§ 10—11.

150 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Пример. Для системы [2]
/г(х, у) = 2х* —ху-
/,(*, y)==
-5* + 1=0, \
-у» = 0 (
найти положительные корни с четырьмя значащими цифрами.
Рис. 37.
Решение. Строим графики функций Д (л;, у) = 0 и /2 (л:, J/) = 0
(рис. 37). Приближенные значения интересующих нас корней есть
Для применения метода итерации запишем нашу систему в
таком виде:
==щ(х, у).
Найдем частные производные
дх
где Ж = 0,43429,
ду
1 +
зм
V
Ограничиваясь окрестностью

Л 9] МЕТОД ИТЕРАЦИИ ДЛЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ
будем иметь:
~дх~
151
2,3 + 5
t -./,4B,1 + 5) —
Г 2
<0,54;
ду
~дх~
W
3,6
¦./3,4B,1 + 5)-!
' К 2
<0,27;
1 +
3.0,43
3,4
<0,42;
= 0.
Отсюда
*Ы + |*^|< 0,54 + 0,42 = 0,96 <
< 0,27 + 0 = 0,27 < 1.
E)
Следовательно, если последовательные приближения (хп, уп) не
покинут области R (что легко обнаружить в процессе вычислений),
то итерационный процесс будет сходящимся.
Относительная близость суммы D)
к единице дает основания предполагать, Таблица 5
что итерационный процесс в данном слу- Значения последователь-
чае будет сходиться сравнительно мед- ных приближений хп и уп
ленно. Приступаем к вычислению
последовательных приближений по формулам
(л = 0, 1, 2, ...).
Соответствующие значения
последовательных приближений помещены в
таблице 5.
Таким образом, можно принять
Е = 3,487; т) = 2,262.
Замечание. Вместо рассмотренного процесса
последовательных приближений C) иногда удобнее пользоваться «процессом
Зейделя»:
п
0
1
2
3
4
5
6
Хп
3,5
3,479
3,481
3,484
3,486
3,487
3,487
Уп
2,2
2,259
2,260
2,261
2,261
2,262
2,262
v Уп)
= 0, 1, 2,
Метод итерации для общих систем рассмотрен в главе Х111
(§§ 8-Ц).

152
АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
§ 10. Метод Ньютона для системы двух уравнений
Пусть хпУ уп — приближенные корни системы уравнений
F(x, jf) = O; О(х, у) = 0, A)
где F и О—непрерывно дифференцируемые функции. Полагая
получим:
= 0. I
B)
Отсюда, применяя формулу Тейлора и ограничиваясь линейными
членами относительно hn и кпУ будем иметь:
Если якобиан
то из системы C) находим:
1
yn
Л) Ру*
Уп) Оу\
= 0. \
C)
Уп)
S (*п* Уп)
1
Следовательно, можно положить:
1
„, Уп) Fyixn, Уп)
# Уп) ОЛ*п'У«)
хп, Уп) F(xn, yn)
ха, Уп) G(xn, yn)
xn> Уп)
1
„, Уа) Fy{xn, Уп)
G(xn,yn) О'у(х„,уя)
F'x(xn, yn) F(xn, yn)
О'Лхп, У„) G(xn, yn)
«я. Уп)
г = 0, 1, 2, ...)•
D)
E)
F)
F',
Исходные приближения х0, у0 определяются грубо приближенно.
Пример. Найти вещественные корни системы
F (х, у) == 2xs —у* — 1=0;
G(x, у)==ху3—у—4 = 0.
A)
Решение. Графическим путем найдем грубо приближенные
значения корней:

МЕТОД НЬЮТОНА ДЛЯ СЛУЧАЯ КОМПЛЕКСНЫХ КОРНЕЙ
153
Подставив в систему A), получим:
/41,2; 1,7) = — 0,434;
0A,2; 1,7) = 0,1956.
Вычислим якобиан
6л:2 — 2у
у* Зху
2 —
отсюда
8,64 —3,40
4,91 9,40
По формуле D) вычисляем h0:
= 97,910.
и —
1
97,910
—0,434 —3,40
0,1956 9,40
3,389
:97,910
= 0,0349;
отсюда по формуле F) находим:
,0349 = 1,2349.
По формуле E) вычисляем k0:
*« = —
1
97,910
8,64 —0,434 [
4,91 0,19561
= — 0,0390;
отсюда по формуле F) находим:
-у1= 1,7 — 0,0390= 1,6610.
Повторяя этот процесс с полученными значениями корней,
получим:
дг2= 1,2343; J2 = 1,6615 и т. д.
Метод Ньютона для общих систем рассмотрен в главе XIII
(§§ 1—7).
§ 11. Метод Ньютона для случая комплексных корней
На практике (например, при решении линейных
дифференциальных уравнений) может встретиться надобность в уточнении
комплексных корней данного уравнения
/(*) = 0. A)
Для этой цели иногда можно использовать метод, аналогичный
методу Ньютона.
Допустим, что f(z)(z = x-\-iy, /2 = —1) — аналитическая
функция в некоторой выпуклой*) окрестности U ее простого
изолированного нуля
С = 5 +/л (ЛС) = о, /'@=^=0),
*) То есть любые две точки, принадлежащие окрестности U, являются
концами отрезка, также принадлежащего U.

154 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
который, вообще говоря, является комплексным. Пусть zn —
приближенное значение корня, принадлежащее окрестности U, и
— уточненное значение корня. Применяя разложение в ряд Тейлора
в точке zn и считая, что f{zn+1)^0 с точностью до Azl, будем
zn
иметь:
отсюда
Таким образом, отправляясь от какого-нибудь значения z0, шаг за
шагом можно получать дальнейшие приближения корня по формуле
*«+i=*B-F7Fl (п = °> *- 2> •••)• О)
Если zn?U (л=1, 2, ...) и последовательность {zn} сходится,
то предел
является корнем уравнения A). Действительно, переходя к пределу
при п—> сх) в равенстве C), будем иметь:
Иш /BЯ)
lim -ги ., = lim «г„—^-^тт т
ИЛИ
fc~6 г (О*
Следовательно,
Для оценки погрешности приближенного значения zn
предположим, что
\ff(z)\^m1>0 при z?U.
Тогда для данной функции
w=/(z)
в достаточно малой /?-окрестности корня ? существует однозначная
обратная функция
определенная в некоторой окрестности |ге;|<р, производная
которой, как известно, есть
dw~l' (г)' ^'

§ 11] МЕТОД НЬЮТОНА ДЛЯ СЛУЧАЯ КОМПЛЕКСНЫХ КОРНЕЙ
Предполагая, что |/(^„)|<Р, имеем:
155
, E)
fit)
где t — текущая точка, пробегающая прямолинейный отрезок между
точками /(?) = 0 и f(zn) (рис. 38). Так как 11| < р, то \/~г(t)\<R
и, следовательно,
Отсюда на основании формулы E) будем
иметь:
•@I
Приведем без доказательства
достаточные условия существования корня
уравнения A), вытекающие из теоремы
Островского [8], [9].
Теорема. Если функция f(z) аналитическая в замкнутой
R-окрестности точки zQ} причем выполнены неравенства:
Рис. 38.
1)
2)
3)
4)
1
t: (*o>
Н'о)
f!
при |^ — 2Г0|
то уравнение A) ajweer единственный корень g в области \z — zo\^R
и процесс Ньютона C), определяемый начальным приближением zo>
сходится к этому корню, г. в.
Быстрота сходимости процесса характеризуется оценкой
— I и.21*-1
9 J r0
G)
Пример. Приближенно найти наименьшие по модулю корни
Уравнения
= «*—0,2*+1 ==0. (8)

156 АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ [ГЛ. IV
Решение. Здесь
/'(*) = ** —0,2.
Так как f'(z) = 0 при z = In 0,2 « — 1,79 и
/(—оо)=+оо, /(*)><>, /( + оо)=+оо,
то уравнение (8) действительных корней не имеет.
За начальное приближение искомого корня § примем наименьший
по модулю корень z0 уравнения
ег+\=0;
отсюда можно положить:
Дальнейшие приближения zn(n=\, 2, 3, .,.) корня ?
последовательно определяем, применяя формулу C):
. 0,2ш 5 .
ит'д-
Результаты вычислений с точностью до 0,001 приведены в таблице 6.
Таблица 6
Уточнение комплексных корней по методу Ньютона
п
0
1
2
3
4
5
3,142/
2,618/
0,153+2,658/
0,109+2,646/
0,107+2,650/
0,107+2,646/
-0,868+0,5/
— 1,030+0,541/
-0,978+0,535/
-0,981+0,525/
—0,977+0,534/
f Ы
—0,628/
0,132-0,024/
—0,061+0,009/
0+0,006/
—0,002—0,005/
+0,002+0,004/
-1,2
— 1,068+0,5/
—1,230+0,541/
—1,178+0,535/
—1,181+0,525/
-1,177+0,534/
-0,524/
0,153+0,040/
^0,044-0,012/
—0,002+0,004/
-0,000-0,004/
Для вычисления ez при z — x-\-iy использовалась известная
формула
ег = ех (cosy -f i sin у).
Полагая
5 » 2г5 = 0,107 + 2,646/,
будем иметь:
/(^в) = 0,002 + 0,004/.
Приближенно считая

ЛИТЕРАТУРА К ЧЕТВЕРТОЙ ГЛАВЕ 157
на основании формулы F) получаем погрешность
!С_,.|»Л(!^-0>«>;-^« 0,004.
Ввиду того, что левая часть уравнения (8) при вещественных z
принимает вещественные значения, то это уравнение имеет также
сопряженный корень
?sz 0,107—2,646/,
равный по модулю корню ?. Действительно, имеем:
Я» =7@ = о.
Замечание. Другой способ решения уравнения A) — это
сведение его к системе двух действительных уравнений. Полагая
в уравнении A) и выделяя действительную и мнимую части
функции f(z)y будем иметь:
) = «(*, y)+iv(x, jf) = O,
где и и v — действительные функции. Отсюда получаем, что
уравнение A) эквивалентно системе
v(xy jf) = O. (
(9)
Уточнение корней системы вида (9) рассмотрено в §§ 9 и 10.
Заметим, что этот новый способ годится также и в случае
неаналитичности функции f(z).
Литература к четвертой главе
1. Я. С. Б е з и к о в и ч, Приближенные вычисления, Гостехиздат, изд. 6,
1949, гл. VI.
2. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
1934, гл. IX, X.
3. Э. Уиттекер и Г. Робинсон, Математическая обработка
результатов наблюдений, ОНТИ, 1935, гл. VI.
4. Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, т. I, Гостехиздат, 1957, гл. IV.
5. Г. П. Толе то в, Курс математического анализа, т. I, Гостехиздат, 1954,
гл. VII.
6. А. О. Гельфонд, Исчисление конечных разностей, Гостехиздат, 1952,
гл. V.
7. Д. А. В е н т ц е л ь, Е. С. Вентцель, Элементы теории
приближенных вычислений, Изд. ВВИА им. Жуковского, 1949, гл. 3, § 4.
8- A. Ostrowski, Матем. сборник 2 A937).
9. Л. В. Канторович, О методе Ньютона, Труды матем. ин-та
им. В. А. Стеклова XXVIII A949), 104—144.

ГЛАВА V
СПЕЦИАЛЬНЫЕ ПРИЕМЫ ДЛЯ ПРИБЛИЖЕННОГО РЕШЕНИЯ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 1. Общие свойства алгебраических уравнений
Рассмотрим алгебраическое уравнение я-й степени (п^\)
Р(х) = аох* + а1хп-1+...+аЛ = О9 A)
где коэффициенты а0, av ..., ап—действительные числа, причем
В общем случае переменную х будем считать комплексной.
Основная теорема алгебры. Алгебраическое уравнение
п-й степени A) (а следовательно, и полином Р(х)) имеет ровно п
корней, действительных или комплексных, при условии, что каждый
корень считается столько раз, какова его кратность [1], [2].
При этом говорят, что корень ? уравнения A) имеет кратность 5
(т. е. ? есть s-кратный корень), если
B)
Комплексные корни уравнения A) обладают свойством парной
сопряженности.
Теорема 1. Если коэффициенты алгебраического уравнения
A) — действительные, то комплексные корни этого уравнения попарно
комплексно-сопряженные, т. е. если ? = а+/(} (a, {$ —
действительные) есть корень уравнения A), кратности s, то число ? = a—/j5
также является корнем этого уравнения и имеет ту же кратность 5.
Отметим, что модули этих корней одинаковы:

§ 1]
ОБЩИЕ СВОЙСТВА АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
159
Следствие. Алгебраическое уравнение нечетной степени с
действительными коэффициентами имеет по меньшей мере один
действительный корень.
Нетрудно дать грубую оценку модулей корней уравнения A).
Теорема 2. Пусть
A = max{\ax\, \аг\, ..., |ая|},
где ak — коэффициенты уравнения A).
Тогда модули всех корней
xk(k=\, ..., п) уравнения A)
удовлетворяют неравенству
т. е. корни этого уравнения на
комплексной плоскости |От] (х ~ Ц- щ)
расположены внутри круга
Рис. 39.
(рис. 39).
Доказательство. Полагая |лг| > 1, из формулы A) имеем:
\at\\x\n—A{\x\"-l + \x\—*+ ... + 1) =
= !ап!!л:!"-Л.
1*1-1
Отсюда, если
т. е. если
получаем, что
\аа\ —
ж I — 1
D)
\Р(х)\>0.
Таким образом, значения дг, удовлетворяющие неравенству D),
заведомо не являются корнями уравнения A). Следовательно, все
корни xk уравнения A) удовлетворяют противоположному неравенству
Следствие. Пусть апФ0 и
В=шах{|о0|, |ах|, ...,

160 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Тогда все корни xk(k~\> 2,..., п) уравнения A) удовлетворяют
неравенству
, „ ,. 1
1 +
В
• = /¦,
\ап\
т. е. корни уравнения A) расположены в круговом кольце
r<\x\<R
(рис. 40).
В самом деле, полагая
1
будем иметь:
где
E)
1
~У1
Рис. 40.
Корни ^ = —(А=1, ..., л) полинома Q(,y) в силу нашей
теоремы удовлетворяют неравенству
1 ^ Л \ В
откуда
*i >
1+1
!=1, . . ., П).
Замечание. Числа г и R являются соответственно нижней
и верхней границами положительных корней уравнения A).
Аналогично числа —/? и —г служат соответственно нижней и
верхней границами отрицательных корней уравнения A).
Если
лг1? х2, ..., хп
— корни уравнения A), то для левой части его справедливо
разложение
Р(х) = ао(х-х1)(х—х2)...(х-хп). F)
Отсюда, производя перемножение биномов в формуле F) и
приравнивая коэффициенты при одинаковых степенях х в левой и

§ 1] ОБЩИЕ СВОЙСТВА АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 161
правой частях равенства F), получим соотношения между корнями
и коэффициентами алгебраического уравнения:
~^~
G)
Левые части равенств G) представляют собой суммы сочетаний
корней уравнения A) по одному, по два и т. д.
Пример 1. Корни xv лг2, лг3 кубического уравнения
удовлетворяют условиям:
х^х^х^ = — г.
Если учитывать кратности корней, то разложение F)
принимает вид
где xv x2i...,xm (т<,п) — различные корни уравнения A) и
ах, а2, ..., ат — их кратности, причем
Производная Я'(л:) выражается следующим образом:
Р '(х) = aQ (х - xj"*- *(х - хгуь-1 ... (х - х J«* -1Q (дг),
где Q (лг) — полином такой, что
Q(^)=^0 при ft=l, 2, ..., w.
Поэтому полином
является наибольшим общим делителем полинома Я(лг) и его
производной Р*(х). Как известно, полином R(x) может быть найден
с помощью алгорифма Евклида [1]. Составляя частное
получим полином
/{х) = Аох»+А1*я-1+...+Ат (8)
6 Б. П. Демидович и И. А. Марой

162 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
с действительными коэффициентами Л0 = д0, Av ..., Ат> корни
которого х1У х2, ..., хт различны.
Таким образом, решение алгебраического уравнения с кратными
корнями сводится к решению алгебраического уравнения более
низкой степени с различными корнями.
Полное число корней xv л;2, ..., х# уравнения
= О,
расположенных на комплексной плоскости внутри простого
замкнутого контура Г (рис. 41), можно определить на основании принципа
аргумента [4], который состоит в следующем: если полином Р(х)
не имеет корней на замкнутом контуре Г,
то число корней N этого полинома внутри
контура Г в точности равно изменению
ArgP(x) при положительном обходе кон-
тура Г, деленному на 2я, т. е.
причем каждый корень считается столько
раз, какова его кратность.
Если уравнение контура Г есть
(/ — параметр), то для определения числа N на плоскости XOY
строят кривую
X=X(t), Y=Y(t) @</<Г), . (К)
где
(X(t), Y(t) — действительные функции), и подсчитывают, сколько
оборотов N кривая К делает вокруг начала координат.
Пример 2. Определить число корней уравнения
=0, (9)
содержащихся внутри круга |jc|<2.
Решение. Полагая
будем иметь:
Р(х) = 8 (cos / + / sin 0s — 6 (cos t + i sin t)+\=*
= (8 cos 3/ - 6 cos / + 1) +1 (8 sin 3/ — 6 sin t).
Отсюда
* = 8cos3/ —6cosf+l,
K=8sin3/-6sin*.
(K)

§ 2] ГРАНИЦЫ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 163
Таблица 7
/
X
Y
0
3
0
*т
—4,22
±5
*т
—10
±5,22
1
* 3
15
Т5.22
_5я_
± 6
6,22
±5
±я
J
0
Построив по точкам кривую К (см. таблицу 7), легко убедиться,
что кривая три раза окружает начало координат (рис. 42). Поэтому
N=3 и, следовательно,
уравнение (9) имеет внутри круга у
| х | < 2 три корня.
§ 2. Границы действительных
корней алгебраических
уравнений
В этом параграфе мы будем
рассматривать полиномы вида
Р (х) = аохп + аххп'г +
• ()
с действительными
коэффициентами д0,
anJ
где
0, lf , nJ д
^О. Нашей целью является
установление границ, по
возможности тесных для
положительных и отрицательных кор-
ней^ A
^2
уравнения
B)
Рис. 42.
причем вопрос о существовании этих корней здесь ие затрагивается.
Заметим, что можно ограничиться нахождением верхней границы R
лишь положительных корней уравнений вида B). В самом деле,
«аряду с уравнением B) рассмотрим вспомогательные
алгебраические уравнения
6*

164 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
и пусть верхние границы их положительных корней соответственно
есть Rv /?2 и /?8. Тогда число -g-, очевидно, есть нижняя граница
положительных корней уравнения B), т. е. все положительные
корни х+ этого уравнения, если они существуют, удовлетворяют
неравенству
Аналогично числа —R2 и ^— являются соответственно нижней
и верхней границами отрицательных корней уравнения B), т. е.
все , отрицательные корни х~~ этого уравнения, если таковые
имеются, удовлетворяют неравенству
Укажем некоторые простые приемы нахождения верхней
границы R положительных корней уравнения B), причем некоторые
из них приведем без доказательства.
Теорема Лагранжа. Пусть а0 > 0 и ak(k^*\)— первый
из отрицательных коэффициентов*) полинома Р(х). Тогда за
верхнюю границу положительных корней уравнения B) может быть
принято число
еде В — наибольшая из абсолютных величин отрицательных
коэффициентов полинома Р(х).
Доказательство. Положим л;>1. Если в полиноме Р(х)
каждый из неотрицательных коэффициентов av ..., аЛ-1 заменить
нулем, а каждый из остальных коэффициентов аЛ, ak+v ..., ап
заменить отрицательным числом —Д то от этого полином A)
может лишь уменьшить свое значение и мы будем иметь неравенство
Р(х) ^ аохп-
= аохп—В
Отсюда при х > 1 получим:
Р(х) JL* ?^1*
—k+l
*) Если такого коэффициента нет, т. е. все коэффициенты полинома
Р(х) неотрицательны, то полином Р (х) не имеет положительных корней.

Л 3] МЕТОД ЗНАКОПЕРЕМЕННЫХ СУММ 165
Следовательно, при
будем иметь:
/>(*)> О,
т. е. все положительные корни х* уравнения B) удовлетворяют
неравенству
+<R
§ 3. Метод знакопеременных сумм
Идея метода Лагранжа может быть обобщена следующим
образом: пусть полином Р(х) расположен по убывающим степеням
переменной х, причем его старший коэффициент а0 > 0.
Представим Р(х) в виде знакопеременной суммы
Р (х) «Qt (х) - Q2 (x) + Q3 (x) - Q4 (x) + ... +Q2m_x (x)-Q2m (*),
где Qx(x) — сумма последовательных членов полинома Р(х) с
положительными коэффициентами, начиная с аохп, —Q2W — сумма
последовательных членов полинома Я (л:) с отрицательными
коэффициентами, непосредственно примыкающих к членам первой
суммы, и т. д., причем последнее слагаемое —Q2m(x) или состоит
из членов с отрицательными коэффициентами, или тождественно
равно нулю.
Обозначим через Cj (y=l, 2, ..., т) положительные числа
такие, что
(У=1, 2, ...,/й). Тогда за верхнюю границу положительных
корней уравнения B) § 2 можно принять число
/?==тах(с1, с2, ..., ст). B)
В самом деле, положим:
где
jf^O (s=\, 2, .... p + q),
причем 6<1/)>0(/=l, 2, .... т).

166 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Полагая х > О, имеем:
Q2/-i (*) -Q2/ (х) = xn*-p+
Из формулы C) ясно, что функции Qtf-i(x)—Q2f(x){J=\, 2, ..., т)
возрастают при возрастании х. Следовательно, при х > с;. > О
имеем:
Отсюда при х > R получаем:
m
S О,
т. е. все положительные корни х+ уравнения B) § 2
удовлетворяют условию
Пример. Определить границы действительных корней уравнения
2л;6 — ЮОлг2 + 2х— 1 = 0. D)
Решение. Здесь о0 = 2и Л = тах A00, 2, 1) = 100. Поэтому
верхняя граница R положительных корней уравнения D), согласно
теореме 2 из § 1, есть
Применяя теорему Лагранжа, учитывая, *что
ал = а3 = —ЮО и В= max A00, 1) = 100,
будем иметь значительно лучшую оценку для верхней границы
положительных корней
2 ~~
Наконец, применяя метод знакопеременных сумм, находим:
2л:5 — 100л:2 = 2л:2 (л;8 — 50) > 0
при х > ?/50 (например, при х > 3,7) и
2х— 1=2 ( л:— YJ >0 при х > 0,5.
Следовательно, можно принять
Я = max C,7; 0,5) = 3,7.

с 4] МЕТОД НЬЮТОНА 167
Для определения нижней границы г положительных корней ураз-
нения D) положим:
Тогда уравнение D) примет вид
j,6_2y4-j-100y8 —2 = 0.
Последовательно получаем:
jr6 —2>*==У(у — 2)>0 при
—2= 100(у3 — 0,02)>0 при
Следовательно,
B; 0,3) = 2
Для нахождения границы отрицательных корней в уравнении D)
положим:
лг= —z.
Отсюда
2z*+\0z2 + 2z+\=0. D')
Так как коэффициенты уравнения D') положительны или равны нулю,
то это уравнение не имеет положительных корней, а следовательно,
данное уравнение D) не имеет отрицательных корней.
§ 4. Метод Ньютона
Теорема Ньютона. Если при х = с>0 полином Р(х) и
все его производные Р' (лг), Р"(лг), ..., Р{П)(х) неотрицательны:
Р<Л>(с)^0 (А = 0, 1, 2, ..., л), A)
причем Р{п) (с) = п\ а0 > 0, то R = c может быть принято за верхнюю
границу положительных корней уравнения
Р(*) = 0. B)
Доказательство. При лг>с, учитывая неравенства A), на
основании формулы Тейлора имеем:
Следовательно, все положительные корни х+ уравнения B)
удовлетворяют неравенству
X ^гв С*

168 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Замечание. При практическом применении теоремы Ньютона
методом проб (используя, например, схему Горнера) отыскивают
монотонно возрастающую последовательность положительных чисел
О < сх < с2 < ... < ?„
для которых справедливы неравенства
/>«-»(<:!)> О,
Такие числа заведомо существуют, так как для ао>О имеем:
Рт(х)-++оо (/и = 0, 1, 2, ..., я-1)
при х—»-+оо. Окончательно можно принять с = сп.
Действительно, так как
то функция Р(п~1) (х)—возрастающая и, следовательно, при х > сг
мы будем иметь:
Р{п'1] (х) > Р<"-» (с^^О.
Из последнего неравенства вытекает, что функция Р*п~2) {х) —
возрастающая в промежутке [cv + оо), и поэтому при а: > сг^сх
получаем:
Проводя последовательно это рассуждение, мы, наконец, убедимся,
что Р(х)—возрастающая функция в промежутке [сп-1, +°°) и,
следовательно, при лг>сл^сп-1 имеем:
Значит, х+ ^ сп.
Пример. Рассмотрим приведенное в примере § 3 уравнение
Р {х) = 2*5 — 100л:2 + 2х—1=0.
Здесь
Р' (л:)=10лг4 —200л: + 2,
Р" (лг) = 40лг3 — 200,
Р'" (х) = 120л;2,
PIV (лг)==240лг,
Pv (x) = 240.

я 5] число действительных корней полинома 169
Очевидно, Р"'(х)>0, Plv(x)>Oy Р* (х)>0 при х > 0. Имеем:
Я" (х) = 40 (х3—5) > 0 при лг^2.
Примем с1 = с2 = с3 = 2. Так как
Я'B)= 10-16 — 200.2 + 2 < 0,
то определяем знак числа
Я'C) = 10-81— 200-3 + 2 >0.
Можно принять с4^3. Далее, имеем:
РC) = 2.243—100-9 + 2.3 — 1 < 0;
поэтому вычисляем:
ЯD) = 2-1024—100-16 + 2-4—1 > 0.
Значит, с5 = 4. Итак, верхняя граница положительных корней
данного уравнения есть
Я = 4.
Оценка по методу Ньютона получилась точнее, чем приведенная выше
оценка по методу Лагранжа, но менее точная, чем оценка по
способу знакопеременных сумм (см. пример § 3).
§ 5. Число действительных корней полинома
После того как установлены границы положительных и
отрицательных корней алгебраического уравнения
. Р(*) = 0, A)
где Р(х)—данный полином, возникает вопрос о числе
действительных корней данного уравнения на некотором известном интервале (а,Ь).
Общую ориентировку о числе
действительных корней уравнения
A) на интервале (я, Ь) дает график
функции у = Р(х) (рис. 43), где
корнями х1У х2Ух3 являются абсциссы
точек пересечения графика с осью Ох.
Отметим простые особенности
целого полинома.
1) Если Р(а)Р(Ь) <0} то на
интервале (а, Ь) имеется -нечетное
число корней полинома Р(х) с
учетом их кратностей.
2) Если Р(а)Р(Ь)>0, то на Рис 43
интервале (а, Ь) или не имеется
корней полинома Р(х), или таких корней существует четное число.
Полностью вопрос о числе действительных корней алгебраического
Уравнения на данном промежутке решается методом Штурма [1J, [2].

170 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Предварительно введем понятие о числе перемен знаков в
числовой системе.
Определение. Пусть дана упорядоченная конечная система
действительных чисел, отличных от нуля:
с±, c2J ..., сп (п^2). B)
Говорят, что для пары рядом стоящих элементов cki ck+1 системы B)
имеется изменение знака, если эти элементы обладают
противоположными знаками, т. е.
и нет изменения знака, если знаки их одинаковы, т. е.
Общее число изменений знаков всех пар соседних элементов ckJ
ck+1 (ft=l, 2, ..., п—1) системы B) называется числом перемен
знаков в системе B).
Для данного полинома Р(х) составим систему Штурма
Р{х), Рг{х), ..., />,(*), .... РЛ{х), C)
где Рг(х) = Р' (х), Р2(х)—взятый с обратным знаком остаток при
делении полинома Р(х) ньРг(х), Pz (x) — взятый с обратным знаком
остаток при делении полинома Рх (х) наЯ2 (а:) и т. д. Полиномы Pk (x)
(k — 2y ...,/») могут быть найдены с помощью несущественно
видоизмененного алгорифма Евклида, причем, если полином Р {х) не имеет
кратных корней, то последний элемент Рт (х) системы Штурма
есть отличное от нуля действительное число. Заметим, что элементы
системы Штурма можно вычислять с точностью до положительного
числового множителя.
Обозначим через N(c) число перемен знаков в системе Штурма
при лг = с, при условии, что нулевые элементы этой системы
вычеркнуты.
Теорема Штурма. Если полином Р(х) не имеет кратных
корней и Р(а)фО, Р(Ь)=^=0, то число его действительных корней
N(a, b) на интервале a<zx < Ь в точности равно числу
потерянных перемен знаков в системе Штурма полинома Р(х) при переходе
от х — а до х = Ь, т. е.
N(a, b) = N{a) — N(b). D)
Следствие 1. Если Р@)=7^=0, то число Af+ положительных
и число Л/_ отрицательных корней полинома ^(л:) соответственно
равны
N+=N@)—N(+oo)
и
N_=N( — oo)-W(O).

§ 61
ТЕОРЕМА БЮДАНА — ФУРЬЕ 171
Следствие 2. Для того чтобы все корни полинома Р (х)
степени пу не имеющего кратных корней, были действительны,
необходимо и достаточно, чтобы выполнялось условие
ЛГ( — оо)—
Таким образом, если
Р (х) = аохп + аххп^ + ... + ав,
где ао>О, товсе корни уравнения Я(лг) = О будут действительны
тогда и только тогда [1], когда: 1) система Штурма имеет
максимальное число элементов п+\, т. е. /я = я, и 2) выполнены
неравенства Pk( + oo)>0 (Л=1, 2, ..., л), т. е. старшие
коэффициенты всех функций Штурма Pk(x) должны быть
положительны.
Пример. Определить число положительных и число
отрицательных корней уравнения
=0. E)
Решение. Система Штурма имеет вид
= лг4 —4лг+1,
отсюда
//( — 00) = 2,
Следовательно, уравнение E) имеет:
N+ = 2—0 = 2
положительных корней и
ЛГ_ = 2—2 = 0
отрицательных корней. Поэтому два корня уравнения E) —
комплексные.
С помощью системы Штурма можно отделять корни
алгебраических уравнений, разбивая интервал (а, Ь), содержащий все
действительные корни уравнения, на конечное число частичных
интервалов (а, Р) таких, что
§ 6. Теорема Бюдана — Фурье
Так как построение системы Штурма, вообще говоря, требует
громоздких вычислений, то на практике ограничиваются более
простыми частными приемами подсчета числа действительных корней
алгебраических уравнений.

172 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Уточним подсчет числа перемен знаков в числовой системе.
Определение. Пусть дана конечная упорядоченная система
действительных чисел
с г с A)
где сгф0 и спф0.
С одной стороны, назовем нижним числом перемен знаков N
системы A) число перемен знаков в ее соответствующей подсистеме,
не содержащей нулевых элементов. __
С другой стороны, назовем верхним числом перемен знаков N
системы A) число перемен знаков в преобразованной системе A),
еде нулевые элементы
(cft_! Ф О, cft+/ Ф 0) заменены элементами cft+? (i = 0, 1, 2, ...,/— 1)
такими, что
k+r B)
Очевидно, что если система A) не имеет нулевых элементов, то
число N перемен знаков в этой системе по смыслу совпадает с ее
нижним N и верхним N числами перемен знаков:
вообще же говоря,
Пример 1. Определить нижнее число и верхнее число
перемен знаков в системе
1, 0, 0, -3, 1.
Решение. Игнорируя нули, получаем:
Для подсчета N, согласно формуле B), составляем систему
1, —е, е, —3, 1,
где е > 0. Отсюда __
Теорема Бюдана — Фурье. Если числа а и Ь (а < Ь) не
являются корнями полинома Р(х) степени п, то число N(a, b)
действительных корней уравнения
Я(ДГ) = О, C)
содержащихся между а и Ь, равно минимальному числу AN
перемен знаков, потерянных в системе последовательных

§ 61 ТЕОРЕМА БЮДАНА — ФУРЬЕ 173
производных
я/м* переходе от х = а к х = Ь, или меньше числа AN на четное
число, г. е.
N(a, b) = AN—2k,
где ___
AN = N(a)-N(b)
и N (я) — нижнее число перемен знаков в системе D) при х=а,
N(b)—верхнее число перемен знаков в этой системе при х = Ь
())
())
Предполагается, что каждый корень уравнения C) считается
столько раз, какова его кратность. Если производные f***(x)
(Л=1, 2, ..., п) не обращаются в нуль при х = а и лг = &, то
подсчет знаков упрощается, а именно:
Следствие 1. Если AAf=O, то между а и b нет
действительных корней уравнения C).
Следствие 2. Если AN=1, то между а и b имеется ровно
один действительный корень уравнения C).
Замечание. Для подсчета числа потерянных знаков AN в
системе D), пользуясь схемой Горнера, составляем два разложения:
E)
- ¦ F)
Пусть N(a) — нижнее число перемен знаков коэффициентов
разложения E) и соответственно N(b)—верхнее число перемен знаков
коэффициентов разложения F). Так как
^ Ь^ <*-0, 1,2, ...,«),
то знаки чисел ak и рЛ совпадают со знаками системы D) при
х = а и х = Ь. Поэтому
= N{a)—N(b).
Пример 2. Определить число действительных корней уравнения
Р(лг) = лг3— х2 + 2х — 3 = 0 G)
в интервале @, 2).

174 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Решение. Здесь N @), очевидно, есть число перемен знаков
в системе чисел
-3, 2, -1, 1,
т. е.
Разложение PB-\-h) получается с помощью применения схемы
Горнера
1—1 2 +3 1 2
2 2 8
1
1
1
1
1
2
3
2
5
4 5 |
6
10
Следовательно, NB) есть число перемен знаков в системе чисел
5, Ю, 5, 1,
т. е. NB) = 0.
Отсюда
AN=N@)—N{2) = 3.
Таким образом, уравнение G) имеет в интервале @, 2) три или
один действительный корень.
Теорема Декарта. Число положительных корней
алгебраического уравнения
Р(х) = а0хп + а1хп~1+...+ап = 0 (а0ф0) (8)
с учетом их кратностей равно числу перемен знаков в системе
коэффициентов
яо> av «2» •••> я* (9)
(где коэффициенты, равные нулю, не учитываются), или меньше
этого числа на четное число.
Теорема Декарта представляет собой применение теоремы Бю-
дана — Фурье к интервалу @, + °°)- В самом деле, так как
) = klan_k (? = 0, 1, ..., /г),
то система (9), с точностью до положительных множителей, есть

§ 6] ТЕОРЕМА ВЮДАНА—ФУРЬЕ 175
совокупность производных Р(к) @) (/5 = 0, 1, 2, ..., п), записанная
так, что порядки их убывают. Поэтому число перемен знаков в
системе (9) равно N@), причем коэффициенты, равные нулю, не
учитываются. С другой стороны, производные Р(А)(+оо)(^ = 0Л,2, ...,п)>
очевидно, имеют один и тот же знак и, следовательно, N ( + оо) = 0.
Поэтому имеем:
причем на основании теоремы Бюдана —Фурье число
положительных корней уравнения (8) или равно AN, или меньше AN на четное
число.
Следствие. Если коэффициенты уравнения (8) отличны от нуля,
то число отрицательных корней уравнения (8), с учетом их кратно-
стей, равно числу постоянств знакэ в системе (9) его
коэффициентов или меньше этого числа на четное число.
Доказательство этого утверждения непосредственно следует
из применения теоремы Декарта к полиному Р( — лг).
Укажем еще необходимый признак вещественности всех корней
полинома.
Теорема Гюа. Если уравнение
ai>xn+a1xm-l + a%x*-*+... +ап = 0 A0)
имеет действительные коэффициенты и все корни его действительны,
то квадрат каждого некрайнего коэффициента этого уравнения
больше произведения двух его соседних коэффициентов, т. е.
выполнены неравенства
al>ak-iak+i (* = !> 2, ..., л—1).
Следствие. Если при каком-нибудь k выполнено неравенство
то уравнение A0) имеет по меньшей мере одну пару комплексных
корней.
Пример 3. Определить состав корней уравнения
— 12лг2+104лг-20 = 0. A1)
Решение. Так как
(— 12)а < 8104,
то уравнение A1) имеет комплексные корни и, следовательно, число
вещественных корней этого уравнения не больше двух. В ряде
коэффициентов уравнения (И) имеется ДМ=3 перемен знаков и

176 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
АР=\ постоянств знаков. Отсюда на основании теоремы Декарта
и следствия к ней, учитывая наличие комплексных корней, делаем
вывод: уравнение A1) имеет один положительный корень, один
отрицательный корень и пару комплексных корней.
§ 7. Идея метода Лобачевского — Греффе
Рассмотрим алгебраическое уравнение я-й степени
где ао=^О. Предположим, что корни xv лг2, ..., хп уравнения A)
таковы, что
J' B)
т. е. корни различны по модулю, причем модуль каждого предыдущего
корня значительно больше модуля по-
следующего*). Иными словами, мы
предполагаем, что отношение любых
двух соседних корней, считая в по-
рядке убывания их номеров, есть ве-
личина, малая по модулю, т.е.
г
I
\
\
\ У \
11
C)
Рис. 44.
где )ел|<е и е—малая величина.
Такие корни для краткости будем
называть отделенными (рис, 44).
Воспользуемся теперь соотношениями между корнями и
коэффициентами уравнения A) (§ 1)
X 4-х 4- 4-Х = — S
*) Если коэффициенты уравнения A) действительны» то из условия B)
следует, что все корни уравнения A) действительны.

Л J] ИДЕЯ МЕТОДА ЛОБАЧЕВСКОГО—ГРЕФФЕ
Отсюда в силу допущений C) мы получаем:
177
D)
где Ev Е2, ..., Еп—малые по модулю величины по сравнению с
единицей. Пренебрегая в равенствах D) величинами Ek (k = 1,2, ..., /г),
будем иметь приближенные соотношения
аг
ххх2.. .хп — ( l)n^f •
E)
Отсюда находим искомые корни
F)
Иными словами, если корни уравнения A) отделены, то они при*
ближенно определяются из цепи линейных уравнений
причем точность этих корней зависит от того, насколько малы по
модулю величины гк в соотношениях C).
Чтобы добиться отделения корней, исходя из уравнения A),
составляют преобразованное уравнение
„("Оу" 4- a<m)vn~l 4- 4- aSm) = 0 п\
«о ¦* * 1 + » • • • • л * \1)
корнями которого ух, у2, ...,уп являются /я-е степени корней
хг> Х2> •••! хп уравнения A), т. е.
Лв^Г (к=*> 2, ..., я). (8)

178 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Если корни уравнения A), которые мы считаем расположенными
в порядке убывания модулей, являются различными по модулю, то
корни уравнения G) при достаточно большой степени т будут
отделенными, так как
Например, пусть
При /я =100 будем иметь:
оо.
и, следовательно,
-^- = 3,2- Ю3; -^- = 2,5. Ю-18.
У1 Уг
Обычно в качестве показателя т берут степень числа 2, т. е.
полагают т = 2р, где р — натуральное число, а само преобразование
производят в р приемов, каждый раз составляя уравнение, корнями
которого являются квадраты корней предшествующего уравнения.
Приближенно вычислив корни ук (k= I, 2, ..., я), из формул (8)
можно определить и корни исходного уравнения A), Точность
вычислений зависит от того, насколько малым является отношение
модулей соседних корней преобразованного уравнения.
Идея этого метода вычисления корней принадлежит Лобачевскому,
практически удобная схема вычислений была предложена Греффе.
Достоинством метода Лобачевского — Греффе является то, что
при применении этого метода нет необходимости изолировать корни.
Нужно лишь избавиться от кратных корней с помощью приема,
указанного в § 1. Само вычисление корней ведется однообразным
регулярным способом. Как мы увидим далее, метод годится также
и для нахождения комплексных корней. Неудобство метода состоит
в необходимости оперирования с большими числами. Кроме того,
отсутствует достаточно надежный контроль вычислений и
затруднена оценка точности полученного результата.
Заметим, что если корни уравнения A) различны, но модули
некоторых из них близки между собой, то сходимость метода
Лобачевского — Греффе весьма медленная. В этом случае такие корни
следует рассматривать как равные по модулю и применять
специальные приемы вычисления.
§ 8. Процесс квадрирования корней
Покажем теперь, как можно просто составить уравнение, корнями
которого являются квадраты корней данного алгебраического
уравнения, взятые со знаком минус. Последнее обстоятельство вызывается
соображениями удобства, чтобы по возможности избежать появления

§ 8] ПРОЦЕСС КВАДРИРОВАНИЯ КОРНЕЙ 179
отрицательных коэффициентов. Процесс перехода от корней
лгЛ (/5=1, 2, ..., п) к корням
для краткости будем называть квадрированием корней*
Пусть
О)
— данное уравнение, где ^
Обозначая через xv лг2, ..., хп корни этого уравнения, будем
иметь:
Р (х) = ао(х — хх) (х — х2) ... (х — хп).
Отсюда
Следовательно,
Р(х)Р(-х) = (-\)па1(х*-х1)(х*-х1)...(х*-х*п). B)
Полагая
У=-х2,
в силу формулы B) получим полином
Q(y) = P(x)P(-x)t
корнями которого являются числа
Уи=-х\ & = л> 2> ••- Л)-
Так как
то, производя перемножение полиномов Р(х) и Р(—хO будем иметь:
Следовательно, интересующее нас уравнение есть
Q(y) = Аоуя + Aiyn-i + A2yn~*+ ... + Л„ = О,
где
= а0%
= а\ —

180 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Короче можно записать:
где предполагается Оу = 0 при s<0 и $ > я.
Правило. Яры квадрировании корней каждый коэффициент
преобразованного уравнения равен квадрату прежнего коэффициента,
минус удвоенное произведение соседних с ним коэффициентов, плюс
удвоенное произведение следующих в порядке близости
коэффициентов и т. д., причем если нужный коэффициент отсутствует, то он
считается равным нулю.
§ 9. Метод Лобачевского — Греффе для случая
действительных различных корней
Пусть корни xv х2, ..., хп уравнения л-й степени с
действительными коэффициентами
а^ + а^+.^+а^О A)
действительны и различны по модулю. Расположим их в порядке
убывания модулей:
Последовательно применяя процесс квадрирования корней,
составляем уравнение
/ +Vя'1+...+*» = 0, B)
корнями которого служат числа
yk=-xf (*=1, 2, ..., п). C)
Если р достаточно велико, то корни yv у2, ..., уп являются
отделенными и на основании результатов § 7 могут быть определены
из цепи линейных уравнений
Отсюда получаем:
лгА = ±2{/^=У^ (Ы,2 я); D)
знаки корней xk определяются грубой прикидкой, при подстановке
в данное уравнение, или на основании соотношений между корнями
и коэффициентами уравнений. Процесс квадрирования корней обычно

§ 9] МЕТОД ЛОБАЧЕВСКОГО ГРЕФФЕ ДЛЯ РАЗЛИЧНЫХ КОРНЕЙ 181
продолжается до тех пор, пока удвоенные произведения не
перестанут влиять на первые главные члены коэффициентов
преобразованного уравнения.
Правило. Процесс квадрирования корней следует прекратить,
если коэффициенты некоторого преобразованного уравнения в
пределах точности вычислений равны квадратам соответствующих
коэффициентов последующего преобразованного уравнения за счет отсутст*
вия удвоенных произведений.
Действительно, если преобразованное уравнение,
соответствующее степени 2р+\ имеет вид
и выполнены соотношения
ck~b\ (& = 0, I, 2, ..., л),
то, очевидно, получаем:
111+1
Таким образом, при этих обстоятельствах мы не сможем увеличить
точность вычисления корней.
Так как при применении метода Лобачевского — Греффе
коэффициенты преобразованных уравнений, вообще говоря, быстро растут,
то полезно выделять порядки их, записывая коэффициенты в
стандартной форме а«10т, где |а|<10 и m — целое число. При
вычислениях, требующих большой точности, выгодно пользоваться
логарифмами (см. [5]).
Пример. Методом Лобачевского — Греффе найти корни
уравнения
= 0. E)
Решение. Результаты вычислений с четырьмя значащими
цифрами помещены в таблице 8.
Останавливаясь на 64-й степени корней, будем иметь:
— 3,445.1017 -х? + 2,486.1029 = О,
— 2,486- 1О29.л;з4+ 1=0.
Отсюда
- | У2.Ц6 1Оч
— =*= \ 3,445 Ш '

182 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Таблица 8
Вычисление действительных корней
методом Лобачевского — Греффе
Логарифмируя, получим:
\г\х1\=щ- 17,53719 = 0,27402;
lg | лга | = ^ • 11,85831 = 0,18528;
лг3 j = JL . (— 29,39550) =Т,54070,
и, следовательно,
Степени
1
2
4
8
16
32
64
128
X9
1
1
1
1
1
1
1
1
*8
0
°\
Ч
6
36 \
-18}
18
3,24. ЮМ
—1.38102 (
1,86 -10а
3,460-10* \
—0,945.10* |
2,515-10*
6,325-108 1
—0,447.108 \
5,878.108 1
3,455.10» \
—0,010.10"/
3,445-10"
1,187.1035\
0 /
1,187.10s6
X
—3
о/
9
81\
-12/
69
4.76Ы0М
-0,036-10*/
4,725-10*
2,233-10П
0 /
2,233-107
4,986.101* \
0 /
4,986-101*
2,486.1029\
0 /
2,486-102»
6,180.10й \
0 /
6,180-1058
X*
1
1
1
1
1
1
1
1
лгг = ± 1,879;
хг = ± 1,532;
*3 = ± 0,347.
Для определения знаков корней заметим, что согласно правилу
Декарта уравнение E) имеет один отрицательный корень и два

§ 10] МЕТОД ЛОБАЧЕВСКОГО — ГРЕФФЕ ДЛЯ КОМПЛЕКСНЫХ КОРНЕЙ 183
положительных корня*), причем
*!+*« +¦*« = <>. <6)
Поэтому наибольшим по модулю должен быть отрицательный
корень, и мы окончательно имеем:
лг1== —1,879;
х2 = 1,532;
xz = 0,347;
причем соотношение F) выполнено в пределах заданной точности.
Для сравнения приводим точные значения корней, полученные по
формуле Кардана:
хх = 2 cos 160° = — 1,87938;
*2 = 2 cos 40° =1,53208;
лг3 = 2 cos 80° = 0,34730.
Заметим, что в нашем случае вычисление корней несколько
упростилось благодаря тому, что крайние коэффициенты уравнения
равны 1. Вообще, при применении метода Лобачевского —Греффе
рекомендуется предварительно преобразовывать уравнение так, чтобы
старший коэффициент уравнения был равен 1, а свободный член
уравнения был равен ±1 (см. [5]).
§ 10. Метод Лобачевского — Греффе для случая
комплексных корней
Обобщим теперь понятие отделения корней.
Пусть корни xv лг2, ..., хп уравнения
аххп-*+...+ап = 0 A)
удовлетворяют условиям
|>ll>-..>|*J. B)
Иными словами, предполагается, что корни уравнения A) можно
разбить на две категории (группы):
• > Хп>
*) Мы учитываем, что уравнение Р (лс)==зх3 — 3*-4-1=0 имеет
положительные корни, так как Р @) > 0 и Р A) < 0.

184 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
так, что модули корней первой категории весьма велики по
сравнению с модулями корней второй категории (см. рис. 45, где корни
содержатся в заштрихованных областях, а внутренность незаштри-
хованного кругового кольца свободна
от корней — «зона пустыни»).
Выпишем первые т соотношений
между корнями и коэффициентами
уравнения A):
1ХВ
• • +Хт-1Х
Рис. 45.
...+*„-
...*„)= (-lI"^.
• • • + *«-i*« — 7ГГ »
Пренебрегая в последних равенствах взятыми в скобки
относительно малыми по модулю членами, получим приближенные
соотношения
«1
C)
Отсюда следует, что корни xv лг2, .. .,хт первой категории (с
большими модулями) приближенно являются корнями уравнения
= 0. D)
Из оставшихся неиспользованных п — т соотношений между
корнями и коэффициентами уравнения A) получаем:
• • -*
т + 1
• • • Т-*и-1Я-1- • -Хп — \
гх2.. *хтхт+1.. .хп — (— 1)" -^ .

§ 10J МЕТОД ЛОБАЧЕВСКОГО — ГРЕФФЕ ДЛЯ КОМПЛЕКСНЫХ КОРНЕЙ 185
Отбрасывая в последних равенствах относительно малые по модулю
члены, будем иметь приближенные соотношения
. . .Х
. . .Х
~Г • • • ~Гхп) == ( *) ~~^ »
Отсюда, используя последнее соотношение в формулах C), находим:
i • • •
E)
Следовательно, корни хт+1, хт+2, ..., хп второй категории (с
малыми модулями) приближенно являются корнями уравнения
amxn-m + am_lXn-m-i+...+an = 0. F)
Таким образом, в наших условиях уравнение A) распадается на два
уравнения более низких степеней, каждое из которых приближенно
определяет корни, принадлежащие одной из категорий.
Рассуждая по аналогии, заключаем, что если корни
уравнения A) могут быть разбиты на р категорий
•^1» ^2» • • • > хтх\
•••» хmi*
••» хтр
так что выполнено условие
т« е. модули корней, принадлежащих более низким категориям,
значительно превышают модули корней, принадлежащих более высоким
категориям (можно сказать, что эти корни являются отделенными

186 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
в групповом смысле), то корни каждой категории приближенно
могут быть определены из соответствующих уравнений
ат% = О,
.. + ат%+тл = 0,
G)
степени которых соответственно т19 т2У .«., /»я. В частности, если
корни уравнения A) полностью отделены, то уравнения G) —
линейные; паре комплексных корней при отсутствии других корней того же
модуля будет соответствовать квадратное уравнение в совокупности
уравнений G) и т. д.
Мы ограничимся здесь рассмотрением простейших случаев, когда
уравнение A), коэффициенты которого считаются действительными,
имеет одну пару комплексных корней или же две пары комплексных
корней с различными модулями, причем модули действительных
корней различны и отличны от модулей комплексных корней. С более
общими случаями можно познакомиться в книгах Крылова [5] и
Скарборо [6].
§ 11. Случай пары комплексных корней
Пусть
(и и v действительны, v=?0) — комплексные корни уравнения A)
§ 10, причем все остальные корни xk (k=?m, k=fcm-\-\) этого
уравнения действительны и удовлетворяют условию
l*il>l*2|>-.->l*JH**+il>--->KI- B)
Применяя процесс квадрирования корней, составим уравнение
V+^i/1-1 + ...+*. = о,
корнями которого являются:
При достаточно большом натуральном р действительные корни
Уг> • • •> Ут-v Ут+%> • • •> Уп бУДУт разделены с большой степенью

§11] СЛУЧАЙ ПАРЫ КОМПЛЕКСНЫХ КОРНЕЙ 187
точности- и могут быть определены из линейных уравнений
Отсюда получаем:
уж
Процесс квадрирования корней прекращается, когда в
коэффициентах bv ..., bm_v bm+v ..., ?„ при следующем шаге пропадают,
в пределах заданной степени точности, удвоенные произведения. Что
касается коэффициента ЬтУ то в его состав, вообще говоря, не
входят исчезающие удвоенные произведения. Может даже случиться,
что эти произведения превалируют над квадратом и коэффициент Ьт
имеет меняющийся знак. Это обстоятельство служит характерным
признаком наличия комплексных корней или корней с равными
модулями в уравнении A) § 10, причем ведущий себя необычным образом
коэффициент Ьт указывает место таких корней в ряде модулей B).
Заметим, что рассматриваемое уравнение заведомо имеет
комплексные корни, если коэффициент Ът меняет знак; так, при наличии
лишь действительных корней все коэффициенты преобразованных
уравнений, очевидно, неотрицательны.
Согласно общей теории корни ут и ут+1, соответствующие
комплексным корням хт и xm+v приближенно удовлетворяют
квадратному уравнению
Обратим внимание, что коэффициент Ьт является средним.Так как
¦***ft+i = «* + *f =г*»
где
— общий модуль комплексных корней, и
то по свойству корней квадратного уравнения имеем:
Отсюда определяем квадрат модуля комплексных корней
C)

188 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Действительную часть и комплексных ^корней проще всего найти,
воспользовавшись соотношением
Отсюда
0 ^
k 7= m + i
и, следовательно,
¦--?Нг 2" **• <4)
k jt m+i
Зная в силу формулы C) общий модуль г комплексных корней,
находим коэффициент v их мнимой части
г> = Уг2 — и2. E)
По формулам D) и E) определяем искомые комплексные корни
Можно также искать комплексные корни в тригонометрическом
виде
*«, ш + 1=Г(СО8ф±/81Пф).
Пример. Найти корни уравнения [7]
** + *»—10** —34*— 26 = 0. F)
Решение. Результаты вычислений с четырьмя значащими
цифрами приведены в таблице 9.
Из таблицы 9 видно, что в пятом преобразованном уравнении
(степень корней 25 = 32) действительные корни хг и л:4 (считая
в порядке убываний модулей) являются отделенными. Эти корни
можно найти из двучленных уравнений
,005-1019 = 0,
— 2,704
Отсюда
*! = ±'/2,005.
Логарифмируя, будем иметь:
1« I * I
I §5 • 19-.S0211 = 0,60319;
¦*«I =^ ' B,27898 — 0,43201) = 0,05772.

§ 11]
СЛУЧАЙ ПАРЫ КОМПЛЕКСНЫХ КОРНЕЙ
Вычисление комплексных корней
методом Лобачевского — Греффе
189
Таблица 9
Степени
¦
2
4
8
16
32
64
X*
1
1
1
1
1
1
1
i)
21
441\
—239/
209
4,368.104\
2,380.10*/
6,748.10*
4,554. ЮМ
-0,078.10е/
4,476-10»
2,003. №\
0,002.10"/
2,005-101»
4,020-1038\
0 /
4,020-10а8
—10
100^
68 }
-52)
116
1,346. ЮМ
-2,671-10*>
0,135.10*1
-1,190.10*
1,416-ЮМ
-1,035.108>
0,009.108)
3,90 -107
1,521-Ю15
-9,748-101*
0
8,227-
6,768.
4,655-
0
2,113.
4,465-
1,084-
0
1015
1031
1031
1031
10е2
10ез
—6,38-10е2
—34
1156\
—520/
636
4,045.105\
—1.568106/
2,477-Юв
6,135.1010\
1,088.1010/
7,223.1010
5,216.1021\
-0,016. 1021/
5,200.1021
2,704-10«\
0 /
2,704. Ю43
7,312.108в\
0 /
7,312.108в
-26
676
4,570-Ю5
2,088-10*
4,360-102а
1,90Ы046
3,614-1090
Следовательно,
*! = :? 4,010; л:4 = ± 1,142.
Грубой прикидкой убеждаемся, что корень л^ —положительный,
а корень аг4 —отрицательный. Таким образом, окончательно имеем:
а:1==4,010; л:4=—1,142.
Так как преобразованный коэффициент при х2 меняет знак, то
данное уравнение имеет комплексные корни х = х2 и х = хв, которые
определяются из трехчленного уравнения
2,005. \019у2 + 2,113- \0пу + 2,704-10^ = 0,
где
Согласно общей теории модуль корней

190 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ |ГЛ. V
находится по формуле C)
«/2,704
У 2,005 Ш *
Отсюда
lg г2 = ~. B4,43201—0,30211) = 0,75406
и, следовательно,
г2 = 5,6763.
Полагая
из соотношения
получим:
« = ^-(-1-4,010+1,142)= -1,934.
Коэффициент мнимой части v определяется по формуле
v = У г2 — u* = V 5,6763—3,7404 = |/ 1,9359 = 1,395.
Следовательно,
лг23=г —1,934 ±1,395/.
Заметим, что корни дг2 и лг8 можно также определить из
соотношений между корнями и коэффициентами уравнения F), а именно,
имеем:
ХХ ~Ь Х% ~Г XZ "г «^4 === — * >
ЛГ1ЛГ2Л:3ЛГ4 ^ —26.
Отсюда, использовав найденные выше значения хг и х4, получим:
лг2 + *3= —3,869;
лг2лг3 = 5,677.
Поэтому лг2 и дг3 можно найти как корни квадратного уравнения
решив которое, будем иметь:
*2,з= -1,934 ± 1,391/.
§ 12. Случай двух пар комплексных корней
Пусть уравнение A) § 10 допускает две пары комплексных корней:

12) случай двух пар комплексных корней 191
с различными модулями (uv vv и2, v% действительны и ^
г/2=^=0), причем все остальные корни х1{]фку j^k+\, }фту
:ф.т^. \) этого уравнения действительны, различны по абсолютной
величине, не равны нулю*) и отличны по модулю от комплексных
корней, т. е.
l*i I > l*t I >•• ..>l^-il> 1-^*1 = l**+i I>--->I*J =
H*. + il>.-.>l*J>0. 0)
Как обычно, производя квадрирование корней рассматриваемого
уравнения до некоторой степени 2Р, получим преобразованное
уравнение
корнями которого являются числа
При достаточно большом натуральном р обнаружится, что при
переходе к степени 2Р+1 некоторые коэффициенты Cj нового
преобразованного уравнения
будут представлять собой, в пределах заданной точности, квадраты
соответствующих коэффициентов bf предшествующего
преобразованного уравнения. При нашем предположении A), мы в конце концов
получим:
Cj=b) при у = 0, 1, 2, ..., ft—
Это обстоятельство позволяет установить место комплексных корней.
Заметим, что достаточным признаком наличия двух пар
комплексных корней уравнения A) § 10 служит изменение знаков
коэффициентов Ьк и Ьт для различных показателей 2Р.
Действительные корни Xj рассматриваемого уравнения
определяются из двучленных уравнений
Отсюда
*у = ± У jjL
*) Нулевые корни могут быть выделены предварительно.

192 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Комплексные корни xk, xk+1 и хт, хт+1 соответственно
определяются из трехчленных уравнений
*+**« = <> B')
т+Ьт+1 = 0. B")
Введем обозначения:
Г___ I \я I <+ I
1 — \хк I — l-^A + ll
Учитывая, что
rx =*
из уравнений B') и B") можно вычислить квадраты модулей
комплексных корней
Для определения действительных частей и1 и и2 комплексных корней
воспользуемся соотношениями между корнями и коэффициентами
уравнения A) § 10, а именно, имеем:
х2х3 ... хп + хгх8 ... хп+ ... +ххх2 ... дг^1 = (- If1 2а=!
и
Х1хг • • • хп — \ ч ?~ •
Разделив первое равенство на второе, получим:
Кроме того,
Отсюда, учитывая соотношения

§ 12] случай двух пар комплексных корней 193
имеем следующую линейную систему уравнений:
•Л ^ «L_Ya' [ C)
9 I о """"™ О/. О >
г\ тъ п J
где a—сумма действительных корней и а' —сумма обратных величин
действительных корней, т. е.
k+i, m, m + i
«¦= Е '
ft+i, m, m+i
X/
Найдя из системы C) их и яа, определяем коэффициенты vt и
мнимых частей комплексных корней по формулам
Таким образом, окончательно находим:
Пример. Методом Лобачевского — Греффе решить уравнение [7]
0. D)
Решение. Применяя процесс квадрирования корней до 16-й
степени и производя вычисления с точностью до четырех значащих
цифр, получим результаты, приведенные в таблице 10.
Легко видеть, что при следующем преобразовании средний
коэффициент будет равен квадрату своего прежнего значения. Поэтому
мы прекращаем процесс квадрирования корней. Так как для 16-й
степени среди коэффициентов преобразованного уравнения имеются два
отрицательных коэффициента, то уравнение D) допускает две пары
комплексных корней:
которые соответственно удовлетворяют трехчленным уравнениям
*32+ 1,359- 10блг1в +5,720-10» = 0
и
5,720.109.#
Б. П. Демидович и И. А. Марон

194 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Таблица 10
Вычисление двух пар комплексных корней
методом Лобачевского — Греффе
Степени
1
2
4
8 '
. 16
X*
1
1
1
1
1
X9
0
01
—8
64 1
—44/
20
4-102 1
—5,24 -lO2 j
—1,24 .102
1,538-10* \
—15,128.10* /
—1,359-105
X*
4
б/
22
4841
—240 >
18 J
262
6,864-10*1
0,684-10* >
0,016-10* J
7,564-10*
5,723.10» 1
—0,003-10» }
о J
5,720-10»
X
—3
9\
—24/
-15
2251
-396 /
—171
2,924.10*1
—4,244.10*/
—1,320.10*
l,743.108\
—9,927-108/
—8,184.108
x°
3
9
81
6,56M03
4,305-107
Отсюда определяем квадраты модулей этих корней:
Гб» = 4,072
1 зле как
~ = 0,2456; -V=1.3574,
то на основании системы C) для нахождения действительных
частей uL и иг корней имеем систему
Отсюда
0,2456^+ l,3574i/2 = 0,5.
tf1== ^0,4497;
и2 = 0,4497.

§ 13] метод бернулли 195
Используя найденные квадраты модулей г\ и г\ корней, определяем
коэффициенты vt и v2 мнимых частей корней:
vx = Vr\-u\ = 1,967;
Таким образом, корни уравнения D) имеют вид
z 1,967/
дг3| 4 = 0,450 ±0,731/.
§ 13. Метод Бернулли
Пусть дано алгебраическое уравнение
= 0 (а0 ф 0), A)
корни которого #х, лг2, ... , хп различны.
На основе коэффициентов ак (& = 0, 1, ..., п) построим так
называемое конечно-разностное уравнение
"оУп^ + *1У*+1-1+'--+аМ = 0 (/ = 0, 1, 2, ...), B)
которое представляет собой рекуррентное соотношение,
связывающее любые, следующие друг за другом, п-\-\ членов бесконечной
последовательности
Л> Уху У%> • ¦ • > Л. • • • C)
Последовательность C) ву.=/(/) (/ = 0, 1, 2, ...), члены которой
удовлетворяют конечно-разностному уравнению B), называется
решением этого уравнения. Для построения решения^- достаточно задать п
его начальных значений уф yv ... , уПж1; остальные члены уп>
Уп+г> • • • шаг за шагом можно определить из уравнения B).
В теории конечных разностей [8] доказывается, что если корни х1У
х2У ..., хп алгебраического уравнения A) различны, то любое
решение конечно-разностного уравнения B) имеет вид
*п (/ = 0, 1, 2, ...), D)
где С1У С2, ..., Сп — произвольные постоянные. Таким образом,
Уравнение A) по отношению к уравнению B) является
характеристическим. Постоянные Clf С2, ... , Сп могут быть определены
из начальных условий:
Уг = ClXl + С2х2 + ... + Спхп,

196 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Теорема. Пусть алгебраическое уравнение A) имеет
единственный наибольший по модулю корень хг. Тогда отношение
двух последовательных членов yi+1 и у{ решения
конечно-разностного уравнения B) стремится, вообще говоря, к пределу,
равному xv т. е.
Шп^^д; F)
/-*• У1 г
Доказательство. Пусть
Предполагая, что корни xk (&=1, 2, ..., п) различны, из
формулы D) имеем:
Отсюда
fl
/Q\
Если Ci^O, то, переходя к пределу в формуле (8) при /—^ оо
и учитывая, что в силу неравенств G) имеют место предельные
соотношения
будем иметь:
У(
Замечание 1. Если при неудачном выборе решения окажется,
что Ct = 0, а С2=7^0» то предел F) будет равен следующему
наибольшему по модулю корню уравнения A).
Замечание 2. Если для решения^, отношение ^?! колеблется,
а//
не стремясь к пределу, то возникает подозрение, что уравнение A)
имеет комплексные корни, наибольшие по модулю.
Замечание 3. Производя в уравнении A) замену переменной
методом Бернулли можно найти отличный от нуля наименьший по
модулю корень уравнения A).

§ 13] метод бернулли 197
Таким образом, для приближенного нахождения наибольшего
по модулю корня хг уравнения A) можно пользоваться формулой
1 Уi-x *
где / достаточно велико.
Для практического применения метода Бернулли нужно задать
произвольные числа уф уг, ... , уп_1У а затем, пользуясь формулой
Уп+(=-1т(апУ1 + ап-1У1-1+ .-• +вьУя+?-1) (/ = 0, 1, 2, ...),
"О
вычислить последовательность чисел уп, уп+±, уп+2> ••• и
отношения -^-, ik±S, ?п±$у ... Если отношение Уя+* при возрастаю-
Уп-1 Уп Уп + 1 Уп+i-l
щем I обнаруживает тенденцию приближения к некоторому числу ?,
то последнее принимается за наибольший по модулю корень xt
уравнения A). В противном случае весьма вероятно, что уравнение A)
имеет несколько корней, наибольших по модулю, или, что менее
вероятно, что для начальной системы чисел у0У yv ... , уп_х
коэффициент Сх = 0.
Если известно грубое значение а наибольшего по модулю корня xlf
то для ускорения сходимости процесса выгодно положить:
Л^ЬЛ^а» ••• » JV-i^a —
Заметим, что метод Бернулли сводится к повторению однообраз*
ных операций и поэтому удобен для реализации на счетных машинах.
Начальные значения у{ (/ = 0, 1, ..., л —1), вообще говоря,
могут быть взяты произвольно. Обычно берут уо=у1= ,.. =уп_2 — 0;
вуи_1 = 1. Хильдебрант [9] предложил выбирать у{ так, чтобы все
коэффициенты С{ в формуле D) были равны 1. В этом случае,
при наличии единственного наибольшего по модулю корня
уравнения A), процесс -^- заведомо сходится при /—* оо.
Метод Бернулли может быть применен также для вычисления
комплексных корней уравнения A) [10].
Пример. Найти наибольший по модулю корень xt уравнения
—5 = 0.
Решение. Соответствующее конечно-разностное уравнение
имеет вид
(/ = 0, 1, 2, ...). (9)
Произвольно берем значения
По формуле (9) подсчитываем значения yt при / ^ 5. Найденные
значения приведены й таблице 11.

198 СПЕЦИАЛЬНЫЕ ПРИЕМЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. V
Таблица 11
Нахождение корней алгебраического уравнения методом Бернулли
1
5
6
7
8
9
Vi
-5
25
—125
625
—3120
Vi
Vi-i
—5
—5
—5
-4,992
i
10
11
12
13
Vi
15 575
—77 750
388 125
—1 937 500
Vi
Vi-\
—4,992
—4,928
—4,99196
—4,991948
Остановившись на у1В1 будем иметь:
Й-H
--¦¦»««•
Отсюда, учитывая у12, приближенно можно положить:
#!=—4,99195.
В заключение отметим, что в последнее время появились новые
методы решения алгебраических уравнений, обладающие удобными
вычислительными схемами (метод Лина, метод Н. В. Палувера
и др.) [10].
Литература к пятой главе
1. А. Г. Курош, Курс высшей алгебры, Гостехиздат, М.—Л., 1946,
гл. 7 и 8.
2. Г. М. Ш а п и р о, Высшая алгебра, Изд. 4, ГУПИ, М., 1938, гл. III и VL
3. Д. Граве, Элементы высшей алгебры, Киев, 1914, гл. X.
4. Б. А. Фукс и Б. В. Шабат, Функции комплексного переменного,
Гостехиздат, М. —Л., 1949, гл. VII.
5. А. Н. Крылов, Лекции о приближенных вычислениях, Изд. 2,
Изд-во АН СССР, 1933, гл. II.
6. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
М. — Л., 1934, гл. X.
7. Б. К. Млодзеевский, Решение численных уравнений, ГИЗ, М.,
1924, гл. IV.
8. А. О. Гельфонд, Исчисление конечных разностей, Гостехиздат, 1952,
гл. V.
9. F. В. Н i I d e b г a n d, Introduction to numerical analysis, New York —
Toronto—London, 1956.
10. В Л. За гу скин, Справочник по численным методам решения
алгебраических и трансцендентных уравнений, Физматгиз, 1960.

ГЛАВА VI
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
§ 1. Улучшение сходимости числовых рядов
Говорят, что ряд
+... A)
сходится медленно, если нужно взять весьма большое число членов
ряда, чтобы получить его сумму с заданной степенью точности.
Например, пусть требуется найти сумму ряда
+ +..+^+... B)
с точностью до 10~в. Для я-го остатка ряда имеем оценку
Следовательно, наша точность будет гарантирована, если мы
возьмем сумму 1000 000 членов ряда, что практически невозможно.
Поэтому ряд B) при решении поставленной задачи следует
рассматривать как медленно сходящийся ряд.
Таким образом, непосредственное нахождение суммы медленно
сходящегося ряда с заданной точностью е, вообще говоря,
затруднительно или даже практически невыполнимо. Поэтому важное значение
приобретают преобразования рядов, улучшающие их сходимость.
Мы здесь ознакомимся с преобразованием Куммера [3], [4], в ряде
случаев полезным для нашей цели.
Пусть ряд A) сходится и сумма его равна А Подберем
вспомогательный сходящийся ряд
+ ... (Ьп?=0), B')

200 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
сумма которого В известна, причем такой, что существует
lim %L = q=?Q. C)
Тогда имеем очевидное равенство
или
A = qB-{- 2 ian — Я&п)< W
В частности, если ап~Ьп, то q = 1 и мы имеем:
со
Следовательно, нахождение суммы ряда A) в общем случае
заменяется нахождением суммы ряда
00
2 (я„—qbn)< E)
Остаток ряда E) /?# может быть записан в следующем виде:
где ert= 1 — q-^—^0 при л—^оо.
Поэтому, вообще говоря, ряд E) сходится быстрее исходного
ряда A). Основная трудность применения преобразования Куммера
состоит в удачном подборе вспомогательного ряда B').
Покажем применение этого преобразования для
знакоположительного ряда A), члены которого ап есть рациональные функции
целочисленной переменной п, т. е.
'^+.-.+Pg (п ' ' ~ш)' F)
где р и q—целые неотрицательные числа и а0 > 0, Ро > 0. Для
сходимости ряда с общим членом F) необходимо и достаточно,
чтобы имело место неравенство

§ 1] УЛУЧШЕНИЕ СХОДИМОСТИ ЧИСЛОВЫХ рЯДОВ 201
В этом случае
(по меньшей мере!).
Рассмотрим вспомогательные ряды
(т=1, 2, ...). G)
/1 = 1
Так как
1
(П+Ч ' ! 1,
т |_я (п+1).. ,(я+/«—1) (л+1) (я + 2)...(я^-m)J
т
то
N
Следовательно,
(8)
Используя идею Стирлинга, общий член ряда, определяемый
формулой F), представим в виде конечной суммы обратных факториалов
где Av A%, ..., Am — неопределенные коэффициенты и
a^m)—остаточный член. Подберем коэффициенты А( (/=1, 2, ..., /я) так,
чтобы
*) Говорят, что ап есть бесконечно малая порядка не меньше т
относительно —;
я
если
Если при этом с Ф 0, то ал—бесконечно малая точно порядка т
относительно --.
я

202
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. VI
Для этого достаточно коэффициенты А^ последовательно
определять по формулам
Ах= [\тп(п+\)ап,
п(п+
(9)
Согласно общей схеме за вспомогательный ряд B) примем:
OD 0D
?*""?• Ln(»+i)+»(»+i)
причем очевидно, что
ton fa =1
л-»-се *п
Так как быстрая сходимость дополнительного ряда 2 Л«т)
обнаруживается, вообще говоря, лишь при достаточно большом #, то
практически удобно выполнять указанное преобразование, начиная
лишь с некоторого члена ряда ар+1. Полагая
+1
П=1
Л=р+1
ап,
будем иметь:

§ 1J УЛУЧШЕНИЕ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ 203
4t я
д(/й)
В частности, при /»—^oo, учитывая что а(ят)и?0, получим
ложение Стирлинга
Пример. Найти сумму ряда
с точностью до 0,001.
Решение. Положим:
Имеем:
1 — ^1 J
Следовательно,
/i*-f 3ft2+ 2/1 — л*—2/га-.п—2—па— 1 дг—3
л (л+1) (л+ 2) («2 +1) /г (л+1) (/1 + 2)
На основании формул A0) и A1) получим:
Так как при я^»3 имеем
/г —3

204 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
то
со со
п—3 ^ Cdx 1 . 1
n
Отсюда следует, что число слагаемых в сумме A2') можно взять
N=10, причем эти слагаемые нужно вычислять с четырьмя
десятичными знаками в узком смысле. Таким образом, имеем:
S& 1,25+ ( — 0,1667)+ ( — 0,0083)+ 0 + 0,0005+ 0,0004 +
+ 0,0002 + 0,0002 + 0,0001 + 0,0001 + 0,0001 = 1,0766,
причем, приняв во внимание, что сумма четырех первых слагаемых
точная, для абсолютной погрешности результата получим оценку
Д < 1.10-з+7.1-М-4 < 0,7-Ю-з.
Отсюда, округляя, находим значение
5 «1,077
с предельной абсолютной погрешностью
Д = 0,7- Ю-з + 0,4.10"8= 1,1 • Ю-3.
Заметим, что для остатка данного ряда A2) имеем оценку
J
N
Отсюда /V ^э 2000, т. е. без преобразования для достижения той
же точности нужно взять примерно 2000 членов ряда.
Замечание. Для приближенного вычисления суммы ряда A)
с общим членом F) можно использовать также ряды
«X 00 00
2—б; Z-in4 —go' Z* пв — 945 И Т# Д#
Л=1 Л=1
Вообще говоря,
У -L-t
2 Bр) ! '
где Вя(л=1, 2, ...) —числа Бернулли [5], [6], определяемые
символической формулой

§ 21 улучшение сходимости степенных рядов 205
в которой после развертывания по биному Ньютона полагаем Вп =^ Вп.
В частности, имеем:
(см. гл. XVI, § 11).
§ 2. Улучшение сходимости степенных рядов
методом Эйлера — Абеля
Рассмотрим сходящийся степенной ряд
S A)
где f(x) — сумма ряда.
Пусть радиус сходимости R ряда A) конечен и отличен от нуля.
Не нарушая общности рассуждения, можно считать, что # = 1*).
Запишем ряд A) в следующем виде:
/(*) = ао + лгф(*), B)
где
/1 = 0
Умножая обе части равенства C) на бином 1—л;, получим:
(l-*)q>(*)= S aB+1*n- S att+1xn+K D)
/1 = 0 /1 = 0
Полагая во второй сумме п-\-\=т и учитывая, что сумма не
зависит от обозначения индекса суммирования, будем иметь:
Поэтому
оо оо
= «о + 2 К+1 - в.) хп = а0 + 2 Двп*".
/1 = 0 /1 = 0
где
*) В самом деле, если 0 < R < оо и /?^6 i, то, полагая t = -& .получим
степенной ряд относительно переменной t с радиусом сходимости р=»1.

206 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
— конечные разности первого порядка коэффициентов ап
(подробнее о конечных разностях см. гл. XIV, § 1). Следовательно, из
формул C) и D) выводим:
/1 = 0
и, значит,
т.
/1 = 0
Указанное преобразование степенного ряда называется
преобразованием Эйлера—Абеля. Аналогично, применив преобразование
ос
Эйлера—Абеля к степенному ряду 2J &апхП> находим:
л=©
где
Д2я„ = А (&ап) = Аап+1 - Аап
— конечные разности второго порядка коэффициентов ап. Отсюда
на основании формулы E) получаем:
/ 0 \
/1 = 0 \ /1 = 0
Повторяя последовательно р раз преобразование Эйлера — Абеля,
будем иметь:
У д хп - а° 1 * Afl° 1 1 х*-1**
7и и„х —j х A~*х)**Ф9т A х)Р
/1 = 0

§ 2J УЛУЧШЕНИЕ СХОДИМОСТИ СТЕПЕННЫХ РЯДОВ 207
где
дЧ, = ля-Ч+1-л*-Ч (п=о, 1, 2, ...)
— конечные разности р-го порядка коэффициентов ап, а Д*яо(й = О,
1,2,...) — последовательные конечные разности коэффициентов ап
при /г = 0. Таким образом,
где положено Д°ао = ао. Формулу F) выгодно применять тогда, когда
конечные разности Арап при п—>оо имеют более высокий порядок
убывания/ чем коэффициенты ап. Это обстоятельство встречается
нередко. Например, если ап = —, то получим:
т. е. здесь Аап при п—^оо убывают быстрее, чем ап.
В частности, если ап--Р(п)> гдеР(я) — целый полином степени
р—1, то формула F) дает в конечном виде сумму ряда
Р(п) хп = ? Д*Р@) _-^_ (| «| < 1), G)
так как
Формула F) теряет смысл при лг=1. Применительно к этому
случаю можно видоизменить преобразование Эйлера — Абеля.
Полагая х = — *, будем иметь:
= 2
Возвращаясь к прежней переменной, получим:
.._?_r
Формула (8) имеет- смысл и при лг=1.

208 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
Пример 1. Найти с точностью до 0,001 сумму ряда
при х =— 1.
Решение. Применим преобразование Эйлера два раза (/?
Имеем:
1
—•"л ~ih-i n (п+2
п п+1 п (Г
Следовательно,
1 1
) (п+3) (л + 1)(л + 2)
2
2
2 6
)(я+2)(я + 3) („+1)(„ + 2)(я + 3)(я + 4)
Отсюда на основании формулы F) получаем:
Ту
""" 4 + 12+ 2 * 24 2 * 120" 2 # 360 2 * 840 +
"*" 2 * 1680 2 * 3024+ 2 # 5040 ''#
Ряд A0) — знакочередующийся с монотонно убывающими по
модулю членами. Поэтому, если мы остановимся на члене
У * 3024 ^ 2016'
то остаток ряда R по модулю не будет превышать первого
отброшенного члена:
^ 3 1 1 ^, о - гк — л

§ 2] УЛУЧШЕНИЕ СХОДИМОСТИ СТЕПЕННЫХ РЯДОВ
Таким образом, беря два запасных знака, имеем:
209
/( — 1) = 0,25000+ 0,08333+ 0,06250 — 0,01250 + 0,00417 —
— 0,00179 + 0,00089 — 0,00050 = 0,38610
с абсолютной погрешностью
А < 5-~ 10 + 3. 10~4 < 4. 10~4.
Округляя найденное число до трех знаков, получим
приближенное значение/(— 1) = 0,386 с предельной абсолютной погрешностью
Д < 4-10~4+ 1.10~4 =y • 10-».
Точное значение суммы есть:
/(— 1)==2 1п2 —1 = 0,38630...
Заметим, что если непосредственно вычислять число/(—1),
пользуясь рядом (9), то для достижения указанной точности
пришлось бы взять примерно сорок пять членов этого ряда.
Пример 2. Найти сумму ряда
== 2 (п*
Решение. Имеем:
Составим таблицу 12.
Таблица 12
Таблица конечных разностей
п
0
1
2
Р(п)
1
3
7
ДЯ (л)
2
4
Д*Р (л)
2
По формуле G) получаем:

210 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
§ 3. Оценки коэффициентов Фурье
Тригонометрическим рядом Фурье данной функции /(#)( —я<
<лг<я)*) называется ряд
A)
коэффициенты которого ап% Ьп (коэффициенты Фурье функции f(x))
вычисляются по формулам
я
ая~ §f(x)cosnxdx (я = 0, 1, ...), B)
—Я
N • я
Ь« = Т lf(x)smnxdx (л = 1, 2, ...). B')
—Я
Достаточным условием существования ряда Фурье функции /(х)
является интегрируемость этой функции на отрезке [ — я, я]. В этом
случае коэффициенты Фурье B) и B') имеют определенные конечные
значения."
Может оказаться, что полученный ряд Фурье расходится или
сходится к другой функции. Приведем без доказательства [1], [7]
условия, при выполнении которых тригонометрический ряд Фурье
сходится к функции f(x) во всех точках непрерывности последней.
Теорема сходимости. Если функция f(x) кусочно
непрерывна и кусочно дифференцируема на отрезке [—я, я]» то ее ряд
Фурье сходится на всей числовой оси и сумма его S(x) есть
периодическая функция с периодом 2я, равная
+O> C)
в любой точке лго€(—я, я) и S(±n) = 2~1[f ( — я + 0) + /(я-0)].
В частности, S(xo) = f(xo), если в точке х = х0 функция
непрерывна, т. е. если /(*0-0)=/(*о + °)=/(*о)-
Если, сверх того, функция f(x) — периодическая с периодом 2я,
то ее ряд Фурье сходится для каждого значения х0 и имеет сумму C).
При выполнении условий теоремы сходимости очевидно, что
ап—>() и Ьп—>0 при п—>оо. Дадим более точные оценки коэффи-
*) Для простоты формулировок мы рассматриваем функцию,
определенную на отрезке [ — я, я]. Общий случай функции <р (t), заданной на отрезке
[а, Ь], может быть сведен к нашему при помощи линейной замены

§ 3] ОЦЕНКИ КОЭФФИЦИЕНТОВ ФУРЬЕ 211
циентов Фурье, накладывая известные ограничения на поведение
функции /(х).
Определение. Говорят, что функция f(x), заданная на
отрезке [ — я, я], принадлежит классу периодичности С(Я|>, если:
1) f(x) непрерывна на отрезке [ — щ я] вместе со своими производи
ними до m-го порядка включительно',
2)/<*>( —я + 0)=/(А)(я — 0) для & = 0, 1, 2, ..., т% т. е. на
концах отрезка [ — я, я] должны совпадать значения функции f(x)
и ее m первых производных.
Из условий 1) и 2) следует, что периодическое продолжение
функции f(x) принадлежит классу С{т)( — сю, -f оо).
Лемма. Если функция f(x) принадлежит классу периодично-
сти С{Щ на отрезке [ — я, я] (короче, f(x) ?С{Щ [ — я, я]), то ее
коэффициенты Фурье ап и Ьп есть бесконечно малые при п—> оо
порядка выше m относительно —, т.е.
п
Доказательство. Проинтегрируем по частям m раз правые
члены следующих равенств:
л
§f(x)cosnxdx (« = °. 1....). W
—я
п
Полагая и=/(х) и dv = cosnxdx, находим du=f/(x)dx и
v= — sinnx. Следовательно, по формуле интегрирования по частям
п
имеем:
л
ап = -1 \—/(х) sin nxY f /' (х) sin nx dx =
я
— я
*) Запись ач = о (-^] обозначает, что lim

212 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
Применяя еще раз интегрирование по частям и учитывая, что
/'( — я)=/' (я), получим:
я
+тг$/'(*) COS (-?.2+**)<**]}
я
я
ejw? J/"(*)cos
-я
и т. д.
После /я-кратного интегрирования по частям в формулах D) и D')
будем иметь:
я
(т
-я
Аналогично
-я
Интегралы
я
еп = ~ J /('"' (*) cos [ -^-
-Я
Я
— Я
с точностью до знака являются коэффициентами Фурье непрерывной
по условию функции /(/й) (#). Как известно, коэффициенты Фурье
непрерывной функции независимо от того, сходится или нет ее ряд
Фурье, стремятся к нулю при неограниченном возрастании их
номера*). Поэтому
гп—**0 и ел—>О при п—>оо.
*) Это следует из того, что для любой кусочно непрерывной функции f (x)
с коэффициентами Фурье ап и Ьп (п = 0, 1, 2, ...) имеет место неравенство
Бесселя [7]
2 Я
00
Следовательно, ряд 2 (ая + ^л) сходится иая—>О; Ьп—>Оприп—> оо.

§ 4] МЕТОД А. Н. КРЫЛОВА ДЛЯ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ 213
Но так как
и bn—J[rn
то коэффициенты Фурье ап и Ьп функции f(x) являются бесконечно
малыми более высокого порядка по сравнению с -^:
Этот результат был положен А. Н. Крыловым в основу метода
улучшения сходимости рядов Фурье.
Замечание. Если /(т) (х) удовлетворяет условиям теоремы
сходимости, то легко доказать, что
В этом случае для коэффициентов Фурье функции / (х) получается
лучшая оценка:
и Ьп=
§ 4. Улучшение сходимости тригонометрических рядов Фурье
методом А. Н. Крылова
Пусть функция f(x) на отрезке [ — я, л] кусочно непрерывная
имеет кусочно непрерывные производные /(|)(дг) (/=1,2, ...,/я)
до m-го порядка включительно. Тогда в силу теоремы сходимости
(§ 3) функцию f(x) во всех ее точках непрерывности можно
представить тригонометрическим рядом Фурье
A)
где ап и Ьп — коэффициенты Фурье, определяемые формулами B)
и B') из § 3. В общем случае коэффициенты ап и Ьп ряда A)
медленно стремятся к нулю, и практически пользоваться этим рядом
затруднительно, а тем более недопустимо почленно
дифференцировать ряд A), что бывает нужно при решении некоторых задач,
в частности при применении метода Фурье.
Идея метода А. Н. Крылова [8] состоит в том, что из
функции f(x) выделяется элементарная функция g(x) (обычно
представляющая собой кусочно полиномиальную функцию), имеющая те же
разрывы, что и функция/(jc), причем ее производные g<() (x) (/ = !»

214
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[гл. vt
2, ..., т) до т-то порядка включительно обладают такими же
разрывами, как и соответствующие производные /{i) (лг) данной
функции /(лг), и, сверх того, такая, что
(/ = 0, 1, 2, ...,т).
В таком случае разность
будет принадлежать классу периодичности
Обозначая через ап и |5W (n = Q, 1,2, ...) коэффициенты Фурье
функции ф (лг), получим:
[¦??+zL (ancos nx+Pn s*n лл:) »
2 «=i J
B)
где ап и prt — бесконечно малые при п—> сх> порядка выше, чем т,
относительно —, т. е. ряд B) будет, вообще говоря, быстро
сходящимся. Этот ряд можно дифференцировать почленно по меньшей
мере m — 2 раза.
Покажем, как по заданной функции f(x) практически строится
вспомогательная функция ^(а:) [9]. Для этого рекуррентным спосо-
&
Г
I
-г*
Рис. 46.
бом построим на отрезке [ — 2я, 2я] последовательность функций
ao(jt), (TxW» ••••<^mWi обладающих следующим свойством:
(fc = 0, 1,2, ...,/я), причем так^х, что производные о47) (лг) (у = 0,
1, ..., ft —1) непрерывны на отрезке [ —2я, 2я].
Функцию о0 (лг) определим следующим образом:
при — 2я<лг<0,
при 0<лг<2я, (*)
при лг = — 2я, 0, 2я,
2
О

§ 4} МЕТОД А, Н. КРЫЛОВА ДЛЯ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ 215
Ее график изображен на рис. 46. Эта функция нечетная, поэтому
ее ряд Фурье содержит только синусы кратных дуг:
о0 (х) = 2 ьп sin пх>
где
л=1
л
я—х cos
Следовательно,
. ч sin х , sin 2x . . sin nx ,. /|гч
^oW = i—I—2—•"* • •"!—~ + # • • E*
Очевидно, что функция о0(х) имеет разрыв в точке лс = О со
скачком, равным п:
M+°)-<M-0)=^-(--J)==jt.
Поэтому функция
имеет в точке х0 такой же скачок, как и функция <то(лг):
яНл;0 + 0)--яМ*0-0) = я,
причем точка разрыва— единственная на отрезке [—я, п].
Функцию ах (л;) определим формулой
х
<*1 (X) = С1 + I а0 (*) dx> F) F
о
где сг — некоторая постоянная.
Интегрируя почленно ряд E), получим:
0 /2 = 1
Постоянную сх подберем так, чтобы свободный член ряда G)
•был равен нулю

216 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
Отсюда
[ГЛ. VI
Ряд 2* ^2» очевидно, является свободным членом ряда Фурье
к
функции j а0 (л;) dx> Отсюда, пользуясь формулой D), имеем:
о
да Л X Л
о о
Поэтому
Следовательно,
причем
1 /я* я3\ я2
6 *
(8)
J (X) = .
при
при -
График функции ог (х) изображен на рис. 47. Функция ох (х)
непрерывна на отрезке [—2я, 2л], но ее производная Oi(x) = oQ(x)
Рис 47.
имеет разрыв в точке лг = О, причем

§ 4] МЕТОД А. Н. КРЫЛОВА ДЛЯ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ 217
Таким же образом определяются функции
где произвольные постоянные cv с2, ... , ст подбираются так, чтобы
свободный член соответствующего ряда Фурье был равен нулю, т. е.
постоянные сй(&=1, 2, ..., т) последовательно находятся из
условий
Функции ok(x) (ft= 1, 2, ...,/») и все производные до (k—1)-го
порядка включительно непрерывны на отрезке [—2я, 2я]. При этом,
так как а^ (х) = о0 (л:), то
о[к)(+0)-о[к)(-0)=л (ft=l, 2, ..., я»),
т. е. производная &-го порядка функции ak(x) имеет разрыв при
х = 0 со скачком я. Отсюда следует, что функция tyk{x) =
= ok(x—xQ)(—n^x ^ n), полученная сдвигом функции ok(x),
имеет разрыв лишь &-й производной в точке х = х0:
Пусть теперь
х{х\ х[°\ ..., Xk°J — точки разрыва f(x);
x(i\ xi1*, ..., *i\} — точки разрыва/'(лг);
х[т\ хТ\ ..., хТ2—точки разрыва /(т>(*),
причем некоторые из этих точек могут повторяться.
Для соответствующих скачков функции и ее производных введем
обозначения
(/ = 0, 1, ..., т; у=1, 2, ...,

218 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. VI
Определим функцию g(x) (функция скачков) формулой
s=km h
... +Е-5гог.(*-лГ)). (9)
S=l
Функция g(x) обладает следующими свойствами:
1) в точках х[°\ х{2°\ ...^х^ функция ^(л:) имеет разрывы,
причем скачки ее в этих точках равны скачкам функции f(x)
в соответствующих точках:
-Go (лгу—лгу —0)] «.
2) производная g*l)(x) (/=1, 2, ..., т) разрывна в точках
\ x»\ ...» •**?. причем
т. е.
3) при хф-х^ функция g(x) имеет непрерывные производные
всех порядков.
Пусть
Ф (*)=/(*)-*(*). (Ю)
В силу первого и второго свойств следует, что
т. е.
Ф (а:) ? С{т) Г зт л1.
Таким образом, для разложения функции f{x) можно
воспользоваться быстро сходящимся рядом Фурье B). Заметим, что,

§ 4J МЕТОД А. Н. КРЫЛОВА ДЛЯ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ 219
пользуясь разложениями
sin п (jc—х[0))
п
и1\* xs )— 4
легко написать разложение в ряд Фурье функции g(x). В итоге
мы получим, что ряд Фурье функции f(x) состоит: а) из медленно
сходящейся части, элементарно суммирующейся к функции g(x)> и
б) из быстро сходящегося остатка, представляющего ряд Фурье
функции <р(х)?Ст[— я, я].
Замечание. Если на концах отрезка [—я, я] предельные
значения функции/(лг) или ее производных /'(л;), ..., /(Л)(лг) (k^)
не совпадают между собой, т. е.
/«>(_я + 0)^/@(Я-0) (/ = 0, 1, 2, ..., ft),
то точки дг = — я и х = п следует считать точками разрыва
функции f(x) или соответственно производных f{l)(x).
Предполагая, что функция f(x) периодически продолжена за
пределы отрезка [—я, я] с периодом 2я, получаем, что скачок
производных в точках лг = — я и л; = я один и тот же и равен
*<'>=/<'>(_ я + 0)— /(/>(я—0).
В силу периодичности функции at (x) имеем:
сг,(* + я) = а,(л;—я),
причем функция а/^лг + я) на отрезке [—я, я] допускает две точки
разрыва (# = — я и л: = я) с одним и тем же скачком, равным я.
Поэтому в формулу (9) нужно включить только одну концевую точку,
например х = — я. В самом деле, на основании формулы (9) скачок
производной ^1) (х) в точке х = — я равен
В силу периодичности g*l) (x) эта производная имеет тот же скачок
и при л: = я. Следовательно, при составлении разности
где учтена лишь точка х = — я, снимается разрыв/-й производной
Функции ф(#) как в точке х = — я, так и в точке х — п.

220
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[гл. vi
Пример. Методом А. Н. Крылова улучшить сходимость ряда
Фурье функции (рис. 48а)
fix)
f *2 + l
\ х2
при —я<лг<0,
при 0<л;<я.
Решение. На отрезке [—л, я] функция f(x) в силу
замечания имеет точки разрыва: хг~ — я; х2 = 0; лг3==я. Вычисляя
коэффициенты Фурье, получим:
•Ч "о
при п нечетном;
ЯП
при п четном.
Следовательно, ряд Фурье функции /(х) имеет вид
k=o
Сходимость ряда A1) —плохая, так как коэффициенты Ьп = о( — \
убывают медленно. Из функции J (х) выделим функцию скачков g(x)
так, чтобы q>(x) = [f(x)-g(x)]?C{m>[—ny я].
i
Л л
Рис. 486.
Подсчитаем скачки Л/о) нулевого рода в точках лгу (у = 1, 2, 3):

§ 4] МЕТОД А. Н. КРЫЛОВА ДЛЯ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ 221
На основании формулы (9), учитывая замечание, получаем;
или
при —я <л:<0 и
. ч 1 я—(#+я) 1 я—х 1
при 0 < лг<я.
Вычитая из функции f(x) функцию скачков g(x)t получаем
функцию
непрерывную на отрезке [—я, я] (рис. 486). Так как
sin пх
П
то
— y LJ)lshinx—^V ±si
я 2u n
/1 = 1
sin
Следовательно,
причем коэффициенты преобразованного ряда Фурье имеют порядок
Убывания o(jp\ .
Заметим, что если из функции f(x) выделить функцию скач-
ков g(x) с точностью до разрывов производной, то остаток

222 улучшение сходимости рядов [гл. vi
будет тождественно равен нулю, т. е. мы получим точную сумму
ряда A0).
Замечание. Метод А. Н. Крылова применим также к рядам
Фурье периода 7=2/. В самом деле, пусть функция f(x) задана
в основной области а — /<лг<а + /. Произведя линейное
преобразование
получим функцию F(t)=f(a -] t\ периода 2я, определенную
в стандартной области —Ж / < я.
§ 5. Приближенное суммирование тригонометрических рядов
Пусть мы имеем сходящийся тригонометрический ряд
ос
2 (яЛ cos nx + bn sin nx) = S(x), \\)
сумма которого S(x) неизвестна. Требуется приближенно с
некоторой наперед заданной точностью вычислить эту сумму.
Очевидно, что чем быстрее стремятся к нулю коэффициенты ап
и Ьп ряда A), тем меньше его членов нужно взять, чтобы обеспечить
заданную точность. Поэтому, прежде чем приступить к подсчету
суммы, желательно улучшить сходимость данного ряда. Для этого
обычно пользуются следующим приемом: из данного ряда выделяют
некоторый тригонометрический ряд, сумма которого g(x) известна,
так, чтобы оставшийся ряд
B)
имел более быструю сходимость, чем исходный.
Если
ТО
00
g (х) = S К cos пх + Ьп sin пх),
GO
S(x) = g (х) + 2 (а„ cos пх + р„ sin пх), C)
где
(/1 = 0, 1, 2, ...).

§ 5J ПРИБЛИЖЕННОЕ СУММИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ 223
В простейших случаях для построения функции g(x) можно
использовать рассмотренные выше разложения:
00
i sin пх
00
sin пх . ч 2зх2д:—
o{x)
Esin пх
12
Иногда полезны также разложения [7]
где ^^=1,202056903...
/1 = 1
Пример. Найти сумму ряда
с точностью до 0,001.
Решение. Коэффициенты ряда Ьп~ 2^_1 имеют порядок
убывания О{ — Ь так как l*m ( йи : —) = 1. Улучшим сходимость задан-
\ П ) п-^оо \ п П )
ного ряда. Очевидно, что
п п / 1\ 1 Л 1,1 \ 1 1
где
n 1,1

224
Тогда
Но
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
sin ля
|ГЛ. VI
sin л*
Таким образом,
= а0 (х) + а2 (л;)
Пусть N—число членов ряда ^уп sinnx, которые нужно взять,
чтобы его остаток /?# удовлетворял неравенству
< 0,001.
Найдем число N. Имеем:
00
Решая неравенство тлт*" < 0,001, получим, что достаточно взять
=5. Следовательно, с заданной точностью имеем:
5
sin ла:
зх—х
Литература к шестой главе
1. Г. М. Фихтенгольц, Основы математического анализа, т. II, Гостех-
издат, 1956, гл. XV и XXIV.
2. А. Марков, Исчисление конечных разностей, Изд. 2, Матезис, 1910,
гл. II.
3. Г. С а л е х о в, Вычисление рядов, Гостехиздат, 1955, гл. I и III.
4. Я. С. Без и ко вич, Исчисление конечных разностей, ЛГУ, 1939, гл. IX.
5. А. О. Гель фонд, Исчисление конечных разностей, Гостехиздат, 1952,
гл. IV.
6. В ал л е-П у с сен, Курс анализа бесконечно малых, т. II, ГТТИ, 1933.
7. Г. П. Толстов, Ряды Фурье, Гостехиздат, 1951, гл. I—V
8. А. Н. Крылов, Лекции о приближенных вычислениях, Изд. 6,
Гостехиздат, 1954, гл. V.
9. Л. В. К а н т о р о в и ч, В. И. Крылов, Приближенные методы высшего
анализа, Изд. 3, Гостехиздат, 1949, гл. I.

ГЛАВА VII
АЛГЕБРА МАТРИЦ
§ 1. Основные определения
Система тп чисел (действительных или комплексных),
расположенных в прямоугольной таблице из т строк и п столбцов,
а1г а12 а13
а21 а22 а23
ат1 ат2
<*2П
*тп
A)
называется матрицей (числовой). Строки и столбцы таблицы A)
называются рядами матрицы.
Числа a{j (*'= 1, 2, ..., m\ j= 1, 2, ..., п)> составляющие
данную матрицу, называются ее элементами. Здесь первый индекс /
обозначает номер строки элемента, а второй/—номер его столбца.
Для матрицы A) часто употребляется сокращенная запись
(/==1, 2, ..., т\ у=1, 2, ..., п)
или
причем говорят, что матрица А имеет тип тХп.
Если т = пу то матрица называется квадратной порядка п.
Если же пг=^=п, то матрица называется прямоугольной. В частности,
матрица типа \Хп называется вектором-строкой, а матрица типа
аи XI—вектором-столбцом. Число (скаляр) можно рассматривать
как матрицу типа 1x1. Квадратная матрица вида
аг 0 0 ... О
О а2 0 ... О
6 6 6 ... аи
B)
называется диагональной и обозначается кратко так: [av a2, .. .,&„]¦
8 Б. П. Демидович и И. А. Марон

226
АЛГЕБРА МАТРИЦ
[ГЛ. VII
В случае, если 0^=1 (/ = 1, 2, ..., п), то матрица B)
называется единичной и обозначается обычно буквой Е, т. е.
о о
1 О
0 0 0
Введя символ Кронекера
0,
1,
если
если
'=Л
можно записать
Матрица, &се элементы которой равны нулю, называется нулевой
и обозначается через 0. Если желают указать еще число строк и
столбцов нулевой матрицы, то употребляют обозначение 0^,
С квадратной матрицей А = [fl/Д,, п связан определитель
(детерминант)
Чг
*22
Чп
Не следует отождествлять эти два понятия: матрица представляет
собой упорядоченную систему чисел, записанную в виде
прямоугольной таблицы, а ее определитель det А есть число,
определяемое по известным правилам, а именно:
det А =
C)
где сумма C) распространена на всевозможные перестановки
(alf a2, ..., ап) элементов 1,2, ..., п и, следовательно, содержит л!
слагаемых, причем х = 0, если перестановка четная, и н = 1, если
перестановка нечетная.
§ 2. Действия с матрицами
А. Равенство матриц
Две матрицы А = [а^] и В=[Ьц] считаются равными: А = В,
если они одного и того же типа, т. е, имеют одинаковое число
строк и столбцов, и соответствующие элементы их равны, т, е.

§ 2]
ДЕЙСТВИЯ С МАТРИЦАМИ
•227
Б. Сумма и разность матриц
| одинакового типа
Суммой двух матриц A = [atj] и В=
С[] го
р у эл
т. е. cij=ai/ + biJ. Таким образом,
Су у р [tj] [^|
называется матрица С=[с(/] того же типа, элементы которой Сц
равны суммам соответствующих элементов a(J и bif матриц А и В,
+ b Т б
21
22
> • • • tnti ' mn —
Из определения суммы матриц непосредственно вытекают
следующие ее свойства:
2)
3)
Аналогично определяется разность матриц
\п
\п
"л2
В. Умножение матрицы на число
Произведением матрицы Л = [#-] на число а (или произведе-*
нием числа а на матрицу А) называется матрица, элементы которой
получены умножением всех элементов матрицы А на число а, т. ©•
Аа — аА =
аа
11
Z21
аа
аа
аа
аа
Из определения произведения числа на матрицу непосредственно
вытекают следующие его свойства:
2) 0Л =
3) а(рЛ) = (а
4)
5) а
(здесь ^4 и В — матрицы; а и р — числа).
Заметим, что если матрица Л —квадратная порядка л, то
8*

228
АЛГЕБРА МАТРИЦ
[ГЛ.VU
Матрица
называется противоположной. Нетрудно видеть, что если матрицы А
и В одинаковых типов, то
А—В =
В).
Пусть
Г. Умножение матриц
А =
1 2
«21 «22
... a
ln
пт2 • • • ап
pi ЬР2 ... bpqA
— матрицы типов соответственно тхп и pxq. Если число
столбцов матрицы А равно числу строк матрицы В, т. е.
й=Р. A)
то для этих матриц определена матрица С типа mXq, называемая
их произведением:
С==
ст\ ст2-
где
==1> 2, ...эт; У= 1, 2,
Из определения вытекает следующее правило умножения матриц:
получить элемент, стоящий в i-й строке и j-м столбце
произведения двух матриц, нужно элементы i-й строки первой
матрицы умножить на соответствующие элементы j-го столбца
второй и полученные произведения сложить.
Произведение АВ имеет смысл тогда и только тогда, когда
матрица А содержит в строках столько элементов, сколько
элементов имеется в столбцах матрицы В. В частности, можно перемножать
квадратные матрицы лишь одинакового порядка.

§ 2J
Пример 1.
ДЕЙСТВИЯ С МАТРИЦАМИ
229
ГЗ 2 8 1]
l=[l-403j
5 =
Г2 —In
1 О
О 1
L.3 1.
3.2+2.1+8-0+ЬЗ 3-(—1)+2-(—3) + 8.1 + Ь1 *
Ь2 + (—4). 1+0-0+3-3 1-(—!) + (—4).(—3)+0'1+3-1
Пример 2.
7 14
1
4
7
2
5
8
3
6
9
•
1
2
3
=
Ы + 2.2 + 3-3
14
32
.7.1+8.2+9-3 J 1_50.
Матричное произведение обладает следующими свойствами:
1) А(ВС) = (АВ)С; 3) (А + В)С=АС+ВС;
2) а(АВ) = (аА)В; 4) С(А-\-В) = СА + СВ
(А, В и С—матрицы; а — число).
Равенства 1) — 4) понимаются в том смысле, что если одна из их
частей существует, то другая часть также существует и они равны
между собой.
Произведение двух матриц не обладает переместительным
свойством, т. е., вообще говоря, АВ=/=ВА, в чем можно убедиться на
примерах.
Пример 3.
Тогда
Г1 2] Г5 61
А=\ ; Д=
L3 4j L7 8J
1 Г23 341
J L31 46j
19 221
*3 50j
т. е. здесь АВфВА.
Более того, может даже случиться, что произведение двух матриц,
взятых в одном порядке, будет иметь смысл, а произведение тех же
матриц, взятых в противоположном порядке, смысла иметь не будет.
Так, например, если
Г 3 2 1
Л=|!?М: 5= 2 18
4 3 0

230
АЛГЕБРА МАТРИЦ
[ГЛ. VII
ТО
АВ
Г19 13 71
= [46 31 19J '
а ВА не существует.
В тех частных случаях, когда АВ = ВА, матрицы А и В
называются перестановочными (коммутативными). Так, например, как
нетрудно убедиться, единичная матрица Е перестановочна с любой
квадратной матрицей А того же порядка, причем
Таким образом, единичная матрица Е играет роль единицы при
умножении.
Если А и В — квадратные матрицы одного и того же порядка, то
det (АВ) = det (ВА) = det A. det В.
Эта формула вытекает из правила перемножения определителей.
Например, для матриц, приведенных в примере 3, имеем:
19
43
23
31
22
50
34
46
1
3
1
3
2
4
2
4
5
7
5
7
б
8
б
8
§ 3. Транспонированная матрица
Заменив в матрице
А =
а1Х
<*1П
типа /wX# строки соответственно столбцами, получим так
называемую транспонированную матрицу
11 «21 ••• a ml'
типа пхт. В частности, для вектора-строки
а^К а, ... ая]
транспонированной матрицей является вектор-столбец
а =
La-

4] ОБРАТНАЯ МАТРИЦА 231
Транспонированная матрица обладает следующими свойствами:
1) дважды транспонированная матрица совпадает с исходной:
2) транспонированная матрица суммы равна сумме
транспонированных матриц слагаемых, т. е.
3) транспонированная матрица произведения равна произведению
транспонированных матриц сомножителей, взятому в обратном
порядке, т. е.
Действительно, элемент /-й строки и у-го столбца матрицы (АВ)'
равен элементу у-й строки и г-го столбца матрицы АВ, т. е.
ajxbu + aJ2b2i + ... + a!nbni.
Последнее выражение, очевидно, представляет собой сумму
произведений элементов i-й строки матрицы В' на соответствующие
элементы у-го столбца матрицы А\ т. е. равно общему элементу
матрицы В!А'.
Если матрица А — квадратная, то, очевидно,
Матрица Л = [<2/;] называется симметрической, если она
совпадает со своей транспонированной, т. е. если
А' = А. A)
Из равенства A) вытекает, что: 1) симметрическая матрица —
квадратная (щ = п) и 2) элементы ее, симметричные относительно
главной диагонали, равны между собой, т. е.
Произведение
ап =
очевидно, представляет собой симметрическую матрицу, так как
С «= (АЛ*)' = (А')' А = АА' = С.
Например,
Г1 2 31 \l t\ — Г 12+22 +32 1-4+2.5 + 3.61 _ Г14 321
L4 5 6J [^ gj "~ L 4-1+5.2+6.3 4а + 52 +62 J ~ [32 77J*
§ 4. Обратная матрица
Определение 1. Обратной матрицей по отношению к
данной называется матрица, которая, будучи умноженной как справа*
та и слева на данную матрицу, дает единичную матрицу.

232
АЛГЕБРА МАТРИЦ
[ГЛ. VII
Для матрицы Л обозначим обратную ей матрицу через Л. Тогда
по определению имеем:
ЛЛ-1 = Л-М = ?1, A)
где Е — единичная матрица.
Нахождение обратной матрицы для данной называется обращением
данной матрицы.
Определение 2. Квадратная матрица называется неособенной,
если определитель ее отличен от нуля.
В противном случае матрица называется особенной, или
сингулярной.
Теорема. Всякая неособенная матрица имеет обратную
матрицу.
Доказательство. Пусть дана неособенная матрица л-го
порядка
ап а12 ... а1п
а21 а22 ... а2п
L ап
где
Составим для матрицы Л так называемую присоединенную (или
союзную) матрицу
Л21 ... Ап1
B)
где Ац—алгебраические дополнения (миноры со знаками)
соответствующих элементов я,у(/, /=1, 2, ..., п).
Заметим, что алгебраические дополнения элементов строк
помещаются в соответствующих столбцах, т. е. произведена операция
транспонирования.
Разделим все элементы последней матрицы на величину
определителя матрицы Л, т. е. на Д:
Л и
Л
А
А
А
^п2
А
Ащ Агп
А А
Апп
А
C)
Докаисем, что матрица Л* есть искомая обратная матрица: Л* = Л.
Как известно, 1) сумма произведений элементов некоторого ряда
(Строки или столбца) определителя на алгебраические дополнения

§4]
ОБРАТНАЯ МАТРИЦА
233
этих элементов равна определителю и 2) сумма произведений
элементов некоторого ряда определителя на алгебраические дополнения
соответствующих элементов параллельного ряда равна нулю, т. е.
J]<Vl/* = M D)
D')
где
6;,=
при / =
О при
На основании этих свойств, составляя произведение А4*, будем
иметь:
АА*.
а21 а 22
Д А '•• Д
«12 А%% Ап
ДА ••* Д
_ А А
1 0 ... О
О 1 ... О
О 0 ... 1
E)
Итак, АА* = Е.
Формулу E) можно вывести короче, если воспользоваться
сокращенными обозначениями
Учитывая соотношение D), получим:
Аналогично можно удостовериться, что
Следовательно, Л* = Л", т. е.
где

234
АЛГЕБРА МАТРИЦ
[ГЛ. VII
Замечание 1. Для данной матрицы Л ее обратная матрица Л
единственна. Более того, всякая правая обратная (левая обратная)
матрица матрицы А совпадает с ее обратной матрицей Л (если
последняя существует).
Действительно, если
то, умножая это равенство слева на А, получим:
или
Аналогично доказывается, что если
Поэтому при проверке соотношения A) достаточно ограничиться
лишь одним равенством.
Замечание 2. Особенная квадратная матрица обратной не
имеет. Действительно, так как матрица А — особенная, то
Из равенства A) имеем:
det Л-det Л = det E = 1,
т. е.
0=1?!,
что невозможно. Утверждение доказано.
Пример. Для матрицы
1 2 3
Л =
— 2—4 -5
найти обратную матрицу.
Решение. Так как определитель
1 2 3
_2 —4 —5
3 5 6
1 2 3
0 0 1
0 —1 —3
то матрица Л неособенная.
Составим присоединенную матрицу
1 3 2
1
0

§4J
ОБРАТНАЯ МАТРИЦА 235
Разделим все элементы матрицы Л на Д—1 и получим:
13 2 1
—3 —3 ~1
2 1 О
Рекомендуется проверить, что действительно
Укажем некоторые основные свойства обратной матрицы.
1. Определитель обратной матрицы равен обратной величине
определителя исходной матрицы. Действительно, пусть
Учитывая, что определитель произведения двух квадратных матриц
равен произведению определителей этих матриц, получим:
Следовательно,
1
~~ det A *
2. Обратная матрица произведения квадратных матриц равна
произведению обратных матриц сомножителей, взятому в обратном
порядке, т. е.
В самом деле,
Значит, В"ХА есть обратная матрица для АВ.
В более общем случае
АА
) = Ар Ар—i . . ,
3. Транспонированная обратная матрица равна обратной от
транспонированной данной матрицы:
Действительно, транспонируя основное соотношение Л~М==?Э
получим:

236
АЛГЕБРА МАТРИЦ
[ГЛ. VH
Отсюда, умножая последнее равенство слева на матрицу- (Л'),
будем иметь:
(A') A' (A^Y^(AYlE
или
что и требовалось доказать.
Замечание. С помощью обратной матрицы легко решаются
матричные уравнения
АХ=В и YA = B.
Действительно, если
, то
и У=ВА'1.
§ 5. Степени матрицы
Пусть А — квадратная матрица. Если р—натуральное число, то
полагают:
р раз
Дополнительно уславливаются, что Л° = ?, где ?—единичная
матрица. Если матрица А неособенная, то можно ввести
отрицательную степень, определив ее соотношением
Для степеней матрицы с целыми показателями справедливы
обычные правила:
2)
Неквадратную матрицу, очевидно, в степень возводить нельзя.
Пример 1. Пусть
О ... (Г
О си ... О
А -=
Тогда
Л) 0 ...а„
а^ О ... О*
О а?... О
О О ...oj

§ 6]
РАЦИОНАЛЬНЫЕ ФУНКЦИИ МАТРИЦЫ
Пример 2. Найти
0 10 0
0 0 10
0 0 0 1
L.0 0 О 0J
Решение. Имеем:
0
0
0
0
1
0
0
0
0
1
0
0
о-
0
1
0_
2

0
0
-0
1
0
0
0
0
1
0
0
0"
0
1
0_
0 10 0
0 0 10
0 0 0 1
L0 0 0 0.
0 0 10
0 0 0 1
0 0 0 0
_о о о о.
237
Если А и В— квадратные матрицы одного и того же порядка,
причем АВ = ВА, то справедлива формула бинома Ньютона
Пусть
§ 6. Рациональные функции матрицы
#21 #22 • • • #2/1
Wl #«2 •••#/!
— произвольная квадратная матрица порядка п. По аналогии
с формулами элементарной алгебры определяются целые
рациональные функции матрицы X:
Р(X) = А0Хт + А^Хт"х + ... + АтЕ (правый полином);
Р(Х) = ХтА0 + Хт-1А1 + ... + ВАт (левый полином),
где Лу (v = 0, 1, ... , т)—матрицы типа тХп или соответственна
типа пХт и Е—единичная матрица порядка п.
Вообще говоря, Р(Х)фР(Х).
Можно ввести также дробные рациональные функции матрицы Х$
определив их формулами
где Р(Х) и Q(X)—матричные полиномы и det[Q(X)]=?0.

238 АЛГЕБРА МАТРИЦ [ГЛ. VII
Пример. Пусть
где X—переменная матрица второго порядка. Найти Р ( п ) •
Решение. Имеем:
_ Г° °1 j. Г-1 °1_ Г° П - Г" -1!
40 oj^L I oj Li о J [о oj •
§ 7. Абсолютная величина и норма матрицы
Неравенство
А^В A)
между матрицами A = [aij\ и В=[Ьц] одинаковых типов
обозначает, что
B)
В этом смысле не всякие две матрицы сравнимы между собой.
Под абсолютной величиной (модулем) матрицы Л = [а;у] будем
понимать матрицу
\ []
где | пц |—модули элементов матрицы А.
Если А и В—матрицы, для которых операции А -\- В и АВ имеют
смысл, то:
а) \А + В\^\А\ + \В\;
б) \АВ\*?\А\.\В\;
в)
(а — число).
В частности, получаем:
(р — натуральное число).
Под нормой матрицы А = [а^] понимается действительное
число |]Л||, удовлетворяющее условиям:
а) ||Л||^0, причем |И|| = 0тогда и только тогда, когда -4 = 0;
б) ||аЛ|| = |а| ||Л|| (а —число) и, в частности, ||—^|| =
в)
г)

§ 7] АБСОЛЮТНАЯ ВЕЛИЧИНА И НОРМА МАТРИЦЫ 239
(Л и В — матрицы, для которых соответствующие операции имеют
смысл). В частности, для квадратной матрицы имеем:
где р — натуральное число.
Отметим еще одно важное неравенство между нормами матриц Л
и В одинакового типа. Применяя условие в), будем иметь:
\\B\\ - ||А + (В-Л)||< \\A\\ + ||Д- А\[.
Отсюда
\\А-В\\ = \\В-А\\2*\\Щ\-\\А\\.
Аналогично
1И-В1|
Следовательно,
Назовем норму канонической, если дополнительно выполнены
условия:
д) если А = [аи]9 то
причем для скалярной матрицы А = [л11] имеем 1И!|=|л11|;
е) из неравенства |Л|^|?|(Л и В—матрицы) следует
неравенство
В частности, ||Л|| = [| | А 11|.
В дальнейшем для матрицы А = [ai;] произвольного типа мы
будем рассматривать главным образом три легко вычисляемые нормы:
Т|а,у| (т-норма);
2) И|, = тах2|«//| A-норма);
Пример. Пусть
Г1 2 31
1=4 5 6.
L7 8 9J
Имеем:
1И||„ = maxA+2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max F, 15, 24) = 24;
1И114 =max'(l + 4 + 7, 2 + 5 + 8, 3 + 6 + 9) = max A2, 15, 18) = 18;
И1* =j/"la + 22 + 3a + 4a + 5a + 6a + 72 + 82 + 9a =
1 =/285 ж 16,9.

240 АЛГЕБРА МАТРИЦ
В частности, для вектора
[гл. vii
X —
эти нормы имеют следующие значения:
bi\9
(абсолютная величина вектора). Если компоненты вектора
действительны, то имеем просто
Для норм \\A\\m, \\A\\t и \\A\\k проверим выполнение условий а) —г).
Непосредственно очевидно, что условия а) и б) выполняются.
Удостоверимся, что для этих норм выполнено условие в). Пусть
= [аи] и B=[bif]f причем матрицы А и В—-одинаковых типов*
Имеем:
max
max
Аналогично
Далее,
\\А + В\\к -
Применяя известное неравенство Коши *)
*) Приведем доказательство неравенства Коши

§ 7] АБСОЛЮТНАЯ ВЕЛИЧИНА И НОРМА МАТРИЦЫ 241
будем иметь:
in+в\\к ^ -j/21^/'2+|/"j?l*//la = иА и*
Таким образом, для всех трех норм условие в) выполнено.
Проверим теперь выполнение условия г). Пусть матрица А = [a(j]
типа т'Хп\ а матрица B=[fyy] типа т"хп". Для возможности
перемножения первой матрицы на вторую необходимо, чтобы т" — п\
причем матрица АВ будет иметь тип т'Хп".
Имеем:
Щ
I /=ils=l
{2 S
где а5 и ^ (s=l, 2, ... , л)—произвольные комплексные числа. Пусть
X — действительная переменная. Рассмотрим очевидное неравенство
где ср^—некоторые действительные числа. Обозначая через cts и bs числа,
сопряженные с as и bsi будем иметь:
bse%) (ask + FS<T %) =
) X + bsbs = | as |2^2 + 2 Re {asbse"f"^) *, +1 *, |».
Отсюда неравенство (>|с) примет вид
s=i s=l
Если положить
то
Re (

242
АЛГЕБРА МАТРИЦ
[гл. vh
Аналогично
ft'
Далее,
и, следовательно,
Так как левая часть последнего неравенства в силу исходного
неравенства (#) неотрицательна при любых вещественных X, то соответствующее
квадратное уравнение не может иметь различных действительных корней.
Поэтому дискриминант уравнения
il
т. е.
S=l
Отсюда и подавно
п
s = i
I»,I"-
S=l S=l
Если числа а$ и ^ действительны, то получаем просто

я 7] АБСОЛЮТНАЯ ВЕЛИЧИНА И НОРМА МАТРИЦЫ 243
Применяя неравенство Коши и учитывая, что т" = п', будем иметь
/т' п" / п'
ZZIZkiv
/
тп' п' гп" п"
ZZ*/ia=VMiiMifiiu=ii A и*-и в
Следовательно, для рассматриваемых норм условие г) выполнено.
Покажем, что нормы || А ||л, \\А\\1 и j| Л ||ft — канонические.
Если Q>Pq — наибольший по модулю элемент матрицы А —
типа т'хп', то, очевидно, имеем:
/гп' п'
ZZK
Таким образом,
|в//К|вл1<1ИН. (*=т> *> *)•
Кроме того, если Л = [а1Х], то
1И11, = 1ИII* = 11^11* = ! «ill-
Далее, если | А \ < \В\, где Л = [ai}] и В= [*,7], то | atj\ < |6,7|.
Из определения норм ||.<4||ю, ||^||г и ||^4||л очевидно, что имеют
место неравенства
IIЛ II, < IIЯ ||, (* = «, /, к).
Кроме того, для любой из этих норм имеем:
II Л II, = 111 ^ III, [s = m, /, k).
Таким образом, условие е) также выполнено.
Следовательно, доказано, что нормы || А ||л, |] А \\г и || А \\к —
канонические.
Отметим, что если матрица Е—единичная, порядка л, то

244
АЛГЕБРА МАТРИЦ
[ГЛ. VII
§ 8. Ранг матрицы
Пусть дана прямоугольная матрица
~ап а12 ... Яш"
#21 ^22 • • • ^2/1
Если в этой матрице выбрать произвольным образом k строк
и к столбцов, где k<^m\n(my n), то элементы, стоящие на
пересечении этих строк и столбцов, образуют квадратную матрицу
порядка k. Определитель этой последней матрицы называется
минором к'ГО порядка матрицы А.
Определение. Рангом матрицы называется максимальный
порядок минора матрицы, отличного от нуля. Иными словами,
матрица А имеет ранг г, если:
1) найдется по меньшей мере один ее минор г-го порядка,
отличный от нуля;
2) все миноры матрицы А порядка r-f 1 и выше равны нулю.
Ранг нулевой матрицы, т. е. матрицы, состоящей из нулей,
считается равным нулю. Разность между наименьшим из чисел тип
и рангом матрицы называется дефектом матрицы. Если дефект равен
нулю, то ранг матрицы — наибольший из возможных для данного типа.
При нахождении ранга матрицы полезно придерживаться
следующего правила:
1) переходить от миноров меньших порядков (начиная с миноров
первого порядка, т. е. элементов матрицы) к минорам ббльших
порядков;
2) пусть найден минор D г-го порядка, отличный от нуля, тогда
нужно вычислить лишь миноры (г + 1)-го порядка, окаймляющие
минор D. Если все эти миноры равны нулю, то ранг матрицы
равен г; если же хотя бы один из них отличен от нуля, то эту
операцию нужно применить к нему, причем в этом случае ранг матрицы
заведомо больше г.
Пример. Найти ранг матрицы
2—4 3 10
1_2 1—4 2
0 1—13 1
^4—7 4 — 4 5 _
Решение. Минор второго порядка, стоящий в левом верхнем
углу этой матрицы, равен нулю. Однако в матрице содержатся и
отличные от нуля миноры второго порядка, например
—4 3
—2 1
?=0,

§ 9]
ПРЕДЕЛ МАТРИЦЫ
245
причем окаймляющий его минор третьего порядка
2—4 3
1—2 1=1
О 1 —1
и оба минора четвертого порядка, окаймляющие минор D'', равны
нулю:
2
1
4
—4
—2
[м 7
3
1
4
1
— 4
—4
2
1
0
4
_4
— 2
7
3
1
4
0
2
5
Таким образом, ранг матрицы равен трем, а дефект 4 — 3=1.
§ 9. Предел матрицы
Пусть имеется последовательность матриц
(*=1,2, ...) A)
одного и того же типа тхп (/=1, 2, ..., т; у=1, 2, ..., п).
Под пределом последовательности матриц Ак понимается матрица
А = lim Ak=[ lim д(*П. B)
Последовательность матриц, имеющая предел, называется сходящейся.
Лемма 1. Для сходимости последовательности матриц Ah
(&=1, 2, ...) к матрице А необходимо и достаточно, чтобы
|| А — Лл||—*0 при k—>oo, C)
г<5е || Л ||—любая каноническая норма матрицы А. При этом
lim || Л4 || = || Л ||.
Действительно, если
ТО
при k > N (е).
Отсюда
|A-AJ<b/,
где /—матрица типа тхп, все элементы которой равны единице,
В силу свойств нормы имеем:
следовательно,
при
lim || А-АЛ ||=0.
k -> 00 '
D)

246 АЛГЕБРА МАТРИЦ [ГЛ. VII
Обратно, пусть выполнено условие C). Тогда при k > N(e) имеем:
и, следовательно,
lim а&) = пц,
т. е.
к -*¦ оо
Кроме того, если Ак—>Л, то имеем:
I МП — ЦЛЙ|| |<||Л — Ак\\—+0 при /5—юо.
Поэтому
lim || Ак || = || Л ||.
/г-* во
Следствие. Последовательность Ак—> () при к—*оо тогда и
только тогда, когда
lim || Ак || = О,
где Ц Ак ||—какая-нибудь каноническая норма.
Легко убедиться, что если
lim Ак = А и lim Вк = 5,
то:
а) lim (Ак ± ?ft) = Л ± S,
б) lim (Л^) = ЛБ,
/? —> 00
в) НтЛ^1 = Л (uetA=pzO)y
к —> оо
в предположении, что соответствующие операции имеют смысл. В
частности, если С—постоянная матрица такая, что возможны
перемножения САк и АкС(к=\, 2, ...), то
lim CAb = СА
lim АкС=АС.
Лемма 2. 'Для сходимости последовательности матриц
Ак(к--=\, 2, ...) необходимо и достаточно, чтобы был выполнен
обобщенный критерий Кдши, а именно: для всякого е > 0 должен
существовать такой номер N = N(e)y что при k>N, p > О
\\Ак+р-Ак\\<г} E)
гДе II II — любая каноническая норма.

§ 10] матричные ряды 247
Действительно, если справедливо неравенство E), то для каждого
элемента a\f матрицы Ak будет выполнен критерий Коши (см. гл, 111,
§ 4) и, следовательно, существует
lim Ak = [ lim
L*-*oo lJ J
Обратно, если существует
A = lim Ak,
то в силу леммы 1
||Л — <<4Л || — **0 при к—юо
и, значит, будет иметь место неравенство E).
§ 10. Матричные ряды
Пользуясь понятием предела матрицы, можно ввести в
рассмотрение матричные ряды
oo N
2ЛА= lim 2^*> 0)
Л = 1 N -* <х> k = i
где Ak — матрицы одного и того же типа.
Если предел A) существует, то матричный ряд называется
сходящимся^ и матрица, полученная в пределе, называется суммой
этого ряда. Если предела A) не существует, то матричный ряд
называется расходящимся и ему не приписывается никакой суммы.
Необходимое условие сходимости матричного ряда.
Теорема 1. Если матричный ряд A) сходится, то
lim Ak = 0.
Доказательство. Пусть
Если ряд A) сходится, то существует конечный предел
S= lim Sh.
ft-* 00
Имеем:
откуда
lim Ак= lim Sk— lim Sk_x = 5—5=0.
к -* со Л-> oo &-> oo
Матричный ряд A) называется абсолютно сходящимся, если
сходится ряд

248 АЛГЕБРА МАТРИЦ [ГЛ. VII
Теорема 2. Абсолютно сходящийся матричный ряд есть ряд
сходящийся.
Доказательство. Пусть
Тогда
Так как матричный ряд B) сходится, то по определению каждый
со
из числовых рядов 2 I а\Т I (*#==Ь 2, ..., т\ у = 1, 2, ..., п)
является сходящимся. Отсюда в силу известной теоремы из теории ря-
00
дов сходятся также, и притом абсолютно, все ряды2а// (/ = 1» -.., /»;
k=i
у=1, ..., п)у т. е. существует предел
N
S= litn Sm = lim ^i A*.
и, значит, матричный ряд A) сходится.
Для грубого анализа сходимости матричного ряда A) можно
пользоваться приведенным ниже достаточным условием.
Теорема 3. Если \\A\\—любая каноническая норма и
числовой ряд
S и л* и ' ' C)
k=i
сходится, то матричный ряд A) также сходится и притом абсолютно.
Доказательство. Пусть
] (*=1, 2, ...)•
Рассмотрим числовые ряды
(/=1, 2, ..., т\ у==1, 2, ..., п). Так как
то каждый из рядов D) сходится и притом абсолютно.
Следовательно, матричный ряд
в силу определения также сходится, причем сходимость — абсолютная.

§ 10J матричные ряды 249
В приложениях важное значение имеют матричные степенные
ряды: правые
2 АкХк E)
/г = 0
и левые
2 *Ч, E')
где ЛГ— квадратная матрица порядка я. В первом случае Ak—
матрицы типа тхп или числа (например, Ak могут представлять собой
векторы-строки); во втором случае Ak — матрицы типа пХт или
числа (например, Ak могут быть векторами-столбцами).
Теорема 4. Если г — радиус сходимости скалярного степенного
ряда
Sii4kii*\ (в)
6 = 0
где \\Ak\\ (& = 0, 1, 2, ...)—какая-нибудь каноническая норма,
то матричные степенные ряды E) и E') заведомо сходятся при
\\Х\\<г. G)
В частности, матричный степенной ряд
с числовыми коэффициентами ak(k = 0, 1, 2, ...) сходится при
\\Х\\<г,
где г — радиус сходимости степенного ряда
Доказательство. Так как
и а*** и < и л* и и* н\
то при выполнении неравенства G) ряд
jSiiVfu
сходится. Следовательно, в силу теоремы 3 степенной ряд E)
также сходится.
Аналогичное рассуждение справедливо для ряда E').
Второе утверждение теоремы следует из того, что если ah —
число, то

250 АЛГЕБРА МАТРИЦ [ГЛ. VII
Теорема 5. Геометрические прогрессии
А + АХ+ АХ2 + ... + АХ* + ,.. (8)
и
А + ХА + Х2А + ... +Х*А+ ..., (8')
где X—квадратная матрица, сходятся, если
\\Х\\<1. (9)
При этом
со
2 AXfc = A(E — X)'1
Действительно, в силу теоремы 4 при наличии условия (9)
геометрическая прогрессия (8) сходится, т. е. существует конечная
матрица
S= 2 АХ*.
Рассмотрим тождество
А (Е + Х + Х2+ ... +Xk) {E — X) - A (E—Xk+1). A0)
Переходя к пределу при k—*оо в равенстве A0) и учитывая, что
в силу условия (9)
Х*+1-+0 при ?-->оо,
будем иметь:
S(E—X) = AE = A. A1)
В частности, полагая А = Е в равенстве A1), получим:
где
Отсюда
Так как det5x конечен, то
det(fi—
и, следовательно, матрица Е—Х — неособенная, т, е. существует

с 10J матричные ряды 251
Умножая обе части равенства A1) справа на (Е—Х)> получим
окончательно:
Аналогично доказывается, что
при
\\Х\\<1.
Следствие. Если \\X\\ < 1, то существует обратная матрица
Сверх того, если |J?|| = 1, то
Замечание. Если ||X\\ < 1, то нетрудно оценить норму
остатка матричного ряда (8).
Имеем:
Аналогично для ряда (8') имеем:
Матричные ряды дают возможность определить транщендентл
ные функции матрицы. Например, полагают
причем можно доказать, что ряд A2) сходится для любой
квадратной матрицы X.

252
АЛГЕБРА МАТРИЦ
[ГЛ. VII
§ 11. Клеточные матрицы
Пусть дана некоторая матрица А. Разобьем ее на матрицы
низших порядков (клетки или блоки) с помощью горизонтальных и
вертикальных перегородок, идущих вдоль всей матрицы. Например,
ап аи
«21 «22
«13
«23
_«31 «32 1 «33 _
где клетками являются матрицы
Тогда матрицу А можно рассматривать как сложную матрицу,
элементами которой служат клетки:
Q
Матрица, разбитая на клетки, называется клеточной или блочной.
Понятно, что разбиение матрицы на клетки может быть
осуществлено различными способами. Частным случаем клеточных матриц
являются квазидиагональные матрицы
где клетки А{ (/=1,..., s) есть квадратные матрицы, вообще
говоря, различных порядков, а вне клеток стоят нули. Отметим, что
Другой важный частный случай клеточных матриц
представляют окаймленные матрицы
Ап-х
где
«21
а12

А 1 1 ] КЛЕТОЧНЫЕ МАТРИЦЫ 253
— матрица порядка п—\\
2» п —матрица-столбец;
V = [я * а 9 ... аи „ ,1 — матрица-строка и аип — число.
Клеточные матрицы одинакового типа и с одинаковым
разбиением условимся называть конформными. Удобство клеточных матриц
состоит в том, что действия над ними совершаются формально по
тем же правилам, что и над обыкновенными матрицами.
А. Сложение и вычитание клеточных матриц
Если клеточные матрицы
B)
конформны, т. е. p — r\ q = s и клетки Atj и B(j имеют одинаковый
тип, то
Г
= \
l
В самом деле, чтобы сложить матрицы А и В, надо сложить
соответствующие элементы их, но очевидно, что то же самое
получится, если мы сложим соответствующие клетки этих матриц.
Аналогично производится вычитание клеточных матриц.
Если А — клеточная матрица A) и а — число, то имеем:
[аАц аЛ12 ... аА1д1
.
аАр1 аАр2...аАрд1
Б. Умножение клеточных матриц
Пусть клеточные матрицы А и В имеют структуру
соответственно A) и B), причем # = г.
Предположим, что все клетки Ац и Bjk (/ = 1, 2, ..., р\ /=1,
2, . . ., q-t k~\y 2, . . ., s) таковы, что число столбцов клетки Ац
Равняется числу строк клетки Bjk. В частном случае, если все
клетки Atj и В(у — квадратные и имеют один и тот же порядок,

254
АЛГЕБРА МАТРИЦ
[ГЛ. VII
то это предположение заведомо выполняется. Тогда можно
доказать, что произведение матриц А и В есть клеточная матрица
С =
Ср2 ... Cps-
где Cik = AnBlk + Ai2B2k+...+AigBgk(i=\, 2, .... р; k = \,
2, ..., s), т. е. матрицы А и В перемножаются так, как будто
на месте клеток находятся числа [2].
Пример. Перемножая клеточные матрицы
А =
В=
t
2
I
I
t
i
^2^
P
T
Q
-2^
S
U
получим матрицу вида
t
2
PR + QT
+-2-+
PS + QU
Особенно просто производится сложение и умножение кв«зидиа-
гональных матриц. Если
Аг
As
•

Я 12J ОБРАЩЕНИЕ МАТРИЦ ПРИ ПОМОЩИ РАЗБИЕНИЯ НА КЛЕТКИ 255
и порядки матриц Ац В;A = 1, 2, ..., $) одинаковы, то,
очевидно, имеем:
At + Bx
•
Ав + В8
АгВх
•
ASBS
§ 12. Обращение матриц при помощи разбиения на клетки
Пусть для данной неособенной числовой матрицы А требуется
найти обратную матрицу Л. Разобьем матрицу А на четыре
клетки:
. -,,J. r) au(r, s)~\
L«2l(S, Г) <Z22(S, в) J '
Здесь в скобках указаны порядки соответствующих клеток,
причем r-{-s = ny где п — порядок матрицы Л. Будем искать
обратную матрицу А^1 также в виде четырехклеточной матрицы
Л г) р13 (г, s)
_P2i(«> r) p22(s, s)
Тогда, так как А~гА = Еу то, перемножая эти матрицы, получим
четыре матричных уравнения
A)
где Ег и ?^ — единичные матрицы соответствующих порядков.
Решив эту систему, определим клетки матрицы А. Для решения
системы A) используем способ исключения неизвестных. Умножая
справа первое уравнение системы A) на af^a^ и вычитая из
результата умножения второе уравнение этой системы, получим:

256 АЛГЕБРА МАТРИЦ
Отсюда находим:
Р1 о — —¦— ОС OS-» q I Own о "~—~ С^
[ГЛ. VII
Аналогично из третьего и четвертого уравнений системы A)
будем иметь:
Здесь, конечно, предполагается, что соответствующие операции
имеют смысл. Введем в рассмотрение матрицы
B)
п _. у „ у^
Тогда формулы для клеток C^ (/, /=1, 2) можно записать
проще:
—-те-1.
Формулы A) определяют клетки матрицы Л при условии,
что а и 8 существуют. Вычисления удобно расположить в виде
следующей схемы [4]:
X=c4ilai2
е-1
«21
^ = а21(ХГ11
a22
«12
e = a22 — Yal2
-e-»y е-»
Этот метод полезно применять, если матрица an легко обратима.

§ 12] ОБРАЩЕНИЕ МАТРИЦ ПРИ ПОМОЩИ РАЗБИЕНИЯ НА КЛЕТКИ
Пример 1. Обратить матрицу
257
1
0
—3
—5
0
1
4
-6
3
5
0
2
—4
6
2
0
Решение. Положим
1 0
Применяя приведенную выше схему, будем иметь:
З -4
О 2
3
5
16
—47
—4
6
34
—11
—3
-5
1
0
-3
—5
4
-6
0
1
4
—6
0
2
3
5
— И
47
2
0
—4
6
—34
16
Отсюда
1422
_i_rir 16 34
1422 |_ 5 6 J [ —47 —11
1422
236 146
202 104
]¦
-iy_ 1 Г 16 341Г-3 4~U l
Г ~ Т422 L -47 -11 J [ -5 -6 J ~- 1422
,-iv« i Г 236 1461Г-3 41__L_
0 Г ~1422 L —202 104 J |_ -5 — 6 J """ 1422
196 -122
~1438
86
681
-1432 J *
Для контроля произведение XQ XY вычисляем двумя способами:
xQ^Y^iXQ-^y и re-1r=.Y(e~1r).
По общей схеме имеем:
1
1422
- —16 68
86 —10
218 140
L —196 122
—236 —146 п
202 —104
16 34
—47 —И J
Б- П. Демидович и И. А. Марон

258
АЛГЕБРА МАТРИЦ
[ГЛ. VH
Частным случаем изложенного метода является так называемый
метод окаймления. Сущность его заключается в следующем. Пусть
дана матрица
«1л
Л =
ani...ann
Образуем последовательность матриц
«и
«11 «12 «13
«21 «22 «23
«31 «32 «33
«11 «12 «13
«21 «22 «23
«31 «32 «33
«41 «42 «43
.Я
-"а
_ «31 «32
«14 "
«24
«34
«44
-«41
«13
«23
«33 _
«42 «43
«14 "
«24
«34
«44 J
и т. д. Каждая следующая матрица получена из предыдущей при
помощи окаймления. Обратная ко второй из этих матриц SJ
находится непосредственно:
А
«21
А
А
«и
A J
где
9 — аЛ
При помощи матрицы
5а,
применив к 53 приведенную выше
схему вычисления, можно получить 57\ а затем при помощи S^1
аналогично получить S^1 и, наконец, 5^ = Л.
Метод окаймления становится непригодным, если одна из
промежуточных матриц S( является особенной. Положение может быть
исправлено с помощью перестановки строк матрицы [5].
Пример 2. Найти обратную матрицу для матрицы
1 4
0 —1
3 1
1 -2
3'
—1
2
1
Решение, Здесь
S2 =
= s;

§ 12] ОБРАЩЕНИЕ МАТРИЦ ПРИ ПОМОЩИ РАЗБИЕНИЯ НА КЛЕТКИ
Схема вычисления S^1 имеет следующий вид:
X
в
251
13
—3
1
36
3 1
1 4
0—1
3 11
0
1
3
—36
Y О
15 _143
12 36
JL IL
4 12 J
Следовательно,
г
1
2
1
4
1
12
1
36
1
12
11
36
13
36
1
12
1
36
J
Для вычисления S1 служит следующая схема:
X
e-1
4
9
2
3
1
9
9
22
1
1
12
1
4
1
12
1
6
-2
1
36
1
12
11
36
31
18
. 5
13
36
1
12
1
36
7
18
1
3
r>
z
22
9
Г
1
33
1
22
1
132
31
99
31
66
31
396
7
99
7
66
7
"~396
-
J

260
АЛГЕБРА МАТРИЦ
[ГЛ. VII
Следовательно,
5
44
9
44
4
44
3
44
15
44
17
44
10
44
31
44
19
44
1
44
2
44
7
44
2
11
3
11
1
22
9
22
1
44
-5
9
4
15
17
10
19
1
—2
—8
—12
2
_ 3 -31 -7
18 J
§ 13. Треугольные матрицы
Определение. Квадратная матрица называется треугольной,
если элементы, стоящие выше (ниже) главной диагонали, равны
нулю. Например,
hi
0
Lo о ... *„„
где t(j = 0 при / > у, есть верхняя треугольная матрица. Аналогично
п 0 ... О
21 ^22 • • • ^
где tn==0 для />/, есть нижняя треугольная матрица.
Диагональная матрица является частным случаем как верхней,
так и нижней треугольной матрицы. Определитель треугольной
матрицы равен произведению ее диагональных элементов, а именно:
если T—[tij] — треугольная матрица, то очевидно, что detT =
= tliLt22.. ,tnn. Поэтому треугольная матрица является неособенной
только тогда, когда все ее диагональные элементы отличны от нуля.
Можно доказать, что: 1) сумма и произведение треугольных
матриц одинакового типа и одной и той же структуры, т. е.
одновременно только верхних или только нижних, есть также треугольные
матрицы того же типа и общей структуры; 2) обратная матрица
неособенной треугольной матрицы есть также треугольная матрица
того же типа и структуры. Пользуясь последним обстоятельством
мы легко можем обращать треугольную матрицу.

§ 13] ТРЕУГОЛЬНЫЕ МАТРИЦЫ
Пример 1. Обратить матрицу
261
Решение. Положим
А'
Перемножая матрицы А и Л", будем иметь:
Г1 О О"!
1=1 2 0 .
Ll 2 3J
Пн 0 0 1
l-i = h2X t22 о .
Отсюда последовательно находим:
^22 — 2 *
* L-
32 Q '
Следовательно,
л-1-
1
2
0 0"
4 •
_ j_
3 3
Имеет место важная теорема [3].
Теорема. Всякую квадратную матрацу
ап а12
а21 а22
а2п
^П\ ап2
имеющую отличные от нуля главные диагональные миноры
«11 «12
«21 «22
можно представить в виде произведения двух треугольных матриц
различных структур (нижней и верхней), причем это разложение
будет единственным, если заранее зафиксировать диагональные
элементы одной«из треугольных матриц {например, положить их
равными 1).

262 АЛГЕБРА МАТРИЦ [ГЛ. VII
Не приводя доказательства теоремы, ограничимся указанием
способа отыскания элементов искомых треугольных матриц. Пусть
A = TtTv A)
где
B)
есть нижняя треугольная матрица порядка п;
7*2 = Ы> ci/ = ° для
есть верхняя треугольная матрица порядка п. Перемножая эти
матрицы, в силу формулы A) получим:
2 */*«*/=*// С У=Ь 2, ..., л). D)
Система D) в силу условий B) и C) принимает вид
^bikckj=aif при />/ (/=1, 2, ..., и) D')
и
^bikckf^aif при /</ (/=1,2, ..., п— 1). D")
Системы D') и D") в силу их особой структуры легко решаются
с точностью до диагональных элементов Ьц и си. Для
определенности можно положить ^. = 1 (/=1, 2, ..., п).
Пример 2. Представить матрицу
Г 1 —1 21
А= -1 5 4
L 2 4 14 J
в виде произведения двух треугольных матриц 7\ и Тг.
Решение. Л=7\72. Будем искать Тг и Г2 в виде
Пи О О"! Г1 rl2 r13l
T^Uu *2* 0 и Г,= 0 1 r23 L
L^l *32 ^33 J L0 0 1 J
Г 1 —1 21 Пи tnrl2 tnrn T
— 1 5 4 I = I ^21 *21Г12 + *22 ^21Г13 + ^22Г23 J J
L 2 4 14J L'31 ^31^12 + ^32 ^13+^23+^33 J
Имеем:
откуда

§ 14] ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ
Решив систему, получим:
fu=l; *«=-!; ^3i = 2;
263
Г12
— 1;
Таким образом,
i = 2;
1 О
— 1 4
2 6
Г23 — 2
1 —
О
О О
1
Пользуясь представлением квадратной матрицы A (det Л
в виде произведения двух треугольных матриц, можно указать еще
один способ вычисления обратной матрицы А~19 а именно, если
ТО
л-1
Si —
Обратные матрицы для треугольных, как мы видели выше,
находятся сравнительно просто.
§ 14. Элементарные преобразования матриц
Следующие преобразования матриц носят названия элементарных:
1) перестановка двух строк или столбцов;
2) умножение всех элементов какой-либо строки (столбца) на
одно и то же число, отличное от нуля;
3) прибавление к элементам какой-либо строки (столбца)
соответствующих элементов другой строки (столбца), умноженных на одно
и то же число.
Две матрицы называются эквивалентными, если одна получается
из другой с помощью конечного числа элементарных преобразований.
Такие матрицы не являются, вообще говоря, равными, но, как можно
доказать, имеют один и тот же ранг [6].
Легко убедиться, что каждое элементарное преобразование
квадратной матрицы А равносильно умножению последней на некоторую
неособенную матрицу. При этом, если преобразование производится
над строками (столбцами) матрицы Л, то множитель должен быть

264
АЛГЕБРА МАТРИЦ
[ГЛ. VII
левым (правым) и представлять собой результат применения
соответствующего элементарного преобразования к единичной матрице [6].
Например, переставляя в матрице
А =
«11 «12 «13
«21 «22 «23
«31 «32 «3
вторую и третью строки, будем иметь эквивалентную матрицу
А =
«П «12 «13
«31 «32 «33
«21 «22 «2;
Та же матрица А получится, если в единичной матрице
1 О О
О 1 О
О 0 1
переставить вторую и третью строки и полученную матрицу
1
0
0
0
0
1
0
1
0
умножить слева на матрицу Л, т. е. А = ЁА.
Аналогичным способом производят и другие элементарные
преобразования. Заметим, что если в равенстве АА~г = Е совершать
одинаковые преобразования строк матриц Л и ? до тех пор, пока
матрица А не превратится в единичную, то будем иметь ЁАА~1 = Е,
где Ё—преобразованная единичная матрица. Отсюда, так как ЁА = Е>
получим Л = Д т. е. обратная матрица А представляет собой
преобразованную единичную матрицу. На этом основан способ
вычисления обратной матрицы при помощи преобразования строк [4].
§ 15. Вычисление определителей
Элементарные преобразования матрицы дают наиболее удобный
способ вычисления определителя этой матрицы. Пусть, например,
«11 012 -. «1
Я21 «22 ... «2
ап1 ап2 ... ап
A)

§ 15J ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ
Предполагая, что а1Х Ф О, будем иметь:
265
Ап = аг1
" 1 «12
«21
77" а22
а2п
2м „„,... „„„
«11
Отсюда, вычитая из элементов а/у., принадлежащих у-му столбцу
2), соответствующие элементы первого столбца, умноженные
на аХу, получим:
1 0 ... О —
«11
««1
дA)
W2/l
где
2/1
7(D
№ = а„-
К определителю Д„_1 применяем тот же прием. Если все элементы
йц ф u (/ = 1, z, . . ., П),
то окончательно находим:
ДA) (/I—1) /О\
я = а11а22 ••• й/ггг • (О)
Если в каком-нибудь промежуточном определителе ДИ_Л левый
верхний элемент a^lf й+1 = 0, то следует переставить строки или
столбцы определителя An_k так, чтобы нужный нам элемент был
отличен от нуля (это возможно всегда, если определитель Д=^=0).
Конечно, при этом следуетучесть изменение знакаопределителя АЯ_Л.
Можно дать более общее правило. Пусть определитель Кп = det [a{J]

АЛГЕБРА МАТРИЦ [ГЛ. VII
преобразован так, что а^=1 {apq — главный элемент), т.е.
0,1
v...
f\ ... V
anl ... an? ... anJ
Тогда
где Art.1 = det[aJ/)] есть определитель (я —1)-го порядка,
получающийся из Ап путем выбрасывания р-й строки и q-то столбца с
последующим преобразованием элементов по формуле
т. е. каждый элемент а|у} определителя &пж1 равен
соответствующему элементу а^ определителя Дя, уменьшенному на произведение
его мроекцийъ aiq и apj на отброшенные столбец и строку
исходного определителя. Доказательство этого положения легко вытекает
из общих свойств определителей [7].
Пример. Вычислить
1 -1 2
2
1
5
1
3
4
—2
1
1
2
—3
2
4
3
5
3
3
1
— 1
2
А,-
Решение, Принимая за главный элемент #15=1, будем иметь:
-2—3-3 3 —ЬЗ 1 —(—1>-3 4—2-3
1 _з.1 4 — Ы 2 — <—1)-1 3 —2-1
5 -3.(~1) -2 -1.(-1) —3 — (—1) (—1) 5 -2-(-1)
«1 —3.2 1 — Ь2 2 —(—1J 3 —2-2
11
2
8
7
0
3
— 1
1
4
3
—4
4
2
ш
7
2

ЛИТЕРАТУРА К СЕДЬМОЙ ГЛАВЕ
2G7
Далее, принимая за главный элемент а24=1 и применяя
аналогичное преобразование, получим:
-15
22
— 9
6
—22
2
10
—25
7
— 9
-15
22
— 9
3
10
—11 —25
ш
7
2.(—1K+2
12
—77
—11
52
:446.
Заметим, что число умножений и делений, нужных для
вычисления определителя л-го порядка, равно [8]
п — 1
Литература к седьмой главе
1. О. Шрейер и Е. Шпернер, Теория матриц, ОНТИ, 1936, § 1, 2.
2. А. Мальцев, Основы линейной алгебры, Изд. 2, Гостехиздат, 1956.
3. В. Н. Ф а д д е е в а, Вычислительные методы линейной алгебры, Гостех*
издат, 1950.
4. Р. Фрезер, В. Дункан, А. Кол л ар, Теория матриц и ее прило»
жения к дифференциальным уравнениям и динамике, ИЛ, 1950.
5. Б. В. Булгаков, Колебания, Гостехиздат, 1954, гл. I.
6. Е. С. Ляпин, Курс высшей алгебры, Учпедгиз, 1953, гл. IX.
7. Э. Уиттекер и Г. Робинсон, Математическая обработка резуль*
татов наблюдений, ОНТИ, 1935, гл. V.
8. Д. К* Фаддеев и В. Н. Фаддеев а, Вычислительные методы линей*
ной алгебры, Физматгиз, 1960, гл. II.

ГЛАВА VIII
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 1. Общая характеристика методов решения систем
линейных уравнений
Способы решения систем линейных уравнений в основном
разделяются на две группы: 1) точные методы, представляющие собой
конечные алгорифмы для вычисления корней системы (таковы,
например, правило Крамера, метод Гаусса, метод главных элементов,
метод квадратных корней и др.), и 2) итерационные методы,
позволяющие получать корни системы с заданной точностью путем
сходящихся бесконечных процессов (к числу их относятся метод
итерации, метод Зейделя, метод релаксации и др.).
Вследствие неизбежных округлений результаты даже точных
методов являются приближенными, причем оценка погрешностей
корней в общем случае затруднительна. При использовании
итерационных процессов, сверх того, добавляется погрешность метода.
Заметим, что эффективное применение итерационных методов
существенно зависит от удачного выбора начального приближения
и быстроты сходимости процесса.
§ 2. Решение систем с помощью обратной матрицы.
Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными
аХ1хх + аХ2х2
а1пхп = bv
а%пхп = *а,
A)
Обозначим через
ll «12 ••• «1
21 «22 ••• <*2
ап1 ап2 ... ап
B)

§ 2] РЕШЕНИЕ С ПОМОЩЬЮ ОБРАТНОЙ МАТРИЦЫ. ФОРМУЛЫ КРАМЕРА 269
матрицу из коэффициентов системы A), через
"V
C)
—-столбец ее свободных членов и через
X z=z
(¦>
— столбец из неизвестных (искомый вектор). Тогда система A)
кратко может быть записана в виде матричного уравнения
Ах = Ь. E)
Совокупность чисел xv х2, ..., хп (или, короче, вектор х),
обращающих систему A) в тождество, называется решением этой
системы, а сами числа х(— ее корнями.
Если матрица Л— неособенная, т. е.
det Л =
аи а12
а21 а22
.. а2п
... апп
F)
то система A), или эквивалентное ей матричное уравнение E), имеет
единственное решение.
В самом деле, при условии detA=?O существует обратная
матрица Л. Умножая обе части уравнения E) слева на матрицу Л,
получим
или
х — л а. {()
Формула G), очевидно, дает решение уравнения E), причем так
как каждое решение имеет вид G), то решение единственно.
'Пример 1. Решить систему уравнений
2xL —
= 15.

270 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Решение. Запишем систему в матричной форме
[гл. viii
L 2 -1 4jbsJ L 15 J
Определитель матрицы А данной системы
det Л =
3—10
—2
1 1
2—14
= 5^=0.
Вычисляя обратную матрицу Л"*1, получим:
l ± —L
1 5 5
2 I2 -1
^5 5
0 T
Отсюда
*1
4_
5
12
5
\_
5
3_
5
\_
5
5
0
15
=
2
1
3
Значит, хг = 2; х2=\; *3 = 3.
Для матрицы А порядка п > 4 непосредственное нахождение
обратной матрицы Л* требует много времени. Поэтому формула G)
редко употребляется на практике.
Пользуясь формулой G), легко получить формулы для неизвестных
системы A). Как известно (гл. VII, § 4),
А~1л
где
[^п Л21 ... Ап1 1
А\п А2п ... Апп J
— матрица, союзная с А (Л/у- — алгебраические дополнения
элементов д.Л. Поэтому

§ 2] РЕШЕНИЕ С ПОМОЩЬЮ ОБРАТНОЙ МАТРИЦЫ. ФОРМУЛЫ КРАМЕРА 271
ИЛИ
где
••• , i-l
(8)
anl
*n,i-l bn V
— определители, получающиеся из определителя А [формула F)]
путем замены его/-го столбца столбцом свободных членов системы (I).
Из равенства (8) получаем формулы Крамера
X9 =
Д '
(9)
Следовательно, если определитель системы A) А ^О, то система
имеет единственное решение х, определяемое матричной формулой G)
или эквивалентными ей скалярными формулами (9).
Пример 2. Решить систему линейных уравнений
^4=-5,
Решение. Определитель этой системы
А =
2
i
0
1
1
-3
2
4
—5
0
—i
—7
1
-6
2
6
= 27^0.
Вычисляя дополнительные определители, получим:
8 1—51
9—3 0—6
—5 2—1 2
0 4—76
= 81;
8—5
9 0
5—1
0—7
1
-6
2
6
= —108;

272
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIII
2
1
0
1
2
1
0
1
1
—3
2
4
1
з
2
4
8
9
—5
0
—5
0
—1
-7
1
—6
2
6
8
9
-5
0
= -27;
= 27.
Отсюда
Аз
Л "
27
7 :
¦1;
_А_4_27
Х*~ А — 27 ~~ ''
Таким образом, решение линейной системы A) с п неизвестными
сводится к вычислению (я+1)-го определителя порядка п. Если
число п велико, то вычисление определителей является трудоемкой
операцией. Поэтому разработаны прямые приемы нахождения корней
линейной системы.
§ 3. Метод Гаусса
Наиболее распространенным приемом решения систем линейных
уравнений является алгорифм последовательного исключения
неизвестных. Этот метод носит название метода Гаусса. Для простоты
рассуждений ограничимся рассмотрением системы четырех
уравнений с четырьмя неизвестными
п\\Х\
013*3
= а
\ 5»
A)
Пусть а1Х ФО (ведущий элемент). Разделив коэффициенты
первого уравнения системы A) на дп, получим:
041*1 + 042*2 + 043*3 + 044*4 = 046-
13*3 + ^14*4 =
B)
где
Ъ --'

§ 3] МЕТОД ГАУССА 273
Пользуясь уравнением B), легко исключить из системы A)
неизвестную xv Для этого достаточно из второго уравнения системы A)
вычесть уравнение B), умноженное на а21) из третьего уравнения
системы A) вычесть уравнение B), умноженное на аг11 и т. д.
В результате получим систему из трех уравнений
+4^4 = ^5, \ (П
где коэффициенты а\}] (it /^2) вычисляются по формуле
аф^ац — анЬу (/, У>2).
Разделив, далее, коэффициенты первого уравнения системы (Г)
на «ведущий элемент» а^, получим уравнение
где
Исключая теперь х2 таким же способом, каким мы исключили лгг,
придем к следующей системе уравнений:
где
Разделив коэффициенты первого уравнения системы (Г;) на
«ведущий элемент» а^, получим:
где
3
Исключив теперь лг3 аналогичным путем из системы (Г;)> будем
иметь:
где

274 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Отсюда
аC)
U44
Остальные неизвестные последовательно определяются из
уравнений B"), B') и B):
Х1 = Ь1Ь —
Таким образом, процесс решения линейной системы по методу
Гаусса сводится к построению эквивалентной системы B), B'), B"),
B'"), имеющей треугольную матрицу. Необходимым и достаточным
условием применимости метода является неравенство нулю всех
«ведущих элементов». Вычисления удобно поместить в таблицу 13.
Приведенная в ней схема называется схемой единственного деления.
Процесс нахождения коэффициентов Ь^гг) треугольной системы
обычно называется прямым ходом, процесс получения значений
неизвестных— обратным ходом.
Прямой ход начинается с выписывания коэффициентов системы,
включая свободные члены (раздел А). Последняя строка раздела А
схемы представляет собой результат деления первой строки раздела
на «ведущий элемент» аХ1. Элементы а<*> (/, /^ 2) следующего
раздела схемы (раздел А±) равны соответствующим элементам aif
предшествующего раздела без произведения их «проекций» на
ряды раздела Л, содержащие элемент 1 (т. е. на первый столбец
и последнюю строку).
Последняя строка раздела At находится путем деления первой
строки раздела на «ведущий элемент» а^. Аналогично строятся
следующие разделы. Прямой ход заканчивается, когда мы дойдем
до раздела, состоящего из одной строки, не считая
преобразованной (раздел А3 в нашем частном случае).
При обратном ходе используются лишь строки разделов Ah
содержащие единицы {отмеченные строки), начиная с последней.
Элемент Ь^ из раздела А31 стоящий в столбце свободных членов
отмеченной строки раздела, дает значение лг4. Далее, все остальные
неизвестные х{ (/ = 3, 2, 1) шаг за шагом находятся с помощью
вычитания из свободного члена отмеченной строки суммы
произведений ее коэффициентов на соответствующие значения ранее
найденных неизвестных. Значения неизвестных последовательно
выписываются в последний раздел В. Расставленные там единицы помогают
находить для x-t соответствующие коэффициенты в отмеченных
строках.

§ 3]
МЕТОД ГАУССА
Схема единственного деления
275
Таблица 13
«11
«21
«31
«41
1
Х%
«12
«22
«32
«42
*11
1
1
«13
«23
«33
«43
&13
4?
ЧУ
«й
НУ
аB)
¦«5S
1
1
*4
аи
«34
а«4
4У
HV
1
1
Свободные
члены
«15
^25
«35
«45
*U
«BV
«CV
«iV
ьBУ
«325'
(Xt)
Xi
x3
x2
Xl
S
«ie
«se
o3e
«49
bib
«Й
*iV
»iV
ХЛ
хл
*-\
Разделы
схемы
л»
В
Для контроля вычислений используются так называемые
«контрольные суммы»
=1. 2, .... 5),
C)
помещенные в столбце ]?] и представляющие собой сумму элементов
строк матрицы исходной системы A), включая свободные члены.

276 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Если а{6 принять за новые свободные члены в системе A), то
преобразованная линейная система
4
2 **/*/ = «/в (' = 1. 2> 3> 4) D)
будет иметь неизвестные */} связанные с прежними неизвестными Xj
соотношениями
xf = xf+l (У=1, 2, 3, 4). E)
В самом деле, подставляя формулы E) в уравнение D), в силу
системы A) и формул C) получим тождество
4 4 6
2 **>*/+/2 «*/ = 2!«// = «/е (У=Ь 2, 3, 4).
Вообще, если над контрольными суммами в каждой строке
проделывать те же операции, что и над остальными элементами
этой строки, то при отсутствии ошибок в вычислениях элементы
столбца 2 равны суммам элементов соответствующих
преобразованных строк. Это обстоятельство служит контролем прямого хода.
Обратный ход контролируется нахождением чисел *у, которые
должны совпадать с числами *у+1.
Пример. Решить систему
7,9*! + 5,6*2 + 5,7*3 — 7>2лг4 = 6,68;
4,3*x + 4,2*2 - 3,2*3 + 9,3*4 = 8,6;
3,2*! — 1,4*2 — 8,9*з + 3,3*4 = 1.
Решение. В раздел А таблицы 14 впишем матрицу
коэффициентов системы, ее свободные члены и контрольные суммы. Далее,
заполняем последнюю (пятую) строку раздела Л, деля первую
строку на 7,9 (на ап).
Переходим к заполнению раздела Ах таблицы. Взяв любой
элемент раздела А (не находящийся в первой строке), вычитаем из
него произведение первого элемента его строки на последний
элемент столбца, к которому он принадлежит, и записываем на
соответствующее место в разделе Аг схемы. Например, выбрав
я4з= —8,9, будем иметь:
eDV = «48—«41*18= —8,9 — 3,2.0,72152= —11,20886.
Чтобы получить последнюю строку раздела А1У делим все члены
первой строки этого раздела на я^——10,82531. Например,
A)_а<218> . -5,33292
23 ~~~^
23 ~~~^ -10,82531
8

§ 3]
МЕТОД ГАУССА
277
Таблица 14
Решение системы по схеме единственного деления
ч
7,9
8,5
4,3
3,2
1
1
5,6
—4,8
4,2
—1,4
0,70886
—10,82531
1,15190
—3,66835
1
5,7
0,8
—3,2
-8,9
0,72152
-5,33292
—6,30254
-11,20886
0,49263
—6,87000
—9,40172
1
1
1
х*
-7,2
3,5
9,3
3,3
—0,91139
11,24682
13,21898
6,21645
—1,03894
14,41573
2,40525
—2,09836
—17,32294
1
1
Свободные
разделы
6,68
9,95
8,6
1
0,84557
2,76265
4,96405
—1,70582
—0,25520
5,2580J
—2,64198
—0,76536
—9,83768
0,56790
0,56790
0,42630
0,12480
0,96710
s
18,68
17,95
23,2
—2,8
2,36456
—2,14876
13,03239
—10,36658
0,19849
12,80374
—9,63845
—1,86372
—27,16062
1,56790
1,56790
1,42630
1,12480
1,96710
Разделы
схемы
А
Лг
А2
Аз
В
Аналогичным путем заполняются остальные разделы таблицы.
Например,
4 — #44 #42 024 =
= 6,21645 —( — 3,66835).(—1,03894) = 2,40525,
Для нахождения неизвестных используем строки, содержащие
единицы, начиная с последней (отмеченные строки). Неизвестное дг4
представляет собой свободный член последней строки раздела Л8:
д:4 = АЙ} = 0,56790.
Значения остальных неизвестных дг3, х2, хх получаются
последовательно в результате вычитания из свободных членов отмеченных

278 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
строк суммы произведений соответствующих коэффициентов b\j] на
ранее найденные значения неизвестных.
Имеем:
х3 = Ь(Ц - b{il*i = - 0,76536 — (— 2,09836) -0,56790 = 0,42630;
24#4 ""23*3 =
= — 0,25520 - (— 1,03894) • 0,56790 — 0,49263 • 0,42630 = 0,12480;
xx = bl5 — buXt — b13x3 — bl2x2 = 0,84557 —(— 0,91139) X
XO,5679O-0,72152-0,42630 —0,70886.0,12480 = 0,96710.
Итак,
^ = 0,96710; #2 = 0,12480; #3 = 0,42630; д;4== 0,56790.
Текущий контроль вычислений осуществляется с помощью
столбца 2» над которым производятся те же действия, что и над
остальными столбцами.
В результате: 1) сумма элементов каждой строки схемы (не
принадлежащих столбцу ]?]) должна быть равна элементу этой строки
из столбца 2; 2) корни хь соответствующие столбцу 2, должны
быть на единицу больше соответствующих корней системы.
Кстати, если учесть единицы, написанные в разделе В, то опять
получится, что и в этом разделе элементы столбца 2 являются
суммами элементов отвечающих им строк. В нашем случае первое и
второе условия выполняются с точностью до единицы последнего
разряда. Следовательно, почти достоверно, что вычисления
выполнены правильно.
Заметим, что если матрица системы —симметрическая, то
соответствующие части разделов Ау А1У Л2, ... схемы единственного
деления также получаются симметрическими. Это обстоятельство
можно использовать для упрощения таблицы.
Нетрудно оценить число N арифметических действий,
необходимых для решения линейной системы с п неизвестными методом
Гаусса [5] (не учитывая контроля).
Для прямого хода требуется следующее число умножений
и делений:
и столько же вычитаний. Для обратного хода потребуется п ^п*""* '
умножений и делений и такое же количество вычитаний. Следова-

§ 4J
УТОЧНЕНИЕ КОРНЕЙ
279
тельно, общее количество арифметических действий в методе
Гаусса есть
при п> 7.
Таким образом, время, необходимое для решения линейной
системы методом Гаусса, примерно пропорционально кубу числа
неизвестных. Например, для решения методом Гаусса системы 100
линейных уравнений со 100 неизвестными на быстродействующей
машине, выполняющей 104 операций в секунду, потребуется время
Т= 106 • 10~4 = 100 сек.
Фактическое машинное время будет значительно больше ввиду
наличия в программе, кроме арифметических действий, других
операций (переадресация, логические операции, пересылки,
формирование и др.).
§ 4. Уточнение корней
Полученные методом Гаусса приближенные значения корней можно
уточнить. Покажем, как это делается, если поправки корней малы
по абсолютной величине.
Пусть для системы
найдено приближенное решение х0. Полагая
X = Хо + б,
для поправки 6=
L6J
корня х0 будем иметь уравнение
или
где г^Ь — Ах0 — невязка для приближенного решения лг0. Таким
образом, чтобы найти 6, нужно решить линейную систему с прежней
матрицей А и новым свободным членом е =
. Для этого доста-
точно к основной схеме вычислений присоединить столбец 8
свободных членов и преобразовать его по общим правилам. Поправки б1э
б2, . . . , бп, как обычно, определяются из отмеченных строк, причем
коэффициенты при этих неизвестных поправках уже имеются готовыми

280
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[гл. vui
в таблице. Заметим, что преобразованные коэффициенты матрицы Л
можно не уточнять, так как при малых невязках соответствующие
ошибки будут обладать более высоким порядком малости.
Пример. Решить методом Гаусса с тремя знаками (например,
на счетной линейке или вручную) систему
—х2— Х3 = 11,33;]
= 42.
A)
Используя полученные значения как начальные приближения,
уточнить корни до 10~4.
Решение. Применяем обычную схему единственного деления
(таблица 15), выполняя все действия с тремя значащими цифрами.
Таблица 15
Уточнение корней, вычисленных методом Гаусса
6
— 1
— 1
1
1
— 1
6
— 1
—0,167
5,83
-1.17
1
1
—1
— 1
6
—0,167
— 1,17
5,83
—0,200
5,60
1
Свободные
члены
11,33
32
42
1,89
33,9
43,9
5,80
50,7
9,05
9,0475
7,62
7,6189
4,67
4,6661
15,33
36
46
2,56
38,6
48,6
6,60
56,3
10,05
8,62
Невязка е
—0,02
0
— 0,01
— 0,0033
— 0,0033
— 0,0133
— 0,0006
—0,0140
—0,0025
—0,0011
—0,0039
Имеем приближенные значения корней:
дг^0) = 4,67; 40) = 7,62; 40

§ 5J МЕТОД ГЛАВНЫХ ЭЛЕМЕНТОВ 281
Подставляя эти числа в данную систему A), вычисляем
соответствующие невязки (т. е. разности между правой и левой частями системы A))
?<<»__ 0,02; еB0) = 0; е?в)=-0,01.
Используя эти значения в качестве свободных членов (таблица 15),
получаем поправки корней
6[О) = - 0,0039; б2@> = - 0,0011; бC0) = - 0,0025.
Отсюда находим уточненные значения корней
*!== 4,6661; лг2 = 7,6189; лг3 = 9,0475,
причем невязки равны
6t= —2- Ю-4, d2 = 2-10-4, 63 = О.
Иногда требуется определить возможную ошибку Ах корня х
линейной системы по известным малым ошибкам АА и АЬ матрицы А
системы и ее свободного члена Ь.
Имеем:
Ах = Ь B)
и
{А + АА) (х + Ах) = Ь + АЬ. C)
Отсюда, пренебрегая малым членом АА*Аху получим:
или
ААх = АЬ-ААх. D)
Таким образом, для приближенного нахождения Ах можно
использовать схему Гаусса для основной системы B), пополнив эту схему
новым столбцом свободных членов АЬ—А Ах,
§ 5. Метод главных элементов
Пусть дана линейная система
A)
аппхп = ап%

282
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. V1I1
Рассмотрим расширенную прямоугольную матрицу, состоящую
из коэффициентов системы и ее свободных членов,
а22
... a>\q ... aln
... а2д ... а2п
.. ain aiy
... а
Pf ••• а
• • • a
рп ар, и + 1
Выберем ненулевой, как правило, наибольший по модулю, не
принадлежащий к столбцу свободных членов {цфп-\-1) элемент apq
матрицы М, который называется главным элементом, и вычислим
множители
для всех ^
Строка с номером р матрицы М, содержащая главный элемент,
называется главной строкой. Далее, произведем следующую
операцию: к каждой неглавной строке прибавим главную строку,
умноженную на соответствующий множитель /я,- для этой строки. В
результате мы получим новую матрицу, у которой q-й столбец состоит
из нулей. Отбрасывая этот столбец и главную р-ю строку, получим
новую матрицу Ж11) с меньшим на единицу числом строк и столбцов.
Над матрицей М{1) повторяем те же операции, после чего
получаем матрицу М^\ и т. д. Таким образом, мы построим
последовательность матриц
Ж,
последняя из которых представляет двучленную матрицу-строку;
ее также считаем главной строкой.
Для определения неизвестных хг объединяем в систему все
главные строки, начиная с последней, входящей в матрицу М^п"х\
После надлежащего изменения нумерации неизвестных получается
система с треугольной матрицей, из которой легко шаг за шагом
найти неизвестные данной системы A). Метод главных элементов
всегда применим, если определитель системы
ап ... а1п
ап1 ... апп

§ 6] ПРИМЕНЕНИЕ МЕТОДА ГАУССА ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ 283
Заметим, что метод Гаусса является частным случаем метода
главных элементов, а схема метода Гаусса получается, если за
главный элемент всегда выбирать левый верхний элемент
соответствующей матрицы.
§ 6. Применение метода Гаусса для вычисления определителей
Пусть
А =
а21
... ап
A)
B)
Рассмотрим линейную систему
Ах = 0. C)
При решении системы C) по методу Гаусса мы заменяли матрицу А
треугольной матрицей В, состоящей из элементов отмеченных строк,
bL2 bn ... bln
О 1 b^ ... b^
.о* 6 * V Y..' i
В результате получалась эквивалентная система
Элементы матрицы В последовательно получались из элементов
матрицы А и дальнейших вспомогательных матриц Av Л2, ..., АПтт1
с помощью следующих элементарных преобразований:
1) деления на «ведущие» элементы alv а{Ц, ..., a^f^i которые
предполагались отличными от нуля, и
2) вычитания из строк матрицы А и промежуточных матриц At
(/=1, 2, ..., л—1) чисел, пропорциональных элементам
соответствующих ведущих строк. При первой операции определитель матрицы
также делится на соответствующий «ведущий» элемент, при
второй— определитель матрицы остается неизменным. Поэтому
det A
Следовательно,
E)
т. е. определитель равен произведению «ведущих» элементов для
соответствующей схемы Гаусса. Отсюда заключаем, что приведенная

284
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIII
нами в § 3 схема единственного деления может быть
использована для вычисления определителей, причем столбец свободных
членов тогда становится излишним.
Заметим, что если для какого-нибудь шага элемент а/'"* = 0 или
близок к нулю (что влечет за собой уменьшение точности
вычислений), то следует соответствующим образом изменить порядок строк
и столбцов матрицы.
Пример. Вычислить определитель
7,4 2,2 —3,1 0,7
1.6 4,8 —8,5 4,5
4.7 7,0 —6,0 6,6
5,9 2,7 4,9 —5,3
Решение. Используя элементы определителя
схему единственного деления (таблица 16).
Д, составляем
Таблица 16
1-й столбец
|7,4|
1.6
4,7
5,9
1
Вычисление определителя методам
2-й столбец
2,2
4,8
7,0
2,7
0,29729
4,32434
5,60274
0,94599
1
3-й столбец
-3,1
—8,5
—6,0
4,9
—0,41891
—7,82974
-4,03112
7,37157
—1,81062
F,11331
9,08440
1
4-й столбец
0,7
4,5
6,6
-5,3
0,09459
4,34866
6,15543
—5,85808
1,00562
0,52120
-6,80939
0,08526
—7,58393
Гаусса
V
7,2
2,4
12,3
8,2
0,97297
0,84326
7,72705
2,45948
0,19500
6,63451
2,27501
1,08526
—7,58393
А=—1483,61867
А
Аг
л2
А3

§ 7] ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА 285
Перемножая «ведущие» элементы (заключенные в рамки), получим:
Д = 7,4.4,32434-6,11331-( — 7,58393)= —1483,61867.
Обратим внимание на следующее обстоятельство. Для того чтобы
решить систему п линейных уравнений с п неизвестными по
формулам Крамера, нужно вычислить л+ 1 определителей л-го порядка.
Между тем для вычисления одного определителя п-то порядка по
схеме единственного деления требуется почти такой же объем работы,
как и для полного решения системы уравнений. Поэтому пользоваться
формулами Крамера для численного решения линейной системы при
п > 3, вообще говоря, нецелесообразно.
§ 7. Вычисление обратной матрицы методом Гаусса
Пусть дана неособенная матрица
Для нахождения ее обратной матрицы
Л"* = [*//] B)
используем основное соотношение
АА-* = Е, C)
где Е — единичная матрица.
Перемножая матрицы А и Л", будем иметь п систем уравнений
относительно п2 неизвестных xtj
п
где
1, когда /=/,
О, когда
Полученные п систем линейных уравнений для у=1, 2, ..,, «?
имеющих одну и ту же матрицу А и различные свободные члены,
одновременно можно решить методом Гаусса.
Пример. Найти обратную матрицу А'1 для матрицы
г1,8 -3,8 0,7 -3,7
-___ 0,7 2,1 —2,6 —2,8
7,3 8,1 1,7 —4,9
1,9 —4,3 -4,9 —4,7

286
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIII
Решение. Составим схему с единственным делением. При этом
будем иметь четыре столбца свободных членов (таблица 17).
Заметим, что элементы строк обратной матрицы получаются в обратном
гюрядке.
Таблица 17
Вычисление обратной матрицы методом Гаусса
1,8
0,7
7,3
1,9
1
1
—3,8
2,1
8,1
-4,3
-2,11111
3,57778
23,51110
-0,28889
1
1
0,7
-2,6
1.7
-4,9
0,38889
-2,87222
-1,13890
-5,63889
-0,80279
17,73557
-5,87081
1
1
*•)
-3,7
-2,8
-4,9
-4,7
-2,05556
-1,36111
10,10559
-0,79444
-0,38043
19,04992
-0,90434
1,07411
5,40155
1
/-1
1
0
0
0
0,55556
-0,38885
-4,05551
-1,05554
-0,10868
-1,50032
-1,08694
-0,08459
-1,58355
-0,29316
0,23030
-0,03533
-0,21121
/ = 2
0
1
0
0
0
1
0
0
0,27950
-6,57135
0,08074
-0,37108
-2,09780
-0,38837
0,04607
0,16873
-0,46003
/¦в
0
0
1
0
0
0
1
0
0
1
0
0,05638
0,33100
0,06128
-0,00944
0,01573
0,16284
/=4
0
0
0
1
0
0
0
1
0
0
1
0
1
0,18513
-0,19885
-0,08920
0,26956
2
-4,0
-1.6
13,2
—11,0
-2,22223
-0,04440
29,42228
-6,77776
-0,01241
29,71405
-6,78134
1,67539
3,05456
0,56540
1,06809
1,06013
0,76266
На основании результатов таблицы 17 получаем:
-0,21121 -0,46003 0,16284 0,26956
-0,03533 0,16873 0,01573 -0,08920
0,23030 0,04607 —0,00944 —0,19885
-0,29316 -0,38837 0,06128 0,18513,

§ 8] МЕТОД КВАДРАТНЫХ КОРНЕЙ
Для проверки составим произведение
287
•1,8—3,8 0,7—3,7-]
0,7 2,1 —2,6 —2,8
7,3 8,1 1,7—4,9
1,9—4,3 —4,9 — 4,7_
--0,21121 -0,46003 0,16284 0,26956-
—0,03533 0,16873 0,01573 —0,08920
0,23030 0,04607 —0,00944 —0,19885
_— 0,29316 -0,38837 0,06128 0,18513.
• 0,99997 0,00000 —0,00001 0,00000п
—0,00025 0,99997 —0,00002 —0,00039
—0,00808 —0,01017 0,99982 0,00009
0,00000 0,00000 0,00000 1,00048_
= ? — Ю-
Г0,03 0,00 0,01 0,00-
0,25 0,03 0,02 0,39
8,08 10,17 0,18 —0,09
0,00 0,00 0,00 —0,48.
Мы видим, что благодаря округлению обратная матрица
получилась не вполне точной. Ниже мы укажем (см. § 15) метод
исправления элементов приближенной обратной матрицы.
§ 8. Метод квадратных корней
Пусть дана линейная система
A)
где А = [аA\ — симметрическая матрица, т.е. Л' = [яу7] = Л. Тогда
матрицу А можно представить в виде произведения двух
транспонированных между собой треугольных матриц
B)
где
0
0
tZ...
0 ...
t«n-
и Г' =
Jin
0 .
i .
.. 0
.. 0
.. tn
г=
Производя перемножение матриц 7" и Т, для определения
элементов ty матрицы Т получим следующие уравнения:
'i A/
t if
(КЛ
¦}

288 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Отсюда последовательно находим:
[ГЛ. VIII
-2 *%
k=i
t-1
C)
t. y = 0 при
Система A) имеет определенное единственное решение, если
(/=1, 2, ...,я), так как тогда
Коэффициенты матрицы Т будут действительны, если tf( > 0. В
дальнейшем мы, вообще говоря, не будем предполагать это последнее
условие выполненным.
При наличии соотношения B) уравнение A) эквивалентно двум
уравнениям:
Т'у = Ь и Тх=у,
или в раскрытом виде
D)
J_ f x -V- -X-1 X = V
*ппХп=Уп-
E)
Отсюда последовательно находим:
а > 1)
F)

§ 8]
МЕТОД КВАДРАТНЫХ КОРНЕЙ
289
с -М±
X: = -
k-i + x
Ui
(Кп).
G)
Изложенный способ решения линейной системы носит название
метода квадратных корней. Так как матрица Л — симметрическая,
а матрица Г—верхняя треугольная, то в вычислительной схеме можно
записывать только -^ (п + 1) верхних коэффициентов а^ и //у. (/ ^у).
При вычислениях применяется обычный контроль с помощью сумм,
причем при составлении суммы учитываются все коэффициенты
соответствующей строки.
Заметим, что если для некоторой $-й строки имеем /g2s < 0, то
соответствующие элементы tsJ будут мнимыми. Метод формально
применим и в этом случае.
При практическом применении метода квадратных корней прямым
ходом с помощью формул C) и F) последовательно вычисляются
коэффициенты ttj и у{ (/=1, 2, ...,/z), а затем обратным ходом
с помощью формулы G) находятся неизвестные х{ (/ = /г, п — 1, ..., 1).
Пример. Методом квадратных корней решить систему уравнений
Зх1 + 4х2 — 5х3 + лг4—Злг5 = 5,4;
— 2хг — 5лг2 + Злг3 — 2л:4 + 2хь = 5,0;
= 3,3.
— 2хх — Зх2 + 2х3 + Зл;4
Решение. Записываем коэффициенты а^ и свободные члены ^.
данной системы в начальный раздел Л таблицы (таблица 18)и
подсчитываем столбец 2- Применяя формулы C) и F), последовательно
переходя от строки к строке, вычисляем коэффициенты t-j и новые
свободные члены у{ и, таким образом, заполняем раздел Б таблицы.
Например,
t
35
2 —(—2)( —2) —( —0,4472Q(—
Для контроля подсчитываем столбец 2« На основании формул
G) находим значения неизвестных лг^ и контрольные величины
10 Б. П. Демидович и И. А, Марон

290
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[гл. vm
Таблица 18
Решение линейной системы методом квадратных корней
аи
1
3
2
0
-2
*и
1
-6,0978
-5,0973
3
4
—5
1
—3
tit
3
2,2361/
—2,2016
-1,2017
аи
2
-5
3
—2
2
-2
—0,4472/
0,8944/
—6,8011
—5,8004
аи
0
1
—2
5
3
tu
0
-0,4472/
2,0125/
3,0414
—0,8996
0,1007
аи
—2
—3
2
3
4
t*
-2
-1,3416/
1,5653/
2,2194
0,8221/
0,1998
1,1992
h
0,5
5,4
5,0
7,5
3,3
Ух
0,5
—1,7471/
—7,5803/
—2,2928
0,1643*
0,5
5,4
1,0
14,5
7,3
2
0,5
—1,7471/
-3,1081/
2,9679
0,9859/
*/
Разделы
схемы
A
Б
В
. = Х;+\У помещая их в разделе В, Например,
ЛГ« ==:
— 7,5803/ —Ь5652/«0Л998—2,0125/-(—0,8996)
0,8944/
§ 9. Схема Халецкого
= —6,8011.
Для удобства рассуждений систему линейных уравнений
запишем в матричном виде
Ах = Ьу A)
где Л =
квадратная матрица порядка п и
[«1,/1+1 "I
— векторы-столбцы. Представим матрицу А в виде произведения
нижней треугольной матрицы В~[Ьц] и верхней треугольной
матрицы С=[с,у] с единичной диагональю, т. е.
А = ВСУ B)

§ 9]
где
СХЕМА ХАЛЕЦКОГО
291
в=
bu О ... О
b21 b22 ... О
1 с12
О 1
О 0 ... 1
Тогда элементы #/у. и с/7- определяются по формулам
C)
'
t-l
D)
Отсюда искомый вектор х может быть вычислен из цепи
уравнений
Ву = Ьу Сх=у. E)
Так как матрицы В и С—треугольные, то системы E) легко
решаются, а именно:
F)
«,-л- 2
к*л (/<л).
G)
Из формул F) видно, что числа yt выгодно вычислять вместе
с коэффициентами c(j. Этот метод получил название схемы Халец-
кого. В схеме применяется обычный контроль с помощью сумм.
Заметим, что если матрица А — симметрическая, т. е. dy^u/i, то
cu-bit
Схема Халецкого удобна для работы на вычислительных
машинах, так как в этом случае операции «накопления» C) и D) можно
проводить без записи промежуточных результатов.
10*

292 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Пример. Решить систему
— 4х4= — 12;
— *4 = 1;
— *эХд = о.
Решение (см. таблицу 19).
В первый раздел таблицы 19 впишем матрицу коэффициентов
системы, ее свободные члены и контрольные суммы.
Далее, так как Ьп = аA (i=l, 2, 3, 4), то первый столбец из
раздела 1 переносится в первый столбец раздела П.
Чтобы получить первую строку раздела II, делим все элементы
первой строки раздела I на элемент л11 = ^11> в нашем случае на 3.
Имеем:
с1% = 1 = 0,C);
с -6-2-
«is = y-2f F).
Переходим к заполнению второго столбца раздела II, начиная
со второй строки. Пользуясь формулами C), определяем bj2:
*и = ви-*иси=1-(-5.1) =4 = 2,66F);
= 0-2-1 = —1 = 0,F);
^42 = «42 —*4lC12 = 5 — 1 • — = 5-g- = 5, C).
Далее, определяя с2у(/=3, 4, 5, 6) по формулам D), заполняем
вторую строку раздела II:
-5). (-1)] -I;
= 4 [( — 17) —( — 5»^] ={

§ 9]
СХЕМА ХАЛЕДКОГО
293
•г
4
(M
H
*
*
CO
7
CO
15
Q
«14
*
CM
a
«и
i
1
CO
1
«24
«23
«21
CO
7
о
«34
ё
ё
1
CO
1
со
e
I
Q
«44
«N
«41
CO
s
CO
666^
o*
8
8
CO
CO
о
33333
CO
о
—
CO
<o
Я
о3
о*
о"
ю
о
ю
о*
-§-
СО
*¦
Т
°
о
cf
-—-
1
7
^_
1
СО
1
СМ
о"
со
СО
133333
1
-
-о
о?
—•
СЧ
7
Ю
7
со
—
СО
СО
н
III

294
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIU
Затем переходим к третьему столбцу, вычисляя его элементы Ь%г
и ?34 по формулам C) и т. д., пока не будет заполнена вся
таблица раздела II. Таким образом, заполнение раздела II происходит
способом «елочки»: столбец — строка, столбец — строка и т. д.
В разделе III, пользуясь формулами F) и G), определяем yi
и *, (/=1, 2, 3, 4).
Текущий контроль осуществляется с помощью столбца 2» над
которым производятся те же действия, что и над столбцом
свободных членов.
§ 10. Метод итерации
При большом числе неизвестных линейной системы схема
метода Гаусса, дающая точное решение, становится весьма сложной.
В этих условиях для нахождения корней системы иногда удобнее
пользоваться приближенными численными методами. Изложим здесь
один из этих методов — метод итерации.
Пусть дана линейная система
A)
Введя в рассмотрение матрицы
au a12 ... aln
«21 «22 • • • «2Л
... an
-Xn -i
ь*
систему A) коротко можно записать в виде матричного уравнения
Ах = Ь. (V)
Предполагая, что диагональные коэффициенты
(/=1, 2 п),
разрешим первое уравнение системы A) относительно ^.второе —
относительно хг и т. д. Тогда получим эквивалентную систему
B)

§ ю
где
МЕТОД ИТЕРАЦИИ
295
' = — ТТ. ПРИ
и а/7 = 0 при i=y (/,/=1, 2, . ,.,/z).
Введя матрицы
ап а12
Р2
систему B) можем записать в матричной форме
* = p + ajt. B')
Систему B) будем решать методом последовательных
приближений. За нулевое приближение принимаем, например,
столбец свободных членов х{0) = |3.
Далее, последовательно строим матрицы-столбцы
(первое приближение),
(второе приближение) и т. д.
Вообще говоря, любое (&4-1)-е приближение вычисляют по
формуле
x{k+1) = $ + ax(k) (? = 0, 1, 2, ...)• C)
Если последовательность приближений л:@), д:A), ..., хш, ...
имеет предел
*= lim xKk\
то этот предел является решением системы B). В самом деле,
переходя к пределу в равенстве C), будем иметь:
lim
lim
ИЛИ
т. е. предельный вектор х является решением системы B'), а
следовательно, и системы A).
Напишем формулы приближений в развернутом виде:
C')
= 0;г = 1, ...,п;к = 0, 1,2,...).

296 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Заметим, что иногда выгоднее приводить систему A). к виду B)
так, чтобы коэффициенты аи не были равны нулю. Например,
уравнение
1 ПО v П 1^*- 9 7
для применения метода последовательных приближений естественно
записать в виде
*х = 2,7 — 0,02*г + 0,15*а.
Вообще, имея систему
п
2 <*//*/= *1 (/ = 1, 2, ... , п),
7=i
можно положить:
<*ц = аи + а>и »
где а$ =? 0. Тогда данная система эквивалентна приведенной системе
п.
*i = h + 2 «//*/ («= 1. 2» • • • » ^)»
/=i
где
B)
U Ciii CL: t
Поэтому при дальнейших рассуждениях мы не будем, вообще
говоря, предполагать, что a,.f = 0.
Метод последовательных приближений, определяемых
формулой C) или C'), носит название метода итерации. Процесс
итерации C) хорошо сходится, т. е. число приближений, необходимых
для получения корней системы A) с заданной точностью, невелико,
если элементы матрицы а малы по абсолютной величине. Иными
словами, для успешного применения процесса итерации модули
диагональных коэффициентов системы A) должны быть велики по
сравнению с модулями недиагональных коэффициентов этой системы
(свободные члены при этом роли не играют).
Пример 1. Решить систему
4*х +0,24*2-0,08*з = 8,
f 3*2 — 0,15*з = 9,
\ — 0,08*2 + 4*3 = 20
методом итерации.

МЕТОД ИТЕРАЦИИ
297
Решение. Здесь диагональные коэффициенты 4; 3; 4 системы
значительно преобладают над остальными коэффициентами при
неизвестных. Приведем эту систему к нормальному виду B)
х± = 2 — 0,06лг2 + 0,02лг3, '
л;2 = 3 — 0,03*!+ 0,05*з, E)
х3 = 5 — 0,01*! + 0,02лг2. I
В матричной форме систему E) можно записать так:
Ч = 3 + -0,03 0 0,05 \х2 L
ЧА L5J L—0.01 0,02 0 J UJ
За нулевые приближения корней системы D) принимаем:
^.@) су, «-(О) О, л~(й) С
Xi —Z, Х2 = О, ЛГ3 =0.
Подставляя эти значения в правые части уравнений E), получим
первые приближения корней:
х[1] =2-0,06.3 + 0,02.5= 1,92;
л:^ = 3 — 0,03.2 + 0,05 • 5 = 3,19;
xl1] = 5—0,01-2 + 0,02.3 = 5,04.
Далее, подставляя эти найденные приближения в формулу E)
получим вторые приближения корней:
х[2) = 1,9094; дгB2) = 3,1944;
лгC2) = 5,0446.
После новой подстановки будем
иметь третьи приближения корней:
х[в) = 1,90923; х[3) = 3,19495;
43> = 5,04485 и т. д.
Результаты вычисления помещены
в таблице 20.
Замечание. При применении метода итерации (формула C))
нет необходимости за нулевое приближение л;@) принимать столбец
свободных членов. Как будет доказано ниже, сходимость процесса
итерации зависит только от свойств матрицы а, причем при
выполнении известных условий, если этот процесс сходится при каком-
нибудь выборе исходного начального приближения, то он будет
сходиться к тому же предельному вектору и при любом другом
то (о)9ТОГ° начального приближения. Поэтому начальный век-
Р * в процессе итерации может быть взят произвольным.
Вычисление
Та
решения
блица 20
линейной
системы методом итерации
k
0
1
2
3
2
1
1
1
92
9094
90923
2
3
3
3
-Г
19
1944
19495
5
5,04
5,0446
5,04485

298 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Целесообразно за компоненты начального вектора выбирать
приближенные значения корней системы, находимые грубой прикидкой.
Сходящийся процесс итерации обладает важным свойством само-
исправляемости, т. е. отдельная ошибка в вычислениях не
отразится на окончательном результате, так как ошибочное
приближение можно рассматривать как новый начальный вектор.
Отметим, что иногда бывает удобнее подсчитывать не сами
приближения, а их разности. Введя обозначения
лс*)_л(А-1) (k = 0, 1, 2,
из формулы C) имеем:
x(k) F)
и
x(k) = ^ + ax{k-1K G)
Отсюда, вычитая из равенства F) равенство G), получим:
Д<*+1> = a (x{k) - x{k~l)) = аД<*>,
т. е.
Д(*+1> = аД(*> D=1, 2, ...). (8)
За нулевое приближение принимаем:
ДС0) = *<°\ (9)
тогда т-е приближение есть
*(Ш>= 2 Д<*>. A0)
Если, как обычно, положить А@) = л;<0) = р, то равенство (8)
будет выполнено и при k = Q. В противном случае равенство (8)
при 4 = 0 не имеет места. Отсюда вытекает такая методика
вычисления этого варианта итерации:
1) если Д(о) = д:со) = р, то
= 0, 1, 2, ...)
2) если же Af0) == х{0) ф$, то находим
и полагаем
** * (*=1, 2, 3, ...).

§ 101
Следовательно,
МЕТОД ИТЕРАЦИИ
299
Пример 2. Решить систему
3^ + 5*, —2*,= 1,
лг1-4лг2+ 10лг3 = 0.
Решение. Приведем систему A1) к виду B):
xt= —\,5 + 0,5лг2 — 0,5лг3;
^ = 0,2-0,6^
(И)
дг3= —
Здесь
а =
' 0 0,5 —0,5
—0,6 0 0,4
—0,1 0,4 0
—1,5
0,2
0
Пользуясь формулами (8) и (9), получим:
--1,5"
0,2
0
да» _ад<0)_
" 0 0,5
—0,6 0
—0,1 0,4
-0,5"
0,4
0
"-1,5"
0,2
0
=
,1 '
0,9
0,23
0,1
0,9
0,23
=
0,335"
0,032
0,350 _
О 0,5 —0,5
—0,6 0 0,4
_—0,1 0,4 О
и т. д. Результаты записываем в таблицу 21.
Таким образом, приближенные значения корней есть
хх= — 1,235; лг, = 1,089; лг„ = 0,560.

300
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIII
Таблица 21
Вычисление решения линейной
системы видоизмененным методом
итерации
(метод накопления)
Недостатком этого варианта метода итерации является
систематическое накопление ошибок при увеличении числа слагаемых, в
результате чего могут возникнуть значительные погрешности искомых
корней. Кроме того, ошибка,
допущенная в вычислениях,
повлияет на окончательный
результат. Поэтому надежнее
пользоваться первым вариантом метода
итерации.
Замечания о точности
расчета. Если все коэффициенты и
свободные члены данной системы
являются точными числами, то
решение ее методом
последовательных приближений может быть
получено с любым заранее заданным
числом т верных десятичных
знаков. При этом в значениях
последовательных приближений
следует удерживать т-\-\
десятичных знаков и
последовательные приближения вычислять до их
совпадения, после чего нужно
округлить результат на один
знак. Если коэффициенты и
свободные члены данной системы являются приближенными числами,
написанными с р знаками, то решение этой системы производится,
как в случае точных чисел, с точностью до /» = /? знаков.
Приведем без доказательства достаточное условие сходимости
процесса итерации (доказательство см. гл. IX, § 1).
Теорема. Если для приведенной системы B) выполнено по
меньшей мере одно из условий
k
0
1
2
3
4
5
6
7
8
9
2
—1,500
0,100
0.335
—0,159
^0.020
0.010
0,002
—0,004
0,000
0,001
—1,235
0,200
0,900
0.Q32
—0,061
0,011
0,009
—0,004
0,000
0,002
0,000
1,089
А(Л)х.
0,000
0,230
0,350
—0,021
-0,008
0,006
0,003
—0,001
0,000
0,001
0,560
1)
или
2)
I «.-/
< 1 (/=1, 2,
G=1, 2,
п)
то процесс итерации C) сходится к единственному решению этой
системы, независимо от выбора начального приближения.
Следствие. Для системы
(i-1, 2 n)

§ И] ПРИВЕДЕНИЕ СИСТЕМЫ К ВИДУ, УДОБНОМУ ДЛЯ ИТЕРАЦИИ 301
метод итерации сходится, если выполнены неравенства
К/1 (' = !> 2, .... я),
т. е. если модули диагональных коэффициентов для каждого
уравнения системы больше суммы модулей всех остальных коэффициентов
(не считая свободных членов).
§11. Приведение линейной системы к виду, удобному
для итерации
Теорема сходимости (§ 10) накладывает жесткие условия на
коэффициенты данной линейной системы
Ах = Ь. A)
Однако, если deMr^O, то с помощью линейного
комбинирования уравнений системы A5) последнюю всегда можно заменить
эквивалентной системой
*, B)
такой, что условия теоремы сходимости будут выполнены.
В самом деле, умножим уравнение A) на матрицу D = A~l—e,
где е = [е^] — матрица с малыми по модулю элементами. Тогда
будем иметь:
(A~l — e)Ax = Db
или
ху C)
где а = еЛ и P = D6. Если |е^| достаточно малы, то очевидно, что
система C) удовлетворяет условиям теоремы сходимости.
Умножение на матрицу D эквивалентно совокупности
элементарных преобразований над уравнениями системы. Задача заключается
в том, чтобы прийти к стандартному виду C) с наименьшей
затратой труда.
Практически поступают следующим образом. Из заданной системы
выделяют уравнения с коэффициентами, модули которых больше
суммы модулей остальных коэффициентов уравнения. Каждое
выделенное уравнение выписывают в такую строку новой системы, чтобы
наибольший по модулю коэффициент оказался диагональным.
Из оставшихся неиспользованных и выделенных уравнений
системы составляют линейно независимые между собой линейные
комбинации с таким расчетом, чтобы был соблюден указанный выше
принцип комплектования новой системы и все свободные строки
оказались заполненными. При этом нужно позаботиться, чтобы
каждое неиспользованное ранее уравнение попало хотя бы в одну
линейную комбинацию, являющуюся уравнением новой системы.
Поясним все сказанное на примере.

302 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ, Ylli
Пример. Систему
(Л)
(Б)
(В)
(Г)
привести к виду, годному для применения метода итерации.
Решение. В уравнении (Б) коэффициент при *3 по модулю
больше суммы модулей остальных коэффициентов, поэтому можно
принять это уравнение за третье уравнение новой системы.
Коэффициент при хх в уравнении (Г) также больше суммы модулей
остальных коэффициентов уравнения (Г), поэтому можно принять
это уравнение за первое уравнение новой системы. Таким образом,
новая система имеет следующий вид:
(I) io*1 + 2*2-*3+2*4 + 4 = O,
(Н)
(III) хх — 2*2 — 5*3 + *4 — 2 = 0,
(IV)
Анализируя данную систему, легко заметить, что для получения
уравнения (II) с максимальным по модулю коэффициентом при *2
достаточно составить разность (А)—{В):
(II) *l + 5*2 + *3 + O*4-l=O.
Теперь в новую систему вошли уравнения (Л), (Б) и (Г), поэтому
в уравнение (IV) обязательно должно войти уравнение (В) данной
системы. Подбором убеждаемся, что за уравнение (IV) можно взять
линейную комбинацию 2 (Л) — (Б) + 2 (В) — (Г), т. е.
(IV) Здгх + 0х2 + 0л;3 - 9лг4 — 10 = 0.
В итоге получим преобразованную систему уравнений I—IV,
эквивалентную исходной и удовлетворяющую условиям сходимости
процесса итерации. Разрешив эту систему относительно
диагональных неизвестных, будем иметь систему
^ = 0,2*! +0*2 —0,2*з + 0*4 +0,2;
*3 = 0,2*1 -0,4*2 + 0*з +0,2*4-0,4;
*4 = 0,333*! + 0*2 +0*з +0*4 —1,111,
к которой можно применить метод итерации.

? ]2] МЕТОД ЗЕЙДЕЛЯ 303
§ 12. Метод Зейделя
Метод Зейделя представляет собой некоторую модификацию
метода итерации. Основная его идея заключается в том, что при
вычислении (k+ 1)-го приближения неизвестной х{ учитываются уже
вычисленные ранее (Л+1)-е приближения неизвестных хг, лг2, ..., лг;-1.
Пусть дана приведенная линейная система
Выберем произвольно начальные приближения корней
стараясь, конечно, чтобы они в какой-то мере соответствовали
искомым неизвестным
•*и хг> • • • » хпт
Далее, предполагая, что &-е приближения х^ корней известны,
согласно Зейделю будем строить (&+1)-е приближения корней по
следующим формулам:
/=*
„ 2 B/4nn (*-0. 1, 2, ...).
Заметим, что указанная выше (§ 10) теорема сходимости для
простой итерации остается верной для итерации по методу Зейделя
(см. гл. IX, §§ 3—7).
Обычно метод Зейделя дает лучшую сходимость, чем метод
простой итерации, но, вообще говоря, он приводит к более громоздким
вычислениям. Процесс Зейделя может сходиться даже в том случае,
если расходится процесс итерации. Однако это бывает не всегда.
Возможны случаи, когда процесс Зейделя сходится медленнее
процесса итерации. Более того, могут быть случаи, когда процесс
итерации сходится, а процесс Зейделя расходится [1] (см. гл. XI, § 6).

304 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. VIII
Пример. Методом Зейделя решить систему уравнений
10*!
Решение. Приведем эту систему к виду, удобному для
итерации,
*!== 1,2 — 0,1лг2 — 0,1-^s»
аг2= 1,3 — 0,2*! — 0,1*3;
*з=1,4 —0,2*!—0,2*2.
В качестве нулевых приближений корней возьмем:
*ie)=l,2; *<0) = 0; х<°> = 0.
Применяя процесс Зейделя, последовательно получим:
лг11} = 1,2 — 0,1-0 —0,1-0 =1,2;
л:B1)= 1,3 — 0,2-1,2 — 0,1-0 =1,06;
х[1]= 1,4-- 0,2-1,2 — 0,2-1,06 = 0,948;
х i2 =1,2-0,1-1,06-0,1.0,948 = 0,9992;
*</> =1,3-0,2- 0,9992 — 0,1 • 0,948 = 1,00536;
42) = 1,4—0,2 0,9992 —0,2-1,00536 = 0,999098 и т. д.
A)
(И)
Результаты вычислений с точностью до четырех знаков
помещены в таблице 22.
Та
бл
ица 22
Нахождение корней линейной
системы методом Зейдел!
к
0
1
2
3
4
5
1
1
0
0
1
1
,2000
,2000
,9992
,9996
,0000
,0000
0
1
1
1
1
1
2
,0000
,0600
,0054
,0001
,0000
,0000
0
0
0
1
1
1
1
4ft)
,0000
9480
9991
0001
0000
0000
Точные значения корней: д:1=1; л:2^1; лг3 = 1 -

§ 13]
СЛУЧАЙ НОРМАЛЬНОЙ СИСТЕМЫ 305
§ 13, Случай нормальной системы
Определение 1. Целый однородный полином второй степени
от п переменных называется квадратичной формой этих
переменных. В общем случае квадратичная форма имеет вид
и (xv х%9 ..., хп) = а1гх\ + а22х\ +...+ аппх\ +
_1} пхяят1ха, A)
где a{j(i,/=1, 2, ..., п) — постоянные числа, причем для удобства
соответствующие коэффициенты при / Ф j взяты в четной форме 2пц*
Приравняв и постоянной с, получим уравнение центральной
поверхности второго порядка
и (xv х2} ..., хп) — с
в л-мерном пространстве.
Если положить
au = aJit B)
т, е. 2пц = пц-\-аyv то формулу A) короче можно записать
следующим образом:
Матрица
A = [*ij] C)
носит название матрицы квадратичной формы (Г). В силу
условия B) матрица А будет симметрической, т. е. совпадет со своей
транспонированной матрицей. Наоборот, для всякой симметрической
матрицы А = [йц] можно построить соответствующую
квадратичную форму (Г),
Определение 2. Квадратичная форма A) называется
положительно (отрицательно) определенной, если она принимает
положительные (отрицательные) значения, обращаясь в нуль лишь при
хх = х2 = ... = хп = 0.
Если u(xv x2i ..., atJ —положительно определенная
квадратичная форма, то уравнение
u(xlf лг2) ..., дгя) = с (с>0)
представляет собой уравнение эллипсоида. Заметим, что в этом случае
%>0 (/=1, 2, ..., я),
так как
аи = иA, 0, ..., 0)>0,
а22 = и@, 1, .... 0)>0,

306 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. Viil
Определение 3. Назовем линейную систему
п
2 aijxj^bi (/=1, 2, ..., п) D)
/
нормальной, если: 1) матрица коэффициентов А = [ау] —
симметрическая, т. е. aLj=^ajh 2) соответствующая квадратичная форма
п п
и= 2 2 ai/xix/ — положительно определенная.
Нормальные системы встречаются при решении многих вопросов,
например, в способе наименьших квадратов, при нахождении
направлений главных осей эллипсоида и т. д.
Нормальную систему D) приведем обычным способом к
специальному виду
где
2 {}ф1) и р<=
Теорема 1. Если линейная система D) — нормальная, то
процесс Зейделя для эквивалентной ей приведенной системы D')
всегда сходится.
Доказательство см. главу XI, § 5, а также [2].
Способ приведения линейной системы к нормальному виду
указывается следующей теоремой.
Теорема 2. Если обе части линейной системы
Ах=Ь E)
с неособенной матрицей А = [а^] умножить слева на
транспонированную матрицу А' = [пу;], то полученная новая система
А'Ах = А'Ь F)
будет нормальной.
Докажем сначала, что матрица А'А есть симметрическая
матрица. В самом деле, имеем:
Теперь докажем, что квадратичная форма, соответствующая матрице
Л'Л,—положительно определенная. Составим квадратичную форму
с матрицей А'А:
п п п
u(xv лг2, .... х„)= 2 S
1 = 1 /=i 4

я ]4] МЕТОД РЕЛАКСАЦИИ 307
Изменяя порядок суммирования, получим:
п п п
п п
2 akixr S ak
Так как значение суммы не зависит от обозначения индекса
суммирования, то
п / п \ 2
«= 2 ( 2 <**,•*,• ) ^ о.
Согласно предположению det A = det [a/y] ^= 0. Поэтому
однородная система
л
2 **/*/ = 0 (ft=l, 2, ..., /г)
имеет лишь нулевые решения. Следовательно,
u(xv х2, ...,#„)> 0 при 1^1 11
Теорема доказана.
§ 14, Метод релаксации
Пусть имеем систему линейных уравнений
а11*1 + а12*2 + « • • + а\пХп = I
Преобразуем эту систему следующим образом: перенесем
свободные члены налево и разделим первое уравнение на —alv второе
на —а22 и т. д. Тогда получим систему, приготовленную к релак*
сации,
B1
где
-Xl+ Ь12х2 + ... + Ь1пхп-f- сг = 0,

308
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
[ГЛ. VIII
Пусть jc@> = {х^\ *B0), ..., *?»)— начальное приближение
решения системы B). Подставляя эти значения в систему B),
получим невязки
7 = 2
п
I F 2
Л-1
C)
Если одной из неизвестных *<°> дать приращение 6*^0), то
соответствующая невязка /??°> уменьшится на величину 8*<s°), а все
остальные невязки Що) (i=?s) увеличатся на величину #/,Д*^0>. Таким
образом, чтобы обратить очередную невязку /?<х> в нуль, достаточно
величине *<0) дать приращение
&*(•> = /?(•),
и мы будем иметь:
^ При
Метод релаксации (по-русски: метод ослабления) [3], [4] в его
простейшей форме заключается в том, что на каждом шаге обращают
в нуль максимальную по модулю невязку путем изменения значения
соответствующей компоненты приближения. Процесс заканчивается,
когда все невязки последней преобразованной системы будут равны
нулю с заданной точностью. Вопрос о сходимости этого процесса
мы оставляем без рассмотрения [4].
Пример. Методом релаксации решить систему [3]
2х2—
— 2*3 = 7,
D)
производя вычисления с двумя десятичными знаками.
Решение. Приводим систему D) к виду, удобному для
релаксации
- хг + 0,2
- хг + 0,1
.-*з + 0,
,2лг8 + 0,6 = 0,
+ 0,2*з + 0J = 0,
,1*2 + 0,8 = 0.

§ И]
МЕТОД РЕЛАКСАЦИЙ
309
Выбирая в качестве начальных приближений корней нулевые
значения
находим соответствующие им невязки
/?<•> - 0,60; RW « 0,70; RM = 0,80.
Согласно общей теории полагаем:
Отсюда получаем невязки
flu> = RW 4. о,2 • 0,8 = 0,60 + 0,16 = 0,76;
Ш = RW + 0,2 -0,8 = 0,70 + 0,16 = 0,86;
Таблица 23
Решение линейной системы методом релаксации
S
0
0,93
0,07
1,00
*i
0,60
0,16
0,76
0,17
0,93
—0,93
0
0,04
0,04
0,03
0,07
—0,07
0
0
0
0
х2
0
0,86
0,13
0,01
1,00
0,70
0,16
0,86
-0,86
0
0,09
0,09
0,04
0,13
—0,13
0
0,01
0,01
0
0,01
—0,01
0
х3
0
0,80
0,18
П П9
1,00
л.
0,80
—0,80
0
0,09
0,09
0,09
0,18
—0,18
0~
0,01
<ш
0,01
0,02
—0,02
0
0

310 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. Х1Ц
Далее, полагаем
6*^ = 0,86
и т. д. Соответствующие результаты вычислений приведены в
таблице 23.
Суммируя все приращения &<*> (/ = 1, 2, 3; & = О, 1, ...),
получим значения корней
хг = 0 + 0,93 + 0,07 = 1,00;
лг2 = 0 + 0,86 + 0,13 + 0,01 = 1,00;
лг3 = 0 + 0,80 +0,18 +0,02 =1,00.
Для контроля подставляем найденные значения корней в
исходные уравнения; в данном случае система D) решена точно.
§ 15. Исправление элементов приближенной обратной матрицы
Пусть имеем неособенную матрицу А и требуется найти
обратную матрицу А. Положим, что мы получили приближенное
значение обратной матрицы О0жА~г. Тогда для улучшения точности
можно воспользоваться методом последовательных приближений
в специальной форме. В качестве предварительной меры
погрешности используем разность
Если F0 = 0, то очевидно, что О0 = Л, поэтому, если модули
элементов матрицы Fo малы, то матрицы А и Do близки между
собой. Будем строить последовательные приближения по формуле
Д* = Д*-1 + Д*-Л-1 (*=1. 2, 3, ...), A)
причем соответствующая погрешность есть
Fk = E-ADk.
Оценим быстроту сходимости последовательных приближений.
Имеем:
Аналогично
и, вообще,
=I, 2, 3,

§ 15] ИСПРАВЛЕНИЕ ЭЛЕМЕНТОВ ПРИБЛИЖЕННОЙ ОБРАТНОЙ МАТРИЦЫ 311
Докажем, что если
J^oKfO. C)
где \\F0\\ — какая-нибудь каноническая норма матрицы Fo (гл. VII,
§ 7), то процесс итерации A) сходится, т. е.
lim Dk = A-K
Действительно, из формулы B) имеем:
«Щ1<11М2Й<^
Поэтому
и, следовательно,
lim Fk = lim (E — ADk) = i
ИЛИ
т. е.
lim Dи== J\ lm === ^4 «
Таким образом, утверждение доказано.
В частности, используя /я-норму (гл. VII, § 7), получаем, что
если элементы матрицы F0 = [f^] удовлетворяют неравенству
= E — Fo,
где п — порядок матрицы и 0^^< 1, то процесс итерации A)
заведомо сходится.
Предполагая неравенство C) выполненным, оценим погрешность
Так как
то
Отсюда
Для /я-нормы или /-нормы имеем ||?||=1, и поэтому

312
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Таким образом,
или
l-q
[гл. vui
D)
E)
где норма понимается в смысле /«-нормы или /-нормы. Из
формулы D) следует, что сходимость процесса A) при <7<^1 очень
быстрая.
На практике процесс уточнения элементов обратной матрицы
прекращают, когда обеспечено неравенство
где е — заданная точность.
Пример. Исправить элементы приближенной обратной
матрицы, полученной в примере § 7 на стр. 286.
Решение. Для матрицы
f-1,8 —3,8 0,7 —3,7-
0,7 2,1 —2,6 —2,8
7,3 8,1 1,7 —4,9
lf9 —4,3 —4,9 — 4,7,
методом Гаусса получена приближенная обратная матрица
Г—0,21121 ^-0,46003 0,16284 0,26956-]
—0,03533 0,16873 0,01573 —0,08920
0,23030 0,04607 —0,00944 —0,19885
—0,29316 —0,38837 -0,06128 0,18513
причем
AD0=E— Ю-8-
[-0,03 0,00 0,01 0,00-
0,25 0,03 0,02 0,39
8,08 10,17 0,18 —0,09
0,00 0,00 0,00 —0,48
Отсюда
= Е-
, = 10-3-
~0,03 0,00 0,01 0,00
0,25 0,03 0,02 0,39
8,08 10,17 0,18 —0,09
0,00 0,00 0,00 —0,48
Для дальнейшего уточнения элементов матрицы Do
воспользуемся итерационным процессом
?>ft+i = Dk+DkFk, Fk = E-ADk (k = 0, 1, 2, ...).

15] ИСПРАВЛЕНИЕ ЭЛЕМЕНТОВ ПРИБЛИЖЕННОЙ ОБРАТНОЙ МАТРИЦЫ 313
Так как
q--=\\F0\\t= 10-40,03+ 10,17)- 1,02-10-*
то процесс итерации быстро сходится.
Имеем:
—0,21121 —0,46003 0,16284 0,26956-
—0,03533 0,16873 €,01573 -0,08920
0,23030 0,04607 —0,00944 —0,19885
—0,29316 —0,38837 —0,06128 0,18513
X
0,03
0,25
8,08
0,00
0,00
0,03
10,17
0,00
= 10
с
,01 0,00-i
0,02 0,39
0,18 —0,09
0,00 —0,48_
—
- 1,19 1,64
0,17 0,16
—0,06 —0,09
0,39 0
,61
0,02
0,01
0,00
0,00
-о,
о,
0,
-о,
32
11
11
24
Отсюда
Г—0,21121 —0,46003 0,16284 0,26956-]
—0,03533 0,16873 0,01573 —0,08920
0,23030 0,04607 —0,00944 —0,19885
_—0,29316 —0,38837 0,06128 0,18513_
Г 1,19 1,64 0,02 —0,32-]
0,17 0,16 0,01 0,11
—0,06 —0,09 0,00 0,11
0,39 0,61 0,00 —0,24,
-—0,21002 —0,45839 0,16286 0,26924-
—0,03516 0,16889 0,01574 —0,08909
0,23024 0,04598 —0,00944 —0,19874
,—0,29277 —0,38776 0,06128 0,18489
Ю-3-
Можно считать
так как
= ?—10~5-
-2—2 13
0 2—10
3 4-5 1
10 0 1

314 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. \'Щ
-2
0
3
1
—2
2
4
0
1
—1
—5
0
з -
0
1
1
На основании формулы D) для погрешности имеем оценку
Так как
|1 Do 1; = 0,46003 + 0,16873 + 0,04607 + 0,38837 < 1,07
то окончательно имеем:
цд-!-^!, <Т=Т1^Ш=%. 8-10-» <9.10-».
Замечание. Подбор приближенной обратной матрицы может
Сыть осуществлен различными способами. В частности,
используется способ обращения матриц, указанный в главе VII, § 12.
В заключение главы отметим следующее. В настоящее время
разработаны многие другие методы решения системы линейных
алгебраических уравнений (Метод Перселла, эскалаторный метод [6J,
метод Ричардсона [7] и др.)
Литература к восьмой главе
1. В. Н. Ф а д д е е в а, Вычислительные методы линейной алгебры, Гостех-
издат, 1950, гл. II.
2. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
1934, дополнение I.
г. М. Дж. Сальвадор и, Численные методы в технике, ИЛ, М., 1955,
гл. 1, § 10.
4. Современная математика для инженеров, под ред. Э. Ф. Беккенбаха,
ИЛ, М„ 1958, гл. 15.
5. X. Л. Смолицкий, Вычислительная математика (конспект лекций),
ЛКВВИА им. Можайского, Л., 1960.
6. Д. К. Фаддеев и В. Н. Фаддеев а, Вычислительные методы
линейной алгебры, Физматгиз, 1960, гл. II,
7. И. С. Берез и н и Н. П. Жидков, Методы вычислений, Физматгиз,
1959, гл. VI.

ГЛАВА IX»
СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ
ДЛЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 1. Достаточные условия сходимости процесса итерации
Пусть мы имеем приведенную линейную систему
Г Pi
A)
— заданные матрица и вектор и х =
— искомый вектор.
Теорема. Процесс итерации для приведенной линейной
системы A) сходится к единственному ее решению, если какая-нибудь
каноническая норма матрицы а меньше единицы, г. е. для
итерационного процесса
x^^fi + ax*-» (*=1, 2, ...)
(х@) произвольно) достаточное условие сходимости есть
|| а ||<1. B)
Доказательство. Отправляясь от произвольного
вектора л:@), строим последовательность приближений
A)
Отсюда
x{k) ==
+
сЛс
@).
C)

316 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. IX
Так как при ||а(| < 1 имеем ||аА||—-*0 при к—*оо, то (см. гл. VII,
§ Ю)
lim аЛ = 0
lim
fc-*oo
Поэтому, переходя к пределу при k—юо в равенстве C), получим:
д:=Нт *<*> = (?—а)'1 $. D)
& -»¦ оо
Этим доказана сходимость итеративного процесса. Кроме того, из
равенства D) имеем:
или
т. е. предельный вектор .я является решением системы A). Так как
матрица системы A) ?—а — неособенная, то решение х
единственно.
Следствие 1. Процесс итерации для системы A); сходится,
если:
а) ||«IL t ,-r
ИЛИ
n
б) || a
или
B) \\ a II k~
В частности, процесс итерации заведомо сходится, если элементы
матрицы а удовлетворяют неравенству
где л —число неизвестных в системе A).
Действительно, а), б) и в) являются простейшими
каноническими нормами матрицы а.
Следствие 2. Для системы
2*1/*/ = ** ('=1. 2, ..., п) E)

§ 2] ОЦЕНКА ПОГРЕШНОСТИ ПРИБЛИЖЕНИЙ ПРОЦЕССА ИТЕРАЦИИ 317
процесс итерации сходится, если выполнены неравенства:
а') |%|> 2'К7| (/=1, 2, .... л)
или
п
Jj i=l lJ
где штрих у знака суммы означает, что при суммировании
пропускаются значения i—j\ т. е. сходимость имеет место, если модули
диагональных элементов матрицы ^4 = [«/у] системы A) или для
каждой строки превышают сумму модулей недиагональных элементов
этой строки, или же для каждого столбца превышают сумму
модулей недиагональных элементов этого столбца.
В самом деле, при наличии неравенства а'), очевидно, выполнено
соответствующее неравенство а) следствия 1.
Для доказательства второго утверждения в системе E) положим:
*• .^_ * / / ___ 1 о **\
Л | —— ^^""" 11> —— 1, ^ j •••, /* I}
где Zi — новые неизвестные. Тогда получим систему
'jzj = bi (/ = 1, 2, ..., л), E)
для которой процесс итерации сходится или расходится
одновременно с процессом итерации для исходной системы E). Приведя
обычным способом систему E') к специальному виду A) и
используя условие б) следствия 1, получим достаточное условие
сходимости процесса итерации для системы E):
2
JJ
(;=1, 2, ..., п)
или
K/I>J3'K! u=h 2, .... я).
§ 2. Оценка погрешности приближений процесса итерации
Пусть д:(Л-1) И x{k) (k^\)— два последовательных приближений
решения линейной системы je = aje-fp. При р^\ имеем:
A)

318 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ (ГЛ. IX
Так как
и
то
и, следовательно,
|| xi«+u_*1»> || < ||«|| (I jc^-**--» 1| <
< IIаII *"*//л**4-" — jcc*>Л при да>*>1.
Поэтому из формулы A) получаем:
l|ja|| * И-
Переходя в последнем неравенстве к пределу при р—>оо, получим
окончательно:
при л ^s 1, или
11 г# II
||*—-л || < 1 —||а|| " ~"~ "•
Если
||а||<у»
то предыдущая формула принимает вид
т. е. в этом случае, если
то и
II *• *¦<*> ll <s р
В общем случае, если в процессе вычислений будет
обнаружено, что
|| х( ) — х{ } || ^ —у- е,
где q= || а \\ < 1, то
и, таким образом,
z& (/=1, 2, ..., л).

§ 2J ОЦЕНКА ПОГРЕШНОСТИ ПРИБЛИЖЕНИЙ ПРОЦЕССА ИТЕРАЦИИ 319
При этом предполагается, конечно, что последовательные
приближения Х^ (/=0, 1, ..., k) вычисляются точно, т. е. в них полностью
отсутствуют погрешности округлений..
Из формулы B), используя полученные выше оценки для нормы
разности двух последовательных приближений, будем иметь:
[I ^ Г<*> II <Г М а 'I || «*A> «.@) ||
II •* л II **= 1 цац И* •* II •
В частности, если выбрать
ТО
Следовательно,
Пример. Показать, что для системы
!— *2 + 2*3"" 3*4 =
*!+10*2— *8+ 2лг4 =
B0
C)
2*2+ *з + 20*4==15
процесс итерации сходится. Сколько итераций следует выполнить,
чтобы найти корни системы C) с точностью до 10~4?
Решение. Приводя систему C) к специальному виду, получим»
*1== 0,1*2 -0,2*з +0,3*4;
*2 = — 0,1*х +0,1*з —0,2*4 +0,5;
C')
а==
*4 = — 0,15*! — 0,1*2 —0,05*3 + 0,75.
Отсюда матрица системы
г 0 0,1 -А),2 0,3 -]
-0,1 0 0,1 —0,2
—0,1 —0,15 0 0,05
_0,15 —0,1 —0,05 0
Используя, например, норму ||аЦ„ получим:
|| а У,= max @,35; 0,35; 0,35; 0,55) = 0,55 < 1.
Следовательно, процесс итерации для системы C') сходится.

320 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. IX
За начальное приближение корня х примем:
- 0, -
v@)_A_ °»5
Х -р- -0,5
0,75_
Отсюда
ПРИ, = 0 + 0,5 + 0,5 + 0,75=1,75.
Пусть k — число итераций, необходимое для достижения
заданной точности. Применяя формулу B'), будем иметь:
\Х
Iх
1 1 — 1/ <х |
Отсюда
и
{k+ 1) lg 0,55 < \g 45— lg 175-4,
т. e.
—(ft+1 )• 0,25964 < 1,65321—2,24304-4 = —4,58983.
Следовательно,
... ^ 4,58983. ,
*+ l > 0^5964 ^17'7
И
k> 16,7.
Можно принять &=17.
Следует отметить, что теоретическая оценка числа итераций,
необходимых для обеспечения заданной точности, практически
оказывается весьма завышенной.
§ 3. Первое достаточное условие сходимости процесса Зейделя
Теорема. Если для линейной системы
х = ах+^ , A)
выполнено условие
Н«П«<1. B)
где
п
2
то процесс Зейделя для системы A) сходится к единственному ее
решению при любом выборе начального вектора х{°К

§ 3] ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ ПРОЦЕССА ЗЕЙДЕЛЯ 321
Доказательство. Пусть x{k) = hc&\ ...,#<*>} —Л-е при-»
ближение процесса Зейделя. Имеем:
!*> = 2 «,/*}« + 2 cdjxf-» + рг (8)
(/=1, 2, ..., я; й=1, 2, ...).
При выполнении условия B) система A) допускает единственное
решение x—{xv ..., хп), которое может быть найдено, например,
методом итерации. Имеем:
*/=2а,7*/ + р\ (/=1,2,...). D)
Вычитая из равенства D) равенство C), получим:
отсюда
f —1 п
¦*/ •*} ^* aJ| ai/ II1*/ л/ T ^J I ^i/ I I лI—x) I \y)
(/=1, 2, .... я).
Согласно смыслу принятой нормы
поэтому
C/'==l, 2, ..., л). Следовательно, из неравенства E) выводим:
*-*'*-1'!!*,. . F)
где
Рг = 2К7| и ?,= 2|а//1-
Пусть s = $(k) есть то значение индекса /, для которого
\x,-xM\ = max\xt-x^\ = \\
Полагая i = n неравенстве F), получим:
||*
или
ax\xt-x^\ = \\x-x^\\ m.
Отсюда
\\х-^\\т^»\\х-*к-»\\т, G)
^ Б. П. Демидович и И. А. Марон

322 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. IX
где
|i = maxy^j—. (8)
Покажем, что
Действительно, так как
п
*\!1 i (мп
ТО
Qi < II а II т—Pi
и, следовательно,
Я1 ^ Иа\\ т — Р1^~\\ъ\\т—Р/И а>1 m П ^ 1Г
1—Р/ 1 —Р/ 1 — Pi
Поэтому
Из неравенства G) вытекает, что
м-
и, следовательно,
Ига *<*> = *,
тем самым сходимость процесса Зейделя к искомому решению
доказана.
Замечание. Так как для метода итерации мы имеем
||х-***1 II<II «II.II*-*"""II.
а для метода Зейделя получим
где (Л ^ || а || т% то в условиях теоремы 1 сходимость процесса Зейделя
в общем несколько лучше, чем сходимость процесса простой
итерации. Из формулы (8) следует, что в этом случае, при применении
метода Зейделя, систему A) выгодно располагать так, чтобы первое
уравнение системы имело наименьшую сумму модулей коэффициентов
?i2 li/|
§ 4. Оценка погрешности приближений процесса Зейделя
по т-норме
Пусть х{к) и х{к+1)—две последовательные итерации процесса
Зейделя. Применяя к этим итерациям преобразования,
использованные при доказательстве теоремы § 3, получим неравенство,
аналогичное неравенству G) из § 3:

§ 5] ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ ПРОЦЕССА ЗЕЙДЕЛЯ 323
Отсюда
При р—> <*> будем иметь:
lira x{k+p) =
и, следовательно,
^1«и И** Х III»»
где
В частности, из полученного неравенства выводим:
\\* -
т. е.
§ 5. Второе достаточное условие сходимости процесса Зейделя
Теорема. Если для линейной системы
дс = ад: + Р A)
выполнено условие
где
п
\\а\\ 1~тах 2j \aitI»
/ '=1
то процесс Зейделя сходится к единственному решению системы A)
при любом выборе начального вектора.
Доказательство. Пусть
(ft) '-1 п
t jZi a>ijXj -f- Zj<XijXj -\- Pj. (f = i, z,..., n, к = I, z,..,). (Z)
11*

324 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. IX
Для точного решения x = {xlf лг2, ... , хп}, которое существует
и единственно, имеем:
1-1 П
*i = 2 <*//*/ + S. «//*/ + Р/• C)
Вычитая из равенств C) соответствующие равенства B), получим:
1
Отсюда
Щ, (xj-
/1 /г
I Xi — Xi I < 2j I «/у 11^/ — ^/ I + 2rf I «/y I I Xj — -^У I
(/ = 1, 2,...,/г).
Просуммировав последние неравенства, будем иметь:
2 \*,-хП< S S l«,7lU/-4ft) I+ 2 S le/ylk/-*^!.
или, меняя порядок суммирования, получим:
Sk-4'Wsi*/-*?! S l«,7l+2U/-^f-1)ISl«//|. D)
i = l /=i i = /+l /=i У г = 1
Положим
1=1
Очевидно,
отсюда
Неравенство D) принимает вид
п п п
«=1 ' " /=1 } J /=1
ИЛИ
п п
У A—5.) \х-—-X{-k)\^ У, t \x--
iA J , J l ^/=i J J

§ 6] ОЦЕНКА ПОГРЕШНОСТИ ПРИБЛИЖЕНИЙ ПРОЦЕССА ЗЕЙДЕЛЯ 325
Так как
то далее имеем:
п
У, у 1 ~~~«jyj J *vy ¦"""" Л»у I 5
п
^ \\OL\\i j?j A—Sj) j Xi — Xj [• F)
Отсюда, переходя к пределу при &-~»оо и учитывая, что [|a||j<l,
получим:
Следовательно,
Шп ^«^ G=1, 2,..., л),
что и требовалось доказать.
§ 6. Оценка погрешности приближений процесса Зейделя
по /-норме
Пусть
п
Использовав преобразования, аналогичные примененным при
доказательстве теоремы предыдущего параграфа, для двух
последовательных итераций x)k) и x^k+1) получим неравенство (F) § 5)
где в силу неравенства E) из § 5
Отсюда
Далее имеем:

326 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ
Отсюда при р~->оэ получим:
я
Ум с \ I *- ^k) I — Pqft
^¦^ / • / * * 1"~*р
или
(ГЛ. IX
SI у
ik) 1
p
где
5 = max5/ = max 2 la//l«
Так как из формулы A) вытекает, что
то справедлива также оценка
п
§ 7. Третье достаточное условие сходимости процесса Зейделя
Теорема. Если для линейной системы
выполнено условие
то процесс Зейделя для системы A) сходится к единственному ее
решению при любом выборе начального вектора.
Доказательство. Пусть
Х1

§ 7] ТРЕТЬЕ ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ ПРОЦЕССА ЗЕЙДЕЛЯ 327
— соответственно точное решение системы A) и р-е приближение
(р = 0} 1, 2, ...) процесса Зейделя для этой системы. Имеем;
1-1 п
*i = 2 «//*/+ 2 */
и
(i = l, 2, ... , л). Отсюда
и, следовательно,
Применяя неравенство Коши (гл. VII, § 7) к сумме всех слагаемых,
стоящих в фигурной скобке, будем иметь:
I^yjl/} B)
где
п
Суммируя неравенства B) по / от 1 до п, получим:
п п i-l n n
I-*/—-*/ I ^^ 2s\x~xi I +Z Zs\xXi
Изменяя индекс суммирования в левой части и порядок
суммирования в правой части последнего неравенства, будем иметь:
$\*,-*Г\%<%\х,-*Г\ш 2 •/ + 2l*y-*ri)li
' = 1 /=i /=/+1 |=1
Пусть
*/= 2 si% Гу-2^ (У=1, 2, ... ,/2—1)
2

328 СХОДИМОСТЬ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. IX
Очевидно,
п п п
J J i=l 1=1 /=1 l/
Пользуясь этими обозначениями, неравенству C) можно придать вид
п п п
vi |д. х^\2 <L ^S-\x лг-р) I2 4- S Т Iх-~
или
I
На основании формулы D) получаем:
7> = ||a||S-.5/<|la||J-||a||j5/=||a||J(l-5/).
Поэтому
%(\S,)\x/-xf)\*<i\\a\\\ ?(l-Sj)\xf-x{jp-l)\\ E)
/=1 /=1
Из неравенства E) при р>1 последовательно выводим:
2 (\-S,) | Xj-хГ I2 < (||a||jy S
Так как ||a||fc<;l, то отсюда будем иметь:
lim %(\-8,)\х,-хР\* = Q,
р -> СС /г= 1
и, следовательно, учитывая, что 0^5у<1 (У=1, 2, ... ,/г),
подучим:
lim xf = xf (У=1, 2, ...,я),
что и требовалось доказать.
Замечание. Погрешность итераций х{р)(р = 1, 2, ...)
оценивается аналогично тому, как это было сделано в § 6.
Литература к девятой главе
1. В, Н. Фаддеев а. Вычислительные методы линейной алгебры, Гостех-
издат, М. — Л., 1950, гл. II, § 17 и 19.

ГЛАВА X
ОСНОВНЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ
§ 1. Понятие линейного векторного пространства
Определение. Упорядоченная совокупность п чисел
x = (xv x2i ... , хп), вообще говоря, комплексных, называется
точкой или вектором n-мерного пространства, а числа хг, х2, ... , хп
называются координатами вектора х[1], [2], [3]. В качестве
примеров векторов укажем следующие:
1) свободные векторы на плоскости или в трехмерном
пространстве будут соответственно двумерными или трехмерными векторами
в смысле данного выше определения;
2) всякое решение любой системы линейных уравнений с п
неизвестными будет /z-мерным вектором;
3) если дана матрица из п строк и m столбцов, то ее строки
будут /ю-мерными векторами, столбцы—л-мерными векторами.
Два вектора x = (xv х2, ... , хп) и y = (ylf у2, ... , уп)
считаются равными тогда и только тогда, когда совпадают их
координаты, стоящие на одинаковых местах, т. е. если xt^yt при
/=1, 2, ... , п.
Обозначим вектор @, 0, ... , 0) через 0 и назовем его нулевым
вектором.
Суммой векторов х = (х1У дг2, ... , хп), у = (yv у2, ..., уп)
называется вектор
х2+у2; ...;хп+уп),
координаты которого суть суммы соответствующих координат
слагаемых векторов. Сложение векторов подчиняется
перестановочному и сочетательному законам:
2)
Аналогично определяется разность векторов хну. Вектор — х,
удовлетворяющий условию (—л;) + д: = 0, называется
противоположным вектору jc. Легко показать, что
х-у = х + (—у).

330 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Произведением вектора х = (хг, x2i ... , хп) на число k
называется вектор
tcX ^=
Из этого определения вытекают следующие свойства
произведения вектора на число:
1) b{x±y)=*kx±ky;
2) (k±l)x = kx±lx;
3) k(lx) = (kl)x;
4) Ojc = 0;
5) \x = x;
6) (_i)X==_Xf
где k и /—произвольные числа, а л: и у — векторы.
Для векторов х и у естественно определяется линейная
комбинация
ах+$>у
(а, Р —числа), как вектор с координатами ал;у+|}уу(/= 1, 2, ... , п).
Любая совокупность /г-мерных векторов, рассматриваемая с
установленными в ней операциями сложения векторов и умножения
вектора на число, не выводящими за пределы этой совокупности,
называется линейным векторным пространством. В частности,
совокупность всех /г-мерных векторов образует я-мерное векторное
пространство Еп.
§ 2. Линейная зависимость векторов
Определение 1. Векторы лтш, х{2\ ... , х{Щ пространства Еп
йазываются линейно зависимыми, если существуют числа cv с2,..., ст>
не все равные нулю и такие, что
c1x<" + c2*<2> + ... + ce,*(m> = 0. A)
Пусть, например, стф0. Тогда из равенства A) будем иметь:
где
Y/ = ~2 (У = 1, 2, ... ,m —1).
Таким образом, данные векторы линейно зависимы тогда и
только тогда, когда один из них является линейной комбинацией
остальных.
Если же равенство A) возможно в единственном случае, когда
с1 = с2 = ... = ст = 0, то векторы х{1\ х{2\ ... , хкщ называются

§ 2J ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 331
линейно независимыми, т. е. векторы линейно независимы тогда
и только тогда, когда никакая линейная комбинация их, не все
коэффициенты которой равны нулю, не является нуль-вектором.
Заметим, что среди линейно независимых векторов, очевидно, не
должно быть нуль-вектора.
Пример 1. Для случая трехмерного векторного пространства Е3
линейная зависимость двух векторов х к у означает, что они
параллельны некоторой прямой, а линейная зависимость трех
векторов х9 у и z — что они параллельны некоторой плоскости.
Отметим, что если часть векторов линейно зависима, то вся
совокупность векторов также линейно зависима.
Пусть имеется совокупность векторов
*"> = (*<'\ *</>, ...,*<") (у=1, 2,...,/»).
Тогда для определения постоянных ck(k—\, 2, ... , m) в силу
равенства A) получаем систему
Если эта система имеет ненулевые решения, то данные векторы
линейно зависимы. В противном случае они линейно независимы.
Рассмотрим матрицу координат
Л7
гA) М) Лт
Пусть г — ранг этой матрицы. В алгебре доказывается [2], что
система B) имеет ненулевые решения тогда и только тогда, когда
r<w. Следовательно, векторы ха), jcB), ... , х{Щ линейно зависимы,
если r</w, и линейно независимы, если г = т (больше т ранг г,
очевидно, быть не может).
Отсюда вытекает, что ранг матрицы X дает нам максимальное
число линейно независимых векторов, содержащихся в данной
совокупности векторов.
Таким образом, если ранг матрицы X равен г, то среди
векторов-столбцов x(j) (/= 1, 2, ... , т): 1) найдется г линейно
независимых и 2) каждые г+1 векторов (г+1</и) из этой совокупности
линейно зависимы. То же самое справедливо относительно векто-
ров-строк (лг!1*, ... , х\т)) A = 1, 2, ... , п) матрицы X.

332 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Пример 2. Исследовать на линейную зависимость систему
векторов:
-1, 1, -Ь 1);
О, 2, 0, 1);
> = A, -5, -1, 2, -1);
Xе" = C, -6, 2, 1, 1).
Решение. Составляем матрицу координат
- 1 1 1 3i
_1 о —5 —6
12—1 2
—10 2 1
1 1 —1 1J
Для определения ранга г матрицы X проведем некоторые
элементарные преобразования, а именно, вычитая из четвертого столбца
матрицы сумму трех первых, получаем:
Хсо
Отсюда заключаем, что все определители четвертого порядка
матрицы X равны нулю. Очевидно, что имеются миноры третьего
порядка матрицы X, отличные от нуля. Следовательно, г = 3, и
так как ранг матрицы меньше числа векторов, то векторы jcA),
х{2), х{3\ хш линейно зависимы. В данном случае это ясно, так как
1 1
1 0
1 2
1 0
1 \
1
—б
—1
2
\
0
0
0
0
0
Теорема 1. Максимальное число линейно независимых
векторов п-мерного пространства Еп в точности равно размерности
этого пространства.
Доказательство. Прежде всего, в пространстве Еп имеются
системы из п линейно независимых векторов. Такова, например,
совокупность п единичных векторов (ортов):
^ = A, 0, 0,..., 0);
*?2 = @, 1, 0,..., 0);
ея=@, 0, 0,..., 1).
Так как если
то очевидно, что сг = с2 = ,.. = сп = 0.

§ 21
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 333
Покажем, что если число векторов jcA), хк2\ ..., х1т больше
п(т> п)> т0 они обязательно линейно зависимы. Действительно,
матрица координат этих векторов имеет тип п х т и, следовательно,
ранг ее r^min(/z, m)=/z</». Отсюда следует, что эти векторы
линейно зависимы.
Определение 2. Любая совокупность п линейно независимых
векторов ^-мерного пространства называется базисом, этого
пространства.
Теорема 2. Каждый вектор п-мерного пространства Еп
может быть представлен, и притом единственным образом, в виде
линейной комбинации векторов базиса.
Доказательство. Пусть х ? Еп и ех, г2, .. ., еп — базис
пространства Еп. В силу теоремы 1 векторы х, sv е2, ..., гп
линейно зависимы, т. е.
сох + схгх + с2е2 + ... + спеа = 0, C)
где некоторый коэффициент у^ у)
В равенстве C) коэффициент со=^О, так как в противном случае
мы бы имели
где Су^О (у^ 1), что противоречит линейной независимости
векторов ev в2, ..., е„. Следовательно, мы можем разрешить равенство C)
относительно х:
* = SA + ?aea+...+gII8li, D)
где
? ?l ? ??
Таким образом, любой вектор х пространства Еп есть линейная
комбинация векторов базиса. Разложение D) единственно. В самом
деле, если имеется другое разложение
* = Б1в1 + &л + ...+ 5«в*, D')
отличное от первого, то, вычитая из равенства D) равенство D'),
получим:
где по меньшей мере один из коэффициентов^ — 2/=7^0.
Равенство E) невозможно, так как векторы базиса линейно независимы.
Следовательно, существует только одно разложение вида D).
Геометрическая иллюстрация. Для случая трехмерного
пространства формула D) эквивалентна разложению вектора х по
направлениям трех данных векторов е,, с2 и гч общего положения
(Рис. 49).

334 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Определение 3. Если ev е2, ..., вп есть базис л-мерного
пространства и
то числа
называют координатами вектора х в данном
базисе bv е2, ..., еп. Заметим,
что координаты вектора
есть координаты его в базисе
ортов
Рис. 49.
(у=1, 2, ..., л),
где 6п;Г—символ Кронекера.
Следовательно, имеем основное
разложение
х = ххех + х2е2 +...+ хпеп. F)
., п) будем называть исходным
Базис ортов ^(у=1, 2,
базисом пространства.
Определение 4. Совокупность Ek векторов из /z-мерного
пространства Еп называется линейным подпространством
пространства ЕпУ если выполнены
следующие условия:
Ek пУ
следует
1) из х
Х+у k
2)изх ? Ek следует ах € ?*•
где а — любое число. В частности,
0?Ек.
Следовательно Ek можно
также считать векторным
пространством. Максимальное числой
линейно независимых векторов
в пространстве Ek называется
размерностью этого подпростран-
ства.
рис
Из теоремы 1 следует, что k*^n. Таким образом, в
пространстве Еп могут быть подпространства: Ег — одного измерения, Е2 — двух
измерений и т. д. до Еп — п измерений (само пространство).
Нулевой вектор 0 можно рассматривать как пространство нулевого
измерения.
Пример 3. В обычном трехмерном пространстве Es
подпространство Ег одного измерения является прямой; подпространство^
двух измерений —п л о скост ью (рис. 50).

§ 3] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 335
Теорема 3. Если zv Z2, ..., zk —векторы п-мерного
пространства Еп, то полная совокупность векторов
х = axzx + аггг +...+ akzk, G)
где а; (У= 1, 2, ..., k) — произвольные числа, представляет собой по-
дпространство пространства Еп, причем, если векторы zv Z2t .. •, zk
(k^n) линейно независимы, то размерность этого подпро-
странства равна k.
Обратно, всякое подпространство Ек пространства Еп совпадает
с совокупностью всех линейных комбинаций линейно независимых
векторов zly z2, ... ,zk этого подпространства (базисные векторы).
Доказательство. Справедливость первого утверждения
теоремы проверяется непосредственно.
Докажем второе утверждение теоремы. Пусть х ? Ек ихне
является линейной комбинацией базисных векторов zvz2, ...,«л. Тогда
очевидно, что векторы л^, zv z2y ..., zk линейно независимы, и, таким
образом, в пространстве Ек имеется й-f-l линейно независимых
векторов. Но последнее обстоятельство невозможно, так как согласно
предположению максимальное число линейно независимых векторов
пространства Ek равно k.
Следовательно, при каком-нибудь выборе чисел av aa, ..., ак
имеем:
х == axzx + a2z2 +...+ akzkf
что и требовалось доказать.
Следствие. Совокупность векторов х9 определяемых
формулой G), представляет собой наименьшее линейное пространство,
содержащее векторы zx, Z2> ...,Zk (так называемое пространство,
порожденное векторами гх> г2, .••, Zk) или пространство,
натянутое на векторы zx, z2f ..., Zk).
§ 3. Скалярное произведение векторов
Пусть в л-мерном пространстве Еп имеем векторы
д: = (дг1, лг2, .... хп) ny = (yvy2, ..мЛ)«
Будем считать, что координаты векторов—комплексные числа:
где / = 1/^Т; у=1, 2, ..., п.
Введем сопряженные величины
Тогда очевидно, что

336 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Под скалярным произведением двух векторов понимается число,
равное
^/ A)
Скалярное произведение обладает следующими свойствами.
1. Свойство положительной определенности. Скалярное
произведение вектора самого на себя есть неотрицательное число,
которое равно нулю тогда и только тогда, когда вектор равен нулю.
В самом деле, из формулы A) имеем:
Очевидно, что @, 0) = 0. Наоборот, если (х, х) = 0, то лгу = О
(У=1, 2, ..., п) и, следовательно, х = 0.
2. Эрмитова симметрия. При перестановке двух множителей
скалярное произведение заменяется сопряженным. Действительно,
пользуясь теоремами о сопряженной величине суммы и сопряженной
величине произведения*), имеем:
(У, х) = j^y,*/* ^ 2J*/JV = \%x/l) =(*' У)*-
Следовательно,
(У, х) = (xf у)*. B)
3. Скалярный множитель, стоящий на первом месте, можно
выносить за знак скалярного произведения, т. е.
(ах, jO = a(x, У). C)
Доказательство этого свойства непосредственно вытекает из
формулы A).
Следствие. Скалярный множитель, стоящий на втором месте,
можно выносить за знак скалярного произведения, заменяя его
сопряженным. Имеем:
(х, ау) = (*у, *)* = [a(j>, *)]* = <** (дт, x)* = a»(x, у).
Итак,
(х, aj>) = a*(x, у).
4. Свойство дистрибутивности. Если первый или второй векторы
представляют собой сумму двух векторов, то скалярное произведение
*) Мы здесь воспользовались следующими теоремами:
а) сопряженная величина суммы равна сумме сопряженных величин
слагаемых;
б) сопряженная величина произведения равна произведению сопряжен*
ных величин сомножителей.

§ 3J СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 337
этого вектора есть сумма соответствующих скалярных произведений
слагаемых этого вектора. В самом деле, пусть
где **={х{*\х{*\ .... *^)(*=1, 2).
Исходя из определения суммы векторов, согласно формуле A)
получаем:
т. е.
(*A> + *<2\ jO = (*A\ Д>) + (*B), у). D)
Далее,
= (^У1}) + (^У2)). E)
Формулы D) и E) легко распространяются на любое конечное
число векторов, а именно:
/ т I \ m I
B *(/>' 2УАJ 2
Кроме введенного /г-мерного комплексного пространства,
полезно рассматривать п-мерное вещественное (действительное)
пространство, т. е. совокупность векторов с вещественными
координатами.
В действительном «-мерном пространстве скалярное произведение
равно сумме произведений соответствующих координат векторов
(, j) 2л <
7=1
Рассмотренные выше свойства скалярного произведения
формулируются так:
1) (*> *)^0, причем если (х, jc) = O, to jc = O;
2) (*, JF) = (jp, л);
3) y) = (jf, ay) = a (x, y) (a действительно);

338 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
С помощью скалярного произведения можно дать определение
и основных метрических понятий в /2-мерном пространстве: длины
вектора и угла между парой векторов.
1. Длина вектора. Длиной вектора в /г-мерном пространстве
называется неотрицательное число
Очевидно, что это определение согласуется с понятием длины
вектора в трехмерном пространстве.
2. Угол между векторами. Углом <р между парой векторов х
и у называется тот угол (в пределах от 0 до 180°), для которого
Для векторов в трехмерном пространстве это определение
согласуется с обычным выражением угла между векторами через
скалярное произведение. Можно доказать, что справедливо
неравенство AJ
Поэтому угол между векторами в вещественном пространстве будет
действителен.
§ 4. Ортогональные системы векторов
Определение 1. Два вектора хну пространства ?я
называются ортогональными^ если их скалярное произведение равно
нулю, т. е.
(х9у) = 0. A)
Если векторы не нулевые, то ортогональность означает, что
угол между ними равен —-. Нулевой вектор, очевидно,
ортогонален любому вектору пространства.
Таким образом, ортогональность есть обобщенное свойство
перпендикулярности.
Определение 2. Система векторов д:A), х{2\ ..., х{Щ
называется ортогональной^ если любые два вектора системы
ортогональны друг другу, т. е.
{хи\ x{k>) = 0 при ]фк.
Заметим, что если вектор хA) ортогонален векторам #B), ..., хт,
то этот вектор ортогонален также любой линейной комбинации
последних векторов, иными словами, вектор х{1) ортогонален
пространству, натянутому на векторы лсB), ..., ximK Действительно,
если
(<*> (Л>) = 0 при * =

§ 4] ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ВЕКТОРОВ 339
то имеем:
(т \ т
*(u. 2 cft*<*> = 2 el (x«\ *<*>) = О,
где с2, ..., сл — произвольные постоянные.
Теорема. Ненулевые попарно ортогональные векторы д;ш,
х{2\ ...» *(Я1) линейно независимы.
Доказательство. В самом деле, пусть
..'+ cw*<m) = 0. B)
Умножая скалярно обе части равенства B) на хA\ получим:
или, так как
(х{1\ хA))ф0 и (х^, x(J)) = 0 при ]ф\, то с* = 0 и сг = 0.
Совершенно так же доказываем, что с2 = 0, ..., ст = 0.
Следовательно, векторы лгш, д;B), ..., х{т) линейно независимы.
Следствие. В я-мерном пространстве Еп ортогональная
система содержит не более п векторов.
Определение 3. Базис ev ?2> •••» % пространства Еп
называется ортогональным, если базисные векторы попарно
ортогональны, т. е,
(ер еА) = 0 при }фк (у, А=1, 2, ..., п).
Если, сверх того, векторы 8у(у=1, 2, ..., /г) —единичные, то
ортогональный базис называется нормированным (короче, ортонор-
мированным). В этом случае имеем:
где буА —символ Кронекера.
Простейший ортонормированный базис пространства ?п, как
нетрудно убедиться, представляет собой систему ортов
*! = (!, 0, 0, ..., 0),
^2==@, 1, 0, ..., 0),
ел = @, 0, 0, ..., 1),
образующих исходный базис.
Ортогональный базис ех, е2, ..., гп всегда можно нормировать,
разделив каждый из векторов 8.- на его длину. Полученные новые
векторы
образуют ортонормированный базис.

340 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Выразим координаты вектора х в ортонормированном базисе
ev e2, ..., ъп. Если
то, умножая скалярно равенство C) справа на Ер получим:
?, = (*, в,) (У=1, 2, ..., п). D)
По аналогии с векторной алгеброй можно сказать, что
координаты вектора в ортонормированном базисе равны проекциям вектора
на соответствующие векторы базиса.
Возводя равенство C) в квадрат, будем иметь:
= 221& (в,, ч) = 2 U) = 2 I Б/ Р. E)
/el /e=:t /=1 /el
т. е. квадрат длины вектора равен сумме квадратов модулей его
проекций на базисные ортонормированные векторы (аналог теоремы
Пифагора). В частности, если пространство Еп—действительное,
то формулу E) можно записать без модуля:
п
(л, л) — ^j \gy) . ^o ;
§ 5. Преобразования координат вектора
при изменениях базиса
Пусть е19 е2, ..., еп и ех, е2, ..., ел — два базиса одного
и того же линейного пространства Еп. Каждый вектор нового
(второго) базиса Еу имеет в старом (первом) базисе ej некоторые
координаты sip stJ% ..., «„/), т. е.
/ VV j^n (У= U 2, . . ., П). (I)
Неособенная матрица 5= [s(j] называется матрицей перехода от
старого базиса к новому **). Эта матрица является
транспонированной по отношению к матрице, задающей преобразование базиса.
Пусть х — данный вектор. Обозначим через лг,- координаты этого
вектора в старом базисе и через |?- — его координаты в новом базисе.
*) При обозначении координат на первом месте указывается номер
соответствующего старого базисного вектора, а на втором — нового
базисного вектора.
*•) Определитель det S Ф (У, так как в противном случае векторы elf
е2, . . ¦, еп были бы линейно зависимы.

§ 5] ПРЕОБРАЗОВАНИЯ КООРДИНАТ ВЕКТОРА ПРИ ИЗМЕНЕНИЯХ БАЗИСА 341
Очевидно, что
Отсюда, подставляя во вторую сумму выражение A) для еу,
получим:
п п п п п
Следовательно, в силу линейной независимости векторов elf
е21 ..., еп находим:
/=1
B)
Если обозначить
* =
и \ =
ill
то соотношение B) можно переписать в следующем матричном виде:
Х = о§, (О)
т. е. вектор в старых координатах (базисе) равен матрице перехода S
(или транспонированной матрице, задающей новый базис),
умноженной на вектор в новых координатах.
Из формулы C) получаем:
l = S~*x. D)
Отметим один важный частный случай, аналогичный
преобразованию прямоугольных координат. Пусть старый базис е1У е2, . ..,?„
и новый базис bv e2, ..., гп действительны и ортонормирова-
ны, т. е,
(eh «/) = в„ E)
и
(в,, ey) = 6fy, E')
где 8{j — символ Кронекера.
Тогда из формулы A) вытекает:
{I, У=1, 2, ..., п),
F)
*) Иными словами, мы рассматриваем вектор х в новых координатах
как преобразованный вектор, отнесенный к старому базису.

342 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
т. е. элементы матрицы перехода 5 являются направляющими
косинусами и могут быть заданы таблицей 24.
Таблица 24
Косинусы углов между ортами двух базисов
Орты новой системы
•
Орты старой системы
S12
•
Нп
Чг
Чг
•
Чп
...
• • •
...
• • •
*П1
«»2
•
Подставляя выражение A) в формулу E'), в силу формул E)
получим:
/ п п \ п
т. е. 1) суммы парных произведений соответствующих направляющих
косинусов различных координатных осей новой ортонормированной
системы равны нулю и 2) сумма квадратов направляющих косинусов
для каждой новой координатной оси равна единице. Отсюда
E, G)
т. е. матрица перехода от одного ортонормированного базиса к
другому ортогональна (подробнее об ортогональных матрицах см. § 6).
§ 6. Ортогональные матрицы
Определение. Действительная матрица Л называется
ортогональной^ если ее транспонированная матрица А совпадает с
обратной А
-1
т. е.
или
A)
B)
Ортогональная матрица имеет следующие свойства.
1. Строки (столбцы) ортогональной матрицы попарно
ортогональны.

* 7]
ОРТОГОНАЛИЗАЦИЯ МАТРИЦ
343
Действительно, если
п
9 то из равенства B) имеем;
® при
2. Сумма квадратов элементов каждой строки (.столбца)
ортогональной матрицы равна 1.
Из равенства B) при /=/ получаем:
S«&= 2*1 = 1.
3. Определитель ортогональной матрицы равен ±1.
В самом деле, на основании равенства B) имеем:
Отсюда, так как
и, следовательно,
и det?=l, то
4. Транспонированная и обратная матрицы ортогональной матрицы
суть также ортогональные матрицы. Это свойство непосредственно
вытекает из формул A) и B).
§ 7. Ортогонализация матриц
Пусть имеем матрицу с действительными элементами
ап а12 ... ain"
а21 а22 ... а2п
• • • «Л
Столбцы матрицы А будем рассматривать как векторы
f=l, 2, ..., п).
Следовательно, эту матрицу можно записать в таком виде:
а(Л)

344 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Теорема 1. Всякую действительную неособенную матрицу А
можно представить в виде произведения матрицы с ортогональными
столбцами на верхнюю треугольную матрицу, г. е.
Л DT
где R — матрица с ортогональными столбцами и Т—верхняя
треугольная матрица с единичной диагональю.
Доказательство. Для простоты доказательство теоремы
проведем для случая, когда порядок матрицы я = 3. Однако
рассуждения будут иметь общий характер. Пусть
у
а18'
Запишем эту матрицу в виде
Рис. 51.
где
— векторы-столбцы.
Так как матрица А — неособенная, то векторы аа\ а{2\ а{В)
линейно независимы.
Действительно, если бы эти векторы были линейно зависимы,
то в det А один из столбцов являлся бы линейной комбинацией двух
других и, следовательно, det А = 0, что невозможно.
Будем искать матрицу R также в виде
где r(J) (/=1, 2, 3) — искомые ортогональные столбцы.
Положим
гA) = аш.
A)
Далее, вектор аB> раскладываем на составляющие t12r{1) и г12),
из которых первая направлена по вектору гA), а вторая
перпендикулярна (ортогональна) к нему (рис. 51), т. е,
B)
B')
где
(г'
ш
Аналогично вектор аC) раскладываем на три составляющие ls\
t23r{2) и гC), из которых первые две направлены соответственно по

§ 7] ОРТОГОНАЛИЗАЦИЯ МАТРИЦ 345
векторам гA) и гB), а последняя перпендикулярна как к вектору га>,
так и к вектору гB) (рис. 51), т. е.
где
(гш, гC)) = 0 и (г<2>, г<3)) = 0. C')
Из построения ясно, что векторы гA), г<2) и гC> будут взаимно
перпендикулярны. Определим из системы B) и C) как векторы
гB) и г<з>} так и коэффициенты t;j. Умножая скалярно обе части
уравнения B) на гA) = аA>, в силу условия ортогональности B')
получим:
(а<2\ rA>) = *X2(rA\ га>),
причем
(гA\ гш)=^0.
Следовательно,
, _ (q<»f г»*)
Заметим, что в силу неособенности матрицы Л вектор гA> = ^
и поэтому (гA), гA))=^=0. Кроме того, гB>^0, так как в противном
случае векторы аа) и аB) были бы линейно зависимы.
Аналогично, умножая скалярно обе части уравнения C)
последовательно на гA> и г<2), в силу условий ортогональности B') и C')
получим:
«>
Отсюда, учитывая, что (гш, гш)т^0 и (гB), г<2)) ?= 0, будем
иметь:
(д(»>, г<») . . (а(8), Г»>)
Легко проверить, что так построенные векторы гш, г<2) и г<3>
попарно ортогональны. Таким образом, окончательно имеем:
a™ = t12rA>+r™, \
где
">) (
= 0 при

346 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Очевидно, что система D) эквивалентна матричному уравнению
аи а12
а21 а,л
°31 #82
an
«23
«88_
=
Г11 Г12 'l3
Г21 '» '23
''З! ^82 '88
•
' 1
0
0
'12
1
¦0
tu~
ИЛИ
где /? = [г,.у] — матрица с ортогональными столбцами, а 7* =='
верхняя треугольная матрица с единичной диагональю.
Пример. Ортогонализировать столбцы матрицы
ГО 1 21
Решение. Положим
E)
Тогда
.0,4.
Теперь найдем
г<2>:
= ас»_^ 2гA)= 2 -0,4 1 U 1,6
LoJ L2 J L-0,8j
Для определения г(8) вычислим /13 и /23. Имеем:
. (о», Н») 2.0+(M+b2__2_
Отсюда
r<3'=a(S> — tlsra)—t.
Итак,
А
)= 0 —0,4 1 —0,3 1,6 = -0^88 .
L 1 J L2J L-0.8J L 0,44 J
ГО 1 1,7 ПГ1 0,4 0,4-1
= I 1 1,6 -0,88 0 1 0,3 ,
L2 -0,8 0,44J1.0 0 1 J

§ 71
ОРТОГОНАЛИЗАЦИЯ МАТРИЦ
347
причем векторы
« Г?1 « Г !Л Г lf7l
ГA)= 1 ; гB)= 1.6 I- гC) = I— 0,88
L2J L—0,8j * L 0,44J
попарно ортогональны, в чем можно убедиться непосредственной
проверкой.
В некоторых случаях выгоднее ортогонализировать не столбцы,
а строки матрицы, рассматривая их как соответствующие векторы.
Пусть А' — транспонированная матрица для данной матрицы
А — приведена к виду
F)
где R — матрица с ортогональными столбцами и Т—верхняя
треугольная матрица с единичной диагональю. Транспонируя
равенство F), получим:
G)
где Т — нижняя треугольная матрица и /?' — матрица с
ортогональными строками. Таким образом, указанный выше прием
ортогонализации столбцов матрицы годится также и для ортогонализации
строк, и мы имеем теорему.
Теорема 2. Всякую действительную неособенную матрицу
можно представить в виде произведения нижней треугольной матрицы
с единичной диагональю и матрицы с ортогональными строками.
Укажем еще один прием ортогонализации строк матрицы, иногда
практически более удобный [5]. Пусть дана действительная
неособенная матрица
ап а12
а21 а22
Из каждой 1-й строки матрицы Л, начиная со второй, вычтем ее
первую строку, умноженную на некоторое число Хп (/ = 2, ..., /г),
зависящее от номера строки. В результате будем иметь
преобразованную матрицу
XV
4V
¦е1
-«U
V
где ej») =
при/=1 и
— Хпа1у при

348 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Подберем множители Хп так, чтобы первая строка матрицы ЛA)
была ортогональна ко всем остальным строкам этой матрицы. Имеем:
2 а$
Отсюда
2'
= 2, .... Я).
Над матрицей ЛA) проделываем аналогичную операцию, а именно:
первые две строки ее оставляем неизменными, а из каждой 1-й строки,
где /^3, вычитаем вторую строку матрицы ЛA\ умноженную
на число к;г (/ = 3, ..., п). Получаем новую матрицу
... а\
<2)
• • • **пп -1
где a^^
^^ при / = 1, 2 и а<2) = а^— *,,2a<ty при
Так как первая строка матрицы ЛB> совпадает с первой строкой
матрицы ЛA) и все остальные строки матрицы Л<2) представляют
собой линейные комбинации строк матрицы ЛA), ортогональных
первой строке матрицы Лш, то строки матрицы ЛB) будут также
ортогональными к ее первой строке. Выберем множители ki2 так, чтобы
строки матрицы ЛB), начиная с третьей, были ортогональны ко
второй ее строке. Получаем:
№^
Отсюда
= 3, • • •)
(А)

§ 7]
ОРТОГОНАЛИЗАЦИЯ МАТРИЦ
349
Указанный выше процесс продолжаем до тех пор, пока не
получится матрица
аи а12 ••• ат
(л-1) fl(/i-l) п^
*21 2 *•• и2П
а
(n-i)
все строки которой попарно ортогональны:
-v^O при кф1.
Матрица Л("~1) = ^ с ортогональными строками получилась
из данной матрицы А в результате цепи элементарных
преобразований. Поэтому справедливо равенство
# = ЛЛ, (8)
где Л—неособенная матрица, которая в нашем случае является
нижней треугольной матрицей.
Матрицу Л легко восстановить, проделав над единичной
матрицей Е все элементарные преобразования, совершенные над
матрицей Л. Из формулы (8) имеем окончательно:
где Г=Л" — нижняя треугольная матрица.
Укажем некоторые свойства матриц с ортогональными рядами.
Лемма. Если столбцы действительной матрицы составляют
ортогональную систему векторов, то произведение транспонированной
матрицы на саму матрицу равно диагональной матрице.
Доказательство. Пусть A = [a{j]—данная матрица.
Требуется доказать, что Л'Л = Д где А' = [#уЧ.] — транспонированная
матрица А и
D =
dn О
О d23
— диагональная матрица.
О 0 ... dnn\
Полагая D=[dij]t согласно правилу умножения матриц имеем:
k=i
Отсюда, так как ahi~— координаты г-го вектора ащ и akj —
координаты /то вектора a{J\ получаем:
= 0.

350 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Следовательно, D=[d^]— диагональная матрица.
Следствие. Произведение действительной матрицы с
ортогональными строками на транспонированную матрицу равно
диагональной матрице, т. е. AA' = D.
Теорема 3. Всякая неособенная действительная матрица А с
ортогональными столбцами представляет собой ортогональную
матрицу, умноженную справа на диагональную матрицу.
Доказательство. В силу леммы имеем:
Л'Л = Д (9)
где D = [dij] — диагональная матрица. Если Л = [а,.у], то, очевидно,
Пусть
О (/ = 1, 2, .... л)
~Pl 0 ... О "
О ра ... О
Loo ...Рв_
Очевидно, что D = d2. Из формулы (9) имеем A'A—d2, откуда
Так как
= d-i, то
Следовательно, матрица Ad^ — U ортогональна и, значит,
А = Ш, A0)
что и требовалось доказать.
Следствие. Неособенную действительную матрицу с
ортогональными строками можно представить в виде произведения
диагональной матрицы на ортогональную матрицу.
Действительно, пусть А — матрица с ортогональными строками;
тогда Л' — матрица с ортогональными столбцами. В силу формулы A0)
имеем А' = Ш, где U— ортогональная матрица и d — диагональная
матрица, которая может быть определена из соотношения
АА = d2.
Отсюда получаем:
где If — также ортогональная матрица.

§ 8J ПРИМЕНЕНИЕ МЕТОДОВ ОРТОГОНАЛИЗАЦИИ К РЕШЕНИЮ СИСТЕМ 351
Замечание. Чтобы данную действительную неособенную
матрицу А с ортогональными столбцами (строками) преобразовать
в ортогональную, достаточно нормировать ее столбцы (или
соответственно строки), т. е. элемент каждого столбца (строки)
разделить на корень квадратный из суммы квадратов элементов этого
столбца (строки). Например, если A = [atj\ есть матрица с
ортогональными столбцами, то матрица
А = [а{/1
где 0// =
матрица.
(*, /=1» 2, ..., л), есть ортогональная
§ 8. Применение методов ортогонализации к решению систем
линейных уравнений
А. Первый способ (ортогонализация столбцов)
Пусть имеем систему линейных уравнений
Ах = Ь A)
с действительной неособенной матрицей А. Ортогонализируя
столбцы матрицы Л, получим матрицу /?, причем A = RT, где
Г—верхняя треугольная матрица. Имеем:
RTx = b. B)
Умножая слева на /?' обе части равенства B), получим:
R'RTx = R'b. C)
Но, как известно, i?'/? = D, где D—диагональная матрица.
Вводя обозначение i?'6 = p, будем иметь:
откуда
Матрица D", обратная диагональной, находится легко, а именно,
если
~du О ... О
?> =
то
О d22... О
_ 0 0 ... dnn_
d^ 0 ... О
о d;2K..o

352 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Относительно просто находится также обратная матрица 7*"*1
треугольной матрицы 7*.
Пример 1. Методом ортогонализации столбцов решить систему
уравнений
0,4*! + 0,Зл;2 — 0,2лг8 = 2;
0,6^-0,5*2 + 0,3*3 = 2,5;
0,3*!+ 0,2*2 + 0,5*з= П.
Решение. Представим матрицу А данной системы в виде
произведения матрицы R с ортогональными столбцами на треугольную
матрицу с единичной диагональю:
I'll '12 '131П ^12 К*1
'•1 '22 '2* 0 i Xn\
'31 '32 '33 J L0 0 i J
Полагаем:
ГA)==
Имеем:
га>
Г0,4-|
= 0,6 I
Lo,3j
По формулам D) предыдущего параграфа находим:
(аB))Ги))_ 0,12-^0,3 + 0,06 0JI2
0,61 и> ^о/>
rB) =
.tl>)
г °
-o
o,
,3'
,5
16 + 0
1
+ 0.
,36 + 0
r
1967
,09
•0,'
0,(
Контроль:
,37871 0,1515
,3820 =-0,2292 \ = 0;
,2590J 0,0777
-0,08+0,18+0,15 0,25
Г0,4ГГ 0,
^ о,6 -0,3
L0,3j L 0,2
0,07574—0,11460+0,12950
[-0,21 Г0,41 Г 0,37871 Г-0,29901
0,3 -0,4098 0,6 +0,1714-0,3820 = -0,0114 ,
0,5j L0,3j L 0,2590j L 0,4215j
Контроль:
(rA\

§ 8] ПРИМЕНЕНИЕ МЕТОДОВ ОРТОГОНАЛИЗАЦИИ К РЕШЕНИЮ СИСТЕМ 353
Таким образом,
Г0,4 О,
1= 0,6 -0,
L0,3 0,
0,3787 -0,29901 Г1 -0,1967 0,40981
3820 -0,0114 0 1 -0,1714 I
2590 0,4215JL0 0 1 J
R .
По формуле D) имеем:
где D =/?'/?—-диагональная матрица и
-[.14
Для матрицы D и ее обратной матрицы D" получаем такие
значения:
D
Далее,
[0,61 ООП Г1,64 001
О 0,35 0 и D-1= 0 2/81 О I
О О 0,2672J L0 О 3,75J
Г 0,4 0,6 0,3 ]Г2 ] Г5,6 1
/?'ft = 0,3787 -0,3820 0,2590 2,5 = 2,67 I
[-0,2990 -0,0114 0t4215JLll J U,08J
Наконец, обычным приемом подсчитываем:
1 0,1967 -0,37611
0 1 0,1714 I
0 0 1 J
В итоге получим:
[1 0,1967 -0,37611Г1,64 0 0 1 Г5,6 1 Г 5,02381
0 1 0,1714 0 2,810 2,67 = 10,0475 I
0 0 1 JLO 0 3,75jL4,08j L15,0087J
Следовательно,
^==5,0238; л:2= 10,0475; лг3= 15,0087;
точные значения корней: л:1==5; х2 = \0; лг8=15,
Б. Второй способ (ортогонализация строк)
Пусть дана система
Л* = &, E)
где det^=^O.
Преобразуем строки системы E) с помощью приема, указанного
в предыдущем параграфе, так, чтобы матрица А перешла в матрицу R
•2 Б. П. Демидович и И А. Марон

854 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
с ортогональными строками. При этом вектор Ь перейдет в какой-то
вектор $. В результате получим эквивалентную систему
#* = &. F)
Следовательно,
x = R-^. G)
Как известно, RR' = D — d2, где*/ — диагональная матрица, и/? = dU>
где U—ортогональная матрица. Поэтому
#-i = (dU)'1 = U-Ч'1 = U'd'd'* = (dU)'d~2 = R'd~* = R'D'1.
Таким образом, на основании формулы G) окончательно имеем:
x = R'D-*b (8)
где
(9)
Используя формулу (8), можно избежать наиболее трудоемкого
процесса нахождения обратной матрицы для недиагональной матрицы.
Наличие матрицы D не вносит усложнения, так как
D—диагональная матрица. Формула (9), нужная по существу, может быть
использована также и для контроля.
Пример 2. Методом ортогонализации строк решить систему
уравнений
3,00*!+о, 15лг2—0,09*3 = 6>°°; '
0,08^ + 4,00^ — 0,16*3=12,00;
0,05*!+ 0,30лг2 +5,00лг3 = 20,00. j
(I)
Решение. По формулам предыдущего параграфа определяем
множители:
л 3,00.0>08+0,15»4>004-(-0>09).(-0,16)__0>8544_
Л*1- 3,002 + 0,152 + 0,092 — 9,0306 "~
. 3,00-0,05+0,15-0,30—0,09-5,00 0,2550
Л 92 "" 9,0306 ~~
Сохраняя первое уравнение системы (I), из каждого следующего
вычитаем первое, умноженное на соответствующие множители Kit
(/ = 2, 3):
3,00*!+ 0,15*2—0,09*s = 6,00; \
— 0,2038*1 + 3,9858*2-0,1685*3= 11,4324; } (II)
0,1346*! + 0,3042*2 + 4,9975*3 = 20,1692. J
Для системы (II) определяем множитель
__—0,2038-0,1346 + 3,9858-0,3042-^0,1685-4,9975 0,3430 __nftOi5
"~ 020382 + 398582 + 016852 "5,9565"" '

§ 8J ПРИМЕНЕНИЕ МЕТОДОВ ОРТОГОНАЛИЗАЦИИ К РЕШЕНИЮ СИСТЕМ 355
Сохраняя два первых уравнения системы (И), из ее третьего
уравнения вычитаем второе, умноженное на множитель Я82:
(III)
3,00*х
—0,2038*х + 3,9858*2 — 0,1685*3 = 11,4324;
0,1390*!+ 0,2185*2+ 5,0011*з =19,9234.
Матрица
Г 3'
- -0,
L *.
00 0,15 —0,09 "
2038 3,9858 —0,1685
1390 0,2185 5,0011.
имеет ортогональные строки. Для контроля составляем матрицу
[9,0306 0,0017-0,00021 Г9,0306 0, 0 1
0,0017 15,9565 -0,0018 « 0 15,9565 0
-0,0002 —0,0018 25,0780J LO 0 25,0780J
Применяя формулу (8), получим:
Г 3,00 —0,2038 0,13901
* = R'D~lP = 0,15 3,9858 0,2185 X
L_0,09 -0,1685 5,001 lj
[0,1107 0 0 1Г 6,00 1 Г 1,9571
0 0,0626 0 11,4324 =3,126.
0 0 0,0399J Ll9,9234J L3,803j
Следовательно,
Х-* ==: 1 ,с/сД/ у Ло О, 1ZU, Ло ——¦ OfOKJO»
В. Третий способ (метод ортогональных матриц)
Пусть линейная система приведена к виду
/?* = ?, (Ю)
где /?==[г^] — неособенная матрица с ортогональными строками и
ГР/1
—вектор свободных членов.
Умножая каждое уравнение системы A0) на нормирующий
множитель
п
12*
7
1 г (/ = 1,2, .... л),

356 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
получим систему
A1)
где R = [jjt^r^yj—ортогональная матрица и
— новый вектор свободных членов.
Из уравнения A1) будем иметь:
§ 9. Пространство решений однородной системы
Рассмотрим однородную линейную систему
alxxx + ахгх% +...¦+• а1пхп = 0;
A2)
= 0;
A)
или, короче,
где A = [atj\ и д: =
— искомый вектор.
Если det ЛфО, то в силу формул Крамера система A) имеет
единственное нулевое решение д: = 0.
Пусть deM~0. В этом случае система A) имеет бесконечное
множество решений (в том числе и ненулевые).
Из формулы (Г) вытекает: 1) если х — решение уравнения (Г),
то сх, где с —произвольная постоянная, есть также решение этого
уравнения; 2) если д:A) и х{2) — решения уравнения (Г), то сумма
*ш + *B) есть также решение этого уравнения.
Действительно, если
А*г = О,
то
Следовательно, сх — решение однородной системы A).
Аналогично, если
А*A) = 0 и
то
т. е.
А (х™ + х™) = Ахп) + Axi2) =0 + 0 = 0,
x{i)-~ также решение однородной системы A),

§ 9] ПРОСТРАНСТВО РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ 357
Отсюда получаем, что любая линейная комбинация решений
однородной системы A) есть также решение этой системы.
Следовательно, совокупность всех решений однородной системы A)
образует векторное пространство, которое называется пространством
решений. Справедлива теорема.
Теорема. Если п — число неизвестных однородной системы A)
и г есть ранг ее матрицы А, то размерность пространства решений
равна k = n — r.
Базис пространства решений называется фундаментальной
системой решений. Если для системы A) известна фундаментальная
система решений
*«> = (*<*>, *U>, ..., *(!>),
то все ее решения содержатся в формуле
х = ctxa) + са*<2> + ... + сй*<*> B)
или, более подробно,
х, =
где сг> с2, ..., ск — произвольные постоянные числа.
Для нахождения фундаментальной системы решений в матрице Л
выделяют минор r-го порядка бг, отличный от нуля. Пусть
8,=
а12 ... а1г
ап ап ... ак
Этого всегда можно добиться путем перестановки уравненийсистемыA)
и изменения нумерации ее неизвестных. Тогда легко доказать, что
уравнения системы A), начиная с (г+1)-го, являются следствиями
первых г уравнений этой системы, т. е. они удовлетворяются, если
будут удовлетворены г первых уравнений системы A). Поэтому
достаточно рассмотреть подсистему
аг1хг + а12х2 + ... + alrxr =—a1% r+1xr+1 — ... — alnxn,
хг = — a2t г+1л:г+1 — ... — а2пхп,
г2х2 +... + апхг^ - ап г+1хг+1— .. .-arnxn,
определитель которой бг отличен от нуля.

358 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
В системе C) значения неизвестных
можно считать произвольными. Разрешив систему C) относительно
неизвестных xv лг2, ..., лгг, получим:
... +a2kcki
D)
где at.y(/=l, 2, ..., г; у=1, 2, ..., ^)—вполне определенные
постоянные.
Кроме того,
I
D')
Си.
Формулы D) и D') дают полную систему решений системы A).
За фундаментальную систему решений можно принять:
arl
1
0
0
_0 __
, X —
ai2
«Г2
0
1
0
_ 0 _
О
О
О
•
1
Эти последние решения могут быть найдены непосредственно из
системы C), если в ней последовательно полагать:
х
г+1"
*• — Of — ! у — *• О»
Пример. Найти фундаментальную систему решений системы
однородных уравнений
^4=0'
E)

§ Ю1
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ
359
Решение. Ранг матрицы системы E) г = 2, причем
1 —1
1 1
= 2^0.
Поэтому два последних уравнения системы E) являются
следствием двух первых. Решаем подсистему
+ *4>1
-3*4.j
Полагая сперва лг3=1; л;4 = 0, а затем лг3 = 0 и ЛГ4==Ь
получим два линейно независимых решения
.A)
f_A 1 i oY
[ 2 ' 2 ' ^ 0>
*B> = (-l, -2, О, 1),
которые образуют фундаментальную систему решений системы E).
Векторы jcA) и х{2) образуют базис пространства решений
данной системы, и все ее решения определяются формулами
лг1= —3ct—с2,
2clf
где сг и с2—произвольные постоянные (здесь для удобства первая
постоянная взята в виде 2сг).
§ 10. Линейные преобразования переменных
Пусть х1У х2, ..., хп—некоторая система переменных величин,
а Ух* Уы •••> Уп — Другая система переменных величин, связанная
с первой следующими соотношениями:
A)
где Л» Л» •••> /„ — заданные функции.
Переход от системы х19 лг2, ..., хп к системе yv y2, ..., уп
будем называть преобразованием.
Определение. Преобразование A) называется линейным, если
новые переменные yv уг> т.., уп являются линейными однородными

360 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
функциями старых переменных xv хг,
У\ ==s a\\*\ Jr а12*2 + ¦ • • + а1пХп>
B)
где а?у(/= 1У 2, . .., /г; у=1, 2, ..., л) — постоянные.
Линейное преобразование B) однозначно определяется своей
квадратной матрицей коэффициентов (матрицей преобразования)
ап al2...aln
а21 а22...а2п
ап\ ап2...ап
Обратно, имея квадратную матрицу ^ = [#//], можно построить
линейное преобразование, для которого эта матрица служит матрицей
коэффициентов. Таким образом, между линейными преобразованиями
и квадратными матрицами существует взаимнооднозначное
соответствие.
Системы переменных хг, х2, ..., xnuyv j/2, ..., уп можно
рассматривать как векторы-столбцы
и v =
одного и того же векторного пространства Еп. Поэтому
преобразование B) отображает пространство Еп на самого себя или на свою
правильную часть.
Пример 1. Преобразование
переводит пространство/^ в подпространствоуг~у2 размерности 1.
Соотношения B) эквивалентны одному матричному соотношению
у = Ах. C)
Действительно, по правилу умножения матриц мы имеем:
Ух
У2

§ 101
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ
361
Отсюда на основании понятия о равенстве матриц получаем
формулы B). Согласно формуле C) матрицу А можно рассматривать как
оператор линейного преобразования.
Линейное преобразование, как легко убедиться непосредственно,
обладает двумя основными свойствами:
1) постоянный множитель можно выносить за знак оператора
линейного преобразования, т. е.
А (ах) = аАх;
2) оператор линейного преобразования от суммы нескольких
векторов равен сумме операторов от этих векторов, т. е.
Как следствие имеем:
А (ах + рг) = аАх + §Az
(х> z — векторы, а и р— скаляры).
Пример 2. Пусть на плоскости Охххг
каждому вектору
-и
ставится в соответствие вектор
'-[?]•
являющийся проекцией вектора х на ось Охг (преобразование
проектирования) (рис. 52). Показать, что данное
преобразование—линейное, и найти матрицу преобразования.
Решение. Очевидно, имеем:
Рис. 52.
и, следовательно, преобразование проектирования является
линейным. Матрица преобразования есть
Выясним смысл элементов a(j матрицы преобразования Л.
Рассмотрим единичные векторы (орты), направленные по осям
координат Oxv Одг2, ..., Охп:
гот
1
•» еп~
LoJ

362 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
«11
«21
«nl
«12-
«22-
*.«¦
••«in
••«2Я
X
0
i
Ц
a
f=\, 2, ..., л).
{-since, cosoc}
Таким образом, а^ представляет собой /-ю координату
преобразованного у'-го единичного вектора.
Пример 3. Пусть на плоскости Оххх2 каждый
радиус-вектор х заменяется той же длины радиусом-вектором у,
повернутым относительно первого на
угол а (преобразование вращения)
(рис. 53).
Показать, что данное
преобразование—линейное, и найти
матрицу преобразования.
Решение. С вектором у
свяжем координатную систему
¦" ОУьУа» которая повернута отно-
и "' *' сительно координатной системы
Рис. 53. Охгх2 на угол а. Так как
координаты вектора^ в системе Оу^у2,
очевидно, есть хх и х2, то координаты этого вектора в старой
системе Охгх2 по известным формулам аналитической геометрии
выразятся следующим образом:
D)
уг = ATjCos a — x2 sin a,
у2 = jic1sin a -f- *2 cos a-
Таким образом, преобразование вращения есть линейное, и его
матрица имеет вид
л — fcosa —sinal
[sin a cos aj"
Можно иначе решить задачу: в результате преобразования
единичный вектор ev очевидно, переходит в вектор {cos a, sin а}, а
единичный вектор е2 — в вектор {— sina, cosa}. Следовательно,
согласно сказанному выше матрица преобразования есть
. __ Fcosa —sinal
~~ [sina cosaj '
и мы снова приходим к формулам D).

§ 10} ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ 363
Определим следующие действия над линейными
преобразованиями А и В: 1) сложение А-\-В\ 2) умножение на
скаляр аЛ; 3) умножение (композиция) ВА с помощью
естественных соглашений:
E)
2) (аА)х-=а(Ах); E')
3) (ВА)х = В(Ах), E")
где х — вектор.
Легко проверить, что если А и В — линейные преобразования,
то результирующие, преобразования А-\-В, аА и ВА также
линейные.
Имеет место следующий принцип: каждому действию 1) —3) над
линейными преобразованиями соответствует такое же действие
над матрицами этих линейных преобразований, т. е. формулы
E), E'), E") можно понимать в буквальном смысле.
Для доказательства ограничимся третьим случаем E")
[формулы E) и E') проверяются более просто].
Пусть нам требуется последовательно выполнить два линейных
преобразования:
F)
Уп = + + )
с матрицей Л = [а(у] и
с матрицей B=[~ljr
Обозначим через C=[cf.y] матрицу композиции этих
преобразований в указанном порядке, т. е. переход от переменных х, *;.,, ,хп
к переменным zv z%y . .., zn. Коротко записывая преобразования F)
и G) в
Ук= S akjxj (Л=К 2 п).
F')

364 сведения из теории линейных векторных пространств [гл. х
и подставляя формулу F') в формулу G'), получим:
*i=%bil 2 *h/x})e 2 */ 2 *'***>• (8)
Таким образом, коэффициент при лгу в выражении для zi% т. е,
элемент Сц матрицы С, имеет вид
ct/ =
2
k-i
• • • +bina
inanf
Мы видим, что элемент матрицы С, стоящий в 1-й строке и у-м
столбце, равен сумме произведений соответствующих элементов i-й
строки матрицы В и /-го столбца матрицы Л, т. е, совпадает
с соответствующим элементом произведения матрицы В на матрицу^.
Следовательно, С=ВА.
Пользуясь матричными обозначениями, доказательство можно
провести значительно проще. Пусть
г*1
ГУг!
1/2
-Уя-
и z =
— соответствующие векторы. Из формул F) и G) имеем:
у = Ах и z = By.
Отсюда
Следовательно, матрица результирующего преобразованияС—ВА.
Пример 4. Найти результат последовательного выполнения
линейных преобразований:
Решение. Напишем матрицы преобразований
5—1 3
1 —2 О
О 7—1
л В=
2 0 1
О 1 —5
0 2 0

§ 111
ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ
365
Перемножая эти матрицы, получим матрицу результирующего
преобразования
2
0
0
0
1
2
1
—5
0
5
1
0
— 1
— 2
7
3
0
— 1
=
10
1
2
5
-37
— 4
5
5
0
Следовательно, искомое линейное преобразование имеет
следующий вид;
— 5лг3;
§11. Обратное преобразование
Пусть данное линейное преобразование
ух = а11лг1 + а12лг2 +... + а1ях
Уг = «21*1 + «22*2 + • • • + ««Л. |
A)
Л = ««1*1 + ««2*2 + • • • + «„Л
переводит систему переменных xv лг2, ..., хп в систему перемен-
ных yv у» ..., уп.
Определение. Преобразование, переводящее систему
переменных yv j/2, ..., уп в систему переменных лг1э л:2, ..., лгп,
называется обратным по отношению к преобразованию A).
Формулы обратного преобразования мы получим, разреши»
систему A) относительно переменных xv лг2, ..., хп.
Пусть Ау (/, у = 1, 2, ..., п) — алгебраические дополнения
элементов a(j матрицы А = [пу] и
Умножая уравнения системы A) соответственно на A1V Atv... ,
и складывая, в силу известной формулы будем иметь:
Аналогично выводим:

366 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ПЬ X
Отсюда
B)
Таким образом, обратное преобразование линейного
преобразования также является линейным (если оно существует).
Теорема. Линейное преобразование имеет однозначное
обратное преобразование тогда и только тогда, когда матрица
данного преобразования — неособенная. Обратное преобразование
линейного преобразования есть линейное, и его матрица
является обратной по отношению к матрице исходного
преобразования.
Доказательство. Если Л = [д17] — матрица
преобразования A) и A = deti4r^O, то обратное преобразование существует
и определяется формулами B). Матрица обратного преобразования,
очевидно, равна
Если А = 0, то, как известно из алгебры, уравнения A) нельзя
однозначно разрешить относительно переменных xv х2, .. •>•*„•
Следовательно, однозначного обратного преобразования не существует,
причем обязательно найдутся значения переменных yv у2,... ууп, для
которых не существует соответствующих значений переменных
х1У дг2, ..., хп. Линейное преобразование в этом случае называется
вырожденным.
Замечание 1. Запишем преобразование A) в матричной
форме
У = Ах% C)
где Л = [<*//] — матрица преобразования; х ну—векторы-столбцы.
Если преобразование Л — невырожденное (det A =^=0), то
существует обратное преобразование
x = A'*y> D)
и каждому вектору х из л-мерного пространства Охг дг2.. ,хп, в силу
формулы C), соответствует один и только один вектор у
этого пространства, т. е. формула C) преобразует пространство
Охгх2.. ,хп в самого себя.
Если преобразование А — вырожденное (deti4 = 0), то
формула C) преобразует пространство Оххх2.. .хп в подпространство
низшего числа измерений.

§ 12] СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ 367
Пример. Рассмотрим преобразование проектирования (§ 10,
пример 2), определяемое матрицей
Lo oj •
Здесь матрица А — особенная и преобразование у = Ах переводит
пространство Охгх2 в координатную ось Oxv
Замечание 2. Будем понимать под Ех тождественное
преобразование, оставляющее вектор х неизменным.
Так как из соотношений
yz=z Ax u jc = A~ly
следует
y = AA"~ly и jc = И
то
§ 12. Собственные векторы и собственные значения матрицы
Пусть дана квадратная матрица А = [пу]. Рассмотрим линейное
преобразование
У = Ах, A)
где х и у — л-мерные векторы (столбцовые матрицы) некоторого,
вообще говоря, комплексного «-мерного пространства.
Определение 1. Ненулевой вектор называется собственным
вектором данной матрицы (или определяемого ею линейного
преобразования), если в результате соответствующего линейного
преобразования этот вектор переходит в коллинеарный ему, т. е. если
преобразованный вектор отличается от исходного только
скалярным множителем.
Иначе говоря, вектор хфО называется собственным вектором
матрицы Л, если эта матрица переводит вектор х в вектор
Ах = Хх. B)
Число X, стоящее в равенстве B), называется собственным значе*
наем, или характеристическим числом, матрицы А, соответствующим
данному собственному вектору х.
Пример 1. Рассмотрим преобразование проектирования в
двумерном пространстве Охххг% определяемое матрицей
П 0]
1=М-

368 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Здесь собственными векторами являются: 1) ненулевые векторы х,
направленные по оси Oxv с собственным значением A^a^l и
2) ненулевые векторы у, направленные по оси Олг2, с собственным
значением Л2 = 0 (рис. 54).
Теорема 1. В комплексном векторном пространстве каждое
линейное преобразование (матрица) имеет по меньшей мере один
действительный или комплексный
собственный вектор.
Доказательство. Пусть А —
матрица линейного преобразования.
Собственные векторы матрицы А
являются ненулевыми решениями
матричного уравнения
или
О *, D— &?)* = 0, C)
ис* ' где матрица А — КЕ называется
характеристической матрицей. Уравнение C)
представляет собой линейную однородную систему, которая имеет
ненулевые решения тогда и только тогда, когда определитель
системы равен нулю, т. е. должно выполняться условие
det (Л->?) = (). D)
Определитель D) называется характеристическим (вековым)
определителем матрицы Л, а уравнение D) называется
характеристическим (вековым) уравнением матрицы А. В развернутом виде
характеристическое уравнение D) запишется следующим образом:
аи—Я а12 ... а1п
«21 «22 —^ ••¦ «2/1
ап1 ап2 ... апп—К
D')
или
Я»-(т1Г-1+а2Г-2-...+(-1)в-Ч-^ + (-1)Х = 0. E)
Полином, стоящий в левой части уравнения E), называется
характеристическим полиномом матрицы А. Коэффициенты его
aI(/=l,2, ...,я) определяются по следующим правилам.
Коэффициент а± равен сумме диагональных элементов матрицы А, т. е.
o1 = 2Laii' Это число называется следом матрицы А и обознача-
/=i
ется так: a1 = Sp^. Коэффициент а2 есть сумма всех
диагональных миноров второго порядка матрицы А. Вообще, коэффициент oh

§ 12] СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ 369
есть сумма всех диагональных миноров /5-го порядка матрицы А.
Наконец, свободный член ап равен определителю матрицы А:
Характеристическое уравнение E) есть алгебраическое
уравнение п-Pl степени относительно X и, следовательно, как
доказывается в алгебре, имеет по меньшей мере один действительный или
комплексный корень. Пусть Я1? Ла, ..., кт (т ^ п) — различные
корни уравнения E). Эти корни называются собственными значениями,
или характеристическими числами, матрицы А7 а совокупность всех
собственных значений называется спектром матрицы А. Возьмем
какой-нибудь корень Я = Яу- и подставим его в уравнение D).
Тогда будем иметь (А — Х;Е) х = 0 или, в развернутом виде,
(^11 — ^7*) "^1 ~^~ ^12*^2 ~Ь • • • "Г" ^1«*^и==: ^»
F)
Так как определитель системы F) det(-4 — Xy-?) = 0, то эта
система заведомо имеет ненулевые решения, которые и являются
собственными векторами матрицы Л, соответствующими собственному
значению Ху-. Если ранг матрицы А — XfE равен r(r</z), то
существует & = л — г линейно независимых собственных векторов
ft 2/)
отвечающих корню Xj. Теорема доказана.
Замечание. Можно доказать, что число линейно независимых
собственных векторов, отвечающих одному и тому же корню
характеристического уравнения, не превышает кратности этого корня.
Отсюда, в частности, следует, что если корни характеристического
уравнения E) различны, то каждому собственному значению
соответствует с точностью до коэффициента пропорциональности один
и только один собственный вектор.
Пример 2. Найти собственные значения и собственные
векторы матрицы
Г2 1 П
1=1 2 1 .
Ь 1 2J
Решение. Составим характеристическое уравнение матрицы А:
[2-Х. 1 1 1
1 2-Х 1 =0.
1 1 2-rJ

370 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЯ. X
Отсюда (к— 1JD — Я) = 0 и Я.1==Я2 = 1; А^4-
Возьмем кх = 1 и подставим в уравнение
у = 0. G)
Имеем:
С i Ой
ИЛИ
(8)
Так как ранг матрицы системы (8) г=1, то два ее уравнения
являются следствием третьего (что, впрочем, очевидно). Поэтому
достаточно решить уравнение
Положив хг = с1; х2 = с2, получим:
где ct и с2 — любые числа, не равные нулю одновременно.
В частности, выбирая сперва сг = 1; с2 = 0, а затем сх = 0;
с2=1, будем иметь простейшую фундаментальную систему
решений, состоящую- из двух линейно независимых собственных
векторов матрицы А:
*¦¦
-[_;] -
Все остальные собственные векторы матрицы А% соответствующие
характеристическому числу Л,х = lt являются линейной
комбинацией этих базисных векторов и заполняют плоскость, натянутую на
векторы хКХ) и jcB' (исключая начало координат).
Возьмем теперь A,s = 4. Подставляя это значение в уравнение
G), получим:
П -1 ЛЯ-
или
— 2х2 + хя = О,
¦2лг3 = 0.
О)

§ 12] СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ 371
Ранг матрицы системы (9) г = 2, причем левый верхний минор
-I'M
Следовательно, третье уравнение системы есть следствие двух
первых, поэтому можно ограничиться системой из первых двух
уравнений:
Отсюда
= 0, \
= 0. j
I 1 11 I —2 11 1—2 II
1—2 l| I I l| I 1 —2|
или
Х1 Х2 Х3 -. ~ ^ у. V— /*
-g- — -g- — -g- , т. е. хг — хг — ха — с,
где с — постоянная, отличная от нуля.
Положив с = 1, получим простейшее решение, реализующее
собственный вектор матрицы А:
¦(:}
Определение 2. Линейное подпространство Ek(k^п)
называется инвариантным относительно данного линейного
преобразования
если каждый преобразованный вектор этого подпространства также
принадлежит ему, т. е. из x?Ek следует Ax?Ek.
Очевидно, что доказательство теоремы 1 полностью остается в
силе, если рассматривать линейное преобразование, определяемое
матрицей А, в некотором инвариантном пространстве.
Теорема 1'. Каждое линейное преобразование, определенное
на инвариантном подпространстве комплексного векторного
пространства, имеет по меньшей мере один собственный вектор.
Отметим еще одно важное свойство собственных векторов.
Теорема 2. Собственные векторы матрицы, соответствующие
попарно различным между собой собственным значениям, линейно
независимы.
Доказательство. Пусть Л —данная матрица и
*,*</> (у=1, 2, ..., /»), A0)
где
</>^О и Ь)ФК при

372 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Допустим, что
схха) + с2х<2) + •.. + стхт = О, A1)
где || + ||+
Пусть для определенности сг^0. Применяя к равенству A1)
преобразование Л, в силу формул A0) будем иметь:
Отсюда, умножая равенство A1) на Хт и вычитая из
полученного равенства равенство A2), находим:
Далее, из равенства A3) аналогичным приемом можно исключить
вектор х{т~г) и т. д. В результате, исключая векторы
л , Аг , . . ., л ,
получим:
Но последнее равенство невозможно, так как ни один из
сомножителей его левой части не равен нулю. Следовательно, наше
допущение ложно и собственные векторы лсA), х{2\ ..., х{т)
линейно независимы.
Следствие. Если все собственные значения матрицы А
порядка п попарно различны, то отвечающие им собственные
векторы этой матрицы в числе, равном л*), образуют базис
соответствующего /г-мерного пространства.
§ 13. Подобные матрицы
Определение. Две матрицы, соответствующие одному
и тому же линейному преобразованию в различных базисах,
называются подобными.
Если матрица А подобна матрице S, то пишут А с/>#. Выведем
условие подобия двух матриц. Пусть матрица А в некотором базисе
реализует линейное преобразование
у = Ах. A)
В новом базисе (в новых координатах) это же линейное
преобразование будет описываться другой матрицей В:
4 = **. B)
где
ВспА.
*) Предполагается, что для каждого собственного значения берется
один собственный вектор-

§ 13] ПОДОБНЫЕ МАТРИЦЫ 373
Обозначим через 5 матрицу перехода от новой системы к
старой, т. е. пусть
x = S|, jy-A), C)
где
Подставив формулы C) в уравнение A), получим:
Отсюда, умножая слева последнее равенство на обратную
матрицу 5, будем иметь:
D)
Сравнивая формулы D) и B), получим:
E)
Относительно матриц А и В, связанных соотношением E),
говорят, что матрица В получается из матрицы А путем
преобразования с помощью матрицы S. Таким образом, заключаем, что две
матрицы подобны тогда и только тогда, когда одна получается из
другой путем преобразования с помощью некоторой неособенной
матрицы.
Из равенства E) выводим A — SBS, т. е. если матрица В
подобна матрице Л, то и, наоборот, матрица А подобна
матрице В. Отметим некоторые свойства преобразования с помощью
матрицы 5.
1. Преобразование суммы равно сумме преобразований:
2. Преобразование произведения равно произведению
преобразований сомножителей:
3. Преобразование обратной матрицы равно обратной матрице от
преобразов анной:
4. Преобразование целой степени (положительной или отрицав
тельной) равно той же степени преобразования:
Теорема 1. Подобные матрицы имеют одинаковьсе
характеристические полиномы.

374 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Доказательство. Пусть ВопА. Требуется доказать, что
det (А — КЕ) = det (?— IE).
Так как
B^S^AS (det S ФО),
то
det (Я— КЕ) = det [S~l (A — КЕ) S] =
= det S det (A — КЕ) det 5 = det {A — А.Е) *).
Итак,
det(B —X?) = det(i4-
Следствие 1. Подобные матрицы имеют одинаковые следы
и одинаковые собственные числа (включая их кратности).
Следствие 2. Свойство вектора быть собственным для
данного линейного преобразования не зависит от выбора базиса.
В самом деле, пусть
Ах = Кх (х
Если в новом базисе вектор х эквивалентен вектору ?, то имеем:
где S — матрица перехода.
Отсюда AS§ = XS§ и, следовательно, 5"М5^ = Л§, т. е. ?есть
собственный вектор для матрицы B=S~1ASor>A1 описывающей
в новом базисе наше линейное преобразование.
Замечание. Так как характеристический полином,
собственные значения и собственные векторы одинаковы для всех матриц,
реализующих данное линейное преобразование, то они называются
соответственно характеристическим полиномом, собственными
значениями и собственными векторами самого линейного преобразования.
Теорема 2. Если данная квадратная матрица порядка п имеет
п линейно независимых собственных векторов, то, приняв последние
за базисные, получим диагональную матрицу, подобную данной.
Доказательство. Пусть имеем квадратную матрицу А. Из
ее собственных векторов ev e2> ..., еп образуем базис. Так как
векторы 01 — собственные, то
Aef = Xfef G=1, 2, ..., п).
*) Мы здесь пользовались известными теоремами (см. гл. VII, § 2 и §4):
1) определитель произведения двух квадратных матриц одинакового порядка
равен произведению определителей этих матриц, 2) определитель обратной
матрицы равен обратной величине определителя исходной матрицы.

§ 14] БИЛИНЕЙНАЯ ФОРМА МАТРИЦЫ 375
Рассмотрим любой вектор х нашего пространства. Раскладывая
его по базисным векторам е^ (/=1, 2, ..., п), будем иметь:
2 jj
где Xj — координаты вектора х в данном базисе.
Применяя преобразование А к вектору х, получим новый вектор
п
у = Ах = А 2 XjCj
или, так как преобразование А линейное,
п п
у = 2 XjAej= 2 */*/*/•
Отсюда видно, что координаты вектора у в данном базисе есть
yj^ljXj (y=l, 2, ..., л)
или
где 6yft — символ Кронекера.
. Следовательно, в новом базисе матрица преобразования есть
диагональная матрица
или, в развернутом виде,
TXj 0 0 ... О
л== о х2 о ... о
.о о o,.U
Следствие. Всякую квадратную матрицу, собственные
значения которой попарно различны, путем преобразования подобия
можно привести к диагональному виду.
Этот результат вытекает непосредственно из теоремы 2
предыдущего параграфа.
§ 14. Билинейная форма матрицы
Пусть A = [ujk] — действительная квадратная матрица и х,у —
векторы я-мерного комплексного пространства. Составим скалярное
произведение
(Ах, у) = 2 (ах)}у) - 2 2

376 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [iVU X
Выражение A) называется билинейной формой матрицы Л.
Выведем одно важное свойство билинейной формы. Сумма A),
очевидно, будет иметь прежнее значение, если изменить порядок
суммирования и одновременно взаимно поменять обозначения
индексов суммирования. Поэтому получим:
п п
(Ах, ji)=S2 l
Запишем полученную сумму в виде скалярного произведения
(ах, л=2 2 **/*>*=( 2 2 **
Таким образом,
(Ах, у) = (х, Л», B)
т. е. в скалярном произведении A) действительную матрицу А
можно переставлять с первого места на второе, заменяя ее
транспонированной.
Следствие. Если матрица А — действительная и
симметрическая (Л' = Л), то
(Ах, jr) = (*. Ay), C)
т. е. в скалярном произведении действительную симметрическую
матрицу можно переставлять с первого места на второе.
§ 15. Свойства симметрических матриц
Теорема 1. Все собственные значения симметрической матрицы
с действительными элементами — действительные.
Доказательство. Пусть А, — собственное значение
матрицы Л и х — соответствующий собственный вектор, т. е.
Ах^Кх (хфО). A)
Так как Af=^At то
(Ах, х) = (х, Ах)
или в силу равенства A)
(Kxf #) = (*
Отсюда
к(х, х) = А* (л:, х).
Собственный вектор по определению — ненулевой, поэтому
(х, Х)ФО
и, следовательно, Я = А.*, т. е. X — действительное число.

§ 15] СВОЙСТВА СИММЕТРИЧЕСКИХ МАТРИЦ 377
Следствие. Характеристическое уравнение для
действительной симметрической матрицы имеет только действительные корни.
Теорема 2. Собственные векторы действительной
симметрической матрицы, соответствующие различным собственным значениям,
ортогональны между собой.
Доказательство. Пусть А — действительная
симметрическая матрица. Рассмотрим два собственных вектора хи) и лг(/>,
соответствующие собственным числам Х( и \j (\.фХ^ш Имеем:
= К:ХК B)
- hjX . \О)
Составим скалярное произведение
Отсюда в силу равенств B) и C) получаем:
D)
Так как на основании теоремы 1 собственное число \, — дей-
ствительное, то А/ = Лу.
Следовательно, из формулы D) имеем:
Я, —
(
Но
поэтому
т. е. собственные векторы х{1) и x{J) ортогональны между собой.
Замечание. Собственные векторы симметрической матрицы
с действительными элементами можно полагать действительными.
Теорема 3. Всякую действительную симметрическую матрицу
при помощи преобразования подобия можно привести к
диагональному виду.
Доказательство. Ограничимся при доказательстве для
наглядности случаем трехмерного пространства ?3.
Пусть дана симметрическая матрица А третьего порядка. Как
известно, всякая матрица имеет по меньшей мере один собствен*
ный вектор (§ 12, теорема 1). Обозначим через ег собственный
вектор матрицы А. Так как эта матрица — симметрическая, то
вектор ег можно выбрать действительным.
Рассмотрим все векторы х, ортогональные к вектору ех% т. е.
такие, что
(*. *t)-o. E)

378 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Покажем, что эти векторы образуют инвариантное
подпространство Е2 относительно преобразования А (рис. 55).
В самом деле, прежде всего, если х?Е2 и у?Е2, т. е.
то для любых чисел аир имеем:
и, следовательно,
Таким образом, множество векторов, удовлетворяющих условию E),
образует линейное пространство, причем легко убедиться, что
измерение этого пространства равно
двум.
Пусть теперь х ? Е2. Рассмотрим
скалярное произведение
(Ах,
т. е.
В силу теоремы Г (§ 12)
в двумерном пространстве Е2 также
существует собственный вектор е2
матрицы А. Будем теперь
рассматривать векторы х, ортогональные
как к вектору elt так и к вектору е2,
Рис. 55. т- е- такие» чт0
Аналогично предыдущему доказывается, что эти векторы
образуют одномерное пространство Ег, инвариантное относительно
преобразования А. В пространстве Ег снова имеется собственный
вектор ег матрицы А Векторы ег> е2> е3, будучи попарно
ортогональными, линейно независимы между собой. Таким образом, мы
построим ортогональный базис пространства Ед, состоящий из
собственных векторов матрицы А.
Обозначим через Яу собственные значения, соответствующие
собственным векторам е^ В силу теоремы 2 из § 13 матрица Л данного
линейного преобразования в собственном базисе ev e2i e3 будет
диагональной, причем в нашем случае
Г** 0 0 1
: 0 Я2 0 .
Lo о b8j
Л =
Аналогично доказывается теорема и в общем случае.

§ 15] СВОЙСТВА СИММЕТРИЧЕСКИХ МАТРИЦ 379
Следствие 1. Для всякого линейного преобразования с
действительной симметрической матрицей существует ортогональный
базис, состоящий из действительных собственных векторов данной
матрицы, в котором матрица преобразования — диагональная.
Следствие 2. Если матрица—-симметрическая, то каждому
собственному значению ее соответствует столько линейно
независимых собственных векторов, какова кратность этого собственного
значения.
Теорема 4(экстремальное свойство собственных
значений). Пусть А — действительная симметрическая матрица и
v Я2, ..., Яп),
где кг, Я2, ..., Кп — все собственные значения матрицы Д.
Тогда для любого вектора х справедливо неравенство
% (л:, х) ^ (Ах, *)< Л (jc, х). F)
Доказательство, В силу следствия 1 к теореме 3
существует система собственных векторов е1У е2, ..., еп матрицы А:
(у=1, 2, ..., л),
образующих нормированный ортогональный базис пространства Еп.
Тогда любой вектор х можно представить в виде
где х19х2, .. .,хп — координаты вектора х в данном базисе. Отсюда
Ах = х1Ае1 + х2Ае2 + ... + хпАеп = ^х^ + К2х2е2 + ..
Учитывая ортогональность векторов базиса, будем иметь:
/ п п \ п п
(Ах, х) = ( 2 XjXje/t 2 xkek) = 2 2 ^,X/xl (e
\/=i *=i / /=i*=i
^/» «v =
т. е.
п
{Ax, *)=
Заменяя в равенстве G) Ay на наименьшее значение Я, получим:
п
(Ах, х)^К 2l*/i* = M*. X).

380 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
Аналогично, подставляя в равенство G) вместо Яу наибольшее
значение Л, находим:
Их, *)<Л 2 !*,!¦== Л(*,*).
Таким образом, неравенство F) доказано.
Следствие. Минимальное собственное значение Я и
максимальное собственное значение Л симметрической действительной
матрицы А являются соответственно наименьшим и наибольшим
значениями квадратичной формы
и = (Ах, х)
на единичной сфере (х, х) = 1.
Действительно, полагая (х, jc) = 1b неравенстве F), будем иметь:
Я<(Лх, х)<Л.
Кроме того, если Лх = Ях, то
{Ах, х) = (Ял, х) = Я;
аналогично, если А* = Лх, то
(Ах, х) = (Лх, х) = Л.
Таким образом,
Я = min (Ах, х) при (х, х) == 1
и
Л = max (А*, х) при (х, х) = 1.
Действительную симметрическую матрицу Л = \atj\ назовем
положительно определенной, если соответствующая квадратичная форма
п п
и = (Ах, х) = 2 S
(si/el
является положительно определенной (гл, VIII, § 13), т. е. для
любого вектора хфО имеем:
(Ах, х) > 0.
Теорема 5. Действительная симметрическая матрица является
положительно определенной тогда и только тогда, когда все
собственные значения ее положительны.
Доказательство. Если А — действительная симметрическая
матрица и ее собственные значения Яу таковы, что Яу>0(/=1,
2, ..., п), то на основании формулы G) из доказательства
предыдущей теоремы имеем:
2

§ 16] СВОЙСТВА МАТРИЦ С ДЕЙСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ 381
где x = {xv дг2, ...,лг„). Отсюда при хфО получим:
{Ах, х) > О,
т. е. матрица А—положительно определенная.
Обратно, пусть А—действительная симметрическая
положительно определенная матрица.
В силу теоремы 1 все ее собственные значения Xv Я2, ...Дй
действительны, причем
является наименьшим значением квадратичной формы и-=(Ах, х)
на сфере (х,х) = \. Так как сфера (х, х)~ 1—компактное и
ограниченное множество и квадратичная форма и непрерывна и
положительна на этой сфере, то по теореме Вейерштрасса наименьшее
значение и существует и также положительно, т. е.
Я>0.
Отсюда и подавно
А.у >0 при /=1,2,..., л.
Приведем без доказательства условия положительной
определенности действительной матрицы [2].
Теорема 6. Для положительной определенности
действительной матрицы А~\а{^ где а^=ад} необходимо и достаточно,
чтобы были выполнены условия Сильвестра:
к Л ^ п. А аП Л12
пц а12 ... а1п
«21 «22 .- (*%П
т. е. действительная симметрическая матрица А положительно
определенная тогда и только тогда, если все главные диагональные
миноры ее определителя detA строго положительны.
§ 16*- Свойства матриц с действительными элементами
В дальнейшем мы, как правило, будем рассматривать матрицы
Л = [«/у], элементы которых ai7- действительны; такие матрицы
называются действительными или вещественными.
Пусть A~[a{f] — действительная квадратная матрица порядка л,
Так как ее характеристическое уравнение
det(i4

382 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ [ГЛ. X
есть полином с действительными коэффициентами* то корни
Я-р Я2, ..., Хп характеристического уравнения, представляющие
собой собственные значения матрицы Л, в случае их комплексности
попарно сопряжены (гл. V, § 1), т. е. если Ks есть собственное
значение матрицы А, то сопряженное число Я* также является
собственным значением матрицы А и имеет ту же кратность.
Действительная матрица может не иметь действительных
собственных значений. Однако в одном важном случае, когда элементы
матрицы положительны, гарантируется существование хотя бы
одного действительного собственного значения [6].
Теорема Перрона. Если все элементы квадратной матрицы
положительны, то наибольшее по модулю собственное значение ее
также положительно и является простым корнем
характеристического уравнения матрицы, причем ему соответствует собственный
вектор с положительными координатами.
Собственные векторы действительной матрицы А с различными
собственными значениями в общем случае комплексные и не
обладают свойством ортогональности. Однако, привлекая собственные
векторы транспонированной матрицы А\ можно получить так
называемые соотношения биортогональности, которые для случая
симметрической матрицы эквивалентны обычным соотношениям
ортогональности.
Теорема 1. Если матрица А — действительная и собственные
значения ее попарно различны, то существуют два базиса {Xj} и
{х'.} пространства EnJ состоящих соответственно из собственных
векторов матрицы А и собственных векторов транспонированной
матрицы А\ удовлетворяющих следующим условиям биортонормировки:
3 при ]фку
1 при /=А.
Доказательство. Пусть Ях, Я2, ..., Яп —собственные
значения матрицы А. Так как матрица А — действительная, то, как мы
знаем, собственные значения ее — попарно сопряженные, т. е. наряду
с собственным значением Яу сопряженное число Я! также является
собственным значением матрицы А. Обозначим через Xj (/'= 1,2,..., п)
соответствующие собственные векторы матрицы Л, т. е.
(/=1,2, ...,/2). A)
Векторы {лгу} образуют базис пространства Еп (§ 12, теорема 2,
следствие).
Так как определитель не изменяет своего значения при замене
строк столбцами, то
det (А—КЕ) = det {А — КЕ)

§ 16] СВОЙСТВА МАТРИЦ С ДЕЙСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ 383
и, следовательно, транспонированная матрица А* имеет те же
собственные значения Яу, что и матрица А. Пусть x'.(j= 1,2 ..., п) —
собственные векторы матрицы Л', соответствующие сопряженным
собственным значениям к* т. е.
А'хг*к)х) (У=1,2, ...,л). B)
Векторы {х.} также образуют базис пространства Еп.
Базисы {Xj} и {х',} биортогональны, а именно:
(Хр х'к) = 0 при ]фк. C)
Действительно, с одной стороны, имеем:
(Ахр xk) = (\jxp xk) = Xf (Xp x'k). D)
С другой стороны, учитывая вещественность матрицы Л, получаем:
{AxJt xk) = (хр A'x'k) - (xj9 Vkxk) = Xk (X;, xk). E)
Из равенств D) и E) выводим:
Так как Xj^kk при ]фк, то из равенства F) вытекает равенство C).
Покажем, что векторы {Ху} и {jr.) можно нормировать так, чтобы
(*,,*;) = ! (/=1, 2, ...,п). G)
В самом деле, разлагая вектор х;- по векторам базиса {x'v х'2, ..., jcrt},
будем иметь:
Отсюда, учитывая условие биортогональности C), получим:
(*/f Xj) = c\ (Х/} Х[)+...+С* (XJ% Х])+...
• • • + сп (•*/> *'п) =с/ (*/» х
поэтому
Взяв вместо векторов jc^ , ...,лсг^ векторы —^ jc^ , ..., —^лг^
а1 ап
чим требуемую нормировку G), так как
^(*/>*')==V<Z/==1 (y=1, 2, ...,«).
Таким образом, если собственные значения действительной
матрицы А различны, то для собственного базиса {xf} матрицы А

384 СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНЫХ ВЕКТОРНЫХ nPOCTPAHCfВ [ГЛ. X
всегда можно найти собственный базис {х)} транспонированной
матрицы А' такой, что
где bJk — символ Кронекера.
Следствие. Если матрица А — действительная и
симметрическая (Л' = Л), то можно положить: x) = Xy{j=\f 2, ..., л),
где Xj — нормированные собственные векторы матрицы А (см. § 15).
Тогда
(*/» **) = */*•
Выведем еще так называемое билинейное разложение матрицы А.
Теорема 2. Пусть А — квадратная действительная матрица и
(/=1, 2, ..., л) — ее собственные векторы, рассматриваемые как
матрицы-столбцы^ и
(&= 1, 2, ..., п) — соответствующие*) собственные векторы
транспонированной матрицы А', рассматриваемые как матрщы-строки%
причем выполнены условия биортонормировки (8):
Иу, /Vfc ) = AkAj — ОуЛ. (У)
Гог<9а илгдег жесго соотношение
где Х19 Я2, ..., Я„ — собственные значения матрицы А.
Доказательство. Рассмотрим матрицы
Х1п
и Х' =
... х„
1_ х1П ... хпп
состоящие соответственно из столбцов Xj(j=l, ..., я) и строк
*•*(*=!, .... л).
В силу равенства (9) будем иметь:
\? х'ыхЛ =[X/X'l] = [b/i] = E,
(И)
где Е— единичная матрица. Так как матрица X состоит из линейно
*) То есть отвечающие тем же собственным значениям матриц А и А\

ЛИТЕРАТУРА К ДЕСЯТОЙ ГЛАВЕ 385
независимых столбцов, то она — неособенная, т.е. дегХфО и,
следовательно, существует обратная матрица X", На основании
равенства A1) (см. гл. VII, § 4, теорема, замечание 1) имеем:
Х^ = Х\
Отсюда вытекает, что
XX = ?,
и, таким образом, мы получаем вторые соотношения биортогональ*
ности [7]
2ед* = 6,7. A2)
Используя эти соотношения, имеем:
\ +... + ХпХп = [xnxtl] + [xttx',t] + ... )
т. е.
Е= Х1Х1+Х2Х2+ ... +ХпХп.
Умножая это равенство слева на матрицу А и учитывая, что
AXj-XjXj (/=1, 2, ..., я),
очевидно, получим равенство A0).
Обратим внимание на то, что в формуле (lO)^Yy иЛ/(/ = 1, 2,...,л) —
собственные векторы матриц Л и Л', соответствующие одному и
тому же собственному значению Яу«, вопреки обозначениям
теоремы 1, где Xj и х)—собственные векторы матриц А и А',
соответствующие комплексно сопряженным собственным
значениям kj и Я/.
Литература к десятой главе
1. Г. Е. Шилов, Введение в теорию линейных пространств, Гостехиздат,
М —Л., 1952, гл. I—IX.
2. И. М. Гельфанд, Лекции по линейной алгебре, Изд. 2., Гостехиздат,
М.—Л., 1951, гл. I—II.
3. А. И. Мальцев, Основы линейной алгебры, Гостехиздат, М.—Л.,
1948, гл. I—III.
4. А. С. Хаусхолдер, Основы численного анализа, ИЛ, 1956, гл. II.
5. Ю. А. трейдер, Решение систем линейных алгебраических
уравнений, Докл. АН СССР, б A951).
6. Ф. Р. Га н т м а х е р, Теория матриц, Гостехиздат, М., 1953, гл. VIII.
7. В. Н. Фаддее в а, Вычислительные методы линейной алгебры,
Гостехиздат, М.— Л., 1950, гл. I.
¦3 б. П. Демидович и И. А. Марон

ГЛАВА XI*
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СХОДИМОСТИ
ИТЕРАЦИОННЫХ ПРОЦЕССОВ ДЛЯ СИСТЕМ
ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 1. Сходимость матричных степенных рядов
Теорема 1. Матричный степенной ряд
A)
с числовыми коэффициентами ak сходится, если все собственные
значения Xv Я2, ,.., Кп матрицы X расположены в замкнутом круге
сходимости | х \ ^ R (рис. 56) скалярного
степенного ряда
со
akx B)
Рис. 56.
причем собственные
значения, лежащие на окружности круга
сходимости, простые и являются точками
сходимости ряда B).
Ряд A) расходится, если хотя бы
одно собственное значение матрицы X
находится вне замкнутого круга
сходимости ряда B), или имеется собственное
лежащее на окружности круга сходимости.
значение матрицы X,
для которого ряд B) расходится.
Доказательство. 1) Пусть матрица X такова, что
к,

поПредположим для простоты, что собственные значения
(/—1, 2, ..., п) матрицы X—простые. Тогда матрица X с
мощью неособенной матрицы 5 может быть приведена к
диагональному виду

§ 1] СХОДИМОСТЬ МАТРИЧНЫХ СТЕПЕННЫХ РЯДОВ 387
Введем обозначения
т
2*
Я*) == K
Имеем:
C)
Так как числа Xj расположены внутри круга сходимости степенного
ряда B) или совпадают с точками сходимости этого ряда,
принадлежащими окружности круга сходимости, то существуют конечные
пределы
(У=1, 2, ..., п).
Поэтому, переходя к пределу при т—»-оо в формуле C), получаем:
D)
т. е. матричный ряд A) в точке X сходится.
Можно доказать также, что утверждение теоремы верно и для
случая кратных собственных значений Яу, на чем мы
останавливаться не будем [1].
2) Пусть, например, хотя бы одно собственное значение Хг
матрицы X таково, что
\
Так как Хх лежит вне круга сходимости степенного ряда B), то
/т №г) при т—>>оо не имеет предела. Из формулы C) следует,
что Fm(X) при т—*оо также не имеет предела, т.е. ряд A) в
точке X расходится.
оо
Аналогичный результат получается, если | Xjl | = 7? и ряд У\акКг
*=о
расходится.
Замечание. Из формулы D) следует, что если ЛгДа, ..., Хп
есть простые собственные значения матрицы Ху то /(AJ, /(Ха), ...
/(*«), где
13*

388 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
являются собственными значениями функции
В частности, собственными значениями матрицы ?& являются числа
Ах, . . . , ЛЛ.
Теорема 2. Матричная геометрическая прогрессия
E+X+X*+...+Xk+..., E)
где X — квадратная матрица порядка п, сходится тогда и только
тогда, когда все собственные значения
lf = kj(X) С/= 1, 2, ..., п)
матрицы X расположены внутри единичного круга
\lf\<\ G=1, 2, ..., п), F)
причем если ряд E) расходится, то Xk-7*+0 при k—юо.
Доказательство. Действительно, так как для
соответствующего степенного ряда
радиус сходимости /?~1, причем при |лг| = 1 ряд G) расходится,
то в силу теоремы 1 геометрическая прогрессия E) сходится лишь
при выполнении условий F).
Если ряд E) расходится, то
l^l^l G=1, 2, ..., л).
Отсюда, предполагая для простоты, что собственные значения
Яр ..., Хп различны, будем иметь:
где vS—неособенная матрица. Поэтому
и, следовательно, Xky^0 при /f—юо. Последнее утверждение
остается справедливым и при наличии кратных значений Ау, на чем
мы останавливаться не будем.
• "Теорема 3. Модуль каждого собственного значения Х19 . .., кп
квадратной матрицы X не превосходит любой ее канонической
нормы, т. е.
11 (У=1. 2 я).

§ 2] ТОЖДЕСТВО ГАМИЛЬТОНА — КЕЛИ 389
Доказательство. Положим
и рассмотрим матрицу
где 8 > 0. Очевидно,
Следовательно (гл. VII, § 10, теорема 5) ряд
сходится.
Отсюда в силу теоремы 2 заключаем, что собственные значения
M-i» ..., М-,, матрицы Y удовлетворяют неравенствам
(у=1, 2, .... я).
Но из формулы (8) вытекает, что
P/=fTih </=*• 2, .... я).
Следовательно,
(/=1, 2, .... п)
или, ввиду произвольности числа 6,
что и требовалось доказать.
§2. Тождество Гамильтона — Кели
Теорема. Всякая квадратная матрица X является корнем
своего характеристического полинома, т. е. если
где яр (А.) = det (XjE1 — Х)у то
Доказательство. Пусть все собственные значения kv
Я2, ..., Яи матрицы Аг, т.е. корни характеристического уравнения
г|)(Х) = О, различны. Тогда матрицу X с помощью некоторой
неособенной матрицы S можно привести к диагональному виду

390 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
Так как \\>{Х) представляет собой частный случай матричного
степенного ряда, то на основании формулы D) из § 1 имеем;
Но, очевидно,
Поэтому
(У=1, 2, ..., п).
, 0, ,.., 0]5 = 0.
Если характеристическое уравнение \];(л) = 0 имеет кратные корни,
то их можно рассматривать как .пределы несовпадающих корней
при бесконечно малых возмущениях коэффициентов уравнения [1].
В результате теорема обобщается и на этот случай.
§ 3. Необходимые и достаточные условия сходимости
процесса итерации для системы линейных уравнений
Используя собственные значения матрицы а=[а//], можно дать
необходимые и достаточные условия сходимости процесса итерации
для линейной системы
л; = ал: + р, A)
где
rPi 1
и х==
Теорема. Для сходимости процесса итерации
B)
при любом выборе начального вектора хш и любом свободном
члене Р необходимо и достаточно, чтобы собственные значения
матрицы а, т. е. корни характеристического уравнения
det (а — ХЕ) = 0,
были по модулю меньше единицы.
Доказательство. Из формулы B) получаем:
- x{k) = (E+a + a?+ ... +a*~1)P + <z**(e). C)
Отсюда следует, что сходимость процесса итерации B) при
произвольных р и х{0) эквивалентна сходимости матричной
геометрической прогрессии
=2 а*.
D)

§ 51 необходимые и достаточные условия сходимости 391
В силу теоремы 2 из § 1 геометрическая прогрессия D) сходится,
если все собственные значения Kf(J= 1,2, . . ., п) матрицы а
удовлетворяют неравенствам
|Яу|<1 (у=1, 2, .... п). E)
Так как при этом а*—> () при k—*оо, то из формулы C) вытекает,
что процесс итерации сходится при любых р и х@\ т. е. существует
lira x{k)=-x,
А-> со
где х—, очевидно, решение системы A).
Если неравенства E) не выполнены, то ряд D) расходится. В таком
случае при некотором выборе начального вектора д:@) процесс
итерации, очевидно, также расходится.
Таким образом, для сходимости процесса итерации B)
необходимо и достаточно, чтобы все корни А15 Я2, ..., Ая
характеристического уравнения
—Я «
12 .- «!«
а22 ^ • • • а2п
= 0
удовлетворяли условиям: |Яу-|<1 (/=1, 2, ..., /г).
Следствие. Для сходимости процесса итерации B)
достаточно, чтобы ^
1|аЦ<1, F)
какова бы ни была каноническая норма (ср. гл. IX, § 1).
Действительно, в силу теоремы 3 из § 1, на основании
неравенства F) получаем неравенства E).
Замечание. Рассмотрим линейную систему
Ах = Ь, G)
где Л = [#1у] и 6=[^ ... Ьп]—вектор-столбец.
Пусть
гаг1 0 ... О п
D\ О а22 ... О \фОт
L V " 6 ' .'.." ' а/ш J
Для приведения системы G) к специальному виду A) обычно
полагают:
Отсюда
= b — (A—D)x,

392 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
и так как detD = ana22 ... аппхф0} то
Можно принять
Таким образом, для сходимости обычного процесса итерации для
линейной системы G) при любом свободном члене Ь и любом
начальном векторе xi0) необходимо и достаточно, чтобы все корни Ях,
Я2, ..., Кп характеристического уравнения
были по модулю меньше единицы. Пользуясь теоремой об
определителе произведения двух матриц, уравнение (8) можно
преобразовать следующим образом:
det D-1 det [(D — A) — №] = 0
или
т. е.
a2n
§ 4. Необходимые и достаточные условия сходимости
процесса Зейделя для системы линейных уравнений
Для линейной системы
х = ах + р,
Г Pi 1
где а = [а,у] и р =
, рассмотрим процесс Зейделя
A)
(k) ___ yi* tk) , VI Лк-i) . о и 1 9
/=1 /=/
при произвольном начальном векторе
г г@) 1
.., п; к = 1, 2, . ..)

§ 4] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ 393
Положим
где
в
[О 0 ... О От г ац а12 ... аХп 
«21 0 ... О О С= 0 ^ •• а2« I
««1 ««2 '•' ««,«-1 oJ L V 'о' \'..'апп J
Тогда процесс Зейделя в матричном виде можно записать
следующим образом:
х{к)^=Вх{к)-\Сх{к) + ^ F=1,2, ...). B)
Теорема. Для сходимости процесса Зейделя B) для си~
стемы A) при любом выборе свободного члена {J и начального
вектора хш необходимо и достаточно, чтобы все корни Xv .. ., Хп
уравнения
1 — ^ а12 ... (iin
= 0 C)
были по модулю меньше единицы.
Доказательство. Из формулы B) вытекает:
(Е- В) xik) = Cx{k~l) + р. ч D)
Матрица Е — В — неособенная, так как
det(E — ?) = !.
Поэтому равенство D) можно записать в виде
^*> = (?_B)-ic*<*-i> + (?--fl)-ip. (8)
Отсюда ясно, что процесс Зейделя эквивалентен процессу
простой итерации, примененному к линейной системе
В силу теоремы предыдущего параграфа, для сходимости
итерационного процесса E) необходимо и достаточно, чтобы корни
Ац, ..., Хп характеристического уравнения
det [(? — S)-i С— Щ = 0 F)
удовлетворяли условиям
|Х,|<1 (у=1, 2, ..., л).
Уравнение F), очевидно, равносильно уравнению C),

394 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
Замечание. Пусть
Положим
G)
ап О ... О
О а22 ... О
О ' *0* '..'. а"
?=0.
Для применения метода Зейделя систему G) обычно записывают
в форме
Dx^(D — A)x + b
или
X = D'1 (D — А) х + D~lb. (8)
Положим
где
о о ... о о
а21 0 ... О О
ап2 ••• «
Л, «-1
/~>
О 0 ... О
Тогда
где
и С = —
причем треугольные матрицы В я С реализуют разбиение матрицы
системы (8), необходимое для применения процесса Зейделя. На
основании формулы C) сходимость процесса Зейделя для
системы G) зависит от свойств корней уравнения
ЯЛЬ] = 0. (9)
Уравнение (9) можно заменить эквивалентным уравнением
или
... а2
ап1% a
= 0.
A0)

§ 5] СХОДИМОСТЬ ПРОЦЕССА ЗЕЙДЕЛЯ ДЛЯ НОРМАЛЬНОЙ СИСТЕМЫ 395
Таким образом, для сходимости процесса Зейделя для системы G)
при любом свободном члене Ь и любом начальном приближении д:@)
необходимо и достаточно, чтобы все корни kf уравнения A0)
удовлетворяли условиям
\kf\<l (/=1, 2, ..., п).
§ 5. Сходимость процесса Зейделя для нормальной системы
Теорема. Для нормальной системы обычный процесс Зейделя
сходится при любом выборе начального вектора.
Доказательство. Пусть линейная система
Ax = h A)
— нормальная, т. е. матрица Л —[а/у]— симметрическая и
положительно определенная.
Положим
где
а1г 0
0 а2г
— диагональная матрица,
0 0
О 0
а21 0
ап1 ап%
•нижняя треугольная матрица,
0 а±2
0 0
0 0
а1п
а2п
0
— верхняя треугольная матрица, являющаяся ввиду симметричности
матрицы Л транспонированной по отношению к матрице V. Тогда
имеем:
(D+V+V*)x = b.
Отсюда
Dx = h-~{V-\-V*)x
и, следовательно,
х - D~lh-D'1 (V+ V*) х% B)

396 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
где
г«- ° - °п
"о -L ... . о
а22
о о
1
«лп J
Согласно предыдущему процесс Зейделя для системы A) или
эквивалентной ей системы B) строится следующим образом:
(ft=l, 2, ...),
C)
где
и С= —
Для сходимости процесса в силу теоремы предыдущего параграфа
необходимо и достаточно, чтобы все собственные значения Я матрицы
М=(Е — В)'1 С
были по модулю меньше единицы.
В нашем случае имеем:
Пусть е — единичный собственный вектор матрицы Ж,
соответствующий собственному значению Я, т. е.
или
Отсюда
и, следовательно,
V*e = — k(D+V)e.
(V*e, e) = — \[(D+V)e, e]
. __ (V*e, e)
Введем обозначения
(De, e)-\-(Ve, e) '
n
{De, e) = 2 ajj I ej |2 = о > О
(Vey е) = а + ф
(аир действительны и i = }/— 1).

§ 6] СПОСОБЫ ЭФФЕКТИВНОЙ ПРОВЕРКИ УСЛОВИЙ СХОДИМОСТИ 397
Ввиду того, что матрица V* является транспонированной по
отношению к матрице V, получаем:
(V*e, е) = (е, Ve) =
Поэтому
и, следовательно,
Используя положительную определенность матрицы Л, будем иметь:
(Aet e) = {De, e) + (Ve, e) + (V*e, e) =
т. е.
G-f-a>— a. E)
Далее, учитывая положительность числа сг, очевидно, имеем:
Таким образом, всегда выполнено неравенство
а + а > |а|. F)
Отсюда для членов дроби D) будем иметь:
т. е.
что и требовалось доказать.
§ 6. Способы эффективной проверки условий сходимости
Для проверки условий теорем сходимости итерационных процессов
нужно иметь эффективные критерии, позволяющие определять,
удовлетворяют ли корни к19 к2, . . ., Хп данного алгебраического полинома
1 0)
требованию
|*,|<1 (У=1, 2, .... я) B)
или не удовлетворяют ему. Этот вопрос можно просто разрешить,
воспользовавшись известными условиями Гурвица [2].

398 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
Т'е орема Гурвица. Пусть коэффициенты pk (k = О ,1, ..., п)
полинома A) действительны, причем
Рз
0
0
Ро
Р2
0
0
0
Pi
0
0
0 ..
Ро ••
0 ..
0 ..
. 0
. 0
• Рп
. 0
0
0
Рл-1
0
0
0
Рл-2
Рп
— матрица п-го порядка, строки которой представляют собой
расширенные последовательности коэффициентов полинома A)
где положено pk~0 при k < 0 и k > п. Тогда все корни Я1Э
п Кп полинома A) имеют отрицательные вещественные
части
ReXy < О
=1, 2, .... /г)
(т. е. расположены в левой полуплоскости комплексной плоскости
Х=а-|-гР) в том и только том случае, если главные диагональные
миноры матрицы М положительны, т. е.
Pi Ро
Рг Р2
C)
Пример 1. Для квадратного трехчлена
условия Гурвица таковы:
Ро > 0, Рг > 0, р2 > 0.
Нас интересует вопрос, когда корни полинома A) удовлетворяют
условию B), т. е. лежат на комплексной плоскости К внутри
единичного круга
С помощью дробно-линейной функции

§ 6] СПОСОБЫ ЭФФЕКТИВНОЙ ПРОВЕРКИ УСЛОВИЙ СХОДИМОСТИ 399
внутренность единичного круга | X | < 1 преобразуется в левую
полуплоскость Re A < 0. При этом наш полином A) принимает вид
Следовательно, корни полинома A) тогда и только тогда
расположены внутри единичного круга, когда вспомогательный полином
удовлетворяет условиям Гурвица C), причем знак выбирается так,
чтобы старший коэффициент
Пример 2. Рассмотрим квадратный трехчлен
f{b) = V + pl+q, D)
где р и q действительны. Вспомогательный полином имеет вид
Из условий Гурвица получаем:
Рассмотрим случаи:
а) ?<1, тогда q>— р— 1 и q>p— 1;
б) 0>1, тогда <7<—р—1 и <7<р—1, что невозможно.
Следовательно, уравнение D) имеет корни А,1, к2, по модулю
меньшие единицы, тогда и только тогда, когда
|*1<1. E)
Так как при п — 2 характеристическое уравнение матрицы а
имеет вид
12
а
21
или
Я2 — (а11 -[- а22) к + det а = О,
то для сходимости соответствующего процесса итерации для
системы двух уравнений необходимо, чтобы
|deta[<l.

400 ДОПОЛНИТ. СВЕДЕНИЯ О СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ [ГЛ. XI
Области сходимости процесса обычной итерации и процесса Зей-
деля, вообще говоря, перекрываются. Можно привести примеры
линейных систем, для которых процесс обычной итерации сходится,
а процесс Зейделя расходится, и
обратно [3].
Пример 3. Рассмотрим линейную
систему
х = ах + $ F)
с кососимметрической матрицей
—я р
(р и q действительны).
Характеристическое уравнение
матрицы а имеет вид
-я р—
Рис. 57.
или
Отсюда
Для сходимости метода обычной итерации необходимо и достаточно,
чтобы
т. е.
(область А на рис. 57).
Для метода Зейделя уравнение, определяющее сходимость,
имеет вид
р — X q
или
G)
На основании результатов примера 2 для того, чтобы корни Кг и Я2
уравнения G) удовлетворяли условиям
необходимо и достаточно выполнение неравенств
откуда
\р\<1,

ЛИТЕРАТУРА К ОДИННАДЦАТОЙ ГЛАВЕ 401
(область В на рис. 57). Так как области А и В частично
перекрываются, то отсюда следует, что для системы F) можно выбрать
коэффициенты р и д, во-первых, так, чтобы метод итерации
сходился, а метод Зейделя расходился (например, р=—0,5; # = 0,6),
и, во-вторых, так, чтобы, наоборот, метод Зейделя сходился, а метод
итерации расходился (например, /? = 0,5; #=1).
Литература к одиннадцатой главе
1. В. И. Смирнов, Курс высшей математики, т. 3, ГТТИ, М.—Л., 1933,
гл. VII.
2. А. Г. К У р ош, Курс высшей алгебры, Гостехиздат, М. —Л., 1946, гл. VIII.
3. В. Н. Фаддеев а, Вычислительные методы линейной алгебры,
Гостехиздат, М. — Л., 1950, гл. II.

ГЛАВА XII
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ
ВЕКТОРОВ МАТРИЦЫ
§ 1. Вводные замечания
При решении теоретических и практических задач часто
возникает надобность определить собственные значения данной матрицы Л,
т. е. вычислить корни ее векового (характеристического) уравнения
det(i4 —*.?) = (), A)
а также найти соответствующие собственные векторы матрицы Л,
Вторая задача является более простой, так как если корни
характеристического уравнения известны, то нахождение собственных
векторов сводится к отысканию ненулевых решений некоторых
однородных линейных систем. Поэтому мы в первую очередь будем
заниматься первой задачей—вычислением корней характеристического
уравнения A).
Здесь в основном применяются Два приема: 1) развертывание
векового определителя в полином /z-й степени
с последующим решением уравнения D(A.) = O одним из известных
приближенных, вообще говоря, способов (например, методом
Лобачевского—Греффе, гл. V, §§ 7—12) и 2) приближенное определение
корней характеристического уравнения (чаще всего наибольших по
модулю) методом итерации, без предварительного развертывания
векового определителя.
В этой главе будут изложены основные методы решения
поставленной общей задачи, причем мы начнем с развертывания вековых
определителей.
§ 2. Развертывание вековых определителей
Как известно, вековым определителем матрицы Л = [а(у]
называется определитель вида
аП К а12 •• • а1п
ап1 ап2 ... апп—%

§ 2]
РАЗВЕРТЫВАНИЕ ВЕКОВЫХ ОПРЕДЕЛИТЕЛЕЙ
403
Приравнивая этот определитель нулю, получаем
характеристическое уравнение
Если требуется найти все корни характеристического уравнения,
то целесообразно предварительно вычислить определитель A).
Развертывая определитель A), получаем полином /z-й степени
B)
где
а, =
есть сумма всех диагональных миноров первого порядка матрицы Л.
есть румма всех диагональных миноров второго порядка матрицы А;
flp«
— сумма всех диагональных миноров третьего порядка матрицы А
и т. д. Наконец,
on = det A
Легко убедиться, что число диагональных миноров k-ro порядка
матрицы А равно
п(п—\). ..{n —
___
1 о
=1, 2, ...,
Отсюда получаем, что непосредственное вычисление
коэффициентов характеристического полинома B) эквивалентно вычислению
определителей различных порядков. Последняя задача, вообще
говоря, технически трудно осуществима для сколько-нибудь больших
значений п. Поэтому созданы специальные методы развертывания
вековых определителей (методы А. Н. Крылова, А. М. Данилевского,
Леверье, метод неопределенных коэффициентов, метод интерполяции
и др.) (см. [1]). В следующих параграфах мы изложим некоторые
из этих методов.

404
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
§ 3. Метод А. М. Данилевского
Сущность метода А. М. Данилевского [1] заключается в
приведении векового определителя к так называемому нормальному виду
Фробениуса
—Ь Р2 Рз ... Рп
1 —Л ' 0 ... 0
0
1 — к
0
A)
0 0 0 ... —
Если нам удалось записать вековой определитель в форме A),
то, разлагая его по элементам первой строки, будем иметь:
D (X) = (Pl -1) {-X)"-i-p2 (-X)»-*+Ps (_А)»-з _ ... +(_l)»-ip,
ИЛИ
D (X) = (-1)" (X" -Plkn-1 -М"-2 - Р^" - ... -/>„)• B)
Таким образом, развертывание векового определителя,
записанного в нормальной форме A), не представляет затруднений.
Обозначим через
Л =
данную матрицу, а через
а1п
1 0 ... О О
.0 0 ... 1 О
- подобную ей матрицу Фробениуса, т. е.
a2i а22
Р2
О
где 5 — неособенная матрица.
Так как подобные матрицы обладают одинаковыми
характеристическими полиномами, то имеем:
det {А — ХЕ) = det (Р—
C)
Поэтому для обоснования метода достаточно показать, каким
образом, исходя из матрицы Л, строится матрица Р. Согласно
методу А. М. Данилевского, переход от матрицы А к подобной ей
матрице Р осуществляется с помощью п — 1 преобразований подобия,
последовательно преобразующих строки матрицы Л, начиная с
последней, в соответствующие строки матрицы Р.
Покажем начало процесса. Нам нужно строку

§ 3]
МЕТОД А. М. ДАНИЛЕВСКОГО
405
перевести в строку 0 0 ... 10. Предполагая, что аП1 и-1 =?0,
разделим все элементы (п—1)-го столбца матрицы А на #„,„-!•
Тогда ее п-я строка примет вид
ап1 аяа ... 1 апп.
Затем вычтем (п—1)-й столбец преобразованной матрицы,
умноженный соответственно на числа ап1, ап2У ..., аппУ из всех
остальных ее столбцов.
В результате получим матрицу, последняя строка которой имеет
желаемый вид 0 0 ... 10. Указанные операции являются
элементарными преобразованиями, производимыми над столбцами матрицы Л.
Произведя эти же преобразования над единичной матрицей, получим
матрицу
1 0 ... 0 0
0 1 ... 0 0
где
при
1
D)
Отсюда заключаем (см. гл. VII, § 14), что произведенные
операции равносильны умножению справа матрицы уИи_х на матрицу >4,
т. е. после указанных преобразований получим матрицу
~ ЬХ1
ъ%1
^2, И-1
0
Ри-1,2
0
1
0 -
E)
Используя правило умножения матриц, находим, что элементы
матрицы В вычисляются по следующим формулам:
aii n-imn-i, j ПРИ
F)
Однако построенная матрица В = АМп_1 не будет подобна
матрице А. Чтобы тшгеть преобразование подобия, нужно обратную
матрицу Mn-i слева умножить на матрицу В:

406
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Непосредственной проверкой легко убедиться, что обратная
матрица Mnli имеет вид
1 0 ... О От
0 1 ... О 0 m
_ Л • V'/
"/11 а«2 ••• ап.п-1 апп
_ О 0 ... 0 1
Пусть
Следовательно,
C~Mn-iB. (8)
Так как, очевидно, умножение слева матрицы NQ-\ на матрицу В
не изменяет преобразованной строки последней, то матрица С имеет
вид
я-1,2
0
О 0 ... 1 0 J
Перемножая матрицы Mnli G) и В E), будем иметь:
cit = blf при 1</<я — 2
(9)
A0)
A0')
Таким образом, умножение M^it на матрицу В меняет лишь
(я — 1)-ю строку матрицы В. Элементы этой строки находятся по
формулам A0) и A0'). Полученная матрица С подобна матрице Л
и имеет одну приведенную строку. Этим заканчивается первый этап
процесса.
Далее, если cn_h п_2фО, то над матрицей С можно повторить
аналогичные операции, взяв за основную (п — 2)-ю ее строку.
8 результате получим матрицу
С двумя приведенными строками. Над последней матрицей продел*а-
ваем те же операции. Продолжая этот процесс, мы, наконец,
получим матрицу Фробениуса
если, конечно, все п — 1 промежуточных преобразований возможны.
Весь процесс может быть оформлен в удобную вычислительную
схему, составление которой покажем на следующем примере.

§ 3] МЕТОД А. М. ДАНИЛЕВСКОГО 407
Пример. Привести к виду Фробениуса матрицу
-12 3 41
2 12 3
3 2 12
4 3 2 1
Решение. Вычисления располагаем в таблицу 25.
В строках 1—4 таблицы 25 помещаем элементы пц{1% /=t,
4
2, 3, 4) данной матрицы и контрольные суммы aib = 2 ац ('—Ь
2, 3, 4) B). Отмечаем элемент я43 = 2, принадлежащий третьему
столбцу (отмеченный столбец). В строке I записываем элементы
третьей строки матрицы Мп г = МВ1 вычисляемые по формулам D)
и D'):
2
__О42 _L 1 К'
1 1 л -
Сюда же (строка I таблицы 25) помещаем элемент
д46 10 -
полу.чаемый аналогичным приемом из контрольного столбца 2.
Число —5 должно совпасть с суммой элементов строки I, не
входящих в контрольный столбец (после замены элемента твз на —1).
Для удобства число —1 записываем рядом с элементом /я33, отделяя
от последнего чертой.
В строках 5—8 в графе М~х выписываем третью строку
матрицы Af"\ которая в силу формулы G) совпадает с четвертой
строкой исходной матрицы А, В строках 5—8 в соответствующих
столбцах выписываем элементы матрицы
вычисляемые по двучленным формулам F) для неотмеченных
столбцов и по одночленной формуле F') для отмеченного столбца.
Например, для первого столбца имеем:
(—2) = —5;
(—2)-— 2;
и т. д.

408
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Таблица 25
Вычислительная схема метода А. М. Данилевского
Номер
строки
1
2
3
4
I
5
6
Z3
8
|7'|
II
9
|10
11
12
110*
III
14
15
16
13'|
м-*
м-1
А
3
2
1
/ИГ1
м2
-24
—15
И
19
6
5
34
24
1
1
2
3
4
2
—5
2
1
0
—24
—1,600
—1
1,2
0
0
' 16
0,167 |-1
—0,167
1
0
0
4
Сто лбцы
2
2
1
2
3
—1,5
—2,5
—2
0^,5
0
—0,067|
—1
0,167
0,133
1
0
5
-0,833
1
0
1
0
40
матрицы
3
3
2
1
...21
0,5 —1
1,5
1
0,5
1
11
0,733
—0,333
—0,467
0
1
34
—5,667
5,333
0
0
1
56
4'
4
3
2
1
—0,5
2,5
2
1,5
0
19
1,267
-0,^67
—0,533
0
0
24
—4,000
3,333
0
0
0
20
2
10
8
8
10
—5
-3,5
—1
3,5
1
—9
—0,600
—1,833
0,333
1
1
69
-11,500
9,500
1
1
1
120
2'
о со to ел
—2
0,2
0
1
9,667
0
1
1

§ 3J МЕТОД А. М. ДАНИЛЕВСКОГО 409
Преобразованные элементы третьего (отмененного) столбца
получаются с помощью умножения исходных элементов на юза = 0,5.
Например,
613 = 30,5=1,5;
623 = 2-0,5 = 1;
Ь33= 1-0,5 = 0,5;
643 = 2-0,5=1.
Заметим, что ^последняя строка матрицы В должна иметь вид
0 0 10.
Для контроля пополняем матрицу В преобразованными по
аналогичным двучленным формулам с т35 = — 5 соответствующими
элементами столбца 2. Например,
.(—5)= — 5;
(—5)- — 2;
(-5) = 3;
Полученные результаты записываем в столбце 2' в
соответствующих строках. Прибавив к ним элементы третьего столбца, будем
иметь контрольные суммы
*/в=2*// (*=1. 2> 3, 4)
для строк 5—8 (столбец 2).
Преобразование М^1, произведенное над матрицей кидающее
матрицу С = М^1 Ву изменяет лишь третью строку матрицы Д т. е(.
седьмую строку таблицы. Элементы этой преобразованной строки 7'
получаются по формуле A0), т. е. представляют собой суммы
парных произведений элементов столбца /И", находящихся в строках
5—8, на соответствующие элементы каждого из столбцов матрицы
В, Например,
с81 = 4 (—5) + 3 (-2) + 2.1 = — 24
и т. д.
Те же преобразования производим над столбцом S:
с35 = 4(—3,5) + 3(—1) + 2-3,5+ 1-1 = — 9.
В результате получаем матрицу С, состоящую из строк 5, 6,
7', 8 с контрольными суммами 2, причем матрица С подобна
матрице А и имеет одну приведенную строку, 8. Этим заканчивается
построение первого подобного преобразования С — М1

41(Г
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Далее, приняв матрицу С за исходную и выделив элемент с22 =
= — 15 (второй столбец), продолжаем процесс аналогичным образом.
В результате получаем матрицу D = yWJ1CAf2, элементы которой
расположены в строках 9, 10', 11, 12, содержащую две
приведенные строки. Наконец, отправляясь от элемента d21 = 6 (первый
столбец) и преобразуя матрицу D в подобную ей, получаем
искомую матрицу Фробениуса Р, элементы которой записаны в строках
13', 14, 15, 16. На каждом этапе процесса контроль осуществляется
с помощью столбцов 2 и 2'.
Таким образом, матрица Фробениуса будет:
Р=
'4 40 56 20"
10 0 0
0 10 0
0 0 10
Отсюда вековой определитедь, приведенный к нормальному виду
Фробениуса, запишется так:
4 — А
1
0
0
40
1
0
56
0
х
1
20
0
0
—Ь
или
= Я4 — 4Х3 — 40Я2
§ 4. Исключительные случаи в методе А. М. Данилевского
Процесс А. М. Данилевского происходит без всяких осложнений,
если все выделяемые элементы отличны, от нуля. Мы остановимся
сейчас на исключительных случаях, когда это требование
нарушается.
Допустим, что при преобразовании матрицы Л в матрицу
Фробениуса Р мы после нескольких шагов пришли к матрице вида
0
0
J) 0 ... 0 ... 1
причем оказалось, что йкч л_х = 0.
Тогда продолжать преобразование по методу А. М. Данилевского
нельзя. Здесь возможны два случая.
0
0
i ••• dkk
... 1
... 0
... dk
... 0
... 0
л-i dktl
0
0

§ 5] ВЫЧИСЛЕНИЕ СОБСТВ. ВЕКТОРОВ ПО МЕТОДУ А. М. ДАНИЛЕВСКОГО 411
1. Пусть какой-то элемент матрицы D, стоящий левее нулевого
элемента dktkmmmV отличен от нуля, т. е. dkl^=0, где /<&—1.
Тогда этот элемент выдвигаем на место нулевого элемента dktkmal,
т. е. переставляем (k—1)-й и /-й столбцы матрицы D и
одновременно переставляем ее (k—1)-ю и 1-ю строки. Можно доказать, что
полученная новая матрица D' будет подобна прежней. К новой
матрице применяем метод А. М. Данилевского.
2. Пусть dk? = 0 (/=1, 2, ..,,&—1), тогда D имеет вид
Oil
0
0
0
0
0
0
@)
c*-i, ft-i
0
0
0
cftft
i
0
... СЛ^ n_!
... 0
... 1
о п
0
В таком случае вековой определитель det(D—ХЕ) распадается
на два определителя
det (D — кЕ) = det (Dx — Я?") det (D2 - IE).
При этом матрица D2 уже приведена к канонической форме
Фробениуса и поэтому det(D2 — ХЕ) вычисляется сразу. Остается
применить метод А. М. Данилевского к матрице Dv
§ 5. Вычисление собственных векторов по методу
А. М. Данилевского
Метод А. М. Данилевского дает возможность определять
собственные векторы данной матрицы Л, если известны ее собственные
значения. Пусть X — собственное значение матрицы Л, а
следовательно, и собственное значение подобной ей матрицы Фробениуса А
Найдем собственный вектор y — (yvy^ -. >>Уп) матрицы Я,
соответствующий данному значению X: Ру = Ху. Отсюда (Р— ХЕ)у = 0 или
Pi —A
1
0.
p%
—\
1
Рз .-•
0 ...
—I ...
Pn
0
0
—А,
Уз
= 0.

412
наХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Перемножая матрицы, получим систему для определения
координат yv у2, ...,уп собственного вектора у:
= 0,
-о,
0)
Система A)—однородная. С точностью до коэффициента
пропорциональности решения ее могут быть найдены следующим
образом. Положим уп= 1. Тогда последовательно получим:
B)
Таким образом, искомый собственный вектор есть
Обозначим теперь через х собственный вектор матрицы Д
соответствующий значению Я. Тогда, очевидно, имеем:
Преобразование /tjv совершенное над у, дает:
0
.0
1
0
... т1п '
... 0
... 1
У\
Уъ
•
•
Уп
1
_ Уп _ -
Таким образом, преобразование Мг изменяет лишь первую
координату вектора. Аналогично преобразование М2 изменит лишь вторую
координату вектора М^у и т. д. Повторив этот процесс п — 1 раз,
получим искомый собственный вектор х матрицы А.
§ 6. Метод А. Н. Крылова
Приведем метод развертывания векового определителя,
принадлежащий А. Н. Крылову [2] и основанный на существенно иной
идее, чем метод А. М. Данилевского.

§ 61
Пусть
МЕТОД А. Н. КРЫЛОВА
413
A)
— характеристический полином (с точностью до знака) матрицы Д.
Согласно тождеству Гамильтона — Кели (гл. XI,. §2), матрица А
обращает в нуль свой характеристический полином; поэтому
= Q. B)
Возьмем теперь произвольный ненулевой вектор
Умножая обе части равенства B) справа на У0), получим:
Положим:
>=1, 2, ..., п);
тогда равенство C) приобретает вид
= 0
ИЛИ
?
у
Уп
"Pi
Ра
C)
D)
E)
E)
где
= 0, 1, 2, ..., л).
Следовательно, векторное равенство E) эквивалентно системе
уравнений
(я-1) , v(i-2) , • (о) (л) /. | л п\ <а\
из которой, вообще говоря, можно определить неизвестные
коэффициенты pv p2, ...,/?„•

414 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Так как на основании формулы D)
?\
(fc=l,2, ..., л), то координаты у?
следовательно вычисляются по формулам
yik\
,у(п* вектора у{к)
по= l, 2,
я).
G)
Таким образом, определение коэффициентов р^
характеристического полинома A) методом А. Н. Крылова сводится к решению
линейной системы уравнений F), коэффициенты которой
вычисляются по формулам G), причем координаты начального вектора
произвольны. Если система F) имеет единственное решение, то ее
корни pv р2, . . ., рп являются коэффициентами характеристического
полинома A). Это решение может быть найдено, например, методом
Гаусса (гл. VIII, § 3). Если система F) не имеет единственного
решения, то задача усложняется [1]. В этом случае рекомендуется
изменить начальный вектор.
Пример. Методом А. Н. Крылова найти характеристический
полином матрицы (см. § 3)
rl
2
3
4
2
1
2
3
3
2
1
2
4~
3
2
1
Решение. Выберем начальный вектор
О
О
О

§61
МЕТОД А. Н. КРЫЛОВА
415
Пользуясь формулами G), определим координаты векторов
= 1,2,3,4).
Имеем:
1
2
3
4
2
1
2
3
3
2
1
2
4-
3
2
1
rl -
0
0
0
-11
2
3
_4
« = Ауа> =
Ауа> =
1
2
3
4
2
1
2
3
3
2
1
2
4-
3
2
I
- 1 -|
2
3
4
—
гЗО-i
22
18
20
у 3) __
уB) __
1
2
3
4
2
1
2
3
3
2
1
2
4-]
3
2
1
гЗО-
22
18
20
г208-т
178
192
242^
1
2
3
4
2
1
2
3
3
2
1
2
4-
3
2
1
-208-
178
192
242_
-2108-1
1704
1656
1992
Составим систему F):
«/'а1'
уУ
Pi
P2
Ps
Pa
У?
которая в нашем случае имеет вид
-208
178
192
242
30
22
18
20
1
2
3
4
1-
0
0
0_
"Pi"
р%
Ръ
Pi-
r-2108-i
1704
1656
_1992^
Отсюда
Решив эту систему, получим:
Pi = —4; />2= — 40;
= — 56; р4 = —20.

416 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ . XII
Следовательно,
40А2 -56А.—20,
что совпадает с результатом, найденным по методу А. М.
Данилевского (§ 3).
§ 7. Вычисление собственных векторов по методу А. Н. Крылова
Метод А. Н. Крылова дает возможность просто найти
соответствующие собственные векторы [1].
Для простоты ограничимся случаем, когда характеристический
полином
D (Я) = Хп +Р1ХП +...+Рп A)
имеет различные корни Х19 Я2, ...,ЯЯ. Предположим, что
коэффициенты полинома A) и его корни определены. Требуется найти
собственные векторы х{1\ jcB>, ..,.,д:(Л), отвечающие соответственно
собственным значениям Ях, Я2, ..., Яи,
Пусть уо), У1) = ЛУО), ...,yn-J) = /4w-yo) —векторы,
использованные в методе А. Н. Крылова для нахождения коэффициентов
/?/.(/= 1, 2, ..,,/z). Разлагая вектор У0) по собственным векторам
x{t) (/=1, 2, ..., /г), будем иметь:
/о) =
спх(п\
B)
где ct (i = 1, 2, ..., п) — некоторые числовые коэффициенты. Отсюда,
учитывая, что
получим:
Пусть
У»» ClXj-V» + с-^Г1*'2» + ... + е,^-1^"».
(Я) = Х-
C)
D)
(/=1, 2, ...,/х) — произвольная система полиномов. Составляя
линейную комбинацию векторов У""", У п~2\ ...,У0) с
коэффициентами 1, qlmmi, ...,?„-!,,•, в силу соотношений B) и C) находим:
cn<fi (К) ^(М)-

§ 8]
МЕТОД ЛЕВЕРРЬЕ
417
Если положить
то, очевидно,
и
Формула E) при этом принимает вид
(/=1, 2, .,.,/2),
1 = 0 при
F)
,_!, ,У0) (/=1,2,..., я). G)
<ур, (Я,.) *"> =у-
Таким образом, если ^=^=0, то полученная линейная комбинация
векторовy/|-i)jy/I)j ,..,уо) дает собственный вектор х{1) с
точностью до числового множителя. Коэффициенты q^{ (/=1, 2, ...
#..,я—1) могут быть легко определены по схеме Горнера
§ 8. Метод Леверрье
Этот метод раскрытия векового определителя основан на
формулах Ньютона [3] для сумм степеней корней алгебраического
уравнения.
Пусть
Ь кя\п1 . A)
— характеристический полином данной матрицы Л = [ау] и Ax, Х2,...
..., \п — полная совокупность его корней, где каждый корень
повторяется столько раз, какова его кратность.
Положим
Тогда при
Отсюда
(? = 0, 1, 2, ...,
п справедливы формулы Ньютона [3]
*-i+• • •+Р*-Л=: — kpk (k = 1,2,
/>i = — *i,
Л). B)
C)
Если суммы $lt 52, ..., 5П известны, то с помощью формул C) можно
шаг за шагом определить коэффициенты pv р2, ..., рп
характеристического полинома A).
14 Б. П. Демидович и И. А. Марон

418
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Суммы s±i sz, ...,«?„ вычисляются следующим образом: для sx
имеем (гл. X, § 12):
т. е.
= SP Ay
si = 2 ап-
D)
Далее, как известно (гл. XI, § 1), Я*, A.J, .. .Д* являются
собственными значениями матрицы Ak. Поэтому
т. е. если
то
E)
Степени Ak = Ak~lА находятся непосредственным перемножением.
Таким образом, схема раскрытия векового определителя по
методу Леверрье весьма простая, а именно: сначала вычисляются Ak
(?=1, ,2, . ..,/*)— степени данной матрицы А, затем находятся
соответствующие^—суммы элементов главных диагоналей матриц Л*
и, наконец, по формулам C) определяются искомые коэффициенты
Метод Леверрье весьма трудоемок, так как приходится
подсчитывать высокие степени данной матрицы. Достоинство
его—несложная схема вычислений и отсутствие исключительных случаев.
Пример. Методом Леверрье развернуть характеристический
определитель матрицы (см. § 3)
г! 2 3 4-
2 12 3
3 2 12
4 3 2 1
Решение. Образуем степени Ак
Имеем:
12 3 4
2 12 3
3^12
4 3 2 1
Г1 2 3 4-
2 12 3
3 2 12
4 3 2 1
= 2, 3, 4) матрицы А.
ЗО 22 18 20i
22 18 16 18
18 16 18 22
20 18 22 30

§ 9]
ПОНЯТИЕ О МЕТОДЕ НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
419
ЗО 22 18 20
20 18 16 18
18 16 18 22
20 18 22 30
208 178 192 242п
178 148 154 192
192 154 148 178
242 192 178 208
-1 2 3 4
2 12 3
3 2 12
-4321
-12 3 4
2 12 3
3 2 12
4 3 2 1
208 178 192 242п
178 148 154 192
192 154 148 178
242 192 178 208
2108 1704 1656 1992-]
1704 1388 1368 1656
3656 1368 1388 1704
1992 1656 1704 2108
Заметим, что не было необходимости вычислять Л4 полностью,
достаточно было найти лишь главные диагональные элементы этой
матрицы.
Отсюда
sx = SpA = 1 + 1 + 1 + 1 = 4;
s2 = БрЛ2 = 30 + 18 + 18 + 30 = 96;
208+148+H8 + 208712;
= 2108 +1388 +1388 + 2108 ==6992.
Следовательно, по формулам C) будем иметь:
= —*i = —4;
-4.4) = —40;
y
—56;
Ра = —т
5+/Vi) =
1
= — -j-F992—4*712 —40-96—56-4) =-
¦20.
Таким образом, мы получаем уже известный результат (см. § 3):
1—1 —2 —3 —4
_4 —3 —2 ^—1
§ 9. Понятие о методе неопределенных коэффициентов
Развертывание векового определителя можно также осуществить
при помощи нахождения достаточно большого количества его
числовых значений.
Пусть
D (Я) = Xй +р1К»-1 +...+/>„ A)
14*

420
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
есть вековой определитель матрицы Л, т. е.
Дели в равенстве A) последовательно положить Х = 0, 1, 2, ...
...,л—1, то для коэффициентов pi (/ = 1, 2, ...,я) получим
систему линейных уравнений
B)
Отсюда
= D(/i—1)—D@)—(я—1)
Из системы C) можно определить коэффициенты р;(/=1,
2, . ..,#) характеристического полинома A).
Вводя матрицу
1 1 ... 1
... л —1
и векторы
ОA)—О@) — Iя
DB)—D@)~ 2"
Ра
систему C) можно записать в виде матричного уравнения
CnP=D; D)
отсюда
p=c:1d.
E)
Заметим, что обратная матрица Сп 1 зависит только от порядка п
векового определителя и может быть найдена заранее, если
приходится иметь дело с массовым раскрытием вековых определителей
одного и того же порядка.

§ 11] НАХОЖДЕНИЕ НАИБОЛЬШЕГО ПО МОДУЛЮ СОБСТВЕННОГО ЗНАЧЕНИЯ421
Таким образом, применение этого метода сводится к вычислению
числовых определителей
D/ h\ _. А л4- / ЬР А\ IЪ 0 10 ti —— 1 \
и нахождению решения стандартной линейной системы D).
§ 10. Сравнение различных методов развертывания
векового определителя
Об относительной эффективности различных методов
развертывания векового определителя можно судить по приведенной ниже
таблице 26 [4], в которой указаны количества действий, требуемых
каждым из рассмотренных методов, в зависимости от порядка
определителя.
Таблица 26
Количество действий, используемых различными методами
развертывания векового определителя, в зависимости от порядка его
Метод

Непосредственное
развертывание
Данилевского . .
Крылова • • . .
Леверрье ....
Неопределенных
коэффициентов

Интерполирования*)
¦) См. гл. XIV, § 23-
Порядок
3


ний—делений У—Д
12
14
67
41
67
46


ний-вычитаний
С-В
10
12
38
27
41
38
4
У-Д
60
42
179
153
171
125
С-В
46
36
118
114
116
102
5
У-Д
320
92
389
414
364
279
С-В
238
80
280
330
265
230
7
У-Д
13 692
282
1287
1791
1 189
972
с-в
10 078
252
1022
1533
945
826
9
У-Д
986 400
632
3 209
5 228
2 966
2525
с-в
725758
576
2 688
4 644
2 481
2202
Из этой таблицы видно, что для развертывания вековых
определителей порядка выше пятого наиболее выгодным, с точки зрения
количества действий, является метод А. М. Данилевского.
§ 11. Нахождение наибольшего по модулю собственного
значения матрицы и соответствующего собственного вектора
Пусть имеем характеристическое уравнение
Корни этого уравнения Я1э Я2, ..., Кп являются собственными
значениями матрицы А. Пусть им соответствуют линейно независимые

422
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
собственные векторы д:ш, лсB\ ..., х{пК Укажем некоторые
итерационные методы вычисления наибольшего по модулю собственного
значения матрицы Л, не требующие раскрытия ее векового
определителя.
Случай 1. Среди собственных значений матрицы Л есть одно,
наибольшее по модулю. Для определенности предположим, что
так что наибольшим по модулю является первое собственное
значение. Очевидно, для действительной матрицы наибольшее по
модулю собственное значение Хг действительно. Заметим, что такой
случай имеет место, если матрица А—«действительная и элементы ее
положительны (гл. X, § 16, теорема Перрона).
Укажем приближенный способ вычисления корня Xv Возьмем
произвольный вектор у и разложим его по собственным векторам х^
матрицы А:
где С/(У=1, 2, ..., п) — постоянные коэффициенты. Произведя
преобразование А над вектором у, будем иметь:
Отсюда, так как х^ есть собственный вектор преобразования Л,
т. е. AxU) — %jX^, получим:
тУ* находим:
B)
., еп (не обя-
Ay назовем итерацией вектора у.
Последовательно образуя итерации Ау% Л2у, .,
(m-я итерация).
Выберем в пространстве Еп~{у} базис ev e2,
зательно единичный). Пусть
=УМ> (*=1, 2, 3, ...)

§ 11).НАХОЖДЕНИЕ НАИБОЛЬШЕГО ПО МОДУЛЮ СОБСТВЕННОГО ЗНАЧЕНИЯ 423
где yim)(i=\t 2, ..., п) — координаты вектора у{т) в выбранном
базисе.
Разлагая собственные векторы дг<у> по векторам базиса, будем
иметь:
Отсюда, подставляя ^выражение C) в формулу B), получим:
или, изменяя порядок суммирования,
Коэффициент при et есть /-я координата вектора у{Щ.
Следовательно, можно написать:
yr^CjXtjkf. D')
Аналогично
Разделив вторую сумму на первую, будем иметь
E)
Предположим, что сх=^0 и лга^=О. Этого можно добиться,
выбирая надлежащим образом исходный вектору и базис (ev ег> ..., ^л).
Преобразуем выражение E) следующим образом:
Отсюда, переходя к пределу при т—*оо и учитывая
неравенства A), получим:

424 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
(так как lim (jf) = 0 при у> 1 ) или приближенно
i ^
точнее,
Взяв достаточно большой номер итерации т, мы сможем с
любой степенью точности определить по формуле G) наибольший по
модулю корень Хх характеристического уравнения данной матрицы Л,
Для нахождения этого корня может быть использована любая
координата вектора у{т\ в частности, можно взять среднее
арифметическое соответствующих отношений.
Замечание 1. В исключительных случаях, при неудачном
выборе начального вектора у, формула F) может не дать нужного
корня или даже вообще может не иметь смысла, т. е. предел отно-
{)
y
шения ¦ 1 ¦ может не существовать. Последнее легко заметить
у(т)
по «прыгающим» значениям этого отношения. В таких случаях сле-
^дует испробовать другой начальный вектор.
Замечание 2. Для ускорения сходимости итерационного
процесса F) иногда выгодно составлять последовательность матриц
Отсюда находим:
где m — 2k. Затем, как обычно, полагаем:
^i^^p- C=l, 2, .... п).
Вектор укщ — Ату приближенно представляет собой собственный
вектор матрицы Л, соответствующий собственному значению Xv

§ 1 1] НАХОЖДЕНИЕ НАИБОЛЬШЕГО ПО МОДУЛЮ СОБСТВЕННОГО ЗНАЧЕНИЯ 425
В самом деле, из формулы B) имеем:
где лс(Л (у=1, 2, ..., я) — собственные векторы матрицы А.
Отсюда
Ату = cj
Так как ( ^ 1 —>() при т—*оо (/> 1), то при достаточно
большом /я с любой степенью точности будем иметь:
т. е. Ату лишь числовым множителем отличается от собственного
вектора д:ш и, следовательно, также является собственным
вектором, соответствующим тому же самому собственному значению Хг.
Пример, Найти наибольшее собственное значение матрицы
Г4 1 01
1=1 2 1
Lo 1 lj
(8)
и соответствующий ему собственный вектор.
Решение. Выбираем начальный вектор
-[!]¦
Составляем таблицу 27.
Таблица 27
У
1
1
1
Ау
5
4
2
Вычисление первого
А*у
24
15
6
А*ц
111
60
21
А*у
504
252
81
А* у
2268
1089
333
собственного
А* у
10161
4779
1422
А'у
45433
21141
6201
значения
А* у
202833
93906
27342
А9 у
905238
417987
121248
4 038939
1 862460
539235

426 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Остановившись на итерациях А*у~у{® и А1Оу =у{Ш, получаем
значения
У^ 4038939
905238
186246Q
1T7987
539235
yJ») ~ 121248
Следовательно, приближенно можно принять:
Хх = 1 D,462 + 4,456 + 4,447) = 4,455 « 4,46.
В качестве первого собственного вектора матрицы Л можно взять:
Г40389391
Агоу = 1862460 I
L 539235J
Нормируя его, окончательно получим:
[0,901
0,42 I
O,12J
Случай 2. Наибольшее по модулю собственное значение
матрицы А является кратным.
Пусть
Из формулы E) имеем:
Отсюда, если с1лг11+...+^^^=0, учитывая, что
\5г) —^

§ 11] НАХОЖДЕНИЕ НАИБОЛЬШЕГО ПО МОДУЛЮ СОБСТВЕННОГО ЗНАЧЕНИЯ 427
получим:
Ш+х)
lim ^—Г^Х1 (/=1, 2, .... п)
или, точнее,
Таким образом, указанный выше способ вычисления к1 применим
и в этом случае.
Как и прежде,
представляет собой один из приближенных собственных вектороо
матрицы Л, соответствующих значению kt. Изменяя начальный
вектор у, мы, вообще говоря, получаем другой линейно независимый
вектор матрицы Л. Заметим, что в этом случае не гарантировано,
что нашим приемом будет определена вся совокупность линейно
независимых собственных векторов матрицы Л для значения kv
Для случаев 1—2 можно указать более быстрый итерационный
процесс нахождения наибольшего по модулю собственного значения XL
матрицы А} а именно: образуем последовательность матриц
Л, Л2, Л4, Л8, ..., Л2*.
Как известно (гл. X, § 12),
аналогично
где m = 2k. Ограничиваясь для простоты случаем 1, имеем:
отсюда
При т—»-оо получаем:
\kt\= lira
т. е.
где т достаточна велико.

428 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Чтобы избежать извлечения корней высокой степени, можно найти
Тогда
Отсюда, учитывая относительную малость | Ха |, ..., |ХЛ| по
сравнению с I Кг I, получим:
Xx^Sp Лт+1/$р А'\
§ 12. Метод скалярных произведений для нахождения первого
собственного значения действительной матрицы
Для отыскания первого собственного значения Ях действительной
матрицы А можно указать несколько иной итерационный процесс,
являющийся иногда более выгодным. Метод основан на образовании
скалярных произведений
(ft=l, 2, ...), где А—матрица, транспонированная с матрицей А,
и у0 — выбранный каким-либо образом начальный вектор.
Переходим теперь к изложению самого метода.
Пусть А — действительная матрица и Я1? Л2, ..., Кп — ее
собственные значения, которые предполагаются различными, причем
\к\>\к\>..->\к\-
Возьмем некоторый ненулевой вектор yQ и с помощью
матрицы А построим последовательность итераций
Для вектора у0 образуем также с помощью транспонированной
матрицы А вторую последовательность итераций
^ (ft=l, 2, ...), B)
где у\ = у0.
Согласно теореме 1 главы X, § 16 в пространстве Еп выберем
два собственных базиса {Xj} и {х/} соответственно для матриц А
и А\ удовлетворяющих условиям биортонормировки:
(х0 х]) = Ьи, C)
где Axi = Xixi и Ах) — к]х) (/, У=1, 2, ..., л). Обозначим
координаты вектора у0 в базисе {Xj} через а17 ..., ап, а в

§ 12J - МЕТОД СКАЛЯРНЫХ ПРОИЗВЕДЕНИЙ 429
базисе {jcj-}— через Ьг, .. ., Ьп, т. е.
^o = ?i+ • • • +ап*п и Л = *1<+ • - ¦ +Ьпх'п.
Отсюда
^ = Л'*у0 = 2J W*; (Ы;2, ...). D')
Составим скалярное произведение
4^ = 1 /=1 /
Отсюда в силу условия ортонормирования находим:
Аналогично
Следовательно, при агЬ^=^0 имеем:
(ги^Г^г+^^ч...!^;^-1 1+ iW )'
Таким образом,
Этот метод особенно удобен для симметрической матрицы Л,
так как тогда А' = А, и мы имеем просто
и, следовательно, здесь нужно построить только одну
последовательность yk = Aky0 (к= 1, 2, ...).
Пример. Методом скалярных произведений найти наибольшее
собственное значение матрицы (§11)
Г4 1 01
= \ 12 1.
L0 1 lj
Решение. Так как матрица А—симметрическая, то достаточно
построить лишь одну последовательность итераций Afcy0 F = 1,2,...).

430 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Выбирая за начальный вектор
У о = И >
можно использовать результаты таблицы 27. Например, при^~5
и к~ 6 имеем:
[2 268"! Г10 16П
1 089 и А*у0 = 4 779 .
333 J L 1 422 J
Отсюда
(Аьу0, А*уо) = 2268-10 161 + 1089«4779 + 333-1422 = 28 723 005
и
(А*у0, А*у0) = 10 1612 + 47792 + 14222 = 128 106 846.
Следовательно,
1 ~ <Л6-Уо' А*Уо) _ 128 106 846 _
1Л/ (Л%, АУО) 28 723 005 —*^°>
что совпадает в написанных знаках со значением, найденным прежде
с помощью А1Оуо (см. § 11).
Замечание. Методы нахождения наибольшего по модулю корня
характеристического уравнения (§11) можно использовать для
нахождения наибольшего по модулю корня алгебраического уравнения
xn+j>1x»-1+...+pa = 0. (9)
Действительно, уравнение (9), как легко непосредственно
проверить, является вековым для матрицы (ср. §3, матрица Фробениуса)
0 0 ..." 1 0
т. е. уравнение (9) эквивалентно уравнению
Если уравнение (9) не имеет нулевых корней, то аналогичным
способом может быть определен наименьший по модулю корень этого
уравнения, а именно, при />и=^0, полагая —=уг получим:
Обратная величина наибольшего по модулю корня уравнения A0),
очевидно, даст нам наименьший по модулю корень уравнения (9).

§ 13]
НАХОЖДЕНИЕ ВТОРОГО СОБСТВЕННОГО ЗНАЧЕНИЯ
431
§ 13. Нахождение второго собственного значения матрицы
и второго собственного вектора
Пусть собственные значения Xy(j—\t 2, ..., п) матрицы А
таковы, что
\К\>\К\>\К\> — >\К\> A)
т. е. имеются два отличных друг от друга, наибольших по модулю
собственных значения Хг и Х2 матрицы А. В таком случае приемом,
аналогичным разобранному выше (§ И), можно приближенно найти
второе собственное значение Х2 и отвечающий ему собственный
вектор х{2).
Из формулы B) § 11 имеем:
Ату =
Ат+1у =
B)
C)
Исключим из формул B) и C) члены, содержащие кг. Для этбго
из равенства C) вычтем равенство B), умноженное на А,1# В
результате получим:
ВД.-^i) л<">. D)
Для краткости введем обозначение
АкАту = Ат+1у—\Ату,
E)
причем выражение E) будем называть Х-разностью от Ату. Если
с2^=0, то очевидно, что первое слагаемое в правой части
равенства D) является ее главным членом при т—>оо, и мы имеем
приближенное равенство
Отсюда
Пусть
F)
G)
Ату =ут =

432 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Из формул F) и G) выводим:
А2 » \m-i =5о—~~ l^-i (/=1, 2, ... , л). (8)
Пользуясь формулой (8), можно приближенно вычислить второе
собственное значение А2. Заметим, что на практике ввиду потери
точности при вычитании близких чисел иногда выгоднее номер
итерации k для определения А2 брать меньшим, чем номер
итерации т для определения Xv т. е. целесообразно полагать:
(k < m),
(9)
где k — наименьшее из чисел, при котором начинает сказываться
преобладание Я2 над следующими собственными значениями.
Формула (9), вообще говоря, дает грубые значения для Я2. Заметим,
что если модули всех собственных значений различны между собой,
то при помощи формул, аналогичных формуле (9), можно вычислить
и остальные собственные значения данной матрицы. Однако
результаты вычислений будут еще менее надежны.
Что касается собственного вектора х{2\ то, как вытекает из
формулы F), можно положить:
jcB)» A^jA A0)
Имеется распространение данного метода на случай кратных
корней характеристического уравнения [1].
Пример. Определить дальнейшие собственные значения и
собственные векторы матрицы (см. пример из § 11)
Г4 1 ОТ
1=1 2 1I
Lo I ij
Решение. Для нахождения второго
примем k = 8. Имеем (см. таблицу 27):
собственного значения
45 433
21 141
6201
А*у
202 833
93 906
27 342
А°у
905 238
417 987
121 248
Составляем Я-разности по формуле
(/=1, 2, 3),

§ 13]
НАХОЖДЕНИЕ ВТОРОГО СОБСТВеННОГО ЗНАЧЕНИЯ
433
где ул = Л{у. Для каждого из столбцов принимается свое
значение Kv а именно: Хх = 4,462; Х1 = 4,456; Я1== 4,447 (таблица 28).
Таблица 28
Вычисление второго собственного значения
202 833
93 906
27 342
КА'у
202 722
94 204
27 576
111
—298
—234
905238
417 987
121 248
905 041
418 445
121 590
197
-458
-342
Отсюда получаем:
<8) 197
тг\ ===TiT == Ь78;
,.(8)
_-4Б8_1 -.
„(8)
Следовательно, приближенно можно принять:
_-342 , ,е
г-234~'
,46)^ 1,59.
В качестве второго собственного вектора можно принять:
Ах,
Нормируя этот вектор, получим:
Г 1971
А*у= -458 I
L-342J
[0,331
—0,76 I
-0,56j
Так как матрица А — симметрическая, то векторы х{1) (§ 11) и х{2)
должны быть ортогональны между собой. Проверка дает:
(Ха\ *B)) = 0,90-0,33 +0,42-(— 0,76) + 0,12-(—0,56) = 0,09.
Отсюда «ЗС (ха\ х{2)) = 85°, что довольно неточно.
Третье собственное значение Я3 находим па следу матрицы А:
Отсюда
= 7 — 4,46 — 1,59 » 0,95.

434 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Собственный вектор
L *3 J
можно вычислить из условий ортогональности:
0,3343) + (— 0,76) х™ + (—0,56) xiz) = 0. I
Отсюда
или
vC)
I 0,42 0,12
—0,76 -0,56
0,12 0,90
-0,56 0,33
0,90 0,42
0,33 —0,76
x
—0,144 ~~ 0t539 "" —0,818 *
После нормировки окончательно получим:
Г-O.Ul
= 0,53 I
L—0,8lJ
§ 14. Метод исчерпывания
Для определения второго собственного значения матрицы и
принадлежащего ему собственного вектора можно указать еще
один способ, называемый методом исчерпывания [1].
Пусть матрица Л = [аху] Действительна и обладает различными
собственными значениями kv Х2, ,.. , кп, причем
Наряду с матрицей А рассмотрим матрицу
где кг — первое собственное значение матрицы Л,
A)
Чх

14]
МЕТОД ИСЧЕРПЫВАНИЯ
435
— соответствующий собственный вектор матрицы Л,
рассматриваемый как матрица-столбец, и
ХХ — [#11 #21 • • • ХП\\
— отвечающий Кг собственный вектор транспонированной матрицы А'7
рассматриваемый как матрица-строка, причем векторы Хг и Хх
нормированы так, что их скалярное произведение равно единице:
(Xv Хх) = х\хг - 2 хпх'п = 1. B)
/=1
Число к1 и векторы Хг и Хх предполагаются известными.
В развернутом виде матрица Ах записывается следующим
образом:
ахх аХ2 ... аХп
а21 а22 ... а2п
цХ21 . . . Хп1] —
ахх а12
021 а22
_ап1 ап2
21 ••• хпхп1
хпХх
21 ••*
Докажем, что все собственные векторы Xj (j= I, 2, ... , п)
матрицы А являются также собственными векторами матрицы Av
причем соответствующие собственные значения сохраняются, за
исключением Kv вместо которого появляется нулевое собственное
Значение.
В самом деле, используя свойство ассоциативности матричного
произведения и условие нормировки B), имеем:
т. е.
и, следовательно, нуль является собственным значением матрицы Аг.
Далее, при у> 1, учитывая, что
(Л), Хг) = Х\Х1 = О (У = 2, ... , л)
(см. гл. X, § 16, теорема 1), получаем:
Ях (ХМ Xj = Л2А) - Х^ (У^у)
(У=2, ...,/2).

43.6 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Таким образом, для матрицы Ах наибольшим по модулю
собственным значением является А,2. Поэтому для определения Я2 и
соответствующего собственного вектора Х2 можно воспользоваться
указанными выше методами (§§ 11 и 12). Этот прием называется
методом исчерпывания. Например, исходя из произвольного
вектора у0У можно вычислить Х2 по формуле
fc ^ / 1Уо\ (I =1,2,..., я),
причем
Покажем, что для нахождения итераций i4?jr0 (л* = 1, 2,...)
можно воспользоваться формулой
АЪо^^Уо-КХгХ^, C)
позволяющей избежать непосредственного итерирования матрицы Л1#.
_ Действительно, пусть собственные векторы Xj и Xf (/= 1, 2,..., п)
матрицы А и транспонированной матрицы А' удовлетворяют усло^
виям биортонормировки (гл. X, § 16, теорема 2)
где bfk—символ Кронекера. Тогда имеет место билинейное
разложение матрицы А
А = ^ВД + К***'* + • • • + K^JCn. D)
Отсюда
Аг = А - XyXtXi - К2Х2Х2 + ...+ КХп&- E)
Так как
AmXf^kfXf (y=l, 2,...,/г),
то, умножая равенство D) слева на Ат"ху будем иметь:
Лт = AmXix[ + АтХгХг +...+ АтХпХп =
г х2х2 +... + Кхпхп. F)
Аналогично, учитывая, что
A^Xj^kfXj (/-2, 3, ..., п)9

§ 15) ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ СИММЕТРИЧЕСКАЯ МАТРИЦА 437
после умножения равенства E) слева на А™ получим:
А? = А™Х2Х2 + ... + А?ХяХа = Ь™Х2Х2 +..,+ КХпХп. G)
Из формул F) и G) вытекает:
что эквивалентно соотношению C).
§ 15. Нахождение собственных элементов положительно
определенной симметрической матрицы
Приведем итерационный метод одновременного нахождения
собственных значений и собственных векторов положительно
определенной матрицы [5].
Как известно (гл. X, § 15), если действительная матрица
— симметрическая и положительно определенная, то:
1) корни Я1? Я2, ... , Хп ее характеристического уравнения
¦«и—К а12 ... а\п
21 022—^ ... а2п
= 0
A)
действительны и положительны;
2) собственные векторы
Л1
G=1, 2, ...,/г)
могут быть взяты действительными и удовлетворяют условиям
ортогональности
= 0 при
B)
Напишем систему, служащую для определения собственного
вектора х{1):
(Л \ ^.'1/ \ _ л-A) \ \ л а-A) ' (\
(*\\ Л1^*1 "Г ^12** 2 *Т • • • "Т" а1пХП —^>
^ = 0,
111 I I I

438
или
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XU
= ? {anx[l)
> C)
Так как координаты собственных векторов определяются с
точностью до множителя пропорциональности, то одна из них
произвольна, например, за исключением особого случая, можно положить
лгп1>=1. Систему C), вообще говоря, можно решить методом
итерации [5], выбирая подходящие начальные значения х[г'0), Х^]
и полагая
1 T&kZ* i/f inl ' "* ' '
=o, l, 2,...).
Можно также использовать процесс Зейделя. Таким образом,
находятся первый корень характеристического уравнения A)
*i » № D)
и первый собственный вектор
ЛЬ *
JLt. k)
Для определения второго корня к2 уравнения A) и второго
собственного вектора х{2) напишем соответствующую систему уравнений:
Из соотношения ортогональности
= 1. 2, ... , п).
E)
F)

§ 15] ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ СИММЕТРИЧЕСКАЯ МАТРИЦА 439
исключим одно из неизвестных xf\ например
заменится эквивалентной системой
* Тогда система E)
ц х}
'/=1
/ • 10 tt —— *)\
rB)
j
G)
Полагая xJI221 = l, решаем систему G) методом итерации. В
результате будут найдены второй корень Я2 характеристического
уравнения A) и собственный вектор х{2\ причем /2-я координата
этого вектора определяется из условия ортогональности F).
Аналогично отыскиваются остальные корни Яу (у=3, .. . , п)
уравнения A) и соответствующие им собственные векторы xiJ).
Мы не рассматриваем исключительные случаи, которые могут
возникнуть при применении этого метода.
Пример. Для матрицы [5]
Г4 2 21
1= 2 5 1
L2 1 6J
найти корни Яу характеристического уравнения и собственные
векторы х{*К
Решение. Матрица Л является симметрической и положительно
определенной, так как
> 0;
Соответствующая система имеет вид
2 —
"Г"
(/=1, 2, 3).
(8)
Полагая j—l и х^ — 1, получим:
(9)

440
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Систему (9) решаем методом итерации, выбирая начальные
значения
лгA>0) = 1 и дгA'0) = 1
Тогда из последнего уравнения системы (9) будем иметь Я.A0) = 9.
Результаты вычислений приве-
Таблица 29 дены в таблице 29.
Вычисление методом итерации Можно принять
собственных элементов матрицы, „ ft c
отвечающих первому корню *i — °>с
характерического уравнения И
к
0
1
2
3
4
5
6
7
8
9
10
11
i
0,89
0,85
0,83
0,81
0,805
0,806
0,807
0,8074
0,8076
0,8076
0,8077
,Uft)
I
0,89
0,83
0,80
0,78
0,770
0,771
0,771
0,7715
0,7717
0,7719
0,7720
<
9
8,67
8,53
8,46
8,40
8,38
8,383
8,385
8,3863
8,3869
8,3871
8,3874
Положим теперь в
системе (8) /=2. Из условия
ортогональности векторов дгA)
и хB) имеем:
0,8077 х{2) + 0,7720 х{22) +
Отсюда
42) = — 0,8077 х[2) —
—0,7720 xf. A0)
(И)
Подставляя это выражение в систему (8) и полагая jeB2) = l,
получим:
х{? =j^B,3846 Ar(xa)+0,4560),
Х2 = 1,1923 х[2) +4,2280.
Систему A1) решаем методом итерации, полагая:
#<2'0) = 1 и А40) = 5,42.
Результаты вычислений даны в таблице 30.
Можно принять Я2 = 4,4867 и лг^ = 0,2170; л;B2) = 1.
Третья координата определяется из соотношений
ортогональности A0):
42) = — 0,9473,
поэтому
— 0,2170—
—0,9473

§ 15] ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ СИММЕТРИЧЕСКАЯ МАТРИЦА 441
Таблица 30
Вычисление методом итерации собственных элементов матрицы,
отвечающих второму корню характеристического уравнения
k
0
1
2
3
4
5
/2 k)
1
0,52
0,35
0,28
0,25
0,23
x{2k)
Х2
1
1
1
1
1
1
А2
5,42
4,85
4,64
4,56
4,53
4,500
k
6
7
8
9
10
11
x{2k)
0,223
0,220
0,218
0,2174
0,2171
0,2170
x(*k)
1
1
1
1
1
1
4,494
4,490
4,488
4,487
4,4868
4,4867
Третий собственный вектор хC) непосредственно определяется
из двух соотношений ортогональности
0,8077 jc<13> + 0,7720л:23) + а;(з3) = 0, \
0,2170 х[8)+х[в)—0,9473 x(9s) = 0. J
Полагая #1 =1,
Следовательно,
получим
J3)
= — 0,5673; ХГ =—0,3698.
Г 1
= -0,5673
I -0,3698
Из последнего уравнения системы (8) приу = 3 находим также
Хз-2,1260.
Для контроля составим след матрицы А:
Sp A = Kt + K2 + ^з==8,3874 + 4,4867 + 2,1260 =15,0001^4 + 5 + 6.
Заметим, что корни, получаемые процессом итерации, как
правило, расположены в порядке убывания их модулей. Собственные
векторы матрицы определяются с точностью до коэффициентов
пропорциональности, поэтому все решения системы (8) таковы:
8,3874
4,4867
2,1260
0,8077с!
0,2170с2
0,7720с!
—0,5673с3
-0,9473с2
—0,3698с3
сд—произвольные постоянные, отличные от нуля).

442
НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
§ 16. Использование коэффициентов характеристического
полинома матрицы для ее обращения
Выше были приведены способы развертывания векового
определителя матрицы в полином (§§ 3—9). С помощью коэффициентов
этого характеристического полинома и составления степеней Л,
Л2, ..., Л"*" неособенной матрицы Л порядка п сравнительно просто
можно найти обратную матрицу Л"*1. Особенно выгодным в этом
отношении является метод Леверрье (§ 8),
Пусть имеем неособенную матрицу А порядка п. Рассмотрим ее
характеристический полином
A)
B)
C)
det (КЕ—А) = Г + р^"-1 + ... +ря_1Ь +рп.
Согласно тождеству Гамильтона—Кели (гл. XI, § 2) имеем:
Ая Ат1АЕ0
Умножая матричное равенство A) слева на Л, получим:
... +Рп.хЕ).
Отсюда при рп Ф О будем иметь:
Таким образом, если известны коэффициентыхарактеристического
полинома матрицы Л и составлены степени этой матрицы до (я—1)-й
включительно, то обратная матрица А~х легко вычисляется по
формуле C).
Заметим, что если рд = 0 и рп_г =^=0, то для получения формулы,
содержащей Л, векторное равенство A) нужно умножать слева
«а Л и т. д.
Пример. Для матрицы (см. § 8, пример)
А =
12 3 4'
2 12 3
3 2 12
4 3 2 1
найти обратную матрицу А.
Решение. Воспользуемся найденными прежде степенями
матрицы Л (§ 8):
0 22 18 20"
22 18 16 1в
18 16 18 22
20 18 22 30

§ 16] ИСПОЛЬЗОВАНИЕ КОЭФФИЦИЕНТОВ ХАРАКТЕРИСТИЧ. ПОЛИНОМА 443
'208 178 192 242"
178 148 154 192
192 154 148 178
242 192 178 208
Так как характеристический полином матрицы А имеет вид
det (Ы—Е) = Л.4—4А.3 —40А.2—56Х — 20,
то по формуле C) получаем:
1J
-20)
I
0 22
22 18
18 16
20 18
|
-ml
1
-
208 178 192
178 148 154
192 154 148
_242 192 178
18 20"
16 18
18 22
22 30_
— 40
' 04 89 96
89 74 77
96 77 74
J2i 96 89
20 40 60 80*
40 20 40 60
60 40 20 40
80 60
40 20
242
192
178
208
'1 2
2 1
3 2
4 3
12Г
96
89
104_
3
2
1
2
8
0
0
0
4
3
2
0
44
36
J°
0
28
0
0
— 56
44 (

0
0
0
*6
36 32
32 36
36 i
0
0
28
14
0"
0
0
0 28
0
1
0
0
40"
36
44
60_
1
r
0 0T
0 0
1 0
0 1_
-0,4 0,5 0 0, Г
0,5 —I 0,5 О
0 0,5 —1 0,5
0,1 0 0,5 -0,4
Для контроля составляем произведение
-0,4 0,5 0 0,1]
0,5 -1 0,5 0
О 0,5 -1 0,5
0,1 0 0,5 -0,4
1
2
3
4
2
1
2
3
3
2
1
2
41
3
2
1J
1 О О О]
0 10 0
0 0 10
0 0 0 1
= Е.

444 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
§ 17. Метод Л. А. Люстерника улучшения сходимости процесса
итерации для решения системы линейных уравнений
Пусть система линейных уравнений
Ах = Ь A)
приведена к виду, удобному для итерации,
лг-р + алг. (Г)
Согласно методу итерации (гл. VIII, § 8), последовательные
приближения решения х системы (Г) определяются -по формуле
х(т) = $ + ах(т-1) (да=1, 2, ...), B)
где jc@)—произвольный начальный вектор.
Предположим, что собственные значения Xv Х2, ..., Ап матрицы а
различны, причем
\К\>\К\^...>\К\- C)
Процесс итерации B) сходится, если
Первое собственное значение Ях может быть приближенно
определено с помощью указанных выше методов (§§ 11 —12). Как доказал
Л. А. Люстерник [6], используя число Я1Э можно существенно
улучшить сходимость итерационного процессаB)длярешениясистемы(Г).
Покажем, как это делается.
При достаточно большом т приближенно можно положить:
X « Хкт\
Оценим ошибку х—ХШ). При условии сходимости процесса B)
имеем:
т
лг= lira *(<Я) = .*@)+2 (Xik)—Jt1*');
кроме того,
т
Поэтому
[] [] ... D)
Так как
==1> 2, ....

§ 17J МЕТОД Л. А. ЛЮСТЕРНИКА УЛУЧШЕНИЯ СХОДИМОСТИ ИТЕРАЦИИ 445
то
х — *<т> = ат (ха) — лг<0)) + *т\г (х{1) — х{0)) + ... E)
Пусть у19 у21 .. ., ^„ — собственные векторы матрицы а,
соответствующие собственным значениям кг, Я2, ..., кп и образующие
базис пространства Еп. Разлагая вектор х{1) — Х{0) по векторам
этого базиса, будем иметь:
... +СяУа,
где Cj (/=1, 2, ..., п) — некоторые определенные числа. Отсюда
пЬп~1Уп F)
Следовательно, на основании формулы E) находим:
Отсюда, учитывая неравенства C), получим:
). G)
Кроме того, из формулы F) при& = /ю-|-1 выводим:
^«+i>_jfc«)==Cix«y1 + o(X?). ^ (8)
Поэтому
Таким образом, окончательно имеем:
«Л/я)
(9)
Добавочный член =—5 заметно улучшает сходимость
итерационного процесса B).
Так как из формулы (8) вытекает, что
f A0)
то формулу (9) можно заменить следующей:
хъхт + -j^-ixw—x'-1*). A1)

446 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Формула (И) освобождает от необходимости вычислять следующее
по порядку приближение.»
На основании формулы A0) наибольшее собственное значение
Хх может быть определено по формуле.
В случае симметрической матрицы а, пользуясь методом
скалярных произведений, получаем более точную формулу:
В частности, если
ТО
И
Поэтому
^^ (/=1, 2, .... л), A2)
где (адаР)/ и (ат"Р)|- — г-е координаты соответственно векторов <zmp
и а1""*1^. Аналогично, если матрица а — симметрическая, то
Пример. Методом итерации решить систему [1]
0,78*! — 0,02*2 — 0,12*з — 0,14*4 = 0,76;
— 0,02*i + 0,86*2 — 0,04*з + 0,06*4 = 0,08;
— 0,12*1^-0,04*2 + 0,72*3-^0,08*4=: 1,12;
— 0,14*i + 0,06#2 — 0,08*з + 0,74*4 = 0,68,
применив для уточнения корней способ Л, А. Люстерника.
Решение. Приводим систему к виду, удобному для применения
метода итерации:
*! = 0,22*! + 0,02*2 + 0,12*з + 0,14*4 + 0,76;
*3 = 0,12*! + 0,04*2 +0,28*3+ 0,08*4 +1,12;
*4 = 0,14*i — 0,06*2 + 0,08*з + 0,26*4 + 0,68

§ 17] МЕТОД Л. А. ЛЮСТЕРНИКА УЛУЧШЕНИЯ СХОДИМОСТИ ИТЕРАЦИИ 447
или в матричной форме
-0,76 -
0,08
1,12
-0,68.
+
-0,22
0,02
0,12
-0,14
0,02
0,14
0,04
— 0,06
0,12
0,04
0,28
0,08
0,14-
—0,06
0,08
0,26..
хг
xz
A4')
Отсюда
рО,22 0,02 0,12 0,14-]
0,02 0,14 0,04 —0,06
0,12 0,04 0,28 0,08
0,14 —0,06 0,08 0,26j
и р =
0,08
1,12
L0,68J
Так как
||а||ж = max @,50; 0,26; 0,52; 0,54) = 0,54 < 1,
то процесс итерации для системы A4) сходится.
Используя в качестве начального вектора xiQ) вектор Р, для
т-ro приближения х^щ искомого решения
получим следующее выражение:
т
A5)
Таким образом, для вычисления х(ГП) нужно образовывать
последовательные итерации вектора 0 с помощью матрицы а. Имеем:
~0,22
0,02
0,12
.0,14
0,02
0,14
0,04
—0,06
0,12
0,04
0,28
0,08
0,14-
—0,06
0,08
0,26.
-0,76"
0,08
U2
.0,68.
-0,3984-
0,0304
0,4624
.0,3680.
0,22 0,02 0,12 0,14"!
0,02 0,14 0,04 —0,06
0,12 0,04 0,28 0,08
.0,14 —0,06 0,08 0,26^
-0,3984-
0,0304
0,4624
.0,3680.
-0,195264"
0,008640
0,207936
.ОД 86624.
и т. д.

448 НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ [ГЛ. XII
Результаты соответствующих вычислений приведены в таблице 31.
Таблица 31
Последовательные итерации вектора р матрицей а
0,76
0,08
1,12
0,68
ар
0,3984
0,0304
0,4624
0,3680
абр
0,02174095
0,00013570
0,02188361
0,02160525
а6р
0,01043649
0,00003285
0,01047017
0,01040364
а'Р
0,195264
0,008640
0,207936
0,186624
а7р
0,00500961
0,00000792
0,00501763
0,00500170
азр
0,09421056
0,00223488
0,09692928
0,09197568
а8р
0,00240463
0,00000190
0,00240654
0,00240272
а*Р
0,04527913
0,00055572
0,04589292
0,04472340
fe = o
1,532746
0,122009
1,972937
1,410737
В формуле A1) примем /я = 8. Так как матрица а —
симметрическая, то для вычисления ее первого собственного значения к1
используем метод скалярных произведений. Имеем:
240 4632 +190* + 2406542 + 240 2722
= 500 961-240 463 + 792.190 + 501 763-240 654+500 170-240 272
Отсюда, учитывая, что х{8) —-лгG) = а8р, находим:
-1,532746-
0,122009
1,972937
.1,410737.
12
+ 13
-0,002405-
0,000002
0,002406
„0,002403-
1,534965-
0,122011
1,975159
Л,412955.
Для сравнения приводим значения корней системы A1),
полученные методом Гаусса [1]:
хг = 1,534965; х2 = 0,122010
лг3= 1,975166; дг4= 1,412955.
Таким образом, если х{9) давало значения корней xi (/ = 1, 2, 3, 4)
примерно с точностью МО — 2«10~3, то после поправок

ЛИТЕРАТУРА К ДВЕНАДЦАТОЙ ГЛАВЕ 449
Л. А. Люстерника мы получаем эти корни приблизительно с
точностью до 10~6.
Метод Л. А. Люстерника улучшения сходимости может быть
применен также к процессу Зейделя. Как известно, процесс Зейделя
для системы B) представляет собой процесс итерации для
равносильной системы
где матрица ах однозначно определяется через матрицу а (см. гл XI,
§ 3), а именно, если
где В—нижняя треугольная матрица с нулевой диагональю и С—
верхняя треугольная матрица, то
Поэтому, если |(|Я) (/» = 1, 2, ..^-—последовательные приближения
по Зейделю корня х системы B), то можно положить:
где \ix — наибольшее по модулю собственное значение матрицы аг.
Отметим, что существуют также и другие методы улучшения
сходимости итерационных процессов для решения систем линейных
уравнений, например, метод М. К. Гавурина [7], [8], метод А. А.
Абрамова [9].
Литература к двенадцатой главе
1. В. Н. Фаддеев а, Вычислительные методы линейной алгебры, Гостех-
издат, М., 1950, гл. III.
2. И. М. Гельфанд, Лекции по линейной алгебре, Изд. 2, Гостехиздат,
М. — Л., 1951, добавл. I.
3. А. Г. К у рош, Курс высшей алгебры, Гостехиздат, М. — Л., 1946, гл. VI.
4. Гарольд Вейленд, Представление векового уравнения в виде
многочлена, УМН II, вып. 4 B0) A947), 128—158.
5. В. Э. Милн, Численный анализ, ИЛ, 1951, гл. II.
6. Л. А. Л юс тер ни к, Труды Матем. ин-та им. В. А. Стеклова, 20 A947),
стр. 49.
7. М. К. Г а в у р и н, Применение полиномов наилучшего приближения к
улучшению сходимости итеративных процессов, УМН, 5:3 C7) A950),
156—160.
8. И. С. Б е р е з и н и Н. П. Ж и д к о в, Методы вычислений, Физматгиз,
1959, т. 2, гл. VIII.
9. Д. К. Фаддеев и В. Н. Фаддеев а, Вычислительные методы линейной
алгебры, Физматгиз, 1960, гл. IX.

ГЛАВА XIII
ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ
§ 1. Метод Ньютона
Рассмотрим, вообще говоря, нелинейную систему уравнений
/i(*i, *2> ...» *л) = 0
/2 (xv х2, ..., хп) — 0
0)
с действительными левыми частями.
Запишем короче систему A). Совокупность аргументов xv
*2> ...» хп можно рассматривать как /г-мерный вектор
Аналогично совокупность функций fv /2, ..., /я представляет собой
также л-мерный вектор (вектор-функцию)
f •==•
Г!Г
Поэтому система A) кратко записывается так:
/(*) = 0. (Г)
Для решения системы (Г) будем пользоваться методом
последовательных приближений.
Предположим, что найдено р-е приближение
1 , Л-2 > • • • ) ХП

§ 1]
МЕТОД НЬЮТОНА
451
одного из изолированных корней х = (лг1, Х2, *.., хп) векторного
уравнения (Г). Тогда точный корень уравнения (Г) можно
представить в виде
B)
= (8Aр), е(/\ ..., е^) — поправка (по г р е шн ость корня).
Подставляя выражение B) в уравнение (Г), будем иметь:
/(*<"> + 8">) = 0.
C)
Предполагая, что функция f(x) непрерывно дифференцируема
в некоторой выпуклой области, содержащей х и д:<я, разложим
левую часть уравнения C) по степеням малого вектора г{Р\
ограничиваясь линейными членами,
е<л = о
D)
или, в развернутом виде,
Л(^Г + еГ.^ Г
г{р)
tflXt\Xl > *2 9 • • •» ХП ) ?2
>, ... f xip>
V,
"T/ /we\^i » «^2 * • • • > -^л / e2 "Г • • •
n
v.
Из формул D) и D') вытекает, что под производной f (x)
следует понимать матрицу Якоби системы функций f1% /2, ..., /
относительно переменных xv х2, ..., xnJ т. е.
дхг дхг * * * дхп
дх~1 Ъх^ дх~п
_дхх дх2 " * # дхп^
15»

452 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХГ11
или в краткой записи
/' (х) = W(x) =
(/, у= 1,2,..., п).
Система D') представляет собой линейную систему относительно
поправок e\p)(i=\t 2, ..., п) с матрицей W(x)9 поэтому
формула D) может быть записана в следующем виде:
Отсюда, предполагая, что матрица W(x{P)) — неособенная, полу-
чим:
Следовательно,
= 0, 1, 2, ...
E)
(метод Ньютона).
За нулевое приближение дг@) можно взять грубое значение
искомого корня.
Пример 1. Приближенно найти положительные решения системы
уравнений (ср. гл. IV, § 9)
/х (xv х2) = хх + 3 lg хг — х\ = 0, \
l9 х2)е=2х1 — х1х2 — 5х1+\=0. )
ft(x
Решение. Кривые, определяемые системой F), пересекаются
приблизительно в точках Мх A,4; —1,5) и М2 C,4; 2,2). Исходя
из начального приближения
= ГМ1
L2.2J '
вычислим вторые приближения корней, производя вычисления с
точностью до четырех десятичных знаков. Полагая
Jr 0Д5441
- Lo36OoJ •
имеем:
[2.3,42—3,4-2,2—5-3,4+1
Составим теперь матрицу Якоби
Cffi Ofi
дхг дх2
-дхх дх2-
xi

§ и
МЕТОД НЬЮТОНА
453
где М — 0,43429. Отсюда
|_4.3,4-2,2-5 -3,4 J L6'4 ~3'4J
причем
Следовательно, матрица W (хт) — неособенная. Составим
обратную ей матрицу
т* \ / "~~ А I С Л 1 OQOO I •
v Д L— 6,4 l,3o32J
Используя формулу E), получим:
уA)_Р»Я 1 I"-3*4 4»4 1Г 0,1544]_
"" L2,2J 23,4571 L— 6,4 1,3832J [—0,3600J ""
] _ Г3,4] Г0,0899] _ Г3,4899
J ~ [2,2J + [о,О633] " L2»2633
_ Г3,4] 1 Г—2,10896
L2,2j 23,4571 L— 1,486O4
Аналогично находятся дальнейшие приближения. Результаты
вычислений приведены в таблице 32.
Таблица 32
Последовательные приближения корней системы F)
0
1
2
3
3,4
3,4899
3,4891
3,4875
0,0899
— 0,0008
— 0,0016
х2
2,2
2,2633
2,2621
2,2616
0,0633
— 0,0012
— 0,0005
Останавливаясь на приближении jcC), будем иметь:
^ = 3,4875; *2 = 2,2616,
причем
- Г0'0002]
~ [o,ooooj#
Пример 2. Методом Ньютона приближенно найти
положительное решение системы уравнений
исходя из начального приближения

454 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Решение. Имеем:
Отсюда
[0,25 + 0,25 + 0,25 — 11 Г- 0,251
0,50 + 0,25 — 2,00 = -1,25 L
0,75-2,00 + 0,25 J L—1.00J
Составим матрицу Якоби
W(x) =
Имеем
W{xm)
[2х 2у 2г1
4х 2у -4 .
6* —4 2z J
Г1 1 П
= 2 1 -4
L3 -4 ij
1 I 1
2 I —4
3 ~4 1
:—40.
Находим обратную матрицу
_L
-15
- 14
-11
-5
— 2
7
— 5
6
j
8 8 8
L 1 _A
20 20 20
И _2. JL
40 40 40
По формуле E) получаем первое приближение
л ^ дрСО) _ уг-1 (xm)f{Xm) ==
0,5
0,5
3
8
7

loll
40
1
8
1
20
—7
40
1
8
-3
20
1
40
-0,25
-1,25
-1,00
[0,5] Г 0,3751 Г0,8751
0,5 + 0 =0,500
0,5j L—0f125J LO,375J

§ II
МЕТОД НЬЮТОНА
455
Далее вычисляем второе приближение х{2\ Имеем:
Г0,8752+0,5002+0,375а - П ГО,
f(x{1)) = 2-0,8752+0,5002 — 4-0,375 = О,
1>0,8752 — 4-0,500 + 0,3752 J LO,
[2-0,
4-0,
6-0,
0,156251
28125
43750J
875
875
875
2-0,500
2-0,500
2-0,375
— 4
2-0,375.
1,750
3,500
5,250
Отсюда
det
1 0,7501
1 -4 L
— 4 0,750 J
1,750
3,500
5,250
0,750
— 4
0,750
1,750
1,750
12,250
1
0
О
0,750
— 4,750
3,750
= —64,75
-__ 15,25 —3,75
— 23,625 —2,6250
^—19,25 12,25
-4,75 1
9,625 .
-1,75 J
Используя формулу E), получаем:
— 3,75
— 2,6250
12,25
Е
[0,8751 Г0.085191 ГО,
0,500 — 0,00338 = О,
O,375J L0,00507j Lo,
— 4,75
9,625
— 1,75
[0,085191
\00338
',00507
156251
28125 ==
43750J
0,789811
2 И
36993J
Аналогично находятся дальнейшие приближения:
[0,785211 Г0,0000П
0,49662 , / (X{S)) == 0,00004
0,36992 J LO, 00005 J
и т. д. *
Ограничиваясь третьим приближением, получим:
х = 0,7852; ^ = 0,4966; 2 = 0,3699.

456 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
§ 2. Общие замечания о сходимости процесса Ньютона
В § 1 был дан формальный аспект метода Ньютона. Условия
сходимости этого метода для системы исследованы Виллерсом,
Стениным, Островским, Канторовичем и др. Ниже излагается частный
случай теоремы Л. В. Канторовича (теорема 1) [1] о сходимости
процесса Ньютона в функциональных пространствах применительно
к конечным системам нелинейных уравнений, причем для простоты
рассуждений используются более грубые оценки. Следуя Л. В.
Канторовичу, устанавливаем также быстроту сходимости процесса
Ньютона, единственность корня системы и устойчивость процесса по
отношению к выбору начального приближения (теоремы 2— 4). Как
частный случай получается теорема Островского [2] о сходимости
процесса Ньютона для уравнения с аналитической комплексной
правой частью.
В дальнейшем совокупности функций будет удобно рассматривать
как вектор-функцию или матричную функцию. Для облегчения
изложения обобщим понятие производной на эти случаи.
Пусть x = (xv ..., хп) и
где /,€(?" (/=1, 2, ..., п).
Определение 1. Под производной f(x) понимается матрица
Якоби системы функций ft (i = 1,... ,я) по переменным xv ..., хп,
т. е.
A)
Матричную функцию
F(X) = \
можно рассматривать как совокупность т вектор-функций
Поэтому под производной F'ix) естественно понимать совокупность
F'{x) = [F[(x) ... F'r(x)],

§ 2] ОБЩИЕ ЗАМЕЧАНИЯ О СХОДИМОСТИ ПРОЦЕССА НЬЮТОНА 457
где
хл дх»
dxnJ
— матрицы Якоби (ft=l, 2,..., г).
Определение 2. Если F(x) =
трица типа пхг и /и(х) ?CA), то
—функциональная
магде
1, 2,..., п; k=\y 2,..., г).
В частности, если вектор-функция f(x) = [/Дл;)] такова, что
^2>, то
где
В этом параграфе для оценки матриц мы будем пользоваться
/гс-нормой (гл. VII, §7), причем значок т для краткости опускается,
а именно:
дх
\\f (х)\\ = max || Wk(x)\\ = max j max ? | |Щ | J
и т. п.
Аналогично
* /=i
dti,(x)
*) Так как, очевидно, для любой конечной совокупности чисел
имеем:
max
iax / max а, Л = max а,у

458 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
Предварительно выведем несколько оценок для m-норм разностей
значений матричных функций, аналогичных формуле конечного
приращения, которые окажутся полезными в дальнейшем (ср. [1]).
Лемма 1. Если
nx) = [ft,(x)] (лхг),
где ffj(x) непрерывны вместе со своими частными производными
первого порядка в выпуклой области, содержащей точки х и
х + Ах, то
• Ц/7' (|)||, C)
где | = jc + 8Ajc, О<0<1 и норма матриц понимается в
смысле т-нормы.
Доказательство. Применяя формулу Тейлора, получим:
где 1/у=л; + 6/уДх, 0<в/у< 1; /==1, 2, ..., п\ у=1, 2, ..., л
Отсюда, фиксируя х и х-\-Ах, будем иметь:
:tnax
дхь
Так как число пар (*, j) конечно, то найдется пара (р, q) такая,
что
max
dxk
п ,
*=!'
max
dxk
где \ = \pq.
Таким образом,
что и требовалось доказать.

§ 2J ОБЩИЕ ЗАМЕЧАНИЯ О СХОДИМОСТИ ПРОЦЕССА НЬЮТОНА 459
Следствие 1. Если
/(*>'
-Jn <*)-
то
II/(*+ А*)—/(х)|| < IIД*||-11/45I1.
где | = х + 9 Ддг и 0 < 9 < 1.
Здесь г= 1.
Следствие 2. При / (лг) ? С*2) имеем:
||/' (х + дх) -/' (jr)|| < nUx\\ \\f E)||.
и о < е < к
где | =
Лемма 2.
в выпуклой области, содержащей точки X и лг + Д^, го
||/(* + Аж) -/(х) -/ (х) ьх\\ < 1 /i||дх||2. !!/• AI1, D)
1
Доказательство. Используя двучленную формулу Тейлора,
получаем:
И[/« (ж + Дж) -/, (ж) -dfi (ж,-)]11
: *2~П1<1Х |
E)
где 1, =

460 ПРИБЛИЖЕННОЕ РеШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Так как
dxjdxk
i.i
dxq dxk
max
dxjdxk
то из неравенства E), учитывая смысл нормы, получаем:
т11А*11'11/ЧШ,
где 1 = |_ =
§ 3*. Существование корней системы и сходимость
процесса Ньютона
Теорема 1. Пусть дана нелинейная система алгебраических
или трансцендентных уравнений с действительными
коэффициентами
/(*) = 0, A)
где вектор-функция
fn(xu . . .,xn
определена и непрерывна, вместе со своими частными
производными первого и второго порядков, в некоторой области со, т. е.
Положим, что х{0) есть точка, лежащая в со вместе со своей
замкнутой Ж-окрестностью:
= { || х - X
™
Ж} с 0),
г&е норма понимается в смысле m-нормы *) (см. гл. VII, § 7),
причем выполнены следующие условия:
*) То есть если А = [ау], то

§ 3J СУЩЕСТВОВАНИЕ КОРНЕЙ И СХОДИМОСТЬ ПРОЦЕССА НЬЮТОНА 461
1) матрица Якоба W(x)= \-J^\ при x = Xm имеет
обратную Го= W-1(xl0)), где ''
2) ||1
m?uc
при i, j= 1, 2, . .., n и x %
4) постоянные Ло, ?0 w С удовлетворяют неравенству
цо = 2лЛоввС^1. B)
Тогда процесс Ньютона
C)
(р — 0, 1, 2, ...) при начальном приближении Хш сходится и
предельный вектор
лг*= lim xm
решение системы A) такое» что
||дг*-дг@)||<2В0<^.
Доказательство. Введем обозначения
max | ^+1> — 4Р) |»
p = 0, 1, 2, ...).
Из формулы C) имеем:
-^Л|| = max |
Исходя из условий 1) — 4), получим оценки для величин Г и
Рассмотрим сначала случай /?=1. Используя условие 2), имеем
,л )\\ ^s ^»о ^= ^^»
*) Иными словами, если W (х@)) = [а/7Ь то Г0=Г-1 (ж<0))= Г^'1 ,
где Л/у—алгебраические дополнения элементов а^ и A = det[a/yJ и,
следовательно,

462 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
следовательно,
и
(ш) с
2
Для оценки T1 = W~1(xa)), воспользовавшись соотношением
ВIВ1А\ представим эту величину в виде
T^lWix^^Wix^r^ir^ix^r^r^ D)
Учитывая условие 1) теоремы, имеем:
\\E-r0W(x™)\\ - ||Г0 [W(х™)- W(х™)}\\ <
Так как из условия 3) вытекает, что
"'«•-???1Ж1<<1
то в силу следствия 2 к лемме 1 получаем:
поэтому
Следовательно (гл. VII, § 10, теорема 5, следствие), существует
обратная матрица
)]-* = {Е- (E-T0
причем, так как \\Е|| ==||Е\\т= 1, то
||[Г0Г (дс»»)]-1!! < 17—< 2. E)
т
Теперь из формулы D) выводим:
II Гг II < II [Г0Г (ж™)]-11| Г ||0 || < 2А„ = А„ F)
Далее, из формулы C) следует:
) - х@)) = 0.
Отсюда на основании леммы 2 будем иметь:
\ п Ц *«>-*«¦> ||* ||/' (I) || < I пЕ%,С,

§ 3} СУЩЕСТВОВАНИЕ КОРНЕЙ И СХОДИМОСТЬ ПРОЦЕССА НЬЮТОНА 463
где
{1) — дг@)) и 0<в<
Поэтому, учитывая неравенство F), получим:
^^ = Bl. G)
Итак, для точки д:A) мы имеем:
и, кроме того,
где
Отсюда получаем:
±oC=til^\. (8)
Следовательно, мы снова находимся в условиях теоремы с той
только разницей, что вместо окрестности Uffl(x{0)) имеем
окрестность Uffl(xil)), вложенную в первую.
~Г
Повторяя аналогичные рассуждения, мы установим, что
последовательные приближения xiP)(p~ 1, 2, ...) имеют смысл и таковы,
что
причем
где постоянные Л и Вр связаны между собой рекуррентными
соотношениями
3 2Г
J
-1 J
(9)
=l, 2, ...). (Ю)

464 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XII!
Покажем, что для последовательности приближений х{Р) (р = 0,
1, 2, ...) выполнен критерий Коши (гл. VII, § 9). Действительно,
при q > 0 имеем:
Поэтому
если р> N и ^> 0? что эквивалентно критерию Коши. Отсюда
следует, что существует
Убедимся теперь, что х* есть решение системы A). Из
соотношения C) имеем:
Переходя в этом равенстве к пределу при р—*оо и учитывая, что
при этом
*i/h-i> _*<*_> О,
а также, что W(xiP)) непрерывна и ограничена в f/^f (xi0)), будем
иметь:
lim/(*<*>) = 0.
р -> ю
Отсюда в силу непрерывности функции /(лс) получим:
f( lim др^\=/(х#) = О,
т. е. лс* есть решение системы A). Кроме того,
l-* —«* II 2
р=0 р=о
Теорема доказана полностью.
Замечание 1. Если f(x) gCB)(o) ив области о> система A)
имеет простое решение х*, т. е. такое, что
/(**) = 0, /'(**) = W (х*)Ф О,
то для каждой точки х{0\ достаточно близкой к х*, условия
теоремы 1, очевидно, будут выполнены.

§ 4] БЫСТРОТА СХОДИМОСТИ ПРОЦЕССА НЬЮТОНА 465
Для проверки условия 2) полезно отметить, что Во дает оценку
расхождения начального и первого приближений процесса Ньютона:
1 о/ \х /II — II* —х I
и поэтому это неравенство легко может быть проверено, как только
будет найдено приближение хаК
Замечание 2. Аналогичные формулировки для теоремы
сходимости получаются, если вместо нормы ||Л ||Л использовать нормы \\A\\t
или || А \\к.
§ 4*. Быстрота сходимости процесса Ньютона
Теорема 2. Если выполнены условия 1) —4) теоремы 1 из § 3,
то для последовательных приближений х{Р) (р = 0, 1, 2, ...)
справедливо неравенство
II**-
где Jt* — решение системы и fi0 определяется формулой B) из § 3.
Доказательство. Используя соотношения (9) и A0) из § 3,
имеем:
|i, - 2пАрВрС=2п • 2Ар_г . 1 ^гВр^С^ *
Отсюда получаем
Далее,
Поэтому
о 1 ..2Р-1 1 ..г?-8
Так как

466 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
то при q > I имеем:
Отсюда, учитывая, что цо<1, получаем:
Переходя к пределу при q—>-оо, окончательно находим:
где
Таким образом, при \i0 < 1 сходимость процесса
Ньютона—сверхбыстрая. В частности, при р = 0 будем иметь:
§ б*. Единственность решения
Теорема 3. При наличии условий 1) — 4) теоремы 1 аз § 3
в области
A)
содержится единственное решение системы A) (§ 3).
Доказательство. Пусть, кроме решения дс* системы A)
из § 3, определяемого процессом Ньютона, имеется другое
решение х** этой системы такое» что
Последовательные приближения х{Р) (р = 0, 1,2, ...) процесса
Ньютона содержатся в окрестности A) и удовлетворяют условию
Wp (xiP+1) - х{р>) - О,
где

§ 5] ЕДИНСТВЕННОСТЬ РЕШЕНИЯ 467
Отсюда, учитывая, что
/(***)=о,
получаем:
и, следовательно,
где
Г — IF""
1 р— wp
Производя оценку по норме, будем иметь:
Согласно обозначениям § 3 (см. теорему 1)
II Г, || < Л,.
Применяя лемму 2 из § 2, получим неравенство
*)/(*(Я)^(л**^яI1<
где постоянная С определена из условия 3) теоремы 1. Поэтому
^ (/> = 0, 1,2, ...). О)
Полагая р = 0 в неравенстве C) и используя неравенство B),
получим:
i 2nA0BlC,
или, вводя числа, определяемые соотношениями
находим
0 = 2В1. E)
Аналогично при р—\ из формул C), E) и D) выводим:
И х** _ЖB) || ^^ nAiC || х** _хи> ||* ^ 2лЛх^С= р,^ = 2В2.
Вообще,
И ***-*<« || <2fi, (р = 0, 1, 2, ...)• F)
Так как на основании формулы B) из § 4 величина Вр—>0при
р—>оо, то, переходя к пределу в неравенстве F), будем иметь:
т. е. решение системы A) в области ||;е—х*т \\ *^2В0 единственно.

468 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Замечание. Если область Uffl(xm)> такова, что
то в расширенной области A)
||х_ж«»||<-рВ0 G)
не имеется других решений системы A), кроме х*.
Действительно, предполагая, что в области G) находится
решение х** системы A) (§ 3) и повторяя рассуждения теоремы, мы
получим неравенство вида C)
|| *** -х{р+1) || <у пАрС\\ х**-х'Р) ||2,
где х{Р) (р = 0, 1, 2, ..^ — последовательные приближения
процесса Ньютона с начальным приближением х{0). Отсюда, так как
\\Л X |j ^»—-?50,
то, используя числа №р+1 = 1*>1, последовательно имеем:
<*• * ** л с R2
X —х || ^ *
и т. д.
Вообще,
|| *••-*<" || <Ав, (Р = О, 1, 2, ...).
Так как
и
то
(8)
Последнее соотношение можно также непосредственно получить из
формул A) и B) (§ 4).

§ 6] УСТОЙЧИВОСТЬ СХОДИМОСТИ ПРОЦЕССА НЬЮТОНА 469
Таким образом,
Следовательно,
х**= lim x{p) = x*,
что и требовалось доказать.
§ 6*. Устойчивость сходимости процесса Ньютона
при варьировании начального приближения
Теорема 4. Если выполнены условия 1) — 4) теоремы 1 из
§ 3 и
\io = 2nAQBoC< 1, то процесс Ньютона сходится к
единственному решению х* системы
A) (§3) в основной области
\\х — х{0) || < 2В0 при любом
выборе начального приближения
х'т из области
A)
1т±
Док азательств о.По
аналогии с введенными выше
обозначениями
и To^
введем обозначения
и Г; = (
. 58.
Покажем, что в точке хП0) будут выполнены условия,
аналогичные условиям 1) — 4) теоремы 1.
Используя обозначения и метод доказательства теоремы 1, имеем:
Отсюда, учитывая неравенство A), получим:

470 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Следовательно,
|| (Гв!Г;)-1 И = || [Е-{Е-Г0&0)Г* II <
^ 1 ^ 1 4 .„
Поэтому существует
и
Далее, выводам:
f ) II ^ II Го |
IV7 ( *.'@) v*0)\ II _1_ II V -Pi %Л0) \ II _L II %»г@) *-^°>
w О \Л * / II ~Т~ II * о/ \"* / II ~Г И Л •*
^ "о* о^^ II ^ —^ II "Т""о"т1'^ ^ II
^ +161X0+8-8^0
Отсюда, используя неравенство B), имеем:
На основании неравенств C и D) получаем:
Кроме того,
2В +1| х(в'-*<»» ||< Щ 50
и, значит, и подавно
25'<°
Таким образом, в точке лг'@) полностью выполнены условия
теоремы 1, причем
(рис. 58).

§ 7] МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА 471
Поэтому процесс Ньютона
где
fp=W~*(x'W) (/> = 0, 1,2, ...),
сходится к некоторому решению х'* системы A) § 3, лежащему
в области U%b' (х'{0)). На основании формулы E)
Но в силу замечания к теореме 3 предыдущего параграфа в области
U*bc(x{0)) имеется единственное решение х* основной си-
стемы A). Поэтому
*'* = **
и
х*= Птх'{р\
р-+ со
что и требовалось доказать.
Замечание. Если 2В0 < Ж и \i0 < 1, то для начального
приближения д:@) всегда имеется окрестность, любая точка которой может
быть принята за начальное приближение процесса Ньютона,
сходящегося к искомому решению х*.
Действительно, пусть
2В0
где д> \. Полагая
получим, что в силу теорем 1 и 4 для любого начального
приближения х'{0\ удовлетворяющего условию
соответствующий процесс Ньютона будет сходиться к решению х*
системы A).
§ 7. Модифицированный метод Ньютона
При построении процесса Ньютона
) (Р = 0, 1, 2, ...) A)
существенным неудобством является необходимость для каждого шага
наново вычислять обратную матрицу W~* (x{f)). Если матрица'W~x(x)

472 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
непрерывна в окрестности искомого решения х* и начальное
приближение дг@) достаточно близко к jc*, то приближенно можно положить*
и мы, таким образом, приходим к модифицированному процессу
Ньютона
B)
(р = 0, 1, 2, .. .), где |@)==дг@). Заметим, что для процессов A) и B)
первые приближения д:A) и |A> совпадают между собой, т. е.
Сходимость модифицированного процесса Ньютона B)
исследовалась Л. В. Канторовичем [1].
Теорема. Если выполнены условия 1) — 4) теоремы 1 из § 3 и
то модифицированный процесс Ньютона B), определяемый
начальным приближением ^0) = лг@), сходится к решению х* системы
причем
Up (р = 0, 1,2, ...), C)
где норма понимается в смысле т-нормы.
Доказательство. Рассмотрим вектор-функцию
где Го= W-l
Очевидно,
(р = 0, 1, 2, ...). D)
Кроме того,
F'(x)=E-rof'(x); E)
отсюда, в частности,
F' (xiO)) = E—rof (х{0)) = Я—Е=0. F)
Методом математической индукции докажем, что все
приближения |(/>) (р= 1,2,...) содержатся в 2Я0-окрестности точки jc@), т. е.
Действительно, при р= 1 равенство G) очевидно, так как в силу
условия 2) теоремы имеем:
|| |<1> - х™ \\ = Ц дгA) - х™ Ц < Во.

§ 7J
МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА
473
Пусть теперь для некоторого р выполнено неравенство G). Тогда,
используя лемму 2 (§ 2), имеем:
дш || = || F(!</»)_хт ,| в „ |ся_г0/(§«)-*«» || =
= II Го [/(S(*>)- W(x^) (^>-дг(о))] || < || Г0/(лг<°>) || +
+ II Го {/(!<*>) -/(х«>) - W (лг<°>)
< Во + ±
Используя неравенство G), находим:
что и доказывает наше утверждение.
Так как условия теоремы 1 (§ 3) предполагаются выполненными,
то система /(лг) = О имеет корень дг* такой, что || лг* — дг@)|| < 2В0.
Рассмотрим разность л:*--!^, где р^1. Учитывая, что
(в) II. (8)
и используя лемму 1 (§ 2), имеем:
II х* - V» || = || F (jr») - F (V-»)
где 0 —точка отрезка [лг*, l^"3].
Далее (см. § 2, лемма 1, следствие 2)
II F @) || -1| F (в) - F' (х@)) Ц < /г || в -лг@) || max || F" (ч)||, (9)
где t| —точка отрезка [0, jc<0)]. Из формулы E) имеем:
4
где б;у — символ Кронекера и Го = [у//Ь Поэтому
Следовательно,
п

474 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
и, значит, на основании (9),
Так как точка в, очевидно, принадлежит 2?0-окрестности точки дг@\то
||в-лг«»||<2Я0
и, таким образом,
II ^ (в) || < 2лЛвВ0С= |хв. (Ю)
Учитывая неравенство A0), из неравенства (8) выводим:
откуда
| х* _ |(о> || = уР ц х* _
При ц.в < 1 из последнего неравенства вытекает, что
lim 1^ = х*.
р -*• оо
Теорема доказана полностью.
§ 8. Метод итерации
Пусть дана система нелинейных уравнений специального вида
где функции ф1? ф2, ..., <рп действительны, определены и непрерывны
в некоторой окрестности ш изолированного решения (аг*,^^ ..., х*п)
этой системы.
Введя в рассмотрение векторы
X = (XV ЛГ2, ..., Хп) И ф(Х) = (ф!(Х), ф2(ЛГ), ..., фл(ДГ)),
систему A) можно записать более кратко:
Х = <Р{Х). B)
Для нахождения вектор-корня дг* = (х1) х2, ..., хп) уравнения B)
часто удобно использовать метод итерации
Х<я+1> = <?(*<*>) (р = 0, 1, 2, ...), C)
где начальное приближение jc@)«jt*. Сходимость этого процесса
будет исследована ниже. Заметим, что если процесс итерации C)
сходится, то предельное значение
= lim xm DJ
р -> оо

§ 8J метод итерации 475
обязательно является корнем уравнения B). Действительно,
предполагая, что соотношение D) выполнено, и переходя к пределу
в равенстве C) при р—*оо, в силу непрерывности функции <р(лг)
будем иметь:
lira x{p+l) = <f( lim х{р)),
т. е.
Таким образом, | есть корень векторного уравнения B).
Если, сверх того, все приближения х{р) (р = 0, 1, 2, . ..)
принадлежат области ши х* — единственный корень системы B) в со,
то, очевидно,
*
Метод итерации может быть применен также к общей системе
0, E)
где f(x) — вектор-функция, определенная и непрерывная в
окрестности 0) изолированного вектор-корня х*. Например, перепишем
эту систему в следующем виде:
где Л — неособенная матрица. Введя обозначение
* + Л/(лг) = ф(х), F)
будем иметь:
Х = <((Х). , G)
К последнему уравнению легко применяется обычный метод
итерации C).
Если функция f(x) имеет непрерывную производную f'(x) в со,
то из формулы F) вытекает:
В следующих параграфах будет доказано, что процесс итерации
для уравнения G) быстро сходится, если <р' (х) мала по норме.
Учитывая это обстоятельство, выбираем матрицу Л так, чтобы
<р' (дг@)) =*E + Af (Х{О)) = 0;
отсюда, если матрица /' (лг@)) — неособенная, будем иметь:
Заметим, что это, в сущности, модифицированный процесс Ньютона,
примененный к уравнению E) (см. § 7).
В случае, если det/' (jc@)) = 0, то следует выбрать другое
начальное приближение jt*0).

476 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
Употребляются также иные способы замены системы E)
эквивалентной ей системой G).
Пример. Методом итерации приближенно решить систему
(8)
Решение. Из графического построения видно (рис. 59), что
система (8) имеет два решения, отличающихся только знаком.
Ограничимся нахождением положительного решения. Из чертежа
усматриваем, что за начальное приближение положительного решения
системы (8) можно принять:
Рис. 59
del/'(дг@))
— 1,8-
— 2,43= —4,23.
Так как матрица /' (лг<0)) — неособенная, то существует обратная
матрица
Таким образом,
Положим
_1_ Г" ~ 1
4,23L-2,43 1,8 J '
Тогда система (8) будет эквивалентна стандартному матричному
уравнению
(9)

§ 91
ПОНЯТИЕ О СЖИМАЮЩЕМ ОТОБРАЖЕНИИ
477
Пользуясь формулой D), находим для решения системы (9)
последовательные приближения:
L*20)J 4'23L2'43 ^8 JL 40'3—40> J
__ ГО,9] 1_ П 1 ] ГО,060] _ ГО,9] _ Г 0,06831 _ Г0.8317] #
" [o,5J 4,23 L2,43 —1.8J [o,229J ~ |0,5j [—0,0630j ~~ [o,563OJ f
,2)_f 0,83171 ^Г1 1 1 [0,83172 + 0,5630^-1]
X L0,5630J 4,23[2,43 —1,8 J [ 0.83173—0,5630 J
_ Г0,8317] Г—0,0049] _ [0,8268] .
~~ L0,5630 J L 0,0003 J "" [0,5633 J '
C)_ Г 0,8268] _ Г 0,0007] _ Г 0,8261 ] #
X ~~ [ 0,5633 J L °.0002 J "" [0,5631 J ;
82611 Г 0,0000]
5631 J L—0,0005 J
u>_ [0,8261] Г 0,0000] __ [0,8261 ]
Х ~~ [ 0,5631 J L—0,0005 J ~" [ 0,5636 J
и т. д.
Ограничиваясь четвертым приближением, имеем корни
#! = 0,8261; лг2 = 0,5636,
причем
с точностью до 10~4.
/(*) = [2;00001
]
0002J
§ 9*. Понятие о сжимающем отображении
Пусть дана нелинейная система
y1 = (f1(xv x2t ..., хп),
A)
где функции <plf ф2, ..., ф„ определены и непрерывны в известной
области G действительного /z-мерного пространства Еп (гл. X, § 1),
причем значения их (j^j^i • • -> У„) "Ри \xv лг2, ...,лгЛ) g О
заполняют некоторую область & d En. Система A) устанавливает ого-
бражение области О на область G'. Введя векторы
•
~У1'
-Уп-
"Ф1"
1-ф„-
систему A) коротко можно записать следующим образом:

478 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
В пространстве Еп введем каноническую норму Ц-jf ||,
удовлетворяющую обычным условиям. Например, можно положить;
или
или
И Т. П.
Отображение A) или A') называется сжимающим в области G,
если существует правильная дробь q такая, что для любых двух
точек хг, лг2€Оих образы ^ — ф^) и ^а = ф(ДГ2)
удовлетворяют условию
\\У1-У2\\<Я\\Хг-Х2\\, B)
1). B')
Рассмотрим нелинейное векторное уравнение
* = Ф<ж), C)
эквивалентное нелинейной системе уравнений специального вида
•*1 == Фх \-^1> Х%ч • • • > -^л)»
дг2 = ф2(х1э лг2, ..., лгл),
Решение х* этого уравнения, если оно существует, является
неподвижной точкой преобразования A). Для нахождения х* построим
итерационный процесс
Ф) (р-1, 2, ...), D)
где дг10)€О.
Теорема 1. Пусть область О замкнута и отображение A)
является сжимающим в О, г. ?. выполнено условие B). Тогдау
если для итерационного процесса D) все последовательные
приближения xm?G (р = 0, 1, 2, ...), то 1) независимо от выбора
начального приближения хт процесс D) сходится, т. е. существует
X* = lim x{Pht E)
р -> о©
2) предельный вектор х* является единственным решением
уравнения C) в области G; 3) справедлива оценка
< ?|| *<«-*«»||. F)

§ 9] ПОНЯТИЕ О СЖИМАЮЩЕМ ОТОБРАЖЕНИИ 479
Доказательство. 1) Для доказательства сходимости
последовательности приближений х{р) (р = 0, 1, 2, ...) применим крате*
рай Коша (см. гл, VII, § 9). Имеем:
> _*</>+*-!> ||. G)
Используя соотношение D) и «условие сжатости» B'),
последовательно получаем:
| дг<1> —ж™ II, (8)
где s^O. Поэтому, усиливая правую часть неравенства G), будем
иметь:
— ДГ<
0) |
или, воспользовавшись формулой для суммы членов геометрической
прогрессии, находим:
**k A) ~^@) II < Y^rq II *(Ь -х™ ||. (9)
хР II <? II ^ ~^ II < Y^rq II * -х
Так как 0^#<1 и, следовательно, qp—+ 0 при р—>- сх>, то из
формулы (9) вытекает, что для всякого е>0 существует Ы=Ы(г)
такое, что при /?>N(e) и k>0 будет справедливо неравенство
-*<" ||<ef
т. е. для последовательности х{р) (р = 0, 1, 2, ...) выполнен
критерий Коши. Поэтому существует:
дг* = tim x{p\
причем jc*?G в силу замкнутости области О.
2) Вектор ж* является решением уравнения C), так как,
переходя к пределу при р-+оо в равенстве D) и учитывая
непрерывность в О вектор-функции <p(JC), будем иметь:
iltn Ar(/>)=<p( Hm
P -f <X> p -+ 00
. A0)
Это решение единственно в О. Действительно, пусть X*' есть
другое решение уравнения C), т. е.
Ж*'=ф (**'). (И)

480 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
Вычитая из равенства A0) равенство A1), получим:
**~**'=<р(д;*)--ф (**'),
отсюда
||х#-д^'|| = 11ф(*#)-Ф(**/I!<^Цл#-л*'||
или
(l-tf)||x»_*»'H<0. A2)
Так как 1—q > 0, то неравенство A2) может иметь место лишь
при || а:* — л;*'|| = 0, т. е. тогда, когда jt* = Jt*'. Таким образом,
другого решения уравнения C) в области G быть не может.
3) Переходя к пределу при & —* оо в неравенстве (9), получим
оценку F).
Теорема 1 доказана полностью.
Замечание 1. Если область О совпадает со всем
пространством ЕпУ то условие x{p)?G (р = 0, 1, 2, ...), очевидно,
становится излишним.
Замечание 2. Используя неравенства
из формулы G) будем иметь:
Отсюда при k—> сю получим:
||*#-*ич||<т^||*1Л-*«'-и||. A3)
\
В частности, если О^^^-у, то из формулы A3) следует,
что при
справедливо неравенство
В условии теоремы 1 требуется, чтобы все приближения хкр)
принадлежали фиксированной области G. На практике это
обстоятельство иногда затруднительно проверить. Поэтому мы приведем
несколько видоизмененную формулировку теоремы 1.
Теорема 2. Пусть отображение A) является сжимающим
в замкнутой области G} и g—ограниченная область, лежащая в G
вместе со своей ^-окрестностью (в смысле введенной нормы), где

§ 10] ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ ПРОЦЕССА ИТЕРАЦИИ 481
D — диаметр области g и q —соответствующий коэффициент в
неравенстве B). Тогда, если
x{0)?g и хР = у(х™)€&
то итерационный процесс D) сходится и справедливы заключения
теоремы 1.
Доказательство. Очевидно, достаточно доказать, что все
последовательные приближения содержатся в области G:
др^бО (р = 2, 3, ...). A5)
Доказательство будем проводить методом математической
индукции.
Прежде всего, по условию теоремы л:@) ? О и xa)?G. Пусть
теперь *(J)?G (s = 0, I, . .., р). Так как
= 0, 1, 2, ...,р).
то на основании неравенства (8) имеем:
Поэтому
Следовательно, xip+1) € О.
Таким образом, свойство A5) установлено и мы находимся в
условиях теоремы A). Теорема 2 доказана.
Замечание. Условия теоремы 2 равносильны следующим: пусть
( A) {) )
р р у у
д:@> ? О и л:A) € Ф причем || хA) — х{0) || ^"D. Если расстояние точки л:A)
до границы Г области О не больше г~~^ т0 итерационный
процесс D) сходится. q
§ 10*. Первое достаточное условие сходимости процесса итерации
Рассмотрим действительную приведенную систему
*2> •••> Хп)>
х2, ..., хя),
0)
или в матричном виде
где
Ф1 (Jf) 1
16 Б. П. Демидович и И. А. Марон

482 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Предполагается, что вектор-функция <р (х) определена и непрерывна
вместе со своей производной <р' (х) = -Д-Ч в выпуклой
ограниченной замкнутой области GcEn.
В этом параграфе мы будем пользоваться двумя нормами:
Относительно области G введем нормы:
|| Ф'(*) ||( = max || <р'(*)!!„ B)
Й
||ф'(ДР)||ц = тах||ф'(л)||р C)
xeG
где
C')
Теорема. Пусть функции ф(дг) и ф'(лг) непрерывны в
области О, причем в G выполнено неравенство
# — некоторая постоянная.
Если последовательные приближения
{р — 0, 1, 2, ,..) «в выходят из области О, го процесс итерации E)
сходится и предельный вектор
является в области G единственным решением системы A).
Доказательство. В силу теоремы 1 предыдущего
параграфа достаточно показать, что отображение
у-ф(д:) F)
при наличии условия D) является сжимающим в области Gb смысле
ш- нормы.

§ 11]ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ ПРОЦЕССА ИТЕРАЦИИ 483
Пусть х1У X2?G и >>,- = Ф (.*,•) A = 1, 2). На основании
следствия 1 к лемме 1 из § 2 имеем:
р' A)
Отсюда
где O^.q<C\, что и требовалось доказать.
Следствие. Процесс итерации E) сходится, если
' (х) ||,.
дх,
(' = 1, 2, ..., п)
G)
при
Очевидно, из системы неравенств G) вытекает условие D) теоремы.
Замечание. На основании теоремы 1 из § 9 для
приближения хКР) получаем следующую оценку:
Ч-q
\ха)-х{
.0I
(р = 0, 1, 2, ...),
где ха) =
§ 11*. Второе достаточное условие сходимости
процесса итерации
Прежде чем переходить к доказательству теоремы сходимости,
использующей нормы Цср' (аг)||ц, выведем предварительно одну оценку
для разности значений вектор-функции, аналогичную теореме
о среднем и представляющую также самостоятельный интерес.
Лемма. Если еектор-функция
непрерывна, вместе со своей производной f (x)y в .выпуклой области,
содержащей тонки х и х-\-Ах, то
\\f(x + Длг) — f(x) ||, < \\ Ддг Ц,- II/' A) Н|э (!)
где | = дг + вАх и 0<6< 1.
Доказательство. Рассмотрим вспомогательную функцию
Ф @=2 ч [А (х+1 адг) -/, (*)],
/=1
где 0 ^ t ^ 1 — скалярный аргумент и в| — система чисел,
принимающих значения—1, 0, 1. Очевидно, Ф^0) = 0. Применяя теорему

484 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Лагранжа о конечном приращении функции, получим:
где l-jc + еАл: и 0 < в < 1.
Отсюда, учитывая, что |е^
будем иметь:
п п
У V
1=1/=1
Так как
дх
7
дх,
max
/1,- A)
дх.
B)
дх
= ИГ E) II/,
то, усиливая неравенство B), получаем:
п п
= II/' A) Иг S I Lxj | = ||/' (I) ||,. || Дд: Ц,.
Полагая в последнем неравенстве
/,(jf)] (/-1, 2, ..., /г),
-Л(*)К11/'EIМ1Аж|||,
,< НА* II ,11/4*) Hi,
окончательно находим:
п
т. е.
что и требовалось доказать*).
*) Если непосредственно применить теорему о среднем к каждой
компоненте вектора f(x + Ax)—f(x), то получается оценка, зависящая от
значений производных '' в различных точках |f- (/ = 1, 2, . . ., /г)
интервала (лс# д;+ Ах). Неравенство B') показывает, что можно ограничиться
значениями производных ^ **' в одной и той же точке |g (лг#

§ 12] МЕТОД СКОРЕЙШЕГО СПУСКА (МЕТОД ГРАДИЕНТА) 485
Теорема. Пусть вектор-функция <p(JC) непрерывна, вместе
со своей производной <р' (х), в ограниченной выпуклой замкнутой
области G и
|1ф'(*)|1п<?<1. C)
где q — постоянная. Если х{0) ?G и все последовательные
приближения
xiP+v = v{XiF>) (P = O| 1, 2, ...) D)
также содержатся в G, то процесс итерации D) сходится к
единственному решению уравнения
* = Ф(*) E)
в области G.
Доказательство. Докажем, что отображение у = (р(х)
является сжимающим в G в смысле /-нормы.
Пусть xv x2^Guyi==ff(xi) (/=1, 2). Используя лемму, имеем:
где
Так как
|| Ф' A) Ц, < max || <р' (*) ||, = || Ф' (х) ||„
xeG
то из неравенства F) получим:
где 0^^ < 1.
В силу теоремы из § 10 теорема является доказанной.
Следствие. Процесс итерации D) сходится к единственному
решению уравнения E), если при x?G выполнены неравенства
О G)
(/=1, 2, ..., п).
Замечание. На основании теоремы из § 10 для
приближения х{Р) имеем следующую оценку:
где ха) =
§ 12*. Метод скорейшего спуска (метод градиента)
Пусть име-ем систему уравнений

486 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
или в матричной форме
B)
где /=
fnJ
Предположим, что функции f. действительны и непрерывно
дифференцируемы в их общей области определения. Рассмотрим функцию
= 2
C)
Очевидно, что каждое решение системы A) обращает в нуль
функцию U(x); наоборот, числа х1У хг, ..., хп, для которых
функция U(x) равна нулю, являются
корнями системы A).
Будем предполагать, что система A)
имеет лишь изолированное решение,
которое представляет собой точку строгого
минимума функции U(x). Таким образом,
задача сводится к нахождению минимума
функции U(x) в я-мерном пространстве
Еп = {xv х%, ..., хп).
Пусть х—вектор-корень системы A)
и Jt@) — его нулевое приближение. Через
точку х{0) проведем поверхность уровня
функции U(x). Если точка хш достаточно
близка к корню х, то при наших
предположениях поверхность уровня
U(x) = U(xi0))
Рис. 60.
будет похожа на эллипсоид.
Из точки д:<0) двигаемся по нормали к
поверхности U(x) = U(x{0)) до тех пор, пока
эта нормаль не коснется в некоторой точке ха) какой-то другой
поверхности уровня (рис. 60)
Затем, отправляясь от точки ха), снова двигаемся по нормали
к поверхности уровня U(x) = U(x{1)) до тех. пор, пока эта
нормаль не коснется в некоторой точке д:B) новой поверхности
уровня U(x) = U(x{2)I и т. д.
Так как U(xyQ)) > U(x{1)) > U(x™) > ..., то, двигаясь по
такому пути, мы быстро приближаемся к точке с наименьшим зна-

§ 12}
МЕТОД СКОРЕЙШЕГО СПУСКА (МЕТОД ГРАДИЕНТА)
487
чением U (дно «ямы»), которая соответствует искомому корню х
системы A). Обозначим через
d
dJL
_дхп-
градиент*) функции U(x).
Из векторных треугольников OM0MV ОМ^^, .. ¦ заключаем, что
+ (р-0, 1, 2, ...)¦
Остается определить множители Я Для этого рассмотрим
скалярную функцию
Функция Ф(Я) дает изменение уровня функции U вдоль
соответствующей нормали к поверхности уровня в точке х{р\ Множитель
Я = Я надо выбрать таким образом, чтобы Ф (Я) имела минимум. Беря
производную по Я и приравнивая ее нулю, получаем уравнение
Наименьший положительный корень уравнения D) и даст нам
значение %р. Уравнение D), вообще говоря, нужно решать численно.
Поэтому укажем метод приближенного нахождения чисел Я . Будем
считать, что Я—малая величина, квадратом и высшими степенями
которой можно пренебречь. Имеем:
Разлагая функции /4- по степеням Я с точностью до линейных
членов, получим:
ф <*>=2 Г/, (*<'ч-
/si L
*) Градиент функции U {х) (обозначается grad U или yUt где символ v
называется наблой) есть вектор, приложенный в точке дг, имеющий
направление нормали п к поверхности уровня функции в данной точке в
сторону возрастания U и длину, равную j-.
Справедлива формула
где
= l, 2, ...» л)—орты пространства Еп.

488 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
где
dfi Г dfi dfi df( 1
дх \_дхх ' дх2 ' " # *f дхп J
Отсюда
м
X
Ф' (*) = -2 ? Г/, (*">)-я^i
/=1 L
Следовательно,
К - i==1
V"~ я
где
4-
dx
-матрица Якоби вектор-функции /.
Далее, имеем:
Отсюда
где ^'(a;) — транспонированная матрица Якоби.
Поэтому окончательно
E)

§ 12] МЕТОД СКОРЕЙШЕГО СПУСКА (МЕТОД ГРАДИЕНТА) 489
где для краткости положено
причем
(р==0> 1, 2, ...)• F)
Если допустить, что функция /(лг) дважды непрерывно
дифференцируема в окрестности искомого корня х> то можно
получить более точные формулы для поправок &х{р) = х(р+Л)—х{р)
(см. [7]).
Пример. Методом скорейшего спуска приближенно вычислить
корни системы
* + *2-2*/г = 0,1;
=— 0,2;
расположенные в окрестности начала координат.
Решение, Имеем:
хт = \ 0 .
Здесь
Гл:+*2—2r/z — 0,1 ~.
/=|у—*/2 + Зл:2 + 0,2
Г1+2* —2г —2у1
= \ Зг 1 — 2г/ За: I
L 2у 2х 1+2г J
Подставляя нулевое приближение, будем иметь:
Г -0,П Г 100-1
/»>= 0,2 и «70= 0 1 0 =?.
L -0,3j L 0 0 lj
По формулам E) и (б) получаем первое приближение
Г 0>11
>= —0,2 I
L 0t3j

490 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Аналогично находим второе приближение х{1). Имеем:
Г 0,13 -| Г 1,2 -0,6 0,4]
/«)= 0,05 ; wx = \ 0,9 1,4 0,3 I
L 0,05 J L-0,4 0,2 l,6j
Г 0,1811
Г/«>= 0,002
1 L 0,147J
[0,27481
0,2098
O,1632J
Отсюда
Следовательно,
0,13.0,2748 + 0,05-0,2098 + 0,05.0,1632
1*1s
0,27482 + 0,20982 + 0,16322
0,054374
: 0,14619797
= 0,3719
Г 0,П Г 0,1811 Г 0,03271
= -0,2—0,37119. 0,002 = -0,2007 I
L 0,3J L 0,147j L 0,2453J
Для контроля вычислим невязку
[0,032 1
—0,017 I
-0,007 J
§ 13. Метод скорейшего спуска для случая системы
линейных уравнений
Рассмотрим систему линейных уравнений
п
21 o-ijXt—bx = 0,
/„=2 «„,*,-*„ =о
0)

§ 131 МЕТОД СКОРЕЙШЕГО СПУСКА ДЛЯ СЛУЧАЯ ЛИНЕЙНОЙ СИСТЕМЫ 491
с действительной матрицей Л==[а(/] и столбцом свободных членов
6 =
Тогда
f=Ax—b
dx
... а„
Следовательно,
где г =Ах{р)—ft—невязка вектора х{р) и
(V АА'гр)
= 0, 1, 2, ...)
B)
C)
rp-(AA'rip, AA'rp)
(ср. [5], [6]). .
Применение формул B) и C) приводит к громоздким
вычислениям. Поэтому на практике часто вместо «скорейшего спуска»
пользуются просто «спуском», добиваясь минимума функции
U=z(Ax — ft, Ax — b).
« При этом число шагов процесса, обеспечивающих заданную
точность корней системы A), вообще говоря, возрастает; однако можно
добиться того, чтобы вычисление каждого шага было более простым.
В общей постановке полагают:
X = х л-рУ (Р== 0) м 2, .. .),
где у{р) — произвольный вектор, направленный наружу поверхности
уровня U= const, проходящей через точку х{р\ т. е.
—Ь = Лаг^>—
Имеем:
Один из возможныхпутей определения скалярного множителя А,-
исходит из требования [7]
Отсюда

492 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ.
В зависимости от выбора вектора у{р) получаются те или иные
расчетные схемы. В частности, если матрица А = А' — положительно
определенная (гл. X, § 15), то, полагая у(р) — г, будем иметь:
Г
(Агггр)ГР
= 0, 1, 2, ...), причем (grad С/{*<*>), yiP))
Пример. Методом скорейшего спуска решить систему уравнений
, rp)>0 при
8*!—х, —2*8 = 2,3;
D)
Решение. Так как в матрице системы преобладают
диагональные элементы, то в качестве начального вектора Jt<0) примем
вектор, координаты которого представляют собой округленные
значения корней системы:
8*! = 2,3;
= -0,5;
6*3 = —1,2;
Отсюда, например,
0,3
—0,05
-0,2
L 0,3 .
Следовательно,
Далее,
8—1—2 О
О 10 1 2
-10 6 2
3—1 2 12 J
8 0—1 3
-1 10 0 —1
-2162
0 2 2 12
- 0,3 "I
—0,05
-0,2
_ 0,3 J
Г 2'31
-0,5
—1,2
L 3,7 J
'0,55-
0,4
0,3
-0.45J
,55
0,4
0,3
.0,45-
,45"
3,0
2,0
-6,8 _
AA'ro =
—1 —2
10 1
0 6
—1 2
0 "
2
2
12 .
,45"
3,0
2,0
.6,8 J
6,6 "
45,6
20,15
.98,95-

§ 13] МЕТОД СКОРЕЙШЕГО СПУСКА ДЛЯ СЛУЧАЯ ЛИНЕЙНОЙ СИСТЕМЫ 493
Применяя формулу C), получаем:
м — (го> ЛА'го) __
о> ЛЛ'г0)
__ 0,55-36,6 + 0,4-45,3 + 0,3-20,15 + 0,45-98,95 _'
Отсюда
0,3
0,05
0,2
0,3 J
— 0,006 532
5,45
3,0
2,0
_6,8
0,2644
—•0,0696
—0,2131
L 0,2556 J
причем
' 0,3109
0,1020
0,1684
—0,1966 J
Аналогично находятся дальнейшие приближения
вующие невязки:
и
соответст0,2351 "
—0,0849
—0,2147
0,2863 -
» Г2 —
~0,0956"
0,0087
0,2493
-0,0967-
*<*>=
4b*(D)
" 0,2296 "
—0,0842
—0,2251
_ 0,2748 -
" 0,2266 '
—0,0792
—0,2379
. 0,2875 _
" 0,2228 "
—0,0810
—0,2430
. 0,2823 _
> г3 —
, г4 =
0,0712 "
—0,0280
0,1692
-—0,0806 _
,0680~
0,0354
0,1211
..0,0334-
" 0,0493 "
0,0013
0,0839
--0,0493 -
и т. д.

494 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. ХШ
Заметим, что в данном случае процесс приближений сходится
медленно: после пятого приближения мы еще далеки от точных корней
системы D), равных х1 = 0,2; х2 =—0,1; ж3= — 0,3; лг4 = 0,3.
§ 14*. Метод степенных рядов
Пусть дана нелинейная система
(Л=1, 2, ..., л), где функции fk— аналитические в окрестности
изолированного решения х* = (х*х, л:*, ...,.*;*).
Рассмотрим более общую систему [8]
^(*1. *и •••» *п> Я) = 0 B)
(ft=l, 2, ..., л), зависящую от действительного параметра Я и
такую, что при Я = 0 система B) решается непосредственно, а при
Я=1—тождественна системе A), т. е.
(Л=1, 2, ..., п). Параметр Я следует вводить так, чтобы
зависимость функций Fk от X была по возможности простой. Например,
если Jt(o) = (х[°\ х[°\ ..., х(пй)) — грубое приближение решения, то
можно положить:
± (^_,Г>) ^р+я ГЛ (х)-± (*,-*<«>) Цр] =0
(*=1, 2, ..., л), где
Мы будем предполагать, что Fk—аналитические функции от Я при
|Я|<1.
Пусть при |Я|^1 система B) имеет простое аналитическое
решение Xj(X) (/=1, 2, ..., /г), которое при Л=1 совпадает
с лг* (у=1, 2, ..., л). Положим
где л:(.0) (у=1, 2, ..., л) — известное решение системы B) при
Я = 0. Разлагая функции Xj (Я) в ряд Тейлора в точке Я = 0,
получим:
?.. (y=i, 2, ..., п). C)

§ 14J МЕТОД СТЕПЕННЫХ РЯДОВ 495
Для определения коэффициентов лг'(о) продифференцируем по
параметру Я равенство B):
п
Й-^ + Ж^0 (ft = L 2 п). D)
Полагая х = хш и Я=0, будем иметь:
Отсюда, если
находим лг'.(О).
Далее, дифференцируя по к равенство D), получим:
п п п
Д2Г
Отсюда при х = хш и Я = 0 находим:
п п
дх, xf ({J> -—ZtZ* дХ/дХ(
0) ,(Q d4k (x«>; 0)
Так как ДГу(О) известны, то из системы E) можно определить
лг*(О). Аналогично вычисляются производные лг'" @), #^@), ...
Заметим, что матрица коэффициентов при старших производных
оказывается все время одной и той же и равна матрице Якоби
функций Flt F2, ..., Fn относительно переменных xv дг2, ..., хп при
x, = ty (У=1, 2 п) и Л = 0.
Предполагая, что ряды C) сходятся при Я=1, окончательно
находим:
x*=x/{l)=*x/@)+x'i{0)+±[xm,{0)+... G=1. 2, ..., д). F)
Недостатком метода является сложность вычислений в общем
случае производных высших порядков. Кроме того, сходимость
ряда F) может быть недостаточно быстрой.

496 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ [ГЛ. XIII
При применении метода не обязательно предполагать
аналитичность функций Xj(k) (y=l, 2, ...,#), а именно: вместо ряда
Тейлора можно воспользоваться формулой Тейлора, оборвав ряды
Xj (X) на некоторой степени Xs и оценив их остатки по известным
формулам (гл. III, § 4).
Литература к тринадцатой главе
1. Л. В. Канторович, О методе Ньютона, Труды Матем. и-та им. Сте-
клова, XXVIII, М.~ Л. A949), 104-144.
2. A. Os trow ski, Сборник работ памяти Д. А. Граве, 1940, стр. 213.
3. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
М.—Л., 1934, гл. IX.
4. Д. А. Вентцель, Е. С. Вентцель, Элементы теории
приближенных вычислений, Изд. ВВИА им. Жуковского, М., 1949, гл. III, § 8.
5. В. Э. Милк, Численное решение дифференциальных уравнений, ИЛ,
1955, гл. IX.
6. А. С. Хаусхолдер, Основы численного анализа, ИЛ, 1956, гл. III.
7. Э. Бут, Численные методы, Физматгиз, М., 1959.
8. Современная математика для инженеров, под редакцией Э. Ф. Беккен-
баха, ИЛ, М., 1958, гл. XIV. Ч. Мор рей, Нелинейные методы.

ГЛАВА XIV
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
§ 1. Конечные разности различных порядков
Пусть
— заданная функция. Обозначим через Ax = h фиксированную
величину приращения аргумента (шаг). Тогда выражение
Ay=Af(x)=f{x + Ax)—f(x) A)
называется первой конечной разностью функции у. Аналогично
определяются конечные разности высших порядков
Апу^А(Ап^у) (л = 2, 3, ...).
Например,
Пример. Построить конечные разности для функции
считая шаг Алг = 1.
Решение. Имеем:
АпР(х) = 0 при л>3.
Обратим внимание, что конечная разность третьего порядка
функции Р(х) постоянна.
Вообще, справедливо утверждение: если
+а1хл-*+ ... +ап
полином л-й степени, то АпРп (x) = n\aohn = const, где Ax = h.

498 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. X[V
Действительно, имеем:
Раскрыв по биному Ньютона круглые скобки, легко убедиться, что
АРп(х) представляет собой полином (п—1)-й степени:
где
Рассуждая аналогично, приходим к выводу, что вторая разность
А'гРп(х) есть полином (п — 2)-й степени:
причем
Проводя последовательно аналогичные рассуждения, мы в конце
концов установим, что
АпРп (x)=nlaohn = const.
Как следствие получаем:
Д^Яп(дг) = 0 при s>n.
Символ А (дельта) можно рассматривать как оператор, ставящий
в соответствие функции у=/(х) функцию Ay=f(x-}-Ax)—f(x)
(Ах постоянно). Легко проверить основные свойства оператора Д:
2) Д (Си) = С Д«(С— постоянная);
3) A
где m и п — целые неотрицательные числа, причем по определению
полагают А°у=у.
Из формулы A) имеем:
отсюда, рассматривая Д как символический множитель, получим:
/(* + Д*) = A + Д)/(*). B)
Последовательно применяя это соотношение п раз, будем иметь:
C)

§ 1] КОНЕЧНЫЕ РАЗНОСТИ РАЗЛИЧНЫХ ПОРЯДКОВ 499
Воспользовавшись формулой бинома Ньютона*), окончательно
выводим:
п
где
ст^п(п—\) ... [п — (т —1I
— число сочетаний из п элементов по т.
Таким образом, с помощью формулы D) последовательные
значения функции f(x) выражаются через ее конечные разности
различных порядков.
Воспользовавшись тождеством
А/ 1 I А \ 1 /К\
= \ 1 —р ?Л) —~ I \О)
и применяя бином Ньютона, получаем:
- ... +1-1OD
Отсюда в силу формулы C) будем иметь:
...+{— \)nf{x). F)
Формула F) дает выражение конечной разности п-то порядка
функции f(x) через последовательные значения этой функции.
Пусть функция f(x) имеет непрерывную производную /{п)(х)
на отрезке [лг, х-\-пАх]. Тогда справедлива важная формула
Anf(x) = (Ax)nf{n) (x + Qn Ax), G)
где ¦ 0<в<1.
Формулу G) проще всего доказать, используя метод
математической индукции.
В самом деле, при /г=1 мы получаем теорему Лагранжа о
конечном приращении функции и, следовательно, формула G) верна.
Пусть теперь при k < п имеем:
Akf(x) = (Ax)kfk) (x + Vk Ax),
где
*) Законность применения формулы бидема Ньютона предоставляем
обосновать читателю.

500 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Тогда
= (Ax)k [fk) [x + Ах + 9'ft Дл:) —/<*> (х + Q'k Ax)].
Применяя теорему Лагранжа к получившемуся приращению
производной f{k)(x), будем иметь:
Ak+1f(x) = (Дл:)* Ах/{к+1) (х + Э'й Дл: + 6" Дл:),
где 0<6"< 1. Полагая
^+eff__9 (8
k+l "u> { }
окончательно получим:
Ak+1f(x) = (Дл:)*+1/(*+1) (x + Q(k+l) Ax),
причем, очевидно,
0<9<1.
Таким образом, установлен переход от k к &+1 и, следовательно
формула G) доказана.
Из формулы G) имеем:
л д*)=
Отсюда, переходя к пределу при Дл:—>0 и предполагая, что
производная /(п> (л:) непрерывна, получим:
= lim
Следовательно, при малых Дл: справедлива приближенная формула
§ 2. Таблица разностей
Часто приходится рассматривать функции y=f(x)r заданные
табличными значениями У(—/(Х() для системы равноотстоящих
точек л:^(/==0, 1, 2, ...), где
Ддг^. = xi+1—х{ =-h~ const.
Конечные разности последовательности у{ естественно
определяются соотношениями
i =¦ A (Ayi) = Ayi+l—Ayit

§ 2] ТАБЛИЦА РАЗНОСТЕЙ
Из первого равенства имеем:
501
Отсюда последовательно выводим:
Использовав формулу бинома Ньютона, получим:
Таблица 33
Горизонтальная таблица разностей
Обратно, имеем:
Д"<у» = [0 + Д)-1Гл =
= A + /S)nyr-Cl(\+A)-1yt+
ИЛИ
X
х0
Xl
х2
У
Уо
У\
У*
Ау
Аг/о
Af/i
А*/2
А.4
Д202
Д8л
Д8«/2
Например,
Таблица 34
Диагональная таблица разностей
i + l—У!
и т. д. Заметим, что для
вычисления л-й разности Д"^,-
нужно знать л+1 членов
У/> Л+1. •... У(+п Данной
последовательности.
Конечные разности различных порядков удобно располагать
в форме таблиц двух видов: горизонтальной таблицы разностей
(таблица 33) или диагональной таблицы разностей (таблица 34).
Пример!. Составить горизонтальную таблицу разностей функции
-1 A)
X
Хо
Xl
*2
х3
У
Уо
Ух
У2
Уз
*У
А#о
A#i
А#2
ь*у
АЧ
A^i
А*У
A3t/o
от начального значения дго = О, приняв шаг * = 1.

502
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Решение. Полагая лго = О, л:1=1, лг2 = 2, находим
соответствующие значения уо =—1, yl = 21 у2 = \3. Отсюда имеем:
Эти значения заносим в таблицу (таблица 35). Так как наша
функция есть полином третьей степени, то третья разность ее постоянна
Таблица 35 <см- § !> и Равна
Горизонтальная таблица разностей Д JPf = 2«3! = 12.
кубической функции A) Поэтому дальнейшее
заполнение таблицы 35 можно
производить при помощи
суммирования, используя формулы
к
0
1
2
3
4
5
у
—1
2
13
44
107
214
ьу
3
11
31
63
107
163
8
20
32
44
56
68
Д*?
12
12
12
12
12
12
= 0, 1, 2, ...),
(/=1, 2, ...),
(' = 2,-3, ...).
Ступенчатой ломаной отмечены исходные данные для составления
таблицы.
Замечание. При составлении таблицы разностей возможны
случайные ошибки вычислителя. Посмотрим, как отразится на значениях
разностей ошибка е в значении уп. Составляя соответствующую
диагональную таблицу разностей, получим таблицу 36.
Из таблицы 36 видно: 1) если уп содержит ошибку, то
ошибочными являются также разности
и т. д.; 2) в ft-e разности Д*^ ошибки входят со знакопеременными
биномиальными коэффициентами, а именно, ошибки соответственно
имеют значения
Cje,
и, следовательно, абсолютное значение максимальной ошибки &-й
разности быстро растет вместе с номером разности; 3) для каждой
конечной разности Аку сумма ошибок с ' учетом их знаков равна

§ 2)
ТАБЛИЦА РАЗНОСТЕЙ
503
Таблица 36
X
У
У»-*
Уп-t
Уп-г
У„ч
Уп+2
Ауп-ч
**.
//
нулю, а сумма абсолютных величин ошибок равна |е|«2л. Таким
образом, даже незначительная ошибка в значении функции приводит
к значительным ошибкам в ее разностях высокого порядка. Заметим,
что максимальная ошибка разностей Аку в случае диагональной
таблицы разностей находится в той же горизонтальной строке, что
и ошибочная табличная величина *уп, или же в верхней и нижней
соседних строках.
Рассмотренный закон распространения е-ошибки в таблице
конечных разностей дает возможность в некоторых случаях установить

504 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
наличие и место ошибки, а также ее числовое значение, что
позволяет исправить таблицу.
Таблицы разностей обычно составляются с точностью до
некоторого фиксированного десятичного разряда. Если функция у=/(х)
имеет непрерывные производные до т-го порядка, то при достаточно
малом шаге /г = Ах ее конечные разности до т-то порядка
включительно изменяются плавно, причем разность m-ro порядка почти
постоянна в пределах данных десятичных разрядов. Нарушение
последнего условия на каком-нибудь участке таблицы при отсутствии
особенностей функции, вообще говоря, свидетельствует о наличии
вычислительной ошибки.
Установив максимальное отклонение m-й разности от нормы,
можно определить место этой ошибки в столбце значений
функции^ в предположении, что: 1)эта ошибка—одиночная и заключается
в неверном подсчете одного значения функции и 2) при вычислении
конечных разностей новых ошибок не было. Если такая ошибка
в таблице разностей обнаружена, то исправление ее может быть
осуществлено с помощью значений разностей. Покажем, каким
путем это достигается, причем для простоты ограничимся случаем
постоянства разностей второго или третьего порядка.
Пусть ошибочное табличное значение есть уп-\-е, где индекс п
установлен, а величина ошибки е неизвестна.
Если третьи разности практически постоянны, то вторые разности
образуют арифметическую прогрессию, и поэтому верное значение
второй разности Д2^..! будет равно среднему арифметическому
трех смежных ошибочных разностей:
так как члены, содержащие 8, сокращаются.
По найденному верному значению второй разности А2уп_1 можно
найти величину ошибки е, а именно: эта ошибка будет равна
полуразности между исправленным и ошибочным значениями разности
Верное же значение самой функции уп найдем из тождества
Для контроля следует снова вычислить конечные разности.
Пример 2. Исправить ошибку в таблице 37.
Решение. Здесь плавный ход вторых разностей максимально
нарушается при л; =19. Имеющаяся ошибка распространяется на

§ 3]
ОБОБЩЕННАЯ СТЕПЕНЬ
505
три строки, объединенные фигурной скобкой. Находим среднее
арифметическое значение второй разности для средней из трех
объединенных строк
Таблица 37
Таблица разностей, содержащая
— 4) = 0. одиночную ошибку
Отсюда
е = ~ [0 — 0,008] = — 0,004.
Внося исправление в
табличное значение у для лг— 19,
получим:
X
15
16
17
18
19
20
21
22
23
У
13,260
14,144
15,028
15,912
16,79BN
17,680
18,564
19,448
20,332
Ау
884
884
884
88@L
88(8L
ооч
884
884
ьгу
0
0
(-4H
(8H
(-4H
0
0
Ошибка
^ е
Ь
= 16,792 —(—0,004) =
*= 16,796.
После исправления получаем
таблицу с плавным изменением
первых разностей и
постоянной второй
разностью(неверные цифры взяты в скобки).
Отметим, что указанным
методом можно исправить лишь
отдельные вычислительные ошибки или описки. Для устранения же
большого количества ошибок, могущих появиться по разным
причинам, а также для уменьшения накопления ошибок, возникающих
в результате неточностей самих вычислительных методов и
округления промежуточных результатов до данного числа знаков,
применяются специальные приемы «сглаживания» [1].
§ 3. Обобщенная степень
В дальнейшем нам понадобится понятие об обобщенной
степени [1].
Определение. Обобщенной ^-степенью числа х называется
произведение п сомножителей, первый из которых равен х, а каждый
следующий на h меньше предыдущего:
= x(x—h)(x—2h) ... [лг —(л —1)й],
0)
где h—некоторое фиксированное постоянное число.
Показатель обобщенной степени обычно записывается в
квадратных скобках. Полагают лгго1=1.

S€6 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
При й = 0 обобщенная степень A) совпадает с обычной
Вычислим конечные разности для обобщенной степени, полагая
Ax = h. Для первой разности имеем:
= (x + h)x ... [л: — (л — 2) h]— x {x — h) ... [х — (п — 1) А] =
т. е.
Ax[n] = nhx[n-1]. ¦ B)
Подсчитываем вторую разность:
A*xw = Д (Ахт) = Д (лАд:111-11) = лА • (я — 1) hxln'2] =
Итак,
Методом математической индукции легко доказать общую
формулу
Akx[n] = n(n-\) ... [л—(k— \)]hkx{n'k\
где ft=l, 2, ..., л.
Очевидно,
AVn3 = 0 при Л>п.
Из формулы B) вытекает также простая формула конечного
суммирования. Пусть
— равноотстоящие точки с шагом А
**+i — ^ = A (i===0» Ь 2 ...).
Рассмотрим сумму
1 = 0
Так как в силу формулы B) имеем:

§ 41
то
ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛИРОВАНИЯ
507
—x0
[n + i]
Итак,
C)
Формула (З) аналогична формуле Ньютона —Лейбница для целой
положительной степени.
§ 4. Постановка задачи интерполирования
Простейшая задача интерполирования [2] заключается в
следующем. На отрезке [а, Ь] заданы п+\ точки х0, xv .. ., хп, которые
Рис. 61.
называются узлами интерполяции, и значения некоторой
функции /(#) в этих точках
/0*о)=.Уо.
Требуется построить функцию Z7^) {интерполирующая
функция), принадлежащую известному классу и принимающую в узлах
интерполяции те же значения, что и f(x)> т. е. такую, что
Геометрически это означает, что нужно найти кривуюy = F(x)
некоторого определенного типа, проходящую через заданную
систему точек М((х19 у() (/ = 0, 1, 2, ...) (рис. 61).
В такой общей постановке задача может иметь бесчисленное
множество решений или совсем не иметь решений.

508 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Однако эта задача становится однозначной, если вместо
произвольной функции F(x) искать полином Рп (х) степени не выше л,
удовлетворяющий условиям B), т. е. такой, что
Полученную интерполяционную формулу
обычно используют для приближенного вычисления значений данной
функции f(x) для значений аргумента лг, отличных от узлов
интерполирования. Такая операция называется интерполированием
функции f(x). При этом различают интерполирование в узком смысле,
когда ~х ? [х0, хп], т. е. значение х является промежуточным между
х0 и хп, и экстраполирование, когда х ? [лс0, хп]. В дальнейшем
под термином интерполирование мы будем понимать как первую,
так и вторую операции.
§ 5. Первая интерполяционная формула Ньютона
Пусть для функции y~f(x) заданы значения у{=/(х() для
равноотстоящих значений назависимой переменной: х{=х^+Ш (/=0,
1, 2, ..., я), где h — шаг интерполяции. Требуется подобрать
полином Рп (х) степени не выше п, принимающий в точках хг
значения
P.i*t)=yt (' = 0, 1, .... п). A)
Условия A) эквивалентны тому, что
при т = 0, 1, 2, ..., п.
Следуя Ньютону, будем искать полином в виде
Рп № = ао + ai (х — х0) + а2 (х—х0) (х—х1) +
+ аь (х—х0) (х—хг) (х—х2) -]Г ...
х — х0)(х—х1) ... (х—хЯтт1). B)
Пользуясь обобщенной степенью, выражение A), запишем так:
n 0 10 i0
+ аа(х-х0У*+...+ая{х-х0)т. B')
Наша задача состоит в определении коэффициентов а,(/=0, 1,2, ...,п)
полинома Рп (х). Полагая лг = лг0 в выражении B'), получим:

§ 5] ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА 509
Чтобы найти коэффициент av составим первую конечную разность
Полагая в последнем выражении х = х0, получим:
APn(xQ)^Ay0^=a1h;
откуда
А
~~ II Л •
Для определения коэффициента а2 составим конечную разность
второго порядка
— l)nh*an(x
Положив х— х0, получим:
откуда
п
а2~" 2Т7? •
Последовательно продолжая этот процесс, мы обнаружим, что
где положено
01 = 1 и А°у=у.
Подставляя найденные значения коэффициентов а{ в выражение B'),
получим интерполяционный полином Ньютона
•••+от-<*-*.)[/11- С3)-
Легко видеть, что полином C) полностью удовлетворяет требованиям
поставленной задачи. Действительно, во-первых, степень полинома
Рп (х) не выше п, во-вторых,
Р„ (**) =Л + пг {хк-х.) + ?$ {хк-х0) (хк-хх) +...
••• н
=1. ? я).

510 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Заметим, что при h—>Q формула C) превращается в полином
Тейлора для функции у.
В самом деле,
л A* \dxkj
Кроме того, очевидно,
lim(x—xo)W = (x—xo)n.
Отсюда при h—*0 формула C) принимает вид полинома Тейлора:
Р„(х)=У(х0)+/(х0)(х-х0)+ ... +У—р1{х-х0Г.
Для практического использования интерполяционную формулу
Ньютона C) обычно записывают в несколько преобразованном виде.
Для этого введем новую переменную q по формуле
тогда
(/ = 1, 2, ..'., л).
Подставляя эти выражения в формулу C), получим:
...+ д^„ D)
где ^= 'УТ^- представляет собой число шагов, необходимых для
достижения точки х, исходя из точки х0. Это и есть
окончательный вид первой интерполяционной формулы Ньютона.
Формулу D) выгодно использовать для интерполирования
функции у =/(х) в окрестности начального значения
Хо> где q мало по абсолютной величине.
Если в формуле D) положить я=1, то получим формулу
линейного интерполирования:
При л = 2 будем иметь формулу параболического или квадратич-t
ного интерполирования:
Pi (X) = yQ + q A>o + ^^ Д 'Л-

§ 5]
ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
511
Если дана неограниченная таблица значений функции у, то
число п в интерполяционной формуле D) может быть любым.
Практически в этом случае число п выбирают так, чтобы разность Anj/j
была постоянной с заданной степенью точности. За начальное
значение х0 можно принимать любое табличное значение аргумента х.
Если таблица значений функции конечна, то число п ограничено,
а именно: п не может быть больше числа значений функции у,
уменьшенного на единицу.
Заметим, что при применении первой интерполяционной формулы
Ньютона удобно пользоваться горизонтальной таблицей разностей,
так как тогда нужные значения разностей функции находятся
в соответствующей горизонтальной строке таблицы.
Пример 1. Приняв шаг h = 0,05, построить на отрезке
[3,5; 3,6] интерполяционный полином Ньютона для функции у = ех,
заданной таблицей
X
У
3,50
33,115
3,55
34,813
3,60
36,598
3,65
38,475
3,70
40,447
Решение. Составляем таблицу разностей (таблица 38).
Заметим, что в столбцах разностей, следуя обычной практике, мы
не указываем десятичные разряды (которые ясны из столбца
значений функции). Так как разности третьего порядка практически
постоянны, то в формуле D) полагаем /z = 3. Приняв л;0 = 3,50,
д>0 = 33,115, будем иметь:
Таблица 38
,087
^=^
Таблица разностей функции
+ 0,005
или
/>а(х) = 33,115 +1.698? +
где
+ 0,00083? (? — \)(q—2),
X
3,50
3,55
3,60
3,65
3,70
у
33,115
34,813
36,598
38,475
40,447
ьу
1698
1785
1877
1972
ьгу
87
92
95
Ь*у
5
3
Пример 2.
вероятностей
В таблице 39 приведены значения интеграла

512
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[гл. xiv
Применяя первую интерполяционную формулу Ньютона,
приближенно найти ФA,43).
Решение. Дополняем таблицу 39 конечными разностями
функции у до третьего порядка включительно.
За х0 принимаем ближайшее табличное значение к искомому
значению х = 1,43, т. е. полагаем
Таблица 39 л л ^ , ^ л
л;0=1,4. Так как h = 0,1, то
Таблица разностей функции j 43 j ,
у = Ф(х) д= ' од • =0,3.
Подставляя в формулу D),
получим:
уж 0,9523 + 0,3-0,0138 +
0,3@,3—1) д
+ 21
X
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
У
0,8427
0,8802
0,9103
0,9340
0,9523
0,9661
0,9763
0,9838
0,9891
0,9928
0,9953
375
301
237
183
138
102
75
53
37
25
А2у
—74
-64
—54
-45
-36
-27
—22
-16
-12
10
10
9
9
9
5
6
4
-(—0,0036) +
+
0,3 @,3-1) @,3-2)
= 0,95686.
(Табличное значение:
Ф A,43) =--0,9569, см.
«Таблицы функций» Янке и Эмде.)
На практике часто
встречается надобность для
функции, заданной таблично, подобрать аналитическую формулу,
представляющую с некоторой точностью данные табличные значения
функции. Такая формула называется эмпирической, причем задача
построения ее неоднозначна.
При построении эмпирической формулы следует учитывать общие
свойства функции. Если из таблицы разностей будет обнаружено,
что л-е разности функции для равноотстоящих значений аргумента
постоянны, то в качестве эмпирической формулы можно взять
соответствующую первую интерполяционную формулу Ньютона.
Пример 3. Построить эмпирическую формулу для функции j/,
заданной таблицей
X
У
0
5,2
1
8,0
2
10,4
3
12,4
4
14,0
5
15,2
Решение. Составляя таблицу разностей (таблица 40),
убеждаемся, что вторая разность постоянна. Используя
интерполяционную формулу Ньютона в форме C) и учитывая, что А=1, будем

§ 5]
иметь:
ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
513
или
^ = 5,2 + Злг—0,2л:2.
Пример 4. Найти сумму квадратов
натуральных чисел от 1 до п.
Решение. Очевидно, имеем:
Ои i 1 ¦"¦"*w„
Отсюда
и, следовательно, Sn можно искать в виде полинома третьей
степени относительно п.
Для определения разностей Таблица 40
ASV A*S±
Конечные разности
нужно вычислить три значения Sv S% и S9. функции у
Имеем:
с» *
О1= I,
Отсюда
причем
Применяя первую интерполяционную формулу Ньютона и
учитывая, что
получим:
Д51 = 5—1=4,
Д52==14—5 = 9,
Д251==9—4 = 5,
X
0
1
2 '
3
4
5
У
5,2
8,0
10,4
12,4
14,0
15,2
2,8
2,4
2,0
1,6
1,2
—0,4
—0,4
—0,4
—0,4
или
17 Б. П. Демидовнч и И. А. Марон

514 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИИ [ГЛ. XIV
§ 6. Вторая интерполяционная формула Ньютона
Первая интерполяционная формула Ньютона практически неудобна
для интерполирования функции вблизи конца таблицы. В этом
случае обычно/ применяется вторая интерполяционная формула
Ньютона. Выводом этой формулы мы и займемся.
Пусть имеем систему значений функции
У1=У(*д (* = 0, 1, 2, ...,п)
для равноотстоящих значений аргумента
Построим интерполирующий полином следующего вида:
Рп (х) = Ч + а1 \х—*п) + а2 (Х—*п) (X~Xn-l) +
а3 {х — хп) {х—хп_г) (х—хп_2) +...
или, используя обобщенную степень, получаем:
+ а3 (х—ха_ъ)М + ...+ая (х-хг)Ы. A)
Наша задача состоит в определении коэффициентов а0, av a2,
а& • •.» ап таким образом, чтобы были выполнены равенства
Pn&d^yi (/ = 0, 1, 2, ..., п).
Для этого необходимо и достаточно, чтобы
Д'>„ (*„-*) = А'Л-f (/ = 0, I, #.. f я). B)
Положим х = хп в формуле A). Тогда будем иметь:
Ря(хп)=Уп = *»
следовательно,
Далее, берем от левой и правой частей формулы A) конечные
разности первого порядка
Отсюда, полагая х = хп^г и учитывая соотношения B), будем
иметь:
Следовательно,

§ 6] ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА 515
Аналогично составив вторую разность от Рп{х), получим:
>B (*) = в22! Ь* + аа3 • 2А* (х -лгй_2)Ш + ...
... +ann(n-\)h*(x-x1)i"-*h
Полагая х = хп_2, находим:
и, таким образом,
а2— 21 /г2 '
Характер закономерности коэффициентов а{ достаточно ясен.
Применяя метод математической индукции, можно строго доказать, что
Подставляя эти значения в формулу A), будем иметь окончательно:
-тр&-хя)...(х-х1). D)
Формула D) носит название второй интерполяционной формулы
Ньютона.
Введем более удобную запись формулы D). Пусть
тогда
и т. д.
Подставив эти значения в формулу D), получим:
..Ач+п-\) А„
.,. + Аи D}
Это и есть обычный вид второй интерполяционной формулы
Ньютона, Для приближенного вычисления значений функции у
полагают:
17*

516
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Пример 1. Дана таблица значений ^ = lgх семизначных
логарифмов
X
1000
1010
1020
1030
1040
1050
у
3,0000000
3,0043214
3,0086002
3,0128372
3,0170333.
3,02A893
Найти lg 1044.
Решение. Составляем таблицу разностей (таблица 41).
Таблица 41
Конечные разности функции у = lg x
X
1000
1010
1020
1030
1040
1050
У
3,0000000
3,0043214
3,0086002
3,0128372
3,0170333
3,0211893
Д/у
43 214
42 788
42 370
41961
41560
-426
-418
—409
-401
Д3/
2
9
8
Примем
тогда
А •~-Х
лг„=1050,
1044—1050
1 = _
= —0,6.
Используя подчеркнутые разности, в силу формулы D') будем иметь:
lg 1044 = 3,021 1893+ (—0,6) -0,0041560 +
+ (-о.Щ-(-о,б+1).0|0000401
(-0.6Н-0,6+1)-(-0,6+2) t
= 3,0187005.
В полученном результате все знаки верные.
Как первая, так и вторая интерполяционные формулы Ньютона
могут быть использованы для экстраполирования функции, т. е. для
нахождения значений функции у для значений аргументов х}
лежащих вне пределов таблицы. Если х < х0 и х близко к xQ} то

§ 6]
ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
517
выгодно применять первую интерполяционную формулу Ньютона,
причем тогда
Если же х > хп и х близко к хп> то удобнее пользоваться второй
интерполяционной формулой Ньютона, причем
Таким образом, первая интерполяционная формула Ньютона обычно
используется для интерполирования вперед и экстраполирования
назад, а вторая интерполяционная формула Ньютона, наоборот,—
для интерполирования назад и экстраполирования вперед.
Заметим, что операция экстраполирования, вообще говоря, менее
точна, чем операция интерйОлирова-
ния в узком смысле слова.
Пример 2. Имея таблицу
значений функций jj = sinAr в пределах
от х = 15° до дг = 55° с шагом
h = 5° (таблица 42), найти sin 14°
и sin 56°.
Решение. Составим таблицу
разностей (таблица 42). Мы видим,
что третьи разности функции у
практически постоянны, и поэтому
можно ограничиться ими.
Для вычисления sin 14° примем:
Таблица 42
Таблица разностей функции
- *0=15°
отсюда
и х =14°;
14°—15е
= —0,2.
X
15°
20°
25°
30°
35°
40°
45°
50°
55°
У
0,2588
0,3420
0,4226
0,5000
0,5736
0,6428
0,7071
0,7660
0,8192
832
806
774
736
692
643
589
532
Ь*у
-26
-32
-38
—44
-49
—54
-57
—
А*У
—6
-6
-6
—5
-5
-3
Применяя первую интерполяционную формулу Ньютона и используя
подчеркнутые разности, будем иметь:
sin 14° = 0,2588 + (—0,2) - 0,0832 + (~°'2J[(~1>2) (—0,0026) +
+ (-0,2) (-1,2) (-2,2) (_0>0006) = о,2419.
о!
По таблицам sin 14° = 0,24192.
Для отыскания sin 56° положим:
отсюда
п = оо и х == оо ,
, 56°-55°_02

518
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Применяя вторую интерполяционную формулу Ньютона
и.используя дважды подчеркнутые разности, будем иметь:
sin 56° = 0,8192+ 0,2-0,0532+ ^Ь?(—0,0057) +
+-0,2.1,2.2,2 (—0,0003) = 0,8291.
По таблицам sin 5*6° = 0,82904.
§ 7. Таблица центральных разностей
При построении интерполяционных формул Ньютона
используются лишь значения функции, лежащие по одну сторону от
выбранного начального значения, т. е. эти формулы носят
односторонний характер.
Таблица 43
X
•**
Л,
X*
х*
У
У-<
У-з
У-*
У-t
h
!tt
У»
У*.
У*
&У-*
Ау-г
&У*
Ау*
*2у
&'У~*
*К
***
**У,
Ь*Уг
й'у-,
&'У,
*У,
&*У-4
*Ь*У-г
е?у
N. У
ь*у-г
аУ,
7&'У-*
tfy.»

§ 8] ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ ГАУССА 519
Во многих случаях оказываются полезными интерполяционные
формулы, содержащие как последующие, так и предшествующие
значения функции по отношению к начальному значению ее.
Наиболее употребительными из них являются те, которые содержат
разности, расположенные в горизонтальной строке
диагональной таблицы разностей данной функции, соответствующей начальным
значениям х0 и у0, или в строках, непосредственно примыкающих
к ней. Эти разности Ay^lt Aj0, A2y~v ... называются центральными
разностями (таблица 43), где
= 0, ±1, ±2, ..,), Л =/(**),
—Ал и т. д.
Соответствующие интерполяционные формулы носят название
интерполяционных формул с центральными разностями, К числу их
относятся формулы Гаусса, Стирлинга и Бесселя [3].
§ 8. Интерполяционные формулы Гаусса
Выведем сначала интерполяционные формулы Гаусса.
Пусть имеется 2/z+l равноотстоящих узлов интерполирования
где
(/ = — п, —(п—1), ...,#—1),
и для функции y=f(x) известны ее значения в этих узлах
Требуется построить полином Р(х) степени не выше 2л такой, что
Р{хг)=уг при / = 0, ±1, ..., ±п.
Из последнего условия вытекает, что
Д*/>(*,) = Д*Л A)
для всех соответствующих значений / и А.
Будем искать этот полином в виде
Р (х) = а0 + аг {х—х0) + аг (х — х0) (х —хг) +
+а3 (х—х^) (х—х0) (х — хг)+аА (х — х^) (х — х0) {x — xj X
X (х — *а) + л6(* —*-2) (•* — *-1)(*—**)(* —*i)(x—X2)+ --<
B)

520 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Вводя обобщенные степени, получим:
o, C)
Применяя для вычисления коэффициентов а({1~0, 1, .. ¦, 2л)
тот же способ, что и при выводе интерполяционных формул Ньютона,
и учитывая формулу A), последовательно находим:
Далее, введя переменную
и сделав соответствующую замену в формуле C), получим первую
интерполяционную формулу Гаусса
, ^ + 2) (g+1) <?(«? —1)(g—2) Л5
-1 gi " у~% "•"••••
—") «а»
•••"*". Bл—1)! ^ ^-(n-ijf Bft)| " >-»
D)
или, короче,
+ ffi A'J»., + ''^''"'
где x = xo + qh и ^ Я(д ) [^( )]
Первая интерполяционная формула Гаусса содержит центральные
разности
(см. таблицу 43, где эти разности образуют нижнюю ломаную строку
по ходу стрелки). Аналогично можно получить вторую
интерполяционную формулу Гаусса, содержащую центральные разности
4У-1>

§ 10} ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА БЕССЕЛЯ 521
(в таблице 43 эти разности образуют верхнюю ломаную строку
по ходу стрелки).
Вторая интерполяционная формула Гаусса имеет вид
1 (y + 2)(y + l)g(g-l)A^ | ^ ^
•••-г
Bл —1)!
+ щ\
или, в сокращенных обозначениях,
1)... (^ —Я+1) д2« ,
\ д у-*
•••^ Bм —1)!
где
§ 9. Интерполяционная формула Стирлинга
Взяв среднее арифметическое первой и второй
интерполяционных формул Гаусса D) и E) (§ 8), получим формулу Стирлинга
i |j Л Jf.2i gj 2 f"
Bл—1)!
J|T2
где
Легко видеть, что
P(Ar.)=^t. при f = 0, ± 1, •.., ±я.
§ 10. Интерполяционная формула Бесселя
Кроме формулы Стирлинга, часто употребляется формула Бес-
селя. Для вывода этой формулы воспользуемся второй
интерполяционной формулой Гаусса E) (см. § 8).

522 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ (ГЛ. XIV
Возьмем 2/г + 2 равноотстоящих узлов интерполирования
с шагом А, и пусть
Л ==/(**) (' = — «. ..., л+1)
— заданные значения функции ^у=/(х).
Если выбрать за начальные значения x — xQ и jj=^0, то,
используя узлы* лгл(& = 0, ±1, ..., ±л), будем иметь:
Примем теперь за начальные значения х~хх иу=ух и
используем узлы л;1+л (& = 0, ±1, ..., ±я). Тогда
причем соответственно индексы всех разностей в правой части
формулы A) возрастут на единицу. Заменив в правой части формулы A)
q на q—1 и увеличив индексы всех разностей на 1, получим
вспомогательную интерполяционную формулу
t
Взяв среднее арифметическое формул A) и B), после несложных
преобразований получим интерполяционную формулу Бесселя
I Ут)) ^(^-1)^+1)^-2) Д«у_а + Д4У-1 ,
Г—о" Н (9-1) G + 1) (9-2)
51

§ 10J. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА БЕССЕЛЯ 523
¦ q(q-l)(q+\)(q-2)(q + 2)(q-3) А'у_3 + Ь*У_2 .
2
Да +1v
где
Интерполяционная формула Бесселя C), как следует из способа
получения ее, представляет собой полином, совпадающий с данной
функцией y=f(x) в 2/Z + 2 точках
В частном случае, при я=1, пренебрегая разностью A3J>_i, имеем
формулу квадратичной интерполяции по Бесселю
ИЛИ
где
В формуле Бесселя все члены, содержащие разности нечетного
порядка, имеют множитель q—-^; поэтому при # = -j формула C)
значительно упрощается:
8 2 1
128 2 Т024 5 Ь • • •
...+(-1)п1±Ц?
Этот специальный случай формулы Бесселя называется формулой
интерполирования на середину. Если в формуле Бесселя C) сделать
замену переменной по формуле q—-<г=А то она приобретает более

524 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
симметричный вид
р м -
BЙ)!
Х
C')
§ 11. Общая характеристика интерполяционных формул
с постоянным шагом
Давая общую характеристику интерполяционным формулам,
обметим следующее: при построении интерполяционных формул Ньютона
в качестве начального значения х0 выбирается первый или последний
узел интерполирования; для центральных же формул
интерполирования начальный узел является средним. Приведенная ниже схема
(таблица 44) показывает используемые разности в основных
интерполяционных формулах, причем для удобства обозрения во второй
интерполяционной формуле Ньютона изменена нумерация индексов.
Более детальное рассмотрение интерполяционных формул
показывает, что при |#|^0,25 целесообразно применять формулу Стир-
линга, а при 0,25^^^0,75—формулу Бесселя. Первую и вторую
интерполяционные формулы Ньютона выгодно применять тогда, когда
интерполирование производится в начале или соответственно в конце
таблицы и нужных центральных разностей не хватает [4].
Пример 1. Значения интеграла вероятностей [3]
даны в таблице '45. Найти Ф @,5437).

§ И] ОБЩАЯ ХАРАКТЕРИСТИКА ФОРМУЛ С ПОСТОЯННЫМ ШАГОМ 525
Таблица 44
X
х.г
X,
X,
X,
*t
У
У-2
У-,
|-
ч
У<
У»
Уз
&У
Ьу-,-'

—-f ^
ЛУ*
__|
^Д'уо
Агу,
ь'у*
^у-"Г
&'У-,
\
—4*A y~f"m'
*'у,
^ у-,
k
?fy-t
-
Примечание
Z* формула
Ньютона
-+»Формула
Стирлинга
- Формула
бвссш
%ч** h формула
Ньютона
Таблица 45
Таблица разностей функции ^ =
X
0,51
0,52
0,53
0,54
0,55
0,56
0,57
У
0,5292437
0,5378987
0,5464641
0,5549392
0,5633233
0,5716157
0,5798158
At,
86 550
85 654
84 751
83 841
82924
82 001
А*у
-896
-903
—910
-917
—923
А*у
—7
—7
—7
-6

526
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
(ГЛ. XIV
Решение. Таблицу 45 дополняем конечными разностями данной
функции у = ф(х). Принимаем дго=*=О,54 и х = 0,5437, тогда
„_*—х0 __ 0,5437—0,54 л Q_
Ч ~— 0^1 -и>э'-
1 3
Так как -^ < q < -^, то воспользуемся формулой Бесселя C'), Имеем:
р = ?—1 = 0,37-0,50 = —0,13;
отсюда, используя подчеркнутые разности, получаем: ,
Ф @,5137) ^5549392 + 0,5633233 ,
2
+ (—0,13) 0,С
+-0,18@,0169-0,28) . (_0;0000007) =
= 0,55913125 — 0,00108993 + 0,00001065 = 0,5580520.
Пример 2. Имея таблицу 46 значений полного эллиптического
интеграла
dx
/"l—sin2 a sin2 x
найти #G8°30').
Таблица 46
Значения полного эллиптического интеграла /С(а)
а
75°
76°
77°
78°
—
79°
80°
81°
82°
83°
84°
К (а)
2,76806
2,83267
2,90256
2,97857
3,06173
3,15339
3,25530
3,36987
3,50042
3,65186
АК
6 461
6989
7601
8 316
9166
10191
11457
13 055
15 144
/
528
612
715
850
1025
1266
1598
2 089
А*К
84
103
135
175
241
332
491
19
32
40
66
91
159
13
8
26
25
68
—5
18
—1
43

§ 12]
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
527
Решение. Полагаем х0 = 78°; А = 1 °; х = 78° 30'; отсюда
q = 0,5. Если воспользоваться формулой Бесселя для
интерполирования на середину, то, ограничиваясь разностями пятого порядка,
будем иметь:
/С G8° 300 =2,97857 + 0,5.8316-10-5-0,125.^±^*1° +
2$
+ 0,023437.22+22. 10~5 = 2,97857-0,04158 —0,000978 +
+ 0,000008=3,019180.
Для сравнения применим теперь формулу Стирлинга
КG8° 30') = 2,97857 + 0,5 7601+8316. ю-» +
.125715-10-5 —0,0625-^|^. 10"8 —0,0078.32-10-8-Ь
,0117 • Щ^.10-* = 2,97857 + 0,039792 +
+ 0,000894 — 0,000074 — 0,000002 + 0,000001 =3,019181,
§ 12. Интерполяционная формула Лахранжа
Выведенные нами в предыдущих параграфах интерполяционные
формулы пригодны лишь в случае равноотстоящих узлов
интерполирования. Для произвольно
заданных узлов интерполирования
пользуются более общей
формулой, так называемой
интерполяционной формулой Лагранжа.
Пусть на отрезке [а, Ь] даны
л+1 различных значений аргу- У
мента: xQ, xv х2У ..., хп и
известны для функции у=*
соответствующие значения:
«Л. ...» /К*в)=Уп- Рис. 62а.
Требуется построить полином Ln (x) степени не выше п, имеющий
в заданных узлах х0, xv ..., хп те же значения, что и функция
f(x), т. е. такой, что
(рис. 62а).
= 0, 1,2, ...,л)

528
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Решим сначала частную задачу: построим полином /?,- (лг) такой, что
Pi (Xj) = О ПРИ /Vs * и Pi (*i) = 1
(рис. 626).
Короче эти условия можно записать следующим образом:
1, если /=/; /1Ч
где б|у — символ Кронекера.
«г,
Рис. 626.
Так как искомый полином обращается в нуль в п точках лг0,
xv ..., Xi_v *i+v ...» хп> то он имеет ви^
Pi \л) — ^i \л "™-Л'О/ \Л "~Л1/ • « • \Л ~~Л/-1/ \Л "~"Л1 + 1/ • • • \Л~""^nh \*)
где Oj — постоянный коэффициент. Полагая x — xt в формуле B)
н учитывая, что /?г (агх-)= 1, получим:
—Хх) ... (ЛГ4- — Ximml
Отсюда
1
Подставив это значение в формулу B), будем иметь:
Pi (*^) ==: \"/" ' ' \'" '/" ' "' \/ \ / ' \ * iy)
Теперь перейдем к решению общей задачи: к отысканию
полинома Ln (х)х удовлетворяющего указанным выше условиям Ln {Х() =,У/.
Этот полином имеет следующий вид:
D)

§ 12] ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА 529
В самом деле, во-первых, очевидно, степень построенного
полинома Ln(x) не выше п и, во-вторых, в силу условия A) имеем:
п
Ln(Xj)='%Pi(Xj)yi=Pj(Xj)yj=y/ (/ = 0, 1 я).
1 — 0
Подставив в формулу D) значение Pi(x) из C), получим:
п
L ix\ = V v **~*о) (*—**>• "(^^
Это и есть интерполяционная формула Лагранжа.
Докажем единственность полинома Лагранжа.
Предположим противное.
Пусть Ln (х) — полином, отличный от Ln{x), степени не выше п
и такой, что
M*i)=J\* С-0, 1, .... п).
Тогда полином
степень которого, очевидно, не выше л, обращается в нуль в л-fl
точках х0> xv x29 ..., хп, т. е.
Qn{x)~0.
Следовательно,
Ln(x)~Ln(x).
Отсюда, в частности, следует, что если узлы интерполирования —
равноотстоящие, то интерполяционный полином Лагранжа совпадает
с соответствующим интерполяционным полиномом Ньютона.
Заметим, вообще, что все построенные выше интерполяционные
формулы получаются из интерполяционной формулы Лагранжа при
соответствующем выборе узлов,
Формуле E) Лагранжа можно придать более сжатый вид. Для
этого введем обозначение
Дифференцируя по х это произведение, получим:
п
Полагая # = #г(i = 0, 1, 2, ..., л), будем иметь:
Внося выражения F) и G) в формулу E), получим:

530 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Следует отметить, что формула Лагранжа в отличие от
предыдущих интерполяционных формул содержит явно yif что бывает
иногда важно.
' Рассмотрим два частных случая интерполяционного полинома
Лагранжа.
При п = 1 мы имеем две точки, и формула Лагранжа
представляет в этом случае уравнение прямой у = Lx (at), проходящей через
две заданные точки:
где а, Ь — абсциссы этих точек.
При я = 2 получим уравнение параболы y = L2(x), проходящей
через три точки:
(х-Ь)(х-с) (х-а)(х-с) (i-g)(i-ft)
У — (а—Ъ) (а—с)Уо f F—а) F—с)Уг "*" (с—а) (с—*)л>
где а, й, с — абсциссы данных точек.
Пример 1. Для функции у = sinnx построить
интерполяционный полином Лагранжа, выбрав узлы
х0 = 0, хг = -g-, лг2 = ~2".
Решение. Вычисляем соответствующие значения функции:
Применяя формулу E), получим:
4
или
Пример 2. Дана таблица значений функции У=/(х)[3]:
У
321,0
322,8
324,2
325,0
Вычислить значение /C23,5).
2,50651
2,50893
2,51081
2,51188

§ 13] ВЫЧИСЛЕНИЕ ЛАГРАНЖЕВЫХ КОЭФФИЦИЕНТОВ 631
Решение. Положим дг = 323,5; л = 3. Тогда по формуле E)
будем иметь:
,то ~ C23,5-322,8) C23,5-324,2) C23,5-325,0) 9 ^к* .
Я323'5) = C21-322,8) C21-324,2) C21-325) 2'50ЫИ +
. C23,5^-321) C23,5—324,2) C23,5^-325) ~ клопо г
+ C22,8—321) C22,8—324,2) C22,8~-325)ji~
, C23,5-321) C23,5-322,8) C23,5-325) 9
4324,2—321) C24,2—322,8) C24,2—325) '
C23,5—321)C23,5—322,8)C23,5—324,2) о kiiqq_
+ C25—321) C25—322,8) C25—324,2) •^'Ollbb
= — 0,07996 +1,18794 +1,83897 — 0,43708 = 2,50987.
§ 13*. Вычисление лагранжевых коэффициентов
Укажем схему, облегчающую вычисление коэффициентов при
^.(/ = 0, 1, 2, ..., п) в формуле Лагранжа, так называемых
лагранжевых коэффициентов
Т(П) /уч __ (* — *о) (X — Хг). . <(-y — ^/_i) (X —
или в более компактной записи
где
Формула Лагранжа при этом имеет вид
Отметим, что форма лагранжевых коэффициентов инвариантна
относительно целой линейной подстановки x~at-\-b (a, b постоянны
и афО). Действительно, положив в формуле A)
(/=0, 1, ...,л),
после сокращения числителя и знаменателя на а", получим:
или
где
что и требовалось доказать»

532 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Для вычисления лагранжевых коэффициентов может быть
использована приведенная ниже схема, особенно удобная при применении
счетной машины. Сначала располагаем в таблицу разности
следующим образом:
\^ Л/* 'V'* Л^ \** А/* ^* ^*
—*о
лг2 дгх
Art л:
X ¦ Jt
г ... х
—х»
хп
-хп.
Обозначим произведение элементов первой строки через Do,
второй— через ?>! и т. д. Произведение же элементов главной диагонали
(в схеме эти элементы подчеркнуты), очевидно, будет Пй+1(д;).
Отсюда следует, что
L("»(Ar) = 5«^i?l (/ = 0, 1, ...,я). D)
Следовательно,
п
1;!:- E)
В случае равноотстоящих точек лаграижевы коэффициенты
могут быть приведены к более простому виду.
В самом деле, полагая
х = хо + th,
будем иметь:
tfo:=O, <!=!, ..., tn = n.
Отсюда
@ = (—1Г-1 Л (л —0 !
Подставив эти выражения в формулу C'), получим:
где
( )
Отсюда
±?-\Г->-^.У1, G)

§ 13]
где
ВЫЧИСЛЕНИЕ ЛАГРАНЖЕВЫХ КОЭФФИЦИЕНТОВ
дг—дг0
533
Задача интерполирования в случае постоянного шага А
облегчается еще тем, что имеются таблицы для лагранжевых
коэффициентов (см. [5]), так что фактически все вычисления сводятся
к умножению табличных коэффициентов на соответствующие
значения функции yt и к суммированию.
Пример 1. Для функции у~у(х) дана таблица значений
X
У
t
0,05
0,9512
1
0,15
0,8607
3
0,20
0,8187
4
0,25
0,7788
5
0,35
0,7047
7
0,40
0,6703
8
0,50
0,6065
10
0,55
0,5769
11
Найти j>@,45).
Решение. Для упрощения вычислений полагаем:
Тогда значения новой переменной t, соответствующие узлам
интерполирования, будут 1, 3, 4, 5, 7, 8, 10, 11. Нам нужно найти
значение^ при # = 0,45, т. е. при t = 9. Полагая t = tt (* = 0, 1, •.., 7),
вычисления располагаем iio приведенной ниже схеме (таблица 47).
Таблица 47
Схема вычисления лагранжевых коэффициентов
/
0
1
2/
3
4
5
6
7
2
3
4
6
7
9
10
—2
И
1
2
4
5
7
8
П(9) =
—3
-1
1*1
1
3
4
6
7
-4
2
-1
ш
2
3
5
6
=3840
0 5**)
-6
-4
-3
-2
1
3
4
—7
-5
-4
—3
*-1
ш
2
3
—9
—7
—6
-5
—3
—2
Г=П
1
-10
—8
-7
—6
—4
-3
—1
га
Di
-725760
26 880
—7 560
5 760
—3 456
2520
11340
-80 640
yt
0,9512
0,8607
0,8187
0,7788
0,7047
0,6703
0,6065
0,5769
t
h
m
-0,013M0-*
0,3202.10"*
—1,0829.10-*
1,3520-10-*
-2,0390-10-*
2,6530.10"*
0,5348.10"*
—0,0716.10-*
?= 1,6535-10-*

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
534
Отсюда
у @,45) = П (9) X 2Г — П (9)%s = 3840' Ь6535 • 10 = 0,6349.
Пример 2. Функция )> = cosa; задана таблицей [5]
[гл. xiv
X
У
i
X
У
t
0
0
5,0
,283662185
0
5,4
,634692876
4
0
0
5,1
,377977743
1
5,5
,708669774
5
0
0
5,2
,468516671
2
5,6
,775565879
6
0
0
5,3
,554374336
3
5,7
,834712785
7
Найти cos 5,347.
Решение. Сделаем замену переменной по формуле
Тогда значения переменной t, соответствующие узлам
интерполирования, будут 0, 1, 2, 3, 4, 5, 6, 7, а искомое значение х = 5,347
перейдет в /==3,47. Учитывая, что узлы /,==/ (/ = 0, 1, ..., 7) —
равноотстоящие, вычисления можно произвести по указанной выше
схеме (таблица 48).
Таблица 48
Схема вычисления лагранжевых коэффициентов для случая
равноотстоящих узлов интерполирования
i
0
1
2
3
4
5
6
7
Xi
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
У1
0,283662185
0,377977743
0,468516671
0,554374336
0,634692876
0,708669774
0,775565879
0,834712785
П = 42,8848749
3,47
2,47
1,47
0,47
-0,53
-1,53
-2,53
—3,53
-1
7
-21
35
—35
21
—7
1
—0,08174702
1,07119198
—6,69309530
41,28319523
41,91368048
—9,72684003
2,14583444
—0,23646254
S« 69,67575724

§ 14] ОЦЕНКА ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ ЛАГРАНЖА 535
Из таблицы 48 имеем:
П C,47) = П C,47—/) = 42,8848749
На основании формулы G) получаем:
cos 5,347 = ур • П C,47) -S = 0,592864312.
§ 14. Оценка погрешности интерполяционной формулы Лагранжа
Для функции y~f{x) мы построили в § 12 интерполяционный
полином Лагранжа Ln(x), принимающий в точках xQy xv ..., ха
заданные значения
J>o=/(*o)> J>i=*/(*i)» •••» Я» =/(*«)•
Возникает вопрос, насколько близко построенный полином
приближается к функции f(x) в других точках, т. е. как велик
остаточный член
Для определения этой степени приближения наложим на
функцию y=f(x) дополнительные ограничения. Именно, мы будем
предполагать, что в рассматриваемой области а ^х^.Ь изменения х,
содержащей узлы интерполирования, функция f(x) им^ет все
производные /'(лс), f"{x), ..., /{П+Х)(х) до (л+1)-го порядка
включительно.
Введем вспомогательную функцию
u(x)=f(x)-Ln(x)-kUn+1(x)t A)
где
П„+1 (лг) = (л: — хо)(х—хг). ..(л— хп)
и k—постоянный коэффициент, который будет выбран ниже.
Функция и(х), очевидно, имеет л-j-l корень в точках
Подберем теперь коэффициент k так, чтобы и(х) имела (л
корень в любой, но фиксированной точке х отрезка [а, Ь], не

536 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
совпадающей с узлами интерполирования (рис. 63). Для этого
достаточно положить
Отсюда, так как Пп+1(х)^0, то
При этом значении множителя k функция и(х) имеет п + 2
корня на отрезке [а, Ь] и будет обращаться в нуль на концах
каждого из отрезков
[хОу Xj], [xv х2]> ..., [xty лг], [дг, xi+1], ,.M [хп_г, хп].
Применяя теорему Ролля к каждому из этих отрезков, убеждаемся,
что производная и[ (х) имеет не менее п+ 1 корня на отрезке [а, Ь].
Рис. 63.
Применив теорему Ролля к производной и'(х), мы убедимся,
что вторая производная tC (x) обращается в нуль не менее п
раз на отрезке [а, Ь\.
Продолжая эти рассуждения, придем к заключению, что на
рассматриваемом отрезке [а, *] производная и{П+1)(х) имеет хотя бы
один нуль, который обозначим через |, т, е. иG|+1)(?) = 0.
Из формулы A), так как
Ц(г) = О и
имеем:
При дг = ! получаем:
Отсюда
Сравнивая правые части формул B) и C), будем иметь:

§ 15J ОЦЕНКИ ПОГРЕШНОСТЕЙ ИНТЕРПОЛЯЦИОННЫХ ФОРМУЛ НЬЮТОНА 537
т. е.
f{I)-Lu{x) = ?^Пв+1<*). D)
Так как х произвольно, то формулу D) можно записать и так:
где ? зависит от л: и лежит внутри отрезка [а, Ь].
Отметим, что формула E) справедлива для всех точек
отрезка [а, Ь]у в том числе и для узлов интерполирования.
Обозначая через
шах
мы получаем следующую оценку для абсолютной погрешности
интерполяционной формулы Лагранжа:
\КпМ\-\/М-1п(х)\^^ф\Пп+1(хI F)
где
П„+1 {х) = (х—х0) (x—xj.. .(х-хп). F')
Пример. С какой точностью можно вычислить ]А 15 с^омЪщью
интерполяционной формулы Лагранжа дл^ функции у~ j/дг, выбрав
узлы интерполирования дго = 100, лг1=121, дг2=144?
Реш ен Hje. Имеем:
4 т 1
Отсюда
Ж8 = тах|/"| =-|--Д== = |-.1О-5 при 100<лг<144.
На основании формулы F) получаем:
l^aK-J* 10"Б-^-|(lt5 —100)A15—121)A15—144)| =
= 4 • 10-15-6-29 да 1,6-10"8.
§ 15. Оценки погрешностей интерполяционных формул Ньютона
Если узлы интерполирования лг01 xv ..., хп — равноотстоящие,
причем
*/+i—xt = h (/ = 0, 1, 2, ..., л —1),
то, полагая

538 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ {ГЛ. XIV
на основании формулы E) из предыдущего параграфа получим
остаточный член первой интерполяционной формулы Ньютона
Ra (х) = hn".q ^"^V) ,(<?~w)/("+1> (i), 0)
где ?•— некоторое промежуточное значение между узлами
интерполирования х01 xv ..., хп и рассматриваемой точкой х. Заметим,
что для случая интерполирования в узком смысле слова ? € [#о» хпЪ
при экстраполировании возможно, что ? ? [дг0, агп].
Аналогично, полагая в формуле E) из § 14
х—хп
получим остаточный член второй интерполяционной формулы
Ньютона
где g—некоторое промежуточное значение между узлами
интерполирования дг0, xv ..., хп и точкой лг.
Обычно при практических вычислениях интерполяционная
формула Ньютона обрывается на членах, содержащих такие разности,
которые в пределах заданной точности можно считать постоянными.
Предполагая, что Ди+1у почти постоянны для функции у=/(х)
и h достаточно мало, и учитывая, что
приближенно можно положить:
/<л+1> /t\
J \Ъ)
В этом случае остаточный член первой интерполяционной формулы
Ньютона равен
В этих же условиях для остаточного члена второй
интерполяционной формулы Ньютона получаем выражение
Пример 1. В пятизначных таблицах логарифмов даются
логарифмы целых чисел от #=1000 до а; =10 000 с предельной
абсолютной погрешностью, равной у10~Б, Возможно ли линейное
интерполирование с той же степенью точности?

§ 16J ОЦЕНКИ ПОГРЕШНОСТЕЙ ЦЕНТРАЛЬНЫХ ИНТЕРПОЛЯЦИОННЫХ ФОРМУЛ 539
Решение. Полагая
будем иметь:
, м „ м
у'=- ку'=-—9
где М = 0,43. Отсюда
Из формулы A) при я = 2и &=1 получаем оценку для
погрешности линейного интерполирования:
Так как при 0^.q^.\ имеем
то окончательно получаем:
Следовательно, линейное интерполирование вполне допустимо*
Пример 2. Оценить погрешность, получающуюся при
приближении функции f(x) = sinx интерполяционным полиномом пятой
степени Рь (x)f совпадающим с данной функцией при значениях
аг = О°, 5°, 10°, 15°, 20°, 25°.
Решение. Здесь /F) (х) = —sin лс; поэтому |/(в) (х) \ ^ 1. На
основании формулы A) имеем:
| sin *-/>,(*) |«'
<М* [*-&) (*-й) (*-fr) (*-f) (*-•&) I •
Например, при х =12° 30' = arc 0,21816 получим:
| sin л: — />5 (лг) |< 2,2 • 10-».
§ 16. Оценки погрешностей центральных интерполяционных
формул
Приводим без доказательства остаточные члены для формул
Стирлинга и Бесселя [3].
а) Остаточный член интерполяционной формулы Стирлинга.
Если 2/z — порядок максимальной используемой разности таблицы и
х ^ [*о — nh> хо + nh]> то

540 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
где
Если же аналитическое выражение функции f(x) неизвестно, то
при h малом полагают:
б) Остаточный член интерполяционной формулы Бесселя. Если
2л+1—порядок максимальной используемой разности таблицы
и х?[х0—nh% хф +(л+!)*]• то
где
же функция f(x) задана таблично и шаг h мал, то принимают:
"Л\~/~ 2Bп+2)!
... (?2-Л2) [?-(«+1)].
В частности, при ? = -б- получаем погрешность при интерполировав
нии на середину
р ^ i (?) / i\»+
JC«~ Bn+2)! 1 ^
или
Л»^ 2Bд+2)! ^
Если положить
! [1.3-5... Bл+1)]«
*
nn+i[b3-5... Bn+l)]>
*/ 22W+2
то формула для остаточного члена формулы Бесселя принимает вид
§ 17. О наилучшем выборе узлов интерполирования
Анализируя формулу E) из § 14, мы видим, что погрешность Rn (x)
формулы Лагранжа представляет собой, с точностью до числовой
постоянной, произведение двух множителей, из которых один, fin+1) ({¦),
зависит от свойств функции f{x) и не поддается регулированию,

§ 17] О НАИЛУЧШЕМ ВЫБОРЕ УЗЛОВ ИНТЕРПОЛИРОВАНИЯ 541
а величина другого, Пя+1 (лг), определяется исключительно выбором
узлов интерполирования.
При неудачном расположении узлов интерполирования ^верхняя
грань модуля погрешности Rn{x) (F) § 14) может быть весьма
большой. Например, если мы сконцентрируем узлы хг вблизи одного
конца отрезка [а, Ь], то Rn{x) при / = 6 — а> 1, вообще говоря,
будет велик в точках лг, близких к другому концу отрезка. Поэтому
возникает задача о наиболее рациональном выборе узлов
интерполирования х{ (при заданном числе узлов п) с тем, чтобы находящаяся
в нашей власти часть погрешности — полином Пи+1 (лг) имел
наименьшее максимальное значение по абсолютной величине на отрезке [а, #],
или, как коротко говорят, «наименее отклонялся от нуля на [а, #]».
Эта задача была решена русским .математиком П. Л, Чебышевым
[2], [6], который доказал, что наилучший выбор в указанном смысле
узлов интерполирования дается формулой
Ь+а , Ь—ар
где
t ^л*. 2* + !^ (/ = 0 12 н)
— нули так называемого полинома Чебышева Тп+1(х). В этом
случае мы будем иметь:
Интересно отметить, что эти узлы не являются равноотстоящими,
а сгущаются около концов отрезка. Даже при таком подборе узлов
в общем случае нельзя гарантировать, что абсолютная величина
погрешности будет сколь угодно мала при достаточно большом п.
Сделаем общие замечания об определении погрешностей
интерполяционных формул. Если максимальные разности практически
постоянны, то результат интерполирования в узком смысле обыкновенно
имеет столько верных десятичных знаков, сколько их есть в
табличных данных, и поэтому оценка погрешностей не обязательна. При
пользовании интерполяционной формулой Лагранжа нет возможности
следить за ходом конечных разностей, и поэтому следует, если это
возможно, оценивать остаточный член.
Если функция /(х) задана таблично и аналитическое выражение
ее неизвестно, то оценка погрешности интерполяционного полинома,
строго говоря, является невозможной. Действительно, для данного
полинома теоретически можно построить бесчисленное множество
различных функций, совпадающих с этим полиномом в данной
системе узлов. Таким образом, в промежуточных точках отклонение
интерполяционного полинома от функции может быть каким угодно.

542 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
Однако, если природа функция такова, что график ее представляет
собой плавную кривую, то приближенно погрешности
интерполирующих полиномов с большой степенью уверенности можно определять
на основании значений конечных разностей высших порядков по
приведенным выше формулам.
§18. Разделенные разности
При построении таблицы разностей мы до сих пор предполагали,
что значения аргумента функции—равноотстоящие, т. е. имеют
постоянный шаг. Однако на практике встречаются также таблицы
для неравноотстоящих значений аргумента, т. е. таблицы
с переменным шагом. Например, такой характер часто имеют
эмпирические данные. Для таблиц с переменным шагом понятие конечных
разностей обобщается, а именно: вводятся так называемые
разделенные разности.
Пусть функция у = /(х) задана таблично и х0, xv лг2, ...—•
значения аргумента, а уф у1% у2, ...—соответствующие значения
функции, где разности
не равны между собой.
Орошения
(/ = 0, 1, 2, ...) называются разделенными разностями первого
порядка. Например,
Аналогично определяются разделенные разности второго порядка
xi+%-xt
(/ = 0, 1, 2, ...). Например, ч
л л
и т. д.
Вообще, разделенные разности п-го порядка получаются из
разделенных разностей (п—1)-го порядка с помощью рекуррентного
соотношения
± A)
t=l, 2, ...; / = 0, 1, 2, ...).

§ 18]
РАЗДЕЛЕННЫЕ РАЗНОСТИ
543
Заметим, что разделенные разности не меняются при перестановке
элементов, т. е. представляют собой симметрические функции своих
аргументов. Например,
и т' д*
Разделенные разности обычно располагаются в таблицу
приведенного ниже вида (таблица 49).
Таблица 49
Таблица разделенных разностей
ч
х%
Ч
х*
4
>/
Уо
Ух
У*
Уз
У*
Разделенные разности
1-го пор:
1*0» *li
[Xl, Х2]
[х%, х9]
2-го пор.
[Xq, Xi, x%]
\Х±у X2t Х$\
[X* XS, X*]
3-го пор.
[#о> х±, х2, х$\
[хъ х2, х3, х^\
4-го пор.
[х0, Xi, xit дс3, х4]
Пример. Составить разделенные разности для функции,
заданной следующей таблицей:
X
У
0
132,651
0,2
148,877
0,3
157,464
0,4
166,375
0,7
195,112
0,9
216,000
Решение. Последовательно применяя формулу A), будем иметь
148,877-132,651 -
= о11о
0» xi\ ~
it *2J
q 2—0 = о
157,464^148,877
0,3—0,2 — Я
85,87181,13 -
—q з_о— ^ '
и т. д. Результаты вычислений приведены в таблице 50.

544
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Таблица 50
X
0
0,2
0,3
0,4
0,7
0,9
Разделенные разности функции
у
132,651
. 140,877
157,464
166,375
195,112
216,000
1-й пор.
81,13
85,87
89,11
95,79
104,44
2-й пор.
15,8 ч
16,2
16,7
17,3
У
3-й пор.
1
1
1
4-й пор.
0
0
§ 19. Интерполяционная формула Ньютона
для неравноотстоящих значений аргумента
Пользуясь понятием разделенных разностей, интерполяционную
формулу Лагранжа можно представить в виде, аналогичном первой
интерполяционной формуле Ньютона. Докажем предварительно одну
лемму, представляющую также самостоятельный интерес.
Лемма. Если у — Р(х) есть полином п-й степени, то его
разделенная разность (п-\-\)-го порядка тождественно равна
нулю, т. е.
[Л, Д-0, Л-j, . ..* *п\
для любой системы различных между собой чисел х, xQ, xv ..., хп.
Действительно, если Р(х) — полином л-й степени, то
является полиномом (я— 1)-й степени относительно лг. Далее,
[х, xot Xl] = Pix'Xl>lZ^iXotXl)^P(x, *„, хг)
представляет собой полином (п—2)-й степени относительно х.
В самом деле, функция Р(х, xQ) — Р(хо> д;1) = Р(лг, лг0)—P{xv x0)
имеет корень лг==д:1 и, следовательно, на основании теоремы Безу
полином Р(х, х0) — P(xot хг) без остатка делится на двучлен х—xt,
С помощью аналогичных рассуждений убеждаемся, что
есть полином нулевой степени, т. е.
лг
0,

§ 19] ФОРМУЛА НЬЮТОНА ДЛЯ НЕРАВНООТСТОЯЩИХ ЗНАЧЕНИЙ АРГУМЕНТА 545
Отсюда
[х> лг0, ..., хп\ ===—-—=-=0.
Пусть теперь Р(х) — полином Лагранжа степени п такой, что
(/==0, 1, ..., п)у где у=/(х) — данная функция. Обозначим через
Я(аг, аг0), Р(х, лг0, хх), ..., Р(х, лг0, ..., дг^) последовательные
разделенные разности полинома Р(х). Имеем:
Р(ЛГ0, Xv ЛГ2) — [XQ> XV Xih V /л\
• • I
PIy y v \ fv v
' \ло> Л1> • • • > л«/ — L**0' ли • • • >
кроме того, на основании леммы
Р(х, лг0, ..., ^я) = 0. C)
По определению получаем:
отсюда
D t **\ —. D / v \ 1 D / v. *у \ / v» «/» \ i *i\
Из определения разделенных разностей следует, что
Л Лт
Отсюда
P(jc X х \ Р(х у \ -4-
+ (x-xJP(x, х0, .... хя) F)
(т = \, 2, ..., я).
Используя формулу F), из формулы E) последовательно выводим:
Р (X) = Р(Х0) + Р(X, Ха) (X -ЛГ0) =
0, xv x2)(x — xQ)(x--xl)+...
0) Xv ..., ХП)(Х—ХЬ)(Х — ХХ) ... (ЛГ— Ar^!)
+ Р{х, х0> ..., дря)(др—дро)(^—-^i) ••• (х—хп)*
18 Б. П. Демидович и И. А. Марон

546
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
или, учитывая равенства B) и C), окончательно получаем
интерполяционную формулу Ньютона для неравноотстоящих значений
аргумента
G)
(8)
где !• — промежуточное значение между точками дг0, xv .. •, хп и х.
П р и мер. Составить интерполяционный полином для функции
y=f(x), заданной таблицей
„. xv ..., хп](х—х0){х—хг) ... (*—*,,-i
Погрешность формулы G), как обычно, равна
X
У
0
0,3989423
2,5069
0,3988169
5,0154
0,3984408
7,52270
0,3978138
С помощью этого полинома найти /C,7608).
Решение. Находим разделенные разности функции у (таб
лица 51).
Таблица 51
Разделенные разности функции у
X
0
2,5069
5,0154
7,5270 ,
0,3989423
0,3988169
0,3984408
0,3973138
1-й пор.
—500
-1499
-2496
2-й пор.
-199
-199
3-й пор.
0
Используя формулу G), находим:
у = 0,3989423 — 0,0000500* — 0,0000199л: (х — 2,5069).
Отсюда
у C,7608) = 0,3989423 — 0,0000500-3,7608 —
- 0,0000199.8,7608. C,7608 - 2,5069) =* 0,3986604,

§ 20] ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ ДЛЯ РАВНООТСТОЯЩИХ УЗЛОВ 547
§ 20. Обратное интерполирование для случая
равноотстоящих узлов
Пусть функция y=f(x) задана таблично.
Задача обратного интерполирования заключается в том, чтобы
по заданному значению функции у определить соответствующее
значение аргумента х.
Остановимся сначала на случае равноотстоящих узлов. Здесь
обычно используется метод последовательных приближений.
Предположим, что функция f(x) монотонна и данное значение^
содержится между yo=f(xo) и j;1=/(a:1).
Заменяя функцию у первым интерполяционным полиномом
Ньютона, будем иметь:
отсюда q = <p(q), где
За начальное приближение принимаем:
Тогда, применяя метод итерации, получим:
' ?. = Ф (?•-!) (»=!. 2> •••)., A)
Если f(x}?Cin+l)[a, b], где отрезок [а, ^содержит узлы
интерполяции, и iiiiar h достаточно мал, то.этот процесс сходится, т. е.
где q—истинное решение. :
На практике процесс итерации продолжают до тех пор, пока
не установятся цифры, соответствующие требуемой точности,
причем полагают q&qs, где qs—последнее приближение* .
Найдя q> определяем затем х из формулы
'-=?-«¦¦
отсюда
18*

548
ИН?ЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Пример 1. Используя значения функции y--\gx, данные в
таблице
X
У
20
1,3010
25
1,3979
30
1,4771
найти значения х такое, что y = \gx= 1,35.
Решение. Составляем таблицу разностей.
Таблица 52
Конечные разности функции у
X
20
25
г 30
у
1,3010
1,3979
1,4771-
969
792
ь?у
-177
Принимая у0— 1,3010, будем иметь:
= у—у0 = 1,35—1,3010 = 490 ^0
Далее, удерживая три знака после запятой, последовательно
получаем:
qx = 0,506 —2^69" ' °7506 ^ "" 0M06^ == °'506"" 0}°23 = °>483;
.0,483 A - 0,483) = 0,506 -0,023 = 0,483.
? = 0,483.
= 20 + 0,483-5 = 22,42.
Принимаем
Отсюда
По таблице антилогарифмов имеем х = 22,39. Значительное
расхождение вычисленного значения и точного объясняется тем, что
шаг А = 5 велик.
Мы применили метод итерации для решения задачи обратного
интерполирования, пользуясь первой интерполяционной формулой
Ньютона. Но совершенно аналогично можно применить этот способ
и к другим интерполяционным формулам: ко второй формуле
Ньютона, к формулам Стирлинга, Бесселя и др. Покажем это на
следующем примере.

§ 20] ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ ДЛЯ РАВНООТСТОЯЩИХ УЗЛОВ 549
Пример 2. В таблице 53 приведены значения интеграла
вероятностей [3]
При каком значении х интеграл у равен ~?
Таблица 53
Значение интеграла вероятностей
X
0,45
0,46
0,47
0,48
0,49
0,50
У
0,4754818
0,4846555
0,4937452
0,5027498
0,5116683
0,5204999
л*
91737
90897
90046
89185
88316
А**
—840
—851
—861
—869
—11
—10
— 8
1
2
Решение. Дополняем таблицу 53 конечными разностями
функции v. Ближайшим табличным значением для аргумента лг, соответ-
ствующим значению функции У^-^, является аго = О,47. Здесь
удобно применить формулу Бесселя.
Имеем *0 = 0,47; h = 0,01; j> = 0,5.
Подставляя эти значения в формулу (8) из § 7 и используя
соответствующие табличные данные, получим:
0,5 = 0,4982475 + 0,0090046
^ (
ИГ
B)
Отсюда, разделив обе части равенства B) на 0,0090046 и
изолировав член, содержащий р в первой степени, будем иметь:
,85-10-бр(р2 — 0,25). C)
В качестве первого приближения параметра р возьмем:
ра) = 0,194623.

550
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Подставив р{1) в выражение C), получим второе приближение:
р{2) = 0,194623 + 4,753-Ю [@,194623J — 0,25]+ , \
+ 1,85-10-*. 0,194623- [@,194623J — 0,25] =
= 0,194623 —0,001008 — 0,000001=0,193614.
Аналогично, подставляя рB) вместо р в формулу C), получим третье
приближение:
рC> = 0,193612.
Так как имеем совпадение первых пяти знаков после запятой, то
процесс итерации считается законченным.
Далее, последовательно находим:
^ 0,47 + 0,0Ь 0,693612 = 0,47693612.
Это значение верно до шестого десятичного знака.
§ 21. Обратное интерполирование для случая
неравноотстоящих узлов
Задача обратного интерполирования функции для случая
неравноотстоящих значений аргумента лг0, хх% ..., хп непосредственно
может быть решена с помощью интерполяционной формулы Лагранжа.
У»
У
Уг
—:иг*
Рис. 64.
Дли этого достаточно принять переменную у за независимую и
написат* формулу, выражающую х как функцию у (рис. 64}
-Ух) (У—У*)- - ЛУ—yi-i) (У—yj+i)- - Лу—Уп
/— У\)
—У1+1)--.(У1—Уп) *

§ 22]
НАХОЖДЕНИЕ КОРНЕЙ
551
где У(=/(хг) (/ = 0, 1. ..., п). Можно также, считая^
аргументом, использовать интерполяционную формулу Ньютона для
неравноотстоящих значений аргумента (см. § 19):
где [jr0, ух}% [у09 ух, у%1 ..., [у0> ух, ..., jg — соответствующие
разделенные разности,.
Пример. Решить пример 2 из § 20 с помощью формулы Ла-
гранжа для обратного интерполирования [3].
Решение. Ограничимся четырьмя значениями:
л;0 = 0,46; ^ = 0,47; лг2 = 0,48; лг4 = 0,49-
Полагая
будем иметь следующую таблицу:
X
и
0,46
—153445
0,47
—62548
0,48
27498
0,49
116683
Данное значение У=~2 соответствует а = 0. Применяя формулу B),
где у заменено на и, получим:
62548. (—27498) • (— 116683)
— 153445+62548). ( —153445— 27498). ( — 153445 —116683)
153445. ( —27498) (— 116683) ft .
'(—62548+153445). ( — 62548—27498).(—62548 —116683) * U'4/ "
•0,46 +
153445 - 62548»(— 116683)
B7498 + 153445) • B7498 + 62548) • B7498 — 116683)
153445-62548-(—27498)
>0,48 +
k.0,49 =
^ A16683+153445).A16683 + 62548).AЦ683—27498)
= — 0,020779 + 0,157737 + 0,369928 — 0,029950 = 0,476936.
§ 22. Нахождение корней уравнения методом обратного
интерполирования
Отметим в заключение, что решение уравнения
/(*).= 6 .
можно свести к задаче обратного интерполирования. Для этого
нужно составить таблицу значений функции у=/(х) и построить
соответствующую таблицу конечных разностей для значений лг,

552
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
близких к корню. А затем применить приемы обратного
интерполирования, отыскивая значение л;, соответствующее у = 0.
П р и м е р. По данной таблице значений функции Бесселя<у=70(^)
X
У
2,4
0,0025
2,5
-0,0484
2,6
—0,0968
найти с точностью до 10~3 корень уравнения /o(je) = O, лежащий
в интервале B,4; 2,6).
Решение. Составляем таблицу разностей (таблица 54).
Таб л ид а 54
Конечные функции бесселевой
функции д> = /<>(*)
X
2,4
2,5
2,6
У
0,0025
—0,0484
—0,0968
-509
—484
ь?у
25
Полагая jj = O и лго = 2,4; ^0 = 0,0025, на основании приведенной
выше в § 20 формулы A) получаем:
= 0,049 - -
Принимаем
отсюда
По таблицам
}ш- 0,049 -0,951 =0,049-0,001 =0,048;
¦0,048-0,952 = 0,049 —0,001=0,048.
q = 0,048;
= 2,4 + 0,048-0,1=2,405.
х = 2,4048.

§ 23J МЕТОД ИНТЕРПОЛЯЦИИ ДЛЯ РАЗВЕРТЫВАНИЯ ВЕК. ОПРЕДЕЛИТЕЛЯ 553
§ 23. Метод интерполяции для развертывания векового
определителя
Интерполирование функций может быть использовано д^я
развертывания векового (характеристического) определителя (см. гл. XII)
где А = [аи1
Выберем равноотстоящие узлы
д0 = о, л^ = 1, ..., hn~?i
и для определителя D(X) вычислим соответствующие значения
Составляя горизонтальную таблицу разностей для
последовательности чисел D@), D(l), ..., D(n), обычным приемом находим
разности A'D@)(/ = 0, I, ..., n). Отсюда, применяя первую
интерполяционную формулу Ньютона, получим полиномиальное выражение
для векового определителя
Если положить
то после несложных преобразований получаем формулу A. A. Map-
нова
п п
' C)
Для облегчения вычислений по формуле B) составлены таблицы
коэффициентов cmi [8J.
В более общем случае, если в качестве узлов интерполирования
взять числа X. = a + ih(t = Of 1, ..., п)> то формула C) примет вид
. D)
Хотя изложенный здесь метод интерполяции и требует
трудоемких вычислений л+1 определителей я-го порядка, тем не менее
этот метод удобен своей простой вычислительной схемой. Кроме
того, он применим к развертыванию определителя более общего
вида
где //у (Я) — целые полиномы от X.

554
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Пример. Пользуясь методом интерполяции, раскрыть
характеристический определитель
1-Х 2 3 4
2 1-Я 2 3
3 2 1-Х 2
4 3 2 1—>
(ср. гл. XII, § 3, пример).
Решение. Последовательно вычислим D (i) при / = 0, 1, 2, 3, 4.
Имеем:
D@)=— 20, ?>A)= —119, DB)=—308,
D C) =? — 575, D D) = — 884.
Конечные разности Д'?)@) (/=0, 1, 2, 3, 4) приведены в
таблице 55.
Таблица 55
Конечные разности чисел П(Х)
к
0
1
2
3
4
D (к)
-20
-119
-308
-575
-884
АО (Я,)
—99
-189
-267
-309
Д*?> (К)
—90
-78
—42
Д«О (Л)
12
36
Д*/> (X)
24
Так как
11 ~~Л>
Я(Л,—1) _ X2 X
2! "" 2 2
I — 1ИХ—2)____>
3! "" <
А1
2
3 •
^(Л,—1) (Я,—2)(Х—3) _ Я4 ¦ X3
4! "" 24 4 + 24
А
4 '
то из формулы B) получаем:
сп= 1;
^22 == "о" > ^^2 ===
С33 === "g" > С23 ==
^4i — 24 ' ^^4
3 '
И
Т

§ 24]
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
555
Отсюда, применяя формулу Маркова C), будем иметь:
I = D @) + [сиДО @) + с12Д2? @) + с13Д3?> @) + с14Д4? @)] А,+
+ [с22Д*Д @) + с23ДЮ @) + c^D @)] Х^ +
HD@)X4 =
=-20+(-99.1
4+12
.1-24.1)
X
.-^Л4=— 20-56Я — 40Х2-
§ 24*. Интерполирование функции двух переменных
Пусть функция
задана на системе равноотстоящих точек (л^., j;y) (/, у==0, 1,2, .
где
xi = x0 + lhi у.^уц+jk,
причем
h =Длг/ = const; k = Д^у — const.
Для краткости введем обозначения
..),
Значения функции z можно оформить в виде таблицы с двумя
входами (таблица 56).
Таблица 56
Значения функции двух переменных
Уо
Уг
У%
•
03
Z\\
. . .
•
Интерполирование функции двух переменных
т. е. нахождение ее нетабличных значений, можно
последовательно проводить по каждому переменном// х и у в отдельности. Пусть,
например, требуется найти значение-

556
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XIV
Интерполируя надлежащим образом выбранные функции одной
переменной х:
где yk жу> находим значения fk(x). Для этого используются
соответствующие строки двойной таблицы. Рассматривая полученные
значения fk(x)—f(x> Уь) как значения функции f(x, у) единственной
переменной у, с помощью одной из интерполяционных формул
находим искомое значение f(x,y)—F.
Можно также производить интерполирование в обратном порядке.
Пример. Значения функции последействия
/(лг, у)=
даются следующей таблицей (см. Янке и Эмде, «Таблицы функций»):
У
0
0
0
X
\
,00
,05
,10
2
2
2
0.4
,500
,487
,456
1
1
1
0.7
,429
,419
,400
1
0
0
1,0
,000
,995
,981
Найти /@,5; 0,03).
Решение. Составляем таблицы 57а, 576 и 57в, используя
строки данной двойной таблицы.
Таблица 57^ [ у = 0,05 | Таблица 676
0
0
1
X
,4
.7
,0
2
1
1
f
,500
,429
,000
Д/
—1
—0
,071
,429
Д*/
0,642
X
0,4
0,7
1,0
f
2,487
1,419
0,995
д/
—1,068
—0,424
д*/
0,644
у=0,10
Т а б л и ц а 57в
X
0,4
0,7
1,0
f
2,456
1,400
0,981
д/
—1,056
—0,419
Д*/
0,637

§ 25]
ДВОЙНЫЕ РАЗНОСТИ ВЫСШИХ ПОРЯДКОВ
557
Так как для этих таблиц
? = 0,7-0,4 = 0,3,
то, принимая лг0 = 0,4, будем иметь:
_*—хо__0,5—0,4_ 1
Я~~ h ~ 0,3 " е
Отсюда, используя первую интерполяционную формулу Ньютона,
последовательно получим:
/о -/@,5; 0) = 2,500-1. 1,071 + 3 ^ 3 ^0,642 = 2,072;
Л =/@,5; 0,05) = 2,487—у. 1,068——0,644 = 2,069;
Л =/@,5; 0,10) = 2,456—у. 1,056 — -.0,637 = 2,033.
Составляем таблицу найденных значений (таблица 58).
Таблица 58
0
0
0
У
,05
,10
2
2
2
/
,072
,069
,033
Af
. —0,003
—0,036
А*/
—0,033
Принимая /5 = 0,05 — 0 = 0,05 и уо = О, получим:
0,03^0 3
Отсюда
/@,5; 0,03) = 2,072—1> 0,003+
0,033) = 2,074.
§ 25*. Двойные разности высших порядков
Для функции z=sf{xfy)f заданной двойной таблицей {г/;-}, можно
определить частные конечные разности
Л А/ = ^+i»y—*// и
Повторно применяя эти операции, получим двойные разности вые-,
ших порядков
nZif) = A^n
nynZif

558 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ [ГЛ. XIV
где положено Д04^^^^. Например,
= Ах (A2yyZif) = Ах (ги м - 2ziy/+1 + zu) -
l,j) — (Zl,J+2 — 2zi,/
§ 26*. Интерполяционная формула Ньютона
для функции двух переменных
Используя разности функции двух переменных z=f(x, у), можно
построить интерполяционный полином, аналогичный
интерполяционному полиному Ньютона. Пусть Р (лг, у) — целый полином такой, что
№fip[xo,y*) = &r***n A)
(/», /г = 0, 1, 2, ...), Положим, что Р(х,у) разложен но
обобщенным степеням разностей х—х0 и у—yQi т. е.
{x—хо){х—хг) +
+ с1г (х-х0) (у -у0) + с02 (у -у0) (у -~уг) +... B)
Полагая х"=х0 и у=у0, в силу условия A) будем иметы
Р (хо> У о) ^ ^оо == соо*
Составляя для полинома Р(хуу) конечные разности первого порядка,
получим:
Отсюда, полагая х = х0 и у—уф на основании условия A) будем
иметь:
т. е.
Далее, подсчитывая для полинома Р(х, у) конечные разности
второго порядка, найдем:
^.-У) = 2!с'

§ 26] ФОРМУЛА НЬЮТОНА ДЛЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 559
Отсюда при х = х0 и у=у0 получим:
0,у0)-А2+%0 = 2!с20/г2,
0> У о) ц
уу(х<» Уо) = до+2*оо = 2! с02к\
т. е.
Аналогично находятся дальнейшие коэффициенты разложения B).
Подставляя найденные значения коэффициентов в формулу B),
получим интерполяционный полиномщдля функции двух переменных
] ... C)
При интерполировании функции f{xty) полагают:
Для удобства вычислений обычно вводят переменные
тогда
и т. д. Отсюда формула C) принимает вид
*«*оо + (рЛ1+%о"
где
Если положить р = 0 или ^ = 0, то формула D) перейдет в
соответствующую интерполяционную формулу Ньютона.
Пример. Пользуясь интерполяционной формулой D), 1&йти
/=/@,5; 0,03) для функции /(лг, у)} рассмотренной в примере
из § 24.

560
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
{ГЛ. XIV
Решение. Принимая х0 = 0,4; у0 = 0, составляем для
функции / таблицы конечных разностей первого порядка (таблицы
59а и 596).
Таблица 59а
'•-2
Д'+"/„,
777
—0,429
—0,424
—0,419
Таблица 596
—0,013
(.1
-о,
-о,
010
019
—0,005
—0,014
Отсюда находим конечные разности второго порядка
да+»/00 = Д1+0/10 - Д1+о/оо „ _ 0,429 - (-1,071) = 0,642;
Д1+1/оо = Д1+о/О1 - А1+о/оо 1,068 - (-1,071 ) = 0,003
или
Д1+1/м = Д0+1/10 - До+1/оо = — 0,010 - (- 0,013) = 0,003;
А0+а/оо = Ao+1/oi - До+1/оо = - 0.031 - (- 0,013) = - 0,018.
Так как
х—х0
то, применяя формулу D), получим:
/=2,500+-i-(-l,071)+-|-(-0,013) +
+i[f(-i)'°'642+244>0'003+
+Т* (—т)(-°'018)] =2,500 — 0,357 — 0,0078-0,0718 +
+ 0,0006 + 0,0021 = 2,067.
Сравнивая с ответом /=2,074, полученным первым способом,
мы видим, что цифры тысячных являются ненадежными.

ЛИТЕРАТУРА К ЧЕТЫРНАДЦАТОЙ ГЛАВЕ 561
Литература к четырнадцатой главе
1. Э. Уиттекер и Г. Робинсон, Математическая обработка
результатов наблюдений, ГТТИ, М.—Л., 1933, гл. I.
2. В. Л. Гончаров, Теория интерполирования и приближения функций,
ГТТИ, М.—Л., 1934, гл. I, §§ 18—21.
3. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
М.—Л., 1934, IV, разд. II.
4. В. М. Б р а д и с, Теория и практика вычислений, Учпедгиз, М., 1935,гл. IX.
5. В. Э. Милн. Численный анализ, ИЛ, 1961, гл. III, VI.
6. Е. Я. Ремез, Общие вычислительные методы чебышевского
приближения, Изд. АН УССР, 1957, ч. 1, гл. I.
7. Математический практикум на счетно-вычислительных приборах и
инструментах. Под общей редакцией Н. А. Леднева, «Советская наука»,
М., 1959, гл. III.
8. В. Н. Фаддее в а, Вычислительные методы линейной алгебры, Гостех-
издат, М.— Л., 1950, гл. III, §27.

ГЛАВА XV
ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
§ 1. Постановка вопроса
При решении практических задач часто нужно найти
производные указанных порядков от функции y=:f(x)t заданной таблично.
Возможно также, что в силу сложности. аналитического выражения
функции f(x) непосредственное дифференцирование ее
затруднительно, В этих случаях обычно
прибегают к приближенному
дифференцированию.
Для вывода формул
приближенного
дифференцирования заменяют данную функцию
f(x) на интересующем
отрезке [а, Ь\ интерполирующей
функцией Р (х) (чаще всего
полиномом), а затем полагают:
/(*)=/*(*)
A)
Рис. 65.
при
Аналогично поступают при нахождении производных высших
порядков функции f(x).
Если для интерполирующей функции Р(х) известна погрешность
R(x)=f(x)-P(x),
то погрешность производной Р (х) выражается формулой
г (*) =/' (*)-/* (дг) = #' (дг), ' B)
т. е. погрешность производной интерполирующей функции равна
производной от погрешности этой функции. То же самое справедливо
и для производных высших порядков.
Следует отметить, что, вообще говоря, приближенное
дифференцирование представляет собой операцию менее точную, чем
интерполирование. Действительно, близость друг к другу ординат двух
кривых
и Y=P(x)

§ 2] ФОРМУЛЫ, ОСНОВАННЫЕ НА ПЕРВОЙ ФОРМУЛЕ НЬЮТОНА 563
на отрезке [а, Ь] еще не гарантирует близости на этом отрезке их
производных f (х) и Р (х), т. е. малого расхождения угловых
коэффициентов касательных к рассматриваемым кривым при
одинаковых значениях аргумента (рис. 65).
§ 2. Формулы приближенного дифференцирования» основанные
на первой интерполяционной формуле Ньютона
Пусть имеем функцию у (х)> заданную в равноотстоящих точках
х{ (/==0, 1, 2, ..., п) отрезка [а9 Ь] с помощью значений yt=f(Xi).
Для нахождения на [я, Ь] производных у' = /' (х), у" =f'(x) и т. д.*)
функцию у приближенно заменим интерполяционным полиномом
Ньютона, построенным для системы узлов х07 х17 ...,
Имеем:
У {х)=
где
д = х-^ и h*=Xtoi-Xt (/-0,1,...).
Производя перемножение биномов, получим:
Так как
dx^dq* dx h dqy
то .
<2>
Аналогично, так как
та
1 Г {- (q- Г) A^0-f %-~;Г^ " А%+ ... I -. C)
*) Само собой разумеется, что, заранее должно быть известно о
существовании соответствующих ггроизводнызс фувдщади* /(*)> иначе выкладки
носят иллюзорный характер.

564 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ [ГЛ. XV
Таким же способом в случае надобности можно вычислить и
производные функции у(х) любого порядка.
Заметим, что при нахождении производных у' (х), уп (дг), ...
в фиксированной точке х в качестве х0 следует выбирать
ближайшее табличное значение аргумента.
Иногда требуется находить производные функции у в основных
табличных точках xt. В этом случае формулы численного
дифференцирования упрощаются. Так как каждое табличное значение можно
считать за начальное, то положим лг = лг0, # = 0; тогда будем иметь:
D)
E)
Если Pk {x) — интерполяционный полином Ньютона, содержащий
разности Ау0, А2у0, ..., А*у0, и
RM{x)=y[x)-Pk(x)
— соответствующая погрешность, то погрешность в определении
производной есть
Как известно (гл. XIV, § 15),
_ hk+i q(q—\)...(q—k)
где g — некоторое промежуточное число между значениями дг0, xv
##., xk1 х. Поэтому, предполагая, что у (х) ^С4*4*2), получим:
Отсюда при 'л; = л0 и, следовательно, при q — Он учитывая, что
Ч"ЛЧ—Ь)]я=о = ( — 1)*А!, будем иметь:

§ 2]
ФОРМУЛЫ, ОСНОВАННЫЕ НА ПЕРВОЙ ФОРМУЛЕ НЬЮТОНА
565
Так как У*+1)A) во многих случаях трудно оценить, то при А
малом приближенно полагают:
и, следовательно,
G)
Аналогично может быть найдена погрешность Rk (аг0) для второй
производной у (лт0).
Пример 1. Найти уг (ЬО) функции ^ = lgAr, заданной таблично
(таблица 60).
Таблица 60
Значения функции у
X
50
55
60
65
и
1,6990
1,7404
1,7782
1,8129
Л,
414
378
347
Л»,
—36
—31
д..
5
Решение. Здесь h = 5. Дополняем таблицу 60 столбцами
конечных разностей (десятичные разряды, как обычно, не указы*
ваются; они определяются десятичными разрядами значений функции).
Используя первую строчку таблицы, на основании формулы D),
с точностью до разностей третьего порядка, будем иметь:
/ E0)« j @,0414 + 0,0018 + 0,0002) = 0,0087.
Для оценки точности найденного значения заметим, что так как
табулированная выше функция есть y = \gx, то
М 0,43429
Следовательно,
/E0) = 2^^=0,0087.
Таким образом, результаты совпадают с точностью до четвертого
десятичного знака.

566
ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
[ГЛ. XV
Пример 2. Путь y=f(t), пройденный прямолинейно
движущейся точкой за время t, дается следующей таблицей [1]:
1
0
1
2
3
4
5
6
7
8
9
Время ti в сек.
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
Путь y(ti) в см
0,000
1,519
6,031
13,397
23,396
35,721
50,000
65,798 .
82,635
100,000
Используя конечные разности до пятого порядка включительно,
приближенно найти скорость V=-^- и ускорение ^=-^~ точки
для моментов * = 0; 0,01; 0,02; 0,03; 0,04.
Решение. Составляем таблицу разностей (таблица 61).
Таблица 61
Конечные разности функции y=f (t)
i l
0 i
1
2
3
4
5 ¦,
6
7
8
9
1/&19
4,512 i
7,366
9,999
12,325
14,379 \
15,798
16,837
17,365
~-
2,9§3
2,854 :
2,633 ,
2,326
1,954
fl;619
1,039
0,528
AVi
—0,139
—0,221
—0,307
—0,372
—0,435
—0,488
—0,511
—
A4«t
—0,082 ^
-0,^86
—0,065
—0,063
—0,045
—0,031
—
--§,004
0,021 s
0,002
0,018
0,014
—
Полагая ft = 0,01 и применяя формулы D) и E), получаем
приближенные значения величины скорости V (см/сек) и величины
ускорения W (см/сек2). Например,
К@) = 100A,519— 1,496 — 0,046 + 0,020 — 0,001) = — 0,4 см/сек,
W@) = 10 000 B,993 + 0,139 — 0,075 + 0,003) = 30600 см/сек*.
Соответствующие значения V и W помещены в таблице 62.

§ 3]
ФОРМУЛЫ, ОСНОВАННЫЕ НА ФОРМУЛЕ СТИРЛИНГА
Таблица 62
Значения скорости V и ускорения W
для закона движения y=f(t)
567
t
0,00
0,01
0,02
0,03
0,04
V
0,4
303,6
596,3
873,2
1121,7
w
30600
29780
28780
26250
23360
V
0,00
303,08
596,98
872,66
1121,9
w
30462
30001
28625
26381
23340
Заметим, что табулированный закон движения дается формулой
,= 100A-СО8^У
Отсюда
dy 5000я . 50 %t
=T* = -9-Sin —
50я*
Для сравнения точные значения V и W приведены в правой поло-
вине таблицы 62.
Отметим, что можно вывести также формулы приближенного
дифференцирования, исходя из второй интерполяционной формулы
Ньютона.
§ 3. Формулы приближенного дифференцирования, основанные
на формуле Стерлинга
Выведенные в § 2 формулы численного дифференцирования для
функции у в точке х = х0 обладают тем недостатком, что они
используют лишь односторонние значения функции при лг>лг0.
Относительно ббльшую точность имеют симметрические формулы
дифференцирования, учитывающие значения данной функции у как прил: > лг0,
так и при х < лг0. Эти формулы обычно называются центральными
формулами дифференцирования. Мы ограничимся выводом одной
из них, взяв за основу интерполяционную формулу Стирлинга.
Пусть ..., лг_8> *-2> х-1> хо> xi> xv xz> ...—система
равноотстоящих точек с шагом лг/+1 — х( = Л и ^1.=/(лг|) —
соответствующие значения данной функции у=/(х). Полагая

568 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ [ГЛ. XV
и заменяя приближенно функцию у интерполяционным полиномом
Стерлинга, будем иметь:
У (х) = 4 QjS
О)
где для краткости введены обозначения
2
и т. д.
Из формулы A), учитывая, что
получаем:
В частности, полагая ^ = 0, будем иметь:
2 2
И

§ 3]
ФОРМУЛЫ, ОСНОВАННЫЕ НА ФОРМУЛАХ СТИРЛИНГА
569
Пример 1. Найти У A) и у A) для функции у=у(х),
заданной таблицей 63.
Таблица 63
Значения функции у ==у (х)
X
0,96
0,98
1,00
1,02
1,04
у
0,7825361
0,7739332
0,7651977
0,7563321
0,7473390
А*
—86029
—87355
-88656
-89931
-1326
—1301
—1275
л..
25
26
л.»
1
Решение. Составляя разности функции у (таблица 63) и
используя подчеркнутые члены, на основании формулы C) будем иметь:
87 355+88 656 1Л_7 1 25+26 1Л_7 . 1 1 1Л.
= —50-(88 005,5+ 4,2 + 0). 10= —0,4400485.
Для проверки заметим, что табулированная функция есть
функция Бесселя нулевого индекса y = J0(x).
Как известно,
7; A) = —Л (х) |x«i = — 0,4400506.
Аналогично, используя дважды подчеркнутые члены и применяя
формулу C'), будем иметь:
= — 2500-1301-10-7 = — 3,2525- 10"l = — 0,325250.
Для сравнения приведем получающееся на основании соотношений
между бесселевыми функциями точное значение
= 0,4400506 — 0,7651977 = — 0,325147.
Таким образом, численное нахождение второй производной есть
операция, вообще говоря, менее надежная, чем первой.
3 а м еч а н и е. Иногда требуется найти экстремум дифференцируе*
мой функции у=у(х), заданной таблично. Для этого необходимо,

570
ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
[ГЛ. XV
чтобы в точке экстремума х было выполнено равенство у' (лг) = О.
Приравняв нулю производную У (х) в формуле B), методом
последовательных приближений находим соответствующее значение^. Отсюда
причем значение^ вычисляется по формуле A) или по какой-нибудь
другой интерполяционной формуле. Найденное значение у является
экстремумом функций, если в окрестности точки х вторая рдзность дг^
сохраняет постоянный знак.
Пример 2. Найти нуль производной функции y^J1 (x),
заданной таблицей 64.
Таблица 64
Значение функции у=^(х)
X
1,80
1,82
1,84
1,86
1,88
1,90
у
0,5815170
0,5817731
0,5818649
0,5817926
0,5815566
0,5811571
2561
918
1
—723
—2360
—3995
—1643
—1641
—1637
-1635
Д*0
2
"¦"
4
2
Дополняем таблицу 64 конечными разностями функции у.
Решение. Принимаем дго= 1,84. Используя подчеркнутые
разности, на основании формулы B) будем иметь:
ИЛИ
0 = 97 — 1641$+ -§-?а.
Отсюда
1641
D)
Отбрасывая малый нелинейный член, получим первое приближение:

§ 4] ФОРМУЛЫ, ВЫРАЖЕННЫе ЧЕРЕЗ ЗНАЧЕНИЯ В РАВНООТСТОЯЩИХ ТОЧКАХ 571
Уточняя это значение, из формулы D) получим второе
приближение:
^2)^1)+^A)]2591Ь10+
= 5,91 Ы0-2 + 3,2-10 = 5,91 ЬЮ-2.
Следовательно, можно положить:
? = 0,05911.
Отсюда
x = xo + qh =1,84 + 0,05911.0,02=1,8411822.
Таким образом,
7; A,8411822) = 0.
§ 4. Формулы численного дифференцирования
для равноотстоящих точек, выраженные через
значения функции в этих точках
Пусть точки х0, xv лг2, ..., хп — равноотстоящие, т. е.
xux~Xi = h (' = 0, 1, 2, ..., /г—1),
и пусть для функции у=у(х) известны значения У(*=у(Х() (/ = 0,
1, ..., п). Для данной системы узлов х{ построим
интерполяционный полином Лагранжа (гл. XIV, § 12)
п
где
Пц+i (*) = (*—*•)(*—*i)...(* — хп).
Тогда
Полагая
получим:
И
(л:^—аг0) (A:f. — хх). ..{xi—xi^1){xi—
Следовательно, для полинома Лагранжа Ln(x) имеем выражение
<в «(п-<)

572 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ [ГЛ. XV
Отсюда, учитывая, что
dx_h
получаем:
Аналогично могут быть найдены производные высших порядков
данной функции у(х). Для оценки погрешности
rn(x)=y'(x)-L'n{x)
воспользуемся известной формулой погрешности интерполяционной
формулы B) (гл. XIV, § 14)
К С*) =у (x)-Ltt (х) = ^§- Пя+1 (*), D)
где | = ? {х) — промежуточное значение между точками дг0, xv . . о хп
и х.
Предполагая, что у(х) ?Оп+2\ выводим:
Отсюда, учитывая формулу A), получаем погрешность производной
в узлах
К (*,) - (- D-1*- ^qf^y+M (i). E)
где ? — промежуточное значение между лг0, лгх, . #м д;п,
I. Произведем расчет для п = 2 (три точки). Из формулы B)
получаем:
Отсюда, учитывая, что ^- = А, будем иметь:
В частности, для производных

§ 4] ФОРМУЛЫ, ВЫРАЖЕННЫЕ ЧЕРЕЗ ЗНАЧЕНИЯ В РАВНООТСТОЯЩИХ ТОЧКАХ 573
получим следующие выражения:
с соответствующими погрешностями:
Приведем без доказательства формулы дифференцирования для
четырех и пяти точек [3], справедливость которых читатель легко
может проверить самостоятельно.
II. и = 3 (четыре точки).
III. /г = 4 (пять точек).
Ш (-3
ш CVo-
Ш (-Л + 6^i -18уа + 10у8 + 3yt) -gy» (g);
(8Л
Рассмотрение формул I — III показывает, что если число точек
нечетно и производная берется в средней точке, то соответствующая

574 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ [ГЛ. XV
формула численного дифференцирования выражается более просто
и обладает повышенной точностью.
Ниже приводятся для случая п = 2 и п — 4 формулы таких
центральных производных [3], причем для выявления -'симметрии
изменена нумерация точек (рис, 66):
I. л = 2.
где у.=у(х() и / = —1, 0, 1;
II, п = 4.
где jr|a=jr(*,) и / = — 2, —1, 0, 1, 2.
§ 5. Графическое дифференцирование
Задача графического дифференцирование заключается в
построении по заданному графику функцииу=/(х) графика ее производной
Пусть дан график функции y=f(jt) (рис. 67).' Для ггостроёния'
в известном масштабе / графика ее производной выбираем на данной
кривой достаточно густую сеть точек 1, 2, 3, 4, 5, .. '.,
включающую по возможности характерные для графика точки. В этих
точках с возможной тщательностью строим касательные к графику
функции, проводя их «на глаз». Далее, на оси Ох выбираем точку Р( — /, 0)
(полюс) и проводим параллельные соответствующим касательным
прямые РГ, Я2', ЯЗ', Я4', Р5\ ... до пересечения их с осью Оу*
Отрезки оси Оу: 0Г, 02', 03', 04', 05', ... представляют собой
соответственно величины, пропорциональные значениям производной
y'=f'(x) в выбранных точках, т. е. являются ординатами графика
производной. В самом деле, например, для точки 1 из рис. 67 имеем:
Аналогичные результаты получаем для всех других точек. Поэтому
точки пересечения Г, 2", 3", 4", 5", ... параллелей, проходящих
через точки Г, 2', 3', 4', 5', ..., с соответствующими вертикалями,
проходящими через точки касания 1, 2, 3, 4, 5, •,., принадлежат
графику производной y = lf'(x).

§ 6] ПОНЯТИЕ О ПРИБЛИЖЕННОМ ВЫЧИСЛЕНИИ ЧАСТНЫХ ПРОИЗВОДНЫХ 575
Соединяя точки Г, 2", 3", 4", 5",... линией, характер которой
учитывает положение промежуточных точек, мы приближенно
получим график производной У в масштабе /. Если выбрать /=1, то
график производной получится в натуральном масштабе.
Для увеличения точности графического построения рекомендуется
сначала определять направление касательной, а затем намечать точку
касания. Для этого график
данной функции разбивают
Iй на небольшие участки, мало
отличающиеся от
прямолинейных. Рассмотрим один
из таких участков АВ
(рис, 68). Построим
семейство хорд, параллельных
секущей АВ.
Геометрическое место середин этих
Рис. 67.
Рис. 68.
хорд представляет собой кривую /С, пересекающую график функции
в точке С, касательная в которой параллельна секущей АВ. Таким
приемом на каждом участке можно найти точку и соответствующее
направление касательной. Дальнейшее построение выполняется
указанным выше способом.
За указаниями более детального характера следует обратиться
к специальной литературе (см., например, [5]).
§ в*. Понятие о приближенном вычислении частных производных
Если функция z=f(x, у) задана на прямоугольной сетке
(/f /=0, 1, 2, ...), то ее приближенно можно представить
интерполяционной формулой (гл. XIV, § 26)
A)

576 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ [ГЛ. XV
где
и &m+nzQ0 = A™mJ?z @, 0) —смешанные двойные разности.
Из формулы A) легко находятся частные производные
d?__cte ^р \_дг дг^дг d^ \_дг
дх dp* dx h dp* ду dg* dy k dq
и т. д.
Литература к пятнадцатой главе
1. А. Н. Крылов, Лекции о приближенных вычислениях, Изд. 6, Гостех-
издат, М., 1954, стр. 228.
2. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
М.-Л., 1934, гл. VII.
3. В. Э. Милн, Численный анализ, ИЛ, М., 1951, гл. IV.
4. Ш.Е.Микеладзе. Численные методы математического анализа, Гостех-
издат, М., 1953, гл. XII.
5. К. Р у н г е, Графические методы математических вычислений, ГТТИ,
М.—Л., 1932, гл. III, § 14.

ГЛАВА XVI
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
§ 1. Общие замечания
Если функция f(x) непрерывна на отрезке [а, Ь] и известна ее
первообразная F(x), то определенный интеграл от этой функции
в пределах от а до b может быть вычислен по формуле Ньютона —
Лейбница
ъ
§f{x)dx = F(b)-F{a), A)
а
где F'(x)=f(x).
Однако во многих случаях первообразная функция F (х) не может
быть найдена с помощью элементарных средств или является
слишком сложной; вследствие этого вычисление определенного интеграла
по формуле A) может быть затруднительным или даже практически
невыполнимым.
Кроме того, на практике подынтегральная функция f(x) часто
задается таблично и тогда само понятие первообразной теряет смысл.
Аналогичные вопросы возникают при вычислении кратных
интегралов. Поэтому важное значение имеют приближенные и в первую
очередь численные методы вычисления определенных интегралов.
Задача численного интегрирования функции заключается в
вычислении значения определенного интеграла на основании ряда
значений подынтегральной функции.
Численное вычисление однократного интеграла называется меха»
нической квадратурой, двойного — механической кубатурой.
Соответствующие формулы мы будем называть квадратурными и куба-
турными формулами.
Мы сначала остановимся на численном вычислении однократных
интегралов. Обычный прием механической квадратуры состоит
в том, что данную функцию f(x) на рассматриваемом отрезке
[а, Ь] заменяют интерполирующей или аппроксимирующей
функцией ф (х) простого вида (например, полиномом), а затем приближенно
19 Б. П. Демидович и И. А. Марон

578 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
полагают:
ь ь
J J (*)**• B)
Функция ц>(х) должна быть такова, чтобы интеграл \ (p(x)dx
а
вычислялся непосредственно.
Если функция f(x) задана аналитически, то ставится вопрос
об оценке погрешности формулы B).
Рассмотрим более подробно применение для этой цели
интерполяционного полинома Лагранжа (гл. XIV, § 12).
Пусть для функции y=f(x) известны в /г+1 точках лг0, xv
х2, ..., хп отрезка [а, Ь\ соответствующие значения
Л*/)=-Л (' = 0, 1, 2, ..., п). C)
Требуется приближенно найти:
По заданным значениям yt построим полином Лагранжа
где
Пл+1(д:) = (лг-л:0)(аг-л;1)...(л:—хп),
причем
^»(^)=Л (' = 0. 1. 2, ..., п).
Заменяя функцию f(x) полиномом Ln(x), получим равенство
ъ ь
§f(x)dx = §Ln(x)dx + Rnm E)
а а
где Rn[f] — ошибка квадратурной формулы E) (остаточный член).
Отсюда, воспользовавшись выражением D), получаем приближенную
квадратурную формулу
ь п
^ F)

§ 1] ОБЩИЕ ЗАМЕЧАНИЯ 579
Если пределы интегрирования а и Ь являются узлами
интерполирования, то квадратурная формула F) называется «замкнутого типа»,
в противном случае — «открытого типа».
Для вычисления коэффициентов Ai заметим, что
1) коэффициенты А( при данном расположении узлов не зависят
от выбора функции f(x);
2) для полинома степени п формула F) — точная, так как тогда
Ln(x) = f(x); следовательно, в частности, формула F) —точная при
у = х* (? = 0, 1, ..., л), т. е. Rn[xk] = 0 при 6 = 0, I, . .., п.
Полагая у — х F = 0, 1, 2, ..., п) в формуле F), получим
линейную систему из /2+1 уравнений
п
'о == 2u ™fr
«=о
п
1Х = ^2j ^ix'
4,-^4*7,
где
(8)
.... л),
из которой можно определить коэффициенты Ло, Л1? #. ., Ап [1], [2J.
Определитель системы (8) есть определитель Вандермонда
Заметим, что при применении этого метода фактическое
построение полинома Лагранжа Ln(x) является излишним.
Простой метод подсчета погрешностей квадратурных формул
разработан С. М. Никольским [3].
Пример. Вывести квадратурную формулу вида
()()D) (9)
о
Решение. Полагая в формуле (9)
у = хк (Л-0, 1, 2)
и учитывая, что
1 1
19*
о

580 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
получим систему
"!=sT^0~'~~2*i^1~'~T ^2)
Т в 16 Л° + Т Л1 + Тб А*
Отсюда
°~~3' 1"~~'3"> 2~~Т
и, следовательно,
Квадратурная формула A0) открытого типа и является точной для
всех полиномов степени не выше второй.. Нетрудно убедиться, что
формула A0) дает правильный результат и при j> = лг3. Поэтому эта
формула является точной также для полиномов третьей степени.
§ 2. Квадратурные формулы Ньютона — Котеса
Пусть для данной функции у =f(x) требуется вычислить интеграл
Выбрав шаг
Ъ-а
h
разобьем отрезок [а, Ь] с помощью равноотстоящих точек
хо = а, xt = x0 + ih (/=1, 2, ..., л-1), хп = Ь
на п равных частей, и пусть
у(=/(х() (/-0, 1, 2, ..., п).
Заменяя функцию у соответствующим интерполяционным
полиномом Лагранжа Ln(x), получим приближенную квадратурную формулу
хп п
A)
i
где А( — некоторые постоянные коэффициенты.

§ 2J КВАДРАТУРНЫе ФОРМУЛЫ НЬЮТОНА—КОТЕСА 581
Выведем явные выражения для коэффициентов At формулы A).
Как известно (гл. XIV, § 12),
/=0
где
PiW— (xi—xQ)(xi—xl)...(xi—xud(xi—xi+1)...(Xi~-xa) ( '
Введя обозначения
?==?и?9 D)
и
будем иметь (ср. гл. XV, § 4, формулу B)):
Л- F)
Заменяя в формуле A) функцию ^ полиномом Ln(x), в силу
формулы F) получим:
или, так как
q = х~~хо ? dqz=z? y
то, сделав замену переменныхвопределенном интеграле, будем иметь:
О
Так как
, Ь—а
то обычно полагают:
где
— постоянные, называемые коэффициентами Котеса (см.,
например, [1], [4]).
19* Б. П. Демидович и И. А. Марон

582
приближенно^ интегрирование Функций
[гл. xvi
Квадратурная формула A) при этом принимает вид
Ь п
(8)
где
(/-0, 1, ..,, п).
Нетрудно убедиться, что справедливы соотношения:
( = 0
2) Я,. = Я„_,..
§ 3. Формула трапеций и ее остаточный член
Применяя формулу G) предыдущего параграфа, при я = 1 имеем:
н Г
отсюда
Рис. 69,
Мы получили известную формулу трапеций для приближенного
вычисления определенного интеграла (рис. 69).
Остаточный член (ошибка) квадратурной формулы A) равен
Предполагая, что у ?Сг)[а, Ь]у выведем простую формулу для
остаточного члена. Будем рассматривать R — R(h) как функцию шага h;
тогда можно положить:
xo+h
Дифференцируя эту формулу по h последовательно двараза, получим:
-У (*•)] -у/

§ 4] ФОРМУЛА СИМПСОНА И ЕЕ ОСТАТОЧНЫЙ ЧЛЕН 583
it
и
Я"(А) =4/(* + *) У' (* + *) if (* + *) = У(
причем
Отсюда, интегрируя по А и используя теорему о среднем,
последовательно выводим:
h h
R' (h)=R' @) + j R" (t) dt=-±§ if (дг0 +1) dt =
0
где Ехб^о» + )
R (A) = Я @) + j ^ (/) dt = -1
о
где 5€(аг0, xo + h).
Таким образом, окончательно имеем:
Й=1|/К), ' B)
где I ? (дг0, дг^.
Отсюда, в частности, следует, что если ву">0, то формула A)
дает значение интеграла с избытком, если же у" <0 — то с д
статком.
§ 4. Формула Симпсона и ее остаточный член
Из формулы G) § 2 при я = 2 получаем:
о
2
о
2
19»*

584 приближенное интегрирование функций [гл. xvi
Следовательно, так как х2—лсо = 2А, имеем:
>'Лр = 40'в + *У1+Л). О)
Формула A) носит название формулы Симпсона. Геометрически
эта формула получается в результате замены данной кривой jj =/(#)
параболой у = Z2 (jut), прохр-
дящей через три точки
^о(*о> УоЬ Mt(xv yt) и
Мг (аг2, Л) (рис. 70).
Остаточный член формулы
St
Симпсона равен
R = ^ydx-
h
^_ Предполагая, что^у ? СD> [a, ft],
^ аналогично тому как это
делалось для формулы трапеций,
Рис* 70* выведем более простое
выражение для /?. Фиксируя
среднюю точку хг и рассматривая i? = /?(A) как функцию шага А(А^О),
будем иметь:
Отсюда, дифференцируя функцию R(h) по А последовательно три
раза, ^получим:
R' (А) = [у (Xl + Щ +у (xt- А)]-1 [у (Xl-h)+4y {xt) +y (atx+A)]-
= 4 [y (*x - A) +y (xt + k)] -
Л- (A) = | [ -/ (*x - A)
Xl + A)] -
+ A)] -~ \y"
1у*

§ 4] ФОРМУЛА СИМПСОНА И ЕЕ ОСТАТОЧНЫЙ ЧЛЕН 585
h nf f ф 2Л2
где 18€(^1 —А»
Кроме того, имеем:
Последовательно интегрируя R'" (А), используя теорему о среднем,
находим:
где Е» €(-*?1 —*»
А
-4^IV ffii) J *з d* = -T8
где
0
где I^(x1 — hy xt + h).
Таким образом, остаточный член формулы Симпсона равен
Я=—?j>ivF), B)
где Е € ( )
о
Следовательно, эта формула является точной для полиномов не
только второй, но и третьей степени, т. е. формула Симпсона при
относительно малом числе ординат обладает повышенной точностью.

586 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
§ 5. Формулы Ньютона — Котеса высших порядков
Производя соответствующие вычисления при/г = 3, получим из
формулы G) § 2 квадратурную формулу Ньютона
ЗА,
(правило трех восьмых).
Остаточный член формулы A) равен [2]
п __ ЗА5 IV,?.
К— 80 У (*>>
A)
где ?€(#<>' •**)»* т- е» ПРИ одинаковом шаге формула Ньютона,
вообще говоря, менее точна, чем формула Симпсона.
Дальнейшие квадратурные формулы Ньютона —Котеса
приведены в [1], [2]. Остаточные члены этих формул даны Стеффенсеном
(см. [1], [5J, [6]).
Заметим, что ошибка формулы Ньютона —Котеса сл+1
ординатами при достаточной гладкости функции y=f(x) по меньшей
мере имеет порядок [1], [6]
где е( yj—целая часть дроби ^ .
Отсюда видно, что в смысле порядка точности квадратурные
формулы с нечетным числом ординат являются более выигрышными.
Коэффициенты Котеса
Таблица 65
п
1
2
.3
4
5
6
7
8
ft.
1
1
1
7
19
41
751
989
ft,
1
4
3
32
75
216
3577
5888
ft2
1
3
12
50
27
1323
—928
ft,
1
32
50
272
2989
10496
ft.
7
75
27
2989
—4540
ft.
19
216
1323
10496
ft.
41
3577
—928
ft,
751
5888
ft.
989
Общий

знаменатель Af
2
6
8
90
288
840
17280
28350
Приводим для справок таблицу коэффициентов Котеса
(таблица 65). Для удобства записи коэффициенты Котеса для каждого п
представлены в виде дробей
I
N

§ 5] ФОРМУЛЫ НЬЮТОНА — КОТЕСА ВЫСШИХ ПОРЯДКОВ 587
с общим знаменателем N. Для контроля заметим, что
2 Ht = N.
Следует обратить внимание на то, что коэффициенты Котеса при
больших п могут быть отрицательными (см., например, п = 8).
Пример. Вычислить
применяя формулу Ньютона—Котеса с семью ординатами (п = 6).
Решение. Полагая шаг
п~ 6 ~~ 6 >
составляем приведенную ниже таблицу значений (таблица 66), где
для удобства принято /^ = 840//^
Таблица 66
( Вычисление интеграла по формуле
Ньютона— Котеса
i
0
1
2
3
4
5
6
*i
0
1
6
1
3
1
2
2
3
5

1
У1
1
6
7
3
4
2
3
3
5
6
11
1
2
Hi
41
216
27
272
27
216
41
hyt
41
185,142857
20,25
181,333333
16,2
117,818182
20,25
581,994372
Отсюда
^ 856 * 58 * >994372 = 0.6933.

588 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Точное значение
/= In 2 = 0,69315 ...
Так как коэффициенты Котеса при большом числе ординат весьма
сложны, то практически для приближенного вычисления определенных
интегралов поступают следующим образом: разбивают промежуток
интегрирования на достаточно большое число мелких промежутков и к
каждому из них применяют квадратурную формулу Ньютона — Котеса
с мальГм числом ординат (см., например, [7]). Получаются формулы
более простой структуры, точность которых может быть произвольно
высокой.
В следующих параграфах мы рассмотрим примеры таких формул.
§ в. Общая формула трапеций (правило трапеций)
Для вычисления интеграла
ь
\ydx
а
разделим промежуток интегрирования [а, Ь] на п равных частей
[лг0, лгх], [xlf х2], ..., [xn_v xn] и к каждому из них применим
формулу трапеций (см. § 3 A)). Полагая Л = -^ и обозначая через
yi^=f(xi) (/ = 0, 1, ..., п) значения подынтегральной функции в
точках л;,-, будем иметь:
ь
§у dx = -J (у0 +yt) + 4 {ух +у%) + ... + 4 (уп.г +уп)
а
ИЛИ
Геометрически формула A) получается в результате замены
графика подынтегральной функции у=?/(х) ломаной линией (рис. 71).
Если у б СB) [а, *], то остаточный член квадратурной формулы A)
в силу B) из § 3 равен
ydx—\iyt.x+yt)
где

§ 7} ОБЩАЯ ФОРМУЛА СИМПСОНА (ПАРАБОЛИЧЕСКАЯ ФОРМУЛА) 589
Рассмотрим среднее арифметическое
). C)
Очевидно, |х заключается между наименьшим т2 и наибольшим
Мг значениями второй производной у" на отрезке [а, Ь], т. е.
Так как у" непрерывна на отрезке [а, Ь], то в качестве своих
П
значений на [а, Ъ\ она принимает все промежуточные числа между т2
и Мг, Следовательно, найдется точка \ ?[а, Ь] такая, что
!*=/"(&).
Из формул B) и C) имеем:
где |? [а, *].
§ 7. Общая формула Симпсона (параболическая формула)
Пусть п — 2т есть четное число и yi—f[xi) (/ = 0,1,2, ...,я) —
значения функции^ =f(x) для равноотстоящих точек a = jt0, xv ...
.. #J xn = b с шагом
&—а 6—а
Л = = ~2— .
Применяя формулу Симпсона (§ 4, A)) к каждому удвоенному
промежутку 00, *2], |>2, *4], .,., [д:2,л.2, ^2J длины 2h (рис. 72),

590
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XVI
будем иметь:
ь
Отсюда получаем общую формулу Симпсона
Введя обозначения
формулу A) можно записать в более простом виде:
ь
Jу их = -g- [CV0 +^Л) + 4а2 + 2а2].
а
(П
Если j> g СD) [а, й], то ошибка формулы Симпсона на каждом
удвоенном промежутке [#2&-2> X2k\ (^= Ь 2, ...,/») на основании § 4,
B) дается формулой
где Ел€(^2*-2> *а*)- Сумми-
руя все эти ошибки,
получим остаточный член общей
формулы Симпсона в виде
iv
1
Рис. 72.
Так как ^1V (x) непрерывна на отрезке [а, Ь], то найдется точка
I ? [а, 6] такая, что
i
Поэтому будем иметь:
/пЛ5 1V «.,
6—а)
Г8б
]V
^
где

§ 7] ОБЩАЯ ФОРМУЛА. СИМПСОНА (ПАРАБОЛИЧЕСКАЯ ФОРМУЛА) 591
Если задана предельная допустимая погрешность г > О, то,
обозначив
будем иметь для определения шага h неравенство
(*-я)щ^4<е;
отсюда
У (Ь-а)
т. е. h имеет порядок ?/е.
Во многих случаях оценка погрешности квадратурной формулы
Симпсона A) по формуле B) весьма затруднительна. Тогда обычно
применяют двойной пересчет с шагами h и 2й и считают, что
совпадающие десятичные знаки принадлежат точному значению интеграла.
Можно указать еще один практически удобный способ подсчета
ошибки квадратурной формулы Симпсона. Предполагая, что на
отрезке [а, Ь] производная у™ (х) меняется медленно, в силу
формулы B) получаем приближенное выражение для искомой ошибки
где коэффициент М будем считать постоянным. Пусть 2Л и 2Я —
приближенные значения интеграла
полученные по формуле Симпсона соответственно с шагом h и
шагом Я=2А. Имеем:
Отсюда
15 *
За приближенное значение интеграла / целесообразно принять
исправленное значение
Заметим, что если число делений п кратно 4, то для вычисления
суммы 2Я можно воспользоваться имеющимися табличными
значениями, делая выборку значений через одно.

592 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Пример. С помощью формулы Симпсона вычислить интеграл
1
/Г* dx
о
приняв л= 10.
Решение. Имеем 2т =10. Отсюда
Результаты вычислений приведены в таблице 67.
V4
Таблица 67
Вычисление интеграла по формуле Симпсона
i
0
1
2
3
4
5
6
7
8
9
10
2
Xi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0,90909
0,76923
0,66667
0,58824 r
0,52632
|3,45955| (a,)
|^o=l,00000|
0,83333
0,71429
0,62500
0,55556
|0,50000=~ t/n|
[2,728181 (a2)
По формуле (Г) получаем:
А» 4 (У*+Уя + 4ох + 2о%) = 0,69315.
C)
Подсчитаем погрешность результата C). Полная погрешность /?
складывается из погрешности действий Rx и остаточного члена /?2.
Очевидно,
2
/= о
где А- — коэффициенты формулы Симпсона и 8 — максимальная
ошибка округления значений подынтегральной функции.
В нашем случае
Rx = пЫ = {Ь-* а) е = 1 ¦ -• Ю-5 = 0,5.10^5.

§ 8] ПОНЯТИЕ О КВАДРАТУРНОЙ ФОРМУЛЕ ЧЕБЫШЕВА 593
Остаточный член оценим по формуле B). Так как
ТО
/V = (-l)(-2)(-3)(-4)(l+*)-*= 24j.
v* » */
Отсюда
max |/v | = 24 при 0<лг<1
и, следовательно,
Таким образом, предельная полная погрешность есть
/? = 0,5.10-5+l,3-10-5 = l,8.1<r5< 0,00002
и, значит,
/=0,69315 ±0,00002.
§ 8* Понятие о квадратурной формуле Чебышева
Рассмотрим квадратурную формулу
где В} — постоянные коэффициенты.
Чебышев предложил выбрать абсциссы tt таким образом, чтобы:
1) коэффициенты В{ были равны между собой;
2) квадратурная формула A) являлась точной для всех
полиномов до степени п включительно.
Покажем, как могут быть найдены в этом случае величины Bt
и t(. Полагая
и учитывая, что при /(tf) = l будем иметь
2 = 2 В"
1=1
отсюда получаем:
4
Следовательно, квадратурная формула Чебышева имеет вид
4

594
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XVI
Для определения абсцисс tt заметим, что формула B), согласно
условию 2), должна быть точной для функций вида
Подставляя эти функции в формулу B), получим систему
уравнений
C)
2(п+1) '
„из которой могут быть определены неизвестные fj (/ = 1, 2, ¦.., /г).
Чебышев показал, что решение системы C) сводится к нахождению
корней некоторого алгебраического уравнения степени п [6], [8].
В таблице 68 приведены значения корней t( системы C) для п = 2,
3, ..., 7.
Таблица 68
Значения абсцисс tt в формуле Чебышева
п
2
3
4
5
i
i;2
i; з
2
1* 4
2;3
2; 4
3
и | «
ТО, 577350
ТО,707107
0
ТО ,794654
ТО, 187592
ТО, 832498
ТО, 374541
0
6
7
i
1;б
2; 5
3; 4
1; 7
2; 6
3; 5
4
/«
ТО, 866247
ТО, 422519
ТО, 266635
Т0,883862
Т0,529657
ТО,323912
0
Заметим, что система C), как показал С. Н. Бернштейн, при
л = 8 и п 2^10 не имеет действительных решений. В этом состоит
принципиальный недостаток квадратурной формулы Чебышева.
Пример 1. Вывести формулу Чебышева с тремя ординатами
3)
( )
Решение. Для определения
систему уравнений
абсцисс ^(/=1, 2, 3) имеем
D)

§ 8J ПОНЯТИЕ О КВАДРАТУРНОЙ ФОРМУЛЕ ЧЕБЫШЕВА 595
Рассмотрим симметрические функции корней
Из системы D) имеем:
Отсюда заключаем, что tt есть корни вспомогательного уравнения
или
Следовательно, можно принять:
Таким образом, соответствующая формула Чебышева имеет вид ч
Чтобы применить квадратурную формулу Чебышева к интегралу
вида
следует преобразовать его с помощью подстановки
х— 2 i 2"Г,
переводящей отрезок а^х^Ь в отрезок —1^?^1. Применяя
к преобразованному интегралу формулу Чебышева B), будем иметь:
*2 E)
п
а 1-1

596
где
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
Ъ-\-а } b—с
<- 2 "• 2~
[ГЛ. XVI
F)
и /,-(/ = 1, 2, ..., п) — корни системы C) (помещены в
таблице 68).
Квадратурная формула Чебышева употребляется главным образом
в кораблестроении.
Пример 2. Вычислить интеграл
по формуле Чебышева с пятью ординатами (п = 5),
Решение. Введем обозначение
Таблица 69
Вычисление интеграла
по формуле Чебышева
*
1
2
3
4
5
S
0,08375
0,31273
0,50000
0,68727
0,91625
. их
0,0773
0,2382
0,3333
0,4073
0,4781
1,5342
имеем:
Г 1 г
где в силу формулы F)
= ^ -J-.1..(_ 0,83250) = 0,08375;
:4=1—л;2 = 0,68727;
^==1—^ = 0,91625.
Соответствующие значения у. = /(х() (/= 1, 2, 3, 4, 5)
подынтегральной функции помещены в таблице 69.
Отсюда
/ = -^.1,5342 = 0,3068.
Для сравнения приводим точное значение интеграла с шестью
значащими цифрами
/=0,306846...

§ 9]
КВАДРАТУРНАЯ ФОРМУЛА ГАУССА
§ 9. Квадратурная формула Гаусса
597
В этом параграфе нам потребуются некоторые сведения о
полиномах Лежандра. Полиномы вида
называются полиномами Лежандра.
Отметим важнейшие свойства полиномов Лежандра [1]:
я
2) ^ Рп (x)-Qk (х) dx = 0 (k< л), где Qk (х) — любой полином
-1
степени ky меньшей п;
3) полином Лежандра Рп (х) имеет п различных и действительных
корней, которые расположены на интервале (—1, 1).
Ниже приводим первые пять полиномов Лежандра и их графики
(рис. 73):
Рг (х) = 1C^-
= ^ C5л:4 - ЗО*2 + 3).

598 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Перейдем сейчас к выводу квадратурной формулы Гаусса.
Рассмотрим сначала функцию y=f @, заданную на стандартном
промежутке [ — 1; 1]. Общий случай легко свести к нашему путем
линейной замены независимой переменной.
Поставим задачу: как нужно подобрать точки tv t2y ..., tn
и коэффициенты Av Л2, ..., Ап, чтобы квадратурная формула
1=1
была точной для всех полиномов f(t) наивысшей возможной
степени ЛЛ
Так как в нашем распоряжении имеется 2л постоянных tt и А{
(/=1, 2, ..., л), а полином степени 2л —1 определяется 2л
коэффициентами, то эта наивысшая степень в общем случае, очевидно,
равна М=2л — 1.
Для обеспечения равенства A) необходимо и достаточно, чтобы
оно было верным при
Действительно, полагая
будем иметь:
1
2 ck I tk<"= 2
C*ssl 6 = 0 < = 1
Таким образом, учитывая соотношения:
( 2
j
при *
= !z±e fe+T
"*" [ 0 при h нечетном,
заключаем, что для решения поставленной задачи [2], [3], [6]

§ 9J КВАДРАТУРНАЯ ФОРМУЛА ГАУССА
достаточно определить /, и At из системы 2л уравнений
п
f=i
л
599
C)
Система C) —нелинейная, и решение ее обычным путем
представляет большие математические трудности. Однако здесь можно
применить следующий искусственный прием.
Рассмотрим полиномы
f(t) = tkPn(t) (& = 0, 1, ..., л—1),
где Pn(t) — полином Лежандра.
Так как степени этих полиномов не превышают 2л—1, то на
основании системы C) для них должна быть справедлива формула A) и
i=i
С другой стороны, в силу свойства ортогональности полиномов
Лежандра (свойство 2)) выполнены равенства
X
J tkPa(t)dt = O при k<n,
-1
поэтому
E)
Равенства E) заведомо будут обеспечены при любых значениях Ai9
если положить
/>„('<) = 0 . (i=l, 2 л), F)
т. е. для достижения наивысшей точности квадратурной формулы A)
в качестве точек ti достаточно взять нули соответствующего
полинома Лежандра. Как известно (свойство 3)), эти нули действительны,
различны и расположены на интервале (—1, 1). Зная абсциссы ti%

600 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
легко можно найти из линейной системы первых п уравнений
системы C) коэффициенты А{ (/ = 1, 2, ..., п). Определитель этой
подсистемы есть определитель Вандермонда
П
и, следовательно, At определяются однозначно.
Формула A), где /, — нули полинома Лежандра Pn(t) и А({1 =
= 1, 2, ...,я) определяются из системы C), называется
квадратурной формулой Гаусса.
Пример 1. Вывести квадратурную формулу Гаусса для случая
трех ординат (л = 3).
Решение. Полином Лежандра третьей степени есть
Приравнивая этот полином нулю, находим корни
tx = — "j/y « —0,774597;
2 0;
/3 = у у» 0,774597,
Для определения коэффициентов Av A2, А3 в силу C) имеем
систему:
отсюда
л-А-1 л-1
/лг — лз — 9 * 2 ~™ 9 '
Следовательно,
Для справок приводим (таблица 70) приближенные значения
абсцисс tt и коэффициентов А( в квадратурной формуле Гаусса A)
для л=1—8 (см. [1], [4], [6]).
Неудобство применения квадратурной формулы Гаусса состоит
в том, что абсциссы точек t( и коэффициенты Ai — вообще говоря,
иррациональные числа. Этот недостаток отчасти искупается ее
высокой точностью при сравнительно малом числе ординат.

§ 9] КВАДРАТУРНАЯ ФОРМУЛА ГАУССА 601
Рассмотрим теперь использование квадратурной формулы Гаусса
для вычисления общего интеграла
ь
[f(x)dx.
в
Делая замену переменной
получим:
Применяя к последнему интегралу квадратурную формулу Гаусса A)
будем иметь:
ь
a iszl
где
#/ = —9—I—о"-'/ (/==1, 2, ..., л), (8)
^ — нули полинома Лежандра Яи@» т- е.
Остаточный член формулы Гаусса G) с л узлами выражается
следующим образом [1], [6]:
""- [Bп)!Р B/г + 1)
отсюда получаем:
'15750
: 3472875 \~2
1237732650 V~2
}
648984486150 V 2
3/.A2) /?\ « т п

602 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
Пример 2. Вычислить интеграл
[гл. xvi
применяя формулу Гаусса с тремя ординатами (л = 3).
Таблица 70
Элементы формулы Гаусса
п
1
2
3
4
5
6
7
8
1
1; 2
1;3
2
1; 4
2;3"
1; 5
2; 4
3
1;б
2; 5
3;4
1;7
2; 6
3;5
4
1;8
2; 7
3;6
4; 5
0
=F 0,57735027
Т 0,77459667
' 0
Т 0,86113631
Т 0,33998104
? 0,90617985
Т 0,53846931
0
=F 0,93246951
q= 0,66120939
Т 0,23861919
Т 0,94910791
q= 0,74153119
=F 0,40584515
0
Т 0,96028986
Т 0,79666648
Т 0,52553242
=F 0,18343464
Al
2
1
4 = 0,55555556
— = 0,88888889
0,34785484
0,65214516
0,23692688
0,47862868
0,56888889
0,17132450
0,36076158
0,46791394
0,12948496
0,27970540
X), 38183006
0,41795918
0,10122854
0,22238104
0,31370664
0,36268378
Решение. Имеем а = 0 и >=1. В силу формулы (8) и
таблицы 70 абсциссы точек с точностью до пяти значащих цифр будут

§ 9]
КВАДРАТУРНАЯ ФОРМУЛА ГАУССА
603
иметь следующие значения:
^з^у + у^з^ 0,88730.
Соответствующие коэффициенты формулы G) в нашем случае будут:
Г -~Ь~~аЛ
W— 2 l
2
—а
2 9 ~ 18"
: 0,27778;
С3
-j'J-=4=0l44444;
4-§— тв = 0,27778.
Дальнейшие вычисления сведены в таблицу 71.
Таблица 71
Схема вычисления интеграла по формуле Гаусса
i
1
2
3
0,11270
0,50000
0,88730
У1
1,10698
1,41421
1,66571
Ci
0,27778
0,44444
0,27778
0,30747
0,62853
0,46270
1,39870
Следовательно,
= 1,39870.
Для оценки остаточной погрешности R3 можно воспользоваться
формулой
Полагая
1
/(х) = у 1 + 2х = A + 2л;) *,
имеем:
11
= — 945A

604 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Отсюда
max |/1в>(л:) | = 945 при
и следовательно,
I Кз I ^ 15750 V 2 ) ~ 2000 *
Заметим, что точное значение интеграла есть
/ = /3—i« 1,39872.
§ 10. Некоторые замечания о точности квадратурных формул
Рассмотренные нами квадратурные формулы имеют следующую
структуру:
где #lf лг2, ..., л:,, —данная система узлов из отрезка
интегрирования [a, ft], ^ — некоторые известные постоянные коэффициенты
и R[f] — остаточный член.
При одном и том же числе ординат точность различных
квадратурных формул различна.
Пример. Сравнить точность различных квадратурных формул
с тремя ординатами для интегралов
/= J/2H^d* = 2/3-_| = 2,797435...
-1
Решение. Применяя формулу Симпсона, получим:
[ ^ ^[/2^ + 4/2+ 0 + /2+1] = ~ 8,428905 = 2,809635.
Формула Чебышева дает такой результат:
= 1-4,220097 = 2,813398.
Наконец, формула Гаусса приводит к следующему значению:
/« 0,555566 (/2—0,774597 + /2 + 0,774597) +
+ 0,888889 /2+ == 2,797460.
Таким образом, здесь формула Гаусса оказывается наиболее
точной.

§ 10J НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТОЧНОСТИ КВАДРАТУРНЫХ ФОРМУЛ 605
Мы ограничимся исследованием квадратурных формул е
равноотстоящими узлами; к числу их относятся наиболее
распространенные формулы: трапеций, Симпсона, Ньютона — Котеса. В этом
случае точность квадратурной формулы в основном характеризуется
порядком остаточного члена
R = O(hm), B)
где
и__Ь—а
— шаг (п — число делений) и m — натуральное
число. Например, для формулы трапеций имеем
(§ 3):
R{/]= -^ А2/* (?),
поэтому /я = 2; для формулы Симпсона (§ 4)
отсюда /я = 4. Квадратурная формула считается
тем точнее, чем больше число т; в этом смысле
формула Симпсона является более точной,
нежели формула трапеций. Качество формулы
обнаруживается при достаточно малом шаге /г.
Отсюда вовсе не следует, что в конкретных
случаях более грубая квадратурная формула при
одном и том же шаге не может дать лучших
результатов, чем более точная. Например, для
функции (рис. 74)
/¦(*) = — 8 + 45л:2 — 25л:4
имеем:
/=
При h = 1 формула трапеций дает точное значение
1 у/A) = 6-
Рис. 74.
тогда как формула Симпсона при А=1 не обеспечивает даже знака
интеграла:
/f/A) + 4/(°)+/A)]
Точность квадратурной формулы при фиксированном числе узлов
существенно зависит от расположения этих узлов. При неудачном
расположении узлов квадратурная формула может дать сильно

606
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XVI
искаженные результаты. Например, для функции у=/(х),
изображенной на рис. 75, выбирая равноотстоящие узлы а — х0У хг, х2,
Jt3, лг4 = 6 и пользуясь соответствующей формулой Котеса для пяти
ординат, получим: _
тогда как очевидно, что />0.
Не представляет большого труда построить аналогичные примеры
для любой квадратурной формулы с произвольным числом ординат.
Вообще, при наличии значительного числа нулей
подынтегральной функции f(x) или при большом числе экстремумов ее (т. е когда
имеется много нулей
производной /'(#)), благодаря
неизбежным большим значениям
старших производных точность
квадратурных формул сильно
понижается. Поэтому шаг h
у///л 'следует выбирать так, чтобы
%f|jfo он был намного меньше рас-
%^~~Фх4 ^ стояний между соседними
нулями функции f(x) и ее
производной /' (#). Для этого
рекомендуется основной
отрезок интегрирования [а, Ь]
разбить на частичные отрезки
[а, р], внутри каждого из
которых функции f(x) и f'(x)
сохраняют постоянный знак (если это возможно), и производить
вычисление интеграла частями, выбирая для каждого частичного
отрезка, вообще говоря, свой шаг. В более сложных случаях нужно
учитывать также поведение производных высших порядков /(Л> (х)
(п ^2). Для общей ориентировки полезно предварительно построить
график подынтегральной функции y=f{x). Если функция сильно
колеблющаяся, то следует применять специальные приемы
вычислений. Разработаны также общие приемы увеличения точности
квадратурных формул [9].
При нахождении полной предельной погрешности квадратурной
формулы A) следует учесть также погрешность суммирования Rx.
Пусть слагаемые f{Xj) (/=1, 2, ...,л) вычислены с абсолютной
погрешностью, не превышающей е, а коэффициенты А{
квадратурной формулы являются точными положительными постоянными.
Тогда можно положить:
Рис. 75.
C)

§ 111
ЭКСТРАПОЛЯЦИЯ ПО РИЧАРДСОНУ
607
Так как квадратурная формула A) верна для /(лг) =
*
, то
= b-a=
/=1
Поэтому из формулы C) имеем:
Следовательно, полная предельная погрешность квадратурной
формулы без учета заключительной погрешности округления равна
где |/?[/]| — погрешность метода, которая может быть определена
указанным выше способом.
Заметим, что если подынтегральная функция y=f(x) задана
таблично значениями y.=f(Xi) (/== 1, 2, ..., я), то, строго говоря,
мы лишены возможности оценить точность квадратурной формулы
A). Дело в том, что через конечную систему точек М^х^у^
можно провести бесчисленное множество кривых у~/(х) (рис. 76),
ограничивающих на данном
отрезке [а, Ь] различные
площади, т. е. интеграл
априори может иметь
совершенно произвольное значение
(см. рис. 76). Пользование
в этом случае квадратурными
формулами допустимо лишь
тогда, если нам в какой-то
мере известны
неиспользованные промежуточные значения подынтегральной функции и ее общие
свойства, позволяющие судить о характере графика функции.
§ 11*. Экстраполяция по Ричардсону
Если для квадратурной формулы A) § 10 известен порядок
остаточного члена R = R[f]> то для определения величины R можно
использовать метод двойного пересчета. Пусть

608 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
где
п
(п — число делений); тогда приближенно можно положить:
^ A)
где М—некоторая величина, которую для данной подынтегральной
функции f(x) будем считать постоянной на промежутке
интегрирования [я, Ь]. Выберем два различных шага
Лх и А2 ,
где пх и п2 (п2 > пг) — количество частичных отрезков в первом
и во втором случаях.
Обозначим через 1п% и 1п% соответствующие приближенные
значения интеграла /. Из формулы A) имеем:
y B)
, B')
где Rnt и /^ — соответствующие остаточные члены. Отсюда
и, следовательно,
На основании формулы A) получаем выражение для остаточного
члена
V n J пп-п" '
в частности при А = А2, т. е. при п = п2, имеем:
Пользуясь поправкой C), в силу формулы B'), для интеграла /
получаем уточненное значение:

§ 11] ЭКСТРАПОЛЯЦИЯ ПО РИЧАРДСОНУ 609
Таблица 72а
Экстраполирование для случая формулы трапеций
п/п
1
2
3
4
п/п
1
2
3
4
л
I = \ sin * dx
0
2
0
7
/ = \ *а in x dx
1 f dx
0
0,429
0,0051
—8,2254
—0,0428
1,571
0,877
185,7090
0,9695
U
1,896
0,881
179,5385
0,9389
0,104
0,0011
—2,0549
—0,0122
2,004
0,8823
177,4819
0,9286
<
2,000
0,8821
177,4836
0,9267
—0,004
—0,0002
0,0017
—0,0019
Этот прием называется экстраполяцией по Ричардсону [10], Введя
обозначение
будем иметь:
где
hu nz = Ins + Р (/я, —
E)
F)
Коэффициенты р табулированы для различных значений а и а».
Заметим, что для формулы трапеций т = 2, а для формулы Симп-
сона т = 4. Частный случай формулы E) был приведен в § 7.
Покажем, что если 1Пх ф. /rt2, то 1Пх п% всегда лежит вне отрезка
Действительно, если
*пг ^> *пх*

610 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Таблица 726
Экстраполирование для случая формулы Симпсона
Mb
п/п
1
2
3
4
п/п
1
2
3
4
п
/ — \ sinxdx
0
0
7
3
Г л
JB5-*»)a/t
0
t-/-/t
—0,094
0,0021
0,0296
—0,0044
2,094
0,7833
177,454
0,0577
/4
2,004
0,7853
177,481
0,0541
-0,
0,
о,
—0,
004
0001
0026
0008
'м
2,010
0,7855
177,483
0,0538
. 1
2,000
0,7854
177,4836
0,0533
-0,010
—0,0001
0,0006
—0,0005
то из формулы E) имеем:
Если же
то из той же формулы E) получаем:
Таким образом,
т. е. /„„„2 получается из 1Пх и /Ла в результате операции
экстраполирования. Этим и объясняется название способа.
Если /Л1 = /|2г, то, очевидно,

§ 12] ЧИСЛА БЕРНУЛЛИ 611
Можно показать, что при достаточной гладкости
подынтегральной функции f(x) порядок остаточного члена для 1Пи Пг равен по
меньшей мере т+\.
Замечание. В таблицах 72а и 726 приведены примеры на
экстраполирование по Ричардсону.
Из таблицы 72а и 726 видно, что для функций, не имеющих
особенностей, экстраполирование, как правило, повышает точность
вычислений.
Можно также вывести более точные формулы экстраполирования,
использующие значения 1по 1п% и 1п% искомого интеграла,
соответствующие трем различным шагам
K=b~=f- (* = 1. 2, 3)
и учитывающие два первых члена разложения остаточного члена
квадратурной формулы [10].
§ 12*. Числа Беряулли
Рассмотрим функцию
Воспользовавшись известным разложением
можно записать:
х *» *«xV* ()
1М 21^3!^"Ф ^21^3!^'"
Отсюда ясно, что функция f(x) в окрестности д: = 0 допускает
разложение в степенной ряд, который для удобства дальнейших
выкладок представим в следующем виде:
где Б0=/@)==1. Для определения остальных коэффициентов
разложения Ви(л=1, 2, ...), носящих название чисел Бернулли,
используем получаемое на основании формулы B) тождество

612 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Производя перемножение степенных рядов и приравнивая нулю
коэффициенты при положительных степенях переменной лг, будем
иметь бесконечную систему линейных уравнений
Яо 1 П /и 19 3
или, умножая на (я+1)! и учитывая, что
(п+\)\ г к 1Ъ 1
получим:
l + 1=0. D)
Если условно положить
Bk = B\ E)
то формулу D) кратко можно записать в следующем
символическом виде:
или, заменяя п+\ на л,
—В* = 0. F)
Полагая л = 2, 3, 4, ... в формуле F), получим бесконечную
систему уравнений
5В4 + 1(Ш8 + 10В2 + 5БХ + 1 = О,
G)
Отсюда последовательно находим:
#1 = — у; B2 = -jr-; #з = 0; В4 = — §0^ Вь = 0;
#п = 0; #12 = — 2730; ^is^0» ^ = "» ^б^0»
о 3617 д _n> R _43867. о _п. о __ 174611
^1в==~Ю"; ^17~и> ^18 — 98"' ^19~и» ^20— 330"
и т. д.
Таким образом, числа Бернулли могут быть шаг за шагом
определены из символической формулы F), причем после развертывания
бинома по правилу Ньютона степени чисел В должны быть заменены
числами Бернулли с соответствующими индексами.

§ 13] ФОРМУЛА ЭЙЛЕРА — МАКЛОРЕНА 613
Функция A) называется производящей функцией чисел Бернулли.
Воспользовавшись обозначением E), разложение C) символически
можно записать следующим образом:
е*-1~* '
Из структуры системы G) очевидно, что все числа Бернулли
рациональны. Кроме того, обнаружилось, что числа Бернулли с
нечетными индексами, кроме Bv равны нулю. Докажем это свойство
в общем виде. Учитывая, что
1
имеем:
Очевидно,
JL х
2 +е 2
есть функция четная. Поэтому ее разложение (8) содержит лишь
четные степени переменной х и, следовательно,
Вп = 0 при п = 3, 5, 7, ...
Числа Бернулли находят применения во многих вопросах. В
частности, они используются в важной формуле Эйлера—Маклорена,
к выводу которой мы переходим.
§ 13*. Формула Эйлера — Маклорена
Пусть ^=/(лг) —некоторая функция, определенная в области
х^х0. Рассмотрим оператор конечной разности
Д/(*) =¦/(* + *>-/(*).
где h — фиксированная положительная величина. Под обратным
оператором -г- от функции f(x) естественно понимается функция
^(лг), удовлетворяющая конечно-разностному уравнению
AF(x)=f(x). A)
Таким образом, из уравнения A) имеем:

614 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Если функция f(x) рассматривается на множестве
равноотстоящих точек
где Ax( = xi+1—xt = h (/ = 0, 1, 2, ...), то обратный оператор
F(xt) =-д-/(#/) легко построить. Действительно, составим
конечную сумму
?(¦*<)= 2 Я*/) (/-1,2,...),
причем будем условно считать, что S(xo) = 0. Очевидно, получаем:
AS (xt) = 5 (лг/+1)-5 (*,) =/(*,.). C)
С другой стороны, согласно уравнению A) имеем:
AF (*,.)=/(•*/)• D)
Вычитая из равенства D) равенство C), находим:
д [F(x.) -?(*,.)] = 0
при / = 0, 1, 2, ... Следовательно, разность Г(Х;)— S(Xi) не
зависит от индекса i и мы можем положить:
отсюда
где F(x0) — произвольная постоянная величина. Итак,
х/(^/) = /7^о) + 5(лг/), E)
т. е. обратный оператор для конечной разности есть оператор
конечного суммирования.
Введем теперь оператор дифференцирования
Под обратным оператором -^- понимается операция
интегрирования
Используя ряд Тейлора, находим:

§ 13] ФОРМУЛА ЭЙЛЕРА — МАКЛОРЕНА 615
Следовательно,
Д = (ел*> — 1).
Отсюда для обратного оператора -^- получаем следующее выражение:
1 1
Умножая обе части последнего равенства на AD, имеем:
«>4 hD
В правой части получалась производящая функция для чисел Бер-
нулли. Поэтому
или более подробно
Интегрируя равенство F) в пределах от х = х0 до х=хп и
используя формулу E), будем иметь:
«ЛИ
л -1 /1—1
/
/=о /=о
- т у wdx +
Учитывая, что

= — 4- и B2k+1 = Q при ^=1, 2, ..м

616 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
получаем формулу Эйлера—Маклорена
т
- Е <ШЛ2*[/B*-" К)-/12*"" (*,)] + /?,«, G)
где /?2/я— остаточный член. Запись формулы G) в виде
бесконечного ряда не всегда законна, так как ряд может расходиться.
Подставляя значения чисел Бернулли, будем иметь:
\ у20 (Уп У° ' 30240 ^п У° ' * * *
^i1^*»)-/'—"(*•)] +Л... (8)
Остаточный член формулы Эйлера — Маклорена имеет вид [6]
«2m- ПП B/П + 2)!
где l?(xQ, xn).
Формулу Эйлера —Маклорена (8) используют для приближенного
вычисления определенных интегралов, а также для приближенного
суммирования значений функций при равноотстоящих значениях
аргумента. Действительно, из формулы (8) мы имеем:
i as 0
пг
Щ] [ B^т F).
(9)
Пример 1. Используя формулу Эйлера — Маклорена,
приближенно вычислить определенный интеграл
1
/= \ (sin* — \nx-\-ex)dx.
Решение. Разделим отрезок [0, 2; 1], например, на восемь
промежутков, беря h = 0,1 и полагая
х/==0,2 + /.0,1 A = 0, 1, ...,8).

13]
ФОРМУЛА ЭЙЛЕРА — МАКЛОРЕНА
617
Результаты вычислений соответствующих значений функции f(x) =
= sin дг — \пх + е* приведены в таблице 73.
Таблица 73
Значения функции f(x)*=sinx—\пх+е*
X
/W
X
fix)
0,2
3,02951
0,7
3,01435
0,3
2,84936
0,8
3,16605
0,4
2,79754
0,9
3,34830
0,5
2,32130
1,0
3,55975
0,6
2,89759
Отсюда
4-Я*о) +/(*»)+• • • +/(*,)+ у/(*8) = 24,1894.
Ограничиваясь производной пятого порядка, имеем:
= cos *-!
/"'(*) = — cos x-j9
Следовательно,
/'@,2) = — 2,7985; /'(!) = 2,2586;
f" @,2) = — 249,7587; /'" A) = 0,1780;
f @,2) = — 74 997,7985; /v A) = —20,7415.
Подставив найденные значения в формулу (8), получим:
/=24,1894-0,1 — —f^-* B,2586 + 2,7985) +
+1^.@,1780 + 249,7587) _№.(_ 20,7415+ 74 997,7985) =
= 2,41894 - 0,00421 + 0,00004 = 2,41477.
Непосредственное интегрирование дает:
/ = [ — cos х—лс (In л: — 1) + е*] |j,a л;
Пример 2. Найти сумму
1.1.1. ,1
20 Б. П. Демидович и И. А. Марон

618 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Решение. В нашем случае
: h 2' * 51; дг 99
Находим производные нечетного порядка от функции f(x):
/»<*>—?¦
Подставляя в формулу (9) и ограничиваясь производной седьмого
порядка, получим:
х* - 2 J x* + 2 V51» + 99V + 3 V51« 99»)
15 \ 51* 99» у ^ 21 V 51» 997 У 15 V519 99»
= 0,004 753 416 + 0,000 243 490 +
+ 0,000 002 169 — 0,000 000 001 = 0,004 999 074.
Согласно формуле (9), где нужно положить h = 2, п = 24, /» = 4,
ошибка полученного результата есть
р 94.. 910.^12. /^A°) /?\ <^ 94.. 910. А . J_ ^ У ^
§ 14. Приближенное вычисление несобственных интегралов
Интеграл
ь
$/(*)** A)
а
называется собственным, если
1) промежуток интегрирования [а, А] конечен;
2) подынтегральная функция f(x) непрерывна на [а, Ь].
* В противном случае интеграл A) называется несобственным.
Рассмотрим сначала приближенное вычисление несобственного
интеграла
\f(x)dx B)

§ 14] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ 619
с бесконечным промежутком интегрирования, где функция f(x)
непрерывна при а^дг<оо.
Интеграл B) называется сходящимся, если существует конечный
предел
lim \f(x)dx,
и по определению полагают:
ое Ь
[f(x)dx = lim [f{x)dx.
C)
(*)
Если предел C) не существует, то интеграл B) называется
расходящимся, и такой интеграл считается лишенным смысла. Поэтому,
прежде чем приступить к вычислению несобственного интеграла,
нужно предварительно убедиться, пользуясь известными признаками
сходимости [10], что этот интеграл сходится.
Чтобы вычислить сходящийся несобственный интеграл B) с
заданной точностью с, представим его в виде
E)
В силу сходимости интеграла число Ь можно выбрать столь
большим, чтобы имело место неравенство
\f(x)dx
2 #
F)
Собственный интеграл
lf{x)dx
можно вычислить по одной из квадратурных формул. Пусть 5—при-
G)
ближенное значение этого интеграла с точностью до 4-, т. е.
Mf{x)dx-S
Из формул E), F) и G) имеем:
^/(x)dx-S
а
т, е. поставленная задача будет решена.
20*

620 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ , [гЛ. XVI .
Предположим теперь, что промежуток интегрирования [а, ,Ь\
конечен и подынтегральная функция f(x) имеет конечное число точек
разрыва на [я, Ь]. Так как в наших предположениях промежуток
интегрирования можно разбить на частичные промежутки с единственной
точкой разрыва подынтегральной функции, то достаточно разобрать
лишь случай, когда на [а, Ь] имеется единственная точка разрыва с
функции /(#), причем второго рода*).
Если с есть внутренняя точка отрезка [а, Ь]> то по определению
полагают:
• Ь /c-6t Ь \
$/(*)***= lim J f(x)dx+ S fix)dx\f (8)
и в случае существования этого предела интеграл называют
сходящимся, в противном случае—расходящимся. *
Аналогично определяется сходимость несобственного
интеграла (8), если точка разрыва с подынтегральной функции f{x)
совпадает с одним из концов промежутка интегрирования [а, Ь].
Для приближенного вычисления с заданной точностью е
сходящегося несобственного интеграла (8), где точка разрыва eg (a,*),
выбирают положительные числа бх и б2 столь малыми, чтобы имело
место неравенство
+Ь2
\f{x)dx
л
Затем по известным квадратурным формулам приближенно вычисляют
собственные интегралы
с-64 Ь 4
J f(x)dx и S f(x)dx. (9)
¦ а с+Ь2
*) Если с—точка разрыва первого рода, т. е. существуют конечные
односторонние пределы
f(c — O)= lim l(x) и f(c + O)= lim f(x),
то можно положить:
ь с ь
где
/ f{x), если а<х<с\ f ffc+O), если х=с;
bW1 f(c-O), если х=с; И М*}~1 f(x), если С<х<6;
причем функции fг (х) и Jf2W являются непрерывными соответственно на
отрезках [а, с] и [с, Ь]. Таким образом, наш интеграл сводится к сумме двух
собственных интегралов.

§ 15] МЕТОД Л. В. КАНТОРОВИЧА ВЫДЕЛЕНИЯ ОСОБЕННОСТЕЙ 621
Очевидно, если St и 52 —приближенные значения интегралов (9)
с точностью до -|-, то
с точностью до 8. Если точка разрыва с подынтегральной функции/(лг)
является концевой для промежутка интегрирования [а, Ь], то методика
вычисления очевидным образом видоизменяется.
§ 15. Метод Л. В. Канторовича выделения особенностей
Часто для приближенного вычисления интеграла от разрывной
функции полезным оказывается метод Л. В. Канторовича выделения
особенностей [1], [6], [10]. Идея этого метода состоит в том, что
из подынтегральной функции/ (л:) выделяют некоторую функцию g(x),
имеющую те же особенности, что и функция/(л;), элементарно
интегрирующуюся на данном промежутке [я, Ь] и такую, чтобы разность
f(x)—g(x) была достаточно гладкой на отрезке [а, Ь]. Например,
где
Тогда будем иметь:
ь ь ь
а а а
где первый интеграл берется непосредственно, а второй без труда
вычисляется с помощью стандартных формул.
Мы рассмотрим применение этото метода для вычисления
интеграла вида
ь
A)
где xQ ? [я, А], 0 < а < 1 и ф (х) непрерывна на отрезке [я, Ь].
Пусть ф(я) €С<да+1)[а, #], т. е. ф(#) имеет на отрезке [а, Ь]
непрерывные производные до (/я+1)-го порядка включительно.
Используя формулу Тейлора, будем иметь:
X^ B)
А = 0
где
F 6 К *))•

622 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Отсюда для интеграла A) получим:
ь „ ь ь
~° а
т
где
Из формулы C) вытекает, что
(по меньшей мере!), следовательно, интеграл E) является собственным
и может быть вычислен с любой степенью точности по подходящей
квадратурной формуле.
Метод Канторовича применим также к несобственным интегралам,
подынтегральная функция которых имеет несколько точек разрыва
рассмотренного типа. В этом случае для вычисления интеграла
достаточно разбить промежуток интегрирования на части, содержащие
лишь одну особую точку подынтегральной функции, и
воспользоваться свойством аддитивности интеграла.
Пример 1. Приближенно вычислить несобственный интеграл [11]
7 "
Решение. Подынтегральная функция
JL 1
имеет на отрезке 0, -^ единственную особую точку х = 0.
Разложим в ряд Тейлора по степеням х функцию
с точностью до лс4. Применяя бином Ньютона, будем иметь:

§ 15] МЕТОД Л. В. КАНТОРОВИЧА ВЫДЕЛЕНИЯ ОСОБЕННОСТЕЙ
Отсюда
623
1
Т з
)
где
1
Т б
5 С Т
i
Т ±
2
715801
= 1,5691585 + 4
F)
Собственный интеграл G) вычисляем по формуле Симпсона,
Таблица 74
Вычисление интеграла
по формуле Симпсона
i
0
1
2
3
4
5
6
7
8
9
10
2
0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
У2/-1
0,000000
0,000056
0,000624
0,003225
0,011588
0,015493
Уг/
|0,000000|
0,000009
0,000216
0,001508
0,006316
|0,020239|
0,008049
приняв я = 10 и шаг Л = -^- = 0,05. Результаты вычислений с
точностью до шести знаков приведены в таблице 74.

624 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Отсюда
/^J-@,020239 + 4-0,015493+ 2-0,008049) =
в^. .0,098309 = 0,0016385.
Следовательно, в силу формулы F) имеем:
1,5691585 \
'=+0,0016385 }-1.6707970.
Заметим, что интеграл / находится эле ментарно и его точное
значение есть
/=у= 1,5707963...
Замечание, В некоторых случаях несобственный интеграл
может быть преобразован в собственный с помощью замены
переменной или интегрирования по частям.
Пример 2. Преобразовать в собственный интеграл
Решение. Полагая в интеграле (8) х =—, получим интеграл
с конечными пределами
1 1
dx
Г
J
(9)
но имеющий особенность при л: = 0.
Производя надлежащее интегрирование по частям, будем иметь:
причем оставшийся интеграл есть собственный, и применение к нему
квадратурных формул не встречает затруднений. Употребляются
также другие приемы преобразования несобственных интегралов [6].
§ 16. Графическое интегрирование
Задача графического интегрирования состоит в следующем: по
данному графику непрерывной функции^; =/(#) требуется построить
график ее первообразной функции

§ 16]'
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
625
Иными словами, нужно построить такую кривуюy = F(x), ордината
в каждой точке х которой численно равна площади криволинейной
трапеции с основанием [а, х], ограниченной данной кривой у=/(х).
Для приближенного построения графика первообразной функции
у = F (х) разбиваем площадь соответствующей криволинейной
трапеции, ограниченной кривой J> =/(#), на узкие вертикальные полоски
с помощью ординат, проведенных в точках лг0, х19... (а = лго<
...) (рис. 77). Каждую из таких полосок заменяем,
F(x)
Рис. 77.
используя теорему о среднем,, равновеликим (по возможности)
прямоугольником с тем же основанием и высотой, равной /(|f), где
\i (/=1, 2, ...) — некоторая промежуточная точка /-го по счету
отрезка [#/-1, х(], т. е. полагаем:
где
^xL (/=1, 2,...).
Значения первообразной функции

626 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
в точках хх можно подсчитать методом накопления:
Xi *i-i Xi
J7 (*«) = $ /(*)<& = $ f(x)dx+l f(x)dx =
(*|-*Л) («'=1, 2,...). A)
Пусть Mx(%v /(Ei)), M2(%2, /(?a))> • • • —соответствующие точки
кривой y=f(x). Проектируя их на ось Оуу получим точки М%,
М2\ ... (рис. 77).
Выберем теперь полюс Р с расстоянием ОЯ= 1 и проведем
лучи РМх, РМ2, ... Искомую линию y = F (x) приближенно
можно заменить ломаной N0NxN2N8 ... с вершинами NQ (х0, 0),
Nx(xv /"(^i)), A^2(^2» F(x2))f*" Последовательные звенья этой
ломаной будут параллельны соответствующим лучам, а именно:
N^WPMl; NxN2\\PM'2; N2Nz\\PMz\... В самом деле, угловой
коэффициент звена Ni^1Ni на основании формулы A) равен
X
в силу же построения угловой коэффициент луча СШ* есть
*i —
—1——/Последовательно,
Nt.MWOM A=1,2,...).
Таким образом, технически построение графика функции y = F(x)
может быть осуществлено так: из точки N0(xQ, 0) проводим
прямую NONX, параллельную лучу ОМ[, до пересечения в точке Nx с
вертикалью х = хх;ъз точки Nx проводим прямую NXN2> параллельную
лучу ОМ'2, до пересечения в точке N2 с вертикалью лг = д;2 и т. д.
Следует отметить, что при применении данного метода
графического интегрирования точки дг,(/ = О, 1 ...) не обязательно брать
равноотстоящими. Для увеличения точности построения рекомендуется
характерные точки графика интегрируемой функции (нули, точки
экстремума, точки перегиба) обязательно включать в состав точек лг,-.
Графическое интегрирование обладает, вообще говоря, малой
точностью. Поэтому этот прием полезно использовать тогда, когда
требуется иметь общее представление об интеграле функции или когда
подынтегральная функция задана графически и ее аналитическое
выражение нам неизвестно.

§ 17]
ПОНЯТИЕ О КУБАТУРНЫХ ФОРМУЛАХ
627
§ 17*. Понятие о кубатурных формулах
Кубатурные формулы или, иначе, формулы численных
кубатур предназначены для численного вычисления двойных
интегралов [1].
Пусть функция z=f(xyy) определена и непрерывна в некоторой
ограниченной области а (рис. 78). В этой области а выбирается
система точек (узлов). М({х{, уг) (/=1, 2,..., N). Для
вычисления двойного интеграла
с, у) dx dy приближенно
полагают:
$$/(*, y)dxdy =
(а)
A)
Рис. 78.
Чтобы найти коэффициенты Аь потребуем точного выполнения
кубатурной формулы A) для всех полиномов
(*•>)= 2 ск1хку1,
B)
степень которых не превышает заданного числа п. Для этого
необходимо и достаточно, чтобы формула A) была точной для
произведения степеней
х*у*
(А, / = 0, 1, 2, ... , п; k + l^n).
о Полагая в A) /(лс, у) =xkyl, будем иметь:
г
о
г
1
И
(а)
(*,/== 0, 1,2, ...,*;
C)
2
Рис. 79.
—>- Таким образом, коэффициенты At фор-
* мулы A), вообще говоря, могут быть
определены из системы линейных
уравнений C).
Для того чтобы система C) была определенной, необходимо,
чтобы число неизвестных N было равно числу уравнений. Отсюда,
составляя «решетку показателей» (рис. 79), получаем:

628
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[ГЛ. XVI
Остается открытым трудный вопрос о наиболее рациональном
выборе узлов для данной области.
Можно указать еще один достаточно общий прием вычисления
двойного интеграла. Пусть область интегрирования ограничена
непрерывными однозначными кривыми
У = Ч>(*)> J = ¦(¦*)
D)
и двумя вертикалями х=а, х = Ь (рис. 80).
Расставляя по известным правилам в двойном интеграле
(а)
пределы интегрирования, будем иметь:.
У
f(x,y)dy.
= { f(x,y)dy. E)
. F)
Применяя к однократному интегралу, стоящему в правой части
равенства F), одну из квадратурных формул, получим:
G)
(о)
где #,-€[#» b] (i— 1, 2, ... , п) и А( — некоторые постоянные
коэффициенты. В свою очередь значения
F(xt)=l f(xhy)dy
ыогут быть также найдены по некоторым формулам квадратур
F(xi)= J
где fi|y — соответствующие постоянные.

§ 18J
КУБАТУРНАЯ ФОРМУЛА ТИПА СИМПСОНА
629
Из формулы G) выводим:
\\ /С*, y)dx tfy =
()
\\
(a)
где А{ и Btj — известные постоянные.
Геометрически этот метод эквивалентен вычислению объма 7,
выражаемого интегралом D) с помощью поперечных сечений.
Для кубатурных формул тица (8) сохраняют силу с
соответствующими видоизменениями общие замечания, относящиеся^ вычислению
однократных интегралов (см. § 10).
§ 18*. Кубатурная формула типа Симпсона
Пусть сначала область интегрирования есть прямоугольник
(рис. 81), стороны которого параллельны осям координат. Каждый
из промежутков [а, А] и [ft, В] //
разобьем пополам точками
и соответственно
где
Всего, таким образом, получим девять точек (xi% yj) (/, У=0,
1, 2, ..., 9). Имеем:
- А В
$$/(*, y)dxdy = \dx\f{x% y)dy. A)
{R) ' a b
Отсюда, вычисляя внутренний интеграл по квадратурной формуле
Симпсона, находим:
, уг)+/{х,
А А
J
; •
J

630 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [ГЛ. XVI
Применяя к каждому интегралу снова формулу Симпсона, получим:
у) dxdy = j {[/ (*0, у0) + 4/ (*!, у9) +/(¦*» У о)] +
+ 4[/(*0. Уд+ */(*!* Уд +/(*«. Л)] +
или
я
y)dxdy=h±
оэЛ)+/(*«»Л)+/(^о.Л)
> B)
Формулу B) будем называть кубатурной формулой Симпсона.
Следовательно,
я
hk
/ (х, jr) dx dy = 'f(c0 + 4Oj + 16a2),
B')
где 0О—:сумма значений подынтегральной функции/(дг, j;) в
вершинах прямоугольника R, <уг — сумма значений / (дг, у) в с е р е д и-
нах сторон прямоугольника R, o2=f(xi> Ух) — значение функции
/(дг, у) в центре прямоугольника R. Кратности этих значений
обозначены на рис. 81.
Пример 1. Применяя кубатурную формулу Симпсона,
вычислить двойной интеграл [7]
4,4 2,6
Решение. Берем
. 4,4-4
'•И
dxdy
и fe=
Соответствующие значения подынтегральной функции
z~—помещены в таблице 75.
. Таблица 75
Вычисление двойного интеграла
по формуле Симпсона
2,0
2,3
2,6
4,0
0,125000
0,108696
0,096154
4,2
0,119048
0,103520
0,0915751
4,4
0,113636
0,0988142
0,0874126*

§ 18] КУБАТУРНАЯ ФОРМУЛА ТИПА СИМПСОНА 631
Применяя кубатурную формулу B), получим:
/ = ^^[@,125000+0,113636+0,096154 + 0,0874126) +
+ 4@,119048 + 0,108696 + 0,0988142 + 0,0915751) +
+16-0,103520] = 0,0250070.
Точное значение этого двойного интеграла будет:
4,4 2.6
Г Г dxdy_^]u 131n ljl==o,0953108.0,262364=:0,0250061.
4 2
Следовательно, остаточная погрешность
Д = 10,025006 — 0,02500701 = 0,0000009^10~в.
Если размеры прямоугольника R{a^x^A; Ь^у^В} велики,
то для увеличения точности кубатурной формулы B) область R
разбивают на систему прямоугольников, к каждому из которых применяют
кубатурную формулу Симп-
сона.
Положим, что стороны
прямоугольника R мы
разделили соответственно на п
и т равных частей; в
результате получилась
относительно крупная сеть пт
прямоугольников (на рис.82
вершины этих
прямоугольников отмечены более
крупными кружками).
Каждый из этих
прямоугольников в свою очередь разделим на четыре равные части. Вершины
этой последней мелкой сети прямоугольников примем за узлы Мц
кубатурной формулы. "
Пусть
2п
и в - ь
2т
Тогда сеть узлов будет иметь следующие координаты:
Xi^^ + ih (л:0 = а; / = 0, 1, 2, ..., 2п)
и
СУо = *;У=О, 1, 2, ..., 2т).

632 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
Для сокращения введем обозначение
[ГЛ, XVI
Применяя формулу B) к каждому из прямоугольников крупной
сети, будем иметь (рис. 82):
п т
Y*lL Hftu 2У+Л/+2, v+/«+i. ¦/+* +
/=0/=0
, 2/+/2I+2, 2/ + 1+/2/ + 1, 2/+2+Л1,
(R)
Отсюда, делая приведение подобных членов, окончательно находим:
2я 2т
где коэффициенты
матрицы
т
/ = 0 /=0 ;
являются соответствующими элементами
1 4 2 4 2 ,.. 4 2 4 1"
4 16 8 16 8 ... 16 8 16 4
2 84 84... 84 82
2 84 84... 84 82
4 16 8 16 8 ... 16 8 16 4
1 4 2 4 2 ... 4 2 4 1
Если область интегрирования а —криволинейная, то строим
Рис. 83. ^
прямоугольник /?за, стороны которого параллельны осям
координат (рис. 83). Рассмотрим вспомогательную функцию
/(*, у), если (лг, у)€с>
О , если (х

ЛИТЕРАТУРА К ШЕСТНАДЦАТОЙ ГЛАВЕ 633
В таком случае, очевидно, имеем:
ЭД/(*> y)dxdy=^f*(Xjy)dxdy.
(о) (R)
Последний интеграл приближенно может быть вычислен по общей
кубатурной формуле C).
Литература к шестнадцатой главе
1. Ш. Е. Микеладзе, Численные методы математического анализа,
Гостехиздат, 1953, гл. XIII, XVIII.
2. В. Э. Милн, Численный анализ, ИЛ, 1951, гл. IV.
3. СМ. Никольский, Квадратурные формулы, Физматгиз, М., 1958.
4. А. Марков, Исчисление конечных разностей, изд. 2. Матезис, 1911,
гл. V.
5. И. Ф. Стеффенсон, Теория интерполяции, М.—Л., 1935.
6. И. С. Б е р е з и н и Н. П. Жидков, Методы вычислений, Физматгиз,
М., 1959, т. I, гл. III.
7. Дж. Скарборо, Численные методы математического анализа, ГТТИ,
1934, гл, VII.
8. А. Н. Крылов, Лекции о приближенных вычислениях, изд. 2, ИАН
СССР, 1933, гл. III.
9. В. И. Крылов, Приближенное вычисление интегралов, Физматгиз,
М., 1959.
10. М. Дж. Сальвадор и, Численные методы в технике, ИЛ, М., 1955.
П. Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, 1948, Гостехиздат, т. 2, гл. IX, XIII.

ГЛАВА XVII
МЕТОД МОНТЕ-КАРЛО
§ 1. Идея метода Монте-Карло
Обычный путь решения задачи состоит в том, что указывается
алгоритм (последовательность действий), с помощью которого
искомая величина / находится или точно, или с заданной погрешностью.
А именно, если через Д, /2, ...,/„, ... обозначить соответствующие
результаты последовательно накопляющихся действий, то
/=Um/B, - A)
причем в случае конечного числа операций процесс обрывается на
некотором шаге. Здесь процесс вычислений является строго
детерминированным: два различных вычислителя при отсутствии
ошибок приходят к одному и тому же результату.
Однако встречаются задачи, где построение такого рода
алгоритма практически невыполнимо или сам алгоритм оказывается
чрезмерно сложным. В этих случаях часто прибегают к моделированию
математической или физической сущности задачи и использованию
законов больших чисел теории вероятностей. ОценкиД,/^, ...,/„,..•
искомой величины / получаются на основании статистической
обработки материала, связанного с результатами некоторых
многократных случайных испытаний. При этом требуется, чтобы случайная
величина fn при п—>оо по вероятности сходилась к искомой
величине / [1], [2], т. е. для любого е >0 должно иметь место
предельное соотношение
1, B)
где Р обозначает соответствующую вероятность.
Выбор величины fn обусловливается конкретными особенностями
задачи. Например, часто искомую величину/трактуют каквероятность
некоторого случайного события (или, более общо, как математическое
ожидание некоторой случайной величины). Тогда частоту fn
появления события при п соответствующих случайных испытаниях (или
соответственно эмпирическое среднее значений случайной величины) вши-

§ 2] СЛУЧАЙНЫЕ ЧИСЛА 635
рокихпредположенияхможнорассматриватькаквероятностнуюоценку
искомой величины. Возможны также и другие варианты. Заметим, что
в этих случаях вычислительный процесс является
недетерминированным, так как он определяется итогами случайных испытаний.
Способы решения задач, использующие случайные величины,
получили общее название метода Монте-Карло, Более точно под методом
Монте-Карло [3], [4], [5], [6] понимается совокупность приемов,
позволяющих получать решения математических или физических
задач при помощи многократных случайных испытаний. Оценки искомой
величины выводятся статистическим путем и носят вероятностный
характер. На практике случайные испытания заменяются
результатами некоторых вычислений, производимых над случайными числами
(см. § 2).
Эффективное применение метода Монте-Карло стало возможным
после появления быстродействующих электронных машин, так как
для получения достаточно точной оценки искомой величины
требуются выполнение вычислений для весьма большого количества
частных случаев и последующая статистическая обработка колоссального
числового материала. Заметим, что при пользовании методом Монте-
Карло нет необходимости знать точные соотношения между данными
и искомыми величинами задачи, а достаточно лишь выявить тот
комплекс условий, при наличии которого соответствующее явление имеет
место. Это обстоятельство делает возможным использование метода
Монте-Карло для решения логических задач.
Из математических задач, для которых разработано применение
метода Монте-Карло, отметим следующие: решение систем линейных
уравнений, обращение матриц, нахождение собственных значений
и собственных векторов матрицы, вычисление кратных интегралов,
решение задачи Дирихле, решение функциональных уравнений
различных типов и др. Метод Монте-Карло успешно используется также
для решения задач ядерной физики. Заметим, что для решения
одной и той же конкретной задачи схема применения метода может быть
существенно различной.
В этой главе будет рассмотрено вычисление кратных интегралов и
решение систем линейныхуравненийметодомМонте-Карло. Что
касается других указанных задач, то сведения о них можно почерпнуть в
специальной литературе (см., например [3], библиография; а также [6]).
§ 2. Случайные числа
При практическом применении метода Монте-Карло случайные
испытания обычно заменяют выборкой случайных чисел.
Определение 1. Величина называется случайной, если она
принимает те или иные значения в зависимости от появления или не*
появления некоторого случайного события.
Случайная величина X задается законом распределения
Ф

636 МЕТОД МОНТЕ-КАРЛО [ГЛ. XVII
где я —любое действительное число и Ф(лг) — известная функция
(функция распределения). Значения случайной величины называются
случайными числами.
Определение 2. Если случайная величина имеет заданный
закон распределения [1], [2] (равномерный, нормальный и т. п.), то
будем говорить, что соответствующие случайные числа
распределены по этому закону.
Пусть числа xv х2, ... лг„, ... являются значениями одной
и той же случайной величины X при независимых между собой
испытаниях с повторяющимися условиями. Тогда последовательность
случайных чисел
к,} A)
будем называть случайной, с соответствующим законом
распределения. В дальнейшем, как правило, мы будем рассматривать
равномерно распределенные на единичном отрезке 0^#^1 случайные
последовательности A). Если (а, 6) —любой промежуток*) из
отрезка [0, 1] и уя = гя(а, Ь) — число элементов конечной
подпоследовательности xv х2, ..., хпУ принадлежащих промежутку (а, Ь)%
то для равномерно распределенной последовательности A) имеет
место предельное соотношение
Шв Щ-й=Ь-а, B)
т. е. предельная относительная частота равномерно
распределенной на [6,1] последовательности {хп} для каждого частичного
промежутка (а, Ь) равна длине этого промежутка.
Если случайная последовательность {хп} равномерно
распределена на отрезке [0, 1], то линейное преобразование
уя = А + {В-А)хя (л=1, 2, ...), C)
где А и В—данные числа, приводит к случайной
последовательности {ya}i равномерно распределенной на отрезке [А, В].
Вообще, имея случайную последовательность {хп}, равномерно
распределенную на отрезке [0, 1], можно построить случайную
последовательность {уп} с заданным законом распределения Ф(у). А
именно, пусть
У
У
— соответствующая функция распределения**), где ф(^)—плотность
вероятности. . -
*) Концы а и Ь по договоренности могут как включаться в
промежуток (а, р), так и не включаться в него.
**) Если уп <п = 1, 2, ...)содержатся в конечном отрезке A<,y<,Bt то,
как обычно, полагают Ф(#) = 0 при у ? [А9 В].

§ 2] СЛУЧАЙНЫЕ ЧИСЛА
Для простоты будем предполагать, что функция
637
непрерывна и строго монотонна (рис. 84). Тогда для каждого хп,
определяя уп из уравнения
- хп = Ф(уп) (л=1, 2, ...),
получим случайную последовательность {уп}, имеющую заданный
закон распределения Ф(у). А именно, по способу построения, для
Уз
0\ ^Тп
Рис. 84.
У,
последовательности {у^ будет справедливо предельное соотношение
lim
D)
где vn (a, b) — число элементов конечной подпоследовательности
У±> •••> Уп> принадлежащих произвольному промежутку (а, Ь).
В частности, полагая
этим способом получим каноническую нормально распределенную
(гауссову) случайную последовательность {уп}> соответствующую
случайной величине Y с математическим ожиданием Л1У=0 и
дисперсией /)У=1. Линейное преобразование
*я = аУп+с (/г=1» 2, .,.)
дает нормально распределенную случайную последовательность {zn}f
соответствующую случайной величине Z, для которой
математическое ожидание MZ=c и дисперсия /)Z = o2.

638 . МЕТОД МОНТЕ-КАРЛО [ГЛ. XVII
§ 3. Способы получения случайных чисел
Для выработки случайных чисел можно использовать результаты
случайныхфизических процессов (например, бросание игральной кости,
вращение рулетки, вспышки в счетчике Гейгера, шум при
электрических передачах и т. п.). Имеются также готовые таблицы
случайных чисел (см., например, [7], [8]).
Строго говоря, при пользовании механическими приспособлениями
для получения случайных чисел нет абсолютной уверенности, что мы
имеем дело со случайными событиями с заданным распределением
вероятностей. Поэтомуполученныйматериалобычно подвергается
статистической «проверке на случайность». В этом смысле надежнее
употреблять случайные числа из таблиц, где такая проверка уже
проделана; однако использование таблиц случайных чисел для решения
задач на электронных цифровых машинах часто связано с серьезными
неудобствами [9].
Для решения задач методом Монте-Карло обычно требуется весьма
большое количество случайных чисел. Эти числа практически
наиболее удобно получаются с помощью специальных датчиков
случайных чисел, подключаемых к машине. Действие этих датчиков
регулируется случайными физическими процессами (например,
радиоактивным распадом, шумами в электронных лампах и т. п.) [9].
Так как воспроизводство случайных чисел, отвечающих данной
теоретической модели, есть процесс весьма тонкий и сложный, то на
практике часто ограничиваются получением так называемых
псевдослучайных чисел, в основных чертах похожих на соответствующие
случайные. Источниками (датчиками) псевдослучайных чисел служат
достаточно сложные математические алгорифмы. В дальнейшем под
термином «случайное число» мы будем понимать как случайные, так
и псевдослучайные числа, если различие между ними не имеет
существенного значения.
- Укажем некоторые простые приемы получения случайных чисел,
в обобщенном смысле, равномерно распределенных на отрезке [0, 1].
Для простоты будем предполагать, что эти числа представляют собой
правильные десятичные дроби с фиксированным количеством
десятичных знаков после запятой, например s (s-разрядные десятичные
дроби), т. е. могут быть записаны в виде
*~ ю "
\.
где &1 (/=!, 2, ..., 5) —цифры этого числа, принимающие
значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для составления таблицы случайных чисел вида A), равномерно
распределенных на [0, 1], достаточно указать способы получения
цифр ai с соблюдением следующих условий:
" а) а есть случайная выборка из системы чисел 0 — 9, причем
все указанные значения равновероятны;

§ 3] СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ ЧИСЕЛ 639
б) выбор предыдущей цифры at никоим образом не влияет на
выбор последующей а1+1.
Для получения 5-разрядного случайного числа такая выборка
производится 5 раз.
Система выбора, удовлетворяющая условиям а) и б), практически
может быть реализована многими способами. Рассмотрим некоторые
из них.
1. В урну опускают десять одинаковых перенумерованных шаров
с номерами 0 — 9. Из урны последовательно извлекается шар и
записывается его номер а. После каждого извлечения шар возращают
в урну и перед каждым следующим тиражом все шары в урне
перемешиваются.
2. Одновременно бросают две игральные кости. Если пг и п2 —
числа выпавших очков (nv л2= 1, 2, 3, 4, 5, 6) соответственно на первой
и второй костях (кости должны быть различаемыми), то очередная
цифра а случайного числа берется равной остатку от деления суммы
6G2! — 1) + л2 на 10, где /^«Сб, т. е. а есть целое
неотрицательное число, меньшее 10, удовлетворяющее сравнению*),
6(/2х— l) + /22E=a(mod 10). B)
Если /*! = 6, то кости перебрасываются. Из формулы B) вытекает,
что цифра а с равной вероятностью может принять любое значение
от 0 до 9 (см. [7]).
3. Берется ^-разрядное целое число. Число возводится в квадрат
и выбираются средние 5 его разрядов; затем процесс повторяется.
Если s достаточно велико, например s^ 10, то выбираемые разряды
могут быть приняты за наборы элементов 5-разрядных
псевдослучайных чисел [3].
Для получения последовательности псевдослучайных чисел можно
также использовать умножение многозначного числа на постоянный
множитель и извлечение средних разрядов или возведение
многозначного числа в квадрат и приведение результата по модулю некоторого
достаточно большого простого числа.
4. Псевдослучайная последовательность {хп} вырабатывается с
помощью процесса [10]
где
ио=1,
5. Используется десятичное разложение положительного
иррационального числа
где ро—целая часть числа оо и (а>)— его дробная часть. j
*) Запись azzsb (mod k) (a, b, k — целые числа) обозначает, что разность
a-— b делится без остатка на /г. '

640
МЕТОД МОНТЕ-КАРЛО
[ГЛ. XV»
Для получения случайной последовательности {хп} полагают:
лгп = (лш) (л=1, 2,...).
Если требуется случайная последовательность, состоящая из
^-разрядных чисел, то в числах (то) ограничиваются соответствующими
разрядами.
Для решения некоторых задач нужно иметь несколько случайных
последовательностей
В этом случае выбирают т линейно независимых положительных
иррациональностей о»!, <о2, ..., <ода и полагают:
(*=1, 2, .;., щ; й=1, 2, ...).
Можно также взять одну равномерно распределенную случайную
последовательность {хп} и произвести из нее т выборок:
2, X
m+2»
\Хт> Xtm> X3m> • • • Ь
беря числа не подряд, а через /я элементов. Очевидно, таким
образом, мы будем иметь т равномерно распределенных
подпоследовательностей.
С помощью этих и других методов составлены таблицы
случайных чисел. В таких таблицах обычно даются случайные
десятичные цифры; из них легко можно конструировать случайные числа
определенного разряда. Для примера приводим часть одной из
таблиц (см.[7]) пятиразрядных случайных чисел (таблица 76).
Таблица 76
Случайные числа, равномерно распределенные
на отрезке [0, 1]
0,57705
0,71618
0,73710
0,70131
0,16961
0,53324
0,43166
0,26275
О;05926
0,66289
0,35483
0,09393
. 0,30304
0,55186
0,64003
0,20514
0,00188
0,55709
0,86977
0,31303
0,11578
0,93045
0,93011
0,42844
0,52906
0,09461
0,99602
0,69962
0,31311
0,27004
0,65339
0,93382
0,05758
0,00336
. 0,88222
0,98585
0,52103
0,91827
0,07069
0,13928
0,66674
0,99279
0,24202
0,94010
0,60981
0,13094
0,35193
0,64560
0,64559
, 0,68008

§ 4] ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО 641
§ 4. Вычисление кратных интегралов методом Монте-Карло
Пусть функция
y = f(*i, *a, ..., хт)
непрерывна в ограниченной замкнутой области S и требуется
вычислить m-кратный интеграл
(S)
**>
dx
A)
Геометрически число / представляет собой (т + 1)-мерный объем
прямого цилиндроида*) в пространстве Охгх2 ... хту, построенного на
основании S и ограниченного
сверху данной поверхностью у ,Уш*Ш
y = f{x)t где х = (х19 х» ...
..., хя) (рис. 85).
Преобразуем интеграл A)
так, чтобы новая область
интегрирования целиком
содержалась внутри единичного /я-мер-
ного куба. Пусть область 5
расположена в /ю-мерном
параллелепипеде
а,.<*,.< Л, B)
(/ = 1, 2, ..., т).
Сделаем замену переменных
Рис. 85.
(/=1, 2, .,., m).
Тогда, очевидно, m-мерный параллелепипед B) преобразуется в т-мер-
ный единичный куб
0<?,<1 (/ = 1, 2, ..., т) D)
и, следовательно, новая область интегрирования а, которая
находится по обычным правилам, будет целиком расположена внутри
этого куба (рис. 86).
Вычисляя якобиан преобразования будем иметь:
L_ ax О ... О
О А2—а2 ... О
О
О
^(А1—а1)(А2—а2) ... (Ат—ат).
*) Точнее, алгебраический объем, где предполагается, что части
цилиндроида, расположенные выше гиперплоскости Од^л^, ...» хт*
имеют'положительную меру, а ниже—отрицательную.

642
Таким образом,
МЕТОД МОНТЕ-КАРЛО
i, Et, • ¦•,
(а)
[ГЛ. XVII
E)
где
xfiai + W'
Введя обозначения
и
1 = (!i> ?2» • • • э 1т)
запишем интеграл E) короче в следующем виде:
' = $$••¦
(О)
(О)
Мы укажем два способа вычисления интеграла E') методом
случайных испытаний.
Первый способ. Выбираем т равномерно распределенных
на отрезке [0, 1] последовательностей случайных чисел:
Щ\ ЕЬ!)..... Щ}\..Л
Точки М,ШП, 1?\ .... Eiw)) У = ». 2. •••) можно Рассматривать
У^/
Рис. 86.
Рис. 87.
как случайные. Выбрав достаточно большое число N точек
М1У Ж2, ..,, М^\ проверяем, какие из них принадлежат области a

§ 4] ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО 643
(первая категория) и какие не принадлежат ей (вторая категория).
Пусть (рис. 87)
1) М^а при / = 1, 2, ..., п F)
и
2) М^а при / = л+1, п + 2, ..., N F')
(для удобства мы здесь изменяем нумерацию точек!). Заметим, что
относительно границы Г области а следует заранее договориться,
причисляются ли граничные точки или часть их к области а, или не
причисляются к ней. В общем случае при гладкой границе Г это не
имеет существенного значения; в отдельных случаях нужно решать
вопрос с учетом конкретной обстановки.
Взяв достаточно большое число п точек Л^-бсг, приближенно
можно положить:
отсюда искомый интеграл выражается формулой
G)
где под а понимается m-мерный объем области интегрирования а.
Если вычисление объема а затруднительно, то можно принять:
отсюда
В частном случае, когда а есть единичный куб (а=1), проверка
становится излишней, т. е, n = JV и мы имеем просто
1 N
Для проверки условий F) и F') обычно исходят из
аналитического задания границы Г области а. В простейшем случае, если
поверхность Г задана уравнением
ФF)=0, (8)
где при ф(?)<0 точка %?o и при <р(|)>0 точка l?o, мы имеем:
1) если ф(/И<) < 0, то точка М{ — первой категории и 2) если
ф(Ж?) > 0, то точка М{— второй категории. Точки М{9 для которых
q>(Mi) = 0, причисляются к первой или второй категории по
соглашению. Заметим, что уравнение (8) можно заменить любым
равносильным ему уравнением, что иногда дает возможность значительно

644
МЕТОД МОНТЕ-КАРЛО
[ГЛ. XVII
облегчить выкладки. Так, например, неравенство для круга
х2 +у2—х—у + -i < О
удобнее заменить эквивалентным
так как второе неравенство проверяется проще.
Если область а — стандартная и задана неравенствами:
b/
(9)
то для определения принадлежности случайной точки М (%г, ?2>
..., ?т) к первой или второй категории проверяют выполнение
этих неравенств.
Таблица 77
Схема определения принадлежности случайной точки М (?lt . . ., lm)
к стандартной области (9)
...
к
Ei
к
8
Практически это удобно делать по схеме, приведенной в
таблице 77. Здесь
( если
если Б, € [|п Б|]
(i=l, 2, ..., /») и 6 = 8^2 ...ей. Очевидно,
если 8=1, то М ? а;
если е = 0, то М ? а.
A,
|0,

§ 4] ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО 645
Заметим, чтр если е/ = 0 (/<т), то дальнейшие значения
e/+i» • • -1 8/» можно не подсчитывать, так как они не повлияют на
окончательный результат. Значение функции y = F (M) подечиты-
вается только для тех точек М, для которых е=1. Затем для
вычисления интеграла / используется формула G).
Пример. Методом Монте-Карло приближенно вычислить интеграл
dxdy, A0)
(or)
где область интегрирования а определяется следующими
неравенствами:
i
(рис. 88).
Решение. Интеграл A0) дан
в приведенном виде, т. е. область
интегрирования а расположена в
единичном квадрате
Для решения задачи воспользуемся
таблицей случайных чисел (таблица 76),
рассматривая каждую очередную пару
чисел таблицы как соответствующие координаты х и у случайной
точки М (л:, у). Так как вычисление носит иллюстративный характер,
то ограничимся Af=20 случайными точками, причем координаты их
для простоты округлим до трех десятичных знаков. Результаты
вычислений приведены в таблице 78, где положено
Отсюда
=¦¦-0.
= 1-3,837 = 0,96
и, следовательно, по формуле G), учитывая, что а=-т", имеем:
/=*ср . а = 0,96 • j=0,24. A1)
Если приближенно принять
±—JL-.JL
С^ N ~2б~5
то получим:
/«0,96
=0,19,

646
МЕТОД МОНТЕ-КАРЛО
[ГЛ. XVU
Таблица 78
Вычисление двойного интеграла A0) методом Монте-Карло
X
0,577
0,737
0,170
0,432
0,059
0,355
0,303
0,640
0,002
0,870
0,116
0,930
0,529
0,996
0,313
0,653
0,058
0,882
0,521
0,071
S
X
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
0,500
X
1,000
1,000
1,000
1,000
1,000
,000
1,000
1,000
,000
,000
1,000
1,000
,000
,000
,000
1,000
,000
,000
1,000
1,000
1
1
0
0
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
0
У
0,716
0,701
0,533
0,263
0,663
0,094
0,552
0,205
0,557
0,323
0,930
0,428
0,095
0,700
0,270
0,934
0,003
0,986
0,918
0,239
0
0
0
0
0
0
0
0
0
0
У(х)
0,154
0,474
0,280
0,740
0,860
0,058
0,992
0,306
0,764
0,042
0
0
1
1
1
0
1
0
0
0
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
0
0
0
0
4
2
0,452
0,855
1,048
1,482
3,837
Заметим, что точное значение интеграла
Is=si ™ 0>22;
поэтому относительная погрешность результата A1) равна
а 0,24 —0,22 _по>
Конечно, тут число точек N = 20 недостаточно, чтобы статистические
закономерности могли проявиться в должной мере, но тем не менее
для грубой ориентировки получен удовлетворительный результат.
у у
Второй способ. Если функция
?
2,

неотрицательна,
лк V в
то интеграл E) можно рассматривать как объем те-
i-мерном пространстве ОБх?а*. ХтУ> т» е.
(V)
где область интегрирования V определяется условиями

§ 4J ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО 647
Пусть
-' - A3)
A4)
Введя в интеграле A2) новую переменную
получим)
(о)
где новая область v есть цилиндроид пространства ОБхБа... Бшл»
построенный на области а и ограниченный снизу гиперплоскостью
т) = 0 и сверху
гиперповерхностью
(рис. 89). В силу
неравенства A3) объем v целиком
лежит в (т +1 )-мерном кубе
(/==1, 2, ..., т),
Возмьем теперь т + \
равномерно распределенных на
[О, 1] случайных
последовательностей
Рис. 89.
соответствующие элементы которых будем рассматривать как
координаты случайных точек
адд брч-.-.
= 1,2, ...)
^пространства О^Ег...^тт]. Если из общего числа N случайных
точек п принадлежит объему v, а ЛА—/г не принадлежит этому
объему, то при достаточно большом числе N приближенно полагают:
A5)
т. е. *
где точка М с одинаковой вероятностью может занимать
положения М19 М2> ..., Ж^. Выполнение соотношения

648 МЕТОД МОНТЕ-КАРЛО [ГЛ. XVII
проверяется аналогично тому, как было указано в первом способе.
Заметим, что если а есть единичный куб 0 < ?, < 1 (/ = 1, 2, ...,/»),
то для точки Мг (Ц1\ ..., Цт), т],.), все координаты которой
предполагаются принадлежащими единичному отрезку [0, 1,] достаточно
проверять лишь выполнение соотношения
Рассмотрим теперь общий случай, когда функция
F(l) =
—-знакопеременная. Пусть
B, A6)
где Ъ и В—неотрицательные числа. Положим
• тогда будем иметь:
(а)
(а) (а)
где функция r\~F(Q в силу неравенства A6) удовлетворяет
неравенствам
Интеграл
... \dodr\
(о) ()
может быть вычислен способом, указанным выше.
Для оценки приближенного равенства *)
? A7)
предположим сначала, что мы имеем дело с идеальными
случайными равномерно распределенными последовательностями точек Щ
(/=1, 2, ...), координаты которых принадлежат единичному
отрезку [0, 1].
На основании теоремы Бернулли, применяя неравенство Чебышева,
будем иметь:
*) Множитель В не имеет существенного значения.

§ 4] ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО 649
Задавшись для данного г гарантийной вероятностью
1-6, A9)
из неравенства A8) получаем, что условие A9) заведомо имеет место,
если
4^=б- B°)
Отсюда выводим:
Таким образом, точность оценки
при заданной предельной вероятности ее обратно пропорциональна
корню квадратному из числа испытаний, т. е. е = О[ -f=). Это
обстоятельство обусловливает сравнительно медленную сходимость
метода Монте-Карло: например, чтобы уменьшить погрешность
результата в 10 раз, число испытаний нужно увеличить в 100 раз! Если
точность оценки г и гарантийная вероятность 1 —б заданы, то из
формулы B0) выводим необходимое число испытаний
N <22)
Например, при е = 0,001 и 6 = 0,01 имеем:
N = 25 000 000.
Оценка B2) является завышенной и может быть значительноулучшена!
Отметим одно важное обстоятельство: число испытаний N не
зависит от размерности интеграла /0 и поэтому метод Монте-Карло
выгодно применять для вычисления кратных интегралов высоких
размерностей, где применение обычных кубатурных формул встречает
значительные затруднения. Например, для приближенного вычисления
обычным путем 10-кратного интеграла, распространенного на
единичный объем, при выборе шага h = 0,1 понадобится сумма,
содержащая примерно 1010 слагаемых!
При практическом применении метода Монте-Карло для
вычисления кратных интегралов обычно пользуются 5-разрядными
равномерно распределенными случайными последовательностями. В этом
случае дробь ^г, если TV велико, будет близка не к истинному
объему /0, а к некоторому фиктивному объему /'0, приближенно
21 Б. Л. Демидович и И. А. Марон

650 МЕТОД МОНТЕ-КАРЛО [ГЛ. XVII
представляющему собой относительную меру числа точек М с
координатами вида
(/=1, 2, ..., in; *,, k = 0, 1, 2, ..., 10*),
попавших в объем v (ср. § 3), причем /0, строго говоря, зависит
от того, причисляются ли граничные точки к объему v или нет.
Полная погрешность результата оценивается следующим образом
(см. [2]):
Первое слагаемое \Г0 — 10\ правой части неравенства B4)
представляет собой обычную вычислительную погрешность,
получающуюся при замене интеграла /0 интегральной суммой,
соответствующей разбиению объема v на элементарные кубические ячейки, вершины
которых принадлежат сетке B3). Величину этой погрешности можно
оценить с помощью неравенства
|/'о-/о|<?-^ B5)
где v — верхняя интегральная сумма (в нашем случае для
интеграла A7) просто объем описанного ступенчатого тела) и v — нижняя
интегральная сумма (т. е. объем вписанного ступенчатого тела).
Величина погрешности |/'о—/0| существенно зависит от разрядности
5 случайных чисел, и если граница тела v кусочно гладкая, то эта
погрешность при достаточно большом s может быть сделана сколь
угодно малой. Неудобство от увеличения разрядности состоит в том,
что возрастает объем работы, так как вычисления приходится
производить с дополнительными знаками. Второе слагаемое \Г0—^
правой части неравенства B4) называется погрешностью выборки
и может быть оценено вероятностным путем с помощью теоремы
Бернулли, как указано выше.
§ 5*. Решение систем линейных алгебраических уравнений
методом Монте-Карло
Рассмотрим линейную систему
Некоторым способом приведем систему A) к специальному виду
*/=2а/у*/+Р* (/=1, ... ,л). B)

§ 5] РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 651
Введя матрицу а = [аи] и векторы
Xz=='
систему B) можно записать в матрично-векторной форме
Будем предпологать, что все собственные значения матрицы а по
модулю меньше единицы. В частности, достаточно считать, что
какая-нибудь каноническая норма матрицы а подчинена неравенству
||а||<1. ¦ C)
В этом случае система B') имеет единственное решение, которое
может быть найдено методом итерации (гл. VIII, § 10).
Подберем систему множителей tty таким образом, чтобы числа /fy,
определяемые уравнениями
удовлетворяли следующим условиям:
1) fty^O, причем рц>0 при а^ф0\
2) Sfty<I (/=!,..., п).
Пусть
п
pit Л+1 = 1 — S pij (/=1,..., п).
Кроме того, условно положим
pn+\,j = 0 при j<Cti-\-\
и
Рп+\, п+\ = 1.
Рассмотрим теперь некоторую блуждающую частицу, обладающую
конечным числом возможных и несовместимых состояний
Эта частица такова, что с вероятностью р^ (/, /=!,..., /2+1)
переходит из состояния S{ в состояние Sp независимо от прошлых
состояний и с неопределенностью будущих. Состояние* 5rt+i —Г
(«граница» или «поглощающий экран») является особым и
соответствует полной остановке частицы, так как в силу условия /fo+i,y = 0
(у=1,..., п) переходы из состояния Sn+i в состояние Sj при
21*

652 МЕТОД МОНТЕ-КАРЛО [ГЛ. XVII
невозможны. Таким образом, процесс блуждания
прекращается, как только частица первый раз попадает на границу Г.
Описанная смена состояний обычно называется дискретной цепью
Маркова*) с конечным числом состояний [2]. Числа рц называются
переходными вероятностями, а матрица
Pll ••• Pin Pi, n + l
Рп\ • •• Рпп Рп, и + 1
О ... О 1
представляет собой матрицу перехода состояний {S,} (закон цепи).
Пусть Si — некоторое фиксированное состояние, отличное от
граничного (/<Ся+1). Рассмотрим случайное блуждание частицы,
начинающееся в данном состоянии vS/=5io и после ряда
промежуточных состояний Sitf Siti . . . , *S/m заканчивающееся на границе
5/м+1 = Г. Таким образом, S/m(/#>0) есть состояние частицы,
непосредственно предшествующее выходу ее на границу. Совокупность
состояний
для краткости будем называть траекторией. Пусть
^—случайная величина, зависящая от случайных траекторий Г,-,
начинающихся в состоянии S{ (функционал траектории Т(), и
принимающая для траектории E) значение
. -VtM_tiJiM* F)
где Ру (/ = /0, /а, ..., im) — соответствующие свободные члены
приведенной системы B).
В частности, если г^;- = 1, то имеем просто
?(*•/) = Р/. + Р*. + . .. + Р,„. F')
По теореме умножения вероятностей траектория Th а
следовательно, и значение ?{Г,-), реализуется с вероятностью
где /0 = / и т + 1
Теорема. Математические ожидания
Xt (/=1, 2, ..., п)
являются корнями системы B).
*) Точнее, простой однородной [2J.

§ 5] РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 653
Доказательство. Траектории Th начинающиеся из
состояния Sh в зависимости от первого шага можно разбить на 1
категорий
...};
т. е. частица, начав блуждание из состояния Sit при первом шаге
может переходить или в состояние Sv или в состояние 6'2 и т. д., а
затем через некоторое число шагов закончить блуждание на границе.
Если частица имеет траекторию
где ]фп-\-\, то случайная величина Х( в силу формулы F)
примет значение
где Гу — некоторая траектория с начальным состоянием 6у.
В том случае, когда частица сразу попадает на границу Г,
т. е. траектория имеет вид Tiy n+1 = {Siy Sn+1}f то
Вероятность того,что траектория Т( есть траектория типа
очевидно, равна рц.
В силу определения математического ожидания имеем:
мх, = SI G»Л77) = 22 U
? i T
Если у<я+1, то траектория T(j состоит из отрезка (Sh Sf)
и некоторой траектории Гу. Поэтому />(Г//)=р/уРG'у). При
у=/1-|-1 имеем:
Кроме того, так как каждой траектории Т[;- при /</х + 1
однозначно соответствует траектория Tj и обратно, то суммирование по
траекториям Т(, для у=1, 2, ..., л можно заменить
суммированием по траекториям Т^
Отсюда, учитывая формулу (8), получаем:
= 2 2№<
/=1 T,

654 МЕТОД МОНТЕ-КАРЛО (ГЛ. XVII
или
Но, очевидно,
%1{Ъ)Р(Т;) = МХЛ (y=l, 2, ..., п).
Кроме того, ^^>(^/)=1 и
п п+1
^Pi,IlP(Tj) + piin^= 2 Р,7=1.
Следовательно,
AUf,= ^«iyAUfy + р, (/=1, .... п\
где al7
Теорема доказана.
Замечание. При доказательстве теоремы предполагалось, что
математические ожидания
¦к» — АЛ V IS , 1 м\
•*? —— IllS\ I \i — 1, а..,/*)
существуют. Можно доказать, что при выполнении условия C)
случайные величины Х( обладают конечными математическими
ожиданиями.
Из доказанной теоремы следует, что корни системы B) можно
рассматривать как математические ожидания случайных величин
Хх, , Хп. Для экспериментального определения величины
х{ = МХ; организуют TV случайных блужданий, со случайными
траекториями Г/(*)(А=1, ..., N) с начальным состоянием 5,- и
каждый раз регистрируют значение %(Т{{к)) случайной величины Х^
Предположим, что испытания независимы между собой и
величина Xi имеет ограниченную дисперсию. Тогда в силу теоремы
Чебышева [1], [2] при N достаточно большом с вероятностью, сколь
угодно близкой к 1, будет справедливо неравенство
где е — заданная предельная погрешность. Таким образом, корни
системы B) приближенно могут быть определены по формулам
N
№*'). О)

§ 5] РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 655
В частности, этим способом можно обращать матрицы вида
А = Е—а, A0)
где ||а||<1 и ?=[8,у]--единичная матрица. Для этого заметим,
что элементы обратной матрицы
л-1-ад
являются корнями линейной системы
**/ С У=1. .... п).
Отсюда получаем, что элементы каждого столбца
xljy • • •» xnj t/^li • • •» п)
матрицы А'1 определяются из линейной подсистемы
п
На основании предыдущего, отправляясь из состояния 5/=*S/e,
при фиксированном j получаем случайную величину Х{, со
значениями
6/ (Ti) = Kf + в/1^Л + ... + &imf°Uii • • • **«-t <m>
где Г{ = {5,0, 5/lt ..., 5/тАт+1 = Г} и числа т;^ таковы, что pi/f
определяемые из уравнений OLl/=pijVijy представляют собой
вероятности перехода из состояния S{ в состояние Sy,
Математические ожидания МХц — Хц дадут искомые элементы матрицы А.
Покажем теперь, как практически возможно организовать
случайное блуждание частицы с заданными вероятностями перехода рц.
Для простоты продположим, что рц суть десятичные дроби с
общим знаменателем 10*($ — натуральное число):
где /Д| ^2» •••> ^i, п+1"~целые неотрицательные числа, причем
Рассмотрим частицу, имеющую начальное состояние St.
Пусть {а:} есть 5-разрядные числа, меньшие единицы, равномерно
распределенные на отрезке [0, 1], например, элементы из соответ
ствующей таблицы случайных чисел. Произведем розыгрыш
случайного числа х. Если окажется, что выполнено неравенство

656 МЕТОД МОНТе-КАРЛО \ГЛ. XVII
то будем считать, что частица переходит из состояния Sj в
состояние 51# Далее, если
то полагаем, что частица переходит из состояния 5j в состояние S2.
Аналогично определяются остальные переходы. В частности, частица
попадает на границу 5Л+1 = Г, если случайное число х таково, что
lQs
На основании данного соглашения ясно, что количества
благоприятных случаев для переходов Sj—*Sj (у=1, 2, ..., п-\-\)
пропорциональны соответственно числам
причем эти случаи равновероятны. Поэтому вероятности перехода
PiSi^Sj)^^ =PiJ (/=1, ..., п; у=1, ..., п+\).
Выбирая последовательность случайных чисел и руководствуясь
указанным выше правилом, получаем случайное блуждание частицы
с фиксированным начальным состоянием и данными вероятностями
перехода. Для достижения нужной точности корней (в
вероятностном смысле) следует рассмотреть достаточно большое количество
независимых блужданий.
Пример. Методом Монте-Карло решить систему уравнений
^ = 0,1*!+ 0,2*,+ 0,7; ^
*, = 0,2*!-0,3*.+ 1,1. f lU)
Решение. Можно положить
2i .
Отсюда матрица перехода есть
,
о,
0
1
2
0,
0
2|
3J
0,7
0,5
1
где элементы первой строки представляют собой соответственно
вероятности перехода из состояния 5Х в состояния Slt 52 и 53 = Г,
а элементы второй строки — из состояния S2 в состояния Slt 52 и Sa,
причем «кайма» соответствует границе Г.
Так как элементы матрицы П кратны 0,1, то можно использовать
одноразрядные случайные числа, цифры которых рекрутируются из

§ 5] РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 657
Таблица 79
Нахождение неизвестного хх системы A2)
методом Монте-Карло
n/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Случайное
число х
0,5
0.7
0,7
0.0 \
о,5;
0,7
о!б}
о|в}
0.7
0,3
0.7
о.И
0.0 \
0,7 |
0,0,
0.1
о.з
0,1
0.1
0.6 J
0,9
0,6
0,1 \
0,5/
0,3
0,3
0.2 \
0.4
0.4 1
0,3 (
0,1
0,6 J
0,6
0,2 \
0,6 )
Траектория
блуждания
s -+г
Si-+ Г
st-+r
Si~+ Г
sx-> г
s, ->• г
^> s2 ^> s22-^
-+ st-+f
s
Значение случайной
величины Л,
0,7
0,7
0,7
0,7 + 0.7
0,7
0,7+1,1
0,7+1,1
0,7
0,7
0,7
0,7 + 1,1+0,7
0,7 + 0,7+1,1-
- ij _ о,7 ~ 1,1
0,7
0,7
0,7+1,1
0,7
0,7
0,7+1,1 -1,1 +
+ 1,1 — 1,1—0,7
0,7
0,7+1,1

658 МЕТОД МОНТЕ-КАРЛО [ГЛ. XVCI
какой-нибудь случайной последовательности, например являются
элементами случайных чисел из таблицы 76 (§ 3).
Полученные результаты для 20 случайных блужданий с начальным
состоянием Sx приведены в таблице 79. Случайное число х
обеспечивало переходы состояний согласно следующей инструкции:
I. Для начального состояния Sx:
1) если 0<лг<0,1, то St — Sx;
2) » 0,1<*<0,3, » St-+S2;
3) » 0,3<л;<1, » Sx-+r;
II. Для начального состояния S2:
1) если 0<лг<0,2, то S2 -* Sx;
2) » 0,2 < х < 0,5, » S2-+S2;
3) » 0,5<лг<1, » S2-+T.
В последнем столбце таблицы 79 помещены значения случайной
величины Xv вычисленные по формуле F). Отсюда
хг=МХг& 1B0-0,7 + 0,7 + 4.1,1) -0,96.
Аналогично вычисляется неизвестное лг2.
Заметим, что точные корни системы A2) суть хг = \ ил;2 = 1.
Для решения алгебраических линейных уравнений по методу
Монте-Карло используются также другие способы [11].
Литература к семнадцатой главе
1. Е. С. В е н тце л ь,Теория вероятностей, Физматгиз, M.t 1958, гл. I — VI
2. Б. В. Гнеденко, Курс теории вероятностей, Гостехиздат. М.—Л.,
1950, гл. I —VI,
3. А. С. Хаусхолде р, Основы численного анализа, ИЛ,М., 1956, гл. VIII.
4. В. Э. Мил н. Численное решение дифференциальных уравнений.
Приложение В, ИЛ, М., 1955.
б, Ю. А. Шрейдер, Метод статистических испытаний (Монте-Карло),
~ Приборостроение, №7 A956).
6. Современная математика для инженеров. Под ред. Э. Ф. Беккенбаха,
ИЛ, М., 1958. Дж. В. Браун, Методы Монте-Карло.
7. Ф. М. Морз и Дж. Е. Кимбел л, Методы исследования операций,
Сов. радио, М., 1956, гл. VI, § 4.
8. М. Кадыров, Таблицы случайных чисел, Изд. Среднеазиатского гос.
ун-та, Ташкент, 1936.
А. И.
9. А. И. Китов и Н. А. Криницкий, Электронные цифровые
машины и программирование, Физматгиз, М., 1959, гл. VIII.
10. Дейвис, Рабинович, Опыты по вычислению кратных интегралов
методом Монте-Карло. Реферативный журнал (математика) № 2 A957),
1835.
11. Ю. А. Шрейдер, Решение систем линейных алгебраических
уравнений по методу Монте-Карло. Вопросы теории математических
машин, сб. I, Физматгиз, М., 1958.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абрамова А. А. метод 449
Абсолютная погрешность 17
Аналитическая функция 86
Базис пространства 333
— — ортонормированный 339
Бернулли метод 195
— числа 64
Бесселя неравенство 212
— формула интерполяционная 522 , 623
Билинейная форма матрицы 376
Биортогональность 382
Бюдана—Фурье теорема 172
Вековое уравнение 368
Вековой определитель 403
Вектор матрицы собственный 367
— нулевой 329
— /г-мерный 329
Вектор-столбец 225
Вектор-строка 225
Вектор-функция 450
Векторы линейно зависимые 330
Величина обратная 101
Верные десятичные знаки 23
Вероятностная оценка погрешности 51
Действительные корни уравнения 159 ,
163 , 165. 167 , 169 , 180
Декарта теорема 174
Десятичные знаки верные 23
Детерминант матрицы 226 , 264 , 283 , 380а
402 , 403 , 421
Дефект матрицы 244
Диагональная матрица 225
— таблица разностей 501
Дифференцирование графическое 574
— приближенное 562
— численное 571—573
Дроби подходящие 56 , 57
— — , закон составления 57
Дробь рациональная 79
— цепная 53 , 54
— — бесконечная 64 и д.
— — — расходящаяся 64
— — — сходящаяся 64
— — , звено 53
— — конечная 53 !
Единичная матрица 226
Единственность корня системы нелиней*
ных уравнений 466
— — уравнения 113
— решения системы нелинейных
уравнений 466
Гавурина М. К. метод 449
Гамильтона—Кели тождество 3S9
Гаусса метод 268 , 272
— формула интерполяционная 520
— — квадратурная 600
Герона процесс 104
Главная строка 282
Главный элемент 268 , 282 ,
Горизонтальная таблица разностей 501
Горнера схема 74
— — обобщенная 77
Границы действительных корней 165 , 167
Графическое дифференцирование 574
— интегрирование 624
— решение уравнения 116
Гурвица теорема 398
— условия 397
Гюа теорема 175
Цанилевского метод 403 , 404 , 410 , 411 , 421
Датчики случайных чисел 638
Двойной пересчет 607
Двойные разности высших порядков 557
Действительная матрица 381
Задача теории погрешностей обратная 43
Закон распространения ?-ошибки в таб»
лице конечных разностей 503
— цепи 652
Звено цепной дроби 53
Зейделя метод 268 , 303
— процесс 151
Знаки верные 25
Значения собственные матрицы 421 , 431
— — — , свойство экстремальное79
Интеграл несобственный 618
— — расходящийся 619 , 620
— — сходящийся 619 , 620
— собственный 618
Интегралы кратные , метод Монте-Карло
641
Интегрирование 577
— графическое 624
Интерполирование в узком смысле 538
— вперед 517
— на середину 523
— назад 517
— квадратичное 510

660
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Интерполирование линейное 510
— обратное для случая неравноотстоящих
узлов 550
— — — — равноотстоящих узлов 547
— параболическое 510
— функций 507
— — двух переменных 555
Интерполяционная формула — см.
Формула интерполирования
Итерация 100. 135 , 268 , 294
Лежандра полиномы 597
Линейная зависимость векторов 330
— комбинация векторов 330
— система 306
Линейное векторное пространство 329
— подпространство 334
— преобразование 359
Лобачевского—Граффе метод 176
Логарифмическая функция 92
Люстерника метод 444
Каноническая норма матрицы 239
Канторовича Л. В. метод 621
Квадратичная форма 305
Квадратная матрица 225
Квадратный корень 104
Квадратура механическая 577
Квадратурная формула 578
Квадрирование корней 179 , 180 , 181
Квазидиагональная матрица 252
Клеточная матрица 252
Комбинация линейная векторов 330
Комбинированный метод 132
Комплексные корни 158
Конечно-разностное уравнение 195
Конечные разности 497
— — второго порядка 206
— — первого порядка 206
— — порядка р 207
Контроль вычислений заключительный 15
— — текущий 15
Конформные матрицы 253
Корень квадратный 104
— — , обратная величина 108
«— кубический 108
— полинома действительный 169
— системы линейных уравнений 269
— уравнения 112
Корни линейной системы , уточнение 279
— уравнения в групповом смысле 186
— — действительные 159 , 163 , 165 , 167 ,
169 , 180
— — комплексные 158 , 183 , 186 , 190
— — — , пара комплексных корней 186
— — — , случай двух пар 190
— — кратные 158
— — , отделение 112
— — отделенные 176
Косинус 95
— гиперболический 98
Косинусы направляющие 342
Котеса квадратурная формула 580
— коэффициенты — см. Коэффициенты
Котеса
Коэффициенты Котеса 581 , 586
— Лагранжа 531
— Фурье 210
Крамера правило 268
— формулы 271
Кратность корня 158
Кратные интегралы 641
— корни 158
Кронекера символ 226
Крылова А. Н. метод 213 , 412 , 421
Кубатура механическая 574
Кубический корень 108
Куммера преобразование 199
Лагранжа коэффициенты 531
— теорема 164
.—- формула интерполяционная 529 , 535
Леверрье метод 417
Маклорена ряд 86
Маркова формула 553
— цепь 652
Матриц равенство 226
— сумма и разность 227
— умножение 228
Матрица 225
— , величина (модуль) 238
— действительная 38i
— диагональная 225
— единичная 226
— квадратичной формы 305
— квадратная 225
— квазидиагональная 252
— клеточная 252
— неособенная 232
— , норма 238 , 239
— нулевая 226
— обратная 231
— — , уточнение 310
— окаймленная 252
— ортогональная 342
— особенная (сингулярная) 232
— перехода к новому базису 340
— , предел 245
— присоединенная 232
— противоположная 228
— прямоугольная 225
— , ранг 244
— , рациональная функция 237
— симметрическая 231 , 376
— — положительно определенная 380
— сингулярная — см. Матрица
особенная
— , степень 236
— транспонированная 230
— треугольная 260
— , умножение на число 227
— Фробениуса 404
— характеристическая 368
— , элементарное преобразование 263
— Якоби 451
Матрицы конформные 253
— подобные 372
— равные 226
— эквивалентные 263
Матричный ряд 247
Медленная сходимость ряда 199
Метод Абрамова А. А. 449
— Бернулли 195
— Гавурина М. К- 449
— Гаусса 268 , 272 , 283
— главных элементов '268 , 281
— градиента — см. Метод скорейшего
спуска
— границ 48 , 49
— Данилевского развертывания векового
определителя 403. 404 , 410 , 411 , 421
— двойного пересчета 607
— Зейделя 268 , 303
— знакопеременных сумм 165
— интерполяции развертывания векового
определителя 403. 421 , 553

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
661
Метод исчерпывания 434
— итерации 100 , 135 , 268 , 294
— — для системы двух уравнений 148
— — — — нелинейных уравнений 474
— Канторовича Л. В. выделения
особенностей 621
— касательных — см. Метод Ньютона
— квадратных корней 268 , 289
— комбинированный 132
— Крылова А. Н. 213 , 412 , 421
— — развертывания векового
определителя 403 , 421
— — , собственные векторы матрицы 416
— — улучшения сходимости
тригонометрических рядов Фурье 213
— Леверрье 417
— — развертывания векового
определителя 403 , 421
— Лобачевского—Греффе 176
— — — для случая действительных
корней 180
—• — — — — комплексных корней 183
— Люстерника улучшения сходимости
процесса итерации для решения
системы линейных уравнений 444
— Монте-Карло 635
— — вычисления кратных интегралов
— — , решение систем линейных
уравнений 650
— неопределенных коэффициентов 419
— Ньютона 123 и д. , 167
— — видоизмененный 131 ид.
— — для системы двух линейных
уравнений 152
— — — случая комплексных корней
153
— — решения систем нелинейных
уравнений 450 , 452
— — — — — — модифицированный
472 и д.
— обратного интерполирования для
решений уравнений 551
— окаймления 258
— ослабления — см. Метод релаксации
— половинного деления 118
— последовательных приближений — см.
Метод итерации
—- релаксации 268 , 307
— Ричардсона 314
— скалярных произведений 428
— скорейшего спуска для решения
системы линейных уравнений 490
— — — — — — нелинейных уравнений
(метод градиента) 485
— степенных рядов для решения системы
нелинейных уравнений 494
— Штурма 169
— хорд 119
— Эйлера-—Абеля 205
— эскалаторный 314
Механическая квадратура 577
— кубатура 577
Минор матрицы 244
Модуль матрицы 238
Монте-Карло метод 635
Направляющие косинусы 342
Начальная погрешность 21
Невязка приближенного решения 279
Неособенная матрица 232
Неподвижная точка преобразования 478
Неполное частное цепной дроби 54
Несобственный интеграл 618
Норма матрицы 1238
— — каноническая 239
Нормальные системы линейных
уравнений 310
Нулевая матрица 226
Ньютона метод — см. Метод Ньютона
— теорема 167
— — интерполяционная 510 , 515
— — квадратурная 580 , 586
Обратная величина 101
— задача теории погрешностей 43
— матрица 231
Обратное интерполирование 547 , 550
— преобразование 365
Обращение матрицы 232 , 255 , 442
~ — методом Гаусса 285
Окаймленная матрица 252
Округление 24
Определитель 226 , 264 , 283
— вековой (характеристический) 380 ,
402
_ __ , развертывание 403 , 421
Ортогонализация матриц 343
— столбцов 351
Ортогональная матрица 342
— система векторов 338
Основная теорема алгебры 158
Особенная матрица 232
Остаток ряда 80
Остаточная погрешность 21
Отделение корней уравнения 112 ид.
Относительная погрешность 49
Отображение сжимающееся 478
Отрицательно определенная квадратичная
форма 305
Оценка погрешности вероятностная 51
— — процесса Зейделя 323 , 325
— — _ итераций 315
Оценки коэффициентов Фурье 211
Ошибка приближенного числа 17
Параболическая формула 589
Переход к новому базису 340
Переходные вероятности 652
Перрона теорема 382
Плотность вероятности 636
Погрешность абсолютная 17
— — разности 33
— — суммы 31
— действий 15
— задачи 20
— интерполяционных формул Ньютона
537
— __ — Лагранжа 535
— квадратурных формул 604
— метода 16 , 20
— начальная 21
— округления 15 , 21 , 24
— остаточная 21
— относительная 19 , 25
— — корня 39
— — произведения 35
— — степени 39
— — частного 38
— предельная 19
— — практическая 51
— приближений итерационных 138 , 317
— — процесса Зейделя 322 , 325
— произведения 35
— разности 33
— суммы 31

662
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Погрешность суммы относительная 28 , 29 ,
— формулы квадратурной 606
— центральных интерполяционных
формул 539
— частного 38
Подобие матриц 372
Подпространство линейное 334
Подходящие дроби 56 , 57
— — , закон составления 57
Показательная функция 88
Полином 74
— интерполяционный Лежандра 597
— — Ньютона 509
— характеристический матрицы 368
Половинное деление 118
Положительно определенная квадратичная
форма 305
— — матрица 380
Порядок матрицы 225
Правило Крамера 268
— трех восьмых 586
Предел последовательности матрицы 245
Предельная погрешность 19
Преобразование вращения 362
— Куммера 199
— линейное 359
— матриц 263
— обратное 365
— проектирования 361
— Эйлера—Абеля 206
Приближенное вычисление частных
производных 576
— число 17
Принсгейма матрица 68
Принцип аргумента 162
— равных влияний 43
Присоединенная матрица 232
Произведение вектора на число 330
— векторов скалярное 336
— матриц 227 , 228 , 253
Пространство линейное векторное 330
— решение однородной системы 356
Противоположная матрица 228
Процесс Герона 104
— Зейделя 151
Прямоугольная матрице 225
Равенство матриц 226
Развертывание вековых определителей
402 и д.
Разделенные разности 542
— — , таблица 543
Разложение в цепную дробь рациональной
функции 71
е* 72
tg* 72
— матрицы билинейное 384
Размерность пространства 332
Разности конечные 497
— — второго порядка 206
— — двойные высших порядков 557
_ __ первого порядка 20о
— — разделенные 542
— — центральные , таблица 519
— __ частные 557
_ _ р-го порядка 207
Разность матриц 227 , 253
Ранг матрицы 244
Рациональная дробь 79
— функция матрицы 237
Релаксация 268 , 307
Решение конечно-разностного уравнения
195
Решение уравнений графическое 1*6
и д.
Ричардсона метод 314
— экстраполяция 609
Ряд Маклорена 86
— матричный 225 , 247 , 249
— Тейлора 86
— тригонометрический 247
— числовой 80
— — сходящийся 80
Сжимающееся отображение 478
Символ Кронекера 229
Симметрическая матрица 231 , 376
Симметрия эрмитова 336
Симпсона формула 584
— — общая 58
Сингулярная матрица 232
Синус 95
— гиперболический 98
Система векторов ортогональная 338
— двух уравнений 152
— линейная нормальная 306
— линейных уравнений , корни 269
— — — , метод Монте-Карло 650
— — ^- , методы точные 268
— нормальная 310
Скалярное произведение векторов 336
Скорость сходимости процесса Ньютона
для системы 465
—. уравнения 128
След матрицы 360
Случайная величина 635
Случайные числа 635
— — , способ получения 638
Собственное значение матрицы 367
— — — второе 431
_ __ _ первое 421
Собственные векторы , метод Данилевского
— _ , — Крылова 416
— значения матрицы 421 , 431
— — — , свойство экстремальное 379
— элементы положительно определенной
симметрической матрицы 437
Собственный вектор матрицы 367
— интеграл 618
Соотношения биортогональности 362
Спектр матрицы 369
Степенной ряд (ряд Тейлора) Ы
— ¦*- матричный 386
Степень матрицы 236
— обобщенная 505
Стирлинга формула дифференцирования
567
— — интерполяционная 521
Строка главная 282
Сумма векторов 329
—матриц 227 , 253
— матричного ряда 247
— числового ряда 80
Суммирование приближенное
тригонометрических рядов 222
Схема вычислительная 13
— Горнера 74
— — обобщенная 77
— единственного деления 274
— — — , таблица 275
— Халецкого 291
Сходимость процесса Зейделя 320 , 322 ,
326 , 392
— — — для нормальной системы
линейных уравнений 395
— — итерации 136 и д.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
663
Сходимость процесса итерации для систем
линейных уравнений 315 , 390
— — — — — нелинейных уравнений
481 , 483
— — Ньютона для систем нелинейных
уравнений 456 , 460 , 465 , 469
— — — , скорость 128 , 465
— — — , устойчивость 469
— ряда матричного 247 , 386
— — — абсолютная 247
Таблица конечных разностей функции
j/=lg* 516
— предельной относительной
погрешности (определение по числу верных
знаков) 29
— разностей горизонтальная 501
— — диагональная 501
— — разделенных 543
функции у=гех 511
— — —. #=sin х 517
— распространения е-ошибки в таблице
конечных разностей 503
— центральных разностей 519
— числа верных знаков в зависимости от
предельной относительной погрешности
30
Тангенс 96
— гиперболический 99
Тейлора ряд 86
Текущий контроль вычислений 115
Теорема Бюдана—Фурье 172
— Гурвица 398
— Гюа 175
— Декарта 174
— Ньютона 167
— основная алгебры 158
— Перрона 382
— Принсгейма 68
— Штурма 170
Тождество Гамильтона—Кели 389
Точка неподвижная преобразования 478
Транспонирование матрицы 230
Трансцендентные функции матрицы 217
Треугольная матрица 260
Тригонометрические ряды 222
Узлы интерполирования 507 , 541
Улучшение сходимости ряда 86 , 199
— — — степенного методом Эйлера —
Абеля 205
— — — Фурье методом Крылова 213
Уравнение вековое 368
— конечно-разностное 195
— — .решение 195
— матрицы характеристическое 195 , 368
Условие сходимости процесса Зейделя
второе 322
— — — — первое 320
— — — — по /-норме 326
Условия Гурвица 397
Устойчивость сходимости процесса
Ньютона при варьировании начального
приближения 469
Уточнение корней линейной системы
279
— обратной матрицы 310
Формула интегрирования Эйлера—Мак«
лорена 616
— интерполирования квадратичного 510
— — Бесселя 522
— — — квадратичная 523
— — — на середину 523
— — Гаусса вторая 520
— — — первая 521
— — Лагранжа 529
-— — — , оценка погрешности 535
— — линейного 510
— — Ньютона вторая 515
— — — для значений аргумента
неравноотстоящих 546
— — — для функции двух переменных
559
— — — , оценка погрешности 538
— — — первая 509 , 510
— — —.— , дифференцирование 563
— — — — , оценка погрешности 538
— — —с разделенными разностям»
546
— — параболического 510
— — Стирлинга 521
— квадратурная 578
— — Гуасса 600
— — Котеса 580
— — Ньютона 580 , 586
— — Чебышева 593
— кубатурная 627
— — типа Симпсона 629
— Маркова , \. А. 553
— параболическая 589
— погрешности общая 41
— Симпсона 584
— — общая 589
— — , остаточный член 585
— Стирлинга , Дифференцирование 567
— трапеций 582
— — общая 588
— — , остаточный член 588
Формулы дифференцирования
центральные 567
— — численного 571
— интерполяционные с постоянным
шагом 525
— — с центральными разностями 519
— Крамера 271
— Ньютона — Котеса 581
— — — высших порядков 586
Фробениуса матрица 404
— нормальный вид опеределителя 404
Функции матрицы рациональные 237'
— — трансцендентные 251
Функция двух переменных 555
— , заданная таблицей 46
— интерполирующая 507
— матричная 456
—- распределения 636
— утГ 88
— y=\gx 92 , 516
— р—sin к 517
Фурье коэффициенты 210
Халецкого схема 291
Характеристический определитель
матрицы 380
— полином матрицы 368
Характеристическое уравнение 195
Форма квадратичная 305
— матрицы билинейная 370
Центральные формулы дифференцировав
ния 567

664
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Цепная дробь 53 , 54
— — бесконечная 64
— — — расходящаяся 64
— — — сходящаяся 64
— — , звено 53
— — конечная 53
Цепь Маркова дискретная 652
Цифра значащая 22
— сомнительная 25
Частное неполное цепной дроби 54
Частные производные 575
— разности 557
Чебышева формула квадратурная 593
Числа случайные 635 , 638
Численное дифференцирование 571
Число Бернулли 64
— вер них знаков произведения 37
— — — частного 39
— действительных корней полинома 169
— перемен знаков системы чисел верхнее
172
— — — — — нижнее 172
— приближенное 17
— — , погрешность 17
— характеристическое 367
Числовой ряд 80
Член й-го звена цепной дроби 53
Шаг интерполяции 508
Штурма метод 169
— теорема 170
Эйлера — Абеля метод 205
— — — преобразование 206
Эйлера— Маклорена формула
интегрирования 616
Эквивалентность матриц 263
Экстраполяция Ричардсона 609
— — для случая формулы трапеций 609
— — формулы Симпсона 610
Экстраполирование 508
— вперед 517
— назад 517
Экстремальное свойство собственных
значений матрицы 379
Элемент главный 268 , 282
— матрицы 225
Элементы собственные положительно
определенной симметрической матрицы
437
Эрмитова симметрия 336
Якоби матрица 451