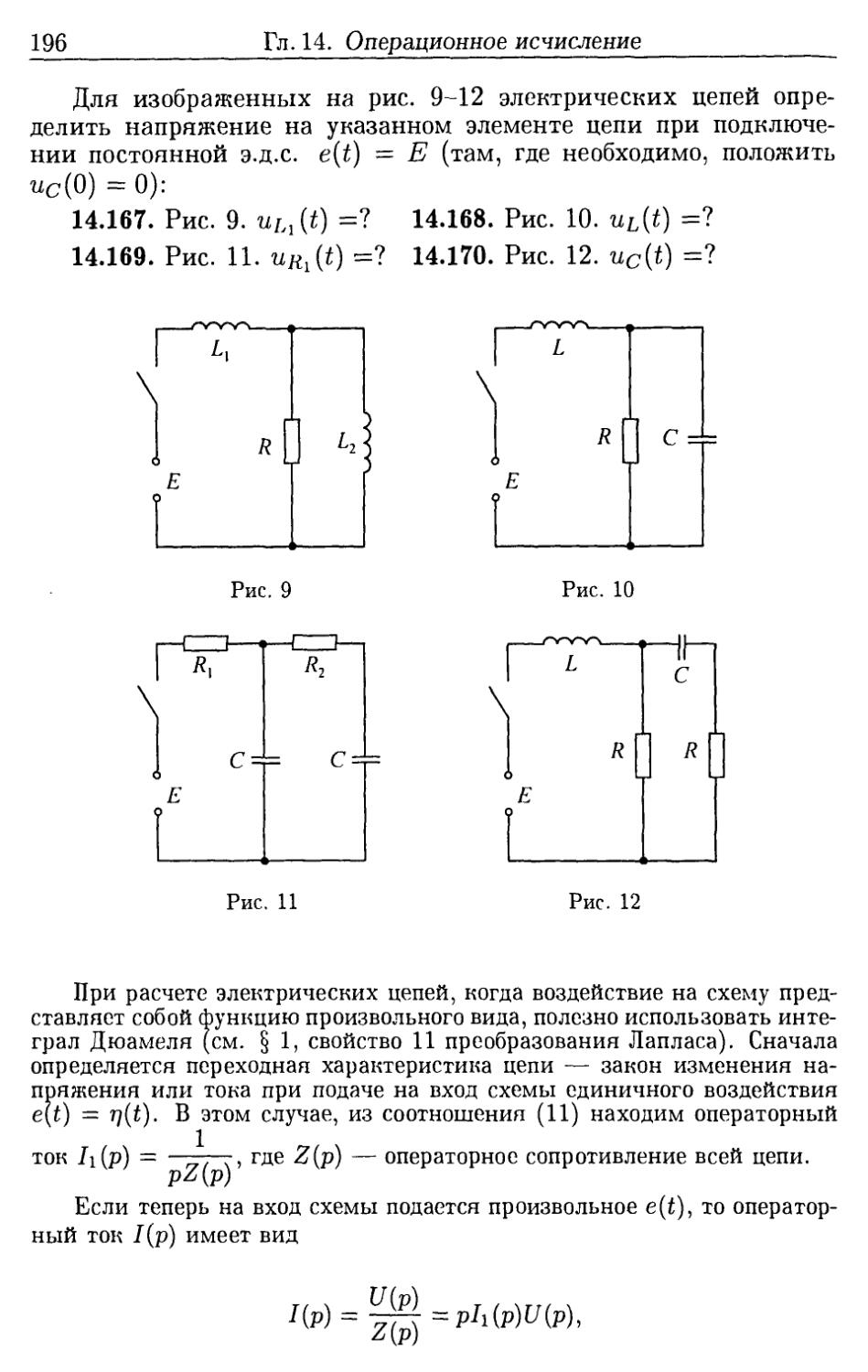
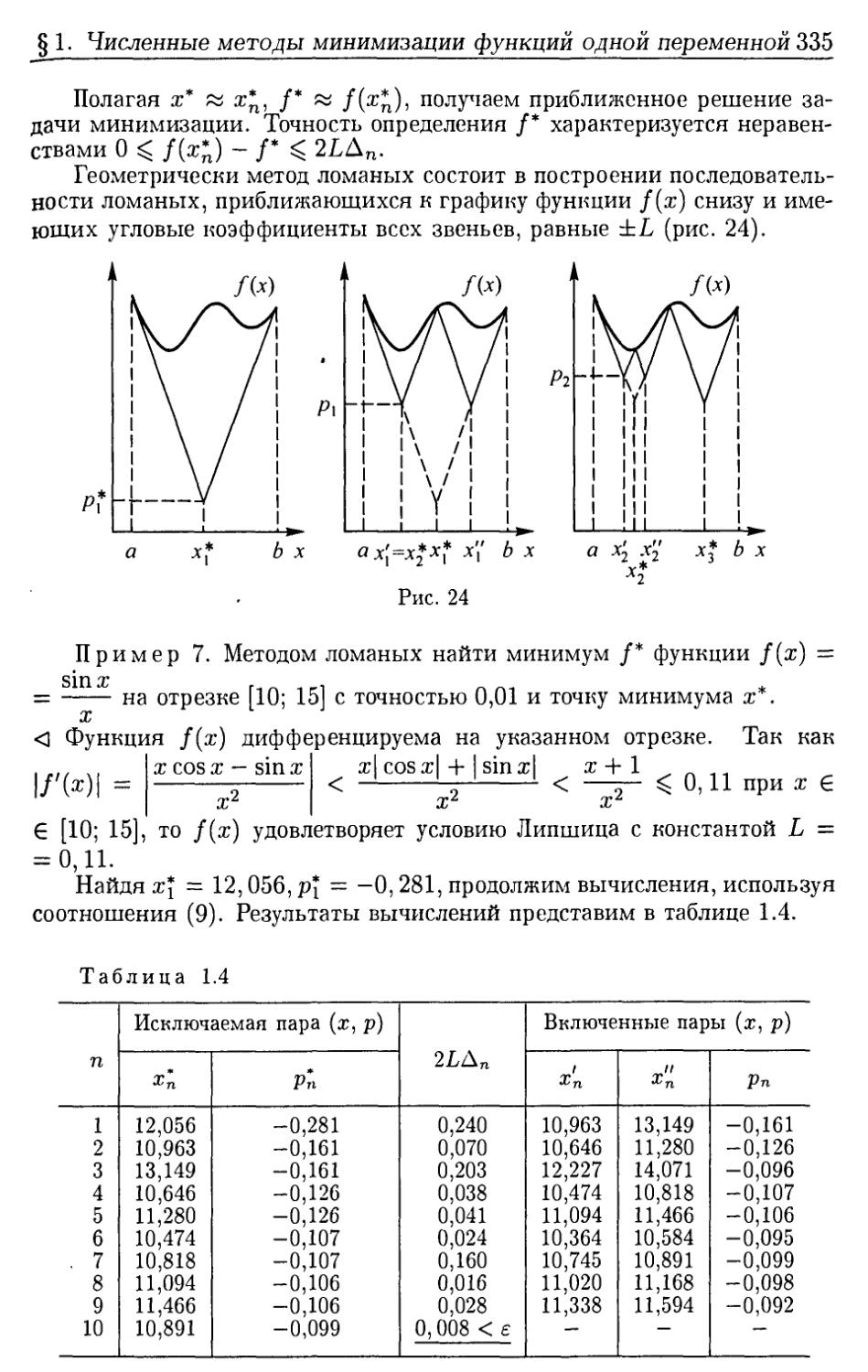
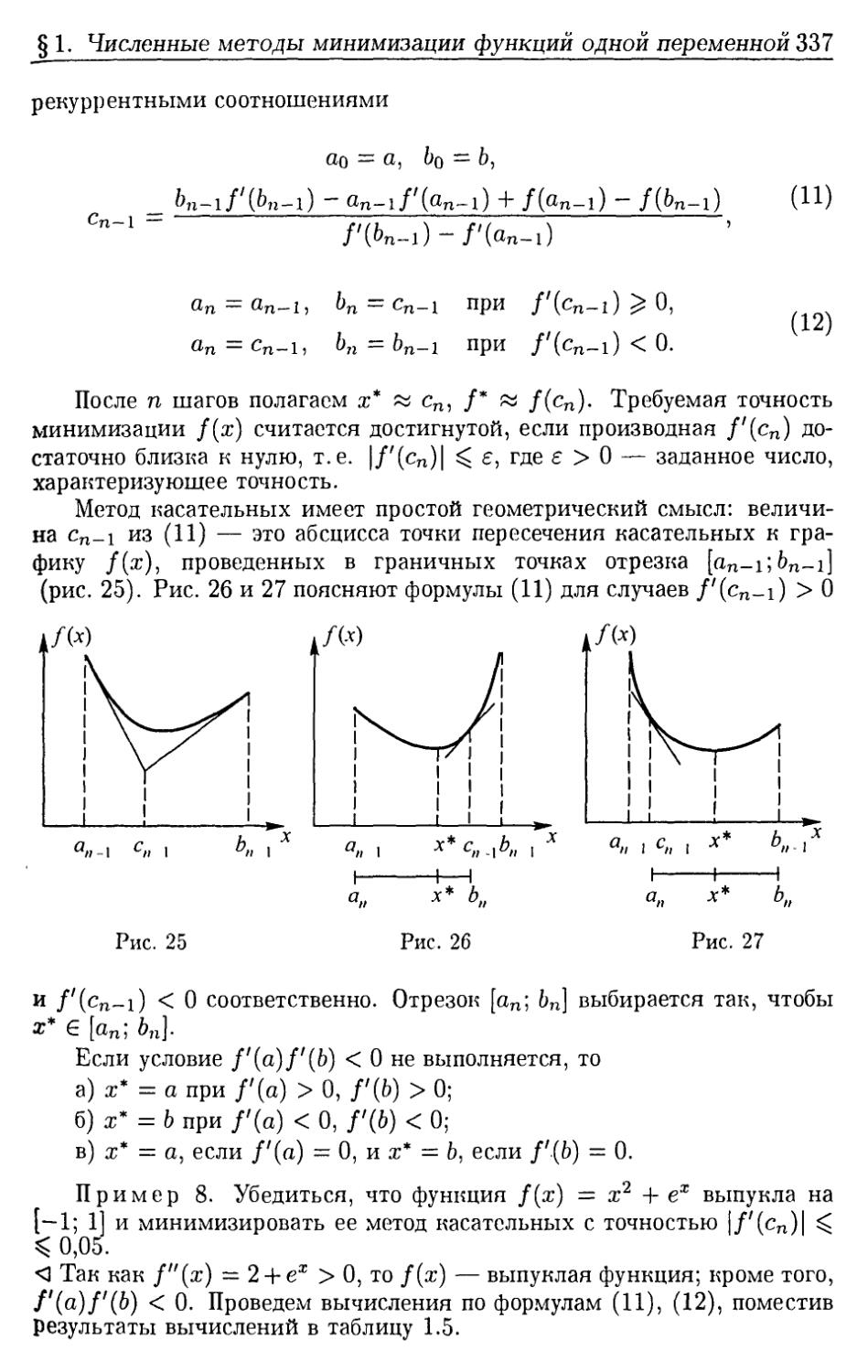
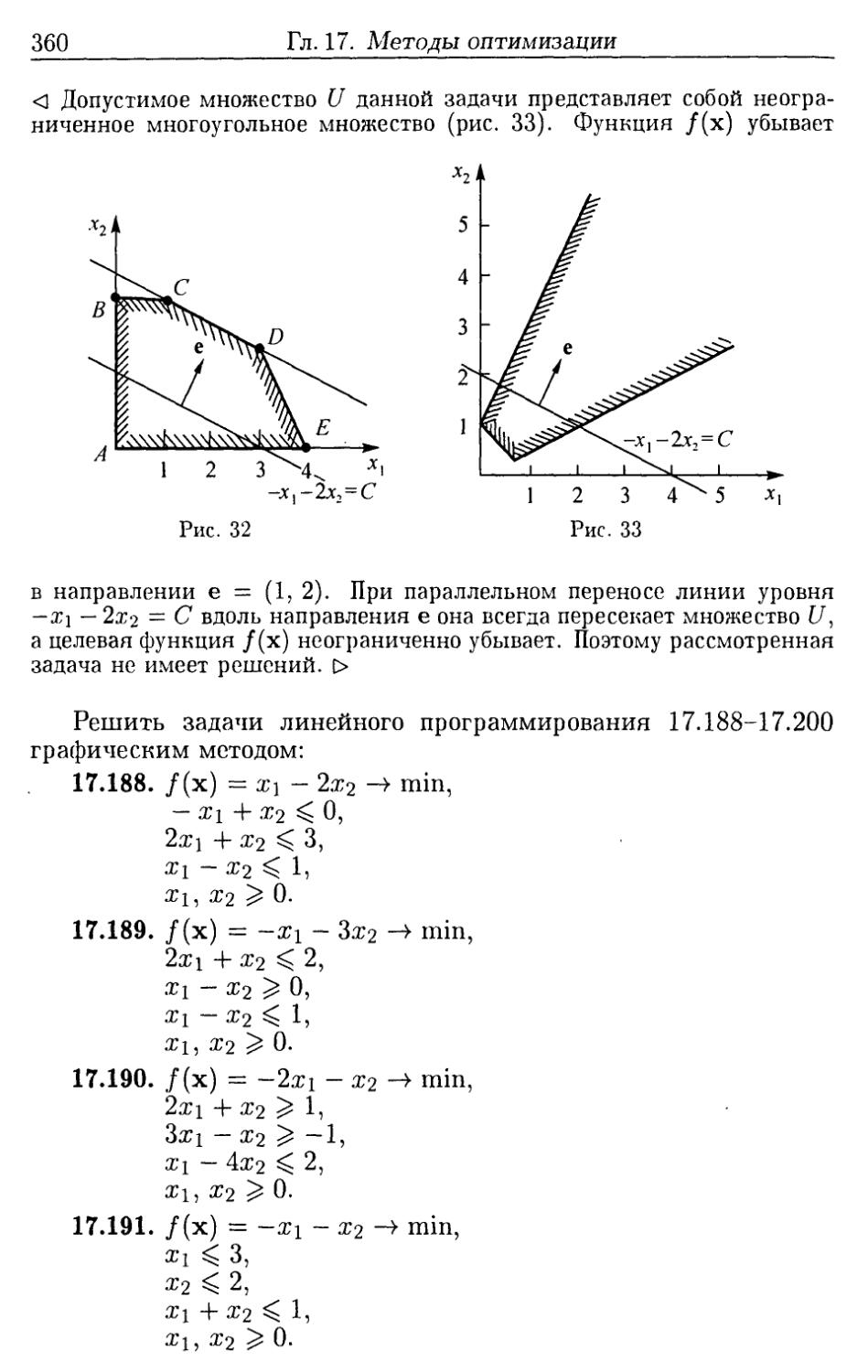
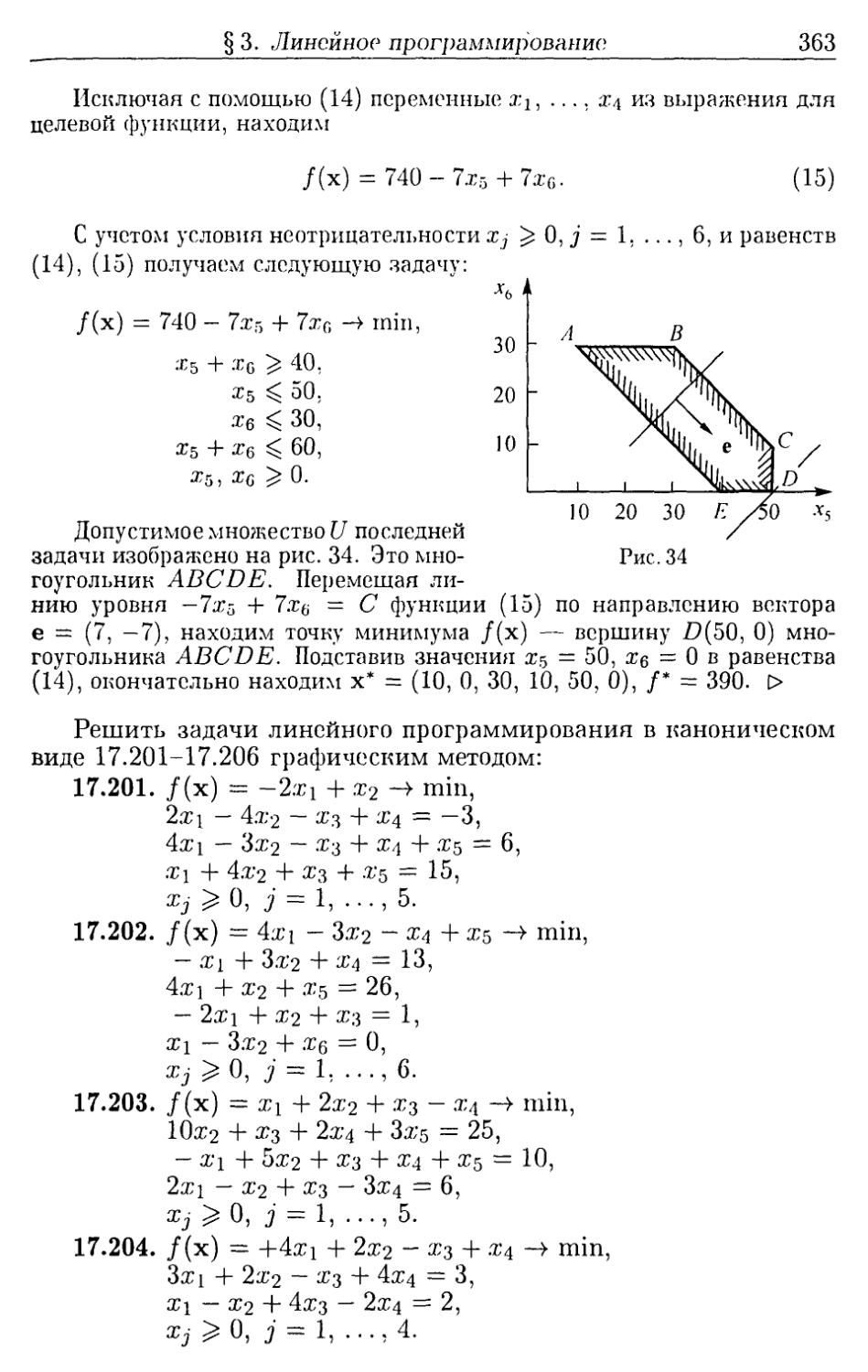
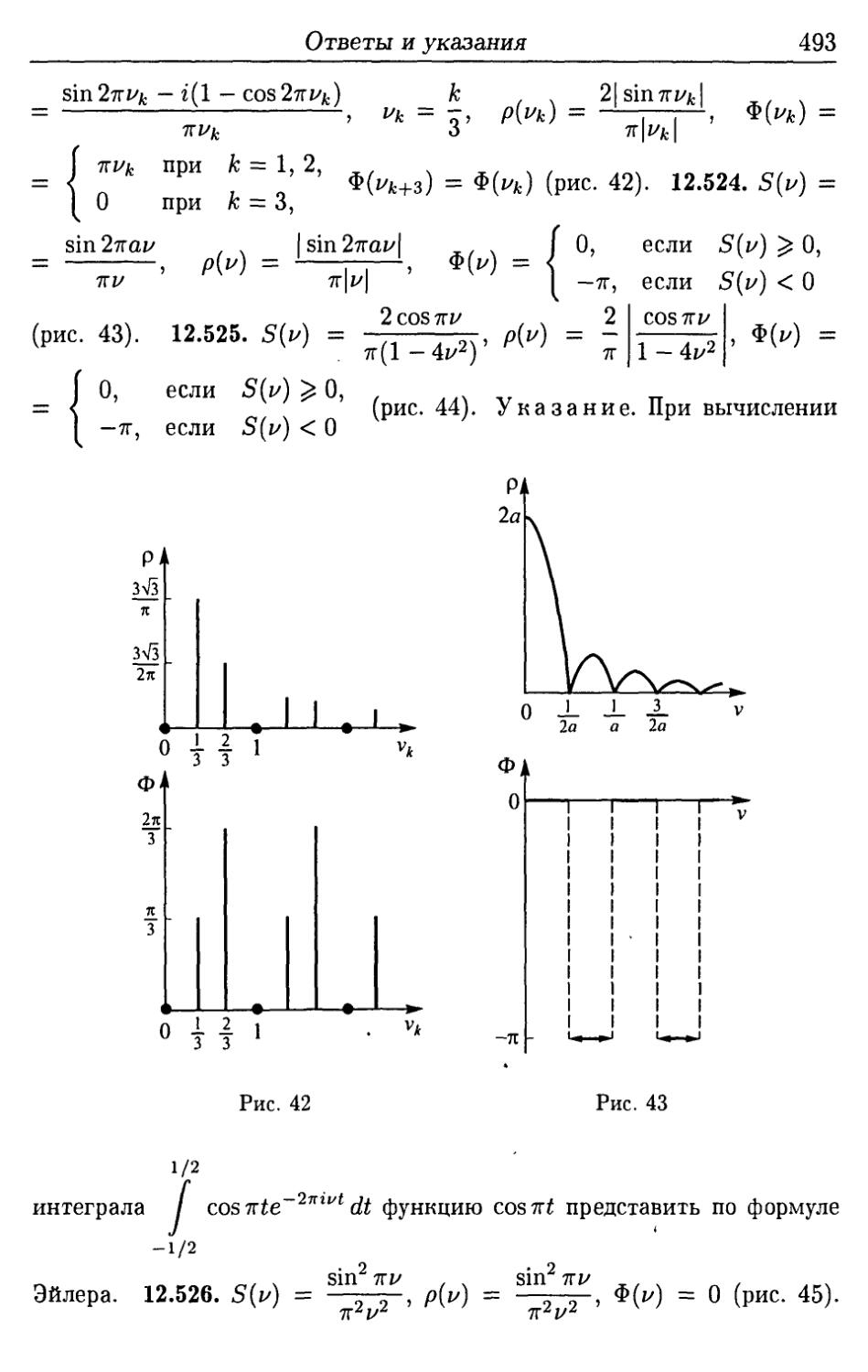
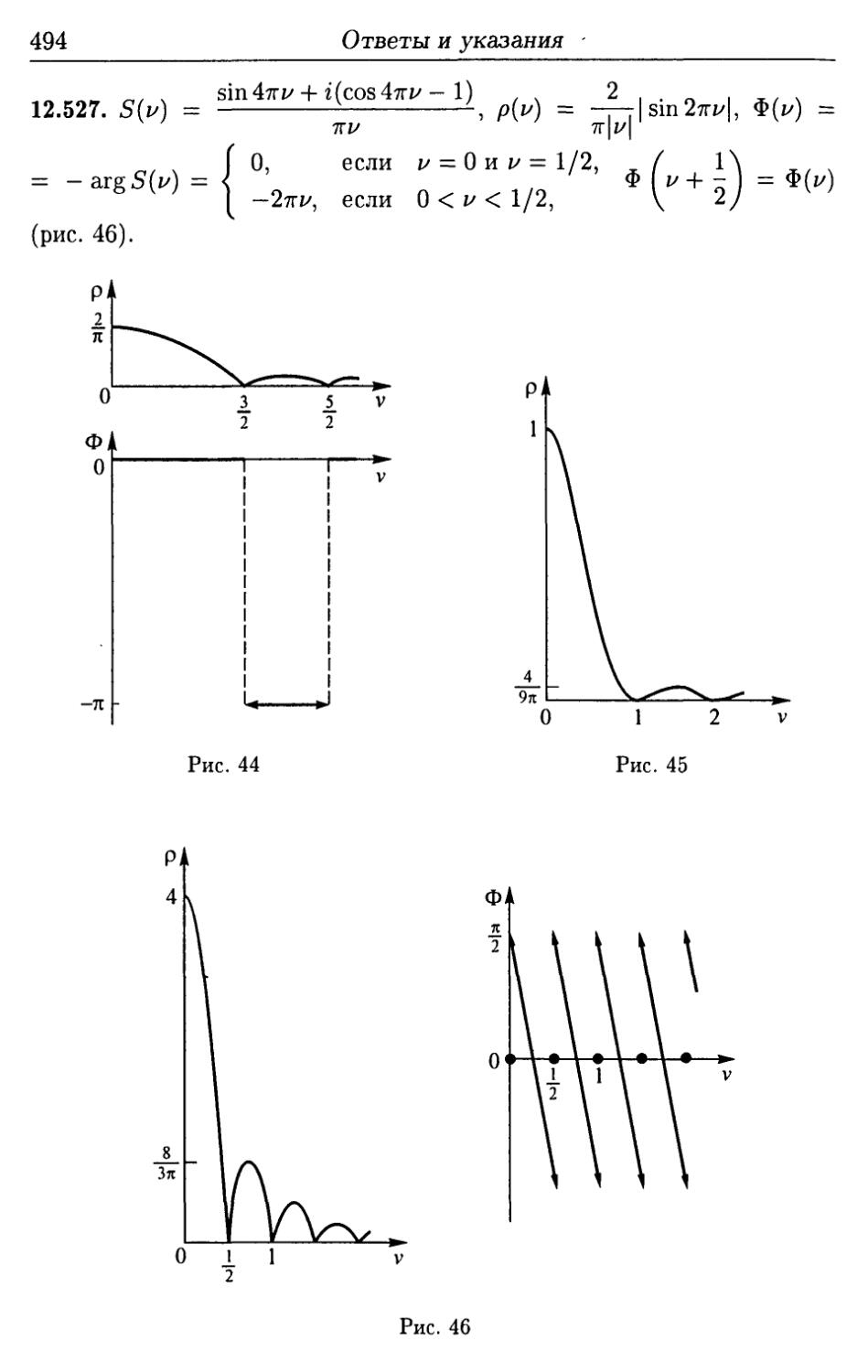
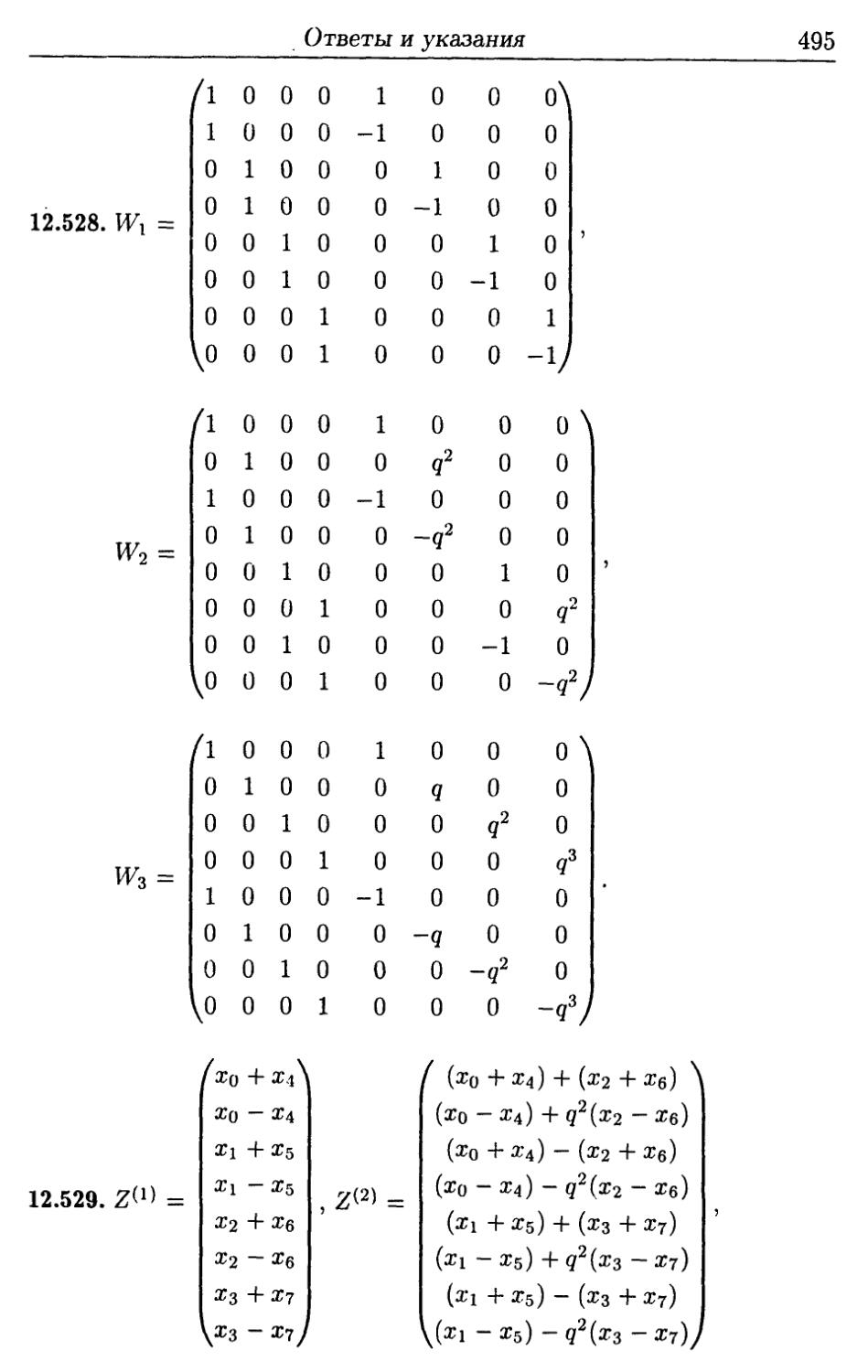
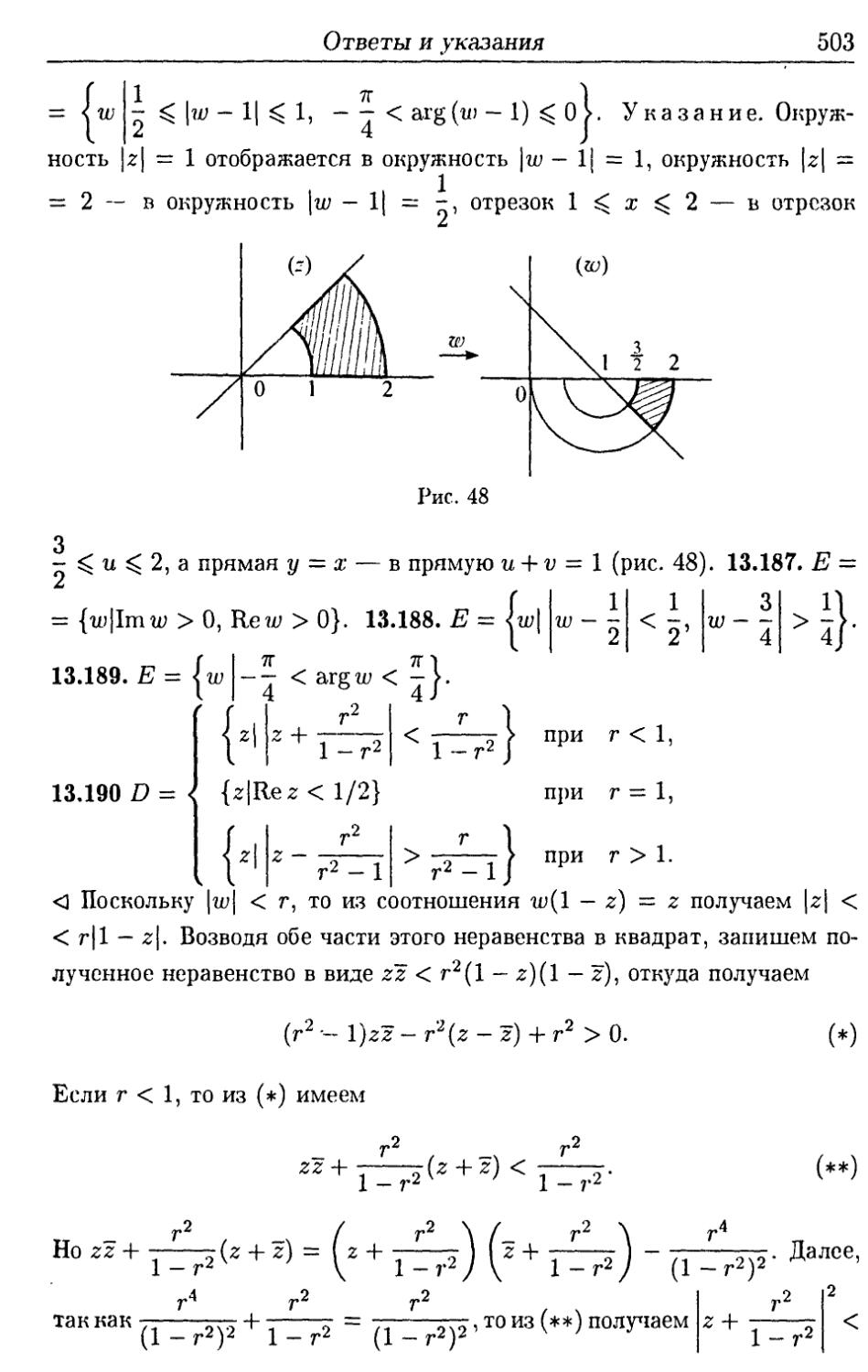
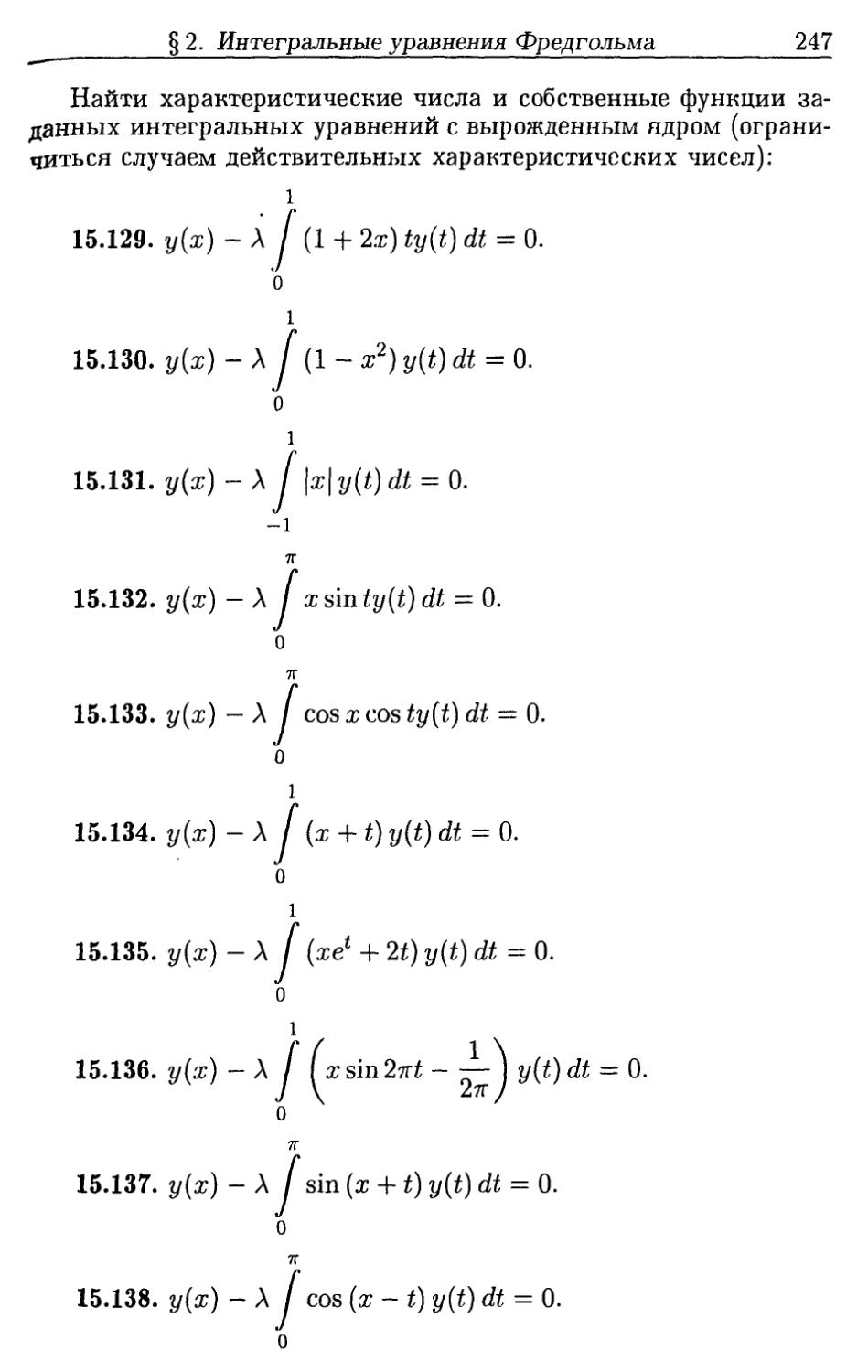Author: Ефимова А.В. Поспелова А.С.
Tags: математика задачи по математике
ISBN: 5-9405-036-7
Year: 2002
Text
СБОРНИК ЗАДАЧ ПО МАТЕМАТИКЕ
ДЛЯ ВТУЗОВ
3
Под редакцией А. В, Ефимова и А. С. Поспелова
Москва
Издательство
Физико-математической литературы 2002
ББК 22.1
С 23
УДК 51(075.8)
Коллектив авторов:
А. В. ЕФИМОВ, А. Ф. К АРАКУЛИН, А. С. ПОСПЕЛОВ,
С. В. ФРОЛОВ, В. В. ЛЕСИН
Сборник задач по математике для втузов. В 4 частях. Ч. 3: Учебное пособие для втузов / Под общ. ред. А. В. Ефимова и А. С. Поспелова. — 4-е изд. перераб. и доп. —М.: Издательство Физико-математической литературы, 2002.—576 с.—ISBN 5-94052-036-7 (Ч. 3).
Содержит задачи по специальным разделам математического анализа, которые в различных наборах и объемах изучаются в технических вузах и университетах. Сюда включены такие разделы, как векторный анализ, ряды и их применение, элементы теории функций комплексной переменной, операционное исчисление, интегральные уравнения, уравнения в частных производных, а также методы оптимизации. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения.
Для студентов высших технических учебных заведений.
Учебное издание
ЕФИМОВ Александр Васильевич, КАР АКУЛИН Анатолий Федорович, ПОСПЕЛОВ Алексей Сергеевич, Фролов Сергей Васильевич, ЛЕСИН Виктор Васильевич
СБОРНИК ЗАДАЧ ПО МАТЕМАТИКЕ ДЛЯ ВТУЗОВ
Часть 3
Редактор Л. А. Панюшкина
Корректор Т. С. Вайсберг
Компьютерная графика М. Н. Грицук
Компьютерный набор и верстка Е. А. Митченко
ИД №01389 от 30.03.2000
Гигиеническое заключение № 77.99.02.953.Д.003724.07.01 от 05.07.2001
Подписано в печать 29.08.2002. Формат 60x88/16.
Печать офсетная с готовых диапозитивов.
Усл. печ. л. 36. Уч.-изд. л. 40,7. Тираж 7000 экз.
Заказ № 4086.
Издательство Физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Отпечатано в полном соответствии с качеством предоставленных диапозитивов на ГИПП «Вятка»
610033 г. Киров, ул. Московская, 122
ISBN 5-94052-036-7 (Ч..З)
ISBN 5-94052-033-2
© Коллектив авторов, 2002
© Физматлит, оформление, 2002
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ ТИТУЛЬНЫХ РЕДАКТОРОВ ........................... 7
ОТ АВТОРОВ ................................................. 8
Глава 11. Векторный анализ.................................. 9
§ 1. Скалярные и векторные поля. Градиент................ 9
1. Геометрические характеристики скалярных и векторных полей. 2. Производная по направлению и градиент скалярного поля
§ 2. Криволинейные и поверхностные интегралы............ 13
1. Криволинейный интеграл 1-го рода. 2. Поверхностный интеграл 1-го рода. 3. Криволинейный интеграл 2-го рода. 4. Поверхностный интеграл 2-го рода
§ 3. Соотношения между различными характеристиками скалярных и векторных полей................................. 28
1. Дивергенция векторного поля и теорема Гаусса-Остроградского. 2. Вихрь векторного поля. Теорема Стокса.
3. Оператор Гамильтона и его применение. 4. Дифференциальные операции 2-го порядка
§ 4. Специальные виды векторных полей................... 35
1. Потенциальное векторное поле. 2. Соленоидальное поле. 3. Лапласово (или гармоническое) поле
§ 5. Применение криволинейных координат в векторном анализе .................................................... 41
1. Криволинейные координаты. Основные соотношения.
2. Дифференциальные операции векторного анализа в криволинейных координатах. 3. Центральные, осевые и осесимметрические скалярные поля
Глава 12. Ряды и их применение............................. 47
§ 1. Числовые ряды...................................... 47
1. Сходимость ряда. Критерий Коши. 2. Абсолютная и условная сходимость. Признаки абсолютной сходимости. 3. Признаки условной сходимости
4
Оглавление
§ 2. Функциональные ряды.................................... 61
1. Область сходимости функционального ряда. 2. Равномерная сходимость. 3. Свойства равномерно сходящихся рядов
§ 3. Степенные ряды......................................... 68
1. Область сходимости и свойства степенных рядов. 2. Разложение функций в ряд Тейлора. 3. Теорема единственности. Аналитическое продолжение
§4. Применение степенных рядов.............................. 80
1. Вычисление значений функций. 2. Интегрирование функпий.
3. Нахождение сумм числовых рядов. Убыстрение сходимости.
4. Интегрирование дифференциальных уравнений с помощью рядов. 5. Уравнение и функции Бесселя
§ 5. Ряды Лорана............................................ 93
1. Ряды Лорана. Теорема Лорана. 2. Характер изолированных особых точек
§ 6. Вычеты и их применение ............................... 100
1. Вычет функции и его вычисление. 2. Теоремы о вычетах и их применение к вычислению контурных интегралов. 3. Применение вычетов к вычислению определенных интегралов. 4. Принцип аргумента
§7. Ряды Фурье. Интеграл Фурье............................. 111
1. Разложение функций в тригонометрические ряды Фурье.
2. Двойные ряды Фурье. 3. Интеграл Фурье. 4. Спектральные характеристики ряда и интеграла Фурье. 5. Дискретное преобразование Фурье (ДПФ)
Глава 13. Теория функций комплексной переменной .............. 125
§ 1. Элементарные функции.................................. 125
1. Понятие функции комплексной переменной. 2. Основные элементарные функции комплексной переменной. 3. Предел и непрерывность функции комплексной переменной
§ 2. Аналитические функции. Условия Коши-Римана........... 134
1. Производная. Аналитичность функции. 2. Свойства аналитических функций
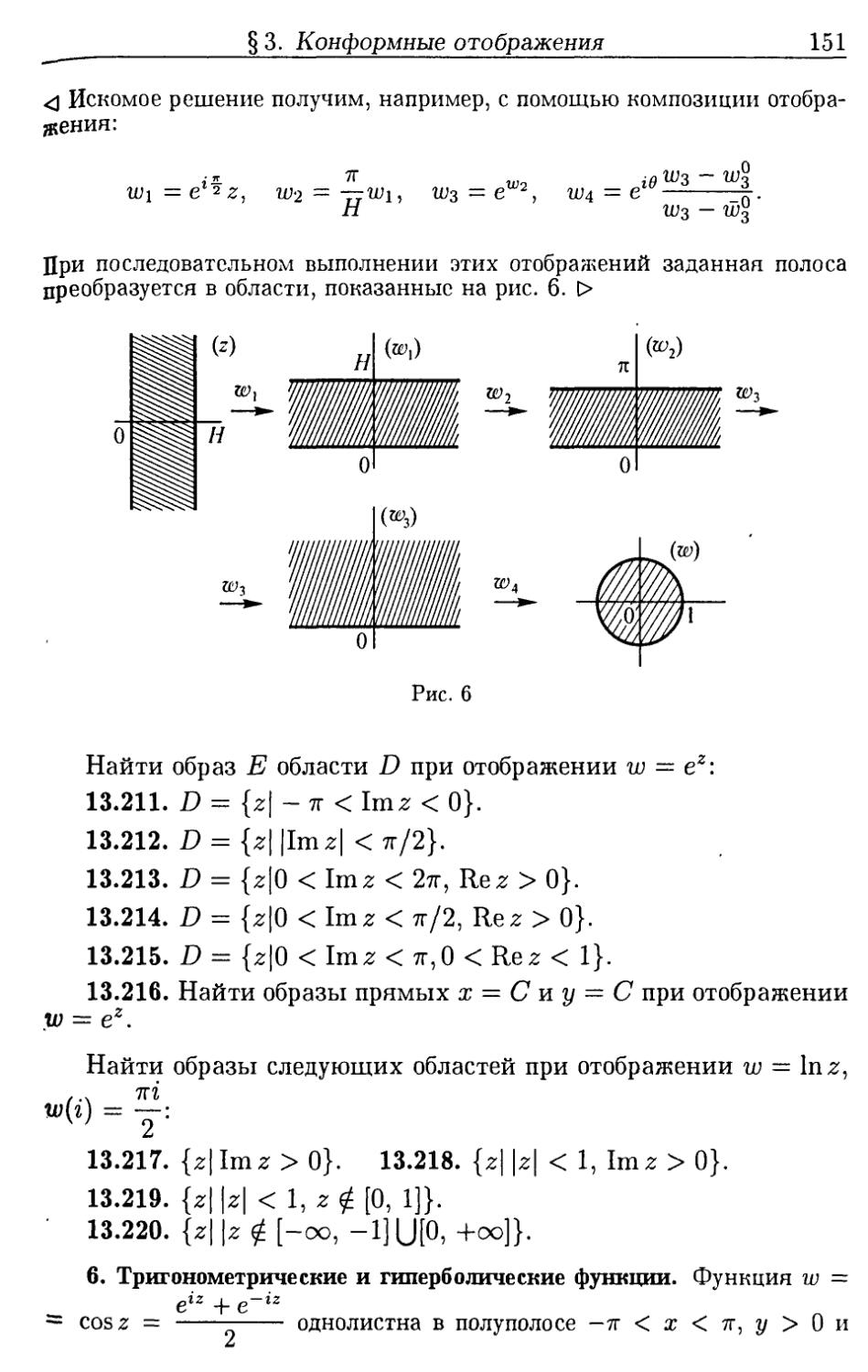
§ 3. Конформные отображения . . ....................... . . . 140
1. Геометрический смысл модуля и аргумента производной.
2. Конформные отображения. Линейная и дробно-линейная функции. 3. Степенная функция. 4. Функция Жуковского. 5. Показательная функция. 6. Тригонометрические и гиперболические функции
§4. Интеграл от функции комплексной переменной............ 152
1. Интеграл по кривой и его вычисление. 2. Теорема Коши.
Оглавление
5
Глава 14. Операционное исчисление ........................... 163
§ 1. Преобразование Лапласа............................... 163
1. Определение и свойства преобразования Лапласа. 2. Расширение класса оригиналов
§ 2. Восстановление оригинала па изображению ............. 172
1. Элементарный метод. 2. Формула обращения. Теоремы разложения
§ 3. Применения операционного исчисления.................. 179
1. Решение линейных дифференциальных уравнений и систем уравнений с постоянными коэффициентами. 2. Решение линейных интегральных и интегро-дифференциальных уравнений.
3. Интегрирование линейных уравнений в частных производных. 4. Вычисление несобственных интегралов. 5. Суммирование рядов. 6. Применение операционного исчисления при расчете электрических цепей
§4. Дискретное преобразование Лапласа и его применение . . 198
1. Z-преобразование и дискретное преобразование Лапласа.
2. Решение разностных уравнений
Глава 15. Интегральные уравнения ...................... 210
§1. Интегральные уравнения Вольтерра................ 210
1. Уравнения Вольтерра 2-го рода: основные понятия, связь с дифференциальными уравнениями. 2. Метод последовательных приближений. Решение с помощью резольвенты. 3. Уравнения Вольтерра 2-го рода типа свертки. 4. Уравнения Вольтерра 1-го рода
§ 2. Интегральные уравнения Фредгольма.................... 232
1. Основные понятия. Метод последовательных приближений и резольвента для уравнений Фредгольма 2-го рода. 2. Решение уравнений Фредгольма 2-го рода с вырожденным ядром.
3. Характеристические числа и собственные функции. Теоремы Фредгольма. 4. Уравнения Фредгольма 2-го рода с симметричным ядром
§3. Численные методы решения интегральных уравнений 259
Глава 16. Уравнения в частных производных .................. 267
§1. Основные задачи и уравнения математической физики . 267
1. Вывод уравнений и постановка задач математической физики. 2. Приведение уравнений к каноническому виду
§ 2. Аналитические методы решения уравнений математической физики.............................................. 275
1. Метод Даламбера. 2. Гильбертовы пространства. Ортогональные системы. 3. Ортогональные ряды. 4. Метод Фурье решения уравнений математической физики
6
Оглавление
§ 3. Приближенные методы решения дифференциальных уравнений в частных производных........................... 301
1. Основные понятия метода сеток. 2. Численное решение краевых задач методом сеток
Глава 17. Методы оптимизации ........................... 323
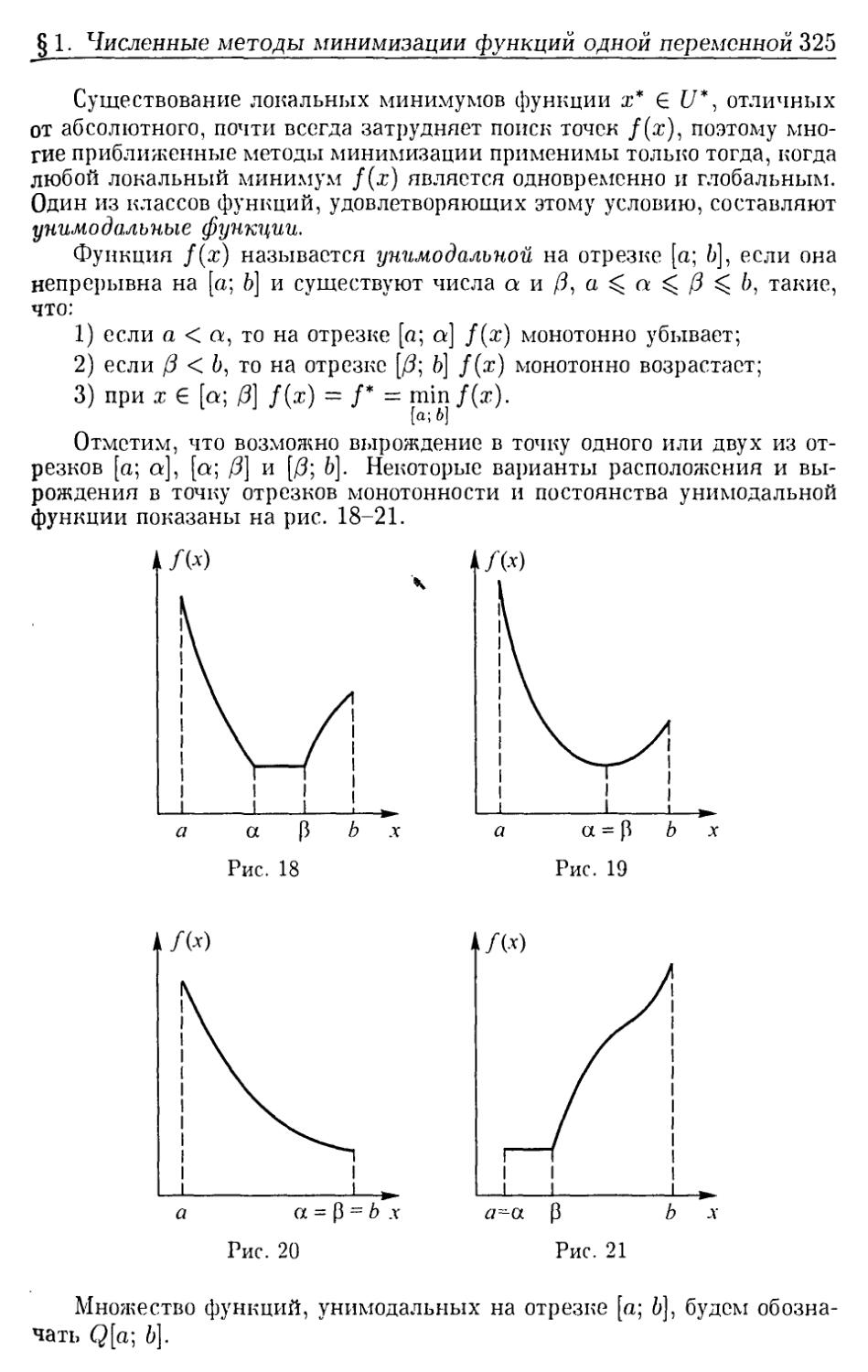
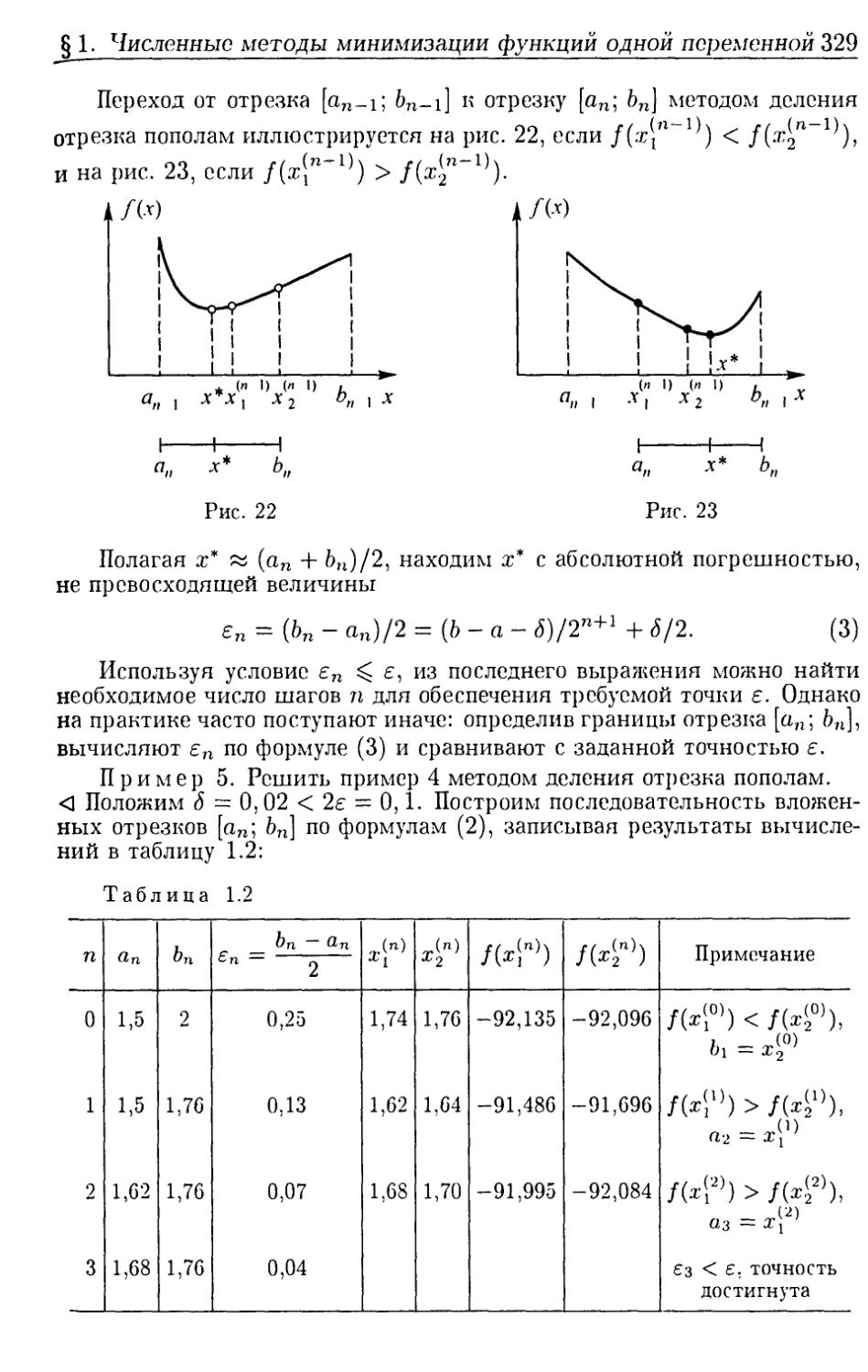
§ 1. Численные методы минимизации функций одной переменной ............................................... 323
1. Основные понятия. Прямые методы минимизации. 2. Методы минимизации, основанные на использовании производных функции
§ 2. Безусловная минимизация функций многих переменных 340 1. Выпуклые множества и выпуклые функции. 2. Методы безусловной минимизации, основанные на вычислении первых производных функции. 3. Методы безусловной минимизации, использующие вторые производные функции
§ 3. Линейное программирование....................... 353
1. Постановки задач линейного программирования. Графический метод решения. 2. Симплекс-метод решения задачи линейного программирования. 3. Целочисленное линейное программирование
§ 4. Нелинейное программирование..................... 386
1. Задачи, сводящиеся к линейному программированию. 2. Методы возможных направлений. 3. Градиентные методы решения задач нелинейного программирования. 4. Методы штрафных и барьерных функций
§ 5. Дискретное динамическое программирование........ 419
§ 6. Вариационное исчисление......................... 435
1. Предварительные сведения. Простейшая задача вариационного исчисления. 2. Обобщения простейшей задачи вариационного исчисления. 3. Задачи с подвижными границами. 4. Задачи на условный экстремум. 5. Прямые методы вариационного исчисления
ОТВЕТЫ И УКАЗАНИЯ ...................................... 467
СПИСОК ЛИТЕРАТУРЫ....................................... 575
ПРЕДИСЛОВИЕ ТИТУЛЬНЫХ РЕДАКТОРОВ
Настоящее издание «Сборника задач по математике для втузов» подверглось значительной перестановке глав и их распределению по томам. В результате первый том содержит алгебраические разделы курса высшей математики, в том числе векторную алгебру и аналитическую геометрию, определители и матрицы, системы линейных уравнений, линейную алгебру и новый раздел — общую алгебру.
Второй том полностью посвящен изложению основ математического анализа, дифференциальному и интегральному исчислениям функций одной и нескольких переменных, а также дифференциальным уравнениям.
В третьем томе собраны специальные разделы математического анализа, которые в различных наборах и объемах изучаются в технических вузах и университетах. Сюда относятся такие разделы, как векторный анализ, элементы теории функций комплексной переменной, ряды и их применение, операционное исчисление, методы оптимизации, уравнения в частных производных, а также интегральные уравнения.
Наконец, четвертый том содержит теоретические введения, типовые примеры и циклы задач по теории вероятностей и математической статистике.
Указанные выше изменения составляют лишь структурную переработку Сборника, никоим образом не затрагивая ни расположения материала внутри соответствующей главы, ни последовательности нумерации примеров и задач.
В смысловом отношении авторы внесли только следующие изменения. Во всех разделах Сборника исключены теоретические введения и циклы задач, связанные с численными методами. Дело Й том, что в настоящее время существует целый ряд программных Оболочек, каждая из которых реализует достаточно полный набор Стандартных методов приближенного решения задач, а основные Навыки работы с компьютером можно приобрести уже в школе. Авторы посчитали также необходимым добавить один новый раздел «Основы общей алгебры» и предложить цикл задач по тензорной алгебре в разделе «Линейная алгебра» в первый, «алгебраический» ,^ом Сборника. Это связано с тем, что круг идей и методов общей Алгебры все глубже проникает в наукоемкие отрасли промышлен-
8
Предисловие
ности и, следовательно, становится необходимой частью образования и подготовки специалистов по инженерным специальностям.
Кроме отмеченного выше, авторами выполнена стандартная техническая работа по исправлению ошибок, описок и других неточностей, учтены также все замечания, возникавшие в процессе работы с предыдущими изданиями Сборника.
А. В. Ефимов, А. С. Поспелов
ОТ АВТОРОВ
5 ноября 2001 года умер Александр Васильевич Ефимов — один из авторов и бессменный титульный редактор всех четырех изданий настоящего Сборника задач.
До последних дней своей жизни он продолжал активно работать над подготовкой рукописи настоящего издания к печати.
Авторский коллектив Сборника выражает глубокие соболезнования семье и близким Александра Васильевича.
Глава 11
ВЕКТОРНЫЙ АНАЛИЗ
§ 1. Скалярные и векторные поля. Градиент
1. Геометрические характеристики скалярных и векторных полей. Дусть D — область в пространстве двух, трех или п измерений. Говорят, что в области D задано скалярное поле, если в D задана скалярная функция точки и(Р) = u(ti, х2, ..., хп) = u(r), называемая функцией Воля (г — радиус-вектор точки Р(х\, х2, ..., тп)). Если каждой точке Р G D поставлен в соответствие вектор а(Р) = а(г), то говорят, что & области D задано векторное поле, определяемое векторной функцией а(Р) = a(a;i, х2, ..., хп) = а(г).
Простейшими геометрическими характеристиками скалярных полей являются линии уровня и(х, у)=Св пространстве двух измерений, поверхности уровня, или эквипотенциальные поверхности, и(х, у, z) = je (7 в пространстве трех измерений и гиперповерхности уровня tl(xi, ..., хп) = С в пространстве п > 3 измерений. Простейшими геометрическими характеристиками векторных полей являются векторные линии и векторные трубки. Векторной линией называется ли-ния, касательная к которой в каждой точке имеет направление соответствующего ей вектора поля. Векторные линии для векторного поля & = axi 4- ayj 4- azk определяются системой дифференциальных уравне-ний
dx _ dy dz
ах(х, у, z) ау{х, у, z) а2(х, у, z)
'^аналогично для плоских и многомерных полей). Векторной трубкой указывается поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (даже частично) с какой-либо векторной линией.
Определить вид линий или поверхностей (гиперповерхностей) ^уровня следующих скалярных полей:
11.1. и = у2 + х. 11.2. и = ху.
11.3. и = у/х. 11.4. и = х 4- у 4- z.
11.5. и — х2 4- у2 — z2. 11.6. и = х2 + у2 — z.
11.7. и = xi 4- Х2 4- £з + 11.8. и = х2 4- х^ + х2 4- х2.
Найти векторные линии следующих полей:
11.9. а = yi — xj. 11.10. а = zi — у].
11.11. а = yi 4- j. 11.12. а = г = zi.4-?/j + zk.
11.13. а = [г, с] (с — постоянный вектор).
10
Гл. 11. Векторный анализ
<1 Пусть с = ai + bj+ ск. Тогда
к
i J я у a b
а = [г, с] =
z = (су - bz)i 4- (az — ex')] 4- (bx — ay]k.
c
Дифференциальные уравнения векторных линий поля а имеют следующий вид: dx _ dy _ dz су — bz az — ex bx — ay
Умножая числитель и знаменатель первой дроби на х, второй на у и третьей на z, находим
xdx _ у dy _ zdz сху — bxz ayz — сху bxz — ayz
Складывая почленно и используя свойство пропорции, окончательно выводим:
dx _ dy _ dz _ xdx + у dy + zdz су — bz az — ex bx — ay 0
Следовательно,
x dx 4- у dy 4- z dz = 0,
или
d(x2 + y2 4- z2) = 0.
Отсюда получаем, что 2 . 2 . 2
X +у + Z£ = С{.
Аналогично, умножая числитель и знаменатель первой дроби на а, второй на 6, третьей на с и складывая почленно, находим
dx _ dy _ dz _ a dx 4- bdy 4- c dz .
cy — bz az — ex bx — ay 0
Следовательно,
a dx 4- b dy 4- c dz = 0,
или
ax 4- by 4- cz = C2
Таким образом, уравнения векторных линий имеют вид
Г х2 4- у2 4- z2 = С2 (С1 0),
( ах 4- by 4- cz = С2.
Векторные линии поля а представляют собой окружности, являющиеся сечениями сфер х2 + у2 + z2 = С2 плоскостями ах + by + cz = С2, перпендикулярными вектору с. с>
§ 1. Скалярные и векторные поля. Градиент 11
i j к
11.14. а = ~ + - + —.
X у Z
11.15. а — (у — z)i + (z — z)j + (х — y)k.
11.16. а — .Tiei + Х2&1 + ^464-
11.17. Найти векторную линию поля а = — yi + хj + 6к, проходящую через точку Р(1, 0, 0).
11.18. Найти векторную линию поля а = z2i — y3j + z2k, проходящую через точку Р( 1/2, — 1/2, 1).
11.19. Определить вид векторных трубок:
а) в задаче 11.12; б) в задаче 11.15.
2. Производная по направлению и градиент скалярного поля. Пусть S = cosa-i4-cos/3-j+cos7-k — единичный вектор данного направления s, Го = ^oi + 3/oj + -Zok — радиус-вектор точки Ро(^о, Уо> zo)- Производная Скалярного поля и(Р) в точке Ро по направлению s, обозначаемая через ди
определяется соотношением ds
ди u(r0 + rs) - u(r0)
— = lim-----------s-------
os г—>0 т
И характеризует скорость изменения функции и(Р) в направлении s.
Л ди
Производная — вычисляется по формуле ds
ди ds
_ ди
_ дх
—о
ди cos а 4- —
COS/3 + — dz
—о
cos 7.
=0
(1)
Градиентом скалярного поля и(Р), обозначаемым символом grad и, Называется вектор, проекциями которого на координатные оси являются Соответствующие частные производные функции и(Р), т.е.
, ди. ди. ди^ ,п.
grad и = — 1 + —j + —к. (2)
дх ду dz
Диалогично определяется производная по направлению и градиент для Д-мерных скалярных полей.
Исходя из выражения производной по направлению (1) и определения градиента (2), доказать следующие свойства градиента.
11.20. Производная поля по направлению s равна скалярному Произведению градиента поля на единичный вектор данного направления, т. е. равна проекции градиента на данное направление
= (gradu, s) = Igrad tz| cos 99, os
£де tp — угол между градиентом и вектором s.
12
Гл. 11. Векторный анализ
11.21. Направление градиента есть направление наибыстрейшего возрастания функции поля.
11.22. В каждой точке поля градиент направлен по нормали к соответствующей поверхности уровня в сторону возрастания потенциала поля, т. е.
, । ди
где п — направление нормали к поверхности уровня в сторону возрастания функции поля.
11.23. Пусть и = м(ж, у, z) и v = и(ж, у, z) — дифференцируемые функции, с — постоянная. Доказать следующие соотношения: a) grad (и + v) = grad u + grad v;
б) grad (с + и) = grad и;
в) gradfcu) = с grad и;
г) grad (ш?) = v grad?/ + ц grad и (см. пример 4 § 3);
д) grad(un) = 7mn-1grad'iz;
. , / и \ v grad и — и grad v , „
е) grad - = —----------2------, v ± 0.
Найти градиенты следующих скалярных полей:
11.24. u = |r|. 11.25. ц = In|г|.
11.26. и — (а, г); а — постоянный вектор.
11.27. и = (а, г)(Ь, г); а, b — постоянные векторы.
10.28. и = |[а, г]|2; а — постоянный вектор.
Пусть г = |г| = у/х2 + у2 + z2. Показать, что:
11.29. (gradu(r), г) — и'(т)г.
11.30. [gradu(r), г] = 0.
Найти производные от следующих полей в заданных точках по заданному направлению:
11.31. и = х2 + -у2 в точке Ро(2, —1) по направлению вектора £
PqPi, где Pi(6, 2).
11.32. и = -х2 — -у2 + z в точке Pq(2, 1, 1) по направлению
х — 2 у — 1 z — 1
прямой —-— = —-— = —-— в сторону возрастания поля.
11.33. и = х2 + х2 - х^ + х2 в точке Pq(1, 3, 2, -1) по направлению вектора а — 2ei + — 2е4.
§ 2. Криволинейные и поверхностные интегралы 13
11.34. Найти производную скалярного поля и = 1/|г| по направлению его градиента.
2 2 2
Z
11.35. Найти производную скалярного поля и = —х + 77 + а2 о2 с2 в точке Р(а, Ь, с) по направлению радиус-вектора этой точки.
11.36. Найти угол между градиентами поля и — х2 + 2у2 — z2 в точках Pi(2, 3, т-1) и Р2(1, —1, 2).
11.37. Найти скорость и направление наибыстрейшего возрастания поля и = xyz в точке Ро(1, 2, 2).
11.38. Найти единичный вектор нормали к поверхности уровня поля и = х2 + 2ху — Ayz в точке Ро(1, 1, —1), направленный в Сторону возрастания поля.
11.39. Найти стационарные точки поля и = 2х2 — 4ху + у2 — — 2yz + Qz.
Убедиться в ортогональности линий уровня полей:
11.40. и = х2 — у2, v = ху.
11.41. и = 2х2 + у2, v = у2/х.
Убедиться в ортогональности поверхностей уровня следующих полей:
11.42. и = х2 + у2 — z2, v = xz + yz.
11.43. и = х2 + у2 — 2z2, v = xyz.
11.44. и = х2 + х% — х2 — х2, v = Х1Х3 + Х2Х4, w = Х1Х4 — Х2Х3.
Найти семейство линий наибыстрейшего возрастания для следующих полей:
11.45. Плоского поля и = х2 — у2.
11.46. Трехмерного поля и = xyz.
11.47. Трехмерного поля и = х2 + у2 — z2.
£ 2. Криволинейные и поверхностные интегралы
1. Криволинейный интеграл 1-го рода. Пусть АВ — дуга кусочно гладкой кривой, и(Р) — заданное на АВ скалярное поле, А = Aq, Al, А2, ..., An_i, An = В — произвольное разбиение дуги АВ и Р„ (г = 1, 2, ..., п) — произвольные точки на частичных дугах AV-\AV^ длины которых обозначим через Asp. Если существует предел после-п
довательности интегральных сумм u(Pp)Asl/ при шахДзр 0 (и p=i v
п -> оо), который не зависит ни от способа разбиения дуги АВ точками Ар, ни от выбора точек Рр на частичных дугах Ap_iAp, то этот предел
14
Гл. 11. Векторный анализ
называется криволинейным интегралом 1-го рода от функции и(Р) по кривой АВ и обозначается через
u(P)ds = / и(х, у, z)ds
АВ
АВ
(ds — дифференциал дуги), т. е.
АВ
и(Р) ds
п
= lim / u(PIz)Asp.
max As„—>0 v 1>=1
(1)
Если функция u(P) непрерывна на AB, то интеграл (1) существует.
Физически интеграл (1) можно рассматривать как массу кривой АВ. Вычисление интеграла (1) сводится к вычислению определенного интеграла. Например, если уравнение дуги АВ задано в виде х = x(t), у = y(t), z = z(t), t0 < t < й, то
ti
У u(P)ds = У u(x(t), y(t), z(t))yjx,2(t) + y,2(t) + z,2(t) dt. ab to
Криволинейный интеграл 1-го рода не зависит от того, в каком направлении проходится дуга АВ, иными словами,
и(Р) ds = / u(F) ds.
АВ
ВА
Пример 1. Определить массу М первого витка винтовой линии х = a cost, у = asint, z = ht, если плотность р(Р) в каждой ее точке пропорциональна длине радиус-вектора этой точки.
< Так как р = kr = ку/х2 +у2 + z2, то в точках винтовой линии р = ку/а2 + h2t2. Первому витку отвечает изменение параметра t от 0 до 2тг и
ds = уж'2 + у'2 + z'2 dt = \/а2 + h2 dt.
§ 2. Криволинейные и поверхностные интегралы
15
Отсюда
27Г
М = j ку/а2 + Д2 л/а2 + h2t2 dt = о
(4. ___________ fl2 _________
-ya2 + h2t2 + — In (ht + \/а2 + h2t2)
2 2n
, l / 2 i Л 2Д2 . °2 1 27Г,г + +4?r2/l2
= к v a2 + h2 \ Try a2 + 4тг2Л2 + — In \ 2n
a
В задачах 11.48-11.54 вычислить следующие криволинейные интегралы Ьго рода:
11.48. (х + у) ds, где С — контур треугольника АВО с вер-
С
шинами А(1, 0), B(0, 1) и 0(0, 0).
/ds
====, где С — отрезок прямой, соединяющий
\/х2 + у2 + 4
с
точки 0(0, 0) и А(1, 2).
11.50. Уxyds, где О — контур квадрата |ж| + |?/| = a (a > 0).
С
11.51. У у2 ds, где О — первая арка циклоиды х = a(t — sint), с
у = а(1 — cost).
11.52. J y/x2 +y2 ds, где C — дуга развертки окружности x = С
= a(cost + tsint), у — a(sint — tcost) (0 C t С 2тг).
11.53. [ dS- , где C — дуга линии x = t,y = t2/л/2, z = t3/3 J x + 3z
c
от <9(0, 0, 0) до B(y/2, y/2, 2>/2/3).
11.54. У (x2 + y2)ds, где C — дуга логарифмической спирали С
г = ae3ifi от точки А(а, 0) до точки 0(0, 0).
16
Гл. 11. Векторный анализ
11.55. Найти массу всей астроиды х = aeos3£, у = asin3£, если плотность р(Р) в каждой ее точке Р выражается формулой р(Р) = где к > 0 — коэффициент пропорциональности.
11.56. Найти массу всей кардиоиды г = a(l + cos</)), если плотность р(Р) в каждой ее точке Р выражается формулой р(Р) = = ку/г, где к > 0 — коэффициент пропорциональности.
11.57. Найти массу всей лемнискаты г2 = a2 cos2<£>, если плотность р(Р) в каждой ее точке Р выражается формулой /1(Р) = кг, где к > 0 — коэффициент пропорциональности.
11.58. Найти массу дуги конической винтовой линии х = = ae*cos£, у = ae*sin£, z = aet, если плотность р в каждой ее точке выражается формулой р = ке1 (где к > 0 — коэффициент пропорциональности), от точки 0(0, 0, 0) до точки А(а, 0, а).
11.59. Найти, с какой силой масса М, равномерно распределенная вдоль окружности х2 + у2 = a2, z — с, притягивает точечную массу т, помещенную в начале координат.
11.60. Найти массу четверти окружности х2 + у2 = г2, расположенной в первом квадранте, если плотность ее в каждой точке пропорциональна абсциссе этой точки (коэффициент пропорциональности а).
11.61. Найти массу полуокружности х2 + у2 = г2, расположенной в верхней полуплоскости, если плотность ее в каждой точке пропорциональна кубу ординаты этой точки (коэффициент пропорциональности /3).
2. Поверхностный интеграл 1-го рода. Пусть G — кусочно гладкая поверхность, и(Р) — заданное на G скалярное поле, Gi, G?, • • •, Gn — произвольное разбиение поверхности G на частичные поверхности, площади которых равны Zkcri, До-2, • • •, и пусть Ру (u = 1, 2, ..., п) — произвольные точки на частичных поверхностях G». Если существу-
п
ет предел последовательности интегральных сумм £) и(Ру) ПРИ р=1
maxdiamcr^ —> 0 (и п —> оо), который не зависит ни от способа раз-р
биения поверхности G на частичные поверхности, ни от выбора точек Pv на этих частичных поверхностях, то этот предел называется поверхностным интегралом 1-го рода от функции и(Р) на поверхности G и обозначается через
§ 2. Криволинейные и поверхностные интегралы 17
(da — дифференциал площади поверхности), т.е.
Уu(P) da =
G
п
lim V ulJPv) bay.
max diam av —>0 1
v P=1
(2)
Если u(P) непрерывна на G, то интеграл (2) существует. Вычисление интеграла (2) сводится к вычислению обычного двойного интеграла. Допустим, что прямая, параллельная оси Oz, пересекает поверхность G лишь в одной точке, т.е. уравнение поверхности имеет вид z = z(x, у), и пусть G проектируется на плоскость Оху в область D. Элемент day Площади D выражается в виде da\ = da cos 7, где 7 — острый угол, который нормаль к поверхности G составляет с осью Oz:
Таким образом,
и(х, у, z) da =
G
//“<*’ у, zlx, =
D
2
dx dy.
Если прямая, параллельная оси Oz, пересекает поверхность G в двух или Фрлее точках, то G разбивается на части, каждая из которых пересекается Ь прямой, параллельной оси Oz, лишь в одной точке. Интегрирование Следует выполнять по каждой из полученных частей.
Вместо плоскости Оху поверхность G можно проектировать на плос-8Йости Oxz или Oyz.
Для двусторонних поверхностей поверхностный интеграл 1-го рода Мю зависит от того, по какой стороне поверхности он берется. Физический смысл поверхностного интеграла 1-го рода зависит от физического характера данного скалярного поля: он может определять массу, распределенную по данной поверхности, электрический заряд и т. д.
Пример 2. Определить статический момент относительно плоскости Оху и положение центра масс однородной полусферы G (плотнос-3?И 1): х2 + у2 + z2 = R2 (х 0).
*3 Имеем
18
Гл. 11. Векторный анализ
где D — круг х2 + у2 Я2, z = 0. Так как на полусфере xdx + уdy + + zdz = 0, то
dz _ х dz _ у dx z ’ dy z
откуда
убг2 + т/2 + z2 _ R
z у/R2 — х2 — у2
и
’2 = 7гЯ3.
D
D
G
Определим теперь координаты центра масс полусферы. В силу симметрии
хо = Уо = 0.
Далее, так как площадь Q поверхности полусферы G есть 2л R2, то
МХу R
20 2
Пример 3. На всей поверхности конуса с высотой h и радиусом основания а распределены электрические заряды. В каждой точке поверхности плотность заряда пропорциональна аппликате этой точки (е = kz). Вершина конуса — в начале координат, его ось направлена по оси Oz. Определить суммарный заряд всей поверхности конуса.
<1 Суммарный заряд основания конуса равен произведению его площади ла2 на плотность точечного заряда, т.е. kh. Таким образом, Еосн = = кла2Н. Заряд боковой поверхности G определяется интегралом
-^бок.пов = kz da.
G
h2
Уравнение поверхности конуса г = 77 + у2), 0 z h. Дифферен-
а2
h2 у
и>
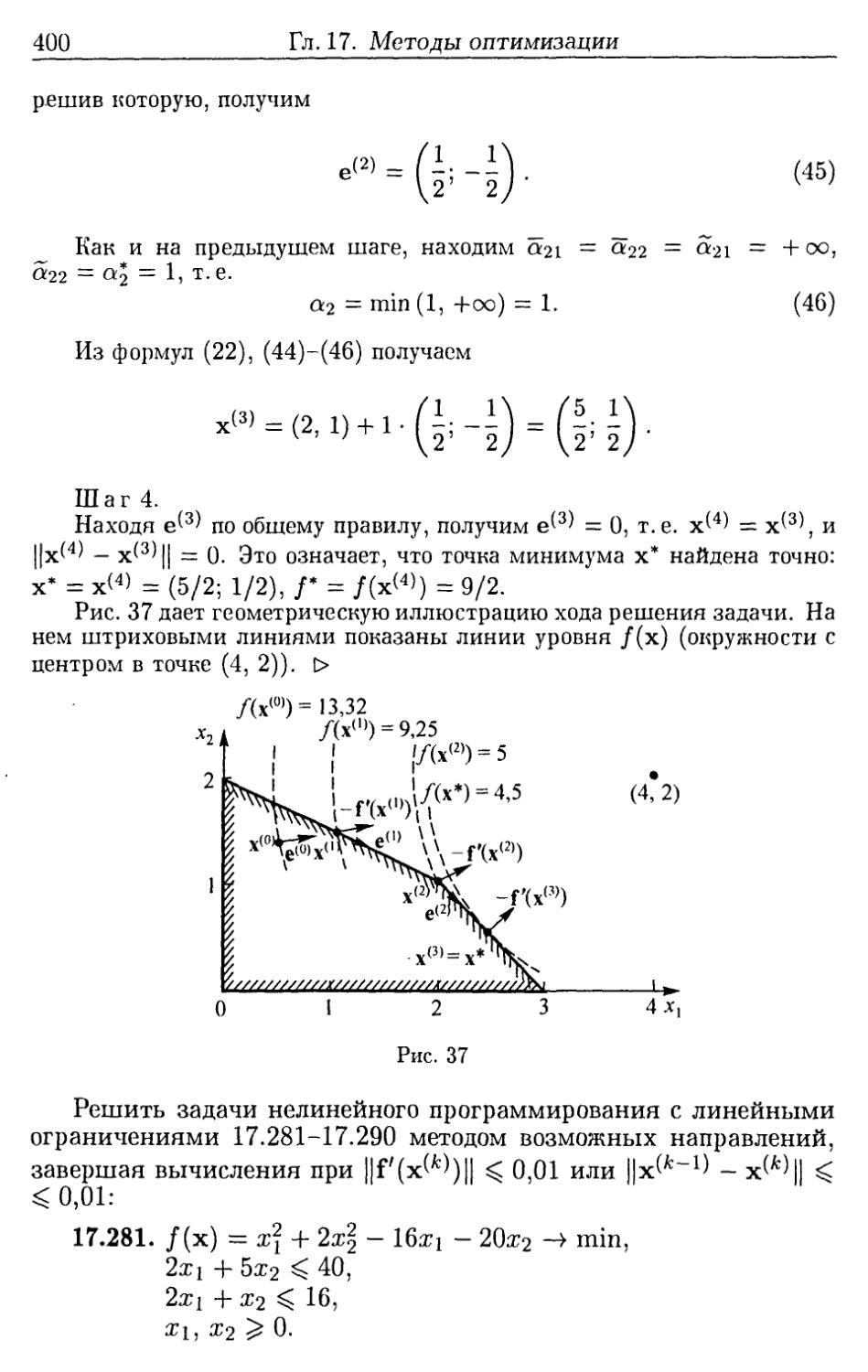
a2 z
Д2 dz ti2 х dz
пируя, находим zdz = —(a; dx + у dy), откуда — = a2 dx a2 z ду
следовательно,
0z\2
dx J + \ dy /
h4 х2 + у2
a4 z2
а
§ 2. Криволинейные и поверхностные интегралы
19
Поэтому
Ябок.пов = к jj zda = Ц у/х2 +у2 dxdy,
G D
где D — круг x2 + у2 a2, z = 0. Переходя к полярным координатам, получаем:
khVa2 + h2 f f 2 . . khy/a2 + h2 f . Г 2 , ^бок.пов =---------- r dr dip =--------—------ dip ir dr =
D oo
= ^-kyrahy/a2 + h2. 0
Находим весь заряд:
E = Еосн + Ебок.пов = kna2h + -knahy/a2 + h2 =
О kyrah . n r~z--------------—
=—-—(3a + 2y«2 + h2). >
О
Вычислить следующие поверхностные интегралы 1-го рода:
11.62. Цx2yz da, где G — часть плоскости х + у + z = 1,
G
лежащая в первом октанте.
11.63. jу/х2 + у2 da, где G — часть поверхности конуса G
X2 + у2 = z2, 0 z 1.
11.64. II (х2 + у2 + z2) da, где G — сфера х2 + у2 + z2 = 1.
G
11.65. II (х + у + z) da, где G — часть сферы x2+y2+z2 = a2, G
Лежащая в первом октанте.
11.66. Определить массу, распределенную на части поверхности гиперболического параболоида 2az = х2 — у2, вырезаемой цилиндром х2 + у2 = а2, если плотность в каждой точке поверхности равна A;|z|, где к > 0 — коэффициент пропорциональности.
11.67. Определить момент инерции однородной (плотности 1) боковой поверхности конуса z = у/х2 + у2 (0 z а) относительно оси Oz.
20
Гл. 11. Векторный анализ
11.68. Определить суммарный электрический заряд, распределенный на части поверхности двуполостного гиперболоида z2 = = х2 + у2 + a2 (a < z < ал/2), если плотность заряда в каждой точке пропорциональна аппликате этой точки (е = kz).
11.69. Определить массу, распределенную по поверхности куба |я| С а, \у\ С a, |z| С а, если поверхностная плотность в точке Р(х, у, z) равна ky/\xyz\, где к > 0 — коэффициент пропорциональности.
11.70. Определить суммарный электрический заряд, распределенный на части поверхности параболоида 2az = х2 + у2, вырезаемой из него цилиндром х2 + у2 = а2, если плотность заряда в каждой точке равна к^/z, где к > 0 — коэффициент пропорциональности.
3. Криволинейный интеграл 2-го рода. Пусть на дуге АВ кусочно гладкой кривой задано векторное поле а = a(r) = ах(х, у, z)i + + ау(х, у, z)j+az(x, у, z)k, пусть А = Ао, Ai, А2, ..., An^i, Ап = В — произвольное разбиение дуги АВ на частичные дуги, Р„ (у = 1, 2, ..., ..., п) — произвольные точки на дугах Ap_iAp, а Дгр — приращение радиус-вектора г(Р) на концах дуги A^-jAp. Тогда, если суще-п
ствует предел последовательности интегральных сумм ^2 (a(Fp), Дгр) р=1
при max |Дгр| —> 0 (и п —> оо), который не зависит, ни от способа раз-
биения дуги АВ на частичные дуги, ни от выбора точек Pv на этих частичных дугах, то этот предел называется криволинейным интегралом 2-ео рода по дуге АВ и обозначается через
f (a, dr) = f axdx + aydy + az dz, AB AB
t. e. (3)
/П
(a, dr) = lim V (а(РД ДгД
max |Дг„I—>0 '
v P=1
AB
Здесь (a, dr) и (a(Pp), Arp) — скалярные произведения векторов. Если вектор-функция а(Р) непрерывна на АВ, то интеграл (3) существует.
Интеграл (3) называют также линейным интегралом вектора а(г). Аналогично определяются линейные интегралы в плоских и многомерных векторных полях. Если даны параметрические уравнения дуги АВ:
§ 2. Криволинейные и поверхностные интегралы 21
х = я(<), У = y{t\ z = z(t), t0 то
У (a, dr) = У (ax(x(t), y(t), z(t))x'(t) + ay(x(t), y(t), z(t))y'(t) +
AB t0
+ az(x(t), y(t), z(t))z'(t)) dt. (4)
Здесь to и ti — значения параметра t, отвечающие точкам А и В. В отличие от криволинейных интегралов 1-го рода, линейные интегралы (3) зависят от направления, по которому совершается интегрирование
вдоль дуги АВ:
У (a, dr) = — У (a, dr).
ВА АВ
Простейший физический смысл линейного интеграла — работа силового доля а = а(г) при перемещении в нем материальной точки по кривой
АВ из точки А в точку В.
Пример 4. Найти работу силового поля F = xi + yj + zk при перемещении материальной точки вдоль первого витка конической винтовой линии х = ae* cost, у = aelsmt, z = ае1 из точки А(0, 0, 0) в точку В(а, 0, а).
<] Так как dx = ае1 (cost — sini) dt, dy = ael(sint + cost) dt, dz = ael dt и
(F, dr) = x dx + у dy + z dz =
= a2e2t((cos t - sin t) cos t + (sin t + cos t) sin t + 1) dt = 2a2e2t dt, то, учитывая, что t = — oo в точке А и t = 0 в точке В, имеем
о
У (F, dr) = 2а2 У e2tdt = a2. >
ав ~°°
Замечание. Этот пример можно решить проще, если учесть, что в данном случае (F, dr) = (г, dr) = -d(r2), причем г = |г| = 0 в точке А и г = а\/2 в точке В. Имеем:
I (F, dr) = i
АВ
О
ау/2
О
= а2
22
Гл. 11. Векторный анализ
Линейный интеграл вектора а, взятый по замкнутому контуру С, называется циркуляцией вектора поля по данному контуру и обознача-
ется символом a - dr. Направление обхода контура указывается зйра-с
нее, причем положительным считается обход против часовой стрелки, а отрицательным — по часовой стрелке.
Для плоских векторных полей а = ax(x, у)1 4- ау(х, y)j имеет место следующее утверждение:
Если векторная функция а = ах(х, y)i + ay(x, y)j непрерывна вместе дах дау а i i
с производными —— и -г-2- в замкнутой области G ~ GII С, то Оу ох
// (^~^)dxdy = fa^- + aydy G С
(формула Грина).
Пример 5. Вычислить криволинейный интеграл
(j) (х + у) dx - (х - у) dy, с
где С — окружность х2 + у2 = г2.
< Применяя формулу Грина, можем записать
£ (х + у) dx - (х - у) dy = Ц (-1 - 1) dx dy = -2тгг2, . с кс
так как dxdy есть площадь круга Кс: х2 +у2 г2. О
кс
11.71. Вычислить работу силового поля F = yi — xj при перемещении материальной точки вдоль верхней половины эллипса 2 2
X, у
^2 + ^2 = 1 из точки А(а, 0) в точку В(—а, 0).
11.72. Вычислить линейный интеграл j (a, dr), если а = y2i + 6в
+ a?2j, 0(0, 0), В(1, 1), по следующим путям:
а) отрезок прямой ОВ-, б) дуга параболы х2 = у; в) дуга параболы у2 = х; г) ломаная О АВ, где А(1, 0); д) ломаная ОСВ, где 0(0, 1).
§ 2. Криволинейные и поверхностные интегралы 23
11.73. Вычислить циркуляцию вектора а — yi — ж] вдоль окружности (х — xq)2 + (у — ?/о)2 — R2 в отрицательном направлении.
11.74. Вычислить линейный интеграл f (a, dr), если а = zi +
ОА
4- ху + ук, уравнение дуги О А: г = ti + i2j + А, 0 t 1.
11.75 . Вычислить линейный интеграл j (a, dr), если а =
ОА
=2 — yzi + xzj + хук, О А — первый виток винтовой линии х = — acost, у = asini, z = ht (0 t 2тг).
11.76 **. Вычислить циркуляцию вектора а = zi + жj + ук по окружности ж2 + у2 + z2 = R2,x + y + z = R,B положительном Направлении относительно орта к.
11.77 . Вычислить циркуляцию вектора а = yi — zj + жк вдоль X2 + У2 , 2 2
эллипса —------F z* = а , у = х в положительном направлении
относительно орта i.
11.78 . Вычислить работу силового поля F = 2ж?/1 + ?/2j — ж2к При перемещении материальной точки вдоль сечения гиперболоида Ж2 + У2 ~ 2z2 = 2а2 плоскостью у = х от точки (а, а, 0) до точки (а\/2, ау/2, а).
Используя формулу Грина, вычислить интегралы:
11.79 . У (ж2 — у2) dx + (ж2 + у2) dy, где С — контур, образо-С
Званный полуокружностью у = у/г2 — х2 и осью Ох.
11.80 . У (ж + у)2 dx — (ж — у)2 dy, где С — контур, образован-С
Ный синусоидой у = sin ж и отрезком оси Ох при 0 ж тг.
11.81 . $ x2ydx — xy2dy.
Х2+у2=Г2
11.82 . У (ж + у)2 dx — (ж2 + у2) dy, где С — треугольник с вер-! С
шинами 0(0, 0), А(1, 0) и В(0, 1).
24
Гл. 11. Векторный анализ
4. Поверхностный интеграл 2-го рода. Гладкая поверхность G в трехмерном пространстве называется двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на поверхности G и не имеющему общих точек с ее границей, возвращается в первоначальное положение. Выбор определенной стороны поверхности, т. е. выбор направления нормали к поверхности, называется ориентацией поверхности.
Пусть G — кусочно гладкая ориентированная поверхность и а = = Qx(x, у, z)i + ау(х, у, z)j + az(x, у, z)k — векторное поле. Разобьем поверхность G на частичные поверхности Gi, G2, . , Gn, площади которых обозначим через Астр (у = 1, 2, ..., п), а площади частичных поверхностей G^, снабженных единичными нормалями п^Р») в точках Р„ € Gu, — через (т.е. считаем каждую такую площадь вектором длины Дегр и направления п|/(Р1/)). Тогда, если существует предел п
последовательности интегральных сумм ^2 (a(-PV), ^аи) ПРИ is-i
тахсНатсгр -» 0 (и п -» оо), который не зависит ни от способа раз-1/
биения поверхности G на частичные поверхности, ни от выбора точек на этих частичных поверхностях, то этот предел называется поверхностным интегралом 2-го рода по поверхности G и обозначается через
УУ (a, da) = УУ ах dydz + ау dxdz + az dxdy, (5) G G
т. e.
[[ (a, da) = lim (а(Р„), Дсг^).
J J maxdiama^O ’
G v P=1
Если поле a(P) непрерывно на G, то интеграл (5) существует.
Поверхностный интеграл 2-го рода называют также потоком векторного поля а(Р) через поверхность G. Его можно интерпретировать как количество жидкости или газа, протекающего за единицу времени в заданном направлении через поверхность G. Переход к другой стороне поверхности меняет направление нормали к поверхности, а потому и знак поверхностного интеграла 2-го рода.
Вычисление поверхностного интеграла 2-го рода сводится к вычислению поверхностного интеграла 1-го рода
//(a’da)=//(a’ n)dCT=J G G < [У (ax cos a 4- ay cos /3 + az cos 7) dcr, (6)
где n = (cos a, cos /3, cos 7) — единичная нормаль к поверхности, или к
§ 2. Криволинейные и поверхностные интегралы
25
вычислению суммы трех линейных интегралов
УУ (a, da) = ± УУ ax(x(y, z), у, z)dydz ± G Di
Ц ау(х, у(х, z), z) dxdz± az(x, у, z(x, y))dxdy, D2 D3
где Pi, D2 и P3 — проекции G соответственно на плоскости Oyz, Oxz и Оху, а х(у, z), у(х, z) и z(x, у) — выражения, полученные из уравнения поверхности G разрешением относительно соответствующих координат.
Пример 6. Найти поток вектора г = xi 4- yj 4- zk через часть ж2 у2 Z2
поверхности эллипсоида — + — + — = 1, лежащую в первом октанте, а2 о2 с2
В направлении внешней нормали.
<1 Имеем в силу (6)
II ^^=11 G G
(х cos а + у cos /3 + z cos 7) da.
Так как в первом октанте внешняя нормаль эллипсоида со всеми осями координат образует острые углы, то все три направляющих косинуса Неотрицательны. Поэтому
jУ (г, da) = xdydz +
G Di
Ц у dxdz + II zdxdy =
D? D3
о „14. лаЬс
= 3t, = 3'8'3 “
(каждый из интегралов по Pi, Рг и Р3 определяет объем одной восьмой Пасти эллипсоида). О
Пример 7. Найти поток вектора а = x2i — z/2j + z2k через всю поверхность тела x2+y2+z2 ЗЯ2, 0 z \/х2 4- у2 — R2 в направлении внешней нормали.
*3 Имеем:
II (a, da) = II (х2 cos а — у2 cos /3 4- z2 cos 7) da =
G G
G
IIУ2 cos/3 da + II z2 cos 7 da.
G G
26
Гл. 11. Векторный анализ
Заданная поверхность ограничена сверху сегментом сферы х2 4- у2 4-2 = 3R2, с боков — частью поверхности гиперболоида х2 + у2 — z2 = = R2, снизу кругом х2 4- у2 R2, z = 0 (рис. 1). На плоскости Oyz и Oxz поверхность С? проектируется дважды с разных сторон. Поэтому, в силу симметрии поверхности относительно этих плоскостей, а также учитывая знаки подынтегральной функции на каждой стороне, можем записать:
9
х cos а
у2 cos /3 da = 0.
G G
На плоскость Оху сферический сегмент проектируется в круг (область D'3) х2 4-4- у2 2R2, часть поверхности гиперболо-
ида — в кольцо (область Р3) R2 х2 +у2 2R2, а нижним основанием
служит лежащий в этой плоскости круг (область D^') х2 4- у2 R2. Но для сегмента сферы cos 7 > 0, для гиперболоида cos 7 < 0, а на нижнем основании z = 0. Поэтому
I (a, da) = z2 cos 7 da G G
I (3R2 — x2 ~ y2) dxdy — У (x2 + y2 — R2)dx dy.
D'3 D3
Для вычисления интегралов перейдем к полярным координатам:
2тг Ry/2
(ЗЯ2 — х2 — у2) dx dy = I dip I (3R2 — r2)r dr = 4л R4,
D3 0 0
2тг, Ry/2 4
II (x2 +y2 - R2) dxdy = I dp I (r2 - R2)r dr = D” OR
Таким образом, окончательно находим:
II (a, da) = ^R4.
G
О
В задачах 11.83-11.86 вычислить поверхностные интегралы 2-го рода:
§ 2. Криволинейные и поверхностные интегралы
27
11.83.
, где G — верхняя сторона части плоскости
G
х 4- у + z = а, лежащей в первом октанте.
f f dxdy „ , 9 9
11.84. / / ---, где G — внешняя сторона сферы х 4- у 4-
G
4- z2 = а2.
11.85. /
, где G — внешняя сторона части поверхно-
G
Н
сти параболоида z = —z(x2 + у2), х 0, у 0, z Н.
R£
, где G — внешняя сторона полусферы х2 4-
11.86.
G
'4- у2 4- z2 = R2,
11.87. Найти поток вектора а = a?2i4-?/2j4-2k через всю поверх-ность тела — ух2 4- у2 z Н в направлении внешней нормали.
11.88. Найти поток вектора а = 2ш1 — yj через часть поверхности цилиндра я24-?/2 = R2, д:^0, ?/^0, О^г^Я, в направлении внешней нормали.
11.89. Найти поток вектора а = a?2i 4- ?/2j 4- z2k через часть поверхности параболоида —х(х2 4- у2) = z, z Н, в направлении R£
внутренней нормали.
11.90. Найти поток вектора а = z2i — ?/2j 4- z2k через часть Сферы х2 4- у2 4- z2 = R2, х 0, у 0, z 0, в направлении внешней нормали.
11.91. Найти поток вектора а = zi 4- yj - 2zk через всю поверхность куба |ж| а, |?/| а, |z| а в направлении внешней Йормали.
11.92. Найти поток вектора а — 2rc2i 4- 3?/2j 4- z2k через всю Поверхность тела \/дт2 4- т/2 z Спешней нормали.
11.93. Найти поток вектора Я ©ерхности параболоида z = -
№ = R, z = 0, х = 0, ориентированной в соответствии с направлением орта к.
11.94. Найти поток вектора а = z2i 4- ?/2j 4- zk через часть
’2 — х2 — у2 в направлении
a = xi + yj 4- zk через часть по-~^х(х2 — у2), вырезаемую плоскостями
28
Гл. 11. Векторный анализ
поверхности параболоида z = — (ж2 — у2), вырезаемую цилиндром Rz
х2 + у2 = R2, ориентированной в соответствии с направлением орта к.
§ 3. Соотношения между различными характеристиками скалярных и векторных полей
1. Дивергенция векторного поля и теорема Гаусса-0 стр огр адского. Дивергенцией £или расхождением) векторного поля а = а(г), обозначаемой через diva, называется скалярная величина, равная пределу отношения потока векторного поля а через замкнутую поверхность Хр к величине vp объема тела, ограниченного этой поверхностью, при vp —> О, т. е. при условии, что поверхность стягивается в точку Р:
(div а) р
= lim — (п) (a, da). vP~>0 Vp JJ
Sp
(1)
Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля, «исходящего» из точки Р, т. е. мощность источника (при (diva)p > 0) или стока (при (diva)p > 0), находящегося в точке Р.
В трехмерном евклидовом пространстве дивергенция непрерывно дифференцируемого поля выражается следующим образом:
da% d(iy daz
div а + —.
ох оу OZ
Теорема Гаусса-Остроградского. Поток векторного поля а(г) через замкнутую поверхность X, лежащую в этом поле, в направлении ее внешней нормали, равен тройному интегралу по области V, ограниченной этой поверхностью, от дивергенции этого векторного поля, т. е.
Е
divadv.
Пример 1. Используя теорему Гаусса-Остроградского, найти поток вектора а = x3i+y3j + R2zk через всю поверхность G тела z Н в направлении внешней нормали.
< Имеем diva = 3(ж2 4- у2) + R2. Поэтому
^(x2+s/2)«:
(3(х2 + j/2) + R2)dv.
§ 3. Характеристики скалярных и векторных полей 29
Для вычисления тройного интеграла перейдем к цилиндрическим координатам. Уравнение поверхности примет вид z = Hr2/R2,
V
2тг R Н
4- у2} 4- R2) dv = У d<p у (Зг2 4- В2) г dr j dz — о о Яг2
~Rr
Г / Hr2
= 27Г / (Зг2 4- Л2) ( Н - —7-
J \ R£
о
г dr =
R
= [ (R4 4- 2Л2г2 - Зг4) г dr = ttIIR4.
Rz J
о
>
11.95. Найти div (xyi 4- yzj 4- zxk).
11.96. Найти div—
{/(x + y + z)2
11.97. Найти дивергенцию векторного поля а = a?2?/i4-^?/2j+2;2k в точке Р(2, 2, —1).
11.98. Найти дивергенцию градиента скалярного поля и = *= x3y2z в точке Р(1, —1, 1).
11.99. Магнитное поле, создаваемое электрическим током силы I, текущим по бесконечному проводу, определяется формулой
Н(Р) — Н(а?, у) = 21 Вычислить divH(P).
х2 4- у2,
11.100. Найти дивергенцию векторного поля а = [с, г], где с — достоянный вектор.
11.101. Найти div(r[c, г]), где с — постоянный вектор.
Используя теорему Гаусса-Остроградского, решить следующие Задачи:
11.102. Доказать, что поток радиус-вектора г через любую кусочно гладкую замкнутую поверхность в направлении внешней Йюрмали равен утроенному объему тела, ограниченного этой поверхностью.
11.103. Найти поток вектора а = a?3i 4- ?/3j — z3k через всю Поверхность куба О^г^ав направлении
внешней нормали.
11.104. Найти поток вектора а = г/г через всю поверхность сферы х2 4- у2 4- z2 = R2 в направлении внешней нормали.
30
Гл. 11. Векторный анализ
11.105* . Найти поток вектора а = 2зй + yj — zk, направленный в отрицательную сторону оси Ох, через поверхность части параболоида у2 + z2 = Rx, отсекаемой плоскостью х = R.
11.106. Распространить понятие потока и дивергенции на случай плоского (двумерного) поля и сформулировать теорему Гаусса-Остроградского для этого случая.
11.107* . Используя решение предыдущей задачи, преобразовать циркуляцию вектора по замкнутому контуру L в плоском поле в двойной интеграл по площади, ограниченной этим контуром.
11.108. Найти с помощью теоремы Гаусса-Остроградского поток вектора а = a?2?/i + :ry2j + xyzk через всю поверхность тела ж2 + у2 + z2 R2, х 0, у 0, z 0 в направлении внешней нормали.
11.109. Найти поток вектора а = x2yi — xy2j + (x2 + y2)zk через всю поверхность тела х2 + у2 R2, 0 z Н в направлении внешней нормали.
2. Вихрь векторного поля. Теорема Стокса. Вихрем векторного поля а = а(г), обозначаемым rota, называется вектор, который в каждой точке Р дифференцируемости поля определяется следующим образом:
(пр rot а)р = lim — (р (a, dr}.
<тр —>0 СГр
Здесь s — единичный вектор произвольного направления, 1р — малый замкнутый контур, окружающий точку Р, лежащий в плоскости, перпендикулярной к вектору s и обходимый в положительном по отношению к вектору s направлении, стр — площадь области, ограниченной контуром 1р', предел ищется при условии, что контур 1р стягивается в точку Р. В трехмерном пространстве rot а через декартовы прямоугольные координаты вектора а = axi 4- ayj + azk выражается следующим образом:
_ —у j : I г —* _ —| j । [ —у _ —* ду dz ) \dz дх ) \ дх ду
Теорема Стокса. Циркуляция дифференцируемого векторного поля а по произвольному кусочно гладкому замкнутому контуру L равна потоку вектора rota через поверхность G, ограниченную этим контуром L:
(2)
§ 3. Характеристики скалярных и векторных полей
31
или в координатной форме
У (ax dx + ciydy + az dz) =
L
f f (daz dciy \ , - f дсьх daz \ , ( da.y dax \ , »
= / / ------л dydz + ----dxdz+ dxdy.
J J \ oy oz ) \oz ox J \ox oy J
G
При этом единичный вектор п нормали к поверхности G направлен в Такую сторону, чтобы обход контура L производился в положительном по отношению к п направлении.
Пример 2. Проверить ответ задачи 11.76 при помощи теоремы Стокса.
<| Так как а = zi 4- xj 4- ук, то rota = i 4- j 4- к. За поверхность G, ограниченную контуром L, примем сам круг, образованный сечением шара х2 4- у2 4- z2 R2 плоскостью х 4- у 4- х = R. Центр круга ОДЛ/З, Л/3, .R/3); его радиус R\ = Ry/'l/S. Единичный вектор нормали n = (i 4- j 4- k)/\/3. Так как (rota, п) = З/у/З = у/3, то находим
У (a, dr) = (rot a, n) do = х/З J^Jdo — у/З-xR2 = — l G G
Пример 3. Найти циркуляцию вектора а = yi — 2zj 4- xk вдоль эллипса, образованного сечением гиперболоида 2х2 — у2 4- z2 = R2 плоскостью у = х, в положительном направлении относительно орта i. Ответ проверить при помощи теоремы Стокса.
О Параметрические уравнения заданного эллипсах — Rcost, у = Rcost, £ = R sin t. Для обхода в заданном направлении параметр t надо изменять от 0 до 2тг. Следовательно,
•
® (a, dr) = Ф у dx — 2z dy 4- х dz =
L L
2тг
= R2 У (- sin t cos 14- 2 sin21 4- cos2 t) dt = ЗтгR2. о
Применим теорему Стокса. Имеем rota = 2i — j — к. За поверхность G, ограниченную контуром L, примем часть секущей плоскости, лежащей внутри эллипса. Единичный вектор нормали, направленный в
1 . 3
нужную сторону, имеет вид n = -т=(1 -J). Поэтому (rota, п) = и 2 2
Ф (a, dr) = [ [ (rota, da) = [ [ (rota, n)do = -7= [ [ do = -у=тг ab.
32
Гл. И. Векторный анализ
Но так как эллипс имеет полуоси a = R\/2 и b = R, то
L
= rot —
11.110. Найти rot xyz(xi 4- уj 4- 2k).
11.111. Найти rot (Р(ж, y)i 4- Q(x, y)j).
11.112. Показать, что магнитное поле Н(Р) (см. задачу 11.99) в области своего определения является безвихревым.
11.113. Найти ротор поля [а, с], если а = z2i 4- ?;2j — ,x,2k и с - i - j + 2k.
„ xi 4- у] 4- zk
11.114. Найти rot —•... = t-у x2 4- У2 + Z2
11.115* . Жидкая среда вращается с угловой скоростью ш = = олД + cjyj +<vzk вокруг оси, проходящей через начало координат. Найти вихрь поля скоростей этой среды.
11.116. Вывести формулу Грина (см. ответ к задаче 11.107), применяя теорему Стокса к двумерному векторному полю а = — Н- О’уЗ •
11.117. Пользуясь формулой Грина, убедиться в том, что площадь Q плоской области D. ограниченной кусочно гладким контуром L, можно найти при помощи любого из трех следующих интегралов: Q — j) xdy = — $ у dx = - j) xdy — у dx.
L L L
11.118. Используя последнюю формулу предыдущей задачи, найти площади фигур, ограниченных следующими кривыми:
а)* петлей Декартова листа ж3 4- у2, — Ъаху — 0;
. а2 о Ь2 . о
б) эволютой эллипса х = — cos t, у = — sm° t (а и о — полуоси эллипса, с = х/о2 — б2).
11.119. При помощи теоремы Стокса найти циркуляцию вектора а = z2i 4- z2j 4- ?/2k по сечению сферы х2 4- у2 4- z2 = R2 плоскостью х + у + z^Rb положительном направлении относительно орта к.
11.120. Найти циркуляцию вектора а — z3i 4- z3j 4- y3k по сечению гиперболоида 2х2 — у2 4- z2 = R2 плоскостью х 4- у = 0 в положительном направлении относительно орта i. Проверить при помощи теоремы Стокса.
11.121. Найти циркуляцию вектора а = ?/2i 4- ху] 4- (х2 4- т/2)к по контуру, вырезаемому в первом октанте из параболоида х2 4-4- у2, = Rz плоскостями т = 0, ?/ = 0, z — R в положительном
§ 3. Характеристики скалярных и векторных полей 33
направлении относительно внешней нормали параболоида. Проверить при помощи теоремы Стокса.
3. Оператор Гамильтона и его применение. Все операции векторного анализа можно выразить при помощи оператора Гамильтона — символического вектора V (читается — набла), определяемого равенством
V7 ‘д . д
dx оу dz
Применяя известные операции умножения вектора на скаляр, скалярного и векторного произведения двух векторов, находим:
. .ди .ди , ди _ ди . , . , _
grad и = 1—+j—+k— = Vu; — = (s, gradu) = (s, Xu) - (s, X)u\ dx dy dz ds
dar day da, .
div a = —- + —* + —- = V, a ;
dx dy dz
f da ~ day rot a = ------—
\ dy dz
ddj. da, \ . / day —---------- + —-
dz dx J \ dx
dax dy
i j k AAA dx dy dz ax ay az
По аналогии с производной по направлению от скалярной функции
ди ds
вводится понятие производной по направлению единичного вектора s от векторной функции а(г). Именно,
— = (s, V)a = (s, gradflaji + (s, grada^)] + (s, gradajk -
dax. day. да,Л
-x-i+ + -д-к.
ds ds ds
Производные по направлению произвольного (не единичного) вектора с отличаются от производных по направлению единичного вектора только тем, что в них входит дополнительный скалярный множитель |с|:
(с, Х)и — (с, grad и),
(с, V)a = (с, gradaz)i + (с, grada^)] + (с, grada2)k.
С помощью оператора Гамильтона удобно выполнять дифференциальные операции векторного анализа над сложными выражениями (произведение двух или более скалярных функций, произведение скалярной функции на вектор, скалярное и векторное произведения векторов и т.п.).
34
Гл. 11. Векторный анализ
Следует лишь помнить, что это оператор дифференцирования произведения.
Пример 4. Найти градиент произведения двух скалярных функций и и V. < Имеем
grad (uv) = V (uv) = V (uv) + V (uv)
(стрелка указывает функцию, на которую «действует» оператор). Но
V(uv) = vVu = vgradu,
V(uv) = uVv = ugradv.
Таким образом, grad uv = v grad u + u grad v. >
Пример 5. Найти rot [а, с], где c — постоянный вектор.
< Так как по известной формуле векторной алгебры [а, [Ь, с]] — (а, с)Ь —
4,
— (а, Ь)с, то, учитывая соотношение [V, [а, с]] = 0, имеем:
rot [а, с] = [V, [а, с]] = [V, [а, с]] + [V, [а, с]] = (V, с) а -(V, а)с.
-I- 4.
Но (V, с) а— (с, V) а, а это есть производная вектора а по направлению вектора с. Далее, (V, а)с = c(V, а) = с div а.
Таким образом, rot [а, с] = (с, V)a — с div а. >
Выполнить следующие дифференциальные операции (с — постоянный, а и b — переменные векторы):
11.122 . Найти div (си) и div(au).
11.123 **. Найти grad (а, с) и grad (а, Ь).
11.124 . Найти div [а, с] и div [а, Ь].
11.125 *. Найти rot (cu), rot (аи) и rot [а, Ь].
4. Дифференциальные операции 2-го порядка. Можно образовать пять дифференциальных операций 2-го порядка:
1) div grad u = (V, V)u = V2u = A u (лапласиан функции);
2) rot grad u — [V, V]u;
3) grad div a = V(V, a);
4) div rot a = (V, [V, a]);
5) rot rot a == [V, [V, a]].
Кроме того, операцию V2 можно применять и к векторным полям, т.е. рассматривать операцию V2a.
Вторая и четвертая операции приводят к нулю:
rot grad u = [V, V]u = 0, div rot а = (V, [V, a]) = 0.
§ 4. Специальные виды векторных полей
35
Это следует из векторного смысла оператора V: в первом случае формально мы имеем векторное произведение двух коллинеарных векторов, а во втором — смешанное произведение компланарных векторов.
11.126. Получить выражения для
div grad u = V2w,
grad div a = V(V, a), rot rot a = [V, [V, a]], V2a = V2axi + V2ayj + V2azk
через производные скалярного или векторного полей.
11.127. Найти grad diva, если а = i;3i + y3j + д3к.
11.128. Найти rot rot а, если а = ху2i + ?/z2j 4- д.т2к.
11.129. Найти V2a, если а = (у2 + z2)xi 4- (т2 4- z2)yj 4-
4- (х2 4- ?/2)гк.
11.130. Найти div grad (uv).
11.131. Найти grad div (wc) и grad div (wa) (c — постоянный, a — переменный вектор).
11.132. Найти rot rot (uc).
§ 4. Специальные виды векторных полей
1. Потенциальное векторное поле. Векторное поле а = а(г) называется потенциальным, если вектор поля а является градиентом некоторой скалярной функции и — и(Р):
a(r) = grad u(P). (1)
Функцию и(Р) в этом случае называют потенциалом векторного поля. Необходимым и достаточным условием потенциальности два?кды дифференцируемого в односвязной области поля а(г) является равенство нулю вихря этого поля:
rot а = 0. (2)
Пример 1. Проверить, что вихрь трехмерного векторного поля а = grad и тождественно равен нулю (функцию и(Р) предполагаем дважды дифференцируемой).
m . du. du. ди.
<] Так как а = grad и = —1 4- —J 4- — к, то, учитывая равенство дх ду dz
смешанных производных 2-го порядка, получаем
. ( д (ди\ д (ди\ \ .
rot а = rot grad w= - — -— — i4-
уду уdz J dz уду J J
( д (ди\ d (du\ \ . ( д (ди\ d(du\\
4- — —-------— 14- — —------— k = 0. >
ydz ydxJ dx ydz J J ydx уду J ду у dx J J
36
Гл. 11. Векторный анализ
В п. 4 предыдущего параграфа это равенство было получено с использованием свойств символического вектора набла.
Потенциальное поле обладает следующими свойствами.
1. В области непрерывности потенциала поля линейный интеграл от вектора поля, взятый между двумя точками поля, не зависит от пути интегрирования и равен разности значений потенциала поля в конце и начале пути интегрирования
в в
У (grad ц, dr) = У du — u(B) — u(A)
А А
(3)
(использована легко проверяемая формула (gradu, dr) = du).
2. Циркуляция вектора поля по любому замкнутому контуру, целиком лежащему в области непрерывности поля, равна нулю.
3. Если поле а потенциально, то потенциал поля и(Р) в произвольной точке Р может быть вычислен по формуле (3):
р
и(Р) =
(a, dr) + С,
(4)
причем С — и(А), что легко получается подстановкой в (4) вместо переменной точки Р фиксированной точки А.
Для вычисления интеграла (4) можно выбрать любой путь — проще всего в качестве такого пути выбрать ломаную со звеньями, параллельными осям координат, соединяющую точки А и Р. За точку А удобно принимать начало координат (если оно лежит в области непрерывности поля).
Пример 2. Найти потенциал поля а = 2a??/i + (ж2 — 2?/;?)j - ?/2k. < Убедимся, что поле потенциально:
daz дау дах daz дау дах
~о~ ~ “я- — — -х— — 0, -j—- — —— — 2х.
Оу oz oz ох ох Оу
Следовательно, rota = 0.
За путь интегрирования примем ломаную ОАВР, где 0(0, 0, 0), А(Х, 0, 0), В(Х, У, 0), Р(Х, У, Z). Находим:
(a, dr) = 2ху dx 4- (ж2 — 2yz)dy — у2 dz.
§ 4. Специальные виды векторных полей
37
Так как на [ОЛ] имеем у — z = 0, dy = dz = 0, 0 х 4 X, то
(a, dr) = 0.
Аналогично, на [АВ] имеем х = X, dx — 0, z = 0, dz = 0, 0 у У, поэтому в Y
У (a, dr) = У X2 dy = X2Y.
А О
На [ВР] имеем х = X, у = Y, dx = dy = 0, 0 z Z, значит,
р z
У (a, dr) = - У У2 dz = -Y2Z. в о
Таким образом, и(Х, У, Z) = X2Y — Y2Z + С. Возвращаясь к переменным х, у, z, получаем
и(Р) = х2у - y2z + С. >
Замечание. Изложенный метод отыскания потенциала поля применяется при решении таких эквивалентных рассмотренной задач математического анализа, как восстановление функции двух, трех и п переменных по их полным дифференциалам, а также при интегрировании дифференциальных уравнений в полных дифференциалах.
Найти потенциалы следующих плоских и трехмерных полей: 11.133. а = (Зх2у — y3)i + (ж3 — 3a?T/2)j.
sin 2х cos 2у • i 4- cos 2х sin 2у • j y/cos2 x sin2 у + sin2 x cos2 у
11.135. a = (yz — xy)i + ^xz — x2 9\ ^+vz) j + (xy + y2z)k.
q<j* (i A • 1 (i 11.136 . a = 1 x i 4- - x2 J \x z A . 2 ) J + У J 1 r-< 1 k.
11.137*. a = f 4 - 4 - \y2 Z2 X6 J . ( Z x 2xz' 22 y3 у j +
\;r2 y2 2ж?;\ , + ~Г k. z6 J
38
Гл. 11. Векторный анализ
11.138*. Доказать, что во всюду непрерывном потенциальном векторном поле векторные линии не могут быть замкнутыми.
Если в плоском потенциальном поле есть точки, в которых поле теряет свойство непрерывности (так называемые особые точки), то циркуляция по замкнутому контуру, окружающему такую точку, может быть отлична от нуля. В этом случае циркуляция по контуру, обходящему данную особую точку один раз в положительном направлении, не зависит от формы контура и называется циклической постоянной относительно данной особой точки.
Аналогичными свойствами обладают трехмерные поля с особыми линиями, вдоль которых поле теряет свойство непрерывности.
— у\
11.139 . Убедиться в потенциальности поля а = —---Опре-
xz 4- yz
делить его особую точку и ее циклическую постоянную.
11.140 *. Доказать сформулированное выше свойство о том, что циркуляция по замкнутому контуру, окружающему особую точку, не зависит от формы контура.
11.141 *. Воспользовавшись формулой (4) для определения потенциала поля, убедиться в том, что потенциал плоского поля, имеющего особые точки, будет многозначной функцией.
2. Соленоидальное поле. Векторное поле а = а(г) называется соле-ноидальным, если дивергенция этого поля равна нулю: diva = 0.
Для трехмерного поля это условие можно переписать в виде
div а -
дах dav да~ дх ду dz
= 0.
В таком поле в силу теоремы Гаусса-Остроградского равен нулю поток вектора поля через любую замкнутую поверхность. Исключение может быть только в случае наличия в таком поле особых точек (в которых вектор поля не определен и дивергенция поля, если ее определять в такой точке при помощи формулы (1) § 3, отлична от нуля). В этом случае поток через замкнутую поверхность может быть отличен от нуля, но будет иметь одно и то же значение для всех замкнутых поверхностей, окружающих данную группу особых точек.
Пример 3. Доказать, что для любого дважды дифференцируемого трехмерного векторного поля а = а(г) поле вихрей соленоидально.
< Имеем
rot а =
dz J
daz \ . / дау дах \ dx J \ dx dy J
§ 4. Специальные виды векторных полей
39
Учитывая равенство смешанных производных 2-го порядка, получаем
д (да, дау\ д (дах да~\
div rot а = — —Z +— +
дх у ду dz ) ду \ dz дх J
д ( дау дах \
+ V И/ - -7Г = 0- > dz у дх ду J
В п. 4 предыдущего параграфа это соотношение доказано с помощью оператора набла.
11.142. Доказать, что в соленоида льном поле поток вектора через замкнутую поверхность, не содержащую внутри особых точек, равен нулю.
Проверить соленоидальность следующих полей:
11.143.
11.144.
а = (х2у + ?/3)i + (ж3 - z?/2)j.
а = я?/2! + :z;2?/j — (х2 + ?/2)zk.
(х + у) In г
ху
(я;2 — ?/2)дк (х2 4- у2)^/2
а =
11.145.
а =
11.146.
х . у .
1 4---J -
yz XZ si-yj , у/х2 + у2
11.147*. Доказать, что в соленоидальном поле поток вектора поля через поперечное сечение любой векторной трубки (определенный в одном и том же направлении) сохраняет постоянное значение.
3. Лапласово (или гармоническое) поле. Векторное поле называется лапласовым (или гармоническим), если оно одновременно и потенциальное, и соленоидальное, т. е. если
rot а н О и div а = 0. (6)
Пример 4. Доказать, что потенциал и двумерного или трехмерного лапласова поля является гармонической функцией двух или трех / д2и д2и д2и д2и д2и \
переменных т. е. у— + = ° или = 0) •
\ dxz ду2 дх2 ду2 dz2 /
< Действительно, имеем
1- j- j &2и &2и
div а = div grad и = 7—5- + = О
дхл ду£
для двух переменных,
д2и &2и &2и
div а = div grad и = = °
дх2 ду1 dz2
для трех переменных.
40
Гл. 11. Векторный анализ
Пример 5. Показать, что потенциал поля сил тяготения, возникающего в пространстве, окружающем некоторую точечную массу, равен к/г {к > 0 — коэффициент пропорциональности) и что поле сил тяготения лапласово.
<1 Поместим начало координат в центре притяжения. Тогда
, к 1 xi + yj + zk кг
а = grad - = /с grad == = -к —------------= -~т-
г у/ж2 + у2 + z2 (ж2 +у2 +22)3/2 f3
Но это — вектор силы притяжения. Действительно, он направлен к центру притяжения, поскольку —г/г — единичный вектор радиус-вектора точки Р(г), направленный к началу координат, а его модуль равен Аг/г2, т.е. обратно пропорционален квадрату расстояния от центра притяже-г
ния. Покажем, что diva = —A;div — — 0. Имеем:
кт.
Х (х2 + у2 + Z2)3/2 ’
дах х2 + у2 + z2 - Зж2 у2 + z2 - 2ж2 дх (ж2 + у2 + г2)5/2
Аналогично, дау х2 + z2 — 2у2 daz х2 + у2 — 2z2 ~ду = ~к = ~к ’
и потому
+ + = -4((!/2+^-2^) + (^+22-2!/2) + (^+!/2-2Z2)) =0.
ох оу OZ г*
Итак, поле сил тяготения лапласово. >
11.148 . Доказать, что плоское векторное поле, потенциалом которого служит функция u = In г (г = у/ж2 4- ?/2), лапласово.
11.149 *. Для гармонических в области G функций и и w доказать следующие формулы Грина:
9 /г U~d~ ~ /// (Srac*w5 gradw)cw
S G
(первая формула Грина),
(вторая формула Грина),
§5. Применение криволинейных координат в векторном анализе 41
#d(uw) п f f f / ! , ч ,
—-— do = 2 / / / (grad u<, grad w) dv
S G
(третья формула Грина).
Являются ли гармоническими следующие функции:
1 1
11.150. и = - = -==.
Г аД2 + у2
11.151. и - г — х = уж2 4- у2 — х.
11.152. u = Ах + By + С.
11.153. и = Ах2 4- 2Вху 4- Су2.
11.154. и = Ах3 4- ЗВх2у 4- ЗСху2 4- Dy3.
11.155. и = Ах 4- By 4- Cz 4- D.
11.156. u = ацх2 4- ацу2 4- a33z2 4- Za^xy 4- 2a^xz 4- 2й23^-
11.157. u = ащх3 4- a.2223/3 4- а333д3 4- Защ^У + Зац3ж2г 4-4- 3ai22-'r?/2 4- За223?Д 4- За133дд2 4- 3«233^2 + ^a^xyz.
§ 5. Применение криволинейных координат в векторном анализе
1. Криволинейные координаты. Основные соотношения. В пространстве задана система координат, если каждой точке Р поставлена в соответствие тройка чисел <?i, q%, <73, причем различным тройкам чисел отвечают различные точки пространства. Числа д15 q?, q% называют координатами (или криволинейными координатами) точки Р = P(qi, q?, <7з)-Наиболее употребительными являются следующие системы координат:
1) Декартова прямоугольная система координат. Здесь q\ = х — абсцисса точки P. q2 — у — ордината и д3 = z — аппликата.
2) Цилиндрическая система координат. Здесь за q^ принимается расстояние г от точки Р до оси г, Qi = г (0 г < 4-оо), q? = — угол,
составленный проекцией радиус-вектора ОР на плоскость Оху с положительным направлением оси Ох (0 < 2тг), a q3 = z — аппликата
точки Р.
При этом цилиндрические координаты связаны с декартовыми прямоугольными координатами при помощи формул
х — г cos 99, у = г sin 99, z — z
и, обратно, ----- у
г = 4- у2, tg9? = —.
х
3) Сферическая система координат. Здесь qi = г — длина радиус-вектора точки Р (0 г < 4-оо), <72 = & — угол между положительным направлением оси Oz и радиус-вектором ОР точки Р (0 0 тг)1),
*) Иногда за координату уг сферической системы принимают угол между --------------►
радиус-вектором ОР и плоскостью Оху (см. Часть 2, гл. 9, § 2).
42
Гл. 11. Векторный анализ
9з = (р — угол между положительным направлением оси Ох и проек---------------------->
цией радиус-вектора ОР на плоскость Оху (0 < 2тг). Имеют место
формулы:
х = г sin 0 cos <р, у = г sin в sin <р, z = г cos О и, обратно,
riTx—2 ; " ~2~ a z . у
г = у/ хЛ + уЛ + z2, cost/ = , tg <р = —.
у/ X2 + у2 + Z2 х
Линия, вдоль которой изменяется только одна координата qi, называется координатной qi-линией, а единичный касательный вектор к этой линии, направленный в сторону возрастания, qi — единичным координатным ортом eqi в точке Р (д°, q2, q3). Аналогично определяются 92- и д3-линии и единичные орты е92, е9з.
Если векторы е91, е92, е93 попарно ортогональны в любой точке пространства, то соответствующая система криволинейных координат qi, q2, 9з называется ортогональной.
Пусть Р (91,92,93) — произвольная точка пространства,
Р (gi + Agi, д2, 9з) — точка, лежащая на gi-линии точки Р, и | PPi | — длина дуги PPi. Тогда число
№1
Li = lim Aqi—>0 Agi
называется коэффициентом Ламе координаты gi в точке Р. Аналогично определяются коэффициенты Ламе Ь2 и L3 координат 92 и 93.
Если точка Р (х, у, z) имеет криволинейные координаты qi = — Qi(.x, У, •?)> 92 = 92(2, У, z), q3 = q^x, У, z), то дифференциалы радиус-векторов drq„ координатных линий и дифференциалы их дуг dsq^ определяются с помощью равенств
дх ду dz
dr q — 1— dqv + j — dqv 4- k~ dq^ — L/L,eq dq^, dq„ dqv dqv
(y = 1, 2, 3), где Lv — коэффициенты Ламе.
Множество точек P(gi, 92, 9з)> для которых одна из координат постоянна, называется координатной поверхностью.
Дифференциалы площадей координатных поверхностей определяются по формулам
daqi = L2L3dq2dq3, daq2 = L]L3dqidq3, daq3 = LiL2dqidq2, а дифференциал объема
dv = LiL2L3dqidq2dq3.
§ 5. Применение криволинейных координат в векторном анализе 43
Найти вид координатных линий и координатных поверхностей и построить их в произвольной точке для следующих случаев:
11.158. Для декартовой прямоугольной системы координат.
11.159. Для цилиндрической системы координат.
11.160. Для сферической системы координат.
Вычислить коэффициенты Ламе:
11.161. В декартовой прямоугольной системе координат.
11.162. В цилиндрической системе координат.
11.163. В сферической системе координат.
Найти дифференциалы дуг координатных линий, дифференциалы площадей координатных поверхностей и дифференциал объема:
11.164. В декартовой прямоугольной системе координат.
11.165. В цилиндрической системе координат.
11.166. В сферической системе координат.
2. Дифференциальные операции векторного анализа в криволинейных координатах. Указанные операции определяются следующими формулами:
1 du 1 du 1 du gradw -
diva = ~~ -—-{L2L3aqx} + (L1L3a<l2) + —-(LiL2ag3)
LlL2L3 \dqi dq2 dq3
(здесь a — *4- aq2eq2 *4*
1 f d /T . d \ Ifd fOta " L^L~3 \d^L3aq^ ~ ^L2a<^) eqi + TjT3 \d^Liaq^ ~
d A Ifd d \
~ ~d^ 3aq3ye<i2 + LiL2 \dq^ 2(lq^~dqf^
1 / d (L2L3 du\ d (LrLsduX
LxL2L3 \dqi \ L] dqi J dq2 \ L2 dq2 J
d /L\L2 du\\ dq3 \ L3 dq3 ) )
Для цилиндрических координат r, ip и z найти выражения:
11.167. gradu. 11.168. Au.
11.169. diva. 11.170. rota.
44
Гл. 11. Векторный анализ
Для сферических координат г, в, ip найти выражения:
11.171. gradu. 11.172. Ди.
11.173. diva. 11.174. rota.
Пример 1. Перейти к цилиндрическим координатам в выражении zi + yj - zk ..
векторного поля а = и найти div а и rot а.
у х2 + у2 + z2
< Так как в данном случае zi 4- yj — г, то
rer — zez а — .
\/г2 + г2
По формулам, полученным при решении задач 11.169 и 11.170, находим:
, 1 / д(гаг) даф daz
div а - -
Г \ ОТ dp oz
1 ( 2r(r2 + г2) - г3 (г2 + z2) - z2 г \ (г2 + г2)3/2 (г2 + г2)3/2
2г2
(г2 + г2)3/2 ’
rota =
1 daz (даг
т dp dr ;r + \ dz
2r z
(Г2+г2)3/2^- >
11.175. Вывести формулы:
А Г 1 d<LiLk} М + 1 Г 1 Г 1
a) dive^ = —-----д2---; б) rote^ = — [gradL^, e^J.
Ь1Ь2Ьз oq»
11.176. Используя формулы, выведенные при решении задачи 11.175, найти diva и rot а для единичных координатных векторов цилиндрической системы координат:
а) а = ег; б) а = е^; в) а = е2.
11.177. Решить задачу, аналогичную 11.176, для сферической системы координат:
а) а = ег; б) а = ео; в) а =
11.178. Найти все гармонические функции вида:
a) u = f(r)- б) u = f(p)- в) u = f(z)
(г, р, z — цилиндрические координаты).
11.179. Найти все гармонические функции вида:
a) u = f(r)- б) и = /(6>); в) u = f{tp) (г, в, <р — сферические координаты).
§ 5. Применение криволинейных координат в векторном анализе 45
11.180. Перейти к сферическим координатам в выражении ска-2xy(z2 -х2 -у2) „
лярного поля и =----------5----- и наити u, grad и и V и.
хл + уЛ
11.181. Перейти к цилиндрическим координатам в выражении
2xyz + [х2-у2) „ 2
скалярного поля и =-----. — -----и наити и, gradti и V и.
у/х2 + у2
11.182. Перейти к сферическим координатам в выражении век-— yi
торного поля а = - , --- —г и найти a, div а и rot а.
у/х2 + у2 4- z2
11.183. Перейти к цилиндрическим координатам в выражении векторного поля а = xzi + yzj — zy/x2 + iy2k и найти a, diva и rot а.
3. Центральные, осевые и о се симметрические скалярные поля. Скалярное поле называется центральным, если функция поля и = и(Р) зависит только от расстояния точки Р поля от некоторой постоянной точки — его центра. Если начало координат поместить в центр поля, то функция и примет вид
и = u(r) = -I- ?/2 + Z2).
При исследовании таких полей целесообразно пользоваться сферическими координатами. Поверхностями уровня такого поля будут сферы с центром в центре поля, и потому эти поля часто называют сферическими.
Скалярное поле называют осевым, если функция поля и(Р) зависит только от расстояния точки поля Р от некоторой оси. Если принять эту ось за ось Oz и обозначить расстояние от точки Р до нее через г, то функция и примет вид
и = и(г) — и(у/х2 + у2).
При исследовании таких полей целесообразно пользоваться цилиндрическими координатами. Поверхностями уровня таких полей являются круговые цилиндры, оси которых совпадают с осью поля. Эти поля называют также цилиндрическими.
Если функция и(Р) скалярного поля принимает одни и те же значения в соответствующих точках всех полуплоскостей, проходящих через одну и ту же прямую (ось поля), то такое поле называют осесимметрическим. Поверхности уровня такого поля — поверхности вращения, оси которых совпадают с осью поля. Если ось поля принять за ось Oz, то при исследовании таких полей целесообразно пользоваться либо сферическими, либо цилиндрическими координатами. Функцию и = и(Р) можно в этом случае представить либо в виде
и - и(г, 0)
46
Гл. 11. Векторный анализ
(в сферических координатах), либо в виде
u = u(r, z)
(в цилиндрических координатах).
Замечание. Градиенты центральных, осевых и осесимметрических полей образуют векторные поля того же характера — центральные, осевые и осесимметрические.
Найти градиенты и лапласианы следующих полей:
11.184. и = /(г), г = \/х2 + у2 + z2.
11.185. u = г = у/х2 + у2.
11.186. u = F(r, 0) (г, 0 — сферические координаты).
11.187. u — F(r, z) (г, z — цилиндрические координаты).
Глава 12
РЯДЫ И ИХ ПРИМЕНЕНИЕ
§ 1. Числовые ряды
1. Сходимость ряда. Критерий Коши. Выражение
оо
U1 + U2 + . . . + ип + . . . = 'У Un, (1)
71=1
где (iZfc)fceN — заданная числовая действительная или комплексная последовательность, называется числовым рядом. Конечные суммы
5i=«i, S2 = ui + «2, • • • ,Sn = щ 4- u2 -I-Fun,... (2)
называются частичными суммами ряда (1).
Если существует конечный предел последовательности частичных сумм (2) S = lim Sn, то ряд (1) называется сходящимся, а число S — п—>оо
суммой ряда (1).
Критерий Коши. Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого е > 0 существовало N = N(e} такое, что для всех п > N и р = 1, 2, ... выполнялось неравенство
1‘S'n-f-p *5*п| = 4“ ^n-f-2 4” " ’ ’ 4” Wn-f-p| Е.
Необходимый признак сходимости. Если ряд (1) сходится, то
lim ип = 0.
п—>оо
~ 1
Пример 1. Показать, что ряд > —.---------- сходится, и найти его
' п(п + 1) п=1 х '
сумму.
< Так как дробь —-----— представима в виде
х\х + 1)
1 _ 1________1_
х(х + 1) х х 4-1 ’
48
Гл. 12. Ряды и их применение
то частичную сумму ряда можно записать следующим образом:
$п 1-2~*'2-3 + 3- 4'*' (п - 1)п n(n + 1)
-.I 1_1 i_i 1___________________1 1_________L__i________1
2 2 3 + 3 4 + ’ + п — 1 п, + п п + 1 п+1
Следовательно,
lim Sn = lim I 1--------- 1=1,
71—>oo n—>oo \ 72 + 1 /
т.е. заданный ряд сходится и его сумма равна 1. [> оо
Пример 2. Исследовать на сходимость ряд qn и в случае схо-п=0
димости найти его сумму. < Имеем
Sn = 1 + q + q2 + ... + qn 1.
Если q = 1, то Sn = n, т.е. lim Sn = оо, и, следовательно, ряд расхо-п—>оо
дится. Пусть теперь q ф 1, тогда
. l-9n 1 qn — 1 — 1 1
1-q 1-q 1-q
Положим q = гё1^, тогда qn = rnetn,fi. При 0 < г < 1 имеем
lim qn = lim гпегп^ = О, п—>оо п—>оо
qn 1
т.е. lim -----= 0, откуда lim Sn = ------. Если же г > 1, то гп —> оо
п—>оо 1 — q п—too 1 — q
qn и, следовательно, конечного предела lim ----, а значит, и предела по-
n—t<x> 1 — q
следовательности частичных сумм не существует. Наконец, при г = 1 и £0 (mod27r) предел
lim егп,р = lim (cos ткр + i sin nip) n—too n—too
(а потому и предел lim Sn) также не существует, и—>схэ
ОО
Таким образом, ряд qn, члены которого составляют бесконечную 71 = 0
геометрическую прогрессию с первым членом 1 и знаменателем q, сходится при |g| < 1 и его сумма равна --и расходится при |g| 1. [>
§ 1. Числовые ряды
49
Пример 3. Доказать, что гармонический ряд
расходится, хотя его члены стремятся к нулю при п —> оо.
<0 Рассмотрим разность частичных сумм с номерами 2п и п. Имеем
1 1 1
S-2n — Sn — —- Н----—“ +
п + 1 п + 2 2п
Заменяя каждое слагаемое меньшей величиной 1/2п, получаем
1 1 1 _ 1 _ 1
2п 2п + 2п П 2п 2
Это неравенство означает, что при р = п для гармонического ряда не выполняется критерий Коши и, следовательно, ряд расходится. |>
Показать, что следующие ряды сходятся, и найти их суммы:
ОО 1 12.1. У — — ' п(п + 1)(п 72=1 + 2)' 12.2. оо о У-2—. 4п2 — 9 72=2
ОО 1 12 3 V - • • £^(2п - 1)(2п + 1)' 12.4. ул 2п + 1 п(п2 — 1) 71 = 3 v ’
ОО 12.5*. у 372 72=1 12.6. y.(l+i)n Z—< 2п 72 = 0
Используя критерий Коши или необходимый признак сходимости ряда, установить расходимость следующих рядов:
ОО 1 оо
12.7. у -- . 12.8. V
£1 л/п(п+1) £{" +2
ОО
12.9. £(-1)".
72=1
ОО
12.10. £
72=1
еп п10
12-11. £
72=1
(2 +»)" п2п
оо
12.12.
72=1
п + in
П
12.13. Доказать, что если члены сходящегося ряда умножить на одно и то же число, то его сходимость не нарушится.
50
Гл. 12. Ряды и их применение
оо оо
12.14. Доказать, что если ряды УУ un и УУ vn сходятся и их
72=1 72=1
(X)
суммы соответственно и и v, то сходится и ряд УУ (un + vn), при-72=1
чем его сумма равна i/4-v. Привести пример, когда обратное утверждение не имеет места.
12.15. Доказать, что отбрасывание конечного числа членов ряда не влияет на сходимость этого ряда (но влияет на сумму!).
2. Абсолютная и условная сходимость. Признаки абсолютной сходимости. Ряд (1) называется абсолютно сходящимся, если сходится ряд из модулей членов этого ряда, т.е. сходится ряд
ОО
1«1| + 1^21 + • • . + |wn| + . . . = У2 l^nl-n=l
(3)
Если ряд (1) сходится, а ряд (3) расходится, то ряд (1) называется условно сходящимся.
Признаки сравнения рядов. Если члены ряда (1) для всех
ОО
n > No (N 1) удовлетворяют условию |мп| Ьп, причем ряд УУ Ьп
П—1 сходится, то ряд (1) сходится абсолютно. Если же для п > N\ члены ряда (1) удовлетворяют условию 0 < сп |un|, причем ряд
ОО
У2 сп расходится, то ряд (3) расходится, т. е. ряд (1) не сходится п=1 абсолютно.
Пример 4. Зная, что ряд УУ —--------—• сходится (см. пример 1),
п=1 4* )
LX? ~| установить сходимость ряда > —.
п=1
оо 1 оо 1
<1 Так как 52 — = 52
п—1 п=0
то, учитывая неравенства
1 1
(п 4- I)1 2 п(п + 1) ’
n = 1, 2, ...,
LAJ ~| по признаку сравнения убеждаемся в сходимости ряда —. ' п2 п—1
§ 1. Числовые ряды
51
На практике более эффективным оказывается следующий
ОО
Предельный признак сравнения. Если ряд vn сходится п—1
абсолютно и существует конечный предел lim
п—>0
Ип
Vn
= q < +оо, то
ряд (1) также сходится абсолютно. Если же члены рядов ип и ип — действительные положительные числа и
п 1- ип
О < lim — < 4-оо, n-»oo уп
ОО оо
то ряды ип и vn либо оба сходятся, либо оба расходятся. п~1 п—1
Пример 5. Исследовать на сходимость ряд
Зп2 - 2 п4 4- 5п
(4)
1
<] Так как ряд ~ сходится (см. пример 4) и так как п=1
Зп2 — 2 1 о , п
hm —-----— : — = 3^0.
п->оо пл 4- on nz
то ряд (4) также сходится. С>
Пример 6. Исследовать на сходимость ряд
2п 4- 5
Зп2 — 2п
(5)
<] Так как
2п + 5 1 2
11т : - = ’
7i->oo Зп2 — 2п п 3
ОО 1
а гармонический ряд > — расходится (см.
z—' п
п=1 расходится. о
Признак Даламбера. Если члены ряда (1) таковы, что существует конечный предел
пример 3), то и ряд (5)
lim
п—>оо
Цп+1
52
Гл. 12. Ряды и их применение
то при 0 I < 1 ряд (1) сходится абсолютно, при I > 1 — расходится, а при I — 1 требуется дополнительное исследование.
Пример 7. Исследовать на сходимость ряд
(6)
TJ п3 (п +1)3
<] Имеем ип = —, un+i = —-—п— и " 9П ' on+1
.. u„+i (n +1)32" 1
lim ----= lim ——, = -
n->oo Пп п->оо 2n+1nd 2
Таким образом, ряд (6) сходится. >
Признак Коши. Пусть lim ?/|un| = I. Тогда если 0 I < 1, п—>оо
то ряд (1) сходится абсолютно, если I > 1, ряд (1) расходится, а при
I = 1 требуется дополнительное исследование.
Пример 8. Исследовать на сходимость ряд
<] Имеем ип
2п + 5\
Зп — 1 /
2n—1
, поэтому
lim ^/|un| = lim n—>oo n—>oo
2— —
2n + 5\
3n- 1/
Следовательно, данный ряд сходится. D>
При использовании признака Коши бывает полезна следующая формула Стирлинга'.
е12п ,
о < е < 1.
Пример 9. Исследовать на сходимость ряд
Е
П=1
2П • п!
пп
§ 1. Числовые ряды
53
О Имеем:
lim У|ип| = lim fl—>оо п—>оо
Z _1_
= - lim (2тгтг)2n e n—>oo
б 12n2
т.е. ряд сходится. D>
Интегральный признак Коши. Пусть функция f(x) положительна и монотонна при х 1, и пусть для всех п € N имеет место равенство f(n) — |un|. Тогда числовой ряд (3) сходится (т. е. ряд (1) сходится абсолютно) или расходится одновременно с несобственным интегралом
+оо
У f(x)dx,
а 1.
Пример 10. Выяснить, при каких значениях параметра р сходится ряд Дирихле
П=1
<] Так как функция f(x) — — удовлетворяет условиям интегрального хр
признака Коши, то исследование сходимости ряда Дирихле сводится к +оо /dx
—. Но хр
1
lim
Ь—>+оо
lim In b = +оо
b—>+оо
ь1-р 1
lim ---------------= 4-00
Ь->+oo 1 — P 1 — P
k 6—>4-00 \p — 1 (p— l)bp-1
при p = 1,
при 0 < p < 1,
1
---- при p > 1.
p-1
Отсюда заключаем, что ряд Дирихле сходится при р > 1 и расходится при р 1. >
54
Гл. 12. Ряды и их применение
12.16. Доказать, что всякий абсолютно сходящийся ряд является рядом сходящимся.
12.17. Доказать, что члены сходящегося ряда можно группировать, не меняя их порядка, произвольным образом.
12.18. Доказать, что члены абсолютно сходящегося ряда можно переставлять произвольным образом; при этом сумма ряда не изменится.
Используя признак сравнения или предельный признак срав-
нения, исследовать на сходимость следующие ряды:
19 I О оо 1 19 9П оо
Z_^ Зп — 2 Z_^
71=1 71=1
ОО ОО
12.21. Е п Зп3 — 1 12.22. Е
71=1 71=1
ОО ОО
12.23. Е . 7Г sin —. и 12.24. Е
71=1 71=1
ОО ОО
12.25. Е п2 tg6 —. п 12.26. Е
71 = 3 71=1
12.27. ОО Е 71 = 2 Inn vn 12.28.
оо оо
12.29. Е 71=1 2 (п 4- 1)3П 12.30. Е 71=1
э — 71
п2 4- 3 4п3 4- 5п
____1_ (2п —
cos у/п 4- i sin y/ri n2
признаком
1
Пользуясь следующие ряды: оо
12.31.
71=1
3 . „
12.33. т 4-—- + ...+
1 1-4
ОО t; ЕП —. 571 71 = 1
п2 4- 5
271
3-5
1-4
Даламбера, исследовать на сходимость
00 п
12.32. V 2-—' п!
71 = 1
3 • 5 ... (2n + 1)
12.36.
71=1
g2n+1 п\
1-4...(Зп-2)
12.35. f
71= 1
12.37. £
п=2
(Зп4-1)!
8пп2
1 • 3 • 5... (2п — 1) 22п(п - 1)!
§ 1. Числовые ряды
55
12.38. £
71=1
sin in 3n
12.39. У
n=l
Пп
nl(e — i)n
п2
оо
Используя признак Коши, исследовать на сходимость следующие ряды: оо / i \ 71
Е/ — 1 1
у 2п + 1J п—1 '
оо 1 / 1 \ и2
12.42. У — | 1 + - ) 2п к nJ n—L 4
ОО / \ 2п
12.44. £Уй(-2Ц) 2-—' у 4п — 3 J
71=1 '
71=1 ' '
00 1 / 1 \ п2
12.43. У — I 1 + - )
Зп у п /
71=1
оо / 1 \ и
12.45. > п | arcsin — )
У п J 71=1
°° / к \к / к \^/2
12.46. У ип, где u2k-i = ( 7-. ". , u2k = ( -----г
\2к + 1/ У ЗА: — 1/
П = 1
12.47. £
П=1
n + 2i V (1 + i)n + 3/
12.48. 52
П=1
i(2n + г) А” 4п )
Используя интегральный признак Коши, исследовать на сходимость следующие ряды: ОО |
12.49. У-----12.50.
2—< п In п п—2
оо 1 оо
12.51. У-—. 12.52. У-------—-----
z—'ninn nlnmlnlnnr
71 = 2 71 = 3 V ’
Исследовать на сходимость ряды:
оо
12.53. У
71=1
ОО
12.55. У
71=1 ОО
12.57. £
71=1
ОО
12.59. У
71=1
пп (2п — 1)п-1
56
Гл. 12. Ряды и их применение
12.61. 100 4-
100 • 103 ( 100 • 103... (97 + Зп)
1-5 + + 1 • 5 • 9... (4п - 3)
1-11 1-11-21 1-11-21... (10п — 9)
12.62. 1 +-----4----------+ ... Н-----------------------
3! 5! (2п - 1)!
1 1-5 1-5-9 1 • 5 • 9... (4п — 3)
1W- 2 + ГГб + 2-4-6-8-10+-•+ (4^2)Й +
12.64. £
п=2
\/п + 1 — \/п — 1
12.65.
п=2
1 \ п(п-1)
П — 1 \ к 7
/1 / 1 \\
12.66. V (In -х-р - In ( sin ) I.
\ п2/0 \ п2/5) J
п=1 х v '
12.67.
71=1
(п!)2 (И?
12.68. 52 si
П=1
7Г sm
оо
12.71. £
71 = 1
12.70. 52
71 = 3
1
n Inn In Inn
Зп -п!
Пп
12.72*. 52
71 = 1
en • n! nn
12.73. 2 4- +
1 • 5
2-5-8
1-5-9
2-5-8...(3n - 1)
l-5-9...(4n-3)
~ „100
12.74. V —
Z_> 2n 71=1
12.76. 52
71=1
2n- l\n
5n 4- 3 J
12.77. 52
71=1
n \71
n 4- 2 J
12.78. ---+----------+---------------+ ... 4-
100 100•102 100 • 102-104
l-4-7...(3n-2)
’ ’ ’ + 100 • 102... (98 4- 2n) + ‘
§ 1. Числовые ряды
57
12.79. оо Е у/п 12.80. оо Е
713 + 1
п= 1 71 = 2
оо 1 оо
12.81. Е п=2 1 п У1п3 71 12.82. Е П=1
оо оо
12.83. Е 1 12.84. Е
у/п + i
П=1 П=1
12.85. оо Е (2 + i)n • 71 2n 12.86. оо Е
П=1 П=1
2П
12.87. Исследовать на
сходимость
уп
(Зп + 1)(2УН-1)‘
1
1
оо 1
—------— при раз-
n_2
и а.
1
личных действительных значениях р
12.88. Исследовать на сходимость ряд > - . , .д
7“^nP(lnn) (1п1ппг при различных действительных значениях р, а и Д.
12.89. Убедиться в том, что признак Даламбера неприменим к 00 2fc-1 2к
ряду Un’ где U2k'1 = ~зЛ~’ U2k = зР тогда как пРизнак Коши П=1
показывает, что этот ряд сходится.
3. Признаки условной сходимости. Признак Лейбница. Пусть члены ап знакочередующегося ряда
di — а-2 + а,з — ад + ... + ап 4* ...
действительны, монотонно убывают, т. е.
di > 02 > • • • > ап > ... ,
lim ап = 0.
п—>оо
(7)
(9)
Тогда ряд (7) сходится, причем для его суммы S имеет место оценка S < Qi.
Пример 11. Исследовать на сходимость ряд
ОО
Ем)
7l+l 1 71
58
Гл. 12. Ряды и их применение
< Так как ап = — > -------- = an+i, n = 1, 2, ..., и lim — = 0, то
П П + 1 п—>оо п
выполнены условия (8) и (9), и данный ряд сходится. Ряд из абсолют-
ОО |
ных величин членов, т.е. ряд > —, расходится. Следовательно, ряд 1 п
П=1
ОО 1
^2 (—1)п+1 — сходится условно. О
П=1
Признак Абеля-Дирихле. Пусть члены последовательности (Ьп) монотонно убывают: bi > &2 > • • • > Ьп > ... и lim bn = О, п—>оо
а частичные суммы Sn = ai + а? + ... + ап, п = 1, 2, ... , ограничены в совокупности, т. е.
п
*=1
< М для всех п Е N.
ОО
Тогда ряд У2 апЬп сходится.
П=1
Пример 12. Исследовать на сходимость ряд
ОО
k=l
sin кх к
х Е R.
<] Очевидно, что в точках х — тк все члены ряда равны нулю, т.е. при х = ттг ряд сходится и его сумма равна нулю. Пусть теперь х ^0 (mod??). Подсчитаем сумму
п Л п
Е. 1 V—\ ж
sin кх =------2 2 sin — sin кх =
fc=i 2sin-fc=1 I 2 *
1
о • х
2sln2
X ( 1\
cos----cos n + - ж
2 \ 2/
2 sin
2
Отсюда заключаем, что для любых n = 1, 2, ... и х £0 (modfr)
И
У2 sin кх
2 1
I . х I ~ I . th
2 sm — sin-
I 21 I 21
§ 1. Числовые ряды
59
/1\ V 1
Далее, последовательность — монотонно убывает и lim — = 0. WziGN 71^00 n
Таким образом, при х ^0 (тобтг) выполнены условия признака Абеля-оо . ,
Esin кх
—-— сходится. Следовательно, ряд сходится К
k=L
при любом х. [>
Исследовать на абсолютную и условную сходимость следующие ряды:
оо
12.90. £(-ф
71=1
ОО
12.92. 22 о
5п — 2
1
Зп - 1
п
71=1
„ 1 1-4 1-4-7
' 12-95.
71 = 2 оо
1 О П<7 \ л / 1\п
1
71 = 3
ОО
71=1
ОО
12.101.
п2
71=1
ОО
12.103. 22
71 = 3
12.91. УЦС.
2—' пуп
71=1
22. / 2п - 1 \ п
Зп + 2 J
72=1
,1-47...(Зп-2)
’ 3-5-7...(2п + 1)
ОО ,
у (-1)"---------------
1 1-3-5...(2п-
71=1 ОО
1 О ПО \ Л ( 1 >71-1
п Inn (In Inn)3
71-1 if
2n‘
71=1
оо
1
па
1
71
n In П\/1п1пП
oo
12.104.
71=1
OO
12.Ю6. 22
71=1 OO
12.108. V .
к 3
71 = 1
sin па
in
п
2 + i\n
12.100.
12.102.
тг=2
71=1
. 7ГП sin — 4
п
оо
12.105*. 22
71=1
ОО
12.107. V | Л
\ 2 ,
71=1 ' '
ОО Есоэшд
—------
971
71=1
п
О • \ 71
3 — г \
1
п — 1пп
2
60
Гл. 12. Ряды и их применение
оо
Убедиться в том, что к рядам У un с указанными ниже чле-п=1
нами (к 6 N) нельзя применить признак Лейбница. Исследовать эти ряды на сходимость другими способами.
12.110* . u2k~l = ~7г=г--Г’ и2к =-----/ ----•
у/с + 1 + 1 4-1 - 1
1 1
12.111. Uok—i = —------, u2k =---------•
ЗА+ 2 ЗА; — 1
1 1
12.112. u2k-i = и2к =
ОО оо
12.114* . Доказать, что из сходимости рядов У^ |оп |2 и УУ |5П|2 п=1 п=1
оо
следует абсолютная сходимость ряда У^ anbn.
п=1
оо оо оо
Произведением по Коши рядов У ап и У^ЬП называется ряд У сп, п=1 П=1 П=1
члены которого получены по формулам
п Сп — (Lkbri—k+l, к=1
Исследовать на сходимость произведение по Коши следующих рядов:
оо - ОО - 00-00 1
12.115* *. и У-. 12.116*. И У (-1)
п2 2п п2 п
71=1 71=1 71=1 71=1
°° ( Л\П ОО - ОО - ОО -
12.117* . уЦ^и V А. 12.118*. У 1и У-.
п2, п п Пп
П=1 71=1 71=1 71=1
ОО
12.119. Доказать, что если ряд У ап сходится абсолютно, а
71=1 ОО
ряд УУ Ьп сходится, то произведение по Коши сходится.
П=1
§ 2. Функциональные ряды 61
Пусть — произвольная числовая последовательность,
п оо
sn = — частичные суммы сходящегося ряда У^ a Rn =
к=0 к=0
оо
= ик — остаток этого ряда. Проверить справедливость со-к=п+1
отношений (называемых преобразованиями Абеля): п п— 1
12.120. У ukvk = У (vk - vk+i)Sk - viSo + vnSn. k=i k=i
n n— 1
12.121. {Дк ^к+1)^к &т) 4* Vn(Sn Sm).
k=m+l k=m+l
n n
12.122. UkVk— [yk Vk—i)Rk—i 4- Ufn+lRm VnRn-k=m+l k—m+2
12.123. Доказать, что для остатка Rn знакочередующегося ряда (7), удовлетворяющего условиям признака Лейбница, справедливо неравенство |7?n| < an+i-
§ 2. Функциональные ряды
1. Область сходимости функционального ряда. Пусть функции fn(z)i n € N, определены в области D. Выражение
ОО
/1(г) 4- /2(г) + ... + fn(z) 4-... = У fn(z), z^D, (1) n=l
называется функциональным рядом. Если для zq € D числовой ряд 00
У fn(zo) сходится, то говорим, что функциональный ряд (1) сходится П=1 оо
в точке Zq. Если в каждой точке z € D\ С D числовые ряды У fn(z) п=1
Сходятся, то ряд (1) называется сходящимся в области D\.
Критерий Коши. Для того чтобы функциональный ряд (1) был сходящимся в области Dy, необходимо и достаточно, чтобы для •любого е > 0 и любого z G Di существовало N = N(e, z) такое, что
|/п4-1 (^) 4- fn+2 (z) 4- ... 4- fn+p[z) | < £
бля всех п > N(e, z) и р € N.
G2
Гл. 12. Ряды и их применение
Для определения области абсолютной сходимости функционального ряда (1) следует воспользоваться либо признаком Даламбера, либо признаком Коши. Именно, если
lim
п—>оо
/п+1
= К?)
ИЛИ
lim У|/п(г)| = l(z), n—>oo
то для определения области абсолютной сходимости ряда (1) следует решить функциональное неравенство l(z) < 1, а для определения области расходимости — функциональное неравенство l(z) > 1. При этом для изучения поведения ряда в граничных точках получаемой области, т.е. в точках, описываемых уравнением l(z) = 1, требуется дополнительное исследование.
Пример 1. Найти область сходимости функционального ряда
ул (-Ф+1 7l3’V5 + 2)n’
х е к,
х > —2.
< Так как 1/п(^)1 — ----7=-— — =
' пЗ»У+ + 2)п
Коши, имеем
и х > —2, то, применяя признак
1
lim г/-----= lim
п->°° ]/ пЗпу/(х + 2) п п—>оо
3(ж + 2)1/2 з^/а; + 2'
Следовательно, ряд сходится, если — 3v<FT2
< 1, т. е. при х >----.
17 °° j
При х = - — получаем знакочередующийся ряд (-l)n+1~, который У ' п
71=1
сходится по признаку Лейбница. Таким образом, область сходимости ряда — полуинтервал [—17/9, +оо). >
Найти области сходимости рядов (х G R). Исследовать ряды на абсолютную сходимость.
оо
12.124.
71=1 ОО .
12.126. V—.
П = 1
12.125. ^2
12.127. f
71=1
cos nx
Пу/n
1
nl(x + 3)n ’
§ 2. Функциональные ряды 63
ОО ОО / V
12.128. У п\ 12.129. У (хп +---------).
п2пхп J
п=1 n=l z
оо . оо
ES1I1ПХ v—' „ X
. 12.131. > xntg—. епх----------/ -J °
П=1 П=1
ОО ОО ч
12.132. y\rv?I. 12.133. J2—. П=1 П=1
Пример 2. Найти область сходимости функционального ряда оо «г—'. П
У 7-----У, г е С.
б-' (г — г)п п=1
.< Применяя признак Даламбера, можем записать неравенство
lim
п—1ОО
(z — i)n+1n
(п + 1)(г — г)п
<1,
откуда заключаем, что ряд сходится абсолютно вне круга радиуса 1 с центром в точке г, т.е. при |г — г| > 1. На окружности |г — г| = 1 ряд, очевидно, расходится. >
Найти области абсолютной сходимости рядов (г 6 С):
12.134. ОО 1 ОО 1 У —Ц-. 12.135. У . г-2)п ^ф + 1п П=1' ' П=1
12.136. °° „оп 00 у 12.137. У . (г — Зг)2п п=1 п=1 ОО 1 оо
12.138. у -ye~nz2. 12.139. УпеП2. п=1 п=1
оо оо / . \ п
12.140*. ]Г(-1)пп~2. 12.141*. (^~П
п=1 „=Лг + г/
12.142*. У
П=1
/ г-2 у \1-2г/
zn
12.143*. У : „У
2. Равномерная сходимость. Сходящийся в области D\ функциональный ряд (1) называется равномерно сходящимся в этой области, если Для любого £ > 0 найдется N = N(s) такое, что для остатка ряда (1)
ОО
^п(г) = 52 k = n+l
64
Гл. 12. Ряды и их применение
при всех n > N(e) и z G Di имеет место оценка
|Яп(г)1 < £-
Критерий Коши равномерной сходимости. Для того чтобы функциональный ряд (1) был равномерно сходящимся в области D\, необходимо и достаточно, чтобы для любого е > 0 существовало N — N(e) такое, что для всех n > N(e) и z € D\ выполнялись неравенства
|/п+1 (•2’) 4" /п+2('2;) + . • • + /п+р(-^)| < Е, р = 1, 2, . . .
Пример 3. Найти область сходимости ряда
оо
£>п-гп+1),
п=0
сумму ряда и показать, что во всей области сходимости ряд сходится неравномерно.
<] Так как частичные суммы ряда имеют вид
Sn(z) = ^(zk ~ zk+l) = 1 - zn+1,
k=0
то можем заключить, что lim Sn(z) существует только при Ы < 1 ив п—>оо
точке z = 1, т.е. областью сходимости ряда является область
А = {z||z| < 1 и z - 1},
причем сумма ряда равна
S(z) = lim Sn(z) = ( * ПРИ ,Z| < 15
4 ' n-><x> к [ О при Z - 1.
Остаток ряда Rn{z) = S(z) — Sn(z) имеет вид
_ f zn+1 при |z| < 1, \ 0 при z = 1.
Отсюда заключаем, что существуют £0 > 0 и N(eq) такие, что для любого
п > N(eq) найдется zn например, выбирая £q = |#n(Zn)| = | > ^- Это
такое, что |zn| < 1, но |.Rn(zn)| > £о- Так, 1
- и zn = ——el<fin, <рп — произвольно, имеем 4 2^
означает, что во всей области сходимости Dx равномерной сходимости нет. Заметим, однако, что в любой области
§2. Функциональные ряды
65
Dr = {z||z| г < 1} ряд будет сходиться равномерно, так как для любого е > 0 найдется N = N(e) = такое, что для всех z € Dr и п > N(e) имеем |Z?;i(z)| = |z|n+1 rn+1 < е. >
Признак В е й е р ш т р а с с а. Пусть функциональный ряд (1) сходится в области Di, и пусть существует сходящийся знакоположи-
ОО
•тельный числовой ряд У ап такой, что для всех z € D\ и для п > Л о 71=1
члены ряда (1) удовлетворяют условию
|Л (z)| (In-
Тогда ряд (1) сходится абсолютно и равномерно в области D\.
ОО
Ряд 52 называется мажорирующим для ряда (1).
77=1
°°^ ^77
Пример 4. Найти область сходимости ряда У — и показать, что z—п2 77=1
в этой области ряд сходится равномерно.
<] Воспользуемся признаком Даламбера. Имеем
lim п—
Zп+1н2
(п + l)2Zn
/Следовательно, в круге |z| < 1 ряд сходится. На границе круга, т.е. при |z| = 1, получаем сходящийся ряд:
Значит, исходный ряд сходится для всех |z| <2 1
в замкнутом круге |z| 1.
Но так как
\ш\
|г|н < 1 п2 "" п2 ’
ТО ряд сходится абсолютно и равномерно. >
Найти область сходимости и область равномерной сходимости Указанных рядов (л; Ей, z Е С):
00 ОО z___. х n_|_ 1
12.144. У(-1рп-х. 12.145. У \ } .
v п(х + 2 п
71=1 71=1
ОО • ОО / i \ т/.
12.146. 12.147. У til-.
п2 2-~‘ х + п
п=1 п=1
66
Гл. 12. Ряды и их применение
___ anz
12.148.
п2
оо
П=1
12.149. 52(-1)п
П = 1
П2
12.150. n~z
П=1
12.151. 52
П=1
1
п
X2
—z—, х Е К, сходится аб-
12.152*. Доказать,
ЧТО ряд
п=0 солютно во всех точках, но не равномерно в любом промежутке, внутри или на границе которого находится точка х = 0.
ОО 9
12.153. Доказать, что ряд \ (—1)пу—-, х Е Ж, сходится
(1 4" X ) п=0
абсолютно и равномерно на всей числовой оси, тогда как ряд из абсолютных величин членов данного ряда (ряд задачи 12.152) на всей числовой оси сходится неравномерно.
12.154. Используя принцип максимума модуля аналитической функции, доказать, что если члены ряда (1) являются аналитическими в области D функциями и непрерывными в замкнутой области D = D + Г и если ряд (1) сходится равномерно на Г, то он сходится равномерно в замкнутой области D (вторая теорема Вейерштрасса).
12.155. Найти область сходимости и область равномерной сходимости, а также сумму ряда
V ( 1 1
V 1 4- zn 14- zn+1
n=0
3. Свойства равномерно сходящихся рядов. Сформулируем ряд свойств в виде задач.
12.156. Доказать, что если члены равномерно сходящегося в области Di функционального ряда (1) умножить на одну и ту же ограниченную в области D± функцию </?(z), то равномерная сходимость ряда не нарушится.
12.157. Доказать, что если функции fn(z) непрерывны в области D\ и ряд (1) равномерно сходится в этой области, то его сумма /(г) непрерывна в области D\.
12.158. Доказать, что если функции /п(г) непрерывны в области D\ и ряд (1) равномерно сходится в этой области, то его можно почленно интегрировать по любой кривой I. целиком лежащей в
§ 2. Функциональные ряды
67
области Pi, т.е. имеет место равенство
12.159* . Доказать, что если на отрезке [а, Ь] функции fn(x) оо
дифференцируемы, функциональный ряд 52 /п(ж) сходится, а ряд п=1 оо
из производных 52 /п(ж) равномерно сходится, то исходный ряд
П=1
можно почленно дифференцировать, т.е. имеет место равенство
оо \ ' оо
52 = 52лм-
.П=1 / П = 1
Для равномерно сходящихся рядов из аналитических функций имеет место
Теорема Вейерштрасса. Если члены функционального ряда (1), т. е. функции fn(z), являются аналитическими в области D функциями и в любой замкнутой подобласти Dy С D ряд (1) сходится равномерно, то:
а) сумма ряда (1), т.е. функция f(z), является аналитической в области D-,
б) ряд (1) можно почленно дифференцировать любое число раз, т. е. справедливы равенства
оо
/<‘)(г) = ЕЛ4^)’ >= = 1,2,..., z е D\ (2) п — 1
в) в любой замкнутой подобласти Dy С D полученные в результате дифференцирования ряды (2) сходятся равномерно.
12.160. Используя утверждение задач 12.157, 12.158 и теорему Морера (теорема, обратная теореме Коши), доказать утверждение а) теоремы Вейерштрасса.
12.161. Воспользовавшись формулой Коши для производной и Утверждением задачи 12.158, доказать утверждение б) теоремы вейерштрасса.
68
Гл. 12. Ряды и их применение
§ 3. Степенные ряды
1. Область сходимости и свойства степенных рядов. Ряд
ОО
Co+C1(z~Zo)+C2(z-Zo)2 + ...+Cn(z~Zo)n + ... = Сп(г ~ Z°}n (i) n=0
называется степенным по степеням z — zq. В частности, ряд
оо
Со + "Ь C‘2Z2 + ... + cnzn + ... = cnzn (2)
71=0
является степенным по степеням z. С помощью замены z — Zq = Z ряд (1) сводится к ряду (2).
Теорема Абеля. Если степенной ряд (2) сходится в точке z = Zi /О, то он абсолютно сходится для всех z таких, что |г| < < |zi|, причем сходимость будет равномерной в любом замкнутом круге |г| г < |zi|. Если же ряд (2) расходится в точке z = z^, то он расходится и для всех z таких, что |г| > |гг1-
Из теоремы Абеля следует, что областью сходимости степенного ряда является круг с центром в начале координат (с центром в точке го), радиус которого может быть определен применением либо признака Далам-бера, либо признака Коши, т.е. из условий
или
lim п—7оо
Cn+1Zn+1 cnzn
= |г| lim
тг—>оо
Cn+l
Сп
lim \/\cnzn\ = |г| lim 77 —7 00 71—700
< 1
Отсюда для вычисления радиуса R круга сходимости получаем соотно
шения
1
lim
7—700 Сп
или R = — •-—т= lim у|сп| п—юс
Пример 1. Исследовать на сходимость ряд
(г + 2)2 (г + 2)4 (г + 2)2п _ (г + 2)2п
1-3 + 4 • З2 +-’-+ п23п + • • • - п2 . зтг
П=1
<1 Применим признак Даламбера:
(г + 2)2п (г + 2)2(п+1>
Un " n2-3” ’ Un+l ~ (п + I)2 • 3"+!
§ 3. Степенные ряды
69
и
lim
п—>оо
(г + 2)2(п+1)п2 .Зп
(п + l)23n+1(z + 2)2п
|z + 2|2 п2
3 Д™ (п + 1)2
|г + 2|2
3
Отсюда заключаем, что ряд сходится в круге |z + 2| < уЗ. Далее на границе круга, т. е. при |z + 2| = УЗ, имеем
П=1
(* + 2)2 п2 Зп
а это означает, что ряд абсолютно сходится в замкнутом круге \z + 2| Уз, причем сходимость в этом замкнутом круге равномерная. >
12.162. Сформулировать теорему Абеля для ряда (1).
12.163* . Установить, что степенной ряд (1) обладает следующими свойствами:
а) в круге сходимости \z — zq| < R сумма степенного ряда /(г) является функцией аналитической;
б) в круге сходимости \z — zq| < R степенной ряд можно почленно дифференцировать любое число раз, причем продифференцированные ряды имеют тот же самый круг сходимости;
в) ряд (1) можно почленно интегрировать по любой кривой, лежащей в круге сходимости, причем интеграл зависит только от начала и конца кривой интегрирования, а ряд, полученный из ряда (1) в результате интегрирования от zq до z, имеет тот же круг сходимости \z — zo| < R.
12.164* . Пусть степенной ряд (1) сходится в круге \z — ^ol < R-R > 0, и /(г) — сумма этого ряда. Показать, что значения производных в точке zq можно выразить через коэффициенты ряда (1) по формулам /^(zq) = n\cnj n — 0, 1, ...
п2 • 2п ‘
п(* + 2)2\ п
2п+1(г-4)п
Найти область абсолютной сходимости и области равномерной сходимости следующих рядов (г е С). Заменяя в этих рядах (кроме 12.179, 12.181, 12.187-12.189) z на х G К, исследовать их на абсолютную и равномерную сходимость.
12.100. > —-—-—. 12.100. > -. -.
п2 • 2n п 2п\/2п + 1
п—1 п=1
оо
12.167. £(-1)
П=1 оо
12.168. £(-l)n+1
П=1
70
Гл. 12. Ряды и их применение
12.169.
71=1
12.171.
71=1
2n(z-2)2n п
12.173. 22
71=1
(Зп —2)2П’
12.175. 22 (- 1)п+1пг" п=1
12.170. 52 (-1)” п=1
12.172. 52
п=1
12.174. 22
п=1
(г - 3)2га (2п 4- 1)3п‘
(п!)2гп
(2п)! '
12.176. 52(-1)п
п=1
nzn
Зп — 2
12.177. 52
71=1
(2п + 1)гп п!
П
4п — 1
12.178. 22
71=1
2п(г-1)п.
12.179. оо 52 nl(z-i)n. п=1 12.180. £1 3"(2n + l)
12.181. Е (z + i)n Пп 12.182. £ (3n + l)(z-l)".
тг= 1 71=1
12.183. оо Е 71=1 к } (2 z - 3)" n 4-1)4’ „2 ~71 12.184. 4 n! 71=1
ОО ,71 00 Jin— 1
12.185. Е (-1)” - v 7 п2п • Inn 12.186. V-Ti 8n+1nln3 n
71 = 2 71=2
12.187. оо Е (z - 2i)2n (n 4" l)2n EE -+ 7^2n+l 12.188. У ” H+1)
71 = 1 \/tz 1 х/ 71 = 1
12.189. ОО Е 71=1 (1 4- i)n(z (n 4- l)(n + i)n + 2) ' ^2пп!г2п 12.190. > ——. 2n I 71=1 V 7
12.191. ОО Е 71=1 /2n — 1\ 2n+l ( ~ OO । -1)". 12.192. V—zn. 2-^ n" 71=1
\3n 4-2/
12.193. 52 (-!)п+1
71=1
2п(г-3)2п~1 п(п 4-1)
12.194. 52
п=1
(г + З)” пДг
§ 3. Степенные ряды
71
12.195. £
п=2
(г - 3)2п n2n In2 п
12.196. J2(-l)n
П=1
п + 1
2п — 1
(г + 3)п.
оо
12.197. 52n!Z!.
П = 1
00 ^п2
12Л99- S^'
12.201. £^.
Z—/ Пп п—1
12.198. £
п=1
nn(z — 5)п
(Зп + I)10 ’
оо
12.200. ^2n2zn2.
п=0
12.202. £к±2£2.
п2
п=1
2. Разложение функций в ряд Тейлора. Имеет место следующая
Теорема Тейлора. Функция f(z), аналитическая в круге \z — zq| < R, однозначно представима в этом круге своим рядом Тейлора
OQ
f (%) — ^n(z Zq) ,
п=0
коэффициенты которого определяются по формулам1)
/(п)(г0)
f(d)
dp,
п ~ 0, 1, ...
Следствие. Если функция f(z) аналитична в области D и zq € D, то в круге |z —z0| < R (го, D), где R(zq, D) — наименьшее расстояние от точки zq до границы области D или до ближайшей точки z', в которой f(z) не аналитична, f(z) может быть представлена в виде степенного ряда
ОО
f(z) = 52сп(^°)(г - zQ)n, (3)
п=0
коэффициенты которого определяются по формулам
г , , _ /(п)(го)
Сп(го) — ।
п!
1 2тгг
(р - Z0)n+1
п = 0, 1, ...
h-z0l=r
г<Л(20, D)
Если zq = 0, то ряд Тейлора называют также рядом Маклорена.
Здесь и далее для записи криволинейных интегралов по замкнутому контуру (контурных интегралов) мы используем обычный знак интеграла.
72
Гл. 12. Ряды и их применение
Пример 2. Разложить функцию f(z) = shz в ряд по степеням z (т.е. в ряд Маклорена).
пл 1 е2 — e~z
< Так как sh z = --------- является аналитической во всей плоскости,
то по теореме Тейлора ее ряд Маклорена будет сходиться к ней во всей плоскости. Имеем
(sh z)(2n+1) = ch z, n = 0, 1, ... ,
(sh = shz, n € N.
/2"(0) n /<2"+1>(0) 1
Следовательно, c2n = -77-77- = 0, a c2n+i = -77——777 = ——777, и
(2п)! (2п + 1)! (2n +1)!
искомое разложение имеет вид
00 г2п+1
sh z — —----—-, z 6 С. >
(2п + 1)! n=O v '
3 а м с ч а н и е. Если рассматривать ряд Тейлора функции /(ж) действительной переменной, т. е. ряд
/(п)(зю) п\
(х - х0)п,
то для справедливости равенства (3) (при z — х и zq = до) необходимо и достаточно, чтобы остаточный член формулы Тейлора Rn(x) стремился к нулю при п —> ос. Остаточный член может быть записан, например, в форме Лагранжа
Rn[x) - -Г - £0~ -/(п+1)(ж0 + 0(ж - до)), где 0 < 6 1,
(п + 1)!
или в форме Коши
Л„(х) = (Ж ~ (1 ~ /(|1+11 (*о + - то)),
или в какой-либо другой форме.
Пример 3. Разложить в ряд Тейлора по степеням х функцию ех.
< Функция /(ж) = ех бесконечно дифференцируема и (ez)^1’ = сх. Следовательно, /(п)(0) = 1. Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
-±_______ео*
(п + 1)! ’
о е 1.
§ 3. Степенные ряды
73
На любом конечном отрезке х G [—а, а], а > 0, имеем
lim |7?п(ж)| = lim
I—>оо п—>оо (71 + 1J!
cn lim -------— = О,
а потому для любого х Е К
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:
~2 00
. Z Z V—* Z
a)e~ = l+ £+ — + —г + ... = 5—,2бС.
2! 71! z—' 71!
n—Q
~2 2п 00 22п
6)cosz = 1+ (_1Г._+ ... = g(_ir__,2SC.
23 „2/1+1 00 22п+1
В) sinz = z-- + ... + (-ir?5-^ + ... = £(-i)»— ' п—О ' '
zEC.
2 71 п
г) 1п(1 + 2) = 2-Д + ... + (-1)«+>г- + ... = £(-1)"+‘Д, |2| < 1.
^.3 ^2н4-1
д) aretgz = Z - — + 4- (-1)'г+15~~;
О ZTb J
г2п+1
2/1 4- 1
И < 1.
ч/ xzv . а(а — 1) п cv(a - 1)... (а - n + 1) „
е) (1 + z)а = 1 + az + - —г2 + ... + ----------L--------------’-zn +
2! n!
— 1) • • • (a — 714*1) 7,
Lf-------------Lzn, |z| < 1, a G K\N
71=1
(в случае, когда a = m E N, функция (1 + z)m раскладывается по биному Ньютона в многочлен, причем разложение имеет место во всей плоскости).
ж) при а = —1 из с) получаем бесконечную геометрическую прогрессию со знаменателем —z:
-------= l- z + z2-z3 + ... + (-l)nz11 4- ... , |z| < 1. 14-2----1
Пример 4. Разложить в ряд по степеням 2 4-3 функцию In (2 — 5z).
74
Гл. 12. Ряды и их применение
< Рассмотрим сначала следующее преобразование данной логарифмической функции:
(5
1 ~ 17^ + 3)
= In 17 + In 1 -
5(z + 3)\
17 J'
5
Воспользуемся разложением г) для In (1 + «), полагая и = — — (г + 3).
Так как разложение г) имеет место при |п| < 1, то наше разложение 5 ,
будет иметь место при —|г + 3| < 1. Таким образом,
/ \ 1
In (2 - 5г) = In 17 + (-l)n+1 (-^(г + ЗП =
= 1п17-£
П=1
5 \ п(г + 3)п
17/ п
\z + 3| <
17
5 '
Заметим, что на действительной оси в точке х = 2/5 ряд расходится (гармонический ряд), а в точке х = —32/5 по признаку Лейбница сходится. Следовательно, [—32/5, 2/5) — промежуток сходимости на действительной оси. >
Часто для разложения функций в ряд удобно пользоваться дифференцированием или интегрированием известных разложений, а при разложении рациональной дроби разложить ее на простейшие.
Пример 5. Получить разложение г) для функции f(z) = In (1 + z). < Имеем
In (1 + z) = f
J 1+^7
о
где путь интегрирования не охватывает точку z — — 1. Заметим, что
функция ----- при |tj| < 1 является суммой геометрической прогрессии
1 + Т)
со знаменателем —тр т.е.
причем, если |т/| < |г| < 1, то ряд сходится равномерно и его можно
§ 3. Степенные ряды
75
почленно интегрировать. Поэтому для z таких, что |г| < 1, имеем:
In (1 + z) =
z
О
dx]
1 + Т]
= 52 / (-77)n^ = n=° Jo
zn+1
n + 1
n—1
t>
~ it
n+1 ___
П
Прихмср 6. Разложить в ряд по степеням z функцию
f( } - z<2 ~2z + 19
(z — 3)2(2z + 5)'
<] Разложим f(z) на элементарные дроби. Имеем
2г+ 5 + (г-3)2’
По формуле суммы геометрической прогрессии
1 _ 1 1 / ыЛ
2z + 5 5 п 2г $2^ } ' 1 1 2’
1 + — п=0 х 7
2 21 2 V' (z\n
z — 3~ 3i_£ ""з^Ы ’ И<3
1 3 п=0
Замечая, что / 2 V _ 2
\г — 3 J (z — З)2 ’
и учитывая утверждение б) задачи 12.163, получим
2 _ 2 у nzn—1
(z - З)2 “ 3 Зп
П = 1
(п + l)zn 3^+i
l2l — 3.
вкладывая ряды для -------- и ---—г, имеем
2z + 5 (z - З)2
ОО
/(") = £
п=0
2(” + 1)У„
3»+2 I >
|г|
5
2
76
Гл. 12. Ряды и их применение
Пример 7. Разложить в ряд по степеням х (х € R) функцию
X
Г sinzz Д.т) = / --------du.
J u о
<] Зная разложение функции sin и
в)), имеем
ОО
к=0
u2k+i
(2А: + 1)!
(см. разложение
а потому, используя свойство в) задачи 12.163, получаем
/. ОО « 9Z. ОО 91.-1. 1
Sin It , 14*: f u J V^z isk X
u S /(2^ + 1)! ’ (2*+ 11(24 + 1)’
Q К--U Q К--V
X € R. >
Используя теорему Тейлора (формулу Тейлора с остаточным членом в какой-либо форме для функций действительной переменной), разложить в ряд по степеням z следующие функции, проверив тем самым справедливость соответствующих соотношений из а)-е):
12.203. е2. 12.204. cos г. 12.205. sin^. 12.206. (14-г)а.
12.207. 22. 12.208. sin (z - у). 12.209. cos2 z.
\ 4/
Написать первые три ненулевых члена разложения в ряд по степеням z следующих функций:
12.210*. tg z. 12.211.—!—. 12.212. thz. 12.213. ez cos z. cos z
Используя разложения основных элементарных функций а)-ж), а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд по степеням z и указать области сходимости полученных рядов2):
12.214. e~z\ 12.215. sin2 z. 12.216.-^. 12.217.-^—.
4 + г2 3 + 4г
2)См. также задачи 12.289-12.294.
§ 3. Степенные ряды
77
-j о I -|
12.218. \/27 - z. 12.219. ,......... . 12.220*.
V^+l2 U - 2)2
12.221. -------—. 12.222. (1 - z)e~2z. 12.223. ch г.
1 + z - 2г2 v }
12.224. 12.226. sin 2г 4- 2г cos 2г. In (1 4- z — 2г2).
12.228. In (г 4- \/1 4- z2).
12.231. У e-r?2/2 dp.
12.233* 0 г cos г — sin г
г2
12.225. sin 2г cos 2г.
12.227. In (г2 4-Зг 4-2).
12.229. arctg2. 12.230. агсзтг.
Z
/• 2
sinrr , -----dp.
1]
Разложить функции в ряд по степеням г — гд и определить области сходимости полученных рядов:
12.235. г3 - 2г2 - 5г - 2, г0 = -4. 12.236. —, г0 = 2.
1 — г
12.237. —, г0 = Зг.
1 — г
12.238. , г0 = 3.
г2 — 6г 4- 5
12.239. , z0 = —4. 12.240. г0 = 1.
г2 4- Зг 4- 2
12.241* . 4т, z0 = 2. 12.242. ег2-4г+1, г0 = 2.
г2
12.243. ze2z~z\ г0 = 1.
12.244. sin (г2 4-4г), гд = —2.
12.245* . In(5г 4-3), г0 = 1.
12.246. In (г2 4- 6г 4- 12), г0 = -3.
Найти области сходимости указанных рядов и их суммы:
12.247. J2(-l)n(n4- 1)(п4-2)гп. 12.248. ^п(г4-1)п. 72 = 0 71=1
ОО / q\
12.249. ~~ i"- 12.250. (-1)”а~2п~2г2п, а / 0.
п=0 П п=0
12.251. ^2(-1)п(п4-1)г2”.
п=0
78
Гл. 12. Ряды и их применение
3. Теорема единственности. Аналитическое продолжение. Сформулируем теорему единственности.
Если функции f(z) и g(z) аналитичны в области D и если на множестве различных точек (zn)n^, имеющем предельную точку aED, выполняются равенства f(zn) = g(zn), п G N, то f(z) = g(z) всюду на D.
Пусть функция /(г) аналитична в области D. а функция g(z) аналитична в области Di такой, что пересечение D П D\ = D2 содержит последовательность различных точек (гп)пе^5 имеющую по крайней мере одну предельную точку а G D2. Пусть, кроме того, f(z) = g(z) для z G D2. Тогда функция
р/ ч _ I ДЛЯ Z E D’ 2 1 g(z) для z £ Dx\d2
называется аналитическим продолжением функции f(z) с области D на область Di\D2.
Пример 8. Доказать, что если функция f{z) непрерывна в области /1\ (-1)п
D, содержащей точку z — 0, и если f — I =----для п — п0 +1, п0 +
\п J п
+ 2, ..., то f(z) не аналитична в области D (no 1 — целое).
<] Так как f(z) непрерывна в D, то на отрезке действительной оси она
1 1
также непрерывна, а в соседних точках х = — и х =---, п > По, она
п п + 1
принимает значения разных знаков. Поэтому существуют точки хп G
Е (——г, — ], в которых f(xn) = 0, причем хп —> 0. Следовательно, + 1 nJ
в точках хп Е D функция f{z) совпадает с аналитической функцией g(z) = 0, а так как f(z) 0, то f(z) не может быть аналитической функцией. >
Пример 9. Доказать, что функция
1 z zn
9(г) = _—+ ^_—^ + ...+ (l_2)n+1 + ...
является аналитическим продолжением функции
f(z) = 1 + 2z + 22г2 + ... + 2nz11 + ...
<] Определим область сходимости рядов для g(z) и f(z). Имеем
_____ / \z\n lim \ ::—-г
п—>оо у |1 —
Z
1 - Z
< 1
и
lim y/\2nzn\ = 2\z\ < 1, n—>oo
§ 3. Степенные ряды
79
т.е. ряд для g(z) сходится в области D\ — {z|Rcz < 1/2} (см. задачу 12.143), а ряд для /(г) — в области D2 = {г| |г| < 1/2}.
Определим суммы этих рядов в указанных областях:
1 / z У \
</(z) = i I 1 + 1-----7l V2 + • • .
а 1 — 2 \ 1—2 (1 — Z)z J
1 1 1
1 - 2 i______Z 1 - 22
1 — 2
И
/(2) = Г^
Так как D2 С £>i и в области D2 справедливо тождество /(2) = g{z\ то функция g{z) является аналитическим продолжением функции /(2) с области D2 на область D\. >
12.252 . Доказать, что при любом а 0 и |а| Ф 1 функциональное уравнение /(2) = f(az) не имеет решения, аналитического в точке z = 0 и ее окрестности, отличного от /(2) = const.
12.253 *. Доказать теорему единственности в том случае, когда Уг ЕЕ D g(z) = 0, т. е. доказать следующую теорему: если аналитическая в области D функция /(2) обращается в нуль в точках (zjQjteN, лежащих в области D и таких, что lim z^ = а 6 D, то к—>оо
V2 G D f(z) = 0.
12.254. Будет ли аналитической в точке z = 0 и ее окрестности функция f(z), если она при всех целых n > tiq удовлетворяет / 1 \ . ТТЛ
соотношению т — = sin —-1
) 2
Найти аналитические в окрестности точки 2 = 0 функции /(z),
удовлетворяющие условиям:
12.255. f ( i ) = —-—, n е N.
\ n J 2n 4-1
12.256. fl~] = f (-i I = i пеК
\7l J \ П/ nZ
n
— является
oo
12.257. Показать, что функция g(z) = УУ
n=0
\ 1 \ /z\n
аналитическим продолжением функции f(z) = - ~ 1 • Найти
z \ z /
n=0
аналитическое выражение этих функций в общей части областей сходимости рядов.
80
Гл. 12. Ряды и их применение
12.258. Показать,что функция
является аналитическим продолжением функции f(z) = zn
— у ( — 1)” —. Найти аналитическое выражение этих функций в п=1
общей части областей сходимости рядов.
§ 4. Применение степенных рядов
1. Вычисление значений функций. Разложения а)-ж) и.з § 3 позволяют получать значения соответствующих функций в заданных точках с любой точностью.
Пример 1. Найти число е с точностью до 10~5.
<] Подставив х = 1 в разложение функции ех, имеем
Оценим остаток
ОО
Е
к = п + 1
1
к\
1 п\п
Следовательно, равенство
1 грешность, равную ——. п\п
е = — имеет предельную абсолютную по-
к=О
Найдем п, для которого —— < 0,00001, или п'.п
п\п > 100000. Получаем п
8 1
8. Вычисляя 2 + > 77
к\
к=2
и округляя, находим
ответ с требуемой точностью е = 2, 71828. D>
12.259. Определить, сколько нужно взять членов в разложении функции In (1 4- ж),чтобы вычислить In2 с точностью до 10~4.
§ 4. Применение степенных рядов
81
12.260. Определить, сколько нужно взять членов ряда в разложении функции cos ж, чтобы вычислить cos 10° с точностью до 10 .
12.261. С какой предельной абсолютной погрешностью можно
вычислить
(32 + 4)1/5
= 2
взяв три члена биномиального ряда?
j.3 ^.5
12.262. При каких х многочлен х —— 4- дает значение функции sin ж с точностью до IO’4?
12.263. Какова предельная абсолютная погрешность равенства
Г7.--- X X1
2а 8сг
при вычислении V5?
Используя соответствующие разложения, вычислить указанные значения функций с точностью до 10-4:
12.264. Те.
12.267. sin 12°.
1 12.265.
е
12.268. cos 1.
12.266. sin-.
5
12.269* . sin 1000.
12.270*. </520. 12.271*. л/15. 12.272*. </700.
12.273*. In2.
12.274. arctg-i=.
12.275 . 7о(О,5), где 10(х) = ]Г(-1)‘
/с=0
22k(k')2
12.276 . shl. 12.277. chi.
В задачах 12.278-12.287, используя разложения в степенные ряды, требуется составить на фортране подпрограммы-функции Для вычисления значений указанных функций с заданной предельной абсолютной погрешностью. Использовать параметры X, EPS, где X — аргумент, EPS — предельная абсолютная погрешность. Имена подпрограмм выбрать не совпадающими с именами соответствующих стандартных подпрограмм-функций.
12.278 *. у = sin ж. 12.279. у = cos.?;. 12.280*. у = ех.
12.281 *. у = (1 4- х)а. 12.282. у = In (1 4- х).
1 4- х
12.283*. у = In-----. 12.284. у = arctg.T.
1 — х
82
Гл. 12. Ряды и их применение
12.285. у = I0(x) (см. задачу 12.275).
12.286. у = sh.T. 12.287. у = сЬд.
12.288. Составить на фортране программу решения одной из задач 12.264-12.277, применяя подпрограммы-функции, полученные при решении задач 12.278-12.287. В программе предусмотреть сравнение результатов, вычисленных с помощью составленной подпрограммы-функции и с помощью стандартной подпрограммы-функции, входящей в библиотеку обязательных подпрограмм.
2. Интегрирование функций. Разлагая подынтегральную функцию /(f) в степенной ряд, можно, используя теорему об интегрировании сте-
X
пенных рядов, представить интеграл f (i) dt в виде степенного ряда и о
подсчитать величину этого интеграла с заданной точностью при любом значении х из интервала сходимости полученного ряда.
/ —/2 Пример 2. Разложить функцию е dt
о
в степенной ряд по сте-
пеням х. оо L , j’’1,
< Используя разложение ех = , ~j^->
k=o
получим
на всей числовой оси. Применяя почленное интегрирование, находим
о
h (2£ + l)/H
Разложить указанные функции в степенные ряды по степеням х:
12.289. 12.290 1
.It ъДх J д
о о
X X
12.291. I cos«2<ft. 12.292. / , ” .
J J ч/ГТД
О о
§ 4. Применение степенных рядов
83
X X
12.293. У IQ(t)tdt (см. задачу 12.275). 12.294. f di. о о
Вычислить интегралы с точностью до 10 3 4
0,3
12.295. / -dt.
J t о
12.297.
12.299.
12.296.
12.298.
12.300.
В задачах 12.301-12.305, используя разложения в степенные ряды, составить на фортране подпрограмму-функцию для вычисления указанных интегралов с заданной предельной абсолютной [погрешностью. Параметры: X, EPS, где X — верхний предел интегрирования, EPS — предельная абсолютная погрешность.
X X
/sin i 2/2
----dt. 12.302. erfa? = —7= / dt.
t v7r J
о 0
12.303.
0
12.304. 12.305.
J t J t
0 0
12.306. Используя подпрограммы-функции, полученные при решении задач 12.301-12.305, составить на фортране программу решения одной из задач 12.295-12.300.
3. Нахождение сумм числовых рядов. Убыстрение сходимости. При Нахождении суммы числового ряда вычисляют его частичную сумму, для которой величина остатка ряда не превосходит заданной абсолютной погрешности. Используя известные разложения в степенные ряды, сумму
Числового ряда в некоторых случаях можно выразить в виде значения Функции в определенной точке.
84
Гл. 12. Ряды и их применение
Доказать указанные равенства:
1 1
12.307. > т------Tv;---------г =-------
1 (а + к)(а 4- к + 1) а + п к=п
1
12.308*. V ---------—-----------------------гг =
{а. + fc)(a + к + 1)(а + к + 2)
1
2(а + n)(a + n + 1)
1
12.309*. V т------------------77-------------г -
j" (а + к)(а + к + 1)... (а + к + р)
=----------------------------- (р е N).
р(а + п)... (а + n + р — 1)
1"+11 = 1п2.
п
оо
п=1 оо 1
12.311* . V (~1)Пп------7 = Т-
v ’ 2п + 1 4
п=0
Найти суммы рядов, не вычисляя частичных сумм:
ОО 1 ОО 1 оо
12.312. V-----—. 12.313. V (—1)п —-
п • 2П (п\
п=1 п=0
оо г 1 12.315. / —--------
J (2n + l)32n+1 п=0
оо
12.317. [ (-1Y1-------^7-Т7.
J v 7 Зп • (2п)!
77=0
12.314. V—. п! 71=1
12.316.
12.318.
ОО
[ (_ПП-----1---
I 1 J (2п + 1)!
п=0
оо
Г 2П
J
п=0
При нахождении суммы числового ряда требуется брать большое число членов, если остаток этого ряда медленно стремится к нулю. Такой ряд следует преобразовать в ряд, остаток которого стремится к нулю быстрее. Данное преобразование называется убыстрением сходимости ряда. Одним из методов убыстрения сходимости является метод Куммера. Неизвестная сумма А сходящегося ряда
(1)
ОО
к—1
§ 4. Применение степенных рядов
85
вычисляется по формуле
ОО
А = qB + 52 (ак ~ Qbk), k=i
(2)
ОО
где В — известная сумма ряда 52 Ък такого, что существует предел к=1
q = lim ^-0 0.
к—>оо bk
Ряд оо
J2 (ак ~ (3)
fc=i
сходится быстрее, чем исходный ряд (1), т.е. остаток ряда (3) есть бесконечно малая более высокого порядка, чем остаток ряда (1).
оо 1
Пример 3. Найти сумму ряда 52 с точностью Д° Ю-3.
/С к=1
<1 Выясним, сколько членов данного ряда нужно взять для достижения требуемой точности. Оценивая остаток (см. задачу 12.307), получаем
52 < Е _ n Е 4- и п < в’
fc=n+l fc=n+l v ' к=п v '
откуда следует, что п > 1000, т.е. для достижения указанной точности требуется взять 1001 член исходного ряда.
Улучшим сходимость ряда. Положив в формуле (2)
ак = Ьк = k(k + lY Q=1, йк~ qbk = k2(k+iy
находим (см. задачу 12.307 при а = 0 и п — 1):
СЮ J ОО | ОО J ОО 1
52У2 = Еk(k + y + 52к2(к+у = 1+Еk2(k+i)'
Применим формулу (2)
Сложив ак = ьк
к2 {к + 1)
для преобразования
1
к(к + 1ук + 2У Q
ряда > -т-г.-—,
^F(/c + l)
= 1 и ak - qbk =
86
Гл. 12. Ряды и их применение
= ~х~,-----г;----г. Тогда, учитывая (4), имеем (см. задачу 12.308 при
к2(к + 1)(к + 2)
а = 0 и n = 1):
ОО | ОО | ОО 1
52 дЕ = 1 + 52 fc(fc + l)(fc + 2) +252 к2(к + 1)(к + 2) = fc=l k=l k=l
1 2V 1
+ 2-2 + ^F(i + l)(fc + 2)'
OO |
Вычисление суммы ряда свелось к вычислению суммы ряда /с=1
Оценивая остаток
ОО
Е
/с=п+1
оо
1
к2(к + 1)(к + 2У
Е
к=1
1
k2(k + iyk + 2}
к=п+1
1
(fc-l)fc(fc+ !)(& +2)
00 1 1
v__________-__________=_______________
~ к(к + !)(& + 2)(к + 3) Зп(п + 1)(п + 2) ’
2 1
получаем —т < 0,001, откуда п3 > - • 2000 « 666,7, или п 9, т.е. Зя? 3
требуемая точность достигается при п = 9. Следовательно,
оо 1 1 9 ।
Утт = 1 + т+ 2У ТТЛ------ГЛГТпХ = 1 + 0,25 + 2 • 0,1975 = 1,645.
к2 4 к2(к + 1)(к + 2)
1
к2(к + 1)(к + 2Y
ОО
Применив преобразование (2) еще раз к ряду
к=1 можно было бы еще более улучшить сходимость. >
В задачах 12.319-12.323, применяя преобразование Куммера, найти суммы указанных рядов с точностью до 10“4, взяв для этого не более 10 членов получившегося ряда. Использовать соотношения
ОО 1 ОО 1 / 1 \
= и = И - cw <₽>!)• 71=1 71=1 ' '
§ 4. Применение степенных рядов
87
Значения дзета-функции взять из таблицы
С(р)
2
3
4
5
1,6449340668
1,2020569032
1,0823232337
1,0369277551
6 1,0173430620
7 1,0083492774
8 1,0040773562
ОО 1 с»
12.319*. V -5—12.320*. V sin2-.
п2 4-1 п
П—1 72=1
12.321*.
п=1
12.322*.
п=1
1
п(5п + 3)
оо 1
12.323* . V (-1)п+1-—
' Зп 4
п=1
12.324. Составить на фортране программу решения одной из задач 12.319-12.323.
4. Интегрирование дифференциальных уравнений с помощью рядов. Степенные ряды широко применяются при решении дифференциальных уравнений. Для целого ряда дифференциальных уравнений показано, что решение y(t) представимо в виде степенного ряда
оо оо (A:) Z \
у(х) = ^ак(х - х0)к - xQ)k, (5)
А=О к=0
коэффициент которого можно определить с учетом заданного уравнения различными способами?
а) Пусть требуется найти решение уравнения у" = f(x, у, у'), удовлетворяющее условиям у(хо) = уо, у'(хо) — У1, причем функция /(х, У, у') в точке (.то, уо, i/i) имеет частные производные любого порядка. Тогда коэффициенты у^к\хо) ряда (5) определяются путем последовательного дифференцирования исходного уравнения и подстановки в вето xq и найденных уже значений ?/'(.то), у''(хо), ...
Пример 5. Найти решение уравнения у" — х2у, удовлетворяющее Условиям ?/(0) = 0, т/(0) = 1.
Имеем y(Q) = 0, y'(Q) = 1, из заданного уравнения находим у"(0) = 0.
88 Гл. 12. Ряды и их применение
Далее, дифференцируя уравнение, имеем
у"' =2 х2у' + 2ху, У1Х = х2у" + 4ху' + 2г/, уУ = х2у'" + (уху" + 6/,
y(k+2) = х2урУ> +2кху^к~^ + к(к —
ОО у(ж) = V
и при х — 0 получаем отсюда
/*+2)(0) = к(к - 1) у(*~2)(0), к = 2, 3, ...
Так как ?/(0) = у"(0) = т/'"(0) = 0 и у'(0) = 1, то
/4п)(0) = т/4,г+2)(0) - /4п+3)(0) = О
и
т/(4п+5)(0) = (4п + 2)(4п + 3) ?j(4n+1)(0) =
= 2-3-6-7...(4?t + 2)(4n + 3), neN.
Следовательно,
2 • 3 • 6 • 7... (4гг + 2)(4п + 3) 4п+1 (4п + 1)! Х
По признак}’ Даламбера полученный ряд сходится при любых х е К, т.е. определяемая этим рядом функция у(х) является решением заданного уравнения при любых х. >
Найти решения уравнений, удовлетворяющие заданным условиям:
12.325. у" = х2у. т/(0) = /(0) = 1.
12.326. у" = -х2у' - 2ху + 1, т/(0) = 7/(0) = 0.
Найти первые 5 членов разложения решения дифференциального уравнения в степенной ряд:
12.327. 7/ = 2cost - тт/2; ту(О) = 1.
12.328. у" = -2ху, 7/(0) = /(0) = 1.
12.329. у" = у cost + т, т/(0) ~ 1, г/'(0) = 0.
б) Если исходное дифференциальное уравнение линейно относительно искомой функции и ее производных, причем коэффициент при старшей производной в точке xq отличен от нуля, то решение следует искать
§ 4. Применение степенных рядов
89
в виде ряда (5) с неопределенными коэффициентами ад, к = 0, 1, ... Законность такого метода вытекает из утверждения, доказываемого в аналитической теории дифференциальных уравнений, которое мы приведем для уравнения 2-го порядка.
Теорема 1. Если в дифференциальном уравнении
Ро<Д) у" + Pi Ыу' + РгО) у = /(т)
(6)
функции ро(х), Pi(x), Р2(х) и f(x) аналитичны в окрестности точки Хо иро(хо) ф 0, то существует решение уравнения (6). представимое
ОО
в виде степенного ряда у(х) = У^ а^. (.т — д’о)А •
к=о
Пример 6. Найти решение (в виде степенного ряда) уравнения
у" - ху' + у = 1,
(удовлетворяющее условиям </(0) = ;</(0) = 0.
<| Ищем решение в виде ряда у(х) — У^ адхк, в котором в силу условий
к=о
ОО
до(0) = ?/'(0) = 0 имеем а0 — — 0- Следовательно, у(х) = У^ адхк.
к—2
^Подставив это выражение в уравнение, получаем
У^ к(к - 1)акХк~2 - У^ какХк -I- У^ вкХк = 1.
к=2 k=2 k=2
Отсюда находим, что 2 • 1 • а-2 = 1, т.е. а> = -—и
(к -I- l)(fc -I- 2)щ.+2 = (к - 1)ад. для к = 1, 2, ...
Так как (р = 0, то a2m+i = 0 для всех т — 0, 1, ..., а для к = 2m, т = 1, 2, ..., получаем рекуррентную формулу
(2m - l)a2„t _
а2(ш+1) “ (2m + l)(2m + 2)’ ™ ' ’ ' " '
Из которой выводим равенства
_ (2m - 1)!! a?(m+1) - (2т + 2)! •
90
Гл. 12. Ряды и их применение
Следовательно, искомое решение имеет вид
_ , V (2ш~ 1)!!г2»1+2
2 (2m+ 2)!
т=Л
причем полученный ряд сходится при всех х Е К. >
Используя степенные ряды, проинтегрировать следующие дифференциальные уравнения:
12.330. у" + ху' + у = 1, у(0) = 1/(0) = 0.
12.331. у" — ху' + у = х, у(0) = 1/(0) = 0.
12.332. у” + ху' + у = х, у(0) = 0, i/(0) = 1.
в) Если коэффициент при старшей производной в линейном уравне-
нии в точке xq обращается в нуль, то следует воспользоваться следующей теоремой.
Теорема 2. Если в дифференциальном уравнении
Ро(х)у" +Р1(х)у' + р2(х)у = 0 (7)
функции ро(х), Р1(т) и р2(х) аналитичны в окрестности точки хо, причем точка xq является нулем порядка s функции рв(х), нулем порядка не ниже s — 1 функции pi(z) и нулем порядка не ниже s — 2 функции р2(х), то решение уравнения (7) в окрестности точки хо существует и представляется в виде обобщенного степенного ряда
ОО
у(х) = (х- хоу ^2 ak(x - x0)k,
k=0
где ао / 0 и г Е К.
Пример 7. Найти решение (в виде обобщенного степенного ряда) уравнения
ху" + у' + ху — 0,
удовлетворяющее начальным условиям т/(0) = 1, у'(0) = 0.
< Коэффициенты уравнения удовлетворяют условиям теоремы 2, поэтому ищем решение в виде обобщенного степенного ряда
ОО оо
у(х) = хГ ^akxk = '^Takxk+r, а0 / 0.
k=o k=o
Имеем
ОО
у' = 52 + r)akxk+r~\
оо к~°
у" = 52 + г)(^ + г — 1)акхк+г~2.
fc=0
§ 4. Применение степенных рядов
91
Додставляя эти ряды в уравнение, получаем
(А: + г)(к + г - 1)акХк+г~г + к~о
+ (к + r)ajta?+r-1 + У2 akXk+r+l = О, fc=o к—о
т.е.
т2аохг~1 + (г + l)2aixr + ((^ + г)2(1к + ак-2)хк+г~1 = 0.
к=2
Отсюда следуют равенства
г2е0 = 0, (г + 1)4 = 0, (к + г)2аь + afc-2 = 0.
Цо условию По 7^ 0- Следовательно, г = 0, а тогда
ai = 0 и к2аь = — flfc-2, к = 3, 4, ...
Из этих равенств заключаем, что й2т+1 — О для всех тп = 0, 1, ... Учитывая начальное условие = 1, заключаем, что ао = 1, и имеем рекуррентную формулу
______ О-2т-2 а2т ~ ” (2m)2 ’
Jf3 которой получаем
Следовательно, искомое решение запишется в виде
°° т2тп
уСд;) = 1 + 52 (-1)-^—Ж£К. > т=1 ' '
Найти общее решение дифференциального уравнения в виде Обобщенного степенного ряда:
12.333* . ху" + 2у' + ху = 0.
12.334. 4ху" + 2у' + у = 0.
5. Уравнение и функции Бесселя. Частным случаем уравнения (6), Коэффициенты которого удовлетворяют условиям теоремы 2, является Уравнение Бесселя
х2у" + ху' + (х2 — У2}у = 0.
(8)
92
Гл. 12. Ряды и их применение
Его решениями являются цилиндрические функции Бесселя первого рода порядка у
/х\2к
о° I — 1
/Дх) = «JV g (-1)\!(у + 1)(1/ + 2)... (м + *) (9)
и для нецелых I/
/х\2к
00 I —) .»
I-^x^a^x р g (-!)* _ ^(2 - г/)... (fc - i/)'
Если же у — целое число, у = п, то вторым частным решением уравнения Бесселя (8) является функция Неймана (или Вебера), определяемая из соотношения
ЛГ . . Iv(x) C0SZ/7T - /_р(а?)
Nh(x) = lim ——------;---------'^-L,
v-+n Sini/7T
являющаяся цилиндрической функцией второго рода порядка п. Постоянная в формулах (9) и (10) берется обычно следующая:
+оо
где Г(1/) = e~xxl/~l dx — гамма-функция Эйлера, о
12.335. Используя представление (9) для 1ц{х\ доказать следующие соотношения:
=x"v1(x), (12)
ах
d (1у&)\
dx \ xv J xv
12.336. Исходя из соотношений (12) и (13), вывести соотношения
217
4-1 (ж) 4- Iv+x{x) = —Iv(x), X
- /р+1(я;) = 2/^(ж).
§ 5. Ряды Лорана
93
12.337* . Используя представление (9) и значение из (11), выразить /_1/2(^) и Д/2(^) через элементарные функции.
12.338. Доказать, что если 1и(х) — решение уравнения (8), то lv(ax) является решением уравнения
х2у" 4- ху' 4- (ск2я;2 — и2)у = 0. (14)
Записать общее решение уравнения (14).
Используя результат задачи 12.338, найти общие решения уравнений:
12.339. ху" + у' + 4ху = 0.
12.340. 9х2у" 4- Эху' 4- (36ж2 - 1)т/ = 0.
12.341. х2у" 4- ху' 4- (Зж2 — 4)у = 0.
12.342. х2у" 4- ху' 4- [9х2 — — ] у — 0.
\ 25/
§ 5. Ряды Лорана
1. Ряды Лорана. Теорема Лорана. Рядом Лорана называется ряд
+оо
^2 сп(г - 20)п; (1)
п=—оо
При этом ряд
-1
/1(*)= 52 Сп(г-2О)П п=—оо
Называется главной частью ряда Лорана, а ряд
оо /2(2) = 52сп(г-г0)п п=0
‘— правильной частью. Если
lim У|с_п| = г < R = =—Ц===, n->o° hm г/ сп
п—>оо
*о областью сходимости ряда (1) является кольцо К — {z|0 г < < \z — *о| < R}- В этом кольце К сумма ряда /(г) = /1(2) 4- /2(2)
94
Гл. 12. Ряды и их применение
является функцией аналитической, причем коэффициенты ряда сп связаны с функцией f(z) посредством формул
(2)
|т)-2о| = г'
где г < г' < R.
Пример 1. Найти область сходимости и сумму ряда Лорана
°° -и 1
ЕТ1 Tl\Z — 1)
2n(z - l)n+1 + Зп
n=l V ' П=1
<1 Применяя признак Коши к каждому из этих слагаемых, имеем
I п 1
11Ш г/ ;-----------;—— = —--------------
72->оо у 2n|z - l|n+1 2|z — 1|
и
< 1
lim
п—>оо
n\z — 1|п-1
Зп
< 1.
z - 1
~ 3
Отсюда заключаем, что областью сходимости исходного ряда является кольцо
К = {z|l/2 < |z — 1| < 3}.
Замечая, что слагаемые являются производными от рядов
-1
и
п=О
зп п=О
можем записать, что в
кольце К
n
2n(z - l)n+1
Зп
,п=О
1_____
- 1)п
.п=О
Зп
= -2р—1-
\2z-3
1 2(z - 1) /
з у _ 3 2
4-z/ ~ (4 — z)2 + (2z — 3)2
1
§ 5. Ряды Лорана
95
Таким образом, суммой данного ряда является функция 3 2 1
= (4 - г)2 + (2г — З)2 ’ 2 ~ 11 3’ >
Теорема Лорана. Если функция f(z) аналитична в кольце Q<Cr<|z — zq|<7?. то в этом кольце она единственным образом представима в виде ряда Лорана ________
+оо / Д—-Х\ у р
f(z) = 52 cAz~zo)n, / / ) X
п— — оо ‘ [ \ Гу / / X
коэффициенты которого вычисляются по I ? /
формулам (2). V С*^ V' Y'n J
Следствие. Пусть /(г) аналитична в -------'
много связи ой области D, ограниченной кон-г> — Рис. 2
ууром 1 и внутренними контурами 7Г ,
..., 7“ (рис. 2). Если точка z0 лежит внутри (или на границе) одного из внутренних контуров 7„ и величина г = max|z0 ~ т/| меньше расстояния R от zo до остальной части границы области D или до точки, в которой f(z) не аналитична, т.е.
О г = max ho — 7/| < R — min \zq — z/|,
t?€7u 77£rU71U...U7v_iU7u + iU...U7m
то в кольце г < \z — zq\ < R функция /(2) может быть представлена ее рядом Лорана
f(z) = 52 с»(г0)(2 - 20)n, r<\z-z0\<R,
коэффициенты которого cn(z0) определяются по формулам (2).
Рядом Лорана для функции f(z) в окрестности точки z = 00 называется ряд
4- ОС'
л*) = 52 CnZ" п~ — оо
' Ч-сх
или 52 — аУг
, 71= —ОС
(3)
Сходящийся в некотором кольце г < |г| < 4-ос (соответственно г < |z — а| < +оо), при этом главной частью ряда Лорана является оо /ос \
ряд 52 cnz'1152 Cn^z ~ ’а пРавильн°й — ряд
п=1 \п=1 /
О /О
52 c,i^n ( 12 Cn^z ~ °Уг
П=—ОО
n——OQ
96
Гл. 12. Ряды и их применение
Пример 2. Разложить в ряд Лорана по степеням z функцию /(д) = 1
г(1 - г)’
<1 Так как аналитичность функции нарушается в точках z = 0 и z = 1, то областью сходимости ряда Лорана будет кольцо 0 < |г| < 1. Замечая.
что при п < -2 функция —-Z—---------- аналитична в круге |г| < р < 1.
гп+2(1 — z)
можем записать, что
:п = т [ —ттд--------г dz = 0 для п = -2, -3
2тгг J zn+2(l - z)
\z\=P
Далее, применяя формулу Коши для функции <p(z) = водных, для и —1 можем записать
и ее произ-
1 Г tp(z) _ </n+1)(0) _ 1 (п + 1)!
2тп J zn+2 (п 4- 1)! (п + 1)! (1 — д),,+2
Таким образом, для 0 < |г| < 1
1 1 00
= --------? = - + £г'‘> О)
2О -2) 2 +о
т. е. главная часть содержит один член, а правильная - - бесконечное число членов. >
Вычисление контурных интегралов (2), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются искусственные приемы. Так, в примере 2 функцию /(г) можно было бы представить в виде суммы дробей, т.е.
1 1
1
г(1 - г)
1 -г’
причем первое слагаемое является уже разложением в ряд Лорана по степеням г, а второе слагаемое есть сумма геометрической прогрессии со знаменателем z, т.е. имеем разложение (4).
Найти области сходимости и суммы следующих рядов: Е1 л пгп2п
----—. 12.344. > ------—-.
(д-2п
п=0 п=1
00 п+3 “2
12.345.^2----Г-’ 12-346- 52 (п + -г)п.
п=0 ’ п—-оо
§ 5. Ряды Лорана
97
Найти области сходимости рядов:
12.347.
П=1
(z + i)2n 2п(п + 1)
4п2 \
3n(z + i)n J
12w УЧ i z
\.Зп(тг2 + 1) (z — 2i)n n=l
00 .
12.349. У* .
Z-/ nnzn n=L
00 / 2 \
12.351. £ ( j I
\ О J
12.350.
n=l
2n + i V 4n(z 4-1)/
Найти все разложения указанных функций в ряды Лорана по степеням г —го и установить области сходимости полученных разложений:
1 . 1
12.352. г0 = 1. г(г-1) 19 Ч^Ч* — г>г\
1^.000 . . , л-о — ОО. г(г- 1)
12.354. г0-2. (г — 2)(г 4- 3) 1 12.355. г0 = -3. (г - 2)(г -4- 3)
12.356. 9 , го — оо. г2 — 4 г 4- 1 12.357. — г0 = 1. г2-Зг + 2’ г3
12.358. -2- - - - г0 - 2. г2 — Зг 4- 2 г 19 4^Q*
, л-о — оо. г2 — 2г + 1 г4
12.360. ——, г0 = -1. (Z + I)3 1—361. + ~о — оо.
12.362. , г0 = i. Zz + 1 12.363. —г. го = оо. г2 + Г
19 ЧКД* Z i 19 4fiV 1
(г2 + I)2 „ л л cos г l^.dOo . 9 9, х-о — оо. (г2 + 1) cos г
12.366. , го — 0. Z6 12.367. —г0 = оо. Z6
1 12.368. sin го = 2. г — 2 12.369. г2е\ г0 = 0. г2 — 4г
12.370. г2е*, го = оо. 12.371. cos , г0 - 2. (г-2)2
98 Гл. 12. Ряды и их применение
1 z И- 1
12.372. -у—, 20 = 1. 12.373. -у-------z0 = i-
z- + z zL + zz — о
12.374. —тс, г0 = 0.
(г2 + 4)(г2 + 1)’
12.375. -г-~2 л/ 2 n ’ z° = 0’ (z^ — 4)(zz — 1)
12.376. Найти три первых члена разложения функции f(z) =
= sin------ в ряд Лорана в окрестности точки zg = оо. Какова
1 — z
область сходимости этого ряда?
2. Характер изолированных особых точек. Точка zq называется правильной точкой для аналитической в области D функции f(z), если су-
ОО
шествует степенной ряд cn(zo)(z — zo)n с радиусом сходимости
п=0
r(zo) > 0 такой, что в общей части круга сходимости \z — zq| < r(zo) и области D сумма этого ряда <£2o(z) совпадает с f(z). Точки, не являющиеся правильными, называются особыми.
Точка zq называется изолированной особой точкой функции f(z), если f(z) — однозначная аналитическая функция в кольце 0 < \z — zq| < < R, a zq — особая точка.
Аналогично, точка zq = оо называется изолированной особой точкой функции f(z), если f(z) — однозначная аналитическая функция в кольце г<\г\<(юиг = оо — особая точка.
Изолированная особая точка zq функции /(г) называется: устранимой особой точкой, если существует конечный предел
lim /(z) = а оо;
2—1—0
полюсом порядка т 1, если для функции g(z) = точка Zq f(z)
является нулем порядка т, т.е. g(z) имеет вид g(z) = (z — z0),7V(2)’ ip(z0) 0 (очевидно, что если z0 — полюс, то lim /(z) = оо);
Z->Z0
существенно особой, если lim /(z) не существует.
Z—>Zo
Исследование характера бесконечно удаленной особой точки удобнее
1
проводить путем замены z = -, с помощью которой бесконечно удаленту
ная точка z = оо переходит в точку т/ = 0.
Пример 3. Найти все особые точки функции
ч 1
z) = ——-
е* + 1
и определить их характер.
§ 5. Ряды .Лорана
99
<] Особыми точками являются точка z = 0 и точки, в которых знаменатель обращается в нуль.
Имеем е = 4- 1 — 0 и с = — -1 = е2ктг+л1, т. е. 4- 1 — 0. если — =
— (2m + 1 )тгг, т G Z, причем эти точки являются нулями 1-го порядка.
Следовательно, в точках zm = —-------;—;, т G Z, функция /(г) имеет
(2т 4- 1)7гг
полюсы 1-го порядка. Точка z — 0 не является изолированной особой точкой, так как она является пределом полюсов, ибо lim zm — 0. >
771
12.377 *. Доказать, что отсутствие в разложении (1) главной части, т.е. равенство нулю всех коэффициентов сп с отрицательными номерами (п = —1, —2, ...), является необходимым и достаточным условием того, что точка zq является устранимой особой точкой функции f(z).
12.378 *. Доказать, что наличие в главной части разложения ;(1) не более тп 1 членов, причем с_ш 0, а с_п = 0 для п mH, есть необходимое и достаточное условие того, что точка '«го является полюсом порядка т для функции f(z).
12.379 *. Доказать, что если zq — существенно особая точка функции f(z), то существует последовательность точек (zn), Jim zn = zq. такая, что lim /(z7l) = ос.
Л—>ОО ' n—>oo
12.380 *. Опираясь на результат задачи 12.379, доказать, что «вели zq — существенно особая точка функции f(z), то для любого комплексного числа А Ф оо существует последовательность точек Нш zn(A) = zq, такая, что lim f(zn(A)) = A.
П-+ОО n-too
12.381 . Установить области сходимости правильной и главной частей разложения Лорана (3) в окрестности бесконечно удаленной Йочки.
Указать все конечные особые точки заданных ниже функций и определить их характер:
1 z 4- 2
12.382 . —--—. 12.383. ------—-----—.
(г2 4- г)3 z(z + 1)(г — I)3
1 z
12.384. -—. 12.385. -----------— ------—.
smz (z + 1)(г — 2)3(г + г)5
12.386. ------г. 12.387. ------Д--------.
г2 sin (г—1) (z 4- 1)3(ег — 1)
7Г
12.388. ~ . 12.389. ------5_.
sin 2г tgz — 1
100
Гл. 12. Ряды и их применение
12.390. tg2 2. 12.391. е^-з*.
1 1 t£ (z — 1)
12.392. cos------. 12.393. tg-------. 12.394. —~-
2 +2г ° 2 — 1 2-1
1— C0S2 sin 2 _ „„„ 1
12.395. -----5--. 12.396. —r-. 12.397. -—-.
22 25 ez - 3
Для заданных ниже функций выяснить характер бесконечно удаленной особой точки (устранимую особую точку считать правильной):
z2 12-398’ 5-2.2' 12.401. 1 - z + 2z2. 12.404. e* 4- 2z2 - 5. З25 — 5z + 2 t z 12.399. — -. 12.400. —r. 22 + 2 - 4 1 - З24 12.402. e'2. 12.403. cos 2. 12.405. eA. 12.406. .
12.407. e~2z + З23 - 2 + 8.
§ 6. Вычеты и их применение
1. Вычет функции и его вычисление. Если функция f{z) аналитична в некоторой окрестности точки zq, за исключением, хможет быть, самой точки 2о, то вычетом функции /(2) относительно точки zq, обозначаемым res [f (z); zq], или выч [/(z); zo], называется число, равное значению интеграла —^-7 [ где С — некоторый простой замкнутый кон-
2ттг J с
тур, лежащий в области аналитичности /(z) и содержащий внутри себя только одну особую точку zq. В качестве С удобно брать окружность \р — zq| = р достаточно малого радиуса р.
Вычет функции совпадает с коэффициентом с_] разложения /(z) в ряд Лорана по степеням z — zq, т.е.
выч [У(z); z0] = c-i = -L [
Z7TZ J
|ij-zo |=p
Если zq = 00 — изолированная особая точка функции f(z), то
выч[/(г); 00] = — / f(rf)dr], ZTTl J
§ 6. Вычеты и их применение
101
где СR = {т]\ \tj\ = R}, R достаточно велико и обход контура — по часовой стрелке. Заметим, что если
/с*)= 52 СпгП' г < и < +°°’ п—— оо
Сп = [ 4+1^’ П = 0’ ±1’ •••’
2ттг J T]n±L 1ч1=р>г
то
выч[/(г); оо] = —c_i.
Если z0 — полюс 1-го порядка функции /(г), то
выч[/(г); z0] = lim (z -z0)f(z), Z-+ZQ
<p(z) причем если f(z) представима в виде f(z) = —— -
гдес^о) 7^ 0, ^(^о) =
= 0, i^'(zq) 0, то
выч [/(г); z0] =
<Р(*о) ^'Uo)’
Если Zq — полюс порядка гп 2 функции f(z), то
выч[/(г); z0] =
1 dm-l((z-ZQ)mf(z))
(m — 1)! dzm~l
e
z2 + 9’ 32 ’
Пример 1. Найти выч
<1 Так как точка zq = 3i является полюсом 1-го порядка, то
выч
егг
z2 4-9
g’Z
* 2
; Зг = lim (z - 3i)~——---------— = — = ~тг^-
z-^Зг (z 4-Зг) (z — Зг) 6г 6eJ
Пример 2. Найти выч
cos 2z 1 (г-1)з;
<l Точка zq = 1 является полюсом 3-го прядка, поэтому
выч
cos 2z 1
- 1 Г — 2! I1™ dz2
3 cos2z
(г-х) (ГЛр
= - lim (—22 cos 2z) = —2 cos 2. [>
2 7
102
Гл. 12. Ряды и их применение
При м о р 3. Найти выч |_е z~2; 2j.
<1 Точка z0 = 2 является существенно особой, поэтому для нахождения з
вычета найдем коэффициент c_i разложения ez~'2 в ряд Лорана по степеням z — 2. Так как
л 3 1 ( 3 \2 „ ,
е!.!=1 + _ + _(—_) +.... 0 < |г - 2| <+сю,
то c_j — 3. Следовательно,
выч с7722; 2 = 3. >
Найти вычеты указанных ниже функций относительно каж-
дого из ее полюсов, отличных от оо:
12.408. д2 + 1 z-2 ‘ 12.409.
12.410. 7 7\-, n 6 N. (z - l)n 12.411.
12.412. 1 z(l — e2z) 12.413.
12.414. ------------------. 12.415.
( 7Г\ 2 /
V " 2 )
(д2 + I)2 ’
1 д3(д2 + 4)2
1
1 •
snu — -
• о 2 sin2z
(2+1)4'
е2
12.416. -х——-. 12.417. tgz. 12.418. etg2 z.
zl\zl + 9)
12.419.
cos3 z z3
z2 + z — 1 1
12.420. 12.421.
z2(z - 1) z(l — z2)
1 cos4z
12.422. — 12.423.
z2 - z5 (д - 2)6
Найти вычеты функций относительно точки zq = 0:
12.424. et 12.425. cos -. 12.426. sin z z
Найти вычеты функций относительно точки zq = оо:
12.427. sin-. 12.428. -----12.429*.
z (z - 1)2(д2 4-1) z2+9
12.430. 12.431. д cos2—. 12.432. sin i
zb - 1 z z - 1 z
§ 6, Вычеты и их применение
103
2. Теорема о вычетах и их применение к вычислению контурных интегралов.
Первая теорема о вычетах. Если функция f(z) аналитична в области D, за исключением изолированных особых точек zi, ^2, .2дг, лежащих в этой области, то для любого простого замкнутого контура С С D, охватывающего точки Zi, z?, . . . , zn,
N
dr) = 2тгг 52 выч [/(г); zk\. fc=i
Вторая теорема о вычетах. Если f(z) аналитична во всей комплексной плоскости, за исключением изолированных особых точек 21, 22, ..., 2дг-1 и zn — оо, то
N
52 выч [/(2); 2fc] = 0.
k=i
Пример 4. Вычислить интеграл / ——-</2, где С — {2| |2| = 3}. J 2 4- 4
с+
< Так как внутри контура С находятся две особые точки подынтегральной функции — полюсы 1-го порядка 21,2 = ±2г, то, применяя первую теорему о вычетах, можем записать
dz = 2ггг выч
— 2тгг
е 2г\
4г )
7Г
— (е2г — е-2г) = тгг sin 2 = 7rsh2z. >
Пример 5. Вычислить интеграл
/dz
210 4- 1' |z|=2
<1 Подынтегральная функция /(2) =
——- имеет десять особых то-2iU 4-1
(2fe+l)7ri
чек г/. = е ю , к = 0, 1, ..., 9, являющихся простыми полюсами,
104
Гл. 12. Ряды и их применение
лежащими на единичной окружности. Так как разложение функции в окрестности бесконечно удаленной точки имеет вид
1
z10 + 1
г10
_1____1_ _1_
г10 220 + г30
1 < |г| < +оо,
ТО — С-1 = выч
00
= 0. Поэтому, применяя вторую теорему о
1
г10 + 1 ’
вычетах, можем записать, что
9
52выч
fc=0
1 (2fe-H)7Ti
----------• р 10
210 + Г
-- -выч
оо = 0.
1
г10 + 1
Таким образом,
9
I = 2ттг 52 выч
fc=0
1 (2fe-H)7ri
----------• Р 10
г10 + Г
= 0. >
Используя теорему о вычетах, вычислить следующие интегралы:
/* dz
12.433. / —где С = {z| |z - 1| = 1}.
J г4 + 1
с-
/z dz
с+
/* ez dz
12Л35' J гД^ + 9)’ГДеС={2||г| = 1}-
с+
12.436* . У q dz, где С = {д| |z| = 4}.
с+
12‘437‘ J ГДС С = = 1}, тг — нату-
с+
ральное число и 0 |а| < 1 < |&|.
§ 6. Вычеты и их применение
105
12.438*.
с+
dz
(z — a)n(z — 6)n
, где С = {z| |z| = 1}, n — нату-
ральное число и0^ |а| < |6| < 1.
12.439. / sin - dz, где С = {z| |z| = г > 0}.
J z
с+
Г dz
12.440. у __ 1)2(г2 + 1) ’ ГДе & = 121 — < О-
с+
12.441.
z + 1
ez + 1
dz, где С ~ {z| |z| = 4}.
12.442.
dz, n G N.
12.443. У znez dz, n G N.
f z2 dz 12.445. / —я--------------.
J sin'5 z cos z
И=5
12.444.
12.446.
1 - ez2 , —-------- dz.
ez dz
z4 + 2z2 + l'
Г ( 1 2 \
12.447. / sin -7 + ez cos z] dz. J \ z ) M=i
//* z^ dz ztgnzdz. 12.449. / —:-------------.
J 2г4 + 1
kl=i |*|=i
3. Применение вычетов к вычислению определенных интегралов.
2 я
а) Интегралы вида f R(sinx, cost) dx, где R — символ рациональ-о
ной функции, с помощью замены z = егх приводится к контурным интегралам от рациональных относительно z функций.
Пример 6. Вычислить интеграл Пуассона
2я
Др) = I О
dx
1 - 2р cos х + р2 ’
IpI / 1-
106
Гл. 12. Ряды и их применение
егх + в гх
<1 Производя замену z — егх, dz = ietx dx — izdx, cosx = ----------
1 z + -— z _
2
z2 + 1
—-—, получаем
dz . f dz
---------------—----— — — 2, I ---------------------
( z2 + l Л J -pz2+p2z + z-p
IZ 1-p--------- +p2] |z|=l
\ Z J
/dz
” 77 г
|2| = 1 p(z-p)(z- -
\ р
Так как при любом p, |р| 1, внутри круга |г| < 1 находится только один
корень знаменателя подынтегральной функции, то при |р| < 1 имеем:
2тгг2
----выч
Р
1
----7—
(z~p\z~p)
27Г
1 — р2 ’
а если |р| > 1, то
Др) =
2тгг2
----выч
р
1 1
/ х ( 1\ ’ Р
(z~p)
27Г р2 — 1
Др) =
Таким образом,
Цр) =
2тг
1 — р2 27Г р2 - 1
при |р| < 1,
при |р| > 1.
Н-оо
б) Интегралы вида /(ж) dx, где /(ж) — функция, непрерывная
— ОО
на (—оо, +оо), аналитическая в верхней полуплоскости, за исключением конечного члена особых точек z^, Z2, ..., z^, лежащих в конечной части верхней полуплоскости, и удовлетворяющая для достаточно больших |z| условию
М
М>0, <5 > 0.
§ 6. Вычеты и их применение
107
В этом случае
= 2m выч [/(г); г/,.].
(1)
/dx
(z2 + 9)2
<1 В верхней полуплоскости функция /(г) = - - —— имеет один полюс [z2 4- 9)2
М
2-го порядка в точке z0 = Зг, и f(z) С —- для достаточно больших |г|.
И
Поэтому
-----Зг
dx
——7 = 2тггвыч —-——г, <js — + 9)2 [(/2 + 9)2’ J
= 2m((z — Зг)2 —— dz V (z2 +
d
= 2m —
3i dz
4гтг
~ О + Зг)3 ;
г=3г
1 \
(г +3г)2 J ;=3. ~
4гтг 7Г
-(6г)2 = 54'
Замечание. Формула (1) справедлива и в том случае, когда функция /(г) имеет вид f(z) = etazF(z)^ где а > 0, а функция F(z) аналитична на действительной оси, в верхней конечное число особых точек z^, г2, ..., z^
полуплоскости имеет лишь и lim F(z) = 0.
Пример 8. Вычислить инте
X sin X , ---------------- dx.
2 — 2x + 10
<1 Подынтегральная функция является мнимой частью функции хегх
~т.------—, значение которой совпадают со значениями на действитель-
хл — 2х + 10
Z • Z
ной оси функции /(г) = ——-———егг. Функция F(z) = ——-——— zz — 2z + 10 zl — 2z + 10
имеет в верхней полуплоскости полюс 1-го порядка в точке zq = 1 + Зг и lim F(z) — 0, т.е. выполнены сформулированные в замечании условия,
108
Гл. 12. Ряды и их применение
а потому можем записать:
—------------- dx = 2тп выч
х2 - 2х + 10
zezz
z3-2z + 10;1 + 3i'
- 2 .(l + 3i)ei(1+3i> _ я 3+j _
~ 2(l + 3i-l) ~ 3(1 + З’,е • “
~ —e~3(cos 1 — 3sin 1 + i(3cosl + sin 1)). О
Таким образом,
я; sin я; , _ Г хегх , тте 3 ,п .
—— —- ах = Im / —— — ах = —-—(3cosl + sml. х2 - 2х + Ю J х2 - 2х + 10 3 v <
Заметим, что одновременно мы вычислили интеграл
ж cos я; , _ [ хегх , ire 3 . „ „ . „ ч
^ = Ке J ?-^+i0</l = ~(cOS1“3slnl)- *
—ОО
Используя один из рассмотренных выше методов, вычислить определенные интегралы: 27Г /dx -------------------, а > 1. а + cos х о
27Г
12.451.
/dx
(а + b cos х)2 ’ о
а > b > 0.
12.452.
/cos2 Зх
----------z- dx, а > 1.
1 — 2а cos х + а2
о
12.453.
о
cos х dx
1 — 2а sin х + а2 ’
0 < а < 1.
§ 6. Вычеты и их применение
109
2я
/sin2 х dx , ----------, а > b > 0. а 4- b cos х
о
27Г
12.455. J* ctg (ж — a) dx, Ima > 0. о
12.456.
dx.
+oo
12.457. I ( QdX- , n G N.
J (д?2 4-l)n 5
— 00
4-оо
124кЯ f dx
J (rr2 -f-а2)(ж2 + 52) о
4-oo
12.459. [ rf'dX2}1, « > 0.
J (xz 4- azy о
4-ос
/x dx
7~o--'л---77777-
(x2 + 4x 4- 13)2 — 00
a > 0, b > 0.
4-oo л
f x4 4" 1
12.461. / ~—- dx.
J x6 + 1
4-o°
12.462. f a > 0. b > 0.
J (a + ta;2)4’ — 00
12.463.
/a; sin я: , f xcosx
-z----------dx. 12.464. / -------7 dx.
x2 4- 4x 4- 20 J x2 4- x 4- 1
— 00 —00
4-oo
/x sin ax , л , —-7 dx, a > 0, b > 0.
x2 + b2
о
12.466.
x 4- 1) sin 2x , ?--------^dx.
x2 4- 2x 4-2
4-oo
f (xs 4- 5x) sinx , 12.467. / \----------—-dx.
J x4 + 10z2 4- 9
-oo
12.468.
f (2x3 4- 13z) .
/ ~—?? sin x dx J x4 4- 13z2 4-36
— oo
по
Гл. 12. Ряды и их применение
12.469.
12.470.
4-ос
/’ cos х t
/ ~~л-------о-----Г ^Х
J хА 4- 5л;2 + 4
о
4. Принцип аргумента. Пусть функция /(д) в области D, ограниченной простым замкнутым контуром С. имеет конечное число N нулей и конечное число Р полюсов, где каждый нуль и каждый полюс считаются столько раз, какова их кратность, причем на контуре С не имеет ни нулей, ни полюсов. Тогда разность и = N — Р равна числу оборотов радиус-вектора w = f(z) при обходе точкой z контура С.
Если f(z) — аналитическая в D функция, то Р — 0 и ш = N.
Пример 9. Найти число нулей многочлена p(z) = z3 — 3z 4- 1, лежащих в правой полуплоскости.
<] Рассмотрим контур С, состоящий из полуокружности Cr радиуса R, лежащей в правой полуплоскости, и отрезка мнимой оси [—iR, iR], и для достаточно большого R применим к этому контуру принцип аргумента.
Так как
p(z) = z3 (1 - + ДЛ , (2)
у z^ z6 J
то очевидно, что при обходе точкой z контура Cr против часовой стрелки arg г получает приращение тг, а потому arg (г3) получит приращение Зтг (Cr отображается в кривую w = R3e'^, —Зтг/2 Зтг/2). Так как
второй сомножитель в (2) для достаточно больших R близок к 1, то и приращение аргумента этого множителя мало. Пусть теперь z = it, т.е. точка z движется по мнимой оси от точки iR до точки —iR. Тогда
p(it) — u + iv = 1 - i(t3 4- 3t), т.е. u = 1, v = -t3 — 3t.
Это означает, что при изменении t от R до —R при R -> +оо argp(-i7) изменяется на 7г (от —тг/2 до тг/2). Таким образом, общее приращение argp(z) при обходе контура равно 4тт, а это означает, что N — 2, т.е. в правой полуплоскости многочлен p(z) = z3 — 3z + 1 имеет два нуля. >
Для данных многочленов найти количество корней, лежащих в правой полуплоскости:
12.471 *. p(z) = z‘l 4- 2д3 + Зд2 4- z + 2.
12.472 . p(z} = 2д4 - Зд3 + Зд2 - д + 1.
12.473 . p(z) = д4 4- д3 4- 4д2 4- 2д 4- 3.
12.474 *. Доказать, что если функции /(д) и ip(z) аналитичны в замкнутой области D = 1)4-Г и для точек р 6 Г справедливо неравенство |(/Д?7)| < |/(?/)|, то число нулей функции Р(д) = /(д) 4-4- <p(z), лежащих в области D, совпадает с числом нулей функции f (д) (теорема Р у ш е).
§ 7. Ряды Фурье. Интеграл Фурье
111
12.475 *. Доказать основную теорему высшей алгебры: многочлен pn(z) = a(]Zn + aizn~[ -I-1- an степени n имеет в плоскости
(д) точно n нулей.
Опираясь на теорему Руше (задача 12.474), найти число нулей данных функций в указанных областях:
12.476 *. F(z) — z5 + 2z1 2 + 8z + 1: а) в круге |г| < 1; б) в кольце 1 < И < 2.
12.477 . F(z) = z3 — 5z + 1: а) в круге |г| < 1; б) в кольце 1 |г| < 2: в) в кольце 2 С |z| < 3.
§ 7. Ряды Фурье. Интеграл Фурье
1. Разложение функций в тригонометрические ряды Фурье. Тригонометрическая система функций
1, cos х, sin х, cos 2х, sin 2т, ..., cos пх, sin пх, ...
является ортогональной на отрезке [—тг, тг] (как, впрочем, и на всяком отрезке длины 2тг), т.е. интеграл по этому отрезку от произведения любых двух различных функций этой системы равен нулю.
7Т
Если /(т) € Ь(-7Г, 7г) (т.е. j )/(т)|<2т < +оо), то существуют
числа
= — [ f(x) cos kx dx, bk = — / f(x) sinkxdx, k = 0, 1, ...,
7Г J 7Г J
называемые коэффициентом Фурье функции /(т); ряд
ОО
SW = у + (ak cos кх + bk sin кх) (1)
k—\
называется рядом Фурье функции f(x). Члены ряда (1) можно записать в виде гармоник
ak cos кх + bk sin кх = Ak cos (кх — pF)
с амплитудой Ak = \/al + b'i, частотой cok — к и фазой pk = arctg —.
О'к
Для функции f(x) такой, что /2(т) G L(—7г, тг), справедливо равенство Парсеваля
1 Г 2 00
- / /2(т) dx = у + У2 (4 + bl).
тс J 2 77?
112
Гл. 12. Ряды и их применение
Если же f(x)eL в виде
L !_\ 2’2/
то коэффициенты Фурье записываются
1/2 1/2
2 Г .. . 2лкх , . 2 Г ... . Чъкх ,
otk = J / /(ж) cos ——dx, Pk = у / f(x)sin--—dx,
—1/2 -1/2
а ряд Фурье — в виде
а0 ( 2якх . 2хкх\ .2^
S(x) = ~ + 22 (CHCOS——+&sin ——\ = 22 Ске ' fc=l ' ' k= — oo
(2)
(3)
Последний ряд называется рядом Фурье в комплексной форме. Здесь
;/2
ск = у У /(ж)е~г^ dx, fc = 0, ±1, ...,
-//2
и для к О ак - ifik otk + ifik
Ck 2 ’ 0—k 2
Суммы рядов (1) и (3) имеют соответственно периоды 2тг и I.
Функция f(x) называется кусочно гладкой на отрезке [а, Ь], если сама функция f(x) и ее производная f'(x) имеют на [а, Ь] конечное число точек разрыва 1-го рода.
Теорема. Если периодическая функция f(x) с периодом I кусочно гладка на отрезке [—1/2, 1/2], то ряд Фурье (3) сходится к значению f(x) в каждой ее точке непрерывности и к значению (/(ж + 0) + + /(ж — 0))/2 б точке разрыва, т. е.
1 +оо
-(/(я+о) + /(ж-о)) = 22 с^^-
k~ — oo
(4)
Если, дополнительно, /(ж) непрерывна на всей оси, то ряд (4) сходится к f(x) равномерно.
Пример 1. Разложить в ряд Фурье функцию
/(ж) = sign Ж, —7Г < Ж < 7Г, и, пользуясь разложением, найти сумму ряда Лейбница
ю ”г х
§ 7. Ряды Фурье. Интеграл Фурье
113
О Так как функция нечетная, то (см. задачу 12.479)
ак = 0, к = 0, 1, ...,
2 7. . 2 / cosmcl71,
Ьь = — / sign х sm nxdx = — (--------------------
7Г J 7Г \ п 1о
о
2 ,
= ----(1 — СОЗП7Г) —
7ГП
4
7г(2т — 1) о
при п = 2гп — 1, F ’ п € N.
при п = 2m,
Следовательно, при — тг < х < тг
signa; --
4 ул sin (2m — 1)а;
тг 2m — 1 m=l
откуда при х — тг/2 получаем
4 ул (-l)m+1 тг " 2m — 1 ’
т. е.
' (-1)™ _ т
' 2m + 1 4
12.478. Доказать, что если f(x) имеет период I, то при любом о Е К
о,+/
У dx a
I 1/2
f(x)dx = f(x)dx. 0 —1/2
12.479. Записать выражения коэффициентов Фурье (2) для четной и нечетной функций на [—1/2, 1/2].
Разложить периодическую с периодом I функцию в ряд Фурье, построить графики его первых частичных сумм Sq(x), Si(х), S2(x) и $з(х) и найти значение S(xq) суммы полученного
ряда в заданной точке ху
12.480. f(x) = <
1 при
0 при
0 < X < 7Г,
—тг < х < 0,
I = 2тг, Xq = тг.
114
Гл. 12. Ряды и их применение
12.481. /(.т) = — при 0 < х < 2тг, I = 2тг, xq — —.
12.482. f(x) = |т| при х G (—1, 1), I — 2, xq = 1.
Разложить в ряд Фурье следующие функции периода I:
12.483. f(x) = | cos rr|, —tv < x < л; I = 2л.
12.484. /(т) — x2, —tv < x < л; I = 2л.
— 1 — т <2 x О
. ’ n ' ’ I = 2т.
1, 0 < х < т;
12.486. /(т) = | sinт|, —л х л; I — 2л.
12.487. f(x) = 2т, 0 < х < 1; I = 1.
12.488. f(x) = 10 - т, 5 < х < 15; I = 10.
12.489. f(x) = sin ат, —л < х < л, I = 2tv.
12.490. /(т) = cos ат, —л < т < л, I = 2л,
12.491. /(т) = shaT, —л < т < л, I — Ък.
12.492. /(т) = ch ат, —л < т < л, I = 2л.
Доопределяя необходимым образом заданную в промежутке (0, а) функцию до периодической, получить для нее: а) ряд Фурье по косинусам, б) ряд Фурье по синусам.
12.493. /(т) = т 6 (0, In2).
J 1, 0 < т л/ ;W = (o, */2<Х< Дх) = / Х' ° Ж 5
v ' [ 2 — т, 1 < т <
/(т) = TsinT, т 6 (0,л).
1,
2.
12.495.
12.496.
12.497.
12.498.
12.500. /(.т) = т, т е (О, Z).
л
-, т G (0,л).
12.499. /(т) = — — т, т 6 (0, л).
12.501. Используя ряд Фурье, полученный в задаче 12.482, найти суммы следующих рядов:
ОО j _ А, 2к + 1
а) (2п + 1)2; б) (4k + 1)2(4* + 3)2'
71 = 0 k = 0
12.502. Используя ряд Фурье, полученный в задаче 12.497, най-
ОО 1
ти сумму ряда (—l)fe+1 —.
A:=l
§ 7. Ряды Фурье. Интеграл Фурье
115
12.503. Используя равенство Парсеваля для функции задачи
СЮ 1
12.481, найти сумму ряда 5 -у.
П-- I
12.504* . Зная выражение ядра Дирихле
п
. 2n + 1 sm--------
2
к=1
2 sin —
2
найти выражение ядра Фейера ?п(х):
п
1 п
— У п + 1 7—' к=0
к \
—- COS кх.
. п + 1/
к=1 х 7
12.505. Используя равенство Парсеваля для функции задачи
сю 1 сумму ряда V —. ' п1 п=1
12.484, найти
12.506. Зная выражение для ядра Дирихле (см. задачу 12.504), получить интегральное представление для частных сумм
п
Sn(f, х) = у- + ^2 (ak cos кх + Ьк sinкх) к=1
ряда Фурье функции f(x) периода 2л.
12.507. Зная выражение для ядра Фейера (см. задачу 12.504), получить интегральное представление сумм Фейера
<м/,
к=0
функции f(x) периода 2л.
12.508* *. Используя полученное в задаче 12.507 выражение для сумм Фейера crn(f-> х)у показать, что для непрерывной на оси функции f(x) в каждой точке х Е [—л, л] справедливо соотношение lim сггг(/, х) = f(x).
п~>сю
116
Гл. 12. Ряды и их применение
2. Двойные ряды Фурье. Если функция /(я, у) имеет период I по переменной ж, период h по переменной у, непрерывна и имеет непре-df Of d2f „
рывные частные производные —, -;г- и -—— в прямоугольнике К — ох оу ох оу
— {(я, у)\ — 1/2 < х < 1/2, —h/2 < у < h/2}, то /(ж, у) представима двойным рядом Фурье
Е. / 2тгтх 2тту
Лт,п am,n cos —— cos ——- +
„ \ th,
т,п=О 4
, . 2irmx 2imy 2тгтх . 2тгпу
+ Omn Sin COS —----1- Cmn COS ; Sin —:-----F
l h I h
, . 2тгтх . 2imy
+ dm,n sin —-— sin —— l h
где
{1/4 при m = n = 0,
1/2 при m > 0, n = 0 или m = 0, n > 0,
1 при m > 0, n > 0
и при m 0, n 0
4 f f t. . 2ivmx 2тту t t am,n - 'ifr f\x> У)cos —j— cos dx dy,
к
i 4 f f ,/ x . 2тгтх 2тгп1/ , , bm,n -'т J\x^ У)sin —]— cos dx dy,
к
4 Г [ .. . 2ътх . 2xny , ,
cm,n = / / J{x,y) COS —-— sin —— dx dy,
к
i 4 f f r/ x . 2тгтх . 2тгпу , , dm,n - J\X> У) Sln —I— Sln dx dy,
к
В комплексной форме ряд Фурье для f(x, у) записывается в виде
4-оо f(x, у) = ст,пе27гг(^+^),
т,п=~ оо
где
cm,n = jj f(x, ?/)е_27гг(л^+'^) dxdy, т, n G Z.
к
§ 7. Ряды Фурье. Интеграл Фурье
117
Пример 2. Разложить в двойной ряд Фурье функцию /(ж, у) = ху в квадрате — тг < х < тг, —тг < у < тг.
<] Принимая во внимание четность или нечетность подынтегральных функций, находим
am,n = -^ jjxU cos mx cos ny dx dy =
1
х cos mx dx = 0, m, n 0;
bm,n
1
7Г2
x sin mxdx = 0, m,
(-m,n
1
7Г2
x cos mx dx = 0, m,
j -±
т.п — о 7Г2
x sin mxdx =
4
о
у sin nydy j x sin mx dx = о
4 / cos ny _y--------------
7Г2 \ П
sin ny
n2
0
4 7r(-l)n+1
7Г2 П
\ / cos mx
—x-------
/ \ m о/ \
s'mmx m2
4
mn
m
о
о
Следовательно, при х Е (—тг, тг), у 6 (—тг, тг)
ОО ху = 4 ^2 (-l)m+n m,n=l
sin mx sin ny
mn
Разложить в двойной ряд Фурье следующие функции: 12.509. f(x, у) = ху при 0 < х < 2тг, 0 < у < 2тг, I = h = 2тг.
118
Гл. 12. Ряды и их применение
12.510. f(x, у) =
I — h = 2тг.
12.511. f(x, у) = h = 4.
12.512. Цх, у) =
I = 2, h = 2тг.
тг — х тг — у
----- . ---- ПрИ _< х < < у < 7Г,
2 2
х2у при — 1 < х < 1, — 2 < у < 2, I = 2.
/ \ 2
( к -у \
х ------ I при — 1 < X < 1, — тг < у < тг,
3. Интеграл Фурье. Если функция /(£) абсолютно интегрируема на (—оо, +оо), т.е. f(t) G L(-oo, +оо), и кусочно гладка на каждом конечном отрезке действительной оси, то она представляется в виде интеграла Фурье
N 4-оо
/W = s(/(«+O) + /(t-O)) = lim [ f(y)e2’“'td^= [ fMe^d^,
2 W->4-oo J J
—N —oo
(5) где
4-oo
f(0 = f f(t)e~2’M dt. (6)
Преобразование (6), которое будем обозначать 5[/], называют прямым, а (5) — обратным преобразованием Фурье, выраженным в комплексной форме. В действительной форме эти преобразования записываются в виде:
а(и>) =
4-оо
f(t) cosutdt,
(7)
(прямое) и
4-оо
У (а(сс) cos ait + b(u) sin uif) du о
(8)
(обратное), и = 2тги.
Если функция f(t) четная, то (7) и (8) записываются в следующей симметрической форме:
.— 4-ос
ЗчгС/] = /с(^) = у | У f(f)cosutdt о
(9)
§ 7. Ряды Фурье. Интеграл Фурье
119
и
f(t) =
cos ait du
(Ю)
и называются парой косинус-преобразований Фурье. Если же /(£) нечетная, то имеем пару синус-преобразований Фурье
г— “Foo
&[/] = А(^) = у | У f (С sinaitdt
о
и
/(«) =
fs(ai) sinivtdai.
о
Пример 3. Найти преобразование Фурье для функции f(t) =е-а1*1, а > 0.
<] Подставляя заданную /(£) в (6), получаем
> 0 4-oo
е-а|«|е-2тгг^^ = f e-(2iriv-a)t dt ± f e~(2^+a)t dt =
о
т. е.
1 (a —27rii/)t
---Т~~е а — 2ти
1
------
a + 2ттгг/
(2тгг1/4-а)(
1______
a — 2тггг/ ' a + 2тггг/
2а
а2 + 4тг2г/2 ’
2а
Ul J а2+47г2г/2’
Подставляя это выражение в (5), получаем
g27rii/t ф /• giwt
"o 4 о т dr — /
'2 -I- 4тг2г/2 7Г j а2 +ш2
2а
cos ait
-dai = — , „
|2 7Г J a2 + u>'
о
о
О
1
Последнее равенство следует из того, что
N
sin ait
smait , f
------т dai = lim / v2 + ai2 TV—>+oo J
— N
„ dai = 0. C> a2 + ai2
120
Гл. 12. Ряды и их применение
Пример 4. Найти преобразование Фурье для функции
= а > 0.
<3 Так как функция /(f) четная, получим пару косинус-преобразований Фурье. Потому воспользуемся формулами (9) и (10). Используя результат задачи 8.192, получаем
e~Q<2
1
—т=е 4« coswt
о
, 1 f
du) = —7= / е cos ivtdu;. [> л/тГО J
о
Найти преобразование Фурье в комплексной форме для функций:
12.513. f(t) = sign(t — а) — sign (f — 6), b > a.
12.514. /(<) = [ h (1 — — } при \t\ < a, 1 \ a / 1 0 при \t\ > a.
12.515. /(t) = 1 cosat при |f| < л/a, 0 при |f| > тг/a, a >
12.516. f(t) = 1 signf при |f| < 1, 0 при |f| > 1.
Найти пару косинус- или синус-преобразований Фурье указанных функций:
12.517*. /(f) = -д, а > 0.
v 7 а2 -И2
12.518*. /(f) =
t а2 +t2
, а > 0.
12.519. /(f) = te~l\
12.520. /(f) = cos(3t, a > 0.
12.521. Доказать, что преобразование (6) является непрерывной функцией, причем lim /(z/) — 0.
>±оо
§ 7. Ряды Фурье. Интеграл Фурье
121
4. Спектральные характеристики ряда и интеграла Фурье. Спектральной функцией ряда Фурье или спектральной плотностью называется отношение коэффициента Фурье функции /(ж) периода I
Ck - с(^)
//2
у У* f(u)e~2ni,/kUdu, -Ч‘>
vk = у
/г € Z, к приращению частоты
л
Ai/fc = —-—
т. е.
//2
$Ы = Ч^ = [ f(u)e~2”il'l‘u du.
&vk J
~1/2
Амплитудным спектром p(vk) называется модуль спектральной функции, а фазовым спектром Ф(рк) — взятый с обратным знаком аргумент спектральной функции, т. е.
рЫ = 1Ж)1 = гк(М1
и
Ф(^) = -argS(^).
На графиках и Ф(^) обычно строят только ординаты р и Ф в точках Ok и спектр называют линейчатым.
Пример 5. Найти спектральную функцию ряда Фурье и построить амплитудный и фазовый спектры для функции
' О
/(ж) = < 1 k О
при х G (-2, -1), при жб (-1,1), f(x + 4) = f(x\ при х € (1, 2).
<] Имеем Vk = к/4 и
2 1 .
/г p — 2nWkX 1
J(;r)e-2KW dx = / 1 • dx = ———
J -2mvk _
—2 -1
j e‘2nwk _ e~‘2itWk
7ri/fc 2г
sin 27ri/fc
7TZ/fc
122
Гл. 12. Ряды и их применение
Следовательно,
Рп
4_ _ 7Г
f \ lev м |sin27rr/fc|
РЫ = |$И)| = -ф^->
= -argS(i/fc) =
О, если sin 27rz/jt О,
—тг, если sin 2'Ki'k < 0.
Графики p{vk) и $(yk) представлены на рис.З. С>
Спектральной функцией интеграла Фурье называется прямое преобразование Фурье
4-оо
$(р) = /(,/)= //Ие-2'-1 л. (п)
—оо
Величина р(у) — |S(p)| называется амплитудным спектром, а величина 4>(z/) = — arg S(v) — фазовым спектром.
Найти спектральные функции 5(^) или и построить амплитудные и фазовые
спектры следующих функций:
' 0 при t G (-2Г, -T),
12.522. /(<) = < — 1 при t G (-T, 0), .. л_. . 1 при tG(O, T), /(* + 4T) =/(*). 4 0 при t G (T, 2T),
12.523. /(t) = < 2 при t G (0, 1), r/ (О при ielu), /(‘ + 3) = /W.
12.524. /(t) = < ^ПРИ '*!<“’ a > 0. 0 при |t| > 0,
12.525*. f(t) = ( cos7t£ при |i| 1/2, { 0 при |t| > 1/2. 1 4-1 при t G (-1, 0),
12.526. /(i) = < 1 — t при t G (0, 1), w 0 при |i| > 1.
12.527. /(i) = < r 2 при t G (0, 2), k 0 при t G (-oo, 0) U(2, +oo).
§ 7. Ряды Фурье. Интеграл Фурье
123
5. Дискретное преобразование Фурье (ДПФ). Аналитическое вычисление преобразования Фурье (спектральной функции) (11) и обратного преобразования (5) вызывает, как правило, значительные трудности. Разработаны методы их численной реализации, одним из которых является так называемое дискретное преобразование Фурье:
т 27V-1
Ж) = Ь = ^£/Ые''т, n = 0, 1, (12)
1-0
Т 1
где tk = (Т — длина заданного интервала) и гп = п—. Обратное 21\ 1
к (12) преобразование имеет вид
2JV-1
fW =xt = - 52 УпС'-тУ £ = 0, 1,, 21V - 1. (13)
п=0
Преобразования (12) и (13) выполняются с помощью так называемых быстрых алгоритмов (БПФ), состоящих в том, что если 2N = гут? .. Лп, rv — целые 2, то матрица преобразования (12) (или (13))
W =
( 1 1
1 Q
1 Q2
\ 1 g2yv-1 ' q2(27V_1)
1
q2 q4
1 \
g2(2N-l)
g(2N-l)2 у
где q — е~г^ — для (13)), представляется в виде произведения п квадратных матриц Wy порядка 2N,
W = WnWn_l...W2Wl,
(14)
имеющих каждая по г у -2N отличных от нуля элементов. Умножение матрицы Wy (у — 1, 2, ..., п) на вектор-столбец Z = (го, zi, ..., Z2/v-i)T за счет отбрасывания умножения на нули может быть произведено за Ту • 2N операций комплексного умножения на множители qk и сложения. Все ДПФ (12) вычисляется тогда за (и Ч-ггН----hrn)27V таких операций
и умножения конечного результата на множитель Т/2N.
Если 2N = 2п (г 1 = Г2 = ... = гп = 2), то в качестве матрицы Wm = = (С1™Ь, У = 1’ 2, • • •, 2п, для разложения (14) можно взять матрицу, элементы которой выражаются следующим образом (q = е~г2п-2); пусть у ~ 0, 1, ..., 2n~m - 1 и р = 1, 2, ..., 2"г-1, тогда
(т) _ (?тг) _ 1
Су2гп+ц,у-2т~1+ц ~ Си-2,п+2т~1+ц,у-2т~1~
124
Гл. 12. Ряды и их применение
Д™) - Дт) - л//1'1)2" т
L'v-2m+ii,2n-1+v-2m-1+ii L't/.2nl+2m~1+M,2n-1+i/-2Tn-14-/2 4 ’
(15) = 0 для остальных пар (к, j}.
12.528. Выписать матрицы Wi, W2 и W3, соответствующие формулам (15) при 2N = 23 = 8.
12.529. Пусть X = (д?о, #1, • • •, ^?)т- Составить произведения Z^ = WiX, Z& = W2Z^ = W2(WlX) и Z& = W3ZW = = W3(W2Wix). Сравнить полученный результат с произведением WX.
Для конечной последовательности комплексных чисел (а?о, Xi, ..., ..., xjv—1) ДПФ по формуле (12) можно представить в виде
1 п—1
= N (п = 0’ 1’ •••’ N~ 1)’ IV
k-0
а обратное ДПФ (ОДПФ) — в виде
N-1
E2nink ,, „ _ .
yne N (к = 0, 1, ..., N - 1).
п=0
Обозначим кратко ДПФ и ОДПФ соответственно
У = 3[Л'] и Х = 3-1[У],
гае X = (х0, ib ..., xN-i)т, Y - (j/0, тл.j/w-i)’.
Глава 13
ТЕОРИИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
§ 1. Элементарные функции
1. Понятие функции комплексной переменной. Множество точек Е расширенной комплексной плоскости (z) = C(J{oo) называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству. Связное открытое множество точек комплексной плоскости называется областью и обозначается через D, G и т.п. Область D называется односвязной, если ее граница является связным множеством: в противном случае область D называется многосвязной.
Если каждому комплексному числу z, принадлежащему области D, поставлено в соответствие некоторое комплексное число w, то говорят, что в области D определена комплексная функция ш = /(z).
Пусть z = х + iy и w = и + w. Тогда функция w — f(z) может быть представлена с помощью двух действительных функций и = и(х, у) и v = v(x, у) действительных переменных х и у:
w = /(г) = и + iv = и(х, у) + iv(x, у),
где
и(х, у} - Re/(z), v(x, у) = Im /(z).
Пример 1. Указать область, определяемую условием |z| — Imz < 1.
<1 Так как |zj — \/х2 + у2 и Imz == у, то получаем неравенство
Vх2 4- у2 - у < 1
или
yjx2 4- у2 < 1 4- у.
Из последнего неравенства следует, что у > — 1. Возводя обе части неравенства в квадрат, находим х2 4- у2 < 1 4- 2у 4- у2. Следовательно, искомая область определяется неравенством у > -(х2 — 1), т.е. представляет собой открытое множество точек, ограниченное графиком параболы у ~ -(х2 — 1) и содержащее точку 0(0, 0). >
Пример 2. Найти действительную и мнимую части функции /(z) = iz2 - z.
126
Гл. 13. Теория функций комплексной переменной
< Полагая z — х 4- iy, находим
/(г) = и(х, у) 4- iv(x, у) = i(x 4- iy)2 - (ж - iy) =
= i(x2 — у2 4- 2ixy) — (х — iy) = —ж(1 4- 2у) 4- i(x2 — у2 4- у).
Таким образом,
Re f(z) = u(x, у) = —ж(1 4- 2у), Im f(z) = v(x, у) = х2 4- у2 4- у. >
Описать области, заданные следующими соотношениями, и
установить, являются ли они односвязными:
13.1. |г — г0| < R.
13.2. 1 < |г-г| < 2.
13.3. 2 < |г — i\ < 4-оо.
13.5. \z — zo| > R-
13.7. Im(zz) < 1.
13.4. О < Re(2iz) < 1.
13.6. О < |г4-г| < 2.
о „ 1 1
13.8. Re - > -. z 4
Указать на комплексной плоскости множества точек, удовлетворяющих указанным соотношениям:
г 4- 1
13.9*. Im-----; = 0. 13.10. \z - i\ 4- \z + i\ < 4.
z — i
z — 2г
13.11. Re------ = 0. 13.12. \z - 51 - \z 4- 5| < 6.
z 4- 2г . ' 11 1
13.13. arg Z~~ Z~ = 0. 13.14*. arg —- = 0. z — ^2 z 4- г
Записать с помощью неравенств следующие открытые множества точек комплексной плоскости:
13.15. Первый квадрант.
13.16. Левая полуплоскость.
13.17. Полоса, состоящая из точек, отстоящих от мнимой оси на расстояние, меньшее трех.
13.18. Внутренность эллипса с фокусами в точках 1 4- г, 3 4- г и большой полуосью, равной 3.
13.19. Внутренность угла с вершиной в точке zo раствора тг/4, симметричного относительно луча, параллельного положительной мнимой полуоси.
Для следующих функций найти действительную и мнимую части:
13.20. f(z) = iz + 2z2. 13.21. f(z) = 2i - z 4- iz2.
7 4- } 7 1
13.22. f(z) = — . 13.23. f(z) = - +
г — z i z
§ 1. Элементарные функции
127
13.24. f (г) = Re (г2 4- г) 4- г Im (г2
Z2 4- Z 4- 1 iz 4- z
13.25. f(z) =
Определить функцию w = f(z) по известным действительной и мнимой частям:
13.26. и(х, у) = х + у, v(x, у) = х - у.
О Если z — х 4- iy и z — х — iy, то х = -(z 4- z)
и у = ~ 2). Тогда
/ х 1 / -х г / —х 1 ~г 1 4- г _
Щх, у) = х + у = -(z + z) - -(z - z) = ——z + у;
, ч 1 z _4 if 1 + i 1 - i _
v(x, y) = x-y = ~(z + z) + -(z - z) = ~Y~z + -y Z.
Следовательно,
/(z) = u(x, y) + iv(x, y) = -y-z 4- -y-z + -yiz + -y iz = f 1 — г 1 4- i Л /1 4- i 1 - i , = “ + ”!r+ ~ + ~T = (
Таким образом, f(z) = (1 +i)z.
Рассмотренный в задаче метод позволяет в общем случае получить для функции комплексной переменной выражение, зависящее от z и z. >
13.27. u(x, у) — х2 — у2 — 2у — 1, ц(ж, у) — 2ху 4- 2х.
13.28. и(х, у) = х—у~ t-1, = УТ у '2~1-
ZJ.Z yi X- + уг
1 1 *
13.29. и(х. у) = —, v(x, у) = х У
Функция w = f(z) называется однолисгпной в области D, если любым различным значениям zi zo, взятым из области D. соответствуют различные значения функции /(zi) f^z?)-
Найти области однолистности следующих функций:
13.30. /(z) = z2.
<1 Пусть zi = и Z2 — pze1^2. Найдем условие, при котором zf = z'^, Хотя zi z-2- Имеем Р|вг2,р1 = р2ег2<р2. Отсюда заключаем, что pi = р2, Д 2<р2 = 2y?i 4- 2кл (к = 0,1). Так как zi z2, то = </?i 4- тг. Таким ^бразом, область однолистности функции w = z2 не должна содержать Внутри себя точек, модули которых совпадают, а аргументы отличаются
128
Гл. 13. Теория функций комплексной переменной
на тг, т.е. областью однолистности является любая полуплоскость, например Re z > 0 или Im z > 0. (>
13.31. f(z) =zn.,nE N. 13.32. f(z) = ez.
13.33. /(г) = e*iz. 13.34. /(г) = z + j.
Геометрически заданную на D функцию /(z) можно рассматривать как отображение области D плоскости (z) на некоторое множество G плоскости (w), являющееся совокупностью значений f(z), соответствующих всем z Е D.
Пример 3. Исследовать отображение, осуществляемое линейной функцией w = az + b.
Это отображение можно рассматривать как композицию трех простейших отображений. Действительно, положим
wi = |a|z,
w2 = etargawi, w3 = w2 + b.
Тогда нетрудно видеть, что w = w3 ow2 Из геометрического смысла произведения и суммы комплексных чисел ясно, что отображение Wi есть отображение растяжения (сжатия при 0 < |a| < 1), отображение w2 представляет собой поворот всей плоскости (wi) относительно начала на угол = arg а и, наконец, отображение w3 есть параллельный перенос плоскости w2 на вектор, изображающий комплексное число Ъ. с>
Найти образы указанных точек при заданных отображениях: 13.35. zq = 1 + г, w = z2 + г.
1 Ч-
13.36. Zq — —-—, W — (z — г)2.
_____ i Imz
13.37. z0 = 1 - w =--------.
2 z
13.38. z0 = 3 - 2г, w = т.
z
13.39. Найдите образы координатных осей Ох и Оу при отображении w = -— z — г
Для отображений, задаваемых указанными функциями, найти образы линий х = С, |z| = R, argz = а и образ области |z| < т, Imz > 0 :
13.40. w = z2. 13.41**. w = -.
z
Один из наиболее употребляемых способов задания функций — задание с помощью формулы — в случае функций комплексной переменной часто приводит к многозначным функциям.
§ 1. Элементарные функции
129
Говорят, что в области D определена многозначная функция w ~ f(z), если каждой точке z € D поставлено в соответствие несколько комплексных чисел w.
V2 г-
Пример 4. Найти все значения функции w =-----------y/z в точке
zo = г-
<] Так как |i| = 1 и arg г = тг/2, то в соответствии с определением корня n-й степени из комплексного числа (см. Часть 2, гл. 5, § 5) находим
Wk =- е^^+2к^, к = 0, 1.
Таким образом,
v2 Ki у2 7г . 7Г .у2 w0 = — - е = — - cos - - г sin - = -г—,
у2 5тг,- у2 5тг . . б7г /- ,у2
wi = —----е 4 = —----cos——г sin — = У 2 + г —-. >
2 2 4 4 2
Найти все значения следующих функций в указанных точках: 13.42. W = Z + tfz, Zq = —1.
13.43. W = Zq = i.
yjz — г
13.44. W = \/l — \/z, Zq = —I.
13.45. w = \/i + \/z, Zq = —1.
Найти Arg f(z), если z — rel<p:
13.46. /(z) = z2. 13.47. f(z) = z3.
13.48. f(z) = \/z+T. 13.49. f(z) = v/T^S.
13.50. f(z) = Vz2 - 4. 13.51. f(z) = y/(z-2)/(z + 1).
2. Основные элементарные функции комплексной переменной. Следующие функции (как однозначные, так и многозначные) называются основными элементарными:
1. Дробно-рациональная функция
aozn + ai zn 1 +---h an
-------------:------:—, П, Г bozm + blZm~l + + bm'
Частными случаями этой функции являются: а) линейная функция
az + b, a, b € С, а 0;
130
Гл. 13. Теория функций комплексной переменной
б) степенная функция
zn, п 6 N;
в) дробно-линейная функция
-— а, Ь, с, d Е С, с 7^ 0, ad — be 0; cz + d
г) функция Жуковского
2. Показательная функция
е2 = eI(cosy + i sin у).
3. Тригонометрические функции
sin г = ^(etz ~ е ггУ
sin г
tg2 =------,
cos г
cosz — ^(ег2 + e tz),
etgz =
cos z sin z
4. Гиперболические функции
sh z — ^(e2
, shz
th 2 — ——, ch z
к h Z
chz — -(e2 н
, ch 2
cth 2 = ——. sh2
5. Логарифмическая функция
Ln г = In |г| + i(arg2 + 2/стг).
Функция Ln 2 является многозначной. В каждой точке г, отличной от нуля и оо, она принимает бесконечно много значений. Выражение In |2| 4-+ г arg2 называется главным значением логарифмической функции г обозначается через In 2. Таким образом,
Ln 2 — In z + 2km.
6. Общая степенная функция
za = eaLnz, а ЕС.
§ 1. Элементарные функции
131
Эта функция многозначная, ее главное значение равно ealnz. Если a =
= —, п G N, то получаем многозначную функцию — корень n-й степени п
из комплексного числа:
= n^ = el(lnb~|+i-(arg2+2^)) =
7. Общая показательная функция
а2 = e2Lna, a G С.
Главное значение этой многозначной функции равно е21пп. В дальнейшем при a > 0 полагаем az = е21па.
8. Обратные тригонометрические функции Arcsinz, Arccos z, Arctgz и обратные гиперболические функции Arshz, Archz, Arthz. Определения этих многозначных функций рассмотрены в примере 7 и задачах 13.70-13.74.
Отображения, осуществляемые некоторыми элементарными функциями и простейшие свойства этих функций будут рассмотрены позднее (в § 3); здесь ограничимся только вычислением конкретных значений этих функций.
Пример 5. Вычислить sin г.
<3 Имеем:
егг — е гг е 1 — е1 е1 — е 1
sin г = ------—-----=----------—---= г-------------= г sh 1. >
2г 2г 2
Пример 6. Вычислить сЬ(2-Зг). О Имеем:
g2 — Зг I g—2+Зг |
ch(2 — Зг) —------------= -(e2(cos3—isin3)+e-2(cos3-Hsin3)) =
= cos 3 ch 2 — isin3sh2. >
Пример 7. Найти аналитическое выражение для функции Arccos z при любом комплексном z. Вычислить Arccos 2.
<1 Так как равенство w = Arccos z равносильно равенству cosw = z, то giw g~iw
можем записать z —----------. Отсюда находим
e2iw - 2zeiw 4-1=0.
Решая это квадратное относительно elw уравнение, получаем
eiw = z 4- y/z2 - 1
132
Гл. 13. Теория функций комплексной переменной
(здесь рассматриваются оба значения корня). Из этого равенства находим iw = Ln (z + x/z2 — 1), т. е.
w = Arccos z =
Отсюда получаем
Arccos 2 = -i Ln (2 ± х/з) = —i In (2 ± х/З) + 2Аттг. >
13.52. Используя данное выше определение функции е2, доказать, что ez имеет чисто мнимый период 2?ri, т. е. е2+27Гг = е2.
Выделить действительную и мнимую части следующих функций:
13.53.
13.55.
13.57.
13.54. w = e^+i)2.
13.56. w = sh (z + 2i).
13.58. w = 3V2.
= e1 z
w
w = sin (z — i).
w = tg (z + 1).
Доказать тождества: 13.59. siniz = ishz. 13.61. tg iz = i th z.
Вычислить значения функции в указанных точках: 13.62. cos (1 + i).
13.60. cos iz = ch z.
13.63. chi.
13.64. sh(—2 + i).
13.65. Ln(-l).
13.68. ctg7ri.
Получить аналитические выражения для указанных ниже функций и для каждой из них найти значение в соответствующей точке zq (см. пример 7):
13.70.
13.71.
13.72.
13.73.
13.74.
13.66. Ini.
13.67. Ln
13.69. thTri.
= Arcsine, Zq = i.
= ArctgZ, Zq = i/3.
= Arshz, Zq = i.
- Arch Z, Zq = — 1.
= Arth Z, Zq = 1 — i.
Найти значение модуля и главное значение аргумента заданных функций в указанных точках:
w = sinz, Zq = тг + iln3.
2 z
w = ze, zq = —тгг.
w - 1 + ch2 Z, Zq = i In 2.
w = th 2, Zq — 1 + iTT.
13.75.
13.76.
13.77.
13.78.
w w w w w
§ 1. Элементарные функции
133
Найти все значения ступеней:
13.79. 2\ 13.80. (-1)\
13.81. (1 + г)\ 13.82. (-1)А
13.83. (3 - 4г)1+\ 13.84. (-3 + 4г)1+\
Решить уравнения:
13.87. ez - i = 0. 13.88. eix = cos лх (x € К).
13.89. in (z - i) = 0. 13.90. sh«z = -1.
3. Предел и непрерывность функции комплексной переменной. Число
А. / оо называется пределом функции f(z) при z —> zq и обозначается А = lim /(г), если для любого е > 0 найдется д = д(е) > 0 такое, что z-»zo
для всех z го, удовлетворяющих неравенству |г — zq\ < д, выполняется неравенство
|/(г) - А| < е.
Говорим, что lim /(г) = оо, если для любого R > 0 найдется д = z—>zo
= <5(Я) > 0 такое, что для всех z zq таких, что — го| < д, выполняется неравенство
1/0)1 > R-
. Следует иметь в виду, что для данной функции /(г) существование предела по любому фиксированному пути (z -> zq) еще не гарантирует существование предела f(z) при z -> г0.
Пример 8. Пусть /(г) = Показать, что lim /(г) не
существует.
< Для предела при г —> 0 по любому лучу reltp имеем
1 / reilfi lim — -----------—
г-»о 2г \ re~l'p
re'** reitp
= sin
т.е. эти пределы различны для различных направлений — они заполняют сплошь отрезок [—1, 1], и, следовательно,
Z
Z
Z
z
Не существует. О
Функция /(г) называется непрерывной в точке zq, если она определена в этой точке и lim f(z) = f(z0).
Z~+ZQ
134
Гл. 13. Теория функций комплексной переменной
Функция f(z), непрерывная в каждой точке области D, называется непрерывной в этой области.
Функция f(z) называется равномерно непрерывной в области D, если для любого е > 0 найдется 6 = <5(г) > 0 такое, что для любых точек 21 и 22 из области D таких, что |2i - 221 < <5, выполняется неравенство |/(21) - /(22)| < Е.
13.91. Используя логическую символику, записать данное выше определение непрерывности функции в области.
Вычислить следующие пределы:
22 - 412 - 3 COS 2
13.92. hm---------. 13.93. hm-—-.
z-^i 2 — г 2->0 ch 22
13.94. lim /in\ . 13.95. lim ch2 + ishz eiz + 2
Доказать непрерывность на всей комплексной плоскости следующих функций:
13.96. w = 2. 13.97. w = |2| Re 2.
13.98. w = ez. 13.99. w = cos |2|.
Как доопределить данные функции в точке 2 = 0, чтобы они стали непрерывными в этой точке:
влоо. /(2) = U.101. /(2) =
13.102. /(2) = 13.103. /(2) = z/\z\.
13.104. Доказать, что функция /(2) = непрерывна в полукруге 0 < |2| 1, | arg2| л/2, но не является равномерно
непрерывной в этом полукруге, а в любом секторе 0 < |2| < 1, | arg2| <а< 7г/2 она равномерно непрерывна.
§ 2. Аналитические функции. Условия Коши-Римана
1. Производная. Аналитичность функции. Если в точке z Е D существует предел
то он называется производной функции /(2) в точке z и обозначается tn \ df^
через f (z) или ——.
dz
Если в точке z € D функция /(2) имеет производную f'(z), то говорим, что функция /(2) дифференцируема в точке 2.
§ 2. Аналитические функции. Условия Коши-Римана
135
Функция f(z), дифференцируемая в каждой точке области D и имеющая в этой области непрерывную производную f'(z), называется аналитической в области D. Будем также говорить, что f(z} аналитическая в точке Zq € D, если f(z) является аналитической в некоторой окрестности точки zq.
Для того чтобы функция f(z) = и(х, у) + w(x, у) была аналитической в области D, необходимо и достаточно существование в этой области непрерывных частных производных функций и(х, у) и и{х^ у), удовлетворяющих условиям Коши-Римана
ди(х, у) _ ди(х, у)
дх ду ’ m
ди(х, у) = dv(x,y) J
ду дх ’
или, в полярных координатах,
5w(rcos</?, г sin 99) 1 ди(г cos 99, rsint/?)
dr r dip
du(r cos p, r sin p) _ 1 du(r cose/?, rsinp) ' '
dr r dp
При выполнении условий (1) или (2) производная f'(z) может быть записана соответственно:
/'(Z) _ ди .ди _ ди .ди ди .ди _ ди .ди дх + 1 дх ду 1 ду дх 1 ду ду 1дх'
или ... . г f ди .ди\ 1 / ди .ди\ . t. /(г) = Д^ + ’^ = (4)
Формулы дифференцирования функций комплексной переменной аналогичны соответствующим формулам дифференцирования функций действительной переменной.
Пример 1. Доказать, что функция f(z) = e2z аналитична и найти
Г^. <1 Имеем g2z _ e2z(cos 2^ j sjn 2yj,
т. е. ц(ж, у) = e2x cos 2y, u(x, y) = e2x sin 2y.
Поэтому = 2e2x cos2y, =-2e2x sin2y, — = 2e2x sin 2y, — = 2e2x cos 2y. дх y dy y
136 Гл. 13. Теория функций комплексной переменной
Следовательно, условия (1) выполняются во всей плоскости, и по первой из формул (3)
(e2z)' — 2е2х cos 2у + i2e2x sin 2у = 2е2х (cos 2у + i sin 2у) = 2e2z. t>
Пример 2. Показать, что функция w — г3 аналитична во всей комплексной плоскости (кроме z = 00).
<1 Действительно, имеем z = reltp и
w = z3 = r3f31^ = г3 cos З99 + ir3 sin З99,
причем
ди „9 „ dv „ 9 . „
— = 3r cos3w, — — 3r sm3<^, dr or
— = -3r3 sin3<p, — =3r3cos3cp, dip d<p
t. e. при любом конечном z = relip выполнены условия (2). Применяя первую из формул (4), имеем
f'(z) = (z3)' = -(Зг2 cos3</2 + гЗг2 sinЗ99) = 3z2. t> z
Пример 3. Показать, что логарифмическая функция w = Ln2 аналитична во всех конечных точках, кроме z = 0, причем
(Ln z)' = -. z
<1 Так как
Ln z = Inr -I- i(ip + 2/c7f),
то имеем:
du _ 1 dv du _ dv _
dr r’ dip dip dr
т. e. выполнены условия (2), и по первой из формул (4) находим
Аналитические функции находят применение при описании различных процессов.
Пример 4. Рассмотрим плоское безвихревое течение идеальной несжимаемой жидкости. Пусть vx(x, у) и vy(x, у) — компоненты вектора скорости v течения вдоль осей х и у, и пусть
V(z) = vx(x, у) - ivy(x, у) (5)
§ 2. Аналитические функции. Условия Коши-Римана
137
— комплексная скорость течения. Показать, что У(д) — аналитическая функция.
<0 Из несжимаемости жидкости следует, что дивергенция вектора скорости тождественно равна нулю, т.е.
, dvy .. п дх ду
(6)
Далее, течение является безвихревым тогда и только тогда, когда ротор его вектора скорости равен нулю, т. е.
^-^ = 0. (7)
ду дх
Но равенства (6) и (7) являются условиями Коши-Римана для функции (5), т.е. комплексная скорость V(z) является аналитической функцией комплексной переменной z = х + iy. [>
Выяснить, в каких точках дифференцируемы функции:
13.105* . w = z. 13.106*. w = Лед. 13.107. w = zlm z.
13.108. w = zRcz. 13.109**. w = |д|. 13.110. w = \z - 1|2.
13.111* . Предполагая выполненными условия Коши-Римана (1) в декартовых прямоугольных координатах, доказать справедливость условий Коши-Римана (2) в полярных координатах и справедливость формул (4) вычисления производной в полярных координатах.
Проверить выполнение условий Коши-Римана (1) или (2) и в случае их выполнения найти f'(z):
13.112. /(д) = e3z. 13.113. /(д) = shz.
13.114. /(д) = zn, n G Z. 13.115. /(д) — cosz.
13.116. f(z) = 1п(д2). 13.117. f(z) = sin-.
13.118* . Пусть /(д) — аналитическая функция в области D.
Доказать, что если одна из функций
и(х, у) = ЛеДд), v(x, у) = 1т/(д),
Ф, у) = |/М|, 0(х, у) = axgf(z)
сохраняет в области постоянное значение, то и f(z) = const в D.
2. Свойства аналитических функций. Ряд свойств, характерных для Дифференцируемых функций действительной переменной, сохраняется и для аналитических функций.
13.119. Доказать, что если /(д) и g(z) — аналитические в области D функции, то функции /(д) ± g(z), f(z) • g(z) также аналитичны в области D, а частное f(z)/g(z) — аналитическая функция
138 Гл. 13. Теория функций комплексной переменной
во всех точках области D, в которых g(z) ф 0. При этом имеют место формулы
13.122. f(z) = z-e~z.
e2 -4- 1
13.124. f(z) =
ez — 1 ez
13.126. f(z) =
13.128. /(2) =-------
cos z — sin z
(/№(*))' = /'ЙрЫ + K^g\z), (' =
13.120. Пусть f(z) — аналитическая в области D функция с областью значений G = {f(z)\z 6 D}, и пусть функция tp(w) аналитична в области G. Доказать, что F(z) = <p[f (г)) — аналитическая в области D функция.
Используя утверждение задачи 13.119, найти области аналитичности функций и их производные:
13.121. f(z) = tg£.
13.123. /(г) = т^-.
13.125. f(z) =-----------
tg Д + CtgZ
13.127. /(z) = cthz.
13.129. Доказать, что действительная и мнимая части аналитической в области D функции f(z) = u(x, у) + iv(x, у) являются гармоническими в этой области функциями, т. е. их лапласианы равны нулю:
d2u d2u d2v d2v
Au "Д 9 Н- "Д к 0, Av — у Н- ~ 2 0-
oxz Oyz oxz oyz
13.130. Получить выражение лапласиана Au в полярных координатах (и = и(г, (^)).
Заметим, что заданием действительной или мнимой части аналитическая в области D функция определяется с точностью до произвольной (комплексной) постоянной. Например, если и(х, у) — действительная часть аналитической в области D функции f(z), то
(*. у)
У -и'у dx + u'x dy,
(*О, Уо)
где (хо, у о) — фиксированная точка в области D и путь интегрирования также лежит в области D.
§ 2. Аналитические функции. Условия Коши-Римана 139
Пример 5. Проверить, что функция и = х2-у2-Бх+у + 2 является действительной частью некоторой аналитической функции /(г) и найти
<1 Так как
^ + ^ = 2-2 = 0
дх2 ду2
во всей плоскости, то и(х, у) — гармоническая функция, а тогда
(я,у) X
v(x, у) = У (2у - 1) dx 4- (2ж - 5) dy = j (2у0 — 1) dx 4-
(жО,Уо) ZO
У
4- У (2ж - 5) dy = (2т/0 - 1)(ж - ж0) 4- (2ж — 5)(у — т/0) =
Уо
= 2ху - х - Бу + Бу0 + х0 - 2хоуо, т. е.
и(ж, у) = 2ху — х - Бу + С и
f(z) = х2 - у2 - Бх + у + 2 + i{2xy — х — Бу 4- С) —
— (ж2 — 2гжт/— I/2) — 5(ж + г?7) + (—жг+ у) 4-24-С'г = z2 — Бг — iz + 2 + Ci. [>
Пример 6. Показать, что функция вида
ц(ж, у) = а(ж2 4- у2) + Ьх + су + d, a 7^ О,
не является действительной (или мнимой) частью никакой аналитической функции.
<] Действительно, это следует из соотношения
д2и д2и . .
Проверить гармоничность приведенных ниже функций в указанных областях и найти, когда это возможно, аналитическую функцию по данной ее действительной или мнимой части:
13.131. и(х, у) = ж3 — Зж?/2, 0 < |д| < 4-ос.
13.132. п(ж, у) = 2exsiny, 0 |д| < +оо.
13.133. ц(ж, у) = 2ху + 3, 0 |д| < +оо.
13.134. v(x, у) = arctg —, 0 < |z| < 4-оо.
140 Гл. 13. Теория функций комплексной переменной
13.135. и(х, у) = —z-х — 2т/, 0 < Ы < 4-оо.
хг 4- yz
13.136. u(x, у) = х2 — у2 + ху, 0 С \z\ < 4-оо.
13.137. v(x, у) = ху, 0 < \z\ < +сю.
§ 3. Конформные отображения
1. Геометрический смысл модуля и аргумента производной. Пусть w = f(z) — аналитическая в точке zq функция и f'(zo) 0. Тогда /с = |/'(г0)| геометрически равен коэффициенту растяжения в точке z0 при отображении w = f(z) (точнее, при k > 1 имеет место растяжение, а при к < 1 — сжатие). Аргумент производной <р = axgf'(zo) геометрически равен углу, на который нужно повернуть касательную в точке zq к любой гладкой кривой L, проходящей через точку zq, чтобы получить касательную в точке Wq = f(zo) к образу L' этой кривой при отображении w = f(z). При этом, если <р > 0, то поворот происходит против часовой стрелки, а если ср < 0, то по часовой.
Таким образом, геометрический смысл модуля и аргумента производной состоит в том, что при отображении, осуществляемом аналитической функцией, удовлетворяющей условию f'(z0) 7^ 0, к = \f (z0) | определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке Zq, а <р = arg/'^o) — угол поворота этого элемента.
Пример 1. Найти коэффициент растяжения к и угол поворота ср в точке zq = 1 — i при отображении w = z2 — z.
<1 Так как w' = 2z — 1 и w'\z=i-i = 1 - 2г, то
к = |1 — 2г| = х/5 и ср = arg (1 - 2г) = — arctg2. >
Найти коэффициент растяжения к и угол поворота ср для заданных отображений w = f(z) в указанных точках:
13.138. w = z2, zq = х/2(1 4- г). 13.139. w = z2, zq = i.
13.140. W = Д3, Zq = 1 + i. 13.141. W = Z3, Zq = 1.
13.142. w = sinz, zq = 0. 13.143. w = ie2z, zq —
Выяснить, какая часть комплексной плоскости растягивается, а какая сжимается при следующих отображениях:
13.144. w = 1/z. 13.145. w = е2-1.
13.146. w = In (г + 1). 13.147. w = z2 + 2z.
Найти множества всех тех точек zq, в которых при следующих отображениях коэффициент растяжения к = 1:
13.148. w = (z - I)2. 13.149. w = z2 - iz.
1 4- iz
13.150. w =--------. 13.151. w = — z3.
1 — iz
§ 3. Конформные отображения
141
Найти множества всех тех точек zq, в которых при следующих отображениях угол поворота ф = 0:
i 1 + iz
13.152. w = —. 13.153*. w = ——.
z 1 — iz
13.154. w = z2 + iz. 13.155. w = z2 — Iz.
2. Конформные отображения. Линейная и дробно-линейная функции. Взаимно однозначное отображение области D плоскости (г) на область G плоскости (w) называется конформным, если в каждой точке области D оно обладает свойствами сохранения углов и постоянства растяжений.
Критерий конформности отображения. Для того чтобы отображение области D, задаваемое функцией w — f(z), было конформным, необходимо и достаточно, чтобы f(z) была однолистной и аналитической в области D функцией, причем f'(z) 0 всюду в D.
В дальнейшем образ области D при отображении функцией w = f(z) обозначается через Е либо через f(D).
Пример 2. Показать, что отображение, осуществляемое функцией w — z3, конформно в области
D = {z| 1 < |z| < 2, 0 < argz < 2тг/3}.
< Необходимо проверить, что заданная функция является аналитической, однолистной в D и что всюду в D f'(z) 7^ 0. Аналитичность функции w = z3 показана выше (см. пример 2 § 2), соотношение w' = 3z2 ф 0 для любого z € D очевидно. Однолистность следует из того, что область D содержится в угле с вершиной в начале координат и величиной 2ж/3 (см. задачу 13.31). [>
Выяснить, какие из заданных функций w = f(z) определяют конформные отображения указанных областей D:
13.156. w = (z + i)2, D = {z|l < |z + z| < 3, 0 < argz < Зл/2}.
13.157. w = \z\2, D = {д||д| < 1}.
13.158. w = ez, D = {д|0 < Imz < 2тг}.
1 / 1\ (1 1
13.159. w = - \ z — ), D = < z - < Ы < 1 >.
2 \ z / I 2 J
13.160. w = (z - I)3, D = {z\ \z - 1| < 1}.
Отображение, осуществляемое линейной функцией w = az + b, рассмотрено выше (см. пример 3 § 1). Оно представляет собой композицию растяжения (гщ = |a|z), поворота (u?2 = e’argawi) и параллельного переноса (юз = W2 + Ъ). Обратная к линейной функции также есть линейная
функция z = —w------. Так как w' = а 0, то отображение w конформно
а а
ВО всей расширенной плоскости, причем имеет две неподвижные точки b ,
21 = ------ (при а 1) И 22 = оо.
1 — a
142
Гл. 13. Теория функций комплексной переменной
Пример 3. Выяснить, существует ли линейная функция, отображающая треугольник с вершинами 0, 1, i в плоскости (z) на треугольник с вершинами 0, 2, 1 -I- i в плоскости (w).
<1 Заметим, что треугольник с вершинами 0, 1, i подобен треугольнику с вершинами 0, 2, 1 4- г, причем вершина в точке z\ = 0 соответствует вершине в точке Wi = 1 4- г, вершина в точке — 1 — вершине в точке w-2 = 0 и вершина в точке z^ = i — вершине в точке w3 = 2. Выполним последовательно преобразования:
a) wi = e’57r^4z — поворот около начала координат на угол а = против часовой стрелки;
б) W2 = x/2wi — гомотетия с коэффициентом к = \/2;
в) w3 — w<2 4- (1 4- г) — параллельный перенос на вектор, изображающий комплексное число 1 4- i.
В результате треугольник с вершинами 0, 1, i отображается на треугольник с вершинами 0, 2, 1 4- г, а осуществляющая это отображение целая линейная функция имеет вид
w = w3 о W2 о wi = z 4- (1 4- г) =
/ х/2 л/2 \
----i — I z 4- 1 4- i = (1 4- г)(1 - z). >
13.161. Доказать, что отображение, осуществляемое целой линейной функцией, имеет две неподвижные точки (совпадающие, если а — 1).
Для указанных ниже отображений найти конечную неподвижную точку zq (если она существует), угол поворота <р и коэффициент гомотетии к\
13.162. w = 2z + 1. 13.163. w = iz 4- 4.
13.164. w = ег4 z — е~г4. 13.165. w = az + b.
Дробно-линейная функция
az 4- b w = —
cz 4- a
ad — be 0, c 0,
осуществляет конформное отображение расширенной плоскости (z) на расширенную плоскость (w). При этом под углом между кривыми в точке z = оо понимается угол в точке z* = 0 между образами этих кривых.
* 1 тт
полученных путем отображения z — -. Простейшей дробно-линейной z
/ х 1
функцией (отличной от линейной) является функция w = -, которая мо-Z
жет быть представлена в виде композиции инверсии относительно еди-
ничной окружности wi = - и комплексного сопряжения W2 = гГц. Про-
Z
стейшая дробно-линейная функция отображает окружности плоскости (z)
§ 3. Конформные отображения
143
в окружности плоскости (w) (прямая линия считается окружностью бесконечного радиуса). Так как общая дробно-линейная функция представляется в виде композиции линейной функции wi = cz + d, простейшей 1 be — ad a
дробно-линейной w? = — и снова линейной w3 =--------4- - , то она
Wi с с
также отображает окружность в окружность.
Дробно-линейная функция w = w(z) вполне определяется заданием образов трех точек. Именно, если zi -4 wi, z-2 -4 w-2 и z3 -4 W3, то
w — wi w3 - W2 _ z - Zi z3 — Z2
W - W2 w3 - Wi Z - Z2 z3 - Zi
(1)
Замечание. Если одна из точек , Z2 или z3 либо wi, W2 или w3 является бесконечно удаленной, то в формуле (1) все разности, содержащие эту точку, следует заменить единицами.
Пример 4. Найти образ окружности х2 + у2 = 2х при отображении 1 w — z
<] Полагая z = х 4- iy, имеем х = - (z 4- z), у = —(z — z). Подставив эти значения в уравнение окружности, находим
х2 4- у2 — 2х = z • z — (г 4- z) = О,
1
и после замены z — — имеем w
WW W W
т. е. w 4- w = 1. Если w = и 4- iv, то w 4- w = 2и. Таким образом, окружность х2 4- у2 - 2х = 0 преобразуется в прямую и = 1/2, параллельную мнимой оси. >
Пример 5. Найти дробно-линейное отображение, переводящее точки —1, г, г 4- 1 в точки 0, 2г, 1 — г.
<1 Используя формулу (1), имеем
w — 0 1 — г — 2г_г4-1 г 4-1 — г
w — 2г 1 — г — О z — i i 4- 1 4- 1 ’
откуда
w 1 z 4-1
w — 2г 5 z — г
144 Гл. 13. Теория функций комплексной переменной
Найти образы следующих линий при отображении w =
z
13.166. Окружности х2 4- у2 = у/3.
13.167. Прямой у = —х/2.
13.168. Прямой у = х — 1.
13.169. Окружности х2 4- у2 4- 2х — 2у 4-1 = 0.
13.170. Доказать, что проходящая через начало координат окружность А(х2 4- у2) 4- 2Вх 4- 2Су = 0 преобразуется функцией w = z в прямую, а любая прямая Вх 4- Су 4- D = 0 — в окружность, проходящую через начало координат.
Найти дробно-линейное преобразование по заданным условиям: 13.171. Точки г, 1, 1 4- г переходят в точки 0, оо, 1.
13.172.
13.173.
13.174.
Точки 1 и г неподвижны, а точка 0 переходит в оо.
1 о 5 3.
Точки - и 2 неподвижны, а - 4- -г переходит в оо.
2 4 4
Доказать, что дробно-линейное преобразование w
az 4- b
= —-j—имеет две неподвижные точки. При каком условии эти точки совпадают? Когда бесконечно удаленная точка является неподвижной?
Точки zi и z-2 называются симметричными относительно прямой, если они лежат на перпендикуляре к этой прямой по разные стороны от нее и на равных расстояниях.
Точки z\ и z-2 называются симметричными относительно окружности, если они лежат на одном луче, выходящем из центра этой окружности, по разные стороны от нее и так, что произведение расстояний от этих точек до центра равно квадрату радиуса.
Точки М и N, симметричные относительно прямой или окружности в плоскости (г), отображаются дробно-линейной функцией в точки М' и /V', симметричные относительно образа этой прямой или окружности в плоскости (w).
13.175. Найти точки, симметричные с точкой 14-г относительно окружностей:
а) |г| - 1; б)* \z-i\ = 2.
z — i
13.176. Для отображения w =-----: найти образ точки, симме-
z 4“ 1
тричной точке 1 — i относительно:
а) прямой у = х; б) окружности \z — 1| = 3.
Пример 6. Найти отображение круга |г| < 1 на круг |w| < 1 такое, чтобы точка z = а(|а| < 1) отображалась в центр круга w = 0.
<1 Запишем дробно-линейное отображение в виде
w = д
Z-ZQ
Z — Z1
§ 3. Конформные отображения
145
Так как точка z = а переходит в точку w = 0, то zq = а, а так как симметричной с точкой w = 0 является точка w = <х>, то z\ является симметричной с точкой z — а относительно окружности |г| = 1, т.е.
= —. Поэтому a z — a w = да---------------------------
az — 1
Далее, точки окружности |г| = 1 переходят в точки окружности |w| = 1, а поэтому при z — eltfi имеем
1 = W
е1* — а
аег^ — 1
Но
eltp — а 2 (eltp - а)(е г<р — а) _ 1 4- |а|2 - eltfia — е l'fia eitfia — 1 (е^а — 1)(е_^а - 1) |а|2 4- 1 — е^а — е~г^а
Следовательно, |^се| = 1, т.е. да = егв, и искомое отображение имеет вид
za — 1
Для отображения (2) единичного круга на себя найти параметры а и 0 по заданным условиям:
13.177. w(l/2) = 0, argw'(l/2) = 0.
13.178. w(0) = 0, argw'(O) = тг/2.
13.179. w[zq) = 0, argw'(zo') = тг/2.
13.180. Доказать, что функция
w _ ® Irna > 0, (3)
z — а
осуществляет отображение верхней полуплоскости на единичный Круг.
Определить параметры а и 0 в формуле (3) по заданным условиям:
13.181. w(i) = 0, argw'(i) = —тг/2.
13.182. w(2i) = 0, argw'(2i) = тг.
13.183. w(zq) = 0, argw'^o) = тг/2.
Найти образ Е области D при заданном дробно-линейном отображении:
13.184. D = {д| Re z > 0, 1тд > 0}; w=-----.
z 4- i
146 Гл. 13. Теория функций комплексной переменной
13.185* . D = (z|0 < argz < w =-----------.
I 1 4 J z - 1
13.186* . D = (z|l \z\ 2, 0 argz w = 1 4- -.
I 4 j z
1 — z
13.187. D = {z| |z| < 1, Imz >0}; w = i-------.
1 4- z
z — 1
13.188. D = {z|0 < Rez < 1}; w —--------.
% 2
13.189. D — двуугольник (круговая луночка), заключенный
£
между окружностями \z — 1| = 1, \z — i| = 1; w =----------
Z " 1 z
13.190* *. Найти область D в плоскости (z), которая при ото-£
бражении w = -------преобразуется во внутренность круга |w| < г
1 — z
плоскости (ш).
3. Степенная функция. Отображение, осуществляемое степенной функцией w = zn (п 6 N, п 2), является конформным в любом
' '2Ъг 2(& 4- 1)тг 1
---- < argz < >, к = 0, 1, ..., ft — 1 (кроме ft--ft I
угле D =
точки z = 0), причем образом этого угла является вся плоскость (w) с . 2кл
разрезом по положительной части действительной оси (лучу argz =--------
2(к 4- 1)тг
соответствует верхний, а лучу argz = ----------- — нижний край раз-
ft
__ • / tp + Zkir \
реза). Обратная функция w = qz = yre1' n где к = 0, 1, ..., ft — 1, г = |z|, = argz, является, как известно, многозначной. Ее однозначная ветвь (выделяемая заданием образа одной из точек) отображает плоскость (z) с разрезом по неотрицательной части действительной оси на соответствующий угол
Е =
2кл 2(к 4- 1)тг
< argw < ft-----------------ft
где к = 0, 1, ..., ft — 1 — фиксировано.
Пример 7. Найти отображение внутренности двуугольника с вершинами zi и z-2, образованного окружностями С\ и 64, на единичный круг.
гг Z~ Z\ 21 4- Z2
<1 Преобразование wi =--------- отображает точку z = —-— в точку
wi = 1, точку z = zi — в нуль, а точку z = z? — в бесконечность. Таким образом, отрезок, соединяющий точки Zi и z?, отображается на положительную действительную полуось. Дуги окружностей, образующие двуугольник, отображаются в лучи argwi = атг и argwi = — /Зтг. Следовательно, область D отображается на сектор Ex = < argwi < ал)
§ 3. Конформные отображения 147
-------------------------------------------------------1------------
(ср- с задачей 13.189). Повернем этот сектор на угол (Зя, т.е. произведем преобразование w-2 = и возведем полученную функцию в степень
(3 + а'
W3 = (w2)^+“.
Сектор отобразится в верхнюю полуплоскость. Функция
W4
Лв ^3 ~ wg
W3 — W3
осуществляет отображение полуплоскости на единичный круг. Величины и в определяются дополнительным заданием отображения
Рис. 4
точки zq в точку w = 0 и условием arg w'(го) = 7. Окончательно, w = = W40W30 w-2 о wi (рис. 4). >
Найти функцию, отображающую заданную область D плоскости (г) на верхнюю полуплоскость (в ответах указана одна из .функций, осуществляющих указанное отображение, причем если функция многозначна, то имеется в виду одна из ее однозначных Ветвей):
13.191. D = {г||г| < 1, \z - 1| < 1}.
13.192. D — {z\ — 7г/4 < argz < тг/2}.
13.193. D = {г| |г| < 1, 1шг > 0}.
13.194. D = {г| |г| > 1, Im г > 0}.
13.195. D = {г| \z\ < 2, 0 < arg г < тт/4}.
148
Гл. 13. Теория функций комплексной переменной
1 / 1 \ 1
4. Функция Жуковского. Имеем w = - z -I— I, w' = -
2 \ z J 2
13.196. D = {z| |z| > 2, 0 < arg г < Згг/2}.
13.197. D = {z| |z| < 2, Imz > 1}.
13.198. D = {z||z| < 1, |z 4- г| < 1}.
13.199. D = {z||z| < 1, |z4-i| > 1}.
13.200. D = {z\ |z| > 1, \z 4- i\ < 1}.
13.201. D — плоскость (z), разрезанная по отрезку [—г, г].
13.202. D — плоскость (z), разрезанная по отрезку, соединяющему точки 1 4- i и 2 4- 2г.
13.203. D — плоскость с разрезом по лучам (—оо, —R] и [R, 4-ос), R > 0.
13.204. D — полуплоскость Imz > 0 с разрезом по отрезку, соединяющему точки 0 и ih (h > 0).
z* 2 — 1
z2
Функция Жуковскогоосуществляет конформное отображение как внешности, так и внутренности единичного круга плоскости (z) на плоскость (ш) с разрезом по отрезку [—1, 1]. Полная плоскость (z) отображается на двулистную риманову поверхность, склеенную крест-накрест по разрезам [-1, 1].
Обратная функция
z = w 4- а/w2 — 1
двузначна, причем каждая ветвь осуществляет отображение плоскости (w) с разрезом по отрезку [—1, 1] на внутренность или на внешность единичного круга в плоскости (z).
Пример 8. Найти образ полярной сетки р = const и </? = const при преобразовании плоскости (z) с помощью функции Жуковского.
<1 Полагая z — ре1***, имеем
1 ( 1 _i(A If 1\ .1 f 1\ .
w = и 4- iv = - ре * -I—е ) = - I р 4— cost/? 4- г~ \ р-sin</2.
2 \ Р / 2 у р/ 2 \ р/
^Конформное отображение, осуществляемое функцией w = - ( z Ч— ),
2 \ z J было использовано впервые Н. Е. Жуковским в качестве метода получения одного класса аэродинамических профилей, названных профилями Жуковского. Профили Жуковского отображаются на круг, для которого можно легко решить задачу обтекания, а это дает возможность исследовать обтекание крыла самолета.
§ 3. Конформные отображения
149
Следовательно,
1 ( 1\ 1 / 1\ .
и = - \ р + - I COS р, V = - р---1 sin р,
2 у рJ 2 у рJ
и для р 1 имеем
cos2 р sin2 р
(4)
(5)
Из этих равенств заключаем, что окружности |г| = р 1 отображаются / ч 1 ( 1\ , 1 ( О
в эллипсы плоскости (w) с полуосями a = - р 4— ) и о = - р--
2 \ р) 2 \ р )
при р > 1 или b = (- — р ) при р < 1. Лучи р = const в плоскости
\ Р /
(z) преобразуются в плоскости (w) в гиперболы с полуосями a = | cos <р| И Ъ = | sin<р|.
Заметим, что фокусные расстояния с = ya2 — Ь2 эллипсов (4) и ci = т=. \/a2 +Ь2 гипербол (5) равны 1, т.е. (4) и (5) — семейства софокусных Эллипсов и гипербол. >
Пример 9. Найти отображение плоскости (г) с разрезами по отрезку, соединяющему точки 0 и 4г, и по отрезку, соединяющему точки 2i и 2 4- 2г, на внутренность единичного круга |w| < 1.
<] Искомое отображение w находим в виде композиции пяти отображений. Функция wi = z — 2г переводит точку z = 2г в начало координат, а функция W2 = el%wi осуществляет поворот плоскости (гщ) на угол гг/2. Точка z = 4г переходит в результате этих отображений в точку W2 = —2, Точка z = 2г — в точку w? = 0, точка z = 2 4- 2г — в точку — 2i, а точка z = 0 — в точку w% = 2. Далее, в результате отображений w% —
•и Wi = ws/4 разрез отображается в отрезок [—1, 1] плоскости (гид), и, наконец,
w5 = ю4 4- i/wj - 1,
отображает внешность отрезка [—1, 1] на внутренность единичного круга, причем выбирается та ветвь этой функции, которая при гщ = оо обращается в нуль. Итак, w = W5 о W4 о W3 о W2 о wi (рис. 5).>
В задачах 13.205-13.207 найти образцы заданных областей при
отображении w = -
150
Гл. 13. Теория функций комплексной переменной
13.205 . Внутренности круга |z| < R при R < 1 и внешности круга |z| > R при R > 1.
13.206 . Внутренности круга |z| < 1 с разрезом по отрезку [1/2, 1].
Рис. 5
13.207 . Внутренности круга |z| < 1 с разрезом по отрезку [-1/2, !]•
13.208 *. Найти отображение круга |z| < 1 с разрезом по отрезку [1/3, 1] на круг |w| < 1.
13.209 *. Найти отображение области D = {z|Imz > 0, \z\ > R} (верхняя полуплоскость с выкинутым полукругом) на верхнюю полуплоскость.
2 2
у
13.210 *. Отобразить внешность эллипса — 4—- — 1 (а > Ь) а2 1г
на внешность единичного круга.
5. Показательная функция. Функция w = е2 однолистна в любой полосе шириной менее 2тг, параллельной действительной оси. Она отображает полосу —оо < х < 4-оо, —7Г < у < 7Г в полную плоскость (w) с разрезом по действительной отрицательной полуоси. Вся плоскость (z) отображается на бесконечнолистную риманову поверхность. Обратная функция z = Ln w = Inw + 2тгтгг, п = 0, ±1, ..., однозначна на этой ри-мановой поверхности, а ее главное значение In w = In |w| 4- i argw определяет конформное отображение всей плоскости (w) с разрезом (—оо, 0] на полосу —7г < Imz < тг шириной 2тг, параллельную действительной оси.
Пример 10. Найти отображение полосы шириной Н, 0 < Rez < Н, параллельной мнимой оси, на единичный круг плоскости (ш).
§ 3. Конформные отображения 151
О Искомое решение получим, например, с помощью композиции отображения:
i* wo i0w3-W§
W\=e 2z, w-2 — —гщ, W3 = e 2, W4 = e -------H?.
H W3 — W3
При последовательном выполнении этих отображений заданная полоса преобразуется в области, показанные на рис. 6. >
Рис. 6
Найти образ Е области D при отображении w = ez:
13.211. D = {z| — тг < Imz < 0}.
13.212. P = {z||Imz| <7г/2}.
13.213. D = {z|0 < Imz < 2тг, Rez > 0}.
13.214. D = {z|0 < Imz < тг/2, Rez > 0}.
13.215. D = {z|0 < Imz < 7r,0 < Rez < 1}.
13.216. Найти образы прямых x = С и у — С при отображении w = ez.
Найти образы следующих областей при отображении w = Inz, «(») =
13.217. {z|Imz > 0}. 13.218. {z| |z| < 1, Imz > 0}.
13.219. {z||z| < 1, z £ [0, 1]}.
' 13.220. {z| |z £ [-oo, -1] U[0, +oo]}.
6. Тригонометрические и гиперболические функции. Функция w = eiz 4- e~iz
== cosz = -------- однолистна в полуполосе —7г<а;<7г,?/>0и
152
Гл. 13. Теория функций комплексной переменной
отображает эту полуполосу на плоскость (w) с разрезом (—оо, 1]. Ри-манова поверхность этой функции более сложная, чем у предыдущих, так как склеивание листов происходит отдельно по лучу (—оо, — 1) и по отрезку [—1, 1].
Функция w = sin z сводится к предыдущей с помощью соотношения /7Г \ т. •
sinz = cos \ 2 ~ z)- 8Шг и cosz СВОДЯТСЯ и гиперболические функции: sh z = —i siniz, ch z — cosiz.
13.221* *. Найти образ E полуполосы D = {г|0 < Roz < тг, Im г > 0} при отображении w = cos z.
13.222. Найти образы прямых х = С, у = С при отображении w = chz.
13.223. Найти образ Е прямоугольника D = {z| — % < Re 2 < < тг, — h < Imz < h, h > 0} при отображении w = cosz.
§ 4. Интеграл от функции комплексной переменной
1. Интеграл по кривой и его вычисление. Пусть I — дуга направленной кусочно гладкой кривой в плоскости (г), точки Zk Е I, k = 0, 1, ..., п, разбивают дугу I на частичные дуги, на каждой из которых выбрано по одной точке к = 1, ..., п. По определению полагаем
/п
f(z)dz- lim (1)
max|Azfc|->0 '
I
при условии, что предел в правой части (1) существует и не зависит ни от способа разбиения дуги I на частичные дуги, ни от выбора точек Если функция f(z) непрерывна на I, то интеграл (1) существует.
Если f(z) = ц(ж, y)+iv(x, у), то вычисление интеграла (1) сводится к вычислению двух криволинейных интегралов 2-го рода
У f(z)dz = u(x, у) dx - v(x, у) dy + i v(x, у) dx + u(x, у) dy. (2) / i i
Пример 1. Пользуясь определением (1), вычислить j Rezdz, где i
I — радиус-вектор точки 1 + i.
<] Разбиваем радиус-вектор точки 1+г на п равных частей, т. е. полагаем
k к 1
Zk = -+г-, &Zfc = -(l + i), к - 0, 1, ..., п, п п п
и пусть £к — Zk- Тогда интегральная сумма запишется в виде
V—"к . V—"к 1 + i 1 + г V—"к к 1 + г гг(?г + 1)
> ,Rezfc Azk = У хк----=------У - = —-------~
z—' n n n n2 2
k—1 k=l k=l
§ 4. Интеграл от функции комплексной переменной
153
Следовательно,
р , г («+ l)(n + 1)
Кеггй = lim --------------
п->оо 2п
1 + ?
Пример 2. Используя представление интеграла в форме (2) и правила вычисления криволинейных интегралов 2-го рода, вычислить интеграл У \z\zdz, где I — верхняя полуокружность |г| = 1 с обходом против I часовой стрелки.
<1 Имеем
У \z\z dz = У + y2(xdx + у dy) + i j у/х2 + у2 (—у dx + xdy). i i i
Переходя к параметрическому уравнению кривой х = cost, у = sin2, О t тг, и учитывая, что у/х2 + у2 — |г| = 1 в точках кривой, получаем
j \z\z dz = j (— cost sin t 4- sin/cost) dt + i у (sin2 t + cos2 t) dt — m. > l о о
Если дуга l задана параметрическим уравнением z — z(t), причем начальная и конечная точки дуги соответствуют значениям параметра t = to и t = ti соответственно, то
У f(z)dz = У f(z(t))z'(t)dt.
i t0
(3)
ПримерЗ. Используя формулу (3), вычислить интеграл j (z + z) dz, i
где I — дуга окружности \z\ = 1, тг/2 arg г Зтг/2.
<1 Положим z(t) = e1t, тг/2 t Зтг/2. Тогда z'(t) = iezt и, используя формулу (3), находим:
I
Зтг/2
(z + z)dz= [ [elt + e~lt)ielt dt — i \ y-e2lt + t
J \2г
тг/2
Зтг/2
— 7П. > тг/2
154 Гл. 13. Теория функций комплексной переменной
Непосредственным суммированием вычислить следующие интегралы:
13.224. у*Im.zdz, где I — радиус-вектор точки 2 — i.
I
13.225. У |z| dz, где I — радиус-вектор точки —2 — Зг.
I
13.226. Доказать, что при изменении направления пути интегрирования интеграл изменит знак, т. е.
У f(z) dz = - У f(z) dz.
l+ l-
13.227. Доказать, что если ai и О2 — постоянные, то
У fai/i(2)+02/2(2)) dz = У /i(z)d^ + o2 У /2(2) dz.
1 1 1
13.228. Доказать, что если кривая интегрирования I является объединением кривых li и /2, т0
У f(z)dz = У f(z)dz + У f(z)dz.
1 h l2
13.229* . Доказать, что имеет место оценка
У f(z)dz
1
l/(2)| ds,
где ds — дифференциал дуги.
Вычислить интегралы по заданным контурам:
13.230. У (2г + l)zdz, I = {z| |z| = 1, 0 arg z тг}.
I
13.231. У Imzdz, I = {(ж, у)\у = 2х2, 0 х 1}.
I
13.232. / {iz2 — 2z) dz, I = {z| |z| = 2, 0 arg z тг/2}.
/
§ 4. Интеграл от функции комплексной переменной 155
13.233. j Re (z + z2) dz, I = {(ж, y)\y = 2x2, 0 < x < 1}.
l
13.234. У (z2 — z) dz, I = {г| \z\ = 1, л < arg z < 2%}.
I
. 13.235. У zez dz, I — отрезок прямой от точки zq = 1 до точки
zi = i-
13.236. У ez dz, I — отрезок прямой от точки zq = л до точки 1
z\ = —гл.
13.237. У z Im (г2) dz, I = {г| Re z = 1, |Im z\ < 10}.
l
13.238. У Re (cos z) sinzdz, I = {z| Re z = л/3, |Im z\ 1/2}.
i
13.239. У cos z dz, I — отрезок прямой от точки zq = л до точки 1 л
г1 = 2+г'
13.240. У sh zdz, I — отрезок прямой от точки zq = In 2 до
1
точки = In 10 + лi In 5.
13.241. У Im г2 Re23 dz, I — {(т, y)\y = За?3, 0 x 1}.
i
13.242. У ~ dz, I = {z| |z| = 1,0^ argz < тг/2}. i
Пусть в области D задана многозначная функция w — f(z)- Однозначная функция w = <p(z), аналитическая в области D, называется однозначной ветвью функции f(z), если для любой точки zq Е D значение ¥>(z0) принадлежит множеству значений функции f(z) в точке z = zq, т.е. <p(zq) Е {/(zq)}. Многозначная в области D функция может иметь как конечное число однозначных ветвей (например, w = y/z), так и бесконечное (например, w = Ln г).
Точка z комплексной плоскости, обладающая тем свойством, что обход вокруг нее в достаточно малой окрестности влечет за собой пере-
156 Гл. 13. Теория функций комплексной переменной
ход от одной ветви многозначной функции к другой, называется точкой ветвления (разветвления) рассматриваемой многозначной функции. Так, точками ветвления многозначной функции w = tfz являются точки z — 0 и z — оо. В каждой из своих точек ветвления многозначная функция принимает только одно значение, т. е. различные однозначные ветви функции в этих точках совпадают.
При интегрировании многозначной функции необходимо выделять ее однозначную ветвь. Во всех задачах ниже это достигается заданием значения многозначной функции в некоторой точке контура интегрирования.
Вычислить интегралы по заданным контурам:
13.243. j ^=, 1 = Р|Н = 1, 1 1 .Уз _ 2+’Т' <] Функция \/z является многозначной где = arg г. Условию У1 = — | + i-t ветвь этой функции, для которой к = так как arg 1 = 0) —тг/2 argz тг/2}, УТ = , к = 0, 1, 2, Ъ — удовлетворяет та однозначная 1. Действительно, при к = 1 (и
У1 = е1(0+2я) =е^ Полагая теперь z(y>) = е \/z = е и, следовательно, тг/2 71 Г dz _ Г iel{p d<p J \/~z J ез(^+27Г) J / — тг/2 —7Г -~ 2 Г dz 13.244. / --, l = {z / jV o' 5_l Z7T . . Z7T 1 ,yj 3 = cos — + г sin — = — + г —. 3 3 2 2 lip (—тг/2 тг/2) на кривой /, находим i^+270, z'(ip) =iei<p, /2 Г / 1 \ 3 3 ) • f f e i dip = /2 Y) Я/2 3. _ilL _i7r. 9 .зуз = 2(e ~e ) = 4’Z~ * -я/2 Z Ч Я |г| = 1, 0 arg£ тг}, У1 = 1.
_____§ 4. Интеграл от функции комплексной переменной_________157
13.245. У \fedz, I = {z| |z| = 1, тг/2 < argz < %}, у/1 = —1. I
/Ln 2z
-----dz, I = {z| |z| = 1, 0 arg z тг/2}, z
i
Ln 1 = 2m.
13.247. / Lnzdz, I = {z| |z| = 1}, Lnz = 'y-i.
J
I
13.248. У zn Ln z dz, n G N, I = {z| |z| = 1}, Ln(—1) = 7n. i
2. Теорема Коши. Интегральная формула Коши. Если функция f(z) аналитична в односвязной области D, ограниченной контуром Г, и 7 — замкнутый контур в D, то
У di] = 0. (4)
7
Если, дополнительно, функция /(z) непрерывна в замкнутой области D = £>Ur, то
/(77) dr] = 0
г
(теорема Коши).
Если функция /(z) аналитична в многосвязной области D, ограниченной контуром Г и внутренними по отношению к нему контурами 71, ..., 7^, и непрерывна в замкнутой области D = D (J Г+ (J 7f U • • • [J 7^, где знаки в верхних индексах означают направления Обходов (рис. 7), то
/ k /М dr] = 0 (5)
Уг+и и 7-7
(теорема Коши для многосвязной „ _
«к \ гис. 7
области).
Если функция /(z) определена и непрерывна в односвязной области D и такова, что для любого замкнутого контура 7 С D
f(r])dr] = 0,
158
Гл. 13. Теория функций комплексной переменной
то при фиксированном zq Е D функция
Z
= У Ж dr]
20
является аналитической в области D, причем Ф'(г) = f(z).
Функция Ф(г) называется первообразной или неопределенным интегралом от f(z), причем если F(z) — одна из первообразных для /(г), то
22
У f<J])dr] = Г(г2) - F(zx).
21
Если f(z) аналитична в области D, z0 Е D и у G D — контур, охватывающий точку z0, то справедлива интегральная формула Коши
fM = /-/ — dv- (6)
2т J г]~ zQ т
При этом функция f(z) имеет всюду в D производные любого порядка, для которых справедливы формулы
/<Ч(2) = 2от/ О) -/И+1 d’1, & = (7)
7
Пример 4. Доказать, что если f(z) — аналитическая и ограниченная в выпуклой области D функция, то для любых двух точек Zi и г2 из этой области имеет место оценка
У dr]
шах|/(г)| |г2 - z1\. z^D
О Из выпуклости области следует, что если Z\ G D, z2 Е D, то и отрезок, соединяющий эти точки, также принадлежит области D. Из теоремы Коши следует, что в качестве пути интегрирования можем взять именно этот отрезок, а потому, применяя оценку задачи 13.229, имеем
У ftifidr]
max|/(z)|
ZE.D
- \z2 - Zi|max|/(z)|. О z^D
Пример 5. Вычислить интеграл
/dr]
1 + Г]2 о
= F(z) - F(0),
если путь интегрирования не охватывает ни одну из точек zi)2 = ±г.
§ 4. Интеграл от функции комплексной переменной
159
г/ ч 1
zi Так как подынтегральная функция j(z) = ------- является аналити-
1 + г2
ческой всюду, кроме точек г1>2 = ±г, то интеграл F(z) имеет смысл во всех точках, кроме z = ±г, и при условии, что путь интегрирования не проходит через эти точки. Следовательно, если путь интегрирования не охватывает ни одну из точек Zi,2 = +г, то в качестве одной из
1 первообразных для функции
можно взять однозначную функцию
/’(z) = arctgz, и, учитывая, что arctgO = 0, имеем
arctgz =
drj
1 +т]2‘
>
о
Пример 6. Вычислить интеграл
. ггтг Sin —-______2_ z2 + 1
dz.
<1 Запишем интеграл в виде
. izir sm —
2
^ti-dz z - i
и, используя формулу Коши (6), находим
I =
2тгг
. izn
sm~F
sin
= 2тгг —
z + i
Пример 7. Вычислить интеграл
|z —2|=3
TF—П dz‘ zJ(z — 1)
<1 Так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках z\ = 0 и г2 — 1, то рассмотрим Многосвязную область Р, ограниченную окружностью Г = {г| |г-2| = 3} и внутренними контурами 7! = {г| |г| = р} и 72 — {г| |г — 1| — р}
160
Гл. 13. Теория функций комплексной переменной
(0 < р < 1/2). Тогда в этой области D функция f(z) = ется аналитической, и по формуле (5) можем записать:
явля-
Применяя теперь соответственно формулы (7) и (6), находим
е*
z - 1 , 2дг
—-— dz = —— z3 2!
Z \ " е 1 . ez(z2 — 4г + 5) = тгг = —5 тгг
Z - 1) (z- I)3 z=Q z=0
e7^3
—— dz = z — 1
= 2тгег.
Z=1
Таким образом, I = ni(2e — 5). t>
Вычислить интегралы:
13.249. j / ez dz, I = {(z, y)\y = z3, 1 < x 2}. 1
13.250. J / sinzdz, I = {z\z = t2 + it, 1/2 t 3/2}. 1
13.251. / £2COS£C?£, I — отрезок прямой ОТ ТОЧКИ Zq = i до
ТОЧКИ £1=1.
13.252. 1 / tgzdz, I = {(z, y)\x = y2,o^y 1}.
I 13.253*. У (z - £0)n dz, n — целое число, I = {д| \z - z0| = R}. 1
13.254. I (z — zq)71 dz, n — целое число, I = {д| \z - z0| =
Im (Z - Zq) >0}.
§ 4. Интеграл от функции комплексной переменной
161
13.255. Вычислить интеграл / (г
1) cos z dz по произвольной
кривой /, соединяющей точки zq = 7Г и z\ =
Зтг.
—г
13.256* . Какие значения принимает интеграл
dz
—р если в
качестве I брать произвольные кривые, соединяющие точки zq = 1
l±S
2 '
и zi =
Вычислить интегралы (обход контуров — против часовой стрелки):
P2z
———.dz.
z — 7гг
С?2 f dz
ITT в) j IT?' |z| = l/2 |z-i|=l |z+z|=l
7Г2 . 7Г2
|z-l| = l |z|=4
Г dz f cos z
13.261. ф ———. 13.262. ф —-------~ dz.
J z2 4-2^ J z2 — ix2
1*1=3 1*1=4
r sh-(z + i)
13.263. ф —f—-— dz.
J z2 - 2г
|z| = l f sin 2 sin (2 — 1) , 13.264. ф --------r-3----- dz.
I z2 — 2 |z(=2
Г
13.265. ® ---—r-----—т, где:
J (z-l)3(z + l)3’
a)C = {z||z-l| = l}; 6) C = {z||z + l| = l};
В)С = МН = Я,Л#1}.
162
Гл. 13. Теория функций комплексной переменной
)г+г] = 1
13.268.
13.269.
z—21=3
sin г , / sh2 z ,
-----— dz. 13.267. Ф —dz. (z + г)3 J z3
|г|=1
. 7TZ sin — --------4----- (z-mz-з) •
che™z J
2з _ 422 dz-
fin /* e1/2
13.270. ф -7 cos--------- dz. 13.271. Ф —z-------—z dz.
j z3 z + 1 j (z2 + 4)2
|z|=l/2 |z-2|=1
13.272. Доказать теорему о среднем: если функция /(z) аналитична в круге |z — zq| R и непрерывна в замкнутом круге |z — zq| R, то значение функции в центре круга равно среднему арифметическому ее значений на окружности, т. е.
2тг
Ц*о) = [ f(zo + RetO)M
Z/R J
о
f
177-Zo |=Я
где ds — дифференциал дуги.
13.273* . Известно, что если /(z) const — аналитическая в области D и непрерывная в замкнутой области D = D |J L функция, то max|/(z)| достигается только на границе области (прин-zeD
цип максимума модуля). Доказать, что если, кроме того, Vz £ G Df(z) 7^ 0, то и min|/(z)| достигается также на границе.
z£D
13.274. Используя формулу (6) для доказать теорему Ли-увилля: если f (z) — аналитическая и ограниченная во всей плоскости (z) функция, то /(z) = const.
Глава 14
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
§ 1. Преобразование Лапласа
1. Определение и свойства преобразования Лапласа. Преобразованием Лапласа функции /(£), t 6 К (которая, вообще говоря, может принимать и комплексные значения), называется функция F(pj комплексной переменной р, определяемая следующим равенством:
+оо
F(p)=[e-pif(ejdt (1)
О
Оригиналом называется всякая функция f(t), удовлетворяющая следующим условиям:
1) /(О — 0 при t < 0, причем принимается, что /(0) = /(4-0);
2) существуют такие постоянные а и М, что
|/(i)| <Meat при t>0 (2)
(величина op = infer называется показателем роста функции /(£));
3) на любом конечном отрезке [0, t] функция f(t) может иметь лишь конечное число точек разрыва, причем только 1-го рода.
Если /(0 — оригинал, то стоящий в правой части равенства (1) Интеграл Лапласа сходится абсолютно и равномерно в полуплоскости Rep а > ctq. При этбм функция F(p) является аналитической в полуплоскости Rep > его и называется изображением функции /(£).
Соответствие между оригиналом f(t) и его изображением F(p) символически записывается в виде F(p) = f(t).
Пример 1. Найти показатель роста многочлена f(t) = antn +... 4-+ Oj t 4- ng •
- < Заметим, что для любого а > О
antn-----+аП + а0 _
lim ------------------= 0.
t—>4-00 efft
Значит, для любого а > 0 существует такое число М = М(а), что выполняется неравенство:
\antn 4- • • • 4- apt 4~ uq| <С М(сг)еа^, t > 0.
Следовательно, op = inf а — 0.
<7>0
164
Гл. 14. Операционное исчисление
Заметим, что при <т = по — 0 неравенство (2) не выполняется. >
Пример 2. Найти изображение функции Хевисайда
Ф) = |
1,
О,
t о, t < 0.
< Так как функция Хевисайда является оригиналом с показателем роста сто — 0, то
+оо
p(i) = j e~pt dt = о
-Л-”'
+oo
0
1
P
p
при Rep > 0. t>
Всюду в дальнейшем под заданной с помощью формулы функцией /(i) будем понимать произведение этой функции на функцию Хевисайда р(£), т.е. считать f(t) =0 при t < 0.
Проверить, являются ли следующие функции оригиналами, и найти их показатели роста:
14.1. /(i) = е3*+2. 14.2. /(i) = е<3.
14.3./« = е- 14.4. Ж = {
14.5. /(£) = In (i + 1). 14.6. /(i) = t\
14.7. /(i) = isin -. 14.8. f(t) =
Используя формулу (1), найти изображения для следующих
оригиналов: 1, 0 t < 2,
14-9. f(t) = / -1, 2 t < 3, 0, 3 < t ( t, 0 t < 2,
14.10. /(t) = • i(4-i), 2 t < 4, 1 I 0, 4^t
14.11. Ш = ь V V/ V/ о ь
14.12. /(*) = < f i(2 - i), 0 t < 2, 10, 2 < L
§ 1. Преобразование Лапласа
165
1, 0 $ 1 : t < : t < 1, 2,
14.13. 7(t) = < 3-i, 2 $ : t < 3,
< 0, 3 $ : t.
7Г
sini о < 1 < 2’
2, 7Г Зтг
— (тг — i), c t < —,
14.14. /(1) = < 7Г 2 ' 2 ’
Зтг
sini, ~2 t < 2тг,
< o, 2тг t.
Свойства преобразования Лапласа:
1. Свойство линейности. Для любых постоянных Ск, к — 1,
2, ..., п,
И п
^Ckfk(t) = ^CkFk{p), Rep> max {(Л, сг2, сгп}_ к=1 к=Л
2. Теорема подобия. Для любой постоянной a > О
1 / Р \
f(at) = —F [ — ) , Rep > aa0. a \a/
3. Теорема смещения. Умножению оригинала на eat, a Е Ж, соответствует смещение аргумента изображения на а, т. е.
eQ</(0 .— F(P ~ q)j Re (р - а) > (т0.
4. Теорема запаздывания. Запаздыванию оригинала на т соответствует умножение изображения на е~рг, т.е.
Tj(t - r)f(t - т) = e~pTF{p), Rep>a0.
5. Дифференцирование оригинала. Если f(t) и ее производные к = 1, 2, ..., являются оригиналами, то для любого
к = 1, 2, ..., п
/<‘>(<) = pbptp) - (р‘-7(0)+р‘“7'(0) + + А-1 >(0)).
В частности, Г^=р^(р)-/(0), Rep > aQ.
б. Интегрирование оригинала:
t
f f(r) dr = Rep > (To-
J P
о
166
Гл. 14. Операционное исчисление
7. Дифференцирование изображения. Умножению оригинала на множитель t соответствует умножение изображения на —1 и дифференцирование его по аргументу р:
= п = 1,2, ...
8. Интегрирование изображения. Если —— является оригиналом, то
ОО |ло = I F(4)dq. р
9. Дифференцирование и интегрирование по пара-аг
метру. Если f(t, a) = b (р, а) и функции —-- и / fit, a) da,
da J
рассматриваемые как функции переменной t, являются оригиналами, то
df(t, a) _. dF(p, a)
da ’ da
02 02
У f(t, a) da == У F(p, a) da.
ai ai
и
10. T еорема Бореля об изображении свертки. Свертке
оригиналов
t t
/1 * /2 = I fi(r)f2(t — r) dr = I fa(t- r)f2(r) dr о о
соответствует произведение изображений, т.е.
/1 * Ь .= Fl(p)F2(p).
11. Интеграл Дюамеля. Если f(t) = F(p) и g(t) = G(p), то pF(p)G(p) = f(O)g(t) + (/' * g)(t) = g(G)f(t) + (д' * f)(t).
Зная изображение функции Хевисайда p(t) = - (см. пример 2), Р
можно с помощью перечисленных выше свойств 1-11 построить таблицу изображений основных функций:
§ 1. Преобразование Лапласа
167
№ F(p) № М) F(p)
1 ^(0 1 6 sin /3t P
Р p2 4- P2
2 tn 1 7 ch (3t P
п! рп-+* 1 pl _ @2
3 at 1 8 sh pt P
р — а p2 _ @2
4 /п 1 Pat 1 9 eat cos /3t p — a
п\ (р — a)n+1 (p — a)2 + /32
5 cos (3t Р 10 eat sin /3t P
р2Р2 (p - a)2 4- (32
С помощью свойств преобразования Лапласа и таблицы основных изображений можно найти изображения большинства функций, встречающихся на практике.
Пример 3. Найти изображение функции sin3 t.
<] Имеем по формуле Эйлера
sin3 t =
/elt — е 1 /3(ezf — е lt)
\ 2г / 4 \ 2г
g t ____ g 311
2i J
3 • . 1 •
— - sin t —- sin 3t.
4 4
Используя свойство линейности и формулу 6 таблицы, находим:
.3.31 13 6
sint — — • ----— — - ~ ---
4 р2 4- 1 4 р2 4- 9 (р2 Ч- 1) (р2 -Ь 9)
Пример 4. Найти изображение функции t2 cos 2t.
<] Используя формулу Эйлера и формулу 4 таблицы изображений, получаем:
t2cOS2t = lt2(e2-' + e-2-‘) = ^_
1
(р 4- 2г)3
р3 - 12р
(р2 -I- 4)3 ’
Заметим,что изображение указанной функции можно было бы получить и другим способом, а именно, дважды дифференцируя изображение cos2i. >
Пример 5. Найти изображение функции Si £ =
функцию называют интегральным синусом).
о
168
Гл. 14. Операционное исчисление
<1 Используя теорему интегрирования изображения, находим
sin t f dp я
= / -у— = arctgq = - - arctgp.
t J q 2
Отсюда по теореме интегрирования оригинала получаем t / \
f sin Г , 1 I 7Г \
Si t = / ---dr = - — — arctgp . >
j r p \ 2 I
о ' '
t
Пример 6. Найти изображение функции j cos (t — т)е~2т dr. о
<1 Используя теорему Бореля об изображении свертки, получаем
t
/ cos(t — т)е~2т dr — cost * e~2t = —---—r-------. t>
7 (P2 + W + 2)
о
Пример 7. Найти изображение оригинала /(t), если
_ ( sin t при 0 SC t < тг, ~ | 0 при t 7Г.
< Используя функцию Хевисайда и учитывая, что = 1 при t тг, функцию /(t) запишем в виде
/(t) = sint 4- p(t — тг) sin (t — тг).
Пользуясь формулой 6 таблицы и теоремой запаздывания, получаем
. 1 е~пр 1 + е-пр
Р\р) — 7 "I ----7 — —\—• О
р2 + 1 р2 + 1 р2 + 1
14.15* . Доказать следующие теоремы о связи «начальных» и «конечных» значений оригинала изображения. Если /(t) = F(p), то
а) /(0) = Р^(р)
р—>оо
и (если существует конечный lim /(t) — /(+оо))
t->+oo
б) /(+оо) = limpF(p).
р-»0
§ 1. Преобразование Лапласа
169
14.16. Доказать следующие соотношения1):
tn
а) — cos fit = nA
Re((p + /3i)n+I) (p2 + /32jn+i
tn
6) — sin (3t = nl
Im ((p + (3i)n+l)
^ + ^n+i
Найти изображения заданных функций:
14.17. |i2 4-1.
14.19. e~l + 3e-2li + t2.
14.21. cos2 t.
14.23. sh3t
14.25. sh3icos2i.
14.27. sin i — i cost
14.29. t2e~l.
14.31. e2t cos t.
14.33. £2ch2t
14.35. te~l sh t.
t
14.37. y* (t — r)2 cos 2т dr. о
14.39’. [C±L^dr.
J T
0 14.41. / dr.
J T 0
Г e/3r _ ear 14.43. / ------dr.
J т о
14.18. t2 - -e*. 2
t 14.20. 2 sin t — cos -. n 2 14.22. sin2 (i — a).
14.24. chi sin t 14.26. ich2t
14.28. -(chisini + shicosi). id
14.30. i3e2<.
14.32. e~l sin21.
14.34. te~l sini. t
14.36* . Уe~~rdr. о t
14.38. У те1~т sin (i — r) dr. о
t
С 1- e~T 14.40. / --------dr.
J T о t 1л ла* [ cos/5т-cos ar 14.42 . / ---------------dr.
J r о
!) Здесь обозначения Re и Im подчеркивают тот факт, что действительная и мнимая части соответствующего комплексного многочлена берутся условно, т.е. р считается вещественным числом.
170
Гл. 14. Операционное исчисление
Найти изображения дифференциальных выражений при заданных начальных условиях:
14.44. TIV(i) 4- 4a;/"(i) + 2x"(t) — 3x'(t) — 5; a;(0) = rr'(O) = = щ"(0) = щ"'(0) = 0.
14.45. xl"(t)+Qx"(t) +x'(t)—2x(t)\ t(0) = я/(0) = 0, x"(Q) = 1.
14.46. x"(t) 4- 5x'(t) — 7x(t) 4- 2; a;(0) = а, ж'(0) = 0.
Используя теорему запаздывания, найти изображения следующих функций:
14.47. p(i - l)ei-1. 14.48. p(i - 2) sin2 ((t - 2)/2).
14.49*. r){t — l)ie(. 14.50*. rj(t — sini.
14.51. f(t) = ( 1 при 0 t < т, t 0 при t т
(единичный импульс, действующий в течение промежутка времени от t = 0 до t = т).
14.52. /(г) = < 0 при t < Ту 1 при Т t < Т 4- г, 0 при t Т 4- т
(запаздывающий единичный импульс). h
14.53. /(t) = < т h при т t < 2т, (i — Зг) при 2т t < Зг, т 0 при 0 Зт. sini при 0 t < тг/2,
14.54. f(t) = < — cost при тг/2 t < Ту 0 при t 7Г.
14.55. /(f) = <! h при 0 t < 1, he~^~^ при t 1.
14.56. /(f) = J sini при 0 i < Ту sh (i — тг) при i т.
14.57*. Доказать,что если f(t) — периодическая функция с пе-
риодом 1у то 1 F^= f e~pt^dt-0
§ 1. Преобразование Лапласа
171
Используя результат задачи 14.57, найти изображения периодических функций (аналитические формулы определяют заданные
функции на периоде [0, /]):
14.58. Ш = ( п П₽“
J v ’ [0 при
О t < т, т t < Т-
1 = Т
(периодическая последовательность единичных импульсов).
14.59. f(t) = sin/3t при 0 < t < д//3; I = тг/(3 (т.е. f(t) = = | sin^|).
14.60. /(t) = -j [ sini L 0 При 0 : при ТГ с t -t < <Т; 1 = Т.
14.61. /(t) = 1 [ h 1 —h при 0 при С : t < : t < с, 2с- 1 = 2с.
14.62. /(£) — — t при с
( h
—t
14.63. /(t) = 1 с
c
I = 2с.
при с t < 2с; тг тг
14.64. /(£) = cos fit при 0 t < —, I = —2. Ш Z_Z 4&JC/
14.65. /(£) = | sinij, I = 2тг.
2. Расширение класса оригиналов. Класс оригиналов можно расширить, включив в него функции, которые могут быть неограничены в окрестности конечного множества точек, но такие, что интеграл Лапласа от них тем не менее в некоторой полуплоскости Rep > ор сходится абсолютно. К числу таких обобщенных оригиналов относится степенная функция /(t) = tp при р > — 1, функция InZ и некоторые другие. В частности, к такому классу относится всякая функция f(t), которая в некоторых точках t = tk (к = 1, 2, ..., п) является бесконечно большой порядка, меньшего единицы, т.е. такая, что lim (t — tk)rkf(t) = 0 при t-*tk
некотором гь < 1, и если вне некоторых окрестностей точек tk она удовлетворяет условиям, при которых функцию можно считать оригиналом.
Пример 8. Найти изображение F(p) функции f(t) = tp, р > — 1.
-f-oo
< Имеем F(p) = f e~pttp dt или, после подстановки pt = г, о
F'">=
+оо
j е~ттр' dr =
Г(//+ 1) рм+1
о
172
Гл. 14. Операционное исчисление
тх • 1 2А
Итак’ гЦГГц =
Замечание. Если р — целое положительное число, то Г(/1 4- 1) — = р\, и мы приходим к формуле 2 таблицы изображений.
Пример 9. Найти изображение функции /(f) = fMInt, р > -1.
<J Из соответствия параметру р получаем
Г(н 4- 1)
= —-——— с помощью дифференцирования по
(£^±22_1пА.
рм+1 F рм+1 у Г(/14-1) J
В частности, положив р = 0, с учетом того, что Г(1) = 1, Г'(1) = —7 (7 = 0,577215 ... — постоянная Эйлера), получаем
7 4-lnp In t =--------.
Р
Найти изображения функций:
14-66-= rfJT+l)’
„ ... ^eQtInf
14.6 . /(f) = M > ~ •
14.68. /(f) = eat Inf. 14.69. /(f) = f^
14.70.
14.71.
14.73.
f^
——— cos^f, P>-1. Г(/14-1)
f(f) = TV \ n sin^’ > -1’ Г(/1 4-1)
/(f) = cosfit • Inf. 0 1
14.72. f(t) = sin(3t • Ini. при 0 t < a,
Ht) =
k \/t — a
при
§ 2. Восстановление оригинала по изображению
1. Элементарный метод. Во многих случаях заданное изображение можно преобразовать к такому виду, когда оригинал легко восстанавливается непосредственно с помощью свойств преобразования Лапласа и таблицы изображений.
2) Здесь под функцией комплексной переменной 1/рр+1 понимается та из ветвей этой многозначной функции, которая на вещественной положительной полуоси комплексной плоскости (р) принимает вещественные значения, т. е. 1/рр+1 = е_^+1)1пр. Аналогичное замечание относится к изображениям функций £peQt, £peQtln£, t^cos^t,
§ 2. Восстановление оригинала по изображению
173
Для преобразования изображения широко используется в этом случае метод разложения рациональной дроби в сумму простейших.
Пример 1. Найти оригинал для функции
F (р) = р2 + 2р + 5
<j Первый способ. Выделяя полный квадрат в знаменателе и далее, используя табличное изображение для sin^t и теорему смещения, получаем:
1 1 1 2 . 1 п
р24-2р4-5 “ (р4-1)24-4 “ 2 (2 4- 1)2 4- 4 ~ 2е Sm
Второй способ. Раскладывая дробь в сумму простейших и используя изображение для eai, получаем
1 _ J_ / 1______________1 \
р2 4- 2р 4- 5 4г \р — (—1 4- 2г) р — (—1 — 2г) /
т 1 __р 1
= —(е(-1+2гД — e(-1~2*)i) — -e~f----------— -е-1 sin2t. >
• 4гv 7 2 2г 2
Пример 2. Найти оригинал для функции F(p} = —---------—.
(р2 4- I)2
<] Первый способ. Раскладывая дробь в сумму простейших, получаем
1 1
(р2 4-I)2 (р - г)2(р 4-г)2
1 /_1______г 1 1
4 \р — г р4-г (р — г)2 (р 4- г)2
= —^-(ielt — ie u + telt + te lf) = ^(sint - icost). 4 2
Второй способ. Заметим, что
i _ _j_ / 1 у
(р2 4- I)2 2р \р2 4- 1J ’
причем согласно теореме о дифференцировании изображения
/ 1
\р2 4- 1
= tsint.
174
Гл. 14. Операционное исчисление
Применяя теперь теорему об интегрировании оригинала, находим
1 1/1 \ 1 Г 1
—------ =----—------ — - г sin т dr = - (sin t — t cos t).
(p1 2 + l)2 2p \p2 4-1 / ' 2 / 2V 7
о
Используя теорему Бореля об изображении свертки,
Третий способ, получаем
1
1 _______________
(p2 4- l)2 p2 4- 1
„ 1— = sin t * sin t = p2 4- 1
о
— sin t [ cos r sin rdr — cos t j sin2 r dr — - (sin t — t cos t). 0
• о
p2e 2p p3 * 4- 1
Пример 3. Найти оригинал для функции р2
<J Найдем сначала оригинал для дроби ——причем в отличие от двух р3 4-1
предыдущих примеров разложение дроби в сумму простейших произведем в множестве действительных чисел.
Имеем:
р2 р2 1/1
р3 4-1 (р 4- 1)(р2 - р 4- 1) 3\р+1
2р- 1
р2 _ р 1
1
3
1
1 п Р~ 2
р+ 1 + / 1\2 3
у ~ 2J + 4
i I е 1 4- 2е^2 cos
О \ Z
А теперь, применяя теорему запаздывания, учтем сомножитель е 2р. Окончательно находим:
2 2 р 1 / о
•“ ~ 2Хе-(<-2) + 2е^~2) cos ~(t - 2)). >
р3 4- 1 3 2
Найти оригиналы для заданных функций:
14.74. -—Ц14.75. ------------i------.
(р-1)2 (р4-1)(р-3)
14.76. -—;------. 14.77. - - J 9----.
р2 4- 4р 4- 3 р3 4- 2р2 4- р
§ 2. Восстановление оригинала по изображению
175
14.78. - 9- -—. р2(р2 4- 1) 14.80. —=——-. (р2 - 4)(р2 4-1) 14.82. . р3 4- 1 е-2р 14.84. —. р/ 1 е-Р Зе~4р 14.86. -4- 4--ТГ—г. р — 2 р pz 4- 9 2р 4- 3 14.79. —- - . р15 4- 4pz 4- 5р 14.81. -7^—^. (р2 4- 4)2 14.83. . р4 + 4 е~2р 14.85. —. (р4-1)3 р 2ре~р 14.87. — р2 4- 4 р2 — 4
2. Формула обращения. Теоремы разложения. Если f(t) — оригинал и F(p) — его изображение, то в любой точке непрерывности /(t) справедлива формула обращения Меллина
ст+гоо
Л*) = Л [ F(p)eptdp, 21W J
где интегрирование производится по любой прямой Rep = ст, ст > сто-
Замечание. Во всякой точке to, являющейся точкой разрыва функ-
ций /(t), правая часть формулы Меллина равна -(/(t0 — 0) 4- /(to 4- 0)).
Непосредственно применение формулы обращения часто затруднительно, и обычно пользуются теоремами разложения, являющимися следствиями из нее:
Первая теорема разложения. Если функция F(p) аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням 1/р имеет вид
ОО
n=0 7
то функция
ОО
/(t) =
n=0
£ n!
t 0 (/(t) = 0 при t < 0)
является оригиналом, имеющим изображение F(p).
Вторая теорема разложения. Если изображение F(p) является однозначной функцией и имеет лишь конечное число особых точек р\, р2, ..., рп, лежащих в конечной части полуплоскости Rep ст0, то п
Ж = £ ВЫЧ [e^F(p); рк].
k=i
176
Гл. 14. Операционное исчисление
Если, в частности, F(p) =
Рт(р)
QM ’
где Рт(р) и Qn(p) — много-
члены степеней т и п соответственно (n > т), pi, р?, ..., рг — корни
многочлена Qn(p) с кратностями, соответственно равными li, I2, ..., 1Г (Zi 4- I2 + • • • + 1г — ^)? то
Т ж = Е k=\
1 d1^
—-----—- hm ——
(tfc - 1)! р->рь dpik
(1)
Если все коэффициенты многочленов Рт(р) и Qn(.p) — действительные числа, то в правой части (1) полезно объединить слагаемые, относящиеся к взаимно сопряженным комплексным корням; сумма каждой пары таких членов равна удвоенной действительной части одного из них.
В частном случае, когда все корни pi, рг, • • •, Рп многочлена Qn(p) простые, используя формулу для вычисления вычета относительно полюса первого порядка (см. с. 101), получим
п ж = £ k=l
Pm(Pk) Pkt
Q'M
(2)
Пример 4. Найти оригинал функции F(p) = -е ₽.
Р
< Первый способ. Разложение функции F(p) в окрестности точки р = оо имеет вид
1 1 00 1 00 1
F(p) = -е-р = - V (-1)п-г- = У (-1)П-Дгг р р t—* п\рп п\рп+х
1 г n=0 1 n=O г
Поэтому, в соответствии с первой теоремой разложения, оригиналом для
00 tn
F(p) является функция f(t) = У (-1)п—— п=0 'П''
= /о(2дЛ) (/о — функция
Бесселя первого рода с нулевым индексом).
Второй способ. Воспользуемся второй теоремой разложения. Для этого надо найти вычет функции -epte~1/p относительно ее единствен-Р
ной особой точки р = 0 (это существенно особая точка), т.е. коэффициент при 1/р разложения этой функции в ряд Лорана в окрестности точки р = 0. Имеем
-epte~1/p = ( 1 4- pt 4- ~л~ 4- • • • 4- 4- ... ) х
р \ 2! n! J
/111 , 1
XI - 4- . „ 4- • • • 4- ( —1) —:——
\р р2 2!р3 n!pn+1
§ 2. Восстановление оригинала по изображению
177
Выделив в произведении рядов члены, содержащие 1/р, найдем:
f(t) = выч -epte 1//р\ 0 =
LP
= 1 " f + (^2 + •1 • + + • • • = >
В этом примере решение, использующее первую теорему разложения, оказалось более простым, чем решение при помощи второй теоремы разложения.
Пример 5. Найти оригинал для функции F(p) = —------——.
(р2 4- /32У
<1 Воспользуемся второй теоремой разложения. Функция F(p) имеет два полюса 3-го порядка р = и ее оригинал определяется равенством
f(t)= выч
Ppt _____-______• Qi
+ ВЫЧ
ept
(р2 + 02У’
— 2Re ( выч
Рр1
-------------• Bi [(р2 ч- z?2)3 ’
Имеем:
ept
выч l(j>2 + /Я3'10г. =
_ 1 .. d2 / _ «з ept \ _ 1 d2 / ept \ _
“ 2! Д™ dp2 \{P Pi) (p2 + /32)3J ~ 2 Л dp2 Цр + fii)3 J ~
_ i ( t2ePt Qte0t 12e₽f A _
- 2 p Vt + fti)2 ~ (p + 3i)4 + (t + #)5 / ~
t2e0it 3te0it 2>e0it
~ ' 16/33г " 16/34 + 16/34
(при дифференцировании мы воспользовались формулой Лейбница для производной произведения). Выделив действительную часть этого выражения и удвоив ее, получим
, _ t2s\n/3t 3i cos /3t 3sin/3£
f = 8/33 8^4 + 8^5 ' >
Пример 6. Найти оригинал для функции F(p) = - .
178
Гл. 14. Операционное исчисление
<j Знаменатель дроби здесь имеет только простые корни pii2 = ±1, р3 4 = ±г. Поэтому в соответствии с формулой (2) получаем
4 1 1 / pit p-it \
/(t) = у -~.epkf = -(е* -е-' + — + —— I =
4р3 4 \ г3 (-г)3)
1 е1 - е 1
2 2
1 е*' - е-“ 1, , t .
= -(shi_sln(). >
Этот пример можно было решить, исходя из разложения —------ =
р4 - 1
_ 1 / 1_________1 \
2 \р2 — 1 р2 4- 1 /
Пользуясь первой теоремой разложения, найти оригиналы для заданных функций: 1 1
14.88. - cos -. р р
14.90. — In^ii. 2р р — 1 1 --1-
14.92 . -----е р-1
р- 1
Пользуясь второй теоремой разложения или с помощью разложения на элементарные дроби, найти оригиналы для заданных функций:
14-93- F= ^75- 14-94- F(Р) = (Р + D(p - 2)(р2 + 4) •
14.95. F(p) = где Q(p) = (р - pj(p - р2)... (р - рп) и Q\P)
все числа pk попарно различны.
14.96. F(p) = (р4 -р^
14.98. F(p) = —2.
(р4 - I)2
Р3
(р2 4- I)3 р2 4- 1 р2(р2 — I)2 р3
14.100. F(p) =
14.102. F(p) =
14.104. F(p) =
14.89. sin-.
P
14.91. -e1^2
P
р 4- 2
1
14.97. F(p) = „ ? лх.
(p2 4- l)2(p2 — 4)
14.99. F(p) = .
pD — 1
14.101. F(p) = -y-l—T-
pz — 4p 4- 3
14.103. F(p) = r _P
p4 — 5p2 4- 4
(p4-l)(p4+4)-
§ 3. Применения операционного исчисления
179
§ 3. Применения операционного исчисления
1. Решение линейных дифференциальных уравнений и систем уравнений с постоянными коэффициентами. Для того чтобы найти решение x(t) линейного дифференциального уравнения с постоянными коэффициентами
4- А1Ж^г-1) 4- • • • 4- anx = f(t) (1)
(где f(t) — оригинал), удовлетворяющее начальным условиям
т(0) = зд, х'(0) = ^............................ (2)
следует применить к обеим частям этого уравнения преобразование Лапласа, т.е. от уравнения (1) с условиями (2) перейти к операторному уравнению
(рп 4- 4- • • • 4- an)X(p) 4- Q(p) = F(p),
где X(p) — изображение искомого решения, F(p) — изображение функции /(£), a Q(p) — некоторый многочлен, коэффициенты которого за-висят от начальных данных xq, х0, ..., Xq и который тождественно равен нулю, если х0 = х'о = = ХдП~^ = 0. Решив операторное уравнение относительно АДр):
Х(р) =
F(p) - Q(p) Цр)
(L(p) = pn 4- aipn 1 4- • • • 4- an — характеристический многочлен данного уравнения) и найдя оригинал для Х(р), мы получим искомое решение x(t). Если считать xq, х'о, ..., х^1"^ произвольными постоянными, то найденное решение будет общим решением уравнения (1). Совершенно аналогично решаются и системы линейных дифференциальных уравнений с постоянными коэффициентами. Отличие будет лишь в том, что вместо одного операторного уравнения мы получим систему таких уравнений, которые будут линейными относительно изобра?кений искомых функций.
Пример 1. Найти общее решение уравнения х" 4- 2х' 4- х = te~l, а также его частное решение, удовлетворяющее начальным условиям
~ 1, Я0 ~ 2-
<1 Пусть x(t) == Х(р), тогда
ж'(0 =рХ(р) - х0, x"(t) =р2Х(р) -рх0 - х'о.
По таблице изображений находим te~l = -----—, и операторное урав-
(р+1)2
нение имеет вид
(р2 4- 2р 4- 1)Х(р) - (р + 2)ж0 - х'о = - J -~2 .
(р4- I)2
180
Гл. 14. Операционное исчисление
Отсюда находим
%(р) = —т£о 4* 7-----4" 7--------ТТТ"
(р+1)2 (Р+1)2 (Р+1)4
Для отыскания оригинала в данном случае проще всего представить X (р) в следующем виде:
Жр + х'о Хо
Y( \ _ (р 4- 1) 4- 1 1 / 1 _
Х(₽) (р+1)2 0 (р+1)2 0 (р+1)4
_ 1
(р4- I)4 ' (р4- I)2 ' р+ 1
Пользуясь таблицей изображений, находим общее решение
x(f) = 4- (я?о 4- х'0)1е~* 4- хое~1
о’
Обозначив xq = С\, ж0 4- х'о = Ci, его можно записать в виде
x(t) = i(3e-l + (Ci +C2t)e-‘. О
Частное решение, удовлетворяющее заданным начальным условиям,
a:(t) = ^!3е *4-(14-3£)е *. > О
Пример 2. Проинтегрировать уравнение х"4-х = f(t) при нулевых начальных условиях, если
о < t <
/(О =
-(7Г-С 7Г
при
при
при
7Г
2’
<1 Запишем /(£) с помощью единичной функции Хевисайда:
/(t) = (l-4(t-^))^-
/ / 7Г \ \ 2
(р (t - тг) -nG — ^)) -G = \ \ Z / /Л
2 / / 7Г\ / 7Г\ . . . ч\
= - И - 2т? И - (t - -) 4- T](t - 7Г)(! - тг)) .
7Г х X Z / X Z / Z
§ 3. Применения операционного исчисления
181
Пользуясь теоремой запаздывания, отсюда находим
2 1 - 2е~ ?р 4-f(t) = F(p) =-------------------
7Г р2
Так как начальные условия нулевые, то, полагая x(t) == Х(р), приходим к операторному уравнению
. 2 . 2 1-2е-^ + е-^
(р2 4- 1)Х(р) = -7Г
р2
из которого после несложных преобразований находим
2 /1
Х(р) = — (1 — 2е~%р + е~пр} -у
7Г \р2
Так как ——z------= t—sin £, то, снова применяя теорему запаздывания,
р2 р2 + 1
находим
*(*) = | ((£ - sin i) -2ri(t- ((t ~ - sin (t - 4-
4- T](t - 7t)((£ - тг) - sin (t - Д')),
т.е.
2
— (t — sint) 7Г
X(f) = <
— (— sin t — 2 cos t — t + тг) 7Г
4
— cos t
7Г
при
при
при
t 7Г. >
Пример 3. Найти решение системы
х' 4- у = е*, х 4- у' = е~1
при начальных условиях ж(0) = хо, т/(0) = уо.
<1 Пусть x(t) == Х(р), y(t) = У(р), тогда x'(f) = рХ(р) - х0, у' (£) = .=’ pY(p) — уо, и получаем операторную систему
рХ(р) - х0 4- Y(p) = —, Р- 1
pY(р) - уо 4- Х(р) = ——. р 4- 1
182
Гл. 14. Операционное исчисление
Решая систему, найдем
vr ч _ Р 1 , Р2 + 1
р^-1Х° р2 - 1^° + (р2 - I)2 ’
ч _ Р , 1 -^0 2Р р2^1Уо + р2_1 (р2_1)2
и, следовательно,
( x(t) = xodit — yosht + tcht, | y(t) = y0 ch t + (1 — xq) shi — t shi. >
Найти общие решения дифференциальных уравнений:
14.105. х" + 9.т = cos 3i. 14.106. х" — 4я/ + 4х = e2t.
14.107. х" + 2xr — te~2t. 14.108. х" + х' — 2х = е1.
14.109. х" + х' — е~* sini.
Найти решения дифференциальных уравнений при заданных начальных условиях:
14.110. х'" + х = 0; я(0) = 0, ж'(0) = — 1, ж"(0) = 2.
14.111. х" + 2х' + х = е-*; я(0) = 1, я/(0) = 0.
14.112. х" + 3x' = e~3t-, ж(0) = 0, ж'(0) = — 1.
14.113. х" — 2х' + 2х = sini; ж(0) = 0, я/(0) = 1.
14.114. х" + 4х = sin2t; я(0) = 1, д/(0) = —2.
14.115. х" — 9.т = shi; я(0) = —1, д/(0) = 3.
14.116. хт — х" = е*; я(0) = 1, я/(0) = ж"(0) = 0.
14.117. :rIV — х = shi; я(0) = я/(0) = ^"(О) = 0, д/"(0) = 1.
14.118. х'" + Зх" + Зх1 + х = te~l\ я(0) = .т'(0) = ^"(О) = 0.
Найти при нулевых начальных условиях решения следующих дифференциальных уравнений:
14.119. х' + х = f(t), где /(«) = •{ J 12< 2’
14.120. х" + х = /(1), где /(() = { ™S( ‘ <
14.121. х" -x’ = f(t), где 7(t) = | ° | { < 11
{1 при 0 i < 1,
-1 при 1 i < 2,
О при i 2.
14.123* *. С помощью интеграла Дюамеля доказать следующее утверждение: если xi(t) — решение уравнения х^ + + a\x^n~^l + ••• + anx = 1 при нулевых начальных условиях
§ 3. Применения операционного исчисления
183
(#(0) = х'(0) = ••• = х(п ^(0) = 0), то решением уравнения »("> + «1 х(П' -1)+ ...+о nx = f(t) при тех же начальных условиях является функция
t t
x(t) = У - т)(/т = д?1(/)/(0) + у* f'(r)x}(t-T) dr 0 0
(J(f) — произвольный оригинал).
Замечание. Результат задачи 14.123 позволяет находить решение линейного дифференциального уравнения с постоянными коэффициентами при нулевых начальных условиях, не находя изображения правой части этого уравнения.
Пользуясь результатом задачи 14.123, найти решения следующих дифференциальных уравнений:
, 1 „ 1
14.124. х — х = 14.125. х — х = -----?.
е* + 3 1 + е1
14.126. х" -х' = —14.127. х" + х = -—-—-.
1 + еь 2 + cos t
14.128. х" + х = e~t2.
Найти общие решения систем дифференциальных уравнений
14.129. х" + у' = t, 14.130. х" + у1 = sht — sint, у" — х' — 0. у" + х1 — cht — cos t.
Найти решения систем дифференциальных уравнений при заданных начальных условиях.
14Л31' х + у' - 0: = 11 !/(0) = -L
14.132. 2х" + х — у1 = — 3 sin х + у' = — sin t;
z(0) - 0, z'(0) = 1, 7/(0) = 0.
14.133. х" - т/' = 0, х — у" = 2 sin i;
z(0) = -1, z'(0) = 7/(0) = 7/'(0) = 1.
14.134. x" - 7/' = 0, x' — y" = 2 cos Z;
z(0) - 7/z(0) = 0, Ж'(0) = 7/(0) = 2.
14.135. x" - у' = е\
x' + y" -y = 0;
z(0) = l, 7/(0) = -l, z'(0) = 7/'(0) = 0.
где /i(t)
у' + х =
Г t
= < 7Г - t
I о
14.138. х" - у = О,
У" -х = /(t),
при тг/2 при
где f(t) = <
184 Гл. 14. Операционное исчисление
14.136. х" + у' = 2 sin t-
у" + z' = 2 cos t,
z" _ x — 0;
z(0) = z(0) = 7/(0) = 0, z'(0) = 7/(0) = -1, /(0) - 1.
Проинтегрировать при нулевых начальных условиях системы дифференциальных уравнений:
С 1 при 0 С t < ТГ, t 0 при t тг,
< тг/2, : t < ТГ, t 7Г.
1 При 0 t < ТГ,
— 1 при 7Г t < 2%, 0 при t 2тг.
2. Решение линейных интегральных и интегро-дифференциальных уравнений. Используя теорему свертывания, можно легко найти изображения решений интегральных уравнений Вольтерра 1-го и 2-го рода (а в простейших случаях по найденному изображению найти и само решение) в том случае, когда ядром в соответствующем уравнении служит функция вида K(t — г), где K(t) — оригинал. Этот метод применим и к интегро-дифференциальным уравнениям с таким же ядром.
Пример 4. Найти решение уравнения Вольтерра 1-го рода
cos (t — r)x(r) dr = t cos t.
о
< Пусть x(t) = X(p); так как
. _• P 4 < - P2 ~ 1
C0Sf--p2 + 1’ U0S<- (p2 + 1)2’
[ cos (t - r)x(r) dr =
J P2 + 1
0
(по теореме свертывания), то приходим к операторному уравнению
рХ{р) _ р2 - 1
р2 + 1 (р2 + I)2 ’
откуда
V( ) = Р2 ~ 1 2Р - 1
{Р) P(P2 + 1) р2+1 р'
Таким образом, x(t) = 2cost — 1. t>
§ 3. Применения операционного исчисления
185
Пример 5. Найти решение уравнения
t
х" + х = sin t + у* sin (t — т)х(т) dr о
при начальных условиях я:(0) = 0, ж'(0) = 1. О Полагая x(t) = Х(р), имеем
x"(t) = р2Х(р) - 1, sin t =
f . . . . . , Х(р)
/ sin (t - т)х(т) dr = —-
J P2 + 1
0
Получаем операторное уравнение
(p2 + l)X(p) - 1 =
рл + 1 pz + 1 или
((p2 + I)2 - l)A(p) = p2 + 2.
Отсюда находим X(p) = 1/p2 и x(t) — t. >
Решить следующие интегральные и интегро-дифференциальные уравнения: t
14.139. f ch (i — т)х(т) dr = ch t — cos t. о
t.
14.140. 3 J sh (i — t)x(t) dr = x(t) — .
о t
14.141. У el~T sin (t — т)ж(т) dr = x" — x’ + e*(l — cos i); о
z(0) = ш'(0) - 1. t
14.142. У sh (t — t)x(t) dr = x” — x' + -ishi; ж(0) = 1, о
®'(0) = 0.
186
Гл. 14. Операционное исчисление
Проинтегрировать уравнения Абеля:
14.143.
14.144.
= 7Г.
О
-1.
3. Интегрирование линейных уравнений в частных производных. Применение операционных методов для интегрирования линейных уравнений в частных производных рассмотрим на примере.
Пример 6. Найти решение уравнения
d2z
т; -г - + z = sin х cos у, дх ду
удовлетворяющее условиям г(0, у) = sin у, z(x, 0) = 0 (х G [0, +оо),
у е [0, +оо)).
< Переходим к операторному уравнению относительно аргумента у, полагая z(x, у) = Z(x, р). Отсюда
dz
— = pZ(x, р) - z(x, 0) = pZ(x, р),
ду
Q2 z д
= ^pZ(z, р» = pZ'x(x, Р)
(по теореме о дифференцировании операторных соотношений по параметру). Получаем операторное уравнение:
ч psinx р) + Z(X, р) = -
Pz + 1
. Р
так как cosp = —--------
р2 + 1
Интегрируя полученное дифференциальное уравнение по аргументу х, находим
2
Z(x, р) = C^e-i + -(рГ^)2- sinx - cos х.
В силу начального условия z(x, 0) = 0 и теоремы о связи начального значения оригинала и конечного значения изображения мы должны иметь lim pZ(x, р) — z(x, 0) = 0, откуда находим lim pCi(p) = 0, причем р—>оо р—>оо
если Ci(p) =' <р(р), то <р(0) — 0 (в силу той же теоремы). Запишем теперь Z(x, р) в следующем виде:
. 1 _£ Р . 1 (Р2 + 1) + (р2 - 1)
Z(x, р) = pCi (р)-е - + (-7^ * - 2-----------------cos
§ 3. Применения операционного исчисления
187
Цо так как
pCi (р) = <р'(р), -е“ р = /о(2\/Т?7)
Р
(см- решение примера 4 из § 2), р 1 р“ — 1
т? •= 2^’ (Tw=ycos?7’
Ю находим:
у
х(х, у) = У </>'Щ10(2у/х(у - £)) dt + о
1 . 1, .
4- -р sin р sin ж — -(smp 4- ycosy) cos я; = .
у
= У <р' (t)Io(2\/x(y - t)) dt- | sin у cos x - ^y cos (x + y) о
(первое слагаемое получено по теореме свертывания оригиналов). Так как То (0) = 1, то, полагая х = 0, находим:
Г ,, ч , 1 . 1 . . 1 . 1
/ <р (t)dt - -snip - —ycosy = <р(у) - -smy- -ycosy = sinp
J & & u
0
3 1
(по начальным условиям); поэтому <p(p) = -sin?/ 4- -pcosp, <p'(p) =
n 1 •
= 2cosy — -ysmy, и окончательно находим
?/
У ^2 cos t — ~t sin tJ Io(2\/x(y — i)) dt — о
1 . 1
- - sin ycosx - -у cos (x 4- у). t>
Проинтегрировать следующие линейные уравнения в частных Производных:
d2 z dz
14.145. — - — 4- z = cos ж; z(0, у) = р, z'x(0, у) = 0.
oxz оу
z dz
14.146. —- - — - a2z = f(x)- г(0, у) = -у, 4(0, у) = 0.
dxz dy
— Ri(x, i),
(5)
— Gu(x, i),
188 Гл. 14. Операционное исчисление
14.147* *. Уравнения длинной линии в случае отсутствия потерь (линейное сопротивление R и утечка G равны нулю) имеют вид:
du(x, t) О
дх dt ’ /дх
di(x, t) _ du(x, i)
dx dt ’
где u(x, t) - напряжение, i(x, i) — ток в точках линии в момент времени t, L — индуктивность и С — емкость, отнесенные к единице длины. Найти решения уравнений (3), удовлетворяющие начальным условиям
и(х, 0) = i(x, 0) = 0 (4)
и граничному условию
u(0, i) = q(t) = Esmcnt.
14.148. В уравнениях длинной линии . du(x, i) di(x, i)
дх dt
di(x, t) _ du(x, t)
dx dt
в случае линии без искажений, величины R, L, С и G связаны R G , .
соотношениями — = — = v. Найти решения уравнений (5),
Li Су
удовлетворяющие начальным условиям (4) и граничному условию и(0, i) = g(i) = E(r/(i) - z?(i - т)), т > 0.
4. Вычисление несобственных интегралов. Один из способов вы-4-оо
числения несобственных интегралов вида dt основан на приме-
о нении теоремы операционного исчисления о связи «конечного» значения оригинала и «начального» значения изображения: если </>(£) = Ф(£) и существует конечный предел lim </>(£) = </>(+оо), то lim </>(£) = t—>+оо t—>4-oo
= </>(+oo) = ПтрФ(р) (см. задачу 14.15). р—>о
Из этой теоремы и соотношения t [ fmdt = -F(P) J p
о
§ 3. Применения операционного исчисления 189
4-оо при условии сходимости интеграла f(t) dt следует соотношение
о
4-оо
I f(t)dt = F(Q). (6)
о
4-оо тт „ „ f sin i ,
Пример 7. Вычислить интеграл I —j—dt.
о
™ 1
<1 Так как t = —-, то по теореме интегрирования изображения имеем
р2 + 1
ОО
sin t [ dq 7Г
~Г -=7^=2-arCtgP’ р
поэтому по формуле (1) находим
Пусть функции
4-оо
/(£, и) и V’W — J u) du о
являются оригиналами и f(t, u) = F(p, u). Тогда, применяя теорему об интегрировании по параметру, будем иметь
4-оо
7(i) = Ф(р) = У <p(u)F(p, u) du. о
Поэтому, если интеграл, определяющий Ф(р), можно вычислить, то для 4-оо
отыскания интеграла j u) du достаточно найти оригинал для
о
Ф(р), т.е. 4-оо 4-оо
J <p(u)f(t, u) du = J <p(u)F(p, и) du. (7)
о
о
190
Гл. 14. Операционное исчисление
+ ос
/cos tu du q2 Zjl ? 2~ ' 0
p2
О Имеем costu = —-----Поэтому (по формуле (7))
р*- + u2
Н-оо 4-оо
/costudu , f pdu _
a2 + u2 ’ J (p2 + u2)(a2 + u2)
о о
4-00
p f f du \ _
p2 — a2 J \a2 + u2 p2 + u2/ о
_ p тг/l 1\ _ 7Г 1
p2 — a2 2 \ a p J 2a p + a
Ho —-— == e~at. Отсюда p + о
4-ос
/costudu 7Г nt --------r = 7Te a1 + u2 2a
о
Еще один способ вычисления несобственных интегралов при помощи операционного исчисления дает
Теорема Парсеваля. Если fi (i) = F[ (р), /2 (О = F2 (р) и функции Fi(p) и F2(p) аналитичны при Re/; 0, то
4-оо 4-оо
У /i(u)F2(u)du = У Fi(v)f2(v)dv. (8)
о о
При этом из сходимости одного из этих интегралов следует сходимость другого3).
4-ос
/g—au sin /Зи ------------du, а > 0.
и о
<1 Имеем e-aZsin/^ = --------, rdt) = Полагая fi(u) =
(р + а)2 + /З2 р
= e~QUsin/3u, F2(u) = имеем F^v) = -——- •- -, f2(v) = p(v). и (v + a)2 + p2
3)Если для одной из функций Fi(p) или F2(p) условие аналитичности выполнено лишь при Rep > 0, то сходимость одного из интегралов может не иметь места.
§ 3. Применения операционного исчисления
191
Поэтому по формуле (8)
/3p(v) dv
dv
о о
(77(11) = 1, так как v > 0). Но
о
о
dv v 4-
v2 л '02 = arctg —-a)2 + /32 p
тг a (3
- - arctg — - arctg-.
2 р a
о
Таким образом,
f e sin /3udu (3
/ -------= arctg a > 0. >
Ju a
о
Вычислить несобственные интегралы, используя формулу (6): 4-оо
14.149. I a0>o
О
4-оо
14.150*. У tpe~at\ntdt, <а > О, р > -1. о
Вычислить несобственные интегралы, используя формулу (7): 4-оо 4-оо
ч . f u sin tu du f -tu2 ,
14.151. / —5------5-. 14.152. e tu du.
J ил + or J
о 0
Вычислить несобственные интегралы, используя теорему Парсеваля (формула (8)):
4-оо / -au _ е~/3и ---------------du, a, (3 > 0. x/u
о
f sinau-sin(3u
14.154. / --------7=------du, a, p > 0.
J Ux/U
о
+r°e-QX2 _ e~/3x2
14.155*. / ---------------dx, a,l3>0.
J Xr
0
192
Гл. 14. Операционное исчисление
5. Суммирование рядов. Методы операционного исчисления могут быть использованы при суммировании числовых и функциональных рядов.
Пример 10. Пусть f(t) = F(p) (область аналитичности F(p): ОО
Rep к\ Доказать, что сумма S ряда (±l)nF(n) может быть най-п=к
дена по формуле
s .(„) (.,
J 1 =F е f о
e~plf(t)dt. Имеем: ---------—
1 =F е_£
о
Поэтому
ОО
= £(±1)»е-"‘.
n=k
(±1)‘ f = [ /(«)f;(±l)ne-nldi =
J 1Te J
о о n=fc
OO
= E(±i)
n=k
e-”7(t)dt = ^(±l)"F(n). >
0
Используя формулу рядов: оо
14.156**. ^2-----
71=1 ( п
0),
найти
суммы следующих числовых
п
ГУ’
2 — - )
4/
2n + 1
оо 2
14.157**. У'' arctg —.
71=1
14.158*. (п2 + 1)(„2 + 2„ + 2)'
71=1
ОО „
14-159*- ^arctg-^- - .
z—' nz + Зтг + 1
71=1
Пример 11. Пусть f(t) = F(p) (область аналитичности F(p): Rep 0). Пусть, кроме того, Ф(£, х) — производящая функция бесконечной последовательности функций <pn(z), т.е.
ОО
Ф(*> я) = 52 Pn(x)tn.
71=0
§ 3. Применения операционного исчисления
193
Доказать, что сумма S(x) сходящегося на [а, 6] функционального ряда оо
^2 F(n)ipn(x) может быть найдена по формуле
п=0
, x)f(t)dt.
(Ю)
о
О Имеем:
+?° +2° оо
I Ф(е~1, x)f(t) dt = / f(t) ^Tipn(x)e~nt dt =
* T> — П
+oo
У’п(^) I e~rltf(t)dt-'^2^n(x)F(n)-S(x'). >
Jo n=
Используя формулу (10), с помощью подходящей производящей функции просуммировать следующие ряды:
14.160*. (-1)”
71 = 0
д,2?1+1
2n + 1
14.161*.
71 = 1
l-3...(2n —1)
2 • 4...2п
jj2t1+ 1
2п + 1
14.162.<.£^, ж6(0,^).
71 = 1
ОО
14.163*. х 6 (0, я).
6. Применение операционного исчисления при расчете электрических Цепей. Методы операционного исчисления широко используются при расчетах процессов, протекающих в электрических цепях. Пусть i(t) и u(t) — соответственно ток и напряжение в цепи. Применение операторного метода основано на справедливости законов Кирхгофа для операторных тока I(p) = i(t) и напряжения U(p) = u(t). На основании закона Ома для основных элементов электрической цепи могут быть записаны следующие соотношения:
uR(t) = Ri(f)
194
Гл. 14. Операционное исчисление
для сопротивления R,
/ ч г di(t)
«it = L-^-
di
для индуктивности L и
i
uc(i) = 77 / i(r)dr + uc(0)
С* J
0
для емкости С. Переходя к изображениям, отсюда получаем
uR(p) = ПЦр),
Ul(p) =pLI(p) -
Uc(p) = ~77j(p) + "MO)-pO p
Используя закон Ома в операторной форме, для произвольного участка цепи можем записать
Г(р) = Z(p)i(p), (11)
где Z(p) — операторное сопротивление указанного участка цепи. Для участков с сопротивлением R, индуктивностью L или емкостью С при нулевых начальных условиях операторное сопротивление имеет, соответственно, вид:
Z/Др) = R, ZL(p) = Lp, Zc(p) = •
Ср
При ненулевых начальных условиях к имеющимся в цепи источникам э.д.с. добавляются дополнительные источники. Величины э.д.с. допол-
нительных источников определяются запасами энергии в индуктивности и емкости и равны в операторном виде, соответственно, 2л(0) и
--цс(0).
Р
Соотношение (11) является основным для расчетов заданного участка цепи в операторной форме.
Пример 12. Найти ток i(t) в цепи, изображенной на рис. 8 при подключении постоянной э.д.с. e(i) = Е. Начальные условия нулевые.
< Так как (e)t — Е = Е/р, то, используя соотношение (11), находим:
Z(p)/(p) = Е/р,
(12)
§ 3. Применения операционного исчисления 195
где операторное сопротивление Z(p) цепи, изображенной на рис. 8, имеет вид
Z(p) = ZL(p) 4- Zc(p) + Zn{p) = Lp + ™ + R, Cp
в силу нулевых начальных условий. Подставляя полученное выражение для Z(p) в (12), находим
Е Е
J(p) pZ(p)
Lp2 + Rp+
С
------• (13)
4L2 J
Для отыскания оригинала i(t) следует рассмотреть три случая в зависимости от вида корней квадратного трехчлена в правой части выражения (13).
1 R2
—— > -гут, тогда по формуле 10 таблицы изображений LC 4х>
Пусть находим
Е _JLt . / 1 R2
= м 2 sm v ~
Lv LC ~ 4L2
п 1 Д2
ПуСТЬ LC = 4Р
тогда воспользуемся формулой 3 той же таблицы:
., Е R t «(t) -- — te IL1.
Lj
Наконец, если
1 R2
—— < 777’ то комбинируя формулы 8 и 3, находим:
Х-/(_7 4x7
?(i) =
LC
, Гй2 1~
Ге'“ shVT^-Zc(- *
14.164. Найти ток г(£) в ДС-цепи (последовательно включены сопротивление R и емкость С) при подключении постоянной э.д.с. e(f) = Е, если wc(0) = uq.
14.165. Найти ток i(t) в RL-цепи. (последовательно включены сопротивление R и индуктивность L) при подключении постоянной э.д.с. e(t) — Е.
14.166. Найти ток г(<) в цепи, изображенной на рис. 9, при подключении постоянной э.д.с. e(t) = если г/с(0) — uq.
196
Гл. 14. Операционное исчисление
Для изображенных на рис. 9-12 электрических цепей определить напряжение на указанном элементе цепи при подключении постоянной э.д.с. e(t) = Е (там, где необходимо, положить М0)=0):
14.167. Рис. 9. uL1(f) =? 14.168. Рис. 10. uL(t) =?
14.169. Рис. 11. uRl(t) =? 14.170. Рис. 12. uc(t) =2
Рис, И
Рис. 12
При расчете электрических цепей, когда воздействие на схему представляет собой функцию произвольного вида, полезно использовать интеграл Дюамеля (см. § 1, свойство 11 преобразования Лапласа). Сначала определяется переходная характеристика цепи — закон изменения напряжения или тока при подаче на вход схемы единичного воздействия e(t) = r/(f). В этом случае, из соотношения (11) находим операторный
ток 11 (р) = , где Z(p) — операторное сопротивление всей цепи.
pZ(p)
Если теперь на вход схемы подается произвольное e(i), то операторный ток 1(р) имеет вид
1(р) = —г = pIi(p)U(p),
§ 3. Применения операционного исчисления
197
где U(p) = e(t). Применяя формулу Дюамеля, окончательно находим:
t
i(t) = e(0)ii(£) + У e'(r)zi(i - г) dr =
о
t
= + У e'(t - r\ii (г) dr = e(O)z'i(f) 4- e' * iy. (14)
о
Пример 13. Найти ток в RL-цепи при подключении э.д.с. e(f) = = ем*.
О Сначала определяем переходную характеристику цепи, в данном случае ток zi(£), возникающий в ЯЛ-цепи при подключении э.д.с. e(i) = 77(f). Имеем (см. ответ к задаче 14.165)
й(0 = (1 -е"тЛ .
Для определения тока z(f) воспользуемся формулой (14). Предварительно вычислим второе слагаемое:
е' * ц
У e'(t — t)zi (г) dr = о
Теперь окончательно находим
i(t} = e(O)ii(t) 4-е' *iy =
1-е 4- - ---чу - е
\ /
14.171. Найти ток в 7?£-цепи при включении синусоидальной э.д.с. e(f) = Esincvt.
198
Гл. 14. Операционное исчисление
14.172. Найти ток в ЛС-цепи, в которую при нулевых начальных условиях подключена э.д.с. e(f) = Е1е~сн1.
14.173. К электрическому контуру, изображенному на рис. 8, д / 1 R2 \
подключена э.д.с. вида e(t) = ( —— > —— ). Найти ток
\LC 4L2)
в контуре (начальные условия нулевые).
§ 4. Дискретное преобразование Лапласа и его применение
1. Z-преобразование и дискретное преобразование Лапласа. Z-преобразованием числовой (действительной или комплексной) бесконечной последовательности (ап) называется функция комплексной переменной F(z), определяемая при |z| > R = lim 1У|ап| рядом Лорана п—too
(1)
и аналитически продолженная в круг |z| < R. Если последовательность (ап) удовлетворяет условию |an| < Меап (М > 0, а — постоянные), то функция F(z) будет аналитической в области |z| > eQ, т.е. вне круга с центром в нулевой точке и радиусом R = еа.
Формула (1) дает разложение F(z) в ряд Лорана в окрестности бесконечно удаленной точки (являющейся правильной точкой F(z)), поэтому для восстановления последовательности (цп) по ее /-преобразованию надо F(z) любым способом разложить в ряд Лорана в окрестности бесконечно удаленной точки; в частности, можно воспользоваться формулой для определения коэффициентов этого разложения (см. формулу (2) § 5 гл. 12)
й-п.
n~l dz
(2)
(С — контур, внутри которого лежат все особые точки функции F(z)4)).
Пример 1. Восстановить (ап) по ее /-преобразованию F(z) =
(г — a)(z — Ь)
"*) Формула (2) является фактически формулой обращения /-преобразования.
§ 4. Дискретное преобразование Лапласа и его применение 199 — -----------------'--------------------'-------'-----
<] Имеем:
1 1/1 1 \
(z - a)(z — b) a-b\z-a z — b
(a - b)z \ i
\ z
an-l _bn-l
1 _ 1 an-bn
л b a - b z1l+1 1---/ п=0
z /
Таким образом, an =----------при n 1, ао = 0. О
a — о
Введем вместо последовательности (ап) решетчатую функцию f(n), полагая an = f(n). По-прежнему f(n) удовлетворяет условию |/(п)| < < MeQn, и примем дополнительно, что f(n) = 0 при п < 0; такие решетчатые функции будем называть дискретным оригиналом. Дискретное преобразование Лапласа функции f(n) мы получим, если в Z-преобразовании положим z = eq:
ОО
*”(?) = £№)?-"’• (з)
п=0
Связь между дискретным оригиналом /(н) и его изображением F*(g)
обозначают символом /(n) .—' F*(q) (иногда пишут F*(q) = D[f(ri)]). Изображение F*(q) — функция комплексной переменной с периодом 2л, при этом в основной полосе —л < Im q л она аналитична при Re q > а. Таким образом, все ее особые точки лежат в этой полосе слева от прямой Reg = а.
Из формулы (3) вытекает следующая формула обращения дискретного преобразования Лапласа:
74-7Г1
/(n) = xF [ F'Wdq. (4)
27Г? J
у—Tri
Пример 2. /(п) = ап, найти F*(g). оо 1 е9
<3 Имеем F*(q) = ane~nq = ----------- = —-—: а потому ап .—’
1 - ae~q eq - а
n=0
—' ~~q--‘ Полагая а = 1, получим 1П = п (п) .—’ ——t>
Свойства дискретного преобразования Лапласа (всюду ниже предпо
лагается /j(n) .—: F*(g)):
1. Л инейност ъ: r г
г- ^CjF-kq).
j=l J=1
200 Гл. 14. Операционное исчисление
2. Формула смещения:
еап/(п) ~ F*(q-a).
3. Формулы запаздывания и опережения:
a) /(n-fc) - e~kttF*(q), (к — 1 \
F\q)- J2/(r)e"r<7 I. г=0 /
4. Дифференцирование по параметру:
_ .. . . 5/(n, F) . dF*(q, х)
Если f(n, х) — F (q, х), то —-- .---------.
дх дх
5. Дифференцирование и интегрирование изображения:
dk
a) nkf(п) —’
ОО
б) — [ (F*(s) — f(O))ds (»>1).
П J
Q
6. Изображение конечных разностей оригинала:
fc-i
Afc/(n) •— (e7 - - eq (e7 - Ar/(0).
r—0
7. Изображение конечных сумм оригинала. Если
9(n) = то g(n) —
к=0
8. Умножение изображений. Если
/1(п) */2(n) = 53/i(r)/2(n-r) г=0
(это — так называемая «свертка» оригиналов), то
/1(п) * /2(п) ’ F*(q) F^q\
§ 4. Дискретное преобразование Лапласа и его применение 201
Приведем таблицу изображений основных решетчатых функций:
№ /(тг) F’(«)
1 /(тг) _ Г С, п 10, п = 0, #о С
2 т?(тг) _ f 1, тг >0, eq
t 0, п < 0 eq - 1
3 пп eq
eq — a
4 ПП eq
е eq — ea
5 eq
(e? — I)2
6 п2 eq(eq + 1) (еЛ — I)3
7 п{п — 1) = С* eq
2! 2 (e*? — I)3
8 п(п -1)...(п- к + 1) eq
kl к\ - l)^1
9 sin (Зп eq sin /3
e2q _ 2e<? cos(3 + 1
10 cos (Зп eq(eq — cos(3)
e2q _ 2e<? cos(3 + 1
11 sh (Зп eq sh (3
e2? — 2e9 ch (3 + 1
12 ch (Зп eq{eq - ch/3)
е2ч _ 2eq ch (3 + 1
13 тг [*] an s-tK tTe =с“ e</+ka
(eq - eQ)/c+1
13' тг[,£] ди a ~ Сп( 1п akeq
(eq — a)fe+1
202
Гл. 14. Операционное исчисление
Пример 3. Найти изображение функции /(n) = ean sin /Зп.
<1 Применяем теорему смещения (свойство 2) и, используя формулу 9 таблицы изображений, находим
—Q cir> /3
ean sin /Зп — F(q - a) = =
v > e2(q-a) _ 2e‘/-Qcos$ + 1
eq+a sin /3
e2q — 2eq+a cos (3 + e2a
В частности,
an sin (3n = en ln a sin /Зп .—'
aeq sin /3 e2q — 2aeq cos/? + a2
t>
Найти изображения следующих решетчатых функций:
14.174 . f(n) = ean cos/Зп. 14.175. f(n) = an cos (3n.
14.176 . f(n) = n2ean. 14.177. f(n) = n2an.
14.178 ’. f(n) = -(- ~fe!1)--tl = С*,,.
14.179 *. /(n) = (П +fc™)W = C*+m. 14.180». /(n) =
Пример 4. Найти решетчатую функцию f(n) по ее изображению eq
F*^ = (е2</ _ 9)2 •
<1 Первый способ. Разложим на простейшие дроби функцию
Г*(<?) 1
е» (е2«-9)2’
положив eq = z:
1 _ _1_ / 1 1 \ i / ! 1 \
(г2 - 9)2 “ 36 \(г - З)2 + (г + З)2; 108 - 3 “ z + 3/ ’
Таким образом:
e2q 1 / 3eq 3eq eq eq \
(e2q - 9)2 " 108 \(е«/ - 3)2 + (eq + 3)2 ” eq - 3 + ^+3) '
Но по формулам 3 и 13' таблицы изображений имеем:
eq - 3 ’
eq
еч +3
(-3)",
3eq . Qn 3eq (eq - 3)2 ' ’ (eq + 3)2 ’
§ 4. Дискретное преобразование Лапласа и его применение 203
Отсюда после элементарных преобразований находим:
е(1
(е2(/ - 9)2
. Зп~3(п — 1)(1 - (~1)п) 4
Второй способ. Переходим к Z-преобразованию (полагая eq = z): ея z
—------—- = ————. Используя формулу обращения (2) и применяя
(е2(/ — 9)2 (г2 - 9)2
теорему о вычетах, получаем
________~п
(г2-9)2
dz —
Но
= выч
__________• ч (г2 - 9)2 ’
+ выч
(г2 - 9)2 ’
гп j d / zn \ _
(г2 - 9)2 ; 3J = Г-S Tz \(z + 3)2 J =
/ nzn~l 2zn \
= inn -----— — -----—
гчз\г + 32 (г + 3)3/
(n - 1) • 3n“3
4
Аналогично,
выч
г" . ,1 _ , (n-l)3"-3
(г2-9)2’ Jj ( > 4
Суммируя эти вычеты, приходим к прежнему результату. О
Найти решетчатые функции по их изображениям е?
14.181. F*(q) = ------
(е? - 1)(е2(? - 4)
14.182. F*(q) =
14.183. F*(9) -
еЧ
е4(? 4- 1 ’
e2q
е2<7 _|_ 2е<7 + 2 ’
п— 1
Пример 5. Найти сумму Sn = cosk/3.
k—0
<1 Используем свойство 7 дискретного преобразования Лапласа:
/(я) —
e^-cosff) =
e2q — 2eq cos /3 + 1
204
Гл. 14. Операционное исчисление
поэтому F*(q)
Sn . ~
eq(eq — cos /?)
eq — 1 (eq — l)(e2<* — 2eq cos (3 + 1)' Разлагая на простейшие множители дробь
eq — cos (3
(eq — l)(e2q — 2eq cos(3 + 1) и добавляя множитель eq, находим
eq (eq — cos (3) _ 1 / eq eq(eq — 2 cos/3 — 1)\
(eq - l)(e2<? — 2eq cos/? + 1) 2 \e9 — 1 e2q - 2eq cos/3 + 1)
eq
Ho ——- .—’ i?(n) (формула 2 таблицы изображений). Следовательно,
eq(eq - 2cos/? - 1) _ eq(eq - cos/?) eQ(l + cos/?)
e2q — 2eq cos (3 + 1 e2q ~ 2eq cos /3 + 1 e2q — 2eq cos (3+1
1 + COS0 . о
.— cos (Зп---;—-— sin (Зп.
sin/?
Таким образом,
Sn = j(r)(n) - cos(3n + ctg | sin (3n) =
' . (3 . 2n - 1
sin - + sin —-—(3
2 sin —
2
. n(3 n — 1 sm — cos -y-. (3 sin —
2
1). О
Найти следующие суммы: n-1 k\r] ""j
k=r
к=г
п—1
14.185. ^2ksink(3.
к=0
п—1
14.186* . J2/c2(n- к)2.
к=1
Пример 6. Найти сумму степенного ряда
У' (cos + sin tn = 1 + \/2t + t2 - i4 - \/2t5 — t6 \ 4 4 /
n=0
§ 4. Дискретное преобразование Лапласа и его применение 205
<] Данный ряд сходится при |t| < 1, так как
lim г/|ап| = 1. Заменяя t п—>оо
-п \ ПЛ
на е q, приходим к дискретному изображению функции f(n) = cos — + П7Г
+ sinT:
оо
n*/ \ - П7Г\
F (g) = У (cos — + sm — Je q n=0
Ho
n 7Г
COS----
4
eq
eq
7Г - COS —
4
e2(i — 2eq cos — + 1
4
n • 7Г eq sin — _________________4 e2(i — 2eq cos -7 + 1 4
. П7Г sin — .—
4
(см. формулы 9 и 10 таблицы изображений). Поэтому (</2\ v/2
е«_ +еч
j\ni = cos —- -1- sin .--------------7=------- =
J 4 4 е2ч - у/2еч +1
e2q
e2q - л/2еч + 1 ’
Отсюда, возвращаясь к аргументу t, находим
1
t 2
S(t) =---------7=— ------—---------7=----.
t~2 - \/21-1 + 1 1 - t\/2 + t2
О
Найти суммы следующих степенных рядов: оо
14.187. Vs'm^rtn.
6
п=0
оо
14.188. V' (cos--sin—)t’
4Л 3 ЗУ
2. Решение разностных уравнений. Пусть дано уравнение
аояДп + k) + a\x(n + к — 1) + • • • + аьх(п) —
(5)
(ао, di, ..., ajt — постоянные) с заданными (или произвольными) начальными условиями: х(0) = х0, х(1) = Х[, ..., х(к-1) = Xk-i • Правая часть уравнения (5) — решетчатая функция </?(n) — предполагается оригиналом.
Полагая х(п) .—: X*(q) и применяя формулу опережения (свойство 3,6)), составляе1М операторное уравнение (оно линейно относительно -Y*(g)) и определяем из него X*(g). Затем одним из способов, изложенных в п. 1, по изображению найдем искомое решение x(ri).
206
Гл. 14. Операционное исчисление
Если исходное уравнение было задано не через последовательные значения неизвестной функции, а через ее конечные разности, т. е. имеет вид
Ь0Хкх(п) + Ь1Ак~1 х(п) + • • • + bkx(ri) = (6)
то вследствие громоздкости формул для отыскания изображений конечных разностей решетчатых функций (п. 1, свойство 6) его следует предварительно преобразовать к виду (5) при помощи известных формул, связывающих конечные разности функции с ее последовательными значениями:
Дгж(п) = х(п + г) - С'х(п + г -1) + С^х(п + г - 2) Н-h (-1)гж(п). (7)
Аналогично решаются и системы разностных уравнений.
Пример 7. Решить уравнение жп+2~xn+i +хп — 0, xq = 1, х\ =2. <1 Полагаем хп .—' X*(q). По формуле опережения находим:
Хп+1 - - х0) = eq(X*(q) - 1) = e*X*(g) - eq,
хп+2 e2’(.V(?) - х0 - Xle~") = e^X^q) - 1 - 2е“’) =
= е2"Х’(д)-е2я -2s''.
Внося эти выражения в исходное уравнение, приходим к операторному уравнению
(е29-е9 + 1)Х*(д) = е29+е9.
Таким образом,
е2т + eq
Х'^ =
ТГ 1
Так как cos — — sin — = —-, to X*(q) запишем в следующем виде: О Z О Z
3 2
Л-'(9) =
е</ (е</ - j) + 1е</ e2q _ 2е<7 • ^ + 1
eq I eq — cos
a • 71 eq sin —
3
e2q _ 2е<? COS + 1 о
Отсюда по формулам 10 и 11 таблицы изображений п. 1 находим
ПТГ /- . пл п . 2п + 1
хп — cos — + v 3 sin — = 2 sin-------------ТГ. >
3 3 6
Замечание. Записать ответ в форме хп = 2cos—-—тг нельзя, так как в этом случае получим xq = 0 1 (по условию равенства нулю
решетчатой функции от отрицательного аргумента).
§ 4. Дискретное преобразование Лапласа и его применение 207 — —--------- ---------------------------------------.-------------
Пример 8. Решить уравнение xn+2 ~4xn+i + 4хп — Зп при произвольных начальных условиях xq, Xi.
<] Полагая хп .—’ Х*(д) и используя приведенные при решении примера 1 изображения
хп+1 eqX*(q) - xoeq, хп+2 e2c,X*(q) - x0e2q - х^ея, приходим к операторному уравнению
(e2q - 4eq + 4)Ar*(g) - а?ое2<7 - (a?i - 4а?0)е9 = ~—z
eq — 6
eq \
поскольку по формуле 3 таблицы п. 1 Зп .—’ ------- . Отсюда находим
eq 3 /
eq
,/*/ ч £ов2(/ , . ч eq
Х ~ (eq - 2)2 + (eq - 2)2 (eq - 3)(е<? - 2)2 ‘
1
Разлагая дробь ——3)^—2)^ на пРостейшие’ имеем
= ХО _ 2)2 + Си - 4zo - 1) _ 2у2 - еЧ _ 2 + eQ _3
Но
е’
-7-^ 3 -
eq — 3
2е?
---— — п-2п,
• 9п
eq - 2 ‘
2p2q
(е» - 2)2 ' " * ’ (е« - 2)2 ~ + 1)2"+I
(последнее соотношение следует из предыдущего по формуле опережения). Переходя от X*(q) к оригиналу, находим:
2
xn = x02-tl2n+1 + -—• 2" - 2П + 3" =
= ~ -- п 2” + (х0 - 1)2" + 3" = (Ci + С2п)2" + 3". о
Пример 9. Решить систему разностных уравнений
•^п+2 Уп — 0, Уп+2 + Хп — 0
при начальных условиях xq ~ уо = 1, a?i = \/2, yi = 0.
208
Гл. 14. Операционное исчисление
<1 Полагая хп .—’ X*(q), Уп —: ^*(?) и по формуле опережения имеем:
х„+г ~ е2 * 4 *’(Х-(?) - г» - г>е~’) = е2’Х*(?) - е2’ - 75е’,
!/п+2 — e2'l(Y'(q') — у0 — У\е ’) = е2’У’(<;) - е2’.
Получаем систему операторных уравнений
е29Х*(д) - У*(д) = е2’ + л/2е9, е2<7У*(д) + X*(q) = e2q.
Так как e4q + 1 = (e2q + \/2eq + 1)(е2(/ — \/2eq + 1), то решение этой системы запишется в виде
X*(q) =
e4q + \/2е3<г + e2q
е4<? + 1
У*(д) =
е4<? _ e2q
e4q + 1
e2q
e2q — \/2 • е9 + 1?
e2q -V2eq
e2q - \/2eq + 1‘
Применяя формулу опережения, имеем:
7Г
2q eq • eq sin -
----------------— y/2---------------4----
e2q — \/2eq + l e2q _ 2eq cos - + 1
4
4’
e2q -V2eq e2q ~ \/2eq + 1
eq (eq — cos — I — eq sin — \4/4
e2q - 2eq cos ~ + 1
4
П7Г . П7Г /- (n+ 1)7T
.— cos —------sin —— — v 2 cos ------------
4 4 4
Следовательно,
2 sin -----
4
yn = y/2 cos-----------. >
Решить следующие линейные разностные уравнения:
14.189. Жп+2 — Зяп+i — 10a?n = 0; xq = 3, a?i = —1.
14.190. xn+2 + xn+i + xn = 0; xq = 1, x\ = -1.
/- 1 л/З
14.191. xn+2 - v3 xn+i 4- xn = 0; x0 = -, a?i = —.
14.192. xn+2 ~ 3^4-1 +2жп = 0; начальные условия произвольные.
§ 4. Дискретное преобразование Лапласа и его применение 209
14.193. хп+з - Зхп+2 4- 3zn+i - хп = 2”; х0 = xi = 0, х2 = 1.
14.194. zn-f-2 — 5rrn-f-i 4- 6xn = 2 • 4П; начальные условия произвольные.
Решить системы линейных разностных уравнений:
14.195. xn-j-i хп 4* уп — 3 ,
4“ 2т:п = 3 , Xq 3, у0 = 0.
14.196. 5xn-]-i 12хп Ул — 0,
5?/п4-1 — ~ 13уп = 0;
начальные условия произвольные.
Глава 15
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Интегральные уравнения Вольтерра
1. Уравнения Вольтерра 2-го рода: основные понятия, связь с дифференциальными уравнениями. Линейным интегральным уравнением Вольтерра 2-го рода называется уравнение
X
?/(ж) = f(x) + У К(х, t) y(t) dt, а
(1)
где у(х) — искомая функция, а К(х, t) и f(x) — известные функции, определенные соответственно в треугольнике a^x^b, a^.t^.x и на отрезке [а, 6]. Функция К(х, t) называется ядром интегрального уравнения (1), функция /(ж) — свободным членом этого уравнения.
Решением уравнения (1) называется всякая функция у(х), х G [а, &], подстановка которой в это уравнение обращает его в тождество. Вопрос о существовании и единственности решения решается различным образом в зависимости от свойств ядра К(х, t) и свободного члена /(ж), а также от того, в каком классе функций ищется решение. Всюду в дальнейшем, если не оговаривается противное, мы будем предполагать, что функции К(х, t) и /(ж) непрерывны в своей области определения. При этом условии уравнение (1) имеет, и притом единственное, решение в классе функций, непрерывных на [а, &].
Интегральные уравнения Вольтерра 2-го рода используются обычно при описании динамики различных процессов в системах. В частности, всякая задача Коши для линейного дифференциального уравнения
dny Xdn~xy . ...
+ +'" + =
у{х0) = уа, у'(ха) = У!,... ,у1-п~1}(х0') = !/„_] может быть сведена к решению некоторого линейного интегрального уравнения Вольтерра 2-го рода.
Пример 1. Составить интегральное уравнение, соответствующее задаче Коши
и"+2и'+и = х2, и(0) = 1, и'(0) — О-
§ 1. Интегральные уравнения Вольтерра
211
<3 Положим и"(ж) = у(х). (2)
Интегрируя (2) с учетом начальных условий, последовательно находим
X X
и' (ж) = и' (0) + У y(t)dt = У y{t)dt^ (3)
о о
X S X
и(х) = и(0) + У ds У y(t)dt~l + У (х — t)y(t) dt. (4) оо о
Подставляя (2)-(4) в исходное дифференциальное уравнение, получаем
X [ X \
?/(ж) + 2 у t/(t) dt + I 1 + У (х — dt j = x2, о \ о /
или
X
у(х) = х2 - 1 - У (2 4- х - dt. (5)
о
Таким образом, показано, что если и(х) — решение исходной задачи Коши, то функция у(х) = и"(х) удовлетворяет интегральному уравнению (5). Обратно, если у(х) — решение этого уравнения, то функция «(ж), определяемая соотношением (4), удовлетворяет как исходному дифференциальному уравнению, так и начальным условиям. Следовательно, рассматриваемая задача Коши эквивалентна интегральному уравнению (5). >
Проверить, что данные функции являются решениями соответствующих интегральных уравнений:
х
15.1. у(х) = е2з;, у(х) = ех 4- f ex~ty(l}dt.
о
X
15.2. у(х) = хех3/\ у(х} = х + j xty{t) dt.
о
/х2 \
15.3. у(х) = е х ( — 4- i I . \ л J
X
у(х) = е~х + У е“^“^ sin (х — t)y(t) dt.
о
212 Гл. 15. Интегральные уравнения
Составить интегральные уравнения, соответствующие следующим задачам Коши:
15.4. и' + 2хи = ех, т/(0) = 1.
15.5. и" - 2и' + и = 0, и(2) = 1, и'(2) = -2.
15.6. и" — sinz • и' + ехи = х, ti(0) = 1, 7i'(0) = —1.
15.7. и"' + хи = ех, u(0) = 1, ti'(0) = ц"(0) = 0.
15.8. tiiv + и" - и = 0, 71(0) = Т1'(0) = 71"(0) = 0, 71"'(0) = 1.
15.9* . Показать, что задача Коши для линейного дифференциального уравнения с постоянными коэффициентами
dny d^y . .
TH + Й17^Г + ---+апУ = f W, dxn dxn 1
УоЫ = y0, y'(x0) = т/1,... ,т/(п-1)(з;о) = Уп-1 сводится к интегральному уравнению вида (1) с ядром
JL (г_+\к-1
К(х, t) = ’
зависящим лишь от разности х — t своих аргументов (интегральное уравнение типа свертки, см. и. 3).
Задача Коши для произвольного дифференциального уравнения 1-го порядка вида
у'= f(x, у), у(х0)=у0 эквивалентна в общем случае нелинейному интегральному уравнению Вольтерра
X у(х) = т/о + У f(x, ytfftdt. Xq
Аналогично, задача Коши для произвольного дифференциального уравнения n-го порядка, разрешенного относительно старшей производной, т/(п) = f(x, у, у', ... , у{п~1}), у(х0) = уо, у'Ы =У1, • • • , У^Чхо) = Уп-1
может быть сведена к системе нелинейных интегральных уравнений Вольтерра.
Пример 2. Составить систему интегральных уравнений, соответствующую задаче Коши
у" = 2у - у'2, у(0) = 1, у'(0) = 0.
§ 1. Интегральные уравнения Вольтерра
213
< Полагая yi(x) = у (х), у2(х) = у'(х), сведем исходную задачу к задаче Коши для нормальной системы 2-го порядка
у[ = У2, У2 = %У1 - уЪ ЫО) = 1, 2/г(0) = 0.
В свою очередь, полученная система дифференциальных уравнений с учетом начальных условий эквивалентна системе интегральных уравнений
X X
= 1 + У y2(t)dt, у2(х) = У (2pi(f) - yl(t)) dt. > о о
Составить интегральные уравнения или системы уравнений, соответствующие следующим задачам Коши:
15.10. у' = 1 4- х sin т/, 2/(?г) = 2д.
15.11. т/ = -1 + Зя2 4- у2, ?/(1) = 1.
15.12. у" = х + у2, у(0) = 1, У'(0) = 2.
3 9
15.13. у"’ = -ху'2, у(0) = —3, у'(0) = 1, у"(0) =-1.
15.14. у'" = х + ху2 - у'2, у(0) = 1, у'(0) = у"(0) = 0.
Во многих случаях решение интегрального уравнения Вольтерра 2-го рода (или системы таких уравнений) в свою очередь может быть сведено “к решению некоторой задачи Коши для обыкновенных дифференциальных уравнений. Укажем здесь два способа, посредством которых это может быть сделано.
а) Если в исходном интегральном уравнении (1) ядро К(х, t) и свободный член f(x) имеют непрерывные производные К'(х, t) и f'(x), то это уравнение может быть продифференцировано (один или несколько раз), что и позволяет в ряде случаев свести его к задаче Коши для некоторого обыкновенного дифференциального уравнения.
Пример 3. Решить интегральное уравнение
X
y(x)=sinx + У sin (ж — t) y(t) dt. (6)
о
<] Последовательно дифференцируя интегральное уравнение, получаем
X
у’(х) = cos х 4- У cos (х — i) y(t) dt, о
X
у"(х) = — sin х 4- у(х) — У sin (х — t) y(t) dt. о
(7)
(8)
214 Гл. 15. Интегральные уравнения
X
Исключая из уравнений (6) и (8) интеграл f sin (х — £) y(t) dt, получаем о
для неизвестной функции у(х) дифференциальное уравнение у"(х) = 0. Из (6) и (7) находим начальные условия: ?/(0) — 0, y'(ty — 1. Следовательно, у(х) = х. >
Рассмотренный прием всегда приводит к цели в том случае, когда ядро К(х, t) имеет вид многочлена по степеням бинома х — t (см. задачу 15.9).
Пример 4. Решить интегральное уравнение
X
у(х) = х + 2 sin х — 1 — j\x — t) y(t) dt. (9)
о
<1 Дважды дифференцируя уравнение (9), получаем
X
y'tyc) = 1 + 2 cost — y(t)dt, (10)
о
y"(x) = — 2 sinx — y(x). (11)
Уравнение (11), или в стандартной форме
у" + у = —2 sinT, (12)
и есть дифференциальное уравнение для функции у(х). Начальные условия найдем из (9) и (10) при х = 0:
2/(0) = -1, ?/'(0)=3. (13)
Решая задачу коши (12), (13), находим
у(х) = 2 sin х + (х — 1) cos х,
что и является решением исходного интегрального уравнения. >
б) Пусть исходное интегральное уравнение (1) имеет вид
п \
52pi(z)<7i(O ) 2/(0^ (14)
i=i /
(уравнение с вырожденным ядром).
Запишем его следующим образом:
X П /»
у(х) = f(x) + ^Pi(x) / qi(t)y(t)dt. (15)
З/О) = /(т) +
§ 1. Интегральные уравнения Вольтерра
215
Вводя функции х
щ(х) = У qi(t)y(t)dt, о
...................................... (16)
X
ип(х) = У qn(t)y(t)dt о
и подставляя их в (15), заключаем, что решение интегрального уравнения (14) имеет вид
у(х) = f(x)+ ^Pi(x)ui(x). (17)
i=i
Далее, дифференцируя соотношения (16) и подставляя вместо у(х) выражение (17), получаем для неизвестных функций Ui(x) систему дифференциальных уравнений
п
и\ (х) = Q1 (х) f(x) + 91 (я) Pi (я) щ (х),
2=1
П
u'n(x) = Qn(x)f(x) +^qn{x}pi{x)Ui{x}.
i=l
Из (16) при х = 0 находим начальные условия: ui(0) = ... = un(0) = 0. Определив функции и^х) и подставив их в (17), получим решение у(х) интегрального уравнения (14).
Пример 5. Решить интегральное уравнение
X /ch t -—y^dt. СП X
о
X
<1 Полагая и(х) = f chty(t)dt, получим о
у<х> =1+
Далее, дифференциальное уравнение для и(х) имеет вид
и'(х) — chxy(x) = ch ж i 1 + -Д-ц(х) )
\ сп я: J
Или
и1 — и = ch ж.
216
Гл. 15. Интегральные уравнения
Решая это уравнение с учетом начального условия и(0) = 0, находим ц(т) = ~(хех + sh х), откуда
1 хех + sh х
2 ch ж
Решить интегральные уравнения, сведя их предварительно к обыкновенным дифференциальным уравнениям: х
15.15. у(х) = ех + у* y(t)dt. о X
15.16. у(х) = 1 -!- У ty(t) dt. о X
15.17. у(х) = ------- -|- [ sin (х — t) y(t) dt.
1 + xz J о x
15.18. y(x) = e~x cos x — f cos xe~^x~^ y(t) dt. о x
15.19. y(x) = 4ex + 3x — 4 — j (x — t) y(t) dt.
о
X
15.20. y(x) = x — 1 + У (x — £) y(t} dt. о x
15.21. y(x) = sin x + | У (x — t)2y(t) dt. о x
15.22. y(x) = chx — f sh(x — t) y(t) dt. о X
15.23. y(x) = x + У (4 sin (x — t) — x -I-1) y(t) dt. о x
15.24. y(x) = 1-1- У ((x — t)2 — (x — t)) y(t) dt.
о
§ 1. Интегральные уравнения Вольтерра
217
2. Метод последовательных приближений. Решение с помощью резольвенты. Метод последовательных приближений применительно к линейному интегральному уравнению Вольтерра 2-го рода
X
у(х) = f(x) + У К(х, t) y(t) dt a
заключается в следующем. Строится последовательность функций уо(х~), yi(x), ... , yn(x)i • • •, где нулевое приближение уо(х) — произвольная функция, а последующие приближения определяются с помощью рекуррентного соотношения
X
Уп(х) = /(ж) + УК(х, tjyn-^tjdt, п = 1, 2, ... a
Если ядро К(х, t) и свободный член f(x) непрерывны соответственно при а^Цхина отрезке [а, 6], то построенная таким обра-
зом последовательность приближений уп(х), п = О, 1, ..., при п -» оо сходится к единственному непрерывному решению интегрального уравнения.
Обычно полагают уо(х) = /(ж), однако это вовсе не обязательно: удачный выбор нулевого приближения часто позволяет ускорить сходимость последовательности уп(х') к точному решению.
Пример 6. Методом последовательных приближений решить уравнение
X у(х) = 1 - У (ж - t)y(t)dt. о
<1 Положим
Тогда
Уо(х) = 1-
7
у^х) = 1- / (х - t) dt = 1 - у, О
// /2 \ 2 4
(х - t) - -J dt = 1 - у + у. О
Для n-го приближения получим
гу»2 Л»4
^) = 1-2! + 4Г-6!+- + (-1>"(ад
218
Гл. 15. Интегральные уравнения
откуда 00 2k
у(х) = lim уп(х) = =
П-+ОО (Zk)'.
Решить интегральные уравнения методом последовательных приближений:
15.25. у(х) = 1 4- У у {t) dt, уо(х) = 0.
о
2 Х
15.26. у(х) = у + х- У y(t) dt,
о
х2
а) Уо(х) = 1, б}у0(х) = ~ + х.
х
15.27. у(х) ~ 1 — х2 4- xy(t) dt,
о
а) Уо(х) = 1 - х2, б) у0(х) = 1.
х
15.28. у(х) = 1 + У xy(t)dt, уо(х) = 1.
о
х
15.29. у(х) = 14- У ty(t)dt, у0(х) = 1.
о
х
15.30. у(х) = 1 4- У tpy(t) dt, у0(х) = 1, р = О, 1, 2, ...
о
X
15.31. у(х} = х - У (ж - i) y{fy dt, уо(х) = 0. о
х
15.32. у(х) = 14- У (х - t) y(t) dt, у0(х) = 0.
о
х
15.33. у(х) = 21 + f 2x-ly(t) dt, у0(х) = 0.
О
х
15.34. у(х) = 1 4- х2 — У о
y(t)dt, y0(x) = Q.
§ 1. Интегральные уравнения Вольтерра
219
В задачах 15.35-15.37 методом последовательных приближений найти для заданных нелинейных уравнений Вольтерра второе приближение у?(хУ в качестве нулевого приближения взять Уо W = 0:
X
15.35. у(х) = У (t2 - y2(t))dt. о х
15.36. у(х) = х — 7г + t sin y(t) dt.
о
x
15.37. y(x) = У dt.
b
Часто вместо одного уравнения рассматривают семейство уравнений
X
у(х) = 7(z) + А У K(x,t) y(t) dt, a
соответствующих различным значениям числового параметра Л. Предполагая, что А фиксировано, будем решать уравнение (18) методом последовательных приближений, взяв в качестве нулевого приближения у о (z) = /(.г). Тогда получим
X X
У1 (х) = + А У K(x,f) /(f) dt = f(x) + A / Ki (z, t) f(f) dt,
a a
где
Ki(x, t) = K(x, t\,
У2(х) = /(z)+A/K(x, t) f(f) dt+X2 j a a
s
a
= f(x) + A j K\ (z, f} /(f) dt + X2 j a a
j Ki (z, i) /(f) dt + A2 у a a
220
Гл. 15. Интегральные уравнения
где
К2(х, t) =
S
j К(х, s) Ki(s, t) ds. t
Вообще,
X
n Г
УтАх) = f(x) + ^X3 / Kj(x, t) f(t) dt =
где
X
Kj(x, t) = У K(x, s) Kj-i(s, t) ds, j = 2, 3, ... , (20)
t
Ki(x, t) = K(x, t).
Ядра Kj(x, t) называются повторными или итерированными. Если ядро К(х, t) непрерывно, то ряд
R(x, t, A) = ^Xj~iKj(x, t) (21)
j=i
при любых фиксированных значениях А сходится (равномерно относительно х G [а, 5] и t G [0, я:]) к функции R(x, t, А), называемой резольвентой ядра К(х, t). Следовательно, соотношение (19) в пределе при п —> оо переходит в формулу
X
у(х) = f(x) + А У R(x, t, A) f(t) dt, (22)
а
выражающую решение интегрального уравнения через резольвенту.
Пример 7. Найти резольвенту R(x, t, А) ядра К(х, t) = х и, используя ее, решить интегральное уравнение
X
у(х) =х - У xy(t) dt.
о
< Из рекуррентных соотношений (20) получаем
Ki (х, t) = х,
х2 - t2 xs ds = х--------
2
/С2(т, t) =
§ 1. Интегральные уравнения Вольтерра 221
X X
К(х, s) Ki(s, t) ds = t t
X X
[ [ s2 — t2 1 / x2 — t2
Кз(х, t) = / K(x, t) Kzis, t)ds = / xs—-— ds = x • - ( —-—
t t
Вообще, можно проверить (например, методом математической индукции), что
„ , ч 1 (x2-t2\j'x
Kj(x,t)-x 2 J
Подставляя это выражение для итерированных ядер в формулу (21), найдем резольвенту
00 \J-1 /~2 4-2 \j-1 2 2
EAJ I X — t \ \ x—t2
0^1)! \—2— ) = xe 2
Найдем теперь решение заданного интегрального уравнения. В рассматриваемом случае А = — - и f(x) — х, поэтому на основании (22) получаем
t/(z) =
-
4 • t dt = х - хе
= хе *4 . >
Найти резольвенты для следующих ядер:
15.38. К(х, t) = 1.
15.40. К(х. t) = х2.
15.42. К(х, t) = xt2.
15.44. К(х, t) = 2shx~sht.
t2 — t + 1
15.46. K(x, t) = -9-------
v ’ x2 - x + 1
15.39. К(x, t) = t.
15.41. K(x, i) = xt.
15.43. K(x, t) = ex~l.
1 4- x2
15.45. K(x, t) = —-2--1 +
15.47. K(x, t) = v ’ chi
15.48. Показать, что для произвольного ядра вида К{х, t) = == xptq, где р и q — некоторые положительные целые числа, ре-
зольвента имеет вид
др+<?+1 _{Р+<?+1
R(я, i, А) = xptqeA р+я+i
222
Гл. 15. Интегральные уравнения
15.49. Показать, что для произвольного ядра вида К(х, £) = К (.т)
= , K(t) 0, резольвента имеет вид
Л(ж’ *’ Л) = кУеЛ(1 °'
Найти с помощью резольвенты решения следующих интегральных уравнений:
X
15.50. у(х) — 1 — ty(t)dt.
о
X
15.51. у(х} — х + xty(t) dt.
о
ir
15.52. у(х) = sin ж + 2 ex~ly(t) dt.
о
X
15.53. у(х) = ch х + —^y(t)dt.
о
15.54. у(х) = ——+ / ——^y(t)dt.
1 + хл J 1 + X1 о
3. Уравнения Вольтерра 2-го рода типа свертки. Интегральное уравнение Вольтерра 2-го рода вида
X
y(x) = f(x) + У К(х - t)y(t)dt, (23)
a
в котором ядро К(х, t) = K(x — t) зависит лишь от разности аргументов, называется уравнением типа свертки. Если в (23) а — конечное число, то, не ограничивая общности (см. задачу 15.65), можно считать а = О, что мы и будем предполагать в дальнейшем.
Для решения уравнений типа свертки используется преобразование Лапласа.
Предположим, что функции f(x) и К(и) — оригиналы (см. гл. 17, § 1, п. 1). Можно показать, что в этом случае решение у(х) также будет оригиналом и, следовательно, к обеим частям уравнения (23) можно применить преобразование Лапласа. Полагая
y{x)=-Y(p), №=F(p), K(u)=k(p)
§ 1. Интегральные уравнения Вольтерра
223
и используя теорему о свертке, согласно которой j К(х — t) y(t) dt = о
К(р) У(р), получим
Y(p) = F(p) + K(p)Y(p),
откуда
У(р) =
l-K(p)’
Оригинал y(x) для У(р) будет решением интегрального уравнения.
Пример 8. Используя преобразование Лапласа, решить интегральное уравнение
X
у(х) = 1 + У ch (ж - t) y(t) dt.
о
< Так как 1 = - и chu = —-----, то, применяя к обеим частям задан-
р р2 — 1
ного уравнения преобразование Лапласа и используя теорему о свертке, получим
y(p) = ; +
р р£ — 1
Отсюда
р2 — 1
Y(p) = ( 2 П
Р(Р -Р~ 1)
1 1
Р + / 1\2 5
~4
и, следовательно, у(х) = 1 + ~^=еа'/2 sh >
Vo 2
С помощью преобразования Лапласа найти решения заданных уравнений типа свертки:
15.55. у(х) = ех — х — 1 + )
о
х 2
15.56. у(х) = — + / (х - t) y(t) dt.
о
224 Гл. 15. Интегральные уравнения
X
15.57. у(х) = хе2х - f dt.
о
х
15.58. у(х) = sin ж 4- cos (x — t)y(t)dt.
о
х
15.59. у(х) = ех 4- sin (я - t) y(t) dt.
о
X
15.60. у(х) = sin ж — у* sh (х — t) y(t) dt.
о
х
X2 If
15.61. у(х) = — + ~ / (x-t)2 y(t) dt.
£ £ J
0
x
15.62. y(x) = e2x 4- У (x — t)ex~f y(t) dt.
0
X
15.63. y(x) = 1 4- У cos (x — f) sin (x — t} y(t) dt.
о
x
15.64. y(x) = 1 4- x cos x — sin x 4- (x — t) sin (x — t) y(t) dt.
о
15.65. Показать, что если y(x) — решение уравнения (23) с а =4 0, то функция у*(х) — у(х 4- а) удовлетворяет уравнению
х
У*(х) = f*(x) + У К (х -t) у* (t) dt, о
где /*(я) = f(x 4-а).
15.66. Показать, что для ядра К(х, t) = К (х — t) все итерированные ядра, а следовательно, и резольвента также зависят лишь от разности аргументов х — t.
Решение уравнений типа свертки можно провести и несколько иным способом, а именно — путем использования преобразования Лапласа для нахождения резольвенты. В самом деле, резольвента ядра t) = = К(х — t) зависит лишь от разности аргументов (см. задачу 15.66) и,
§ 1. Интегральные уравнения Вольтерра
225
следовательно, решение уравнения
X
у(х) = /(ж) + У К(х - t) y(t) dt о
можно записать в виде
X
у(х) = /(ж) + У R(x - t) f(t) dt, о
(24)
(25)
где R(x — t) = R(x, t, 1), a R(x, t, Л) — резольвента ядра K(x, t) = = K(x — t). Применяя к обеим частям уравнений (24) и (25) преобразование Лапласа, получим
У(р) = F(p) + к(р) m У(р) = Ftp) + R(p) F(p),
откуда
Л(р) = . (26)
1 - К(Р)
Оригинал R(u) = R(p) определяет резольвенту R(x — t), зная которую, из (25) найдем и решение уравнения.
Пример 9. С помощью резольвенты найти решение уравнения
2 [ _ ж—t V 3
y(f) = l + -j= е sin—(х-t) у (t)dt. yoJ
о
< В рассматриваемом случае К (и) =
2 — и/2 • V3
—т=е ' sin—и и
х/3 2
К(Р) =
1
р2 + р + 1 ‘
Из (26) получим R(p) = ~ ^3 = 1 - е и, т. е. R(x - i) =
= 1 — е~^х~1\ Учитывая, что f(x) = 1, с помощью (25) находим решение
X
у(х) = 1 + У (1 - dt = х + е~х. > о
226
Гл. 15. Интегральные уравнения
Найдя резольвенту с помощью преобразования Лапласа, решить следующие интегральные уравнения:
X
15.67. у(х) = i + У е~2^ • y(t) dt.
о
х
1 f о
15.68. у(х) = 2 + - / (х — t)3 y(t) dt.
о
X
15.69. y(x) = e~x + у* sin (x — t) y(t) dt.
о
X
15.70. y(x) = e”2 4- f (1 — y(t) dt.
о
x /—
f i —i v3
15.71. y(x) = 1 + / e~ 2 cos —-(x — t) y(t) dt.
J £
0
Используя преобразование Лапласа, решить систему уравнений типа свертки:
15.72. yi(x) = -1+1 о
х
У yi(t) dt. о
15.73. У1(х) = —х + I о
У2 (%) = —Зх2 + X — 5 I
о
0
15.74. ух(х) =х + J y2(t)dt, о
х3
У2(х) = — + 2х - 1 -о
о
§ 1. Интегральные уравнения Вольтерра
227
X X
15.75. yi(x) = ех - У yi(t)dt + 4; f ex~ly2(t)dt, о о
X X
у2(х) = 1 - У е'^х~^уi(i) dt + У y2(t)dt. о о
X X
15.76. yi(x) = X + У y2(t) dt, у2(х) = 1 - У 7/1 (f) dt, о о
х
Уз(х) = sin ж + iy (x-tjy^t) dt. о
4. Уравнения Вольтерра 1-го рода. Линейным интегральным уравнением Вольтерра 1-го рода называется уравнение вида
X
У К(х, t)y(t)dt = f(x), а
W)
где у(х) — искомая функция, а К(х, t) и /(ж) — заданные функции, определенные соответственно в треугольнике а х, t b, t х и на отрезке [а, Ь]. Классическим примером уравнения этого типа является уравнение Абеля
1 ~^Ldt = f(X), J у/X — t
О
а также его обобщение с ядром вида К(х, t) = ---—, 0 < а < 1,
имеющим интегрируемую особенность при х = t. В настоящем пункте ограничимся рассмотрением уравнений, для которых ядро К(х, t) и свободный член /(ж) непрерывны всюду в своей области определения.
К уравнениям Вольтерра 1-го рода приводит, например, следующая важная задача, часто встречающаяся на практике. Пусть задана некоторая линейная динамическая система, x(t) — ее входной, a y(t) — выходной сигналы. Тогда, как известно, зависимость y(t) от x(t) может быть записана в виде
-j-оо
y(t) = У g(t, т)х(т)6т,
— ОО
(28)
где g(t, т) — весовая функция, определяемая свойствами системы. Если в частности, выполнено условие физической реализуемости (т.е.
228
Гл. 15. Интегральные уравнения
g(t, т) — 0 при т > t) и система находилась в покое до момента времени t0 (т.е. x(t) — 0 при t < to), то (28) принимает вид
t
y(t) = У g(t, т)х{т)(1т. (29)
to
Если теперь требуется по известному выходному сигналу восстановить внешнее воздействие, то мы приходим к уравнению Вольтерра 1-го рода (29) относительно x(t) при заданной функции y(t).
В отличие от уравнений Вольтерра 2-го рода, решение уравнения Вольтерра 1-го рода (27) существует только в том случае, когда свободный член f{x) удовлетворяет ряду дополнительных условий, зависящих в каждом конкретном случае от свойств ядра 7Г(ж, t).
В частности, каково бы ни было ядро, необходимым условием существования решения, как это видно из (27) при х = 0, является равенство f(a) =0.
Пример 10. Найти условия разрешимости в классе непрерывных функций и решение уравнения
/(х — t}n 1
————-y(t)dt = f(x), п = 1, 2, ... , х € [0, с]. (30)
I71
о
< Предположим, что непрерывное решение у(х) существует. Тогда из (30) следует, что /(0) = 0 и существует непрерывная производная f'(x), х Е [0, с]. Дифференцируя (30) последовательно п раз, получаем
Г (х —
о
х
У y(t) dt = /(п-1)(ж), о
у(х) = f(n\x).
Таким образом, если непрерывное решение у(х) существует, то функция /(ж) имеет непрерывные производные до n-го порядка включительно, причем
/(0)=/'(0) = ... = /<"-1>(0) = 0; (31)
при этом решение единственно и должно иметь вид у(х) = f^n\x). Подставляя в (30) у(х) = f^n\x) и п раз интегрируя по частям с учетом
§ 1. Интегральные уравнения Вольтерра
229
соотношений (31), найдем, что функция у(х) = f^n\x) действительно является решением исходного уравнения (проверьте!). >
Если ядро К(х, t) и свободный член f(x) (f(a) = 0) уравнения (27) дК(х, 0 г// х
таковы, что существуют непрерывные производные --- и f (х) и,
дх
кроме того, функция К(х, х) 0 всюду на [а, 6], то уравнение (27) эквивалентно уравнению Вольтерра 2-го рода и, следовательно (см. п. 1), имеет единственное непрерывное решение. В самом деле, предполагая существование непрерывного решения и дифференцируя (27) с учетом перечисленных условий, получаем
/дК(х, t) . ч ч
—- y(t) dt = f (ж)
a
ИЛИ
. . f'M [ 1 дК(х, t} . . , .
= FT----\ + / FT--7—й—(32
К(х, х) J К(х, х) дх
a
т.е. у(х) есть решение уравнения Вольтерра 2-го рода (32). Обратно, непосредственной проверкой убеждаемся, что решение уравнения (32) при условии /(а) = 0 удовлетворяет и исходному уравнению (см. задачу 15.77).
Пример 11. Решить уравнение
X
У (2 + ж2 — i2) у($) dt = х2, о
сведя его к уравнению Вольтерра 2-го рода. < Дифференцируя это уравнение, получаем
X
2у(х) + У 2xy(t) dt = 2х о
или
X
у(х) = х — У xy(t) dt о
— уравнение Вольтерра 2-го рода. Ядро К(х, £) = —х вырождено и,
X
полагая u(x) = j y(t) dt, получаем о
у(х) — х — хи(х), и'(х) = у(х) =.х — ху(х}
230
Гл. 15. Интегральные уравнения
или
и' + хи = х, и(0) = 0.
Отсюда и(х) = 1 — е~х /2 и у(х) = хе~х /2. >
Если в исходном уравнении Вольтерра 1-го рода (27) К(х, х) = О на [а, Ь], то после дифференцирования этого уравнения снова получается уравнение 1-го рода, и т- при выполнении соответствующих условий — можно повторить описанный выше прием. При этом, однако, следует всякий раз внимательно учитывать отмеченные выше ограничения на свободный член, необходимые для разрешимости уравнения.
Пример 12. Решить уравнение
X
sin (ж — t) y(t) dt = ех — 1. (33)
о
< Условия существования и непрерывности производных для ядра и свободного члена здесь выполнены. Дифференцируя дважды, получаем
X
У cos (ж — t) y(t) dt = ех, (34)
о
X
у(х) — У sin (ж — t) y(t) dt = ех. (35)
о
Уравнение (35) есть уравнение Вольтерра 2-го рода и оно имеет единственно непрерывное решение у(х) = 2ех — х — 1, которое может быть найдено, например, операционным методом. Однако функция у(х) = = 2ех — х — 1 не удовлетворяет исходному уравнению, в чем можно убедиться непосредственной подстановкой. Дело здесь в том, что уравнение (34) не имеет решения, так как = 1^0. А поскольку решение уравнения (33) должно удовлетворять уравнению (34), то и исходное уравнение (33) не имеет решения. >
15.77. Доказать, что решение уравнения (32), в котором /(а) = = 0, является решением и уравнения (27).
Решить заданные уравнения Вольтерра 1-го рода, сводя их к уравнениям 2-го рода:
X
15.78. I (х — t) y(t) dt = ех — х — 1.
15.79. / ех ty(t)dt=—.
о
§ 1. Интегральные уравнения Вольтерра
231
I
15.80. I y(t) dt = х. о
I
15.81. У sin (х — t) y(t) dt = 1 — cos x. о
x
15.82. У sh (x — t) y(t) dt = shx — x. b
X
15.83. У (x-t)2y(t)dt = x\ о
x
15.84. У (z — t)2 y(t) dt = ж3 + x2. о
X
15.85. / (1 + x — t) y(t) dt = ~e~x sinz. / 2
о
r x2
15.86. / (1 - x2 + t2) y(t) dt = —.
J **
0
15.87. J (2t - x) y(t) dt = x3 - 1.
1
Решить уравнения Вольтерра 1-го рода типа свертки, применяя преобразование Лапласа непосредственно к заданному уравнению (см. также п. 3):
X
15.88. У (х — i) y(t) dt = ch x — 1. о
X
15.89. у sin (x — t) y(t) dt = ^x4. о
X
15.90. / cos (x — t) y(t) dt = x sin x.
о
232
Гл. 15. Интегральные уравнения
X
15.91. / sh (я; - t) y(t) dt = 2 sin2 b
X
15.92. У (x — t) sin (x — t) y(t) dt = sin2 x. о
X
15.93. j' (x — t)ex~l y(t) dt = ~e2x — xex — |. о
x
15.94. У ex~f cos (x — t) у(t)dt = xex. b
X
15.95. [ ex~l sh (.t — t) y(t) dt = ~e2x — -я — 7. J v ’yv ’ 4 2 4
0
X
15.96. У (x — t) sh (x — t) y(t) dt = x ch x — sh x. 0
X
15.97* . У y/x - ty(t) dt = x3y/x. b
§ 2. Интегральные уравнения Фредгольма
1. Основные понятия. Метод последовательных приближений и резольвента для уравнений Фредгольма 2-го рода. Линейными интегральными уравнениями Фредгольма называются уравнения вида
у(х)
К(х, t)y(t)dt = f(x)
(1)
(уравнения 2-го рода) и
ь
К(х, t)y(t)dt = f(x)
(2)
(уравнения 1-го рода). В (1) и (2) у(х) — искомая функция, а ядро К(х, t) и свободный член f(x) предполагаются заданными соответственно в квадрате а х, t b и на отрезке [а, 6]. Если, в частности,
§ 2. Интегральные уравнения Фредгольма
233
К(х, t) = 0 при а < х < t, то уравнения (1) и (2) превращаются в уравнения Вольтерра 2-го и 1-го рода соответственно.
Мы ограничимся рассмотрением уравнений Фредгольма 2-го рода, наиболее интересных и важных для приложений.
Далее будем предполагать, что пределы интегрирования а и 6 в (1) — конечные числа, а функции К(х, t) и f(x) либо непрерывны в своей области определения, либо, в более общем случае, удовлетворяют условиям
ь ь
j j |К(х, t)|2 dx dt = В2К < Ч-оо. (3)
a a
b
У\f(x)\2dx < 4-00. (4)
a
Если f(x) = 0 всюду на [a, 6], то уравнение Фредгольма 2-го рода (1) называется однородным, в противном случае оно называется неоднородным. Решением уравнения (1) будем называть всякую функцию у(х) класса (a, b), обращающую это уравнение в тождество относительно х € [а, 6].
Обычно рассматривается не одно уравнение (1), а семейство уравнений ь
у(х) - А У К(х, t) y(t) dt = f(x), • (5)
a
зависящих от числового параметра А, который может принимать как действительные, так и комплексные значения. В отличие от уравнений Вольтерра 2-го рода, существование и единственность решения уравнения (5) существенно зависят от значения параметра А (см. подробно об этом в п. 3). В настоящем пункте рассмотрим случай, когда число А удовлетворяет условию
/ ь ь \ -1/2
|А| < — = ( Уj \К(х, t)\2 dxdt\ (6)
\a a /
(точнее, |A| < AJ, где Ai — наименьшее по модулю характеристическое число уравнения (5), см. п. 3).
При условии (6) уравнение (5) имеет единственное решение (непрерывное, если непрерывны К(х, Р) и /(т)), которое может быть найдено методом последовательных приближений подобно тому, как это делается в^лучае уравнений Вольтерра 2-го рода (см. п. 2 § 1). А именно, перепишем уравнение (5) в виде
ь
у(х) = f{x) 4- А [ К(х,Р) y(t) dt
234
Гл. 15. Интегральные уравнения
и далее, выбрав произвольно нулевое приближение уо(х), построим последовательность уп(х), п = 1, 2, ..., полагая
6
Уп(х) - + А У К(х, t) yn-i(t) dt, п Е N.
a
Если число А удовлетворяет условию (6), то при п —> оо последовательность уп(х) сходится (в общем случае в метрике £2(0, 6), а в случае непрерывного ядра и равномерно на [а, 6]) к точному решению у(х).
Пример 1. Методом последовательных приближений решить уравнение 1
у(х) ~ У = s^n7ra:-о
<] В данном случае, полагая А = 1/2иК(ж, t) = l, имеем
1 1
11 \К(х, t)\2dxdt = B2K = 1
о о
и, следовательно, условие |А| < \]Вк выполнено. Приняв ?/о(ж) = зттгж, последовательно находим
1 1
т/i (ж) = sin лх + - / уо (t) dt = sin лх + - / sin irt dt = sin лх -I—,
2 J 2 J тг
о 0
Уч{х) = sinTTZ + i y*y\(t)dt 0
= sin 7ГЖ +
. 11
cti = sin 7гж -I-f- —,
7Г 2%
Уз(х) = sin7ra; + -
У У2 (x) dt = sin 7ГЖ + j 0
dt =
1 1 1
8Ш7га; + - + — + —.
7Г 2% 227Г
Вообще,
!/n(a:)=sinM+-+- + ... + —
§ 2. Интегральные уравнения Фредгольма
235
откуда
.. . . . 1^1. 2
lim уп{х) = smnx + — > —г = sinлх Н—. п—>оо 7Г 2—2Л 7Г
k=0
Поэтому решением уравнения является функция
/ ч . 2
у(х) = 8Ш7Гя; Н—, 7Г
в чем можно убедиться непосредственной проверкой. >
Методом последовательных приближений найти решение заданных уравнений Фредгольма 2-го рода, предварительно убедившись, что условие (6) выполнено:
1
15.98. у(х) — xty(t) dt — 2х.
о
7Г
15.99. у(х) + ~ [ cos2 ty(t) dt = 1.
7Г J
о
1
15.100. у(х) — л У (1 — х) s'm2nty(t) dt = -(1 — х). о
7Г
15.101. у(х) — У sinxy(t) t dt = 2 sinrc.
о
7Г
15.102. у(х) + I (cos (х + 0 + cos (х ~ £)) dt = cos х.
2тг J о
Если в качестве нулевого приближения выбрать свободный член уравнения (5), т.е. уо(х) = f(x), то для n-го приближения получается общая формула (см. также § 1, п. 2)
п Ь
Уп(х) = f{x) + Kj(x, t) /(t) dt =
3 = l a
n € N, (7)
236
Гл. 15. Интегральные уравнения
где итерированные ядра определяются соотношениями
ь
К\(х, £) = К(х, t), Kj(x, t) = У К(х, s) t) ds, j = 2, 3, ...
a
(8)
При |Л| < \/BK ряд
R(x, t, A) = AJ-1 Kj(x, t) (9)
сходится и функция R(x, t, А), называемой резольвентой ядра K(x, t). Следовательно, (7) в пределе при п —> оо переходит в формулу
ь
у(х) = f(x) + А У R(x, t, A) f(t)dt, (10)
a
выражающую решение интегрального уравнения через резольвенту.
Замечание. Понятие резольвенты как функции R(x, t, А), с помощью которой по формуле (10) определяется решение интегрального уравнения, сохраняет смысл для любых значений А, при которых это уравнение однозначно разрешимо. Метод последовательных приближений и формула (9) дают представление для резольвенты в виде ряда по степеням А (называемого рядом Неймана), годное лишь в области |А| < 1/Вк.
Существует, однако, общий метод нахождения резольвенты — метод определителей Фредгольма, который в принципе позволяет построить резольвенту для любого значения А, при котором интегральное уравнение имеет единственное решение. Этот метод здесь не рассматривается.
Пример 2. С помощью итерированных ядер найти резольвенту и решение интегрального уравнения
1
у(х) ~ / 7+72 dt = 1 + х2-
111 и J JL L
о
X
<] В данном случае К(х, t) = -——
1 + tz вании (8) получаем
и для итерированных ядер на осно-
К^х, t) = К(х, t) = —^77, 1 +
§ 2. Интегральные уравнения Фредгольма
237
1 1
Кз(х, i) = / s)K2(s, t)ds = -—- / =
/ X j JL u> JL "j" l
о 0
/ln2\2 x
= \T J 1 + t2’
X
1 + t2'
Поэтому резольвента ядра равна
ОО ОО /» \ j —• 1
EX 4 — 1 ТГ 7 \ V“^ (In % \ Ж 1 X
A Kj(x, t) ( -2~'Ч 1 । ^2 “ In2 1 4-12 ’
j=i j=i 4 7 1 - —A
причем этот ряд сходится в области
2 |А|<Ы2- (11)
Заметим, что в рассматриваемом случае
11 1 1 2
В^ = / ^dxdt = 11 (1 + t2)2 dxdt = 0 0 0 0
т. е. условие (6) приводит к неравенству
И < 2\ZtIt <12)
V 7Г + 2
6 2
Так как 2\ ----- < :—, то из сравнения (11) и (12) видно, что в рас-
V тг + 2 In 2
сматриваемом случае область сходимости ряда Неймана для резольвенты шире, чем это гарантируется условием (6) (в соответствии с замечанием на с. 236).
Далее, для заданного уравнения А = j—- и, следовательно,
X
y-q—Решение уравнения на основании (10) равно
R I х, t,
1
1 Г х 2
у(х) = 1 + X2 + —- / 2——(1 + t2) dt = 1 + —-х + х2. >
In 2 J 1 + tz In 2
0
238
Гл. 15. Интегральные уравнения
Методом итерированных ядер найти резольвенту и решение заданных интегральных уравнений:
7Г
sin х.
о 1 In 2 f
15.104. y(x) 2x+ty(t) dt = x.
La J 0 1
15.105. y(x) + тг y* я sin27rt?/(t) dt — cos 2лх. о i
15.106. y(x) - | I о 7t/2
- У sinj;costт/(t) dt = 1. о
и L(x, t) называются ортогональными в квадрате выполняются условия
е х
Ядра К(х, t) а х, t b, если
ь
ь
= 0
a
a
для всех a х, t Ь. Если, в частности, ядро К(х, t) ортогонально самому себе, то для него второе итерированное ядро Къ(х, t) = 0 всюду в квадрате a х, t Ь. Следовательно, для такого ядра ряд Неймана для резольвенты сходится при любых значениях А, а сама резольвента совпадает с ядром К(х, £).
Пример 3. Методом итерированных ядер найти резольвенту и решение интегрального уравнения
COS ЛХ COS 3?г£ y(t) dt = COS 37ГЖ.
< Ядро K(x, t) = cos лх cos 3nt ортогонально самому себе:
(cos ЛХ COS Зтгз) (COS 7ГЗ cos Зтгt) ds = 0.
§ 2. Интегральные уравнения Фредгольма
239
Поэтому резольвента R(x, t, А) — cos лх cos Зтг£ и решение заданного уравнения имеет вид
1
у(х) = cos Зтгх + j cos лх cos2 Зтг£ dt = cos Зтгж + COS 7ГЖ. > -i
15.108. Доказать, что если ядра L(x, t) и М(х, t) ортогональны, то резольвента ядра К(х, t) = L(x, t) + М(х, t) равна сумме резольвент L(x, t) и М(х, i), т.е.
Rk(x, t, А) = Rl(x, t, А) + Rm(x, t, A).
Используя ортогональность ядер и результат задачи 15.108, решить интегральные уравнения:
1
// з \
Ж \ 1 ~ 2 / dt ~
о
1
15.110. у(х) — у* sin2Tnn/(i) t dt = х.
о
7Г
15.111. у(х) — У sin (т + 2г) y(t) dt = х.
—л
1
15.112. у(х) ~ л I (%2 + 1 + xt) y(t) dt = 1.
О J
-1
7Г
15.113. у(х) + —- / (х sini + sin2T) y(t) dt = sin(a:).
4тг J
~л
2. Решение уравнений Фредгольма 2-го рода с вырожденным ядром. Ядро К{х, t) называется вырожденным, если оно имеет вид
п
j=i
Соответствующее интегральное уравнение
ь / п \
I yf&dt = f(x) (13)
a \J = 1 /
240
Гл. 15. Интегральные уравнения
решается путем сведения к системе линейных алгебраических уравнений следующим образом.
Перепишем уравнение (13) в виде
п
У И - ^Pj^Sj = /(я), (14)
7=1 I
где неизвестные Sj определяются через искомое решение у(х) равенствами
ь
Sj = J dt, j = (15)
a
Умножая тождество (14) последовательно на qt(x), j = 1, 2, ... , п, и далее интегрируя обе части на отрезке [а, Ь], с учетом (15) получим для неизвестных чисел Si следующую систему линейных алгебраических уравнений:
п / Ь \ b
Si - I / qi(я) Pjds Sj = / qi(x)f(x)dx, i = 1, 2, ... , n.
1 \a / a
(16) Введем обозначения
ь b
aij = j qi(x)pj(x)dx, fi = j qi(x) f(x)dx. (17)
a a
Тогда система (16) запишется в виде
п
Si ^ijSj fii i — 1)2, • . . , П, (1$)
7=1
или в матричной форме (Е - A)S = F, (19)
где Е — единичная матрица, А = (aij)pj=1, S = (si, ... , sn)T, F = = (Л, - - -, А)т-
Если si, ... , sn — какое-нибудь решение системы (18), то в соответствии с (14) функция
п
У И = f(x) + ^РАх) Sj (20)
7—1
§ 2. Интегральные уравнения Фредгольма
241
будет решением исходного интегрального уравнения (13). Если же система (18) несовместна, то и интегральное уравнение не имеет решения. Этот метод применим, конечно, и в том частном случае, когда уравнение (13) однородное, т.е. f(x) = 0.
Пример 4. Решить уравнение
— sin х sin t + t ) y(t) dt = sin 2x.
7Г J
<] Ядро K(x, t) = — sin т sin t + t — вырожденное. Полагая 7Г
Pi (я) = -sin ж, р2(т) = 1, 7Г ql(t)=sint, qz(t)=t,
по формулам (17) вычисляем
ТГ
f 1 . 2 1 1
ап = / — sin xdx — 1, J тг
— тг тг
o2i = / — х sin xdx = 2,
J я
х • sin 2х dx = —тг.
Система (19) принимает вид
/ О О W Si \ / 0 \
\ —2 1 Д S2 ) ~ { -тг J ’
ее общее решение: si = С, s2 = — тг + 2С, где С — произвольная постоянная. Следовательно, любая функция вида
С (1 \
у(х) = sin 2х -I-sin я; - тг + 2С = sin 2т + С I - sinx + 2 — тг
тг X тг /
есть решение заданного интегрального уравнения и других решений это Уравнение не имеет. >
Пример 5. Решить уравнение
о
242
Гл. 15. Интегральные уравнения
<1 Следуя изложенному выше общему методу, запишем это уравнение в виде
у(х) — У. у/х s = х,
1
где s — y/ty(t)dt. Умножая обе части на у/х и интегрируя, получаем о
1 1
s — 2 У xdx- s = У д,3у/2 dx,
о о
или s — s = 2/5. Последнее уравнение не имеет решения относительно s, следовательно, исходное интегральное уравнение также не имеет решения. [>
Найти все решения или установить неразрешимость заданных уравнений Фредгольма 2-го рода с вырожденным ядром:
2тг
15.114. у(х)----I cos х sin ty (i) dt = sin я.
тг J
о
i
2e f
15.115. y(x)------—- I chxy(t)dt = 1.
ez — 1 J
о i
24 г / з \
15.116. y(x) - — I (1 - x2) (1 - -tj y(t) dt = x.
о
i
15.117. y{x) — J (1 + x) cos 2тг£т/(£) dt = x.
о
тг/4
15.118. y(x) ~ y* tg ty(t) dt — cos2 x.
о
1
15.119. y(x) ~ 4 f xt2y(t) dt = 0.
о
1
15.120. y(x) + У* exty(t) dt = 0.
о
§ 2. Интегральные уравнения Фредгольма 243
1
15.121. у(х) — у* (2х — t)y(t) dt = cos 27гж. b
15.122. у(х) - У (1 + 2xt)y(t) dt = -|(z + 3). о
1
//3 \
( -xt + x2(t — 1) j y(t) dt = 0.
-1 7Г 15.124. y(x)------[ cos2(x — t)y(t) dt = sin2rr.
7Г J 0 1
15.125. y(x) + [ (x - y/i)y(t) dt = ^x + \/x - 7. J 3 6
о 7Г
15.126. y(x) — — [ cos (x — t)y(t) dt = 0.
7Г J —7Г 1
15.127. y(x) — 3 (x2t2 + 4xt + 1) • y(t) dt = 2тг2 cos 2тгж.
о
1
15.128. y(x) — У (xt + x2)y(t) dt = 0.
-1
3. Характеристические числа и собственные функции. Теоремы Фредгольма. Значения параметра Л, при которых однородное уравнение
ь
у(х) — Л У К(х, t) y(t) dt = 0 (21)
a
имеет ненулевые (нетривиальные) решения у(х) 0, называются характеристическими числами этого уравнения или ядра К(х, £), а каждое Ненулевое решение — собственной функцией, соответствующей характеристическому числу Л. Заметим, что число А = 0 не является характеристическим, так как при А = 0 уравнение (21) имеет лишь нулевое Решение. Если А — характеристическое число, то число у = 1/А называется собственным числом интегрального уравнения. При этом у 0.
244
Гл. 15. Интегральные уравнения
Из результатов п. 2 следует, что в случае уравнения с вырожденным ядром
г f п \
у(х)-Х I ^Pj^q^t) I y(t)dt = 0 (22)
a v=1 /
всякое решение имеет вид
п
= X^Sjp^x), (23)
i=i
где S = (si,...,sn)T — решение однородной системы
(Е - AA)S = 0 (24)
ь
с матрицей А = (а^), aij = j qi(x)pj(x), i, j = 1, ..., n. Заметим, что a
если заменить А на 1/ju, то система (23) принимает вид
(А - pE)S = 0, p/Q. (25)
Отсюда следует, что собственные числа интегрального уравнения (22) совпадают с отличными от нуля собственными числами матрицы А, а собственные функции определяются соотношением (23), где S = ($i, ..., sn)T — соответствующие собственные векторы этой матрицы.
Пример 6. Найти характеристические числа и собственные функции уравнения
1
у(х) — X (xt — 2х2) y(t) dt = 0.
о
<1 Ядро К(х, t) = xt — 2ж2 вырожденное. Полагая
Р1(х) = х, рз(х) = —2х2,
q2(t) = l,
найдем элементы матрицы А в (25):
Оц
021
1
[ 2 1 1
/ х dx = -,
J д
о
1
f я 1
/ xdx = -,
о
012 —
«22 —
—2 [ ж3 dx = — х, J 2’
о 1
—2 / х2 dx = —.
J 3 о
§ 2. Интегральные уравнения Фредгольма
245
Характеристическое уравнение для определения собственных чисел матрицы А имеет вид
1 1
3 М 2
1 2
det (Л — рЕ) =
2 1 1 / 1V л
+F+36 " Г+б) “°’
2 3 Д
откуда р, = —1/6 — единственное собственное число матрицы А. Соответствующие собственные векторы находим из системы уравнений
А + S = 6 7
/1
2 2
1 1
\ 2 2 /
общее решение которой si = С, s? = С, где С — произвольная постоянная. Следовательно, окончательно получаем, что заданное интегральное
X 1
уравнение имеет единственное характеристическое число А = — = —6, а соответствующие собственные функции имеют вид
у(х) = —6(si£ — 2s2^2) = С(х — 2х2),
где С — произвольная постоянная. [>
Интегральное уравнение может вообще не иметь характеристических чисел (например, в том случае, когда ядро К(х, t) вольтерровское или, в случае вырожденного ядра, матрица А в (24) нулевая) либо не имеет действительных характеристических чисел.
Пример 7. Найти характеристические числа и собственные функции уравнения 7Г
у(х) — А х cosi у (£) dt = 0.
— 7Г
<3 Имеем
у(х) — Xxs = 0,
s = / costy(t) dt,
откуда
п
s — As lx cos x dx = 0.
7Г
Ho j x cos x dx = 0, поэтому при любом А последнее уравнение имеет — 7Г
только одно решение: s = 0. Следовательно, при любом А интегральное
246
Гл. 15. Интегральные уравнения
уравнение имеет только тривиальное решение, т.е. не имеет характеристических чисел. [>
Пример 8. Найти характеристические числа и собственные функции уравнения
7Г
у(х) — Л sin (ж — Д) y(t) dt = 0.
— 7Т
<1 Ядро
К(х, t) = sin (ж — Д) = sin ж cos t — cos ж sin t
выро?кденное, причем можно положить
Р1(ж)=8П1ж, pz(x) = — соэж,
Qi(i) = cos i, qz(t) = sin(i);
/ 7Г \ 2
матрица A = I aij = j qi(x)Pj(x) dx j имеет вид
\ -тг / ij—i
характеристическое уравнение
det (A - pE) = | % | = p2 + 7Г2 = 0
имеет только комплексные корни дм,2 — ±гтг. Найдем соответствующие собственные векторы. Для р\ = in
Для р2 = —in
(A + i.E)S„ = ^ 7;)Й)„2 = (о)>
GVMD- (27)
Окончательно заключаем, что заданное интегральное уравнение действительных характеристических чисел не имеет, но имеет два комплекс-х 1 1 г
ных характеристических числа Л1,2 = - ~ Тг—. Соответствующие
ДМ,2 п
собственные функции имеют вид (см. (26) и (27))
У\(ж) = Ai(Ci sin ж — iCi cos ж) = А\егх,
У2 (ж) = А2 (С*2 sin ж -I- гСг cos ж) = А2в~гх, где Ai и Аг — произвольные комплексные постоянные. [>
§ 2. Интегральные уравнения Фредгольма
247
Найти характеристические числа и собственные функции заданных интегральных уравнений с вырожденным ядром (ограничиться случаем действительных характеристических чисел):
15.129. y(x) - A I (1 + 2x) ty(t) dt = 0. b
i
15.130. y(x) - А У (l-я?2) y(t) dt = 0. о
1
15.131. y(x) — А У \x\y(t)dt = 0.
-1
15.132. y(x) — Л j xsintyff) dt — 0. о
15.133. y(x) — A j cos x cos ty(t) dt = 0. о
1
15.134. y(x) — A y* (x +1) y(t) dt = 0. о
i
15.135. y(x) -XУ (xel + 2i) y(t) dt = 0. о
i
15.136. ytx) — A [ I xsin2Trt — —- j y(t)dt = 0.
J \ 2д J
о
15.137. у(х) — Л j sin (д + t) y(t) dt = 0. о
15.138. y{x) — A / cos (x — t) y(t) dt = 0.
о
248
Гл. 15. Интегральные уравнения
Для уравнений Фредгольма 2-го рода вида
ь
у(х) - Л У Х(ж, t) y(t) dt = f(x), a
(28)
где a и b — конечные числа, а ядро K(x, t) и свободный член /(ж) интегрируемы с квадратом в области а ж, t b и на отрезке [а, Ь\ (в частности, непрерывны), справедливы следующие теоремы Фредгольма (при формулировке которых мы ограничимся случаем действительного ядра К(х, £)).
1. Однородное уравнение
ь
у(х) - Л / Х(ж, t) y(t) dt = О
(29)
имеет либо конечное, либо счетное множество характеристических чисел\ если этих чисел счетное множество, то они стремятся к бесконечности.
2. Если Л — характеристическое число, то уравнение (29) и сопряженное ему однородное уравнение
У И - X
К*(х, t) y(t) dt — О,
(30)
a
где К*(х, t) = К(х, t), имеют одно и то же, и притом конечное, число линейно независимых решений.
3. Альтернатива Фредгольма: либо неоднородное уравнение (28) имеет одно и только одно решение для любой функции f(x) G € 1/2(a, 6), либо соответствующее однородное уравнение (29) имеет по крайней мере одно нетривиальное решение. (Другими словами, если число Л не является характеристическим, то уравнение (28) имеет, и притом единственное, решение для любой функции /(ж) € £2(0, 5).)
4. Если Л — характеристическое число, то для того чтобы уравнение (28) имело решение, необходимо и достаточно, чтобы свободный член /(ж) был ортогонален любому решению у*(х) однородного сопряженного уравнения (30), т. е.
ъ
У /(ж)?/(ж) dx = 0. а
Проиллюстрируем теорему Фредгольма на примере интегрального уравнения с вырожденным ядром.
§ 2. Интегральные уравнения Фредгольма
249
Пример 9. Исследовать решения интегрального уравнения
(ж2 cos t + х sin t) y(t) dt = cos x
(31)
в зависимости от значений параметра Л.
<] Решение интегрального уравнения сводится к решению неоднородной системы
(Е - AA)S = F, (32)
где
ь
A = (aij), dij = У qi(x)pj(x}dx, i, j = 1, 2, ..., n, a
HF = (/l,...,/n)
имеем
' b \
fi = J' Qi(x) f(x)dx |. В рассматриваемом случае
< ft
Pi (ж) = ж2,
<7i (t) = cos t,
р2(-т) = x, д2(ж) - sin t,
П] i — / cos ж • ж2 dx = 4л,
0,12 — / cos ж • x dx = 0,
a2i — / sin ж • x2 dx = 0,
(Z22 = sinx xdx = —2%,
cos2 xdx =
тг,
smxcosxdx = 0.
Система (32) имеет вид
1 — 4% A
(33)
Характеристическое уравнение
det (Е - АЛ) = (1 + 2тгА)(1 - 4дА) = 0
1 1
Имеет корни Ai = — и А2 = ——, являющиеся характеристическими 4л 2л
Числами соответствующего однородного уравнения.
250
Гл. 15. Интегральные уравнения
При любом А , — — система (33) имеет единственное решение 4% 2тг
’ 7Г
si = —, s2 = 0;
1 - 4тгА
соответствующее решение интегрального уравнения:
, . Ал- 2 X / 1 1
„W = cosx + __х, Л/-,
При А = Ai = из (33) получаем
4%
/0 0\
lo -1 W _ w • \ 2/
Эта система, а вместе с ней и исходное интегральное уравнение решения не имеют.
При А = А2 = — 1/(2тг) система (33) принимает вид
/3 0\ /зА _ /7г\ ко oj U2/ “ W
и имеет решения si = тг/3, S2 = С. Соответствующие решения интегрального уравнения таковы:
у(х) = COS Ж -I- А2(31Ж2 -I- 32ж) = cos ж — ^ж2 + Сх,
где С — произвольная постоянная. [>
Исследовать решения заданных уравнений с вырожденным ядром при различных значениях параметра А:
1
15.139. у(х) — A f ж(1 + /) y(t) dt = х2.
о
1
15.140. у(х) — A f xy(t)dt = з1п2тгж.
о 1
/3 (1 + 2ж) ty(t) dt = 1 — -х.
о 1
15.142. у(х) — A f х sin 2тг£г/(£) dt = х.
о
§ 2. Интегральные уравнения Фредгольма
251
4
15.143. у(х) — Л f tgty(t) dt = ctgx.
TV
15.144. y(x) — arccos ty(t) dt = -y
./ v 1 — x2
о
7Г
15.145. y(x) — Л f sinz cos ty(t) dt — cosx.
о i
15.146. y(x) — А У (1 + xt) y(t) dt = sin7rz.
-i
1
/1 3
(x + t) y(t) dt = - + -x. Z Z
-1
7Г
15.148. y(x) — А У cos (x + t) y(t) dt = 1. о
4. Уравнения Фредгольма 2-го рода с симметричным ядром. Ядро К(х, t) называется симметричным, если оно удовлетворяет условию
К(х, t) = K(t, х)
для всех а х, t Ь.
Для симметричных ядер, удовлетворяющих условию
ь ь
У У |А”(ж, t)|2 dxdt < +оо, а а
дополнительно к основным теоремам Фредгольма (см. п. 3) справедливы следующие утверждения:
1. Симметричное ядро, отличное от тождественного нуля, имеет по крайней мере одно характеристическое число.
2. Характеристические числа симметричного ядра действительны, а собственные функции, соответствующие различным характеристическим числам, ортогональны.
На практике часто встречается случай, когда интегральное уравнение с симметричным ядром является решением некоторой самосопряженной однородной краевой задачи для обыкновенного дифференциального уравнения. В таких случаях нахождение характеристических чисел и собственных функций ядра сводится к решению указанной краевой задачи.
252
Гл. 15. Интегральные уравнения
Пример 10. Найдите характеристические числа и собственные функции ядра
К(х, /) =
t(x + 1), (i + 1)х,
0 х t 1,
О t х 1.
(34)
<1 Заметим, что ядро (34) симметричное. Действительно, из (34) следует
К(х, i) =
x(t + 1), (х + l)t,
О t х 1,
О х t 1.
(35)
Сравнивая (34) и (35), видим, что К(х, t) = K(t, х) для любой пары (х, t).
Однородное интегральное уравнение
- А
К(х, i) y(t) dt = О
(36)
с ядром (34) запишем следующим образом:
у(х) = А
(t + 1) y(t) dt + (x + 1)
(37)
Далее, дважды продифференцируем (37):
(X
У (£ + 1) y(t) dt + х(х + 1) у(х) + о
1
У tyW
X
dt — (х + 1) ху(х)
(38)
у"(х) = А((х + 1) у(х) - ху(х)) = Ху(х). (39)
Таким образом, число А и функция ylx) таковы, что
У" - ХУ = 0. (40)
Найдем теперь краевые условия, которым должна удовлетворять искомая функция у(х). Для этого, подставляя в (37) и (38) х = 0 и х = 1,
§ 2. Интегральные уравнения Фредгольма
253
получим
2/(0) = А У ty(t)dt, о
1
2/'(0) = А У ty(t) dt, о
2/(1) = А У (t + 1) y(f) dt, о
i
2/'(1) = А У (t + l)y(t) dt, о
откуда
Х/(0) = 2/'(0), у(1)=у'(1). (41)
Соотношение (40) и (41) образуют в совокупности однородную краевую задачу, решая которую, найдем характеристические числа и соответствующие им собственные функции исходного интегрального уравнения.
Рассмотрим три случая.
1) А = 0. Уравнение (40) принимает вид
У" = о,
его общее решение:
у(х) = С1 + С2х. (42)
Используя краевые условия (41), получим для нахождения постоянных Ci и С2 систему
С\=С2, с\ + с2 = с2, которая имеет единственное решение Ci = 0, С2 = 0. Следовательно, краевая задача, а вместе с ней и уравнение (36) при А = 0 имеют лишь тривиальное решение у(х) = 0, т.е. А = 0 не является характеристическим числом. Впрочем, это можно было заметить сразу из уравнения (36): если в нем А = 0, то у(х) = 0.
2) А = си2 > 0. Уравнение (40) имеет вид
у"-Ш2у = 0, его общее решение:
у(х) = С\е“х + С2е~“х.
Краевые условия (41) приводят к системе
+ С2 — шС\ — шС2, Cie“ + С2е~“ = uCie“ - шС2е~ш
Или, в матричной форме,
1 —
1 4- си
e-tJ + cue-tJ
(43)
254
Гл. 15. Интегральные уравнения
Эта система имеет нетривиальные решения в том и только в том случае, когда выполняется условие
1 — СО 1 + СО _ /1 Wi I \ 1 1 _
е~“+ше~ш ~ + М е-о> -
= —2(1 — со)(1 4- со) shco = О,
т. е. со = ±1 (со2 > 0!), или Л = со2 = 1.
При со = 1 из (43) получаем
/О 2 \ (СЛ _ /ОХ /СЛ _ /0\ \0 2/е) (С2) - и tc2) - VM ’
откуда у(х) = Ciex, С\ — произвольная постоянная.
Аналогично, при со = — 1 получаем
откуда у(х) = х, Съ — произвольная постоянная.
Таким образом, А = 1 — характеристическое число ядра (35), соответствующая ему линейно независимая система собственных функций состоит из двух функций yi = ех, у2 = е~х, а любая собственная функция имеет вид у(х) = С\ех + C^e-*, где С\ и С2 — произвольные постоянные.
3) А = —со2 < 0. В этом случае уравнение (40) имеет вид
у" -4— со2// = 0,
его общее решение:
у(х) = Ci cos сох + С2 sin сох.
Краевые условия (41) приводят к системе
Ci = шС2,
С1 cos со + С2 sin со = —coCi sin со + С0С2 cos со
или, в матричной форме,
1 cos со + со sin со
-W \ (СЛ /04
sincj - ucvsujj \С2) W
(44)
Эта система имеет отрицательные решения в том и только в том случае, когда co2sinco — 0, т.е. соп — ттп, п = ±1, ±2, ..., или Ап = -со2 = = — л2п2, п G N.
§ 2. Интегральные уравнения Фредгольма
255
При ш = 7Г72, п = ±1, ±2, ..., из системны (44) получаем
/ 1 -7ГП /0\
к(-1)п -7гп(-1)^ \С2) - ко; ’
откуда Су = 7гпС, С2 = С и у(х) = С(лпсо$ттх + зштгпа;), где С — произвольная постоянная ип = ±1, ±2, ... Заметим, однако, что в этом выражении для у(х) переход от п к — п приводит лишь к смене знака, т.е. к изменению константы С. С учетом этого получаем, что каждому из характеристических чисел Хп = —тг2п2, п € N, соответствует одна базисная собственная функция уп — лп созлпх + зтлпх. п € N, а любая собственная функция имеет вид
у(х) = С(лп cosimx + sinyrna;), п G N,
С — произвольная постоянная.
Подводя итог, заключаем, что для заданного ядра задача о характеристических числах и собственных функциях имеет следующее решение:
Ао = 1, у0Л=ех, Уо,2 = е~х,
Хп = —л2п2, уп = лп cos лпх + sin лпх, п Е N. >
Для заданных симметричных ядер найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения:
15.149. К(х, t) = {
{—х, 0 х t.
—t, t х 1.
15.151. К(х, t) = { J i1’ °t<*
I v 1 , b Jb
( costsinrr, (K<
15.152. K(x, t) = < .
v [ sint cos x, t
r,z x f sintcosx,
15.153. K(x, t) = < , . , .
v [ cos t sin X, t
r sin (t — 1) sin a;
15.154. K(x, t) = ) . sin,1 „
sint sin (x — 1)
t,
t,
sin 1
256
Гл. 15. Интегральные уравнения
Ish (t — 1) sh#
shtsh(f - 1)
sh 1 ’
0 x t,
t x 1.
15.156. K(x, t) = sin|a; — t|, 0
{—e (ch a;
v , -x — chte ,
0 x t, t x 2.
Если задано неоднородное интегральное уравнение
у(х) - Л / 7Г(х, 0 у{€) dt = /(.т)
(45)
с симметричным ядром К(х, t) = /С(£, х), удовлетворяющим условию ь ь
У |Щж, £)|2 dxdt < +оо, а а
то его решение в общем случае может быть найдено следующим образом. Пусть
А1, Аг, ... , Ап, ... (46)
— последовательность характеристических чисел ядра К(х, i), а
У1(х), у2(х), ... , уп(х), ... (47)
— соответствующая ортонормированная последовательность собственных функций. При этом в последовательности (46) каждое характеристическое число выписывается столько раз, каков его ранг, т.е. число линейно независимых функций, соответствующих этому характеристическому числу.
Если параметр А в уравнении (45) не совпадает ни с одним из характеристических чисел An, п = 1, 2, ..., то решение этого уравнения (существующее и единственное в силу 3-й теоремы Фредгольма для любой правой части /(х)) дается формулой
ОС -
7/(х) = /(х) 4- А Уп(а:), (48)
п= 1
где ь
f(x)yn(x)dx, п = 1, 2, ...
(49)
§ 2. Интегральные уравнения Фредгольма
257
Если же параметр А совпадает с одним из характеристических чисел, имеющих ранг г, т.е.
— ^т+1 — ^т+2 — • • • — Ат_|_
для некоторого т, то решение существует в том и только в том случае, когда функция /(ж) ортогональна ко всем собственным функциям, соответствующим данному характеристическому числу, т.е. выполнены г условий
ь
У f(x) Уп(х) dx = 0, п = т + 1, т + 2, ... , т + г. (50) a
В этом случае уравнение имеет бесконечное множество решений, имеющих вид
у(х) = /(s) + А
fn
An A
Уп(х') “b ClУт+1 (^) • • •
..., m+r
• • • + СгУт+Лх), (51)
где Ci, ... , Cr — произвольные постоянные.
Пример 11. Найти все решения неоднородного интегрального уравнения
у[х) - А / K(ar, t) y(t) dt = 2 ~ sin I’
t (52)
f cost sin x, 0 < x < t, K(s, t) = { .
( Sint COSS, t X 7Г,
при различных значениях параметра А.
<1 Характеристические числа и соответствующие им собственные функции ядра (52) имеют вид (см. задачу 15.152)
Ап — — 1 4-
/2п4- 1\2
V 2 J
. 2п 4-1
Уп = sm —-—ж,
п = 0, 1, 2, ...
Заметим, что в данном случае каждое характеристическое число имеет ранг г = 1, а последовательность собственных функций ортогональна, но не нормирована на отрезке [0, тг]: нормированные собственные функции имеют вид
/2 . 2п + 1 п Л п
Уп = \ ~ sm —-—х, п = 0, 1, 2, ...
V тг 2
258
Гл. 15. Интегральные уравнения
7Г X
По формулам (49) для /(х) = — — sin — получаем
. х\ [2 . 2п +1 ,
- sm — Н / — sm —-— х dx = 2/V тг 2
При Л Ап, п = 0, 2, ..., уравнение имеет единственное решение
ОО
И*) = 4 -sm2
n=0
. 2n + 1
1 sm ~Y~X
Xn — A 2n 4* 1
При A = Ao = — 3/4 в силу ортогональности f(x) к собственной X
функции уо(х) = sin - получаем бесконечное множество решений вида
ЗЛ)
у(х) = — - — sin — — - >
yv ’ 4 2 2 4
п=1
. 2п + 1 sm —-—х
2
п(п + 1)(2п + 1)
+ Csin^,
где С — произвольная постоянная.
Наконец, при А = An, п = 1. 2, ..., уравнение решения не имеет. >
Найти решения неоднородных уравнений Фредгольма 2-го рода с симметричным ядром при различных значениях параметра А (характеристические числа и собственные функции соответствующих ядер см. в задачах 15.149-15.157):
1
15.158. у(х) — А У К(х, t) y(t) dt — 1, о
(t — l)rr, 0 x t(x — 1), t x 1.
§ 3. Численные методы решения интегральных уравнений 259
/7Г
К(х, t) y(t) dt = sin 7г.т cos —x, о
f — x, 0 < x t,
( — t, t X 1.
7Г
15.160. y(x) — X К(x, i) y(t) dt = x — л, b
f sin t cos x, 0 x C t,
K(x, t) = 4
( cos t sin a;, t x тг. 7Г
15.161. y(x) — A j - sin |a; — 11 y(t) dt = 1.
о
§ 3. Численные методы решения интегральных уравнений
Существуют различные методы численного решения интегральных уравнений: метод конечных сумм, метод моментов, метод коллокации и др. Ниже будут рассмотрены два из них — метод конечных сумм и метод моментов.
Пусть задано интегральное уравнение Фредгольма 2-го рода (ср. § 2, п. 1 настоящей главы)
?/(т) - А
К(х, t)y(t)dt = f(x),
(1)
где у(х) — искомая функция, К(х, t) и f(x) — известные функции, определенные в прямоугольнике а х, t Ь и на отрезке [а, 6] соответственно, А — параметр, не равный собственному числу соответствующего однородного уравнения.
Метод конечных сумм. Этот метод основан на приближенном вычислении определенного интеграла с помощью некоторой квадратурной формулы
F(x) dx = ^T^AiF(xi) dx + Rr, (2)
где Xi, i — 1, 2, ..., n, — точки отрезка [a, b], Ai, i = 1, 2, ..., n, — числовые коэффициенты, не зависящие от выбора функции F(x), и Rp — ошибка формулы (2), порожденная приближенным вычислением интеграла. В случае равноотстоящих узлов Xi = а + (г — l)h, i = 1, ..., п,
260 Гл. 15. Интегральные уравнения
где h =-----, коэффициенты Ai в приближенных формулах (2) имеют
п — 1
следующие значения:
1) для формулы прямоугольников
Ai = h, i = 1, 2, ..., п - 1, Ап = 0;
2) для общей формулы трапеций
— Ап — h/2, А2 = ... = An_i = h]
3) для общей формулы Симпсона при п = 2т + 1
= А2т+1 = /г/3, А2 — А4 = . . . = А2т — 4Ь/3, A3 = А~у -- ... = A2;n^i = 2/г/З.
Вводя обозначения
Уi; j ) /(pi) fi> Л J 1? 2, . . . , 72,
интегральное уравнение (1) на основании формулы (2), в которой ошибка Rf отброшена, можно заменить системой тг линейных алгебраических уравнений относительно неизвестных — приближенных значений точного решения у(х} в узлах хр
п
yi 'У Ajkijyj — fi, i — 1,2, ..., тг. (3)
j=i
Система (3) может быть решена одним из численных методов линейной алгебры, например, методом Гаусса.
Найдя yi из (3), для решения у(х) получаем из уравнения (1) приближенное аналитическое выражение
п
У(х} = /(ж) + А ^2 AjK(x, xj) yj.
j=i
Пример 1. Используя квадратурную формулу Симпсона, методом конечных сумм найти приближенное решение уравнения
1
у(х) - 0,5 У xel{y) dt = е~х. о
В вычислениях положить п = 3.
< Выбираем равноотстоящие узлы xi = 0, = 0,5, хз = 1. Значения
ядра К(х, t) = хе1 и правой части /(а;) = е~х в точках (xi, tj) и Xi соответственно оформим в виде таблиц:
§ 3. Численные методы решения интегральных уравнений 261
Таблица значений Kij = tj)
ч Xi
0 0,5 1
0 0 0,5 1
0,5 0 0,8244 1,6487
1 0 1,3592 2,7183
Таблица значений Д =/(xt)
Xi 0 0,5 1
1 0,6065 0,3679
Квадратурная формула Симпсона (см. (3)) в нашем случае имеет вид
F(x)dw i(F(0) + 4F(0,5) + F(l)),
О
так как h = 1/2, Л = h/3 = 1/6, А2 = 4Н/3 = 4/6, А3 = h/З = 1/6.
Для определения приближенных значений i = 1, 2, 3, решения у(х) в узлах Xi согласно (3) получим, используя таблицы значений и fi, следующую систему линейных уравнений:
У\ = 1,
- ^(0,оу, +3,2976^ + 1,35921/3) = 0,6065, (4)
Уз - <^(91 + 6,5948J/2 + 2,7183г/з) = 0,3679.
После упрощения система (4) перепишется в виде
У1 = 1,
0,7252?/2 - 0, ИЗЗт/з = 0,6482, (5)
0,54961/2 - 0,7735г/з = -0,4512.
Решая систему (5), находим
2/1 = 1, 3/2 = 1,1079, уз = 1,3706.
Следовательно, приближенное решение интегрального уравнения выражается формулой
у(х) = е~х + 1, ООЗх.
Заметим, что точное решение уравнения есть у(х) = е~х 4- х. >
262
Гл. 15. Интегральные уравнения
Изложенный выше метод применяется также для приближенного решения интегрального уравнения Вольтерра 2-го рода
X
К(х, t)y{t)dt = f(x),
a £ х b.
В последнем случае полагают, что
Ki:i = 0, j > I.
Действительно, уравнение Вольтерра с ядром К(х, t) можно свести к уравнению Фредгольма с ядром К* (х, t), вводя функцию
К*(х, t) =
7<(z, t), О,
a t х, х < t.
Метод моментов. В методе моментов приближенное решение у интегрального уравнения ищется в виде суммы f(x) и линейной комбинации линейно независимых на отрезке [а, 6] функций <рх(х), • • •,
..., ¥п{х), т.е.
И
у(х) = уп(х) = f{x) + ^2
г=1
(6)
где С], С'2, .. •, сп — некоторые постоянные. Подставляя (6) в (1), получаем невязку
11 п ~
R[yn(x)] = ^сг<р^х) - X'^Ci'ipi^x) -- X К(х, t) f (t) dt, (7)
1=1 г=1 ft
где
ь
ipitx') = / К(х, t) dt, i = 1, 2, ... , n.
Согласно методу моментов коэффициенты Ci, i = 1, 2, ... , п определяются из условий ортогональности невязки ко всем функциям <Р\\х), <Pz(x), ..., <рп(х). Эти условия дают следующую систему линейных уравнений:
ь
/ R[yn(x)]ipi(x)dx = 0, i = 1, 2, ... , п,
§ 3. Численные методы решения интегральных уравнений 263
или в силу (7)
п cj (aij ~ = ^7i > I = 1, 2, . . . , П, (8)
J=1
где
ь otij = У (fii(x)<pj(x)dx, a
b b
/3ij = У dx IК (ж, t) pj(t) dt,
a a
b b
7i = У da; У K(x, t) f(t) dt. a a
Если определить D(X) = det (a^ — АД7) системы (8) отличен от нуля, то коэффициенты ci, 02, ... , сп определяются однозначно. Подставляя их найденные значения в (6), получаем приближенное решение исходного интегрального уравнения.
Замечание. Для удобства вычислений интегралов систему (8) иногда формируют, используя условие ортогональности невязки (7) к некоторой иной системе функций, отличной от системы ipi (а;), </?2, • • • • • • , </?п(ж).
Пример 2. Найти приближенное решение уравнения
1
у(а;) = У К(х, t)y(t)dt = 1, о
где
f (t — l)rr, 0 х t, К(х, t) = l '
I t(x — 1), t X 1.
< Используя выражение для ядра К(х, t), перепишем уравнение в виде
( X 1 \
j* t(x - l)y(t) dt + У (t - 1) xy(t) di j =1.
0 x J
Положим y(x} = = 1 + Cix + c^x2. Тогда невязка R [i/з(ж)] имеет
264
Гл. 15. Интегральные уравнения
вид
RMx)] =
= С]Х + с2х2
/ 4 с2 , ( х4
~ 12+МТ
х(х — I)2 + _
Из условия ортогональности невязки Я[у2(ж)] к функциям жиж2 получаем следующую систему:
1
У R [у2(ж)] xdx — О, о
1
У R [?/2(ж)] х2 dx = 0. о
После вычисления интегралов и некоторых преобразований получим следующую систему линейных уравнений для определения и с2:
0,3555ci + 0, 3146с2 = -0,1167, 0,2638ci + 0, 2417с2 = -0,025.
Решая эту систему, находим a = 0,027, с2 = -0,029. Приближенное решение исходного интегрального уравнения имеет вид у(х) = 1 + + 0,027ж - 0,029ж2. t>
Замечание. Мы не приводим оценок точности приближенного решения для изложенных методов ввиду довольно громоздких выкладок. Изложение этих вопросов можно найти в специальной литературе1).
Решить интегральные уравнения методом конечных сумм, либо методом моментов. В методе моментов использовать функции у)к(х) — хк, & = 0, 1, 2, ... , п:
1
' 15.162. у(х) — 4 У sin2(rrt2) y(t) dt = 2ж — тг. о 1
15.163. у(х) - У earcsin y(t) dt = tg х. о
^См., например, Березин И.С., Жидков Н.П. Методы вычислений. — Т. 2. — М.: Физматгиз, 1962, гл. 10, § 10.
§ 3. Численные методы решения интегральных уравнений 265
1
15.164. у(х) — У tg е0,1^2^ y(t) dt = etg (x + 5). о
i
15.165. y(x} — У sin (x + 1/ ?/(i) dt = x2 + 5.
о
1
15.166. y(x) — - / (x2 + sinzi) y(t) dt = cos 2x.
О J
0
1
15.167. y(x) + - f xln(x2 + 10£2 + 3) y(t) dt = x2 + 3z.
о
i
15.168. y(x) — 5 У tg e0,lf:r y(t) dt ~ cos2 x.
о
1
15.169. y(x) — [ (1 + sin ext) у(t) dt = -(x + 8).
J O
0
1
15.170. y(x) - 3 У (x2t2 + ext + 1) y(t) dt = cos 2x.
о
i
15.171. y(x) + 5 У ext+t2 y(t) dt = In (1 + x).
о
1
15.172. y(x) + У (x sini — \4) y(t) dt = cos 3x.
о
i
15.173. y(x) — У (xt + rr2 cosi) y(t) dt = x — 2.
о
1
15.174. y(x) — У (x + 3)ext+t y(t) dt = x(ex + 2).
о
66 Гл. 15. Интегральные уравнения
1
15.175. у(х) — - / cos In ((й 4- 5)rr) y(t) dt = sinrr.
5 J о i
15.176. y(x) — y* (5zarcsin£ - In (t + 8)) y(t) dt = x2 + 8. о
1
15.177. y(x) — 4 У xex2+tx y(t) dt = e2x 4- 8. о i
15.178. y(x) 4- У cos 2ir(x2 4- tx) y(t) dt — x2 4- sin x. о
i
15.179. y(x) — 4 У (x2t 4- sinxt 4- In (t 4- 4)) y(t) dt = ex2 4- 8. о
X
15.180. y(x) - У (x — sin xt) y(t) dt = sin x, 0 C x 1. о
x
15.181. y(x) — У (1 4- x2t — etx) y(t) dt = e2x 4- x, 0 < x < 1. о
X
15.182. y(x) — У sin (3rr — %tx) y(t) dt = 1 — 2 cos x, 0 C x 1. о
x
15.183. y(x) - [ et3x2-5tx y(t) dt = e3x + 9, 0 x < 1.
0 x
15.184. y(x) — У (x In (t 4- 8) - t) y(t) dt = ^e2x 4- x, 0 x 1. о
Глава 16
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Основные задачи и уравнения математической физики
1. Вывод уравнений и постановка задач математической физики. Многие задачи механики, физики, широкий круг инженерно-технических задач приводят к исследованию дифференциальных уравнений с частными производными второго порядка, являющихся частным случаем так называемых уравнений математической физики.
Их вывод опирается на механические или физические законы. Из всего многообразия таких задач мы ограничимся лишь несколькими простейшими, иллюстрирующими некоторые методы построения математических моделей реальных физических или механических процессов.
Пример 1. Вывести уравнение распространения тепла в изотропном твердом теле.
<] Обозначим температуру тела в точке М(х, у, z) в момент времени t символом и(х, у, z, t). Как известно, в теле происходит движение тепла от более нагретых частей к менее нагретым. В теории теплопроводности принято, что количество тепла AQ, проходящего через некоторый элемент поверхности Дет, лежащий внутри данного тела, пропорционально дпдг, где ДП — поток вектора grad и через элемент Д<т, т.е.
AQ = &ДПД£. (1)
Здесь к — к(х, у, z) — коэффициент теплопроводности.
Выделим внутри тела произвольный объем V, ограниченный гладкой замкнутой поверхностью S, и составим уравнение теплового баланса для выделенного объема. Пусть Qi — количество тепла, входящего в V через поверхность S за промежуток времени (£, t + Д^). Тогда из (1) следует, что
Qi = k(M)(gradu, da) At.
Е
Обозначим Q? количество тепла, выделяемого или поглощаемого в объеме V за промежуток (t, t + Д£) вследствие имеющихся в этом объеме источников (или стоков), плотность которых, т.е. количество поглощаемого или выделяемого тепла за единицу времени в единице объема,
268
Гл. 16. Уравнения в частных производных
обозначим F(x, у, z, i). Ясно что
Q2 = УУУ F(x, у, z, t) dv St,
V
а тогда, используя формулу Гаусса -Остроградского, для общего количества тепла, приходящего в объем V за промежуток времени (t, t + St), получаем выражение
Qi +Q2 = Щ div (A: grad u) dv St + УУУ F\x, y, z, t) dv St. (2) V V
С другой стороны, на изменение температуры объема тела V за время (t, t + St) на величину Stu = u(x, у, z, t + St) - u(x, y, z, t) «
du(M, t)
«--------Ai необходимо затратить следующее количество тепла:
dt
Qe = JЦ [u(x, у, z + St) - u(x, у, x, i)]7(x, у, z) p(x, y, z) dv « allhpTtdv&t’ (3) V
где 7 = 7(M) — теплоемкость вещества, а р = р(М) — его плотность. Но Qi + Q2 = Q3, а потому из (2) и (3) следует соотношение
ш w
V
— div (A:gradu) — F(x, у, z, t) dv = 0.
Так как объем V произволен, а подынтегральная функция непрерывна, то отсюда следует, что в любой момент времени t должно выполняться соотношение
Эи
^р —- = div (A: grad и) + F(M, t). (4)
dt
Это уравнение (4) называется уравнением теплопроводности неоднородного изотропного тела. Если тело однородно, то 7, р и к постоянные и уравнение (4) запишется в виде
du .2 ( d2u d2u d2u\ .. .
~dt = a + dy^ + ~dt2J+ г’
где
/А: .. . 1 . .
a = \ , f(x, y, z, t) = ~F(x, y, z, t). >
V 7P 7P
§1. Основные задачи и уравнения математической физики 269
Для вычисления температуры тела и(х, у, z, i) в любой точке тела и в любой момент времени t недостаточно решения уравнения (4) или (5). Из физических соотношений следует, что необходимо знать еще распределение температуры внутри тела в начальный момент времени (начальное условие) и тепловой режим на границе тела (граничное условие). Точно так же и для решения других задач математической физики требуется знание начальных (если процесс нестационарный) и граничных условий. Поэтому под постановкой задачи в дальнейшем подразумевается выбор функции, характеризующей исследуемый физический процесс, вывод (или выбор) соответствующего этому процессу уравнения, установление граничных условий и формулировка начальных условий.
Пример 2. Поставить задачу об определении температуры однородного изотропного стержня 0 х / с теплоизолированной боковой поверхностью, если его начальная температура есть некоторая функция х, а на концы стержня подается извне заданный тепловой поток.
<1 Температура стержня зависит только ст координаты точки х G [О, I] и времени t, т.е. и = и(х, t). Внутри стержня источники тепла отсутствуют, т.е. F(x, у, z, t) = 0. Поэтому уравнение (5) принимает вид ди(х, t) 9д2и(х, t) 9 к тт
-------— а—х—;—, гДе а — —• Начальное условие записывается в ot-----дх2 ур
виде и(х, 0) = <р(х), 0 х I, где <^(.т) — заданная функция. Граничные условия имеют вид
<(0, 0 = -7y-Qi(0, <(М) = Л<72(£), о < t < 00, ко ка
где а — площадь поперечного сечения стержня, Qi(t) и #2(0 — тепловые потоки (количество тепла, поступающего в единицу времени) в стержень через его концы. Таким образом, имеем задачу:
Найти решение и(х, t) уравнения
ди(х, t) 2д2и(х, t) 2 к
—тс—=а —, а = —, 0 < t < оо, (6)
dt их2 ур
удовлетворяющее условиям:
и(х, 0) = <р(х) (начальное условие),
<(0, 0 = -7у-?1(0>
। а (граничные, или краевые, условия). [> (7)
0 = ту <72 (О ка
Рассмотренная в примере 2 задача относится к так называемым смешанным задачам, в которых участвуют как начальные, так и граничные условия. Граничные условия (7), наложенные на значение производной и'х(х, t), называют условиями второго рода. Рассматриваются также
270
Гл. 16. Уравнения в частных производных
задачи с условиями первого рода, наложенными на значения функции iRx, t),
u(0, t) = u(l, t) = (8)
и с условиями третьего рода, наложенными как на значения функции и(х, t), так и на значения производной и'х(х, t),
= ^i(0, х=0
/ <9и \
— + du \ох J
= ^2(f). х—1
(9)
Условия (9) означает упругое закрепление в точках х — 0 и х = I.
Кроме смешанной задачи достаточно часто встречается задача Коши, состоящая в отыскании решения и(х, t) в области —оо < х < оо, 0 < t < < оо, удовлетворяющего только начальным условиям (например, условию и(х, 0) = <р(х) для уравнения (6)).
16.1 **. Вывести уравнение малых колебаний закрепленной на концах х = 0 и х = I натянутой струны, т. е. свободно изгибающейся в плоскости горизонтальной тонкой нити. Действующая на струну сила натяжения Т значительно больше силы тяжести, т. е. действием силы тяжести можно пренебречь.
16.2 . Используя уравнение задачи 16.1, поставить задачу о вынужденных колебаниях закрепленной на концах х = 0 и х = I горизонтальной однородной струны, если в момент t = 0 струна имела форму <р(х), 0 х I, и скорость струны в каждой ее точке задается функцией 'ф(х).
16.3 *. Используя уравнение задачи 16.1, поставить задачу о свободных колебаниях закрепленной на конце х = I горизонтальной однородной струны, левый конец которой (при х — 0) движется так, что касательная в этом конце (при х —> +0) в любой момент времени горизонтальна. В момент t = 0 струна имела формулу <р{х), а скорость каждой точки равна нулю.
16.4 **. Рассматривая однородную двухпроводную линию равномерно распределенных индуктивностей, сопротивлений, емкостей и утечки, вывести волновое уравнение, называемое также уравнением длинной линии. (Ввести величины: L — индуктивность, С — емкость, R — сопротивление, G — коэффициент утечки, которые считать отнесенными к единице длины.)
16.5 . Используя уравнение задачи 16.4, поставить задачу об отыскании закона изменения напряжения и силы тока в длинной линии (0 х < ос) без потерь (т.е. R = G = 0), если известны начальные напряжение <р(х), сила тока ^{х}, а напряжение в точке х = 0 постоянно и равно Eq.
17.6*. Воспользовавшись уравнение (6) примера 2, поставить задачу о распределении температуры внутри однородного изотропного стержня, начальная температура которого равна uq, при свободном внутреннем теплообмене, если в левом конце его (при
§ 1. Основные задачи и уравнения математической физики 271
х = 0) поддерживается постоянная температура uq, а через правый конец (при х — I > 0) происходит теплообмен с окружающей средой, температура которой задана функцией <p(t).
16.7. На границе бесконечного изотропного однородного цилиндра, направляющая которого — кривая L — лежит в плоскости, перпендикулярной образующей, поддерживается температура, зависящая только от положения точки на L. Используя уравнение (5) примера 1, поставить задачу об установившемся стационарном распределении температуры внутри цилиндра (плоская задача Дирихле).
2. Приведение уравнений к каноническому виду. Общее уравнение второго порядка относительно функции u(xi, х%, ... , хп) неизвестных Xi, Х2, ••• , хп имеет вид
п
, хп)
i,j=l
д2и dxi dxj
( ди ди
"b f 1*^1) • • • ) ^П, д 5 • ’ ‘ ) д
у dxi дхп
= 0.
(10)
Методы решения таких уравнений и характер описываемых этими уравнениями процессов зависят от вида квадратичной формы
71
aij(Xi, ... , Xn)titj (11)
г, j—1
в каждой точке Мо(х°, ... , т°) некоторой области D n-мерного пространства.
Как известно, выбором линейного преобразования матрица (агДхЧ, ... , t°))”j=1 квадратичной формы (11) может быть приведена к каноническому (диагональному) виду, причем согласно закону инерции число положительных, отрицательных и равных нулю коэффициентов канонического вида матрицы не зависит от способа диагонализации.
В соответствии с этим уравнение (10) в точке Mq (в области D) называется уравнением эллиптического типа, если все п коэффициентов канонического вида квадратичной формы одного знака, т. е. квадратичная форма (11) является положительно либо отрицательно определенной в точке Mq (соответственно в области D). К уравнениям эллиптического типа обычно приводят задачи о стационарных тепловых процессах, об отыскании гармонических в области D функций.
Уравнение (10) имеет гиперболический тип в точке Mq (в области D), если в точке Mq (соответственно в области D) п — 1 коэффициент канонического вида квадратичной формы (11) имеет один знак, а один коэффициент противоположен им по знаку. К уравнениям гиперболического типа приводят различные задачи о колебательных процессах. В более общем случае уравнение (10) имеет ультрагиперболический тип, если т коэффициентов канонического вида квадратичной формы одного знака, а остальные п — т — противоположного.
212
Гл. 16. Уравнения в частных производных
Наконец, уравнение (10) имеет в точке Мо (в области D) параболический тип, если в точке Мо (соответственно в области D) хотя бы один из коэффициентов канонического вида квадратичной формы (И) равен нулю. Такие уравнения описывают процессы распространения тепла, диффузии и некоторые другие.
В случае двух независимых переменных х и у уравнение (10) обычно записывается следующим образом:
. .д2и . д2и . .д2и ( ди ди\
а(х, у)—+2Ь(х, У)д^+с(х, (z, у, u, = 0.
(12)
Соответствующая ему квадратичная форма имеет вид
а(т, y)tl + 2b(x, y}tit2 + с(ж, y)t}.
Тип уравнения (12) .может быть определен и без приведения квадратичной формы к каноническому виду. Именно: уравнение (12) имеет в точке Мо(жо, уо) (в области D)
эллиптический тип, если ас — Ь2 > 0, гиперболический тип, если ас—Ь2 < 0, параболический тип, если ас — Ь2 = 0
в точке Мо (соответственно в области D).
Уравнение
а(х, у) dy2 — 26(т, у) dx dy + с(х, у) dx2 =0 (13)
называется характеристическим для уравнения (12), а его общие интегралы
<^(ж, у) = С, i/i(x, у) = С
— характеристиками.
Характеристики линейного уравнения в частных производных второго порядка (12) используются для приведения его к каноническому виду. Для уравнения гиперболического типа (ас - Ъ2 < 0) характеристики действительны и различны. Полагая £ = (р(х, у) и г] = 'ipfx, у), приводим уравнение (12) к виду
или
д2и дг]
+ $ С г], и,
ди ди\ _
(14)
д2и д2и д^~д^
ди ди \
др) =0,
1 1
если положить дополнительно а = ~(£ + rf), /3 = -(£ — rf).
(14')
§ 1. Основные задачи и уравнения математической физики 273
Для уравнения эллиптического типа (ас — Ь2 > 0) характеристики комплексные и комплексно сопряжены (<р(я, у) = ф(х, ?/)). Полагая С = + ^х' у^ = 3/) и У = у) - ф(х, у)) -
= Im<^(z, ту), уравнение (12) приводим к виду
d2u d2u
+ dtf +
Ф2
6 Vi u,
du du \ d^ ’ dyJ
= 0.
(15)
В случае уравнения параболического типа (ас — Ь2 =0) имеется только одна характеристика <р(х, у) = С. Полагая £ = <р(х, у) и у = = у), где ф(х, у) — произвольная функция, независимая с <^(ж, у)
А /Л
0 1, получаем
ФХ Фу J
т. e. якобиан I =
d2u ( du du\
—+Ф3 (j, ту, u, —, — j
- 0.
(16)
Уравнения (14), (14'), (15), (16) называются каноническими.
Рассмотренный метод приведения уравнения (12) к каноническому виду (14)—(16) и решение полученного уравнения носит название метода характеристик.
Так как для каждого типа канонических уравнений разработаны определенные методы как аналитического, так и численного решения, то задача приведения уравнений (12) к каноническому виду представляет практический интерес.
Заметим, что в различных областях тип одного и того же уравнения (12) может быть различным.
Пример 3. Определить тип уравнения
2 2
У2и"х + Х2и" - —и1 - —их = 0 у у у у х
(17)
и привести его к каноническому виду.
<3 Так как ас — Ъ2 = у2х2 > 0 во всех точках, не лежащих на прямых х = 0 или у = 0, то в любом открытом квадранте заданное уравнение имеет эллиптический тип. Составим характеристическое уравнение
у2 dy2 + х2 dx2 = 0.
Оно имеет комплексно сопряженные общие интегралы у2 + ix2 = к и У2 — ix2 = к. Поэтому полагаем £ = у2 и у = х2. Тогда имеем
их — и'А + и'Х1'х = U't] 2^,
иу = иА + иА = 2у,
и"х = ЩА + uwVX) 2х + и'п 2 = u”v • 4ж2 + 2и'у,
иуу = (и'1А + 2у + и'с2 = u'U 4^2 + 2Ч-
274 Гл. 16. Уравнения в частных производных
Подставив эти значения в исходное уравнение, получим
2 2
у^АхГи'^ 4- 2и'?) 4- х2{^у2и'^ 4- 2п^) - ~2уи'^ - ^2хип = О,
т.е. 4т2?/2(?/''?/ 4- и'^ — 0. Сокращая на 4т2?/2 0, приходим к уравне-
нию канонического вида и'^ + и''1Г} — 0. Отсюда заключаем, что решение уравнения является гармонической функцией по переменным £ и ?/. >
В задачах 16.8-16.18 определить тип уравнений и привести их
к каноническому виду:
16.8.
16.9.
d2u г д2и дх2 ° дх ду д2и д2и -----1- 4--- дх2 дх ду
д2и
4- 4---
ду2
= 0.
д2и ди ди dyz дх ду
= 0.
16.10.
д2и д2и <Э2и дх2 дх ду + ду2
-.п ^2и о / ^2‘и ^2и 16.П. х 4- 2^ху +у - дх/ дх ду dyz 1 ( у \ ди V = °-
~ о \ ~г ~ УУ ] 2 \\/х v J
г,д2и д2и 9д2у Ifil? о/ Оги 1 rpt & = 0.
J-О.Ал. у „ ^Ху q । <л о dxz дх ду dyz 7д2и ->д2и п ди 16.13. у2^~х - - 2т— = 0. dxz dyz дх д2и д2и 1 ди 1 ди
16'и'ХУдх2 + ду2 + 2Удх 2у ду -.«ir д2и д2и 9 д2и = 0 в области т f ди ди' 0, у > 0.
dxz дх ду dyz _ _ д2и д2и 16.16. - ттг—= 0. dxz dyz д2и д2и CtgT — + — \дх ду' ) - 0.
16.17. т—ч 4- т-—т = 0 в области т dxz dyz ^0.
д2и 9д2и
4- 2т?/—— 4- у2^~2 = 0. дх ду dyz
16.18. А дх/
16.19**. Найти общее решение уравнения из задачи 16.8.
16.20. Найти общее решение уравнения из задачи 16.9.
16.21. Найти общее решение уравнения из задачи 16.11.
16.22. Найти общее решение уравнения из задачи 16.15.
16.23. Найти общее решение уравнения из задачи 16.18.
§ 2. Аналитические методы решения уравнений
275
§ 2. Аналитические методы решения уравнений математической физики
1. Метод Даламбера. Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый в этом случае методом Даламбера. В основе его лежит тот факт, что с помощью замены £ = х + at, р = х — at уравнение
преобразуется в уравнение — = 0 (см. задачу 16.5), которое имеет об, ОТ]
общее решение Д£, р) = Ф(£) + ^(т/), где Ф и F — произвольные дважды дифференцируемые функции. Для определения этих функций Ф и F, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным х и t, то решение имеет вид
Дх, t) = Ф(х + at) + F(x — at).
Здесь F(x — at) характеризует прямую волну (кривая F(x) смещается вправо со скоростью а), а Ф(.т + at) — обратную волну (кривая Ф(т) смещается влево со скоростью а).
Если рассматривается задача Коши для бесконечной струны — оо < < х < оо, то по заданным начальным условиям
и{х, 0) = Дх), u't(x, 0) = гДх) (2)
определяются функции Ф и F и искомое решение {формула Даламбера)
x+at
1 1 Г
Дх, t) = ~[Дх — at) + Дх + at)] + — / Дг) dz.
r— at
(3)
Пример 1. Найти решение Дх, t) задачи Коши ( —оо < х
д‘2и д2и . дДх, 0)
= -к~у, Дх, 0 = cosx, -----------— = 0.
dt2 дх2 dt
<] Используя формулу Даламбера (3), имеем
Дх, t) = |[cos(t — t) + cos(x + i)] = cos x cos t. I>
Используя формулу Даламбера, найти решения u{x, t) следующих задач Коши (—оо < х < оо, Q < t < оо):
276
Гл. 16. Уравнения в частных производных
16.24. Найти решение уравнения u"t = uxx при начальных условиях и(х, 0) =----, u't(x, 0) = 0.
16.25. Найти решение уравнения u"t = uxx при начальных sin х .. х
условиях и{х, 0) =----, ut(x, 0) = ---%.
X 1 + X1
16.26. Найти решение уравнения u”t = ^хх при начальных
у UJIUOKI/IA V у 14" 2 ’ ? ' O1JL1 • 16.27. Найти решение уравнения u"t = и" ^хх при начальных
условиях ц(ж, 0) 16.28. Найти 1 1 4- х2 ’ решение u'tix, 0) = cos X. уравнения u'[t = ихх при начальных
2
условиях и(х, 0) = е~х , u't(x, 0) = у—-—%
16.29*. Найти закон свободных колебаний бесконечной струны,
если начальная скорость каждой ее точки равна нулю, а начальное отклонение задается функцией
10
х
2к — х
при х 6 (—оо, 0) U (2/, оо), при х G (0, /), при х G (/, 2/).
Построить на чертеже профиль струны в моменты времени t = = l/2a и t = l/a (а — входящая в уравнение (1) постоянная).
16.30* . Найти решение уравнения u"t = а2ихх при начальных условиях и(х, 0) = (р(х) = 0,
(0 при
—а при а при
|т| > h,
—h < х < 0, 0 < х < h.
Построить профиль струны в моменты времени t = h/{2a) и t = = 3h/(2a).
В случае полубесконечной струны кроме начальных условий (2), заданных при 0 х < оо, необходимо добавить еще граничное условие (конец струны предполагается в точке х = 0)
u(0, t) = 0 (4)
для закрепленной в точке х = 0 струны,
<(0, Г) = О (5)
§ 2. Аналитические методы решения уравнений
277
для свободного конца в точке х = О,
г/f,. (0, t) - /ш(0, t) = О
для упругого закрепления в точке х = 0.
Из условий (2) и (4) следует, что <^(0) = 0.
В случае однородных граничных условий (4) или (5) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (4), т.е. </?(—х) = —<р(х), 1р(-х) = —'ф(х), и четным образом для условия (5), т.е. <р(—х) = <^(ж), V>(-x) ~ ^(ж).
Э^и д2и
Пример 2. Найти решение уравнения -г-у = а2-—-, ot2 дх2
0 х < оо,
, 9 ди(х, 0) . о
О < t < оо, удовлетворяющее условиям и\х, (J) = х, ——--- = sin х,
u(0, t) = 0.
<1 Продолжим функции <£>(т) = х2 и V'(z) — sin2 х на отрицательную полуось нечетным образом:
<^1(я) =
при
при
х О, х < 0;
{sin2 х при ж > О,
— sin х при X < U.
Тогда по формуле Даламбера (3) решение запишется следующим образом:
ж+at
dz =
x+at
1 f . 2 j — / sin zdz 2a J
при t
+ at)2 - (ж — at)2] +
sin2 z dz при
>0,
x2 + a2t2 -f- ----cos2zsin2at при t -,
2 4a a
1 x
2axt + — \2x — sin 2x cos 2at] при t > — > 0. > 4a a
278
Гл. 16. Уравнения в частных производных
Замечание. Как следует из формулы Даламбера (3) и уравнения (1), входящая в условие (2) функция ср(х) должна иметь вторую производную, а функция ip(x) — первую. Однако в последующих задачах мы будем рассматривать функции <^(ж) с угловыми точками, а функции i/i(x) — с точками разрыва, предполагая тем не менее, что определяемая по формуле (3) функция является решением (вообще говоря, обобщенным) исходного уравнения (1). Это объясняется тем, что путем незначительных изменений функции ср и можно сделать достаточно гладкими и полученные для этих сглаженных функций по формуле (3) решения и*(т, t) будут мало отличаться от ц(т, t).
Используя метод продолжения и формулу Даламбера, найти решения следующих задач:
16.31. В области 0 z < оо, 0 < £ < оо найти решение уравнения (1), удовлетворяющее условиям
и(х, 0) = 0, щ(х, 0) = sinz, ?/т(0, t) = 0.
16.32. В области 0 z < оо, 0 < £ < оо найти решение уравнения (1), удовлетворяющее условиям
✓
и(х, 0) = у--j-—2, u't(xi 0) — 0, гДО, t) — fl-
16.33. В области 0 а: < оо, 0 < £ < оо найти решение уравнения (1), удовлетворяющее условиям
и(х, 0) = 0, ut(x, 0) = - 9, г/(0, t) = 0.
1 4- хл
16.34. В области 0 z < оо, 0 < t < оо найти решение уравнения (1), удовлетворяющее условиям
^2
ц(д:, 0) 2? H‘t(xi А) ’ о’ А-
1 + X* 1 + Х£
16.35. В области 0 С х < оо, 0 < t < ос найти решение уравнения (1), удовлетворяющее условиям
и(х, 0) = е х , ut(x, 0) = sinz, г/(0, t) — 0.
16.36. В области 0 z < оо, 0 < £ < оо найти решение уравнения (1), удовлетворяющее условиям
{7VX
sinT при .г-е [0,/],
0 при х G (/, оо),
u't(x, 0) = 0, u(0, £) = 0.
Построить график решения в моменты t = l/(4a) и t = 81/(4a).
§ 2. Аналитические методы решения уравнений 279
16.37. Полуограниченная струна (u(0, t) = 0) в начальный момент имеет форму м(.т, 0) = 0 и начальную скорость
m = J с п₽" х е [°- ')-’ (0 при х € [/, оо).
Найти форму струны для момента времени t = l/a и I = 51/а, где а — входящая в уравнение (1) константа.
2. Гильбертовы пространства. Ортогональные системы. Одним из наиболее распространенных аналитических методов решения уравнений математической физики является так называемый метод Фурье, который опирается на свойства ортогональных систем и ортогональных разложений. Поэтому изложению метода Фурье мы предпосылаем ряд задач на свойства ортогональных систем, ортогональных рядов и на решение краевых задач обыкновенных дифференциальных уравнений.
Пусть в векторном пространстве U введено скалярное (внутреннее) произведение (х, у) векторов х 6 U и у 6 U (см. Часть 1, гл. 3, § 1, п. 3), удовлетворяющее условиям:
1) (X, У) = (У, X),
2) (Х1 + х2, у) = (xi, у) + (х2, у),
3) (Ах, у) = А(х, у), А е О,
4) (х, х) 0, причем (х, х) = 0 <-> х = 0.
Нормой элемента х Е U, обозначаемой ||х||, называется число, равное ^/(х, х), т.е. ||x|j2 — (х, х). Последовательность векторов {xn} С U называется фундаментальной, если она удовлетворяет условию: для всех е > 0 существует N = N(e) такое, что для любых ni, n2 > N(e) выполняется неравенство ||хП1 — хП2|| < е. Пространство U называется полным, если любая фундаментальная последовательность векторов {хп} этого пространства имеет предел хо 6 U. Полное линейное векторное пространство со скалярным произведением называется пространствам Гильберта и обозначается буквой Н.
16.38 *. Доказать, что удовлетворяющее условиям 1)-4) скалярное произведение есть непрерывная функция относительно сходимости по норме, т.е. если ||хп — х|| —> 0 и ||уп — у|| -> 0 при п -> оо, то и I(хп, уп) - (х, у)| -> 0 при п оо.
16.39 . Доказать, что линейные операции над векторами гильбертова пространства Н непрерывны, т.е. если ||хп — х|| —> 0, 1|Уп ~ У|| —> 0 и последовательность чисел Хп —> А (п —> оо), то 11(хп + Уп) ~ (х + у)|| -> 0 и ||Апхп - Ах|| -> 0.
16.40 *. Доказать, что конечномерное евклидово пространство является полным.
16.41 . Пусть I2 — векторное пространство бесконечных последовательностей х = (xi, Х2, ..., хп, ...) с действительными (ком-оо
йлексными) компонентами хп, п 6 N, причем |дп|2 < 00. До-
п=1
280
Гл. 16. Уравнения в частных производных
оо
казать, что соотношение (х, у) = задает скалярное про-
71=1
изведение в пространстве
16.42 . Доказать, что счетное множество В = {en, n G N; еп = = (0, ..., 0, 1,0, ...образует ортонормированный базис в пространстве I2 относительно скалярного произведения задачи 16.41.
16.43 *. Доказать, что I2 является пространством Гильберта.
16.44 . Пусть £2 (а, Ь) — пространство заданных на [а, Ь] ком-ь
плекснозначных функций f(x) таких, что | / (z) |2 dx < 00. Счи-
a
Ь
тая известным, что из условия j\f(x)\2dx = 0 следует f(x) = a
= 0(х\ где 0(х) — нулевой элемент пространства £2(0., Ь), доказать, что если f(x) G L2(a, 6), g(x) G £2(a, b), то соотноше-b
ние (/, g) = f f(x)g(x) dx определяет скалярное произведение в a
L^a, b). Написать неравенство Коши-Буняковского в L2 (а, 6), называемое также неравенством Шварца (см. Часть 1, с. 122).
16.45 *. Доказать, что последовательность непрерывных функций
(—1 при t G [—1, — 1/п],
nt при t G [—1/п, 1/п],
1 при t G [1/п, 1]
фундаментальна в пространстве непрерывных на отрезке [—1, 1] / 1 х 1/2
функций с нормой ( f (/(£) “ fi'(i))2 dt j , но не имеет предела. \-1 /
Таким образом, это пространство не является полным.
16.46. Пусть £2(а’ — пространство заданных на [а, Ь] функ-
ь
ций /(ж) таких, что j\f(x)\2p(x)dx < 00, где весовая функция а
р(х) 0 и может обращаться в нуль только в отдельных точках
§ 2. Аналитические методы решения уравнений
281
Доказать, что если /(z) G Lp2(z, 6), </(z) G 6), то соотношение
ь
(Л £/) = У /Шх)р(х) dx
a
определяет скалярное произведение в L^a, Ь) (см. условие задачи 16.44).
Система функций {(рп(х)}^=0, заданных на отрезке [а, Ь], называется ортогональной на [а, Ь], если
а) <рп(х) G L2(a, b), п - 0, 1, ...; ь
\ f i \ i \ Г 0 при m / п,
б) (<^п, 4>т) - J <Рп(х) <pm(x) dx - | 0 при т = п
а
Система функций {<^?l(z)}^_0 называется ортогональной на [а, 6] с весом p(z), если
а) <рп(х) € Lp2(a, b), п = 0, 1, ...;
ь
/( 0 при т п, Vn(x) фт(х) р(х) dx = < , . п
V dn 0 при т — п. а
Если dn = 1 для всех п = 0, 1 ..., то система называется ортонор-мированной на [а, Ь] или соответственно ортонормир овинной на [а, Ь] Свесом р(х).
На примерах следующих задач убедиться в существовании ортогональных и ортогональных с весом систем функций:
16.47. Доказать, что тригонометрическая система функций
1, cosz, sinz, cos2z, sin2z, ..., cosnz, sinnz,
ортогональна на отрезке [—д, д], а система
1 cos z sin z л/2д’ л/д ’ \А ’
cos пх sin пх
ортонормирована на [—д, д].
. Л тт Г 1 °°
16.48. Доказать, что система функций s cos —— > ортого-
I I Jп=0
нальна на отрезке [О, I].
. Л тт f . 2%nz 1
16.49. Доказать, что система функций < sin —-— > ортого-I ) тбМ
Нальна на отрезке [0, 1/2].
282 Гл. 16. Уравнения в частных производных
16.50. Пусть система функций fo(x), /1(.т), ..., fn(x), ... из L‘2(a, Ъ) линейно независима на [а, Ь]. Доказать по индукции, что построенные по рекуррентной формуле функции
Ых)
П/о||’
п—1
fn(x) - ^2 (/п,
=
п-1
fn — ^2 Р’^р’к
к~0
n = 1, 2, ...,
образуют ортонормированную на [а, Ь] систему (метод ортогонализации Шмидта).
16.51. Используя метод ортогонализации Шмидта (см. задачу 16.50), найти первые четыре функции (ортонормированные полиномы Лежандра Pq(x)^ Pi(x), Pz(x) и Рз(тт)), полученные при ортогонализации системы степеней 1, ж, х2, ... на отрезке [~1, 1]-
16.52. Используя метод ортогонализации Шмидта (см. задачу 16.50), найти первые 4 функции, получаемые при ортогонализации системы степеней 1, х, х2, ... на отрезке [—1, 1] с весом р(х) =
= (ортонормированные полиномы Чебышева).
v 1 — х2
16.53* . Ненормированный полиномы Чебышева с коэффициентом 1 при старшей степени имеют вид
То(.т) = 1, Тп(х) — —4т cos (narccos т), —1 < х < 1
2П *
(n G N). Доказать, что система {Тп(т)}^_0 ортогональна на [—1, 1] z ч 1
с весом р1х) = —7- — .. vTT?
16.54. Используя метод ортогонализации Шмидта (см. задачу 16.50), найти первые 3 функции, полученные при ортогонализации системы степеней 1, т, х2, ... на отрезке [0, 1].
Функции Радемахера гп(х) определяются следующим образом:
гп(т) — sign sin 2п+17гт, п = 0, 1, ...,
§ 2. Аналитические методы решения уравнений
283
где
(1 при х > О,
О при х = О,
— 1 при х < О.
16.55. Построить графики функций Радемахера гп(ж) для п — = 0, 1, 2, 3.
16.56. Показать, что при д > v каждый интервал постоянства функции г|У(т) содержит четное число 2[L~V интервалов постоянства гм(ж).
16.57. Доказать ортонормированность системы {гп(я?)}^_0 на отрезке [0, 1].
Функции Уолша IV,г(х), х Е [0, 1], в нумерации Пэли определяются следующим образом:
Wo(.r) = 1, W2k(x) = гк(х), /г = 0, 1,
и если н = 2П’ + 2П2 + ... + 2n", rii > п2 > • • > п„ 0, то
У У
И'п(ж) = JJ ИМя) = П rnfc(z), fc=l A'=l
где гп(т) — функции Радемахера, причем в точках разрыва
= ^[И „(х + 0) + 1И„о - 0)].
16.58. Построить графики функций Уолша VPn(z) для п = 0, 1, ..., 8.
16.59. Доказать ортонормированность системы {РИП W}~=o на отрезке [0, 1].
16.60* *. Пусть J„(x) — решение уравнения Бесселя х2у" + 4- ху' + (х2 - v2)y = 0, а — корни Л(гс). Доказать, что
система функций { Д|У(д^т)}^_1 ортогональна на отрезке [0, 1] с весом р(х) = х.
Отыскание решения у(х'), х 6 [а, 6], уравнения
(к(хУ(х)У - q(x)y(x) + Хр(х)у(х) = 0, (6)
Удовлетворяющего однородным краевым условиям одного из типов
1) ?/(а) = УУ) = 0,
2) у'У) - у'(IV) = 0,
284
Гл. 16. Уравнения в частных производных
3) у(х) ограничено при х -> а H-О и х -> b -О, будем называть задачей Штурма-Лиувилля. При этом предполагаем, что функции к(х), q(x) и р(т) непрерывны на отрезке [а, Ь], причем к(а) = к(б) — 0 в случае условия типа 3), к(х) > 0, q(x) 0, р(х) > 0 и р(х} ограничена для х Е [а, 6].
В общую задачу Штурма-Лиувилля краевые условия 1)-3) могут входить и в некоторых линейных комбинациях.
Нетривиальные решения у(х) ^0 уравнения (6), удовлетворяющие одному из краевых условий 1)—3), существуют не при всех А. Значение А*, при котором существует нетривиальное решение у*(х) задачи Штурма-Лиувилля, называется собственным числом уравнения (6), а соответствующее ему решение у*(х) — собственной функцией.
Заметим, что собственные функции yi(x) и у2(х) задачи Штурма-Лиувилля, соответствующие различным собственным числам Ai ^2, ортогональны на [а, Ь] с весом р(х), т.е.
ь
(У1, Уг) = У yi(x)y2(x)p(x) dx = 0.
а
Найти собственные числа и собственные функции следующих задач:
16.61* *. у"- Ху = 0, 7/(0) = 7/(0 = 0.
16.62. у" - Ху = 0, /(0) = у'(1) = 0.
16.63. у" -Ху -0, 7/(0) = 7/(0 = 0.
16.64. у" - Ху = 0, 7/(0) = т/G) = 0.
16.65* *. у”(г) 4- ^/(г) +ш2?/(г) = 0, т/(Л) = 0.
3. Ортогональные ряды. Пусть Ф = — ортонормиро-
ванная на [а, 6] система функций, а функция f(x) G £2(а, 6). Тогда существуют числа
ь
сп = cn(J) = (/, </?п) = У f(x)<pn(s)dx, п = 0, 1, ..., а
называемые коэффициентами Фурье функции f(x) по системе Ф. Ряд с этими коэффициентами
ОО /(ж) ~ 52сп(^п(т) п=О
называемые ортогональным разложением или рядом Фурье функции /(ж) по системе Ф.
§ 2. Аналитические методы решения уравнений
285
Если система Ф только ортогональна, а не нормирована, то
ь
1 f ь /
п = 0, 1, ...
а
a
16.66. Используя результат задачи 16.60 (см. решение), найти выражение коэффициентов Фурье-Бесселя функции /(т) 6^(0, 1) (р{х) = х) по системе х)}к^.
16.67* . Нормированные полиномы Лежандра Рп(х) (см. задачу 16.51) можно определить также соотношением {формула Род-рига)
п
.2\п
п = 0, 1, ...
п\2п dxn
они образуют ортогональную на [—1, 1] систему, т.е. 1 ( 0 при m п,
/ Pn{x)Pm(x) dx = < 2
-1 ( 2т1 + 1 Р
Найти первые 4 коэффициента разложения функции /(.т) = |ж|, — 1 < х < 1, если известно, что РЛх) = 1, Р\(х) = ж, РЛх) = = Зт2/2 - 1/2, Ръ(х) = 5я3/2 - Зя/2.
16.68. Записать выражение коэффициентов Фурье функции
/(а;) 6 1, 1) \ р{х) = ] по системе полиномов Чебы-
\ v 1 — х2 J
шева (см. задачу 16.53).
16.69. Для функции /(т) — х на отрезке [0,1] вычислить первые четыре коэффициента ее разложения по системе Уолша в нумерации Пэли.
п
16.70* . Доказать, что частные суммы Sn(f, х) = ск<рк(х) к=0
разложения функции f(x) по системе Ф дают решение следующей задачи о наилучшем среднеквадратичном приближении: в множестве
{п
ВД = (^кфк (^)
fc=0
286
Гл. 16. Уравнения в частных производных
«полиномов» Тп(х) по системе Ф порядка не выше п найти тот, который дает минимум интегралов
min ТпЕЛ/п
ь
У [/W -Tn(x)]2dx. a
16.71. Используя результат задачи 16.70, вывести неравенство Бесселя для конечных сумм
и для бесконечных рядов
f(x)dx.
16.72. Написать неравенство Бесселя задачи 16.71 для коэффициентов Фурье функции f(x) периода 2 л по тригонометрической системе {1, cos пт, 8шпт}пе^.
Ортогональная система Ф = {</?п(т)}^=0 называется полной, если из равенства
ь
!х = 0, п — 0, 1, ...,
следует, что /(т) = 0 почти во всех точках отрезка [а, 6].
Для полных ортонормированных систем неравенство Бесселя обращается в равенство Парсеваля
Рассмотренные ранее тригонометрические системы, система Уолша, система функций Бесселя, системы полиномов Лежандра и Чебышева являются полными.
16.73. Каков смысл неравенства Бесселя и равенства Парсеваля в конечномерном евклидовом векторном пространстве?
16.74* . Доказать, что система функций Радемахера не является полной на отрезке [0, 1].
§ 2. Аналитические методы решения уравнений
287
4. Метод Фурье решения уравнений математической физики. Метод Фурье, широко используемый при решении ряда задач математической физики, состоит в следующем. Искомая функция, зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной или нескольких переменных. По-
сле подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, часть из которых вместе с краевыми условиями исходной задачи являются краевыми задачами Штурма-Лиувилля. Искомое решение представляется рядом по произведениям собственных функций этих задач Штурма-Лиувилля.
Пример 3. Найти отклонение u(x, /) от положения равновесия за-
крепленной на конце х — 0 однородной горизонтальной струны, правый конец которой при х = I перемещается так, что касательная к
струне остается постоянно горизонтальной. В
1 117ГТ 4тгж
мени струна имела форму —sin ——— cos ,
15 21 21
начальный момент вре-начальные скорости от-
сутствовали.
<] Предполагая, что струна совершает малые колебания, получаем следу-
ющую смешанную краевую задачу: найти решение уравнения свободных
колебаний струны
d2u _ 2d2u 2 _ То dt2 a dx2 ’ p
(7)
удовлетворяющее начальным условиям
1 . 117ГЖ 47ГТ du(x, 0)
(*’0)= 15S,n^TC0Slr (8)
и граничным условиям
w(0,/) = 0, <(/,0=0. (9)
Решение этой задачи ищем в виде произведения u(x.t) = X(x)T(t), подставляя которое в (7), находим
Х(х}Т" (t) — a2 X" (x)T(t).
Разделив обе части этого уравнения на а2Аг(ж)Т(/), получаем
Т"(0 _ Х"(х) a2(t) ~ Х(х) ’
(Ю)
Каждое отношение в (10) зависит от своей переменной, поэтому равенство возможно только в том случае, когда каждое из этих отношений
постоянно.
Полагая
= А и используя граничные условия (9),
получаем задачу Штурма-Лиувилля
Х"(х) - АХ(х) = 0, А(0) = Х'(Г) = 0,
288
Гл. 16. Уравнения в частных производных
Л /2Аг — 1 V собственными числами которой являются числа лк = — I ———тг I .
. 2/с — 1
а собственными функциями — функции Хк(х) = sin———тгх, к = 1,
2, ... (см. задачу 16.63). „ / х
Подставив в (10) вместо отношения „его значение А& =
Х(х)
f2k — 1 \2
= — I ———тг 1 , получим при каждом к = 1, 2, ... уравнение
/2^ — 1 \
Г(С = О,
общим решением которого является функция
2А; — 1 2к — 1
Tfc(i) = Ак cos - 7tqZ + Вк sin..—- vat.
Таким образом, решениями уравнения (7), удовлетворяющими граничным условиям (10), являются функции
Uk(x, t) = Tk(t)Xk(x) =
f л 2к - 1 „ . 2к - 1 \ . 2к - 1
— I Ак cos ———я at + Вк sm ———я at I sin ———тг.т,
к = 1,2, ...
Из линейности уравнения (7) следует, что любая линейная комбинация этих уравнений, т. е. формально составленный ряд
. х Л 2fc — 1 „ . 2/c-l \ . 2Л; — 1
щх, t) = > I Ak cos ———7rat + Bk sin ———irat I sin ———тгх (11) k=l 4 7
при условиях на коэффициенты Ак и Вк, допускающих возможность его двукратного почленного дифференцирования по t и по х, также является решением уравнения (7), удовлетворяющим граничным условиям (9).
Потребуем, чтобы представленное рядом (11) решение u(x, f) удовлетворяло также граничным условиям (8), т.е. чтобы
, 1 . Идж 4тгх . 2к — 1
«(ж, 0) = — sin cos — = 2. Ak sm ~оГ~™
к=1
и
du(x, 0) dt
= o = S k=l
2к - 1 „ . 2k - 1
———яаВк sin ———ях.
21 21
§ 2. Аналитические методы решения уравнений 289
f 2к - 1
по системе < sin-----—лх
I 21
Из этих равенств заключаем, что если числа являются коэффициентами Фурье функции
. 1 . 117гх 4тгт 1 / 7лх 15тгяА
= Issin ITcos 1Г = 30 Vin 1Г + s,n-2Г)
оо
, т.е. если А^ = 0 при к 4 и к / 8, k=i
a At = As — 1/30 и если Bk = 0 для всех к = 1, 2, ..., то функция
1 / 7ле1 . 7лх lonat 15тга?
U(x, t) = - (cos — s.n — + cos — s.n —
является искомым решением уравнения (7). t>
16.75. Найти отклонение u(x, t) от положения равновесия закрепленной на концах х = 0 и х = I однородной горизонтальной 1
струны, если в начальный момент струна имела форму - sin —у—, а начальные скорости отсутствовали.
16.76. Найти отклонение u(x, t) от положения равновесия закрепленной на концах х = 0 и х — I однородной горизонтальной струны, если в начальный момент точки струны находились в положении равновесия и ей была придана начальная скорость 1 . б-ттд?
3sin-T’
16.77. Найти отклонение u(x, t) от положения равновесия закрепленной на конце х = I однородной горизонтальной струны, левый конец которой при х = 0 перемещается так, что касательная к струне остается горизонтальной, если в начальный момент
1 Зтг.т
струна имела форму -cos—-, а начальная скорость отсутство-_ У 21
вала. ।
16.78. Найти отклонение u(x, t) закрепленной на концах х = 0 и х — I однородной горизонтальной струны от положения равновесия, если в начальный момент струна имела форму параболы с вершиной в точке х = Z/2 и отклонением от положения равновесия Л, а начальные скорости отсутствовали.
Указание. Решить уравнение колебаний закрепленной на концах струны u't't — a2u”x при начальных условиях
. 4hx(l — ж) du(x, 0)
• 4^=0.
16.79. Найти колебания закрепленной на концах х = 0 и ж = I однородной горизонтальной струны, находящейся в поло
290
Гл. 16. Уравнения в частных производных
жении равновесия, если в начальный момент времени ударом молоточка в точке х = Z/З ей сообщается постоянная начальная скорость
1 7Г
ди(х, 0) _ dt ~ I Vq при х~ 3 1 < 2/? 7Г
0 при х~ 3 > 2Л’
где тг/h — ширина молоточка.
16.80. Найти закон свободных колебаний закрепленной на конце х = 0 однородной горизонтальной струны, если правый ее конец при х = I перемещается так, что касательная к струне остается постоянно горизонтальной. В начальный момент струна находилась в положении равновесия и ей была придана начальная скорость u't(x, 0) = simrx/l.
Указание. Граничными условиями в данном случае являются условия u(0, t) = = 0, а системой собственных функций является
дх
f . я(2к — 1)т )
система < sm---—----->
I 2/ J fceN
16.81. Закрепленной в точке х = I однородной горизонтальной струне, левый конец которой в точке х = 0 может перемещаться с горизонтальной касательной, придана начальная скорость v =
— Найти закон ее свободных колебаний, если в началь-
, , . . 7ГХ
ный момент она имела форму (р[х) = sin —
Указание. Системой собственных функций задачи является система ( я(2к — 1)т 1
1COS----21-----
16.82. На концах однородного изотропного стержня длиной I поддерживается нулевая температура. Предполагая, что стенки стержня теплоизолированы от окружающей среды, найти закон распределения температуры в стержне, если известно, что в начальный момент имелось следующее распределение температуры:
j; (I — дЛ
и(х, 0) = uq---т,—, где wq = const.
xz
Указание. Решить уравнение распространения тепла u't = a2u'^.x.
16.83. Один конец стержня (при х = 0) поддерживается при постоянной нулевой температуре, а второй (при х = I) теплоизолирован от окружающей среды (т.е. производная от u(x, t) по х
§ 2. Аналитические методы решения уравнений 291
на этом конце равна нулю: u'x(l, t) = 0). Найти закон распределения температуры внутри стержня, если начальная температура задана функцией
( 0 при 0 < х < 1/2, u(x,0) =<р(х) = I
t uq при 1/2 < х < I.
Указание. Системой собственных функций является система
л(2к — 1)х )
21 I
> keN
16.84* *. Однородная прямоугольная мембрана (0 х I, 0
у т), закрепленная вдоль всего контура, лежащего в горизонтальной плоскости, и имеющая в начальный момент форму и(х, у, 0) = <р(х, у), начала колебаться с начальной скоростью i4(z, у, 0) = -0(т. у). Найти закон свободных колебаний мем-
браны. Получить решение в случае <р(х, у) = sin —-- sin —-, I m
i()(x, у) = 0, если натяжение мембраны То равно ее поверхност-нои плотности р, т.е. a — — — 1.
Р
16.85* . Точкам закрепленной по контуру однородной квадратной мембраны со стороной I, находящейся в начальный момент в положении равновесия, придали начальные скорости u't(x, у, 0) =
. лх . 2лу тт
= sin — sin—Найти закон свободных колебаний мембраны.
16.86* . Закрепленной по контуру однородной квадратной мем-_ . . _ . лх . лу
оране со стороной I. придали форму и(х, у, 0) — sin —sin—. Найти закон свободных колебаний, если начальная скорость точек мембраны постоянна и равна a/l, где а, — входящая в уравнение колебаний постоянная.
16.87* *. Найти стационарное распределение температуры в прямоугольнике D = {(т, г/)|0 х а, 0 у Ь}, если на границе прямоугольника поддерживается заданная температура:
и(х, 0) — и(х, Ь) = 0, х G (0, а),
7/(0, у) = <р(у) = у(Ь - у), и(а, у) = 'ф(у) = sin у,
У е (0, Ь).
292
Гл. 16. Уравнения в частных производных
16.88* . Найти решение и(х, у) уравнения Лапласа Ди = и"х -у + Нуу = 0в прямоугольнике D — {(z, ?/)|0 х а, 0 у Ь}, удовлетворяющее следующим краевым условиям:
х ,, х / \ Эи(х, 0) du(x, b)
^(0, У) = У[Ъ ~ у), и(а, у) = ——— = —~— = 0.
16.89. Найти решение и(х, у) уравнения Лапласа Ди = 0 в прямоугольнике D = {(я, ?/)|0 х а, 0 у Ь}, удовлетворяющее условиям
и(0, у) = а, и(а, у) = ау,
du(x, 0) _ du(x, b) _ dy
16.90* *. Найти свободные колебания закрепленной по краю однородной круглой мембраны радиуса /, если в начальный момент отклонение в каждой точке определялось равенством u(r, ср, 0) =
= qIq в котором /11 — первый положительный корень,
10(х), а начальная скорость мембраны равна са, где а — постоянная, входящая в уравнение колебаний мембраны.
16.91* *. Найти закон стационарного распределения температуры внутри бесконечного кругового цилиндра радиуса R, если на его поверхности поддерживается заданная температура:
u(r, cp)\r=ri = f(cp) = sin ср.
В случае, когда исходное уравнение в частных производных является неоднородным, т.е. в характеризуемом этим уравнением физическом процессе имеются внешние силы и источники, предварительно находится система собственных функций соответствующего однородного уравнения и решение ищется в виде ряда по этим собственным функциям с переменными коэффициентами.
Пример 4. Найти форму u{x, t) (отклонение от положения равновесия) закрепленной на конце х = 0 однородной струны, правый конец которой имеет горизонтальную касательную и на которую действует внешняя сила с плотностью F(x, t) 0. В начальный момент t = 0 струна имела форму ср(х) и каждая точка имела скорость 'ф(х'). Найти и(х, /) при условии, что ср(х) — tplpF) = 0, a F(x, t) = а2 = То/р.
< Предполагая, что струна совершает малые колебания, имеем следующую первую краевую задачу: найти решение н(х, /) уравнения вынужденных колебаний струны
d2u od2u , То ,
= а\-2 + F(x,t), а2 =—, (12)
otz ах/ р
удовлетворяющее граничным условиям
u(0,t) = 0, ^Д)=о (13)
их
§ 2. Аналитические методы решения уравнений
293
и начальным условиям
(14)
(15)
м(.г, 0) = </>(ж), = 'Ф(х).
Чтобы найти собственные функции однородного уравнения u‘tt — = a2u”x с граничными условиями (13), положим u(x, t) = X(x)T(t) и после разделения переменных получим уравнения
Т" X"
а2Т~ х с граничными условиями
Х(0) = Х'(/) = 0. (16)
Решая уравнение X" — XX = 0 с краевыми условиями (16), находим соб-х /тг(2Ат—1)\2
ственные числа Хк = — I ---—-----I и соответствующие собственные
функции
. л(2к — 1)ж ,
- к G N
21
(17)
(см. задачу 16.63).
Рассматривая t как параметр, разложим функцию F(x, t) в ряд по f . л(2к — 1)ж 1 системе < sin-----------> :
I 2/ J
а / х тг(2А: — 1)ж F(x, i) = 524fc(f)sm--------,
k=i
где i , . х 2 /' z . . я(2к — 1)ц , Ak(t) = J / 0sin--------------------------dv, к € N.
о
Будем искать решение уравнения (12) в виде ряда . . . л(2к — 1)ж
?/(ж, t) = ----------, (18)
k=i
подставляя который в (12) (считаем, что c^(i) таковы, что возможно Двукратное почленное дифференцирование по х и по t) и сравнивая коэффициенты при одинаковых гармониках, получаем бесконечную систему дифференциальных уравнений второго порядка относительно функций ck{t\. тг2п2(2к — 1 )2
<-(0+ --4Р--Lck(t) = Ak(ep кек (19)
294
Гл. 16. Уравнения в частных производных
Из начальных условий (14) следует, что функции Ck(t) должны удовлетворять условиям
Е. . . 7Г( - IX
Ск (0) sill---------
к—\
и
и (х, 0) = Цх) = cfc(0) sm-----------------.
t=i
Пусть
i
/n. 2 f . . . 7t(2At — l)v , ,ЛЛ.
Ы°) = J J </>(4 8111-------dv (20)
о
и
I
4(°) = k 6 N’ (21)
0
t. e. Ct (0) и c'k (0) являются коэффициентами Фурье соответственно функций и 'ф(х') по системе (17). Найдем теперь решения q(£) уравнений (19), удовлетворяющие условиям (20) и (21), и, подставляя их в ряд (18), получим искомое решение u(x, t).
По условию ip(x) = 1/>(ж) = 0, поэтому
q(0) = 4(0) ~ 0 для всех к G N.
Далее, так как F(x, i) — о2, то
i
. . . . 2 [ 2 . я(2к - l)v
Ak(t) = Ак = - az sin------------—-----dv -
о
2a2 21 тг(2к — l)t> 1 4a2
Г 7г(2А:'- 1) C°S 21 v=0 = 7t(2A: - 1) ’
Поэтому требуется найти решения дифференциальных уравнений
.. 7г2а2(2А; — I)2 4«2
<'(') + —тр—iv (22)
4/ 7г(2А: — 1)
удовлетворяющие условиям
Ck (0) = 4(0) = о.
(23)
§ 2. Аналитические методы решения уравнений
295
Корни характеристического уравнения для уравнения (22) мнимые, поэтому частные решения уравнений (22) ищем в виде q(Z) = ук- Подставив эти значения в (22), найдем, что
16/2
~ тг3(2Л: - I)3 ’
а поэтому общее решение каждого из уравнений (22) запишется в виде
Q-(i) = ak cos
-na(2k — l)i
21
п . ла{2к — l)i + $к sin —
16Z2
+ 7г3(2Ат — I)3 ’
к € N,
и из условий (23) получим
16/2
ct(0) = ак + !r3(2jt_1)3 - 0.
. „ ла(2к — 1)
4(0) = Л + —= о,
т. е. Д = О в «I = -Таким образом,
16/2 , ™ тг3(2Аг - I)3 ’
. . 16Z2
Ск^ ~ тг3(2Л: - I)3
ла(2к — 1)А
1~COS------21-----) =
32/2 . 2 ^а(2к — 1)Z
= tt3(2A: -1)3 Sin 41
и искомое решение имеет вид
32/2
. 2 ла(2к — l)i . тг(2к — 1).т
Sm 41 Sm 21 ' >
16.92*. Для 0 х I и t 0 решить уравнение д2и д2и .
й7 _ а? +з!^_ )
при нулевых начальных и краевых условиях
и(х, 0) = u't(x, 0) = u(0, Z) =- u(l, t) = 0.
16.93*. Для Q^x^lnt^Q решить уравнение d2u эд2и а2 . irat di^=a д^ + ~pS>n~T
LAJ -|
296
Гл. 16. Уравнения в частных производных
при нулевых начальных и краевых условиях
и(х, 0) - u't(x, 0) = zz(O, t) = u(l, t) — 0.
16.94. Найти температуру стержня при 0 х I с теплоизолированной боковой поверхностью, если начальная температура его концов равна нулю, а в точке xq G (0, I) находится сосредоточенный источник с постоянной мощностью Q.
Указание. Требуется найти решение уравнения
du od2u
с нулевыми начальными и граничными условиями w(t, 0) = u(0, t) = = u(l, i) = 0, в котором f(x, t) = Q6(x-xo)/cp, <5(x) — дельта-функция Дирака, с — удельная теплоемкость и р — удельная плотность. При I
2
I
вычислении коэффициентов Ak(t) —
f(y, i) sin —— dv использовать
о
следующее свойство J-функции:
если /(ж) определена и непрерывна в точке .то, то
- x0)dx = f(x0)-
16.95. Для 0^.т^2и£^0 найти решение уравнения
du О2 и . тгх di = dz* +S111T’
удовлетворяющее начальному условию u(x, 0) = 0 и граничным условиям zz(O, t) = 0 и u'x(2, t) — 0.
В примерах 3 и 4 краевые условия являлись однородными (см. определение задачи Штурма-Лиувилля перед задачей 16.61). Если же рассматривается задача с неоднородными краевыми условиями, то с помощью замены u — v + U путем надлежащего выбора функции U задача сводится к решению уравнения относительно функции v уже с однородными краевыми условиями. Выбор функции U определяется видом заданных краевых условий.
Пример 5. Найти закон свободных колебаний горизонтальной струны, правый конец которой при х — I закреплен, а левый при х = 0 / х 7Га^ тт
движется по закону u(0, t) ~ sm ——. Начальные скорость и отклонение равны нулю.
§ 2. Аналитические методы решения уравнений
297
<] Имеем уравнение u"t — aI 2uxx с начальными условиями и(х, 0) —
=. u't(x, 0) = 0 и неоднородными граничными условиями ?z(0, t) =
. -Kat I - х . Kat
= sin -y-, u{l, t) = 0. Произведем замену щх, t) = t\x. t)-j—j— sm —j—. Тогда относительно функции v(x, i) получим неоднородное уравнение
,, 9 к2а2(1-х} . nat
Vu = о —
с начальными условиями v(x, 0) — 0, v't(x, 0) = -—-— и однород-
ными граничными условиями t’(0, t) = v(l, f) = 0. Однородное уравнение v"t ~ a2vxx с этими граничными условиями имеет систему соб-
{. ккх 1
sin —— > , поэтому ищем решение неоднород-
‘ J fceN
ного уравнения в виде
елд j
/ ,\ • ТГгСЖ sin —.
k=i
Подставив это выражение в неоднородное уравнение, получим бесконечную систему уравнений
/ 'ТГ \ 2
T(0+ -H CW) = A(0,
(24)
2a2(l — х) nat . ккх , 2ка2 Kat ---------sin —— sin —— dx = sm ——, причем
где = у / о
из начальных условий имеем
ОО ,
v(x, 0) = ^0,(0) sin-у- = 0, т.е. 0,(0) оо ,
v;(x, 0) = ^Cl(0)sin^ = k=\
следующие условия на С7;(0) и С^(0):
= 0 для всех к G N, и
’T‘e-
I
2 f ла(1 — x) . лкх , 2a ,
C\.(0) — — - / -------—-----sm —— dx = — — для всех к G N.
о
При к = 1 в уравнении (24) имеет место резонанс (см. указание к задаче 16.93), поэтому частное решение ищется в форме Ci(<!) = ( Л Kat . Kat\
= t I A] cos ——h Bi sm —j— j ; подставив его в уравнение, найдем, что
298
Гл. 16. Уравнения в частных производных
Ci(t) = —-~-cos——Используя затем условия Ci(0) = 0 и С{(0) = 2а =----находим, что
х 1 . л at at irat
Ci(t) = --sin —--------------- cos ——.
7Г I I I
2а
Далее, используя условия Сь(0) = 0 и С"к(0) = —~гг, при к 2 получаем IК
следующие решения уравнений (24):
. 2 . irkat 2 . 7rat
a(<) = - 1ДДТГ)sin — + sm —
Подставив эти коэффициенты в ряд для v(x, t), получим искомое решение
. . I — х . irat . .
u(x, t) = —j— sin ——h v{x, t). [>
16.96. В области О О и i О найти решение уравнения u't = a2uxx при начальном условии а (ж, 0) = х/l и граничных условиях г/(0, i) = 0 и u(l, t) = е~Л
Указание. Для приведения неоднородных граничных условий к однородным произвести замену u(x, i) = v(x, t) + хе~1/1.
16.97. В области найти решение уравне-
ния u't = uxx при начальном условии и(х, 0) = 1 и граничных / \ « dull, t)
условиях u(0, t) = е и —-------= 0.
ох
Указание. Для приведения неоднородных граничных условий к однородным произвести замену a(x, t) = ц(дг, t) + е~^.
16.98. Найти закон свободных колебаний горизонтальной струны, левый конец которой при х = 0 закреплен, а правый движется . nat тт
по закону u(l,t) = sm-^y. Начальные уклонения и скорости равны нулю.
Указание. Для приведения неоднородных граничных условий к однородным произвести замену u(x, i) = v(x, i) + у sin
16.99. В области 0 х /, t 0 найти решение уравнения u'i = a2uxx при начальном условии и(х, 0) = — и граничных условиях г/(0, i) = е-*, u(l, i) = 0.
§ 2. Аналитические методы решения уравнений
299
16.100. В области 0 х /, t 0 найти решение u't = u"x при начальном условии и(х, 0) — 1 и граничных u'T(0, t) — 0, u(l, t) =
При решении задачи Коши (в этом случае краевые условия заменены ограниченностью решения на бесконечности) метод Фурье приводит к использованию интеграла Фурье.
Пример 6. Найти закон распределения температуры м(.т, t) в длинном однородном стержне, боковая поверхность которого теплоизолирована и известно начальное распределение температуры и(х, 0) — <р(х) = -т2 = е .
<1 Пренебрегая влиянием температурных условий на концах длинного стержня, будем считать его бесконечным. Поэтому мы имеем следующую задачу Коши: найти решение уравнения
du .,d2u п
— --- а"-г—г, -оо < х < 4*ос, 0 < t < +оо. (2э)
dt dx,
удовлетворяющее начальному условию
и(т, 0) = <р(х) = е
(26)
Предполагаем, что ip(x) абсолютно интегрируема на оси ( —оо, оо). Ищем решение в виде произведения ц(т, t) = X[x)T{f), поэтому уравнение (25) преобразуется к виду
Г X" 2 aXT ~ X ’
(27)
причем отношение отрицательно в силу того, что при t —> оо функция T(i) — е~а 1 не должна возрастать до бесконечности. Правое из отношений (27) приводит к уравнению X" 4- о/2 А" = 0, решениями которого являются функции
А\Д.т) — Л(и>) cos олт 4- B(cj) sin ox,
а потому решениями уравнения (25) являются функции
ww(a:, i) = е~а ш (A(cj) cos та: + В(иа) sinubr).
Если Л(и>) и абсолютно интегрируемы для ш 6 [0, +оо), то интеграл
Н-оо +оо
/Г — 2
ww(x, t) dca = / e aw (Л(ш) cosimx 4- 7?(w) sinevar) dca
о о
(28)
300 Гл. 16. Уравнения в частных производных
можно дифференцировать по параметрам t и х и мы имеем
+оо
u't(x, i) — —а2 У w2e~a ш z(A(w) coscjx + В(сУ) sincjx) dw, о
+ oo
u"x(x, t) = — У е-а w ((A(w) coscut + B(w) sinwt) cL>. о
Следовательно, определяемая интегралом (28) функция u(x, t) является решением уравнения (25), поэтому, если мы выберем
+оо
A(lu) = — / cos LVT dr
7Г J — oo
и +oo
B(lu) = — / <£>(r) sin шт dr,
7Г j — oo
то определяемая интегралом (28) функция w(x, t) будет удовлетворять и условию (26). Таким образом, искомым решением является функция
У 2 ,2 е
о
u
ujx cos шт + sin шх sin wr] dr =
0
е a w 1 coscu(.r — г) cL>.
— oo
0
Используя формулу (см. задачу 9.192)
Г 2 1 I я sA
е yuJ cosdwdw — — e 4->,
J 7
о
вычисляем внутренний интеграл
— 2 2/
е a coscu(x - т
,2
0
§ 3. Приближенные методы решения уравнений
301
а потому
1 .
---7= / iplrie dr. 2av%i J
В нашем случае </?(т) = е т , поэтому
— ОО
В задачах 16.101-16.104 найти решение задачи Коши
du d2u
— = ~°° < х < +°°, 0 t < 4-00,
ot охг
при указанном начальном условии и(х, 0):
{А, 1x1 h, 0, |х| > п.
16.102. и(х, 0) = е~К
{1х|, 1х| h, п к/ 0, |х| > п.
/ х ( %, Ы h,
16.104. u(x, 0) = < . . ,
§ 3. Приближенные методы решения дифференциальных уравнений в частных производных
1. Основные понятия метода сеток. В большинстве случаев получить решение дифференциального уравнения в частных производных с помощью элементарных или специальных функций невозможно. В связи с этим важное значение приобретают приближенные методы его решения. Ниже мы ограничимся рассмотрением краевых задач для уравнений математической физики с двумя независимыми переменными в области D с границей 7, т. е.
Lu ~ a(x, y)uX3. + 2b(x, y)uxy + с(х, y)uyy + d(x, y)u'x +
4-ф, y}u'y 4- g(x, y)u = f(x, у), (x,y)eD, (1)
Ги = <ф, у), (х, у) 6 7, (2)
где а(х, у), Ь(х, у), с(х, у), d(x, у), е(х, у), д(х, у), f(x, у) — известные функции переменных х и у, определенные в области D, Г — некоторый линейный (в общем случае дифференциальный) оператор граничных условий и tp(x, у) — известная функция, заданная на границе 7.
302
Гл. 16. Уравнения в частных производных
Наиболее часто используемым методом численного решения краевой задачи (1), (2) является метод сеток (метод конечных разностей). В методе сеток замкнутая область D = D U 7 заменяется конечным множеством точек — сеткой Dh = Dh U7/i- Точки этого множества называются узлами сетки. Параметр h = (/г, т), шаг сетки, характеризует ее плотность в области D. Обычно при |h| — Vh2 + т2 —> 0 последовательность сеток Dh стремится заполнить всю область D. Производные, входящие в левые части соотношений (1) и (2), заменяются на сетке Dh соответствующими разностными отношениями. В результате получается система линейных алгебраических уравнений
Lh^h ~ fh(x ТП ? Уп), (х ТП 3 Уп ) € Pft,
Г/гП/г — У^/ДЖггг, Уп), \Хт, Уп) £ 77г,
гден/г(жт, yn),(xm, уп) € Dh — искомая сеточная функция, fh(xm, уп), 4>h(xm, Уп) — сеточные функции, заданные на множествах Dh и 7/г соответственно, и L/г, Гh — разностные операторы. Сеточная функция uh, являющаяся решением системы уравнений (3), называется приближенным решением краевой задачи (1), (2) на сетке Dh- Ее значения йт,п = йь(хт, уп) приближенно заменяют в узлах сетки Dh соответствующие значения точного решения й(хт, уп) исходной краевой задачи с некоторой погрешностью дтп = йт,п — й(хт, уп).
Семейство систем уравнений (3), зависящее от параметра h = (h,r), называется разностной схемой. Разностную схему (3) иногда удобно записывать в виде
LhUh — fh,(.Xm, Уп), (Хгп, Уп) £ P/t, (4)
где
( Lh, (%т, Уп) £ Р/г,
I Гh, (Хт, Уп) 7/t,
( fh, (Хт, Уп) Dh, I Ph, (хт, Уп) € 7/1-
Построение разностной схемы (3) или (4) для краевой задачи (1), (2) начинается с выбора сетки, т.е. указывается правило замены области Р и границы 7 сеточной областью Dh- Чаще всего сетка выбирается прямоугольной и равномерной. Для этого проводятся два семейства параллельных прямых: х = хо + mh и у = у^+пт и рассматриваются всевозможные точки попарных пересечений прямых из этих семейств, т. е. точки вида (хт, уп) — (жц 4-тЛ, у§ +пт). Точки (хт, уп), которые принадлежат замкнутой области Р, образуют сетку Dh, являясь ее узлами. У каждого узла (хт, уп) имеется четыре соседних точки: (ж?п-1, уп), (xm+i, уп), (хт, Уп-i), (хт, Уп+i)- Если все эти соседние точки также принадлежат сетке Dh, то узел (хт, уп) называется внутренним, в противном случае узел (хт, уп) называется граничным. Совокупность внутренних узлов образует множество Р/1( а граничных — множество 7/1
§ 3. Приближенные методы решения уравнений 303
(так что Dh — Dh U7h)- Следует отметить, что множество граничных узлов 7ь не обязательно является подмножеством точек границы 7, что приводит к погрешностям при построении сеточной функции <ph из (3). На рис. 13 приведен пример прямоугольной и равномерной сетки
построенной для заданной области D (внутренние узлы сетки здесь отмечены символом *, а граничные — символом •).
После выбора сетки Dh проводится построение сеточной функции fh = (Л, и разностного оператора Lh = (Lh, ГЛ) из (4). Для определения fh в узлах сетки Dh полагают fh(xm, уп) = f(xm, уп), если (хт, Уп) G Dh, fh&m, Уп) = Ч?(хт, уп), если (xm, уп) G yh и (жпг, Уп) € 7, если же граничный узел (хт, уп) 7, то в качестве f(xm, уп) выбирается значение функции tp(x, у) в произвольной точке (ж, у) € 7, отстоящей от узла (хт, уп) на величину, меньшую \h\. Для построения разностного оператора Lh все известные функции, участвующие в явной записи операторов L и Г (например, а(х, у), Ь(х, у) и т.д.), заменяются своими значениями в узлах сетки Dh и обозначаются соответственно через ат, п-> Ът, п и т. д., а частные производные 1-го и 2-го порядков неизвестной функции и(х, у) приближенно заменяются соответствующими разностными отношениями. В результате получаем разностную схему (4), соответствующую краевой задаче (1), (2).
Пример 1. Построить разностную схему для краевой задачи распространения тепла в конечном стержне (0 х I)
u't - = f(x, t), u(x, 0) = <р(х),
u(0, 0 = V’i(i), u(l, t) = V>2(i)-
304
Гл. 16. Уравнения в частных производных
<1 Заметим, что область определения {(.т, i)|0 х I, 0 t < +оо} данной краевой задачи является неограниченной. Поэтому для построения равномерной прямоугольной сетки Dh (которая всегда является конечным множеством точек) поступим следующим образом. Проведем два семейства прямых х = mh и t = пт для некоторых заданных Лит. Очевидно, что точка (xm, tn) принадлежит области определения исходной задачи, если т = 0, 1, ..., г, где г = [i/Л], и п — 0, 1, ... Положим
Dh = {(жт, tn)\m = 0, 1, ..., г, п = 0, 1, ..., s}, (5)
где целое 8 выбирается так, чтобы интервал 0 t ts перекрывал тот временной диапазон, в котором изучается распространение тепла в стержне. Множество внутренних узлов имеет вид Dh — {(хт, tn)\т = 1, 2, ..., г — 1; п = 1, 2, ..., s. В это множество входят и узлы вида (хт, ts), т = 1,2, ..., г — 1, которые мы считаем внутренними, так как наше ограничение t st является искусственным! Соответственно -уь — = Dh\Dh или в явном виде 7^ ~ {(жт, 0)|т = 0, 1, ..., г}U{(0, fn)|n = = 1, 2, ..., s} U {(жг, tn)\, п — 1, 2, ..., s}.
Далее полагаем Uh =
771 5
V’l(in), ^2 (in),
(xm, tn) E Dh,
n = 0; m = 0, 1, ..., r, m — 0; n — 1, 2, ..., s, m = r; n = 1, 2, ..., s.
(6)
' f (Я-771 , tn) ,
Отметим, что в случае, когда l/h не является целым числом, т. е. г — = R/^] < узлы (xr, tn), п = 1, 2, ..., з, не принадлежат граничной полупрямой х = I, у 0. Вместе с тем эти узлы являются граничными, поэтому значения сеточной функции fh в них перенесены с границы.
Для получения разностного уравнения заменим производные разностными отношениями (см. задачи 16.105 и 16.108):
'иДЖт, tn) ~ — (^771,71+1 — ит,п)> Т
in) ~ ^2^(^m+l,n 2um, n 4" Uni—1,71),
где (хт, tn) Е Dh- Следовательно,
1
Lhuh = <
Um, 0,
а2
n+l Um,n) ^2 \U /п+1, п ^Umin 4" Um — т = 1, ..., г — 1; п = 0, 1, ..., 8 — 1, т = 0, ..., г,
(7)
«0,п, П = 1, . . . , 8, , Ur, п, П = 1, . . . , 8.
§ 3. Приближенные методы решения уравнений
305
Подставляя выражение (6) и (7) в (4), получаем искомую разностную схему, которая представляет собой следующую систему линейных алгебраических уравнений:
, 2 1’ ,г п 4“ Щп— 1, п)— f m, tn),
m — 1, ..., г — 1; n — 0, ..., s — 1, Um,о = <p(xm), m = 0, r, Uo,n = n = 1, s,
Ur,n — U — 1, • • . , S.
Эта система состоит из (s + l)(r 4-1) уравнений. Решив ее относительно неизвестных wm,n, тп = 0, ..., г; п — 0, ..., з, найдем сеточную функцию й/t = {um> п}, значения которой в узлах сетки приближенно заменяют значения искомого решения исходной краевой задачи для уравнения теплопроводности. >
Естественно, наибольшие трудности в построении разностной схемы (4) вызывает замена дифференциального оператора L исходного дифференциального уравнения в частных производных (1) разностным оператор ом Lh из (3).
Пусть Uh — конечномерное нормированное пространство сеточных функций i^, заданных на сетке Dh, с нормой ||iift|| = max|np|, где р
Up — координаты вектора иь (индекс и последовательно пробегает все пары индексов (тп, п), нумерующих узлы сетки). Будем говорить, что разностный оператор Lh приближает дифференциальный оператор L, если для любой функции и(т, у), дифференцируемой достаточное число раз, норма сеточной функции (Lu)ft — LhUh стремится к нулю при |h| —> 0, т. е.
||(Lu)ft — ZzftUftU —> 0, |Л| —> 0.
Если, кроме того, выполняется неравенство
||(Lu)ft - LftUft|| С(|< + |т-Г),
где С — константа, не зависящая от h, то порядок приближения разностным оператором равен р по переменной х и q по переменной у.
В частном случае, когда шаги сетки связаны соотношением т = 0(h) (т. е. не являются независимыми) и
||(Lu)ft-LftUft||^C|/i|r,
говорят, что разностный оператор Lh приближает оператор L с порядком приближения 72.
Для определения порядка приближения обычно используется формула Тейлора.
Пример 2. Определить порядок приближения дифференциального оператора Lu = u't - а2и”х разностным оператором из примера 1.
306
Гл. 16. Уравнения в частных производных
< В примере 1 был построен разностный оператор
1
(£/i^/i)m, п — "(^m,n+l n) (^т+1, п 2'1Хттг> + Um-l,n)-
Используя формулу Тейлора, находим
(^т, п+1 ^т, п) — in 4" 7") in))
Т Т
I / \ И / !\
— Uf\xm, tn) + t ),
где tm < t' < tm 4- г, и
. 1 f 1 , . _ 4
n 4" Um— I, n) — t I T МЖп 4" ^п)
h \ h'
- u(xm, tn)) 4- i (u(x - m - h, tn) - u(xm n
in))
h3 —u'"'
24 xxxx
h .. . . h2 ...
tn) T g ^xxx
h2
—u""
2^ xxxx
где xm — h < x" < xm < x' < xm 4- h. Приводя подобные члены в правой части последнего выражения, получаем
д2 (^пг4-1,п
т, п
4" Um— 1, п)
~ tn) 4"
24
(и'1"
\^хххх
III/
'хххх
h
h
2
m ч
6
Следовательно,
(LhUh) тп, п
— Uf {Xm i
' uxx{xm, tn) 4- 2Utt(x
t')~
a2h2
ini
xxxx
III/ xxxx
24
§ 3. Приближенные методы решения уравнений
307
Используя выражение (8), разность между исходным дифференциальным оператором L и заменяющим его разностным L/t в узлах сетки можем представить в виде
(Lu)m,n ii
для некоторых t'(tn < t' < tn + т) и х', х"(х1П — h < xr' < хт < < х' < х,п + Л). Если теперь \u"t(.т, t)\ < ЛЛ и \u""xx(x, i)| < Л/2; то
выполняется неравенство
£'hИh 11 — max|(E?z)m n {IJh.‘^'h}Tn,n\ m,n
My a2h2
т|т|+лг
с(|Л|2 + И)-
2
Следовательно, использованный в примере 1 разностный оператор приближает исходный дифференциальный и порядок приближения по переменной х равен двум, а по t — единице.
Отсюда, в частности, следует, что для того, чтобы порядок приближения был равен двум, необходимо шаги Нит сетки связать соотношением т = ti2.
Замечание. Для облегчения запоминания построенного разностного оператора полезно поставить в соответствие ему «шаблон» — геометрическую картинку расположения узлов сетки, значения в которых связывает разностный оператор при некоторых фиксированных значениях тип. Для разностного оператора из примера 1 шаблон изображен на рис. 14 (проверьте!). >
В задачах 16.105-16.107 определить порядок приближения дифференциального оператора частной производной и'х указанным разностным оператором Lip
16.105. (LhUh)m,7l — — (ит+уп — ит>п) — оператор правосторонней разности.
16.106. п — —(ит п — um-i п) — оператор левосто-
’ Н
ронней разности.
16.107. (Lfluh)m,n = ~(ит+\,п ~ Um-yn) — оператор центральной разности.
В задачах 16.108-16.111 определить порядок приближения заданного дифференциального оператора L второй частной производной указанным разностным оператором L^-.
308
Гл. 16. Уравнения в частных производных
16.108. Lu — Uxx->
— \uni+l,n ~ ^m,n 4" Um_
16.109. Lu — Uyy, kLhUh)m,n —
16.110. Lu — ^xyt {L^U^im^n —
1
— ль (^тп+1,п+1 ~ ^771+1, 77—1 — um—1,77+1 4~ um— 1,77—1)* 4/гт
16.111. Lu — Uxy^ {^Jh'^'h}myn —
- —(
Jl/ (^771+1,714-1 1^777+1, n 4" um,n um,n+l)-
16.112. Построить разностную схему для краевой задачи из примера 1, используя оператор правосторонней разности и оператор, аналогичный приведенному в задаче 16.109. Определить порядок приближения полученного разностного оператора L^ (шаблон приведен на рис. 15):
n + 1)
(т-l, п +1) (т, n +1) (т +1, и +1) п +1-------•-----*------•-----
т
I (ш-1, п) (т,~п} (т +1, п) - /г ,
(mL и)
Рис. 14
Рис. 15
В задачах 16.113 и 16.114 определить, какой дифференциальный оператор и с каким порядком приближается заданным разностным оператором L^:
16.113. (1>/гЦ/г)т,n — 2^(^т+1,тг ^m—1,тг) 4"
4” n тг+l ^771+1,77 4- um —
Zt
16.114. (l>h^h)77i,7i —
(w?7i—l, 77 4“ Wm, 77—1 4~ 2/7724-1, n 4“ Um^ n_|-i 4цт, n
п +1
§ 3. Приближенные методы решения уравнений
309
16.115. Определить, при каком а порядок приближения дифференциального оператора L: Lu = u't — u"x разностным
1 (Lh'U'h)m, n ^m,n)
n+1 ^Um'Ti+l ~ um— У
+ (1 O') (Щп+l, n ^m,n l,n))
будет четвертым no h и первым по т.
Составить разностные схемы для следующих краевых задач:
16.116. = °) = °) =
u(0, t) = *01(0, u(b, t) = D = {(ж, i)|0 х 6, 0 < t < Т}. Q2U Э2и
16.117. Cdx? + ddy^ = f(X' у}' с > °’ d > °’ = У^
D = {(ж, ?/)|0 х Ь, 0 у У}.
Более общим способом построения разностных операторов, приближающих заданный дифференциальный, является метод неопределенных коэффициентов. Этот метод состоит в том, что приближается не каждая производная в отдельности, а сразу весь оператор. Для замены дифференциального оператора разностным в узле (хт, уп) рассмотрим N соседних узлов. Узел (хт, уп) обозначим индексом 0, а остальные рассматриваемые узлы занумеруем числами 1, 2, ..., N. Составим ли-N
нейную комбинацию с неопределенными коэффициентами q,
k=0
где Uk — значение и(х, у) в узле к.
Предполагая функцию и(х, у) дифференцируемой п + 1 раз, разложим и/, по формуле Тейлора в окрестности узла 0. Считая сетку квадратной (г — h), имеем
Ес‘и‘= У
к=О i+j^n 4 d 7
О)
Коэффициенты 7у линейно выражаются через с*. Выберем коэффициенты ck так, чтобы правая часть в равенстве (9) отличалась возможно меньше от значения дифференциального выражения Lu в узле 0, т. е. чтобы коэффициенты при производных в уравнении (1) совпадали с коэффициентами при соответствующих производных в правой части (9), а коэффициенты при старших производных порядка г (2 < г п) в (9) приравняем нулю, т. е.
= 0 для 2 < i + j = г п. (10)
310
Гл. 16. Уравнения в частных производных
Учитывая, что 7^ выражаются через с^, имеем систему уравнений относительно ед,, решив которую, мы получим приближение оператора Lu в узле (m, n): N
^2 ckUk = (Lu)0 +
к=0
Система уравнений (10) относительно сд. может иметь несколько решений, однако достаточно взять одно из них. Используя в случае необходимости достаточно большое число узлов N, можно получить хорошее приближение Lu в узле (т, п).
В задачах 16.118 и 16.119 построить соответствующие разностные операторы методом неопределенных коэффициентов.
16.118. Lu — u"x + 2uxy + 5Uyy. Порядок приближения равен двум (шаблон указан на рис. 16).
< Построим квадратную сетку т. е. выбираем шаг как по переменной х, так и по переменной у равным h. В качестве соседних берем 8 узлов 8
(см. рис. 16), т.е. N = 8. Имеем линейную комбинацию —
к=0
= (Lu)o-
Разлагая и/, по формуле Тейлора в окрестности узла 0, будем иметь
щ = и(х0 + Л, т/о) =uQ+ u'xh + ^h2 + ^h3 + <9(Л4),
u" и'"
U2 = u(x0, y0 + h) = u0 + U1 h + -~h2 + -^-h3 + <9(/i4), y 2! 3!
'll" u'"
«3 = u(x„ - h, y0) = «0 - u’xh + - -^h3 + О(Л4),
Li. O.
u" u'"
u4 = u(z0, y0 - h) = u0 - u' h + -ff-h2------^-h3 + O(7i4),
y 2! 3!
h2
u5 = u(x0 + h, y0 + h) = u0 + u'xh + u'yh + ~^{uxx + + w”y) 4-
+ ~^(u'xxx + 3u’x2y + 3w"'y2 + U'yyy) + О(Л,4),
§3. Приближенные методы решения уравнений 311
U6 — u(xq Д, Уо 4“ ll) Uq Uxll -I- Uyh 4“ ^^xy ”1" ^7/7/) +
b3
4- + 3<'L ~ 3<2 4- <y) 4- 0(h4),
O| ' j/U/O/ л у л у УУУ' ' '
/ I h? II II II
U7 = u(x0 - h, y0 - h) = «0 - u'xh - u'yh 4- -y(uxx 4- 2u”y 4- uyy) -
h3
- + 3<% 4- 3'" 2 4- u'”yy) 4- 0(h4),
h2
V8 = U^Xq 4" h, Уо Л-) — Uq 4* Uxh 2! ^xx ^^xy ^yy)
Л3
+ ^xxx - Щ + 3<> - u'^yy) 4- 0(h4).
Додставим эти выражения в (Lu)q:
(Lw)o == ^о(со 4~ Ci 4- C2 4- C3 4- C4 4- C5 4- се 4- C7 4- c§) 4-
4- u'xh(ci - C3 4- C5 - cq - C7 4- c8) 4- u'yh(c2 - C4 + c$ + Cq - c7 - eg) 4-h2 h2
4- uxx — (ci 4- C3 4- C5 4- c6 4- c7 4- c8) 4- u'yy — (c2 4- c4 4- c5 4- c6 4- c7 4- c8) 4-
2u" Л3
+ -^2(C5 - CO + C7 - c8) 4- ^4''x(ci - C3) +
/j3 /l3
+ 3j'wyyT/(c2 -C4) + -^c5(uxxx 4- 3«^2y 4- 3u"y2 4- u'yyy) 4-
ДЗ
4“ ~q Co( — u'xxx 4- 3w”2y — ^u'xy2 + Uyyy) ~ h3
~ ~^c7(u'xxx 4- 3ux2y 4- Зи^г 4- u'yyy) 4-
+ ~^co(uxxx ~ 3u"2jz 4- 3«”^2 - u'yyy) 4- Я(С1, c2, • • •, c8)/i4 =
— u’xx 4- 2«” 4- 5u'' . ху у у
312
Гл. 16. Уравнения в частных производных
Сравнивая коэффициенты при соответствующих производных, получим систему линейных уравнений для нахождения сд., выбирая при этом i 4-+ j = 3:
Со 4- Ci 4- с-2 4- Сз 4- С4 4- с$ 4- eg + Су 4- eg = О,
С] — Сз 4- С5 — Со — Су 4- Cg = О,
С2 ~ С4 4- С5 4- Cq — Су — Cg = О,
2
Ci 4- Сз 4- сз 4- Со 4- су 4- eg — —,
10
С2 4- С4 4- С5 4- Сб 4- Су 4- Cg — —,
2
С5 Cg Су 4- Cg д2 ’
Ci — Сз 4- С4 4- С5 — Со — Су 4- Cg = О,
С5 4- с6 — Су — Cg - - О,
С5 — с6 — Су 4- eg = О,
С'2 ~ С4 4- С5 4- Cq — Су — Cg = 0.
Систему уравнений (11) решаем методом исключения. Из последних четырех уравнений получим с$ = Су, С2 = С4. Используя эти равенства, из второго и третьего уравнения системы установим, что cq = eg, ci = С3. Можно переписать систему уравнений (11) в следующем виде:
Cq 4- 2ci 4- 2с2 4- 2cs 4- 2со — О, 2ci 4-2с5 4-2сб = 2/Л.2, 2с2 4- 2с5 4- 2сб = 1О/7г2, 2с5-2с6 = 2/h\ {
с4 = О, С-2 = 0.
Решая систему (12), получим следующие значения для искомых постоянных:
с0 = -2/h2, ci = -4//?, с2 = 0, с3 = —4/Л.2, С4 = 0, с5 = 3//?, CQ = 2/h\ Су = ^/К2, cs = 2/h'2.
Окончательно для узла 0 получим
(Z/£7)o ~ (—21/0 ~ 4i/i ~ 41/з 4- З115 4- 2i/g 4- З1/7 4- 2i/g), т. е. для всех внутренних узлов сетки имеет место формула
(Z//il/h)m, п
— 21/т, п 4- 4um+i, п 4- 4//^—1! п
31/т+1,п+1 21/^ — ^ n_|-i 31/т—1)П—1 21/т1П+1.
Порядок аппроксимации второй: г — 1 = п — 1 = 2. t>
§ 3. Приближенные методы решения уравнений
313
16.119. Lu = u'xx + Uyy. Порядок приближения равен двум (шаблон указан на рис. 17).
Рис. 17
Пусть, как и выше, Uh — {й)г(т, п)} — решение разностной схемы, т.е. системы линейных алгебраических уравнений (4). Применение разностной схемы к решению краевой задачи (1), (2) оправдано, если величины й/г(т, п) являются приближенными значениями сеточной функции й(хт, уп), представляющей собой значения неизвестного решения й(х, у) задачи (1), (2) в узлах сетки.
Будем говорить, что разностная схема (4) является сходящейся на решении й(х, у) задачи (1), (2), если при Л -> 0 выполняется условие1)
уп) - Uh(m, п)|| -» 0.
Если дополнительно выполняется неравенство
IRzm, Уп) - uh(m, n)|| < Ahs, (13)
где А — константа, не зависящая от h, то говорят, что скорость сходимости имеет порядок s относительно h.
Сеточная функция й(хт, уп), вообще говоря, не является решением разностной схемы. Поэтому при подстановке ее в левую часть (4) получается выражение
Lh(u(xm, уп)) = Jh +6fh,
где 8/^ называется невязкой или погрешностью аппроксимации.
Если -> 0 при h —> 0, то говорят, что разностная схема (4) аппроксимирует краевую задачу (1), (2) на решении й(х, у). При выполнении дополнительного условия
W7, (14)
где С - константа, не зависящая от h, число а > 0 называется порядком аппроксимации.
Наконец, не менее важным свойством разностных схем является понятие их устойчивости. Разностная схема (4) называется устойчивой,
*) Здесь и в дальнейшем будем считать шаги h и т зависимыми, т.е. т =
314
Гл. 16. Уравнения в частных производных
если существует такое /г0, что для всех h < h0 и любых fh она имеет единственное решение и
11ш|| С11ЛН. (15)
где С — константа, не зависящая от h и правой части f h.
Между рассмотренными понятиями сходимости, аппроксимации и устойчивости существует тесная связь.
Теорема 1. Пусть устойчивая разностная схема (4) аппроксимирует краевую задачу (1), (2) на решении й(т, у} с порядком аппроксимации а > 0. Тогда эта схема является сходящейся и порядок ее сходимости совпадает с порядком аппроксимации.
Пример 3. Для задачи Коши
ut ~ и'х = f(x> ^)> < х < 4-оо, 0 t Т,
и(х, 0) = -оо < х < 4-оо,
построена разностная схема
1 _ _ 1
• \Um,n+l llm,n ) , (^т+1 ,п п) — /т,пэ
Т Г1
m = 0, ±1, ..., ±М- п = О, 1, ..., [Т/т] - 1,
^т,0 — Tmt Ш = О, ±1, . . . , iTVf,
где т = Xh и постоянная А 1. Определить порядок аппроксимации этой схемы и исследовать ее на устойчивость.
<] Сначала покажем, что построенная разностная схема аппроксимирует исходную краевую задачу и определим порядок аппроксимации. Предполагая, что решение й(х, у) задачи Коши имеет ограниченные вторые производные, по формуле Тейлора имеем
п п
[й{хт 4- h, tn) H[xm, in)) — п
— их[хт,
^п) 4- 2Uxx(xm 4- С,
^п) >
О < С < h,
Щт,п+1 йтгп) — 4" т) й[хт. tn)) —
Т
= tn) 4- tn 4- 7}),
О < р < т.
§ 3. Приближенные методы решения уравнений
315
Учитывая соотношение т = АЛ, получаем
"( «т, п+1 Um.n) j \^т+1,п ^т,п) —
T Л
— tn} — Йд.(хП1, 1пУ) + й in + р) ~ + С, ^п)^ •
Погрешность аппроксимации 6fm>n = 1>ь(й(хт, уп\) - fm^n^ следовательно, принимает вид
Sfm,n = <
2^хх^Хт ”1"
0 Фт
Но йт,о - Рт — О для любого т в силу граничных условий. Поэтому норма 6fm п оценивается следующим образом:
Н*Лп,пН
m, n
in + Л) 2^xx^x t'n)
hM—~
2
< max
где M — максимальное значение вторых производных функции й(х, у)
, приходим к неравенству (14).
в области D. Полагая здесь В = М—-—
Следовательно, рассматриваемая разностная схема аппроксимирует исходную задачу Коши и порядок аппроксимации равен единице. (Конечно
же, на решении й(х, у), обладающем ограниченными вторыми производными.)
Отметим, что метод проверки свойства аппроксимации разностной схемы во многом повторяет метод определения порядка приближения разностным оператором дифференциального.
Теперь проведем исследование разностной схемы на устойчивость. Снова используя соотношение т = АЛ, перепишем исходную разностную
схему в виде
Wm,n+i — (1 A)um> п + n -Т Xhfm,ni .
(16)
и)п, о — рт >
где, как и выше, т = 0, ±1, ..., ±М; п = 0, 1, ..., [Т/(АЛ)] — 1.
По условию А 1, поэтому 1 — А 0. В этом случае справедлива оценка
— А)и
т, п 4- Аит+1,п| (1 А)|ц
т, п I + A|um+i,п|
С (1 - A) max {|wm,n|},
316
Гл. 16. Уравнения в частных производных
{|«m+l,n|} 4- Amax{|unl,n| |um+l,n|} =
= max{\um n|, ,n|} max |wm,n|-
— Л/^Птг^Л/
Используя эту оценку, из (16) находим:
|^m, n+1 I 1(1 А)и?П1П 4- Xum+15 n| 4- Xh\fm, n|
ma* JWm,n| + A/illAII, (17)
-M
где \\fh\\ = max |/niin|. Правая часть неравенства (17) от тп не зависит, m, n
поэтому выполняется неравенство
max |um,n+i| max lu^^l + A/iHAll (18)
для любого n = 0, 1, ..., [УДАЛ.)] — 1.
Используя неравенство (18) для оценки первого слагаемого в его правой части, последовательно находим
max |um,n+i| < max. |um,n-i| + 2Ah||AII • • •
.max |um,n-fc'| + (k+ 1)WAII
Mmax |ит1о| + (п4-1)А71||Д|| =
= max' J<Anl + (« + 1)Ah.|J//J|, (19)
— M
так как i/m,o = pm из (16). Теперь заметим, что max \ipm I ll/JI
— M^m^M
и НАН ll/hll- Подставляя эти неравенства в (19), получим
max lum.n+il (1 + (гг 4- 1)Л/г)||/л||
-М^.т^.М
^(1 + [7’/А/1]Л/1)||7лК(1 + 7’)||7„||.
Правая часть полученного соотношения от h не зависит. Следовательно,
max
max
0^n^[T/(Ah)]-2-М^т^М
К,„+1| (1 + Т)||/Л||,
11«</.К(1 + г)11/Л||,
и мы получили искомое неравенство (15) (с С = 1 + Т), означающее по определению, что разностная схема устойчива при А 1.
§ 3. Приближенные методы решения уравнений
317
Так как заданная разностная схема аппроксимирует на решении исходную краевую задачу и устойчива, то при А 1 она является сходящейся и скорость сходимости по теореме 1 имеет первый порядок. >
16.120. Доказать теорему 1.
16.121. Показать, что рассмотренная в примере 3 разностная схема неустойчива при Л > 1.
16.122* *. В области D = {(ж, т/)|0 ж 1, О^т/^У} построить разностную схему первого порядка, аппроксимирующую первую краевую задачу для уравнения гиперболического типа
d2u d2u du du . t
Lu = a-—; - b—y + c— + d— + gu = f, a > 0, b > 0,
dx, dyz dx dy
u| = (p(x), 1yrzQ 7 '
= и|ж=0=Ф(т/), u\x=1=F(y).
y=0
• 16.123*. В области D из задачи 16.122 построить разностную схему второго порядка, аппроксимирующую первую краевую задачу.
16.124 *. В области D построить разностную схему первого порядка, аппроксимирующую третью краевую задачу
Lu = f, u|y=0= <^(ж),
du dy
= 'Ф(х), y-0
du _ . .
= ф(?/), x=0
&+
= T’(y)-
16.125 **. Построить разностную схему второго порядка, аппроксимирующую третью краевую задачу.
16.126 *. Определить порядок аппроксимации разностной схемы задачи 16.117.
В задачах 16.127-16.129 для заданных задач Коши и соответствующих им разностных схем выполнить следующие задания:
1) Выписать разностный оператор и правую часть f h, возникающие при записи этой схемы в виде (4).
2) Нарисовать шаблон для разностного оператора L^.
3) Показать, что разностная схема аппроксимирует соответствующую краевую задачу с первым относительно h порядком на решении й(ж, £), имеющем ограниченные вторые производные.
4) Исследовать разностную схему на устойчивость в зависимости от значений параметра А: т = Xh.
318
Гл. 16. Уравнения в частных производных
16.127. u't - u'x = f(x, £), -оо < х < +оо, 0 < t Т, и(х, 0) = =
~ um,n) ~ ~j~\umyn ~ ~ fm,m
m = 0, ±1, ..., ±М, ^777 ,0 ~ • 5 [Т7Г] !•
16.128. u't + u'x = /(.г, t), -00 < х < +00, 0 t < Г, и(.т, 0) = = <^);
1 1
— (um,n+l ~ um,n) v(um,n ~~ um-l,n) ~ /777,77, Т П,
m = 0, ±1, ..., ±М,
^777 ,0 — ^777, О? 1, • • • •>
16.129. u't + u'x = /(т, Z), —оо < х < +оо, 0 С t С Т, и(х, 0) = =
— (^тп, тг+1 ^771,71) ~7 (^7714-1, п Щп, п) = fm.ni
т h
m — 0, ±1, ..., ±М,
^777,0 — фтПЧ — 0? 1? • • • 1 [Т' I”7"] !•
16.130. Исследовать устойчивость разностной схемы из примера 1.
16.131. Исследовать устойчивость разностной схемы из задачи 16.112.
16.132. Исследовать устойчивость разностной схемы из задачи 16.116.
16.133. Исследовать устойчивость разностной схемы
2^ (^771, 77+ 1 ^777 , 71— 1) ~ ^2 (^777— 1 , 77 ‘^'^'ГП, 77 ^777+1 , n} 1
m = 0, 1, ..., М — 1, п = 0, 1, ..., N — 1, ^777,0 — 9^777 5 ^ 777, 1 = “Фш1 ^0, 77 ~ М, 77 = 0-
2. Численное решение краевых задач методом сеток. Все разностные схемы, применяехмые при решении краевых задач математической физики, делятся на два больших класса — явных и неявных схем. ___________ Под слоем разностной схемы понимается совокупность точек сетки D, лежащих на некоторой горизонтальной (или вертикальной) прямой.
§ 3. Приближенные методы решения уравнений 319
Если значения сеточной функции um,n+i, заданные на (п 4- 1)-м слое, выражаются в явном виде через значения этой же функции на слоях с меньшими номерами, то такая схема называется явной. В противном случае схема называется неявной.
Например, разностная схема, полученная в примере 1, является явной, так как может быть записана следующим образом (см. выражение (7)):
а2т
^т,п+1 — TUm>n 4- '+т+1,п +Ит, п 4" ^т—1,п) “Ь Jm,ni
п 0, 1, ..., s — 1; rn = 1, ..., г — 1,
Wjn,0 — Ш — 0, 1, . . . , Г,
ио,п = Ф1Ы, т = 1, 2, ..., s, иг,п = гФ2^п\ т = 1, 2, ..., s.
Решение получающейся системы линейных алгебраических уравнений трудностей не представляет и осуществляется последовательно, переходом от слоя к слою.
Сложнее обстоит дело с неявными схемами (как в задаче 16.112, например). Для решения соответствующих им систем уравнений удобно применять метод прогонки, т. е. модифицированный метод исключения для решения системы линейных уравнений. Суть этого метода разберем на основе неявной разностной схемы для уравнения теплопроводности (см. задачу 16.112). Введем обозначения
_ а2т к — 2a‘2r — f
®m, n+1 — > ®т, п+1 — 1 4 , 9т, п+1 — Щп, п + fm, п+1 • (20)
Разностную схему из задачи 16.112 перепишем в виде
«О, п — 'Фт, п
Gm, n+lUm—1, п+1 + Ьт, п^т, п+1 ~i~ ®т, n+lUm+l, п+1 = 9т,п+1ч (21)
^k, п = Ф‘2, пч — 0, . . . , 8 1,
^т,0 = Ш — 1, . . . , fc 1.
Система уравнений (21) при каждом фиксированном значении п совпадает с системой
«о = <£,
®п^п—1 4" Ъпип 4- cnun.±i — gn, п — 1, ..., N 1, (22)
Пдг = 1/1,
Для которой справедлива следующая
320 Гл. 16. Уравнения в частных производных
Лемма. Система уравнений (22), коэффициенты которой удовлетворяют неравенствам |bn| 14- |ап| 4- |сп|, разрешима при любых правых частях, и для ее решения справедлива оценка
М max{|< |5i|, ..., |5n-i|, К-
Для системы (21) условия леммы выполнены. Систему уравнения (21) удобно решать с помощью метода, который называется методом прогонки. Будем искать решение системы уравнений (21) при каждом фиксированном п в виде
Пщ — 1,п4-1 ~ Qm,n+lUm,n+l 4" -Нтп.п+Ы И? — • • • ? 2. (23)
Исключая um_i n+i из системы (21), получим
am,n+l .
Um, п+1 — — , uni+l, п+1 “г
Um, п+1 Ч/m, п+1 4" От,п+1
9т, п+1 ~ ит,п+1Нт,п+1 (24)
Um, n+lQm, п+1 4- Ът,п+1
Соотношение (24) связывает значения функций um,n+i, um+i,n+i, поэтому можно записать
Um, п+1 = Qm+l,n+lUm+l,n+l “Ь Нт+1, п+1 • (25)
Сравнивая соотношения (24) и (25), имеем
Ош, п+1
Чт+1,п+1 — — х-j , 5
Um, п+1 Ц/ni, п+1 "г От, п+1
„ (2б)
rj _ 9т, п+1 Um, п+1 т, п+1
Нт+1,п+1 — Л . •
Um, п+1 Ч;т, п+1 "г 0щ,п+1
Соотношения (26) определяют значения всех прогоночных коэффициентов Qm,n, Нт,п- С помощью этих соотношений сетка проходится вверх по т от значения 1 до значения к — 1 при фиксированном значении п. При этом определяются все значения Qm,n? Нт,п на сетке (прямая прогонка). Определив все прогоночные коэффициенты Qm, п, Нт,п, проходят сетку вниз от значения k до 2, последовательно определяя значения ит,п из уравнения (23) (обратная прогонка). Граничное условие при т = 0 определяет начальные значения Q+n+ъ Н1,п+ъ а граничное условие при т = к в общем случае определяет первое значение ид.. Метод прогонки обладает тем свойством, что ошибки округления, получаемые на каждом шаге, не нарастают. Это свойство служит основанием ее широкого применения.
16.134* *. Определить начальные значения прогоночных коэффициентов и значение для решения параболического уравнения
§ 3. Приближенные методы решения уравнений
321
в случае граничных условий
Эп
+ Pin ax
1а;=0
= Ф1,
= Ф2.
х— 1
В задачах 16.135-16.147, используя разобранные выше раз-аостные схемы, найти приближенное численное решение:
d2u d2u 9
16.135. 2—у - 2—у - tx2 dtz pxz
}’u\i=o=x^
— sin re, м| = el t=0
о= 4 cos t. х—2
d2u d2u
16.136. ~&ry = 0, D = {(.T, ?/)|0 X 4 1,
oxz dy£
du
u(0, x) = x, w(0, y) = y, —(x, 0) = 0, u(l, y) = 1 - y.
16.137. ч™ ~ 4uyy = %У, D = {(t, t/)|0 x 2, 0 < у < 1}, x2
4=0= x2 + “4=0= у + 6> 4=o= siny + !’ <=2= Scosy.
16.138. uxx ^Uyy
У O, ^|y=0= x'2’
du 9
-д- + У u ox
= 5?/3 rr=l
- xy = du
d'j »=0
+ 4?/.
0, D = {(z, ?j)|0 < x 1, 0 4
(du \ 9
-д- + yu] = y\ dx J X--=Q
ехУ^ D = {(т, ?/)|0 ^т^2, 0 г/ / du . \
= 1, I -—I- = 5т/,
у=0 \^х / х=0
16.139. uXx 4tz>yy —
111 Л r du
Ч’ Ч7=о~ 4т + 5, —
= cos у.
Задачи 16.140- 16.143 решить, используя явную или неявную схемы:
du Oil
16.140.-----2—2 - х = 0, D = {(.т, т/)|0 < х 2, 0 4 у 1},
ди дх£
I , х । ,
WI п— 1-----, и\ =COSW, и = sinu.
ly=0 2 lx=0 lx=2 J
322
Гл. 16. Уравнения в частных производных
д2и ди d п _ л~2 ~ —Ь 1 — О, D =
дхг ду
2, ^|x-i= е^’ (тГ+и ix-1 \дх
16.142. — 2ихх
9 ди t=Q= х ’ te
du дх
= 0.
х=0
= 0.
х=2
ди
16.143. — dt
t=Q= sin7nc>
“ а? + 8а
0,5и \ дх
( ди
= 0, — 4- 0,5и
х=0 \дх
= 0.
х—1
Решить следующие задачи Дирихле:
16.144. 2ихх 4- иуу = х2 4- 2ху, D = {(ж, ?/)|0 х < 2, 0 < у
Ч- 4=0= 1 + х’ 4=2= 3 - У2' uL=o= 1 + 5У’ 4=1= 6 - х2-
16.145. = -х2 -у2, D = {(z, у) |0 <ж<1, 0<у<
0,4х=о=2^2’ uLi= у2+4У’ 4=0= °’ 4=1= +2ж +2-д2 и д2 и
16.146. ^2+4^2 = siri24/’ D = {(ж> ?/)10 х У + 0 У
п> ’4=о=х’ ху+4=i=5 _ х' 4=о= 5у-
16.147. 2ихх+^иуу+ух = 0. D ~ {(ж, г/)|0 х 2, 0 у 1}, х=о=5^ uU=o= 4у=1=5 —
Глава 17
МЕТОДЫ ОПТИМИЗАЦИИ
§ 1. Численные методы минимизации функций одной переменной
1. Основные понятия. Прямые методы минимизации. Пусть на множестве U С R определена функция f{x). Под минимизацией функции f{x) на множестве U будем понимать решения следующей задачи: найти хотя бы одну точку минимума х* и минимум fx = f{x*) этой функции на множестве U.
Задача нахождения точки максимума и максимального значения функции f{x) сводится к задаче минимизации заменой /(ж) на — f{x), поэтому ниже будут рассматриваться только задачи на минимизацию.
Напомним, что число х* Е U называется точкой абсолютного {глобального) минимума или просто точкой минимума функции f{x) на множестве U, если /(ж*) < /(ж) для всех ж Е U. Значение /* = min /(ж) называется абсолютным {глобальным) минимумом или просто минимумом f{x) на U. Множество всех точек минимума функции /(ж) на множестве U будем обозначать U*.
Число ж Е U называется точкой локального минимума функции /(ж), если существует такое число <5 > 0, что /(ж) /(ж) для всех ж Е
€ U$ = {ж|ж Е U, |ж — ж| < ($}. Значение f{x) называется локальным минимумом f{x). Всякая точка глобального минимума f{x) является и точкой локального минимума этой функции. Обратное, вообще говоря, неверно.
В задачах 17.1-17.4 найти множество точек минимума U* функции f {х) на множестве U:
17.1. f{x) = sin2 7гж, U = R.
17.2. /Щ = |г-г2|, С/ = [-1;2].
17.3. f(x) = cos U = (0; 1].
17.4. f(x) = Р "РИ М U = R.
J v ' (1 при |ж| 1,
17.5. Доказать,что линейная на отрезке [а; Ь] функция f(x) = = Ах 4- В, А 0, достигает минимума на этом отрезке только в точке х = а или х — Ь.
324
Гл. 17. Методы оптимизации
Отметим,что минимум функции f(x) на множестве U может и не существовать, т.е. множество U* может быть пустым. В этом случае используют обобщение понятия минимума — точную нижнюю грань функции /(ж) на множестве U. Пусть /(ж) ограничена снизу на U, т.е. /(ж) А > —оо для всех х Е U. Число /* называется точной нижней гранью функции /(ж) на множестве U (J* = inf /(ж)), если /(ж) /,
при всех ж Е U и для любого £ > 0 найдется точка ж£ Е U такая, что /(же) < f* + £. Для неограниченных снизу функций /(ж) полагают f* = —оо. Если U* 0, то /* — inf /(ж) — f* = min /(ж).
Пример 1. Пусть /(ж) = 1/ж, U = [1; +оо). Показать, что множество U* точек минимума функции /(ж) на множестве U пусто и /* — = inf /(я;) = 0.
< Предположим, что U* 0, т.е. существует хотя бы одна точка минимума ж* Е U функции /(ж) на U. Возьмем произвольное число ж > ж*. Тогда ж Е U и /(ж*) = 1/ж* > 1/ж = т.е. ж* не является точкой минимума /(ж) на U. Полученное противоречие и доказывает, что множество U* точек минимума пусто.
Покажем, что /* = inf /(ж) = 0. Очевидно, для произвольного ж Е Е [1; +оо) справедливо неравенство /(ж) = 1/ж > 0. Далее, пусть е > 0. Возьмем произвольное х£ > max(l/e, 1). Тогда х£ Е U и /(ж£) < е = — О + £. Поэтому /* = 0. > '
Пример 2. Пусть /(ж) =1пж, U — (0; 1]. Найти f* = т!’/(ж).
< Функция /(ж) не ограничена снизу на множестве U, поэтому по определению точной нижней грани полагаем f* = —оо. >
В случае U* = 0 под задачей минимизации /(ж) на множестве U понимают определение f* — inf /(ж), полагая f* — f*. При этом точка минимума ж* не ищется.
В задачах 17.6-17.11 убедиться, что множество точек минимума функции /(ж), заданной на множестве [7, пусто, и найти Л = inf f(x):
и.в.и = R.
17.7., /(ж) = 2ж3 - 9ж2 + 12ж + 5, U = (-ос; 5).
17.8. /(ж) = ж sin ж, U = К.
17.9. /(ж) = агс1^ж, U = (—оо; —1].
17.10. /(ж) = 1ёж, Е/= [—2; 2].
17.11. Дх) = Д-, a) U = (0; 1); б) U = (1; +оо).
111 ж
17.12. Показать, что если min/(ж) существует, то inf/(ж) = = min Дж).
§ 1. Численные методы минимизации функций одной переменной 325
Существование локальных минимумов функции х* Е U*, отличных от абсолютного, почти всегда затрудняет поиск точек /(д), поэтому многие приближенные методы минимизации применимы только тогда, когда любой локальный минимум /(д) является одновременно и глобальным. Один из классов функций, удовлетворяющих этому условию, составляют унимодальные функции.
Функция /(д) называется унимодальной на отрезке [а; 6], если она непрерывна на [а; Ь] и существуют числа а и Д, а а /3 Ь, такие, что:
1) если а < а, то на отрезке [«; a] f{x) монотонно убывает;
2) если (3 < 6, то на отрезке [/3; Ь] /(т) монотонно возрастает;
3) при х Е [а; /3] /(ж) = /* = min f(x).
[а; 6]
Отметим, что возможно вырождение в точку одного или двух из отрезков [а; а], [а; (3] и [$; 5]. Некоторые варианты расположения и вырождения в точку отрезков монотонности и постоянства унимодальной функции показаны на рис. 18-21.
Рис. 21
Множество функций, унимодальных на отрезке [а; 6], будем обозначать Q[a; Ь].
326
Гл. 17. Методы оптимизации
Для проверки унимодальности функции f(x) на практике обычно используют следующие критерии:
1) если функция f(x) дифференцируема на отрезке [а: Ь] и производная f'(x) не убывает на этом отрезке, то f(x) 6 Q[a; 6];
2) если функция f(x) дважды дифференцируема на отрезке [а; Ь] и f"(x) 0 при х G [я; &], то f(x) 6 Q[a; 6].
Пример 3. Показать, что функция /(.г) = ж'1 — 10щ3 4- Збж2 4- 5х унимодальна на отрезке [3; 5].
< Вторая производная функции f{x) равна f"(x) = 12ж2 — 60ж 4- 72. Корни полученного квадратного трехчлена Ж1 = 2 и х2 = 3. Следовательно, f"(x) 0, если х 3 и, в частности, при x 6 [3; 5]. Используя
второй критерий унимодальности, получаем, что /(ж) € Q[3', 5]. >
В задачах 17.13-17.16 убедиться в унимодальности функции /(ж) на указанных отрезках [а; 6]:
17.13. /(ж) = х2 — Зж 4- х In х, [1; 2].
17.14. /(ж) = In (1 4- ж2) — sinх, [0; л/4].
17.15. f(x) = |ж4 + ж2 - 8ж + 12, [0; 2].
17.16. /(ж) = |ж2 — зтж, [0; 1].
17.17. Показать, что любая из точек локального минимума функции /(ж) G Q[a; b] является и точкой ее глобального минимума.
16.18. Показать, что если f(x) Е Q[«; b] и а с < d Ь, то /(ж) Е Q[c; d].
17.19. Пусть f(x) Е Q[ci; b] и a хд < ж2 b. Показать, что
а) если > f(x2), то [/* C [tj; b], а если f(x}) < f(x2), to t/* C [a; ж2];
б) если /(.ti) = f(x2), то отрезок [ip ж2] содержит хотя бы одну точку х* Е U*-,
в) если f(xi) /(ж2), то ж* Е [а; ж2], а при f(x}) > f(x2) имеем х* Е [ж]; 6], где ж* — одна из точек минимума /(ж) на [а; Ь].
17.20. На какие 3 части следует разбить отрезок [—1: 2], чтобы на каждой из них функция /(ж) = ||ж(ж- 1)| - 1| была унимодальной?
17.21. Найти максимальное значение Ь, при котором функция /(.ж) = — ж2 + 5ж — 6 унимодальна на отрезке [—5; 6].
17.22. Будет ли функция /(ж) = аж3 — Зж2 — 10 унимодальной на отрезке [1; 2] при а > 3?
Большую группу приближенных методов минимизации функций составляют прямые методы минимизации, основанные на вычислении
§ 1. Численные методы минимизации функций одной переменной 327
только значений минимизируемой функции в некоторых точках и не использующие значений ее производных.
Метод перебора является простейшим из прямых методов минимизации. Пусть f(x) Е Q[a; b] и требуется найти какую-либо из точек хминимума х* функции /(ж) на отрезке [а; Ь] с абсолютной погрешностью £ > 0. Разобьем [а; Ь] на п равных частей точками деления Xi — a + i(b- а)/п, i = 0, 1, 2, ..., п, где п (Ь-а)/е. Вычислив значения f(x) в этих точках, путем сравнения найдем точку хт, для которой f(xm) = min f(xi). ' (1)
О^г^п
Далее полагаем х* ~ жт, /* « f(xm\ При этом максимальная погрешность еп определения точки х* равна £п = (Ь — а)/п.
Пример 4. Найти минимальное значение /* и точку минимума х* функции /(ж) = ж4 +8ж3 — 6ж2 — 72ж на отрезке [1,5; 2]. Точку ж* найти с погрешностью £ = 0,05.
<1 /(ж) Е Q[l,5; 2], так как /"(ж) — 12ж2 + 48ж — 12 > 0 при ж Е [1,5; 2] (проверьте!).
2 — 15
Выбрав п = = 10, вычислим значения f(xi) = 1,5 + г • 0,05,
0,05
i = 0, 1, ..., 10, поместив их в таблице 1.1.
Таблица 1.1
Xi 1,50 1,55 1,60 1,65 1,70 1,75
f&i) -89,4 -90,2 -91,2 -91,8 -92,08 -92,12
Xt 1,80 1,85 1,90 1,95 2,00
f(xi) -91,9 -91,4 -90,5 -89,4 -88,0
Из таблицы 1.1 находим ж* « 1,75, /* « —92,12. >
17.23. Пусть /(ж) 6 Q[a; 6], хт — точка, найденная из условия (1), ж* — одна из точек минимума /(ж) на [а; Ь]. Показать, что если 1 т п — 1, то ж* 6 [жт_1; жт+1]; если т = 0, то х* G [жо; Ж1]; если т = п, то ж*[жп_1; ж„].
17.24. Пусть отрезок [а; 5] разбит на п частей точками Xi — == а + (b — а)г/п = а + Дг, i = 0, 1, ..., п. Рассмотрев функцию
- --(ж - жт+1 + 6} при ж G [а; жт+1 - 5],
А-<5
-(ж - жт+1 + 5) при . ж G [жт+1 - 6; 6], о
где — 1, 0 < 5 < Д, показать, что абсолютная погреш-
ность определения точки минимума унимодальной функции мето-b — а
Дом перебора может быть как угодно близкой к Д =----= еп.
328
Гл. 17. Методы оптимизации
В задачах 17.25-17.33 методом перебора найти точку минимума .?;* функции /(.?;) на отрезке [а; Ь] с точностью £ и минимум /*:
17.25. /(.г) = х 4- -, [1; 2], е = 0,05.
17.26. /(.т) = х2 - 2х + е~х, [1; 1,5], е = 0,05.
17.27. /(.т) = tgrr — 2 sin ж, [0; тг/4], е — 0,03.
17.28. /(.т) = У1 + + е“2ж, [0; 1], е = 0,1.
17.29. f (x) = д4 + 4д2 - 32д 4-1, [1,5; 2], е = 0,05.
17.30. f(x) = -х7 — х3 4- -х2 — х, [1; 1,5], £ = 0,05.
17.31. /(д) = х3 - 3sinT, [0,5; 1], £ = 0,05.
17.32. f ix) = 5х2 - 8.т5/4 - 20т, [3; 3,5], £ = 0,02.
17.33. /(.?;) = -х3 — 5т4-т1пт, [1,5; 2], е = 0,02.
17.34. Пусть f(x) - - унимодальная дифференцируемая на [а; Ь] функция, причем \ f(x) | М при х Е [а; 6]. Оценить погрешность 6п нахождения минимума /*, методом перебора при разбиении отрезка [а; Ь] на п частей.
Метод перебора, предполагающий предварительный выбор точек хц 2 = 0, 1, ..., п, называется также пассивной стратегией поиска точки минимума х*. На практике точки Xi выбираются заранее, когда удобно провести п4-1 независимых экспериментов по измерению значений /(аг), а последовательное измерение этих значений трудоемко или невозможно, например ввиду нехватки времени. Однако использование уже полученной в предыдущих экспериментах информации о функции f(x) для выбора очередной точки х, измерения (вычисления) /(а;) приводит к более эффективному поиску точки х*. Методы минимизации, в которых точки Xi определяются в процессе поиска точки минимума с помощью найденных ранее значений функции f(x), называются последовательными методами.
Метод деления отрезка пополам является простейшим последовательным методом минимизации. Он позволяет для любой функции f(x) Е Q[a; 6] построить последовательность вложенных отрезков [a; b] D D [ai: 6i] D • • • D [<in-i; 6n-i] D [ап; 6П], каждый из которых содержит хотя бы одну из точек минимума х* функции f(x). Пусть е > 0 — требуемая точность определения точки х*. Выбрав <5 Е (0; 2е), построим последовательности {а„}, {6П}, {а:^} и {ж^}, п = 0, 1, ..., используя рекуррентные формулы ао = а, 6о = 6,
= (an-i + 6n-i - д)/2, j (7г-1)
&п — 1, Ьп — х2 ,
п _ r(n-l) L _ 1
5 — ип—Ij
— (an-i + bn-i 4-(J)/2; (2)
если f(x[n~l}) /(4п-1)), если f(x[n~1}) > f(x{2n~l)).
§ 1. Численные методы минимизации функций одной переменной 329
Переход от отрезка [а„_i; &n-i] к отрезку [ап; 6„] методом деления отрезка пополам иллюстрируется на рис. 22, если f(x\n < f(x2n ^), по г/ (п—1)\ г/ (п—1)\
и на рис. 23, если f[x\ ) > f(x.2 ).
a„ х* b„ a„ i* b„
Рис. 22
Рис. 23
Полагая x* ~ (a„ + 6n)/2, находим x* с абсолютной погрешностью, не превосходящей величины
е„ = (ъ„ - a,,)/"! = (b-a- <5)/2"+1 + Л/2. (3)
Используя условие £п е, из последнего выражения можно найти необходимое число шагов п для обеспечения требуемой точки £. Однако на практике часто поступают иначе: определив границы отрезка [an; Ьп], вычисляют £п по формуле (3) и сравнивают с заданной точностью £.
Пример 5. Решить пример 4 методом деления отрезка пополам.
<1 Положим 6 = 0,02 < 2е — 0,1. Построим последовательность вложенных отрезков [а„; Ьп] по формулам (2), записывая результаты вычислений в таблицу 1.2:
Таблица 1.2
п Ьп й е 1 см -с 11 й Ц) 1 Я-(!П) /й"’) Примечание
0 1,5 2 0,25 1,74 1,76 -92,135 -92,096 < л40)), 61 = х™
1 1,5 1,76 0,13 1,62 1,64 -91,486 -91,696 а> = а//)
2 3 1,62 1,68 1,76 1,76 0,07 0,04 1,68 1,70 -91,995 -92,084 /(х<2)) > (2) аз = т} £3 < £, ТОЧНОСТЬ достигнута
330
Гл. 17. Методы оптимизации
Следовательно, х* « 1,72, и f* ~ /(1,72) = 92,13. >
Для увеличения скорости сходимости метода величину 3 Е (0; 2е) целесообразно выбирать как можно меньшей, однако этот выбор ограничен снизу используемым количеством верных десятичных знаков при задании аргумента х. В любом случае <5 должно быть больше машинного нуля применяемого вычислительного средства.
17.35. Показать, что каждый из отрезков [an; bn\, п — 1, 2, ..., полученных методом деления отрезка пополам, содержит хотя бы одну из точек минимума функции f(x) Е Q[a; Ь].
17.36. Показать, что для f(x) Е Q(a-, b] п шагов метода деления отрезка пополам обеспечивает вычисление точки минимума х* на отрезке [а; Ь] с абсолютной погрешностью, не превосходящей
b — a 5 / 1 \
п 2n+1 2 \ 2П)
17.37. Найти число шагов п метода деления отрезка пополам, необходимое для определения точки минимума функции f(x) Е Е Q[a', b] на отрезке [а; Ь] с точностью £ > 0.
17.38. Достаточно ли вычисления 10 значений функции f(x) Е Е Q[0; 1] для определения ее точки минимума на отрезке [0; 1] с точностью с — 0,02 методом деления отрезка пополам?
17.39* . Сравнить необходимые количества вычисленных значений Nfl и Nn функции f(x) при поиске ее точки минимума на отрезке длины 1 с точностью е = 10~5 методами деления отрезка пополам и перебора соответственно.
В задачах 17.40-17.48 методом деления отрезка пополам найти точку минимума х* функции f(x) на отрезке [а; 5] с точностью е и минимум /*:
17.40. f(x) = х 4- > I1! 2], £ = 0,02.
17.41. f(x) = xsinx + 2cosx, [—5; —4], £ = 0,02.
17.42. f [x) = xA 4- 8r3 - 6z2 - 72z + 90, [1,5; 2], e = 0,05.
17.43. f ix) = x6 4- З?2 + 6x - 1, [-1; 0], e = 0,1.
x2
17.44. f(x) = lO.rlna; —[0,5; 1], e = 0,05.
17.45. f(x) = x2 + 2 (x 1g - - 2), [1,5; 2], e = 0,01.
\ e /
17.46. f(x) = 3z4 - 10? 4- 21a;2 4- 12ж, [0; 0,5], e = 0,01.
2т
17.47. f(x) = — - 2x2, [-3,5; 4,5], e = 0,02.
17.48. f(x) = ex - |ж3 + 2x, [-1,5; -1], e = 0,01.
§ 1 • Численные методы минимизации функций одной переменной 331
Метод золотого сечения также является последовательным методом минимизации. Опираясь на свойства золотого сечения отрезка, этот метод использует найденные значения f(x) более рационально, чем метод деления отрезка пополам (см. задачу 17.53), что позволяет переходить к очередному отрезку, содержащему точку х* после вычисления одного, а не двух значений /(х). Деление отрезка на две неравные части так,что отношение длины всего отрезка к длине большей его части равно отношению длины большей части к длине меньшей части, называется золотым сечением этого отрезка.
Золотое сечение отрезка [я; Ь] осуществляется двумя точками
0 \/з 1
Xi=a +—_—(6-а), х2 = а +—-—(6 — а), (4)
причем Xi есть вторая точка золотого сечения отрезка [a; Хз], а х2 — первая точка золотого сечения отрезка [xi; 6].
Зная одну из точек золотого сечения отрезка [я; 5], другую можно найти по одной из формул
xi = а + Ъ - х2, х2 = а + Ь — Х[. (5)
Пусть /(х) 6 Q[a; 6] и требуется найти точку минимума х* функции /(х) на [а; Ь]. Построим последовательности {а„}, {6П} и {x;l}, п = = 1. 2, ..., следующим образом:
an=an-i, Ьп~х^1~Х\ хп = х\п~1}, если/(xJn'1J) /(х.^-1));
an = х\п~1\ Ь?г = Ьп-г, х,г=4’г-1), если > /(х^'-1)),
(6) п = 2, 3, ..., где ai = а, 1ц = Ъ, х\п и х.™ -- первая и вторая точки
золотого сечения (4) отрезка [an-i; &n-i]-
Для определения чисел я,г, Ьп, хп по найденным an-i, 6n-i, xn_i необходимо выполнить следующие операции:
1) найти одну из точек золотого сечения отрезка [an-i; 6n-i] по известной другой точке хп_1, используя формулы (5) !);
2) вычислить значение /(х) во вновь найденной точке золотого сечения (значение в другой точке x„_i уже вычислено на одном из предыдущих шагов);
3) сравнить значения f(x\n~^) и f(xS)n~1'1) и найти «п. Ън, хп по формулам (6).
Таким образом, на каждом шаге определения an, bn и xn п — 2,3,..., требуется вычисление одного значения /(х). Положив х* ~ хп, найдем
!) При определении х* с большой точностью,чтобы избежать накопления ошибок округления, обычно точки золотого сечения отрезка [an; находят по формулам (4) и в качестве Х1П-1) и х^’’1'1 используют xn-i и ту из найденных точек, которая больше отличается от xn-i-
332
Гл. 17. Методы оптимизации
точку минимума х* с точностью £п:
откуда следует, что число шагов п метода золотого сечения, обеспечивающее заданную точность £ нахождения точки х*, должно удовлетворять неравенству
(7)
Пример 6. Решить пример 4 методом золотого сечения.
< Вычисления проведем по формулам (6), представив результаты в таблице 1.3, где стрелками отмечены сохраняющиеся при переходе к следующему шагу значения.
Таблица 1.3
п £п Яп Ьп (п) ж} ^(п) /uS"’) Примечание
1 0,309 1,5 2 1,691 1,809 -92,049 -91,814 /С40) < /(^2°), Ьг == х^
2 0,191 1,5 1,809 1,618 1,691 -91,464 -92,049 /(г®) > /(т<2>), аз = -Л'1
3 0,118 1,618 1,809 1,691 1,736 -92,049 -92,138 ад = х^
4 0,073 1,691 1,809 1,736 1,764 -92,138 -92,083 /(Ж(14)) < /(^24)), Ь5 = х^
5 0,045 1,736 -92,138 Еп < Е, ТОЧНОСТЬ достигнута
Из таблицы 1.3 получаем ж* « х5 = 1,736, /* « /(ж5) = -92,138. Заметим, что если воспользоваться формулой (7), то необходимое число шагов п можно определить заранее. В нашем случае п 4, 79, т. е. п = 5, и отпадает необходимость во втором столбце таблицы 1.3
3 — v 5
17.49. Показать, что каждая из точек х\ = a 4---(Ь — а)
V5-1 2
и Х2 = a + —-—[о — а) осуществляет золотое сечение отрезка
[а; Ь].
§ 1. Численные методы минимизации функций одной переменной 333
17.50. Пусть и 12 — точки золотого сечения отрезка [а; Ь]. Показать, что X] является второй точкой золотого сечения отрезка [а; х?], а Х2 — первой точкой золотого сечения отрезка [ti; 6].
17.51. Пусть и Х2 — точки золотого сечения отрезка [а; Ь].
а) Доказать, что справедливы равенства .ti = о. + b — д’2, Х2 = = a 4- b — Хд.
б) Найти длины отрезков [а; Х2] и ; 6].
17.52. Найти длину Дп отрезка [an‘, bn], полученного методом золотого сечения при поиске точки минимума х* функции на от-(/— \ п
v 5 — 1 \
—-— I (Ь — а), где
хп — одна из точек золотого сечения отрезка [ап; 6П].
17.53. Сравнить необходимые количества вычисленных значений Nfl и Nc функции f(x) при ее минимизации на отрезке длины 1 с точностью е = 10-5 методами деления отрезка пополам и золотого сечения соответственно.
В задачах 17.54-17.62 методом золотого сечения найти точку минимума х* функции f(x) на отрезке [а; 5] с точностью е и минимум /*:
17.54. f(x) = 2х + i, [0; 1], е = 0,1.
17.55. f(x) = х'{ + 2х2 + 4х + 1, [-1; 0], £ = 0,1.
17.56. f(x) = х5 - 5ж3 + Юж2 - 5х, [-3; -2], е = 0,1.
17.57. /(.ж) = ж2 + Зж(1пж - 1), [0,5; 1], е = 0,05.
17.58. /(ж) = ж2 — 2ж - 2 cos х, [0,5; 1], е = 0,05.
17.59. f (x) = (х + I)4 - 2т2, [-3; -2], е = 0,05.
17.60. f(x) = 3(5 - ж)4/3 4- 2т2, [1,5; 2], е = 0,025.
17.61. /(ж) = —ж3+ 3(1+ ж)[1п (1 + ж) — 1], [-0,5; 0,5], е = 0,05.
17.62. /(ж) = 2 + т2 +т2/3 — In (1 + т2/3)— 2т arctg т1/3, [0,5; 1], е = 0,025.
В прямых методах минимизации, рассмотренных выше, требуется, чтобы функция /(ж) была унимодальной. Если /(ж) этим свойством не обладает, то применение указанных методов приводит, вообще говоря, к неверному результату. Кроме того, во многих случаях доказательство унимодальности функции /(ж) бывает затруднительно.
Метод ломаных является последовательным методом, рассчитанным на минимизацию произвольных (не обязательно унимодальных) функций, удовлетворяющих условию Липшица. Говорят, что функ
334
Гл. 17. Методы оптимизации
ция f(x) удовлетворяет на отрезке [а; Ь] условию Липшица, если существует такое число L > 0 (константа Липшица), что
|/(ж') -/(ж")| Г|ж'- ж"| (8)
для всех х', х" Е [а; 6].
Для проверки условия Липшица на практике используют следующий факт: если функция f(x) имеет на отрезке [а; Ь] ограниченную производную, то она удовлетворяет условию (8), где L тах|/'(ж)|.
[а; Ь]
Пусть функция /(ж) удовлетворяет на [а; /;] условию Липшица с константой L. Опишем метод ломаных для минимизации /(ж).
Полоуким
- fW + Ца + Ь)], = ЙДа) + f(b) + Ца - А)]
и реализуем следующую схему вычислений:
Ш а г 1. Вместо пары чисел (ж*, ) образуем две новые пары (ж^, р\)
и (ж”, pi) следующим образом:
ж'1=ж^-Дь ж'/= ж* + Д1, pi = |[/(тД) +Pi],
где А1 = — Р*]-
Шаг 2. Из полученных двух пар (x[,pi) и (ж'/, pi) выберем ту, у которой вторая компонента минимальна. Обозначим ее (ж2, р2) и исключим из рассматриваемого множества (очевидно, на данном шаге в качестве (ж2, р2) можно взять любую из пар (х\, pi), (жь pi)). Вместо пары (ж2, Р2) добавляем две новые пары (ж2, р-2) и (ж2, Р2), компоненты которых находятся по формулам
ж2 = ж; - Д2, ж2' = ж; + Д2, р2 = |[/(ж2) - р2],
ГДС А2 = ^Жг) ~р^'
В результате получим множество, состоящее из трех пар чисел (ж, р).
Ш а г п. Из п полученных на предыдущих шагах пар (ж, р) выбираем ту, у которой вторая компонента р минимальна. Обозначим ее (ж*, р*). Исключаем эту пару из рассматриваемого множества и добавляем вместо нее две новые пары чисел (ж'п, р„) и (ж”, рп) по формулам
ХП Дп) Я-n ХП Рп Р71] , (9)
гдс А” =
§ 1. Численные методы минимизации функций одной переменной 335
Полагая ж* » ж*, /* « /(ж*), получаем приближенное решение задачи минимизации. Точность определения /* характеризуется неравенствами 0 < /(ж*) - 2£ДП.
Геометрически метод ломаных состоит в построении последовательности ломаных, приближающихся к графику функции /(ж) снизу и имеющих угловые коэффициенты всех звеньев, равные ±L (рис. 24).
Рис. 24
Пример 7. Методом ломаных найти минимум /* функции f (ж) = _ sinjr 0Трезке цд. 15] с точностью 0,01 и точку минимума ж*, ж
< Функция /(ж) дифференцируема на указанном отрезке. Так как \ги\ =
€ [10; 15], то /(ж) удовлетворяет условию Липшица с константой L =
ж cos ж + sin ж ж 4-1 п ----;--1 < —0,11 при ж е
ж2 х£
х cos ж — sin ж ж2
= 0,11.
Найдя ж* = 12,056, р* = -0,281, продолжим вычисления, используя соотношения (9). Результаты вычислений представим в таблице 1.4.
Таблица 1.4
п Исключаемая пара (ж, р) 2ТДП Включенные пары (ж, р)
Рп / *^п ж" Рп
1 12,056 -0,281 0,240 10,963 13,149 -0,161
2 10,963 -0,161 0,070 10,646 11,280 -0,126
3 13,149 -0,161 0,203 12,227 14,071 -0,096
4 10,646 -0,126 0,038 10,474 10,818 -0,107
5 11,280 -0,126 0,041 11,094 11,466 -0,106
6 10,474 -0,107 0,024 10,364 10,584 -0,095
. 7 10,818 -0,107 0,160 10,745 10,891 -0,099
8 11,094 -0,106 0,016 11,020 11,168 -0,098
9 11,466 -0,106 0,028 11,338 11,594 -0,092
10 10,891 -0,099 0,008 < е — — —
336
Гл. 17. Методы оптимизации
Из таблицы 1.4 находим х* и 10,89, /* и /(10,89) = 0,091. Отметим, что /(ж) $ Q [10; 15], поэтому из методов минимизации, рассмотренных выше, в даннОхМ случае применим только метод ломаных. >
17.63. Показать, что если функция /(ж) удовлетворяет условию Липшица (8), то модуль углового коэффициента любой хорды или касательной к графику /(ж) не превосходит константы Липшица L.
17.64. Показать, что если функция удовлетворяет условию Липшица (8), то она непрерывна на [а; Ь].
17.65. Найти наименьшую из констант Липшица функции /(ж) = |ж3 + 2ж2 — 5х + 6 на отрезке: а) [0; 1]; б) [0; 10].
17.66. Показать, что функция /(ж) = ^/ж на отрезке [0; 1] не удовлетворяет условию Липшица.
В задачах 17.67-17.71 методом ломаных найти минимум /* функции /(ж) на отрезке [а; Ь] с точностью е:
17.67. /(ж) = ^ [7; 11], е = 0,01.
х£________
17.68. f(x) = -\/20ж - ж2’ + 0,01 sin ж, [9; И], е = 0,05.
17.69. /(ж) = (0,1ж - 5)8 + cos (0,02ж), [49; 51], е = 0,02.
17.70. fix) = In ж + 0,1 sin (0,1ж), [10; 12], е = 0,01.
17.71. f ix) = (ж-0,9)2 + (х- 1,1)4, [0,8; 1,2], е = 0,05.
2. Методы минимизации, основанные на использовании производных функции. Если вычисление или измерение производных функции f(x) не представляет больших затруднений, то при решении задачи минимизации можно применять непрямые методы, основанные на использовании производных f(x). Во многих случаях эти методы обеспечивают более быструю сходимость, чем прямые методы минимизации.
Метод касательных применяется для минимизации выпуклых дифференцируемых функций. Функция f(x) называется выпуклой на отрезке [а; Ь], если
f[ax’ + (1 — а)ж"] С af(x') + (1 — a)f(x")
(10)
для произвольных х’, х" 6 [а; Ь] и a G [0; 1].
Проверка условия (10) почти всегда вызывает затруднения, поэтому на практике используют следующий критерий выпуклости:
Для того чтобы дважды дифференцируемая на отрезке [а; 6] функция f(x) была выпуклой на отрезке [а; Ь], необходимо и достаточно, чтобы f"(x) 0 при всех х G [а; Ь\.
Опишем метод касательных. Пусть /(ж) — выпуклая дифференцируемая на отрезке [а; 6] функция, причем f(a) • f'(b) < 0. Построим с
§ 1. Численные методы минимизации функций одной переменной 337
рекуррентными соотношениями
^0 -- Ь0 Ь,
bn-if'(bn i) - an-if'(an-i) + f(an-i) ~ (П)
f'(bn-i) - f'(an-i)
an — ап-15 bn — cn—i
при f'(cn-i)^Q,
Qn — Cn — 1) bn — bn—i
при /'(cn_i)<0.
(12)
После n шагов полагаем x* « cn, /* « f(cn). Требуемая точность минимизации /(ж) считается достигнутой, если производная f'(cn) достаточно близка к нулю, т.е. |У’/(сгг)| г, где е > 0 — заданное число, характеризующее точность.
Метод касательных имеет простой геометрический смысл: величина сп_1 из (11) — это абсцисса точки пересечения касательных к графику /(ж), проведенных в граничных точках отрезка [an_i;bn_i] (рис. 25). Рис. 26 и 27 поясняют формулы (11) для случаев /'(cn_i) > О
Рис. 27
и /'(cn-i) < 0 соответственно. Отрезок [an; bn] выбирается так, чтобы
2- G [Яп) ^nJ-
ЕСЛИ условие < 0 не выполняется, то
а) ж* = а при f'(a) > 0, /'(b) > 0;
б) ж* = b при f'(a) < 0, /'(b) < 0;
в) ж* = а, если f'(a) = 0, и ж* = Ь, если f'(b) = 0.
Пример 8. Убедиться, что функция /(ж) = ж2 + ех выпукла на [—1; 1] и минимизировать ее метод касательных с точностью [/'(сп)| 0,05.
<1 Так как /"(ж) = 2 + ех > 0, то /(ж) — выпуклая функция; кроме того, f'(a)f'(b) < 0. Проведем вычисления по формулам (11), (12), поместив результаты вычислений в таблицу 1.5.
338
Гл. 17. Методы оптимизации
Таблица 1.5
п 1>П Cn /'(Cn) Примечание
0 -1 1 0,11586 1,35 /' (c0) > 0, bi = co j'(ci) < o, a-2 = Cl
1 -1 0,11586 -0,41637 -0,173
2 -0,41637 0,11586 -0,14313 0,58 /'(c2) > о, h = C2 |/'(сз)| <0,05, точность достигнута
3 -0,41637 -0,14313 -0,27806 0,02
Из таблицы 1.5 находим х* « сз — 0,278; /* « /(сз) = 0,835. >
17.72. Показать, что если функция f(x) выпукла на отрезке [а; Ь], то на любом отрезке [х'\ .т"] С [а; Ь] график f(x) лежит не выше хорды, проходящей через точки графика с абсциссами х' и х".
17.73* *. Показать,что если /(т) — выпуклая дифференцируемая функция, то любая касательная к графику f (д) лежит не выше этого графика.
17.74. Показать, что выпуклая дифференцируемая на отрезке [а; Ь] функция унимодальна на этом отрезке.
17.75. Показать, что если функция f(x) выпукла на отрезке [а; Ь], то на этом отрезке любая точка локального минимума является и точкой глобального минимума f(x).
В задачах 17.76-17.83, убедившись в выпуклости функции f(x) на отрезке [а; Ь], найти ее точку минимума х* и минимальное значение /* методом касательных, используя в качестве условия достижения требуемой точности неравенство |У'(сп)| С 0,01:
17.76. /(т) = т-1пт, [0,1; 2].
17.77. f(x) = х2 — sinT, [0; тг/2].
17.78. f(x) - х4 4- х2 + х + 1, [-1; 2].
х2
17.79. /(т) = — - cost, [0; 3].
17.80. /(т) = У1 4-т2 + е~2х, [0; 1].
17.81. Да;) = е* + i [0,1; 2].
17.82. /(т) = (х — 4)2 + 1пт, [3; 5].
17.83. /(т) = х4 + е~х, [0; 1].
Метод Нъютонст использующий не только первую, но и вторую производные функции /(ж), при определенных условиях обеспечивает значительно более высокую, чем рассмотренные выше методы минимизации, скорость сходимости к точке минимума х*.
§ 1. Численные методы минимизации функций одной переменной 339
Пусть /(ж) ---- выпуклая дважды дифференцируемая на R функция. Выбрав начальное приближение х$, построим последовательность
__ f (*^77 I ) ТО /Т О\
хп — ^п-1 ~ гц / Г? Н — 1, 2, ... (13)
J
Считая неравенство |//(.т,г)| £ (г — достаточно малое число) условием
достижения требуемой точности вычислений, положим х* ~ тп, /* « -/(м-
При неудачном выборе;хо последовательность (13) может расходиться. Если же точка хц достаточно близка к х*, то эта последовательность сходится к х* достаточно быстро.
Оценка скорости сходимости может быть сформулирована следующим образом. Пусть f(x) — дважды дифференцируемая на К функция, причем f"(x) // > 0 при всех х G Ж и f"(x) удовлетворяет условию
Липшица на R с константой L. Тогда, если начальное приближение .то
удовлетворяет условию q = —— |/'Uo)| < 1, то последовательность (13) 2/z2
сходится к единственной точке минимума х* функции f(x) на 1R, причем
I * I 2П л 1
U - хп\ < ~qz , п = 0, 1, ...
Пример 9. Методом Ньютона найти точку минимума х* и минимальное значение /* функции f(x) — (х — 2)4 - In т с точностью I/UJI «I ю-7.
< Выберем х0 = 3 и проведем вычисления по формуле (13), записывая результаты в таблице 1.6.
Таблица 1.G
п £ п /Un) /'Un)
0 3 -9,86 • 10"2 3,67
1 2,6972477 -0,7558859 0,985
2 2,5322701 -0,8488508 0,208
3 2,4736906 -0,8553636 2,1 10~2
4 2,4663735 -0,8554408 3- 10~4
5 2,4662656 - 0,8554408 5 • 10-8 < IO"7
Окончательно х* % 2,4662656, f* ~ —0,8554408. >
Метод Ньютона часто используется на завершающем этапе минимизации, когда точка минимума х* грубо найдена другим, менее трудоемким методом и требуется найти х* с большой точностью.
В задачах 17.84-17.89 минимизировать функцию /(а?) на всей числовой оси методом Ньютона. Критерием достижения требуемой точности считать выполнение неравенства \fr(xn) | 10-4:
340
Гл. 17. Методы оптимизации
17.84. f(x) = х2 + е х.
17.85. fix) = 2х + е~х.
17.86. f(x) = х2 4- х 4- sin х.
17.87. f(x) = х2 — х 4- е~х.
17.88. f(x) — ех 4- е~2х 4- 2х.
17.89. f(x) = 2х2 4- х 4- cos2 х.
17.90. Найти точку минимума х* функции f(x) одной из задач 17.76-17.83 методом Ньютона, используя в качестве начального приближения решение, найденное методом касательных. Вычисления закончить при |/'(жп)| Ю-6.
•§ 2. Безусловная минимизация функций многих переменных
1. Выпуклые множества и выпуклые функции. Пусть Еп — п-мерное евклидово пространство арифметических векторов х = (ж15 Ж’2, ..., хп). Множество U С 8П называется выпуклым, если вместе с любыми двумя точками гИ1), х^ 6 U оно содержит и отрезок, соединяющий эти точки, т. е.
4- (1 — а)х^ 6 U для всех a € [0; 1]. (1)
Пример 1. Показать, что множество точек х = (Ж1; х^) плоскости U = {(ti ; Ж2)|ж2 4- ж| С 1} выпукло.
< Пусть х^1) = (ж^\ ж^) и х^2) = (ж*2), ж^) G Г, а х = (Ж1, жг) = = ctx^1) + (1 — а)х(2) — точка отрезка, соединяющего точки х^1) и х^2\ |х2 Покажем, что х 6 U. Имеем
рис 2g Используя неравенства (ж^)24-(ж2^)2 1,
i = 1, 2 (так как х^ Е U) и 2ж^ж^ (ЖРЬ2 + (ЖГЬ2, получим ж? +ж^ а2 4- (1 - а)2 4- 2а(1 - а) = 1, т. е. ж е и.
Выпуклость множества U ясна из рис. 28. Так как U — круг, то отрезок, соединяющий любые две точки х^\ х^2) € £7, целиком лежит в U. >
§ 2. Безусловная минимизация функций многих переменных 341
Проверка условия (1) в большинстве случаев требует громоздких выкладок, поэтому на практике при исследовании выпуклости множеств в пространствах £2 и £3 часто используют геометрические иллюстрации, подобные рис. 28.
В задачах 17.91-17.100 установить, являются ли выпуклыми множества U:
17.91. U = {(ti, х2)|2ti 4- х2 2, 2x1 - %2 -2, х2 0}.
17.92. U = {(д?1, х2)\х\х2 > 1, Х[ > 0}.
17.93. U = {(24, ж2)|д;2 > £?}•
17.94. U = {(.ri, x2)|xix2 < 1, xt > 0, х2 > 0}.
17.95. U = {(a?i, х2) |xi ~ ^2 2, х\ 4- х2 4}.
17.96. U = {(.Т1, х2, хз)|хз > х\ + х%}.
17.97. U = {(zi, х2, х3)|хз < х\ 4-т2}.
17.98. U = {(xi, а?2, хз)|.Х1 4- х2 1}.
17.99. U - {(.г‘1, х2, xi)xi 4- х2 4- хз 1, 24 > 0, х2 0}.
17.100. U = /(.ti, х2, ®3)|4 + V + > 1)-
I Z <5 J
Функция f (ж), заданная на выпуклом множестве U С £п, называется выпуклой на этом множестве, если для любых точек хО), х^2) G U и произвольного числа a G [0; 1] справедливо неравенство
/[ах^ 4- (1 — q)x(2)] С af(x^ 4- (1 - а)/(х^2^).
(2)
На практике обычно используют следующий критерий выпуклости функции:
Если /(х) — дважды дифференцируемая на выпуклом множестве U С £п функция и матрица ее вторых производных f"(x) — = (д2 f(x)/dxi dxj) (гессиан) положительно определена при всех х Е U, то функция /(х) является выпуклой на множестве U.
Применяя критерий Сильвестра к матрице вторых производных, .можно сформулировать это утверждение в более удобном для проверки виде:
Если все угловые миноры матрицы fr'(x) положительны при X Е U, то функция /(х) выпукла на множестве U.
Пример 2. Выяснить, является ли функция /(24, х2) = 2.t24-^2 + 4- sin (xt 4- х2) выпуклой в пространстве £2.
342
Гл. 17. Методы оптимизации
<1 Запишем матрицу вторых производных
67W дх^ а2/(х) дх2 дху
а2/(х) \
дх\ дх2
dxl /
/ 4 — sin (art 4- .т2)
\ — sin (з?1 4- х2)
- sin (.п + х2)
2 — sin (xi 4- х2)
Найдя угловые миноры этой матрицы Д1 = 4 — sin (ад 4- х2),
Д2 —
4 — sin (<Ti + £2) — sin (.Ti + я?2)
— sin (яд 4- х2) 2 — sin (ti 4- т2)
= 8 - 6 sin (a?i 4- т2),
убеждаемся, что Д; > 0, i — 1, 2, при всех х е S2, т.е. функция /(х) выпукла. >
Выпуклые функции играют большую роль во многих вопросах оптимизации в связи с тем, что всякий локальный минимум выпуклой функции является одновременно и глобальным.
В задачах 17.101-17.106 убедиться в выпуклости функции /(х) во всем пространстве £п\
17.101. /(ж1, х2} = + х2 — 2ж1ГЕ2 + 6iri — х2 — 2.
17.102. /(ti, х2) = >/1 + х“у + х%.
17.103. /(Ж1, х2) = х2 + х? — cos ———.
17.104. f(xy, х2) = Ху + х? + Ху + х% + xjx^.
17.105. f(xy, х2, х3) = е^?+^+^.
17.106. /(®b я2, жз) — бя2 + 5^2 4- 4^3 + 4.Т1Т2 + 2д>2^з-
В задачах 17.107-17.110 указать множества (У, на которых функции /(х) являются выпуклыми:
т2
17.107. /(х) = —.
17.108. /(х) = sin(iri 4- х2).
17.109. /(х) = X2 4- 2х2 — sin — х2).
17.110. /(х) = Ху 4- а;? 4-------.
1 2 хх + х2
Во многих задачах оптимизации рассматриваются квадратичные п п
функции, т.е. функции вида /(х) — CijXiXj 4-^2rJxJ- Если поло-
г,У=1 j=i
§ 2. Безусловная минимизация функций многих переменных 343
жить qij = Cij + Cji, то получим симметрическую матрицу Q — (qij), с помощью которой можно представить квадратичную функцию в виде
/(х) = j(Qx, х) 4-(г, х), (3)
где х = (xj, х2, ..., хп)т, г = (п, г2, ..., гп)т — векторы-столбцы, (х, у) — скалярное произведение векторов х и у € 8П.
Градиент и матрица вторых производных функции (3) равны grad/(x) = f'(x) = Qx + г, f"(x) = Q = (q2j).
Таким образом, для того чтобы функция (3) была выпуклой в £п, достаточно, чтобы матрица Q была положительно определена.
Пример 3. Пусть /(х) = 2x1 ~ 2xix2 + Зх1Хз + х% — 2х2хз 4- 4х| 4-4- X} 4* 2х2 + Зжз.
а) Найти матрицу Q и вектор г в представлении (3) функции /(х).
б) Найти градиент f'(x).
в) Выяснить, является ли функция /(х) выпуклой.
<1 а) В данном случае сп = 2, q2 = -2, С13 = 3, с22 = 1, с2з = -2,
/ 4 2 3 \ /1\
Сзз = 4, ci = 1, г2 - 2, гз = 3, поэтому Q = -2 2 -2 ,г = 2 .
\ 3 -2 8 / \3/
б) Используя найденные матрицу Q и вектор г, запишем
/4 -2
f(x) = Qx + г = I -2 2
\ 3 -2
3 \ /xi\ /1\
-2 j I Х2 j + I 2 | =
8 / \хз/ \3/
(4з?1 — 2x2 + Зхз 4-1 \
—2xi 4" 2х2 — 2хз 4* 2 | . 3xi - 2x2 4- 8x3 4- 3 /
в) Найдем угловые миноры Д; матрицы /"(х) = Q:
Д1 — 4, Д2 —
4 —2
-2 2
= 4, Дз =
4
-2
3
-2
2
-2
3
-2
8
= 22.
Так как Д; > 0, i = 1, 2, 3, то функция /(х) выпукла в £3. >
17.111. При каких а, b и с функция /(х) = ах\ 4- Ъх\Х2 4- сх^ является выпуклой в £2?
17.112. При каких значениях а функция /(х) = х? 4-^2 + хз + 4- сие 1Z2 выпукла в £3?
В задачах 17.113-17.116 выписать матрицу Q квадратичной функции /(х), найти ее градиент Г(х(°'1) в точке х1-0) и убедиться в выпуклости /(х) в £п:
344
Гл. 17. Методы оптимизации
17.113. /(х) = х2 + 5т1Л2 -4- 3^2 -4- Ж1 — Т2, х(°) = (1, 1).
17.114. /(х) = х2 — ЗгЕ1 Х2 4-10^2 + 5t'i — Зд>2, х^0) = (2, 1).
17.115. /(х) = х2 4- 2х?2 + ^-тз + 2^1 х2 — Х2Х3 4- 2.Т1 4- я?з, х^°) = = (1,0, -1).
17.116. /(х) = X2l-h-X2-hxl-j-X[X2+X[X3-hX2X3 + 5X] — Х2 — З.Т'з, х(°) = (1, 2, 3).
2. Методы безусловной минимизации, основанные на вычислении первых производных функции. Постановка задачи минимизации функции п переменных /(х) ~ f(xi, х%, •., хп) на множестве U С Sn не отличается от постановки в одномерном случае. Если U = £п, то говорят о безусловной минимизации функции /(х).
Для решения задачи безусловной минимизации функции /(х) наиболее часто применяют приближенные методы, в основе которых лежит вычисление производных /(х) первого порядка. Такие методы обычно называют градиентными. В ряде других методов требуется вычисление не только первых, но и вторых производных функции /(х).
Метод градиентного спуска. Пусть /(х) — выпуклая дифференцируемая во всем-пространстве 8п функция и требуется найти ее точку минимума х*. Выбрав произвольное начальное приближение х^0) € £п, построим последовательность
x(^+i) = x(fe) _ Qfcf'(x(*)), k = 0, 1, ..., (4)
где величины > 0 (параметрические шаги) выбираются достаточно малыми для того, чтобы выполнялось условие
k = 0, 1, ... (5)
В качестве условия окончания вычислений обычно используется близость к нулю градиента f'(x^)), т.е. выполнение неравенств
3/(x(fc))
дх{
i 1, 2, ..., п,
или
||Г(х^)|| =
дх{
(6)
2
(e — заданное достаточно малое число), после чего полагают х* « х(А'. f* » /(х(/г)).
Если при некотором к условие (5) нарушается, то шаг в (4) уменьшают (дробят) в заданное число раз до выполнения неравенства (5) и продолжают вычисления.
§ 2. Безусловная минимизация функций многих переменных 345
Пример 4. Минимизировать в функцию /(х) = /(ан, яг2) — = х 1 + 2д?2 + е,Г1+;Г2 методом градиентного спуска, завершив вычисления при \д f / dxi\ 0,05, i = 1, 2.
<] Выбрав начальное приближение х^0) = (0, 0) и «о = 1, построим последовательность (4), записывая результаты вычислений в таблице 2.1.
Таблица 2.1
к TW 4^2 a/(x<fc)) дх 1 а/(х(^) дхч Применение
0 0 0 1 1 1 1
-1 -1 3,145 — — Условие (5) нарушено. Умень-
0 0 1 1 1 0,5 шаем оо в 2 раза
-0,5 -0,5 1,118 — — Условие (5) нарушено. Умень-
0 0 1 1 1 0,25 шаем «о в 2 раза
1 -0,25 -0,25 0,794 0,106 -0,393 0,25 Условие (5)
выполнено
2 -0,2766326 -0,1516326 0,774 0,0983 0,0451 0,25 То же
3 -0,3012259 -0,1629096 0,772 0,0262 -0,023 - Точность достигнута
Итак, х* « (-0,301, -0,163), /* « 0,772. О
Для квадратичной функции (3) формула (4) принимает вид
х(/=+!) — х(*) - + г), k = 0,1,... (7)
В задачах 17.117-17.120 совершить один шаг градиентного спуска (4) из точки х(°) с шагом и сравнить значения /(х^0)) и
17.117. /(х) = х] + 2x1 + еХ1+:Е2, х<°> = (1, 1), а) а0 = 0,1; б) се0 = 0,265; в) ар — 0,5.
17.118. /(х) = 2x^+x2+xiX2+xi+X2, х(°) = (0, 0), a) ev0 = 0,1;
<б) а0 = 0,5; в) «о = 1-
17.119. /(х) = х* + х?2 4- xl + х\Х2 + а^з, = (0, 1, 0), a) qq = 0,1; б) ар — 0,638; в) «о = 10.
17.120. /(х) = exi +(xi +д2 + ге3)2, х^ = (1, 1, 1), а) «о = 0,1; б) сг0 = 0,21268; в) q0 = 1-
346
Гл. 17. Методы оптимизации
17.121. Показать, что если функция /(х) дифференцируема и точке х^ и f'(x^)) ф О, то при достаточно малом шаге из (4) будет выполнено условие (5).
Метод наискорейшего спуска отличается от метода градиентного спуска способом определения величины ak, которая находится из условия
= тшФДа), где Ф^(а) =/[х(А) - аГ(х(/г))]. (8)
а>0
Такой выбор ak обеспечивает максимально возможное уменьшение функции /(х) вдоль направления ее антиградиента —f'(x^^) в точке х^.
Таким образом, для определения ak на каждом шаге метода наискорейшего спуска решается одномерная задача минимизации (8), для чего можно использовать методы, рассмотренные в § 1.
Пример 5. Решить пример 4 методом наискорейшего спуска.
Шаг 1. Положим х^0^ = (0,0), тогда f'(x^) = (1; 1), Ф0(а) = = /(0 — а-1, 0 — а-1) = За2 -Ь е~2а. Для нахождения точки минимума функции Фо (а) используем метод перебора:
а 0,18 0,20 0,22 0,24 0,26
Фо(а) 0,7949 0,7903 0,7892 0,7916 0,7973
т. е. а = а0 = 0,22, откуда х^1) = (о, 0) - 0,22 • (1, 1) = (-0,22, -0,22).
Шаг 2. f'^1)) = (0,204,-0,236), ФДа) = (-0,22 - 0,204а)2 + 4- (—0,22 + 0,236а)2 + е-°’44+°>032а. Минимизируем Ф1(а):
а 0,28 0,30 0,32 0,34 0,36
Ф1(а) 0,77401 0,77384 0,77380 0,77387 0,77401
т.е. a = ai = 0,32, откуда х<2> = (-0,22, —0,22) — 0,32• (0,204, -0,236) = = (-0,2853, -0,1445).
Шаг 3. f'(x(2>) = (8,007, 7,268) • 10~2, Ф2(а) = (-0,2853 - 8,007 х х 10-2)2Ч-(—0,1445 — 7,268-10~2-а)2Ч-е_°’429“15’275’]о 2. Минимизируем Ф2(а):
a 0,20 0,22 0,24 0,26 0,28
Ф2(а) 0,77273 0,77241 0,77240 0,77241 0,77244
т.е. а = а2 = 0,24, х<3) = (-0,3045,-0,1619), f'(x(3>) = (1,821, —2,051) • 10“2, поэтому требуемая точность достигнута и х* « х^3) = = (-0,305, -0,162), /* « /(х<3)) = 0,772. >
§ 2. Безусловная минимизация функций многих переменных 347
Если /(х) — квадратичная функция (3), то величина может быть найдена в явном виде
PW)- ГДС 1'т = ^т+г- <9)
Таким образом, для квадратичной функции метод наискорейшего спуска состоит в построении последовательности {х^} по формулам (7), (9).
17.122* . Показать, что градиенты f'(x^^) и f'(x^'+1^) в последовательных точках итерационного процесса метода наискорейшего спуска ортогональны, т.е. (Г(х^)), f,(x^+1^)) = 0, к = 0, 1, ...
17.123. /(х) = х\ 4- а;2 4- a?i 4- ж2, = (0, 0).
17.124. /(х) = х? + Х[Х2 4- х?, х(°) = (1, 1).
17.125. Дх) = а;2 + 2а;2 + еХ1+Ж2, х^ = (1, 1).
17.126. Дх) = 2д?| 4~ Х% 4~ ^’1^2 + X] 4~ а?2, х(°) — (0, 0).
17.127. Дх) = х'[ + а?2 4~ х% 4* 1Г1Т2 4~ ^2^.3? х(й) = (0, 1, 0).
17.128. Дх) = exi 4- (ху 4- х2 4- а;з)2, х^0^ = (1, 1, 1).
В задачах 17.129-17.144 минимизировать квадратичные функции методом наискорейшего спуска, заканчивая вычисления при
^0,01,^1, 2,..., п:
17.129. Дх) = 7а;2 4- 2ш1ГС2 4- 4- Ж1 — 1О.т2.
17.130. f (х) = За?2 — Зя?1 х2 4- 4а?2 — 2жi 4- х2.
17.131. Дх) = Ху 4- 4#iх2 4- 17а;2 4- Ьх2.
17.132. Дх) = 5а;2 — 4a?ia?2 4- 5а;2 — — х2.
17.133. /(х) = 4а;2 4- 4a;ia;2 4- ба;^ — 17a;i.
17.134. /(х) = 2а;2 — 2a;ia;2 4- За;2 4- a?i — За?2-
17.135. Дх) = 10а;2 4- 3a?i.r2 4- х2 4- 10а?2.
17.136. Дх) — Ху ~ 2х}Х2 4- ба;2 4- a?i — а;2.
17.137. /(х) = 4а;2 4- ба;-2 4- 7а;2 — 2хрх2 4- х\х^ 4- Х[ — х2 4- х^.
17.138. /(х) = 3a;24-4a;24-5a;24-2a;ja;2 —а;]а;з —2.а;2а;з4-а?1-Зд‘з.
17.139. /(х) = а;24-5а?2 4-8а;2 — х\х2+хух^~а;2д,з4-5а;1 — За;24-а?з.
17.140. /(х) = 2a?24-4a;24-8a;24-2a;ia;2 —а;1а;з4-2а;2а;з4-6а:1 —7а;з.
348
Гл. 17. Методы оптимизации
17.141. f (х) = 7х1+4х2 + 6х1-Зх1Х2+Т\Хз-Х2Хз+Х1-Х2 + х:].
17.142. /(х) = Бх? + Зх$ + 2х% + 2XjX2 + XjX3 + Х2Х3 + 5xi + х3.
17.143. /(х) = ЗгЕ| 4-5^2+ 4.т?з 4-2.Т1.Т2 - .Т17;,з - .Т2^з-Г 7а?1+^з.
17.144. /(х) = 4xi-h4x2 + xl-xix2 + 2xix3 4-x2x3-xi-hx2-x:i.
Метод сопряженных градиентов состоит в построении последовательных приближений х^) к точке минимума функции /(х) следующим образом:
x(*+i) = xw -QkP{k\ fc = 0, 1, •••, x^eSn, (10) где x(°) — заранее выбранное начальное приближение, шаг выбирается аналогично (8):
= min$t(a), где (а) =/(x(fc) - ар(/с)), (11)
а>0
а направление спуска — определяется по формуле
p(fc) _ f'(x(fc)) 4. /^р^-1), k = 1, 2, ..., р(°) = f'(x<°)), где
А р/(х^)\2 ||Г(х<‘-))||2 ДА 9х< '
£
г=1 х 7
Таким образом, метод сопряженных градиентов отличается от метода наискорейшего спуска только выбором направления уменьшения функции на каждом шаге (—p(fc) вместо —f'(x^))). Отметим, что из (12) определяется не только антиградиентом —f'(x^^), но и направлением спуска — р(*~О на предыдущем шаге. Это позволяет более полно, чем в градиентных методах, рассмотренных выше, учитывать особенности функции /(х) при построении последовательных приближений (10) к се точке минимума.
Критерием достижения заданной точности вычислений в методе сопряженных градиентов обычно служат неравенства (6). Часто для уменьшения влияния накапливающихся погрешностей вычислений через каждые N итераций (10) полагают /31Пм = 0, т = 0, 1, ..., т. с. производят обновление метода (N — параметр алгоритма).
Для минимизации выпуклой квадратичной функции в £п требуется не более п итераций метода сопряженных направлений.
Приглср 6. Методом сопряженных градиентов найти точку минимума х* функции /(х) = 4- 2з?2 4- — 7з?1 — 7x2-
§ 2. Безусловная минимизация функций многих переменных 349
О /(х) —квадратичная функция, заданная в 82- Поэтому точка х* будет найдена после двух шагов метода сопряженных градиентов.
Шаг 1. Выбрав начальное приближение х^°) = (0, 0), по формулам (9)—(11) находим
р<0) = f (х(О)) = + - 7, XI + 4х2 - 7)|(о) = (-7, -7),
Шаг
Фо^) = 98(2<д2 — а). Из условия Фд(«о) = 0 минимума Фо(<д) получим «о = Отсюда хО) = (0, 0) - |(-7, -7) = Q, / 7 7\
;О)) = \ 4’4/’ откуда с учетом (12) имеем / 7 7\ 1 , „ / 35 21\ „
= (“4’4)+ ^(~7’~7) = (-16’ 16} Поэтому \ 4
-<д2 — 4<д — 392 ) и eti — Окончательно х^2) =
А = —, р(1) 16’ р
Ж Г 1 49 (7
= 32 (2
/7 74 4 ( 35 214 .
- U’ 4/ 7 ( 16’ 16/ -<3’ !)-х • >
17.145. Показать, что при обновлении метода сопряженных градиентов на каждом шаге (т. е. если = 0, k = 1, 2, ...) он переходит в метод наискорейшего спуска.
17.146. Минимизировать одну из квадратичных функций задач 17.129-17.136, совершив две итерации метода сопряженных градиентов из произвольного начального приближения х^0) £ £2.
17.147. Минимизировать одну из квадратичных функций задач 17.137-17.144 с помощью трех итераций метода сопряженных градиентов, используя произвольное начальное приближение х(0) G £3.
17.148. Минимизировать функцию /(д) = x'j 4- х2 4- х$ + х\ — — 2а?2 + 2а;з ~ 2д4 с помощью четырех итераций метода сопряженных градиентов, используя произвольное начальное приближение х<°) G £4.
В задачах 17.149-17.174 минимизировать функцию /(х) мето-
дом градиентов, заканчивая вычисления при
<9/(х^) dxi
1СГ3,
i = 1, 2, ..., п:
17.149. /(х) = т? + 24 4- ех1-И - х} 4- 2.т2.
17.150. /(х) = 4- х2 4- 1 4- |zi - |а;2.
17.151. /(х) = irf 4- 2^2 4- ^1^2 + 2iei 4- Х2-
350
Гл. 17. Методы оптимизации
17.152. /(х) = х2 4- 3j:2 4- cos (д?1 4- 72).
17.153. /(х) = 0 4- 2.7? + х\ 4- ех"+2х2 - ,п - х2.
17.154. ./ (х) = 74 4- 5т2 4- ет1+^.
17.155. /(х) = х\ 4- х2 4- \/2 + х2 4- х?> ~ 2а; 1 + 372.
17.156. Дх) = 27? + Зх2 - 2sin + х2-
17.157. Дх) = In [1 4- Зх2 4- 5.7? 4- cos (а?! - 72)].
17.158. Дх) = х2 4- ет1+ж2 4- 471 4- З.т2.
17.159. Дх) = 74 4- 2x2 + 4^/1 4- 7? 4- 7?.
17.160. Дх) = 2a:i - 5а;2 4-ех1 + 2г2.
17.161. Дх) = 2 ДЗ 4- 7? 4- 27? 4- х^ — Х[ — 73.
17.162. /(х) = х2 4- 2х2 4- 7?7? + х^ 4- еж2+;/з — 72 + 73.
17.163. Дх) = 4л/1 4- 7? 4- 7? 4- 37? 4- Хд — 2х2.
17.164. Дх) = 2х] 4- а4 4- х2х2 4- 73 4- х2х2 4- X] 4- 72.
17.165. Дх) = х2 4- 57? 4- 27? 4- cos (34 — х2 4- 73).
17.166. Дх) = exi+x‘2 4- In (4 4- xj 4- 2х2).
17.167. Дх) = хд 4- х2 - 5.т3 + еМ+'^+^з.
17.168. /(х) = х\ 4- а,’2 4- х2х2 4- \/5 4- а;^ 4- 2а?з 4- 74 4- х^.
17.169. /(х) — 2а;? 4- х2 4- 4а;? — 2 sin ( .
17.170. /(х) = 2у/х2 4- За;^ 4- 3 4- х2х2 — ,'Z?i — х2.
17.171. /(х) = х2 4- а?з 4- ех^+х^+х^ 4- 34 — а;2.
17.172. /(х) - 74 4- х2 + 7’3 + Зу/х2 4- х2 + 1 + ех"+х1
17.173. /(х) = 2a;f 4- 4- sin (71 4- х2) 4- \/3 4- х^ 4- х^.
17.174. /(х) = 74 4- Юх-2 - З73 4- е^+4+^з.
3. Методы безусловной минимизации, использующие вторые производные функции. Если при построении последовательности приближений к точке минимума функции /(х) использовать информацию, содержащуюся в значениях не только первых, но и вторых производных /(х), то при определенных условиях можно обеспечить более быструю, чем в градиентных методах, сходимость этой последовательности.
§ 2. Безусловная минимизация функций многих переменных 351
Метод Ньютона применяется для безусловной минимизации выпуклых дважды дифференцируемых функций. В этом методе последовательные приближения к точке минимума функции /(х) строятся с использованием первых и вторых производных следующим образом:
x(fc+i) = x(fc) _ [/"(xW)]-if'(XW), k = 0, 1, ..., (13)
где х(°) € 8п — начальное приближение, [/"(х^^)] 1 — матрица, обратная матрице вторых производных функции /(х) в точке х^\ Критерием достижения требуемой точности вычислений обычно служат неравенства (6).
Если начальное приближение х^°) достаточно близко к точке минимума х*, то метод Ньютона сходится, как правило, гораздо быстрее методов минимизации, использующих первые производные /(х), поэтохму его часто используют на завершающем этапе минимизации при уточнении приближения к точке х*, найденного другим, более простым методом.
Пример 7. Используя решение примера 4 в качестве начального приближения метода Ньютона, найти точку минимума функции /(х) = = %? + 2а?2 + е^14’^2 с точностью \df(x^)/dxi\ 10“5, i — 1, 2.
<1 Используя результаты решения примера 4, запишем
(0) _ 0,3012259\ — ( 2,622655 A in-2
х ~ ^—0,1629096j ’ 1 ) - \—2,2960057 ’ iU ’
(oh _ <0,39319151 0,62867835A
J ^0,62867835 0,22329787/ •
Найдем
[/"(x(0))]-1
( -0,39319151 у—5,3404226 • 10“2
-5,3404226 • 10~ 0,22329787
откуда
(1) _ 0,3012259\
x - ^—0,1629096j
( 0,39319151
5,3404226 • IO'2
-5,3404226 • 10-‘Л
0,22329787 ) X
( 2,622655 A x 1^—2,2960057
/-0,3127641A
^—0,15638217 •
Вычислив f'(x(1)) = (7,9 -10 6, 7,9 - 10 6), убеждаемся, что условие точности выполнено, т.е. х* ~ х^1^ = (—0,3127641, —0,1563821). >
Модифицированный метод Ньютона обеспечивает более устойчивую сходимость последовательности приближений к точке минимума, чем метод Ньютона.
Если начальное приближение х^°) выбрано недостаточно близким к точке минимума х*, то даже для выпуклой функции /(х) последовательность (13) может нс сходиться к х*. Этот недостаток метода Ньютона
352 Гл. 17. Методы оптимизации
будет устранен, если последовательность приближений {х^} строить по модифицированной формуле
x(fc+i) = х(м _ k = о, i,..., (14)
где ak находится подобно (8) и (11):
$k(ak) = minlt(a),
ct>0
ФЦа) = /{x(fc> -
Кроме того, для последовательности (14) всегда выполняется неравенство y(x(fc+i)) /(х(/г)), k = 0, 1, ..., которое может нарушаться в случае (13).
17.175. Показать, что точка минимума выпуклой квадратичной функции с помощью одной итерации метода Ньютона из произвольного начального приближения х^0) Е 8П.
17.176. Используя результат задачи 17.175, показать, что для нахождения точки минимума выпуклой квадратичной функции достаточно одной итерации модифицированного метода Ньютона при произвольном Е 8П.
17.177. Минимизировать одну из квадратичных функций задач 17.129-17.144 с помощью одной итерации метода Ньютона.
17.178. Минимизировать функцию /(х) из задачи 17.148 методом Ньютона, используя произвольное начальное приближение х(°) Е £4.
17.179. Используя в качестве начального приближения решение одной из задач 17.149-17.174, полученное методом сопряженных градиентов, уточнить это решение с помощью метода Ньютона, заканчивая вычисления при ^/(x^)/^] IO-6, i = 1,
2, ..., тг.
17.180. Показать, что если матрица /"(х^) положительно определена и /'(х (*0) 0, то направлениерк = —[/"(х^))] ^'(х^) является направлением убывания /(х) в точке х^\
17.181. Выбрав произвольное начальное приближение, минимизировать одну из функций задач 17.149-17.174 модифицированным методом Ньютона, используя критерий точности решения |a/(xW)/aa:f| < 10~5, i = 1, 2,
§ 3. Линейное программирование
353
§ 3. Линейное программирование
1. Постановки задач линейного программирования. Графический метод решения. Задача минимизации функции п переменных /(х) = — /(zi, .... хп) на некотором множестве U С £п, не совпадающем со всем пространством £п и заданном с помощью ограничений (равенств и неравенств) на координаты Xj точки х € £„, называется задачей математического программирования. При этом функцию /(х) называют целевой функцией, а множество U — допустимым множеством.
Решение задач математического программирования, как правило, связано со значительно большими трудностями, чем решение задач безусловной минимизации, рассмотренных в § 2.
Простейшим частным случаем задачи математического программирования является задача линейного программирования, состоящая в минимизации линейной целевой функции /(х) = /(^i, ...,хп) =
п
= ^^CjXj на множестве U С £п, заданном системой линейных ограни-
чений (равенств и (или) неравенств) на координаты Xj (j = 1, 2, ..., п).
Задача линейного программирования формулируется следующим образом.
Среди точек х = (a?i, ..., хп) G £п, удовлетворяющих ограничениям
п
^aijXj^bi, i = 1, 2, ..., I- (1)
п
^aijXj^bi i = I + 1, ..., m- (2)
J=i
Xj Z 0,
n
найти me, в которых функция /(x) = ^T^CjXj принимает минималъ-j=i
ное значение, и определить это значение.
Отметим, что в условии задачи линейного программирования могут содержаться неравенства и противоположного, чем в (2), знака, однако такие неравенства легко сводятся к виду (2) умножением на —1.
Если в условии задачи линейного программирования не содержатся ограничения-неравенства (2), т.е. в (1) I = т, то она называется задачей линейного программирования в каноническом виде.
Вводя дополнительные переменные xn+i 0, i = I + 1, ..., т, ограничения-неравенства (2) можно записать в виде равенств
п
^2 aijXj + xn+i =bi, i = I + 1, ..., т.
j=l
354
Гл. 17. Методы оптимизации
Таким образом, любая задача линейного программирования может быть записана в каноническом виде
/(*) = £ min (3) j=i
п
52 aijx3 — bi, i = 1, ..., m, (4)
j=1
Xj > 0. (5)
Часто используется векторная запись задачи (3)-(5):
/(х) = (с, х) —> min,
Ах = Ь, (6)
х О,
где х = (з?1, ..., хп) — вектор неизвестных, с = (ci, ..., сп) — вектор коэффициентов целевой функции из (3), А = (а^) — прямоугольная матрица размера т х n, b — (bi, ..., bm) — вектор правых частей системы (4), ах^О — краткая запись условий неотрицательности (5).
Математические модели многих важных для практики задач оптимизации представляют собой задачи линейного программирования.
Пример 1. Составить математическое описание следующей задачи об оптимальном составе сплава и представить полученную задачу линейного программирования в каноническом виде.
Для приготовления 6о кг сплава с заданными свойствами используют вещества Aj, j = 1, ..., п. В х кг вещества Aj содержится aijX кг химического элемента Bi, i = 1, ..., т. Содержание элемента Bi в сплаве должно заключаться в пределах от fa до bi кг. Стоимость 1 кг вещества Aj составляет Cj руб.
Требуется определить такой состав для приготовления сплава, при котором общая стоимость израсходованных веществ минимальна.
<1 Обозначим Xj количество кг вещества Aj, используемое для приготовления сплава (очевидно Xj 0, j = 1, 2, ..., п). Тогда содержание п
элемента Bi в славе составит 52 кг, а стоимость израсходованных
п
веществ будет равна 52 С7Ж7 руб.
2) Символ /(ж) —> min в записи условия задачи математического программирования используется вместо слов «минимизировать функцию Далее указываются ограничения, определяющие допустимое множество.
§ 3. Линейное программирование
355
Поэтому, с учетом ограничений на содержание элементов Bi в сплаве, для величин :r,j получим следующие неравенства:
11
Pi ^aijXj bi, г = 1,..., т.
•7 = 1
Кроме того, количество сплава должно составлять Ьо кг, поэтому п
= 6°-
Таким образом, математическое описание задачи об оптимальном составе сплава принимает вид
п
/(х) = ^2cixj min>
j=i
n
/^2 aijX3 (?)
J=1 ii
^2aijxj > Pi {i = l, .... rn), (8)
j=i
TI
xj — 60, (9)
j=1
Xj ^0, j = 1, ..., n.
Запишем эту задачу линейного программирования в каноническом виде.
Среди ограничений (7)-(9) на переменные Xj содержится 2т неравенств (7), (8). Для преобразования их в ограничения-равенства введем 2т дополнительных неотрицательных переменных xn+i и xn+m+i, i = 1, ..., т.
Прибавив переменные xn+i к левым частям соответствующих неравенств (7) и вычтя переменные xn+m+i из левых частей неравенств (8), получим задачу линейного программирования в каноническом виде
п
/w = ^2cjxj min’ j=i 11
'У > jxi Т xnjf-i — Ьг,
п
^ijXj xn-i-m~i~i — f3i (7 — 1. ..., т),
n
^2хз = bo, j=i
Xj 0, j = 1, ..., n + 2m. D>
356
Гл. 17. Методы оптимизации
Составить математическое описание задач оптимизации 17.182-17.187, представив полученные задачи линейного программирования в каноническом виде:
17.182. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающиеся составом и стоимостью. Данные от этих сплавах приведены в таблице 3.1.
Таблица 3.1
Компоненты сплава Содержание компонентов в %
сплав № 1 сплав Xs 2
Медь 10 10
Олово 10 30
Цинк 80 60
Стоимость 1 кг 4 6
Получаемый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12,8 кг.
Определить количества Xj, j = 1, 2, сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье.
17.183* . Для изготовления двух видов изделий Л1 и А? завод использует в качестве сырья алюминий и медь. На изготовлении изделий заняты токарные и фрезерные станки. Исходные данные задачи приведены в таблице 3.2.
Таблица 3.2
Виды ресурсов Объем ресурсов Нормы расхода на 1 изделие
изделие Ai изделие Аг
Алюминий (кг) 570 10 70
Медь (кг) 420 20 50
Токарные станки (станко-час) 5600 300 400
Фрезерные станки (станко-час) 3400 200 100
Прибыль на 1 изделие (тыс. руб.) 3 8
Определить количества rrj, j = 1, 2, изделий Aj, которые необходимо изготовить для достижения максимальной прибыли.
17.184. Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице 3.3 указаны: состав поезда
§ 3. Линейное программирование 357
каждого типа, количество имеющихся в парке вагонов различных видов для формирования поездов и максимальное число пассажиров, на которое рассчитан вагон каждого вида.
Таблица 3.3
Поезда Вагоны
багажный почтовый плацкартный купейный мягкий
Скорый 1 1 5 6 3
Пассажирский 1 — 8 4 1
Число пассажиров — — 58 40 32
Парк вагонов 12 8 81 70 26
Определить число скорых Xi и пассажирских .г 2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным.
17.185. Завод производит продукцию двух видов Ai и А2, используя сырье, запас которого составляет b т. Согласно плану выпуск продукции Ai должен составлять не менее 60% общего объема выпуска. Расход сырья на изготовление 1 т продукции Ai и А? составляет соответственно а,] и а? т. Стоимость 1 т продукции Ai и А2 составляет соответственно с\ руб. и сг руб. Определить план выпуска продукции Ai и Аг, при котором стоимость выпущенной продукции будет максимальной.
17.186. В начале рабочего дня автобусного парка на линию выходит Xi автобусов, через час к ним добавляется ж 2 автобусов, еще через час — дополнительно хз машин.
Каждый автобус работает на маршруте непрерывно в течение 8 часов. Минимально необходимое число машин на линии в г-й час рабочего дня (г = 1, 2, ..., 10) равно 6г. Превышение этого числа приводит к дополнительным издержкам в течение г-го часа в размере q руб. на каждый дополнительный автобус.
Определить количества машин xi, Х2, Х3, выходящих на маршрут в первые часы рабочего дня, с таким расчетом, чтобы дополнительные издержки в течение всего рабочего дня были минимальными.
17.187. Процесс изготовления изделий двух видов состоит в последовательной обработке каждого из них на трех станках. Время использования г-го станка составляет bi часов в сутки, i — 1, 2, 3. Время обработки каждого изделия у-го вида, j = 1, 2, на г-м станке равно apj часам. Прибыль от реализации одного изделия j-го вида составляет Cj руб. Составить план суточного впуска изделий так, чтобы прибыль от их производства была максимальной.
358
Гл. 17. Методы оптимизации
Если задача линейного программирования содержит только две переменные, и в ее условии нет ограничений-равенств (1), то такую задачу можно исследовать и решить графически.
Рассмотрим задачу
/(х) = ci Xi + с2.т2 -> min,
(Ю)
ацXi + (1цХ2 bj, i = 1, ..., m, (11)
Xi 0, x-2 0.
(12)
На плоскости (xi, ж2) любое из неравенств (11) определяет полуплоскость, лежащую по одну из сторон от прямой ацх^ + п^2т2 = bi. Для того чтобы определить расположение этой полуплоскости относительно граничной прямой, можно подставить координаты какой-либо точки (при bi 0 проще всего взять начало координат) в соответствующее неравенство (11) и проверить его выполнение.
Таким образом, допустимое множество U задачи (10)—(12) является пересечением первого квадранта х\ 0, т2 0 и полуплоскостей, со-
ответствующих неравенствам (11). Поэтому множество U представляет собой либо:
а) пустое множество, тогда задача (10)-(12) не имеет решений из-за несовместности ограничений (11), (12);
б) многоугольник (рис. 29);
в) неограниченное многоугольное множество (рис. 30).
Для решения задачи (10)—(12) в случае U 0 рассмотрим семейство линий уровня функции /(х) из (10)
CiTi + с2ж2 — С, С — const,
(13)
которые являются параллельными прямыми. Антиградиент — f'(x) = = (—ci, —с2) = е перпендикулярен прямым (13) и указывает направление убывания /(х). Если перемещать параллельно самой себе произвольную прямую (13), проходящую через допустимое множество U, в направлении е убывания /(х) до тех пор, пока эта прямая будет иметь
§ 3. Линейное программирование
359
хотя бы одну общую точку с множеством U, то в своем крайнем положении указанная прямая пройдет через точку множества U, в которой целевая функция /(х) принимает минимальное на U значение.
Пример 2. Используя графический метод, найти решение следующей задачи линейного программирования:
/(х) = —3a?i - 2х2 —> min, + 2х2 7,
2ж1 + х2 8,
Х2 3.
<] Изобразим на плоскости (xi, x2) допустимое множество U данной задачи (многоугольник ABCDE) и одну из линий уровня — ЗЖ1 — 2x2 — С целевой функции (рис. 31). Направление убывания /(х) указывает вектор е = (3, 2). Совершая параллельный перенос линии уровня вдоль направления е, находим ее крайнее положение. В этом положении прямая —3a?i — 2т2 = С проходит через вершину Л(3, 2) многоугольника ABCDE. Поэтому целевая функция /(х) принимает минимальное значение /* в точке х* = (3, 2), причем /* = /(3, 2) = = -13. >
Задача линейного программирования (10)—(12) может иметь и бесконечное множество решений.
Пример 3. Решить задачу линейного
программирования с целевой функцией /(х) = — х^ — 2ж2 и ограничениями на допустимое множество U, взятыми из примера 2.
<3 Множество U построено при решении примера 2. На рис. 32 изображена линия уровня — xi — 2x2 = С целевой функции /(х). В своем крайнем положении при параллельном переносе вдоль направления е — (1, 2) она содержит сторону CD многоугольника ABCDE. Таким образом, все точки отрезка CD являются точками минимума функции /(х) на множестве U. Так как концы С и D этого отрезка имеют координаты (1, 3) и (3, 2) соответственно, то любая точка минимума /(х) представима в виде х* = а(1, 3) + (1 — а)(3, 2) = (3 — 2a, 2 -I- а), где a G [0; 1]. Минимальное значение целевой функции f* = /(х*) = —7. >
В случае неограниченного допустимого множества U задача линейного программирования (10)—(12) может не иметь решения, так как целевая функция на таком множестве может быть не ограниченной снизу.
Пример 4. Решить графическим методом задачу линейного программирования
/(х) = -xi - 2x2 min,
Xi + Х2 1,
2ж1 - х2 -1,
- 2х2 0, Х1, х2 0.
360
Гл. 17. Методы оптимизации
<1 Допустимое множество U данной задачи представляет собой неограниченное многоугольное множество (рис. 33). Функция /(х) убывает
Рис. 32
в направлении е = (1, 2). При параллельном переносе линии уровня —ху — 2x2 — С вдоль направления е она всегда пересекает множество U, а целевая функция /(х) неограниченно убывает. Поэтому рассмотренная задача не имеет решений. >
Решить задачи линейного программирования 17.188-17.200 графическим методом:
17.188. /(х) = X] — 2х2 wiin, — Xi + Х2 < 0, 2гТ1 + Х2 3, Xi - Х2 < 1, ГС1, Х2 0.
17.189. /(х) = —Xi — Згс2 —> min, 2a?i + Х2 2, .Т1 - х2 0,
Xi — Х2 1,
ГС1, Х2 0.
17.190. /(х) = — 2гг1 — Х2 —> min,
2rri + Х2 1, 3^1 - х2 > -1, xi — 4а?2 С 2, Я?1, Х2 0.
17.191. /(х) -= — xi — Х2 -> min, Я-i 3, Х2 2, Х1 + Х2 1, Xi, Х2 0.
§ 3. Линейное программирование
361
17.192. /(х) = — ху — 4^2 —> min,
xi 2,
Xi + 2x2 2,
•^2 < 2,
.7?! +^2^3,
Лд, Х2 0.
17.193. /(х) = — xi — Х2 -» min,
Xi + Х2 1,
XI -Х2 -1,
XI - х2 1,
Х1 2,
Х2 2,
Xl, Х2 0.
17.194. /(х) = —2xi — Х2 —> min,
xi + 2х2 2,
2ГГ1 — Х2 0,
я?1 - 2x2 О,
Х1 - Х2 -1,
Xi, Х2 0.
17.195. /(х) = —xi — Х2 -» min,
2x2 1,
Х1 + Х2 < 3,
д,-] < 2,
Х2 2,
2.Т1 + Х2 2,
XI, х2 0.
17.196. Решить задачу 17.182 об оптимальном составе сплава.
17.197. Найти оптимальный план выпуска продукции в задаче 17.183.
17.198. Определить число формируемых пассажирских и скорых поездов в задаче 17.184.
17.199. Найти оптимальный план выпуска товаров в задаче 17.185, полагая ai = 2, 02 = 1, b = 390, ci = 200, С2 = 300.
17.200. Решить задачу 17.187 со следующими исходными данными:
/0,1
А = = 0,2
\0,3
0,2\ ОД , 0,3/
12\ 10 , 21/
a) ci = 65, С2 = 80; б) ci = 85, С2 = 60.
Графический метод используется также для решения задачи линейного программирования в каноническом виде (3)-(5) с произвольным числом переменных Xj, если число свободных переменных системы уравнений (4) не превосходит двух.
362
Гл. 17. Методы оптимизации
Пусть ранг г матрицы системы ограничений (4) (т.е. матрицы А из (6)) равен рангу расширенной матрицы (А|Ь) этой системы. В противном случае система (4) несовместна и задача линейного программирования (3)-(5) не имеет решения, так как ее допустимое множество U пусто.
Выберем произвольный базисный минор матрицы А. Для определенности будем считать, что этот минор порядка г соответствует первым г столбцам и строкам матрицы А. Если г < т, то уравнения (4) с номерами i = г 4-1, ..., тп являются следствиями остальных уравнений и их следует опустить. Поэтому будем считать, что г = т.
Предположим, что п — т = 2 или п — т — 1. Считая переменные Xj, j = 1, ..., т базисными, а остальные — свободными, решим систему (4), т.е. выразим базисные переменные через свободные, после чего исключим базисные переменные из условия задачи (3)-(5). Для этого полученные соотношения для базисных переменных подставим в выражение (3) целевой функции и запишем условие неотрицательности (5) для всех переменных.
В результате получим задачу линейного программирования вида (10)—(12), эквивалентную исходной задаче и содержащую только свободные переменные исходной задачи, а их число не превосходит двух. Для решения полученной задачи можно использовать графический метод.
Пример 5. Используя графический метод, найти решение следующей задачи линейного программирования в каноническом виде:
/(х) = xi 4- 9^2 + 5хз 4- 3x4 4- 4xs 4- 14x6 -> min,
xi 4- Х4 = 20, х2 4- х5 = 50, х3 + Х6 = 30, Х4 4- х5 4- Хб = 60, Xj ^0, j = 1, ..., 6.
<1 В
данном случае матрица системы ограничений-равенств имеет вид
/1 0 0 1 0 0\
/010010] 0 0 1 0 0 1
\0 0 0 1 1 1/
Ее ранг г = 4 = т, причем минор, образованный первыми четырьмя столбцами, может быть выбран в качестве базисного (проверьте!). Число свободных переменных п — т — 2, поэтому для решения задачи можно использовать графический метод.
Решив систему ограничений-равенств относительно базисных переменных Xj, j = 1, ..., 4, получим
xi = -40 4- х5 4- Хб, х2 = 50 - х5, хз = 30 - х6, х4 = 60 — х5 — х6.
(14)
§ 3. Линейное программирование
363
Исключая с помощью (14) переменные Xi, .... Х4 из выражения для целевой функции, находим
/(х) = 740 - 7х5 + 7хс.
(15)
С учетом условия неотрицательности х3Л>. 0, j = 1, ..., 6, и равенств (14), (15) получаем следующую задачу:
/(х) = 740 — 7х-, 4- 7хс, -> min,
х5 4- xG 40, Ж5 50; xq 30, Xq 4- Xq 60,
Х5, XQ 0.
Допустимое множество U последней задачи изображено на рис. 34. Это многоугольник ABCDE. Перемещая линию уровня —7x5 4- 7xq = С функции (15) по направлению вектора е = (7, —7), находим точку минимума /(х) — вершину 79(50, 0) многоугольника ABCDE. Подставив значения х$ = 50, xG — 0 в равенства (14), окончательно находим х* = (10, 0, 30, 10, 50, 0), /* ~ 390. >
Решить задачи линейного программирования в каноническом виде 17.201-17.206 графическим методом:
17.201. /(х) — —2x1 + X‘i —> min,
2xi “ 4х-2 — х.з + Х4 = — 3,
4xi — Зх2 — х3 + Х4 + Х5 = 6, xi + 4х2 + х3 4- х5 = 15, х3 0, j = 1, ..., 5.
17.202. /(х) = 4xi — Зх2 — Х4 + xs —> min,
— Xi + Зх2 + Х4 — 13,
4xi + + х$ = 26,
- 2xi + Х2 + хз = 1,
xi - Зх2 + х6 = 0, х3 7? 0, j = 1. ..., 6.
17.203. /(х) = xi + 2х2 + хз — х'4 —> min, 10х2 + хз + 2x4 + Зх’5 — 25, - Х1 + 5х2 + Хз + Х4 + Х5 = 10, 2xi — + хз — 3x4 = 6,
х^ 0, j 1, ..., 5.
17.204. /(х) = 4-4xi + 2х2 — Х3 + Х4 —> min, 3xi 4- 2х2 — хз + 4x4 — 3, xi — х2 4- 4хз — 2x4 : 2, х70, j = 1, ..., 4.
364
Гл. 17. Методы оптимизации
17.205. /(х) = —xi — 3x2 ~> min, 2х 1 — Х2 + xq + xq — 10, 2X1 + 2х2 + #4 + Xq = 25, - 2а?1 + Зх2 4- х3 - XQ = 9, б.Т’2 + Х3 + Х4 = 36, Xj 0, j = 1, ..., 6.
17.206. /(х) = -2xi + 2x2 + 3^4 - xq -> min, 3xi — 2x2 — Х3 4- х‘4 = 2, Х1 4- х2 - XQ = 3, 4xi — Х2 + Х4 + Xq = 19, 4xi — Х2 — Х4 4- Xq = 13, xj > 0, j 1, ..., 6.
2. Симплекс-метод решения задачи линейного программирования. Общим методом решения произвольной задачи линейного программирования является симплекс-метод, рассматриваемый ниже.
Пусть ранг г матрицы А = системы ограничений-равенств (4) задачи линейного программирования в каноническом виде совпадает с рангом расширенной матрицы (Л|Ь).
Выберем какой-нибудь базисный минор матрицы А. Для определенности будем считать, что он соответствует первым г столбцам и строкам этой матрицы. Если г < т, то уравнения с номерами i = г + 1, ..., т, являющиеся следствиями остальных уравнений системы, отбросим, полагая в дальнейшем г = т.
Для решения системы уравнений (4) относительно базисных переменных Xj, j = 1, ..., т, с помощью эквивалентных преобразований приведем ее к виду
Х1 . (°) 4" а1,т+1жп1+1 4- • • • -I- Qi0)nXn =4°’,
Х2 4- 'г 4- ' u2, m+lxni+l ' • • + a2°nxn - 3W - ’ (16)
Хт 4” &т, т+1Хт+1 4- • + q(0) X - /3(0) — Pm •
Тогда общее решение системы (4) запишется следующим образом:
xi = д£0) (o) (0) • al,nXn,
x2 = 02 } _ (°) _ Q2, m+lXm+l (°) a2,nxni (17)
X - 3{0) — Pm _ (°) am,m+lXm+1 (0) nxn i
где свободные переменные xm+i, ..., хп могут принимать произвольные значения.
§ 3. Линейное программирование 365
Положив их равными нулю, получим частное решение
xi - х2 = хт = xm+i = хт+2 = • • • = хп = О
х<°) = (,е, (18)
которое назовем базисным решением системы (4). Каждому выбору базисных переменных соответствует свое базисное решение системы (4).
Если все компоненты базисного решения (18) удовлетворяют условию неотрицательности, т.е. если /З^ 0, i = 1, ...,т, то такое
решение называют допустимым базисным решением системы (4) или угловой точкой допустимого множества U задачи линейного программирования (3)-(5). Если среди неотрицательных чисел /3-°) в (18) есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой), а соответствующая задача линейного программирования также называется вырожденной.
В основе симплекс-метода лежит следующий факт:
Если задача линейного программирования (3)--(5) разрешима, то минимум целевой функции /(х) из (3) достигается хотя бы в одной из угловых точек допустимого множества U этой задачи.
Так как различные базисные решения системы (4) соответствуют различным вариантам выбора т базисных из общего числа п переменных Xj, то число допустимых базисных решений (угловых точек) не превышает С™. Поэтому задачу линейного программирования можно решать посредством перебора конечного числа угловых точек допустимого множества U, сравнивая значения целевой функции в этих точках. Однако при большой размерности п задачи линейного программирования этот подход затруднителен. Идея симплекс-метода состоит в направленном переборе угловых точек допустимого множества U с последовательным уменьшением целевой функции /(х).
Описание си мп леке-метода . Предположим, что задача линейного программирования (3)-(5) является невырожденной, а базисное решение (18) — допустимым. Используя соотношение (17), выразим целевую функцию из (3) через свободные переменные Xj, j = т +1, ..., п:
f^=Po}+ 52 (19)
j=m+l где
т т
РоО) Pj0) = CJ- j =m + l, ...,n.
i—1 i-1
Справедливы следующие утверждения:
а) Если в выражении (19) все коэффициенты j = m+1, ..., п, неотрицательны, то в угловой точке (18) достигается минимум целевой функции /(х) из (3) на допустимом множестве U задачи (3)-(5) и этот минимум равен рд°\
366
Гл. 17. Методы оптимизации
б) Если среди отрицательных коэффициентов р^\ j ф 0, из (19) есть такой (например, что в (16) все коэффициенты off О, i — 1, ..., т, то целевая функция /(х) не ограничена снизу на допустимом множестве U и задача (3)-(5) не имеет решений.
в) Если хотя бы один из коэффициентов р^°\ j О, в (19) отрицателен (например, < 0) и при этом среди коэффициентов off в (16) есть хотя бы один положительный, то существует угловая точка х^}>) множества U такая, что /(з^1)) < f(x^).
В случаях а) и б) процесс решения задачи линейного программирования на этом заканчивается. Рассмотрим подробнее случай в). Пусть в (19) коэффициент р\°^ < 0 и в (16) имеются положительные коэффициенты eff. Найдем номер к базисной переменной из условия
/Г 4?
mm
а<?’>0
(20)
где минимум берется по всем номерам г = 1, ...,т, для которых < > о-
Найдем решение системы (4), считая свободными переменные xm+i, • • •, xi-i, х^, xi+i, ..., хп, т.е. поменяв местами свободную переменную xi с базисной переменной X).. Система уравнений вида (16) в этом случае запишется следующим образом:
п / (0) \ (0)
I aij Qil (0) I x3 (0) Хк ~ "i ail ™ + i \ akl / akl
Лф0) (0) &к
" Л(0)’ ак1
п
i = 1, ..., т, i к,
1 .
(0) Xj + (0) Хк (0) ’
akl akl akl
(21)
а зависимость целевой функции от новых свободных переменных примет вид
п ( а(0)\ /?(°)
/И= Е (22)
> = m+l \ ОСщ /
Компоненты нового базисного решения можно найти, приравняв нулю свободные переменные Xj, j = т + 1, ..., п, j I и хь и найдя
§ 3. Линейное программирование
367
при этом условии значения базисных переменных из (21). Базисное решение х^1) является допустимым, т.е. угловой точкой множества U, причем /(х(1)) < /(х(0)).
По знакам коэффициентов в системе (21) и выражении для целевой функции (22) можно сделать одно из трех приведенных выше заключений, как это было сделано для угловой точки х^°\ В случае в) следует совершить переход к очередной угловой точке х^2\ аналогичный переходу ОТ х(°) К Х^, и т.д.
Так как число угловых точек допустимого множества U не превышает С™, то случай в) может повторяться конечное число раз, т.е. в результате конечного числа шагов перехода к новой угловой точке будет либо найдено решение задачи, либо сделано заключение о том, что она не имеет решений.
Реализация описанного выше симплекс-метода значительно упрощается при использовании симплекс-таблиц. Записав коэффициенты уравнений (16) и целевой функции (19) соответствующим образом (см. таблицу 3.4), получим симплекс-таблицу задачи (3)-(5) для угловой точки х(°) из (18).
Таблица 3.4
XI • Хп
Х1 а1,т+1
Xk а(0) к, т-Ь1 Q(°)
Хт а(0) “т, т + 1 •• ТП, 1 а(0) • • ^*771, П №
о(0) Ргп + 1 (о) Pl »(0) • • Рп -р?>
Рассмотрим переход от симплекс-таблицы, соответствующей угловой точке х(°\ к симплекс-таблице для угловой точки х^).
Пусть номера к и I определены так, как это сделано выше. Элемент а также строка и столбец таблицы 3.4, на пересечении которых он стоит, называются разрешающими или опорными. Из формул (21) и (22) следует, что преобразование исходной симплекс-таблицы с опорным элементом (см. таблицу 3.4) приводит к новой симплекс-таблице (таблица 3.5), для определения элементов которой необходимо выполнить следующие операции:
368
Гл. 17. Методы оптимизации
1. Поменять местами переменные Xk и х/, остальные переменные оставить на прежних местах, см. таблицу 3.5.
Таблица 3.5
хк Хп
а?1 а(1) и1,т+1 а(1) ..
XI а(1) 'Ч,т+1 а(1) «к А'1’
Хт &тп, т + 1 - . а(1) • • ctm, п /3<1>
„(1) Рт + 1 р!" ♦ Рп -рР
2. На место опорного элемента поставить 1.
3. На остальных местах разрешающей строки записать соответствующие элементы исходной таблицы.
4. На свободные места разрешающего столбца поставить соответствующие элементы исходной таблицы, взятые со знаком минус.
г тт (1) /э(1) (1)
5. На оставшиеся свободные места элементов а\- , р\ , ' в но-
вой симплекс-таблице записать числа сц,, fa, fa, найденные следующим образом:
5.7 = <4? 40), ft = «S’ • Г - ’ С.
Для упрощения вычислений по этим формулам их можно сформу-(0) (0) (0) (0) /
лировать в виде «правила прямоугольника»: ак1 , akjofa , ait (или (°) /э(°) /э(0) (о) (0) (0) (0) (0)ч /
ак1 , рк , fa a\t, или oikl , ак-, , р) перемножаются (причем
§ 3. Линейное программирование
369
(0) г-
дроизведение, не содержащее опорного элемента берется со знаком минус) и полученные произведения складываются.
6. Все полученные элементы новой таблицы разделить на опорный (о) I
элемент akl' (это можно делать и непосредственно после выполнения операций каждого из п. 2-5).
Пример 6. Решить задачу линейного программирования из примера 5 симплекс-методом, используя в качестве начальной угловой точки базисное решение, соответствующее свободным переменным xi и хз.
<1 Столбцы с номерами 2, 4, 5 и 6 матрицы А системы ограничений-равенств данной задачи образуют базисный минор (проверьте!). С помощью эквивалентных преобразований приводим эту систему к виду (16), где базисными являются переменные х2, Х4, х$ и х^:
х2 + X} 4- хз — 40
Х4 + xi = 20
Х5 - Xi - Хз = 10 х6 + хз = 30.
(23)
Полагая в равенствах (23) свободные переменные xi и х2 равными нулю, находим х2 — 40, Х4 = 20, х& — 30, т.е. базисное решение х(°) = (0, 40, 0, 20, 10, 30). Так как все базисные переменные в х^0) положительны, данное базисное решение является допустимым (т. е. угловой точкой) и невырожденным.
Исключив с помощью (23) базисные переменные в выражении для целевой функции, получим
/(х) = 880 - 7х! - 14х3.
(24)
С помощью равенств (23) и (24) составляем симплекс-таблицу, соответствующую угловой точке х^:
XI Хз
Х<1 1 1 40
Х4 1 0 20
х5 -1 -1 10
х6 0 В 30
—7 -14 -880
Среди коэффициентов j 0, из (19) есть отрицательные — это элементы —7 и —14 последней строки симплекс-таблицы. Следовательно, угловая точка х^°) не является решением задачи.
370
Гл. 17. Методы оптимизации
Для каждого из отрицательных элементов p(j среди соответствующих коэффициентов из (16) (т.е. элементов симплекс-таблицы, сто-- (0)ч
ящих в том же столбце, что и р- ') есть положительные, значит, возможен переход к новой угловой точке х^О с меньшим значением Дх).
Найдем разрешающий элемент. В качестве опорного можно взять любой из столбцов таблицы, соответствующих свободным переменным xi и х3. Выберем, например, столбец при свободной переменной х3.
Разрешающую строку находим в соответствии с (20): так как min (40/1, 30/1) = 30/1, то разрешающей является строка, соответствующая базисной переменной х$. Итак, опорный элемент найден, в симплекс-таблице он обведен рамкой.
Заполнив новую симплекс-таблицу по правилам, описанным выше, получим
Х1 Хб
Х'2 И -1 10
Х4 1 0 20
х5 -1 1 40
Хз 0 1 30
-7 14 -460
Отметим, что значение Дх) в новой угловой точке уменьшилось по сравнению со значением в исходной: 460 вместо 880 (см. элементы в правых нижних углах симплекс-таблиц).
В нижней строке последней таблицы есть отрицательный элемент —7, стоящий в столбце при свободной переменной Xi. Кроме того, в этом столбце имеются положительные элементы, поэтому возможно дальнейшее уменьшение Дх) с помощью очередного шага симплекс-метода.
На данном шаге выбор опорного столбца однозначен и определяется отрицательным элементом —7 последней строки. Разрешающая строка находится из условия (20): так как min (10/1, 20/1) = 10/1, то это строка при базисной переменной х2- Опорный элемент в последней таблице обведен рамкой.
Как и на предыдущем шаге, находим очередную симплекс-таблицу по общим правилам:
Х2 Хб
а?1 1 -1 10
Х4 -1 1 10
х5 1 0 50
Хз 0 1 30
7 7 -390
§ 3. Линейное программирование
371
В этой симплекс-таблице оба коэффициента j 0. в последней строке положительны. Поэтому угловая точка х^2\ соответствующая свободным переменным т-2 и Xq, является точкой минимума целевой функции /(х): х* — х^2) = (10; 0; 30; 10; 50; 0). Минимальное значение f(x) со знаком минус записано в правом нижнем углу симплекс-таблицы, поэтому /* — 390. Сравните эти результаты с решением той же задачи, полученным графическим методом, см. пример 5. >
Замечание. Если задача линейного программирования (3)-(5) вырогкдена, то возможны холостые шаги симплекс-метода, т.е. шаги, в результате которых значение целевой функции не изменяется. При этом теоретически возможно и зацикливание, т.е. бесконечное повторение холостых шагов. Для того чтобы избежать зацикливания, разработаны специальные алгоритмы (антициклины). Однако на практике зацикливание происходит крайне редко, поэтому антициклины мы здесь не рассматриваем.
Решить задачи линейного программирования 17.207 -17.212 симплекс-методом, используя в качестве начальной угловой точки:
17.207. /(х) = — 5я?1 + 4д’2 — хз — Зх4 — 5хз —> min,
Зя? 1 — х2 4- 2xi 4- я?5 = 5,
2.Т1 - Зэ?2 + Хз + 2ж4 + хз = 6, Зз?1 — Х2 + Хз + 3X1 + 2д?5 = 9,
Х} >0, j = l, .... 5; х(°> = (0, 0, 1, 2, 1).
17.208. /(х) = —— х2 — хз — х4 + 4я?5 —> min,
З.Т1 + х2 4- хз - 6д?5 = 7,
2а?1 + х-2 + З.-гз + Зд?4 — 7я?5 = 10,
- 3.7? 1 + Х2 + Хз - 6.Т?4 = 1,
^>0, j = l, 5; х(°> = (1, 2, 2, 0, 0).
17.209. /(х) = 2.Т] + х2 + хз + 7з?4 — 2а?5 —> min,
•7?1 4- х2 - хз + х4 = 1,
2xl + х2 4- хз - х5 = 7,
xi + 2х2 + хз - 7.Х1 + хз = 6,
Xj ^0, j = 1, ..., 5; х<°) = (2; 1; 2; 0; 0).
17.210. /(х) = xi — Зх2 — Зхз 4- 6.7:4 4- З.Т5 —> min,
— 2я?1 4- З.Х2 — 4жз 4- 3xi 4- 2 т: 5 = 1,
— 8я?1 4- 2х2 4- Зхз — 4.7?4 — 4х$ = 1, — a?i — 4д?2 4- 2.т?з — Зт?4 4- З.Т5 = 1, Xj> 0, 7 = 1,..., 5; х<°) = (0; 1; 1; 0; 1).
17.211. /(х) = —2т?1 4- х2 4- 4а?з — х4 — Х3 —> min,
х2 4- 2xi -^5 = 1,
Xi - х4 - хз = 1,
2х2 4- т?з 4- 2д?5 = 4,
<s0, 7 = 1, .... 5; х<°) = (1; 1; 2; 0; 0).
372
Гл. 17. Методы оптимизации
17.212. /(х) = a?i — Х2 — я?з — ^4 — Зя?5 —> min, 2х 1 + 2х2 + &4 + £5 — 3, 3zi — Х2 + 2жз — 2ж5 — 1, — 3^1 + 2жз — Z4 + 2^5 = 1,
Xj>0, j = 1, х<°) = (0; 1; 1; 1; 0).
Решение задачи линейного программирования симплекс-методом начинается с поиска какой-либо угловой точки х^°) допустимого множества U этой задачи.
Метод искусственного базиса нахождения начальной угловой точки х(°) состоит в следующем. Пусть в ограничениях задачи линейного программирования (3)-(5) все bi 0, г = 1, т. Если это не так, то умножим соответствующие уравнения (4) на —1. Введем т дополнительных переменных a:n+i, г = 1, ..., m, и рассмотрим вспомогательную задачу линейного программирования
т
Дх) = ^TjXn+i -> min, i=i
(25)
n
^2 aijxj + xn+i — bi, i = 1, ..., m, (26)
J=i
Xfc 0, k = 1, ..., n + m. (27)
Одной из угловых точек допустимого множества U этой задачи, очевидно, является точка = (0; ...; 0; &i; ...; bm). Поэтому для решения задачи (25)-(27) можно использовать симплекс-метод со следующей начальной симплекс-таблицей:
Xi Х2 • • Хп
Хп+1 ап 012 • • ain Ьх
Хп + 2 а?1 022 а2п Ьг
Хп+т dml Огп2 • • Onin Ътп
Pl Р2 Рп ~Ро
т т
где = - J2 aH, j = • • •, п; ~ро = - bt-
г=1 г=1
Отметим, что решение задачи (25)-(27) всегда существует, так как ее допустимое множество U непусто (х(°) 6 U), а целевая функция (25) ограничена снизу на U (Дх) 0).
Пусть /* = min Дх). Рассмотрим возможные случаи. и
§ 3. Линейное программирование
373
1. f* >0. Тогда допустимое множество U исходной задачи линейного программирования (3)-(5) пусто, т.е. эта задача не имеет решений.
2. /* = 0 и минимум целевой функции /(х) достигается в угловой точке
х = , ..., xn, ; ..., (28)
допустимого множества U вспомогательной задачи. Тогда
х(0) = (Jj; х2; • • •; хп) (29)
есть угловая точка допустимого множества U исходной задачи (3)-(5) и ее можно использовать в качестве начальной угловой точки при решении этой задачи симплекс-методом.
Из (25) видно, что равенство /(х) = /* = 0 возможно только тогда, когда все координаты xn+i, i = 1, ..., m, в (28) равны нулю.
Если задача (25)- (27) невырождена, то это означает, что все переменные Xn+i для угловой точки (28) являются свободными. Опустим столбцы, соответствующие этим переменным в окончательной симплекс-таблице, составленной при решении задачи (25)-(27). Полученная в результате этого таблица будет соответствовать системе уравнений (4), разрешенной относительно т переменных х±, являющихся базисными для угловой точки (28). Поэтому остается заменить в этой таблице последнюю строку на строку коэффициентов целевой функции (3) исходной задачи и продолжить ее решение симплекс-методом из начальной угловой точки (29).
Если вспомогательная задача (25)-(27) вырождена, то в угловой точке (28) некоторые из переменных xn+i, i = 1, ..., т, могут оказаться базисными. Тогда эти переменные следует перевести в свободные с помощью холостых шагов симплекс-метода, выбирая в качестве разрешающих произвольные элементы симплекс-таблиц, отличные от нуля. После этого исходная задача (3)-(5) решается симплекс-методом так, как описано выше.
Пример 7. Методом искусственного базиса найти какую-либо угловую точку допустимого множества задачи линейного программирования, рассмотренной в примере 5, и записать соответствующий этой угловой точке симплекс-таблицу.
<3 Введем дополнительные переменные х7, ..., тщ и запишем условие вспомогательной задачи линейного программирования (25)-(27) для рассматриваемого случая:
/(х) = х7 + х8 + хд + жю -> min,
Xi + Х4 + х7 = 20, х2 + х5 + х8 = 50, х8 + Xq + хд = 30, Х4 + хе + хе + жю = 60, Xk 0, к = 1, ..., 10.
374
Гл. 17. Методы оптимизации
Считая дополнительные переменые ж7, .... жю базисными, запишем симплекс-таблицу этой задачи, соответствующую угловой точке х^ = = (0; 0; 0; 0; 0; 0; 20; 50; 30; 60):
Ж1 Х2 Х8 Х4 хь 1’6
Х7 1 0 0 И 0 0 20
Х8 0 1 0 0 1 0 50
Хд 0 0 1 0 0 1 30
Жю 0 0 0 1 1 1 60
-1 -1 -1 -2 —2 -2 -160
Любой столбец этой симплекс-таблицы может быть выбран в качестве разрешающего, так как элементы ее последней строки отрицательны. Выберем, например, столбец, соответствующий свободной переменной Х4. Тогда разрешающим будет элемент этого столбца, стоящий в первой строке, так как min (20/1, 60/1) = 20/1.
Производя преобразования симплекс-метода, получим такую последовательность симплекс-таблиц (рамками обведены разрешающие элементы) 3):
В нижней строке последней симплекс-таблицы нет отрицательных элементов, а в правом нижнем углу стоит нуль. Следовательно, минимум
3) Столбец симплекс-таблицы, соответствующий вспомогательной переменной Xn+i, вводимой в свободные на каждом шаге метода искусственного базиса, удобнее вычеркивать на данном шаге вместо того, чтобы исключить такие столбцы одновременно в окончательной симплекс-таблице.
§ 3. Линейное программирование
375
у* = 0 вспомогательной целевой функции достигнут и
х(0) = (0; 40; 0; 20; 10; 30)
(30)
есть угловая точка допустимого множества U исходной задачи линейного программирования из примера 5.
Заменив нижнюю строку последней симплекс-таблицы на строку коэффициентов целевой функции исходной задачи, получим симплекс-таблицу этой задачи, соответствующую угловой точке из (30):
Ж1 Хз
Х4 1 0 20
я2 1 1 40
Хб 0 1 30
Z5 -1 -1 10
—7 -14 -880
Отметим, что другие варианты выбора разрешающих элементов в Хюде реализации метода искусственного базиса могли привести к другим угловым точкам допустимого множества U исходной задачи.
Использование х^0) из (30) в качестве начальной угловой точки симп-декс-метода в рассматриваемой задаче иллюстрирует решение примера 6.
Решить задачи линейного программирования 17.213-17.225 Симплекс-методом, находя начальную угловую точку методом искусственного базиса:
17.213. /(х) = —За?1 4- 2x2 — 2жз 4- 2^4 — х$ —> min,
xi 4- Х2 - ж3 = 1,
— Х2 + ^3 + %4 —
Х2 + Х3 + Х5 = 2,
Xj ^0, j = 1, ..., 5.
17.214. /(х) = —6a?i — &Г2 + 4- Зд?4 ~> niin,
2xi + 5x2 4” Х3 4” 2д?4 = 20,
12^1 4- 6x2 4” 2^з 4- Х4 = 72,
х3 > 0, j = 1, ..., 4.
17.215. /(х) = —xi — 4x4 —> min,
— xi — 2x2 4- 2д?з 4- Х4 4- 5х$ = 13,
— 2^1 4- 2x2 4” 4^4 4- хз = 5,
Xi - Х2 4" Хз - Х4 4- 2^5 = 5,
жу > 0, j = 1, ..., 5.
376
Гл. 17. Методы оптимизации
17.216. /(х) = 34xi 4- х2 4- Зхз - 3x4 -> min, 3xi — 2х-2 4- За?з 4- 2x4 = 9, xi 4- 2X2 ~ + ^4 = О,
- Х[ - Х2 + 2хз 4* Х4 = 6, Xj О, j = 1, ..., 4.
17.217. /(х) = -xi 4- 2x2 4- 2хз - х^ -> min,
Xi + Х2 + Хз + Х'4 = 7, — 3xi 4- х2 4” 2хз 4” Х4 = 6, 2xi 4- х2 4- хз - х4 = 2, х3 О, j = 1, ..., 4.
17.218. /(х) = —3x1 4- хз — 2x4 —> min, 15xi 4- 2х2 ~ Зхз — 7x4 4- Х5 = 4, 2xi 4- Х2 4- хз — 2x4 = 3, х3 4- 5x4 4- 2х5 = 7, Xj^O, j = 1, ..., 5.
17.219. /(х) — —Х2 —> min,
xi 4- Х2 > 1, - xi 4- х2 -1, 2xi —^2^0, xi, х2 > 0.
17.220. /(х) = 3xi — 2х2 4- хз -> min, 3xi 4- х2 — 2хз = 2, 4xi 4- Зх2 4- 2хз = 1, х7- 0, j = 1, 2, 3.
17.221. /(х) = —2x1 4- х2 — хз 4- Х5 —> min, — 2x2 4- Х4 4- Х5 = —3, хз — 2x4 — 2, xi 4- Зх2 — х‘4 5,
х\ 4- х2 -3, Xj^O, j = 1, • • •, 5.
17.222. /(х) = —8х] — 2x2 4- 5хз — 15x4 ~> min, — xi 4- Зх2 4- хз 4- 10x4 25,
2xi 4- х2 4- хз 4- 5x4 < 10, lOxi 4- 2x2 4- 2хз — 5x4 26,
х3 0, j = 1, ..., 4.
17.223. Предприятие, располагающее ресурсами сырья трех видов Bi, i = 1, 2, 3, может производить продукцию четырех видов Aj, j = 1, ..., 4. В таблице 3.6 указаны затраты ресурсов Д на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.
§ 3. Линейное программирование
377
Таблица 3.6
Вид сырья Вид продукции
Ai а2 Аз Ад Объем ресурсов, т
Bi 4 5 2 3 60
в2 30 14 18 22 400
Вз 16 14 8 10 128
Прибыль, руб. 48 25 56 30
Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной, при условиях:
а) продукции необходимо выпустить не менее 8 т, продукции Ад — не более 5 т, а продукции и Аз — в отношении 2:1;
б) производственные издержки на 1 т продукции Aj, j = 1, ..., ..., 4, составляют соответственно 3, 9, 12 и 6 руб., а суммарные издержки не должны превышать 87 руб.
17.224. Завод получает 4 вида полуфабрикатов Bi в количествах: — 400 т, Т?2 — 250 т, 7?з — 350 т и В] — 100 т.
В результате смешения этих компонентов получают 3 вида про-цукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для Ai — 2:3:5:2, для А^ — 3:1:2:1, для Аз — 2:2:1:3. Стоимость 1 т продукции Aj составляет: Ai — 12 руб., А^ — 10 руб., Аз — 15 руб.
Составить оптимальный план выпуска продукции по критерию: а) максимальной стоимости выпущенной продукции;
б) максимального использования полуфабрикатов.
17.225. Решить задачу 17.186 об оптимальном графике работы автобусного парка при следующих исходных данных:
i 1 2 3 4 5 6 7 8 9 10
bi 10 20 22 23 25 22 20 15 10 5
Ct 5 5 6 6 6 8 10 15 15 20
3. Целочисленное линейное программирование. Во многих случаях на допустимое множество задачи линейного программирования (3)-(5) накладывается дополнительное требование целочисленности переменных Если этому требованию должны удовлетворять все переменные, то
378
Гл. 17. Методы оптимизации
получаем полностью целочисленную задачу линейного программирования, которая в каноническом виде записывается следующим образом:
п №) = min> J=1
« п
aijXj = bi, i = 1, ..., m, j=i
Xj 0, Xj € Z,
j = 1, ..., n,
(31)
где Z — множество целых чисел.
Полностью целочисленную задачу с двумя переменными можно решить графически, учитывая, что допустимое множество U этой задачи состоит из точек целочисленной координатной сетки, принадлежащих допустимому множеству U задачи линейного программирования без дополнительного требования (31).
Решить полностью целочисленные задачи линейного программирования 17.226-17.234 графическим методом:
17.226. /(х) = xi — 20x2 —> min,
— -Ь 10^2 С 40,
4xi + 2^2 29,
Xj 0, Xj G Z, j = 1, 2.
<1 На плоскости (яд, x?) построим допустимое множество U рассматри-
ваемой задачи линейного программирования без требования целочислен-
ности (многоугольник ABCD на рис. 35) и отметим точки множества U с целочисленными координатами. Совокупность этих точек представляет собой допустимое множество U полностью целочисленной задачи.
Перемещая линию уровня целевой функции /(х) в направлении е = ( — 1, 20) убывания /(х), находим крайнее положение этой линии, в котором она еще имеет непустое пересечение с множеством U. В этом поло-
жении линия уровня проходит через точку В(0, 4), поэтому решение задачи имеет вид х* = (0, 4), /* = min/(x) =- —80.
и
Отметим, что, как видно из рис. 35, точкой минимума /(х) в данной задаче без требования целочисленности является точка <7(5; 4,5),
§ 3. Линейное программирование
379
т.е. х* = (5; 4,5), /* — min/(x) = —85. Отсюда следует, что точкой минимума целевой функции на допустимом множестве U целочисленной задачи не обязательно является ближайшая к решению х* обычной (нецелочисленной) задачи точка множества U с целочисленными координатами. >
17.227. /(х) = — xi — ^2 —> min,
2д“1 4- 3^2 36,
Xi 13,
З.т; 1 4- а?2 > 6,
Xj 0, Xj G Z, 7 = 1,2.
17.228. /(х) = —9.Т] — 11а72 —> min,
4xj 4- З.Т2 < 10,
,Т1 < 5,
xi 4- 2x2 8,
Xj 0, Xj 6 Z, j = 1, 2.
17.229. /(х) = —4a?i — За;2 —> min,
4.7; 1 4- Х2 10,
2.7; [ 4- За;2 8,
Xj 0, Xj G Z, j = l,2.
17.230. /(х) = —а?! — а?2 —> min,
2х{ 4- Зж2 5,
.Ti С 2,
Xj 0, Xj G Z, 7 = 1, 2.
17.231. /(х) = Х2 - а;з min,
Зх2 4- .7;3 4- х4 = 3,
Xi - 2х,2 4" я-’з = 1,
Xj 0, Xj G Z, j = 1, 2.
17.232. /(x) = -a;2 -> min,
3a;i 4- x2 4- a?3 = 12, — 8a; ] 4- 3a;2 4- x4 = 24, x-j 0, x-i G Z, 7 = 1,2.
17.233. В цехе площадью 74 м2 необходимо установить станки, на приобретение которых отпущено 42 тыс. руб.
Существует два типа станков. Станок первого типа стоимостью 6 тыс. руб., требующий 12 м2 производственных площадей, обеспечивает изготовление 70 изделий в смену. Аналогичные характеристики станка второго типа составляют соответственно 4 тыс. руб., 6 м2, 40 изделий в смену.
Найти оптимальный вариант приобретения станков, обеспечивающий максимальное производство изделий в цехе.
17.234. Решить задачу 17.182 об оптимальном составе сплава, предполагая, что сырье каждого вида приобретается в количествах, кратных 1 кг.
380
Гл. 17. Методы оптимизации
Для решения полностью целочисленных задач линейного программирования с произвольным числом переменных используется метод Го-мори. Он состоит в последовательном отсечении от допустимого множества U нецелочисленной задачи частей, не содержащих точек с целыми координатами. Эти отсечения производятся включением в задачу дополнительных ограничений на переменные Xj.
Опишем алгоритм метода Гомори, использующий симплекс-метод.
1. С помощью симплекс-метода находится решение х* задачи линейного программирования без учета требования целочисленности (31). Если для х* условие (31) выполняется, то задача решена. В противном случае среди чисел f3i последнего столбца симплекс-таблицы, определяющей решение х*, есть такие, что {0i} > 0 4).
2. Среди нецелых элементов /3i выбирается произвольный элемент Дг (например, с максимальной дробной частью {Дг}). По r-й строке симплекс-таблицы составляется дополнительное ограничение вида — п
{otrjXj} — {Дг} (здесь, как и выше, для определенности мы
полагаем, что свободные переменные Xj имеют номера т + 1, ..., n). С помощью вспомогательной переменной л?п+1 0 это ограничение пред-
п
ставляется в виде равенства xn+i — {ап} = — {Дг} и вводится в j=m+l
симплекс-таблицу дополнительной строкой
•£n+1 |^п+1, m-j-1 • • • С^п+1, п | Дп+1 ! (32)
где an+iJ = j = т + 1, ..., n; /3n+i = -{Дг}.
Так как /3n+i — — {/3r} < 0, то после дополнения строкой (32) симплекс-таблица перестает соответствовать допустимому базисному решению задачи линейного программирования, которую она описывает.
3. Для перехода к допустимому базисному решению производятся следующие операции:
а) строка с отрицательным свободным членом /3k считается разрешающей (на первом шаге, очевидно, к = n + 1);
б) если все коэффициенты 0, то задача не имеет решения, в противном случае номер I разрешающего столбца находится из условия
Pi • Pj
---- = mm —~:
Ittfctl jakj<0
в) совершается преобразование симплекс-таблицы с опорным элементом осы- Если в новой таблице по-прежнему есть хотя бы один отрицательный свободный член, то описанная процедура повторяется, начиная с операции а), необходимое число раз.
4) Напомним, что всякое действительное число а можно представить в виде а = [а1 + {а)> гДе [°] — целая часть числа а, а {а} = a — [а] — его дробная часть.
§ 3. Линейное программирование
381
Если все элементы /3* вновь полученной симплекс-таблицы неотрицательны, то допустимое базисное решение найдено. Отметим, что выбор опорного элемента аы гарантирует неотрицательность коэффициентов Pj новой симплекс-таблицы. Поэтому найденное допустимое базисное решение является и оптимальным.
4. Если найденное в разделе 3 решение задачи линейного программирования удовлетворяет условию целочисленности, то вычисления завершаются, а если нет, то продолжаются переходом к разделу 2 описания алгоритма.
Описанный алгоритм позволяет найти решение полностью целочисленной задачи линейного программирования, или установить отсутствие решений за конечное число итераций.
Пример 8. Решить задачу 17.226 методом Гомори.
<] Введя дополнительные переменные хз, xt 0, запишем эту задачу в каноническом виде:
/(х) = xi — 20x2 -> min, ~xi 4- 10x2 + хз = 40, 4^1 + 2^2 Я-4 = 29,
Xj 0, х7- € Z, 7 = 1,2.
Отметим, что так как все коэффициенты ограничений-равенств данной задачи целые, то целочисленность исходных переменных Х], х% влечет целочисленность и дополнительных переменных Хз, х$. Поэтому и после перехода к каноническому виду можно рассматривать данную задачу как полностью целочисленную и применить для ее решения метод Гомори.
Одна из угловых точек допустимого множества нецелочисленной задачи очевидна: = (0, 0, 40, 29). Запишем симплекс-таблицу для
этой угловой точки:
Х1 х2
Хз -1 I’io'I 40
Х4 4 2 29
1 -20 0
Решение нецелочисленной задачи находится за две итерации симплекс-метода:
Х1 Хз Х4 Хз
Х2 Х4 -1/10 42/10 1/10 -2/10 4 Х2 -> 21 х\ 1/42 10/42 4/42 -2/42 9/2 5
-1 2 80 10/42 82/42 85
382
Гл. 17. Методы оптимизации
Это решение х* = (5, 9/2, 0, 0), /* = -85 не удовлетворяет условию целочисленности, поэтому дополняем последнюю симплекс-таблицу строкой (32):
X.\ X.3
X-2 1/42 4/42 9/2
Xl 10/42 -2/42 5
X5 -1/42 -4/42 -1/2
10/42 82/42 85
Для перехода к допустимому базисному решению находим разрешающий элемент по описанному правилу и преобразуем симплекс-таблицу:
X.5 x3
X 2 1 0 4
Xl 10 -1 4
X4 -42 4 21
10 1 80
Последняя симплекс-таблица не только соответствует допустимому базисному решению, но и дает решение рассматриваемой задачи: х* ~ = (0, 4), /* = -80.
Отмстим, что дополнительное ограничение, введенное в симплекс-2 4 1
таблицу, имеет вид - — • х3 -. С помощью уравнений
х3 = 40 4- xi — 10л>2, хд = 29 — 4xi — 2x2 перепишем его для переменных xi и Х2‘- х-2 4. Отсюда видно, что дополнительное ограничение
соответствует отсечению от допустимого множества U (многоугольника ABCD на рис. 35) части, содержащей точку х* = (5, 9/2) (вершину С этого многоугольника). >
Решить полностью целочисленные задачи линейного программирования 17.235- 17.250 методом Гомори:
17.235. /(х) = -xi + д‘4 —> min,
— 2ti + Х4 + Т5 — 1,
+ Х‘2 — 2а?4 = 2,
xi + x,i + З.Т4 = 3,
Xj 0, Xj; G Z, j = 1, . . . , 5.
17.236. /(x) = — 2x-[ + 2x2 — Зтз + 3z4 —> min,
x-[ — 2x2 + X4 = 3,
x-2 + - 2t4 = 5,
3t2 + X4 + x5 = 4,
Xj 0, Xj G Z, j = 1, ..., 5.
§ 3. Линейное программирование
383
17.237. /(х) = —X} 4- Х2 — хз 4- Х4 —> min, xi 4- 2жз 4- Х4 = 8, ^1 + ^2 - ям = 4, — xi + 2х2 4- £3 4- 3x4 — 6, Xj о, xj е z, j = 1,..., 4.
17.238. /(x) — —X[ — X2 —> min,
2#i 4- X2 4- X3 = 5, 2xi 4- 3^2 4- X4 = 9, Xj 0, Xj; e Z, j = 1, ..., 4.
17.239. /(x) = xi 4- 2x2 4- £5 -» min,
4- X2 4- X3 4- X4 4- x$ - 5,
4- X3 4- X4 - x$ = 2,
X3 - X4 4- x5 = 1, Xj 0, Xj 6 Z, j = 1, ..., 5.
17.240. /(x) = —4zi — 3^2 min, 2^1 4- 3^2 4- X3 = 8, 4a?i 4- X2 4- X4 = 10, 0) Xj ^5 j 1, • • • , 4.
17.241. /(x) = —xi — X2 —> min,
xi 4- 2x2 4- x3 = 6, 3zi 4- 2x2 4- X4 = 9, Xj 0, x3;£ Z, j = 1, ..., 4.
17.242. /(x) = — X3 -> min, - 6з?2 4- 5^з 4- x$ = 6, 7x2 ~ 4^з 4- X4 = 4, xi 4- X2 4- X3 = 9, Xj 0, Xj G Z, j = 1, ..., 5.
Отметим, что переход к каноническому виду в полностью целочисленной задаче линейного программирования, содержащей ограничения-неравенства п
J=1
не приводит, вообще говоря, к полностью целочисленной задаче в каноническом виде, так как в преобразованных ограничениях (33)
п
O'ijXj “Ь Xn+i — j=l
вспомогательные переменные xn+i не подчинены требованию целочисленности.
Однако если все коэффициенты , bi в (33) — целые числа, то условие целочисленности можно распространить и на xn+i, как это сделано при решении примера 8.
384
Гл. 17. Методы оптимизации
Полностью целочисленную задачу в каноническом виде можно получить также, если в (33) a^, bi — рациональные числа. Для этого следует умножить (33) на общее кратное знаменателей коэффициентов aij, bi (т.е. перейти к целым коэффициентам в (33)) и лишь после этого ввести вспомогательные переменные xn+i.
17.243. /(х) = 3^1 4- 2x2 4- ^з min, xi 4- Зя?2 4- х3 10, 2a?i 4- 4а?з > 14, 2^2 4- хз 7,
Xj 0, Xj G Z, j = 1, 2, 3.
17.244. /(x) = —2a?i — X2 — хз —> min,
ху 4- 2x2 4- 2а?з = 16,
Xi 4- X2 < 7, 3a?i 4- 2^3 > 18, Xj 0, Xj eZ, j = 1, 2, 3.
17.245. /(x) = —4^1 — 3a?2 —> min,
4a?i 4- X2 C 44,
Xi C 22,
X2 < 18,
Xj 0, Xj eZ, j = 1, 2.
17.246. /(x) = Xi 4- 2x2 4- X3 —> min,
1 1 2
^1 + 3Я2 4- -хз 1,
2a?i 4- X2 1,
1 3
-rr2 4- -хз > 1,
Xj 0, Xj El, j = 1, 2, 3.
17.247. /(x) = — Xi — 2x2 — За?з -> min,
2 1 25
Xi 4- -x2 4- -хз < —,
3 2 6
3 2
Xi 4- -X2 4- -Хз < 3, 5 5
Xj 0, Xj eZ, j = 1, 2, 3.
17.248. В цехе размещены 100 станков 1-го типа и 200 станков 2-го типа, на каждом из которых можно производить детали Ai и А2. Производительность станков в сутки, стоимость 1 детали каждого вида и минимальный суточный план их выпуска представлены в таблице 3.7.
§ 3. Линейное программирование
385
Таблица 3.7
Детали Производительность, дет./сут Стоимость 1 детали, руб. Минимальный суточный план
Тип 1 Тип 2
Ai 20 15 б 1510
а2 35 30 4 4500
Найти количества станков г-го типа, г = 1, 2, которые необходимо выделить для производства деталей Xj, j = 1,2, с таким расчетом, чтобы стоимость продукции, производимой в сутки, была максимальной.
17.249. Решить задачу 17.183, считая, что в результате усовершенствования технологического процесса расход меди на изготовление одного изделия Л2 снизился с 50 до 40 кг.
17.250. Решить задачу 17.199 в предположении, что товары Ai и Л2 выпускаются в количествах:
а) кратных 1 кг;
б) кратных 2 кг.
Если требованию целочисленности подчинены не все переменные задачи линейного программирования, то такая задача называется частично целочисленной.
Для решения частично целочисленных задач также используется метод Гомори, но его алгоритм в этом случае отличается видом коэффициентов Qn+i,j в дополнительной строке (32), а именно
{ — агр если arj 0,
{Дг} п
fL'Y/3 }QrJ’ если arj < °’
если переменная Xj подчинена требованию целочисленности, и
если {аг>} < {Дг},
{Дг } /г •> X f 1 Г /Э 1
~ ссли >
для Xj, свободных от этого требования.
Разумеется, вычисления заканчиваются, когда целыми являются нс обязательно все коэффициенты /3i симплекс-таблицы, а только те, которым соответствуют переменные Xi, подчиненные требованию целочисленности.
Решить частично целочисленные задачи линейного программирования 17.251-17.256 методом Гомори:
386
Гл. 17. Методы оптимизации
17.251. /(х) = - 10^2 min,
3zi 4- х2 < 12, — 8a?i + За?2 С 24, Xj 0, х2 € Z.
17.252. /(х) = -xi - х2 -> min,
х\ + 2х2 < 4,
2я?1 +^2^4, Xj 0, xi G Z.
17.253. /(х) = — xi - 4х2 -> min,
х2 4- х3 = 7/2,
xi 4- х2 4- х^ = 7,
- + х2 + х5 = 2,
Xj 0, xi G Z.
17.254. /(x) = —10a?i 4- 5^2 4- 7x3 — 3^4 -» min, — xi — 2x2 4- За?з 4- 3^4 = 3/2, xi 4- x2 4- 7j?3 4- 2j?4 = 7/2, 2a?i 4- 2x2 4- 8Z3 4- x^ = 4, Xj > 0, a?i, x2 6 Z.
17.255. Решить задачу 17.182 об оптимальном составе сплава, предполагая, что сырье второго вида приобретается в количествах, кратных 1 кг, а сырье первого вида — в произвольных количествах.
17.256. Решить задачу 17.199 в предположении, что:
а) товар Ai выпускается в количествах, кратных 1 кг, а товар А2 — в произвольных количествах;
б) товар Ai выпускается в произвольных количествах, а товар А2 — в количествах, кратных 1 кг.
§ 4. Нелинейное программирование
1. Задачи, сводящиеся к линейному программированию. В наиболее общей постановке задача нелинейного программирования формулируется следующим образом:
/(х) -> min, (1)
5i(^) 1,2,...,/, (2)
5i(x) bi, i = I + 1, ..., m, (3)
где /(x), <?i(x), i = 1, ..., m, — заданные (не обязательно линейные) функции п переменных. Отметим, что условие неотрицательности переменных Xj 0, j = 1, ..., п, входящее в постановки многих задач нелинейного программирования, можно записать в виде неравенств (3), положив <7j(x) = —Xj, bj = 0.
§ 4. Нелинейное программирование
387
Некоторые задачи нелинейного программирования сводятся к задачам линейного программирования, методы решения которых описаны в § 3.
Рассмотрим задачу дробно-линейного программирования
п
52 cjxj+с°
/(х) = --------------> min, (4)
52 djXj 4- d0
J=i
п
5 O'ij'Ej — Ь{, — 1, • • • , ^5 (^)
7=1
n
52 aijxj bi, i = I 4- 1, ..., m, (6)
7=1
Xj^Q, j = 1, ..., n. (7)
Будем считать, что во внутренних точках допустимого множества U задачи (4)-(7) знаменатель целевой функции из (4) не обращается в нуль и, следовательно, сохраняет знак. Если этот знаменатель отрицателен, то умножим числитель и знаменатель дроби из (4) на —1 и будем в п
дальнейшем считать, что 52 (^7Ж7 + do > 0 для всех х G U. з=1
(И \
52 djXj 4- do I (очевидно, у0 > 0 при х 6 U) и 7=1 /
введем новые переменные yj = yoXj, j = 1, ..., п.
В новых переменных yj, j — 0, 1, ..., п, задача (4)-(7) принимает следующий вид: п
7( у) = 52 cjyj min’
7=0
52 %'^7 “ ЬгУО = О,
7 = 1 п
52 «174/7 - biye О,
7=1 п
52 ^jyj ~
7=0
Уз > О,
i 1, ..., I,
i — I 4- 1, ..., т,
j = 0, . . . , 71,
(8)
388
Гл. 17. Методы оптимизации
т.е. превращается в задачу линейного программирования (см. § 3). Отметим, что требование уо 0, включенное в условие задачи (8), не ограничивает возможного изменения переменной уо, так как уо > 0 при х е U.
Найдем решение у* = (Уо> • • •, Уп)> f* задачи линейного программирования (8) и, используя равенства
* yj • л х 7*
xj=*, j = f = mm/x)=/,
’ Vo u
(9)
получим решение исходной задачи дробно-линейного программирования
Если г/g = 0, то допустимое множество U задачи (4)-(7) не ограничено и минимум целевой функции /(х) на нем не достигается.
Решить задачи дробно-линейного программирования 17.257-17.266:
17.257. /(х) = min
' xi+ 2х2 + 1
xi — 2x2 2,
2^1 + Х2 + хз = 6, Xj О, j = 1, 2, 3.
<] Знаменатель xi + 2x2 + 1 целевой функции положителен при всех х из допустимого множества U, так как Ti, я?2 0.
Вводя переменные уо = l/(a?i + 2x2 + 1), yj = yoXj, j = 1, 2, 3, получим следующую задачу линейного программирования:
/(г/) = —2г/1 4- г/2 min, У1 ~ 2у2 - 2у0 < 0, 2г/1 - г/2 + Уз ~ 6г/0 = 0, У1 + 2у2 + уо = 1, yj 0, 7=0,..., 3.
Приведя эту задачу к каноническому виду и решив ее симплекс-методом, находим г/g = 1/3, У* = 2/3, у% = 0, г/з = 2/3, /* = -4/3, откуда, используя формулы (9), получаем решение исходной задачи: х* = = (2; 0; 2), /* = -4/3. >
17.258. /(х) = 4a?1 +-ЗХ2 -> min, 2х j -Ь Х2
XI + 2X2 16,
Х1 + Х2 С 10,
Х1 6,
Х2 7, 3?1, Х2 0.
§ 4. Нелинейное программирование
389
17.259. Дх) = ~~ -4 min, М ' 2x2 + 4-1
- xi 4- х2 4- Зх3 = 8, 2xi - х2 - х3 = 4, xj 0, j = 1, 2, 3.
17.260. /(х) = -4 min,
V ' х2 + Зх3
Xi - х2 4- 2х3 = 4, — xi 4- 2x2 4- х3 4- Х4 = 6,
17.261. Дх) = -3— —^2— -> min, J V 7 xi 4- х2 4- 2
Xi 4- X2 4- X4 — 3, 3xi 4- X2 - x% = 4, — xi 4- 3x2 4- X4 = 6, ^•^0, j = 1, ..., 5.
17.262. /(x) = -2^ -^+ £3 minj xi 4- 3x2 4- 5хз
6xi — 3x2 4- хз 4- X4 = 12, 7xi — x2 4- 2хз 12, - 4xi + 2x2 - хз - X5 = 1, xj 0, j = 1, ..., 5.
17.263. /(x) = Xl у —3 - -4 min, 3xi 4- 2x2 + 1
xi 4- x2 4- x3 = 6, 3xi — 2x2 4- X4 = 9, - xi 4- 2x2 4- X5 = 10,
17.264. Дх) = —-> min, JV ’ Xi 4-Зх2 4-2
xi 4- Зх2 - х3 = 7, — 3a?i 4- 4а?2 + а?4 = 17,
.. . — 3xi 4- 2x2 4- 1
17.265. f х =-------Ц-—н
xi Ч- 2х2 4* 3
-11 4- 3x2 ~ Х4 = 10, 2a?i 4- 4х2 — х3 — Х4 = 20, 5xi 4- 2х2 4- Х5 = 35, — 3xi 4- 2х2 + %б ~ 11,
390
Гл. 17. Методы оптимизации
17.266. /(х) =
xi - 2х2 + 3
Д’2 + 2
-> min,
Х[ + Х2 - Д‘3 -= 5, - XI 4- 2X2 1,
— 3X1 + Х2 + Х<1 = 1, — ЗД] + 2х2 Т xq = 11, Xj ^5 j 1, . . . , 4.
Другой важный класс задач нелинейного программирования, решение которых можно найти методами линейного программирования, образуют задачи квадратичного программирования, в которых требуется минимизировать выпуклую функцию (см. § 2) на допустимом множестве, заданном линейными ограничениями, т.е.
/(х) = -(Qx, х) + (г, х) -> min, (10)
п
^aijXj^bi, i = (И)
j=i
Xj 0, j = 1, ..., п. (12)
Здесь Q = (qij) — симметричная матрица размера п х п, г = = (и, • • •, тп) — заданный вектор. Напомним, что если матрица Q положительно определена, то квадратичная функция /(х) из (10) является выпуклой в 8п.
На основании известной теоремы Куна-Таккера [1] точка минимума х* = (х*, ..., ж*) целевой функции /(х) из (10) на допустимом множестве U (И), (12) может быть найдена как решение следующей системы уравнений с дополнительными переменными Xi, xn+i, i = 1, ..., т\ /ij, j = 1, ...п:
п т
Y^qtjXt+rj +^Aia0- - Hj = 0, J = 1, ...,n, (13)
2=1 2=1
П
^aijXj + xn+i = bi, i = (14)
1=1
АгЖп+г = 0, i = jijXj = 0, j = l,...,n, (15)
удовлетворяющее условию неотрицательности
Xj 0, jij 0, j = 1, ..., n; Xi 0, г = 1, ..., m. (16)
Для решения системы (13)—(16) можно использовать метод искусственного базиса (см. § 3), позволяющий найти одну из угловых точек множества, заданного ограничениями (13), (14), (16). Так как эта точка
§ 4. Нелинейное программирование
391
принадлежит указанному множеству, то она удовлетворяет перечисленным ограничениям.
При реализации метода искусственного базиса следует учитывать и условия (15), т.е. не включать в базисные одновременно переменные Xi и xn+i с одним и тем же индексом i и переменные Xj, pj с одинаковым номером j.
Пример 1. Решить задачу квадратичного программирования
/(х) = + 2х| ~ 2т1Ж2 — 2x1 — 6т-2 -> min,
xi + х2 С 2,
-Xi + х-2 С 2,
xi, х2 0.
/ 2 —2\
<] Матрица Q = ( 4 I квадратичной функции /(х) положительно
определена (проверьте самостоятельно!). Система (13)—(16) в данном случае принимает вид
2xi — 2х2 + Ai ~ А2 pi — 2, (17)
—2x1 + 4x2 + Ai + 2А2 — Р2 — 6, (18)
xi + х2 + х3 = 2, (19)
-xi + 2х2 + х4 = 2, (20)
/ziXi = р2х2 = А1Х3 = А2х4 - 0, (21)
xi,...,x4^0; pi,p2^0-, Ai,A2^0.
Будем искать угловую точку множества, определяемого этой системой, методом искусственного базиса. При этом, так как уравнения (19) и (20) легко разрешаются относительно переменных хз и х4, для уменьшения размера симплекс-таблиц дополнительные переменные (Х5 и Хб) вводим только в уравнения (17) и (18), считая базисными переменными начальной угловой точки Х3, х4, Х5 и х$.
Вспомогательную целевую функцию /(х) = Х5 + Хб выразим через свободные переменные Xi, Х2, Ai, А2, pi и р2 с помощью уравнений (17) и (18): /(х) — —2xi — 2Ai — А2 4- pi + Р2 + 8.
Последовательность симплекс-таблиц, приводящих к решению задачи, приведена ниже. Рамками обведены опорные элементы, а те свободные переменные, которые на данном шаге нельзя переводить в базисные из-за условий (21), обведены кружками.
В последней таблице элементы нижней строки неотрицательны, следовательно, минимум вспомогательной целевой функции /* = 0 достигается в угловой точке, соответствующей этой таблице.
Поэтому искомое решение задачи квадратичного программирования имеет вид х* = (4/5, 6/5), /* = f(x*) = 36/5. >
392 Гл. 17. Методы оптимизации
Х| х2 (У) (У) Ц| р2 *1 *4 © ^2 01
*5 2-21-1-10 2 х5 11 1-1-10 4
-2 412 0 -1 6 > Х(' 0-2 1 2 0-1 2
Х3 110 0 0 0 2 х3 [з/2|-1/2 0 0 0 0 1
Л-4 -10 0 0 0 0 2 х2 -1/2 1/2 0 0 0 0 1
0-2-2-11 1 -8 -11-2-11 1 —6
Xj ,Г4 Х| А-2 Ц| Ц2 хз *4 Лб ^2 01 (Нг)
*5 -2/3 4/3 1-1-1 0 10/3 х5 -2/з[То7з1 -1 -3 -1 1 4/3
0 -2 [Т] 2 0-1 2 ~ X, 0-2 1 2 0-1 2
*1 2/3 -1/3 0 0 0 0 2/3 xt 2/3-1/3 0 0 0 0 2/3
Х2 1/3 1/3 0 0 0 0 4/3 х2 1/3 1/3 0 0 0 0 4/3
2/3 2/3 -2-11 1 -16/3 2/3-10/3 2 3 1 -1 -4/3
Замечание. Если задача квадратичного программирования наря-
п
ду с ограничениями-неравенствами (11) содержит и равенства atjxj =
j=i
= bi, то для преобразования их к виду (11) следует выразить из этих равенств какие-либо базисные переменные через остальные и записать условие неотрицательности для базисных переменных.
Например, преобразуем ограничения-равенства
3X1 + Х2 + Х3 + Х4 = 16, -xi + Зх2 - х3 + х4 = 4
к виду (11). Разрешив их относительно х% и а?4, находим х2 — 6 — — 2x1 + х2, Х4 — 10 — a?i — 2х2• Учитывая условие неотрицательности хз 0, Х4 0, получим ограничения-неравенства (11): 2xi — х2 ^6, Xi + 2х2 10.
Решить задачи квадратичного программирования 17.267-17.276:
§4. Нелинейное программирование
393
17.267. Дх) = х\ 4- ^2 — Юж1 — 15x2 —> min, 2х 1 4- Зх2 13, 2xi 4- х2 С 10, X], х2 0.
17.268. /(х) = х2 4- х^ — 20rci — 30х2 ~> min, 5xi 4- 13x2 С 51, 15xi + 7x2 Ю7,
xi, х2 > 0.
17.269. Дх) = х2 — 2xi — х2 —> min, 2xi 4- 3x2 С 6, 2xi 4- х2 4, xi, х2 > 0.
17.270. Дх) = х2 4- Х2 — lOxi — 20x2 -> min, 9xi 4- 8x2 С 72, xi 4- 2x2 С Ю, Xi, Х2 > 0.
17.271. Дх) = X} 4- Х2 — lOxi — 8x2 —> min, 2xi + 3x2 4- хз = 6, Xj > 0, j = 1, 2, 3.
17.272. Дх) = Зх2 + х2 — 3xi ~ 2x2 —> min,
xi 4- 3x2 4- хз 4- Х4 — 16, 3xi — Х2 — хз 4- Х4 = 4, ху > 0, у = 1,..., 4.
17.273. Дх) = х2 4- х2 4- Хз 4- Х2 — 2хз -> min, X] 4- Х2 4- 2хз < 6, Зх] 4- 2x2 4- хз 12, Xj > О, j = 1, 2, 3.
17.274. Дх) = (xi 4- Х2 4- Х3)2 -> min,
X] 4- 2x2 + Зхз 6,
xi 4- х2 1,
Х2 4- х3 1,
ху 0, j — 1, 2, 3.
17.275. /(х) = х22 4- 2Х1Х3 — хз -> min,
xi 4- х2 = 4,
Х2 4-х3 = 8, Xj 0, j = 1, 2, 3.
17.276. Дх) = х2 4- х2 — xi — 2хз -> min,
xi - х2 4- 2х3 = 6, ху 0, j — 1, 2, 3.
394
Гл. 17. Методы оптимизации
Минимизировать в многоугольнике с вершинами (0, 0), (0, 4), (5, 8), (10, 4), (6, 0) следующие функции:
17.277. /(х) = х2 4- ~ 4xi — 6a?2-
17.278. / (х) = х2 + х% - 20a?i - 16я2-
17.279. /(х) = х2 + 2а?2 ~ lO^i — 32z2-
17.280. /(х) = 2х2 + 3^2 ~ — 48ге2-
2. Методы возможных направлений. Основная идея этой группы методов решения задач нелинейного программирования заключается в построении последовательных приближений к точке минимума х* целевой функции /(х) на допустимом множестве 17:
x(fc+i) =Х(М+Qfce(fc)? k = x^EU, ак > 0. (22)
Эти методы напоминают безусловную минимизацию /(х) градиентными методами (см.§ 2).
Вектор е^к\ определяющий направление перемещения (22) из точки x(fc) в точку x(fc+1\ должен удовлетворять следующим двум требованиям:
1. Для достаточно малых ак > 0 точка x(fc+1) из (22) принадлежит множеству U (т.е. задает возможное направление).
2. Для достаточно малых > 0 выполняется неравенство/(x(fc+1)) < < /(x(fc)) (т.е. e^fc) определяет направление убывания /(х)).
Первое условие означает, в частности, что для граничных точек x^fc) допустимого множества U вектор направлен внутрь U.
Величина ак > 0 в (22) выбирается из условия наибольшего убывания целевой функции в направлении^) с учетом требованиях^1) G U.
Рассмотрим сначала метод возможных направлений решения задачи минимизации выпуклой дифференцируемой нелинейной функции /(х) на допустимом множестве U, заданном линейными ограничениями
/(х) —> min,
(23)
п
Y^aijXj ^bi5), г = 1, ..., m, (24)
j=i
Xj 0, j = 1, ..., n.
(25)
Опишем выбор вектора e^fc) = (e^; ...; e^) из (22), определяющего возможное направление убывания функции /(х) в точке x^fc). Рассмотрим возможные случаи.
О Если среди этих ограничений есть равенства, то преобразовать их к виду (24) можно описанным выше способом (см. замечание на с. 392).
§ 4. Нелинейное программирование
395
1. Пусть в точке х^^ все неравенства (24) и (25) выполняются как строгие. Это означает, что х^^ — внутренняя точка допустимого множества U. Тогда
e(fc) = -Г(х(А°), (26)
т.е. определение очередного приближения x(fc+1) из (22) совпадает с итерацией градиентного метода (см. § 2).
2. Пусть хотя бы одно из неравенств (24), (25) в точке х^^ обращается в равенство, т. е. х^) является граничной точкой допустимого множества U. Тогда выбор в соответствии с (26), вообще говоря, невозможен, так как может оказаться, что точка х^+1) из (22) при любом ak > 0 не принадлежит множеству U (е^ из (26) не является возможным в точке x(fc) направлением).
Опишем, как определять возможное направление убывания в этом случае.
Обозначим через Ik и Jk множества индексов, соответствующих ограничениям (24) и (25), которые в точке x(fc) обращаются в равенства, т.е.
= bi >, Jii = - °}-
(27)
Представим компоненты ej- вектора для j Jk в виде
е(Л) _ е(М +
(А:)-~ej
(28)
где
(ft) ej-
0,
(k)-
0,
если 0,
если < 0;
если 0, если < 0.
_e(M
Очевидно, e^+, > 0, и = 0 для всех j Jk-
G) Такое представление для j £ Jk, позволяет находить вектор как решение задачи линейного программирования, содержащей условие неотрицательности переменных, несмотря на то, что его компоненты могут быть отрицательными.
Для j Е Jk представление (28) не используется, так как у вектора определяющего возможное направление, компоненты с номерами j Е Jk не могут быть отрицательными.
396
Гл. 17. Методы оптимизации
Вектор e(fc) = (е^; ...; е^) из (22) ищется как решение следующей задачи линейного программирования:
ft(e(‘>) = (f'(xw), е(Ч) =
jE-h J j£Jk J
(29)
(a(i), ew) = £2 aiieT + 52 ai^e<jk>>+ ~ e(k) ) °’ г’ € Л, (30) i^Jk j£Jk
+ (ад
3=1 jG-Jk j$.Jk
ej^O, jeJt, (32)
4‘)+,e<fc)- >0, j^Jk, (33)
ej‘)+-4‘>-=0, (34)
где а(г) = (an, ..., ain).
Поясним смысл соотношений (29)-(33).
1. Минимуму целевой функции Д(е^) из (29) соответствует минимально возможный с учетом ограничений (30)-(34) угол между искомым вектором и антиградиентом — f'(x^), определяющим направление скорейшего убывания /(х) в точке x^fc\
2. Ограничение (30) для каждого i 6 Ik означает, что вектор
составляет угол
71 (i)
— с вектором а' >
, нормальным к граничной ги-
п
перплоско.сти 2_Jaijxj — допустимого множества U и направленным j=i
вне U.
')Для учета дополнительного условия (34) при решении задачи (29)—(33) (к)+ (k)-
симплекс-методом следует не включать переменные е) ' и е) с одинаковым номером j в число базисных одновременно.
§ 4. Нелинейное программирование
397
Так как точка х^ принадлежит этой гиперплоскости, то условие (30) для любого i € Ik гарантирует, что направление является воз
можным по отношению к г-му ограничению (24) исходной задачи. Рис. 36 поясняет смысл ограничений (30) в двумерном случае.
3. Условие (31) является ограничением на длину вектора и обеспечивает ограниченность снизу целевой функции А(е^) из (29).
4. Неравенство (32) для каждого j € € Jk гарантирует, что направление искомого вектора является возможным по отношению к у-му ограничению (25) ис-
ходной задачи.
5. Соотношения (33) и (34) следуют из представления (28) компонент
3 i Jk. вектора
Опишем теперь, как определить величину перемещения Ok вдоль направления из (22). Для найденного вектора она находится из
условия
/(x(fc) 4-afce(fc)) = min ffx^+ae^),
т. e.
Ckfc = min (tkfci, . . . , O^km. ^fcl > • • • i ^fc), (35)
где otki и ctkj — максимальные перемещения, при которых для точки a;(fc+1) из (22) выполняются соответственно г-е ограничение (24) и j-e ограничение (25), т.е.
4-оо, если (а(г\ е^) 0,
[Ьг — (а(г\ х^)]/(а(’\ e(fc)), если (a^,e<fc>) > 0;
~ ( 4-оо, если 0,
= 1 (fc) / (fc) (fc) / n (37)
( —ж) /е) , если е) < 0, а а*к находится из условия наискорейшего спуска вдоль направления
вектора без учета ограничений (24), (25), т.е.
4>fc(a£) = min ФдДа), где Ф^а) = /(х^ 4- (38)
а>0
Приведем описание к-го шага решения задачи (23)-(25) методом возможных направлений.
1. Подставить х^ в неравенства (24) и (25) и определить множества индексов Д, Jk по формулам (27).
398
Гл. 17. Методы оптимизации
2. Если Ik = Jk — 0, найти вектор из (26), в противном случае определить из решения задачи линейного программирования (29)-(33) с помощью формулы (28).
3. Для найденного вектора определить ak из формул (34)-(37).
4. Найти очередное приближение х^+О по формуле (22).
При выполнений хотя бы одного из условий ||f'(x^^)|| е или ||x(^-i) _x(fc)|| Где £ > 0 — число, определяющее точность решения задачи, вычисления завершают, полагая х* « х^\ /* « /(х^).
Любое из равенств ||/'(х^|| = 0, ||х^-1^ — х^| = 0 означает, что точка минимума х* функции /(х) на множестве U найдена точно: х* = Х^\
Пример 2. Решцть следующую задачу нелинейного программирования с линейными ограничениями методом возможных направлений, завершая вычисления при ||Г(х^^)|| 0,01 или ||x(fc_1) — х^|| 0,01.
/(х) = (а^ - 4)2 + (ж2 - 2)2 -> min, xi 4- х2 < 3, xi + 2х2 < 4, zi, х2 0.
<1 В качестве начального приближения выберем, например, точку х(°> = (0,4; 1,4)' (убедитесь, что х^0) G U).
Шаг 1.
1. Ограничения (24) и (25) в точке х(°) выполняются как строгие неравенства (проверьте!), т.е. х^0) — внутренняя точка множества U, т.е. Io = Jo = 0.
2. В соответствии с (26) находим
е<°> = -/'(х<°>) = (7,2; 1,2). (39)
3. Из формул (36), (37) получаем aoi = 1/1, Q02 = 1/12, 5oi = = <До2 = 4" СЮ.
Определим ag в соответствии с (38), используя условие минимума Ф£>(а) = 0:
Ф0(а) - /(х(°) 4- ае<°)) = (0,4 4- a • 72 - 4)2 4- (1,4 4- a • 1,2 - 2)2, Фо(а) — 107,04а — 53,52 = 0, откуда a.g = 1/2.
Из (35) окончательно находим
а0 = min (1/7, 1/12, 1/2, +оо) = 1/12. (40)
4. Используя равенства (22), (39) и (40), получим
х<‘> = (0,4; 1,4) + 4-(7,2; 1,2) = (1; 1,5). (41)
§ 4. Нелинейное программирование
399
Шаг 2.
1. В точке из (41) второе из ограничений задачи выполняется как равенство, поэтому х^) — граничная точка множества U, причем Л = {2}, Л =0.
2. Задача (29)-(33) для определения принимает вид Д(е(])) = —бе(1)+ _ еП>+ _|_ е^- -> min,
е(П+ _ e(D- + 2е(1)+ _ 2е(1Ь 0,
е(П+ + е(П- + е(1)+ + е(1)-^1?
е<*’+, с'1’’ > 0; е<'>+ е<”- = 0, > = 1,2.
Записав эту задачу в каноническом виде с помощью дополнительных переменных и выбрав эти переменные в качестве базисных, в результате (i)+ q/o (1)- i/о (1)-двух шагов симплекс-метода получим е\ = 2/3, е2 = 1/3, ег — = е^+ = 0, т. е.
3. По формулам (36), (37) находим ап = 3/2, ai2 = 9/2, qi2 = = 5ц = +оо, а* = 156/85, поэтому в соответствии с (38)
4. Очередное приближение х^2^ находим по формуле (22) с учетом (41), (42) и (43):
хИ=М)+1&Ч)=(2;1’- <44>
Шаг 3.
Как и на втором шаге, для определения е(2) получаем задачу линейного программирования
/2(е(2)) = -4е^+ + 4ej2)_ - 2е^+ + 26^" -> min,
е(2)+_е(2)-+е(2)+_е(2)-^0,
еР)+-е;2)-+2е(2)+-2е(2)-^0, em + e(2)- + em + 42)-^i, 42)+, е<2’- > 0; е<2)+-42’-=0, > = 1,2, .
400
Гл. 17. Методы оптимизации
решив которую, получим
е(2) = Л. _1 \ 2’ 2
(45)
Как и на предыдущем шаге, находим а21 — #22 — #21 = + оо, #22 =«2 = 1, т. е.
«2 = min (1, 4-оо) = 1. (46)
Из формул (22), (44)-(46) получаем
х<” = (2, 1) + 1(1; -Г) = (|; Г)-v ’ \2 2/ \2 2/
Шаг 4.
Находя е^3) по общему правилу, получим е^3) — 0, т.е. х^4) = х^3\ и ||х(4) — х^3) || = 0. Это означает, что точка минимума х* найдена точно: х* = x<4> = (5/2; 1/2), /* = /(х<4)) = 9/2.
Рис. 37 дает геометрическую иллюстрацию хода решения задачи. На нем штриховыми линиями показаны линии уровня /(х) (окружности с центром в точке (4, 2)). >
х2
2
1
/(х(0))= 13,32
/(х(|)) = 9,25
I ’ '/(х(2)) = 5
Рис. 37
(4*2)
4 х.
Решить задачи нелинейного программирования с линейными ограничениями 17.281-17.290 методом возможных направлений, завершая вычисления при ||f'(х^)|| 0,01 или ||х^ — Х^Н
< 0,01:
17.281. /(х) = х\ 4- 2^2 — 16a7i — 20j?2 —> min, 2а?1 4- 5а?2 40,
2^1 4- Х2 16, ГГ1, х2 0.
§ 4. Нелинейное программирование
401
17.282. /(х) = xj 4- xj — 18а?1 — 20^2 -> min, ,-ri 4- Х2 < 15, 2a?i -4- 5x2 < 60, Зх 1 4- Х2 С 30, Xl, Х2 0.
17.283. /(х) = (я?1 — 16)2 4- (а?2 — 9)2 —> min, 5a?i 4- 2x2 60,
xi 4- Х2 С 15, xi 4- 4я?2 40,
Х1, Х2 0.
17.284. /(х) = я2 4- xj — £1^2 — За?2 min, xi 4- Х2 < 4, XI, Х2 0.
17.285. /(х) = xj 4- xj - 4^1 - 8а?2 min, 6a?i 4-11^2 + хз 4- 2я?4 = 96, — 2a?i 4- Зя?2 ~ 2ж3 4- Х4 = 8, Xj 3 1, ..., 4.
17.286. /(х) = xj 4- 2a?i - Х2 -> min,
xi 4- Х2 < 15,
xi 4- За?2 4- хз = 30, 5a?i 4- 3j?2 4- Х4 = 60, х3 0, j = l,..., 4.
17.287. /(х) = xj 4- 2xj — 6xi — 32x2 ~> min, Зя?1 + Х2 4- хз = 30, xi 4- Х2 4- Х4 = 15, 2a?i 4- 5я?2 4- £5 = 60, хj ^0, j 1, ...,5.
17.288. /(х) = 2xj 4- 3^1 4- 2x2 4- 4а?з -» min, xi 4- За?2 4- 2а?з 15, 3a?i 4- Х2 4- хз 20, Xj > 0, j = 1, 2, 3.
17.289. /(х) = xj 4- xj, 4- xj 4- xi — 2x2 min, xi 4- 2x2 4- 3j;3 18, 2a?i 4- X2 4- хз 20, Xj > 0, j = 1, 2, 3.
17.290. /(x) = xj - 2a?i 4- 2x2 4- хз -> min, xi 4- 3a?2 4- 2а?з 7, 3a?i 4- X2 4- хз 3, Xj ^0, j = 1, 2, 3.
402
Гл. 17. Методы оптимизации
Метод возможных направлений используется также для решения задачи нелинейного программирования более общего, чем (23)-(25), вида, а именно
/(х) min,
<h(x) 0, г = 1, ..., т,
(48)
где /(х), </г(х) — выпуклые дифференцируемые в £п функции.
Опишем один из вариантов определения необходимого для решения этой задачи вектора из (22) методом возможных направлений, а также укажем критерий окончания вычислений.
1. Выбор вектора Если х^ — внутренняя точка допустимого множества U, т. е. д^х^) < 0, i = 1, ..., m, то вектор определяется так же, как в рассмотренном выше случае линейных ограничений (24), (25), т.е. = -f'(x^).
Если же х^ — граничная точка множества U, т.е. множество индексов
А = = 0} (49)
непусто, то компоненты ej- вектора представляются в виде = (Л)+ (к)-
= 6j — и находятся из решения следующей задачи линейного
(к)+ (к)- ,
программирования с переменными о>, е^' , е - , j — 1, ..., п:
fk = ~°к min,
^/(XW)z (fc)+ (fc)-X, /А
(е/ -ej ) + <r4O,
dfl,(x(fc))
/ (k)+ (k)~x , n
(e) - e) ) -I- ak 0,
+ e<4) )O,
(50)
i G h,
(k)+ (k) — n (k)+ (k)- n • .
^к,еу , e\ 0, e) • e} =0, j = 1, ...,n
Замечание. Для ускорения сходимости метода возможных направлений множество индексов (49) иногда определяют не по точному, а приближенному равенству дДх^) = 0 со все возрастающей точностью Q, т.е. вместо 1к используют множество 1к{Дк} — {«| — ?к д^х^) 0},
где Ек ~> 0 при k -> оо.
§ 4. Нелинейное программирование
403
2. Выбор величины перемещения ak- Величина ак находится по аналогии со случаем линейных ограничений (24), (25) на допустимое множество U, т.е.
ak = ruin(ctfci, ..., акт, <д£),
где а*к определяется из (37), a aki, г = 1, ..., ш, — максимально возможное перемещение вдоль направления с учетом г-го ограничения (48), найденное из условия 4- а^е^) = 0.
3. К])итерий окончания вычислений. Условием достижения заданной точности решения е > 0 задачи (47), (48) методом возможных направлений служит выполнение хотя бы одного из неравенств ||f/(x^^)|| £, (?k £. При выполнении этого условия полагают
х* « х(/с), /* RS /(х(А:)).
Любое из равенств f'(x^) = 0, = 0 означает, что точка минимума
х* функции /(х) на множестве U найдена точно: х* = х^\
Пример 3. Решить следующую задачу нелинейного программирования методом возможных направлений, завершая вычисления при ||Г'(х^)|| < 0,1 или Ok < 0,1:
/(х) = —xi — х-2 -> min,
<7г(х) = xj 4- х% - 25 0.
<1 Функции /(х) и <71 (х) являются выпуклыми (проверьте!) и дифференцируемыми в £п, поэтому можно использовать метод возможных направлений.
Выберем начальное приближение х^0) = (0; 1). Очевидно, х^0) G U.
Шаг 1.
1. Так как ^(х^0)) = —24 < 0, то х^ является внутренней точкой множества U и 1к = 0.
2. Вектор е(°) находим по формуле е(°> = -f'(x(°)) = (1, 1).
3. Найдем максимально возможное перемещение qqi из условия gi (x^°^-f-Qoie^0^) = (04-<Дог 1)24-(14-Qor 1)2 —25 = 20^ 4-2<до1 — 24 = 0, откуда Qoi =3.
Определяя Qq из (38), получим Qq = 4-сю, так как функция Фо(<т) = = /(х(°) 4- ае^0)) = — 2а — 1 неограниченно убывает при а -> 4-оо.
Отсюда находим величину перемещения на первом шаге: Qq — — min (3, 4-ос) - 3.
4. Найдем следующее приближение (22):
х(1) - (0, 1)4-3(1, 1) = (3, 4).
Шаг 2.
1. Поскольку ^(х!1)) = 0, то х^1) — граничная точка множества П и А = {!}•
404
Гл. 17. Методы оптимизации
2. Вектор находим из решения задачи линейного программирования (50):
Л = -о-i min, _em +e(D- _е(1)+ +e(D- +СТ1 0) 6ej1)+ - бе^- 4- 841)+ - 4- ai < О,
= j = i,2.
Решив ее симплекс-методом, получим cti = 1/8, е^+ = 9/16, =
= 7/16,41}- = 4^+ = о, т.е. = (4^+ - ei^ > е2^+ — е2^ )= = (9/16, -7/16).
3. Величину перемещения Qi находим, как и на предыдущем шаге: Qn = 16/65, qJ = 4-оо, т.е. Qi = 16/65.
4. Очередное приближение х^2) находим из (22):
х<2> = (3; 4) + || (^; -1) = (3,188; 3,892).
Шаг 3.
Так как gi(x(2)) = 0, то точка х^ является граничной. Находя е^2) и а2 по общему правилу, получим: ст2 = 0,125, = (0,547; —0,453),
а2 = 0,186. Отсюда х™ = (3,240; 3,809).
Переходя к следующему шагу, найдем стз = 0,094 < 0,1, т.е. требуемая точность достигнута и х* й х^3^ = (3,240; 3,809), /* « /(х^) = = - 7,049. О
Решить задачи нелинейного программирования 17.291-17.298 методом возможных направлений, завершая вычисления при ||f'(x<fc>)|| 0,01 или ак 0,01.
17.291. /(х) = 2ti 4- Х2 -» min, gi (х) = х± 4- т2 - 9 0.
17.292. /(х) = т2 4- ^2 — 12т 1 — 6т2 -> min,
#1(х) = т2 4- ^2 - 16 0.
17.293. /(х) = —xi — 2х2 min, ^i(x) = х\ + х^ - 1 0,
^2(х) = -Xi - Х2 0.
17.294. /(х) = т2 — 2ti — Х2 —> min, ^i(x) = 2т2 4- 3^2 — 6^0.
§ 4. Нелинейное программирование
405
17.295. /(х) = 4xJ + ^2 + 2х2 -> min,
pi (х) = xj + ^2 “ 4х2 0, р2(х) = -xi + х2 - 2 0.
17.296. /(х) = lOxi — х2 -> min,
pi (х) = х^ - 4m 1 + Жо + 3 О,
д2(х) = + 4я?2 — 4я?2 — 4^0.
17.297. /(х) = 4mi 4- Х2 -> min,
Р1(х) = xl + х2 - 1 О, р2(х) = Х1 - Х2 0.
17.298. /(х) = X? — 3^1 + х| -> min, pi(x) = xj - 2х2 О, р2(х) = -Х1 + х2 0.
3. Градиентные методы решения задач нелинейного программирования. Один из подходов к решению задач нелинейного программирования состоит в такой модификации градиентных методов безусловной минимизации (см. § 2), чтобы в процессе построения последовательных приближений к точке минимума учитывались ограничения на допустимое множество.
Ниже рассматриваются два метода минимизации, основанных на этом подходе применительно к решению гладкой задачи выпуклого программирования
/(х) -> min, х G U, (51)
где U С £п — выпуклое замкнутое множество, /(х) — выпуклая дифференцируемая на U функция.
Первый метод (метод проекции градиента). На каждой итерации этого метода предусмотрена процедура возврата очередного приближения градиентного спуска х^+1^ = х^ — ajtf'(x^) на допустимое множество [/, если x(fc+1) U. Такой возврат производится посредством проектирования x^k+l^ на [/, т.е. замены х^+1^ на ближайшую точку множества U.
Определение. Пусть заданы замкнутое множество U С £п и точка z G Еп. Точка zu = Ри(ъ) называется проекцией точки z на множество 17, если p(zu, z) = minp(x, z), xEU
где p(x, у) = ||x —y|| — расстояние между точками х и у в пространстве Еп-
Очевидно, для точки z G U проекция P[/(z) совпадает с z.
Таким образом, в методе проекции градиента последовательные приближения х^ к точке минимума х* целевой функции /(х) на множестве U вычисляются по формулам
х^+О = р[/[х(М - Qfef'(xW)], к = 0, 1, ..., х(0> G U. (52)
406
Гл. 17. Методы оптимизации
В зависимости от способа вычисления из (52) различают несколько вариантов метода проекции градиента, самыми распространенными из которых являются следующие.
1. Qjt находится, как в методе наискорейшего спуска безусловной минимизации (см. § 2), т.е. ФЦоч) = шшФДа), где ~ Лх^ ~ а>0
- Qf'(x(/c))].
2. В предположении, что градиент f'(x) целевой функции удовлетворяет на множестве U условию Липшица, т. е.
||f'(x')-f'(x")||^L||x'-x"||
(53)
для всех х', х" G {/, полагают = а, к = 0, 1, ..., где a — произвольное число из интервала (0; 2/L). Если известна минимальная константа Липшица L из (53), то выбирают, как правило, a — \/L.
Вычисления по формуле (52) завершаются при выполнении одного из неравенств ||f'(x^))|| е или ||х^ — х^-1)|| £, где величина е > 0
определяет точность решения задачи. Окончательно полагают х* х^\ /•«/(х'Ч).
Отметим, что определение проекции P[/(z) для точки z U является самостоятельной задачей нелинейного программирования
п
/(х) = ||х — z||2 = (xj — Zj)2 -> min, х G U, j=i
(54)
решение которой может вызвать затруднения.
В частном случае, когда множество U определяется лишь линейными ограничениями, задача (54) представляет собой задачу квадратичного программирования. Ее решение может быть найдено за конечное число шагов, как описано выше.
Особый интерес при использовании метода проекции градиента представляют такие множества U, для которых задача проектирования решается в явном виде.
Пример 4. Найдите проекцию A/(z) точки z G £п на множество
U =
< х G £„|[|ж(|2 = £х2 С 7?2
, >=1
(замкнутой шар радиуса Ro с цен-
тром в точке 0 в пространстве £п).
<1 Запишем условие задачи (54) для рассматриваемого случая
п
/(х) - УУ (xj — Zj)2 —> min,
J=i
124 я»
(55)
§ 4. Нелинейное программирование
407
Рассмотрим возможные случаи.
1. z G U, т.е. Ro- Тогда P[/(z) = z.
n
2. z U, т.е. 52zj = R2 > R2. Запишем ограничение-неравенство j=i
(55) в виде равенства, добавив в его левую часть дополнительную переменную жп+1 = у2 0. В результате получим задачу на условный минимум (см. Часть 2, с. 214):
п
/(х) = 52 ^хз ~z3^ rnin>
j=i
n
<^(x, у) = 52 x2j + У2 “ Ro = °-J=i
Для ее решения запишем необходимые условия экстремума функции п ( п
Лагранжа L(x, у, А) = (xj ~ zj)2 + I 52 х^з + У2 ~ Ro
>=i V=1
<~ = 2Ху = 0, ду
52+у2 - яо = о-j=l
п
Решив эту систему п + 2 уравнений с учетом предположения 52 zj ~
Rq r
= R2 > Rq, находим Xj = ~Zj, j — 1, ..., n, A = —-1, у = 0, т.е.
R R$
Ro rt х = —z = Roz
Г1
Проверим выполнение достаточного условия минимума Т(х, у, А) в найденной точке. Для этого найдем все частные производные вто-/ \ A (RV Л R Л Q2L OR
рого порядка в точке (х; у; А) = ~z; 0; —----1 : = 2 —,
\ R Ro J дх^ Rq
d2L _ . _ d2L . a2£ _ (R_ \
dx}dy °’ } 1'"" ’ dxidxj °’ J’ 9y2 2 («0 1)’
408
Гл. 17. Методы оптимизации
R * » / R \ п л
Поэтому d2L = 2— dx2 + 2 ( —-------1 \ dy2 > 0 при dx2 + dy2 > 0,
0 7 = 1 '° ' 7 = 1
т. с. достаточное условие минимума выполняется.
Окончательно
P[/(z) = <
п
если
j=i n если г2 > R2. >
7=1
(56)
Если проекция точки z Е £п на допустимое множество задачи нелинейного программирования находится в явном виде, то использование метода проекции градиента для ее решения значительно упрощается.
Пример 5. Решить следующую задачу нелинейного программирования методом проекции градиента, завершая вычисления при выполнении одного из условий ||f')|| 0,01, ||х^-1) — х^0|| 0,01:
/(х) = — xi + х% min, х2 -|- х% 1.
<1 В качестве начального приближения возьмем, например, точку х^ = = (0; 0,05) G U.
Градиент f'(x) = (—1,2ж2) удовлетворяет условию Липшица (53) с константой L — 2, так как
ЦГ(х') - f'(x")|| = У(-1 + 1)2 + (24 - 2х")2 =
= 2|4 - 4'| =5 2||х' - х"||.
Поэтому в (52) можно положить ak = a G (0; 1), k = 0, 1, ..., например, <*k = 0,75.
Шаг 1. Так как f'(x^0^) = (—1, 1), по формуле (52) находим
х(1) = Ри[х^ - af'(x(0))] = Ри[(0; 0,5) - 0,75(— 1, 1)] =
= Pt/[(0,75; -0,25)].
Точка (0,75; —0,25) принадлежит множеству 17, так как 0,752 + 0,252 = — 0,625 < 1, поэтому х(]) = (0,75; -0,25).
Требуемая точность не достигнута, так как Цх^0) — х^Ц = 1,06 > > 0,01.
Шаг 2. Как и на предыдущем шаге, находим
Г(х(1)) = (-1; -0,5), х(2) = /14(0,75; -0,25) - 0,75(-1; -0,5)] =
= Р(4(1,5; 0,125)].
§ 4. Нелинейное программирование
409
Точка (1,5; 0,125) допустимому множеству не принадлежит, потому что 1,52 + 0,1252 = 2,266 > 1. Так как множество U представляет собой замкнутый шар радиуса jRq — 1 с центром в точке 0 в пространстве £2, то, используя результат примера 4, по формуле (56) находим
X2 = Р(/[(1,5; 0,125)1 = = (0,9965; 0,08304).
1 х/1,52 + 0.1252
Требуемая точность не достигнута, так как Цх^1^ — || = 0,298 >
> 0,01.
Результаты остальных шагов метода проекции градиента приведены в следующей таблице:
к Х(Л) ||x(fc-D _x(fc)|| x(fc) -af'(x(fc))
2 (0,9965; 0,0830) 0,298 (-1; 0,1661) (1,7465; -0,0415)
3 (0,9997; -0,0238) 0,107 (-1; -0,0476) (1,7497; 0,0119)
4 (0,99998; 0,00679) 0,031 (-1; 0,0136) (1,74998; -0,00339)
5 (0,99998; -0,00194) 0,0087 Точность достигнута
Из таблицы следует, что х* & = (0,99998; —0,00194), /* «
« f(x^) = —1. Отметим, что точное решение рассматриваемой задачи х* = (1, 0), Г - -1. О
В задачах 17.299-17.303 найти проекцию zp = Pu(z) точки z 6 8П на указанные множества U С 8П:
17.299. U — {х 6 £n\xj0, j = 1, ..., п} (неотрицательный октант пространства £п).
17.300. U = {х 6 Z7i\o,j < Xj bj, j = 1, ..., n} (n-мерный параллелепипед).
{n I
x 6 8n \ (xj — Zj°))2 < Ro 2 (замкнутый шар
J=1 J
радиуса Rq с центром в точке x^0)).
I n
17.302. U — < x 6 8n\ ^^ajXj — b, a = (ai, ..., an) 0
[ J=i
(гиперплоскость с нормальным вектором a).
{n
x G 8n \ i^ajXj b, a = (ai, ... , an) 0
J=1 (полупространство в 8n).
410
Гл. 17. Методы оптимизации
Используя результаты решения подходящих задач 17.299-17.303, решить задачи нелинейного программирования 17.304-17.313 методом проекции градиента. Вычисления завершить при ||x(fc-i) _x(fc)|| 0,01:
17.304. /(х) = xl + 4^2 + 3tiХ2 + 2ti + 16®2 -> min, > 0, Х2 0.
17.305. / (х) = 9®2 + х\ — 54тi + 4®2 —> min, Ti > 0, Х2 0.
17.306. /(х) = ®2 + 9^2 — 12®i — 36®2 -> min, — 1 4, 1 Х2 2.
17.307. /(х) = 2>/1 + ®2 + 2®2 + + ®2 -> min,
5 8, 1 Х2 10.
17.308. /(х) = 2xi + Х2 -> min,
(®1 - 4)2 + (®2 - 2)2 1.
17.309. /(х) = ®2 — 8®i + ®2 “* ю’п, ®1 + (®2 ~ 4)2 9.
17.310. /(х) = ®2 + ®2 + хз + Х1 + х2 + mm, ®1 + Х2 + ®з = 3.
17.311. /(х) = ж2 + ®2 + хз ~ 4®i ~ 6®2 — 2®3 —> min, 2®i + ®з = 2.
17.312. /(х) = (®i — 2)4 + (®2 — I)4 min, 2®i 4- ®2 2.
17.313. /(х) = ®2 — Х2 —> min, 2®i — 2x2 1-
Второй метод {метод условного градиента). Пусть EU — очередное приближение к решению гладкой задачи выпуклого программирования (51), причем f'(x(fe)) ф 0. Тогда в окрестности точки функция /(х) представима в виде
f(x) - /(х«) 4- (f'(x(fe>), х - х^) + о(||х - х^||), и линейная функция
А(х) = (Г(х(А:)), х - х(/с))
является приближением разности /(х)—f{x^) с точностью до величины о(||х — х^Н) в некоторой окрестности точки x^fc\
Поставим вспомогательную задачу минимизации на множестве U линейной функции Л(х), т.е.
Д(х) = (Г(х(Л)), х - х^) -> min, х G U. (57)
§ 4. Нелинейное программирование
411
Пусть х^ — решение этой задачи. Следующее приближение х^‘+1^ к точке минимума х* функции /(х) на множестве U найдем по формуле
х(Л+1) = x(fc) +Qfe(xW afcG(0;l). (58)
В силу выпуклости допустимого множества х^+1^ 6 U.
Величина ак из (58) в различных вариантах метода условного градиента вычисляется по-разному. Опишем два способа определения а^.
1. o<k = min (1, а*к), где ак найдено из условия наискорейшего спуска по направлению х^ — x^h ФаДо<) = тшФ^о), где Фа-(q) = ffx^ 4-
К а>0
4- сДх^ - х^)].
2. В начале выполнения итерации (58) полагают ак = 1, после чего проверяют условие
/(x(fc+1)) < f(x^). (59)
Если оно нарушается, то ак уменьшают (дробят) в 2 раза и повторно проверяют (50). Дробление qa производят до выполнения неравенства (50), после чего переходят к следующей итерации (68).
Условие окончания вычислений по методу условного градиента совпадает с аналогичным условием метода проекции градиента.
Отметим, что вспомогательная задача Q57) является, вообще говоря, задачей нелинейного программирования. Укажем случаи, когда поиск ее решения х^ не представляет затруднений.
1. Допустимое множество U задано линейными ограничениями и условием неотрицательности переменных. Тогда (57) — это задача линейного программирования и ее решение можно найти с помощью симплекс-метода (см. § 3).
2. Допустимое множество U = {х G £n\aj Xj bj. j = 1, ..., n} —
n-мсрный параллелепипед. Тогда
если df(x(k>))/dxj > 0, если df(x^)/dxj < 0, если df(x^k^/dxj, = 0.
(60)
I п
3. Допустимое множество U = < х G '£n| (xj ~ 2/j°^)2 [ i=i
шар радиуса Ro с центром в точке . Тогда
x(k) _ у(о) _
Пример 6. Решить следующую задачу нелинейного программирования методом условного градиента, завершая вычисления при
412
Гл. 17. Методы оптимизации
||х^ - х<*> || 0,1:
/(х) = xj - 4^1 + х% - 2^2 -> min, 0 С xi 1, О С ^2 2.
< В качестве начального приближения выберем, например, точку х^°) = = (0, 0) G U.
Шаг 1. Найдем градиент f'(x) = (2xi - 4, 2x2 - 2) в точке х^°\ f'(x(°)) = (-4, —2). Запишем вспомогательную задачу (57):
Д(х) = (f'(x(°)), х - х(°)) = -4ж1 - 2x2 -> min,
О С xi С 1, 0 < Х2 2.
Это задача линейного программирования, ее можно решить симплекс-методом. Однако проще воспользоваться соотношениями (60), откуда следует х^0) = (1,2).
Найдем qq первым способом. В данном случае
Фо(а) = /[х^ + а(х(°) - х^)] = /(a, 2a) = 5а2 — 8а.
Из условия Фр (а) = 0 находим а = Qq = 0,8. Поэтому ар = min(l, 0,8) = = 0,8.
Вычислим очередное приближение х^1) по формуле (58): х^1) = = (0, 0) + 0,8(1, 2) = (0,8; 1,6).
Так как ||х^°) — х^Н = 1,79 > 0,1, то требуемая точность не достигнута.
Результаты вычислений на следующих шагах метода условного градиента приведены в следующей таблице:
к Х(М х(Л) Oik
1 (0,8; 1,6) 1,789 (1,0) 0,462
2 (0,892; 0,861) 0,745 (1,2) 0,212
3 (0,915; 1,103) 0,243 (1,0) 0,168
4 (0,929; 0,917) 0,187 (1,2) 0,140
5 (0,939; 1,069) 0,152 (1,0) 0,121
6 (0,947; 0,940) 0,129 (1.2) 0,106
7 (0,952; 0,153) 0,113 (1,0) 0,095
8 (0,957; 0,953) 0,1 Точность достигнута
Окончательно х* » х^ = (0,957; 0,953), /* « /(х(8)) = -3,91. О
Решить задачи нелинейного программирования 17.314-17.322 методом условного градиента, завершая вычисления при ||х^_ 1) — — с 0,1:
§ 4. Нелинейное программирование
413
17.314. /(х) = + п?2 — 6^1 — 4п?2 -> min,
Ж1 + х2 2, 2?1, х2 0.
17.315. /(х) = а;2 + 4а?2 — 8a?i ~ 8^2 min, — 2 С х± С 2, 0 < х2 < 3.
17.316. /(х) = e(2xi~x2)2 х2 х2 _ 4Ж1 _ 4Ж2 _> mjn?
О < xi < 1, - 2 < х2 < 3.
17.317. /(х) = In (2 + х\ 4- ^2 “ ^2) + е^1'312)2 -> min,
х\ 3, х2 0.
17.318. /(х) = а?| + а?2 + 6х± — 2х2 —> min, х? + а?2 1-
17.319. /(х) = ж2 + х? — 8a?i + 4а?2 min, (д?1 - I)2 + (х2 - I)2 1.
17.320. /(х) = In (ж2 + ж?; —4ж1 — 6ж2 + 13) — 2ж1 — х2 —> min, (а?1 + 2)2 + 2?2 4.
17.321. /(х) = ж2 + п?2 — 6а?1 — За?2 + 5 —> min,
xi + х2 3, 2a?i + х2 4, х\, х2 0.
17.322. /(х) = In (ж2 + п?2 — 8п71 — 6п?2 + 26) — xi — х2 -4- min, xi + х2 4, О < xi 3,
О < х2 2.
4. Методы штрафных и барьерных функций. Один из подходов к решению задачи нелинейного программирования f(x) -> min, х G U основан на замене этой задачи последовательностью задач безусловной Минимизации
Л(х) =/(х) + </?fc(x)-> min, х G €п, /с = 1, 2, (61)
где </?л-(х) — функции, которые с ростом к во все большей степени учитывают ограничения, определяющие допустимое множество U исходной задачи.
В методе штрафных функций функции (/^(х) подбираются так, чтобы при больших к функция А(х) из (61) мало отличалась от /(х) при х G U и быстро возрастала при удалении точки х U от допустимого множества U.
414
Гл. 17. Методы оптимизации
Определение. Пусть U С £п — заданное множество. Последовательность функций определенных в £п и обладающих свойст-
вом
( 0, если х G U, lim (лЦх) = < , , тт
k-yoo ' [ +оо, если х $ U,
называется последовательностью штрафных функций множества U.
Рассмотрим один из вариантов метода штрафных функций приближенного решения задачи нелинейного программирования
f(x) -> min, Ых) = 0, г = 1, ...,/, (?Дх) 0, i = I + 1, ..., т,
(62)
считая, что функции /(х), (/Дх), г = 1, ..., т, заданы во всем пространстве 8п.
Положим
<ЫХ) = kip(x), k = 1,2,..., (63)
где l т
<?(х) =^9i(*)+ 52 ^+(x)]2, г=1 г=/4-1
если
если
&(х) < О, <7г(х) > 0.
Равенства (63) определяет последовательность штрафных функций допустимого множества задачи (62) (проверьте!).
При определенных условиях последовательность решений задач безусловной минимизации (61), (63) сходится к решению х* задачи (62), поэтому для достаточно больших к полагают х* « x^fc\ f* « /(х^)).
Критерием достижения требуемой точности решения задачи (62) может служить неравенство
||Х(А-’) _ х(/г/2)||
(64)
где е > 0 — число, характеризующее точность, к — четное число.
Для решения задач (61) можно использовать методы безусловной минимизации, рассмотренные в § 2.
Если в задаче (62) /(х) — выпуклая квадратичная функция, а (/Дх), i — 1, ..., т, — линейные функции, то точное решение вспомогательной задачи (61) можно найти из системы линейных уравнений dfk{y-)/dxj = 0, j = 1, ..., п, определяющих стационарную точку функции Л(х).
§ 4. Нелинейное программирование
415
Пример 7. Методом штрафных функций решить следующую задачу нелинейного программирования:
/(х) = 2т2 4- х2 -» min, 01 (х) = -Xi - х2 4- 2 < О, 0г(х) = ху - 2ж2 4- 1 < О, 0з(х) = -2^1 4- з?2 0.
<] Целевая функция /(х) является выпуклой (проверьте!) квадратичной функцией, а ограничения, определяющие допустимое множество задачи, линейны. Поэтому решение х(к) вспомогательной задачи (61) для любого к = 1, 2, ... может быть найдено точно из условия Д(х^) = 0.
Так как функция </?^(х) из (63) в различных областях пространства 8П задана по-разному, то при составлении вспомогательной функции Д(х) следует сделать определенное предположение о расположении ее точки минимума х^.
1. Предположим, что в точке х^ безусловного минимума функции /Цх) все ограничения задачи (65) нарушаются, т.е. ft(xW) > 0, i = 1, 2, 3.
Тогда д^(х^) = i = 1, 2, 3, поэтому считаем, что
Л(х) = /(х) 4- /с[^(х) 4- ^(х) 4- ^(х)] =
= (2 4- 6/с)щ2 4- (1 4- 6Лт)щ2 ~ х2 — 2kxi — Skx2 4- 5к.
Решив систему уравнений
= (4 + 12/с)ж1 — 6Лтщ2 — 2А: = 0, OXi
= -6kxi 4- (2 4- 12к)х2 - 8к = 0, ох2
находим
(k) _ 18&2 + к (k) _ 27/с2 4- 8к
Х1 ~ 27к2 4- Ш 4- 2’ Х2 ~ 27к2 + 18к + 2'
Так как дз(*(к)) = -2х[к} 4- х(2к) = f ~VL. о < 0 ПРИ всех 27к£ + 1о/с 4- 2
к = 1, 2, ..., то предположение <?з(х^) > 0 не подтвердилось.
2. Предположим, что д^х^) 0, i = 2, 3, gi(x^) > 0. Тогда
р+(х(/с)) _ q, г- _ 2, 3; = ^(х^)), поэтому считаем, ЧТО Л-(х) =
= /(х) 4- kg^lx) = (2 4- к)х2 4- (1 4- к)х% 4- 2kxi х2 — 4/сЖ1 — 4/ле2 + 4^, откуда находим
416
Гл. 17. Методы оптимизации
Легко проверить, что сделанное предположение подтверждается, т.е. равенства (66) определяют точку безусловного минимума вспомогательной функции Д(х) из (61) (убедитесь!).
Окончательно находим х* = lim х^ = (-),/* = /(х*) = к—>оо \ 3 3у 3
Отметим, что для решения вспомогательных задач (61) можно было использовать и приближенные (например, градиентные) методы безусловной минимизации (см. § 2). Тогда, если требуемая точность решения задачи нелинейного программирования (65) задана числом е из (64), равным, например, 0,01, то получим х* « х^120) = (0,66 30; 1,3260), /* « /(х^120)) = 2,63 73, так как || x(12O)_x(6O)||=0)0L
Решить задачи нелинейного программирования 17.323-17.332 методом штрафных функций, полагая х*» x^fc^ при ||х^к>) — х^/2^ || < 0,05:
17.323. /(х) = х2 + х| — 20xi — 30x2 —> min,
2xi + 3x2 — 13 0,
2xi + Х2 — 10 0.
17.324. /(х) = х2 4- х^ — 10xi — 15x2 min, 5xi 4- 13x2 — 51 0, 15ti 4- 7х2 - 107 0.
17.325. /(х) ~ х? 4- х? — 5xi — 4x2 min, 2xi 4- 3^2 4- хз = 6.
17.326. /(х) = х2 4- х^ — 5xi — 10а?2 —> min, 9xi + 8^2 - 72 0,
xi 4- 2x2 — 10 0.
17.327. /(х) = х2 — 2ж1 — Х2 min,
2^1 + Згг2 — 6^0,
2^1 + Х2 - 4 0.
17.328. /(х) = х% — 2x2 + 2x1 + > min,
xi + 3x2 + 2хз — 6^0, 3xi + Х2 + хз — 2 0.
17.329. /(х) = — xi + Х2 — 2x2 —> min, Зх2 + 2х2 — 6^0.
17.330. /(х) = х2 + х2 - 6xi — 3x2 -> min, х2 + х2 — 9 0.
§ 4, Нелинейное программирование
417
17.331. /(х) = х? + .7,2 ~ min,
— + .7,’2 О,
.7'1 - 2х2 О.
17.332. /(х) = — Х[ — 4x2 —> min,
Х[ + х\ — 1^0,
- Х1 + Х2 < 0.
В методе барьерных функций исходная задача нелинейного программирования также сводится к последовательности задач безусловной минимизации (61), но функции ^-(х) выбираются таким образом, чтобы при больших к функции Д(х) из (61) мало отличались от /(х) во внутренних точках х допустимого множества U и в то же время при приближении точки х € U к границе множества U эти функции неограниченно возрастали.
Определение. Пусть множество U С 8П задано. Последовательность функций (х)}, определенных во всех внутренних точках множества U, называется последовательностью барьерных функций этого множества, если выполняются условия:
1. lim (£fc(x) = 0 для любой фиксированной внутренней точки х множества U:
2. lim <pk (х^О) = +00 для любой последовательности {х^} вну-г—>оо
тренних точек множества U, сходящейся к какой-либо граничной точке этого множества.
Рассмотрим некоторые варианты метода барьерных функций решения следующей задачи нелинейного программирования:
/(х) -> min, , 7}
,?г(х) < 0, г = 1, ..., п. '
Положим
= —</?(х), к =1,2,..., (68)
К
где
т
р>®, (69)
г=1
ИЛИ
т
(70)
i=l
Выражения (68)-(70) определяют последовательность барьерных функций допустимого множества U задачи (67) (проверьте!).
Пусть х^ — решение задачи безусловной минимизации (61), где функция ^л-(х) определена равенствами (68), (69) или (68), (70). Полагая х* и х^), f* % /(х^9) для достаточно большого к, находим приближенное решение задачи нелинейного программирования (67) мето
418
Гл. 17. Методы оптимизации
дом барьерных функций. Для контроля достигнутой точности решения можно использовать критерий (64).
Пример 8. Решить следующую задачу нелинейного программирования методом барьерных функций, полагая х*«х^ при ||x(fc) _ x(fc/2)|| 0)002:
/(х) = + 2я?2 min,
01 (х) = -з?! + х2 О, 02(Х) = 1 - X! - 3?2 0.
< Используем последовательность барьерных функций (68), (70). Тогда задача (61) принимает вид
Д(х) = а:? + 2х% - ~[In (a?i - з?2) +1п(з?1 + х2 - 1)] -> min, х G £п. к
Решая ее методом Ньютона (см. § 2) при к = 500 и к = 1000, получаем х(50°) = (0,6696; 0,3319), х<100°) = (0,6682; 0,3326). Так как ||х<1000 -- х<500>|| = 1,65 • 10~3 < 0,002, полагаем х* » х<100°) = (0,6696; 0,3319), /* »/(х^1000)) = 0,66 87. >
Решить задачи нелинейного программирования 17.333-17.339 методом барьерных функций, полагая х* « х^ при 11х^ — х^/2) || < 0,05:
17.333. /(х) = а?2 — 2з?2 — —> min,
xj + х2 ~ 0.
17.334. /(х) = а;2 + а?| ~ 10я71 — 8а?2 + 3 —> min,
xi + 2з?2 — 2^0, 2х 1 + Х2 — 2 0.
17.335. /(х) = —2xi + а?2 — а?2 + 2 —> min, 2а;2 + За?2 — 6^0.
17.336. /(х) = а?2 + а?2 — 8a?i — 4а?2 + 3 —> min, а?2 + а;2 — 8 0.
17.337. /(х) = а?2 + а?2 - 3a?i + 1 —> min, а?2 - 2а?2 0, — 2х\ 4- а?2 0.
17.338. /(х) = — xi — 5а?2 —> min,
xi + а?2 — 1 0, — ху + 2x2 0.
§ 5. Дискретное динамическое программирование
419
17.339. f(x) = 9(j;i - 5)2 + 4(Ж2 - 5)2 -> min, а:2 - 2х 1 - Х2 + 1^0,
- xi 4- Х2 - 1 0,
Х\ ~ х2 С 0.
§ 5. Дискретное динамическое программирование
В этом параграфе рассматриваются многошаговые задачи оптимизации, т.е. задачи, оптимизацию в которых можно представить в виде ряда последовательных этапов (шагов).
Предположим, что состояние некоторого процесса или объекта описывается n-мерным вектором х = (зд, х?, ..., хп), или, что то же самое, точкой х пространства £п, которое называют фазовым пространством.
Будем считать, что процесс является N-шаговым, т.е. его эволюция происходит в N этапов (шагов) в соответствии со следующей схемой:
Х(О) xw .
начал ьное \ । к конечное
состояние . м состояние
/с-и шаг
Переход между состояниями на k-м шаге происходит в соответствии с уравнением состояний
Х^ = f(*)(x(A:~1), u^), (1)
где G £т — m-мерный вектор управления, выбираемый на fc-м шаге, f(k)(x, и) — заданная n-мерная вектор-функция аргументов х G G £п, U G От •
Таким образом, предполагается, что в результате А:-го шага процесс переходит в состояние x^fc\ которое определяется только начальным состоянием х^-1) этого шага и выбранным на нем вектором управления и не зависит от «предыстории» процесса до k-ro шага, т.е. от х(°), •. •, х^~2^ и ...,
Показателем эффективности к-ro шага является заданная числовая характеристика (целевая функция этого шага) Л = к =
= 1,2, ...,N.
Предположим, что эффективность всего процесса в целом характеризуется целевой функцией вида
w
J(x, и) = ^2 Л(х(А:-1), uW), (2)
Л-=1
где х = {х(°\ х^\ ..., х^} — набор состояний, называемый (фазовой траекторией процесса, а и = {u^\ и^'2\ ..., — набор векторов
управления, который называется управлением процессом.
Таким образом, рассматриваются только аддитивные целевые функции J, представимые в виде суммы целевых функций шагов Л-.
420
Гл. 17. Методы оптимизации
Предположим далее, что на фазовую траекторию и выбор управлений наложены ограничения
х^ЕХк, к = 1, ..., N - 1, (3)
k = l,...,N, (4)
где Хк и — заданные множества в пространствах 8П и £т
соответственно, причем множество Uk зависит, вообще говоря, от начального состояния к-го шага.
Ограничения на начальное и конечное состояния процесса х'°>ёХ0, х^ёЛ'л,
называются начальными и конечными условиями. При этом множества Xq и Хк С во многих случаях содержат по одной точке (начало и конец фазовой траектории).
Пусть и = {и^\ г/2\ ..., и^)} — управление процессом, удовлетворяющее ограничениям (4) и переводящее его из некоторого начального состояния х^°) G Хо в некоторое конечное состояние x^N^ Е Хк в соответствии с уравнениями (1) с учетом ограничений (3). Обозначим множество всех таких управлений буквой U.
Многошаговая задача оптимизации формулируется следующим образом: среди всех управлений uEU выбрать такое (u* = {i/1)*, U(2)*, ..., UW‘}), для которого целевая функция (2) принимает минимальное или максимальное (в зависимости от смысла задачи) значение.
Управление и* и соответствующая ему фазовая траектория х* называются оптимальными.
Условие многошаговой задачи оптимизации будем записывать следующим образом:
J(x, и) = fc=l u(Z9) -> extr8), (5)
= fW^x^k-1), k = 1, ..., N, (6)
exk, k = 1, ..., N - 1, (7)
E k = 1, ..., N, (8)
x(°) E Хо, x^) E XN. (9)
8) Символом extr мы будем обозначать минимум или максимум соответствующей функции, в зависимости от смысла задачи. Несмотря на то, что задачу на максимум целевой функции J всегда можно свести к задаче минимизации —J min, мы будем рассматривать и задачи на максимум, используя обозначение J —> шах, чтобы математические постановки этих задач соответствовали их прикладному смыслу.
§ 5. Дискретное динамическое программирование
421
К многошаговым задачам оптимизации сводятся многие прикладные задачи.
Пример 1. Сформулировать следующую задачу в виде многошаговой задачи оптимизации (5)-(9).
С помощью ?/-ступенчатой ракеты с заданной стартовой массой М в космос запускается межпланетная станция массой т. За время работы каждой ступени ракета получает добавочную скорость Дц = z), где
у — масса, разгоняемая этой ступенью, z — масса самой ступени. Найти такое распределение общей массы М ракеты между ее ступенями, при котором конечная скорость станции будет максимальной.
<] Обозначим u^k\ k = 1, ..., N, массу к-й ступени, считая от межпланетной станции (т.е. на старте работает ступень массой а в конце разгона — ступень массой
Массу станции вместе с примыкающими к ней к ступенями ракеты обозначим х<Х), к = 0, 1, ..., N. Тогда, очевидно,
x(k) _ x(k-i) u(k), k = l, x(°> = m, = M + m.
Из условия задачи вытекают следующие ограничения на массы х^ и nW: т х^ М 4- т, 0 Л/, т. е.
х^ € Xk = [m; М + т], еик = [0; М],
к = 1, ..., N- 1, к = 1, ..., N.
В результате работы к-й ступени ракеты приращение скорости станции составит поэтому ее конечная скорость будет равна
F(x^k~l\ k=i
Таким образом, рассматриваемую задачу можно сформулировать как многошаговую задачу оптимизации следующего вида:
N
J(x, и) = F(ar^fc-1\ -> max,
Х(Л) _ к = 1, ..., N,
G [m; т + М], к = 1, ..., N — 1, uW G [0; М], k=l,...,N,
х(°) = т, х^ = М + т. >
Сформулировать задачи 17.340-17.349 в виде многошаговых задач оптимизации вида (5)-(9):
422
Гл. 17. Методы оптимизации
17.340. Сумма средств S распределяется между N предприятиями. Выделение к-му предприятию средств в размере и приносит доход Л(м), к = 1, 2, ..., N. Определить, какое количество средств необходимо выделить каждому предприятию, чтобы суммарный доход всех предприятий был максимальным.
17.341. Сумма средств S выделяется предприятию в течение N лет. Прибыль, получаемая предприятием в результате выделения ему средств и в течение к-го года, составляет Jjt(w), к = 1, ..., N. Распределить выделяемые средства по годам таким образом, чтобы суммарная прибыль предприятия за N лет была максимальной.
17.342. Найти N неотрицательных чисел u^k\ к = 1, ..., 7V, сумма которых равна S, а произведение максимально.
17.343. Совхоз производит посевной материал. Ежегодно часть семян продается потребителям, а оставшаяся их часть используется для воспроизводства. Доход от продажи и т семян составляет F(u) руб. Количество посевного материала, оставленное в совхозе, в следующем году увеличивается в А раз (Л > 1). В начале первого года имеется а т семян. В конце N-tq года их производство прекращается. Сколько семенного материала следует продавать каждый год, чтобы доход совхоза за N лет был максимальным?
17.344. Рассмотреть задачу 17.343 в предположении, что в конце N-ro года производство семян не прекращается, и минимальное планируемое их количество к началу (N + 1)-го года составляет b т.
17.345. Планируется производство на двух предприятиях в течение N лет. Начальные средства, предназначенные для выделения предприятиям, составляют S руб. Средства в размере и руб., вложенные в производство на г-м предприятии в начале каждого года, приносят к концу этого года доход Ji(u) руб., а также сумму оставляемую для финансирования дальнейшего производства, i = 1, 2. По истечении каждого года все предназначенные для дальнейшего производства средства перераспределяются между предприятиями.
Найти такой способ распределения средств предприятиям, при котором суммарный доход двух предприятий за N лет будет максимальным.
17.346. Оптовая база вмещает Р т продукции. Запасы продукции могут пополняться и продаваться в начале каждого из N месяцев, причем пополнение предшествует продаже. Хранение 1 т продукции в течение к-то месяца обходится в руб., а продажа того же ее количества в начале к-го месяца приносит доход (3^ руб. Начальное количество продукции на базе составляет а т.
Определить количества продукции, которые в начале каждого месяца следует принимать на хранение и продавать, чтобы суммарная прибыль базы за N месяцев была максимальной.
§ 5. Дискретное динамическое программирование 423
17.347. Рассмотреть задачу 17.346 в предположении, что в начале каждого месяца продажа продукции предшествует ее пополнению.
N
17.348. F(u) = -> min,
k=i
N
^aku^ 6, k=l
> 0, 6 Z, к = 1, ..., N,
где ak 0, к = 1, ..., N, b 0 (сепарабельная9) задача целочисленного программирования с одним линейным ограничением).
N
17.349. F(u) = ^F^^) -> min,
k=i
N
bi, i — 1, ..., m, k=i
0? u{k) e = 1, TV, где ai’k, bi ft, i = 1, ..., m, к = 1, ..., N (сепарабельная задача целочисленного программирования с m линейными ограничениями).
Для решения многошаговой задачи оптимизации (5)-(9) используется метод динамического программирования, основанный на принципе оптимальности Беллмана:
Оптимальная траектория в задаче (5)-(9) обладает тем свойством, что любая ее завершающая часть, начинающаяся с k-го шага, к = 1, ..., N — 1, является оптимальной для остающихся шагов процесса.
Опишем метод динамического программирования.
Заметим прежде всего, что в формулировке многошаговой задачи оптимизации (5)-(9) ограничения на фазовую траекторию (7) и на конечное состояние (9) можно включить в ограничения на выбор управлений, заменив соотношения (7) и (8) следующим эквивалентным ограничением:
и® G Uk(x<k~V) = {uw € Uk\f{k\x^k~^, u<fc)) € Хк}, (10)
к = 1, ..., N.
п
9) Функция п переменных вида <р(х\, ..., хп) = <pi(xi) называется сепа-
i=i
рабелъной.
Если все функции, входящие в условие задачи математического программирования, сепарабельны, то такую задачу называют сепарабельной.
424 Гл. 17. Методы оптимизации
С учетом этого перепишем формулировку задачи (5)-(9) в следующем виде:
N
J(x, и) — и^) -» extr, (11)
uw), к = 1, ..., N, (12)
и(МЦх(м’), fc = l, ...,7V, (13)
x<0’ G Лф. (14)
Предположим, что в результате начальных к — 1 шагов процесс перешел в состояние х^-1Г Рассмотрим задачу оптимизации оставшихся N — к + 1 шагов, аналогичную задаче (11)—(14). Пусть оптимальное управление и*(к) = ..., и(Л')*} последних N — к + 1 шагов и
оптимальная траектория этих шагов х*(к) = {х^-1), х^*, ..., x^jV^*}, начатая из состояния х^-1), найдены.
N
Целевая функция (£(&), и(кУ) = i/1)) последних
i—k
N — к + 1 шагов при х(к) = х*(к), и(к) — и* (к) принимает оптимальное (т. е. минимальное или максимальное) значение, зависящее от начального состояния х(/с-1) фазовой траектории этих шагов, т.е.
extr (т(/с), u(/c)) = j(k\x*(k), и*(к)) = Вл(х^-1^). (15)
Функция Вд,(х^_1^) из (15) называется функцией Беллмана последних N — к + 1 шагов.
Очевидно,
= extr J/v(x(N-1\ i/N)). (16)
uW^JN-l))
Кроме того, функции Беллмана связаны между собой следующими рекуррентными соотношениями, вытекающими из принципа оптимальности:
В^х^-1)) = extr {Bfc+i[f^(x^-1\ u(fc))] + Jfc(x(A’-1\ u^)}, u(fc)€Ofc(x(fc-1))
к = 1, ..., N- 1. (17)
Соотношения (16) и (17), позволяющие последовательно найти функции Беллмана Вд^х^-1)), Вдг_1(х^“2)), ..., Bi (х^), называются уравнениями Беллмана.
Находя функции Bfe(x^-1)), к = N, N — 1, ..., 1, из (16) и (17), мы одновременно определяем и управления и^^*(х^-1^), которым отвечают оптихмальные значения соответствующих величин Zn —
§ 5. Дискретное динамическое программирование
425
и/t = ^fc+i[f^(x^ u(fc))]+Л(х^ u(fc)), k = N—1, 7V-2, ..., 1,
из правых частей равенств (16) и (17):
и^Чх^-1))] =
= extr (18)
Zfc[x(fc-1), U(fc)*(x(fc-1))] =
= extr Zk(?Sk~x'>, u(fc)) = Вл(х^-1)), (19) u(fc)6J7fc(x(fc-’))
k = N — 1, ..., 1.
Управления и^*(х(Л-1)), k = 1, ...,7V, называются условными оптимальными управлениями, а процесс их нахождения — условной оптимизацией. Отметим, что управления и^*(х(*-1)), найденные в соответствии с (19), удовлетворяют принципу оптимальности, т.е. в зависимости от начального состояния х^-1) управление и^*(х(*-1)), k = 1, TV — 1, учитывает оптимизацию не только к-го шага, но и следующих за ним N — к шагов.
Итак, в результате условной оптимизации находятся функции Веллмана Bfc(x(fc_1)) и условные оптимальные управления и^^*(х^-1^), 1, ..., 7V.
После этого можно осуществить безусловную оптимизацию в задаче (11)—(14), т.е. определить искомые оптимальное управление процессом и* = {t/1)*, ..., и оптимальную фазовую траекторию х* — — {х(°)*, ..., х^*} следующим образом.
Так как функция Веллмана 2?i(x(°)) для каждого начального состояния х^0) € Xq равна оптимальному значению целевой функции N шагов, т.е. всего процесса, начатого из состояния х^°\ то оптимальное начальное условие х^°)* € Xq находим из соотношения
ВДх^*^ extr Bi(x(0)) (20)
х(°>ех0
(если множество Xq из (14) состоит из единственной точки х^°\ то полагаем х(°)* = х(°)).
Далее, используя найденные условные оптимальные управления, а также уравнения состояний (12), последовательно находим и^1^*, х^1^*, и(2)*, х<2>*, ..., и^)*, х^* из следующих соотношений:
u(l)* _ u(l)*(x(0)*}? х(1)* = у(1)(х(0)^ и(1)*}?
ц(2)* _ ц(2)* (Х(1)*)? х(2)* = у(2)(х(1)*,
q(^)* — ц(^'г)*(х(^ 1)*), = /(^(х^ 1)*, и(Л0*).
426
Гл. 17. Методы оптимизации
Алгоритм метода динамического программирования.
Этап I (условная оптимизация).
Шаг 1. Находим условное оптимальное управление и^’Дх^-1)) и функцию Беллмана Вдг(х^-1)) в соответствии с (16), (18).
Шаг 2. Используя результат первого шага, находим u(yv-1)*(x(/v~2)) с помощью равенств (17) и (19) при к = N — 1.
Шаг N. Используя результаты (N — 1)-го шага, определяем U(1)*(x^°)) и _E?i(x(°)) в соответствии с (17) и (19) при к = 1.
Этап II (безусловная оптимизация).
Шаг 0. Находим оптимальное начальное состояние х^0)* в соответствии с (20).
Шаг 1. Определяем оптимальные управление i/1)* и конечное состояние х^1)* первого шага процесса по формулам (21).
Шаг 2. Используя результаты предыдущего шага, находим i/2)* и х^2)* в соответствии с (21).
Шаг N. С помощью результатов (N — 1)-го шага определяем и^* и х^* по формулам (21).
Окончательно имеем u* = {и^*, ..., и^)*}, х* = {х(0)*, ..., х^)*}.
Пример 2. Методом динамического программирования решить задачу из примера 1 со следующими исходными данными: N — 3, М = 63, m = 1, F(y, z) = z/y.
О Для указанных исходных данных многошаговая задача оптимизации примера 1 формулируется следующим образом:
к----\ V' и(/с)
J(x, и) = > —г.—— -» max,
k-1
к = 1, 2, 3,
х^ € [1; 64], к = 1, 2,
G [0; 63], к = 1, 2, 3,
я;(0) — 1, a;(N) = 64.
(22)
Определим множества Uk(x(k О) из (10):
= {и^ е [0; 63][®(fc-1) + G [1; 64]} = [0; 64 - я/*"1)], к — 1, 2, 3, так как 1.
Проведем вычисления по методу динамического программирования в соответствии с описанным выше алгоритмом.
§ 5. Дискретное динамическое программирование
427
Этап I (условная оптимизация).
Шаг 1. Из (1G) находим В3(х^2Ч = max —ту. Так как u(3)e[O;G4-z(2)] Х^2>
, uW) = и^/х^2) при всех х№ G [1; 64] является возрастающей функцией аргумента и^3\ то ее максимум достигается при максимально возможном значении т.е.
м(3>*(я/2)) = 64- х(2). (23)
Вз(*М) = Z3(xm, U<3»-(^2))) = (24)
Ш а г 2. В соответствии с (17) при k = 2 с учетом (24) и (22) получаем
/П /64 — я/1) — и^\
В2(жш) = max ------------------г-——т-— + -угг •
м(2)е[0;64-.т(1)] \ ЯД^+Ш2) ХУ1> J
Найдем точку максимума и^Дх^Д функции
Z2(x^ , =
64 — я/1) — г/2)
я/1) + я/1)
на отрезке [0; 64 — я/1)] в зависимости от я/1).
Для определения стационарных точек функции Z2(x^, tA2'1) решим уравнение
0Z2 (нДД2 + 2г?2М1) — (я/1))2 — 64я?Э)
5г/(2) д41)(д;(1) 4-w(2)y2
и™ G [0; 64 — я/1)],
откуда получим
и(2) (ягП^о = 8ч/я/1) — я/1)
(25)
(очевидно, и^2Дх^До G [0; 64 — я/1)], так как я/1) 64).
Сравним значения функции Z2(x^l\ и^2Д в точке г/^я/1)^ из (25) и на концах отрезка [0; 64 — я/1)]:
a) Z2(z(1), 0) = Дуг - 1; б) Z2(x^, 64-я/1)) = 0;
яЛ1;
в) /2(я:(1), ц(2)(.т<1))0) = 2 f~7= - 1\
ЧУЯ))1) /
Отсюда следует, что
Я2(я/]\ 64 - я/1)) /2(я)^\ 0) Z2(x^\ (я/1)^)
428
Гл. 17. Методы оптимизации
при G [1; 64] (проверьте!). Поэтому
и(2)*(ж(1)) — и^2\х^)о = 8\/а/1) — х^
(26)
и
B2(z(1)) = ^2^(1), u(2)*(z(1))] = 2 (~Л= - 1") • (27)
Шаг 3. Учитывая равенства (27) и (22), из (17) при к = 1 получаем
Bi(a;(0)) — max
1Д1) €[0; 64—
+ ж(°)
- 1
у/х(°) + и<М
Как и на втором шаге, исследуя функцию
Zi(a;(0), iz(1)) = 2
8
у/х^ +
+ х(0)
-1
на максимум по г/Э) на отрезке [0; 64 — я/0)] (проведите исследование самостоятельно!), получим
г/1)*^0)) — 4(ж(0))2/3 — ж(°), (28)
В^х^) = 12(ж<0))-1/3 -3. (29) ,
Этап II (безусловная оптимизация).
Шаг 0. Так как множество Хо состоит из единственной точки ж(°) — 1? То полагаем
ж(0)* = 1. (30)
Шаг 1. Из формул (21) с учетом (28), (30) и (22) находим
u(i)* = = 3) ж(1)* = х(о)* + u(i)* = 4
Шаг 2. Аналогичным образом из формул (21), (26) и (22) получаем
и(2)* = ?/2)*(4) = 12, ^(2)* = ^(l)* + и(2)* = 1б
Шаг 3. Используя равенства (21), (23) и (22), находим
г/з>* = ц(3)*(16) = 48, т(3)* = ж(2)* + Ц(3)* = 64.
Окончательно получаем и* = {3, 12, 48}, х* = {1, 4, 16, 64}. Таким образом, массы верхней, средней и нижней ступеней ракеты должны равняться соответственно 3, 12 и 48 единицам. При этом межпланетная станция достигнет максимально возможной в данных условиях скорости, равной В\(х^*') = 9 единицам (см. формулы (29), (30)). >
§ 5. Дискретное динамическое программирование 429
Задача, рассмотренная в примере 2, свелась к непрерывной модели многошагового процесса оптимизации. В этой модели управления и^, векторы состояний и другие величины могут непрерывно изменяться на соответствующих множествах.
Для многих экономических и производственных задач характерной является дискретная модель, предполагающая, что величины, описывающие процесс, могут принимать только дискретный ряд значений. Функциональные зависимости в таких задачах задаются, как правило, в виде таблиц, а не аналитически. Однако общая схема их решения методом динамического программирования остается без изменений.
Пример 3. Общая сумма в 4 млн руб. распределяется между тремя предприятиями в количествах, кратных 1 млн руб. В результате выделения средств k-му предприятию в размере и оно дает доход Л-(и), к = 1, 2, 3, величина которого может быть найдена из таблицы 5.1:
Таблица 5.1
и 0 1 2 3 4
J\(u) 0 5 9 11 12
Ji(u) 0 4 8 12 14
дз(и) 0 7 9 10 11
Распределить средства между предприятиями так, чтобы их суммарный доход был максимальным.
О Обозначив средства, выделенные к-му предприятию (к = 1, 2, 3), символом а сумму средств, выделенных предприятиям с номерами от 1 до к, символом х(к\ сформулируем рассматриваемую задачу как многошаговую задачу оптимизации (11)—(14):
з
J(x, и) = -ь max,
к=\
= x(k О + и^к\ к = 1, 2, 3, Е [0; 4-i(bl>]nZ, к = 1,2,3, = 0, х^ = 4.
Для решения этой задачи применим метод динамического программирования.
Этап I (условная оптимизация).
Шаг 1. Найдем ВДх^) = max J3(u^3h. Так как функ-
гх<3>С[0; 4-z<2)]nZ
ЦИЯ /з(ж(2), является возрастающей функцией аргу-
мента (см. таблицу 5.1), то ее максимум достигается при макси
430
Гл. 17. Методы оптимизации
мальном допустимом значении гД3\ т.е.
= [4 - а;<2)]10). (31)
Отсюда В3(ж(2)) = Z3(.t(2\u(3)*(z(2))) = J3([4 - а/2)]). Значения B3(.r(2^), найденные с помощью таблицы 5.1, представлены в таблице 5.2.
Таблица 5.2
д.(2) 0 1 2 3 4
В3(т(2)) 11 10 9 7 0
Шаг 2. Вычислим
В2(х^^) = max + г/2)) + J2(^2))}.
м(2) е[О; 4 — z(’)]nz
Для нахождения максимума функции и^2'1) = В3(ж^^ +w^2^) +
+ составляем таблицу 5.3 значений этой функции, используя
данные таблиц 5.1 и 5.2.
Таблица 5.3
ж(1) ц(2>
0 1 2 3 4
0 11 14 17 И 14
1 10 13 [Ц] 12 -
2 9 |ГГ| 8 - -
3 В 4 - - —
4 0 - - - —
В таблице 5.3 рамками обведены максимальные по значения функции Z2(a;O)? ц('2)), соответствующие различным значениям
Используя таблицу 5.3, находим функции В2(гг^^) и пред-
ставив их значения в таблицах 5.4 и 5.3.
Таблица 5.4 Таблица 5.5
ж(1) 0 1 2 3 4 х(1) 0 1 2 3 4
B2(z(1)) 19 15 И 7 0 3 2 1 0 0
Шаг 3. Так как .множество Xq состоит из единственной точки а;(0) = о, то найдем только Bi(0) и иО)*(о);
Bi(0) = max {В2(0 + г/1)) + .71 (г/1))}.
м(’)е[о; 4]nz
10) Напомним, что символом [а] обозначается целая часть числа а.
§ 5. Дискретное динамическое программирование 431
Для определения максимума в правой части последнего равенства составим таблицу 5.6 значений функции Z2(0, + ^(гД1)),
которые найдем с помощью таблиц 5.1 и 5.4.
Таблица 5.6
0 1 2 3 4
Z2(0, u(1)) 19 [~20~] [~20~] 19 12
Из таблицы 5.6 видно, что ВДО) = 20, причем u^)*(o) — 1 или гД1)*^) — 2, т.е. в данной задаче существует два оптимальных управления и две оптимальные траектории.
Этап II (безусловная оптимизация).
Ш а г 1. а) Пусть — 1. Тогда аД1)* — аД0)* + — 1.
б) Пусть — 2. Тогда аД1)* — ж(°)* 4- гД1)* — 2.
Ш аг 2. а) Для аД1)* = 1 имеем = гД2)*(1) = 2 (см. таблицу 5.5), ж(2)* — дЛ1)* + гД2)* — 3.
б) Для х^* — 2 получаем гД2)*(2) = 1 (см. таблицу 5.5), =
- дФ)* 4- U(2)* = 3.
Шаг 3. Так как для обеих оптимальных фазовых траекторий я;(2)* = 3, то из (31) находим i№* = гД3)*(3) = 1, а;^3^* = х®* + -I- и(3)* =4.
Окончательно получаем и* — {1, 2, 1} или и* = {2, 1, 1} и соответственно х* = {0, 1, 3, 4} или х* = {0, 2, 3, 4}.
Таким образом, существуют два оптимальных варианта распределения средств предприятиям.
Первый вариант: первому предприятию выделяется 1 млн руб., второму — 2 млн руб. и третьему — 1 млн руб.
Второй вариант: первому — 2, второму — 1 и третьему — 1 млн руб.
В обоих случаях суммарный доход предприятий составит Bi(0) = = 20 млн руб. >
В условиях задачи 17.340 решить задачи 17.350-17.352 об оптимальном распределении средств предприятиям со следующими исходными данными:
17.350. S = 5 млн руб., N = 4. Средства предприятиям распределяются в количествах, кратных 1 млн руб. Функции Л(и), k = 1, ..., 4, заданы следующей таблицей:
и (млн руб.) 0 1 2 3 4 5
Л(ц) 0 1,5 2 3,5 5,5 9
Л(«) 0 3 4,5 5,5 6,5 7,5
Л(«) 0 4 5 5,5 6 9
Л(ц) 0 2 3 4 6,5 8
432
Гл. 17. Методы оптимизации
17.351. S = 5 млн руб., N = 5. Средства распределяются в количествах, кратных 1 млн руб. Функции к — 1, ..., 4, заданы таблицей из условия задачи 17.350, а функция /5(11) — следующей таблицей:
U (млн руб.) 0 1 2 3 4 5
Л(«) 0 3 4,5 6 7,5 3,5
17.352. S — 100 тыс. руб., N ~ 4. Средства каждому предприятию выделяются в количествах, кратных 25 тыс. руб., но не могут превосходить 50 тыс. руб. Функции Л(u), к — 1, ..., 4, заданы следующей таблицей:
и (тыс. руб.) 0 25 50 75 75
J1 (и) 0 12 14 20 28
0 12 18 24 30
0 12 16 24 30
Л(^) 0 8 12 16 24
В условиях задачи 17.341 решить задачи 17.353-17.357 об оптимальном выделении средств предприятию в течение N лет со следующими исходными данными:
17.353. S = 500 тыс. руб., N = 4. Средства, выделяемые в течение каждого года, кратны 100 тыс. руб. Функции Jk(u) представлены в таблице.
и (тыс. руб.) 0 100 200 300 400 500
J1 («) 0 40 70 104 120 136
0 50 80 96 112 124
0 34 76 100 ПО 120
Л (и) 0 60 90 100 110 136
17.354* . Найти решение задачи 17.353, если начальная сумма S
а) уменьшена на 100 тыс. руб.;
б) увеличена на 100 тыс. руб. при следующих дополнительных данных о прибыли предприятия при выделении ему в течение к-го года средств в размере 600 тыс. руб.:
к 1 2 3 4
Л(600) 146 132 130 144
§ 5. Дискретное динамическое программирование 433
17.355. S = 400 тыс. руб., N = 4. Выделяемые в течение k-го года средства кратны 20 тыс. руб. и не могут превосходить 200 тыс. руб. Функции /Ди) заданы таблицей
и (тыс. руб.) 0 20 40 60 80 100 120 140 160 180 200
Jl (и) 0 10 20 40 100 160 180 190 200 210 215
0 20 40 60 80 95 101 102 103 104 105
ад 0 5 10 15 25 37 69 140 225 280 300
Ji(u} 0 30 68 95 140 160 170 175 176 177 178
17.356. S = 300 тыс. руб., N = 3, функции Jk(u), к = 1, 2, 3, определяются следующим образом:
а) Л(ц) = J2(u) = = 10 — IO-3 • (u — 100)2;
6) Jx(u) = /2(ц) = 24 - 6 • 10~4(ц - 200)2, У3(ц) = 16 - 4 x x 10-4(ц — 200)2.
17.357. S = 150 тыс. руб., N = 3, J\(u) = 0,12ц, /2(ц) = = 0,0012ц2, 73(ц) = 0,36ц - 0,0024ц2.
17.358. Найти решение задачи 17.342, если N — 3, S = 9.
17.359. Найти решение задачи 17.342 с произвольными исходными данными.
17.360. Найти решение задачи 17.343, если F(u) = си, с > 0.
17.361. Найти решение задачи 16.343 при следующих исходных данных: F(u) — 0,1ц2, А = 5, a — 4, N = 3.
17.362. Найти решение задачи 17.344, если F(u} — си, с> 0, Л3а > Ъ.
17.363. Найти решение задачи 17.344 при следующих исходных данных: F(u) = 0,1ц2, А = 5, a = 4, b = 5, N = 3.
17.364. Найти решение задачи 17.345 со следующими исходными данными: N = 4, S = 200 тыс. руб., Л(ц) = 0,3ц, ЛИ = 0,4ц, /Ди} = 0,8ц, /2(ц) = 0,5ц.
17.365. Найти решение задачи 17.345 при следующих исходных данных: N = 3, S = 120 тыс. руб., /1(ц) = 0,4ц, /з(и} = = 0,6ц. Выделение средств предприятиям происходит в количествах, кратных 20 тыс. руб., а функции Л(ц) и У2(ц) заданы следующей таблицей:
и (тыс. руб.) 0 20 40 60 80 100 120
Jl(li) 0 5 8 12 14 15 16
<h(u) 0 3 5 8 12 14 15
434
Гл. 17. Методы оптимизации
17.366. Найти решение задачи 17.346 со следующими исходными данными: Р = 10, N = 4, a = 0. Коэффициенты и /3^, к ~ 1, ..., 4, представлены в таблице:
к 1 2 3 4
ось 10 15 10 6
0к 7 12 9 8
Считать, что к концу рассматриваемого периода база должна быть освобождена от продукции.
17.367. Найти решение задачи 17.346 при следующих исходных данных: Р = 12, N — 4, a = 5. Значения коэффициентов ak, Рк-> к — 1> • • • 5 4, приведены в условии задачи 17.366. Считать, что к концу рассматриваемого периода на базе должно остаться 4 т продукции.
Используя результат решения задачи 17.349, решить задачи целочисленного линейного программирования 17.368-17.371 методом динамического программирования:
17.368. F(u) = -4г/1) - Зг/2) —> min,
4г/1) 4- г/2) 10,
2г/1) 4- Зг/2) 8,
u^\ г/2) 0; г/1), г/2) G Z.
17.369. F(u) = — г/1) ——> min,
г/1) 2,
2г/1) + Зг/2) < 5,
г/1), г/2) 0; г/2) 6 Z.
17.370. F(u) = — 9г/1) — Иг/2) —> min,
г/1) 5,
4г/1) 4- Зг/Л2) 10,
г/1) 4- 2г/2) < 8,
г/1), г/2) 0; г/1), г/2) G Z.
17.371. F(u) = — г/1) — 2г/2) — Зг/3) —> min,
6г/1) 4- 4г/2) 4- Зг/3) 25,
5г/1) 4- Зг/2) 4- 2г/3) 15,
> 0; е Z, к = 1, 2, 3.
17.372. Имеется 7 т сырья, пригодного для производства изделий трех видов. Для изготовления одного изделия каждого вида требуется соответственно 1, 2 и 3 т сырья.
§ 6. Вариационное исчисление
435
Расходы Jk(u) на производство и изделий к-го вида, к = 1, 2, 3, приведены в таблице (значения Л(0) характеризуют штраф выплачиваемый в случае, если изделие к-го вида нс производится):
и 0 1 2 3 4 5 6 7
Jl(tt) 40 30 25 21 17 14 И 2
Л (и) 55 40 29 29 ' - - - -
Л(п) 70 50 35 - - - - -
Спланировать выпуск изделий так, чтобы затраты на их производство были минимальны.
17.373. Судно грузоподъемностью 10 т загружается контейнерами трех типов. Массы контейнеров различных типов и стоимости грузов в них составляют соответственно 860 кг, 720 кг, 600 кг и 516 руб., 360 руб., 240 руб. Найти количества контейнеров каждого типа, которые необходимо загрузить, чтобы стоимость грузов на судне была максимальной.
17.374. Имеется 9 однотипных станков, каждый из которых можно наладить на производство изделий одного из трех видов. Зависимость количества изделий каждого вида, изготовленных за смену, от количества станков, занятых для их производства, приведена в таблице:
Число станков
Вид изделия 1 2 3 4 5 6 7 8 9
I 14 18 22 26 32 38 42 48 50
II 10 18 24 28 30 36 40 44 54
III 12 20 26 30 32 36 42 44 50
Найти количество станков, которые необходимо использовать для изготовления изделий каждого вида, чтобы общее число произведенных изделий было максимальным.
§ 6. Вариационное исчисление
1. Предварительные сведения. Простейшая задача вариационного исчисления. Существует ряд прикладных задач оптимизации, в которых качество выбранного решения не удается охарактеризовать с помощью Целевой функции. Числовой показатель качества в этих задачах зависит
436
Гл. 17. Методы оптимизации
от функции (а не от одной или нескольких переменных), определить которую необходимо так, чтобы этот показатель принял минимальное или максимальное значение. Числовыми показателями в указанных задачах являются функционалы.
Определение. Если каждому элементу у = у(х) множества G из некоторого функционального пространства X поставлено в соответствие определенное число J, то говорят, что на множестве G С X задан функционал J(y) = J[?/(t)].
В качестве функциональных пространств X в вариационном исчислении используются пространства Сп[а; 6], которые определяются следующим образом.
Линейное нормированное пространство Сп[а; 6], п = 0, 1, ..., состоит из функций у(х), имеющих на отрезке [а; Ь] непрерывные производные у(к\х) до n-го порядка включительно п), с нормой
п
tolln = 52
к=0
max ж€[а; 6]
\у{к)И\.
Расстояние p(yi, у?) между функциями (кривыми) yi(x) и yz(x) в пространстве Сп[а; 6] определяется формулой
п
p(yi,иОп = foi -wiin = 52 -г/2Ч(я)1> п = о,1,...
Пусть функция у*(х) £ Сп[а; Ь] и е > 0 — произвольное число. Множество функций (кривых) у(х} £ Сп[а; 6], для которых выполняется неравенство
р{у\ У)п < г, называется е-окрестностью n-го порядка кривой у*(х).
Говорят, что функционал Л[у(т)] достигает на кривой у* (х), локального или относительного минимума (максимума), если для всех у(х) из некоторой s-окрестности кривой у*(х) выполняется неравенство
Jfo'CO) №•(*)] > -W)])- (1)
Локальные минимумы и максимумы функционала 7[?/(ж)] называются его локальными экстремумами.
Если (1) выполняется для всех кривых у(х), принадлежащих некоторому множеству G С Сп[а; Ь], то говорят, что на кривой у*(х) достигается абсолютный экстремум функционала J[?/(t)] на множестве G.
Пусть функционал 7[?/(ж)] определен на множестве G С Ci[a; Ь]. Функции у(х) £ G можно рассматривать не только как элементы пространства Ci[a; 6], но и как элементы Со[а; Ь]. Локальный экстремум
и)Под производной у(0\х) нулевого порядка здесь понимается сама функция у(х).
§ 6. Вариационное исчисление 437
функционала <7[з/(ж)] в пространстве Со[а; 6] называется сильным, а в пространстве Ci [а; Ь] — слабым локальным экстремумом. Всякий сильный экстремум функционала является и слабым, а обратное, вообще говоря, неверно.
Отметим, что всякий абсолютный экстремум функционала 7[т/(ж)] является сильным и слабым локальным экстремумом, но не всякий локальный экстремум будет абсолютным.
Сформулируем простейшую задачу вариационного исчисления.
Пусть функция F\x, у, z) имеет непрерывные частные производные' до второго порядка включительно по всем своим аргументам. Требуется среди всех функций у(х) S Cifa; Ь], удовлетворяющих граничным условиям
У(о)=Уо, у(Ь) = уъ (2)
найти ту функцию, на которой достигается слабый экстремум функционала
ь
Ду&] = У F(x, у, y')dx. (3)
а
Другими словами, простейшая задача вариационного исчисления состоит в отыскании на множестве всех гладких кривых, проходящих через точки Мо(а, уо) и Mi(6, ух), той кривой, на которой функционал (3) достигает слабого экстремума.
При решении простейшей задачи вариационного исчисления используется следующая теорема.
Теорема 1. Для того чтобы функционал (3) достигал на функции у(х) € Ci[a; Ь] слабого экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера
(4)
Решения (интегральные кривые) уравнения (4) называют экстремалями функционала (3).
Уравнение (4) в развернутом виде записывается следующим образом:
y"(x)Fyly' + y'(x)Fyy' + Fxy> - Fy = 0.
Если Fyiy> £0, то оно представляет собой обыкновенное дифференциальное уравнение второго порядка, поэтому его общее решение зависит от двух произвольных постоянных, которые находятся с помощью граничных условий (2).
Отметим, что так как всякий сильный экстремум функционала является и слабым, то теорема 1 дает необходимое условие и сильного экстремума функционала (3).
Кроме того, так как абсолютный экстремум функционала (3) на множестве
G = {(т) € б?![а; ь]\у(а) = у0, у(Ь) = ух} (5)
438
Гл. 17. Методы оптимизации
является и локальным экстремумом (сильным и слабым), то теорема 1 определяет необходимое условие абсолютного экстремума функционала (3) на множестве (5).
Таким образом, решение краевой задачи
У(а) = уо, у(Ь) = ух
позволяет найти все кривые возможного экстремума функционала (3) на множестве функций (5).
Пример 1. Найти гладкие экстремали функционала
1
J[y(x)] = У (У>2 ~ 12ж?/) dx, о
удовлетворяющие граничным условиям т/(0) = 0, у(1) = 1.
< 1 В данном случае F(x, у, у') = у' — 12жт/, поэтому уравнение Эйлера(4) имеет вид у" 4- 6х = 0. Его общее решение у(х) = —х3 + С}Х + 0%. Из условий ?/(0) = 0, ?/(1) = 1 получаем систему уравнений для определения Ci и С?'
7/(0) = с2 = о,
у(1) = -1 + Сх+С2==1,
откуда находим С\ = 2, С2 = 0- Следовательно, в рассматриваемой задаче существует единственная экстремаль у(х) = —х3 + 2х. >
Решение задачи (6) существует не всегда, а если оно существует, то может быть не единственным.
Пример 2. Найти гладкие экстремали функционала
2
J\y(x)] = У (2ж - y)ydx, 1
удовлетворяющие граничным условиям т/(1) = 1, у(2) = 3.
< 1 Уравнение Эйлера имеет вид х - у = 0. Так как функция у(х) = х условию т/(2) = 3 не удовлетворяет, данная задача нс имеет решений.
Пример 3. Найти гладкие экстремали функционала
7Г
JMx)] = У (у'2 - y2)dx, о
удовлетворяющие граничным условиям т/(0) = 1, у(дг) = —1.
§ 6. Вариационное исчисление
439
< 1 Уравнение Эйлера имеет вид у" + у = 0, а его общее решение у(х) = = Ci cos х = С2 sin ж.
Используя условия ?/(0) — 1, у (if) = —1, находим у(х) = cos ж 4-4- С sin ж, где С — произвольная постоянная.
Таким образом, данная задача имеет бесконечное множество решений. >
В задачах 17.375-17.384 найти все экстремали функционала J(y), удовлетворяющие указанным граничным условиям:
1
17.375. J(y) = У (у2 + ху) dx; ?/(0) = ?/(1) = 0.
о
7Г
17.376. J(y) = j (4т/ cos х 4- у'2 — у2 dx-, у(0) = у(л) = 0.
о
е
17.377. J(y) = У (2у - x2yf2) dx- у(1) = е, у(е) = 0.
1
1
17.378. J(y) — У (у2 4- уу' + 12ж?/) dx-, ?/(0) = у(1) = 0. о
1
17.379. J(y) = У (еу 4- ху) dx-, у(0) = 0, ?/(1) = 1. о
1
17.380. J(у) — У (у'2 + у2 + ху) dx; у(0) = у(1) = 0. о
1
17.381. J(y) = У (у'2 4- у2 + бу sh2x)dx; у(б) = 0, 2/(1) = 1. о
1
17.382. J(y) = [ (у12 + у2 + lye1) dz; у(0) = 0, у(1) = Т
о
1п2
17.383. J(y) = [ {у’2 + 3y2)e2t dx; у(0) = 0, у(1п 2) = J О
0
440
Гл. 17. Методы оптимизации
Ь
17.384. J(y) = У (?/2 + у2 - 4ys\nx) dx\ y(Q) = 0, y(b) = yY.
b
b
17.385. Показать, что функционал f \p(x)y’ + q(x)y + rir)] dx, a
где p(x) G Ci [a; b], q(x), r(x) e Co[a; b], не имеет экстремумов.
Уравнение Эйлера (4) не всегда интегрируется в квадратурах, а в ряде случаев его решение может вызвать затруднения. Перечислим частные случаи, в которых решение уравнения Эйлера упрощается по сравнению с общим случаем.
1. Функция F из (3) не зависит от у', т.е. F = F(x, у). Уравнение (4) в этом случае принимает вид Fy(x, у) = 0. Это конечное (не дифференциальное) уравнение, его решение не содержит произвольных постоянных и, следовательно, удовлетворяет условиям (2) только в ис-
ключительных случаях.
2. Функция F зависит только от у': F = F(y'). Уравнение Эйлера принимает вид Fy'yi-y" — 0, а его общее решение у(х) = С^х+С?. Таким образом, в данном случае экстремалями функционала J[?/(t)] являются всевозможные прямые.
3. Функция F не зависит от у, т.е. F = F(x, у'). Тогда уравнение (4) записывается в виде —Fy'(x, у1) = 0, откуда получаем первый интеграл уравнения Эйлера Fy'(x, у1) = Ci, т.е. дифференциальное уравнение первого порядка, решив которое, найдем экстремали функционала.
4. Функция F не зависит явно от х, т.е. F = F(y, у1). Уравнение Эйлера принимает вид Fy — Fyy>y' — Fy'y<y" = 0 или (после умножения обеих частей этого равенства на у1) —(F — y'Fy') = 0, откуда получаем первый интеграл уравнения Эйлера F-y'Fyi = С\. Это дифференциаль-
ное уравнение первого порядка можно проинтегрировать, разрешив его относительно у' и разделив переменные, или путем введения параметра.
Найти экстремали следующих функционалов J(?/), удовлетворяющие указанным граничным условиям:
1
17.386. J(y) = У (2еу Г- у2) dx- у(0) = 1, у(1) = е.
о
1
17.387. J(y) = у* (ех+у — у — sina;) dx\ т/(0) = 0, у(1) = —1.
о
§ 6. Вариационное исчисление
441
1
17.388. J(y) = jy^dx; у(0) = О, У(1) = 1. О
} + ?/2
17.389. У(т/) - / У-- dx; т/(-1) = О, 7/(1) = 1.
J У
-1 3/2
17.390. J(y) = У (у'3 + 2х) dx-, у(0) = 0, у Q) = 1. О
1
17.391. J(y) = У (ху' + У2) dx; у(-1) = 1, т/(1) = 0.
-1 2
17.392. J(y) = [ хпу’2 dx, п G N, п 7^ 1; т/(1) = ———, J 1—72
1 nl — п 1
17.393. J(y) = У (у- у'2} dx; т/(0) = т/(1) = 0. о
1
17.394. J(y) = fyy'dx-, у(0) = 1, у(1) = VI. о тг/2
17.395. J(y) = У (2т/ + у2 - т/'2) dx; т/(0) = у = 0. о
В ряде случаев существование абсолютного экстремума функционала (3) на множестве функций (5) и его характер (минимум или максимум) бывают очевидны из физических или геометрических соображений. В таких случаях необходимое условие экстремума, сформулированное в теореме 1, позволяет найти функцию у(х), дающую абсолютный минимум или максимум функционалу (3) на множестве (5).
Пример 4. Найти гладкую кривую на плоскости, соединяющую две данные точки Л/о(а; -<4) и М\(Ь, В) и имеющую минимальную длину.
442
Гл. 17. Методы оптимизации
< Длина дуги гладкой кривой, описываемой уравнением у = у(х) и про-ь___________________________________________________
ходящей через точки с абсциссами а и Ь, равна J yl + у'2 dx.
a
Поэтому данную задачу можно сформулировать следующим образом: найти функцию у(х), минимизирующую функционал
ь
J[yW] = У У1 + у'2 dx (6)
a
в удовлетворяющую условиям у(о) = А, у(Ь) = В.
Уравнение Эйлера для этой задачи имеет вид у"(х) = 0, откуда у = Ci х + (?2. Найдя (71 и (?2 из условий на функцию у(х) при х = а и
В — А
х — Ь, получим у(х) = ---(х — о) + А, т. е. необходимое условие экс-
о — a
тремума функционала (6) выполняется на прямой, соединяющей точки Мо и Му.
Из геометрических соображений ясно, что среди гладких кривых, соединяющих данные точки, кривая минимальной длины должна существовать, а кривая максимальной длины — нет. Поэтому упомянутая прямая и является искомой кривой. >
17.396. Материальная точка перемещается вдоль плоской кривой у = у(х), соединяющей точки Л/о(а, А) и Mi(Ь, В) со скоростью и = ку'. Найти гладкую кривую, время движения вдоль которой из точки Мо в точку Mi будет минимальным.
17.397. Решить задачу 17.396, если Mq — (0, 0), Mi = (1, 1), и = х.
17.398. Среди гладких кривых, соединяющих точки Мо(О, 1) и Л/1(1, 1), найти ту, которая при вращении вокруг оси Ох образует поверхность наименьшей площади.
17.399* *. Задача о брахистохроне. Найти гладкую кривую, соединяющую' точки Mq(0, 0) и Mi(xi, т/i), при скатывании вдоль которой под действием силы тяжести материальная точка, зафиксированная первоначально в точке Mq, переместится в точку Му за минимальное время (трением и сопротивлением воздуха пренебречь).
2. Обобщения простейшей задачи вариационного исчисления. Ниже рассмотрены два обобщения простейшей задачи вариационного исчисления. Первым из них является задача на экстремум функционала 7[т/(я;)], зависящего от производных высших порядков функции у(х}‘-
ь
J[y(x)] = [ F(x, у, yw, ..., у^) dx, (7)
§ 6. Вариационное исчисление
443
где функция F(x, у, ..., имеет непрерывные частные производные вплоть до (п + 1)-го порядка по всем аргументам, а у(х) G Сп[а; 6].
Граничные условия в этой задаче имеют вид
у(.а) — Уо, У{1}(а) = Уо \ ...,у(п)(а) =у(оп),
(о)
у(Ъ) = У1, У(1)(6) = у^\ . • •, у{п)(Ъ} = у[п\
Приведем обобщение теоремы 1 применительно к рассматриваемой задаче.
Теорема 2. Для того чтобы функционал (7) достигал на функции у(х) Е Сп[а; Ь] локального экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера-Пуассона
d d2 dn
Fv - + T^F»<2' - + = °- (9)
dx J dx* J dxn y
Подобно случаю простейшей задачи вариационного исчисления, решения уравнения (9) (экстремали функционала (7)), удовлетворяющие граничцым условиям (8), являются кривыми возможного абсолютного экстремума этого функционала на множестве
G = {у{х) е С„[а; Ь]|»(а) = уо, .... у(п>(а) = Уо‘}, y(b) = У1, •••
Пример 5. Найти экстремали функционала
1
Ж*)] = У (120x7/ - у") dx, о
удовлетворяющие граничным условиям
у(О) = у'(О) = О, </(!) = 1, »'(!) = 6.
< Запишем уравнение Эйлера -Пуассона: у^ = 120х. Его общее решение у(х) = х5 + (Дх3 + С2Х2 + С3Х + С4. Отсюда с помощью граничных условий получаем систему уравнений для определения постоянных Си ..., С4:
С4 =0,
С3 -0,
Ci + С?2 + С3 + С4 = 0,
ЗС} + 2CS + С3 — 1,
из которой находим Ci = 1, С2 = -1, С3 = С4 = 0. Поэтому экстремум функционала может достигаться на кривой у(х) — х5 + х3 — х2. >
444
Гл. 17. Методы оптимизации
В задачах 17.400-17.411 найти все экстремали функционала J(y), удовлетворяющие указанным граничным условиям:
1
17.400. J(y) = J у" dx\ г/(0) = ?/(1) = т/'(1) = 0, ?/'(0) = 1.
о
17.401. J(y) = / (48у — у"2) da; у(0) = у'(0) = 0, у(1) = 1, у'(1) = 4.
1
17.402. J(y) = [ (у"2 -24xy)dx-, у(0) = у'(0) = 0, у(1) = J о
у'(1) = 1.
тг/2 .
17.403. Ду) = [ (у"2 - у'2) dx- у(0) = у'(0) = 0, у (£) = о
(?)=°'
6
17.404. J(y) = [ (у"2 + у'2) dx-, у(0) = у'(0) = у(6) = у'(6) = 0.
17.405. Ду) = I е~ху"2 dx-, у(0) = 0, у'(0) = 1, у(1) = е, У'(1) = 2е.
1
17.406. J(y) = У (x + l)3y"2dx-, у(0) = 1, у'(0) = -1, у(1) =
О
=? =4
тг/2
17.407. Ду) = I (у"2 -у2 + х2) dx-, у(0) = 1, у'(0) = у (0 =
О
= °, у' = -1-
§ 6. Вариационное исчисление
445
1
17.408. J(y) = I у'"2 dx-, у(0) = у'(0) = у"(0) = 0, у(1) = 1, о
у'(1) = 4, у"(1) = 12.
1
17.409. J(y) = [ (у'"2 - у"2) dx; у(0) = у"(0) = 0, у'(0) = 1,
О
7/(1) = ?/(1) = sh 1, г/(1) = chi.
7Г
17.410. J(y) = j (у’"2 -y"2)dx; у(0) = у'(0) = у"(0) = О, О
Т/(7Г) = 7Г, 7/'(тг) = 2, у"(п) = 0.
7Г
17.411. Ду) = [ (у"'2 - у’2) dx; у(0) = у'(0) = у"(0) = О,
О
7/(?г) = у" (л) = sh 7Г, ?/(%) = ch 7Г + 1.
Другим обобщением простейшей задачи вариационного исчисления является задача об экстремуме функционала, зависящего от нескольких функций:
ь
J[yi(x), уп(х)] = УF(x, уДх), ..., уп(х), у'Дх), y'n(x))dx, a
(10) где функция F(...) имеет непрерывные частные производные до второго порядка включительно по всем своим аргументам и yk(x) G (7i[a; Ь], к = 1, ..., п.
Граничные условия в этой задаче имеют вид
Ук{а)=У^\ Ук(Ь) = у{к1\ к = 1,...,п. (11)
Теорема 1 для данного случая обобщается следующим образом.
Теорема 3. Для того чтобы набор функций yi(x), уп(х) Е € (71 [а; 6] доставлял слабый экстремум функционалу (10), необходимо, чтобы эти функции удовлетворяли системе дифф ер енци-.алъных уравнений Эйлера
Fyk ~ TxFy'k = 0, k = 1, ..., п. (12)
446
Гл. 17. Методы оптимизации
Пример 6. Найти функции у\(х) и у2{х) Е С] [а; Ь], на которых может достигаться экстремум функционала
тг/2
J[yi(x), у2(х)] = У (у'2 + у'22 + 2 - 2yYy2)dx о
при граничных условиях yY (0) = 3/2O) = 0, т/i (тг/2) = у2(тт/2) = 1.
< Система уравнений Эйлера имеет вид
у" +?/2=0,
У2 +3/1=0-
Исключая из второго уравнения функцию у2 = —у", получим у^ — -1/1=0. Общее решение этого уравнения имеет вид yi(x) = CYex + + С2е~х + Сз cost; + С4 sinх. Отсюда находим
у 2 (х) — —у"(х) = -С\ех - С2е~х + С3 cos я; + Сд sin х.
Из граничных условий следует, что CY = С2 = С3 = 0, С4 = 1, поэтому i/i (ж) = sin х, у2(х) = sin ж. >
В задачах 17.412-17.419 найти функции у\(х) и у2 (ж) 6 C*i[a; b], на которых может достигаться экстремум функционала J(i/i, i/2) при указанных граничных условиях:
тг/2
17.412. у2) = У (i/2 + у22 + 2yiy2)dx- 3/1 (0) = з/2(О) =
о
= 0, т/i(тг/2) = 1, 1/2(тг/2) = -1.
1
17.413. J(i/i, у2) = У (i/f + i/22 ~ 2yYy2)dx; у} (0) = i/2(0) = 0, b
3/1(1) = sh 1, i/2(l) = -shl.
7Г/2
17.414. <7(3/1, ?/2) = / (У\У2 ~ У\У2) dx\ 1/1 (0) = ?/2(0) = 0, b
?/i(7t/2) = 1, 2/2(tt/2) = -1.
1
17.415. <7(з/1, 3/2) = У (y'Yy2 + yYy2)dx; i/i(0) = i/2(0) = 0, ’ 0
3/1(1) = e, 3/2(l) = 1/e.'
§ 6. Вариационное исчисление
447
1
17.416. У2) = У (у[У2 + 6xyi + 12x2y2)dx- у} (0) = 1/2(0) =
о
= 0, Ш(1) = 1/2(1) = 1.
з
17.417. 7(?л, г/2) = У Wi2 + Уъ + xyiy2)dx-, i/i(l) = 1, г/2(1) =
= г/2(3) = О, Ш(3) = 1пЗ+ 1.
7Г
17.418. J(yi,y2) = У (У12 -у22 + 2у\у2+ 2yi cos х + 2у%) dx, о
2/1(0) = -1, 1/2(0) = 2/2(7г) = 0, у^тт) = 1 + тг.
1
17.419. <7(1/!, у2) = У (у'2 + у'22 + 2y^dx, 1/1 (0) = ?j2(0) = 1, о
yiW = 3/2, i/2(l) = 1.
3. Задачи с подвижными границами. В задачах вариационного исчисления с подвижными границами в отличие от ранее рассмотренных задач граничные условия на функцию у(х), х Е [а; Ь] на концах отрезка [а; Ь] не зафиксированы.
Простейшая задача вариационного исчисления с подвижными границами состоит в определении функции у(х) Е (Л[а; 6] и точек ж0, Xi Е [а; b], Xq < xi, для которых функционал
Х1
J[y(x)] = У F(x, У, y')dx (13)
Хо
достигает слабого 12) экстремума при условиях
у(х0) = ро(хо), y(xi) = 9?i(xi). (14)
(Здесь ро(х'), </?i (я;) Е Ci [a; b], F(x, у, z) — заданные функции и F(x, у, z) имеет непрерывные частные производные до второго порядка включительно по всем аргументам.)
12) Напомним, что слабым называется локальный экстремум в пространстве Ci [а; Ь]. В задаче с подвижными границами на кривой у*(х) с абсциссами концов Xq и Xi функционал (13) достигает локального экстремума в Ci[a; b], если существует число е > 0 такое, что для всех кривых у(х) Е Ci[a; 6] и точек хо и ®i, удовлетворяющих неравенствам ||?/* — t/||i < е, |^о — ^ol < £, |^i — #i| < £, справедливо J[y* (а?)] J[j/(a?)] (локальный минимум) или J[y* (ж)] J[i/(;r)] (локальный максимум).
448
Гл. 17. Методы оптимизации
Эту задачу можно сформулировать и следующим образом. Пусть на плоскости заданы гладкие кривые 71: у — ^о(^) и 72: у — ^i(x). х € [а; Ь]. Требуется найти такую гладкую кривую у = у(х), которая соединяет какую-либо точку кривой 71 с какой-либо точкой кривой 72 и доставляет слабый экстремум функционалу (13).
Приведем обобщение теоремы 1 для простейшей задачи вариационного исчисления с подвижными границами.
Теорема 4. Для того чтобы функционал (13) достигал на функции у(х) Е (71 [а; Ь] слабого экстремума при условиях (14), необходимо, чтобы эта функция удовлетворяла уравнению Эйлера
Fy - j~Fy’ = О у dx у иусловиям трансверсальности
[F + (Ро - = О,
[F + (rf=0. 1 °’
Таким образом, для определения экстремалей в простейшей задаче с подвижными границами необходимо найти общее решение у(х, (7i, С2) уравнения Эйлера, после чего из условий (15) и уравнений
у(х0, Сг, (72) = (М^о), ?/(^i, Ci, (72) = 99i(xi) (16)
определить постоянные (71 и С2 и концы отрезка [хо; 27].
Если на одном из концов искомой кривой у(х) задано обычное граничное условие (у(а) = уо или y(b) = yi), то условие трансверсальности (15) следует записать только для другого конца кривой.
Частным случаем задачи с подвижными границами является задача, в которой задана абсцисса одного из концов кривой у(х), например Х2 = Ь, но граничное условие для х = b отсутствует. Это означает, что граничная точка (Ь, у(ЬУ) кривой у(х) может перемещаться по вертикальной прямой х = Ъ, и вместо второго условия трансверсальности (15) следует записать естественное граничное условие
[Fy']x=b = 0. (17)
Пример 7. Найти экстремали функционала в следующей задаче с подвижными границами:
J[y(x)] = I y/1+y^dx; у(х0) = х% + 2, у(х^ = хъ
Хо
< Так как функция F(x, у, у1} = у 1 + у'2 зависит только от у1, то общее решение уравнения Эйлера имеет вид
у(х) - Cix -I- (72. (18)
§ 6. Вариационное исчисление
449
Запишем условия трансверсальности (15):
Из (18) находим ?/'(хо) = у'(х\) = С\. Отсюда с учетом равенств (16) получаем систему четырех уравнений для определения Ci, С2, и xi
+ С? + (2^о - Ci) г-—= — О, V1 + С{
'/гт^+(1-С1)7Й^=0’
Ci^o + С*2 — Xq 4- 2, С[Х} -Ь С*2 = Xi,
решив которую, находим Ci = — 1, С2 — 11/4, xq = 1/2, xt — 11/8.
Следовательно, уравнение экстремали имеет вид у(х) — —х 4-1 11
11
4 ’
zo = 5,x1 = -.
Отметим, что функционал 7[т/(х)] в данной задаче с подвижными границами представляет собой длину дуги кривой между точками (я?о, ?/(го)) и (я?1, y(xi)). Поэтому геометрический смысл этой задачи состоит в определении гладкой кривой минимальной длины, соединяющей параболу у = х2 4- 2 и прямую у = х. Найденное решение позволяет определить расстояние S между указанными параболой и прямой:
11/8
S = [ v/l + (-l)2dz = 7-
J 8
1/2
2. >
Пример 8. На$ти экстремали функционала в следующей задаче:
7Г / 4
= У (у'2 -y2)dx, у(0) = 1. о
<] В этой задаче отсутствует граничное условие при х = тг/4, следовательно, правый конец кривой у(х) может перемещаться по прямой х = тг/4, и необходимо использовать естественное граничное условие (17).
450
Гл. 17. Методы оптимизации
Уравнение Эйлера имеет вид у" + у = 0, а его общее решение у(х) = = Ci cos ж + Czsinx. Из условия 2/(0) = (7i = 1 находится постоянная (71, а из условия (17) 2у' = — sin^ + (72 cos =0 — постоянная
(72 = 1, откуда у(х) = cos х + sin ж. О
Найти экстремали функционала в следующих задачах с подвижными границами:
XI
17.420. J(y) = У у'2 dx; 7/(0) = 0, y(xi) = -a?i - 1. о
xi
17.421. J(y) = [ у'2 dx; 1/(0) = 0, у(х{) = —-—.
J 1 — xi
о xi
17.422. J(y) = I yjl+^dx-, y(0) = 0, #(ц) = i o 1
17.423. J(y) = У ^/1 + y'2dx; y(xQ) = x%, y(xT) = X1-5. о
1/2
17.424. J(y) = У Q/ - y'2) dx; 1/(0) = 0.
о
i
17.425. J(y) = У (у'2 + 2/) dx-, 2/(1) = 0.
о тг/2
17.426. J(2/) - I (y'2 - y2) dx- 2/(0) = 0.
о
Xl
17.427. J(y) = f (у'2 + у2) dx-, y(0) = 0, y^O = 1.
0
17.428. J(2/) = J ------U—dx- 2/(0) = 1, у(х^ = x, - 1.
о
7Г/4
17.429. 7(2/)= У (у'2 ~ у2 + 4y cos x) dx-, 2/(0) = 0. n
§ 6. Вариационное исчисление 451
К задачам вариационного исчисления с подвижными границами относится и задача Больца, состоящая в определении функции у(х) G Ci [а; Ь], доставляющей слабый экстремум функционалу
ь
J[y(x)] = J' F(x, у, у') dx + f (у(а), у(b)), (19)
а
где f(u, v) — заданная функция, имеющая непрерывные производные по и и V.
Необходимое условие экстремума функционала (19) формулируется следующим образом.
Теорема 5. Для того чтобы функционал (19) достигал на функции у{х) Е (71 [а; 6] слабого экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера
и условиям трансверсальности для задачи Больца
= °> + =°- <20>
I L ду(Ь) JI=t
Условия (20) используются для определения постоянных (71 и С2 из общего решения у(х, (71, (72) уравнения Эйлера.
Пример 9. Найти экстремали функционала
тг/2
= У* (у'2 - y2)dx - Л°) + 2у (тр • о
< Уравнение Эйлера у" 4- у = 0 имеет общее решение
у (х) — Ci cos х 4- С2 sin х. (21)
Записав условия трансверсальности (20)
[2у' 4- 2?/]а;=о = 2[-(7i sin я; 4- С2 cosх 4- (7i cosz 4- С2 sinz]z==o =
= 2(7i + 2(72 = 0,
[2у' 4- 2]а;=7г/2 = 2[-(7i sin х 4- (72 cos х + 1]х=:7Г/2 = -2(71 4-2 = 0, находим (7i = 1, (72 = —1. Таким образом, функция у{х} = cosz — — sinz является единственной кривой возможного экстремума функционала J[?/(z)]. >
452
Гл. 17. Методы оптимизации
Найти экстремали следующих функционалов:
1
17.430. 7Ц= [ y'2ds + y2(0)-2?/2(l).
о
1
17.431. J(y) = У (?/2 4- у2) dx — 2sh 1 т/(1).
о
7Г
17.432. J(y) = У (?/»2 4- у2 — 4z/sinrr) а?ж4-27/2(0)4-2^(тг)—т/2(тг). о
з
17.433. J(y) = У hfy2 dx 4- г/4(0) - 8т/(3).
о
е
17.434. J(y) = У 2у'(ху' + y)dx + Зг/2 (1) - у2(в) - 4т/(е).
1
1
17.435. J(y) = У ех+\у'2 + 2y2)dx + 2у(1)(у(0) + 1).
О
1
17.436. J(y) = У еуу2 dx 4- 4еу(0) +32е“у(1).
о
7Г/2
17.437. 7(т/) = У (У2 - у2) dx 4- z/2(0) - у2 Q 4- 4т/ о
4. Задачи на условный экстремум. Задачи вариационного исчисления, в которых на искомые функции накладываются, помимо граничных условий, дополнительные ограничения, называются задачами на условный экстремум.
Рассмотрим следующую задачу об экстремуме функционала, зависящего от нескольких функций, ъ
..., yn(x)]=jF(x, yi(x), ..., yn(x), y'i(x), ..., у'п(хУ) dx (22) a
с граничными условиями
уМ=у^\ Ук(Ь) = у^\ к = 1, ..., п, (23)
при дополнительных ограничениях, заданных уравнениями связи
4>i(x, У1, ..., уп, у{, ..., у'п) = 0, i = 1, ..., m, m < n. (24)
§ 6. Вариационное исчисление
453
Эта задача вариационного исчисления называется задачей Лагранжа. Введем функцию Лагранжа рассматриваемой задачи
Ь(.г, ?/i, ..., уп, у{, ..., у'п, Ai, ..., Ат) =
F(x, У\, . . . , Ут У it •••, Уп) 4"
771
+ 52Аг(ж)<А(ж, У1, Уп, у{, , у'п), (25) г=1
где Xi(x) € Ci [а; b] — произвольные функции (множители Лагранжа).
При решении задачи Лагранжа используется следующее необходимое условие экстремума функционала (22).
Теорема 6 13). Если функции yi(x), ..., уп(х) доставляют слабый экстремум функционалу (22) при условиях (24), (25), то существуют множители Лагранжа Xi(x), i — 1, ..., т, при которых эти функции удовлетворяют системе уравнений Эйлера
Lyk — ~-Ly> = Q, к = 1,...,п, (26)
ах к
ь записанных для функционала I(yi, ..., ун) = Ldx.
С помощью теоремы 6 решение задачи об условном экстремуме функционала J(y\, ..., уп) сводится к исследованию экстремума функции-, нала 1(у\, ..., уп) без дополнительных условий (24).
При использовании теоремы 6 для решения задачи Лагранжа искомые функции уЛл), к = 1, ..., п, и множители Лагранжа Xi(x), i = = 1, ..., ni, определяются из системы п + т уравнений (26) и (24).
Пример 10. Найти функции у\(х), yi(x), на которых может достигаться экстремум функционала J(y\, у Л) в следующей задаче Лагранжа:
1
д(У1,У1) = У (у{2 +y'22)dx-о
»1(0)=Ы0) = 0, г/1(1) = 2сЫ, г/2(1) = 2shl;
y'l - Уг = 0.
<] Функция Лагранжа данной задачи имеет вид L = у{2 4- у'22 + Х(у{ — — т/з)- Для определения функций yi(x), У2(х) и Х(х) запишем систему,
13) Эта теорема обобщает соответствующий результат для задачи на условный экстремум функции п переменных (см. Часть 2, стр. 214).
454
Гл. 17. Методы оптимизации
состоящую и.з уравнений Эйлера (26) и уравнения связи:
2т/" 4- А' = О,
2^ + Л = О,
У{ ~ Уч = 0.
Исключая из этой системы сначала функцию А(.г), а затем 2/1 (ж), получим у2 - у'2 = 0. Обозначим у'2 буквой г, тогда z" — z = 0. Общее решение этого уравнения z(x) — С\ёх + С2е~х. Отсюда последовательно находим
2/г(^) = У dx = С4ех - С2е~х + С3,
У1(х) = У y2(x)dx = Ciex + С2е~х + С3х + С4.
Для определения постоянных Ci, ..., С4 из граничных условий получаем следующую систему уравнений:
2/1(0) = С4 + С2 + С4 = 0,
2/2(0) = Ci — С2 + С3 = 0,
2/1(1) = С16 + С2е 1 + С'з + С4 = 2 ch 1,
2/2(1) = С4е — С2е 1 + С3 = 2 sh 1,
откуда находим Ci = С2 = 1, Сз = С4 = 0, т.е. в данной задаче функционал J(2/i,2/2) может достигать экстремума при 2/1 (ж) —ёх + + е~х = 2 ch ж, 2/2 = ех — е~х = 2sha;. [>
Найти функции 1/1 (.т), 2/2 (^)5 на которых может достигаться экстремум функционала J(2/i, Уч) в следующих задачах Лагранжа.
7Г/2
17.438. J(2/1, 2/2) = У (2/1 + Уч ~ У[2 ~ У'ч + cos ж) о
2/1(0) = 2/2(0) = 2/1 (тг/2) = 1, 2/2(7г/2) = -1;
2/1 - Уч - sinj; = 0.
1
17.439. J(2/i, 2/2) = f (y'i2 + ^Уч + У2ч) о
У1(О) = —2, у2(0) = 1, V1(l) = -е-1, у2(1) = 0;
г/i - у'22 = °-
§ 6. Вариационное исчисление
455
17.440. <7(z/i, г/2) = J (у[2 + у22 + х3) dx; о
2/1(0) = г/2(1) = 2, г/2(0) = 2/1(1) = 1;
Ух - %У2 + Зж = 0.
1
17.441. J (ух, у2) = У (у2 + у'2 + 1) dx;
У1(0) = у2(0) = у2(1) = 0, У1(1) = 2;
Ух + У2 - 2z2 = 0.
1
17.442. J(yi, у2) = У (у'2 + y%)dx; о
2/1(0) = г/2(1) = О, ?/2(0) = г/1(1) = 1;
Ух ~У2 = 0-
тг
17.443. J(yx, у2) = У (?Д2 - у22) dx; о
2/1(0) = г/2(0) = 2/1 (тг) = 0, 2/г(тг) = тг/2;
Ух - У2 + cos х = 0.
тг/2
17.444. J(ух ,у2)- У (у'2 + у'2 + 2?/iу2) dx; о
2/1(0) = 1, 2/2(0) = -1, Ух (j) = у + 1; 2
Ух + у2 - 4гг = 0. ъ
17.445. J(yY, у2) = У (ух + у2 + У2) dx; a
Ух(а) = Ух°\ У2(а} = У^\ У^Ь) = У]1^ У^) = У2};
Ух + У2 - 1 = 0.
456
Гл. 17. Методы оптимизации
Задача на условный экстремум функционала (22) с граничными условиями (23) при дополнительных условиях
ь
УFi{x,yi, ...,y'n)dx = Ci, i = 1, ..., m и), (27)
a
называется изопериметрической задачей.
Функция Лагранжа данной задачи имеет вид
У\ 1 • • • > Уп-, У\-> • • • 1 Уп-, Ai, ..., Аш) —
т
= F(x, У1, уп, у[, ..., у'п) + ^XiFi(x, ух, ..., уп, у[, ..., у'п), г=1
(28)
где множителями Лагранжа А/, i = 1, ..., т, являются произвольные вещественные числа.
При решении изопериметрической задачи используется следующее необходимое условие экстремума, подобное условию, сформулированному в теореме 6 для задачи Лагранжа.
Теорема 7. Если функции г/1(ж), ..., уп(х) доставляют слабый экстремум функционалу (22) при условиях (23), (27), то существуют числа Ai, ..., Хт (множители Лагранжа), при которых эти функции удовлетворяют системе уравнений Эйлера
Lyk ~ ~dx^y'k ~ 0’ ~ 1’ ’ ' ’ ’ П’
где L — функция Лагранжа (28).
При использовании теоремы 7 для решения изопериметрической задачи функции yk(x), k = 1, ..., п, и множители Лагранжа Аг-, г = = 1, ..., т, находятся из системы п + т уравнений (29) и (27).
Пример 11. Найти функцию у(х), на которой может достигаться экстремум функционала J(y) в следующей изопериметрической задаче:
J(y) = У У'~ dx-о
/7Г ycosxdx = -.
о
14)В данном случае, в отличие от задачи Лагранжа, число дополнительных ограничений не ограничивается условием т < п.
§ 6. Вариационное исчисление
457
<] Функция Лагранжа данной задачи имеет вид L = у'2 + Ху cos х. Из уравнения Эйлера Л cos х - 2у" = 0 находим у(х) = — — cos х + Ci х + С*2. Для определения множителя Лагранжа Л используем дополнительное условие У ^-^cosx + Cix + С2^ cosxdx = -^Л - 2Ci — —, откуда о
g
находим Л = -2-------Ср Таким образом, общее решение уравнения
7Г
4
Эйлера имеет вид у(х) = cos ж -I—Ci cos я: + С\х + С^.
7Г
Постоянные С\ и С2 определяем из граничных условий 2/(0) = 1 + 4 / 4\
+ - Ci +С2 — 1, у (тг) = — 1+ I тг-I Ct +С2 = 1, откуда Ci — С2 — 0.
7Г \ 7Г /
Итак, функционал 7(т/) может достигать экстремума при т/(ж) = = COS Ж. [>
Найти функции, на которых может достигаться экстремум функционала J(yi, ..., уп) в следующих изопериметрических задачах:
1
У y'2dx; о
1
7/(0) = (0), 7/(1) = 1; У xydx = 0. о
1
у* у'2 dx;
о
1 у(0) = у(1) =0; I о
1
J ху dy = 0. о
J у'2 dx; о
7Г
7/(0) = 0, т/(тг) = 1; / у sin х dx = 0.
о
458
Гл. 17. Методы оптимизации
7Г
17.449. J(y) = J ysinxdx:, о
тг
Г 9 3
2/(0) = (0), 2/W = тг; J у' dx = -тг.
о
1
17.450. J(y) = I (у'2 + у2) dx-О
1
г/(0) = 0, 7/(1) = е-1; e~xydx = i(l - Зе-2), о
1
17.451. J(yr, у2) = У*y'ly^dx] о
ш(0) = 2/2(0) = ?/i(l) = 0, 2/2(1) = 1; 1 1
У 2/1 dx — 1, У 2/2 dx = 0. о о
1
17.452. J(2/b 2/2) = У (У1 + yi)dx\ о
ш(0)=2/2(0) = 0, 2/1(1) = 1, 2/2(1) = -3;
1
У 2/'12/2 dx = °-о
1
17.453. J(2/i, 2/2) = У^'ц ?/2^; о
2/1(0) = 2/2(О) = 2/1(1) = 0, 2/2(1) = 1; 1 1
/ ху\ dx = 0, / ху2 dx = 0.
о
о
§ 6. Вариационное исчисление
459
1
17.454. J(y}, у2) = У (у\2 + ?/22) dx\
о
1
2/1(0) = 7/2(0) = 7/1(1) = 2/2(1) = О, У у \y2dx = —2.
о
1
17.455. J(yi, т/2) = У я(т/1 - yz)dx-
о
2/1(0) = 7/2(0) = т/2(1) = о, 7/1(1) = 2;
• 1
г 4
/ y'ly'zdx =
J 5
О
5. Прямые методы вариационного исчисления. Обычные методы вариационного исчисления, при использовании которых задача минимизации функционала сводится к интегрированию уравнений Эйлера-Лагранжа, как правило, приводят к трудоемким вычисленияхМ и поэтому являются малоэффективными. Приближенные численные методы, дающие непосредственное решение вариационной задачи, называются прямыми методами вариационного исчисления. Основная идея прямых методов заключается в том, что вариационная задача рассматривается как предельная для некоторой задачи на экстремум функции конечного числа переменных. Наиболее известными среди них являются методы Ритца, Канторовича и Галёркина. Следует отметить, что прямые методы вариационного исчисления являются также и приближенными методами решения краевых задач дифференциальных уравнений.
Метод Ритца. Пусть требуется найти минимум функционала
ь
J(y) - У F(x, у, y')dx, у(а)=у0, у(Ь)=уг. а
(30)
Идея метода Ритца состоит в том, что значения функционала J(y) рассматриваются не на произвольных допустимых кривых вариационной задачи (30), а лишь на всевозможных линейных комбинациях вида
п
Уп{х) = <р0(х) + ^JCi<pi(x), 1=1
(31)
где ipo(a') = уо, <po(ty = У\ и <Pi(x) — последовательность линейно независимых функций, причем = 0, г = 1, 2, ..., п. Эти
функции называются координатными.
460
Гл. 17. Методы оптимизации
На функциях вида (31) функционал (30) превращается в функцию, зависящую от п переменных Ci, С2, • •, Сп:
<7(Уп(хУ) = Ф(Сь С2, ... ,СП).
Значения Ci, С2, . • •, Сп выбираются так, чтобы функция Ф(С1, Сг,..., ..., Сп) достигала экстремума, т.е. Ci, С2, ..., Сп определяются из системы уравнений
5Ф
——=0, г = 1, 2, ..., п. (32)
uCi
При найденных из системы (32) значениях С*, I = 1, 2, ..., п, приближенное решение вариационной задачи (30) запишется в виде
п
Уп И = <А) (ж) + С* & Iх) • (33)
г=1
Вопросы сходимости минимизирующей последовательности {?/* (гс), х € N} являются сложными. Они изучаются в специальной литературе. Для оценки точности результатов, полученных методом Ритца или другими прямыми методами, обычно пользуются следующим практическим правилом. Вычислив г/* (ж) и г/*+1(ж), сравнивают их между собой в нескольких точках отрезка [а, Ь]. Если в пределах требуемой точности их значения совпадают, то считают, что с требуемой точностью решение рассматриваемой вариационной задачи (30) равно Уп(х)-Если же значения г/* (ж) и Уп+1(х) хотя бы в некоторых из выбранных точек отличаются значительно, то вычисляют Уп±2(х) и сравнивают теперь значения 2/^+1 (ж) и Уп+2(х')- Этот процесс продолжается до тех пор, пока значения г/*+/.(ж) и y„+i.+i(x>) не совпадут в пределах заданной точности.
Пример 12. Найти экстремаль функционала
1
У (У>2 +У2 + Ъху} dx о
(34)
при граничных условиях г/(0) = 0, г/(1) = 0 методОхМ Ритца.
<] Полагаем <ро(-'£) = 0. В качестве координатных функций выбираем <pk(x>) — - хк, к G N. Эти функции удовлетворяют граничным
условиям <рд:(О) = </?k(l) = 0. Выберем п = 2. Тогда в соответствии с (33)
У2(х) = Ci(x2 - х) + С2(z3 - Ж2) (35)
и
г/2 (ж) = Ci (2ж - 1) + С2 (Зж2 - 2х).
(36)
§ 6. Вариационное исчисление
461
После подстановки (35) и (36) в (34) и интегрирования получим
Ф(Сь С2) = J(y2(x)) = iief + + |с22 - ic, - ic2.
30 30 7 6 10
Воспользовавшись необходимыми условиями экстремума функции Ф(С1, С2), находим
дФ дСг = —С1 + —С2 - - = 0, 15 30 6
дФ дС2 (37) = —Ci + -С2 - — = 0. 30 7 2 10
Решая систему (37), получим С* = 69/473, = 1/^3. Следова-
тельно, приближенное выражение у^х) для экстремали г/(ж) имеет вид
t/2*W = ~х) + - ж2) = т|д(77а;3 -8ж2-69ж).
В данном случае существует точное решение поставленной задачи:
у(х) = "2~ 1 (е* -е-х) “ х‘
— 1
Сравним полученное методо.м Ритца приближенное решение у2{х) и точное при некоторых значениях аргумента:
X 0,0 0,2 0,4 0,6 0,8 1,0
у(^) 0,0000 -0,0287 -0,0505 -0,0583 -0,0444 0,0000
У2^) 0,0000 -0,0285 -0,0506 -0,0585 -0,0442 0,0000
Сравнение показывает, что точное и приближенное решения совпадают с точностью до 0,0002. >
В задачах 17.456-17.460 методом Ритца найти приближенное решение задачи об экстремуме указанных функционалов:
2
17.456*. J[y(x)] = у* (у'2 + у2 + 2ху) dx, у(0) = у(2) = 0, о
п = 2. 2
Г / „ х2 — 1 \
17.457*. 7[?/(д?)] — / I ху' —'----------у2 — 2т2у I dx,
J \ х J
1
2/(1) = 2/(2) = 0, п = 2.
462
Гл. 17. Методы оптимизации
1
1\у'2 - у2 -2xy)dx, т/(0) = у(1) = 0,
о
п = 2.
D
2 (du\2\ л ц
+ — dxdy, \°yj /
D = {(ж, у))х О, у
. тг . .. Г [ (f Эи\2 (^и\2 п \ 1 1
17.460*. J[u(x, ?/) = / / — ) + — ) -2u] dxdy,
J J \\oxj \dy) /
D X 7
D = {(x, y)\ — 2 x 2, —2 у 2}, 'tz.|r£> = 0, n = 2.
17.461. Найти методом Ритца приближенное решение дифференциального уравнения у" + х2у = х, у(0) = у(1) = 0. Определить уЦх) и Уз(х) и сравнить их значения в точках х = 0,25 и х = 0,5.
Метод Канторовича. Этот метод применяется для приближенного решения вариационной задачи, когда функционал зависит от функции нескольких переменных. Пусть
D
/ du du\
F [х, у, u, —, — ] dxdy, \ ох оу J
(38)
D = {(*> !/)l° :r $ b, ai(:r) О a2(z)}, u\r„ = у).
При применении метода Ритца к функционалу (38) (см. задачи 17.459-17.460) выбирается следующая система координатных функций: <Ро(х, у), <pi(x, у), ..., <Рп(х, у)- Решение ищется в виде
п
Un(x, у) = (р0(х, у) + ^Ck<Pk(x, у), k=l
где Ck — неизвестные постоянные. В методе Канторовича выражение для экстремали берется в виде
п
un{x, у) = Y^Uk(x)<Pk(x, у), k^l
(39)
где ик(х) — неизвестные функции, определяемые таким образом, чтобы функционал (38) достигал экстремального значения. Отыскание решения в виде (39) позволяет расширить класс экстремалей.
§ 6. Вариационное исчисление
463
(а \ 2 / а \ 2 \
+ f -2uj dxdy, (40) дх J \ду J J
После подстановки (39) в (38) и интегрировании полученного выражения по у получается следующий функционал:
ь
J[un(x, ?/)] = У Ф(ж, щ (ж), ..., un(x), и\ (ж), ..., u'n(x)) dx.
a
Функция и*к(х), к = 1, 2, ..., п, должны удовлетворять системе уравнений Эйлера-Лагранжа
d
~ = °’ А: = 1, 2, п,
к dx к
в приближенное решение и*(х, у) вида (39) — заданным граничным условиям на прямых х = а и х = Ь.
Пример 13. Методом Канторовича найти экстремаль функционала
2/)] = УУ
D
где D = {(а?, т/)| — а х а, -Ь у b}, u|rD = 0, п = 1.
Решение будем искать в виде
щ(х, у) = щ(х)(Ь2 - у2).
Граничные условия на прямых у ± b выполняются. После подстановки щ (ж, у) в (40) и интегрирования по у получаем
Я 16 о /2 8,3 9 8,3 \ ,
—i + ~Ь3и2 - -b3ui dx.
10 О О J
—а
Уравнение Эйлера для этого функционала имеет вид
Находим общее решение этого уравнения:
щ (х) = ch v/%5 f + С2 sh v/%5 7 + 0,5.
о 0
Постоянные Ci и C2 определяем из граничных условий, т.е. t«i(—а) =
/ _______ (1 \ — 1
= ui (а) = 0, откуда = 0 и = - (2 ch -/2^5 - ) \ о/
464
Гл. 17. Методы оптимизации
Окончательно получаем следующее приближенное выражение для экстремали функционала (40):
/ ch У2^5 у \
и*г(х, у) = и^х^Ь2 - у2) = 0,5(Ь2 - у2) 1-—£ • >
\ ch 7 / \ о'
В задачах 17.462 и 17.463 найти приближенное решение метода Канторовича. Положить n = 1:
17.462*. J[u(x, т/)] = УУ (и" % + u'yy — 2и) dxdy, где D =
= {(z> 2/)lkl 1> \у\ О, wlr = °-
17.463*. J[u(x, у)] = +и'уу -2xy)dxdy, где D =
D
= {(z, у)|0 X 1, 0 у 1}, u|r = 0.
Метод Галёркина. Этот метод применяется для отыскания приближенных решений как вариационных задач, так и краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных, в частности, уравнений Эйлера-Лагранжа.
Пусть неизвестная функция и(Р) удовлетворяет в некоторой области D следующей краевой задаче:
L(u(P)) =/(Р), Peg, Г(м(Р)) = 0 на 7 (7 — граница G).
Здесь L — некоторый линейный дифференциальный оператор, Г — линейный оператор граничных условий. Приближенное решение краевой задачи (41) ищется в виде суммы
п ип(Р) = ^ск<рк(Р), k=l
где ск — неопределенные коэффициенты, ^рк(Р) — система линейно независимых непрерывно дифференцируемых функций, удовлетворяющих однородным краевым условиям. Обозначим 6f невязку
<5/= L(un(P)) -/(Р).
Коэффициенты ск определяются из условия ортогональности в области D невязки 6f к функциям ipk(P), к — 1, 2, ..., п:
Аци„(Р))-/(Р)Ь(Р)</Р = 0, fc=l,2, (42)
D
§ 6. Вариационное исчисление
465
Так как оператор L линеен, то (42) запишется в каноническом виде, удобном для вычислений ср.
/ Lta(P))^(P)dP= / !(P)Vk(P)dP, А — 1 / J
или в виде
’*• /» /»
/ л(р)^(р)йр= / f(P)?k(P)dP,
4—1 * *<
гдеА(Р) = Ш(Р)).
Замечание. Можно использовать ортогональность невязки к другой линейно независимой системе функций т/>&(Р) выбираемой из удобства вычислений получаемых интегралов (см. решение примера 14).
Пример 14. Найти экстремаль функционала
Лу) =
— 2ху)dx
при граничных условиях 2/(0) = 0, 2/(1) = 0.
<1 Составить уравнение Эйлера F' —~F' J dx у
= 0, имеем
Ly = f(x), т.е. у" =-х.
(43)
Краевые условия остаются прежними: 2/(0) = 0, 2/(1) — 0- Исходная задача сводится к эквивалентной краевой задаче:
у" = -х, 7/(0) = 0, 2/(1) = 0.
Решение будем искать приближенно методом Галёркина, записывая искомую функцию в виде
у(х) = ж(1 — ж)(А + Вх) = Ая:(1 — х) + Рж2(1 — ж), (44)
где (ж) = ж(1 — х) и <£>2 (ж) = ж2(1 — х). Вычисляя у" и подставляя в левую часть уравнения (43), запишем выражение для невязки 6:
6f = -2А + В(2 - 6х) + х.
Вместо условий ортогональности невязки <5/ к функциям (ж) и (ръ^х) коэффициенты А и В определены из условия ортогональности 6f к функ-
466
Гл. 17. Методы оптимизации
циям = 1 и -ф2(х) = х (функции 1/>1(я:) и ^г(^) линейно независимы на [0, 1] с <Pi(x) и ц>2(ху.
1 1 1
А У -2dx + B У (2-6x)dx = - У х dx,
0 0 0
1 1 1
А У —2х dx + В У (2 — 6т) dx = — У т2 dx.
0 0 0
(45)
Вычисляя интегралы в (46), получим систему уравнений
2А + В = 1/2,
А + В = 1/3.
Решая эту систему относительно А и В, получим
А = 1/6, В = 1/6.
Подставив найденные коэффициенты А, В в формулу (44), найдем искомое приближение для экстремали:
ч 1 /-< \ 1 ч х(1 - т2)
У (х) = - х) + вх (! ~ х) = ——•
Заметим, что в данной задаче найденное приближение совпадает с точным решением ут = т(1 — т2)/6. t>
Методом Галёркина найти решение следующих вариационных задач. Ограничиться приближениями искомой экстремали в виде yn(x) = <p(x)(aQ + Оцх + a,2X2 -|--------------h anxn),
где </?(т) выбирается из условия выполнения граничных условий, а n = 1:
2
17.464. J(y) = У (ху' + у'2) dx, р(0) = 0, р(2) = 0. о
1
17.465. J(y) = У (у2 + у'2 - 2у sinх) dx, р(0) = 0, р(1) = 0. о
1
17.466. J(y) = У (у2 + у’2 + 2уех) dx, р(0) = 0, р(1) = 0. о
ОТВЕТЫ И УКАЗАНИЯ
Глава 11
11.1. Линии уровня — параболы у2 — С — х. 11.2. Линии уровня — гиперболы ху = С (при С = 0 — совокупность координатных осей). 11.3. Линии уровня — прямые у = Сх, х 0. 11.4. Поверхности уровня — параллельные плоскости х + у 4- z = С. 11.5. Поверхности уровня — однополостные и двуполостные гиперболоиды х2 4- у2 — — z2 = ±С2 (при С = 0 — конус х2 4- у2 — z2 ~ 0). 11.6. Поверхности уровня — параболоиды вращения х2 4- у2 = z 4- С. 11.7. Гиперповерхности уровня — четырехмерные параллельные плоскости Х\ + х% + + Х3+Х4 = С. 11.8. Гиперповерхности уровня — четырехмерные сферы х2 +ж2 + жз + х4 = ^2- 11’9* Окружности х2 + у2 = С2. 11.10. Гиперболы ху = С (при С = 0 — совокупность координатных осей). 11.11. Параболы у2 = 2(х + С). 11.12. Прямые у — — = —. 11.14. Линии пересече-
I т п
ния гиперболических цилиндров у2 — х2 = Ci с такими же цилиндрами z2 — х2 = С?- 11.15. Окружности, являющиеся линиями пересечения сфер х2 4- у2 4- z2 = С2 с плоскостями х 4- у 4- z = С-2- 11.16. Прямые четырехмерного пространства, перпендикулярные к оси Охз и ее пере-£1 х2 Х4
секающие: Хз = С. 11.17. х = cost, у = suit, z — bt.
ti 12 м
11.18.------= 1, —И —г = 4. 11.19. а) Конические поверхности с
х z х 2yz
вершинами в начале координат, направляющими которых служат заданные замкнутые кривые; б) тороидальные поверхности, образованные окружностями с центрами на прямой х = у = z, лежащими в плоскостях х 4- у 4- z = С, сечениями которых служат заданные замкнутые кривые. И.24. Л = ? + yJ + Zk . 11.25. 11.26. а. 11.27. а(Ь, г) +
|г| + ^2 + 22 |г|2
4-Ь(а, г). 11.28. 2|а|2г —2(а, г)а. 11.31.13/5. 11.32. 4/\/5. 11.33.14/3. 11.34. 1/|г|2. 11.35. 6/х/а2 +52 +с2. 11.36. cos<£ = -4/\/41.
11.37. = 2\/б, n = -^(2i + j + к). 11.38. ^==(2i + 3j - 2к).
468
Ответы и указания
11.39. Р(3, 3,-3). 11.45. ху = С. 11.46. { „ \
\ X — Z = С2-
11.47. / У~С^Х^ п.48. ^/2 + 1. П.49. In 11.50. 0.
[ z = Съ/х. 2
11.51. ^a3. 11.52. ^[(1 + 4тг2)3/2 - 1]. 11.53. 2=. 11.54. 2^2. 15 о v/ 2 У
11.55. Дьга3. П-56. 2Ьга\/2а- 11.57. кяа2. 11.58.
11.59. - 11.60. аг2. 11.61. ^Дт4. 11.62. х/3/360.
(а2 4- с2)'5'2 3
3 8ка3
11.63. 2\/2тг/З. 11.64. 47Г. 11.65. -ла3. 11.66. ——— (\/2 + 1).
4 15
11.67.7Га--^. 11.68. ^у-(3\/3-1). 11.69. ^ка3. 11.70. ^-а\/а(3\/2-
- In (1 + \/2))- П.71. —лаЬ. 11.72. а) 2/3; б) 0,7; в) 0,7; г) 1; д) 1.
11.73. 2тгР2. 11.74.91/60. 11.75. 2тг2a2h. 11.76. ^Д-. <1 z = R-x-y, у 3
х2 + у2 + (R — х — у)2 = R2, или х2 4- ху 4- у2 = R(x + у). Положим
R(l + t) R(t + t2) R
у = tx. lor да имеем: х = --------у — ----------- — R — ----------,
У 1 +1 +t2 ’ У 1 + t + t2 1 4-1 +t2
Rt
z = — --------. Значению t = 0 соответствует точка A(R, 0, 0), значе-
1 4" t + t2
Ниям t = ±oo — точка B(0, R, 0), значению t = — 1 — точка (7(0, 0, R).
Обходу в положительном направлении относительно оси Oz соответствует
обход ВС AB, т.е. изменение t от —oo через —1 и 0 до 4-оо. Далее, J R(t2 4-20 , RClt 4-1) , , R(t2 - 1 ,
dX ~ dy ~ (l + t + t2)2^' dZ ~ (1 4-1 4-12)2 dt‘
R2(l + 2t + 3t2 + 2t3 + t4) _ R2 dt
(1 + t + t2)2 Получаем zdx + xdy + ydz =
(1 4-1 + t2)3
1
2____
1\2 “
2 J
.2
dt
= R2 —
J 3
— OO —
4
2R2 2t+l +o° 2vR2
= —7= arctg----t=- = -----;=-. >
\/3 v/3 .oo Vs
( 7\
11.77. 2тга2. 11.78. 2^/2-- a3. 11.79. 4r3/3. 11.80. -4тг.
\ /
11.81. -7гг4/2. 11.82.-1. 11.83. a3/6. 11.84.4™. 11.85. 4HP3/15.
Ответы и указания
469
11.86. 7гР4/2. П.87. кПрН/Ь. 11.88. ъ&Н/Ь. 11.89. vR2H2l?>. 11.90. тгЯ4/8. 11.91.0. 11.92. тг/?4. 11.93.-Я2Я/З. 11.94.0. 11.95. т + + y + z. 11.96. -2/(t + ?/ + z)5/3. 11.97.14. 11.98.8. 11.99.0. 11.100.0. 11.101.0, 11.103. а5. 11.104. 4тгР2. 11.105. -2тгР3. Указание. За
мкнуть поверхность, добавив основание параболического сегмента, и вычесть соответствующую ему часть потока. 11.106. Если а = axi 4- nyj, то поток вектора а через дугу АВ определится формулой / (a, n) ds =
АВ
ax dx — ау dy. Теорема Гаусса-Остроградского для плоского поля:
fl
(j) axdy — ау dx =
L
---—— \ dxdy (формула Грина). У ка-
Q
зание. Положить в предыдущей формуле (задача 11.106) ах = ау, d5 _ г>4 jj
ау — -ах. 11.108. —. 11.109.—-—. 11.110. x(z2-?/2)i 4- y(x2-z2)j + o Z
+z(y2 - T2)k. 11.111. | k. 11.113. -2?/i + 2Tj — 2(3z + 2?/)k.
\ ox oy J
11.114. 0. 11.115. roti' = 2w. Указание. Скорость v точки P(r), вра
щающейся с угловой скоростью ш вокруг оси, проходящей через начало координат, равна [си, г]. 11.118. а) а2. Указание. Перейти
к параметрической форме, положив у = tx\ петле соответствует изме-3 а2Ъ2 4 3
нение t от 0 до 4-оо. б) -тг—7-. 11.119. ~"R3. 11.120. -ttR4.
8 сл 3 2
R3
11.121. —. 11.122. div (са) = (с, gradw), div (ам) = wdiva4-(a, gradu).
11.123. grad (a, c) = [c, rota] 4- (c, V)a, grad (a, b) = [b, rot a] 4-
4- [a, rotb] 4- (b, V)a 4- (a, V)b. <1 Найдем предварительно [c, rota]. Имеем: [c, rota] = [с, [V, а]] = (a, c)V — (с, V)a = V(a, с) - (с, V)a. Отсюда V(a, с) = [с, rota] 4- (с, V)a, далее, grad (a, b) = V(a, b) 4-4-
4- V(b, а) и используем предыдущий результат. > 11.124. div [а, с] = ~ (с, rota),div[a, b] = (b, rota) —(a, rot Ь). 11.125. rot(cw) = [gradfl, с], rot(afl) = a rota 4- [gradfl, a], rot[a, b] = (b, V)a — (a, V)b 4- adivb — — bdiva. Указание. См. решение примера 5. 11.126. div grad а =
470
Ответы и указания
= V2u =
д2и д2н д2и
дх2 + ду2 dz2 ’
grad div а = V(V, а) =
<9(div а) . дх г
d(diva).
—5----j +
ду
4- -а- к, rot rot а = [V, [V, а]] = V(V, а) - V2a = grad div a - V2a,
С/ Z
V2a= V2oxi + V2ayj + V2o2k. 11.127. 6r = 6(zi 4-т/j 4-zk). 11.128.0,
11.129. 4r = 4(яч 4- уj 4- zk). 11.130. u div grad v 4- 2(gradw, gradv) 4-
4- vdivgrad?/. 11.131. grad div (wc) — (c, V)gradu, graddiv(ua) =
— u grad diva 4- divagrad u + [grad u, rot a] 4-(grad и, V)a+(a, V)grad?z.
11.132. rot rot (uc) = (c, V)gradw — cV2u. 11.133. x3y — xy3 4- C. ________________________________ 2 2 2
11.134. 2 \/cos2 x sin2 у 4- sin2 x cos2 у 4- C. 11.135. xyz-4- —I- C.
у Z X
11.136. —I- —I— 4- С. Указание. За начальную точку А принять xyz
точку (1, 1, 1) или любую другую точку, не лежащую на осях коорди-....... yz xz ху ~ _г _
нат. 11.137. — 4--7----7 4- С. оказание. См. указание к пре-
яг2 у1 zl
дыдущей задаче. 11.138. <| Если бы во всюду непрерывном потенци-
альном поле могли существовать замкнутые векторные линии, то циркуляция по такой линии не могла бы быть равной нулю, так как произведение (a, dr) вдоль всей линии сохраняло бы постоянный знак, и поэтому (a, dr) 0. О 11.139. Особая точка 0(0, 0), циклическая постоянная равна 2тг. 11.140. Указание. Взять два произвольных замкнутых контура, обходящих данную особую точку: АМА и BNB. Соединить точки М и N отрезком прямой и к сложному контуру AMNBNМА применить формулу Грина. 11.141. Указание. Использовать при определении потенциала пути, обходящие по нскольку раз и в различных направлениях особые точки. 11.147. Указание. Применить теорему Гаусса-Остроградского и учесть, что на боковой поверхности трубки (а, п) = 0. 11.149. Указание. Применить тео-
рему Гаусса-Остроградского и учесть, что для гармонических функций V2u = 0. 11.150. Нет. 11.151. Нет. 11.152. Да. 11.153. Только при А 4- С — 0. 11.154. Только если A + C = B + D = 0. 11.155. Да. 11.156. Только при оц 4-fl22 +®зз = 0. 11.157. Только если ощ 4-«122 4-4" а133 — 0112 + O222 + 0233 — Оцз 4" 0223 4- яззз — 0- 11.158. Линии х У — Уо Z - Zo х - Xq у Z - z0
я;: - = —-— = - Q- линии у: —-— = - = —-—; линии я: - ж0 у - уо z
z: —-— = —-— = -. 11.159. Линии г: р = <£>0, z - z0 (лучи,
Ответы и указания
471
исходящие из точек оси Ог, лежащие в горизонтальных плоскостях); линии <£>: г = го, z = zq (окружности с центрами на оси Oz радиуса ГО) лежащие в плоскостях z = z0); линии z: г = го, р = ро
(прямые, параллельные оси Oz). 11.160. Линии г: 6 — 6q, = ро
(лучи, исходящие из начала координат); линии 0: г = tq, р — ро
(полуокружности радиуса г0 с центром в начале координат, лежащие в полуплоскостях р — ро, проходящих через ось Oz, т.е. мериди
аны). Линии р: г = го, 0 = Oq (окружности радиуса rosin0o с центром на оси Oz, лежащие в горизонтальных плоскостях, т.е. параллели).
11.161. Lx — Ly = Lz = 1. 11.162. Lr = Lz = 1, = r. 11.163. Lr = 1,
Lg = r, — rsinfl. 11.164. dsx = dx, dsy = dy, dsz = dz-, dax =
= dydz, day = dxdz, daz = dxdy, dv — dxdydz. 11.165. dsr = dr,
ds^ = г dp, dsz = dz-, dar = rdpdz, da^ = drdz, daz = г dr dp-, dv = rdrdpdz. 11.166. dsr = dr, dsg = rdO, ds^ = rs'mOdp-, dar = = r2 sin 6 d6 dp, dag = r sin 6 dr dp, da^ = r dr d0-, dv = r2 sin 0 dr dO dp.
du 1 du du
11.167. _ er 4 ~ e^-\~ ez. dr r op dz
11.168. i r
Г dr) 1 d2u d2u dr + r dp2 Г dz2
da^X
- —er + dz ) 1 du
11.171. —er 4- +
г dO
• adu\ smedo) +
11.170.
\r dp
.. . du
ez-
dr d de
11.169. r \ dr dp dz J
/ dar dazX 1 / dlya^) dar
\ dz dr / r \ dr dp
1 du 1 f d f 2du
+ 11.172. -....sinfl— r2—-
rsmOdp r2smU\ dr \ dr
1 d2u\ 1 ( . d 2 ч d ( . da^X
+ • 11.173. - -Sin0—(r2ar) + r—(a0Sin0) +r-^- ).
sin 0 dp2 j r2 sin 0 \ dr dO dp J
_ 1 (d da&\ 1/1 dar d A
11.174. —z—z er + - -----e0 +
rsmO dp J r \sin# dp dr )
+ - [ ^-(rag) ~ | e^. 11.176. a) diver = -, roter = 0; 6) dive^ = 0,
r \ dr dv J r
e . 2
rote^, = —; в) divez = 0, rotez = 0. 11.177. a) diver = -, roter = 0; r r
o) dive# — ----, rote# = —; в) dive^ — 0, rote^, = --------er —
r r r
---eg. 11.178. a) u = Ci Inr 4- C?-, 6) u — C\p 4- C-y, в) u = C\z 4- Съ-
472
Ответы и указания
11.179. а) и = — 4- С2; б) и - Су Intg 4- С2; в) и = Сцр 4- С2.
г 2
11.180. и = г2 sin 2ip cos 20, grad и — 2r ^sin 2<р cos 20er — sin 2ip sin 2#e# 4-
cos2<z>cos2# i . г. г. 9Л> -г.
4-------------е- , V2u = 2 sm 2<р(1 — 2 ctg2 0). 11.181. и = rz sm 2<f> 4-
sin# /
4- r cos 2ip, gradu = (z sin 2<p 4- cos2<^)er 4- 2(zcos2(,s> — sin 299)0^ 4-3?/
4- rsin2<^e,, V2u — —11.182. a = sintfe^, diva = 0, rota =
= - (2cos#er — sinfleo). 11.183. a = rz(e.r — ez), diva = 2z — r.
r
rota = (r + z)e,p. 11.184. grad?/ = f'(r)er = f'(F)-, V2?/ = /”(r) +
4- 11.185. gradu = /'(r)er = /'(r)-, V2u = f"(r) 4-
r r r
11.186. gradu = ди 16F ^9 + е<?’ V и = г д0 d2F 2dF_ dr2 r dr 1 d2F ctg# dF + r2 d0
дг r2 d02
11.187. grad?/ = dF с дг dF г + -д-ег, V2u = dz d2F IdF dr2 r dr d2F + dz2'
Глава 12
1 23
12.1. -. 12.2. —.
4 45
12.3. 1. 12.4. 11
3 6e - e2 - 1
’ ’ 2 (3e - 1)(3 - e)
У к a-
e n 4* en
зание. Использовать формулу Эйлера eosin = -------------. 12.6. 1 4- i.
12.19. Расходится. 12.20. Сходится. 12.21. Сходится. 12.22. Сходится.
12.23. Расходится. 12.24. Расходится. 12.25. Сходится. 12.26. Сходится.
12.27. Расходится. 12.28. Сходится. 12.29. Сходится. 12.30. Сходится.
12.31. Сходится. 12.32. Расходится. 12.33. Сходится. 12.34. Сходится.
12.35. Расходится. 12.36. Сходится. 12.37. Сходится. 12.38. Сходится
абсолютно. 12.39. Сходится абсолютно. 12.40. Сходится. 12.41. Расхо
дится. 12.42. Расходится. 12.43. Сходится. 12.44. Сходится. 12.45. Сходится. 12.46. Сходится. 12.47. Сходится абсолютно. 12.48. Сходится абсолютно. 12.49. Сходится. 12.50. Расходится. 12.51. Расходится.
Ответы и указания
473
12.52. Сходится. 12.53. Сходится. 12.54. Сходится. 12.55. Сходится.
12.56. Сходится. 12.57. Расходится. 12.58. Сходится. 12.59. Сходится.
12.60. Сходится. 12.61. Сходится. 12.62. Сходится. 12.63. Сходится.
12.64. Сходится. 12.65. Сходится. 12.66. Расходится. 12.67. Сходится.
12.68. Сходится. 12.69. Сходится. 12.70. Расходится. 12.71. Расходится. 12.72. Расходится. Указание. un+\/un > 1. 12.73. Сходится. 12.74. Сходится. 12.75. Расходится. 12.76. Сходится. 12.77. Расходится. 12.78. Расходится. 12.79. Сходится. 12.80. Сходится. 12.81. Схо-
дится. 12.82. Расходится. 12.83. Расходится. 12.84. Сходится абсолютно. 12.85. Расходится. 12.86. Сходится абсолютно. 12.87. Если р > 1, то ряд сходится при всех а, а если р < 1, то расходится. Если р = 1, то ряд сходится при a > 1 и расходится при a 1. 12.88. Если р > 1, то ряд сходится при любых а и /3, а если р < 1, то расходится. Если р = 1, то ряд сходится при a > 1 и любых /3 и расходится при a < 1. Если же р = a = 1, то ряд сходится при 0 > 1 и расходится при (3 1. 12.90. Сходится условно. 12.91. Сходится аб-
солютно. 12.92. Расходится. 12.93. Сходится абсолютно. 12.94. Расходится. 12.95. Сходится условно. 12.96. Сходится абсолютно. 12.97. Сходится абсолютно. 12.98. Сходится абсолютно при a > 1, условно — при 0 < a 1 и расходится при а 0. 12.99. Абсолютно сходится. 12.100. Условно сходится. 12.101. Абсолютно сходится при всех a Е К. 12.102. Расходится. 12.103. Сходится условно. 12.104. Сходится абсолютно. 12.105. Сходится условно. Указание. Рассмотреть частичные суммы с номерами 8п, в которых сгруппировать члены с номерами 8k +1 и 8к 4- 5, 8к + 2 и 8к 4- 6, 8к 4- 3 и 8к 4- 7. Убедиться в существовании предела lim Ssn. Далее, как и при доказательстве признака Лейбница, 71—>ОО
1 7ГТ1
воспользоваться соотношением lim — sin — = 0. 12.106. Сходится П-+СО п 4
условно. 12.107. Расходится. 12.108. Абсолютно сходится. 12.109. Расходится. 12.110. Расходится. Указание. Рассмотреть частичные суммы с четными номерами. 12.111. Сходится условно. 12.112. Сходится абсолютно. 12.113. Расходится. 12.114. Указание. Воспользоваться
неравенством |а • Ь\
$ |(|а|1 2 +|6|2).
12.115. Сходится.
<1 Оценим сп.
474
Ответы и указания
Имеем
У —
/с=1
1
1
^.2 . 2п~^+1
1 п\ 2
2 7
Полученные слагаемые являются членами сходящихся рядов Ai УУ ~7= „_1 v2n
1 2n+i
к=1
Ai Аъ
2i п2’
к
к2(п — к 4- 1)
1
12.116. Сходится. Указание. Для оценки сп = у к=1
воспользоваться разложением дроби на простейшие -rz-, , —
к2(п — к + 1) 1 1 /1 1 \
= 7—ГТПл + 7—Г~Й2 Т + —П------------Г и показать, что числа Ьп =
(п + l)kz (п + 1)2 п + 1 —к/
1 п Л 1
= (—l)n+1-----j £2 монотонно убывают по абсолютной величине.
к=1
12.117. Расходится. Указание. Воспользоваться разложением дроби из . 1 А 1
предыдущей задачи на простейшие и оценить члены ап — --------- > —z
п + 1 z—' kz fc=i
А< 1 1
снизу. 12.118. Расходится. Указание. сп = УУ —------------—— > —
к ' \п к "К 1J п
при п 2. 12.124. (О, +оо); абсолютно сходится при х G (1, +оо). 12.125. IR; сходимость всюду абсолютная. 12.126. Расходится во всех точках. 12.127. W\{—3}; сходимость всюду абсолютная. 12.128. (—оо, —1); сходимость всюду абсолютная. 12.129. (—1, —1/2] U (1/2, 1); сходится абсолютно при х G (—1, —1/2) U (1/2, 1). 12.130. [0, +оо) U {&7г|Аг = = —1, —2, ...}; сходимость всюду абсолютная. 12.131. (-2, 2); сходимость всюду абсолютная. 12.132. (0, 4-оо); сходимость всюду абсолютная. 12.133. [1/е, е); сходится абсолютно при х € (1/е, е). 12.134. |г-2| > 1. 12.135. |z+l| > 1. 12.136. |г-3г| > \/2. 12.137. Полуплоскость Rez > 0. 12.138. {z| — тг/4 < argz < тг/4 и Зя/4 < argz <
Ответы и указания
475
< 5тг/4}. 12.139. Re г < 0. 12.140. Re г > 1. Указание. Сравнить выражение |(—с членом п~р ряда Дирихле. 12.141. Im г > 0. Указание. Воспользоваться тем, что дробно-линейная функция w = i0 ? - Zq
= e ----— отображает верхнюю полуплоскость во внутренность еди-
z - ZQ
ничного круга. 12.142. |z| > 1. Указание. При |«| > 1 функция w = ег0 ——отображает внешность единичного круга (|г| > 1) на внутренность (|w| < 1). 12.143. |д/(1 — д)| < 1, т.е. Re г < 1/2. Указание. См. задачу 11.190. 12.144. Сходится при х G (0, +оо), равномерно сходится при х G [а, 4-оо) для любого a > 0. 12.145. Сходится при х 6 (-оо, —3) U [—1, +оо), равномерно сходится при х 6 € (—оо, —3 — J] U [-1, +оо) для любого 6 > 0. 12.146. Равномерно сходится на всей оси. 12.147. Сходится на всей оси, кроме точек х =
= — 1, —2, ... Сходится равномерно на множестве, получающемся из оси после удаления интервалов (—<5*. — к, -к 4- 8'k), к G N, где 8к и 8'к сколь угодно малы. 12.148. Re г 0; сходимость всюду равномерная. 12.149. — 1| 1; сходимость всюду равномерная. 12.150. Сходится
при Бег > 1, равномерно сходится при Re г a > 1. 12.151. Сходится вне круга |г + 2| > 1, равномерно сходится вне любого круга |д + 2| оо 2
> a > 1. 12.152. Указание. Вычислить Rn(x) = > ----—г
' И + x2\k
k=n+l v 7
и показать, что lim Rn(x) = 1 / Rn(0) = 0. 12.155. Ряд сходится в £—>0
области, состоящей из внутренности единичного круга |д| < 1, точки z — 1 и внешности единичного круга |д| дится в объединении замкнутого круга |г| ности круга
[ 1/2 = 1 -1/2
О
> 1; ряд равномерно схо-1 — 7 и замкнутой внеш-\z\ 1 + 8 для любых 7, 8 > 0. Сумма ряда S(z) =
|z| < 1, 12.159. У к азание. Воспользоваться утвер-z -- 1.
при при
ждением задачи 12.158. 12.162. Если степенной ряд (1) сходится в точке z = z\ 7^ zq, то он абсолютно сходится в круге \z - д0| < |д1 — До| и равномерно сходится в любом замкнутом круге \z — z0| С г < 1-1 ~ го|- Если ряд (1) расходится в точке z = zq, то он расходится и вне круга \z — до| > >|д2-г0|. 12.163. Указани е. Для доказательства утверждений а) и б) воспользоваться теоремой Абеля и теоремой Вейерштрасса, а для доказа-
476
Ответы и указания
тельства утверждения в) — теоремой Абеля, утверждением задачи 12.158 ________________ / I I ______ у---
и учесть, что lim \ п = lim у|сп|. 12.164. Указание. Восполь-п-»оо V п 4* 1 п-Юо
зоваться утверждением б) задачи 12.163. 12.165. Сходится абсолютно и равномерно в области \z — 1| 2. 12.166. Сходится абсолютно и
равномерно в области \z 4- 1| 2. 12.167. Абсолютно сходится, если
\z + 2| < 1: равномерно сходится, если \z 4- 2| С г < 1. В точках х = -3 и х = — 1 сходится условно. На отрезке — 3 х — 1 сходится равно-
мерно. 12.168. Абсолютно сходится в области \z — 4| < 1/2; равномерно сходится в области \z — 4| г < 1/2. В точке х = 9/12 сходится условно, в точке 7/2 расходится. На любом отрезке 7/2 < г С х 9/2 сходится равномерно. 12.169. Сходится абсолютно в области |д — 2| 1/\/2; равно-
мерно сходится в области |д—2| г < 1/х/2- В точках 2±-/= расходится. 12.170. Сходится абсолютно в области \z — 3| < \/3; равномерно сходится в области \z — 3| г < \/3. В точках х = 3 ± \/3 сходится условно, и на отрезке 3 — y/З х 34-\/3— равномерно. 12.171. Сходится абсолютно в области |д| < 3, равномерно сходится в области |г| г < 3, в точке
х = — 3 сходится условно, а в точке х = 3 расходится. 12.172. Сходится
абсолютно в области |д| < 1, сходится равномерно в области \z\ г < 1,
в точках х = ±1 расходится. 12.173. Сходится абсолютно в области |д 4- 1| < х/2/3, сходится равномерно в области |z 4- 1| г < х/2/3, схо-
\/2 у/Ъ
дится условно в точке х — — 1 4- — и расходится в точке х = — 1 4- .
12.174. Сходится абсолютно в области \z\ < 4, сходится равномерно в
области |д| г < 4, в точках х = ±4 расходится. 12.175. Сходится абсолютно в области |д| < 1. Сходится равномерно в области \z\ г < 1; расходится на окружности |д| = 1. 12.176. Сходится абсолютно в обла
сти |д| < 1; сходится равномерно в области |д| г < 1; расходится на
окружности |д| = 1. 12.177. Сходится абсолютно во всей плоскости, рав
номерно — в любой ограниченной области. 12.178. Сходится абсолютно в области \z — 1| < 8; сходится равномерно в области \z — 1| г < 8; в точках х = — 7 и х = 9 расходится. 12.179. Расходится во всех точках, кроме точки zq = г. 12.180. Сходится абсолютно в области |г — 3| < \/3, сходится равномерно в области |г — 3| г < х/З, в точках х = 3±\/3 рас
ходится. 12.181. Сходится абсолютно во всей плоскости, равномерно —
Ответы и указания
477
в любой ограниченной области. 12.182. Сходится абсолютно в области \z — 1| < 1; сходится равномерно в области |г— 1| г < 1; на окружности |z — 1| = 1 расходится. 12.183. Сходится абсолютно в области |г — 3| < 4; сходится равномерно в области |г - 3| г < 4; в точке х = 7 сходится условно, в точке х = — 1 расходится. На любом отрезке —1</^а;^7 сходится равномерно. 12.184. Сходится абсолютно во всей плоскости, равномерно сходится в любой ограниченной области. 12.185. Сходится абсолютно в области |г| < 2; сходится равномерно в области \z\ г < 2. В точке х — — 2 расходится, в точке х = 2 сходится условно. На любом отрезке — 2 < I х 2 сходится равномерно. 12.186. Сходится абсолютно и равномерно в области |г| 2. 12.187. Сходится абсолютно в
области \z — 2г| < 2, сходится равномерно в области |г - 2г | г < 2. 12.188. Сходится абсолютно во всей плоскости, равномерно —- в любой ограниченной области. 12.189. Сходится абсолютно и равномерно в области \z + г| -/=. 12.190. Сходится абсолютно во всей плоскости, равномерно — в любой ограниченной области. 12.191. Сходится абсолютно в области \z — 1| < 9/4; сходится равномерно в области \z — 1| г < 9/4; в точках х = —5/4 и х = 13/4 расходится. 12.192. Сходится абсолютно в области |г| < е; сходится равномерно в области |г| г < е; в точках х = ±е расходится. 12.193. Сходится абсолютно и равномерно в области \z - 3| < 1/\/2. 12.194. Сходится абсолютно и равномерно в области \z 4- 3| 1. 12.195. Сходится абсолютно и равномерно в области \z — 3|
<С л/2. 12.196. Сходится абсолютно в области \z 4- 3| < 1, сходится равномерно в области \z 4- 3| г < 1; в точках х = — 2 и х = — 4 расходится. 12.197. Сходится абсолютно в области |г| < 1; сходится равномерно в области |г| г < 1; расходится на окружности |г| = 1. 12.198. Сходится только в точке z = 5. 12.199. Сходится абсолютно и равномерно в области |г| 1. 12.200. Сходится абсолютно в области |г| < 1/2;
сходится равномерно в области |г| г < 1/2; расходится на окружности \z\ = 1/2. 12.201. Сходится абсолютно и равномерно в области |г-2| 1. 12.202. Сходится абсолютно и равномерно в области |z+ 1| С
ОО /Q оо
1. 12.207. V -=- (z In 2f, |z| < +оо. 12.208. V Н1) f ™ Т1 • £ ™
п=О п=0
zn п\
478
Ответы и указания
1 ~ (2z)2n
Н < +оо. 12.209. 1 + - > kl < +оо- 12.210. z +
' 2 (2тг)!
п= I ' 7
2 з 16 5 . | 7Г
+ — zy + —z + ..., Ы < —. Указание. Радиус сходимости этого 3! 5! 2
ряда определяется путем применения следствия из теоремы Тейлора.
12.211. 1 + 1г2 + Аг-1 + ..., |-| < I 12.212. z- ~z' + + ...,
тт ’ ’ 2 4
\z\ < 12.213. 1 + z - -г3 - -г4 + ..., \z\ < +оо. 12.214. 1 - г2 +
21
Jin
+(-1)"у+-
12.216. 22 Ь1)’1
71=0
~| CXJ
+оо. 12.215. -£(-1)
(2г)2п
^п^тг-Н
Зтг+1 ’
ki < г
12.219. -
3
12.218. 3 - £
Л _ 1-3 4
\ 18 + 2-18^
12.220. V 7-l±±z 9/1+2
71=0
71 = 0
2-5.8...(Зп-4) п_2 г ’ |г .'1~\/_1уЛ-3...(2»-1)г2,.
3-г + 1
(г - 2)2 “
|г| < I-
тг! 18п
Указание.
/1=0
^2n-F 1 4п+Г ’
12.222. £(-1Г------------
п~ О
оо
< +оо. 12.224. 22(- 1)п(2тг + 2)
71 = 0 nln-f-l
х 7Х-----7V7Z2n+1, Ы < +оо. 12.
Z2n
|г| < +оо. 12.225. У (-1)
i; при
|г| < +оо. 12.223. 22
71 = 0
22п+1
71 = 0
п 71=1
| 00 71
х = - сходится условно. 12.227. In 2 + 22 (-1)'г+1(1 + 2~п) — , \z\ < 1;
2 п=1 п
(2п - 1)!! г2п+1 при х = 1 сходится условно. 12.228. z + > (— 1) --------------—--------.
k 7 2п • тг! 2п + 1 71=1
00 г2п+1
Ы < 1: при z ~ ±1 абсолютно сходится. 12.229. (—1Уг-------.
2п + 1
71=0
(2тг - 1)!! 22n+1 |г| < 1; при х = ±1 сходится условно. 12.230. z + > -------------------,
2птг! 2п + Г
Ответы и указания
479
\z\ < Г, при х = ±1 абсолютно сходится. 12.231. (—1)п---
1 1 ’ 2пп!(2пН
п=0
оо 4п+2
М < +00. 12.232. £(-l)"2(2J1)!(2n + 1), 14 < +00.
00 о 2n —1
12.233. £(-!)"+'|z|<+oo. Указание. 2C0S7Sln* =
= . 12.234. f;(-l)n+1(- ~£У"~-г, И < +00. Указа-
' ' П=1 ' '
2 sin 2 — 1 + COS 2 /1 — COS 2 \ . _ _____
ние. ------------- = (--------) . 12.235. —78 + 59(2 + 4) —
2J \ 2 /
ОО
-14(2 + 4)2 + (2 + 4)3. 12.236. ^2(-l)n+1(2-2)n, \z - 2| < 1.
п=0
12-237- Е j-~з.г+‘ ’ |2^3!1 < |1-3i| = 12-238- -Е
n=0 V ' k=0
12.242. е“3
п=0
+ (z- l)2n+1),
|z-3| < 2. 12.239. 52 (2~n~‘ - 3“n~‘)(z + 4)n, |z+4| < 2. 12.240.1 + n=0
+ - 1) + Е(-1)п+1^^^(г - l)n, ]z — 1| < 1.
n=2
'n(z — ‘2}n~1 1 /i\'
,12.241. £2 (-l)n+1-, |z —2| < 2. Указание. — = - .
П\2п 00 1 '_________________________________/ , |z| < +oo. 12.243. e 52 (-l)n-((z-l)2n +
П n=0
oo (' A
, |z| < +00. 12.244. 52 (-1)" -7П|(* + 2)4" +
T \ I zn) 1
n=0 \ v ’
+ (£ир(г + 2>4Н - < +~- 12.245.
4 ' / n=l
8 / 5 \
|z— 11 < -. Указание. In (5г + 3) = In 8 + In ( 1 + - (z — 1) ). 5 \ 8 /
(z + 3)2n 2
12.246. In 3 +£ (-l)n+144b lz + 3l < 2- I2-247-14 < 15
4~. 12.249. |z - 3| < 1; -1П г~ при z / 3, z2 z - 3
О при z = 3. 12.250. |z| < |a|; T. 12.251. |z| < 1; --9-?.
a2 + z2 (1 + z2)2
п • Зп
12.248. |2 + 1| < 1;
480
Ответы и указания
12.253. Указание. Представив f(z) в виде ряда по степеням (г - а), т. е. ОО
в виде /(г) = ^cn(z — а)п, из непрерывности /(г) в точке z = а убе-тг—О оо
диться в том, что со = 0. Это означает, что f(z) — (z—a) У^сп(г — a)n-1 = n=l
= (z — a)fi(z), где fi(z) — аналитическая в круге |z — а| < R функция и /i(2fc) = 0> & = 1) 2, ... Отсюда вывести заключение, что cj = 0 и т.д. 12.254. Нет. 12.255. f(z) = z/(z + 2). 12.256. /(г) = г2. 12.257. g(z) = /(г) — 1/(2 — z) в общей части кругов |z| < 2 и \z - г| < < \/5. 12.258. g(z) = f(z) = ln(l+z) в общей части кругов |г| < 1 и \z — 1 — 2г| < 2\/2. 12.259. 10 000 при х — 1 или 10 при х = —0,5.
1 / Д’ \ 4
12.260. Два члена, предельная абсолютная погрешность в < — —j = = 0,0000386 < 0,0001. 12.261. 0,0002. 12.262. |т| < 0,9067. 12.263. 0,002. 12.264. 1,6487. 12.265. 0,3679. 12.266. 0,5878. 12.267. 0,2094.
12.268. 0,5403. 12.269. 0,8269. Указание. Учитывая, что 1000 =
= 318-3,1415926+1,5707963 — 0,5971963, приводим аргумент к величине 0,5971963 € [0, 7г/4] и находим sin 1000 = sin (1,5707963 — 0,5971963) = = cosO,5971963. 12.270. 8,0411. Указание. ^520 = (512 + 8)1/3 =
/ i\i/3 ______ / iX1/2
= 8 (1 + 64/ ’ 12-271* 3’8730- х/15 = хЛб77! = 4 (1 - — j
/ 9 \ 1/4
12.272.5,1437. Указание. </700 = (625 + 75)1/4 = 5 I 1 + — .
у 25/
1 + т
12.273. 0,6931. Указание. Использовать разложение In--------------- —
1 — х
оо 2ti~I-1 *|
= 2Г|---------прит=-. 12.274.0,5236. 12.275.0,9385. 12.276.1,1752.
2п + 1 3
п—О
оо 2п
12.277.1,1276. 12.289. V (-1)п+1^-.
' 2п2
°° т2п+1
12.292. J2(-l)n п—0
(2п + 1)!!т3п+1 2п п!(3п + 1)
12.294. ]Г(-1)П п=0
ж2п+1
(2п + 1)(2п + 1)!
12.291. У(-1)71—4т;---------с-
7 (2п)!(4н + 1)
°° rr2fc+2
12.295. 0,2800. 12.296. 0,1991.
Ответы и указания
481
71=1 '
4 oo /
_>)+E p.
12.297. 0,4802. 12.298. 0,6225. 12.299. 0,7714. 12.300. 0,9461.
12.308. Указание.
______________1______________
(а + k)(a + к + 1)(а + к + 2)
_ 1 /_________1____________________1 _______А
2 \(а + к)(а + к + 1) (а + к + 1)(а + к + 2)) 12.309. Указание. См. задачу 12.308. 12.310. Указание. Разложение в степенной ряд функции In(1 + х) при х = 1. 12.311. Указание. Разложение в степенной ряд функции arctga; при х = 1. 12.312. In 2.
1 \/3
12.313. /0(2). 12.314. е — 1. 12.315.-In2. 12.316. sin 1. 12.317. cos—.
2 3
12.318.е2. 12.319.1,0767. Указание. = С(2) - ((4) + <(6) -
71—1 ОО - сю
— £(8)+У — о—тг. 12.320.4,3226. Указание. У sin2 — = 7г2((2) —
П=1
7Г2 1 7Г4 \
- —+-------г • 12.321. 0,5071. Указание.
п2 3 п4J
ОО 1 ОО 1
У-г—-= С(3) - 2<(6)+4V 12.322.0,0939. Указа-
п3 + 2 п6(п3 4-2)
71=1 71=1
00 1 1 / 1 \ Q / 1 \ Q
»"' L = 5 (1 - 5) «2’-й 1 - ;) <(3)+шх
71= 1
/ I \ оу 00 1
х р-зЛ4)- 12.323. 0,1249. Указа-
00 1 1 2 / 1 \ 4 / 1 \
ние. У (-1)п+1~-------- = ~1п2 — - 1- - С(2) + — I 1 - - С(3) -
Зп + 2 3 9\ 2/ v' 27 \ 4/ v 7
- — fl - Ш) + — У (-l)n+1-------------------.
81 V 81^-1 J n4(3n + 2)
l-2-5-6...(4n + l)(4n + 2) 4n
(4,7)! X +
2-3.6.7...(4n + 2)(4,i + 3) \
+ (4n + l)!
12.326. у(х) = (1'4 ',7,n ,(3P,+ 1))2(3n + 4)x3n+2, x g R.
^0 <3n + 2>!
x2 5x3 3x4
12.327. y(x) = l + 2x - — - -------- + ... 12.328. y(x) = 1 + x -
О x
00
12.325. j/M = E
71 = 0
482
Ответы и указания
х^ х^ х2
- v ~ ТГ + 77 + • 12-329- = 1 + 57 +
3 6 45 2!
00 ZlAm+l „
12.330. у(х) = У —-х2т = 1-е~х /2> х
2т • т!
х3 х5 5ж6
— — — Н“ ...
3! 5! 6!
е К. 12.331. у(х) =
т=1 4 ' тп=1 ' '
х х2т+1, х е Л 12.333. у(х) = Ci + С2 . Указание. Общее х х
решение должно содержать две произвольные постоянные, поэтому из
равенств т(г + 1)ао = 0 и (г + l)(r + 2)ai = 0 выбираем г = —1, тогда о,0 0 и «1 / 0. 12.334. у(х) = Ci cos у/х + С2 sin у/х. 12.337. Ц/2 (ж) =
Г~2~ [~2~
= \ — sin ж, Z_1/2(x) = \ —cos ж. Указание. Использовать равен-
V 7ГЖ ' V т^х
ство Г ( п + | ЛА- 12.338. у(х) = Climax) + С21_и(ах),
\ 2/ 2П'1’1
если v — не целое число и у{х) = Ciln(ax) + С2^п(ат), если v = п —
целое число. 12.339. у(х) = C\Iq(2x) + C2Nq(2x). 12.340. у(х) =
= Cili/3(2x} + C2Z_1/3(2x). 12.341. у(х) = Cil2(xj3) + C2I2 (W3). z-2
12.342. у(х) = Cih/^x) + C2Z_1/5(3x). 12.343. \z - 2| > 1; ——. Z О
2г
12.344. |z + г| > 2; ---—. 12.345. 0 < Ы < +oo; zV/2. 12.346. 1 <
(z - г)2
< \z-i\ < +oo; 1/z2. 12.347.1/3 < \z + г| < yfi. 12.348. 2 < |z — 2г| < 3.
12.349. |z| > 1/e. 12.350. |z + 1| > 1/4. 12.351. 1/2 < |z| < x/3.
1 ОО ОО 1
12-352- ГГ7-Х - D", 0 < |z-l| < 1; £ (~1)"+17—TV-+1' n=O n=l ' '
1 < |z - 1| < +oc. 12.353. 52 -% 1г1 > L n=2 zn
ти замену z = 1/r} и разложить по степеням
Указание. Произвес-
Т]. 12.354. g, 1 -
1 5(z - 2)
00 Kfc
у (-1/------------
} (z-2)*+2’
1 1 X I Q \
I* - 2I > 5- 12-355’ -5(^3) - й £ (V . ° < I- + 31 < 5;
fc=0 ' '
°° ck 00 Ak 1
V 7-------1г + 31 > 5- 12-356. - У -у—|z| > 2. 12.357.--------------------------- -
/уУ (z + 3)fc+2 1 1 z2k+2 11 * * V z - 1
л—О А,—О
Ответы и указания
483
ОО 1 оо «
" 2 52 - ’ о < 1г-11 < 1; г _ i +2 52 <z _ nfc+2 ’ 1г _ 11 >
fc=O k=0 ' 7
О оо
> 1. 12.358. —- + 2 52 (“(* - 2)2fc + (-г - 2)2fc+1), 0 < \z - 2| < 1;
1 /1 1 \ °° к
---9 + 2 У (7--5ш~7------ТдаГ )- 1г“2! > !• 12.359. г2 ^2-^, z — 2 z—' \ (z — 2)2fc (z — 2)2fc+1 j z*
k-0 xv ' v ' ' k=l
1 < |z| < +oo. Указание. После замены z = 1/т] воспользоваться ра-
/ 1 V 1 1 1
венством I I — ---Т- 12.360. -------------- - ------
\1-ту/ (1 — ту)2 (-г + 1)2 (-г + 1)3
z / -1. 12.361. z - 1 + V *—т, 1 < |г| < +оо. 12.362. —------- -
zk 1 1 2(г-г)
12.364.
i 1 kik{z — i)k 1 4(z - i)2 ~ 8 2*
00
12-3в3- ЕЫт- М > L к—О z
- oo
0<|z-i|<2;--^(* + 2)(-i)* 2 k=0
z i ( i у
ние. —t---— = — ~ I ---
(г2 -I- I)2 2 \z2 + 1/
2 A:
------ГГ7Т) 2 < |г-г| < +oo. У к а за-(г — z)fc+1
Для второго разложения воспользо-
ваться заменой
г-7 = W 12.365.
Л=О
1 < |г| < +оо.
Указание, -г-^—— (z2 + l)2
< |z| < +оо. 12.367. У (-1)n75"V, 0 < |г| < +оо. 12.368. J2 (-1)” х п=0 п=0
1 °0 1
X --------тг?---Го-тг, о < Iz - 21 < +оо. 12.369. У —--------0 <
(2тг + 1)!(г — 2)2n+1 n\zn~2
ОО J
< Ы < + оо. 12.370. У —:------т, 0 < |г| < +оо.
1 n\zn~2 1
п=0
1237‘+ г)"(гп)!((. -2),и + (2п+1)
.2,2. £ <-№ - 1)‘(1 - АЛ - ,| < t £ ИИ + к=0 ' ' к=0
484
Ответы и указания
00 /nfc-i «22, (—п*
+ Z briF’1 < |г -11 < 2: s +2fe)' k-H >2.
fc=l ' ' k=0 v 7
1 oo
12.373.
6 fc=O
- 2г) (4 - i)‘+1
3 + 2г \ , (2 + i)k+l )^Z~l
(3 + 2г)£ fc=i
(2 - г)*"1 (z — г)*
OO
+ (3-2i)£
fc=O
(-l)fc(z — z)fc (4 - z)fc+1
|z - г| < д/5;
\/5 < \z - i| <
1
6
1 1
< i^((3 + 2i)(2-i)'‘-1 + (-l)‘-1(3-2i)(4-i)‘-1)7—
6 z—' (z — г
t—1 v
1 / I \
\z-i\ < yi7. 12.374. -£(-l)‘2‘+1 11 - ^1, |z| < 1;
° fc=O ' '
1 ( 00 ( nfc °° ( ПМН-l \ 1 00
ЕШ-ЕЦ^- -ки<2;
<_J \ Az * / О Az
\fc=O fc=O / fc=O
1 f *| OO ~| 00 -,2k \
> 2. 12.375. - z2k f1 “ 4E+U ’ izl < 1; -3 ( z2(Jt+i) + ZL 4H-1 ) ’
fc=O ' ' \fc=O k=Q /
1 A k 1 1 1 К 1
к И <2; з 52 z2(fc+i) > lzl>2-12-376- _^+^2 "6z3+’"’ 1<lzl<+o°-fc=O /Г / \
(----^п-Н И B0C'
h-2o|=p
пользоваться ограниченностью f(z), вытекающей из существования предела lim f(z). 12.378. Указание. Использовать следующее утвер-z—>Zo
ждение: если g(z) = (z — zo)m<p(z), m 1, <£>(zo) ф 0 и <£>(z) — аналитическая функция в окрестности точки zq, то в некоторой окрестности точки zo справедливо разложение - . = bo + bi(z — zo) + ..., где 1 <£(z)
bo = ——г 7^ 0. 12.379. Указание. Провести доказательство от про-<^(z0)
тивного, т. е. предположить, что /(z) ограничена в окрестности точки zo и вывести из этого предположения, что zo — устранимая особая точка. 12.380. Указание. Рассмотреть функцию <£>(z) = ——--------доказать,
/(г) - А
что zo — существенно особая точка для </?(z), и воспользоваться утвер-ОО
ждением задачи 12.379. 12.381. 5"^ cnzn сходится во всей плоскости, а п=1
Ответы и указания
485
оо
ряд cnzn — вне круга |г| > R. 12.382. Точки zi = е-7гг/4 и z2 = п= —оо
= е3?гг/4 — полюсы 3-го порядка. 12.383. Точки z^ = 0 и Z2 = -1 — по
люсы 1-го порядка, а точка z$ = 1 — полюс 3-го порядка. 12.384. Точки
Zk = kit, к G Z, — полюсы 1-го порядка. 12.385. zq = — 1 — полюс 1-го
порядка, zi = 2 — полюс 3-го порядка, Z2 = — г — полюс 5-го порядка. 12.386. z^ =0 — полюс 2-го порядка, Zk = 1 + кя, к Е Z, — полюсы 1-го порядка. 12.387. z^ = — 1 — полюс 3-го порядка, Zk = 2кт, к € Z, — полюсы 1-го порядка. 12.388. zq = 0 и Z2 = тг — устранимые особые точки, Zk = як/2, к = ±1, ±2, ±3, ±4, ..., — полюсы 1-го порядка. 12.389. z0 = тг/4 — устранимая особая точка, Zk = тг(4/с + 1)/4, к = ±1, ±2, ..., —полюсы 1-го порядка. 12.390. Точки Zk — тг(2к+1)/2, к 6 Z, — полюсы 2-го порядка. 12.391. Точка z0 = Зг — существенно особая. 12.392. Точка zq = —2i — существенно особая. 12.393. Точки 2
Zk = 1 Ч----—----—, к € Z, — полюсы 1-го порядка, а точка z = 1 —
7г(2А; + 1)
предельная для полюсов. 12.394. В точке z = 1 устранимая особен-л 7г(2А: + 1) ,
ность, а в точках Zk = 1 -I----------, к 6 Z, — полюсы 1-го порядка.
12.395. В точке zq = 0 устранимая особенность. 12.396. В точке z0 = 0 — полюс 4-го порядка. 12.397. В точках Zk = 1пЗ + 2кт, к G Z, —
полюсы 1-го порядка. 12.398. Правильная точка. 12.399. Полюс 3-го порядка. 12.400. Правильная точка (нуль 3-го порядка). 12.401. Полюс 2-го порядка. 12.402. Существенно особая точка. 12.403. Суще
ственно особая точка. 12.404. Полюс 2-го порядка. 12.405. Правильная
точка.
12.408.
12.409.
12.410.
12.411.
12.412.
12.406. Правильная точка.
выч
' z2 + 1 z-2
2 =5.
z2 выч —------—; г =
(z2 + I)2 г2п выч -----—; 1 =
1(г-1)-’ J
1 ВЫЧ 0 z3(z2 + 4)2
Г 1 выч --------277 5 0
z(l — е2г) к = ±1, ±2, ...
12.407. Существенно особая точка.
1.
--г, выч
4
(z2 + l)2'’
2п(2п — 1)... (п + 2)
1
= — —, выч 32’
1
2’
выч
1
,г3(г2 + 4)2;±2г.
Г 1
; кт
1
64'
____1
2кт'
486
Ответы и указания
12.413. выч
12.414. выч
выч
12.415.
выч
12.416.
выч
выч
12.417.
выч
12.418.
выч
12.419.
выч
12.420.
выч
12.421.
выч
выч
12.422.
выч
выч
12.423.
12.427.
второй
12.433.
sin г 2
Г; (-l)fcg+br
sin 2z
sin 2z
тг \ 2
sin 2z
ez
z2(z2 + 9) ’ 0 ег _r
z2(z2 + 9)’
Л Л
tg ( к + - j тг ; kir] = 0,
3
2
к~, к€%.
7з
7Г
2
1
4
7Г — 2’
4 sin 2
(тг-2Г
4 cos 2
_ 1
~ 9’
3
е2
ВЫЧ [z2(z2 + 9)
ie Зг ~бТ"
= -1, к € Z.
ctg2 z;
г ч 1
COS'5 z Л
ZJ
z2 + z — 1
-г,—=°>
к е ъ.
выч
1
z(l-z2);0]’
----1----1
Л1 - r2V
-У-т;о =o, z2 — z°
z2 _ z5 ’ 1
; Зг
ге3г "бГ’
выч
1
3’
1
2
выч
z2 + z — 1
z2(z-l) ’ 1 = L
4=1
1
z2 - z5 ’
выч
1
z2 - z5 ’
2
1
2’
6
-1 -гУЗ
2
1 -гУЗ
6
cos 4z 2
128 . й ~1Г'П8'
12.428.0. 12.429. -1sh3.
теоремой о вычетах. 12.430.
Л--^2. 12.434. 2ттг. 12.435. 12.436. ^-^sh3. Указание.
2 9 3
выч
-1.
12.424.
1. 12.425. 0. 12.426. 1.
Указание. Воспользоваться
0. 12.431. тг2. 12.432. -1.
______ 2тгг , Л ,г
з . ............
Ответы и указания
487
Воспользоваться второй теоремой о вычетах и результатом задачи 12.429. п(п + 1)... (2,71 — 2) 2т ------------------------------Т,----г;—7• 12.438. 0. Указание. (Ь — а)2п-1 вычетах и соотношением
12.437. (-1)п
Воспользоваться второй теоремой о
выч[/(г); оо] = 0. 12.439. 2тгг. 12.440. 0. 12.441. -4дг. 12.442. 2тгг, п = 2п+1т
= 1; 0,71 = 0,2,3,... 12.443. ----—
(п-1)!
12.444. 2(1 — е~1У)т. 12.445. 2m.
12.446. (cos 1 4- sin 1 + i(sin 1 — cos 1))^-
12.450. —^L==. 12.451. -
У(а2 - Ь2)3
2тг t____________
12.454. ~(а — \/а2 — Ь2). 12.455. т.
п{п + 1)... (2п — 2) __ тг
X
12.447.0. 12.448.0. 12.449. m.
12.452.
i12.453. 0.
1 — а2
12.456. 7г\/2. 12.457. х
12.459. 12.460.
4а 27
тге-4
(sin 2 + 2 cos 2).
' 12'458' 2„6(., • (О'
П-463. 2
к/З sin - — cos -). 12.465. Ye~ab- 12.466. де-2 cos 2. л/3 \ 2 2/ 2
12.467. ^-(е-1+е“3). 12.468.тг(е-2+е~3). 12.469. |е“3. 12.470.7г?~^.
12.471. 2 корня. Указание. p(it) при изменении t от +оо до —оо приращения не получает. 12.472. 2 корня. 12.473. 3 корня. 12.474. Указа-(</?(z)
1 + ~yY~\
12.461.
12.464.
4 з714
при обходе точкой z контура L приращения не получает, ибо
1.
/(Ч) „<=L
12.475.Указание. Рассмотреть функции/(z) = aozn и <p(z) = a1zn" + ... + an на окружности |z| = R достаточно большого радиуса R. 12.476. а) в круге |z| < 1 один нуль; б) в кольце 1 |z| < 2 че-
тыре нуля. Указание. Положить /(г) = 8z в случае а) и /(z) = z5 в случае б). 12.477. а) в круге |z| < 1 один нуль; б) в кольце 1
[z] < 2 нулей нет;
четной: 0k = 0, ak
Z/2
4 f
= 0, 0k ~ - J . о
в) в кольце 2 |z| < 3 два нуля. 12.479. Для
//2
4 С .. . 2ъкх ,
= - f(x) cos—-—dx, а для нечетной: ak = о
О.'тт кт 1
—— dx (к = 0, 1, 12.480. f(x) = - +
488
Ответы и указания
= 1 (рис. 38). 12.481. /М =
2т — 1 2 х—' к
к=1
„(кх я / олх ,/ ч 1 4 cos7r(2m—1)т
SG) = 4 (₽ИС' 39)- 12-482' = 2-^2 (2,„-1)^ '
т=1 ' '
Рис. 38
Рис. 40
Ответы и указания
489
2 4 <^2. f_iU+i ^2
S(l) = 1 (рис. 40). 12.483. - + - > V------------cos2A;x. 12.484. — +
v ’ u 7 ft- ft- 4k2 - 1 3
+ 4 Y cos ta. 12.485. 1 f 5- sin 12.486. * -
k2 я 2k 4-1 т ft-
k—1 k=Q
. ктгх
- 1 f 12.487. i-2 f 12.488.1° f (-1)‘ ft- 4к2 — 1 тг к тг к
k=i fc=i k=i
2sinaft-^. ...ksmkx . _
------- x i_i\k — если a — не целое; sin аж, если a € Z. a2 — k2
12.489.
12.490.
ft-k=i
2 sin атг I
ОО
7Г
если a
\ fc=l
_ „ 2 sh aft-
e Z. 12.491. -------------->
ft- ' fc=i
a cos kx \
—-----— , если a — не целое; cos аж,
а2 — Ar /
t .fcsinfcx 2 shaft- ( 1
----77- 12-492. ------- —
a2 + k2 тг \ 2a
оо
a cos kx\ .
k~.----ту • 12.493. a)
a2 + k2 /
fc=i
(2(-l)fc - 1)A; . kirx
cos (4A: + 3)ж
4 A: + 3
1 ni 2(-l)fc - 1 knx ------1- 2 In 2 > —з—-——— cos —-, In 2--In2 2 + А;2тг2 In 2
,o .1 2 /cos (4k + 1)ж
12.494. a) - + - V ---------b-----H- -
7 2 ft- 6^ \ 4k + 1 k=0 \
1
— + 21n2V In 2
. 4 v—ч 1 . 2 &7Г . , -,n x 1 4
6) — > - sm — sin kx. 12.495. a) ------------------------- x
ft- k 4 2 ft-2
fc=i
1
2
8 . (2k + 1)тгж
6^g(2Twsin---------
™ (-1)* i 16 5^ к
12.496. a) 1+2^——-costa- -cosx, <5) -smz- — (4p _ n2 x
fc=2 k=l V 6 7
1 4 x°°x (—1)^ 2 x°°o / (—I)*"*"1
x 8ш2А;ж. 12.497. a) - 4—- ———cosirkx, 6) —7 I ----------------- +
3 7г2 к2 тг \ к
k=i k—i \
<2((_i\fc__4 00 1
4----И / 9-------- simrkx. 12.498. a) ft-------—-----------— cos (2A: - 1)ж,
A;37t2 J 7 ft- (2k - I)2
00 1 _ 1\fc Л 00 1
б ) У"4------7-----sinkx. 12.499. a) ~У —---------------—- cos (2k - 1)ж,
7 к ft- (2k - l)2
k=0 k=l v ’
6) f^in2te. 12.500. a) | cos T P™,
A:=l fc=l v ’
490
Ответы и указания
О/ 1 JcTTT 71*2 7г 2
б) — V (—l)fc+1 - sin ——. 12.501. а) —, б) -т=. Указание. Рас-
7 тг V 7 k I 7 8 ’ 7 32х/2
К=1
смотреть ряд в точке т0 = 1/4. 12.502. 7г2/12. 12.503. тг2/6.
X
12.504. Указание. Умножив и разделив Dn(x) на 2sin —, получим
1
^п(ж) — х /
2(n + l)sm- Л=о
х . 2х + 1
2 sm — sin---------х
2 2
г. • Х
2 sin -
2
1
4(п + 1) sin2
/ 7 /7 1 \ \ 1 — cos (п + 1)т
х > (cos кх — cos (к + 1)т) =------------------—
к—о 4(п + 1) sin2 -
п + 1 2 sin2 -
2
7Г4
12.505. —
90
12.506.
. 2n + 1 sm——t
+ f(x - t))-— dt.
2 sin -
2
12.507.
. 2n + 1 sm--------
2
2 sin -
2
1 .
7Г(П + 1) J 0
, 2 '«'i A .
sin —-t 2
x -------— dt. 12.508. <] Учитывая, что
2 sin2 -
2
dt =
. 2 sin
7г(п +1)J О
2 t
— dt = 1, 2 sin2 -
2
о
можем записать
о-п(/, х) - /(ж) =
1
7Г(П + 1)
г Sin —-Г
/ (/(ж +1) + f(x - 0 - 2/(ж))------ t~ dt =
о 2sin22
6
- 1 f
7r(n + 1) J О
sin —— t
-t) - 2/(ж))--------~~ dt +
2 sin2 -
Ir.2
1 f sin —— t
/ , n / (f(x + i) + f(x -t)- 2/(t))--------------dt = Ii + I2.
^n + VJ 2 sin2 |
Ответы и указания
491
По заданному е > 0 выберем 8 столь малым, чтобы для 0 t 6 выполнялось неравенство: \f(x + t) + f(x — t) — 2/(x)| < £. Тогда
6 • 2 П + 1 .
2 [ 2 M = £
^ + 1’/2 2sin4 2
<5 • 2 г SHI
^7—rfi < f
J n • 2 1 2
0 Sm 2
2
Далее в силу непрерывности /(ж) имеет место неравенство |/(ж)| М при х € [—тт, д]. Поэтому
ir । / 1 L/ 1 2Л/7Г 7* dt
2 7г(п + 1)/ /2 i \ 2 п + 1 ] t2 (п + 1) 62 '
5 2 - • - 6
Выбирая п столь большим, чтобы т.е. |стп(/, х) - f(x)\ < £. [> ОО
_____ г/ ч 9 Л v^sinmx 12.509. /(ж, у) = тг2 — 2тг 2?-
т=1
2 оо /
4 2
т=1
12.510. f(x, у)
. тгпу sin-----
П
_ 27Г ул 3
т=1
2Мтг2
62
< I’находим 1/21 < I’
оо
у-л sm mx sm пу л тп
т, п=1
-1)п .
----sin пу + п
12.511. f(x, у) = — £ 5—'------------ х
О7Г *—'
П=1 m
sin пу
П
7Г smmx + — >
2
-------sin mx sin пу. тп
16 (-1)”*+”+! . тгпу с, ч
d---г > ------------cos тгтх sm———. 12.512. f(x, у) =
7Г3 , т2п 2 v 7
тп
т, п=1
Н1 2 v2'
— sin тгтх Ч— >
тг 2-—'
т, п—1
(_Ппг+п+1
----------sin ятх cos пу.
тп2
12.513. J[sign (t — a) — sign (t, — b)] = s^n яги(а+ь)
. o л , sm isva
12.514. ^[f] = h-^rr~.
п
п
47Г1/ . 4тг2у / a
12.515. 3[/] = < a2 — 4д2 7Г 0 sin при 2a a
— при У = —.
1 a 2Д
2 sin2 тгу 1 \/27Г
12.516. 3[/] = ТПУ 12.517. a2 +12 — р-ша ~ 2a
1
a2 +12
492
Ответы и указания
wa cos cut dw.
Указание. Для вычисления $с
1
a2 +t2
ис-
пользовать соотношение (*) из примера 3 на с. 248. 12.518. $с
t
a2 +12
~e ша, -z——- = I e ша smutdw. Указание. Использовать co-2 ’ a2 +12 J
о
d Г 1 ' a2 + i2 I duj a2 + t2 _.2. ш
вычислен в задаче 12.517. 12.519. 3s[te 1 j =
отношение &
, где интеграл &
,2
a2 +12 te-S =
।
f Ш . ,,
= \~ / —y=e 4 smcucacu.
V тг J 2>/2
12.520. &[e~a|t| cos pt] = J-
a(ai2 + Д2
2\’
e cos fit = — i
7Г j
0
a2 + P2 + ш2
coswZ dw.
Рис. 41
о
t
t
1
12.522. S(^) = sin2 Tri/fcT, vk = p(yk) = -Д- sin2 тгукТ, -KUk 4T 7Г|РЛ|
{0 при к = 4n,
— при к / 4п п £ (рис. 41). 12.523. S(yk) =
Ответы и указания
493
sh^tti^ — г(1 — cos27TPfc) k . . 2lsin7rp'fc| .
--------------------------------, ^ = 3, = фм =
ТГ^Л
TFZ/fc при к 1, 2, (рис 42). 12.524. S(p) =
О при к = 3,
sin27rap . . I sin 2тгар|
--------, Р^) = П— 1ГУ-----7Г М
ФМ =
(рис. 43).
12.525. S(p) =
2 cos 7Г1/
7Г(1 — 4z/2) ’
О,
-тг, 2
7Г
если S(v) О, если S{y) < О COS7FP 1 — 4р2
, Ф(^) =
О,
—тг,
если S(p) < О
(рис. 44).
Указание. При вычислении
Рис. 42
1/2
интеграла cos Trte~2nu't dt функцию cosTri представить по формуле -1/2
cin2 7Г1/ Эйлера. 12.526. S(p) = —5-5“,
• 2
Sin 7ГР ч .
—5-5-, ф(р) = О (рис. 45).
494
Рис. 45
Рис. 46
Ответы и указания
495
12.528. Wi =
W2 =
W3 =
/1 0 0 0 1 о о о\
1000-1 о о о 0 1 0 0 0 1 о о
0 1 0 0 0 -1 о о
0 0 10 О 0 1 о ’
0010 0 0-1 о
0 0 0 1 О О 0 1
\0 О О 1 О 0 0-1;
/1 000 1 о о о \
0 1 0 0 0 q2 О О
1000-10 00
0 1 0 0 0 —q2 О О
0 0 1 0 0 0 1 0
0 0 0 1 0 0 Од2
0010 О 0-1 о
^0 0 0 1 О О 0 —д2;
/1 000 1 о о о \
О 1 О О 0 q О О
0 0 1 0 0 0 q2 О
0 0 0 1 0 0 0 д3
1000-100 О О 1 О О 0 —q О О
0 0 1 0 0 0 -q2 О
12.529. =
^0 0 0 1 0 0 0 -д3/
(gg _|_ (я0 + ж4) + (ж2 + жб)
Хо — Ж4 (жо - х±) + q2{x2 - ж6)
Х1 + х5 (ж0 + ж4) - (ж2 + х6)
Ж1 ж5 , Z<2> = (жо - Х4) - q2(x2 - х6)
х2 + ж6 (Xi + х5) + (ж3 + ж7)
х2 - ж6 (xi - х5) + д2(ж3 - х7)
Жз + х7 (Ж1 +ж5) - (ж3 +ж7)
\х3 -х7) ^(Ж1 - ж5) - д2(ж3 -ж7);
496
Ответы и указания
( (т0 + х4 + х2 + т6) + (ti + х5 + хз + ж7) \
(то - т4 + Я2х2 ~ q2x6) + (qxi - qx5 + q3x3 - q3x7) (a?o + x4 + t2 - T6) + (g2Ti + q2x5 - q2x3 - q2x7) (t0 - x4 - q2x2 + g2ze) + (tf3£i ~ Q3^5 - qxz + qx7) (x0 + x4 + x2 + x6) - (a?! + x5 + t3 + x7) (t0 - t4 + q2x2 - q2x6) - (qxx - qx5 + g3T3 - g3T7) (т0 + t4 - t2 - t6) - (g2Ti + q2x5 - q2x3 - q2t7) \(t0 - t4 - q2x2 + q2t6) - (g3Ti - q3x5 - qx3 + qx7)/
Глава 13
13.1. Внутренность круга с центром в точке до радиуса R; односвязна.
13.2. Внутренность кольца между окружностями радиусов 1 и 2 с центром в точке zq = г; двусвязна. 13.3. Внешность круга радиуса 2 с
центром в точке zq = i с выколотой бесконечно удаленной точкой; дву
связна. 13.4. Внутренность горизонтальной полосы, заключенной между
пряхмыми у = —1/2 и у = 0; односвязна. 13.5. Внешность круга радиуса R с центром в точке zo; односвязна. Бесконечно удаленная точка z = оо является внутренней точкой этой области. 13.6. Внутренность круга с выколотым центром zo = —г радиуса 2; двусвязна. 13.7. Открытая полуплоскость, определяемая прямой х = 1 и содержа-
щая начало координат. 13.8. Внутренность круга радиуса 2 с центром в
точке (2, 0); односвязна. 13.9. Прямая х — г/+ 1 = 0. Указание. За-
писать
z + 1
----- в виде z — г
(z + !)(-? + г) _ (z + 1)(г + г)
X2 у2 ность эллипса — + —
z = —2i. 13.12. Часть
(z-i)(z + i) \z - г|2
13.10. Внутрен-
— 1. 13.11. Окружность |г| = —2, кроме точки плоскости, лежащая справа от левой ветви ги-
перболы — — — — 1. 13.13. Прямая, проходящая через точки z\ и 9 16
г2, с вырезанным отрезком, соединяющим эти точки. 13.14. Внутрен
ность отрезка, соединяющего точки —гиг. Указание. Воспользоваться равенством arg (—г) = тг + arg г. 13.15. Re г > 0, Im г > 0.
13.16. Rez < 0. 13.17. |Rez\ < 3. 13.18. |г - (1 + г)| + \z - (3 + г)| < 6.
13.19. Зтт/8 < arg (г — zq) < 5тт/8. 13.20. u = 2х2 — 2у2 + у, v = 4ху + х.
Ответы и указания
497
13.21. и = —2ху — х, v = 2 — у + х2 — у2. 13.22. и
2я(1 + д) у
v = —ГГ7Г7 12- 13-23- и = -У - ~2 ~ v х2 + (1 + у)2 х2 + у2
13.24. и = х2 — у2, v = 2ху — 1. 13.25. и =
х2 - (1 4-г/)2
х2 4- (1 + у)2 ’
п 9,I • хл + у2 2(х-у}^ + « + х2 ~ — y2+x + l'),v = ———~(2ху + у — х2 + у2 — х — 1). 13.27. z2 + 2iz-l.
i 2(ж-г/)
13.28. z + -. 13.29. 4z/(z2 — z2). 13.31. Любая область, лежащая внутри z
угла с вершиной в начале координат и раствора не более тг/п. 13.32. Любая область, лежащая в полосе, параллельной действительной оси и шириной не более 2тг. 13.33. Любая область, лежащая в полосе, параллельной мнимой оси и шириной не более 2тг/3. 13.34. Любая область, лежащая либо внутри единичного круга (|д| < 1), либо вне его (|д| > 1). Указание. Равенство zi Н----= г2 4----при z\ / z^ возможно только
21 Z<1
2 1
13.35. Зг. 13.36. —г/2. 13.37. — + -г.
5 5
в случае, когда z<i = — 21 5 12
13.38. — — —г. 13.39. Ось Ох отображается в окружность u2 + v2 = 1. Ось Оу отображается на ось Ои. При этом точка z — i переходит в точку w = оо, а точка z = оо — в точку w = 1. 13.40. Прямая х = С отображается в параболу v2 = 4С2(С2 — и); окружность |г| = R — в окружность |w| = R2, проходимую дважды; луч arg z = a — в луч argw = 2a; полукруг |z| < г, 1тд > 0 — в круг |гд| < г2 с разрезом по отрезку положительной действительной оси. 13.41. <] Точки, лежащие на прямой х — С, записываются в виде z = С + iy, а потому w = 1 С . у С у
= п 7 •" = —2 ~ 2 • Отсюда и = >72-—2 > v = —2 ’
С 4- гу С2+у2 С2+у2 С2+у2 С2+у2
9 о 1 U
и +v = —--------- = —. следовательно, образом прямой х = С является
С2 + у2 С 'll
окружность u2+v2 — — = 0. Образом окружности |z| = R является окруж-С/ 1
ность |w| = Луч arg£ = а, т.е. луч (0, оо-ега) отобразится в идущий R
из бесконечности луч (0, оо • е~га). Полукруг |z| < г, Im г > 0, отобразится в нижнюю полуплоскость с вырезанным полукругом |w| -,
г /2 г- \/2 г-
у (1 - х/2 + г), wi = уН ~ \/2 + г),
Imw < 0.
498
Ответы и указания
W2
/2 2
/2
2
Wi
/2
2
13.44. Wi
- г). 13.43. w0 = ------
2-х/2
У2 + х/2 (cos у + i sin у), = я - arctg (ч/2 - 1); w3 = - \/2 — \/2 (cos у + г sin у),
w2 - - \/2 + л/2 (cos у + i sin у ), </?i
— \/2 — \/2 (cos у + i sin у У W4 =
<P2 = arctg (\/2 + 1). 13.45. Wi = 0, w2 = 1 + i, w3 = -(1 + z).
13.46. 2(99 + А:7г), к G Z. 13.47. 3<p + 2&7г, к G Z. 13.48. +
О
4- 2тг(п + ЗА:)), n = 0, 1, 2, к G Z, sinz/» = - cosip —
a/1 + r2 + 2r cos <p
= —> .l.X.^=-0S(|^ .. 13.49. — + 7r(n + 2k), n = 0, 1, к G Z, sinz/» = yi + r2 + 2rcos^ 2
r sin 99
^/64 + r2 — i6r cos ’
+ 7r(n + 2k), n = 0, 1, к
r2 cos 2<p — 4
1/I6 + r4 - 8r2 cos 2<p
. . 3r sin >p
sm ip — —r ......- 7 ....=
, г cos <р — 8
cosip = f -==
yj 64 + r2 - 16r cos „ . , r2 sin 2w
G Z, smi/; = ---------------------
ib
13.50. +
----- ----------- - - PGS ll) — 16 + г4 — 8г2 cos 2<р ’
13.51. — + 7г(п + 2&), п = 0, 1, к € Z,
sin2 <р + (г2 — 2 — г cos </?)2
, r2 - 2 — r cos ф
cos ip = y-—— —............. .
J9r2 sin2 <p + (r2 — 2 — r cos ip)2
sin?/. 13.54. Rew = ex2~^l~y')2 x
-(i-y)2 sin2z(l — y). 13.55. Re w = sin# x
13.56. Re w = sh x cos (y + 2),
D sin2(l + z)
13.57. Rew = ——------------—-------r, Imw =
ch 2y + cos 2(1 + x)
13.58. Re w = 3*2+«5 cos —x-, Im w —
x2- + y2
13.62. chi cos 1 - zshlsinl. 13.63. cosl.
13.53. Rew = el~x cosy, Imw = —e1-1 x cos2(1— y), Imw = ex2 x ch(l — y), Im w = — cosxsh(l — y).
Im w = ch ж sin (y + 2).
sh 2y ch2z/ + cos 2(1 + x) * .. . у - _ 3 «2+v2 Sm —— .
Xz + Z/z
13.64. — sh2cosl + i ch 2 sin 1. 13.65. (2k + 1)ttz, A- G Z. 13.66. -z.
2 ’
тгг, к G Z. 13.68. zcth.7T. 13.69. 0. 13.70. Arcsinz = = — i Ln (iz 4- \/l — z2), Arcsinz = 2ктг — i In (\/2 — 1), к G Z.
13.67.
Ответы и указания
499
13.71. Arctgz = -^-Ln ; lZ, Arctg j- = ктг + ^Ь2, fc G Z. 2 1 ” о 2
13.72. Arshz = Ln (z + \/z2 4-1), Arshz = ^2/с+^дг, k G Z.
13.73. Arch г = Ln (z + \/z2 - 1), Arch(-l) = (2к + 1)тгг, к G Z.
1 1 -{- z 1 z ( 1 \
13.74. Arthz — -Ln -----, Arth(l - z) = - In 5 + - arctg 2 + I к + - I ттг,
2 1 ““ % 4 2 \ 2 J
4 3%
к G Z. 13.75. |w| = argw = — • 13.76. |w| = тг2, argw = 0. o Z
1 e2 — 1
13.77. |w| = -(3 + cos In 4), argw = 0. 13.78. |w| ~ th 1 = ——-
2 e2 + 1
argw = 0. 13.79. (cos In 2 +z sin In 2)e 2n7T, n G Z. 13.80. е(2/г+1)’Г, к G Z.
_ „ (ob-iX- ( In 2 . . In 2 \ _
13.81. e'2 4' I cos ——I- z sin —— j, к G Z.
\ Z Z j
. ( ( 4\
13.83. 5earctg з +2/г7Г I cos I In 5 — arctg -) + z sin \ \ О/
13.82. e^2^1)™, k G Z.
/ 4\\
I In 5 — arctg - j j, к G Z. \ О/ J
13.84. -5earctg з+(2/с+1)я fcos fin 5 — arctg j + z sin f In 5 — arctg
\ \ J \ о
к G Z. 13.85. e-¥U+8*)5 k G Z. 13.86. ei(1+12^ , к G Z.
13.87. z = i(^+2ki^, fc G Z. 13.88. x = 0. 13.89. z = 1 + z.
13.90. z = 1г+2ктг, к G Z. 13.91. f(z) непрерывна в D, если Ve > 0 Vz G P 35 = 5(e, z) > 0 ((I Az| <5Az + AzgP)=> \f(z + Az) - /(z)| < e).
13.92. -2z. 13.93. 1. 13.94. oo. 13.95. 0. 13.100. /(0) = 0. 13.101. /(0) =
= 0. 13.102. /(0) = 0. 13.103. lim /(z) не существует. 13.105. He z->0 __
Az
дифференцируема ни в одной точке. Указание, lim -— не суще-Дг-^0 AZ
ствует. 13.106. Не дифференцируема ни в одной точке. Указание. При
л > л V 1
Ад = к&х имеем lim -------—— = lim -------т.е. предел не суще-
, Дг^оАх + zAz/ Дх—>о 1 + гк н
ствует. 13.107. Дифференцируема только в точке z = 0. 13.108. Дифференцируема только в точке z = 0. 13.109. Не дифференцируема ни |z + Azl — Izl I Azl
в одной точке. <] В точке z = 0 lim JJ——1 = lim —1 — не
Дг—>0 Az Дг—>0 Az
существует. Если же z 0, то, обозначая ]z] = г, Az — имеем
500
Ответы и указания
|z + Дг| - |z| Дг
I /, 2Др, . , MpV ,
r \ 1 (x cos tp + у sm tp) + — — 1
\ V r* 1 2 3 \ r J
сюда найдем
lim
Др—>0
Дре^
Др
X
— при <р = 0 и
г
. От-
I / Ар г \ 1 + 2—у +
IV г
тг
---при <р = —. таким оора-г--2
2
du dx du dy dx dr + dy dr dv du
-rcos^, т.е. -
dv dv . dv
— costp - — simp и — =
dy dx dtp
1 dv .
- • —. Аналогично проверя-r dtp
lim ----------------—
iAp-»o гДр
\z 4- Дд| = Izl
зом, lim ------;-------не существует. [>
Дг-40 Дг
13.110. Дифференцируема только в точке z = 1. 13.111. Указание. Использовать правила дифференцирования сложной функции двух переменных и(т, у) = u(r cos <р, г simp), v(x, у) = v(rcos<p, r simp) и усло-ВИЯ (1): - = dv = г simp + eta
ется второе из равенств (2). Для получения равенств (4) следует вы-du dv dr dr
разить — и — через производные по г и <р, производные —, —, dx dx dx dy
dtp dtp r-z---- у
—, — получить из равенств г = \Jxz + у, tp = arctg — и подставить dx dy х
найденные выражения в (3). 13.112. (е3г)' = Зё3г. 13.113. (shz)' = = ch z. 13.114. {zny = nzn~x (кроме точки z = 0 при отрицательных n). 13.115. (cosz)' = — sinz. 13.116. (ln(z2))' = -. 13.117. (sin-) =
1 z
= - cos-. 13.118. Указание. Воспользоваться условиями Коши-Ри-
3 3
мана. 13.121. Вся плоскость, кроме точек z — (k + тг, к €
(Цг)' = 13.122. Вся плоскость; f'(z) = е 2(1 — z). 13.123. Вся
.... (1 — z2) cos z — z(l + z2) sin z
плоскость, кроме точек 21,2 = ±г; f (z) =--------—----—------------.
2ez
13.124. Вся плоскость, кроме точек zv — 2тгрг, v € Z; f'(z) = -------—.
(ez — I)2
Ответы и указания
501
13.125. Вся плоскость, кроме точек zv
—у, у € Z; f'(z) = cos 2г.
(Z — 1)
13.126. Вся плоскость, кроме точки z = 0; f'(z) = ——-—-. 13.127. Вся 2 1
плоскость, кроме точек Zk = к € Z; /'(г) =------------у—. 13.128. Вся
sh z
плоскость, кроме точек Zk = | к + - | тг, к € Z; f'(z) = ------------.
\ 4/ 1 - sin 2г
d2u 1 du 1 д2и
13.130. Ди = +-Г^-^.13.131. Ди = 0, v(x, у) - Зх2у-у3 +
дгл г dr г2 д(рл
+ С, /(г) = (х + г?/)3 + Ci = г3 + Ci. 13.132. Ди = 0, и(х, у) =
= 2ех cosy + С, /(г) = 2eI(cos?/ + г sin у) + С = 2е2 + С. 13.133. Ди = = 0, v(x, у) = —ж2 + у2 + С, f(z) = -i(x2 - у2 + 2ixy) + 3 + Ci = = — iz2 + 3 + Ci. 13.134. Ди = 0, и(ж, у) = - In (ж2 + у2) + С, 1 V
f(z) = - In (ж2 + у2) + i arctg — + C = In |г| + i arg г + C = In г + C.
13.135. Ди = 0, и(ж, у) = —уУ— + 2х + С, f(z) = ~—~-2y + 2ix + ж2 + хл + у2
+ Ci = - + 2iz + Ci. 13.136. Ди = 0, и(ж, у) = —^(ж2 — у2) + г 2
? 2 — У
2ху + С, /(г) = z2 — -г2 + Ci — — — z2 + Ci. 13.137. Ди = 0, и(ж, у) - ^(ж2 - у2} + С, /(г) = |г2 + С. 13.138. к = 4, ip = тг/4.
13.139. к = 2, = тг/2. 13.140. к = 6, = тг/2. 13.141. к = 3,
= 0. 13.142. к = 1, = 0. 13.143. к = 2, = тг/2. 13.144. Сжи-
мается область |г| > 1, а растягивается область |г| < 1. 13.145. Сжимается полуплоскость Re г < 1, а растягивается полуплоскость Re г > 1.
13.146. Сжимается область [г-t-11 > 1, а растягивается область |г +1| < 1.
13.147. Сжимается внутренность круга |г + 1| < 1/2, а растягивается у
внешность этого круга. 13.148. |г — 1| = 1/2. 13.149. г — - =1/2.
13.150. |г +г) = \/2. 13.151. |г| = 1/л/З. 13.152. {г|1ш (1 - г)г = 0}, т. е.
прямая у = х. 13.153. {г|1ш (1 + г)(г + г) = 0}, т. е. прямая ж+у +1 = 0.
__ 2 Зтг
Указание. Использовать paBeHCTBoarg —------= —— 2 arg (г + г) = 0
Зтг
и соотношение —— = arg(—1 — г). 13.154. Луч 0 < ж < +оо, у = —1/2.
13.155. Луч 1 < ж < +оо, у = 0. 13.156. Отображение конформно.
13.157. Отображение не конформно. 13.158. Отображение конформно.
502
Ответы и указания
13.159. Отображение конформно. 13.160. Отображение не конформно. 13.162. zo = -1, a = 0, к = 2. 13.163. z0 = 2(1 + i), a =
к = 1. 13.164. zq = - ^ctg^-, a = к = 1. 13.165. При
2 2 8 4
a 1 zq = -----------, a = arg а, к = |а|. 13.166. Прямая v = —3.
1 — a
13.167. Прямая u — 2v = 0. 13.168. Окружность и2 + и2 — и — v = 0.
13.169. Окружность и2 + v2 + 2и + 2v + 1 = 0. 13.171. w = i-------
z — 1
13.172. w = + . 13.173. w = (5 ~ 30г ~ 4, 13Д74. г =
z 4г - 5 - Зг
a - d ± >/(а - d)2 + 4bc „
= ---------—-------------, z\ = Z2 при (a — dy + 4oc = 0. Бесконечно
2c
удаленная точка является неподвижной только при с = 0, т.е. для линейной функции. 13.175. а) -(1 + г); б) 4 + г. У казан ие. Точка 1 + г 1 + 2г
и центр круга г лежат на прямой у = 1. 13.176. a) w|
6) WL-=1-9i= 13Л77-a = I- в = 7Г-
~u, ~ 2
13.183. a = zq, в = тг.
полуокружность). 13.185. Е = < w
5 ’
13.178. a = 0, 0 =
Зтг
13.179. a = z0, 0 = 13.181. a = i, 0 = 0. 13.182. a = 2i, 0 = —.
13.184. E = {w||w| < 1, Imw <0} (нижняя
T J
—, Im w < 0 >
2 |
/1
2
1.
~ 2Z
(рис. 47). Указание. Луч 0 < х < +оо преобразуется во внешность
отрезка 0 и 1, причем точки верхней полуплоскости (г) отображаются в точки нижней полуплоскости (w). Прямая у — х = 0 отобра-— 1 + i 1 - г_
жается в окружность ww-----2~w 4-----2~w ~ т,е‘ в ОКРУЖНОСТЬ
\/2 11
= с центром в точке wq = - — -г. 13.186. Е =
/1 1.
w — - — -г \ 2 2
Ответы и указания
503
fl 7Г )
= < w - |w — 1| 1, — — < arg(w — 1) <С 0 >. Указание. Окруж-
ность z\ = 1 отображается в окружность |w — 1| = 1, окружность |z| = = 2 — в окружность \w — 1| — отрезок 1 х <С 2 — в отрезок
Рис. 48
з
- и 2, а прямая у = х — в прямую u + v = 1 (рис. 48). 13.187. Е =
= {w|Imw > 0, Rew > 0}. 13.188. Е =
П
4]
1
2
1 2’
3
W 4
( г „2
I । т
<Z z + ------
( 1 — r2
13.190 Z? = < {z|Rez<l/2}
Т-~2 f ПРИ
при
г = 1,
.2
{2 >
. r Г I
z\ z-~-- > ——- > при г > 1.
г2 — 1 т2 - 1 J
<] Поскольку |w| < г, то из соотношения w(l — z) = z получаем |z|
< r|l — z|. Возводя обе части этого неравенства в квадрат, запишем полученное неравенство в виде zz < r2(l — z)(l — z), откуда получаем
(г2 - l)zz - r2(z - z) + г2 > 0.
(*)
Если г < 1, то из (*) имеем
„2
_ г
ZZ+ -----2
1 — Г2
г2
1 — т2
_ г2 _
Но zz + --------(z + z) =
1 — г2
^.4 ^.2
так как -------— + --------- -
(1 — Г2)2 1 — Г2 (1 — Г'
г2
1 — г2 г2
г2 \ г4
1 — г2 / (1 — г
то из (**) получаем z +
т2
1 — г2
Далее,
2
504
Ответы и указания
г
1 — г2
2 (
, т. e. D = <г| z +
.2
1 — Г2
1 — г2 J _ г2 Аналогично в случае г > 1 найдем zz-------—~(z
r4 r2 r2
— I)2 r2 — 1 (r2 — I)2
г 1
> —----> (внешность круга).
rz — 1 J
r2 z ~ ~2—7 r2 — 1
г2
г2
z\ Z-r2 — 1
то из (*)
получаем z + z < 1, т.е. D
кость). О
13.192. w
13.195. w
г I
(внутренность круга).
+ z) > —-—-, т.е. г2 — 1
-Z1)3 _ 1
-г2)3’ Z1 ~ 2 /г4-1\2 = е з • гз. 13.193. w = I -- I .
\z - 1)
13.191. w
2г 4- V 3 4- i 2z — -\/3 4- i
Следовательно, D =
Наконец, если г = 1,
z|Rez < (полуплос-. л/3 1 . л/3
“гТ’ 22 = 2+гТ-/ , 1 \ 2
13.194. w =
г4 + 16>12 ЛОЙ +
?Т^) 13Л96-)3 /
I 2z \/3 -j- i
. 13.198. w = — ---------т=---
у 2г — v3 + г
юппп /2г + \/3 + Л
13.200. w = - ---------5=---- .
у 2г - V3 - ij
I z 13.203. w = 5/^4. 13.204. w =
V 2 + 2г - г \ z- R
13.197.
3/2
13.199.
13.201.
2
z - 1
w
w
w
——. 13.202. w = г — z
и2
липса -------7
1 /п IV
~Ar+r)
2
= V z2 + h2. 13.205. Как внутренность круга |г| < R при R < 1, так и внешность круга |г| > R при R > 1 отобразятся на внешность эл-V2
-----------т = 1. 13.206. Плоскость с раз-
4 V R)
резом по отрезку [—1, 5/4]. 13.207. Плоскость с разрезом по лучам 3 / 1
(—сю, —5/4], [1, +оо). 13.208. Один из ответов: w = - I z 4— ] — - + 8 у z J 4
//3 / 1\ 1 \2
+ w(oV + -l—-) —1 (причем выбирается та ветвь, которая точку у у 8 у z J 4 J
z = 0 переводит во внутренность круга |w| < 1). Указание, wi =
1 ( 1\ 3wi - 1 3
= 9 V + “ ’ W2 = -------Q’ W3 = ЛW2’ W4
Zi \ % 1 6 4
1, W =
Ответы и указания
505
If R2\
= W4 оW3оW2оwi. 13.209. w = I z 4-----I. Указание. Произвести
— K z x 1 ( i A
преобразование подобия w\ — — и для отображения w2 = - wi 4--
R 2 \ wi/
проследить за преобразование.м границы области. 13.210. w = -- х
а 4- о
х (г 4- \/z2 — с2), где с = т2 — b2. Указание. Производя преобра-z 1 (1 \ а зование подобия wi = - и определяя R из условий - [ R 4-=
с 2 \ R) с
| ~ 7г) ~ ~’ нах°Дим w2 = wi 4--\/w2 — 1 и W3 = ~^w2. 13.211. E =
= {w|Imw < 0}. 13.212. E = {w|Rew > 0}. 13.213. E = {w||w| > 1, w [1, 4-oo)}. 13.214. E = {w||w| > 1, 0 < argw < j. 13.215. E = = {w|l < |w| < e, Imw > 0}. 13.216. Если w = рег<р, то прямая x = С отображается в окружность р = ес, проходимую бесконечное число раз, а прямая у = С — в луч if = С. 13.217. Е = {w|0 < Imw < тг}. 13.218. Е = {w|Rew <0, 0 < Imw < тг}. 13.219. Е = {w|Rew < 0, 0 < Imw < 2тг}. 13.220. Е = {w|0 < Imw < 2тг, w u + iir для u > 0}. 13.221. E = {w|Imw < 0}. <] Представить cos г = = 4- е~гг) в виде композиции отображений wi = гг, w2 = eW1,
Wi = i ( w2 4- — | (рис. 49). > 13.222. Прямые x — С преобразуются 2 \ w2 )
(ш2)
Рис. 49 и2 v2 1
в эллипсы —- 4- — = 1, где a2 = -(ес 4- е~с)2 = (chС)2, Ь2 а2 Ь2 4
х (ес — е~с)2 = (shC)2, а прямые у = С — в гиперболы - о „ cos2 С
(ар)
1
4 Х
и2
506
Ответы и указания
-------5— = 1. 13.223. Так как область D содержит точки с симметрич-sin С
ными мнимыми частями, то область значений Е имеет два прообраза:
каждый из прямоугольников Di = {г| — тг < Re z < тг, — h < Im г < 0} и D-2 ~ {г| — тг < Re г < ж, 0 < Im г < h} отобразится на нижнюю по-U2 V2
ловину внутренности эллипса ------------Ь -=------ = 1, v < 0.
— (ел + е~л)2 — (ел — е~^)2
4 4
713
13.224. — 1 + 2г. 13.225.-— (2 + Зг). 13.229. Указание. Оценить
интегральную сумму (1) и, учитывая, что |Д^| перейти к пре-
2 8
делу при maxAsfc —> 0. 13.230. —4 + гтг. 13.231. - + 2г. 13.232. - -О о
/ 8 \ 1г
- -+4тт г. 13.233.— — -. 13.234.-2. 13.235. (2 sin 1 - е) +
\ о / oU о
13.238.
8
101(—l)ln5 - 25
20(7f2 + 1)
13.242. -^-4 •
3
х
х
+ г(1 - 2 cosl). 13.236. -г(1 + ew). 13.237.
О ch 1
х (1+ sh 1). 13.239. —-((гт2 - 4) - 4тгг). 13.240.
9 п -ч 51 2304.
х (1 - тг2 + 2тгг). 13.241. - — -
13.244. ^~(~73 +г). 13.245. 72(1 — 72 + г). 13.246.^. 13.247. —2гг.
4 6
2тг/
13.248. ( —1)п+1——-. 13.249. e(ecos8 — cosl) + ie(esin8 — sini).
(11 9 3\ / 93 1 1\
cos - ch - — cos - ch - I + i I sin - sh-sin - sh - 1.
42 4 2/ \ 4 2 4 2/
13.251. (2cosl - sini) +i(3shl -2chi). 13.252. -ln\/sh2 1 + cos 1 +
+ i arctg (tg 1 • th 1). 13.253. £ (z — zo)n dz = < П^И П
J I 2тгг при n = —1.
|z-z0|=fi
Указание. Произвести замену переменной z — zq = Re20.
13.254.
(z — z0)n dz =
0
27?2fc+1 ” 2k + 1
при n = -1,
при n = 2k + 1, k € Z, k -1.
при n = 2k.
Ответы и указания
507
13.255. ^2 —— бЬ — J — i(e3? — 1). 13.256. — (1 + 4k), k € Z. Указа-n 1
ние. В качестве пути интегрирования взять часть окружности z = - + + ^ег<р либо при 0 <р <С тг/2, либо при —Зтг/2 <р <С 0 и добавить любое число оборотов. 13.257. а) 0; б) —8тгг. 13.258. а) 2тгг; б) 0. 13.259. а) 0; б) тг; в) -тг. 13.260. а) тгг; б) 2тгг. 13.261. 0. 13.262. 0. 13.263. тг. 13.264. 0. 13.265. а) б) -^; в) 0. 13.266. -rrshl. 13.267. 2тгг. 8 8
i тг2
13.268. — — тг(тг + 2)\/2. 13.269. — sh 1. 13.270. тг3г. 13.271. 0.
8 2 1
13.273. Указание. Рассмотреть функцию <р(г) = -——г.
Глава 14
14.1. Да; 3. 14.2. Нет. 14.3. Да; 0. 14.4. Да; 0. 14.5. Да; 0. 14.6. Да; 0.
14.7. Да; 0. 14.8. Нет. 14.9. i(H-e~3p-2e~2P). 14.10. -^(2-2ре~2р -р 2р2
11 2
- Зе~2р + е~4р). 14.11. -е_рт(1 — т) +-т(1 — е~рт). 14.12. — (р-1 + р р2 рл
+ е~2р(р + 1)). 14.13. 1(1 - е~р - е~2р + е~3р). 14.14. -^—(1 -pt 1
1 , 2е~%р
е-2р7Г) 4— ——е~2 (1 + е-7гр)--т—(1—е пр). 14.15. У казание.
р(р2 + 1) тгр2
1 + р2 4 - 4р + р3
Воспользоваться теоремой подобия. 14.17. —;—. 14.18. — 7---.
рл 2рД1 — р)
14.19. 1 3 + 1420. -4^.+ 8^-4Р + 2 М21 _^+2
р+1 р + 2 р3 (р2 + 1)(4р2 + 1) р(р2 + 4)
14.22. f о . (р cos 2а - 2 sin 2а) ). 14.23. . 2 \р p2+4v V (р2-1)(р2-9)
14.24. р2 + 2 14.25. 3(р2 - 13) 4 р2 + 4
/ 14 26
р4 + 4 (р2 + 13)2 — 36р2 (р2 — 4)2
2 р2 2 6
14.27. (р2 + I)2 ’ 14.28. - . 14.29. . 14.30. -г.
. Р 4 + 4 (р + 2)л (р - 2)4
14.31. Р 14.32. - 14.33. + + .
р2 — 4р + 5 (р + 1) (р2 + 2р + 5) (р2 - 4)3
14.34. 2(р+1) 14.35. +--Q 14.36. - г. Указание
(р2 + 2р + 2) 2 р2(р + 2)2 р2(2р+1)
508
Ответы и указания
[ е~^-т>)т(1т = е~ъ * t. 14.37. 9. 2-. 14.38. -ут-у~-----------
J р2 (р2 + 4) р2 (р2 — 2р + 2)
о
14.39. In 11----). Указание. Воспользоваться теоремой ин-
2р \ р2)
тегрирования изображения, а затем теоремой интегрирования оригинала. 14.40. -lnfl + -Y 14.41. у- In + 7 • 14.42. j- In Р + .
р \ р/ 2р р — 1 2р р^ + /г
Указание. Воспользоваться теоремой интегрирования по параметру, а 1 р — Ct затем теоремой интегрирования оригинала. 14.43. -In------------
р р-/3 5
14.44. (р4 + 4р3 + 2р2 - Зр)Х (р)-. 14.45. (р3 + 6р2 + р - 2)Х(р) - 1.
2 е~р е~2р
14.46. (р2 + 5р - 7)Х(р) Н-ap- а. 14.47. ---. 14.48. ——.
р р - 1 2р(р2 +1)
тэр (Р 1)
14.49. - —. Указание. rj(t — l)tef = ep(t — l)((t — l)et-1 + ei-1).
(p - I)2
* Л n — P “1“ 1 ». / 7Г \ .
14.50. —e <p —--. Указание, nit—- sint = ri
2 p2 + l 4 4/ 1
x (sin (t — -у) + cos (t — 77У). 14.51. -(1 — e~pT). 14.52. -(1 — e~pT)e~pT. \ \ 4/ \ 4 // p p
7 1
14.53. -^-(l-e~pT-e~2pT + e-3pT). 14.54. ——-(1 -e"^)(l-pe"^). Tp2 P2 + 1
/1 e~p \ 1 2»2e-p7r
14.55. h[------------- I. 14.56. —---1-----——. 14.57. < Положим
\p p(p+l)/ p2 + l p4 - 1
х
14.56.
Тогда /о(^) = 0 (поскольку
/о(<) - "
0,
/(£) = f (t — /) при t I в силу периодичности). Переходя к изображе-I
ниям, отсюда находим То(р) = F(p) — e~ptF(p'), где F0(p) — je~pt f(t) dt. о
1
Следовательно, F(p) = -—----- = v ' 1 - e~pl
1 - e~pT
14.58. —--------
p(l — e~PT)
14.61.
P 2
14.59.
e-ptf(t}dt. >
0
cth^. 14.60.
2/3 he~pc
p(l — e_pc)
1 — e_pZ
р2 + /З2
14.62. А -ср2
1 + e-””
(p2 + 1)(1 - e~»TY
14.63. А Л?-cpz 2
/3
Ответы и указания
509
14.64.
14.67.
(7 —
14.70.
р+/3е % с cthp7r оо 1
------------=—. 14.65. ——14.66. ---г——. (р2 +/32)(1 - е-^) Р2 + 1 (р — а)м+1
1 (г'(^ + 1) __ Л 14кЯ _7 + Ь(р - а)
(p-a)M-i \Г(д+1) • У' 14,68‘ р — а
постоянная Эйлера). 14.69. |(Р + Tf ‘ •
7 2 (р2 + /32)^+1
l(P + W^-(P-ffiF+‘ W+fln^+^+larctgg 2г (р2 + /32)м+1 р2 _|_ ^2
parctg- - /Зу- |1п(р2 + /32) г-
14.72. ----. 14.73. . — е~ар. 14.74. te*.
рг + рл у р
14.75. |(e:u14.76. p~2t sh t. 14.77. 1 - e~l - te~l. 14.78. i -sini.
3 11
14.79. -(1 — e~2t cost — 4sini). 14.80. -(ch2i — cosi). 14.81. -isin4i.
1 / / 73 j 73 \ \ 1
14.82. - I e4/2 | cos —t H—7= sin— t — e~4 . 14.83. -shi sini.
3 у у 2 x/З 2 J I 2
14.84. p(t - 2)(i - 2). 14.85. |p(i - 2)(i - 2)2e-(4"2). 14.86. e24 +
+ p(t - 1) + p(t - 4)sin3(i - 4). 14.87. cos2i - 2p(t - l)ch2(i - 1). 00 f2n 00 f2n
£'-,r»TT>w-
...... у „
~ (2n +l)!(2n +1) J т ^ n!(2n)l
»V“—U Q Kj
14.92. е410(2лЛ). Указание. Применить теорему смещения к оригиналу, полученному в примере 4 из § 2. 14.93. e-24(cost — 2sini). Ill 1 n /
14.94. -e24 — ~e t ~ 77;COS^ — Tsin2i. 14.95. ePkt. 14.96. - x
6 15 10 5 ' 8
«=1
3 17 1
x (chi — cosi) — -(shi — sini). 14.97. —icosi — — sini + — sh2i.
8 10 50 50
1 12// \/3 1
14.98. -i(shi — sini). 14.99. - chi + - ch - cos ——. 14.100. -i2 cosi +
8 3 3 2 2 8
3 1 1
+-isini. 14.101.-(e34 - e4). 14.102. i - 2shi + ichi. 14.103. - x
8 2 3
x (ch2i-chi). 14.104. -7-(ch i + cosi) — 7 ch icosi. 14.105. rr(i) = 10 5
510
Ответы и указания
t ( t2\
= Ci cos3t + C2 sin3t + - sin3t. 14.106. x(t) = I Ci + C2t + — I e2t.
6 \ 2 /
/ /2 । /\ / f \
14.107. x(t) = 01+ 02---------- e~2t. 14.108. x(t) = Oi + - ef +
\ 4 / \ /
+ C2e~2t. 14.109. x(t) = Ci + O2e-t + |e-t(cosf - sint). 14.110. x(t) =
= e5 S*n ~2~ ~ C°S + 6 <’ = ^1 + t + e~l.
2 t 2
14.112. x(t) = -(e-3t - 1) - ~e~3t. 14.113. x(t) = -(1 - e^cost +
У о Э
1 7 t
+ -(l + 6ef) sin t. 14.114. z(t) = cos2t--sin2t--cos 2t. 14.115. x(t) =
~1. 14.111. x(t) =
25 1
= sh 3t - ch 3t - - sh t. 14.116. x(t) = 3 + t + (t - 2)e'. 14.117. x(t} = 24 8
fl f4
= - ch/—- sin f. 14.118. x(t) = —e~l. 14.119. x(t) = 1 —e~l — rdt — 2) x 4 4 24
x (1 — e~^~2)). 14.120. x(t) = sin t + ^(t — 7r)(t — тг) sin (t — тг).
14.121. z(t) = cht — 1 — -r](t - l)(ch(t - 1) - 1). 14.122. x(t) =
e
= 2 ^sin2 — 2r)(t — 1) sin2 * - - + p(t - 2) sin2 . 14.123. <] Уравнению x^ + + • • • + an-ix' + anx = 1 при нулевых началь-
ных условиях соответствует операторное уравнение L(p)Xi(p) = где Р
Xi(p) + xi(t), a L(p) = рп + aipn 1 + ••• + an_ip + an — характе-1
ристический многочлен уравнения. Отсюда L(p) = . Уравне-
нию я;(п) + aix(n~v> + • • • + an-ix' + anx = f(t) при нулевых началь-
ных условиях соответствует операторное уравнение L(p)Ar(p) = F(p), где Х(р) = T(t), a F(p) = /(t)- Отсюда Х(р) = = pXi(p)F(p).
JAP)
С помощью интеграла Дюамеля (см. § 1, свойство 11) получаем x(t) = t t
= Ti(O)/(t)+ У x\ (r)f(t — т)с1т = У x{ — t) dr (так как xi (0) = 0),
о 0
t
или x(t) = /(0)ti (t) + j f'fj^xi (t — r) dr. > 14.124. x(t) = |(e^ — 1) — J 0
t 1 4- 4 1 1 4- pt
— -el + -e4n-----------. 14.125. x(t) = -(ef — 1 — tef) + shtln .
9 9 t 2 2e£
Ответы и указания
511
14.126. x(t) = e*-l-(t + ln2)(ef + l)4-(e41)ln(e' + 1). 14.127. z(t) = t \ \
о I I 2 4" cos t
—-pr 4-cos tin---------. 14.128. x{t\ =
x/3 3 v 7
4 sin t t — -j= arctg
е т>) sin т dr (этот интеграл не выражается через элементарные
—e .
7/(t) = —tsint. 14.133. x(t) = sint — cost, ?/(t) = sint 4
14.134. x(t) = sint 4- sht, y(t) = cost 4- cht. 14.135. x(t) =
о
функции). 14.129. x(t) = Ci +С2 sin t + Сз cos t + t, yt = C4 4- C3 sin t — t2
— C2 cos t 4- —. 14.130. x = Ci 4- C2 sh t 4- C3 ch t, у = - C3 sh t -
— C^cht 4- cht 4- cost 14.131. x(t) — , yff) = —el. 14.132. j.(t) =
— tcost, 4- cost t2
= 14----, y(t) = 1 — el. 14.136. x(t) = — sin t, y(t} = — cos t, z(t) — sin t.
14.137. z(t) = (14-i-sini-cosf)-277 (x - ) — sin [t - 4-
4- 77(i-7r)(-14-(t-7r)4-cos(t - 7r)-sin(t - 7r)), y(t) = (l-t4-sint-cost) — — 2/7 (t - fl - cos (t - 4- T](t - 7г)(1 4- (t - 7r) - sin (t - 7г) -
— cos(t —7г)). 14.138. a:(t) = |(cht 4-cost - 2) - 7/(t — 7r)(ch(t - 7г) 4-4- cos (t - тг) - 2) 4- ^//(t - 2?r)(ch (t - 2тг) 4- cos (t - 2тг) — 2), y(t) = = -(cht-cost)—z/(t-7r)(ch (t - 7r)-cos(t - 7r))4-|z/(t-27r)(ch (t — 2тг) -
2 2 1
- cos (t — 2тг)). 14.139. 2 sint. 14.140. ch 2t--sh 2t. 14.141.
14.142. cht. 14.143. —7:. 14.144. r . . Jrz . 14.145.^,7/) =
Vi 1 (1 4- p) 1 (a 4- p)
= у cos x 4- x sin x. 14.146. z(x, y) = ~ sha(y — t)/(t) dt. a 0
14.147. u(x, t) = q(t — xx/LC} = Esincu(t — xx/LC), i(x, t) = J— x
x q(t—xx/LC) = E^J — sinu^t-xy/LC), t > xx/LC. <] Предполагая, что u(x, t) и i(x, t) и их производные как функции переменной t являются оригиналами, и обозначая U(x, р) =’ u(x, t), 1(ж, р) = i(x, t), получим dU(x,p) dl(x,p) ( .
операторные уравнения —------= —Lpl(x, р), ——— = —GpU{x, р)
512
Ответы и указания
Euj
с граничными условиями q(t) = C/(0, p) = Q(p) = 2~^'^2 . Исключая cPU(ж, p)
I(x, p) из первого уравнения и считая p параметром, находим-—7— =
dx2
= LCp2U(x, р). Отсюда U(x, р) = А(р)ер'^^х+В(р)е~ру^^х. Из физических соображений следует, что при х -> +оо решение U(х, р) ограничено, а потому при Rep > 0 коэффициент при первом слагаемом должен Еи
быть равен нулю, т.е. А(р) = 0. Далее, из условия £7(0, р) = —z-г
р2 + си2
следует, что U(x, р) = —z-а тогда 1(х, р) = — — х
р2 + си2 Lp
дЩх,р) fC Еш тт
x -------- = \ Применяя теорему запаздывания,
ox V L рг +
находим отсюда искомое решение. >
14.148. u(x, i) = Ee~l'y^^x(r](t — x\/LC) — p(i — x\/LC — t)); i(x, i) = Ee-'-jTSx^(t-xVLC)-^t-xVLC-т)). 14.149. In + 7?.
1 <Г'(д + 1) , \ „
—тг --------r;—Ina . Указание. Использовать решение
\Г(р+ 1) /
14.67. 14.151. ^e~at. 14.152.
2
14.155. Va). Указание. В задан-
14.150.
задачи
14.153.
14.154.
ном интеграле предварительно положить х2 = и. 14.156. 2. <) Имеем +оо pi /* e~t
—----------2 = tsh k = 1. Поэтому по формуле (9) S = / -------—t х
(р2 -1) 0
У te ^dt=-(te 2+2е 2)|+°°=2. > о
9 1 1 тт 1
О arctg — ~ arctg--------- — arctg------. Но arctg - =
n— 1 n + 1 p
1 _,sini 1 .sini .
—, arctg------- .= e ---- (по теореме сме-
t p — 1 t
T t , 1
x sh - dt = -2 2
14.157. 77г. 4 sini _ _.____
= , arctg—~=e t——, arctg--------- =
i p+1 i p-1
2 _g c
щения). Следовательно, arctg — =' f(t) = ---sini; k = 1. Поэто-
p2 i
/e e* — e 1 f 1 + e
-----г------sin t dt = / --sin tdt.
1 - e~l t J t
о о
Ответы и указания
513
sini = arctg - + arctg = F(p), F(0) = arctg(+oo) + 4-oo 3 f 1 +
+ arctg 1 = -тг. Следовательно, по формуле (6) / -----
о
— -тг. > 14.158. Указание. — ------------rrir—z-----zv
4 2 (p2 + l)(p2 + 2p + 2)
1 7Г 3
----й—z-----z• 14.159. -. Указание, arctg ——----------p2 + 2p + 2 2 n2 + 3n + 1
— arctg-----см. решение задачи 14.157. 14.160. arctga;.
n + 3
Положить Ф(£, x) =
Ф(£, x) = - , -~-
... . t sin a;
7 1- 2tcosx + t2
Но —-t
t
sin t dt =
1
р2 + 1
1
= arctg ---
п
У казание.
X
-----14.161. arcsine. У к а з а н и е. Положить
1 + x2t
14.162.
7Г — X
. <) Используем производящую функ-
2
tn sin пх. Имеем
Ф(е l, x) —
e 1 sin x
1 — 2e~t cos a; + e~2t ’
- = = f(t), rj(t) = 1 при t 0. Находим по формуле (10):
/e 1 smx dt
-----—-----------— = sin X
1 — 2e~l cos a; + e~lt
о
e 1 dt
о
— cos a:)2 + sin2 x
e — cos x
= — arctg------;------
sin X
-roo ч
. . 1 — COS X
= — arctg (- etg a;) + arctg —:---------
0 sin x
и, так как — arctg (— etg x) = arctg (etg x) = — — x,
arctg
1 — cos x / x\ x
= arctg |^tg -j =
sin a;
. 7Г X
TO T(x) = --x + - = Использовать разложение
7Г — X
2
>
14.163. - In
. Указание.
1 4-1 cos x
1 + 2t cos x + t2
= ^2(-l)nin cosnx, n—O
514
Ответы и указания
положив Ф(£, т)
14.165. (1 -e-f
R k
1 + t COS X
1 + 2t cos x + t2 E -Uq
14.166.
1 R2
ПРИ LC > 4L2 ’
Е — Uq __r_.
—-—te ы
R2 ’ 4L2 R2
LVTc
ПрИ LC ~ 4£2’
14.164. U°e
R
• / 1 e 2Llsinw—-
У L\j
4L2*
, R2Г
X shV4£2_Zc(
при Zc
R2
4L2'
1
___
xVi2 iR2* [LTZZL \ L2 4R2
k 2RLi
при
1
/ 1 L, X^4R2 L2 9/7 /-L-^
V 4Л2 L2
E -Uq
4L2
=e x 1
LC
14.167. Ee~™^l\ cos-- x k Li
. 1 Mi 1 Mi Sm£i V L2 4R2 J при L2 4R2
Li 1 „__l_( / , 1
Гг=й?’ Ee^leh-x
L2 4R2 ’
14.168. ~~^e Д^+С)*. 14.169. E\l-e ^r^1 (ch.V±i^
L + C I I 2C7?2
_ №fl2-2)y4 + fl^ ч/4 + Я^ \\ f((_L_2L
4C2Rl 2CR2 ))' ' ’ ^ЛС 3C
’ v x/L2+4C2 ± y/L2+4C2 v \M2+4C2 Ch 2LRC ‘—4LCIV Sh
2L зсе
Е
14.171. ro „
R2 + L2u2
x e or 1 I t----.
k 2 J
14.173. у
c
. /1 R2 4
X SmV LC 4C2i+J__ LC
14174 e9(e(? -eQ cos/3)
e2q — 2eq+a cos /3 4- e2a
*1 + R sin <jjt — L(jJ cos ijjt^.
^—^-e-At^t-t2 -
~ 4L
. 2 1 1 R2 \
R2 Sm 2 V LC 4L2J‘ 4L2
• 2
14.176.
(e9 — eQ)3
. 14.177.
(е9
2LRC J )'
14.172. x
R
2
===== x
1 R2
LC 4L
e9(e9-acos/3)
I'l. 11 □. ~ T ~ T.
е2ч — 2aeq cos /3 + a2
1
14.178.
. У к а-
Ответы и указания
515
e(m+l)9 e(m+l)q
зание. По свойству 3, а). 14.179. ------при тп < к- -----------—г-
m — 1
У Cr*e(m-r)9 при
Указание. По свойству 3,6).
r=k
14.180. arctg----—. <) Применяем формулу интегрирования изобра-
е9 - cos р
(свойство 5, б)):
женин
sin /Зп п
/е9 sin /3 dq _ f е9 sin /3 dq
e2q — 2e9 cos/3 + 1 J q(e^ — cos /3)2 + sin2 /3 я я
eq — cos /3 = arctg-—-—
sm/3
sin
= arctg------------
ь eq — cos /3
( eq - cos /3
так как arctg-----—
I sin p
14.181. /(n) = -|ln +
14.182. /(n) = sin cos П~^7Г. 14.183. /(n) = (\/2)n+1 cos ~яг-
Указание. Использовать формулы для изображения функций an sin /Зп п(г+11
и ап cos /Зп (пример 3 и задача 14.175). 14.184. ^”"L1
2
14.185. --------(sin/3 — 2п 1 sinп(3 + 2nsin(n — 1)/3) при n 1.
5 — 4 cos р п(п4 — 1)
14.186. --—----. Указание. Использовать формулу умножения изо-
OU
1_1+д
1 t 1 9 г
бражений. 14.187. -------•=---. 14.188. —----—14.189. хп =
2<2_^+1 1-г + г2
-2)п+1). 14,190. хп = —= sin —14.191. хп = V 3 3
= sin -—14Д92. хп = (2х0 - ол)1п + (ал - х0)2п = Сх + С2 • 2п. 14.193. х„ = 2п - (n + 1). 14.194. хп = (ал - 2z0 - 2)3П + (1 - ал + + За;0)2п +4n = Ci • Зп + С2 • 2П + 4п. 14.195. хп = (~1)п + 2п + Зп, уп = 2(—1)п - 2п - Зп. 14.196. хп = ~Х°- ~ -° • 2п + - -° +-° • Зп = 5 5
= Сг2п+С2-Зп, уп = -У~ -2п+3уо~ 6X9 -3n = -Ci-2n+1+C2-3n+1.
5 5
тг е9 — cos /3 = — - arctg----:—-—
2 sin (3
я
1 1 2п~
-2П + — (-2)п = --------
4 12к ' 3
; 14.183. /(п) = (\/2)n+1 cos
= arctg
sin В \
--------п • > е9 - cos pl
Пп-2\ _ in—3
1
7
я
п
t
3
516
Ответы и указания
Глава 15
X X
15.4. у(х} = ех—2х—2xy(t) dt. 15.5. у(х) = 2х—9+j (2 — х 4- £) х о 2
X xyttjdt. 15.6. у{х) = ех(х - 1) - sina; 4- х 4- j {s\nx — ех{х - t))y{t)dt. о
х о
If т3
15.7. у(х) = ех — х — - х(х — tfyfj;') dt. 15.8. у(х) = —----х -
о
Я (ж — t)3 А
х - t — -—I y(t)dt. 15.9.У казание. Воспользоваться фор-о
мулой
dtn-i
a
п—2
a
15.10. у(х) = х + я +
X
х
/ 1 "-.ту [ (x-t^-'y^dt. (п- 1)! J
X X
tsiny(t)dt. 15.11. у(х) = х3 — х 4- 1 4- f y2(t)dt.
тг 1
X X
/2 />
7/2(i) dt, у2(х) = у 4- 2 4- / 7/?(t) dt. 15.13. yi (а;) =
О о
хх х
= - 3 4- У т/2(£) dt, у2(х) = 1 + У y3(t)dt, у3(х) =-1 + f y2(t)dt. 0 0 о
х х
f f X2
15.14. 7/1 (х) = 14- / 7/2(t) dt, 7/2(ж) = / y3(f)dt, y3(x) = — 4-
15.16. y(x) =
4- У ty2(t)dt — У y^ttydt. 15.15. y(x) = ex(x 4- 1). о о
= e^2/2. 15.17. ytx) = y-j-—- 4- a; arctga; — - In (1 4- x2).
= cosare~(a:+sina:). 15.19. у(х) = 2ex — 2cosa; 4- 5sina;.
= - e'x. 15.21. т/(а;) = i I ex 4- 3 cos x 4- 3 sin x — 4e x/2cos^—x 0 \
15.18. т/(я) =
15.20. y(x) =
2 Z)'
15.22. y(x) = 1. 15.23. y(x) = xchx. 15.24. t/(x) = ^ex 4- ^e~x^2 x
Ответы и указания
517
f 1 . 77 Q 77
X —7= sin —~x + 3 COS ~~X \ a/7 2 2
15.25. y(x) = ex. 15.26. y(x) = x.
00 2/c+l r
15.27. y(x') = 1. 15.28. у(х) = l+sV —7—7-77 = l+xex /2 / /2 dt.
(2k 4- 1)!!
0
x2 а;Р + 1
e~. 15.30. y(x) — e ₽+1 . 15.31. y(x} — sina;. 15.32. y(x) =
15.34. y(x) — (1 +a;2)e_2:r. 15.35. уг(х) —
_*1
2 .
3.2_f2 a:3-/3 a.3_f3
teA£-2 . 15.40. а;2ел з . 15.41. xtexs~^ .
15.43. е(л+1)(а;-0, 15.44. 2sh 1-8,1 геА^-^.
15.46. ^~^+1 ел(ж-<). 15.47. ^eA(*-0.
хг — x + 1 ch t
2 3 1 1 2
15.50. e-^". 15.51. xe^. 15.52. ~e3x------cosa; + - sina;. 15.53. ex chx.
5 5 5
ex
---15.55. ex(x - 1) + 1. 15.56. cha; - 1. 15.57. e2x - ex. + x2
\/3
15.58. -7= e1/2 sin—-a;. 15.59. 2ex —x — 1. 15.60. 2 sin a; —a;. 15.61. y(x) = v3 2
2 / 73 7fA 1 14
-e-t sin I ~~x~x + — I • 15.62. -e2x(2x + 3) + -. 15.63. - —
О \ZO/ 4 4 о
15.29. y(x) =
= chx. 15.33. y(x) = (2е)ж.
~ T
15.38.
15.42.
15.45.
15.54.
1 x 3е
1
x7
- —. 15.36. У2(х) = x + a; cos a; — sin a;. 15.37. У2(a;) = 1 — e DO
^(t-x) 15>39<
,4 Л xt2ex 4 .
l+*2cX(*-n
—-cos-УЗж. 15.64.1. 15.67. 2 - e"1. 15.68. chx 4- cosx. 15.69. e~x x
3
/ x2 .
(1 + T;
72
4-V^sin —-x. 15.72. y\(a;) = 1 — 2cosa;, y-Ax) = 2 sina;. 15.73. yi (a;) =
3 6 1 11
= — — -X—— ex(3 cos 2x-4sin2a;), y2(x) = — - + -ex(cos2x + 2sin2x').
25 5 25 5 5
/ 7з 1 \/3 \
15.74. уi (a;) = x + e~x — ex^2 I cos -x~x-7= sin ~x~x I, y2(x) =
\ " v 3 /
x
1 / 75
15.70. -e~? 14-4 ch — x
5 \ 2
72
15.71. 2 — COS ~^~X 4-
-e~x
2 уЗ
4- sin — x. 15.75.1/1 (z) = (a;4-2) sin a;4-(2a;4-1) cos a;,
/1 \ . /1
= -l-4-a;lsina;4-l-
У2&) =
15.76. yi (x) = 2 sina;, a;2
= 2cosx - 1, y3(x) = x. 15.78. ex. 15.79. x - —. 15.80. 1
15.81.1. 15.82. a;. 15.83.3. 15.84. Решения нет. 15.85. e~x ( 7 — sina; ].
\2 J
У2&) =
— a;ln3.
518
Ответы и указания
2 ( 1 А
15.86. хех . 15.87. 3(2ж - 1). 15.88. ch ж. 15.89. а;2 (б+-а;21.
15.90. 2 sin ж. 15.91. 2 cosa; — 1. 15.92. Решения нет. 15.93. ^(е21 “ 1)-(1 \ 15
1Н—а;2). 15.95.1. 15.96.1. 15.97.—а;. У к а з а н ие. Восполь-2 / 4
2
зеваться формулой Г(г + 1) — zV(z). 15.98. За;. 15.99. -. 15.100. 1 — х. О
2 1
15.101. 4sinar. 15.102. -cosx. 15.103. R(x, t. A) = -----y(x) =
= sina;. 15.104. R(x, t. A) = 2x+t-------, y(x) = —-2,c+1 + x.
1 ЗА In 2
~ 21n2 t
15.105. R(x, t, A) = a;sin27r<, y(x) = cos27ra;. 15.106. R(x, t, A) = - ,
1 — A
2
?/(a;) = e~x + x. 15.107. R(x, t, A) = ------- sin x cos a;, y(x) = 1 + 2 sin x.
L — A
15.109. 1 + ^x. 15.110. +-cos2ttx. 15.111. x — 7Гcosa;. 15.112. 7 + 6a;2.
15.113. sina;—-a;. 15.114. sina;+cosx. 15.115. Решения нет. 15.116. x + 6
+ C(1 - a;2). 15.117. x. 15.118. cos2 a; + ——. 15.119. Cx. v 7 2(2 - In 2)
1 /5 A
15.120. 0. 15.121. cos2тга;. 15.122. x + -. 15.123. Cl-x + x2].
15.124. Решения нет. 15.125. 1 + y/x. 15.126. Cicosa; + C2 sin x. 5 6
15.127. 27r2cos27ra; + -(2a;2 - 1). 15.128. 0. 15.129. A = y(x) = О I
3
= C(1 + 2a;). 15.130. A = y(x} = C(1 - a;2). 15.131. A = 1, y(x) =
1 2
= C|a;|. 15.132. A = —, y(x) = Cx. 15.133. A = —, y(x) = Ccosx. 7Г ‘ 7Г
15.134. /ii)2 = I ± -^=; yi,2(x) = C(V^x ± 1). 15.135. //lj2 = 1 ±
2 у 3
±
-(e - l)a; ± 1 . 15.136. A = -2%, y(x) = C.
....... 2 , 4
15.139. При A ± | y(x) = x2 + при
5 2 о — 5A
15.140. При A 2 y(x) = sin27ra;, при A = 2
15.141. При A = 1 — ПрИ A = 6
2 2
15.137. Ai,2 = ±—, 3/1,2(ж) = C(sina; ± cosa;). 15.138. A = —, y(x) = 7Г ’ ~
— Cl COS X + C-2 sin X.
' 6
A = - решения нет. 5
y(x) = sin 2тга; + Cx.
Ответы и указания
519
3 2тг
?/(т) = 1 - -х 4- 0(1 + 2т). 15.142. При Л —2тг у(х) = ------------х, при
2 2тг + А
7Г
Л = -2тг решения нет. 15.143. у(х) = ctgT + —А, А 6 К. 15.144. При
\ / 1 z \ I 7г2А / \ тгА .
А 0 I у(х) = —. 15.145. у(х) = cost + — shit,
I 3 л I
А € К. 15.146. При А -у(х) = shittt 4----------------—а т, при А = -
2 2 1 х 2
1 зА
3 3 \/3
1/(т) = sin7гт + —т 4- С, при А = - решения нет. 15.147. При А ± —
2тг 2 2
/А 1 3
У(х) = - + -т 4-
/3 2’ „ 2 \ у/3
-----д— I (1 4- 2А)т 4-1 4- -А 1, при А = ±— реше-
1 - -А2 \ 3 / 2
3
2 2А 2
ния нет. 15.148. При А ±— т/(т) = 1------------г—sinT, при А = —
7Г 1 । АТТ 7Г
2
у(х) = 1-sinT + Ccost, при А = — решения нет. 15.149. Ап = —тг2п2, 7Г
тг2 2п Ч- 1
уп = sin тгпт, п е N. 15.150. Ап = - — {2к + I)2, уп = sin;r—-—т, п = 0, 1, 2, ... 15.151. Ап = — и2, где cun — корни уравнения си = 1+рЯ2.
I 1 \
т, п = О, 1, 2, ... 15.153. An = 1 - ( J , Уп = п = О, 1, 2, ... 15.154. An = 1 — 7г2тг2, уп = зштгпт, п € N. 15.155. Ап = — 1 — 7г2п2, уп = simmx, п € N. 15.156. Ao = 1, Уо = 1; An = 1 — 4п2, уп = Ci cos2ttx 4- С2 sin2;rT, п G N. 15.157. Ап = = 1 4- си2, где сип — корни уравнения cu = ctg2си, уп = coscunT, п 6 N. 15.158. При А Ап = —7г2п2, nEN,
= ctgcu, уп = coscun(T - 1), п € N. 15.152. Л,
. 2n + 1
Уп = sin—-—
2п + 1
= cos-----X,
2
, . . . v'' 1 4 sin тг(2к 4- 1)т
при Л = Х2т, т € N,
1
У(я) — 1 "Ь ^2m '
к-0
^2&+1 Х2т
4sin7r(2/c 4- 1)т _ . л
------—--------— 4- С sm 2тг тт;
7г(2/с + 1)
при А = A2m+i, т = О, 1, ... решения нет. 15.159. При А Ап
520
Ответы и указания
/ 2п + 1 \
1~2 /
, п = 0, 1, 2, ...
у(х) = sin 7ГХ COS —X
1 . тг
Г1ПГ +
1
А = Ао = - — и А = Ai = 4
п = 2, 3, ..
9тг2
—— решения нет; при А = А
у (х) = sin ях cos —х — X
1 . ТГ
1
. тг(2п + 1) + С sin --—-------
( 2 1 1 \
15.160. При А Хп = 1 — ( -— ) , п = 0, 1, 2, ...,
ОО
у(х) = X - 7Г + A
п=0
2п + 1
• cos —-—х;
при А = Хп решения нет. 15.161. При А = Хп = 1—4тг2п2, п = 0, 1, 2, ..., у(х) = (1 - А)-1; при А = Ao = 1 решения нет, при А = An, п € N,
у (ж) — ;—Ц—Ь cos ^пх + ^2 sin 2пх.
1 Ап
15.162. ’) -3,1459, -3,0518, -2,9692, -2,8983, -2,8387, -2,7903,
-2,7527, -2,7257, -2,7088, -2,7015, -2,7033, -2,7137, -2,7321,-2,7577, -2,7900, -2,8282, -2,8715, -2,9193, -2,9707, -3,0247,-3,0811.
’) Ответы I? задачам 15.162-15.184 приводятся в виде значений функции у (ж) в точках отрезка [0, 1], выбранных с шагом Дж = 0,05, т.е. yk — у(%к} — = у (А: Дж), к = 0, 1, .. •, 20. При решении этих задач методом конечных сумм, либо моментов следует сравнить значения полученного решения с приведенным в точках вида Xk = к • 0,05, к = 0, 1, ..., 20.
Ответы и указания
521
15.163. -4,3533, -4,3578, -4,3031, -4,3688, -4,3747, -4,3806, -4,3863, -4,3914, -4,3956, -4,3985, -4,3998, -4,3988, -4,3950, -4,3877, -4,3759, -4,3585, —4,3341, -4,3008, -4,2563, -4,1974, -4,1198. 15.164. 0,5335, 0,3333, 0,1614, 0,0109, -0,1233, -0,2448, -0,3566, -0,4608, -0,5594, -0,6535, -0,7444, -0,8332, -0,9209, -1,0082, -1,0959, -1,1848, -1,2758, -1,3695, -1,4668, -1,5688, -1,6765. 15.165. 63,0353, 63,9561, 64,8184, 65,6236, 66,3731, 67,0681, 67,7100, 68,2999, 68,8388, 69,3277, 69,7680, 70,1604, 70,5058, 70,8054, 71,0600, 71,2707, 71,4384, 71,5642, 71,6409, 71,6940, 71,6998. 15.166. 1,0000, 1,0135, 1,0172, 1,0111, 0,9955, 0,9709, 0,9376, 0,8963, 0,8476, 0,7921, 0,7306, 0,6641, 0,5933, 0,5192, 0,4428, 0,3651, 0,2870, 0,2096, 0,1340, 0,0610, -0,0083. 15.167. 0,0000, 0,2209, 0,4469, 0,6780, 0,9142, 1,1557, 1,4025, 1,6546, 1,9121, 2,1751, 2,4436, 2,7176, 2,9972, 3,2825, 3,5734, 3,8701, 4,1726, 4,4809, 4,7950, 5,1150, 5,4410. 15.168. 0,3123, 0,2985, 0,2796, 0,2555, 0,2264, 0,1925, 0,1539, 0,1111, 0,0641, 0,0134, -0,0407, -0,0978, -1,1575, -0,2192, -0,2827, -0,3472, -0,4125, -0,4780, -0,6076, -0,6708. 15.169. 2,4334, 2,3247, 2,1981, 2,0532, 1,8890, 1,7072, 1,5056, 1,2843, 1,0430, 0,7813, 0,4988, 0,1951, -0,1303, -0,4778, -0,8480, -1,2413, -1,6584, -2,0997, -2,5659, -3,0576, -3,5754. 15.170. -1,1130, -1,0644, -1,0122, -0,9562, -0,8963, -0,8322, -0,7639, -0,6910, -0,6134, -0,5308, -0,4431, -0,3500, -0,2513, -0,1466, -0,0358, 0,0815, 0,2056, 0,3369, 0,4755, 0,6220, 0,7766. 15.171. 0,9897, 0,9686, 0,9376, 0,8970, 0,8469, 0,7879, 0,7202, 0,6446, 0,5617, 0,4722, 0,3768, 0,2763, 0,1719, 0,0643, -0,0455, -0,1565, -0,2675, -0,3777, -0,4860, -0,5914, -0,6929. 15.172. -0,1988, -0,1636, -0,1312, -0,1016, -0,0744, -0,0497, -0,0273, -0,0071, 0,0110, 0,0270, 0,0410, 0,0530, 0,0630, 0,0711, 0,0774, 0,0818, 0,0842, 0,0848< 0,0834, 0,0802, 0,0750. 15.173. 0,8313, 0,8287, 0,8039, 0,7577, 0,6912, 0,6062, 0,5048, 0,3894, 0,2629, 0,1281, -0,0116, -0,1528, -0,2922, -0,4265, -0,5526, -0,6672, -0,7678, -0,8518, -0,9172, -0,9623, -0,9859. 15.174. -2,0000, -2,0579, -2,1294, -2,2145, -2,3133, -2,4257, -2,5517, -2,6913, -2,8446, -3,0114, -3,1920, -3,3861, -23,5938, -3,8152, -4,0502, -4,2988, -4,5610, -4,8369, -5,1263, -5,4294, -5,7462. 15.175. -2,8204, -2,7112, -2,5946, -2,4700, -2,3366, -2,1938, -2,0408, -1,8768, -1,7009, -1,5122, -1,3096, -1,0922, -0,8587, -0,6050, -0,3388, -0,0497, 0,2607, 0,5939,
522
Ответы и указания
0,9518, 1,3351, 1,7488. 15.176. 4,7481, 4,9997, 5,2563, 5,5178, 5,7844, 6,0560, 6,3326, 6,6142, 6,9008, 7,1924, 7,4890, 7,7906, 8,0971, 8,4087, 8,7252, 9,0468, 9,3734, 9,7050, 10,0416, 10,3832, 10,7297. 15.177. 9,0000, 9,6196, 10,4009, 11,3784, 12,5934, 14,0952, 15,9423, 18,2048, 20,9659, 24,3244, 28,3977, 33,3252, 39,2718, 46,4331, 55,0407, 65,3683, 77,7398, 92,5376, 110,213, 131,300, 156,4264. 15.178. -0,7005, -0,5713, -0,4441, -0,3191, -0,1964, -0,0760, 0,0420, 0,1574, 0,2702, 0,3804, 0,4878, 0,5923, 0,6938, 0,7924, 0,8879, 0,9802, 1,0693, 1,1552, 1,2376, 1,3167, 1,3923. 15.179. 2,0380, 1,8073, 1,5597, 1,2958, 1,0164, 0,7219, 0,4131, 0,0909, -20,243, -0,589, -0,945, -1,310, -1,682, -2,059, -2,440, -2,821, -3,200, -3,574, -3,939, -4,290, -4,6216. 15.180. 0,0000, 0,0501, 0,1004, 0,1517, 0,2027, 0,2556, 0,3076, 0,3625, 0,4151, 0,4717, 0,5247, 0,5823, 0,6349, 0,6926, 0,7443, 0,8008, 0,8508, 0,9053, 0,9535, 1,0059, 1,0499. 15.181. 1,0000, 1,1550, 1,3207, 1,4969, 1,6862, 1,8859, 2,1029, 2,3292, 2,5790, 2,8354, 3,1245, 3,4152, 3,7512, 4,0800, 4,4708, 4,8389, 5,2909, 5,6921, 6,2067, 6,6194, 7,2710. 15.182. -1,0000, -1,0087, -1,0196,
-1,0398, -1,0515, -1,0674, -1,0692, -1,0641, -1,0452, -1,0042, -0,9569, -0,8761, -0,8027, -0,6992, -0,6154, -0,5200, -0,4442, -0,3751, -0,3108, -0,2539, -0,1807. 15.183. 10,0000, 11,0564, 11,6033, 12,5516, 13,1184, 14,0373, 14,5906, 15,4312, 15,9774, 16,7572, 17,3502, 18,1492, 18,8795, 19,8175, 20,7997, 22,0172, 23,3845, 25,0395, 26,9496, 29,2271, 31,8675. 15.184. 0,2500, 0,3279, 0,4112, 0,5029, 0,6005, 0,7127, 0,8301, 0,9712, 1,1155, 1,2966, 1,4771, 1,7136, 1,9427, 2,2555, 2,5495, 2,9672, 3,3491, 3,9123, 4,4129, 5,1786, 5,7222.
Глава 16
d2u(x, t) 9d2u(x,t} 1 _. . . .
16.1. ——— = a ——------------1—r(x, t), где u[x, t) — отклонение
dt2 dx* p
точки струны с абсциссой х от положения равновесия в момент времени t, а2 =Т/р, р —.плотность струны, F(x, t) — плотность распределения действующих на струну внешних сил. <] Пусть a = a(x, t) — острый угол между осью абсцисс и касательной к струне в точке с абсциссой х в момент времени t. Условие малости колебаний означает, что величиной
Ответы и указания
523
2/ к • 1 ди
a (х, t) можно пренебречь, а потому имеем sin а а a, cos а « 1, — = дх
= tga « а. Длина любого участка М\М2 струны в момент времени t выражается формулой
Х1
2 dx,
(ди\2 2
а так как — ~ а ~ 0, то
\дх )
IM1M2I ~ Х2 - Х[ = Дж.
Согласно второму закону Ньютона сумма всех сил, действующих на участок струны М\М‘2, равна по величине и по направлению вектору ускорения этого участка, умноженному на его массу. Вычислим все силы, действующие на этот участок. Плотность распределения внешних сил обозначим через F(x, t), тогда внешняя сила, действующая на MiM2, равна F(x, t)Ax. Далее, силы натяжения 1\ и Т2, действующие на концах Mi и М2, направлены по касательным к дугам в соответствующих точках. Из малости колебаний и из того, что равнодействующая этих сил вызывает только вертикальные перемещения, заключаем, что горизонтальная составляющая равнодействующей равна нулю, т. е. —Т\ cosqi 4- Т2 cos «2 = 0- Так как cos ад a cos а2 ~ 1, то отсюда выводим равенство Ту = Т2 = Т. Следовательно, вертикальная составляющая сил натяжения дается выражением Т sin а2 — Т sin ад и сумма всех сил Fm1m2} действующих на участок MiM2, равна
Fmxm2 — T(sina2 — sinai) 4- F(x, <)Дж.
Но в момент времени t a = a(x) = arctgu'x, а потому
sin «2 — sinai = sina(xi 4- Дж) — sina(xi) =
= cosa(a?i 4- 9 Дж)(а(ж1 4- Дж) — а(ж1)) =
= соза(ж1 +0Дж)(аг^и'Х|;с=а:1+01 А* =
= соза(ж1 4- 9 Дж)
Дж
х=ху+0\ Дх
(О < 9 < 1, 0 < 9Х < 1).
524
Ответы и указания
При наших предположениях cosa(a?i + 0 Ах) « 1 и (^)2|а._а.1+б1 Да.« 0. Таким образом,
_ d2u(xi + @1 Ах, t) . ч * / ч
FM1 м2 а Т-------—--------Ах 4- F(x, t) Ах. (*)
С другой стороны, считая участок материальной точкой (при достаточно малом Ах), имеем
Fmxm-1 = рАх. (**)
Приравняв согласно закону Ньютона выражения (*) и (**) и переходя к пределу при Ах —> 0, для искомой функции u(x, t) получаем дифферен-
u(x, t), определенную при 0 ж Z, и 0 t 4-оо, являющуюся решением уравнения
д2и 2^2« 1 .
aF _ ° + pF<-x’
(а2 = Т/р, Т — натяжение струны, р — плотность струны, F(x, t) — плотность распределения внешних сил) и удовлетворяющую условиям
u(0, t) = u(l, t) = 0 (граничные условия),
и(х, 0) = <р(ж), „ , ч (начальные условия).
= №)
16.3. Найти функцию u(x, t), определенную при 0^ж^/и0^(< Q2u d2u ( Т
<4-оо, являющуюся решением уравнения = a2y—z [а2 — —,Т — ot2 дх* \ р
натяжение, р — плотность струны) и удовлетворяющую условиям
u(l, t) = О,
ММ) дх
и(х, 0) = «/’(ж),
ди(х, 0) dt
(граничные условия),
(начальные условия).
Ответы и указания
525
Указание. Граничное условие при х = 0 получить из отсутствия на этом конце внешней силы и, следовательно, равенства нулю силы натяжения Т, пропорциональной . 16.4. Напряжение u(x, t) и сила
от
тока i(x, t) в точках линии в любой момент времени t должны удовлетворять волновому уравнению
d2w(x, t) _ d2w(x, t) ( dw(x, t)
- LC—+ (LC + ЛС)-^— + RGw(x, t).
<] Рассматриваем двухпроводную линию как систему равномерно распределенных индуктивностей, сопротивлений, емкостей и утечки
(см. рис. 50). Согласно первому закону Кирхгофа (алгебраическая сумма токов, сходящихся в узле, равна нулю) имеем
ди
i(x, t) — i(x + Да?, t) = С + G Ахи(х, t),
ди
где С Ах—----ток через конденсатор, a G Ахи(х, t) — ток утечки. Раз-
дх
делив это равенство на Ах и переходя к пределу при Ах —> 0, получим уравнение
^ = -С^-С«(М). (.)
Далее, согласно второму закону Кирхгофа падение напряжения и(х, t) на участке между х и х 4- Ах состоит из падения напряжения на индуктив-ности LAx—— и из падения напряжения на сопротивле
526
Ответы и указания
нии R Axi(x, t), т. е.
di(x О
u(x, t) — u(x + Ах, t) = L Ах—----- + R Axi(x, t).
Разделив на Ax и переходя к пределу при Ах —> 0, получим уравнение
дх ~ L dt
(**)
Уравнения (*) и (**) называются уравнениями длинной линии. Исключая из этих уравнений i(x, t), приходим к уравнению
d2u d2u du
~ = LC^ + (LC + RG)^ + RGu, (* * *)
dx2 dt2 dt
а исключая u(x, t) — к уравнению
d2i d2i di
~ = LC— + (LC + RG)- + RGi. (****) dxz dt2 dt
Уравнения (* * *) и (****) называют также телеграфными уравнениями. [> 16.5. Найти функции и(х, t) и i(x, t), определенные при 0 х < < 4-оои0^£< +оо, являющиеся решениями уравнения
d?w(x, t) _ d2w(x, t) dx^ ~ ° dt?
и удовлетворяющие условиям
u(x, 0) = (fi(x),
(начальные условия), i(x, 0) = i/)(x)
u(0, t) = Eo,
(граничные условия)
u(+oo, t) = г(+оо, t) = 0
(условия при x = +oo следуют из физических соображений). 16.6. Найти функцию и(х, t), являющуюся решением уравнения
du _ 2^2u
dt а dx2
Ответы и указания
527
и удовлетворяющую условиям
и(х, 0) = Uq
u(0, t) = ио,
(начальное условие)
u'x(l, t)+y[u(l, t) - </>(£)] = 0
(граничные условия),
S At, где S — площадь поперечного сечения стержня, а
Х=1
где 7 — коэффициент теплообмена между стержнем и средой. Указание. Для получения граничного условия при х = I заметим, что количество теплоты, проходящей через конец стержня за время At, равно л , ди' ^<1 = дх
к — коэффициент теплопроводности материала стержня. С другой стороны, Aq пропорционально произведению разности температур u(Z, t) —
— </?(t) на площадь S и на время At, т. е. Aq — h[u(l, t) — (^(t)]^ At, где
h 0 зависит от качества теплоизоляции конца стержня от окружающей h
среды. Сравнивая оба выражения для Aq и обозначая 7 = —, приходим к
к написанному граничному условию. 16.7. Пусть система координат выбрана так, что ось Oz параллельна образующей. Область, ограниченную кривой L в плоскости Оху, обозначим через D. Найти функцию и(х, у), которая для всех точек М(х, у) € D удовлетворяет уравнению
д2и д2и
-----1----= 0 дх2 ду2
т.е. является гармонической в области D, а на границе области, т.е. на кривой L, удовлетворяет условию
где f(x, у) — заданная на L непрерывная функция. Для установивши
шегося теплового процесса — = 0. 16.8. Гиперболический, иёп = 0. ot *'
16.9. Параболический. Выбирая £(х, у) = 2х — у и т)(х, у) = х, после преобразования получаем уравнение и”л -I- Зи^ = 0. 16.10. Эллиптический, u"M + u"v = 0, где ц(х, у) = — Зх — у = Re £(х, у) и v(x, у) ~ 2х = = Im£(ir, у). 16.11. Параболический. Выбирая £ = у/у — у/х и т] = х,
Q2U Л тт
после преобразования получаем уравнение = 0. 16.12. Параболиче-сч/2
528
Ответы и указания
'XX
ский. Выбирая £ = х2 + у2, т] = х при £ ту2, т. е. при у ф 0, получаем 2£ d2u
уравнение 4- --------и'^ = 0. При у = 0 имеем уравнение = 0, а
при х = 0 — уравнение и"х = 0. 16.13. В области D = {(а?, у)\х 0, у ф 0} гиперболический, - 2(^2 J~2j4 = 0- При
х = 0 или у — 0 параболический. 16.14. В области D = {(а?, у)\х > > 0, у > 0} эллиптический, и'^ 4- = 0. При х = 0 или у = О
параболический. 16.15. Гиперболический, и'£ = 0. 16.16. В области D = {(а?, 2/)|а? 0} гиперболический, и'^ — —-(и'^ — = 0.
При х = 0 параболический. 16.17. В области D эллиптический, и'^ 4- и'^ + — и'^ = 0. При х = 16.18. Параболический. Выбирая £(а?, у) = у/х и преобразования получаем уравнение и^(^, ту) = 0.
= <^(4а? — ту) 4- t/j(x — у), где <р(у) и 0(тт) — произвольные дважды дифференцируемые функции. <] Выбирая £(х, у) = 4х — у и ту(а?, у} — х — у,
= Ж 2/)к 0}
0 параболический. ту(а?, у) = у, после 16.19. н(х, у) =
приводим уравнение к виду и'^ = 0 (см. задачу 16.8), последовательно интегрируя которое, находим и'^ = <^о(С) и и(С> ^) — 4>o(£)d£ +
4- 0(уу) = <^(£) 4- 0(ту). Подставив сюда выражения для £(х, у) и ту(а?, у), получим искомое решение. 16.20. и(х, у) = i/)(2x — у)е~3х 4- ip(2x — — у), где </a(v) и ^(у) — произвольные дважды дифференцируемые функции. 16.21. и(х, у) = xip(y/y - у/х) 4- г^у/у - у/х), где </?(v) и 0(ц) — произвольные дважды дифференцируемые функции. 16.22. и(ж, ту) = = Ф(ту — a?4-cos т)-|-Ф(ту — х — cos а?), где Ф(ц) и Ф(п) — произвольные два-жды дифференцируемые функции. 16.23. и(х, у) — \ — }у 4- 01—),
где <р(у) и 0(v) — произвольные дважды дифференцируемые функции. х sin х cos at — at cos x sin at
16.24. u(x, t =------------------------.
x2 — azt*
16.25. u(x, t) =
x sin x cos at — at cos x sin at
x2 — a2t2
1 1 + (a? + at)2
+ 4a П 1 + (a? — at)2
1 Г x + t x — t
16.26. u(x, t) = - [1 + (a. + t)2 + ! + (rc _ <)2
16.27. u(x, 0 = |
1 1
1 + (x + t)2 + 1 4- (x - t)2
+ sin a? sint.
4- sin a? cost.
Ответы и указания
529
16.28. и(ж, t) = е
16.29. Если 0 t
u(x, t) =
т, 1 I
Если — t 2а a
u(x, t) =
•2+t2)•ch2ж^ + l —, то 2a 1. 1 - In -4 1
1/ -(ж + at) при
ж при
I — at при
2l-x при
, 1/ “ 2^"°^ при
О з при
1/ -(ж + at) при
, 1/ t — - (ж + at) при
I — at при
1/ -(ж + at) при
, 1/ /- -(ж-at) при
0 при
4- (а? + tY 4- (х - ty '
—at x at, at x I — at, I — at x I + at, I + at x 21 — at, 21 — at x 21 + at, остальных x.
—at x I — at,
I — at C x C at, at x 21 — at, 21 - at x C I + at, I + at x 21 + at, остальных x.
Если - t < +oo, to a
u(x, t) = <
-(ж + at)
, 1/
I — -\x + at)
1,
-(ж - at)
, 1/
/ - -(ж - at)
О
при —at C x I — at, при I — at С ж 21 — at, при at ж I + at, при I + at ж 21 + at, при остальных ж;
530
Ответы и указания
при
при
при
при остальных ж;
i(J-z) |(®-0 3Z х ~2~2 0
при — I х С О,
при 0 х С Z,
при I х 21,
при 21 <С х С 3/, при остальных х.
Указание. Рассмотреть случаи различного возможного расположения значений х — at и х 4- at на оси х, а именно: если х — at < 0, то х + at может лежать в промежутках (—оо, 0) (О, Z), (Z, 21) и (2/, 4-оо); если 0 < х — at < I, то точка х 4- at может лежать в промежутках (О, I), (I, 21) и (21, 4-оо); если I < х — at < 21, то точка х 4- at может лежать в промежутках (I, 21) и (21, 4-оо); если 21 < х — at < 4-оо, то и х 4- at G € (21, 4-оо). 16.30. Если 0 С t то 2a
( О
при —оо < х — h — at
u(x, t) = <
и
1/
- - (x 4- at 4- h)
—at
при h 4- at x < 4-00,
при — h — at C x at — h,
при at — h C x —at,
при —at x C at,
at
1/
-(-ж 4- at 4- h)
при at x C h — at,
при h — at C x h 4- at.
Ответы и указания
531
h h
Если — t , то 2а a
О
и
1,
--(x + at + h)
1,
-(х + at - h)
х
1,
~{х — at + h)
1
-(—ж + at 4- h)
при —oo < x — h — at при h + at x < +oo, при -h — at C x —at, при —at C x C at — h, при — h + at x < h — at, при h — at x at,
при at x h + at.
При t — имеем a
О при —oo < x C — h — at
и
при h + at ж < +oo,
u{x, t) = <
— - (x + at + h)
1,
-(x + at — h)
0
при — h — at С ж —at,
при — at ж C h — at,
при h — at ж at — h,
0
( h
u ж, —
\ 2a
^(ж — at + h)
1
ж + at + n)
ж
при at — h x at,
при at ж h + at.
f 3h\ , , /ЗЛ при ж e l-oo, —- I (J I —
( 3h h\ при xe (jy,
f h h\
при xe -j,
fh 3h\
при I£ .
532
Ответы и указания
( 3h
u x, —
I ’ 4a
О
х
1
2
1
2
1
2
1
2
7h\ при x € ( -сю, - <_7А 7/р 4 > ЗА
x 4- 4 ) при x € | 1 4 ’ ’ 4
A\ ( 3h А\
x — 4/ при x G | С 4 ’ “ 4/
/ h h'
при x G | \ 4’ 4, 1 5
A\ (h ЗА\
x 4- 4J при x € I \4’ 4 J 1 5
7h\ /ЗА 7h
-I+TJ при х Е 1 <4’4 1 .
7h
4
Указание. Рассмотреть'случаи различного возможного расположения значений х — at и х 4- at: если х — at < — h, то х + at может лежать в промежутках (-сю, —А), (-А, 0), (0, А) и (h, 4-сю); если —h < < х — at < 0, то х 4- at может лежать в промежутках (—А, 0), (0, h) и (h, 4-сю); если 0 < х — at < h, то х 4- at может лежать в промежутках (0, /г) и (А, 4-сю); если h < х — at < 4-сю, то и х 4- at € (А, 4-сю).
16.31. и(ж, t) = <
— sin ж sin at, a
-(1 — cosx cosat),
' 1 о 16.32. u(x, t) = * k 2 16.33. u(x, t) = — In 4a 16.34. u(x, t) = — In 4a f 1 + b . 2 {x 4- at)2 ( {x - at)2
1 4- (x 4- at)2 * 1 4- {x - at)2 (x 4- at)2 (at — x)2
1 4- (x 4- at)2 1 4-(at - x)2 1 4- (x 4- at)2 1 4- {x — at)2 1 4- (x 4- at)2 1 4- {x - at)2 + (x 4- at)2 {x - at)2
1 4- {x 4- at)2 1 4- (ж — at)2 (ж 4- at)2 ( (ж - at)2
1 4- (x 4- at)2 * 1 4- (ж - at)2
при
при
при
при
16.35. u(x, t) — е (l2+a2i2) chaxt 4-
-(1 — cos x cos at) a
1 • , X •
- sin (ж) sm at a
при
при
Ответы и указания
533
16.36. Если 0 t то a
u(x, t) = <
. ях irat sin — cos ——
sin y(a; — at)
0
при 0 x I — at,
при I — at x <C I 4- at,
при I 4- at x < 4-oo.
Если - t < 4-oo, to a
0
при 0 x at — I
u(x, t) = <
и
при I 4- at x < 4-oo,
i sin y(x - at) ii I
при at — I x at 4-1-
0
0
при при при
при при при
I
16.37. Если 0 t < -, to a
u(x, t) = <
ct
с .
—{I 4- at - x)
при
при
при
О х < I — at,
I — at х < I 4- at, I 4- at x < 4-00.
< 0
Если - t < oo, to a
ct
u(x, t) = <
c .
— {J 4- at — x)
0
при
при
при
О х at — I, at — I х < at 4-1, at + l<^.x< 4-oo.
534
Ответы и указания
( I
u z, -
\ О'
( Ы
u z, —
\ а
при о X < . 21,
0 при 21 5 с х * С 4-оо;
cl а при 0 ; X < : 4Z,
2а при 4Z ; х <6/,
0 при 6Z : <: х < 4-ос
16.38. Указание. Выражение (хп, уп) - (х, у) записать в виде (хп, уп- у)+(хп—х, у) и воспользоваться неравенством Коши-Буняковского. 16.40. Указание. Показать, что в произвольном ортонормированном базисе фундаментальность последовательности векторов {хп}пе^ эквивалентна фундаментальности числовых последовательностей их координат. 16.43. Указание. Воспользовавшись результатами задач 16.41 ь
У f(x)g(x) dx < a
и 16.42, доказать полноту пространства 16.44.
b b
У |/(z)|2 dx j |t/(z)|2 dx. 16.45. Указание. Пусть f(x) — произ-a a
вольная функция из [—1, 1] и h(t) — разрывная функция, равная — 1 при t < 0 и 1 при t 0. Неравенства Коши-Буняковского для интегралов (неравенства Шварца, см. задачу 16.44) следует, что
/ i \ 1/2
I [ (f(t) ~ dt | >
\ 1/2
2 dt |
ч 1/2
2 dt |
Показать, что
lim
2 dt = О,
-1
и в силу непрерывности
1
-1
Ответы и указания
535
Отсюда следует, что интеграл
2 dt не может стре-
миться к нулю при п —> оо, какова бы ни была f(t) G 1, 1].
16.51. Р0(х) =
75’ = /Iх’ = /у (*2
I), Aw = О у
= (х3 - 1Д16-52- = 4=>
у О \ 5 / у7Г
T1W = Jfx, f2(x) = у|(2а:2 - 1), TgW — d^-(4x3 — За:). 16.53. Указа-ние. При вычислении интегралов произ
вести замену переменной arccosz = 9.
16.54. <ро(х) = 1, — 2\/3 (х — -),
(^2 (ж) = 6\/5 (х2 — х 4- . 16.55. См.
рис. 51. Вертикальные прямые в точках разрыва проведены только для наглядности. 16.58. См. рис. 52. Вертикальные прямые в точках разрыва проведены для
0
-1 1 0 ro W
S f / ' < . f*.
-1 к / S > к ' 1 V1/
Рис. 51
наглядности. 16.60. <1 Учитывая, что I^ax) есть решение уравнения ху" + у1 + (а2х — - } у = 0 (см. гл. 12, задача 12.338), т.е. урав-\ XJ
нения
а . / о и \
— {ху)+[а х----------)у = О,
dx \ х/
и полагая Za = lyfax) и Ui = 11,(у/11г>х'), можно записать
4-(xZ'a) + (а2х-—} Za = 0
dx \ х )
и
4-W) + (уУУх --}и, = 0.
dx \ х J
536
Ответы и указания
Рис. 52
Умножая первое равенство на Ut, второе на ZQ, вычитая из первого полученного равенства второе и принимая во внимание соотношение - za-i-(xVD = £(zaxu; - xu.z’3, dx dx dx
получим
4-<,xZaU't - xUtZ'a) + - a2)ZM = 0.
dx
Интегрируя это равенство в пределах от 0 до 1 и учитывая, что -^-(Za) = dx
d
= —ly(ax) = aF (ax), приходим к равенству dx
((/4И)2 ~ a2) / Iv{^x}Iv{ax}xdx -
о
Ответы и указания
537
Отсюда при a = f^m получаем
1
У I„(p^x)Iu(p$x)xdx = О, о
а переходя к пределу при a -> найдем
([I^ztfxdx = lim = |[ШМ)]2 / 0. О
a-t^i a2 - (р} ’у 2
16.61. Хк = - ^~у^ j Ук(х) = sin ^у-, к € N. <1 Из общего решения уравнения у(х) = cie4^ -I- С2в~'^ при Л > 0 или у(х) = Cix 4- С2 при Л = 0 и из граничных условий следует, что отличное от тождественного нуля решение этой задачи возможно только при Л < 0 (си-f Ci 4- С2 = 0, стемы < /тт
I <7ie^4-(726
и
G =0,
имеют нулевое решение C2I = 0
Ci = С2 = 0). Поэтому полагаем Л = —си2 и общее решение уравнения запишем в виде у(х) = CiCos шх 4- С2 sin шх. Из граничных условий следует, что С\ — 0 и С2 sin си/ = 0. Это означает, что отличное от тождественного нуля решение задачи возможно только в случае sin си/ = 0, т. е. при ш = uJk = —, к € N. Отсюда и находим собственные числа. Функции ук(х) = sin^-y^, к € N, являются собственными функциями этой задачи. > 16.62. Ло = 0, у0(х) = 1, Хк = - (yy'j , Ук{х) — cos^y^, к е N. 16.63. А* = - ((2*~ 1)яА /о? 1 \2
. (2к - 1)тгт , _
. sin ---—------, к G N.
2к — 1
cost———7гт, к Е N. 16.65. Хк =
16.64. Хк = - 2' 71J , у
/м(0)\2 /м(0)
~ ~ЕГ ’ Z/fc(r) == ~Б~Г ) > где Мг) — функция Бесселя порядка \ lx j \ К I
нуль, а к € N, — ее нули, т. е. /0(м1°Ь = 0. < Если ш — 0, то полу-
чаем уравнение ~(гу"(г) + у'(г)) = 0, или - — (гу1) = 0, решая которое, г г dr
538
Ответы и указания
находим сначала гу'(г) = ci и, наконец, у = ci Inr + C2. Из ограниченности решения при г = 0 следует, что Ci = 0. Используя далее граничное условие y(R) = 0, находим, что С2 = 0, т.е. у(г) = 0. Последнее означает, что ш = 0 нс является собственным числом. Пусть теперь w 0. Произведем в исходном уравнении замену переменной ту = шг. Так как У г = У'^'г = uy'^ у"г = ^у'^, то уравнение преобразуется к виду
и2 [у'^) + -у'тМ) + У^)j = 0, (*)
которое является частным случаем (при у = 0) уравнения Бесселя ., 1 / ( у2\
у 4- -у 4- 1------ ) у = 0.
х \ х1)
Следовательно, решением уравнения (*) является функция Бесселя Jo(^), т.е. решением исходного уравнения является функция ?/(г) = = 1о(мг).
Из граничного условия y(R) = Iq^luR) = 0 находим, что aiR = .
Таким образом, собственными значениями нашей задачи являются чи-/ (о)\2
ела = cj2 = I I , к € N, а собственными функциями — функции \ R I
/ Jo) \
Iq -^-г ]. Замечание. Уравнение \ R I
у" + -у' - ы2у = О г
заменой yi = —у приводится к виду у" 4—у{ 4- w2уi = 0, откуда за-г
ключаем, что уравнение (**) имеет решение у = а потому
для краевой задачи с уравнением (**) легко находим собственные числа
2
и собственные функции. > 16.66. с* = ----?
х)х dx,
/j 0
1 5
k € N. 16.67. Ci = сз = О, Со = -, С2 = -. Указание. Воспользоваться 2 8
четностью функции |ят| и четностью или нечетностью соответствующих полиномов.
dx
71^’С1: =
cos (к arccos х) , ---;- —-dx, к € N.
Ответы и указания
539
16.69. со = -, Ci = — -, ег = — -, Сз = 0. 16.70. Указание. Восполь-2 4 о
зовавшись ортонормированностью функций (х)}^_0, записать инте-
грал в виде
[/(ж) - Тп(х)]2 dx = / /2(ж) dx - 2 ak(f, Ы + 52 =
„ k=0 k=0
b
У f2(x) dx a
^4 + ^(ск~°^2-
Jk=O Ar=o
2 00
16.72. + £ (al -bl)
k=l
16.73. Равенство Парсеваля
означает, что квадрат модуля вектора равен сумме квадратов всех его
координат (в ортонормированном базисе), а неравенство Бесселя — что
квадрат модуля вектора не меньше суммы квадратов некоторых из его
координат. 16.74. Указание. Воспользоваться тем фактом, что функции Уолша Wjt(a;) при к ф 2П (см. определение перед задачей 16.58
и задачу 16.59) ортогональны функциям Радемахера rm(z) = W2m(x).
16.75. u(x,
1 Затг/ Зтг
t) = - cos —-— Sin ~rX.
О V Z
/ . Sant . 5nx
16.76. u(x, t) = —— sm —-— sin —— 15(Z7t I I
/ и 1 За7Г/ 37ГЖ
16.77. u(x, t) = - cos cos —.
16.78.
32/i
<x’ (> = b
k=0
тг(2к + l)at cos-------------
(2к + I)3
. (2k + IWz sin------—
16.79.
( 4vo/ V
k=l
. тгк . тг2к sm — sm —
3 2lh
k2
. Trkat тгкх sm —-— sm —.
16/ °° (—I)*"*"1
16.80. u(x, t) = — g _____ x
. (2k 4- l)7rat . (2k -I- 1)тгж
x sm 2----—-----sm -----———
21 21
540
Ответы и указания
j LAJ
16.81. u(x, t) = — 2^
41 ’
+ ~2-7rJa
k=i
4(-l)fe+1~
16.82. u(x, t)
_________2 (2 к — 1)7T at (2k + 1)(2Лт - 3) C°S 21 +
1 . (2k — l)7rat 1 (2k — 1)тгз7
Sm 21 J C°S 21
(2m 4- 1)тгд7
16.83. u(x, t)
(2&-1)ttJ (2& — I)3 8u0 1 _
7Г3 (2m 4-1)3 6
(2к + 1)тг oo COS----------
4 2k 4-1
4up
7Г k=0
n COS 7Г62
/с—1 n=l
4- Bk, n sin тш
где
. (2k 4- 1)тгж sm--------------
21
irkx . тгпу sm —— sin---------,
I m
тп I Л Г Г 'ТГк*')} 'ТГГ) У
Ak п — -Ю si*1 ~~Г~ s’n-----------dv dz,
’ Im J J I m
о о
Bk
m I
iralm
. irkv , rnz , , sin — sin —— dv dz,
к, n E N.
Зтг2/ 8тг?у
В случае, когда <р(х, у) = sin —— sin-------, i/j(x, у) = 0 и
I тп
1 / 64? • Зтгх . 8яу _
a = I, u(x, у, t) = cos7F\/ — 4---- £ sin —— sin----. <] Предполагая, что
V t2 m2 I m мембрана совершает малые колебания, имеем первую краевую задачу:
найти решение u(x, у, i) уравнения свободных колебаний мембраны
d2u _ 2 /д2и д2и\ 2 _ 'Во dt2 a \ дх2 ду2) ’ р ’
удовлетворяющее начальным условиям
/ / ч ди(х, у, 0)
u(z, у, 0) = ip(x, у), ---—-----= i/j(x, у)
и граничным условиям
и(0, у, t) = u(l, у, t) = u(x, 0, t) = u(x, m, t) = 0.
(1)
(2)
(3)
Ответы и указания
541
Ищем решение в виде произведения
и(х, у, t) = X(x)Y(y)T(t),
подставив которое в (1), получаем
XYT" = a2(X"YT 4- Y"XT).
Разделив это равенство на a2XYT, имеем
Т" X" Y" a2T~ X + Y '
Каждое отношение здесь зависит от своей переменной, а потому равенство возможно только в том случае, когда каждое из этих отношений постоянно. Полагая X"/X = Л, Y"/Y = ци используя граничные условия (3), получаем две задачи Штурма-Лиувилля:
X" - XX = О, Д(0) = Х(1) = 0, (5)
Y" -iiY = О, У(0) = У(т) = 0. (6)
Рассмотрим сначала задачу (5). Как показано в задаче 16.61, собственными числами задачи (5) являются числа Хк = — (тгk/Z)2, а собственными функциями — функции
__ , . . ккх , т .
Хк(х} = sin —j—, к € N. (7)
Аналогично, собственными значениями задачи (6) являются числа р,п = —(тгп/m)2, п € N, а собственными функциями — система функций Уп(?/) — sin {'кпу/тп'), п € N. Подставив в (4) вместо отношений X"/X и Y"/Y их значения — (тгАг/Z)2 и — (тгп/m)2, получим уравнения
решениями которых при различных к и п будут функции
Tk,n(t) = АкуП C0S7F(Z
t + Вк п sin 7га
fc\2
I
/ п \ 2
( —) t. \т/
542
Ответы и указания
Таким образом, решениями уравнения (1), удовлетворяющими граничным условиям (3), являются функции
Из линейности уравнения (1) следует, что и любая линейная комбинация решений (8), т.е. формально составленный двойной ряд
при условии возможности его двукратного почленного дифференцирования также является решением уравнения (2), удовлетворяющим условиям (3). Потребуем, чтобы представленное рядом (9) решение и(х, у, t) удовлетворяло условиям (6), т.е. чтобы
оо оо ,
/ ч л • ^КХ ^ПУ г ч
Щх, ?/, 0) = } } Afc, n sin —— sin--= ip(x, у)
*—' L' l m
k=l n=l
И
oo oo / / , \ 2 о .
~Ч I (n\2 'KKX . nny .
u't(x, y, 0) = 2^Z^Bk’n™\ ( 7 ) + (~) sin—-sin---------='Ф{Х, у).
fc=l n=l V \ /
Из этих равенств заключаем, что если числа Ak,n являются коэффициентами Фурье функции ip(x, у), т.е. если
m I ’
. 4 f f . . . 7rku . 7ГП2 ...
Ak п = — / / ЧлУ, z) sin —r~ sin---dv dz, к, п GN,
’ Im J J I m
о о
Ответы и указания
543
а числа Bjtin7ra у), т. е. если
4
— коэффициентами Фурье функции
Bk,n
m I
. irkv . 7ГП2 , , sin —7- sin--------dv dz,
I m
2 о 0 k, n G N, то ряд (9) является искомым решением задачи 16.84 в общем случае. Если же у) = 0, то все Вк,п = 0, к, п 6 N, а для <р(х, у) = = sinsin имеем Ак,п = 0 при (к, п) / (3, 8) и A3 g = 1. О I тп ’
<Л . I . тгач/б, . 7гж . 2ттп „
16.85. и(х, у, t) = --у= sin—-—tsin — sin——. Указание. Boc-
7гау5 « I I
пользоваться формулами для коэффициентов Ак,п и Вк<п, полученными в задаче 16.84.
\ 7га16 . 7Га\/2М . 7VX . тгу
16.86. и[х, у, t) = cos — ----1——7= sin —;— I sin — sin — 4-
\ I 7T3v2 III I
. яах/(2к 4- I)2 4- (2n 4- I)2
00 00 Sln-------\------------------'—t
VV_____________________T l-.- .... x
SJ JSl (2^ + l)(2n + l)v/(2fc + I)2 + (2n + I)2
. (2k 4- 1)тгж . (2n 4- l);ru
x sin-----— sin 2------1
Воспользоваться формулами для коэффициентов Ак,п и Вк,п, получен
ными в задаче 16.84.
. яку
z . sm у як(а-х)
16.87. и(х, у) = > ----7— ак sh--------;----
v > у/ 7rfca « ъ
k=i sh —7- L b
где
, , якх
4- bk sh --— о
2 f . . . irkv .
ак = 7 1 W) sin ~7~ dv = о J b
о
о
852 7Г3(2ш — I)3 О
ь ( к 2 У . яу . тгку 1
Ьк = 7 / sin — sin —— dy=<
ь j ь ь 0
о
при к = 2m — 1,
при к = 2m, m 6 N;
при к = 1, при к >2.
544
Ответы и указания
<1 Определение стационарного распределения температуры сводится к д2и д2и
решению уравнения Лапласа Ди = —? + = 0 с заданными гранич-
ными условиями. Решение ищется в виде и(х, у) = X(x)Y(y). Тогда X" Y"
имеем уравнения —— = - — = си2 и граничные условия Y(0) = Y(6) = A Y
= 0. Таким образом, задача Y" + си2У = 0, У(0) = Y(b) = 0 приводит к
собственным функциям (см. задачу 16.61) Yk(y) = sin —и собствен-
(7гА>\2 ( ТГ к'\^
— I , к 6 N. Решения уравнений X" — ( — I X = 0 о / \ b J
запишем через гиперболические функции:
, тгкх . , тгкх
Хк(х) = ak ch -j— + bk sh ——. о о
Тогда решение исходного уравнения Ди = 0, удовлетворяющее всем гра-
ничным условиям, запишем в виде
Е/ , тгкх . , 7гАхе\ . тгку
ак ch —— + bk sh —— sin -z—.
\ о о / о
к=1 4 7
Для определения чисел ак и Ьк получаем соотношения
ОО J
и(0, у) = ip(y) = Vat sin fci b
и
/ \ / / \ \ л ( i тгка j тгка\ , тгку
u(a, у) = г/т(у) = > afc ch —— + bk sh -r— sm —, z—' \ b b J b
k=l
из которых находим, что
Лк
b ь
2 [ . . . тгкв . 2 [ .. . . irkv ,
- / ip(v) sm —— dv = - v(b — V) sm —— dv b J b b J b
о о
( 862 , n
= (2m - 1)M “P” k = 2m-l
k 0 при к = 2m, m G N
ь
, тгка , , тгка 2 [ , . . . Trkv , ak ch —— + bk sh —— = - y>(v) sm —— dv.
b b b J b
о
Ответы и указания
545
Из последнего равенства находим bk'
г & ь
. 1 2 /* Trkv , 2 /* Trkv . . тгка
bk = -----— у / 4p(v) sm —— dv — - I ip(v) sin--------------dv ch ——
. тгка b J b b J b b
sh — _ 0 0
b
Подставляя значения ak и bk в ряд для u(x, у), получаем
0(v) sin dv
ь
2 f . . . Trkv , , тгка - / <p(v) sin —— dv ch ——
0 J b b
0
. тгкх y
, тгка sh ——•
. тгку xsin —— = b
ip(v) sin —— dv b
. тгкх , тгка , тгка . тгкх ch —7— sh ch —- sh ——
00 00
. Trkv , . тгкх sin —— dv sh —— b b
. тгку sin ——
0
, тгка
shv
. тгку sm —— г -----г— ak sh
. тгка sh —— L
тгк(а — ж) b
. , тгкх
+ bk sh —— . t> b
52 62
16.88. u(x, y) = + у +
, 2mir(x - a)
Sh b
„ , 2rmra sh —-—
0
2rmry cos —j— b
Указание. Собственными числами соответствующей задачи Штурма-f тгк\ 2
Лиувилля являются числа — I — ) , к = 0, 1, ..., а соответствующие \ о /
тг ку
им собственные функции имеют вид Yk(y) — cos ——, к = 0, 1, ... По-о
/тгк\2
этому уравнение X" — ( — \ X = 0 имеет систему решений Хо(^) =
, ,, , ч . тгкх , . тгкх ,
= аох + Ьо и Xk\x) - ак ch —---F bk sh ——, к G N.
о о
546
Ответы и указания
. . а(6 - 2)
16.89. и(ж, у) = a 4--------—-х —
2a v (2m - 1)7гж
4ab 1 sh 5 (2m - 1)тг?/
тг2 (2m - I)2 , (2m - 1)тга C°S b ni=i sh---------—-—
16.90. u(r, <p, t) = u(r, t) =
+ 2d£
k=l
1
(^)
apkt I
т №A
ч л •
<1 Уравнение u"t = a2Au, где u = u(x, y, t) и Au = uxx 4- u'yy, в полярных координатах (г, <р) записывается в виде (см. задачу 11.168 при и(х, у, z, t) = u(x, у, t)):
d2U _ 2 ( ^U I &U 1 d2u\
dt2 a \ dr2 + r dr + r2 dip2 )
Начальные условия не зависят от <р, поэтому колебания радиальные,
и уравнение принимает вид
<Э2« _ 2 (d2u 1 du\ . .
dt2 a \<9r2 + r dr J
Требуется найти решение u = u(r, t), 0 r l, уравнения (*) при начальных условиях
u(r, 0) = alo ,
uj(r, 0) = ca
и граничном условии u(l, t) = 0.
Ищем решение в виде произведения u(r, t) = R(r)T(t), подставив которое в (*) получаем:
T"R = a2 (TR" 4- -TR' ) , \ T J t. e. ।
T"(t) + -Я'(г)
a2T(t) R(r) X'
Отсюда получаем уравнение
R"(r) + -R'(r)- XR(r) = 0
r
Ответы и указания
547
с граничным условием R(T) = 0. Собственными числами этой краевой задачи (см. ответ к задаче 16.65) являются числа А^ = — ( — ] , k £ N, а собственными функциями — функции Rk(r) ~ 10 Решая уравнение
/ 2
Ч'(0 + а’(у) Tt(t) = O,
получаем
Tk(t) = ак cos —— + /Зк sin —j~.
Следовательно, искомое решение представляется в виде ряда
( a^kt , /э • а^\
~ > ( ак cos ~J~ + @к sin ~Т~ ) Л:=1 ' '
Используя начальные условия, находим
u(r, t)
оо
u(r, 0) = aln (у-г) = 52 ’
(**)
Ut(r, 0) = са = 22
Из ортогональности с весом р(х) = х {z0 на промежутке [0, I] и
од = а и ак = 0 при к 2.
(см. задачу 16.60) системы
из соотношения (**) имеем
Учитывая равенства
о
rdr = l2 j Io(pkv)Io(j2mv)vdv = о
|^2(^о(^))2, т = к,
0, т к,
находим выражения коэффициентов Фурье-Бесселя ук функции /(г) по системе G Nj на отрезке [0, I] (ср. задачу 16.66):
1
о
к G N,
548
Ответы и указания
а тогда из второго начального условия имеем
О _ _____ f т ( P'k \ ,
Р/г 12/ Т1 / \\2 I ' Са " *0 ( / /
a^ik 1г(1^к)У J \ I /
о
Мк 2 ^к
= I (i)VIM dv=/VIoW dv-о о
Но (см. задачу 12.335) vlo(v) = — (vZi(v)) и Z^v) = -Zn(v), а dv
потому
Рк Рк
У vlo(y)dv = У -^-(vli(v))dv = vZi(v)|Jfc = UkhM = о о
т. е.
Л = —А ,, fceN.
Следовательно,
u(r, t) = a cos
Uv
- 2с/ -y——- sin
= о cos ~~“Z0 + 2с/ У
1
к=1 ЙЛЫ81П
16.91. u(r, ср) = Ao + У2 (Акгк cos kip + Bkrk sin kip) = sin tp, где fc=i
2?r
A) = y- [ /(^) dip = 0,
Z7T J
0
2л
Ak = —r / f(tp) cos kip dtp = 0, к G N, 7ГГ1Г J
о
2л 2л
Bi ~ ^r/f^)s'mipdip = Bk = ~-£ У f(ip) sin kip dip о о
Ответы и указания
549
_r „ d2u 1 ди
<] Уравнение Лапласа в полярных координатах имеет вид —т- 4- - — 4-<7г2 г дг
1 д2и
4—— 0 (и не зависит от z). Решение и(г, <^) должно быть огра-г2 дрг
ничено при 0 г R и периодично по т.е. u(r, р 4- 2тг) = и(г, ф). Полагая u(r, р) = Х(г)Ф(<^), приходим к уравнениям
>1 - •«
Решение уравнения Ф"(<^)4-АФ(<^) = 0 должно иметь период 2%, а потому Л = к2, к = 0, 1, ..., и мы имеем
Ф*. = ajt cos кр 4- bk sin kip.
При Л = к2 из левой части (*) получаем уравнение Эйлера
т2Х''(т) 4- тХ'(т) - fc2X(r) = О,
которое путем замены г = ev сводится к уравнению X"(v) = 0 при к = О и к уравнению Х”(у) — k2X(v) = 0 при к 1, решениями которого будут функции X0(u) = aov 4- b0, Хк, i(v) = ekv = rk и Xfci2(v) = e~kv = r~k. При ao ф 0 решение Хо(^) не ограничено при v —> — 00, также не ограничены и решения Хк,1ф) = г~к при 0 < г < R. Следовательно, будем иметь ифг, р) = Ьо, афт, р) = гк(ак cos кр 4- bk sin кр). Вы-СЮ
берем ak и bk так, чтобы функция ц(г, р) = Ьо 4- гк (ак cos кр 4-fc=i
4- bk sinкр) удовлетворяла условию u(R, ф) = f(p), т.е. чтобы f(p) = ОО
= Ьо 4- ^2 Rk(ak cos кр 4- bk sin кр). Для этого следует выбрать Ьо = к=1 2тг 2тг
1 Г 1 г 1
= 2тг ак ~ / f&)coskpdp, к G N, Ьк = х
о о
2тг
х f (р) sin кр dp, к G N. В нашем случае f(p) = sin(</?), а потому
о
Ьо = 0, ак — 0, к G N, bi — — и Ьк = 0 при к 2.
550
Ответы и указания
(2m - l)7rt
16.92. 8/4 со° i 1 . (2m - 1)7гх ’ я5 Е (2m - I)5 I m—1 ' (2m — 1)тг£ 8/4 22. cos (2m — 1)тгж x 3 2 3 =- — > — l—— sm —2 — (x3 - 2хг1 4- I3). тг5 (2m- I)5 I 12v ’ m=l
Указ ание. Последнее выражение получено путем двукратного почлен-
ного и нтегрирования:
X
/ d'r f z п, 8/2 5-л 1 [ [ . (2m — 1)тги 1 v(v-l)dv= У / dx! / sm t dv. J тг3 (2m -1)3 J J I
0 114 m~1 о //2
16.93 . . 2 (1 . nat at nat\ . nx u(x, t) — — I — sm — cos —— sin — 4- 7Г2 \7Г I I I J I 1 V' 1 [ 1 • (2m ~ + 7J-3 m(m — 1) (2m — l)2 ° П I 1 . Trail . (2m — 1)тгж 4- rt sin , sm 2m 4- 1 I I
Указ ание. При решении системы уравнений С*, (t) 4- 1 —— 1 Ck(t) =
= Ак ампли /), к = 2m — 1 — нечетные числа, следует учесть, что частота туды внешней силы совпадает с частотой амплитуды первой гар-
МОНИК форме и, т. е. имеет место резонанс и частное решение следует искать в ~ / nat _ nat\ Ci (£) = /! сц sm —j—h pi cos -j- 1 . .
16.94. . . 201 1 г _/'я±а\2я . nkxo . тгкх 0 = 74—> 77 1 - e k ' sin —— sm ——. Cpn2a2 k2 L J I I k=l
16.95. / A \ 2 / x / 4 \ Л -(1)2Л • ulx, t) = — 1 — e sin—. \7Г/ \ / 4
16.96. u(x, t) (e + g to)2 - (2] Sm I '
Ответы и указания
551
16.97. u(x, t) = е «7* 4-
. (2k + 1)тгж
4 ~ sm - 21
+ 7г^(2А:4-1)[7г(2А:4-1)2-1]
е 4iJ - е ' 21 / 1
16.98. и(х, 0 = J sin +
3/4-1 . Trakt п . 7rat\ . тгкх
—— sin — ----2 sin —- sin ——.
к I 21 J I
16.99. u(x, t) =
1 (*g(2m-l))2f . 7г(2т — l)^
2m — 16 I
4-
2/ ул_____________1___________
% " к(тгак 4- 1)(тгак — /)
. тгкх sin ——.
16.100. u(x, t) = е~1!12 4-
“ e-(^>)2fc-l
’ --//2fc-l V \С03~^-
fc=1 (2fc — 1) I [^—14 -1 1
4-oo
, ч 2Л Г ,2tsma)h
16.101. u(x, /) = — / e £-----------cosuxdu.
ТГ J U
0
4-oo 2
2 f е~ш 1
16.102. u(x, t) = — I —-—-cosuxdw.
тг J cu2 4- 1 о
4-oo •
,л ,лп . f _^2tSm 2 fi 1 . ,
16.103. u(x, t) = — / e --------— hcos—------------sin— ] cosujxdw.
K тг J ш V 2 cu 2 J о
4-oo
<z> . 2 Г _ш2. 1 /sinuh , .
16.104. u(x, t) = — I e —-----------------h cos cun smuxau.
тг J и \ и J
о
552
Ответы и указания
16.105. Первый. 16.106. Первый. 16.107. Второй. 16.108. Второй. 16.109. Второй. 16.110. Второй, если т = Xh. 16.111. Первый, если т = Xh. 16.112.
' Um, п+1 ~ Um,n ^2^771+1,77+! ^Um, п+1 “Ь Um— l,n+l
LhUh = <
01 Uo, п, Wfc, п,
h?
тп — 1, к — 1, п = 0, в — 1, тп = 0, ..., к, п — 0, ..., s;
fh = {
фт 1 iKn, ^2,n,
тп = 1, к — 1, п = О, ..., s — 1,
тп = 0, ..., к,
LhUh — fh. Порядок приближения разностным оператором Lh — второй по h и первый по т. 16.113. Lu = u'x + u'y, порядок приближения — первый по h и второй по г, если г2 = Xh. 16.114. Lu = u”x + u”y, 1 г2
порядок приближения второй. 16.115. a = - —
16.116. Разностные схемы могут быть следующими:
^т, п— 1 2^m+-i>n
а д!
тп = 1, ..., к — 1, П = 1, ..., 8 — 1,
Um, п+1 ^Um,n
'ТП—1, п
LhUfi — <
Um, 01
Um, 1 Um, О
Uq, п;
Uk, п 1
Um, п+1 ^Um,n
n— 1 Q^m+l ,n 2um.
a Д2
m = 1, ..., к — 1, n = 1, ..., s — 1,
771—1, П
LhUh — <
Um, О, Um, 1 Um, —1
п = 0, ..., s,
m — 0, ..., к,
П = 0, . . . , s;
тп — О, ..., к,
2т
Uq, ni
Uk, nt
п = О, ..., s;
Ответы и указания
553
т, п+1,
^пи
'Фт > Ф1,п, Ф2,п,
fh = <
т — 1, к — 1, п = О, 3 — 1,
т = О, ..., к,
п = О, ... ,s, Lhuh - fh.
16.117. т = h, LhUh =
Um+i, n 2umi n H- um—1, n , j w»n, n+i И- n H- Um, n—1
Cm, n № \-am^n —
m = 1, к — 1, тг = 1, ..., s — 1,
< ^т,п{,Хт^ Уп) £
j fm,n, m = 1, ..., к - 1, n = 1, ..., s - 1, ^m,n, (^m) Уп) £ 'Yh’
Замечание. В случае данной области разностные уравнения составляются и для точек yh. 16.119. u,n+i,n+i + um-i,n+i + um-i,n-i + + um+iin_i — 4ит1П = 2h2fmtn- Порядок аппроксимации равен двум. Указание. (Lu)o = cqUq + CiUi + c2U2 + сз^з + C4U4. В силу симметрии уравнения и симметрии шаблона положить = с? = сз = ед = Ь. 16.120. <1 По определению аппроксимации имеем (см. соотношение (14))
где 6fh = Lh(u(xm, уп)) - fh.
Положим £h(xm, уп) = u(xm,yn) - ит,п. Здесь, как и ранее, ц(ж, у) — решение краевой задачи (1), (2), a {um,n} = Uh — решение разностной схемы (4). В силу линейности оператора Lh имеем:
^h^h) — Lh(u(Xrni Уп) 'ат,п) —
— Lh(u(xm, Уп)) Lh(um, п) — Lh^U^Xmi Уп)) f h — hi
т. e. сеточная функция £h(xm, уп) является решением разностной схемы LhUh — Sfh- В силу устойчивости этой разностной схемы (соотношение (15)), а также используя неравенство (*), находим:
1№т, 1/п)|| c\\8fh\\ CBh° = Ah°,
554
Ответы и указания
где А = ВС. Тем самым неравенство (13) установлено, что и доказывает теорему. 16.121. Указание. Для доказательства неустойчивости достаточно рассмотреть разностную схему при некотором выборе правой части fh. Положить /Ш1П = 0 для всех типи ipm = (—l)ms, Е > 0 — некоторое число. Тогда разностная схема запишется в виде:
Wm,n+1 = (1 "Ь AUm-i-i, п,
Мтп.о = (~1)т£.
Получить отсюда, что
um,n = (1 - 2Л)п(-1)т£.
Затем показать, что
Ц«л|| = |1 - 2А|^/<лл>1е.
Если ||/Л|| = max [<pm| = е, то, следовательно, выполняется равен-— М ство
= |1 - 2А|(г/<аа>1 ||7*||.
Сравнивая это равенство и соотношение (15) и учитывая, что
|1 _2Д|(Т/(ЛЛ)1
при h -> 0, получаем, что исходная разностная схема неустойчива.
16.122.
Ащ, п^т, п+1 "Ь Вт>пит^ п— 1 4- Сщ, п "Ь "Ь Вт,пУт-1,п "Ь
п = 1, ...,$ — 1, m = 1, ...,& — 1,
т = 0, ..., к,
п — 0, ..., s;
^т. О,
LhUh = <
Um, 1,
W0, п, u Ilk, П,
fm, п, <Рт j
fh = 4>т +1"Фт,
n = 1, ..., s — 1, m = 1, ..., к — 1,
m = 0, ..., fc,
n = 0, ..., s,
Ответы и указания
555
где
. Ьщ, п . dm, п ^т, п dm_ п
Ат,п ~ т2 । 2т-’ ^т,п ~
Um п Ст п Um п Ст п
т’п h? 2h ’ т’п h2 2h ’
гл 2ctmi п bm< п U'm, п — д2 ' ^_2 9т, п-
16.123.
Wo, m к Uk,7l'
+ 2тВт)о
Dm, Q^Pm — l OV’m]»
где значения коэффициентов те же, что и в задаче 16.122. Указание.
Привлекая еще один горизонтальный ряд, соответствующий п — — 1, du ит 1 ит —1
производную — заменить разностным отношением ----------------.
дУ у=о
Промежуточные значения um_i исключить, используя разностное урав-
нение
LhUh — -Am, п^т, п+1 “I” ^m, п^т, п— 1 Om, nUm-J-1, п 4”
“I” nUm — 1,п 4" Ет> nUm п — fm,n-
При исследовании порядка аппроксимации учесть, что порядок аппроксимации уравнения равен двум. Для исследования порядка аппроксимации разностной схемы необходимо определить порядок аппроксимации начальных и граничных условий.
556
Ответы и указания
16.124. Ат, nUm, п+1 4” Вт,п^т, п—
т, п^т-1, п
т, n.Um+1, п |
Um,n = jm,ny Ul — 1, • . . , к 1, П 1, • . • , S 1.
Um, 1 — (firn “I” '^'Фггц
Uk —1, п
•т,
Ul п — (1 ^1п^)^0, п 4” />Фп, Ufc п — . ± п -у . .
(1 + d2nh) (1 + д2пп)
Значения коэффициентов те же, что и в задаче 16.122.
16.125. Ат,пит, п+1 + ^т,п^т,п-1 + Ст,п^т+1,п 4” DmnUm— 1,п "Ь 4” Ет, nUm, п = fm, Пт Ul, — 1, . . . , А; — 1, 71 — 1, . . . , S 1, Um, 0 — ^Pmi ТП = 0, . . . , к.
Um, 1 = j п [/m,0 4* 2тВт, о'фт ~ Cm^O^m+l
^m,0 4- £>m,0
Dm^O^Pm— 1 EmtQipmj,
^о, nUo, n+i 4" Bq, n/uo, n—1 4- (Co, n 4-Do, n)^i, n 4~ (^on 4” 2/z.JinZ?o, n)^o, n =
~ fo,n 4- 2hDo, пФп, (*)
(-4o,o 4- Bq,q)uq, i =/o,o + StBo.oV’o 4" 2ЛРо,оФо — (Co,o 4- Dq,q)p>i —
— (Eq<0 4- 2h6ioDo,o)(po, (Ak,o 4- Bk,o)uk, 1 = fk,o 4- 2rBk,o^k - 2hCk,oFo — (Ck,o 4- Dk,0)tpk-i -
— (Ek,o — 2h82oCk,o')(Pk,
Ak, n.uk, n-t-i 4- Bk, nUk, n— 1 4" (Ck, n 4- Dk, n)uk—i ,n 4-
4- (Ek,n + 2h62nCk,n)uk,n — fk,n ^hCk,nFn.
Схема (*) имеет второй порядок аппроксимации на решении, обладающем ограниченными четвертыми производными. <1 Заменим входящие в начальные и граничные условия производные центральными разностями. Для аппроксимации граничных условий в узлах (0, п) привлечем еще узлы вертикальных рядов, соответствующие т т = к + 1 (см. рис.53), и запишем следующие соотношения:
= -1 И
^1, п 1, п
п, + — Ф
2п ^fc+1, n “ 1, п , г
“г п —
2h
Ответы и указания
557
Разностные уравнения, аппроксимирующие дифференциальное уравнение задачи 16.122 в узлах (0, п) и (к, п), имеют вид
^О, nWo, п+1 "Ь В0, nWo, п—1 “I” О), n^l, п “Ь Д), nU—l,n Н- -Do, nWo, п — fo, п>
nUk, п+1 Н” В к, nUk, п-1 + Ek, nWfc+l, п Н“ В к, nUk — l,n Н“ Ek,nUk,n — fк, п-
Исключая из этих уравнений u_i,n, Uk+i,n с помощью выражений (**), получим
^0, nWo, п+1 + В0, nWo, п -1 + (Со, п “Ь Dq, п)W1, п Н- (.Do, п Н- 2/1 ^inZ?o, п) Wo, п —
— fo, п Н- 2hD0< nFi, п, (* * *)
k, п^к, п+1 “I” Bk, п^к, п—1 “I” (Ок,п “Ь В к, n'fak — 1, п
“Ь (Ё//с,п 2/lJ2nCfc, n)Uk, п — fk,n ^hCk, п^2, w
Значения решения в узлах (О, 1) и (&, 1) определяются из (* * *) при п = 0. Исключая величины uo,-i> Uk,-i с помощью начальных усло-Uo 1 - Wo,-1 Uk,l~Uk,-l .
вий ------------ = 'фо, ----------- = фп, получим выражения для
2т 2т
определения wo, i, Uk, i
(Ai,о + Bo,o)wo, i = /о,о + ЗтВо^^о + 2/i7?o,o^o ~
— (Со, о + -Do, 0)^1 — (Ё/0,0 + 2/w$io-Do,o)<Ab
(>U,о + Вк,о)ик, 1 = fк,о + ZrBk^k ~ 2hCk,oFo -
— (C&,o + Dk,0)^-1 — (Ek,о - 2h&2oCк,o)^k- t>
558
Ответы и указания
16.126. Порядок аппроксимации равен двум. Указание. Для замены частных производных w"r, u"y использовать разностный оператор из задачи 16.108. Положить т = h.
16.127. 1)
LhUfi —
1
^m, 01
1
h
£ 1hn,n “I” , l,n> h
fm, n 5 pm •
2) Шаблон изображен на рис. 54. 4) Схема неустойчива при любом Л.
16.128. 1) Lhuh =
. , n+l
= Xh
ч Um,0-
Jm,n>
'pm-
2) Шаблон тот же, что и в задаче 16.127. 4) Схема устойчива при Л 1. ( 1 _ 1 (1 Л 1
16.129. 1) LkUk = / A/l“”*'n+I h\X+ J U,n’n +hUm+1'n ,
L ^т,0.
- f fm n,
fh=\ m’ 2) Шаблон изображен на рис. 55. 4) Схема неустой-tpm •
чива при любом Л. 16.130. Схема устойчива при условии т
(т, п + 1) (т, п + 1)
/7 । 1 п । 1 "
(m 1, п) (/я, п) (w, п) (т, п + 1)
m 1 Л 1 я п т + 1
Рис. 54
Рис. 55
16.131. Схема устойчива при любых h, т. 16.132. Схема устойчива при условии ат < h. 16.133. Схема всегда устойчива. 16.134. Прого-. , & 1, п тт п
ночные коэффициенты Qln = — —---------2------, Hi п =-------------,
НР1, п. СЦ, п h(3i^n £Т1,п
Ответы и указания
559
п = 1, ..., s. Значение решения на правой границе, необходимое для обратной прогонки,
Ol2,nHk,n + Ъ&2п 1
77к,п — /, х . > п , 71 1, ... , 8.
<*2,1 (1 — Qk, п) + ЬР2, п '
<] Аппроксимируем граничные условия задачи 16.134 разностными соотношениями
^1,п ~ ^о,п л » / \
(71 п 1 "Ь Pl,nWo,n — ^1,п> (*)
П,
77к,п ^к-1,п . п » п ( \
О2,п--------7-----h P2,nUk,n = $2,п, 71 = 0, . . . , 8. (**)
fl
Полагая в формуле (25) тп = 0, запишем следующее равенство:
^0,n = Ql,n^l,n "Ь ^1,п, П = 1, . . ., 8. (***)
Сравнивая равенства (*) и (***), получим начальные значения прогоночных коэффициентов
__ ^1,П ТТ ___ ^1)П ___
Q1, п > п 1 711, п , п > 71 1, . . . , 8.
•7pi,n <^1, п пр1<п Ctl,n
Для обратной прогонки необходимо знать значение решения на правой границе Uk,n- Для определения этого значения запишем равенство (23) в узле (к, п):
77k— 1,п = Qk+nUk,n 4” 71 = 1, . . . , 8. (****)
Заметим, что все прогоночные коэффициенты определены по формулам (24). Сравнивая равенства (****) и (**), получим систему линейных уравнений
Qk, n'U'k, п 71k —1,п — Hk,ni
(,02, к 4” ЛД2, k^Ttfc, n О2, кТ^к— 1, п = к^2,п-
Uk,n получим как решение этой системы. >
560
Ответы и указания
16.135. h = 0,02; т = 0,01;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 0,0 0,16 0,64 1,44 2,56 4,00
0,2 0,22 0,28 0,82 1,67 2,80 3,98
0,4 0,49 0,48 1,08 1,96 3,10 3,68
0,6 0,82 0,92 1,41 2,33 3,19 3,30
0,8 1,23 1,42 1,82 2,76 3,11 2,79
1,00 1,72 1,97 2,46 2,97 2,88 2,16
16.136. h = 0,01; т = 0,01;
У X
0,0 0,20 0,40 0,60 0,80 1,00
0,0 0,0 0,20 0,40 0,60 0,80 1,00
0,2 0,20 0,20 0,40 0,60 0,80 0,80
0,4 0,40 0,20 0,39 0,59 0,78 0,60
0,6 0,60 0,39 0,37 0,56 0,54 0,40
0,8 0,80 0,57 0,34 0,49 0,28 0,20
1,00 1,00 0,73 0,47 0,20 0,00 0,00
16.137. h = 0,02; т = 0,01;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 1,00 1,16 1,64 2,44 3,56 5,00
0,2 1,20 2,42 2,94 3,82 5,06 4,90
0,4 1,39 3,73 4,33 5,29 6,57 4,61
0,6 1,56 4,15 5,80 6,82 6,53 4,13
0,8 1,72 4,53 7,31 8,37 6,23 3,48
1,00 1,84 4,91 7,94 8,38 5,74 2,70
16.138. h = 0,01; т = 0,01;
У X
0,0 0,20 0,40 0,60 0,80 1,00
0,0 0,0 0,04 0,16 0,36 0,64 1,00
0,2 -0,42 -0,03 0,41 0,93 1,53 3,01
0,4 -1,14 -0,08 0,68 1,52 2,44 7,28
0,6 -3,28 -0,14 0,97 2,12 4,18 14,60
0,8 -10,87 -0,51 1,27 2,75 8,14 26,44
1,00 -40,84 -2,30 1,56 4,20 15,18 44,60
Ответы и указания
561
16.139. h = 0,02; т = 0,01;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 5,00 6,60 8,20 9,80 11,40 13,00
0,2 5,30 6,79 8,39 9.99 11,59 13,12
0,4 5,65 6,98 8,58 10,17 11,77 13,18
0,6 6,19 7,15 8,74 10,33 11,92 13,18
0,8 7,26 7,32 8,89 10,46 12,04 13,09
1,00 9,61 7,57 9,01 10,57 12,03 12,87
16.140. h = 0,02; т = 0,01;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 1,00 0,80 0,60 0,40 0,20 0,0
0,2 0,98 0,84 0,72 0,58 0,42 0,20
0,4 0,92 0,87 0,81 0,72 0,59 0,39
0,6 0,83 0,88 0,88 0,83 0,73 0,56
0,8 0,70 0,86 0,91 0,92 0,86 0,72
1,00 0,54 0,80 0,92 0,98 0,96 0,84
16.141. h = 0,02; т = 0,01;
У X
0,0 0,20 0,40 0,60 0,80 1,00
0,0 0,0 0,04 0,16 0,36 0,64 1,00
0,20 -0,17 0,01 0,01 0,01 0,01 0,00
0,40 -0,72 0,04 0,02 0,01 0,00 0,00
0,60 -1,63 0,10 0,04 0,00 0,00 0,00
0,80 0,97 0,17 0,00 0,00 0,00 0,00
1,00 1,00 0,00 0,00 0,00 0,00 0,00
16.142. h = 0,02; т = 0,01;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 0,00 0,16 0,64 1,44 2,56 4,00
0,2 0,28 0,46 0,83 1,28 1,52 1,27
0,4 0,30 0,42 0,53 0,60 0,54 0,38
0,6 -0,03 0,05 -0,05 -0,24 -0,43 -0,44
0,8 -0,67 -0,61 -0,87 -1,23 -1,47 -1,29
1,0 -1,57 -1,52 -1,90 -2,38 -2,62 -2,21
562
Ответы и указания
16.143. h = 0,01; т = 0,01;
У X
0,0 0,2 0,4 0,6 0,8 1,00
0,0 0,0 0,59 0,95 0,95 0,59 0,00
0,2 0,50 0,54 0,57 0,58 0,57 0,53
0,4 0,60 0,70 0,88 1,10 1,29 1,31
0,6 2,01 2,51 3,54 4,88 6,08 6,31
0,8 8,05 9,90 13,58 18,31 22,41 23,03
1,00 25,35 30,58 40,44 52,78 63,21 64,34
16.144. h = 0,02;
У X
0,0 0,4 0,8 1,2 1,6 2,0
0,0 1,00 1,40 1,80 2,20 2,60 3,00
0,2 2,00 1,05 0,95 1,06 1,44 2,96
0,4 3,00 1,02 0,60 0,59 0,93 2,84
0,6 4,00 • 1,36 0,76 0,67 0,93 2,64
0,8 5,00 2,76 2,12 1,81 1,64 2,36
1,00 6,00 5,84 5,36 4,56 3,44 2,00
16.145. h = 0,02;
У X
0,0 0,20 0,40 0,60 0,80 1,00
0,0 0,0 0,0 0,0 0,0 0,0 0,0
0,20 0,08 0,32 0,51 0,72 0,99 0,84
0,40 0,32 0,72 1,07 1,41 1,78 1,76
0,60 0,72 1,23 1,68 2,12 2,56 2,76
0,80 1,28 1,82 2,65 3,22 3,82 3,84
1,00 2,00 2,44 2,96 3,56 4,24 5,00
16.146. h = 0,02;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 0,0 0,40 0,80 1,20 1,60 2,00
0,20 1,00 0,24 0,35 1,24 0,0 0,0
0,40 2,00 0,34 0,10 0,82 0,0 0,0
0,60 3,00 0,66 0,19 0,47 1,96 0,0
0,80 4,00 1,92 1,34 1,25 2,04 0,0
1,00 5,00 4,60 4,20 3,80 3,40 3,00
Ответы и указания
563
16.147. h = 0, 02;
У X
0,0 0,40 0,80 1,20 1,60 2,00
0,0 0,0 0,63 0,89 1,10 1,26 1,41
0,20 1,00 0,36 0,44 0,54 0,64 1,29
0,40 2,00 0,32 0,26 0,28 0,32 1,20
0,60 3,00 0,83 0,66 0,56 0,45 1,12
0,80 4,00 2,86 2,06 1,69 1,19 1,05
1,00 5,00 4,84 4,36 3,56 2,44 1,00
Глава 17
17.1. U* = Z 17.2. [/* = {О, 1}. 17.3. [/* = ( 1 . k G Ш.
[ 2к — 1 J
17.4. [/* = [-1; 1]. 17.6. = 0. 17.7. Д = -оо. 17.8. Д = -оо.
17.9. Л = -тг/2. 17.10. Л = -оо. 17.11. а) Д = -оо; б) Д = 0. 17.20. [-1; 0], [0; 1], [1; 2]. 17.21. b = 2,5. 17.22. Да. 17.23. Указание. Воспользоваться результатом задачи 17.19. 17.25. х* = 1,4142, /* = 2,8284. 17.26. ж* = 1,156, /* = 0,6609. 17.27. х* = 0,6605,
/* = -0,4501. 17.28. ж* = 0,6565, Г = 1,4653. 17.29. ж* = 1,6702, /* = = -33,5064. 17.30. т* = 1,2963, /* = -1,7557. 17.31. ж* = 0,8241, /* = = -1,6421. 17.32. х* = 3,3532, /* = -47,1447. 17.33. ж* = 1,8411, /* = = - 6,0016. 17.34. 6п 17.37. п log2 Ь-~-“ 17.38. Да.
17.39. NA = 32, Nn = 100001; Nn/NA = 3125. Указание. Использовать результат задачи 17.37, полагая 6 « 0. 17.40. х* = 1,2599, Г = 1,8899. 17.41. ж* = -4,4934, /* = -4,8206. 17.42. х* = 1,6030, /* = -2,1376. 17.43. ж* = -0,7549, /* = -3,6347. 17.44. ж* = = 0,3822, /* = -3,7491. 17.45. ж* = 1,7556, /* = 2,4154. 17.46. х* = = 0,3684, Г = 2,4154. 17.47. х* = 4, /* = -8,9169. 17.48. х* = \/5 — 1
= - 1,5, /* = -1,6519. 17.51. б) х2 - a = b - хх = —(5 - а).
(/— \ п~ 1 v 5 — 1 \
— . 17.53. Na = 32, Nc = 24; NJNC =
= 1,33. 17.54. ж* = 0,7071, /* = 2,8284. 17.55. ж* = -0,6823, /* = = - 0,5814. 17.56. ж* = -2,2340, /* = 61,1806. 17.57. ж* = 0,6488,
564
Ответы и указания
Г = -2,3675. 17.58. ж* = 0,5110, /* = -2,5054. 17.59. ж* = -2,3247, /* = -7,7290. 17.60. ж* = 1,5160, /* = 20,4415. 17.61. ж* = 0, /* = -3. 17.62. ж* = 0,7339, /* = 1,6796. 17.65. a) L = 5; б) L = 135. 17.67. /* = 1,152 х 10~2. 17.68. /* = -10,006. 17.69. /* = 0,523. 17.70. /* = 2,387. 17.71. /* = 1,393 х 10~3. 17.73. <1 Уравнение касательной к графику f(x) в точке (я?о5 f(xo)) имеет вид у = f(xo) + + f'(xo)(x — Xq). По формуле конечных приращений f(x) = f(xo) + + f'(£)(x ~ хо)> где С заключено между х и ж0. Поэтому f(x) — у = = [/'(С) — хо) 0, так как f'(x) не убывает. [>. 17.76. х* = 1,
/* = 1. 17.77. z* = 0,4502, /* = -0,2325. 17.78. /* = -0,3855, /* = = 0,7852. 17.79. ж* = 0, /* = -1. 17.80. ж* = 0,6501, /* = 1,6951. 17.81. z* = 0,7035, /* = 3,4422. 17.82. ж* = 3,8708, /* = 1,3702. 17.83. ж* = 0,5283, /* = 0,6675. 17.84. ж* = 0,351734, /* = 0,827184. 17.85. ж* = -0,693147, /* = 0,6137064. 17.86. ж* = - 0,835430, /* = = -0,879073. 17.87. ж* = 0,738835, /* = 0,284712. 17.88. ж* =
= - 0,175203, /* = 1,908524. 17.89. ж* = -0,443931, /* = 0,765751. 17.91. Да. 17.92. Да. 17.93. Да. 17.94. Нет. 17.95. Да. 17.96. Да.
17.97. Нет. 17.98. Да. 17.99. Да. 17.100. Нет. 17.107. U = {(^, аг2)|ж2 >
> 0}. . 17.108. U = {(ж1, ж2)|(2А; — 1)тг < xi + ж2 < 2/стг, k G Z}.
17.109. U = £2. 17.110. U — {(ж1, ж2)|ж1 + х2 > 0} (J{(a?i, z2)|zi + х2 < < - 17.111. а > 0, 4ас - Ь2 > 0. 17.112. a G (-2; 2).
17.113. Q= f2 5V f/(x(°))=f8Y
у 5 6 J v ’ \ioy
17.114. Q
17.115. Q
17.116. Q
/2
2 \o /2
1
V
17.117. a) = (0,0611; -0,1389), /(x^) < /(X(°)); 6) x^1) = (-1,4881; -2,0181), /(x^) = /(x(°)); в) xW = (-3,6945; -4,6945), /(x^1)) >
Ответы и указания
565
> /(х^). 17.118. а) = (-0,1; -0,1), /(х^) < /(х^0)); б) х^1) = = (-0,5; -0,5), /(х^) = /(х(0)); в) х(1) = (-1; -1), /(х^) > /(х(0)). 17.119. х^ = (-0,1; 0,8; -0,1), /(х^) < /(ж^); б) х^) = (-0,638; -0,276; -0,638), /(х^) = /(х^); в) х^ = (-10, -19, -10), /(х^) > > /(х<°)). 17.120. а) х»1’ = (-0,1437; 0,4; 0,4), /(х^) < /(х^); б) х^ = (-1,4323; -0,2761; -0,2761), /(х^)) = /(х^); в) х^ = = ( — 10,4366; —5; —5), /(х^1)) > /(х^). 17.122. Указание. Воспользоваться необходимым условием минимума функции Фл(а) = /[х^ — - af^x^)] в точке a^- = 0. 17.123. а0 — 0,5. 17.124. «о =
= 0,333. 17.125. Q0 = 0,113. 17.126. а0 = 0,25. 17.127. а0 = 0,236. 17.128. qq = 0,119. 17.129. х* = (-0,2206; 1,0441), /* = -5,3309. 17.130. х* = (0,3333; 0), /* = 0,3333. 17.131. х* = (0,3846; -0,1923), /* = -0,4877. 17.132. х* = (0,1667; 0,1667), /* = -0,1667. 17.133. х* = = (2,55; —0,85), /* = -21,675. 17.134. х* = (0; 0,5), /* = -0,75. 17.135. х* = (0,9677; -6,4516), /* = -32,2581. 17.136. х* = (-0,5; 0), /* = -0,25. 17.137. х* = (-0,1053; 0,0789; -0,0639), /* = -0,1207. 17.138. х* = (-0,1538; 0,1154; 0,3077), f* = - 0,5385. 17.139. х* = = (-2,6028; -0,0198; 0,1050), /* = -6,4658. 17.140. х* = (-1,5865; 0,3221; 0,2981), /* = -5,8029. 17.141. х* = (-0,1112; -0,0292; 0,0308), /* = -0,4435. 17.142. х* = (-0,5236; 0,2028; -0,1698), /* = -1,3939. 17.143. х* = (-1,2867; 0,2317; -0,2569), /* = -4,6319. 17.144. х* = = (-0,0732; -0,2195; 0,6830), /* = -0,4146. 17.148. х* = (0,1; -1; 1), /* = -3. 17.149. х* = (0,2310; -0,3160), /* = 0,5565. 17.150. х* = = (-0,7071; 0,7074), /* = - 0,7071. 17.151. х* = (-0,7592; -0,4053), /* = -1,4428. 17.152. х* = (0; 0), /* = 1. 17.153. х* = (0,2420; 0,1829), /* = 1,7814. 17.154. х* = (-0,1918; -0,9596), /* = -2,3843.
17.155. х* = (0,7358; -0,8580), /* = -1,4001. 17.156. х* = (0,2400; -0,3267), Г = -0,4504. 17.157. х* = (0; 0), /* = 0,6931. 17.158. х* = = (-0,6132; -0,6633), /* = - 1,805. 17.159. х* = (-0,3015; -0,6031), /* = 3,3166. 17.160.x* = (-0,2990; 1,4952), /* = -4,7299. 17.161.x* = = (1,2248; 0; 1,2248), /* = 2,4495. 17.162. х* = (0; 0,1555; -0,4119), /* = 0,6949. 17.163. х* = (—0,3016: 0,6030; 0), /* = 3,3166. 17.164. х* = = (-0,4446; -0,5778; 0,0010), /* = -0,7668. 17.165. х* = (0; 0; 0), /* = = 1. 17.166. х* = (О'; 0°; 0), /* = 2,3863. 17.167. х* = (-0,1907;
566
Ответы и указания
-0,0954; 0,9535), /* = -2,4321. 17.168. х* = (-0,6300; 0; -1,5811), /* = 1,1087. 17.169. х* = (0,2300; 0,4600; -0,1150, /* = -0,4131. 17.170.x* = (1,0610; 0,3539; 0,0011),/* = 2,8284. 17.171.x* = (-0,4041; 0,2235; 0), /* = 0,6600. 17.172. х* = (-0,1912; -0,4081; -0,3602), /* = 3,5056. 17.173. х* = (-0,2136; -0,3328; 0), /* = 1,4461. 17.174. х* = = (-0,1154; -1,1544; 0,3463), /* = -8,3670.
17.182. /(х) = 4т1 + 6я?2 —> min,
0,Ixi + 0,1x2 2,
0,1^1 + 0, 3x2 3,
0,8xi + 0,6х2 7,2,
0,8xi +0,6x2 < 12,8, Xi, Х2 0.
17.183. /(х) = —3x1 — 8x2 —> min,
lOxi + 70x2 < 570,
20xi + 50х2 < 420,
300xi + 400x2 5600, 200x1 + Ю0х2 < 3400, xi, Х2 0. Указание. Максимуму прибыли 3xi +8x2 соответствует минимум противоположной величины.
17.184. /(х) = —626x1 - 656x2 min,
xi + х2 < 12,
xi < 8,
5xi + 8х2 81,
6xi + 4х2 70, 3xi + Х2 26, Х1, Х2 0.
17.185. /(х) = -С1Х1 — С2Х2 -> min,
0, 4xi — 0,6x2 0,
aiXi + О2Х2 Ь, Xi, Х2 0.
8 9 10 10
17.186. /(х) = Х1 Ci + Х2 5+ ci + ж3 Е^-Е Cibi -+ min, 1=1 г=2 г=3 г=1
Xi ^61,
Xi + Х2 62,
xi + х2 + хз > max bi, 3^г^8 ^2+^3^ 69, Хз 5ю,
Xj ^0, j = 1, 2, 3.
Ответы и указания
567
17.187. /(х) = —С1Ж1 — С2Т2 min,
filial + 012^2 61,
021^1 + 022^2 &2,
0-31+ О-32Я-2 63,
Ж1, х2 0.
17.188. х* = (1; 1); /* = -1. 17.189. х* = (2/3; 2/3); /* = -8/3.
17.190. Нет решений. 17.191. Бесконечное множество решений: х* = = (а; 1 - а), где a G [0; 1]; /* = 1. 17.192. х* = (1; 2); /* = -9. 17.193. х* = (2; 2); /* = —4. 17.194. Нет решений. 17.195. Бесконечное множество решений: х* = (2 — а; a 4- 1), где a € [0; 1]; /* = = -3. 17.196. х* = (2; 28/3). 17.197. х* = (1; 8). 17.198. х* = (5; 7). 17.199. х* = (146,25; 97,5). 17.200. а) х* = (20; 50); б) х* = (30; 40). 17.201. х* = (4; 1; 7; 0; 0); /* = -7. 17.202. х* = (5; 6; 5; 0; 0; 13); Г = 2. 17.203. х* = (1; 0; 4; 0; 7); /* = 5. 17.204. х* = (0; 2; 1; 0); /* = 3. 17.205. Бесконечное множество решений: х* — (6 — За; 5 + + а; 6 - 6а; 0; За; 3 + 4а), где а G [0; 1]; /* = -21. 17.206. х* = = (1; 2; 0; 3; 14; 0); /* = -3. 17.207. х* = (1; 0; 2; 0; 2); /* = -17. 17.208. Нет решений. 17.209. х* = (3; 0; 2; 0; 1); /* = 6. 17.210. Нет решений. 17.211. х* = (9/2; 0; 0; 3/2; 2); /* = -25/2. 17.212. х* = = (0; 0; 11/10; 12/5; 3/5); /* = -53/10. 17.213. х* = (2; 0; 1; 0; 1); /* = -9. 17.214. х* = (5; 2; 0; 0); /* = -46. 17.215. х* = (1/2; 0; 6; 3/2; 0); /* = -6,5. 17.216. х* = (0; 1; 3; 1); /* = 7. 17.217. х* = = (1; 0; 3; 3); /* = 2. 17.218. х* = (1/5; 27/5; 0; 7/5; 0); /* = -17/5. 17.219. Нет решений. 17.220. Нет решений. 17.221. х* = (0; 2; 4; 1; 0); /* = —2. 17.222. х* = (3; 0; 0; 4/5); /* = -36. 17.223. а) х* = = (0,8; 8; 0,4; 0); б) х* = (5; 0; 6; 0). 17.224. а) х* = (600; 0; 0); б) х* = = (0; 700; 0). 17.225. х* = (15; 5; 5). 17.227. х* = (13; 3), /* =
= -16. 17.228. х* = (1; 2), /* = -31. 17.229. х* = (2; 1), /* = -11. 17.230. Два решения: х* = (2; 0), х* = (1; 1); /* = —2. 17.231. х* = = (0; 0; 1; 2), /* = -1. 17.232. х* = (1; 9; 0; 5), /* = -9. 17.233. х* = = (3; 6). 17.234. х* = (3; 9). 17.235. х* = (2; 0; 1; 0; 5), /* = -2. 17.236. х* = (0; 0; 11; 3; 1), /* = -24. 17.237. х* = (3; 2; 2; 1), /* = = —2. 17.238. х* = (0; 3; 2; 0) или х* = (1; 2; 1; 1) или х* = (2; 1; 0; 2), /* = -3. 17.239. х* = (1; 3; 0; 0; 1), /* = 8. 17.240. х* = (2; 1; 1; 1),
568
Ответы и указания
f* = -11. 17.241. х* = (2; 1; 2; 1) или х* = (1; 2; 1; 2) или х* = = (3; 0; 3; 0) или х* = (0; 3; 0; 3), /* = -3. 17.242. х* = (1; 3; 5; 3), /* = -5. 17.243. х* = (1; 2; 3), /* = 10. 17.244. х* = (6; 1; 4), г = -17. 17.245. х* = (6; 18), /* = -78. 17.246. х* = (0; 1; 1), /* = 3. 17.247. х* = (0; 0; 7), /* = -21. 17.248. хп = 76, х12 = 24, ж21 = 0, Х22 = 200. 17.249. х* = (7; 7). 17.250. а) х* = (146; 97); б) х* = = (146; 96). 17.251. х* = (3/8; 9), /* = -717/8. 17.252. х* = (1; 3/2), /* = -5/2. 17.253. х* = (3; 7/2; 0; 1/2; 3/2), /* = -17. 17.254. х* = = (1; 0; 1/6; 2/3), /* - -65/6. 17.255. х* = (3; 9). 17.256. а) х* = = (146; 292/3); б) х* = (293/2; 97). 17.258. х* = (6; 0), /* = 2. 17.259. х* = (12; 20; 0), /* = -8/41. 17.260. х* = (0; 0; 2; 4), /* = = - 2/3. 17.261. х* = (3/5; 11/5; 0; 1/5), /* = 5/6. 17.262. х* = (5/2; 11/2; 0; 27; 0), /* = -21/38. 17.263. х* = (0; 0; 6; 9; 10), f* = -3. 17.264. х* = (12/5; 23/5; 46/5; 29/5), /* = -1/91. 17.265. х* = (5; 5; 10; 0; 0; 16), /* = -4/13. 17.266. Нет решений. 17.267. х* = (2; 3), /* = -52. 17.268. х* = (5; 2), /* = -131. 17.269. х* = (2/3; 14/9), /* = -22/9. 17.270.x* = (2; 4),/* = -80. 17.271.x* = (33/13; 4/13; 0), /* = -273/13. 17.272. х* = (1/2; 1; 9/2; 8), /* = -7/4. 17.273. х* = = (0; 0; 1), /* = -1. 17.274. х* = (0; 0; 0), /* = 0. 17.275. х* =
= (1; 23; 25)/6, /* = 143/12. 17.276. х* = (0; 0; 3), /* = -6.
17.277. х* = (2; 3), /* = -13. 17.278. х* = (8; 28/5), /* = -154,24. 17.279. х* = (5; 8), /* = -153. 17.280. х* = (10; 4), /* = -344.
17.281. х* = (29/5; 22/5), /* = - 108,44. 17.282. х* = (7; 8), /* =
= - 173. 17.283. х* = (10; 5), /* = 52. 17.284. х* = (1; 2), /* = -3.
17.285. х* = (2; 4; 8; 16), /* = -20. 17.286. х* = (0; 10; 0; 30), /* =
= -10. 17.287.x* = (3; 8; 13; 4; 14), /* = -137. 17.288.x* = (0; 0; 0), /* = 0. 17.289. х* = (0; 1; 0), /* = -1. 17.290. х* = (1; 0; 0),
/* = —2. 17.291. х* = (-2,683; -1,342), /* = -4,025. 17.292. х* =
= (3,578; 1,789), /* - -37,667. 17.293. х* = (0,447; 0,894), /* = -1,4. 17.294. х* = (0,791; 1,258), /* = -2,214. 17.295. х* = (0; 0), /* = 0. 17.296. х* = (1,005; 0,099), /* = 9,95. 17.297. х* = (0,618; 0,618), /* = 4,090. 17.298. х* = (1; 0,5), /* = -1,75. 17.299. zuj = max (0, zy),
Ответы и указания
569
aj ’
17.300. zuj = < бу,
если Zj < aj,
если Zj > bj, j = 1, ..., n,
Zj, если aj Zj bj.
z, если
17.301. zu = <
I x(°) 4- 7?o(z — x(°))/||z — x(°)||, если
z G U, z£U.
17.302. zu = z—[(a, z)—b]a/||a||. 17.303. Zu = z+max {0, b - (a, z)}a/||a||. 17.304. x* = (0; 0), /* = 0. 17.305. x* = (3; 0), /* = -81. 17.306. x* = = (4; 2), f* = -68. 17.307. x* = (5; 1), Г = 11,29. 17.308. x* = = (3,1056; 1,5528), /* = 7,764. 17.309. x* = (2,1213; 1,8787), /* = = -8,9411. 17.310. x* = (1; 1; 1), /*= 6. 17.311. x* = (0,8; 1; 0,4),
/* = -8,2. 17.312. x* = (0,8; 0,4), /* = 104,987. 17.313. x* = (1; 0,5), /* = 0,5. 17.314. x* = (1,5; 0,5), /* = -8,5. 17.315. x* = (2; 1), /* = -16. 17.316. x* = (1; 2), f* = -3. 17.317. x* = (3; 1), /* = = 2,3026. 17.318. x* = (-0,9487; 0,3162), /* = -5,3246. 17.319. x* = = (1,7071; 0,2929), /* = -9,4858. 17.320. x* = (-2,111; 0,8944), /* = = 1,7603. 17.321. x* = (1,6; 0,8), /* = -3,8. 17.322. x* = (2; 2), /* = -2,2082. 17.323. x* = (2; 3), /* = -117. 17.324. x* = (5; 2), /* = = - 51. 17.325. x* = (33/13; 4/13; 0), /* = -7,385. 17.326. x* = (2; 4), /* = -30. 17.327. x* = (2/3; 14/9), /* = -2,444. 17.328. x* = (0; 1; 1), /* = -1. 17.329. x* = (1,258; 0,791), /* = -2,214. 17.330. x* = = (2,684; 1,342), /* = -11,125. 17.331. x* = (0,5; 1), /* = -1,75. 17.332. x* = (0,618; 0,618), /* = 4,090. 17.333. x* = (1,8388; 0,7862), /* = -2,7933. 17.334.x* = (0,6667; 0,6667),/* = -8,1111. 17.335.x* = = (0,791; 1,258), /* = -0,214. 17.336.x* = (2,530; 1,265), /* = -14,299. 17.337. x* = (1; 0,5), /* = -0,75. 17.338. x* = (0,8284; 0,4142), /* = = - 2,8995. 17.339. x* = (3; 4), /* = 40.
N
17.340. J(x, u) = —> max,
k=i
x(k) _ x(k-l) u(k), k = 1, . . . , N,
e [0; S], к = 1, ..., N - 1, e [0; S], к = 1, ..., N, = 0, x(N>) = S,
570
Ответы и указания
где — средства, выделенные k-му предприятию, х^ — сумма средств, выделенных предприятиям с номерами от 1 до к. 17.341. См. ответ к задаче 17.340, где — средства, выделенные предприятию в к-м году, а — средства, выделенные ему за первые к лет, к = 1, ..., N.
N
17.342. J(x, й) = ^Jk^k~1\ uw) -> max, k=i
х[к^ = , х^ = х2к~^^ • и^к\ к = 1, ..., N,
х[к) G [0; S], к = 1, ..., N- 1,
G [0; 5], к = 1, ..., N,
J0) _ 0 (0) _ г (N) _ s
к к
где х^ = = = 0, к = 1, ..., N — 1,
JN(x(N~^ иЦ =
N
17.343. J(x, и) = -> max,
k=l
x^ = Ax(k~^ — vSk\ A; = 1, ..., TV,
x^ ^0, k = 1, ..., N-l,
v№ € [0; Аж*-1], к = 1, ..., N,
x^ = a, = 0,
где — количество семян, проданных в к-м году, х^ — их количество, оставленное в совхозе к концу к-го года, к = 1, ..., N. 17.344. В ответе задачи 17.343 заменить конечное условие = 0 на условие Ь.
N
17.345. J(x, й) = [Ji(u(fc)) 4- -> max,
к=1
х^ = fifvW) + — и^), к = 1, ..., N,
G [0; к = 1, ..., N,
х^0>) = S, х^^ 0,
где — средства, перераспределяемые в начале к-го года, — средства, выделяемые первому предприятию в к-м году.
Ответы и указания
571
N
17.346. J(x, й) — ^2 (^w2fc) _ akui^) -> max, k=i
x^ = x(<k~1>> + A = 1, ..., TV,
G [0; P], k= 1, ..., TV-1,
u[k) G [0; P — G [0; x^k~1^ + u^], k — 1, ..., N,
x^0>) = a, G [0; P],
где — запасы продукции в начале k-го месяца, и — количества продукции, принятой и проданной в начале к-го месяца соответственно. 17.347. В ответе задачи 17.346 заменить ограничения на управления следующими ограничениями: G [0; xSk~^], G
G [0; Р-ж^-1) + и{к)], к = 1, ..., N.
N
17.348. J(x, u) = -» min,
fc=i
xSO — к = 1, ..., N,
^0, A; = 1, ..., — 1,
> 0, G Z, к = 1, ..., N,
x^0>) = b, 0, к
где x^ = b - a,ji№.
j=i
N
17.349. J(x, u) = '^Fk(u^k'>) -> min, k=l
X(A) — — и^а^, к = 1, ..., TV,
x-k^ 0, i = 1, ..., m, к = 1, ..., N — 1,
> 0, G Z, к = 1, ..., N,
x(0) = b = (bi, ..., bm), x^ 0, i = 1, ..., m, к
где x(fc) и — m-мерные векторы с компонентами х\к>> = Ь{—У~^
j=i
и = aik соответственно, к = 1, ..., N. 17.350. u* = {1, 2, 1, 1},
J* = 12. 17.351. Три решения: й* = {0, 2, 1, 1, 1}, й* = {1, 1, 1, 1, 1},
й* = {0, 1, 1, 1, 2}, J* = 13,5. 17.352. й* = {25, 25, 25, 25}, J* =
= 44. 17.353. й* = {100, 100, 200, 100}, J* = 226. 17.354. а) й* =
ЪТ1
Ответы и указания
= {100, 100, 200, 0}, J* = 186; б) й* = {100, 100, 300, 100}. Указание. Использовать результаты условной оптимизации, полученные при решении задачи 17.353. 17.355. Семь решений: й* = {100, 0, 200, 100},
й* = {100, 40, 180, 80}, й* = {120, 0, 200, 80}, й* = {120, 0, 180, 100},
й* = {120, 20, 180, 80}, й* = {100, 20, 200, 80}, й* = {100,20,180,100};
J* = 620. 17.356. а) й* = {100, 100, 100}, J* = 300; б) й* = {114,3;
114,3; 71,4}, J* = 48,6. 17.357. й* = {0, 150, 0}, J* = 27. 17.358. й* = = {3, 3, 3}, J* = 27. 17.359. й* = {S/N, S/N, ..., S/N}, J* = (S/N)n. 17.360. й* = {0, 0, ..., aAN}, J* = caAN. 17.361. й* = {19,2; 3,84;
0,768}, J* = 38,402. 17.362. й* = {0, 0, ..., aAN - b}, J* = caAN -
- сЬ. 17.363. й* = {19,01; 3,802; 7,604}, .7* = 37,638. 17.364. й{ =
= {200, 160, 128, 0}, = {0; 0; 0; 102,4}, J* = 187,36, где и —
средства, распределенные первому и второму предприятиям соответственно. 17.365. uf = {40; 64; 25,6}, = {80, 0, 0}, J* = 99,84.
17.366. й{ = {10, 0, 10, 0}, = {0, 10, 10, 0}, .7* = 90. 17.367. =
= {7, 0, 12, 4}, = {0, 12, 12, 0}, J* = 111. 17.368. и* = (2, 1),
F* = -11. 17.369. Два решения: и* = {2, 0}, и* = {1, 1}; F* = -2. 17.370. и* = {1, 2}, F* = -31. 17.371. и* = {0, 0, 7}, F* = -21. 17.372. й* = {2, 1, 1}, J* = 115. 17.373. й* = {10, 1, 1}, J* = 5760. 17.374. Четыре решения: й* = {2, 3, 4}, й* = {3, 3, 3}, й* = {1, 4, 4}, й* = {2, 4, 3}; J* = 72. 17.375. у = ^-(а;3 — ж)- 17.376. Бесконечное множество решений: у = (С + х) sina;, С Е 1 17.377. у = е/х — — Ina;. 17.378. у = х3 — х. 17.379. Нет решений. 17.380. у = sha; х , ~ sh2 , • _ „ 1
= —— — —. 17.381. у = sh2a;---------—sha;. 17.382. у = -хех — sha;.
sh 1 2 J sh 1 y 2
17.383. у = ex - e~3x. 17.384. у = S,m6sha; + sina;. 17.386. Нет sh о
решений. 17.387. у = — x. 17.388. у = x. 17.389. у = -(1 + a;). a*2 4
17.390.1/ = (2a;/3)3/2. 17.391.?/ = - — -- + -. 17.392. y = x1
17.393. у — -(x — x2). 17.394. Два решения: у = (a; + l)2/3 и у = В — A
= (За; — I)2/3. 17.395. у = cosa; + sina; — 1. 17.396. у = --(a; — a) +4.
b — a
17.397. у = yA - x2 + 1. 17.398. у = ch (a; - 0 / ch 1. 17.399. < Ha-
Ответы и указания
573
правим ось Оу вертикально вниз. Скорость материальной точки ds/dt = = \/2ду, поэтому время ее движения из точки Mq в точку Mi t =
о
F у'2
—— dx. Так как подынтегральная функция не зависит
У
,/2
явно от а;, то уравнение Эйлера имеет первый интеграл ---------—— —
\/У
/2
У 2
— —= = С или у(1 + у' ) = Ci. Введем параметр t, пола-\]у(1 + у'2}
. С\ Ci . < dy
гая у = ctgi. Тогда у — -----------= — (1 — cos2i): dx = — =
ь 1 + ctg21 2 v . у'
Ci
= Ci(l-cos2i) dt, x = —(2i—sin2f) + C2. Из условия прохождения кривой у(х) через точку Mq(0, 0) находим: = 0. Обозначив 2t через ii, получим уравнения семейства циклоид: х = ~у (ы — sinii), у = — (1 — — cosii). Таким образом, искомая кривая является циклоидой. Постоянная Ci может быть найдена из условия ее прохождения через точку , ?/1). 17.400. у = х(х - I)2. 17.401. у = х4. 17.402. у = ^(а;5 + + За;3 — 2а;2). 17.403. у = х + cosx. 17.404. у = 0. 17.405. у — хех. 17.406. у = —-—. 17.407. у = cosx. 17.408. у = а;4. 17.409. у — shx.
х + 1
17.410. у = х — sina;. 17.411. у = sha; — sina;. 17.412. yi = sina;, У2 = — — sin a;. 17.413. y\ = sh x, y2 = — sh x. 17.414. yi = sin x, y2 = — sin x. 17.415. yi = ex, y2 — e~x. 17.416. yi — x4, y2 = x3. 17.417. yi = In x +1, X
У2 = 0. 17.418. Бесконечное множество решений: yi = — — sina; — cosx —
9
X X
— C sinx4-а;, У2 = — -sinx + C sina;, C 6 IR. 17.419. yi = — +1, y2 = 1.
у = —2a;, xi = 1. 17.421. Два решения: у — ±4x, Xi = у у = x/\/2, xt = ^2. 17.423. у = -x + 3/4, a;0 = 1/2, xx = 23/8. у = -a;(l - a;). 17.425. у = (a;2 - l)/4. 17.426. Бесконечное мно-решений: у = С sin а;, С е К. 17.427. Нет решений. 17.428. у = - (х — I)2, xi — 2. 17.429. у = (а; — j — 1) sina;. 17.430. у = 0.
17.431. у = sha;. 17.432. у = ех 4-sina;. 17.433. Два решения: у = = x/ТП и у = \ 17.434. у = Ina; + 1. 17.435. у = -ех/(е3 + 1).
17.420.
17.422.
17.424.
жество
574
Ответы и указания
17.436. у = 2 In (х + 1). 17.437. у — sinx + cosa:. 17.438. ух = cos ж 4-
4- sin ж, у2 = cos ж — sin ж. 17.439. у\ = (ж — 2)с х, У2 — (1 — х)е
17.440. yi — 2 — ж, у2 = х + 1.
17.442. Нет решения. 17.443. у\
17.441. yi = ж2 4- ж, у2 = х2 — ж.
ж . 1
= -sin ж, у2 — — (sin ж — ж cos ж).
17.444. т/i = ж2 4- cos ж 4- sin ж, у2 = ж2 - cos ж — sin ж. 17.445. Бес-
конечное множество решений: у\ = т/>(ж), У2 — х — 4>(x) 4- у^ 4- у[°^ — а, где -ф(х) 6 Ci[a; 5], если у^ - у[^ — (у^ — у{°^) = b — а\ нет решений при т/.^ - у{1} - (У2°} - 2/$0)) /Ь-а. 17.446. у - |ж3 - |ж. 17.447. у = = бОж3 — 9бж2 + Збж. 17.448. у = (ж — 2зтж)/тг. 17.449. Два решения:
у = х 4- sin х, у = х - sin ж. 17.450. у = хе х. 17.451. т/i — -бж2 + бж,
т/2 = Зж2 — 2ж. 17.452. Два решения: т/i = Зж2 — 2ж, т/2 — Зж2 — бж и 5 3
т/i = —Зж2 4- 4ж, у2 = —Зж2. 17.453. т/i = 0, у2 — -ж3 — -х. 17.454. Бесконечное множество решений: т/i = 2зт/г7гж, т/2 = — 2зшА;7гж, k 6 Z. 17.455. Два решения: т/i = Зж—ж3, т/2 = х3—х и т/i — ж3+ж, т/2 — —ж3+ж.
17.456. т/2(ж) = ж(2 — ж)(—1,3551 + 0,303ж). Указание. Искать реше
ние т/г(ж) = ж(2 — ж)(С1 + Сгж). 17.457. а/* (ж) = 0,3215(ж — 1)(ж — — 2). Указание. Решение искать в виде т/1(ж) = С1(ж — 1)(ж — 2).
17.458. т/2(ж) = ж(1 — ж)(0,192 + 0,171ж). Указание. Решение искать в виде т/г(ж) = ж(1 - ж)(Са + Сгж). 17.459. Мз(ж, у) = ж2 4- у2 + жт/(1 -— ж — т/)(3,0401 — 0,05б2ж(1 + ж)). Указание. Решение искать в виде «з(ж, 7/) = х2 + у2 + С1Ху(1 - X - у) + с2х2у(1 - X - у) + С3х3у(1 - X - у). 17.460. т/i (ж, т/) = 0,0037(ж2 — 4)(т/2 — 4). Указание. Решение искать в виде т/i (ж, т/) = С1(ж2 — 4)(т/2 - 4). 17.461. у% (ж) = ж(ж — 1)(0,1708 + 4- 0,1744ж), т/з = ж(ж - 1)(0,1705 + 0,176ж - ,0,002ж2). Указание. Решения искать в виде т/о(ж) = ж(ж — l)(Ci 4- Сгж), т/з(ж) = ж(ж — l)(Ci 4-4- С2Х 4- С3Ж2). В заданных точках значения 7/2 и 7/3 совпадают с точностью до 0,0001. 17.462. т/i (ж, т/) — 0,3125(ж2 — 1)(т/2 — 1). Указание. Решение искать в виде 7/1 (ж, т/) = С1(ж2 - 1)(т/2 - 1). 17.463. t/J(ж, т/) = = 0,3125жт/(ж — 1)(т/ — 1). Указание. Решение искать в виде т/i (ж, т/) = = 0,3125жт/(ж — 1)(т/ - 1). 17.464. т/(ж) = ж(2 - ж)/4. 17.465. т/(ж) = = ж(1 - ж)(0,140 - 0,144ж). 17.466. т/(ж) = ж(1 - ж)(-0,655 - 0,277ж).
СПИСОК ЛИТЕРАТУРЫ
1. Васильев Ф. П. Численные методы решения экстремальных задач. — М.: Наука, 1980.
2. Кузин Л. Т. Основы кибернетики. — Т. I: Математические основы кибернетики. — М.: Энергия, 1973.
3. Ефимов А.В. Математический анализ (специальные разделы). — Ч. I: Общие функциональные ряды и их приложения. — М.: Высшая школа, 1980.
4. Ефимов А.В., Золотарев Ю.Г., Терпигорева В.М. Математический анализ (специальные разделы). — Ч. II: Применение некоторых методов математического и функционального анализа. — М.: Высшая школа, 1980.
5. Гачев Э.М., Кушниренко А.Г., Тихомиров В.М. Сборник задач по оптимальному управлению. — М.: Изд-во Моск, ун-та, 1980.
6. Колихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. — М.: Высшая школа, 1979.
7. О чан Ю.С. Методы математической физики. — М.: Высшая школа, 1965.
8. Очан Ю.С. Сборник задач по методам математической физики. — М.: Высшая школа, 1967.
9. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по уравнениям математической физики. — М.: Наука, 1972.
10. Араманович И.Г., Левин В.И. Уравнения математической физики. — М.: Наука, 1964.
11. Смирнов М. М. Задачник по уравнениям математической физики. — М.: Наука, 1968.
12. Дьяченко В.Ф. Основные понятия вычислительной математики. — М.: Наука, 1977.
13. Калиткин Н. Н. Численные методы. — М.: Наука, 1978.
14. Марчук Г.И. Методы вычислительной математики. — М.: Наука, 1989.
15. Краснов М. Л. Интегральные уравнения. Введение в теорию. — М.: Наука, 1975.
16. Краснов М. Л., Киселев А.Н., Макаренко Г.И. Интегральные уравнения. — 2-е изд. — М.: Наука, 1976.