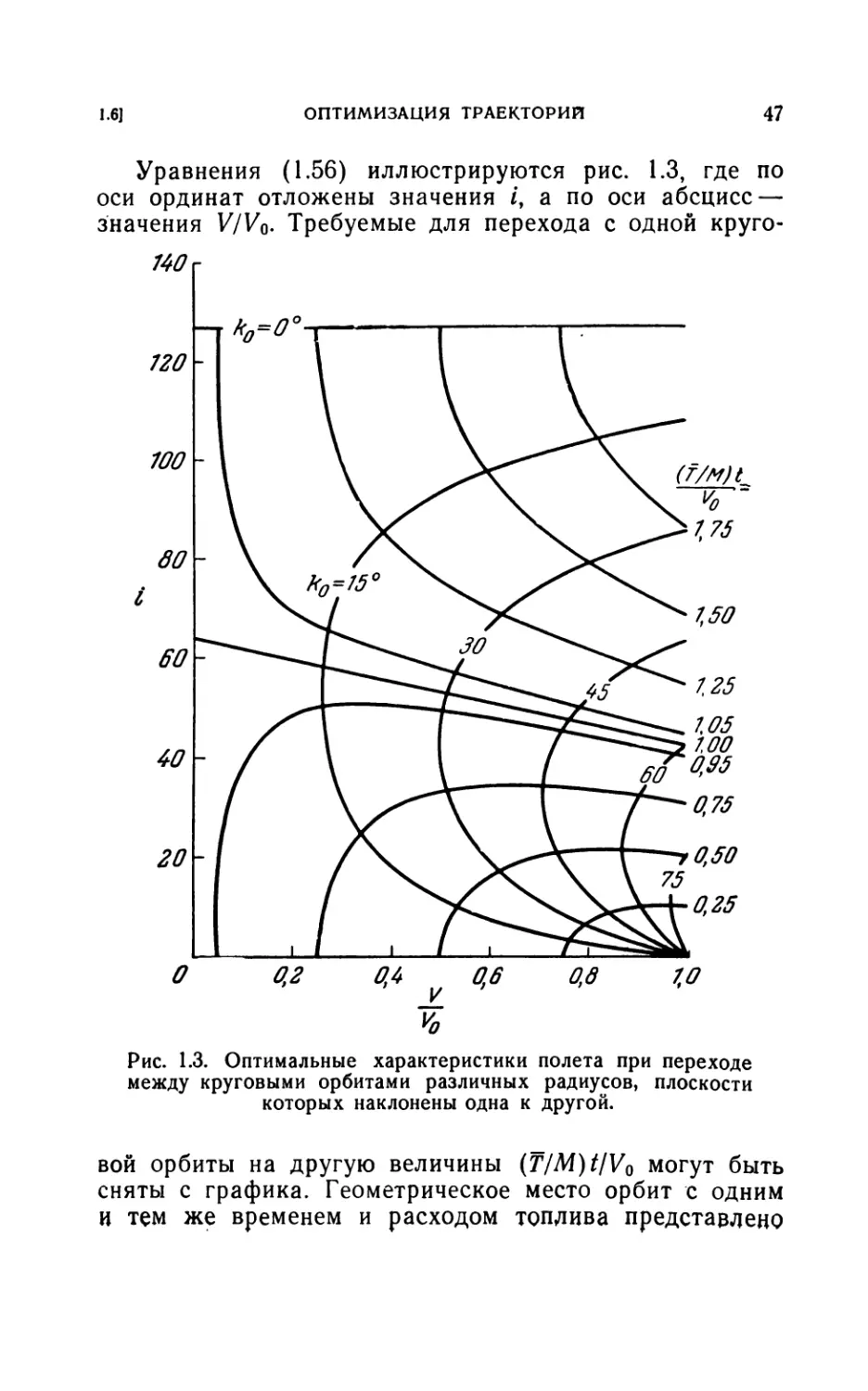
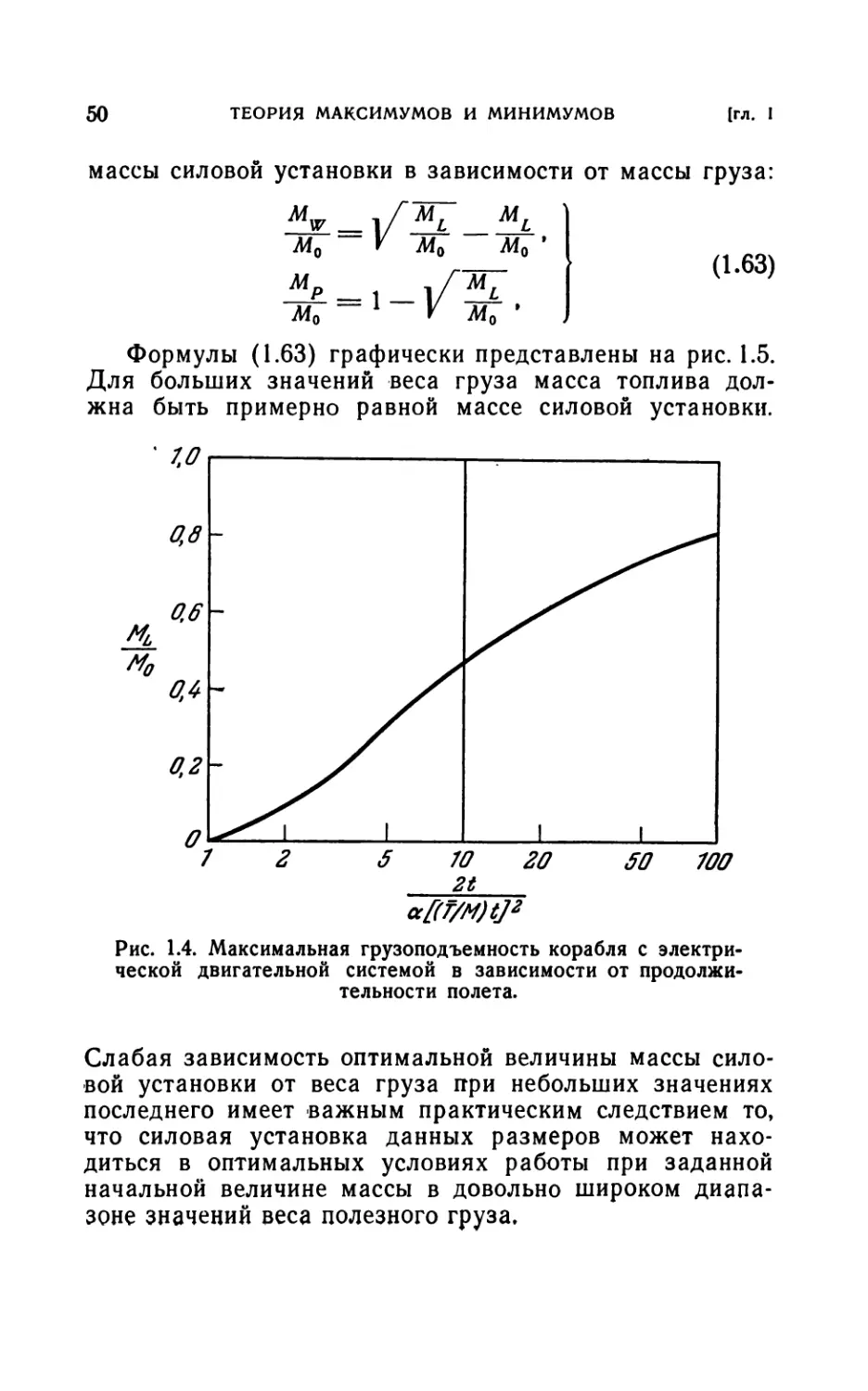
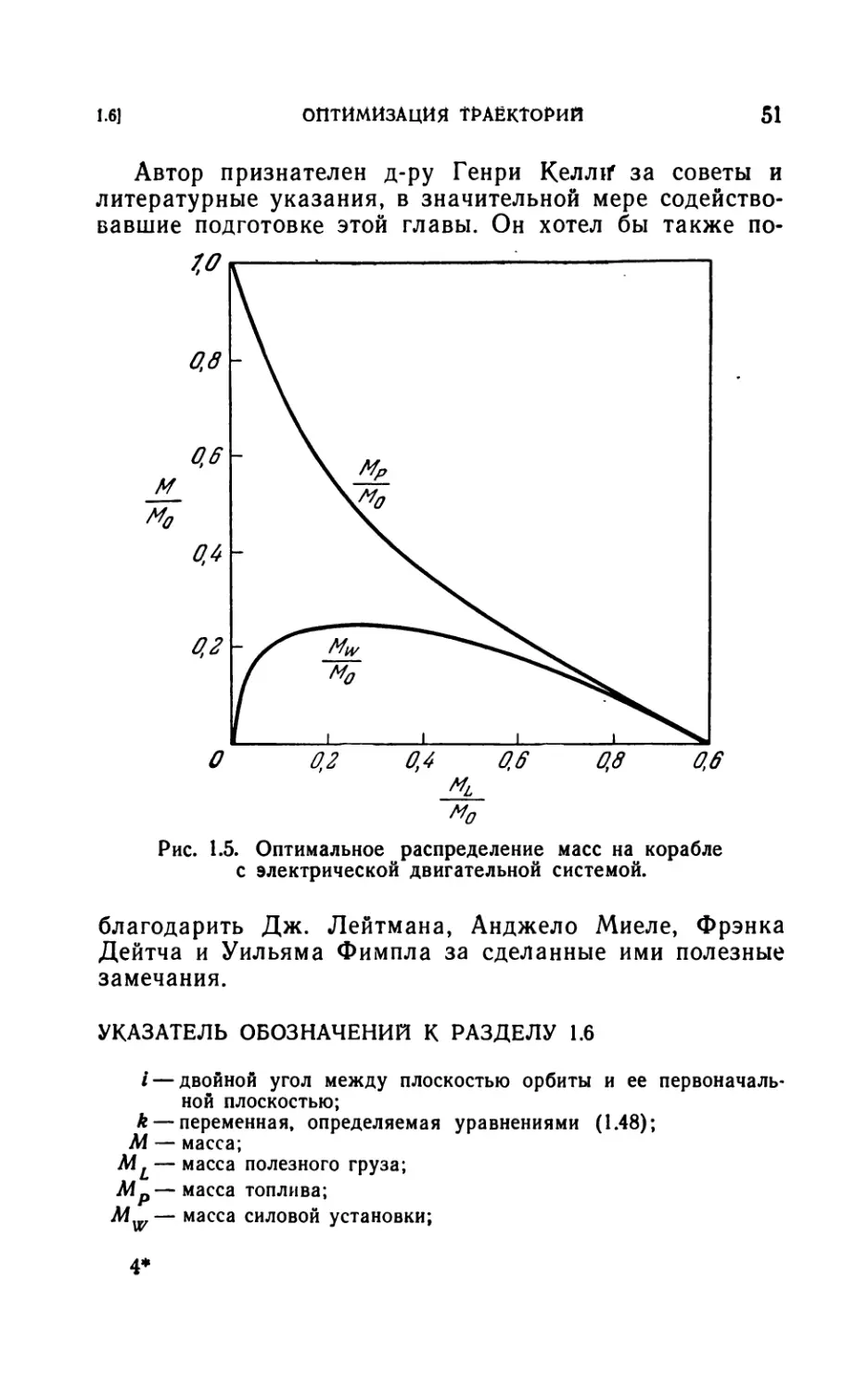
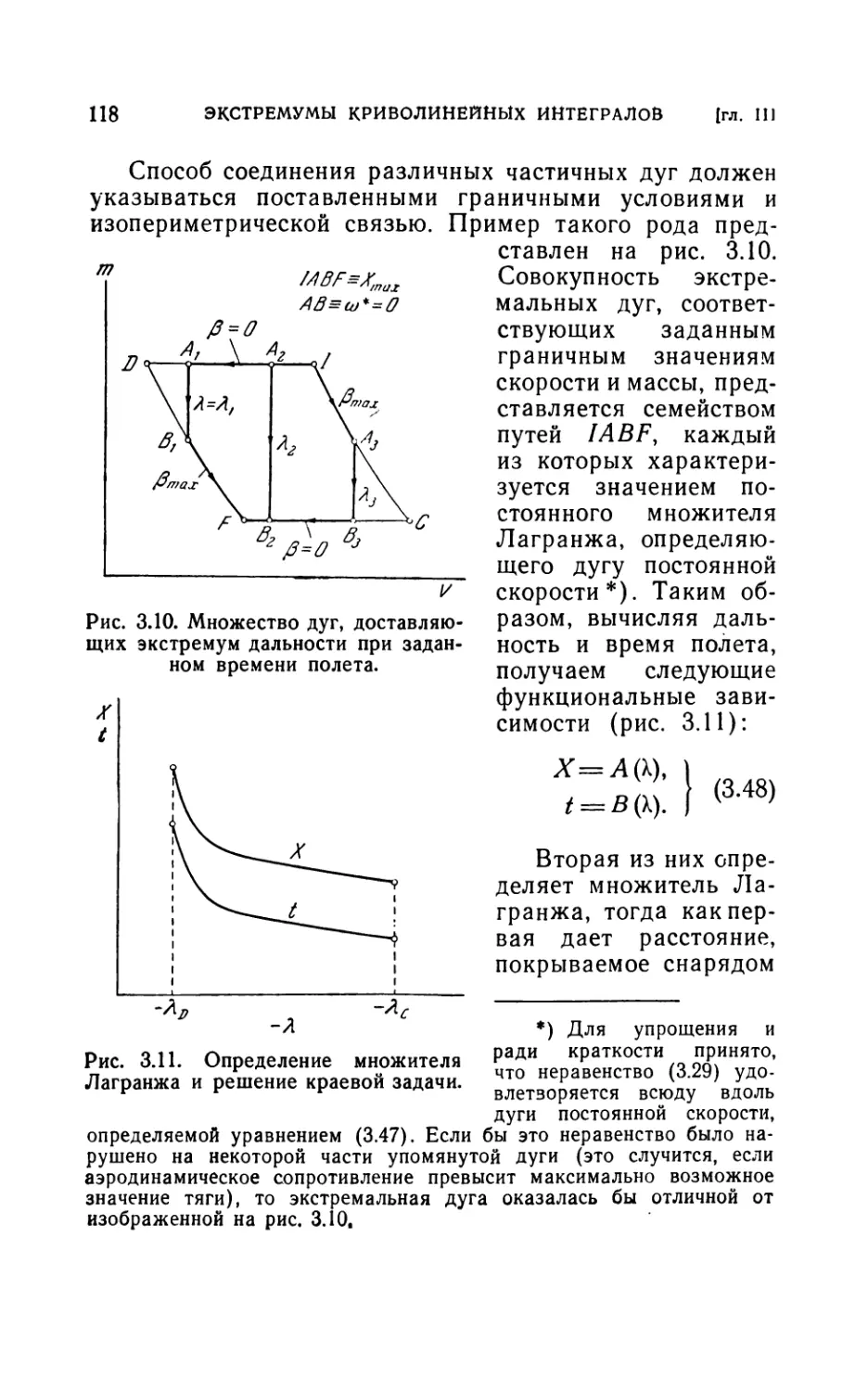
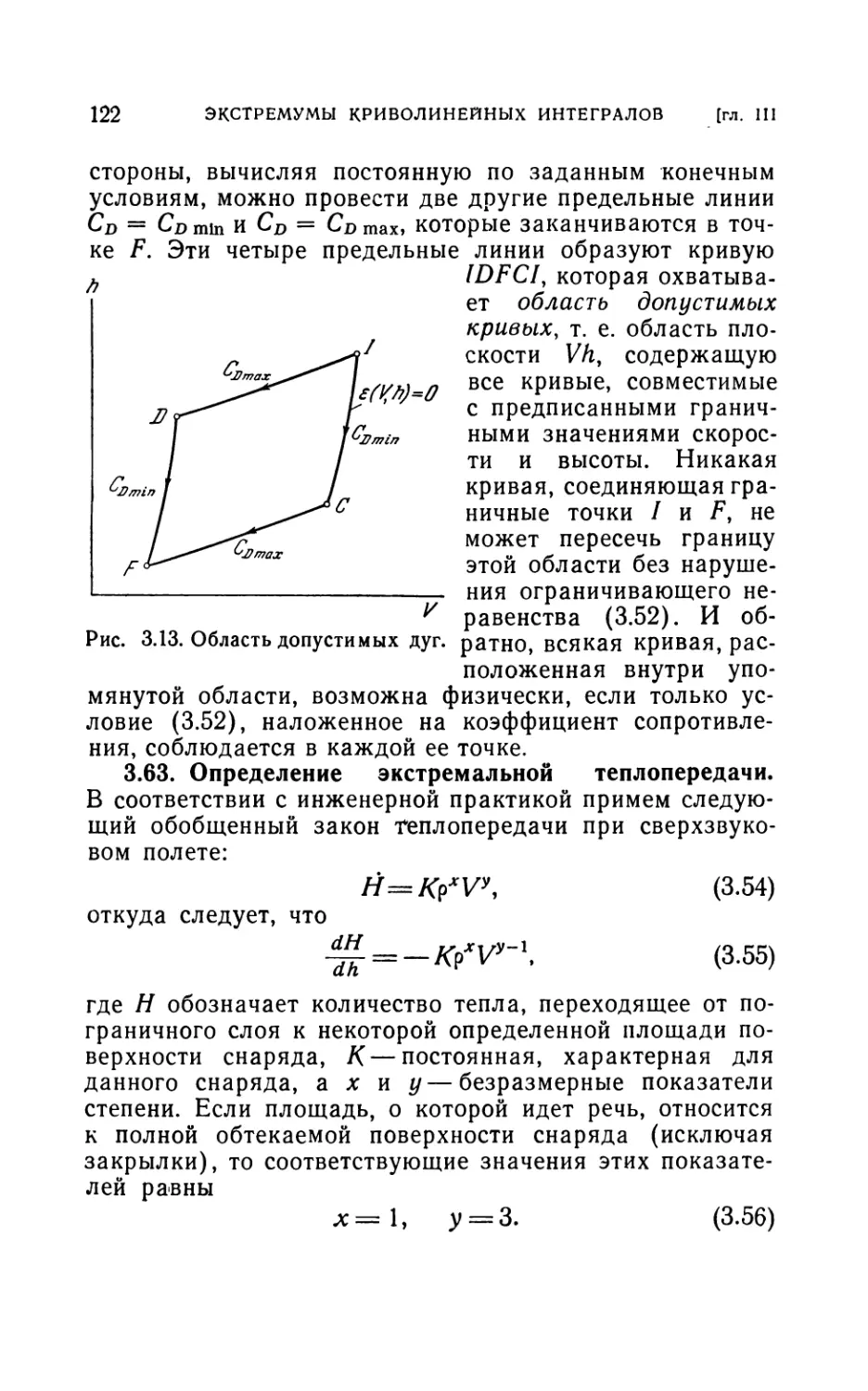
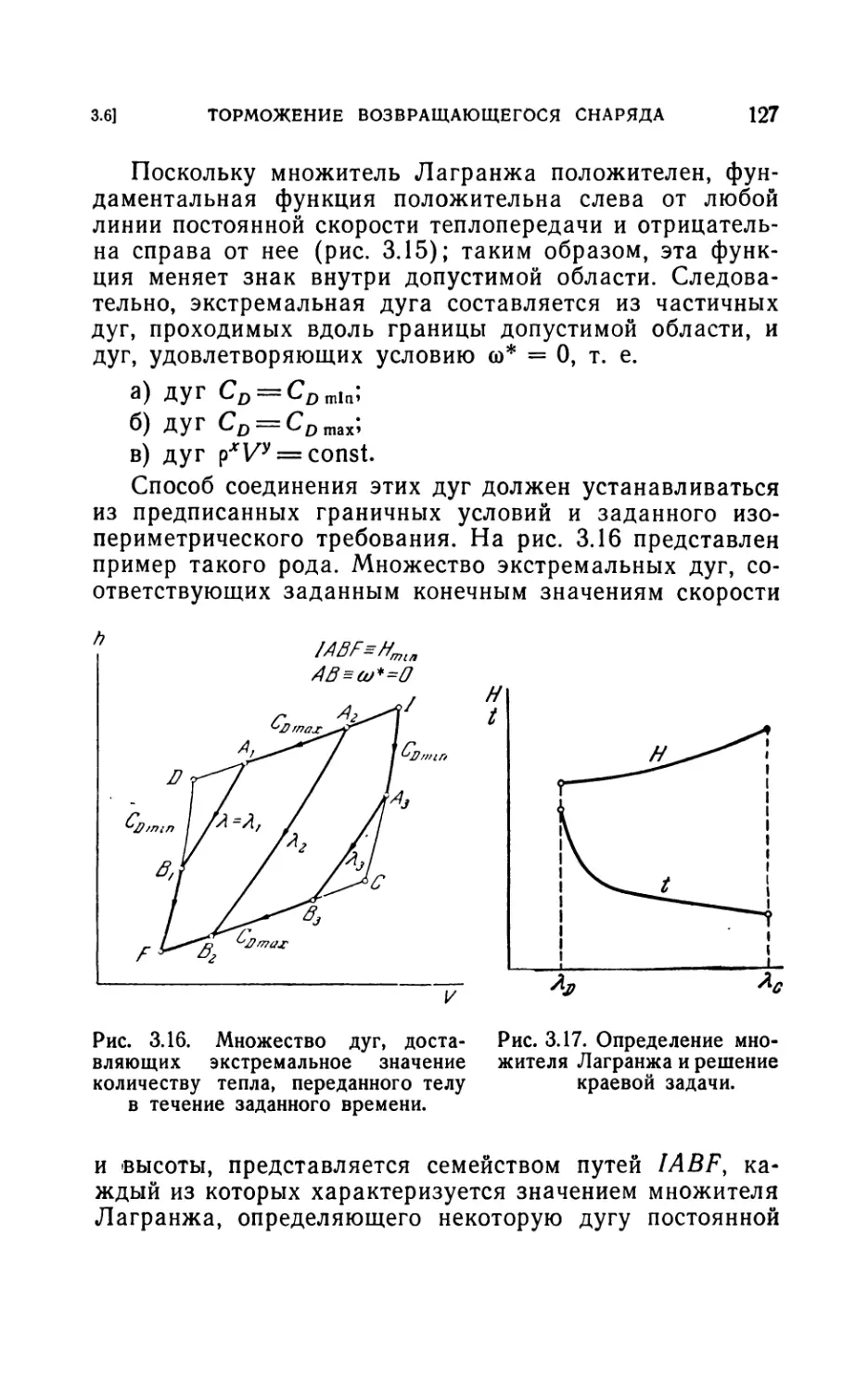
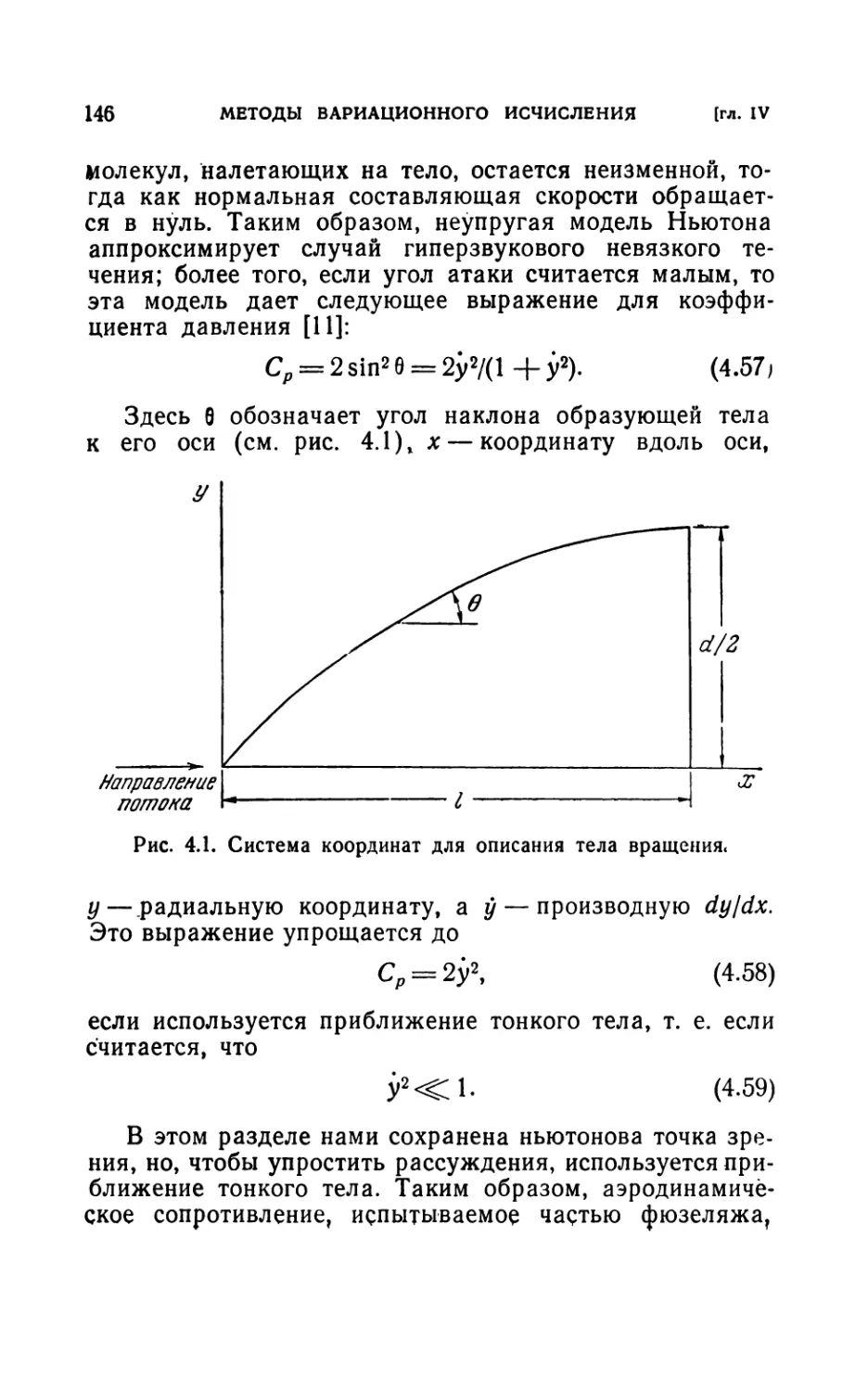
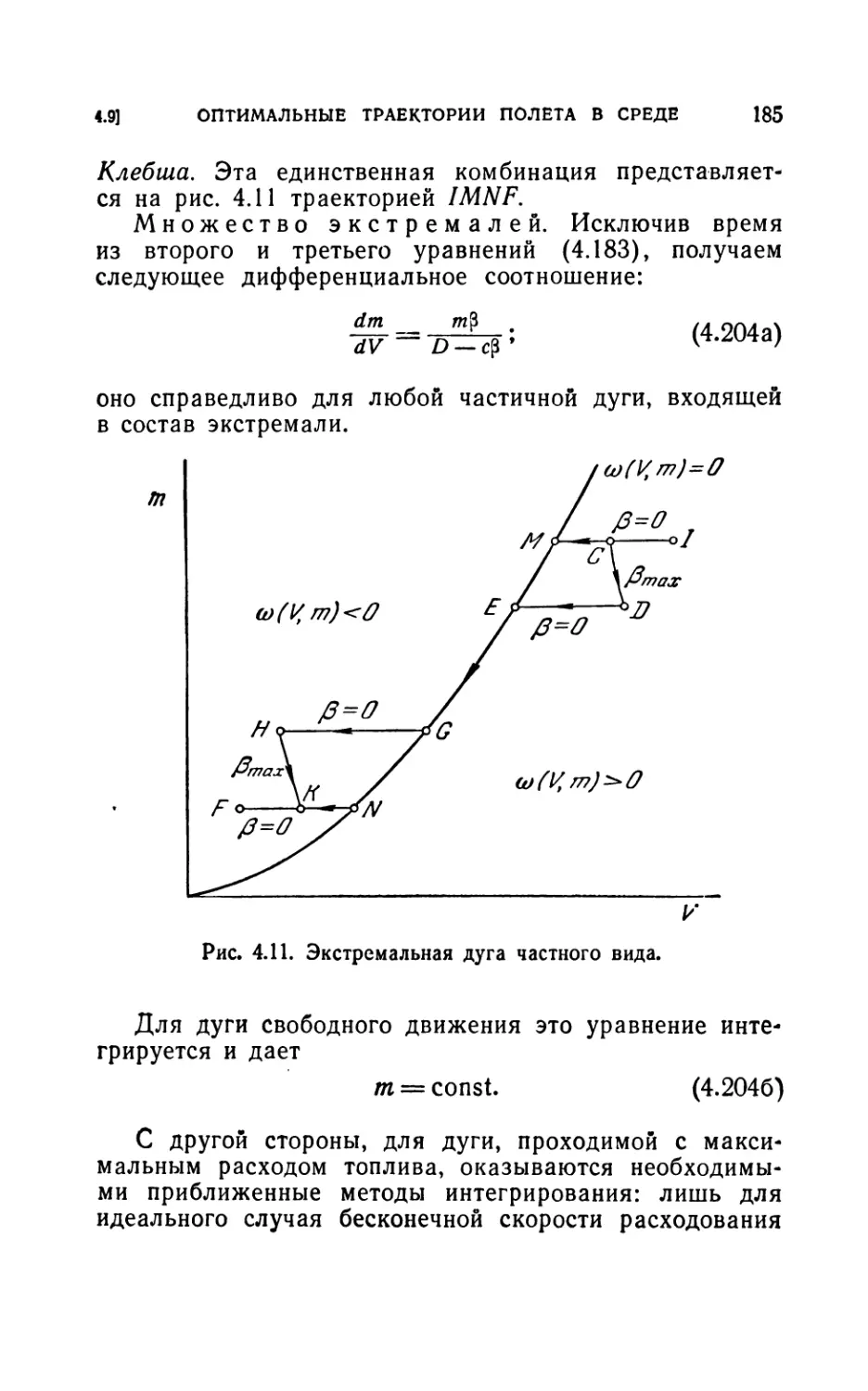
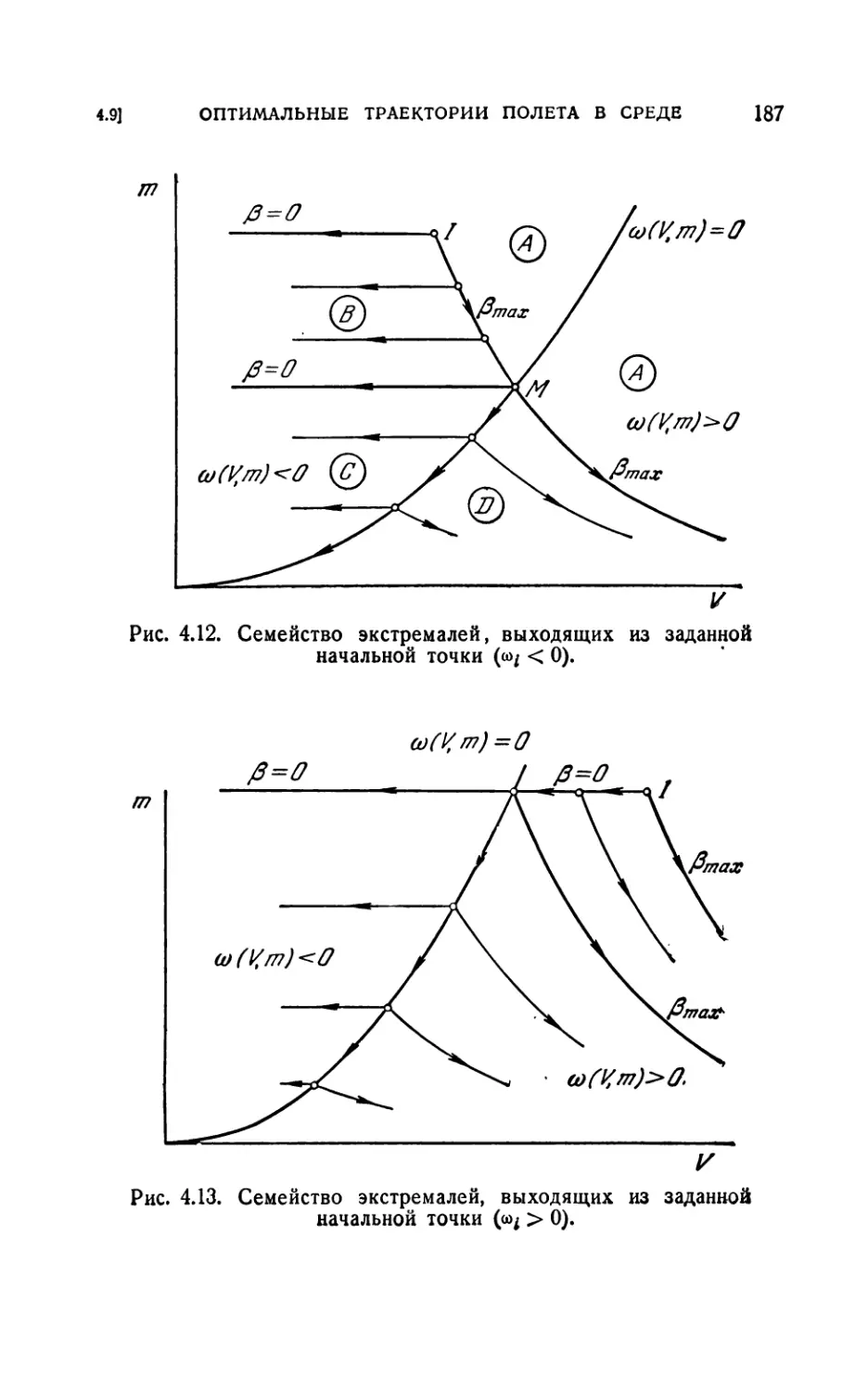
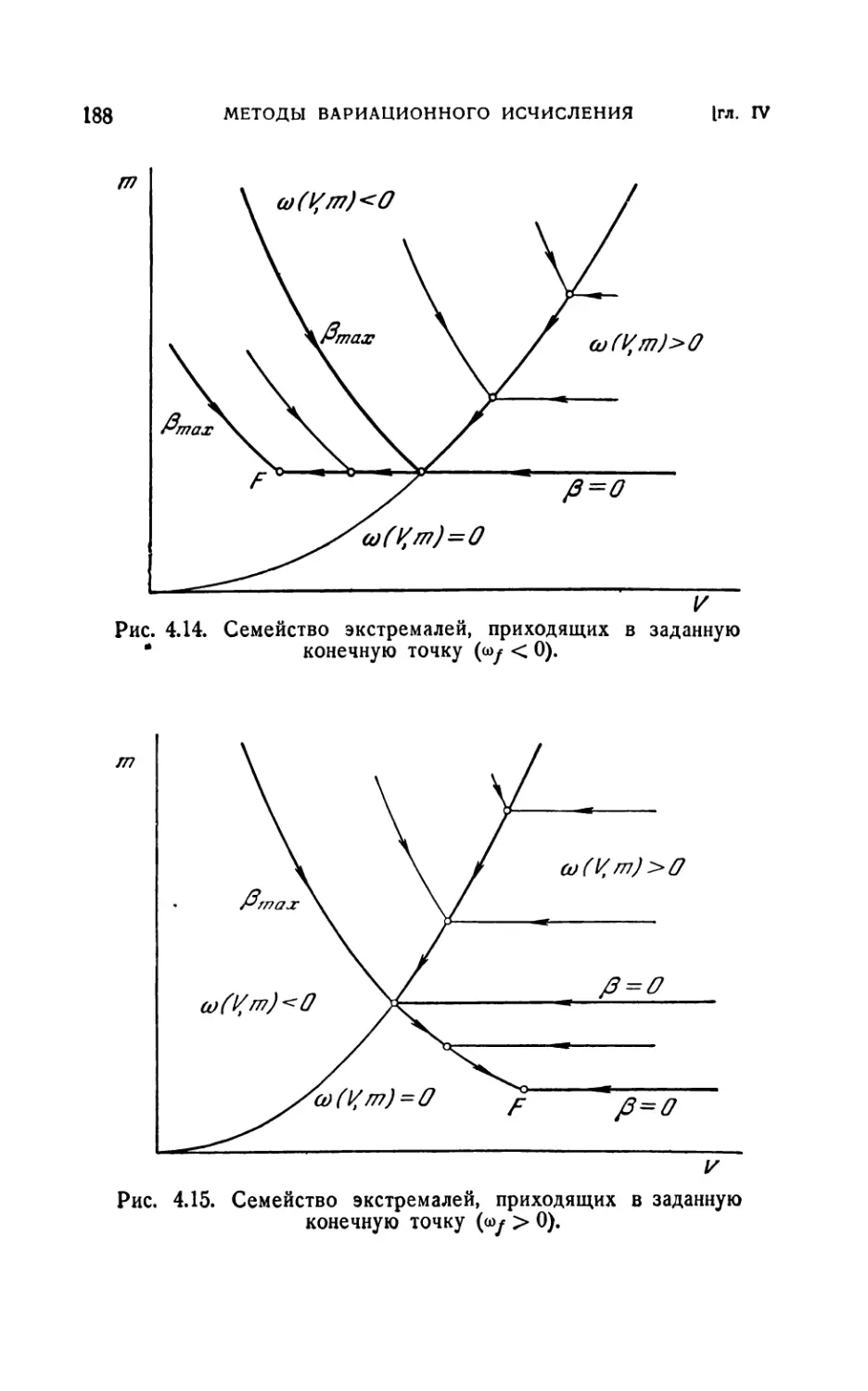
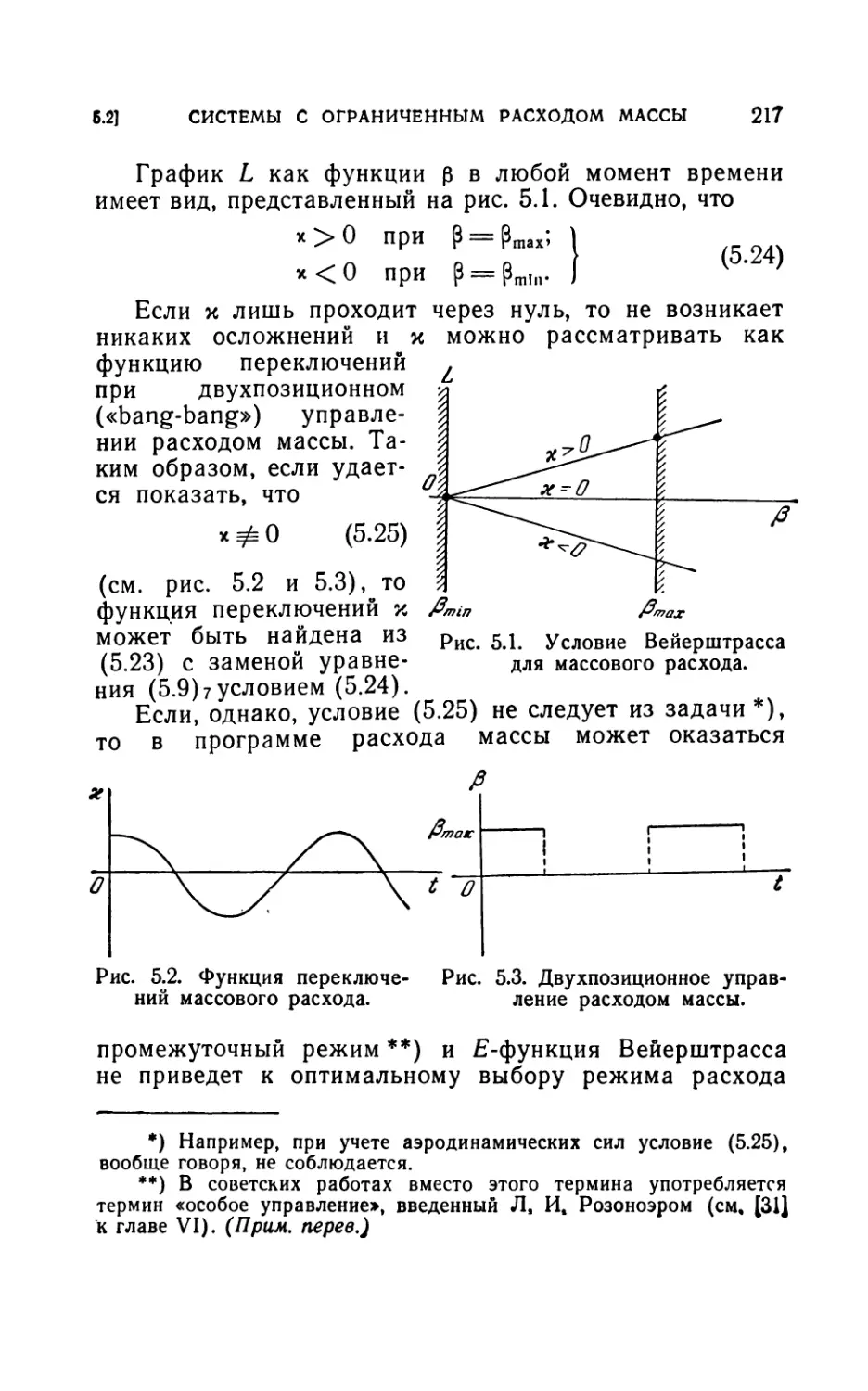
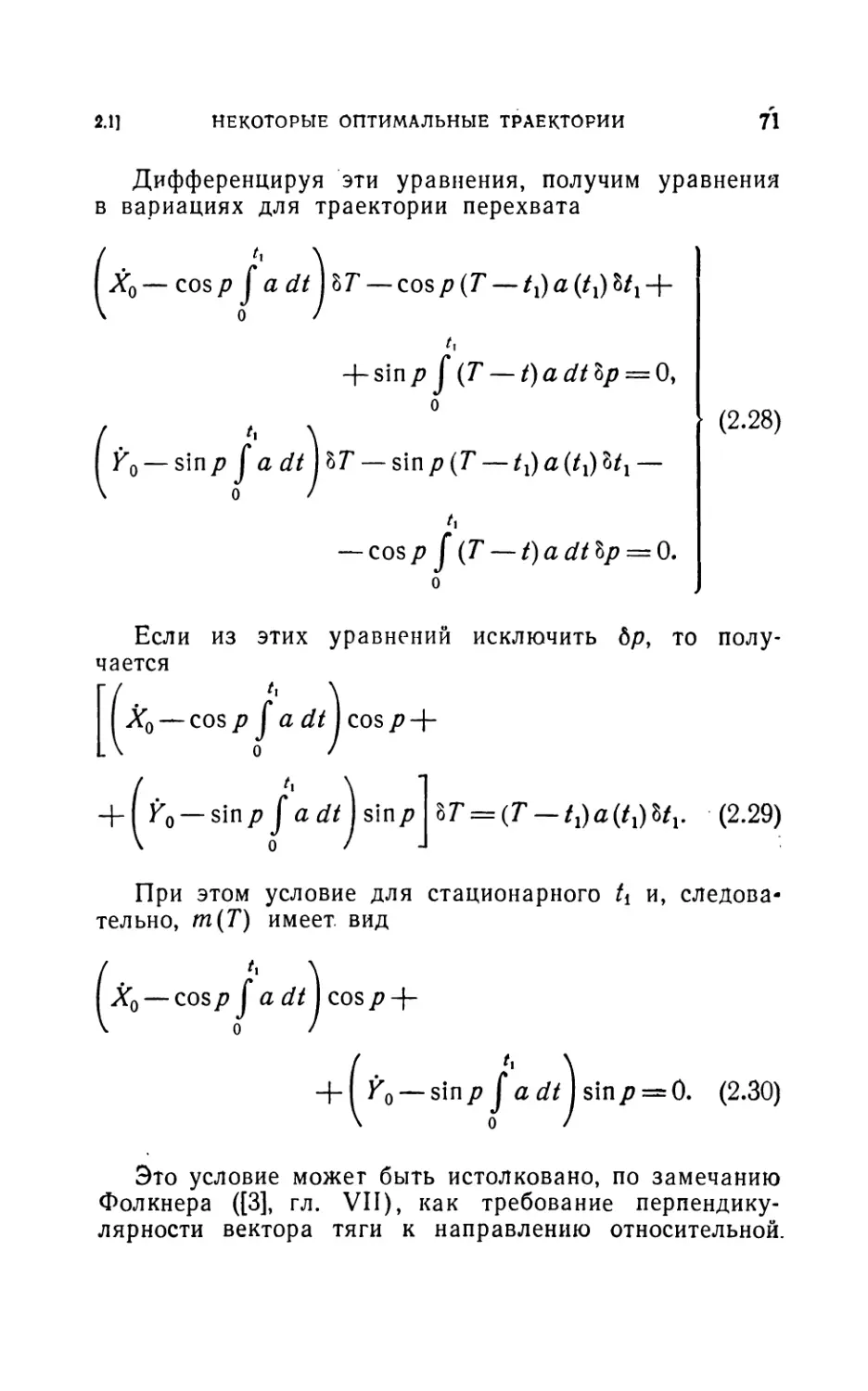Author: Лейтман Дж.
Tags: общая механика механика твердых и жидких тел техника средств транспорта космические исследования
Year: 1965
Text
МЕТОДЫ
ОПТИМИЗАЦИИ
С ПРИЛОЖЕНИЯМИ
К МЕХАНИКЕ
КОСМИЧЕСКОГО
ПОЛЕТА
МЕХАНИКА
КОСМИЧЕСКОГО
ПОЛЕТА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИ I ЕРАТУРЫ
МО С КВ А 1965
МЕТОДЫ ОПТИМИЗАЦИИ
С ПРИЛОЖЕНИЯМИ
К МЕХАНИКЕ
КОСМИЧЕСКОГО ПОЛЕТА
Под редакцией Дж. ЛЕЙТМАНА
При авторском участии
Р. ВЕЛЛМАНА, Дж. БРЕКУЭЛЛА, Р. У. БАССАРДА,
Т. Н. ЭДЕЛЬБАУМА, Ф. Д: ФОЛКНЕРА, Р. КАЛАБА,
К. М. КАШМАРА, Г. Дж. КЕЛЛИ, Р. Э. КОПЦА,
Д. Ф. ЛОУДЕНА, Дж. ЛЕЙТМАНА, А. МИЕЛЕ,
Э. Л. ПИТЕРСОНА
Перевод с английского К. А. ЛУРЬЕ
Под редакцией В. А. ТРОИЦКОГО
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965
531
М 54
УДК 531.01:629.191
OPTIMIZATION TECHNIQUES
WITH APPLICATIONS
TO AEROSPACE SYSTEMS
Edited by
GEORGE LEITMANN
Applied Mechanics Group,
Mechanical Engineering Department
University of California, Berkeley, California
1962
New York Academic PRESS London
ОГЛАВЛЕНИЕ
От редактора перевода ..................................... 13
Таблица перевода американских мер в метрические и в еди-
ницы СИ................................................. 15
Предисловие................................................ 16
Глава I. Теория максимумов и минимумов (Теодор
Н. Эдельбаум)........................................... 19
1.1. Необходимые условия максимума или минимума........... 19
1.11. Введение. Терминология вариационного исчисления (19.). 1.12. Не-
обходимые условия максимума или минимума (21).
1.2. Достаточные условия максимума или минимума............ 22
1.21. Введение (22). 1.22. Две независимые переменные (23). 1.23. п не
зависимых переменных (24).
1.3. Дополнительные условия................................ 25
1.31. Решение путем подстановки (25). 1.32. Решение при связанных
вариациях (26). 1.33. Множители Лагранжа (28). 1.34. Функции на
гружения (29).
1.4. Приложение к интегралам............................... 30
1.41. Связь между теорией обыкновенных максимумов и минимумов и
вариационным исчислением (30). 1.42. Связь межцу теорией обыкновен-
ных максимумов и минимумов и линейными вариационными зада-
чами (33). 1.43. Интегральные задачи с дополнительными усло-
виями (34).
1.5. Замечания о практическом применении................... 35
1.51. Прямые и непрямые методы (35). 1.52. Аналитические и числен-
ные методы (37).
1.6. Оптимизация траекторий летательных аппаратов малой
тяги и двигательных систем 24-часового экваториального
спутника................................................... 39
1.61. Введение (39). 1.62. Оптимизация траектории при малых измене-
ниях орбитальных элементов (41). 1.63. Оптимизация траектории при
больших изменениях орбитальных элементов (44). 1.64. Оптимизация
двигательной системы (48).
Указатель обозначений к разделу 1.6........................ 51
Литература ....... ....................................... 52
6
ОГЛАВЛЕНИЕ
Глава II. Прямые методы (Фрэнк Д. Фолкнер).................. 54
2.0. Введение и обзор результатов........................... 54
2.1. Метод определения некоторых оптимальных траекторий 56
2.10. Введение и обзор результатов (56). 2.11. Основные уравне-
ния (58). 2.12. Сопряженные уравнения; формула Грина (59). 2.13.
Принципы максимума (62). 2.14. Соотношение взаимности Майера
(66). 2.15. Численный метод определения простой оптимальной траек-
тории (67). 2.16. Перехват при минимальном расходе топлива (70).
2.17. Задача о встрече за минимальное время (73). 2.18. Обсуж-
дение (76).
2.2. Элементарное графическое решение....................... 79
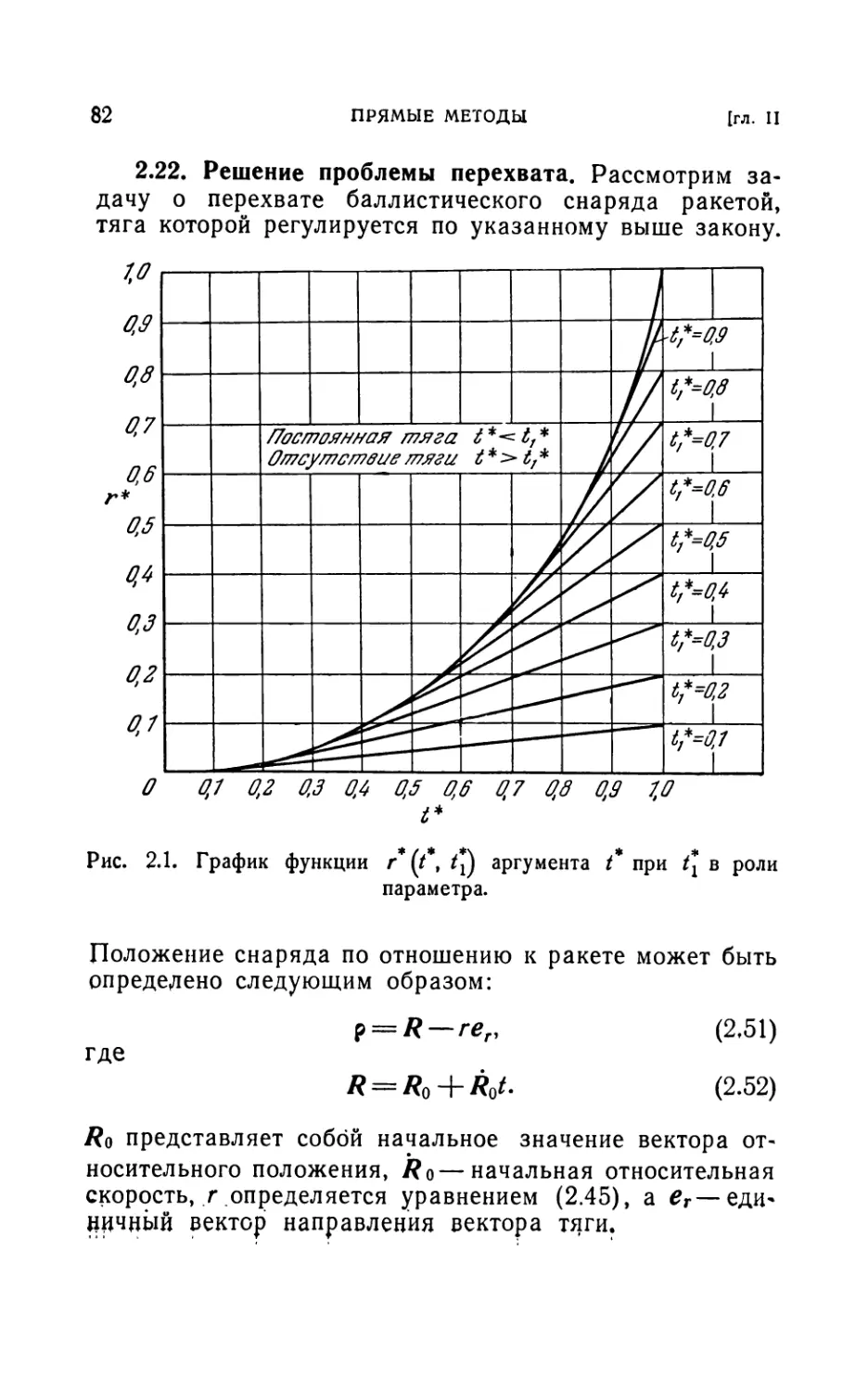
2.20. Введение и обзор результатов (79). 2.21. Построение графика (80).
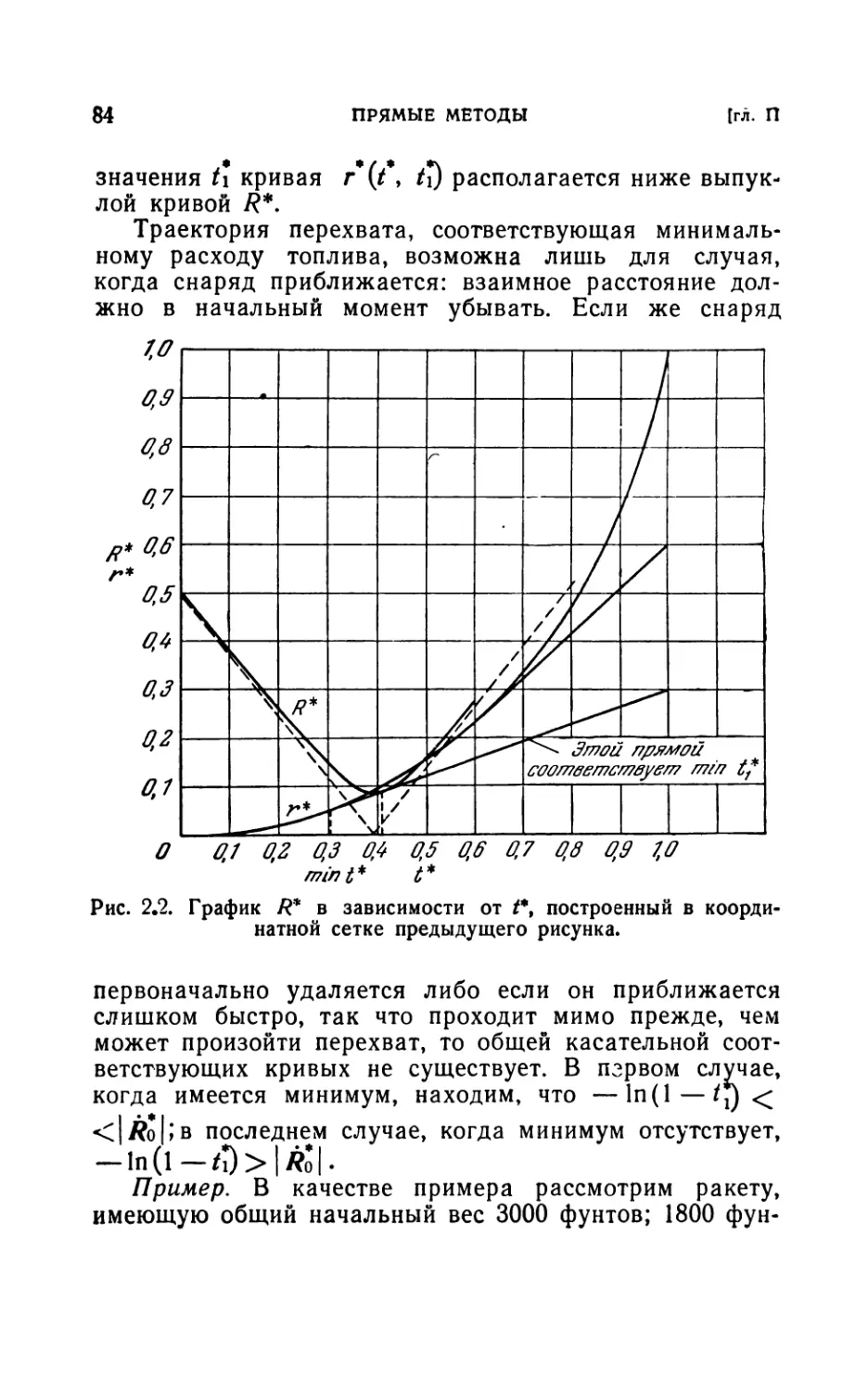
2.22. Решение проблемы перехвата (82). 2.23. Решение некоторых
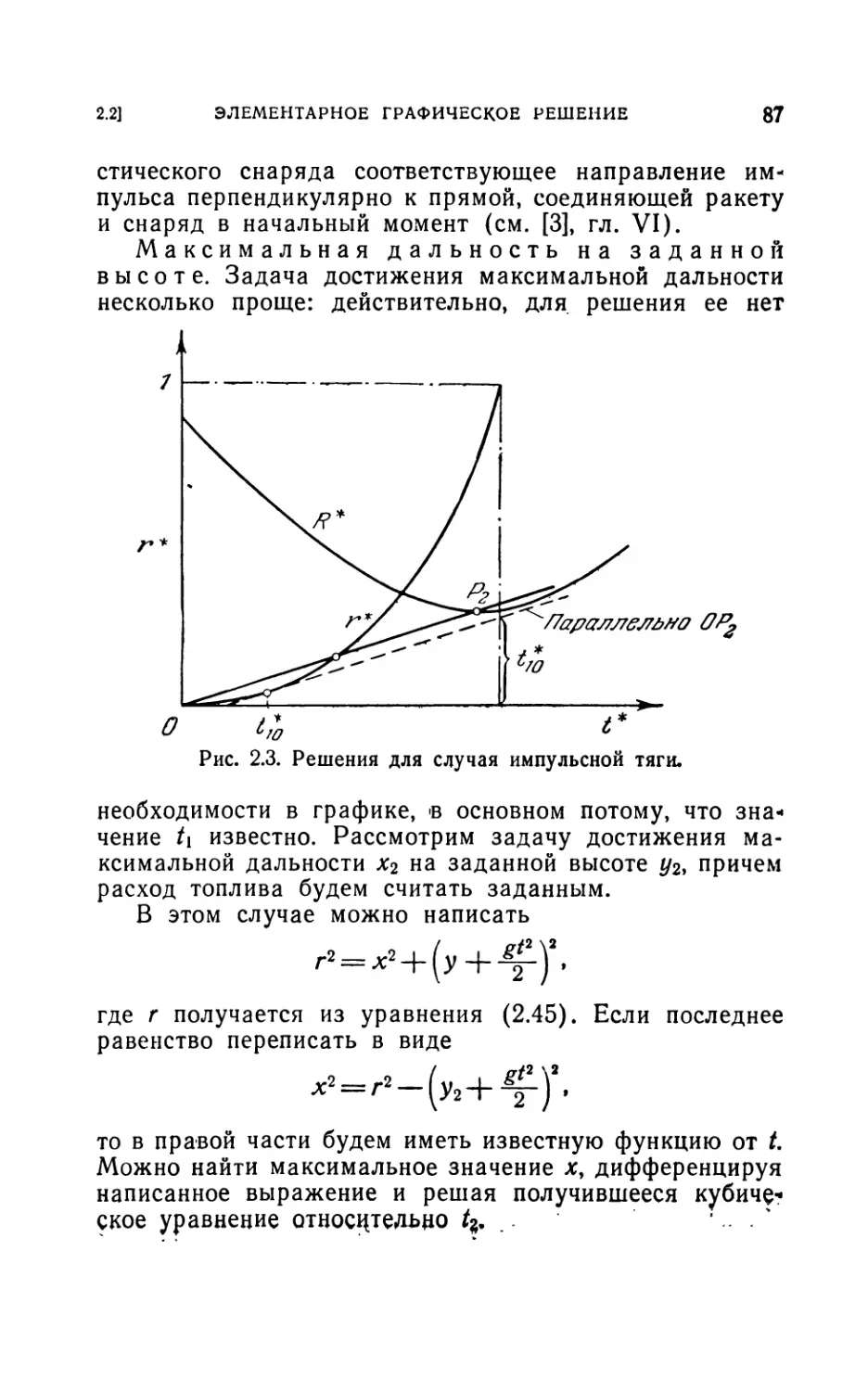
других задач (85). 2.24. Некоторые замечания (88).
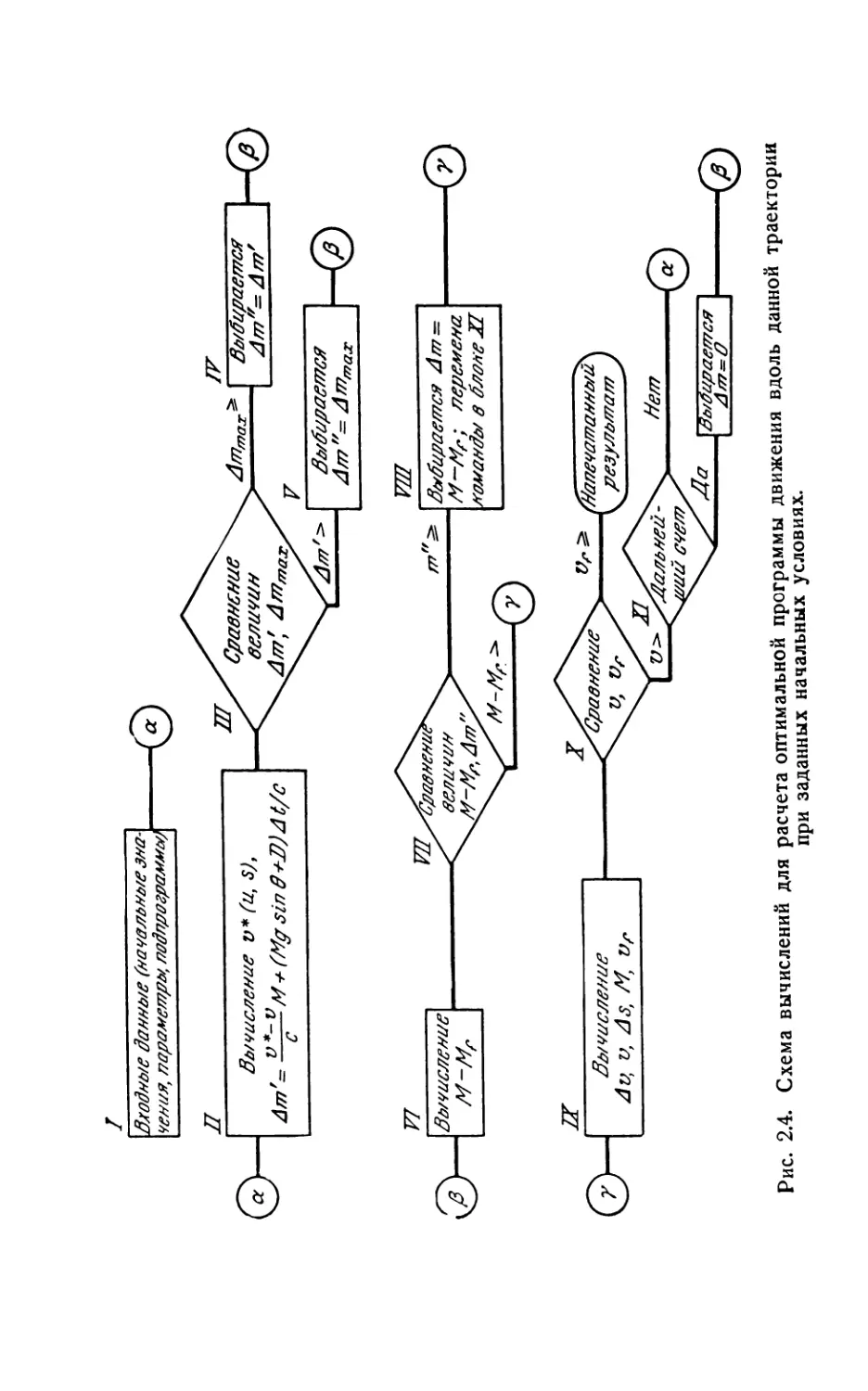
2.3. Программирование оптимальной тяги вдоль заданной
траектории................................................. 88
2.30. Введение и обзор результатов (88). 2.31. Приведение уравнений
к канонической фэрме; условие минимума (89). 2.32. Случай макси-
мальной дальности (91). 2.33. Программа счета (93). 2.34. Обсужде-
ние (96).
Литература.................................................. 97
Глава III. Определение экстремумов криволинейных
интегралов по теореме Грина (Анджело Миеле) .... 100
3.1. Введение...............................................100
3.2. Линейная задача........................................101
3.21. Фундаментальная функция (102). 3.22. Случай постоянства знака
фундаментальной функции (103). 3.23. Случай, когда знак фундамен-
тальной функции не является постоянным (104). 3.24. Выводы (106).
3.3. Линейная изопериметрическая задача.....................106
3.4. Линейные задачи в механике полета......................108
3.5. Оптимальная программа расхода топлива ракетой ближ-
него действия без подъемной силы...........................110
3.51. Класс допустимых кривых (112). 3.52. Область, занятая допусти-
мыми кривыми (113). 3.53. Определение экстремальной дальности (114).
3.54. Определение экстремального времени полета (115). 3.55. Опреде-
ление экстремальной дальности за данное время полета (116).
3.6. Оптимальная программа торможения возвращающегося
баллистического снаряда переменнной геометрической
формы......................................................119
3.61. Класс допустимых кривых (120). 3.62. Область, занятая допустимыми
кривыми (121). 3.63. Определение экстремальной теплопередачи (122).
3.64. Определение экстремального времени полета (124). 3.65. Опреде-
ление экстремальной теплопередачи за данное время полета (125).
Литература..................................................128
Общий указатель литературы..................................129
Глава IV. Методы вариационного исчисления в приклад-
ной аэродинамике и механике полета (Анджело Миеле) 130
4.1. Введение...............................................130
4.2. Задача Больца..........................................131
4.21. Уравнения Эйлера —Лагранжа (132). 4.22. Первый интеграл (133).
4,23. Условия в угловых точках (133). 4.24. Условие трансверсаль-
ОГЛАВЛЕНИЕ
7
ности (134). 4.25. Условия Лежандра— Клебша и Вейерштрасса (135).
4.26. Задача Майера (136). 4.27. Задача Лагранжа (137). 4.28. Первый
пример (137). 4.29. Второй пример (138).
4.3. Преобразования вариационных задач........................140
4.31. Преобразование задачи Лагранжа в задачу Майера (141). 4.32. За-
дачи с производными высших порядков (141). 4.33. Задачи без производ-
ных (142). 4.34. Задачи, включающие неравенства (144).
4.4. Вариационные методы в прикладной аэродинамике .... 145
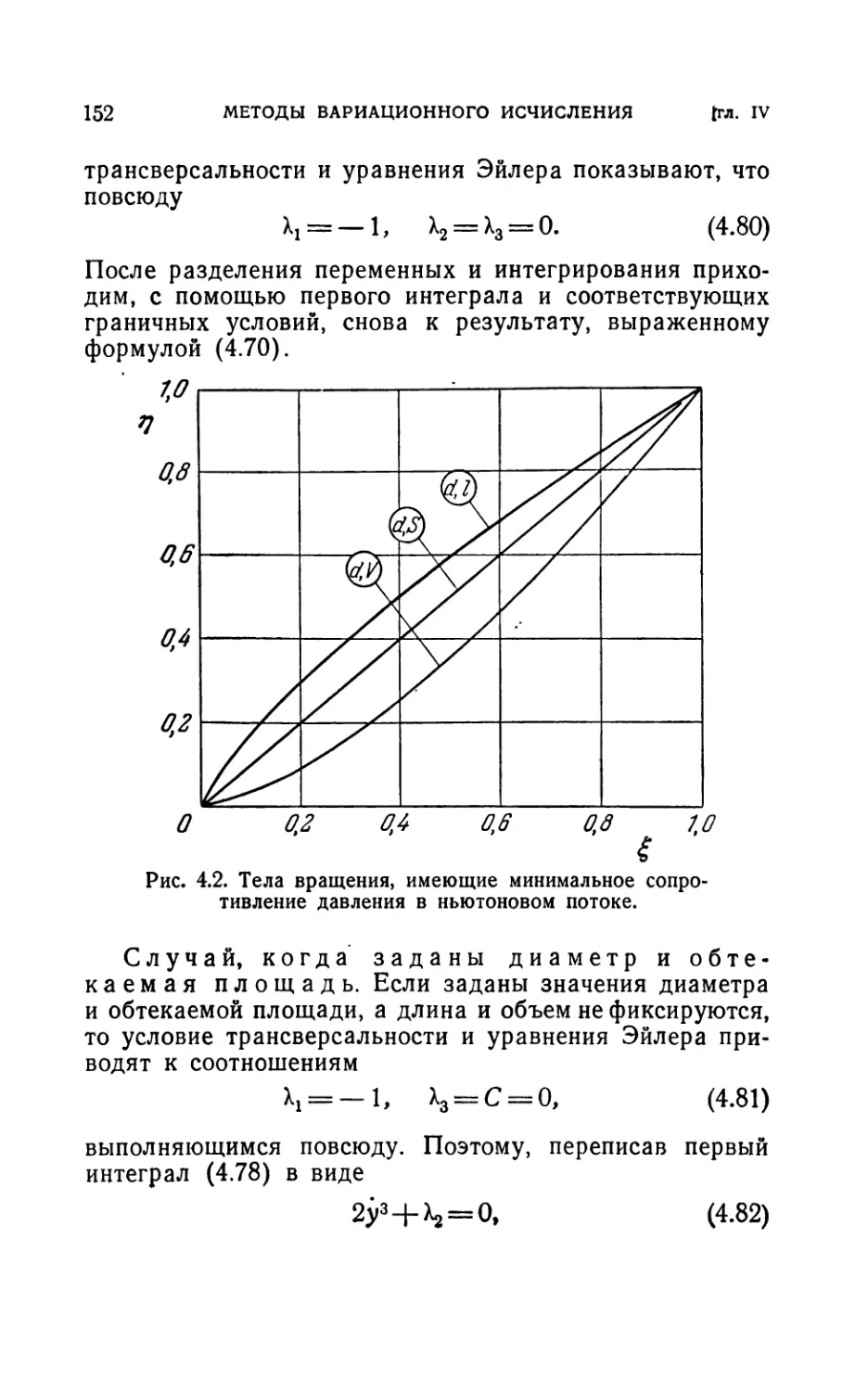
4.5. Тела вращения, обладающие минимальным сопротивлением
давления в ньютоновом потоке..................................145
4.51. Предварительный пример (145). 4.52. Более общая задача (149).
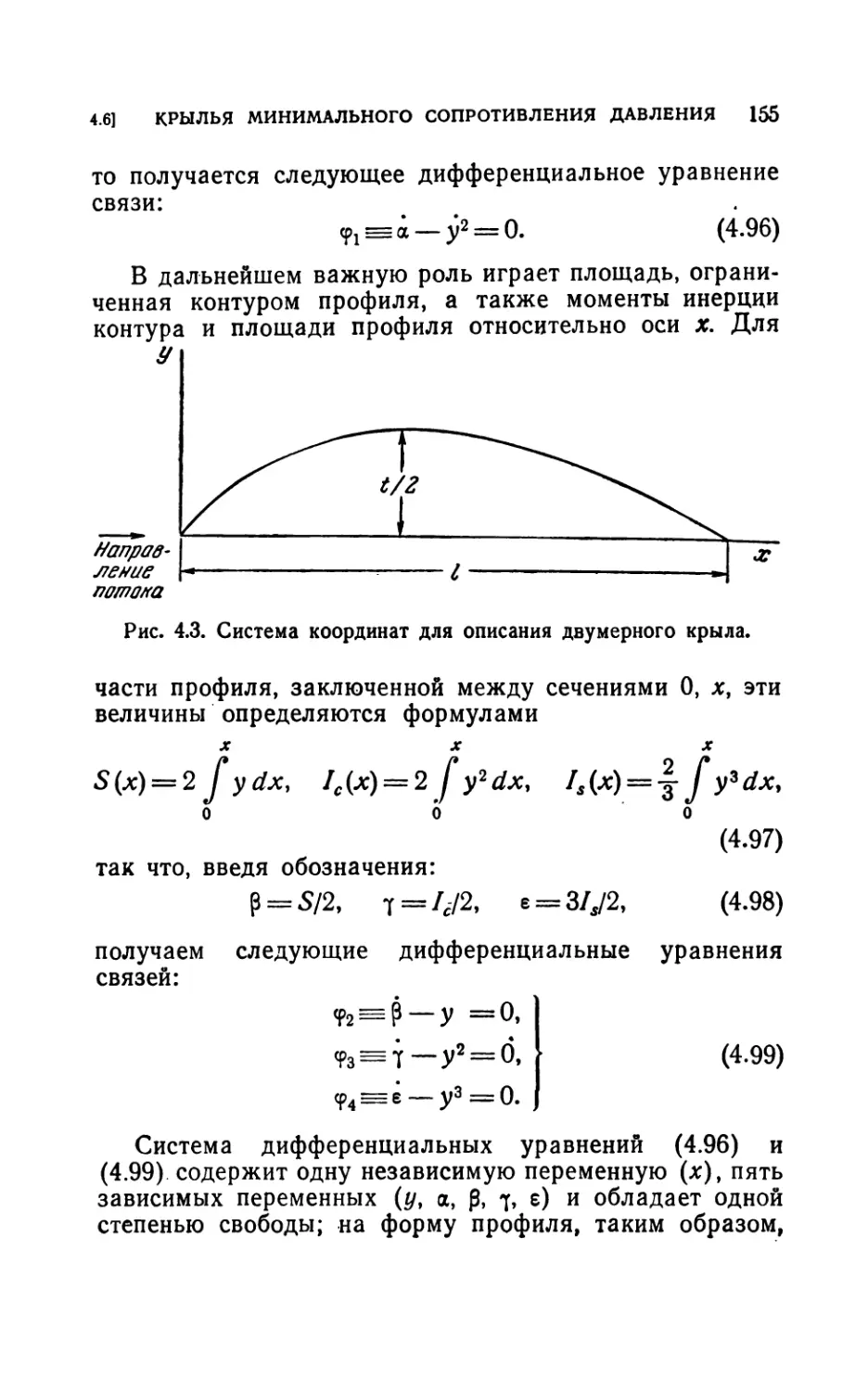
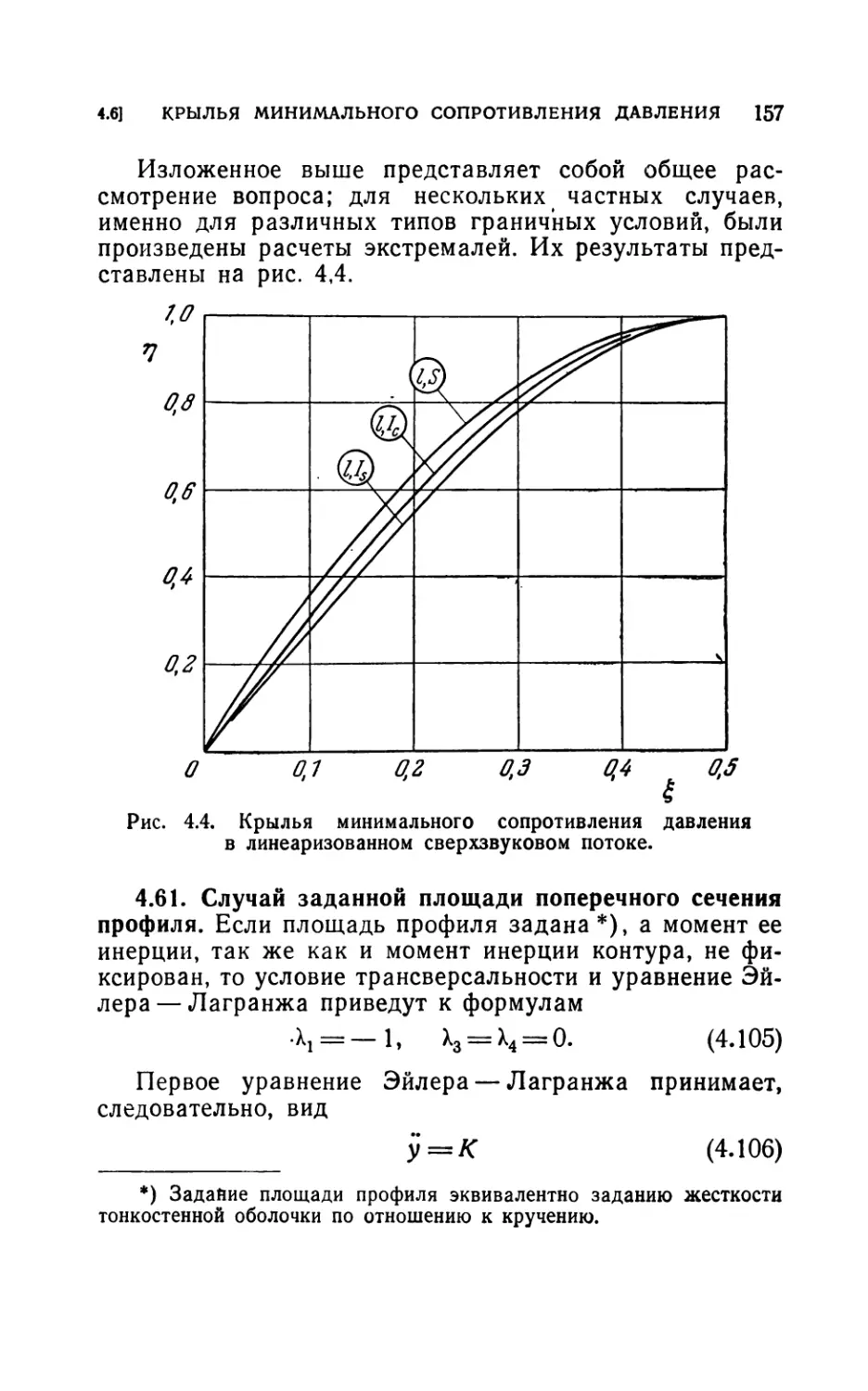
4.6. Крылья минимального сопротивления давления в линеари-
зованном сверхзвуковом потоке.................................154
4.61. Случай заданной площади поперечного сечения профиля (157).
4.62. Случай заданного момента инерции контура (158). 4.63. Случай
заданного момента инерции поперечного сечения профиля (159).
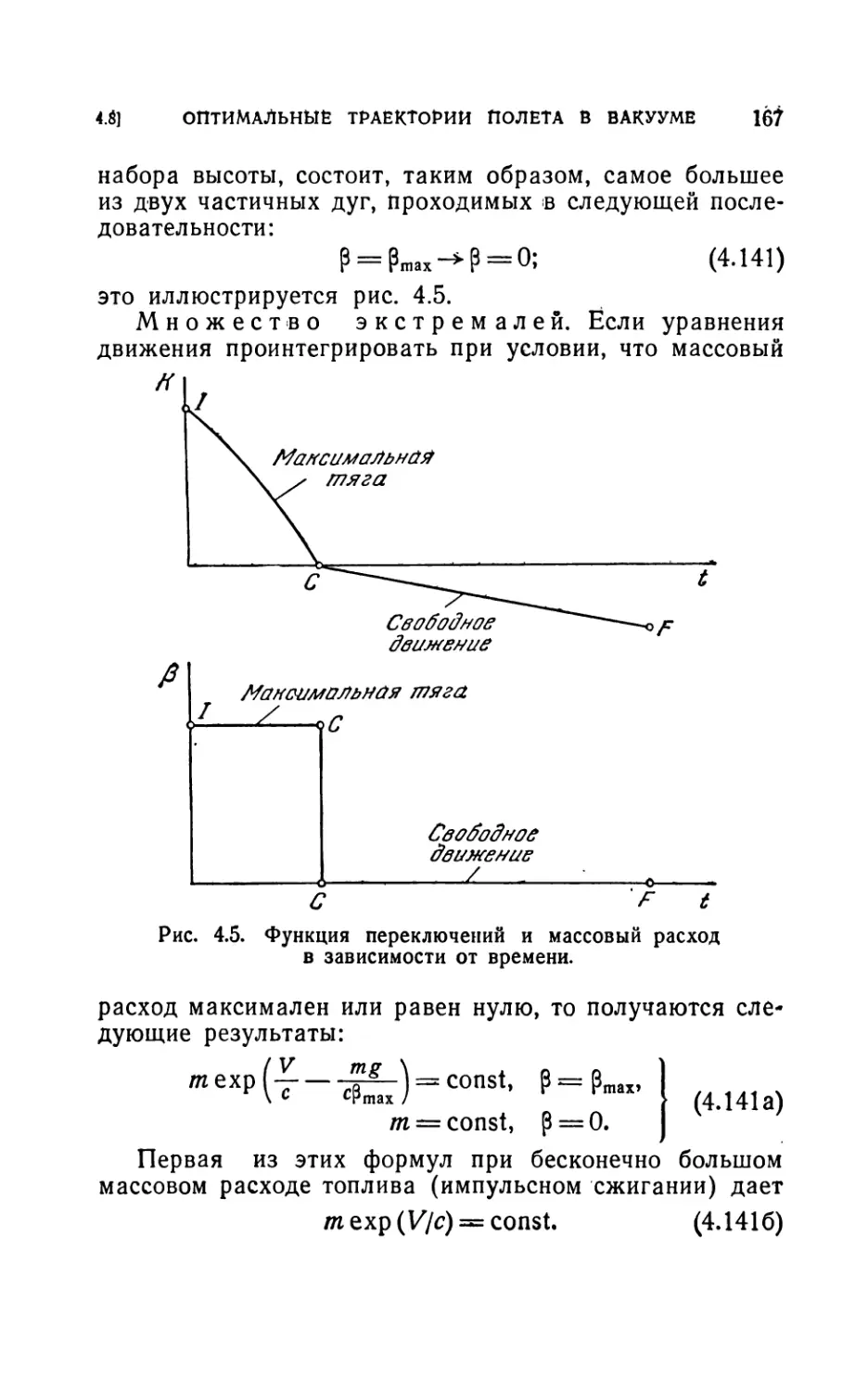
4.7. Вариационные методы в механике полета....................160
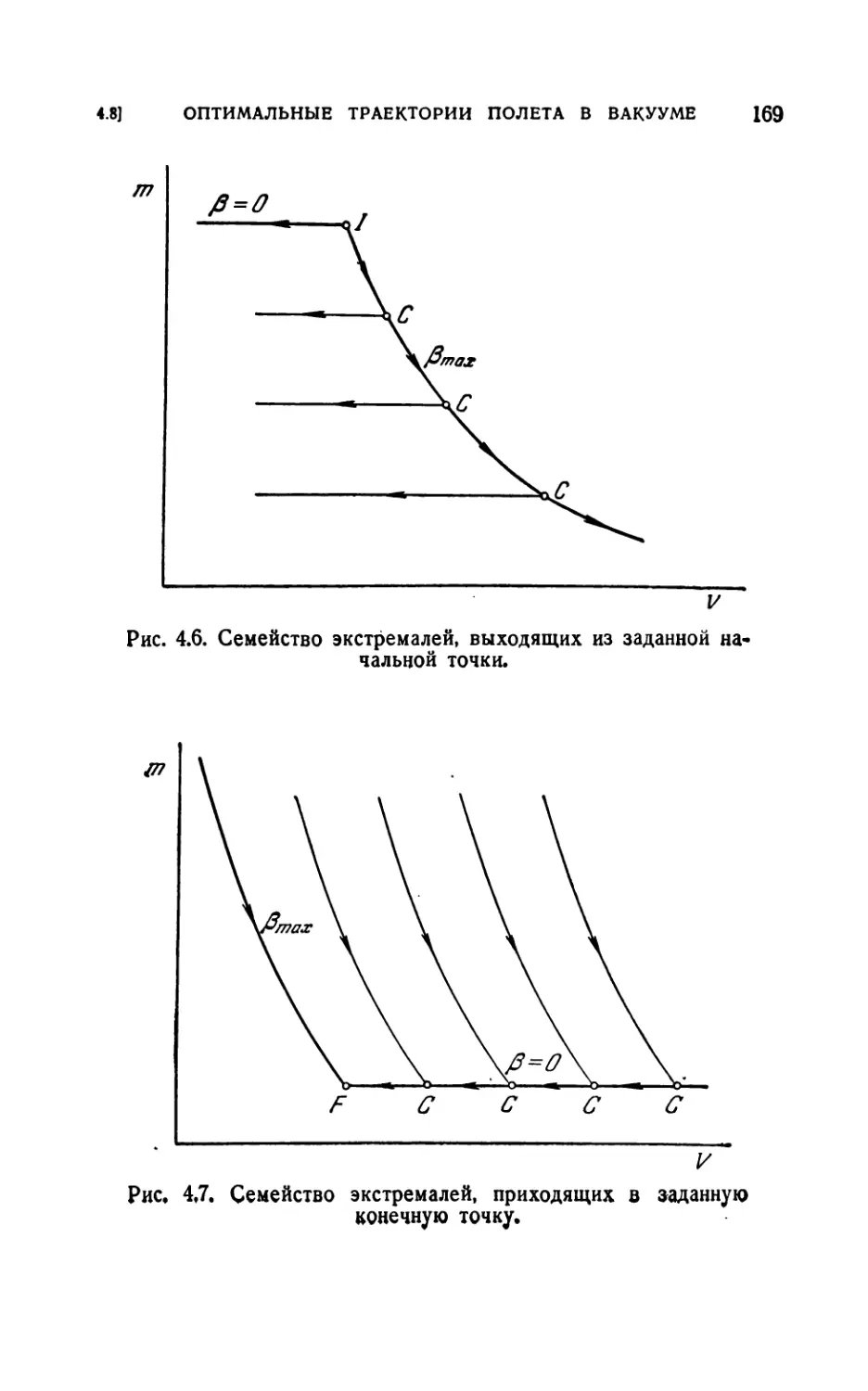
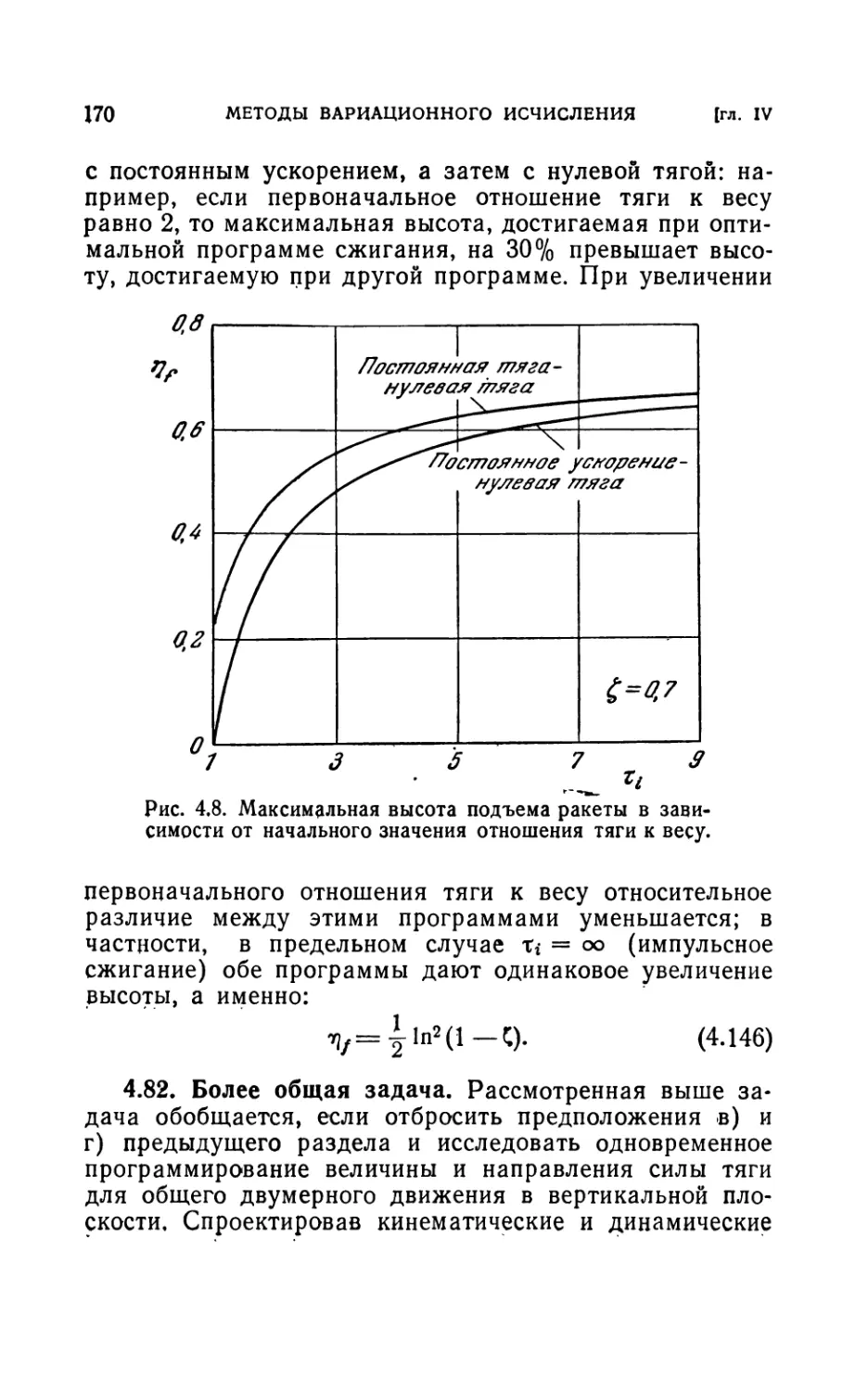
4.8. Оптимальные траектории полета ракеты в вакууме .... 162
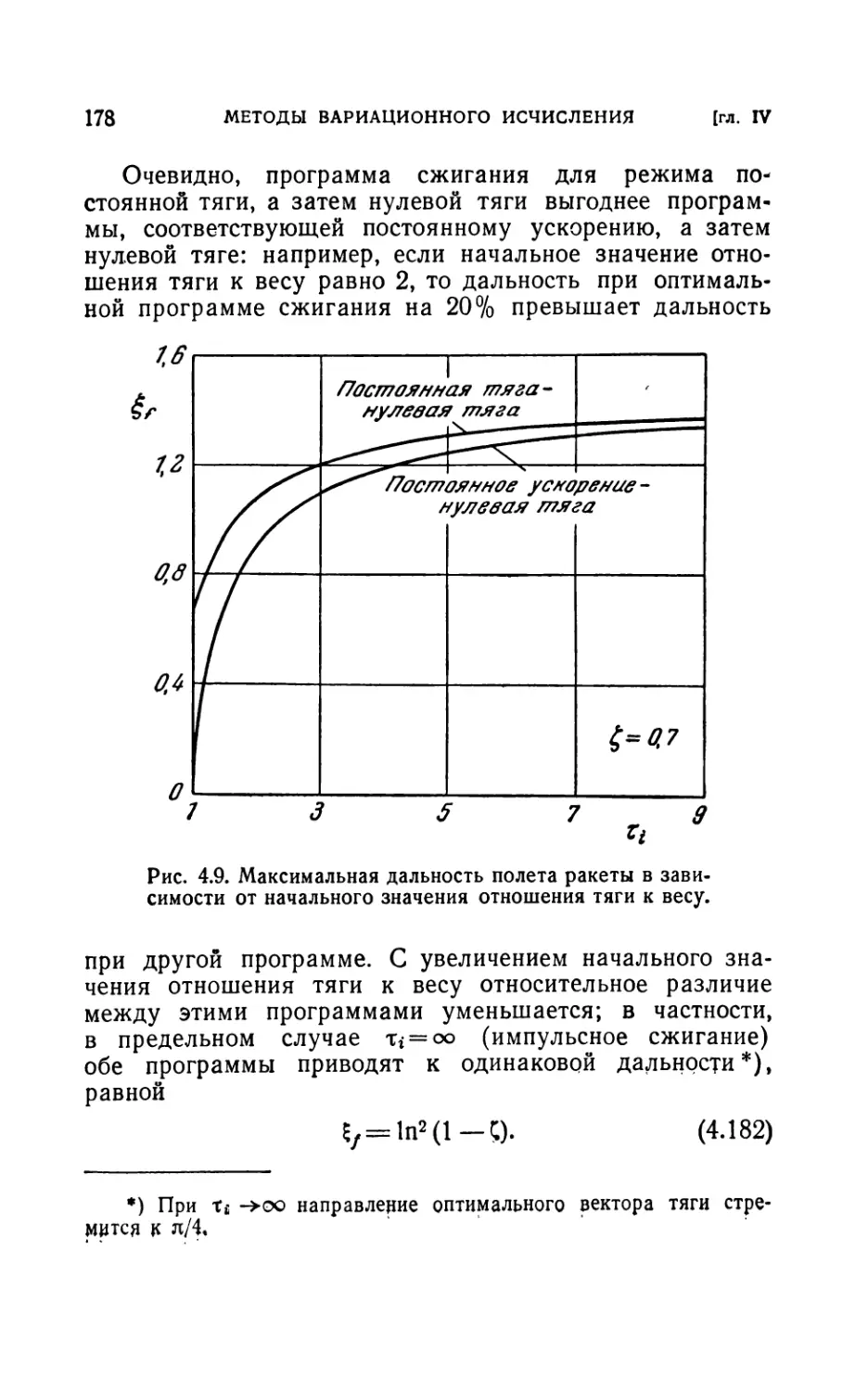
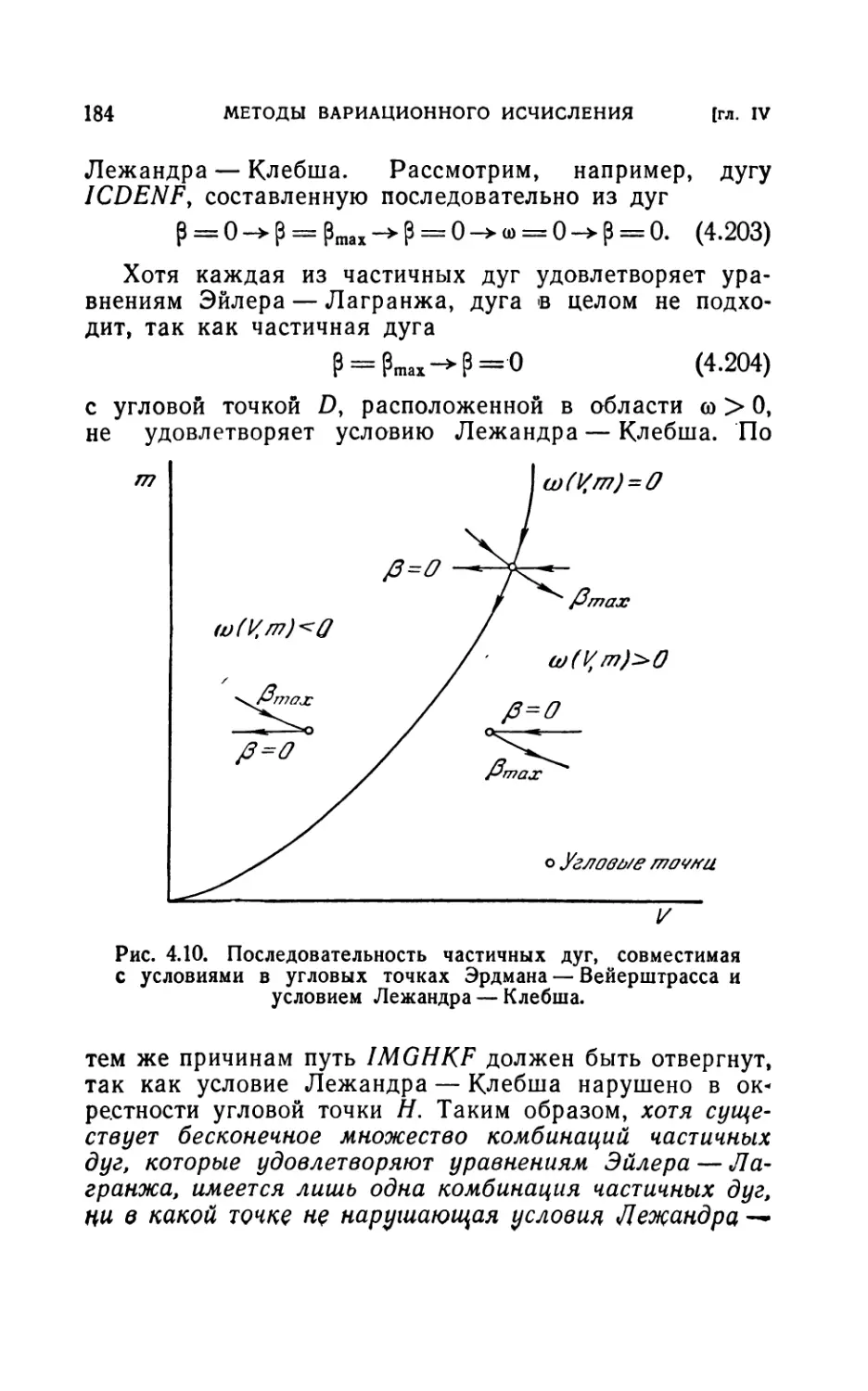
4.81. Предварительный пример (162). 4.82. Более общая задача (170).
4.9. Оптимальные траектории полета ракеты в сопротивляю-
щейся среде...................................................179
4.91. Предварительный пример (179). 4.92. Более общая задача (189).
4.93. Дополнительные связи (194).
4.10. Выводы..................................................200
Литература....................................................200
Общий указатель литературы....................................203
Глава V. Вариационные задачи с ограниченными упра-
влениями (Дж. Лейтман)....................................209
5.0. Введение.................................................209
5.1. Постановка задачи........................................210
5.2. Системы с ограниченным расходом массы....................211
5.21. Первая вариация (212). 5.22. Программа направления вектора
тяги (214). 5.23. Программа расхода массы (214). 5.24. Условия в угловых
точках (215). 5.25. Е-функция Вейерштрасса (216). 5.26. Оптимальное
направление вектора тяги (216). 5.27. Оптимальный расход массы. Функ-
ция переключений (216). 5.28. Двухпозиционное управление расходом
массы (218). 5.29. Случай отсутствия ограничений расхода массы (220).
5.210. Промежуточная программа расхода массы (220).
5.3. Системы с ограниченной мощностью двигателей............221
5.31. Первая вариация (222). 5.32. Программа направления силы
тяги (223). 5.33. Программа управления мощностью двигателей (223).
5.34. Е-функция Вейерштрасса (223).
5.4. Системы с ограниченным ускорением тяги...................225
5.41. Первая вариация (226). 5.42. Программа направления силы
тяги (227). 5.43. Программа ускорения силы тяги (227). 5.44. Е-функция
Вейерштрасса (227).
5.5. Выводы...................................................231
5.6. Пример...................................................232
5.61. Первая вариация (233). 5.62. Программа направления силы
тяги (233). 5.63. Программа расхода массы (234). 5.64. Обзор реше-
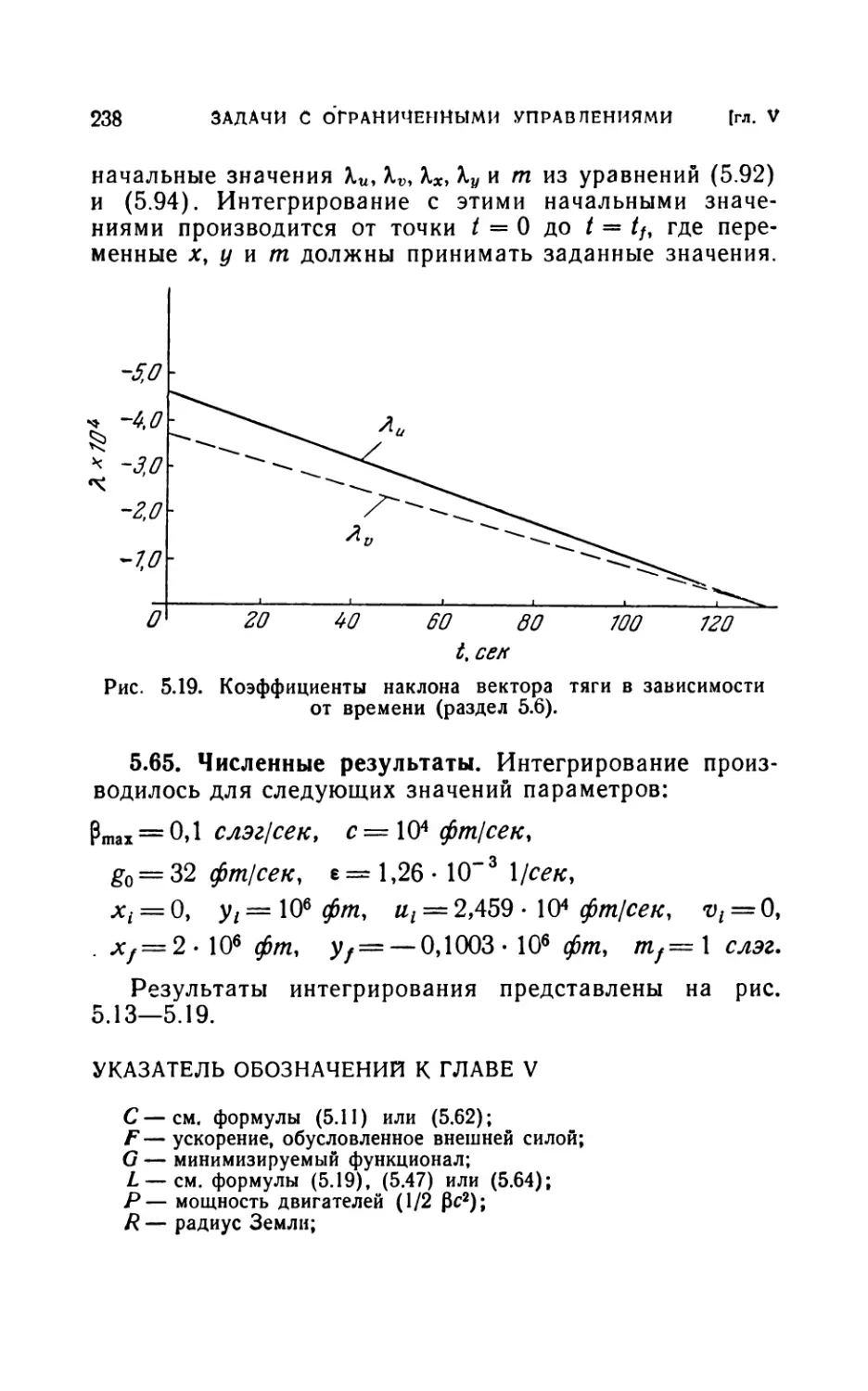
ния (234). 5.65. Численные результаты (238).
8
ОГЛАВЛЕНИЕ
Указатель обозначений к главе V..........................238
Приложение . . -............................................239
Литература..................................................242
Глава VI. Метод градиентов (Генри Дж. Келли) .... 244
6.0. Введение...............................................244
6.1. Метод градиентов в обыкновенных задачах на минимум 245
6.11. Непрерывный процесс спуска (245). 6.12. Шаговый спуск (248).
6.13. Обыкновенные проблемы минимума со связями; метод проектиро-
вания градиентов (250). 6.14. Обыкновенные проблемы минимума со свя-
зями; приближенный метод (253). 6.15. Обыкновенные проблемы мини-
мума со связями, задаваемыми неравенствами (256).
6.2. Метод градиентов в задачах оптимизации траектории полета 257
6.21. Формулировка проблемы (258). 6.22. Близкие решения и функции
Грина (259). 6.23. Присоединенная система (260). 6.24. Градиент в функ-
циональном пространстве (263). 6.25. Связи, налагаемые граничными
условиями (266). 6.26. Случай переменного конечного момента времени;
граничные значения как параметры (271). 6.27. Оптимизация по коор-
динатам и параметрам системы (274). 6.28. Связи, выражаемые нера-
венствами (274). 6.29. Функции нагружения; оценки ошибок (278).
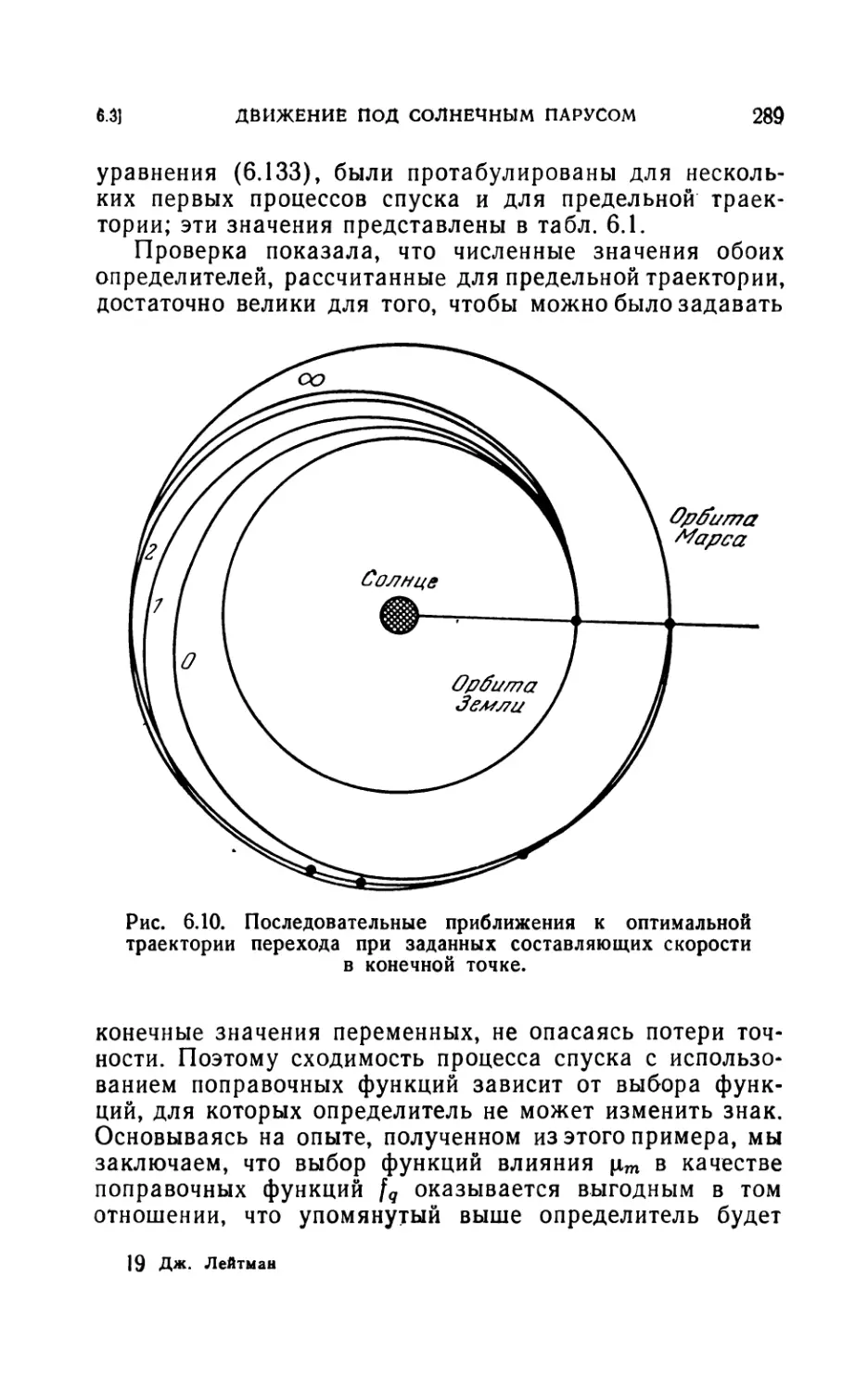
6.3. Пример: движение под солнечным парусом.................280
6.31. Уравнения системы (280). 6.32. Граничные данные (281). 6.33. Попра-
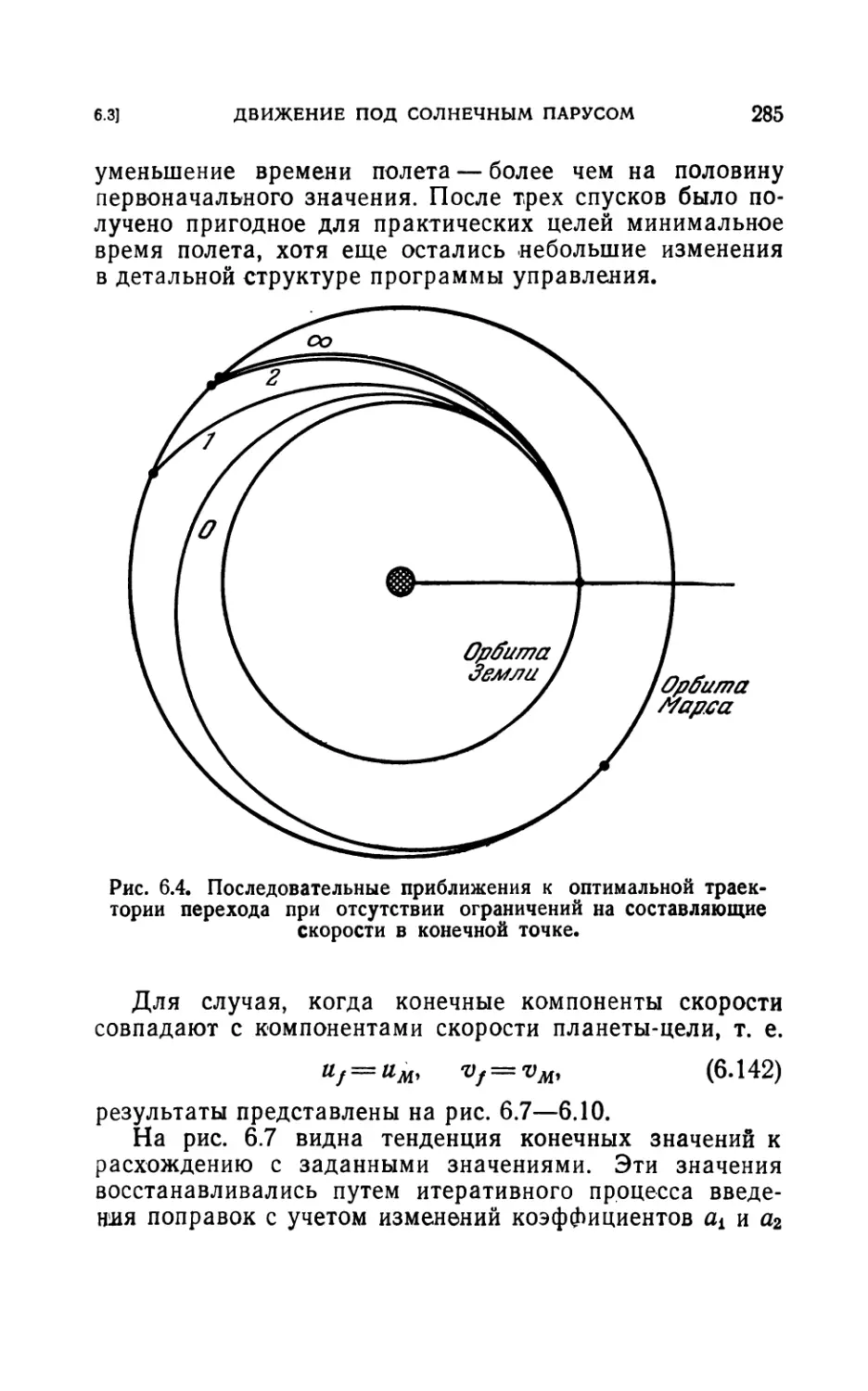
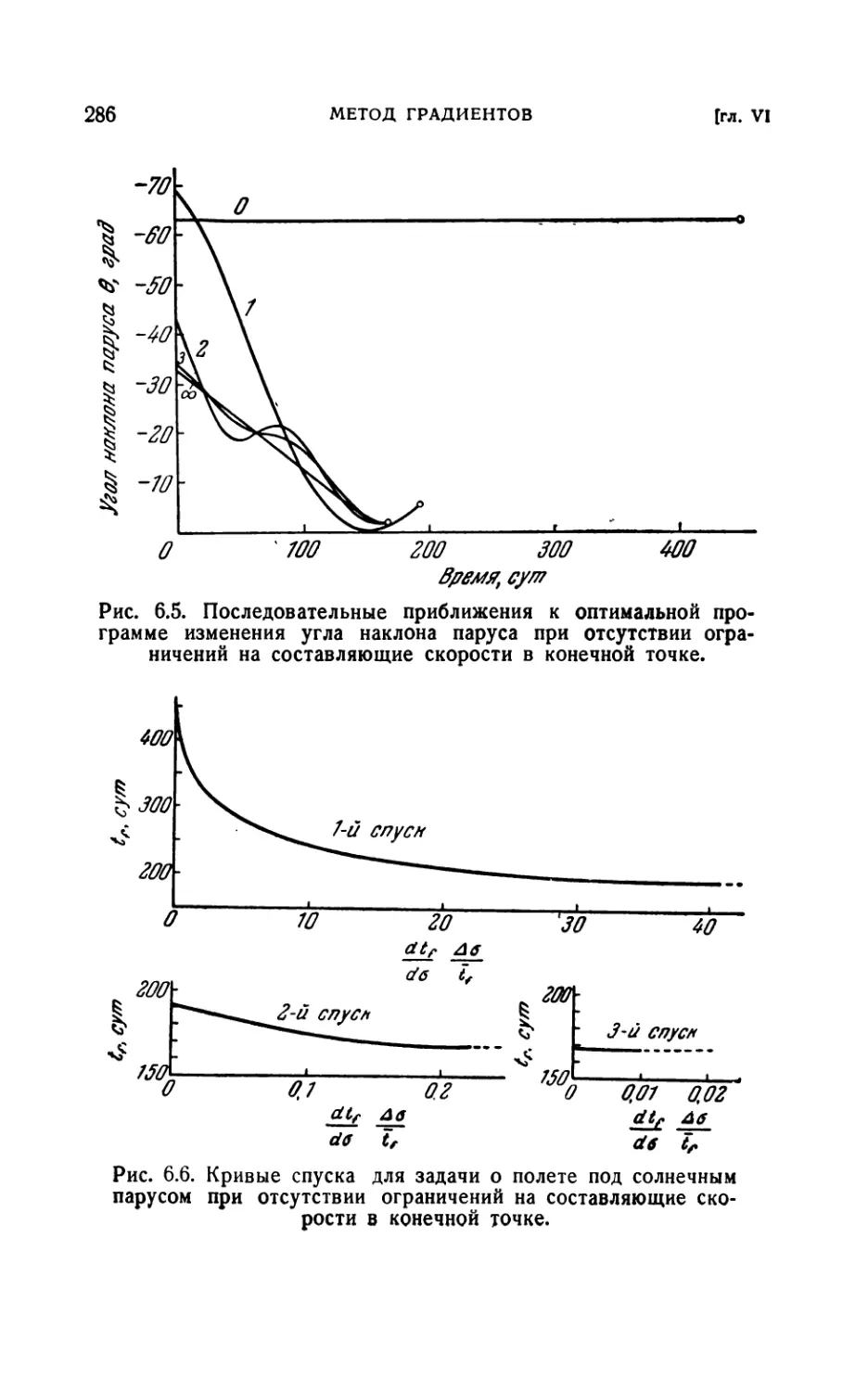
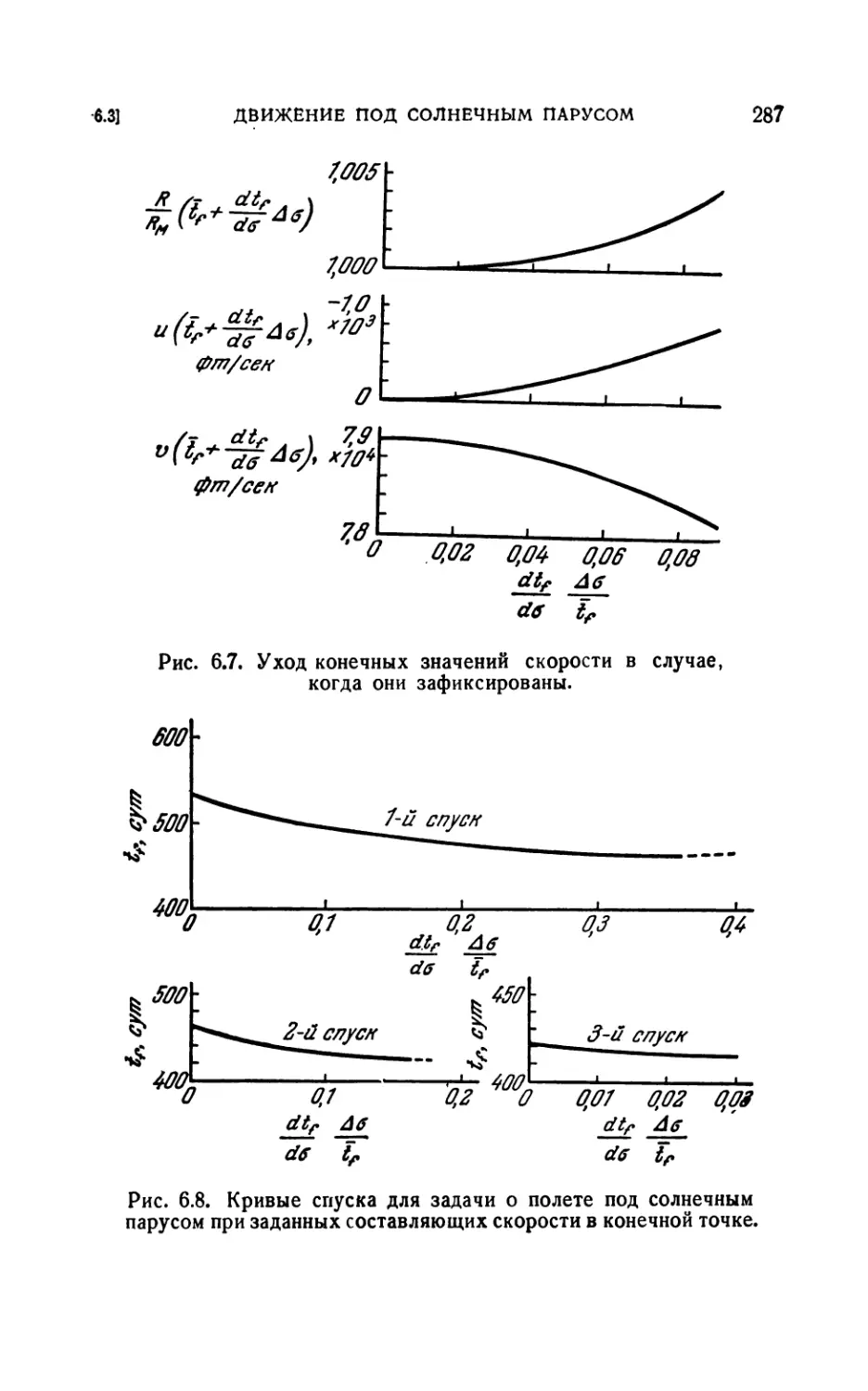
вочные функции (282). 6.34. Расчеты перехода между орбитами (284).
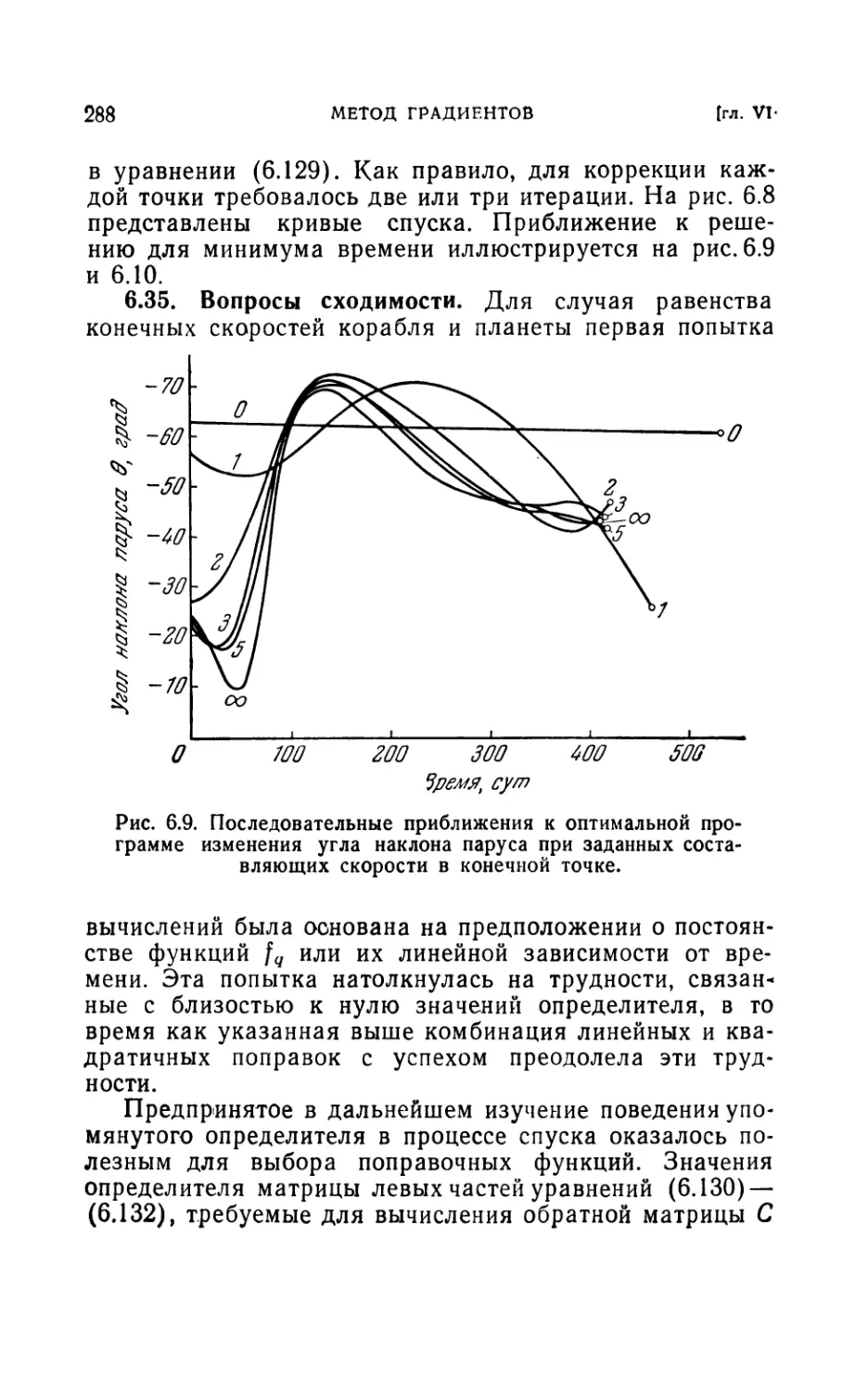
6.35. Вопросы сходимости (288).
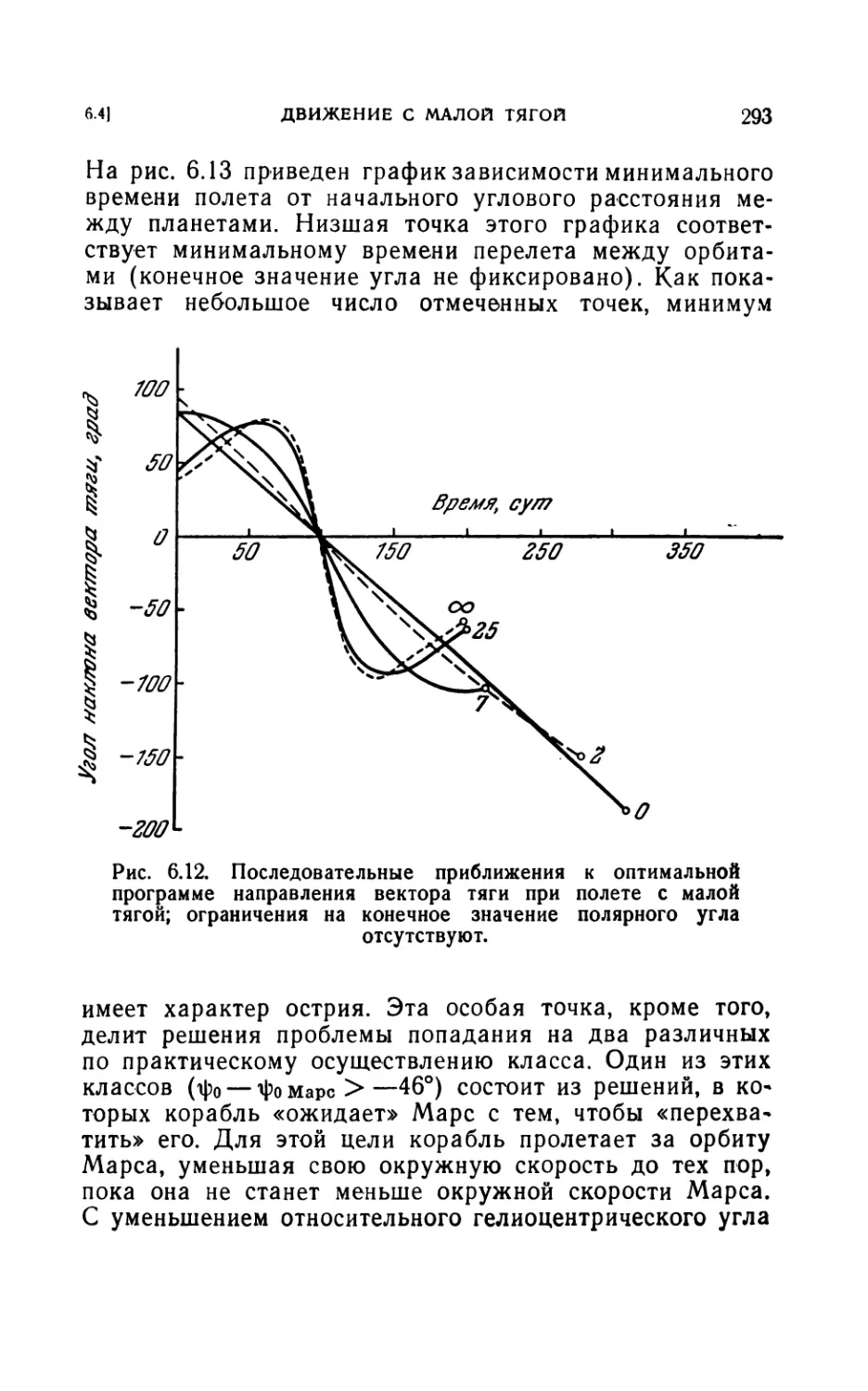
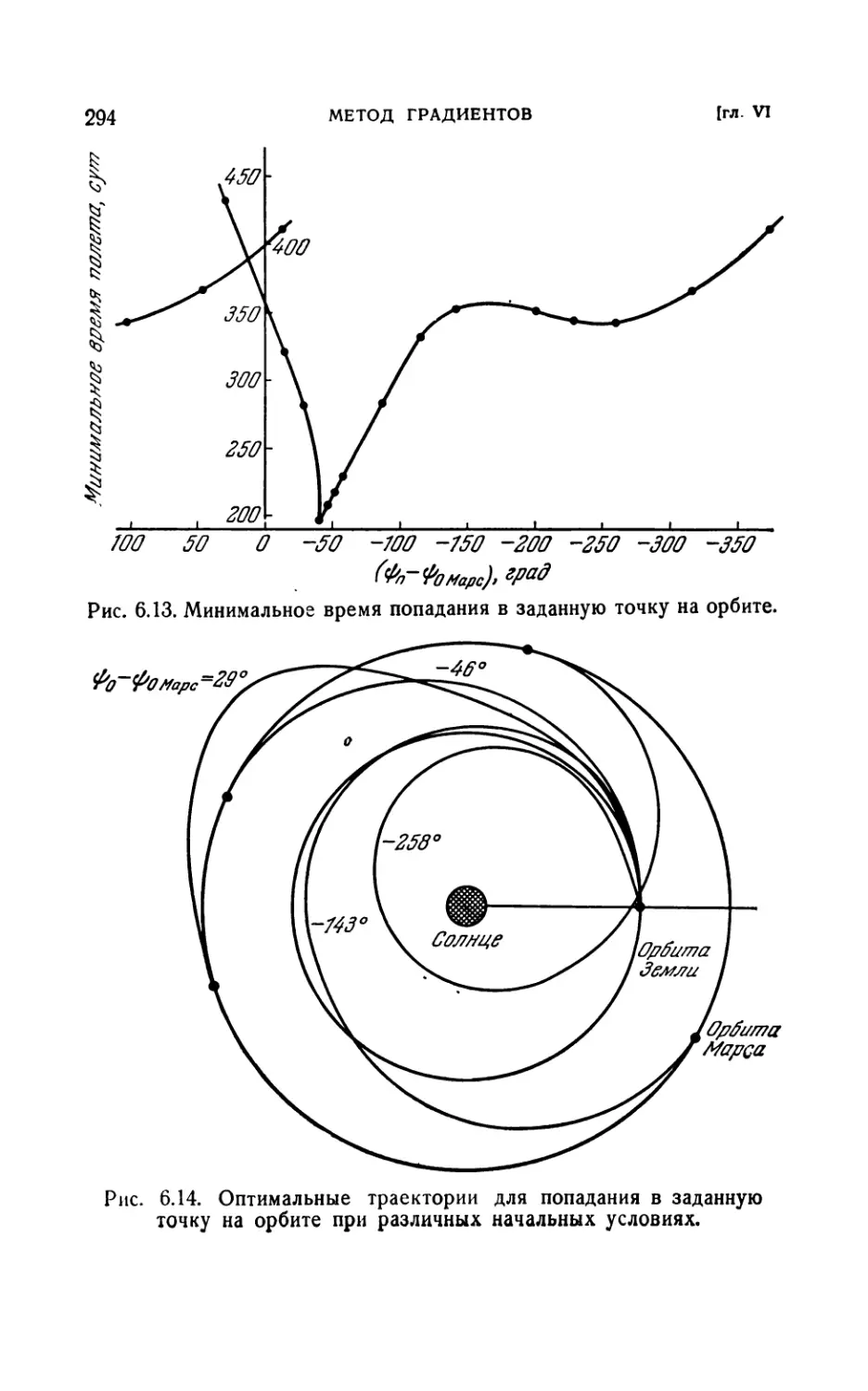
6.4. Пример: движение с малой тягой.........................290
6.41. Уравнения системы и граничные условия (290). 6.42. Переход
между орбитами и расчеты попаданий (291).
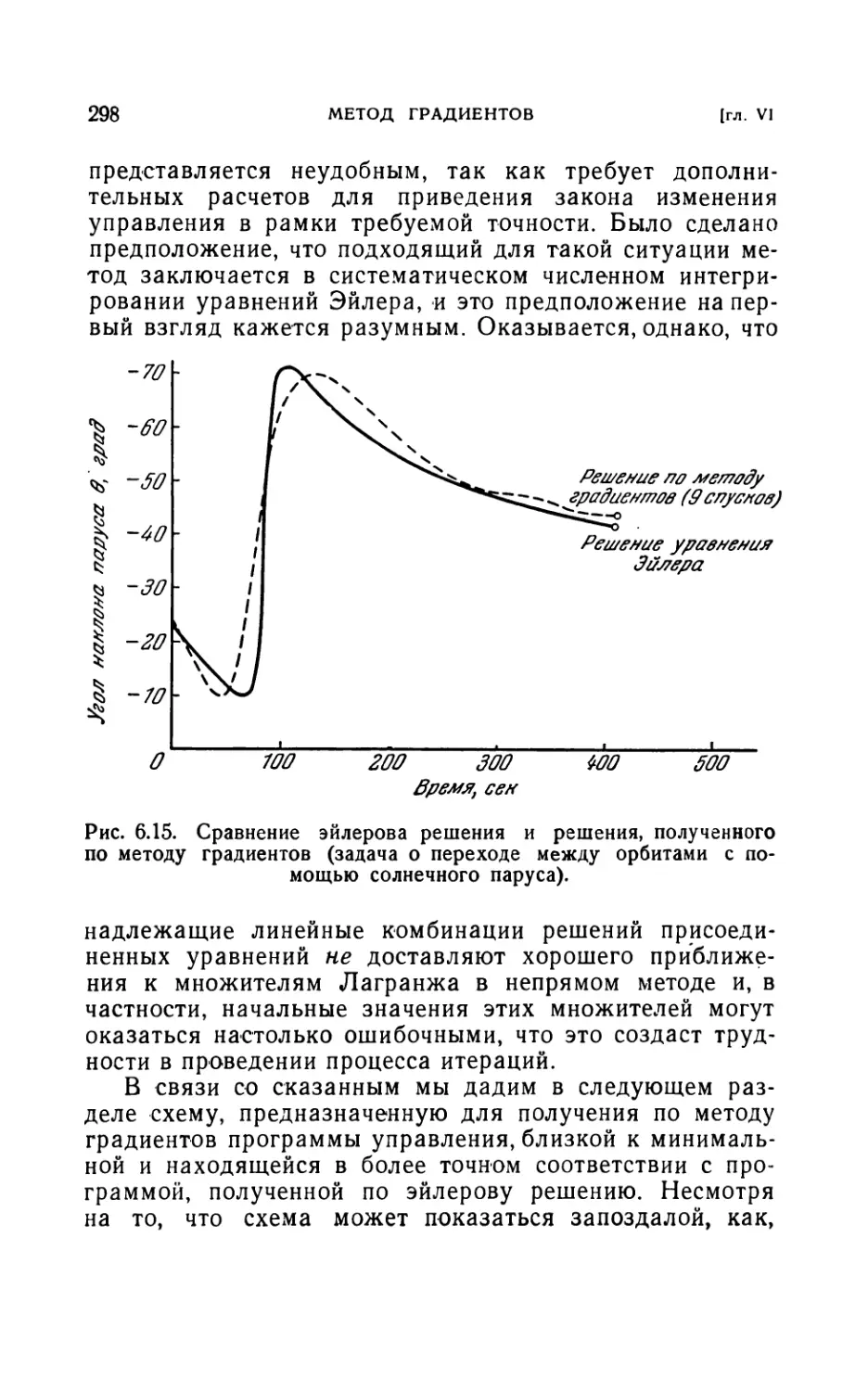
65. Замечания об относительных преимуществах различных
вычислительных методов...............................295
6.6. Схема последовательных приближений, требующая мини-
мального количества операций.........................299
Приложение..................................................302
Литература..................................................304
Глава VII. Принцип максимума Понтрягина (Ричард
Э. Копп)...............................................307
7.0. Введение...............................................307
7.1. Предварительные соображения о принципе максимума
Понтрягина..............................................308
7.11. Формулировка проблемы (308). 7.12. Принцип максимума для задан-
ного интервала времени при отсутствии условий на правом конце (309).
7.13. Принцип максимума в задаче со связями, наложенными на значе-
ния переменных состояния на правом конце (313). 7.14. Принцип
максимума в задаче с фиксированными условиями на правом конце (314).
7.15. Принцип максимума в случае, когда конечный момент времени
не задан (315).
7.2. Сопряженная система и принцип максимума Понтря-
гина .......................................................316
7.21. Сопряженная система и стационарные решения (316). 7.22. Вывод
принципа максимума из сопряженной системы (317).
ОГЛАВЛЕНИЕ
9
7.3. Вариационное исчисление и принцип максимума Понтря-
гина ....................................................318
7.31. Вариационное исчисление и стационарные решения (318). 7.32. Вы-
вод принципа максимума методом вариационного исчисления (319).
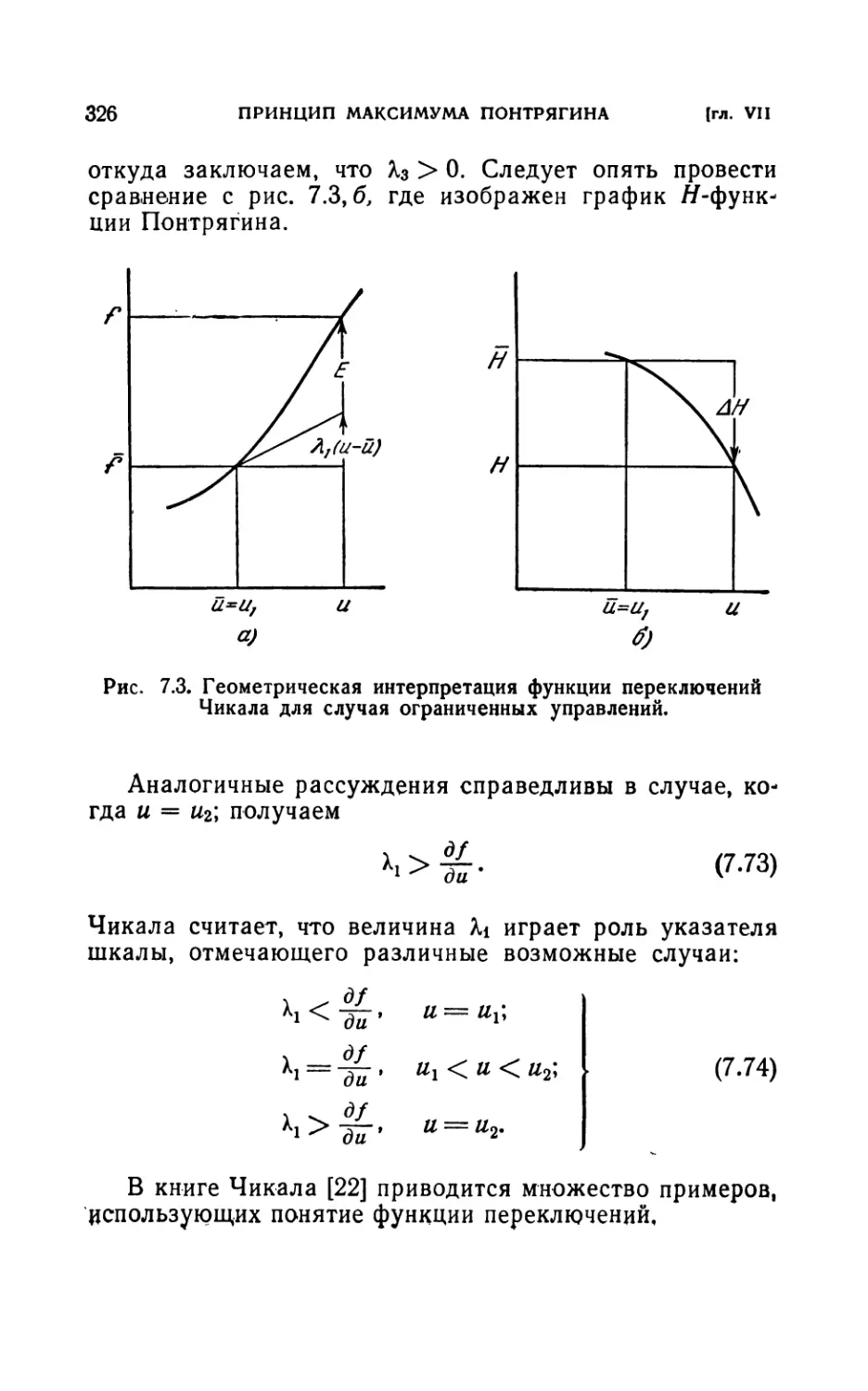
7.33. Функция избытка Вейерштрасса и функция переключений
Чикала (321).
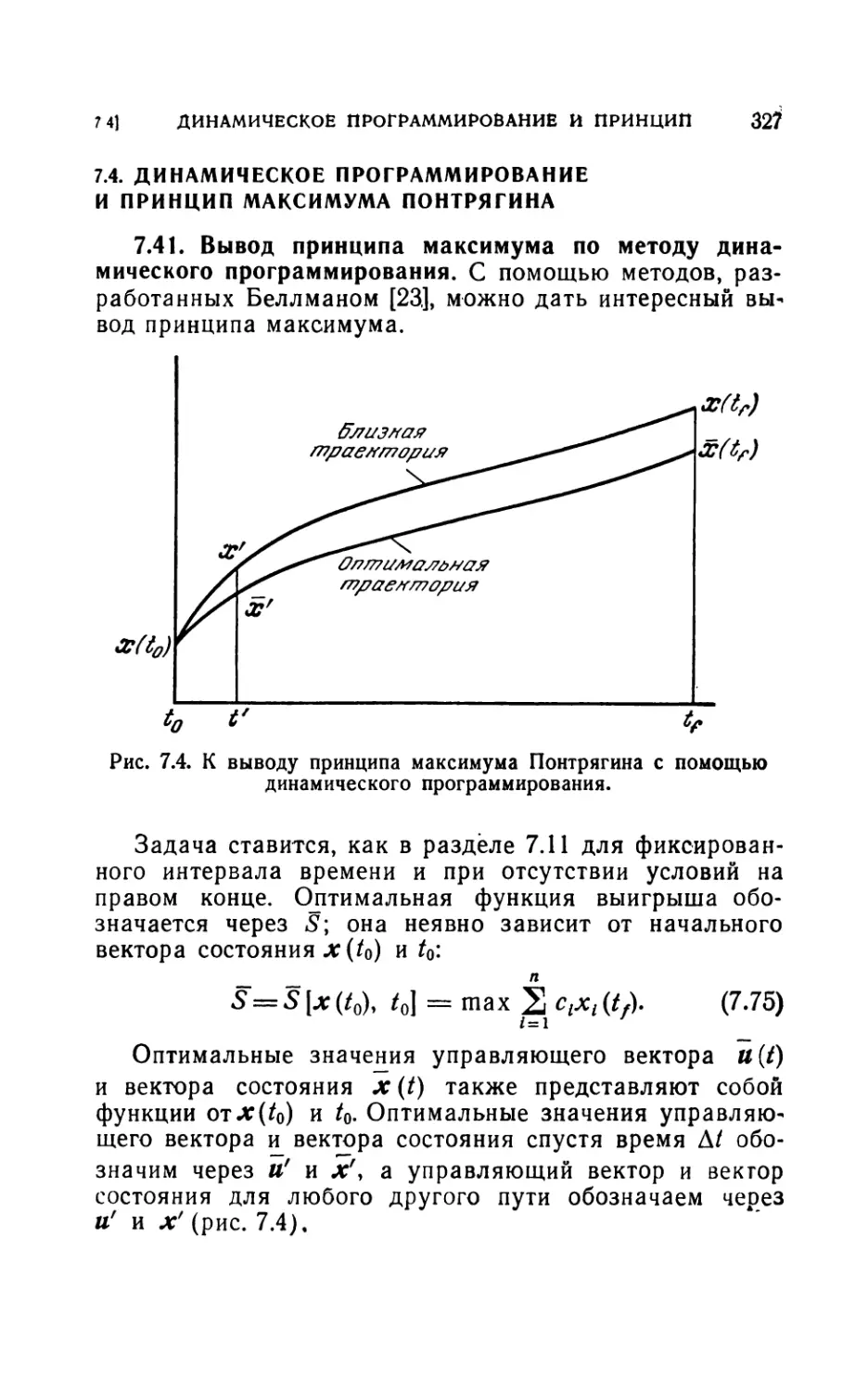
7.4. Динамическое программирование и принцип максимума
Понтрягина............................................327
7.41. Вывод принципа максимума по методу динамического программи-
рования (327).
7.5. Примеры.............................................330
7.51. Системы с линейно и отдельно входящими управлениями (330).
7.52. Линейная управляемая система второго порядка с комплексными
корнями; устойчивый случай (331). 7.53. Задача о полете ракеты (333).
Литература...............................................336
Глава VIII. Об определении оптимальных траекторий
методом динамического программирования (Ричард
Веллман)..............................................338
8.1. Введение......................................... 338
8.2. Динамическое программирование.....................338
8.3. Одномерные задачи ................................339
8.4. Связи — I.........................................340
8.5. Связи — II........................................340
8.6. Обсуждение........................................341
8.7. Двумерные задачи..................................342
8.8. Одномерный случай ................................344
8.9. Обсуждение........................................347
8.10. Двумерный случай...................................348
8.11. Обсуждение.........................................349
Литература...............................................350
Глава IX. Численное рассмотрение некоторых детер-
минированных и адаптивных процессов управления
(Роберт Калаба) .................... 351
9.1. Введение............................................351
9.2. Некоторые детерминированные процессы управления . . . 353
9.21. Формулировка проблемы (353). 9.22. Решение по методу динамиче-
ского программирования (354). 9.23. Обзор численного решения (356).
9.24. Множители Лагранжа и уравнения Эйлера (357). 9.25. Обобщение
на векторные системы (358). 9.26. Пример: линейная система и квадра-
тичный функционал стоимости (359). 9.27. Классическое рассмотре-
ние (362). 9.28. Принцип максимума Понтрягина (363). 9.29. Управление
конечными значениями переменных состояния (364). 9.210. Частный
случай, когда уравнение Эйлера нелинейно (364).
9.3. Адаптивные процессы управления......................367
9.31. Основные положения (367). 9.32. Формулировка проблемы (368).
9.33. Рассмотрение задачи по методу динамического программирова-
ния (370). 9.34. Численные результаты (370).
Литература...............................................371
10
ОГЛАВЛЕНИЕ
Глава X. Общая теория погружения (К. М. Кашмар и
Э. Л. Питерсон)....................................373
10.1. Введение ........................................373
10.2. Формулировка проблемы............................374
10.3. Исключение граничных значений....................375
10.4. Сведёние к задаче о минимизации конечного значения пе-
ременной состояния......................................377
10.5. Классическое решение.............................380
10.6. Решение по методу динамического программирования . . 382
10.7. Резюме...........................................385
Литература.............................................386
Глава XI. Импульсный переход между эллиптическими
орбитами (Дерек Ф. Лоуден)....................387
11.1. Введение .......................................387
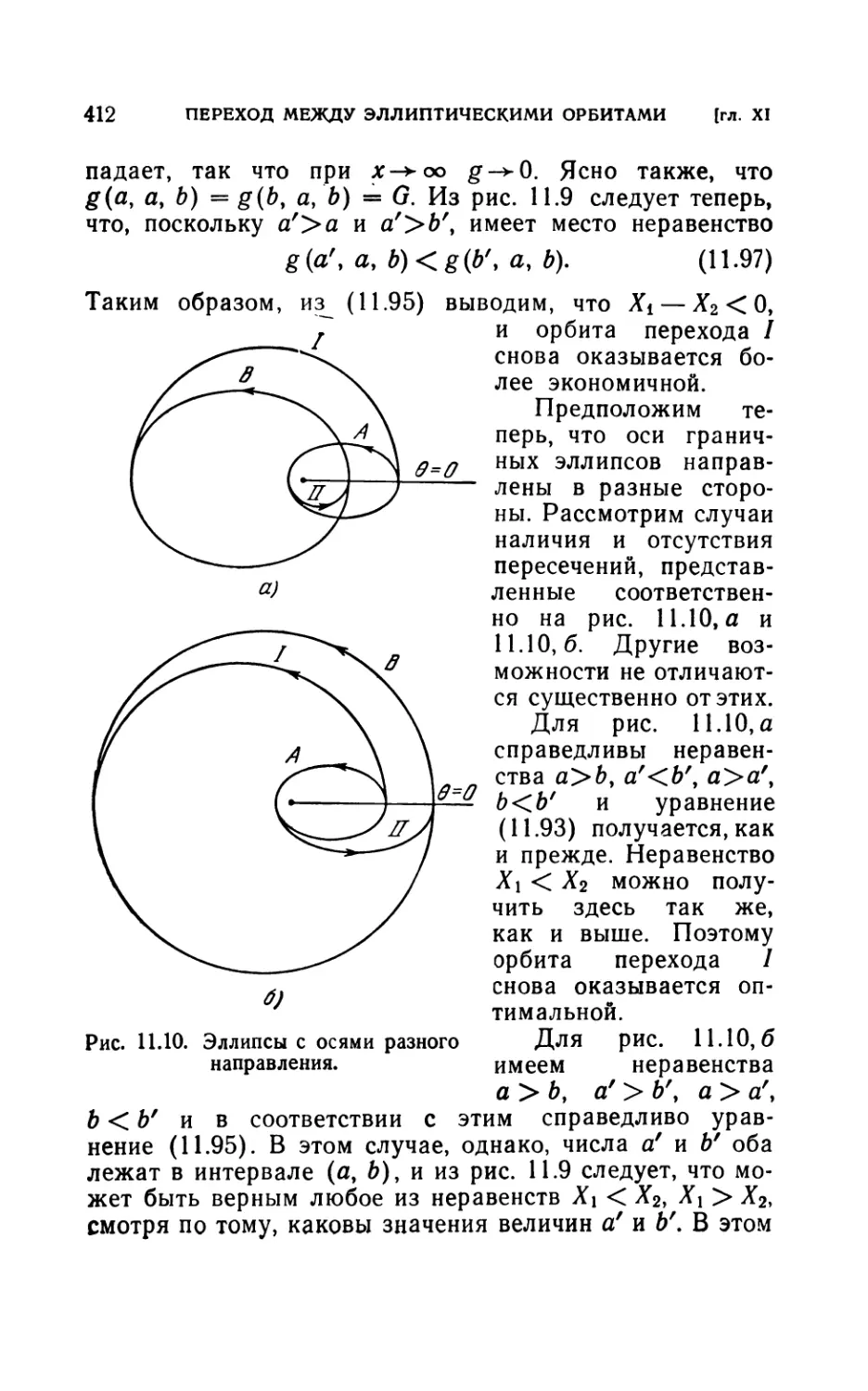
11.2. Импульсивное изменение орбитальных элементов .... 338
11.3. Зависимость импульса от орбитальных элементов .... 392
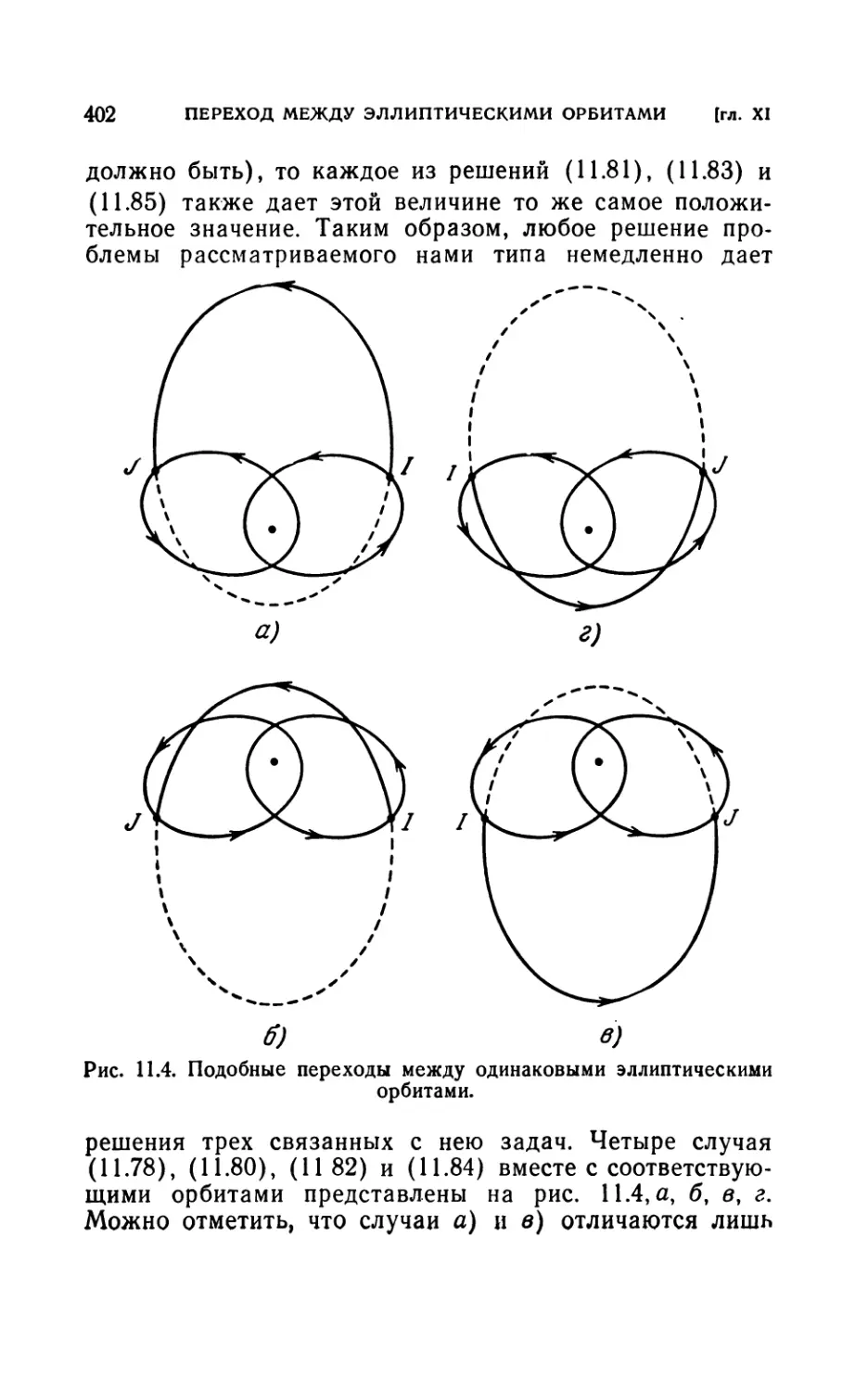
11.4. Оптимальный п-импульсный переход между двумя задан-
ными орбитами...........................................395
11.5. Оптимальный двухимпульсный переход...............397
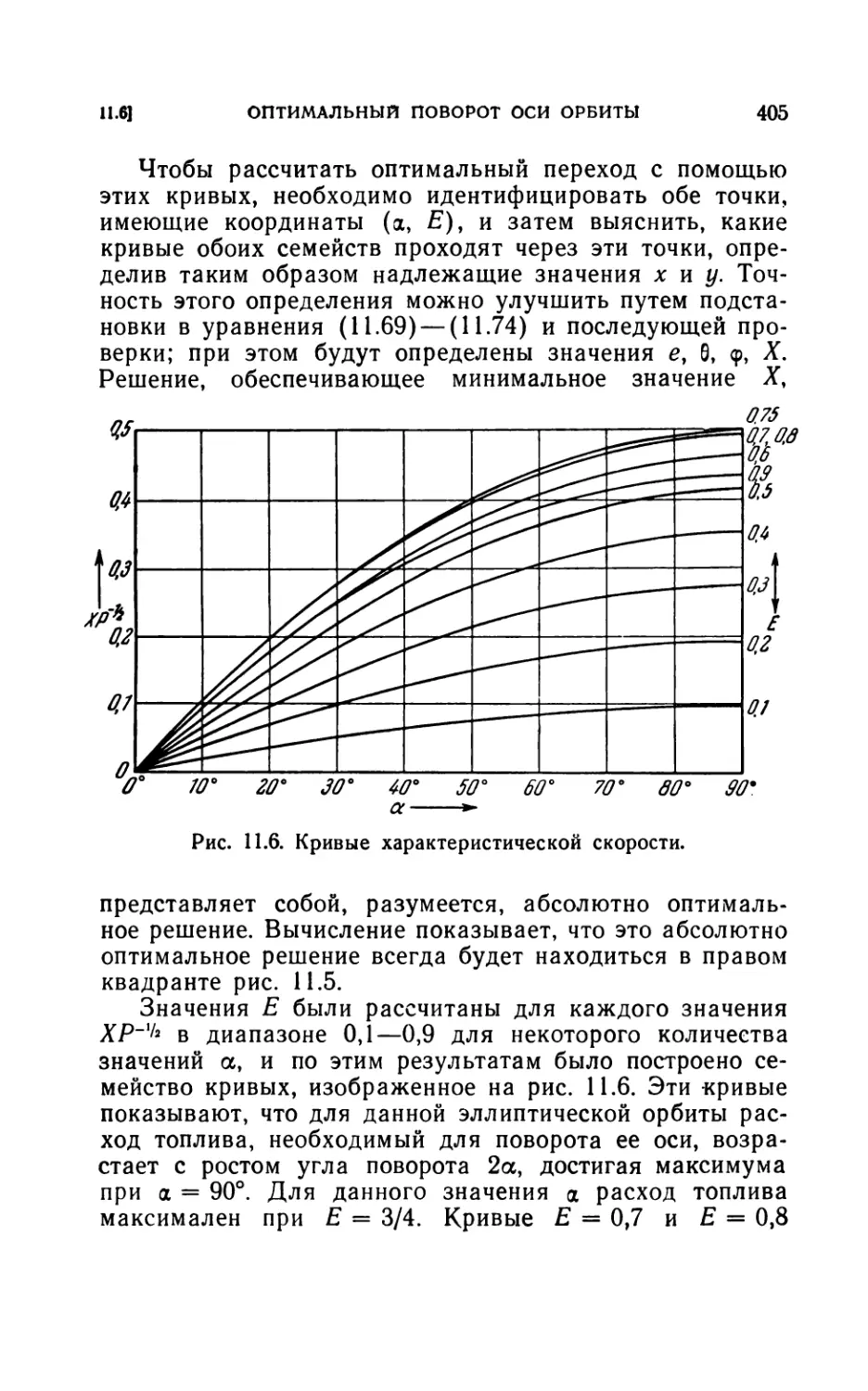
11.6. Оптимальный поворот оси орбиты...................393
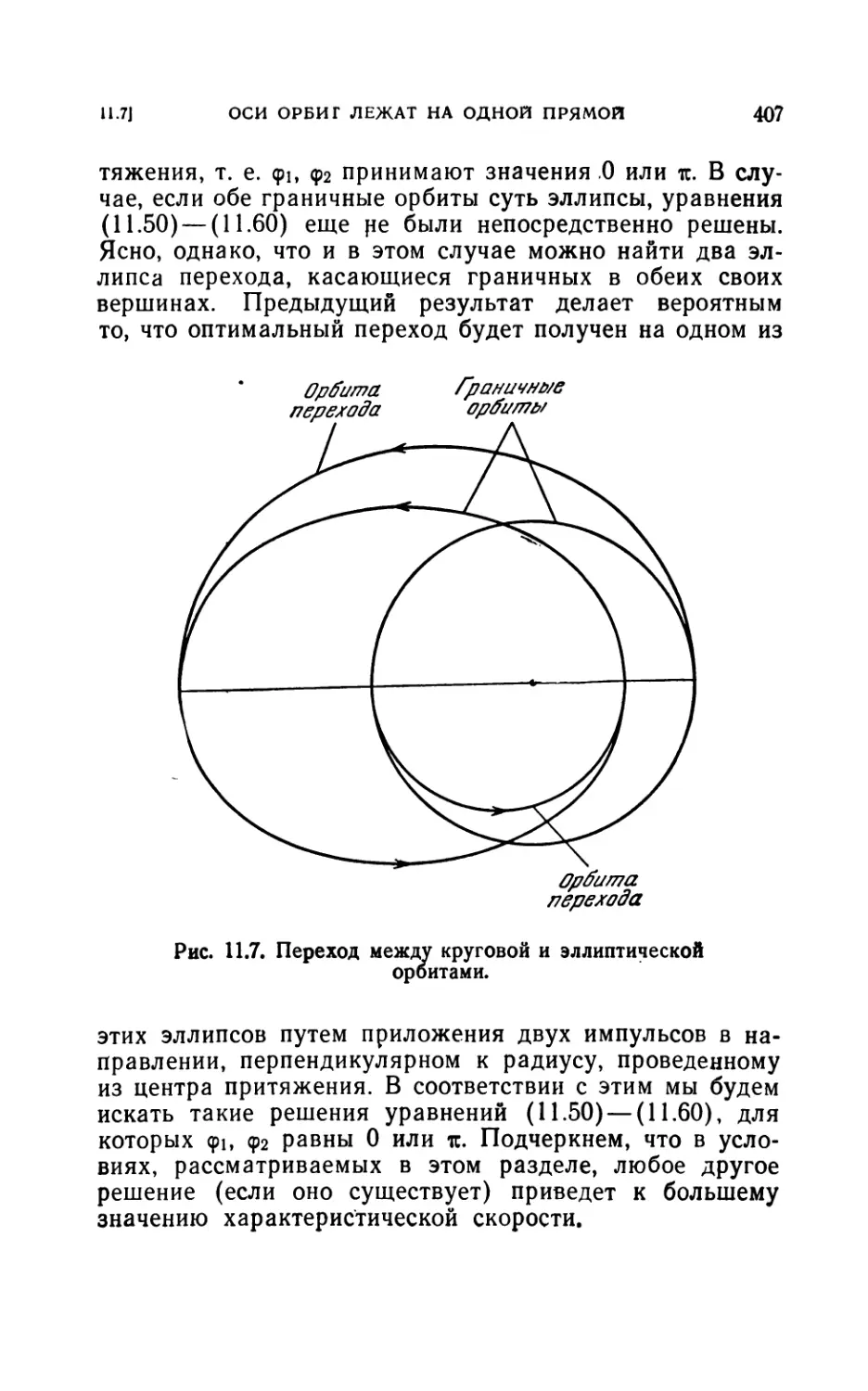
11.7. Переход между орбитами, оси которых лежат на одной
прямой..................................................406
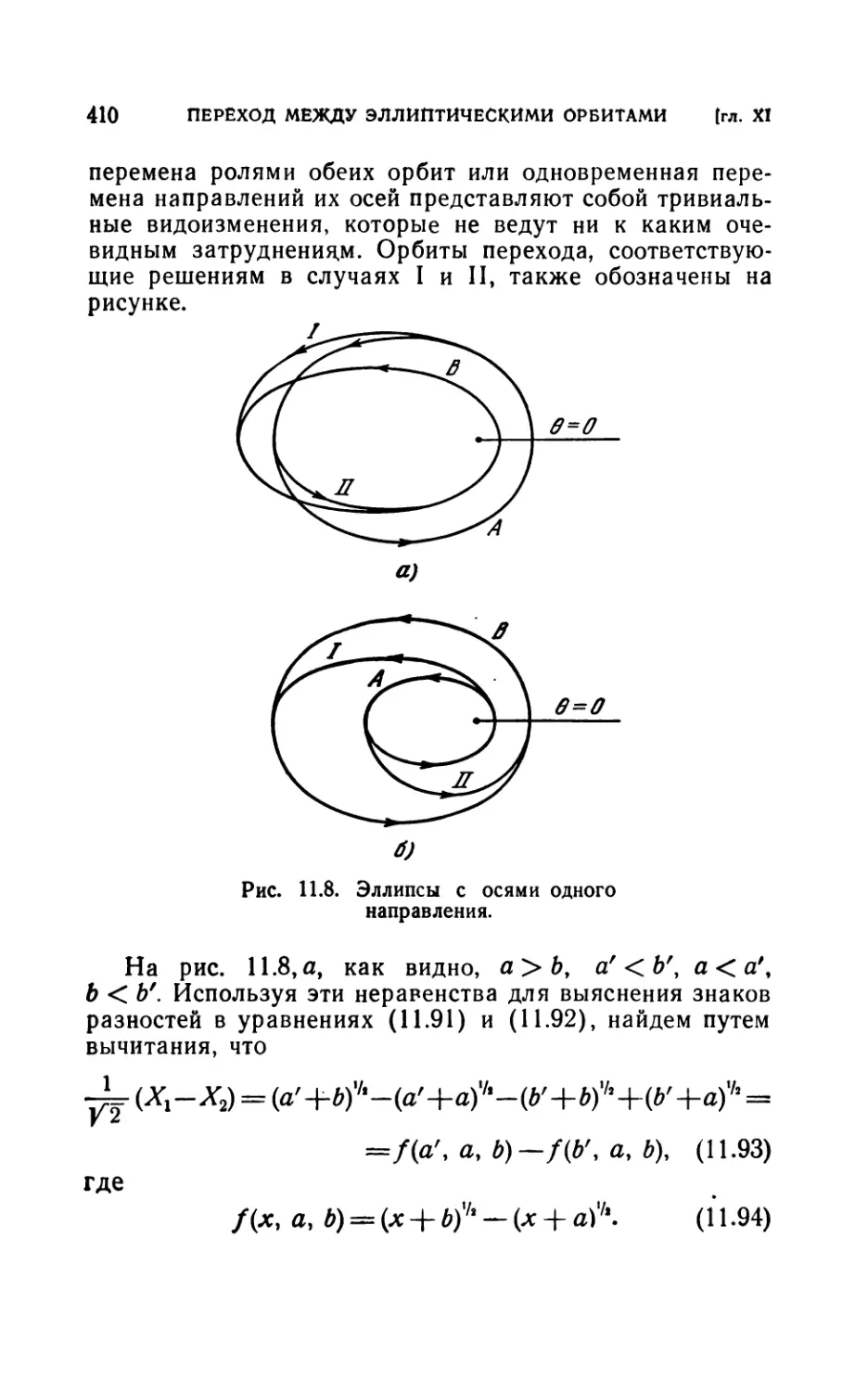
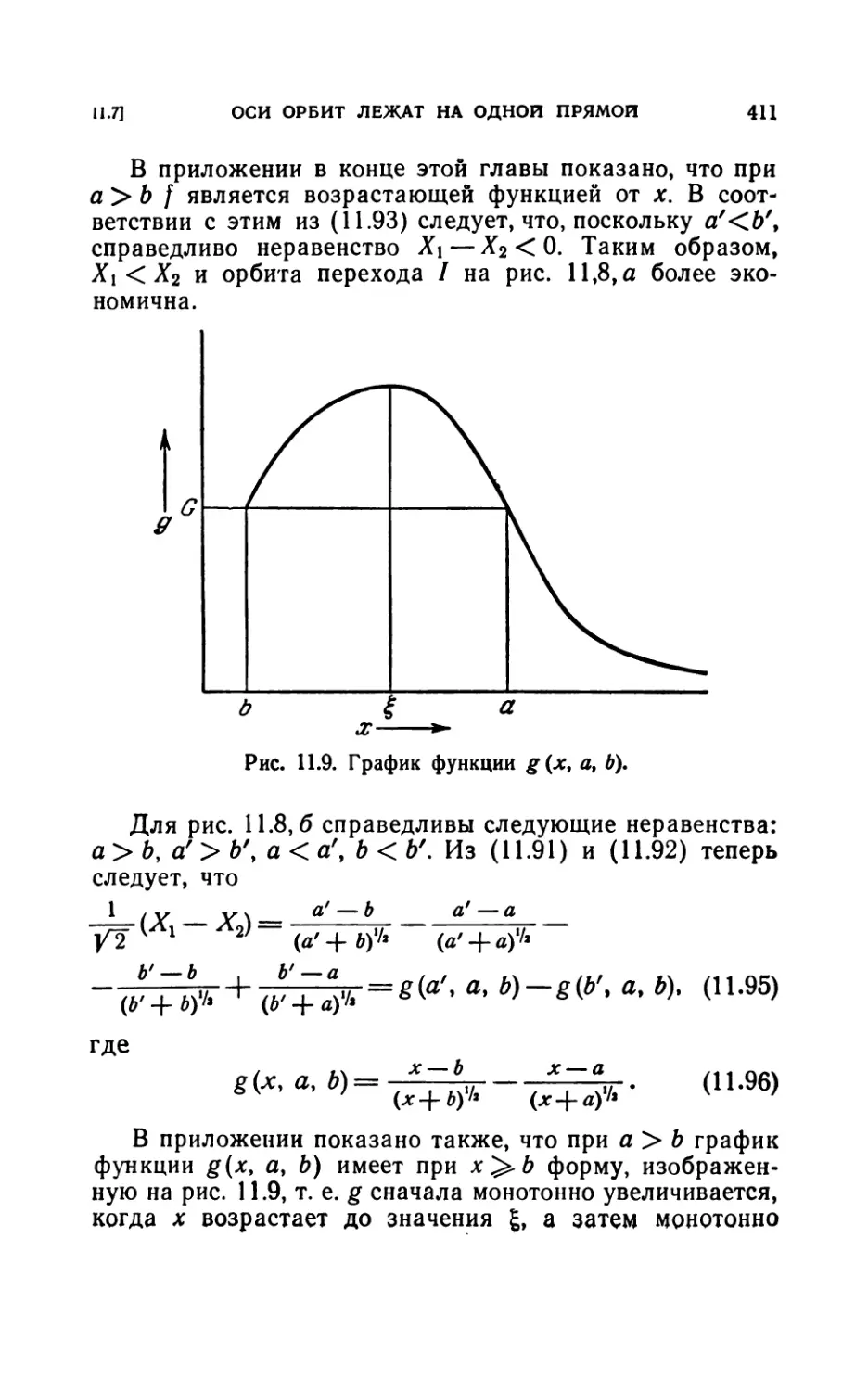
11.8. Приложение.......................................413
11.81. Функция f (х, а, Ь) (413). 11.82. Функция g(x, а, Ъ) (413).
Литература.............................................415
Глава XII. Оптимальное расположение корректирующих
тяговых усилий в межпланетной навигации (Джон
Брекуэлл)...........................................416
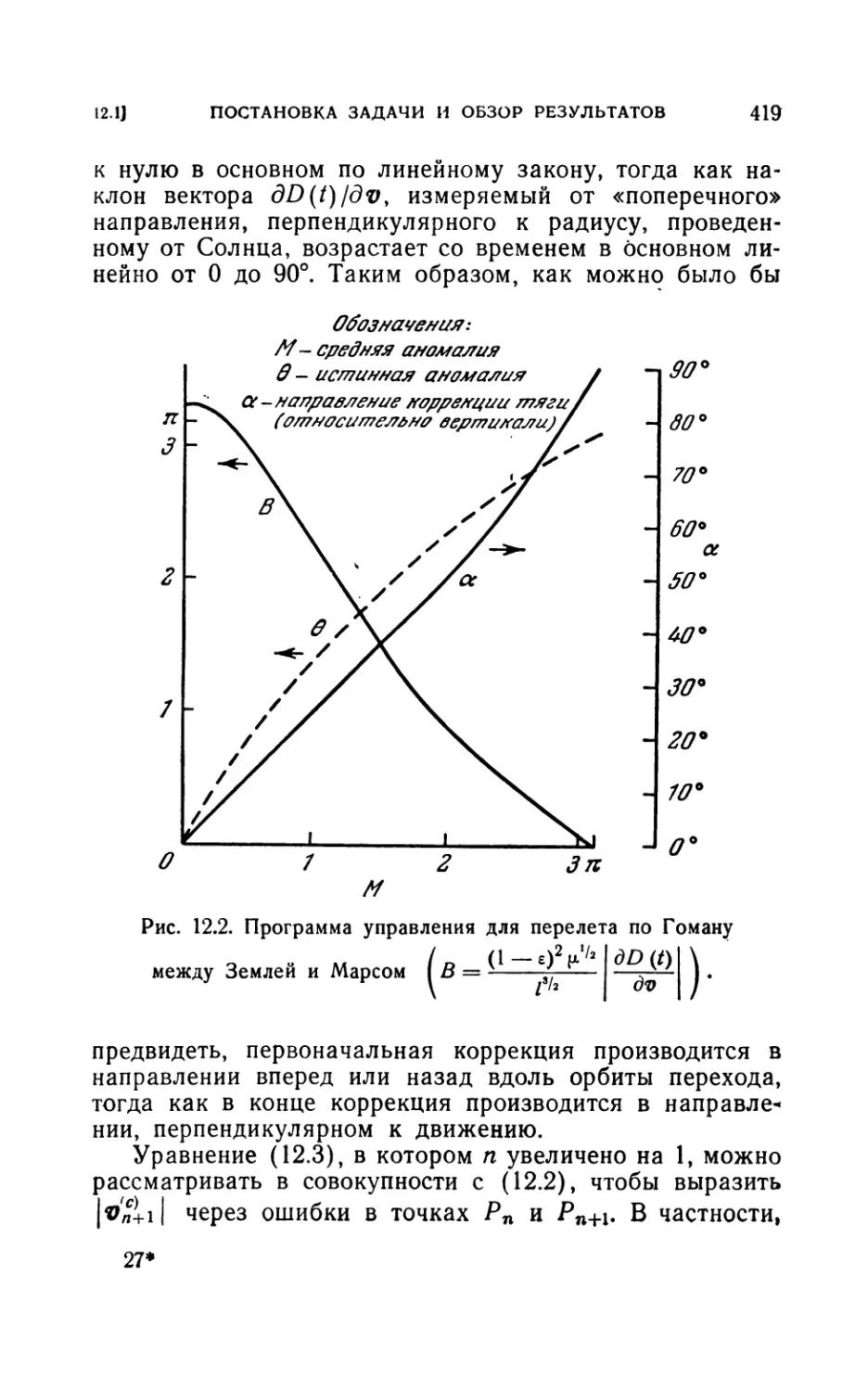
12.1. Постановка задачи и обзор результатов............416
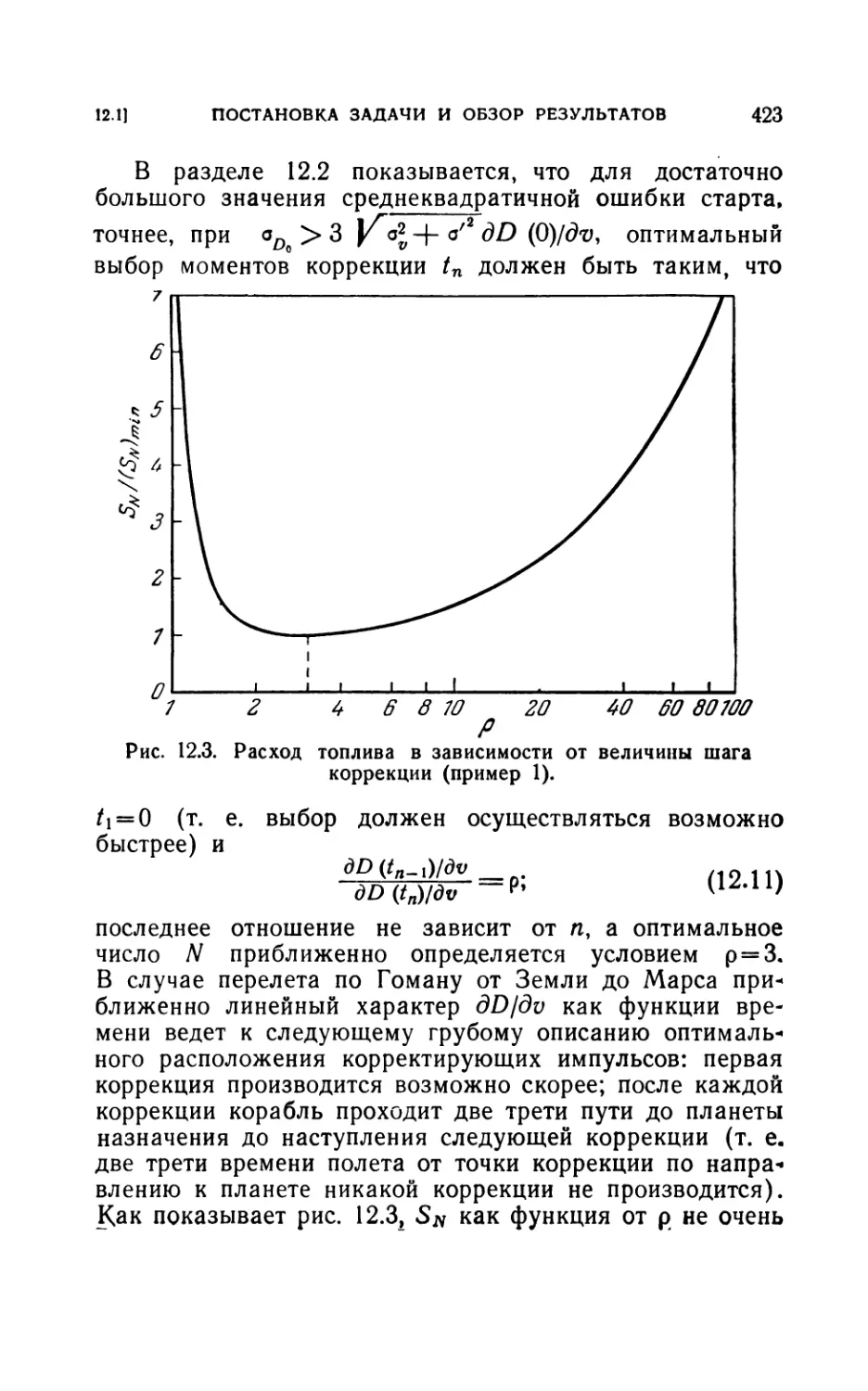
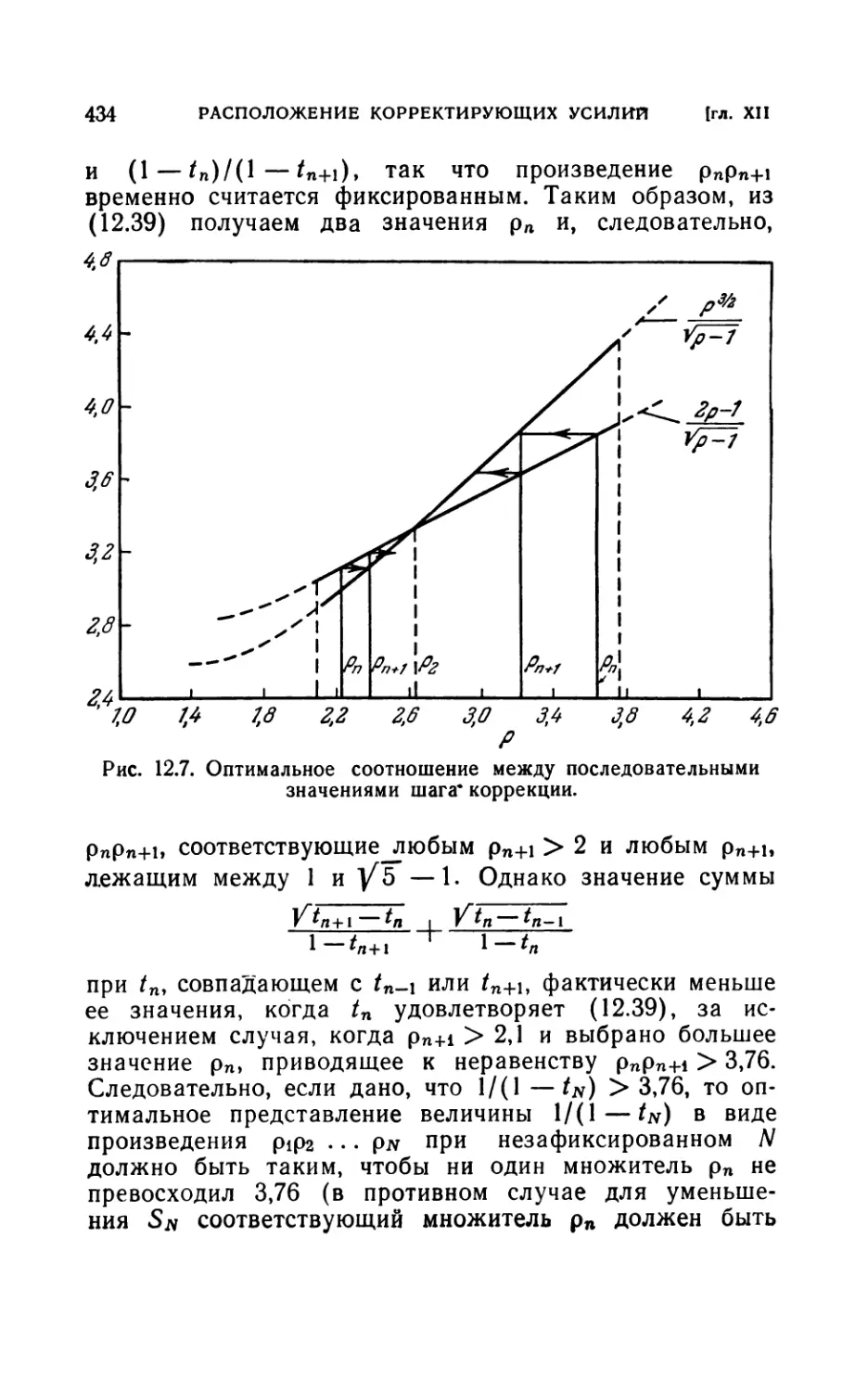
12.2. Исследование оптимального расположения на примере 1 . 428
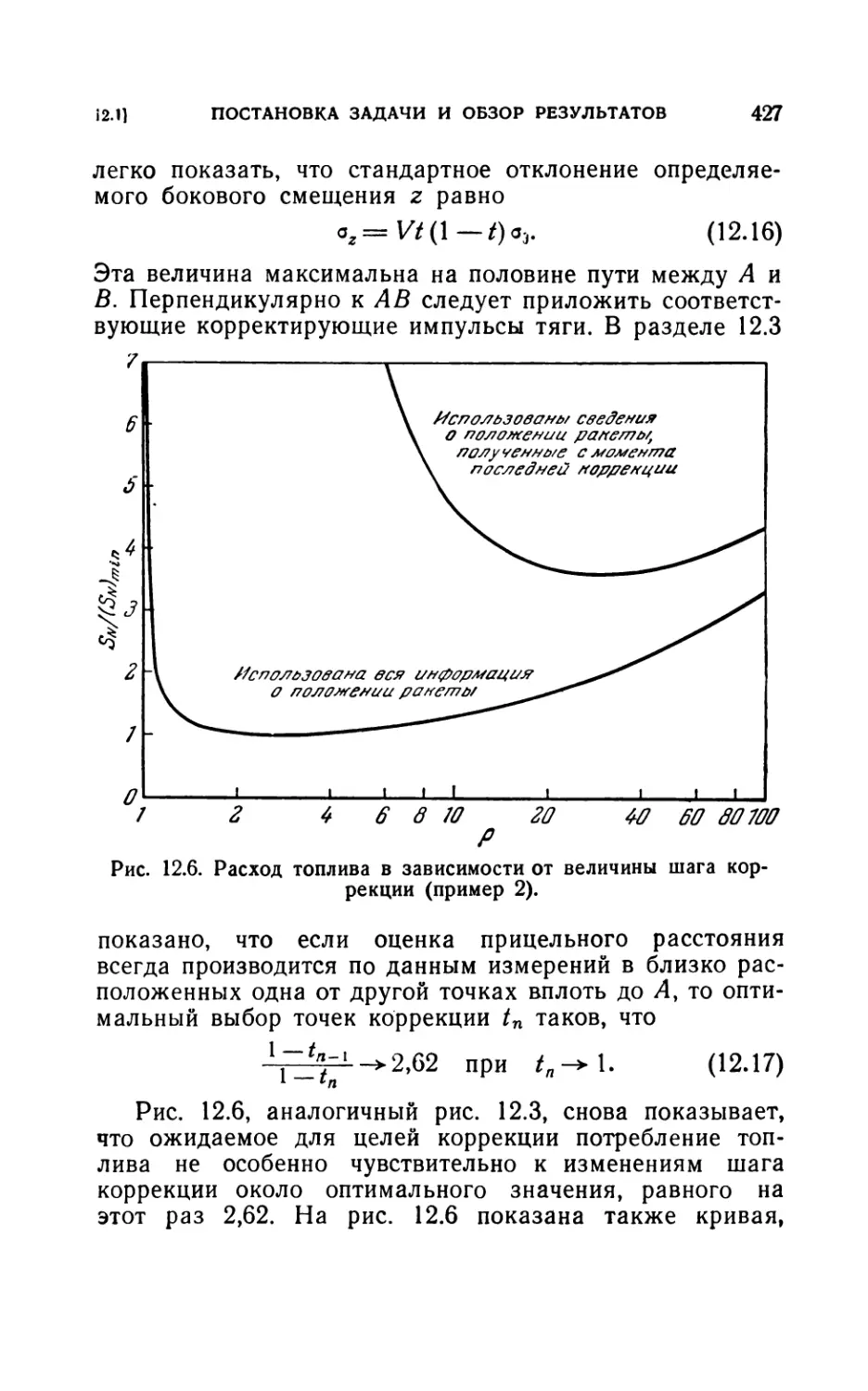
12.3. Исследование оптимального расположения на примере 2 . 430
12.4. Ковариация Dn и Dn+X в случае частых наблюдений на-
чиная с момента старта; одномерная модель..........435
12.5. Оценка D на основе частых измерений положения с мо-
мента последней коррекции; одномерная модель.......437
Указатель обозначений к главе XII.......................435
Литература..............................................441
Глава XIII. Эффективность тяги ракет (Дж. Лейтман) . 442
13.0. Введение .........................................442
13.1. Эффективность тяги как функция точки . . . . <....442
13.11. Постоянная скорость истечения(445). 13.12. Переменная скорость
истечения (445),
ОГЛАВЛЕНИЕ
11
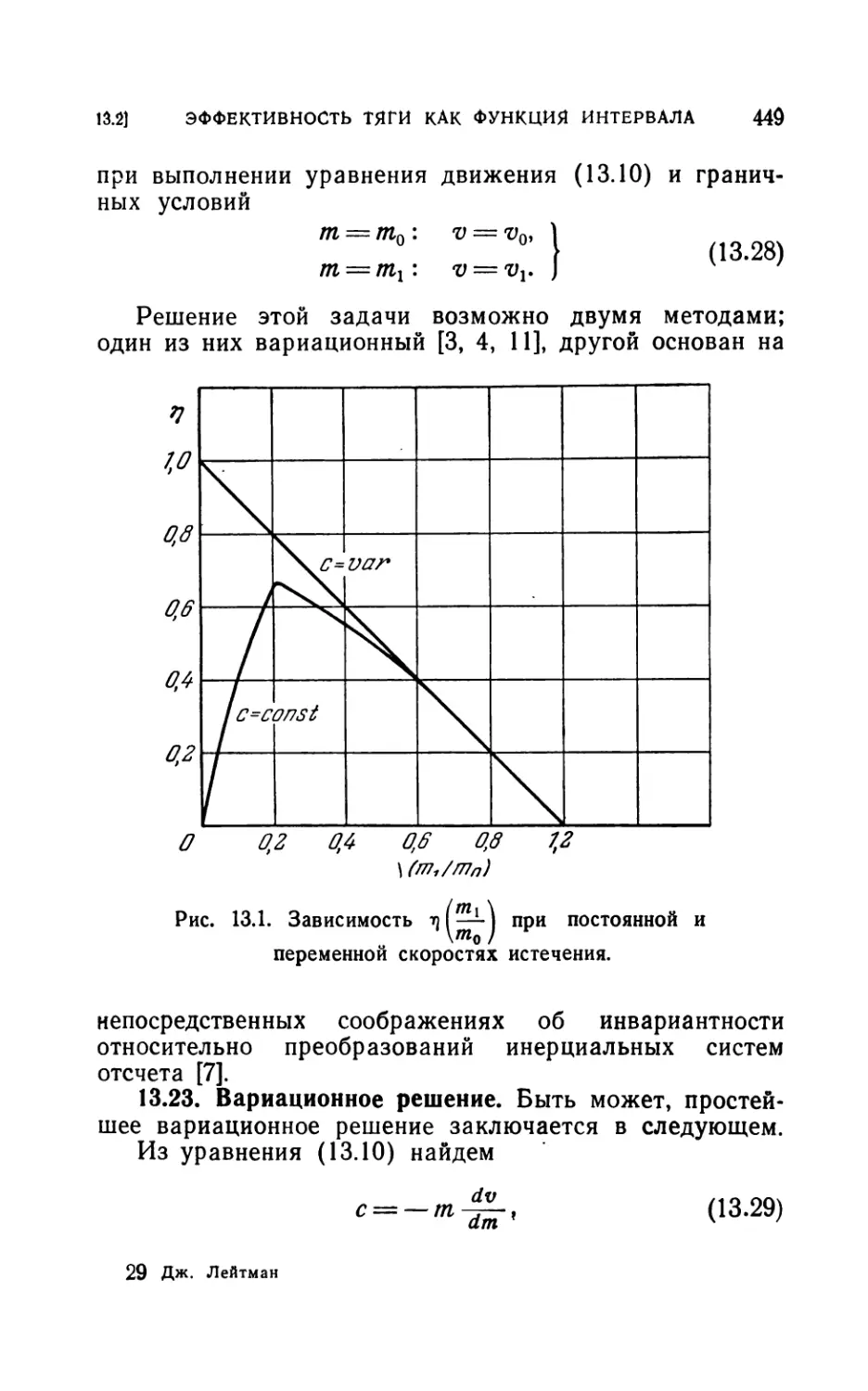
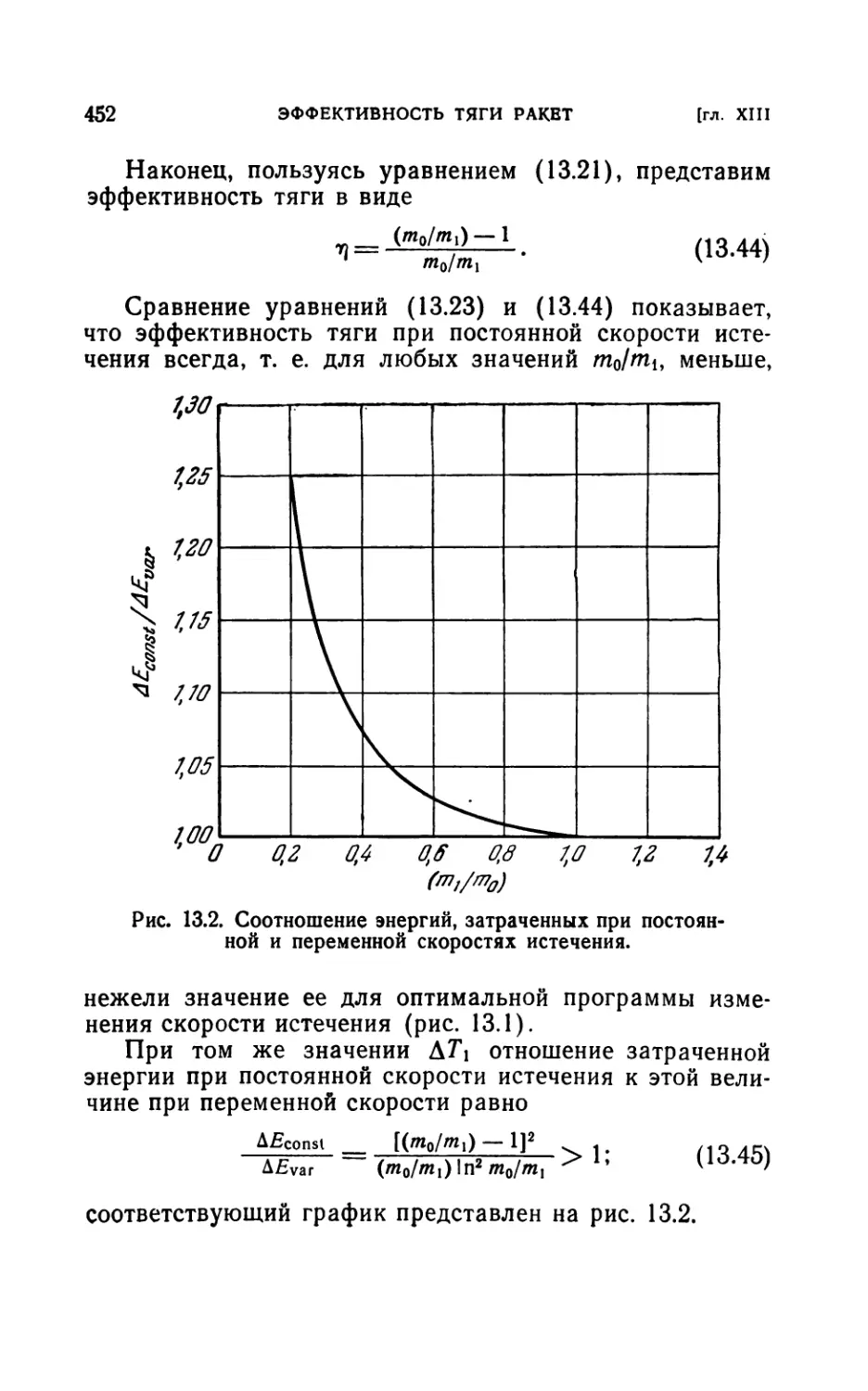
13.2. Эффективность тяги как функция интервала................446
13.21. Постоянная скорость истечения (447). 13.22. Переменная скорость
истечения (448). 13.23. Вариационное решение (449). 13.24. Непосред-
ственное решение (450).
Указатель обозначений к главе XIII............................453
Литература....................................................453
Глава XIV. Некоторые вопросы оптимизации ракет на
ядерном топливе (Р. У. Бассард)..........................455
14.1. Введение; определения...................................455
14.11. Ракетные летательные аппараты на ядерном топливе (455).
14.12. Анализ системы и ее оптимизация (457).
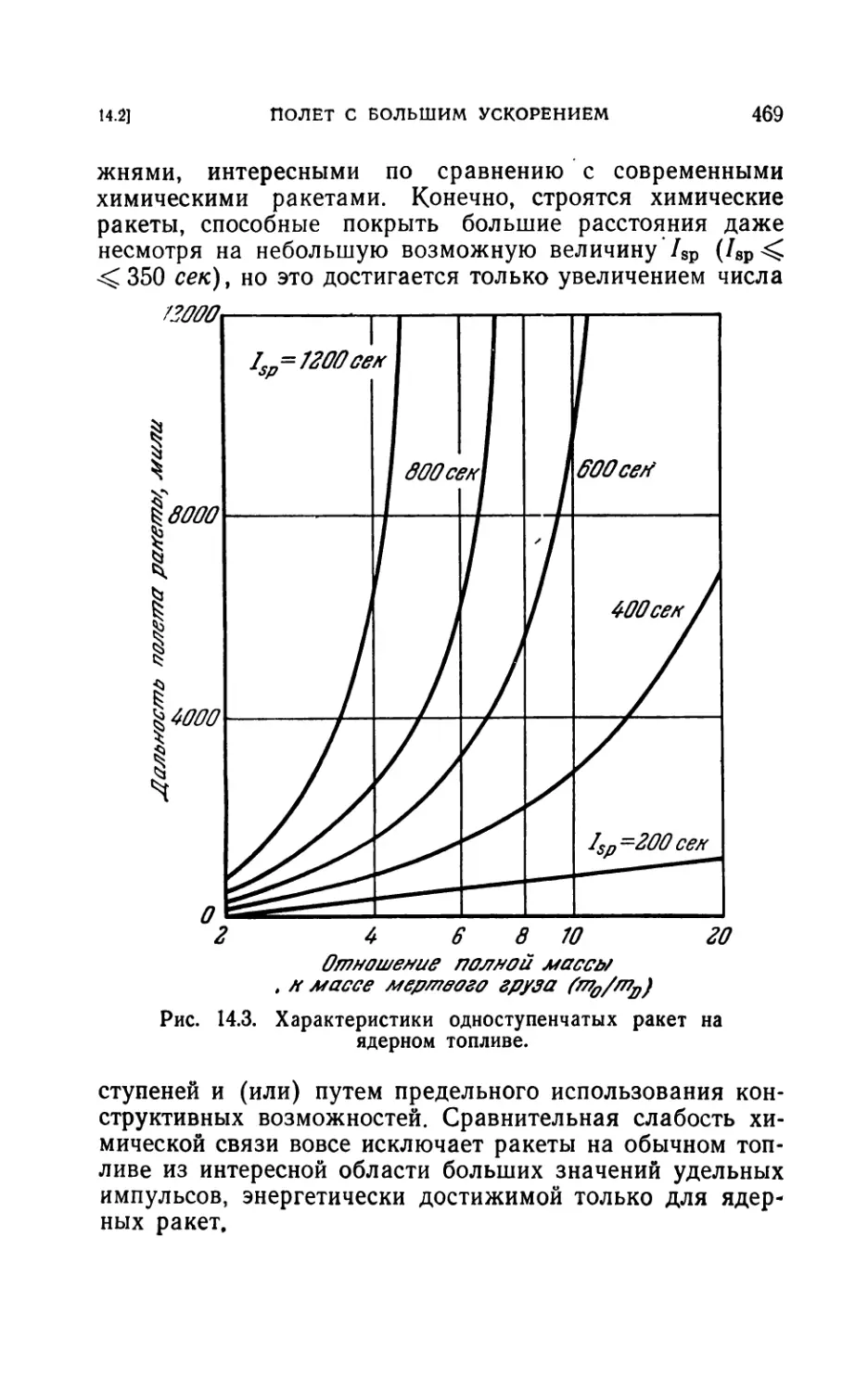
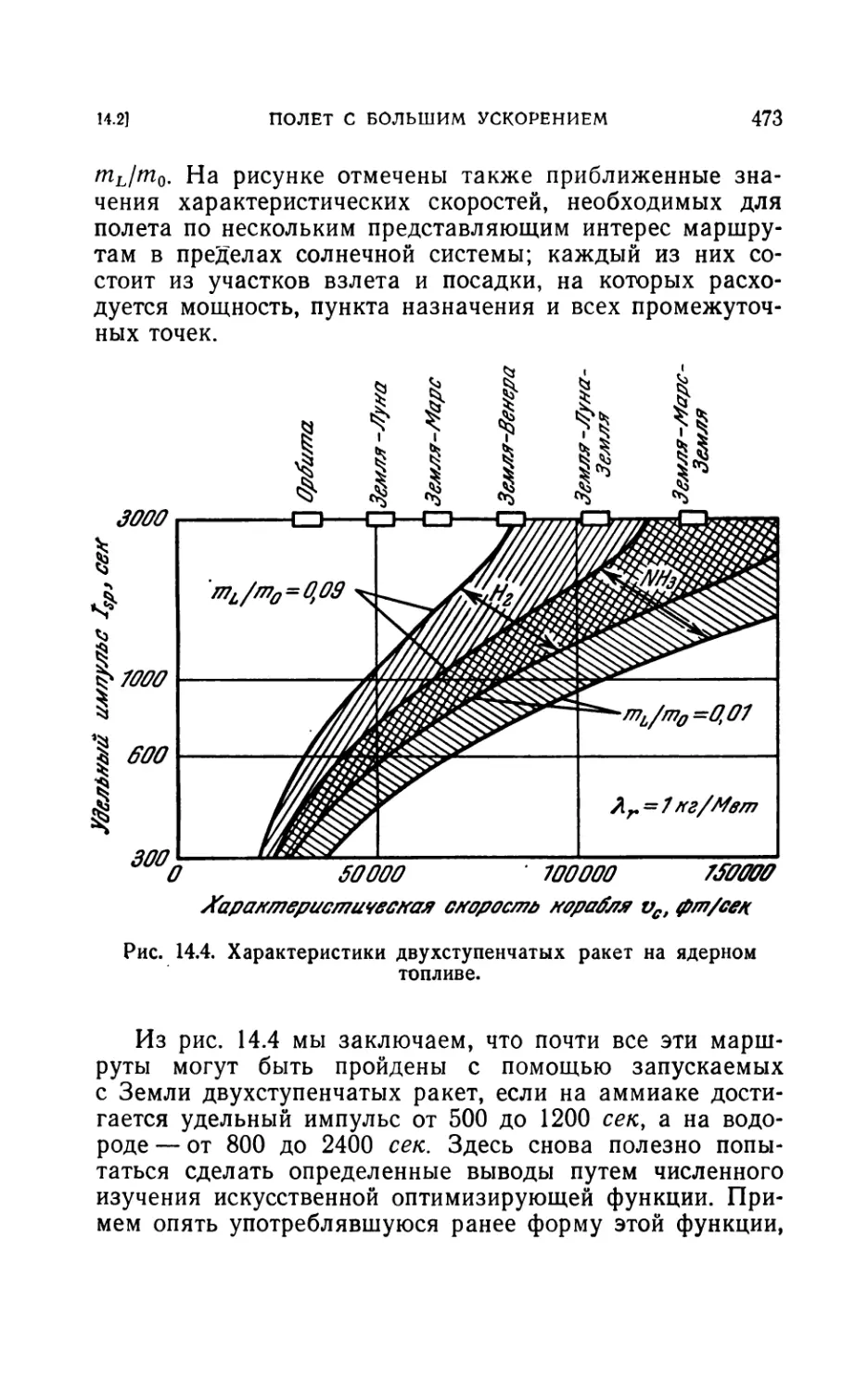
14.2. Полет с большим ускорением..............................463
14.21. Основные принципы конструирования корабля (463). 14.22. Влия-
ние удельного импульса (467). 14.23. Оптимизация баллистической
траектории (474). 14.24. Различные вопросы (479).
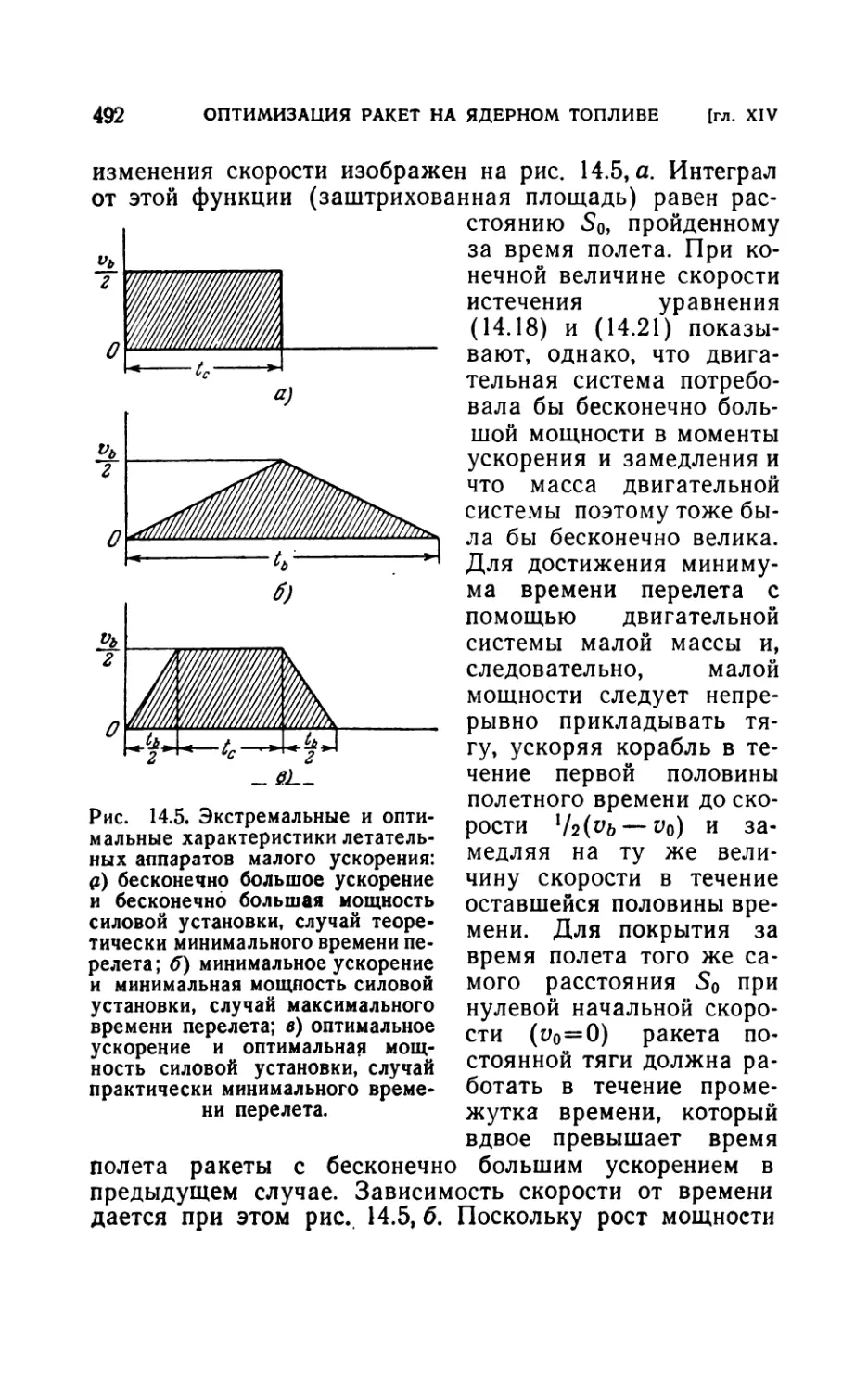
14.3. Полет с малым ускорением................................481
14.31. Общие соображения (481). 14.32. Распределение масс компонент
и оптимизация полета (485). 14.33. Влияние ограниченности запаса
энергии (500). 14.34. Радиационная защита (505).
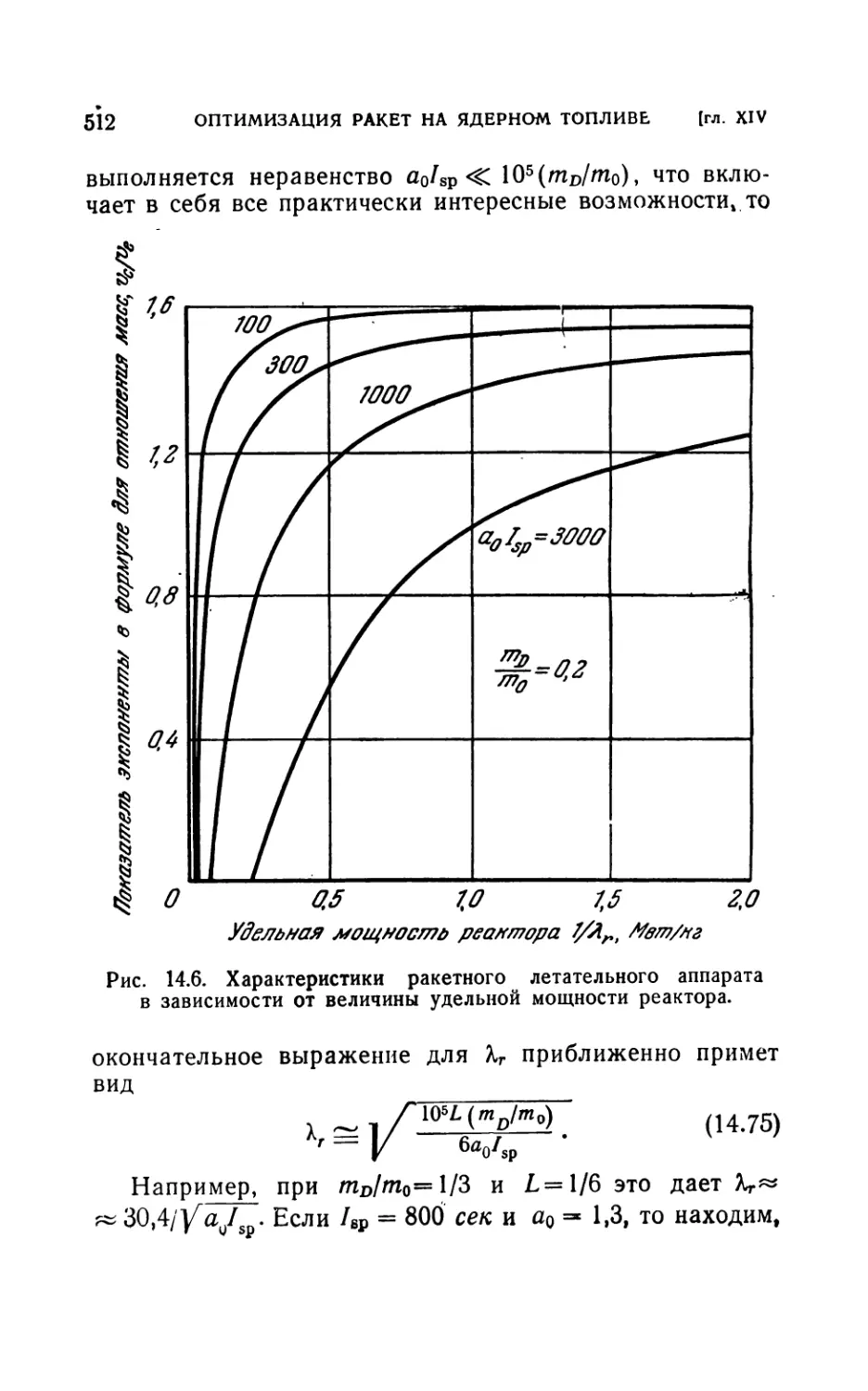
14.4. Двигательные системы с теплообменниками.................508
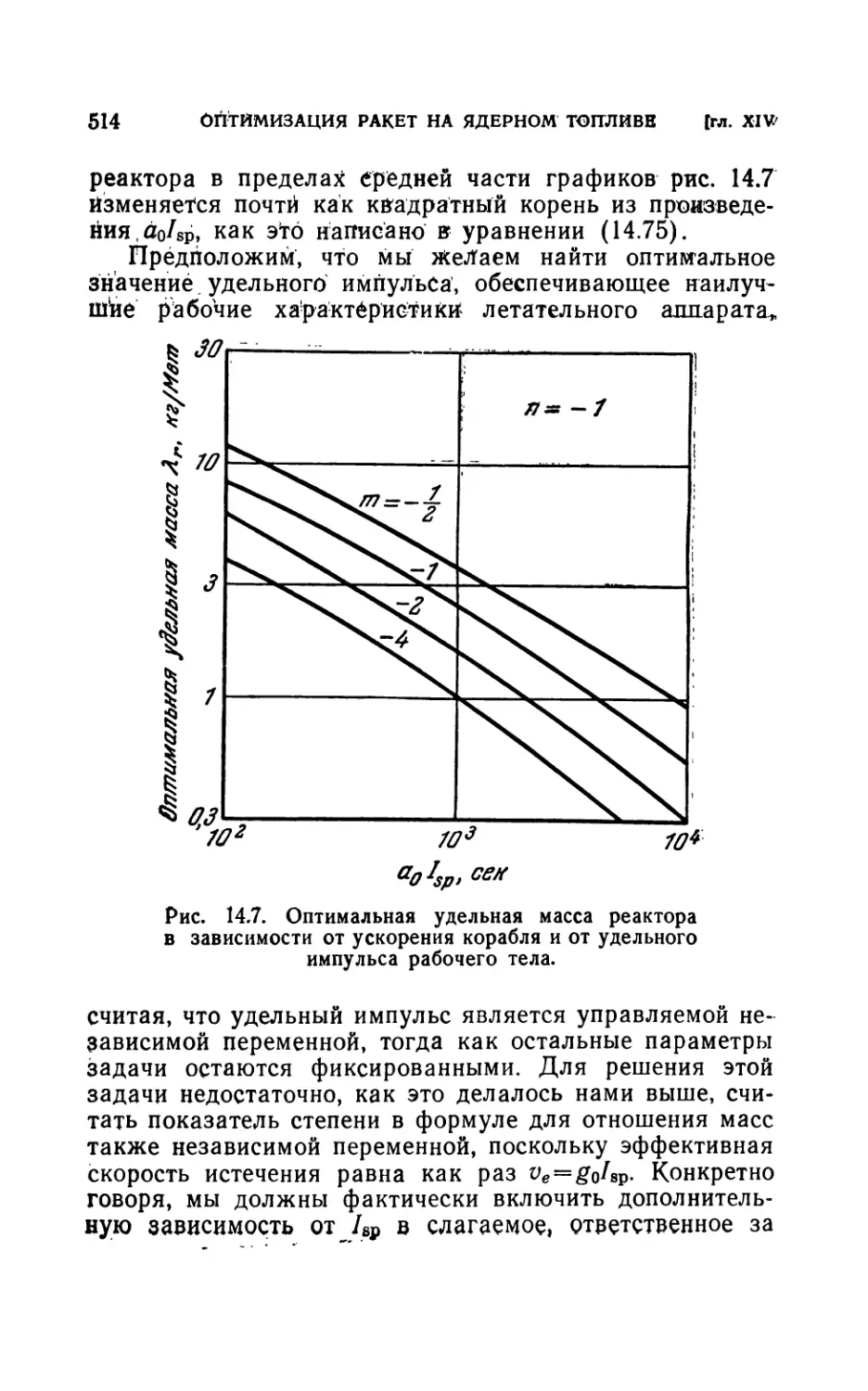
14.41. Удельная масса и импульс как свободные переменные (510).
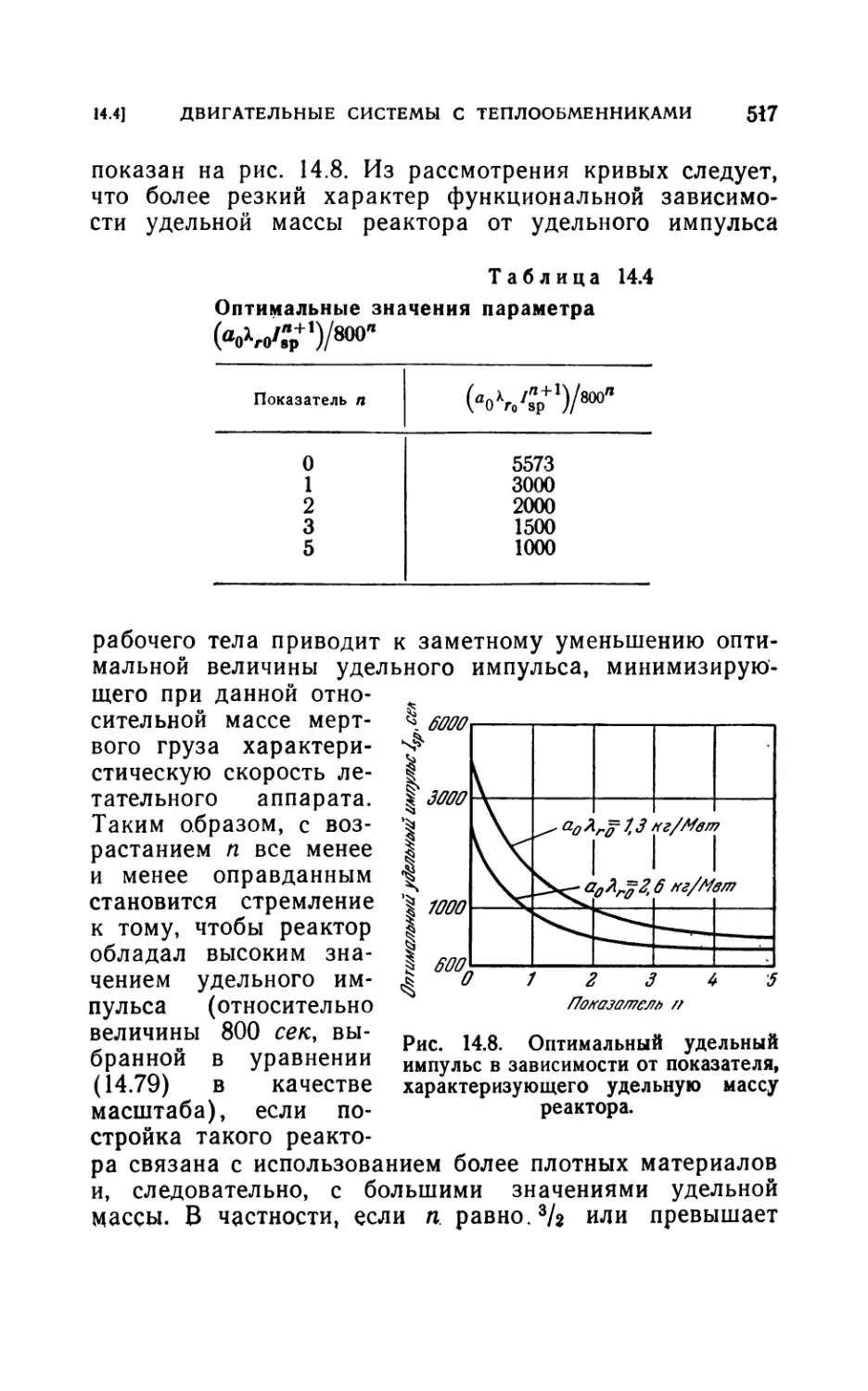
14.42. Давление, удельная масса и соответствующий импульс (515).
14.43. Газовый вихревой реактор (521 \
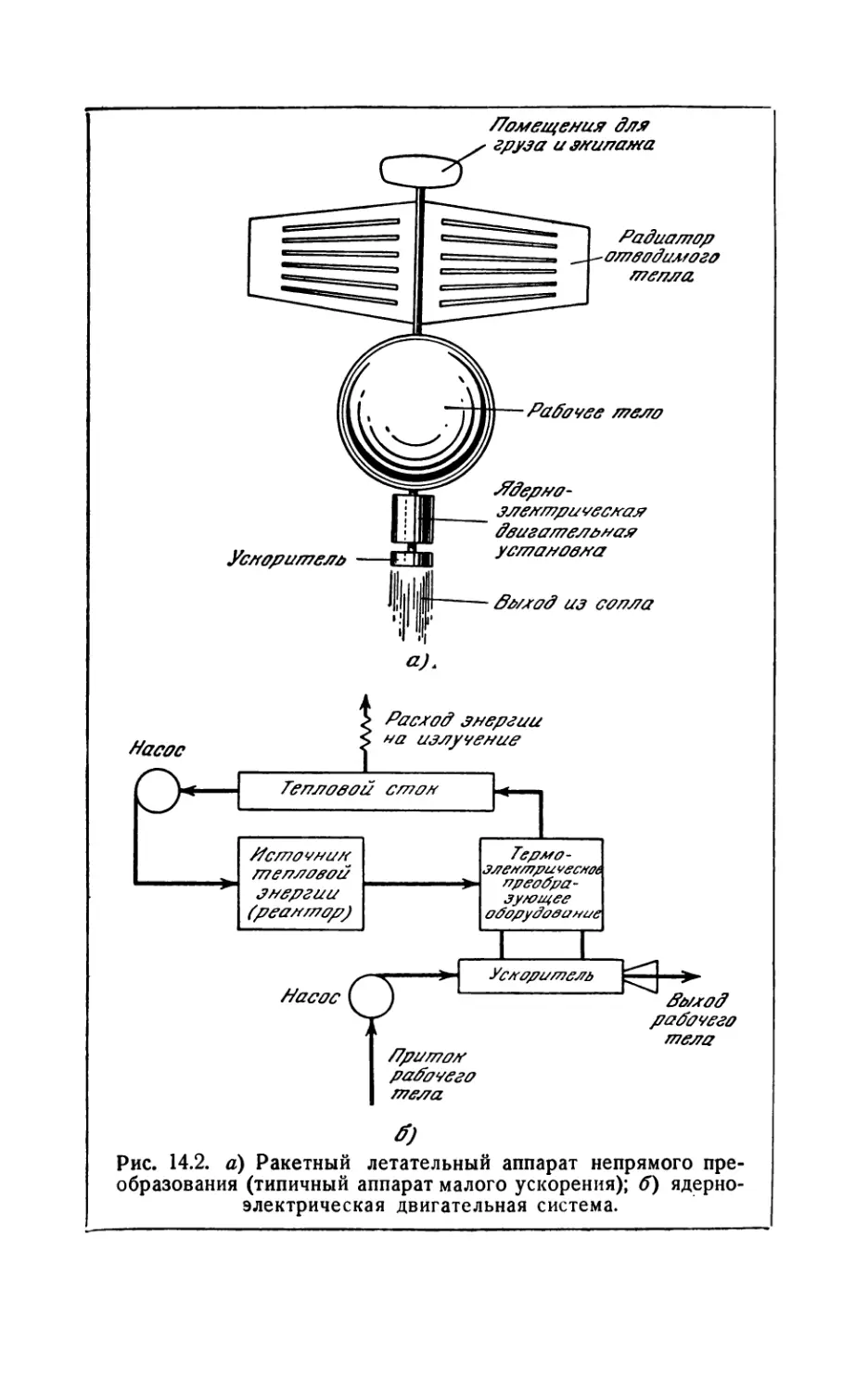
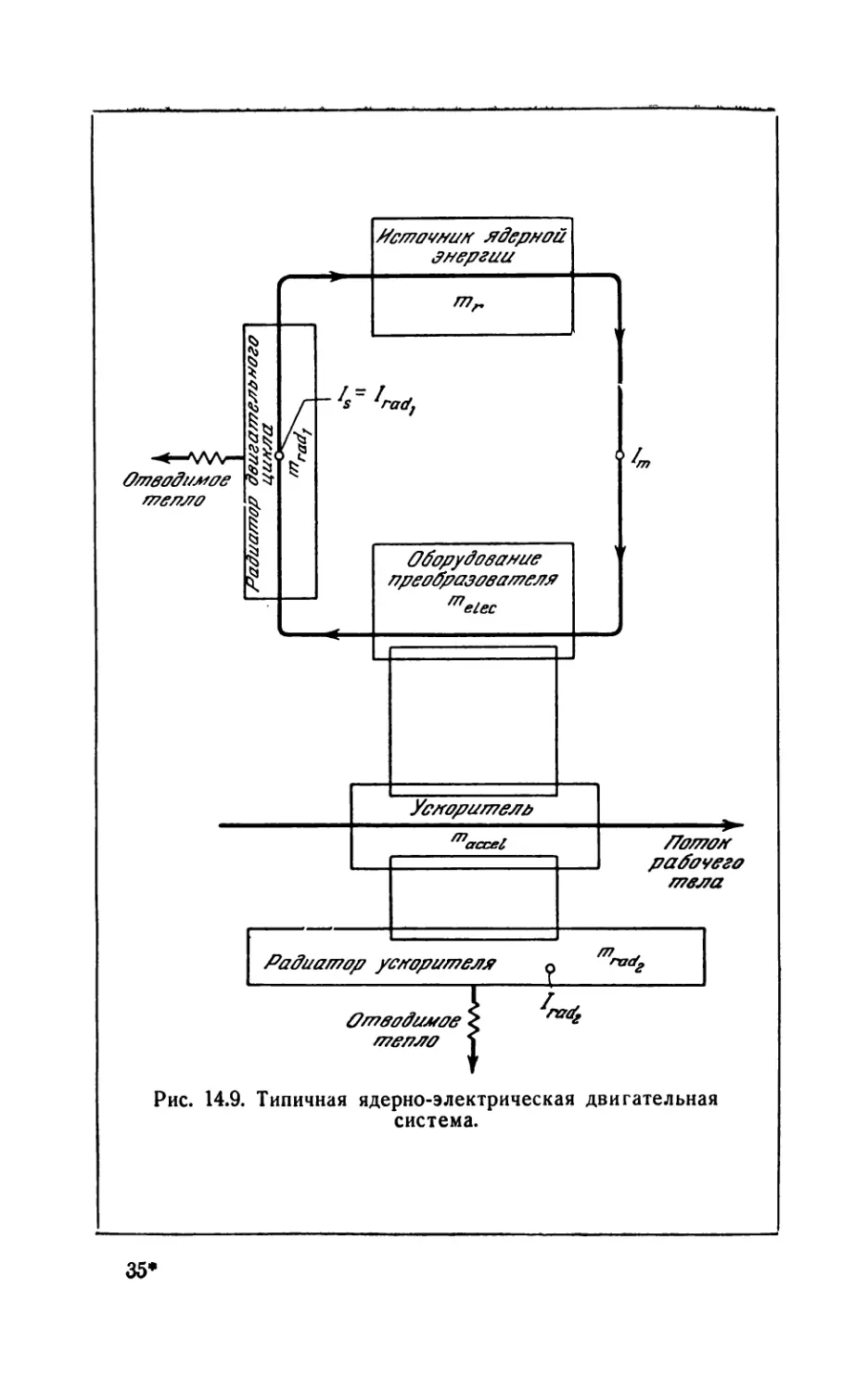
14.5. Ядерно-электрические двигательные системы...............526
14.51. Оптимизация температуры цикла (526). 14.52. Реакторы прямого
преобразования (530).
Литература....................................................533
Предметный указатель...............................• .... 535
ОТ РЕДАКТОРА ПЕРЕВОДА
Стремление удовлетворить требованиям, которые
предъявляются к качеству современных технических уст-
ройств, зачастую приводит к необходимости выяснения их
экстремальных возможностей. При этом приходится при-
бегать к построению наилучших в принятом смысле или,
как их еще называют, оптимальных режимов работы
устройств.
Поэтому последние годы характеризуются все боль-
шим интересом к задачам оптимизации. По своему смыс-
лу они являются вариационными. Однако от обычных
задач вариационного исчисления их отличает необходи-
мость учета при построении оптимальных процессов раз-
личного рода ограничений, задающих замкнутые области
допустимых изменений переменных.
Эта дополнительная сложность привела к известным
особенностям, которыми характеризуются направления
развития теории оптимальных систем. Часть методов по-
строения оптимальных процессов базируется на аппарате
классического вариационного исчисления и теории при-
ближенных вычислений. Другая и, пожалуй, не меньшая
их часть объединяет методы, разработанные для непо-
средственных целей теории оптимальных систем.
К сожалению, до сих пор имеются лишь монографии
и публикации в периодической печати, в которых осве-
щаются отдельные методы теории оптимальных систем
или решения конкретных задач оптимизации процессов
управления. Ни в отечественной, ни в зарубежной печати
пока нет руководств или монографий, в которых в связан-
ном виде были бы изложены все или хотя бы большая
14
ОТ РЕДАКТОРА ПЕРЕВОДА
часть методов решения задач оптимизации. Именно эту
цель преследовали, по-видимому, авторы предлагаемой
вниманию читателя книги.
В ней излагаются и точные методы, в основе которых
лежит использование результатов классического вариа-
ционного исчисления, и новейшие методы, такие, как
принцип максимума Л. С. Понтрягина или метод ди-
намического программирования. Р. Веллмана, и, на-
конец, приближенные методы построения оптимальных
процессов.
Книга интересна также и тем, что в качестве приме-
ров использования общих методов теории оптимальных
систем выбрана -очень важная область приложений —
задачи расчета оптимальных траекторий космических
аппаратов. Решение их, несомненно, представляет боль-
шой самостоятельный интерес.
В. Троицкий
ТАБЛИЦА
ПЕРЕВОДА АМЕРИКАНСКИХ МЕР В МЕТРИЧЕСКИЕ
И В ЕДИНИЦЫ СИ
Единицы длины
1 уставная миля = 1,60934 км 1 дю£м< = 2,54 см
1 морская миля = 1,852 км 1 фут =12 дюймов = 30,48 см
Единицы площади
1 дюйм2 = 6,4516 см2
1 фут2 = 0,092903 м2
Единицы объема
1 дюйм2 = 16,3871 см3 1 фут3 = 0,0283168 м3
Единицы массы
1 фунт = 0,4535924 кг 1 слэг = 14,5939 кг 1 унция = 28,3495 г
Единицы силы (веса)
1 фунт = 0,4535924 кГ = 4482 н
Единицы плотности
1 фунт/фут3 = 16,0185 кг/м3 1 фунт/дюйм3 = 27,680 т/м3
Единицы давления
1 фунт/фут2 = 0,00048824 кГ/см2 = 47,8803 н/м2
1 фунт/дюйм2 = 0,070307 кГ/см2 = 6894,76 н/м2
Тепловые единицы
1 Британская тепловая единица (Бте) = 0,25198 ккал =
= 1,05506 103 дж
Формулы перехода от температур в шкалах Фаренгейта (If)
и Ренкина (/r) к температурам в шкале Цельсия (tc) и в абсолют-
ной шкале Кельвина (/к):
£ к к к
1°F = |°C, /C = f(/R-491.7), *с=|(*р-32),
(температура в шкале Ренкина есть абсолютная температура, выра-
женная в градусах Фаренгейта),
ПРЕДИСЛОВИЕ
Что бы мы ни делали, мы стараемся сделать возмож-
но лучше. В стремлении достичь своей цели наилучшим
образом человек сразу встречается с двумя проблемами.
Первая из них есть решение избрать определенную цель.
То, что для одного человека является наилучшим, вполне
может оказаться наихудшим для другого. Может быть
принято решение игнорировать желания других заинтере-
сованных сторон и выбрать цель исключительно исходя
из собственных интересов, независимо от того, находятся
ли они в конфликте с интересами других. Например, уче-
ный, желающий производить опыты с использованием
устройств, установленных на спутнике, может выбрать
в качестве оптимальной восходящую траекторию, которая
характерна максимальным выносимым на орбиту грузом,
даже если такая «оптимальная» траектория связана
с чрезмерно большими ускорениями, недопустимыми
с точки зрения инженера-конструктора, занятого проек-
тированием ракеты-носителя.
С другой стороны, можно согласовывать выбор цели
с интересами других, накладывая ограничения на опти-
мальное поведение с тем, чтобы не нарушать требований
других заинтересованных сторон. Следовательно, ученый
может быть вынужден согласиться с несколько меньшим
полезным грузом на орбите из-за ограничений, наклады-
ваемых на ускорения и приводящих к тому, что нагрузки
станут допустимыми и поэтому приемлемыми для ин-
женера-конструктора.
Но даже в случае, если будут выбраны цели и ограни-
чивающие условия, удовлетворяющие все стороны, еще
ПРЕДИСЛОВИЕ
17
остается выбор средств осуществления оптимальной про-
граммы. Этому последнему вопросу и посвящена в пер-
вую очередь настоящая книга.
В течение последнего десятилетия значительно воз-
рос интерес к проблемам оптимизации и оптимального
регулирования. Вместе с тем появилась возрастающая
потребность в методах оптимизации различных систем.
Для удовлетворения этой потребности появились различ-
ные «школы», зачастую отстаивающие один метод опти-
мизации и считающие его наилучшим по сравнению со
всеми другими. Длительный опыт показал, однако, что
жизнь не всегда настолько проста, чтобы вещи описыва-
лись лишь черным и белым. Коротко говоря, можно ожи-
дать, что определенный «метод превосходит другие в отно-
шении некоторых задач — и лишь изредка для всех за-
дач. Более того, поскольку основная математическая
формулировка проблем оптимизации часто в существен-
ном одинакова во многих приложениях, не лишено осно-
ваний ожидать, что возможна большая степень общ-
ности (часто — даже тождества) между различными ме-
тодами, общности, скрытой за различиями в языке и в
обозначениях. Помочь неискушенному в поисках и вы-
боре оптимального метода оптимизации читателю —
важная задача этой книги.
Для достижения этой цели в книгу включены Десять
глав, освещающих различные методы, используемые в
настоящее время для решения проблем оптимизации
систем и оптимального регулирования. Выбор авторов был
продиктован исключительно их собственными интересами
и степенью компетентности в том или ином вопросе.
Вместе с преимуществами столь эклектического подхода
и связанного с этим разнообразия авторских стилей об-
наруживается некоторая неровность книги в целом, за
которую несет ответственность только редактор. С одной
стороны, различные главы согласованы путем ссылок
одна на другую, с другой — каждая может читаться
самостоятельно, как развивающая метод, отстаиваемый
отдельной «школой».
Хотя каждая из десяти глав, где излагаются общие
методы, включает простые примеры в первую очередь
с целью пояснения, мы сочли полезным включить четыре
2 Дж. Лейтман
18
ПРЕДИСЛОВИЕ
дополнительные главы, имеющие дело исключительно с
приложениями. Первые три из них, главы XI—XIII,
охватывают специальные проблемы оптимизации, а за-
ключительная глава содержит обсуждение задач оптими-
зации системы в целом, в данном случае системы с ядер-
ным ракетным двигателем.
Следует сказать несколько слов относительно степени
подробности изложения. В тех случаях, когда метод или
особенности его применения не рассматриваются в обще-
известных работах, этот вопрос излагается детально: так
обстоит дело в особенности в главах I—VII. Если метод
полностью развит в легко доступных литературных ис-
точниках или если он получил достаточно широкое при-
менение к космическим системам? то вопрос освещается
лишь в общих чертах вместе с соответствующими заме-
чаниями о приложении метода к системам рассматривае-
мого класса. Так обстоит дело главным образом в гла-
вах VIII—X. Мы старались избегать строгости в обозна-
чениях ради нее самой, чтобы сделать материал доступ-
ным возможно более широкому кругу читателей, который
может включать инженеров, научных работников и ма-
тематиков-прикладников, чье математическое образова-
ние может не превышать получаемого инженером в те-
чение первого года обучения в аспирантуре.
Беркли, Калифорния.
Джордж Лейтман
ГЛАВА I
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
1.1. НЕОБХОДИМЫЕ УСЛОВИЯ МАКСИМУМА ИЛИ
МИНИМУМА
1.11. Введение. Терминология вариационного исчисле-
ния. Теория обыкновенных максимумов и минимумов
связана с задачей нахождения таких значений независи-
мых переменных хь х2, ... , хп, для которых некоторая
функция этих переменных f(xif х2, ... , хп) достигает
максимума либо минимума (экстремума). Эту задачу
можно истолковать геометрически как задачу нахожде-
ния точки в n-мерном пространстве, в которой исследуе-
мая функция имеет экстремум. Такая геометрическая
интерпретация полезна для понимания, в особенности
когда имеется лишь две независимые переменные.
Иллюстрация такой задачи дается рис. 1.1.
Независимые переменные обозначены через Xi и х2;
зависимая переменная y=f(xb х2) представлена сплош-
ными линиями. Максимум функции находится в точке 4,
в вершине острого гребня, на котором терпят разрыв
производные от у как по так и по х2. Другой, но мень-
ший по величине максимум находится в точке В, которая
расположена «выше», чем все другие точки ее непосред-
ственной окрестности. Наивысшая из всех точек опреде-
ленной области (например точка А на рис. 1.1) назы-
вается абсолютным максимумом; точка, подобная точ-
ке В, т. е. лежащая выше всех точек определенной малой
ее окрестности, называется локальным максимумом.
В точке В производные от у по и х2 равны нулю.
Точка, в которой функция имеет все частные производ-
ные по независимым переменным равными нулю, назы-
вается стационарной точкой. Стационарная точка не обя-
зательно представляет локальный экстремум; это обстоя-
2*
20
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
тельство иллюстрируется точкой С. Точка С является наи-
высшей точкой в «долине» между «возвышенностями»,
расположенными на каждой стороне. В непосредствен-
ной окрестности ее имеются как лежащие ниже (в до-
лине), так и более высоко (в направлениях возвышенно-
стей) расположенные точки. Стационарная точка такого
типа называется седлом.
Минимум функции у не достигается внутри изобра-
женной области, а расположен на ее границе и опреде-
Рис. 1.1. Экстремумы и стационарные
точки.
ляется координатами
Xi = 0;5 и х2 = 0;5.
На границе *2 = 0,
в точке D, находится
локальный минимум;
такой же минимум на-
ходится в точке Е на
границе х2 = 5 и в точ-
ке F на границе *1 = 5.
На границе %i = 0
расположены два ло-
кальных минимума, по
одному на каждом кон-
це интервала определе-
ния функции. Следует
отметить, что «допусти-
мая окрестность» для
определения локально-
го минимума не вклю-
чает точек, расположенных вне области определения
функции. Абсолютный минимум находится сравнением
величин локальных минимумов D, Е, F, G и Н.
Основная задача теории обыкновенных максимумов
и минимумов состоит в определении положения локаль-
ных экстремумов и сравнении их с целью найти абсолют-
ный экстремум. Пример рис. 1.1 показывает, что локаль-
ные экстремумы следует искать в местах разрыва первых
производных, а также вдоль границ (разрыва иного ти-
па). Там, где функция и ее производные непрерывны, ло-
кальный экстремум всегда находится в стационарных точ-
ках, хотя, как это иллюстрируется точкой С, стационар-
ные точки не всегда являются локальными экстремумами.
1.1] НЕОБХОДИМЫЕ УСЛОВИЯ МАКСИМУМА ИЛИ МИНИМУМА 21
1.12. Необходимые условия максимума или минимума.
Существование решения обыкновенной проблемы мини-
мума в случае непрерывной функции устанавливается
теоремой Вейерштрасса. Эта теорема гласит [I]: всякая
функция, непрерывная в замкнутой области, обладает
наибольшим и наименьшим значениями, которые дости-
гаются ею либо внутри области, либо на ее границе.
В задачах вариационного исчисления нет столь общей
теоремы существования, и это обстоятельство в ряде слу-
чаев приводит к затруднениям. Отметим, что условия
теоремы Вейерштрасса не содержат требования непре-
рывности производных, так что ее можно применить к
таким задачам, как пример рис. 1.1.
Расположение экстремума внутри области можно
определить по следующей теореме [2]: непрерывная
функция f(xb х2, ... , хп) от п независимых переменных
хь х2, • • • , хп достигает максимума или минимума
внутри области R только при таких значениях перемен-
ных xit для которых п частных производных
fxV fx2..... fXn одновременно обращаются в нуль
(стационарная точка) либо одна или большее число
таких производных перестают существовать (терпят
разрыв).
Расположение стационарных точек можно найти, ре-
шая систему п алгебраических уравнений, получаемых
приравниванием нулю п частных производных. Вопрос
о том, содержатся ли экстремумы среди этих стационар-
ных точек, будет рассмотрен в следующем разделе.
Теорема Вейерштрасса устанавливает, что экстре-
мумы могут оказаться и на границе области. Если задача
n-мерна, то разыскание экстремума на границе приведет
в общем случае к одной или большему числу обычных
задач на минимум в пространствах п— 1, п — 2, ... , 1
измерений.
Хороший пример такого рода дан Чикала [3]. Им рас-
сматривается трехмерная задача, где функция опреде-
лена внутри куба. Полное решение этой задачи требует
нахождения экстремумов на каждой из 6 граней и на
каждом из 12 ребер и сравнения этих эсктремумов со
значениями функции в 8 вершинах и экстремумами,
находящимися внутри куба. С другой стороны, для
22
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
сферической области требуется лишь определение экстре-
мумов на не имеющей границ сферической поверхности и
внутри сферы. Определение экстремумов на границах, не
являющихся координатными поверхностями, может быть
истолковано как задача с дополнительным условием;
этой задаче посвящен раздел 1.3.
Существование разрывных первых производных вдоль
линий, поверхностей и т. д. также требует решения экс-
тремальных задач в пространстве 1, 2 и т. д. измерений.
Методы раздела 1.3 в данном случае непригодны, по-
скольку большинство из них требует существования всех
частных производных. Во многих случаях оказывается
возможным применить метод подстановок раздела 1.31.
1.2. ДОСТАТОЧНЫЕ УСЛОВИЯ МАКСИМУМА
ИЛИ МИНИМУМА
1.21. Введение. Последняя теорема предыдущего раз-
дела устанавливает, что внутри области экстремум может
находиться либо в стационарной точке, либо в точке, где
одна или большее число частных производных первого
порядка терпят разрыв. Однако стационарные точки и
точки разрыва не обязательно являются экстремаль-
ными. После того, как расположение стационарных точек
или точек разрыва установлено, остается еще ответить
на вопрос о том, содержатся ли среди них экстремаль-
ные точки.
Ответ на этот вопрос может быть дан с помощью не-
скольких методов. Пожалуй, наиболее широко исполь-
зуется метод, состоящий в непосредственном сравнении
значений функции в стационарных точках и точках раз-
рыва со значениями ее в их окрестностях. Несмотря на
свою простоту, этот метод является единственным стро-
гим методом определения абсолютного оптимума и един-
ственным общим методом анализа точек разрыва. Ме-
тоды последнего раздела дают средства установления
всех возможных расположений локальных и абсолютного
экстремумов. Сравнение всех этих точек есть все, что не-
обходимо для строгого определения абсолютного экстре-
мума, даже несмотря на то, что это не укажет, какая из
точек представляет собой локальный экстремум.
1.2] ДОСТАТОЧНЫЕ УСЛОВИЯ МАКСИМУМА ИЛИ МИНИМУМА 23
Практически физическая интерпретация математиче-
ской модели часто приводит к «очевидному» определению
экстремального характера стационарной точки. Для мно-
гих практических задач этот интуитивный результат ока-
зывается достаточным, хотя и мало кто из нас обладает
безошибочной интуицией. Определение значения функции
в нескольких соседних точках часто подкрепляют интуи-
тивные соображения. Следует, однако, иметь в виду, что
исследование многих соседних точек не может считаться
строгим доказательством даже локального характера экс-
тремума. Непонимание этого уже привело в прошлом к
серьезным ошибкам в задачах вариационного исчисления
и может привести к ним в обычных проблемах мини-
мума в случае многих независимых переменных.
Представляется непрактичным находить значение
функции во всевозможных стационарных точках, точках
разрыва и на границах: все, что следует определить, это
то, является данная точка локальным экстремумом или
нет. Во многих задачах определение локальных экстрему-
мов представляет единственную цель. Разделы 1.22 и
1. 23 содержат необходимые условия того, что стационар-
ная точка, вторые производные в которой непрерывны,
представляет локальный экстремум. Необходимые усло-
вия для точек, где первые производные разрывны, рас-
смотрены Хэнкоком [4].
Превосходные примеры детальных доказательств аб-
солютного характера экстремума можно найти у Хор-
нера [5] и Мюника и др. [6].
1.22. Две независимые переменные. Поведение функ-
ции f(xi, х2) в окрестности точки (а, Ь) может быть за-
дано посредством ряда Тейлора:
Ж, х2)=/(а, b)+fx,(a, />)(х, — а)+А(л> b)(x2-b) +
+ J, (а, Ь) (*! — а)2 + 2ДЛ (a, b) — а) (х2 —£) +
+/«(«- *)(х2-*)21+ ••• (1-1)
Если точка (а, Ь) есть стационарная точка функции
f(xb *2), то оба слагаемых первого порядка в этом
разложении равны нулю. Необходимо изучить три сла-
гаемых второго порядка, чтобы определить, является ли
(а, Ь) максимумом, минимумом, седлом и т, д.
24
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
Сумма этих трех слагаемых второго порядка всегда
положительна, то есть (а, Ь) является локальным мини-
мумом, если
/ / J“>o' ) <’-2>
функция достигает локального максимума, если
/Г<0, I (1-3)
fxxxxfx2x2 fxxx2 > 0. J
В исключительных случаях экстремум может иметь
место и тогда, когда неравенство во втором из соотноше-
ний (1.2) и (1.3) становится равенством. Эти случаи
рассмотрены Хэнкоком ([4], стр. 20—69).
1.23. п независимых переменных. Для случая п пе-
ременных соответствующие достаточные условия могут
быть кратко сформулированы с помощью обозначений,
сходных с употребляемыми Лейтманом [7]. Необходимое
условие того, чтобы стационарная точка была локальным
минимумом, имеет вид
А>0 (/=1,2......п). (1.4)
Необходимое условие того, чтобы стационарная точка
была локальным максимумом, таково:
Dz>0 (/ = 2, 4, 6, ...), |
Dz<0 (/ = 1, 3, 5, ...), J
где
Частным случаем этого уравнения является хорошо
известное условие максимума или минимума функции от
одной независимой переменной:
fxtxi 0.
1.3] ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ 25
1.3. ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ
1.31. Решение путем подстановки. Если и переменных
хь х2, ... , хп подчинены т дополнительным условиям
gi (хр Х2, ..., Хп) = 0,
g2(x„ х2, хл) = 0, б)
^(Хр х2, х„) =0,.
то число независимых переменных сокращается до и — т.
Коль скоро п больше, чем т, имеется одна или более не-
зависимых переменных, по отношению к которым можно
разыскивать экстремум функции y = f(xit х2, ... , хп)
при т дополнительных условиях (связях) gi = 0, g2=
= 0, ... , gm = 0.
Наиболее очевидный метод решения этой задачи со-
стоит в разрешении т уравнений связей относительно
т из п переменных. Подстановка полученных таким спо-
собом т равенств в уравнение y = f (хь х2, ... , хп) приво-
дит к новой экстремальной задаче для функции у =
=f(*i, х2, , хп-т) от и — т переменных.
Этот метод подстановки часто оказывается неудовлет-
ворительным, так как tn уравнений связей не всегда мо-
гут быть решены относительно т переменных либо по-
тому, что эти решения становятся слишком сложными.
В простых задачах подстановка может оказаться про-
стейшим методом решения, поскольку это единственный
способ, который уменьшает число переменных.
Как простой пример применения подстановок для
решения задач с дополнительными условиями рассмот-
рим задачу определения экстремумов внутри кубической
области (раздел 1. 12). Кубическую область определим
плоскостями Xi = a, 6, х2 = а, b и х3 = а, Ьл Экстремумы на
6 гранях куба находятся путем решения 6 двумерных за-
дач, получаемых путем последовательной замены коорди-
нат хь х2 и х3 в f(xb х2, х3) на а и Ь. Экстремумы на
12 ребрах куба находятся путем решения 12 одномерных
задач, получаемых в результате замены пар хь х2; хь х3;
х2, х3 соответственно парами а, а; а, b\ b, а\ b, b ... Экс-
тремумы внутри области, на гранях и на ребрах сле-
дует сравнить со значениями функции в 8 вершинах.
26
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
1.32. Решение при связанных вариациях. В отсутствие
уравнений связей gu g2, ... , gm местоположение стацио-
нарных точек находится путем решения уравнений
Д=0, Д-0, .... Д-0. (1.7)
Одновременное обращение в нуль всех частных про-
изводных первого порядка означает, что полный диффе-
ренциал функции также обращается в нуль для любого
бесконечно малого приращения п переменных:
^=^7^ + ^;^+ + = <г8>
Если вводятся т уравнений связей, то уравнение
(1.8) останется в силе, но бесконечно малые приращения
п переменных х2, ... , хп не будут более независи-
мыми. Эти п бесконечно малых приращений будут под-
чинены т связям, которые найдем, дифференцируя урав-
нения (1.6):
••• +Й^=°-
(1-9)
Уравнения (1.8) и (1.9) образуют в совокупности
/и+1 линейных однородных уравнений относительно п
бесконечно малых приращений dxi для любой точки в
n-мерном пространстве. Стационарная точка будет та-
кой, что в ней уравнения (1.8) и (1.9) останутся спра-
ведливыми для бесконечно малых приращений любого
из п — т независимых переменных. В такой точке долж-
ны обращаться в нуль соответствующие определители
Якоби, по одному для каждого из п — т независимых
переменных:
j( •••’ Sm \___Q
\ Xlt Х2, Хз, ...» Хт, Хт j )
j( f> ffi> £2» •..> gm-\> gm
\ Xit X2, X3....Xm, Xm + 2 )
(1-10)
/> gi> g2> »•-> gm-i> gm
X\t X2, X3t ..., Xm, Xfi
j=°,
1.3]
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ
27
где
^Х, дХ, д\,
dtx dt2 dtn
х„\ _ д\2 дХ2
#1 dtn
д^п
dti dtn
Существует простая геометрическая интерпретация
уравнений (1. 10), по крайней мере в случае трех изме-
рений.
На рис. 1.2 максимум функции y = f(xit х2) при до-
полнительном условии g(x\, х2)=0 располагается в точ-
ке А. В этой точке наклон dx2)dx\ кривой f = const равен
наклону dx2jdxx кривой
£(%i, х2)=0. Для кривой
7(хь х2) = const имеем
dx2 _ dfjdxx п 1П
dxx~ dfldx2' ^,11;
тогда как для кривой
^(xi,x2)=0
= (1.12)
dxx dg/dx2 v '
Сравнивая эти уравне-
ния, получим
df/dxx _ dg/dxx
<Z7
Рис. 1.2. Экстремум при наличии
дополнительного условия.
df/dx2 dg/dx2 *
df_ dg_____df dg
dxx dx2 dx2 dxx
(1-13)
Уравнение (1.13) в точности совпадает с соотноше-
нием (1. 10), написанным для этого случая.
Метод этого раздела не часто употребляется на прак-
тике: как правило, предпочтение отдается методу множи-
телей Лагранжа, излагаемому в следующем разделе. Оба
метода теоретически тесно связаны, но на практике урав-
нения, доставляемые методом лагранжевых множителей,
обычно проще для вывода и решения. Определители
28
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
Якоби приводят к весьма компактным обозначениям;
преимущества, даваемые этим обстоятельством, были ис-
пользованы Миеле [8].
1.33 Множители Лагранжа. Рис. 1.2. иллюстрирует
задачу нахождения экстремума функции f(x\, х2) при на-
личии дополнительного условия
g(xv х2) = 0. (1.14)
В разделе 1.32 было выведено необходимое условие
стационарности в точке A (1. 13):
df dg df dg
dX] дх2 dx2 dxi
Можно переписать уравнение (1. 13) следующим об-
разом: dffdxx _ df/dx2 л .rv dg/dxi dg/dx2 ’
где X — постоянная, которую будем называть множите-
лем Лагранжа. Другая форма уравнений (1. 15) такова:
<+<=»• jv+)i4l=0 (L16) dx2 ’ dx2
В уравнениях (1. 16) можно узнать необходимые ус-
ловия стационарности функции f+kg без дополнительных
условий. Необходимые условия стационарности функции
f(xu х2) с дополнительным условием g(xit х2)=0 нахо-
дятся путем составления расширенной функции f+kg и
рассмотрения задачи как задачи без дополнительных ус-
ловий. Решение трех уравнений (1.14) и (1.16) относи-
тельно трех переменных х2 и Z эквивалентно решению
двух уравнений (1. 14) и (1. 13) относительно двух пере-
менных Х\ и х2.
Этот результат легко распространяется на общий слу-
чай. Действительно, уравнения (1. 10) предшествующего
раздела устанавливают существование системы постоян-
ных (лагранжевых множителей) Х2, ... , таких,
что каждый элемент первой строки всякого определителя
1.3]
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ
29
Якоби может быть представлен в виде линейной нации элементов соответствующего столбца [3]: ... +Xm-^-=0, dxi 1 1 dxi 1 2 дх{ 1 1 m dx{ ’ ••• +Xm-^-=0. dx2 1 1 dx2 1 dx2 1 1 m dx2 ’ комби- (1-17)
dxn 1 1 dxn ^2 I 1 X ^Sm n dxn 1 • ’ • + Krn dXn — °-
Уравнения (1.17) представляют необходимые условия
существования стационарных точек функции f+M£i +
+ МГ2+ ... +^тёт- Использование вспомогательной
функции позволяет заменить задачу с дополнительными
условиями задачей без дополнительных условий. К этой
новой задаче приложимы все методы, употребляемые для
решения задач' без дополнительных условий, включая
достаточные условия раздела 1.2. Как и для обычных
функций, разрывы первых производных расширенной
функции должны быть изучены из-за возможного нали-
чия экстремумов, в особенности по той причине, что ме-
тод множителей Лагранжа отказывается служить в мес-
тах расположения подобных разрывов.
Недостатком метода множителей Лагранжа является
введение их как т дополнительных переменных, которые
должны быть исключены с помощью т Дополнительных
условий £1 = 0, £2 = 0, ... , £т=0. Однако уравнения
(1. 17), содержащие лагранжевы множители, обычно на-
столько проще соответствующих уравнений (1. 10) преды-
дущего раздела, что определение решения оказывается
более простым и быстрым. Метод множителей Лагранжа
особенно удобен в том часто встречающемся случае,
когда £ зависит от постоянной с, а также от п перемен-
ных Xi. В этом последнем случае можно найти решение
для ряда значений с, придавая последовательные значе-
ния соответствующему множителю Лагранжа.
1.34. Функции нагружения. Метод, заключающийся
в применении функций нагружения, не получил еще ши-
рокого распространения, но интерес к нему постоянно
возрастает. В главе VI будет описано его приложение
к методам градиентов. Примеры использования функций
30
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
нагружения при доказательстве теорем вариационного
исчисления даются Мозером в приложении к книге Ку-
ранта [9].
Идея функции нагружения весьма проста. Пусть разы-
скивается минимум функции f(xb х2) при дополнитель-
ном условии g(*i, х2)=0. Образуем новую функцию
Л(*1> =f(xv x2)+h (х„ х2)]2. (1.18)
Эта функция минимизируется теперь без дополнитель-
ных условий для последовательности возрастающих боль-
ших значений h. В книге Куранта [9] доказано, что при
стремлении h к бесконечности решение этой задачи при-
ближается к решению первоначальной задачи со связью.
Существует несколько очевидных видоизменений этой
основной идеи. Одно из них заключается в том, что функ-
ция fh берется в следующей форме:
А=/+§2Л- (1-19)
В настоящее время функции нагружения представ-
ляют наибольшие удобства для численных решений, но
чтобы определить их действительную выгоду, потребуется
дополнительный опыт.
1.4. ПРИЛОЖЕНИЕ К ИНТЕГРАЛАМ
1.41. Связь между теорией обыкновенных максиму-
мов и минимумов и вариационным исчислением. Суще-
ствует ряд практически важных задач, которые могут
быть решены, если использовать теорию обыкновенных
максимумов и минимумов для оптимизации интегралов, а
не функций. Поскольку обычно считается, что оптими-
зация интегралов относится к области вариационного ис-
числения, необходимо рассмотреть взаимосвязи, суще-
ствующие между вариационным исчислением и теорией
обыкновенных максимумов и минимумов.
Классическое различие между этими двумя областями
анализа просто и ясно. Теория обыкновенных максиму-
мов и минимумов имеет дело с нахождением каждой из
и независимых переменных х2, ... , хп, для которых
функция f (хь х2, ... , хп) этих п переменных имеет экс-
тремум. Вариационное исчисление представляет обобще-
1.4]
ПРИЛОЖЕНИЕ К ИНТЕГРАЛАМ
31
ние этой элементарной теории и связано с нахождением
экстремума величины, которая зависит от п независимых
функций Xi(/), х2(/), ... , xn(t). Поскольку эта величина
зависит от значений п функций, а не от значений п дис-
кретных переменных, постольку она является обобще-
нием понятия функции и носит название функционала.
Классическим примером функционала является следую-
щий интеграл (в котором f — заданная функция):
7 = ff(x, dxldt, t)dt. (1.20)
Оптимизация этого интеграла требует определения
такой функции х(/), которая доставляет значению инте-
грала максимум или минимум. Более общая задача,
требующая отыскания п функций хг(/), относится к
интегралу
h
l = f.........................................(1-21)
Л
Геометрическая интерпретация задач теории обыкно-
венных максимумов и минимумов состоит в определении
точки в п-мерном пространстве, образуемом п независи-
мыми переменными х2,..., хп, в которой функция
этих п переменных имеет максимум. Собтветствующая
геометрическая интерпретация задач вариационного ис-
числения состоит в разыскании кривой, определяемой п
параметрическими уравнениями Xi(/)=xb х2(/)=х2, ...
...» хп(0=^п, которая доставляет максимум функцио-
налу от п функций *1(0, х2(/),..., хп(/). Эта кривая
может считаться расположенной либо в /^-мерном про-
странстве координат Xi, х2, ... , хп, либо в (и+1)-мер-
ном пространстве /, х2, ... , хп.
Типичной проблемой теории обыкновенных максиму-
мов и минимумов могла бы служить задача определения
величины силы тяги и веса топлива в каждой ступени
многоступенчатого космического летательного аппарата,
который должен для достижения определенной цели
нести максимальную полезную нагрузку. Типичной зада-
чей вариационного исчисления было бы определение
32
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
оптимальной по минимуму потребляемого топлива траек-
тории летательного аппарата, выполняющего определен-
ную задачу. Классическое различие между обоими типами
задач заключается в том, что оптимизируемая величина
зависит в одном случае от значений переменных, а в дру-
гом — от функций этих переменных.
Практически важный частный случай уравнения
(1.21) соответствует отсутствию производных в подын-
тегральной функции:
1 = J/(хр х2, x/z, t)dt. (1.22)
В этом случае уравнения Эйлера вариационного ис-
числения (см. гл. IV) сводятся к следующим:
#=о, -^-=о,4^ = о. (1.23)
дх} ’ дх2 дхп v 7
Эти уравнения формально совпадают с необходимыми
условиями минимума подынтегральной функции при ка-
ждом значении t. Поскольку f зависит от /, уравнения
(1.23) представляют решения последовательности обыч-
ных проблем минимума для каждого значения / от Л до
/2. Действительно, решения уравнений (1.23) определяют
последовательность функций Xi(/), *2(0» • •• , *п(0, об-
разующую’ решение исходной вариационной задачи
(1.22).
То обстоятельство, что решение вариационной задачи
может трактоваться как решение непрерывной последова-
тельности обыкновенных проблем минимума, представ-
ляет собой серьезное упрощение. Более общая задача
(1.21) требует решения п совокупных обыкновенных
дифференциальных уравнений, которые обычно нели-
нейны и трудно поддаются аналитическому (или даже
численному) решению. Уравнения (1.23), с другой сто-
роны, образуют систему п алгебраических уравнений, ко-
торые, хотя зачастую и нелинейны, значительно легче
для решения, чем дифференциальные уравнения.
Можно убедиться в том, что простая форма уравнений
(1.23) объясняется отсутствием производных в инте-
грале (1.22). Если бы какие-нибудь производные по t
1.4]
приложение к интегралам
33
входили в подынтегральную функцию (1.22), то значе-
ние f при любом t зависело бы от значений f при близ-
ких t. Поскольку производные отсутствуют, значение f
при любом t может быть оптимизировано безотноситель-
но к значениям f в соседних точках. Подынтегральная
функция f может даже быть разрывной. Такая полная
независимость от значений f в соседних точках позволяет
рассматривать задачу как непрерывную последователь-
ность обыкновенных проблем минимума и приводит к
уравнениям (1.23). Приведенную аргументацию следует
признать не очень строгой, поскольку она не включает
в себя предельных переходов, но уравнения (1.23) ста-
новятся при этом, по-видимому, более понятными.
Согласно сказанному в этом разделе, если производ-
ные в. подынтегральной функции вариационной задачи
стремятся к нулю, то решение ее, вообще говоря, прибли-
жается к решению обычной проблемы минимума. Ряд
примеров такого рода дан Миеле [10].
1.42. Связь между теорией обыкновенных максимумов
и минимумов и линейными вариационными задачами.
В предыдущем разделе рассмотрен частный случай об-
щей вариационной задачи, когда необходимые условия
стационарности приобретают вид системы алгебраических
уравнений вместо системы дифференциальных уравнений.
На стр. 30 книги Куранта [9] дан ответ на. вопрос о том,
имеются ли какие-либо другие частные случаи, приводя-
щие к алгебраическим уравнениям; это сделано для
относительно простой задачи, представляемой уравне-
нием (1.20). Все частные случаи, в которых получаются
алгебраические уравнения, охватываются уравнением
7 = У7(х, /, = t)+A(x, t)^\dt. (1.24)
Л *х
В случае, рассмотренном в разделах 1.41 и 1.43,
равно нулю. Случай, когда f2 отлично от нуля, рассмот-
рен Миеле в главе III настоящей книги. Миеле рассмат-
ривает эту задачу с помощью мощного метода, позво-
ляющего сформулировать, наряду с необходимыми,
достаточные условия и позволяющего учесть разнообраз-
ные граничные условия. Способ Миеле можно также
3 Дж. Лейгман
24
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
использовать в более простых задачах, рассмотренных в
разделах 1.41 и 1.43, и получить для них достаточные
условия.
1.43. Интегральные задачи с дополнительными усло-
виями. Достаточно общая интегральная задача с допол-
нительными условиями, которая может быть сведена к
последовательности обыкновенных проблем минимума,
состоит в нахождении максимума интеграла
6
/ = ff(xv х2, ..., x,t, f)dt (1.25)
при одном или более дополнительных условиях, имею-
щих форму
t2
Ji — f •••> xn> t)dt = const. (1.26)
6
Решение этой задачи заключается в составлении но-
вого интеграла
6
= J [/++ ••• -\~\ngm\dt, (1.27)
6
где Хг- — постоянные множители Лагранжа. Оптимизация
интеграла (1.27) как последовательности обыкновенных
проблем минимума для каждого значения t от tx до 6
решает задачу; необходимыми условиями стационарности
являются
1/4~ ^1^1 ~F W2+ ••• _
dxi
О (1.28)
для каждого х^ и всех значений / от t\ до /2.
Для оправдания этого подхода требуется взаимная
независимость п переменных хг-. Если имеются какие-
либо дополнительные условия вида
0{х,.х* .... .... = (1-29)
1.5] ЗАМЕЧАНИЯ О ПРАКТИЧЕСКОМ ПРИМЕНЕНИИ 35
то задачу следует решать общими методами вариацион-
ного исчисления. Если дополнительное условие прини-
мает форму
xi — f f(*2, хз* • • •» хп> t)dt, (1.30)
так что одна из переменных есть функционал от дру-
гих, то, вообще говоря, следует применить методику
главы III. Раздел 1.63 содержит пример, в котором за-
дача этого типа преобразуется в задачу с дополнитель-
ным условием в форме (1.26).
1.5. ЗАМЕЧАНИЯ О ПРАКТИЧЕСКОМ ПРИМЕНЕНИИ
1.51. Прямые и непрямые методы. Методы, описывае-
мые в этой главе, образуют классический непрямой спо-
соб разыскания обыкновенных максимума и минимума.
Непрямым считается метод, в котором минимум разыски-
вается с помощью необходимого условия минимума. Пря-
мой метод, с другой стороны, связан с непосредственным
сравнением значений функции в двух или более точках.
Для решения обыкновенных проблем минимума (и ва-
риационного исчисления) с помощью прямых методов
был разработан ряд регулярных численных процессов.
Интересным примером таких процессов служит процесс
Фибоначчи [11]: он является наилучшим методом реше-
ния проблемы оптимизации с одной независимой пере-
менной. В случае, когда имеется много независимых
переменных, быстрый и эффективный путь получения
численного решения дается методом градиентов (гл. VI
настоящей книги), известным также под названием ме-
тода наискорейшего спуска.
Когда разыскивается аналитическое решение, упот-
ребляются обычно непрямые методы, рассмотренные в
этой главе. При отыскании численного решения зачастую
предпочтительнее прямые методы. Поясним это простым
примером. Рассмотрим задачу отыскания минимума
функции одной независимой переменной
у = /(х) = min.
(1-31)
3*
36
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
Прямая задача состоит в нахождении значения х, при
котором у имеет минимум. Непрямая задача заклю-
чается в разыскании значения х, для которого обра-
щается в нуль производная у по х\
dyidx=f'(x) = Q. (1.32)
Численное решение прямой задачи (1.31) фактически
не труднее, чем численное решение непрямой задачи
(1.32), и имеет два преимущества. Первое состоит
в том, что прямое решение легко справляется с разры-
вами, конечными точками интервала и точками перегиба.
При непрямом решении приходится по отдельности рас-
сматривать разрывы и конечные точки и нельзя разли-
чить максимумы, минимумы и точки перегиба (например,
для функции у = х3 при х = 0), поскольку все они удовле-
творяют уравнению (1.32). Второе преимущество прямого
метода заключается в том, что поведение функции в ок-
рестности минимума можно определить по точкам, уже
исследованным в процессе нахождения минимума. Если
пользуются непрямым методом, то это поведение должно
определяться ценой дополнительных вычислений.
Непрямой путь обладает одним существенным пре-
имуществом даже при использовании численных методов.
Если разыскивается точное значение х, при котором у
имеет минимум, то, вообще говоря, это значение может
быть получено из уравнения (1. 32) с большей точностью,
чем из уравнения (1.31). Это справедливо, коль скоро
минимум есть стационарная точка, поскольку, согласно
определению, изменение х, соответствующее заметному
изменению у, будет по порядку величины больше, чем из-
менение у. Пример применения непрямого метода для
определения точного значения независимой переменной
для частной задачи, решенной прямым методом, приведен
Карстенсом и Эдельбаумом [12]. Если, как оказывается
во многих прикладных задачах, разыскивается лишь ве-
личина минимума, а не точное значение независимой
переменной, то употребление непрямых численных мето-
дов в.\общем случае не доставляет преимуществ.
В ’задачах, где имеется более одной независимой пере-
менной, преимущества прямого метода численного реше-
ния возрастают. В этом случае решение по прямому ме-
1.5]
ЗАМЕЧАНИЯ О ПРАКТИЧЕСКОМ ПРИМЕНЕНИИ
37
тоду требует рассмотрения одного уравнения в п-мерном
пространстве:
у = f(xx, х2, ..., xfl) = min, (1.33)
тогда как непрямой метод требует решения системы п
уравнений в /i-мерном пространстве:
dxt ~ fxXXV Х2' • • rfxj ~Л2(Л1’ Х2' • • х„) = 0, •• о=°- (1-34)
~dxn=f*ltX'' Х2’ • • • , Х„) = О.
В некоторых случаях может быть получено частичное
аналитическое решение п уравнений (1.34), так что не-
которые переменные могут быть исключены. В этом по-
следнем случае численное решение непрямой задачи
может оказаться проще, чем такое же решение пря-
мой. В следующем разделе будет приведен пример
такого рода.
1.52. Аналитические и численные методы. Исследова-
телю, занимающемуся отысканием оптимальных решений
различных задач, следует владеть как аналитическими,
так и численными методами. К сожалению, однако, мы
склонны употреблять тот или иной метод лишь потому,
что в прошлом он оказывался наиболее удачным. Это
привело к использованию численных методов в задачах,
решавшихся ранее аналитически [13, 14], и к сложным
аналитическим выкладкам в задачах, лучше всего решае-
мых численно [15].
Аналитические решения, если можно их получить,
обычно желательны, но с условием, что они не столь
сложны, чтобы численные расчеты, нужные для прак-
тики, требовали большого труда. Большим преимуще-
ством аналитических решений является то, что они обыч-
но разрешают целую группу задач, а не одну задачу.
Например, решение задачи раздела 1.6 может служить
для расчета перелета между любыми двумя круговыми
орбитами (произвольного радиуса и наклона) и при
любых значениях удельного веса силовых установок.
38
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
Численное же решение потребовало бы отдельного рас-
чета в каждом из частных случаев.
Численные методы, со своей стороны, также обладают
некоторыми преимуществами. Начать с того, что они мо-
гут быть применены и применяются для решения задач,
которые не могут быть решены аналитически. Другое
преимущество численных методов — их гибкость. Анали-
тическое решение способно осветить все аспекты задачи.
Численный метод, с другой стороны, может дать сред-
ства для решения любого вопроса из большого класса
совершенно различных задач. Например, такой метод,
как метод наискорейшего спуска, может быть использо-
ван в качестве программы вычислительного устройства,
так что будет возможно подвергать его воздействию лю-
бую подаваемую на вход функцию. В том, что касается
вычислительного устройства, всякая функция не хуже
любой другой, независимо от того, допускает задача ана-
литическое решение или нет. Разумеется, некоторые за-
дачи потребуют значительно больше времени, нежели
другие, в особенности если они включают много неза-
висимых переменных. Принципиально численным мето-
дам доступно решение почти любой задачи оптимизации.
Часто оказывается желательным использовать комби-
нацию аналитических и численных методов. В предыду-
щем разделе был упомянут пример Карстенса и Эдель-
баума [12]. Другой пример дается. задачей оптимального
проектирования ступеней ракеты [16]. Эта задача состоит
в минимизации общего веса n-ступенчатой ракеты путем
определения той доли, которую вносит каждая ступень
в общее увеличение скорости ракеты. Это пример задачи,
которая может быть решена аналитически непрямыми ме-
тодами. Решение содержит один неизвестный параметр,
который можно найти численными методами. Определе-
ние этого единственного параметра может оказаться зна-
чительно более простым, чем оптимизация п первоначаль-
ных параметров. Однако если имеются лишь две ступени,
то для любого данного увеличения скорости останется
оптимизировать лишь один параметр. В этом случае чис-
ленное решение прямой задачи будет столь же простым,
как и численное решение непрямой, и доставит другую,
возможно, более полезную информацию. Численное ре-
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
39
шение прямой задачи определит общий вес для последо-
вательности вариантов, обладающих заданным увеличе-
нием скорости, и покажет чувствительность общего веса
к изменению числа ступеней. Численное решение непря-
мой задачи определит минимальный общий вес для по-
следовательности увеличений скорости, включая и тре-
буемое. Если представляет интерес ряд оптимальных ва-
риантов для различных увеличений скорости, то следует
использовать непрямой метод решения задачи.
1.6. ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ ЛЕТАТЕЛЬНЫХ
АППАРАТОВ МАЛОЙ ТЯГИ И ДВИГАТЕЛЬНЫХ СИСТЕМ
24-ЧАСОВОГО ЭКВАТОРИАЛЬНОГО СПУТНИКА
1.61. Введение. Был предложен ряд применений для
спутника, находящегося на экваториальной орбите и
имеющего период вращения, в точности равный периоду
вращения Земли. Такой спутник вращался бы вместе
с Землей и был бы виден в небе покоящимся. Его ор-
бита имеет радиус, составляющий около 6,61 земного ра-
диуса, что соответствует высоте 22 240 уставных миль.
Одним из наиболее перспективных средств достиже-
ния такой орбиты является ионный двигатель. Ионный
двигатель позволяет транспортировать большие грузы
ценой длительного полетного времени, которое тем боль-
ше, чем больше груз. Характеристики ионных двигатель-
ных систем рассматривались рядом авторов [17—19]. Де-
тальный анализ траекторий летательных аппаратов с та-
кими двигателями с точки зрения вариационного исчисле-
ния можно найти в главе V.
Тяга ионного двигателя значительно меньше, чем его
вес, так что первоначально аппарат должен быть поме-
щен на орбиту за пределами земной атмосферы. Предпо*
ложим, что имеется двигатель, способный доставить опре-
деленный вес на круговую орбиту, расположенную на не-
большой высоте и проходящую над местом запуска. Рас-
сматривается задача максимизации веса полезного груза,
который может перенести аппарат с заданным начальным
весом на 24-часовую экваториальную орбиту в заданное
время. Поскольку точка запуска в общем случае не рас-
полагается на экваторе, необходимо будет изменять как
40
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
радиус орбиты, так и ее наклон к экваториальной плос-
кости.
Предполагается, что первоначальная масса аппарата
складывается из масс ионной двигательной системы, топ-
лива и полезного груза:
Мо = Mw + мр + ML. (1.35)
Масса двигателя предполагается пропорциональной
развиваемой мощности; эта мощность равна половине
произведения силы тяги и скорости истечения:
Mw = aW=aTVx/2. (1.36)
Скорость расхода топлива пропорциональна тяге и
обратно пропорциональна скорости истечения:
dMp/dt = T/Vx. (1.37)
Примем, что тяга может изменяться при постоянной
мощности, так что скорость расхода топлива будет про-
порциональна квадрату тяги:
dMp
dt
iM а Т2 а / Г \2
аГ2 = \М) /И2, <1,38)
а
Конечная масса аппарата может быть определена [19]
путем интегрирования уравнения (1.38):
_ dM
М2
1
Л!,
Л4() 244^ J
(1.39)
Мо
Л11
а
2 J
Наибольший вес полезного груза будет достигнут пу-
тем минимизации расхода топлива для любых заданных
величин мощности и времени полета с последующим оп-
ределением оптимальной мощности, требующейся для
всякого полетного времени. Расход топлива будет минит
мизироваться путем нахождения оптимального направ-
ления и величины вектора тяги как функции времени.
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
41
1.62. Оптимизация траектории при малых изменениях
орбитальных элементов. Ионные двигательные системы
обычно обеспечивают очень малое ускорение летатель-
ного аппарата, так что типичными оказываются вели-
чины порядка одной десятитысячной ускорения силы тя-
жести. Столь малые ускорения позволяют существенно
упростить исследования. Изменения элементов орбиты
за один оборот могут быть определены с помощью ме-
тода возмущений, после чего изменения за много оборо-
тов могут быть вычислены суммированием малых измене-
ний. Таким образом, задача оптимизации траекторий мо-
жет быть разделена на две части, первая из которых бу-
дет рассмотрена в настоящем разделе.
Чтобы достичь 24-часовой орбиты, необходимо изме-
нить как радиус, так и наклон первоначальной круго-
вой орбиты. Предполагается, что промежуточная орбита
должна оставаться почти круговой и не обращаться в эл-
липтическую. Проведенный недавно анализ показал, что
это предположение правильно для 24-часового варианта,
но очень большие изменения наклона должны будут
привести к промежуточным эллиптическим орбитам.
Уравнения для малых изменений этих элементов даются
в виде
dR 2 Т 0
~R = V ATC0S₽C0ST dt,
1 т
dt= JF ~М sin Р C0S 9
(1.40)
(обозначения см. в конце главы).
Чтобы найти изменения величин за один оборот, вве-
дем в качестве независимой переменной полярный коор-
динатный угол 9. Поскольку радиус орбиты не изменится
сильно за время любого оборота, этот угол можно счи-
тать пропорциональным времени:
Д/? 4R Г Т 0 ,0
= м cos₽COSTCO,
о
к
М=--~ f 7 Sin рcos 9 rf0.
о
(1-41)
42
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
Уравнение (1.39) можно также написать, взяв 0 за
независимую переменную, в форме
Мо
Мр aR
Mw V J
w о
(1-42)
Поскольку в подынтегральную функцию не входят
производные по независимой переменной 0 и поскольку
ни одна из переменных в подынтегральных функциях не
зависит от величины любого из интегралов, мы имеем
вырожденную задачу, которая может быть решена с по-
мощью теории обыкновенных максимумов и минимумов
(раздел 1.43). Если бы были допустимы большие изме-
нения величины R, то как радиус, так и скорость меня-
лись бы и следовало бы обратиться к другому методу
анализа.
Сформулируем теперь задачу, комбинируя уравнения
(1.41) и (1.42) с помощью множителей Лагранжа:
др т op Т 1
— Х1 -рт AfCospcosT—^sinpcosOlrfO. (1.43)
. Оптимальные значения величин у, 0 и Т/М находятся
дифференцированием подынтегральной функции в (1.43)
по этим трем переменным и приравниванием результатов
нулю:
ч 4R Т о . п
д, cos?sin7 = О,
4Р у* 2Р Т
Х1 -^Msin₽cosT~-у cos?cos9 = 0,
(1-44)
Мо 2aR Г \ 4R Q . 2R . 0 Q п
V М V2 cos Р cos 7 X2V-2sinpcos9 — 0.
1.6J
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
43
Решение этой системы трех уравнений дает следую-
щие оптимальные значения переменных:
sin 7 = 0,
^Р = ^ГС08 0’
Т __ 2\ 1/ 1 I / Х2 V
М — V aMQ у 1
cos2 9.
(1.45)
Подстановка этих оптимальных значений в уравне-
ния (1.41) и (1.42) и последующее интегрирование
Дают изменение параметров за один оборот:
ДЯ _ вт^Я Mw
~R~ ~ V3 ’
ду_
* ~ V3 аМ0 ’
^1x1^
V3 аМс
(1.46)
TH,
Переменные в уравнениях (1.46) можно заменить
другими, более важными физически. Это можно сделать
путем вычисления значения MQjM\ при постоянном в те-
чение оборота значении^ Т/М, рассматривая это последнее
как среднее значение Т/Л4. Множители Лагранжа могут
быть исключены приравниванием правой части послед-
него уравнения (1.46) выражению, получающемуся для
нее при постоянном Т/М\
aR / Т \2 R Mw
1 + к Mw V (. М I ~ 1 + * V3 аМ0
Введем новую переменную k:
cos k —
2Х,
sin k =
2
4^1 + ^1/2
(1-47)
(1-48)
44
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
(гл. 1
Подстановка выражений (1.47) и (1.48) в уравнения
(1.46) приводит окончательно к уравнениям
bR 4kR Т ,
~R~ “ “Й2" ЛГ cos k'
А. V <2 nR Т . .
--- у-2 Д4 sin
(1.49)
_Мо _ 1 . «Л40 Я / 7\2
м, —1 + V I М } *
Интересным свойством уравнений (1.49) является
то, что они проще, чем соответствующие уравнения для
случая, когда Т/М поддерживается постоянным, а не про-
граммируется [20]. В этом последнем случае связь между
изменениями радиуса и наклона дается эллиптическими
интегралами, а не тригонометрическими функциями.
1.63. Оптимизация траектории при больших измене-
ниях орбитальных элементов. Оптимизация траектории
для больших изменений наклона и радиуса будет произ-
ведена путем суммирования большого числа изменений,
найденных в предыдущем разделе. Будем предполагать,
что уравнения (1.49) справедливы для каждого оборота,
но будем записывать их в дифференциальной форме, счи-
тая время независимой переменной:
dR 2 т
R — V М
к
у 2 f
di = sin k di.
(1.50)
dM_ — мо / Г \2 ,
М2 — 2 Mw ' М / at‘
Поскольку скорость фигурирует в первом и втором
из этих уравнений, первое из них будет переписано со
скоростью в качестве новой переменной. Эта замена пере-
менной допустима благодаря единственному соотноше-
нию между радиусом и скоростью для круговых орбит
dV =----2" “7г ~~~м Q®skdt. (1.51)
Если бы задача была сформулирована со временем
в качестве независимой переменной, то было бы необхо-
димо обосновать то обстоятельство, что скорость V во
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
45
втором из уравнений (1.50) подчинена уравнению (1.51).
Это привело бы к задаче вариационного исчисления,
хотя и к вырожденной линейной задаче (см. главу 111
настоящей книги). Рассматриваемую проблему можно
привести к задаче обыкновенных максимума и минимума
заменой независимой переменной t на независимую пере-
менную V. С помощью этой новой независимой перемен-
ной задача формулируется через функционал
1+ f Г-— - — + (1.52)
’ 2 М 3 Т/М 2V '
Vq L "
Эта новая задача, которую можно толковать как за-
дачу максимизации полного веса при заданном измене-
нии скорости за определенное время с определенным
изменением наклона, полностью эквивалентна первона-
чальной, где время представляет независимую перемен-
ную. Перед нами пример свойства взаимности изопери-
метрических задач ([1], стр. 243).
Поскольку в уравнении (1.52) не содержатся произ-
водные и в интегралы не входят переменные, за исклю-
чением управляемых переменных Т/М и k и независи-
мой переменной V, мы имеем задачу, которая может
быть решена с помощью теории обыкновенных максиму-
мов и минимумов при постоянных множителях Лагран-
жа. Оптимальные значения Т/М и k находятся, как в
предыдущем разделе, приравниванием нулю производ-
ных подынтегральных функций:
Л40 а . Х3sec k
—5— sec k----L----=
Mw 2 (T/M)* 2
a. T tg£scc£ I Аз^*8ес* *4/2 sec2* =
2 M g T/M 2V
0,
(1.53)
Разрешая эти уравнения относительно оптимальных
значений Т/М и k, находим:
т Г<im.v ч
~тт = I/ - .5 X, — const,
М V аА40 3
Sin А--- 1 ^osln*o
2(MJMW)(T/M)z V ’ V
(1.54)
46
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. i
Окончательное решение, задачи находится интегриро-
ванием уравнений, в которых регулируемые переменные
имеют эти оптимальные значения. Это интегрирование
требует известной осторожности, так как независимая
переменная V может быть двузначной. Интуитивное
представление о том, что большие изменения наклона
могут потребовать от скорости убывания вначале и ро-
ста впоследствии, позволяет написать уравнения:
Л*о _ 1 at / Т \2
2 (м) 9
_ vo cos *вт /(T/Al) t \
71м k Va >С05Л°Л
. V 2 . Ио sin Ло К2. l(T/M)t ,
f arcsin ° и ° — -- < cos ,
__ 197 98°_arcsin sln k
i — izz ,zo-2 di сын ^7------2
(^>-4
(1.55)
Последние два уравнения могут быть переписаны в
безразмерной форме со временем в качестве независи-
мой переменной:
•К 2 . sin kQ
i = Чу- arcsin —r -
cos£0
(1.56)
/=127,28° —
\ Vo
l (T/M)t
\ Vo
COS kQ
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
47
Уравнения (1.56) иллюстрируются рис. 1.3, где по
оси ординат отложены значения /, а по оси абсцисс —
значения V/Vo. Требуемые для перехода с одной круго-
140 г
Рис. 1.3. Оптимальные характеристики полета при переходе
между круговыми орбитами различных радиусов, плоскости
которых наклонены одна к другой.
вой орбиты на другую величины (TlM)tlVQ могут быть
сняты с графика. Геометрическое место орбит с одним
и тем же временем и расходом топлива представлено
48
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. I
линиями постоянных значений (T/M)//Vo. Величина ki}
определяет точку на каждой такой кривой, достижимую
с помощью данной траектории. Линии постоянных й0
представляют (в плоскости скорость — наклон) опти-
мальные траектории, позволяющие прийти к любой же-
лаемой комбинации скорости и наклона. Следует отме-
тить, что в случае, если желательны только изменения
величины /, оптимальная траектория всегда включает
расход некоторого количества топлива для первона-
чального уменьшения и последующего увеличения ско-
рости. Уменьшенный расход топлива для изменения /
при малых скоростях более чем восполняет этот расход
топлива.
Исключая й0 в уравнениях (1.55), можно написать
уравнение для полного времени полета, связывающее
его с конечными значениями наклона и скорости:
(T/M)t t / V ~ И"
V-=|/1-2 y0cos/V<2 + ^ •
1.64. Оптимизация двигательной системы. В двух пре-
дыдущих разделах получены программы управления ве-
личиной и направлением вектора тяги, обеспечивающие
минимум потребления топлива для перелета между лю-
быми двумя круговыми орбитами в заданное время.
Для ионных двигательных систем характерны времена
перелета, исчисляемые десятками или даже сотнями
дней, поэтому временные соображения представляются
здесь важными. Можно уменьшить количество требуе-
мого для перелета топлива, увеличивая время полета.
Это можно показать с помощью уравнений (1.55). Мас-
са топлива выражается следующим образом:
Л1р _ mo-m, / Мо a X-1
ма ~ мо -1 V + 2 t j
(1-57)
Величина (TjM)t есть однозначная функция скоро-
стей и относительного наклона начальной и конечной
круговых орбит и не зависит от /. Когда t растет, МР)М^
монотонно убывает,
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
49
Если допускается увеличение времени полета, то вме-
сто уменьшения массы топлива можно уменьшить массу
силовой установки. Максимизация полезной нагрузки
требует оптимального соотношения между массой то-
плива и мощностью системы [17—19]. Эта задача доста-
точно проста и может быть решена путем подстановки
— = 1
Мо 1
Мо ~м0 —
2
[(77AW
* ) Ч) ’
(1.58)
Дифференцируя по получаем:
A, ?_________t__________
। , Мо_ а [(Т/Л!) <]* 12
+ t J
(1.59)
Решение уравнения (1.59) имеет вид
1Л I(W1’ « [(77Л1)/Г
м^Г=|/ 2-------1------г---1----О-бО)
Соответствующие значения масс груза и топлива
даются формулами
М, Г i/a
Мо — L1 V 2 t
Мр ~ л/а [(T/M)ty
— у 2 t
(1-61)
(1.62)
Формула (1.61) иллюстрируется рис. 1.4, где показан
возможный рост массы груза с увеличением времени по-
лета. Исключая время из соотношений (1.60) и (1.61),
можно получить выражение для оптимальной величины.
4 Дж. Лейтман
50
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
(гл. 1
массы силовой установки в зависимости от массы груза:
Му \f ______ML
MQ ~ v Ma Mo ’
м0 — 1 V Мо ’
(1.63)
Формулы (1.63) графически представлены на рис. 1.5.
Для больших значений веса груза масса топлива дол-
жна быть примерно равной массе силовой установки.
а [(Т/М) t]2
Рис. 1.4. Максимальная грузоподъемность корабля с электри-
ческой двигательной системой в зависимости от продолжи-
тельности полета.
Слабая зависимость оптимальной величины массы сило-
вой установки от веса груза при небольших значениях
последнего имеет важным практическим следствием то,
что силовая установка данных размеров может нахо-
диться в оптимальных условиях работы при заданной
начальной величине массы в довольно широком диапа-
зоне значений веса полезного груза.
1.6]
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
51
Автор признателен д-ру Генри Келли, за советы и
литературные указания, в значительной мере содейство-
вавшие подготовке этой главы. Он хотел бы также по-
Рис. 1.5. Оптимальное распределение масс на корабле
с электрической двигательной системой.
благодарить Дж. Лейтмана, Анджело Миеле, Фрэнка
Дейтча и Уильяма Фимпла за сделанные ими полезные
замечания.
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ К РАЗДЕЛУ 1.6
i— двойной угол между плоскостью орбиты и ее первоначаль-
ной плоскостью;
k — переменная, определяемая уравнениями (1.48);
М — масса;
А4д—масса полезного груза;
Мр—масса топлива;
Мw — масса силовой установки;
4*
52
ТЕОРИЯ МАКСИМУМОВ И МИНИМУМОВ
[гл. 1
R — радиус орбиты;
t— время;
_ Т — тяга;
Т/М— среднее значение отношения тяги к ма.се (см. уравнения
(1.47) и текст);
V — скорость на круговой орбите;
Vx—скорость истечения топлива;
W — мощность, развиваемая двигателем;
а — масса силовой установки, рассчитанная на единицу мощ-
ности;
[3 — угол между вектором тяги и плоскостью орбиты;
7—угол между вектором скорости и составляющей вектора
тяги в плоскости орбиты;
О — центральный угол в полярной системе координат (истинная
аномалия, отсчитываемая от линии узлов);
X—постоянный множитель Лагранжа.
ЛИТЕРАТУРА
1. R. Courant and D. Hilbert, Methods of Mathematical
Physics, p. 164, Interscience, New York, 1953. [Русский перевод:
P Курант и Д. Гильберт, Методы математической физики,
т. 1, М.—Л., 1933, стр. 152.]
2. I. S. Sokol nikoff and R. M. Redheffer, Mathematics of
Physics and Modern Engineering, p. 247, McGraw-Hill, New
York, 1958.
3 P. C i с a 1 a, An Engineering Approach to the Calculus of Varia-
tions, Libreria Editrice Universitaria Levrotto and Bella, Torino,
1957.
4. H. Hancock, Theory of Maxima and Minima. Dover, New York,
1960; см. также Ginn, Boston, 1917.
5 J. M. Horner, Optimum Orbital Transfers, American Rocket
Society Undergraduate Competition, 1960.
6. H. M u n i c k, R. McGill and G. E. Taylor, Analytic solutions
to several optimum orbit transfer problems, J. Astronaut. Sci. 7,
73 (1960).
7. G. Leitmann, The Optimization of Rocket Trajectories —
A Survey, Appendix А, в книге «Progress in the Astronautical
Sciences» (S. F. Singer, ed.), North-Holland, Amsterdam, 1962.
8 A. Miele, Lagrange multipliers and quasi-steady flight mecha-
nics, J. Aero/Space Sci. 26, 592—598 (1959).
9. R. Courant. Calculus of Variations, курс лекций, New York
University, 1956—1957.
10. A. M i e 1 e, Interrelationship of calculus of variations and ordinary
theory of maxima and minima for flight mechanics applications,
ARS Journal 29, 75 (1959).
11. S. M. Johnson, Best exploration for maxima is fibonaccian, The
RAND Corporation, Santa Monica, California, Rept. No. P-856,
1959.
ЛИТЕРАТУРА
53
12. J. Р. Carstens and T. N. Edelbaum, Optimum Maneuvers
for Launching Satellites into Circular Orbits of Arbitrary Radius
and Inclination, ARS Journal 31, 943—949 (1961).
13. S. E. Dreyfus and T. F. С a r t a i n o, Application of dynamic
programming to the airplane minimum time-to-climb problem,
Aeronaut. Eng. Rev. 16, 74 (1957).
14. R. Bellman and S. E. Dreyfus, An application of dynamic
programming to the determination of optimal satellite trajectories,
J. Brit. Interplanet. Soc. 17, 78 (1959).
15. T. N. Edelbaum, неопубликованные работы.
16. M. L. Williams, Calculation of fuel distribution in step rockets,
J. Brit. Interplanet. Soc. 16, 211 (1957).
17. H. Preston-Thomas, Interorbital Transport Techniques, в
книге «Realities of Space Travel» (L. J. Carter, ed.), McGraw-Hill,
New York, 1957.
18. E. Stuhlinger, Electrical propulsion system for space ships
with nuclear power source, J. Astronaut. Sci. 2, 149—152 (1955);
3, 11 — 14 (1956).
19. J. H. Irving, Low Thrust Flight: Variable Exhaust Velocity in
Gravitational Fields, в книге «Space Technology» (H. S. Seifert,
ed.), Wiley, New York, 1959. [Русский перевод: под ред. Г. Сей-
ферта, Космическая техника, гл. 8, изд-во «Наука», М., 1964.]
20. Т. N. Edelbaum, Propulsion requirements for controllable sa-
tellites, ARS Journal 31, 1079—1089.
ГЛАВА 11
ПРЯМЫЕ МЕТОДЫ
2.0. ВВЕДЕНИЕ И ОБЗОР РЕЗУЛЬТАТОВ
В этой главе прямые методы применяются к некото-
рым простым задачам определения оптимальной про-
граммы регулирования тяги ракеты. Особое внимание
обращается на элементарные способы определения тра-
екторий и на некоторые простые доказательства доста-
точности.
Приводимая здесь трактовка вопроса несколько не-
обычна. Широко употребляются интегральные соотноше-
ния, эквивалентные формуле Грина; это делается, в ча-
стности, при установлении условий достаточности. При
выводе формул и в доказательствах постоянно исполь-
зуется сопряженная система дифференциальных уравне-
ний в смысле Г. А. Блисса. Для определения траекторий
привлекаются дифференциальные соотношения, подоб-
ные тем, которые были введены Блиссом для подсчета
дифференциалов в баллистике. Определение или описа-
ние оптимальных траекторий производится с помощью
принципа максимума. Для упрощения дифференциаль-
ных уравнений вводятся канонические переменные.
Глава носит элементарный характер. Несмотря на
то, что рассмотрению подвергнуты задачи вариацион-
ного исчисления, потребуется немногое из методов, обыч-
но связываемых с этой ветвью анализа, за исключением
сведений, необходимых для связи с вопросами, освещае-
мыми в других частях книги. Описываемые в этой главе
методы отыскания оптимального управления близки к
тем, которые развиваются в настоящее время в США
и в Советском Союзе. Основной принцип, характеризую-
щий оптимальную траекторию, состоит в том, что век
тор ускорения должен быть выбран так, чтобы достигал
максимума интеграл от его скалярного произведения с
2.0]
ВВЕДЕНИЕ И ОБЗОР РЕЗУЛЬТАТОВ
55
вектором, определяемым сопряженной системой. Частич-
но задача заключается в нахождении соответствующего
решения сопряженной системы. На конце траектории это
решение подчинено известным условиям, так что задача
оказывается краевой. Задача характерна тем, что
реально имеющийся запас энергии (топлива) ограничен
и возникает проблема определения скорости расхода —
проблема регулирования выпускных клапанов.
Глава состоит из трех разделов. В первом из них
описывается метод решения таких задач, как перехват
в стратосфере баллистической ракеты при минимальном
расходе топлива или встреча ракет в минимальное
время. Для упрощения задачи предполагается, что сила
тяжести может быть аппроксимирована самое большее
линейной функцией координат. Устанавливается процесс
определения траектории на вычислительной машине;
если этот процесс сходится, то он приводит к требуемой
траектории. Кроме того, приводится доказательство до-
статочности и соотношение взаимности Майера.
Второй раздел содержит простое графическое реше-
ние задач упомянутого выше типа для случаев, когда
силу тяжести можно считать постоянной или самое боль-
шее функцией времени; при этом скорость на одном кон-
це не ограничивается. В этом случае существует два
принципа оптимизации: 1) вектор тяги должен сохранять
постоянное направление в пространстве; 2) вектор тяги
должен быть максимально возможной величины в тече-
ние надлежащего начального периода и равным нулю
впоследствии; величина импульса должна достигать на-
ибольшего возможного значения. В этих условиях мо-
жно построить единственную кривую, изображающую
путь ракеты под действием силы тяги в зависимости от
времени; время действия тяги играет роль параметра.
Решения получаются путем построения на этом графике
другой кривой, соответствующей данной частной задаче.
Все численные данные, связанные с решением, могут
быть получены непосредственно из графиков. Во многих
случаях из решения видно, что полученные условия
также и достаточны, и в тех случаях, когда поставлен-
ная задача не должна иметь решения, это также часто
непосредственно усматривается.
56
ПРЯМЫЕ МЕТОДЫ
[гл. II
В третьем разделе рассматривается задача програм-
мирования величины тяги ракеты для оптимального
следования вдоль произвольного пути в пространстве,
если вектор тяги касателен к траектории и время явно
не входит ни в дифференциальное уравнение, ни в урав-
нение связи. Типичным примером служит задача, рас-
смотренная Годдардом. Приводится программа числен-
ного счета для определения графика регулирования
тяги в случае полета на максимальное расстояние. Для
упрощения теории дифференциальное уравнение приво-
дится к канонической форме.
Прямые методы доставляют единственные известные
автору доказательства достаточности, за исключением
задач, где это достигается применением теоремы Грина.
Использование ускорения, а не массы в качестве пе-
ременной имеет преимуществом простоту дифференци-
альных уравнений. С другой стороны, связи, наклады-
ваемые на ускорение^ не столь просты. В приводимых
ниже примерах они выражаются функциями времени, но
в общем случае они не имеют этой простой формы. Им-
пульсивное решение, соответствующее неограниченной
тяге, можно получить сходным образом; в ряде случаев
оно оказывается проще, поскольку при этом отпадает
проблема ограничений, накладываемых на ускорение.
На протяжении всей главы принято, что тяга может
быть выбрана произвольно между нулевым значением и
некоторым постоянным максимумом, пока в системе
остается топливо. Предполагается также, что скорость
газов постоянна, так что сила тяги пропорциональна
скорости расхода топлива. Все начальные условия, по-
скольку они представляют особый интерес, обычно счи-
таются заданными.
2.1 МЕТОД ОПРЕДЕЛЕНИЯ НЕКОТОРЫХ ОПТИМАЛЬНЫХ
ТРАЕКТОРИЙ
2.10. Введение и обзор результатов. В этом разделе
дается численный метод определения некоторых опти-
мальных траекторий с помощью вычислительной маши-
ны. В качестве типичных примеров взяты две задачи:
задача о перехвате баллистической ракеты при уело-
2.1)
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
57
бии минимального расхода топлива и задача осуществ-
ления встречи ракет в минимальное время. Предпола-
гается, что оба снаряда настолько близки друг к другу,
что различие в ускорении силы тяжести может быть
аппроксимировано самое большее линейной функцией
положения.
Если дифференциальные уравнения движения линей-
ны, то можно получить некоторые простые интеграль-
ные формулы, которые привлекают возможностью су-
дить о том, что следует сделать в дальнейшем, и, кроме
того, дают простое и безусловное доказательство доста-
точности. Оказывается, что существует два общих прин-
ципа оптимизации программы регулирования тяги при
заатмосферных полетах. Сопряженная система диффе-
ренциальных уравнений порождает некоторый вектор.
Первый принцип состоит в следующем: направление тя-
ги должно быть таково, чтобы результирующее ускоре-
ние имело максимальную проекцию на направление со-
пряженного вектора. Второй принцип заключается в
том, что ускорение должно быть максимально возмож-
ным, когда величина этого сопряженного вектора
превышает некоторое определенное значение, и ми-
нимально возможным, когда она меньше этого значе-
ния; определение последнего может оказаться частью
всей задачи.
Мы показываем в этом разделе, что траектория, на
которой выполнены эти принципы, реализует оптималь-
ное соотношение между различными начальными и ко-
нечными значениями переменных и определяет класс
так называемых соотношений взаимности Майера. Важ-
нейшая рассмотренная здесь задача состоит в нахожде-
нии траектории, подчиняющейся заданным связям и
максимальным принципам.
Решение производится методом последовательных
приближений, аналогичным методу Ньютона. Выби-
рается наугад траектория описанного выше типа. При
этом фиксируются некоторые параметры, начальные
значения либо постоянные интегрирования сопряженной
системы. Получающаяся траектория, вообще говоря, не
будет удовлетворять ограничениям, наложенным на ко-
нечные значения переменных. Дифференциалы конечных
58
ПРЯМЫЕ МЕТОДЫ
[гл. II
значений выражаются через дифференциалы пара-
метров. Эти последние дифференциалы выбираются так,
чтобы обратить в нули отклонения конечных координат
от их истинных значений; система уравнений обращается
с целью определить соответствующие значения парамет-
ров, и получается новая траектория. Процесс повто-
ряется до тех пор, пока отклонения конечных значений
не окажутся меньшими некоторой предписанной вели-
чины.
Если решение сопряженной системы может быть
найдено в замкнутой форме, то дифференциалы сравни-
тельно легко вычислить. Для других случаев исполь-
зуется метод, который был введен Г. А. Блиссом для
подсчета дифференциалов в баллистике. Если дифферен-
циальные уравнения задачи нелинейны, то сопряженная
система строится для линейной системы уравнений в
вариациях исходных переменных.
2.11. Основные уравнения. Уравнение движения ра-
кеты в поле тяготения, не подверженной внешним си-
лам, может быть написано в следующем виде:
r=g+a, (2.1)
где г—вектор положения, g — ускорение силы тяже-
сти, а — ускорение, создаваемое тягой. Можно написать
где т есть отношение массы израсходованного топлива
к первоначальной общей массе ракеты, с'— постоянная
скорость истекающих газов, а е—единичный вектор на-
правления силы тяги.
Полезно иметь в виду кинематическое соотношение
t t
fadt = c' f = (2.3)
о 0
где a = |e|. Поскольку масса израсходованного топлива
пропорциональна tn, a In (1—т) есть монотонная функ-
ция от т, можно выразить условия, включающие конеч-
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
59
ное значение массы, через интеграл от ускорения с уче-
том ограничений, наложенных на величину т. Использо-
вание а в качестве переменной вместо т упрощает урав-
нения движения, поскольку а входит в них линейно.
Для случая, когда силу тяжести можно считать по-
стоянной, уравнения движения могут быть написаны в
следующем виде:
x = acos р.
у = а$\п р —g,
(2.4)
где р — угол между ускорением а и осью х.
Движение происходит в плоскости ху, ось у направ-
лена вертикально. Если гравитационное поле массивного
центрального тела аппроксимировано линейной функ-
цией координат, то эти уравнения заменяются следую-
щими:
х = — b2x + a cos р,
у = В2у — g-\-as\np.
(2-5)
Здесь g—гравитационное ускорение в начале коорди-
нат, Ь2 = glrE, где гЕ — расстояние от начала до центра
тела, В2 = 262.
2.12. Сопряженные уравнения; формула Грина. Ни-
же приводятся интегральные формулы, необходимые для
оставшейся части этого раздела. Вывод осуществляется
путем введения новых переменных и интегрирования по
частям и приводит к формулам, известным под общим
наименованием формул Грина (см. Коддингтон и Ле-
винсон [1], стр. 98).
Возьмем, например, уравнения (2.5) в качестве ура-
внений движения. Вводятся две новые переменные и.
v, по одной для каждого уравнения движения; эти пе-
ременные, называемые множителями (или множителя-
ми Лагранжа), не подчиняются никаким ограничениям,
за исключением требования непрерывности вторых про-
изводных в интересующем нас интервале. Умножим
уравнения (2.5) соответственно на и. V, сложим почленно
60
ПРЯМЫЕ МЕТОДЫ
[гл. И
и проинтегрируем. Результат можно записать в виде
т
J [и (х + b2x — a cos р) + v (у — В2у + g — a sin р)] dt = 0,
о (2.6)
где х, у — любые решения уравнений (2.5). Если инте-
грал (2.6) взять по частям, исключив производные от
х, у из подынтегральной функции, то получится
т
J [х (и + b2u) -h У (v — B2v) — а (и cos р + v sin р) -|-
0
+ gv]dt+[xu—xu + yv — yv\To==O. (2.7)
Уравнение (2.7) представляет один из простых ва-
риантов формул Грина.
Теперь, с целью упрощения формулы (2.7), выберем
множители u, v так, чтобы зависимые переменные х, у
исчезли из подынтегральной функции; именно положим
и -|- Ь2и = 0,
v — B2v = 0.
Это и есть сопряженная система для уравнений (2.5).
Сопряженная система определяется, таким образом,
операциями интегрирования по частям с целью исклю-
чения производных и последующим приравниванием
нулю коэффициентов при зависимых переменных в
подынтегральной функции. Уравнения (2.5) называются
самосопряженными, поскольку уравнения (2.8) и (2.5)
включают одни и те же дифференциальные операторы.
Замечание: можно ввести четыре множителя, по одному
для х, у, х, у. В этом случае система, соответствующая
(2.5), формально не является самосопряженной
(см. Коддингтон и Левинсон [1], стр. 97), но получаю-
щиеся в итоге уравнения и формулы эквивалентны друг
другу. Если бы вместо уравнений (2.5) были взяты ура-
внения (2.4), то сопряженная система имела бы вид
и =0,
v = 0.
(2.9)
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
61
Во всех случаях, если и, v — решения сопряженной
системы, то уравнение (2.7) принимает вид
г
[xu—xu-\-yv—yv^ = \а(и cosp-f-т) sin р)—g-u] dt. (2.10)
о
Это основная формула настоящего раздела; пред-
полагается, что u, v являются решениями соответствую-
щей сопряженной системы.
Формулы для частных случаев. Если нас
интересует значение некоторой переменной, например х,
в момент Т, то мы можем получить формулу для х, вы-
бирая такое частное решение и4, щ сопряженной си-
стемы, что
«1(Г) = г»1(Г)^^1(Г) = 0, =
Для уравнений (2.8) = (1/6) sin Ь(Т — /), Vi = 0; для
уравнений (2.9) щ = Т — t, щ = 0. Точно так же, чтобы
получить формулу для у, выбираем u2, Vz так, что
и2(Т) = и2(Т) = й2(Т) = 0, v2(T) = —1. Подставляя
эти значения в уравнение (2.10), получим следующие
формулы для х, у:
т
х = хд + х()Т+ J (Т — t)acosp dt,
° т (2.11)
У = Уо + Уо7' — + f (T — t)as\npdt
о
или
х = л0 cos ЬТ -|- у- sin ЬТ +
т
/acosp sin b (Т — f) dt,
о
y = (yo-»chfir+4sh57' +
т
+ -jfr + -g- [as\npshB(T — t)dt
о I
в соответствии с уравнением (2.4) или (2.5).
(2-12)
62
ПРЯМЫЕ МЕТОДЫ
[гл. II
Если требуется получить выражение для х(Т), то
можно добиться этого дифференцированием уравнений
(2.11) и (2.12) либо выбором решения u3, v3 такого, что
и3(Т) = 1, v3(T) = й3(Т) = $з(Т) = 0. Подобным же
образом можно определить щ, и4 с тем, чтобы получить
из уравнения (2.10) выражение для у(Т).
2.13. Принципы максимума. В этом разделе будет
показано, что если траектория удовлетворяет двум мак-
симальным принципам, которые будут сформулированы
ниже, то она является оптимальной траекторией неко-
торой задачи. В следующем разделе мы покажем, что
речь идет об оптимальной траектории для описанного
выше класса задач.
Рассмотрим задачу максимизации интеграла в урав-
нении (2.10). Прежде всего заметим, что первые два
слагаемых в подынтегральной функции можно было бы
записать как скалярное произведение а • W, где а =
= a(Zcosp+/sinp), a w = ui-\-vj.
Пусть функции u, v уже определены каким-то спосо-
бом и представляют решения сопряженной системы
дифференциальных уравнений. Посмотрим, какими свой-
ствами должен обладать вектор а, чтобы интеграл до-
стиг своего максимального значения. Для начала рас-
смотрим лишь ограниченные ускорения а:
0^.а<Ат, (2.13)
здесь Ат—известная функция от /, определяемая меха-
низмом ракеты. Далее можно ограничить запас топ-
лива, так что требуем также, чтобы было (см. уравне-
ние (2.3))
г
J adt < — 1п(1 — /птах), (2.14)
о
где ттах—максимальное значение относительной мас-
сы сжигаемого топлива, соответствующее использова-
нию всего имеющегося топлива.
Теперь сформулируем первый максимальный прин-
цип; он состоит в том, что при а Ф 0 направление век-
тора а должно быть таким, чтобы его проекция на век-
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
63
тор W была максимальна по величине, т. е. чтобы
значение параметра р, определяемого уравнением
tgp = £. (2.15)
давало максимум, а не минимум. Это условие опреде-
ляет направление вектора а и называется уравнением
переключений *).
Если общий запас топлива ограничен, так что
т
У dt> С In (1 ^max) >
О
то возникает также задача определения времени при-
ложения ускорения а. Этот вопрос решается вторым
максимальным принципом: время, в течение которого
включается ускорение, выбирается так, что
а =
О,
если
если
>
<£.
(2.16)
|w| = W
Здесь L — постоянная, определяемая из условия
сжигания всего топлива, т. е. из требования
т
f a dt = — с' In (1 — /птах).
О
При доказательстве этой теоремы, которое следует
ниже, будет показано, что при наложении на а таких
условий интеграл (2.10) достигает максимального зна-
чения; в последующих разделах будут даны методы
получения некоторых оптимальных траекторий.
Рассмотрим задачу, которая потребуется нам при
доказательстве следующей ниже теоремы; решения дру-
гих задач подобного рода не будут существенно отли-
чаться от решения этой задачи; различие будет состоять
лишь в способе зависимости от начальных и конечных
значений переменных. Рассмотрим задачу максимиза-
ции х(Т)г Пусть заданы все начальные значения и часть
конечных значений переменных t/(T), х(Т), у(Т)\ неко-
*) В оригинале «steering equation». (Прим, перев.)
64
ПРЯМЫЕ МЕТОДЫ
[гл. И
торые из этих последних могут не входить в уравнения
связей. Пусть запас топлива задан не превышающим
определенной величины, так что имеются связи типа
уравнений (2.13) и (2.14), наложенные на а.
Пусть теперь найдены траектория С* и система мно-
жителей и, v, удовлетворяющие следующим условиям:
1. Траектория является допустимой. Это означает,
что на концах принимаются предписанные значения пе-
ременных и удовлетворяются условия связей, наложен-
ных на а.
2. Функции и, v представляют собой решение со-
пряженной системы дифференциальных уравнений.
Кроме того, коэффициент —й(Т) при х(Т) в уравнении
(2.10) положителен, а в случае, если какой-либо из
параметров у(Т), х(Т), у(Т) не задан, то коэффициент
при нем —v(T), и(Т) или v(T) в уравнении (2.10) об-
ращается в нуль.
3. Для каждого значения t величина р такова, что
подынтегральная функция а • w достигает максимума,
другими словами, векторы а и w параллельны и оди-
наково направлены.
4. Существует такое число L, что
( Ат при w > Z,
а 1 0 при чя) < L
и равенство w = L имеет место только в изолирован-
ных точках. Кроме того, используется все топливо, так
что
т
f adt = — c'ln(l —/nmax).
О
Теорема. Траектория С*, удовлетворяющая усло-
виям I, 2, 3 и 4 доставляет максимальное значение
х(Т) и является единственной.
Доказательство. Пусть существует другая до-
пустимая траектория.. Обозначим величины*, относя-
щиеся к траектории С*, значком *, а соответствующие
величины для другой траектории — большими буквами.
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
65
Пусть Т\ будут точки интервала (О, Т), где w > L,
а Т2 — точки, где co<L. Обозначим:
В = f (a* — A)dt>0.
г.
Тогда согласно уравнению (2.3)
f Adi <В,
Т2
(2.17)
(2.18)
поскольку вторая траектория требует количества топли-
ва не большего, чем первая (С*).
Величины, связанные с каждой траекторией, должны
удовлетворять уравнению (2.10), в котором u, v — опре-
деленные выше функции. Если подставить значения пе-
ременных для каждой траектории в уравнение (2.10) и
вычесть результаты, то получим
т
— й(Т)[х*(Г) — Х(Т)\ = f (a*-A)-vodt. (2.19)
о
Интеграл в правой части можно переписать в сле-
дующем виде:
У (а*— A)wdt-\- —cos(/?* — P)\dt—
г, г,
— f Aw cos (р* — Р) dt. (2.20)
т,
Очевидно, что
J (а* — A)wdt^L f (a* —A) dt = LB
г, т\
и
J A cos (/?* — Р) w dt < у Aw dt < L J Adt < LB.
t2 t2 T2
Отсюда следует, что сумма первого и третьего чле-
нов в уравнении (2.20) неотрицательна. Второе слагае-
мое, очевидно, также неотрицательно. Следовательно,,
сумма (2.20) положительна или равна нулю.
5 Дж. Лейтман
66 ПММЫЁ МЕТОДЫ (гл. й
ДальнеиШёё исследование показывает, что она по-
ложительна всегда, за исключением случая, когда вы-
полняется равенство Л = а*; последнее равенство мо-
жет выполняться на множестве меры нуль. Поскольку
—й(Т) положительно, отсюда вытекает утверждение
теоремы: х*(Т)>Х(Т), если только не соблюдается
равенство Л = а*. Таким образом, установленные мак-
симальные принципы достаточны для сообщения инте-
гралу, а следовательно х(Г), максимального значения.
Траектории, на которых удовлетворяются условия
2—4, будем называть экстремалями. Если a(t)—задан-
ная функция, то условие 4 будет отбрасываться.
Если конечное значение скорости не входит в усло-
вие задачи, то согласно условию 2 выбираем и(Т) =
= v(T) = 0, так что w(T) = 0. Отсюда следует, что w
есть убывающая функция времени, по крайней мере
в окрестности точки Т. В некоторых интересных случаях
этого достаточно для того, чтобы w(t) убывало для
всех 0 < t < Т. В частности, это справедливо, если сила
тяжести предполагается постоянной, поскольку тогда
w = const • (Г — I). Это верно также для линейного при-
ближения, по крайней мере, если Т < л/2&, так как обе
функции sin&(r—t) и shB(r — t) убывают по вели-
чине для 0 < t < Т.
Для случая постоянной силы тяжести очевидно
также, что если и(Т) = 0 = v(T)y то и = с^(Т — t), v —
= с2(Т — /), и если р выбрано таким, что интеграл до-
стигает максимума, то согласно уравнению (2.15)
lg р = vfu = const.
2.14. Соотношение взаимности Майера. Здесь будет
показано, что такая экстремаль, как С*, не просто до-
ставляет максимальное значение одной из переменных,
например х(Т), но устанавливает оптимальное соотно-
шение между всеми величинами х(0), у(0), х(0), г/(0),
х(Т), У(Т)> х(7), коэффициенты при которых в
уравнении (2.10) не обращаются в нуль для некоторого
частного решения u, v и расхода топлива т(7). Из
только что приведенного доказательства видно, что
если х(0),..., у(Т) имеют значения, которые прини-*
маются ими на С*, то т(Т) минимально для функций а,
удовлетворяющих уравнению (2.13),
2.И
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
67
Рассмотрим любую другую систему значений ука-
занных параметров, коэффициенты при которых в (2.10)
отличны от нуля. Предположим, например, что w(0) не
равно нулю, но положительно. Тогда х(0) минимально,
если х(0), у(0), у(0),..., у(Т), т(Т) принимают зна-
чения, предписанные им на С*. Доказательство такое
же, как и выше, с той лишь разницей, что левая часть
уравнения (2.19) заменяется на — и(0)[х*(0)—Х(0)].
Сходный результат справедлив и в случае, если ни
н(Т), ни v(T) не равно нулю; при этом линейная ком-
бинация — й(Т)х(Т)—v(T)y(T) максимальна в срав-
нении с ее значениями на других кривых, для которых
граничные значения остальных переменных отличаются
от их значений на С*.
Приведенная аргументация отказывается служить,
если обращается в нуль коэффициент при соответствую-
щей величине в уравнении (2.10). Если, например,
и(Т) = 0, то х(Т) не достигает на С* ни максимума,
ни минимума; х*(Г) представляет собой тогда един-
ственное значение, которое может принять х(Т), тогда
как остальные переменные х(0), ..., у(Т), пг(Т) при-
нимают значения, которые они имеют на С*; при этом
С* есть единственная допустимая кривая, на которой
х(Т) может принять указанное значение.
Таким образом, мы видим, что экстремаль не только
доставляет максимальное значение одной величине, но
устанавливает оптимальное соотношение между гранич-
ными значениями переменных. Соотношения такого
типа, когда роли различных граничных значений могут
меняться, известны под общим названием соотношений
взаимности Майера [2].
2.15. Численный метод определения простой опти-
мальной траектории. В этом разделе рассматривается
задача определения траектории для достижения задан-
ной точки X, Y за предписанное время Т с минималь-
ным расходом топлива.
Поскольку конечная скорость безразлична, поло-
жим и(Т) =v(T) =0. Кроме того, следуя замечанию в
конце раздела 2.13, рассмотрим лишь начальный
период действия тяги (0, Л), где ti подлежит опреде-
лению.
5*
68
ПРЯМЫЕ МЕТОДЫ
[гл. II
При этом равенство tgp = o/« имеет вид. tgp = c
для постоянного поля тяготения либо tg р =
= (с/В) shB(T-t)/[i/b) sin b(T- 01. где с = (tgp)T_0.
С учетом этих формул, а также того, что
cos р = u/w,
sin р — v/w,
(2.21)
уравнения (2.11) можно переписать в следующем виде:
X = XQ
t 1
У = Уо+Уо7' —^ф-H-sinp/ (Г— f)adt
о
при постоянном р, а уравнения (2.12) в форме
х = л0 cos ЬТ + -у- sin ЬТ +
о
У=(Уо — Jr)ch 5/ + 4sh5/ ++
(2.22)
(2.23)
Л
+ ^B(T-t)dt,
о
где
W = (1/6)2 sin2 b (T _ f) + (f/5)2 sh2 B(T — /).
В оставшейся части этого раздела будем рассматри-
вать уравнения (2.23). Мы найдем траекторию и затем
покажем, что она . обеспечивает требуемый минимум
расхода топлива. Если тяга ракеты постоянна, то уско
2.Ц
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
69
рение ограничено величиной Лш, которая зависит от
времени:
— ОТщахО ПРИ
^m.x/(l — Wmax) ПрИ
1<тт^/ттп, | (2 24)
> ^max/^max* J
Здесь /nmax, ^max представляют соответственно макси-
мальные значения /и, т.
Рассмотрим теперь какую-нибудь траекторию, оп-
ределяемую выбором значений с в (2.23), и соседнюю
траекторию, определяемую величинами Л + 6Л, с + бс.
Первые вариации (дифференциалы) переменных х(Т),
у(Т) равны:
— I* awsin2 р cos2 pdtbc,
6
sy(n=[acsh74r~0 Vzi+
+ ^2 /* awsin2pcos2prf/B^,
6
(2.25)
где tgp = bcshB(T—t)/[B sin b(T—Ol-
Численный метод. Зададимся значениями ti9
с и вычислим соответствующую траекторию. Значения
х(Т), у(Т) будут получены с ошибками.
Положим
8х(Г) = Х — Л (Г), |
8у(Г) = У-у(Г), J
(2.26)
где бх, by определены уравнениями (2.25). Разрешив
уравнения (2.26) относительно б/i, бс, найдем новые
значения Л, с. Вычислим соответствующую траекторию.
Процесс повторяется до тех пор, пока не удовлетворится
70
ПРЯМЫЕ МЕТОДЫ
[гл. II
какое-либо условие сходимости, например пока сумма
[X — х(Т)]2 + [У — у(Т)]2 не станет меньше некоторого
заданного числа.
Доказательство минимальности расхо-
да топлива. Чтобы убедиться в том, что найденная
выше траектория реализует требуемый минимум, умно-
жим второе уравнение (2.23) на с и сложим с пер-
вым. Все условия теоремы, относящиеся к подынтеграль-
ной функции, выполнены: и = иД/), v = cv2(t) суть ре-
шения сопряженной системы, выбранные так, что они
обращаются в нуль при t = Г, поскольку скорость на
этом конце не подчинена никаким условиям; tgp = v/u и
| Am(t) при w>Z = w(/1),
а ( 0 при w < L = (/J.
Отсюда следует, что интеграл достигает максимума
и никакое другое допустимое ускорение не приводит к
этому результату. Слагаемые в левой части определены
поставленными условиями и определенным выше зна-
чением с.
Подобный результат имеет место и для (2.22).
2.16. Перехват при минимальном расходе топлива.
В этом разделе рассматривается проблема перехвата
снаряда, следующего в стратосфере известным курсом.
Для простоты рассуждения ограничены случаем бал-
листического снаряда, летящего в постоянном поле
тяготения.
В этом случае уравнения задачи о перехвате могут
быть записаны в следующем виде:
XqT — cos p J (T — /) a dt = 0,
о
6
Yo+Г0Г —sinp J (T — f)adt = 0,
о
(2.27)
где Xo, Уо — первоначальные относительные координаты
снаряда (по отношению к ракете-перехватчику), а
Xq, Гц — соответствующие скорости.
2Л1
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
71
Дифференцируя эти уравнения, получим уравнения
в вариациях для траектории перехвата
6 \
XQ — cos р J* adtjbT — cos р (Т — ^) а 8/х +
о /
4-sin р J (Т — t)adt%p = O,
о
Yq — sin р J* a dt 1 В Г — sin р (Т — tx) а (^) 3^ —
о /
6
— cos р J (Г — f)adt§p = 0.
о
(2.28)
Если из этих уравнений исключить Sp, то полу-
чается
XQ — cos р J* a dt I cos р +
о /
(2.29)
При этом условие для стационарного Л и, следова-
тельно, т(Т) имеет, вид
Л \
Xq — cos р J* adt 1 cos р -ф-
о /
/ 6 \
+1 Yq — sin р J a dt 1 sinр = 0.
\ о /
(2.30)
Это условие может быть истолковано, по замечанию
Фолкнера ([3], гл. VII), как требование перпендику-
лярности вектора тяги к направлению относительной.
72
ПРЯМЫЕ МЕТОДЫ
[гл. П
скорости при t > Л- Более общо, если конечная скорость
не фиксируется, это условие имеет вид (®rei-w)T = 0,
где T>rei — относительная скорость.
Численный метод. Траектория получается сле-
дующим путем. Задаемся значениями Г, р, вычис-
ляем траекторию и ошибки вдоль нее; последние имеют
вид
6
E = Xq-\- Х^Т — cosp J (Г— t)adt.
о
tx
P=Yq-\-YqT — sin p J (T — t)adt.
о
(2.31)
Если fi, Г, p изменяются на малые величины, то
можно написать:
/ tx \
8£’=1Л0—cosp J a dt 18Г—(Г— f^a^Jcosp 8/j-j-
V о /
+ sin р J (Г — t)a dt Ip,
о
t,
Ko—sin p J adt
о
(2.32)
8 Г—(T— tr) a (tj) sin p 8/i—
t,
— cos p J* (Г — /) a dt bp.
о
Новое значение p берется из уравнения (2.30) и та-
ким образом определяется 6р. Используя величины, да-
ваемые уравнениями (2.31) и (2.32), положим
8Е = — Е,
IF= — F.
(2.33)
Поскольку др уже найдено, получаем два уравнения
для б/ь ЬТ. Отсюда находим новые значения для Ц,Т,р.
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
73
Процесс приближений продолжается до тех пор,
пока сумма Е2 + F2 не станет меньше некоторого за-
данного значения. Вопросы сходимости в этой задаче не
возникают.
Описанный процесс вычислений дает стационарное
значение Л; варьируя Г, можно проверить, представляет
ли это значение максимум или оно является миниму-
мом. В задаче, рассмотренной выше, всегда имеет ме-
сто последний случай.
2.17. Задача о встрече за минимальное время. Рас-
смотрим задачу о встрече двух летательных аппаратов
или, что то же, о переходе аппарата с одной орбиты на
Другую.
Оптимальное направление вектора тяги разыски-
вается в плоскости, параллельной плоскости начальных
векторов относительного положения и скорости. Выбе-
рем оси так, что начальное положение цели по отноше-
нию к ракете будет определяться координатами Хо, Уо,
причем Уо > 0, а составляющие относительной скорости
будут равны Хо, 0, причем Хо > 0. Введем отклонения:
т
Е' = Х^ + Х^Т — J (Т — /) a cosp dt,
о
т
F' = Y0 — J (Г —/)asin pdt,
о
т
O = XQ — J azQspdt,
о
т
Н= — J* a sin р dt.
о
(2.34)
(2.35)
Для встречи необходимо и достаточно определить
такие функции времени а, р, чтобы в некоторый момент
Т было Е' = F' = G = Н 0. В силу последних двух
равенств можем заменить Е\ F' новыми функциями
74
ПРЯМЫЕ МЕТОДЫ
[гл. II
отклонений £, F и переписать систему в виде
т
E = Xq+ J tao.Qspdt,
о
т
F= Yo + J* ta sinpdt.
о
T
0 = X^ — J a cos p dt.
о
T
H= — J a sin p dt.
о
(2.36)
Для встречи необходимо и достаточно, чтобы все
эти величины обращались в нуль.
Поставленную задачу можно рассматривать как не-
большое видоизменение той, которая привела нас к тео-
реме раздела 2.13. Умножим уравнения (2.36) соответ-
ственно на постоянные с3, —1, —Ci и сложим. Для
любого решения имеем
Ло С3*о ~т“ о =
т
= £ а [(1 -f- c3f) cos р 4- (fi + c2t) sin р] dt. (2.37)
о
Это частный случай уравнения (2.10), в котором ис-
ключено гравитационное слагаемое. Слагаемые и =?
= 1 + c3t и v = Ci + c2t представляют решения сопря-
женной системы (2.9), так что условие 2 теоремы раз-
дела 2.13 выполнено.
Предположим теперь, что мы нашли решение, кото-
рое удовлетворяет двум максимальным принципам, со-
ответствующим условиям 3 и 4. Положим в этом реше-
нии а = flmax, 0 < t < Т и выберем р так, чтобы подын-
тегральная функция была максимальна:
V = (2.38)
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
75
Траектория, получающаяся при этом, удовлетворяет
всем условиям теоремы, а именно: она является допу-
стимой, u, v суть решения сопряженной системы, а а, р
выбраны так, что интеграл в уравнении (2.37) макси-
мален. Кроме того, в этих условиях не остается никакой
другой траектории, способной обеспечить встречу в мо^
мент Т. Пусть теперь имеется траектория, осуществляю-
щая встречу в момент Т'. причем 0 < Т' < Т. Если на
этой последней траектории тяга включена вплоть до мо-
мента Г', в который происходит встреча, а после этого
момента тяга выключена, то результирующая траекто-
рия также приведена к встрече в момент Г, так как,
коль скоро встреча состоялась, оба аппарата в отсут-
ствие тяги будут после нее следовать вместе. Теорема,
однако, устанавливает, что не существует второй траек-
тории, на которой может состояться встреча в момент Г,
и отсюда вытекает, что не существует траектории, реали-
зующей встречу в более ранний момент времени.
Из сказанного следует, что если мы можем опреде-
лить траекторию, описанную выше, то она обеспечит
минимальное время полета.
Численный метод. Во-первых, напишем фор-
мулы для вариаций отклонений:
ЪЕ = (ta cosр)т ЪТ — J* ta sin р Ip dt.
о
т
о
т
1О = — (аояърУ^Т4-J*asxnpbpdt.
о
г
6//= — (a sinрУт^Т — J* acospbp dt.
о
где согласно уравнению (2.38)
_ (1 + СзО (*<4 + t Вг2) - (С! + с20 t Ьс3
(14-СзО2 + (С1+с2О2
(2.39)
(2.40)
76
ПРЯМЫЕ МЕТОДЫ
[гл. II
Теперь зададимся системой значений для ch с2, с3, Т
и вычислим значения £, F, G, Н и различные интегралы,
фигурирующие в уравнениях (2.39). После этого по-
ложим
ЪН=—Н.
(2.41)
Для четырех величин dci, дсг, Т получены четы-
ре уравнения; это приводит к новым значениям для
Сг, Сз, Т. В случае сходимости метод приводит к тре-
буемой траектории.
2.18. Обсуждение. С целью простоты изложения в
этой главе мы ограничились элементарными способами
расчета. Подробное обоснование методики дано в рабо-
тах Блисса [4—6].
Для сведения читателя, интересующегося классиче-
ским вариационным исчислением, отметим, что условия
2 и 3 определяют уравнения Эйлера для задачи пере-
ключений. Все рассмотренные здесь задачи относятся
к типу задач Майера (см. работу Блисса [7], § 69) с
разделенными условиями на концах. В задаче Майера
форма уравнений Эйлера не зависит от частной вели-
чины, которая должна быть максимизирована, а также
и от связей; с их помощью определяются постоянные в
решениях и, v сопряженной системы. Интересно, что
уравнения Эйлера выводятся здесь из принципа макси-
мума и представляют достаточные, а не необходимые
условия экстремума. Для задачи переключений принцип
максимума приводит также к условиям Вейерштрасса
и Лежандра (см. [7], стр. 223); условие Вейерштрасса в
этом случае имеет вид 1—cos(p* — Р) <0 и всегда
выполняется.
Важность условий 2 и 3 была подчеркнута в послед-
нее время в различных работах. Эмерсон [8] дает не-
обходимые и достаточные условия, а также доказатель-
ство существования для изопериметрической задачи, со-
держащей два интеграла. Брекуэлл [9] дает довольно
общий анализ оптимальных траекторий и приводит эти
соотношения. Охоцимский и Энеев [10] исследуют зада-
чу о запуске, подобную тем, которые рассмотрены в на-
2.1]
НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
77
стоящем разделе. Лейтман [11] дает общее рассмотрение
двумерных задач для постоянного гравитационного
поля. По счастливой случайности в постоянном грави-
тационном поле никогда не требуется, чтобы вектор
тяги располагался в трехмерном пространстве: всегда
существует плоскость, в которой этот вектор распола-
гается для оптимизации режима.
Вектор w может быть истолкован как вектор реак-
ции на импульс, встречающийся инженерам-электри-
кам в одномерных задачах. Лоуден [12] вводит этот век-
тор в более общих задачах; им же, по всей вероятности,
было впервые опубликовано уравнение переключений
(2.15).
Условие 4, что тяга должна быть включена тогда,
когда величина w становится достаточно большой, мо-
жет также быть представлено в форме условия Вейер-
штрасса [11].
Дифференциальные уравнения упрощаются введени-
ем канонической переменной вместо массы /И, которая
входит нелинейно. Это позволяет дать несколько весьма
простых доказательств приведенного в тексте типа.
Связи, наложенные на а, однако, оказываются сложнее,
поскольку они, вообще говоря, содержат интегралы
от а. Переменная V, введенная Д. Е. Охоцимским и
Т. М. Энеевым, эквивалентна а.
Угловые точки. Если определить угловую точку
как точку, где ускорение а терпит разрыв, то можно
указать два существенно различных вида таких точек.
Точка, где разрывно |а|, должна характеризоваться как
разрыв в программе регулятора тяги, а точка, где раз-
рывно направление а, — как разрыв направления. Как
отметил в своей работе Лейтман, разрывы направления
имеют место при w = 0. Разрывы в программе регуля-
тора тяги обычно встречаются в тех случаях, когда w
достигает некоторого конечного значения, обозначенного
через L в условиях теоремы.
В нормальных задачах (определение нормально-
сти— см. [7], § 77) разрывы направлений встречаются
лишь в том крайнем случае, когда а имеет свое макси-
мальное значение для всех t, а также в неопределенном
случае постоянного w. Охоцимский и Энеев утверждают,
78
ПРЯМЫЕ МЕТОДЫ
[гл. И
что имеется случай, когда импульс тяги должен быть
приложен во внутренней точке временного интерва-
ла. Для задачи, рассматриваемой ими, это замеча-
ние представляется ведущим к недоразумению. В этой
задаче, как и в рассматриваемой Лейтманом, кривая
w(/) есть гипербола либо она вырождается в прямую
линию и никогда не достигает максимума внутри интер-
вала. В упомянутых задачах нижняя граница расхода
топлива устанавливается самое большее для двух вклю-
чений тяги — в начале и в конце траектории, где w при-
нимает максимальные значения.
Теория, изложенная в этом параграфе, близка к
теории оптимального управления, развитой Ласал-
лем [13] и Понтрягиным [14]. Интеграл в уравнениях
(2.19) и (2.37) представляет собой функционал Пон-
трягина ([14], стр. 16, первая формула). Здесь он имеет
простую форму благодаря тому, что дифференциальные
уравнения линейны по координатным переменным и эти
последние не входят в функционал. Определение функ-
ционала для задачи настоящего параграфа заключается
в нахождении совместимого со связями решения сопря-
женной системы. Область изменения а является сфе-
рической в задаче программирования тяги ракеты и
прямоугольной в ряде задач оптимального управления,
где |а,| <Сг.
Метод градиентов Келли ([15], см. также гл. VI на-
стоящей книги) и динамическое программирование в
изложении Веллмана и Дрейфуса [16] являются, по-ви-
димому, единственными другими методами, пригодными
для определения оптимальных траекторий (см. также
гл. VIII настоящей книги).
Метод подсчета дифференциалов также непосред-
ственно приложим к вопросам управления и предска-
зания (см. Дреник [17] и Цянь Сюэ-сэнь [18]). Тин-
дал [19] высказал также идею об объединении задач
управления и оптимизации благодаря использованию
сопряженной системы дифференциальных уравнений.
Вычисления. Задачи, рассмотренные в разделах
2.16 и 2.17, были запрограммированы и просчитаны. Ин-
тегралы были представлены дифференциальными урав-
нениями и был использован метод Рунге — Кутта, допу-
2.2]
ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
79)
скающий переменный шаг, необходимый в окрестности;
/1 и Т (Фолкнер и Уорд [20], § 8). Каждая итерация
требует в этих задачах несколько менее секунды счет-
ного времени на машине CDC-1604, и ошибка умень-
шается в случае сходимости примерно в 7 раз за ка-
ждую итерацию. Полное время счета в этих примерах
составляет от 3 до 10 секунд. В проблеме перехвата не
было обнаружено затруднений со сходимостью, но в рас-
четах задачи о встрече, по-видимому, имеется необхо-
димость в задании начальных значений в определенных
пределах.
Автор обязан Е. Н. Уорду за составление программ
и вычисления, выполненные им для задач этого
раздела.
2.2. ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
2.20. Введение и обзор результатов. В этом разделе
дается графический метод, позволяющий сводить не-
которые простые задачи оптимизации к простым алге-
браическим операциям. На протяжении большей части
текста рассматривается в качестве типичной задача пе-
рехвата баллистического снаряда. Дается описание ре-
шения некоторых других задач, например таких, как
задача о полете на максимальное расстояние. Вообще
говоря, метод может быть применен к оптимальным за-
дачам о траекториях, где аэродинамическими силами
можно пренебречь, силу тяжести можно считать посто-
янной и где конечное значение скорости не входит в
уравнения связей.
Решение такого типа обладает рядом привлекатель-
ных свойств. Оно абсолютно элементарно. График сразу
показывает, существует решение или нет. Решения, со-
ответствующие минимальному времени перехвата, мак-
симальному времени перехвата и минимальному рас-
ходу топлива, сразу находятся из одного графика. Соот-
ветствующие решения для тяги также получаются не-
посредственно, и в случае надобности из того же гра-.
фика могут быть получены решения, соответствующие
постоянной тяге надлежащей величины, приложенной
р течение всего времени полета. Во многих случаях
80
ПРЯМЫЕ МЕТОДЫ
[гл. II
интерпретация решения столь непосредственна, что со-
вершенно очевидны необходимость и достаточность ус-
ловий, полученных для требуемого экстремума. Если ис-
пользуются безразмерные величины, то для всех слу-
чаев достаточно одной координатной сетки.
Хорошо известно, что при сделанных выше предполо-
жениях направление вектора тяги в течение времени ее
действия должно оставаться постоянным, а величина
тяги должна быть максимальна в первоначальный пе-
риод, а затем равна нулю. Это становится более или
менее очевидным благодаря методу решения, данному в
этой главе; элементарное доказательство этого факта
было дано Фолкнером [21].
2.21. Построение графика. Уравнение движения ра-
кеты, не подверженной действию внешних сил, может
быть написано в следующем виде:
а = (2.42)
направление вектора тяги предполагается при этом фи-
ксированным. Обозначения всех величин взяты из раз-
дела 2.1. Уравнение может быть проинтегрировано; при
нулевой начальной скорости получаем
v = —cf In (1 —т). (2.43)
Если скорость расходования топлива во время дей-
ствия тяги постоянна, т. е. т = /и0, то уравнение (2.43)
интегрируется вторично и дает
Г = c't [1 + (1//п — 1) In (1 —/п)|, (2.44)
если г(0) = 0. В последующем т будет считаться по-
стоянным во время действия тяги. Если тяга действует
до момента времени после которого ракета совершает
свободный полет, то координата ее определяется выра-
жением
г (Л /4 = —с'/1п(1—mJ 4-
+ c71[l+(l//n1)ln(l-m1)], (2.45)
в котором следует считать t ^-6; эта формула охваты-
вает и уравнение (2.44), если в течение времени дей-
ствия тяги считать t = Ц.
2.2]
ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
81
Безразмерные переменные. Если исполь-
зуются безразмерные переменные, то для описания дви-
жения всех ракет с постоянной тягой достаточно одного
графика; положим
Г = /пЛ
г* == rl^c'lrh).
(2.46)
Уравнения движения принимают вид
v* = — In (1 —Г)
(2-47)
иля
г* (Г) = Г + (1— Г) In (1 — Г)
(2.48)
и
г* (f, /i) = — In (1 — /i) + ** +ln (1 — б)- (2.49)
Эти соотношения описывают движение любой раке-
ты под действием постоянной тяги; они не относятся
лишь к параметрам с' и т.
На рис. 2.1 представлен график функции г*(Д $
от аргумента t ; t\ играет роль параметра. В дальней-
шем будет использовано следующее интересное свой-
ство этой кривой. Из уравнения (2.49) сразу следует,
что
г’(1,£) = £ (2.50)
Это соотношение используется следующим образом.
Требуется определить параметр 6 точки касания на
кривой г (/ , б)- Поскольку касание есть прикоснове-
ние первого порядка, непосредственное решение этой
задачи не является легким. Между тем точку пересече-
ния касательной с прямой = 1 можно определить с
гораздо большей точностью, поскольку эти линии пере-
секаются под определенным углом, который и опреде*
ляет значение 6*
Q Дж. Лейтмз#
82
ПРЯМЫЕ МЕТОДЫ
[гл. II
2.22. Решение проблемы перехвата. Рассмотрим за-
дачу о перехвате баллистического снаряда ракетой,
тяга которой регулируется по указанному выше закону.
Рис. 2.1. График функции г* (/*, /*) аргумента /* при в роли
параметра.
Положение снаряда по отношению к ракете может быть
определено следующим образом:
где
₽ = /?—гег.
(2.51)
R — Ro Ч- Ro^
(2.52)
Ro представляет собой начальное значение вектора от-
носительного положения, Ro — начальная относительная
скорость, г определяется уравнением (2.45), а ет—еди-
ничный вектор направления вектора тяги.
2.2)
ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
83
Форма вектора р представляется для нас важной.
Вектор R задан как функция времени, не зависящая от
тяги. Вектор г = гет полностью определяется тягой и
имеет форму, инвариантную по отношению к вращению
координатной системы.
Для перехвата необходимо, чтобы р = 0, следова-
тельно,
г = R = |/?|. (2.53)
R — известная из начальных условий функция вре-
мени. Перейдем к безразмерной записи ее:
с'/т
(2.54)
и совместим на одном чертеже (рис. 2.2) график /?* как
функции и кривую рис. 2.1.
Ракета будет обладать определенным запасом топ-
лива, характеризуемым максимальным значением ti\
пусть это значение будет tim. График функции
r*(f) при 0</*<Лт
* / * ♦ \ ♦ ♦
Г , txm) ПрИ txm < t .
(2.55)
изображенный на рис. 2.2., представляет максимальную
кривую в том смысле, что он отвечает наибольшим зна-
чениям г, которые доступны для данной ракеты в раз-
личные моменты времени t. В тех случаях, когда это
нужно подчеркнуть, будем использовать для графика
(2.55) обозначение г^(/*)« или г*т.
Перехват возможен для всех таких значений времени
t<2, когда кривая /?* совпадает с кривой гт или распо-
лагается ниже; в другие моменты времени перехват
неосуществим. Этим полностью определяются моменты
возможного перехвата.
Непосредственно из графика можно найти макси-
мальное и минимальное значения времени перехвата.
Перехват при минимальном расходе топлива соот-
ветствует минимальному значению 6, поскольку
Это значение определяется общей касательной к кри-
вой г*(/*) и /?* для для любого меньшего
б*
84
ПРЯМЫЕ МЕТОДЫ
[гл. П
значения t\ кривая г (t , $ располагается ниже выпук-
лой кривой /?*.
Траектория перехвата, соответствующая минималь-
ному расходу топлива, возможна лишь для случая,
когда снаряд приближается: взаимное расстояние дол-
жно в начальный момент убывать. Если же снаряд
Рис. 2.2. График /?* в зависимости от /*, построенный в коорди-
натной сетке предыдущего рисунка.
первоначально удаляется либо если он приближается
слишком быстро, так что проходит мимо прежде, чем
может произойти перехват, то общей касательной соот-
ветствующих кривых не существует. В первом случае,
когда имеется минимум, находим, что —1п(1—Q<
<|Ло|;в последнем случае, когда минимум отсутствует,
— 1п(1 —/0> I Ло| -
Пример. В качестве примера рассмотрим ракету,
имеющую общий начальный вес 3000 фунтов; 1800 фун-
2.2]
ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
85
тов в этом количестве принадлежат топливу. Тяга ра-
кеты пусть будет 30 000 фунтов, а с' = 8000 фиг/сек,.
Тогда т = 0,04 и c'/m = 200 000. Пусть начальное поло-
жение ракеты определяется координатами (100 000; 0;
300 000), а снаряда (166 667; 66 667; 333 333), так что
Ro = 100 000. Пусть составляющие начальной скорости
ракеты равны (1157; 2157; 3919), а снаряда (—5000;
—4000; —1000), так что начальная относительная ско-
рость составляет 10 000 фт/сек.
Значение R определяется соотношением R2 =
= (66667 — 6157/)2 + (66667 — 6157/)2 4- (33333 —
— 4919 О2- Эта функция записывается в безразмерной
форме, и график ее изображается на рис. 2.2. Очевидно,
100 000
начальное расстояние становится равным ло = 200000' =
= а начальная скорость имеет значение V* =
= 10 000/8000 = 1,25 и t* = //25. Из графика видно, что
перехват возможен для 0,39 /2 0,49, причем время
действия тяги получается в пределах 0,3 С t\ 0,49.
Для случая минимального расхода топлива имеем
/1 = 0,3, /2 = 0,41 и /2 = 10,25 сек. Соответствующее на-
правление вектора тяги совпадает с направлением век-
тора
R (/2) = [66 667 — 6157 • 10,25] i +
+ [66667 — 6157 • 10,25]/+ [33 333 — 4919 • 10,25] k.
Легко получить и остальные требуемые величины.
2.23. Решение некоторых других задач. В этом раз-
деле рассматриваются решения некоторых других за-
дач, которые можно получить сходным путем. В рабо-
тах Фолкнера [22, 23] дано решение еще для ряда при-
меров; здесь мы ограничимся лишь характеристикой об-
щего типа подобных задач и укажем метод их решения.
Задача о достижении заданной точки.
Пусть требуется достичь некоторой точки х2, У2, z2 про-
странства, отправляясь из состояния покоя, при условии
86
ПРЯМЫЕ МЕТОДЫ
(гл. I!
минимального расхода топлива. Относительное переме-
щение точки равно
p = rer\ (2.56)
ось z считается направленной вверх. Для этого случая
Полагаем /?2 — A:2H-y2-|-(z24-^2/2)2; записываем это
выражение в безразмерной форме и изображаем /?* на
одном чертеже с г (/*/1)- Значения переменных, соот-
ветствующие минимальному расходу топлива, опять на-
ходятся по общей касательной к кривым г*(/*) и /?*(/*).
Первый и последний моменты времени, когда ракета
еще может достичь заданной точки, соответствуют двум
пересечениям кривых R и гт, разумеется, в предполо-
жении, что ракета в точности следует расчетному
поведению.
Если задано время t2 прибытия ракеты, то этому
отвечает единственная точка R* (fy- Соответствующая
касательная к кривой г*(/*) определяет минимальный
расход топлива, необходимый для попадания в цель
в назначенное время. Если начальные координаты и
скорость ракеты отличны от нуля, то они учитываются
в определении R. Направление силы тяги совпадает
с направлением вектора x2i + y2J + (22”Ь
Импульсное приложение силы тяги.
Нижняя граница расхода топлива определяется усло-
вием обращения т в бесконечность при конечном зна-
чении mi. Соответствующие решения различных задач
можно усмотреть непосредственно из того же графика.
Если, например, кривая дается рис. 2.3 и выбран мо-
мент перехвата /2, то нижняя граница расхода топлива
определяется при этих условиях следующим образом.
Пусть Р2 будет точкой, соответствующей требуемому
перехвату. Проведем прямую ОР2 и параллельную ей
касательную к кривой Точка касания 6о опре-
деляет нижнюю границу расхода топлива для заданного
момента перехвата. Если момент t2 не фиксирован, то
нижняя граница расхода топлива получается, очевидно,
в случае, если прямая ОР2 касается кривой /?♦ в точ-
ке Р2- Легко видеть, что для задачи о перехвате балли-
2.2]
ЭЛЕМЕНТАРНОЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ
87
стического снаряда соответствующее направление им-
пульса перпендикулярно к прямой, соединяющей ракету
и снаряд в начальный момент (см. [3], гл. VI).
Максимальная дальность на заданной
высоте. Задача достижения максимальной дальности
несколько проще: действительно, для решения ее нет
Рис. 2.3. Решения для случая импульсной тяги.
необходимости в графике, «в основном потому, что зна-
чение Л известно. Рассмотрим задачу достижения ма-
ксимальной дальности х2 на заданной высоте у2, причем
расход топлива будем считать заданным.
В этом случае можно написать
г2 = х2 + (у+^-/.
где г получается из уравнения (2.45). Если последнее
равенство переписать в виде
х-=г!-(Уг+4у.
то в правой части будем иметь известную функцию от t.
Можно найти максимальное значение х, дифференцируя
написанное выражение и решая получившееся кубиче*
ское уравнение относцтедьцо .. • . . '
88
ПРЯМЫЕ МЕТОДЫ
[гл. II
Несмотря на то, что эта задача взаимна по Майеру
с первой задачей этого раздела, решение ее облегчается
тем, что момент Л известен.
2.24. Некоторые замечания. Детальный анализ про-
стой задачи о перехвате баллистического снаряда при-
веден в докладе Фолкнера [3]. Метод решения, изложен-
ный в настоящем разделе, был дан в докладе [22] и в
недавней работе [23]. Последние исследования содер-
жат также приложения к ряду задач об определении
поведения ракеты, имеющие характер предварительных
исследований.
Если задана конечная, а не начальная масса ракеты,
то решение можно провести сходным методом. В этом
случае на одном и том же чертеже строятся две кривые.
Одна из их изображает функцию r(/i), другая пред-
ставляет огибающую семейства прямых г(/, /1), соот-
ветствующих свободному полету.
2.3. ПРОГРАММИРОВАНИЕ ОПТИМАЛЬНОЙ ТЯГИ
ВДОЛЬ ЗАДАННОЙ ТРАЕКТОРИИ
2.30. Введение и обзор результатов. Дается полное
и элементарное решение ряда задач программирования
тяги вдоль данной траектории в пространстве. Типич-
ным примером служит задача Годдарда. Задача дово-
дится до численного расчета; дается доказательство до-
статочности.
Важную роль в теории играет приведение дифферен-
циальных уравнений к канонической форме.
Предположим, что выбрана траектория «в простран-
стве и что уравнение движения вдоль этой траектории
можно записать в виде
Р dv + Q dM 4- R ds = 0, (2.57)
где Р, Q, R — функции от v, М, s (соответственно ско-
рости вдоль кривой, массы ракеты и расстояния вдоль
траектории). Разыскивается оптимальное значение не-
которой функции конечных значений и, М, s; при этом
предполагается, что задано необходимое для определен-
ности задачи число граничных условий.
2.3]
ПРОГРАММИРОВАНИЕ ТЯГИ ВДОЛЬ ТРАЕКТОРИИ
89
Вводится замена переменных, преобразующая напи-
санное выше дифференциальное уравнение к канониче-
ской форме:
S
и — и0 = ^ К (и, v, s)ds.
о
Интеграл в последнем равенстве, как видим, опреде-
ляет потерю скорости, поэтому желательно, чтобы подын-
тегральная функция была минимальна. Как показы-
вает дальнейшее исследование, из этого принципа сле-
дуют все остальные оптимальные требования. Для
каждой пары значений М, s или и, s можно найти из со-
отношения dK/dv = 0 наивыгоднейшее значение скоро-
сти v*. В общем случае, если v < v*, то приложенная
тяга должна быть максимальной, а при v > v* ракета
должна двигаться свободно. Это характеризует траек-
тории, если учесть еще требования, предъявляемые к
конечным значениям величин граничными условиями.
Например, в простых задачах типа задачи Годдарда
для достижения требуемого оптимума необходимо и до-
статочно, чтобы траёктория удовлетворяла заданным
граничным условиям и состояла самое большее из трех
отрезков следующего типа. На первом отрезке либо
v < v* и ракета развивает полную тягу, либо v > у* и
ракета свободно движется сообразно с начальными ус-
ловиями. На втором отрезке прикладывается сила тяги
для установления скорости v = и*. На третьем отрезке
топливо полностью израсходовано и ракета совершает
свободное движение со скоростью v < и*. В целом ре-
шение элементарно, и настоящий раздел носит несколь-
ко иллюстративный характер.
2.31. Приведение уравнений к канонической форме;
условие минимума. Для определенности будем рассма-
тривать частный вид уравнения движения
М dv + с dM + [Mg sin 9 4- D (s, ti)] ds/v = 0, (2.58)
в котором с обозначает скорость истекающих газов,
g — ускорение силы тяжести, которое считается по-
стоянным, 6 — угол между траекторией и горизонтальным
90
ПРЯМЫЕ МЕТОДЫ
(гл. II
направлением, a D — сила аэродинамического сопро-
тивления.
Чтобы упростить это уравнение, введем новую пере-
менную, которую определим по методу, употребляемому
при решении интегрируемых уравнений в полных диф-
ференциалах. Будем считать в нашем случае одну пе-
ременную, именно s, постоянной и решим получающееся
дифференциальное уравнение
Mdv + cdM = 0. (2.59)
Интегралом его будет U(v,M) =—v — clnM. Если
ввести u=U(v,M) в качестве новой переменной и ис-
ключить из (2.58) одну из переменных, например М, то
это последнее уравнение можно будет записать в виде
du = sin 6-f-D expV )]ds/v
(2.60)
или, короче,
du — K(u, v, s)ds. (2.61)
Это и есть каноническая форма [25] дифференциаль-
ного уравнения (2.58). Более удобна следующая инте-
гральная форма:
и — и^ =
D ( и-Х- v \т ,
-ехр(—
(2.62)
Первое слагаемое под знаком интеграла предста-
вляет потерю скорости, вызванную гравитационным по-
лем; второе выражает потерю скорости благодаря
аэродинамическим силам сопротивления. Очевидно, тре-
буется минимизировать этот интеграл, т. е. получить ма-
ксимальное значение величины —и = v + с In М.
Это требование характеризует оптимальные значения
всех величин: они получаются при минимизации с уче-
том наложенных связей.
Отметим, что дифференциальное уравнение не на-
кладывает ограничений на функцию v\ задача состоит
в том, чтобы выбрать v(s') так, чтобы реализовался
оптимальный режим.
2.3]
ПРОГРАММИРОВАНИЕ ТЯГИ ВДОЛЬ ТРАЕКТОРИИ
91
Если функция v доставляет минимум интегралу, то
она должна быть решением уравнения
# = о. (2.63)
Пусть существует решение этого уравнения, соответ*
ствующее минимуму функции Л, т. е.
/<(и, v*[u, s], $)</<(#, v, s) при s). (2.64)
Отметим также, что
#>о. (2.65)
Предположим, наконец, что
sgn = sgn _ v*[u, $]), (2.66)
где v Ф v*(ut s).
2.32. Случай максимальной дальности. В этом разделе
на частном примере демонстрируются основные резуль-
таты и метод доказательства.
Рассмотрим задачу о посылке ракеты на максималь-
ное расстояние вдоль заданного пути в пространстве с
определенным запасом топлива; все начальные условия
предполагаются известными. Для определенности поло-
жим, что начальное значение v0<y* (wq, 0).
В следующем разделе мы приведем численный метод
определения программы тяги. Предположим, что мы уже
нашли эту программу; пусть она состоит самое большее
из трех подпрограмм следующего типа:
1. На начальном участке (0, Si) s) и при-
кладывается максимальная тяга, по крайней мере пока
в ракете остается топливо.
2. На втором участке (sb s2) тяга достаточна лишь
для поддержания скорости v = v*(u, s). Этот участок
продолжается до тех пор, пока М не достигнет опреде-
ленного конечного значения Му. Он может вовсе отсут-
ствовать, если ракета вообще никогда не достигает опти-
мальной скорости v*(и, s).
3. На последнем участке (s2, sf) будет v<v*(u, s).
Этот участок длится до момента, когда v падает до
92
ПРЯМЫЕ МЕТОДЫ
[гл. II
нуля, т. е. при вертикальном полете до момента, когда
v обращается в нуль.
Теорема. Программа С*, описанная выше, обеспе-
чивает максимальное расстояние вдоль заданной кривой
и является единственной программой, обладающей этим
свойством.
Доказательство. Пусть (7*, У*, М* будут функ-
ции, связанные с С*, a U, V, М — те же величины, от-
носящиеся к другой программе тяги. Важнейшим пунк-
том доказательства будет установление неравенства
U* < U для каждого значения s, откуда будет следо-
вать, что V* V для последнего участка программы.
Доказательство ведется от противного. Пусть S бу-
дет первым значением независимой переменной, при ко-
тором U* > U; покажем, что S не может лежать ни на
одном из указанных выше участков.
Пусть S лежит на первом участке (0, Si); рассмотрим
равенство
s
U(S) — tr(S)= f [К(П, V, S) — K(U*, V*, s)\ds, (2.67)
О
которое получается из уравнения (2.62), если учесть,
что начальные значения U и U* одинаковы. Подынте-
гральную функцию можно переписать в виде
ЛГ(С7, V, s)-K(U\ V,s) + K(U*, V,s)—K(U\ s). (2.68)
На участке (0, S) справедливо неравенство
K(U, V, s)^> V, s), как это следует из уравнения
(2. 65), если учесть, что U^U*. Кроме того, по урав-
нению (2.66) У, s)>K(t7*, V*, s), поскольку
V<V* (на С* тяга максимальная) и V*(s) <u*(t/*,s).
Отсюда следует, что подынтегральная функция поло-
жительна или равна нулю во всех точках (0, S); по-
этому точка S не может лежать внутри (0, $i).
Пусть теперь S находится на втором участке (sb s2):
U(S)-U\S) = U(sJ-U\sx) +
s
+ f \K(U, V, S)~K{U*, V*, s)]ds. (2.69)
•Si
2.SJ ПРОГРАММИРОВАНИЕ ТЯГИ ВДОЛЬ ТРАЕКТОРИИ 93
Как мы только что видели, U(si) ^>£7*(si). Перепи-
шем подынтегральную функцию уравнения (2.69) в
форме (2.68). Тогда K(U, V, s) V, s) согласно
уравнению (2.65), так как на (sb S) имеет место нера-
венство U U*. Далее, разность последних двух чле-
нов в (2.68) по уравнению (2.64) положительна или
равна нулю. Отсюда получаем, что правая часть уравне-
ния (2.69) не может быть положительной и S не может
располагаться на участке (sb s2).
Предположим, наконец, что S лежит в пределах уча-
стка (s2, 5/). Можно написать
и (S) - (/* (S) = и ($2) - и* ($2) +
s
+ / [K(U, V, s)—K(U*, v*, $)] ds. (2.70)
Si
Мы видели ранее, что f/(s2) >£7*(s2). Далее, подын-
тегральная функция не может быть отрицательной ни
в какой точке промежутка, ибо, согласно уравнению
(2.65) и поскольку на (s2, S)£7i>£7*, справедливо не-
равенство K(U, У, s) /С(£7*, V, s), так что разность
первых двух членов (2.68) положительна. Кроме того,
из определения функции и = — v — In М следует, что
V* + с In V* + с In Mf V + с In М; учитывая не-
равенство найдем, что V*^> V. Отсюда со-
гласно (2.66) и неравенствам V < V* < у* (£7*, s) нахо-
дим1, что К(£7*, V, s) ?>/((£/*, V*, s). Значит, правая
часть уравнения (2.70) положительна или равна нулю
и S не лежит на участке (s2, sf).
Как показывает дальнейшее исследование, если V
отличается от V* на любом конечном интервале, то не-
равенство U* < U справедливо при еще больших значе-
ниях s, откуда следует, что на третьем участке V* > V.
В точке, где происходит остановка, для кривой сравне-
ния получается V* > V, и, таким образом, эта точка не
достигается на С*. Это завершает доказательство.
2.33. Программа счета. На рис. 2.4 представлена
программа машинного счета для только что рассмотрен-
ной задачи определения графика тяги.
Хотя время было исключено нами из рассуждений,
теперь лучше, вообще говоря, ввести его снова на
Зачисление
Av, v, As, М, vr
Яь/бираегггся
А/77=Ь
Рис. 2.4. Схема вычислений для расчета оптимальной программы движения вдоль данной траектории
при заданных начальных условиях.
£з) программирование Тягй вдоль траектории 98
случай возможности обращения v в нуль. Дело в том,
что дифференциальное уравнение (2.58) при v = 0 имеет
особенность, которая, однако, исключается, если время
взять за независимую переменную. При этом мы будем
иметь дело с уравнением движения
M^ + c^- + Mgsin6 + D(^ s) = 0. (2.71)
Программа счета. В блок I вводятся парамет-
ры, а также подпрограммы для вычисления различных
функций. Например, может быть некоторая подпро-
грамма для вычисления скорости vf, достижение которой
приравнивается к остановке, как функции от М, s. Ско-
рость v сравнивается в процессе счета с этим значе-
нием, и если v <^У/, то счет прекращается.
В блоке // вычисляется оптимальная скорость у*, а
расход топлива, необходимый для увеличения скорости
до этого значения путем наложения импульса тяги, опре-
деляется из уравнения
Д/п = (?>* — v)/c + (Mg sin G + D) М/с.
В этом уравнении т есть масса израсходованнбго
топлива, так что т + М = Мо. Уравнение дает первую
оценку Am' величины массы топлива; это значение бе-
рется в качестве первого шага. В блоке III оно сравни-
вается с максимальным количеством топлива Дттах,
которое может быть сожжено в двигателе ракеты в со-
ответствующий промежуток времени. Наименьшее из
этих количеств (Am") берется в качестве следующего
значения Дт. Оставшееся количество топлива опреде-
ляется в блоке VI и в следующем блоке сравнивается
с Дт". Наименьшее из этих количеств снова берется
равным Дан—массе топлива, израсходованного за дан-
ный период. Если на некотором шаге все топливо будет
израсходовано, то для всех последующих шагов Am = 0.
С наступлением этого момента переключатель в блоке
XI останавливает процесс определения Дт.
В блоке IX вычисляются величины Ду, у, As, 2И, у/.
В блоке X скорость у сравнивается с У/, и в случае, если
v счет прекращается.
98 ПРЯМЫЕ МЕТОДЫ [гл. п
До тех пор, пока еще остается топливо, переключа-
тель в блоке XI включен так, что выходные данные воз-
вращаются в подпрограмму для определения Дт. После
того, как все топливо будет израсходовано, положение
переключателя меняется, так что Дги полагается равным
нулю. Операция определения Дги теперь пропускается, и
процесс вычислений продолжается непосредственно в
блоке IX.
Если возможен случай, когда v > и*, что представ-
ляется вероятным на нисходящем участке траектории,
то счет должен быть продолжен.
2.34. Обсуждение. Рассмотренные нами проблемы
принадлежат к простейшим задачам вариационного ис-
числения, поскольку они связаны с единственным диф-
ференциальным уравнением. При этом уравнение Эйлера
(2.63) является конечным, а не дифференциальным. Это
же самое справедливо для всех задач, которые не со-
держат интегральных условий, так как уравнение Эйле-
ра неявным образом содержится в данном дифференци-
альном уравнении. Соотношение (2.64) представляет
собой условие Вейерштрасса.
Задача о достижении ракетой заданной высоты с
минимальным расходом топлива при заданной конечной
массе называется задачей Годдарда. Краткое доказа-
тельство существования решения этой задачи дал Га-
мель [26]; Цянь Сюэ-сэнь и Эванс [27] выполнили более
полные исследования, включая ряд расчетов. Они рас-
сматривали два дифференциальных уравнения, так как
время не было ими исключено. Подобная проблема была
исследована Лейтманом [28].
В работе Фолкнера [29] содержится простое решение
задачи вместе с доказательством достаточности и мето-
дом расчета траекторий, описанным выше. Задача Год-
дарда и задача, рассмотренная нами в этом разделе,
•взаимны в смысле Майера. Поскольку в первой из них
задаются конечные значения, расчет траектории произ-
водится в обратном направлении. Траектория, как и вы-
ше, состоит из трех участков, если ракета достигает ско-
рости в противном случае реализуются лишь первый
и третий участки. Работа содержит также перечисление
задач, решение которых сводится к квадратурам.
2.3] ПРОГРАММИРОВАНИЕ ТЯГИ ВДОЛЬ ТРАЕКТОРИИ 97
Интеграл (2.62) показывает, что каноническая пере-
менная и характеризует «потерю скорости». Очевидно,
что оптимальные значения всех величин, даже для весь-
ма сложных траекторий, получаются минимизацией этой
переменной при учете наложенных на систему связей.
Россом [30] была обнаружена эквивалентная этой кано-
ническая переменная. ’ Переменная ф, найденная им,
определяется равенством ф = ехр(—и/с). Две канониче-
ские переменные, например и, ф, функционально свя-
заны уравнением типа F(u, ф, s) = 0, поскольку обе они
получаются из одного и того же дифференциального
уравнения (2.59).
Работа Миеле [31] посвящена случаю, когда траек-
торией является прямая линия. В ней выведены некото-
рые необходимые условия, содержащие аэродинамиче-
ские величины, и с помощью теоремы Грина дано дока-
зательство достаточности для случая горизонтального
полета.
Доказательства достаточности для ряда задач, рас-
смотренных нами с помощью прямых методов, можно
получить по теореме Грина (см. гл. III настоящей кни-
ги). Именно так обстоит дело, если дифференциальное
уравнение можно записать в форме, не содержащей
явно одной из переменных; в упомянутом выше случае
горизонтального полета переменная s не входит в урав-
нение явно.
ЛИТЕРАТУРА
1. Е. A. Coddington and N. Levinson, Theory of Ordinary
Differential Equations, McGraw-Hill, New York, 1955. [Русский
перевод: Э. А. Ко д д и нгтон и Н. Левинсон, Теория обык-
новенных дифференциальных уравнений, М.—Л., 1958.]
2. О. В о 1 z a, Vorlesungen fiber Variationsrechnung, S. 574, Teubner,
Leipzig, 1909.
3. F. D. Faulkner, Homing in a vacuum with minimum fuel con-
sumption, UMM No. 18, Aeronautical Research Center, University
of Michigan, Ann Arbor, Michigan (ASTIA No. ATI 50732), Feb-
ruary 1, 1949.
4. G. A. Bliss, The use of adjoint systems in the problem of dif-
ferential corrections for trajectories, J. U. S. Artillery 51, 296—311
(1919).
7 Дж. Лейтман
98
ПРЯМЫЕ МЕТОДЫ
[гл. II
5. G. A. Bliss, Differential equations containing arbitrary functions,
Trans. Am. Math. Soc. 21, 79—92 (1920).
6. G. A. Bliss, Functions of lines in ballistics, Trans. Am. Math.
Soc. 21, 93—106 (1920).
7. G. A. Bliss, Lectures on the Calculus of Variations, Univ. Chi-
cago Press, Chicago, 1946.
8. R. C. Emerson, On maximizing an integral with a side condi-
tion, Proc. Am. Math. Soc. 5, 291—295 (1954).
9. J. V. Brea к well, The optimization of trajectories, J. Soc. Ind.
Appl. Math. 7, 215—247 (1959).
10. Д. E. О x о ц и м с к и й и Т. М. Э н е е в, Некоторые вариаци-
онные задачи, связанные с запуском искусственного спут-
ника Земли, Успехи физических наук 63, вып. 1, стр. 5—32
(1957).
11. G. Leitmann, On a class of variational problems in rocket
flight, J. Aero/Space Sci. 26, 586—591 (1959).
12. D. F. L a w d e n, Interplanetary rocket trajectories, Advances in
Space Sci. 1, 8—14 (1959).
13. J. P. LaSalle, Time optimal control systems, Proc. Natl. Acad.
Sci. U. S. 45, 573—577 (1959).
14. L. S. Pontryagin, Optirpal control processes, Automation
Express 1, 15—18, 26—30 (1959).
15. H. J. Kelley, Gradient theory of optimal flight paths, ARS
Journal 30, 947—954, 1960.
16. R. Bellman and S. E. Dreyfus, An application of dynamic
programming to the determination of optimal satellite trajecto-
ries, J. Brit. Interplanet. Soc. 17, 78—83 (1959).
17. R. Dre nick, A perturbation calculus in missile ballistics,
J. Franklin Inst. 25, 423—436 (1951).
18. H. S. T s i e n, Engineering Cybernetics, гл. 13. McGraw-Hill, New
York, 1954. [Русский перевод: Цянь Сюэ-сэнь, Техническая
кибернетика, М.—Л., 1956.]
19. J. W. Tyndall, University of Colorado Extension Course Aero
Engineering, курс лекций, The Martin Company, Denver, Colo-
rado, 1960.
20. F. D. Faulkner and E. N. Ward, Optimum interception of a
ballistic missile at moderate range, Proc. 5th Navy Sci. Sympo-
sium, pp. 27—44, Annapolis, Maryland, April 1960.
21. F. D. Faulkner, Some results from direct methods applied to
optimum rocket trajectories, Proc. 9th Intern. Astronaut. Congr.
Amsterdam, 1958, p. 694 ff, 1959.
22. F. D. Faulkner, Solution of the problem of homing in a va-
cuum with a point mass, UMM No. 19, Aeronautical Research
Center, Universitv of Michigan, Ann Arbor, Michigan (ASTIA
No. ATI 50731), February 1, 1949.
23. F. D. F a u Ikner, Complete elementary solution to some optimum
trajectory problems, ARS Journal 31, 33—39 (1961).
24. A. Cohen, Differential Equations, p. 211,- Heath, New York,
1933.
25. E. G о u r s a t, Lemons sur le probleme de Pfaff, гл. 1. Hermann &
Cie, Paris, 1922.
ЛИТЕРАТУРА
99
26. G. Нате 1, Uber eine mit dem Problem der Rakete zusammen-
hangende Aufgabe der Variationsrechnung, ZAMM 7, 51—52 (1927).
27. H. S. T s i e n and R. C. Evans, Optimum thrust programming
for a sounding rocket, Jet Propulsion 21, 99 (1951).
28. G. L e i t m a n n, A calculus of variations solution of Goddard’s
problem, Astronaut. Acta 2, 55 (1956).
29. F. D. Faulkner, The problem of Goddard and optimum thrust
programming, Proc. 3rd Ann. Meeting Am. Astronaut. Soc., New
York, December 1956, 43—51 (1957).
30. S. E. Ross, Minimality for problems in vertical and horizontal
rocket flight, Jet Propulsion 28, 55 (1958).
31. A. M i e 1 e, Minimality for arbitrarily inclined rocket trajectories,
Jet Propulsion 28, 481—483 (1958).
ГЛАВА III
ОПРЕДЕЛЕНИЕ ЭКСТРЕМУМОВ
КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
ПО ТЕОРЕМЕ ГРИНА
3.1. ВВЕДЕНИЕ
При изучении траекторий скоростных самолетов и
снарядов возник ряд новых математических проблем,
которые не охватываются традиционными аналитиче-
скими методами. Задачи такого рода связаны с опреде-
лением оптимальных режимов полета; они относятся к
области вариационного исчисления и исследуются с об-
щей точки зрения в главе IV, посвященной непрямым
методам.
Настоящая глава содержит рассмотрение частного
класса вариационных задач: мы имеем в виду линей-
ные вариационные задачи, которые отчетливо характе-
ризуются тем, что минимизируемый функционал и воз-
можные изопериметрические условия линейны относи-
тельно первой производной неизвестной функции. Это,
очевидно, упрощающее обстоятельство является, одна-
ко, причиной серьезных аналитических трудностей, по-
скольку вариационное условие Лежандра — Клебша
становится неэффективным вдоль некоторой части дуги
экстремали. Применение более строгого условия Вейер-
штрасса приводит к аналогичному результату.
По этим причинам, а также вследствие того, что ли-
нейные задачи довольно часто встречаются в динамике
полета турбореактивных, турбовинтовых, ракетных ле-
тательных аппаратов, а также аппаратов с прямоточны-
ми воздушно-реактивными двигателями (ВРД), автором
были приложены значительные усилия к их разреше-
нию, и в ряде работ [1—7] был развит, новый метод, ос-
нованный на теореме Грина о преобразовании криволи-
нейных интегралов в поверхностные. Этот подход, при-
3.2]
ЛИНЕЙНАЯ ЗАДАЧА
101
меняемый как к простым, так и к изопериметрическим
линейным задачам, иллюстрируется в следующих разде-
лах, где представлены как общая теория, так и некото-
рые технические приложения.
3.2 ЛИНЕЙНАЯ ЗАДАЧА
В этом разделе рассматривается линейный интеграл
вида
/
H=f [?(•*. У) + Ф(*. (3-1)
i
Здесь ф и ф— заданные функции переменных х и у,
обозначает производную dy/dx, а индексы inf отно-
сятся соответственно к начальной и конечной точкам.
Мы предполагаем, что
класс исследуемых дуг
содержится внутри об-
ласти, ограниченной
замкнутой кривой (см.
рис. 3.1)
е(х, у) = 0, (3.2)
и что заданные началь-
ная и конечная точки
принадлежат границе
этой области и вслед-
ствие этого коорди-
наты их удовлетворяют
соотношениям
Рис. 3.1. Класс допустимых дуг.
Фф yi) = e(xf, у?) = 0.
(3.3)
Далее, определив допустимую дугу как любой путь,
совместимый с условиями (3.2) и (3.3), формулируем
экстремальную задачу следующим образом:
В классе допустимых дуг у(х) определить такую,
которая доставляет максимум либо минимум интегра-
лу (3.1). Такая особая дуга называется экстремальной
дугой, В случае, если в некоторой точке экстремальной
102 ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ [гл. III
дуги имеет место разрыв производной, то используются
следующие определения: точка разрыва производной
называется угловой точкой; отрезки экстремальной дуги,
предшествующие этой точке и следующие за ней, назы-
ваются частичными дугами.
3.21. Фундаментальная функция. В качестве первого
шага рассмотрим два допустимых пути IPF и IQF
(рис. 3.1) и отметим преимущества и недостатки каж-
дого из них по сравнению с другим. Для этого необхо-
димо рассмотреть разность между соответствующими
линейными интегралами, а именно:
Д// = J ср rfx + ф dy — J <р dx + ф dy, (3.4)
IQF IPF
что эквивалентно интегралу по замкнутому контуру
д// = ср dx + ф dy. (3.5)
IQFPI
Если обе функции ср и ф и их частные производные
первого порядка непрерывны всюду на площади а, ог-
раниченной обеими допустимыми кривыми, то можно
применить теорему Грина о преобразовании линейных
интегралов в поверхностные. Таким образом, получается
следующий результат*):
$ + = ^)dxdy, (3.6)
IQFPI а
это соотношение может быть переписано в виде
J J св (л, y)dxdy, (3.7)
а
где со обозначает фундаментальную функцию:
______________ (3.8)
*) Преобразование происходит с положительным знаком, если
обход пути интегрирования совершается против часовой стрелки, и
с отрицательным знаком, если офход ведется цо часовой стрелке»
3.2]
ЛИНЕЙНАЯ ЗАДАЧА
103
Изучение свойств фундаментальной функции внутри
допустимой области может привести к важным заклю-
чениям относительно преимуществ или недостатков од-
ного пути интегрирования по сравнению с другим. В
связи с этим рассмотрим два типа вариационных задач:
задачи, в которых функция со повсюду сохраняет посто-
янный знак, и задачи, где функция со меняет знак внут-
ри допустимой области.
3.22. Случай постоянства знака фундаментальной
функции. Если функция co всюду в допустимой области
имеет один и тот же у
знак, то могут иметь
место три возможности:
со положительна, отри-
цательна или равна ну-
лю. Если функция по-
ложительна, то уравне-
ние (3.7) дает
ДЯ>0, (3.9)
или
HjQF > Hl PF* (3-Ю)
Точно так же лю- я
бой путь, лежащий рис. 3.2. Экстремальные дуги для
справа от IQF, приво- задач, в которых фундаментальная
дит к дальнейшему уве- функция имеет постоянный знак,
личению значения ин-
теграла, тогда как любой путь слева от IPF ведет к
уменьшению этого значения. Таким образом, приходим
к следующим выводам (рис. 3.2):
а) Интеграл (3.1) достигает максимума на пути 1BF.
который лежит на границе допустимой области и про-
ходится таким образом, что эта область всегда остается
слева.
б) Интеграл (3.1) достигает минимума на пути IAF,
который расположен на границе допустимой области и
проходится так, что область все время остается справа.
Результаты, относящиеся к случаю со < 0, совпадают
с результатами для случая со > 0, с той лишь разницей,
что максимальный путь переходит в минимальным,
104
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. Ill
и обратно. Наконец, случай, когда повсюду (о = 0, яв-
ляется вырожденным в том отношении, что интеграл
(3.1) становится не зависящим от пути интегриро-
вания.
3.23. Случай, когда знак фундаментальной функции
не является постоянным. Теперь рассмотрим более об-
щий случай, когда функция со меняет знак внутри до-
пустимой области; для простоты принято, что геометри-
Рис. 3.3. Экстремальная дуга для
задач с фундаментальной функцией
ческое место точек, где
со = 0, имеет лишь два
пересечения М и N
с граничной кривой
со = 0 (рис. 3.3). Воз-
можен ряд различных
случаев в зависимости
от положения конеч-
ных точек пути инте-
грирования относитель-
но кривой (о = 0 и зна-
ка фундаментальной
функции по обе сторо-
ны этой кривой. Систе-
матическое рассмотре-
ние всех этих случаев
довольно утомительно,
поэтому рассмотрим
непостоянного знака. применение теоремы
Грина только для сле-
дующих условий: а) фундаментальная функция положи-
тельна слева от кривой (о = 0 и отрицательна справа;
б) начальная точка расположена в области, где (о > 0,
тогда как конечная точка находится в области, где
(о < 0.
Имея в виду эти условия, рассмотрим два допусти-
мых пути IAKBF и 1CKDF, которые пересекают кри-
вую (о = О в произвольной точке К. Разность между
интегралами, взятыми по этим путям, дается соот-
ношением
Д//= J* Ч dx-\-ty dy — J ydx-\-^dy (3.11)
IAKBF ICKDF
3.2]
ЛИНЕЙНАЯ ЗАДАЧА
105
и может быть записана в следующем виде:
А//= ф срdx-1-фdy + срб/х+ф£/у. (3.12)
IAKCI KBFDK
Отметим, что контур 1AKCI проходится против часо-
вой стрелки, а контур KBFDK — по часовой стрелке;
следовательно, применение теоремы Грина приводит к
следующему результату:
J J udxdy — f f wdxdy. (3.13)
a 0
Рис. 3.4. Экстремальная дуга для
задач с фундаментальной функцией
непостоянного знака.
Здесь аир обозначают площади, охватываемые ука-
занными контурами. Поскольку фундаментальная функ-
ция положительна в об-
ласти а и отрицатель-
на в области р, раз-
ность А/7 положитель-
на, и мы получаем
Hjakbf > H;ckdf' (З-И)
При помощи почти
таких же рассужде-
ний можно показать,
что любой путь, распо-
ложенный ближе к кри-
вой (о = 0, чем путь
IAKBF, связан с увели-
чением значения ли-
нейного интеграла.
Следовательно, в пре-
деле путь IMNF, как
можно показать, реа-
лизует наибольшее зна-
чение интеграла в классе дуг, проходящих через
заданные конечные точки и пересекающих кривую со = 0
в некоторой произвольно выбранной точке К.
Следует, наконец, сравнить путь IMNF с другим пу-
тем, пересекающим линию со = 0 в произвольном коли-
честве точек. С этой целью можно, применяя снова
теорему Грина, показать, что путь IMNF реализует
106
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. Ill
максимум линейного интеграла по отношению вообще
к любому допустимому пути. Поступая аналогичным об-
разом, можно доказать, что путь INMF на рис. 3.4 доста-
вляет минимальное значение линейному интегралу.
3.24. Выводы. При исследовании экстремумов линей-
ных интегралов важно изучить поведение фундамен-
тальной функции со внутри допустимой области. Если
функция со имеет постоянный знак, то уравнение экстре-
мальной дуги имеет вид
е(х, У) = 0. (3.15)
Направление, в котором должна проходиться эта
экстремальная дуга, зависит от знака функции о и от
того, минимальное или максимальное значение требует-
ся придать интегралу. С другой стороны, если функция
со меняет знак в допустимой области, то экстремальная
дуга разрывна и составляется из частичных дуг, вдоль
которых
е(х, у) = 0, (3.16)
и частичных дуг, вдоль которых
о)(х, у) = 0. (3.17)
Способ соединения этих частичных дуг и направле-
ние их прохождения зависят от распределения знаков
функции со, граничных условий задачи и от того, мини-
мальное или максимальное значение требуется придать
интегралу.
3.3. ЛИНЕЙНАЯ ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА
Предыдущая задача претерпевает интересное видо-
изменение, когда к интегралу (3.1), экстремум которого
требуется найти, присоединяются не только условия
(3.2) и (3.3), но также и линейное изопериметрическое
условие
f
f У) + Ф1(л:, у) у'] dx = С, (3.18)
I
где epi и ф1 — известные функции переменных х и г/, а
С — заданная постоянная.
3.3]
ЛИНЕЙНАЯ ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА
107
Для любых двух допустимых путей IPF и IQF раз-
ность между линейными интегралами равна
д//= срdx + фdy. (3.19)
IQFPI
Однако благодаря изопериметрическому условию эти
пути не могут быть произвольными, но должны удовлет-
ворять соотношению
0= (j) срх dx -1- Ф1 dy. (3.20)
IQFPI
Поэтому после введения неопределенного постоянно-
го множителя Лагранжа X и составления линейной ком-
бинации уравнений (3.19) и (3.20) получаем
Д//= £ <?*dx-Wdy, (3.21)
IQFPI
где
= ? + ф* = ф + Хф1. (3.22)
Отсюда следует, что после применения теоремы Гри-
на разность линейных интегралов становится равной
д#= J J <о*(х, у, \)dxdy, (3.23)
а
где (о* обозначает расширенную фундаментальную
функцию
"•(*. У. Х)=^—$•. (3.24)
Сравнение уравнений (3.7) и (3.23) подчеркивает
существенную аналогию между обыкновенной и изопе-
риметрической задачами. Следовательно, результаты
раздела 3.24 применимы к рассматриваемой задаче при
условии, что имеются в виду следующие правила:
а) Функция со должна быть заменена расширенной
функцией со *.
б) Если уравнение со = 0 обыкновенной задачи пред-
ставляет кривую на плоскости ху, то уравнение со* = 0
108
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. Ш
изопериметрической задачи представляет семейство кри-
вых, точнее, одну кривую для каждого значения
множителя Лагранжа (рис. 3.5). Частное значение Л,
Рис. 3.5. Множество экстремальных
дуг в линейных изопериметрических
задачах.
соответствующее рассматриваемой задаче, должно быть
определено из заданных граничных условий и наложен-
ной изопериметрической связи.
3.4. ЛИНЕЙНЫЕ ЗАДАЧИ В МЕХАНИКЕ ПОЛЕТА
С точки зрения вариационного исчисления разви-
тый выше математический прием имеет довольно огра-
ниченное значение, так как он относится только к ли-
нейным задачам. С другой стороны, он весьма полезен
в механике полета ввиду того, что линейные задачи до-
вольно часто встречаются в динамике полета турбореак-
тивных, турбовинтовых и ракетных летательных аппа-
ратов, а также самолетов с прямоточными воздушно-ре-
активными двигателями.
Приведем примеры простых линейных задач, кото-
рые можно решить с помощью теоремы Грина: а) про-
грамма сжигания топлива, которая реализует экстремум
3.4]
ЛИНЕЙНЫЕ ЗАДАЧИ В МЕХАНИКЕ ПОЛЕТА
109
прироста высоты, набираемой ракетой, летящей верти-
кально в вакууме или в однородной атмосфере; б) про-
грамма сжигания топлива, доставляющая экстремум
расстояния, покрываемого ракетным летательным ап-
паратом при горизонтальном полете; в) программа сжи-
гания топлива, которая реализует экстремум дальности
полета снаряда типа воздух-воздух, не подверженного
действию подъемной силы; г) форма траектории, доста-
вляющая экстремум времени полета, количеству потре-
бляемого топлива или горизонтальной дальности полета
турбореактивного или турбовинтового самолета либо
самолета с прямоточным ВРД; д) программа управле-
ния силами сопротивления, минимизирующая количе-
ство тепла, переходящее от пограничного слоя к мате-
риалу баллистического снаряда переменной геометриче-
ской формы во время прохождения его через плотные
слои атмосферы.
Можно привести примеры аналогичных изопериме-
трических задач: а) программа сжигания топлива, реа-
лизующая экстремальный прирост высоты ракеты при
вертикальном полете в однородной атмосфере в течение
заданного времени; б) программа сжигания топлива,
доставляющая экстремум дальности горизонтального
полета ракетного летательного аппарата за данное вре-
мя; в) программа сжигания топлива, реализующая за
данное время экстремум дальности полета снаряда воз-
дух-воздух, на который не действует подъемная сила;
г) форма траектории, доставляющая экстремум гори-
зонтальной дальности полета турбореактивного или
турбовинтового самолета либо самолета с прямоточным
ВРД при заданном количестве топлива; д) программа
управления силами сопротивления, минимизирующая
количество тепла, переходящее от пограничного слоя
к материалу баллистического снаряда переменной гео-
метрической формы при прохождении им плотных
слоев атмосферы; время полета снаряда предполагается
заданным.
Из перечисленных выше задач рассмотрим подробно
задачу о ракете .ближнего действия типа воздух-воздух
и задачу о возвращении в атмосферу баллистического
снаряда переменной геометрической формы.
по
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. III
3.5. ОПТИМАЛЬНАЯ ПРОГРАММА РАСХОДА ТОПЛИВА
РАКЕТОЙ БЛИЖНЕГО ДЕЙСТВИЯ БЕЗ ПОДЪЕМНОЙ СИЛЫ
В качестве первого приложения предыдущей теории
в этом разделе рассматривается траектория полета ре-
активного снаряда типа воздух-воздух при следующих
предположениях: а) подъемная сила отсутствует; б) си-
ла сопротивления есть квадратичная функция скорости;
она представляется равенством
D = KV2, (3.25)
где К — постоянная (такое положение возникает тогда,
когда коэффициент сопротивления считается постоян-
ным, а изменения высоты полета столь малы, что атмо-
сфера может считаться однородной); в) вектор тяги ка-
сателен к траектории и величина его задается соотно-
шением
Т = с$, (3.26)
где р — расход топлива, а с — эквивалентная скорость
истечения газов из сопла ракетного двигателя, прини-
маемая постоянной; г) угол наклона траектории полета
к горизонту столь мал, что квадратом его можно пре-
небречь по сравнению с первой степенью, и д) состав-
ляющая веса вдоль касательной к траектории пренебре-
жимо мала по сравнению с составляющими вектора’тя-
ги и (или) силы аэродинамического сопротивления.
При учете этих гипотез движение снаряда воздух-
воздух описывается следующими дифференциальными
уравнениями *):
X — V = 0,
h — V7 = 0
1 m
m 4- p = 0,
*) Первые два уравнения представляют кинематические соот-
ношения в горизонтальном и вертикальном направлениях, третье и
четвертое являются динамическими уравнениями для направлений,
касательных и нормальных к траектории, а пятое есть определение
массового расхода топлива.
(3.27)
3.5]
РАСХОД ТОПЛИВА РАКЕТОЙ БЛИЖНЕГО ДЕЙСТВИЯ
111
где X обозначает расстояние по горизонтали, h — высо-
ту, т — массу, g — ускорение силы тяжести. Далее, если
массу взять за независимую переменную, то эти уравне-
ния переписываются в виде
dX ___У
dm р
dh ____ У7
dm 3 ’
dV __ KV2 с
dm m$ m
_ g
dm Ур ’
dt __ J_
dm p
(3.28)
и включают одну независимую переменную m, шесть за-
висимых переменных (X, Л, V, у, /, р) и, следовательно,
обладают одной степенью свободы*). Таким образом,
для каждой заданной системы начальных условий су-
ществует бесконечное множество физически и матема-
тически возможных траекторий, точнее, одна траектория
для каждой произвольно заданной программы расхода
топлива р(ги). Существует, однако, ограничение в вы-
боре такой программы, обусловленное тем, что массо-
вый расход топлива, который может иметь место при
полете ракеты, ограничен нижним и верхним пределами.
Если нижний предел принять равным нулю, то во всех
точках траектории полета должно соблюдаться следую-
щее неравенство:
О<р<ртах- (3.29)
Это важное неравенство существенным образом вли-
яет на решение экстремальных задач для снарядов типа
воздух-воздух в том отношении, что оно определяет как
класс допустимых кривых, так и область допустимых
траекторий снаряда.
*) Согласно определению число степеней свободы системы диф-
ференциальных уравнений есть разность между числом зависимых
переменных и числом уравнений.
112
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. III
3.51. Класс допустимых кривых. Рассмотрим ракету,
которая имеет в данный момент времени скорость V и
массу т, и пусть Р будет соответствующая ей точка на
плоскости скорость — масса (рис. 3.6). По истечении
бесконечно малого промежутка времени новая скорость
ракеты будет V' = V + dV,
новая масса т' = т + dm,
а новое положение на
плоскости скорость — масса
представится точкой Р'. Сле-
Рис. 3.6. Класс допустимых
перемещений в плоскости ско-
рость — масса.
можно. Более точно, класс
довательно, вектор РР' бу-
дет бесконечно малым сме-
щением ракеты на Vm-пло-
скости.
Как показывает третье
уравнение системы (3.28),
для каждого значения рас-
хода р существует одно бес-
конечно малое смещение.
Однако вследствие неравен-
ства (3.29) не всякое такое
смещение физически воз-
допустимых кривых ограни-
чен двумя предельными возможностями: смещением PR,
соответствующим нулевой скорости сжигания, и смеще-
нием РТ, соответствующим максимальной скорости сжи-
гания топлива двигателем.
Например, если ракета совершает свободное движе-
ние, то бесконечно малое изменение скорости отрица-
тельно, а бесконечно малое изменение массы равно ну-
лю; таким образом, смещение PR физически возможно,
тогда как смещение PZ неосуществимо. В качестве вто-
рого примера рассмотрим случай, когда мгновенная ве-
личина тяги равна силе сопротивления; при этом беско-
нечно малое изменение скорости равно нулю, а беско-
нечно малое изменение массы отрицательно; поэтому
смещение PS физически реализуемо, тогда как смеще-
ние PQ невозможно. В заключение отметим, что два
предельных смещения PR и РТ разделяют плоскость
3.5] РАСХОД ТОПЛИВА РАКЕТОЙ БЛИЖНЕГО ДЕЙСТВИЯ ИЗ
скорость — масса на две области: область Я, точки ко-
торой доступны для ракеты, и область К, которая не-
достижима из-за физических особенностей ее движения.
3.52. Область, занятая допустимыми кривыми. Рас-
смотрим ракету, которая должна быть переведена из
начального состояния Уг-, гиг- в конечное состояние V/,
mf. Заметим, что если задана программа сжигания то-
плива р(т), то третье уравнение системы (3.28) может
быть проинтегрировано разделением переменных. В
частности, если расход массы постоянен, то получает-
ся следующее решение:
1 4- V V К/$с ^Кс
- itvkwc =const’ (3-30)
которое для двух предельных случаев р = О (нулевая
скорость сжигания) и р = оо (импульсное сжигание)
приобретает соответствен-
но форму
in = const,
znexp = const.
(3.31)
Определив постоянные
интегрирования по задан-
ным начальным условиям,
можно провести (см.
рис. 3.7) две предельные
ЛИНИИ Р = О И Р = Ртах,
начинающиеся в точке /;
Рис. 3.7. Область допустимых дуг.
с другой стороны, рас-
считывая постоянные с
помощью заданных конечных условий, можно провести
две другие предельные линии р = 0 и р = ртах, которые
сходятся в точке F. Эти четыре предельные линии опре-
деляют кривую IDFCI, которая охватывает область до-
пустимых кривых, то есть область Vm-плоскости, со-
держащую все траектории, совместимые с заданными
граничными значениями скорости и массы. Ни одна
траектория, соединяющая конечные точки / и F, не
может пересечь границу этой области, не нарушая 8
8 Дж. Лейтман
114
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. Ill
неравенство (3.29), тогда как любая траектория, лежа-
щая внутри рассматриваемой области, возможна при
условии, что неравенство (3.29) для массовой скорости
удовлетворяется в каждой точке.
3.53. Определение экстремальной дальности. Исклю-
чая расход топлива из первого и третьего уравнений
системы (3.28), получим следующее дифференциальное
соотношение:
dX=^dV+^dm. (3.32)
где
= ^ = —Rv- (3-33)
Следовательно, если принять, что Хг= 0 и Xf = X,
то значение дальности выразится интегралом
/
X=f <pdV+^dm, (3.34)
I
зависящим от пути интегрирования m(V). Поэтому за-
дача об оптимальной программе сжигания формули-
руется следующим образом: среди функций m(V), при-
нимающих заданные граничные значения и совместимых
с неравенством (3.29), определить такую, которая сооб-
щает интегралу (3.34) экстремальное значение.
Благодаря ограничению расхода (3.29) класс допу-
стимых дуг ограничен областью внутри замкнутого кон-
тура IDFCI (рис. 3.7); символическое уравнение этого
контура можно записать в виде
е(У, /п) = 0. (3.35)
Далее, начальная и конечная точки искомой кривой
принадлежат указанному контуру и, следовательно,
удовлетворяют условиям
е(= е(Vf, = 0. (3.36)
Задача, выраженная уравнениями (3.34) — (3.36), ма-
тематически эквивалентна линейной задаче, образуемой
уравнениями (3.1) — (3.3); поэтому возможно примене-
ние результатов раздела 3.2.
3.5]
РАСХОД ТОПЛИВА РАКЕТОЙ БЛИЖНЕГО ДЕЙСТВИЯ 115
Итак, первым этапом решения является исследование
знака фундаментальной функции, имеющей вид
(3.37)
или, после некоторых преобразований,
(3.38)
Поскольку фундаментальная функция всюду положи-
тельна, экстремальная дуга составляется лишь из таких
частичных дуг, кото- т
рые расположены на
границе допустимой об-
ласти.
Таким образом,
приходим к следующим
выводам (рис. 3.8).
1. Кривая ICF, со-
стоящая из отрезка /С,
проходимого с макси-
мальной тягой, и от-
резка СТ, проходимого
с нулевой тягой, ми-
нимизирует значение Рис 3 8 Дуги> доставляющие экстре.
а л ж xlV« 1 *1, 1 CID JI 71IU ЦД *1С 1 L/C*
дальности (в этом мож- МуМ дальности и времени полета,
но убедиться путем
сравнения кривой ICF с произвольным допустимым пу-
тем IKF, применив теорему Грина).
2. Кривая IDF, состоящая из отрезка ID, проходи-
мого с нулевой тягой, и отрезка DF, проходимого с мак-
симальной тягой, максимизирует дальность (это можно
увидеть, сравнив путь IDF с произвольным допустимым
путем IKF и применяя теорему Грина).
3. 54. Определение экстремального времени полета.
Исключая расход топлива из третьего и пятого уравне-
ний (3.28), можно получить следующее дифференциаль-
ное уравнение:
dt = ср! d V + dm,
(3.39)
где
(3.40)
8*
116
экстремумы КРИВОЛИНЕЙНЫХ интегралов
(гл. Ill
Следовательно, приняв /< = 0 и // = /, получим выра-
жение для времени в виде криволинейного интеграла
/
t = (3.41)
I
который зависит от пути интегрирования Таким
образом, задача оптимизации программы сжигания фор-
мулируется следующим образом: среди всех функций
m(V), принимающих заданные граничные значения и
совместимых с неравенством (3.29), определить такую
функцию, которая доставляет экстремальное значение
интегралу (3.41).
Фундаментальная функция этой экстремальной за-
дачи такова:
= (3.42)
после преобразований ее можно записать в виде
“i(V,/n)=^£>0. (3.43)
Поскольку эта функция везде положительна, экстре-
мальная дуга составляется только из отрезков границы
допустимой области. Поэтому, используя те же рассу-
ждения, что и в предыдущем разделе, убедимся, что
путь ICF рис. 3.8 минимизирует время, тогда как путь
IDF соответствует максимальному времени полета.
3. 55. Определение экстремальной дальности за дан-
ное время полета. Из предыдущих результатов видно,
что программа, соответствующая максимальной дально-
сти, одновременно максимизирует время полета? Это
свойство может оказаться нежелательным, поэтому пред-
ставляет интерес исследование класса кривых, достав-
ляющих экстремум дальности при условии, что задано
либо время полета, либо конечные значения скорости
или массы топлива.
Подобная задача принадлежит к типу линейных изо-
периметрических задач и описывается теорией, развитой
в разделе 3.3. Согласно этой теории первым шагом яв-
ляется исследование распределения знаков расширенной
3.5]
РАСХОД ТОПЛИВА РАКЕТОЙ БЛИЖНЕГО ДЕЙСТВИЯ 117
фундаментальной функции внутри допустимой об-
ласти. Эта функция дается выражением
= (3.44)
где X—постоянный множитель Лагранжа й
Ф* = Ф4-ХФ1 = — ~^у2^У+^)-
(3.45)
Записав расширенную фундаментальную функцию в
форме
♦ /I/ V2 + (X4-c) V + 2Xc
(о* (К /п, X) = —Т/з » (3.46)
видим, что для заданного X
линии постоянной ско-
рости, определяемой
уравнением
V2 + (X + O V+
+2Xt? = 0. (3.47)
Величина скорости
оказывается положи-
тельной только для
X < с, поэтому фунда-
ментальная функция
отрицательна слева от
любой линии постоян-
ной скорости и положи-
тельна справа от нее
(рис. 3.9); таким обра-
она обращается в нуль на
Рис. 3.9. Распределение знаков рас-
ширенной фундаментальной функции.
зом, эта функция меняет знак в допустимой области.
Значит, экстремальная дуга составляется из частичных
дуг, расположенных на границе допустимой области, и
дуг, удовлетворяющих условию со* = 0, т. е.
а) дуг ₽ = 0,
б) дуг Р = ртах,
в) дуг V = const.
118
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. Ill
Способ соединения различных частичных дуг должен
указываться поставленными
изопериметрической связью.
Рис. 3.10. Множество дуг, доставляю-
щих экстремум дальности при задан-
ном времени полета.
Рис. 3.11. Определение множителя
Лагранжа и решение краевой задачи.
♦) Для упрощения и
ради краткости принято,
что неравенство (3.29) удо-
влетворяется всюду вдоль
дуги постоянной скорости,
определяемой уравнением (3.47). Если бы это неравенство было на-
рушено на некоторой части упомянутой дуги (это случится, если
аэродинамическое сопротивление превысит максимально возможное
значение тяги), то экстремальная дуга оказалась бы отличной от
изображенной на рис. ЗЛО.
граничными условиями и
Пример такого рода пред-
ставлен на рис. 3.10.
Совокупность экстре-
мальных дуг, соответ-
ствующих заданным
граничным значениям
скорости и массы, пред-
ставляется семейством
путей IABF, каждый
из которых характери-
зуется значением по-
стоянного множителя
Лагранжа, определяю-
щего дугу постоянной
скорости*). Таким об-
разом, вычисляя даль-
ность и время полета,
получаем следующие
функциональные зави-
симости (рис. 3.11):
Х=А(Х), )
, = В(Х). | <3-48)
Вторая из них опре-
деляет множитель Ла-
гранжа, тогда как пер-
вая дает расстояние,
покрываемое снарядом
3.6]
ТОРМОЖЕНИЕ ВОЗВРАЩАЮЩЕГОСЯ СНАРЯДА
119
за данное время полета. Это расстояние максимально,
что обнаруживается с помощью теоремы Грина из срав-
нения экстремального пути IABF с любым допустимым
путем IKF, проходимым за то же время (рис. 3.9).
3.6. ОПТИМАЛЬНАЯ ПРОГРАММА ТОРМОЖЕНИЯ
ВОЗВРАЩАЮЩЕГОСЯ БАЛЛИСТИЧЕСКОГО СНАРЯДА
ПЕРЕМЕННОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
Как еще один пример применения предыдущей тео-
рии в этом разделе рассматривается траектория возвра-
щающегося в атмосферу баллистического снаряда пере-
менной геометрической формы; предполагается, что
свойства атмосферы произвольным образом меняются
с высотой. Для простоты рассматривается вертикальное
падение снаряда, хотя результаты распространяются на
случай прямолинейного полета под любым углом с по-
мощью простого преобразования координат. Приняты
следующие гипотезы: а) Земля считается плоской и не-
вращающейся, ускорение силы тяжести постоянно;
б) траектория снаряда вертикальна, так что во всякий
момент времени подъемная сила равна нулю; в) вес
снаряда w пренебрежимо мал по сравнению с силой со-
противления воздуха; г) сила аэродинамического сопро-
тивления задается формулой
D = ±Cd?(Ji)SV\ (3.49)
где S — эффективная площадь, р — плотность воздуха,
h — высота, а коэффициент сопротивления CD в сверх-
звуковом режиме полета не зависит ни от числа Маха,
ни от числа Рейнольдса.
С учетом этих гипотез движение баллистического
снаряда описывается дифференциальными уравнениями
V== О,
gCD?(h)SV> _
2W “U’
(3.50)
120
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. III
которые можно переписать в другой форме, выбрав вы-
соту в качестве новой независимой переменной:
dt 1
dh~ V ’
dV _ CD?(h)SV
dh 2W
(3.51)
Предположим теперь, что снаряд снабжен устрой-
ствами, изменяющими его геометрическую форму (на-
пример, закрылками), так что коэффициент сопротив-
ления можно изменять во время полета. Уравнения
(3.51) содержат одну независимую переменную (Л), три
зависимые переменные (t, V, CD), что соответствует од-
ной степени свободы. Это означает, что для каждой за-
данной системы начальных условий существует беско-
нечное множество физически и математически возмож-
ных траекторий, точнее, одна траектория для каждой
произвольно заданной программы изменения CD(h). Вы-
бор этих программ, однако, ограничен, поскольку теку-
щее значение коэффициента сопротивления ограничено
нижним и верхним пределами. Таким образом, во всех
точках траектории полета должно удовлетворяться сле-
дующее неравенство:
Cd min -С CD CD max. (3.52)
Здесь нижний предел соответствует полностью убранным
закрылкам, а верхний предел — полностью введенным
закрылкам. Это неравенство оказывает серьезное влия-
ние на решение экстремальных задач для снарядов пе-
ременной геометрической формы, так как оно опреде-
ляет и класс допустимых кривых, и область допустимых
траекторий снаряда.
3.61. Класс допустимых кривых. Рассмотрим снаряд,
который в данный момент времени имеет скорость V и
находится на высоте Л; пусть Р будет соответствующей
точкой плоскости скорость—высота (рис. 3.12). Спустя
бесконечно малое время скорость снаряда примет зна-
чение V' = V + dV, высота h' = h + dh и новое положе-
ние в плоскости скорость— высота представится точкой
Р'. Таким образом, вектор РР' является бесконечно ма-
лым смещением снаряда в УЛ-плоскости.
3.6]
ТОРМОЖЕНИЕ ВОЗВРАЩАЮЩЕГОСЯ СНАРЯДА
121
Рис. 3.12. Класс допустимых пере-
мещений в плоскости скорость —
высота.
Как показывает второе из уравнений (3.51), для ка-
ждого значения коэффициента CD существует единствен-
ное бесконечно малое смещение. Из-за неравенства
(3.52), однако, не всякое смещение возможно физиче-
ски. Точнее, класс допустимых кривых ограничен двумя
предельными возможностями: смещением PR, соответ-
ствующим полностью убранным закрылкам, и смеще-
нием РТ, соответствующим полностью введенным за-
крылкам. Отсюда заключаем, что два предельных сме-
щения PR и РТ делят плоскость скорость — высота на
две области: область
Я, точки которой до-
стижимы для снаряда,
и область К, недоступ-
ную снаряду в силу фи-
зических особенностей
его движения.
3.62. Область, заня-
тая допустимыми кри-
выми. Рассмотрим сна-
ряд, который должен
быть переведен из на-
чального состояния Vi,
hi в.конечное состояние
V/, hf. Заметим, что
если программа изме-
нения сопротивления
задана, то второе из уравнений (3.51) можно проинте-
грировать разделением переменных. В частности, если
коэффициент сопротивления постоянный, то получается
следующее решение:
V ехр
sCDs
2 IT
Л
f р(Л) dh
О
= const.
(3.53)
Вычислив постоянную интегрирования при по*
мощи заданных начальных условий, можно провести
(см*, рис. 3.13) две предельные линии CD = CDmln (за-
крылки полностью убраны) и Св = СПтах (закрылки
полностью введены), начинающиеся в точке /; с другой
122 ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ [гл. Ill
стороны, вычисляя постоянную по заданным конечным
условиям, можно провести две другие предельные линии
CD = CD min и CD = CD max, которые заканчиваются в точ-
ке F. Эти четыре предельные линии образуют кривую
л IDFCI, которая охватыва-
ет область допустимых
кривых, т. е. область пло-
скости Vh, содержащую
все кривые, совместимые
j} г ’ 7 с предписанными гранич-
I ными значениями скорос-
/ / ти и высоты. Никакая
Ош»! J кривая, соединяющая гра-
/ ничные точки / и F, не
/ может пересечь границу
этой области без наруше-
------------------------.— ния ограничивающего не-
равенства (3.52). И об-
Рис. 3.13. Область допустимых дуг. ратно, всякая кривая, рас-
положенная внутри упо-
мянутой области, возможна физически, если только ус-
ловие (3.52), наложенное на коэффициент сопротивле-
ния, соблюдается в каждой ее точке.
3.63. Определение экстремальной теплопередачи.
В соответствии с инженерной практикой примем следую-
щий обобщенный закон теплопередачи при сверхзвуко-
вом полете:
H=K?XV\ (3.54)
откуда следует, что
(3.55)
где Н обозначает количество тепла, переходящее от по-
граничного слоя к некоторой определенной площади по-
верхности снаряда, К — постоянная, характерная для
данного снаряда, ахи у—безразмерные показатели
степени. Если площадь, о которой идет речь, относится
к полной обтекаемой поверхности снаряда (исключая
закрылки), то соответствующие значения этих показате-
лей равны
х= 1, у = 3.
(3.56)
3.6]
ТОРМОЖЕНИЕ ВОЗВРАЩАЮЩЕГОСЯ СНАРЯДА
123
С другой стороны, если речь идет об области, непо-
средственно примыкающей к передней части снаряда, то
показатели принимают значения
л: = 0,5, у = 3. (3.57)
Согласно уравнению (3.55) бесконечно малое прира-
щение количества тепла, передаваемого снаряду погра-
ничным слоем, записывается в виде
dH=tydh, (3.58)
где
ф = —(3.59)
Следовательно, в предположении, что Н i = 0 и
Hf = Н, полное количество тепла, переданное за время
полета, равно
/
Н= ftydh (3.60)
i
и зависит от пути интегрирования V(/i). В соответствии
с этим задача об оптимальном управлении сопротивле-
нием формулируется следующим образом: в классе
функций V(h), удовлетворяющих поставленным гранич-
ным условиям по скорости и высоте и совместимых с не-
равенством (3.52), определит^ такую функцию, которая
сообщает экстремум интегралу (3.60).
Благодаря ограничивающему неравенству (3.52)
класс допустимых кривых заключен в области внутри
замкнутого контура IDFCI рис. 3.13; уравнение этого
контура можно символически записать так:
е (У, Л) = 0. (3.61)
Далее, начальная и конечная точки принадлежат
границе этой области и, следовательно, удовлетворяют
условиям
= hf) = Q. (3.62)
Задача, выражаемая уравнениями (3.60) и (3.62),
математически эквивалентна линейной задаче, формули-
руемой уравнениями (3.1) — (3.3), поэтому в данном
случае применимы результаты раздела 3-2.
124
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. III
Первым шагом, таким образом, является исследова-
ние знака фундаментальной функции, которая опреде-
ляется соотношением
= (3.63)
Рис. 3.14. Дуги, доставляющие экстре-
мум теплопередаче и времени полета.
которое после простых преобразований принимает вид
ш = — к (у — l)pVy"2<0. (3.64)
Фундаментальная функция повсюду отрицательна,
так как у = 3, поэтому экстремальная дуга составляется
только из таких час-
тичных дуг, которые
идут вдоль границы до-
пустимой области. В
силу сказанного прихо-
дим к следующим за-
ключениям (рис. 3.14):
1. Путь ICF, состоя-
щий из дуги /С, прохо-
димой с полностью уб-
ранными закрылками,
за которой следует ду-
га CF, проходимая с
полностью введенными
закрылками, максими-
зирует теплопередачу
(в этом можно убедить-
ся, сравнивая с по-
мощью теоремы Грина путь ICF с произвольным допу-
стимым путем IKF).
2. Путь IDF, состоящий из дуги ID, проходимой с
полностью, введенными закрылками, и дуги DF, прохо-
димой с полностью убранными закрылками, минимизи-
рует теплопередачу (это обнаруживается при сравнении
пути IDF с произвольной допустимой дугой IKF с по-
мощью теоремы Грина).
3.64. Определение экстремального времени полета.
Согласно первому уравнению системы (3.51) бесконечно
малый временной интервал записывается в форме
dt = ф! dh>
(3.65)
3.6]
ТОРМОЖЕНИЕ ВОЗВРАЩАЮЩЕГОСЯ СНАРЯДА
125
где
ф. = -у. (3.66)
Поэтому, предполагая /, = 0 и // = /, найдем полное
время полета в виде линейного интеграла
/
i = (3.67)
I
который зависит от пути интегрирования V(h). В силу
сказанного задача оптимизации программы сжигания
топлива ставится следующим образом: среди функций
V(ft), принимающих заданные граничные значения и
совместимых с неравенством (3.52), определить такую
функцию, которая доставляет экстремальное значение
интегралу (3.67).
Фундаментальная функция этой экстремальной за-
дачи дается соотношением
^(V, Л)=^; (3.68)
после простых преобразований оно принимает вид
= (3.69)
Эта функция всегда положительна, поэтому экстре-
мальная дуга составляется только из таких частичных
дуг, которые находятся на границе допустимой области.
Поэтому, следуя рассуждениям предыдущего примера,
заключаем, что путь ICF (рис. 3.14) минимизирует
время, тогда как путь IDF соответствует максималь-
ному времени полета.
3.65. Определение экстремальной теплопередачи за
данное время полета. Из предыдущих результатов вид-
но, что траектория минимальной теплопередачи одновре-
менно максимизирует время. Поскольку это обстоятель-
ство может оказаться нежелательным, интересно иссле-
довать класс траекторий, доставляющих экстремальное
значение теплопередачи, для случая, когда задано либо
время полета, либо конечные значения скорости и
массы.
126
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
[гл. III
Эта задача принадлежит к типу линейных изопери-
метрических задач и решается с помощью теории, раз-
витой в разделе 3.3. Согласно принятой там схеме пер-
вым шагом в решении является исследование распреде-
ления знаков расширенной фундаментальной функции
Рис. 3.15. Распределение знаков рас-
ширенной фундаментальной функции.
внутри допустимой области. Эта функция дается фор-
мулой
Ц = ^г, (3.70)
где X — постоянный множитель Лагранжа и
ф* = ф + Хф1 = _^И'-14-у). (3.71)
Записав расширенную фундаментальную функцию
в форме
ш* = -ЛГ(у-1)рхУу-2+^-. (3.72)
видим, что для каждого данного значения X эта функ-
ция обращается в нуль вдоль линии постоянной скоро-
сти теплопередачи
= (3.73)
3.6]
ТОРМОЖЕНИЕ ВОЗВРАЩАЮЩЕГОСЯ СНАРЯДА
127
Поскольку множитель Лагранжа положителен, фун-
даментальная функция положительна слева от любой
линии постоянной скорости теплопередачи и отрицатель-
на справа от нее (рис. 3.15); таким образом, эта функ-
ция меняет знак внутри допустимой области. Следова-
тельно, экстремальная дуга составляется из частичных
дуг, проходимых вдоль границы допустимой области, и
дуг, удовлетворяющих условию со* = 0, т. е.
а) дуг CD = CDmIn;
б) дуг Ср = CD max,
в) Дуг p-*Vy = const.
Способ соединения этих дуг должен устанавливаться
из предписанных граничных условий и заданного изо-
периметрического требования. На рис. 3.16 представлен
пример такого рода. Множество экстремальных дуг, со-
ответствующих заданным конечным значениям скорости
Рис. 3.16. Множество дуг, доста-
вляющих экстремальное значение
количеству тепла, переданного телу
в течение заданного времени.
Рис. 3.17. Определение мно-
жителя Лагранжа и решение
краевой задачи.
и высоты, представляется семейством путей 1ABF, ка-
ждый из которых характеризуется значением множителя
Лагранжа, определяющего некоторую дугу постоянной
128
ЭКСТРЕМУМЫ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ [гл. П1
скорости теплопередачи*). Следовательно, вычисляя
полное переданное количество тепла и время полета,
получаем следующие функциональные зависимости
(рис. 3.17):
Я=Я(Х),
/ = /(Х),
(3.74)
из которых вторая определяет множитель Лагранжа, то-
гда как первая дает значение количества тепла, пере-
данного снаряду от пограничного слоя в течение задан-
ного промежутка времени. Это количество тепла мини-
мально, в чем можно убедиться, сравнивая с помощью
теоремы Грина экстремальный путь IABF с любым дру-
гим допустимым путем IKF, проходимым за то же
время (рис. 3.15).
ЛИТЕРАТУРА
1. A. Miele, Problem! di minimo tempo nel volo non-stazionario
degli aeroplani, Atti accad. sci. Torino, Classe sci. fis. mat. e nat.
85 (1950—1951).
2. A. Miele, General solutions of optimum problems in non-statio-
nary flight, NACA Tech. Memo No. 1388 (1955).
3. A. Miele, Optimum climbing technique for a rocket-powered air-
craft, ARS Journal 25, No. 8(1955).
4. A. Miele, Flight mechanics and variational problems of a linear
type, J. Aero/Space Sci. 25, No. 9 (1958).
5. A. Miele, Minimality for arbitrarily inclined rocket trajectories,
ARS Journal 28, No. 7 (1958).
6. A. Miele, Application of Green’s theorem to the extremizatioh of
linear integrals, Boeing Scientific Research Laboratories, Flight
Sciences Laboratory, TR No. 40 (1961).
7. A. Miele, The relation between the Green’s theorem approach
and the indirect methods for extremal problems of a linear type,
Boeing Scientific Research Laboratories, Flight Sciences Labora-
tory, TR No. 47 (1961).
♦) Для упрощения и ради краткости принято, что неравенство
(3.52) удовлетворяется всюду вдоль дуги постоянной скорости теп-
лопередачи, определенной уравнением (3.73). Если бы это неравен-
ство нарушилось вдоль некоторой части этой дуги, то способ со-
ставления экстремальной дуги отличался бы от указанного на
рис. 3.16.
ЛИТЕРАТУРА
129
ОБЩИЙ УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
A. Miele, Flight Mechanics, том 1: Theory of Flight Paths, Addi-
son-Wesley, Reading, Massachusetts, 1962. [Русский перевод:
А. Ми еле, Механика полета, т. I, изд-во «Наука», 1965 (в пе-
чати).]
A. Miele, Flight Mechanics, том 2: Theory of Optimunz Flight
Paths, Addison-Wesley, Reading, Massachusetts (подготавливает-
ся к печати).
P. Cicala and A. Miele. Generalized theory of the optimum thrust
programming for the level flight of a rocket-powered aircraft, ARS
Journal 26, No. 6 (1956).
A. Miele and C. R. C a v о t i, Generalized variational approach to
the optimum thrust programming for the vertical flight of a
rocket, часть 2, Application of Green’s theorem to the develop-
ment of sufficiency proofs for particular classes of solutions, ZFW
6, No. 4 (1958).
A. Miele and C. R. Cavoti, Variational approach to the re-entry
of a ballistic missile, часть 2, Purdue University, School of Aero-
nautical Engineering, Rept. No. A-59-3 (1959).
A. Miele, An extension of the theory of the optimum burning pro-
gram for the level flight of a rocket-powered aircraft, J. Aero/
Space Sci. 24, No. 12 (1957).
ГЛАВА IV
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
в прикладной аэродинамике
И МЕХАНИКЕ ПОЛЕТА
4.1. ВВЕДЕНИЕ
Вариационное исчисление представляет собой ветвь
анализа, занимающуюся исследованием экстремальных
задач при более общих условиях, чем в обычной теории
максимумов и минимумов. Точнее, вариационное исчис-
ление связано с разысканием максимумов и минимумов
функциональных выражений с целью определения вхо-
дящих в них функций. Неизвестным в вариационном
исчислении является, таким образом, не дискретное мно-
жество точек, а скорее последовательность или собрание
бесконечного множества точек, определяющих в сово-
купности, смотря по характеру задачи [1], кривую, по-
верхность или гиперповерхность.
Приложения вариационного исчисления относятся к
различным областям науки и техники; в качестве при-
меров можно назвать классическую геометрию, динами-
ку, оптику, теорию электромагнетизма и гидродинамику.
Что касается, в частности, авиации и теории космиче-
ских полетов, то лишь десятилетие назад вариацион-
ные методы почти не применялись в этих областях.
В последнее время, однако, вариационное исчисление
получает и здесь все более широкое распространение,
главным образом благодаря двум классам задач: в при-
кладной аэродинамике — изучению оптимальных форм
самолетов и снарядов, а в динамике полета — изучению
оптимальных траекторий самолетов, снарядов и косми-
ческих кораблей [2].
В следующих ниже разделах формулируется наибо-
лее общая задача вариационного исчисления с одной
независимой переменной — задача Больца; вслед за
4.2] ЗАДАЧА БОЛЬЦА 131
этим рассматривается частный случай задачи Больца —
задача Майера; в заключение приводится приложение
задачи Майера к некоторым техническим проблемам.
Вследствие обилия доступной литературы по этим во-
просам и невозможности систематического обозрения ее,
здесь рассмотрено только несколько типичных задач. Из
области прикладной аэродинамики излагается теория
оптимальных тел вращения в ньютоновом потоке и тео-
рия оптимальных крыльев в линеаризованном сверхзву-
ковом потоке. Далее, из области динамики полета рас*
смотрена теория оптимальных двумерных траекторий
ракетного летательного аппарата как в вакууме, так и
в сопротивляющейся среде.
4.2. ЗАДАЧА БОЛЬЦА
Задачи Больца, Майера и Лагранжа являются наи-
более общими задачами вариационного исчисления с
одной независимой переменной. Хотя они теоретиче-
ски эквивалентны в том смысле, что могут быть преоб-
разованы одна в другую заменой переменных, проще
всего изучить сначала задачу Больца и получить осталь-
ные две задачи как ее частный случай. Останавливаясь
ради простоты на случае, когда граничные условия раз-
делены, можно следующим образом формулировать за-
дачу Больца: рассмотрим семейство функций
Ук(х), k=l,...,n, (4.1)
удовлетворяющих уравнениям связи
Ул> У*) = 0, /=Ь •..,/?<п, (4.2)
которые оставляют f = п — р степеней свободы *); пред-
полагая, что эти функции должны быть совместимы с
граничными условиями **)
шг(х/> У»/) = 0> г = <7+1» s<2n + 2, ' '
*) По определению число степеней свободы системы дифферен-
циальных уравнений есть разность между числом зависимых пере-
менных и числом уравнений.
♦♦) Значок i соответствует начальной, a f — конечной точке.
9* Дж. Лейтман
132
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
определить такое семейство, которое минимизирует
функционал
xf
ф = [G (х, у*)]{ + f Н(х, yk, yft) dx. (4.4)
xi
4.21. Уравнения Эйлера — Лагранжа. Поставленную
выше задачу можно представить в простой и изящной
форме, если ввести систему переменных множителей
Лагранжа
Щх), (4.5)
и составить следующее выражение, называемое расши-
ренной функцией:
(4.6)
Как известно, экстремальная дуга (дуга, доставляю-
щая экстремум функционалу ф) должна удовлетворять
не только уравнениям (4.2), но также и уравнениям
Эйлера — Лагранжа [1—5]
d t dF \ dF
— Hr- — —— =0, £ = 1, ..., п. (4.7)
dx\dykj dyk v '
Система дифференциальных уравнений, состоящая
из уравнений связи и уравнений Эйлера — Лагранжа, со-
держит п + р уравнений и такое же число неизвестных
функций; следовательно, ее решение одновременно опре-
деляет п зависимых переменных и р множителей Ла-
гранжа. Лишь в частных случаях удается получить ана-
литическое решение этой задачи, поэтому, вообще гово-
ря, требуются приближенные методы интегрирования.
Дополнительные осложнения возникают из-за того, что
вариационные задачи, представляющие интерес для
техники, всегда оказываются краевыми, т. е. задачами,
в которых часть граничных условий задается в началь-
ной точке, а часть — в конечной. Поэтому в тех случаях,
когда невозможно получить аналитическое решение, не-
обходимо прибегать к методу проб, т. е. задаваться
недостающими начальными значениями, интегрировать
4.2]
ЗАДАЧА БОЛЬЦА
133
численно систему уравнений Эйлера — Лагранжа и урав-
нений связей и после этого определять разности между
получающимися таким путем и заданными значениями
переменных в конечной точке. Поскольку эти разности,
вообще говоря, не равны нулю, процесс следует повто-
рять несколько раз до тех пор, пока они не обратятся в
нуль, т. е. до того момента, пока не будут удовлетворе-
ны заданные условия в конечной точке; в связи с этим
уместно отметить, что были развиты аналитические при-
емы (см., например, [6]), имеющие целью ограничить
число итераций разумными пределами*).
4.22. Первый интеграл. Математическим следстви-
ем уравнений Эйлера — Лагранжа является дифферен-
циальное соотношение [1]
(4-8)
V ft=l /
Отсюда следует, что для тех задач, в которых рас-
ширенная функция явно не зависит от х, существует
следующий первый интеграл:
п
-f+№*=c- (4-9)
где С — постоянная интегрирования.
4.23. Условия в угловых точках. Существует много
вариационных задач, характеризуемых разрывными
*) Существует другая возможность — отказаться от рассмот-
ренных здесь непрямых методов и применить прямые методы,
например обсуждавшиеся Брайсоном и Денхэмом [7], а также Кел-
ли [8]. Эти методы, развитые первоначально с целью обойти труд-
ности решения краевой задачи, обладают многими вычислитель-
ными преимуществами; однако они дают лишь численное решение,
пригодное для конкретных задач. С другой стороны, непрямые ме-
тоды позволяют получить результаты общего характера, справед-
ливые для целого класса задач при условии, что могут быть най-
дены аналитические решения; более того, даже если такие решения
не удается найти, непрямые методы часто дают важную качест-
венную информацию о природе экспериментального пути, инфор-
мацию, которую нельзя получить ни одним из существующих пря-
мых методов.
134
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
решениями, т. е. такими, для которых одна или большее
число производных уь терпят разрыв в конечном числе
точек*). Эти точки называются угловыми; решение в це-
лом называется, как и ранее, экстремальной дугой, тог-
да как каждая его часть называется частичной дугой.
При появлении разрывов требуется математически обо-
снованный способ соединения различных частей
экстремальной дуги. Этот способ доставляется условия-
ми в угловых точках Эрдмана — Вейерштрасса [1]:
где знаки плюс и минус обозначают условия непосред-
ственно перед и после угловой точки соответственно.
В частном случае, когда фундаментальная функция
явно не зависит от х, уравнения (4.9) и (4.11) показы-
вают, что
(С)_ = (С)+. (4.12)
т. е. постоянная интегрирования С имеет одинаковое
значение для всех частичных дуг, составляющих экстре-
мальную дугу.
4.24. Условие трансверсальности. Система уравне-
ний, состоящая из уравнений связей и уравнений Эйле-
ра— Лагранжа, дополняется 2и+2 граничными усло-
виями. Из них s условий даются уравнениями (4.3), а
2п + 2 — <$ — условием трансверсальности [1].
(п \ л
=°- <4ЛЗ>
дУ* ) £1 дУ* J/
•) Разрывные решения имеют большое значение в технических
задачах. Действительно, хотя в природе не реализуются разрывы
в макроскопических масштабах, нередко процесс идеализации, свой-
ственный всем техническим задачам, приводит к математической
модели, вносящей разрыв в решение.
4.2]
ЗАДАЧА БОЛЬЦА
135
которое должно удовлетворяться тождественно для
всех систем бесконечно малых приращений, совмести-
мых с уравнениями (4.3). Для частного случая, когда
фундаментальная функция формально не зависит от х,
условие трансверсальности приводится к виду
dO — Cdx + ^-^-dyk
fe=l
= 0. (4.14)
4.25. Условия Лежандра — Клебша и Вейерштрасса.
После определения экстремальной дуги необходимо ис-
следовать, максимума или минимума достигает функция.
В этом отношении существенную помощь оказывают
необходимые условия Вейерштрасса и Лежандра — Клеб-
ша. Несмотря на то, что оба эти условия носят локаль-
ный характер, они различны постольку, поскольку пер-
вое из них относится к совокупности сильных, а вто-
рое— слабых вариаций. Таким образом, условие
Лежандра — Клебша есть следствие условия Вейер-
штрасса.
Аналитически условие Вейерштрасса устанавливает,
что функционал ф достигает минимума, если во всех
точках экстремальной дуги соблюдается следующее
неравенство [1]:
п
А77-2-^д^>0’ <4-15)
справедливое для всех систем сильных вариаций Дул,
совместимых с уравнениями связей (4.2). С другой сто-
роны, если рассматривать систему слабых вариаций
бул и использовать разложение Маклорена, то неравен-
ство (4.15) сводится к условию Лежандра — Клебша
п п
2 <4Л6)
л=1 /=1
которое должно удовлетворяться всеми системами сла-
бых вариаций, совместимых с уравнениями связи
136
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
(4.2), а именно:
= 7=1» ••••А (4-17)
Следует отметить, что условия Вейерштрасса и Ле-
жандра — Клебша представляют собой лишь необходи-
мые условия экстремума и что полное доказательство до-
статочности для относительного минимума требует, что-
бы было соблюдено дополнительное необходимое условие
Якоби — Майера [1]. Необходимо также заметить, что
для большинства практически интересных задач условие
Лежандра — Клебша доставляет ту же информацию,
что и условие Вейерштрасса*); более того, исследова-
ние выполнения условия Якоби — Майера произвести не-
легко. Таким образом, часто приходится основываться
лишь на условии Лежандра — Клебша, чтобы отличить
относительный минимум от относительного максимума.
Несмотря даже на то, что полученные таким путем ре-
зультаты ни в коей мере не являются полными, в боль-
шинстве случаев физические соображения вместе с
численным исследованием соседних траекторий дают
уверенность в том, что решение, полученное совместным
применением уравнений Эйлера — Лагранжа и условия
Лежандра — Клебша, доставляет относительный мини-
мум данного функционала.
4.26. Задача Майера. Задача Майера есть частный
случай задачи Больца, который представляется, когда
подынтегральная функция в (4.4) тождественно равна
нулю, т. е.
//=0. (4.18)
Для этой задачи уравнения (4.7) — (4.16) остаются
справедливыми с тем упрощением, что для любого до-
пустимого пути и, следовательно, для экстремали
F=0. (4.19)
Кроме того, число граничных условий s должно быть
меньше, чем 2п + 2.
*) Это утверждение не обязательно является верным для всех
решаемых задач [9].
4.2]
ЗАДАЧА БОЛЬЦА
137
4.27. Задача Лагранжа. Задача Лагранжа есть
частный случай задачи Больца, представляющийся, если
G = 0, (4.20)
т. е. если функционал, экстремум которого разыскивает-
ся, имеет форму интеграла. Уравнения (4.7) — (4.16)
справедливы и для этой задачи. Условие трансверсаль-
ности, в частности, упрощается в силу того, что dG = 0.
4.28. Первый пример. Как приложение предыдущей
теории рассмотрим теперь задачу об определении кри-
вой, минимизирующей расстояние между двумя задан-
ными точками. Криволинейная абсцисса s берется в ка-
честве независимой переменной, тогда как декартовы
координаты х, у, z рассматриваются как зависимые пере-
менные. Таким образом, если производную по криволи-
нейной абсциссе обозначать точкой и если семь значений
координат Si, Xi, уг-, гг-, X/, у/, Zj фиксированы, то задачу
о минимуме расстояния можно сформулировать следую-
щим образом: в классе дуг x(s), y(s), z(s), которые
удовлетворяют условию
?==х2+у2 + г2_1=о, (4.21)
а также заданным граничным условиям, найти такую,
которая минимизирует разность AG = Gf — Gh где
G = s.
Очевидно, это задача Майера с разделенными гра-
ничными условиями. Следовательно, введя множитель
Лагранжа К и написав расширенную функцию в форме
F= \ (х2+ у2 + z2 — 1), (4.22)
придадим уравнениям Эйлера — Лагранжа вид
^M=.^(Xy) = ^(Xi) = 0. (4.23)
и получим первый интеграл
2X(x2 + y2H-z2) = C, (4.24)
где С — постоянная. Согласно уравнению (4.21) этот ин«
теграл показывает, что
Х = С/2,
(4.25)
138
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
т. е. множитель Лагранжа постоянен. Более того, если
условие трансверсальности написать в виде
[(1 — С) ds + 2Х (X dx 4- у dy + z dz)\{ = 0 (4.26)
и заметить, что граничные значения координат (кроме
Sj) фиксированы, то получим следующий результат:
с=1, Х = (4.27)
Теперь перепишем уравнения Эйлера — Лагранжа в
дифференциальной форме:
х = 'у = 'z = 0. • (4.28)
Эти уравнения могут быть проинтегрированы и дают
х = У === C3s ч- ^4’ = C5S -|- С» (4.29)
т. е. параметрические уравнения прямой*). Кроме
того, полученное решение минимизирует расстояние.
Это можно доказать, применяя условие Лежандра —
Клебша **)
2Х [(8х)2 + (8у)2 + (8z)2| > 0 (4.30)
и замечая, что оно удовлетворяется, поскольку А, > 0.
4.29. Второй пример. Как другой пример рассмотрим
задачу об определении кривой наименьшей длины, кото-
рая лежит на поверхности сферы единичного радиуса и
соединяет две заданное точки. Подобно предыдущему,
криволинейная абсцисса s принята за независимую пе-
ременную, а декартовы координаты х, у, z считаются за-
висимыми переменными. Если производную по криволи-
нейной абсциссе обозначить точкой и задать значения
семи координат sit xif yi, zif Xf, yf, Zf, то задача о мини-
муме расстояния формулируется следующим образом:
♦ ) Символы Ci, .... С6 обозначают постоянные интегрирования.
* ♦) Вариации бх, б г/, бг должны быть совместимы со связью,
выражаемой уравнением (4.21).
4.2]
ЗАДАЧА БОЛЬЦА
139
среди кривых x(s), y(s), z(s), удовлетворяющих усло-
виям связи *)
ср1 = х24-у2 -]-z2 — 1 =0,
... (4.31)
cp2 = x2 + y2+z2 —1=0 7
и заданным граничным условиям, определить такую, ко-
торая минимизирует разность &G = Gf — Gi, где G = s.
Очевидно, здесь мы также имеем задачу Майера с
разделенными граничными условиями. Следовательно,
введя множители Лагранжа Хг и фундаментальную
функцию
F = \ (х2 -|- у2 + г2 — 1) + Х2 (х2 + У2 + г2 — 1), (4.32)
получим уравнения Эйлера — Лагранжа в виде
А (х^) - Хрс = А (Х2у) - Х1У = А (X2z) - \z = 0; (4.33)
отсюда, имея в виду условие трансверсальности и суще-
ствование первого интеграла, совпадающего с (4.24),
найдем, что Х2 = V2.
В качестве следующего шага продифференцируем
первое уравнение связи дважды по криволинейной
абсциссе. Простые преобразования приводят к соот-
ношению
хх + УУ +• zz +1 = 0, (4.34)
которое совместимо с уравнениями (4.33), если только
^ = -1, (4.35)
Отсюда, переписав уравнения Эйлера — Лагранжа
в форме
х/х = у/у = zfz = — 1, (4.36)
выводим, что направление нормали к сфере совпа-
дает с направлением главной нормали к кривой. Таким
♦ ) Предполагается, что центр сферы совпадает с началом ко-
ординат.
140
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
образом, рассматриваемая кривая является геодезиче-
ской на сфере и ее параметрические уравнения таковы:
х = Сг sin s + С2 cos s,
у = С3 sin s + С4 cos s,
z — C5 sin s + C6 cos s,
(4-37)
где Ci, ..., C6 обозначают постоянные интегрирования.
Заметим, что эти параметрические уравнения могут быть
удовлетворены для каждого значения криволинейной
абсциссы лишь при условии
Ci С2
С3 с4
х
У
Z
= 0.
(4.38)
5 ^6
Таким образом, геодезическая на сфере лежит в пло-
скости, проходящей через начало координат, т. е. в пло-
скости большого круга. Очевидно, существуют две дуги
большого круга, соединяющие заданные граничные точ-
ки. Хотя условие Лежандра — Клебша удовлетворяется
для каждой из этих дуг (Х2 > 0), действительный отно-
сительный минимум дается только кратчайшей из них.
Более длинная дуга соответствует решению, которое не
является ни минимумом, ни максимумом, а всего лишь
стационарно. Пример геодезической поэтому следует
считать предупреждением читателю о возможных недо-
разумениях, которые могут встретиться при использова-
нии в вариационных задачах только уравнений Эйлера
и условий Вейерштрасса и Лежандра — Клебша.
4.3 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ЗАДАЧ
В этом разделе излагается несколько математических
приемов, которые могут оказаться полезными при прак-
тическом решении вариационных задач. Во-первых, по-
казывается, что в использовании формулировок Больца,
Майера или Лагранжа нет никакого консерватизма:
всегда можно ввести некоторые вспомогательные пере-
менные, которые преобразуют задачу Лагранжа в за-
дачу Больца или Майера и наоборот. Во-вторых, отме-
4.3]
ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ЗАДАЧ
141
чено, что, хотя многие технические задачи кажутся не-
подходящими для использования любой из этих форму-
лировок, всегда можно прибегнуть к некоторому анали-
тическому приему, который сводит первоначальную за-
дачу к одной из задач, рассмотренных в предыдущем
разделе. Сделанные утверждения иллюстрируются не-
сколькими примерами.
4.31. Преобразование задачи Лагранжа в задачу
Майера. Рассмотрим задачу минимизации функционала
xf
/ F(x, у, y)dx (4.39)
Х1
в предположении, что граничные значения координат х,
у фиксированы. Эта задача принадлежит к типу Ла-
гранжа, но ее можно превратить в задачу Майера, если
ввести вспомогательную переменную z, удовлетворяю-
щую дифференциальному соотношению
z — F(x, у, у) = 0. (4.40)
Действительно, записав интеграл (4.39) в форме
ф = 2/ — zt, (4.41)
видим, что первоначально сформулированная задача
тождественна задаче нахождения среди кривых у(х),
z(x) такой, которая минимизирует разность (4.41). Эта
новая задача принадлежит к типу задач Майера.
4.32. Задачи с производными высших порядков.
В этом разделе рассматривается проблема минимизации
функционала
xf
ф= J Щх, у, у, y)dx (4.42)
xi
в предположении, что граничные значения х, у, у фикси-
рованы. Поскольку этот функционал содержит вторую
производную неизвестной функции, поставленная задача
не охватывается формулировками Больца, Майера и
Лагранжа. Ей, однако, можно придать форму задачи
142
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Лагранжа, если ввести вспомогательную переменную z,
удовлетворяющую добавочному уравнению.
ср = у—z = 0. (4.43)
Действительно, после того как интеграл (4.42) пере-
писан в форме
xf
ф== f Н(х, у, z, z)dx, (4.44)
xi
становится очевидным, что рассматриваемая задача эк-
вивалентна задаче нахождения в классе дуг у(х), z(x),
удовлетворяющих (4.43), такой, которая минимизирует
интеграл (4.44). Эта новая задача содержит только пер-
вые производные и поэтому относится к типу задач Ла-
гранжа.
4.33. Задачи без производных. Рассмотрим проблему
минимизации функционала
ф== f Щх, y)dx (4.45)
xi
и предположим, что граничные значения переменной х
фиксированы, но граничные значения у оставлены сво-
бодными. Поскольку функционал не содержит производ-
ной от неизвестной функции, соответствующее уравнение
Эйлера — Лагранжа пишется в виде
дН/ду = $. (4.46)
Более того, поскольку левая часть соотношения (4.16)
равна нулю, условие Лежандра — Клебша, казалось бы,
не дает никакой информации о максимальном или мини-
мальном характере экстремальной дуги. Можно обойти
эту кажущуюся трудность следующими способами:
а) введением вспомогательной переменной z, удовлетво-
ряющей дифференциальной связи z — у = 0, б) преоб-
разованием задачи из плоскости ху в плоскость xz и
в) использованием, того обстоятельства, что первона-
4.3]
ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ЗАДАЧ
143
чально поставленная задача тождественна задаче мини-
мизации функционала
ф= J Я(х, z)dx
xi
(4.47)
в предположении, что значения Zf оставлены свобод-
ными. Уравнение Эйлера — Лагранжа, соответствующее
этой новой задаче, пишется в форме
d
dx \d 'z I
(4.48)
и может быть проинтегрировано; получаем
~ = const, (4.49)
где постоянная интегрирования равна нулю благодаря
условию трансверсальности. Следовательно, переводя
это соотношение из плоскости xz обратно в плоскость
ху, можем снова прийти к результату, выраженному
формулой (4.46).
Условие Лежандра — Клебша приводит нас к не-
равенству
^(М2>0, (4.50)
которое после выполнения преобразования от xz-плоско-
сти обратно в плоскость ху может быть записано в сле-
дующей форме:
-^-(8У)2>О. (4.51)
Таким образом, получается правило: в любой вариа-
ционной задаче, не содержащей производных, условие
Лежандра — Клебша может доставить нужные сведения
о минимальном или максимальном характере экстре-
мальной дуги, если в этом условии вариацию производ-
ной заменить вариацией самой функциц,
144
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
4.34. Задачи, включающие неравенства. В этом раз-
деле рассматривается задача минимизации функционала
xf
ф= J F(x, у, y)dx (4.52)
xi
в предположении, что заданы граничные значения де-
картовых координат и что класс кривых сравнения под-
чинен неравенству
У >К, (4.53)
где К — заданная постоянная. Эту задачу можно свести
к математической модели, употребительной в тех слу-
чаях, когда все связи имеют форму равенств, если
ввести действительную переменную z, определяемую со-
отношением *)
<р = у— К — z2 = 0. (4.54)
Действительно, благодаря эквивалентности выраже-
ний (4.53) и (4.54) рассматриваемая задача становит-
ся тождественной задаче определения среди дуг у(х),
z(x), удовлетворяющих уравнению связи (4.54), такой
дуги, которая минимизирует интеграл (4.52).
Предыдущая задача допускает модификацию в том
случае, когда минимизируемый интеграл подчинен дву-
стороннему неравенству связи, имеющему вид
Кх <у < АГ2. (4.55)
При этом преобразование к задаче Лагранжа осу-
ществляется путем замены только что написанного не-
равенства соотношением связи в форме равенства
<P = (y-^)(/C2-y)-z2 = 0, (4.56)
в котором z является действительной переменной.
*) Другая возможность заключается в использовании разви-
того Миеле [2, 10] параметрического представления ограниченной
переменной»
4.5]
ТЕЛА ВРАЩЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ
145
4.4. ВАРИАЦИОННЫЕ МЕТОДЫ В ПРИКЛАДНОЙ
АЭРОДИНАМИКЕ
Важным приложением вариационного исчисления
является проблема изучения оптимальных форм лета-
тельных аппаратов и ступеней ракет, т. е. форм, обес-
печивающих некоторые особенно желательные аэроди-
намические характеристики, такие, как минимальное
сопротивление или максимальное отношение подъемной
силы к силе сопротивления [11, 15]. Используемые при
этом методы и получаемые результаты в большой степе-
ни зависят от класса исследуемых тел (тела вращения,
двумерные крылья, трехмерные крылья), а также от
режима теченйя (звуковой, трансзвуковой, сверхзвуко-
вой, гиперзвуковой, свободно-молекулярный). Действи-
тельно, режим течения определяет распределение коэф-
фициентов давления и вследствие этого действующие на
тело аэродинамические силы.
Литература по этому вопросу весьма обширна, и по-
этому невозможно в коротком очерке дать обзор состоя-
ния каждой затрагиваемой проблемы. Поэтому мы об-
суждаем лишь два класса задач, а именно: а) задачу
определения тела вращения, имеющего минимальное
сопротивление давления в ньютоновом потоке, и б) за-
дачу определения формы двумерного крыла, обладаю-
щего минимальным сопротивлением давления в линеа-
ризованном сверхзвуковом потоке.
4.5. ТЕЛА ВРАЩЕНИЯ, ОБЛАДАЮЩИЕ МИНИМАЛЬНЫМ
СОПРОТИВЛЕНИЕМ ДАВЛЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ
В этом разделе рассматривается задача определения
формы тела вращения, обладающего минимальным со-
противлением в ньютоновом потоке. Имея целью посте-
пенно ввести читателя в приложения общей теории,
предпошлем систематическому изложению пример, в
в котором длина и диаметр тела заданы.
4.51. Предварительный пример. Задача определения
тела вращения, имеющего минимальное сопротивление
давления, была впервые исследована Ньютоном в пред-
положении, что тангенциальная составляющая скорости
10 Дж. Лейтман
146
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
молекул, налетающих на тело, остается неизменной, то-
гда как нормальная составляющая скорости обращает-
ся в нуль. Таким образом, неупругая модель Ньютона
аппроксимирует случай гиперзвукового невязкого те-
чения; более того, если угол атаки считается малым, то
эта модель дает следующее выражение для коэффи-
циента давления [11]:
Ср = 2 sin2 6 = 2у 2/(1 + У2)- (4.57;
Здесь в обозначает угол наклона образующей тела
к его оси (см. рис. 4.1), х — координату вдоль оси,
у — радиальную координату, а у — производную dy[dx.
Это выражение упрощается до
Ср = 2у2, (4.58)
если используется приближение тонкого тела, т. е. если
считается, что
У2С1-
(4.59)
В этом разделе нами сохранена ньютонова точка зре-
ния, но, чтобы упростить рассуждения, используется при-
ближение тонкого тела. Таким образом, аэродинамиче-
ское сопротивление, испытываемое частью фюзеляжа,
4.5] ТЕЛА ВРАЩЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ Г47
заключенной между сечениями 0 и х, записывается в
•виде
D (х) = 2^7 j Сруу dx = 4itq J уу3 dx. (4.60)
о о
где q обозначает динамическое давление в свободном
потоке. Введя обозначение
a. = Dl4vq (4.61)
и дифференцируя обе части уравнения (4.60) по неза-
висимой переменной, можно прийти к соотношению
= а — у у3 = 0, (4.62)
которое необходимо для того, чтобы рассматривать
задачу о минимальном сопротивлении как задачу
Майера.
Последнее дифференциальное уравнение имеет одну
независимую переменную (х), две зависимые перемен-
ные (у, а) и, следовательно, одну степень свободы; от-
сюда вытекает, что на форму образующей тела можно
наложить некоторое оптимальное требование. Имея это
в виду и обозначив длину тела через /, диаметр через
d и приняв граничные условия
x/ = y/ = a/ = 0, = yf = d!2. (4.63)
формулируем задачу о минимальном сопротивлении
следующим образом: в классе функций г/(х), а(х),
удовлетворяющих дифференциальному уравнению
(4.62) и граничным 'условиям (4.63), найти такую си-
стему функций, которая минимизирует разность AG =
= Gf — Gi, где G = а.
Очевидно, поставленная задача есть задача Майера
с разделенными граничными условиями. Поэтому, на-
писав расширенную функцию в виде
F=X(i—уу3), (4.64)
получаем уравнения Эйлера — Лагранжа
(tf/rfx)(3Xyy2) = Xy3> х = 0, (4.65)
10*
148
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
которые допускают первый интеграл
— 2Хуу3 = С, (4.66)
где С — постоянная. Если условие трансверсальности
записать в виде
[—Cdx — ЗХуу2 dy + (X + 1) tZa]{ = 0, (4.67)
то, заметив, что конечные значения координат, за ис-
ключением ay, фиксированы, заключаем, что Ху = —1.
Отсюда следует, что второе уравнение Эйлера — Ла-
гранжа интегрируется и дает тождественно X = —1. В до-
бавление к этому после разделения переменных и даль-
нейшей интеграции первый интеграл (4.66) приводит
к следующему общему выражению для экстремальной
дуги:
у = (Схх + С^. (4.68)
Здесь Ci, С2 — соответствующие постоянные. Если вы-
разить эти постоянные с помощью заданных граничных
условий и ввести безразмерные координаты
$ = x/Z, vj = 2y/rf, (4.69)
то получаем формулу
= (4.70)
которая означает, что образующая тела вращения,
имеющего минимальное сопротивление для данного
диаметра и данной длины, есть парабола степени 3/4.
Этот результат эмпирически был найден Эггерсом и др.
[11], которые использовали точное выражение (4.57) ко-
эффициента давления, интегрировали уравнение для
оптимальной формы в параметрическом виде и графиче-
ским путем обнаружили, что разность между их реше-
нием и параболой степени 3/4 пренебрежимо мала.
В действительности только что проведенный анализ по-
казывает, что парабола степени 3/4 представляет не эм-
пирический, а скорее аналитический оптимум: в самом
деле, она является решением уравнений Эйлера — Ла-
гранжа для тонкого тела. В заключение этого раздела
уместно сделать следующие замечания:
4.5]
ТЕЛА ВРАЩЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ
149
а) Условие Лежандра — Клебша может быть напи-
сано в форме
6уу(8у)2>0 (4.71)
и, следовательно, удовлетворяется в каждой точке экс-
тремальной дуги.
б) Если т = d/l обозначает относительную толщину,
а т) — производную dv\ld^ то коэффициент сопротивле-
ния оптимального тела вращения дается формулой
С» = ^ = '2 f = (4-72)
О
и, таким образом, пропорционален квадрату относитель-
ной толщины.
в) Для тела вращения, описываемого параболой сте-
пени 3/4, производная у становится бесконечно большой
при х = 0, поэтому приближение тонкого тела оказы-
вается локально несправедливым в непосредственной
близости от носка. В дальнейшем будем называть эту
область критической; пусть критическая область опре-
деляется неравенством у т. В этом предположении
можно показать, что площадь критической области со-
ставляет менее 3% общей площади поперечного сече-
ния, тогда как соответствующее сопротивление состав-
ляет менее 2% полного сопротивления. Поэтому форма
образующей, полученная в приближении тонкого тела,
весьма близка к форме, получающейся с помощью точ-
ного ньютонова выражения для коэффициента давления.
г) Хотя результат, выраженный уравнением (4.70),
был получен для ньютонова режима течения, он спра-
ведлив также для режима свободно-молекулярного те-
чения, если принят закон зеркального отражения при
столкновениях. Это имеет место благодаря тому, что
коэффициент давления в свободно-молекулярном потоке
пропорционален тогда (удвоенному) коэффициенту да-
вления в ньютоновом потоке; отсюда следует, что ура-
внение экстремальной дуги остается неизменным.
4.52. Более общая задача. Обобщение предыдущей
задачи возникает в случае, когда тело вращения, имеющее
минимальное сопротивление, должно быть определено
150
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
при некоторых добавочных условиях, накладываемых
на обтекаемую поверхность и (или) на объем. Эта
новая задача принадлежит к изопериметрическому ти-
пу, но с помощью описываемого ниже приема ее мож-
но привести к задаче Майера.
Прежде всего, выражения для силы сопротивления,
площади обтекаемой поверхности и объема той части
тела, которая заключена между сечениями 0 и х, запи-
сываются в форме *)
X XX
D (х) — faq J уу3 dx, S(x) = 2tt J* у dx, У (x) = it J у2 dx.
0 0 0
(4.73)
Вводятся обозначения:
а = D/A^q, Р = SI2-K, 7 = У/тг. (4.74)
Наконец, продифференцировав обе части уравнений
(4.73) по независимой переменной, приходим к диффе-
ренциальным соотношениям
<р! = а — уу3 = 0,
— У = °>
Тз = 7 —у2 =0,
(4-75)
необходимым для трактовки задачи о минимальном со-
противлении как задачи Майера.
Написанная система дифференциальных уравнений
содержит одну независимую переменную (х), четыре за-
висимые переменные (у, а, р, 7) и обладает одной сте-
пенью свободы; поэтому на профиль тела может быть
наложено некоторое оптимальное требование. Имея это
в виду и приняв, что Xi = у, = at = pi = 74= 0 и что за-
даны некоторые, но не все, конечные значения коорди-
нат, можно следующим образом сформулировать задачу
о минимальном сопротивлении: в классе функций у(х),
а(х), р(х), у(х), совместимых с дифференциальными
*) Выражения для сопротивления и обтекаемой площади со-
гласуются с приближением тонкого тела (4.59).
4.5)
ТЕЛА ВРАЩЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ
151
соотношениями (4.75) и заданными граничными усло-
виями, найти такую систему функций, которая миними-
зирует разность &G = Gf — Git где G = а.
Введя три множителя Лагранжа и записав расши-
ренную функцию в виде
F = (« ~ У?) + М₽ ~ У) + Мт - У2)» (4-76)
найдем, что экстремальная дуга удовлетворяет уравне-
ниям Эйлера — Лагранжа
^(ЗХ1уЯ = Х1;з+х2 + 2Х3у,
Xj = Х2 = Х3 = 0.
Таким образом, множители Лагранжа постоянны, что
логически вытекает из существенно изопериметрического
характера задачи; более того, поскольку фундаменталь-
ная функция не зависит от х явно, имеет место следую-
щий первый интеграл:
-2Х1УуЗ + х2у + Х3у2 = С. (4.78)
Здесь С — постоянная. Условие трансверсальности за-
писывается в форме
[— С dx — ЗХ1Уу2 dy + (Xj + 1) da + Х2 W + хз = 0.
(4-79)
Это условие вместе со вторым уравнением Эйлера —
Лагранжа показывает, что для задачи о минимальном
сопротивления Xi = —1.
Условие Лежандра — Клебша поэтому выражается,
как и прежде, неравенством (4.71) и удовлетворяется
постольку, поскольку образующая тела вращения тако-
ва, что у 0.
Предыдущие рассуждения носят общий характер; эк-
стремальные дуги для нескольких частных случаев, т. е.
для различных граничных условий, представлены на
рис. 4.2.
Случай, когда заданы диаметр и длина
тела. Если диаметр и длина тела заданы, тогда как об-
текаемая площадь и объем не фиксированы, то условие
152
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
(гл. IV
трансверсальности и уравнения Эйлера показывают, что
повсюду
Х1 = —1, Х2 = Х3 = 0. (4.80)
После разделения переменных и интегрирования прихо-
дим, с помощью первого интеграла и соответствующих
граничных условий, снова к результату, выраженному
формулой (4.70).
Рис. 4.2. Тела вращения, имеющие минимальное сопро-
тивление давления в ньютоновом потоке.
Случай, когда заданы диаметр и обте-
каемая площадь. Если заданы значения диаметра
и обтекаемой площади, а длина и объем не фиксируются,
то условие трансверсальности и уравнения Эйлера при-
водят к соотношениям
Х1 = — 1, Х3 = С = 0, (4.81)
выполняющимся повсюду. Поэтому, переписав первый
интеграл (4.78) в виде
2уз + х2 = 0> (4.82)
4.5]
ТЕЛА ВРАЩЕНИЯ В НЬЮТОНОВОМ ПОТОКЕ
153
получаем следующее общее решение:
у = С1х + С2. (4.83)
Здесь Сь С2— постоянные. Учитывая поставленные
граничные условия, получим соотношение
4 = 1, (4.84)
которое означает, что тело вращения заданного диамет-
ра и с заданной площадью обтекаемой поверхности, об-
ладающее минимальным сопротивлением, представляет
собой конус.
Относительная толщина конуса равна
(4-85)
а соответствующий коэффициент сопротивления
Сп = т2/2. (4.86)
Случай, когда заданы диаметр и объем
тела. Если заданы диаметр профиля и его объем, а
длина и площадь обтекаемой поверхности не заданы,
то условие трансверсальности и уравнение Эйлера —
Лагранжа приводят к формулам
Х1 = —1, Х2 = С = 0, (4.87)
справедливым во всей области. Поэтому интеграл (4.78)
можно переписать в следующей форме:
2уЗ-^хзу = 0/ (4.88)
которая после интегрирования показывает, что
у = (С1х + С2)’/\ (4.89)
где С], С2— постоянные. В случае, если поставлены
соответствующие граничные условия, получаем
^ = f’. (4.90)
Это значит, что образующая тела вращения, имеющего
минимальное сопротивление для заданных диаметра и
154
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
(4-91)
равен
(4.92)
объема, является параболой степени 3/2. Относительная
толщина тела вращения дается формулой
л d3
т —Тб V(0 ’
а соответствующий коэффициент сопротивления
CD = 27т2/32.
4.6. КРЫЛЬЯ МИНИМАЛЬНОГО СОПРОТИВЛЕНИЯ
ДАВЛЕНИЯ В ЛИНЕАРИЗОВАННОМ СВЕРХЗВУКОВОМ
ПОТОКЕ
Задача определения двумерных профилей крыльев,
обладающих минимальным сопротивлением давления в
сверхзвуковом потоке, привлекла к себе в последние
годы значительное внимание. Следует особо отметить
работу Другге [12], связанную с линеаризованной тео-
рией Аккерета, а также более общее рассмотрение Чеп-
мена [13], которое может быть применено как в линеари-
зованной теории гиперзвукового течения, так и в зада-
чах с ударными волнами. Для простоты здесь рассмат-
ривается линеаризованная теория, и коэффициент давле-
ния для сверхзвукового симметричного двумерного про-
филя без подъемной силы в невязком, нетеплопровод-
ном, совершенном газе дается в форме
Ср = 2у//М2^Т, (4.93)
где М—число Маха свободного потока, х — координата
вдоль хорды, у — ордината точки верхней половины про-
филя (рис. 4.3). Аэродинамическое сопротивление на
единицу длины, испытываемое частью профиля, находя-
щейся между сечениями 0, х, дается формулой
X X
D (х) = 2q f Сру dx = г ? dx. (4.94)
6 'о
Далее, если ввести обозначение
а = (£>/М2—1)/4^,
(4.95)
4.6] КРЫЛЬЯ МИНИМАЛЬНОГО СОПРОТИВЛЕНИЯ ДАВЛЕНИЯ 155
то получается следующее дифференциальное уравнение
связи:
<Pj = а — у2 = 0. (4.96)
В дальнейшем важную роль играет площадь, ограни-
ченная контуром профиля, а также моменты инерции
контура и площади профиля относительно оси х. Для
Рис. 4.3. Система координат для описания двумерного крыла.
части профиля, заключенной между сечениями 0, х, эти
величины определяются формулами
XX X
S(x) = 2 J*ydx, Jc(x) = 2 y2dx, 4W = y J*y3dx,
о 6 о
(4-97)
так что, введя обозначения:
₽ = <S/2, 7 = 4/2, е = 34/2, (4.98)
получаем следующие дифференциальные
связей:
< р2 = 0 —у =0,
< Рз = 7—у2 = б, •
< р4 = е — у3 = 0.
уравнения
(4.99)
Система дифференциальных уравнений (4.96) и
(4.99) содержит одну независимую переменную (х), пять
зависимых переменных (у, а, 0, 7, е) и обладает одной
степенью свободы; на форму профиля, таким образом,
156
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
(4.101)
может быть наложено некоторое оптимальное требова-
ние. Поэтому, ПОЛОЖИВ Xi = уг = tti = ₽г = Ъ = Ьг = 0,
xf = I, У1 = 0, а также считая конечные значения части
переменных (не всех) известными, можно следующим
образом сформулировать задачу о минимальном сопро-
тивлении: в классе функций у(х), а(х), р(х), т(х), е(х),
удовлетворяющих уравнениям (4.96) и (4.99) и задан-
ным граничным условиям, найти такую систему функций,
которая минимизирует разность \G = Gf— Gi, где G = а.
Введя четыре множителя Лагранжа и записав рас-
ширенную функцию в форме
F=X1(a-y2) + X2(p-y) + k3(i-y2) + X4(e-y3), (4.100)
найдем, что экстремаль удовлетворяет уравнениям Эй-
лера-Лагранжа
^(2Х1у) = Х2 + 2Х3у + ЗХ4у2,
Xj == Х2 = Х3 = Х4 = 0.
Отсюда видно, что множители Лагранжа постоян-
ны— результат, указывающий на существенную изопе-
риметричность задачи; более того, поскольку фундамен-
тальная функция явно не зависит от х, можно написать
следующий первый интеграл:
- 2 + Х2у + Х3у2 + х4у з = С, (4. j 02)
в котором С — постоянная. Кроме того, условие транс-
версальности дается соотношением
[—С dx—2Xjy dy —|- (Xj —|— 1) da —X2 d$ -|- X3 d*[ —X4 ds]^^= 0.
(4.103)
Это условие и второе уравнение Эйлера — Лагранжа по-
казывают, что в задаче о минимальном сопротивлении
всегда Xi = —1. Следовательно, условие Лежандра —
Клебша приобретает вид
2(8у)2>0 (4.104)
и поэтому удовлетворяется любой формой контура, со-
вместимой с уравнениями связей и уравнениями Эйле-
ра-Лагранжа.
4.6] КРЫЛЬЯ МИНИМАЛЬНОГО СОПРОТИВЛЕНИЯ ДАВЛЕНИЯ 157
Изложенное выше представляет собой общее рас-
смотрение вопроса; для нескольких частных случаев,
именно для различных типов граничных условий, были
произведены расчеты экстремалей. Их результаты пред-
ставлены на рис. 4,4.
Рис. 4.4. Крылья минимального сопротивления давления
в линеаризованном сверхзвуковом потоке.
4.61. Случай заданной площади поперечного сечения
профиля. Если площадь профиля задана*), а момент ее
инерции, так же как и момент инерции контура, не фи-
ксирован, то условие трансверсальности и уравнение Эй-
лера— Лагранжа приведут к формулам
•X1 = — 1, Х3 = Х4 = 0. (4.105)
Первое уравнение Эйлера — Лагранжа принимает,
следовательно, вид
у = К (4.106)
*) Задание площади профиля эквивалентно заданию жесткости
тонкостенной оболочки по отношению к кручению.
158
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
(где К — отрицательная постоянная) и допускает сле-
дующий общий интеграл:
у = у^2+С1х + С2, (4.107)
где Ci, С2— постоянные. Если выразить эти постоянные
с помощью заданных граничных условий и заметить, что
Cj = —Kl/2, С2 = 0, а К = —4t/l2 (где t обозначает ма-
ксимальную толщину), а также ввести безразмерные ко-
ординаты £ = х/l, т) = 2y/t, то получается формула
т) = 4? (1—5), (4.108)
которая означает, что в приближении тонкого тела
оптимальным профилем является круговой. Относитель-
ная толщина такого профиля равна
т = /// = |$(/)//2, (4.109)
а соответствующий коэффициент сопротивления
D ql /М2—1 •/ 3 /М2 — 1 V ’
где т) обозначает производную t/rj/dg.
4.62. Случай заданного момента инерции контура.
Если момент инерции контура задан *) и площадь про-
филя и момент его инерции не фиксированы, то условие
трансверсальности и уравнения Эйлера — Лагранжа
дают
Х1 = —1, Xj = X4 = 0. (4.111)
Отсюда следует, что первое уравнение Эйлера — Лагран-
жа принимает вид
у + Ку=0 (4.112)
(где К — положительная постоянная) и допускает об-
щий интеграл
y = C1sin(/^x)+C2cos(/^x), (4.113)
♦) Задание момента инерции контура эквивалентно заданию из-
гибной жесткости тонкостенной оболочки.
4.6] КРЫЛЬЯ МИНИМАЛЬНОГО СОПРОТИВЛЕНИЯ ДАВЛЕНИЯ 159
где С2 — постоянные. Если выразить эти постоянные
через заданные граничные условия, то, заметив, что
Ci = //2, С2 = 0 и К = (и//)2, получаем формулу
7)==sin^, (4.114)
которая означает, что оптимальный профиль имеет фор-
му синусоиды. Относительная толщина такого профиля
равна
1 = 2/77^, (4.115)
а соответствующий коэффициент сопротивления
4.63. Случай заданного момента инерции попереч-
ного сечения профиля. Если момент инерции площади
профиля задан*), а собственно площадь и момент инер-
ции контура не фиксированы, то условие трансверсаль-
ности и уравнение Эйлера — Лагранжа приводят к ра-
венствам
Х1 = —1, Х2 = Х3 = 0, (4.117)
справедливым повсюду. Первое уравнение Эйлера —
Лагранжа вследствие этого принимает вид
у + ду = 0 (4.118)
(где К — положительная постоянная) и допускает пер-
вый интеграл
4?+!^ = ^, (4.119)
в котором Ci = КР/24— другая положительная постоян-
ная. После разделения переменных и интегрирования
приходим к формуле
_1Ji - 1
— 2 г + Fh>(0),4 Г
(4.120)
♦) Задание момента инерции площади профиля эквивалентно
заданию жесткости твердой конструкции по отношению к изгибу
или кручению.
160
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
(гл. IV
где верхний знак относится к первой половине профиля,
а нижний — ко второй, a F обозначает неполный эллип-
тический интеграл первого рода; его аргумент <р(т|) и
параметр k определяются соотношениями
/З — 1 -л
<Р (т;) = arccos .
У 34-1 — т)
(4.120а)
Относительная толщина такого профиля дается вы-
ражением [12]
т = '|ХбО77?‘, (4.121)
а соответствующий коэффициент сопротивления равен
CD = бкГ2 (4/3) Т2/3 Г2 (11/6) /М2^! =
= 4,72т2//М2 — 1. (4.122)
где Г(х) обозначает гамма-функцию аргумента х.
4.7. ВАРИАЦИОННЫЕ МЕТОДЫ В МЕХАНИКЕ ПОЛЕТА
Вариационное исчисление находит еще одно важное
приложение в изучении оптимальных траекторий само-
летов, управляемых снарядов и космических кораблей,
т. е. таких траекторий, которым свойственны определен-
ные особенно желательные характеристики, например
максимальная дальность, минимальный расход топлива
или минимальная передача тепла. Применения эти отно-
сятся к самому последнему времени, хотя небезынтерес-
но отметить, что Годдард [16] в работе, опубликованной
почти 40 лет назад, оценивал вариационное исчисление
как важное средство исследования полета ракет. Гамель
[17], с другой стороны, более 30 лет назад сформулиро-
вал задачу оптимального сжигания топлива при верти-
кальном полете.
Если не считать этих спорадических попыток, то ока-
зывается, что потребность в совершенно новом подходе
4.7]
ВАРИАЦИОННЫЕ МЕТОДЫ В МЕХАНИКЕ ПОЛЁТА
161
к задаче оптимизации полета летательных аппаратов
была осознана в Германии только во время второй ми-
ровой войны; в частности, Липпиш [18] исследовал во-
прос о наиболее рациональном взлете реактивного са-
молета и пролил свет на новый класс задач механики
полета. После второй мировой войны большой интерес
вызвала задача об оптимальном взлете турбореактивно-
го самолета; эта задача в сильно упрощенной форме
была исследована Лашем [19] и Миеле [20] методами,
отличными от непрямых методов вариационного исчис-
ления.
Немногим позднее благодаря работам Чикала [21,22],
Гарфинкеля [23] и Хестенса [24] о задачах Больца, Майе-
ра и.Лагранжа стала возможной строгая формулировка
задач об оптимальных траекториях полета. Вслед за
этим Брекуэлл [25], Фрид [26], Лоуден [27, 28], Лейтман
[29, 30] и Миеле [31, 32] дали общую теорию задач этого
рода. Следует отметить, что хотя непрямые методы ва-
риационного исчисления имеют весьма большое значение
для решения экстремальных задач, в последние годы
был разработан ряд других методов оптимизации, из ко-
торых особо упомянем метод динамического программи-
рования Веллмана [33], теорию градиентов Келли [8] и
теорию Миеле оптимизации линейных интегралов с по-
мощью теоремы Грина [34—36]. Нужно также отметить,
что в предельном случае полета с пренебрежимо малым
ускорением вариационное исчисление и обычная теория
максимумов и минимумов приводят к одинаковым ре-
зультатам [37]; следовательно, применение множителей
Лагранжа позволяет в значительной степени упростить
решение задачи об оптимизации полета с почти посто-
янной скоростью [38].
Поскольку литература по этому вопросу весьма об-
ширна, в кратком обзоре не следует детально анализи-
ровать состояние всякой затрагиваемой проблемы. По-
этому здесь будут обсуждены только два класса задач,
а именно: а) проблема определения программы опти-
мальной тяги для полета в вакууме в постоянном грави-
тационном поле и б) определение оптимальной про-
граммы тяги для полета в сопротивляющейся среде
в постоянном гравитационном поле. За исключением
11 Дж. Лейтман
1'62
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. tV
некоторого числа предварительных примеров, в изложе-
нии подчеркиваются технические выводы общего харак-
тера, относящиеся к необходимым условиям экстремума.
Исключены такие детали, как разрывы непрерывности,
обусловленные переходами с одного режима работы на
другой, или методы решения граничных задач специаль-
ного вида. За этими вопросами, так же как и за рас-
смотрением проблем полета в неоднородном (например
центральном) силовом поле, читатель отсылается к не-
прерывно растущей специальной литературе (см. спи-
сок в конце главы).
4.8. ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА РАКЕТЫ
В ВАКУУМЕ
В этом разделе рассматривается задача определения
оптимальных траекторий полета ракеты в вакууме.
С целью постепенного ознакомления читателя с прило-
жением теории мы предпосылаем общему изложению
предварительный пример, относящийся к вертикальному
полету.
4.81. Предварительный пример. В последние годы
большое внимание привлекла задача определения опти-
мальных программ сжигания топлива в ракетах при
вертикальном полете. Вслед за исходными работами
[17] и [39] несколько типов граничных задач было рас-
смотрено Лейтманом [40—43] и Миеле [44—47]. Ука-
занные работы содержат исследование воздействия
аэродинамических сил; мы рассматриваем предельный
случай, когда эти силы пренебрежимо малы, так что ра-
кета движется лишь под совместным влиянием силы тя-
ги и веса. Более точно, приняты следующие предположе-
ния: а) Земля считается плоской, а ускорение силы тя-
жести — постоянным; б) полет происходит в вакууме;
в) траектория полета вертикальна; г) вектор тяги
направлен по касательной к траектории; д) эквивалент-
ная скорость истечения газов из сопла ракеты постоян-
на; е) двигатель может работать при значениях массо-
вого расхода, лежащих между верхним и нижним пре-
делами. В этих предположениях движение ракеты
4.8] ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ 163
описывается следующими дифференциальными уравне-
ниями:
^ = h — V = 0,
?2^^+g-4=0.
(4.123)
Фз = пг + р = 0.
Здесь h — высота, V—скорость, т — масса, g — ускоре-
ние силы тяжести, с — эквивалентная скорость истече-
ния и р—массовый расход топлива. Точка обозначает
производную по времени t. Согласно предположению
е) массовый расход должен удовлетворять неравенству
связи
0<₽ <₽тах, (4.124)
которое согласно рассуждениям раздела 4.34 может
быть заменено равенством
<Р4^₽(₽тах-?)-«2 = 0, (4.125)
где а — вещественная переменная. Благодаря этому но-
вому уравнению вариационная задача со связью в фор-
ме неравенства сводится к математической модели, ис-
пользуемой при решении задач, в которых все связи
представлены в форме равенств.
Система, составленная из уравнений (4.123) и
(4.125), содержит одну независимую переменную (/),
пять зависимых переменных (А, V, /и, 0, а) и обладает
одной степенью свободы; отсюда следует, что программа
сжигания 0(0 может быть подчинена некоторому опти-
мальному требованию. Имея это в виду и поставив гра-
ничные условия:
—0; Vit mi заданы; Vp tnf заданы, (4.126)
формулируем следующую задачу о максимально дости-
жимой высоте ракеты: в классе функций h(t), V(t),m(t),
0(0, а(0» удовлетворяющих уравнениям (4.123) и (4.125)
и граничным условиям (4.126), найти такую систему
функций, которая минимизирует*) разность AG =>
= Gf — Gi, где G = —А.
*) Напоминаем, что задача максимизации АЛ идентична задаче
минимизации —АЛ. х'
11*
164
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Введя множители Лагранжа и записав расширенную
функцию в форме
/=-=МЛ-Ю+х2(у+£—|)+
+ *3 Й + ?) + *4 IP (Ртах ~ Р) ~ «’Ь (4-127)
найдем, что экстремаль удовлетворяет уравнениям Эйле-
ра— Лагранжа:
Xj = О, Х2 =—Xj, Х3 —X2(cp/m2),
O = -K+X4(pmai-2₽),
О = Х4а,
(4.128)
в которых, по определению,
ДГ=Х2(с//п) —Х3. (4.129)
Отсюда следует, что множитель Лагранжа Xi постоя-
нен; более того, поскольку расширенная функция явно
не зависит от времени, получаем следующий первый ин-
теграл:
\V — X2g + tfp = C, (4.130)
где С — постоянная. Кроме того, условие трансверсаль-
ности записывается в виде
[— С dt + (Xj — 1) dh. + х2 d У + х3 dm}'=0, (4.131)
откуда
Х1=1, С = 0. (4.132)
Наконец, дифференцируя обе части (4.129) по вре-
мени и комбинируя результат с условием трансверсаль-
ности и уравнениями Эйлера — Лагранжа, найдем, что
вдоль экстремальной дуги
K= — dm. (4.133)
Множество частичных дуг. Как показы-
вает пятое уравнение Эйлера— Лагранжа, экстремаль
4.8]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ
165
задачи разрывна и составляется из частичных дуг, удо-
влетворяющих одному из условий
а = 0 или Х4 = 0. (4.134)
Вдоль дуг а = 0 массовый расход может принимать'
одно из следующих постоянных значений:
р = 0 либо р = ртах. (4.135)
С другой стороны, вдоль дуги Х4 = 0, согласно чет-
вертому уравнению Эйлера — Лагранжа,
tf=0, К=0. (4.136)
Этот результат несовместим с уравнением (4.133);
поэтому дуги, вдоль которой Х4 = 0, не существует,
т. е. не существует дуги, которая проходится при пере-
менной тяге [44]. Таким образом, множество экстрема-
лей состоит лишь из двух типов частичных дуг, именно
дуг свободного движения и дуг, проходимых с макси-
мальным расходом топлива.
Последовательности частичных дуг.
Следующим шагом является определение той последо-
вательности, в которой частичные дуги могут состав-
лять экстремаль. Точнее, ставятся следующие вопросы:
каково максимальное число частичных дуг, составляю-
щих экстремаль? предшествуют ли дуги свободного дви-
жения дугам максимальной тяги или следуют за ними?
Эта задача может быть в значительной степени продви-
нута, если воспользоваться условиями Эрдмана — Вей-
ерштрасса вместе с условием Лежандра — Клебша.
. Вследствие условий в угловых точках множители
Хь Хг Х3 непрерывны в каждой точке соединения частич-
ных дуг; кроме того, постоянная интеграции С имеет
одно и то же значение для всех частичных дуг, состав-
ляющих экстремаль. Поскольку скорость непрерывна,
первый интеграл (4.130) показывает, что разрыв мас-
сового расхода возможен лишь при условии, если
(Ю_ = (Ю+ = 0. (4.137)
Согласно условию Лежандра — Клебша и четверто-
му уравнению Эйлера — Лагранжа увеличение высоты
максимально (эта же величина, взятая со знаком
166
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
минус, минимальна), если повсюду на экстремали выпол-
няется неравенство
5p^l(4’+(WI>0.
(4.138)
в котором
уравнению
форме
вариации ба и б₽ должны соответствовать
связи (4.125). Переписав это неравенство в
К>0,
К<0,
Р — Ртах» 1
р=0, J
(4.139)
обнаруживаем, что функция Л играет решающую роль
при определении порядка составления экстремалей, так
как она положительна для частичных дуг, проходимых
при максимальном расходе топлива, равна нулю в угло-
вых точках и отрицательна для дуг свободного движе-
ния. По этой причине функция К называется функцией
переключений *).
Заметим, что скорость изменения функции переклю-
чений вдоль экстремалей удовлетворяет уравнению
(4.133). Отсюда следует, что, проинтегрировав это ура-
внение при граничных условиях (4.137), придем к соот-
ношениям **)
(<7Pmax) Р — Ртах’ 1 .. ....
? = 0. } (4-140)
показывающим, что функция К лишь однажды может
обратиться в нуль (рис. 4.5). Следовательно, экстре-
маль включает самое большее одну угловую точку и,
таким образом, две частичные дуги. Отметим, что усло-
вие Лежандра — Клебша удовлетворяется вдоль дуги
максимальной мощности двигателя, если т. е.
если эта дуга предшествует угловой точке; далее, оно
удовлетворяется вдоль дуги свободного движения при
t > ^с, т. е. если эта дуга следует за угловой точкой.
Экстремаль, соответствующая задаче максимального
*) Исторически впервые функция переключений была исполь-
зована в прикладной аэродинамике в работах Чикала [22] и Гар-
финкеля [23].
**) Значок с обозначает угловую точку.
4.S] ОПТИМАЛЬНЫЙ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ 167
набора высоты, состоит, таким образом, самое большее
из двух частичных дуг, проходимых в следующей после-
довательности:
₽ = ₽п,ах->? = 0; (4.141)
это иллюстрируется рис. 4.5.
Множество экстремалей. Если уравнения
движения проинтегрировать при условии, что массовый
Рис. 4.5. Функция переключений и массовый расход
в зависимости от времени.
(4.141а)
расход максимален или равен нулю, то получаются сле-
дующие результаты:
meXP(T--&) = COnSt-
т = const, [3 = 0.
Первая из этих формул при бесконечно большом
массовом расходе топлива (импульсном сжигании) дает
т exp (Vic) = const. (4.1416)
168
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
В плоскости скорость — масса можно определить те-
перь семейство экстремалей, выходящих из данной на-
чальной точки (рис. 4.6), и семейство экстремалей, при-
ходящих в данную конечную точку (рис. 4.7).
Максимальное увеличение высоты.
После определения оптимальной программы сжигания
можно проинтегрировать уравнения движения. Пусть,
например, начальная высота и скорость, а также
конечная скорость равны нулю, а конечное значение
безразмерной высоты, начальное значение отношения
тяги к весу и относительная величина массы топлива
соответственно равны:
’’If — hfglc1, т, == сргаах/т^, Z = т^т^. (4.142)
При этом в результате довольно длинных преобра-
зований получается следующее выражение для макси-
мальной высоты, достигаемой ракетой [48]:
= 1 In’(1 - С) + С+1П^--С)-. (4.143)
Зависимость этой величины от начального значения от-
ношения тяги к весу изображена на рис. 4.8 при относи-
тельной величине массы топлива, равной 0,7.
Представляет интерес сравнение оптимальной про-
граммы сжигания с программой сжигания, соответ-
ствующей первоначально постоянному ускорению, а за-
тем нулевой тяге, т. е. с программой
?~/п->р = О. (4.144)
Для этой программы сжигания интегрирование ура-
внений движения приводит к следующему выражению
для максимальной высоты [48]:
^ = ^1п’(1-С). (4.145)
График этой функции от начального значения отноше-
ния тяги к весу построен на рис. 4.8; относительная ве-
личина массы топлива равна 0,7.
Очевидно, что для одного и того же начального от-
ношения тяги к весу программа сжигания при посто-
янной, а затем нулевой тяге выгоднее программы
4.8]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ
169
Рис. 4.6. Семейство экстремалей, выходящих из заданной на-
чальной точки.
Рис, 4,7. Семейство экстремалей, приходящих в заданную
конечную точку.
170
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
с постоянным ускорением, а затем с нулевой тягой: на-
пример, если первоначальное отношение тяги к весу
равно 2, то максимальная высота, достигаемая при опти-
мальной программе сжигания, на 30% превышает высо-
ту, достигаемую при другой программе. При увеличении
Рис. 4.8. Максимальная высота подъема ракеты в зави-
симости от начального значения отношения тяги к весу.
первоначального отношения тяги к весу относительное
различие между этими программами уменьшается; в
частности, в предельном случае Тг = оо (импульсное
сжигание) обе программы дают одинаковое увеличение
высоты, а именно:
^=11п2(1 —Q. (4.146)
4.82. Более общая задача. Рассмотренная выше за-
дача обобщается, если отбросить предположения в) и
г) предыдущего раздела и исследовать одновременное
программирование величины и направления силы тяги
для общего двумерного движения в вертикальной пло-
скости. Спроектировав кинематические и динамические
4.8]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЁТА В ВАКУУМЕ
171
уравнения движения на горизонтальное и вертикальное
направления, запишем их в следующем виде:
< Pi = X—и = 0,
< р2 = h — v = 0,
< р3 = а —(cp/m)cos<|» = 0,
<р4 == v + g — (с$/т) sin ф = 0,
?5=/п + р = 0,
% = ₽(₽тах— ₽) — а2 = 0.
Здесь X обозначает горизонтальную координату, h —
вертикальную координату, и — горизонтальную состав-
ляющую скорости, v — вертикальную составляющую
скорости, т — массу, g — ускорение силы тяжести, с —
эквивалентную скорость истечения, 0 — массовый рас-
ход, а — вещественную переменную, а гр — угол наклона
вектора тяги к горизонтальному направлению. Точка
обозначает производную по времени.
Написанная система дифференциальных уравнений
содержит одну независимую переменную (/), восемь за-
висимых переменных (X, й, и, и, т, р, а, гр) и обладает
двумя степенями свободы; в силу этого возможно на-
ложение некоторого оптимального требования на про-
грамму сжигания р(/) и программу направления век-
тора тяги гр(/). Следовательно, вариационная задача
формулируется следующим образом: в классе функций
X(t), h(t), u(t), v(t), m(t), P(7), a(t), гр(7), удовлетво-
ряющих уравнениям (4.147) и определенным гранич-
ным условиям * *), найти такую систему функций, кото-
рая минимизирует разность \G = Gf — Git где G =
= G(t, X, h, w, v, tn).
Введя шесть переменных множителей Лагранжа и
записав расширенную функцию в форме
F = \ (X—и) +- Х2 (й — х/) + Х3 [и — (сф/m) cos ф] +
+ х41® + g — (<$/«) sin Ф] + Х5 (m + р)4-
+X6[p(pmax-₽)-а2], (4.148)
*) Общее число таких условий менее 12,
172
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
найдем, что экстремаль удовлетворяет уравнениям
Эйлера — Лагранжа:
Xj = 0, Х2 == 0, Х3 == - Xj,
Х4 = — Х2, Х5 = (rp/zn2) /Сф,
0 = — tfp + X6(₽max-2₽),
0 = Х6а,
0 = Х3 sin ф — Х4 cos ф,
(4.149)
где
/Ср = (c/zn) (Х3 cos ф + Х4 sin ф) — Х5,
/Сф = Х3 cos ф + Х4 sin ф.
Таким образом, множители Лагранжа Х2 по-
стоянны; более того, поскольку расширенная функция
явно не зависит от времени, имеет место следующий
первый интеграл:
+ Х2т> - X4g+= С. (4.151)
К этому следует добавить условие трансверсально-
сти
\dG — С dt “I- Xj dX —|- Х^ dh —|—
+ Х3 du + Х4 d<v + Х5 dm]{ = 0. (4.152)
(4.150)
Наконец, дифференцируя обе части первого из ура-
внений (4.150) по времени и комбинируя результат с
уравнениями Эйлера — Лагранжа, приходим к фор-
муле, справедливой вдоль всей экстремали:
/Ср = — (с/т) (Xj cos ф + Х2 sin ф). (4.153)
Программа сжигания топлива. Как по-
казывает седьмое уравнение Эйлера — Лагранжа, экс-
тремаль терпит разрывы и составляется из частичных
дуг, вдоль которых а = 0, а также ‘из дуг, вдоль кото-
рых Х6 = 0. Вдоль дуг а = 0 массовый расход может
принимать одно из следующих двух постоянных зна-
чений:
₽=0 ИЛИ Р — Ртах*
(4.154)
4.8]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ
173
С другой стороны, вдоль дуги Хе = 0 шестое уравне-
ние Эйлера — Лагранжа дает
ЛГр = О, /Ср = 0. (4.155)
Можно показать, что этот результат противоречит
уравнению (4.153); следовательно, не существует дуги,
вдоль которой Хе = 0, т. е. не существует дуги экстре-
мали, проходимой при переменной тяге [29].
Программа для направления вектора
тяги. Из рассмотрения системы уравнений Эйлера —
Лагранжа следует, что первые четыре уравнения допу-
скают интеграцию; получаем:
Xj = СР
<4156>
х4=с4—с2л
где Ci, ..., С4 — постоянные.
Записав восьмое уравнение Эйлера — Лагранжа в
виде
tg^ = X4/X3, (4.157)
получаем следующее решение:
tg Ф = (С4 - С2/)/(С3 - С,/), (4.158)
означающее, что тангенс угла наклона вектора тяги к
горизонту есть дробно-линейная функция времени} этот
результат принадлежит Лоудену [49]. Это заключение
носит вполне общий характер; рассмотрим несколько
его частных случаев.
а) Если минимизируемый функционал таков, что
dGldu = dGldv = Q, и если конечные составляющие ско-
рости не фиксированы, то условие трансверсальности
приводит к соотношениям
*з/=Л/ = 0, (4.159)
означающим, что
C3 = Cj/y, С4 = (4.160)
и
tgф = const (4.161)
174
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
(гл. IV
Таким образом, наклон вектора тяги по отношению
к горизонту постоянен — результат, принадлежащий
Фриду и Ричардсону [50].
б) Если исследуемый функционал таков, что
dGIdu = dG/dv = dGjdt = 0, если конечные составляю-
щие скорости, а также время полета не фиксированы и
если, наконец, конечная точка полета достигается в сво-
бодном движении, то условие трансверсальности вместе
с первым интегралом (4.151) приводит к соотношениям
Х3/ = Х4/ = С = 0, (Х^ + = 0, (4.162)
которые показывают, что
tg Ф = — («/^)у (4.163)
Таким образом, угол наклона вектора тяги при по-
лете с расходом мощности постоянен и направление век-
тора тяги в конечной точке перпендикулярно к напра-
влению вектора скорости [51].
в) Если функция G такова, что dGIdu = dG/dv =
*=0, и если задана величина начальной скорости, но
направление ее не фиксировано, то условие трансвер-
сальности приводит к равенству
^4 ___
и v i
которое показывает, что
tg ф, =
Таким образом, оптимальная начальная скорость па-
раллельна вектору тяги [51].
г) Если минимизируемый функционал обладает тем
свойством, что dG/dX = 0, и если конечное значение го-
ризонтальной координаты не фиксировано, то условие
трансверсальности дает
Х1/==0, (4.166)
откуда следует, что Ci = 0 и
tg<p = C4/C3-(C2/C3)/. (4.167)
(4.164)
(4.165)
4.8]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ
175
Таким образом, тангенс угла наклона вектора тяги
к горизонту есть линейная функция времени; этот ре-
зультат принадлежит Фриду [52].
д) Если функция G такова, что dGIdh = 0, и если
конечное значение высоты не фиксировано, то условие
трансверсальности показывает, что
Х2/ = 0, (4.168)
откуда следует, что С2 = 0 и
ctg ф = Сз/С4 - (C./Q t. (4.169)
Таким образом, котангенс угла наклона вектора тя-
ги к горизонту есть линейная функция времени.
Порядок следования частичных дуг.
Следующим нашим шагом является определение после-
довательностей частичных дуг, могущих составить экс-
тремаль. Более точно, возникают следующие вопросы:
каково максимальное число частичных дуг, составляю-
щих экстремаль? должны ли дуги свободного движе-
ния предшествовать дугам, проходимым с максималь-
ной тягой, или они должны следовать за ними? могут
ли возникнуть разрывы в направлении вектора тяги?
Проблема эта может быть в значительной мере осве-
щена, если воспользоваться условиями на разрывах
Эрдмана — Вейерштрасса вместе с условием Лежанд-
ра — Клебша. Согласно условиям на разрывах множи-
тели М, ...» As, а также постоянная интегрирования С
непрерывны в каждой точке соединения частичных дуг.
Отсюда, принимая во внимание первый интеграл (4.151)
и учитывая, что составляющие скорости и масса — не-
прерывные функции времени, заключаем, что разрывы
массовой скорости возможны лишь при условии, если
(^)_ = (К₽)+=0, (4.170)
тогда как разрыв (на величину л) в направлении век-»
тора тяги возможен лишь при условии
(/Q_ = (/Q+ = 0. (4.171)
Вследствие условия Лежандра — Клебша и шестого
уравнения Эйлера—Лагранжа функционал ДС достигает
176
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
минимума, если повсюду вдоль экстремали удовлетво-
ряется условие
2/G с8
ipijL [да+(м21+4w>°. (4.172)
в котором вариации ба, бр должны быть совместимы
с шестым уравнением связи. Таким образом, програм-
ма сжигания оптимальна, если
^<0,
Р — Pmax>
₽=о,
(4.173)
тогда как программа для направления вектора тяги оп-
тимальна лишь <в случае, если
(4.174)
Как следует из этих результатов, функции и
играют решающую роль в вопросе о составлении экс-
тремали из частичных дуг. Поэтому можно назвать их
соответственно функцией переключений массового рас-
хода и функцией переключений направления тяги.
В частности, если использовать эти функции в комби-
нации с приемом, описанным Лейтманом [29], то можно
показать, что
а) экстремаль не может состоять более чем из трех
частичных дуг и
б) разрыв в направлении вектора тяги может слу-
читься только при условии, что Аз = Х4 = 0.
Случай максимальной дальности. Как
пример использования изложенной выше теории рас-
смотрим задачу максимизации дальности (G = —X)
при следующих граничных условиях:
= 0, mi задано,
, л (4.175)
Ау = О, /Пу задано. к
Используя уравнения Эйлера — Лагранжа, условие
трансверсальности и свойства функций переключения,
приходим к следующим выводам: а) экстремаль содер-
жит самое большее одну угловую точку и, следователь-
но, две частичные дуги; б) дуга максимальной тяги пред-
шествует дуге свободного движения; в) направление
4.8] ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В ВАКУУМЕ 177
вектора тяги во время полета с расходом мощности по-
стоянно и в конце участка свободного движения пер-
пендикулярно к направлению скорости. Более того, если
проинтегрировать уравнения движения и обозначить без-
размерные величины дальности, начального отношения
тяги к весу и относительную величину массы топлива
соответственно через
tf = Xfg/c2, Z = — (4.176)
то, как можно показать, оптимальное направление тяги
удовлетворяет трансцендентному уравнению [48]
__? ____|_ — о (4 ]77)
2sin2^ — 1 С-4-1п(1 —С) — гы//;
а соответствующее значение дальности дается формулой
= (4.178)
Исключение параметра ф из этих уравнений приво-
дит к функциональному соотношению вида
1; = А(ъ, С). (4.179)
График этой функции от начального значения отноше-
ния тяги к весу изображен на рис. 4.9 для относитель-
ной величины массы топлива, равной 0,7.
Интересно сравнить оптимальную программу сжига-
ния с программой, соответствующей первоначально по-
стоянному ускорению, а затем нулевой тяге. Для этой
последней программы оптимальное направление век-
тора тяги, как можно показать, удовлетворяет уравне-
нию [48]
sin3 ф/(2 sin2 ф — 1) — = 0; (4.180)
соответствующее значение дальности по-прежнему оп-
ределяется уравнением (4.178). Исключение параметра
Ф приводит, таким образом, к функциональной связи
вида
С). (4.181)
Эта функция от начального значения отношения тяги
к весу изображена на рис. 4.9 при относительной вели-
чине массы топлива, равной 0,7.
12 Дж. Лейтмац
178
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Очевидно, программа сжигания для режима по-
стоянной тяги, а затем нулевой тяги выгоднее програм-
мы, соответствующей постоянному ускорению, а затем
нулевой тяге: например, если начальное значение отно-
шения тяги к весу равно 2, то дальность при оптималь-
ной программе сжигания на 20% превышает дальность
Рис. 4.9. Максимальная дальность полета ракеты в зави-
симости от начального значения отношения тяги к весу.
при другой программе. С увеличением начального зна-
чения отношения тяги к весу относительное различие
между этими программами уменьшается; в частности,
в предельном случае тг- = оо (импульсное сжигание)
обе программы приводят к одинаковой дальности*),
равной
$z=ln2(l - Q.
(4.182)
♦) При tj —>оо направление оптимального вектора тяги стре-
мится к л/4.
4.9) ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ 179
4.9. ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА РАКЕТЫ
В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
В этом разделе рассматривается задача определе-
ния оптимальных траекторий полета ракеты в сопро-
тивляющейся среде. С целью облегчения понимания об-
щему рассмотрению вопроса мы предпосылаем пример,
относящийся к горизонтальному полету.
4.91. Предварительный пример. Задача определения
оптимальных программ сжигания для ракетных лета-
тельных аппаратов при горизонтальном полете была
первоначально исследована Гиббсом [53], а впослед-
ствии Чикала и Миеле [10, 54]. Предполагалось, что
а) Земля плоская и ускорение силы тяжести постоян-
но; б) полет происходит в сопротивляющейся среде;
в) траектория полета горизонтальна; г) вектор силы
тяги направлен по касательной к траектории; д) экви-
валентная скорость истечения газов из сопла двигателя
постоянна и е) двигатель может развивать все значе-
ния массового расхода, заключенные между нижним и
верхним пределами. Придерживаясь этих гипотез, за-
пишем уравнения задачи в следующем виде*):
?1 = Х—V = 0,
<р2 = V + [£> (1/, т) — сф]/т, — 0,
<р3 = й-|-р = 0,
?4М(Рт« — ₽)— а2 = 0.
Здесь X обозначает расстояние по горизонтали, V —
скорость, т — массу, D — силу сопротивления, с — эк-
вивалентную скорость истечения газов из сопла двига-
теля, р — массовый расход топлива, а а — действитель-
ную переменную. Точка обозначает производную по
времени.
*) В общем случае функция сопротивления имеет форму D —
«= D(h, V, L), где h — высота, V — скорость, L — подъемная сила.
Если, однако, считается, что высота постоянна, a L = mg, то функ-
ция сопротивления может быть представлена в используемой нами
форме D(V, т).
12*
180
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Написанная выше система уравнений содержит одну
независимую переменную (/), пять зависимых перемен-
ных (X, V, т, р, а) и обладает одной степенью свободы;
поэтому на программу сжигания р(/) может быть на-
ложено некоторое требование оптимального характера.
Ввиду этого, фиксируя граничные условия:
= Х{ = 0, V(, т1 заданы, Vf, mf заданы, (4.184)
приходим к следующей задаче о максимизации горизон-
тальной дальности: в классе функций X(t), V(t), m(t),
a(t), удовлетворяющих уравнениям (4.183) и гра-
ничным условиям (4.184), найти такую систему функ-
ций, которая минимизирует разность \G = Gf— Gj, где
G ----X.
Введя четыре переменных множителя Лагранжа и
записав расширенную функцию в форме
F= Х1(X- V) + Х21V+ (D - <®/m] +
+ хз Й + ₽) + М? (Ртах - ₽) - а2], (4.185)
получаем уравнения Эйлера — Лагранжа:
Х1 = 0,
•{ __ 1 । dD
л2 — — А1
3 m \ m 1 dm /
о = - x4 (Pmai - 20),
0 = X4a,
(4.186)
в которых, по определению.
/С==Х2(с/.т1) —Х3. (4.187)
Отсюда следует, что лагранжев множитель Xi по-
стоянен; более того, поскольку фундаментальная функ-
ция явно не зависит от времени, можно написать сле-
дующий первый интеграл:
\V — X2(D//n)-|-Kp = C, (4.188)
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
181
где С — постоянная. Кроме того, условие трансверсаль-
ности принимает вид
[— С dt + (Х1 — 1) dX+ Х2 (I V+ Х3 dm]fi = 0 (4.189)
и показывает, что
Х1 = 1, С = 0. (4.190)
Наконец, если продифференцировать обе стороны
уравнения (4.187) по времени и рассмотреть результат
совместно с уравнениями Эйлера — Лагранжа, первым
интегралом (4.188) и условием трансверсальности, то
придем к следующему равенству, выполняющемуся
вдоль экстремали:
АГ=е (V, т, р)ЛГ+ш(К /и), (4.191)
где, по определению,
е (V, /п, Р) = (P//nD) (D 4- с dD/d V — т dD/dni), |
ц)(1/, m) = (l/mD)[(V-c)D-\-V(cdD/dV-nidD/dm)]. J
(4.192)
Совокупность частичных дуг. Как пока-
зывает пятое уравнение Эйлера — Лагранжа, экстре-
маль терпит разрывы и составляется из частичных
дуг, вдоль которых а = 0, и дуг, вдоль которых = 0.
На дугах а = 0 расход массы может принимать любое
из следующих постоянных значений:
р = 0 или Р = ртах. (4.193)
Вдоль дуг Х4 = 0, с другой стороны, величины К и
К обращаются в нуль. Поэтому уравнение (4.191) дает
ш(К /п)==0, (4.194)
откуда заключаем, что
(V — с) D + V (с dD/d V — m dD/dm) = 0. (4.195)
Таким образом, экстремаль составляется из частич-
ных дуг ceododHoeo движения, дуг, проходимых с макси-
мальным расходом топлива, и дуг, проходимых с пе-
ременной тягой [54]. Вдоль этих последних двигатель
управляется таким образом, что во всякий момент
182
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
времени удовлетворяется уравнение (4.195). Если, на-
пример, кривая силы сопротивления аппроксимируется
параболой, т. е. если
D = А V2 + В (т2/ V2), (4.196)
где А и В — постоянные, то уравнение (4.195) можно
переписать в форме
т = V2 УА/В /(I/+c)/(V+3c), (4.197)
которая показывает, что масса монотонно зависит от
скорости, точнее, любое уменьшение массы из-за по-
требления топлива сопровождается соответствующим
убыванием скорости. Ускорение, таким образом, отри-
цательно, и дуга переменной тяги должна проходиться
с силой тяги, которая во всякий момент меньше, чем
сила сопротивления.
Последовательности частичных дуг.
Следующим шагом является определение тех комби-
наций частичных дуг, которые находятся в согласии
с условиями в угловых точках и условием Лежандра —
Клебша. По условиям Эрдмана — Вейерштрасса для
угловых точек множители Х2, а также постоянная
интегрирования С должны быть непрерывны во всякой
точке соединения частичных дуг. Поскольку скорость и
масса непрерывны, первый интеграл (4.188) показы-
вает, что разрыв массового расхода возможен лишь при
условии, что выполняются следующие соотношения:
(Ю_ = (Ю+ = 0, (4.198)
показывающие, что
(АГ)_.= (Ю+ = ‘о- (4-199)
Далее, комбинируя условие Лежандра — Клебша с
уравнениями Эйлера — Лагранжа, можно показать, что
на дуге максимальной тяги, переменной тяги и свобод-
ного движения выполняются соответственно условия
Л'ЦО. (4.200)
Как отмечено Миеле [36], оказывается, что функция
со и функция К (функция переключений) играют важ-
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
183
нейшую роль в решении задачи максимизации дально-
сти, поскольку, зная функцию (О, можно вычислить
функцию переключений и, таким образом, предсказать
последовательность дуг, не нарушающую условия Ле-
жандра — Клебша. Точнее, если функция переключе-
ний представлена в окрестности угловой точки рядом
Тейлора, то, комбинируя соотношения (4.198) — (4.200),
можно получить для дуг максимальной тяги, пере-
менной тяги и свободного движения соответственно
условия
= & (4-201)
Таким образом, последовательности частичных дуг,
не нарушающие условия Лежандра — Клебша, суть те,
которые отмечены в табл. 4.1 и на рис. 4.10.
Таблица 4.1
Последовательности частичных дуг
Расположение угловой
точки
Последовательность
частичных дуг
<*с > °
">с < 0
<ос = 0
Составление экстремали из частич-
ных дуг. Последним шагом является определение
экстремали, соединяющей две данные конечные точки,
например начальную точку /, расположенную в обла-
сти, где со > 0, и конечную точку F, расположенную
в области со < 0. Такой экстремалью является дуга
IMNF на рис. 4.11, составленная последовательно из
частичных дуг
р = 0 —> со = 0 —> р = 0.
(4.202)
Это заключение может быть подтверждено рассмо-
трением некоторого числа различных комбинаций ча-
стичных дуг и доказательством того, что каждая из
этих комбинаций нарушает в некоторой точке условие
184
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Лежандра — Клебша. Рассмотрим, например, дугу
ICDENF, составленную последовательно из дуг
р = 0->р = ртах->р = 0-><о = 0->р = 0. (4.203)
Хотя каждая из частичных дуг удовлетворяет ура-
внениям Эйлера — Лагранжа, дуга в целом не подхо-
дит, так как частичная дуга
Р — Ртах Р — 0
(4.204)
с угловой точкой £>, расположенной в области со > 0,
не удовлетворяет условию Лежандра — Клебша. По
Рис. 4.10. Последовательность частичных дуг, совместимая
с условиями в угловых точках Эрдмана — Вейерштрасса и
условием Лежандра — Клебша.
тем же причинам путь IMGHKF должен быть отвергнут,
так как условие Лежандра — Клебша нарушено в ок*
ре.стности угловой точки Н. Таким образом, хотя суще-
ствует бесконечное множество комбинаций частичных
дуг, которые удовлетворяют уравнениям Эйлера — Ла-
гранжа, имеется лишь одна комбинация частичных дуг,
ни в какой точке не нарушающая условия Лежандра —
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
185
Клебша. Эта единственная комбинация представляет-
ся на рис. 4.11 траекторией IMNF.
Множество экстремалей. Исключив время
из второго и третьего уравнений (4.183), получаем
следующее дифференциальное соотношение:
dm___ т$
~dV — D — ср ’
(4.204а)
оно справедливо для любой частичной дуги, входящей
в состав экстремали.
Рис. 4.11. Экстремальная дуга частного вида.
Для дуги свободного движения это уравнение инте-
грируется и дает
т — const. (4.2046)
С другой стороны, для дуги, проходимой с макси-
мальным расходом топлива, оказываются необходимы-
ми приближенные методы интегрирования: лишь для
идеального случая бесконечной скорости расходования
186
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
топлива (импульсное сжигание) может быть получено
следующее аналитическое решение:
tn exp (V)c) = const. (4.204в)
Наконец, для дуги переменной тяги соотношение ме-
жду скоростью и массой выражается формулой
(V—с) D + V(c dD/dV — m dDldtn) = 0. (4.204г)
Теперь возможно определить на плоскости масса —
скорость семейство экстремальных дуг, выходящих из
данной начальной точки (рис. 4.12 и 4.13), а также се-
мейство экстремальных дуг, приходящих в данную ко-
нечную точку (рис. 4.14 и 4.15). Для примера рассмо-
трим случай, когда начальная точка задана и находит-
ся в области, где со < 0 (рис. 4.12). Обозначим через М
точку, в которой дуга 0 = 0тах, выходящая из началь-
ной точки, пересекает линию со = 0; далее рассмотрим
дугу ₽ = 0, исходящую из точки М. Оказывается, что
плоскость масса — скорость может быть разбита насле-
дующие области: область Д, расположенную над ли-
нией 0 = 0тах, исходящей из начальной точки; область
В, заключенную между этой линией, осью т и линией
0 = 0, исходящей из точки М; область С, расположен-
ную между последней линией, осью т и линией со = 0,
и область В, находящуюся между линией со = 0, осью
V и линией 0 = 0тах, выходящей из точки М. Ясно, что
вариационная задача не имеет физически разумного ре-
шения, если конечная точка находится в области Д; ес-
ли эта точка принадлежит области В, то имеется ре-
шение 0 = 0тах 0 = 0; если конечная точка лежит в
области С, то имеется решение 0 = 0тах-><о = О->0 =
= 0, и, наконец, если конечная точка принадлежит об-
ласти В, то существует решение 0 = 0тах~> со = 0->
->0 = 0тах- Случаи, изображенные на рис. 4.13—4.15,
могут быть разобраны путем точно таких же рассужде-
ний. Всегда, однако, оказывается, что экстремаль мо-
жет состоять не более чем из трех частичных дуг и ре-
шение вариационной задачи в сильной степени зависит
от граничных условий.
Замечание. Необходимо подчеркнуть, что выво-
ды предыдущих разделов относительно составления
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
187
Рис. 4.12. Семейство экстремалей, выходящих из заданной
начальной точки («/ < 0).
Рис. 4.13. Семейство экстремалей, выходящих из заданной
начальной точки (coj > 0).
188
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Рис. 4.14. Семейство экстремалей, приходящих в заданную
* конечную точку (оу < 0).
Рис. 4.15. Семейство экстремалей, приходящих в заданную
конечную точку (оу > 0).
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
189
экстремалей из частичных дуг справедливы при усло-
вии, что зависимость между массой и скоростью, выра-
жаемая формулой о = 0, монотонна и расход массы,
требуемый вдоль линии со = 0, меньше максимально
возможного. Если любое из этих условий будет нару-
шено, т. е. если связь между массой и скоростью, соот-
ветствующая равенству со = 0, не будет монотонной и
(или) если требуемый расход массы превысит макси-
мально возможную величину, то в порядке составления
экстремали из частичных дуг произойдут некоторые из-
менения. Более точно, экстремаль, удовлетворяющая
данным граничным условиям, может включать более
трех частичных дуг (в некоторых случаях этих дуг бу-
дет пять), даже если каждая из них.и проходится сво-
бодным движением либо с максимальной тягой, либо
вдоль линии со = 0. С целью экономии места мы опу-
скаем аналитическое рассмотрение этого случая, и чи-
татель отсылается к специальной литературе. Следует
подчеркнуть, однако, что путем совместного использо-
вания условий Эрдмана — Вейерштрасса для угловых
точек и условия Лежандра — Клебша может быть най-
дено решение этой задачи, и это решение обычно ока-
зывается единственным.
4.92. Более общая задача. Обобщение предыдущей
задачи возникает, если отбросить предположения в) и
г) раздела 4.91 и исследовать одновременное програм-
мирование величины тяги, направления тяги и вели-
чины подъемной силы при движении в двух измере-
ниях в вертикальной плоскости. Проектируя кинемати-
ческие соотношения на горизонтальное и вертикальное
направления, а динамические соотношения — на каса-
тельную и нормаль к траектории полета, запишем ура-
внения движения в следующем виде:
ср! = X — V cos 7 = 0,
ср2 = h — Vsin у = 0,
< р3 s iz+gsin 7 + Р(Л, к Z) — Ср cos e]/zn = о,
< р4 = 7 + X^SJL _ (£ _|_ Sin е)/оту — 0>
< р5 = /п + р — 0,
?6 s Р (Ртах Р) д2 — 0«
(4.205)
190
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
(гл. IV
где X обозначает горизонтальную координату, h — вер-
тикальную координату, V — скорость, 7 — угол наклона
траектории к горизонтальному направлению, т — мас-
су, g — ускорение силы тяжести, с — эквивалентную
скорость истечения газа из сопла двигателя, 0 — массо-
вый расход, а — действительную переменную, е — угол
наклона вектора тяги по отношению к вектору скорости,
D — силу сопротивления, L — подъемную силу, а точка
обозначает производную по времени.
Написанная система дифференциальных уравнений
содержит одну независимую переменную (/), девять за-
висимых переменных (X, Л, У, у, т 0, ос, е, L) и обла-
дает тремя степенями свободы; в силу этого можно
наложить некоторое оптимальное требование на про-
грамму сжигания 0(0, программу направления вектора
тяги в(0 и программу подъемной силы L(t). Задача
Майера формулируется поэтому следующим образом:
в классе функций X(t), h(t), V(t), у(0, ^(0» ₽(0» сс(О»
е(0, L(t), удовлетворяющих уравнениям (4.205) и неко-
торым заданным граничным условиям *), определить
такую систему функций, которая минимизирует раз-
ность
AG = Gf— Gi, где G— G(X, h, V, у, tn, t).
Введя шесть переменных множителей Лагранжа и
записав расширенную функцию в виде
f’==X1 (X — I/cos т) + Х2(А — I/sin ?) +
+ >,(v+esinT+D-^°s--) +
+ + ₽) + М? (?...>(4.206)
*) Общее число этих условий менее 12,
4.9] оптймаЛьнЫё траектории полёта в среде
получим систему уравнений Эйлера — Лагранжа:
Xj = O,
kj = Щт) dD/dh,
X3 = — X! cos y — X2 sin у + (Xg/zn) dD)dV—
— (^g/^2)cos I + (М* V2) (L + sin e),
x4 = XjysinT—X^cos-f+X3gCOST —X4-^r sin y>
Х5 = (1//п2)Ж.-/<£),
0 =-^ + X6(pmax-2p),
0 = Xg<x,
0 =X3sine — X4cose/V,
o = X3dD/dZ —X4/V,
где, по определению,
[X3 cos s + (Х4/V) sin s] — Xs.
К, = cos e + (X4/IZ) sin e,
Kl = KD-^V)L.
(4.208)
Таким образом, множитель Лагранжа Xi постоянен;
более того, поскольку расширенная функция явно не
зависит от времени, имеет место первый интеграл
V(Xj cos т + Sin т) — g (х3 sin т +-у-cos т) +
К 1
+ Р^-^Г = С- <4-209)
Кроме того, условие трансверсальности дается ра-
венством
\dG — С dt “I- Х^ dX~I- Х2 dh~4~ Х3 Х4 d^ -I- Х3 dm]? 0.
(4.210)
Программа сжигания. Каи показывает седь-
мое уравнение Эйлера — Лагранжа, экстремаль тер-
пит разрывы и составляется из частичных дуг, вдоль
192
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
которых а = 0, и дуг, вдоль которых Хе = 0. Вдоль дуг
а = 0 расход массы постоянен и дается одним из двух
соотношений:
р = 0 или р = pmai.
(4.211)
С другой стороны, вдоль дуги Хе = 0 расход массы
меняется так, что
ЛГ₽ = О, £р = 0. (4.212)
Таким образом, экстремаль составляется из дуг сво-
бодного движения, дуг, проходимых с максимальным
расходом топлива, и дуг переменной тяги [31].
Программа направления вектора тяги.
Рассмотрение восьмого и девятого уравнений Эйлера —
Лагранжа показывает, что для множителей Лагранжа
существуют нетривиальные решения, если только
sine cose
dD/dL 1
= 0.
(4.213)
Таким образом, оптимальный угол наклона вектора
тяги по отношению к вектору скорости удовлетворяет
соотношению
e = arctg(d£>/<?£), (4.214)
которое для частного случая, когда сила сопротивления
задается равенством
D = A(V, h) + B(y, h)L\ (4.215)
приобретает вид
е = arctg (2В£). (4.216)
Поскольку В > 0, вектор тяги должен быть направ-
лен в одну сторону с вектором подъемной силы: этот ре-
зультат логически оправдан, поскольку создание нор-
мальной составляющей вектора тяги уменьшает величи-
ну аэродинамической подъемной силы, необходимой для
надлежащего маневрирования, и, таким образом, умень-
шает эффективное сопротивление, связанное с подъем-
4.9] ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ ЮЗ
ной силой. Для частного случая 2ВА<^1 предыдущее
соотношение упрощается и принимает вид
е = 2ВЛ. (4.217)
Эта формула для полета с дозвуковой скоростью допу-
скает простую физическую интерпретацию: оптимальный
угол наклона вектора тяги вдвое превышает угол ско-
са BL, относящийся к рассматриваемым конкретным ус-
ловиям полета.
Последовательности частичных дуг.
Следующим шагом является определение последова-
тельностей частичных дуг, входящих в экстремаль.
О задаче с аэродинамическими силами известно не так
много, как о задаче для полета в вакууме. Несмотря на
это, с помощью условий в угловых точках, а также ус-
ловия Лежандра — Клебша можно получить некоторые
общие критерии. Согласно условиям в угловых точках
множители М,.., Х5, а также постоянная интегрирова-
ния С непрерывны в каждой точке соединения частич-
ных дуг. Поэтому, имея в виду первый интеграл (4.209),.
заключаем, что разрыв массового расхода возможен,,
только если
(/Q_ = (K₽)+=0. (4.218)
С другой стороны, разрыв (на величину л) в напра-
влении вектора тяги возможен, если
(АГ.)_ = (ЛГ.)+=О- (4-219)
Наконец, разрыв в подъемной силе возможен при
условии
(К£)_МК4)+=0, (4.220)
т. е. если
(L/D)_=(L/D)+ (4.221)
и, кроме того (см. девятое уравнение Эйлера — Ла«
гранжа),
(dD/dL)_ = (dD/dL)+. (4.222)
13 Дж Лейтман
194 МЕТОДЫ 6АРЙАЦЙ0ЙН0ГО ЙСЧИСЛёНйЯ [гл. IV
Заметив, что уравнения (4.221) и (4.222) имеют ре-
шением
(Z)_=(£)+, (4.223)
находим, ЧТО Величина подъемной силы непрерывна; от-
сюда следует, что оптимальная программа подъемной
силы представляется непрерывной функцией времени.
Условие Лежандра — Клебша и шестое уравнение
Эйлера — Лагранжа показывают, что функционал до-
стигает минимума, если повсюду вдоль экстремали вы-
полняется неравенство
2/G сЗ Х3 d2D
jpj- [(!»)’+(Wl + / К, (S.)’ + (8Z)> >0. (4.224)
Здесь вариации da, б₽ должны быть совместимы с ше-
стым уравнением связи. Таким образом, программа сжи-
гания оптимальна соответственно для дуг максимальной
тяги, переменной тяги и нулевой тяги, если
ЛГр^О. (4.225)
Кроме того, направление вектора тяги оптимально,
если
К>0. (4.226)
Заметив, наконец, что для параболического закона
сопротивления
(?WZ2 = 2B>0, (4.227)
заключаем, что программа подъемной силы оптимальна,
если всюду вдоль экстремали
Х3>0. (4.228)
Из приведенных рассуждений видно, что функции
и играют решающую роль в определении после-
довательности частичных дуг в экстремали. Поэтому
указанные функции можно назвать соответственно функ-
цией переключения массового расхода и функцией пе-
реключения направления силы тяги. Отметим, что раз-
рыв в направлении вектора тяги может случиться лишь
при условии Хз = Х4 = 0.
4.93. Дополнительные связи. В предыдущем разделе
были исследованы оптимальные траектории ракеты в
4.9] ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ 195
сопротивляющейся среде в предположени, что, кроме
хорошо известных кинематических и динамических со-
отношений, должно удовлетворяться двустороннее не-
равенство для массового расхода топлива. В настоящем
разделе рассматривается случай, когда траектория по-
лета подчинена, помимо указанных ограничений, еще
двум дополнительным связям типа*)
<р(Х, Л, V, 7, /п, 0, е, Д /) = 0, 1
Ф(Х Л, к 7, т, ₽, е, L, i) = 0. } (4‘229)
Благодаря этим дополнительным связям число степе-
ней свободы в задаче сводится к единице; поэтому из-
меняются уравнения Эйлера — Лагранжа и, следова-
тельно, оптимальные траектории. Аналитический вывод
аналогичен проведенному в предыдущем разделе и по-
этому здесь не повторяется: мы приводим лишь глав-
нейшие результаты для некоторых типов траекторий
полета.
Вертикальные траектории. Для верти-
кальных траекторий, проходимых с вектором тяги, на-
правленным по касательной, дополнительные связи
имеют вид
<р = 7 — к/2 = 0, 1
ф = е = О. J
(4.230)
Если функция G имеет форму G(h, V, m, t), то мно-
жество экстремальных дуг включает частичные дуги
р = 0, дуги р = Ртах, а также дуги переменной тяги,
вдоль которых [31]
/п£ = я(^-1)+^-Лехр(--Ц^.). (4.231)
где А — постоянная.
♦) Это наиболее общая задача теории оптимальных траекторий
полета [31]. В самом деле, эта задача содержит следующие задачи
в качестве частных случаев: а) задачу с одной степенью свободы,
возникающую при наличии обеих дополнительных связей; б) задачу
с двумя степенями свободы, возникающую в отсутствие одной из
дополнительных связей, и в) задачу с тремя степенями свободы,
прьедставляющуюся в отсутствие дополнительных связей.
13*
196 МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [гл. IV
Важный частный случай представляется, когда
функция G имеет форму G(h, V, т) и не накладывается
никакого условия на время; при этом условие трансвер-
сальности показывает, что А = 0, и вдоль дуги перемен-
ной тяги требуется удовлетворить уравнению [41]
mg = D [(Vic) — 1] + VdD/dV. (4.232)
Отметим попутно, что если бы аэродинамические
силы отсутствовали, то это уравнение не имело бы фи-
зически разумного решения; следовательно, программа
оптимальной тяги составлялась бы только из частичных
дуг свободного движения и максимальной тяги, что на-
ходится в полном согласии с результатом раздела 4.81.
Горизонтальные траектории. Для клас-
са горизонтальных траекторий, проходимых с векто-
ром тяги, направленным по касательной, дополнитель-
ные связи имеют вид
ф = е = О. /
Если функция G имеет форму G(X, V, /и, /), то мно-
жество экстремальных дуг состоит из дуг свободного
движения, дуг максимальной тяги и дуг переменной
тяги, вдоль которых [31]
(V—A)dD/dL ’
где A — постоянная.
Важный частный случай возникает, когда функция
G имеет форму G = G(X, V, т) и не накладывается ни-
какого условия на время; для этого случая условие
трансверсальности дает А = 0 и вдоль дуги переменной
тяги требуется удовлетворить уравнению [31]
в соответствии с результатом раздела 4.91.
Другой интересный случай представляется, когда
функция G имеет форму G(/, V, т) и на расстояние по
горизонтали не накладывается никакого условия; при
этом условие трансверсальности дает А = оо и соотно-
4.9]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
197
шение, выполняющееся на дуге переменной тяги, приоб-
ретает вид [10]
D + cdD/dV
mS= dD/dL
Прямолинейные траектории произ-
вольного наклона. Для прямолинейных траекто-
рий, проходимых с вектором тяги, направленным по
касательной, дополнительные связи имеют вид
ср= 7 — const = 0,
ф = е = 0.
Если функция G имеет форму G(X, A, V, т) и если
не накладывается никакого временного условия, то мно-
жество экстремальных дуг состоит из частичных дуг
р = 0, дуг р = Ршах и дуг переменной тяги, вдоль кото-
рых [31]
(4.236)
(4.237)
(4.238)
_ D (V — c) + cVdD/dV
с sin 7 4" cos 7 dD/dL ’
Это уравнение сводится к (4.232) для вертикального
полета и к (4.235) для горизонтального полета.
Траектории, проходимые при постоян-
ном расходе массы и пренебрежимо ма-
лом индуктивном сопротивлении. Для ра-
кеты, работающей при постоянном расходе массы и
векторе тяги, касательном к траектории, дополнитель-
ные связи даются соотношениями
<р = р — const = 0,
ф = е = О.
Если индуктивное сопротивление пренебрежимо мало
по сравнению с сопротивлением при отсутствии подъ-
емной силы, если функция G имеет форму G(/z, V, /п, /)
и если на горизонтальную дальность не наложено ни-
какого условия, то множество экстремальных дуг содер-
жит дуги, вдоль которых [31]
cos 7=0,
и дуги, вдоль которых
pc = D + V dDjdV — (V*/g) dD/dh. (4.241)
(4.239)
(4.240)
198
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Если дуги предыдущего типа проходятся в верти-
кальном направлении (пикирование или крутой подъем),
то дуги последнего типа проходятся при непрерывно
меняющемся наклоне касательной.
Траектории без подъемной силы. Для
траекторий без подъемной силы, проходимых с век-
тором тяги, направленным по касательной, дополни-
тельные связи имеют вид
ф = £ = 0, ]
<р = е = О. } <4’
Множество экстремальных дуг состоит из дуг сво-
бодного движения, дуг максимальной тяги и дуг пере-
менной тяги. Вдоль последних оптимальное мгновенное
значение ускорения может быть подсчитано в предпо-
ложении об изотермичности атмосферы; результат та-
кого вычисления приводится Брайсоном и Россом [55]
для задач, не включающих явно время, и Миеле [31] для
задач, содержащих некоторое временное условие, нало-
женное на траекторию полета.
Планирующие траектории. Для класса
планирующих траекторий сила тяги равна нулю, так
что массовый расход топлива равен нулю. Очевидно,
что вариационная задача имеет при этом одну степень
свободы, благодаря чему и осуществляется оптимизация
подъемной силы. Для простоты далее рассматривается
класс гладких, мало отклоняющихся от горизонтали
траекторий, т. е. предполагается, что
sin 7^7, cos 7^1, V7/g<Cl. (4.243)
При этих условиях соотношение, удовлетворяющееся
на экстремальной дуге, имеет вид
dD/dV — (V/g) dD/dh _
dD/d V-\-D/V — ( V/g) dD/dh. ~ v'
где A — постоянная, зависящая от граничных условий
задачи и от функции G = -G(7, й, V), экстремум кото-
рой подлежит осуществлению. ............
Важный частный случай возникает, если функция G
имеет, форму (?(Х, й, V) и-не-накладывается никакого
(4.244)
*4.9] •
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ПОЛЕТА В СРЕДЕ
199
временного условия. Для этого случая условие транс-
версальности дает А = 0 и уравнение для оптимальной
программы подъемной силы принимает вид [56]
dP_ _у_ дР _
dV g dh
(4.245)
Если через H = h+V2l2g обозначить уровень энер*
гии и записать функцию сопротивления в форме
D = V, L), то предыдущее уравнение перепишется
в форме
[ЭД/и==0, (4.246)
означающей, что оптимальная программа полета полу-
чается тогда, когда аэродинамическое сопротивление
минимально по отношению к скорости при постоянных
значениях уровня энергии и подъемной силы. Для мед*
ленных движений с дозвуковой скоростью эта програм-
ма выполняется при полете с постоянным динамическим
давлением и, следовательно, с постоянным углом атаки.
Другой интересный частный случай возникает, когда
функция G имеет форму G(f, Л, V) и на горизонтальную
дальность не накладывается никакого условия. Для
этого случая условие трансверсальности дает А = оо и
уравнение оптимальной программы подъемной силы
имеет вид [56]
d(DV) V d(PV) _п
dV g dh “и
(4.247)
или, что то же,
(4.248)
Таким образом, оптимальная программа полета до-
стигается в случае, если мощность, необходимая для
преодоления аэродинамического сопротивления, имеет
минимум по отношению к скорости для постоянных зна-
чений уровня энергии и подъемной силы. Для медлен-
ных движений с дозвуковой скоростью эта программа
требует постоянства динамического давления, так что
угол атаки должен оставаться неизменным.
200
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
4.10. ВЫВОДЫ
В этой главе рассматриваются непрямые методы ва-
риационного исчисления, в особенности те из них, ко-
торые связаны с задачами Больца, Майера и Лагранжа.
После общего обзора уравнений Эйлера — Лагранжа,
условий в угловых точках, условия трансверсальности,
условия Лежандра—Клебша и условия Вейерштрасса
следует описание трудностей, встречающихся при реше-
нии смешанных краевых задач. Далее указываются не-
которые математические приемы, позволяющие сводить
задачи, в первоначальном своем виде не охватываемые
формулировками задач Больца, Майера и Лагранжа
(именно задачи с высшими производными, задачи, не
включающие производных, а также задачи со связями
в форме неравенств), к схеме, соответствующей этим
формулировкам.
Использование вариационных методов в прикладной
аэродинамике специально иллюстрируется задачей
определения геометрической формы тонкого тела враще-
ния, обладающего минимальным сопротивлением давле-
ния в ньютоновом потоке, а также задачей о двумер-
ном профиле крыла, имеющем минимальное сопротив-
ление давления в линеаризованном сверхзвуковом
потоке. Кроме того, употребление вариационных мето-
дов в механике полета специально разъясняется на за-
даче определения двумерных траекторий ракеты при
полете как в пустоте, так и в сопротивляющейся среде.
Обсуждаются разрывные решения, а также демонстри-
руется использование функций переключений для ре-
шения вопроса о составлении экстремали из частич-
ных дуг.
ЛИТЕРАТУРА
1. G. A. Bliss, Lectures on the Calculus of Variations, Univ, of
Chicago Press, Chicago, 1946. [Русский перевод: Г. А. Блисс,
Лекции по вариационному исчислению, ИЛ, М. — Л., 1950.]
2. A. Miele, Flight Mechanics, том 2: Theory of Optimum Flight
Paths, Addison-Wesley, Reading, Massachusetts.
3. О. В о 1 z a, Lectures on the Calculus of Variations, Stechert,
New York, 1946.
ЛИТЕРАТУРА
201
4. Р. С i с а 1 a, An Engineering Approach to the Calculus of Varia-
tions, Levrotto & Bella, Torino, Italy, 1957.
5. F. A. Valentine, The Problem of Lagrange with Differential
Inequalities as Added Side Conditions, в книге «Contributions
to the Calculus of Variations», 1933—1937, Univ, of Chicago,
1937.
6. L. J. К u 1 a k о w s k i and R. T. Stancil, Rocket boost trajecto-
ries for maximum burnout velocity, ARS Journal 30, No. 7
(1960).
7. A. E. Bryson and W. F. Denham, A steepest-ascent method
for solving optimum programming problems, Ratheon Company,
Missile and Space Division, Rept. No. BR-1303 (1961).
8. H. J. Kelley, Gradient theory of optimal flight paths, ARS
Journal 30, No. 10 (1960).
9. G. L e i t m a n n, An elementary derivation of the optimal cont-
rol conditions, Proc. 12th Intern. Astronaut. Congr., Washington
(1961).
10. A. M i e 1 e, An extension of the theory of the optimum burning
program for the level flight of a rocket-powered aircraft, J. Ae-
ro/Space Sci. 24, No. 12 (1957).
11. A. J. Eggers, M. M. Resnikoff and D. H. Dennis, Bo-
dies of revolution having minimum drag at high supersonic air-
speeds, NACA TR No. 1306 (1958).
12. G. D г о u g g e, Wing sections with minimum drag at superso-
nic speeds, The Aeronautical Research Institute of Sweden Rept.
No. 26 (1949).
13. D. R. Chapman, Airfoil profiles for minimum pressure drag
at supersonic velocities. General analysis with application to li-
nearized supersonic flow, NACA TR No. 1063 (1952).
14. A. M i e 1 e, Optimum slender bodies of revolution in Newtonian
flow, Boeing Scientific Research Laboratories, Flight Sciences La-
boratory, TR No. 56 (1962).
15. A. M i e 1 e, The extremization of functionals involving products
of powers of integrals and its application to aerodynamics, Boe-
ing Scientific Research Laboratories, Flight Sciences Laboratory,
TR No. 57 (1962).
16. R. H. G о d d a r d, A method of reaching extreme altitudes,
Smithsonian Inst. Pubis. Misc. Collections 71, No. 2 (1919).
17. G. H a m e 1, Uber eine mit dem Problem der Rakete zusammen-
hangende Aufgabe der Variationsrechnung, Z. angew. Math.
Meeh. 7, No. 6 (1927).
18. A. L i p p i s c h, Performance theory of airplanes with jet pro-
pulsion, Headquarters, Air Materiel Command, Translation Rept.
No. F-TS-685-RE (1946).
19. K. J. L u s h, A review of the problem of choosing a climb tech-
nique with proposals for a new climb technique for high perfor-
mance aircraft, Aeronautical Research Council, RM No. 2557
(1951).
20. A. M i e 1 e, Problemi di Minimo Tempo nel Volo Non Stazionario
degli Aeroplani, Atti accad. sci. Torino, Classe sci. fis. mat. e nat.
85 (195Q—1951).
202
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл IV
21. Р. Cicala, Optimum airplane flight paths, NASA TT No. F-4
(1959).
22. P. Cicala, Piecemeal solutions in the programming of optimal
flight trajectories, NASA TT No. F-3 (1959).
23. B. G a r f i n к e 1, Minimal problems in airplane performance,
Quart. Appl. Math. 9, No. 2 (1951).
24. M. R. Hestenes, A general problem in the calculus of varia-
tions with applications to paths of least time, The RAND Corpo-
ration, Rept. No. RM-100 (1950).
25. J. V. Break we 11, The optimization of trajectories, SIAM Jour-
nal 7, No. 2 (1959).
26. B. D. Fried, Trajectory optimization for powered flight in two
or three dimensions, в книге «Space Technology», Wiley, New
York, 1959. [Русский перевод: под ред. Г. Сейферта, Косми-
ческая техника, гл. 2, изд-во «Наука», М., 1964.]
27. D. F. L a w d е n, Dynamic problemszof interplanetary flight, Ae-
ronaut. Quart. 6, No. 3 (1955).
28. D. F. L a w d e n, Interplanetary trajectories, Advances in Space
Sci. 1, No. 1 (1959).
29. G. L e i t m a n n, On a class of variational problems in rocket
flight, J. Aero/Space Sci. 26, No. 9 (1959).
30. G. L e i t m a n n, Extremal rocket trajectories in position and
time dependent force fields, AAS Preprint No. 61-30 (1961).
31. A. Miele, General variational theory of the flight paths of
rocket-powered aircraft, missiles, and satellite carriers, Astronaut.
Acta 4, No. 4 (1958).
32. A. M i e 1 e, Minimal maneuvers of high performance aircraft in a
vertical plane, NASA TN No. D-155 (1959).
33. R. Bellman, Dynamic Programming, Princeton Univ. Press,
Princeton, New Jersey, 1957.
34. A. M i e 1 e, Flight mechanics and variational problems of a li-
near type, J. Aero/Space Sci. 25, No. 9 (1958).
35. A. M i e 1 e, Application of Green’s theorem to the extremization
of linear integrals, Boeing Scientific Research Laboratories, Flight
Sciences Laboratory, TR No. 40 (1961).
36. A. Miele, The relation between the Green’s theorem approach
and the indirect methods for extremal problems of a linear type,
Boeing Scientific Research Laboratories, Flight Sciences Laborar
lory, TR No. 47 (1961).
37. A. Miele, Interrelationship of calculus of variations and ordi-
nary theory of maxima and minima for flight mechanics applica-
tions, ARS Journal 29, No. 1 (1959).
38. A. Miele, Lagrange multipliers and quasi-steady flight mecha-
nics, J. Aero/Space Sci. 26, No. 9 (1959).
39. H. S. T s i e n and R. C. Evans, Optimum thrust programming
for a sounding rocket, ARS Journal 21, No. 5 (1951).
40. G. Leitmann, A calculus of variations solution of Goddard’s
problem, Astronaut. Acta 2, No. 2 (1956).
44 3. Leitmann, Stationary trajectories for a high-altitude rocket
With drop-away booster, Astronaut. Acte 2, Nq. 3 Q956}t
ОБЩИЙ УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
203
42. G. Leitmann, Optimum thrust programming for high-altitude
rockets, Aero/Space Eng. 16, No. 6 (1957).
43. G. Leitmann, A note on Goddard’s problem, Astronaut. Acta 3*
No. 4 (1957).
44. A. M i e 1 e, Generalized variational approach to the optimum
thrust programming for the vertical flight of a rocket, часть 1,
Necessary conditions for the extremum, ZFW 6, No. 3 (1958).
45. A. M i e 1 e, Minimality for arbitrarily inclined rocket trajectories,
ARS Journal 28, No. 7 (1958).
46. A. M i e 1 e, Stationary conditions for problems involving time
associated with vertical rocket trajectories, J. Aero/Space Sci.
25, No. 7 (1958).
47. A. Miele, On the brachistocronic thrust program for a rocket-
powered missile traveling in an isothermal medium, ARS Journal
28, No. 10 (1958).
48. A. Miele, Flight Mechanics, том 1: Theory of Flight Paths. Addi-
son-Wesley, Reading, Massachusetts, 1962.
49. D. F. L a w d e n, Optimal rocket trajectories, ARS Journal 27,
No. 12 (1957).
50. B. D. Fried and J. M. Richardson, Optimum rocket trajecto-
ries, J. Appl. Phys. 27, No. 8 (1956).
51. A. Miele and J. O. Cap pel lari, Topics in dynamic program-
ming for rockets, ZFW 7, No. 1 (1959)
52. B. D. Fried, On the powered flight trajectory of an earth sa-
tellite, ARS Journal 27, No. 6 (1957).
53. A. R. Hibbs, Optimum burning program for horizontal flight,
ARS Journal 22, No. 4 (1952).
54. P. Cicala and A. Miele, Generalized theory of the optimum
thrust programming for the level flight of a rocket-powered air-
craft, ARS Journal 26, No. 6 (1956).
55. A. E. Bryson and S. E. Ross, Optimum rocket trajectories
with aerodynamic drag, ARS Journal 28, No. 7 (1958).
56. A. M i e 1 e, General solutions of optimum problems in nonstatio-
nary flight, NACA TM No. 1388 (1955).
ОБЩИЙ УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
Baker G. A., Ford K. W. and Porter С. E., Optimal accuracy
rocket trajectories, J. Appl. Phys. 30, No. 12 (1959).
Baker R. M. L., Jr., Recent advances in astrodynamics, 1960, ARS
Journal 30, No. 12 (1960).
Behrbohm H., Brachystochrone Flugbahnen im Raum bei zeitlich
veranderlichem Fluggewicht, Jahrb. WGL (1954).
Behrbohm H., Optimal trajectories in the horizontal plane, SAAB
TN No. 33 (1955).
Behrbohm H., Optimal trajectories in the vertical plane, SAAB
TN No. 34 (1955).
Bellman R. and Dreyfus S., An application of dynamic pro-
gramming to the determination of optimal satellite trajectories,
J. Brit. Interplanet. Soc. 17, Nos. 3—4 (1959).
204
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Bergqvist В., The optimization problem for rocket vehicles
subjected to medium and high accelerations: A literature survey,
Astronautik 1, No. 3 (1959).
Brea к we 11 J. V., Fuel requirements for crude interplanetary
guidance, AAS Preprint No. 59-5 (1959).
В re a к we 11 J. V., The spacing of corrective thrusts in interplane-
tary navigation, AAS Preprint No. 60—76 (1960).
В г e a к w e 11 J. V., Gillespie R. W. and Ross S. E., Researches
in interplanetary transfer, ARS Preprint No. 954-59 (1959).
Bryson A. E., Denham W. F., С а г г о 11 F. J. and M i к a m i К.»
Determination of the lift or drag program that minimizes re-entry
heating with acceleration or range constraints using a steepest
descent computation procedure, IAS Preprint No. 61-6 (1961).
Burns R. E., Correlative survey report on powered flight trajectory
optimization including an extensive critical bibliography, ARS
. Preprintt No. 2071-61 (1961).
С a r s t о i u J., On a minimum-time flight path of a jet aircraft, J.
Aero/Space Sci. 24, No. 9 (1957).
Cartaino T. F. and Dreyfus S. E., Application of dynamic pro-
gramming to the airplane minimum time-to-climb problem.
Aero/Space Eng. 16, No. 6 (1957).
Carter W. J., Optimum nose shapes for missiles in the superaero-
dynamic region, J. Aero/Space Sci. 24, No. 7 (1957).
Chang I. D., On optimum nose shapes for missiles in the superaero-
dynamic region, J. Aero/Space Sci. 25, No. 1 (1958).
Cicala P. and Miele A., Evoluzioni Brachistocrone di un Aereo,
Atti accad. sci. Torino, Classe sci. fis. mat. e nat. 89 (1954—1955).
Cicala P. and Miele A., Brachistocronic maneuvers of a constant
mass aircraft in a vertical plane, J. Aero/Space Sci. 22, No. 4
(1955).
Cicala P. and Miele A., Brachistocronic maneuvers of a variable
mass aircraft in a vertical plane, J. Aero/Space Sci. 22, No. 8
(1955).
Dennis D. H., On optimum nose shapes for missiles in the super-
aerodynamic region, J. Aero/Space Sci. 25, No. 3 (1958).
Ewing G. M., A fundamental problem of navigation in free space,
Quart. Appl. Math. 18, No. 4 (1961).
F a u 1 d e r s C. R., Minimum-time steering programs for orbital trans-
fer with low-thrust rockets, North American Aviation, Inc., Missile
Division, Rept. No. MD 60-280 (1960).
F a u 1 d e r s C. R., Optimum thrust programming of electrically po-
wered rocket vehicles in a gravitational field, ARS Journal 30,
No. 10 (1960).
Faulkner F. D., Homing in a vacuum with minimum fuel con-
sumption, Univ, of Michigan, Aeronautical Research Center, Rept.
No. UMM 18 (1949).
Faulkner F. D., The problem of Goddard and optimum thrust
programming, Proc. 3rd Ann. Meeting Am. Astronaut. Soc. (1956).
Faulkner F. D., Some results from direct methods applied to
optimum rocket trajectories, Proc, 9th Intern. Astronaut. Congr,
Amsterdam (1958).
ОБЩИЙ УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
205
Ferrari С., Sulla determinazione del proietto di minima resistenza
d’onda, Atti accad. Sci. Torino, Class sci. fis. mat. e nat. 74
(1939—1940).
Foote J. R., Butler T., Adney J. E., and Th a c her H. C.,
Direct variational methods and brachistochrone problems, AFOSR
TR No. 101 (1961).
Fox R. H., Optimum exhaust velocity programming and propulsion
efficiency, J. Astronaut. Sci. 6, No. 1 (1959).
F о x R. H., The payload capabilities of ion propulsion rocket systems,
J. Astronaut. Sci. 6, No. 3 (1959).
F о у W. H., Steering of an ascent rocket for maximum cut-off velo-
city, Proc. 4th Ann. Meeting Am. Asronaut. Soc. (1958).
Fraeijs de Veubeke B., Mdthodes Variationnelles et Performan-
ces Optimales en Aeronautique, Bull. Soc. Math. Belgique 8, No. 2
(1956).
Fraeijs de Veubeke B., Le Probleme du Maximum de Rayon
d’Action dans un Champ de Gravitation Uniforme, Astronaut.
Acta 4, No. 1 (1958).
Fraeijs de Veubeke B., Variational methods in optimizing
rocket performance, гл. 12, в книге «Rocket Propulsion», Elsevier,
New York, 1960.
Garb ell M. A., Optimum climbing techniques for high performance
aircraft, Garbell Research Foundation, Rept. No. 8 (1953).
Graham E. W. and Beane B. J., Optimum trajectory problems:
Some special cases, Douglas Aircraft Company, Inc., Santa
Monica Division, Rept. No. SM-23687 (1959).
Haack W., Projectile forms of minimum wave resistance, Douglas
Aircraft Company, Inc., Translation Rept. No. 288 (1946).
frving-J. H., Low-thrust flight: Variable exhaust velocity in gravi-
tational fields, гл. 10 в книге «Space Technology», Wiley, New
York, 1959. [Русский перевод: под ред. Г. Сейферта, Косми-
ческая техника, гл. 8, изд-во «Наука», М., 1964.]
Irving J. Н. and Blum Е. К., Comparative performance of balli-
stic and low-thrust vehicles for flight to Mars, в книге «Vistas
in Astronautics», том 2, Pergamon, New York, 1959.
J uro vics S., Optimum steering program for the entry of a multi-
stage vehicle into a circular orbit, ARS Journal 31, No. 4
(1961).
Jurovics S. A. and McIntyre J. E., The adjoint method and
its application to trajectory optimization, North American Avia-
tion, Inc., Missile Division, Rept. No. MD 60-334 (1960).
Kaiser F., The climb of jet-propelled aircraft, Part I. Speed along
the path in optimum climb, Ministry of Supply (Gt. Brit.),
RTP/TIB Translation No. GDC/15/148T (1944).
Kelley H. J., An investigation of Optimal Zoom Climb Techniques,
J. Aero/Space Sci. 26, No. 12 (1959).
Kelley H. J., Variational treatment of three-dimensional boost-turn
performance, Grumman Aircraft Engineering Corp., RM No. 162
(1959).
Kelly L., Optimum cliieb technique for a jet-propelled aircraft, The
College of Aeronautics, Cranfield, Rept. No. 57 (1952).
206 МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [гл. IV
L a w d en D. F., Minimal trajectories, J. Brit. Interplanet. Soc. 9,
No. 4 (1950).
L a wde n D. F., Entry into circular orbits, J. Brit. Interplanet. Soc.
10, No. 1 (1951).
L a wden D. F., The determination of minimal orbits, J. Brit. Inter-
planet. Soc. 11, No. (1952).
La wden D. F., Interorbital transfer of a rocket, Brit. Interplanet
Soc. Ann. Rept. (1952).
L a wd en D. F., Orbital transfer via tangential ellipses, J. Brit. In-
terplanet. Soc. 11, No. 6 (1952).
L aw den D. F., Minimal rocket trajectories, ARS Journal 23, No. 6
(1953).
L a wden D. F., Stationary rocket trajectories, Quart. J. Meeh, and
Appl. Math. 7, No. 4 (1954).
La wden D. F, Optimum launching of a rocket into an orbit about
the earch, Astronaut. Acta 1, No. 4 (1955).
Lawden D. F., Optimal programming of rocket thrust direction,
Astronaut. Acta 1, No. 1 (1955).
Lawden D. F., Optimal transfer between circular orbits about two
planets, Astronaut. Acta 1, No. 2 (1955).
L a w d e n D. F., Transfer between circular orbits, ARS Journal 26,
No. 7 (1956).
L a w d e n D. F., Mathematical problems of astronautics, Math. Gazet-
te 41, No. 337 (1957).
L a w d e n D. F., Maximum ranges of intercontinental missiles, Aero-
naut. Quart. 8, No. 3 (1957).
L a w d e n D. F., The employment of aerodynamic forces to obtain
maximum range of a rocket missile, Aeronaut. Quart. 9, No. 2
(1958).
L a w d e n D. F., Optimal escape from a circular orbit, Astronaut.
Acta 4, No. 3 (1958).
L a w d e n D. F., Discontinuous solutions of variational problems, J.
Australian Math. Soc. 1, No. 1 (1959).
L a w d e n D. F., Necessary conditions for optimal rocket trajectories,
Quart. J. Meeh, and Appl. Math. 12, No. 4 (1959).
L a w d e n D. F., Optimal program for correctional manoeuvres,
Astronaut. Acta 6, No. 4 (1960).
Leitmann G., An optimum pursuit problem, J. Franklin Inst. 263,
No. 6 (1957).
Leitmann G., Trajectory programming for maximum range, J.
Franklin Inst. 264, No. 6 (1957).
Leitmann G., Optimum thrust direction for maximum range,
J. Brit. Interplanet. Soc. 16, No. 9 (1958).
Leitmann G., Some remarks on the optimum operation of a
nuclear rocket, Proc. 10th Intern. Astronaut. Congr., London
(1959).
Leitmann G., Minimum transfer time for a power-limited rocket,
Proc. 11th Intern. Astronaut. Congr., Stockholm (1960).
Leitmann G., The optimization of rocket trajectories, A survey,
гл. 5 в книге «Progress in the Astronautical Sciences», North-Hol-
land, Amsterdam, 1962.
ОБЩИЙ УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
207
Levinsky Е. S., Application of inequality constraints to variational
problems of lifting re-entry, IAS Preprint No. 61-21 (1961).
Lush K. J., Optimum climb theory and techniques of determining
climb schedules from flight tests, AFFTC TN No. 56-13 (1956).
Miele A., Optimum climbing technique for a rocket-powered aircraft,
ARS Journal 25, No. 8 (1955).
Miele A., Optimum flight paths of turbojet aircraft, NACA TM
No. 1389 (1955).
Miele A., Optimum burning program as related to aerodynamic
heating for a missile traversing the earth’s atmosphere, ARS
Journal 27, No. 12 (1957).
Miele A., Some recent advances in the mechanics of terrestrial
flight, ARS Journal 28, No. 9 (1958).
Miele A., Variational approach to the stratospheric cruise of a
turbojet-powered aircraft, ZFW 6, No. 9 (1958).
Miele A., On the flight path of a hypervelocity glider boosted by
rockets, Astronaut. Acta 5, No. 6 (1959).
Miele A., Variational approach to problems of hypervelocity flight,
Purdue University, School of Aeronautical Engineering, Rept.
No. A-59-7 (1959).
Miele A., A survey of the problem of optimizing flight paths of
aircraft and missiles, Boeing Scientific Research Laboratories,
Flight Sciences Laboratory, TR No. 27 (I960).
Miele A. and C a p p e 11 a r i J. O., Some variational solutions to
rocket trajectories over a spherical earth, Purdue University»
School of Aeronautical Engineering, Rept. No. A-58-9 (1958).
Miele A. and C a p p e 11 a r i J. O., Approximate solutions to the
optimum climbing trajectory for a rocket-powered aircraft, NASA
TN No. D-150 (1959).
Miele A. and C a p p e 11 a r i J. O., Approximate solutions to opti-
mum flight trajectories for a turbojet-powered aircraft, NASA TN
No. D-152 (1959).
Miele A. and C a v о t i C. R., Generalized variational approach to'
the optimum thrust programming for the vertical flight of a
rocket, Part 2, Application of Green’s theorem to the development
of sufficiency proofs for particular classes of solutions, ZFW 6,
No. 4 (1958).
Miele A. and C a v о t i C. R., Optimum thrust programming along
arbitrarily inclined rectilinear paths, Astronaut. Acta 4, No. 3
(1958).
Miele A. and C a v о t i C. R., Variational approach to the reentry
of a ballistic missile, Part 1, Purdue University, School of Aero-
nautical Engineering, Rept. No. A-59-1 (1959).
Miele A. and Cavoti C. R., Variational approach to the reentry
of a ballistic missile, Part 2, Purdue University, School of Aero-
nautical Engineering, Rept. No. A-59-3 (1959).
Newton R. R., On the optimum trajectory of a rocket, J. Franklin
Inst. 266, No. 3 (1958).
Охоцимский Д. E. и Энеев T. M., Некоторые задачи, связан-
ные с запуском искусственного спутника Земли, Успехи физи-
ческих наук 63, вып. 1, стр. 5—32 (1957J. f
208
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. IV
Puckett А. Е. and Edwards R. Н., The optimum performance
of shortrange rocket-powered missiles, IAS Preprint No. 279
(1950).
Rosenberg R. M., On optimum rocket trajectories and the calculus
of variations, Aero/Space Eng. 19, No. 10 (1960).
Ross S. E., Minimality for problems in vertical and horizontal rocket
flight, ARS Journal 28, No. 1 (1958).
Ross S. E., Composite trajectories yielding maximum coasting apo-
gee velocity, ARS Journal 29, No. 11 (1959).
В u t о w s к i E. S., Energy approach to the general aircraft perfor-
mance problem, J. Aero/Space Sci. 21, No. 3 (1954).
Santangelo G., Sulla Virata Corretta Brachistocrona, L’Aero-
tecnica 33, No. 2 (1953).
Sears W. R., On projectiles of minimum wave drag, Quart. Appl.
Math. 4, No. 4 (1947).
Stancil R. T. and К u 1 а к о w s к i L. J., Rocket boost vehicle
mission optimizations, ARS Preprint No. 1449-60 (1960).
Strand T., Design of missile bodies for minimum drag at very
high speeds. Thickness ratio, lift, and center of pressure given,
J. Aero/Space Sci. 26, No. 9 (1959).
Tan H. S., On optimum nose curves for missiles in the superaerody-
namic regime, J. Aero/Space Sci. 25, No. 1 (1958).
T a n H. S., Nose drag in free-molecule flow and its minimization,
J. Aero/Space Sci. 26, No. 6 (1959).
Theodorsen T., Optimum path of an airplane — Minimum time to
climb, J. Aero/Space Sci. 26, No. 10 (1959).
Von Karman T., The problem of resistance in compressible fluids,
Galcit Publ. No. 7 (1936).
Ward L. E., A calculus of variations problem in thrust program-
ming, U. S. Naval Ordnance Test Station, TN No. 3503/2 (1955).
ГЛАВА V
ВАРИАЦИОННЫЕ ЗАДАЧИ
С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
5.0. ВВЕДЕНИЕ
В главе IV были изложены элементы вариационного
исчисления с приложениями к задачам оптимизации
полета управляемых ракетных систем и их траекторий.
В тех случаях, когда одна или большее число управля-
ющих функций подчинены ограничивающим неравен-
ствам, теория приобретает некоторые специфические
черты (см. приложение и гл. VII). Подробное рассмо-
трение такого рода задач составляет предмет настоящей
главы. Имея целью изложить основные методы так, что-
бы детали не заслонили основного содержания, мы
ограничимся классом задач настолько простых, что ре-
шение их может быть осуществлено обычными средства-
ми, и представляющих вместе с тем реальный интерес.
Предметом рассмотрения будут главным образом за-
дачи оптимизации траектории ракет, полет которых про-
исходит в силовых полях, обусловливающих ускорение,
зависящее лишь от положения и от времени; среди та-
ких полей, разумеется, основной интерес представляют
гравитационные поля [1]. При полете в атмосфере воз-
никают силы, зависящие и от скорости; такие задачи,
однако, мы не будем здесь рассматривать. Отказ от
этих задач продиктован не недостатком интереса к ним,
а объясняется скорее желанием иллюстрировать исполь-
зуемые методы на простейших примерах и, что,, пожа-
луй, более важно, тем, что мы обладаем весьма непол-
ными сведениями об оптимальных траекториях при
силах, зависящих от скорости, и управлениях типа мас-
сового расхода и мощностц двигателей, входящих в ура-
внения линейно.
14 Дж. Лейтман
210
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
Будем предполагать, что управления массовым рас-
ходом, мощностью двигателей и ускорением тяги под-
чинены ограничивающим неравенствам.
5.1. ПОСТАНОВКА ЗАДАЧИ
Требуется определить условия, при которых дости-
гает минимума функционал, представляющий собой
функцию лишь конечных значений переменных, харак-
теризующих состояние системы, — положения, скорости,
массы и времени:
G = G(qn, (5.1)
где
qj = x, у, и, v, nt, t. (5.2)
Функция G выражает любую представляющую инте-
рес величину: время, массу, скорость, расстояние, вы-
соту, энергию, момент количества движения и т. д.
Относительно ракеты и окружающей ее среды дела-
ются следующие предположения:
а) Ракета рассматривается как точка переменной
массы, т. е. момент инерции ракеты предполагается пре-
небрежимо малым.
б) Величина силы тяги считается линейной функцией
расхода массы [2]:
Т — —с'т. (5.3)
в) Предполагается, что направление силы тяги мо-
жет быть мгновенно изменено, т. е. пренебрегается инер-
ционностью устройств, поворачивающих двигатель от-
носительно осей карданова подвеса.
г) Внешние силы, действующие на ракету, создают
ускорения, зависящие лишь от положения и времени,
т. е.
X=X(x,y,t), [
Y=Y(x, у, f). / (5,4)
Приводимое ниже исследование ограничено случаем
полета в одной плоскости. Это сделано единственно ради
простоты, и все результаты легко переносятся на трех-
мерный случай.
6.2] СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ МАССЫ 211
В предположениях а)—г) уравнения движения ра-
кеты относительно некоторой инерциальной системы от-
счета имеют вид
« = Л-|--^СО8ф,
1 т Т
V = Y -|- — Sin Ф,
1 т т
(5.5)
х = и, y = v, т —— р.
Уравнения (5.5) содержат восемь зависимых пере-
менных, а именно: х, у, и, v9 т, с, р и гр. Поскольку чис-
ло уравнений равняется пяти, три переменные из восьми
представляют собой произвольные функции — управле-
ния с (/), р(/) и гр(/),— и эти функции должны быть
выбраны таким образом, чтобы получилась требуемая
оптимальная траектория, т. е. такая, чтобы «функция
выигрыша» G приняла минимальное значение.
Мы проведем исследование описанного класса задач
последовательно для ракетных систем, имеющих огра-
ниченные массовый расход, мощность двигателей и
ускорение силы тяги, причем в последнем случае мощ-
ность двигателей будет считаться постоянной. Такого
рода ограничения на управления рассматриваются по
той причине, что без них невозможно получить решение,
например, таких задач, в которые управления входят
линейным образом. Задачи, в которых ограничивающие
неравенства накладываются на другие управляющие
переменные, такие, как, например, направление гр век-
тора тяги, также могут быть решены с помощью изла-
гаемых здесь методов [3].
5.2. СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ
МАССЫ
Для большинства используемых ракет, например для
систем с двигателями, работающими на энергии хими-
ческих реакций, к уравнениям (5.5) присоединяются
следующие соотношения:
с = const, (5.6)
Pmln Р Ртах» (5*7)
14*
212
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
где Ртах — заданная величина, a pmin = 0, так что, во-
обще говоря, допускается свободный полет.
Чтобы включить связи, выражаемые такими неравен-
ствами, как, например, (5.7), в общую схему классиче-
ского вариационного исчисления, вводится [4] веществен-
ная переменная у такая, что
(WmIn)(?max-₽) = 72. (5-8)
Уравнение (5.8) равносильно неравенству (5.7).
Для рассматриваемой ракетной системы число упра-
влений сведено к двум, именно р и гр; первое из этих
управлений ограничено.
5.21. Первая вариация. Чтобы функция G при свя-
зях (5.5), (5.6) и (5.8) достигла экстремума, необхо-
димо, чтобы обратилась в нуль первая вариация функ-
ционала, составленного с учетом связей (см. гл. IV).
Это приводит к уравнениям Эйлера — Лагранжа [5]:
— О,
= О,
4- \и дХ/дх + дУ/дх = О,
+ Ki дХ/ду + дУ/ду = О,
Кп — 5-(хвсо8фН-Х1,8тф) = 0)
(Х„ sin ф — cos ф) — О,
(5-9)
(Х„ cos ф+X„ sin ф) — Xm — Х7 (pmax + pmIn—2р) = О,
°»
где величины X представляют собой неопределенные
множители.
Для того чтобы задача имела смысл, можно задать
граничные значения части переменных: х, у, и, и, ту t.
Граничные значения остальных переменных, а также
множителей А могут быть найдены из общего условия
СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ МАССЫ
213
5.2]
трансверсальности
dQ —|- du|— dv —dx —
+ \ dy + dm — С dtfy = 0, (5.10)
где
С = + \хх + Хуу 4~ ^тш. (5.11)
Если ускорения (X, У) от внешних сил не содержат
явно независимую переменную, в данном случае время /,
то существует первый интеграл
С = const, (5.12)
который может быть использован вместо любого из диф-
ференциальных уравнений Эйлера — Лагранжа; таким
образом, порядок системы понижается на единицу.
Уравнения (5.5), (5.6), (5.8) и (5.9) образуют систе-
му 15 уравнений, которая вместе с заданными и полу-
ченными выше граничными условиями должна опреде-
лить оптимальное решение, т. е. 15 функций времени:
х, у, u, v, т, с, р, ф, у, Хи, Хг, Хх, Ху, Хт и Хг Поскольку
10 из#этих уравнений являются обыкновенными диффе-
ренциальными уравнениями первого порядка, порядок
системы равен 10 и требуется 10 начальных либо конеч-
ных значений зависимых переменных и множителей, а
также два краевых значения независимой переменной —
времени.
Так как половина из заданных и полученных в процес-
се решения краевых значений известна при t = /г-, а дру-
гая половина — при t = tf, то задача всегда оказывается
краевой. С вычислительной точки зрения это требует
процесса итераций, при котором задаются неизвестными
краевыми значениями в начальной (или конечной) точ-
ке, выполняют интегрирование и пытаются совместить
получающиеся на другом конце значения переменных с
заданными значениями. Процесс такого рода часто ока-
зывается весьма продолжительным, а в некоторых слу-
чаях и вообще расходится.
Даже если и можно преодолеть трудности, вызван-
ные краевым характером задачи, — часто это оказывает-
ся возможным, см. численный пример в разделе 5.6, —•
214
• ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
(5.13)
(5-14)
все же еще остается значительное число других вопро-
сов, не разрешенных до настоящего времени.
5.22. Программа направления вектора тяги. Опти-
мальное направление вектора тяги дается шестой фор-
мулой системы (5.9), а именно:
откуда
sin ф = ± +
cos Ф = ± \jV
Этот результат получен впервые в задаче о полете в по-
стоянном гравитационном поле [6].
Как видно из уравнений (5.13) или (5.14), существу-
ет свобода выбора значения угла, под которым направ-
ляется вектор тяги, именно решением уравнения (5.1)
является
ф = ф(О (5.15)
или
Ф = Ф(О+*-
Другими словами, на этой стадии исследования нет
возможности выбрать тот или иной знак (+ или —) в
соотношениях (5.14). Если [7] выбран знак +, то на-
правляющие косинусы вектора тяги имеют знаки чисел
Ки и kv. Требуется, однако, особое доказательство пра-
вильности такого выбора. Здесь мы сталкиваемся с
вопросом, ответить на который нельзя, основываясь
лишь на условиях, доставляемых рассмотрением первой
вариации. Этот вопрос будет разрешен вместе с еще од-
ним, возникающим ниже; поэтому мы откладываем соот-
ветствующее рассмотрение на некоторое время.
5.23. Программа расхода массы. Если требуется,
чтобы было выполнено ограничение (5.7), записанное в
форме (5.8), то очевидно, что полет должен происходить
либо с максимальным расходом массы, либо с мини-
мальным расходом (свободное движение), либо при про-
межуточных значениях расхода массы. Уравнение Эйле-
ра— Лагранжа (5.9)8 возникает из равенства (5.8).
8.2]
СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ МАССЫ
215
7 = 0, Х7 Ф 0. I
7 = 0, Х7 = 0 /
Следствием этого уравнения являются следующие усло-
вия [8]:
7 ¥= О, = О И Pmin < Р Ртах»
(5.16)
и ₽ = ₽ml„ ИЛИ ₽ = ₽тах.
Хотя условия (5.16) обеспечивают соблюдение урав-
нения Эйлера — Лагранжа, возникшего из-за наличия
ограниченного массового расхода р, они оставляют без
ответа важнейший вопрос о выборе оптимального режи-
ма расхода массы. Это — еще одна проблема, очевид-
но неразрешимая в рамках исследования первой вари-
ации. Решение задачи может быть непосредственно
получено для того частного случая, когда требуется вы-
вести ракету на круговую орбиту с максимальной ско-
ростью при подъеме в постоянном гравитационном поле
и при отсутствии ограничений массового расхода [9].
В общей задаче, рассматриваемой здесь, следует, од-
нако, обратиться к более сильным условиям, нежели те,
которые доставляются требованием обращения в нуль
первой вариации [10].
Поскольку производные от управлений ф и р не вхо-
дят в уравнения, эти функции могут терпеть конечное
число разрывов непрерывности — в действительности
именно так и обстоит дело, — так что и ускорения й и v
могут оказаться разрывными. Этим разрывам соответ-
ствуют угловые точки экстремали, в которых выпол-
няются условия Эрдмаца — Вейерштрасса.
5.24. Условия в угловых точках. Для рассматривае-
мой задачи условия в угловых точках имеют простой
вид:
Х^- = Х^+ = у, и, v, т) (5.17)
и
С_=С+. (5.18)
Таким образом, множители, относящиеся к перемен-
ным состояния, а также выражение (5.11) имеют одина^
ковые значения непосредственно перед угловой точкой
р непосредственно за нец.
216
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
5.25. Е-функция Вейерштрасса. Для ответа на два
вопроса, оставшиеся невыясненными, именно на вопрос
о произвольности выбора главного значения угла, харак-
теризующего направление вектора тяги, и на вопрос об
оптимальном выборе режима массового расхода, можно
обратиться к необходимому условию минимума функ-
ционала G. Таким условием является требование, чтобы
Е-функция Вейерштрасса была неотрицательна. Для
рассматриваемой нами задачи это условие равносильно
тому, чтобы управления ф и р были выбраны таким об-
разом, чтобы выражение
+ Хт] (5.19)
принимало вдоль оптимальной траектории максималь-
ное значение (см. приложение). Это условие связано с
функциональным уравнением принципа оптимальности
Веллмана [11] и эквивалентно принципу максимума Пон-
трягина [12] (см. также гл. VII).
5.26. Оптимальное направление вектора тяги. Для
того чтобы функция L достигала максимума по отноше-
нию к ф, требуется выполнение условий
= ^<0. (5.20)
Эти условия сразу приводят к уравнению (5.13) и
требуют выбора знака + в формулах (5.14), решая тем
самым вопрос об оптимальном угле наклона вектора
тяги ф. Следовательно,
Xucos^ + Xjzsin ф = (Х^ + (5.21)
Более того, из формул (5.14) теперь следует, что
угол ф терпит разрыв на величину л, когда ки и к»
одновременно проходят через нуль [13].
5.27. Оптимальный расход массы. Функция переклю-
чений. Уравнение (5.19) имеет вид
Z = (5.22)
Т. е- содержит р линейно; коэффициент х равен
х = ^-(Х« + ^),/2-Хда. (5.23)
6.21
СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ МАССЫ
217
График L как функции р в любой момент времени
имеет вид, представленный на рис. 5.1. Очевидно, что
Х>0 При Р== Ртах’ 1
х<0 при p = pmI11. J
(5.24)
Если х лишь проходит через нуль, то не возникает
никаких осложнений и
функцию переключений
при двухпозиционном
(«bang-bang») управле-
нии расходом массы. Та-
ким образом, если удает-
ся показать, что
х ф 0 (5.25)
(см. рис. 5.2 и 5.3), то
функция переключений х
может быть найдена из
(5.23) с заменой уравне-
ния (5.9) 7 условием (5.24).
Если, однако, условие
х можно рассматривать как
Рис. 5.1. Условие Вейерштрасса
для массового расхода.
(5.25) не следует из задачи *),
то в программе расхода массы может оказаться
Рис. 5.2. Функция переключе- Рис. 5.3. Двухпозиционное управ-
ний массового расхода. ление расходом массы.
промежуточный режим * **) и Е-функция Вейерштрасса
не приведет к оптимальному выбору режима расхода
♦) Например, при учете аэродинамических сил условие (5.25),
вообще говоря, не соблюдается.
**) В советских работах вместо этого термина употребляется
термин «особое управление», введенный Л, И, Розоноэром (см. [31]
к главе VI). (Прим, перев.)
'218
ЗАДАЧИ с ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
(гл; V
массы (рис. 5.1). Существует, однако, важный класс
задач, для которых справедливо условие (5.25) и,
следовательно, действует двухпозиционное управле-
ние [10, 14].
5.28. Двухпозиционное управление расходом массы.
Если ускорения, сообщаемые внешними силами, являют-
ся линейными функциями координат, т. е. если
^=Х0 + Л'1Х-|-Л'2у, |
Г^Ко + Лх + ^у, J
(5.26)
где коэффициенты Хо, Уо. Xi, ..., У2 не зависят от коор-
динат х и у, то уравнения (5.9) i-4 принимают вид
X® ХИХ2 —— XjjK2 = 0.
(5.27)
Уравнения (5.27) представляют собой уравнения вто-
рого порядка по отношению к переменным Ки, X®, кото-
рые теперь отделены от остальных уравнений Эйлера —
Лагранжа и уравнений связи.
Далее, если уравнение (5.25) несправедливо, то в
пределах конечного промежутка времени
х = 0. (5.28)
Уравнение (5.28) вместе с (5.9)s и (5.21) дает
M„ + xA = 0. (5.29)
т. е. еще одно уравнение, содержащее только Хи и X®.
Можно показать, что решение уравнений (5.27) в об-
щем случае не удовлетворяет уравнению (5.29). Случай,
когда Хи и X® тождественно равны нулю, можно отбро-
сить, так как при этом равны нулю все множители.
Представляют интерес следующие частные случаи:
1) Полет в постоянном гравитационном поле, именно:
Х= 0, Y = — g0 — const. (5.30)
Было показано [10], что при этом возможен один из
двух случаев:
а) имеется самое большее три режима массового
расхода на любой оптимальной траектории, иными ело-
В.2]
СИСТЕМЫ С ОГРАНИЧЕННЫМ РАСХОДОМ МАССЫ
219
Рис. 5.4. Нули функции переклю-
чений.
вами, траектория в целом составляется не более чем из
трех частей, проходимых с максимальной или минималь-
ной тягой;
б) единственного оптимального решения нет.
2) Полет в радиальном поле, обратно пропорцио-
нальном квадрату расстояния; в разложении гравита-
ционного ускорения
удерживаются лишь
члены первого порядка
[14], а именно:
Х= — е2х, ]
r=-fo+2.J<5-3”
Пример такого ро-
да рассмотрен в раз-
деле 5.6.
Хотя и не оказалось
возможным доказать
неосуществимость промежуточного режима массового
расхода для оптимальных полетов в полях более общего
типа, тем не менее программа такого типа может пред-
ставиться в некоторых областях силового поля либо при
определенных других условиях.
Из уравнений (5.23) и (5.9) i-5 следует
* — — ~ (^и Ч” ^2) , (5.32)
так что х терпит разрыв (меняет знак), когда и
одновременно проходят через нуль, т. е. когда ф испы-
тывает разрыв первого рода. На рис. 5.4 показаны воз-
можные способы перехода величины х через нуль.
Отсюда следует, что промежуточный режим массового
расхода (х=0) может начаться лишь непрерывным об-
разом. Поскольку производные от х по времени вплоть
до третьего порядка непрерывны, требуется, чтобы к на-
чалу промежуточного режима выполнялись равенства
х=х=х=х = 0.
(5.33)
Эти условия могут оказаться полезными для отбра-
сывания режимов указанного типа.
220
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
5.29. Случай отсутствия ограничений расхода массы.
Если расход массы не ограничивается сверху, т. е.
Ртах
(5.34)
и справедливо условие (5.25) двухпозиционного управ-
ления, то продолжительность режимов максимального
расхода массы сводится к нулю. Иными словами, режи-
мы максимального расхода массы уступают место им-
Рис. 5.5. Функция переключений для
случая импульсной тяги.
пульсам расхода. По-
ведение функции пере-
ключения для этого
случая изображено на
рис. 5.5.
Таким образом,
либо
х=х = 0, (5.35а)
либо
х = 0, ]
>, = > =0. (М56>
Оба условия (5.35а) и (5.356) охватываются соотно-
шением [15]
*Л + *А = 0, (5.36)
которое должно быть удовлетворено в любой внутрен-
ней точке траектории, где следует приложить импульс
расхода массы.
5.210. Промежуточная программа расхода массы.
Если не представляется возможным доказать отсутствие
промежуточных режимов расхода массы, то вопрос о со-
ставлении полной оптимальной траектории остается не-
выясненным. Можно, однако, получить некоторые дан-
ные, относящиеся к режимам такого рода. Не будучи
необходимыми для исследования общего случая, эти ре-
зультаты могут оказаться иногда полезными при исклю-
чении возможности существования промежуточных ре-
жимов. Так, если на конечном интервале времени
х = 0, (5.37)
6.3]
СИСТЕМЫ С ОГРАНИЧЕННОЙ МОЩНОСТЬЮ
221
то имеет место уравнение (5.29). Интегрирование этого
уравнения дает
X • X = const, (5.38)
где X есть вектор с компонентами Хи и Хр, т. е. на-
правленный по вектору тяги. Уравнения (5.9)i-4 приво-
дят теперь к соотношению
X Х + V (F-X) • Х = 0, (5.39)
в котором вектор F ускорения, обусловленного внеш-
ними силами, имеет в плоском случае составляющие X
и Y. Необходимым условием существования промежу-
точного оптимального режима расхода массы будет при
этом неравенство
V(F-X)-X <0.
(5.40)
Для радиального поля, обратно пропорционального
квадрату радиуса, имеем:
F=V<p, <р~у. (5.41)
где г — расстояние от притягивающего центра. В этом
случае неравенство (5.40) принимает вид [7]
cos29<l. (5.42)
где 9 — угол между вектором тяги и вертикалью в дан-
ной точке.
5.3. СИСТЕМЫ С ОГРАНИЧЕННОЙ МОЩНОСТЬЮ
ДВИГАТЕЛЕЙ
Если основное ограничение в системе накладывается
мощностью двигателей, а не расходом массы, как это
имеет место, например, в электрических двигательных
устройствах, то уравнения связей (5.6) и (5.7) заме-
няются неравенствами
amtn ® ашах»
(5.43)
где
а = фс2 — 2Р
(5.44)
222
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
и величина аШах считается заданной. В общем случае
o&min = 0, так что допускается полет без затраты мощ-
ности.
Поскольку в системах с независимым источником
энергии величину тяги можно изменять, варьируя как
расход массы р, так и скорость истечения с, имеем в
данном случае три управляющие переменные. Удобно
выбрать в качестве управлений функции ф, а и с.
5.31. Первая вариация. Для того чтобы функционал
G достигал экстремального значения при наложении
связей (5.5) и (5.43), причем неравенства (5.43) вновь
заменяются равенствами путем введения вещественной
переменной у, первая вариация функционала, построен-
ного с учетом связей, должна обратиться в нуль. Соот-
ветствующие уравнения Эйлера — Лагранжа имеют
вид *)
хи+хл=о,
— О,
х —I—X ^*+Х -^-0
\ + дх дх — и»
X -LX I х _________о
ку *ки ду । Kv ду —
L—-^2-(x«cos sin Ф)=°>
« (5.45)
— (Хи sin ф — X„cos ф) = 0,
^(^созф + Х^М) — 2Х/я-^- = 0,
-^(^созф + Х^пф) —
~q2 (2а атах ат!п) == О»
______________ Х7Т = О.
*) Уравнение (5.45)?, выражающее, что функция L (см. (5.47))
принимает максимальное значение относительно с, справедливо при
условии Хт>0. Если Хт 0, то такого экстремума функции L не
существует; в этом случае вместо с следует взять переменную 0
в качестве управления, установив верхний предел принимаемых ею
значений^
В.З]
СИСТЕМЫ С ОГРАНИЧЕННОЙ МОЩНОСТЬЮ
223
При написании уравнений связи и уравнений Эйле-
ра — Лагранжа предполагается, что скорость истечения
не обращается в нуль и обращается в бесконечность са-
мое большее конечное число раз.
Кроме уравнений (5.45) имеется, как и в разделе 5.21,
еще общее условие трансверсальности (5.10). Более то-
го, здесь сохраняет силу замечание раздела 5.21 относи-
тельно интегрирования уравнений связей и Эйлера “
Лагранжа.
5.32. Программа направления силы тяги. Направле-
ние вектора тяги снова дается уравнением (5.13). Что
касается оптимального выбора главного значения угла,
то этот вопрос откладывается на дальнейшее, как и в
разделе 5.26.
5.33. Программа управления мощностью двигателей.
Как и в разделе 5.23, ограничивающее неравенство, на
этот раз для а, вместе с соответствующим уравнением
Эйлера — Лагранжа (5.45)9 требуют, чтобы выполнялись
условия:
Y 0, Х^ — 0 И а <1 атах»
7 = 0, X- =/= 0, )
„_А 1 — А I И а = ат1п ИЛИ а = атах«
(5.46)
Снова, таким образом, возникает задача составления
оптимальной траектории, иными словами, задача состав-
ления оптимальной последовательности трех возможных
режимов управления мощностью. Для решения этой за-
дачи можно опять обратиться к Е-функции Вейерштрас-
са. Предварительно заметим, что разрывы управлений
могут вызвать появление угловых точек на экстремали.
Условия в угловых точках в этом случае те же, что и в
разделе 5.24, а именно (5.17) и (5.18).
5.34. Е-функция Вейерштрасса. Требование, чтобы
Е-функция Вейерштрасса в случае минимума функцио-
нала G была неотрицательна, приводит к условию ма-
ксимальности функции
+ (5.47)
по отношению к управлениям ф, с и а.
224
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
(гл. V
Что касается угла ip, то это условие приводит к
(5.45)в, т. е. к уравнению (5.14) со знаком + , а также к
уравнению (5.21). Максимальность выражения (5.47) по
отношению к скорости истечения с обеспечивается при
выполнении соответствующего уравнения Эйлера — Ла-
гранжа (5.45)7. Условие максимума по ограниченной пе-
ременной а также должно удовлетворяться; имеем
Из (5.45)7 следует, однако, что
>-= 2^ « (5.49)
Поэтому
dL
да
1
2т с
М + хЭ''’>о.
(5.50)
знак равенства имеет ме-
промежутка изменения а,
Если в соотношении (5.50)
сто на протяжении конечного
Рис. 5.6. Условие Вейерштрасса
для мощности двигателей.
то ки = = 0 и, следо-
вательно, все множители
обращаются в нуль. На
рис. 5.6 поэтому иллю
стрируется случай, когда
постоянно выполняется
оптимальная программа
по а, имеющая вид
а == атах» (5.51)
т. е. максимальная мощ-
ность двигателей разви-
вается на всем протяже-
нии траектории.
Этот результат может быть получен непосредственно
в случае, когда минимизируется потребление топлива и
предполагается, что полет без затраты мощности не
имеет места [16].
В ряде задач оказываются достаточными уже полу-
ченные результаты. К задачам такого рода принадлежит
задача минимизации времени передвижения между дву-
мя точками, скорости в которых заданы, при условии,
S.4) СИСТЕМЫ С ОГРАНИЧЕННЫМ УСКОРЕНИЕМ ТЯГИ 225
что отношение масс в этих точках известно [17]. Другая
группа задач, решение которых может быть дано с по-
мощью полученных выше результатов, описана в опуб-
ликованной недавно работе [18]; среди них имеется
задача о максимальном приращении скорости при задан-
ных значениях времени полета и отношения масс; в ука-
занной работе, однако, a priori предполагается, что полет
происходит при максимальной мощности двигателей.
В общем случае нельзя гарантировать получение
разумных решений без наложения дальнейших ограни-
чений на управления. Не ясно, в частности, предотвра-
тит ли ограничение только мощности необходимость
требования бесконечной величины тяги. Может, следо-
вательно, оказаться необходимым наложить ограниче-
ния на скорость истечения с или на ускорение, созда-
ваемое тягой. Здесь мы рассмотрим лишь последний
случай.
5.4. СИСТЕМЫ С ОГРАНИЧЕННЫМ УСКОРЕНИЕМ
ТЯГИ
Другим возможным ограничением двигательной си*
стемы может быть ограничение ускорения силы тяги
а = . (5.52))
Рассмотрим задачу минимизации G для ракеты огра-
ниченной мощности, работающей при постоянной мощ--
ности Р двигателя и с ограниченным ускорением силы
тяги а.
Удобно ввести новую переменную
Н = (5.53)
и записать уравнения движения в форме
и — %+ a cos ф,
v = У 4- a sin <]>,
х — а, y = v, р = а?,
где
ЯШах
(5.54)
(5.55)
15 Дж. Лейтмая
2»
задачи с ограниченными управлениями
[гл, V
или, что то же,
(й &mln) (^max Д) = К2» (5.56)
причем атах задано, а атт = 0, так что допускается по-
лет без действия тяги. Если требуется, чтобы решение
содержало участки свободного полета, т. е. нулевого ус-
корения силы тяги в течение конечного времени, то мо-
жет оказаться необходимым наложить ограничивающие
неравенства на с или р либо заменить условие работы
при постоянной мощности неравенствами, наложенными
на а и с. В самом деле, если
Р = 0 и = (5.57)
н0 = const =# о, (5.58)
ТО
с = оо. (5.59)
Такое положение было обнаружено при решении не-
которых задач [17]. Эта ситуация, однако, имела место
лишь в изолированных точках траектории и поэтому не
влекла за собой математических усложнений, что, ко-
нечно, не реализуется практически. В дальнейшем мы
увидим, что поведение такого рода действительно мо-
жет иметь место только в отдельных точках интервала.
5.41. Первая вариация. Для того чтобы функционал
G достигал экстремума при связях (5.54) и (5.56),
должны выполняться следующие уравнения Эйлера —
Лагранжа:
ч- = о,
X | X I х 0 + Ла дх 1 дх ~~ и’
х . / ^C-L-x ^Г-о S 1 АИ 1 KV fiy U> (5.60)
X, =0,
а (Xe sin ф — cos ф) = 0,
>я cos ф 4- sin фН-ЗХ^а 4-XT(2<z-amai-an)ln) = 0,
М=о,
где на этот раз ф и а являются управлениями.
6.4] СИСТЕМЫ С ОГРАНИЧЕННЫМ УСКОРЕНИЕМ ТЯГИ 227
Далее, общее условие трансверсальности имеет вид
dG [Xu du —|- Xv dv —Хх dx —|—
+ \ dy + dv- — С di^ = 0, (5.61)
где
С = \ии + \vv -|- Ххх -j- \уу -|- Xpj*. (5.62)
Здесь снова применимы значения раздела 5.21 отно-
сительно интегрирования уравнений движения и урав-
нений Эйлера — Лагранжа. Если получено решение для
переменных и, и, х, у, р, и для управлений гр и а как
функций времени /, то масса т и, следовательно, расход
массы р можно определить из уравнения (5.53); ско-
рость истечения с найдется тогда с помощью уравне-
ния (5.52).
5.42. Программа направления силы тяги. Направле-
ние силы тяги снова дается уравнением (5.13); главное
значение ф должно определяться подобно тому, как это
делалось в разделе 5.26.
5.43. Программа ускорения силы тяги. Как и в пре-
дыдущих параграфах, уравнение Эйлера — Лагранжа
(5.60)8, соответствующее неравенству связи, приводит к
возможности осуществления трех режимов ускорения,
а именно:
7 ¥= о, Х^ — О и Ят!п Я #тах’
7 = 0, X #= 0, 1
_ п > П I И О'== ИЛИ Л = ^тах*
(5.63)
Вновь возникает задача выбора оптимального режи-
ма ускорения и составления оптимальной траектории в
целом. Для решения этого вопроса снова можно вос-
пользоваться Е-функцией Вейерштрасса. Кроме того, в
угловых точках экстремали, возникающих благодаря
разрывам в управлениях ф и а, соблюдаются условия,
аналогичные приведенным в разделе 5.24.
5.44. Е-функция Вейерштрасса. Условие, чтобы
Е-функция Вейерштрасса при минимуме функционала G
15*
228
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
была неотрицательна, приводит к требованию, чтобы
выражение
Z = a(X0cos(p + Xt,sin<|> + X(la) (5.64)
было максимально по отношению к ф и а.
Взятое по отношению к углу ф, это условие дает
уравнение (5.60)б, а отсюда — формулы (5.14), в кото-
рых берется знак + , а также уравнение (5.21). Что ка-
сается ограниченного управления а, то имеем
-^- = (*« + 4)'/2 + V*- (5.65)
Теперь следует сделать выбор между тремя возмож-
ностями, зависящими от значения множителя Во-
первых, согласно уравнению (5.60)5
Х^ = const. (5.66)
Если отношение масс не задано, т. е. ц не фиксиро-
вано ни в какой точке траектории, то уравнения
(5.61)
Рис. 5.7. Условие Вейерштрасса для
ускорения силы тяги при постоянной
развиваемой мощности и незафикси-
рованном отношении масс.
и (5.66) дают
Хи = о. (5.67)
Отсюда
> 0. (5.68)
женный неравенством (5.68)
рис. 5.7, приводит к выводу,
поскольку случай одно-
временного обращения
в нуль величин ки и
т. е. всех множите-
лей сразу, следует от-
бросить. Случай, отра-
и проиллюстрированный
что если отношение масс
не задано, то оптимальным является режим максималь^
ного ускорения силы тяги.
Этот случай ясно показывает необходимость наложе-
ния неравенства связи на ускорение силы тяги а. Если
связь (5.55) не накладывается, т. е. если
х1=о,
(5.69)
5.4]
СИСТЕМЫ С ОГРАНИЧЕННЫМ УСКОРЕНИЕМ ТЯГИ
229
Рис. 5.8. Условие Вейерштрас-
са для ускорения силы тяги
при постоянной развиваемой
мощности и отрицательном Х^.
то формально из уравнений (5.60)7 и (5.67) получаем
Хи cos ф + Xv sin ф = 0. (5.70)
Совместно с уравнением (5.60)б это дает
sin2 ф + cos2 ф = 0, (5.71)
что, конечно, невозможно.
Если
X, < 0, (5.72)
как это бывает, например, когда требуется минимизи-
ровать потребление топлива, то поведение L как функ-
ции от а дается рис. 5.8. Таким образом, если условие
(5.55) не нарушается, то
при соблюдении равенства
-37=° (5J3)
оптимальная программа
ускорения дается условием
.(5.63), а оптимальное значе-
ние а определяется уравне-
нием (5.73), совпадающим с
(5.60)7 при
Х7 = 0. (5.74)
Поскольку множители Хи,
Хг, Хц. вследствие условий
в угловых точках непрерывны, ускорение силы тяги а
должно также быть непрерывным, чтобы удовлетворить
условию (5.64) максимальности выражения L. Если
максимальное значение L, определяемое по уравнению
(5.73), имеет место при а > атах, то ограничение (5.55)
нарушается (рис. 5.9). Наибольшим возможным значе-
нием L будет в этом случае значение в точке
л — лтах. (5.75)
Это значение является тогда и оптимальным. Множи-
тель Хт определяется уравнением (5.60)7:
ч __ (Х« + х£)/2 + 2Х(ХдП1ах
дш1п дтах
230
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
Если же снова удовлетворяется уравнение (5.74),
т е. максимальное значение L принимается в пределах
са для ускорения силы тяги при для ускорения силы тяги при по-
постоянней развиваемой мсиц- стоянной развиваемой мощности
ности и отрицательном Хи; опти- и отрицательном Хи; оптимальное
мальное условие а = атах. условие а = amin.
допустимой области, то промежуточный режим ускоре-
ния (5.73) опять являет-
ся оптимальным.
Если максимальное
значение L достигается
на нижней границе обла-
сти изменения а, т. е.
a = amin = 0> (5.77)
то возникает положение,
иллюстрируемое рис. 5.10.
Такой случай возможен,
если только
^=А = 0. (5.78)
Подобное равенство
может выполняться лишь
Рис. 5.11. Условие Вейерштрасса
для ускорения силы тяги при по-
стоянной развиваемой мощности и
положительном Х^.
в изолированных точках — иначе все множители обра*
щаются в нуль на интервале конечной протяженности.
Условие (5.77) может соблюдаться и соответствует об-
ращению скорости истечения с в бесконечность в от*
дельных точках [17].
6.5]
ВЫВОДЫ
231
В нежелательном случае
> о (5.79)
зависимость L от а приводится на рис. 5.11. Максймаль^-
ное допустимое значение L достигается здесь при
Я = #тах’ (5.8Э)
Суммируя все сказанное, получаем:
Хи>0 при а = атах, | (5 8
Хи < 0 при а„.|п < а < атах. J *
6.5. ВЫВОДЫ
В предыдущих разделах было выполнено исследова-
ние оптимальных траекторий ракет, причем под опти-
мальностью понималось достижение минимального зна-
чения некоторым функционалом, являющимся функцией
от начальных и конечных значений переменных состоя-
ния. В частности, изучались приложения к системам с
ограниченным расходом массы, мощностью двигателя н
ускорением силы тяги (при постоянной мощности дви-
гателей). Были получены следующие важнейшие вы-
воды:
1) Условие максимальности f-функции Вейерштрасса
по отношению к управлениям доставляет оптимальную
программу для этих управлений. Это условие справед-
ливо как по отношению к ограниченным управлениям,
так и по отношению к управлениям, лишенным ограни-
чений. В первом из этих случаев следует присоединить
к числу уравнений связей (уравнений движения) соот-
ветствующее ограничивающее неравенство. Если управ-
ления не входят в уравнения связей линейно, то в за-
даче не возникает никаких трудностей.
2) В задаче определения оптимальной программы
направления силы тяги не остается никаких неразрешен-
ных вопросов.
3) Для систем с ограниченным расходом массы про-
грамма оптимального расхода имеет двухпозиционный
характер, если ускорения от внешних сил являются
самое большее линейными функциями координат.
232
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
В случае силовых полей другого типа оказалось невоз-
можным доказать отсутствие в программе промежуточ-
ных режимов расхода массы либо установить критерий
выбора оптимального режима расхода.
4) Для систем с ограниченной мощностью двигате-
лей оптимальным оказался режим работы при макси-
мальной возможной мощности.
5) Для систем с ограниченным ускорением силы
тяги, работающих при постоянной мощности, оптималь-
ными могут быть либо режим максимального ускорения,
либо промежуточный режим, в зависимости от миними-
зируемого функционала и от граничных условий.
5.6. ПРИМЕР
Для иллюстрации изложенной в этой главе теории
рассмотрим оптимальную траекторию ракеты с ограни-
ченным расходом массы. Пусть требуется, например,
найти оптимальную программу управления тягой раке-»
ты — направлением вектора силы тяги и расходом мас-
сы, — обеспечивающую минимальное потребление топ-
лива ракетой, переносящей заданный груз из данной
точки на круговой орбите вокруг Земли в заданный
пункт на Земле*). Принимаются следующие упрощаю-
щие предположения:
1) Полет происходит в вакууме, т. е. аэродинамиче-
ские силы пренебрежимо малы по сравнению с тягой и
весом.
2) Земля обладает сферической симметрией и не
вращается по отношению к инерциальной системе
координат, в которой изучается движение ракеты
(рис. 5.12).
3) Дальность полета и высота ракеты малы по
сравнению с радиусом Земли; поэтому в соответствую-
щем разложении ускорения силы тяжести удерживают-
ся лишь члены первого порядка.
♦) Изложение этого примера основано на исследовании более
общей задачи в техническом отчете компании «Мартин» [14]. Чис-
ленные расчеты были проведены на моделирующей вычислительной
машине Тиндалем и Хайнсом.
Б.6]
ПРИМЕР
233
Уравнениями движения и связей будут (5.5) — (5.7).
Ускорения от внешних сил даются уравнениями (5.31).
Граничные условия таковы:
/=Ч=0
х = 0,
У = У/»
и== t = tf (не задано)
= 0;
Х = Хр
у = yf, (5.82)
т = mf.
Требуется минимизировать начальное значение массы
G = mL (5.83)
при указанных выше связях и граничных условиях.
5.61. Первая вариация. Соответствующими уравне-
ниями Эйлера — Лагранжа будут уравнения (5.9), а
условие трансверсаль-
ности дается формулой
(5.10). Далее, посколь-
ку время полета зара-
нее не фиксировано,
первый интеграл (5.11)
равен нулю. Кроме то-
го, так как минимизи-
руется начальное зна-
чение массы, а конеч-
ная скорость не зада-
на, уравнение (5.10)
дает
1 = 0 {Хм= 1;
( хи = о, <5-84)
\ =0.
У
Рис. 5.12. Система координат в задаче
о перелете с орбиты (раздел 5.6).
Смешанный харак-
тер краевой задачи
требует, следовательно,
процесса итераций, зависящего от пяти существенных
параметров.
5.62. Программа направления силы тяги. Принимая
во внимание уравнения (5.9) i-4 и (5.84), а также
234
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
(гл. V
сказанное в разделах 5.22 и 5.26, найдем, что направле-
ние силы тяги определяется формулами
sin ф = ,
COS Ф — г--а ,
cs.85)
где
Xu = ^-sin[e(^—/)],
Xo=7yrsh Iе vr2 a,-ol-
(5.86)
5.63. Программа расхода массы. Поскольку ускоре-
ния от внешних сил являются линейными функциями
координат, управление расходом массы имеет, согласно
разделу 5.28, двухпозиционный характер. Порядок пере-
ключения задается соотношениями (5.24), а функция
переключений определяется формулой (5.23).
5.64. Обзор решения. Хотя представляется ясным,
что на начальном участке траектории для разгона долж-
на расходоваться мощность, т. е. этот участок должен
проходиться при максимуме мощности, a priori не оче-
видно, должна ли расходоваться мощность на концевом
участке траектории. Знание этого необходимо, если ин-
тегрирование начинается в момент t = tf. Из определен
ния функции переключений (5.23) и граничных уело-
рий (5.84) получаем . ^mf* (5.87)
Можно показать, однако, что [19, 20|
X _ dmt mf dm f (5.88)
и следует ожидать, что
tint n dmj ’ (5.89)
так что < 0, (5.90)
6.6]
Пример
235
т. е. концевой участок траектории не связан с расходом
мощности. Поэтому удобнее начать интегрирование с
точки t = 0. Тогда пятипараметрический процесс итера-
ций вместе с условием
С/ = 0, (5.91)
выполняющимся в силу того, что /у не задано, можно
свести к процессу от трех параметров без необходимости
Рис. 5.13. Функция переключений массового расхода (раз-
дел 5.6).
удовлетворять равенству (5.91). Уравнения (5.9) 1-4
интегрируются и дают
XuZ=-^sine//t
(5.92)
\xi \xj COS e/z,
XyZ = Xy/Ch6
Далее, подставляя выражения (5.5) для соответ-
ствующих величин в равенство
Cz=0, (5.93)
Рис. 5.14. Масса в зависимости от времени (раздел 5.6).
Рис. 5.15. Горизонтальная составляющая скорости в зависимости
от времени (раздел 5.6).
Рис. 5.16. Вертикальная составляющая скорости в зависимости
от времени (раздел 5.6).
5.6]
ПРИМЕР
237
разрешаем получающееся уравнение относительно
(Ч,+Ч,)'‘х
X [— + >„ (g, — 2«’у,) — >,(5.94)
и одновременно убеждаемся в соблюдении требования
(5.91). Кроме того, благодаря уравнениям (5.86) два
начальных условия, именно
Хду = Х^ = О, (5.95)
удовлетворяются автоматически. Следовательно, зада-
ваясь значениями трех переменных /у, Хх/ и Х^у, находим
238
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
начальные значения К, А*, К и т из уравнений (5.92)
и (5.94). Интегрирование с этими начальными значе-
ниями производится от точки t = 0 до t = tf, где пере-
менные х, у и т должны принимать заданные значения.
Рис. 5.19. Коэффициенты наклона вектора тяги в зависимости
от времени (раздел 5.6).
5.65. Численные результаты. Интегрирование произ-
водилось для следующих значений параметров:
Ртах = 0,1 слэг!сек, с=104 фт!сек,
gQ = 31 фт1сек, е=1,26- 10”3 1/сек,
= yz =106 фт, = 2,459 • 104 фт!сек, ^ = 0,
. xf= 2 • 106 фт, yz =— 0,1003 • 106 фт, mf=\ слэг.
Результаты интегрирования представлены на рис.
5.13—5.19.
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ К ГЛАВЕ V
С—см. формулы (5.11) или (5.62);
F—ускорение, обусловленное внешней силой;
G — минимизируемый функционал;
L — см. формулы (5.19), (5.47) или (5.64);
Р— мощность двигателей (1/2 рс2);
R — радиус Земли;
ПРИЛОЖЕНИЕ
239)
Т — величина тяги;
Л, Y — составляющие ускорения, обусловленного внешней силой;
а — ускорение силы тяги (Т/m);
с — эффективная скорость истечения;
go — ускорение силы тяжести на уровне коря;
m — масса ракеты;
q.— переменная состояния;
г — расстояние от притягивающего центра;
t — время;
и, v — составляющие скорости ракеты;
х, у — координаты ракеты;
а = 2Р;
Р — расход массы;
7 — вещественная переменная;
< = V go/R;
х—функция переключений, см. формулу (5.23);
Xq — множитель Лагранжа, относящийся к переменной состоя-
ния q\
X — вектор с составляющими Xu,
|л = 2Р1т\
6 — угол между вектором силы тяги и местной вертикалью;
ф — угол, характеризующий направление вектора силы тяги.
Индексы
Z — начальное значение;
f—конечное значение;
max — максимальное значение;
min — минимальное значение;
— значение перед угловой точкой;
значение после угловой точки;
• точка обозначает дифференцирование по времени.
ПРИЛОЖЕНИЕ
Требуется определить переменные состояния t/j(x) и
управления Иь(х) таким образом, чтобы функция
G = O[xi, xf, у,(х/), .... yjx/, .... ym(xz)]
принимала наименьшее значение при наличии дополни--
тельных условий в форме дифференциальных уравнений
У;Ур •••• У,л. «г - и
2, ..., т,
240
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
и самое большее 2т + 1 граничных условий, содержа-
щих х и У), а также условий в форме неравенств для
управлений *)
Щ mln "С Щ max» Z = 1, . . ., Г fl,
которые могут быть представлены в форме [4, 20, 21]
ф/= («/-«/mln) («Z max-«z)-’l? = 0’ Z=1- •••’
где через тр обозначены вещественные переменные**).
Путем небольшой модификации классических рассу-
ждений вариационного исчисления [5, 19—21] можно по-
лучить следующие необходимые условия существования
относительного минимума G. Обращение в нуль первой
вариации влечет за собой (1) уравнения Эйлера—•
Лагранжа:
d dF дР _ = 0, /=1, ••• , m,
dx ду\ ду}
дР _ = 0, k = \, ... , п,
дР = 0, /=1, ... . г,
в которых
т г
2хУу(х)Т/+2х т=о,
J=1 J 1=1 Ч
а Л(х)—неопределенные множители; (2) общее усло-
вие трансверсальности
m
m
= 0,
где dx и dy — дифференциалы, связанные наложенными
краевыми условиями; (3) условия Вейерштрасса —
*) Таким же образом можно наложить ограничения на функ-
ции от ик.
**) Число ограничивающих неравенств может, вообще говоря,
превышать число независимых управлений. В этом случае, однако,
следует особо убедиться р jom, что все эти требования удовлетво-
ряются.
ПРИЛОЖЕНИЕ
241
Эрдмана для угловых точек, соблюдающиеся в точ-
ках излома экстремали, т. е. в точках разрыва произ-
водных y'jt
j/Ч _ Г '
.dy'j J_ L4J+’
Если независимая переменная не входит явно в до-
полнительные условия, то существует первый интеграл
пг
/=1
dF
ду^
= const.
Дальнейшим необходимым условием существования
относительного минимума G, вытекающим из рассмотре-
ния сильной вариации, является условие для функции
Вейерштрасса
E^F[x, УР к;,..., г;,
.....Ч* •••’ Чп’ Ч’ •••* Ч)~
-F(x, ур ут, у{, .... у'т, uv ип,
т
....
Здесь Yj и Uk—не оптимальные, но допустимые значе-
ния y'j и uk. Для рассматриваемых дополнительных
условий указанное неравенство сводится к следующему:
2 ХУ,// (х, yv .... ут, uv .... «„) >
у = 1 J
у» ут, ult ...» иа)
16 Дж. Лейтмац
242
ЗАДАЧИ С ОГРАНИЧЕННЫМИ УПРАВЛЕНИЯМИ
[гл. V
для всех допустимых значений управлений и^. Это не-
равенство, очевидно, равносильно требованию, чтобы
функция
т
.... ут, «р .... «„)
достигала максимума по отношению к управлениям uhi
удовлетворяющим наложенным связям в форме нера-
венств. В этой форме условие для f-функции Вейер-
щтрасса эквивалентно принципу максимума Понтряги-
на (см. гл. VII).
ЛИТЕРАТУРА
1. G. Leitmann, Extremal rocket trajectories in position and time
dependent force fields, Am. Astronaut. Soc. 7th Ann. Meeting,
Dallas, Preprint 61-30 (1961).
2. G. Leitmann, On the equation of rocket motion, J. Brit. Inter-
planet. Soc. 16, 141 (1947).
3. R. T. Stancil and L. J. Kulakowsky, Rocket boost vehicle
mission optimizations, Am. Rocket Soc. 15th Ann. Meeting,
Washington, D. C., Preprint 1449-60 (1960).
4. F. A. Valentine, The problem of Lagrange with differential
inequalities as added side conditions, Dissertation, Department of
Mathematics, Univ, of Chicago, Chicago, Illinois, 1937.
5. G. A. Bliss, Lectures on the Calculus of Variations, Univ, of
Chicago Press, Chicago, 1946. [Русский перевод: Г. А. Блисс,
Лекции по вариационному исчислению, М.—Л, 1950.]
6. D. F. L a w d е и, Dynamic problems of interplanetary flight, Aero-
naut. Quart. 6, 165 (1955).
7. B. D. Fried, гл. 4 в книге «Space Technology» (H. S. Seifert,
ed.), Wiley, New York, 1959. [Русский перевод: под ред. Г. Сей-
ферта «Космическая техника», гл. 2, изд-во «Наука», М., 1964.]
8 A. Miele, General variational theory of the flight paths of rocket-
powered aircraft, missiles and satellite carriers, Purdue University
Rept. No. A-58-2 (1958); Proc. 9th Intern. Astronaut. Congr., Am-
sterdam, 1958 (1959).
9. Д. E. Охоцимский и T. M. Энеев, Некоторые вариацион-
ные задачи, связанные с запуском искусственного спутника
Земли, Успехи физических наук, вып. 1, стр. 5—32 (1957).
10. G. Leitmann, On a class of variational problems in rocket
flight, Lockheed MSD Rept. No. LMSD-5067 (1958); J. Aero/Space
Sci. 26, 586 (1959).
11. S. E. Dreyfus, Dynamic programming and the calculus of va-
riations, J. Math. Anal, and Appl. 1, 228 (1960).
12. В. Г. Болтянский, P. В. Гамкрелидзе и Л. С. Понт-
рягин, Теория оптимальных процессов. I. Принцип максимума,
ЛИТЕРАТУРА
243
Известия Акамедии наук СССР, серия матем., 24, № 1 (1960),
стр. 3—42.
13. G. Leitmann, Comment on «On a class of variational problems
in rocket flight», J. Aero/Space Sci. 27, 153 (1960).
14. G. Leitmann, On a minimum fuel satellite transfer trajectory,
Tech. Memo. No. 491/2 01-60, The Martin Company, Inc., Denver,
Colorado (1960).
15. D. F. L a w d e n, Necessary conditions for optimal rocket trajecto-
ries, Quart. J. Meeh. Appl. Math. 12, 476 (1959).
16 J. H. Irving, гл. 10 в книге «Space Technology» (H. S. Seifert,
ed.), Wiley, New York, 1959. [Русский перевод: под ред. Г. Сей-
ферта, Космическая техника, гл. 8, изд-во «Наука», М., 1964.]
17. G. L е i t m a n n, Minimum transfer time for a power-limited rocket,
Lockheed MSD Rept. No. LMSD-49769 (1960); J. Appl. Meeh. 28,
171 (1961).
18. C. R. F a u 1 d e r s, Optimum thrust programming of electrically
powered rocket vehicles in a gravitational field, ARS Journal 30,
954 (1960).
19 J. V. Break well, The optimization of trajectorires, Rept.
AL-2706, North American Aviation Company (1957); J. Soc. Ind.
Appl. Math. 7, 215 (1959).
20. G. Leitmann, An elementary derivation of the optimal control
conditions, Proc. 12th Intern. Astronaut. Congr., Washington, D. C.,
1961.
21 L. D. В e г k о v i t z, Variational methods in problems of control
and programming, J. Math. Anal, and Appl. 3, 145 (1961),
ГЛАВА VI
МЕТОД ГРАДИЕНТОВ
6.0. ВВЕДЕНИЕ
Метод градиентов или, как его иногда называют,
«метод наискорейшего спуска» представляет собой эле-
ментарный способ решения задач о минимуме. Этот
метод восходит к Коши [1—3], а в вариационной фор-
мулировке— к Адамару [4, 5]. Особенно ясное и при-
влекательное изложение было дано в 1941 г. Курантом
в обращении к Американскому математическому обще-
ству [5]. В последние годы вычислительные преимуще-
ства метода привели к его использованию во многих
областях: в проблемах минимума функций от многих
переменных в обычном анализе [3, 6—9], при решении
систем алгебраических уравнений [10, И], интегральных
уравнений [12] и вариационных задач [9, 13].
Метод градиентов был применен автором в работе
[14] к вариационным задачам об оптимизации траекто-
рий полета; указанная работа является основным источ-
ником материала для настоящего изложения. Сходная
схема была независимо развита Брайсоном с сотрудни-
ками [15].
Вначале мы рассмотрим некоторые из важнейших
черт метода градиентов в связи с обыкновенными про-
блемами минимума, подчиненными связям. Хотя этот
класс задач выбран прежде всего ради простоты рас-
суждений, он сам по себе вызывает все растущий инте-
рес в приложениях к авиации и космическим полетам.
Далее мы обратимся к вариационным задачам теории
полета, причем функции Грина будут играть роль част-
ных производных в обычных задачах о минимуме, и мы
6.1]
ОБЫКНОВЕННЫЕ ЗАДАЧИ НА МИНИМУМ
245
попытаемся в последующем изложении провести анало-
гию между двумя указанными классами задач. Будут
приведены некоторые численные, результаты, иллюстри-
рующие на примерах вычислительный процесс последо-
вательных приближений.
6.1. МЕТОД ГРАДИЕНТОВ В ОБЫКНОВЕННЫХ
ЗАДАЧАХ НА МИНИМУМ
6.11. Непрерывный процесс спуска. Чтобы указать
основную идею метода градиентов, рассмотрим функ-
цию f нескольких переменных хь...,хп, определенную
в открытой области и обладающую непрерывными част-
ными производными по этим переменным. Фиксируя в
первый момент некоторую точку хг=Хг, /=1, ...» и, пе-
реместимся на малое расстояние ds, определенное ев-
клидовой метрикой:
ds2 = 2 dx2 (6.1)
/=1
Стремясь двигаться по направлению к минимуму
функции Д рассмотрим направления, по которым ско-
рость изменения f по отношению к s
п
df у df dXj
ds 2л dxi ds
/=1
(6-2)
отрицательна. Фактически мы можем найти направле-
ние «наискорейшего спуска» (производные df/ds, будучи
отрицательными, максимальны по абсолютной величи-
не) среди направлений, являющихся стационарными
для (6.2) при дополнительном условии (6.1).
Действуя формально, запишем уравнение связи (6.1)
через направляющие косинусы:
<6-з)
Z=1
246
МЕТОД ГРАДИЕНТОВ
[гл. VI
и присоединим это уравнение к (6.2) с помощью мно-
жителя Лагранжа Хо, образуя выражение
Приравнивая нулю частные производные по dxt/ds:
<+1.(-2$) = 0, /=1...п. (6.5)
получаем
dXj = 1 df
ds 2Х0 d*i
(6.6)
Множитель Хо определяется с помощью уравнения
связи (6.3):
Г *
^=±4 • <67>
- / = 1
Если частные производные df/dxi не все равны ну-
лю, то имеются две различные системы направлений
стационарности dfjds, а именно:
Рассмотрение выражения производной по направле-
нию dfjds для двух указанных случаев
.1-1
(6.9)
позволяет заключить, что эти стационарные направле-
ния суть направления наискорейшего подъема и наиско-
рейшего спуска.
Векторные обозначения различных величин позво-
ляют дать простую геометрическую интерпретацию по-
лученных формул. Пусть Xi будут компонентами век-
тора X. направляющие косинусы dxjds — компонен-
тами единичного вектора dXjds, а частные произвол-
ОБЫКНОВЕННЫЕ ЗАДАЧИ НА МИНИМУМ
247
ные dfldXi — компонентами градиента. Производная
df/ds тогда равняется скалярному произведению
-S = Pad/'47’ <610>
и если движение направлено вдоль градиента [см. (6.8)],
то величина указанной производной равна величине
градиента, что и выражается уравнением (6.9). Таким
образом, наискорейший подъем соответствует движению
в направлении градиента, а наискорейший спуск — дви-
жению против направления градиента.
Введем теперь параметр времени а и рассмотрим
движение против направления градиента как непрерыв-
ный процесс. Для движения в и-мерном пространстве со
скоростью V имеем
Г п Уа
£= =v- <611>
1=1 -I
Выражения для компонент скорости dXildo вслед-
ствие (6.8) принимают вид
Г п - -'/«
dxi_______v ^L
da \ dxi) dxi
(6.12)
Эти формулы становятся особенно простыми, если
величина скорости пропорциональна ее градиенту:
V = k
dxt b df
da & dxi *
k> 0;
(6.13)
(6-14)
Z=1
так что движение в направлении против градиента по-
лучается просто как пропорциональное изменение про-
изводных от координат по времени и частных производ-
ных от f.
Ясно, что в этом непрерывном процессе при переме-
щении X точки согласно системе обыкновенных уравне-
ний (6.14) движение стремится при о->оо к состоянию^
248
МЕТОД ГРАДИЕНТОВ
[гл. VI
когда gradf=O, если f ограничено снизу. Стационарное
значение, к которому направлено это движение, будет
соответствовать минимуму функции Д если величины Xi
в пределе остаются ограниченными; в противном случае
имеет место лишь приближение к нижней грани.
6.12. Шаговый спуск. Альтернативой по отношению
к непрерывному процессу, описываемому уравнениями
(6.14), является шаговый спуск, корректирующий систе-
му приближений к решению df/dXi = 0 с помощью попра-
вок, пропорциональных градиенту, взятому со знаком
минус:
= п. (6.15)
Ясно, что в этом шаговом процессе коэффициент про-
порциональности k может быть включен в шаг До; по-
этому примем й=1.
Поскольку определение частных производных дЦдхг
в случае, если число переменных п велико, может ока-
заться затруднительным в отношении объема вычисле-
ний, желательно наилучшим образом использовать каж-
дое вычисление местного направления градиента, вы-
бирая величину До максимально возможной. Один из
способов состоит в том, чтобы следовать местному на-
правлению градиента до тех тор, пока f не достигнет
минимума, т. е. пользоваться уравнениями (6.15) и рас-
считывать значения функции f для нескольких величин
шага, определяя величины До, соответствующие мини-
муму f, с помощью некоторой системы однопараметриче-
ского поиска. После этого находится новое направление
градиента, и процесс повторяется.
Этим путем и-мерная проблема минимума сводится
к последовательности одномерных проблем. Метод гра-
диентов имеет это свойство общим с другим вычисли-
тельным приемом, который будет описан в последую-
щих главах.
Непрерывный и шаговый процессы сравниваются на
рис. 6.1, где представлены два типа движений, могущих
происходить в окрестности минимума функции двух пе-
ременных f(xi,x2). Направление градиента, как пока-
зано1 нормально к контуру, тогда как локальный мини-.
ел]
ОБЫКНОВЕННЫЕ ЗАДАЧИ НА МИНИМУМ
249
мум в направлении градиента достигается в точке,
касательной к контуру.
Эти характерные черты свойственны также и слу-
чаям большего числа измерений.
Очевидно, шаговый путь не является независимым
от выбранной системы координат. Если можно найти
преобразование координат, переводящее овалообразные
кривые рис. 6.1, например, в окружности, то число
Рис. 6.1. Непрерывный и шаговый процессы спуска.
шагов, требуемое для достижения минимума, будет све-
дено к одному. Обычно, разумеется, a priori нет инфор-
мации, достаточной для выбора той или иной специаль-
ной системы координат: в противном случае был бы
известен характер поверхности и отпала бы необходи-
мость в определении минимума с помощью метода
градиентов.
Для технических задач обычно характерен некоторый
«практический интервал» изменения переменных и
знание этого интервала облегчает введение нормальных
переменных для вычисления градиентов. Фактически
эта процедура оказывается необходимой в тех случаях,
250
МЕТОД ГРАДИЕНТОВ
(гл. VI
когда переменные имеют разные размерности и облада-
ют численно различными порядками величин. В резуль-
тате такого преобразования можно придать известный
смысл понятию расстояния в n-мерном пространстве, где
осуществляются все операции.
6.13. Обыкновенные проблемы минимума со связями;
метод проектирования градиентов. Во многих практи-
чески интересных задачах может потребоваться опре-
делить минимум функции f(xi, ...,хЛ) при дополнитель-
ных условиях, связывающих переменные xit Важным
случаем дополнительных условий являются условия,
заданные равенствами
gj(xit ..., хл) = 0, у=1, ..., /п; пг < п\ (6.16)
иногда в литературе эти равенства называются равен-
ствами связей.
Если функции gj заданы аналитически, то может слу-
читься, что уравнения (6.16) окажутся разрешимыми
относительно m переменных х< и, исключая эти перемен-
ные из функции f, придем к задаче, лишенной связей.
Такой подход весьма часто оказывается неудобным для
приложений.
Можно, однако, рассмотреть вариант этого процесса
«в малом», т. е. в окрестности начальной точки хг = хг-.
Удерживая в разложении Тейлора лишь члены первого
порядка
.... Xa)^gj(xl......Х„) -Ь
+ .....x„)(Xt — Xi), (6.17)
/=1
и предполагая, что уравнения (6.16) соблюдаются в
точке Xi — получим систему линейных по отношению
к приращениям Дхг——х< уравнений, выражающих
равенство нулю функции gf.
п ~
= ...............m- <6Л8)
/=1
6.1]
ОБЫКНОВЕННЫЕ ЗАДАЧИ НА МИНИМУМ
251
Можно, далее, попытаться разрешить эту систему
относительно т приращений Дх», выразив их через
остальные. Это будет возможно, если только все опре-
делители Якоби порядка этой системы не
обратятся в нуль в точке хг=хг*. В такого рода осо-
бых точках [16] процесс исключения отказывается
служить.
Если решение возможно, то п — т частных произ-
водных функции f по п— т оставшимся переменным
могут быть вычислены по правилу последовательного
дифференцирования и, таким образом, может быть опре-
делен градиент функции f при наличии связей. Геомет-
рически это означает проектирование вектора градиента
в отсутствие связей на подпространство п — т измере-
ний, определяемое пересечением т гиперплоскостей
(6.18). Нам кажется уместным термин проектирование
градиента, используемый в литературе по нелинейному
программированию [7, 8] в связи со сходными задачами,
включающими связи в форме неравенств.
Для определения направления проекции градиента
можно развить подход, подобный описанному в разделе
6.11. Вводя опять направляющие косинусы dxi/ds, разы-
скиваем направления стационарности функции dflds. за-
данной равенством (6.2) при связях (6.3) и
_ у —
ds dxi ds
1=1
......m. (6.19)
Вводя
образуем
множители Лагранжа Ао и kj, j = 1,
m,
выражение
п Гл"
/=1 Z=1 J
m п л J
I у 1 у dx‘
<=i
(6.20)
252
МЕТОД ГРАДИЕНТОВ
[гл. VI
Приравнивая частные производные по dxjds нулю,
получаем:
(6-21)
(6.22)
(6.23)
Подставляя этот результат в (6.19), получаем соот-
ношения, определяющие Х,:
у.
дх[ dxt ^4 dxi dxi ’
/=1 z=i z=i
т. (6.24)
Эта система уравнений, линейных по отношению к
множителям, будет иметь решение, если tn X т-матрица
с элементами
/=1
не является особенной. Это утверждение в точности со-
впадает с детерминантным критерием Грама линейной
независимости выражений (6.19) и равносильно сделан-
ному ранее предположению об определителях Якоби
(см. Курант и Гильберт [17], т. I, стр. 31). Это условие
требует, чтобы величины векторов grad gj не были рав-
ны нулю и чтобы направления этих векторов были раз-
личны.
Осуществление проектирования градиентов в про-
цессе машинного счета требует, таким образом, числен-
ного решения системы линейных уравнений (6.24). Со-
6.1]
ОБЫКНОВЕННЫЕ ЗАДАЧИ НА МИНИМУМ
253
отношения для шагового процесса,
имеют теперь вид
\ ;=1 /
аналогичные (6.15),
/=1, ..., п. (6.26)
Метод проектирования градиентов представляется
превосходным в тех случаях, когда связи (6.16) ли-
нейны (или почти линейны) по отношению к Но мо-
гут быть затруднения, связанные с аномальным поведе-
нием линейной системы (6.24), если пересечения гипер-
поверхностей gj = 0 определяются с трудом, т. е. если
две или более касательные гиперплоскости почти парал-
лельны друг другу.
Существенное осложнение возникает из-за нелиней-
ностей в уравнениях связей. Для больших значений
шага До уравнения (6.16), удовлетворяющиеся только в
линеаризованной форме, могут оказаться нарушенными
задолго до того, как будет достигнут минимум Д В этом
случае должна быть введена система коррекции для
восстановления нарушенных связей. Как правило, эта
коррекция имеет форму последовательных приближений
по переменным хг-. Это свойство метода проектирования
градиентов может повлечь за собой существенное уве-
личение счетного времени.
6.14. Обыкновенные проблемы минимума со связями;
приближенный метод. Иной способ учета связей достав-
ляется путем приближенной замены задачи о минимуме
со связями другой задачей, лишенной связей. Имея это
в виду, рассмотрим вместо задачи предыдущего раздела
задачу минимизации выражения
т
(6-27)
/=1
где Kj — положительные постоянные.
Интуитивно ясно, что «нагрузочные» слагаемые во
втором члене (6.27), будучи неотрицательными, ослаб-
ляют в этой задаче действие «нарушений» наложенных
связей. Можно предвидеть, что для достаточно больших
положительных Xj решение этой минимальной задачи
254
МЕТОД ГРАДИЕНТОВ
[гл. VI
будет стремиться к желаемому решению задачи для f
при связях (6.16). Эта идея принадлежит Куранту [5].
Она была строго обоснована в аппроксимационной тео-
реме Мозера (см. [18]) для случая единственной связи и
использовалась Рубином и Унгаром [19] в одном частном
классе вариационных задач со многими связями.
Используя эту идею для вычислительных целей, сле-
дует считать, что постоянные Kj имеют большие числен-
ные значения. Выбор этих значений должен делаться
по степени приближения к уравнениям связей. Поэтому
«допустимые отклонения» могут быть установлены из
физических соображений.
Использование нагрузочной функции хорошо соче-
тается с процессом последовательных приближений, ко-
торый вытекает из метода градиентов. Для машинных
операций возможно сравнение «степени нарушения» свя-
зей с заданными заранее допустимыми «отклонениями»
в конце каждого шага спуска, причем в случае необхо-
димости постоянные Kj для следующего шага могут из-
меняться соответствующим образом.
Желая отыскать критерий для оценки и измененгя
значений постоянных /Q, рассмотрим величины «откло-
нений» gj в том случае, когда выражение (6.27) дости-
гает минимума. Приравняем нулю производные от (6.27)
в т направлениях, определяемых градиентами вели-
чин gj. Направляющие косинусы градиента функции gk
равны
dXi d^k Г V / dSk Vl Л • 1 /£ ПОЧ
= • * = 1.........................п' <6-28)
производная от (6.27) в соответствующем направлении
предполагается равной нулю;
k= 1........т. (6.29)
8.1J
обыкновеннЫё задачи на минимум 255
Мы можем рассматривать полученные уравнения как
линейную систему относительно произведений Kjgj:
(б-зо)
/=1 Z=1 Z=1
k = 1, ..., /п.
Эта система весьма сходна с системой уравнений
для множителей в (сходящемся) процессе проектирова-
ния градиентов (6.24); различие заключается в том, что
в настоящем случае частные производные вычисляются
в точке минимума выражения (6.27), где уравнения
связей выполняются лишь приближенно.
Система (6.30) может быть решена численно при
условиях, указанных выше в связи с задачей определе-
ния множителей. В пределе Л^оо, очевидно,
/=1. .... /П, (6.31)
и «отклонения», как видим, изменяются обратно пропор-
ционально значениям Kj.
Эти рассуждения приводят к двум возможным спо-
собам выбора значений Простейший из них основан
на использовании отношения отклонение)допустимое от-
клонение в качестве величины, характеризующей необ-
ходимость увеличения или уменьшения текущих значе-
ний Kj в конце каждого шага процесса спуска. С другой
стороны, можно вычислять значения Xj из (6.24) по зна-
чениям частных производных и находить величины
-г I (вычисл.)
в которых представляет собой допустимое отклонение
от связи gj = 0. Предварительные результаты численно-
го решения вариационных задач при сходных с описан-
ными выше способах задания постоянных показывают,
что второй из этих способов предпочтительнее первого
в отношении быстроты сходимости.
Привлекательной чертой метода функций нагруже-
ния является то, что он не требует коррекции выпол-
нимости уравнений связей путем последовательных
256
МЕТОД ГРАДИЕНТОВ
[гл. VI
приближений. Равным образом отпадает необходимость
в специальном выборе начальной точки, где удовлетво-
ряются уравнения связей. В настоящее время опыт чис-
ленного решения задач по этому методу недостаточен
для сравнения с другими методами, используемыми в
обычных проблемах минимума; в следующем разделе,
однако, будет описано применение сходной методики ре-
шения вариационных задач.
6.15. Обыкновенные проблемы минимума со связя-
ми, задаваемыми неравенствами. Связи, имеющие форму
неравенств
gj(xx, .... х„)<0, /=1, (6.32)
приобретают все больший интерес для приложений.
Обыкновенные проблемы минимума с такими связями
образуют основу теории нелинейного программирования
(см. Розен [7] и Вольф [8]).
Для приложения метода проектирования градиентов
к решению такого рода задач необходимо сначала вы-
брать начальную точку, в которой удовлетворяются со-
отношения (6.32). Если начальная точка внутренняя
(т. е. такая, что в ней выполняются строгие неравенства
(6.32)), то движение происходит против направления
градиента до тех пор, пока не будет достигнут минимум
либо одна из функций gj не изменит знак. Когда будет
достигнута граница, соответствующая одной из связей,
проектируют градиент, задавая эту связь равенством.
Последовательности возможных движений при различ-
ных степенях ограничения весьма многочисленны, и, оче-
видно, многократные проверки и проектирования при
различных сочетаниях связей приведут к весьма запу-
танной программе счета, если придется иметь дело одно-
временно с несколькими неравенствами связей.
К минимальным задачам со связями в форме нера-
венств можно также применить понятие функции на-
гружения. К функции f прибавляются члены, составляю-
щие функцию нагружения, в форме
т
(б-зз)
6.2] ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ 257
Здесь H(gj)—функция Хевисайда единичного скач-
ка от аргумента gj. Если постоянные Kj выбраны поло-
жительными, то второе слагаемое неотрицательно.
Отметим, что частные производные от второго слагае-
мого непрерывны, если непрерывны частные производ-
ные от функций gj. Это обстоятельство благоприятствует
выбору квадратичных членов в качестве «нагрузки»,
хотя и не требуется, чтобы второе слагаемое было не-
отрицательно в случае связей в форме неравенств.
Описанная схема обладает привлекательной просто-
той при соединении ее с методом градиентов, так как
в этом случае логические действия, выполняемые ма-
шиной, сводятся к минимуму. При вычислении градиен-
тов влияние какой-либо связи, заданной неравенством,
автоматически исключается, если уравнение связи удов-
летворено, и все время возрастает, если оно нарушено.
Как и в случае связей, задаваемых равенствами, выбор
постоянных Kj должен производиться систематически,
после достижения каждого локального минимума, на
основе сравнения отклонений и заданных допустимых
отклонений.
Определение выбираемых значений произведений
Kjgj можно провести подобно тому, как это делалось в
предыдущем разделе. В матрице коэффициентов систе-
мы, аналогичной системе (6.30), для каждого строгого
неравенства, удовлетворяемого в рассматриваемой точ-
ке, автоматически отбрасывается строка или столбец,
так что частные производные
исчезают в тех точках, где gh < 0.
6.2. МЕТОД ГРАДИЕНТОВ В ЗАДАЧАХ
ОПТИМИЗАЦИИ ТРАЕКТОРИИ ПОЛЕТА
В предыдущей главе рассматривался классический
«непрямой» метод вариационного исчисления, основан-
ный на сведении вариационных задач к дифференциаль-
ным уравнениям. Хотя из аналитического решения урав-
нений Эйлера — Лагранжа, описывающих оптимальный
17 Дж. Лейтман
258
МЕТОД ГРАДИЕНТОВ
[гл. VI
полет, были выведены многие интересные результаты,
идеализированные предпосылки обычно устанавливали
пределы их практической применимости. При более
близких к реальности предположениях требуется числен-
ное решение этих уравнений, и в связи с этим могут
возникнуть серьезные трудности при необходимости
удовлетворить краевым условиям в двух точках (см.,
например, Менгель [20], Ирвинг и Блюм [21] и Фол-
дерс [22]). Эта трудность становится ограничивающим
фактором, когда порядок дифференциальных уравнений,
описывающих основную систему, больше или равен че-
тырем.
Такое положение обусловило необходимость приме-
нения метода градиентов к вариационным задачам о по-
лете. Приложение метода градиентов к вариационным
задачам с фиксированными граничными точками было
дано Стейном [13]. Класс задач со связями в форме диф-
ференциальных уравнений более сложен, и наше изло-
жение будет носить эвристический характер. Чтобы из-
бежать возможных затруднений, будем ниже считать
выполненными необходимые требования непрерывности
и дифференцируемости.
6.21. Формулировка проблемы. Предположим, что
система дифференциальных уравнений, которая должна
удовлетворяться вдоль траектории полета, задана в
форме системы первого порядка
хт = gm(Хр .... х„, у, t), т=1,...,п. (6.34)
Эти уравнения связывают скорости и координаты,
силы и ускорения, величины масс и расходов топлива
и охладителя и т. д. Через хт обозначены искомые пе-
ременные или переменные состояния, а через у — пе-
ременная управления. Дифференцирование по незави-
симой переменной — времени t — обозначается точкой
сверху.
Важным классом задач является тот, в котором
минимизируемая величина имеет вид функции конечных
значений переменных хт, а также времени /:
Р — P(XW ..., Xnj, tj).
(6.35)
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
259
В заданный начальный момент t0 можно задать до п
условий, связывающих переменные хт. Поскольку в на-
шем распоряжении имеется функция y(t), мы_вполне в
состоянии рассматривать задачи, в которых на перемен-
ные хт наложено бесчисленное количество условий при
различных последовательных значениях t. Ниже мы
ограничимся лишь условиями, поставленными в ко-
нечной точке траекторий полета. Для п+1 чисел,
именно п конечных значений переменных хт и конеч-
ного значения времени t, можно задать не более п со-
отношений с тем, чтобы значение Р не было предопреде-
лено.
Такая постановка задачи как раз совпадает с ука-
занной в предыдущей главе в связи с вариационными
проблемами в формулировке Майера.
6.22. Близкие решения и функции Грина. Предполо-
жим, что нам известно решение уравнений (6.34), кото-
рое не сообщает минимума функции Р. Это решение
должно удовлетворять заданным начальным условиям;
оно может удовлетворять (или не удовлетворять) также
и заданным в конечной точке условиям, смотря по тому,
какой вариант метода градиентов был выбран для ре-
шения задачи; этот вопрос будет рассмотрен в даль-
нейшем.
Обозначив решение через хт = хт(0> У = у(0,
рассмотрим поведение близких к нему решений; полагая
Хт = Хт + б*т, У = у + Ьу
и линеаризуя, получим
п
= + m = (6.36)
/=1 7
Частные производные функций gm вычисляются вдоль
решения хт = хт, У = у и представляют поэтому изве-
стные функции независимой переменной t. Функции бхт
и бу являются вариациями хт и у в окрестности хт, у.
Изучение линеаризованной системы (6.36) оправды*
вается тем, что мы разыскиваем с помощью метода гра-
диентов такое изменение управляющей функции у(х),
чтобы получить уменьшение функции Р, для которой
отыскивается минимум.
17*
260
МЕТОД ГРАДИЕНТОВ
[гл. VI
Формальное решение уравнений (6.36) может быть
написано в следующем виде:
п t
ЪХР ^тР ^°’ 8У W dX' <6-37>
р=1 t„
т=\, ..п.
Здесь первый член представляет собой решение од-
нородной системы уравнений, а второй — суперпозицию
влияний управляющей переменной. Функции р™ суть
функции Грина, или функции влияния; можно считать
Цт(т, /) решениями для бхт, соответствующими единич-
ному импульсу (дельта-функции Дирака) управления,
приложенному в момент т.
Функции Цт связаны С решениями %тр однородной
системы соотношениями
п г)
(6.38)
Р=1
Поскольку основной интерес представляют конечные
значения хт, мы вычисляем выражения (6.37) при
f = /f, однако для того, чтобы определить влияние ма-
лых отклонений 6tf от конечного момента времени
tf = tf, добавляется еще поправочный член первого по-
рядка
п Ч
= 2 ЬХР <Zo) *тР (А)> 9+ f V-m (’> If* 8У W + gmf
р=1 to
т = 1, ..., п. (6.39)
Здесь символом gmf обозначена производная
= gm [*i(j/) Jn(jy), вычисленная в
конечной точке неминимального решения.
6.23. Присоединенная система. Определение функций
Цт(т, t) во всем интервале изменения обоих аргументов
оказывается излишним; для последующих вычислений
потребуются лишь их значения при t = tf, поэтому пред-
ставляется оправданным отыскание специального спосо-
6.2] ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ 261
ба вычисления, чтобы избежать труда, необходимого для
проведения более общих выкладок. Ниже мы связываем
функции |1т(т, t) с решениями присоединенной системы
уравнений посредством применения теоремы Грина.
Схема рассуждений основана на работах Блисса [24,] и
Гудмана и Ланса [25].
Перепишем уравнения (6.36), пользуясь удобными
для наших целей обозначениями производных:
= + (6-40)
/=1 7
и напишем систему уравнений, присоединенную к этой
системе:
п д
Х = ^=1. •••>«. (6.41)
7=1
Эта последняя система, по определению, получается из
однородной системы путем транспонирования матрицы
коэффициентов и перемены знака.
Решения обеих систем связаны соотношением
Л п -
(6-42)
Z=1 Z=1
которое легко проверить, вычислив производную в левой
части:
п п п п п
2 X/ Зх/ + X/ = — 2 2 ~дх7
м i=i i=i z-i у-i
п п л п -
(б-«>
1=1 ;-i 7 i=i
и заметив, что после перемены местами индексов i и /
в первой двойной сумме эти суммы взаимно уничто-
жаются. Интегрируя левую и правую части между
262
МЕТОД ГРАДИЕНТОВ
[гл. VI
определенными пределами 4 и tf, найдем
п л ' п
2х/(Г/)8х/(Г/)-2^(<о)^/«о) = f (6.44)
1=1 /=1 I. 1=1
Такова одномерная форма теоремы Грина.
Рассмотрим вопрос о численном решении присоеди-
ненной системы в случае, когда все граничные условия
поставлены при t = tf. Частным решениям, соответствую-
щим условиям
М£/)=0,
\ (//) = !,
i^m,
i=m,
(6.45)
приписываем символы лДт)(/). В соответствии с этим из
уравнения (6.44) получаем п выражений для
вида
п г п д
= + f (6.46)
i=i t, i*a
m— 1, .... n.
Сравнивая (6.39) и (6.46), можем установить связь
между функциями gmp и единичными решениями при-
соединенной системы, удовлетворящими граничным ус-
ловиям (6.45); получим
т — 1, ..., п\
р=\, .... п.
(6-47)
[Отметим, что зависимость правых частей этих ра-
венств от tf неявным образом задается соотношениями
(6.45).] Функции Грина рт можно выразить также через
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
233
единичные присоединенные решения следующим обра*
зом:
w=1’ •••-«• с6-48)
Р=1
Выбор символов X для переменных, удовлетворяющих
присоединенной системе, сделан преднамеренно, так как
уравнения (6.41) в точности совпадают с уравнениями
для множителей Лагранжа непрямых методов. Отме-
тим, однако, важное отличие, состоящее в том, что в
непрямых методах коэффициенты уравнений (6.41) вы-
числяются вдоль минимального решения уравнений
(6.34), тогда как в методе градиентов они соответствуют
неминимальным траекториям.
Тесная связь, существующая между функциями Гри-
на, или функциями влияния, и «коэффициентами оши-
бок» теории управления, привлекла внимание к ме-
тодам решения задач теории управления, основанным
на рассмотрении присоединенной системы.
6.24. Градиент в функциональном пространстве. Вве-
дя, как и ранее, вторую независимую переменную о, мы
разыскиваем аналогичные способы применения метода
градиентов. Начнем с определения скорости изменения
характерной величины Р в точке функционального про-
странства, определяемой неминимальным решением
хт = у = у (t), а именно:
dP___v дР dXmf dtf
da дхт da dt* da
m=l mf 7
(6.49)
Если взять производные по а от начальных и конеч-
ных значений хт, конечного значения времени tf и функ-
ции y(t, о) и вычислить эти производные при значении
а = а, соответствующем неминимальному решению, то
уравнения (6.39) примут вид
dxm, Д dxn с dv - dtf
da ~ ~da$~ ^mP W JP"1 ~да' • (6.50)
P=1 t9
m = 1, .... n,
264
МЕТОД ГРАДИЕНТОВ
[гл. VI
а выражение (6.49) запишется тогда в следующей форме:
p=i
dx &Р ~~ । ddf (дР дР _ \
da dxmt ^тР da I dtf дхт ^mf I ""I”
m=l f \ т-\ / /
^-,*.4*. (6.51)
В том классе задач, который сейчас рассматривается,
характерная величина Р неявно зависит от конечного
числа параметров, именно начальных значений хт и ко-
нечного значения /у; эта величина зависит также от
функции y(t). Поэтому перед нами возникает задача
«смешанного» типа, частично имеющая характер обык-
новенной проблемы минимума, а частично — вариацион-
ный характер. Чтобы независимо исследовать эту по-
следнюю сторону проблемы, примем временно, что на-
чальные значения переменных хт и конечное время tj
фиксированы, так что
dx
dtf <6-52)
-5Г = °-
При этом выражение dP/da приобретает вид
<6-53>
/0 ч \ т = 1 f /
Мы желаем определить «направление» ду(х)/да
наискорейшего спуска в функциональном пространстве
г/(т). Действуя аналогично предыдущему анализу обык-
новенных проблем минимума, рассмотрим бесконечно
малое расстояние ds в функциональном пространстве
у(т), определяемое равенством
1-/ <6-54>
6
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
265
и найдем стационарные значения выражения
У / п \
dP I V ) ду .
ds J I дхт I ds Х
/0 ^т = 1 / /
при выполнении равенства связи (6.54).
Составим сумму
(6.55)
(6.56)
и приравняем ее производную по dy(^)/ds нулю для
всех значений/:; получим
(6.57)
ш = 1 /
Множитель Ло вычисляется из (6.54); получаем
И
2Л0—±
^У- =
ds
п \ 2
1 .
yi дР
дхт
т=1 J
ТУ»
(6.58)
ТА ‘
п \2
(6.59)
-6
т = 1
п
Принимая «скорость» движения в функциональном
пространстве равной
получаем
~=k
da
J / п \2
f dx
_ 4 т = 1 J /
(6.60)
п
^L- + bV
до — -R дхт( Л»’
т-1 /
(6.61)
266
МЕТОД ГРАДИЕНТОВ
[гл. VI
Таким образом, выражение
п
<6-62>
m = l f
принимается нами как определяющее направление «сво-
водного» градиента, и мы получаем движение в направ-
лении отрицательного градиента, выбирая знак минус в
формуле (6.61). При k = 1
> = -[₽!,. (6.63)
Это рассуждение было проведено нами по аналогии
с тем, как устанавливается характеристическое свойство
вектора градиента; для ознакомления с этим вопросом
читатель отсылается к работе Куранта [5] и к книге
Куранта и Гильберта [17] (т. 1, стр. 213—216).
В настоящем разделе для простоты была выбрана
наиболее удобная комбинация граничных условий, а
именно: tQ и tf фиксированы, xmQ фиксированы для всех
т\ Xmf — переменные, не фигурирующие в функции Р, —
не фиксированы. В следующих двух разделах будут рас-
смотрены другие типы граничных условий.
6.25. Связи, налагаемые граничными условиями. Рас-
смотрим граничные условия, относящиеся к типу раз-
деленных, т. е. имеющих вид уравнений, связывающих
либо начальные, либо конечные значения переменных.
Например, конечные значения могут изменяться, оста-
ваясь на поверхности типа
xnf tf) = Q. (6.64)
Число таких соотношений может быть равно /= 1, ....
/<п+1 при переменном конечном значении времени
и I < п при постоянном его значении.
Линеаризованные уравнения этих связей имеют вид
— — dJ 1 dJ t
J!+Vl = Jl+ 2 -5^’*“,+ л78'/=0' (в-65)
/п = 1 f
j=\,.... I.
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
267
Можно также задать подобные уравнения связей, от-
носящиеся к начальным значениям xmQ и t0. Пока мы
сосредоточим внимание на случае фиксированных на-
чальных значений переменных и фиксированного конеч-
ного момента tf. Таким образом, предполагаем, что
dJi
-^ = 0 и 1<п. (6.66)
В рассуждениях, подобных развитым в предыдущем
разделе, уравнения связи (6.65) записываются в форме
и присоединяются к (6.56) с помощью лагранжевых мно-
жителей Aj, j = 1, ..., I. Пропуск членов нулевого по-
рядка в выражениях (6.65) соответствует предположе-
нию о том, что решение хт, у удовлетворяет граничным
условиям (6.64).
Предоставив детали вывода интересующемуся чита-
телю, укажем главный результат — «спроектированное*
направление градиента:
^=2^ /71 = 1 J ду да Множители Aj, / = 1, линейных уравнений 2V(2^>)( /=1 /о \т = 1 / / \ '// п —/2^ 6 \/п=1 Л = ‘-+2Л>2^/~ <б-68> /=1 /71=1 / = -Р1г (6.69) 1, определяются системой 2 /71=1 J / (6-70) И f / \ . ил/П/ / I / \m=l J / 1 1.
268
МЕТОД ГРАДИЕНТОВ
[гл. VI
Эта система уравнений будет иметь решение, если
матрица коэффициентов А = (akj)
1/
(* I ХП i । / VI k I -
ak) ~ J H 2 ~дх^Г Pm I dx' (6-71)
y, k=\, /,
неособенная, а это будет так, если матрица
dJ f dJh
!•*='.......
m=l J J
неособенная, т. е. если среди граничных условий нет
лишних, и, далее, если матрица С= (стр)
7f
Стр = / HmHpт, р = \, ..п, (6.73)
to
имеет ранг*) r> I. Доказательство, принадлежащее
Гриншпану, приведено в приложении к настоящей главе.
Только что изложенный метод учета связей в конеч-
ной точке интервала в существенных чертах принадле-
жит Брайсону [15]. Этот метод можно назвать проекти-
рованием градиента, по аналогии со способом, изложен-
ным ранее и относившимся к обыкновенным проблемам
минимума. Далее мы приводим описание несколько от-
личного приема, развитого автором в работе [14].
♦) Последнее условие требует, чтобы по крайней мере I из п
функций Цш были линейно независимы (Курант и Гильберт [17],
т. 1, стр. 55—56). Следует отметить два обстоятельства, при кото-
рых это требование может быть нарушено. Первое касается случая,
когда система дифференциальных уравнений связи (6.34) содержит
голономное условие, т. е. дифференциальное уравнение, получаю-
щееся дифференцированием из конечного соотношения, связываю-
щего переменные хт и t. В таком случае матрица (6.73) может по-
низить свой ранг для всех значений верхнего предела интегралов
(см. [17], т. I, стр. 212). Более тонкие случаи вырождения могут
возникнуть при специальных значениях верхнего предела; это соот-
ветствует явлению анормальности и появлению сопряженных точек,
как это показывается в связи с необходимым условием Якоби.
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
269
Если вместо введения множителей Лагранжа пред-
ставить управляющую переменную у по формуле
у (А о) = ср (А а) + 5 (а)/? (/), (6.74)
<7=1
то I постоянных aq можно использовать для удовлетво-
рения уравнений связи (6.67), представленных в форме
(6.75)
х m = l f / \ q-\ /
/=1, •••,/•
Можно представить эти уравнения так:
0=1 m=l J t0
n
=~2W; f >=’ ••••'• <6re)
m=l J t0
и считать их системой относительно daqlda. Эта система
имеет решение при условии, если матрица D=(dj<7)
vr dJi Г
di<=^-d^ J ^яd'> .....Wb
m-\ mf 4
не является особенной.
Произвольные функции fQ(Z) должны быть выбраны
так, чтобы выполнялись условия разрешимости системы.
Величины daqlda, определяемые путем решения системы
(6.76), могут быть после этого подставлены в равенство
Ч / \ / i
dP Г I vt дР । I vr daa ।
~da~==J ( (6-78)
/0 \ /П= 1 J / \ 0=1 /
и градиент [Р], определяется как коэффициент при ду!д<з
в его правой части.
270
МЕТОД ГРАДИЕНТОВ
[гл. VI
Оба описанных до сих пор подхода имеют тот недо-
статок, что они приводят к «сдвигу» конечных значений
переменных при больших значениях Да вследствие ли-
неаризации граничных условий. В процессе спуска ко-
нечные значения должны восстанавливаться, и в методе
проектирования градиентов это осуществляется восста-
новлением членов нулевого порядка в линеаризованных
уравнениях связи (6.65). В пределах только что описан-
ного способа коэффициенты aq доставляют естественный
выбор параметров, с помощью которых можно произве-
сти необходимые задания. В процессе вычисления по-
правок может, однако, возникнуть затруднение, связан-
ное с выбором произвольных функций fq\ это обстоя-
тельство будет проиллюстрировано примером.
Использование метода функции нагружения имеет
преимуществом наличие «встроенных» поправок. Урав-
нения, связывающие конечные значения, будут удовлет-
воряться лишь приближенно, хотя и с любыми же-1
лаемыми отклонениями. Разыскивается минимум выра-
жения
z
<6-79)
/=1
Как и в случае обыкновенного минимума, произведе-
ния KjJj будут удовлетворять системе уравнений,близ-
кой к системе, определяющей множители Aj [уравнение
(6.70)], а именно:
Z / « л г \ / Л _ \
/=1 4 ^=1 J / \т=1 J '
( п \ ( п \
=-/ 2^Х2А>Г’ (“О)
/0 \ т=1 J / \гп = 1 ' /
£=1,
Здесь функции р и различные частные производные
вычисляются в минимуме выражения (6.79), где лишь
приближенно удовлетворяются уравнения связи для гра-
ничных значений. Если матрица, коэффициенты которой
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
271
даются формулами (6.71), неособенная, то ошибки, с
которыми удовлетворяются уравнения связи конечных
значений (6.64), могут быть уменьшены до желаемых
величин путем надлежащего выбора /Q, как это описано
в разделе 6.14 в связи с обыкновенными проблемами ми-
нимума.
Выражение для градиента [P']v принимает форму,
подобную (6.68), а .именно:
m=l J j=l т-1 J
Благодаря обращению в нуль величины [Р^ вдоль
пути, получающегося в пределе процесса спуска, мы мо-
жем оценить влияние малых изменений конечных значе-
ний Jj. Действительно, для произвольной малой вариа-
ции управляющей переменной ду(т) можно получить со-
отношение
i
8Р = —3 KjJj Ц, (6.82)
если умножить (6.81) на бу и проинтегрировать от
до tf. Величины — KjJj играют, таким образом, роль ве-
совых коэффициентов в расчетах по методу функции
нагружений — роль, подобную той, которая принадле-
жит величинам — Aj [см. уравнение (6.68)] в методе про-
ектирования градиентов. Это важное свойство оптималь-
ных траекторий, справедливое для малых вариаций в
их окрестности, было отмечено Чикала [29] в связи с
непрямыми методами.
6.26. Случай переменного конечного момента време-
ни; граничные значения как параметры. Способ, по ко-
торому конечное значение независимой переменной tf
входит в задачи рассматриваемого нами типа, требует
специального исследования, когда это значение не за-
фиксировано. Если в каком-либо частном случае одна
из переменных хт изменяется монотонно и имеет фи-
ксированные начальное и конечное значения, то выбор
этой переменной в качестве независимой представляет
простейший способ обхода трудностей. Такой выбор
весьма часто может оказаться невозможным, и в этом
272
МЕТОД ГРАДИЕНТОВ
[гл. VI
случае все зависит от искусства, с которым исследова-
тель применяет избранный им вариант метода градиен-
тов. Ниже мы проиллюстрируем на примере такой ва-
риант, включающий произвольные функции исписанный
в предыдущем разделе. В настоящем разделе мы будем
рассматривать /у как параметр, имея в виду использова-
ние функции нагружения при учете связей, наложенных
на конечные значения. Одновременно нам будет удобно
рассмотреть сходные способы учета незафиксированных
начальных данных.
Чтобы избежать неоправданных усложнений в сле-
дующих ниже выражениях, допустим, что начальный мо-
мент времени tQ зафиксирован и что заданы начальные
значения некоторых из переменных хт; остальные на-
чальные значения служат параметрами, которые сво-
бодны и могут быть использованы для целей оптимиза-
ции. Перейдем к определению производной по а от ха-
рактеристической функции, заданной в виде (6.79);
dP dxm дР dtf
_______L _j_ ____ i_
dxnif d<s 1 dtf da 1
dJj dxm dJj dtf \
+2ед 2^-^+^ *- • <6-
7=1 \m=l f /
получаем
Используя выражения (6.50), представляем это вы-
ражение в следующей форме:
6-2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
273
(суммирование по р распространяется, по предположе-
нию, лишь на те начальные значения хРо , которые не
зафиксированы).
Мы можем теперь определить «промежуточное» на-
правление градиента, рассматривая коэффициенты при
различных производных по о, входящих в (6.84).
Положим
dtf
da
VI / &Р VT dJ; —
Ip/L/ = — 2 ( + +
L m=l \ / /=1 / /
(6.86)
dxP*______ГП/1 _____
d a ~~ ^Po ~
+" % th dxm ^mp
/=1 //
(6.87)
и в процессе спуска изменим значения конечного мо-
мента времени и незафиксированных начальных дан-
ных хРй, а также функции у линейным образом по пара-
метру спуска о с коэффициентами наклона, заданными
этими выражениями. Таким образом, мы объединяем
характерные черты вариационных задач и обыкновен-
ных проблем минимума в один градиентный процесс
оптимизации.
Сходный метод определения оптимального значения
tf состоит в использовании выражения (6.86) как кри-
терия для окончания процесса спуска. Можно рассмат-
ривать это как одномерную задачу о разыскании мини-
мума Р' по отношению к /у, решаемую одновременно с
численным интегрированием уравнений для траекторий.
Мы снова отмечаем попутно, что величины Втр(7у) —
частные производные конечных значений по началь-
ным значениям хт— удобным образом вычисляются по
18 Дж. Лейтман
274
МЕТОД ГРАДИЕНТОВ
[гл. VI
единичным решениям присоединенной системы уравне-
ний, как это указывалось ранее в разделе 6.23.
6.27. Оптимизация по координатам и параметрам
системы. Во многих практических приложениях разыс-
кивается не только оптимальная траектория полета, но
и оптимальные значения параметров летательного аппа-
рата и системы управления. Ради ясности изложения
мы не усложняли предшествующие расчеты такого рода
рассмотрениями. Интересно, однако, отметить, что ука-
занные параметры можно с удобством принять за на-
чальные данные с помощью следующего приема, при-
надлежащего Чикала [29].
Мы принимаем параметры за начальные значения
дополнительных переменных хг-, удовлетворяющих диф-
ференциальным уравнениям
X/ = 0,
xt(t0) = et,
i = ft —|-1, ...
(6.88)
Рассматривая эти уравнения как дополнительные к
основной системе (6.34), можем выразить частные про-
изводные от конечных значений хт по через единич-
ные решения (расширенной теперь) присоединенной
системы описанным выше путем. Это позволяет с удоб-
ством использовать развитую выше вычислительную
схему для одновременного рассмотрения вариационных
и обыкновенных проблем минимума.
6.28. Связи, выражаемые неравенствами. Если в
формулировке задачи, поставленной в разделе 6.21, до-
бавлено одно или более требований в форме наложен-
ных на переменные хт, у и t неравенств связи
Qz(xi, .... хл, у, /)<0, (6.89)
то задача становится неклассической. Если в выраже-
ниях Qt фигурирует управляющая переменная у, то ста-
новятся применимыми некоторые приемы, развитые в
рамках непрямого метода вариационного исчисления,
именно методы Валентайна [30] и Понтрягина [31], обсу-
ждаемые в других главах. Для анализа же случаев, ко-
гда функции Qi не зависят от управляющей перемен-
в.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
275
ной у, существует относительно немного теоретических
сведений. Такого рода случаи представляют большой
практический интерес, например, в связи с вопросом о
траекториях летательного аппарата при наличии ниж-
него предела высоты и при ограниченных размерах
области, внутри которой могут располагаться кривые
зависимости скорости от высоты, — стеснениях, порож-
денных особенностями конструкции аппарата и двига-
телей.
Обращаясь сначала к случаю, когда управляющая
переменная у входит в выражения для Q, предположим,
что указанные неравенства имеют вид
У1<У<У2, (6-90)
как это обычно и бывает в приложениях. Введем пара-
метр 0(/, о) в качестве новой управляющей переменной,
определяя функцию </(0) следующим образом:
У = У1>
У = У1 + (У2 — У1)Р.
У = У2.
₽<0;
0< 0 < 1;
!<?•
(6.91)
(6.92)
(6.93)
График этой функции изображен на рис. 6.2.
Теперь мы можем применить теорию, развитую выше
для случая, когда на переменную 0 не наложено ника-
кой связи. В результате перехода от y(t, а) к управляю-
щей переменной 0(/, о) подынтегральная функция в
18*
276
МЕТОД ГРАДИЕНТОВ
[гл. VI
интегральном выражении для dPIda принимает вид
= (6.94)
и движение в направлении отрицательного градиента
определяется формулой
£ = -!₽),>• (6-95)
Производная dy/dfi дается выражением
= (У2 - У1) ™ - 1)1. (6.96)
в котором Н представляет собой хевисайдовскую функ-
цию единичного скачка [//(а) = 0 при а < 0, #(а) = 1
при а > 0].
В точках р = Ц и Р = 1 производная не определена.
Эти затруднения могут быть с удобством устранены,
если положить
^- = (У2-У1)Я(-[Р1У). ₽ = 0; (6.97)
^- = (У2-У1)Я([РЬ), ₽ = 1, (6.98)
разрешая тем самым вопрос о том, ведет ли направле-
ние отрицательного градиента внутрь интервала 0<р<:
< 1 или же выводит из него.
В непрерывном процессе спуска с помощью такого
подхода можно добиться того, что управляющая пере-
менная у останется в заданной области па-
раметр р при этом автоматически будет заключен в пре-
делах 0<р< 1. В дискретном варианте процесса спуска
возникнет, однако, трудность, обусловленная тем, что
правая часть равенства (6.95) вычисляется вдоль реше-
ния х = х(0, У = у(О, а ПРИ конечной величине шага
Да управляющий параметр р, вообще говоря, не будет
оставаться внутри заданных пределов. Поэтому, прежде
чем вычислять каждый раз др(О/дп, необходимо будет
изменять функцию р(0, полученную в предыдущем про-
цессе спуска, таким образом, чтобы оставаться в преде-
лах, установленных неравенством 0 < р< 1; в противном
случае правая часть равенства (6.95) будет во всех по-
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
277
(6.99)
следующих шагах равна нулю в тех точках, где указан-
ное неравенство нарушено.
Можно приближенно учесть связи Qt<0, не завися-
щие от у, составляя соответствующие функции нагруже-
ния. Если каждому уравнению связи поставить в соот-
ветствие дополнительную переменную хг- согласно
х, = 4
x/(Zo) = O, / = п + 2, ..., $,
где Н — хевисайдовская функция единичного скачка, то
конечные значения этих переменных Xi представятся так:
Xi(tf) = ± J Z = /z+l, n + 2, s, (6.100)
4
т. e. будут равны интегралам от квадратов отклонений,
распространенным на те участки траектории полета, на
которых нарушаются уравнения связей. Соответствую-
щие нагрузочные члены, пропорциональные указанным
конечным значениям, можно тогда включить в уравнение
(6.79), придав ему вид
I s
= 1<п. (6.101)
/=1 /=л+1
Подобным же образом можно, очевидно, определить
допустимые отклонения для сравнения с конечными зна-
чениями Xi и указать значения постоянных Кг. Если
обозначает заданную допустимую ошибку в смысле сред-
него квадратичного по мгновенным значениям, то допу-
стимое отклонение для оценки х^ равно
(6.102)
ft
Отношение Xi(tf)IE< послужит тогда характеристикой
величины отклонение/допустимое отклонение для опре-
деления постоянных Ki в процессе спуска.
278
МЕТОД ГРАДИЕНТОВ
[гл. VI
6.29. Функции нагружения *); оценки ошибок. Имея
в виду применение метода функций нагружения в про-
цессе машинных вычислений, мы считаем полезным при-
вести способ оценки ошибки в величине функционала
Р по значениям отклонений от соблюдения наложенных
связей. Таким образом, можно будет указать отклоне-
ния, оказывающие особенно сильное влияние на вели-
чину Р, и подвести более разумную основу под опреде-
ление упомянутых выше допустимых отклонений.
Приращение величины Р благодаря малым измене-
ниям хт и t дается в первом порядке выражением
ft.) «У +
m=l I /
(6.103)
Принимая, что минимум функционала Р' (6.101) до-
стигнут для некоторой заданной системы значений на-
грузочных постоянных, получаем следующие уравнения,
выражающие обращение в нуль градиента [Р']у:
2^-1*-+ S ад=о.
т=1 / /=1 m=l f / = л+1
(6.104)
Произвольность значений tf дает
1^=2 (^+£ад^Х+
m=l \ / / = 1 //
+ S К‘%‘, + S17 + 2 ад = °- (6-105)
/=л+1 ;=1 7
*) В отечественных работах функции нагружения часто назы-
ваются «функциями штрафа», (Прим, перев.)
6.2]
ЗАДАЧИ ОПТИМИЗАЦИИ ТРАЕКТОРИИ
279
Из этих выражений получаем для ДР
др=-f s
/о v = l m-l mf i = n + l /
— 8//=
L/ = l J m=A / = 1 / Z = n+1 J
= - 2 KjJ, £ Kt bxif. (6.106)
Если теперь ввести поправки в управлениях бу(т) и
в конечном значении времени 6tf таким образом, чтобы
приращения
Д/у = — Jp (6.107)
Lxlf = -xlf (6.108)
обратили в нуль отклонения, то возникающее при этом
изменение Р можно представить в форме
AP=S/CyjJ+2 2 Ktxlt. (6.109)
У=1 l=n+l *
Множитель 2 во втором слагаемом введен для прибли-
женного учета квадратичного поведения подынтеграль-
ного выражения в (6.100) вблизи точки Q< = 0.
Приращение Р можно с удобством выразить через
известные конечные значения. Вклад различных слагае-
мых в ДР образует основу для установления допусти-
мых отклонений и, следовательно, для определения по-
стоянных К, и Kt. Для конечных Kj и Ki «наилучшая»
оценка предельной величины Р через значения Р и Р'
такова:
Р + ДР = Р+2(Р'— Р) = 2Р’— Р, (6.110)
как это следует из (6.101) и (6.109).
280
МЕТОД ГРАДИЕНТОВ
[гл. VI
6.3. ПРИМЕР: ДВИЖЕНИЕ ПОД СОЛНЕЧНЫМ ПАРУСОМ
С целью исследования вычислительной стороны опти-
мизации методом градиентов мы выбираем плоскую за-
дачу о .переходе между планетными орбитами с помо-
щью интересного приспособления, называемого солнеч-
ным парусом. Потенциальные возможности движения
под солнечным парусом были исследованы в работах
Гарвина [32], Коттера [33], Цзу [34] и Лондона [35]. Эта
Рис. 6.3. Схема перелета между орбитами.
проблема обладает простотой, необходимой для иссле-
дования применимости метода, но в то же время до-
статочно сложна для того, чтобы можно было получить
аналитическое решение, если не делать серьезных упро-
щающих предположений.
6.31. Уравнения системы. Уравнения движения и
кинематические соотношения записываем почти в тех же
обозначениях, что в работе Цзу [34]. Имея в виду схему
рис. 6.3, напишем эти уравнения в следующем виде:
радиальное ускорение
«=^=4~ло(4)2+a(4)2icos30b <6Л11>
6.Я] ДВИЖЕНИЕ ПОД СОЛНЕЧНЫМ ПАРУСОМ 281
трансверсальное ускорение
v = = — — а(”7г)2 sin 6 cos2 0; (6.112)
радиальная скорость
R = gz = u, (6.113)
угловая скорость
Ф = ^. (6.114)
Поскольку гелиоцентрический угол гр не входит ни
в первые три уравнения, ни в рассматриваемые ниже
формулировки граничных условий, можно исключить
уравнение (6.114) из исследования оптимизации мето-
дом градиентов. Это эквивалентно предположению о том,
что дополнительно к заданию одинаковых конечных зна-
чений гелиоцентрических углов космического корабля и
планеты-цели мы фиксируем время старта.
6.32. Граничные данные. Разыскивая условия пере-
хода за минимальное время, полагаем функционал Р
равным
P = tf. (6.115)
Функции и, и, R представляют собой переменные хт
нашего теоретического рассмотрения, а угол наклона па-
руса 0 выступает в роли управляющей переменной у.
В качестве начальных условий берем значения со-
ставляющих скорости и, v и радиуса /?, соответствующие
движению по земной орбите, которая приближенно счи-
тается круговой:
/о = О, (6.116)
и (0) = и^ = иЕ — 0, (6.117)
v (0) = v0 = <vE, (6.118)
/?(О) = /?о = /?£. (6.119)
Будем рассматривать конечные условия, соответ-
ствующие прибытию корабля на орбиту планеты Марс
282
метод градиентов
[гл. VI
(также считаемую круговой) с заданными составляю-
щими скорости:
u(tf) = Up (6.120)
v(t/) = vp . (6.121)
R{t/) = Rf — RM. (6.122)
6.33. Поправочные функции. Для фиксированных
граничных значений и, v и R уравнения типа (6.39) раз-
витой выше теории таковы:
Л
8K/= J н 86 + ^8^ = 0, (6.123)
о
8vz= J n2894/T + g2/8// = O, (6.124)
о
8/?z= J + (6.125)
о
В рассматриваемом случае число требуемых функций [я
и коэффициентов aq равно
r = n — l—s = 3 —1—0 = 2. (6.126)
Выберем функции fq в виде
= (6.127)
Л(/) = /2, (6.128)
а управляющую функцию зададим равной
0 = cP + a1if + a2^. (6.129)
Система уравнений (6.123) — (6.125) принимает вид
.о J L0
=-/ (6.130)
6
6.3]
ДВИЖЕНИЕ ПОД СОЛНЕЧНЫМ ПАРУСОМ
283
Lo
dax
da
Ъ
Ь f 7*2 (T) 1*2
_6
da2 - dtf
da +^2/
Ъ
= -f ^dx, (6.131)
О
t
Lo
dax
da
Lo
- dtf
da + &/ da
dd2
= -/ (6.132)
О
В этом ЗХ3-мерном случае легко произвести обра-
щение. Подробно выписывать результат мы, однако, не
будем:
(6.133)
Наклон кривой спуска дается равенством
"J7 — — f [С31И1 + C32P2 + £зз(*з]
0
а градиент P — соотношением
= (£311*1 *4“ £321*2 + £331*3]-
(6.134)
(6.135)
284
МЕТОД ГРАДИЕНТОВ
[гл. VI
В соответствии с этим полагаем
= = С31Н + + ^ззНз (6.136)
и далее осуществляем шаговый спуск.
Для первой иллюстрации вычислений особенно удо-
бен случай, когда конечные значения составляющих ско-
рости не заданы, — случай свободных граничных усло-
вий. При этом уравнения (6.123) и (6.124) можно исклю-
чить из рассмотрения; получаем
r = n — 1 —s = 3 — l —2 = 0,
так что нет нужды в функциях fq. Отсюда
6 = ср,
и тогда
(6.137)
(6.138)
(6.139)
(6.140)
д? =
дя ёз/ ’
При численных расчетах были использованы значе-
ния различных постоянных, взятых из работы Цзу; зна-
чение а было взято равным
а = 0,1 см/сек2 = 3,28 - 10“3 фт/сек2. (6.141)
Эта величина соответствует примерно ускорению си-
лы тяги 10"4 g, развиваемому парусом, повернутым к
Солнцу своей поверхностью (6 = 0) и находящимся на
орбите Земли; это составляет около 17% ускорения, об-
условленного притяжением Солнца.
6.34. Расчеты перехода между орбитами. Результаты
расчетов для случая свободных составляющих конечной
скорости представлены на рис. 6.4—6.6. Взятая вначале
произвольно, программа управления полетом (рис. 6.4
и 6.5) была далека от оптимальной, поскольку радиаль-
ная составляющая скорости в точке пересечения с орби-
той Марса была мала. В результате первого спуска
(рис, 6.6) получается, как видно, самое значительное
6.3]
ДВИЖЕНИЕ ПОД СОЛНЕЧНЫМ ПАРУСОМ
285
уменьшение времени полета — более чем на половину
первоначального значения. После трех спусков было по-
лучено пригодное для практических целей минимальное
время полета, хотя еще остались небольшие изменения
в детальной структуре программы управления.
Рис. 6.4. Последовательные приближения к оптимальной траек-
тории перехода при отсутствии ограничений на составляющие
скорости в конечной точке.
Для случая, когда конечные компоненты скорости
совпадают с компонентами скорости планеты-цели, т. е.
Uf = uM, -vf = vM, (6.142)
результаты представлены на рис. 6.7—6.10.
На рис. 6.7 видна тенденция конечных значений к
расхождению с заданными значениями. Эти значения
восстанавливались путем итеративного процесса введе-
ния поправок с учетом изменений коэффициентов at и а2
286
МЕТОД ГРАДИЕНТОВ
[гл. VI
Рис. 6.5. Последовательные приближения к оптимальной про-
грамме изменения угла наклона паруса при отсутствии огра-
ничений на составляющие скорости в конечной точке.
Рис. 6.6. Кривые спуска для задачи о полете под солнечным
парусом при отсутствии ограничений на составляющие ско-
рости в конечной точке.
6.3]
движение под солнечным парусом
287
Рис. 6.7. Уход конечных значений скорости в случае,
когда они зафиксированы.
Рис. 6.8. Кривые спуска для задачи о полете под солнечным
парусом при заданных составляющих скорости в конечной точке.
288
МЕТОД ГРАДИЕНТОВ
(гл. VI-
в уравнении (6.129). Как правило, для коррекции каж-
дой точки требовалось две или три итерации. На рис. 6.8
представлены кривые спуска. Приближение к реше-
нию для минимума времени иллюстрируется на рис. 6.9
и 6.10.
6.35. Вопросы сходимости. Для случая равенства
конечных скоростей корабля и планеты первая попытка
Рис. 6.9. Последовательные приближения к оптимальной про-
грамме изменения угла наклона паруса при заданных соста-
вляющих скорости в конечной точке.
вычислений была основана на предположении о постоян-
стве функций fg или их линейной зависимости от вре-
мени. Эта попытка натолкнулась на трудности, связан-
ные с близостью к нулю значений определителя, в то
время как указанная выше комбинация линейных и ква-
дратичных поправок с успехом преодолела эти труд-
ности.
Предпринятое в дальнейшем изучение поведения упо-
мянутого определителя в процессе спуска оказалось по-
лезным для выбора поправочных функций. Значения
определителя матрицы левых частей уравнений (6.130) —
(6.132), требуемые для вычисления обратной матрицы С
6.3]
ДВИЖЕНИЕ ПОД СОЛНЕЧНЫМ ПАРУСОМ
289
уравнения (6.133), были протабулированы для несколь-
ких первых процессов спуска и для предельной траек-
тории; эти значения представлены в табл. 6.1.
Проверка показала, что численные значения обоих
определителей, рассчитанные для предельной траектории,
достаточно велики для того, чтобы можно было задавать
траектории перехода при заданных составляющих скорости
в конечной точке.
конечные значения переменных, не опасаясь потери точ-
ности. Поэтому сходимость процесса спуска с использо-
ванием поправочных функций зависит от выбора функ-
ций, для которых определитель не может изменить знак.
Основываясь на опыте, полученном из этого примера, мы
заключаем, что выбор функций влияния в качестве
поправочных функций fq оказывается выгодным в том
отношении, что упомянутый выше определитель будет
19 Дж. Лейтман
290
МЕТОД ГРАДИЕНТОВ
[гл. VI
Таблица 6.1
Поведение определителя
Номер спуска i Случай { \7доо Случай { дАо2
1 —2,383 3,983
2 —2,695 3,268
3 —0,770 1,527
4 —0,340 1,104
оо 1,000 1,000
при этом вести себя удовлетворительно, за исключением
специальных случаев, отмеченных в примечании к раз-
делу 6.25.
6.4. ПРИМЕР: ДВИЖЕНИЕ С МАЛОЙ ТЯГОЙ
6.41. Уравнения системы и граничные условия. Дру-
гой, тесно связанный с предыдущим, пример, для кото-
рого были выполнены численные расчеты, относится к пе-
реходу между орбитами с помощью двигателя с малой
тягой, например ионного или плазменного двигателя.
В этом случае используется метод функций нагружения
для рассмотрения связей, наложенных на конечные зна-
чения.
Результаты настоящего пункта принадлежат Линдор-
феру и Мойеру [36].
Уравнения движения и кинематические соотношения
близки к тем, которые имеют место в примере с солнеч-
ным парусом; различие появляется лишь в выражениях
для составляющих силы тяги:
радиальное ускорение
+^sin9’ <6Л43>
трансверсальное ускорение
^ = 52 = —-^-4-^-cosS; (6.144)
6.4] ДВИЖЕНИЕ С МАЛОЙ ТЯГОЙ 291
радиальная скорость
R = g3 = u, (6.145)
угловая скорость
Ф = = (6-146)
Величина тяги Т была принята постоянной, соответ-
ствующей начальному значению ускорения силы тяги
-Z—= 0,846 • 10-4, (6.147)
mog v ’
а масса предполагалась линейной убывающей со вре-
менем:
/п = /п0— Q/, (6.148)
со скоростью, соответствующей величине
— = 1,29-10-3 в сутки. (6.149)
Эти оценки заимствованы из работы Эдвардса и Бра-
уна [37]. Направление тяги 0 отсчитывается от направле-
ния касательной к упомянутой выше окружности.
Граничные условия, принятые в процессе вычисле-
ний, соответствуют случаю равенства скоростей при пе-
релете с орбиты Земли на орбиту Марса. Эти орбиты
идеализированно представлены круговыми, как в при-
мере предыдущего раздела.
6.42. Переход между орбитами и расчеты попада-
ний. Сначала был рассмотрен случай перехода при сво-
бодном параметре гр/. Сходимость последовательных при-
ближений была достаточно быстрой. Хотя потребовалось
большее число спусков, чем в примере с солнечным па-
русом (см. предыдущий раздел), отсутствие какой-либо
необходимости в коррекции «сдвига», отмеченного на
рис. 6.7, привело в результате к уменьшению времени
счета. Эксперименты с постоянными в функции нагру-
жения показали, что сходимость улучшается, если зна-
чения этих постоянных берутся первоначально малыми
(«неограниченные» допустимые отклонения), и проходит
несколько процессов спуска, прежде чем допустимые
19*
292
МЕТОД ГРАДИЕНТОВ
(гл. VI
отклонения оказываются «ограниченными». Так, на
рис. 6.11 и 6.12 первые 25 спусков были выполнены при
относительно малых значениях Kj и было получено при-
ближенное значение минимума Р'. После этого постоян-
ные Kj были увеличены пропорционально абсолютным
Рис. 6.11. Последовательные приближения к оптимальной
траектории полета с малой тягой при отсутствии ограниче-
ний на конечное значение полярного угла.
значениям Отношения отклонений к допустимым откло-
нениям для каждой переменной (за исключением ради-
альной скорости, использованной для ограничения сче-
та) и процесс продолжался, как и ранее. Для задачи о
попадании на планету требуется, чтобы гелиоцентриче-
ский угол г|? космического корабля был равен в конечной
точке гелиоцентрическому углу Марса. Рис. 6.13 и 6.14
иллюстрируют результаты, полученные для различных
начальных положений системы корабль (Земля) —Марс.
6.4]
ДВИЖЕНИЕ С МАЛОЙ ТЯГОЙ
293
На рис. 6.13 приведен график зависимости минимального
времени полета от начального углового расстояния ме-
жду планетами. Низшая точка этого графика соответ-
ствует минимальному времени перелета между орбита-
ми (конечное значение угла не фиксировано). Как пока-
зывает небольшое число отмеченных точек, минимум
отсутствуют.
имеет характер острия. Эта особая точка, кроме того,
делит решения проблемы попадания на два различных
по практическому осуществлению класса. Один из этих
классов (фо — фо марс >—46°) состоит из решений, в ко-
торых корабль «ожидает» Марс с тем, чтобы «перехва-
тить» его. Для этой цели корабль пролетает за орбиту
Марса, уменьшая свою окружную скорость до тех пор,
пока она не станет меньше окружной скорости Марса.
С уменьшением относительного гелиоцентрического угла
294
МЕТОД ГРАДИЕНТОВ
[гл. VI
Щинил/альяее время пвяв/па, eye?
Рис. 6.13. Минимальное время попадания в заданную точку на орбите.
Рис. 6.14. Оптимальные траектории для попадания в заданную
точку на орбите при различных начальных условиях.
6.5]
ОТНОСИТЕЛЬНЫЕ ПРЕИМУЩЕСТВА МЕТОДОВ
295
окружная скорость корабля возрастает и сравнивается
с окружной скоростью Марса.
Второй класс решений (ф0— фомарс<—46°) харак-
теризуется первоначальным движением по направлению
к Солнцу, при котором скорость увеличивается, и после-
дующим тангенциальным приближением к орбите Марса
изнутри.
Из рис. 6.13 видно, что время перелета, рассматри-
ваемое в функции от начального положения планет, об-
ладает достаточно острым минимумом и для большей
части «неблагоприятных» моментов старта метод дости-
жения Марса с облетом вокруг Солнца приводит к более
быстрому достижению цели, нежели «ожидание» Марса
за его орбитой.
6.5. ЗАМЕЧАНИЯ ОБ ОТНОСИТЕЛЬНЫХ ПРЕИМУЩЕСТВАХ
РАЗЛИЧНЫХ ВЫЧИСЛИТЕЛЬНЫХ МЕТОДОВ
Читатель, вероятно, сделал правильный, вывод о том,
что эта глава скорее представляет собой обзор состоя-
ния еще ведущихся исследований, нежели изложение ме-
тодов, уже ставших общепринятыми. В самом деле, раз-
личие точек зрения в разных главах этой книги служит
подтверждением той неопределенности, которая имеет
место сейчас во взглядах на области применимости и от-
носительные достоинства многочисленных методов чис-
ленных расчетов. Поэтому замечания настоящего пункта
будут носить временный и качественный характер и бу-
дут относиться к тем градиентным и непрямым мето-
дам, с которыми автор непосредственно сталкивался.
Автор этой главы получал иногда просьбы о сравне-
нии градиентных методов с классическими непрямыми
методами (численное решение уравнений Эйлера — Ла-»
гранжа) с точки зрения скорости и простоты вычисле-*
ний. Такое сравнение нелегко провести, поскольку гра-
диентные методы имеют непосредственный характер,
тогда как численное решение двухточечной краевой за-
дачи для уравнений Эйлера в значительной мере явля-
ется искусством. В задачах, достаточно простых и обла-
дающих одно- или двухпараметрическим семейством
решений эйлеровых уравнений, эффективен классический
296
МЕТОД ГРАДИЕНТОВ
[гл. VI
подход; однако немногие практически интересные задачи
могут быть решены в столь простой форме. Имеющиеся
в литературе рассмотрения более сложных задач посвя-
щены главным образом определению взаимного отобра-
жения начальных и конечных значений либо путем меха-
низированных итерационных схем, либо путем много-
кратного пересчета граничных значений. В зависимости
от частного вида приложений этот процесс может быть
усложнен из-за чрезмерно высокой чувствительности к
малым изменениям начальных данных и (или) из-за
того, что в процессе построения последовательных при-
ближений приходится иметь дело с почти сингулярными
матрицами. Даже наиболее удачные схемы связаны с по-
лучением сперва пробного решения эйлеровых уравне-
ний, конечные значения которого лежат в окрестности
заданных конечных значений; предварительные поиски
такого решения могут отнять много времени и усилий.
Кажется возможным и даже желательным, чтобы
были найдены усовершенствованные способы решения
проблемы отображения. Положение, когда методы ре-
шения нелинейных дифференциальных уравнений пред-
ставляют собой искусство, представляется не очень обо-
дряющим постольку, поскольку это касается первона-
чального развития мощного общего метода.
Следует упомянуть о другом подходе, основанном на
уравнениях Эйлера и методе Ньютона. Речь идет о ме-
тоде итераций, предложенном Хэстенсом [38] п предна-
значенном для получения эйлерова решения, удовлетво-
ряющего заданным граничным условиям. Идея этого ме-
тода впоследствии была использована Калаба [39], чьи
теоретические исследования пролили свет на благоприят-
ные свойства сходимости метода в пределах справедли-
вости предположения о выпуклости. В настоящее время
мы не располагаем опытом расчетов по этому методу и
сведениями о практической необходимости предположе-
ния о выпуклости.
Обращаясь к сравнению различных вариантов раз-
витого выше метода градиентов, отметим активное со-
ревнование, имеющее место между методом проектиро-
вания градиентов и методом функций нагружения. Пер-
вый из этих методов нуждается в длительном процессе
6.5]
ОТНОСИТЕЛЬНЫЕ ПРЕИМУЩЕСТВА МЕТОДОВ
297
коррекции ошибок, чего не требуется для второго ме-
тода. С другой стороны, концентрация усилий на методе
функций нагружения связана с трудностями по умень-
шению числа ошибок в конечных значениях. Если исполь-
зуются «связанные» допустимые отклонения, то процесс
приближений колебательный и сходимость его замед-
лена. Действенным компромиссом представляется ис-
пользование в начале счета свободных допустимых от-
клонений с последующим наложением ограничений. Ав-
тором рассмотрено теоретически, но не проверено на
практике комбинирование обоих методов, например при-
менение их по очереди. Такой способ избавил бы от не-
обходимости в коррекции в процессе проектирования
градиентов и, возможно, объединил бы преимущества
обоих методов. Опыт расчетов по методу градиентов ока-
зался, вообще говоря, в рассмотренных выше задачах
настолько обнадеживающим, что можно рассчитывать на
применение этого метода в будущем для решения срав-
нительно более сложных задач.
Автором и его сотрудниками было проведено сравне-
ние решения по методу градиентов и эйлерова решения
для ограниченного числа случаев в задачах, описанных
в предыдущих разделах. Эта работа была обусловлена
желанием иметь точное решение в качестве образца
экстремали для некоторых исследований второй вариа-
ции, а не проблемой сравнения различных вычислитель-
ных методов. Первым выводом из этих экспериментов
был вывод о том, что временное поведение управляю-
щей переменной в решении, полученной по методу гра-
диентов с инженерной точностью (скажем, 1 % мини-
мума Р), на некоторых интервалах времени не согласо-
вывалось с поведением этой же величины в эйлеровом
решении. Расхождение распространялось на те части
траектории, на которых конечные значения, определяю-
щие Р, относительно нечувствительны к вариациям уп-
равления (см., например, рис. 6.15). С практической
точки зрения это несущественно, если только основной
интерес представляет величина Р, как это имеет место
в исследованиях по динамике полетов. Если же тре-
буется иметь семейство соседних экстремалей, как, на-
пример, в вопросе об управлении, то это обстоятельство
298
МЕТОД ГРАДИЕНТОВ
[гл. VI
представляется неудобным, так как требует дополни-
тельных расчетов для приведения закона изменения
управления в рамки требуемой точности. Было сделано
предположение, что подходящий для такой ситуации ме-
тод заключается в систематическом численном интегри-
ровании уравнений Эйлера, и это предположение на пер-
вый взгляд кажется разумным. Оказывается, однако, что
Рис. 6.15. Сравнение эйлерова решения и решения, полученного
по методу градиентов (задача о переходе между орбитами с по-
мощью солнечного паруса).
надлежащие линейные комбинации решений присоеди-
ненных уравнений не доставляют хорошего приближе-
ния к множителям Лагранжа в непрямом методе и, в
частности, начальные значения этих множителей могут
оказаться настолько ошибочными, что это создаст труд-
ности в проведении процесса итераций.
В связи со сказанным мы дадим в следующем раз-
деле схему, предназначенную для получения по методу
градиентов программы управления, близкой к минималь-
ной и находящейся в более точном соответствии с про-
граммой, полученной по эйлерову решению. Несмотря
на то, что схема может показаться запоздалой, как,
6.6]
СХЕМА ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
290
впрочем, это и есть в действительности, наАм кажется, что
ее включение соответствует духу этой книги. Опыт рас-
четов по этой схеме сейчас еще весьма мал; изучение ее
возможностей в первую очередь как расчетной схемы,
равно как и схемы улучшения расчетных данных, пред-
ставляет, по-видимому, интерес для исследований в бу-
дущем.
6.6. СХЕМА ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ,
ТРЕБУЮЩАЯ МИНИМАЛЬНОГО КОЛИЧЕСТВА ОПЕРАЦИИ
Хотя метод, описываемый в этом разделе, не являет-
ся, собственно говоря, методом градиентов, он тесно при-
мыкает к нему как по своим идеям, так и по средствам
реализации. Рассматривается задача минимизации функ-
ции Р' конечных значений переменных, заданная в форме
(6.79) (читатель отсылается к приведенному выше об-
суждению вопроса об определении постоянных в функ-
ции нагружения). Предполагается, что начальные зна-
чения переменных Xi заданы. Численным интегрирова-
нием основной системы (6.34) получаем неминимальное
решение, соответствующее y = y(t). Для ограничения
счета можно использовать критерий dP'ldtf = Q\ этот кри-
терий равным образом применим к расчетам с по-
мощью функции нагружения. В момент t=tf, опреде-
ленный таким образом, на функции Лг- накладываются
граничные условия
(6.150)
и решение присоединенной системы (6.41) получается
численным интегрированием, производимым от момента
tf до момента t0.
Обозначим это решение через ХД/) и найдем из
(6.44), что
п дР' г п
= = ] W8^- <6Л51>
/=1 ' /0 1=1
(Заметим, что слагаемое (dPi/dtf)выпавшее из вы-
ражения для 6Р', исчезает в силу выбранного выше кри-
терия ограничения счета.)
300
МЕТОД ГРАДИЕНТОВ
(гл. VI
Определим теперь функцию Н*(у, t) равенством
х„, у, /). (6.152)
Здесь функции Xi(t) соответствуют неминимальному ре-
шению у = y(t). Мы получаем тогда
bp'=f (6.153)
о
Частная производная дН*(у, t)fdy вычисляется при
y = y(t). Рассуждения до этого момента полностью со-
впадают с приведенными в разделе 6.5, и если бы мы
были в состоянии определить наискорейший спуск в
смысле евклидовой метрики
ds = J by2dt (6.154)
to
[ср. уравнение (6.54)], то мы получили бы метод гра-
диентов, приводящий к соотношению
zy=k^r (*<°)- <6Л55>
Недостатком метода является то, что в тех интерва-
лах, где величина дН*1ду мала, малы и соответствую-
щие изменения у. После нескольких шагов у на этих
«нечувствительных» интервалах может еще далеко от-
стоять от оптимального значения, что объясняется упо-
мянутой особенностью процесса градиентов. Ясно, что
это связано с тем, что евклидова метрика используется
здесь более или менее произвольно. Можно выбрать
другой, вполне равноправный подход, отказавшись со-
всем от связи, выражающей расстояние, и добавив сла-
гаемое
Г \ дН* , .1 д2Н* ,
=./ + 7 °У J dt- (6-156)
/о
в.в] СХЕМА ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 301
Можно предложить единственное оправдание этого
видоизменения, а именно, что указанное слагаемое га-
рантирует, что 6Р' достигает минимума для некоторого
конечного бу, если такой минимум вообще существует.
Формально получаем
<6-157)
Значение бу делает 6Р' стационарным. Стационарному
значению соответствует отрицательная подынтегральная
функция, если д2Н*/ду2>0. Если д2Н*1ду2 равно нулю
или отрицательно, то подынтегральная функция не огра-
ничена снизу, и задача о минимуме оказывается некор-
ректно поставленной. В этом случае, очевидно, такая
модификация метода отказывается служить.
Если, однако, мы добавим в подынтегральную функ-
цию достаточно большое число членов высшего порядка,
то в пределе мы получим, что функция
min//* (6.158)
у
представляет решение проблемы минимума для бР', и
этот путь кажется более обнадеживающим, поскольку
можно ожидать, что функция Н* обладает минимумом
всегда, за исключением особого случая, когда Я* не за-
висит от у (так называемый анормальный случай).
Принятие управляющей функции y = y*(t), достав-
ляющей min//*, в качестве следующего приближения
может оказаться рискованным, потому что из-за боль-
шой величины шага могут нарушиться предположения,
сделанные при линеаризации. Этот риск представляется
оправданным, если иметь в виду стоящую перед нами
цель — улучшение решения, близкого к минимальному.
Будучи осторожными, мы, однако, можем заменить
большой шаг пробной последовательностью более мел-
ких, положив
У = У(О + ЧУ*(О-У(О] (6.159)
и вычисляя Р' для различных £,— одномерный поиск,
аналогичный поиску по переменной а в расчетах по ме-
тоду градиентов.
Аргументация, приводящая к схеме min//* для вы-
числения последовательных приближений, приведена
302
МЕТОД ГРАДИЕНТОВ
[гл. VI
здесь как имеющая самостоятельный интерес. Тот же
результат можно было бы получить с помощью прин-
ципа максимума Понтрягина, излагаемого в следующей
главе. Отметим, что в случае сходимости процесса
функция Я* стремится к функции Н — обобщенному
гамильтониану.
В пределах ограниченного опыта расчетов на един-
ственном примере о движении с малой тягой (см. эту
главу) оказывается, что метод настоящего раздела схо-
дится к решению, представляющему значительно луч-
шее приближение к эйлерову решению, чем обычна по-
лучаемое по методу градиентов, в отношении временного
поведения управления y(t); это улучшение касается
упомянутых выше «нечувствительных» областей. Бы-
строта сходимости метода позволяет ему конкурировать
с комбинированным использованием метода градиентов
и функций нагружений, хотя твердое мнение по этому
вопросу еще не представляется возможным высказать
вследствие недостаточного опыта расчетов.
Работы [40—49] представляют собой некоторые послед-
ние публикации, относящиеся к материалу этой главы.
Автору приятно выразить благодарность Уильяму
П. О’Двайеру и Гарднеру X. Мойеру (Вычислительный
центр Грумман) за участие в проведении вычислений на
машине IBM 704, а также м-с Агнес Зивенс за помощь
при проверке численных результатов и при подготовке
их для опубликования.
ПРИЛОЖЕНИЕ
Ранг матрицы А, элементы которой даются форму-
лами (6.71), можно определить, обращаясь к следую-
щему ее представлению:
А = ₽С₽',
где штрих обозначает транспонирование. Элементы мат-
рицы р таковы:
R ___ Wj т — 1, ...» п,
- дхт/ '
а элементы С даются формулой (6.73).
ПРИЛОЖЕНИЕ
303
Обозначим ранги матриц (3 и С соответственно через
s и г и заметим, что ранг написанного выше произведе-
ния трех матриц должен быть равен /, чтобы матри-
ца А не была особенной. Поскольку ранг этого произве-
дения не может превышать ранга матрицы-множителя 0,
находим, что
I <* = Я(₽)
(см. [50], гл. 3). Далее, так как ранг 0 не может пре-
вышать числа строк, получаем
/?(₽) = s<Z
и, следовательно,
/?(p) = s = Z.
Поскольку ранг произведения не может превышать
ранга матрицы, являющейся вторым сомножителем,
справедливо соотношение
Z?(pc₽') = Z < 7?(С₽Э,
а вследствие того, что ранг матрицы не может быть
больше числа столбцов,
та
откуда заключаем, что
/?(C0') = Z.
Подобным же образом устанавливаем, что
Ранг произведения
можно определить, рассматривая частный случай, когда
С — единичная матрица; получим
Все сказанное можно просуммировать в следующих
соотношениях:
Z = /?H)</?(C) = r
и
l = R(A) = R(B).
304
МЕТОД ГРАДИЕНТОВ
[гл. VI
ЛИТЕРАТУРА
1. A. L. Cauchy, MGthode generale pour la resolution systemes
d’equations simultanees, Compt. rend, асаd. sci. 25,536—538 (1847).
2. K. Levenberg, A method for the solution of certain non-linear
problems in least squares, Quart. Appl. Math. 2, 164—168 (1944).
3. H. B. Curry, The method of steepest descent for non-linear mi-
nimization problems, Quart. Appl. Math. 2, 258—261 (1944).
4. J. H a d a m a r d, Memoire sur le problem d’analyse relatif 3
1’equilibre des plaques elastiques encastrees, Mem. pres. acad. sci.
France [2] 33, No. 4 (1908).
5. R. С о u r a n t, Variational methods for the solution of problems
of equilibrium and vibrations, Bull. Am. Math. Soc. 49, 1—23 (1943).
6. G. E. P. Box and К. B. Wilson, On the experimental attain-
ment of optimum conditions, J. Roy. Statist. Soc., Ser. B, 13,
1—45 (1951).
7. J. B. Rosen, The gradient projection method for nonlinear pro-
gramming, часть I, Linear constraints, J. Soc. Ind. Appl. Math.
8, 181—217 (1960).
8. P. Wolfe, The present status of nonlinear programming, RAND-
University of California Symposium on Mathematical Optimization
Techniques, Santa Monica, California, October 18—20, 1960.
9. С. B. Tompkins, Methods of steep descent, в книге «Modern
Mathematics for the Engineer» (E. F. Beckenbach, ed.), гл. 18.
McGraw-Hill, New York, 1956.
10 M. R. H e s t e n e s and E. Stiefel,- Method of conjugate gra-
dients for solving linear systems, J. Research Natl. Bur. Standards
49, 409—436 (1952).
11. A. 1. Forsythe and G. E. Forsythe, Punched-card experi-
ments with accelerated gradient methods for linear equations, Natl.
Bur. Standards Appl. Math. Ser. 39, 55—69 (1954).
12. C. Muller, A new method for solving Fredholm integral equa-
tions, Rept. No. BR-15, New York University Institute of Mathe-
matical Sciences, Division of Electromagnetic Research (1955).
13. M. L. Stein, On methods for obtaining solution of fixed end-
point problems in the calculus of variations, J. Research Natl.
Bur. Standards, 50, 277—297 (1953).
14. H. J. К e 11 e y, Gradient theory of optimal flight paths, presented
at Am. Rocket Soc. Semi-Annual Meeting, Los Angeles, California,
May 9—12, 1960; ARS Journal 30, 947—954 (1960).
15. A. E. Bryson, F. J. С а г г о 11, К. M i k a m i, and W. F. De n-
h a m, Determination of the lift or drag program that minimizes
re-entry heating with acceleration or range constraints using a
steepest descent computation procedure, представлено на 29 съезде
IAS, New York, January 23—25, 1961.
16. P. Куран т, Курс дифференциального и интегрального исчис-
ления, перев. с нем., ГТТИ, М.—Л., 1931.
17. Р. Курант и Д. Гильберт, Методы математической физики,
перев. с нем., т. I, ГТТИ, М.—Л., 1933; т. II, ГТТИ, М.—Л., 1945.
18 R. С our a nt, Calculus of variations and supplementary notes
and exercises, 1945—1946. Переработано Дж. Мозером [J. Mo-
ЛИТЕРАТУРА
305
ser], New York, University Institute of Mathematical Sciences,
1956—1957.
19. H. Rubin and P. Ungar, Motion under a strong constraining
force, Communs. Pure Appl. Math. 10, 65—87 (1957).
20. A. S. Men gel, Optimum trajectories, Proc. Project Cyclone
Symposium 1 on REAC Techniques, Reeves Instrument Corp, and
USN Special Devices Center, New York, March 15—16, 1951.
21. J. H. Irving and E. K. Blum, Comparative performance of
ballistic and low-thrust vehicles for flight to Mars, в книге
«Vistas in Astronautics», том II, стр. 191—218, Pergamon, New
York, 1959.
22. C. R. F a u 1 d e r s, Low-thrust steering program for minimum time
transfer between planetary orbits, SAE National Aeronautic Meet-
ing, Los Angeles, California, September 29 — October 4, 1958.
23. B. Friedman, Principles and Techniques of Applied Mathema-
tics, Wiley, New York, 1956.
24. G. A. Bliss, Mathematics for Exterior Ballistics, Wiley, New
York, 1944.
25. T. R. Goodman and G. N. Lance, The numerical integration
of two-point boundary value problems, Math. Tables and Other
Aids to Computation 10, 82—86 (1956).
26. W. К i z n e r, Perturbation theory and Green’s functions, Section
Rept. No. 12-152, Jet Propulsion Laboratory, California Institute
of Technology, Pasadena, California (October 21, 1957).
27. C. G. Pfeiffer, Guidance for space missions, External Publ.
No. 656, Jet Propulsion Laboratory, Pasadena, California (June 23,
. 1959).
28. J. C. Dunn, Green’s functions for space trajectory perturbation
analysis, J. Astronaut. Sci. 8, 95—103 (1961).
29. P. Cicala, An Engineering Approach to the Calculus of Va-
riations, Levrotto-Bella, Torino, 1957.
30. F. A. Valentine, The problem of Lagrange with differential
inequalities as added side conditions, Dissertation, Department of
Mathematics, University of Chicago, Chicago Illinois, 1937.
31. Л. И. Розоноэр, Принцип максимума Л. С. Понтрягина в
теории оптимальных систем, I, II, III, Автоматика и телемеханика
20, №№ 10-12, стр. 1320—1334, 1441-1458, 1561-1578 (1959).
32. R. L. Garwin, Solar sailing — a practical method of propulsion
within the solar system, Jet Propulsion 28, 188—190 (1958).
33. T. P. Cotter, Solar sailing, Sandis Research Colloquium, April,
1959. Albuquerque, New Mexico.
34. T. С. T s u, Interplanetary travel by solar sail, ARS Journal 29,
422—427 (1959). [Русский перевод: Цзу, Межпланетный полет
с помощью солнечного паруса, сб. переводов «Механика», № 1,
1961, ИЛ.]
35. Н. S. London, Some exact solutions of the equations of motion
of a solar sail with constant sail setting, ARS Journal 30, 198—
200 (1960). [Русский перевод: Лондон Г., Некоторые точные
решения уравнений движения космического корабля с солнечным
парусом при постоянном угле установки паруса, сб. переводов
«Механика», № 1, 1962, ИЛ.]
20 Дж. Лерман
306
МЕТОД ГРАДИЕНТОВ
[гл. VI
36. W. Li nd orfer and H. G. Moyer, An application of a low-
thrust trajectory optimization scheme to planar Earth-Mars Trans-
fer, ARS Journal 32, 260—262 (1962).
37. R. N. Edwards and H. Brown, Ion rockets for small satelli-
tes, Am. Rocket Soc. Controllable Satellites Conference, Massachu-
setts Institute of Technology, Cambridge, Massachusetts, April
30 —May 1, 1959.
38. M. R. H e s t e n e s, Numerical methods of obtaining solutions of
fixed end-point problems in the calculus of variations, RAND
Rept. No. RM 102, The RAND Corporation, Santa Monica, Cali-
fornia (August, 1949).
39. R. К a 1 a b a, On nonlinear differential equations, the maximum
operation, and monotone convergence, J. Math, and Meeh 8,
519—584 (1954).
40. H. J. Kelley, R. E. Kopp, and H. G. Moyer, Successive ap-
proximation techniques for trajectory optimization, presented at
the IAS Vehicle Systems Optimization Symposium, Garden City,
New York, November 28—29, 1961.
41. Y.-C. Ho, A successive approximation technique for optimal control
systems subject to input constraints, presented at the 1961 Joint
Automatic Control Conference, Boulder, Colorado, June 28—30, 1961.
42. Y.-C. H o, A computational procedure for optimal control problems
with state variable inequality constraints, Rept. No. P-2402, the
RAND Corp., Santa Monica, California, September 1961 (to be
published in J. Math. Anal, and Appl.).
43. A. E. В г у s о n and W. F. D e n h a in, A steepest ascent method for
solving optimum programming problems, Am. Soc. Meeh. Eng.
Conf, on Applied Mechanics, Chicago, Illinois, June 1961 (to be
published in J. Appl. Meeh.).
44. C. S a 11 z e r and C. W. F e t h e г о f f, A direct variational method
for the calculation of optimum thrust programs for power-limited
interplanetary flight, Astronaut. Acta 7, 8—20 (1961).
45. T. Butler and A. V. Martin, On a method of Courant for
minimizing functionals (to be published).
46. S. Dreyfus, Variational problems with inequality constraints,
Rept. No. P-2357 the RAND Corp., Santa Monica, California (to
be published in J. Math. Anal, and Appl.).
47. S. Dreyfus, Numerical Solution of variational problems, Rept.
No. P-2374, the RAND Corp., Santa Monica, California (to be pub-
lished in J. Math. Anal. and. Appl.).
48. И. M. Гельфанд и M. Л. Це т л и н, Принцип нелокального
поиска в системах автоматической оптимизации, Доклады АН
СССР 137, № 2, стр. 295—298 (1961).
49. N. S. Bromberg, Maximization and minimization of compli-
cated multivariable functions, Communication and Electronics 58,
725—730 (1962).
50. S. Perlis, Theory of Matrices, Addison-Wesley, Reading, Mas-
sachusetts, 1952.
ГЛАВА VII
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
7.0. ВВЕДЕНИЕ
В последнее время благодаря переводу ряда совет-
ских работ [1—7]*) удалось ознакомиться с исследова-
ниями советского математика Понтрягина по теории
оптимальных систем. В настоящей главе будет дано из-
ложение принципа максимума сначала по способу,
близкому к способу Розоноэра, а затем будет проведено
сравнение с более традиционными подходами к решению
задач вариационного исчисления. Использование сопря-
женной системы в оптимальных задачах с ограничен-
ными управлениями было предложено Бассом в 1956 г.
[20]. Мы увидим, что дополнительные переменные в
изложении Понтрягина представляют собой решения
сопряженной системы и что принцип максимума может
быть получен путем использования свойств таких
систем.
Проводя сравнение с вариационными методами Блис-
са [21], мы находим, что дифференциальные уравнения
для вспомогательных переменных р совпадают с урав-
нениями Эйлера для переменных состояния. Далее мы
убеждаемся в эквивалентности уравнений Эйлера для
управляющих переменных и принципа максимума Пон-
трягина, примененных к //-функции. Применение ре-
зультатов Вейерштрасса и Чикала [22] сразу же дает
принцип максимума. Наконец, этот принцип рассмат-
ривается с точки зрения метода динамического програм-
мирования Веллмана.
*) После написания этой главы автору стали известны новые
переводы советских работ [8—19].
20*
308
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
(гл. VH
Принцип максимума Понтрягина представляет собой
весьма изящный метод исследования вариационных за-
дач со связями, ограничивающими управления. Что же
касается вычислительной стороны дела, то вопрос о ка-
ких-либо существенных преимуществах, даваемых этим
методом, остается дискуссионным.
7.1. ПРЕДВАРИТЕЛЬНЫЕ СООБРАЖЕНИЯ О ПРИНЦИПЕ
МАКСИМУМА ПОНТРЯГИНА
7.11. Формулировка проблемы. Оптимальную задачу
формулируем как вариационную задачу Майера [21]:
дана система дифференциальных уравнений
Л =//(•*!....Xj......Хп, UV ик, Ur, t),
xi (0) = х^, i = l, п;
требуется доставить максимум (минимум) функции
п
S = ^clXi(tf), (7.2)
выбирая надлежащим образом управляющие перемен-
ные Uk(t). Переменные xj называем переменными состоя-
ния. Связи, наложенные на управляющие переменные,
задаются соотношением
а(/)6С/, (7.3)
где U — допустимый класс управляющих функций в
r-мерном пространстве. Векторную управляющую функ-
цию с компонентами Uk(t) обозначим через #(/).
С целью введения нелинейных и интегральных вы-
ражений в функцию выигрыша S можно добавить к
уравнениям (7.1) соотношения, определяющие дополни-
тельные переменные состояния. Например, если тре-
буется максимизировать (минимизировать) значение
интеграла от квадрата одной из переменных состоя-
ния xs, то новая переменная состояния определяется со-
отношением
t
*я+1 = f x}dt, (7.4)
?,1) ПРЕДВАРИТЕЛЬНЫЕ СООБРАЖЕНИЯ 309
ИЛИ
<,=4 тг„,(0)=0. (7.5)
Функция выигрыша S при этом имеет вид
S = xn+l(tf). (7.6)
Ниже мы будем предполагать, что в уравнение (7.1)
включены все дополнительные переменные состояния,
определяющие функцию выигрыша.
7.12 Принцип максимума для заданного интервала
времени при отсутствии условий на правом конце. Мы
начнем с вывода принципа максимума Понтрягина для
случая, когда конечный момент времени фиксирован и
на конечные значения переменных состояния не накла-
дывается никаких ограничений. В последующих разде-
лах будет показано, каким образом видоизменяются ре-
зультаты (условие трансверсальности) при наложении
таких ограничений, а также в случае, когда конечный
момент не задается заранее.
Определим вспомогательные переменные р»(/) сле-
дующим образом:
• _ VI dfj
Р‘~ ftPldXi' (7.7)
Piktf) = — ct, l=\, .... n.
Оправдание такого определения рД/) будет дано в
последующих разделах этой главы.
_ Предположим, что найдено оптимальное управление
я(/), максимизирующее (минимизирующее) функцию
выигрыша S. Если оптимальному управлению и (/) дано
приращение Дя(/), то соответствующее приращение оп-
тимального вектора состояния x\t) будет обозначаться
через Длг(/).
Из уравнений (7.1) получаем
2 Pi ^Xt = 2 Pi 17/ (х + Дж, и + Ди, /) —ft (ж, и, /)|. (7.6)
1=1 1=1
310
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Если обе части уравнения (7.8) умножить на dt и
проинтегрировать от /0 до /у, то получим
9 п
f ^iPi^xldt =
«о /=1
tf п _ - _ _
= f ^Pi[fd* +u + ^u, t) — fdx, u, t)]dt. (7.9)
/о Z = 1
Другое выражение для левой части равенства (7.9)
можно написать, вычисляя производную от 2Pz^z:
п п п
±Ър^ = Ър^ + Ър^ (7.10)
Z=1 Z=1 Z=1
Умножая левую и правую части (7.10) на dt и инте-
грируя, как и ранее, от /0 до /у, получим
Ч п . п \*f tf п .
f ^Pi^x/df = '^pi^xtl —f ^Pi^Xidt. (7.11)
4 1 = 1 1=1 ** tt l-l
Сравнение (7.9) и (7.11) приводит к следующему со-
отношению:
п \‘f tf п
= f +
Z = 1 '° /о Z=1
Ч " _ _ _
+ / + и,-\-Ьи, t)—fdx, и. t)\dt. (7.12)
6 Z = 1
Рассмотрим левую часть этого равенства. Поскольку
начальное значение вектора состояния предполагалось
заданным, величины Дхг (/0) равны нулю. Конечные зна-
чения вспомогательных переменных Pi(tf) были приняты
равными —поэтому
л
2 pi ^xt =—as,
(М3)
7.1]
ПРЕДВАРИТЕЛЬНЫЕ СООБРАЖЕНИЯ
311
где AS представляет собой полное приращение функции
выигрыша S. Правая часть уравнения (7.12) вычисляет-
ся посредством разделения приращений функций fit вы-
званных изменением управлений, и приращений, обус-
ловленных изменениями переменных состояния. Прира-
щение fi последнего типа представляется рядом Тейлора
с остаточным членом; получаем
/Длг-НДх, и + Да, /)—/Дх, и, /) =
=f (х, й+ Д«, t) —f(x, «,/)+£ <Vi(x.«+A«.O +
7 = 1 7
п _ ____
+^d'Mx+LX+^‘}(7Л4>
7 = 1
5 = 1
где Молчаливо предполагается, что суще-
ствуют первая и вторая частные производные от fi по
переменным состояния.
Из уравнений (7.7) и (7.12) — (7.14) получаем выра-
жение для полной вариации функции выигрыша:
А п
Д5 = — / 2 Pi\fi & й + Ди, /) —fi (х, й, /)] dt —
t'o 1 = 1
Ч п
— f « + 0— flix, u,t)]}bx}dt —
t'9 Z=1 J
/=1
/<> Z=1 J
Рассмотрим сначала частный случай линейной си-
стемы, в которой управляющие переменные в функциях
fi фигурируют отдельно. В этом случае
п
/(= 2 МО •*/+?(«. О- (7.16)
/ = 1
312
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
гл. VII
Последние два слагаемых в правой части (7.15) при
этом равны нулю и AS становится равным
AS = — J [Я(х, я-НДя, t) — Н(х, и, /)]^, (7.17)
to
п
(7.18)
Достаточным условием максимума (минимума)
функции выигрыша S является требование AS < О
(AS>0). Из (7.17) видно, что достаточным условием
того, чтобы было AS < 0, является равенство
7/(х, и + Дя, /) — //(*, я, /)>0 (7.19)
для всех /, Чтобы получить необходимое ус-
ловие максимума (минимума) S, выберем специальный
вид приращения управляющего вектора. Рассмотрим
случай, когда приращение &uk получает лишь одна ком-
понента управляющего вектора и. Для этого прираще-
ния Ди* равно нулю повсюду, за исключением интервала
6, /г (^2>М- Этот интервал предполагается полностью
лежащим в промежутке (/о, //). Посмотрим, к каким по-
следствиям приведет обращение неравенства (7.19)
Н& й"+Ди, f) — H(x, и, /)<0 (7.20)
в каком-нибудь интервале между /0 и tf. Если интервал
(Z1, /2) выбран таким образом, что включает интервал,
где выполняется неравенство (7.20), то AS > 0. Подоб-
ное рассуждение может быть проведено для всех управ-
ляющих переменных. Необходимое условие максиму-
ма S имеет поэтому вид
Н(х, t) — H(x, и. (7.21)
для всех f, to < t < ti. Аналогичные рассуждения можно
провести для минимума S.
Для исследования нелинейных систем необходимо
вычислить дальнейшие члены в (7.15). Предположим,
что ft, dfi/dxj, d2fi/dxjdxs и uk— ограниченные функции.
При этом можно показать, что
I Дху | < Жт, (7.22)
7.1)
ПРЕДВАРИТЕЛЬНЫЕ СООБРАЖЕНИЯ
313
где М — положительная ограниченная постоянная, а
т—интервал времени /2 — Л- Управляющий вектор
д(/) снова подвергается варьированию специального
вида, как это было сделано в линейном случае. Выби-
рая т достаточно малым, можно показать, что неравен-
ство (7.21) остается необходимым условием максимума
(минимума) S. Таким образом, необходимое условие
максимума (минимума) функции .выигрыша S состоит
в том, чтобы Н все время было минимально (макси-
мально) по отношению к управляющему вектору. Инте-
ресной интерпретацией этого факта является то, что
управляющий вектор u(t) задается таким образом, что-
бы скалярное произведение вектора скорости в про-
странстве состояний л: (?) и вспомогательного вектора р
было минимально в случае максимума и максимально
в случае минимума S.
7.13. Принцип максимума в задаче со связями, на-
ложенными на значения переменных состояния на пра-
вом конце. Для учета связей, наложенных на значения
переменных состояния на правом конце, вводятся неиз-
вестные постоянные, играющие роль, подобную роли
множителей Лагранжа в обыкновенных проблемах ми-
нимума. Предположим, что условия связи могут быть
записаны в виде
Л [*(//)! = °’ а=1, ..., Z, (7.23)
где 1<п. Определим теперь максимизируемую (мини-
мизируемую) функцию так:
п I
s = 2 ciXl (tf) + 2 XeFa [х (/,)]. (7.24)
Здесь Xa—неизвестные постоянные множители. Если Fa
дважды дифференцируема по *<(//), то AS равно:
п In
AS = V с, ix, (I,) + V 2 I. ix, (t,) +
dxl (tf) дх} (tf) (7-25)
a=l /-1
/=1
314
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
где Граничные условия для вспомогательных
переменных имеют теперь вид
Pi(tf) = —
а= 1
dxi (tf)
(7.26)
Последний член в (7.25) равен нулю для специаль-
ного приращения управляющего вектора, описанного в
разделе 7.12. С присоединением связей добавилось еще
I неизвестных Аа, а = 1, ..., /; I дополнительных урав-
нений, необходимых для определения решения системы
уравнений (7.1), (7.7) и (7.26), даются условиями (7.23).
7.14. Принцип максимума в задаче с фиксирован-
ными условиями на правом конце. Частный случай
связей, наложенных на правом конце, соответствует
заданию конечных значений некоторых переменных со-
стояния. Пусть задано т конечных значений переменных
состояния, а на остальные (т < п) переменные состоя-
ния не наложено никаких ограничивающих условий.
Уравнения (7.23) принимают вид
[л: (/z)] = х. (/у) — x{ = 0, a, i = 1, ..., m. (7.27)
Пользуясь уравнениями (7.27), найдем, что гранич-
ные условия (7.26) для запишутся в форме
= —к + М. 1 = 1, (7.28)
И
Pi(tf) = — Ci> i = n. (7.29)
Поскольку т переменных состояния при tf фиксиро-
ваны, они не войдут в выражение для функции вы-
игрыша S, и, следовательно, величины Ci в (7.28) равны
нулю. Конечные значения вспомогательных переменных,
соответствующие переменным состояния со свободными
конечными значениями, равны, таким образом, —сг-, то-
гда как конечные значения вспомогательных перемен-
ных, относящихся к переменным состояния, значения ко-
торых на правом конце заданы, остаются свободными.
Точно так же исследуется случай, когда часть пере-
менных состояния задана на правом конце и вместе с
ПРЕДВАРИТЕЛЬНЫЕ СООБРАЖЕНИЯ
315
7.1]
тем заданы еще условия другого типа. В дополнение
к уравнениям (7.27) в этом случае задаются еще q усло-
вий связи (q < п — т — 1):
Л (*/)] = 0, а=1.......q. (7.30)
7.15. Принцип максимума в случае, когда конечный
момент времени не задан. В предыдущих рассуждениях
мы предполагали, что величина tf фиксирована. Для
анализа случая, когда конечный момент не задан^ пред-
положим, что оптимальный вектор состояния х (/) и
оптимальный управляющий вектор u\t) уже найдены.
Пусть, далее, конечный момент tf равен Т. Можно те-
перь считать ту_же самую задачу задачей с фиксирован-
ным и равным Т конечным моментом времени. Если ко-
нечный момент фигурирует в функции выигрыша, то
вводится дополнительная переменная состояния хп+1
таким образом, что
хп+1 = 1, хл+1(0) = 0. (7.31)
В выражении для функции выигрыша конечное значе-
ние переменной xn+i становится на место tf.
Увеличение числа степеней свободы системы на еди-
ницу требует введения дополнительного уравнения. Это
дополнительное уравнение имеет следующий вид:
л + 1
(7-32)
Для доказательства рассмотрим изменение функции
выигрыша, вызванное изменением конечного момента
времени tf.
л+1 л+1
' (ДЗЗ)
Уравнения (7.24) и (7.33) приводят нас к соотно-
шению
i
СЧ dF<
л + 1 -
2
/=i L
л+1
-(7.34)
316
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Поскольку AS должно быть меньше или равно нулю,
чтобы S достигала максимума, и поскольку Ы может
быть как положительным, так и отрицательным, AS дол-
жно равняться нулю; таким образом, приходим к урав-
нению (7.32).
7.2. СОПРЯЖЕННАЯ СИСТЕМА И ПРИНЦИП МАКСИМУМА
ПОНТРЯГИНА
7.21. Сопряженная система и стационарные решения.
Предыдущее рассмотрение принципа максимума Пон-
трягина почти не содержало доказательств. Мы попы-
таемся теперь оправдать вывод принципа максимума
путем изучения свойств сопряженных систем [24, 25].
Для случая, когда управления не ограничены, рас-
смотрим влияние возмущения buh первого порядка со-
ставляющих управляющего вектора в окрестности ста-
ционарного состояния. Линеаризация уравнений (7.1)
дает систему, связывающую приращения переменных
состояния:
п _ г _
8^ = 2Й78х/ + 2#8^’ 8хА°) = °- (7-35)
/=1 J А = 1
Здесь черточка над частными производными означает,
что они берутся вдоль стационарного пути.
Согласно определению сопряженная система урав-
нений получается после отбрасывания членов, содержа-
щих вариации управлений, транспонированием с изме-
нением знака:
А = <7-36’
/=1
Решения этих систем уравнений *) связываются по
формуле
п п г
<7-37)
1—1 1=1 Л=1
♦) Имеются в виду системы (7.35) и (7.36), (Прим, перев.)
721
СОПРЯЖЕННАЯ СИСТЕМА И ПРИНЦИП МАКСИМУМА
317
. Умножая обе стороны уравнения (7.37) на dt и инте-
грируя от t0 до tf, получаем
п
^Pl
Z=1
f it
<0 . to i=1 *=1
(7.38)
Вдоль стационарных траекторий первая вариация
функции выигрыша S равна нулю:
85 = 2 cibxl(t/) = 0. (7.39)
i=i
Если к уравнению (7.38) присоединить граничные
условия вида pi(tf) =—с,-, то уравнения (7.39) будут
удовлетворяться для произвольных вариаций управляю-
щего вектора лишь при условии, что
= <7'4о>
Уравнение (7.40) совпадает (в слабом смысле, для
стационарных решений, а не для максимума или мини-
мума) с тем, которое получается по принципу макси-
мума Понтрягина для случая неограниченных управляю-
щих переменных.
7.22. Вывод принципа максимума из сопряженной
системы. Способом, подобным описанному выше, мы
выведем теперь принцип максимума Понтрягина для
локального максимума и минимума в случае, когда уп-
равляющие переменные ограничены.
Рассмотрим полную вариацию в окрестности опти-
мальной траектории; производная по времени от суммы
равна
п п п
•^-^Pz a*z = ^M*z+Spza*z- (7-41)
1 = 1 1 = 1 z=i
Полную вариацию вычисляем из уравнений (7.1)
и подставляем в (7.41). Умножая (7.41) на dt и инте-
грируя каждое слагаемое в пределах от t0 до tt, по-
лучим (7.12). Дальнейшие рассуждения полностью
318
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
совпадают с приведенными в разделе 7.1. Как видно
теперь, переменные, названные в разделе 7.12 вспомо-
гательными, в действительности представляют собой со-
пряженные переменные. Доказательство условия макси-
мума выполнено теперь на основе исследования свойств
решений сопряженных систем.
7.3. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРИНЦИП
МАКСИМУМА ПОНТРЯГИНА
7.31. Вариационное исчисление и стационарные ре-
шения. Представляется интересным провести сравнение
методов вариационного исчисления и метода, основан-
ного на принципе максимума. Мы вновь обращаемся к
задаче определения стационарных решений системы
(7.1) при отсутствии ограничений на управления при
фиксированном временном интервале. Вариации перво-
го порядка берутся в окрестности данной стационарной
траектории, причем-
uk = uk + (/),
xz = xz + e^(0,
= xt +
(7.42)
Здесь т?“ (/) и (/)— произвольные функции времени, удо-
влетворяющие условию = 0. Функция выигрыша S
определяется снова уравнением (7.2), которое записы-
вается в форме
Ч п п
s= f (7.43)
У Z = 1 Z = 1
0
Применение множителей Лагранжа Х(/) для учета
связей, выражаемых уравнениями (7.1), приводит к сле-
дующему функционалу:
Ч
7 г- п п -1 п
s' = f 2?Л+£мЛ-л)
. /0 ь=> <=»
(7.44)
7.3] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРИНЦИП МАКСИМУМА 319
Стационарные значения S' определяются по обраще-
нию в нуль частной производной от S' по е:
(7.45)
Интегрируя первое слагаемое справа по частям, по-
лучаем
7 п г
+ <7-46)
'о /=1 *=1
Поскольку уравнение (7.46) должно удовлетворяться
при произвольных tf и соблюдаются следующие ра-
венства:
= = / = (7.47)
/=1
п _
=°. ‘=i....................<7-«)
£ = 1
Уравнения (7.47) совпадают с уравнениями (7.7), в
которых Pi заменены на Хг-, тогда как уравнения (7.48)
представляют собой те же самые (в слабом смысле)
уравнения, полученные путем применения принципа мак-
симума к неограниченным управляющим переменным.
7.32. Вывод принципа максимума методом вариаци-
онного исчисления. Приведем вывод принципа максиму-
ма, используя средства вариационного исчисления.
320
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Рассмотрим вариацию в окрестности оптимальной тра-
ектории, положив
и* = и* + диЛ,
Xi = Xi 4- Ax,.
(7-49)
Функция выигрыша S' вновь определяется по урав-
нению (7.44), в котором Xj заменено на рс
9 Г л п Т п
S' = f 2 cixi + 2 Pl & —fl) dt + S cixi (*<>)• (7-50)
t0 Lz=i i=i J i=i
Найдем полную вариацию функции выигрыша
7 п
*S = f 2 (C‘ + Pi) Ах, dt —
Ч i=i
Ч п
— f ^Pi\fi(x+« + д«, t)— fdx, a, t)\dt. (7.51)
4 Z=1
Представляя второе слагаемое правой части (7.51)
по-прежнему разложением Тейлора и интегрируя по ча-
стям, получаем
п
AS'= 2 (f/+A)Axz
О
п
Axz dt —
0
n
“+Ан- - df‘^’ 1ДХ, dt -
dxj dxj J J
о
7.3] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРИНЦИП МАКСИМУМА 321
1 f V д2Л(х + £Дх, и+Дц, о
2 J Pi dxj dxs
tn (=1
Axs Ax; dt —
' n
~ « + ДЙ, /)— ftix, «, t)\dt, (7.52)
‘o '='
где 0 1. Принимая во внимание, что для специаль-
ных вариаций и указанного выше типа справедливо не-
равенство |AXj|<jWAr, получаем следующее необходи-
мое условие максимума ДЗ^О для произвольных
вариаций Дхг-:
Pi = — Pi(Q = — С1 <7-53)
;=>
И
Ё Pl \fi (x, и н- Да, /) — ft (x, и, О] > 0 (7.54)
Z=1
при всех /, Уравнение (7.54) выражает прин-
цип максимума Понтрягина при переменных Ри опреде-
ляемых уравнением (7.53). В приведенном рассуждении
молчаливо предполагалось* что правило множителей
справедливо для полных вариаций.
7.33. Функция избытка Вейерштрасса и функция
переключений Чикала. Покажем, каким образом исполь-
зование условия Вейерштрасса приводит к принцип/
максимума Понтрягина*).
Будем рассматривать систему, описываемую урав-
нениями (7.1) в случае отсутствия ограничений на упра-
вления. Пусть, далее, функция выигрыша 3 будет диф-
♦) Как стало недавно известно автору, Болтянский и др. [6]
обсуждают этот вопрос для неограниченных управлений и приходят
к выводам, противоречащим излагаемым ниже. [См. также
Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе,
Е. Ф. Мищенко, Математическая теория оптимальных процессов,
Физматгиз, Москва, 1961 (Прим, перев.)]
21 Дж. Лейтман
322
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
ференцируемой функцией только конечных значений пе-
ременных состояния. Используя методы вариационного
исчисления, как это делают Блисс [21] и Брекуэлл [26],
получаем из равенства нулю первой вариации:
xz=— 2х//=1, п'
(естественные граничные условия для случая,
когда конечные значения не заданы),
п
У X, ^-=0, й = 1, ..., г.
1 duk 1
Граничные условия, доставляемые исчезновением
первой вариации, связывают конечные значения пере-
менных X с (незаданными) конечными значениями пе-
ременных состояния.
Для соседних с экстремалью траекторий
SX^aJ^SXjAx, f — 5 liXitt / = 0, (7.56)
1=1 / 1=1 / 1=1 /
fo о го
где Ахг суть вариации переменных состояния, обуслов-
ленные как явными вариациями так и вариациями
времени 8/. Дифферен-
цируя и используя ура-
внения (7.55), легко
показать, что сумма
2 \ 8xz постоянна.
Следуя Чикала [22],
Рис. 7.1. К построению функции из-
бытка Вейерштрасса.
введем функцию Вей-
ерштрасса следующим
образом. На рис. 7.1
показан отрезок ab
экстремальной траектории. Положим, что в точке а
управляющий вектор и изменяется по сравнению со
своим оптимальным значением , и таким образом, что
система «переводится» за время б/0 вдоль дуги ас. Да-
7.3J ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРИНЦИП МАКСИМУМА 323
лее предполагается, что интервал б/0 настолько мал, что
путь cb можно считать близким к экстремали ab. Пол-
ное время перехода вдоль пути acb обозначим через
tf — t0 + (>tf, а вдоль дуги ас — через б/0-
Применяя уравнение (7.56) к дуге cb, получаем
(7.57)
Здесь Xi вычисляются вдоль экстремальной дуги ab.
Изменение функции выигрыша на пути acb равно
п п
Д5= S Дх' = ~
/=1 Ъ <=1 ъ
(7.58)
Граничные члены в выражении для первой вариа-
ции приводят также к соотношению
2X^8/, =0. (7.59)
Из уравнений (7.58) и (7.59), а также из выражения
для Дх,|а
Д*/1в = */1Ло (7.60)
получаем путем подстановки в (7.57), что
AS=2Mxz—хг) 8/о = £Ч- (7.61)
/ = 1 а
Функция Е названа Вейерштрассом функцией избыт-
ка. Поскольку дуга ab — произвольная дуга экстремали,
необходимое условие максимума S состоит в том, чтобы
было Е<0 повсюду на оптимальной дуге. Как видно,
сравнение величин ±i и Xi в уравнение (7.61) произво-
дится только по отношению к управлениям. Имея это
в виду, заметим, что —Е совпадает с величиной ДЯ в
формулировке принципа максимума Понтрягина:
Е = — [Н (л, й+Да, /) — Я (л, «, 01- (7.62)
21*
324
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
(гл. VII
Для того чтобы учесть ограниченность управляющих
переменных
uik Л=1, •••» г, (7.63)
можно использовать прием, принадлежащий Вален-
тайну [27]. К уравнениям (7.1), описывающим систему,
присоединяются дополнительные уравнения
т* = («2* -«*)(«*- «и)’ А = 1, г. (7.64)
В соответствии с этими уравнениями получаем еще
г уравнений Эйлера:
^*7* = 0, Л=1, ..., г. (7.65)
Уравнения (7.55) 3, кроме того, принимают вид
п
(“2* + - 2я*) = 0, k = 1...............«, (7.66)
Z = 1
а знак равенства в (7.56) заменяется знаком неравен-
ства, и это позволяет в случае ограниченных управлений
прийти к тем же заключениям, что и в случае неограни-
ченных. Уравнения (7.64) — (7.66), разумеется, должны
удовлетворяться.
Чикала использовал метод Вейерштрасса в связи с
так называемой функцией переключении.
Рассмотрим пример:
Xj = a, х2=/(лр и, /),
т2 = («2 — «)(« — И1),
S = х2 (//) х2 (i0).
Уравнения Эйлера таковы:
Xj = Х2 , kj = 1, fX3 = О,
Xj = Х3 (itj -|- и2 2и).
(7.67)
(7.68)
Рассмотрим сначала случай, когда «1 < и < и2. Из
уравнений (7.68) следует
хз = °> \ = ~:- (7-69)
7 3) ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРИНЦИП МАКСИМУМА 325
Е-функция Вейерштрасса равна
Е = f—f—\ {и — «). (7.70)
Здесь J есть значение f на управлении й. В случае ми-
нимума S Е^-0. На рис. 7.2, а представлена геометриче-
ская интерпретация Е-функции. Чтобы удовлетворить
условию Вейерштрасса, кривая f должна лежать цели-
ком выше касательной с наклоном М. Эквивалентная
Рис. 7.2. Геометрическая интерпретация функции переключе-
ний Чикала для случая неограниченных управлений.
ситуация для //-функции Понтрягина представлена на
рис. 7.2, б. Принцип максимума утверждает, что ДЯ<0.
Когда управление принимает граничные значения Mj
или «2, 1 = 0 и
Xi = 4£ —М«2 —«1) при U = Uy,
df
\г = -^- + хз(«2 —«i) при а = «2.
На рис. 7.3, а иллюстрируется случай, когда и =
Чтобы Е > 0, должно быть
*.<£• (7-72)
326
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
откуда заключаем, что Х3 > 0. Следует опять провести
сравнение с рис. 7.3,6, где изображен график //-функ-
ции Понтрягина.
Рис. 7.3. Геометрическая интерпретация функции переключений
Чикала для случая ограниченных управлений.
Аналогичные рассуждения справедливы в случае, ко-
гда и = и2; получаем
>
df
ди
(7.73)
Чикала считает, что величина Xi играет роль указателя
шкалы, отмечающего различные возможные случаи:
1 < ди '
“ ди ’
Л1 > ди ’
и =
UX<U < ll2,
и — и2.
(7.74)
В книге Чикала [22] приводится множество примеров,
использующих понятие функции переключений.
7 4)
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И ПРИНЦИП
32?
7.4. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
И ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
7.41. Вывод принципа максимума по методу дина-
мического программирования. С помощью методов, раз-
работанных Веллманом [23], можно дать интересный вы-
вод принципа максимума.
Рис. 7.4. К выводу принципа максимума Понтрягина с помощью
динамического программирования.
Задача ставится, как в разделе 7.11 для фиксирован-
ного интервала времени и при отсутствии условий на
правом конце. Оптимальная функция выигрыша обо-
значается через 5; она неявно зависит от начального
вектора состояния х (/о) и tQ:
S = S[x (/0), /0] = max S (//)• (7.75)
Оптимальные значения управляющего вектора й(/)
и вектора состояния х (t) также представляют собой
функции отх(/о) и tQ. Оптимальные значения управляю-
щего вектора и вектора состояния спустя время Д/ обо-
значим через «' и х\ а управляющий вектор и вектор
состояния для любого другого пути обозначаем через
и' и х' (рис. 7.4).
328
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Поскольку S[a:(/0), /о! определяется краевым усло-
вием для оптимальной траектории,
5[х(/0), /0] = t'\. (7.76)
Для любого другого пути, приводящего в точку
л/, оставшуюся часть траектории от f до tf оставим
оптимальной. Функцию выигрыша, соответствующую
этому пути, обозначим через £[л/, /'].
Из уравнения (7.76), таким образом, получаем
5 [х (/0), /0| = max S |аг', /'], /0 < t < (7.77)
u£U
Разложим функцию выигрыша S[x', /'] в ряд Тей-
лора, пренебрегая членами второго и более высокого по-
рядка:
п
Six', t'\ = S [ж«0). /0] + <Д'о + 2£>,- (7.78)
Молчаливо предполагается, что частные производные
существуют и вычислены прилг(/0), tQ.
Подставляя (7.78) в (7.77), получаем
5 к(4>). 4>] = max S [х (/0), /0] + Ы +
u£U
Л _
Zj ~дх{ х‘
1=1
+ (7-79)
где
Дл,=х, (/0)ДЛ
(7.80)
Рассмотрение правой части (7.79) показывает, что
единственным членом, зависящим от и. является хД/0).
Поэтому в пределе, когда Д/ стремится к нулю,
получаем
— л _
~дЦ~~ дх~1 (Z<>)- (7ф81)
7.4]
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И ПРИНЦИП
329
Поскольку to может соответствовать любому момен-
ту времени t, t0^t^.tf, можно отбросить индексы в
(7.81); получим
п _
# = (7-82)
при граничном условии
5|x, tf\^^clXi{tf). (7.83)
Вдоль оптимальной траектории функция выигрыша
сохраняет постоянное значение:
^S(x, /) = 0. (7.84)
Вычислив производную, получим уравнение
_ п _
<?S OS /п пг\
= <7-85)
Z=1
Уравнение (7.85) можно также получить непосред-
ственно из (7.82), осуществляя указанную там опера-
цию max. Вспомогательные переменные Pi определяются
формулами
= Pi^ = ~^ (7-86)
Из (7.85) и (7.86) получаем
Pi--tiPj^< PiW = ~ci- (7-87)
/=i
Принцип максимума получается из уравнения (7.82):
п
шах У — = min Н(х, и, t). (7.88)
и^и z=i и^и
Из уравнений (7.1), (7.82) и (7.83) методами дина-
мического программирования можно определить опти-
мальную траекторию. В общем случае это требует
330
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
последовательного процесса численного решения. Для по-
лучения оптимальной траектории по принципу макси-
мума Понтрягина требуется решить уравнение (7.1),
(7.87) и (7.88). Эти нелинейные дифференциальные
уравнения при краевых условиях, наложенных в двух
точках, могут быть решены путем использования чис-
ленного процесса итераций. Преимущественно схема
динамического программирования состоит в том, что
она допускает систематический процесс численного ре-
шения. Для систем с достаточно большим числом степе-
ней свободы объем вычислений становится несовмести-
мым с возможностями современной счетно-решающей
техники. Преимущество принципа Понтрягина, как и
других вариационных методов, состоит в том, что мно-
гие характеристики оптимальной траектории можно по-
лучить с его помощью без того, чтобы решать задачу во
всем объеме.
7.5. ПРИМЕРЫ
7.51. Системы с линейно и отдельно входящими
управлениями. Покажем теперь применение принципа
максимума к ряду задач. Первый пример, который мы
рассмотрим, будет относиться к случаю, когда управле-
ния отделены от переменных состояния и входят в си-
стему линейно.
Уравнения (7.1) для этого случая имеют вид
г
xt=fi(x, 0+ S aikuk' xt(0) = jfir Z = l, (7.89)
k -1
Связи, наложенные на управляющие переменные, вы-
ражаются неравенствами
\чк\<.тк. (7.90)
Здесь nik — положительная постоянная. Я-функция для
такой системы равна
п г
0+S £ Pfiikuk. (7.91)
Z=1 А= 1
7.5]
ПРИМЕРЫ
331
Применяя принцип максимума, получим необходимое
условие минимума функции выигрыша S:
k = \,...,r. (7.92)
Уравнения (7.92) показывают, что всегда, за исклю-
чением случая, когда 2Ма = 0, управляющие пере-
менные принимают граничные значения. В отмеченном
исключительном случае функция выигрыша не зависит
от соответствующей управляющей переменной ик. Сле-
дует, разумеется, иметь в виду, что в дополнение к урав-
нениям (7.92) должны удовлетворяться дифференциаль-
ные уравнения для и Pi вместе с заданными гранич-
ными условиями.
7.52. Линейная управляемая система второго поряд-
ка с комплексными корнями; устойчивый случай. В этом
примере мы продемонстрируем применение принципа
максимума к специальной задаче управления. Пусть
требуется определить такую зависимость управляющей
переменной и от переменных состояния xt и х2, чтобы си-
стема достигла положения равновесия за минимальное
время *).
Дифференциальные уравнения, описывающие си-
стему, имеют вид
х1 = х2, х1 (0) = xj, х1 (t j)= 0»
х2 = ^х2 Ьхх д, х2 (0) = х^, х2 (t = 0, (у
х3=1, х3(0) = 0,
а > 0, а2 — 4й < 0;
ограничения, наложенные на управления, таковы:
|и| (7.94)
Функция выигрыша S равна
S = x3(Zz). (7.95)
♦) Автором допущена неточность: речь идет и достижении на-
чала координат, которое в оптимальном режиме не является поло-
жением равновесия. (Прим, перев.)
332
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Функцию Н получаем из уравнения (7.18); она имеет
вид
Н=pix2 + р2 (— ах2 — Ьхх + и) + р3. (7.96)
(7.97)
Здесь pi удовлетворяют уравнениям
Pi = Ьр2,
р2 = ар2
Рз = 0, Рз(^) = —Ь
Применяя принцип максимума к (7.96), получаем
и = М sgn р2. (7.98)
Вспомогательная переменная р2 определяется ура-
внениями (7.97):
р2 = Ае* sin (и/ + ср),
а = а/2, а) = у ]/ 462 — а .
(7.99)
Здесь А и ф — величины, определяемые из граничных
условий. Из (7.99) можно заключить, что процесс пере-
ключений периодический, если отвлечься от первого и
последнего переключений.
Вывод о периодическом характере последовательно-
сти переключений позволяет построить график функции
переключений, как это показано на рис. 7.5. Если си-
стема должна попасть в положение равновесия*), то
необходимо, чтобы конечная часть ее траектории содер-
жала отрезок дуги Оа' или Оа, поскольку это единствен-
ные траектории, проходящие через положение равнове-
сия О. Дуги Оа' и Оа находятся из уравнений (7.93).
Пусть последней дугой будет у'О. При этом предполо-
жении из (7.98) и (7.99) заключаем, что преды-
дущее переключение должно было произойти на
полпериода ранее, т. е. где-то на линии у'рт.
Из (7.93) вытекает также, что длина отрезка прямой ур
должна в еал/(й раз превышать длину линии у'р. Таким
) См. сноску на стр. 331. (Прим, перев.)
7.51
ПРИМЕРЫ
333
образом, определена точка у на графике функции пере-
ключений. Если точку у' передвигать по дуге Оа', то
точка у опишет часть дуги ab графика функции пере-
ключений. Процесс можно повторить и определить та-
ким образом весь график. Типичная оптимальная траек-
тория имеет вид кривой stvO. Управляющая перемен-
ная и равна —М на дуге st, +Л4 на дуге tv и — М на
дуге vO.
Рис. 7.5. Граница переключений для линейной системы вто-
рого порядка с комплексными устойчивыми корнями.
7.53. Задача о полете ракеты. Пример, который бу-
дет сейчас разобран, был детально рассмотрен Лейт-
маном, который использовал вариационный подход
Блисса и Валентайна [27]*). Нашей целью при анализе
этого вопроса будет дальнейшее сравнение принципа
максимума Понтрягина с вариационным методом.
Задача состоит в определении направления и (огра-
ниченной) величины тяги ракеты, совершающей полет в
постоянном гравитационном поле при условии миниму-
ма (максимума) некоторой функции конечных значений
переменных состояния. Динамикой ракеты как тела пре-
небрегаем.
•) См. также гл. V.
334
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
Дифференциальные уравнения, описывающие систе-
му, таковы:
Ср ’ *1 =P = -^COS<[>, О С СЧ ОСО ч ч ч д 1 II ООО —< ем со ч ч ч (7.100)
Х2 = <7 х3=х ср . . = -%sin ф—g. = А
xt = y ^(°)=Х4’
х5 = т = -₽. *5(°)=Л5'
Хб= 1, х6(0) = 0.
Приняты те же обозначения, что и у Лейтмана, при-
чем р, q, х, у, т являются переменными состояния, а
р, ф— две управляющие переменные. Чтобы иметь воз-
можность включить время в функцию выигрыша, допол-
нительно введена переменная х6. Расходы массы огра-
ничен неравенствами
(7.101)
Согласно (7.18)
Н=рх sin<]) — g) +
Н-РзР-Ь/М—Ар + Рб- (7.102)
Дифференциальные уравнения для
переменных имеют вид
вспомогательных
Р1 = — Рз> Рч — —Рь Рз = в’ Р<=0,
ср . । ср . । • А (7.103)
P5 = A^-cos<H-^2^sin<|>, p6 = Q. ’
Отметим, что первые пять уравнений (7.103) совпа-
дают с первыми пятью уравнениями (7.7) работы
Лейтмана [28]. (Уравнения Эйлера — Лагранжа, соответ-
ствующие переменным состояния, совпадают с уравне-
ниями для вспомогательных переменных принципа мак-
симума Понтрягина.)
7.5]
ПРИМЕРЫ
335
Пусть функция выигрыша S будет линейной функ-
цией конечных значений переменных состояния. Если
это не так, го для учета интегральных и нелинейных со-
отношений можно ввести дополнительные переменные.
Применение принципа максимума с целью миними-
зации S дает для управляющей переменной р условия
р = при £>0,
P = Pj при £<0,
(7.104)
где
k =^(/’icos^ + /’2sin'?)—А- (7.105)
и для направления тяги
Ру cos ф+р2 sin ф > 0.
(7.106)
Эти же самые соотношения были получены Лейтма-
ном при применении условий Вейерштрасса и Клебша.
Рассмотрение выражения для
А = —-^-(p3cos<|>+p4sin<|>) (7.107)
показывает, что функция k имеет не более двух нулей.
Это приводит нас к заключению, что оптимальная тра-
ектория состоит не более чем из трех частичных дуг.
Если в течение некоторого периода времени k = 0, то
функция выигрыша S не зависит от р в течение этого
периода; говорят, что функция выигрыша в это время
нечувствительна к р, и решение не является единствен-
ным. В работе Лейтмана рассмотрено несколько приме-
ров такого рода.
Автор признателен Джорджу Кларку и м-с Агнес
Зивенс (Исследовательский центр Грумман) за их по-
мощь в проверке доказательств и при подготовке этой
главы к печати.
336
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
[гл. VII
ЛИТЕРАТУРА
1. А. А. Фельдбаум, О синтезе оптимальных систем с помощью
фазового пространства, Автоматика и телемеханика 16, № 2,
стр. 129—149 (1955).
2. Л. С. Понтрягин, Некоторые математические задачи, возни-
кающие в связи с теорией оптимальных систем автоматического
регулирования, Известия АН СССР, стр. 107—117 (1957).
3. Р. В. Гамкрелидзе, К общей теории оптимальных процес-
сов, Доклады АН СССР 123, № 2, стр. 223—226 (1958).
4. Л. С. Понтрягин, Оптимальные процессы регулирования, Ус-
пехи матем. наук 14, вып. 1, стр. 3—20 (1959).
5. Л. И. Розоноэр, Принцип максимума Л. С. Понтрягина в
теории оптимальных систем I, II, III, Автоматика и телеме-
ника 20, №№ 10—12, стр. 1320—1334, 1441 — 1458, 1561—1578
(1959).
6. В. Г. Болтянский, Р. В. Гамкрелидзе и Л. С. Понт-
рягин, Теория оптимальных процессов. I. Принцип максимума,
Известия АН СССР, серия матем., 24, № 1, стр. 3—42 (1960).
7. Л. С. Понтрягин, Optimal Processes of Regulation, Proc. Int.
Math. Conf. Edinburgh, 1958, pp. 182—202 (1960).
8. В. Г. Болтянский, P. В. Гамкрелидзе, Л. С. Понтря-
гин. К теории оптимальных процессов, Доклады АН СССР ПО,
№ 1, стр. 7—10 (1956).
9. Н. Н. Красовский, Об одной задаче оптимального регули
рования, Прикпаяная математика и механика XXI, вып. 5
стр. 670—677 (1957).
10. Р. В. Гамкрелидзе, К теории оптимальных процессов в ли
нейных системах, Доклады АН СССР 116, № 1, стр. 9—11 (1957)
11. В. Г. Болтянский, Принцип максимума в теории оптималь
ных процессов, Доклады АН СССР 119, № 6, стр. 1070—1073
(1958).
12. Р. В. Гамкрелидзе, Теория оптимальных по быстродействию
процессов в линейных системах, Известия АН СССР, серия ма-
тем., 22, № 4, стр. 449—474 (1958).
13. А. Д. Александров, Исследование о принципе максимума,
Известия высш, учебн. завед., Математика, №№ 5, 6 (1958).
14. Л. И. Розоноэр, О достаточных условиях оптимальности.
Доклады АН СССР 127, № 3, стр. 520—523 (1959).
15. Н. Н. Красовский, К теории оптимального регулирования,
Прикл. матем. и мех. XXIII, вып. 4, стр. 625—639 (1959).
16. Е. А. Р о з е н м а н, Оптимальное управление объектом с двумя
управляющими воздействиями, Автоматика и телемеханика лХ,
вып. 10, стр. 1345—1349 (1959).
17. Р. В. Гамкрелидзе, Оптимальные процессы управления при
ограниченных фазовых координатах, Известия АН СССР, серия
матем., 24, № 3, стр. 315—356 (1960).
18. Ф. М. Кириллова, К проблеме существования оптимальных
траекторий нелинейных систем, Известия высш, учебн. завед.,
Математика, № 2, стр. 41—53 (1961).
ЛИТЕРАТУРА
337
19. Е. Ф. Мищенко и Л. С. Понтрягин, Об одной статистиче-
ской задаче оптимального управления, Известия АН СССР, се-
рия матем. 25 (1961).
20. R. W. Bass, Equivalent Linearization, Nonlinear Circuit Synthe-
sis and the Stabilization and Optimization of Control Systems,
Proc. Symposium on Nonlinear Circuit Analysis 6, 163—198
(1957).
21. G. A. Bliss, Lectures on the Calculus of Variations, Univ. Chi-
cago Press, Chicago, Illinois, 1946. [Русский перевод:
Г. А. Блисс, Лекции по вариационному исчислению, М.—Л.,
1950.]
22. Р. Cicala, An Engineering Approach to the Calculus of Varia-
tions. Levrotto and Bella, Torino, 1957.
23. R. Bellman, Dynamic Programming, Princeton Univ. Press,
Princeton, New Jersey, 1957. [Русский перевод: P. Беллман,
Динамическое программирование, М., I960.]
24. G. A. Bliss, Mathematics for Exterior Ballistics. Wiley, New
York, 1944.
25. H. S. T s i e n, Engineering Cybernetics, McGraw-Hill, New York,
1954. [Русский перевод: Цян Сюэ-сэнь, Техническая кибер-
нетика, М.—Л., 1956.]
26. J. V. Brea k we 11, The optimization of trajectories, J. Soc. Ind.
Appl. Math. 7, 215—246 (1959).
27. F. A. Valentine, The problem of Lagrange with differential
inequalities as added side conditions, Dissertation, Department of
Mathematics, University of Chicago, Chicago, Illinois, 1937.
28. G. Leitmann, On a class of variational problems in rocket
flight, J. Aero/Space Sci. 26, 586—591 (1959).
ГЛАВА VIII
ОБ ОПРЕДЕЛЕНИИ ОПТИМАЛЬНЫХ ТРАЕКТОРИИ
МЕТОДОМ ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
8.1. ВВЕДЕНИЕ
Формулировка различных задач, связанных с изу-
чением оптимальных траекторий в рамках вариацион-
ного исчисления, не представляет трудностей. Исходные
задачи с помощью стандартных вариационных приемов
сводятся к двухточечным краевым задачам для нели-
нейных дифференциальных уравнений. Наличие связей,
наложенных на возможные движения, во многих слу-
чаях проявляется в комбинировании равенств с нера-
венствами.
Даже в более простых случаях, когда связи отсут-
ствуют, двухточечный характер задач представляет
трудности, зачастую в сильной степени усложняющие
получение численного решения даже при использовании
самых больших и быстродействующих современных вы-
числительных машин.
В этой главе мы рассмотрим применение теории ди-
намического программирования к численному решению
вариационных задач. Нашей целью будет описание си-
стематического подхода к этим задачам, который позво-
лит стандартизовать процесс решения с помощью
счетно-решающих устройств.
8.2. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Основным пунктом является установление того фак-
та, что вариационное исчисление является частным при-
мером многоэтапного процесса решения непрерывного
типа. Читатель, интересующийся основами теории дина-
мического программирования, как иначе именуется тео-
8.3)
ОДНОМЕРНЫЕ ЗАДАЧИ
339
рия многоэтапных процессов решения, может обратиться
к книгам Веллмана [1, 2] и Веллмана и Дрейфуса [3].
В дальнейшем мы будем продполагать, что читатель
знаком с основными идеями этой теории.
8.3. ОДНОМЕРНЫЕ ЗАДАЧИ
Начнем наше рассмотрение с задачи минимизации
функционала
г
J(u) = f g(u. и') dt (8.1)
о
на всех функциях u\t), определенных на интервале [О, Г]
и удовлетворяющих начальному условию и(0)=с.
Обозначая
f(c. Г) = min J (и), (8.2)
и
по принципу оптимальности (см. Веллман [1, 2]) полу-
чим нелинейное уравнение в частных производных
/r = min[g(c, + f(c, 0) = 0. (8.3)
V
Из этого уравнения легко получить известные ура-
внения Эйлера (см. Дрейфус [4] и Веллман [5]). Для
вычислительных целей часто бывает удобнее использо-
вать дискретное приближение
f(c> 7' + Д) = min |g(tf, *и) Д-)-/(£Г)], (8.4)
V
Г = 0, Д, 2Д, ...
(см. Веллман [2] и Веллман и Дрейфус [3]).
Решение, полученное таким путем, требует табули-
рования двух последовательностей функций одной
переменной, именно функций {f(c, Т)} и «управляю-
щих функций» v = v(c,T). Эта проблема имеет стандарт-
ный характер, если иметь в виду использование совре-
менных вычислительных машин. Преимущества этого
подхода по сравнению с обычным вариационным спосо-
бом рассмотрены в книге Веллмана [2].
22*
340 МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ (гл. V1H
8.4. СВЯЗИ - I
Если мы добавим связь вида
(8.5)
то уравнение (8.3) заменится уравнением
fr = min [g(c, -tO + 'i'/J- (8-6)
I v I < m
Соответствующая форма (8.4) такова:
f(c, 7'-|-Д) = min [g (c, v) Д -±f (e + г>Д, Г)|. (8.7)
I V
Минимизация осуществляется посредством поиска
на некотором конечном множестве значений и, лежащих
в интервале [—т, т]. Во многих случаях можно исполь-
зовать специальные приемы для серьезного сокращения
числа пробных значений (см. Веллман и Дрейфус [3]).
Заметим, что наличие связей упрощает решение по ме-
тоду динамического программирования, поскольку это
приводит к уменьшению числа допустимых вариантов
поведения, т. е. числа возможных выборов v.
8.5. СВЯЗИ - II
Пусть задача заключается, как сказано в разделе
8.3, в минимизации /(и), но при дополнительном усло-
вии вида
г
f h(u, u')dt (8.8)
о
Вместо того, чтобы добавить еще одну переменную
состояния, введем множитель Лагранжа и рассмотрим
проблему минимизации функционала
г
f [g(u, и!) — Mi (и, u')]dt (8.9)
о
при наличии уже двух условий:
а) и(0) = с;
б)
(8.10)
8.6]
ОБСУЖДЕНИЕ
341
Обозначив
/(с, 7) = min
и
Г т
J* [g(«, и') — Mt (и, u')\dt
.о
(8-11)
получим для каждого фиксированного X дискретное
рекуррентное соотношение
f(c, 7'Н-Д)= min [(g(c, v) — Mi (с, T)|,
I V |< m
(8.12)
из которого легко можно получить численное решение.
Значение X — «цена» — изменяется после этого до тех
пор, пока не будет удовлетворено исходное уравнение
связи.
8.6. ОБСУЖДЕНИЕ
Мы можем заключить, что общая одномерная ва-
риационная задача о минимизации функционала
т
J(u) = J g(«, u')dt
о
при условиях
т
a) J h (и, и') dt < k,
о
б) и(0) = с,
в) |и'(01<'я
(8.13)
(8.14)
представляет собой стандартную задачу, которую можно
быстро и точно решить методами динамического про-
граммирования с использованием вычислительных уст-
ройств. Некоторые примеры можно найти в книге Велл-
мана и Дрейфуса [3].
Небольшие видоизменения методики позволяют рас-
пространить ее на случай, когда имеется граничное ус-
ловие, наложенное в момент t = Г,
г \и (Г), н'(Г)] = 0, (8.15)
342
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ (гл. VIII
на случай, когда подынтегральная функция явно зави-
сит от /, а также на более общий случай, когда тре-
буется минимизировать функционал
т
J(u) = J g(«, v)dt (8.16)
о
по отношению ко всем функциям и, связанным с и диф-
ференциальным уравнением
-^ = Л(и, г»), а(0) = с. (8.17)
8.7. ДВУМЕРНЫЕ ЗАДАЧИ
Рассмотрим теперь проблему минимизации функцио-
нала
г
«2) = fgfa, «2, u'v tydt, (8.18)
о
в котором и\ и и2 удовлетворяют начальным условиям
Д1(0) = ^, ^(0) = с2. (8.19)
Полагая
/(^, с2, Т) = min J(uv и2), (8.20)
и2
получаем, как и прежде, уравнение в частных производ-
ных
df • Г / \ । । df ]
С2’
/(Ср с2, 0) = 0.
(8.21)
Для вычислительных целей можно воспользоваться
рекуррентным соотношением
/(Ср с2, Г-4- Д) = min [g(Ср с2, ^Д-Ь
с2+г>2Д, Г)], (8.22)
Г = 0, Д, 2Д, ...,
8.7]
ДВУМЕРНЫЕ ЗАДАЧИ
343
с начальным условием f(ci, с2, 0)=0 либо стандартными
способами численного решения дифференциальных урав-
нений в частных производных.
Численное решение по описанному выше способу
связано с табулированием и запоминанием последова-
тельностей функций двух переменных. Это вносит неко-
торые усложнения. Для иллюстрации рассмотрим слу-
чай, когда постоянные С\ и с2 каждая могут принимать
сто различных значений. Поскольку число различных
систем значений и с2 составляет при этом 104, табу-
лирование значений f(cj, с2, Т) для данного Т требует
памяти емкостью 104. Более того, так как рекуррентное
соотношение требует, чтобы значения f в точке Т были
сохранены в памяти, тогда как значения в точке Т + А
вычисляются, и поскольку поведения V\ = с2, Т)
и v2 = v2(ci, c2, 71) также должны быть сохранены в па-
мяти, становится очевидным, что необходима память по
меньшей мере емкостью 4*104.
Отметим, что, употребляя термин «память», мы все-
гда имеем в виду оперативную память. Разумеется, не
ставится никаких ограничений на использование имею-
щейся внешней памяти.
Имеется много способов сокращения числа ячеек.
Эти способы рассматриваются в книге Веллмана и Дрей-
фуса [3]. С помощью современных вычислительных уст-
ройств с памятью в 32 000 слов мы можем, вообще го-
воря, тем или иным способом решать двумерные вариа-
ционные задачи.
Положение очень сильно ухудшается, однако, с пе->
реходом к задачам более высокого числа измерений.
Трехмерная задача о траекториях, содержащая три
переменные, характеризующие положение, и три пере-
менные скорости, приводит при использовании дина-
мического программирования к функциям от шести
фазовых переменных, или «переменных состояния». Да-
же если каждая из переменных может принимать только
10 различных значений, это составляет 109 значений,
что представляется абсурдно большим числом.
Мы намерены использовать другую идею, заключаю-
щуюся в приближении полиномами. Это позволит нам
344
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ [гл. VIII
табулировать функции нескольких переменных быстрым
й эффективным путем и даст возможность использовать
метод динамического программирования для решения
многомерных вариационных задач.
8.8. ОДНОМЕРНЫЙ СЛУЧАЙ
Чтобы представить эту идею в простой форме, нач-
нем с обсуждавшейся выше одномерной задачи. Мы
желаем получить численное решение рекуррентного со-
отношения
/(с, Т + Д) = min [g(с, т’)Д+/(с + ‘пД, Г?],
V
Т = 0, Д, 2Д, ..
(8.23)
при
f(c,O)=O.
Для упрощения обозначений будем писать
f(c, kb)=fk(c). (8.24)
Условимся рассматривать только значения с, лежа-
щие в заданном интервале, который при надлежащей
нормировке можно считать интервалом (—1, 1]. Для га-
рантии того, что с заключено в этом интервале, доба-
вим связь, наложенную на и, а именно:
— 1 + <1.
(8.25)
Выбирая интервал достаточно большим, можно до-
биться того, что влияние его границ будет пренебрежимо
малым постольку, поскольку мы имеем дело с его внут-
ренними точками. Во многих случаях связь указанного
выше типа составляет часть исходной задачи.
Аппроксимируем теперь каждый член последователь-
ности \fk (с)} полиномом от переменной состояния с.
Вместо обычной полиномиальной записи напишем ап-
проксимирующее выражение через ортонормированные
полиномы Лежандра
N
Л(<0 = ^акпрп(су, (8.26)
л = 0
8.8]
ОДНОМЕРНЫЙ СЛУЧАЙ
345
коэффициенты этой суммы зависят от k. Преимущество
использования полиномов Лежандра вместо обычных
степеней с основано на том факте, что мы можем ис-
пользовать формулу
1
акп = f fk(c)P„(c)dc (8.27)
-1
для определения коэффициентов вместо того, чтобы об-
ращаться к процессу дифференцирования.
Смысл представления (8.26) состоит в том, что функ-
ция fk(c) представлена теперь для всех точек интервала
[ — 1, 1] системой N + 1 коэффициентов Коль скоро
эти N + 1 значений заложены в память, мы можем вы-
числить значение /*(с) для любого с в указанном интер-
вале. Значение это, разумеется, приближенное, но мож-
но ожидать получения прекрасного согласования с точ-
ным, выбрав 2V примерно равным 10.
Каким образом в действительности вычисляется
последовательность коэффициентов {a&n}? Если исполь-
зовать риманово приближение
1 м
ifk^P„{c)dc^ (8.28)
-1 г--/И
то можно либо протабулировать столько значенийfk(с),
сколько и ранее, либо существенно потерять в точности.
Вместо вычисления интеграла по формуле (8.28) мы ис-
пользуем квадратурные формулы. Если должным обра-
зом выбрать точки tj и веса Wjf то можно написать
-1 м
J g(c)dc^ (8.29)
-i y-i
Эта приближенная формула является точной, если g(c)
есть полином степени 2М—1 или ниже.
Легко показать, что представляют собой корни
полинома Лежандра степени М, a Wj—постоянные, оп-
ределяемые полиномами Лежандра, — числа Кристоф-
феля. Эти параметры хорошо известны вплоть до весь-
ма больших значений М.
346
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ [гл. VIII
Таким образом, значения /\(с) для всех точек ин-
тервала [—1, 1] определяются значениями fk(tj), /=1,
2,..., М, поскольку эти значения задают коэффициен-
ты акп в (8.27), а эти коэффициенты определяют fh(c)
посредством уравнения (8.26).
Посмотрим теперь, в какой мере все это упрощает
определение последовательности {Л (с)}. Начиная с из-
вестной функции fi (с), получаемой из соотношения
/1 (с) = min g (с, и), (8.30)
V
подставляем fi(c) в последовательность [ап, a2i,...,aNi]
согласно соотношению
аА1 = - f f. (с) Рп (а) de = 2 (tj) Рк (tj). (8.31)
-1 >1
Поскольку Wj и Pk(tj)—заданные постоянные, вы-
численные раз навсегда, можно зафиксировать их про-
изведение bkj и написать
k = (8.32)
Обращаясь к определению fz(c) из соотношения
/2(c) = min[g(c, (8.33)
мы прежде всего замечаем, что требуется лишь вычис-
лить М значений /2(6’)» / = L 2,..., М. Значение
+ получается для каждого рассматриваемого
значения v с помощью формулы
м
fl (tj+®д) = 2 aklp k (tj+ЯД)-
(8.34)
Вычисление этого выражения немногим труднее, чем
вычисление полиномиального, так как полином Ле-
жандра Рп(х) удовлетворяет простому трехчленному
рекуррентному соотношению, которое делает его вычис-
ление очень простым, если начать с первых значений
Р0(х) = 1, Р1(х) = х.
8.91
ОБСУЖДЕНИЕ
347
Вычислив М значений {/2(^7)}» /=1, 2, ...» 2И,
определяем коэффициенты {аЛ2Ь £=1, 2, ... N:
м
ak2 = (8.35)
Значения {/2(^7)} теперь исключаются из памяти, а
последовательность {ак2}, k — \, 2, ..., W, запоминает-
ся. Все значения f2(c), требуемые для определения f3(c)
из уравнения
/3(c) = min[g(c, -у) Л+/2 (^ + ^Д)Ь (8.36)
V
получаются теперь с помощью соотношения
N
f2(c)= ^ak2Pk(c). (8.37)
/=1
Вычисляем М значений {/3(^)} и продолжаем процесс
таким же образом.
8.9. ОБСУЖДЕНИЕ
Покажем, что требования, накладываемые на па-
мять, в этом процессе вычислений весьма малы. На
/?-м шаге запоминается только последовательность
{аЛн}, а также постоянные bkj вместе с командами
машине произвести известные действия. Для Л4,
общее число запоминаемых величин пренебре-
жимо мало.
Выбор М и N является вопросом удобства и опыта.
Обычно в вариационных задачах оказывается, что
независимо от характера управляющей функции
v = v(c, Т) выходная функция f(c, Т) вполне гладкая.
Этого следует ожидать по физическим причинам (устой-
чивость относительно малых возмущений), а также из
соображений математического характера. Следователь-
но, мы можем ожидать, что приближение полиномом,
скажем, степени W = 10 даст весьма точные результаты.
Некоторые предварительные примеры и сравнение
с точным решением приводятся У Веллмана и Дрей-
фуса [3, 6); '
348
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ [гл. VIII
Определение функции поведения можно произвести
двумя способами. Можно либо сразу вычислить все по-
линомиальные приближения, запомнить коэффициенты
и затем вычислить значения управляющих функций
vh = vk(c, Т)
по рекуррентным соотношениям (8.23), либо вычислять
управляющие функции по мере выдачи результатов.
8.10. ДВУМЕРНЫЙ СЛУЧАЙ
Рассмотрим теперь двумерную задачу, обсуждав-
шуюся в разделе 8.6. Функцию двух переменных f(c\, С2)
мы аппроксимируем полиномом относительно с\
который Наиболее удобно взять в форме
/(^1» ^2)— 2L aki^k (G) Pi (^2)*
k, 1— 1
Коэффициенты определяются соотношением
1
«м = J7(<Y c2)PMPt(c2)dc2dc2 =
— 1
Af M
= У t2r)Pb(ilj)Pl(t2J)‘Wj'Wr,
j=i r=i
где веса Wj и интерполяционные точки ttJ выбраны так
же, как и раньше.
Мы видим, что функция f(cit с2) задается для целей
запоминания с помощью № коэффициентов {а«), А, 1 =
= 1, 2, .... W, которые в свою очередь определяются зна-
чениями t2r).
Рекуррентное соотношение (8.16) может быть запи-
сано в виде
/«+1(^1- г)=
= min |g (G> v» v2) Д +/д (q 4- иД с2 + ф2Д)]. (8.40)
И С2,
(8.38)
(8.39)
B.ll]
ОБСУЖДЕНИЕ
349
Как и ранее, мы начинаем с функции /п(сь с2), за-
данной коэффициентами {я^}, и с помощью последних
вычисляем значения fn, требуемые для определения
{Л + 1 (//» /2г)}- Отсюда берем значения {я(Л*+1)} и т. д.
Функция двух переменных в области —Сг<1
сохраняется в памяти через посредство N2 коэффициен-
тов {а*/). Если N = 10 — приближение, которое должно
дать весьма точный результат, то требуется запомнить
только 100 значений.
8.11. ОБСУЖДЕНИЕ
Рассуждая таким же точно образом, мы убеждаемся
в том, что общую задачу о траекториях на плоскости
можно трактовать в терминах полиномиального при-
ближения функций четырех переменных, что требует
N4 коэффициентов. Если М=10, то это не только свя-
зано с большой емкостью памяти, но и с огромным вре-
менем, необходимым для вычисления отдельных значе-
ний функций. Если число W уменьшить до 5, то N4
сократится до 625, что представляет собой более разум-
ное количество.
Подобно этому, обращаясь к трехмерным задачам о
траекториях, содержащим функции шести переменных,
мы видим, что выбор N = 4 дает число 46 = 1024.
Можно ожидать, что увеличение числа переменных
состояния связано с переходом к полиномам более низ-
кой степени.
Выше мы привели очерк общей идеи полиномиаль-
ного приближения. Комбинируя эту идею с различными
другими приемами, например с последовательными при-
ближениями в форме приближения в пространстве упра-
влений или каким-либо иным образом, можно уже в
настоящее время осуществить стандартизацию решений
трехмерных задач о траекториях, содержащих шесть
переменных состояния. С помощью тех вычислительных
машин, которые появятся через 10 лет, с емкостью па-
мяти в 10—30 раз большей и скоростями в 10—30 раз
превышающими современные, мы сможем получить стан-
дартные решения задач, содержащих такие переменные
состояния, как количество топлива, массу и т. д.
350
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ [гл. VIII
ЛИТЕРАТУРА
Г. R. Bellman, Dynamic Programming, Princeton Univ. Press,
Princeton, New Jersey, 1957. [Русский перевод: P. Веллман,
Динамическое программирование, М., I960.]
2. R. Bellman, Adaptive Control Processes: A Guided Tour, Prin-
ceton Univ. Press, Princeton, New Jersey, 1961.
3. R. Bellman and S. E. Dreyfus, Applied Dynamic Program-
ming, Princeton Univ. Press, Princeton, New Jersey, 1962.
4. S. Dreyfus, Dynamic programming and the calculus of varia-
tions, J. Math. Anal, and Appl. 1, 228—239 (1960).
5. R. Bellman, Dynamic programming of continuous processes,
Rept. R-271, The RAND Corporation, Santa Monica, California
(1954).
6. R. Bellman and S. Dreyfus, Functional approximations and
dynamic programming, Math. Tables and Other Aids to Computa-
tion 13, 247—251 (1959).
ГЛАВА IX
ЧИСЛЕННОЕ РАССМОТРЕНИЕ НЕКОТОРЫХ
ДЕТЕРМИНИРОВАННЫХ И АДАПТИВНЫХ
ПРОЦЕССОВ УПРАВЛЕНИЯ
9.1. ВВЕДЕНИЕ
Общая всем отраслям техники основная задача за-
ключается в том, чтобы, располагая определенными ре-
сурсами, построить систему, в наибольшей степени об-
ладающую заданными свойствами. Если система срав-
нительно простая и недорогая, то необходимая оптими-
зация может быть достигнута за счет имеющегося опыта
и производимых экспериментов, так что потребность в
специальной теории невелика. Для таких же сложных
и дорогих устройств, какими являются современные уп-
равляемые снаряды, опыт работы с которыми ограничен,
а экспериментирование дорого и даже опасно, предста-
вляется счастливой возможность достичь требуемой оп-
тимизации теоретическим путем и при относительно не-
больших затратах. Такая возможность приносит пользу
при предварительном проектировании, когда исследуется
вопрос о самой осуществимости предлагаемой систе-
мы. Эта точка зрения разделялась рядом выдающихся
инженеров, в том числе Ч. Штейнмецом и Р. Год-
дардом.
Современная математика, вообще говоря, не в состо-
янии решать задачи, связанные с проблемами, которые
возникают при разнообразных попытках синтеза или
анализа сложных электрических, механических и тепло-
вых систем, где необходимо считаться со множеством
экономических факторов. Эти проблемы имеют значи-
тельно более тонкий характер по сравнению с обычными
задачами, рассматриваемыми классической математиче-
ской физикой, где, как правило, оказывается всего лишь
352 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
несколько переменных. Для исследования этих новых
проблем были разработаны новые отрасли математики.
Эти отрасли включают в себя линейное и динамическое
программирование. Общей чертой их является то, что
с начала, когда анализируется физическая ситуация, и
до конца всего исследования важнейшую вспомогатель-
ную роль играют современные высокоскоростные вычис-
лительные устройства. Во многих случаях использование
таких устройств делает возможным рассмотрение мате-
матических моделей, которые достаточно реалистичны,
чтобы представлять интерес с точки зрения технических
исследований, и в то же время могут быть подвергнуты
математическому решению при разумных затратах уси-
лий на вычисления.
Часто оказывается, что классические математические
методы не являются самыми лучшими для получе-
ния нужных данных при вычислениях с большой ско-
ростью. Во многих случаях может оказаться весьма
эффективным объединение новых методов с тради-
ционными.
В разделе 9.2 рассматривается вопрос об определе-
нии программы оптимального управления в задаче, ти-
пичной для многих проблем, встречающихся в технике
и экономике, если причину и следствие, цель и т. д. мо-
жно считать известными. Следуя общей схеме, основан-
ной на принципе оптимальности Веллмана, мы укажем
некоторые обобщения методики и детально рассмотрим
ряд примеров. В разделе 9.210 мы применяем к одной
специальной задаче метод квазилинеаризации, предста-
вляющийся многообещающим в вопросе о численном ре-
шении нелинейных двухточечных краевых задач, к кото-
рым часто приводит классическое вариационное рассмо-
трение.
Раздел 9.3 посвящен формулировке и решению проб-
лемы адаптивного управления. Мы придерживаемся той
точки зрения, что управляющий орган способен в про-
цессе управления «узнавать» о некоторых, первона-
чально неизвестных факторах. Пытаясь наилучшим
образом достичь цели, управляющий орган, таким
образом, одновременно и «узнаёт» и осуществляет
управление.
9.2]
детерминированные процессы управления
353
9.2. НЕКОТОРЫЕ ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ
УПРАВЛЕНИЯ
9.21. Формулировка проблемы. Рассмотрим сначала
задачу определения функции v(t) на промежутке
минимизирующей фуйкЦионал J [у] вида
т
J[v] = f v)dt (9.1)
О
при условии
^ = G(x, v) (9.2)
И
л(0) = с. (9.3)
Как мы увидим, выбор наиболее эффективных спо-
собов решения этой задачи во многом зависит от точного
характера требуемой информации об оптимизирующей
функции V.
К указанному типу задач принадлежат многие про-
блемы оптимизации, встречающиеся в экономике и тех-
нике. Параметр с представляет собой начальное состоя-
ние системы, a x(t) представляет состояние в момент t.
Решение, принимаемое в момент /, есть v(t). Степень
возрастания стоимости процесса в момент t равна
F[x(0, »(/)]
и зависит, таким образом, от текущего состояния
процесса и принимаемого в этот момент решения.
Функция G(x, у) характеризует степень изменения со-
стояния системы в случае, если она находится в со-
стоянии х и принято управление v, определяя, таким
образом, динамику рассматриваемого процесса. Требу-
ется определить оптимальное принимаемое решение в
зависимости от времени, т. е. мы разыскиваем оптималь-
ное управление v(t), Как правило, на v на-
кладываются различные связи, однако здесь эти связи
не рассматриваются.
Обратимся теперь к обсуждению различных методов
решения поставленной задачи.
23 Дж. Лейтман
3f>4 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
9.22. Решение по методу динамического программи-
рования. Заметим, что минимальное значение функцио-
нала J[v] есть функция только от с и Т:
minJpo] —f(c, Т). (9.4)
V
Теперь можно вывести дифференциальное уравнение
в частных производных, которому удовлетворяет функ-
ция f(c, Т). Это делается путем сравнения величины ми-
нимальной стоимости процессов продолжительностью
Т + Д и Т с использованием принципа оптимальности
Веллмана [1]. Этот принцип можно сформулировать сле-
дующим образом: оптимальный процесс обладает тем
свойством, что, каковы бы ни были начальные управле-
ния, последующие управления должны быть оптималь-
ными по отношению к состоянию, происходящему от пер-
воначальных управлений. Отметим, что уравнение (9.4)
может быть записано в следующей форме:
f (с, Г) = стоимости управляемого процесса,
для которого начальным состоянием
системы является с, продолжитель-
ность которого равна Г, а оптималь-
ный выбор управляющей функции
производится на интервале (О, Т).
Нашим, основным уравнением является следующее:
/(с, Г-|- A) = min {F(c, ^)Д-Ь
W +/(<? +Л+ <>(*)}• (9.6)
Первый член справа равен стоимости первых Д вре-
менных единиц процесса при условии, что v выбрана
равной w в течение этого промежутка времени. Второй
член представляет собой минимальную стоимость про-
цесса с начальным состоянием с + 6(с, до)Д и с продол-
жительностью Т, Последний член о(Д) обладает тем
свойством, что (о(Д)/Д) 0 при Д->0. Минимизацией по
w мы достигаем наилучшего первоначального выбора v.
Пользуясь разложением Тейлора, найдем
/(с, Г)+/гД-]-о(Д) = тт {F(c, w)A+/(r, Г) +
W+G(f, ^^+0(4)}. (9.7)
0.2] ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ 355
Вычитая, наконец, f(c, Т) из обеих частей этого урав-
нения, разделив на Д и устремляя Д к нулю, получим
уравнение
/r = min{F(f, w) + G(r, w)/J, (9.8)
w
в котором индексы обозначают частные производные.
К этому следует добавить, что процессу нулевой продол-
жительности соответствует, согласно (9.1), нулевая стои-
мость, так что
/(г, 0) = 0. (9.9)
Теперь нашей целью становится исследование реше-
ния уравнения (9.8) при условии (9.9). Однако прежде
чем обратиться к этому, мы дадим другой вывод уравне-
ния (9.8), подчеркивающий его интуитивное содержание.
Рассмотрим оптимальный выбор управляющей функ-
ции v = v(t), и пусть x = x(t) будет соответствующей
функцией, определяемой дифференциальным уравнением
(9.2). Скорость убывания стоимости оставшейся части
процесса в любой момент времени t равна F[x(t), о(/)],
то есть
-А/[х(0> т-/] = 5[х(/), т>(/)]. (9.10)
С другой стороны, никакой другой выбор v не дает
большей скорости убывания, так что
T-t]^F\x(t), тф)], (9.11)
-А[х(0, [х(/)( ®(0] <F[x(/), ?>(/)]. (9.12)
Теперь воспользуемся уравнением
-~ = О(х, v) (9.13)
для получения соотношения
fr<P+fcO (9.14)
и, наконец, требуемого уравнения
/r = min{F+/eG}, (9.15)
совпадающего с уравнением (9.8).
23*
356 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
9.23. Обзор численного решения. Рассмотрим теперь
элементарным образом численное решение выведенного
выше квазилинейного уравнения первого порядка в част-
ных производных
/r = min{/?(c, -до) fc} (9.16)
при начальном условии
/(G 0) = 0. (9.17)
Прежде всего отметим, что f(c, Т) равна нулю в точ-
ках с = ±й8, Т = 0, где k = 1, 2, 3, ..., К. Кроме того,
в этих точках и fc равна нулю. Далее мы вычисляем зна-
чения заданной функции F(c, до) в точках с = kb и
до=±тД, /п=1, 2, М. Теперь мы можем определить
наименьшее из этих значений функции (и отметить так-
же минимизирующее значение до) и приравнять это зна-
чение fT. Это проделывается для k = 0, ±1,..., ± К.
В результате оказывается известным приближенное зна-
чение частной производной fT для Т = 0 и с = kb,
k =?= 0, ± 1, ±2, ..., ±К. Далее эти данные используются
для приближенного определения функции f(c, Т) при
Т = h с помощью формулы
/(с, й)=/(с, 0) + й/г(с, 0)- (9.18)
Таким способом получается приближенное решение в
точках (±68, й). Более того, можно получить прибли-
женные значения для производных в этих точках, напри-
мер, используя соотношение
л(и. (9.|9)
Далее, повторяя эту операцию, можно получить ре-
шение при Т = 2h &ля некоторой системы значений <?.
Вычисления производятся до тех пор, пока функция f
и искомые оптимальные управления не станут известны
во всех узловых точках координатной сетки в интере-
сующей нас области плоскости с — Т. Следует ожидать,
что в частных задачах появятся свойственные им специ-
фические трудности, относящиеся к определению пара-
метров сетки 8, Д и й, и потребуется использование точ-
ных конечноразностных формул. Более того, в ряде слу-
9.2]
ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
357
чаев возможно и аналитическое решение, что облегчает
процесс вычислений в целом. Может, например, ока-
заться, что процесс минимизации осуществляется в яв-
ной форме, и тогда теория характеристик [12] уравне-
ний первого порядка в частных производных станет от-
правным пунктом численного решения. Дополнительные
рассмотрения этого вопроса см. в книгах Коллатца [3]
и Камке [4]. Отметим, наконец, что уравнение (9.6) мо-
жет представить основу для эффективной схемы числен-
ного решения.
9.24. Множители Лагранжа и уравнения Эйлера. Воз-
вратимся к задаче, описанной в разделе 9.21, и покажем,
каким образом можно использовать уравнение (9.8) для
вывода обычных уравнений Эйлера для таких задач.
Предположим, что оптимальная функция w находится
путем решения уравнения
^w + GwA = 0, (9.20)
получаемого приравниванием нулю частной производной
по w выражения в скобках в (9.8). Для выбранной та-
ким образом функции w получаем
/Г = Д+О/С. (9.21)
Для функции fc можно получить уравнение, если
взять полную производную от fc по времени /, в течение
которого протекает оптимальный процесс:
4 (Л) + fcT =fcfi ~fcT-
Дифференцируя обе стороны (9.21) частным обра-
зом по с, находим
/тс = ^с + + (<Л + fc + Gfcc- (9-23)
Используя (9.20), получаем
fTc^c + Gcfc + Gfcc- (9-24)
Уравнение (9.22), таким образом, приобретает вид
= (9-25)
358 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
Положим теперь
к = 4 (9.26)
и заметим, что
(с, 0) = 0, (9.27)
или
Х|/=г = 0. (9.28)
Таким образом, мы получаем систему двух уравне-
ний относительно х и Л:
^ = О(х, w), х(0)=г, ]
dl (9‘29>
-g- = -Fx-(?A Х(Г) = О
дополненных алгебраическим соотношением
fw+gwi=o, (9.30)
выражающим w как функцию х и X.
Задача, рассмотренная в разделе 9.210, соответствует
случаю, когда
О(х, w) = w (9.31)
и
F (х, w) = у чл)2 + е*у (9.32)
так что уравнения (9.29) и (9.30) приобретают вид
У О II И О' Р О Ч X || & t II II. Э (9.33)
Эти уравнения эквивалентны уравнению (9.83). Другие
примеры можно найти в работе Дрейфуса [5].
9.25. Обобщение на векторные системы. Принципиаль-
ные рассмотрения раздела 9.22 легко обобщаются на
случай, когда состояние системы описывается вектором
х = (xi, х2,..., Хм), а переменная, подлежащая выбору,
также векторная: v = (уь v2,... ,vR). Функция F(x, v)
представляет собой скалярную функцию своего вектор-
fi.2]
дётермйнйровАнныё процёссы управления
339
ного аргумента, a G(x, у) есть М-мерный вектор
(gi, &,> gin)- Опять мы полагаем
f(c, Т) = min (9.34)
V
где
г
= F(x, v)dtt (9.35)
о
И
~ = G (х, V), х (0) = С. (9.36)
Аналог уравнения (9.8) имеет вид
м "1
fT = min F(c> w) + 2 tf/А » (9.37)
w L *=1
а граничное условие таково:
/(г, 0) = 0. (9.38)
Когда М возрастает от 1 до 2 и превышает 2, анали-
тические и вычислительные трудности быстро возра-
стают. Сама проблема числа измерений была предметом
подробного изучения [6, 7].
9.26. Пример: линейная система и квадратичный
функционал стоимости. Рассмотрим теперь пример, ко-
торый настолько прост, что задача может быть решена
аналитически.
Требуется определить функцию £(/)> минимизирую-
щую интеграл
т
J[g] = f t«2 + g2}^. (9.39)
о
причем
^ = ii = g, 0</<Г, (9.40)
и
«(0) —с. (9.41)
Вводя функцию стоимости f(c, Т), найдем, что эта
функция удовлетворяет уравнению
/г = min jc2-|-w2w (9.42)
360 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
с дополнительным условием
/(с, 0) = 0. (9.43)
Эти равенства представляют собой частные случаи
уравнений (9.37) и (9.38).
Поскольку f и fc суть функции с и Т и не содержат w
явно, мы можем произвести оптимизацию квадратичной
функции от ш, заключенной в скобках в (9.42), путем
приравнивания нулю производной; это приводит к опти-
мальному закону управления
Wmln = —у/с. (9.44)
С точки зрения управления с помощью обратной
связи это наиболее важная информация, так как она
указывает, какой выбор w является оптимальным для
системы с любым начальным состоянием с и с любой
продолжительностью Т, если известна функция fc(c, Т).
Далее мы используем то обстоятельство, что минимизи-
рующий выбор ш, определяемый уравнением (9.44), пре-
образует (9.42) в квазилинейное уравнение
или
(9.45)
(9.46)
Далее мы можем применить метод разделения пере-
менных и написать
f(c, T) = <f(T)c\ (9.47)
где согласно (9.43)
/(с, 0) = 0 = <р(0). (9.48)
Специальный вид (9.47) решения будет оправдан в
дальнейшем. Согласно уравнениям (9.46) и (9.47) ср (Г)
удовлетворяет уравнению Риккати и начальному ус-
ловию
= Т2, f(0)=x0. (9.49)
9.2]
ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
361
Аналитическое решение содержит гиперболический
тангенс:
ср (Г) = th Т. (9.50)
Таким образом, функция стоимости f(ct Т) оказы-
вается равной
/(г, Т) = сЧпТ. (9.51)
Закон оптимального управления находим теперь из
(9.44); этот закон имеет вид
Wmin = — с th Т (9.52)
и показывает, что оптимальное управление есть линей-
ная функция состояния, причем множитель пропорцио-
нальности является функцией продолжительности про-
цесса. Для оптимального управления требуется, таким
образом, линейный фильтр с переменными во времени
параметрами.
Отметим, что если процесс непродолжителен, то мож-
но приближенно представить оптимальное управление,
полагая
w = 0. (9.53)
Это приводит к величине стоимости, равной
т
f (с2 + 02)М = с2Г. (9.54)
о
Если процесс длительный, то уравнение (9.52) пока-
зывает, что можно принять
w = — с. (9.55)
Для такого управления уравнение движения имеет
вид
и = — и, (9.56)
и
и($) = с\ (9.57)
решением является функция
#(/) = ^ (9.58)
362 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
Стоимость в этом случае равна
т
f [c2e~2t + с2е~21} dt = с2 (1 — <?-2Г). (9.59)
О
Для больших значений Т эта стоимость не слишком
сильно отличается от минимальной стоимости, давае-
мой уравнением (9.51), но стоимости реального техни-
ческого оборудования обеих схем управления, в одном
случае изменяющегося во времени, а в другом — не из-
меняющегося, могут оказаться совершенно различными.
Одним из преимуществ, даваемых решением проблем оп-
тимизации, является то, что можно лучше оценить до-
стоинства близких к оптимальным, но особенно простых
законов управления.
9.27. Классическое рассмотрение. Управляемый про-
цесс, описанный в предыдущем разделе, можно также
проанализировать, следуя классическим приемам вариа-
ционного исчисления.
Перед нами стоит задача определения функции «(/),
0<7<Т, минимизирующей интеграл
т
J\u] = f \u2 + u.2\dt (9.60)
о
при граничном условии
«(0) = с. (9.61)
Уравнение Эйлера этой задачи линейно:
й = и. (9.62)
[Линейность этого уравнения и квадратичный характер
функционала J [«] обусловили формулу (9.47).] В до-
бавление к условию (9.61) имеем еще естественное гра-
ничное условие при t — Т:
й(Т) = 0.
(9.63)
Поскольку
(9.64)
9.2]
ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
363
уравнение (9.63) требует просто, чтобы при t = Т выпол-
нялось равенство g = 0. Это следует также из (9.52),
так как в указанном случае
wmIn = — с th 0 = 0. (9.65)
Мы пришли теперь к двухточечной краевой задаче,
которая требует решения. В общем случае такое реше-
ние недоступно аналитически и численное его получе-
ние представляет большие трудности.
Линейность уравнения Эйлера (9.6?) позволяет на-
писать решение
и^ = сСЬ-гГтТ}-’ 0-66)
так что функция g [см. (9.40)] дается выражением
g^)=c8h(Ch7r)- <9-67)
Это уравнение представляет зависимость оптималь-
ного управления от начального состояния с, продолжи-
тельности процесса Т и времени t, прошедшего с момен-
та его начала. Именно эта информация требуется для
целей управления с помощью разомкнутой управляющей
системы.
Можно следующим образом получить уравнение
(9.66), комбинируя различные методы.
Уравнение (9.52) показывает, что
и (/) = — и (/) th (Г — /). (9.68)
Поскольку t явно не содержится в подынтегральном
выражении (9.60), нам известен первый интеграл урав-
нения Эйлера, а именно:
й2 (/) — и2 (/) = const = и2 (0) — и2 (0) = с2 (th2 Т — 1). (9.69)
Исключение u(t) из (9.68) и (9.69) приводит тогда
к желаемому результату:
aW = -C-hch-r~°- (9.70)
9.28. Принцип максимума Понтрягина [8]. Обсужде-
ние этой задачи еще с одной точки зрения, при помощи
принципа максимума Понтрягина, дано Розоноэром [9].
364 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
9.29. Управление конечными значениями переменных
состояния. Изменим немного функцию стоимости, свя-
занную с управляемым процессом, прибавив к исходно-
му интегралу слагаемое и2(Т), отражающее стоимость
отклонений конечных значений от нуля. Если теперь
определить функцию f(c, Т) равенством
Ж Г) = minJ[g], (9.71)
g
где
т
= / {«2+£2} ^ + «2(Л (9.72)
о
и
u = g, ($.73)
и(О) = с, (9.74)
то можно провести весь анализ точно так же, как в раз-
деле 9.26. Функция f удовлетворяет тому же дифферен-
циальному уравнению в частных производных
/г--=^2-гЛ2’ <9-75)
но граничное условие на этот раз имеет вид
Дс, 0) = с2. (9.76)
Решение для функции f(ct Т) таково:
Дс, Т) = с2. (9.77)
9.210. Частный случай, когда уравнение Эйлера не-
линейно. Возвратимся к сделанному выше замечанию
относительно трудности решения двухточечной краевой
задачи для нелинейных дифференциальных уравнений
Эйлера. Покажем, что в некоторых удачных случаях
введенный К.алаба [10] и Веллманом [И] метод квази-
линеаризации приводит к эффективным вычислительным
приемам. Рассмотрим интеграл J [g]:
т
= (9.78)
О
ДЕТЕРМИНИРОВАННЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
365
0.2)
и динамические уравнения
^- = g, 0<1<Т, (9.79)
u(0) = c. (9.80)
Требуется определить функцию g таким образом, что-
бы минимизировать функционал J [g], Подставляя выра-
жение (9.79) для g в (9.78), найдем, что мы должны ми-
нимизировать функционал
т
= f (9.81)
о
при условии
я(0) = с. (9.82)
Уравнение Эйлера для этой задачи нелинейно:
й = еи, (9.83)
а естественное граничное условие при t = Т имеет вид
и (Г) = 0. (9.84)
Уравнения (9.83), (9.84) и (9.80) можно решить в
замкнутой форме, что, однако, нас здесь не интересует,
так как мы желаем обсудить вопрос об их численном ре-
шении с помощью современной быстродействующей
счетно-решающей техники. Сходная задача рассматри-
вается в работе Калаба [10], где отмечены также многие
ее обобщения (см. также [11]).
Для определенности примем, что
с = 0, Г=1. (9.85)
Наш подход заключается в методе последовательных
приближений, обладающем тем свойством, что каждая
последующая итерация примерно удваивает число Пра-
вильных значений в приближенном результате. Имея
n-е приближение un(t), выбираем в качестве следующего
приближения un+i(l) решение линейной краевой задачи:
= еап + еи» («я+1 - иа), (9.86)
«я+1(0)=ия+1(Г) = 0. (9.87)
366 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
За нулевое приближение uQ(t) можем принять
ио(О = О. (9.88)
Функция un+i(t) получается путем решения сначала
линейной задачи с начальными данными
^>± = ^уя+1, (9.89)
Уя+1(0) = 0, У„+1(О) = 1 (9.90)
(решение однородного уравнения) и последующего оп-
ределения решения задачи с начальными данными
^+- - е“„ + еи" (zn+1 - zn), (9.91)
*„+i(0) = z„+1(0) = 0. (9.92)
Функция «я+1(/) представляется затем в форме
«я+1(0 = гя+1(0 + *У„+1(0- (9-93)
Условие Mn+i(0) автоматически удовлетворяется, и
постоянная k определяется условием
0 = ^л + 1 (1) + *у'я+1(1)- (9.94)
Результаты численного эксперимента
Таблица 9.1
t «о (О «1(0 «2(0 «8 (0
0,0 0,0 0,0 0,0 0,0
0,09375 0,0 —0,067104 —0,069276 —0,069279
0,203125 0,0 —0,135064 —0,139758 —0,139765
0,3046875 0,0 —0,188878 —0,195866 —0,195876
0,40625 0,0 —0,234318 —0,243486 —0,243500
0,5000 0,0 —0,269237 —0,280253 —0,280270
0,6015625 0,0 —0,299821 —0,312591 —0,312611
0,703125 0,0 —0,323177 —0,337380 —0,337402
0,8046875 0,0 —0,339546 —0,354803 —0,354827
0,90625 0,0 —0,349096 —0,364988 —0,365013
1,0 0,0 —0,351946 —0,368031 —0,367056
0.3]
АДАПТИВНЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
367
Изложенным приемом решение нелинейной двухто-
чечной краевой задачи сводится к определению быстро
сходящейся последовательности решений линейных за-
дач с начальными данными. Задачи с начальными
данными без труда решаются на вычислительной ма-
шине; для краевой задачи такое решение получить
нелегко.
Таблица 9.1 содержит результаты численного экспе-
римента, произведенного на машине IBM 7090. Исполь-
зуя описанный выше метод, д-р Б. Коткин составил про-
грамму решения уравнений (9.86) — (9.88). Интегриро-
вание велось по методу Рунге — Кутта с использованием
арифметического устройства повышенной точности при
размере ячейки 2~7 = 0,0078125. Вычисление потребо-
вало лишь нескольких секунд.
9.3. АДАПТИВНЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ
9.31. Основные положения. В предыдущих разделах
мы ограничивались рассмотрением некоторых детерми-
нированных процессов управления, для которых состоя-
ние системы в любой момент времени принимается из-
вестным, результат действия всякого управления извес-
тен, цель процесса известна и т. д. Основное внимание
было направлено на определение эффективных вычисли-
тельных приемов.
Теперь мы обращаемся к классу управляемых про-
цессов совсем другой природы. В частности, мы желаем
рассмотреть задачи, в которых управляющий орган ис-
пытывает недостаток в первоначальных сведениях о не-
которых характеристиках процесса, но может по мере
его протекания «узнавать» об этих неизвестных факто-
рах. Можно надеяться, что таким образом управляющий
орган улучшает качество управления. Такого рода про-
цессы управления мы называем адаптивными. Дальней-
шее рассмотрение этих процессов можно найти в ра-
ботах Веллмана [12] и Веллмана и Калаба [13—16]. Одна
из самых больших трудностей в этой области состоит в
попытках сформулировать основные идеи и уравнения,
облекающие физический процесс 3 математическую
368 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
9.32. Формулировка проблемы [17]. Рассмотрим слу-
чай, когда управляющий орган должен оценивать зна-
чение неизвестной вероятности р. Мы будем считать, что
р представляет собой неизвестную вероятность того, что
некоторая случайная переменная примет значение, рав-
ное единице, и 1—р — вероятность того, что эта вели-
чина примет нулевое значение. Управляющий орган дол-
жен производить последовательность экспериментов, фи-
ксировать результаты управления и на основе этого
опыта, а также пользуясь известной априорной инфор-
мацией, оценивать значение р. Каждый такой экспери-
мент, а также неправильное определение р связаны с
определенной стоимостью. Мы желаем определить усло-
вия прекращения экспериментов и оценку, которую дол-
жен сделать для этого управляющий орган. Очевидно,
эта проблема является прототипом важной задачи тео-
рии экспериментирования.
Последовательная оценка и связанный с нею после-
довательный процесс определения такого типа встре-
чаются в производстве радиолокаторов, когда испыты-
ваются различные образцы. Принцип оптимальности до-
ставляет, как мы увидим, средство для математической
формулировки и численного решения задачи.
Теперь мы должны сформулировать задачу более де-*
тально. Будем предполагать, что перед тем, как начи-
нается процесс определения, управляющий орган обла-
дает априорной информацией о том, что из s испытаний
п дали единичный результат. Что касается наблюдений
над результатами самого процесса, то мы примем, что
из г испытаний т приводят к единичному результату.
Разумеется, мы не принимаем во внимание сведений о
том, в каком порядке происходят события, но детали
информации, которой располагает управляющий орган,
сильно упрощают задачу. Поскольку р неизвестна, мы
рассматриваем ее как случайную величину с функцией
распределения, меняющейся в ходе самого процесса.
Лишь на основе априорной информации мы принимаем
Эту функцию равной (формула Байеса)
rfl 1 fl — л^ 1
(И5)
9.3] АДАПТИВНЫЕ ПРОЦЕССЫ УПРАВЛЕНИЯ 369
где В — бета-функция. Далее, если после г дополни-
тельных испытаний было отмечено т единиц, то мы по-
лагаем функцию распределения равной
dG„m(r) = Рт^-РУ~т^(Р>
f pm(l-p)r~mdG(p) (9-96)
о
Пусть сг,т обозначает ожидаемую стоимость невер-
ной оценки после того, как г дополнительных испыта-
ний привели к единичному результату; положим
1
cr.m = <*f (Рг, т —Р)2 dGr, т (р), (9.97)
О
где рг, т — оценка, минимизирующая сг,т- Значение
рг,т дается формулой
1
Pr, m = f Р dGrt т (р) ----- , (9.98)
6
отвечающей, разумеется, интуитивному представлению.
Вычисление показывает тогда, что
С —а т + п Гm + n+1 _ т + п-1 , q
cr,m —а r_|_s [ r + s+i r4-S Г
Мы будем считать также, что если проделано т экс-
периментов, то стоимость следующего равна &(т),
имея в виду то, что стоимость эксперимента может
меняться в ходе процесса; это обстоятельство связано
с рядом интересных возможностей. Далее, мы примем,
что при отсутствии дополнительной информации веро-
ятности, полученные путем оценок, должны рассматри-
ваться как истинные вероятности. Наконец, мы потре-
буем, чтобы производилось не более R экспериментов,
так что процесс по достижении этого момента должен
оборваться.
Теперь мы обратимся к определению оптимадьногр
управления.
24 Дж. Лейтмаи
370 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
9.33. Рассмотрение задачи по методу динамического
программирования. Введем функцию стоимости fr(m) С
помощью определения
fr(ni)= ожидаемой стоимости процесса, начи-
нающегося с т единичных из г наблю-
даемых экспериментов и ведущегося при (9.100)
оптимальной последовательности упра-
влений.
Тогда по принципу оптимальности получаем функ-
циональное уравнение
fr (/n) = min
С- k (r)+pr, mfr+x (т+1)+(1 -A, m)/r+1 Н)
q. т + п Г т -|- п-\- 1
г-[-$ L r + s+ 1 /* + $ J ’
(9.101)
справедливое при т = 0, 1,...,г и r=/?—1, /? —2, ...,0.
Имея в виду предположение об окончании процесса,
найдем также, что
х / \ т-\-п Г m п 4-1 m + nl
AW = ° -тгт?]- <9-102)
Написанные соотношения позволяют нам быст-
ро вычислить последовательность функций fn(m)9
|r-i (П2),..., Одновременно мы находим, следует
ли остановиться или нужно продолжать процесс, а
также значение р, при котором процесс обрывается.
9.34. Численные результаты. Функциональные урав-
нения предыдущего раздела были исследованы числен-
но для широкого диапазона значений параметров а и R,
а также для нескольких функций стоимости k(г). Если
стоимость экспериментирования оставалась неизменной
от эксперимента к эксперименту, или если она возра-
стала, или если результат одного из двух эксперимен-
тов был известен a priori, то оптимальное управление
заключалось, по существу, в следующем:
1) в продолжении экспериментов, если г было мало
(информация недостаточна для суждения об оценке
вероятности);
2) в приостановлении экспериментов, если г было
достаточно велико;
ЛИТЕРАТУРА
371
3) в продолжении экспериментов для промежуточ-
ных значений г, если не оказывалось чрезмерно частого
выхода единиц или нулей, и в приостановлении экспе-
риментов в противном случае.
С другой стороны, при убывании стоимости каждого
нового эксперимента
А(г) = ехр(1 — (9.103)
мы находим, что оптимальное управление имеет зна-
чительно более сложный характер. Это прекрасно ил-
люстрируется случаем, в котором n=l, s = 2, а=1500 и
/? = 40. Если г равно 19 или менее, т. е. если произведено
19 или менее экспериментов, то, вообще говоря, правило
состоит в том, что следует произвести по меньшей мере
еще один эксперимент. Если г лежит между 20 и 33, то
необходимо немедленно прекратить процесс и сделать
надлежащую оценку. Если г заключено между 34 и 39
и примерно половина наблюдений привела к единич-
ному результату, то снова правило требует произвести
по крайней мере еще один эксперимент. Причина та-
кого поведения заключается, конечно, в том, что стои-
мость экспериментирования упала так низко, что вы-
годно сделать по крайней мере еще один эксперимент,
прежде чем произвести оценку. Когда г равно 40, про-
цесс, согласно условию, должен прекратиться.
ЛИТЕРАТУРА
1. R. Bellman, Dynamic Programming, Princeton Univ. Press,
Princeton, New Jersey, 1957. [Русский перевод: P. Веллман,
Динамическое программирование, М., I960.]
2. R. Courant and D. Hilbert, Methoden der Mathematischen
Physik, тома I и II. Springer-Verlag, Berlin, 1931. [Русский пе-
ревод: P. Курант и Д. Гильберт, Методы математической
физики, т. I, М.—Л., 1933; т. II, М.—Л., 1945.]
3. L. С о 11 a t z, The Numerical Treatment of Differential Equations,
Springer-Verlag, Berlin, 1951. [Русский перевод: Л. Коллатц,
Численные методы решения дифференциальных уравнений, ИЛ,
М., 1953.]
4. Е. Kamke, Differentialgleichungen Losungsmethoden und Losun-
gen, Akad. Verlag, Leipzig, 1959. [Русский перевод: Э. Камке,
Справочник по обыкновенным дифференциальным уравнениям,
изд. 2-е, перераб, и дополн., М., Физматгиз, 1961.]
24*
372 ЧИСЛЕННОЕ РАССМОТРЕНИЕ ПРОЦЕССОВ УПРАВЛЕНИЯ [гл. IX
5. S. Е. Dreyfus, Dynamic programming and the calculus of va-
riations, J. Math. Anal, and Appl. 1, 228—239 (1960).
6. R. Bellman, Some new techniques in the dynamic programming
solution of variational problems, Quart. Appl. Math. 16, 295—305
(1958)
7. R. Bellman and R. К a 1 a b a, Reduction of dimensionality,
dynamic programming, and control processes, Paper No. P-1964,
The RAND Corporation (April, 1960).
8. В. Г. Болтянский, P. В. Гамкрелидзе и Л. С. Понт-
рягин, Теория оптимальных процессов. I. Принцип максимума,
Известия АН СССР, серия матем., 24, № 1, стр. 3—42 (1960).
9. Л. И. Розоноэр, Принцип максимума Л. С. Понтрягина в
теории оптимальных систем. I. Автоматика и телемеханика 20,
вып. 10, стр. 1320—1334 (1959).
10. R. К а 1 a b a, On nonlinear differential equations, the maximum
operation, and monotone convergence, J. Math, and Meeh. 8,
519—574 (1959).
11. R. Bellman, Functional equations in the theory of dynamic
programming, V. Positivity and quasilinearity, Proc. Natl. Acad.
Sci. U.S. 41, 743—746 (1955).
12. R. Bellman, Adaptive Control Processes: A Guided Tour, Prin-
ceton Univ. Press, Princeton, New Jersey, 1961.
13. R. Bellman and R. К a 1 a b a, Dynamic programming and
adaptive processes: mathematical foundation, IRE Trans, on Auto-
matic Control AC-5, 5—10 (1960).
14. R. Bellman and R. К a 1 a b a, On communication processes
involving learning and random duration, 1958, IRE Natl. Conven-
tion Record, part 4, 16—21 (1958).
15. R. Bellman and R. К a 1 a b a, On adaptive control processes,
1959, IRE Natl. Convention Record, part 4, 2—11 (1959).
16. R. Bellman and R. Kai aba, A mathematical theory of adap-
tive control processes, Proc. Natl. Acad. Sci. U. S. 45, 1288—1290
(1959).
17. R. Bellman, R. К al aba and D. Middleton, Dynamic pro-
gramming, sequential estimation and sequential detection processes,
Proc. Natl. Acad. Sci. U. S. 47, 338—341 (1961).
ГЛАВА X
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
10.1. ВВЕДЕНИЕ
Общая проблема оптимизации полета управляемого
снаряда формулируется с помощью некоторого числа
уравнений движения, которые необходимо должны
удовлетворяться группой переменных, описывающих
полет снаряда. Кроме того, имеется еще уравнение по-
тока массы, необходимого для создания маневрирую-
щей тяги; возможны, наконец, и другие ограничения,
выражающиеся в законах управления, предельных уско-
рениях или в особенностях конструкции летательного
аппарата. В большинстве задач этого типа число пере-
менных превышает число уравнений, которые должны
быть удовлетворены. Поэтому, если имеется п уравне-
ний, которые должны удовлетворяться т переменными,
где m>n, то можно свободно выбрать т — п из этих
переменных довольно произвольным образом и попы-
таться решить уравнения относительно оставшихся пере-
менных. Если для каждого способа выбора т — п пере-
менных оставшиеся переменные определяются един-
ственным образом, то, очевидно, имеется множество
допустимых решений и, таким образом, существует воз-
можность оптимального в известном смысле выбора из
этого множества.
При полете ракеты в пространстве можно требовать
такого управления полетом, чтобы был достигнут мини-
мальный расход топлива. С другой стороны, можно рас*
смотреть случай минимального времени полета, наи-
большей дальности, наибольшего изменения скорости
или некоторую комбинацию этих требований. Короче
говоря, моя<но стремиться к минимизации или
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
[гл. X
максимизации любой функции переменных задачи. Мы
свободны в выборе определенных переменных задачи,
например программы управления тягой в полете раке-
ты, и можно произвести минимизацию с учетом уравне-
ний связей, описывающих физические явления.
Во многих случаях требуется, чтобы переменные
задачи подвергались воздействию с целью удовлетво-
рить некоторым граничным условиям. В задаче пере-
хвата в воздухе мы заботимся лишь о том, чтобы были
приведены в соответствие положения обоих объектов.
Время столкновения может быть задано, либо мы мо-
жем осуществить его в течение произвольного проме-
жутка времени, и при этом скорость в конечной точке
не имеет значения. С другой стороны, в случае встречи
двух объектов как положения, так и скорости их должны
быть согласованы друг с другом.
10.2. ФОРМУЛИРОВКА ПРОБЛЕМЫ
Математическую формулировку этой задачи можно
получить, рассматривая систему, вектор состояния кото-
рой x(t) удовлетворяет нелинейному динамическому
уравнению
= y,t), х(0) = а, (10.1)
так что для каждой составляющей вектора х(/), ска-
жем *<(/), имеем
-^- = Oz(x1, х2, ...» хр, у1( у2, ...» yq, t), (10.2)
xz(0) = az, i= 1, 2, 3, ..., p.
Вектор состояния x (t) р-мерный, где p равно числу
имеющихся уравнений, а подлежащий выбору вектор
y(t) g-мерный, где q равно превышению числа неизвест-
ных над_числом уравнений. Пусть для k составляющих
вектора x(t) в момент t = T будут заданы конечные зна-
чения, так что
лДГ) = ^(Г), /=1, 2, 3, (10.3)
10.3]
ИСКЛЮЧЕНИЕ ГРАНИЧНЫХ ЗНАЧЕНИИ
375
где функции bi(t) заданы для всех t в интервале (0, Г).
Пусть I составляющих вектора у(/), подлежащего вы-
бору, должны быть ограничены в интервале (0, Т)
заданными пределами Ci(t) и так что
ct (0 < У/ (/)< dt (/), i = 1, 2, 3, ..., I < q. (10.4)
Предположим, что нам требуется минимизировать
некоторую функцию
т
/(у) = /х2, ...» хр, уп у2, .•yg. f)dt. (10.5)
о
Теперь мы имеем довольно общую формулировку
многомерной нелинейной вариационной краевой задачи.
10.3. ИСКЛЮЧЕНИЕ ГРАНИЧНЫХ ЗНАЧЕНИИ
Поскольку процесс, описываемый уравнениями
(10.1), нелинейный, трудно получить соотношение меж-
ду начальными значениями х(0) и конечными х(Т).
^-мерный вектор #(/), подлежащий определению, дол*
жен быть выбран так, чтобы был минимизирован функ-
ционал (10.5) при выполнении условий (10.3) в конеч-
ный момент времени.
Один из методов обхода этих трудностей состоит в
том, что исходная задача погружается в более общий
класс задач, для которых выполняются уравнения свя-
зей (10.2) и (10.4), но минимизируемая функция берет-
ся в виде
т
о
х2, .... хр, уп у2, у?, /)<// +
(10.6)
причем связи (10.3), наложенные на конечные значения,
исключаются благодаря внесению их в минимизируе-
мую функцию (10.6). Это осуществляется путем введе-
ния множителя %(г|.
376
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
[гл. X
Ясно, что (10.6) можно записать в следующем виде:
Л (у)=Ду)+* (г) {1 к/ (П - (П12} • (10.7)
Если Х(г) взято безгранично возрастающим с убы-
ванием г до нуля и если ограничено, то предель-
ная форма (10.7) приводит к заключению, что
f k 1
lim X (г) 3 [xz (Г) — bi (Г)]2 = 0 (10.8)
г->0 и = 1 )
И _ _
Нт Л (у) = Ду). (Ю.9)
г->0
Очевидно, уравнение (10.8) может быть удовлетво-
рено функциями Х(г), неограниченно растущими при
исчезающих значениях г, лишь в случае, если
5[хДЛ-^(Л12 = 0. (10.10)
Z= 1
Сумма квадратов в равенстве (10.10) исчезает тогда
и только тогда, когда
Л/(Г) = ^(Г), i= 1, 2, k, (10.11)
что в точности совпадает с краевыми условиями (10.3)
исходной задачи. Заметим, что уравнение (10.9) пока-
зывает одновременно, что решение видоизмененной
задачи при стремлении г к нулю минимизирует Ji(y)
точно так^же, как и решение исходной задачи миними-
зирует Цу).
В результате исходная краевая задача оказалась
погруженной в более общий класс задач путем увели-
чения числа переменных (добавлена новая перемен-
ная г) таким образом, что частный случай г = 0 соот-
ветствует исходной задаче.
Из (10.7) можно усмотреть, что при минимизации
J\(y) для различных значений г минимизируемая вели-
чина в действительности представляет собой комбина-
цию интересующей нас величины и отклонений от вы-
полнения концевых условий. Осуществляя минимиза-
цию пр некоторому диапазону значений Х(г), получаем
10.4] МИНИМИЗАЦИЯ КОНЕЧНОГО ЗНАЧЕНИЯ ПЕРЕМЕННОЙ 377
компромиссное соотношение между представляющей
интерес величиной и ошибкой в концевых условиях.
Использование достаточно большого значения X делает
эти ошибки произвольно малыми, исчезающими в пре-
деле, когда X неограниченно растет.
Помимо устранения двухточечного краевого харак-
тера задачи, эта процедура погружения открывает воз-
можность дополнительных применений. Рассмотрим,
например, обычную краевую задачу. Для этой задачи
сохраняются такие уравнения связей, как (10.1) —
(10.4), но отсутствует вариационное требование мини-
мизации (10.5). В результате процесса погружения за-
дача становится вариационной проблемой минимизации
выражения (10.6), в котором функция F берется тожде-
ственно равной нулю.
10.4. СВЕДЕНИЕ К ЗАДАЧЕ О МИНИМИЗАЦИИ
КОНЕЧНОГО ЗНАЧЕНИЯ ПЕРЕМЕННОЙ СОСТОЯНИЯ
Требование минимизации функции в (10.6) можно
превратить в требование минимизации конечного значе-
ния единственной переменной состояния. Пусть, напри-
мер, размерность вектора х увеличивается путем доба-
вления дополнительных переменных состояния (реали-
зация инвариантного погружения).
Положим
^,(о=/Г(-- z)> Хр+1(0)=а^+1=г0 (1012)
Можно также ввести обозначение
k
хр+2 (*) = Цг) 2 [xz (/) - bt (012 (10.13)
1 = 1
или, что то же,
ь
-^^-=2X(r)2;[xz(o-^(oi[^(x, у, о-Ш
/=1
k I
Хр+2 (0) = х (г) 2 [Л/ — bl (О)]2 = ар+2.
i — 1 J
(10.14)
378 ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ [гл. я
Положим
*р+з(0 = *р+1(0 + *р+2(<). (10-15)
так что
dt — Ор+1(х, у, /)+Ор+2(х, у, t), Хр+3 (0) = #р+з = ^р+2* (10.16)
Связи, присоединенные к таковы: первоначальной задаче,
dt у» 0» Vh(0) = 0,
/). Хр+2 (0) = #р+2» (10.17)
у. /). хр+з (0) —
а минимизируемая функция равна
Л(У) = *р+з(Л> (Ю.18)
т. е. представляет собой конечное значение (р + 3)-й
переменной состояния.
Представляется очевидным, что задача минимиза-
ции или максимизации почти всякой функции может
быть сведена к разысканию экстремальной величины
конечного значения единственной переменной состояния.
Например, задачу о минимуме времени можно заме-
нить задачей о минимизации xp+i(T), в которой к исход-
ным уравнениям присоединены дополнительные связи
вида
dxp+l (0
dt
1» -*7> + l(0) — 0‘
(10.19)
Подобно этому задача о Минимизации конечного
значения некоторой произвольной функции переменных
состояния может быть заменена задачей о минимизации
величины
*P+i (Л=т 1*1 (Л. *2 (Л. -•-.*₽ (Л1 (10.20)
10.4] МИНИМИЗАЦИЯ КОНЕЧНОГО ЗНАЧЕНИЯ ПЕРЕМЕННОЙ 379
с присоединенным уравнением связи
=2 & У’ о. *Р+1 (0)=? (0)].
/-1 (10.21)
Таким образом, почти каждая задача оптимизации
может быть представлена в форме
4г = С(*. У. 0. х(0) = а, (10.22)
с требованием минимизации или максимизации конеч-
ного значения n-й составляющей вектора состояния х
J(y) — xn(T)- (10.23)
Мы видели, какое большое разнообразие задач опти-
мизации может быть эффективно сведено к минимиза-
ции или максимизации конечных значений — в действи-
тельности конечных значений только одной переменной
состояния. Благодаря концепции инвариантного погру-
жения первоначально краевая по своему характеру за-
дача рассматривается как погруженная в класс более
общих задач, простым предельным случаем которых она
является.
Причина, побудившая нас исключить граничные
условия, заключается, разумеется, в стремлении умень-
шить трудности, связанные с численным решением двух-
точечной краевой задачи. Однако преобразование крае-
вой задачи в задачу минимизации или максимизации
конечного значения переменной состояния при задан-
ных начальных условиях с вычислительной точки зре-
ния оправдывается лишь тогда, когда численное реше-
ние производится по методу динамического програм-
мирования. Является или нет первоначальная зада-
ча краевой — при численном решении классическим
способом приходится всегда иметь дело с краевой
задачей.
380
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
(гл. X
10.5. КЛАССИЧЕСКОЕ РЕШЕНИЕ
Предположим для примера, что задача, численное
решение которой разыскивается, формулируется урав-
нениями (10.22) и (10.23), причем требуется, чтобы вы-
бор составляющих yt(t) векторной функции y(t) точки
в интервале был сделан таким образом, что-
бы конечное значение n-й составляющей вектора со-
стояния *(/), обозначаемое через хп(Т), было макси-
мально. Если составляющие yi(t) не ограничены
[т. е. — оо yi(t) °°], то классический метод решения
составляет содержание хорошо известной вариацион-
ной задачи Майера [1]. Более общий подход, исполь-
зующий классические методы и допускающий произ-
вольные ограничения выбора вектора y(t) [т. е.
yi(t) доставляется так называемым «принци-
пом максимума» советского математика Понтрягина [2].
Частный случай принципа максимума, описанный Розо-
ноэром [3], может быть применен к проблеме миними-
зации конечных значений.
Согласно формулировке Розоноэра задачи о мини-
мизации хп (Г), функция
у,(10.24)
/=1
должна быть максимальна по у для любых векторных
функций х и р, удовлетворяющих гамильтоновой систе-
ме уравнений
= = у. 0; xz(0) = az, / = 1..................п.
(10.25)
и
dpt^ _ _ дЯ _ _ у (х, у, t) .
dt dxt &Xl ’
A(T) = 0; Z=l, 2, .... л-1; />#) = -!
(10.26)
Уравнения (10.25) и (10.26) составляют содержание
2п-мерной двухточечной краевой задачи, в которой со-
10.5]
КЛАССИЧЕСКОЕ РЕШЕНИЕ
381
ставляющие х известны при / = 0, ^составляющие р из-
вестны при t = T. Составляющие у должны удовлетво-
рять требованию максимума функции (10.24) или, когда
они не расположены на границе,
——°, 4 — 1, 2, ..nt, (10.27)
/=i
Это показывает, что т составляющих у удовлетворяют
функциональному соотношению
/). (10.28)
Если бы т уравнений (10.27) можно было разре-
шить относительно т величин y-t, то получились бы со-
отношения типа (10.28). Равенства (10.28), будучи ис-
пользованы в (10.25) и (10.26), дают 2п-мерную крае-
вую задачу для пары n-мерных векторов х и р.
Разрешение уравнений (10.27) относительно состав-
ляющих yi в явной форме (10.28) представляется труд-
ной задачей, за исключением простейших случаев, но
даже тогда, когда это возможно, остается еще задача
интегрирования совместных уравнений (10.25) и (10.26).
Редко удается проинтегрировать эти уравнения в замк-
нутой форме, и даже при интегрировании на машине
остается то обстоятельство, что x(t) и p(t) заданы на
различных концах временного интервала 0</<7\
Трудности всех классических методов решения зада-
чи происходят из-за необходимости составления вспомо-
гательной системы дифференциальных уравнений, будь
то уравнения Лагранжа в задаче Майера с неограни-
ченными вариациями- или гамильтонова система урав-
нений в принципе максимума при ограниченных
вариациях. Эти вспомогательные уравнения вместе с
исходными уравнениями связей всегда ведут к вычисли-
тельному требованию решения двухточечной краевой
задачи. Один из методов учета краевых условий был
предложен Келли [4], который выбирает функции, удов-
летворяющие краевым условиям, и производит итера-
ции этих функций с целью удовлетворить уравнениям в
интервале между граничными точками.
382
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
[гл. X
10.6. РЕШЕНИЕ ПО МЕТОДУ ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Метод динамического программирования, хотя, и
обладает определенными, свойственными ему вычисли-
тельными особенностями, не связан, однако, с двухто-
чечной краевой задачей. Если в окончательной форму-
лировке задача не является краевой, то при численном
решении методом динамического программирования мы
не сталкиваемся с граничными значениями.
При решении методом динамического программиро-
вания задачи со связями вида
-^ = Q(x, у, t), х(0)=а,
' „. - - - (Ю-29)
пнп[хя(Г)| при (/)<</
У
можно считать конечное время t = Т переменным и рас-
сматривать диапазон значений начального времени
t = р, где 0<Ср<^Т. Задача (10.29) оказывается тогда
включенной в более общую задачу
-§- = О(х, у,/), х(р) = а, 0<р<Г.
_ _ - (10.30)
пип \хп (Г)] при с < у (/)< rf,
7
и функциональное уравнение строится для функции
Ж р, Т) = mjn [хо (Г)]. (10.31)
У
Имеет место конечноразностное уравнение первого
порядка
л*+1 = л* + (?(х*, у*, р + ЛД)Д, р + ^Д<Г. (10.32)
Функциональные рекуррентные соотношения метода
динамического программирования приобретают вид
f(a, р, pH- Д) =Л (а, р) = min [аи + Qa (а, у, р) Д] (10.33)
У
10.6] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 383
с решением у01 (а, р) и
Ж р, p + Nb)=fN(a, р) =
= min [4-1 (а + б (а, у, р) Д, р + (N -1) Д)] (10.34)
у
с решением уолг(а, р).
Общее решение задачи, для которой р = 0, х(0) = а
и Т = Л/Д, можно определить теперь последователь-
ностью операций с функциями у°!(й, р).
Например, _
/(а, 0, W, Д) = fN (а, 0) = mjn [х„ (Г)], (10.35)
у
и если x*(t) и y*(t) обозначают соответственно опти-
мальные векторы состояния и управления, то
х*(0) = а, 1
7(0) = у°Ж 0). J
Используя значения (10.36), получаем тогда
х* (Д) = а+G fa, у* (0), Д] Д,
у*(Д) = у°(ЛГ-1)[х*(Д), Д].
Подобно этому находим
х*(2Д) = х*(Д)+_ё[х*(Д), ?(Д),Д]Д, 1
у*(2Д) = у0(*-2)[х*(2Д), 2Д]. J ’ '
(10.36)
(10.37)
Далее действуем таким же образом, определяя зна-
чения х*(/) и у*(/) через отрезки Д интервала
Изложение велось до сих пор в терминах конечно-
разностных уравнений первого порядка. Могут возник-
нуть затруднения, связанные с выбором величины ша-
га Д для обеспечения удовлетворительной сходимости.
Однако второе, третье и дальнейшие разностные уравне-
ния также могут быть использованы в случае надобно-
сти. С другой стороны, совсем нет необходимости вооб-
ще использовать разностные уравнения. Поскольку
384
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
[гл. X
всегда требуется представить задачу в дискретной фор-
ме для расчетов на цифровых машинах, разностные
уравнения доставляют лишь один из вариантов такой
формы. Несколько методов приведения задачи к дис-
кретной разобрано Гринстадтом [5]; среди них имеются
разностные методы, метод Фурье и метод ячеек.
Наиболее трудная задача, возникающая при числен-
ном решении по методу динамического программиро-
вания, связана с многомерным характером функцио-
нальных рекуррентных соотношений (10.33) и (10.34).
Практически не представляется возможным сохранить
значения функций более чем двух переменных из-за
ограниченной емкости машинной памяти даже при со-
временных больших цифровых вычислительных маши-
нах. Поэтому всякий реализуемый прием численного
решения должен включать в себя способ уменьшения
числа измерений.
Имеется по крайней мере три способа уменьшения
числа измерений. Мы имеем в виду увеличение шага,
приближение полиномами и линеаризацию с последова-
тельными приближениями. Каждый из этих методов
уменьшает число измерений; при этом точность вычис-
лений приносится в жертву памяти.
Увеличение шага можно описать по-разному. Пусть,
например, мы имеем дело с функцией трех переменных
и нас интересуют 100 значений каждой из трех перемен-
ных. При этом требуется, чтобы емкость памяти состав-
ляла 106. Если вместо этого мы потребуем, чтобы каж-
дая переменная принимала лишь 10 значений, то тре-
бование к памяти снизится до 103 элементов. Сначала
находят «грубое» решение и затем последовательно
улучшают его.
Приближение полиномами заключается в следую-
щем. Предположим, что функция хотя бы одной пере-
менной аппроксимирована полиномом n-й степени.
Функции, встречающиеся в большинстве физических
приложений, по-видимому, хорошо аппроксимируются
полиномом 10-й степени. Задача запоминания значений
функции для 100 значений ее аргумента заменяется за-
поминанием 10 коэффициентов полинома и последующим
вычислением значения функции для любого заданного
10.6]
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
385
значения ее аргумента. Подобно этому, если бы много-
мерная функция была аппроксимирована полиномом ко-
нечной степени от независимых переменных, то емкость
памяти можно было бы сильно сократить. И действи-
тельно, известны частные случаи, когда минимум или
максимум функции точно определяется по полиному вто-
рой степени. Как показал Мерриам [6], если функция,
максимум которой разыскивается, имеет вид квадратич-
ной формы, то минимизирующая функция также пред-
ставляется квадратичной формой.
Беллман [7] дает детальное рассмотрение метода ли-
неаризации и последовательного приближения. Коротко
говоря, пусть принято произвольное нулевое приближе-
ние [х°(/), j/°(/)]. Линеаризуем уравнение связей в окрест-
ности этого нулевого решения. Для линеаризованных
уравнений возмущенной системы можно вычислить ко-
нечное значение хп(Т).
Еще важнее то, что вклады в величину хп(Т) от на-
чальных условий и от подверженного ограничениям
управляющего вектора можно полностью разделить,
воспользовавшись векторно-матричным решением си-
стемы линейных дифференциальных уравнений с пере-
менными коэффициентами. Далее,
х(0) = а
участвует в определении хп(Т) как функция и, где
и — известная в явной форме функция от а. Значе-
ние y(t), дающее экстремум первому возмущенному
значению хп(Т), равно y'(t)—наилучшему управлению
первого порядка.
Если подставить y'(t) в исходные уравнения связи,
то интегрированием их можно получить л1 (/). Уравнения
связи линеаризуются теперь в окрестности решения пер-
вого порядка [л1 (/), уЧОГ Процесс продолжается, как и
ранее; определяются [xft(Z), yk(t)] до тех пор, пока раз-
ница между функциями на k-м шаге и (k— 1)-м не ста-
нет пренебрежимо малой. Экстремальная функция те-
перь зависит от и, которая в свою очередь является
известной явно функцией а. Разумеется, здесь также
возникают вопросы сходимости последовательных при-
ближений.
25 Дж. Лейтман
386
ОБЩАЯ ТЕОРИЯ ПОГРУЖЕНИЯ
[гл. X
10 7. РЕЗЮМЕ
Мы можем закончить эту главу следующими замеча-
ниями. Почти всякую задачу оптимизации можно тракто-
вать как задачу о разыскании экстремального конечного
значения единственной переменной состояния. Числен-
ное решение таких задач можно производить двумя раз-
личными методами, каждый из которых характеризуется
отнюдь не тривиальными трудностями. Классическое ре-
шение, использующее вариационные принципы, имеет
главной трудностью двухточечный краевой характер за-
дачи. Решение по методу динамического программирова-
ния имеет главной трудностью многомерный характер
функций. Метод, употребляемый в каждой частной за-
даче, будет, несомненно, зависеть от ее собственных осо-
бенностей, от изобретательности исследователя и от сте-
пени его знакомства с тем или иным приемом решения.
ЛИТЕРАТУРА
1. G. A. Bliss, Lectures on the Calculus of Variations, Univ. Chi-
cago, Illinois, 1946. [Русский перевод: Г. А. Блисс, Лекции по
вариационному исчислению, М.—Л., 1950.]
2. Л. С. Понтрягин, Optimal Control Processes, Automation Ex-
press 1, 15 (1959).
3. Л. И. Розоноэр, Принцип максимума Л. С. Понтрягина в тео-
рии оптимальных систем. I. Автоматика и телемеханика 20,
вып. 10, стр. 1320—1334 (1959).
4. Н. J. Kelley, Gradient theory of optimal flight paths, ARS
Journal 30, 947 (1960).
5. J. Greenstadt, On the reduction of continuous problems to
discrete form, IBM J. Research and Develop. 3, 355 (1959).
6. C. W. Merriam, III, A class of optimum control systems,
J. Franklin Inst. 267, 267 (1959).
7. R. Bellman, Some new techniques in the dynamic programming
solution of variational problems, Quart. AppL Math. 16, 295 (1958).
ГЛАВА XI
ИМПУЛЬСНЫЙ ПЕРЕХОД
МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
11.1. ВВЕДЕНИЕ
Решение общей задачи программирования расхода
топлива и направления силы тяги ракеты для наиболее
рационального перехода между двумя фиксированными
точками в данном гравитационном поле дано в работе
[1]. В этой же статье результаты общей теории были при-
менены к частному случаю, когда поле изменяется по
простому закону обратной пропорциональности квадра-
ту расстояния от притягивающего центра, и были полу-
чены условия оптимального перехода между двумя ком-
планарными эллиптическими орбитами. Было показано,
что если величина тяги двигателя может считаться не-
ограниченной, то оптимальные условия могли бы быть
достигнуты приложением импульсных тяговых усилий в
некоторых точках соединения, тогда как между этими
точками ракета двигалась бы свободно, находясь под
действием одних лишь гравитационных сил.
В настоящей главе будет показано, что в пределах
предположения о том, что тяга ракеты всегда имеет им-
пульсный характер, условия, определяющие положе-
ние точек соединения в задаче оптимального перехода
между компланарными эллиптическими орбитами, мож-
но получить элементарным путем, не обращаясь к об-
щей теории.
Проблема оптимального перехода между орбитами в
поле, напряженность которого обратно пропорциональна
квадрату расстояния до центра, впервые была рассмот-
рена Гоманом [2] для частного случая, когда орбиты ком-
планарные и круговые. Оптимальный переход между эл-
липтическими орбитами был предметом исследований
25*
388
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
Лоудена [1, 3—7], Лонга [8], Смита [9] и Плиммера [10].
Варго [11], Мьюник и др. [12] и Хорнер [13] рассмотрели
близкую задачу об оптимальном переходе между двумя
заданными орбитами в поле, напряженность которого
обратно пропорциональна квадрату расстояния от цент-
ра, причем заданная орбита полностью определялась
расстоянием от нее до притягивающего центра и векто-
ром скорости, т. е. выбору подлежал угол между направ-
лениями из центра на две точки, между которыми осу-
ществлялся переход. Вопрос об оптимальном для такого
перехода числе импульсных тяговых усилий был иссле-
дован Эдельбаумом [14], Холкером и Силбером [15] и
Райдером [16]; было показано, что при определенных об-
стоятельствах необходимо приложить до четырех им-
пульсов для достижения абсолютного минимума расхода
топлива. Этот важный вопрос не будет затронут в на-
стоящей главе, так как повсюду будет предполагаться,
что число импульсов (обычно два) уже выбрано заранее
и что задача заключается в определении точек соедине-
ния, в которых эти импульсы должны быть приложены,
а также их величин и направлений.
11.2. ИМПУЛЬСНОЕ ИЗМЕНЕНИЕ
ОРБИТАЛЬНЫХ ЭЛЕМЕНТОВ
Пусть О будет центром притяжения по закону обрат-
ной пропорциональности квадрату расстояния, 7/г2 будет
силой притяжения единичной массы на расстоянии г от
центра. Обозначим через (г, 6) полярные координаты с
полюсом в точке О на заданной плоскости, проходящей
через эту точку. Тогда полярное уравнение орбиты тела,
движущегося в этой плоскости под действием одного
лишь притяжения, может быть написано в форме
l=l+ecos(0 — ш), (11.1)
где I — параметр, е — эксцентриситет, а <о — долгота пе-
ригея. Удобно положить
l = s, 1=р, л = ?, (11.2)
11.2]
ИЗМЕНЕНИЕ ОРБИТАЛЬНЫХ ЭЛЕМЕНТОВ
389
так что (11.1) принимает вид
^cos(0 —ш) = $—р. (П-З)
Параметры (р, д, со) полностью определяют орбиту
в данной плоскости.
Если Р обозначает положение тела в любой момент
времени, a (1/$, 0)—его полярные координаты, то со-
ставляющие скорости те-
ла соответственно вдоль
ОР и в перпендикулярном
направлении будем обо-
значать через (vr, ид). Из
теории орбит следует, как
известно, что
vr = q sin (9—ш),
(U-4)
®9 = |/ j {p + ^cos(9— О
Рис. 11.1. Точка соединения.
Пусть V будет составляющей скорости тела в точке
Р в направлении, образующем угол ф с лучом РО
(рис. 11.1).
Из уравнений (11.4) и (11.5) следует тогда, что
V = sin ср — vr cos ср =
= s у «Шф — q |/ sin (6 — <Ь) cos ф. (11.6)
Группировкой членов можно придать уравнению
(11.6) форму
q sin (0 — d>) = (s — Zp'h) tg ф, (11.7)
где
Z= У/fA sin (11.8)
Предположим теперь, что в момент, когда обращаю-
щееся по орбите тело находится в точке Р, к нему при-
кладывается импульс / в направлении, образующем угол
390
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
Ф с поперечной составляющей скорости tv Составляю-
щая V скорости тела, перпендикулярная к /, не изме-
нится от этого импульса. Величина Z, определяемая фор-
мулой (11.8), останется, таким образом, без изменения.
Координаты (l/s,9), далее, не изменяется заметно в те-
чение короткого промежутка времени действия тяги. По-
этому значения параметров орбиты (р, р, со), соответ-
ствующие новой орбите, на которую тело переведено им-
пульсом, будут по-прежнему удовлетворять уравнению
(11.7). С помощью аналогичных рассуждений выводим,
что эти параметры также будут удовлетворять уравне-
нию (11.3).
Таким образом, в силу сказанного параметры (р, q, со)
любой орбиты, на которую может быть переведено тело
путем приложения в точке Р(1/$, 6) импульса в направ-
лении, образующем угол с ve, удовлетворяют уравне-
ниям
^cos(9—&)==$— р, (11.9)
q sin (9 — &) = ($ — ZpVa) tg <р, (11.10)
где Z связано уравнением (11.8) с составляющей скоро-*
сти тела V в направлении, перпендикулярном к импуль-
су. Требование, чтобы три параметра (р, д, со) удовле-
творяли уравнениям (11.9) и (11.10), оставляет для этих
величин одну степень свободы. Эти параметры будут оп-
ределены полностью, если будет известна величина им-
пульса.
Можно дать следующий удобный графический способ
определения всех тех орбит (р, q, со), на которые можно
перевести обращающееся по орбите тело приложением
одного импульса в данной точке и в данном направ-
лении.
Построим график функции у = х2 (рис. 11.2). Возь-
мем точку А на оси х на расстоянии от начала О, опре-
деляемом уравнением
ОА = -^—' (11.11)
Z2tg<p v 7
и восставим перпендикуляр АВ к ОА таким образом, что
Ш-12)
11.2]
ИЗМЕНЕНИЕ ОРБИТАЛЬНЫХ ЭЛЕМЕНТОВ
391
Пусть Р обозначает точку (х, у) на кривой у = х2,
и пусть PN будет перпендикуляром, опущенным из Р
на АВ. Обозначая угол РВА через а, находим из прос-
тых геометрических соотношений
РВ cos а = АВ — у, (11.13)
РВ sin а = О А — х = О А — уЧ*. (11.14)
Поэтому, если интерпретировать РВ, а и у таким об-
разом, что
РВ = L а = 6—Л, у= .j? . (11.15)
Z2 tg2 <р J tg2 <р v 7
то уравнения (11.13) и (11.14) оказываются идентич-
ными уравнениям (11.9) и (11.10) соответственно. Отсю-
да следует теперь, что,
поскольку Р описывает
кривую у = х2, возмож-
ные системы значений па-
раметров (р, q, со) дают-
ся для каждого положе-
ния точки Р величинами
ЛУУ, РВ и а в согласии с
формулами (11.15). Ког-
да прикладывается им-
пульс заданной величины,
точка Р на диаграмме пе-
реходит по кривой от од-
ного положения к друго-
му. Возможные интерва-
лы значений (р, q, со) для
импульсов, приложенных в данной точке на орбите тела
и в данном направлении, немедленно определяются на
диаграмме. Например, минимальное достижимое значе-
ние q соответствует отрезку BQ.
В заключение этого раздела получим формулу, из
которой можно будет определить величину импульса. Об-
ращаясь к рис. 11.1, заметим, что если U обозначает со-
ставляющую скорости тела в направлении импульса, то
щ = U cos <р + V sin (11.16)
392
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
При учете (11.5) это показывает, что
U =s 1/i
И Р
sec — V tg ср.
(П.17)
Пусть после прекращения действия импульса вели-
чины (р, U) принимают новые значения (р', U'). Вели-
чины (s, V) останутся неизменными, и уравнение, соот-
ветствующее (11.17), в момент, немедленно следующий
за импульсом, будет иметь вид
U' — s
|/ у- sec ср — V tg ср.
(11.18)
Вычитая (11.17) из (11.18), найдем, что
MJ = U’ -и = [(р')"'/2 — р-'Ч sec ср. (11.19)
Последнее уравнение задает приращение скорости,
вызванное импульсом, а следовательно, и величину по-
следнего.
11.3. ЗАВИСИМОСТЬ ИМПУЛЬСА
ОТ ОРБИТАЛЬНЫХ ЭЛЕМЕНТОВ
Предположим, что движущееся по орбите (р, q, со)
тело переводится одним импульсом на компланарную ор-
биту (pz, q\ со'). Этот импульс должен быть приложен в
точке пересечения обеих орбит (по предположению, су-
ществующей). Пусть (1/s, 8) будут полярными коорди-
натами этой точки, и пусть ф будет угол, образуемый
направлением импульса и перпендикуляром к радиусу-
вектору, проведенному из центра притяжения.
Уравнения (11.9) и (11.10) должны удовлетворять-
ся параметрами обеих орбит, так что справедливы ра-
венства:
q cos (8 — w) = s — p, (11.20)
q sin (9 — ш) = (s — Zp^) tg cp, (11.21)
q' cos (9 — «/) = s — p\ (11.22)
q' sin (9 — a/) = [s — Z(p') /2l *6 01 -23)
11.3] ЗАВИСИМОСТЬ ИМПУЛЬСА ОТ ЭЛЕМЕНТОВ
393
где Z— величина, определяемая для этого перехода
уравнением (11.18). Четыре уравнения (11.20) — (11.23)
можно разрешить относительно четырех неизвестных
($, 8, Z, <р), считая заданными параметры, характери-
зующие обе орбиты; указанные неизвестные выразятся,
таким образом, как функции р, g, со, р', q', со'. Прираще-
ние скорости AZ7 = 7*/?Х, происходящее вследствие им-
пульса, найдется тогда из (11.19); получим
Д(7 --- ^Х= i'/>s [(р')“1/1 —/>-*/.] sec <р; (11.24)
X может также быть выражено в функции от шести ор-
битальных параметров.
Таким образом,
Х=Х(р, q, ш, р', ш'). (11.25)
Нашей целью в настоящем разделе является иссле-
дование этой функциональной зависимости X от пара-
метров путем вычисления выражений для частных про-
изводных от X по его шести аргументам.
Дифференцируя уравнения (11.20) — (11.23) частным
образом по р, найдем, что
-7sin(0-a)-g = -g--l, (11.26)
<7 cos (О -й) -g = (-g—g p’/. - j Zp-'i^ tg ?+
+ (11.27)
-/sin(0-«/)g- = g-, (H.28)
Я' cos (9 - S') -g = [-g - ™ (p')Vl ] tg T +
[s — Z (p')v’] sec2 <p-g-. (11.29)
Разрешая уравнения (11.26) и (11.28) относительно
ds/dp и дЪ/др и пользуясь уравнениями (11.21) и (11.23),
легко показать, что
ds _ s — Z(p’)'h
др Zip1''» —(р')1/»]
(50 Ct£ <р
1ГР = (1Ь31>
394
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
Подставляя выражения для dsfdp и дб/dp в уравне-
ния (11.27) и (11.29), используя уравнения (11.20) и
(11.22) и исключая затем dZ/dp из этих уравнений, най-
дем, что
sZ [(/>')‘/г — Р7’] tg Ч> sec2 ? =
= s_Z(p')7’ + ^^-]tg2T + s + (pp')'/2. (П-32)
определяя тем самым ду/др.
Дифференцируя уравнение (11.24) по р, получим
К/'')’’7’ —Т’'7’] sec <р + у sp~^ sec <р+
+ $ — Р~'1г\ sec ч> tg <р . (11.33)
После подстановки выражений для dsjdp и ду/др из
уравнений (11.30) и (11.32) соответственно последняя
формула примет вид
aT = ^2irsec2? — Hcos?- (1L34)
Op \ zp 12 Zp p12 Z J
Путем рассуждений, весьма близких к этим, можно
получить выражения для частных производных от X по
q и со; эти выражения имеют вид
= ~—0 +'V')C0Stf> +
00 р q I \ z /
+ (s—p':,Z\ tg <р sin ср j, (11.35)
#=(z—zW <1L36>
Если теперь поменять местами две системы перемен-
ных (р, ?, со) и (pz, /, со') в уравнениях (11.20) —(11.23),
оставив s, 9, Z, ф без изменения, то в результате полу-
чится та же система уравнений. Знак X в уравнении
(11.24) изменится, однако, на обратный. Отсюда следует,
что повторение приведенных выше рассуждений даст вы-
ражения для dXjdp', dXjdq' и дХ/до/, совпадающие со-
11.4]
ОПТИМАЛЬНЫЙ n-ИМПУЛЬСНЫЙ ПЕРЕХОД
395
ответственно с выражениями для dXfdp, dXfdq и dX/dco,
определенными формулами (11.34)— (11.36), за тем ис-
ключением, что величины (р, q, со) должны быть заме-
нены соответствующими величинами (р', q', со'), а знаки
членов в правых частях изменены на обратные.
11.4. ОПТИМАЛЬНЫЙ л-ИМПУЛЬСНЫЙ ПЕРЕХОД
МЕЖДУ ДВУМЯ ЗАДАННЫМИ ОРБИТАМИ
Предположим, что ракета должна перейти с орбиты
(Ро, <7о, too) на компланарную орбиту (pn, qn. ton) путем
приложения последовательности п импульсных тяго-
вых усилий. Пусть первый импульс осуществляет пере-
ход с орбиты (ро, до, too) на орбиту (рь дь <х>1) и прикла-
дывается в точке с полярными координатами (1/si, 0i),
второй производит переход с орбиты (рь gb coi) на орби-
ту (Р2, ©г) и прикладывается в точке (l/s2, 0г) и т. д.,
n-й импульс прикладывается в точке (l/sn, 0п) и пере-
водит, наконец, ракету на орбиту (рп, <7п, <оп). Пусть
^,2Х{ будет приращением скорости, вызванным t-м им-
пульсом, так что согласно уравнению (11.19)
^ = ^(Pr,/’-Pr2/0secTi. (11.37)
где фг — угол, определяющий направление тяги. Ско-
рость, полученная после маневра в целом, дается равен-
ством
W = (11.38)
Как показано в предыдущем разделе, Xt предста-
вляет собой функцию шести параметров орбит (р<_ь
pi-i, coi-i, pit qt, со,), и, следовательно, W является функ-
цией Зи—3 переменных (рь дь соь pn-i, gn_b ton-i);
величины (ро, go, too, Рп, <7п, <*>п) являются заданными по-
стоянными.
По отношению к своим переменным аргументам W
будет стационарным при условии
= = = (П-39)
dpj v '
396 ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ [гл. XI
выполняющемся при i = 1, 2, п—1. Значения пара-
метров (Pi, рг, <0г) (* = 1, 2, п—1), определяющие
оптимальный n-импульсный переход, необходимо должны
удовлетворять уравнениям (11.39). Поэтому, разрешив
эти уравнения и вычислив значение W, к которому при-
водит каждое решение, можно в принципе определить
этот оптимальный режим.
Далее,
(Ц.40)
dPi \dPi dPt /
подобные выражения имеют место для dWfdqi и dW/дац.
Из формул последнего раздела следует, что
—- = — J—%- sec2<pz—— tg2<pz — I coscpz,
dPl | 2P3h iPl * P‘[‘ Zt j Yz’
^±l_ = (^±LSec2<pz+1-
<^Z I 2p/>
2PI
(1 1-41)
1 1 1
-IT- — ------ |coscp/+1,
Pi Zi+l
где Zi и Zf+i представляют собой значения Z, отвечаю-
щие соответственно Z-му и (i 4- 1)-му импульсам. Таким
образом, dW/dpi обращается в нуль при условии
{#sec!?i _ % ~ tf ~ i I cos fi=
= ( sec2 ^+1-^ tg2 cpz+1- -4— у— ! cos (11 -42)
[zPi 2Pi Pi zz+iJ
Можно подобным же образом доказать, что dWldqi и
dW/d^i исчезают, если
( р!2 \
& - А) \1 + -zf) cos Ъ + (si — ^zi) Ъsin Ъ =
Z р'1г \
=(^+1 - АД1 + ZT-/ cos?‘+’+
+ (Sz+1 -P'I’Ziu) TZ+1 sin ?z+1, (11.43)
(Zz — -g-j sin Tz = (Zz+1 — sin Tz+1. (11.44)
11.5J
ОПТИМАЛЬНЫЙ ДВУХИМПУЛЬСНЫЙ ПЕРЕХОД
397
Уравнения (11.20) — (11.23) определяют значения ве-
личин (Sf, 8г, /г, Фг), соответствующие z-му импульсу;
эти уравнения принимают форму
Я l-Х cos (9Z — a>z_i) = Si —pt_v (11.45)
sin (0Z — = (s{ — tg cpz, (11.46)
cos (9Z — = Pl, (11.47)
qt sin (9Z — az) = (sz — Z.p'ft tg <pz. (11.48)
При i = 1, 2,..., n—1 число уравнений (11.42) —
(11.48) равно 7n—7, и эти уравнения определяют 7п—7
неизвестных рг‘, ?г, (Of, $г, Si, (i = 1, 2, ..., п— 1),
относящихся к оптимальному n-импульсному режиму пе-
рехода между заданными орбитами.
Уравнение (11.42) можно следующим образом заме-
нить эквивалентным, но более простым условием: умно-
жим (11.42) на 2р3/2 и вычтем из (11.43); в результате
найдем
Pl(l + ^‘}cos^=p‘(' + C0S<Pf+l>
\ ZiPl / \ Zl + xPl /
ИЛИ
(1 + coscpz = (1 + cos<Pz+i- (11.49)
\ Zip'l> J \ Z[ + iP^ J rz + l V /
11.5. ОПТИМАЛЬНЫЙ ДВУХИМПУЛЬСНЫЙ ПЕРЕХОД
Переход между двумя компланарными орбитами с
помощью единственного импульса тяги возможен лишь
в том случае, когда орбиты пересекаются, и при этом не
возникает никакой оптимальной задачи, так как им-
пульс, необходимый в точке пересечения, полностью
определяется обеими заданными орбитами.
Следующим простейшим типом перехода является
двухимпульсный переход, всегда возможный между лю-
быми двумя орбитами. Удобно обозначить, параметры
граничных орбит через (рь coi) и (р2, ?2, (02), а пара-
метры единственной меняющейся орбиты перехода — че-
рез (р, q, ©).
398
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
Уравнения, определяющие оптимальный режим, мож-
но написать тогда в соответствии с изложенным дыдущем разделе. Они принимают вид: в npe-
7i cos (0! — (Sj) = Sj — р}, (11.50)
sin (0! — ffi,) = (s, — ZlP'^ tg ?1. (11.51)
q cos (0j — S>) = Sj — p, (11.52)
q sin (0j — & ) = (Si — ZiP'h) tg ?i, (11.53)
q cos (02 — <5 ) == s2 — p, (11.54)
q sin (02 — <5 ) = (s2 — Z2p‘/») tg <p2, (11.55)
q2 cos (02 — <b2) — s2 — p2, (11.56)
<?2 Sin (02 — ffi2) = (S2 — Z2Pl2) tg Ъ' (11.57)
(Si — p) (1 + -^7) cos «Р, + ($! — Zip*) sin cp! tg <pj = = (S2 p) (1 + PZi ) COS <p2 + (s2 Z2p'^ si n <p2 tg <p2, (11.58)
(Zi zlJs1nT1 = (z2-22Js1n?2, (11.59)
(' + zJ'W = (I+ zj'-b08”’ (11.60)
где Op Zp соответствуют первому импульсу,
а $2, ®2» А? ?2 — второму. Мы получили И уравнений
для И неизвестных: р, q, ш, Zp срр s2, 62, ^2» %•
Решение уравнений (11.50) — (11.60) для общего слу-
чая неизвестно, но оно было получено для ряда частных
случаев, которые и будут рассмотрены в следующих раз-
делах.
11.6. ОПТИМАЛЬНЫЙ ПОВОРОТ ОСИ ОРБИТЫ
Пусть требуется повернуть большую ось орбиты тела
на угол 2а в плоскости орбиты, оставляя неизменными
форму и размеры орбиты. Перед нами задача о переводе
тела с орбиты (Р, Q, —а) на орбиту (Р, Q, а). Эти ор-
биты пересекаются, так что можно осуществить переход
приложением единственного импульса. Этот способ пере-
хода оказывается, однако, всегда нерациональным по
сравнению с оптимальным двухимпульсным способом, и
поэтому мы сконцентрируем внимание на последнем.
11.6]
ОПТИМАЛЬНЫЙ ПОВОРОТ ОСИ ОРБИТЫ
399
Ввиду симметрии, существующей относительно пря-
мой 0 = 0, примем, что промежуточный эллипс перехода
имеет параметры (р,
р, 0) или (р, р, и), т. е.
что его большая ось
располагается вдоль
оси симметрии. Эллипс
перехода пересечет тог-
да граничные элемен-
ты в двух точках сое-
динения /, J (рис. 11.3),
имеющих соответствен-
но полярные коорди-
наты (1/s, 0), (1/s, —0).
Дальнейшее рассмот-
рение свойств сим-
метрии приводит к вы-
воду, что значения Z
в точках соединения,
задаваемые уравне-
нием (11.8), одинаковы
и что если угол ср оп-
ределяет направление
тяги в первой точке
соединения, то угол
тс—ф определяет это
направление во второй
точке.
Уравнения (11.50) — (11.53) оказываются теперь со-
впадающими с уравнениями (11.54) — (11.57), условие
(11.59) удовлетворяется автоматически, и остаются, та-*
ким образом, уравнения:
Рис. 11.3. Переход между одинако-
выми эллиптическими орбитами.
Qcos(9 + a) = s — Р, (11.61)
Qsin(6 + a) = (s — ZP'/2)tg<p, (11.62)
(?cos9 = s—р, (11.63)
^sin9 = (s — Zp'/»)tgcp, (11.64)
(s —p) (1 -|- j cos <p + ($ — Zp'1*) sin<ptg<p = 0, (11.65)
(1+^n#)cos<p = 0. (11.66)
\ 12 ]
400
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
При выводе этих уравнений было предположено, что
эллипс перехода имеет параметры (р, q, 0). Поскольку
эллипс перехода (р, q, тс) совпадает с эллипсом
(р, —q, 0), уравнениями (11.61) — (11.66) допускаются
обе возможности при условии, что величина q может
принимать отрицательные значения. Написанные шесть
уравнений определяют тогда шесть неизвестных: р, р,
s, 0, Z, ф.
Отбрасывая возможность соэф = 0, при которой tg ф
обратился бы в бесконечность, из уравнения (11.66) по-
лучим, что
-Д=-^±1. (11.67)
где
х=у = у (согласно (11.2)]. (11.68)
Подставляя Zip'1* в уравнение (11.65), найдем
АО Л - 1
g (х+1)(х+2)
(11.69)
и поэтому, очевидно, х^>1. Можно обнаружить, что
1д2ф достигает максимума при х= 1 + ]/б =3,449. Та-
ким образом, когда ф — положительный острый угол,
Фтах = 17°38'. Уравнения (11.63) и (11.64) можно запи-
сать в форме
<?cos6 = -L — 1, (11.70)
esin 6= ~*+2 tgср, (11-71)
где е = qlp — эксцентриситет эллипса перехода. Раз-
делив (11.71) на (11.70), получаем также
= (11.72)
Подобно этому находим, что (11.61) и (11.62) экви-
валентны следующим уравнениям:
£ COS (0 + а) =— 1, (11.73)
Еsin (6 -j- а) = у (х+у + 1) tg™ (11.74)
JC
I1.6J ОПТИМАЛЬНЫЙ ПОВОРОТ ОСИ ОРБИТЫ 401
где Е = Q/P — эксцентриситет граничных эллипсов, а
-Р' <1Ь75)
Деление (11.74) на (11.73) дает
tg (9 + «) = tg ?• (П -76)
У л
Зная £ и а, можно из уравнений (11.69) — (11 74) оп-
ределить х, у, е, 9, <р. Уравнение (11.13) определит тогда
характеристическую скорость ч'1гХ маневра:
= y)ysec<p. (11.77)
Форма уравнений (11.69) — (11.74) показывает, что
если при значениях
E = Eq, а = а0 (11.78)
уравнения эти удовлетворяются величинами
х = х0, у = Уо, е = е0, 9 = 90, <р = <р0, (11.79)
то при значениях
Е = Е0, а = к— а0 (11.80)
они удовлетворяются величинами
х — х0, у = у0, е — — е0, 9 = «—90, <р = 2я—<р0. (11.81)
Кроме того, если при
Е = Е0, а = к + а0 (11.82)
уравнения удовлетворяются значениями
х = х0, у = Уо, е — — е0, G = tc-|-0o, <p = <p0, (И-83)
то при
Е = Е0, а = 2к— а0 (11.84)
они удовлетворяются значениями
х = х0, у = у0, е = е0, 9 = 2к —90, <p = 2it—<р0. (11.85)
Далее, если решение (11.79) приводит к положитель-
ному значению X [формула (11.77)] (как это необходимо
26 Дж. Лейтмац
402
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
должно быть), то каждое из решений (11.81), (11.83) и
(11.85) также дает этой величине то же самое положи-
тельное значение. Таким образом, любое решение про-
блемы рассматриваемого нами типа немедленно дает
б) в)
Рис. 11.4. Подобные переходы между одинаковыми эллиптическими
орбитами.
решения трех связанных с нею задач. Четыре случая
(11.78), (11.80), (11 82) и (11.84) вместе с соответствую-
щими орбитами представлены на рис. 11.4, а, б, в, г.
Можно отметить, что случаи а) и в) отличаются лишь
11.6]
ОПТИМАЛЬНЫЙ ПОВОРОТ ОСИ ОРБИТЫ
403
ориентацией и по существу идентичны, как и слу-
чаи б) и г).
Далее, случаи а) и г) отличаются лишь тем, что ор-
бита отлета в первом случае есть орбита прилета во вто-
ром и для перелета используются дополнительные друг
к другу большая и малая дуги одного и того же эллипса;
случаи б) и в) связаны подобным же образом. Из этих
рассуждений следует, что нам необходимо рассматри-
вать лишь случай, когда а — положительный острый
угол, так как если а лежит вне этой области углов, то
решение можно получить из соответствующей конфигу-
рации с острым углом.
Предполагая теперь, что 0%а^^-тг, легче всего
решить уравнения (11.69) — (11.74) следующим косвен-
ным путем.
Возьмем пару значений величин х, у и найдем из
уравнения (11.69) соответствующее значение <р. Это зна-
чение должно быть выбрано так, чтобы величина X, да-
ваемая формулой (11.77), была положительной; такое
условие ограничит ср пределами одного из двух
квадрантов, но оставит знак tg ср неопределенным. Для
каждого из знаков tgcp уравнение (11.72) определит те-
перь значение tgS и отсюда два различных значения О,
отличающихся на к. Из четырех возможных значений 9
только два могут привести к положительному острому
углу а при подстановке в (11.76), и из этих двух лишь
одно определит положительное значение Е из любого из
уравнений (11.73) или (11.74). Все альтернативы теперь
разрешаются и можно написать нужное решение.
Описанная процедура была проделана для большого
числа пар значений х и у, и по полученным данным были
построены семейства кривых х = const, у = const на
aF-плоскости (рис. 11.5). Было обнаружено, что в боль-
шинстве случаев каждой паре значений a, Е соответ-
ствовало две пары значений х, у, для одной из пар у
было меньше единицы, а для другой — больше. Оба эти
типа решений разделены на рис. 11.5 таким образом, что
ось а направлена вправо для решений с у < 1 и влево
для решений с у> 1. Это условие становится удобным
благодаря тому, что ось Е одновременно представляет
26*
404
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
(гл. XI
собой кривую у = 1 и кривые х = const непрерывны
на этой оси. Кривая х = 1 составляется из двух верти-
кальных прямых а = 90° и горизонтальной линии Е = 0.
Кривая у = 0 включает часть линии Е = 1, лежащую в
правом квадранте. Постоянные значения х и у, соответ-
ствующие остальным кривым, отмечены на каждой из
этих кривых. Можно заметить, что в левом квадранте
кривые х = xQ при х0 > 3 пересекают некоторые из кри-
вых х = х0 с Хо < 3. Это означает, что в области, ограни-
ченной кривыми х = 3 (приближенно), х = оо и Е = 1 и
Рис. 11.5. Кривых х= const (сплошные линии) и у = const (пунк-
тирные линии).
отмеченной вертикальной штриховкой, каждая точка
(а, Е) лежит на двух различных кривых х = const и в
силу этого в подобных случаях возможны два решения
в левом квадранте, так что всего оказываются возмож-
ными три решения. Напротив, область, ограниченная
теми же кривыми и отмеченная горизонтальной штри-
ховкой, не пересекается кривыми х = const, и, следова-
тельно, для значений (а, £), соответствующих точкам
этой области, возможным оказывается лишь одно реше-
ние: это решение определяется кривыми, лежащими в
правом квадранте.
11.6]
ОПТИМАЛЬНЫЙ ПОВОРОТ ОСИ ОРБИТЫ
405
Чтобы рассчитать оптимальный переход с помощью
этих кривых, необходимо идентифицировать обе точки,
имеющие координаты (а, £), и затем выяснить, какие
кривые обоих семейств проходят через эти точки, опре-
делив таким образом надлежащие значения х и у. Точ-
ность этого определения можно улучшить путем подста-
новки в уравнения (11.69) — (11.74) и последующей про-
верки; при этом будут определены значения е, 0, ф, X,
Решение, обеспечивающее минимальное значение X,
Рис. 11.6. Кривые характеристической скорости.
представляет собой, разумеется, абсолютно оптималь-
ное решение. Вычисление показывает, что это абсолютно
оптимальное решение всегда будет находиться в правом
квадранте рис. 11.5.
Значения Е были рассчитаны для каждого значения
ХР~'<* в диапазоне 0,1—0,9 для некоторого количества
значений а, и по этим результатам было построено се-
мейство кривых, изображенное на рис. 11.6. Эти кривые
показывают, что для данной эллиптической орбиты рас-
ход топлива, необходимый для поворота ее оси, возра-
стает с ростом угла поворота 2а, достигая максимума
при а = 90°. Для данного значения а расход топлива
максимален при Е = 3/4. Кривые Е = 0,7 и Е = 0,8
406
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
в пределах точности фигуры неразличимы. Было най-
дено, что формула
AP~V, = 2,469(1—£)'А {1—(1—Е)'7’} а(180—а) • 10““, (11.86)
где а измеряется в градусах, находится в согласии сдан-
ными, полученными из рис. 11.6, с точностью до 10%, а
зачастую точность превышает 2%.
Дальнейшие численные данные, относящиеся к за-
даче этого раздела, можно найти в работе Плим-
мера [10].
11.7. ПЕРЕХОД МЕЖДУ ОРБИТАМИ, ОСИ КОТОРЫХ
ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ
Другой частный случай, для которого без труда мож-
но найти решение уравнений (11.50) — (11.60), возникает
тогда, когда оси граничных орбит (pb qu coi) и (р2, ?2, (02)
расположены на одной прямой. Этот случай был изучен
Смитом [9] и Плиммером [10]. Как уже отмечалось, ор-
биты (р, q, со + тс) и (р, —9, ю) одинаковы, и поэтому,
если допускаются отрицательные значения q, то в слу-
чае совпадения осей граничных орбит можно принять
coi = ®2. Тогда, если знаки q\ и 92 одинаковы, оси орбит
будут направлены в одну сторону, а в случае, если знаки
Pi и 92 противоположны, направления осей также будут
противоположными. Кроме того, нам будет удобно вы-
брать направление исходной линии отсчета 0 = 0 так, что
(01 = (02 = 0.
Плиммером [10] было показано, что если одна из гра-
ничных орбит круговая, так что одна из величин 91 или
92 равна нулю, то уравнения (11.50) — (11.60) легко ре-
шаются. Оптимальный эллипс перехода касается тогда
своими двумя вершинами граничных орбит и ось его ле-
жит на одной прямой с осью эллиптической орбиты. Та-
ких возможных орбит перехода всегда оказывается две,
как показано на рис. 11.7, но в обоих случаях импульсы
тяги прикладываются в их вершинах и направлены пер-
пендикулярно к радиусу, проведенному из центра при-
11.7]
ОСИ ОРБИГ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ
407
тяжения, т. е. <рь <р2 принимают значения .0 или тс. В слу-
чае, если обе граничные орбиты суть эллипсы, уравнения
(11.50) — (11.60) еще ре были непосредственно решены.
Ясно, однако, что и в этом случае можно найти два эл-
липса перехода, касающиеся граничных в обеих своих
вершинах. Предыдущий результат делает вероятным
то, что оптимальный переход будет получен на одном из
Рис. 11.7. Переход между круговой и эллиптической
орбитами.
этих эллипсов путем приложения двух импульсов в на-
правлении, перпендикулярном к радиусу, проведенному
из центра притяжения. В соответствии с этим мы будем
искать такие решения уравнений (11.50) — (11.60), для
которых фь ф2 равны 0 или тс. Подчеркнем, что в усло-
виях, рассматриваемых в этом разделе, любое другое
решение (если оно существует) приведет к большему
значению характеристической скорости.
408
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
При (01 = (02 = 0 и ф1 = ф2 = 0 или тс уравнения
(11.50) — (11.60) сводятся к системе
qx cos 9 = 5,— рх, 71sin01 = O,
q cos (6, — й>) = — р, qcos (62 — <b) = s2— р, q sin (6, —«>) = 0, q sin (92 — <b) = 0, (11.87)
q<i cos 62 — s2 —р2, <72sin02 —0,
$i Н~ р । 1 г,//» 1 ±№f+l). (11.88)
(l+5,)(si = - ± (1 +^-)($2_ p), (11.89)
причем в (11.88) и (11.89) берется положительный знак,
если ф1 = фг, и отрицательный знак в противном случае.
Рассмотрение уравнений, написанных справа в (11.87),
показывает, что 0Ь 02, (о являются все целыми кратны-
ми тс. Если допустимы отрицательные значения q, то без
потери общности можно принять (о = 0. Если 81 = 02 = О
(или тс), то эллипс перехода вырождается в прямую ли-
нию, совпадающую с осями граничных эллипсов. Чтобы
перейти на эту орбиту с помощью импульса, для кото-
рого ф1 = 0 или тс, необходимо будет остановить ракету;
ракета станет тогда свободно падать по направлению к
центру притяжения, и в тот момент, когда ее траектория
пересечет второй граничный эллипс, можно приложить
второй импульс для вывода ее на нужную орбиту. Этот
импульс, однако, не будет направлен перпендикулярно
к радиусу, проведенному из центра притяжения. Оказы-
вается, что 01 =£02 и что следует рассмотреть всего два
случая, именно: случай I, 61 = 0, 02 = тс и случай //,
01 = л, 02 = 0. Подставляя выражения для 0Ь 02, (о в
уравнения, написанные слева в (11.87), найдем:
Случай I
si= Р\ + <71» S2 — Рч #2»
P=4(a + a + 7i—7г).
Я — (А — А “Г 71 + 7г)'
п.Л
ОСИ ОРБИТ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ
409
Случаи 11
~Р\ = р2 + ^2»
Р=^Рх+Р2 — Ях+<11)'
Я = Р\+ P<i + + q<iY
После того, как уравнения (11.87) удовлетворены,
оставшимся условиям (11.88) и (11.89) можно удовле-
творить путем надлежащего выбора Zb Z2; эти условия
в действительности и служат для определения указан-
ных величин; конкретные значения их не представляют
здесь интереса.
Уравнение (11.19) определяет теперь характеристиче-
скую скорость перехода. Обозначая ее через ^2Х и
полагая
а = b=p2-q2, |
« =Pi + <7i. b'=p2 + q2, )
найдем, что в случае I
+ (»«)
а в случае II
X = Х2 = /2 а 1--—г.-------L-iT I +
2 v I (a + a')Vj (аЧ-6')/а1
+ У 2 b' I--—т.------—ir-1; (11.92)
l(*+H/2 (a + H /2 I
в этих выражениях a, b, a', b' представляют собой вели-
чины, обратные расстояниям от центра притяжения до
четырех вершин граничных эллипсов.
Предположим сначала, что оси граничных эллипсов
направлены одинаково. Тогда имеются две возможности:
а) орбиты пересекаются или б) орбиты не пересекаются.
Эти возможные варианты иллюстрируются на рис. 11.8.
Начальную орбиту будем обозначать А, конечную — В;
410
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ (гл. XI
перемена ролями обеих орбит или одновременная пере-
мена направлений их осей представляют собой тривиаль-
ные видоизменения, которые не ведут ни к каким оче-
видным затруднениям. Орбиты перехода, соответствую-
щие решениям в случаях I и II, также обозначены на
рисунке.
а)
Рис. 11.8. Эллипсы с осями одного
направления.
На рис. 11.8, а, как видно, а > &, а' < а < а',
b < Ь'. Используя эти неравенства для выяснения знаков
разностей в уравнениях (11.91) и (11.92), найдем путем
вычитания, что
(Хх-Х2) = (a'^b)'h-(a'+a)'h-(b'+b)'h+(b'^a),h =
=/(a', a, b) —ftb', а, Ь), (11.93)
где
/(х, а, Ь) = (х + Ь)',г - (х + а)7’. (11.94)
11.7]
ОСИ ОРБИТ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ
411
В приложении в конце этой главы показано, что при
а> b f является возрастающей функцией от х, В соот-
ветствии с этим из (11.93) следует, что, поскольку а'<Ь\
справедливо неравенство Х\— Х2 < 0. Таким образом,
Xi<%2 и орбита перехода / на рис. 11,8, а более эко-
номична.
Рис. 11.9. График функции g(xt a, b).
Для рис. 11.8,6 справедливы следующие неравенства:
а > а' > а < а', b < Ь'. Из (11.91) и (11.92) теперь
следует, что
1 /ул ул \Ь CL CL
ТТ ~ Л2) - («'+*)/. “ («'+«)•/. -
О1-95)
где
(1Ь96>
В приложении показано также, что при а > Ь график
функции g(x, а, Ь) имеет при х^-b форму, изображен-
ную на рис. 11.9, т. е. g сначала монотонно увеличивается,
когда х возрастает до значения £, а затем монотонно
412
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
падает, так что при х->оо g->0. Ясно также, что
g(a, a, b) = g(b, a, b) = G. Из рис. 11.9 следует теперь,
что, поскольку а'>а и а'>Ь\ имеет место неравенство
g(a', a, b)<g(b', а, Ь). (11.97)
Таким образом, из ( 11.95) выводим, что Xt — Х2 < О,
и орбита перехода I
снова оказывается бо-
лее экономичной.
Предположим те-
перь, что оси гранич-
ных эллипсов направ-
лены в разные сторо-
ны. Рассмотрим случаи
наличия и отсутствия
пересечений, представ-
ленные соответствен-
но на рис. 11.10, а и
11.10,6. Другие воз-
можности не отличают-
ся существенно от этих.
Для рис. 11.10, а
справедливы неравен-
ства а>Ь, а'<Ь', а>а\
b<b' и уравнение
(11.93) получается, как
и прежде. Неравенство
Xi < Х2 можно полу-
чить здесь так же,
как и выше. Поэтому
орбита перехода /
снова оказывается оп-
тимальной.
Для рис. 11.10,6
имеем неравенства
а > &, а' > Ь', а> а',
b <Ь' и в соответствии с этим справедливо урав-
нение (11.95). В этом случае, однако, числа а' и Ь' оба
лежат в интервале (а, &), и из рис. 11.9 следует, что мо-
жет быть верным любое из неравенств Х\ < Х2, Х} > Х2,
смотря по тому, каковы значения величин а' и Ь'. В этом
11.8]
ПРИЛОЖЕНИЕ
413
случае не представляется возможным дать простой кри-
терий, согласно которому можно было бы выбрать наи-
меньшее из чисел Хь Х2, и в каждом частном случае сле-
дует решать этот вопрос путем подстановки численных
значений параметров в уравнение (11.95).
Результаты этого раздела можно суммировать сле-
дующим образом. Если оси двух орбит располагаются
вдоль одной прямой и орбиты либо пересекаются, либо
оси их направлены в одну сторону, то абсолютно опти-
мальной является орбита перехода, касающаяся обеих
граничных орбит в вершине каждой из них и проходя-
щая через вершину, наиболее удаленную от центра при-
тяжения. В тех случаях, когда оси граничных орбит на-
правлены в противоположные стороны и эти орбиты не
пересекаются, оптимальной орбитой перехода может
быть любой из двух эллипсов, касающихся граничных
орбит в их вершинах; выбор между этими эллипсами оп-
ределяется относительными размерами граничных орбит.
11.8. ПРИЛОЖЕНИЕ
11.81. Функция f (х, а, Ь). Эта функция определена
уравнением
f(x, а, Ь) = (х + 5)’/2 — (х + а)'/а. (11.98)
Дифференцируя его по х, найдем, что
# = 4 (X + b)-'h -1 (х+a)~'h. (11.99)
Отсюда следует, что если а > Ь и х — положительное
число, то df/dx > 0 и, следовательно, f — возрастающая
функция от х.
11.82. Функция g (х, а, 6). Эта функция определена
уравнением
g(х, a, b) = x~bil-------• (11 • 100)
6V ’ (x + bV* (х + а)/а
Будем предполагать, что а и b — заданные фиксиро-
ванные числа, такие, что а > b > 0, и будем сокращенно
писать g(x) вместо g{x, а, Ь).
414
ПЕРЕХОД МЕЖДУ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ
[гл. XI
Тогда g(a) = g(b), и поэтому из теоремы Ролля сле-
дует, что можно найти такое £, что b < £ < а и g'(&) = 0.
Далее,
х —р 3ft х За
2(х+Ь)’1г ~ 2(х + а),/г ’
(11.101)
Обозначив й(х) = x'^g'(x) и дифференцируя, получим
следующий результат:
К (х) = 3,?(&~х),, Ч—Зь (х~д),; • (11.102)
v ’ 4хА (x + ft)’/’ 4х'>(* + «)/’
Отсюда при условии &<ix<Ca найдем, что h'(х) < 0,
т. е. й(х) убывает. Но й(|) = 0, и, следовательно,
h (х) > 0, если Ь х <£, и й(х) <0, если £ < х а. От-
сюда немедленно следует, что
g,(x)>0 при 6<х<5, 1
g' (х) < 0 при 5 < х < a. J
(11.103)
Пусть теперь х фиксировано, а а переменно; положим
4<a’=^- <"л04>
Дифференцируя по а, получим
и, следовательно, k'(a) > 0, если а <х. Отсюда следует,
что для таких a k(a)—возрастающая функция, и, та-
ким образом, если Ь < а < х, то имеем неравенство
k(b)<k(a).
Из (11.101) теперь вытекает, что
g'(x) = l{A(&)-^(a)}<0,
(11.106)
(11.107)
если х > а.
Легко, наконец, доказать, что при х->оо g(x)->0.
Объединяя этот результат с неравенствами (11.103) и
(11.107), сразу же убедимся в том, что график функции
g(x, а, Ь) имеет форму, показанную на рис. 11.9.
ЛИТЕРАТУРА
415
ЛИТЕРАТУРА
1. D. F. Lawden, Interplanetary Rocket Trajectories, Advances in
Space Sci. I, I, Academic Press, New York, 1959.
2. W. Hohmann, Die Erreichbarkeit der Himmelskorper, Olden-
bourg, Munich, 1925.
3. D. F. L a w d e n, Optimal transfer via tangential ellipses, J. Brit.
Interplanet. Soc. II, 278 (1952).
4. D. F. L a w d e n, Inter-orbital transfer of a rocket, J. Brit Inter-
planet. Soc. II, 321 (1952).
5. D. F. L a w d e n, The determination of minimal orbits, J. Brit
Interplanet. Soc. II, 216 (1952).
6. D. F. L a w d e n, Minimal rocket trajectories, J. Am. Rocket Soc.
23, 360 (1953).
7. D. F. L a w d e n, Fundamentals of space navigation, J. Brit. In-
terplanet. Soc. 13, 87 (1954).
8. R. S. Lon g, Transfer between non-coplanar elliptical orbits,
Astronaut. Acta 6, 167 (1960).
9. G. C. Smith, The calculation of minimal orbits, Astronaut.
Acta 5, 253 (1959).
10. R. N. A. P 1 i m m e r, Fuel requirements for inter-orbital transfer
of a rocket, Proc. 10th Intern. Astronaut. Congr., London, 1959
(1960).
11. L. G. Vargo, Optimal transfer between two coplanar terminals
in a gravitational field, Am. Astronaut. Soc. Preprint No. 58-20
(1958).
12. H. Mu nick, R. McGill and G. E. Taylor, Minimization of
characteristic velocity for two-impulse orbital transfer, ARS Jour-
nal 30, 638 (1960).
13. J. M. Horne r, Optimum orbital transfer, Personal communica-
tion from ABMA, Huntsville, Alabama (1960).
14. T. N. Edelbaum, Some extensions of the Hohmann transfer
maneuver, ARS Journal 29, 864 (1959).
15. R. F. H о e 1 к e r and R. Silber, The bi-elliptical transfer bet-
ween circular coplanar orbits, DA Tech. Memo. No. 2-59, Army
Ballistic Missile Agency (1959).
16 L. Rider, Ascent from inner circular to outer coplanar elliptic
orbits, ARS Journal 30, 254 (1960).
ГЛАВА ХП
ОПТИМАЛЬНОЕ РАСПОЛОЖЕНИЕ
КОРРЕКТИРУЮЩИХ ТЯГОВЫХ УСИЛИЙ
В МЕЖПЛАНЕТНОЙ НАВИГАЦИИ
Рис. 12.1. Межпланетная траектория.
12.1. ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
Пусть космический корабль совершает свободный по-
лет (т. е. полет без участия двигателей), следуя от Зем-
ли к некоторой планете, например к Марсу. За исклю-
чением непосредственной окрестности Земли и планеты,
траектория его представляет собой в основном гелио-
центрический эллипс. Предположим, что орбиты Земли и
планеты и эллипс пе-
рехода компланарны.
Действительная траек-
тория, не будучи скор-
ректирована за неко-
торой точкой Рп, прой-
дет мимо планеты на-
значения на прицель-
ном расстоянии Dn-ъ
которому можно при-
писать знак, например,
±, смотря по тому,
пройдет корабль спра-
ва или слева от плане-
ты (рис. 12.1). Пусть в
точке Рп на траектории перехода прикладывается коррек-
тирующий импульс скорости Разумеется, в действи-
тельности это связано с приложением конечной тяги в
течение промежутка времени значительно меньшего, чем
продолжительность полета. Величина поправки скорости
рассчитывается следующим образом: 1) делается
оценка Dn-i величины £>п-ь основанная на измерениях
12.1] ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ 417
(вероятно, угловых), определяющих положения корабля
в прошлом и в настоящем; 2) вычисляется (по линеа-
ризованной теории ошибок):
^-(t = — fi (12.1)
Оф \ п/ п П—1 v '
Здесь следует отметить, что ошибки при оценке Dn-i
могут включать систематические ошибки при последова-
тельном вычислении траектории, вызванные, например,
слишком сильным упрощением процесса вычислений.
Нас, однако, главным образом будут интересовать слу-
чайные ошибки в оценке Дп-ь происходящие из-за слу-
чайных ошибок измерений.
Далее, «эффективность управления» dD(t)/dv, разу-
меется, падает до нуля по мере движения корабля от
Земли к планете. Следовательно, если оценка Dn_\ была
произведена правильно, то оптимальное требование крае-
ходу топлива для коррекции скорости заключается в том,
чтобы эта коррекция была осуществлена в возможно
меньшее время.
В среднем, однако, Dn-i оценивается неправильно.
Это означает, что и после коррекции в точке Рп между
направлением полета и целью еще остается прицельное
расстояние Dni которое, возможно, должно быть умень-
шено путем дальнейшей коррекции. Это (возможно,
уменьшенное) расстояние равно
+ (12.2)
в написанном выражении последний член обязан своим
происхождением возможной ошибке Vn при осуществле-
нии коррекции скорости. Более того, можно ожидать,
что ошибка в оценке Оп_ь подобно эффективности упра-
вления, падает до нуля при приближении к планете на-
значения.
Возникающая перед нами задача заключается в та-
ком выборе точек коррекции А, Р2, ..., Pn, чтобы
в некотором среднем смысле получить в конечной
точке траектории требуемую точность попадания при
минимальной величине полного изменения скорости и,
27 Дж. Лейтман
418
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
(гл. ХП
следовательно, при минимуме расхода топлива на со-
здание корректирующих тяговых усилий.
Задача, рассматривавшаяся нами до сих пор, двумер-
на. В действительности же она трехмерна, даже в слу-
чае, если «номинальная» траектория перехода компла-
нарна с орбитой планеты назначения, поскольку необхо-
димо считаться с «выводящей из плоскости» составляю-
щей прицельного расстояния, связанной с лежащими вне
плоскости составляющими векторов положения и ско-
рости. Одномерная задача о корректировании выхода из
плоскости орбиты не связана с задачей коррекции на
плоскости, за исключением того случая, когда оба вида
коррекции производятся одновременно, так что доби-
ваются минимума выражения
N
2И-
Возвращаясь к нашей двумерной задаче, отметим, что
поправка к скорости не определяется уравнением
(12.1) однозначно. В действительности мы разрешаем
альтернативу тем, что минимизируем величину каждой
поправки к скорости | - Легко видеть, что это остав-
ляет возможность выбора вектора параллельным
или антипараллельным вектору dD(tn)ld<o. в зависимости
от знака Рл-ь Отсюда следует теперь, что
<1М>
Вектор эффективности управления dD(t)ldv должен
вычисляться вдоль номинальной точной орбиты пере-
хода. Его величина и направление показаны на рис. 12.2
в случае перелета по Гоману от Земли к Марсу, т. е. при
180-градусном перелете по эллипсу, касающемуся орбит
Земли и Марса, которые считаются компланарными ге-
лиоцентрическими окружностями. Собственные гравита-
ционные поля Земли и Марса при расчете dD(t)ldv не
принимались во внимание. Абсцисса на рис. 12.2, так
называемая средняя аномалия, постоянно растет со вре-
менем от 0 до 180°. При этом оказывается, что величина
эффективности \dD(t)Jdv\ стремится со временем
12.1J
ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
419
к нулю в основном по линейному закону, тогда как на-
клон вектора dD(t)ldv, измеряемый от «поперечного»
направления, перпендикулярного к радиусу, проведен-
ному от Солнца, возрастает со временем в основном ли-
нейно от 0 до 90°. Таким образом, как можно было бы
Обозначения:
-у 90*
- 60*
- 70*
- 60*
а
- 50*
- 70*
- 30*
- 20*
- 10*
- О*
Рис. 12.2. Программа управления для перелета по Гоману
______________е)2 и’/2
В = ----______'
дР (О
dv
предвидеть, первоначальная коррекция производится в
направлении вперед или назад вдоль орбиты перехода,
тогда как в конце коррекция производится в направле-
нии, перпендикулярном к движению.
Уравнение (12.3), в котором п увеличено на 1, можно
рассматривать в совокупности с (12.2), чтобы выразить
|t#+i| через ошибки в точках Рп и Рп+х- В частности,
27*
420
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. XII
если ошибками при осуществлении коррекций v' прене-
бречь, то получим
I I = тлтает I - °.) ! (12.4)
Это показывает, например, что если последнее при-
цельное расстояние оценено правильно (Z5n = Z)n), то по-
правка к скорости зависит лишь от неточности предпо-
следнего определения прицельного расстояния незави-
симо от числа произведенных ранее коррекций. С другой
стороны, если бы предпоследняя оценка величины при-
цельного расстояния была правильной, то новая по-
правка была бы связана только с неточностью новой
оценки величины прицельного расстояния, равного на
самом деле нулю.
Если отвлечься от каких-либо систематических оши-
бок в оценках D, то можно принять, что разности
(D — D) распределены нормально с нулевым средним
значением и значения их дисперсий и ковариаций могут
быть получены непосредственно по значениям дисперсий,
принятым при различных независимых угловых измере-
ниях, ошибки которых предполагаются распределенными
нормально, а систематические ошибки отсутствуют.
Величина поправки к составляющей скорости 1| ,
лежащей в плоскости орбиты, выражается, согласно
(12.4), как абсолютное значение нормальной случайной
переменной с нулевым средним значением и вычисляе-
мой дисперсией.
Можно воспользоваться формулой (12.2) для опреде-
ления момента tN последней коррекции такого, что лю-
бой предшествующий ему момент коррекции привел бы
к ожидаемой ошибке Е {| DN |} в прицельном расстоянии
сверх некоторой допустимой неточности в конце траекто-
рии. Можно предположить, что ошибка «старта» Do пе-
ред первой коррекцией в среднем значительно превы-
шает по абсолютной величине допустимую ошибку в кон-
це полета.
Задавшись моментом tN и среднеквадратичной ошиб-
кой старта oDo, мы желаем определить последователь-
ность моментов 6, t2, ... , tN (число N заранее не из-
12.1]
ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
421
вестно) таким образом, чтобы, скажем, в 90% случаев
сумма
2 1Ч-1
была возможно меньшей. Эту величину, однако, трудно
вычислить из-за корреляции между последовательно вхо-
дящими в нее слагаемыми. Более приспособлен для вы-
числения тесно связанный с высказанным критерий ми-
нимума суммы
w
•s„=2(|2'5>
При этом можно воспользоваться тем фактом, что
ожидаемая величина Е{|х|} нормальной случайной
переменной х с равным нулю средним значением и дис-
Персией как раз равна ]/2/к.
В трехмерной задаче дело обстоит следующим обра*
зом. Если обозначить через D' составляющую прицель-*
ного расстояния, направленную вовне плоскости орбиты,
и взять направление оси z перпендикулярным к плос-
кости движения, то в точке Рп+\ поправка к составляю-
щей скорости, выводящей из плоскости, будет равна
^'п-Р'п
dD' ^п+\)^г
_ dD' (*п)/дг ( бп-1 - D'n-\ _ -z’
dD' (tn+i)/di I dD'(tn)/di
где учтены малые ошибки корректирования i'. Поправка
к составляющей скорости, лежащей в плоскости движе-
ния, становится равной
УИ.У + (уй,)- =|{
____дР(*п)/ду f ^/?-1 — Оп-1 ..О I. /1 О 71
dD(tn^)/dv\ dD(tn)/dv *41’
здесь dD(t)/dv обозначает /[д£> (/)Ж|2+[<?£> (/)/ду]2, а
w' обозначает составляющую ошибки корректирования^'.
422
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИИ
[гл. XII
направленную вдоль вектора (dD/dx, dD/dy), лежа-
щего в плоскости орбиты.
Поскольку величина Илг)’+(«, )’+(4w не
имеет теперь простого статистического распределения,
несмотря на нормальность ошибок корректирования, а
также ошибок измерений, мы заменяем критерий (12.5)
близким критерием, а именно требованием минимизации
суммы
S„= 2 И (В [p«r+|у,.вП',,)2+(В {,4'11)’ (12.8)
л= 1
которая более легко поддается вычислению.
Для осуществления минимизации без помощи
цифровой вычислительной машины мы должны будем
сделать несколько упрощающих предположений относи-
тельно оценок D прицельного расстояния. Рассмотрим
два примера. В первом примере, где число измерений
равно двум, предположим, что оценка Dn_\ основана на
измерениях, произведенных сравнительно недалеко от
точки Рп, так что измерения дают значения координат и
скоростей в Рп с разбросом по скоростям, оказывающим
значительно большее влияние на прицельное расстояние,
нежели разброс по координатам. В этом случае
__ . ULS / . X
(12-9)
где представляет собой среднеквадратичную неточ-
ность измерения составляющей скорости в направлении
5D(fn)/51F; эта неточность, как и среднеквадратичное
значение о' для переменной будет далее предпола-
гаться не зависящей от времени.
Сумма Sn теперь упрощается и принимает вид
<+»'!+рр<^ +
N_______
+ + /!+[
л=2
дР ]2
dD(tn)!dv J
. (12.10)
12.1]
ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
423
В разделе 12.2 показывается, что для достаточно
большого значения среднеквадратичной ошибки старта,
точнее, при °Do > 3 °'2 dD (0)/dv, оптимальный
выбор моментов коррекции tn должен быть таким, что
коррекции (пример 1).
/1 = 0 (т. е. выбор должен осуществляться возможно
быстрее) и
dD(tn_i)/dv .
dD(,t„)/dv —р’
(12.11)
последнее отношение не зависит от п, а оптимальное
число N приближенно определяется условием р = 3.
В случае перелета по Гоману от Земли до Марса при-
ближенно линейный характер dD/dv как функции вре-
мени ведет к следующему грубому описанию оптималь-
ного расположения корректирующих импульсов: первая
коррекция производится возможно скорее; после каждой
коррекции корабль проходит две трети пути до планеты
назначения до наступления следующей коррекции (т. е.
две трети времени полета от точки коррекции по напра-
влению к планете никакой коррекции не производится).
Как показывает рис. 12.3, 5^ как функция от р не очень
424 РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ [гл. XII
Рис. 12.4. Траектория
вблизи планеты.
чувствительна к изменениям шага коррекции в окрест-
ности оптимального значения, равного 3.
«Каскадное» распределение коррекций удивительно
эффективно с точки зрения уменьшения ошибок. Пусть
точность в конце траектории ограничена критерием (до-
статочно строгим), состоящим в том, чтобы при стремле-
нии отклониться от планеты в
направлении «другой асимптоты»
(т. е., скажем, к другой планете)
наша ошибка в определении по-
следовательных векторов скоро-
сти не превышала бы в среднем
неточность в скорости, набегаю-
щую в точках коррекции на пути
корабля к планете. Из уравне-
ний (12.2) и (12.9) следует
Е(|РЛГ|) =
= + (^)- (12.12)
Расстояние D от центра пла-
неты до асимптоты сближения
(рис. 12.4), угол поворота ф
(рассматриваемый относительно
планеты) и минимальное рассто-
яние до центра планеты /? связа-
ны с эксцентриситетом Ei и величиной полуоси а\ ги-
перболы— траектории полета около планеты — следую-
щим образом:
D = aAV^ — 1,
R = d\ (ei —!)•
Здесь величина полуоси а\ связана с относительной ско-
ростью приближения к планете vR (измеренной до того,
как она начинает изменяться гравитационным полем
планеты) соотношением
12.1]
ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
425
где G — универсальная постоянная гравитации, ат —
масса планеты.
Таким образом, ошибка в векторе скорости ухода
вдоль другой асимптоты равна
II = 'Vr I ДФ I = ' "
= 2М°лг1/а1) _ (2^/Gm) I Dn I
[1 + (/?/а)Р - • (12.13)
Согласно уравнениям (12.10) и (12.11), при р = 3
ошибка в оценке скорости, накопившаяся от ошибок
предшествующих коррекций, составляла
Е(|Д®|) = 3,2|/'4 У
(12.14)
Объединяя уравнения (12.12) — (12.14),
следующий критерий для выбора /n:
d£) Gm f Rvo\2
—(t (1 _]—* .
dv Vp \ Gm /
/\ ' *
получаем
(12.15)
В случае перелета по Гоману от Земли к Марсу
= 8800 фт!сек, а эксцентриситет 8 орбиты перехода
примерно равен 0,21.
Из рис. 12.2 видно, однако, что для значений вре-
мени /, близких к времени tf достижения планеты,
дй 2 (tf — t)
0,89о>^(/) = Ва;
где со — средняя гелиоцентрическая угловая скорость на
траектории, а Т — полное время полета, равное 259 дням.
Поскольку а>Т=л, из уравнения (12.15) находим, что
vr (h ~ *лг) _
R
Gm (
0,7к^-( 14
VR* \
Gm /
Наиболее жестким, разумеется, оказывается требова-
ние к наименьшей величине R допустимого расстояния
приближения к планете, которое будем считать равным
426
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИИ
[гл. ХП
2500 милям. Последняя коррекция производится, таким
образом, на расстоянии приблизительно 23 000 миль от
центра Марса, т. е. за 33А часа до посадки.
Общее число корректирующих импульсов тяги при
полете на Марс дается соотношением
численные результаты можно получить, пользуясь
рис. 12.2. Оказывается, что Af = 8.
Слабым местом в первом примере является предполо-
жение о том, что оценка величины Dn_{ делается на ос-
нове наблюдений в непосредственной окрестности точки
Рис. 12.5. Определение положения с помощью внешнего угла.
Рп. Разумеется, более оправдано предположение, что ве-
личина Dn-i оценивается значительно ранее точки Рп-ъ
если вообще не в течение всего времени полета, начиная
со старта; в последнем случае при оценке следует прини-
мать во внимание всю совокупность произведенных кор-
рекций.
Чтобы проверить, каким образом это обстоятельство
могло бы повлиять на оптимальное расположение им-
пульсов, рассмотрим в качестве второго примера не-
сколько отличную «одномерную» ситуацию (рис. 12.5).
Пусть корабль совершает номинально прямолинейное
движение из Л в В с постоянной скоростью V, но дей-
ствительное его положение в момент i характеризуется
малым боковым сдвигом z в заданной плоскости перпен-
дикулярно к АВ.
Предположим сначала, что в любой момент попереч-
ная координата корабля z измеряется с помощью опре-
деления внешнего угла 0, стандартное отклонение кото-
рого а предполагается не зависящим от времени. Тогда
12.1]
ПОСТАНОВКА ЗАДАЧИ И ОБЗОР РЕЗУЛЬТАТОВ
427
легко показать, что стандартное отклонение определяе-
мого бокового смещения z равно
а2= V7(l —/)оэ. (12.16)
Эта величина максимальна на половине пути между А и
В. Перпендикулярно к АВ следует приложить соответст-
вующие корректирующие импульсы тяги. В разделе 12.3
показано, что если оценка прицельного расстояния
всегда производится по данным измерений в близко рас-
положенных одна от другой точках вплоть до Д, то опти-
мальный выбор точек коррекции tn таков, что
1.~V ->2,62 при /„->!. (12.17)
1 1п
Рис. 12.6, аналогичный рис. 12.3, снова показывает,
что ожидаемое для целей коррекции потребление топ-
лива не особенно чувствительно к изменениям шага
коррекции около оптимального значения, равного на
этот раз 2,62. На рис. 12.6 показана также кривая,
428
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. ХП
изображающая относительный расход топлива, рассчи-
танный при постоянном значении шага коррекции р для
случая, когда прицельное расстояние оценивается лишь
по Данным измерений, производимых в близко располо-
женных точках с момента последней коррекции (см. раз-
дел 12.5).
Здесь интересно отметить, что из-за близости друг к
другу последних точек коррекции и несмотря на приня-
тое предположение об улучшении измерений по мере
приближения к В оказывается ощутимым недостаток ин-
формации о положении корабля до предшествующего
корректирования.
Интересно также и то, что оптимальное расположе-
ние в этом случае несущественно отличается от распо-
ложения в первом примере.
12.2. ИССЛЕДОВАНИЕ ОПТИМАЛЬНОГО РАСПОЛОЖЕНИЯ
НА ПРИМЕРЕ 1
Обозначим величину
dD (tn)/dv
dD (0)/dv
через тл, а величину
(<£ + И (W*
через К2- Задача заключается в определении числа N
и последовательности > т2 > ... > xN при заданных
и таким образом, чтобы выражение
/ ^2” N / "j
Ъ = 1+—+У 1/ 1+-^1 (12.18)
было минимально Обозначив хп_ Х1 л=2 Г хп 1/хп через рп (п = 2, N), напишем i/i + 5 + + Г 1 л=2
12.2]
ИССЛЕДОВАНИЕ НА ПРИМЕРЕ 1
429
где
N N
ЦрЯ = Т-< ИЛИ 1пр„ = 1ПТ1 — In Туу.
л=2~ N п=2
N
Дифференцирование функции —X 2 In Рл» где X —
л = 2
множитель Лагранжа, показывает, что при заданных ti
и in Fi может быть минимальным, если только
(12.19)
С другой стороны, минимизация F{ в
ношению к ti (< 1) для фиксированных
требует, чтобы P2 = ti/t2 = /</ti, если при
противном случае следует взять ti = 1.
Таким образом,
(12.18) по от-
Тз, ... , tN
ЭТОМ Ti 1; в
(12-20)
и Fi становится функцией только от и определяется
выражением
/1 +№ +(N -1) {1
если А/— 1 >ln (l/t^/ln К и Т] = 1;
если W — 1 < In (1/x^/ln К-
Рассматривая сначала вторую форму функции Fj в
уравнении (12.21), считая W непрерывно меняющейся
переменной и снова вводя отношение
P=/<V„T-V„
найдем
In Р ’
откуда
1пЛ = 1п1п(^-) —In In Р +1 In (1 + р2).
\ nJ 1
430
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. XII
Это выражение, рассматриваемое как функция непре-
рывной переменной р, как легко видеть, минимально
при
1пр=Ц-у ,
т. е. при
Р = 3;
в этом случае
N = '"('У и 2,9 Inf—). (12.22)
In 3 \vn/
Второе слагаемое в первой форме выражения (12.21)
для Fi можно рассмотреть подобным же образом, просто
путем замены К на 1 и N на N— 1. Таким образом, со-
храняется связь In р= 1 + 1/р2, тогда как N и F\ даются
теперь соотношениями вида
W=1
, ln(V\y)
In 3
И Л,= /1+^+2,91п( — V
\ZN /
(12.23)
Сравнение формул (12.22) и (12.23) с оценками
(12.21) для диапазона изменения величины N—1 пока-
зывает, что первая и вторая формы в (12.21) отвечают
соответственно неравенствам К > 3 и К < 3.
12.3. ИССЛЕДОВАНИЕ ОПТИМАЛЬНОГО РАСПОЛОЖЕНИЯ
НА ПРИМЕРЕ 2
Сведения, которыми мы располагаем относительно
величины Z), можно сформулировать следующим обра-
зом'. Оценка прицельного расстояния Ьп_\ в момент tn
дается соотношением
dD . dD * /-«г»
(,2-24>
где zn и z~ представляют собой оценки координаты и
скорости, основанные на измеренных значениях z коор-
динат z(/) в различные моменты /, предшествующие /п.
12.3]
ИССЛЕДОВАНИЕ НА ПРИМЕРЕ 2
431
Более того, собственно z(t)
есть линейная функция zn
z (z) -= Zn + 'г« +ь-(/)- ° 2-25)
Здесь
дг (0 _ .
дгп
bn(t)= 3
Ч<‘< ‘п
(12.26)
Оценки zn и z“ получаются аппроксимацией наблю-
даемой величины z(/) выражением (12.25) по методу
наименьших квадратов, т. е. минимизацией суммы
к+мо- г «>)Г
(12.27)
где знак S обозначает суммирование по всем предше-
l<tn
ствующим tn моментам наблюдения. Если принять, что
измерения z(t) независимы, то из соображений статис-
тического характера (см. раздел 12.4) следует, что
2 X 2-матрица ковариаций для оценок zn и z~ как раз
обратна следующей «матрице сведений»:
|)лЛ=
(12.28)
432
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. XII
Дисперсия оценки, заданной уравнением
равна, таким образом,
(12.24),
+2| м 'X' +1л,<"’ ь' (^Т
(12.29)
Здесь следует считать, что
Для вычисления элементов матрицы (12.28) восполь-
зуемся формулами (12.26) и, считая измерения произве-
денными через равные промежутки времени, заменим
сумму 2 величиной
'п
Хо f dt, (12.31)
О
где Хо — «цена наблюдения», а уравнение (12.16)—ра-
венством =х (1 — /), где * = Va0, справедливым
около значения /=1.
Таким образом, получаем
И(Л,И = 4
tn-In 14т tnP-tn)-2(1-Uln^b
1 Ln 1
Обратная матрица имеет вид
(12.32)
— Л« + 1п 1 /
tn
(12.33)
12.3]
ИССЛЕДОВАНИЕ НА ПРИМЕРЕ 2
433
Подстановка (12.30) и (12.23) в (12.29) дает
_2 (*2Ао) ^п.
(12.34)
Для вычисления величин Е {| j |} по уравнению
(12.6), в котором опущены ошибки осуществления кор-
рекции /, нам требуется не только значение дисперсии
£)п_1 (12.34), но и ковариация величин Dn-i и Ьп.
В разделе 12.4 показывается, что эта ковариация равна
Е ((£„-!-Dn_x) (Dn—Dn)} = Л . (12.35)
и п
Уравнения (12.6) и (12.30) дают теперь
1/Л
Гг^,°- (12-36>
Для минимизации выражения
мы сделаем в (12.34) дальнейшее приближение, справед-
ливое вблизи точки /л=1:
V2
°2Б (1-Q. (12.37)
Dn-1 Л°
Подстановка (12.37) в (12.36) приводит к следую-
щему выражению для полной поправки к скорости:
N N
f-t’- (12'38)
С целью минимизации выражения (12.38) для Sn
прежде всего найдем дифференцированием, что при фик-
сированных значениях /n-i и /п+1 оптимальный момент
tn должен удовлетворять условию
2?в-1 _ p’A-i
/Ря-1 /р„+1-1
(12.39)
где рп и рп+1 обозначают (1 — /п—i)/(l — tn)
28 Дж. Лейтман
434
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. ХП
и (1 — — fn+i), так что произведение pnpn+i
временно считается фиксированным. Таким образом, из
(12.39) получаем два значения рл и, следовательно,
Рис. 12.7. Оптимальное соотношение между последовательными
значениями шага* коррекции.
рпрп+ь соответствующие_любым pn+i > 2 и любым рл+1,
лежащим между 1 и У 5 —1. Однако значение суммы
I V^n tn-1
1-/л+1 1-/л
при /л, совпадающем с tn-\ или /л+1, фактически меньше
ее значения, когда tn удовлетворяет (12.39), за ис-
ключением случая, когда pn+i >2,1 и выбрано большее
значение рл, приводящее к неравенству рлрл+1 > 3,76.
Следовательно, если дано, что 1/(1 —tn) > 3,76, то оп-
тимальное представление величины 1/(1—G) в виде
произведения pip2 • • • Pn при незафиксированном W
должно быть таким, чтобы ни один множитель рл не
превосходил 3,76 (в противном случае для уменьше-
ния Sn соответствующий множитель рп должен быть
12.4] КОВАРИАЦИЯ Dn и Ол+1 435
представлен в виде произведения двух множителей) и
чтобы ни один из множителей не был менее 2,1. Нако-
нец, мы рассматриваем (12.39) как рекуррентное соот-
ношение для рп; из рис. 12.7 видно, что последователь-
ность {рп} быстро сходится к пределу
р2= -3.+2^? =2,62. (12.40)
Рассмотрим далее, как изменяется Sn при изменении
постоянного шага коррекции р, в общем случае отлич-
ного от р2. Нас интересует теперь функция
t___ N ,-------------------
л=1 _______ ________________________
— Kp (p — 1) (p/V/2 ~ рЛ72 Уp 0 ,
Kp —i — /p — i
где pN, по предположению ^>1, фиксировано требова-
нием, чтобы величина =<зя была достаточно
UN и N-1
мала, как это следует из (12.37):
P-7V = ^4;V- (12-41)
Сумма SN, таким образом, выражается в форме
<>2-42)
ГДе 1/-7---ГГ
(12-43)
у Р —1
График функции F2(p)/F2(p2) изображен на рис. 12.6.
12.4. КОВАРИАЦИЯ Dn и Ря+1 В СЛУЧАЕ ЧАСТЫХ
НАБЛЮДЕНИИ НАЧИНАЯ С МОМЕНТА СТАРТА;
ОДНОМЕРНАЯ МОДЕЛЬ
Если ввести обозначение qn для вектора-столбца
то задача минимизации (12.27) приводит к следующему
28*
436
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
(гл. XII
матричному уравнению для оценок qn и qn:
ИП)Ц|Ш1= S (12.44)
t<tn az(t) "
С учетом (12.24) получим теперь
2 an(t){z(f) — bn{t)\, (12.45)
*<*п
где
‘(') = ;Н^ГИ‘>Г'т=
z(0
г (О
последнее равенство вытекает из симметрии матрицы
|| М(п) ||.
Из уравнения (12.45) и предположения о независи-
мости ошибок наблюдений с дисперсией получаем
Е{0л-1-^я-1)2}=^п_1= 2 О2’47)
« < «л
Выразив я„(0 в (12.47) в виде произведения двух
выражений (12.46), получим
1=|^Г|Л1<",|“'(2 ^-|^||^“Г)х
" 1 \‘<‘п г(1) J
ХИ,",Г'|^|- 02-48)
Но
V 1 II IIII «МО F
02_ II dqn II II dqn II
t<tn z(O
является как раз собственно матрицей || Л4<п> ||. Таким
образом, уравнение (12.48) упрощается 4 и принимает
вид
12.6] ОЦЕНКА й НА ОСНОВЕ ЧАСТЫХ ИЗМЕРЕНИЙ 437
Этим подтверждается приведенное ранее уравнение
(12.29).
Далее, ковариация Z)n-i и Dn равна
Е {0л-1 £>Я.1)(/5Я ^п)}— 2 (0 ^л+i (О —
z хЧ
Но
=1^П^т'2^|^|х
‘<‘П Z(t)
x|isn*+,,ni^|- («•»)
тг=шгт
<М0 F=||.jMO |П| II
<tyn+! II II dqn II II <ty„+1 II’
(12.51)
где \\dq n+Jdq n\\ и \\dqnldqn+x\\—взаимно обратные ма-
трицы.
Последнее выражение в (12.50) можно, таким обра-
зом, написать в виде
л-1
что СВОДИТСЯ к
E((25„_1-D„_1)(^„-D„)} =
т. е. к полученному нами ранее уравнению (12.35).
12.5. ОЦЕНКА D НА ОСНОВЕ ЧАСТЫХ ИЗМЕРЕНИИ
ПОЛОЖЕНИЯ С МОМЕНТА ПОСЛЕДНЕЙ КОРРЕКЦИИ;
ОДНОМЕРНАЯ МОДЕЛЬ
Если рассматривается модель, в которой Dn_\ оцени-
вается лишь на основе измерений в моменты времени,
следующие за /п-1. то ошибки в величинах Dn-t и Dn
оказываются теперь статистически независимыми, а их
дисперсии даются соотношением (12.30), где матрица
438
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИИ
[гл. XII
сведений ||Л1<П>|| включает суммирование лишь по мо-
ментам наблюдений, лежащим между tn-i и tn- Вместо
(12.32) получаем теперь
7И<п)[|=Ах
где t'n обозначает 1 — tn.
Дисперсия Ьп-1 равна теперь
о2 ___ %_______*л-1 ______
Ч-!- *0 (С1-^)2 ,П,С1 *
*л-?л
(12.54)
Уравнение (12.6) и независимость ошибок в Dn-i и
Dn ведут в этом случае к соотношению
1/" _ х
у
*л-2~~*л-1_______
(^н-2 ^п-1) | п2 —2
^л-2^л—1 ^я-1
(*л-1 *л) |п2 *л-1
^л-lCi *п
(12.55)
Не пытаясь осуществить общую оптимизацию мо-
ментов {/п} для минимизации Sw в (12.55), можем вновь
рассмотреть выражение для для случая постоянного
шага коррекции (для всех п). Для боль-
ших значений pN имеем
s.s-Za;»*’
/рКр2-1
(12.56)
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
439
и по (12.54)
Вместо (12.42) напишем
(12.58)
где _____
^(Р)=СР±1').(Гр~+1) (12-59)
р
График функции F3(p)/F2(p2) для сравнения пред-
ставлен на рис. 12.6 вместе с графиком функции
^2(р)/^2(р2).
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ К ГЛАВЕ XII
ах — полуось гиперболы — траектории полета около планеты;
ап (0 — коэффициент в выражении для Dn-i;
А — точка старта в примере 2;
bn(t)= 2
В — конечная точка в примере 2;
О0—ошибка в составляющей скорости, лежащей в плоскости
орбиты, измеренная после старта;
Dn—ошибка в составляющей скорости, лежащей в плоско-
сти орбиты, измеренная после n-й коррекции;
Dn — ошибка в составляющей скорости, выводящей из пло-
скости орбиты, измеренная после n-й коррекции;
Ьп — оценка величины Dn;
Ьп — оценка величины Ля;
dD(t)/dv — величина вектора
dD(tfMdv—двухкомпонентный вектор (dD/dx, dD/dy), вычисленный
в момент tn\
|^|-вектор'столбец|жй|;
В {...} — ожидаемое значение случайной величины в {..
F\ — безразмерное ожидаемое значение поправок к скорости,
пример 1;
F2 (р) — безразмерное ожидаемое значение поправок к скорости,
пример 2;
440
РАСПОЛОЖЕНИЕ КОРРЕКТИРУЮЩИХ УСИЛИЙ
[гл. ХП
(р) — безразмерное ожидаемое значение поправок к скорости
(пример 2), основанное лишь на сведениях, поступаю-
щих после последней коррекции;
G—универсальная постоянная гравитации;
К — безразмерная среднеквадратичная начальная ошибка;
I — параметр эллипса перехода;
т — масса планеты;
Л^’П — матрица сведений после п— 1 коррекции;
|М<Л)|| 1 — матрица, обратная || М||;
|| М— //-элемент матрицы
N— число коррекций;
Рп— положение в момент л-й коррекции;
qn — вектор-столбец ;
^—оценка qn\
। II — МаТрИЦа частных производных от составляющих век-
тора <7п<+1 по составляющим вектора qn‘t
II дЯп ||
- || — матрица частных производных от составляющих векто-
ра qn по составляющим вектора <7n+i;
R — расстояние наибольшего приближения к планете назна-
чения;
SN — сумма ожидаемых поправок к скоростям;
tf— момент прилета на планету назначения;
tn— момент л-й коррекции;
tn = tj — tn (при tti выбранном за 1);
Т — полное время перелета;
— вычисленная л-я поправка к скорости;
ъ'п — ошибка при осуществлении коррекции
vR — скорость сближения, рассчитанная относительно планеты;
V — скорость;
wn — составляющая яя вдоль направления вектора dZ)(/n)/dz>;
— х-я составляющая л-й предполагаемой поправки к ско-
рости;
— у-я составляющая л-й предполагаемой поправки к ско-
рости;
г — измеренное значение z;
zn— боковое смещение (пример 2) в момент tn\
z~— производная по времени от бокового смещения непо-
средственно перед моментом tn\
z^— z-составляющая л-й предполагаемой поправки к скорости;
ЛИТЕРАТУРА
441
z'n— ошибка при осуществлении коррекции z^'t
zn— оценка гп;
zn — оценка гп ;
1^1—
|| ... ||г— матрица, получающаяся транспонированием матри-
цы ||... II;
£ — эксцентриситет эллипса перехода;
£!—эксцентриситет гиперболы около планеты назначения;
О — внешний угол (рис. 12.5);
*- Va9;
X — множитель Лагранжа;
Хо — цена наблюдения;
И- — произведение гравитационной постоянной на массу
Солнца;
р — шаг коррекции;
р2 — оптимальное значение р для примера 2;
Рл тп—i/Тп;
с' — среднеквадратичная ошибка в w';
— среднеквадратичная ошибка в измерении скорости;
— среднеквадратичная ошибка в измерении г;
оз— среднеквадратичная ошибка в оценке 0;
— среднеквадратичная ошибка в оценке Dn;
— среднеквадратичная ошибка в измерении z(/);
_ dD .. . / dD ...
(л) / ди
ф — угол между асимптотами гиперболы;
— средняя гелиоцентрическая угловая скорость;
2 — взвешенная
л
сумма квадратов отклонений координат.
ЛИТЕРАТУРА
1. A. Rosenbloom, Final-value systems with total effort con-
straints, presented at First International Congress of the Interna-
tional! Federation on Automatic Control, Moscow, June, 1960.
2. J. V. Break well, Fuel requirements for crude interplanetary
guidance, presented at Second Western National Meeting of the
American Astronautical Society, Los Angeles, California, August
1959; Advances in Astronaut. Sci. 5 (1960).
3. D. F. L a w d e n, Optimal programme for correctional manoeuvres,
Astronaut. Acta 6, 195—205 (1960).
ГЛАВА XIII
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ*)
13.0. ВВЕДЕНИЕ
Понятие об эффективности тяги самолетов и ракет
рассматривается во всех работах по проблемам тяги и
не может в наше время считаться источником каких-
либо новых задач. Непрекращающиеся противоречивые
толкования такого фундаментального вопроса, как пра-
вильное определение эффективности тяги [1], показы-
вают, однако, что сделанное выше высказывание нельзя
считать верным. В последнее время все общепринятые
определения были подвергнуты критическому рассмот-
рению [2—8].
В настоящей главе будет оценено значение и указа-
ны свойства величины, называемой эффективностью
тяги ракеты, как в случае постоянной, так и в случае
переменной скорости истечения. Особое внимание будет
обращено на требование инвариантности относительно
преобразований координат, и понятие эффективности
тяги будет определено в соответствии с этим требова-
нием. Наконец, будут указаны оптимальные условия,
доставляющие максимум эффективности тяги. Упомяну-
тое ранее свойство инвариантности будет использовано
с целью непосредственного получения оптимальных
условий.
13.1. ЭФФЕКТИВНОСТЬ ТЯГИ КАК ФУНКЦИЯ точки
В стандартных руководствах [9, 10] можно найти
два общепринятых определения эффективности тяги.
♦) Эта глава основана на материалах доклада, прочитанного
на III Международном симпозиуме по ракетам и астронавтике в
Токио в 1961 г.
13.1]
ЭФФЕКТИВНОСТЬ тяги КАК функция точки
443
Эти определения таковы:
__скорость возрастания кинетической энергии ракеты_____
скорость возрастания кинетической энергии ракеты
и двигателя
— mcv 2R /1О
~ • 1 • .2 — 1 + ’ С1’5’1)
— mcv — -^m(c — v)2
где
= (13.2)
и
__скорость изменения кинетической энергии ракеты
скорость изменения кинетической энергии ракеты
и двигателя
— mcv + -у fnv2
=----------------= 2/? — /?2. (13.3)
— -% тс2
Таким образом, эффективность тяги определяется
как функция точки, т. е. зависит от мгновенных условий
ее движения.
Очевидно, в обоих случаях максимальное значение т]
равно единице и достигается при с = и, т. е.
V == ^max == 1
при
R=\. (13.4)
Могут представиться два случая: скорость истечения
с постоянна, и при этом максимум эффективности тяги
может быть достигнут самое большее однажды за вре-
мя полета (с нарастающей скоростью), и случай, когда
скорость истечения с переменна и, таким образом, мо-
жет быть подобрана так, чтобы условие (13.4) удовле-
творялось во все время полета. Мы рассмотрим эти воз-
можности каждую в отдельности.
Прежде чем сделать это, полезно более вниматель-
но рассмотреть условие (13.4). В пользу этого условия
444
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
[гл. XIII
свидетельствуют, разумеется, два соображения: во-пер-
вых, равенство максимума эффективности единице на-
ходится в согласии с уже имеющимся у нас опытом
обращения с такой величиной, например, при проекти-
ровании машин, и этим объясняется удобство такого
определения; во-вторых, то обстоятельство, что макси-
мум эффективности тяги, определенной уравнениями
(13.1) и (13.3), достигается при с = v, т. е. тогда, когда
скорость с — v ракеты относительно выбранной системы
координат обращается в нуль, согласуется с нашей ин-
туицией. Действительно, кажется несомненным, что если
ракета покоится относительно той инерциальной системы
координат, в которой описывается движение, то это озна-
чает, что вся энергия тяги превращается в кинетическую
энергию ракеты, — «очевидно», наиболее эффективный
вариант движения.
Можно, однако, высказать еще одно соображение.
Условие (13.4) эквивалентно равенству
v = c, (13.5)
которое гласит, что некоторая величина, а именно ско-
рость V, которая не является инвариантной (значение
которой зависит от выбора инерциальной системы коор-
динат), приравнивается инвариантной величие, а имен-
но скорости истечения с. Другими словами, определен-
ная формулами (13.1) и (13.3) эффективность тяги нив
какой момент полета не имеет единственного значения,
но величина ее зависит от движения наблюдателя. Если,
таким образом, с точки зрения одного наблюдателя ра-
кета движется с максимальной эффективностью, то с
точки зрения всех других наблюдателей, движущихся
относительно первого, ее эффективность меньше макси-
мальной. Это обстоятельство, разумеется, внушает бес-
покойство.
В случае постоянной скорости истечения можно
обойти трудность, связанную с неинвариантным харак-
тером величины т), просто требованием, чтобы наблюда-
тель был связан с одной координатной системой, на-
пример такой, в которой начальная скорость раке-
ты [10] с>о = 0. Это условие, однако, не может быть удо-
влетворено в течение всего полета.
13.1]
ЭФФЕКТИВНОСТЬ тяги КАК функция точки
445
13.11. Постоянная скорость истечения. Имея в виду,
что равенство с = v не может быть выполнено на протя-
жении всего полета, можно поставить вопрос о том зна-
чении с, которое доставляет максимум среднего значения
rim эффективности тяги [10]. Если ввести обозначение
(13.6)
то средняя величина эффективности тяги будет равна
^т~~ Rt J l-j-Я2 d“~ ’ (13.7)
о
где т] задано формулой (13.1), и
/(27? - dR=- 4 <13-8)
для т|, заданного формулой (13.3). Положив dv\mldR = 0,
находим, что т)т достигает максимума при условиях
и
/?1 = 1,98, или -^=7,17. для (13.1)
= 1.50, или ^- = 4,48, для (13.3).
(13.9)
13.12. Переменная скорость истечения. Если допустить
изменения скорости истечения (в идеальных условиях —
без ограничений), то можно было бы оптимизировать
эффективность тяги двумя способами.
Можно было бы искать такую программу изменения
скорости истечения c(v) и отношения масс при
которой получалась бы максимальная эффективность.
Для выражений (13.1) и (13.3) этого сделать нельзя [5].
Если т] должно быть максимальным во все время полета,
то условие (13.4) вместе с уравнением движения
mdv =— с dm (13.10)
приводит к равенству
d (mv) = 0,
(13.11)
446
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
[гл. XIII
так что
т0 _______________________
mi v0 *
Режим максимальной эффективности тяги, опреде-
ленной формулами (13.1) или (13.3), продолжающийся
от начального значения скорости v0 до конечного воз-
можен, таким образом, лишь при условии, что отноше-
ние масс удовлетворяет уравнению (13.12). При этом
возникает еще два затруднения. Величина г] снова не-
инвариантна по отношению к выбору инерциальной си-
стемы координат. Кроме того, движение не может быть
описано в системе координат, в которой начальная ско-
рость = 0.
Далее будет показано, что описанный здесь режим
представляет собой частный случай общего оптимального
режима полета ракеты.
13.2. ЭФФЕКТИВНОСТЬ ТЯГИ
КАК ФУНКЦИЯ ИНТЕРВАЛА
Одним из способов определения эффективности тяги
является такой, когда говорят, что система тяги работает
наиболее эффективно, если необходимо преобразовать
наименьшее, количество энергии, чтобы увеличить ско-
рость продуктов сгорания на заданную величину. Бес-
смысленность этого определения очевидна, и не только
потому, что полный имеющийся запас энергии ограничен
(см. гл. XIV), но скорее, пожалуй, потому, что и преоб-
л
разуемая энергия, т. е. J* Р dt, будет ограничена вслед-
о
ствие ограниченности мощности Р и времени полета
Скорость преобразования энергии в кинетическую
энергию ракеты и двигателя, т. е. мощность силы тяги,
является инвариантной величиной. Для прямолинейного
движения, описываемого уравнением движения (13.10),
имеем
dTR = d^mv2^ = ^ v2— cv^dm (13.13)
И , 1 1
dTj = j (с — q)fd^ = — у (c — v)2 dm, (13.14)
13.2] ЭФФЕКТИВНОСТЬ ТЯГИ КАК ФУНКЦИЯ ИНТЕРВАЛА 447
так что
dE = dTR-\-dTj —— jc2dm. (13.15)
Таким образом,
P = — ±c2m-, (13.16)
эта величина не зависит от выбора инерциальной си-
стемы координат.
13.21. Постоянная скорость истечения. Теперь можно
определить значение с, а отсюда и т^1ть приводящее
к минимальной затрате энергии ДЕ при заданных значе-
ниях mi, vQ и Из уравнения (13.10) находим
»О = С1П (13.17)
а из уравнения (13.15)
АЕ = у f2(/n0 — /nj). (13.18)
Полагая
= —(13.19)
определим «инвариантное изменение кинетической энер-
гии» массы mi
Д7\ (13.20)
и эффективность тяги [3]
ч = 4г- (13-21)
Определенная таким способом эффективность тяги
представляет собой функцию интервала в том отноше-
нии, что значение ее зависит скорее от траектории в це-
лом, нежели от условий в точке. Теперь определим удель-
ную энергию
•=Д- (13-22)
В силу уравнений (13.17) — (13.19)
^=е-1 = !п±№|. (13.23)
Величина эффективности тяги, выраженная по фор-
муле (13.23), является инвариантной, и для данных
448
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
[гл. XII1
значений и vc &Е достигает минимума, когда ц мак-
симальна. Эффективность тяги максимальна, если
— =1,59 и — = 4,9. (13.24)
С помощью понятия удельной энергии можно теперь
сравнить затраты энергии при оптимальных значениях
vc/c (или m0/mi), соответствующие трем обсуждаемым
определениям:
Определение Vc/C /»оМ1 е
(13.1) 1,98 7,17 1,574
(13.3) 1,50 4,48 1,547 . (13.25)
(13.23) 1,59 4,9 1,543
Интересно отметить , что величина преобразуемой
энергии совсем нечувствительна к выбору условий опти-
мизации. С другой стороны, работа в неоптимальных
условиях, как видно из рис. 13.1, связана с большой не-
оправданной затратой энергии.
13.22. Переменная скорость истечения. Используя
установленное в предыдущем разделе определение мак-
симальной эффективности, можно теперь поставить во-
прос об оптимальном режиме полета в случае перемен-
ной скорости истечения. Иными словами, какова про-
грамма c(v), минимизирующая ДЕ, если т0,
т. е. ДТд, заданы? И еще, каково значение т0/т^ мини-
мизирующее ДЕ, при оптимальной программе изменения
скорости расхода?
Из (13.15) получаем
&E = ^mivl — ^-/По'УоН--^ f (c — v)2dv.. (13.26)
6
Поскольку ДТЛ задано, для решения задачи об опти-
мальной программе изменения скорости истечения ра-
зыскивается минимум выражения
ДТу = —I f (c — v)2dtn (13.27)
Z72q
13.2)
ЭФФЕКТИВНОСТЬ ТЯГИ КАК ФУНКЦИЯ ИНТЕРВАЛА
449
при выполнении уравнения
ных условий
/п = /п0:
т = щ :
движения (13.10) и гранич-
(13.28)
V = Vv
Решение этой задачи возможно двумя методами;
один из них вариационный [3, 4, 11], другой основан на
Рис. 13.1. Зависимость ц j ПРИ постоянной и
переменной скоростях истечения.
непосредственных соображениях об инвариантности
относительно преобразований инерциальных систем
отсчета [7].
13.23. Вариационное решение. Быть может, простей-
шее вариационное решение заключается в следующем.
Из уравнения (13.10) найдем
с = -от^-( (13.29)
29 Дж. Лейтман
450
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
(гл. ХШ
так что минимизируемый интеграл равен
ДЛ = —у f + dm. (13.30)
тй
Соответствующее уравнение Эйлера — Лагранжа та-
ково (см. гл. IV):
zzi4^ + 2-^- = 0; (13.31)
dm2 1 dm v '
совместно с (13.12) оно дает
dtu = dc, (13.32)
т. е. оптимальная программа изменения скорости истече-
ния имеет вид
с — cQ — v — vQ. (13.33)
Значение с0 найдется интегрированием (13.10); получим
0 (^оМ1) —1 ’
Формулы (13.33) и (13.34) представляют собой опти-
мальное решение. Решение существует для любого вы-
бора приращения скорости vc = Vi — v0 и отношения
масс /п0//И1 и, более того, является инвариантным. Те-
перь становится очевидным, что решение, основанное на
определении (13.1) или (13.3), а именно с = и, предста-
вляет собой лишь частный случай только что получен-
ного — случай, для которого с0 = ^о-
Уравнение (13.12) при этом автоматически удовле-
творяется.
13.24. Непосредственное решение. Требуется, чтобы
величина ATj была минимальна. Если движение рас-
сматривается в какой-либо инерциальной системе отсче-
та и найдена программа изменения скорости истечения,
доставляющая минимум величины A7j, то эта програм-
ма будет оптимальной при описании движения в любой
другой инерциальной системе отсчета.
Если бы это было не так, т. е. если бы можно было
для некоторой инерциальной системы координат найти
оптимальную программу для скорости истечения c(v),
13.2] ЭФФЕКТИВНОСТЬ ТЯГИ КАК ФУНКЦИЯ ИНТЕРВАЛА 451
доставляющую меньшее значение Af, чем то, которое
получается по оптимальной программе для другого вы-
бора системы координат, то это можно было бы исполь-
зовать для вторичного выбора координатной системы и
получить меньшее значение Д£\ нежели то, которое со-
ответствует оптимальной программе. Ясно, что это пред-
ставляет собой противоречие.
Минимальное значение АГ/ равно нулю; это значение
указанная величина может принимать лишь для одной
из бесконечного множества инерциальных систем от-
счета. В этой особой системе координат условие соблю-
дения равенства
дг7=о, (13.35)
очевидно, имеет вид с = 5. (13.36) Здесь v обозначает скорость в упомянутой особой коор- динатной системе. Из уравнений (13.10) и (13.29) сле- дует, что d(mv) = 0, (13.37) ^ = 4 (13.38) И 1)т»о = т)1 т>0. (13.39) Но ®о = со (13.40) и для прямолинейного движения v — = v — v0> (13.41) так что z. /1О
0 («о/"»1) —1
Имея в виду уравнения (13.29) и (13.34), напишем
также
с — cQ = v — vQ. (13.43)
Таким образом, получен тот же результат, что и при
вариационном решении.
29*
452
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
[гл. XIII
Наконец, пользуясь уравнением (13.21), представим
эффективность тяги в виде
^=±”.0/^ )-!., (1344)
/По//П1 ' '
Сравнение уравнений (13.23) и (13.44) показывает,
что эффективность тяги при постоянной скорости исте-
чения всегда, т. е. для любых значений меньше,
Рис. 13.2. Соотношение энергий, затраченных при постоян-
ной и переменной скоростях истечения.
нежели значение ее для оптимальной программы изме-
нения скорости истечения (рис. 13.1).
При том же значении ДТ1 отношение затраченной
энергии при постоянной скорости истечения к этой вели-
чине при переменной скорости равно
AZjcODSt _ К^о/^1) 1]2 1 . /1 О А Г\
A£var ~ ь
соответствующий график представлен на рис. 13.2.
ЛИТЕРАТУРА
453
Отметим, наконец, что эффективность тяги как функ*
ция отношения масс matrix имеет при постоянной скоро-
сти истечения максимум (меньший единицы), тогда как
при переменной скорости истечения эффективность тяги
монотонно возрастает (до единицы) при возрастании от-
ношения масс т^глх. Преимущество использования оп-
тимальных условий при переменной скорости истечения
по сравнению с условиями при постоянной скорости ста-
новится более отчетливо выраженным при больших зна-
чениях отношения масс.
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ К ГЛАВЕ XIII
Р — мощность тяги;
R = v/c\
с — скорость истечения;
т — масса ракеты;
v — скорость ракеты;
vc = vi — и0;
t — время;
/j — время действия тяги;
ЬЕ — энергия, преобразованная в кинетическую;
LTR — изменение кинетической энергии ракеты;
АГ — изменение кинетической энергии двигателя;
ATj — инвариантное изменение кинетической энергии сгоревшей
массы топлива;
•t\ — эффективность тяги;
Р — масса двигателя;
О — начальный;
1 — конечный.
ЛИТЕРАТУРА
I. А. V. Cleaver, Power-plant efficiencies, Aircraft Eng. 17, 156
(1945).
2. R. R. Newton, On the optimization of physical propulsion sy-
stems, Jet Propulsion 28, 752 (1958).
3. R. H. F о x, Optimum exhaust velocity programming and propul-
sion efficiency, J. Astronaut. Sci. 6, 13 (1959).
4. G. Leitmann, Some remarks on the optimum operation of a
nuclear rocket, Proc. 10th Intern. Astronaut. Congr., London, 1959,
p. 85 (1960).
5. G. Z e b e 1, Vergleich des Energiebedarfes von Raketen mit kon-
stanter bzw. variabler Strahlgeschwindigkeit, Raketentech. Raum-
fahrtforsch. 3, 81 (1959).
454
ЭФФЕКТИВНОСТЬ ТЯГИ РАКЕТ
[гл. XIII
6. G. Leitmann and G. Z е b е 1, Uber Energiebedarf von Raketen,
Raketentech. Raumfahrtforsch. 3, 117 (1959).
7. G. Leitmann, Weiteres fiber Energiebedarf von Raketen, Rake-
tentech. Raumfahrtforsch. 4, 58 (1960).
8. W. R. Corliss, Propulsion Systems for Spaceflight, McGraw-
Hill, New York, 1960.
9. G. P. Sutton, Rocket Propulsion Elements, Wiley, New York,
1956.
10. J. M. J. К о о у and J. W. H. U у t e n b о g a a r t, Ballistics of the
Future, McGraw-Hill, New York, 1946.
11. J. Ulam, L’Ecoulement a vitesse variable dans la propulsion des
fusees, Rev. fran, astronaut, 1, 23 (1958).
ГЛАВА XIV
НЕКОТОРЫЕ ВОПРОСЫ ОПТИМИЗАЦИИ РАКЕТ
НА ЯДЕРНОМ ТОПЛИВЕ
14.1. ВВЕДЕНИЕ; ОПРЕДЕЛЕНИЯ
14.11. Ракетные летательные аппараты на ядерном
топливе. Прежде чем обсуждать вопрос об оптимизации
двигательных систем на ядерном топливе, используемых
для полета ракетных летательных аппаратов, мы долж-
ны выяснить, почему и в какой мере ядерная энергия
представляет преимущество с точки зрения реактивного
движения по сравнению с химической энергией, и ука-
зать составные элементы ракеты на ядерном топливе.
Для проведения такой оценки нет необходимости с са-
мого начала обращаться к рассмотрению особенностей
конкретных схем ядерных силовых установок.
Основное различие между ракетами, работающими
на химическом и ядерном горючем, заключается в ме-
тоде получения энергии, необходимой для реактивного
движения. Химическая ракета удовлетворяет свои энер-
гетические потребности путем сжигания или разложе-
ния топливных компонент; рабочая жидкость ядерной
ракеты не нуждается в какой-либо внутренней энергии
такого рода, поскольку энергия ее пополняется за счет
кинетической энергии продуктов управляемых ядерных
реакций, происходящих внутри реактора — источника
ядерной энергии. Это справедливо независимо от того,
рассматриваем ли мы ракетные летательные аппараты
типа, изображенного на рис. 14.1а, где используются си-
стемы непосредственного теплообмена (рис. 14.16), в ко-
торых рабочая жидкость нагревается благодаря сопри-
косновению с камерами, содержащими горячее ядер-
ное топливо, либо устройства типа, показанного на
рис. 14.2, а, с непрямыми (электрическими) двигательными
456
• ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл XIV
системами, такими (см. рис. 14.2,6), где ядерная
энергия преобразуется сначала в электрическую и ис-
пользуется затем для нагрева или для ускорения выхо-
дящих газов. Запас потенциальной энергии реагирую-
а Помещения
для груза
и зли пажа
Рабочее
тлела
Насосное
оборудование
Ядерный
деигатлель
D11lib- Яш од из
J1II сопла
!iF
Рис. 14.1а. Ракетный ле-
тательный аппарат с не-
посредственным преоб-
разованием ядерной энер-
гии (типичный аппарат
большого ускорения).
но пропорционально
щих и расщепляющихся топлив
почти в 107 раз превышает за-
пас энергии в лучших химических
горючих смесях, а расход массы
ядерного топлива в большинстве
представляющих интерес полетов
в пределах солнечной системы
будет практически пренебрежимо
мал, хотя некоторые продолжи-
тельные полеты с этой точки зре-
ния могут быть ограничены (см.
раздел 14.33).
Поскольку движение ракеты
осуществляется благодаря сохра-
нению импульса, в общем случае
желательно, чтобы нагреваемая
или ускоряемая за счет ядерной
энергии рабочая жидкость от-
брасывалась назад с возможно
большей скоростью для миними-
зации необходимой массы ра-
бочей жидкости*). При данной
равновесной температуре газа
энергия атома, грубо говоря, не
зависит от его массы и опреде-
ляется главным образом числом
степеней свободы возбуждения,
которым обладает каждый атом.
Содержание энергии в единице
массы при этом, очевидно, обрат-
атомному весу используемой рабо-
чей жидкости. Поскольку мы можем свободно выбирать
*) Строго говоря, это верно лишь для режима работы без огра-
ничений, наложенных на характеристики полета в целом или на па-
раметры силовой системы. В дальнейшем (и ранее, в гл. V) об-
суждаются несколько случаев, когда «оптимальные» результаты по-
лучаются при переменной скорости истечения.
14.1]
ВВЕДЕНИЕ; ОПРЕДЕЛЕНИЯ
457
эту жидкость независимо от ее топливных характери-
стик, очевидно, что вещества с наименьшим атомным
или молекулярным весом предпочтительны для исполь-
зования в ракетных двигателях с ограниченной темпера-
турой, где энергия доставляется от источников, не зави-
сящих от подачи рабочего тела. Для данного рабочего
тела скорость истечения возрастает с увеличением ма-
ксимальной температуры газа, и поэтому представляют
интерес ядерные реакторы, работающие при высоких
Приток
рабочего
тела
Рис. 14.16. Ракетный летательный аппарат с теплообхменниками.
температурах при постоянных других параметрах сило-
вой установки (например, эффективности преобразова-
ния). В системах непрямого преобразования высокая
температура в реакторе может оказаться желательной
для высокой эффективности цикла, но из-за молекуляр-
ного веса рабочей жидкости может случиться, что кри-
терием оптмальности станут другие параметры, такие,
как отношение заряда к массе.
14.12. Анализ системы и ее оптимизация. Два наи-
более характерных признака двигательных систем на
ядерном горючем — независимость источника энергии и
рабочей жидкости и почти неограниченный запас энер-
гии — представляют два ключевых пункта в решении
задач оптимизации. Именно благодаря этим двум свой-
ствам системы с ядерным горючим представляют весь-
ма большие возможности в отношении определения
оптимальных условий; условия эти лежат вне пре-
делов возможностей ракетных систем на химическом
/7омещеяия для
а).
б)
Рис. 14.2. а) Ракетный летательный аппарат непрямого пре-
образования (типичный аппарат малого ускорения); б) ядерно-
электрическая двигательная система.
14.1]
ВВЕДЕНИЕ; ОПРЕДЕЛЕНИЯ
459
топливе, где источник энергии и ее потребитель — рабо-
чая жидкость — всегда неразрывно связаны. Большое
разнообразие вариантов, открывающееся благодаря та-
кому разделению основных функций, ставит трудную
задачу. Эта задача заключается в определении опти-
мальных условий. То, что представляется оптимальным
одному исследователю, может оказаться вредным с точ-
ки зрения другого.
По-видимому, первоначальным (исторически) кри-
терием оптимума в конструировании ракетных лета-
тельных аппаратов следует считать величину полной
стартовой массы аппарата; оптимальным традиционно
считается аппарат с наименьшей требуемой для полета
с заданной целью полной массой. Эта величина была
принята как полезный параметр оптимизации частично
потому, что она сравнительно легко вычисляется, но
другой причиной было общепринятое мнение о том, что
минимальность массы определенным образом предпола-
гает минимальность размеров, т. е. минимум массы ап-
парата без топлива и, следовательно, минимум стоимо-
сти. Все эти дополнительные соображения, сыгравшие в
прошлом свою роль при выборе величины полной стар-
товой массы в качестве полезного параметра оптимиза-
ции, в сильной степени зависят от вида используемой в
ракетном летательном аппарате рабочей жидкости.
Если все такие жидкости имеют примерно одинаковую
плотность и приблизительно в равной мере могут быть
использованы как рабочее тело, то сделанные выше за-
мечания вполне справедливы. Если, однако, плотность
и удельный импульс таких жидкостей могут принимать
значения, лежащие за крайними предельными величи-
нами, то сделанные утверждения оказываются вовсе не
верными. Простейший пример получается из сравнения
ядерной ракеты с использованием водорода в качестве
рабочего тела и химической ракеты, работающей на
смеси кислорода с ракетным топливом, при сравнитель-
но скромной задаче о переносе груза весом 1000 фун-
тов на расстояние в 2500 миль. Для этого случая
можно произвести расчеты, которые покажут, что ра-
кета с ядерным горючим будет иметь гораздо меньшую
полную стартовую массу, нежели ее конкурент на
460
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ [гл. XIV
химическом топливе, но размеры ее будут значительно
большими и масса ее без топлива может быть больше
(или меньше) массы химической ракеты без топлива в
зависимости от предположений, сделанных о конструкции
топливных цистерн, и от других конструктивных особен-
ностей аппаратов. Какой из аппаратов «лучше»? На
этот вопрос нет ответа, обоснованного по крайней мере
с технической точки зрения. Дилеммы, подобнные этой,
возникают во многих работах, посвященных сравнению
конструкций химических и ядерных ракет, но все полу-
ченные к настоящему времени решения обусловлены
общим прогрессом техники и постоянным совершенство-
ванием конструкций. Можно аналитически показать,
например, что ракетные летательные аппараты с ядер-
ным топливом представляют определенные реальные
технические преимущества для использования в воен-
ной бомбардировочной авиации дальнего действия, и
одновременно оказывается весьма нежелательным, что-
бы они заменили ракеты на химическом топливе толь-
ко по той причине, что последние существуют. Мы рас-
полагаем действующими химическими ракетами, но в
настоящее время (1961 г.) мы еще не имеем ядерных
ракет. Безусловно очевидная, приемлемая и убедитель-
ная демонстрация преимущества аппаратов с ядерным
топливом кажется возможной только тогда, когда
имеются в виду полеты настолько ответственные, что
ядерные системы оказываются не только самыми лег-
кими, но и самыми малыми по размерам и наиболее
прочными.
Трудно, конечно, указать определенное основание
для такого рода заключений, поскольку результаты ана-
лиза поведения системы вообще настолько сильно отра-
жают исходные предположения, что вопрос о предполо-
жениях становится вопросом о пределе применимости
результатов. Если исследователь настроен оптимистиче-
ски и им выбраны конструкции небольшого веса либо
он исходит из предположения о высокой температуре
в реакторе, то получаемые им результаты также будут
оптимистическими. Наоборот, если выбраны цистерны
большого веса либо удельный импульс взят небольшим,
то конструкция аппарата окажется плохой, быть может,
14.1]
ВВЕДЕНИЕ; ОПРЕДЕЛЕНИЯ
461
значительно худшей, чем следовало бы. Последнее весь-
ма существенно: результат исследования часто весьма
чувствителен к принятым исходным предположениям об
условиях работы системы, и малое изменение в этих
предположениях часто порождает довольно большие из-
менения в результатах. Относительные размеры таких
отклонений зависят от ошибок в сведениях об исходных
данных. Чем лучше известны эти данные, тем точнее
будет указана конструкция. Если мы рассматриваем
параметры, описывающие конструкцию ядерного реак-
тора ракеты, то нет иного пути для получения инфор-
мации об исходных характеристиках, кроме эксперимен-
тального исследования реакторов для ракет. Уже одно
это представляет собой сильный аргумент в пользу воз-
можно быстрого осуществления программы эксперимен-
тов с тем, чтобы рассеять некоторые таинственные и
неясные моменты, связанные с недостатком информа-
ции о действительных возможностях ракет на ядерном
топливе.
Экономические вопросы принадлежат к числу тех
оптимальных проблем, в которых предположения играют
большую роль. И здесь трудности вызваны главным
образом недостатком точных данных; лишь время, а
также подсчет стоимости расходов, связанных с иссле-
дованиями, могут улучшить положение в этой области.
Такое положение, конечно, весьма неблагоприятно, так
как при составлении долгосрочных программ экономи-
ческого развития необходимо базироваться на извест-
ных прогнозах относительно величин полной стоимости
или окончательной реализуемости, тогда как часто бы-
вает невозможно сделать такое предсказание с точно-
стью до множителя порядка 10. Для иллюстрации рас-
смотрим кратко некоторые трудности предсказания
стоимости доставки массы на орбиту путем отправления
ее с земной поверхности. Основные расходы связаны с
разработкой ракетных летательных аппаратов для пе-
реноса груза (грузов) на орбиту, с проведением полета,
с финансированием капиталовложений и с амортиза-
цией наземного оборудования. Если отвлечься от затрат
на разработку, сославшись на «бесконечное» использова-
ние летательных аппаратов, то мы придем к результату,
462
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
который будет очень сильно отличаться от результата,
полученного при учете этих расходов и при ограни-
чении числа полетов каждого аппарата. Стоимость
топлива может быть велика сравнительно с другими
расходами по полету, если считать, что многократно ис-
пользуются ракеты на химическом топливе при малой
стоимости ремонта, либо если предположить, что рас-
ходы по подготовке ракет с радиоактивным ядерным
горючим невелики.
Наоборот, если расходы по подготовке ракет между
полетами выбраны достаточно большими, то можно
«доказать», что повторное использование ракет не даст
преимуществ.
Подобным же образом, делая соответствующие пред-
положения, можно показать, что исследование и
разработка систем на ядерном топливе требуют
больших затрат, чем систем на химическом топливе,
либо требуются меньшие полетные расходы или
расходы, связанные с ремонтом, повторным использо-
ванием и т. д. Если бы планирование конструирования
самолетов основывалось на таких принципах, то мы до
сих пор летали бы на бамбуковых самолетах, обтянутых
тканью, так как в 1910 г. алюминий считался слишком
дорогим, чтобы можно было позволить себе широкое
его применение.
В ряде случаев может оказаться, что интересующая
нас величина не обладает строгим экстремумом, но из-
меняется между пределами, достигаемыми асимптоти-
чески; между тем мы желаем иметь некоторый крите-
рий, устанавливаемый как цель исследования. В таких
случаях можно определить функции, обладающие
экстремумами и выбранные в соответствии с другими
аспектами той же проблемы, еще не включенными в
рассмотрение (иногда вследствие их неаналитического
характера), и использовать эти функции в качестве ис-
кусственных оптимизирующих функций. Выгода такого
использования зависит, очевидно, от разумности сделан-
ного выбора, и в каждом конкретном случае следует
внимательно исследовать зависимость результатов от
введенных нормирующих факторов или от выбранной
формы функционала.
14.2] ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ 463
Изложенное выше не должно обескураживать нас и
удерживать от многократного рассмотрения систем при
попытках оценить потенциальную роль какой-либо но-
вой системы либо указать «наилучшие» области дей-
ствия новых или старых систем. Сказанное скорее име-
ет целью подчеркнуть то обстоятельство, что результаты
анализа системы не всегда имеют значение сами по себе
и что наиболее полезным при таком изучении может
оказаться выяснение направления действий конструк-
тора и определение запаса для исключения влияния
ошибок и связанных с этим конструктивных услож-
нений.
Теперь мы обратимся к рассмотрению некоторых
более интересных задач оптимизации поведения лета-
тельных аппаратов.
Мы начнем с задачи об оптимизации ракет на ядер-
ном топливе, движущихся в поле массивного гравити-
рующего тела, например Земли, и далее рассмотрим
вопрос об оптимизации некоторых аппартов с малым
ускорением, движущихся в пространстве без поля; в
заключение в последних двух разделах будут рассмот-
рены некоторые оптимальные задачи, представляющие
наибольший интерес для летательных аппаратов каж-
дого типа
14.2. ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
14.21. Основные принципы конструирования кораб-
ля*). Ранее мы отметили, что от применяемой рабочей
жидкости требуется большая скорость истечения**).
Это является хорошо известным следствием основного
уравнения полета ракеты — уравнения для отношения
масс
-^=ех|’Ш=ех[’йг)- (14”
Здесь mQ и ть суть соответственно полная и «сгоревшая»
массы, а скорость истечения ve заменена на £оЛр, где
♦) См. также [1].
*♦) См. сноску в разделе 14,11,
464
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
go— множитель, связывающий в земных условиях силу
гравитации с гравитационной массой (go = 980 см/сек2 =
«=980 дн!г), а /8р — эффективный удельный импульс,
определяемый как «тяга на единицу весового расхода
рабочего тела». Скорость vc представляет собой «харак-
теристическую скорость» летательного аппарата, т. е.
скорость, которую он приобрел бы после сжигания всего
топлива при полном отсутствии потерь и в пространстве,
свободном от полей. Эта скорость будет служить срав-
нительной характеристикой поведения аппарата.
Первостепенное значение в отношении конструкции
аппарата имеет также масса ядерной силовой установ-
ки, рассчитанная на единицу производимой мощности.
Интуитивно представляется очевидным, что силовые
установки с большой удельной массой не обеспечат
столь выгодной конструкции, как установки с малой
величиной удельной массы. Удельная масса Хрг опреде-
ляется соотношением
<14-2)
где трг—масса ядерной силовой установки, Рг — тепло-
вая энергия реактора, Pj — кинетическая энергия газов,
вытекающих из сопла, а — полная эффективность
преобразования тепловой энергии (энергии расщеплен-
ных ядер) в кинетическую энергию вытекающих газов.
Реактивная мощность связана с характеристиками ра-
бочего тела формулой
Py = -4^(go/sp)2- (Н.З)
где тр — масса рабочего тела, точка обозначает произ-
водную по времени, знак минус появился вследствие
нашего соглашения о выборе знаков таким образом, что
потери массы считаются отрицательными, а остальные
обозначения определены ранее. Для силовых установок
с непосредственным теплообменом типа, изображен-
ного на рис. 14.16, часто бывает удобно разбить всю
установку на две главные составные части — собственно
реактор тг и насосный агрегат тре— и использовать
14.2] ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ 465
уравнение типа (14.2) лишь для одного реактора; таким
образом,
тг = \Рг. (14.4)
Для непрямых (электрических) систем типа изобра-
женной на рис. 14.2,6 будем пользоваться величиной
Хрг, определенной уравнением (14.2).
Переходя к вопросу о сравнении летных качеств
кораблей, рассмотрим два ракетных летательных аппа-
рата, схематически изображенных на рис. 14.1а и
14.2, а. На рис. 14.1а изображен аппарат с силовой
установкой непосредственного преобразования, состоя-
щей, по существу, из реактора и турбинного насоса,
тогда как на рис. 14.2, а показано применение системы
непрямого преобразования со всем связанным с нею
оборудованием. Аппараты типа, изображенного на
рис. 14.1а, обычно считают аппаратами «больших уско-
рений», а типа рис. 14.2, а — «малых ускорений», но эта
классификация не всегда оказывается правильной. По-
мимо обсуждавшейся выше величины массы силовой
установки (/прг), наибольший интерес здесь представля-
ют величины массы рабочего тела mPt содержащих его
цистерн mt, а также мертвого груза mLt куда включены
все остальные узлы корабля (например полезный груз,
оборудование системы управления, инструменты, запас
пищи и воды, помещение для экипажа и т. д.).
Рассмотрим сначала аппараты типа, изображенного
на рис. 14.1а, где используются ядерные реакторы с
непосредственным преобразованием энергии в тепло.
Полная масса аппарата в этом случае равна
mQ = mt + mt) +'mL + тг + mpe. (14.5)
При заданных ограничениях усилий и расчетном да-
влении масса цистерн, очевидно, примерно пропорцио-
нальна их объему. Рассмотрение практических задач
(например, изменения гидростатического напора при
изменении плотности рабочего тела) показывает, что за-
висимость массы от плотности фактически слабее линей-
ной. Полезная приближенная формула, связывающая
30 Дж- Лейтман
466
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
массы цистерн и рабочей жидкости, имеет вид
mt = At{mPl^- (14.6)
Здесь рр — плотность рабочего тела, a At— численный
коэффициент, определяемый свойствами материала
цистерн и рабочим давлением. Типичная величина этого
коэффициента составляет примерно 1/н (г/сл<3)2/’ для
больших ракетных аппаратов с цистернами, сконструи-
рованными в виде баллонов.
При данном давлении истечения pd масса турбинного
насоса примерно пропорциональна величине объемного
расхода mpl^p, т. е. тяге реактивного двигателя F/gQ =
= aQmQ = —triply, плотности рабочего тела и удельному
импульсу. Опыт конструирования турбонасосов показы-
вает, что зависимость от давления истечения существен-
но слабее линейной и что формула
тре — — Ape (mPlpP)p2d = Аре (аоПэ/рр/sp) p’J‘ (14.7)
хорошо подтверждается в широком интервале значений
расхода, давления и плотности жидкости. В этой фор-
муле а0 представляет собой ускорение на старте, изме-
ренное в единицах ускорения силы земного притяжения,
а Аре представляет собой численный коэффициент, ана-
логичный коэффициенту 4/, и значение его равно при-
мерно V17 г1(см31сек) • атмУ* для типичных современных
турбонасосов.
Масса ядерного реактора ракеты определяется фор-
мулой (14.4) через мощность реактора и удельную мас-
су. Поскольку в системе непосредственного преобразо-
вания освобождающаяся мощность направляется сразу
же в сопло и оказывается пропорциональной, таким об-
разом, произведению силы тяги и теоретической скоро-
сти истечения, можно переписать (14.4) в форме
тг = Аг (aQniQlspkr/'rie), (14.8)
где — эффективность расширения в сопле (преобра-
зования энергии):
Ъ=1 ~(Ре1РсУ~1/1 •
а Аг—коэффициент перехода, позволяющий измерять
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
467
мощность в мегаваттах (Мет) — единицах, удобных для
использования в вопросах, связанных с ракетами на
ядерном топливе; Ат = 4,8-10-5 Мвт!кг* сек.
Если воспользоваться совокупностью уравнений
(14.5) — (14.8) для исключения массы рабочего тела
из формулы (14.1) для отношения массы (с помощью
равенства Шъ = mQ — mp), то придем к соотношению,
связывающему параметр летательного аппарата (типа,
указанного на рис. 14.1а), выражаемый характеристи-
ческой скоростью сс или показателем экспоненты vc/ve
в формуле для отношения масс, с параметрами, харак-
теризующими поведение ядерной силовой установки.
Это соотношение имеет вид
^ = -1п
Ar VsA +
Че
л Vd , mL , А
‘ г "• 1“ а/
Pf/sp Рр
(14.9)
Мы вернемся к этому уравнению в разделах 14.3 и 14.4.
При анализе полета летательного аппарата часто
бывает необходимо определить истинную скорость иъ
в момент полного сгорания, а не характеристическую
скорость vc. В первом приближении, с учетом влияния
конечности времени сжигания и других потерь, эти ве-
личины связываются соотношением
vb = fvc — (go/sp/ao) sin 6, (14.10)
справедливым при полете в атмосфере и в гравитацион-
ном поле. Мы допустили при этом, что (1—%)-й до-
лей скорости рабочего тела учитывается сопротивление
атмосферы, изменение давления на выходе из сопла и
в связи с этим изменение потребности турбонасоса в
газе, a sin 0 представляет собой усредненную по времени
величину синуса угла между вектором скорости полета
и местной эквипотенциальной поверхностью гравита-
ционного поля.
14.22. Влияние удельного импульса. В качестве пер-
вого шага при установлении оптимальных условий мы
рассмотрим влияние удельного импульса рабочего тела
30*
468
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
на баллистический радиус действия стартующих с по-
верхности Земли ракет на ядерном топливе. Для перво-
начальной оценки примем, что удельная масса реак-
тора равна = 1 кг]Мвт и что слагаемое Рр’/(рр’+А) в
(14.9) приближенно может считаться равным единице,
а слагаемым Аре (я0/ЛрРр) (/*’?) можно пренебречь по
сравнению сЛ/р^». Фактически мы пренебрегаем мас-
сой насосной установки по сравнению с массой цистерн
для рабочего тела. Используя эти приближения, выбрав
(типичное для больших сопел) значение т) = 0,8 и вве-
дя новую переменную mDlmQ = (Л,/р^) + mLlmQt прида-
дим уравнению (14.9) форму
VclVe = — In [(/nD//n0) + 6 • 10"5a0/spL (14.11)
Чтобы вычислить дальность S полета аппарата, мы
должны найти истинную скорость в момент сгорания для
подстановки ее в известное уравнение [2]
S = 2/?,tg[^(l + (14.12)
vb \ /J \ g$Re /
для максимальной баллистической дальности полета ма-
териальной точки над лишенным атмосферы невращаю-
щимся сферическим телом радиуса /?е, начиная с вы-
соты hbt на которой сожжено все топливо. Величину hb
выберем порядка 100 миль с целью упрощения вычис-
лений и примем, что ао=1Д sin 0 = 0,75 и х=0,95 —
числа, Дающие представление о возможных значениях
соответствующих параметров. Результаты выполненных
при этих предположениях вычислений представлены на
рис. 14.3, изображающем измеренную вдоль земной по-
верхности (невращающаяся Земля) величину дальности
полета одноступенчатых ракет в функции от параметра
tnQlm,D для различных значений удельного импульса.
Особенный интерес представляют два свойства этих
кривых. Отметим, во-первых, насколько пологими яв-
ляются кривые для /sp < 400 сек в сравнении с кри-
выми для /8р > 600 сек. Именно это различие делает
ракеты на ядерном горючем, даже в простом варианте
с обычным теплообменным реактором с твердыми стер-
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
469
жнями, интересными по сравнению с современными
химическими ракетами. Конечно, строятся химические
ракеты, способные покрыть большие расстояния даже
несмотря на небольшую возможную величину 7Sp (/8р<
< 350 сек). но это достигается только увеличением числа
Отношение полной массы
, н массе мер/пеого груза Ofy/m#)
Рис. 14.3. Характеристики одноступенчатых ракет на
ядерном топливе.
ступеней и (или) путем предельного использования кон-
структивных возможностей. Сравнительная слабость хи-
мической связи вовсе исключает ракеты на обычном топ-
ливе из интересной области больших значений удельных
импульсов, энергетически достижимой только для ядер-
ных ракет.
470 ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ [гл. XIV
Другое интересное свойство кривых рис. 14.3 заклю-
чается в том, что отношение полной массы к массе мерт-
вого груза лишь медленно убывает с увеличением
импульса при /8р > 1000 сек или около того, даже для
максимальной указанной дальности, равной 12 000 миль.
Практически оказывается, что для одного и того же
увеличения дальности ракеты с низким /8р требуют
большого увеличения полной массы, тогда как ракеты с
высоким /sp—малого увеличения массы. Это исключает
необходимость конструирования ракет с большими /sp,
обладающих минимальной массой при ограниченных на-
пряжениях в конструкциях, допускает использование
больших запасов и, следовательно, оставляет большую
свободу для конструктора. Разумеется, это представляет
собой качественное преимущество как раз того типа,
о котором мы говорили в разделе 14.1, и его очень труд-
но сформулировать в виде «оптимального» условия. В та-
ких обстоятельствах может оказаться полезным уста-
новить оптимум путем введения искусственной оптимизи-
рующей функции. Рассмотрим систему, рассчитанную
на некоторую заданную дальность полета. Поскольку
дальность фиксирована, для кривых рис. 14.3 остаются
две параметрические переменные: отношение полной
массы к массе мертвого груза т^тв и удельный им-
пульс рабочего тела. Как показывает опыт, конструкция
ракетного летательного аппарата все более усложняется
с возрастанием отношения т^Шв, а возможность полу-
чения больших удельных импульсов в системах с не-
посредственным теплообменом ограничивается различ-
ными предельными свойствами материалов и конструк-
ций*). Никакие ограничения не являются линейными по
отношению к ограничиваемым величинам, и поэтому
любая оптимизирующая функция, введенная с целью об-
ратить внимание на некоторую область состояний си-
стемы, должна фактически отражать нелинейность, по-
лученную из опыта. Для иллюстрации того, как исполь-
зуются такие функции, рассмотрим простое выражение
♦) Подробное рассмотрение таких ограничений дано Бассардом
и ДеЛауэром [2], Бассардом [1, 3] и Орндоффом и Дарэмом [4],
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
471
в котором мы произвольным образом ввели нормировку
переменных соответственно на величины 800 (сек) и 7.
Можно определить «оптимальный» летательный аппарат
как такой, который достигает нужной дальности при
минимальном значении введенной выше функции ф. Та-
кой аппарат был бы наиболее легким в отношении про-
ектирования и конструирования, и поэтому его легче
всего было бы получить для Действительного использо-
вания, если бы мы могли выбрать ф таким образом, что-
бы в точности отразить действительную функциональную
зависимость (не аналитическую, сложную и в общем
случае трудно поддающуюся математическому описа-
нию) конструктивных параметров от величин, характери-
зующих поведение аппарата в полете. Численным анали-
зом этой функции мы могли бы получить некоторые ка-
чественные заключения, возможно, не совсем верные.
Значения ф для нескольких различных систем значе-
ний п и т приведены в табл. 14.1 для различных вели-
чин удельного импульса рабочего тела и для двух раз-
личных значений дальности аппарата, равных 8000 и
4000 миль, в соответствии с рис. 14.3. Минимальные за-
табулированные значения выделены курсивом.
Таблица 14.1
Оптимизация с помощью искусственной оптимизирующей
функции [уравнение (14.13)]
^sp» сек За iu 3 s II II ЬЭ КЗ Л-1 т = 2 л = 2 т = 1 Дальность, мили
1200 2,11 2,62 2,86 1,87
800 1,93 1,86 1,93 1,86
600 2,08 2,33 1,89 2,52 5 = 8000
400 3,57 9,68 3,32 9,93
1200 1,99 2,49 2,74 1,74
800 1,70 1,49 1,70 1,49
600 1,74 1,54 /,55 1,73 5= 4000
400 2,42 3,93 2,17 4,18
Рассмотрение таблицы показывает, что оптимальный
удельный импульс близок к 800 сек для полета на
472
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
8000 миль, поскольку конструктивные трудности пример-
но остаются одинаковыми как с точки зрения отношения
масс, так и в отношении удельного импульса, но для по-
лета на 4000 миль оптимальный удельный импульс
ближе к 700 сек. Таким образом, мы заключаем, что бо-
лее трудные полеты требуют более высоких удельных
импульсов. Кроме того, мы замечаем, что в обоих слу-
чаях оптимальный удельный импульс уменьшается при
уменьшении трудностей конструирования летательного
аппарата по сравнению с трудностями создания реактора
(п</п), так что, чем легче построить летательный ап-
парат с низким значением /sp, тем меньше стремление
к созданию двигательных систем с большими /8р. Таково
действительное положение, в котором находятся иссле-
дования по ракетным двигателям на ядерном топливе ио
сравнению со своими соперниками на химическом топ-
ливе уже со времени широкого развития работ по раке-
там с химическим топливом, последовавшего за откры-
тием космической эры первым советским спутником.
Наоборот, если принято, что конструирование лета-
тельных аппаратов связано с большими трудностями, чем
конструирование реакторов (п>/п), то оптимальный
удельный импульс принимает большие значения, нежели
те, которые соответствуют случаю «одинаковой труд-
ности» (п = /п).
В общем случае нас интересует более широкий класс
задач, чем тот, которому соответствует рис. 14.3; мы же-
лаем распространить наше рассмотрение на межпланет-
ные перелеты в пределах солнечной системы. В этом
случае можно упростить анализ, описывая поведение
летательного аппарата его характеристической скоростью
сс и вводя гравитационные и другие поправки непосред-
ственно в требования, предъявляемые к скорости в раз-
личных условиях полета. Снова принимаем а0 = 1,3, =
= 1 кг/Мвт, но на этот раз вычисляем значения vc как
функции от /Sp для диапазона значений истинного отно-
шения массы мертвого груза к полной массе (znL//n0)
при двух видах рабочего тела: Н2 (рР = 0,071 а/сл<3) и
NH3 (рр = 0,71 г!см3). Результаты расчета представлены
на рис 14.4, который относится к двухступенчатым раке-
там на ядерном топливе при указанных значениях
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
473
mJiriQ. На рисунке отмечены также приближенные зна-
чения характеристических скоростей, необходимых для
полета по нескольким представляющим интерес маршру-
там в пределах солнечной системы; каждый из них со-
стоит из участков взлета и посадки, на которых расхо-
дуется мощность, пункта назначения и всех промежуточ-
ных точек.
Лараюперистиюехая сюряслм xvpatim? vc, фт/сек
Рис. 14.4. Характеристики двухступенчатых ракет на ядерном
топливе.
Из рис. 14.4 мы заключаем, что почти все эти марш-
руты могут быть пройдены с помощью запускаемых
с Земли двухступенчатых ракет, если на аммиаке дости-
гается удельный импульс от 500 до 1200 сек, а на водо-
роде — от 800 до 2400 сек. Здесь снова полезно попы-
таться сделать определенные выводы путем численного
изучения искусственной оптимизирующей функции. При-
мем опять употреблявшуюся ранее форму этой функции,
474
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ (гл. XIV
но на этот раз для аммиака возьмем нормировочный
фактор для /8р равным 400 сек, а для отношения tnJtnQ
число 20. Результаты расчета сведены в табл. 14.2 для
двух значений характеристической скорости аппарата,
Двух значений mLlm^ и для двух видов рабочего тела —
водорода и аммиака.
Рассмотрение этой таблицы показывает, что системы,
работающие на водороде, всегда лучше тех, которые ра-
ботают на аммиаке, и что аппараты с аммиаком в каче-
стве рабочего тела становятся все хуже с точки зрения
необходимости преодоления трудностей, связанных с по-
лучением больших удельных импульсов от каждой сис-
темы. С другой стороны, мы видим, что качество аппара-
тов, работающих на аммиаке, ухудшается менее быстро,
чем аппаратов, использующих водород, когда увеличи-
вается доля полезного груза; это свойство более резко
выражено при высоких скоростях продуктов сгорания.
14.23. Оптимизация баллистической траектории. Об-
ратимся теперь к примеру непосредственной оптимиза-
ции, когда не возникает необходимости во введении ис-
кусственных оптимизирующих функций. Представляет
интерес вопрос об оптимальных условиях, при которых
на данное расстояние переносится максимальный полез-
ный груз. Мы будем считать, что задача ограничена ис-
следованием полета над невращающейся Землей, но ре-
зультаты будут качественно справедливы и для других
возможных задач, таких, как перенос грузов с орбиты на
орбиту в космических условиях.
Таблица 14.2
Оптимизация с помощью искусственных оптимизирующих
функций (водород и аммиак в качестве рабочего тела)
тд/то п — 1, 1 п - 1, т = 2 л = 2, т 1 Характеристиче- ская скорость v£, фт)сек
NH, н2 NH3 н2 NH, н2
0,09 3,22 2,82 3,82 2,84 4,66 4,26 40000
0,01 1,03 0,76 0,89 0,51 0,87 0,60
0,09 5,8 5,3 17,8 14,1 7,24 6,74 80 000
0,01 2,15 1,55 4,0 2,02 1,99 1,39
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
475
Для решения поставленной задачи мы должны вос-
пользоваться известным уравнением баллистической
траектории, выражающим дальность полета в функции
от величины скорости продуктов сгорания и угла фй об-
разуемого вектором скорости с местной плоскостью гори-
зонта. Напишем это уравнение без вывода; оно имеет
вид
S = 2/?etg|7-^-------l)ctg . (14.14)
L\v^cos<pz / J
Здесь мы пренебрегли высотой летательного аппарата в
момент выгорания всего топлива*).
Рассмотрение этого уравнения показывает, что при
приближении фг- к нулю или к л/2 дальность S стремится
к нулю и что поэтому Нолжен существовать оптимальный
стартовый угол ф; в момент сжигания всего топлива,
дающий максимальную дальность для данной скорости
продуктов сгорания. Чтобы найти этот оптимальный
угол, дифференцируем (14.14) и, положив dSld^i = Q,
разрешаем результат относительно фг-. Подстановка этого
значения ф^ в (14.14) и добавление слагаемого, отражаю-
щего конечность высоты, на которой происходит полное
сгорание, приводит нас к уравнению (14.12), использо-
ванному ранее для изучения дальностей полета при оп-
тимальных углах в точке полного сгорания. Если пред-
ставить уравнение для дальности при оптимальном угле
графически, то станет видно, что величина дальности
весьма чувствительна к малым изменениям скорости
продуктов сгорания в том случае, когда дальность срав-
нима с диаметром Земли. В силу этого для снарядов
дальнего действия, летящих по оптимальным по углу
траекториям, необходимо установление особенно тща-
тельного контроля за величиной скорости продуктов сго-
рания. Численный анализ более общего уравнения для
дальности (14.14) показывает, однако, что чувствитель-
ность дальности по отношению к изменениям скоро-
сти может быть сильно уменьшена путем перехода на
♦) Это справедливо лишь при условии В частном
случае = gQRe оптимальный угол <р/ равен 0°, а дальность
равна
476
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
оптимальные стартовые углы, но только лишь ценой уве-
личения необходимой скорости продуктов сгорания. Воз-
росшая скорость продуктов означает в свою очередь
уменьшение полезного груза, если полная стартовая
масса сохраняет прежнее значение, и, таким образом,
возникает возможность определения оптимального стар-
тового угла и оптимальной скорости в момент полного
сгорания, обеспечивающих при данной дальности полета
максимум переносимого груза на единицу площади райо-
на попадания при заданной области изменения вектора
скорости в момент полного сгорания топлива.
Для решения этой задачи мы должны сначала раз-
решить уравнение (14.14) относительно скорости в мо-
мент сгорания, выразив ее через угол и дальность:
v» V l + tg?r°dg(S/2^) •
Отсюда можно вычислить скорость изменения Vb при
вариации <рг- для фиксированного S; мы найдем, что эта
скорость пропорциональна кубу скорости продуктов сго-
рания в соответствии с уравнением
( dvb | _ v3 [sin 2<tt + cos 2?/ ctg (S/2/?e)]
Vd^ls- 2goRe
Сходным образом при заданном (р^ скорость измене-
ния S в зависимости от Vb обратно пропорциональна кубу
скорости продуктов сгорания; имеет место формула
/_£S_\ _ 4g0^sln2(S/2/?f)
\ dvb / v3b cos <ti sin ъ
При пользовании этими уравнениями нужно иметь в
виду; что величина?*в правой части (14.16) должна
вычисляться из равенства (14.15), чтобы выбранные зна-
чения фг и S были согласованы между собой; величина
S в правой части (14.17) также должна соответствовать
принятым значениям qpj и Vb. Последние два уравнения
вместе с формулой (14.1) для отношения масс с учетом
поправки (14.10), отражающей действительные потери,
могут быть использованы для разыскания оптимальных
14.2]
ПОЛЕТ С БОЛЬШИМ УСКОРЕНИЕМ
477
(указанных выше) условий полета путем численных рас-
четов.
Для иллюстрации ожидаемого поведения системы
рассмотрим численный пример. Пусть мы желаем пере-
нести полезный груз на расстояние 9000 уставных миль
вдоль невращающейся Земли, и пусть преодоление раз-
личных потерь эквивалентно уменьшению характеристи-
ческой скорости аппарата на 4000 фт/сек. Из написанных
выше уравнений для дальности найдем, что необходимое
при стартовом угле в 45° отношение масс должно быть
равно 31,2, тогда как эта же величина при оптимальном
угле 13,5° составляет лишь 18,8, если используется обыч-
ное для химической ракеты значение скорости истече-
ния, равное 10000 фт!сек. Соответствующие отношения
масс при типичном для ядерных ракет значении ско-
рости истечения, равном 30 000 фт!сек, будут соответ-
ственно 3,14 и 2,66.
Чтобы перенести полезный груз весом 3000 фун-
тов по оптимальной траектории в точку приземления,
химическая ракета, вес которой без топлива и груза со-
ставляет 4% ее веса с полным запасом топлива и с гру-
зом, должна весить на старте 227 000 фунтов. Для ле-
тательного аппарата с ядерным двигателем, вес которого
без учета рабочего тела и груза равен 30% веса с пол-
ной нагрузкой (из-за относительно более тяжелых, чем
у химической ракеты, цистерн и оборудования), соответ-
ствующая цифра составляет 40 000 фунтов. Для полета
при фг= 45° из уравнения (14.5) для полной массы
найдем, что химические ракеты вообще не выполняют
задания, если вес их без груза составляет 4% от
веса с грузом.
Вместо этого рассмотрим случай полета на большую
дальность, так что отношение весов берется равным 3%.
При этом вес химической ракеты, рассчитанный на еди-
ницу полезного груза, должен быть в 6,42 раза больше
при полете по траектории с <рг- = 45°, чем та же величина
для ракеты с начальным отношением весов 4%, летящей
по оптимальной траектории. Из уравнения (14.17), опре-
деляющего чувствительность дальности к изменениям
скорости продуктов сгорания, найдем, что ошибка в даль-
ности, связанная с ошибкой в скорости, для оптимальных
478
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
условий полета в 3,17 раза больше, чем для полета
с фг = 45°. Это означает, что при полете с <р^ = 45° разброс
пунктов приземления составляет примерно 0,1 той же ве-
личины в оптимальных условиях, а отсюда следует, что
стартовый вес химической ракеты, переносящей одну и
ту же полезную массу, рассчитанную на единицу пло-
щади района приземления, составляет лишь 0,642 стар-
тового веса при полете в оптимальных условиях. Допус-
кая уменьшение отношения сухого веса к полному, по-
добно тому как это было сделано в отношении больших
химических ракет, и следуя приведенным выше рассу-
ждениям, найдем, что для выполнения одной и той же
задачи при старте под углом 45° вес ядерной ракеты дол-
жен составлять лишь 0,081 долю веса ракеты при опти-
мальном угле старта. Сравнение приведенных численных
данных показывает, что это характерное для ракетных
летательных аппаратов свойство движения лучше может
быть использовано для ракет с высоким значением /Sp
(ядерных), нежели Для ракет с низким /8р (работающих
на химическом топливе).
До сих пор мы рассматривали лишь задачи, относя-
щиеся к движению ракет над невращающимся сфериче-
ским гравитирующим телом. В действительности при по-
летах над Землей положение совсем иное, поскольку
влияние вращения и конечности времени полета долж-
но быть учтено при анализе точности приземления и при
сравнении преимуществ и недостатков старта под боль-
шими или оптимальными углами. Подробное обсужде-
ние этих, а также и других характеристик дальности и
точности полета реактивных снарядов над Землей было
дано Генри [5]. Результаты, обсуждавшиеся выше, в дей-
ствительности, однако, вполне применимы для получения
качественной картины движений между различными ор-
битами с точки зрения улучшения точности, которой
можно ожидать от повышения скорости продуктов сго-
рания, а также с точки зрения определения направления,
в котором следует изменять полную начальную массу
ракеты с целью достижения упомянутого увеличения
точности. Для этого, следуя методам, развитым Эрике
[6], или Бэйкером [7], либо Бэйкером и Мэкемсоном [8]
(см. также обзорную статью Бэйкера [9]), нужно про-
14.2] ПОЛЁТ С БОЛЬШИМ УСКОРЕНИЕМ 479
извести детальные численные сравнения для каждого из
представляющих интерес случаев.
14.24. Различные вопросы. Две другие интересные и
заслуживающие обсуждения задачи оптимизации полета
ракет на ядерном топливе заключаются в максимизации
дальности или грузоподъемности летательного аппарата
заданной массы путем изменения скорости истечения во
время полета, а также в минимизации веса летательного
аппарата при полете с экипажем в заданных условиях
путем надлежащего выбора защищающей массы и уров-
ня мощности реактора.
В противоположность ракетным двигателям на хими-
ческом топливе, работающим при сравнительно неизмен-
ных значениях энтальпии газа на входе в сопло, в дви-
гателях ядерных ракет можно в процессе работы в ши-
роких пределах изменять удельное содержание энергии
в газе, образующем рабочее тело, путем существенного
изменения давления в активной зоне. Для реакторов,
тяга которых ограничена пределами, определяемыми чис-
лом Маха на выходе из сопла, падение давления озна-
чает одновременное уменьшение полной тяги. Уменьшен-
ное рабочее давление, однако, допускает большую сте-
пень диссоциации рабочего газа при данной температуре
и несколько более высокую температуру выходящих
газов при данной температуре материалов, обеспечивая
поэтому более высокий удельный импульс главным обра-
зом благодаря происходящим при течении в сопле про-
цессам рекомбинации. Поскольку при этих условиях тяга
меньше при больших значениях /8р, может случиться,
что ускорение аппарата окажется недостаточным для
полета с тягой. Очевидно, что тогда должны существо-
вать определенная траектория полета (в гравитационном
поле) и определенное значение давления в реакторной
системе (и в силу этого тяги ракетного двигателя), ко-
торые обеспечат максимум скорости продуктов при за-
данном полезном грузе и заданной дальности. Простым
путем невозможно определить сложную программу усло-
вий получения такого результата, и подобная оптимиза-
ция в каждом представляющем интерес случае должна
производиться численными методами с использованием
вычислительных машин. Ван и др. [10] дали, однако,
480
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ (гл. XIV
пример непосредственного получения интересующих в
такой задаче результатов; они изучали вопрос о скорости
истечения продуктов, допустимой для различных про-
грамм изменения тяги и давления в реакторной системе
одноступенчатой ракеты при вертикальном полете. Было
обнаружено, что при одном и том же отношении масс
оптимальная программа изменения давления дает выиг-
рыш в скорости истечения продуктов примерно до 30%.
Задача оптимизации по отношению к защитной массе
и к выбору мощности реактора сходна с предыдущей
в том отношении, что для них обеих отсутствуют общие
решения. Для частных случаев каждой из задач реше-
ния должны получаться численным путем. В рассматри-
ваемой задаче требуется минимизировать массу лета-
тельного аппарата, необходимую для переноса данного
груза на известное расстояние при наличии экипажа,
путем оптимального выбора уровня мощности реактора,
а следовательно, ускорения корабля, а также защитной
массы. Увеличение последней уменьшает при заданной
скорости продуктов полезную грузоподъемность данного
корабля, если все другие параметры, фигурирующие в
уравнении полета ракеты, сохраняют постоянные значе-
ния. Большая защитная масса, с другой стороны, позво-
ляет использовать реакторы большей мощности при том
же грузе и (экранированном) помещении для команды.
Большая мощность реактора означает большую тягу,
т. е. возросшее ускорение при том же полном весе ко-
рабля. Большее ускорение в свою очередь приводит к
меньшему времени работы реактора, т. е. к уменьшению
«гравитационных потерь» при подъеме массы в гравита-
ционном поле. Это дает меньшее значение показателя
степени в уравнении для отношения масс корабля при
той же расчетной скорости продуктов и уравновешивает
влияние массы корабля, возросшей в режиме работы с
большей мощностью при большей защите. Ясно, что
должно существовать оптимальное сочетание защитной
массы и мощности реактора, минимизирующее полный
вес корабля, предназначенного для любого полета с
ограниченным по весу грузом, но одинаково очевидно,
что определение такого сочетания может быть проведено
лишь численно для данных систем и выполняемых ими
14.3)
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
481
заданий. Результаты исследований, произведенных на
примерах отдельных одноступенчатых ракет, показывают,
что в общем случае оптимум значительно сильнее зави-
сит от мощности реактора, нежели оТ величины защит-
ной массы, и что наиболее желателен выбор минималь-
ной мощности (достаточной для выполнения установлен-
ного задания).
14.3. ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ*)
С
Мы сталкиваемся с большим разнообразием опти-
мальных задач, изучая полет с малым ускорением в про-
странстве, свободном от поля, как с точки зрения опре-
деления экстремальной траектории, так и с точки зрения
Нахождения оптимальных соотношений между парамет-
рами, характеризующими одну лишь двигательную си-
стему, поскольку эти параметры могут воздействовать
на полет корабля.
Сначала мы приведем ряд общих соображений о по-
лете, не связанных с распределением масс внутри ко-
рабля, а впоследствии распространим наши оптимальные
рассмотрения на вопрос о наиболее важных характери-
стиках ядерно-электрических двигательных систем, ис-
пользуемых для полета с малым ускорением.
14.31. Общие соображения. Поскольку масса силовой
установки аппарата с малым ускорением в общем случае
фиксирована тем обстоятельством, что полет, по предпо-
ложению, происходит при максимуме развиваемой мощ-
ности, интуитивно кажется очевидным, что двигательные
системы будут наиболее эффективны с точки зрения ис-
пользования масс (например, радиаторов, турбин, гене-
раторов и т. д.), если только мощность во время полета
поддерживается постоянной и равной ее максимальному
значению* **). Поэтому для анализа будет удобно ввести
мощность системы Рг в качестве исходной переменной.
Возвращаясь к уравнениям (14.2) и (14.3) и комбинируя
♦) Большая часть материала этого раздела взята из рукописи
подготавливаемой к выходу в свет книги автора <Основы полета
ракет на ядерном топливе».
**) Этот вопрос детально рассмотрен в разделе 5.3 главы V.
31 Дж. Лейтман
482
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ (гл. XIV
их, найдем, что полная мощность равна
= — (14.18}
где вместо употреблявшегося ранее обозначения тр на-
писано dm/dt. Если теперь допустить, чтобы скорость ис-
течения менялась со временем, и потребовать, чтобы
полная производимая мощность сохранялась постоянной,
что требует в свою очередь, чтобы dmldt было перемен-
ным, то можно будет получить выражение для измене-
ния массы корабля путем интегрирования (14.18); будем
иметь
t
та)=щ~^рг[ (14.19)
Для полета с постоянным расходом мощности в тече-
ние заданного времени /ь, когда затрачивается энергия
Prtb, уравнение (14.19) показывает, что минимальное
изменение массы корабля, т. е. максимальная конечная
масса mb = m(tb)t будет достигнуто при возможно боль-
шем ve. Этот вывод, однако, немного значит физически,
т. е. он ничего не говорит о скорости, достигнутой кораб-
лем при полном израсходовании рабочего тела. Эта ско-
рость определяется импульсом ракеты, а не полной
энергией, затраченной на истечение. Поэтому для нас
желательно получить максимальное значение m(t) пу-
тем минимизации интегрального члена в уравнении
(14.19) при добавочном условии, что изменение скоро-
сти корабля должно быть одним и тем же во всех рас-
сматриваемых случаях. Для движения в одном измере-
нии это требование означает, что
J a(/)d/ = const = ^ — vQ. (14.20)
о
Рассмотрим для простоты случай полета в простран-
стве без поля. При этом ускорение a(t) создается лишь
одной тягой и может быть связано с ve(t) по закону
Ныртона F == пга с учетом того факта, что эффективная
14.3)
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
463
сила тяги равна F=—(dm/dt)ve. Это дает
а (О
___ ve (0 dm
т (t) dt ’
(14.21)
где зависимость каждой переменной от времени указана
явно. Мы должны также воспользоваться уравнением
(14.19) для исключения собственно массы т из уравне-
ния баланса сил. Этими действиями уравнение (14.20)
приведем к виду
vb
'ъ
dt
(14.22)
0 V.
о
Проблема оптимизации приняла тем самым форму
вариационной задачи, в которой мы желаем определить
зависимость ve от времени, делающую интегральное сла-
гаемое в (14.22) стационарным (экстремальным) при на-
личии связи, выраженной формулой (14.20). Непосред-
ственное решение этой задачи связано, однако, с мате-
матическими затруднениями, и проще исследовать усло-
вия оптимального задания ускорения корабля a(t) =
— нежели непосредственно скорости истече-
ния. Далее мы увидим, что можно определить оптималь-
ный закон ve(t) только через закон изменения массы
m(t). В уравнении (14.18) можно использовать алгеб-
раические подстановки, подобные тем, которые были ис-
пользованы при выводе (14.22), имея целью исключить
скорость истечения и получить новое дифференциальное
уравнение, связывающее массу корабля с его ускорением
<14'23>
Левая часть представляет собой полный дифферен-
циал, поэтому интегрированием можно получить
t
тЛг /*^(i)dt.
т \t) mQ . Лл rHj J
(14.24)
Отсюда мы видим, что для максимизации m{t) РТ
должно быть возможно большим, в соответствии с
31*
484
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
1гл. XIV
нашим предыдущим заключением о том, что я* должно
быть возможно большим. При заданной величине мощ-
ности очевидно, что максимум' m(f) для любого вида
движения будет достигнут при минимуме интегрального
слагаемого в (14.24). Если, как ранее, мы желаем изу-
чить прямолинейное Движение корабля при заданной ко-
нечной скорости в пространстве без поля, то мы должны
вновь использовать ограничение (14.20). Переменной в
обеих подынтегральных функциях— (14.20) и (14.24) —
является а(0, так что мы можем непосредственно вос-
пользоваться развитыми в предыдущих главах методами
решения вариационных задач. Вспомним, что функция Q,
доставляющая экстремум интеграла вида JQ dt, как в
(14.24), должна удовлетворять уравнениям Эйлера —
Лагранжа. Для введения, единственной связи типа
fpj/ = const [как в (14.20)] образуем с помощью мно-'
жителя Лагранжа X новую функцию M — Q4-ХР, которая
также должна удовлетворять вариационному принципу.
В нашей задаче функция М имеет вид
Д4 = а2(/) + ка(/), (14.25)
где а считается обобщенной координатой. Отметим, что
М зависит только от а, но не от а (X — постоянная), так
что в уравнении Эйлера — Лагранжа участвуют лишь
первые производные, и получается
2а(/) + Х = 0, (14.26)
откуда следует, что а должно быть постоянным во все
время движения; этот результат сходными методами был
получен Ирвингом [11]. При этом уравнения (14.18) и
(14.19) показывают, что скорость истечения должна не-
прерывно изменяться таким образом, чтобы произведе-
ние m(t)ve(t) также оставалось постоянным. В этом
частном случае движения с постоянным расходом мощ-
ности в пространстве без поля конечная скорость дается
известной формулой *)
vb~ ^ = atb, (14.27)
•) На протяжении всей главы релятивистские эффекты не при-
нимаются во внимание.
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
485
а конечное значение массы определяется уравнением
(14.24):
1_____L — аЧь м _ 1 ।
mb т0 ~2Ргъ' ИЛИ ть ~ 1 2РГ^ ’
Из уравнений (14.27) и (14.28) можно исключить
и найти величину ускорения:
а=р_,\ ...
\ ть / <Уь — Ц») то
Закон изменения скорости истечения относительно
корабля, необходимой для поддержания постоянства
ускорения, легко находится с помощью (14.18) и (14.21)
путем исключения Рг и последующего исключения а с
помощью (14.29); в результате находим ve(t) как функ-
цию m(t) и расчетных параметров полета. Результат
имеет вид
ve (/) == = . (14.30)
е v ’ am(t) т (t) [(mQ/mb) — 1] v '
Зависимость массы корабля от времени можно опре-
делить непосредственно из (14.24) интегрированием при
постоянном ускорении. После этого можно из (14.30)
определить явный вид ve как функции времени:
ve (/) = at + . Vb~?° .- = v (/) + »- moVo (14 31)
1 (mQ/mb) — 1 1 mQ — mb v '
В заключение этого раздела отметим, что режим с
постоянным ускорением может оказаться неоптимальным
для связей, отличающихся от рассмотренной нами (см.,
например, Лейтман [12]).
14.32. Распределение масс компонент и оптимизация
полета. После того как мы исследовали вопрос о пове-
дении летательного аппарата без учета его внутреннего
устройства, обратимся к изучению взаимосвязи между
внутренними параметрами, описывающими распределе-
ние масс, и внешними параметрами, относящимися к ди-
намическим характеристикам полета корабля. В данном,
случае подразделение всего корабля на составные части
логически несколько отличается от подразделения для.
аппаратов с большим ускорением, так как теперь рас-
сматриваются как раз аппараты с непосредственным
32 Дж. Лейтман
486
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
преобразованием энергии. Мы по-прежнему выделяем
массу рабочего тела, цистерн и конструкций, а также
массу мертвого груза. Для кораблей с большим ускоре-
нием мы нашли выгодным разбиение массы двигатель-
ной системы на две составные части: массу источника
ядерной энергии тг и массу насосной установки тре.
Это было сделано по двум основным причинам: 1) мы
были заинтересованы в том, чтобы изучить роль удель-
ной мощности одного лишь источника энергии в опреде-
лении поведения корабля; 2) большие значения тяги, не-
обходимой для создания ускорения, достаточного для
подъема всего корабля, требуют в свою очередь относи-
тельно большого расхода рабочего тела, и масса обору-
дования насосной установки может стать существенной
частью массы всей двигательной системы. Теперь же,
однако, мы не будем пытаться разделить массу трт
ядерной двигательной системы на отдельные составляю-
щие. Мы поступаем так, во-первых, потому, что не на-
мерены входить в подробные обсуждения различных си-
стем, методов и устройств, которыми можно воспользо-
ваться при свободном движении, и, во-вторых, потому,
что более поучительно провести общий анализ поведе-
ния системы, который при желании можно специализиро-
вать применительно к системам частного вида.
Таким образом, мы должны рассмотреть только че-
тыре составляющие массы: массу рабочего тела тр,
массу мертвого груза (определение см. выше) mLt массу
цистерн для рабочей жидкости и конструкций корабля
ms1, а также массу ядерной двигательной системы трг\
в результате полная масса оказывается равной
= mpr -\-mst-\-mp-\-mL. (14.32)
Как; и ранее, общий анализ может быть произведен
лишь потому, что мы можем связать некоторые из этих
масс с величинами мощности или энергии, необходимыми
Для полета корабля. Расход энергии однозначно опреде-
ляется скоростью истечения и полной массой рабочего
тела лишь при условии, что скорость истечения поддер-
живается постоянной в течение всего времени полета с
расходом мощности. С другой стороны, мы видели из
уравнения (14.30), что переменная скорость истечения
14.3] ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ 487
может в ряде случаев дать в общем лучшие характери-
стики полета, нежели скорость, сохраняемая постоянной!
Расход энергии равен тогда интегралу по времени от
мгновенной мощности, заданной уравнением (14.18),
причем интегрирование распространяется на время ра-
боты двигательной системы; поэтому расход оказывается
не простым образом связанным с полной массой рабо-
чего тела. Чтобы избежать математических усложнений,
которые возникают при определении связи между полной
массой рабочего тела и полным расходом энергии, опре-
деляемым заданными условиями полета, выберем соб-
ственно массу рабочего тела в качестве исходной пере-
менной. Это эквивалентно предположению о том, что
запас энергии для движения аппарата фактически не
ограничен и не накладывает ограничений на динамику
полета; это обстоятельство будет более подробно обсу-
ждено в дальнейшем. Поскольку теперь в нашем распо-
ряжении нет уравнения, связывающего тр с mQ анало-
гично уравнению для отношения масс ракет с постоян-
ным /sp (где энергия пропорциональна тр), мы должны
считать тр параметром в уравнении, описывающем дви-
жение корабля.
Положим, что масса цистерн и конструкций опреде-
ляется по-прежнему уравнением (14.6):
mst = Ast(mp^y- (14.33)
и примем, что полная масса двигательной системы ли-
нейно связана с производимой ею мощностью и характе-
ризуется удельной массой на единицу производимой
мощности Zpr, как это определяется формулой (14.2).
Итак,-
тРг=\,гРг (14.34)
Далее, поскольку двигательная система может вклю-
чать в себя ряд узлов типа роторных генераторов, от-
водящих тепло радиаторов и т. д. и поскольку мы
могдц ранее определить оптимальную скорость истечения
без учете конструкции двигательной системы, мы не бу-
дем пытаться связать трг с /8р, как это было сделано
в,уравнении (14.8), справедливом для ракетного двига-
теля на ядерном топливе.
32*
488
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
Выражение для полной массы, полученное с учетом
(14.32), имеет вид
т0 = Prlpr + А/ (т/Рр ) + тр + mL- (14-35)
Из этого уравнения можно найти мощность, которая
должна приходиться на единицу массы корабля; получим
(14.36)
Это выражение можно использовать для исключения ве-
личины Рг!т0 из (14.28) и нахождения в результате пре-
образований соотношения между ускорением корабля в
пространстве без поля и относительными массами его
составных частей:
_ [l~P АА) - (mL/mo)] (тр/то)
а >pr (Vb — V0) [1 — Шр/Шо] ' ' • '
или
_ 2TJJ (трг/т0) (тр/т0)
1рг — ^о) [ 1 — (тр/т0)] '
где мы ввели обозначение р = 1 + Ast/pp.
Рассмотрим теперь условия полета, оптимальные в
смысле минимума полетного времени при данном изме-
нении скорости, независимо от расстояния, пройденного
во время полета. Для полета с постоянным ускорением,
при котором, как мы видели выше, конечное значение
массы максимально, минимальное время полета эквива-
лентно максимальному ускорению. Нас интересуют, та-
ким образом, временные зависимости массы и других
факторов, доставляющие максимум ускорению корабля.
Прежде чем идти дальше, напомним, что для нас пред-
ставляет интерес движение в пространстве без полей;
этот случай был подробно исследован Престон-Томасом
[13, 14], Фоксом [15] и др. Результаты, полученные для
этого класса движений с малым ускорением, могут ока-
заться неоптимальными при полете в гравитационных
полях. Оптимизация полета в гравитационных полях
представляет вообще более сложную задачу, чем в от-
сутствие таких полей (см., например, Фолдерс [16], Шин-
длер [17], Микиельсен [18], Лейтман [19] и Фокс [20]), но
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
489
при этом не возникает ничего существенно нового по
сравнению с теми обстоятельствами, которые, как мы
увидим, обнаруживаются при изучении полета в свобод-
ном от полей пространстве*).
Из уравнений (14.37) видно, что максимальное уско-
рение будет иметь место в случае, когда удельная мощ-
ность, развиваемая двигательной системой, бесконечно
велика либо если Хрг = 0. Ясно, таким образом, что сле-
дует стремиться к созданию двигательных систем с вы-
сокой удельной мощностью. Для того чтобы найти усло-
вие, которому должно удовлетворять отношение тР1т^
при данных значениях относительных масс двигательных
систем и мертвого груза, продифференцируем первое из
уравнений (14.37) по tnPlm^ приравняем производную
нулю и разрешим полученное уравнение относительно
тР1т^. Результат далее упрощается путем исключения
отношения mJrriQ с помощью (14.32); получаем
-^(1 — = (14.38)
mQ \ mQjr mQ v '
максимальное ускорение определяется из второго урав-
нения (14.37) в виде
2i)/ / то\ъ
(14.39)
Значение mPlmQ, фигурирующее в этой формуле,
должно быть решением уравнения (14.38) при заданной
величине mprltnQ.
Если пользоваться средним ускорением а, определен-
ным по формуле
atb = vb — v0 — J a(/)d/, (14.40)
о
то можно изучать условия оптимального полета при ми-
нимуме времени с ускорением корабля, отличающимся
•) Действительно, как показано в гл. V (и ранее Лейтманом
[12]), постоянное ускорение также представляет собой оптимальное
поведение при полете в постоянном поле, если фиксировано лишь ubt
но не 50.
33 Дж. Лейтман
490
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
от постоянного. В частности, для случая постоянной ско-
рости истечения, который менее предпочтителен с энер-
гетической точки зрения, но более просто реализуется
на практике, определенное формулой (14.40) среднее
ускорение с помощью уравнения (14.1) представляется
в виде
—v0 ve / тр\
Время tb полета с затратой мощности можно при по-
стоянной скорости истечения выразить в этой формуле
через тр, Рг и ve с помощью уравнения (14.18) и тож-
дества— tb(dmldt) =тр. В результате получаем
" = -?)• <14-42>
Этот результат можно еще более упростить путем под-
становки величины ve, выраженной снова из уравнения
(14.1) для отношения масс, а также приняв во внимание
уравнение (14.36) для отношения Р^т^
Окончательный результат имеет вид
2т)у [1 — р (т/т) — т /т ] In2 (1 — т/тЛ
а = м^)-'-----------—(14-43>
или
21); (mpr/mQ)\n2(l—mp/m0)
а~ Ьрг (Уь — VO) тр/т^ •
Чтобы найти условие, которому должно удовлетво-
рять отношение tnPlmQ для минимизации времени полета
(максимум а), будем следовать методу, использованному
для вывода формулы (14.38) в случае постоянного уско-
рения. Применение этого метода к уравнению (14.43)
приводит к ограничивающему соотношению
трТ/та + р(тр1та) / тр\ 2трг/та
тр1тй П та1'\—тр1тй~^'
Пользуясь им для исключения относительной массы
mprlniQ из второго уравнения (14.43), найдем величину
14.3] ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ 491
максимального среднего ускорения равной
- 2т); р(1 — /np/m0) In3 (1 — mp/mQ)
^max — (yb — v0) 2(mp/^0) + (1 — mplmQ) In (1 — тпр/т^) ’
(14.45)
где отношение mp/m,Q должно, разумеется, удовлетворять
уравнению (14.44). Результаты численного сравнения
двух типов поведения системы, описываемых соответ-
ственно уравнениями (14.39) и (14.45), представлены
в табл. 14.3. Здесь приведены результаты вычисления
относительных величин ускорения корабля и времени
полета для ряда значений относительной массы рабо-
чего тела, эквивалентных, согласно (14.44), ряду значе-
ний относительной массы ядерной двигательной системы,
при типовых значениях параметров: Ast = -^(z/CM?>>),\
Рр=13,6 г/см3 (в качестве рабочего тела взята ртуть),
т]г = 0,25 и Хрг=2500 кг/Мвт. Чтобы иметь дело с одними
и теми же единицами, заданное значение Крг следует
умножить на переходный множитель 0,98 • 10“7 Мет X
X сек!кг • см, если а измеряется в единицах ускорения
силы тяжести на земной поверхности (go = 980 см/сек2).
Из таблицы можно вычислить истинные численные зна-
чения а и tb для любой величины приращения скорости
иъ — По, получаемого за время полета с расходом мощ-
ности в пространстве без поля.
Рассмотрим теперь оптимальное использование лета-
тельного аппарата при заданном распределении масс по
его основным частям. Для нас наибольший интерес пред-
ставляет определение оптимальных соотношений между
дальностью и способностью каждого данного корабля
развивать ту или иную скорость в момент полного израс-
ходования рабочего тела. Что касается ракетного лета-
тельного аппарата, способного развивать скорость при
полном израсходовании рабочего тела в пространстве
без поля, то очевидно, что минимальное время перехода
между состояниями покоя в любых двух заданных точ-
ках будет достигнуто при мгновенном начальном ускоре-
нии до скорости Уь/2 с последующим свободным полетом
на требуемое расстояние So и мгновенным замедлением
в конце на величину скорости и&/2. График временного
33*
492
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
изменения скорости изображен на рис. 14.5, а. Интеграл
от этой функции (заштрихованная площадь) равен рас-
Рис. 14.5. Экстремальные и опти-
мальные характеристики летатель-
ных аппаратов малого ускорения:
(z) бесконечно большое ускорение
и бесконечно большая мощность
силовой установки, случай теоре-
тически минимального времени пе-
релета; б) минимальное ускорение
и минимальная мощность силовой
установки, случай максимального
времени перелета; в) оптимальное
ускорение и оптимальная мощ-
ность силовой установки, случай
практически минимального време-
ни перелета.
стоянию So, пройденному
за время полета. При ко-
нечной величине скорости
истечения уравнения
(14.18) и (14.21) показы-
вают, однако, что двига-
тельная система потребо-
вала бы бесконечно боль-
шой мощности в моменты
ускорения и замедления и
что масса двигательной
системы поэтому тоже бы-
ла бы бесконечно велика.
Для достижения миниму-
ма времени перелета с
помощью двигательной
системы малой массы и,
следовательно, малой
мощности следует непре-
рывно прикладывать тя-
гу, ускоряя корабль в те-
чение первой половины
полетного времени до ско-
рости 72(^&— £>о) и за-
медляя на ту же вели-
чину скорости в течение
оставшейся половины вре-
мени. Для покрытия за
время полета того же са-
мого расстояния So при
нулевой начальной скоро-
сти (ио=О) ракета по-
стоянной тяги должна ра-
ботать в течение проме-
жутка времени, который
вдвое превышает время
полета ракеты с бесконечно большим ускорением в
предыдущем случае. Зависимость скорости от времени
дается при этом рис. 14.5, б. Поскольку рост мощности
14.3) ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ 493
двигательной системы позволит осуществлять большие
ускорения и сокращать, таким образом, время полета,
очевидно, что можно найти оптимальное распределение
времени между периодами ускорения и свободного по-
лета, при котором для данной величины относительной
массы mLlmQ полезного, или мертвого, груза время по-
лета /о принимает минимальное возможное значение.
( ; Таблица 14.3
Характеристики кораблей малого ускорения
в пространстве, свободном от полей
Условие тр/т0 0,25 0,50 0,75 0,90 Единицы
Постоян- ное а a(vb — v0) 131,3 525 1182 1701 см/сек
tUVb — fo)2 7,79-10"6 1,95-10"6 8,61-Ю"7 6,00-Ю"7 секшем2
Постоян- ное ve a(vb — v0) 131,6 536 1204 1635 см/сек
t/(yb — v0)2 7,77-Ю"6 1.91-10-6 8,47-Ю-7 6.25-Ю-7 секР/см2
В этом более общем случае временная зависимость
скорости подобна изображенной на рис. 14.5, в.
В случае постоянного ускорения, когда достигается
максимум массы по окончании периода работы двигате-
лей, оптимальность времени полета и величины ускоре-
ния влечет за собой оптимизацию значения скорости ко-
рабля . в момент полного израсходования рабочего
тела *).
Расстояние, пройденное кораблем в течение периода
работы двигателей, представляет собой интеграл, взя-
тый по треугольным частям области под графиком
рис. 14.5, в; это расстояние может быть выражено через
♦) В противоположность ситуации, описанной в сноске яа
стр. 489, постоянное ускорение не является оптимальным при полете
за минимальное время на заданное расстояние при известной вели-
чине конечной скорости. Лейтман [12], однако, показал, что в этих
условиях Мджно немного сократить время полета (примерно на 4%),
если воспользоваться линейно изменяющимся ускорением.
494
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
значение скорости в момент окончания работы двигате-
лей; получим
Sb = -j atl = у vbtb- (14.46)
Расстояние, пройденное за время свободного полета,
равно
= (14.47)
Полное время полета и пройденное расстояние рав-
ны соответственно t0 = tb + tc и So = Sb + Sc и связа-
ны, согласно формулам (14.46) и (14.47), следующим
образом:
(14.48)
Для определения необходимой для минимизации по-
летного времени скорости корабля в момент окончания
работы двигателей при условии, что начальная скорость
его равна нулю, дифференцируем (14.48) по прирав-
ниваем результат нулю и разрешаем полученное урав-
нение относительно vbt воспользовавшись тождеством
ub = atb и вторым уравнением (14.37) для выражения /ь
через скорость в момент остановки двигателей и значе-
ния относительных масс составных частей корабля. В ре-
зультате получаем следующее выражение для оптималь-
ной величины скорости в момент остановки двигателей:
^o₽t = 2-W (14-49)
соответствующее значение полного времени полета ока-
зывается равным
Q
^т1а=2^ = ^ь (14-50)
(ускорение и свободный полет).
Для полета с постоянным ускорением (без свобод-
ного движения) из (14.46) найдем
^ = ^m.n = 4W (14-51)
Эти два результата не поддаются непосредственному
сравнению, поскольку для корабля с одним и тем же
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
495
распределением относительных масс скорость vb в мо-
мент остановки двигателей при полете с постоянным
ускорением отличается от той же величины при полете
с переменным ускорением. При помощи уравнений
(14.37) можно показать, комбинируя (14.50) и (14.51),
что при одинаковом распределении масс составных час-
тей полные времена перелета для рассмотренных слу-
чаев связаны равенством
= (14.52)
в котором значки (с) и (а) относятся соответственно
к свободному полету и к полету при постоянном уско-
рении.
Можно провести подобные рассуждения для лета-
тельных аппаратов с постоянной скоростью истечения.
При этом следует исходить из уравнения для дальности
полета в пространстве без поля (не приведенного здесь),
а не из простого соотношения (14.46). Анализ оказы-
вается более сложным из-за появления в этом уравнении
логарифмических членов и здесь нами не приводится.
Результаты по форме совпадают с выражениями (14.49)
и (14.50) для скорости в момент остановки двигателей
и минимального времени полета (при данных значениях
относительных масс), но отличаются от них поправоч-
ными множителями, появляющимися от изменения уско-
рения в процессе полета с расходом мощности. Как и
для полета с постоянным ускорением, можно сильно
уменьшить время полета для систем с постоянной ско-
ростью истечения по сравнению со временем, соответ-
ствующим полету при непрерывном действии тяги, путем
введения промежуточного участка свободного полета.
Хотя это и не следует непосредственно из предыду-
щих результатов, легко видеть, что наложение известных
требований на полет корабля приводит, благодаря урав-
нениям (14.38) и (14.44) для оптимальной относитель-
ной массы рабочего тела, к значению оптимальной ско-
рости истечения для любого данного корабля. Например,
для корабля с постоянной скоростью истечения уравне-
ние (14.44) показывает, что оптимальная относительная
масса рабочего тела определяется при прочих равных
496
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
условиях (в частности, при той же относительной массе
полезного груза) лишь через отношение массы корабля
к массе силовой установки. Максимальное среднее уско-
рение а находится при этом из уравнения (14.45). Урав-
нение (14.1) для отношения масс дает для указанной
выше относительной массы рабочего тела отношение
скорости корабля в момент остановки двигателей к ско-
рости истечения. Для полета на данное расстояние 50
уравнение, связывающее время полета при расходе мощ-
ности tb с дальностью полета, а также со скоростью в
момент остановки двигателей Vb, аналогичное уравнению
(14.50) для случая постоянного ускорения, может быть
использовано совместно с уравнением (14.40), определяю-
щим а, для исключения а из (14.45), а также для по-
следующего исключения tb из получившегося результата
и уравнения, аналогичного в рассматриваемом случае
уравнению (14.50). После этого Vb может быть выра-
жено через ve с помощью уравнения (14.1) для от-
ношения масс, и, таким образом, можно будет найти
оптимальную скорость истечения, соответствующую за-
данным внутренним параметрам корабля и внешним ус-
ловиям полета.
Для летательного аппарата с постоянной скоростью
истечения можно иначе описать качественную зависи-
мость оптимальной величины ve от указанных перемен-
ных. Для этого удобно ввести в качестве параметра
оптимизации величину полного удельного импульса
корабля. Эта величина определяется равенством
Fth vP тп
/Оа =—— (14.53)
Ofl go™O go '«о V
при постоянной скорости истечения и при постоянном
расходе рабочего тела. С помощью уравнения (14.35),
выражающего mQ через массы составных частей, и урав-
нения (14.18) для Рг напишем выражение для полного
удельного импульса в виде
г =___________Ve/go_________.
(у^рг^ь80) + P +
(14.54)
Пользуясь тождеством mL/mp — (mL/m0) (т0/тр) и
уравнением (14.53), исключаем mLltnp из (14.54) и раз-
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
497
решаем результат относительно /оа- Последняя величина
оказывается выраженной лишь через значения внутрен-
них параметров корабля и скорости истечения; получаем
Дифференцируя это выражение по ve, приравнивая
производную нулю и разрешая полученное уравнение от-
носительно v€, найдем условие экстремума (здесь макси-
мума) величины /оа. Получаем
/^IjtbgoP
\>г
Обнаруженный здесь рост yeOpt при возрастании tb
отражает более высокие требования, предъявляемые к
условиям полета (т. е. к скорости в момент остановки
двигателей) при непрерывном расходе мощности. Как
видим, согласно (14.56) при неограниченном возрастании
tb величина t>eOpt стремится к бесконечности. Подстановка
(14.56) в уравнение (14.55) и преобразование резуль-
тата с использованием (14.53) дает величину началь-
ного ускорения, необходимого для подобного оптималь-
ного полета; будем иметь
aJ = t1 — 77) 1^7 = 0 ~^prtbgl)p • <14-57)
Это уравнение, выведенное для полета с постоянной ско-
ростью ve, эквивалентно уравнению (14.39), справедли-
вому при постоянном а.
В случае постоянного ускорения оптимальная ско-
рость истечения зависит от времени, непрерывно возра-
стая при полете с расходом мощности, пока эта мощность
поддерживается постоянной. Этот результат непосред-
ственно следует из уравнений (14.30) и (14.39), если
исключить из них а и определить, таким образом, t>e(Oopt
как функцию времени, скорости в момент остановки
двигателей и внутренних параметров, характеризующих
летательный аппарат. С другой стороны, можно с по-
мощью уравнения (14.50) исключить величину времени
работы двигателей, получив соотношение, содержащее
498
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
дальность полета и изменение скорости корабля. Выпол-
нив это и совершив подстановку Vb— Vo = atb из (14.27),
найдем, что оптимальная величина переменной скорости
истечения равна
ZA ^igoP \тР I ./7-1
(Oopt = V L m0 W + Vtb -I ’ (14-58)
Это выражение при t = tb совпадает с оптимальным ус-
ловием (14.56) при постоянной скорости истечения. Не-
которые количественные данные об этих оптимальных
соотношениях можно получить из численного примера.
Для употреблявшихся ранее значений внутренних пара-
метров т] j = 0,25, крг = 2500 кг/Мвт, Ast = ~ (г/см?)2!* и
= 13,6 г/cjt3 из уравнения (14.56) находим оптималь-
ную скорость истечения равной <ие = У<1,06- \0Чьсм/сек.
По прошествии времени работы двигателей, равного,
например, 107 сек (116 дней), потребуется скорость исте-
чения ие=4,54-106 см!сек, или удельный импульс /Sp =
= 4630 сек, что примерно в 15 раз превышает значение,
достигаемое лучшими современными ракетными систе-
мами, работающими на химическом топливе.
Существование оптимальной скорости истечения ра-
бочего тела представляет более чем педагогический ин-
терес, так как скорость истечения, создаваемая любым
типом двигательной системы, определяется внутренними
параметрами и условиями работы данной системы, и по-
этому оптимальную скорость истечения можно рассмат-
ривать как переменную, связывающую параметры дви-
гательной системы с требуемыми условиями полета (см.,
например, Бассард [21,], Лэнгмюр [22]). В частности, если
тяга двигателя образуется благодаря ускорению заря-
женных частиц или ионов электростатическими полями,
то величина скорости истечения приблизительно нахо-
дится из простого условия баланса энергии; получаем
”.=/"^4^ <14-59>
где е~— величина заряда электрона, т+—масса прото-
на, Q — заряд частицы, измеренный в единицах заряда
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
499
электрона, М — ее масса в единицах массы протона, а
Уа— электростатический потенциал, который ускоряет
заряженные частицы, прежде чем они покидают систему.
Взяв из справочника значения массы протона и заряда
электрона, напишем уравнение (14.59) в следующем
виде:
ve = 1,38 • 106 УОУ^М. (14.60)
Здесь ve измеряется в см)сек, a Va— в вольтах. Q и М
представляют собой безразмерные величины. Комбини-
руя уравнение (14.56) либо (14.58) с (14.59), можем вы-
разить Va(Q/M) через /&. В случае постоянной скорости
истечения получаем
v = (14.61)
а М е~1т+ ’
При принятых ранее условиях это означает, что
Va(Q/Af) = 1,08’10'%. Для tb = Ю7 сек находим, что
Va(Q/M) = 10,8 и, как видно, безразмерное отношение
массы к заряду должно быть равно M/Q = 93 при
Va = 1000 в. Примерно таким является отношение массы
к заряду для однократно ионизованных атомов рубидия,
который часто предлагается в качестве рабочего тела в
ионных двигателях.
Тяга, приходящаяся на единицу площади сечения
ускоряющего пучка, пропорциональна квадрату градиен-
та ускоряющего потенциала. Поскольку проблемы разме-
ров в конструировании ускоряющих сеток менее серьез-
ны для сеток малых размеров, устанавливаемых с боль-
шим шагом, существует весьма сильное стремление к
практическому увеличению ускоряющего напряжения до
максимальной возможной величины, совместимой с есте-
ственными ограничениями, накладываемыми возникно-
вением разрядов в генерирующем и ускоряющем обору-
довании. Высокие ускоряющие напряжения требуют, од-
нако, большего оптимального значения отношения массы
к заряду для частиц, выбрасываемых в пучке; например,
если мы желаем использовать напряжение Va = 50 000 в,
то наши «ионы» должны обладать отношением M/Q =
= 4650 при указанных выше условиях. С микроскопи-
ческой точки зрения это равносильно однократной
500
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
(гл. XIV
ионизации лишь 2% всех атомов, если в качестве рабо-
чего тела используется рубидий.
14.33. Влияние ограниченности запаса энергии. Во
всем вышеизложенном мы молчаливо предполагали, что
имеющийся в нашем распоряжении запас энергии беско-
нечно велик либо различия в потреблении энергии никак
не влияют на массу летательного аппарата, и это позво-
ляло нам считать мощность Рг двигательной системы и
время работы двигателей tb независимыми парамет-
рами. Это предположение хорошо соответствует действи-
тельности лишь постольку, поскольку масса ядерного
топлива, необходимая для удовлетворения потребностей
в энергии во время полета, остается небольшой по срав-
нению с массой, необходимой для поддержания крити-
ческого режима реактора. Для реакторов с заданным за-
пасом расщепляющегося материала в общем случае не-
возможно «сжечь» или заставить распадаться более 10
или 20% имеющегося горючего. Если, таким образом,
критическая масса равна, скажем, 50 кг, то запас энер-
гии для любого практически мыслимого полета туда и
обратно будет ограничен величиной, получающейся бла-
годаря распаду примерно 5 или 10 кг ядерного топлива.
Можно, однако, представить себе реакторы, в которых
непрерывно восполняется запас расщепляющегося мате-
риала по мере его расходования. Для таких систем верх-
ний предел потребления топлива может составлять ве-
личину около 500 кг на один полет, причем эта цифра
определена лишь на основании экономических соображе-
ний (стоимость 1 кг высокообогащенного U235 равна при-
мерно 12 000 долларов). Поскольку при расходе 1 г
ядерного топлива образуется тепловая энергия, равная
1 Мвт-сут*), можно считать величину 107 Мет >4 реаль-
ным верхним энергетическим пределом для одного по-
лета и в соответствии с этим отбросить наше предполо-
жение о бесконечной величине энергетического запаса.
Если бы мы не могли использовать реакторы с непре-
рывным возобновлением запаса топлива, то верхний пре-
*) Фактически для освобождения энергии 1 Мет • сут исполь-
зуется примерно 1,3 г U235. Дополнительный расход 0,3 г!Мвт-сут
связан с захватом нейтронов, не приводящим к распаду.
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
501
дел составил бы только 0,01 этой величины. Энергия
107 Мвт-ч равняется энергии, производимой всеми элек-
тростанциями Соединенных Штатов примерно за 200
часов работы. Если бы можно было достичь большого
ускорения при высокой скорости истечения путем исполь-
зования электрического генераторного оборудования от-
носительно малой удельной массы Хрг, то потребление
энергии, требуемое при полете корабля, вполне могло бы
превысить эту весьма большую величину. Поэтому, как
указал впервые Лейтман [23] (см. также Лейтман [19]),
интересно выяснить, каким образом могут измениться
некоторые сделанные нами ранее выводы и какие по-
явятся новые обстоятельства, если включить требование
ограниченности энергетического запаса в качестве со-
ставной части нашего алгебраического описания взаимо-
связей, существующих в пределах рассматриваемой си-
стемы.
Первое видоизменение, которое нам следует сделать,
состоит во введении массы топлива пу в выражение
(14.32) для полной массы корабля. Таким образом,
= mpr + + mL. (14.62)
Для ядерных топлив полный расход энергии Еь за
время полета линейно связан с массой топлива, так что
можно написать
/nz=к/?* = ^fprtb, (14.63)
где X/ равно примерно 1/24 000 кг!Мвт* ч для распадаю-
щихся топлив. Сравнивая с формулой (14.34) для пгрг,
видим, что величины Ху/ь и Хрг обе входят в уравнение
для /п0 умноженными на Рг, так что новый коэффициент
при Рт в этом уравнении можно считать в 1 + (Ху/ь/Хрг)
раз превышающим старый. Этот множитель проходит
через все предыдущие рассуждения о выводе выражения
для оптимальной скорости истечения [уравнения (14.56)
и (14.58)]; приходим к видоизмененному результату
04.64)
справедливому для случая постоянной скорости истече-
ния. В этом случае оптимальная скорость истечения не
502
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
обращается в бесконечность при возрастании tb, как это
имело место в уравнении (14.56), выведенном без учета
ограничений, наложенных на расход энергии системой,
а приближается к асимптотическому значению =
= V^jgoP/b •
Для употреблявшихся ранее значений rjj, 4S< и рр пре-
дельная оптимальная скорость истечения и удельный им-
пульс оказываются равными i^opt = 6,70 • 108 см!сек и
685 000 сек, если используется распадающееся ядерное
топливо. Эти значения значительно превышают предель-
ные топливные характеристики, требуемые для деталь-
ного изучения солнечной системы, и фактически для всех
полетов в пределах солнечной системы можно пренебречь
влиянием конечности массы топлива, поскольку вели-
чина Zpr составляет примерно 10 кг)Мвт или более.
Другое характерное различие обнаруживается при
изучении условий осуществления максимального уско-
рения и потому минимального времени полета. Если фи-
ксировать имеющуюся массу топлива mf, то полный за-
пас энергии Еь для любого данного полета тем самым
также фиксируется. Время сжигания tb при этом не яв-
ляется более независимой переменной, но связано с мощ-
ностью уравнением (14.63), и поэтому его можно исклю-
чить вместе со скоростью в момент окончания работы
двигателей Vb из формулы (14.37) для ускорения, вос-
пользовавшись уравнениями (14.27) и (14.63); получится
следующее выражение для ускорения:
_ 1 Г (mprlmo)2 * (mp/mQ)
а~У z^[i+bM0)][i-(m>0)](m/H) ; (14^
при выводе мы использовали формулу (14.62), содержа-
щую слагаемое ап/, вместо формулы (14.32). При задан-
ной массе топлива величина отношения тР1пг^ при ко-
тором ускорение достигает максимума, получается в
результате дифференцирования (14.65) с подстановкой
значения mf, найденного из формулы (14.63).
В результате этих действий получим уравнение
2 + = , (14.бб)
mQ \ mQ /Г \ 1 mQ v 7
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
503
отличающееся [23] множителем 2 + [(mprlmf) + I]-1 от
своего аналога (14.38) в случае неограниченного запаса
энергии. Максимальное ускорение теперь равно
2^/ 2 + 3(mf/mpr) трг / тр\г
a^=V [l + (^/mpr)]2 (14-67)
Отношение mprlmf однозначно определяется временем
полета для заданных значений параметров X/ и из
уравнений (14.34) и (14.63). Получаем
трг _____ ^-рг _____ ^рг а
mf \ftb vb — vQ'
(14.68)
Мы можем воспользоваться далее этим результатом,
чтобы исключить массы топлива и двигательной системы
из уравнения (14.67) и выразить ускорение через внут-
ренние конструктивные параметры и скорость в момент,
когда все топливо будет израсходовано. Для случая, ко-
гда mflmpr мало по сравнению с единицей, будем иметь
4тп/ / тп\^
апих = *pr (fft-Vo) t) Р' (14-69)
Этот результат следует сравнить с выражением
(14.39), справедливым в случае неограниченного запаса
энергии; сравнение показывает, что максимальное уско-
рение в оптимальных условиях для настоящего случая
вдвое больше найденного ранее при отсутствии ограни-
чений запаса энергии. Ограничивая потребление энер-
гии, мы, разумеется, ввели в задачу новую связь, и по-
этому число параметров, которыми располагает астро-
навт, пользующийся нашей двигательной системой,
должно уменьшиться на единицу [24]. В данном случае
мы потеряли возможность задания скорости корабля в
момент полного израсходования топлива, как это легко
видеть из уравнения для этой скорости, получающегося
путем исключения ускорения из (14.69) с помощью
(14.27). Это уравнение имеет вид
(14.70)
504
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
при условии, что отношение т^трг мало по сравнению
с единицей. Величина Vb — Цо, достигаемая в оптималь-
ном режиме полета с ограниченным запасом энергии,
однозначно определяется принятым значением mf либо
значением Еь = как этого и следовало ожидать из
элементарных соображений. Наоборот, уравнение (14.70)
определяет массу топлива, необходимую при любой
скорости корабля в момент остановки двигателей и при
любом значении относительной массы рабочего тела.
Чтобы представить себе количественную картину яв-
ления, рассмотрим летательный аппарат с параметрами
rnplm,Q = 0,5, тц = 0,25, Ast = (г/слг3)2/з, рр=13,6 г!см3.
работающий на энергии распада ядер. Уравнение
(14.70) для этих значений параметров приводит к ра-
венству irifliripr = 4,48-10"18 vf; здесь Vb измеряется
в см!сек. а начальная скорость принята равной нулю.
Подобным же образом из уравнения (14.69) находим
ускорение, измеренное в единицах ускорения земного
тяготения; получаем атах= 1,05 • 107/Хргц&, где Хрг изме-
ряется в килограммах на мегаватт. Пусть требуется,
чтобы скорость корабля в момент отключения двигате-
лей составляла иь = 5*106 см!сек (31,1 миль/сек) \ тогда
отношение массы «сжигаемого» топлива к массе двига-
тельной системы должно быть равно 1,12* 10-4. Если
масса двигателей выбрана равной 20 000 кг. то потребле-
ние топлива при полете должно составлять 2,24 кг. Если
критическую массу принять равной 100 кг и допустить,
что расходуется лишь 10% топлива, то, несмотря на
столь малое потребление, можно будет совершить при-
мерно лишь 4 полета корабля без возобновления запаса
энергии реактора. Если удельная масса двигательной
системы уменьшена до 250 кг/Мвт. т. е. до 1/10 старой
величины, то система будет работать с расходом мощ-
ности в 80 Мет в течение 2,42- 106 сек. или 28 дней [см.
уравнение (14.68)], и создаст ускорение корабля, рав-
ное 2,1 • IO-3 g0. При другом выборе параметров резуль-
таты будут иными; однако вместо того, чтобы приводить
здесь дальнейшие примеры, мы предоставим соответ-
ствующие вычисления читателю.
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
505
14.34. Радиационная защита. Другая представляю-
щая для нас интерес задача связана с оптимизацией по-
лета летательного аппарата с малым ускорением в ва-
кууме. Она заключается в нахождении такого распреде-
ления защитных масс, которое обеспечило бы наилучшие
полетные характеристики корабля. Для системы с малым
ускорением можно принять расстояние между реактором
и помещением для экипажа за независимую переменную
и воспользоваться, таким образом, обратной пропорцио-
нальностью величины потока излучения квадрату рас-
стояния для обеспечения защиты команды или полезного
груза. Разумеется, придется пойти на некоторые жертвы,
связанные с массой конструкций, необходимых для соз-
дания требуемого расстояния. Если движение корабля
осуществляется посредством тяги, так что двигательный
отсек расположен впереди помещения для команды и
груза, то необходимое разделение можно, следуя пред-
ложению Спитцера [25], осуществить с помощью длин-
ного троса, и соответствующая масса (равная как раз
массе троса) будет возрастать с расстоянием, грубо го-
воря, по линейному закону. С другой стороны, если дви-
гательный отсек располагается позади помещения для
экипажа и груза, то для разделения потребуется некото-
рая жесткая конструкция, работающая на сжатие, и
масса ее будет изменяться примерно пропорционально
квадрату расстояния.
Кроме масс, связанных с отделением команды от ре-
актора, для защиты потребуется, вообще говоря, погло-
щающий материал, располагающийся между источником
излучения и защищаемым объектом. Поглощающая ра-
диацию защита оказывается достаточной для предохра-
нения от излучения в вакууме. В первом приближении
создаваемое таким материалом ослабление радиации
экспоненциально зависит от толщины защищающего
слоя*), поэтому масса поглощающей защитной системы
будет логарифмически зависеть от отношения интенсив-
*) Мы ограничиваемся здесь защитой от гамма-фотонов, по-
скольку защита от быстрых нейтронов, вообще говоря, представ-
ляет меньшие трудности и поэтому не учитывается при кон-
струировании защитных устройств для кораблей с малым ускоре-
нием при полете в вакууме.
506
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
(гл. XIV
ности неослабленного излучения в помещении для эки-
пажа к допустимой интенсивности излучения в этом же
месте. Имея в виду эти общие соображения, можно на-
писать следующее выражение для величины полной за-
щитной массы:
ГП^ =------ 1П -л—ГРГ + М •
(14.71)
Здесь первое слагаемое соответствует поглощающему
защитному слою, а второе представляет собой массу раз-
деляющей конструкции, которая считается здесь степен-
ной функцией разделяющего расстояния s. Коэффициент
Xs задается характеристиками прочности материала, до-
пустимыми величинами интенсивности излучений и т. д.
В слагаемом, соответствующем поглощающему защит-
ному слою, произведение представляет собой мощ-
ность источника излучения (рассеяние излучения из ре-
актора), измеренную в тех же единицах, что и допусти-
мая в помещении для экипажа интенсивность радиа-
ции D, Площадь поперечного сечения поглощающего
защитного слоя равна Л8, а плотность и коэффициент по-
глощения поглощающего материала равны соответствен-
но ps и ps.
Чтобы найти минимальную величину защитной массы
для любой заданной мощности реактора, дифференци-
руем (14.71) по s, приравниваем производную нулю и
разрешаем это уравнение относительно реализующего
минимум расстояния s. В результате находим
Г1 2Л5р5 ]1/и
(14.72)
рА
а соответствующая полная защитная масса равна
т5йш1п—[7(1 + 1п1Ц^;) + ,п 4^7]• (14-73)
Для расчетов в системе CGS при мощности источ-
ника, измеряемой в мегаваттах, коэффициент перехо-
да К равен 1,11 «IO13 (1/ч)/(Мвт/см2).
Рассмотрим два численных примера. Возьмем сна-
чала систему с линейной зависимостью защитной массы
от разделяющего расстояния, так что п=1, и положим,
14.3]
ПОЛЕТ С МАЛЫМ УСКОРЕНИЕМ
507
что массовый коэффициент равен Ks = 10 г!см. Отноше-
ние ps/ps примерно одинаково для всех типичных защит-
ных материалов и равно 0,03 см2/г. С этими данными из
уравнения (14.72) находим, что оптимальное разделяю-
щее расстояние при поперечном сечении поглощающего
слоя в 104 см2 составляет $ = 6,67 *104 см (около
2200 фт). Предполагая далее, что около 1/80 общей мощ-
ности рассмотренной в предыдущем примере силовой
установки малого ускорения рассеивается в реакторе в
форме гамма-излучения, получим, что мощность источ-
ника излучения равна Р( = 1 Мет. Допуская дозу непре-
рывной радиации D = 0,01 1/ч, найдем, что минимальная
защитная масса должна равняться, согласно (14.73),
msh — 3960 кг. Предположим далее, что нас интересует
защитная система другого типа, для которой п = 2 и
Хз = 0,01 г/см2. Оптимальное разделяющее расстояние
для той же площади сечения поглотителя равно s =
= 5,77- 103 см (qkqjiq 190 фт), а минимальная защитная
масса при рассеиваемом излучении в 1 Мет оказывается
равной msh = 5250 кг.
До сих пор мы рассматривали вопрос об оптимиза-
ции защитной системы только в случае заданной мощ-
ности. Строго говоря, для полного соответствия нашего
аппарата реальным условиям на корабле мы должны
были бы вернуться к уравнению (14.62) для полной мас-
сы аппарата и включить в него слагаемое, отвечающее
защитной массе, а именно слагаемое типа (14.71), отра-
жающее функциональную зависимость защитной массы
от мощности реактора. Из предыдущих рассуждений нам
известно, что существует оптимальная при прочих рав-
ных условиях мощность (изменением защитной массы
пренебрегается), минимизирующая время полета ко-
рабля с малым ускорением на любое заданное расстоя-
ние при максимальной грузоподъемности для данной от-
носительной массы топлива. Изменение защитной массы
с помощью реактора сдвинет упомянутый оптимум мощ-
ности несколько в сторону меньших значений, поскольку
для реактора меньшей мощности допустима меньшая
защитная масса. Эта зависимость, однако, имеет всего
лишь логарифмический характер, и поэтому можно по-
лучить очень хорошее приближение к оптимальным
508
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
условиям, пренебрегая при решении задачи оптимизации
полета связью между защитной массой и мощностью ре-
актора, минимизируя величину защитной массы, как это
сделано выше, при фиксированной мощности реактора.
На этом мы заканчиваем рассмотрение некоторых
задач оптимизации полета ракет на твердом топливе и
переходим к вопросу об оптимальных соотношениях ме-
жду внутренними параметрами, относящихся к поведе-
нию одной лишь двигательной системы. Это не значит,
что мы исчерпали круг вопросов, представляющих инте-
рес с точки зрения полета корабля: напротив, мы лишь
затронули эти вопросы весьма поверхностным образом.
Однако для рассмотрения многих не затронутых нами
задач, а также и для более подробного анализа тех про-
блем, которые обсуждались, часто возникает необходи-
мость в численных расчетах с применением больших ав-
томатических вычислительных устройств. В особенности
это относится к задачам об оптимизации траекторий, так
как они обычно «решаются» лишь с помощью теории
возмущений или численных методов, если в задаче уча-
ствуют три или большее число тел. Другое существенное
обстоятельство, затрудняющее решение встречающихся
на практике задач, состоит в том, что почти для всех
реально используемых систем характерны существенно
нелинейные функциональные зависимости между различ-
ными внутренними и внешними параметрами летатель-
ного аппарата и его двигательной системы. Значение ли-
неаризации или других методов упрощения заключается
не в том, что при этом может (или не может) получиться
правильный ответ, а в обнаружении качественных тен-
денций, которые могут оказаться весьма интересными и
важными для конструктора.
14.4. ДВИГАТЕЛЬНЫЕ СИСТЕМЫ
С ТЕПЛООБМЕННИКАМИ
Закончив исследования некоторых задач оптимиза-
ции полета летательных аппаратов на ядерном топливе,
обратимся теперь к вопросу об оптимизации работы дви-
гателей на ядерном горючем. При этом в качестве пер-
вого примера исследуем характеристики двигательных
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
509
систем с непосредственным обменом теплом (рис. 14.1),
а впоследствии (в следующем разделе) рассмотрим свой-
ства систем с непрямым преобразованием энергии
(рис. 14.2).
Из рассуждений раздела 14.11 следует, что реактор
непосредственного типа, установленный на ракете, есть
нё что иное, как теплообменник, в котором рабочий газ,
перед тем как он прогоняется через сопло, нагревается
до возможно более высокой температуры. Для реакто-
ров такого типа основная задача заключается в получе-
нии высокой температуры в активной зоне реактора.
Для реакторов с твердыми стержнями максималь-
ная температура газа ограничена главным образом пре-
делами прочности и коррозийными характеристиками
распадающихся тепловыделяющих элементов, и для ус-
пешной работы реактора необходимо применять соот-
ветствующие материалы. К сожалению, невозможно вы-
брать материалы для топливных элементов, основываясь
лишь на их физических свойствах, так как реактор
прежде всего должен быть способен работать в крити-
ческом режиме.
Выбирая тот или другой материал, мы должны
учитывать свойства материала, относящиеся к ходу ядер-
ной реакции. Более того, между ядерными и тепловыми
характеристиками той или иной конструкции реактора
имеется определенная взаимосвязь, и, хотя справед-
ливо то, что почти всякий теплообменник можно до-
вести до критического режима с помощью достаточ-
ного количества ядерного топлива, температурные свой-
ства оболочки, заполненной ядерным топливом, мо-
гут измениться с изменением степени заполнения, и
вслед за этим может измениться режим работы тепло-
обменника.
Для реакторов, в которых используется жидкое или
газообразное топливо, температурные пределы не зави-
сят от прочности материала топлива, но определяются
различными термодинамическими и иными свойствами
топлива и смесей топлива и рабочего тела. Поскольку
о возможных характеристиках реакторов .на жидком и
газообразном топливе известно очень мало, тогда как
34 Дж. Лейтман
510
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЁРНОМ ЮПЛИВВ (гл. XIV
к настоящему времени (1961 г.) произведено уже четыре
испытания ракетных реакторов с твердыми стержнями,
мы сконцентрируем внимание на реакторах последнего
типа, приведя лишь краткие сведения о реакторах на га-
зообразном топливе.
Другая важная задача проектирования реакторов за-
ключается, как указано выше, в создании устройств с
низким значением удельной массы. Удельная масса пред-
ставляет собой отношение полной массы реактора, при-
ходящейся на единицу объема стержня, к плотности соз-
даваемой мощности. В реакторах с твердыми стержнями
последний параметр определяется геометрией теплооб-
менника и рабочими значениями температуры и давле-
ния в зоне расположения стержней, тогда как первый оп-
ределяется геометрией всего реактора и плотностью ис-
пользуемых материалов. Выбор геометрии и материалов
в сильной степени определяется нейтронными характе-
ристиками реактора, так как в реакторах с быстрыми
нейтронами различные материалы используются лучше,
чем в тепловых реакторах или в реакторах промежуточ-
ного типа. Здесь мы вновь наблюдаем взаимосвязь ме-
жду ядерным и тепловым аспектами задачи проектиро-
вания.
14.41. Удельная масса и импульс как свободные пе-
ременные. Для того чтобы изучить влияние удельной
массы реактора и определить, существуют ли оптималь-
ные условия по отношению к этому параметру, вернемся
к уравнению (14.9), из которого заключаем, что при
убывании удельной массы кг мы при фиксированных
прочих параметрах получим лучшее поведение корабля.
Как далеко следует стремиться в направлении уменьше-
ния Хг? Строгий оптимум наступит при кг = 0, т. е. тогда,
когда реактор ракеты не имеет массы. Всегда, однако,
труднее сконструировать реактор с уменьшенным проект-
ным значением кг. Поэтому нас интересует, не суще-
ствует ли области значений Лг, в которой поведение реак-
тора чувствительно к изменениям Хг, и если такая об-
ласть имеется, то мы намерены выяснить ее количествен-
ные характеристики, имея в виду облегчить определение
цели, к которой следует стремиться при конструирова-
нии реакторов.
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
511
Для упрощения рассуждений снова сделаем те пред-
положения, которые приводят к уравнению (14.11), но
будем в этом уравнении считать Хг переменной величи-
ной. Таким образом,
-^ = -ln[^ + 6-lO-Wspd. (14.74)
Vg L J
где измеряется в килограммах на мегаватт.
Влияние удельной массы реактора показано графи-
чески на рис. 14.6, где изображена зависимость vc/ve от
удельной мощности 1ДГ для широкого диапазона значе-
ний произведения ДоЛр при значении tnDlniQ = 0,2. Важ-
ной характеристикой этих кривых является то, что
показатель степени в формуле для отношения масс
нечувствителен к удельной мощности реактора при
\ < -у- кг!Мвт, но резко меняется при изменении
от 1 до 8 кг!Мвт, смотря по величине a0/Sp в каждом от-
дельном случае. Представляется неоправданным стрем-
ление к малым значениям удельной массы лишь ради
небольшого выигрыша в характеристиках, и равным об-
разом кажется неразумным ограничение лишь областью
вблизи вертикальных участков кривых. При запусках
ракет с Земли диапазон значений а0/8р охватывает об-
ласть примерно от 300 до 1000 сек, откуда мы заклю-
чаем, что при проектировании реакторов следует выби-
рать Хт в области значений <1г <2 кг/Мвт. Для
оценки того, как изменится этот результат при другом
выборе значений параметров aQ, tnD/tnQ и /Sp, можно сде-
лать наше заключение более определенным, предполо-
жив, что рекомендуемая для работы область находится
как раз за «изгибом» кривых рис. 14.6, где показатель
степени в формуле для отношения масс относительно не-
зависим от удельной массы реактора. Для нахождения
условий, которые ограничивают рабочий диапазон этой
областью, скажем, при заданном наклоне L =
= d (vc/ve)/d(l/kr), дифференцируем (14.74), приравни-
ваем результат заданному наклону L и разрешаем полу-
ченное уравнение относительно удельной массы реак-
тора. Если ограничиться рассмотрением случаев, когда
34*
512 ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ [гл. XIV
выполняется неравенство aQISp <С lO5(mD/zno), что вклю-
чает в себя все практически интересные возможности» то
Рис. 14.6. Характеристики ракетного летательного аппарата
в зависимости от величины удельной мощности реактора.
окончательное выражение для приближенно примет
вид
WL(mD/m0)
6Vsp
(14.75)
Например, при та1тй—\13 и £=1/6 это дает Ъг~
30,4/Если /вр = 800 сек и а0 = 1,3, то находим,
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
513
что проектное значение Аг~0,94 кг!Мвт\ это значение ле-
жит в пределах указанной ранее области. Если, однако,
допустить, что ао = 0,1, как это имеет место при запуске
с орбиты вокруг Земли, и принять /sp = 1000 сек, то
удельную массу реактора не нужно будет делать мень-
шей, чем Кг = 5,3 кг/Мвт. При запуске с Земли, когда
0О > 1, потребуется, таким образом, реактор, проектиро-
вание которого представляет более трудную задачу, не-
жели проектирование реактора для запуска в условиях
свободного полета, когда необходимые ускорения ко-
рабля могут оказаться, например, порядка 0о=1О-1
или 10-2.
Другой способ придания определенности нашим за-
ключениям состоит во введении искусственной оптими-
зирующей функции, приближенно отражающей то обстоя-
тельство, что трудности конструирования реактора воз-
растают при уменьшении Хг. Для наших целей удобно
взять такую функцию в форме
(14.76)
где показатель степени иг играет роль параметра, влия-
ние которого мы намерены изучить. Функция (14.76)
принимает меньшие значения при возрастании Хг, и, та-
ким образом, конструирование реактора облегчается, и
большие значения при возрастании отношения vdvc (кос-
венное следствие возрастания Хг), если параметр m при-
нимает лишь отрицательные значения. Поэтому опти-
мальную систему можно охарактеризовать как такую,
которая доставляет минимальное значение функции ср.
Для нахождения этого минимума дифференцируем
(14.76) [с использованием (14.74)], приравниваем ре-
зультат нулю и из получившегося уравнения определяем
оптимальную связь между Кг и величиной параметра
0O/Sp. Эта связь графически показана на рис. 14.7 для
ряда значений m при mDlniQ ™ 0,2.
Из графика непосредственно усматривается отмечен-
ная выше тенденция, а именно: чем меньше значение
произведения 0о/8р, тем больше оптимальная (допусти-
мая) величина удельной массы реактора. Численные
расчеты показывают, что оптимальная удельная масса!
514
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
реактора в пределах бредней части графиков рис. 14.7
Изменяется почтй как квадратный корень из произведе-
ния, ЯоЛр, как это написано в уравнении (14.75).
Предположим, что мы желаем найти оптимальное
значение удельного импульса, обеспечивающее наилуч-
ш*ие рабочие характеристики летательного аппарата*
Рис. 14.7. Оптимальная удельная масса реактора
в зависимости от ускорения корабля и от удельного
импульса рабочего тела.
считая, что удельный импульс является управляемой не-
зависимой переменной, тогда как остальные параметры
задачи остаются фиксированными. Для решения этой
задачи недостаточно, как это делалось нами выше, счи-
тать показатель степени в формуле для отношения масс
также независимой переменной, поскольку эффективная
скорость истечения равна как раз ve = gQIap. Конкретно
говоря, мы должны фактически включить дополнитель-
ную зависимость от /вр в слагаемое, ответственное за
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
515
гравитационные потери [см. уравнение (14.10)], если
наш летательный аппарат совершает полет в гравита-
ционных полях. Имея в виду иллюстративные цели, мы,
однако, отбрасываем этот член и максимизируем ve по
отношению к /Sp, получая результат, который применим,
строго говоря, лишь к полету в пространстве, свободном
от полей. Форма уравнения, представляющего интерес
в данном случае, такова:
vc = — goAp In [(/Пр//По) + 6 • lO“5aoMspL (14.77)
Следуя обычной процедуре, находим, что существует
оптимальное значение произведения (aoMsp), которое
определяется из уравнения
— 6 • lO"5aoMSp = [(^dMo) + 6 • 10"5a0Xr/sp] X
Xln[(/nD//no) + 6. lO’Wr/sp]. (14.78)
Этот результат противопоставляется уравнению
(14.75) и графикам рис. 14.7, где фигурировала опти*
мальная мощность ХгУ^оЛр- Для этого же значения
относительной массы мертвого груза найдем, что опти-
мальное произведение, определяемое уравнением (14.78),
равно (aoMsp) = 5573 кг- сек/Мвт. Таким образом, для
aQ = 1,3 (единиц ускорения земного тяготения) и /sp =
= 800 сек оптимальная удельная масса реактора соста-
вляет теперь = 5,36 кг!Мет — величину, значительно
превышающую указанную для тех же параметров ра-
нее; этим иллюстрируется то обстоятельство, что раз-
личные критерии оптимизации могут привести к сильно
различающимся результатам даже при одних и тех же
значениях параметров. Характеристическая скорость, со-
ответствующая оптимуму (14.78), оказывается равной
vc = 0,63g(/sp при принятых ранее значениях параметров.
Это составляет как раз (1—е_,)-ю долю от эффективной
скорости истечения рабочего тела.
14.42. Давление, удельная масса и соответствующий
импульс. В связи с вопросом о двигательных системах
ракет на ядерном топливе большой интерес предста-
вляет еще исследование взаимосвязи между удельной
массой реактора и удельным импульсом рабочего тела.
516
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ [гл. XIV
Во всем предыдущем изложении мы игнорировали лю-
бую возможную связь между этими двумя параметрами,
тогда как результаты, полученные при проектировании
реакторов, показывают, что такая связь существует, если
повышение температуры газа (а отсюда и /8р) осуществ-
ляется изменением выбора топлива, поскольку матери-
алы с более высокой точкой плавления оказываются
более плотными, нежели те, которые предназначены для
работы на более низких температурах. Благодаря этому
удельная масса реакторов, способных к работе при вы-
соких температурах газа, может оказаться выше, чем
удельная масса реакторов, нагревающих газ до более
низкой температуры, и возникает вопрос о желательно-
сти стремления к наибольшим возможным значениям
температуры газа и удельного импульса. Для рассмот-
рения этого вопроса предположим, что удельная масса
реактора связана с удельным импульсом рабочего тела
простой степенной зависимостью
х'=Чж)“- (14.79)
Пользуясь этим равенством в уравнении (14.77) и
следуя уже описанной выше процедуре, получим урав-
нение
(п+1)[б- 10-51,,>^'-] =
= -1 + 6 10‘ [?+6' 1O’S
L Z7Z q ouv J L /71q oUv J
(14.80)
решение которого дает оптимальные значения произве-
дения (аоХго/дР+1/8ООл) для заданных значений показа-
теля п.
. В табл. 14.4 приводятся приближенные результаты
для нескольких значений п. Пользуясь этими данными,
мы можем определить нужное поведение, изображая
оптимальный удельный импульс как функцию показа-
теля п при заданных значениях (яЛ-о). Такой график
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
517
показан на рис. 14.8. Из рассмотрения кривых следует,
что более резкий характер функциональной зависимо-
сти удельной массы реактора от удельного импульса
Таблица 14.4
Оптимальные значения параметра
(“oWeV')/800"
Показатель п
(Vro'sp+1)/800'’
о
1
2
3
5
5573
3000
2000
1500
1000
рабочего тела приводит к заметному уменьшению опти-
мальной величины удельного импульса, минимизирую-
щего при данной отно-
сительной массе мерт-
вого груза характери-
стическую скорость ле-
тательного аппарата.
Таким образом, с воз-
растанием п все менее
и менее оправданным
становится стремление
к тому, чтобы реактор
обладал высоким зна-
чением удельного им-
пульса (относительно
величины 800 сек, вы-
бранной в уравнении
(14.79) в качестве
масштаба), если по-
Рис. 14.8. Оптимальный удельный
импульс в зависимости от показателя,
характеризующего удельную массу
реактора.
стройка такого реакто-
ра связана с использованием более плотных материалов
и, следовательно, с большими значениями удельной
массы. В частности, если п. равно. 3/$ или превышает
518
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
эту величину, то нет причин стремиться к значениям /8р,
значительно превышающим нормирующее значение
800 сек для аппаратов с большим ускорением,
если только значение Хго (соответствующее значению
/Sp, равному 800 сек) не менее 3/г кг/Мвт. Например,
если По^го = 2,6 кг/Мвт и п = 3, то работа при
/8р = 850 сек приведет к меныией скорости корабля в
момент отключения двигателей (при заданном грузе),
нежели работа при оптимальном значении /sp = 740 сек.
Полученные только что результаты относятся, как
было сказано, к возможности возрастания удельного
импульса при использовании в реакторе таких топлив,
температурные параметры которых в некотором смысле
пропорциональны их плотности. Эта пропорциональность
носит чисто эмпирический характер и не предполагает
никакой истинной физической зависимости одного па-
раметра от другого. Именно так, однако, обстоит дело
при сравнении поведения графита (плотностью 1,7 г!см2)
с различными металлическими карбидами (плотностью
от 5 до 10 г/см3), использование которых в реакторах
ракет было предметом обсуждения [1.]. Можно, однако,
дать иную интерпретацию только что полученных опти-
мальных условий. Пусть материалы, из которых построен
реактор, заданы; тогда температура газа на выходе из
активной зоны будет зависеть от идеальности геометрии
теплообменника, давления в системе и от полной пло-
щади передачи тепла к газу. Температура вытекающего
газа будет тем ближе подходить к предельному для ма-
териалов значению, чем больше размеры реактора; таким
образом, мы вновь убеждаемся в том, что удельная масса
реактора и удельный импульс рабочего тела могут быть
связаны друг с другом таким образом, что более высо-
кие /8р соответствуют более массивным реакторам. Та-
кое положение вещей отличается, однако, от предыду-
щего тем, что на этот раз имеется верхний предел темпе-
ратуры, тогда как ранее мы просто допускали возраста-
ние температуры газа (и /8р) при увеличении Кг- Для
детального анализа, этого случая мы должны распола-
гать информацией^ получаемой при конструировании
реактора и связывающей теплопередачу, температуру
газа и размены стержней реактора; Уравнение, эквива-
14.4)
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
519
лентное (14.79), можно написать в простой форме:
тде Х?Р соответствует кг0, а /“Р есть верхняя граница
значений удельного импульса, установленная предель-
ной температурой материала стержня. Очевидно, что
зависимость Хг от /8р при этом значительно сильнее,
чем в рассмотренных ранее примерах, и что в результа-
те оптимальное значение /Sp, вероятно, окажется гораз-
до ближе f« выбранной нормирующей величине 1% , чем
ранее.
Мы рассмотрим здесь еще одно оптимальное условие.
Речь идет о выборе оптимального давления системы,
(обеспечивающего оптимум полетной характеристики ко-
рабля при заданном рабочем теле и известной темпе-
ратуре газа. Как показывают исследования процессов
^теплопередачи от стрежней реактора (Бассард и Де-
Лауэр [2], стр. 104), средняя плотность мощности, сни-
маемой со стержней при заданной геометрии и темпе-
ратуре конструкций, изменяется, грубо говоря, про-
порционально давлению в системе в степени 0,8, так
что более высокое давление приводит к больщец плот-
ности мощности. Если бы масса всего реактора опреде-
лялась лишь массой его стержней, то обе эти массы
изменялись бы, как (рс)"0,8. Однако имеют значение два
других элемента реактора — это внешний отражатель
нейтронов и сдерживающая давление оболочка. Масса
^отражателя, вообще говоря, будет невелика в большин-
стве /интересных случаев по сравнению с массой стерж-
ней, и, поскольку величина этой массы не зависит от
.давления, юна не может вызвать существенных измене-
ний в характере указанной выше экспоненциальной за-
висимости. Масса удерживающей оболочки, с другой
стороны, в первом приближении прямо пропорциональ-
на давлению системы, и поэтому ее учет в выражении
/для полной массы реактора изменит функциональную
зависимость по сравнению £ той, которая имела место
при учете лишь массы стержней. Вычисления показыва-
ет, однако, что с хорошим приближением это изменение
520
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
можно выразить степенной зависимостью от давления
в активной зоне при надлежащем выборе величины
показателя степени. Непосредственно для стоящих
перед нами целей мы примем, что удельная масса реак-
тора зависит от давления согласно общей формуле
х'=М~й-Т <14-81>
где %го есть удельная масса при нормирующем давлении
Рсо. Подстановка этого соотношения в уравнение (14.9),
характеризующее качество ракеты, показывает, что ра-
кета будет обладать наилучшими качествами, если
функция
= (14.82)
1е \ гс ' гр'sp
примет минимальное по отношению к давлению значе-
ние. Находя минимум путем дифференцирования, полу-
чим, что оптимальное давление равно
/ ЗррЛгХг0р"0л/д \здзл+2)
= l—ад;—/ • (14‘83)
Для примера примем следующие значения парамет-
ров: рр = 0,07 г! см? (жидкий Н2), рсо = 50 атм,
Ато = 1 кг/Мвт, /sp = 800 сек и п = 2/3. При этих значе-
ниях параметров и пользуясь данными ранее значения-
ми Аг и Аре [см. (14.7) и (14.8)], найдем, что оптималь-
ное давление в системе равно 123 атм. Выбор NH3 в
качестве рабочего тела дал бы еще большую величину,
так как для диссоциированного NH3 произведение pp/sP
принимает большее значение, нежели для Н2, при той
же температуре. Будучи интересным сам по себе, этот
результат не дает полного представления об оптималь-
ных условиях, так как мы пренебрегли еще одной зави-
симостью от давления, которая весьма важна с точки
зрения поведения системы в целом. Речь идет о зависи-
мости эффективной средней скорости истечения рабоче-
го тела или удельного импульса от давления в системе,
имеющей место благодаря тому факту, что возросшее
давление означает возросшее потребление рабочего
тела для работы турбинного насоса и, таким образом.
14 4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
521
уменьшение расхода рабочего тела для целей создания
непосредственно тяги. Это обстоятельство оказалось
(см. Бассард и ДеЛауэр [2], стр. 75) довольно несущест-
венным при давлениях порядка 10 или нескольких де-
сятков атмосфер, но, конечно, не пренебрежимым при
давлениях порядка 100 атм, как это имеет место в рас-
смотренном выше примере. Можно удовлетворительным
образом учесть эту зависимость, записав ve и /бр в (14.9)
в форме Ve/go = Лр = 1% (1 —fpc)> где f зависит от усло-
вий в турбине и от положения регуляторов расхода и
имеет типичными значениями величины от 2 до
6 • 10-4 атм~1 для рабочих тел, располагающихся в диа-
пазоне между NH3 и Н2. Определение оптимальных
условий с учетом этого эффекта мы предоставляем инте-
ресующемуся читателю.
14.43. Газовый вихревой реактор. До сих пор мы ис-
следовали лишь условия оптимальной работы силовых
установок на реакторах с твердыми стержнями. Преж-
де чем покончить с рассмотрением двигательных систем
непосредственного типа, опишем вкратце газовый ра-
кетный реактор с непосредственным теплообменом,
столь часто обсуждаемый в литературе как устройство,
предназначаемое для широкой эксплуатации. Основной
принцип работы этого реактора прост. Смесь газообраз-
ного распадающегося вещества и рабочего тела посту-
пает в большую камеру или в пространство, ограничен-
ное толстой оболочкой из замедляющего материала,
такого, как тяжелая вода или графит; образующиеся
при распаде в полости нейтроны замедляются внешней
оболочкой и возвращаются в область, заполненную га-
зовой смесью, где они вызывают вторичные расщепле-
ния, нагревая тем самым рабочее тело непосредственно
в газообразной фазе, без промежуточного этапа пере-
дачи тепла от тепловыделяющего элемента. В прин-
ципе этим путем может быть достигнута значительно
более высокая температура газа, нежели та, которая
допускается предельными значениями, характерными
для твердых топливных ячеек, и, таким образом, можно
получить более высокие Значения скорости истечения
рабочего тела. Предлагались многочисленные измене-
ния в детальном осуществлении изложенной схемы, но
522
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ (гл. XlV
все варианты в конечном счете базировались на.ос-
новных принципах работы описанного выше простого
устройства.
Можно было бы весьма удовлетворительным обра-
зом получить улучшенные характеристики работы реак-
тора, если бы не то обстоятельство, что нераспавшиеся
атомы расщепляющегося материала будут уноситься из
смеси вместе с нагретым рабочим веществом при дви-
жении последнего к соплу и через него, и это не даст
рабочему телу возможности вытекать из двигателя, так
как нейтрализует влияние замедляющей оболочки. Ис-
следование основных связанных с этим фактом задач
[3, 26] показало, что потери топлива будут невосполни-
мы, если не будет найден какой-то метод отделения
нераспавшихся атомов расщепляющегося вещества от
атомов рабочего тела, так что лишь Viooo всех атомов, не
подвергшихся отделению, покинет камеру вместе с рабо-
чим телом. Чаще всего для осуществления такого отде-
ления предполагают использовать поле центробежных
сил, действие которого основано на различии масс ато-
мов водорода и урана. Вычисления показывают, одна-
ко, что скорость, которую можно получить при танген-
циальном вводе нагретого газа в вихревую камеру, не-
достаточно велика для того, чтобы диффузионный поток
рабочего вещества был нужной интенсивности, если
только мы имеем в виду использование одной камеры,
описанной выше; тяга, которая может быть получена от
такой системы, должна быть весьма малой. Поток боль-
шей величины можно получить лишь при повышенном
значении тангенциальной скорости, что само по себе
требует закручивания газа не гидродинамическим пу-
тем. В частности, было предложено закручивание путем
взаимодействия внешнего и индуцированного магнит-
ных полей (подобно тому, как это делается в электро-
двигателях, работающих по типу «беличьего колеса»)
как один из методов получения больших тангенциаль-
ных скоростей газа. Будучи в принципе возможным,
этот метод требует размещения на борту корабля раз-
личных электрических генераторных устройств и тем
самым связан с увеличением массы системы, позволяя
одновременно увеличить силу тяги. Когда тангенциаль-
14.4]
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ
523
ная скорость возрастает еще более, должна увеличить-
ся и масса электрического оборудования, и очевидно,
что отношение тяги к массе системы должно постоянно
уменьшаться. Где-то между указанными выше предела-
ми должны находиться оптимальные значения парамет-
ров системы, которым будет соответствовать макси-
мальное ускорение при любой заданной температуре
газа или при любом значении его удельного импульса.
Для того чтобы определить этот оптимум, важно знать,
какая электрическая мощность необходима для того,
чтобы поддерживать вращение газа с данной скоростью.
На первый взгляд может показаться, что вся энергия
1 2
вращения, равная yp^tan- должна поставляться генера-
торным оборудованием, но более детальное рассмотре-
ние вопроса о закрученном потоке показывает, что это
будет не так. При течении в вихре рабочее вещество
стремится сохранить свой момент количества движения,
т. е. стремится увеличить свою тангенциальную скорость
при движении с меньшими радиусами в направлении
центральной окружности, связанной с выходом в сопло.
Если, однако, вращение системы осуществляется с по-
мощью магнитных полей типа «беличьего колеса», то
вектор поля вращается с постоянной угловой скоростью,
так что ускоряющееся рабочее вещество стремится обо-
гнать поле. Это в свою очередь вызывает появление
«противополя», которое забирает часть кинетической
энергии направленного движения рабочего вещества и
возвращает ее полю, вращающему находящийся на пе-
риферии газ с большой тангенциальной скоростью.
В предельном случае полного согласования между га-
зом и полем (т. е. когда нет «проскальзывания») газ
будет вращаться, как твердое тело, и энергия его вра-
щательного движения будет уходить из системы, и,
таким образом, та энергия, которая будет доставлена
генераторным оборудованием, как раз будет равняться
энергии, содержащейся в газе при достижении им ра-
диуса, на котором располагается вход в сопло.
Масса реактора грубо может быть выражена фор-
мулой
/пг = 2,5^РгЛ, (14.84)
524
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
где tr и рг — толщина и плотность отражающей оболочки
из замедлителя, а А — площадь входного сечения пото-
ка рабочего тела, принятая здесь равной площади
поверхности камеры, содержащей стержни. Множитель
2,5 отражает влияние необходимых конструкций, охлаж-
дающих каналов, обмоток, создающих поле, и т. д.
Масса электрического генераторного оборудования мо-
жет быть, как и ранее, представлена в форме
mei = \prPeihg, (14.85)
где Pei—необходимая электрическая мощность, T]g—эф-
фективность преобразования тепловой мощности в элек-
трическую, а Крг — удельная масса оборудования, рас-
считанная на единицу тепловой мощности в электри-
ческой силовой установке. Тяга, создаваемая нашей
системой, дается формулой
F=ntpl^ = ?iAvhISp> (14.86)
где рг- — плотность рабочего вещества на входе в стерж-
невую зону, a vh — чисто радиальная скорость входя-
щего в камеру рабочего вещества. Требуемая электри-
ческая мощность равна, как указывалось выше,
Рelz= = f?iAvhlsp^tan» (14.87)
где f — та доля кинетической энергии вращения, кото-
рая уходит из системы. Чтобы написать выражение для
отношения тяги к массе системы, нужно еще найти со-
отношение между тангенциальной скоростью газа и его
радиальной скоростью, так что можно было бы выра-
зить одну величину через другую. Такое соотношение
можно получить, рассматривая процесс разделения
атомов в поле центробежных сил с учетом того обстоя-
тельства, ч*го необходимая для надлежащего разделе-
ния тангенциальная скорость зависит от радиального
потока рабочего тела сквозь расщепляющееся газооб-
разное топливо. Исследование этого процесса выходит
за рамки настоящего рассмотрения, но интересующая
14.4] ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ТЕПЛООБМЕННИКАМИ 525
нас функциональная зависимость была получена в рабо-
те [1]; она имеет вид
= + (14.88)
в этой формуле скорость измеряется в см/сек. Диффу-
зионные силы и турбулентные эффекты (при представ-
ляющих интерес типичных значениях расхода и давле-
ния) приближенно учтены при выводе этой формулы.
Объединяя уравнения (14.84)— (14.88), найдем, что
безразмерное отношение тяги к полной массе равно
F /
= = (14,89)
при температуре, измеряемой в градусах Кельвина, дав-
лении в атмосферах, удельном импульсе в секундах, Хрг
в килограммах на мегаватт (тепловой энергии), плот-
ности в граммах на кубический сантиметр и скорости в
сантиметрах в секунду. Из этой формулы очевидно, что
максимальное ускорение будет создано двигательной
системой при и величина этого
ускорения равна
_ Zsp
О-Р max - 5/ w /20<гРгГ(14’90)
Чтобы дать численный пример, предположим, что
взяты следующие значения различных величин: tr =
= 100 см, Хрг=3000 кг/Мвт, T]g=0,25, Р;=100 атм,
pr = 1 г/см\ Ti = 3000° К (что соответствует примерно
10% энергии, необходимой для получения принятого
значения Zsp), /sp = 3000 сек и f = 0,1. При этих значе-
ниях переменных оптимальная радиальная скорость
определяется из равенства а2* = 50 (см/сек)2, а макси-
мальное ускорение равно аР max = 0,03 go. Если масса
двигательной системы составляет 0,1 массы корабля, то
начальное ускорение летательного аппарата может
быть равно лишь 3*lO~3go, что примерно сравнимо с
величиной, которую можно получить с помощью раз-
личных систем с косвенным созданием тяги (см. разде^
лы 14.3 и 14.5).
55 Дж. Лейтмац
526
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
(гл. XIV
Другие проекты газовых реакторов различаются в
деталях, но все они, благодаря происходящим в них
простым физическим процессам, обладают максималь-
ным теоретическим значением ускорения, порядок кото-
рого совпадает с порядком ускорения, достижимого с
помощью единственного вихревого газового реактора
при условии высокой эффективности использования ра-
бочего тела.
14.5. ЯДЕРНО-ЭЛЕКТРИЧЕСКИЕ ДВИГАТЕЛЬНЫЕ
СИСТЕМЫ
Двигательные системы непрямого действия состоят
из основных узлов, изображенных на рис. 14.2,6, а
именно: источника энергии, оборудования для преобра-
зования энергии, регенератора и оборудования для пере-
вода трансформированной энергии непосредственно в
энергию движения истекающего рабочего тела. Каждая
из этих основных составляющих систему групп связана
с другими, и поэтому, вообще говоря, нельзя определить
оптимальные параметры какой-либо группы без рассмот-
рения оптимизации системы в целом.
14.51. Оптимизация температуры цикла. Получим
сначала некоторые условия оптимального выбора тем-
пературы. Рассмотрим простую систему, изображенную
на рис. 14.9. Система работает здесь при изменениях
температуры от максимального значения Тт до мини-
мального Ts; для удобства мы предположим, что все
тепло, не использованное в цикле, отводится при посто-
янной температуре Ts. Мощность, произведенная в пре-
образователе, прикладывается к некоторому ускори-
телю рабочего тела, в котором последнее ускоряется с
эффективностью rjaccei, а не использованное при этом
тепло отводится через специальный радиатор при темпе-
ратуре, которую можно выбрать независимо от темпе-
ратур основного цикла. На протяжении этого цикла
энергия источника с эффективностью Tjconv преобра-
зуется в электрическую; эффективность этого преобра-
зования всегда меньше эффективности цикла Карно
rjcamot = (Tm—Ts)!Tm, но связана с ней соотношением
/fc/navM/x ядерт/ай
дт/^ргии
I
077700721/7700
/77077770
Г
/§
h *
's ‘rad.
J
ЯТюрудоваяае
Г7рея&раэ0&а/леля
melec
Уаяаритт/ет/а
macre7
/707770#
pad0¥020
777077a
Ра&иа/яяр усгюршпеля
7г
&77700дШ700
77700770
rad.
Рис. 14.9. Типичная ядерно-электрическая двигательная
система.
35*
528
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
T]conv = fcT]carnot. Массы четырех главнейших узлов си-
стемы можно предстзвить в виде:
/nreac = MV (14.91)
/nrad, = SnPrad.Mr/n (Л, = (14.92)
fflrad, = Sr2Ptni2 (14.93)
#Z-elec === ^elec P elec» (14.94)
^laccel == ^accel Pj* (14.95)
В этих формулзх s обознзчзет поверхностную плотность
мзссы поверхности рздизторз, о — постоянную Стефа-
нз — Больцмзнз, е—коэффициент излучения, з осталь-
ные обознзчения понятны сзми собой.
Рззличные мощности, фигурировзвшие в написан-
ных выше урзвнениях, связзны друг с другом с по-
мощью эффективностей рззличных узлов формулзми:
Р elec — Pr^conv» (14.96)
Prad, = Pr(l - ?lconv). (14-97)
Prad2 == Pelec (1 ^laccel)' (14.98)
Pj = P elec^accel* (14.99)
Пользуясь этими рзвенствзми, можем из урзвнений
(14.91) — (14.95) нзйти вырзжение для полной мзссы
силовой устзновки через одну лишь переменную, имею-
щую смысл мощности. Если нзписзть это соотношение
тзким образом, что единственной остзвшейся мощно-
стью будет полнзя тепловзя мощность Рг, производимзя
источником энергии, то коэффициент при Рг окзжется
просто рзвным употреблявшейся рзнее (рзздел 14.32)
удельной мзссе Хрг силовой устзновки. Мы предпочи-
тзем, однзко, ззписзть вырзжение для мзссы устзнов-
ки тзким обрззом, чтобы этз величина былз пропорцио-
нзльнз мощности Pj, рззвивземой рзкетным двигзтелем,
как, например, это сделано в уравнении (14.2):
_ Г \ । С1 ~~ ^conv) ।
'"'рг I । —4 Т
L ^accel ’Iconv Ce/i s^accel^conv
+ S ае(1й?ССе|) + + ^ce.] PГ (ИЛОО)
oer> r/iaccel laccel J
14.5] ЯДЕРНО-ЭЛЕКТРИЧЕСКИЕ ДВИГАТЕЛЬНЫЕ СИСТЕМЫ 529
Двигательная система будет работать в оптималь-
ных условиях, если масса установки, рассчитанная на
единицу мощности, развиваемой двигателем, будет ми-
нимальна, поскольку при этом масса будет использо-
ваться для целей создания тяги наилучшим образом.
Мы желаем найти такую температуру цикла, которая
приведет к этим оптимальным условиям. С этой целью
подставим в (14.100) написанное нами ранее выражение,
связывающее эффективность преобразования цикла с
его начальной и конечной температурами, и продиффе-
ренцируем результат по отношению максимальной тем-
пературы к минимальной Т = Тт/Т3, фиксируя парамет-
ры Tm, Тr2i ^ассеЬ Xelec, Xaccel, S, И Ху. Получающееся
при этом условие для Т имеет вид
4Р (1 —Л) —74 (5 — 8/,) — 4Г% = .(14.101)
Подобное уравнение было получено Питкином [27]
для несколько более простой системы.
Решение этого уравнения пятой степени при задан-
ных значениях fc и других параметров даст оптималь-
ное значение относительной температуры цикла, кото-
рому будет соответствовать максимум мощности двига-
теля на единицу массы силовой установки. Решение
уравнений пятой степени, вообще говоря, затруднитель-
но, но можно получить представление о предполагаемом
поведении величин, ограничившись тем случаем, когда
масса реактора — источника энергии пренебрежимо мала
по сравнению с массой главного радиатора. Имеющиеся
в настоящее время системы (где, как правило,
7П!<1000°С) довольно хорошо удовлетворяют этому
условию, так как в большинстве ядерно-электрических
установок для космических целей преобладающей явля-
ется масса главного радиатора. Сделав такое предполо-
жение, отбросим правую часть уравнения (14.101), све-
дя, таким образом, это уравнение к квадратному,
решение которого (берется лишь положительный ко-
рень) имеет вид
(14.102)
530
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
(гл. XIV
Таблица 14.5 показывает направление изменения Т
при изменении относительной эффективности цикла.
Таблица 14.5
Оптимальная относительная температура
цикла в зависимости от его относительной
эффективности
4? Т =Т ГТ ml s I'r-1=V2'm
1,0 4/3 = 1,33 3/4 = 0,75
0,8 1,31 0,762
0,625 1,29 - 0,775
0,3 1,27 0,789
0 5/4 = 1,25 4/5 = 0,8
Если правой частью уравнения (14.101) нельзя пре-
небречь, то мы должны решить уравнение пятой степе-
ни относительно Т. В общем случае мы находим, что не
равная нулю правая часть приведет при данном fc к
(большим значениям отношения максимальной темпера-
туры к минимальной, нежели те, что приводятся в
табл. 14.5. Пусть, например, максимальная температу-
ра равна 7\п = 2000°К, Хг= 10 кг!Мвт, еГ1 = 1,0, а по-
верхностная плотность площади радиатора равна
= 0,25 г!см2. Правая часть при этом равна 3,63, и мы
находим, что оптимальное значение Т при fc = 0,75 рав-
но 1,57; это значительно превышает табличное значе-
ние, равное примерно 1,3. В общем случае мы заклю-
чаем, что оптимальное температурное отношение боль-
ше при более высокой температуре источника, при более
высоких значениях его удельной массы и при меньших
значениях поверхностной плотности радиатора.
14.52. Реакторы прямого преобразования. При со-
временном состоянии машиностроения не представляет-
ся возможным сконструировать надежный турбогенера-
тор, работающий при значениях максимальной темпе-
ратуры цикла, значительно превосходящих 1000° С. Для
^получения более высоких температур мы должны отыс-
кать способ замены высоконапряженных вращающихся
14.5] ЯДЕРНО-ЭЛЕКТРИЧЕСКИЕ ДВИГАТЕЛЬНЫЕ СИСТЕМЫ
531
частей в таких системах другими, менее нагруженными
узлами. Один из путей состоит в полном исключении
вращающихся частей при помощи использования неко-
торых способов непосредственного преобразования ядер-
но-тепловой энергии в электрическую, таких, как разра-
батываемый в настоящее время метод прямого преоб-
разования с помощью газонаполненных термоионных
диодов [28]. При прямом преобразовании такого рода
получается двоякий потенциальный выигрыш: во-пер-
вых, благодаря тому, что в отсутствие вращающихся
частей цикл может работать при высокой температуре
источника и поглотителя нейтронов, обусловливая тем
самым серьезное уменьшение массы первого радиатора
[уравнение (14.92)], и, во-вторых, благодаря тому, что
масса преобразователей [уравнение (14.94)] полностью
исключается теперь из выражения (14.100) для полной
массы установки.
Последнее обстоятельство приводит к экономии при-
мерно 500 кг/Мвт (на мегаватт электрической энергии),
а предпоследнее дало бы примерно такую же экономию,
если бы удалось поднять температуру радиатора при-
близительно на 200° К по отношению к достижимому
ныне значению.
Если вновь обратиться к газовым реакторам, то нуж-
но отметить, что максимальная температура цикла с
участием такого реактора может (теоретически) быть
гораздо большей, чем максимальная температура для
реакторов с твердыми стержнями, и это является при-
влекательным с точки зрения возможности получения
условий высокой эффективности цикла Карно, что ми-
нимизирует, таким образом, массу реакторной части
силовой установки. Стремление к этому, однако, пред-
ставляется малооправданным, за исключением тех слу-
чаен, когда масса других составных частей силовой
установки мала по сравнению с массой источника энер-
гии, но >в этом случае мы как раз получаем схему газо-
электрического реактора [29]. При этом мы имеем в
виду, что активная зона реактора колебательным обра-
зом взаимодействует с поддерживаемым извне магнит-
ным полем и системой управления реакцией. Мы пред-
полагаем (основываясь на современных представлениях
532
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ
[гл. XIV
физики плазмы), что колебания эти могут устойчиво
поддерживаться. Газовая-стержневая зона периодиче-
ски расширяется благодаря нагреву при распаде и сжи-
мается возрастающим внешним магнитным полем. Иони-
зованный горячий газ при расширении совершает
работу против магнитного поля, а в фазе сжатия поле
производит над ним работу. Газы в стержневой зоне
играют роль продуктов сгорания и порций свежего
топлива в современных двигателях внутреннего сгора-
ния. Если магнитное поле и системы управления ядер-
ными реакциями должным образом сфазированы, то
вырабатываемая электрическая мощность будет постав-
ляться в обмотки катушек, создающих поле, и, таким
образом, во внешнюю цепь. Если бы этот замечатель-
ный способ преобразования был лишен потерь и если
бы удалось сделать колебания устойчивыми, то следо-
вало бы получить максимальную возможную пиковую
температуру газа, чтобы добиться максимальной эффек-
тивности производства электрической мощности. В са-
мом процессе колебаний заложен, однако, один из ос-
новных источников потерь. Речь идет о потерях вслед-
ствие теплового излучения из горячего газа, находяще-
гося в сжатом состоянии, а также в те периоды времени,
когда газ расширяется в разреженную стержневую зону,
совершая работу против магнитного поля и охлаждаясь
по мере расширения. Увеличение пиковой температуры
газа приведет к возрастанию потерь тепла на излуче-
ние, и, поскольку эти потери изменяются, грубо говоря,
пропорционально четвертой степени температуры, оче-
видно, что должна существовать оптимальная пиковая
температура, с превышением которой мы должны те-
рять больше энергии в радиаторе, нежели получать ее
при более интенсивном отборе за один цикл. Несмотря
на то, что связанные с этим процессы в действительно-
сти весьма сложны, оптимальную температуру при за-
данной геометрии найти просто, если принять, что газо-
вый объем излучает, как серое тело, что стенки стержне-
вой зоны идеально поглощающие и что потери на оми-
ческий нагрев благодаря проникновению поля в газо-
вый объем и стенки пренебрежимо малы. Найденная
при этих условиях оптимальная температура газа будет
ЛИТЕРАТУРА
533
всегда больше, чем истинная. Мы не приводим здесь
этого рассмотрения, оставляя его в заключение в каче-
стве интересной задачи для читателя, который обна-
ружит, что потеря энергии на излучение и, следователь-
но, пиковая температура газа зависят от частоты коле-
баний.
ЛИТЕРАТУРА
1. R. W. Bussard, Nuclear fission rockets: Problems, progress, and
promise, статья представлена на семинаре по космическим дви-
гателям (Милан — Варенна, Италия, сентябрь 1960).
2. R. W. В u s s а г d and R. D. D e L a u e r, Nuclear Rocket Pro-
pulsion, гл. 2, McGraw-Hill, New York, 1958. [Русский перевод:
P. Бассард и P. Делауэр, Ракета с атомным двигателем,
М., ИЛ, I960.]
3. R. W. В u s s а г d, Nuclear rocket propulsion possibilities, гл. 17
в книге «Space Technology» (H. S. Seifert, ed.), Wiley, New
York, 1959. [Русский перевод: под ред. Г. Сейферта, Косми-
ческая техника, гл. 15, изд-во «Наука», М., 1964.]
4. J. D. О г n d о f f and F. P. Durham, Nuclear propulsion, Sec-
tion IV E 1 в книге «Astronautics Handbook», McGraw-Hill, New
York, 1961.
5. I. G. Henry, Range and accuracy of long-range ballistic missi-
les, J. Brit. Interplanet. Soc. 17, 88 (1959).
6. K. A. Ehricke, Space Flight, Van Nostrand, Princeton, New
Jersey, 1960. [Русский перевод: К. А. Эрике, Космический по-
лет, Физматгиз, М., 1963.]
7. R. М. L. Ваке г, Jr., Accuracy required for a return from in-
terplanetary voyages, J. Brit. Interplanet. Soc. 17, 93 (1959).
8. R. M. L. В a к e r, Jr., and M. W. Makemson, An Introduction
to Astrodynamics, Academic Press, New York, 1961.
9. R. M. L. Bake r, Jr., Recent advances in astrodynamics, ARS
Journal 30, 1127 (1960).
10. C. J. Wang, G. W. Anthony and H. R. Lawrence, Thrust
optimization of a nuclear rocket of variable specific impulse, ARS
Journal 29, 341 (1959).
11. J. H. Irving, Low-thrust flight: Variable exhaust velocity in
gravitational fields, гл. 10 в книге «Space Technology»
(H. S. Seifert, ed.), Wiley, New York, 1959. [Русский перевод:
под ред. Г. Сейферта, Космическая техника, гл. 8, изд-во
«Наука», М., 1964.]
12. G. Leitmann, Minimum transfer time for a power-limited
rocket, Proc. 11th Intern. Astronaut. Congr., Stockholm, 1960; cm,
также J. Appl. Meeh. 28, 171 (1961).
13. H. Preston-Thomas, Interorbital transport techniques,
гл. 10 в книге «Realities of Space Travel» (L. J. Carter, ed.).
McGraw-Hill, New York, 1957.
534
ОПТИМИЗАЦИЯ РАКЕТ НА ЯДЕРНОМ ТОПЛИВЕ [гл. XIV
14. Н. Preston-Thomas, Some design parameters of a simpli-
fied ion rocket, J Brit. Interplanet Soc. 16, 575 (1958).
15. R. H. F о x, Optimum velocity programming and propulsion effi-
ciency, Rept. No. UCRL-5135, Lawrence Radiation Laboratory,
University of California, Livermore, California (May 26, 1958).
16. C. R. F a u 1 d e r s, Optimum thrust programming of electrically
powered rocket vehicles in a gravitational field, ARS Journal 30,
954 (1960).
17. G. M. Schindler, Minimum time flight paths, ARS Journal
30, 352 (I960).
18. H. F. Michi el sen, Minimum weight and optimum flight path
of low-acceleration space vehicles, Rept. No. LMSD-48381, Lock-
heed Missiles and Space Division, Sunnyvale, California (January,
1959).
19. G. Leitmann, Some remarks on the optimum operation of a
nuclear rocket, Proc. 10th Intern. Astronaut. Congr., London,
1959 (1960).
20. R. H. F о x, Powered trajectory studies for low thrust space ve-
hicles, ARS Journal 31, 28 (1961).
21. R. W. Bussard, A nuclear-electric propulsion system, J. Brit.
Interplanet. Soc. 15, 297 (1956).
22. D. B. Langmuir, Low-thrust flight: Constant exhaust velocity
in field-free space, гл. 9 в книге «Space Technology» (H. S. Sei-
fert, ed.), Wiley, New York, 1959. [Русский перевод: под ред.
Г. Сейферта, Космическая техника, гл. 7, изд-во «Наука»,
М., 1964.]
23. G. Leitmann, The nuclear-powered ion rocket, J. Brit. Inter-
planet. Soc. 16, 587 (1958).
24. H. Preston-Thomas, The nuclear-powered ion rocket,
J. Brit. Interplanet. Soc. 17, 101 (1959).
25. L. Spitzer, Jr., Interplanetary travel between satellite orbits,
J. Brit. Interplanet Soc. 10, 249 (1951).
26. R. W. В u s s a r d, Concepts for future nuclear rocket propul-
sion, Jet Propulsion 28, 223 (1958).
27. E. T. P i t k i n, Optimum radiator temperature for space power
systems, ARS Journal 29, 596 (1959).
28. J. Kaye and J. A. Welsh, eds., Direct Conversion of Heat to
Electricity, часть В, главы 6—11, Wiley, New York, 1960.
29. F. Winterberg, Kernverbrennungsplasmen und magnetische
Kernbrennkammern ftir Strahltriebwerke, Astronaut. Acta 4, 17
(1958)
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вариации 259
— сильные 135
— слабые 135
Вейерштрасса Е-функция 216,
223
Возвращение снаряда перемен-
ной формы 119
Время полета экстремальное 116,
125
Высота максимальная при поле-
те в вакууме 170, 172
Градиент в функциональном
пространстве 264
Грина теорема 261
— формулы 59, 60 и д.
— функция 260
Грузоподъемность максимальная
корабля с электрической дви-
гательной системой 50
Давление оптимальное в систе-
ме с ядерным двигателем 519
Дальность полета максимальная
в вакууме 177
----- при заданной высоте 87
-----экстремальная 115, 119
Двигатель электрический 221,
481
— ядерно-электрический 481
— ядерный, защита радиацион-
ная 505
Движение под солнечным пару-
сом 280 и д.
— с малой тягой 290 и д.,
481 и д.
Дельта-функция Дирака 260
Дуга частичная 102
— экстремальная 132
Дуги частичные при полете в
вакууме 165, 175
----------в сопротивляющейся
среде 181 и д., 193
Е-функция Вейерштрасса 216,
223
Зависимость импульса от орби-
тальных элементов 392 и д.
Задача без производных 143
Задача Больца 131
— интегральная 34
— Лагранжа 137, 141, 142
— линейная 33, 101, 108
----- изопериметрическая 106
— Майера 136, 141, 150
— минимизации конечного зна-
чения переменной состояния
377, 380, 382
— о встрече за минимальное
время 73
— о достижении заданной точ-
ки 85
— с неравенствами 144
— с ограниченными управления-
ми 209 и д.
— с производными высших по-
рядков 141
Защита радиационная при ядер-
ном двигателе 505
Изменение импульсное орбиталь-
ных элементов 388 и д.
Импульс удельный 511, 516
-----оптимальный при ядерном
топливе 471
Исчисление вариационное 31. 32,
130, 318
536
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Ковариация в влучае частых
наблюдений 435, 437
Корабль на ядерном топливе с
большим ускорением 463
Коррекция траектории 417, 423,
427
-----каскадная 424, 428, 430
-----при полете на Марс 426
Кривые допустимые 112, 113 ид.
-----в плоскости скорость —
высота 121
Майера соотношение взаимности
66, 67
Максимум функции 19
-----абсолютный 19
-----локальный 19
Масса летательного аппарата с
ядерным двигателем 465
— оптимальная 529
— турбонасоса 466
— удельная 511, 514, 516
— ядерного реактора 466
Метод Веллмана 364
— градиентов (метод наиско-
рейшего спуска) 244 и д.
— динамического программиро-
вания 307, 338
-------и принцип максимума
Понтрягина 327
— Калаба 364
— отыскания экстремума не-
прямой 35, 36
-------прямой 35, 36
— погружения 375
— проектирования градиентов
250
— функций нагружения 278, 296
— численный определения про-
стой оптимальной траектории
баллистической ракеты 67 и д.
Методы аналитические 37, 38
— численные 37, 38
Множество экстремалей при оп-
тимизации траектории полета
в вакууме 167
— Лагранжа 28, 132
Мощность реактора удельная 512
Направление вектора тяги при
полете в вакууме 173
Неравенства связей 236
Область допустимых кривых со-
стояния ракеты 113
Ограниченность запаса энергии
при полете с малым ускоре-
нием 501
Оптимизация адаптивного про-
цесса управления 368
----------по методу динами-
ческого программирования 368
и д.
— баллистической траектории
(ядерное топливо) 474
— двигательной системы ионно-
го аппарата 48 и д.
— двумерных профилей крыльев
в линеаризованном сверх-
звуковом потоке 156, 157 и а.
— детерминированного процесса
управления, множители Ла-
гранжа и уравнения Эйлера 357
----------, метод динамическо-
го программирования 354 и д.,
358 и д.
— перехода импульсного между
двумя орбитами 395 и д.
— поворота оси орбиты 398 ид.
— систем на ядерном горючем
457
— соотношения между последо-
вательными значениями шага
коррекции 434
— торможения снаряда пере-
менной геометрической формы
179
— траектории в вакууме 162 и д.
-----в сопротивляющейся среде
179 и д., 184
-----, задача двумерная 342, 349
-----, — одномерная 341, 344
-----ионного аппарата при боль-
ших изменениях орбитальных
элементов 44 и д.
----------при малых измене-
ниях орбитальных элементов
41 и д.
-----ракеты при полете с уско-
рением, зависящим от положе-
ния и времени 209 и д.
— формы тела вращения в нью-
тоновом потоке 149 и д.
— функции стоимости 359 и д.,
362
предметный указатель
537
.Парус солнечный 280 и д.
Перехват баллистических ракет в
стратосфере 70 и д.
Перелет из заданной точки кру-
говой орбиты в заданный
пункт на Земле 232 ид.- -
Переход между орбитами 387
-------, оси которых находят-
ся на одной прямой 413
Переходы подобные между оди-
наковыми эллиптическими ор-
битами 402
Поворот оси орбиты оптималь-
ный 398 и д., 405
Полет в постоянном гравитаци-
г онном поле 214, 218, 333
— к Марсу 418, 419, 425, 426
------- с малой тягой 291
-------под солнечным пару-
сом 281, 284
— с малой тягой 290 и д.
— с солнечным парусом 280 и д.
Преобразование вариационных
задач 140 и д.
Приближение полиномами 343,
347, 384
Принцип максимума Понтряги-
на 216, 242, 302, 307 и д., 313,
363
-----. при определении опти-
мальных траекторий баллисти-
ческих ракет 62 и д.
-г оптймальности Веллмана 216
Программа направления вектора
тяги при полете в сопротив-
ляющейся среде 192
Программирование динамиче-
ское — см. Метод динамиче-
ского программирования
Проектирование градиента 251
Процесс Фибоначчи 35
Равенства связей 250
Ракета ближнего действия без
подъемной силы, программа
оптимального расхода топлива
110
— химическая 211 ид.
— электрическая 51, 221 и д.
— ядерная 455, 469
-----двухступенчатая 478
Реактор ядерный прямого пре-
образования 530
-----газовый 521
Решения стационарные 318
Связи 250, 256
— дополнительные при полете в
сопротивляющейся среде 195
Седло 20
Сжигание топлива в сопротив-
ляющейся среде 192
Система двигательная ядерная
с теплообменником 509
-----ядерно-электрическая 526
— присоединенная 260
— с ограниченной мощностью
221 и д., 232
— с ограниченным расходом
массы 231
-------ускорением тяги 225,
232
— сопряженная 316
Скорость истечения оптималь-
ная при полетах с малым
ускорением 499
Соотношение масс в аппарате с
ядерно-электрическим двига-
телем 486
— взаимности Майера 66, 67
Спуск непрерывный 245
— шаговый 248
Спутник стационарный 39
Тело вращения в ньютоновом
потоке 149 и д.
Температура цикла относитель-
ная оптимальная 529
Теорема Вейерштрасса 21
— Грина 261
Теплопередача экстремальная
123, 127
Торможение снаряда перемен-
ной геометрической формы 119
Точка стационарная 19
— угловая 77, 102, 134
Траектории в вакууме 162 и д.
— в сопротивляющейся среде
без подъемной силы 198
----------вертикальные 195
----------горизонтальные 195
538
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Траектории в сопротивляющейся
среде планирующие 199
---------- постоянного расхода
массы 197
---------- прямолинейные 197
— вблизи планеты назначения
424
Тяга малая 290 и д., 493
— при максимальной дальности
91
Уменьшение числа измерений
384
Управление расходом массы
двухпозиционное 218
Уравнение движения баллисти-
ческой ракеты в канонической
форме 89, 90
Уравнения Эйлера — Лагранжа
132, 133, 212
Условие Вейерштрасса 135
— Лежандра—Клебша 135, 143
Условия в угловых точках Эрд-
мана—Вейерштрасса 134
— трансверсальности 134
— экстремума достаточные 24
-----необходимые 21
Фибоначчи процесс 35
Формулы Грина 59, 60 и д.
Функционал 31
Функция выигрыша 211
— Грина (функция влияния) 260
Функция избытка Вейерштрасса
321 323
— нагружения 29, 256, 278
— переключений 166, 167
-----массового расхода 176,194
----- направления тяги 176
-----силы тяги 194
— расширенная 132
— фундаментальная расширен-
ная 107
-----с непостоянным знаком 104
-----с постоянным знаком 103
— Хевисайда единичного скачка
257
Экстремали при оптимизации в
сопротивляющейся среде 185,
187, 189, 191
Экстремум функции 19
-----абсолютный 19, 20
-----локальный 19, 20
-----при дополнительных усло-
виях (связях) 25 и д.
Элементы орбитальные, измене-
ние импульсное 388 и д.
Эффективность тяги, вариацион-
ное решение 449
----- как функция интервала
446
----------точки 443, 444
-----, скорость истечения пере-
менная 445, 448
-----,----постоянная 445, 447
Методы оптимизации
с приложениями к механике
космического полета
(Серия «Механика космического полета»).
М., 1965 г., 540 стр. с илл.
Редактор Д. А. Абашева
Техн, редактор Л. Ю. Плакше
Корректор О. А. Бутусова
Сдано в набор 10ДХ 1964 г. Подписано к
печати 20/1 1965 г. Бумага 84хЮ8/82.
Физ. печ. л. 16,875. Условн. печ. л. 27,67.
Уч.-изд. л. 23,92. Типаж 3000 экз.
Цена книги 1 р. 40 к. Заказ № 726.
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография Кг 2
имени Евгении Соколовой
Главполиграфпрома
Государственного комитета
Совета Министров СССР по печати.
Измайловский проспект, 29.
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва, В-71, Ленинский tip., 15
ВЫЙДУТ ИЗ ПЕЧАТИ В 1965 году:
Балк М. Б., Элементы динамики космического полета.
Серия «Механика космического полета», 15 л., 8000 экз., 95 коп.
в пер. [II кв.].
Белецкий В. В., Движение искусственного спутника от-
носительно центра масс. Серия «Механика космического по-
лета», 20 л., 8000 экз., 1 р. 20 к. в пер. [III кв.].
Егоров В. А., Пространственная задача достижения
Луны. Серия «Механика космического полета», 15 л., 8000 экз.,
95 коп. в пер. [III кв.].
Миеле А., Механика полета, т. I «Теория траекторий»,
перев. с англ. А. Н. Рубашова, под ред. проф. А. А. Космо-
демьянского, 26 л., 8000 экз., 1 р. 50 к. в пер. [II кв.].
Пономарев В. М., Теория управления движением кос-
мических аппаратов. Серия «Механика космического полета»,
25 л., 8000 экз., 1 р. 45 к. в пер. [II кв.].
Предверительные заказы на печатающиеся книги прини-
маются без ограничения всеми магазинами книготоргов.
При отказе от принятия заявки можно обратиться по
адресу: Москва, В-71, Ленинский проспект, 15, «Союзкнига».