Author: Дегтярь В.Г. Пегов В.И.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника монография подводные лодки гидродинамика баллистические ракеты ракетные стартовые системы
ISBN: 5-93419-006-7
Year: 2004
ФГУП
«ГРЦ «КБ им. академика В. П. Макеева»
В. Г. Дегтярь, В. И. Пегов
ГИДРОДИНАМИКА
БАЛЛИСТИЧЕСКИХ РАКЕТ
ПОДВОДНЫХ ЛОДОК
Монография
Миасс
2004
УДК 629.762.2.085.5
Д26
Дегтярь В.Г., Пегов В.И.
Гидродинамика баллистических ракет подводных лодок:
Монография. — Миасс: ФГУП "ГРЦ "КБ им. акад. В.П. Макеева",
2004. - 256с.: ил.
Монография содержит общую постановку задачи гидродинамики мор-
ских баллистических ракет, вывод системы дифференциальных уравнений и
кинематические соотношения, необходимые для описания пространственного
движения ракет, движущихся внутри взволнованной жидкости. Получены об-
щие выражения действующих на ракету гидродинамических сил и моментов
через значения коэффициентов присоединенных масс ракеты и производных по
времени от этих коэффициентов. Разработаны приближенные и численные ме-
тоды расчета гидродинамических характеристик при режимах сплошного и ка-
витационного обтекания ракет, приведены результаты параметрических расче-
тов гидродинамических характеристик для наиболее характерных внешних об-
водов ракет. Исследованы газодинамические и тепловые процессы, протекаю-
щие при выходе ракеты из шахты.
Монография адресуется специалистам, работающим в области создания
ракетных стартовых систем.
ISBN 5-93419-006-7 © Федеральное государственное унитарное
предприятие "Государственный ракетный центр
"КБ им. академика В.П. Макеева" (ГРЦ "КБ
им. академика В.П. Макеева"), 2004
Предисловие
Монография охватывает широкий круг вопросов, включающих в себя
разработку гидродинамических схем старта и теоретические основы гидро-
динамики и динамики подводного старта баллистических'ракет подводных
лодок. В ней обобщен теоретический и экспериментальный материал много-
численных исследований самих авторов, а также освещены и систематизиро-
ваны результаты многих исследований, проведенных в научно-
исследовательских институтах и опытно-конструкторских бюро в процессе
создания ряда морских стратегических ракетных комплексов, находящихся в
настоящее время на вооружении Военно-Морского Флота
Одной из главных особенностей книги является ее практическая на-
правленность: приводимые в ней теоретические результаты изложены в виде
конечных формул, а результаты расчетов - в виде графиков и таблиц, кото-
рые непосредственно используются в практике проектирования ракет. Доста-
точно полно освещаются также полуэмпирические методы оценки гидроди-
намических характеристик ракет, основанные на систематизации и обобще-
нии экспериментальных данных. Вместе с тем, в книге отражены новейшие
методы численно-аналитического исследования задач гидродинамики с по-
мощью высокопроизводительных ЭВМ, которые в настоящее время приме-
няются при проектировании подводных аппаратов.
В монографии получила дальнейшее развитие, применительно к гидро-
динамическим схемам старта, общая методология проектирования и конст-
руирования баллистических ракет. При проектировании ракет одна из клю-
чевых проблем заключается в адекватном учете особенностей гидродинами-
ки подводного старта. На начальной стадии необходимо представить в общих
чертах гидродинамическую схему старта, определить физико-механическое'
взаимодействие подсистем ракеты, а также свойства, которыми должна обла-
дать баллистическая ракета на всевозможных режимах старта и движения
под водой. Это зависит прежде всего от особенностей конструкции и силовой
установки ракеты. Определив основные функции систем ракеты в зависимо-
сти от гидродинамических характеристик ракеты, можно перейти к тому, как
гидродинамик и конструктор должны координировать свои усилия для дос-
тижения общей цели. Работа обычно начинается с предварительной оценки
на основе упрощенных уравнений, в которые последовательно вносятся
уточнения по результатам экспериментальной отработки подводного старта
ракет. Оптимальным способом окончательной доводки систем старта при
проектировании является математическое моделирование пространственного
движения ракеты как системы с шестью степенями свободы, для которого
нужно знать все гидродинамические характеристики и присоединенные мас-
сы ракеты.
Мы надеемся, что эта книга будет полезна широкому кругу специали-
стов научно-исследовательских институтов и опытно-конструкторских бюро,
а также преподавателям, аспирантам и студентам, специализирующимся в
области гидродинамики и ракетно-космической техники.
Авторы
Введение
Морские баллистические ракеты, стартующие из. пусковых шахт под-
водных лодок, испытывают максимальные силовые нагрузки на шахтном и
подводном участках траектории. Именно эти нагрузки определяют, как пра-
вило, требования к прочности БРИЛ и системе ее управления. Наиболее дос-
товерными исследованиями гидрогазодинамики подводного старта БРПЛ яв-
ляются экспериментальные. Однако экспериментальная отработка новой
конструкции требует больших материальных и временных затрат, поэтому
создание эффективных методов расчета гидрогазодинамических характери-
стик и действующих на БРПЛ нагрузок очень важно для практики проекти-
рования. В то же время теоретический анализ гидрогазодинамических про-
цессов, сопровождающих движение БРПЛ под водой, представляет большие
трудности как при разработке математических моделей нестационарных про-
цессов, так и при решении соответствующих краевых задач. В зависимости
от принятой схемы старта и участка траектории расчетная модель движения
должна учитывать различные доминирующие факторы (например, наличие
свободной поверхности при кавитационном обтекании) при достаточно про-
стой постановке задач.
Известные в настоящее время расчетные модели зачастую основаны на
упрощающих предположениях, недостаточно полно соответствующих физи-
ческой картине движения и введенных исключительно с целью преодоления
математических трудностей при решении начально-краевых задач. Как пра-
вило, тело считается тонким, газ в каверне — неподвижным, движение жидко-
сти — установившимся, форма надшахтной газовой полости предполагается
заранее известной и т.д. Такие решения носят оценочный характер и требуют
детальной опытной проверки.
Обширные экспериментальные и теоретические исследования по гид-
рогазодинамике старта БРПЛ проводятся в ГРЦ "КБ им. академика В.П. Ма-
кеева", филиале НАГИ, НИИ механики МГУ, ЦНИИ им. академика
А.Н. Крылова, 1-м ЦНИИ МО, ВМА им. Н.Г. Кузнецова, ЦНИИМаш, БГТУ,
НИИ ПММ при ТГУ и ряде других организаций.
В решение проблем гидродинамики и динамики подводного старта
внесли большой вклад В.П. Макеев, В.Н. Челомей, Г.В. Логвинович, Ю.Л.
Якимов, Е.Н. Мнев, М.Г. Щеглова, О.П. Шорыгин, С.В. Шахрис, Н.Ф. Там-
булов, Е.Н. Капанкин, А.Д. Жаботинский, Б.И. Полетаев, В.А. Хотулев, П.П.
Тихонов, Л.А. Бондаренко, И.Б. Богоряд, А.П. Шальнев, Б.А. Соснин,
И.Н. Заболотнов, А.А. Болдырев, Ю.П. Кабанов, Э.Е. Либин, Г.А. Степанен-
ко и другие.
В ГРЦ “КБ им. академика В.П. Макеева” разработаны и в течение мно-
гих лет используются в инженерной практике математические модели, алго-
ритмы и комплексы программ расчета гидродинамических и газодинамиче-
ских параметров и динамики подводного старта ракет. Однако до настоящего
времени нет подробного, полного и систематического изложения постановки
и математической формулировки с единых позиций одновременно задач гид-
5
родинамики, газодинамики и динамики, методов их решения, описания алго-
ритмов и их программной реализации для всего подводного участка траекто-
рии. Цель настоящей монографии заключается в обобщении многолетнего
опыта применения математического моделирования гидродинамических и
газодинамических процессов и динамики ракет при создании и отработке ря-
да ракетных комплексов в ГРЦ "КБ им. академика В.П. Макеева" и ликвида-
ции отмеченного недостатка.
С удовлетворяющей практику проектирования точностью определены
гидродинамические характеристики и нагрузки на БРПЛ при безотрывном ее
обтекании потоком идеальной жидкости на различных участках траектории:
при прохождении через верхний срез шахты, движении в безграничной жид-
кости и выходе из нее. Эти задачи решены методом потенциала простого
слоя, а также вариационными методами, численная реализация которых осу-
ществляется с помощью пакета алгоритмов и программ, позволяющих полу-
чить приближенные решения задачи.
Проанализированы физические процессы и общие подходы к расчету
гидродинамических нагрузок при старте из затопленной шахты ПЛ. Разрабо-
тана и апробирована методика учета влияния образующихся при старте газо-
вых полостей.
Предложен метод расчета присоединенных масс ракеты в затопленной
водой шахте. Метод позволяет учитывать пространственную картину тече-
ния, форму носовой части и прямого кормового среза ракеты, величину
кольцевого зазора шахты. Решение краевой задачи для потенциала скорости
проводится в канонической области, переход в которую осуществлен с по-
мощью конформного преобразования. Затем краевая задача решается в кано-
нической области с помощью метода конечных элементов. Приводятся ре-
зультаты параметрических расчетов присоединенных масс по разработанно-
му методу. Реализован численный метод расчета гидродинамических нагру-
зок на ракету с учетом влияния спутного потока, возникающего как при стар-
те из затопленной, так и незатопленной водой (сухой) шахты.
Разработан новый подход к решению задач о потенциальном течении
идеальной жидкости со свободными границами, основанный на оригиналь-
ном алгоритме конформного отображения области течения с границами про-
извольной формы на прямоугольник с фиксированными сторонами. Краевая
задача решается каким-либо методом в этом прямоугольнике. Обратный пе-
реход от канонической области к физической плоскости осуществляется чис-
ленно-аналитически. В отличие от известных конечно-разностных методов и
метода интегральных уравнений предложенный подход позволяет аналити-
чески учесть особенности решения в точке схода потока с кавитатора, в бес-
конечно удаленной точке и не требует решения вопроса о замене бесконеч-
ной области конечной.
Важное значение для рационального выбора схема старта имеют рабо-
ты по расчету динамики возникающих при старте БРПЛ газовых полостей и
связанных с ними гидродинамических нагрузок. В постановке задачи расчета
газовых полостей наиболее полно учитываются главные физические факторы
6
(влияние сил земного тяготения, геометрическая и динамическая нелинейно-
сти течения, отсутствие касательных напряжений на свободной поверхности)
и конструктивные особенности конкретной схемы старта (газоприход в по-
лость через кольцевые зазоры, от генераторов в головной части ракеты; ди-
намика выхода БРПЛ из шахты и др.)- Несмотря на ряд упрощающих поста-
новку задачи допущений (осреднение термодинамических параметров газа
по объему, неподвижность газа, неучет хода носителя, замена корпуса БРПЛ
бесконечным цилиндром в случае старта из затопленной шахты и др.), мате-
матическая модель остается очень сложной, чтобы получить точные количе-
ственные данные.
Разработан алгоритм расчета деформаций поперечных сечений кавер-
ны и распределенных нагрузок при кавитационном обтекании ракеты с углом
атаки. Расчет формы и положения поперечных сечений с учетом наличия
твердого тела осуществляется методом конформных отображений. Распреде-
ленные гидродинамические нагрузки сравнены с экспериментальными зна-
чениями. Разработан приближенный метод расчета гидродинамических на-
грузок в области несимметричного смыкания каверны на круговой цилиндр.
Приближенное решение находится в плоском кольцевом слое в случае, когда
радиус поперечного сечения каверны в области смыкания близок к радиусу
цилиндра, а радиальная скорость смыкания каверны намного превышает ско-
рость поперечного потока. Получено, что в области смыкания нормальная
гидродинамическая нагрузка имеет знакопеременный характер, а коэффици-
ент С" в процессе смыкания принимает значения, намного превышающие
2,0, и значение 2,0 при полном смыкании каверны на цилиндр.
Разработанные алгоритмы и программы позволяют рассчитать геомет-
рию газовой полости и гидродинамические нагрузки для старта как из сухой,
так и затопленной шахты, и являются достаточной основой для решения но-
вого класса задач о вытеснении жидкости из шахты, движении БРПЛ при на-
личии головной и кормовой каверн и т. д.
В целом достигнутый уровень теоретических и экспериментальных ме-
тодов исследования гидродинамики подводного старта позволяет наиболее
полно учитывать влияние основных физических факторов при проектирова-
нии БРПЛ.
Монография состоит из восьми глав. В первой главе ставятся задачи
исследования, вводятся системы координат, изложены основные динамиче-
ские законы движения твердого тела и уравнение для давления в жидкости. В
гл. 2 рассматриваются вопросы силового воздействия невязкой жидкости на
Движущееся в ней тело, выводятся дифференциальные уравнения обтекания
тела невязкой жидкостью и граничные условия, вводятся основные динами-
ческие параметры жидкости, присоединенные массы тела. В гл. 3 приведены
характеристики гравитационных волн и постановка задачи гидродинамики
при движении тела во взволнованной жидкости. В гл. 4 выводятся диффе-
ренциальные уравнения неуправляемого пространственного движения тела
внутри взволнованной жидкости, рассматриваются вопросы представления
7
позиционных гидродинамических сил через кинематические параметры дви-
жения тела. Гл. 5 посвящена численному методу расчета гидродинамических
коэффициентов и присоединенных масс тела вращения, в ней выводятся ин-
тегральные уравнения метода потенциала простого слоя и все формулы, не-
обходимые для расчета гидродинамических параметров. В гл. 6 приводятся
методы и результаты расчета гидродинамических нагрузок и присоединен-
ных масс при старте ракеты из затопленной шахты. Гл. 7 посвящена методам
и результатам расчета кавитационного обтекания ракет. В гл. 8 рассматрива-
ются вопросы газодинамики, тепломассообмена и движения ракеты в шахте,
выводятся дифференциальные уравнения продольного движения в шахте.
8
Глава 1
Постановка задачи. Системы координат.
Основные динамические законы движения твердого тела в пространстве
§ 1. Постановка задачи исследования и гидродинамические схемы
обтекания ракет
В связи с созданием баллистических ракет подводных лодок с середи-
ны 50-х гг. прошедшего столетия в нашей стране были начаты исследования
научно-технических проблем подводного старта. В результате возникло но-
вое крупное научное направление в прикладной гидродинамике - гидроди-
намика ракет. Подводный запуск БРПЛ осуществляется из шахт подводных
лодок, погружаемых на стартовую глубину Н и движущихся с заданной ско-
ростью W при волнении моря различной балльности В. Слой воды высотой Н
является, с одной стороны, естественным защитным экраном, обеспечиваю-
щим скрытность расположения подводной лодки, с другой — требует допол-
нительных массовых и энергетических затрат для его преодоления. Подвод-
ный участок траектории ракеты включает в себя несколько последователь-
ных участков: выхода из шахты, движения в воде и пересечения свободной
поверхности воды. Научные исследования подводного старта БР включают в
себя изучение гидродинамических и газодинамических процессов в пусковой
шахте, гидродинамических нагрузок и начальных возмущений ракеты на
шахтном участке траектории, гидродинамических сил с учетом волнения мо-
ря при свободном движении ракеты в воде и пересечении ею поверхности
воды. Для всех этих процессов характерна ярко выраженная нестационар-
носгь, многие проблемы связаны с двухфазностью (жидкость - газ) обтека-
ния ракеты, влиянием газовых полостей на характер гидродинамических
процессов.
Благодаря теоретическим и экспериментальным совместным исследо-
ваниям в НИИ и КБМ (ныне Государственный ракетный центр "КБ им. ака-
демика В.П. Макеева") были достигнуты значительные успехи в понимании
сложных физических процессов, сопровождающих подводный старт БРПЛ,
разработаны методы моделирования и расчета основных гидрогазодинамиче-
ских процессов, протекающих при старте в шахте, движении в воде и при пе-
ресечении БРПЛ поверхности воды.
Выход ракеты из шахты осуществляется с помощью энергетического
средства старта: порохового аккумулятора давления, стартового или марше-
вого двигателя. Расходные характеристики ЭСС определяются из условия
получения максимальной полезной работы при заданных ограничениях по
величинам допустимых продольных перегрузок, действующих на ракету на
шахтном участке движения. Это требует довольно плавного изменения се-
кундного расхода продуктов сгорания с примерно линейным во времени ха-
рактером его возрастания после выхода на режим. В отечественной практике
9
старт на жидкостном реактивном двигателе осуществляется только из затоп-
ленной водой шахты, так как температура продуктов сгорания ЖРД достига-
ет очень больших значений (~35ОО К) и непосредственное воздействие газо-
вых струй на шахту, пусковую установку и ракету недопустимо. Охлаждение
выхлопных газов водой наряду с постепенным нарастанием массового расхо-
да позволяет значительно снизить давление газов в подракетном объеме. Для
ликвидации гидроудара при запуске ЖРД непосредственно у среза сопел ор-
ганизуется газовый колокол (например, с помощью сжигания пороховой
шашки), затем поочередно, с некоторым интервалом по времени, запускают-
ся два рулевых блока ЖРД, через некоторый промежуток времени - еще два
рулевых блока. Основной двигатель ЖРД запускается при прохождении ра-
кетой более половины длины шахты. Ракета движется в шахте под действием
тяги двигателя и так называемой поршневой силы, обусловленной избыточ-
ным давлением выхлопных газов в подракетном объеме [13].
Подводный старт первых БРПЛ осуществлялся из затопленных перед
стартом пусковых шахт. Гидродинамическая схема при режиме сплошного
обтекания ракеты приведена на рис. 1.1. Из шахты ракета выходила под дей-
ствием собственного двигателя и повышенных давлений в шахте в набегаю-
щий за счет движения ПЛ поперечный поток жидкости и двигалась на шахт-
ном, свободном участках траектории и при пересечении поверхности воды в
режиме сплошного обтекания. Под действием поперечного потока жидкости
возникали значительные боковые гидродинамические силы и изгибающие
моменты, вызывающие значительные угловые отклонения при неуправляе-
мом движении ракеты на подводном участке траектории.
пересечение свободной
свободное движение
ракеты, статическая
неустойчивость
Рис. 1.1 Гидродинамическая схема при режиме сплошного обтекания
Вызванное волнением моря движение жидкости приводило к дополни-
тельным возмущениям на ракету. Как правило, на подводном участке траек-
тории на ракету действуют наибольшие при полете ракеты нагрузки, ракета
под водой получает наибольшие возмущения параметров движения. Участок
10
траектории в воде в значительной степени влияет на тактико-технические ха-
рактеристики БРПЛ, конструктивно-компоновочные решения, требуемые па-
раметры системы стабилизации движения ракеты под водой и т.д. Ограниче-
ния на габариты ракет из-за их размещения на ПЛ привели к необходимости
более высокой плотности компоновки ракеты в пусковой шахте, уменьше-
нию зазора между ракетой и шахтой, более полной носовой части ракеты, не-
возможностиустановки гидродинамических органов управления и стабили-
зации (например, хвостового оперения)./Всё это привело к статической неус-
тойчивости ракет. Одновременно, в связи с более полными головными час-
тями ракет, возросли изгибающие моменты и поперечные силы [11,19, 30].
Выполнение требований по прочности корпуса ракет и, следовательно,
обеспечение допустимых гидродинамических нагрузок, удовлетворение тре-
бований по безударному выходу ракеты из шахты и стабилизации движения
ракеты под водой привело к необходимости ограничения скорости ПЛ в мо-
мент старта, балльности моря и в целом к ограничению начальных условий
старта. Улучшение тактико-технических характеристик последующих ракет-
ных комплексов стало возможным благодаря расширению условий старта как
по скорости хода ПЛ, так и по балльности моря и привело к необходимости
реализации принципиально новых способов старта и новых гидродинамиче-
ских схем обтекания ракет, позволяющих снизить гидродинамические на-
грузки и возмущения при движении ракеты в шахте, обеспечить статическую
устойчивость и уменьшить значения углов отклонения от вертикали и угло-
вых скоростей ракеты.
В КБМ были проведены проектно-конструкторские проработки, экспе-
риментальные и расчетно-теоретические исследования и выданы техниче-
ские задания на НИР по новым способам старта БРПЛ. В результате проект-
ных и научно-исследовательских работ было выявлено, что наибольший по-
ложительный эффект достигается при переходе от режима сплошного обте-
кания к режиму кавитационного (двухфазного) обтекания БР. Кавитацион-
ный способ старта осуществлен на морских комплексах с твердотопливными
ракетами РСМ-45 и РСМ-52. Ракета РСМ-45 разработана в КБ "Арсенал" под
руководством П.А. Тюрина, ракета РСМ-52 — в КБМ под руководством
В.П.Макеева. Старт БР осуществляется из незатопленной шахты ПЛ. Кави-
тационный способ старта заключается в применении кавитационных схем
обтекания БР путем формирования каверны за счет установки на носке БР
кавитатора и источника газа (газогенератора). Для создания каверн нужных
размеров на РСМ-45 и РСМ-52 используется массовый расход газов как но-
сового ГГ, так и газов, истекающих из подракетного объема шахты (рис. 1.2)
[9-12,17,30-32].
При кавитационном способе старта БР выходит сначала в газовый пу-
зырь, а при прохождении кавитатором верхней границы пузыря на БР начи-
нает формироваться присоединенная газовая каверна. При этом носовая ка-
верна частично захватывает газы из пузыря. В процессе натурной экспери-
ментальной отработки РСМ-52 с плавстенда и экспериментальной подводной
лодки с целью улучшения гидродинамических характеристик ракет на под-
11
водном участке траектории в КБМ был разработан ряд предложений по орга-
низации двухфазного газожидкостного обтекания БР, а также ряд кавернооб-
разующих устройств. Весьма существенным является то, что на комплексе с
ракетой РСМ-52 герметизация пусковой шахты осуществляется с помощью
головной части ракеты с весьма полными обводами, имеющей поперечные
размеры, превышающие размеры миделя ракеты, то есть носовая часть раке-
ты выполняет роль герметизирующей мембраны. Для такой полной компо-
новки носовой части комплексное решение проблем гидродинамики БР -
снижение боковых гидродинамических нагрузок и возмущений на шахтном
участке траектории, обеспечение устойчивости движения БР - может быть
достигнуто путем создания режима кавитационного или газоструйного обте-
кания ракеты (рис. 1.2) [17, 30]. При использовании газоструйной защиты но-
совая часть каверны деформируется интенсивными газовыми струями, вы-
пускаемыми в носовой части БР. С помощью газовых струй (коэффициент
интенсивности Q) появляется возможность дополнительно регулировать
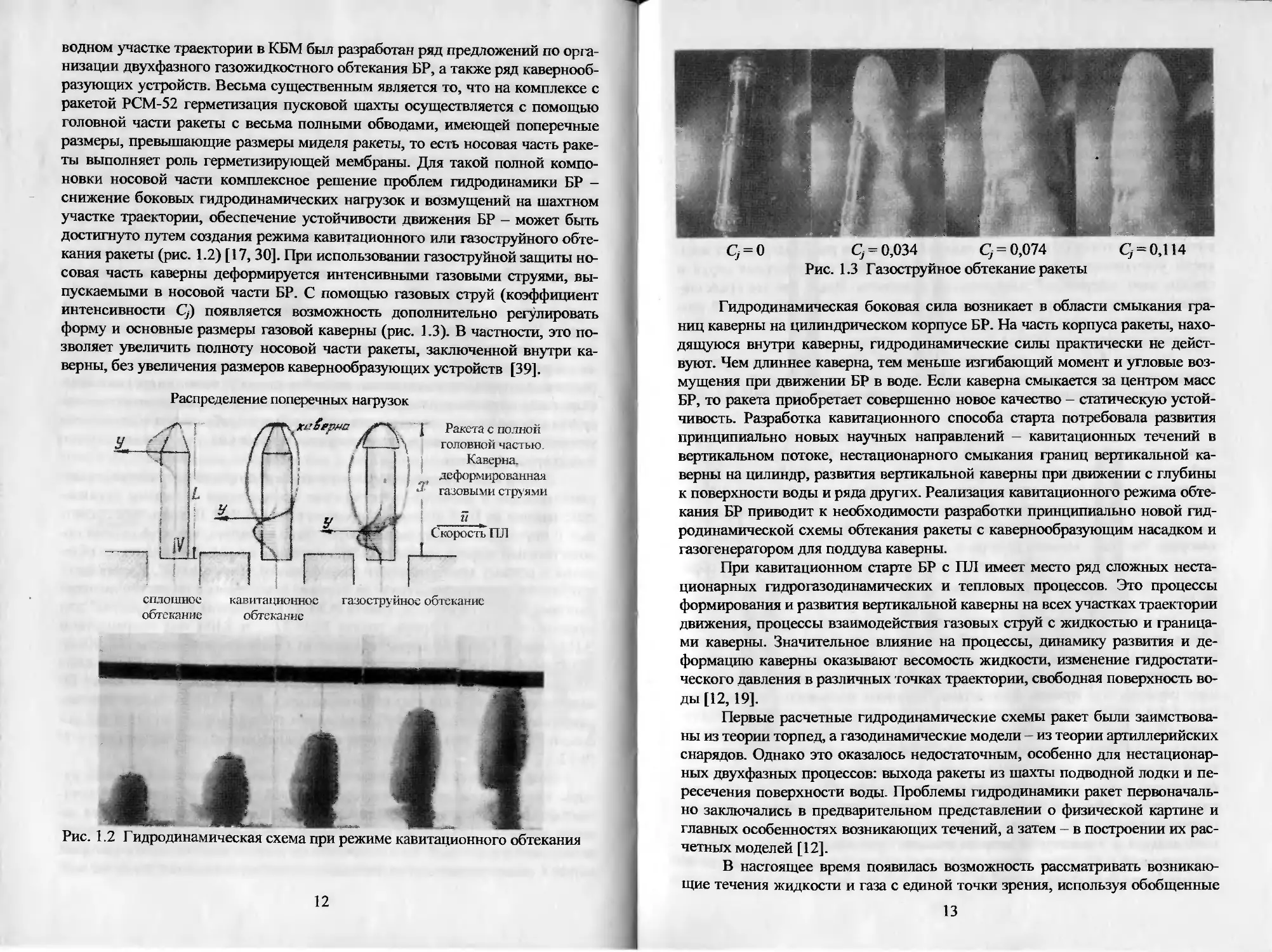
форму и основные размеры газовой каверны (рис. 1.3). В частности, это по-
зволяет увеличить полноту носовой части ракеты, заключенной внутри ка-
верны, без увеличения размеров кавернообразующих устройств [39].
Распределение поперечных нагрузок
сплошное
обтекание
кавитационное газоструйнос обтекание
обтекание
Рис. 1.2 Гидродинамическая схема при режиме кавитационного обтекания
12
Cj = O Cj = 0,034 Cj = 0,074 Q = 0,114
Рис. 1.3 Газоструйное обтекание ракеты
Гидродинамическая боковая сила возникает в области смыкания гра-
ниц каверны на цилиндрическом корпусе БР. На часть корпуса ракеты, нахо-
дящуюся внутри каверны, гидродинамические силы практически не дейст-
вуют. Чем длиннее каверна, тем меньше изгибающий момент и угловые воз-
мущения при движении БР в воде. Если каверна смыкается за центром масс
БР, то ракета приобретает совершенно новое качество - статическую устой-
чивость. Разработка кавитационного способа старта потребовала развития
принципиально новых научных направлений — кавитационных течений в
вертикальном потоке, нестационарного смыкания границ вертикальной ка-
верны на цилиндр, развития вертикальной каверны при движении с глубины
к поверхности воды и ряда других. Реализация кавитационного режима обте-
кания БР приводит к необходимости разработки принципиально новой гид-
родинамической схемы обтекания ракеты с кавернообразующим насадком и
газогенератором для поддува каверны.
При кавитационном старте БР с ПЛ имеет место ряд сложных неста-
ционарных гидрогазодинамических и тепловых процессов. Это процессы
формирования и развития вертикальной каверны на всех участках траектории
движения, процессы взаимодействия газовых струй с жидкостью и граница-
ми каверны. Значительное влияние на процессы, динамику развития и де-
формацию каверны оказывают весомость жидкости, изменение гидростати-
ческого давления в различных точках траектории, свободная поверхность во-
ды [12, 19].
Первые расчетные гидродинамические схемы ракет были заимствова-
ны из теории торпед, а газодинамические модели - из теории артиллерийских
снарядов. Однако это оказалось недостаточным, особенно для нестационар-
ных двухфазных процессов: выхода ракеты из шахты подводной лодки и пе-
ресечения поверхности воды. Проблемы гидродинамики ракет первоначаль-
но заключались в предварительном представлении о физической картине и
главных особенностях возникающих течений, а затем - в построении их рас-
четных моделей [12].
В настоящее время появилась возможность рассматривать возникаю-
щие течения жидкости и газа с единой точки зрения, используя обобщенные
13
струйные, вихревые и кавитационные модели и, в частности, кавитационную
модель как модель течения с искусственной кавитацией.
За все время исследований накоплен большой экспериментальный ма-
териал, касающийся движения в воде и выхода ракеты из воды, который
служит основой для создания теоретических и численных моделей сложных
нестационарных двухфазных течений. Основным элементом анализа являет-
ся подход, существенно опирающийся на аналитические или численные мо-
дели невязкой жидкости - струйные и кавитационные схемы для нестацио-
нарных течений и движения тела с изменяющейся геометрией. Благодаря
этому можно реализовать более простые расчетные модели отрывного и ка-
витационного течений, в которых влияние вязкости и реальных свойств жид-
кости учитывается в рамках представлений теории турбулентных струй и
следов, явно содержащей эмпирические константы. Везде, где это представ-
лялось уместным, авторы старались проследить возможности моделей раз-
личного уровня и указать проверочные способы вычислений. Эти расчетные
модели реализованы на ПЭВМ [7-17].
На рис. 1.4 — 1.6 приводятся основные расчетные схемы режима
сплошного обтекания при выходе ракеты из шахты в набегающий поток во-
ды, скорость которого равна скорости хода подводной лодки. Поверхность
лодки заменена плоским экраном.
На рис. 1.4 диаметр шахты равен диаметру ракеты. Это наиболее про-
стая модель из приведенных. На рис. 1.5 представлена более близкая к реаль-
ной модель, когда между ракетой и шахтой есть кольцевой зазор. Ракета
движется в шахте по опорно-ведущим поясам. Приведенная на рис. 1.6 мо-
дель учитывает дополнительно формирование у среза шахты сначала газово-
го пузыря, а затем, после выхода кормы ракеты из пузыря, - донной газовой
каверны. Расчеты газового пузыря и донной каверны проводятся с целью
уточнения гидродинамического воздействия на ракету. Газовый пузырь обра-
зуется после разрушения мембраны, которая герметизирует объем шахты
[9,19,30].
При выходе ракеты из шахты газы из кольцевого зазора поступают в
объем газового пузыря, однако наиболее интенсивный его рост происходит
после выхода из шахты кормы ракеты. В это время давление газов в шахте,
как правило, превышает давление окружающей среды, и газ из шахты начи-
нает перетекать в пузырь. Вследствие большого массового расхода газов
(рис. 1.6а) давление в пузыре возрастает и становится больше гидростатиче-
ского (Рст), свободная граница пузыря приобретает значительные радиаль-
ные скорости, радиус пузыря растет. При выходе кормы тела из пузыря часть
газов захватывается телом, и за его кормой образуется донная газовая кавер-
на, которая имеет форму, близкую к цилиндрической (рис. 1.6в). По мере
роста газовых объемов давление газов в них падает и становится меньше
гидростатического. Вследствие разрежения радиус газового пузыря начинает
уменьшаться, и в некоторый момент времени происходит полное схлопыва-
ние пузыря (R = 0), объем донной газовой каверны полностью отделяется от
объема шахты (рис. 1.6г) [19, 30].
14
Рис. 1.4 Выход ракеты из шахты (диаметр шахты равен диаметру ракеты)
Рис. 1.5 Выход ракеты из шахты
(между ракетой и шахтой есть кольцевой зазор)
После этого нижняя часть донной каверны разрушается, а верхняя со-
храняется на всем последующем участке движения вплоть до выхода кормы
ракеты из воды (рис. 1.6д). На рис. 1.7а и 1.76 представлена наиболее простая
15
гидродинамическая модель пересечения БР поверхности воды, когда не учи-
тывается деформация свободной поверхности. На рис. 1.7в представлена мо-
дель ударного струйного воздействия на днище БР. Спутная струя воды по
схеме Эфроса образуется при смыкании свободных границ донной газовой
Рис. 1.6 Формирование и развитие газового пузыря и донной
Рис. 1.7 Пересечение поверхности воды
16
Рис. 1.8 Формирование каверны при газоструйном обтекании
Как уже отмечалось [12, 19, 30], одним из способов снижения гидроди-
намического воздействия на ракету является переход от режима сплошного
обтекания к режиму кавитационного обтекания ракеты. С этой целью в об-
ласть динамического разрежения на поверхности ракеты подают газ и фик-
сируют фронт схода струй воды с носка. В результате на поверхности ракеты
2 Зак. 3686
17
формируется присоединенная газовая каверна (рис. 1.2, 1.8). Для фиксации
переднего фронта каверны применяют кавитатор, который обтекается водой.
Ниже кавитатора свободные границы охватывают всю носовую часть ракеты,
которая полностью находится в газовой полости и исключается из взаимо-
действия с водой (рис. 1.2, 1.8) [17, 30 - 33]. Смыкание границ каверны про-
исходит на цилиндрическом корпусе ракеты, так что только кавитатор и ниж-
няя часть цилиндра обтекаются водой, а оставшаяся часть поверхности тела
обтекается газом, давление которого по всей этой поверхности примерно
одинаково. На кавитаторе формируется гидродинамическая сила сопро-
тивления, при смыкании границы каверны на цилиндр — боковая гидродина-
мическая сила.
При движении ракеты под водой на нее действуют следующие силы:
— массовые силы — вес и сила плавучести ракеты;
— гидродинамические силы, распределенные по поверхности ракеты и
обусловленные воздействием окружающей воды;
— газодинамические силы, создаваемые выхлопными горячими газами
энергетического средства старта;
— реактивная сила двигателя ракеты (в том случае, если он работает).
Решение общей задачи гидродинамики проводится в предположении о
возможности разделения действующих на ракету гидродинамических сил на
составляющие потенциальной и вязкой природы. Из теории волн известно,
что морское волнение достаточно хорошо описывается с помощью концеп-
ции потенциального движения невязкой жидкости: силы трения слабо влия-
ют на характеристики свободных, в частности, прогрессивных, волн, а ветро-
вые волны, согласно спектральному методу, могут быть представлены су-
перпозицией простых гармонических волн. На этом основании предполагаем,
что в общей задаче о движении ракеты при волнении главная роль принад-
лежит силам потенциальной природы, что позволяет широко использовать
потенциальные методы описания движения невязкой несжимаемой жидкости
при выяснении структуры действующих на ракету гидродинамических сил.
Влияние вязкости в необходимых случаях учитываем с помощью эмпириче-
ских поправок, вводимых в формулы для гидродинамических сил и моментов
по результатам экспериментов.
Наиболее полной характеристикой безвихревого движения жидкости
является потенциал скорости: если он найден, то можно определить все ки-
нематические и динамические параметры как на поверхности тела, так и в
окружающей жидкости.
Общую гидродинамическую задачу о движении ракеты во взволнован-
ной жидкости путем априорной линеаризации будем приводить к следующей
гидродинамической задаче. Потенциал скорости абсолютного движения
жидкости, выраженный в координатах подвижной системы, отыскивается как
решение уравнения Лапласа в области, ограниченной поверхностями ракеты,
подводной лодки и свободной поверхностью жидкости в положении ее рав-
новесия. Линейность граничной задачи позволяет представить искомый по-
тенциал в виде суммы потенциала скорости набегающих волн, который счи-
18
тается заданным, и потенциала скорости возмущенного движения жидкости,
который обусловлен движением ракеты и находится при решении гидроди-
намической задачи. В конечном итоге задача гидродинамики заключается в
нахождении гидродинамических коэффициентов (СХ,Сy,mz,Cy ,т“,Су
и присоединенных масс (2ц, 222, 22б, ) и их распределения по длине раке-
ты при движении ее в шахте, затем в воде и при пересечении поверхности
воды.
Задача динамики подводного старта заключается в определении кинема-
тических параметров пространственного движения ракеты при заданных на-
чальных условиях старта, массо-центровочных и гидродинамических харак-
теристиках ракеты. Решение ее состоит в выводе системы дифференциаль-
ных уравнений движения ракеты в воде, разработке алгоритма интегрирова-
ния и программной реализации его на ПЭВМ. В результате расчетов динами-
ки ракеты определяют проектные параметры рассматриваемого способа
старта, такие, как требуемая ширина кольцевого зазора между корпусом ра-
кеты и стенкой шахты, силовые характеристики амортизации и режимы ра-
боты энергетического средства старта, обеспечивающие на шахтном участке
движения несоударение корпуса ракеты с конструктивными элементами пус-
ковой установки, шахты и подводной лодки и стабилизацию движения раке-
ты в воде и после выхода ее из воды.
При разработке математического моделирования процессов старта ста-
вится задача по наиболее полному учету условий подводного старта: конст-
руктивно-компоновочных особенностей ракеты и пусковой установки, вида
энергетического средства старта и его режимных параметров, силовых ха-
рактеристик применяемой амортизационно-стартовой системы, амплитудно-
частотных характеристик волнения моря и качки подводной лодки.
§ 2. Системы координат и кинематические характеристики,
определяющие положение ракеты в пространстве
В общем случае пространственное движение ракеты может быть пред-
ставлено суммой поступательного движения центра масс и вращательного
движения вокруг центра масс. Для количественного задания поступательного
и вращательного движений применяют следующие системы координат
(рис. 1.9):
O0X0Y0Z0 — начальная (стартовая, инерциальная) система координат.
В момент старта ее начало совпадает с центром масс ракеты, ось ОйХй на-
правлена вверх по вертикали в точке старта, ось О0У0 - по горизонтали в на-
правлении кормы ПЛ, O0Z0 — дополняет систему координат до правой. В
Дальнейшем начало этой системы координат вращается вместе с Землей, а
оси ее не изменяют первоначального положения относительно инерциально-
го пространства;
2'
19
OX0Y0Z0 — полуподвижная система координат, начало которой в про-
цессе движения совпадает с полюсом (центром масс), а оси параллельны
осям инерциальной системы. Эта система служит для отсчета углов поворота
ракеты вокруг центра масс;
OXYZ — связанная с ракетой система координат. Ее начало совмещено
с центром масс ракеты, ось ОХ направлена вдоль продольной оси симмет-
рии ракеты, ось OY - в направлении, противоположном ходу ПЛ в момент
старта, ось OZ — образует правую систему координат.
а
Рис. 1.9 Схема движения ракеты
в шахте (а), в воде (б), при пересечении поверхности воды (в)
• Поступательное движение ракеты определено, если известно измене-
ние во времени координат центра масс в инерциальной системе координат
x0=x^t)- у0=у0(О; z0=z0(o. (i.i)
Угловое положение связанной системы координат относительно инер-
циальной задают при помощи трех углов Эйлера. Эйлеровы углы выбирают-
ся так, что система OXYZ, первоначально совпадающая с OXGYGZ(i, пере-
водится в окончательное положение тремя последовательными поворотами
вокруг каждой из осей, занимающих новое положение после каждого пово-
рота.
20
Последовательность поворотов приведена на рис. 1.10. Первый поворот
осуществляется против часовой стрелки вокруг оси ОХ на угол второй —
вокруг оси OY на угол у/, третий - вокруг оси OZ на &.
х, ад,
Рис. 1.10 Ориентация связанных осей относительно инерциальных
Таким образом, пространственное положение ракеты будет известно,
если определено изменение во времени проекций центра масс на оси инерци-
альной системы координат и изменение во времени Эйлеровых углов
JT0=^0(Z); У0=У0(Х); Z0=Z0(f); (1.2)
y/=yAt)\
Они определяются в результате решения шести дифференциальных
уравнений движения ракеты: трех уравнений поступательного движения и
трех уравнений вращательного движения. Уравнения движения удобно запи-
сывать в проекциях на оси связанной системы координат.
В результате их решения определяются проекции линейной и угловой
скоростей на оси связанной системы координат
Uy, uz, (Оу, Ct)z. (1.3)
Далее, используя таблицу направляющих косинусов между осями свя-
занной и инерциальной систем координат, определяют проекции скорости
центра масс на оси инерциальной системы. Интегрируя последние, получают
координаты центра масс тела в инерциальной системе. Затем определяют уг-
лы Эйлера ф, у/, & через проекции угловой скорости на оси связанной систе-
мы <Ох,(Оу,(Ог.
21
Построим таблицу направляющих косинусов между осями инерциаль-
ной и связанной систем координат (таблица 1.1).
Таблица 1.1
X У Z
Ао аи 012 013
Уо <221 О22 О23
Zo О31 O32 озз
Косинусы углов между осями выражаются через углы Эйлера. Для оп-
ределения направляющих косинусов повернем систему OX0Y0Z0 из своего
первоначального положения, совпадающего с положением инерциальной
системы, на углы (р,у/, 9, обозначим два промежуточные положения связан-
ной системы через OXi У ( Z\ и ОХ2 Y2Z2 и запишем проекции вектора в со-
ответствующей системе координат через его проекции в последующей:
У0=А’1; А\ =Z2cos^ + Z2sin^;
Уо =y1cos^>-Z1sin<p; Yt =Y2;
Zo = У| sin^J + Z, cos<p; Zj = -X2 sin^ + Z2 cos^; (1.4)
X2 = X cos9 - У sin 9;
Y2 = X sin 9 + У cos 9;
Z2 = Zj.
Выполнив соответствующие подстановки, получим в окончательном
виде выражения для проекций вектора в инерциальной системе координат
через проекции его в связанной системе [19]:
Хо =ArcoSi9cos^/-ysinl9cos^ + Zsin^;
Уо = X sin9cos<p + У cos5cos^> + X cos&sin^sin^ —
-ysin^sin^sin^-Zsin^cos^; (1.5)
Zo = У sin $sin#> + У cos.9sin#> - X cosi9sin у cosy +
+ У sin 5 sin cos ^> + Zcos^cos^j.
Таким образом, выражения для направляющих косинусов имеют вид:
ап =cos5cos^; а12 =-sin<9cos^; а13 = sin^;
а21 =sin<9cos^ + cosi9sin^sin#>;
а22 =cos<9cos<p-sin.9sin^sin^>; а23 =-sin^>cos^; (1.6)
а31 = sin^sin^ - cos^sin^cos^;
а32 =cos<9sin^> + sin19sin^cos#>; а33 =cos^cos^>.
Связь между координатами и углами стартовой (инерциальной) систе-
мы координат OoXoYqZo и связанной с телом системы координат OXYZ нахо-
дится с помощью следующей системы дифференциальных уравнений
^о=а1Л+а12^+«1з1>г;
Zo = + a-nVy + о23ог 1 (1-7)
22
Z0=a3lux+a32vy+a33vz;
ф = (сох cos & - со sin &)—-—;
cos^
ф = сох sin# + соу cos#;
# = coz - (сох cos# - соу sin#)zg^.
(1.8)
§ 3. Основные динамические законы движения твердого тела
При рассмотрении движения твердого тела большую роль играет ряд
величин, связанных с его кинематическими и массовыми характеристиками.
К их числу относятся: вектор количества движения Q , вектор момента коли-
чества движения и кинетическая энергия Т. Если движение тела задано век-
тором скорости полюса иа и вектором угловой скорости вращения со (рис.
1.11), то, выделив бесконечно малую массу dm, можно для элементарных ве-
личин dQ, dKa и dT написать:
_ — - _ 1 г
= vdm\ dKa=rxudm; dT = — v dm, (1.9)
где и — абсолютная скорость выделенного элемента, равная
и=иа+а>хг. (1-10)
Подставив это значение в выражение (1.9) и проинтегрировав по всей
массе тела, найдем:
Q = ffo + ® х г }dm\
(М)
Ка = J[^ х (ц, + ® X Г (1-11)
(М)
Т = — J(ufl + И) х г )2 d/n.
2 (М)
dQ
23
Предполагаем, что система xyz, начало которой расположено в
полюсе А, может иметь произвольную угловую скорость, которую обозначим
а>е. В том частном случае, когда а>е = а>, система xyz будет жестко связана с
телом. Если же = 0, то оси xyz движутся поступательно вместе с полюсом.
Не останавливаясь на деталях преобразований величин (1.11), приведем лишь
их окончательные выражения.
Проекции вектора количества движения:
Qx M^VojA'dlyZc <ЧУс)
Qy соусе CQZc) MUq>s (1.12)
Qz = ^/(t^+fiVc-^c) = Mvcz,
где M- масса тела;
(Цс, Оу, со, - проекции угловой скорости тела на оси xyz;
хс, Ус, zc — координаты центра масс тела относительно выбранного по-
люса;
Vox, voy, Vaz, va, Vey, va - проекции скоростей полюса и центра масс.
Проекции вектора момента количества движения:
/Q- A/(ycL^ Zcllqy) + JxxQx АхуОу JxzQz,
Ку = M(zcVm - XcV^) + Jyy(£>y - JyzOy - JyzGy, (113)
Kz hd^XcVay ycVax) JzzQ: JzxQx Jzytlly
Отметим, что входящие в эти формулы осевые и центробежные момен-
ты инерции тела (Jm Jyy, при произвольной его форме и при лю-
бом значении aie являются переменными величинами и лишь при
toe = (О (т. е. для связанных осей) они постоянны. В этом случае целесообраз-
но направлять оси координат по главным осям инерции для выбранного по-
люса, тогда все центробежные моменты инерции будут равны нулю. Форму-
лы (1-13) упростятся и примут вид:
^х Kf(ycVaz Zctlay) + JxGy,
Ку = MiZcUaz-XcVaA + JyOiy, (1.14)
Ai(xcVay ycVax) + ^zQ,
где J„ Jy и Jz — главные моменты инерции.
Выражение кинетической энергии твердого тела, в общем случае его
движения, имеет вид
П)
»az
(О
Т = ^М\р2ах+^ау
(115)
+ +Jyy(°2y +Jzza>2 -^ху^у ~2Jy2(0y(0z -2Jzx0)za>x).
Первый член определяет кинетическую энергию поступательного дви-
жения вместе с полюсом, последний - вращательную вокруг него и средний
- взаимную энергию. Если полюс принят в центре масс, то взаимная энергия
24
пропадает. При условии, что оси xyz, являясь главными, жестко связаны с те-
лом и полюс не совпадает с центром масс,
(1.16)
Юау ^az
СОу СО.
Ус *с
Непосредственное сравнение формул (1.15), (1.13) и (1.12) позволяет
написать следующие, важные для дальнейшего, соотношения:
57 „ дТ
Qx =——; Э»ах Ках=—; (1Л7) дсоу к - дТ
В дальнейшем для составления дифференциальных уравнений движе-
ния твердого тела неоднократно придется иметь дело с двумя динамически-
ми законами: количества движения и моментов количества движения. Не
входя в подробности их вывода для различных систем координат, считаем
все же полезным привести некоторые принципиальные соображения, отно-
сящиеся к механической системе, состоящей из п материальных точек и дви-
жущейся относительно некоторой неподвижной системы координат.
Пусть z-я точка системы имеет массу /и, (рис. 1.12). Ее положение отно-
сительно неподвижной системы координат OoXoYoZ0 определяется радиусом-
25
вектором rt, и к ней приложены две группы сил: внутренние и внешние. Рав-
нодействующая первой из них , второй - Fd>.
Для каждой точки системы в соответствии со вторым принципом Нью-
тона можно написать
r^-^F^ +F^. (1.18)
Суммируя по всем точкам, найдем
(О dt (О (О
Так как внутренние силы входят в систему попарно равными, прямо
противоположными и каждая пара направлена по одной прямой, то их гео-
метрическая сумма равна нулю и предыдущее равенство можно переписать
так:
—У^, —= УЛ(<,).
Л(0 ' (О
Но векторы
df"i 'E'ie'l
>mi—- и > F> ’
dt_ ft '
суть количество движения системы Q и главный вектор действующих на нее
внешних сил V. Поэтому
^- = Г(е). (1.19)
dt
Это и есть закон количества движения системы в неподвижных коор-
динатах. Для получения закона моментов умножим векторно радиус-вектор
г, на правую и левую части равенства (1.18), после чего просуммируем их по
всем точкам системы
У rt X т, = У X F^ + У rt X F^.
(9 dt (i) (,)
Оба члена правой части суть главные моменты внешних и внутренних
сил, причем последний из них равен нулю в силу указанного выше свойства
внутренних сил. Левая часть может быть представлена в виде
d2rt
dt2
У rt хт,
(О
где — вектор момента количества движения системы относительно непод-
вижной точки Од.
Таким образом, векторная форма закона моментов количества движе-
ния в неподвижной системе координат
= (1.20)
at
26
Чаще всего приходится встречаться с формой законов, отнесенной к
подвижным осям, начало которых совмещено с произвольной точкой тела, а
сами они либо перемещаются поступательно, либо вращаются с некоторой
угловой скоростью. Не входя в подробности вывода, приведем лишь оконча-
тельные выражения законов.
Для осей XoYoZ0, поступательно движущихся вместе с полюсом А, име-
ем закон количества движения
^- = Г(е); (1.21)
dt
закон моментов количества движения
+ = (1.22)
dt
где Q — вектор количества движения твердого тела;
Ка — вектор момента количества движения относительно точки Л;
иа — вектор скорости полюса;
V(е) - главный вектор внешних сил;
~ главный момент внешних сил относительно точки А.
Для осей Axyz, вращающихся с угловой скоростью а>е, соответственно
получим:
+ = (1.23)
at
^+йехКа + »ах()=ТУ. (1.24)
dt
Проекции векторов Q и Ка вычисляются по формулам (1.12), (1.14).
Выпишем основную систему дифференциальных уравнений движения
твердого тела. Предположим, что оси Axyz, в которых рассматривается дви-
жение, имеют некоторую (вообще говоря любую) угловую скорость <ое, а на-
чало А жестко связано с произвольной точкой тела. Назвав орты осей буква-
ми i, j, к и приняв во внимание формулы (1.17) для векторов, входящих в
законы (1.23) и (1.24), получим:
- - дТ - дТ г дТ
Q =i-----+ 1---+ к------;
диау dvaz
уу - дТ - дТ гдТ
да>х дй)у d(Dz
V^=iVx+jVy + kVz;
lyf* =iLax+ JLay +
27
Тогда законы (1.23) и (1.24) можно переписать так:
£ dt (х ST -ST г ЗТ> i + 1 + к < Э»ах д»ау Suaz> + 1 “>ех дТ j ^>еу ST к coez ST =ivx+]vy+kvz-,
^ах
d(T ST -.ST гдт"
— i +1 + к
dty Sa>x S(oy Sco.
i
Юех
ST
S(OX
к к
j i j
^ey coez + ^ax Vay
ST ST ST ST ST
S(Oy Scoz d»ax SUay ^az
= iLax + jLay + kLaz.
Приравнивая выражения, стоящие множителями при одинаковых ортах
справа и слева, получим две группы уравнений. Первая представляет собой
закон количества движения
d ST + (Oey ST ~^ez ^ay
dtSv^ ^az
d ST dt Suay ST d»ax ~^ex ^-=V- ^az У
d ST dtSv^ + (°ex ST d»ay -^ey SVax "
(1-25)
а вторая — закон моментов количества движения
d ST ST ST ST ST ,
J д ^еу д ®ez Д + Vay uaz —
dt Э(ОХ S(O, S(t) SUa, SlL
d ST ST ST ST ST т
+ сое, а>ех +и,,---и„„-----= L
dt Scoy---------------------------------------Эсох-Scoz-Su^
d ST ST ST ST -- г
~Т т— + юех -----со — + ------и -— = L.
dt Scoz Scoy Л Scox оиау Л диах
Приведенная форма законов выражена через кинетическую энергию
тела. Поэтому в дальнейшем (гл. 4) при составлении дифференциальных
уравнений будем пользоваться суммарным выражением кинетической энер-
гии тела и жидкости. Можно динамические законы (1.25) и (1.26) выражать
не через кинетическую энергию, а через динамические параметры Q и Ка,
как это и делают некоторые авторы. В этом случае следует разложить по ор-
там величины Q и Ка (формулы (1.23) и (1.24)) и воспользоваться форму-
лами (1.12) и (1.13). Отметим, что для вывода дифференциальных уравнений
часто пользуются второй лагранжевой формой.
28
К написанным системам уравнений необходимо добавить шесть кине-
матических уравнений, из которых три связывают проекции иа с углами
скольжения и атаки, а три другие - проекции вектора угловой скорости тела
ю с углами Эйлера у/, $и <р.
Уравнения (1.25) и (1.26) самые общие. Из них могут быть получены
различные частные случаи. Например, если движение рассматривается в по-
ступательно движущихся осях, то нужно отбросить члены, содержащие мно-
жители а>ех, (Ogy и а>а, так как они равны нулю.
Если движение изучается в связанных осях, то нужно положить
G>ex= ac=(a.t и ед^ед,
направив, кроме того, для упрощения выражения кинетической энергии оси
xyz по главным осям инерции.
Если рассматривается случай вращения твердого тела вокруг непод-
вижной точки (йа =0), то для связанных с телом осей xyz, направленных по
главным осям инерции, можно написать из (1.16):
дТ да>х , ц,=0 = JХО)Х, дТ ди^ - = м(а>угс -<л); 1
дТ ' Jу&}у9 дТ = M(cozxc -®л);
5®^ Ц,=0 диау
' дТ' doz / ц,=0 = JZ(OZ, дТ = м(б)хус — CDyX^.
Следовательно, уравнения (1.26) и (1.25) примут вид:
dcOy / х
Jу ~dt z ~ J*~ h»
Jz^-(jx-Jy)<i)xa>y = Lz (1.27)
at
и
М<ох(а)уУс + едгс) -Мхс{а2у
M<oy(cozzc }-Мус((о2 +&XJ 1=Г,;
Ma>z\a)xxc + ^уУс, )-Mzc(ax 1=г,.
Первая группа есть система дифференциальных уравнений вращения
твердого тела вокруг неподвижной точки в форме уравнений Эйлера. Она
служит для определения проекций угловой скорости (сц, (Оу, щ), а следова-
тельно, и эйлеровых углов (по формулам (1-8)).
Вторая группа (1.27) позволяет найти реакцию неподвижной точки, ес-
ли из первой группы найдены проекции угловой скорости ед, ау и ау
29
Уравнения (1.25) и (1.26) вместе с шестью кинематическими уравне-
ниями вполне определяют движение тела при том условии, что правые части
(1.25) и (1.26), т. е. проекции главного вектора и главного момента сил, дей-
ствующих на тело, являются (в общем случае) известными функциями вре-
мени, кинематических параметров и их производных. В дальнейшем будем
заниматься преимущественно рассмотрением движения тела в жидкости. То-
гда к числу действующих на него сил следует отнести: вес тела, Архимедову
силу, силы гидродинамического воздействия жидкости и тягу, создаваемую
движителем.
Условно принято силы воздействия жидкости на движущееся в ней те-
ло разбивать на две группы. В гидродинамике установлено, что вязкость
жидкости, обуславливающая появление в ней сил трения, проявляется только
в тонком слое, охватывающем движущееся тело, который называется погра-
ничным. В нем происходит резкое изменение скорости частиц жидкости, за
счет чего появляются значительные силы трения и вихреобразование. Глав-
ный вектор и главный момент сил, вызванных действием пограничного слоя,
характеризуют и наиболее важную первую группу сил воздействия жидко-
сти. Они зависят от величины вектора скорости полюса, углов атаки и
скольжения и проекций угловой скорости на оси координат. Подробно силы
воздействия вязкой жидкости рассмотрим в гл. 4.
Вторая группа сил, с которыми жидкость действует на тело, вызвана ее
движением вне пограничного слоя. Здесь с вязкостью жидкости можно не
считаться и полагать ее идеальной. Основная причина появления этих сил
лежит в преодолении сил инерции всех частиц жидкости. Они рассмотрены в
гл. 2, 5,6.
В связи с увеличением скорости движения тела следует учитывать воз-
можность возникновения кавитации корпуса. Кавитацией называют явление
вскипания жидкости у стенки обтекаемого тела вследствие местного пони-
жения давления в потоке. С возникновением кавитации нарушается сплош-
ность потока и изменяется силовое воздействие жидкости на тело.
В дальнейшем при рассмотрении силового воздействия невязкой и вяз-
кой жидкости на движущееся в ней тело будем предполагать, что кавитация
отсутствует. Чтобы не ошибиться в расчетах, надо установить условия воз-
никновения кавитации для тел.
На рис. 1.13 представлено распределение скоростей и давлений по об-
воду одного из тел при обтекании его осесимметричным потоком жидкости.
Скорость выражается через безразмерный коэффициент скорости к = —, а
Ц>
давление — через безразмерный коэффициент давления
( \2
y = £z£o=1_ У.1
л, 2 ’
РЦ> 14) )
2
где рр, Ц) - давление и скорость в набегающем потоке;
р, V- давление и скорость в соответствующей точке на обводе.
30
Величины к и / зависят от формы обвода, положения выбранной точки
на обводе, а также от угла атаки а. Будем полагать а = 0.
При изучении кавитации вводится коэффициент местного разрежения
[21]
Рис. 1.13 Распределение коэффициентов скорости и давления по длине тела
Коэффициент £ представляет собой величину падения давления в рас-
сматриваемой точке у обвода по сравнению с давлением р0 в невозмущенном
потоке, выраженную в долях скоростного напора.
Как видно из рис. 1.13, на корпусе имеются участки пониженного дав-
ления. Минимальное давление р^п наблюдается на носке в точке, соответст-
вующей максимальному значению коэффициента £
2
Anin=A)-^4nax- (1-28)
Из последней формулы видно, что при прочих равных условиях с рос-
том скорости Vq давление рпШ1 уменьшается и, вообще говоря, может принять
сколь угодно малое значение. Если р^т достигнет величины pj- давления на-
сыщенных паров воды при данной температуре ее, то вода у носка тела заки-
пит. Скорость Ц), соответствующая началу кавитации, называется критиче-
ской скоростью. Из формулы (1.28) при pmin=p(/получим
1 Л'ттах
гдеро =pa+yh;
ра - атмосферное давление, Па;
у, р- весовая и массовая плотность воды, Н/м3, кг/м3;
h — глубина погружения тела, м.
31
Изменение величины pd в зависимости от температуры воды t приве-
дено в табл. 1.2.
Таблица 1.2
t,°C 100 50 30 20 10 0
р<!,кПа 101,3 12,3 4,3 2,3 1,2 0,6
Величина зависит от геометрии обвода и угла а. Например, при
а = 0 для сферического носка = 0,67 и при р = 1020 кг/м3, h = 4 м и
pd — 2,3 кПа по формуле (1.29)
/2/101300 + 10003 • 4 - 2300) ,
1---------------------— = 20,37 м/с.
V 1020-0,67
Из сказанного ясно, что момент возникновения кавитации на обводе
зависит как от геометрии тела (//ах), так и от параметров потока, обтекающе-
го его, - (vq, ро, pd). Величина //и может быть рассчитана численным мето-
дом, изложенным в гл. 5.
Склонность потока к кавитации характеризуется числом кавитации
2
которое по физическому смыслу представляет собой запас давления в потоке
над уровнем начала кавитации, выраженный в долях скоростного напора. Не-
трудно понять, что некавитирующие обводы должны удовлетворять условию
//ах <
Следовательно, чтобы подобрать некавитирующие обводы, необходимо ус-
тановить связь между геометрией обвода и £пих-
§ 4. Уравнение для давления в жидкости относительно подвижных осей
Нами используется гипотеза о потенциальном обтекании тела, и давле-
ние будем определять из уравнения Коши-Лагранжа, которое обычно запи-
сывается в неподвижной системе координат. Неподвижную систему коорди-
нат обозначим через систему F, а подвижную систему координат с центром
О' - через F'. Точка О'движется с поступательной скоростью U и вращает-
ся с угловой скоростью /» .
Если точка А, радиус-вектор которой относительно точки О'равен г,
жестко связана с F' то она имеет скорость
V -U + й>хг.
Пусть q и q' - скорости частицы жидкости А в момент времени t, ус-
тановленные наблюдателями, находящимися соответственно в системах F и
F'. Тогда
q=q' + U + ахг.
32
Для безвихревого движения несжимаемой жидкости уравнение Коши-
Лагранжа имеет вид
— + 192+£> + ^ = С(/),
Ро 2 dt
где Q— потенциал массовых сил.
Частная производная — вычисляется при изменении только времени t
и, следовательно, относится к фиксированной точке в пространстве.
Если наблюдатель связан с F', а точка А неподвижна в системе F, то
наблюдателю будет казаться, что эта точка движется со скоростью (- V ). Ес-
ли движение относительно F потенциальное, то q = \(р и скорость измене-
ния <р в неподвижной относительно F точке вычисляется наблюдателем, свя-
занным с системой F', следующим образом
dt dt
Здесь производная —— берется в подвижной системе F'. Следователь-
ft
но, уравнение Коши-Лагранжа примет вид
— + 192+Z2 + ^-KV^ = C(z).
Ро 2 &
Пусть qr есть скорость жидкости в системе F'. Тогда
qr = q -V =Vq)-V.
Таким образом, найдем
—q2 - VV<p = -(? - V)2 - -V2 = —q2 --V2.
2 2 2 2 2
Следовательно, уравнение Коши-Лагранжа для давления относительно
системы F', то есть в подвижной системе координат, может быть записано в
виде [23,25,29]
-^+l92+fi + ^->2=C(Z).
р0 2 ft 2
Постоянная интегрирования C(Z) равна отношению давления в жидко-
сти на достаточном удалении от тела к плотности жидкости ро'.
C(t)=P д,/р0. Поэтому окончательное выражение для отношения разности
давления (Р-Р к р0 в подвижной системе координат представим равенст-
вом
(1.30)
Ро dt 2
3 Зак. 3686
33
Глава 2
Силовое воздействие невязкой жидкости на движущееся в ней тело
§ 1. Постановка задачи гидродинамики прн движении тела
в спокойной воде
Движение жидкости, образующееся за счет перемещения в ней любого
твердого тела, будет рассматриваться в осях xyz (рис. 2.1), жестко связанных
с телом и имеющих начало в произвольной точке. Жидкость принимается
безграничной, несжимаемой и невязкой, а ее движение - потенциальным. В
этой главе рассматривается движение тела в спокойной, т.е. невзволнованной
воде, параметры волнения моря учитываются в следующих главах.
Рис. 2.1 Схема движения тела в спокойной воде
С точки зрения сил движение жидкости возникает за счет давления, ко-
торое каждая точка наружной поверхности тела оказывает на жидкость. Оче-
видно, каждая точка поверхности испытывает то же давление, но направлен-
ное в обратную сторону. Основная задача, решению которой посвящена на-
стоящая глава, это определить главный вектор и главный момент указанных
давлений с целью введения их в дифференциальные уравнения движения те-
ла. Обратим внимание на природу рассматриваемых сил. Движущееся тело
вызывает появление скоростей покоящихся вначале частиц жидкости, поэто-
му давление наружной поверхности тела на жидкость должно преодолевать
34
только ее инерцию. Других сил не будет ввиду отсутствия вязкости, несжи-
маемости и безграничности жидкости. В силу этого воздействие невязкой
жидкости на движущееся в ней тело носит инерционный характер, вследст-
вие чего соответствующие силы и называют силами инерционной природы.
Переходя к вопросу о количественном определении сил, заметим, что
это можно выполнить различными путями:
1) определив поле скоростей в жидкости, найти распределение давле-
ний по поверхности тела, и суммированием нагрузок, происходя-
щих от этих давлений, вычислить результирующие силы;
2) вычислить силы из теорем количества движения и моментов коли-
чества движения, т.е. тех теорем, которые позволяют непосредст-
венно определить силовое взаимодействие между телом и жидкой
средой, если известна скорость любой точки последней;
3) рассматривая жидкость как механическую систему и определив по-
ле ее скоростей, найти главный вектор и главный момент сил инер-
• ции.
В дальнейшем будем пользоваться последней из трех указанных воз-
можностей. Приведем основные относящиеся сюда формулы.
Если обозначить главный вектор и главный момент сил инерции всей
массы жидкости буквами V 1 и L„ , а главный вектор и главный момент сил
воздействия наружной поверхности тела на жидкость через V и La, то по
принципу Даламбера
Г7+К=0; LJa+La=Q. (а)
С другой стороны, главный вектор и главный момент сил воздействия
жидкой среды на тело, которые обозначим через V2 и L2, по принципу ра-
венства действия и противодействия равны
v2=-v-, L^-T^.
Но тогда из выражений (а) следует, что
V2=V}- L2=LJa, (2.1)
т. е. силовое воздействие невязкой жидкости определяется главным вектором
и главным моментом сил инерции всей жидкости. Они находятся из законов
количества и момента количества движения
VJ =_^Ql_^xq .
dt V2
LJa=^-d>*K2-v*Q2. (2.2)
dt
Здесь Q2 и K2 - количество и момент количества движения жидкости
во всем безграничном объеме;
а>- угловая скорость тела (или, что то же, осей xyz);
и - линейная скорость начала координат (полюса А).
3’
35
Формулы (2.2) определяют, в главных чертах, ход дальнейшего изло-
жения. Необходимо:
1) определить скорость любой точки жидкости;
2) вычислить векторы количества движения и момента количества
движения Q2 и К2,
3) подставить (при заданных и и я>) найденные величины в правые
части формул (2.2).
Остановимся теперь на постановке задачи гидродинамики. Безвихревое
движение невязкой жидкости, вызванное движением в ней твердого тела, ха-
рактеризуется потенциалом скорости, который обозначим через <р (х, у, z).
Тогда проекции скорости произвольной точки жидкости на оси xyz будут:
(23)
да да да
и =—! ; и, -—
х дх у ду z dz
Следовательно, сам вектор скорости
и . . .
дх ду dz
или, в обозначениях теории поля,
й = grad(3.
Напомним, что градиентом скалярной функции
(2.4)
(2.4')
<р называется вектор,
направленный по нормали к поверхности уровня (<з=const) в данной точке и
численно равный быстроте роста функции <р в направлении нормали, т. е.
ип=&ъ&<рп=—.
ап
Дифференциальное уравнение для отыскания потенциала <р выводится
из уравнения неразрывности (уравнение Лапласа)
дх2 ду2 dz2
Для его определения необходимы граничные условия, которым должен
удовлетворять потенциал <р на наружной поверхности тела и в бесконечно-
сти.
1. В силу непроницаемости поверхности движущегося в жидкости тела
и безотрывности обтекания нормальная составляющая скорости частиц жид-
кости, соприкасающихся с поверхностью £2 тела, должна в любой момент
времени совпадать с нормальной составляющей соответствующей точки по-
верхности. В противном случае жидкость отрывалась бы от поверхности или
проникала бы сквозь нее. Следовательно,
36
где ип - проекция на нормаль к поверхности /2 скорости точки В тела
О „
(рис.2.1), а — - нормальная составляющая скорости частицы жидкости,
дп
прилегающей к этой точке поверхности.
Из кинематики известно, что распределение скоростей точек твердого
тела вполне определяется заданием вектора скорости полюса и и угловой
скорости вращения а>. Для скорости любой точки В поверхности имеем
формулу
иь = и + <у хгь,
где г ь — радиус-вектор точки В относительно полюса Л.
Если обозначить через п орт внешней к поверхности тела нормали, то
нормальная составляющая скорости точки В определится выражением
ип = п-иь = п - и + п- (&*.гь)
или
и„ = п • и + ю • (zj, х п ).
Таким образом, первое граничное условие имеет вид
— = п- и + а хп). (2.6)
дп
2. В бесконечном удалении от поверхности тела, т. е. при г —>оо, жид-
кость находится в покое, т. е. скорость любой ее точки равняется нулю.
Следовательно,
.. дф дф дф _
lim— = lim^- = игл— = 0,
г-»® дх г-*° ду '->“> dz
где
r = ^x2 + у2 +z2 .
Можно показать, что при этом условии потенциал скорости в беско-
нечно удаленной точке равен нулю, т. е.
^=0. (2.7)
Таким образом, для определения поля скоростей жидкости служит
дифференциальное уравнение (2.5) с граничными условиями (2.6) и (2.7). За-
дача в значительной степени упрощается следующим, введенным Кирхго-
фом, представлением потенциала
ф=+ <Pivy + ф^ +фцах+ Ф5<оу + <z>6®z • (2-8)
При таком представлении зависящие от времени величины (и и ё7)
отделены от ф1, которые связаны только с формой поверхности тела. В са-
мом деле, из выражения (2.8) следует, что, например, функция q\ представ-
ляет собою потенциал скорости при условии, что тело поступательно дви-
жется с постоянной скоростью, равной единице, вдоль оси Ах:
*4=1; vy = vz=Q-, a>x=a>y=a>z=Q.
Ясно, что при этом условии поле скоростей жидкости зависит только от фор-
мы тела. Аналогичный смысл имеют фг и фг. Точно также ф^ соответствует
37
потенциалу скорости <р при вращении тела относительно оси х с единичной
угловой скоростью, а ф5 и ф6 - при вращении вокруг осей у и z. В связи со
сказанным функции ф1 получили название единичных потенциалов.
В силу того, что величины vx ,—,a>z могут принимать любые значения,
можно записать дифференциальные уравнения единичных потенциалов
э^+^.+0^=о ...6
‘ Эх2 Эу2 5z2
Граничные условия на наружной поверхности определяются из (2.6),
если в него вместо <р подставить формулу (2.8), а правую часть выразить че-
рез проекции векторов на оси. Получим
дд\ дф2 дф, <Э(34 <Э(з5 <Э% , п.
l> —— + U —— + и7—^ + т —— + <ov—^ + CD——= (2.10)
х дп у дп 2 дп х дп у дп z дп
= ихпх + иупу + uznz + O)x(ynz -zny)+ a>y(znx -xnz)+ (i)z{xny -ynx),
где x, у, z - проекции радиуса-вектора точки В на оси (координаты точки на-
ружной поверхности);
пх, пу, nz - проекции орта нормали на те же оси, равные:
пх = cos(n , xj=a;
пу = cos (п , yj=/?; (2.11)
nz =cos(h , z)=y.
Из выражений (2.10) и (2.11) получаем искомые граничные условия для
единичных потенциалов: ф 5^ —- = а\ —- ^_= л. дп ’ дп дп ’ дп - у COS (и , zj- ZCOS (и , у)= yy-z/}\ = zcos(n , x)-xcos(n, z}=za-xy; / Л \ ( л \ = xcosb y)-ycosh xj=xfl-ya. (2-12)
Подставляя далее формулу (2.8) в формулу (2.7), находим, что
при г->оо grad#», = О,0>; = 0, i = 1,2,...,6. (2.13)
Таким образом, задача об определении потенциала (а, а следовательно,
и поля скоростей, сводится к определению шести гармонических функций
<Pi, удовлетворяющих каждая своим граничным условиям (2.12) и (2.13).
Этими условиями функции q)t определяются однозначно.
§ 2. Основные динамические параметры жидкости
Допустим, что для тела, движение которого задано векторами U и а,
найдены все шесть единичных потенциалов <р{. Тогда по формуле (2.8) опре-
делится потенциал ф, а по (2.4) — вектор скорости любой точки жидкости.
Рассматривая жидкость как механическую систему и зная скорость любой ее
точки, можно найти и динамические параметры жидкости: Q2 - вектор коли-
чества движения, К2 — вектор момента количества движения и Т2 - кинети-
ческую энергию. Но тогда соотношениями (2.1) и (2.2) решается наша глав-
ная задача — определение сил воздействия невязкой жидкости на движущееся
в ней тело. Таким образом, необходимо развернуть выражения для величин
Qi t ^2 И ^2-
Если выделить в жидкости произвольный элементарный объем dV, по-
ложение которого относительно начала подвижной системы координат ха-
рактеризуется радиусом-вектором г, а скорость — вектором й, то для него
можно написать
dQ2 = updV, dK2 = rx updV; dT2 = ^u2pdV,
где p — плотность жидкости, принимаемая во всех ее точках одинаковой.
Интегрируя по всему безграничному объему жидкости, получим выра-
жения искомых динамических параметров:
Q2 = p\udv-,
v
K2=p^rxudV; (2.14)
у
T2=lpJM2JK.
z v
Если принять во внимание формулу (2.4'), то можно написать:
C2=pJgrad^dK;
v
ЛГ2 = pjrxgrad^dK; (2.15)
v
'l2=^p№ad(p)2dV.
z v
преобразования этих интегралов в поверхностные воспользуемся
Двумя положениями:
а) обобщенной теоремой Гаусса
J = J ФИ, (а)
у (<) nt
гп₽ 17 г „ - <Э - <Э - <Э
где у - оператор Г амильтона, имеющий вид i — + j-\-k —;
дх ду dz
L — любая линейная функция;
38
39
п - вектор наружной нормали к поверхности тела.
Знак £ в правой части показывает, что интегрирование нужно про-
водить по всем поверхностям П, ограничивающим объем;
б) формулой Остроградского - Грина
[ (coAf + grad со- grad f)dV = Y Г co—dQ, (б)
v (О Д дп
где со и f- произвольные функции координат, непрерывные до вторых про-
изводных.
Учитывая по (2.4‘), что w=grad^? = V^ и полагая в формуле (б)
со = f = <р, а также принимая во внимание, что на поверхности шара беско-
нечного радиуса <р = 0, можно выражениям (2.15) в соответствии с формула-
ми (а) и (б) придать вид:
Qi = Р ^пП;
п
K2 = pfy>(rxn)d/2; (2.16)
я
T2=-pbp^-dn.
2 Г^оп
Здесь интегрирование производится по наружной поверхности движу-
щегося тела.
Подставляя вместо <р его выражение (2.8) и учитывая граничные усло-
вия (2.12), получим:
Qlx = Р jWx + <№у + <Рз»2 + <Р4<ОХ + <Ps(Oy + W»z)^T^ i
п у дп
Qiy=р + <Pi»y + Wz + <р<р>х + tp&y + ^6®z ; (2.17)
я у дп
Q12 = Р jWx + <Р»у + <P1»Z + (Р^х + <Рз°>у + <Pffl>z\^-dPl
О дп
И
o
K2x = P f(<*Wx + <P2»y + <P3°z + 4>^x + <P5°>y + ^z)~df2 ;
n y dn
к2у = P ((«’I+ ^y + ^z + ^4®x + (ps^y + ^6®z dn; (2.18)
Q urt
K2z = P ffe^X + <P2»y + <Pl»z + <№x + <№y + W«z )^jdQ .
я y dn
Для сокращения письма введем обозначения:
6zx=^l’ Qly — ^2’ G2z=?^3’ ^2x=A’ ^2y~^5’ ^2z = A’
^x=Q\, ^у=Ч2\ ^x=94; <»y=?5; ®z=?6-
Тогда формулы (2.17) и (2.18) примут вид
40
(2-19)
(2.20)
(2-21)
(2.22)
л,=р\ |Е <ад*|^7^=Е л,кЯк,
a V=i ) on t=i
i=\,2,...,6,
*=1,2,....6,
где
Ък=р\ <Pk^~d&-
h dn
Величины Aik носят название присоединенных масс.
Формулы (2.19) могут быть представлены в развернутом виде
Qix =Лл++Лб®г;
Qly ~ ^2\Ux + ^22Uy + ^23*4 + ^24®х + /^25<иу + ^26®г >
Qiz = Л1Ух + ^32uy + ЛзЗ*4 + ^ЗА^х + ^ЗЗ^у + Лб®г
И
&2х = Л4\их + Л42иу + Аз*4 + + Лц®? + Л46&г ’
^2у = Л1Цс + ^52 + ^53^4 + ^ЗА^х + ^ЗЗ^у + ^56®z 5
K2z = Л^х + >^2*4 + Лз*4 + ^64ах + ^3&y + Лб^г -
Отсюда следует, что динамические параметры жидкости зависят, во-
первых, от кинематических параметров твердого тела (й и а) ), отражающих
его движение в функции времени, и, во-вторых, от системы постоянных ко-
эффициентов Aik, характеризующих форму наружной поверхности тела в
смысле обтекания ее жидкостью.
В отношении величин Aik отметим следующее. Прежде всего обратим
внимание, что принятый двойной индекс надо понимать следующим обра-
зом. Первая цифра указывает, на какую ось проектируется вектор, причем
оси х соответствуют цифры 1 (для вектора Q2 ) и 4 (для вектора К2), оси у - 2
и 5 и оси z — 3 и 6. Вторая цифра обозначает, от какого движения произошла
та или иная проекция, причем цифры 1, 2, 3 соответствуют поступательному
движению вдоль осей х, у и z, а 4, 5 и 6 - вращательному вокруг тех же осей.
Можно показать, что из 36 коэффициентов Aik, входящих в формулы
(2.21) и (2.22), неравными друг другу будут лишь 21, так как имеет место ра-
венство
(2-23)
Обратимся к определению выражения кинетической энергии жидкости.
Согласно третьей формуле (2.15), а также выражениям (2.19)
Т2=^Р$ Ч>~^ = \р\ (е ФкЧк Е ^4. W
2 дп 2 я <=i dn )
что можно переписать таким образом:
1 6 6
Г2=^Е E^f^^ (2 24)
2 I =i *=| п дп
или, учитывая формулу(2.20),
41
1 6 6
(2.25)
2 i=l м
Если, заменив буквы q их значениями, развернуть формулу (2.25), то
можно, сгруппировав соответствующим образом члены, установить, что ки-
нетическая энергия жидкости состоит из трех частей:
1) кинетической энергии поступательного движения
= Лц1% + ^22^ + Аз^г + ^^2UxUy + 2^3^^ + ^^3\UzUx’ (2.26)
2) кинетической энергии вращательного движения
2Т2(2) = Л^х + + ^6<У2 + 2245гахй?? + 2Л56<оуй)2 + 2^4®Z0X; (2.27)
3) взаимной кинетической энергии
+ Л\$О>у + )+ Ь>ДАд®х + + Аб®? ) +
+ сДАд^х + + Afi^z)
Из написанных выражений следует, что коэффициенты имеют раз-
мерности:
Л1к при i = 1, 2, 3 и к = 1, 2, 3 - размерность массы;
при/ = 1, 2, 3 и к=4, 5, 6 - размерность статических моментов
масс;
А< при» =4, 5, 6 и к = 4, 5, 6 — размерность моментов инерции масс.
Нетрудно видеть, что величины коэффициентов Л1к зависят от положе-
ния начала и направления осей координат. Последнее можно выбрать так,
чтобы
Лг =Лз = Аз =0.
Соответствующие направления называются главными. Помимо этого
должным подбором начала координат можно добиться того, чтобы
Я15=Аъ Аб=—Аб> Аб=Ад-
Отвечающая этим равенствам точка называется центральной. Для цен-
тральной и главной системы отсчета число различных коэффициентов при-
соединенных масс уменьшается до 15.
В заключение настоящего параграфа заметим, что между кинетической
энергией жидкости Т2 и проекциями векторов Q2 и К2 имеет место связь,
легко усматриваемая из формул (2.21), (2.22) и (2.25) (или (2.26), (2.27) и
(2.28)), если последнее соотношение дифференцировать по qt и сравнивать с
соответствующими выражениями (2.21) или (2.22), а именно:
5т2. _ат2.
8их да>х
П - дТ2 . к _ дТ2
_дТ2. _дТ2
V2z - “ > Л2г - ~ -
OV, 0(0.
(2.29)
42
§ 3. Силовое воздействие невязкой жидкости.
Присоединенные массы А* тела
Допустив, что все присоединенные массы определены (этот вопрос
рассмотрен ниже), нетрудно решить интересующую нас задачу о силовом
воздействии идеальной жидкости на движущееся в ней тело, воспользовав-
шись для этого соотношениями (2.2). Если разложить входящие в них векто-
ры по ортам осей xyz, то проекции главного вектора и главного момента сил
воздействия можно представить в виде:
И2я = - avQ2z + а>.Qiy:
at
dQlv
v2y =-^~- oj-.Qi, + a&iz; (2.30)
at
v12 =-^r~ - ^Qiy + Qix
dt
и
Az.v = ~ K2z + Qlz + 402, i
at
dK2v
Цу = - (o7K2x + <oxK2z - vzQ2x + vxQ2z, (2.31)
^2z = - ^xK2y + ЮуК2х ~ VxQ2y + VyQ2x.
Подстановка сюда формул (2.21) и (2.22) приводит к явному выражению сил
и моментов воздействия жидкости через кинематические параметры движе-
ния тела и присоединенные массы. Однако этих соотношений не приводим -
во-первых, потому что они слишком громоздки и, во-вторых, потому что
большинство тел, движение которых приходится рассматривать, обладает
одной или двумя плоскостями симметрии, вследствие чего указанные соот-
ношения значительно упрощаются. В самом деле, допустим, что плоскость
хАу тела (рис. 2.1) служит плоскостью симметрии. Тогда при изменении зна-
ков V., а)х и картина обтекания тела не меняется. Следовательно, не
должно измениться и выражение суммарной кинетической энергии жидко-
сти. Этого можно добиться, если в формулах (2.26), (2.27) и (2.28) сделать
нулями Aik в тех членах, которые меняют знак при указанных изменениях
знаков проекций скоростей. Из этих соображений следует, что в нуль обра-
щаются присоединенные массы
Аз, А 4, As, Аз, Ад, As, Ав, Ав, Аб-
При этом кинетическая энергия жидкости принимает вид
43
^2 ~уА1^х + ~^22V} +~^33Uz + ^12UxUy + Аб^х®г +
+ A26UyCl)z + Aj4Dzfi>x + Аз*4®, + Аз®х®, +
1 2 1 2 1 2
+—АддСОх + у As®, + у Ae®z ,
а проекции векторов Q2 и К2:
Q2x=^x+^y+^z>
@2у = АгРх + ^22Vy + Аб®г »
б2х=Аз^+А4®х+А5®,’
Силовое воздействие жидкости определится подстановкой этих выражений в
формулы (2.30) и (2.31).
Аналогично, если плоскость xAz служит плоскостью симметрии, то об-
ратятся в нуль величины [35]
Аг, Л14, Аб, Аг, Л34, Аб, Аг, А54, Аб,
соответственно чему из формул (2.21) и (2.22):
К2х = Аги, + Ам®х + Аб®г’’
^2 у = А Ах + АзРг + As®, 5
^2z = АгР, + Ад®х + Аб®г •
К2х = АиЦ + ^44 ®х + As®,;
&2у ~ As^z + Аэ®х + As®,i
^2z = АбУх + АбР, + Аб®г -
(2.32)
(2-33)
(2-34)
2
С?2х = А Ах + АзУг + Аб®,’
С?2, = ^22°у + ^4®х + Аб®г
0.2г = А Ах + Аз^г + As®, ’
Если, наконец, тело имеет две плоскости симметрии (хАу и xAz ), то не
обращаются в нуль лишь восемь коэффициентов:
Ац, Аг, Аз, А4, As, Аб, Аб, As,
и, следовательно,
Т2 = у (а 1°х + АгР* + Аз^г + ^44®^ + As®J + +
+ 2A6f,®z +2Ast>z®,),
(2.35)
^2x
&2у = As®y + As^zi
Aiz = Аб®г + ^26иу
(2.36)
а потому по (2.29)
бгх = Ai^xi
Сг, = Аг^, + Аб®г;
Q2Z = Аз^г + As®,;
Этот случай представляет для нас большой практический интерес, так
как если верхние и нижние перья вертикальных стабилизаторов мало отли-
чаются друг от друга по форме и площади, то тело вращения с оперением
можно считать телом, имеющим две плоскости симметрии.
Если вертикальные и горизонтальные стабилизаторы одинаковы, то
можно показать, что имеют место соотношения:
Аг = Аз; Ae = As, Аб = _As- (2.37)
Для голого корпуса тела вращения (без стабилизаторов) А44=0, так как
тело, имеющее осевую симметрию, при вращении вокруг оси симметрии не
приводит в движение окружающую его невязкую жидкость.
44
Числовые значения присоединенных масс зависят от ориентировки ко-
ординатных осей относительно тела. Вместе с тем, так как мы имеем дело со
вполне определенным движением тела, характеризуемым параметрами и и
, то его обтекание будет также определенным, не зависящим ни от какой
координатной системы. На этом факте и основан пересчет величин Aik из од-
ной системы координат в другую. В самом деле, если взять выражение кине-
тической энергии жидкости в некоторой системе координат и заменить в нем
составляющие линейной и угловой скоростей через аналогичные величины в
новой системе, то после необходимых преобразований получим искомые
формулы перехода. Рассмотрим два наиболее часто встречающихся случая:
поворот осей и перенос начала для плоского движения. Конечно, всякие иные
случаи могут быть легко рассмотрены при помощи аналогичных рассужде-
ний.
Рис. 2.2 Поворот системы координат
Допустим, что движение тела происходит в плоскости хАу. Тогда в со-
ответствии с формулами (2.26), (2.27) и (2.28) кинетическая энергия жидко-
сти может быть выражена
2Т2 = ^,<4 + 2^2^ + + 2Лб^®г + • (а)
Если в системе осей х’у' (рис. 2.2) проекции скорости полюса будут
и ty, то можно написать:
их = их' cos#-Ру sin#,
иу = их- sin# + Ру cos#.
45
Подставляя эти выражения в формулу (а) и группируя члены, найдем
значение кинетической энергии в новых осях. Очевидно, соответствующие
коэффициенты при проекциях скоростей и будут искомыми значениями Я в
осях х'у'. Не приводя подробности всех указанных преобразований, напишем
окончательные значения :
Л^ = Лц cos2 в+Л22 sin2 6 + 2Л,2 sin #cos#;
^22 =Лц sin2 # + >222cos2^_ 2^ sin^cos#
Л 2 = (Л22 - A1 )sin ^cos 6 + Л2cos 2#;
^6 =^66>
Л[6 = Лц, cos# + 2г6 sin 0,
Л^6 = -Л^ь sin# + т?26 cos#.
Рис. 2.3 Параллельный перенос осей
Для случая параллельного переноса осей (рис. 2.3) связь между проек-
циями скоростей в старой и новой системах выражается
"х = их + b(Oz’ vy = иу' ~ а(°г-
После подстановки в формулу (а) и преобразований, аналогичных ука-
занным, найдем:
Л'1=Ль Л'б = Лб +^Л1 ~а^2’
Л22 = ^22 J Лгб = -^26 + — (2.39)
Лзз = А,б ~ -^66 + *2Л1 + °2~ ZabAft + 2/Ц6 — 2а>?26.
46
Пересчет присоединенных масс в случае одновременного переноса и
поворота осей можно проводить последовательно, применяя формулы (2.38)
и (2.39).
§ 4. Приближенное определение присоединенных масс
для тела вращения с кормовыми стабилизаторами
Рассмотрим удлиненное тело вращения с вертикальными и горизон-
тальными стабилизаторами, расположенными в кормовой части. Их протя-
женность обычно не превышает одного калибра. Относительно плоскости
вертикальных стабилизаторов тело всегда симметрично.
В соответствии со сказанным выше нужно определить следующие при-
соединенные массы:
^И’^22^^33’^44’^55^66’^26 И •
Удобнее всего их находить алгебраическим сложением присоединен-
ных величин для голого корпуса и оперения.
Один из наиболее простых и распространенных приближенных мето-
дов определения присоединенных масс голого корпуса основан на так назы-
ваемой гипотезе плоских сечений. Ее суть заключается в том, что при попе-
речном обтекании удлиненного тела считают каждое его сечение находя-
щимся в плоском потоке, т.е. гипотеза предполагает отсутствие продольного
растекания жидкости. Но тогда, если рассматривать движение в поперечном
направлении и считать известной присоединенную массу для каждого сече-
ния, то суммированием всех присоединенных масс по длине тела определя-
ется присоединенная масса для соответствующего направления. Аналогично
суммированием статических моментов и моментов инерции элементарных
присоединенных масс находятся две другие величины Я.
Пусть Л(х) присоединенная масса поперечного сечения тела при его
движении вдоль оси Ау. Тогда в соответствии со сказанным выше
Ч>
4> = fax)dx,
ч
где X] и х2 — координаты носовой и кормовой оконечностей.
Присоединенные статические моменты и моменты инерции выразятся
х2 х2
формулами: = fxA(x)dx; Я£6 = jx2A(x)dx.
ч ч
Имея в виду, что поперечные сечения тела суть окружности, можно на-
писать Л(х) = лрг2(х), поэтому
47
х2
^22 - ЛР р2 (x)dx = pV0;
ч
*2
= яр Jx • r\x}dx = /?Кохо;
ч
ч
4б = яр [x2r2 (x)dx = рУ012в,
ч
где Fo - объем голого корпуса;
хо и i2o - координаты центра объема тела и его радиус инерции относи-
тельно принятой оси.
Будем считать радиус инерции 1^ тела относительно оси, проходящей
через центр объема, приближенно равным
iZo = (0,25-0,26)1,
где L - длина тела.
Имея в виду, что голый корпус тела есть тело вращения, для остальных
присоединенных масс
^33=^25 ^55=^6б! ^44=0; ^26=_^35- (2.42)
Переходя к определению присоединенных величин оперения (рис. 2.4),
обратим внимание на то, что присоединенная масса сечения (левая часть
рис. 2.4), обтекаемого плоскопараллельным потоком вдоль оси Ау, может
быть найдена по формуле
(2.40)
(2-41)
1
1
Л = я(г+с)2 1-----=--г-----j- ,
L а+о2 (i+^)4J
с
Поэтому, используя ту же гипотезу плоских сечений, можно написать
48
Л%" =яр f(г + с)i 2 * • <fdx;
х2
х3
Л^ = лр Jx • (г + с)2^/х;
*2
(2.43)
х3
л^п = яр Iх2 (г + с)2 фх,
х2
„ , 1 1
где 6=1---------=- +---—J-.
(1 + сг)2 (1 + сг)4
Следует иметь в виду, что вычисленные по формулам (2.43) присоеди-
ненные величины включают в себя и часть голого корпуса, заштрихованную
на рис. 2.4. Но в формулах (2.40) уже учтены эти величины, поэтому из (2.43)
их нужно исключить. Способ этого исключения приведен ниже в числовом
примере.
Суммированием выражений Л для корпуса и оперения находим значе-
ния Л22, Л26, Ае для всего тела. Те же значения будут иметь Л#, As и As>
если справедливы формулы (2.42).
Для присоединенной массы оперения можно получить прибли-
женное аналитическое выражение, если соблюдены два условия: 1) обвод те-
ла на участке О-В (рис. 2.4) считается прямолинейным; 2) оперение нераз-
движное, так что величину г + с в формуле (2.43) можно считать постоянной
и равной го (полукалибр). В соответствии с формулами (2.43) и (2.40)
i
= xpf(r + c)2
о
1____
+ (1 + <г)4
1---------7
(1 + а)2
i
dx-np\r2dx.
о
Так как
то
=^c’fr02G-^-+^->bx-^ofr2rfx
о \ го го ) о
или
/6 2 Л2
Аг7 = яр J11 —2 fgdx.
ol го J
Если, как сказано выше, считать го постоянным, то при отнесении ко-
ординаты х к длине оперения I можно написать
В силу того, что участок обвода тела в пределах оперения считаем
прямолинейным (рис. 2.4),
4 Зак 3686
49
(г2 “И)
r = rl + -у- X.
Введем новую переменную:
с _ г _ rl , г2~г1*
г0 г0 г0
Тогда
UJ Г2-ГХ
При — = 0 £= —, а при— = 1 £=— .поэтому
I г0 I г0
г2
r0 r0 ъ
Интегрируя и выполняя очевидные преобразования, получаем формулу
или
fin_ лго1 J'i-'i 2г23-Г!3 1г25-Г!5
L г0 3 г0 5 'О J
Го го
Таким образом, для шести из упомянутых выше восьми присоединен-
ных масс способы вычисления установлены. Остается определить две: Лц и
Л^. Приближенное представление о величине Лц можно получить, заменяя
тело эквивалентным эллипсоидом вращения, для которого имеется точное
решение. В табл. 2.1 дано значение коэффициента присоединенной массы
К
эллипсоида вращения при различных удлинениях.
Таблица 2.1
L D 1 1,5 2 2,51 2,99 3,99 4,99 6,01 6,97 8,01 9,02 9,97 00
Ки 0,5 0,305 0,209 0,156 0,122 0,082 0,059 0,045 0,036 0,029 0,024 0,021 0,0
Присоединенный момент инерции определяется формой кормовой
части. Если считать, что она соответствует рис. 2.4, то по гипотезе плоских
сечений
50
I
Ли =
о
где - присоединенный момент инерции при вращении контура вокруг оси
х. Для этого случая имеется точное решение, в результате которого
1 14
(1 + гг)4
1
,4
4
2 '
(1 + <7)4.
Тогда
4
1----------1—
, 1
4 о
. (1+О4.
Обычно стабилизаторы выполняются так, что их кромки параллельны
продольной оси тела. В этом случае на большей части длины стабилизаторов
сумма r+с постоянна, в связи с чем
4 о
где £, =
1____
(1+О-)4
1
4
2 "
. 0 + ^)4.
Так как эта величина при любом сг всегда меньше единицы, то можно
написать
Л-(г + с)4/
<44 < 4
(2.44)
4'
51
Глава 3
Характеристики гравитационных волн и постановка задачи
гидродинамики при движении тела во взволнованной жидкости
§ 1. Характеристики плоских регулярных волн
Волновые движения возникают под действием внешних возмущений и
представляют процесс их распространения в жидкости. В зависимости от то-
го, какие силы способствуют волнообразованию, волны можно подразделить
на гравитационные, капиллярные и упругие [2, 36].
Гравитационные волны возникают вследствие того, что жидкость на-
ходится в поле силы тяжести; выведенная из состояния равновесия внешни-
ми возмущениями, она совершает колебания. К гравитационным относятся
ветровые волны, волны, вызываемые движением тел, волны внутренние, воз-
никающие на границе раздела жидкостей с разной плотностью или в неодно-
родных (стратифицированных) жидкостях, волны цунами, а также прилив-
ные, создаваемые притяжением Луны и Солнца.
Рис. 3.1 Характеристики плоских правильных волн
Капиллярные волны обусловлены действием сил поверхностного натя-
жения и имеют вид ряби, порождаемой ветром или движением тел. Они мо-
гут существовать одновременно с гравитационными.
Упругие волны возникают вследствие сжимаемости жидкости; к ним
относятся звуковые и взрывные волны.
Поверхностные волны с периодически повторяющимися характеристи-
ками называются правильными или регулярными. Если картина волнового
движения одинакова в параллельных плоскостях, то такие волны называются
плоскими. В отличие от плоских волны ветровые имеют трехмерный харак-
тер, однако знание характеристик плоских волн способствует описанию
трехмерного волнения. На рис. 3.1 показаны плоские правильные волны.
Профиль волны в плоскости, перпендикулярной образующим, описы-
вается такими основными характеристиками, как длина Я, высота h и период
т. Длиной А волны называется расстояние между соседними вершинами или
подошвами; высота h волны представляет расстояние от подошвы до верши-
ны. Величина a = h!2 правильных периодических волн является их амплиту-
52
дой. Угол ав, образуемый касательной к данной точке профиля с горизон-
тальной поверхностью покоящейся жидкости, называется углом взволнован-
ной поверхности или волнового склона. Максимальное значение угла волно-
вого склона (в градусах) можно определить по формуле
ав =51,?>nhl Л.
Промежуток времени т между прохождением через неподвижную вер-
тикаль последовательных вершин или подошв волны называется ее перио-
дом. Отношение а>= 2я/тпредставляет частоту волны. Волны можно подраз-
делить на прогрессивные и стоячие. Профиль прогрессивных волн переме-
щается в пространстве со скоростью с, которая называется скоростью их рас-
пространения или фазовой скоростью; у регулярных волн с - Мт. К прогрес-
сивным относятся ветровые и корабельные волны.
Профиль стоячих волн не перемещается в пространстве и лишь изме-
няет свои ординаты в данной его области; такие волны могут возникать, на-
пример, в результате отражения прогрессивных волн от берегов.
Ветровые волны и волны, вызываемые движением тел в жидкости или
действием импульсов давления на ее поверхность, называются вынужденны-
ми. Рассматривают также свободные волны, характеристики которых не из-
меняются с течением времени, а высота зависит от начальных условий их
возникновения; к ним близки волны морской зыби. Влияние вязкости жидко-
сти на процессы формирования и затухания волн обычно не велико, поэтому
теорию волн большей частью разрабатывают, полагая жидкость невязкой, а
ее движение потенциальным.
Рассмотрим основы теории прогрессивных волн. В этом случае потен-
циал скорости (fa, у, z, t) в неподвижной системе координат, имеющей нача-
ло на невозмущенной свободной поверхности, удовлетворяет уравнению Ла-
пласа Л<р= 0, а также кинематическому и динамическому граничным услови-
ям на свободной поверхности при z = Q(x, у, t) и непротекания на плоском
дне водоема
д<р = 8(р д£в । 8<р 8^в , .
Sz 8х дх 8у ду dt
д(р 1 (8<р | । 8(р | । 8(р ] „ „ „ , ч
—— + — + — +gG=°; (3-1)
I AS I I I I « I О V £» J V Z
2 V йх 7 \°У ) \8z )
— = 0 при z = -H.
8z
Система граничных условий (3.1) используется при разработке нели-
нейной теории волн. Уравнения (3.1) несколько упрощаются в случае пло-
ских прогрессивных волн (см. рис.3.1), где потенциал <fa, z, t) и 4в(х, t). Раз-
работка нелинейной теории связана с большими математическими трудно-
стями.
53
Более простой является линейная теория, основанная на предположе-
нии, что волны имеют относительно малые амплитуды и параметр
( Я A3 h ,
— — «1.
\Н) Я
В этом случае задача сводится к решению уравнения А<р= 0 с соблюде-
нием упрощенных граничных условий, отнесенных к невозмущенной по-
верхности при z = 0:
_ 1 Э2у> __\дср
Sz g dt2 ’ В g dt ’
а также на дне при z = -Н: dcpldz = 0 . Система уравнений (3.2) является, наря-
ду с уравнением Лапласа, линейной и допускает применение метода суперпо-
зиции решений.
Потенциал плоских прогрессивных волн относительно малой амплиту-
ды, распространяющихся вдоль положительного направления оси х, имеет
вид [36]
(3-2)
(3-3)
(3-4)
d%
<р =---—ch£(z + Н )sin(/cx - cot),
cochkH
где к = 2л/А - частота формы волны, характеризующая число волн, уклады-
вающихся на отрезке оси х длиной 2тг м. Профиль £в(х, t) волн, соответст-
вующий этому потенциалу:
= acos(fcc - cot)
с углами волнового склона
2ли .
tgaB =-----sm(fcc - cot) ~ ав.
Я
Частота волн связана с их длиной зависимостью
со2 = gkMH,
а скорость распространения волн
\2л Я
Частицы жидкости движутся по замкнутым эллиптическим траектори-
ям, уравнение которых
х-х0
ch^(z0 + Н)
МН
= 1,
z-zp
chZ:(z0 + Н)
° shkH ,
где хо и Zo - координаты равновесного положения частиц.
Характерной особенностью волн относительно малой амплитуды явля-
ется то, что их длина и фазовая скорость не зависят от амплитуды. Энергия
волн, приходящаяся на участок длины, равный Я, представляет сумму кине-
тической Тж и потенциальной Пж энергии (в рассматриваемых волнах
Тж ~ Пж):
54
Э=Тж + Пж=^Л. (3.5)
Перенос энергии в волнах происходит с так называемой групповой скоро-
стью Uf-
_с( 2Ш 1
A sh2A//J’
т. е. в общем случае «г < с.
В предельном случае для жидкости неограниченной глубины, когда
Н-» -<ю, потенциал и другие характеристики волн имеют вид
<р =—sin(fcc - щ<); (3.6)
со
со2 = gk, т.е. т = 0,8-/Л и Л = 1,56т2;
с = JgAllTC = 1,25л/Я;
иг=с/2.
Уравнение ординат свободной поверхности и формула для вычисления энер-
гии совпадают с выражениями (3.4) и (3.5). Траектории частиц в случае глу-
бокой жидкости имеют вид окружностей с уравнением
(x-xo)2+(z-z0)2=a2e2ho.
По мере увеличения глубины погружения радиусы траекторий убывают:
г = ае А .
Скорость движения частиц по данной окружности постоянна:
„ 2«о
2тг -г-
и = —ае .
г
При zo = 0 и / с = 2ла /Ли, следовательно, и « с.
В другом предельном случае, когда Н « Л, согласно этой теории
иг= с, а скорость распространения волн
c = -jgH.
Давление в жидкости при волнах относительно малой амплитуды вы-
числяется с помощью зависимости
д<р
Р = Рат+^-Р~^^
ot
где ср определяется согласно выражениям (3.3) или (3.6).
На скорость распространения волн, особенно при малой их длине, мо-
гут оказать влияние силы поверхностного натяжения. Для жидкости, имею-
щей глубину Н, поверхностное натяжение ап, скорость распространения
волн с учетом влияния капиллярности
If стп 2л\,2лН
У^2л- р Л ) Л
55
Существует минимально возможная скорость cmin распространения капил-
лярных волн; в случае глубокой воды cmin = 0,235 м/с.
С помощью нелинейной теории получить зависимости, описывающие
характеристики волн конечной амплитуды в замкнутом виде, не удается. По-
тенциал скорости плоских нелинейных прогрессивных волн можно предста-
вить в виде ряда (p=hq\ +h1<p2 +h3^ +..., где <рп - потенциалы последова-
тельных приближений. Теория второго приближения, в которой сохранены
первые два члена этого ряда, позволила Вигелю для жидкости конечной глу-
бины получить потенциал
йЯ ch fc(z +/7) 3 яй2 ch2k(z + Н) . ... .
?=Ч------sin(fa ~ +77-----?4.ц sm2(fa- at),
2г shA77 16 г sh кН
где первое слагаемое соответствует линейной теории. Ординаты волн второ-
го приближения определяются соотношением
~ й ,, . лй2f, з А , ,,,
£в =—cos(fcc - at) +- 1 +--5— cth кН cos2(fcv - at).
2 4л\ 2sh кН)
Рис. 3.2 Профили волн по линейной
(1) и нелинейной (2) теории
На рис. 3.2 сопоставлены ординаты этого профиля с профилем волн по
линейной теории. Траектории частиц в нелинейных волнах незамкнуты, и
скорость переноса воды в направлении волн, убывающая по глубине, состав-
ляет
_лг2й2 ch2k(z + H)
Un ~ 2тЛ sh2 кН
Характерной особенностью волн конечной амплитуды является связь
скорости их распространения не только с длиной, но и с амплитудой. Ско-
рость распространения таких волн на глубокой воде можно определить по
формуле Л. Н. Сретенского
[gA (2яа^ 1Г2лиУ
с= — 1+ ------ +- ------
Ц2л- \А J 2{ A J
56
§ 2. Статистические характеристики ветровых волн и сведения
о волнении в некоторых районах моря
Реальное ветровое волнение имеет сложную форму, изменение которой
во времени и пространстве носит неправильный, нерегулярный характер,
создающий у наблюдателя впечатление хаотичности движения масс воды.
Причина этого заключается, главным образом, в турбулентности ветрового
потока над морем, закономерности которого описываются методами теории
вероятности и математической статистики. Поэтому и характеристики ветро-
вых волн тоже могут рассматриваться как случайные величины и изучаться с
помощью статистико-вероятностных методов [36].
Различают три типа морского волнения:
1) волнение, вызываемое и поддерживаемое ветром, действующим на
свободную поверхность воды;
2) волны зыби, остающиеся после прекращения действия ветра или
выходящие за сферу его действия;
3) смешанное волнение - результат наложения более молодых ветро-
вых волн на зыбь или систему ветровых волн, образовавшихся ра-
нее.
Согласно ГОСТ 18451 - 73 основные элементы ветровых волн опреде-
ляются следующим образом:
высота волны - превышение вершины волны над соседней подошвой
на волновом профиле, проведенном в генеральном направлении распростра-
нения волн;
длина волны - горизонтальное расстояние между вершинами двух
смежных гребней на волновом профиле, проведенном в генеральном направ-
лении распространения волн;
длина гребня — горизонтальное расстояние между подошвами двух
смежных ложбин на волновом профиле, проведенном перпендикулярно к ге-
неральному направлению распространения волн;
период волны - интервал времени между прохождением двух смежных
вершин волн через фиксированную вертикаль;
скорость волны — скорость перемещения гребня волны в направлении
ее распространения, определяемая за короткий интервал времени порядка
периода волны;
уклон взволнованной поверхности - угол между горизонтальной прямой
и касательной к волновому профилю в некоторой его точке.
Считая эти элементы случайными величинами, зависимости между ни-
ми наиболее полно определяют с помощью функций распределения. Разли-
чают два вида таких функций: одни описывают разнообразие элементов волн
при фиксированной балльности волнения (или силе вызвавшего его ветра) и
называются функциями распределения при квазистационарном волнении или
просто функциями распределения, другие характеризуют разнообразие эле-
ментов волн за длительные промежутки времени, исчисляемые годами, и на-
зываются режимными функциями распределения. В расчетах мореходных ка-
57
честв судов используются в основном функции распределения при квазиста-
ционарном волнении, на которых мы и остановимся.
Теоретическими и экспериментальными исследованиями установлено:
функция распределения F(x), характеризующая вероятность того, что эле-
менты волн равны заданной величине х или превышают ее, (называемая так-
же функцией обеспеченности) определяется общей формулой
(3.7)
к~
F(x°) = exp - Л
где х° - нормированное по среднему значению (х° = х/х), х - среднее зна-
чение элемента волн х. Значения А и к - параметров, полученных в результа-
те обобщения натурных данных, - приведены в табл. 3.1 [2,36].
Таблица 3.1. Значения параметров Л и А: функции распределения
Элементы волн А к
Высота h 0,785 2
Период т 0,712 3
Длина 2 и длина гребня L 0,757 2,3
Распределение значений высоты волн подчиняется закону Рэлея
(рис. 3.3); параметры распределения периодов зависят от спектрального со-
става волнения и могут несколько отличаться от указанных.
Рис. 3.3 Распределение высоты волн глубокого моря:
1 - гистограмма; 2 - теоретическая кривая
Формула (3.7) определяет разнообразие элементов волн заданной обес-
печенности по отношению к средним элементам волн. Поэтому, задавшись
обеспеченностью (вероятностью превышения) по формуле (3.7) или по соот-
ветствующей ей табл. 3.2, легко найдем, во сколько раз элемент волны задан-
ной обеспеченности больше (или меньше) среднего элемента волн.
Например, из табл. 3.2 следует, что при обеспеченности волн, равной
3%, высота волны h3%, фигурирующая в шкале балльности Главного управ-
ления гидрометеорологической службы (ГУ ГМС), в 2,11 раза больше сред-
ней высоты волн. Эта шкала служит для визуальной оценки интенсивности
58
волнения; она приведена в табл. 3.3. Наибольшая высота волн, принимаемая
равной высоте волны с обеспеченностью 0,1%, превышает среднюю в 2,97
раза.
Таблица 3.2 Зависимость отклонения относительно средних
элементов волн от обеспеченности
нормированные элементы волн Обеспеченность, %
0,1 1 3 5 10 30 50 70 90 95
Высота 2,97 2,42 2,11 1,95 1,71 1,24 0,94 0,67 0,37 0,26
Период -Р 2,13 1,86 1,70 1,61 1,48 1,19 0,99 0,79 0,53 0,42
Длина Я0 и длина гребня £° 2,62 2,19 1,95 1,82 1,62 1,22 0,96 0,72 0,42 0,31
Таблица 3.3 Шкала балльности волнения
Балл степени волнения Высота волны, 113%, м Словесная характеристика волны Балл степени волнения Высота волны, h3%, м Словесная характеристика волны
0 0 Отсутствует V 2,0-3,5 Сильное
I До 0,25 Слабое VI 3,5-6,0 »
II 0,25-0,75 Умеренное VII 6,0-8,5 Очень сильное
III 0,75-1,25 Значительное VIII 8,5-11,0 » »
IV 1,25-2,0 » IX 11,0 Исключительное
В зарубежной практике для оценки интенсивности волнения часто
применяется понятие «значительной высоты» волн, которая определяется как
средняя от одной трети наиболее высоких (из всей совокупности) волн. Это
понятие используется для визуальной оценки состояния моря: по мнению
иностранных океанографов, именно такие волны четко фиксирует на поверх-
ности моря невооруженный глаз наблюдателя.
Между средней высотой волн Л и «значительной высотой» hi/3 суще-
ствует соотношение:
Л]/3 =1,6Л ,
откуда высота волны 3%-й обеспеченности
^з% = М3й|/з
Таблица 3.4 Соотношение между значениями средней высоты
и обеспеченностью волн
Обеспе- ченность, % Обеспе- ченность, % й|/п /Л Обеспе- ченность, % Л1/л/А
1 2,68 10 2,02 70 1,24
3 2,39 30 1,63 90 1,08
5 2,24 50 1,41 95 1,05
59
Таким образом, высота волны Л3%, фигурирующая в шкале балльности
волнения ГУГМС, заметно превышает значительную высоту волн. Это нуж-
но иметь в виду при оценке степени балльности волнения с использованием
данных визуальных наблюдений. Соотношение между средней высотой волн
и средней высотой hy„ заданного числа наиболее высоких волн при разной
обеспеченности приведено в табл. 3.4.
Распределение элементов смешанного волнения в общем случае может
отличаться от устанавливаемого формулой (3.7); для высоты волн это отли-
чие, как показывают натурные данные, обычно незначительное; закон рас-
пределения периодов при указанных в табл. 3.1 параметрах может заметно
отличаться от приведенного.
Иногда обеспеченность высоты волн выражают с помощью формулы,
вытекающей из распределения Рэлея:
' Ь2
Г(Л) = ехр
(3.8)
где D^- дисперсия волновых ординат. Отсюда любая характерная высота
волны оказывается пропорциональной корню квадратному из дисперсии —
стандарту высоты волны. В частности, средняя высота волны
Л =2,5^,
высота волны 3 %-й обеспеченности
Лз% = 5,з7^,
значительная высота волны
Таблица 3.5 Значения повторяемости волнения в различных районах
Наименование бассейна Повторяемость (в %) при балльности волнения
0-Ш IV-V VI и более
Океаны:
Атлантический 41 39 20
Индийский 44 36 20
Тихий 43 38 19
Моря:
Балтийское 81 18 1
Баренцево 63 23 7
Берингово 70 27 10
Каспийское 77 18 5
Охотское 63 27 10
Северное 55 33 12
Черное 76 19 5
Японское 70 25 5
60
Таблица 3.6 Распределение повторяемости волн 3%-й обеспеченности
Море Время года 1 Высота волн, м
0-1,25 1,25-2,0 2,0-3,0 3,0-5,0 5,0-7,0 более 7
Балтийское Зима 64 15 11 8 2 0,5
Весна 81 9 7 3 0,5 0
Лето 84 8 5 3 0,5 0
Осень 72 12 9 6 1 0
Средняя за год 75 11 8 5 1 0
Баренцево Зима 36 17 16 21 7 3
Весна 53 15 13 15 4 0,5
Лето 72 11 9 7 1 0
Осень 50 14 14 17 4 1
Средняя за год 53 14 13 15 4 1
Каспийское Зима 67 12 11 8 2 0,5
Весна 78 9 8 4 1 0
Лето 78 9 8 4 1 0
Осень 69 12 11 7 1 0,5
Средняя за год 73 10 10 6 1 0,5
Охотское Зима 40 21 18 14 4 3
Весна 56 18 14 7 3 2
Лето 66 15 10 6 3 0
Осень 42 20 17 12 5 4
Средняя за год 51 19 15 9 4 2
Черное Зима 71 13 8 4 2 1
Весна 87 6 4 2 1 0
Лето 88 6 3 2 1 0
Осень 79 11 5 3 2 0
Средняя за год 80 10 5 3 2 0,5
Японское Зима 53 15 14 12 3 3
Весна 64 15 10 7 3 1
Лето 69 15 8 5 3 0
Осень 60 16 11 8 4 1
Средняя за год 62 15 11 8 3 1
Зима: декабрь - март; весна: апрель - сентябрь - ноябрь май; лето: июнь - август; осень:
61
Для оценок мореходности судна в определенном водном бассейне ха-
рактерные балльность и элементы волн следует назначать с учетом повто-
ряемости волнения различной интенсивности как в среднем за год, так и по
временам года. Значения повторяемости волнения различной балльности в
важнейших бассейнах Мирового океана, осредненные по всем временам го-
да, приведены в табл. 3.5. Данные таблицы показывают, что наиболее бур-
ными являются океаны, наиболее спокойными — закрытые моря. Последнее
объясняется двумя причинами: во-первых, длина участков поверхности моря,
на протяжении которых действует ветер одного направления (длина разго-
нов), в закрытых морях сравнительно невелика; во-вторых, повторяемость
штормов того направления, на котором существует достаточно большая дли-
на разгонов, гораздо меньше, чем повторяемость штормов в данном бассей-
не. Распределение повторяемости волн 3%-й обеспеченности в разные вре-
мена года в морях, омывающих берега России, приведено в табл. 3.6.
§ 3. Спектральный метод исследования и структура морского
ветрового волнения
Спектральный метод исследования и расчета морских волн основан на
суперпозиции простых гармонических волн, в качестве которых принимают-
ся плоские прогрессивные волны относительно малой амплитуды. Если нере-
гулярное волнение имеет двумерный характер, т. е. длина гребней очень ве-
лика, то ордината волнового профиля
со
В = COS(V - (Of + <5j),
i=l
где dj и St — амплитуда и начальная фаза i-й спектральной составляющей
волнения; к, и — ее волновое число и круговая частота; х — горизонтальная
координата, отсчитываемая в направлении бега волн; t — время.
Трехмерный характер ветровых волн можно отразить, складывая пло-
ские прогрессивные волны, распространяющиеся в различных направлениях.
Обозначив через угол, образуемый направлением бега i-й гармонической
составляющей с осью ох, в результате сложения бесконечно большого числа
таких составляющих получим
cos[*f (xcos5y - у sin^) - co^t + . (3.9)
i=i 7=i
Отсюда видно, что ординаты поверхности моря z = £в(х, у, 0 меняются
как в направлении бега волн (координата х), так и вдоль их гребней в направ-
лении оу, перпендикулярном к ох.
Для количественной оценки процесса волнения с помощью представ-
ления (3.9) используются энергетические соотношения. В соответствии с
теорией плоских прогрессивных волн энергию каждой i-й гармонической со-
ставляющей волнения, входящей в структуру (3.9) и имеющей j-е направле-
ние, можно представить в виде = pga^ /2. С другой стороны, обозначив
62
через s удельную энергию волн, приходящуюся на единицу площади поверх-
ности моря, определим энергию i-й гармонической составляющей с у-м
направлением на бесконечно малых интервале частот Ла> и угле распростра-
нения АЭ как Ец = s (to, 3) А<оА9. Тогда амплитуда этой составляющей
l2s(<v,3) г--------т _ _ s((0,3)
a{i= —------<JA(o-A& или, вводя обозначение о> =------, можем запи-
\ Pg Pg
сать:
ау = ^28^,3)^ А(о-АЗ. (3.10)
Тем самым амплитуды гармонических составляющих волнения опре-
деляются через его удельную энергию.
Функция 8^(а>,3), характеризующая распределение удельной энергии
волн по частоте и направлениям распространения, называется двумерной
спектральной плотностью волнения или двумерным энергетическим спек-
тром. С его помощью можно количественно оценивать трехмерное морское
волнение. Проинтегрировав функцию 8^((1),3) по всем возможным углам
распространения •?, например, от 0 до 2л, получим одномерный энергетиче-
ский спектр называемый также частотным. Он служит для описания
двумерного волнения либо колебаний уровня воды в точке. Размерность
спектральной плотности Ь2Т. В зарубежной литературе энергетическим спек-
тром иногда называют величины S{to,3), а иногда 2s(a>,3)l g, от чего суть
структурного представления морского волнения, конечно, не меняется.
Однако зависимость (3.10) определяет процесс изменения ординат вол-
нового профиля (3.9) не полностью: неизвестны фазы отдельных гармониче-
ских составляющих. В спектральном методе считается, что в интервале углов
от 0 до 2 я-эти фазы равновероятны; тем самым в описание морского волне-
ния в явном виде вносится элемент теории вероятности. Это позволяет уста-
новить количественные зависимости между спектральными и статистиче-
скими характеристиками волнения, рассматриваемого как случайный про-
цесс, т. е. как случайная функция времени.
В большинстве практических приложений, связанных с изучением
морского волнения и мореходных качеств судов, оказывается достаточным
знать основные вероятностные характеристики случайных функций времени
- математическое ожидание, дисперсию и корреляционную функцию. Слу-
чайная функция £B(t) называется стационарной, если ее вероятностные ха-
рактеристики не зависят от времени t. Следовательно, математическое ожи-
дание gB(t) и дисперсия такой функции - величины постоянные, а кор-
реляционная функция /?(г) зависит только от временного интервала г. Слу-
чайная функция обладает эргодическим свойством, если ее вероятностные
характеристики, вычисленные по множеству реализаций, равны соответст-
вующим характеристикам, найденным по одной продолжительной реализа-
ции.
63
В теории стационарных случайных процессов получены соотношения
между спектральной плотностью процесса 5^(<у) и его корреляционной
функцией 7?(z) [36]:
Sf(a>)=— p?(r)cos<yr dr; R(f)= JSf(ft>)cos®rdfi>. (3.11)
к о 0
Зная одну из этих величин, легко определить другую. Для использова-
ния зависимостей (3.11) при изучении морского волнения последнее нужно
считать стационарным случайным процессом. Это несправедливо, если рас-
сматривать процесс ветрового волнения в целом, начиная с ранних стадий
его развития и кончая затуханием или обращением в мертвую зыбь. Однако
при практической оценке мореходных качеств судов обычно интересуются
характеристиками квазистационарного волнения, т. е. волнения определен-
ной балльности. Эти характеристики оцениваются по регистрации процесса
за ограниченный промежуток времени (порядка 30 мин), в течение которого
математическое ожидание и дисперсия волнения изменяются, как правило,
незначительно. Поэтому с некоторой долей условности запись волнения ука-
занной продолжительности можно рассматривать как реализацию стацио-
нарного случайного процесса и результаты ее обработки использовать на ос-
нове теории стационарных случайных процессов.
Рис. 3.4 Распределение ординат волн глубокого моря
Анализ многочисленных записей волнения, проведенный разными ис-
следователями в различных бассейнах, показывает, что ординаты ветровых
волн глубокого моря практически всегда распределены в соответствии с
нормальным законом Гаусса. Это иллюстрирует рис. 3.4, на котором эмпири-
ческое распределение — гистограмма ординат волн — сопоставлено с теорети-
ческой кривой Гаусса (плавная кривая). То, что процесс волнения является
нормальным (гауссовым) случайным процессом, можно показать и теорети-
ческим путем, используя одну из основных теорем теории вероятности -
центральную предельную теорему. Применяя эту теорему, а также пред-
ставления (3.9) и (ЗЛО), нетрудно установить связь между дисперсией волно-
вых ординат и двумерным энергетическим спектром:
64
D( = f \S((co)d<od9. (3.12)
O-JT
Переходя к одномерному (частотному) спектру, получим
D(=X\S({cd)da . (3.13)
о
Эта формула является частным случаем зависимости (3.11) для корре-
ляционной функции, если в последней принять т= 0. Но высота волны рас-
пределена по закону Рэлея и связана с дисперсией формулой (3.8); следова-
тельно, формулы (3.10) и (3.13) определяют связь между такими статистиче-
скими характеристиками нерегулярного волнения, как средняя высота, или
высота волны заданной обеспеченности, и его энергетический спектр.
Для установления более сложных зависимостей между статистически-
ми и спектральными характеристиками волнения используется понятие мо-
мента спектра. Моментом порядка г частотного спектра 5^(<у) называют ве-
личину
dar, г>0. (3.14)
о
Понятие момента двумерного спектра удобнее ввести, представив ор-
динату поверхности моря, покрытой трехмерными волнами, в виде
<й(0 = £ iaU COS(W,X - Vjy - (Oyt + Sy ),
<=l >1
где и = к cos 9, v= к sin 9, а к - волновое число в направлении 9.
Энергия каждой составляющей, приходящаяся на бесконечно малый
1 2
интервал волновых чисел AunAw.—pga (ut,Vj) = s(u,v)Au • Ли, где s(u, и) -
удельная энергия волн. Поэтому функцию
f pg 2Ли-Аи
характеризующую распределение удельной энергии в зависимости от волно-
вых чисел ни и, тоже называют двумерным энергетическим спектром.
Между спектрами S^{a>,9) и S^(u,u) существует простая связь. Так,
для случая глубокой воды, когда и =(<у2 Ig)-cos9; и=(а>21 g)-sm9, имеем
SAeo,9)=^-SA — cos«9,-~— sin А (3.15)
g \g g )
Теперь можно ввести, аналогично понятию момента частотного спек-
тра, понятие момента двумерного спектра. Моментом порядка р, q спектра
S^(u,v) называют выражение вида
mpq= J ^S^u,v)upu4dudv. (3.16)
5 Зак 3686
65
Из формул (3.13) и (3.14) видно, что момент нулевого порядка (г = 0)
частотного спектра определяется той же формулой, что и дисперсия волно-
вых ординат, т.е.
mo = Dc.
Значит, статистические характеристики высоты волны однозначно вы-
ражаются через момент спектра нулевого порядка. В частности, средняя вы-
сота волны
h =2,5д/й^;
высота волны с обеспеченностью р%
hp%=fn(.p)^,
где в соответствии с законом Рэлея
/я(р)=2[-21п(Л/о/100)]’/2.
Для определения среднего периода подсчитываются промежутки вре-
мени между последовательными прохождениями процесса <f(Z) через нулевое
(среднее) положение, или, как говорят, нули функции Если ее ординаты
распределены по закону Гаусса, то средний период
т = 2fr^D^/D^.,
где - дисперсия производной dgldt. Тогда с учетом спектрального пред-
ставления (3.9), (3.10) и формулы (3.12) получим
I1'2
J ^S^{a>,&)da)dS
г = 2я ------------------- .
J ^S^(a>,ff)a>2da>d,9
Интегрируя по направлениям распространения спектральных состав-
ляющих и переходя к частотному спектру, в соответствии с выражениями
(3.13) и (3.16) найдем
г = 2я^тп0 / ти2 ,
где момент спектра второго порядка
ОО
«2 = lS^(cd)a)2da).
о
Таким образом, средний период волн однозначно определяется момен-
тами частотного спектра нулевого и первого четного порядков. Рассматривая
вместо процесса изменения волновых ординат <ГВ(/) процесс <Г5(0, можно
подсчитать средний промежуток времени между двумя последовательными
максимумами
т = 2л’Л/т2/»14, (3.17)
где момент спектра четвертого порядка
со
ТП4 = |5^(<у)<у4£/<у.
о
Формула (3.17) учитывает возможное наличие вторичных экстремумов,
в частности, отрицательных максимумов, обращенных выпуклостью к нуле-
вой средней линии процесса £"в(0- Число отрицательных максимумов опре-
деляется формулой
/ = |р-(«2/л/,Ио"14)]-
Число I связано с характеристикой ширины спектра £ зависимостью
где
е=т11-(т11тот4 ).
Таким образом, подсчитав моменты нулевого, второго и четвертого по-
рядка, можно количественно оценить ширину спектра.
Для установления связи между пространственными характеристиками
волнения и энергетическим спектром используются понятия моментов спек-
тра в форме (3.16). Средняя длина волны
^ = 2л-7/Я00/от2Пт»
а средняя длина гребня
L = 2^V"I00/"I2mm >
где
ОО ОО
»loo= J $Sf(u,u)du du;
=|["I20 +-J(m20 - "’ог)2 +4zmi2i +"2o2];
w2min = |[w20 - л/Оиго -*”02)2 +4zMn + '«ог];
ОО ОО
/и20 = J ^S^(u,u)u2du du;
оо оо
mn = j jSf(u,u)uu du du; •
CO OO
m02 = J fS^-(u,u)u2du du.
Отсюда легко найти среднее значение показателя трехмерности волне-
ния AIL . Зная энергетический спектр волнения, нетрудно рассчитать прак-
тически все необходимые для оценок мореходных качеств средние характе-
ристики волн, по которым с учетом законов распределения элементов волн
(см. § 2) вычисляются высота, период, длина заданной обеспеченности.
66
5*
67
Для двумерной спектральной плотности в практических расчетах
обычно используется приближенное представление, базирующееся на обоб-
щении экспериментальных данных:
где S^(a>) - частотный спектр волнения; - его угловой спектр.
Таким образом, для определения двумерной спектральной плотности
можно вычислять частотный и угловой спектры по соответствующим рас-
четным формулам. Гораздо обстоятельнее изучен частотный спектр, анализ
которого базируется на записях волнографов, накопленных за последние де-
сятилетия в большом количестве.
Существуют два основных способа получения аналитических зависи-
мостей одномерной спектральной плотности волнения от частоты. Первый из
них, широко применяющийся как океанографами, так и судостроителями, со-
стоит в построении расчетных формул непосредственно для спектральной
плотности на основе анализа записей волнения и структурных зависимостей,
правильно отражающих физические особенности волнообразования. Второй
способ, применявшийся в 50-е годы, по-видимому, только судостроителями,
заключается в предварительном анализе корреляционной функции, получен-
ной по записям волнографа, аппроксимации ее приближенной аналитической
зависимостью и последующем выводе формулы для частотного спектра из
соотношения (3.15). Таким путем были получены, например, формулы Н. Н.
Рахманина и Г. А. Фирсова, которые широко использовались при оценке мо-
реходности.
Остановимся подробнее на первом способе, применявшемся рядом ав-
торов для построения приближенных формул, отражающих зависимость час-
тотного спектра от спектральной частоты и параметров, характеризующих
состояние моря в штормовую погоду. В качестве этих параметров некоторые
авторы принимали характеристики ветра над морем (волнообразующие фак-
торы), другие — характерные элементы волн, чаще всего их среднюю высоту
и средний период (или частоту).
Первая по времени аналитическая формула для частотного спектра бы-
ла получена Нейманом:
, ( 2д2
SAco) = Сео6 ехр----
со и
(3-18)
где постоянная С = 4,8 м2 -с’5. Как видно, этот спектр однопараметрический;
он зависит только от средней скорости ветра й и не содержит других волно-
образующих факторов, таких как длина разгона или продолжительность дей-
ствия ветра. Принято считать, что он отвечает идеальным условиям предель-
ного развития волн. Для таких условий между высотой волн 3% -й обеспе-
ченности и средней скоростью ветра справедливо соотношение
= 0,00935м2,5.
Следовательно, в формуле (3.18) вместо и в качестве параметра можно вве-
сти Лз„/о, получив модифицированный спектр Неймана. Этот спектр при раз-
68
ных hy,A приведен на рис. 3.5. Он хорошо отражает физическую суть явления:
чем больше характерная высота волн (или скорость вызвавшего их ветра),
тем больше удельная энергия волнения и тем выше расположена кривая
спектральной плотности.
Рис. 3.5 Модифицированный частотный спектр Неймана
Максимальной ординате спектра отвечает частота а>тт = 0,816 glи . По мере
удаления от данной частоты ординаты кривой быстро уменьшаются, причем
зоне а> <«Упих отвечает гораздо более интенсивное снижение спектральной
плотности, чем зоне а» а>тт. Это объясняется тем, что в зоне длиннопери-
одных спектральных составляющих, где значения скорости ветра и волнения
выравниваются, передача энергии ветра волнам затруднена, а для состав-
ляющих, фазовая скорость которых равна или больше средней скорости вет-
ра, она вообще отсутствует.
Другое выражение для частотного спектра предельно развитого волне-
ния было предложено Пирсоном и Московитцем на основе спектрального
анализа большого числа волнограмм, которые были записаны в Северной
Атлантике на английских и американских кораблях погоды; оно имеет вид
,4"
5г(<у)=2^~ ехр
(О
(3.19)
где а= 0,0081; /7= 0,74; w - средняя скорость ветра на высоте 19,5 м над по-
верхностью моря.
Попытка отойти от модели полностью развитого волнения путем учета
Длины разгона и продолжительности действия ветра была предпринята Вэ-
ном. Обобщив различные эмпирические данные, он пришел к следующей
формуле для частотного спектра:
Si(fi>) = KtaT(> ехр(- (3.20)
69
с'уп р.3/2
где К, = 7,5-104см2 с5; Л, =--------- 8-
'—1= V"
(t — продолжительность действия ветра, с; и - его скорость, м/с; tm = 232и).
Чтобы учесть зависимость спектра от длины разгона волн х (в метрах),
в формуле (3.20) вместо Л, следует подставить величину
, _ 82,3gs/3
х~7 \
,г~ 1 X
у/х----1=.
----, гдех<хт; xm=l,41w2.
«4/3
Представление частотного спектра в зависимости от волнообразующих
факторов удобно для последующего вычисления статистических характери-
стик волнения. Если этот спектр нужен для вычисления спектральной плот-
ности элементов какого-либо случайного процесса, обусловленного действи-
ем волн, например, качки корабля, то удобнее представлять его в зависимо-
сти от характерных параметров волн (средняя высота, средние период или
частота, высота заданной обеспеченности, период или частота, отвечающие
максимуму спектра). Последние задаются исходя из известных океанографи-
ческих сведений о волнении в данном бассейне или из специфических усло-
вий решаемой инженерной задачи, например, из условия определения наибо-
лее неблагоприятных параметров качки. Из ряда выражений, полученных в
такой форме, приведем наиболее распространенные в инженерной практике.
Формула Ю. М. Крылова для линейного частотного спектра, выведен-
ного на основании теоретических соображений:
/ ..\-7
ехр -0,78:
-4“
£Дй>) = 0,0795А2? =
\со,
где т — средний период волн; со- средняя частота волн.
Формула А. И. Вознесенского - Ю. А. Нецветаева
\б Г
й,пм*- ехр -1,5
со J I
где m0 = Df - момент нулевого порядка; со^ - частота, отвечающая макси-
муму спектра.
Формула, рекомендованная II Международным конгрессом по конст-
рукции и прочности судов:
_ . . 9,43 (сотм
Sc{co) =—т0 -аи-
(О I со
2л-У
(3.21)
(3.22)
(1 V
S (й>) = 0,0175Л^г
\тсо)
где йз% — высота волны 3 %-й обеспеченности.
Формула, рекомендованная 12-й Международной конференцией опы-
товых бассейнов:
ехр -0,44
\тй)
(3.23)
70
S^-(a>) = Ata>5 exp
(3-24)
8,l-103g2
где 4=---------—
4
3,11-IO4
K4
, К - коэффициент, зависящий от степени
развитости волнения: для полностью развитого волнения К = 1, для разви-
вающегося волнения К < 1 (достигает 0,6), для мертвой зыби К> 1 (достигает
1,7).
Исследование структуры частотного спектра, проведенное И.Н. Дави-
даном, показало, что она неоднородна и в широком диапазоне частот не мо-
жет быть точно отражена ни одной из приведенных формул. В спектре суще-
ствуют три области: основного максимума (0 < со <соп), переходная
(соп < /у< <ур) и равновесная (<у> сор). В каждой из них ординаты спектраль-
ной плотности волнения могут быть рассчитаны по формулам
\5
^тах
х5
^тах ]
<У )
S({co) = 6со^т0(соп)со~6 ехр! -1,2
• при СО<СОП-,
S(co„)~ S(con)
SAco) = S(con')+-Е----—(со-соп) при соп <со<а>р;
S<(<w) = 7,8-10-3g2<y"5 при со>сор,
Л2гу3-0,Зж®
где тп(соп) =----7----;
2^+0,3<Э
=1,04^-(1 + 2-10~3г);
^тах=0:
0,06
(О
Однако на практические оценки мореходности различие в частотных
спектрах, рассчитанных по разным формулам, в большинстве случаев влияет
незначительно. На рис. 3.6 сопоставлены кривые одномерной спектральной
плотности, рассчитанные по формулам Неймана, Г.А. Фирсова и II Между-
народного конгресса по конструкции и прочности судов.
Здесь же нанесена кривая эмпирического спектра, полученная
А.И. Вознесенским и Ю.А. Нецветаевым по результатам анализа натурных
записей волнения. Несмотря на заметное различие кривых в низкочастотной
зоне и в районе максимума спектра, вычисленные по ним с помощью спек-
трального метода амплитуды бортовой качки 2%-й обеспеченности оказались
одного порядка и разница между ними не превысила 20%.
Расчетные зависимости для углового спектра , характеризующе-
го распределение удельной энергии волн по направлениям распространения
спектральных составляющих, базируются на анализе результатов аэросте-
71
реофотосъемки и записей самоориентирующихся волномерных буев, позво-
ляющих измерять уклоны в двух взаимно перпендикулярных направлениях.
Рис. 3.6 Сопоставление различных частотных спектров для 6-балльного
волнения, рассчитанных по формулам А.И. Вознесенского и
Ю.В. Нецветаева (1), Г.А. Фирсова (2), II Международного конгресса
по конструкции и прочности судов (3), Неймана (4)
Наиболее простой и распространенной в инженерных расчетах являет-
ся формула:
^(^) = -cos2 & ,
(3.25)
где т.е. элементарные волновые гармоники, бегущие навстречу
средней скорости ветра, отсутствуют. Эта формула справедлива при умерен-
ном волнении. В случае сильного шторма рекомендуется формула
5<(19) = ^-со84.9 . (3.26)
Оказалось, что в зависимости от балльности волнения, а также от ста-
дии его развития угловой спектр приближенно описывается функцией
cos" i9, где для ветровых волн 2< п < 5, а для мертвой зыби п достигает 10.
Более детальные исследования структуры углового спектра показали,
что он зависит и от спектральной частоты:
л( 1,8
1,8
5^ = 2 4
1,8
(cos^p,
(3.27)
)
где 6\=(о1ф - безразмерная частота. Таким образом, = f(a>,3).
Согласно результатам натурных наблюдений угловой спектр зависит
также от интенсивности волнения и может быть определен по формуле
72
s(W=
K^exp -K|^ -2
(^+1)
(3.28)
'J
2(щ, +1) Л-exp -л ,
I L 2(<ц+1)2.
2
где а\ = <у/<утах, а параметр К зависит от волнового числа = (о^ /g,
отвечающего максимуму частотного спектра, и уменьшается с увеличением
последнего; в частности, при кт1а =0,016 рад/м К = 8, при =0,036 рад/м
К = 5,при Атах =0,144 рад/м К = 3.
Рис. 3.7 Распределение удельной энергии волн по частотным
и угловым интервалам
Для получения двумерной спектральной плотности волнения нужно
частотный спектр, вычисленный по одной из формул (3.19) - (3.24), умно-
жить на угловой, определяемый формулами (3.25) - (3.28). В итоге основная
часть энергии волн будет сосредоточена в довольно узком угловом и частот-
ном диапазонах вблизи максимума спектра. Это иллюстрирует рис. 3.7, на
котором показано распределение спектральной плотности волнения по угло-
вым и частотным интервалам.
Энергетический спектр смешанного волнения существенно отличается
от рассмотренного: он, как правило, имеет два максимума, которые прибли-
женно соответствуют максимумам каждой из волновых систем, составляю-
щих смешанное волнение. Максимум спектра зыби обычно располагается в
низкочастотной области, максимум ветровых волн — в зоне более высоких
частот.
На спектральный состав морского волнения заметное влияние оказыва-
ет ограниченность водоема, в частности, близость берега и мелководье. Тео-
ретическое исследование на базе теории рефракции нерегулярных волн и
спектральный анализ синхронных записей волнения в разных точках при-
брежной зоны позволили выяснить, как изменяются частотный и угловой
спектры при выходе волн на мелководье.
73
Рис. 3.8 Сопоставление частотных спектров волнения
на глубокой воде (1) и мелководье (2). Расчетный спектр (3)
На рис. 3.8 приведены эмпирические частотные спектры волнения на
глубокой воде (кривая 1) и в прибрежной зоне (кривая 2) при относительной
глубине водоема Н/ =0,2 (Н- глубина воды, - средняя длина волн на
глубокой воде) и угле между направлением береговой черты и генеральным
направлением фронта волн 20° < а < 40°. Там же изображен соответствую-
щий расчетный спектр (кривая 3). Видно, что удельная энергия волн при вы-
ходе на мелководье заметно уменьшается.
Рис. 3.9 Угловые спектры волнения
на глубокой воде (1) и мелководье (2)
На рис. 3.9 показаны эмпирический угловой спектр волнения на глубо-
кой воде (кривая 1), расчетный угловой спектр на мелководье (кривая 2) при
777^0= 0,2 и а = 50°, а также экспериментальные точки для соответствую-
щих значений этих параметров. Очевидно, процесс трансформации волн в
прибрежной мелководной зоне сопровождается заметным сужением углового
74
спектра и приближением характера волнения к двумерному. Эмпирические и
расчетные данные хорошо согласуются, поэтому рассматриваемый процесс
можно описывать линейной спектральной моделью. По мере приближения к
берегу каждая спектральная составляющая частотного и углового спектров
деформируется по законам гидродинамической теории волн без значитель-
ных потерь энергии, вплоть до начала обрушения гребней, которое наступа-
ет, согласно натурным данным, при h =0,5 Н. Это условие можно предста-
вить и в более удобной для расчетов форме
ho6plh0 =0,5^/^,
где йс - средняя высота волн к началу обрушения гребней; h0 — средняя
высота волн на подходе к прибрежной зоне; Зй =Л0//!() - условная средняя
крутизна волн. При h > ho6p волны разрушаются, процесс перестает быть ста-
ционарным, и закономерности, вытекающие из спектральной теории, теряют
силу. Для этой зоны аналитические выражения, определяющие динамическое
действие волнения, отсутствуют, и при оценке пользуются эмпирическими
данными, полученными в океанографии, гидротехнике и теории корабля.
§ 4. Выбор расчетного спектра волнения
Известно большое число формул, предложенных различными исследо-
вателями для аналитического описания энергетических частотных спектров
волнения. Как показывает анализ, различия этих спектров обусловлены,
главным образом, влиянием условий волнообразования (продолжительность
действия ветра, разгон, гидрологические условия и т. д.) и ограниченностью
экспериментального материала, что не позволяет рассматривать их как уни-
версальные, хотя многие из спектров несомненно являются достоверными
аппроксимациями результатов измерений волнения.
На основании имеющихся в настоящее время данных в качестве типич-
ного частотного спектра реального морского волнения рекомендуется двух-
параметрический спектр вида
Z \6
£,(«) = 9,43^-НМ ехр
(£> I (О J
где т0 = D%~ дисперсия волновых ординат; со=2л1т - средняя частота вол-
нения, определяемая по точкам пересечения волнового профиля с нулевой
линией; - частота максимума спектра; т - средний период волнения.
Для спектра (3.29) соотношение характерных частот равно
й)т =0,ТПс5.
Максимальная безразмерная ордината спектра sm = S^m(i)lmG = 2Д0; ширина
спектра £ = 0,75. График спектра изображен в виде безразмерной функции
8^со)а)1тй = f(a)la>m) на рис. 3.10.
75
Рис. 3.10 График энергетического спектра морского волнения
Применяемые в зарубежной практике спектры Пирсона - Московица,
Бретшнайдера, II Международного конгресса по конструкции судов (1971) и
12-й Международной конференции опытовых бассейнов (1969), по существу,
не имеют отличий от спектра (3.29) и могут быть представлены в аналогич-
ной форме:
5Д<у) = Я^Р^-1 ехр ,
а> V а> J V ю J
где А = 6,99-7,06; В = 1,24 - 1,25, к = 5, п = 4.
Для полного описания спектра волнения (3.29) достаточно определить
два параметра: соответствующие заданной интенсивности волнения диспер-
сию ординат волн и их средний период т. Согласно принятой в СССР
шкале степени волнения ГУ ГМС 1953 г. (табл. 3.3) интенсивность волнения
определяется по высоте волны с обеспеченностью (вероятностью превыше-
ния) 3%. Поэтому для вычисления дисперсии волновых ординат по заданной
высоте волны используется зависимость
= 0,143(0,5Л3% У = 0,0358й3% . (3.30)
Входящее сюда значение Лз% выбирается по шкале степени волнения в соот-
ветствии с заданными условиями расчета. Следует заметить, что при исполь-
зовании формулы (3.30) и шкалы степени волнения ГУ ГМС 1953 г. величина
Лз% должна определяться без учета вторичных волн, соответствующих экс-
тремумам волнового профиля, обращенным к нулевой линии. Для определе-
ния среднего периода волнения рекомендуется использовать график
(рис. 3.11), полученный по результатам обработки волномерных наблюдений
на различных морях и океанах.
76
Рис. 3.11 Связь между средним периодом и характерной высотой волн:
1 — развитое волнение; 2 — развивающееся волнение;
3 - затухающее волнение
График дает представление о зависимости т - f(hy/„) на разных стади-
ях развития ветрового волнения в открытом море. Как видно, при заданном
значении Л3% возможны различные значения среднего периода волнения, ле-
жащие в пределах заштрихованной на графике зоны. Середина этой зоны
(кривая 1) хорошо согласуется с соотношением для вполне развитого волне-
ния
г = З3д/^з% .
Для учета индивидуальных особенностей акватории соотношение меж-
ду величинами Л3% и т следует определять по данным океанографических
наблюдений. С целью получения относительно неблагоприятного спектра из
числа возможных для волнения заданной силы из значений среднего периода
выбирается такое, при котором максимум спектра располагается по оси час-
тот возможно ближе к максимуму амплитудно-частотной характеристики
рассматриваемого процесса.
Таблица 3.7. Основные параметры расчетного энергетического спектра мор-
ского волнения
Параметр Степень волнения, баллы
3 4 5 6 7 8
Высота волны Л3%, м 1,25 2,0 3,5 6,0 8,5 11,0
Средний период волн т, с 3,7 4,5 6,0 7,8 9,2 10,5
Дисперсия волновых ординат D& м2 0,056 0,143 0,438 1,29 2,58 4,33
Средняя частота волнения а, с’ 1,70 1,39 1,05 0,805 0,683 0,570
Частота максимума спектра с'1 1,32 1,08 0,809 0,626 0,531 0,433
Примечание. Высоты волн соответствуют верхним пределам диапазонов шка-
лы степени волнения.
77
Спектральная плотность углов волнового склона рассчитывается по
формуле
5а(<у) = g 2c^S^{a))51^>2 = 34Д2<у45^(<у), градус. (3.31)
Для описания трехмерного волнения спектральная плотность волновых
ординат определяется выражением
S^{(O,a) = mS^(a>)cosn а,
где а- текущее значение угла, определяющее направление распространения
спектральных составляющих трехмерного волнения ( -90° < а< 90°); -
частотный спектр волнения.
Коэффициенты тип могут принимать следующие значения:
п.............1 2 4
т.............0,5 2/л 8/Зтг.
Спектральная плотность углов волнового склона определяется выра-
жением, аналогичным (3.31).
Изложенный способ определения энергетического спектра волнения
дает удовлетворительные результаты при выполнении сравнительных расче-
тов качки судов или проверке на действие морского волнения конструкций,
частотные характеристики которых отличаются широкой полосой пропуска-
ния и имеют достаточно большие значения в зоне максимума спектра волне-
ния. Однако на практике могут встречаться случаи, когда спектральная плот-
ность выходного процесса формируется, главным образом, за счет низкочас-
тотных составляющих спектра волн (0,4 < а>< ц^,). Это может быть, если
обследуемый объект представляет собой фильтр низких частот, т. е. имеет
полосу пропускания в диапазоне 0 — a>i, где частота <Оу < <ц„. В этом случае
выбор расчетного спектра требует особого внимания. Недостаток данных о
низкочастотном диапазоне спектров волнения и разнообразие возможных в
действительности видов волнения не позволяют дать исчерпывающие реко-
мендации по этому вопросу. В качестве одного из возможных методов ис-
пользуется описание волнения с помощью суммы двух спектров, один из ко-
торых определяет волнение в зоне максимума и в высокочастотной зоне, а
второй - в зоне низких частот:
(®) = ^i(®) + ^^г(^У) •
Первое слагаемое соответствует основному спектру, а второе — допол-
нительному спектру
( \8 Г ( \4
Л’2(^) = 173-()2- —1 ехр -2,0рМ ,
а>2 ( со J V со J
параметры которого определяются следующим образом: zn02 = 0,130wioi,
(Ц„2 = 0,70^; й>2 = 0,82zyml, где тОу и сом - характеристики основного спек-
тра.
Из условия постоянства расчетного значения дисперсии волнения
wioi = 0,8850^-; прочие параметры спектра 5^(<у) определяются по рекоменда-
циям, изложенным выше.
78
Выбор параметров дополнительного спектра базируется на имеющемся
в настоящее время экспериментальном материале, анализ которого позволяет
считать, что вызванное ветром морское волнение практически не содержит в
своем составе гармоник, частота которых была бы меньше частоты максиму-
ма спектра более чем в 2,5 - 3 раза. Наличие в спектре гармоник с более низ-
кой частотой может быть объяснено сейсмическими и приливными колеба-
ниями или иными малообследованными волнообразующими факторами.
Параметры дополнительного спектра могут оказать существенное
влияние на результаты расчета, объектом которого является фильтр низких
частот. Поэтому рекомендуемый способ описания волнения должен коррек-
тироваться с учетом особенностей обследуемого объекта, требований к точ-
ности и надежности расчетов и тех новых сведений о свойствах морского
волнения, какие могут быть установлены в будущем.
По аналогии с изложенным приемом сложение двух спектров с незави-
симым выбором их параметров может применяться для расчетов воздействия
на судно смешанного волнения, т. е. двух волновых систем, одна из которых
представляет собой зыбь, накладывающуюся на ветровое волнение. Однако в
настоящее время имеется крайне мало экспериментальных материалов, кото-
рые могут быть положены в основу этого метода.
§ 5. Общая постановка задачи гидродинамики
при движении тела во взволнованной жидкости
Будем предполагать, что параметры волнения моря известны и внесе-
ние тела в жидкость в целом не сильно влияет на характеристики волнения.
Реальное морское волнение представляет собой сложный нерегулярный про-
цесс. Влияние его на движущееся тело проявляется в силовом воздействии
скоростей и ускорений волнового движения частиц воды. Учет этого воздей-
ствия в значительной мере определяется методом описания волнения. Спек-
тральный метод описания реального морского волнения основывается на
представлении его в виде суммы элементарных волновых систем различной
амплитуды, частоты и направления распространения. Как видим из § 3, 4
этой главы, распределение энергии между этими системами характеризуется
энергетическим спектром. Спектральный метод описания волнения позволя-
ет представить его в виде непрерывного физического процесса, в связи с чем
в расчетах подводного старта этот метод получил применение при статисти-
ческой оценке параметров старта.
В проектных расчетах применяется наиболее простой и наиболее изу-
ченный предельный случай для жидкости неограниченной глубины, когда
воздействие реальной волны заменяется воздействием гармонической волны.
При движении тела в воде при нерегулярном волнении используют следую-
щие характеристики стационарного случайного процесса: дисперсию D„, вы-
соту волны с заданной степенью р% обеспеченности Лр%, средний период Тср,
спектральную плотность S^. В отечественной практике оценка интенсивно-
сти волнения производится по шкале степени волнения, в основу которой
79
положена высота волны 3%-й обеспеченности (Л3%). Потенциал скорости
волнового движения жидкости принимается при этом для жидкости неогра-
ниченной глубины. Однако даже при принятых упрощающих предположени-
ях при решении гидродинамической задачи сталкиваемся со значительными
математическими трудностями. Поэтому общая гидродинамическая задача
при движении тела во взволнованной жидкости путем априорной линеариза-
ции приводится к более простой линейной граничной задаче. Потенциал ско-
рости Ф^х0,у0, z0, t) движения жидкости, выраженный в координатах старто-
вой системы, отыскивается как решение уравнения Лапласа в области, огра-
ниченной свободной поверхностью жидкости в положении равновесия, т.е.
плоскостью xD= Н, и смоченной поверхностью тела [23, 36].
Граничное условие на свободной поверхности = 0) приобретает вид
Линейность граничной задачи приводит к представлению искомого по-
тенциала Ф$ в виде суммы
6
Ф5=Фн.+Ф/, + ^Л>
т-1
где Фн - потенциал скорости свободных набегающих волн, который считает-
ся заданным; Фа - потенциал скорости диафрагмированного волнового дви-
жения; (рт = <рт(х$, у0, z0) - функции, характеризующие ту часть потенциала
скорости возмущенного движения жидкости, которая обусловлена движени-
ем тела в покоящейся воде. Обычно такая постановка гидродинамической за-
дачи проводится в теории качки судов. Однако целесообразно объединить
два последних слагаемых в правой части и искомый потенциал представить в
виде
6
Ф5=Ф. + Е^т> (3-32)
т=1
где Фу,- заданный потенциал скорости волн, а (рт = ^т(%о,Уо, z0) - единичный
потенциал, характеризующий часть потенциала, которая обусловлена движе-
нием тела во взволнованной жидкости. Теперь вместо двух неизвестных по-
тенциалов приходим к одному неизвестному.
Потенциал скорости движения жидкости Ф$ удовлетворяет уравнению
Лапласа
21Ф5 = 0
в области, занятой жидкостью и ограниченной ее свободной поверхностью и
смоченной поверхностью тела. На свободной поверхности должны выпол-
няться кинематическое и динамическое граничные условия. Наиболее общий
вид кинематических граничных условий на свободной поверхности жидкости
~Г^в(хо • То ’Z0 'f)~ 0,
at
а на смоченной поверхности тела
80
^-/2(xo,yo,zo,t)=O,
at
(3.33)
где уравнение свободной поверхности
С В (Х0 ’ Го >20 ’0 = 0 ,
а уравнение смоченной поверхности тела
•#CWo>W)=0-
В задачах о движении твердого тела в невязкой жидкости условие
(3.33) обычно представляют в виде равенства нормальных составляющих
скоростей жидкости и тела
бФс
—~ = ”п>
дп
(3.34)
где п - нормаль к смоченной поверхности, ц, - нормальная составляющая
скорости тела.
Динамическое граничное условие на свободной поверхности жидкости
состоит в равенстве давления атмосферному во всех точках этой поверхно-
сти: р=ра. Давление в невязкой жидкости при безвихревом движении опреде-
ляется интегралом Коши-Лагранжа, который в стартовой системе координат
записывается в виде
d<I>s р
Р = Ра+Р&0-р—±-£-
Ot 2
^sY+(W|2
8Уо ) I &о ,
5х0 ,
Будем считать, что при большом углублении от свободной поверхно-
сти волновое движение затухает, а очень далеко от источника возмущений -
тела - оно вырождается в заданную систему набегающих волн, скорости ко-
торых ограничены, то есть должны выполняться условия: ГФх —> 0 при
z0 —> оо, ограничен при —> оо. Начальное положение тела опре-
деляется координатами его центра масс tjo, Со и тремя эйлеровыми углами
<pq, де, в момент t = 0 и начальными скоростями , %, £"0, > Фо > Фо •
При решении задачи о движении тела во взволнованной жидкости
удобнее использовать связанную систему координат, в которой можно сфор-
мулировать граничную задачу.
Граничное условие (3.34) в связанной системе Oxyz представляется в
виде
бФс _ _ /------ — \ —
—^- = У0-И + (й?хГ0)-И,
дп
где v0(t>x,i>y,v2) - вектор скорости начала О связанной системы координат,
принятого за полюс; aj(tox,ay,aO - вектор угловой скорости вращения во-
круг мгновенной оси, проходящей через этот полюс, f0(x,y,z) - радиус-
вектор точки поверхности тела относительно полюса О. В проекциях на оси
связанной системы координат это условие можно записать соотношением
6 Зак. 3686
81
= F,a + V20 + V3y + V4(yy - z0)+V5 (za - xy)+V6(x/3 - ya), (3.35)
on
где Ki = vx, V2 = vy, V3 = uz, Vi = fii, V5 = tOy, V6 = лх - проекции векторов u0 и
л л л
со на координатные оси, a = cos(n,x); ft = cos(n,y); у - cos(n,z) - соответ-
ствующие направляющие косинусы.
Граничное условие (3.34) на поверхности тела с учетом представления
потенциала скоростей Ф$ в виде суммы (3.32) можно записать как
дп дп h т дп'
Производная по нормали от известного потенциала скорости волн
дФ
—— определяется по формуле
дп
дФ
~^-=^адФк,-п = и{а + и2Р + и2у. (3.36)
дп
Составляющие вектора скорости волнового потока й{их,и2,и3) рассчи-
(3.37)
(3.38)
тываются в полюсе тела.
В работах Якимова Ю.Л. при расчете динамики тела во взволнованной
дФ
жидкости используется выражение для —— в виде, приведенном в формуле
дп
di 1- ЭФ5 дФ„
(3.36). Граничное условие на поверхности тела —----— с учетом выра-
зи дп
жений (3.35) и (3.36) представляется тогда как
ЭФс ЭФ
on on
+Ул(уг- zP)+ V5(za - ху)+ Г6(хД - уа)
Существенным недостатком его является то, что в нем не учитываются
изменения иг, «з вдоль корпуса тела и решение зависит от того, в какой точке
берутся значения и2, щ. Для ликвидации этого представим составляющие
волнового потока иг, Щ в виде линейных зависимостей от координаты х [19]
ди2
и2+-к-х = и2+х-и2х,
дх
ди3
мз +—~
3 дх
ди2 ди,
где w2x = и изх = ~ производные от составляющих вектора скорости
С/Л ох
волнового потока и2 и и3 по координате х в полюсе тела. Подставляя равенст-
дФ
ва (3.38) в (3.36), найдем уточненное выражение для ——
дп
82
= ща + (м2 + х u2x)fi + (м3 + х и3хУ
дп
На профилированном носке тела у и z изменяются от нуля до радиуса
цилиндра, а а, наоборот, с их ростом уменьшается от единицы (при у = z - 0)
до нуля на цилиндре, при этом координата х измеряется от центра масс тела,
расположенного на расстоянии ~0,6 L от носка. Поэтому мржно считать, что
на теле ya « х, za « х, и вместо граничного условия (3.37) записать уточ-
ненное граничное условие на поверхности тела в виде
дФ
дп дп (3.39)
+ (у у - zy?)+(V5 -и5)(га-ху)+(У6-и6 )(xfi - у а),
где дополнительно введены обозначения и5 = -м3х и и6 = w2x •
Функции <рт, характеризующие потенциал скорости возмущенного
движения жидкости, которая обусловлена движением тела во взволнованной
жидкости, должны удовлетворять граничным условиям на смоченной по-
верхности тела
= ^.= в- д,Рз -у
’ дп ’ дп (340)
^£-=yy-zfr, ^=za-xy; ^- = хР~уа.
дп дп дп
д<р
Полученные выражения для —— (i = 1,2,..., 6) совпадают с их значе-
дп
ниями при движении тела в спокойной воде (2.12).
Потенциал скорости абсолютного движения жидкости Ф$ будет нахо-
диться по формуле
6
0.41)
i=i
где в соответствии с формулой (3.39) приняты следующие сокращения
U\ = V\ — U\, U2 — V2 — Ui, U3 = V3 — из', Ut, = И4; U$ = V3 — щ", Ub = V6 — u6.(3.42)
Таким образом, гидродинамическая задача о движении тела во взвол-
нованной жидкости сводится к гидродинамической задаче о движении тела в
спокойной воде. Полученное решение для тела, движущегося в спокойной
воде, - (^, фз, ... , - транспонируется в решение для движения во взвол-
нованной жидкости с помощью простых формул (3.41), (3.42). В соответст-
вии с выведенными нами формулами (3.41) и (3.42) уточнится выражение для
кинетической энергии жидкости при движении тела во взволнованной жид-
кости: вместо формулы (2.25), справедливой при движении тела в спокойной
воде, получим выражение
1 6 6
T2=-l1XWUk. (3.43)
Z. 1=1 fc=l
В последнюю формулу входят как скорости волнового потока, так и
градиенты его скоростей вдоль оси тела.
6*
83
Как уже отмечалось, при движении ракеты в воде при нерегулярном
волнении используются следующие характеристики стационарного случай-
ного процесса x(t): высота волны заданной р% обеспеченности hp% и средняя
длина волны Л Обычно на практике оценку интенсивности волнения прово-
дят по высоте волны 3%-й обеспеченности (Л3%). Потенциал скорости Фк для
жидкости неограниченной глубины и волнения 3%-й обеспеченности запи-
шем в виде [19]
Фю = sin(£y© cost? + kz0 smq-a> t), (3.44)
2to
где q - курсовой угол, измеряемый между направлением движения ПЛ и
направлением волны (рис.3.12), х©, уо, z© — координаты центра масс ракеты в
стартовой системе.
Рис. 3.12 Схема определения курсового угла q
Полученная нами формула для Фк (3.44) более полно учитывает усло-
вия старта ракеты и позволяет рассчитывать скорости и ускорения жидкости
на всем подводном участке траектории ракеты. Далее на основании формулы
(3.44) получим выражения для составляющих скорости волнового движения
жидкости сначала в стартовой системе координат
1 , к(х0-Н) . ( .
w10 =—^-=—hy,/owe sm\kyoce>sq+kzosmq-<i)t+£o),
oXq 2
84
u20=:-^-=—h3V(iKk^Xo co^ky0cosq+kz0sinq-tot+£0)cosq, (3.45)
5y0 2
дФ№ 1 фъ-я) z, , . ч .
ы30 =——=—hJ%(oe cos(ky0cosq+kz0smq-tot+£0)smq.
5z0 2
Затем, используя значения направляющих косинусов (1.6), осуществим
переход от скоростей в инерциальной системе координат к скоростям в свя-
занной системе координат
Щ = ОцЩо + Я21«20 + «31«30i
«2 ~ «12«10 + «22«20 + «32«30! (3.46)
Из = авМю + Ягз«2о + «зз«зо-
В дифференциальные уравнения движения ракеты (гл. 4) входят волно-
вые ускорения жидких частиц, рассчитанные в связанной системе координат
du{ du2 du2
dt' dt’ dt
Проводя дифференцирование no t выражений (3.46) и используя фор-
мулы пересчета скоростей из инерциальной в связанную систему координат,
найдем выражения для ускорений жидких частиц в связанной системе коор-
динат
^«1 _ „ ^«10 „ ^«20 , _ ^«30 , dall , ^«21 ,, , ^«31 ,, .
dt 11 dt 21 dt 31 dt dt 10 dt 20 dt 30’
£^2_-д dul0 | Д du20 I д du30 dal2 da22 ^«32 . fl 471
dt “a‘2 dt+a22 dt +“32 dt+ dt “lo+ dt “2o+ dt “30’ (3-47)
du3 dul0 , „ du20 . du30 . dal3 , ^«23 ,, , ^«33 ,,
dt " 13 dt 23 dt 33 dt dt ‘° dt “2° dt
где производные составляющих скорости представляются в виде
^«10 «20 «30 ^«20 dUjn
——=~(0——=-(0—2!-; ——=6aW|0cosg; ——=6WW|Osin^.
dt cosq smq dt dt
Входящие в дифференциальные уравнения градиенты волновых скоро-
стей найдем как производные от сложных функций
5W|o ^«20 Si/зо I'
ai2^ + fl[22 Л +°32^- -
vXq ^-^0 J
' - Зщо dl/20 .
du2
U2x =^-
dx
dx0
dx
.f „ ^10 , „ ^«20 , ^30 , | „ —ш , „ -xu „ —M
+ al2~Z--+ a22~Z--+ «32~^-- П7~+ “12^----+ «22“^-+ «32----
v dy0 dy0 dy0 J dx '
5w10
«13^—+ «23
, —xu । _ —30 ^Уо , I u? , zu
'23 "T— + «33 ---+ «13 -T +«23 — + «;
5i/10
>3 a
dux
du-
“ 3y0
du,
U3x=^ =
dx
S«20
du-
dx
Sz0
dx
v “ dz0
^2o.+a33^f30. _
dx0 dx0 ?
I _ ^«ro _l „ ^«20
3z0
5z0
8z0
dtp
dx
'зо | dzo .
dx ’
5y0
5y0 J dx
, ^30
33*^
5z0 ,
85
^'о ^Уо dZg л. л.
Учитывая, что —- = дп, —- = д21, —- = a3t, и проводя дифференци-
dx dx dx
рование по х0, уо, z0 формул (3.45), получим выражения для градиентов ско-
ростей и производных от них по времени
И2х » Л{Я12И1 + Д||Н2 - Н1о[«п«12 + («22COS9 + fl32sinq)(n21cosq + n3lsinq)]};
w3l = Л{Д1зМ1 + ДцД3 - Wio[anai3 + (n2icosq + fl33sinq)(n2|Cosq + n31sinq)]};
du3 du3x , ( du, da,-, du-, da,,
—r=------=-k<a,3—L+u.-——+a,.——+u3—LL-
dt dt 1 13 dt 1 dt 11 dt 3 dt
dut da^, du
dt 1 dt dt ’ ° dt
- (д13 + (a23 cosq + a33 sin q\a2l cosq + a3i sinq)]-
at
da*3 daxx fda23 da-i-* * ^z \
~м1о aH~7^+ai3"^+l“^costf+~^sintf 1(^21 cos<7 + 03isin<7)+
dci')] da^ii . । 1
___rno/iJ___ILoin /j I S'
dt 1 dt Jjj
_ f dux dax j du2 dax i
I12 <ft 1 dt 11 dt 2 dt
dat 3 da.
dt ’ 13 dt
(. 1Ш71 •
a23 cos# + a33 sm#)| —^-cos#+—-^-sin#
^du2x
dt dt
(3.48)
+ ^22 COSq + дз2 sin#)(a21 cos# + a3| sin#)]-
dt
da,2 da,, f da-,-, da-,-, .
-U|0 Дц—r^+a12—7*-+ —I—cosq+—~-smq (n21cosq + fl3Ismq)+
L dt dt \ dt dt )
e . da-,, da-,, . ") 1
+(fl22cosq + fl32sinqi——cosq+——sinq >.
k dt dt Jjj
Входящие в выражения (3.47) и (3.48) производные по времени от на-
правляющих косинусов вычисляются по следующим формулам:
da, । da, da,,
—=д12гдг-д13щу; -^-=д|3®х-дп<уг; -^-=aix(oy-al2(ox-,
da-,, del-,-, da-,-,
-^- = «22^7-«23®/ -^- = «23®х-«21®г; -^- = «21®y-«22®x;
da-,, da-,-, da-,-,
-^- = a32®z-«33®y; -^- = «33®х-«31®г; -^- = «3l®T-a32®x-
86
Глава 4
Дифференциальные уравнения неуправляемого
пространственного движения ракеты
Выведем уравнения движения ракеты для двух случаев: сначала для
более простого — движения в спокойной воде и затем - для движения во
взволнованной жидкости.
§ 1. Общая форма дифференциальных уравнений движения
Дифференциальные уравнения пространственного движения получим,
исходя из законов количества и моментов количества движения, приведен-
ных в §3 гл. 1. Движение относим к связанной с телом системе координат
(xyz).
Д ля триедра осей xyz угловая скорость 0)е равна угловой скорости тела
л?. Динамические параметры тела обозначим буквами Q и К, в отличие от
соответствующих динамических параметров невязкой жидкости, для кото-
рых в гл. 2 были приняты обозначения Q2 и К2 - При этих условиях исходные
законы имеют вид
^- + ®xQ=F' (4.1)
at
и
dK'+iDxK,=L’. (4.2)
dt 1
Буквами V и L' обозначены главный вектор и главный момент сил,
приложенных к телу со стороны невязкой и вязкой жидкости, веса, Архиме-
довой силы. Для главного вектора и главного момента сил давления невязкой
жидкости справедливы общие выражения
at
и
£' -VxQ2.
dt
Подставив их в формулы (4.1) и (4.2), после переноса в левую часть по-
лучим
^- + axQ=V; (4.3)
dt
—+axK + vxQ2=M, (4.4)
dt
87
где Q = Qt + Q2 - суммарное количество движения тела и всей окружающей
ее невязкой жидкости;
К =К, + К2 — суммарный момент количества движения относительно на-
чала координат;
V и М — главный вектор и главный момент всех сил, приложенных
к телу, кроме уже учтенных сил воздействия невязкой жид-
кости.
При составлении дифференциальных уравнений нужно иметь скаляр-
ную форму законов (см. формулы (4.3) и (4.4)), получаемую проектировани-
ем всех входящих в них векторных величин на оси xyz. При этом удобно
пользоваться формулами (2.29), позволяющими связать проекции Q и К с
суммарной кинетической энергией Т:
Qy =
Qz =
ST, ST2 ST ST, ! ST2 ST _
Svx Svx Svx’ Sax Sa>x Scdx ’
ST, | dT2 ST . _ ST, ! ST2 ST
Svy Svy Suy' Say Say S<oy
ST, । ST2 _ ST . Svz Svz Svz' _ ST, । ST2 ST S(oz Scoz Sa>z
Обозначая далее через i, j, к орты осей, можно написать
- т ST -ST -ST
Q =i----+ J---+k-----;
Svx Suy Svz
- ST -ST r ST
К =t----+j----+ k----.
Sax Sa>y Sa>z
Подставим эти векторы в формулы (4.3) и (4.4) и одновременно разло-
жим все остальные векторы по тем же ортам:
| ? ST
dt
у ST
dt
-ST гдт
. 1--+к-----
дб)х да>у Soz
-ST гдТ
J---+ к--
Svx диу Svz
i ST j a>y ST к ST -Vx-i + Vy-'j ¥Vz-k-,
^Vx Svy
i ^x ST S&x 1 (Oy ST Scoy к ST Sa>z + i ^x ST2 Svx j Vy ST2 Suy к ST2 ^z =
= M x • i + M j + Mz к.
88
Сопоставляя выражения при одинаковых ортах слева и справа, придем
к искомой скалярной форме законов:
d ВТ dtdvy ВТ + а д»х ~ах °L=V. Bvz yt (4.5)
d ВТ dt Buz ВТ + ат Виу ~ыу °L=v- Bvx
d ВТ ВТ + — Baz ~(Ог ВТ вт2 вт2
dt Вах Сх-. Сх„ 1V1 у « Вау у Bvz Виу
d ВТ ВТ +e°2Bax ВТ ВТ2 ВТ2 1) —I) — —/w ’ (4-6)
dt Вау ' Baz z Bvx Л Bvz y’
d ВТ dt Baz ВТ + гуг да ~шу ВТ BT2 BT2 + ь> —-~UV—-=M,. Ba Buv y Bvx л у Л
Здесь производные по времени — берутся от величин, вычисленных в
dt
подвижной системе координат, V (Vx,Vy,Vz) и M{Mx,My,Mz} есть главный
вектор и главный момент всех сил, приложенных к телу, кроме сил воздейст-
вия невязкой жидкости.
Чтобы воспользоваться этими соотношениями для вывода дифферен-
циальных уравнений, необходимо иметь развернутые выражения для сум-
марной кинетической энергии.
Найдем эти величины. Приводим их в виде, удобном для дальнейшего
использования:
а) Кинетическая энергия тела
Ту = ^М(»2Х + и2 + 4^)+ + Jy^y + Л®2 )-
б) Кинетическая энергия невязкой жидкости (формула (2.35)) при дви-
жении тела в спокойной воде
Т2 = |(Л1^ +^У + + + ^гау +
+— (Лм^х++) •
б1) Кинетическая энергия невязкой жидкости при движении тела внут-
ри взволнованной жидкости (формула (3.43))
Гг=|(Л Д2+Л^22 + Лз^з2)++
+ 1(Я44С/42+Л55С752 +Лб^б).
89
в) Суммарная кинетическая энергия при движении тела в спокойной
воде
Т = 7] + Г2 = |(М + \, )v2 + |(М + Л>2)г?2 + |(М + Язз)^ +
1 2 1 2 1 2
+ a^vo), + Л35ш» +-(Jx + Л44 )сох +-(JУ+Л55}ю +-(Л +Я66 )буг; (4.7)
’ 2 2 2
в'; Суммарная кинетическая энергия при движении тела внутри взвол-
нованной жидкости
Т' = 7] + Т2' = ^Л/(г>2 + V2 + v:)+ + Jya>2 + Jza>2)+ (4.8)
Д2 + ДД2+ДД2)+ WJ6 + л,5и3и5 + |(я44п42 + л55г2 + я66г62).
Выражения для Ui(i= 1,2,..., 6) приведены в формулах (3.42), из кото-
рых следует, что производные по совпадающим направлениям равны едини-
це
<^ = 1; = М = 1; ЗД=1- 5Д=11
Эк,. ’ dv„ ’ Эк ’ Э<у ’ Эйл ’ Э(У7
х у z х у Z
, ди, ди2
по другим - производные равны нулю (например, —L = —- = 0).
Эку Экх
§ 2. Позиционные силы и моменты воздействия вязкой жидкости
В гл. 2 рассматривалось силовое воздействие идеальной (т.е. лишенной
вязкости) жидкости на движущееся тело. Полученные результаты показыва-
ют, что в общем случае неустановившегося движения твердого тела в иде-
альной жидкости определение силового воздействия сводится к нахождению
коэффициентов присоединенных масс. В частном случае установившегося
прямолинейного движения это воздействие сводится только к моменту, ре-
зультирующая сила сопротивления отсутствует. Последнее обстоятельство
находится в явном противоречии с практикой, в гидродинамике это противо-
речие получило название парадокса Даламбера-Эйлера. На самом деле при
установившемся прямолинейном движении твердого тела в жидкости равно-
действующая сил реакции отлична от нуля. Это несоответствие теории и
практики обусловлено неучетом вязкости жидкости.
Однако применение схем потенциального обтекания с отрывом, на-
пример, схемы Кирхгофа, позволяет более полно решить гидродинамиче-
скую задачу. В прикладной гидродинамике, на основании проведенных экс-
периментальных исследований были апробированы и применены различные
схемы обтекания и разработаны методы расчета. Наиболее рациональные из
них были внедрены в практику гидродинамических расчетов. Так, в резуль-
тате проведенных экспериментальных и теоретических исследований гидро-
динамическая задача о выходе ракеты из шахты была сведена к задаче о по-
тенциальном обтекании удлиняющегося тела. Для определения сил потенци-
90
ального происхождения условно борт ПЛ заменен бесконечной плоской пла-
стиной, предполагается также, что диаметр шахты равен диаметру цилинд-
рического корпуса ракеты. Потенциал скорости течения ищется методом, ос-
нованным на распределении гидродинамических особенностей (диполей) по
оси тела вращения. Метод применим только для тонких тел с коническим
носком. Часто ракета имеет притупленную форму носка. Численное решение
в общем случае для тела с любой формой носка получено с помощью распре-
деления особенностей по поверхности тела. Решению гидродинамической
Рис. 4.1 Гидродинамическая компоновка тела:
1 — корпус тела; 2 — обтекатель, 3 — выступающие над корпусом
тела элементы, 4 - кормовой срез (днище)
Отличительной особенностью корпуса тел, выходящих из-под воды,
является сочетание профилированной носовой части и цилиндрического кор-
пуса, заканчивающегося в корме плоским срезом, а также наличие высту-
пающих над корпусом элементов конструкции (рис. 4.1). Такая форма корпу-
са не является хорошо обтекаемой, так как плоский срез с острыми кромками
в кормовой части вызывает срыв потока за телом. Для создания расчетной
модели обтекания корпуса и схемы расчета сил существенно знать, как фор-
мируется течение в кормовой части тела.
При малых местных углах атаки жидкие струи сходят с кормы по каса-
тельной к образующей поверхности цилиндрического корпуса в месте распо-
ложения плоского среза при произвольном нестационарном движении тела.
Математически это предположение в нашем случае сводится к тому, что за
телом был введен бесконечный след в виде цилиндрической каверны. Им-
пульс, сообщенный потоком жидкости телу, передается затем формирующе-
муся за телом следу. Введение за телом бесконечного следа позволяет для
вычисления сил использовать методы теории тонкого тела:
- плоских сечений, который после введения гипотезы о сходе струй с
задней кромки может быть распространен на все сечения тела,
вплоть до кормового среза;
— описания движения с помощью потенциала гидродинамических
особенностей, распределенных по длине тела и следа.
Расчеты показывают, что при вычислении потенциала или распределе-
ния нагрузки по длине тела существенное значение имеет след, простираю-
щийся только на расстоянии одного-двух диаметров позади тела, т.е. след,
практически только что оставленный телом. Ранее оставленный след, даже и
91
бесконечной длины, оказывает весьма слабое влияние, и поэтому его форма
и поведение вдалеке от тела становятся несущественными. Гипотеза о плав-
ном сходе струй с задней кромки позволяет получить только линейную часть
гидродинамической силы; для определения нелинейных составляющих при-
ходится вводить дополнительные предположения. Для определения вязкой
составляющей нормальной силы используется, например, аналогия между
пространственным пограничным слоем тела вращения и нестандартным по-
граничным слоем, формирующимся за цилиндром. Для определения вязкой
нелинейной составляющей будем пользоваться результатами эксперимен-
тальных исследований.
Воздействие жидкости на тело сводится к силам, непрерывно распре-
деленным по его поверхности, которые характеризуются величинами нор-
мального р и касательного т напряжения в каждой точке поверхности тела. В
общем случае эта пространственная система сил приводится к главному век-
тору R (X, Y, Z) и главному моменту М (Мх, Му, Mz) в связанной системе.
Гидродинамические коэффициенты Сх, Су, Cz, тх, Шу, т2 являются сложными
функциями кинематических параметров. Определение этих функций сопря-
жено со значительными трудностями. Эти коэффициенты обычно разлагают
в ряд Маклорена по угловой скорости и удерживают в разложении только
члены первого измерения в предположении, что угловые скорости малы [16]:
Л г
7 2
Р»2 е .
Z = сг|
\(o=0
. дСх дСх дС
ш=0 + <»х + <»г
да)х дй)„ да),
дС дСу
——со, + -О),
да)х да)у у
dCz dCz
----- О) +-- О),
да),-да>у у
дСу
доз,
Му =
"Ф=о +
дт, дт,
—z~—^~a)x + -——^~
да)у
дту
доз
дту
дсо,
Mz= ™z\s=o +
эс2
да),
дт
а).
О),
да).
дт
o)x+-—^a)y+-—^a)z
дй)у дй)г
дт, дт,
а)х +---а), +---со,
дсох да), у da)z
Л у у
дт,
Р»2 s .
2 м’
\ 2
Ри С .1.
2
. 2
PV С 7.
| 2 М ’
2
2
(4.9)
M
Первые члены разложений определяются при со = 0, представляют со-
бой проекции силы и момента при поступательном движении тела и носят
название позиционных сил. Прочие слагаемые определяют добавки к этим
силам, появившиеся вследствие вращения тела. Эти добавки носят название
вращательных производных гидродинамических сил. Представление гидро-
динамических силы и момента в формуле (4.9) соответствует широко распро-
страненной в настоящее время гипотезе стационарности, когда предполагает-
ся, что гидродинамические коэффициенты полностью определяются мгно-
92
венными значениями кинематических параметров и не зависят от предысто-
рии движения.
Если тело симметрично относительно плоскости XOY, то
дСу дСу дт2 дтх Q
3«у„ дюх дт
Если тело симметрично относительно плоскости XOZ, то
3CZ SCZ дт дт дт
--— =----— =-— =---— =--— — и.
дсох da>z дау дах дсо2
Можно считать, что вращение тела не вызывает продольной силы, то
есть полагать, что
дСх _ дСх _ дСх _ q
дтх да>у да>2
Введем безразмерную угловую скорость со =------
и
и примем следую-
щие обозначения:
_а _ дСу _ р _ gCz _
у ~ да ' 1 ~ др'
аг дСу дтх
у да2 дах
р дтх р
тх =———; mv
х дР у
а у дт. а у
дау
дту
~др'
дС2 .
дй)у '
а дт2
т2 =—-
да
дт.
dmz
(4.Ю)
Общие выражения для гидродинамических сил и моментов:
Q = -X = Cxp^-SM-
Y = Cy(a)p^-SM +^pSMLmzv,
Z^Cz{P)p^-SM+-C^pSMLmyv, (4.11)
= mx(a,P)p—SML + - mxx pSMl}vcox;
My = my(P)p^-SML + ±т?р5мЬ2шу
1 7
Мг =т2(а}р—$мк+-тю2'pSML va2.
С учетом вязкости при развитом турбулентном пограничном слое на основа-
нии имеющихся экспериментальных данных для удлиненных тел вращения
получим следующие зависимости:
с/«)=с;а+й,«2; cz(/7)=cf^+M2;
а и- 1 I \ Р п а — 2 (4-12)
т2(а}=тп2а+Ьххца ; ту(а)=туP+bp^a ,
93
где приближенно можно считать Ь{ =-Ь2 =—Лц = L4/D есть удлинение ци-
Зтг
линдра тела, хц=хц1 L, хц- координата середины цилиндра, отсчитываемая
от центра масс тела.
Целесообразно привести знаки гидродинамических коэффициентов:
С" >0; Cf <0; т% >0; т“ >0; CJ >0; Cj <0; mJ <0; mJ <0.
Для тела, близкого по форме к телу вращения, возникновение гидроди-
намического момента вокруг продольной оси вызвано выступающими
над корпусом надстройками. Коэффициент момента крена т х определяется
проливками моделей в гидродинамических трубах или испытаниями моделей
в гидроканалах.
Рис. 4.2 Схема расчетов при определении коэффициента тх
(вид с носка тела), плоскость I - III тела параллельна диаметральной
плоскости ПЛ в момент выхода, плоскость
П - IV перпендикулярна диаметральной плоскости
Схема замеров при испытаниях в гидродинамических трубах приведена
на рис. 4.2, где центральный угол <рТ измеряется между меридиональной
плоскостью испытываемого выступающего на высоту h элемента и направ-
лением набегающего бокового потока иг. В результате экспериментальных
исследований определяется боковая гидродинамическая нагрузка на вы-
ступающий элемент конструкции. Исходя из нее, находится максимальное
значение коэффициента момента крена т“ по формуле
(4.13)
94
гДе hb^y-
, hb = R + h/2, R - радиус в сечении тела, Sb - боковая
площадь выступающего элемента, L - характерная длина тела, Sm - площадь
миделя тела. По результатам статистической обработки систематических
экспериментальных исследований момента крена одного обтекателя на телах
вращения получены эмпирические зависимости коэффициента гидродинами-
ческой нагрузки Сь от h, приведенные на рис. 4.3 и в табл. 4.1. На рис. 4.4
представлена эмпирическая зависимость тх от (рт в виде функциикото-
рая изменяется в диапазоне от +1 до -1.
Таблица 4.1 Зависимость 10 Сь от h для различных типов обтекателей
h 1 2 3 4 5 6
0 0 0 0 0 0 0
0,01 0,029 0,045 0,049 0,054 0,075 0,103
0,02 0,050 0,067 0,073 0,080 0,100 0,159
0,03 0,064 0,082 0,087 0,094 0,116 0,186
0,04 0,073 0,091 0,096 0,103 0,126 0,201
0,05 0,079 0,097 0,102 0,110 0,132 0,208
0,06 0,084 0,102 0,107 0,116 0,138 0,213
0,07 0,088 0,106 0,111 0,121 0,142 0,216
0,08 0,092 0,109 0,114 0,125 0,146 0,218
0,09 0,096 0,111 0,116 0,128 0,150 0,220
На рис. 4.3 нагрузка зависит от места расположения обтекателя на теле
(на носке, на цилиндре) и от относительной длины обтекателя. Каждому виду
обтекателя присвоен индекс от 1 до 6 (1с = 1, 2,..., 6). Наименьшая нагрузка
получается на обтекатель, установленный на расстоянии 0,257* от начала ци-
линдра, его индекс "1" (к = 1), наибольшая нагрузка - на обтекатель, распо-
ложенный на носке тела (1с = 6). Поэтому в исходных данных для расчета тх
необходимо наряду с Л, Sb и начальным углом установки обтекателя (рг ука-
зывать индекс обтекателя в соответствии с рис. 4.3. Полученную экспери-
ментальным путем нагрузку С“ для обтекателя (см. рис. 4.3) сравним с не-
сущей способностью крыла. Удлинение обтекателя Я очень мало (Я=h/l4! Из
теории крыла известно, что для крыльев предельно малого удлинения
С=2а2 и——-4а,
у да
так что при а = 10° получим
—^=0,7 —или ^=0,012 —.
да рад да град
95
Рис. 4.3 Экспериментальная зависимость боковой нагрузки
на обтекатель от безразмерной высоты обтекателя h (вид с носка)
96
Из рис 4.3 следует, что теоретическое значение С“ достигается, на-
пример, при Г/1Ч = 0,5 и h = 0,068. Это свидетельствует о том, что обтекатель
имеет некоторую аналогию с крылом предельно малого удлинения, а вид эм-
пирических зависимостей С“ (Л) определяется влиянием образующегося на
поверхности тела пограничного слоя и интерференцией корпуса тела. Наи-
большая интерференция имеет место на носовой части тела, Где коэффициент
интерференции достигает двух единиц. Эмпирическую зависимость тх от (zy-
можно выразить с достаточной точностью с помощью ряда Фурье
/(^y)=0,624sin^r +0,435sin2p-0,069sin3^r -0,05sin4^?r -
-0,052sin5(z>7 -0,024sin6<pr -0,018sin7<z>, -0,0178sin8^>r.
Тогда зависимость коэффициента mx от оу, <рт и безразмерной высоты обте-
кателя h запишется в виде
тх(От’Фт) — ^hk^^b^bf(Фт )•
Здесь нагрузка определена по рис. 4.3 в зависимости от h в соответствии
с присвоенным обтекателю индексом к. При наличии на теле нескольких, на-
пример, п обтекателей, используется принцип суперпозиции и суммарное
значение тх? находится как алгебраическая сумма всех и слагаемых
тх£ =^S'hkiaT^bi^lbif^Ti 0-15)
1=1
с учетом начального угла расположения i-ro обтекателя .
Центральный угол поворота плоскости набегающего потока
(рис.4.2) и угол атаки ат в этой плоскости рассчитываются по формулам
arcsin при uy>Q',
Ur
я-arcsin при ьу<0;
<Рт =
ат =arcsin
и
где Uy, иг и Ur — нормальная, боковая и радиальная проекции полной скорости
потока и.
На основании формул (4.14), (4.15) определен коэффициент тх* в
предположении линейной зависимости тх от юх в малом диапазоне измене-
ния Цгу— <ргоУ.
тх“^х
/(^го)
где производная от f по ^ определена в соответствии с формулой (4.14)
7 Зак. 3666
97
f(<pT)=-^—-Qfi>2Acosq)T +0,869cos2^>,. -0^08cos3^r -0,198cos4^r -
-0,258cos5^r -0,146cos6^r 0,126cos7^r -0,142cos8^r. (4.16)
На рис. 4.4 приведены графики для функций j[(pT),f\(pr), рассчитанных
по формулам (4.14), (4.16). Сравнение расчетных значений Д^) с экспери-
ментальными показывает, что ошибка аппроксимации не превышает 2%.
В инженерных расчетах обычно полагают равным нулю (т°‘ =0),
что мало сказывается на результатах расчетов.
Так называемая отрицательная плавучесть тела находится как разница
его веса Mg и Архимедовой силы А
Р = Mg - А.
Проекции и моменты отрицательной плавучести на оси связанной сис-
темы координат рассчитываются по формулам
Рх = -ацР', Ру = -апР\ Pz = -ai3P, Lx = 0, Ly = -al3xAA', Lz = anxAA, (4.17)
где значения коэффициентов ап, ai2, а13 рассчитываются по формулам (1.6),
хА - координата х центра объема тела относительно центра масс тела.
Рис. 4.4 Аппроксимационные зависимости f (<рт) и/'(^’г)
Остановимся теперь на методике расчета гидродинамических сил на
выступающие элементы конструкции, которые могут иметь форму паралле-
лепипеда, овала, полусферы, пластины и других. Предполагаем, что линей-
ный размер элемента h мал в сравнении с радиусом тела (й « /?) и внесение
его в поток несущественно изменяет поле скоростей. Гидродинамическую
силу на выступающий элемент F(X,Y,Z) найдем по общепринятым форму-
лам
2
Х = Сх ^-s-
х 2
98
Y^CyPo^S^ (418)
2
Z = C2^S„.
Для выступающих поясов оценку коэффициента Су проведем на осно-
вании обобщения экспериментальных данных. Как правило, выступающий
элемент обтекается турбулентным потоком с отрывом струй, так что импульс
от тела передается формирующемуся за телом турбулентному следу, и для
коэффициента Су справедлива оценка по линейной теории
Су = С“-а\ (4.19)
С“ =2.0,
где размерность С“ равна 1/рад, а есть местный угол атаки, и в качестве ха-
рактерной площади необходимо брать площадь поперечного сечения высту-
пающего элемента S7.,. Полученные по формулам (4.18) силы на выступаю-
щие элементы суммируются с действующими на тело гидродинамическими
силами (4-П).
§ 3. Система дифференциальных уравнений продольного
и углового движения осесимметричного тела в воде и
при пересечении свободной поверхности воды
Приведенными формулами (4.7) - (4.20) исчерпываются все необходи-
мые соотношения для составления дифференциальных уравнений движения
на основе законов (4.5) и (4.6).
Обратимся сначала к составлению левых частей. С этой целью выпи-
шем значения Q*, Qy, Q7, Ку, Кг.
При движении тела в жидкости, используя выражение (4.7) для Т, най-
дем, что
Qy = ^-=(M+A22)u + ^(Dz;
dvy
dv2
и (4.20)
KJC=^ = (Jx+Z44X;
к у = ~ = (jу + Л» ;
7’
99
Kz =T— = (JZ +Лб>2 + Л26»у
д(Ог
При движении тела во взволнованной жидкости, используя выражение (4.8)
для Т’, найдем
Qx=^Mvx+^Ux-
°UX
I/ Uy
Q'z=^-- = Muz +A^U3 +Л35и5
cu2
и
(4-21)
(4.22)
дТ' . т . .
Кх — — — (Jx + А^)ах;
о<ух
= Jy(i)y + + ^5С/3;
+ Лб^б + Аб^2 •
O(DZ
Если использовать выражения Qx, Qy, Q, Кх, Ку, Kz, то уравнения (4.21) мож-
но представить в более наглядной форме:
п' _ 8Т' _ п 1 .
Qx - ~ -Qx
^х
-8Т' -Г> 2 3
Оу _ ~Qy~ Лги2 ~ 4гбиб>
Qz - ~Qz~ ^33U3 - AsU5’
K'x = — = KX;
^ax
v, _^T'
A^, — — Ay /<55W5 Лу5и3,
V' 8T' V 2 1
Kz ~/l66U6_/‘26U2-
Из последней системы следует, что при учете волнения появляются до-
полнительные члены, которые представляют собой произведения присоеди-
ненных масс тела Лл и значений ик, характеризующих поле скоростей
взволнованной жидкости.
Подставив выражения (4.20) в левые части законов (4.5) и (4.6) и обо-
значив их соответственно буквами Ах, Ау, Az, В„ Ву, В2, для движения тела в
спокойной воде после несложных преобразований получим
100
Ах=(М + Л11)^~ + (М + Л33)и2а -
at
- (л/ + АгХу», + ^y - +u*^’
+A« ~+(w + \ I k®2 - (л/ + Л33 \>z6)x -
at at
(4-23)
л,=(м+AjA"-*+Aik
at at
- +A1 + ц +ay ;
Дс =(A + A»)-^"1"^ ~^y + ^66~^s}°)2(ay +
+ (Аз - АгН^ + (Аб + Ъ&уЯу - 4&z)+ (4-24)
ВУ =(jy + Аз)^+ Аз^ + (Л -л +^ - АбК*>2 +
at at
+ (А 1 - Аз К^2 - А6^®х - Аз W + <4 >
Д=(Л+Аб)-^—+Ав -~г-+(л - А+As - Ач)6^ +
at at
+ (Аг - AI \xv + A6"x®2 + Аз*4«4 + «4 + Vy ^г-
at at
По поводу этих выражений можно отметить следующее.
Задачи прикладной гидродинамики сводятся к трем основным: выходу
ракеты из шахты, движению ракеты в воде и пересечению ракетой поверх-
ности воды. Гидродинамическая задача о выходе ракеты из шахты сводится
к задаче о выходе тела в поток жидкости через плоский бесконечный экран.
При введении зеркального отображения приходим к гидродинамике удли-
няющегося в обе стороны тела. При введении гипотезы о плавном сходе
струй воды с цилиндрического корпуса в месте расположения плоского сре-
за и формировании за телом бесконечного следа систему «тело + след»
можно рассматривать как тело с изменяющейся во времени геометрией. Та-
ким образом, основные задачи гидродинамики при выходе сводятся к гид-
родинамике тела с изменяющейся во времени геометрией. Поэтому в урав-
нениях остаются слагаемые, содержащие производные по времени от при-
Г^А
соединенных масс тела —-
I dt
101
В дальнейшем эти производные войдут составной частью в гидродина-
мические коэффициенты и на этом основании не будут учитываться в диф-
ференциальных уравнениях.
Позиционные силы и вращательные производные моментов, как пра-
вило, определяются продувками модели в аэродинамических или проливками
в гидродинамических трубах либо испытаниями на ротативных установках
или в гидроканалах. Естественно, что при этом автоматически учитывается и
воздействие невязкой жидкости, которое сводится к моментам при стацио-
нарном движении тела с постоянным углом атаки или постоянной угловой
скоростью. Поэтому необходимо их вычесть из правой части или, что то же,
прибавить противоположные по знаку члены:
Для : (^зз ^a)uyvz и (Я22
Для Br: (Лн-Лвкл и (Язз-Лпкл;
и Лз51\й>/’ (4.25)
ДляВ2: (Лг2-Л1Х^ и (Л1 ~^22)их°у '>
и
Для существенного упрощения дифференциальных уравнений будем
считать, что тело близко по внешним обводам и массо-центровочным харак-
теристикам к телу вращения. Отступления от тела вращения обусловливают-
ся в основном технологическими погрешностями, а также выступающими
над корпусом тела надстройками.
Для удлиненного тела вращения (Л > 5) величины Ли и Л ввиду их
малости можно опустить в тех слагаемых, где они входят в сумме с Л55 или
Л66 и с Jy или Jz. Также будем полагать, что Jy = Jz и Л55 = Л66, =-^26,
^зз ~ ^22 •
Сначала остановимся на выводе уравнений движения тела в спокойной
воде. Принимая во внимание все сказанное, перепишем выражения для Ах,
Ay,..., Bz в виде:
Ах = (М + Я,,)^- + (М + Яг2){vz<o -v со z)-Л^о2 +a>2)+vx;
dt at
Ау = (М + Л22) У + А26 2 + (М + Яп )uxa>z — (М + Л22 )vz<ox + ^2бахау +
at at
+ Vy^ + a)z^-
у dt dt
at at
+ 4б®х^2 + «4 ~~ - <Oy
dt dt
— t Г - \ d(0
Bx = (Jx + ^44 )~3-* 60x —J— ’
dt dt
(4.26)
102
By = (Jz + Лб)^ - Лб - Аб^х - (Л + ЛбХ^г +
bz={Jz+Лб)^-+Лб ~ - АбЧ^х+(Л+ЛбХ^у +
at at
+ а,^+и^26.,
Z dt У dt
В этих выражениях подчеркнуты слагаемые, которые учитываются в
гидродинамических силах и моментах и поэтому в дальнейшем выводятся из
дифференциальных уравнений движения ракеты.
Правые части законов (4.5) и (4.6) найдем с учетом формул (4.11),
(4.12), (4.14), (4.16)- (4.19), (4.25):
VX=R^- ^CxPSuu2 - an(Mg - Л);
Vv =\Cy^fS^ -^СаугpSMLva)z-al2(Mg-A);
Vz = l-Ct(fl)pSHv Лс?рвыЬишу-al3(Mg-A); (4.27)
Mx =\tnxpSMLu2 + mu*pSMl}uax,
z
My =\™у<Я)/£„1л +\m”y Рвм^Шу ~al3AxA;
Mz =^m2(a)pSuLu pSuL2 u&2 +ai2AxA.
Итак, левые и правые части скалярных законов (4.5) и (4.6) получены.
Следовательно, искомые дифференциальные уравнения движения тела вра-
щения в спокойной воде будут:
1.
2.
3.
(М + ,)^ + (М +Ля)(и2еоу - иусо2} - (а>2у + ю22) =
~ В-ду—-^CxpSutJ -au(Mg-А),
(М + /?22+ Лб + (М + Яц)ихй}2-(М + ^22 )uzMx + ^(Охт =
at at
+~CyzpSMuLa>2 -an(Mg-A);
du da)
(M + y?22 + (M + )иуй)х ~(М + Л^их(оу+ =
=^C2(^)pSMu +^C2rpSuLu(oy -al3(Mg-A);
(4.28)
103
4.
5.
6.
(Л + = LmxPSubv2 + pSMl}ua>x;
at 2 2
t/бУ., л dv
(А+Лб)“^“ ^6 ~Z~ ~ (Jz + " ^2биуШх =
at at
=^my(P)pSMLv +^yypSuL2 vcoy-aI3AxA;
(Л + Лб)^ + ^26 + (Л + ЛбК®, " A?6^z®z =
dt dt
=^nz(a)pSuLv +|«C pSML2 v(oz +anAxA.
Полученные уравнения (4.28) являются дифференциальными уравне-
ниями неуправляемого пространственного движения тела в спокойной воде.
Чтобы система (4.28) была замкнутой, к ней необходимо добавить ки-
нематические уравнения (1.7), (1.8) и следующие соотношения:
V
а = arctg(—-) - для угла атаки;
Р = arcsin— — для угла скольжения;
и
Г~2 2 1
v = у/их + vy + иг - для полной скорости центра масс тела.
Теперь перейдем к выводу дифференциальных уравнений движения
тела во взволнованной жидкости. Используем выражение для суммарной ки-
нетической энергии (4.8) и в соответствии с формулами (4.5) и (4.6) и сказан-
ным выше найдем производные (4.21).
Подставив выражения (4.21) в левые части (4.5) и (4.6), получим для
движения тела внутри взволнованной жидкости:
А'х = (М + +ад~ад)-
- C)z (м иу + ад + ад ) - А, + и, ^1;
ш at
A'y = (M+^')d^-+^(lc^+a>z(Mvx + ад)- (0x{Mv2+ад - ад)-
ад—-46—+^2“+<Л—;
dt dt 2 dt 6 dt
л; = (м + +0х(м»у + ад+ад)-
at at
+ (4.29)
а/ at at at
В'х = (jx + 244)^ -ад)+^(ад +ад)+
104
+ Л^Щ-и^У ^{uyU,+u2Uby шх^--
в'у=(Л +Лб)^-+4А -J^y
+ — U\(^oJLf3 + Л^\Uxu3 -U\(Л22и3 — ) -
-Лб—+Лб—+и5^-и3^; '
dt dt 5 dt 3 dt
B'z =(JZ +Лъ6)^-+Л26^+а,х(Лга,у+Лыи5-A^U3 -Лха>уУ
— 2 +(71(^22^2 +Лгб^б)~Л1^Г1Ц2 + и\(Л22и2 +^26^6^ —
-Лб—-Лб—+*4—+u2^.
dt dt 6 dt 2 dt
В этих выражениях аналогично формулам (4.26) подчеркнуты слагае-
мые, которые учитываются в гидродинамических силах и моментах и в даль-
нейшем выводятся из дифференциальных уравнений движения ракеты во
взволнованной жидкости.
Аналогично формулам (4.27) найдем правые части в случае движения
внутри взволнованной жидкости:
vx = В.ДУ-\cxpSMU2-ail(Mg-A)-
Vy=^Cy(a)pSMU2 +^Cy!pSMLUU6-an(Mg-Ay,
Vz =^C2(P)pSMU2 У-С2Ур8мЬииз-a^Mg-A)-, (4.30)
Mx = X-mxPSMLU2 + ^pSML2U^x-
My =^my(^)pSMLU2 +|/n7pSuL2UU5 -al3AxA-,
=^m2(a)pSMLU2 +^т2г pSML2UU6 +al2AxA.
Отличие равенств (4.30) от (4.27) связано с учетом параметров волнового по-
тока:
Ui=UcosPcosa; U2 = -C/cos/7sina'; t/3=f/sin/?;
U = ^U2 + U2 +U3 ; a - arctg^- j; p=arcsin^y^.
Однако, как будет показано в следующем параграфе, значения гидро-
динамических коэффициентов и присоединенных масс для обоих случаев (с
волнением и без него) будут одинаковыми.
Теперь на основании выражений (4.29) и (4.30) можно записать урав-
нения движения тела вращения во взволнованной жидкости:
105
(Л/ + Я,, )^-+^y(Mu2 +a22u3
-^=R„y-X-CxPSMU2-au(Mg-A);
(М + Я22) ' + Аж-—*-+ (02(М Ux + ЛцС/])-<ух(л/и2 +^22^3 -^26^5)“
at at
Ле?,pSMLUU6-al2(Mg-A);
Ш (ll £ x*
(м + Я22)——--Л^——^-+ О)х(м Uy + ^22^2 + ^26^б)~ ау(МUx +Л1^1)-
at at
+|c? pSMLUUs-al3(Mg-A);
at at Z Z
(Jx + A„)^ = -mxpSMLU2 + —mxxpSMl}Ua>
(Л + ^f,6)~t~~^16~t~~(°x{^z(Oz + Лб^6 +Лб^2 ~^x(Oz)+^l\^\U'i ~
at at
-и1(^-Я2би5)-Ям^+2Л26^Лпгу^)р8мьи2 +
at dt 2
ЛтЮ; pSML2UU5-al3xAA- (4.31)
(Л +Лб)^+Лб +A^s - W3 -j^yY^u^+
+и1(Я21и2+Л2биб)-^6^-2Л26^=
dt dt
=^z(^)pSMLU2 +~m22 pSML2UU6 +al2xAA.
Для приближенного учета волнового давления удвоены произведения
. du2 . du3 . du3 . du2
Л22 —г-, ^22 —~ > Лб —~ и Лб —~ соответственно во втором, третьем, пятом
dt dt dt dt
и шестом уравнениях.
Таким образом, система (4.31) записана для движения тела вращения в
воде с учетом волнения, а также пересечения поверхности воды. В последнем
случае все гидродинамические коэффициенты и присоединенные массы за-
висят от длины вышедшей из воды части тела. Параметры волнения в (4.31)
Щ, “2, «з, us, ив, а также производные от них по времени, рассчитываются по
формулам (3.46) - (3.48).
106
§ 4. Приближенный метод расчета гидродинамических коэффициентов
Этот теоретический метод расчета может применяться для приближен-
ной оценки гидродинамических характеристик тонкого тела вращения с за-
остренной формой носка.
Полученные формулы (4.25) и (4.26) позволяют перейти к одному из
основных вопросов проводимых нами теоретических исследований - к выво-
ду формул для гидродинамических коэффициентов. Общие выражения для
гидродинамических сил приведены в формулах (4.11). В качестве характер-
ного линейного размера примем радиус цилиндрической части тела R. Связь
присоединенных масс тела Aik с коэффициентами присоединенных масс Kik
выразим равенствами:
Л^ЪрЯ'К", ^2=SpR3K22-, ^=\6pR*K2p, A66 = 32pR5K(6,
вид которых выбран с целью упорядочивания численных значений Кл для
удлиненных тел.
Согласно первому уравнению (4.26) для АЛи первому уравнению (4.11)
найдем, что при движении тела вращения в спокойной воде
CxP~SM=~vx-^--,
2 at
и далее согласно второму уравнению (4.26) для Ауи второму
(4.11)
уравнению
(4.32)
(4.33)
Cy(a)p^-SM +^C^pSMRd)zv=-vy^-(oz^.
2 2 dt dt
Аналогично и для третьих уравнений (4.26) и (4.11)
с.(P)p^-SM + ~CzypSMR(0yv = -V2 + а)у
2 2 dt dt
При составлении этих и последующих уравнений учитывали, что гидродина-
мические силы и моменты будут заноситься в правые части дифференциаль-
ных уравнений движения тела.
Будем полагать, что зависимость присоединенных масс от времени
выражается через некоторый параметр I, который может быть, например,
продольным перемещением полюса тела относительно взволнованной жид-
кости 1 = lT - Z], где 1Т = fv.pt, /] = (и^г, так что — = vx - щ = Ц. В спокой-
J J dt
ной воде, когда Wi=Zi=O, / есть продольное перемещение полюса тела.
Тогда производная от Кл по времени t будет иметь выражение
dKjk dKjk
dl 1 dl
dKik _ dKjk dl
dt dl dt
Вывод формул для гидродинамических коэффициентов проведем сначала для
участка выхода тела в спокойной воде. Будем полагать углы а и Р малыми,
а зависимости гидродинамических коэффициентов от а и р - линейными:
107
Cy(a) = Cya; Cz(P) = Cf ,
= mf- P\ mz(a) = mz a и т.д.
В результате на основании равенств (4.32), (4.33) найдем, что
С = 16
х я <п ’
c;=-cf=-^-; (4.34)
я al
СШг =—Са>г -
у z я dl
При выводе уравнений для коэффициентов гидродинамического момента
(mz, т^‘и т.д.) необходимо дополнительно учитывать выведенные из Ву и
Bz члены (4.25). В результате исходные уравнения для определения mz, ту
и т.д. запишутся в виде
my(P)p^SMR+^my'pSMR2v<i>y = (Л2-^)vxvz ~^их<оу-<»y^+uz^;
£ til Ul
mz(a)P^-SMR+^^pSuR2ua}z -cdz^-u^.
2 2 dt dt
Откуда найдем выражения для производных от коэффициента гидродинами-
ческого момента по углу аги угловым скоростям a>z и юу:
<=^=-(к22-*11+2^М; (4.35)
а/ )
"V =т/ =-----\К26 + 2—^\.
я V dl )
Рассчитанные по формулам (4.34), (4.35) значения гидродинамических
коэффициентов составляют основную их часть. Имеющие место эксперимен-
тальные поправки на их значения отражают нелинейные зависимости этих
коэффициентов от кинематических параметров. Так, в формулах (4.12) вве-
дены поправки Ь{п Ь2 на Су(а) и Cz(fl). Влияние экспериментальных по-
правок существенно проявляется только при больших углах атаки или
скольжения (a, fl> 0,25 рад).
Используя полученные нами выражения (4.29) и (4.30) и проводя ана-
логичный вывод для движения тела во взволнованной жидкости, получим,
что выражения для гидродинамических коэффициентов сохраняются такими
же, как и для движения тела в спокойной воде. Этот результат полностью со-
ответствует проведенной нами в § 2 гл. 3 постановке гидродинамической за-
дачи: гидродинамическая задача о движении тела внутри взволнованной
жидкости сводится при использовании относительных кинематических пара-
метров к гидродинамической задаче о движении тела в спокойной жидкости.
Таким образом, если решена задача о потенциальном обтекании тела
или присоединенные массы тела определены каким-либо методом, то полу-
108
ченные нами формулы (4.34) и (4.35) позволяют полностью решить гидроди-
намическую задачу, то есть рассчитать все необходимые для решения задачи
динамики гидродинамические коэффициенты.
Наиболее простым методом определения присоединенных масс являет-
ся метод плоских сечений, когда жидкость разбивается на элементарные слои
плоскостями, перпендикулярными оси тела вращения, и течение жидкости в
каждом слое определяется поперечным движением элемента тела (цилиндра)
в слое. Распределение поперечной присоединенной массы по длине тела
—— равно произведению плотности воды на площадь рассматриваемого ce-
de
чения тела S: —— = pS. При этом продольная присоединенная масса 2ц и ее
dx
производная по / считаются малыми и полагаются равными нулю. Такой
подход справедлив только для тонкого тела, имеющего заостренную носовую
часть в виде, например, конуса.
Тогда при выходе из шахты схематизированного тела вращения "ко-
нус-цилиндр" с общей длиной Z, высотой конуса й и единичным радиусом
цилиндра {Sm = л) найдем зависимости для коэффициентов присоединенных
масс от длины вышедшей части тела I
jr ft IT 1
^22=—р- при/<й; ЛГ22 =—(/——й) при/>й;
л 3 I3
"ри^л’
Я26 (/-|Л)ХТ -1(2/2 -й2) при/>й;
16 3 4
(4.36)
16
„ л-/3(/2 1 , хЛ
=----=-----хт1+— при l<h ~,
66 32й2^5 2 т 3 ) Р
7lh( h2 1 . хЛ Л I3 — h3 .,2 ,2\ 2zi i\ 1^1
= ~ —ч------Хг(/ -А ) + xrG-A) при/>й,
I J Л- J
где Хт — координата центра масс тела, отсчитываемая от его носка.
В соответствии с полученными формулами (4.36) найдем производные
от коэффициентов К22, Кгь, Кы> по /:
18
при I < h;
при I > й;
109
при I < h;
при / > h;
при I < Л;
при I > h.
(4-37)
Подставляя эти выражения в формулы (4.34), (4.35), найдем зависимо-
сти гидродинамических коэффициентов от длины / вышедшей из шахты час-
ти тела:
Щ/ = ту
(4.38)
2,0 при l>h;
при /<Л;
? 1
-2 (/-хг)2+(/-|й)хг-1(2/2-й2
при I > й;
(4-39)
Полученные выражения (4.38) - (4.40) обычно применяют при проведе-
нии приближенных гидродинамических расчетов для тонких тел, имеющих
заостренную форму носка. Заметим, что равенство Су = 2,0 выполняется тем
точнее, чем больше /. Более того, при больших / (1/R >10) это равенство
можно применять в качестве критерия точности численных методов расчета.
После выхода тела из шахты за его кормой будет формироваться след в
виде донной газовой каверны и гидродинамические коэффициенты будут
иметь постоянные значения, определяемые вторыми равенствами (4.38) -
(4.40) при l=L:
Сау =-С^ = 2- С? = -С? = 2(Z - хг);
ПО
= -2 (L-xrf +(L-h)xT -|(2Z? -Й2) ,
m? =m^‘
при этом производные от коэффициентов К22, К26, К&> по I также будут иметь
постоянные значения, рассчитываемые по формулам
^22_=£; ^26=—fxT-L); ^- = —(L-xT)2.
dl 8 dl 161 T dl 32
(4.41)
При выходе тела из воды изменение присоединенных масс в зависимо-
сти от / в системе “тело+след” происходит за счет разностей изменения при-
соединенных масс формирующегося за телом следа и вышедшей из воды
части тела, то есть определяется как разность
соответствующих производ-
ных, записанных формулами (4.41) и (4.37):
^26.
dl
при l<h;
при I > h;
при / < h;
при l>h;
(4-42)
Используя полученные выражения (4.42) и подставляя их в формулы
(4.34) и (4.35), получим следующие выражения для гидродинамических ко-
эффициентов при выходе тела из воды:
при l<h;
О
при / > h;
111
-(L-l)(L + l-2xT) при l>h.
На рис. 4.5 для иллюстрации приведены графики коэффициентов сил и
моментов С“, т“, Cyz, в зависимости от длины вышедшей из шахты
(воды) части тела I, при этом расчет проведен для тела вращения, имеющего
Рис. 4.5 Зависимости гидродинамических коэффициентов при выходе
из шахты и из воды от длины / вышедшей части тела
Проведенное нами сравнение результатов расчетов с эксперименталь-
ными данными [1] показывает, что расхождение стационарных характери-
стик тел вращения, имеющих заостренную носовую часть в виде конуса, не
превосходит 15—20%, а вращательных производных — 20-25%. В проектных
расчетах погрешности гидродинамических коэффициентов не должны пре-
вышать 10%. Поэтому для обеспечения требуемой точности расчетов гидро-
динамики разрабатываются численные методы, погрешности которых не пре-
вышают погрешностей определения гидродинамических коэффициентов на
экспериментальных установках и составляют 5—7%. Кроме того, численные
методы позволяют получить более полные данные, например, распределение
давления по поверхности тела и присоединенные массы тела.
112
§ 5. Инженерный метод расчета донной газовой каверны
Как видно из рис. 1.9а, 1.96, при выходе тела у среза шахты формиру-
ется газовый пузырь, а после выхода кормы тела из пузыря — донная газовая
каверна.
Расчеты донной газовой каверны проводятся с целью уточнения донно-
го давления при движении тела в воде непосредственно после выхода его из
шахты. Начало расчета - с формирования у среза шахты газового пузыря,
форма которого близка к форме полусферы (рис. 1.6а) [14,15].
Расчетная модель разработана при следующих упрощающих предпо-
ложениях:
- форма пузыря близка к полусферической, а форма донной каверны
близка к цилиндрической с диаметром, равным диаметру цилиндри-
ческой части тела;
— давления газов в пузыре и донной каверне равны и находятся из
уравнения состояния газов: после выхода кормы тела из шахты дав-
ление в шахте и пузыре выравнивается за счет перетекания газов.
Расчет перетекания газов из шахты в пузырь проводится по форму-
лам Сен-Венана;
- температуры газов в пузыре и донной каверне равны температуре
окружающей воды;
- температура горячих газов в шахте после выхода из нее кормы тела
остается постоянной на протяжении всего времени формирования
донной каверны (рис. 1.6а, б, в, г).
— отделение донной каверны от шахты происходит при схлопывании
газового пузыря (рис. 1.6 г).
Дифференциальное уравнение для расчета газового пузыря запишется
в виде
d Rn _ ?п ~рст 3 f dRtl А .4 43
dt2 RnP 2Rn к dt j
где Per ~ гидростатическое давление на уровне среза шахты. Давление в пу-
зыре находится из уравнения состояния
рп = ™nRnTn (4.44)
Vn
Объем пузыря Vn рассчитывается с учетом находящейся в нем части
тела 4Кги верхнего свободного объема шахты AVK:
Vn=^Rl-AVT+AVK. (4.45)
При разгерметизации объема шахты массовый расход газа через обра-
зующееся проходное сечение 5 из шахты в пузырь —у— рассчитывается в
dt
соответствии с формулами Сен-Венана:
8 Зак. 3686
113
(4.46)
Объем донной каверны У^он до начала схлопывания пузыря находится по
Удон - (XК *П
формуле
(4-47)
где Хк есть расстояние от кормы до среза шахты (рис. 1.6в).
В соответствии с принятыми предположениями температуру газов в га-
зовом пузыре и донной каверне будем полагать равной температуре окру-
жающей жидкости (7)к), а температура газов в шахте Тк находится расчетным
путем и принимается равной температуре газов в момент выравнивания дав-
ления в объеме шахты с давлением в газовом пузыре. Давления в донной ка-
верне, пузыре и шахте после выравнивания давлений вплоть до схлопывания
пузыря считаются одинаковыми и находятся по формуле
> _р - тг^К^К
К П Ук+^п
(4.48)
где // = (КкТкУШпТп), тг - масса газов, содержащихся в шахте, пузыре и ка-
верне, рассчитываемая как интеграл от массового расхода ПАД (тйг) по фор-
муле
t
тпг = тг0 + . (4.49)
о
В этой формуле есть суммарная масса газов в верхнем свободном
объеме шахты в начальный момент времени t ~ 0, соответствующий моменту
запуска ПАД. При разгерметизации шахты происходит интенсивный рост пу-
зыря, и радиальная скорость его положительна (Rn >0).
Схлопывание пузыря начинается с момента изменения знака скорости
его границы, когда скорость Rn становится отрицательной (Яп< 0). В этот
момент достигается максимальный радиус пузыря Rjim. В процессе схлопы-
вания уменьшается Rn, а образующаяся за телом цилиндрическая каверна
вследствие преимущественно радиальных скоростей жидкости начинает со-
общаться с пузырем через коническую горловину. Коническая поверхность
имеет основание 5W, а вершину - в центре пузыря (рис. 1.6 г). Объем донной
каверны при схлопывании пузыря рассчитывается по формуле
Кйда=(Хк-Rn)SM +^LM -Rn)S^ (4 50)
Кцм л
При движении носка тела в пузыре и выходе носка тела из пузыря ди-
намическая осевая сила от действия пузыря Xn,(t) в z-м сечении носка
114
(s, < /н) с площадью поперечного сечения S, и на цилиндрической части тела
(s, > 1н) рассчитывается по формулам
(f)=(.Pn ~ Рст )$1 ПРИ < 4ь
^щ(О=(^л _^ст)^м при5,->/н- (4.51)
После выхода носка тела из пузыря (I — lH> Rn) Хп№) находится по
формулам
D
- Per Я при Si < In,
D
^л.(0=74-(^ ~Pct)Sm при st > lH, (4.52)
где I - длина вышедшей из шахты части тела; 1Н- длина носка тела.
После выхода кормы тела из пузыря полагаем Xni(t) = 0.
Расчет донной каверны проводится до полного схлопывания пузыря
(Rn=0). Полученные значения Рп, начиная от момента выхода нижнего опор-
но-ведущего пояса тела из шахты до момента схлопывания пузыря, исполь-
зуются в процессе счета для уточнения сопротивления тела.
§ 6. Метод расчета воздействия струи жидкости на
днище ракеты при движении ее в воде и пересечении
поверхности воды
После пережатия газовой полости часть газов захватывается донным
срезом ракеты и за ней формируется присоединенная газовая каверна, а дру-
гая часть газов остается в контейнере. За кормой ракеты реализуется разре-
жение, и при захвате газов там возникает течение с развитой кавитацией.
Действительно, кормовой срез обычно близок к плоскому срезу, то есть ци-
линдрический корпус ракеты заканчивается острой кромкой с нулевым ра-
диусом кривизны. На этой кромке происходит отрыв пограничного слоя, и
основной поток движется по криволинейной траектории, огибая заполнен-
ную газом зону отрыва. На основании теоретических и экспериментальных
исследований установлено, что наиболее близкими к физической картине ка-
витационного обтекания кормы ракеты из всех возможных являются схема
Жуковского-Рошко и схема Эфроса. Остановимся сначала на схеме Жуков-
ского-Рошко (рис. 4.6), которая построена на введении замыкателя в корме
каверны при одновременном обращении движения, то есть кавитационное
обтекание начинается с замыкателя и заканчивается на донном срезе. С по-
мощью приведенных на рисунке эмпирических формул и формул теории
тонкого тела можно построить приближенную форму донной каверны. Так,
например, если принять <т= 0,2, а замыкатель в виде диска (сХо =0,82), то в
соответствии с эмпирическими зависимостями, приведенными на рис. 4.6,
rn = R(/2,2, Ln = 37?о ~ 1 >5По.
В случае, если <т= 0,15, на основании приведенных формул получим
следующие оценки:
8*
115
rn — Rt/2,9, Lk — 3,4 Ro — 1,7£>о.
Видим, что длина донной каверны по схеме Жуковского-Рошко при измене-
нии числа кавитации от 0,15 до 0,20 не превосходит двух калибров тела.
оо К
2
= C^o<1 + g>
Гп V
LK 1,92-Зет
п
Hpnx<dmdn = 2rn
С =0,82
*0 ’
I X Р
R='n 1+3-
I rJ
Теория тонкого тела при x>dn
(RR'jlnR^
2
R2=GX + f,2
г/лЛо "
Л|х=г/я=1,9г„, 4
п
=0,27
Рис. 4.6 Расчетная схема Жуковского-Рошко
Однако схема Жуковского-Рошко основывается на искусственном
приеме — введении замыкателя - и не отражает всех особенностей в зоне
смыкания границ каверны. В частности, схема Жуковского-Рошко не учиты-
вает образование обратной струи при смыкании в концевой зоне границ ка-
верны. При опытах в вертикальной гидродинамической трубе в концевой зо-
не каверны за сферой хорошо видна обратная струя, которая движется внутрь
каверны.
С помощью высокоскоростной киносъемки присоединенной газовой
каверны установлено, что как сама каверна, так и возвратная струя нестацио-
нарны, а процесс их образования и последующего затем разрушения близки к
циклическому процессу. Вследствие существующих возмущений изменяется
скорость и направление обратной струи, и она может ударять по свободной
поверхности каверны, разрушая ее, или по донному срезу тела, где давление
может локально резко повышаться.
Исходя из этого, можно заключить, что воздействие обратной струи на
донный срез тела носит случайный характер. В настоящем разделе даются
оценки максимально возможного воздействия обратной струи наднище.
Кинограммы часто используют для определения скоростей, ускорений
и толщины обратной струи. Если известны объем каверны, промежуток вре-
мени между моментами отрыва и скорость возвратного течения, то можно
рассчитать толщину обратной струи, считая, что отрыв каверны происходит
в момент заполнения всей каверны жидкостью. Скорость возвратного тече-
ния будет такой же, как и скорость течения вдоль свободной поверхности
раздела, т.е. она будет равна скорости потока, умноженной на (1+о)1/2. Тол-
щину обратной струи можно определить также и другим способом. Скорость
заполнения каверны обратной струей зависит от количества движения, кото-
рое требуется, чтобы развернуть основную массу жидкости параллельно на-
правляющей поверхности. В рассматриваемом нами случае, когда каверна не
охватывает все тело, увеличение сопротивления тела равно изменению коли-
чества движения обратной струи.
Толщина обратной струи рассчитывается непосредственно по измене-
нию количества движения. Для той части жидкости, которая образует обрат-
ную струю, уравнение количества движения имеет вид [21]
и2
=pQ(p<c +Ц>),
где Лст- разность коэффициентов сопротивления тела при бескавитационном
обтекании и обтекании при наличии присоединенной каверны, $м = «£^/4 -
площадь поперечного сечения тела (цилиндра), р- плотность жидкости, и„-
скорость невозмущенного течения, Q = nDti>o - объемный расход в обратной
струе, t>0 =и00л/1+<т - скорость возвратного течения, D - диаметр тела (ци-
линдра), t - толщина обратной струи (рис. 4.7). Это уравнение можно привес-
ти к виду
Рис. 4.7 Расчетная схема Эфроса
117
116
Л-D
AcrD
в^+ст+л/Г+ст) * 8(2+l,5o-)’
Толщина обратной струи t и ее диаметр d связаны очевидным равенст-
вом
D \D
По имеющимся экспериментальным данным приближенно можно при-
нять, что за кормой тела d/D = 0,25. Скорость натекания обратной струи на
днище равна ц>. Таким образом, полный скоростной напор qo на днище при
натекании обратной струи
2 2 2
а площадь зоны воздействия на днище давления струи соизмерима с площа-
дью лг/2/4, то есть Sm/16.
Как наблюдалось в опытах, аналогичное повышение давления на дни-
ще может реализовываться также и после выхода кормы тела из воды. Тогда
донная каверна соединяется с атмосферой и вдоль свободной границы кавер-
ны из-за весомости жидкости начинает действовать сжимающее давление.
Это приводит к динамическому процессу смыкания границ донной каверны и
образованию центральной водяной струи, которая достигает днища тела и
оказывает на него ударное силовое воздействие (рис. 4.8). Приведенные вы-
ше оценки для возвратной струи будут справедливы и в этом случае, то есть
скоростной напор на днище тела будет рассчитываться по приведенной выше
формуле.
Рис. 4.8 Воздействие на днище струи воды
2
при смыкании свободных границ каверны: q=(1+<у)р~
118
Глава 5
Численный метод расчета гидродинамических коэффициентов и
присоединенных масс тела вращения
§ 1. Постановка задачи гидродинамики при
прохождении тела через экран
Будем рассматривать тело вращения, состоящее из цилиндрического
корпуса и притупленной носовой части. Профилированная носовая часть вы-
полнена в виде сегмента сферы и конических или оживальных переходников.
Для сильно вытянутых тел вращения, имеющих заостренную носовую
часть, гидродинамические характеристики определяются в настоящее время
по методу плоских сечений или по методу, основанному на распределении
гидродинамических особенностей по оси симметрии тела. В методе плоских
сечений используется гипотеза о плоскопараллельности течения в попереч-
ном сечении тела, когда продольным растеканием жидкости можно пренеб-
речь. Методы, основанные на распределении гидродинамических особенно-
стей по оси симметрии тела, применимы только к телам, для которых огра-
ничен угол наклона касательной к меридиональному сечению. Таким обра-
зом, метод плоских сечений и метод, основанный на распределении гидроди-
намических особенностей по оси тела, нельзя применять для расчета гидро-
динамических характеристик ракет, имеющих обычно притупленную форму
носка.
Следует также отметить, что при проведении прочностных расчетов
ракеты наряду с суммарными значениями гидродинамических коэффициен-
тов необходимо знать их распределение по длине и давление на поверхности.
Эту задачу для тела с притупленной формой носка возможно решить лишь с
помощью численного метода, реализованного в виде программы для ПЭВМ.
Применяемый в настоящей работе метод позволяет рассчитывать гидродина-
мические характеристики при выходе ракеты, являющейся телом вращения с
произвольной формой носка. Будем определять гидродинамические характе-
ристики только для вышедшей части корпуса ракеты.
Часть корпуса ракеты, вышедшая из шахты, обтекается несимметрич-
ным потоком жидкости, обусловленным вертикальным движением ракеты и
ходом ПЛ. На этой части корпуса формируются нормальные и продольные
гидродинамические нагрузки. В результате действия нормальных сил проис-
ходит отклонение продольной оси ракеты от вертикали и вращение корпуса
ракеты относительно некоторой поперечной оси.
Выход ракеты из шахты можно характеризовать следующими кинема-
тическими параметрами: продольной скоростью Vx, длиной вышедшей части
I, угловой скоростью вращения /2 и углом отклонения оси ракеты от вертика-
ли у Величины V„ £2, упри движении ракеты в шахте изменяются от нуле-
вых значений в момент трогания до некоторых максимальных значений в
момент выхода кормового среза ракеты из шахты.
119
Отклонения продольной оси ракеты от вертикали невелики, и для уп-
рощения задачи будем считать, что ракета движется вертикально. Линейные
размеры ракеты на порядок меньше размеров ПЛ, поэтому корпус ПЛ можно
заменить бесконечной плоской стенкой. В узком кольцевом зазоре между
корпусом ракеты и шахтой расположены пояса горизонтальной амортизации
ракеты и другие элементы. Из-за малости проходной площади кольцевого за-
зора влиянием спутного потока жидкости из кольцевого зазора пренебрежем
и будем считать диаметр шахты равным диаметру цилиндрической части
корпуса ракеты.
Как и при движении тела в безграничной жидкости, при выходе ракеты
из шахты действующие на нее гидродинамические силы можно разделить на
силы потенциального происхождения и силы, связанные с отрывом погра-
ничного слоя и образованием вихрей, т.е. силы вязкого происхождения. Си-
лы потенциального и вязкого происхождения будем рассчитывать независи-
мо друг от друга.
При сделанных предположениях задача определения гидродинамиче-
ских характеристик ракеты при выходе ее из шахты движущейся под водой
ПЛ сводится к задаче об обтекании тела вращения, проходящего через жест-
кий экран перпендикулярно его плоскости в полупространство, заполненное
жидкостью, движущейся параллельно экрану с постоянной скоростью W,
равной скорости хода объекта.
В настоящей работе для нахождения параметров потенциального обте-
кания тела вращения, проникающего через плоский экран в поперечный по-
ток жидкости, применяется метод источников, непрерывно распределенных
по выступающей над экраном и омываемой жидкостью поверхности тела со.
Принятая расчетная схема приведена на рис. 5.1.
Для характеристики движения тела вращения в идеальной несжимае-
мой жидкости достаточно знать обтекание для трех простых движений [28]:
- поступательного вдоль оси х со скоростью V\ = 1 (i = 1);
— поступательного вдоль оси у со скоростью К2 = 1 (i = 2 );
- вращательного вокруг поперечной оси, параллельной оси z, со ско-
ростью ~ 1 (i=6 ).
Суммарный потенциал вызванного движения жидкости определяется
по формуле
Ф=2?ч(К1^| + К2^2СО5 0+Кб^бСО8 0); (5.1)
где R4 - характерный линейный размер (радиус цилиндрической части тела);
<Р\, ф2, <Рб ~ безразмерные потенциалы при простом движении;
К,=АЧ-<Л.
120
Рис. 5.1 Расчетная схема: 1-поверхность тела;
2-жесткий экран; 3-поверхность зеркального отображения тела
121
Наряду с декартовой системой координат xjyiZi, связанной с телом, с
единичными векторами i\,j\,ki, необходимо ввести также декартову систему
координат xyz, связанную с твердым экраном, с единичными векторами
i,j,k. Поскольку задача прохождения тела через жесткий экран решается
раздельно для дискретных положений тела относительно экрана, то удобнее
при рассмотрении для каждого положения совместить эти системы, как это
показано на рис. 5.1. Будем пользоваться также цилиндрической системой
координат х, г, 0, ось х которой совпадает с декартовой, а у = rcos0, z = rsin0.
Потенциалы при каждом простом движении удовлетворяют уравнению
Лапласа
ЛФ,=0, i = 1,2,6. (5.2)
При выдвижении тела через жесткий экран в идеальную несжимаемую
жидкость граничное условие на омываемой поверхности тела а> выражает
совпадение нормальной составляющей скорости точки Р поверхности тела и
жидкой частицы, прилегающей к точке Р:
= 1<(Р) й(Р), /=1,2,6. (5.3)
О
На плоскости экрана а>эк должно выполняться условие непротекания
= 0, /=1,2,6. (5.4)
При удалении в бесконечность потенциалы должны стремиться к нулю
Ф,->0 при Jx1 + у1+ Z1
Таким образом, приходим к внешней задаче Неймана.
Здесь ¥,(Р) — скорость точек поверхности тела при соответствующем
простом движении, й(Р) - нормаль к поверхности тела <о, направленная
внутрь жидкости, пэк - нормаль к поверхности экрана
Нормальную составляющую скорости точки тела Р определим сле-
дующим образом.
Распределение скоростей твердого тела вполне определяется заданием
линейной скорости одной точки этого тела Vo и угловой скорости вращения
тела. Выбирая в качестве такой точки некоторый полюс А, лежащий на оси
симметрии тела на расстоянии хА от его носка, и обозначая через £2 вектор
угловой скорости вращения тела, для скорости К(Т’) произвольной точки Р
тела будем иметь формулу
К(Р) = К0 +/2хг,
где г есть радиус-вектор точки Р относительно полюса Л. Или в развернутом
виде
сФ[
дп
дФ1
дпж
122
У(Р) = (-У}1 -V2j -V3k) +
x-xA
j k
122 f23
rcos0 rsm.0
После раскрытия последнего выражения и группировки членов полу-
чим
V(P) = (-Kf + P22r sin О - 123r cos 0)i + (-К2 + (х - хА )123 -12/ sin 0) j +
+ (~К3 +12/ cos 0 -122 (х - хА ))к.
Итак, для плоского движения тела вращения будут иметь место сле-
дующие выражения:
при i= 1 К|(Р) = -K]i;
при г=2 V2(P) = -V2i ; (5.5)
при1=6 F6(P) = [-ircos^ + 1(х-хл)]-123.
Если за параметр принять длину дуги s образующей тела вращения, от-
считываемую от точки пересечения оси симметрии с поверхностью носка те-
ла и возрастающую в направлении экрана, то образующую тела вращения
можно представить в параметрической форме, выражая цилиндрические ко-
ординаты ее точек в виде функции независимой переменной s:
x=x(s), r=r(s).
При этом производные по s обозначим
, дх , дг
X =—, г = —.
ds ds
Введем систему координат п,т,Ь, связанную с точкой тела Р, единич-
ные векторы которой направлены: п — по нормали к поверхности тела, ? —
по касательной к меридиональной кривой тела, проходящей через точку Р в
сторону возрастания s, b - по вектору п х ? и образующий с векторами п, ?
правую систему координат. Единичные векторы п,т,Ь выражаются через
единичные векторы декартовой системы координат по формулам
п =-r'i + x'cos# j + x'sin#&;
f = x'i + r'cos0 j + r'sin0k; (5.6)
b =-sin# ] + cos0k.
Следовательно, граничное условие (5.3) перепишется в виде
=Г1(Р)-и(Р)=г'.К1;
дп ш
= V2(P) п{Р) = —х' • У2 • cos#; (5.7)
= V6 (Р) -п(Р) = [г/ + х'(х - хА )] 123 • cos0.
дФ2(Р)
дп
8Ф6(Р)
дп
123
Здесь при вычислении скалярных произведений векторов 1<(Р),и(Р)
использованы их выражения (5.5), (5.6) через единичные векторы декартовой
системы координат. Принятая параметрическая форма задания образующей
тела позволяет представить поверхность вращения произвольной формы.
Поставленную задачу можно решить с помощью замены обтекания те-
ла обтеканием системы гидродинамических особенностей, а именно: источ-
ников, непрерывно распределенных по поверхности тела со.
Влияние жесткого экрана будем учитывать путем введения дополни-
тельной системы особенностей, распределенных по поверхности зеркального
отображения тела симметричного плоскости экрана. Граничное условие
(5.4) будет выполнено, если интенсивность источников, распределенных по
поверхности зеркального отображения тела, принять равной по величине и
знаку интенсивности соответствующих источников, заменяющих тело.
Таким образом, положим, что источники непрерывно распределены по
поверхности тела и его зеркального отображения со + со* с поверхностной
плотностью //(0), которая является функцией переменной точки Q поверх-
ности тела. Обозначим через R расстояние от рассматриваемой точки по-
верхности Р с цилиндрическими координатами х, г, текущей точки по-
верхности Q с координатами £ р, Л
К = [(х-£)2 +(rcos£-pcosi?)2 +(rsin#-psini9)2]2\
Абсолютный потенциал скорости для каждого простого движения тела
Ф,(Р) будет иметь выражение
Ф,(Р) = - f , i=l,2,6, (5.8)
где dco=pd3da есть элемент поверхности;
<т -значение параметра s, характеризующее текущую точку Q
поверхности;
p,(Q)- поверхностная интенсивность источников при i-м простом
движении тела.
Потенциал течения, полученный интегрированием элементарных ис-
точников с расходом pid со по поверхности, называется потенциалом просто-
го слоя. Подынтегральное выражение (5.8) стремится к бесконечности при
сближении точек Р и Q (R —> 0 ), расположенных на поверхности, и интеграл в
этом выражении является поэтому несобственным. Нормальная производная
потенциала простого слоя (5.8) в рассматриваемой точке поверхности Р име-
ет разрыв, и величина скачка нормальной производной равна произведению
2 л- на значение плотности в точке Р, то есть 2 сгр,{Р):
^Р- = 2^(Р)+ \pi{Q)^P-d<o, (5.9)
где вектор R равен
R=(x-g)i +(rcos^-pcosi9)j + (rsin0-psinff)k. (5.10)
124
Поскольку интенсивности на зеркальном отображении равны интен-
сивностям в соответствующих точках на теле, то уравнение (5.9) можно пе-
реписать в виде
^^=2л-//,(Р)+ jAi(e)
Rn(P) R.n(P)
R3
R3.
da), (5.11)
где
7L = (х - (21 - ^))- i + (г cos О-pcos0)j + (rsin0- psin^)^;
R = [(х - ^)2 + r2 +p2 - 2rpcos(0 - ;
Л = [(x - (2/ - ^))2 + r2 + p2 - 2rpcos(0 - .
Решение p,(s, ff), i= 1, 2, 6, будем искать в виде:
pl(s,0) = pi(s)-, p2(s,0) = p2(s)-cos0, p6(s,0) = p6(s)-cos0.
Вместо p(s) удобно рассматривать функции g,(s), связанные c p(s) со-
отношениями:
(5-12)
g, = 2лг—, i= 1,2, 6,
т.е. gi(s,0) = gi(s\, g2(s,0) = g2(s) cos0, g6(s,0) = g6(s)-cos0.
Тогда граничные условия (5.7) можно переписать в виде:
R-n R> n , ,о
d(7-d&
(5-13)
r 2>r0J0J
или, проведя соответствующие преобразования, представить их следующим
образом:
R3 R3
Si2x
gx(s) = rr'~ — j fgi(cr)
о 0
r Slln к • n
g2 (-s) = ~x'r - J J g2 (o-)cos S +
2>rcos^o о [_ R
r S,2jr к n
g6 (S) = r[rr' + x'(x - XA )] - — — J J g6 (o-)COS —j- +
ZZTCOScz q q xv
Здесь Si — длина дуги образующей выступающей над экраном части те-
ла.
Таким образом, получены неоднородные интегральные уравнения
Фредгольма второго рода для определения неизвестных функций gi(P)
(i= 1, 2, 6). Составленные интегральные уравнения (5.14) эквивалентны урав-
нениям Лапласа (5.2) вместе с граничными условиями (5.3), (5.4), поскольку
всякое потенциальное течение, вызванное движением твердого тела в жидко-
сти, может быть сконструировано с помощью системы источников.
Определив из уравнений (5.14) функции g,(s,0), а следовательно, и
Pi (s, 0), можно легко рассчитать все поле течения.
R-n R, n ,n ,
—r— d0da;
R-n
R3
’"Lo Я
дз -^-^rfa;(5.14)
, R-n R. n
R
,3
Л3
d0-da.
125
§ 2. Вывод интегральных уравнений метода потенциала простого слоя
Теперь более подробно остановимся на выводе интегральных уравне-
ний потенциала простого слоя. В качестве исходных уравнений примем
уравнения (5.14) предыдущего параграфа, которые с учетом выражений для
скалярных произведений векторов R, R, и единичного вектора п
R n=x'r- r'(x -£)- x'pcos(& - г?);
Rtn = x'r—r'[x - (2Z - £)] - х'р cos(# - г?)
запишем в следующем виде:
gi(s)=fio(s)~ fg,(^fc0(s,«r)+K'’,o(s,a)]rfo-, i= 1,2,6, (5.15)
О
где обозначено:
/10 = гг'’ flD = ~rx'’ foo = rlrr' + х'(х - хА)];
Ki0(s,a) и K*0(s,ст) - ядра этих интегральных уравнений. При этом введены
2тг X
следующие обозначения для ядер:
0 [(х-£)2 + г2 + /> -2r/?cos(0-
г’/ \ г 2Г {х7 -/[х - (2/-£)]-xpcos(#-$)}</#
— J------------------------------------
2л- 0
1- ’
г2 + р2 —2rpcos(0- г?)}2
„ , , • г 1Л, r '(x-^)-x7?cos(^-z?)]coszV?9
R-2o\s^) - — — J — ----—5—;
ZTTCOS# п Г , э •> F
с-£) +r +р -2rpcos(#-$)p
'[х - (2/ - £)]- x'pcos(0 - z?)cos г%/г?
[2/ - +r2 + р2 - 2rpcos(# - г?)}2
2я
K20(s,a)=—-— [
27TCOS0 □
Легко видеть, что ядра:
K20(s,a).
Сначала выведем формулы для интегралов К10(5,ст), K20(s,cr). Введем
следующее обозначение:
Откуда следует, что
0--б = 2а, 0 = О-2а, d$ = -2da. (5.17)
В дальнейшем нам потребуются следующие зависимости, полученные с ис-
пользованием обозначения (5.16):
1 + cos(# - г?) = 1+cos 2а = 2 cos2 а;
1 - cos(0 - г?) = 1 - cos 2а = 2 sin2 а;
(5.18)
(5.19)
126
cosi9 = cos(6*-2«)=cos^-2cos^sin2 a-2 sinor cos a sin 0\ (5.20)
sin <9 = sin(<9- 2a)=sin в - 2 sin #sin2 a-2 sin acosacos 0. (5.21)
Сделаем также следующее преобразование:
(х - £)2 + г2 + р -2r/?cos(^-19) = (х - £)2 + (г + /з)2 -4r/?cos2 а.
Введем обозначения:
П = J(^-^)2+(^-Z’)2; г2 = J(x-<ff + (г+ р)2;
4гр *rp ri=r2~rt.
(x-tf+(r + p)2 г2 г2 г2 ’
1.2 1
b = x’(r- p)-r\x-g).
Выражение для ядра ЛГ10 (ж, а) запишем в виде
[xr-/(x-^)-x/cos(g-J)] dS
[(х - О2 + г2 + р2 - 2r/?cos(6’ - .9)]2
Ь + х'Д1 - cos(# -19)^19
[(х - £)2 +r2 + р2 - 2rpco^0 - .9)]2
d&
2 + р2 - 2rpcos{0-19)]2
l-cos(£-.9)__________d&
2 + р2 - 2rpcos(0- i9)p
= —\---------
+^e2j---------
О Г/ f\2 L
Введем пределы интегрирования:
0Г=--, 0г=--л,
2 2
и ядро Kw(s,a) с учетом (5.16), (5.17), (5.19), (5.22) запишется в виде:
„ < \ rb в\ — 2da
(5.22)
, 2
-4sm a da
' ^2
2^
127
где через Jj и J2 обозначены следующие интегралы:
. da sin2 a da
71" 'Тг —~ V I —?"*
61 f -Jl + р2 sin2 а | 611 -J1 + р2 sin2 а |
Эти интегралы вычисляются с помощью полных эллиптических интегралов
\ do
первого рода Л (к )= . = и второго рода
ол/1-А:2 sin2 О
л
2 ----2--Т~ Г1-г1
Е(к )= pvl-A: sin 0d0 с модулем к2 = — 1 .
о г2
Итак, имеем [6]:
Jl=-2E(k2)'Jl-k2 ; (5.23)
лЛ,5‘П'°^ у, -~2^^ №)-42)]. (5.24)
Ь (V1 + Р2 sin2 а J к
Теперь, используя соотношения (5.23), (5.24), можно записать
/С10 (л,<т)=-* [- rb-J\- 2rx'p • J 2 ] = A(BGt + x'G2 ),
I TA5
лг2 Vl-A;
где дополнительно введены обозначения:
^2 тг^(х - ё,}2 + (г + р)2
_ 2rb _ 2rb
= Т=(хЧ92+(г-р)2;
G.=E{k2)-
128
G2=K(k2)-E(k2).
Аналогично вычисляется интеграл для зеркального отображения:
где введены обозначения:
G; = E(V);
G2 =K(kl)-E(k2);
r' = V[* - (2/ - £)F + (r - z7)2;
r2* = VIх - (2/ - £)]2 + (r+z7)2;
b* =x'(r-p)-r'[x-(2/-^)];
*2
kl=\-^.
h
Таким образом, видим, что ядро ^(ж,©-) (как и все другие ядра зер-
кального отображения) рассчитывается так же, как и X^10(s,ст), если в форму-
лах заменить (х-4Э на [х-(21-].
Учитывая равенства (5.16), (5.17), (5.20), получим выражения:
9 Зак 3686
129
0г
-2rxp J
0,
sin2 ada
I 2 2
1 + p sin a
1
_ sin3 acosada
-2tg6 Jv— »
Ml + p1 sin2 a j
[-6r(J, -2J2 -2tg6J3)-2rxp(J2 ~2J4 -2Zgfl75)].
0г
~2!
01
sin ada
f 2 • 2
1 + p sm a
^r23\vl- к1 J
Здесь обозначены интегралы
_ sinacosada
sin3 acosada
2 • 2
+ р sin а
01
2*2 Г
+ p sin a I
которые равны нулю (J3 = J5=0 ). Вычислим интеграл Je, [ 6 ]:
j sin4 ada
0i M1+ p2sin2a
к2
С учетом равенств (5.23) — (5.26) найдем, что
K20(s,<t)=A(BHx+x' Н2).
где обозначено:
k'2=l-k2; Hx =
Л1-
(5.26)
(5.27)
§ 3. Вывод формул для расчета относительных скоростей
и потенциалов
Пусть U -вектор относительной скорости жидкости в точке Р поверх-
ности тела по отношению к подвижной системе координат п,т,Ь, связанной
с телом; V = V0+P2*.f — вектор переносной скорости точки телаР по отно-
шению к неподвижной системе координат. Тогда вектор суммарной скорости
жидкости в точке Р по отношению к неподвижной системе координат можно
записать в виде:
u=V+U.
(5.28)
130
Умножим скалярно обе части равенства (5.28) на векторы гиб:
Ut = -V-t+u-t; (5.29)
Ub=-V-b+6-b,
где представления векторов г и b приведены в формулах (5.6), а вектора V -
в выражении (5.5). Вектор U удобно представить в виде:
U = г (и1гЦ + и21У2 cos# + и6гИ6 cos#)+ 6(ы2йК2 sin# + w6Z)K6 sin#),
где и1Т и ий - безразмерные компоненты относительных скоростей по осям г
и Ь. Далее будем считать все линейные размеры отнесенными к R4. Так как
К(-6=0; F2-6 = F2sin#;
V6-b = -(х - хА )Л3 sin# = —(х - хА )^-sin# = -(х - хА )К6 sin#, (5.30)
то
K|-r=-F(x'; V2-T = -E>r'cos#;
V6 • f = -V6 cos#[rx' - r'(x - xA )]
C7-r = K1wlj.,i=l; U • f = VtuiTcos#, i=2,6;
U-b -Vxu{b,i=\\ U b =К(иа8т#, i=2,6.
Можно записать следующие выражения:
R-т R»-T
R3
R*
Rb R.b
R3 R3
dod9, i = 1,2,6;
dad 9, i = 1,2,6.
- - vi St2t
Ц-f =T^JJg.
о о
_ у St2n
‘J.-fe=5zffg.
“00
Равенства (5.29) (с учетом (5.30) - (5.34)) перепишем в виде:
1 S,2f
+ Jgl(<
2л- 0J 0J
S,2x
«2r = r- + j f g2 (o-)cos 9
2;rcos# о о
R • f R, • i
J
dud9
R3 R
^- + ^-\iad9,
R
(5.31)
(5-32)
(5.33)
(5-34)
(5.35)
и
1
“6r
= [rx' - r'(x - xA)] + 1 J J g6(a)cos#
dad9\
3
] 5/2л-
«26 = "I + -1. ~ f f g2 (C-)COS5
2л sin# q p
Rb R,b'
R3 R^3
dad9
R,b , ,n
, .-----=— dtxd9
R3 R^3
(5.36)
9*
131
U(,b = (х - xj+ -—— J J g6(o-)cos5
2fl-sin0 j
Rb R,b ,
—z- +----z- dad&’,
R R’ .
где (с учетом (5.6), (5.10))
R • т = x'(x - £)+r'[r - pcos(3 - 5)],
Rt • т = x jx - {11 - £)]+r '[r - p cos(# - 5)],
Rb = psin(#-5); Rt-b = psm(3-&).
По аналогии с формулами (5.15) соотношения (5.35) и (5.36) перепи-
тем в виде:
uiT(s) = fn (s) + Jg, (o-)^,! (s,a) + К*л (s,o-)]do-, r=l, 2, 6,
0
где
1 P т 1 2” f
K"M = — J-r^; <1(s,a) = — J-^9; (5.37)
2n „ R 2n J R.
v / \ 1 R-T njn v* t \ 1 R»'T ojo
K2l{s,o) = ------ J——cos&A9; K2x{s,a)=-------- \—^-cosSd&\
2л cos 0 о p 2;rcos0 „ R,i
K6l(s,a) = K2X{s,o); K*6X(s,o) = K2i{s,a);
/и(«) = x'; /21 (s) = r'; f6l(s) = rx'-r,(x-xA) (5.38)
Utb(s) = fi2(s)+^(а^Ка(з,а) + К*2(5,а)^а, i = 2,6; (5.39)
0
где
Kn(S,<?)=—j4Acos&^; (5.40)
2fl-sm# 0 R
K(,2{s,a) = K22{s,o)-, /22(«) = -1; /б2(«) = Х-ХЛ-
Для тела вращения uxb (s) = 0.
Проведем вычисление ядра (s, <т), приведенного в формуле (5.37):
((s = 1 2J c + r'p[l-cos(0-.9)] = 1 [с + Ir'psin2 a\-2da) =
° Ь2 _ 2гр[1 - cos(£ - б1]^ 2я fl [r22-4rpcos2a]2
_ 1 е|[с + 2г'р sin2 g]cta _ 1 ^[с + 2r'р sin2 ctjctar _
п J г 2 . 2 пг2 J (1-Л2 cos2 а)
4 [r2-4rpcosza]2 24 v '
132
где и J2 приведены в формулах (5.23) и (5.24) и, кроме того, введено но-
вое обозначение:
с = х(х-^)+г(г-р).
Теперь можно записать, учитывая интегралы (5.23) и (5.24):
2с
Kn(s,a) = A 4
C-Gi+—G2 ,
где учтено, что
Г/
,2
и
_ „ 2с
а также введено обозначение: С = —.
Таким образом, получили, что ядро Ки (s,a) равно:
Kn(S,a)=/-2f^fd0=A(cGl +-бД
о R I r J
Вычислим ядро K2l{s,a), приведенное в (5.38):
1_______).
Гт/ГТЛ 4
(5-41)
K2l(s,a) =------------
3,
7TCOS0-T2 j
*j(c + 2r 7>sin2 afa - 2 sin2 or -
(l 4. r>2 sin
7T<X>S0-r
-'/>sin a jcos 3da _
2.2^
+ p sin ay
2tg0smacosa}cos0da __
=------/ У; [с(~ Л + 2^2 + 2/gfi73)+2т'/?(- J2 + 2J4 + 2tg0/s)],
71 Г23р/1 - t2 j
где интегралы Jx, J2, JJ4, J5 были уже вычислены ранее. Учитывая эти ин-
тегралы, получим:
133
По аналогии с K2^(s,d) зависимость (5.42) можно переписать в виде:
(5-42)
= А |Я1С+— Н2
4г',
Вычислим ядро K22(s,a). Используя равенства (5.16), (5.17), (5.20),
найдем, что
где введено обозначение
7 sin2 ar cos2 ardor
Jf> - у-
(1 + p2 sin2 a)2
Вычислим интеграл J6 [6]:
где обозначено
H3 = Л[(1 + Ar'2 )К(к2 ) - 2Е{к2 )].
к
Итак, получили, что
Kn(s,a)=^-.
г
Далее сомножитель 1 /г вынесем за знак интеграла и будем считать,
что
К22 = А • Н3 ; К22 = А* Н3. (5.43)
Тогда выражения (5.39) перепишутся в виде:
1 Sl г .
иа> = fa + - Jg, №2 (s,a)+К*2 (s,cruder, i = 2,6;
r о
где
/22(л)=-1; f61(s)=X-XA.
При этом следует иметь в виду равенства
K*62(s,a)=K22(s,a). (5.44)
Выведем формулы для потенциалов Фь Ф2, Фе- Используя формулы
(5.8) для потенциала простого слоя и учитывая зеркальное отображение,
можно записать следующие выражения:
Piffi = ~ J J g‘f — + —lodod.9 для i=l;
о о 2лр L* R*J
cos# = -Yjg‘^COS19f_L + —Icdod# дляi = 2,6.
oJoJ I* R.J
Формулы (5.45) также перепишем в виде:
1 (л 1 Л
1 f Jg2(a-)cos/-^ + -^-]dad^;
2 л-cos 0 q q у R Rm J
1 s,2jr fl ] A
^б(0=~э f Jg6(o-)cosd — + — Hod#.
2^cos6' q q у R Rm J
Введем обозначения для ядер:
„ ( ч 1 2pd.9 *( 1 1 2(d&
КаМ=— J—; Kl2(s,a)=— J—;
2л о R 2л $ R*
,o Z \ 1 2f COS .9
-d&\ K22(s,cj-)=------I——-dff-,
R v ' 2fl-cos0 0J R,
о
1 2| cosi9
22TCOS^ J
^62(s,a)= K22(s,a\, K62(s,a)= K22(s,o).
Тогда формулы для вычисления потенциалов запишутся в виде:
g
^i(s)=-^2(-s,o-)]^, i=12,6.
о
(5-45)
(5.46)
(5.47)
(5.48)
Нетрудно показать, что ядра Ki2{s,a), i=2, 6, в выражениях для по-
тенциалов (5.47) совпадают с ранее полученными равенствами (5.43), (5.44).
Вычислим ядро Kn{s,o), приведенное в формуле (5.47). Для этого нам
понадобятся некоторые интегралы, которые вычислим предварительно [6]:
J7= J =-2a/1^F7C(A2); (5.49)
Q-fl + p sin ar
_n. (550)
0^1 +p2 sin2 ar
134
135
2r sin ada 2-71-A:2 rtn„,t 2Ч Р/,2Ч1
J9 = J । у, =—72—Г K(k )~E(k )J- (5-51)
e, + p sin a *
Учитывая равенства (5.49) - (5.51), получим:
^2(s,ff)=^-G5, G3=2tf(it2). (5.52)
§ 4. Основные расчетные формулы
На основании результатов предыдущих параграфов этой главы приве-
дем для удобства пользования основные расчетные формулы. Для вычисле-
ния гидродинамических характеристик тела вращения необходимы суммар-
ные значения относительной скорости U на поверхности тела вращения.
Формулу для ее расчета представим в виде
U = т(и1тУ} + н2тИ2 cos# + u6tV6 cos#) + b(u2bV2 sin# + w66K6 sin#), (5.53)
где uiT и - безразмерные компоненты относительных скоростей по осям т
и Ь.
Решение р, (i= 1,2, 6) будем искать в виде
//,(«,#) = p,(s); p2(s,6) = p2(s)cos#; р6 = p6(s)cos#.
Вместо Pi(s) будем рассматривать функции g,(s), связанные с р, со-
отношениями
g. - 2лг—, i= 1,2,6.
°* у
Интегральное уравнение для функций g,(s) запишется в виде:
St СО = /о (s) “ U (о-)[^,о + *7o (^с)]^, i = 1,2,6.
0
Здесь для известных функций fi0(s) используются соотношения
/ю="'; /20=-"’; /ео = 4"'+х’(х-хл)].
В ядра интегральных уравнений входят следующие выражения:
Г1 = J(x-^)2+(r-p)2 ; < =Л/[х-(2/-^)]2+(г-р)2;
г2 = /х-^)2+(Г + р)2 ; т2 = + ;
6 = х'(г-р)-г'(х-£);
с = х'(х-£) + г'(г-р);
Также введены сокращения
Z=-L; в=^;
ПГ2 яг2 г2
Тогда можно записать
Kjo = (BG| + x'G2 )А;
К2о = ^бо=(ВЯ1+х'Я2)Л;
=х'(г - р) - г'[х - (21 - £)];
с* = х'[х - (21 - £)] + г'(г - р).
с=~-, С*=^-.
♦ 2 _2 *2
Kt0=(B*G* +х'в2)А*;
К20 = К60 =(В Н\ + х Н2 )А .
136
Функции G,,G2,G| ,G2,Hx,H2,Hx ,Н2 выражаются через полные эллин-
2 2
тические интегралы первого рода К(к ) и второго рода Е(к ) с модулями
2 2 *2 »2
Г2 Г2
по формулам:
Gx=E(k2); Gt=E(kl);
G2 = [К(к2 ) - Е(к2 )]; G2 = [К(к2 ) - Efk2 )];
н; =-Jj[(l + K!)E(*.!)-2«2K(t.2)];
К*
Н2 = -^[(1 + Зк'2 )К(к2 ) - (3 + к'2 )Е(к2 )];
к
Н2 = -^[(1+ЗЛ12 )К(к* ) - (3 + к? )Е(к' )],
к*
где к'2=1-к2; к'2=1-к2.
Формулы для вычисления и(т, uib и <pt имеют вид
s,
“iAs)=fn(s) + Jg/o-MKflCs.CT) + KiX(s,a)]da, i= 1,2,6;
о
I si ,
uib(s) = fi2(s) + - jg,(CT)[A:,2(s,o-) + Ki2(s,a)]da, i=2,6;
s>
^(s) = - ]gi(a)[Ki2(s,a) + Ki2(s,<?)]dcr, i=2,6.
0
При этом для тела вращения ихь =0, безразмерные компоненты переносной
скорости fXi =х'; f2x=r'; /61 = rx'-r'(x - хА ); f22=-l; fa=x-xA.
Для ядер интегралов введены обозначения
Klx(s,a) = (CGl +~G2)A; KXi(s,a) = (C'Gx +-G2)A ;
т г
Kl2(s,a) = G3A; KX2(s,cr) = G3A ;
K2l(s,a) = (CHl +-H2)A; K22(s,a) = H3A;
r
K2l(s,a) = K6l(s,a) = (C*Hx +—H2)A*; Kn(s,a)=H3A*,
r
где дополнительно вводятся сокращения
G3=K(k2); G3=K(kl);
'У
К
'у
Н*3 =-5-[(1 + Л12да.2)-2Е(Л.2)].
к
В концевой точке (s=0) при продольном обтекании безразмерный по-
тенциал вычисляется по формуле
s,
о
1
[(х-$)2 + р2]2
[(х-(2/-£))2 + Р2]2
§ 5. Формулы для расчета гидродинамических коэффициентов
Пусть и (х, у, z, t) есть поле скоростей, обусловленное волнением моря,
а Ф&(х, у, z, f) - его потенциал, тогда выполняется равенство й = grad .
Предположим теперь, что в некоторую точку внешнего потока (х, у, z),
которая имела скорость u(x,y,z,t), внесено тело, поперечные размеры кото-
рого R таковы, что выполняется неравенство:
|К • grad|i/||«|к -й|,
где V - скорость внесенного тела. Это неравенство означает, что скорости
внешнего потока, которые были бы при отсутствии тела в этом месте, мало
меняются на протяжении тела R.
В соответствии с приведенной в гл. 3 постановкой гидродинамической
задачи суммарный потенциал скоростей движения жидкости Ф£, вызванного
внешним волновым потоком й и движением тела V, находится как сумма
потенциала внешнего потока Ф w и потенциала обтекания тела Ф [36]:
Ф2 (x,y,z ,1) = Фи (x,y,z,t) + Ф(х,у,г,1). (5.54)
Тогда интеграл Коши-Лагранжа в неподвижной системе координат в
принятой расчетной схеме (рис. 5.1) можно записать в виде:
^fr+^T+|lgrad0K,|2 +||ёгадф|2 + ёга^Ф(у ^Ф+^-+₽(/-х)=^-,
St St 2 2 р0 ро
или с учетом (5.54)
^^+||^ФЛ|2+^-+g(Z-x) = ^-.
St 2 Ро Ро
Здесь частные производные по времени от потенциалов находятся в непод-
вижной системе координат. В подвижной, связанной с телом системе коор-
динат частная производная по времени находится по формуле:
д'ФЕ дФ£ _ дФЕ . -
—^ = —f- + q-Ve=—^ + &ad^-Ve.
dt dt dt
138
Здесь <? = grad Ф^- - абсолютная скорость жидкости, вызванная движением
тела и волнением моря, Ve - вектор переносной скорости, выражение для ко-
торого в рассматриваемом плоском движении имеет вид:
Ve =i(-Vx -Z?3rcos#) + j(-V2 + /23(х- xj).
С учетом последних равенств уравнение Коши-Лагранжа запишется сле-
дующим образом:
5/ р0 2 рй
Относительную скорость жидкости обозначим через qr
и уравнение Коши-Лагранжа в случае движения тела во взволнованной жид-
кости примет вид:
й А 2 А
Из последнего равенства найдем выражение для разности давления, отнесен-
ной к плотности воды ро,
Ро St 2
которое практически совпадает с полученным в § 3 гл. 1 для движения тела в
покоящейся жидкости (1.30).
Для рассматриваемого плоского случая (рис. 5.1) (И3=И4=К5=0) по-
тенциал скоростей жидкости на поверхности тела с учетом используемых
нами граничных условий, приведенных в § 5 гл. 3, записывается в виде:
Ф£ = R((Vl+(К2 -w2>2cos#+(*6 - “б >6 cos#), (5-55)
где введены безразмерные потенциалы <рх, р2, <рь по формулам:
ФI=R(^'l-u1)pl; Ф2 = Я(И2-н2)(р2со8#; Ф6 = fl(K6-u6>6cos#,
причем V6=/23 R. Здесь щ, и2, щ - параметры волны, рассчитываемые по
формулам (3.46), (3.48).
В соответствии с рассматриваемой схемой выхода введем следующие
соотношения для скоростей
__ у —и
Vl-ul = VAcosa; K2-«2=K^sina; /2 = —-------
Va
где VA = -щ)2 + (К2 - и2 )2 и угол атаки находится из выражения:
( V2-и2У
<r = arctg —---- .
Тогда формула (5.55) для потенциала Ф2приобретет более простой вид:
Ф£ =RVa(^ cosa + <р2 sinacos# - Р2<рь cos#). (5.56)
Введем следующие безразмерные величины
139
V6~u6.
'А
dV2 R dV2 .
di ~ dt ’
Й=^ =
Уг
(Л v^- v2=^-,
R ' VA Va _
_ щ _ u2 dVt R dVx
Wi=—; m2=—; У=—L=—v—L;
У А У A dt V} dt'
j. _ _ R dux _ du2 _ R du2
U'~ dt ~ VA dt ' U2~~dT~V% dt '
R d/2 p dVA R dVA
dt VA dt
. da R da _ xA
a~~^~VA~dt' Xa~~R' R
Фг=—,
RVa
У a dt ’
_ X у I
R R
Ч
а также найдем, что
тТ” dVA R Г/Ту . ч /т>
Уа = " ui )cos« + (у2 “
а Уа
«Jcosa + CKj -u2)sma.
Единичные потенциалы (р\, <)>i, зависят от длины вышедшей части
тела I и угла отклонения оси симметрии тела от вертикали % которые, в свою
очередь, зависят от времени f.
I = l(t); /= Х0-
Поэтому производные по времени от единичных потенциалов выража-
ются формулой:
d^ _ d(Pi dl dtp, dy _ d<pt
dt dl dt dy di dl
dl
где — = V. =cosa + u,.
di 1 1
Будем рассматривать практически вертикальный выход тела, когда
угол /мал (/< 0,1), то есть производные от потенциалов по углу у будут не-
велики и ими можно пренебречь:
^«0, i=1,2,6.
dy
С учетом последнего соотношения равенства (5.57) перепишутся сле-
дующим образом:
~(cosa + ux)+^^‘ i=l,2,6, (5.57)
5/ dt
^- = ^-(cosa + u}),
где введено обозначение (d, =^-, i = 1,2,6.
dl
Теперь соотношение для производной —с использованием (5.56)
dt
примет вид:
140
Q ф 2 Г—----- —
-- = VA |КЛФГ + (- q\ sin a + <p2 cos a • cos 0)a - £2<pb cos в +
+ cos« + <p'2l sin« • cos*? - ^^cos^cos# + U|)]. (5.58)
В соответствии с принятыми обозначениями запишем выражение для
квадрата вектора переносной скорости Ке2:
Ие2 =И^{(й| + cos«)2 + (i/2 + sin«)2 + 2(2у3 -Л)[Г(ц + cos«)cos*?-
-(м2 +sina)(x-хл)]+(й>3 -/2)2[r2cos26'+(x-x4)]}. (5.59)
Аналогично для квадрата вектора относительной скорости жидкости
^2 имеем следующее выражение:
(5.60)
<?2 = VA [w2r cos2 а + 2ulT cos«(w2r sin a - /2/6r)cos*?+
+ (i/2rsin«-Z2z6r)2 cos2 0 + (u2b sina - &U6b) sin2 *?].
С учетом полученных соотношений (5.58) - (5.60) найдем выражение
для коэффициента давления
2(р-рю)
рУ}
На омываемой поверхности тела при выходе его во взволнованную
жидкость через жесткий экран:
2(р—.ф^ + 2a'(^sin«-p2cos«cos#) + 2/2%cos0-
Pova _
- 2(cos а + й} cosa + <z>2, sin а • cos в -<р'ы£2 cos (?)+
+ (й| + cos«)2 +(й2 + sin«)2 + 2(л73 - /2)[г(п, + cos«)cos6>-
-(w2 + sino')(x-x4)]+(6J3 -/2)2[r2cos26'+(x-хл)2]-
- u2r cos2 a - [2w, Tu2 T cos «sin a - 2 w, Tu6 TS2 cos «]cos в+
+ [- w2r sin2 «+2w2rM6r/2sin«- ulT.
+ [- ulb/22 + 2«24u6fc/2sin« - w2fc sin2 a
./^Jcos2 0+
r]sin20-^f, (5.61)
Fr
у
где Fr = - число Фруда.
Перейдем теперь к определению сил, которые действуют на твердое
тело при выходе его через плоский экран.
Главный вектор сил давления F и главный их момент М А относитель-
но полюса А находятся по формулам:
F = - ffpndur, МА = - fjp(fA х n)d(o;
СО (D
где d a>=rd Ods - элемент поверхности тела вращения.
141
Для тела вращения ограничимся вычислением проекций Q, N главного
вектора сил F на оси связанной с телом системы координат и момента Mz
относительно оси z
S, 2лг S, 2я
Q- j ^prr'd6Us; N = -j ^px'rcos0d6ds;
0 0 0 0
S,2n
Mz = - J p[rr' + x'(x - xA )]/?cos0d0ds
о 0
и коэффициентов этих сил и момента по формулам:
А»Х
rpeSM=xR2.
Расчет коэффициентов проводился по формулам:
1
cx=v~i iprr'dais’
о о
1 S12л-
Сп =------j Jpx'rcos^^dy;
SM о о
1 s‘ 2я
mz = - j |/эг[гг' + х'(х - хА )]cos 0d6ds,
V о о
где коэффициент давления р приведен в равенстве (5.61).
Подставляя в эти формулы выражение для коэффициента давления р
из равенства (5.61) и проводя интегрирование по углу 6?от 0 до 2 л, получим
выражения для коэффициентов Сх, С„ и mz.
Присоединенные массы тела вращения Лц,Л22’Лб иЛб вычисляются с
учетом представления (5.55) по формулам
s,
Лц = -2^о0Л farr'ds;
о
^22 j^2rx ds’
0
S,
Лб=-^ол2
о
S,
Л66 = ~^Р0Р2 И"' + Х'(Х - ХА )кбЛ
0
Соответствующие этим присоединенным массам безразмерные коэф-
фициенты присоединенных масс вводятся с помощью следующих зависимо-
стей:
к- - ^11 JZ - ^2 .
8АЯ3 8АЯ3
142
(5.62)
(5.63)
гг _ ^26 . If _ ^66
26 16р0Я4 ’ 66 32р0Я5’
Введем обозначения:
СХО \2<Ригг'^>
ЛМ О
О
С =— (ufrr'ds;
xi е J ,г
О
Si
О
л s‘
G3 KM2rM6r +U2bU(>b}rr'ds-,
О
т- S>
Cx.=-^-\^lT^u1bb)rT,ds.
О
Тогда коэффициент сопротивления тела при прохождении его через эк-
ран во взволнованном потоке жидкости будет рассчитываться по формуле
Сх =^^LL(r/)cosa-dsina)+[(Ml +cosa)2 +(u2 +sina)2]>j2 -
- CXo cosa^u, + cosa) - CX| cos2 a - CXi sin2 a +
+ 2CX3/2sina-CX4/22 +2(«i +cosa)(ta3 -/2) — -(/ -xA)r2 +
+ (<у3 -/2)'
ГТ)2 1_ + (/-_7л)2-2+1т(2^_-) _
4 л
-b-’ <5-64)
nFr
- Г(Ы к
где г, =-!--безразмерный радиус поперечного сечения тела на уровне эк-
Л
— 1 Г 2 j с ''С ~
рана; тт = ]лг ах - безразмерный объем вышедшей части тела;
хс=— = —-— §nr2xdx - безразмерная координата центра объема вышедшей
Л Лтр q
части тела.
Выражение для коэффициента нормальной силы имеет вид
С„ = ^^~22 (р. sina + acosa) + ^^^26-(Кл/2 + £1) +
л л
+ СЯ1 sinacosa + С sina(i7| + cosa) + СП1£2 cosa + + cosa) -
~^^<э3(й|+cosa), (5.65)
л
где коэффициенты поперечной присоединенной массы К22 и присоединенно-
го статического момента К26 приведены в равенствах (5.62);
143
2я 2я
= -z- ; Cn2 = -z- yp'uX'rds;
\ 0 0
2ks,( , J 2ns,f , , 2rT
cn3=—^- JMirM6r* rds5 cn4 = -ТГ ]^6ix rds + —L. (5.66)
0 \ о n
Затем запишем выражения для коэффициента mz
mz = sina + dcosa)+ (кл/2 + /?)+
+ sinacosor+mZ2 sina(M, + cosor) + wZs/2cosa + mZi/2(ux + cosa) -
-2й>3(и] +cosa) -------(хА-хс) ,
4 л
где коэффициенты присоединенного статического момента Л?26 и присоеди-
ненного момента инерции приведены в равенствах (5.62);
271"
mZl = V11“1гм2г["' + *'(* - хА )]г<*;
О
27^
тг2 = Т1№ + х'(х ~ хА )>Л;
О
2/^
mz3 = j«lrM6r["'+x'(x ~ xA )hfc;
0
2я5'г , r , i , Гг/ 2гг
= “’>6/1" +Jc(x-x^)jrds+ -------------~{xA-xc}
n 4 я
(5.67)
тч:
О
Исходя из полученных формул для Сх, С„ и mz, найдем их выражения
при стационарных условиях (РА =/2 = а = 0) и при движении в покоящейся
ЖИДКОСТИ (W] = н2 = w6 = 0)
Сх = г,2 -(С, +СХ )cos2 a-Cr sin2 а+2Сх /2sinar-Cr /22;
Л I X AQ f Л2 -*3 Хд ’
сп = (С„, + сп2 )sinacostf + (С„3 + С„4 )/2cosa;
mz=(mZi +mZ2)sinacosa + (mZ3 + mZ4)/2cosa.
Откуда найдем производные от С„ и mz по а а /2:
д£2
dtnz
dQ
т.
_ «1 п2 ’
а=П=О
'-'п
а=Я=й
«з »4 ’
= mZl+mZi-, m
a=Q=0
= т7 +т
__ z3
«-Л=0
п
дСп
да
dmz
да
Распределения коэффициентов С„ и mz по длине тела х при установив-
шемся движении и при ненулевых параметрах движения и волнения запи-
шутся
144
dCn dC“ . . dC” -
—- = —— sin a(cos a + ut) + —— /2(cos a+ux);
dx dx dx
dm7 dm" . , _. dm” — _
—- = —— sina(costz +1/|) + —— Z2(cos«+ux),
dx dx dx
в соответствии с формулами (5.66), (5.67) приведем распределения по длине
с учетом равенства x'ds-dx и обозначения drldx = гх
dC" 2т, ,
dx sM
(5.68)
dC” 2т , . /с 691
dx SM
dm" 2m , , .. . ..
—7— = + Mir«2r )("x + (x - xA ));
dx SMR
dm” 2m , , .. , 44
—Г" = - <Ры - W|r“6r)("x + (x - xA )).
dx SMR
Гидродинамические свойства обтекаемого тела наряду с перечислен-
ными коэффициентами характеризует также коэффициент центра давления
Cd, рассчитываемый по формуле
ш
Cd =хА +—
а л
'-'п
При обтекании тела вязкой жидкостью возникают касательные напря-
жения. В практических расчетах вязкую составляющую продольной силы
определяют как для плоской пластины, смоченная боковая поверхность ко-
торой равна боковой поверхности тела. Коэффициент сопротивления для
продольно обтекаемой пластины определяется в области ламинарного тече-
ния, т.е. для чисел Рейнольдса
Re, <5-105... 106,
у
по закону Блазиуса
а в области турбулентного течения, т.е. для Re, >106, по закону Прандтля-
Шлихтинга
Cf =
0,455
(IgRe,)258 '
Коэффициент составляющей продольной силы от сопротивления тре-
ния Cxf тогда найдется по формуле
10 Зак. 3686
145
где SMEPi = ,SUErj - площадь меридионального сечения выступающей
над экраном части тела.
Здесь использовано выражение для боковой поверхности тела враще-
ния
С — г Ъ
‘-’бок, ” ‘-’мер, •
Следовательно, коэффициент продольной силы Сх£ при выходе в жид-
кость тела вращения через жесткий экран определится как сумма составляю-
щих от сил давления (5.64) и сил трения Сху
СХ£ = Сх + .
Вихревая составляющая нормальной силы возникает в связи с форми-
рованием и отрывом пограничного слоя и последующим развитием за цилин-
дрическим корпусом тела возвратного течения при пронизывании неподвиж-
ного слоя жидкости носовой частью и цилиндрическим корпусом тела.
Вследствие этого нормальное сопротивление некоторого узкого кольца ци-
линдрического корпуса при движении тела с углом атаки может быть при-
ближенно принято таким же, какое возникает на таком же кольце бесконеч-
ного цилиндра, начавшем двигаться импульсивно и прошедшим путь, рав-
ный расстоянию, пройденному этим кольцом тела в неподвижном жидком
слое перпендикулярно оси цилиндра. В результате экспериментальных ис-
следований установлено, что формирование на цилиндрическом корпусе
вихревых сил происходит с запаздыванием и постоянное их значение дости-
гается по истечении некоторого интервала времени от начала движения, за
который формируется пограничный слой, происходит его отрыв и устанав-
ливается возвратное течение за цилиндром. Сопоставление двух значений
вихревых сил, сосчитанных с использованием в одном случае полученного
коэффициента сопротивления при импульсивном движении и в другом - ко-
эффициента сопротивления цилиндра при установившемся движении, пока-
зывает, что в первом случае вихревые силы несколько меньше. Однако экс-
перименты проведены для докритических чисел Рейнольдса
(Re = 0,64-105...1,28-105), тогда как натурным условиям соответствуют закри-
тические числа (Re = 2-106...6-10б), что не позволяет воспользоваться резуль-
татами опытов при расчете натурных изделий.
Поэтому в расчетах будем пользоваться значениями коэффициента со-
противления бесконечного цилиндра Cg при установившемся движении, ко-
торые зависят от числа ReK при поперечном обтекании. При развитом тур-
булентном пограничном слое Cg = 0,35. В соответствии с изложенным вихре-
вую составляющую нормальной силы Cnf будем определять по формуле
Cnf=C6Snsm2 а, (5.70)
где Sy -5ц /SM, Sy - площадь меридионального сечения цилиндрической
части тела.
Коэффициент нормальной силы определится как сумма
146
С„г=С„ + СиГ. (5.71)
При движении с углом атаки без вращения с учетом равенств (5.71) и
(5.70) выражение для С„г приобретает вид
C„r = Са sinacosa + CKS„ sin2 а. (5.72)
nz, п U Ц v '
В соответствии с последней формулой, считая вихревую составляю-
щую приложенной к центру меридионального сечения цилиндрической части
корпуса тела Хц, из уравнения моментов получим зависимость коэффициента
центра давления от угла атаки
СаСи sinacosa + CKSuxtJ sin2 а
_ б--Ц~Ц--------, (5.73)
(-пЕ
где5д = 2{1-1нос)Кц, хц=^-, хц = 1-^-.
Кц Z
§ 6. Методы вычислений
Остановимся более подробно на методах вычислений при решении за-
дачи обтекания потенциальным несжимаемым потоком идеальной жидкости
тел вращения.
При расчете плотностей источников, скоростей и потенциалов имеют
место особенности в подынтегральных функциях. Так, при расчете скорости
при и—>s, £->х имеют место два типа особенностей: 1п|х- £| и
все остальные несобственные интегралы имеют только логарифмическую
особенность 1п|х - . Для интегрирования с особенностями можно использо-
вать замену переменных [28]
Л(£) = т—। signtf - х),
у £ - х| + CL
где L - характерная длина;
С - постоянная величина, значение которой равно единице (С = 1).
Элемент дуги в новых переменных будет равен
Зависимость ст от h определяется соотношением
a-s = sign(A)---у, (5.74)
1-Л
и вблизи особой точки узлы интегрирования распределяются с постоянным
шагом h.
После замены интегрирование по новой переменной проводится по
формуле трапеций. Если выделить особенность для главного значения несоб-
ственного интеграла с помощью введения квадратурной формулы типа Гаус-
147
10*
са, то наряду с повышением точности вычислений это приведет к значитель-
ному усложнению расчетов.
Таким образом, одним из важных моментов при проведении вычисле-
ний является выделение главного значения несобственного интеграла, ядро
которого при сг—>5 стремится к бесконечности.
Обычно замена переменных используется лишь на участке вблизи осо-
бой точки (s=ст) |$ - <т| < 0,05 L. Поэтому интегрирование на этом участке и
вне его проводится по разным формулам, что приводит к значительному ус-
ложнению алгоритма расчета.
В настоящей работе для упрощения всего вычислительного процесса
не станем переходить к новым переменным вблизи особой точки, хотя будем
увеличивать плотность расположения узлов интегрирования при приближе-
нии к ней. Расположение узлов интегрирования на
участке |s-cr|<y
опре-
деляется при этом по формуле
aj=s +
J2'Si
2-103-2j2 ’
j=l,2,...,20,
где знак принимается для точек, расположенных выше (cr7 <s ), и знак “+”
- для точек, расположенных ниже особой точки (oj > s).
Вне этого участка узлы интегрирования расположены в расчетных точ-
ках. По существу при увеличении плотности расположения узлов в окрестно-
сти особенности по последней формуле, позволяющей ослабить особенности
подынтегральных функций в несобственных интегралах, использована зави-
симость, аналогичная (5.74), и достигается при этом такая же точность вы-
числений. Однако вычисление интегралов в нашем случае проводится по
всему участку интегрирования от 0 до s( по одним и тем же формулам
Jg(<7)K(s,aX<7 = £(gfcKfc + gfc).
О k=[
где g*=g(o*) yiKk=K(sМ/ - количество узлов интегрирования
для выступающей длины /.
Для нахождения интенсивностей g, (i = 1, 2, 6) источников, распреде-
ленных по поверхности выступающей части тела, необходимо решить инте-
гральные уравнения (5.15) для каждого простого движения (например, мето-
дом последовательных приближений). За начальное приближение интенсив-
ностей следует принимать свободные члены соответствующего интегрально-
го уравнения.
Алгоритм метода последовательных приближений довольно прост при
реализации на ПЭВМ, так как практически не требует введения дополни-
тельных операций. Однако в процессе апробации его было отмечено, что ко-
личество итераций значительно возрастает (до 20-30) при малой высоте вы-
ступания тела над экраном (/ < R), а для тел с неплавными обводами (с точ-
ками излома или участками отрицательного наклона касательной к профилю
148
тела) процесс сходимости и вовсе может нарушаться. В связи с этим для
расширения пределов применимости метода, а также повышения его точно-
сти и надежности, решение системы интегральных уравнений (5.15) будем
искать по методу Фредгольма, то есть систему интегральных уравнений све-
дем к эквивалентной системе алгебраических уравнений
Л| igi+ai2g2+ai3g3 + — +a\MgM =
a2lg2 + fl22g2 + fl23g3+--- + fl2AfgAf = ^2j
............................................... (5.75)
«MlgM + «M2g2 + aM3g3+.--+aMMgM = Ьм-
Расчет элементов матрицы проводится по формулам
s*r • 1
ajk = sjk + Ki0(Sj,a)\iu,
Sk-l
[1 при j = к Г z . • 1
где 8jk ={ ; IA',()(s,,cr) + Kj0(s,o-)l - ядра интегральных уравне-
1 [0 приj*k
ний (5.15) в j-й расчетной точке;
bj - свободный член интегрального уравнения, то есть bj =fy(Sj:).
Первая строка матрицы соответствует первой расчетной точке (/ = 1),
вторая строка - второй (/ = 2) и так далее. При выводе формул считали, что
весь промежуток интегрирования по 5 от 0 до st разбивается на отдельные ок-
рестности расчетных точек по формулам
‘ 1/ ч . 1,
sk-\ ~ 2^Sk 2 + ~ 2+ Sk ’
где sk.2, sk.\, sk - координаты к-2, к-1, к-х расчетных точек. При выводе фор-
мул для элементов матрицы ajk предполагали также, что на каждом интервале
от до s*k интенсивности g,{o)(i=l, 2,6) принимают постоянные значения,
так что зависимость gi(o) получается в виде ступенчатой функции. Получен-
ная система алгебраических уравнений (5.75) решается методом Гаусса.
При расчете относительных скоростей жидкости и потенциалов будем
формировать матрицы и затем проводить вычисления. Например, при вычис-
лении и1т сначала формируем матрицу в виде
&п bl2...blN
^21 ^22—®2N
9
IPwi ^N2—^NN
где bjk рассчитываются аналогично ajk по формуле
bjk= J[j:11(j7,<7)+ki*i(^,o-)]</ct.
S’k-x
Затем, используя bjk, найдем, что для J-й расчетной точки
N
ЩА^) = /и(5у.)+Хёк^к-
к=1
149
Аналогично находятся И2Й и6г, а также u2h, иы> и (ft (/ = 1, 2, 6). При этом
используем ядра К22, К62 и Ki2 (i = 1, 2, 6) соответственно. При расче-
те и2т, и2ь, иы свободные члены/2i,^i и/22,/б2 рассчитываются по фор-
мулам (5.38) и (5.40). Проведенные проверочные расчеты показывают, что
применение метода Фредгольма для решения системы интегральных уравне-
ний позволяет значительно повысить точность расчетов и расширить рамки
применимости численного метода.
§ 7. Результаты расчета гидродинамических коэффициентов
и сравнения с экспериментом
По разработанной программе на ПЭВМ выполнены параметрические
расчеты гидродинамических коэффициентов, проведено сравнение расчет-
ных значений с экспериментальными данными. На рис. 5.2 показаны расчет-
ная и экспериментальная зависимости коэффициента Су от длины I вышед-
шей части при углах атаки 10° и 20°. Видно, что результаты расчетов удовле-
творительно согласуются с экспериментом.
Исследование гидродинамических коэффициентов при вращательном
движении тела («-0; 12^0) С£/, для рассматриваемой задачи вообще
ранее не проводилось ни экспериментальным, ни теоретическим методами,
dtf
На рис. 5.3 приведено распределение —— при 1=20 по длине тела, состоя-
dx
щего из острого конуса (/г =4,705, угол раствора 2/3 =24°) и цилиндра. Там
же нанесены значения, соответствующие движению тела в безграничной
жидкости и рассчитанные М.Г.Щегловой и Г.В.Махортых по приближенному
методу, основанному на распределении особенностей по оси тела и следа,
справедливому для сильно вытянутых тел с заостренным носком [38].
При расчете обтекания тела безграничным потоком жидкости обычно
используются гипотеза о плавном сходе струй с задней кромки цилиндриче-
ского корпуса и предположение о сохранении в каждом плоском слое, пер-
пендикулярном оси тела, образующегося следа импульса, сообщенного ему
кормовым сечением. Здесь вдоль следа распределяются гидродинамические
особенности (диполи), интенсивность которых принимается постоянной и
равной интенсивности на кормовом срезе.
В носовой части тела (рис. 5.3) наблюдается удовлетворительное соот-
dCy R
ветствие расчетов ——, а при приближении к экрану в численном решении
dx
dC°
нагрузка ——остается практически постоянной величиной, в расчете же для
dx
безграничной жидкости вблизи кормового сечения тела наблюдается ее
уменьшение.
150
I
5.2 Сравнение расчетных и экспериментальных зависимостей коэффициента
Су от длины I вышедшей части
151
Рис. 5.3 Сравнение расчетов по численному методу и приближённому методу для тела вращения,
состоящего из цилиндра и острого конуса (2/?= 24°), при I = 20 и хА = 10
152
~ dCy
Разница в суммарном значении С за счет несовпадения —— в кор-
dx
мовой части составляет примерно 4% (ЛС^ «0,7 при значении С^=16,7).
- dC> к
Несоответствие сравниваемых значении —— вблизи кормового сечения
dx
объясняется влиянием экрана.
Следует отметить также, что для тела с цилиндрическим корпусом при
достаточном удалении носка (Z>10) влиянием экрана можно пренебречь. На
этом основании для сравнения будут привлечены результаты экспериментов,
полученные для движения тела в безграничной жидкости. Так, для сравнения
расчетных значений коэффициента Сх используются результаты дренажных
испытаний тела вращения, имеющего полусферический носок и цилиндриче-
ский корпус, в аэродинамической трубе при нулевом угле атаки (рис. 5.4).
Рис. 5.4 Сравнение расчета —— с результатами эксперимента
dx
для тела, состоящего из цилиндра и полусферы
На практике часто встречаются компоновки со сложной формой носка,
с точками излома образующей. Однако использование в расчете х' и г' квад-
ратичных интерполяций приводит к автоматическому сглаживанию профиля
тела вблизи точки излома. В качестве примера рассмотрим тело вращения с
цилиндрическим корпусом и носком, состоящим из двух конических поверх-
153
dC“
ностей и скругления. На рис. 5.5 приведена распределенная нагрузка ——,
dx
рассчитанная для / ~ 20, когда влиянием стенки можно пренебречь и сравни-
вать результаты вычислений с данными эксперимента для движения тела в
безграничной жидкости. В частности, на рис. 5.5 приведены результаты ин-
тегрирования давления, замеренного в аэродинамической трубе ЦАГИ при
малой скорости потока (и = 45м/с). Результаты расчетов и экспериментов на
рис. 5.4, 5.5 удовлетворительно согласуются.
Рис. 5.5 Сравнение расчета —— с результатами эксперимента для
dx
тела, состоящего из цилиндра, конических переходников и сегмента сферы
Существующие приближенные методы, метод плоских сечений и ме-
тод, основанный на распределении особенностей по оси тела, распространя-
ются на тела вращения с острым наконечником и цилиндрическим корпусом.
С целью выявления границ их применения вычислено распределение
dCy
— для тел с цилиндрическим корпусом и носком в виде острого конуса
dx
(h =1,5; 2,5; 5,0) при длине выступающей над экраном части тела I = 20, когда
jc;
влияние экрана на величину —— практически перестает сказываться (рис.
dx
5.6). Из сравнения результатов вычислений можно заключить, что прибли-
женный метод при h =5,0 дает, с точки зрения совпадения с численным ре-
154
шением, удовлетворительные результаты, а при h =1,5; 2,5 погрешности его
достигают больших значений (порядка 30 ... 70%). Расчеты этих форм приве-
дены также в виде графиков местного коэффициента продольного растекания
жидкости /?(х) (рис. 5.7). Из графиков рис. 5.6, 5.7 видно, что наибольшее от-
личие 7/(х) от единицы (ту(х) = 1 соответствует предположению о плоско-
параллельности течения в каждом поперечном сечении - методу плоских се-
чений) наблюдается для А = 1,5, и для этой же формы носка реализуются
dC“
наибольшие погрешности при вычислении---- по приближенному методу.
dx
Отсюда следует, что по приближенному методу получаются удовлетвори-
тельные результаты в тех случаях, когда становятся приемлемыми предпо-
ложения метода плоских сечений.
dC“
На рис. 5.8 - 5.10 проводится сравнение распределений —----- и
dx dx
коэффициента т](х) для тел вращения с различной формой носка: у наиболее
притупленного из них носок состоит из плоского среза и плавного скругле-
ния радиусом 7?о = 0,5, контуры других представляют собой семейство ожи-
вал (/?«,= 1; 2; 4), включая полусферу (Ro =1). Для наиболее притупленного
155
dC°
носка (Rq = 0,5) получаются и самые большие, максимальные, значения ——
dx
dCn
и —Значения коэффициента ^(х) получаются наименьшими на носке,
dx
что связано с концевым эффектом при поперечном обтекании тела вращения;
причем вблизи стенки этот эффект проявляется наиболее сильно.
Рис. 5.7 Коэффициент т](х) для тел вращения, состоящих
из цилиндра и острых конусов (Л = 1,5; 2,5; 5)
В табл. 5.1 приведены гидродинамические коэффициенты С“, Cdo,
С°, mf, С, СХ2 при различных значениях / для этих тел вращения. Из таб-
лицы следует, что с увеличением I, начиная с I = 10, значения коэффициентов
С“, Cdo, С^, СХ2 остаются практически неизменными, то есть при больших /
(/ > 10) влияние экрана ослабевает и практически перестает сказываться. Зна-
чения коэффициентов C>J и (по модулю) увеличиваются при удалении
носка от экрана, при этом Су меняет знак. Наибольшие значения коэффици-
ента Cdf> получаются для более вытянутых тел.
156
Рис. 5.8 Распределение —— для тел вращения с различной формой носка (7?0 = 0,5; 1; 2; 4)
157
Рис. 5.10 Коэффициент т/х) для тел вращения с различной формой носка (Ло = 0,5; 1; 2; 4)
I
I
I
I
I
I
I
I
I
I
I
I
I
Таблица 5.1
0,5 1 1,5 2 3 5 7,5 10 12,5 15 0,81 1,39 1,60 1,72 1,85 1,88 1,94 1,96 1,97 1,97 0,53 1,21 1,53 1,67 1,81 1,88 1,95 1,97 1,98 1,98 0,22 0,71 1,21 1,55 1,76 1,87 1,95 1,97 1,99 1,99 0,13 0,44 0,83 1,22 1,66 1,83 1,95 1,97 1,99 1,99 1,01 0,96 0,94 0,94 0,99 1,05 1,13 1,14 1,14 1,14 1,00 1,00 1,01 1,03 1,10 1,19 1,25 1,28 1,29 1,29 0,70 0,96 1,12 1,22 1,32 1,43 1,51 1,53 1,55 1,55 0,49 0,80 1,07 1,35 1,55 1,71 1,82 1,85 1,88 1,88 -3,32 -8,57 -10,08 -10,52 -10,37 -8,45 -4,79 -0,85 3,28 7,53 -2,78 -6,78 -8,73 -9,48 -9,55 -7,70 -4,06 0,03 4,27 8,66 -1,23 -2,75 -4,62 -6,64 -8,20 -6,81 -3,03 0,84 5,10 9,58 -0,64 -2,19 -3,24 -5,72 -7,83 -6,42 -2,25 1,65 6,07 10,65 mi ’dy о 00 о? 00 Г- Г" 40 Ml г<у М1 00 о? 40 Ml М1 Су Ch СМ^ МТ 40 00 СП Ml Tt xf СП vcy см о —у ОО (N Ml СП Оу сМ^ Оу СМ~ Ml" Ch СП 40 in ’t 't c*y ^y Г-y mi О? Г? 1Л r 40 40 Ml M1 Г"у ^ly o' —Г 40' r- 40 mi m r-y oo го о VO О 40 40 MT \Г CM VO о сч —у VO с<Г CM Ml CM ’ <4 сь. ch M- oo < -r CM —< 0,61 0,91 0,94 0,95 0,97 0,97 0,97 0,97 0,97 0,97 0,53 0,89 0,95 0,97 0,98 0,98 0,98 0,98 0,98 0,98 0,26 0,59 0,86 0,96 0,99 0,99 0,99 0,99 0,99 0,99 0,11 0,35 0.59 0,80 0,95 0,98 0,99 0,99 1,00 1,00 1,21 1,71 1,84 1,92 1,98 1,99 1,99 2,00 2,00 2,00 1,07 1,67 1,81 1,89 1,97 1,98 1,99 1,99 2,00 2,00 0,44 1,14 1,66 1,84 1,96 1,98 2,00 2,00 2,00 2,00 0,22 0,66 1,16 1,60 1,94 1,98 2,00 2,01 2,01 2,01
3 ® Л ° ° g O' ft; V c 1. Cc Г еЧ < II II II ООО ? «S ft; ft; М- ? 'L "о I £ *2- —• cm ? "o >U I 0° ft; ft; ft; ? Ill ft: ft! ft; M 1 0 1 < —• cm > II II it о © о % «К
и и и zu/- u °*
160
Для рассматриваемых компоновок рассчитанные значения коэффици-
ентов присоединенных масс Л.22 и при различных / приводятся в табл. 5.2.
Здесь же помещены значения коэффициента Лп, они убывают при удалении
носка от экрана и, естественно, для более притупленного тела
(Ro = 0,5) оказываются наибольшими. Для различной длины выступающей
над экраном части поверхности тела с полусферическим носком (/?0 = 1)
представлены также отношения Я22 и Лы к соответствующим величинам, по-
лученным по методу плоских сечений, - Лщ = > Лб = А>6 ^ббле ~ и
значения поправки на растекание rj, определяемой по теоретико-
экспериментальной формуле Пабста
i/Ry
п= 1
J+WRj
1-0,425
1+ (///?, )2
(5.76)
Обычно в формуле Пабста используется отношение длины тела к его шири-
не. Однако в нашем случае, при использовании в решении зеркального ото-
бражения тела, т.е. при наличии экрана, при поперечном обтекании происхо-
дит как бы удвоение длины выступающей над экраном части тела. Поэтому в
формуле (5.76) взято отношение длины выступающей части тела к радиусу, а
не к диаметру цилиндрической части тела (l/R^. Поскольку значения ту близ-
ки к полученным нами более точным методом значениям то в инженер-
ных расчетах при определении Л22 (для тела, проникающего в жидкость че-
рез жесткий экран) по методу плоских сечений можно поправку вычислять
формулой (5.76). Удобно также и при счете коэффициента использовать
те же значения rj, имея в виду, что значения будут при этом несколько
завышенными. Для разных тел (7?0 = 0,5; 2; 4) значения и Л66 получаются
примерно такими же, как и для тела с полусферическим носком.
Необходимость учета сил вязкого происхождения возникает не только
при проведении теоретических расчетов, но и при экстраполяции результатов
модельных экспериментов на натурные условия. Условие физического подо-
бия при учете эффекта вязкости жидкости заключается в равенстве числа
Рейнольдса для модели и явления в натуре. Как правило, размеры модели в
несколько раз меньше натурных, и для сохранения числа Re необходимо ли-
бо увеличить скорость модели, либо пропорционально уменьшить кинемати-
ческий коэффициент вязкости ц оба пути практически неосуществимы. Так,
на испытываемых моделях, наоборот, скорость обычно меньше, чем в натур-
ных условиях, а модельные опыты проводятся в той же среде (в воде), что и в
условиях натуры. Известно, что при проведении модельных испытаний число
Рейнольдса на 1 - 3 порядка меньше натурного, что приводит к увеличению
эффекта вязкости в модельных условиях. Эти обстоятельства вносят большие
затруднения при нахождении составляющих сил вязкого происхождения.
11 Зак. 3686
161
Таблица 5.2
00 -н оо Tfr 40 40 Tfr СП О СЧ О 40 00 00 СП СП СП СП —« -< г- —< О <> Г; СП CH СЧ ГЧ ГЧ VI СП 04 СП СЧ 04 с4 of (N г- о V4 Tt сП ГЧ »—< l-Н «-Н «-Н 04 оо Jn о о о о on о г 40 V4 ’tf П о o' о" о Г- Tfr V (И N о о о о ОО —< ITJ СЧ СЧ —' о о’ o’ о" о СП 40 (N •—< —’ о о о о’ о" о" о 0.66 1.37 1.99 2.51 3.30 4.09 4.25 4.41 5.56 8.67 0.34 0.99 1.60 2.12 2.91 3,70 3.86 4.03 5,17 8.28 0,11 0,51 1,05 1,56 2,35 3,14 3,30 3,47 4,61 7,72 0,04 0.29 0.63 1,04 1,81 2,60 2,76 2,93 4,07 7,18 00 04 О 04 о" 40 04 о" СП 04 o' 00 о" 00 o' 04 40 o' 40 о' О МП о о~ 0,26 0,45 0,56 0,63 0,72 0,79 0,79 0,80 0,81 0,87 0,37 0,55 0,67 0,74 0,83 0,90 0,94 0,95 0,96 0,97
*п О — CS Tfr 4= 4= ЦД «Ч <4 «Ч <4 О —< СЧ Т1- Ч !’ IL " «ч «ч «ч «ч II 0? см и о? X© н>
о г-—« й к ХО <м О w—<
162
Рис. 5.12 Зависимость коэффициентов Су и от угла атаки для
модельных (Сх ~ 1) и натурных (Сх = 0,54) условий
Зависимости составляющей коэффициента нормальной силы С#, про-
исхождение которой связано с вязкостью жидкости, и суммарного коэффи-
циента Су от угла атаки а(0 <а< 20°) вычислены при проникновении в жид-
кость через жесткий экран ранее рассмотренного нами тела с цилиндриче-
ским корпусом и полусферическим носком (7?о =1) для /=3,0и/=15 (рис.
5.12). Оценки проведены для модельных экспериментов и натурных условий,
причем предполагалось, что модельным условиям соответствуют докритиче-
ские числа Рейнольдса (ие<2-105), а натурным условиям - сверхкритиче-
163
11*
ские числа Рейнольдса (Ке>2-106). Согласно экспериментальным данным
(рис. 5.11) (из технического отчета NACA) для докритических чисел Рей-
нольдса коэффициент Сх = 1, для сверхкритических - Сх « 0,54.
Из рассмотрения графиков рис. 5.12 видно, что составляющая Су воз-
растает с увеличением угла атаки и составляет от суммарного коэффициента
для модельных условий при / =15и«=10° примерно 45%, а при а =20° -
около 60%; для натурных условий эти значения примерно в два раза меньше;
при I = 3 для модельных и для натурных условий значения невелики. От-
сюда можно заключить, что эффект вязкости жидкости наиболее сильно ска-
зывается при больших углах атаки и больших I, причем для условий модель-
ных экспериментов составляющая вихревого происхождения значительно
превышает ее значения, соответствующие натурным условиям. Без учета
влияния вязкости (при Сх = 0) зависимости Су от а при / = 3 и / = 15 будут
линейными.
Рис. 5.11 Зависимость коэффициента сопротивления бесконечного
цилиндра от числа Рейнольдса (данные NACA, технический отчет)
164
Глава 6
Методы и результаты расчета присоединенных масс
и нагрузок на ракету при старте
§ 1. Анализ гидродинамических нагрузок при старте ракеты
из затопленной шахты
Подводный старт морских баллистических ракет производится как из
затопленных, так и сухих шахт подводных лодок. Способ старта из затоплен-
ных шахт ПЛ является традиционным для отечественного ракетостроения и
осуществляется обычно с помощью маршевого двигателя при сплошном ре-
жиме обтекания.
Остановимся сначала на особенностях гидрогазодинамических процес-
сов. На основании анализа экспериментальных данных было установлено,
что особенности гидродинамических процессов связаны с формированием
струйных течений жидкости, газовых полостей в шахтном объеме и окру-
жающей жидкости, изменением положения их границ, разгерметизацией
шахтного объема и последующим затоплением его водой. Схема обтекания
ракеты на различных этапах движения ее под водой при старте из затоплен-
ной шахты приведена на рис. 6.1 [30].
1 — корпус ракеты; 2 — стенка шахты; 3 — граница раздела сред;
4 - амортизационные пояса; 5 - донная каверна
165
Значительные гидрогазодинамические нагрузки на ракету возникают
при запуске двигателя в затопленной шахте. После прорыва мембраны двига-
теля в подракетном объеме начинается интенсивное взаимодействие горячих
выхлопных газов с водой; в результате образуется газовая полость, давление
в которой в начальный момент может выравниваться с давлением в камере
сгорания двигателя. Для снижения начального пика давления у мембраны
двигателя организуют некоторый начальный объем (например, так называе-
мый воздушный колокол).
Затем образуется газовая струя, которая проникает в жидкость и расте-
кается по днищу шахты. В результате в подракетном объеме формируется
интенсивное циркуляционное течение парогазоводяной смеси, давление ко-
торой быстро повышается и становится больше статического давления на
глубине старта.
Под действием избыточного давления и тяги двигателя ракета выходит
из шахты; одновременно избыточным давлением вытесняется столб воды из
кольцевого зазора и образуется спутная струя (рис. 6.1а). Скорость спутного
потока в начале выхода из-за удержания ракеты на пусковом столе несколько
больше, затем становится меньше и в конце выхода ракеты из шахты снова
превышает скорость ракеты. Осушение кольцевого зазора происходит до вы-
хода ракеты, и, начиная с этого момента, над срезом шахты формируется га-
зовый пузырь. Особенно интенсивный наддув его шахтными газами и рост
объема происходит в момент выхода кормы ракеты из шахты, когда вырав-
нивается давление газов в объемах шахты и газового пузыря, то есть давле-
ние в пузыре становится больше статического давления на уровне среза шах-
ты (рис. 6.16). В дальнейшем, с ростом объема газового пузыря, давление в
нем падает и изменяется во времени по закону, близкому к закону затухаю-
щих колебаний. Форма образующегося пузыря остается близкой к полусфе-
ре. Это подтверждается как опытными данными, так, в частности, и прове-
денными нами численными исследованиями процесса разгерметизации
шахтного объема. Так что при движении в шахте и некоторое время после
выхода из нее кормовая часть ракеты обтекается газовой средой.
После прохождения границы пузыря за кормой ракеты образуется ци-
линдрический газовый след, в течение некоторого промежутка времени со-
общающийся с газовым пузырем. Вследствие большой продольной скорости
ракеты интенсивно растет объем следа, возникает значительное разрежение
газового объема и на некоторой высоте над срезом шахты происходит его пе-
режатие. Начиная с этого момента, образуются две газовые полости: верхняя
захватывается ракетой, и в следе за ней образуется присоединенная дониая
газовая каверна, а нижняя остается у среза шахты и определяет начальные
условия затопления (рис. 6.1 в).
При движении ракеты в воде возможно возникновение кавитации на ее
носовой части. В самом деле, дренажные испытания моделей ракет показы-
вают, что минимальные значения коэффициента давления для существую-
щих профилированных носовых частей достигают —0,5 (Рт;п » -0,5). Давле-
ние же насыщенных паров при температуре 20°С составляет всего
166
0,002 МПа, и при скорости ракеты около 25 м/с кавитация на носке может за-
рождаться при расстоянии от него до свободной поверхности менее 10 м; за-
тем размеры зоны кавитации растут при приближении к поверхности воды.
Описанные особенности гидрогазодинамических процессов непосред-
ственно определяют условия обтекания ракеты и формирования гидродина-
мических нагрузок на нее при выходе из шахты и последующем движении
под водой.
Обратимся к случаю выхода ракеты из шахты. Для простоты будем
считать, что движение происходит в плоскости хОу и угол разворота ракеты
в шахте незначителен по величине. На рис. 6.2 приведен этот случай движе-
ния, где поверхность ПЛ представлена в виде плоскости (Si). Границу разде-
ла сред "газ - жидкость" (S3) также считаем плоской.
Смоченные поверхности ракеты (So) и шахты (Si) изменяются с течени-
ем времени. Положение ракеты относительно шахты в плоскости хОу опре-
деляется двумя независимыми параметрами: координатой носка х0 и боковым
смещением Ь.
Третьим независимым параметром является координата границы раз-
дела сред X]. Экспериментальные исследования гидродинамических нагрузок
на шахтном участке показывают, что за короткий промежуток времени выхо-
да из шахты на поверхности ракеты не успевает полностью сформироваться
вихревая система и влиянием ее в гидродинамических расчетах можно пре-
небречь. Тогда течение жидкости можно считать потенциальным и при опре-
делении главного вектора гидродинамических сил, действующих на ракету
при движении в шахте, исходить из закона сохранения количества движения
167
[23]. Такой подход использован, в частности, М.Г. Щегловой и Г.В. Махор-
тых при определении гидродинамических характеристик удлиненных тел
вращения при произвольном движении в безграничной жидкости со следом в
виде донной каверны [38].
В качестве контрольной поверхности возьмем сферу Е с очень боль-
шим радиусом. Количество движения жидкости в охваченном контрольной
поверхностью объеме т (рис. 6.2) в момент t есть
К = р gra dtpdr = tfppndS - ffppndS,
Г X Sq+Sj tS'j+S'j
где <p- потенциал вызванного течения жидкости в неподвижной системе ко-
ординат; п - орт внешней нормали к поверхностям So, S2, S3 и X. Полное
изменение количества движения частиц жидкости в объеме г за промежуток
времени от t до t + dt будет равно
dK=d fjppndS- jfppndS- tfppndS-
X dSo dS,
- ff d(p^ndS)+^pVVndSdt.
S()+S| +S2+S3 E
Здесь последнее слагаемое учитывает количество движения частиц, вошед-
ших и вышедших через контрольную поверхность за промежуток времени от
t до t + dt. Функция <р является сложной функцией времени, координат и трех
независимых параметров х0, Х] и Ъ, которые, в свою очередь, также зависят от
времени.
Поперечное смещение не вызывает деформаций поверхностей So, Sb S2
и S3, поэтому dS0 и dSi представим в виде цилиндров с образующими
(х0 — xx)dt и (—xx)dt. Второй и третий интегралы в равенстве (6.1) преобра-
зуем к виду
(6.1)
2л
flppndS=pR0(x^-xI)dt J(pi)^Xi d0\
dSo О Ц
2л
^p^xidS=-pRixxdt |(<гй) d0.
dS, 0 r=%
Проводя для интегралов по поверхности 21 те же оценки, что и в работе
[23], получим выражение для главного вектора сил давлений
fI d(nR& д<р
\/С Ot OXq oxl ob J
2л
+ZzRo(Xo -x,) f(<zw)x^, d0-
0 r-R0
So+Si+Sj
2л- _
~рК\Хх [(<т)х=х^0+(Рд -Р,)^п* +А ,
о
где Рд - давление в газовой полости; Рх - гидростатическое давление на
уровне поверхности S2.
168
^о+^г -
So+Si
Здесь проведено интегрирование по поверхности раздела, на которой выпол-
няется условие постоянства давления
(6-2)
и выделена массовая сила; А — вектор силы плавучести части ракеты, нахо-
дящейся выше уровня х = Х\, R - функция координаты х профиля ракеты,
R = Л(х). Составляющие вектора F в направлении осей х и убудут равны
1 d(nYRp) . dp . dp dpi„ „2
---------- + xonx + x,nx — + bnx — dS + (Pn - P. )^R. + A,;
r dt 8x0 1 Xdx} x db] д 1 1
ff Г1 d^nyR<P> dp . dtp t dpi
-n rr -—77—+w>T+x‘n>T+bn>^ dS+
R dt dxg dxt db
1Я 1Я
+pR0(x0-x}) \(nyp)x=Xi d0-pRoxx J(ny^)x=X] d0+Ay. (6.3)
0 r=R0 0 r=Rt
Ракета является вытянутым телом вращения с профилированным нос-
ком, а донное давление на шахтном участке обычно в 1,5-2 раза превышает
статическое, так что в формуле для Fx основной вклад вносит сумма двух по-
следних слагаемых, которые выражаются в конечном виде.
На границе раздела сред (х = xj nv = cos 6* на цилиндре и nv = -cos О на
стенке шахты, а при малом смещении ракеты в кольцевом зазоре и выполне-
нии условия постоянства давления (6.2) потенциал весьма слабо будет зави-
сеть от 0, так что
\(p)x=Xl cos0i0=(.p)x=Xi jcos0J0=O;
о r=Ro 0 r=Ro r^Ro о
2яг 2л 2л
f(fmy)x^d0=-f(P)x=x, cosbti0=-(p)x=xi Jcos^=0.
0 r=R, о г=К| г=К| О
Поэтому формулу (6.3) запишем в виде
„ ff Г1 d(nyRp) - dp . dp t .
dxo dxt db J
(6.4)
R dt
So+St
Из выражения (6.4) следует, что при использовании наиболее простой
постановки задачи о гидродинамических нагрузках, когда предполагается ра-
венство диаметров ракеты и шахты, учитываются только два первых слагае-
мых в подынтегральном выражении, и нагрузка, как покажем далее, получа-
ется при этом завышенной. Третье слагаемое наряду с первыми двумя учи-
тывается при исследовании влияния спутного потока воды. При истечении
струи в окружающую жидкость (Vcn >0) боковая нагрузка на ракету снижа-
ется (обозначим коэффициент С" при этом через С“+), а в случае разреже-
ния газов в шахте и реализации водопада (Усп <0) — наоборот, увеличивается
(С* ). Из приведенных расчетов следуют оценки
169
где С^о - коэффициент С“, получаемый без учета влияния спутного потока.
Влияние спутного потока проявляется при малой длине вышедшей части ра-
кеты, когда носок находится у среза шахты.
Влияние четвертого слагаемого проявляется в основном на находящей-
ся ниже среза шахты омываемой части ракеты. Основываясь на решении
плоской задачи, можно заключить, что гидродинамическая нагрузка на эту
часть действует в направлении, противоположном относительному смеще-
нию ракеты в шахте, и приводит к уменьшению общей нагрузки, так что в
инженерных расчетах вследствие малых смещений ракеты в шахте четвер-
тым слагаемым в формуле (6.4) можно пренебречь.
После выхода границы раздела сред из кольцевого зазора начинает
формироваться надшахтный газовый пузырь, скорость сноса b которого
близка к скорости ПЛ, b^U (рис. 6.16). При большом избыточном давлении
газов в пузыре скорость его расширения R больше скорости сноса U, так что
замыв ракеты жидкостью происходит только в верхней части пузыря; зона
замыва имеет малую протяженность.
Исходя из общей формулы (6.1), проводя те же оценки для контроль-
ной поверхности £ и учитывая, что на плоскости пу = 0, найдем выражение
для Fy в этом случае:
Fy=4 +4 -
Ш с CIL о
Используя сферическую систему координат (иу =-sinA cos^,
dS=R2sinAdAd0), оценим второе слагаемое
[[p<pnydS=-4nRR Jsin2 AdA |(<4>)г=л cosOdd -
dt s} оо
я12
-р [sin2AdA {Г— (R2<p)+bR2^
J «V a*Jr=jR
cosOdd.
0
Здесь интегрирование по полярному углу А проводится от 0 до л/2, т. е. в ин-
тегралы включена и зона замыва, где значение А близко к нулю (А и 0) и, сле-
довательно, вклад этой части в интегралы незначителен. Вне зоны замыва
потенциал сносимой вниз по потоку полусферы при наличии плоскости бли-
зок к потенциалу пространственного источника, который является функцией
только от г. Поэтому при интегрировании по в получаются нулевые значе-
ния внутренних интегралов, интеграл по в целом обращается в нуль и вы-
ражение для Fy приобретает такой же вид, как и при движении тела в без-
граничной жидкости [23]:
Fy=Jt\\p(PnydS- <6-5)
170
Для оценки дополнительной боковой гидродинамической силы AFy,
обусловленной несимметрией надшахтного газового пузыря, определим ин-
дуцированную им боковую дополнительную скорость жидкости AUy и рас-
пределим вдоль оси цилиндра диполи, линейную мощность которых поло-
жим равной 2пАиуа2. Исходя из того, что форма пузыря близка к полусфере и
в присутствии плоскости, заменяющей поверхность ПЛ, динамика его границ
описывается с помощью введения пространственного источника мощностью
4я7?2R с центром в точке (О, Ь, 0). Тогда AUy является функцией от координа-
ты х
ж, =
где b - расстояние от центра полусферического пузыря до оси цилиндриче-
ской части ракеты (рис. 6.16).
При малом боковом смещении, когда b « х, с некоторым завышением
скорости можно принять более простую зависимость
AU =^.
С учетом последнего равенства потенциал на поверхности цилиндра
(д/у2 + z2 =а) будет иметь следующий вид:
(p(x,0,f)=—ba3R2R- f---, + [--. = cos#.
2 1-”£3Л*-£)2+а2Г л^Лх-О2+а2Г.
Здесь с учетом влияния корпуса ПЛ, представляемого нами плоско-
стью, диполи распределены также и по зеркальному отображению ракеты
(первое слагаемое). Кроме того, для простоты пределы интегрирования взяты
равными радиусу пузыря и бесконечности, так как подынтегральное выраже-
ние очень быстро, как 1/£6, стремится к нулю.
После интегрирования найдем, что
<p(x,9,f) = bR-A f(x,R )cos0,
2а
где f(x,R ) = /0(х) + /,(x,R ) - f2(x,R ),f (/ = 0, 1,2) являются функциями
от безразмерных х и R (x=x!a,R =R!a). Для упрощения письма далее
черточку будем опускать и запишем
пч 1 4 3 1-4*2 24
f;(x,R)=—. =----------;
(1=1,2) 2 V1 + (4 -х)2 2(1 + * ) R
(6-6)
(6-7)
171
. 11 1 5x 2x4-25x2+3 „ 2x2-13
Af ~ Э-----T -------------------э”i-----R;X---—— '
/?21 + х2 Я,(1 + х2)2 (1 + x2)3 (1 + x2)3
।-----f---------i (6.8)
B, = 1+x2 -xR, + V(l+x2)[(«,.-x)2+1J;
Rt = (-1)1+,Я.
Для вычисления главного вектора гидродинамических сил, действую-
щих на тело при неустановившемся движении в идеальной жидкости, вос-
пользуемся формулой (6.5). Выражение для погонной нагрузки, обусловлен-
ной несимметрией надшахтного газового пузыря, с учетом равенств (6.5) -
(6.8) после несложных преобразований запишем окончательно в виде
dCy = bR2R + bR2R + 2bRR2 - _ bR^_(^_ _
dx a2UV ’ ’ a2UV\dt dt У
где & 4 .3 j)
д, zVi+w-x)2 24+и-«,)!Г 2<1+* >П^'
Производные по времени Л, и Д в соответствии с выражением (6.8)
имеют вид
2/?, 1_____R' 5х • 2х2-13
R? 1 + х2 Я2(1 + х2)2 'Х(1 + х2)3’
I i+P
Bi=-xRi+Ri(Ri-x) —-----------(6.11)
у1 + (/?,-х)2
Д =(-1),+‘К.
При выводе формулы (6.9) считали, что угол атаки мал и а = -U/V,
V-скорость ракеты.
Расчеты проведены для одного из ракетных комплексов, влияние
шахтных процессов на гидродинамические характеристики ракеты на кото-
ром в процессе испытаний оказалось столь значительным, что потребовалось
принять конструктивные меры для их снижения. При этом радиус, скорость и
ускорение границы пузыря определяются путем интегрирования по времени
уравнения Рэлея
R\ р 2 )
где Рп - давление газов в пузыре; Ро - статическое давление на глубине
старта.
В табл. 6.1 приведены безразмерная скорость V , безразмерное давле-
ние Рп в зависимости от безразмерного времени t. Здесь же приведены рас-
стояние I от кормы ракеты до плоскости и полученные в результате решения
значения радиуса пузыря R и суммарные значения С“£.
172
При l = 40 вода полностью вытесняется из кольцевого канала, кормо-
вой срез ракеты находится еще в шахте (/=—2). Давление газов в шахте
больше статического, и с этого момента у среза шахты начинает формиро-
ваться газовый пузырь, который одновременно сносится поперечным пото-
ком (Ь =С7/д/Р0/ /?=0,12).
Таблица 6.1
а\ р 40 42 44 46 48 50 52 54 56
Рп-Рп/Р0 1,65 1,46 1,20 1,18 0,75 0,67 0,60 0,60 0,69
v=v/Jpoip 1,01 1,06 1,10 1,14 1,15 1,16 1,17 1,18 1,19
Р'п 2,3 1,92 1,40 1,36 0,50 0,34 0,20 0,20 0,38
1 = 11а -2,0 0,22 2,55 4,98 7,45 9,95 12,47 15,01 17,80
R = Rla 1 2,27 3,45 4,42 5,11 5,45 5,45 5,10 4,77
са ^уХ 1,08 -0,28 0,36 1,17 1,93 2,13 2,15 2,09 2,02
При t = 42 корма ракеты выходит из шахты, давление газов в пузыре
резко падает и при 7 = 46,8 становится равным (Рп =1), а затем и меньше
статического (Рп <1). Для достаточно удлиненного тела, очевидно, можно
предположить, что погонные нагрузки на носовую и кормовую части ракеты
формируются независимо друг от друга: нагрузка на носовую часть опреде-
лена по методу потенциала простого слоя [14, 15], а на кормовую часть, обу-
словленную несимметрией газового пузыря, - по формулам (6.9) - (6.11). Из
приведенных на рис. 6.3 графиков видно, что нагрузки на кормовую и носо-
вую части имеют противоположные знаки и в промежутке времени t от 41
до 44 суммарный коэффициент С“£ близок к нулю, а коэффициент момента
mzs(mzs = ~cyACd ~ 0>5)), наоборот, примерно вдвое превышает его значе-
ние при обтекании тела сплошным потоком (т“с п = 0,75) (рис. 6.4). Упро-
щенно можно сказать, что на ракету действует в этом случае пара сил.
Кроме того, за счет газового пузыря уменьшаются смоченная поверх-
ность и присоединенный момент инерции ракеты. Поэтому ракета получает
дополнительные угловые возмущения в плоскости тангажа из-за газового пу-
зыря как за счет увеличения гидродинамического момента, так и за счет
уменьшения суммарного момента инерции ракеты. Расчеты показывают, что
максимальный дополнительный возмущающий момент достигает 9 кН-м и
время его действия после выхода кормы ракеты из шахты составляет 0,26 с,
что удовлетворительно согласуется с результатами испытаний в натурных
условиях (8 -10 кН-м и 0,2 - 0,3 с).
173
Дополнительно рассмотрено еще два расчетных случая: в первом избы-
точное давление газов в пузыре было увеличено вдвое (Рп' в таблице), а в
другом оценена эффективность одного из способов снижения возмущающего
момента с помощью обтюрации половины кольцевого зазора у среза шахты с
подветренной стороны. Из графиков рис. 6.4 видно, что увеличение избыточ-
ного давления вдвое приводит к незначительному (на 15 - 25%) увеличению
дополнительного возмущающего момента, что свидетельствует о нелиней-
ном возрастании его от Рп.
При описанном способе снижения возмущающего момента газовый пу-
зырь смещается первоначально навстречу боковому потоку, так что началь-
ное боковое смещение пузыря отрицательное, Ьо = -0,5. Дополнительный
возмущающий момент (t = 40...42,2) становится при этом отрицательным, а
затем по мере роста t и b увеличивается и становится положительным.
174
Дополнительный, возмущающий, момент при этом способе уменьша-
ется более чем в два раза, что и было подтверждено результатами натурных
испытаний ракетных комплексов.
§ 2. Методы расчета присоединенной массы ракеты
при движении в шахте
Присоединенные массы ракеты при ее поперечном движении в затоп-
ленной водой шахте рассчитываются обычно по методу плоских сечений, ко-
гда пренебрегают продольным растеканием жидкости. Решение плоской за-
дачи дано в работе Е. Н. Капанкина [20]. В настоящем разделе присоединен-
ные массы рассчитываются в самой общей постановке: проводится учет про-
странственной картины течения, формы носовой части и прямого кормового
среза ракеты, смещения оси ракеты от оси шахты, величины кольцевого зазо-
ра между ракетой и стенкой шахты, а также вида нижней границы жидкости.
Введем прямоугольную систему координат Oxyz (рис. 6.5) с началом в
точке пересечения оси ракеты с днищем шахты S$, ось Oz направим верти-
кально вверх по оси ракеты, ось Ох — вдоль вектора поперечной скорости w0,
ось Оу направим так, чтобы система координат была правая. Движение иде-
альной несжимаемой жидкости, вызванное поперечным движением тела, бу-
дем считать потенциальным; потенциал скорости (рО, z, 0) должен удовле-
творять в области течения уравнению Лапласа
1 Э Г 1 Э2<р + д2 <р _д
гэД drj г2 д02 dz2
(6.12)
и следующим граничным условиям:
— = 0 на S2,S4,S5, (6.13)
дп
— = -uocos0cosy на So = 8\ + , (6.14)
дп
<р —> 0 при удалении в бесконечность,
где у - угол между касательной к профилю тела и его осью симметрии
(рис. 6.5). Вследствие трехмерности задачи вычисление потенциала (р непо-
средственно в физической области течения представляет значительные труд-
ности, поэтому решение задачи (6.12) - (6.14) будем проводить в канониче-
ской области, переход в которую осуществим с помощью конформного пре-
образования.
С этой целью в каждой поперечной плоскости физической области те-
чения введем комплексную переменную z = х + iy и осуществим дробно-
линейное конформное отображение [20]
z-a,
о)=-а2-----L
z — а2
(6.15)
175
которое выбрано таким образом, что радиус Rt цилиндрической части ракеты
остается без изменения. Радиус шахты в преобразованной области тече-
ния находится по формуле
. (6.16)
здесь координаты и а2 определяются выражениями
а1=(Л-л/я2-1)Л1; =(А + л/л2-1)Я„ A = -2 ~R' ~b ,
2Rtb
где b — смещение оси ракеты от оси шахты; R2 — радиус шахты в физической
области.
В результате преобразования (6.15) неконцентрические окружности в
каждом поперечном сечении физической области переходят в концентриче-
ские окружности для соответствующих поперечных сечений преобразован-
ной области (рис. 6.5, 6.6). В результате неосесимметричная физическая об-
ласть течения становится осесимметричной, за исключением носка ракеты, в
нижней части которого, расположенной вблизи цилиндрического корпуса,
наблюдается незначительное искривление оси, а в верхней - несколько более
сильное. Но поскольку верхняя часть в силу краевого эффекта вносит незна-
чительный вклад в присоединенную массу и рассматриваемые поверхности
близки друг к другу, то будем переносить граничные условия с преобразо-
ванной поверхности на осесимметричную.
Уравнение Лапласа (6.12) для преобразованной области течения при-
мет вид
1 5 ( др\
pH2 дру др)
1 д2 <р t d2(t> =
р2Н2д/32 дх2
(6.17)
176
,, _ „ If f syY f&Y K
где коэффициент Лямэ Hx =-. — + — + — с учетом преобразова-
Vk^Z7/ \др) \др)
ния (6.15) равен
тт fl2(°2~al)
~ 2 2 9
р + 2/w2cos/?+a2
а граничные условия (6.13), (6.14) запишутся следующим образом:
^=0 на S'2,S'S'5,
дп 2 4 3
f=~=-ujA2 -1 (1 + ЛСО!^? cos/ HaS0=S1'+S;,
дп (А + cos fl)
> 0 при удалении в бесконечность.
(6.18)
(6.19)
(6.20)
Рис. 6.6 Преобразованная область течения
Для приближенного решения краевой задачи (6.17) - (6.20) воспользу-
емся формулой метода Галеркина [22], согласно которой запишем следую-
щее условие, эквивалентное соотношениям (6.17) - (6.20):
ггРгГдГ д (1 д<р] д( ,,2J
JJ) J 8<pdfl\dpdz=b. (6.21)
«До1Л\ SPJ dfppdfi) dz\ dz J] J
Вариационную задачу (6.21) будем решать с помощью представления
искомого потенциала в виде тригонометрического ряда
<^Z’,z,/7)=f;0KG9,z,/7)cosK/?, (6.22)
к=1
где функции Фк(р, z) - неизвестные коэффициенты ряда Фурье. Приведенное
разложение потенциала в ряд Фурье допустимо вследствие того, что заданная
на поверхности ракеты S'o = S, + Sj нормальная скорость жидкости предста-
вима в виде
12 Зак. 3686
177
f = Xfkc0SK/7, (6.23)
fc=l
где коэффициенты ряда Фурье с учетом формулы (6.20) равны
fk=— (f voskfidf! = (-1)* ка*-1 (1 - а2 )u0 cos/. (6.24)
л о
Ряд Фурье для функции Я2, входящей в соотношение (6.21), имеет
следующий вид:
h 00
tf2=-^-+XAmcos»i/?,
Z- m=l
где коэффициенты разложения равны
1 2п , Эе2
hm=-\H1xc^mpdp=-r^—ri
(6.25)
(6.26)
а
т
d
т= 0,1,2,
В равенстве (6.26) введены обозначения
Ог(а2~а1). j_
7 7 9 "
р +02 Р +а^
Подставляя разложения (6.22) и (6.25) в вариационное соотношение
(6.21) и проводя соответствующие выкладки, получим
r 2f Г s
д Г 1 д<р
о LSP
2Х”2
2 ’
(6-27)
д_
др) dfl^pdfl) dz
' д
к2
’ dz)
h0 82Фк
2 dz2
(6.28)
5/2
где коэффициент Л</2 определяется из выражения (6.26) при т = О.и равен
*=iL^
ко_ =
с2
Л2Р/2
(6.29)
\ а2 )
С учетом равенства (6.28) соотношение (6.21) перепишем в виде
к2 . hQ д2Фк
—Фк + р——±
р к 2 dz2
*=i
—I
др
dpdz>&t>k =0,
(6.30)
«2
S/2
откуда следует, что оно распадается на следующие соотношения, не связан-
ные между собой (ряд осесимметричных вариационных задач):
f(T5f ЭфЛ к2. к0д2ФкЛ^ , , п
— р-г1- +-—фк + р—---------------------Л
\i дрГ др) р к dz2 к^
(6.31)
к= 1,2, 3,....
178
Выражение (6.31) после интегрирования по частям и введения функционалов
“ z X 2 —
„ _1 г( (ЗФЛ Лд
\ к1 > t
+—Ф2к pdpdz+fkfokpdl (6.32)
ho ( дФк
2 dz
перепишется в виде
#>0, *=1,2,3,..., (6.33)
т.е. решение краевой задачи свелось к решению ряда осесимметричных задач
по минимизации функционалов (6.32), которую осуществим с помощью из-
вестного метода конечных элементов [22, 34]. Для этого область течения в
плоскости р, z разобьем на треугольники. Обозначим через Фк> неизвестные
функции, каждая из которых определена на своем z-м треугольном элементе,
тогда искомые функции Ф^р, z) можно представить в виде суммы
ф*(/^2)=Еф*г)(/Лг), к= 1,2,3,..., (6.34)
где п — общее количество треугольных элементов.
Функции Фк^(р,г) в пределах элементов аппроксимируются через уз-
ловые неизвестные {Ф*} и функции формы [лг^] следующим образом [34]:
ФР=[^О](Ф*}» *=1,2,3,..., z= 1,2,3,..., и. (6.35)
С учетом выражения (6.34) функционалы (6.32) представятся в виде со-
вокупности функционалов
Fk=±F^,
(6.36)
где обозначено
I2 । к0(дФ^
| + 2
pdA^+fk ^pdLw. (6.37)
/<>
dz
1
Л А'
Заметим, что ниже в основном используются обозначения и сокраще-
ния, принятые в работе [34], причем
— приведено в равенстве (6.29);
1 О
. 2 J Z
dN^~
5/2
dN^
- матрица градиентов функций формы.
. dz .
В матричном виде соотношение (6.37) перепишем следующим образо
2л(о[_
(638)
12’
179
Для минимизации функционалов (6.38) на множестве узловых значе-
ний {Ф*} необходимо выполнить равенства (и - общее количество элементов
в области течения)
SF, " FP
к= 1,2,3,.... (6.39)
з{ф*}
Последние соотношения представим в матричном виде
^T=Zfc')Kl+h(,)})=0, к= 1,2,3,..., (6.40)
где введены обозначения
+ (6.41)
л“> /> Р
Й°)=Л НТ^(0- (6-42)
Если ввести матрицы
(6.43)
i=l i=l
то соотношения (6.43) примут вид
[**]&}=&}> к= 1,2,3,.... (6.44)
Таким образом, задача минимизации функционалов (6.38), а тем самым
и краевая задача (6.17) — (6.20), окончательно сведена к решению ряда систем
линейных уравнений (6.44) относительно неизвестных узловых значений
функций Ф*>
Приведем вид матриц (6.41) и (6.42) треугольного элемента для случая
линейной аппроксимации функций Ф^(р,г). Матрица (6.41) треугольного
элемента, полученная приближенно по значениям /?в его центре,
— btb2 6Д1 Гс,^ qc2 qcjl 1 л Г2 1 11
и=£ b^b^ bjb-^ 1 ”0 Р С2С1 с2с2 с2с3 + 1 2 1 , (6-45)
4А ^3^2 Ь2ЬЪ 2 А А 5'зС1 с3с2 с3с3. /712 1 1 2
где — - значение функции (6.29) в центре элемента; А - площадь элемента;
р - значение координаты р в центре элемента. Матрица (6.42) треугольного
элемента представляется следующим образом:
о
2Rt+Rj
R^lRj
(6.46)
где L - длина стороны элемента; Л„ Rj - радиальные координаты узлов i, j,
взятых на границе тела.
Безразмерная присоединенная масса ракеты при ее поперечном движе-
нии в шахте определялась по формуле
180
>?22 -
—Т—
^rRiLuls'o дп
(6.47)
где интегрирование ведется по поверхности So = Sj + , S', и S'3 - соответ-
ственно носовая и цилиндрическая поверхность ракеты.
С учетом соотношений (6.20), (6.22), (6.23) равенство (6.47) запишется
в виде ряда
<6-48)
RyLu0 k=i о
где fK = kak~l (1 - а2 )и0 cos у; L - длина ракеты.
Значения функций ФК, входящих в подынтегральное выражение (6.48),
получаются в результате решения ряда систем линейных уравнений (6.44).
Количество членов ряда в формуле (6.48) для достижения заданной точности
вычисления возрастает с увеличением безразмерной величины смещения оси
ракеты от оси шахты Ь . Значительный рост числа членов ряда наблюдается
при приближении ракеты к стенке шахты (30 - 50 членов).
Описанный способ вычисления присоединенной массы ракеты был
реализован в виде программы для ПЭВМ. Для разбиения преобразованной
области течения р, г использовалось 1800 треугольных элементов, взаимо-
связанных в 1001 узловой точке. Ширина полосы глобальных ленточных
матриц [/GJ в равенствах (6.44) получалась в расчетах равной 13. Результаты
расчетов, полученные по разработанной программе, представлены на рис.
6.7-6.13.
Сначала были проведены расчеты безразмерной присоединенной мас-
сы цилиндрического тела с прямыми срезами при поперечном движении его
в трубе в зависимости от величины смещения b (0 < b < 1,0) для различных
удлинений 2(0,25 < Я <10).
Результаты расчетов, проведенные для Ry = 1,0 и R2 = 1,1, приведены на
рис. 6.7. Из рисунка видно, что присоединенная масса цилиндра существенно
зависит от его удлинения Л, а при одинаковом удлинении - от величины
смещения Ь. Чем меньше удлинение, тем больше отличается присоединен-
ная масса по величине и характеру изменения от аналитической кривой, по-
лученной по работе [20] для случая цилиндра бесконечного удлинения (пло-
ская задача), и наоборот. При приближении цилиндра к стенке трубы при-
соединенная масса начинает резко расти.
181
Рис. 6.7 Зависимость присоединенной массы цилиндра от его смещения
в трубе для различных удлинений
При малых удлинениях цилиндра присоединенная масса слабее зависит
от величины b и начинает значительно возрастать лишь при приближении
цилиндра к стенке трубы. Были проведены также расчеты, показывающие,
что при возрастании радиуса R2 присоединенная масса существенно умень-
шается и стремится к ее значению в бесконечной жидкости.
На рис. 6.8 приведены графики изменения присоединенной массы ра-
кеты в зависимости от величины кольцевого зазора шахты 8= R2- R[ для за-
данных поперечных смещений Ь=0; 0,5; 0,9. В расчетах было принято:
Л = 5,0; 0,1 < 8 < 1,0. Из рисунка следует, что присоединенная масса значи-
тельно возрастает при уменьшении 8 от 0,3 до 0,1. При заданном значении 8
присоединенная масса тем больше, чем больше величина смещения b .
Рис. 6.8 Зависимость присоединенной массы от величины кольцевого
зазора для фиксированных смещений
182
На рис. 6.9 представлены кривые изменения присоединенной массы ра-
кеты в зависимости от расстояния I между кормовым срезом ракеты и дни-
щем шахты для различных смещений b (Ь = 0; 0,5; 0,9) и радиусов шахты R2
= 1,1; 1,25. Как видно из рисунка, влияние днища шахты на величину Л22 на-
чинает сказываться приблизительно при значениях I < 0,5. Это влияние тем
сильнее, чем меньше величина 8, и наоборот.
Рис. 6.9 Изменение присоединенной массы в зависимости от расстоя-
ния между кормовым срезом ракеты и днищем шахты
Л /
для различных поперечных смещений ракеты (т]= )
Были проведены также расчеты для оценки влияния на присоединен-
ную массу ракеты перемещающейся вверх по задонному объему и кольцево-
му зазору шахты нижней свободной границы жидкости, граничащей с газо-
вой средой (см. рис. 6.10, 6.11).
Расчеты были проведены при 2= 5,0 и 8= 0,1, b = 0; 0,5; 0,9. Измене-
ние присоединенной массы на рис. 6.10 приведено в зависимости от верти-
кальной координаты zo, отсчитываемой от среза кормы ракеты до подвижной
свободной границы жидкости, при этом координата z0 > 0 соответствует по-
ложению свободной границы выше, а координата z0 < 0 - ниже среза кормы
ракеты. Из рис. 6.10 следует, что при движении свободной границы жидкости
в задонном объеме (при z0 < 0 ) присоединенная масса при заданном значе-
нии b остается практически постоянной, незначительно уменьшаясь при
приближении границы к срезу кормы ракеты; при дальнейшем движении
свободной границы вверх по кольцевому зазору присоединенная масса раке-
ты Л22 уменьшается до нуля, причем до zo » 5,0 уменьшение идет приблизи-
тельно по линейному закону, а при z0 > 5,0 линейный закон изменения нару-
шается.
183
Рис. 6.10 Зависимость присоединенной массы ракеты от положения
свободной нижней границы жидкости
На рис. 6.11 приведены распределения присоединенной массы по длине
ракеты для различных положений свободной границы жидкости (z0 = 0; 3; 5;
7; 8), а также для случая, когда свободная граница, находящаяся на уровне
среза кормы (при z0 = 0), заменяется на твердую. Из сравнения распределе-
ний присоединенной массы по длине ракеты для двух видов нижней границы
жидкости видно, что кривые распределений существенно отличаются друг от
друга в кормовой части ракеты.
Рис. 6.11 Распределение присоединенной массы по длине ракеты для
случаев, когда нижняя граница жидкости является свободной или жесткой
На рис. 6.12 приведены результаты расчетов, показывающие влияние
на присоединенную массу Я22 формы носовой поверхности ракеты. Расчеты
проведены для ракет с удлинениями Л= 5, 10, причем рассмотрены случаи,
184
когда носовая часть является цилиндром с прямыми срезами или полусфе-
рой. Из сравнения кривых для этих случаев видно, что влияние формы носо-
вой части ракеты на присоединенную массу незначительно, при этом влияние
тем меньше, чем больше удлинение ракеты, и наоборот.
На рис. 6.13 приведено изменение присоединенной массы для смеще-
ния b ®0 в зависимости от удлинения цилиндрического тела вращения с
прямыми срезами. Видно, что с увеличением 2 кривая изменения присоеди-
ненной массы асимптотически приближается к кривой, полученной по работе
[20] для Л = оо.
Рис. 6.12 Зависимость присоединенной массы от формы носовой части
тела для различных его удлинений
Рис. 6.13 Зависимость присоединенной массы цилиндрического тела
с прямыми срезами от его удлинения при фиксированном смещении
(7=1,1, 6=0)
185
§ 3. Метод расчета гидродинамических нагрузок на ракету
с учетом спутного потока
Подводный старт ракеты из пусковой шахты подводной лодки сопро-
вождается сложными физическими процессами, которые определяют течение
окружающей жидкости, а следовательно, и гидродинамические нагрузки на
ракету. В частности, при старте ракеты как из затопленной шахты, так и из
сухой, формируется спутный поток: в первом случае - при вытеснении из
кольцевого зазора содержащейся в нем воды избыточным давлением вы-
хлопных газов в подракетном объеме, а в другом - при истечении из кольце-
вого зазора газового потока и формировании в окружающей жидкости над-
шахтной газовой полости.
Используемые на практике методы расчета гидродинамики ракет осно-
вываются на предположении о равенстве диаметров ракеты и шахты и не
учитывают влияние спутного потока. Однако имеющиеся эксперименталь-
ные данные свидетельствуют о необходимости учета при определенных ус-
ловиях этого фактора.
Здесь изложен численный метод расчета гидродинамических нагрузок
на ракету с учетом влияния спутного потока. При решении задачи ограни-
чимся такими числами Эйлера, при которых на носовой части ракеты еще не
возникает кавитация и она вместе с прилегающей к ней цилиндрической ча-
стью обтекается сплошным потоком. При этом кормовая часть корпуса раке-
ты может обтекаться газовым потоком. На рис. 6.14 приведены схемы выхода
ракеты из затопленной (схема А) и сухой (схема Б) пусковой шахты подвод-
ной лодки.
Рис. 6.14 Схемы обтекания при выходе ракеты из шахты в спутном потоке:
А - выход из затопленной шахты; Б - выход из сухой шахты
186
Для упрощения задачи будем также считать в схеме А параметры спут-
ного потока известными на уровне бесконечной плоскости, с помощью кото-
рой здесь представляем поверхность подводной лодки, т.е. на поверхности S2
нормальные скорости известны. В схеме Б будем считать границу образую-
щейся надшахтной газовой полости близкой к плоскости, скорости ее извест-
ными, так что граничные условия с нее будем переносить на плоскость (схе-
ма А).
Очевидно, что это предположение справедливо для начальной стадии
развития газовой полости. Также будем считать жидкость идеальной и не-
сжимаемой, а вызванное течение жидкости - потенциальным.
Используем декартову xyz и цилиндрическую хгв системы координат.
Обычно форма ракеты близка к форме тела вращения, поэтому ограничимся
осесимметричным телом и двумя простыми поступательными движениями:
вдоль оси х со скоростью Ki (i = 1) и вдоль оси у со скоростью К2 (i = 2).
Суммарный потенциал вызванного течения жидкости Ф (х, г, 0) запишем в
виде потенциалов
Ф(х, г, 0) - Ф1 (х, г, 0)+Ф2 (х, г, О),
где Фь Ф2 - потенциалы скоростей при i -м простом движении.
Граничным условием потенциала скоростей для каждого простого
движения является условие равенства нормальных скоростей соответствую-
щих частиц жидкости и точек смоченной поверхности тела S]
= К,> i=l,2, (6.49)
si
и точек плоскости (S2 + S3)
=Uni, i=\,2, (6.50)
где п - внешняя нормаль к поверхности тела или плоскости. Кроме того, по-
тенциалы Ф, стремятся к нулю при удалении в бесконечность:
Ф,-> 0 при г-> оо, 1=1,2. (6.51)
В соответствии с принятыми выше предположениями
дФ,
дп
дФ1
дп
Гп1=Г, sin/ на $1»
К„2 = V2 COS/COS 6? на S|, (6.52)
[о на на s2, S3,
U„2=0 на52и53,
где у- угол касательной профиля тела; /3- некоторый параметр, характери-
зующий отношение скорости спутного потока к скорости тела
V, ’
Для численного решения краевой задачи воспользуемся формулой ме-
тода Галеркина, согласно которой запишем следующие два условия, эквива-
лентные сформулированной выше краевой задаче:
187
д(1дФкЛ д ( дФ\
+ —-----— 4-г---—
д0\г дх ) йх\. дх )_
&PKd6tirdx=0,
4=1,2.
(6.53)
Исходя из вида граничных условий (6.49), (6.50), (6.52), решение будем ис-
кать в форме
Ф!(х,г,0)=^(х,г),
Ф2(х,г,0)=р2(х,г)со80. (6.54)
Кроме того, поскольку решение находим в конечной области, внешняя
граница которой расположена на достаточном удалении от шахты, то усло-
вие (6.51) запишем в виде
(6.55)
где интенсивность точечного пространственного источника q находится с
помощью интеграла по поверхности S2
<1 = \Un2ds-,
s2
S4 — некоторая полусферическая поверхность, расположенная на конечном
удалении от носка тела (порядка 10 радиусов тела).
Подставляя выражения (6.54) в условия (6.53) и проводя интегрирова-
ние по 6, а затем интегрирование по частям, получим
^1+S2
rdrdx= ^f2r8<p2dS,
s.
j г L dr дх дх
L dr dr г2 дх дх
(6.56)
(6.57)
где
jV|Sin/ на
на S2,
^=12cos/ на 5j.
При выводе уравнений (6.53), (6.54) в силу условий (6.55) полагалось,
что вариации потенциалов на поверхности St равны нулю:
8<Р\ = 0; 6</>i -- 0.
Таким образом, исходная краевая задача сведена к решению двух осе-
симметричных вариационных задач для двух функций: pi(x, г) и ^(х, г).
Равенства (6.53) и (6.54) запишем коротко в виде 8Ft = 0, <5F2 = 0, где
функционалы F и F2 представим в виде:
1 Г/о \2
2'
rdrdx + f^ fardS,
. йх 7 J s1+s2
2"
rdrdx + /2 fardS.
J $1
Минимизацию функционалов будем проводить с помощью метода ко-
нечных элементов. Для этого область течения, ограниченную снаружи полу-
Р2 =
I2 1 2
I +~2^2 +
188
сферической поверхностью St, разобьем на треугольные элементы. При ин-
тегрировании по меридиональной плоскости течения наряду с граничными
условиями (6.49), (6.50), (6.52) на поверхности тела и стенке используем так-
же условие (6.55) на ограничивающей поверхности 54. Вычисление потен-
циалов скоростей было реализовано в виде программы для ПЭВМ.
Распределения гидродинамических коэффициентов вычисляем по
формулам
dC“
-3- = 2г^21+и1ги2т),
dx
dm" „( dr Y , 4
dx k dx J
где Xo ~ координата полюса тела;
' d<Pi г
<р21 = - частная производная от потенциала по /;
щ п «2г - касательные составляющие относительной скорости на
поверхности ракеты (при 1=1,2).
Расчеты выполнены при варьировании двух параметров:
где t7i - скорость спутного потока, V\ - продольная скорость ракеты;
Л 2~ ^2 ’
где /?2 - внешний радиус потока, Ru - радиус цилиндрической части корпуса
ракеты.
В расчетах величина /7 изменялась от -2 до 2 (-2 < /?< 2). Отрицатель-
ные значения /3 могут реализоваться в случае старта из сухой шахты при
большой степени обтюрации кольцевого зазора и незначительном перетека-
нии газов из подракетного объема в кольцевой зазор. Тогда разгерметизация
шахты может происходить при разрежении газов в объеме кольцевого зазора
и возникновении так называемого "водопада". Как следует из опытных дан-
ных, скорость падающего потока можно с удовлетворительной точностью
определить при этом по формуле, вытекающей из формулы Торричелли,
I
где Ро — статическое давление; Рг — давление газов в кольцевом зазоре; р -
плотность воды.
Положительным же значениям (3 соответствуют такие способы старта,
когда под воздействием избыточного давления из кольцевого зазора вытес-
няется жидкая или газовая среда.
При старте из затопленной шахты величина второго параметра Р2 ха-
рактеризует в основном отношение радиуса шахты к радиусу цилиндриче-
ской части ракеты, а при старте из сухой шахты величина Р2 обычно превы-
шает радиус шахты. В расчетах отношение R2 изменяется в диапазоне от 1
189
до 2 (1 < R2 < 2). Заметим, что рассматриваемые здесь случаи /?= О, а также
R2 =1 соответствуют используемым в настоящее время методикам, когда не
учитывается влияние спутного потока.
Расчеты выполнены для ракеты, состоящей из цилиндрического корпу-
са и полусферического притупления.
dC“
На рис. 6.15 приведена нагрузка —— для различной длины вышедшей
dx
части I, на рис. 6.16 даны графики зависимости с“ от / (Z =—) при различ-
R4
ных сочетаниях параметров [3 и R2.
Рис. 6.15 Погонная нагрузка при выходе ракеты из шахты при I =2,4:
1-Д=2, Я2=2; 2-Д= 1,^=2; 3-р= 1, Я2=1,5;
4- Д=0или К2=1; 5-/?=-1,/?2 = 2
При отсутствии спутного потока (/?= О или R2 =1,0) полученные гра-
фики полностью совпадают с данными без учета спутного потока. Значения
нагрузки и С“ при отрицательных (3 лежат выше, а при положительных
Р - ниже этих значений. Наибольшее влияние спутного потока наблюдается
при меньших значениях I. Ограничиваясь 10%-й точностью, можно сказать,
что это влияние распространяется до I* = 5Ry.
Явление "водопада" (J3<0) вызывает увеличение нагрузки и С“ - и тем
больше, чем больше |/?|. Наоборот, спутный поток при /? > 0 приводит к
уменьшению нагрузки и С“. Для коэффициента т“ наблюдаются те же за-
кономерности, что и для С“. В табл. 6.2 проведено сравнение безразмерной
интегральной характеристики при различных сочетаниях параметров Д и
190
R2, где обозначено
Величина Jр наиболее полно характеризует уровень гидродинамиче-
ских нагрузок на рассматриваемом участке движения.
Рис. 6.16 Зависимость коэффициента С“ от длины вышедшей части I:
Р=2, R2=2', 2- P=1,R2=2', 3- Р= 1, Я2 = 1,5;
4- р=Ъ или Л2 = 1; 5- Р=-\, Rl=2', 6- p=-2,R2=2
Таблица 6.2
р=-2 Д—1 Д=0 Д=1 1=2
я2=1 1 1 1 1 1
^2 =1,5 1,19 1,10 1 0,90 0,80
Я2=2,0 1,37 1,18 1 0,82 0,63
Значение Jp=\ получается без учета влияния спутного потока (Р= О
или /?2=1)- Наименьшее для рассмотренных вариантов значение J^=0,63,
соответствующее случаю наименьшего нагружения ракеты при старте, полу-
чается при Р= 2 и R2 = 2, а наибольшее значение 7^ = 1,37 и соответственно
наибольшие нагрузки - при р= -2 и R2 = 2.
191
Из полученных данных следует, что спутная струя (/?> 0) может слу-
жить эффективным способом снижения гидродинамических нагрузок, осо-
бенно в начале выхода ракеты из шахты подводной лодки (/ = 57?,), и, наобо-
рот, реализация при старте "водопада" (/?< 0) может привести к значитель-
ному увеличению гидродинамических нагрузок.
192
Глава 7
Методы и результаты расчета кавитационного обтекания ракеты
§ 1. Расчет кавитационного обтекания ракеты
Приближенный расчет кавитационного обтекания ракеты можно про-
вести методом плоских сечений, который нашел широкое применение в тео-
рии глиссирования, развитой Г.В. Логвиновичем [26]. В рамках этого метода
Э.В. Парышевым рассмотрена задача о нестационарном глиссировании ци-
линдра в сужающейся части тесной каверны.
Согласно гипотезе Г.В. Логвиновича о независимом расширении попе-
речных сечений задачу о кавитационном обтекании ракеты под углом атаки
можно свести к плоской гидродинамической задаче отдельно для каждого
сечения.
Развитие принципа "независимости расширения" на неосесим-
метричные случаи с помощью метода возмущений проведено в работах [3, 4,
27]. Однако этот метод нельзя непосредственно использовать в том случае,
когда в потоке жидкости, кроме каверны, присутствует еще и тело, имеющее
твердые границы, например, корпус ракеты за кавитатором. Конкретное по-
перечное сечение каверны может либо пересекаться с телом, либо нет, или
содержать его внутри себя. В общем случае это приводит к решению матема-
тической задачи в области достаточно сложной геометрической формы.
Расчет формы и положения поперечных сечений с учетом наличия
твердого тела может осуществляться в этом случае методом конформных
отображений. Распределенные гидродинамические нагрузки определим по
полю давления, полученному из решения плоской задачи.
На рис. 7.1 показаны возможная геометрическая конфигурация, пред-
ставляющая собой профиль меридионального сечения каверны, и одно из по-
перечных сечений, отстоящее на расстояние z от кавитатора.
а) Меридиональное сечение б) Поперечное сечение
Рис. 7.1 Профиль меридионального сечения каверны
и одно из поперечных сечений
13 Зак. 3686
193
Согласно принципу "независимости расширения" это сечение разви-
лось из круга, пробитого кавитатором в момент прохождения данного слоя
жидкости, под влиянием двух факторов: расширения и сноса. Закон расши-
рения (зависимость площади от времени) будем считать известным из фор-
мул Г.В. Логвиновича. Тогда, в соответствии с принципом "независимости
расширения", течение жидкости в каждом поперечном сечении потока следу-
ет считать плоским. Это в большой степени облегчает решение гидродина-
мической задачи, поскольку трехмерная задача сводится к последовательно-
сти плоских нестационарных гидродинамических задач с переменной грани-
цей области.
Но при определении поля давления имеется принципиальное затрудне-
ние, связанное с предположением о плоскопараллельном течении. Из-за пе-
ременности площади поперечных сечений каверны потенциал скорости на
большом расстоянии и его производная по времени, а также давление возрас-
тают по логарифмическому закону. Это противоречие, как и обычно при ис-
пользовании метода плоских сечений, может быть преодолено только путем
добавочных предположений относительно поведения потенциала скорости на
больших расстояниях, где он уже не описывается решением плоской гидро-
динамической задачи.
Расчет эволюции поперечных сечений каверны в процессе их сноса бо-
ковым течением предполагает знание закона расширения или просто формы
осесимметричной каверны. Она зависит от числа кавитации и, для весомой
жидкости, от числа Фруда. Приближенная теория Г.В. Логвиновича дает
простую формулу для вида осесимметричной каверны.
Введем декартову систему координат Oxyz так, что ее начало совпадает
с центром кавитатора, а ось Oz направлена по оси симметрии в направлении
силы тяжести. Тогда зависимость числа кавитации от расстояния до кавита-
тора дается формулой
где о(0)
R„
^0
- число кавитации на уровне кавитатора;
- радиус кавитатора;
Fr = /'° - число Фруда;
т/29Л;
Wo — скорость кавитатора.
Форма каверны зависит от о(0) и Fr
R(z)=-Jl + z-0,31<r(0)z2 - z3 Z(10Fr2). (7.1)
Эта формула отличается от известной формулы Г.В. Логвиновича уче-
том влияния числа Фруда. Полагая в ней R =1 и определяя положительный
корень квадратного уравнения, получим следующее выражение для длины
каверны:
L = -^2,4 Fr4 cr(0)+10Fr2 -1,55Fr2 <т(0). (7.2)
194
Расчет формы осесимметричной каверны по формуле (7.1) показывает
не только качественное, но и хорошее количественное совпадение в пределах
10%, если сравнивать с некоторыми случаями численного расчета (рис. 7.2).
Рис. 7.2. Сравнение рассчитанных профилей каверн:
-----численный метод;---приближенное решение
В поперечных сечениях, перпендикулярных оси симметрии, постановка
плоской гидродинамической задачи показана на рис. 7.3. Ось Ох направлена
по вектору скорости сноса бокового течения п0, а ось Оу - перпендикулярно к
ней. В силу симметрии течения относительно оси Ох показана только верх-
няя половина. Круг ВСЕ представляет собой поперечное сечение корпуса ра-
кеты радиуса Ro. Линия CD — поперечное сечение каверны. В какой-либо оп-
ределенный момент времени t потенциал скорости <г(х, у, f) должен удовле-
творять уравнению Лапласа во внешней области по отношению к контуру
BCD и граничным условиям: нормальная скорость равна нулю на корпусе ра-
кеты и на оси Ox (АВ, DA), то есть —=0 на ВС, АВ, DA; на границе каверны
дп
CD задано значение потенциала скорости р=/
На большом удалении поток должен иметь скорость щ, поэтому потен-
циал должен стремиться к значению и^х: $>—>иох при yjx2+y2 -> оо.
Этих условий достаточно для определения потенциала скорости, но
площадь сечения каверны при этом будет оставаться постоянной, если поток
считать регулярным на бесконечности. Поэтому наложим дополнительно те-
чение от источника переменной по времени интенсивности, который будет
отвечать за изменение площади поперечных сечений каверны. Будем считать,
что закон изменения площади сечений известен и вытекает из формулы (7.1).
Если в определенный момент времени значение потенциала на границе
каверны известно (<р=f), то, решая гидродинамическую задачу, можно опре-
делить скорость точек границы и таким образом прогнозировать ее положе-
ние в следующий момент времени. Из условия постоянства давления на гра-
да>
нице каверны можно найти граничное значение — и, следовательно, новое
dt
значение потенциала на передвинутом контуре. После чего расчет повторяет-
ся снова, что дает возможность пошагового определения эволюции попереч-
ного сечения каверны. В качестве начального условия этого процесса за кон-
тур каверны принимается круг радиуса Ro с центром в начале координат, на-
13’
195
чальное значение потенциала равно нулю. Введем безразмерные величины
y = y/RK-, r=tW0!RK-, U0=u0IW0,
4^=|(cr+Mo+(Vp)2)
ат 2
где за единицу длины принят радиус кавитатора RK, за единицу скорости -
скорость кавитатора Wo- В безразмерном виде (черту над буквой опускаем)
полная производная потенциала по времени на границе каверны будет равна
(7-3)
Решение краевой задачи для потенциала скорости будем находить ме-
тодом конформных отображений, в результате чего физическую область пе-
реведем в вертикальную полосу, решение в которой может быть получено
аналитическим методом. Сначала физическую плоскость z переводим в об-
ласть zi (рис. 7.3) по формулам
*о2
Z
zi
(7.4)
или в координатном виде
$ '
х2+Д
Г, $
yt=y 1--77Ч
При этом круг корпуса тела переходит на участок вещественной оси
х,: -2Rq < X] < 2Rq . Краевая задача в плоскости zj имеет вид, показанный на
рис. 7.3. Точки контура CD (поверхность каверны) при этом пересчитывают-
ся по формуле (7.4) так же, как и точки поверхности корпуса.
Обратное преобразование имеет следующий вид:
z=^1+^i2-4/Jo2). (7.5)
В координатном представлении формулу (7.5) можно записать в виде
Х = ЯХ1+^Л2_4/г°2У ^ = |(у1+лМ2“х12)’
А = 1(^+(Х1-2^)2 + 3/y2+(xl+2R0)2).
Далее область zj отобразим на верхнюю полуплоскость z2 (рис. 7.3),
считая, что контур CD задан координатами его точек и аппроксимируется
ломаной линией. Это преобразование осуществляется известной формулой
Кристоффеля-Шварца для отображения прямолинейных многоугольников.
Контур CD при этом ложится на вещественную ось х2, причем точка С пере-
ходит в начало координат.
196
Область (!,-* ~>)
I g.o &Л
: „ _____ df i
i& I
M I
\ C _ r s
JtJJHIJ fll unit |»IJ 1 linnimmnn Hill 11ШГ1ЛШ UH
° r-x
КвноническО!> область
9~ue^t*as^
A^—®e}
Рис. 7.3 Схема решения задачи в плоскости
Если контур CD задан п точками, то в области z2 они переходят соот-
ветственно в точки
у2 = 0; х2 = ah а2, а3,...,а„.
Вычисление этих значений (прообразов вершин линии CD) произво-
дится методом П.П. Куфарева [24]. Одновременно этим же методом произво-
дится пересчет точек корпуса ракеты на участке ВС.
Наконец, отобразим верхнюю полуплоскость z2 в вертикальную полу-
полосу <о= у + iA(рис. 7.3) с помощью формул
z2 = ^-(1 - cos а>); (7.6)
х2 =^-(l-ch2cos/); у2 =^-sh2sin/.
Границе каверны CD в области ео отвечает нижняя сторона по-
197
луполосы: 2=0; 0< у< л. Из (7.6) при 2 = 0 получим зависимость
/=2arctg
поэтому прообразам вершин линии CD будут в со отвечать точки
2 = 0; /t = 2arctg J———
(7-7)
Точки корпуса ракеты (участок ВС) будут лежать на левой стороне по-
луполосы, т.е. на линии /= 0. Они имеют координаты
ап
/= 0; 2 = 21n 1—— +
Краевая задача для потенциала скорости во всех областях имеет одина-
ковый вид вследствие инвариантности уравнений Лапласа и граничных усло-
вий при конформных отображениях. В области со изменится только условие
на бесконечности в соответствии с формулой (7.6), так как при больших зна-
чениях 2 она дает
а 1
х2----~^е cos/.
Если считать, что граничное значение потенциала скорости {ср=f) за-
дано в точках контура CD в физической плоскости, то эти значения перено-
сятся в точки д (7.7) канонической области со. В дальнейшем, однако, при
разложении в ряд Фурье возникает необходимость вычисления граничного
значения потенциала в точках, равномерно расположенных по оси /на уча-
стке 0 < / < л. Для пересчета значений граничного потенциала в эти точки
приходится применять интерполяцию.
Для потенциала скорости в области со можно записать аналитическое
выражение
<p{y,A)=q0A-—и0 sh2cos/+ ^/ке~кл cosA:/, (7.8)
2 t=o
если известны коэффициенты Фурье функции/(^
/(/)=Z/* cos*/.
*=0
Последние можно определить, например, методом быстрого преобра-
зования Фурье. Из выражения (7.8) следует, что оно удовлетворяет уравне-
нию Лапласа и необходимым краевым условиям, в том числе и условию на
бесконечности. В это решение добавлен член q0A, который не влияет на гра-
ничные условия и соответствует логарифмическому источнику интенсивно-
сти <у(г). Для определения его интенсивности рассмотрим производную пло-
щади поперечного сечения каверны по безразмерному времени:
^=2(*Л,
Jr C}D дп
где интегрирование производится в физической плоскости (рис. 7.3). В полу-
198
полосе «у эта формула имеет вид
dS = Лдр^
dr ^дЛ
Подставляя в нее выражение (7.8), получим
dS .
JT24-
Так как для осесимметричной каверны S = л/?2 и 7?(z) задается формулой
(7.1), то для интенсивности q0 получим выражение
9o(r)=i 1-0,62<т(0)г-0,3 -М .
2l iFrJ )
Составляющие скорости
дю дю
u=-L-, и=—^-
дх ду
в физической плоскости выражаются через потенциал, заданный в области а>,
формулами
2
дрдх дрду
ду ду дЛ дЛ
дрду ^др дх
ду ду дЛ дЛ
da
2
(7.9)
dz
da
Применение этих формул возможно всюду, кроме точек, лежащих на
границе каверны, так как она аппроксимирована ломаной линией и в верши-
нах имеет слабые особенности. Но на границе каверны, так же, как и на кор-
пусе ракеты, потенциал скорости и функция тока непрерывны. При этом
имеют место соотношения
д<р_д<р dl dip др _ др dl
ду dl ду' дЛ ду dl ду’
dl
и=
ду dl ду’ дЛ ду
дх дх dl ду ду dl. dz
ду dl ду’ ду dl ду’ da ду'
и =
где / - длина контура в физической плоскости. Подставляя эти значения в
выражение (7.9), получим следующие формулы:
дрдх дрду
и~~дГд1+~дГд1’ (710)
_дрду~др дх
u~~drdi ~дГдГ
которые позволяют вычислять скорости во всех точках, в том числе и в точ-
ках границы каверны.
Функция тока у\у, Л) определяется как сопряженная с потенциалом
(7.8) функция:
199
И/,Л)=-ЯйГ + vMo ch ^sinr + Yfke кЛ .
k=l
Для вычисления скоростей удобно принять разностные аналоги формул
(7.10).
Распределенная гидродинамическая нагрузка рассчитывалась по фор-
муле
dC я —
—-=2/?0 [Pcos/J///,
t/z J
где в - центральный угол сечения тела, а коэффициент давления
Р =(Р- Рк)/pWq находился по формуле
P = 67_2|^+Ho2-(v^)2.
от
При переходе к новому шагу по времени координаты точек границы
каверны пересчитываются в соответствии с вычисленными скоростями
(7.10), а новые значения потенциала — исходя из уравнений (7.3). Оказалось
более удобным это делать не в физической плоскости, а в области z\ (рис.
7.3), так как тогда легко избежать особенности, имеющей место в точке схода
границы каверны с тела. Связь между скоростями в этих областях получает-
ся, если продифференцировать формулу (7.4).
Расчет эволюции границы каверны в таком режиме показал, что ее точ-
ки сгущаются к левому краю (рис. 7.3), и аппроксимация контура ломаной
линией постепенно становится неудовлетворительной. Чтобы избежать этого
эффекта, проводится корректировка контура, целью которой является вырав-
нивание расстояний между вершинами ломаной линии.
Расчет эволюции поперечных сечений производится до тех пор, пока
каверна не схлопнется, при этом значение z соответствует длине каверны, ко-
торая дается уравнением (7.2). Устойчивость счета зависит от величины шага
по времени, который должен быть достаточно малым, и от числа точек на
контуре границы каверны. Обычно достаточно произвести 20 шагов до пол-
ного сжатия, т.е. производить расчет с шагом 0,05, а число расчетных точек
на границе каверны задавать более 20 (в расчетах обычно брали от 21 до 31
точки).
Результаты расчетов сравнивали с известными экспериментальными
исследованиями кавитационного обтекания тел вращения с углом атаки.
Расчетные значения распределенных нагрузок, а также суммарных сил
и моментов по методу плоских сечений получаются больше эксперименталь-
ных примерно на 30%, что, очевидно, связано с существующим эффектом
поперечного растекания жидкости, поэтому на расчетные значения ввели по-
правочный коэффициент, равный 2/3. С учетом этого коэффициента на рис.
7.4 приведены результаты сравнения распределенных гидродинамических
нагрузок для различных условий обтекания, на рис. 7.5 - коэффициентов
нормальной силы и на рис. 7.6 - профилей деформированных каверн.
200
Рис. 7.4 Сравнение погонных нагрузок в невесомой жидкости
при угле атаки 8°: -----расчет,------эксперимент
Из рис. 7.4 следует, что в целом приближенные расчеты, выполненные
по разработанному методу с учетом поправочного коэффициента, удовлетво-
рительно согласуются с экспериментальными данными. Погонная нагрузка
обычно имеет ярко выраженный максимум: если следовать принципу "неза-
висимости расширения", она возникает вниз по потоку на некотором рас-
стоянии от кавитатора, имеет крутой передний фронт, достигает своего мак-
симального значения, а затем резко падает.
Проведенные методом плоских сечений расчеты для полубесконечного
тела (цилиндра) показывают, что следующий за пиком спад нагрузки не свя-
зан с кормовым эффектом, как это может показаться из анализа эксперимен-
тов. Как правило, в корме каверны нагрузка становится отрицательной, одна-
ко она невелика и может реализоваться при достаточно большом удлинении
тела (около 10 калибров).
На рис. 7.5 сравниваются расчетные и экспериментальные значения ко-
эффициента нормальной силы, они также удовлетворительно согласуются.
201
Из рис. 7.6 следует, что деформированные расчетные профили весьма похо-
жи на экспериментальные.
Учитывая сложность поставленной задачи и отсутствие аналогичных
решений, можно считать полученное решение удовлетворительным и ис-
пользовать его в практических расчетах.
Рис. 7.5 Сравнение коэффициентов нормальной силы:
--------------расчет; ----эксперимент
202
§ 2. Теоретическое исследование гидродинамических нагрузок
при несимметричном смыкании каверны на круговой цилиндр
Большой практический интерес представляет несимметричное обтека-
ние ракеты в режиме частичной и развитой кавитации, когда передний фронт
газовой каверны фиксируется точкой схода струй с кавитирующего насадка,
а кормовая часть ее заканчивается областью несимметричного смыкания на
поверхности ракеты. Гидродинамическая сила формируется при этом на смо-
ченной части поверхности: на наветренной стороне кавитирующего насадка
и в области смыкания каверны на корпус ракеты.
Теоретическое решение задачи о кавитационном обтекании тела в на-
стоящее время получено только для осесимметричного случая. В этом разде-
ле разработан приближенный метод расчета подъемной силы и момента от
нее в области несимметричного смыкания каверны на круговой цилиндр.
Разобьем всю область течения жидкости секущими плоскостями и при-
ближенное решение задачи будем искать в плоском слое. Предположим так-
же, что кавитирующий насадок является диском или близким по форме к не-
му, а корпус ракеты - круговым цилиндром (рис. 7.7).
Рис. 7.7
1 - кавитирующий насадок; 2 - граница носовой каверны; 3 - область несимметричного
смыкания каверны; 4 - цилиндрический корпус
Кавитирующий насадок, проходя сквозь плоскость жидкости, порожда-
ет элемент каверны, который расширяется по инерции, преодолевая внешнее
избыточное давление. Через некоторый промежуток времени запас кинетиче-
ской энергии исчерпывается, поперечное сечение каверны достигает макси-
мальной площади, после чего начинает постепенно сужаться. Сечение кавер-
ны, кроме того, испытывает сопротивление жидкости и сносится поперечным
потоком. Наконец наступает такой момент, когда сечение каверны коснется с
наветренной стороны поверхности тела (рис. 7.7, сеч. А) и начнется несим-
метричное смыкание каверны на поверхность тела (рис. 7.7, сеч. Б). При вер-
тикальном движении тела, если форма кавитирующего насадка близка к дис-
203
ку, поперечное сечение каверны на протяжении всего своего развития,
вплоть до момента начала смыкания на тело, остается близким к круговому, а
скорость сноса его близка к скорости поперечного потока [26]. В этом случае
в момент подхода контура сечения к цилиндру в плоском слое реализуется
течение, близкое к изображенному на рис. 7.7, сеч. А, где 7?10 - радиус на-
чального сечения каверны, который в начале взаимодействия сечения кавер-
ны с цилиндром (t = 0) больше радиуса тела RT, радиальная же скорость гра-
ницы Лю отрицательна (Л10 <0). Составляющую продольной скорости тела
обозначим через V, а через U - поперечную составляющую, они считаются
здесь неизменными в процессе смыкания.
Известно, что потенциал скоростей при расширяющейся или сужаю-
щейся плоской каверне выражается через логарифмический потенциал и для
изменения площади сечения каверны требуется бесконечная энергия. Поэто-
му, следуя работе [26], решение будем искать в конечной области, а именно в
кольцевом слое, ограниченном в начальный момент снаружи круговой ци-
линдрической поверхностью S2 радиуса Л20, а изнутри — поверхностью St ра-
диуса 7?10 (Л10 < R20), равного в начальный момент радиусу каверны. Кроме
того, будем считать жидкость идеальной невесомой и несжимаемой, а вы-
званное течение жидкости - потенциальным. На поверхности каверны SK, как
обычно, должно выполняться условие постоянства давления
^=^(0,
где PK(f) - давление газов в каверне. При t > 0 на поверхности S\ возникает
поверхность контакта тела с жидкостью, размеры которой будут постепенно
расти и определяться величиной центрального угла 1вс (рис. 7.8).
На смоченной части поверхности тела ST должно выполняться условие
непротекания, т.е. производная от искомого потенциала скоростей <зпо нор-
мали п должна удовлетворять равенству
=UtosO. (7.11)
ЗН Sr
В качестве внешней ограничивающей поверхности примем некото-
рую свободную поверхность, аналогичную, например, наблюдаемой в гидро-
204
динамических трубах с открытой рабочей частью. Граничное условие на этой
свободной поверхности невесомой и несжимаемой жидкости можно записать
в виде
=|i>22(^), (7.12)
dt s2
где 0) — абсолютная скорость жидкости на свободной поверхности. Про-
водя интегрирование последнего уравнения по времени, найдем для каждого
момента времени распределение потенциала на поверхности S2
(7.13)
Таким образом, решение поставленной задачи сведено к нахождению в
кольцевом слое потенциала скоростей <р, удовлетворяющего уравнению Лап-
ласа и граничным условиям (7.11) - (7.13). Эта все еще сложная задача может
быть решена с помощью, например, какого-либо численного метода. Однако
здесь ограничимся сугубо приближенным решением, поэтому дополнительно
предполагаем:
1) в начальный момент времени RT и Ri0 близки по величине;
2) величины До и U такие, что в процессе смыкания каверны на тело
изменяющаяся во времени поверхность каверны остается всегда
близкой к поверхности тела, так что граничное условие с поверх-
ности каверны можно сносить на поверхность тела;
3) как и в начальный момент времени, в процессе всего процесса
смыкания все точки свободной границы каверны имеют некото-
4)
В
рую одинаковую радиальную скорость, определяемую, например,
из решения другой задачи; очевидно, это предположение выполня-
ется тем точнее, чем больше отношение |Л;0 /[/|;
в начальный момент внешнюю ограничивающую поверхность, как
и внутреннюю, можно принять близкой к поверхности кругового
цилиндра с радиусом R20, а в соответствии с предположением (2) в
процессе смыкания каверны будем считать ее форму такой же и
радиус ее переменным по времени - Л2(0-
силу сделанных упрощающих допущений граничное условие на
внутренней поверхности кольца приближенно можно записать в виде
Bn Sr дг
-0С<0<0С,
0Г <0<2тт-0г
= fAt,0),
St
(7-14)
U cos0,
где =
а дифференцирование по п заменено дифференцированием по г. Искомый
потенциал скоростей в кольцевом слое удовлетворяет на внутренней поверх-
ности граничному условию (7.14), на внешней - условию (7.13).
Введем в плоском слое декартову Оху и полярную Ог0 системы коор-
динат с началом в центре тела (см. рис. 7.7). Ось у направим вдоль прямой,
соединяющей центры кругового цилиндра и сечения каверны. Положитель-
205
где
ной будем считать внутреннюю к поверхности S = St + S2 нормаль п. Введем
комплексную переменную z. Очевидно, что потенциал скоростей ф является
гармонической функцией и удовлетворяет граничным условиям (7.13), (7.14).
Введем комплексный потенциал а> = ф+1ф (где ф— функция тока) и разло-
жим его в плоскости z в кольце R} < г < R2 в ряд общего вида [25]:
a=qlnz + c0 + £(c„zn+c_nz_"), (7.15)
л=1
q = m + iF; c„ = a„ + ib„, c.n = a.„ + ib.„, z = re,e = rcos0+ irsin0,
\nz=\nr + i0,
также найдем, что
qlnz = mlnr - Г0 + <(Г1пг+ m0)\
= r/,(a„cosn0 - b„sinn0) + </(Z>„cosw^ + a„sin n0}\
c_nz~n =-^-(a_n cosn0+b_n sinn#) +—(b_n cosn0-a_n sinn0).
rn rn
Выделяя в выражении (7.15) действительную часть и считая течение
бесциркуляционным, т.е. Г= 0, получим выражение для потенциала в кольце
00 f д
ф(г,0,1)=т!пг+ао+Ц апг" 4-^-
» (ь \
cosm?+£l —sinn6*.
л-1 \ Г J
В силу симметрии течения относительно у потенциал является четной
функцией, так что должно выполняться условие Ьп = Ь.„ = 0.
Для определения коэффициентов т, а„ и а.„ из выражения (7.16) найдем
величину д<р1дг при г = RT и воспользуемся граничными условиями (7.13),
(7.14):
(7-16)
Л-1
дф
дг
^r=R2
^=—+^(папгп '-na_nr ” ')cosn0;
дг г „=|
= V" + Е(иаХ’' - «а-иЯт"“1 \osn0=f}(t,0)
r=RT Щ n=l
“Г a 'I
= znlnl?2 +flo +£ «„Я” 4—7 cosn0=f2(t,0).
"=1k T?2 ,
Коэффициент m и коэффициенты ряда Фурье для
дф _дф
5 ~5г
(7-17)
(7-18)
=/10,<7) и (з|г=д=f2(t,0)
r=RT
дп
определятся по формулам
~-f/,(/,0)^;
&Т о
nanR”'-na^Rj"-' =-l/j(Z,^)cos«^;
аЛ+^- = -]/2(^СО8И^.
206
Введем коэффициенты к®, к^:
=-J/1(/,/?)^=-sin^ +^^Rl,
Л й Л Л
к,(,) = - f/l(^)cos^ = — +—26,'Х 2^' sin^, (7.19)
Яо Л’у. 2 ) л
при п > 1
Лц ЛА л-1 л+1 ) пл
^=-\f2{t,0)d0-
^0
при л > О
k^=-{f2{t,0)cosn0d0. (7.20)
^0
Из формул (7.17) и (7.18) с учетом (7.19) и (7.20) получаем систему ал-
гебраических уравнений для определения коэффициентов
m=RTk^\ а0=к^-l^RT\nR2, (7.21)
п
anR2n +а =R2k[2\ П.22)
Из системы (7.22) получаем выражения для коэффициентов
л =----------=-?—5—(7К.+1^° +л/^<2)); (7.23)
" n(R2n + R}n) т " 2 " ' 4
а „ =--z-i—=— (nR2Rrnk^ -R^R^k™).
и(Л2п+Л2л) 2 Т п т 2 " '
(7-24)
С учетом соотношений (7.16), (7.21), (7.23) и (7.24) получим выражение
для потенциала
<p(r,0,t) = Лд2) + k^RT lnr/R2 +
। ^R2n +nR^n^)rn+(nR^k^-R^)r-n cosjig
(7.25)
На основании общего выражения (7.25) найдем все необходимые в
дальнейшем функции: потенциалы <p(Rr, О, t) на окружности r = RT и
^(/?2, 0, t) на окружности r = R2, а также касательную составляющую скоро-
сти и т при r = Rr, касательную и радиальную составляющие скорости при
г = R2:
<p(RT,0,t) = ^о2) + }rt ,n'5’-
207
л=1
1-J2”
1 + J2"
cos^+2J и
n „=1
----x-cosnj;
1 + J2"
p(R2,e,t)=k^ + ^^2)c°snJ;
n=l
V’i(l)^-• ZJ nVi(2) п^П д
= 2У<п ---z-smnJ-2yA? ’---—smnJ;
n i . е2и Z-< л - „2л ’
r=RT л=1 1 + l> л=1 1 + О
_i_dtp
~~r~dO
dtp
dr
r=R2
. (1) „ . (1) J" +1 „ 8 J (2) 1 — J2" «
= J+2^fc„ -—-^cosnJ+ —Ynk\ }-—^-cosnJ;
n=l 1 + p
1 dtp
U ,-s =----—
г'г-Кг гве,
= -^^2)Hsin«J,
Л=1
где 8=RT! R2.
Известно, что в аэродинамических трубах с открытой рабочей частью
при обеспечении 10%-й точности аэродинамических коэффициентов величи-
на Jue должна превышать 0,25 (8< 0,25) [20], поэтому будем считать, что 8 в
нашем случае не превышает 0,25, и в полученном приближенном решении
ограничимся членами, имеющими порядок 8, и пренебрежем членами поряд-
ка 82 и выше.
Кроме того, заметим, что коэффициенты к^ согласно формулам (7.19)
имеют нулевой порядок малости (<5°), а коэффициенты к(2) согласно форму-
лам (7.20) - второй порядок малости ( J2). Действительно, в начальный мо-
мент времени абсолютная скорость границы поверхности S2 согласно закону
сохранения массы равна ur0 = R20 = 80До (8> = Rt / R20) и пропорциональна
Jo- Значения потенциала на S2, определяемые в последующие моменты вре-
мени путем интегрирования по времени уравнения (7.12) при нулевом на-
чальном значении, будут пропорциональны J2. Следовательно, и коэффици-
енты к™, являющиеся коэффициентами разложения функции <г>(/?2, 0, t) в
ряд Фурье, также согласно формулам (7.20) будут иметь порядок J2.
С точностью до членов второго порядка малости последние выражения
примут более простой вид
<p(RT,e,t) = k®RT In J- RTYk^^^--, (7.26)
n=i n
tp(R2,e,t) = Q-, (7.27)
«Г lr-/fr = Ekn) sin« <9; (7-28)
И=1
=k^8- «rU2=0. (7.29)
208
Отметим, что входящий в выражение (7.26) ряд является абсолютно
сходящимся, а в выражение (7.28) - неабсолютно сходящимся, и для дости-
жения необходимой точности (до 0,02) требуется более 100 членов ряда.
Из формул (7.29) следует, что ограничивающая внешняя поверхность с
точностью до членов второго порядка малости будет оставаться в процессе
всего смыкания каверны близкой к круговой цилиндрической поверхности с
изменяющимся во времени радиусом, а значение потенциала на ней будет ос-
таваться близким к нулевому значению. Это находится в соответствии с ра-
нее принятыми допущениями.
Уравнение (7.28) используем для нахождения центрального угла 20с,
соответствующего замытой части поверхности тела:
= siring +-^-sin<9c.
at Кт n-i
В силу симметрии течения относительно оси у в начальный момент
£с0 = ^со = 0 и ДОЯ выхода из нулевой точки необходимо задать некоторый
ненулевой угол 0^ Ф 0. В расчетах обычно задавалось значение 0& » 1°.
Для вычисления гидродинамических сил, действующих на круговой
цилиндр при смыкании на него каверны, определим количество движения
жидкости В в замкнутом объеме между поверхностями S) и Sy.
В =-р fffdids,
S1+S2
где р - плотность жидкости.
Для единичной длины поверхностей Si и 5^:
2л- 2х
Ву=-р ^<p{RT,0,t){-cos0)RTd0-р ^<p{R2,0,t)cos0R2d0-,
о о
2 л 2л
Bz =-р \<p{RT,0,t)s\n0RTd0~р \<p{R2,0,t){-sm0)R2d0.
о о
Используя выражение (7.26) для <p(Ri, 0, t) и учитывая, что согласно
выражению (7.27) <з(/?2, О, t) = 0, найдем окончательно
Ву=-р^к^\ Bz = 0,
где к^ находится по формуле (7.19).
Гидродинамическую силу PY, действующую на единичную длину ци-
линдра, получим из выражения
= (7-30>
dk^ 2 Г d0 - .
где —— = — (Ueos0c -Rl)cos0c—--.RjSin#. .
dt я\_ dt
Гидродинамическую подъемную силу ракеты Y и момент от нее М от-
носительно начальной точки замыва найдем как результат интегрирования по
слоям:
14 Зак. 3686
209
M- jPyxdx,
о
Y = ]Pydx;
о
где Lc - длина замытой части ракеты. Перейдем к безразмерным величи-
« « - - tU с
нам, обозначив безразмерный путь цилиндра через у =—, безразмерную
скорость - через = Rt IU и безразмерное ускорение границ каверны - че-
рез Л1=^-/?1. Введем также безразмерное значение k/1’ = к^ IU и угол
атаки а, который считается здесь малой величиной (tg а » «). Тогда найдем,
что
о rfy tga’
м^р^и2^-^-,
г dy tga
__ у
здесь ус = —, ус - координата замытой части тела,
(7.31)
[(cos вс - Ri )cos 0свс - Rx sin вс ].
Учитывая, что U= Va, получим
Y=p7rR}V2^-,
M=p^TV2]y^-dy,
о Ф
здесь учтено, что (0)=0, а вс соответствует у=ус.
Из выражения (7.31) найдем производную от коэффициента подъемной
силы по углу атаки С“:
(7.32)
Са -
у рл1$У2а
а из формулы (7.32) - для производной коэффициента момента С":
га _ 2М _ 2 V dk,(1) ~
рлк^У2а а dy У'
Учитывая выражения (7.19) и (7.30), найдем, что
Са =-(2dc +sin20c -4Д sin0c);
7t
- 2Р 4 Г - 1
Ру = pnR U2 = ~ Rl )cos^^ “ sm^J-
(7.33)
(7.34)
210
Остановимся коротко на качественном анализе полученных результа-
тов.
1. Безразмерная нагрузка в области смыкания каверны на круговой ци-
линдр имеет знакопеременный характер. Действительно, из формулы (7.34)
следует, что в начале смыкания, когда вс ~0, 7^ = 4//r(l-Д)Д, и так как
dQ/dt>Q и (1-Д)>0, то Д>0. В конце смыкания, когда вс^ л,
Ру=41 я(\ + R\)d3cl dy, и так как в конце смыкания обычно Д <0,а |д|»1,
— — Л
то Ру < 0. Нулевое значение Ру достигается при — < вс < л.
2. В начале смыкания Су =0 (6) » 0), а в конце смыкания (0С & л)
Су =2,0. Это совпадает с известным результатом Г.В. Логвиновича [26] при
частичном замыве тела, когда каверна полностью смыкается на тело. Однако
из формулы (7.33) следует, что в процессе смыкания С° принимает значе-
ния, превышающие 2,0. Действительно, вследствие того, что Ру имеет знако-
переменный характер: в начале смыкания Ру >0 , а в конце смыкания Ру <0,
максимальное значение С“(С“тах) достигается в момент, когда 7^=0, и ве-
личина Сутах определяется величиной Д в этот момент.
Этот вывод особенно важен для переходных кавитационных режимов.
В частности, заслуживает особого внимания участок движения ракеты в шах-
те, когда происходит смыкание каверны при формировании носовой газовой
каверны, а значение Сутах по имеющимся опытным данным может достигать
значений, в несколько раз превышающих значение 2,0. Также С" значитель-
но больше 2,0 при переходе от режима частичной кавитации к режиму разви-
той кавитации, когда длина каверны становится больше длины тела, а вели-
чина угла вс в кормовом сечении меньше л (вс < л).
3. Коэффициент центра приложения подъемной силы Cd находится из
выражения
1 Ус
откуда следует, что величина его обратно пропорциональна углу атаки. При
этом следует учитывать, что отсчет производится от начальной точки кон-
такта каверны с цилиндром (см. рис. 7.7, х = 0).
В результате проведенных теоретических исследований получены но-
вые закономерности по формированию гидродинамических сил в области не-
симметричного смыкания каверны на круговой цилиндр.
14’
211
§ 3. Метод и результаты расчета гидродинамических
нагрузок при кавитационном обтекании ракеты
Задача о кавитационном обтекании ракеты на основании сформулиро-
ванного Г.В. Логвиновичем принципа независимости расширения попереч-
ного сечения каверны сводится к смешанной краевой задаче в кольцевом
слое [26].
Внешний радиус кольца находится также на основании "принципа не-
зависимости". Учитывая, что потенциал скоростей в кольцевом слое имеет
выражение
^20
для быстропротекающих процессов на внутреннем кольце (г = /?|0) найдем,
что
^=-^=^=(адо+Ло)1п^-.
Р ot R20
Исходя из этого же принципа, получим
Р<х, — Рк_ а Э (л7^0) а п п \
Сопоставляя два последних равенства, найдем, что
аг
R20 _ 2Сх
RW
Принимая во внимание, что для диска Сх = 0,82, а эмпирический коэф-
фициент а принимает значения от 1,5 до 1,9 (а = 1,5...1,9), получим, что от-
ношение изменяется в соответствии с изменением коэффициента а от 4
до 9 и среднее его значение составляет 6,5. В расчетах принималось началь-
но
ное значение отношения -^-=5,0. В процессе сужения радиус сечения ка-
Но
верны стремится к единице, а внешнее кольцо изменяется при этом значи-
ло
тельно медленнее, поэтому в конце смыкания отношение —— стремилось к
Но
своему среднему значению 6,5 или несколько превосходило его.
Краевая задача в кольцевом слое жидкости с использованием метода
конечных элементов сводится к эквивалентной вариационной задаче отыска-
ния минимума функционала F [22]:
где / - часть границы области Т, вдоль которой задана нормальная производ-
ная потенциала скорости. Функционал (7.35) является исходным выражением
212
в методе конечных элементов. Способ получения из функционала (7.35) сис-
темы линейных алгебраических уравнений метода конечных элементов при-
веден, например, в работе [22].
Согласно этому способу, функционал F записывается в матричном ви-
де:
где
F= \rndl,
х £ 1
Э=Г’ оЛ
О 1J’1[ахду]’ дп'
На отдельном i-м элементе потенциал <р аппроксимируется в виде
р(,) =[лг(,)]{Ф},
где [л^] — функции формы,
[Ф] - множество неизвестных узловых значений потенциала (р в облас-
ти течения, тогда {?(,)}=[в(г)]{ф} , где [в(,)] содержит производные от функ-
ции формы.
Теперь для функционала на i-м элементе можно записать выражение:
F(,)= Д1{Ф}т(в(/)Р[а(в(/)]{Ф}<М + J?(’)^(O]r{0}d£,
Л(.> 2 ДО
где Л® - площадь i-ro элемента,
L® — длина границы i-ro элемента.
Для минимизации функционала F необходимо выполнение соотношения:
8F р
6{Ф} мб{Ф} ’
n
где F=£Fw,tf- число конечных элементов в области течения.
i=l
В результате можно записать следующее соотношение:
/)[в(‘)]г[ф(‘)]{Ф}лл+
и\ф1 л(0 до
где введены обозначения
к(‘} =
{/(0}=
Окончательная система уравнений после минимизации функционала
получается в виде:
или [Я]{Ф}={Г}, (7.36)
где обозначено:
213
MN (737)
i=l
Таким образом, задача сведена к нахождению неизвестных значений
потенциала {Ф} из системы линейных алгебраических уравнений (7.36).
Согласно МКЭ, вся область течения в плоском кольцевом слое разби-
валась на треугольные элементы с узловыми точками в вершинах треуголь-
ников и с линейной аппроксимацией потенциала внутри элементов. Сетка
конечных элементов показана на рис. 7.9. В процессе расчета изменяется по-
ложение тела относительно свободной границы каверны, а также деформи-
руются границы каверны. Разбиение области течения проводится автомати-
чески по специально разработанной для ПЭВМ программе.
Рис. 7.9 Сетка разбиения области течения
Задача нахождения неизвестных значений потенциала скорости мето-
дом конечных элементов в узлах области течения решалась на каждом вре-
менном шаге при следующих начальных и граничных условиях (рис. 7.9):
- условие непротекания на смоченной поверхности цилиндра Г|:
= t7cos#; (7.38)
бн Г1
- на оси симметрии (граница Д ):
=0; (7.39)
дп г4
214
- условие постоянства давления на границе Г2.
(7.40)
где сг- число кавитации;
V - абсолютная скорость жидкости на свободной границе;
- на внешней границе кольцевого слоя Гз :
(7.41)
- при t = 0
Л20
(7.42)
V2
Ло
V2 +V2
при / = 0,
при />0.
(7-43)
(7-44)
Таким образом, на каждом временном шаге решалась для точек границ
каверны Г2 следующая система дифференциальных уравнений в обезразме-
ренном виде (R? = 1, С/=-1):
dt 2'
dx
—=VX,
dt x
dt y’
dR2 _ RjoRjo
dt R2
dt
где x, у - координаты точек каверны;
Vx, Vy - компоненты скорости жидкости V на границе каверны, при этом
величины Vx, Vy находились методом наименьших квадратов с
использованием значений потенциалов в точках жидкости, бли-
жайших к точкам каверны;
С“ — коэффициент подъемной силы при стационарном глиссировании
цилиндра по поверхности каверны, определенный по коэффици-
енту давления Р;
р = 2Х . 2
pU2nR2r п
2 _
= — <Tsin0c + [Pcos6tf# — коэффициент гидродинами-
ке о
ческой силы, действующей на единицу длины цилиндра;
- — коэффициент давле-
дп )
ния, рассчитываемый в подвижной системе координат £, ту, связанной с ци-
2(Р-Ра>) = 2д9>
pU2 St
1 дГ \дп.
215
линдром;
вс - центральный угол замытой части цилиндра;
у
д - ~ - длина дуги текущей точки;
da
Rz - текущий радиус внешнего кольца каверны.
По разработанной программе на ПЭВМ проведены параметрические
расчеты при значениях начального радиуса сечения каверны «ю = 1,1...2,0 и
начальной радиальной скорости смыкания сечения каверны До=-1...-1О.
Динамика смыкания границ каверны представлена на диаграммах рис. 7.10.
Рис. 7.10 Диаграмма смыкания границы сечения каверны на цилиндр:
a) «w=l,l; До =-5,0;< = 0; 0,01; 0,02; 0,03; 0,04;
б) «ю = 1,5; До =-3,0; t = 0; 0,02; 0,04; 0,06; 0,08; 0,10; 0,12; 0,14; 0,16; 0,18; 0,20;
0,22; 0,24;
в) «ю = 1,5; До =-5,0; t = 0; 0,01; 0,02; 0,03; 0,04; 0,05; 0,06; 0,07; 0,08; 0,09; 0,10;
0,11; 0,12; 0,13; 0,14;
г) «ю = 1,5; До =-10; t = 0; 0,01; 0,02; 0,03; 0,04;; 0,05; 0,06; 0,07; 0,08;
д) «ю = 2,0; До =-3,0; «=0; 0,01; 0,03; 0,05; 0,07; 0,09; 0,11; 0,13; 0,15; 0,17;
е) «ю = 2,0; До =-5,0; t = 0; 0,01; 0,03; 0,05; 0,07; 0,09; 0,11; 0,13; 0,15; 0,17;
ж) «ю = 2,0; До =-Ю; t = 0; 0,01; 0,02; 0,03; 0,04; 0,05; 0,06; 0,07; 0,08.
Из рис. 7.10 видно, что при До <-1,0 полное смыкание сечения кавер-
216
ны на цилиндр происходит при “тесном” зазоре между полостью и телом. В
случае же, когда Л10 <1,5, при расширении зазора с подветренной стороны
образуется газовый шлейф.
В процессе проведения расчетов было выявлено, что значение
— 2Х
Рх=----—у при различных значениях Лю и До изменяется в очень широ-
pU 7tRT
ком диапазоне, и для удобства графического представления результатов
вместо и / были использованы комплексы Д'и Р:
fr. ,й ,р
t
t =—,
т
где Т - период инерционного смыкания сечения каверны, определяемый со-
отношением:
2^о
Зависимости P*(t') для различных Л10 представлены на рис. 7.11 -
7.14. Для выбранных комплексов Р^ и Г при одинаковом зазоре (Лю- 1) по-
лучаются весьма близкие значения зависимостей Д*(Р) при До =-3;-5, что
свидетельствует об удачном выборе комплексов Р^ и Р, и это может быть
полезным при обобщении результатов расчетов.
Рис. 7.11 Погонная нагрузка при Л,о =1Д
217
При =-1 для всех рассмотренных зазоров величина имеет наи-
большие значения. Из условия соответствия зависимостей (Р) при малом
зазоре и <-1,0 следует, что нагрузка Р при этих условиях обратно про-
порциональна Т и прямо пропорциональна относительной начальной скоро-
сти Полное смыкание сечения каверны на цилиндр происходит
также при малом зазоре и Rl0 < -1.
Рис. 7.12 Погонная нагрузка при R10 = 1J25
В других случаях, когда /?10 > —1,0, а также больших зазорах
(7?10 - 1) > 0,5, происходит либо глиссирование цилиндра по деформирован-
ной поверхности каверны, как это видно из диаграмм для /?10 = 2,0
(рис. 7.10, д), либо за зоной смыкания цилиндра образуется газовый шлейф
(рис. 7.10, ж), где погонная нагрузка еще не нулевая и вносит свой вклад в
суммарную гидродинамическую силу. Из-за трудности реализации числен-
ной схемы деформация шлейфа здесь не рассматривалась.
218
К
R
1 ч ***** • * 4
ч..„ ж» •
—1—а л * ' *• л л х .
i * ' ж •
о о,г о.ч о.б o.t
Рис. 7.13 Погонная нагрузка при Я]0 = 1,5
Рис. 7.14 Погонная нагрузка при Я10 =2,0
Обратимся теперь к физическим аспектам смыкания сечения каверны
на цилиндр. Так как при полном смыкании сечения каверны погонная на-
грузка имеет знакопеременный характер, то наибольшие значения суммарной
гидродинамической силы будут в случае смыкания вблизи кормового среза
ракеты, когда на ее цилиндрическом корпусе реализуется только положи-
тельная часть нагрузки. Как следует из результатов многочисленных экспе-
риментальных исследований, именно в таких случаях реализуются макси-
219
мальные значения Су (С“).
Полное смыкание сечения каверны на цилиндр может реализоваться
как в случае горизонтального движения, так и в случае вертикального дви-
жения ракеты.
На рис. 7.15 проведено сравнение результатов расчетов с эксперимен-
том для коэффициента нормальной силы С“тах.
В целом рассматриваемая здесь задача относится к типичным модель-
ным задачам, позволяющим объяснить результаты экспериментов. В частно-
сти, полученные распределения Р позволяют объяснить реализацию значи-
Рис. 7.15 Сравнение расчетных значений С“шах
с экспериментальными
220
Глава 8
Газодинамика и тепломассообмен при старте.
Дифференциальные уравнения движения ракеты в шахте
§ 1. Общая постановка задач газодинамики и тепломассообмена
при старте и картина течения газов в шахте
С целью упрощения математического описания газодинамических про-
цессов при старте вводится обычно ряд предположений:
- течение газов в свободных объемах отсутствует, изучаются только
средние значения давлений и температур, смешение и выравнивание
температур и давлений продуктов сгорания топлива с газом проис-
ходит мгновенно;
- процесс истечения газов считается квазистационарным, расход газов
через кольцевой зазор рассчитывается по формуле Сен-Венана;
- смесь газов принимается равномерной по составу и подчиняющейся
уравнению состояния для идеального газа.
Методики расчета газодинамических параметров предназначены для
расчета различных схем старта ракеты с ПЛ при выходе с помощью ПАД и
ДУ.
Рассмотрим газодинамические процессы в задонном объеме, кольце-
вом зазоре и надшахтной газовой полости. Весь свободный объем шахты в
соответствии с расположением поясов амортизации и обтюрации будем раз-
бивать на ряд характерных объемов, в которых производится осреднение га-
зодинамических параметров. При подводном старте изделий с частичной об-
тюрацией истекающие через кольцевой зазор "ракета-шахта" продукты сго-
рания взаимодействуют с окружающей водой, образуя надшахтную газовую
полость с колебательным характером изменения давления, обусловленным
инерционностью воды и упругостью газов пузыря. Колебательный характер
изменения давления у верхнего среза шахты оказывает влияние на внутри-
шахтные процессы.
Из опытов установлено, что величина энергетических потерь в шахте
при минометном старте может достигать 20 - 30% общей энергии, посту-
пающей от источников продуктов сгорания. Одним из распространенных
приемов при математическом описании процессов старта является разделе-
ние задач газодинамики и тепломассообмена на самостоятельные задачи.
При этом учет влияния теплообмена проводится корректировкой энергопри-
хода в объемы шахты - например, путем введения коэффициента, учиты-
вающего теплопотери, в величину температуры торможения газов, посту-
пающих в объем шахты. Значение этого коэффициента обычно подбирается
из условия совпадения расчетных данных с результатами испытаний. Опре-
деленные таким образом коэффициенты являются переменными по времени
величинами и зависят от режима работы источника продуктов сгорания. Ре-
221
шение второй задачи по определению теплового воздействия на ракету и
шахту в свою очередь требует знания газодинамических параметров потока,
то есть обе задачи являются взаимосвязанными и влияющими друг на друга.
При совместном рассмотрении процессов газодинамики и теплообмена
уравнение теплообмена в задонном объеме можно записать в виде
^=J±Nu(T0-Tw) + m:r-+^(T^ -7^)1,
dt t 2
где S - суммарная площадь омываемых газом поверхностей, включая боко-
вую поверхность шахты; Л - теплопроводность газа; £ - характерный размер;
То - температура газа; Tw - температура стенки шахты; е?, £у - степени чер-
ноты газа и стенки; <т- постоянная Стефана - Больцмана.
Число Нуссельта Nu, характеризующее интенсивность конвективного
теплообмена, определяется из выражения
V С т
7Vu = O,O3Reo’8Pr/3 М- ,
nJ
где Re - число Рейнольдса; Рг - число Прандтля.
Экспериментальные исследования, проведенные на крупномасштабных
моделях и натурных стендах, показали, что интенсивность теплообмена в за-
донном объеме существенно превышает интенсивность теплообмена в глад-
ких трубах при наличии в них однородного турбулентного потока. На осно-
вании сравнения экспериментальных значений коэффициента теплоотдачи с
расчетными, полученными по известной формуле Гухмана-Илюхина, были
введены поправочные коэффициенты Кап^, Касд для старта изделий с помо-
щью ПАД или стартового двигателя
>т0 82 ( rji \0»35
а=0,0206СРГСТ (g • цгсг )0,18 — I —~ I Калоед >
\1w )
W = 30,Зе051*"- = 74-е'1-36^.
Причиной трудностей, возникающих при попытках строгого учета теп-
лообмена в расчетных методиках, является достаточно сложная картина те-
чения, реализующаяся при старте и зависящая от типа применяемых старто-
вых устройств.
В практике проектирования рассматривается широкий круг возможных
схем старта. Отметим здесь основные особенности различных схем с точки
зрения процессов газодинамики и тепломассообмена. Так, если старт ракеты
осуществляется с применением ПАД и запуском ДУ после выхода из шахты,
то движение ракеты в шахте будет происходить только за счет сил давления.
В случае применения стартовых двигателей или маршевого двигателя первой
ступени необходимо учитывать тягу и ее изменение от противодавления. Тип
источника продуктов сгорания, его расположение, схема подачи рабочего га-
за, химический состав продуктов сгорания будут также влиять на газодина-
мические и тепловые параметры.
222
Другим определяющим фактором является схема расположения амор-
тизации ракеты. Пояса горизонтальной амортизации могут располагаться на
ракете или шахте. Газодинамические и тепловые процессы в минометной
схеме старта существенным образом зависят от обводов поясов амортизации,
их расположения, степени обтюрации кольцевого зазора. В соответствии с
этими особенностями принимается та или иная схематизация течения. Влия-
ние вертикальной амортизации выражается посредством упругих сил на пу-
ти, соизмеримом с величиной деформации элементов вертикальной аморти-
зации. В пусковых установках применяются также различные устройства
удержания, фиксирующие ракету на пусковом столе до достижения опреде-
ленной величины поршневой силы. При "сухом" способе старта с ПЛ для
герметизации верхнего среза шахты применяется жесткая или эластичная
мембрана; известны также устройства, обеспечивающие равномерное откры-
тие шахты посредством хода ракеты. Процессы раскрытия верхнего среза
шахты и формирования надшахтной газовой полости при подводном старте
существенным образом влияют на газодинамические параметры в свободных
объемах шахты.
Кроме того, для уменьшения гидродинамических нагрузок на ракету
при старте с движущейся ПЛ могут применяться различные устройства,
обеспечивающие двухфазное обтекание ракеты на подводном участке траек-
тории, например, газогенераторы наддува газовой каверны. Эти особенности
обтекания оказывают влияние на изменение давления как на корпусе ракеты,
так и в шахте, что требуется учитывать при расчете гидродинамических на-
грузок и кинематических параметров движения ракеты на шахтном участке.
Более плотная компоновка ракеты и элементов стартовой системы в ограни-
ченном объеме шахты ПЛ, усложнение геометрии трактов приводит к ло-
кальным неравномерностям газодинамического и теплового воздействия.
Наличие узкого кольцевого зазора между ракетой и шахтой позволяет
приближенно рассмотреть задачу о течении газа в кольцевом зазоре в дву-
мерной плоской постановке, при которой за координаты берутся длина вдоль
образующей ракеты х и расстояние по окружности у. Одним из наиболее дос-
тупных и простых методов изучения двумерных установившихся дозвуковых
и сверхзвуковых течений является метод газогидравлической аналогии (ГГА)
[37], согласно которому движение мелкой воды в открытом русле аналогично
течению газов с показателем адиабаты, равным 2,0 (к=2,0). Хотя такое от-
личие от к реальных газов вызывает отличия в количественных результатах,
все же гидравлическая аналогия оказывается полезной для качественного
изучения двумерных установившихся течений. Модель для испытаний в гид-
ролотке представляет собой развертку боковой поверхности ракеты с уста-
новленными на различных расстояниях имитаторами поясов горизонтальной
амортизации. На вход в канал непрерывным потоком подается вода, уровень
которой может варьироваться в зависимости от условий эксперимента. Высо-
та уровня жидкости в кольцевом зазоре устанавливается с помощью заслонки
гидролотка и также может варьироваться.
223
В результате проведенных экспериментальных исследований выявле-
но, что в случае равномерной установки амортизаторов в кольцевом зазоре
между поясами амортизаторов наблюдаются следующие четыре характерные
зоны течения (рис. 8.1):
— в каналах между амортизаторами;
— на участке смешения струй, истекающих из этих каналов;
- в зазоре "шахта-изделие" после участка смешения (зона стабилизи-
рованного течения);
- участок перестройки течения перед входом в каналы следующего
пояса амортизации.
а) Равномерная установка амортизаторов;
б) Неравномерная установка амортизаторов
Рис. 8.1 Схематизация картины течения газов в кольцевом зазоре
224
I I
Ввиду относительно небольшой протяженности зоны 1 —— <0Д
\ Ab, )
толщина пограничного слоя, формирующегося на боковых поверхностях
амортизаторов, относительно невелика —— «1 I, поэтому профиль скоро-
I У1 )
сти в выходном сечении между амортизаторами близок к равномерному. В
общем картину течения в этой зоне можно представить следующим образом.
Струи, истекающие из зазоров между амортизаторами, расширяются и на оп-
ределенном расстоянии взаимодействуют между собой. В месте слияния
струй статическое давление довольно резко возрастает, что приводит к воз-
никновению вторичных течений. Вниз по потоку течение быстро выравнива-
ется, постепенно переходя к стабилизированному. Струи в области перед
точкой слияния ведут себя независимо друг от друга. Для ближнего поля те-
чения нарастание ширины струи происходит по линейному закону, как и в
случае одиночных струй.
Результаты экспериментальных исследований при равномерной уста-
новке амортизаторов показали, что при фиксированном перепаде давления
длина участка смешения струй 12 не зависит от ширины проходных сечений,
а зависит в основном от ширины самих амортизаторов и составляет
4...6 Лдм. Аналогичные результаты по длине переходного участка течения бы-
ли получены Марстерсом при изучении взаимодействия двух плоских парал-
лельных турбулентных струй.
При увеличении противодавления на выходе из кольцевого зазора дли-
на переходного участка уменьшается (рис. 8.2) примерно по линейному зако-
ну
£2»|б,3-2Л—
I ^0 7
Это объясняется тем, что при распространении струи в более плотной
среде ядро постоянной скорости укорачивается, а в менее плотной - удлиня-
ется.
В случае неравномерного расположения амортизаторов, характеризуе-
у.
мого отношением — (рис. 8.1), длина второго участка увеличивается в мес-
У1
тах напротив широких протоков кольцевого зазора, а в местах его большего
загромождения возникают зоны вихревых и возвратных течений.
15 Зак. 3686
225
Рис. 8.2 Изменение длины переходной зоны /2
в зависимости от противодавления (yi I уг = 1)
На рис. 8.3 приведена полученная из экспериментов зависимость отно-
сительной длины участка перестройки течений 1г=1г!от величины
У\1 У2- Длина переходного участка 12 приближенно может быть аппроксими-
рована линейной зависимостью
= 6,3 - 2,5—Y0,22 + 0,78—1
I poA Уг)
Длина участка перестройки течения перед входом в каналы следующе-
го пояса амортизации во всех экспериментах составляла
k a2h(M
и практически не зависела от перепада давлений.
Неравномерность проходных сечений может привести к тому, что дли-
на переходного участка /2, будет близка или превышать расстояние между
соседними поясами амортизаторов AL t.
В этом случае зона стабилизированного течения вырождается и в коль-
цевом зазоре по всей длине в зонах напротив широких протоков имеют
место ярко выраженные струйные течения. На соседних участках в зонах на-
против узких протоков возникают вихревые и возвратные течения.
226
Для подтверждения полученной методом ГГА качественной картины
течения и проверки соотношений по длинам переходных участков были про-
ведены экспериментальные исследования с использованием пространствен-
ной модели (М=1:10) на установке (рис. 8.4), состоящей из форкамеры 1, в
которую поступал воздух из магистрали высокого давления, модели шахты 2
и модели ракеты 3 с установленными на ней двумя поясами амортизации 4 и
одним поясом обтюрации 5, расположенном в нижней части модели.
Необходимое противодавление на выходе из шахты создавалось до-
полнительным поддувом газов в емкость, окружающую модель ракеты и
шахты.
Методика эксперимента строилась в предположении квазистационар-
ности процессов. Варьировались следующие параметры:
- положение ракеты относительно шахты;
- степень обтюрации кольцевого зазора;
- давление в форкамере;
- давление среды на выходе из шахты.
Отношение давления на выходе из кольцевого зазора к давлению в за-
___________ р
донном объеме Р = —— составляло 0,2 ... 0,66. На модель ракеты наносился
визуализационный состав. В процессе эксперимента при выходе на стацио-
нарный режим замерялось давление в 30 - 40 точках на изделии и шахте с
помощью манометров.
15*
227
Рис. 8.4 Схема экспериментальной установки
На рис. 8.5 приведена типичная фотография реализуемой в кольцевом
зазоре картины течения при у1 /у2=16, когда зона равномерного течения от-
228
сутствует. При всех исследуемых режимах в плоскостях I и III (напротив ши-
роких протоков) отчетливо видны интенсивные струйные течения на всем
промежутке между первым и вторым поясами амортизаторов. В плоскостях
II и IV реализуется сложное вихревое течение.
При увеличении степени обтюрации струйные течения становятся бо-
лее отчетливыми, при этом, чем больше перепад давления между входным и
выходным сечениями кольцевого зазора, тем выше по потоку перемещается
система вихревых и возвратных течений (плоскости II и IV на фотографиях
рис. 8.5).
Рис. 8.5 Картина течения газа в кольцевом зазоре
229
В верхнем поясе амортизаторов поток перемешивается и течение ста-
новится близким к равномерному.
Сравнение длины переходного участка с аналогичными данными,
полученными методом гидроаналогии (см. рис. 8.3), показывает их удовле-
творительное совпадение.
Анализируя полученные экспериментальные результаты по картине
течения газов в кольцевом зазоре, можно сделать вывод, что картина течения
в основном определяется конструктивным заполнением кольцевого зазора,
т.е. геометрическими факторами, и слабо зависит от величины внешнего про-
тиводавления. Неравномерность проходных сечений вдоль окружности зазо-
ра между ракетой и шахтой оказывает значительное влияние на характер те-
чения.
Немаловажным вопросом, особенно при расчетах процесса теплообме-
на в задонном объеме, является изучение картины течения, зависящей как от
используемых стартовых устройств, так и от положения ракеты в шахте. С
этой целью были проведены эксперименты на гидролотке и пространствен-
ной модели (М=1:12,5). В экспериментах изучалась картина течения, реали-
зуемая для случаев старта ракеты с помощью односоплового и многосопло-
вого двигателя первой ступени и старта с использованием ПАД. Для послед-
него случая исследовалось влияние некоторых конструктивных особенностей
(различные отражательные козырьки и щитки) на газодинамическую картину
течения. Отношение диаметра ракеты к диаметру шахты во всех эксперимен-
тах составляло ^¥/ =0$. В результате проведенных экспериментальных
исследований выявлено, что в задонном объеме картина течения зависит от
положения ракеты в шахте и характеризуется глубиной проникновения струй
f.cmp- При расстояниях от среза сопла до днища, шахты меньших £стр, и
старте с помощью односоплового двигателя можно выделить следующие ха-
рактерные участки течения:
натекания струи на днище шахты;
растекания потока вдоль боковой поверхности шахты;
вихревых течений, омывающих днище ракеты.
При старте с помощью многосоплового стартового двигателя картина
течения несколько усложняется. Дополнительно в центральной части днища
шахты возникают участки стекания направленных навстречу друг другу те-
чений, формирующих отраженный в сторону днища ракеты поток, оканчи-
вающийся вихревыми течениями.
При расстояниях от среза сопла до днища шахты, больших £стр, кар-
тина течения меняется. В данном случае в зоне от (,стр до днища шахты
формируются системы вихревых течений. В зоне между нижним срезом ра-
кеты до 1стр картина течения аналогична описанной выше.
230
На рис. 8.6 приведены данные по глубине проникновения струи в зави-
симости от отношения давлений в камере и задонном объеме.
Здесь же нанесена расчетная кривая по формуле, полученная для диа-
пазона dp/ < 0,7,
/«ш
р С р \ С р /
-^- = 5+2/ -0,062,
^кр v 1 J к J
которая дает удовлетворительное совпадение с экспериментом.
Рис. 8.6 Зависимость глубины проникновения струи от отношения
давлений в камере и задонном объеме:
---------------------расчет, J - эксперименты
На рис. 8.7 приведено изменение скорости набегающего потока у дни-
ща шахты и/итах в сечении, где Р^Р2, в зависимости от расстояния между
срезом сопла и днищем шахты у /da. При расстояниях, меньших tcmp, с воз-
растанием у lda происходит уменьшение скорости примерно по линейному
закону
и 1 У
----= 1-а—,
^тах
где «шах - скорость потока в сечении отрыва в сопле. При у >£стр величина
скорости составляла
= 0,2 ...0,3
^тах
и практически не зависела от расстояния у !da.
231
Umax
Рис. 8.7 Изменение скорости потока у днища шахты в зависимости от
положения ракеты
Отметим характерные особенности картины течения при старте с по-
мощью ПАД. По газодинамической схеме можно выделить две группы ПАД:
с центральным расположением сопла и с группой сопел, расположенных на
его боковой поверхности по окружности. ПАД устанавливают на специаль-
ное основание и крепят к опорному фундаменту на днище шахты. Централь-
ное сопло ПАД направляют к днищу шахты, тем самым исключается прямое
воздействие струи на ракету, а днище шахты защищают специальным покры-
тием или экраном. Для изменения направления струи и уменьшения ее теп-
лового и силового воздействия могут применяться различного рода отража-
тельные щитки.
Если опорный фундамент основания ПАД сделан заподлицо с поверх-
ностью днища шахты, то вне фундамента уже не формируется вихревое те-
чение, а струя растекается вдоль боковой поверхности шахты.
При применении ПАД с боковым расположением сопел струи натека-
ют на цилиндрическую поверхность шахты и, растекаясь, формируют тече-
ния, аналогичные описанным в первом случае.
Во всех вариантах у днища ракеты и боковой поверхности ПАД имеют
место зоны вихревых течений.
Естественно, хотя рассмотренные выше примеры не охватывают все
возможные случаи применения источников продуктов сгорания, тем не менее
они позволяют отметить основные характерные особенности картины тече-
ния. К ним можно отнести наличие участков натекания струй на днище или
цилиндрическую поверхность шахты, участков вихревых течений и участков
растекания и стекания потока.
232
Ниже будет дан анализ влияния отмеченных особенностей течения на
распределение газодинамических и тепловых параметров в задонном объеме
и кольцевом зазоре "ракета-шахта".
§ 2. Дифференциальные уравнения продольного движения ракеты
при старте из затопленной водой шахты
На рис. 8.8 схематично изображено положение ракеты в затопленной
водой шахте перед запуском ЖРД. Сначала организуется газовый колокол
(например, с помощью сжигания пороховой шашки), затем поочередно за-
пускаются два рулевых блока ЖРД, через некоторый промежуток времени
еще два рулевых блока (всего 4 рулевых блока); основной двигатель ЖРД за-
пускается при прохождении ракетой более половины длины шахты. Под дей-
ствием тяги двигателя и избыточного давления сначала в газовом колоколе, а
при сходе ракеты с пускового стола и всем подракетном объеме, ракета на-
чинает двигаться в шахте. Продольная скорость ее нарастает во времени
примерно по линейному закону, а избыточное давление за днищем ракеты
обычно не превосходит гидростатического на глубине старта. Под действием
избыточного давления вода через кольцевой зазор вытесняется из шахты.
Рис. 8.8 Схема расположения ракеты в затопленной водой шахте:
1 - ракета, 2 - шахта, 3 - рулевые блоки, 4 - основной блок ЖРД,
5 - пояса резинометаллических амортизаторов, 6 - газовый колокол,
7 - пусковой стол
Уравнение движения ракеты можно записать, основываясь на уравне-
ниях динамики, подробный вывод которых дан в гл. 2 и 4. Как уже отмеча-
лось, узкий кольцевой зазор между ракетой и шахтой позволяет представить
233
задачу о течении воды в кольцевом зазоре в двумерной плоской постановке,
при этом за координату х берется длина вдоль образующей ракеты, за у -
расстояние по окружности. Воспользуемся интегральной теоремой о количе-
стве движения жидкости, считая, что вследствие малой ширины кольцевого
зазора давление поперек него примерно постоянно. Рассмотрим плоскую
твердую решетку, в которой имеются щели шириной, сравнимой с толщиной
решетки, расположенные на одинаковом расстоянии друг от друга (рис. 8.9).
Рис. 8.9 Расчет сопротивления решетки в однородном потоке
Если такую решетку поместить под прямым углом к установившемуся
потоку со скоростью U, то на ее тыльной стороне жидкость будет вытекать в
виде множества струй; эти струи смешиваются, а в конечном счете снова об-
разуется однородный поток с той же скоростью U. Таким образом, здесь
применим анализ внезапного расширения трубы, и, следовательно, вытека-
ние жидкости из отверстий в решетке сопровождается общим уменьшением
константы Бернулли на величину
1 \2
|р[/2 , (8Л)
2 < а )
где а - отношение площади отверстий в решетке к площади решетки.
С другой стороны, течение вверх по потоку от решетки и в отверстиях
таково, что, как нетрудно убедиться с помощью элементарных расчетных
оценок, вязкость в нем не играет важной роли (если размер отверстий не
слишком мал) и, как правило, для него применима теорема Бернулли. Следо-
вательно, величина (8.1) равна разности между значениями констант Бернул-
ли для областей далеко вверх и далеко вниз по потоку от решетки; но так как
скорости потока в обоих этих областях равны U, то величина (8.1) равна так-
же разности давления в них. Таким образом, с учетом (8.1) можно заключить,
что средняя сила сопротивления в расчете на единицу площади решетки так-
же определяется величиной (8.1). Введем понятие коэффициента гидравличе-
ского сопротивления £, величина которого согласно формуле (8.1) найдется
по формуле [5]
234
В нашем случае а есть отношение площади проходного сечения в поя-
се амортизации к общей поперечной площади кольцевого зазора. Если пояса
амортизации расположены на достаточном расстоянии друг от друга, то об-
щее гидравлическое сопротивление всего кольцевого зазора можно найти как
сумму гидравлических сопротивлений отдельных установленных в нем поя-
сов. В соответствии с этим суммарный коэффициент сопротивления кольце-
вого зазора ^представится в виде
N
где N- количество поясов. При выходе ракеты из шахты количество поясов в
кольцевом зазоре будет уменьшаться, и соответственно будет уменьшаться и
&
Система уравнений, описывающая движение ракеты в шахте, пред-
ставляется в виде двух дифференциальных уравнений
*р =(Кду + 4Р'$м -Cxq-SM -FTP +A-G-Fyd) ;
= P(h-xe) '
(8.2)
В приведенных уравнениях приняты следующие обозначения:
хр,хв - ускорение ракеты и столба воды (высотой й) в кольцевом зазоре, Яду
- тяга двигателя, Ар - превышение давления в газовом колоколе над гидро-
статическим на глубине старта, FTP — сила трения при скольжении ракеты по
поясам резинометаллической амортизации, F^ - сила удержания ракеты на
пусковом столе, действующая до момента разрыва связи. Для замыкания сис-
темы (8.2) найдем текущий объем колокола
Г + 'Хр+^кз 'Хд,
массу газов в колоколе
и давление парогазовой смеси в газовом колоколе по уравнению Клапейрона
Pr=(w/7+wr)/?Fcw.
Здесь тп~ масса образующегося пара, ТСм~ температура парогазовой смеси.
Определенные трудности расчета связаны с оценкой величины давле-
ния, для получения которой требуется знать эффективную поверхность со-
прикосновения частиц воды и газа и коэффициент теплообмена. При прове-
дении расчетов предполагали, что за счет кинетической энергии струи двига-
теля вода, находящаяся за днищем ракеты, расщепляется на множество мел-
ких шариков с некоторым спектром радиусов, которые в свою очередь по-
крыты газовыми более мелкими пузырьками. Эта методика была неодно-
235
кратно апробирована в практике создания ряда ракетных комплексов и дала
положительные результаты. Для определения величины давления Р также
широко использовались результаты модельных испытаний на газодинамиче-
ских стендах разрабатываемых комплексов, которые потом проверялись и
уточнялись по результатам натурных испытаний. В целом можно заключить,
что температура парогазовой смеси для созданных комплексов обычно близ-
ка к температуре насыщенных паров при реализующемся за днищем ракеты
давлении. Температура насыщенных паров находится по эмпирической зави-
симости
Тп = 10^0Д^,
где Рг - давление газов в газовом колоколе, измеряемое в Па. Значение газо-
вой постоянной R рассчитывается при этом как среднемассовое значение га-
зовых постоянных выхлопных газов и пара.
§ 3. Газодинамика и продольное движение ракеты
при старте из сухой шахты
Рассмотрим вертикальное движение ракеты в шахте ПЛ. Начало систе-
мы координат поместим в плоскости верхнего среза шахты, а ось у направим
вверх. '
Вдоль оси у на ракету будут действовать следующие силы:
Fn - поршневая сила; R(P) - тяга двигателя; Gp - вес ракеты; FpeaK - си-
ла реакции вертикальной амортизации; сила гидродинамического сопротив-
ления при движении ракеты; сила, возникающая за счет перепада давления
на поясах горизонтальной амортизации.
В этом случае уравнение вертикального движения ракеты можно запи-
сать в виде
dl) _
(m + ^)—l = Fn + 0°R(P) + Д1£(/?-Рм-SP )SOET^t -
(8.3)
v2
-XFmP.+F^Ayy-C^S,-Gp,
где у - путь, пройденный ракетой;
Fn = - ^и+1 )S„ -(Ph- Р„+1 )SH - ;
(0-при старте на ПАД;
[1-при старте на ДУ;
(0- пояса горизонтальной амортизации расположены на шахте;
[1 —пояса горизонтальной амортизации на ракете;
|0-приу>/;;
[1 - при у < ;
(/, - расстояние от верхнего среза шахты до i-ro пояса амортизации, если по-
236
h
SH =
sh =
следние установлены на ракете, или расстояние от нижнего среза цилиндри-
ческого корпуса ракеты до i-ro пояса амортизации при расположении их на
шахте).
Сила реакции вертикальной амортизации задается таблично как функ-
ция пути ракеты F^^ = fly) и полагается равной нулю при полном разжатии
элементов вертикальной амортизации. В FpeaK дополнительно включается си-
ла разрушения разрывных болтов, удерживающих ракету на пусковом столе.
Параметры Рь /?и Sh определяются следующим образом:
Ph -при подводном старте,
0,101 МПа - при надводном старте;
SH — при подводном старте,
Sp - при надводном старте;
р —при подводном старте,
рн =1,25^--при надводном старте;.
м
SK - при наличии кавитатора и R<y0 + у,
• Sp - при наличии кавитатора и R > у0 + у,
Sp - без кавитатора ;
(рн„ ~ Рв8У) " при R < у0 + у,
Р„+1-при R>y0+y,
(рв-при F<y0+y,
1Рл+1-при R>y0+y.
Здесь R - радиус надшахтного газового пузыря, рассчитываемый по
формуле Рэлея, уо - высота носка ракеты над срезом шахты в исходном по-
ложении, Sp - площадь миделя ракеты.
Для определения газодинамических параметров продуктов сгорания в
задонном объеме ракеты применим подход, основанный на использовании
уравнений термодинамики переменного количества газа.
Энергетический баланс смеси газов в задонном объеме согласно пер-
вому закону термодинамики можно представить в виде
d{Gi)~ VdP = dQ,
где G — суммарный вес рабочей смеси в задонном объеме;
dQ — количество полученной системой теплоты.
Из выражения для удельной энтальпии di=Cpdt имеем
di _ „ dT к dT
dt р dt к-1 dt
Используя уравнение состояния
PV=GRT
h
(8-4)
(8.5)
(8.6)
и полагая теплофизические характеристики к и R зависящими от времени,
выражение (8.5) можно записать следующим образом:
237
(8.8)
di РУ к (IdV \ dP \ dG 1 dR\
dt G (k-I)If dt + P dt G dt R dt J ( '
Подставив последнее уравнение для дифференциала энтальпии в уравнение
первого закона термодинамики (8.4) и произведя несложные преобразования,
для изменения давления в задонном объеме получим
dP 1Г, ,\( dQ .dG} 1 dV 1 dG \ dR\
dt FL \dt dt J \y dt G dt R dt).
При определении баланса массы в задонном объеме будем полагать,
что ее изменение может происходить за счет следующих факторов:
— поступления продуктов сгорания от стартового или маршевого дви-
гателей, пороховых аккумуляторов давления, специальных газоге-
нераторов, либо различных их комбинаций;
- термохимического разрушения теплозащитных материалов поверх-
ности ракеты, днища и стенок шахты;
- возможного парообразования некоторого количества находящейся в
задонном объеме воды;
- утечки рабочей смеси через кольцевой зазор "ракета-шахта", а также
через специальные газоотводные устройства.
Таким образом, уравнение баланса массы можно записать в следующем
виде
+ ZGpa3j -YGym,K + G„, (8.9)
«< i j k
где ^Gnpi - суммарный секундный приход продуктов сгорания в задонный
i
объем; ~ суммарный секундный приход массы за счет разрушения
j
теплозащитных покрытий ракеты и шахты; _ суммарный секундный
к
расход массы из задонного объема; Gn - секундный приход массы за счет
парообразования воды.
Уравнение теплового баланса для данной системы имеет вид
dQ _ х-1 л1 v .•/' , dQxuM dQw dQn f
d,—л~' (810)
где iot - удельная энтальпия продуктов сгорания, поступающих в задонный
с dQxuu-----------------------------------------------dQw dQ
объем;----—— приход тепла за счет химических реакции; — — - со-
dt dt dt
ответственно потери тепла на теплообмен и испарение жидкости.
Продифференцировав уравнение состояния (8.6), для температуры
среды в задонном объеме получим следующее уравнение
dT (\dP IdR IdH
— 1 I-------------, I О. Ill
dt--------------------------------------------{P dt R dt у dt)
238
где у = — — удельный вес, определяемый из уравнения
dY_i(dG
dt~V\dt 7 dt)
(8-12)
Уравнения, характеризующие изменение теплофизических характери-
стик среды, записываются с учетом их осреднения по весу Отдельных компо-
нентов смеси
ср = А; +^0^+CpeGe
+YRJGpa}J + ReGe |.
«и i )
Для проведения расчетов на ПЭВМ удобнее иметь дифференциальную
запись этих соотношений
' c +c ^+c
^J^pj+^p. dt pn dt
dCn. _, dCnl dCm dC
npf dt + dt 6 dt " dt J’
+ ^'«^ + R-^7 + R"^' +
Cj । j dl dl
Gnp'‘ dt ^Gpta j dt Ge dt Gn dt
at \j j j
+ YGnp,i
i
dR 1
dt
(8-13)
(8-14)
Для показателя адиабаты к =
£j>
Ср
из соотношения Прандтля-Майера
R = Ср-Cv имеем
dR ( \sdCP
j к (к_1)—~
dK^dt dt
dt Cp-R
(8.15)
Уравнения для изменения пути ракеты в шахте и величины задонного
объема имеют вид:
f = (8.16)
dt 4 dt' 1 ’
Расход газов С>т^из задонного объема через к отверстий площадью Sk опре-
деляется по формулам Сен-Венана:
239
* I K-l
к-1
K+l
э Л к
к I
"PT
(8.18)
2
» V
k
2gK
2
=
к
J К 4-1
( 2 A «-I
\K + ly
P\ K+1V1
при -^->| —— I
к
Система уравнений (8.3), (8.7) - (8.18) представляет собой замкнутую систе-
му обыкновенных дифференциальных уравнений для расчета газодинамиче-
ских параметров в задонном объеме изделия при известных значениях теп-
лофизических характеристик компонентов рабочей смеси и параметров, оп-
ределяющих процессы тепломассообмена.
При расчете газодинамических параметров в задонном объеме тепло-
физические характеристики рабочей смеси обычно осредняются по весу вхо-
дящих в смесь компонентов. В качестве входных величин используются их
значения на срезе сопла источника продуктов сгорания и для находящегося в
свободном объеме шахты воздуха. При таком подходе не учитываются воз-
можные процессы догорания, диссоциации и рекомбинации, играющие за-
метную роль при применении высокотемпературных топлив. Суммарная ве-
личина энергии, выделяемая или поглощаемая при протекании химических
реакций, зависит от состава, количества реагирующих веществ и условий
протекания данной химической реакции. То есть, помимо решения уравне-
ний газодинамики, позволяющих получить давление и температуру в задон-
ном объеме, которые в свою очередь зависят от величины тепловых эффек-
тов химических реакций, необходимо решать задачу по расчету состава и те-
плофизических свойств рабочей смеси, которые однозначно определяются
давлением и температурой.
Изложенная выше система уравнений справедлива для случая расчета
замороженного состава.
В случае расчета равновесного состава из системы уравнений газовой
динамики необходимо исключить уравнения (8.7), (8.8), (8.13) - (8.15).
Уравнение для удельной энтальпии рабочего тела согласно первому за-
кону термодинамики записывается в виде
df 1 Г
dt' (7
1 IV"1 A А Т"1 z-» dQw • dG Tr dP I
~ pa},jlT3IIJ ~^fiym,kltk ~T г , + , p
'* J. t j к dt dt dt J
давление определяется по уравнению состояния для идеального газа
(8.19)
А
Уравнение баланса массы рабочего тела с учетом утечки газа и разру-
шения материала теплозащитного покрытия
= Tfinpf + •
al i ; к
240
Система уравнений газовой динамики замыкается уравнением движе-
ния (8.3) и уравнением для определения потерь тепла .
dt
Элементарный химический состав рабочего тела определяется из соот-
ношения между количеством продуктов сгорания и количеством газа, остав-
шегося в задонном объеме после утечки первоначального газа Go,
к-°^.
G.
Величина К определяется интегрированием уравнения
«/£_ _______j_________k______J_____
dt ~ G
Для выполнения термодинамических расчетов необходимо знать хими-
ческий состав (условную формулу) рабочего тела.
Пусть условные формулы продуктов сгорания, продуктов разрушения
материала ТЗП и первоначального газа в задонном объеме соответственно
имеют вид
4'>... л<‘>... 4т>
ЧТ biT ЬтТ
...4> ...4т>
Ч73П °ПЗП °тТЗП
... 4‘>... <>,
40 40 °тО
где Л® - символ /-го химического элемента,
bi - количество атомов /-го химического элемента в условной формуле
рабочего вещества.
Тогда значение Ь, для рабочего тела определяется по формуле
Z>, = [qbiT + (1 — q )biT3n ]K + bi0,
™ g = л,----------------•
^np,i + Z_| ^-pa3,j
• J
Приход массы продуктов разрушения при известном значении тепло-
dQw , ,
вого потока qw = —— определяется с использованием эффективной энталь-
dt
пии разрушения материала по зависимости
Ус = У
раз,] 2-j т ’
J j •’зфф
зфф=-А + B(i - iw ),А,В- const, Sj — площадь поверхности материала ТЗП).
При этом энтальпия продуктов разрушения /^ для каждого из компонен-
тов определялась при температуре, соответствующей температуре разруше-
ния материала ТЗП.
Определение термодинамических параметров рабочей смеси проводи-
лось по известному методу расчета химического равновесия при Р,Т= const.
16 Зак. 3686
241
Общая система уравнений записывается в виде:
уравнения диссоциации (закона действующих масс)
1пру - ^ац=0, j=1,2,...,/;
(8.20)
уравнения сохранения вещества
1+п, -1пЛ/г-1п/>, =0;
(8.21)
уравнение закона Дальтона
1п£р,-1пр = 0,
(8.22)
где i,j — индексы независимого и зависимого компонентов соответственно,
к - номер индивидуального вещества в конденсированном состоянии с
числом молей в этом состоянии ПК$ ,
q — индекс любого индивидуального вещества,
1-при j = k (nj=Pj)
0-при j*k.
Уравнение диссоциации газовой фазы конденсированных веществ име-
ет вид (8.20), логарифмы давления насыщенных паров определяются выра-
жением
(8.23)
< =^ехр{1590(П-^(Г)]/Л0 -[/“(Т)-У°ДГ)]/7?07’}.
Выражение для констант равновесия
\nKpj ----——-гг,— = Лт)-
(8.24)
(8.25)
7?0 RqT
Уравнение для удельной энтальпии
/ = Е”Л + > (8-26)
где nj, и, - числа молей j-ro продукта реакции и i-ro независимого компонен-
та.
Решение системы уравнений (8.20) - (8.25) производилось численным
методом Ньютона в два этапа. Сначала решалась система уравнений (8.20) -
(8.25) для заданных Р, Т, а затем уточнялась температура с использованием
уравнения (8.26).
Величина АТ вычислялась по формуле
ат=--^—Л
ЗТ)Р
После этого по уравнению состояния (8.19) уточняется давление, затем
расчет повторяется до заданной точности
<10‘3.
Значение равновесных характеристик рабочей смеси определялось из
соотношений
242
S".cr. -|-X”»ci., ।
51nT
dlnT
i ( Sin//
rldlnT
4«=U177j
*” r1 ’
7 Срз
u-1 1 ' I
Значения логарифмов констант равновесия 1пКр, и функций определя-
лись интерполяцией табличных значений.
Как показали результаты расчетов, зависимости указанных характери-
стик от реальных значений температуры и давления несущественны, и их
можно не учитывать при расчетах газодинамических параметров.
16’
Принятые сокращения и основные обозначения
БРПЛ ГГА ГДХ ГУГМС ду МД нгг ЖРД ПАД пл РМА РМК сд тзп ЭСС - баллистические ракеты подводных лодок - газогидравлическая аналогия - гидродинамические характеристики - Главное управление гидрометеорологической службы - двигательная установка — маршевый двигатель - носовой газогенератор - жидкостный ракетный двигатель - пороховой аккумулятор давления - подводная лодка - резинометаллическая амортизация - резинометаллическое кольцо - стартовый двигатель - теплозащитное покрытие - энергетическое средство старта
OqXoIoZo OXoKoZo OXYZ V, Vu Vy, vz - стартовая (инерциальная) система координат - подвижная система координат - связанная с телом система координат - вектор линейной скорости центра масс тела и его составляющие в связанной системе координат
CO, COX. (Oy, COZ - вектор угловой скорости центра масс тела и его составляющие в связанной системе координат
Q L R,X,Y,Z - вектор количества движения тела - вектор момента количества движения тела - вектор гидродинамической реакции и его составляющие
М, Мх, Му, Мг ~ вектор гидродинамического момента и его составляющие
сх - коэффициент тангенциального сопротивления тела в связанной с телом системе координат
cn,cz ту, mz g Н Т, t М L, 1 D %С9 Ус* Zc - коэффициенты нормальной и боковой силы - коэффициенты моментов рыскания и тангажа - ускорение свободного падения - глубина старта - температура, время - масса тела - длина тела, длина вышедшей части тела - диаметр тела - координаты центра масс тела относительно полюса (центра объема) тела
Sm ^z S - площадь миделя - главные моменты инерции тела - длина дуги образующей тела
244
Кду А,хл А Л Ку Ок р T,j,ic т п г,х, е г’,х' а Р а - тяга двигателя - Архимедова сила и координата точки ее приложения — плотность воды - присоединенная масса - коэффициент присоединенной массы — число кавитации - гидродинамическое давление - единичные векторы (орты) — единичный вектор касательной к поверхности тела - единичный вектор нормали к поверхности тела - цилиндрические координаты - производные от г и х по длине дуги я — угол атаки - угол скольжения — амплитуда волны
ав к he (he=2a) & F D, Sc - угол волнового склона - частота формы волны (волновое число) — высота волны — ордината волны - функция распределения - дисперсия волновых координат — энергетический спектр волнения (спектральная плот- ность)
и, и — горизонтальная и вертикальная составляющие вектора скорости волнового потока
И, Ui, U2, и} — вектор скорости волнового потока и его составляющие в связанной системе координат
и5, и6 — градиенты составляющих вектора скорости волнового потока в связанной системе координат
& к2 т2 Ср, Су л - вектор количества движения жидкости - вектор момента количества движения жидкости - кинетическая энергия жидкости - теплоемкости газа при постоянных давлении и объеме — теплопроводность газа
Литература
1. Белоцерковский С.М., Табачников ВТ. Экспериментальное исследова-
ние стационарных и нестационарных характеристик тел вращения
//Труды ЦАГИ. - 1963. - Вып. 896.
2. Бородай И.К., Нецветаев Ю.А. Качка судов на морском волнении. - Л.:
Судостроение, 1969.
3. Буйвол В.Н. Тонкие каверны в течениях с возмущениями. - Киев: Пау-
кова думка, 1980.
4. Буйвол В.Н., Журавлев Ю.Ф., Капанкин Е.Н. Возмущенное движение
тонких пространственных каверн И В кн.: Неустановившиеся течения
воды с большими скоростями. - М.: Наука, 1973.
5. Бэтчелор Дж. Введение в динамику жидкости. - М.: Мир, 1973.
6. Грандштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и про-
изведений. - М.: Наука, 1971.
7. Гузовский Л.Г. Численный анализ кавитационных течений: Препринт //
Ин-т теплофизики Сиб. отд. АН СССР, 1979, № 40.
8. Гульнев С.И., Капанкин Е.Н. Об особенностях кавитационного обтека-
ния тел кавитационным потоком жидкости И Ученые записки ЦАГИ. -
1975. - Т. VI. - № 2.
9. Дегтярь В.Г. Методология проектирования стартовых систем балли-
стических ракет подводных лодок. И Космонавтика и ракетостроение.
2002.-Вып. 3(28).
10. Дегтярь В.Г. Методы расчета и практика применения энергетических
средств старта баллистических ракет подводных лодок. // Космонавтика
и ракетостроение. - 2003. - Вып. 4.
И. Дегтярь В.Г. Методы решения задач динамики и стабилизации балли-
стических ракет подводных лодок. И Космонавтика и ракетостроение. -
2003. -Вып. 4.
12. Дегтярь В.Г., Мнев Е.Н., Чемодуров В.Т. Подводный старт баллистиче-
ских ракет морского базирования. - ФГУП ГРЦ "КБ им. академика В.П.
Макеева" при участии ГУП "ВИМИ", 2001.
13. Дегтярь В.Г., Мошкин И.Ю., Пегов В.И. Численный метод расчета не-
стационарных газовых полостей в жидкости. // В сб. Проблемы проекти-
рования неоднородных конструкций. - Миасс, 2000.
14. Дегтярь В.Г., Пегов В.И. Математические модели гидродинамики ракет
// Математическое моделирование: Сб. научно-методических трудов. -
Челябинск: ЮУрГУ, 2003.
15. Дегтярь В.Г., Пегов В.И. Методы математического моделирования гид-
родинамики ракет // Известия РАРАН, М. - 2003. - Вып. 1.
16. Дегтярь В.Г., Пегов В.И. Позиционные силы и моменты при воздействии
на ракету вязкой жидкости И РКТ, сер. XIV, 2001. - Вып. 45. - Миасс,
2001.
246
17. Дегтярь В.Г., Пегов В.И. Результаты экспериментальной отработки ка-
витационного способа старта ракет. И РКТ, сер. XIV, 1999. - Вып. 1(43),
4.2. - Миасс, 1999.
18. Дегтярь В.Г., Пегов В.И. Теоретическое исследование гидродинамики
тела вращения при выходе его из цилиндрической полости. И В сб. Про-
блемы проектирования неоднородных конструкций. — Миасс, 1999.
19. Дегтярь В.Г., Пегов В.И. Теоретическое исследование гидродинамики
морских баллистических ракет. И Космонавтика и ракетостроение. -
2001.-Вып. 22.
20. Капанкин Е. Н. Удар кругового цилиндра в жидкости с внешней жесткой
или свободной границей в виде окружности. Учет влияния границ пото-
ка в аэродинамических трубах. // Труды ЦАГИ. - 1969. - Вып. 1154.
21. Кнэпп Р., Дейли Дж., Хэммит Ф. Кавитация. - М.: Мир, 1974.
22. Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидко-
сти. - Л.: Судостроение, 1979.
23. Кочин Н.Е. и др. Теоретическая гидромеханика: Ч. I. - М.: Гостехиздат,
1963.
24. Куфарев П.П. Об одном методе численного определения параметров в
интеграле Кристоффеля-Шварца. И ДАН СССР. - 1947. — Т. 57.
25. Ламб Г. Гидродинамика. - М., 1947.
26. Логвинович Г.В. Гидродинамика течений со свободными границами. -
Киев: Наукова думка, 1969.
27. Логвинович Г.В., Буйвол В.Н. и др. Течения со свободными поверхно-
стями. - Киев: Наукова думка, 1985.
28. Маслов Л.А. Методы расчета обтекания тела вращения любой формы
при произвольном движении в идеальной жидкости. // Ученые записки
ЦАГИ. - 1970. - Т. I. - № 2.
29. Милн-Томсон Л.Н. Теоретическая гидродинамика. - М.: Мир, 1964.
30. Пегов В.И., Тихонов Н.Н. Гидродинамика морских ракет. // В сб. Балли-
стические ракеты подводных лодок России. - Миасс, 1994.
31. Полетаев Б.И. Математические модели динамики движения ракеты на
подводном участке кавитационного старта с подвижного носителя. И В
кн. Проблемы машиноведения и машиностроения. Межвузовский сбор-
ник, Санкт-Петербург. - 2001. - Вып. 24.
32. Полетаев Б.И. Физическая трактовка и экспериментальные исследования
гидродинамических характеристик ракеты при ее движении на подвод-
ном участке в режиме кавитационного обтекания. // В кн. Проблемы ма-
шиноведения и машиностроения. Межвузовский сборник. Санкт-
Петербург. — 2001. — Вып. 24.
33. Рождественский В.В. Кавитация. - Л.: Судостроение, 1977.
34. Сегерлинд Л. Применение метода конечных элементов. - М.: Мир, 1979.
35. Седов Л.И. О неустановившемся движении внутри жидкости тела вра-
щения. // Труды ЦАГИ. - 1940. — Вып. 515.
36. Справочник по теории корабля. Т. 1, 2, 3. / Под ред. Я.И.Войткунского,
А.А.Русецкого. - Л.: Судостроение, 1985.
247
37. Сунцов Н.Н. Методы аналогии в аэрогидродинамике. - М.: Физматгиз,
1958.
38. Щеглова М.Г., Махортых Г.В. Гидродинамические характеристики и
распределение нагрузки на удлиненных телах вращения при произволь-
ном движении. // Труды ЦАГИ. - 1970. - Вып. 1237.
Оглавление
Предисловие.................................................3
Введение....................................................5
Глава 1. Постановка задачи. Системы координат. Основные
динамические законы движения твердого тела
в пространстве.............................................9
§ 1. Постановка задачи исследования и гидродинамические
схемы обтекания ракет.......................................9
§ 2. Системы координат и кинематические характеристики,
определяющие положение ракеты в пространстве................19
§ 3. Основные динамические законы движения твердого тела....23
§ 4. Уравнение для давления в жидкости относительно
подвижных осей..............................................32
Глава 2. Силовое воздействие невязкой жидкости на движущееся
в ней тело.........................................34
§ 1. Постановка задачи гидродинамики при движении
тела в спокойной воде.......................................34
§ 2. Основные динамические параметры жидкости...............39
§ 3. Силовое воздействие невязкой жидкости. Присоединенные
массы тела..................................................43
§ 4. Приближенное определение присоединенных масс для тела
вращения с кормовыми стабилизаторами........................47
Глава 3. Характеристики гравитационных волн и постановка задачи
гидродинамики при движении тела во взволнованной
жидкости..................................................52
§ 1. Характеристики плоских регулярных волн................52
§ 2. Статистические характеристики ветровых волн и сведения
о волнении в некоторых районах моря........................57
§ 3. Спектральный метод исследования и структура морского
ветрового волнения.....................................,...62
§ 4. Выбор расчетного спектра волнения.....................75
§ 5. Общая постановка задачи гидродинамики при движении тела
во взволнованной жидкости...................................79
Глава 4. Дифференциальные уравнения неуправляемого
пространственного движения ракеты..................87
§ 1. Общая форма дифференциальных уравнений движения .......87
§ 2. Позиционные силы и моменты воздействия вязкой жидкости.90
§ 3. Система дифференциальных уравнений продольного
и углового движения осесимметричного тела в воде и при
пересечении свободной поверхности воды......................99
§ 4. Приближенный метод расчета гидродинамических
коэффициентов............................................107
§ 5. Инженерный метод расчета донной газовой каверны........113
249
§ 6. Метод расчета воздействия струи жидкости на
днище ракеты при движении ее в воде и пересечении
поверхности воды.......................................115
Глава 5. Численный метод расчета гидродинамических
коэффициентов и присоединенных масс тела вращения..........119
§ 1. Постановка задачи гидродинамики при прохождении тела
через экран................................................119
§ 2. Вывод интегральных уравнений метода потенциала
простого слоя..............................................126
§ 3. Вывод формул для расчета относительных скоростей
и потенциалов..............................................130
§ 4. Основные расчетные формулы............................136
§ 5. Формулы для расчета гидродинамических коэффициентов...138
§ 6. Методы вычислений.....................................147
§ 7. Результаты расчета гидродинамических коэффициентов и
сравнения с экспериментом..................................150
Глава 6. Методы и результаты расчета присоединенных масс
и нагрузок на ракету при старте............................165
§ 1. Анализ гидродинамических нагрузок при старте ракеты
из затопленной шахты.......................................165
§ 2. Методы расчета присоединенной массы ракеты при движении
в шахте....................................................175
§ 3. Метод расчета гидродинамических нагрузок на ракету
с учетом спутного потока...................................186
Глава 7. Методы и результаты расчета кавитационного обтекания
ракеты.....................................................193
§ 1. Расчет кавитационного обтекания ракеты................193
§ 2. Теоретическое исследование гидродинамических нагрузок
при несимметричном смыкании каверны на круговой цилиндр....203
§ 3. Метод и результаты расчета гидродинамических нагрузок при
кавитационном обтекании ракеты.............................212
Глава 8. Газодинамика и тепломассообмен при старте.
Дифференциальные уравнения движения ракеты в шахте.........221
§ 1. Общая постановка задач газодинамики и тепломассообмена
при старте и картина течения газов в шахте.................221
§ 2. Дифференциальные уравнения продольного движения ракеты
при старте из затопленной водой шахты......................233
§ 3. Газодинамика и продольное движение ракеты
при старте из сухой шахты..................................236
Принятые сокращения и основные обозначения.................244
Литература.................................................246
250
ДЛЯ ЗАМЕТОК
МОНОГРАФИЯ
ДЕГТЯРЬ Владимир Григорьевич, ПЕГОВ Валентин Иванович
ГИДРОДИНАМИКА БАЛЛИСТИЧЕСКИХ РАКЕТ
ПОДВОДНЫХ ЛОДОК
Ответственный редактор С.Т. Калашников
Технический редактор Т.В. Тукачева
Литературный редактор ЛА Осипова
Компьютерный набор: А.И. Едунова, Н.И Корнева, Г.В. Чесалкина
Сдано в набор 16.11.2003. Подписано к печати 6.04.2004.
Формат 60x90/16. Бумага офсетная.
Уч-изд. листов 10,4. Тираж 1000 экз.
Заказ № 3686.
ФГУП "ГРЦ “КБ им. акад. В.П.Макеева",
456300, г. Мнасс, Челябинская обл., Тургоякское шоссе, 1
Отпечатано с оригинала-макета заказчика
в ФГУП "Издательство "Челябинский Дом печати",
454080, г. Челябинск, Свердловский пр., 60.