Author: Игдалов И.М. Кучма Л.Д. Поляков Н.В. Шептун Ю.Д.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника междупланетные соединения (междупланетные полеты) космонавтика (аэронавтика) ракеты
ISBN: 966-7985-81-4
Year: 2004
И. М. Игдалов, Л. Д. Кучма,
Н. В. Поляков, Ю. Д. Шептун
РАКЕТА
КАК ОБЪЕКТ УПРАВЛЕНИЯ
2004
И. М. Игдалов, Л. Д. Кучма,
Н. В. Поляков, Ю. Д. Шептун
РАКЕТА
КАК ОБЪЕКТ УПРАВЛЕНИЯ
Под редакцией академика
С. Н. Конюхова
Допущено
Министерством образования и науки Украины
как учебник для студентов
высших учебных заведений
Днепропетровск
АРТ-ПРЕСС
2004
УДК 629.76 (075.8)
ББК 39.62я73
И26
Допущено Министерством образования и науки Украины
27.01.2004 № 1/11-295
Научные рецензенты:
акад. НАН Украины В. С. Будник;
д-р техн, наук, проф. Н. Д. Коваленко
(ИТМ НАН Украины)
Книга посвящена вопросам теории и практики динамического проектирования
в ОКБ-586 (ГКБ «Южное») МБР и PH КА, построенных по нетрадиционным схемам или
с оригинальными техническими решениями («глобальная» ракета с орбитальной ГЧ, пер-
вая РГЧ, PH на базе боевых ракет I и II поколений и др.).
По результатам анализа военно-политической обстановки 60-х годов XX века показа-
на необходимость создания III поколения ракетных комплексов на основе решений,
принципиально отличных от «классических» (минометный старт жидкостных ракет,
в т. ч. тяжелого класса, РГЧ ИН, БЦВМ, ПУ высокой защищенности и др.).
Аналогично - середина 70-80-х годов - необходимость создания ракет IV поколения
в т. ч. твердотопливных РТ-23 среднего класса, управляемых путем отклонения ГО (ДУ II
и Ш ступеней со стационарными соплами без «рулевых» органов). Ракеты РТ-23 эксплуа-
тируются как в шахтном, так и в уникальном железнодорожном вариантах базирования.
Книга предназначена для студентов вузов и специалистов в области ракетно-
космической техники.
Игдалов И. М., Кучма Л. Д., Поляков Н. В., Шептун Ю. Д.
И26 Ракета как объект управления: Учебник /Под ред. акад. С. Н. Ко-
нюхова. - Д.: АРТ-ПРЕСС, 2004. - 544 с.
ISBN 966-7985-81-4
Книга присвячена питаниям Teopii i практики динам!чного проектування в ОКБ-586
(ДКБ «П!вденне») МБР i PH КА, побудованих за нетрадицшними схемами чи з оригшаль-
ними техшчними р!шеннями («глобальна» ракета з орбпальною ГЧ, перша РГЧ, PH на
баз! бойових ракет I i II поколшь та ш.).
За результатами анал!зу вмськово-полпично! обстановки 60-х poxis XX стол!ття по-
казана необхщшсть створення III поколшня ракетних комплексе на основ! р!шень, прин-
ципов© вщмшних вщ «класичних» (мшометний старт рщинних ракет, у т. ч. важкого кла-
су, РГЧ IH, БЦОМ, ПУ високо! захищеност! та ш.).
Аналопчно - середина 70-80-х роюв - необхщшсть створення ракет IV поколшня,
в т. ч. твердопаливних РТ-23 середнього класу, керованих шляхом вщхилення ГО (ДУ II
i III ступешв з! стацюнарними соплами без «кермових» оргашв). Ракети РТ-23 експлуа-
туються як у шахтному, так i в ушкальному зал!зничному вар!антах базування.
Книга призначена для студент!в вуз!в i фах!вщв в облает! ракетно-косм!чно! техшки.
УДК 629.76 (075.8)
ББК 39.62я73
ISBN 966-7985-81-4 © Игдалов И. М., Кучма Л. Д,
Поляков Н. В., Шептун Ю. Д., 2004
© АРТ-ПРЕСС, 2004
СПИСОК СОКРАЩЕНИИ
АН
ББ
БД
БЖРК
БО
БРДД
БЦВК
БЦВМ
Вд(Вб)
ГКБЮ
Академия наук
Боевой блок
Боевое дежурство
Боевой железнодорожный ракетный комплекс
Боевое оснащение
Баллистическая ракета дальнего действия
Бортовой цифровой вычислительный комплекс
Бортовая цифровая вычислительная машина
Вероятное (срединное) отклонение по дальности (направлению)
Государственное конструкторское бюро «Южное»
им. академика М. К. Янгеля (новое название ОКБ-586)
Головная часть
Днепропетровский государственный (национальный) университет
ГЧ
ДГУ (ДНУ)
AT (I, L, Z и др.) Предельное (2.7 СКО) отклонение соответствующего параметра
ЖРД
КА
КВ
КВО
КП
КСП ПРО
лки
МБР
мпд
огч
ОКБ
ОС
ПАД
ПРО
ПУ
ПФ яв
РГЧ
РК
PH
СКО
СУ
СУРТ
тз
ТПК
ттт
ттх
ФТФ (ФТИ)
цвк
ШПУ
яв
Жидкостный ракетный двигатель
Космический аппарат
Контакт выхода ракеты из ТПК
Круговое вероятное отклонение
Командный пункт
Комплекс средств противодействия ПРО
Летно-конструкторские испытания
Межконтинентальная баллистическая ракета
Максимальная прицельная дальность
Орбитальная головная часть
Особое конструкторское бюро
Одиночный старт
Пороховой аккумулятор давления
Противоракетная оборона
Пусковая установка
Поражающие факторы ядерного взрыва
Разделяющаяся головная часть
Ракетный комплекс
Ракета-носитель
Среднее квадратическое отклонение
Система управления
Система управления расходом топлива
Техническое задание
Транспортно-пусковой контейнер
Тактико-технические требования
Тактико-технические характеристики
Физико-технический факультет (институт)
Цифровой вычислительный комплекс
Шахтная пусковая установка
Ядерный взрыв
3
Посвящается
85-летию
Днепропетровского национального университета
и 50-летию
Государственного конструкторского бюро «Южное»
им. академика М. К. Янгеля
ПРЕДИСЛОВИЕ
Работам по развитию реактивной техники в СССР в середине 1946 г.
был официально присвоен статус важнейшей государственной задачи.
Решение практической части этой задачи было возложено на вновь
созданные в Москве и Подмосковье специализированные научно-
исследовательские и опытно-конструкторские организации, а научное со-
провождение работ - на головные НИИ Министерства вооружения и Ми-
нистерства обороны с широким привлечением институтов Академии наук
(академики А. Ю. Ишлинский, М. В. Келдыш, Н. Н. Моисеев, Д. Е. Охо-
цимский, Б. Н. Петров, В. А. Трапезников и др).
Все организации были укомплектованы квалифицированными специа-
листами и видными учеными с предприятий смежных отраслей науки
и техники. Руководили разработками - каждый по своему профилю -
ставшие в дальнейшем Героями и дважды Героями Социалистического
Труда и академиками: В. П. Бармин, В. П. Глушко, В. И. Кузнецов, Н. А. Пи-
люгин и М. С. Рязанский. Они все входили в первый Совет Главных кон-
структоров, созданный и возглавляемый академиком С. П. Королевым -
руководителем головного предприятия по созданию ракетных комплек-
сов-ОКБ-1 МВ.
В результате уже в процессе создания первых советских жидкостных
ракет дальнего (для тех лет) действия Pl, Р2, Р5М и особенно первой
межконтинентальной - легендарной Р7 - был накоплен научный потенци-
ал в виде проектов, отчетов, диссертаций и т. п. по динамике ракет и их
динамическому проектированию.
В связи с проведением всех работ в режиме строжайшей секретности
открытые публикации некоторых результатов научных исследований
в области динамики ракет стали появляться только в середине пятидесятых
годов в виде статей в изданиях Академии наук. Это были труды Н. Н. Мои-
сеева [110 - 1953 г.], Г. С. Нариманова [114 - 1956 г.], [115 - 1957 г.],
Д. Е. Охоцимского [119 - 1956 г.], Б. И. Рабиновича [127 - 1956 г.] и др.
В эти же годы и в зарубежных журналах публикуются научные статьи
по отдельным вопросам динамики тел с полостями, заполненными жидко-
4
стью (авторы Abramson Н. N., Ransleben G. Е.» Chu W. Н.» Garza L. R.,
Bauer H. F. и др.).
В конце пятидесятых годов появились первые несекретные книги, со-
держащие некоторые материалы о ракете как объекте управления - рабо-
ты А. С. Локка [101] и В. И. Феодосьева, Г. Б. Синярева [153]. Обе работы
носили общетехнический характер.
Создание в Украине, на Урале и в Москве новых центров по разработке
ракетных комплексов с жидкостными ракетами дальнего действия, а также
потребность в учебно-методическом материале для подготовки специа-
листов данного профиля в ряде вузов страны вызвали в середине 60-х - на-
чале 70-х годов большой поток фундаментальных работ по динамике ра-
кет как объектов управления. Это монографии К. С. Колесникова [87],
Н. Н. Моисеева и В. В. Румянцева [111], Г. Н. Микишева и Б. И. Рабино-
вича [106], [107], К. А. Абгаряна и И. М. Рапопорта [1], А. А. Лебедева
и Л. С. Чернобровкина [96], а также труды по баллистике ракет - Р. Ф. Ап-
пазова, С. С. Лаврова и В. П. Мишина [14], А. А. Лебедева и Н. Ф. Герасю-
ты [95] и ряд других работ. Краткий обзор литературы приводится ниже во
«Введении», а библиография - в «Списке использованной литературы».
Упомянутые основополагающие труды безусловно являлись теорети-
ческой базой для решения практически всех задач динамики ракет, но по-
строенных по «классическим» схемам, принятым в мировой практике ра-
кетостроения в 50-60-е годы.
В то же время академиками В. С. Будником
и М. К. Янгелем, начиная с первых разработок, бы-
ло выбрано направление на создание ракетных ком-
плексов по нетривиальным схемам. Так, в 1953 г.
еще коллективом отдела Главного конструктора за-
вода № 586 во главе с В. С. Будником был разрабо-
тан первоначальный эскизный проект ракеты стра-
тегического назначения с ЖРД, работающим на вы-
сококипящих компонентах топлива. Ракета Р-12, при
дальности стрельбы в ~2 раза большей, чем у Р-5М,
управлялась автономной инерциальной системой
без радиоуправления и радиокоррекции.
Будник
Василий Сергеевич
(1913)
Учитывая перспективность выбранного направления создания боевых
ракетных комплексов, для его реализации 10 апреля 1954 года было при-
нято решение о преобразовании ОГК завода в Особое конструкторское
бюро № 586. Под руководством Главного конструктора - начальника
ОКБ-586 М. К. Янгеля и его первого заместителя В. С. Будника в период
до 1969 г. были созданы два поколения оригинальных комплексов боевых
ракет дальнего действия, в том числе «глобальной» (дальность стрельбы
5
до 40 000 км) ракеты с орбитальной ГЧ - 8К69 и ракеты 8К67П с первой
трехблочной РГЧ. Наряду со сданными на вооружение шестью РК перво-
го поколения и тремя - второго были разработаны и доведены до ЛКИ
комплекс МБР среднего класса 8К66 и до завершения летных испытаний -
мобильный грунтовый комплекс комбинированной МБР сверхлегкого
класса 8К99 (стартовый вес 30 тс). Одновременно было закончено проек-
тирование и начаты ЛКИ четырех ракетно-космических комплексов, по-
строенных на базе созданных боевых ракет.
В 1968-1969 гт. М. К. Янгель разработал, обосновал и начал реализа-
цию принципиально новой концепции вооружения ракетных войск стра-
тегического назначения (РВСН).
Цель - при минимизации затрат повышение в десятки раз защищенно-
сти РК от ЯВ и в несколько раз - боевой эффективности ракет в условиях
активной ПРО.
Средства - минометный старт из ТПК, РГЧ, ЦВК, мощный КСП
ПРО и т. д.
Результат - до конца жизни М. К. Янгеля (октябрь 1971 г.) - заверше-
ние в полном объеме проектно-конструкторской разработки и начало экс-
периментальной отработки третьего поколения РК - жидкостных ракет:
тяжелого класса - 15А14 (Р-36М) и легкого класса - 15А15 (МР-УР100).
Генеральным конструктором КБ «Южное» (с 1971 г.) академиком.
В. Ф. Уткиным была успешно завершена разработка и сдача на вооруже-
ние комплексов ракет 15А14 и 15А15, а также созданы по принятой док-
трине РК того же поколения, но с улучшенными ТТХ - соответственно
ракеты 15А18 и 15А16.
В восьмидесятые годы были созданы непревзойденные по своим ТТХ
боевые комплексы IV поколения с жидкостной ракетой тяжелого класса
15А18М («Сатана») и с трехступенчатой твердотопливной ракетой сред-
него класса 15Ж60, а также не имеющего аналогов в мировой практике
БЖРК с ракетой 15Ж61. Обе твердотопливные ракеты управлялись
принципиально новым способом - путем отклонения головного отсека
при стационарных без органов управления соплах двигателей II и III сту-
пеней.
Одновременно был создан полностью автоматизированный с уникаль-
ными эксплуатационными и тактико-техническими характеристиками ра-
кетно-космический комплекс PH среднего класса 11К77 («Зенит-2»). Ос-
новными отличиями этой PH как объекта управления являлись тандемная
схема с большим удлинением (отношение длины ракеты к ее диаметру со-
ставляло 14,6) и управление I ступенью путем отклонения камер марше-
вого двигателя (тяга, создаваемая каждой камерой около 200 тс).
6
Герасюта
Николай Федорович
(1919-1987)
Влияние далеко не полного перечня оригинальных технических ре-
шений на облик и ТТХ ракеты как объекта управления рассмотрены на
конкретном примере во «Введении» книги.
Очевидно, что динамическое проектирование таких ракет потребова-
ло существенного дополнения и преобразования основополагающей на-
учно-теоретической базы применительно к практике работы КБ.
Проблемы, возникавшие при создании всех РК,
успешно решались коллективом, возглавляемым
профессором Н. Ф. Герасютой. За 10-15 лет им была
создана научная школа, насчитывающая 5 докторов
и более 40 кандидатов наук, в том числе более
20 канд. техн, наук по динамике ракет как объек-
тов управления: Н. Н. Андреев, Н. Г. Белецкая,
В. В. Брикер, А. И. Баулин, В. В. Горбунцов,
Н. Е. Зыков, В. А. Ларин, Г. Л. Мадатов, А. А. Ма-
нойленко, В. М. Морозов, Н. М. Полякова,
Е. А. Серый, Г. М. Резник, М. А. Якушкин и др.
Большинство ученых школы Н. Ф. Герасюты обеспечивали учебный про-
цесс либо на правах штатного совместительства, либо являясь штатными
сотрудниками, в т. ч. заведующими кафедрами САУ и РТС Физико-
технического института ДНУ [135], а также были основой при создании
соответствующего подразделения в Институте технической механики
(ИТМ) НАНУ. В результате оба института активно участвовали в решении
насущных задач динамики ракет, возникавших в процессе создания пер-
спективных РК.
Весь процесс создания РК, а также сопровождающее и обеспечиваю-
щее этот процесс динамическое проектирование проходили в самом тес-
ном контакте с головными институтами отрасли (ЦНИИмаш - НИИ-88)
и заказчика (НИИ-4 МО), а также со смежными специализированными
НИИ и КБ, без участия которых вообще немыслимо выполнение таких
работ.
Кроме вышеназванных ученых, головных институтов и создателей
теоретической основы динамики ракет [14, 106, 107, НО, ИЗ, 114, 115,
116, 119, 127], необходимо отметить неоценимую помощь и поддержку
КБЮ, оказываемые в течение многих лет директором ЦНИИмаш про-
фессором Ю. А. Мозжориным.
Реализация в СУ нетрадиционных технических решений коллективом
НИИ автоматики и приборостроения обеспечивалась благодаря Гене-
ральному конструктору системы управления, руководителю института -
академику Н. А. Пилюгину и его заместителю - профессору М. С. Хит-
рику. Яркими примерами являются: отказ от систем радиоуправления
7
и радиокоррекции в СУ БРДД стратегического назначения, создание СУ
ракет, управляемых путем отклонения головного отсека; реализация в СУ
МБР легкого класса минимальной прицельной дальности 1000 км, для че-
го II ступень ракеты должна была совершать эволюции, близкие к фигу-
рам высшего пилотажа [19]; создание систем управления с уникальными
ТТХ на базе многомашинного вычислительного комплекса для ракет-
носителей «Зенит-2» и, особенно, «Зенит-З SL» программы «Морской
старт» и др.
Аналогично решались проблемы динамики ракет в ОКБ-692 (КБ Электро-
приборостроения) во главе с академиком НАНУ В. Г. Сергеевым и его за-
местителем в то время профессором Я. Е. Айзенбергом (впоследствии -
руководителем НПО «Хартрон»). Здесь примерами могут служить созда-
ние СУ ракеты с первой РГЧ за 8 месяцев от начала разработки до пуска,
а также реализация минометного старта жидкостной ракеты тяжелого клас-
са, создание СУ PH, построенных на базе боевых ракет, и многое другое.
Отдельные специфические задачи и используемый математический
аппарат для их решения, в полной мере изложенные в вышеуказанных
фундаментальных трудах, помещены в соответствующих главах настоя-
щей книги для придания ей цельности и для избавления читателя от необ-
ходимости обращения к этим источникам многолетней давности.
Книга предназначена для студентов старших курсов «ракетных» фа-
культетов вузов и для инженеров и научных работников соответствующих
специальностей, а «Введение» и отдельные главы (например, 3, 5, 6, 11,
12, 13 и др.) могут представлять интерес для широкого круга технической
интеллигенции.
Для изучения специальных глав настоящей книги необходимо обла-
дать знаниями в объеме вузовских программ по курсам: высшая матема-
тика, теоретическая механика, теория автоматического регулирования,
основы ракетной техники и аэрогидродинамики.
Авторы выражают глубокую благодарность:
Е. А. Джуру - за большую помощь и активную поддержку, которые
обеспечили написание и издание книги;
В. М. Морозову - за помощь в редактировании и предоставление мате-
риала для главы 14;
Б. В. Дмитриеву, написавшему по просьбе авторов главу 15;
М. И. Галасю - за высказанные замечания по рукописи книги;
А. А. Манойленко - за предоставленные материалы для раздела 13.5;
В. Л. Тихонову, В. В. Швалевой, С. Г. Безгубой - за помощь при ком-
пьютерном оформлении рукописи.
8
ВВЕДЕНИЕ
Задачей современных МБР или РКН является доставка ББ или КА
в заданную точку на поверхности Земли или космического пространства
соответственно. Для решения этой научно-технической проблемы даже
в общей постановке требуются, как минимум, энергетическая установка
мощностью миллионы киловатт и устройства прецизионного управления
с относительными погрешностями 10’5-ь10’6 измеряемой величины (ско-
рости, времени и др.). Задача существенно усложняется за счет целого
ряда ограничений, условий и требований, во многих случаях противоре-
чивых.
Сведение воедино всех накладываемых условий, ограничений и тре-
бований осуществлялось в процессе проведения головными институтами
Министерства обороны военно-технической научно-исследовательской
работы, исходными позициями которой являлись прогноз стратегической
обстановки в мире и состояния систем вооружений на 10-20 лет вперед.
Результаты такой НИР представлялись в форме достаточно объемного
документа, называемого «Тактико-технические требования МО» к созда-
ваемому конкретному ракетному или ракетно-космическому комплексу
в целом и его основным частям, одной из которых является МБР или PH
КА соответственно.
ТТТ утверждались и согласовывались министрами обороны и воен-
но-промышленного комплекса, а также головными разработчиками. Та-
ким образом, ТТТ являлись документом государственного уровня, тем
более, что главные характеристики комплекса вводились в соответст-
вующее постановление правительства, подписывавшееся первым лицом
государства. Очевидно, что невыполнение отдельных требований этого
документа приводило к весьма нежелательным последствиям.
Основными ТТТ МО, определяющими облик и характеристики боево-
го ракетного комплекса и ракеты как объекта управления, являлись (пе-
9
речень в порядке и объеме, приведенным в книге «Ракеты и космические
аппараты конструкторского бюро «Южное» [131]):
• тип ракетного комплекса;
• тип пусковой установки;
• способ старта ракеты;
• класс и тип ракеты;
• вид боевого оснащения;
• тип системы управления;
• максимальная прицельная дальность стрельбы;
• точность стрельбы;
• обобщенный показатель надежности и его составляющие;
• время пуска из полной боевой готовности;
• стойкость ракеты к поражающим факторам ЯВ в полете;
• гарантийный срок нахождения на БД;
• условия боевого дежурства ракеты;
• условия боевого применения.
Примечание*, аналогичные по своему существу требования содер-
жались в ТТТ, предъявляемых к космическому ракетному комплексу
и ракете-носителю космических аппаратов.
Например, вместо требований к виду боевого оснащения и величине
МПД задавался: «Вес космических аппаратов, выводимых на круговую
орбиту высотой 200 км и наклонением 90°- 12 тс» (для КРК К11К77).
Вместо требования по точности стрельбы задавалось: «КРК должен
обеспечивать точность выведения КА, характеризующуюся следую-
щими ошибками выведения на круговую орбиту высотой 200 км - по
высоте орбиты ДН^±3,5 км; по периоду обращения ДТ^±2,5 с; по углу
наклонения плоскости орбиты Л1^±2угл. мин.» и т. п.
Рассмотрение и анализ ТТТ проведем на примере созданного в конце
семидесятых годов прошлого столетия и долгие годы лучшего в мире бое-
вого комплекса межконтинентальной баллистической ракеты, как наибо-
лее сложного. Этот ракетный комплекс так называемого III поколения
имел индекс 15ПО18 с ракетой 15А18 или РС-20Б и явился базой для соз-
дания ракеты-носителя «Днепр», успешно эксплуатируемого в междуна-
родных коммерческих программах.
Степень влияния на облик и параметры ракеты как объекта управления
перечисленных основных ITT проводится раздельно для каждого из них.
1. Ракетный комплекс - стационарный, с высокозащищенными
(до 100 кг/см2) от наземного ЯВ одиночными шахтными автоматизи-
рованными пусковыми установками (типа «ОС»). При этом пусковые
10
установки располагаются удаленными на несколько километров от
командного пункта и между собой. Заданный тип старта отличается:
• от наземного, т. е. с пускового стола, устанавливаемого в определен-
ной точке на поверхности Земли;
• от шахтного защищенного (~2 кг/м2), с расположением в непосредст-
венной близости трех ПУ и одного КП;
• от мобильного старта - грунтового, железнодорожного и др.
Для удовлетворения предъявленному требованию необходимо, чтобы
комплекс ракеты, устанавливаемой в ШПУ типа «ОС», обеспечивал в про-
цессе БД
- возможность проведения дистанционного контроля:
• параметров температурно-влажностного режима;
• степени загазованности окружающей ракету среды парами ком-
понентов топлива;
• готовности ракеты и ее систем к проведению пуска в заданное
время путем периодических (с допустимым интервалом) проверок
соответствующих параметров комплекса;
- прием зашифрованной команды на проведение пуска ракеты (при
этом должна быть обеспечена практически абсолютная невозмож-
ность проведения несанкционированного пуска - степень «защиты»
10’8-109.);
- проведение пуска ракеты через заданное время с момента получения
на ПУ боевой кодограммы. Для осуществления пуска необходимо
проведение ряда операций в строго определенной последовательно-
сти, не допускающей никаких отклонений от заданной циклограммы.
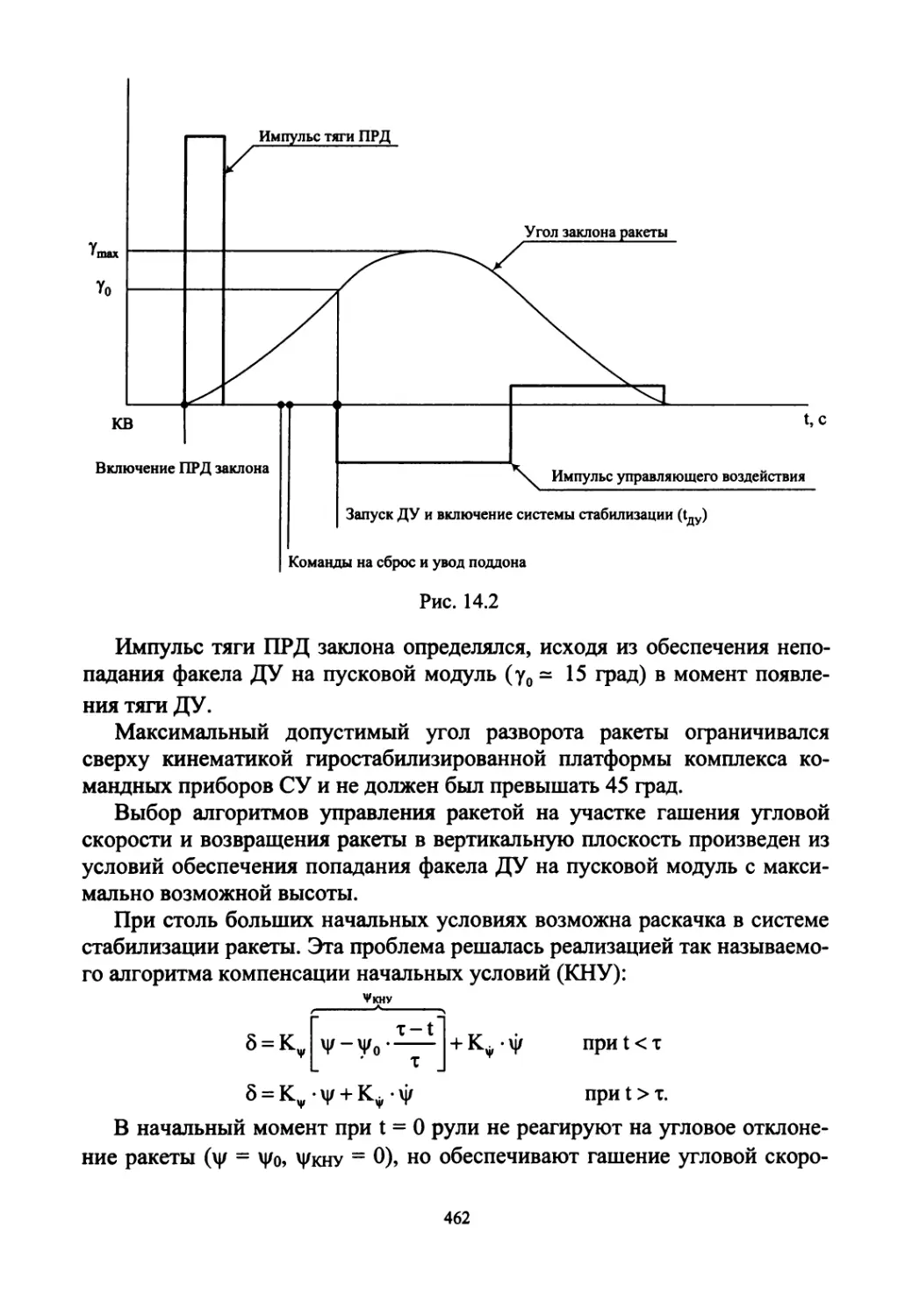
2. Способ старта ракеты - минометный, из ТПК с помощью ПАД'а.
Такой тип старта жидкостной МБР тяжелого класса был реализован
впервые в мировой практике ракетостроения. Это одно из радикальных тех-
нических решений по ракетному комплексу, определивших возможность
выполнения весьма жестких ТТТ и, в частности, требования по п. 1, путем
уменьшения размеров ПУ за счет исключения оголовка шахты, внутреннего
стакана, газоходов, газоповоротных решеток и др.
Ракета как объект управления в этом случае превращалась в комплекс
ракеты, поскольку он представлял единое целое:
- двухступенчатая ракета со ступенью разведения, установленная
в ТПК, на котором закреплены «наземная» проверочно-пусковая ап-
паратура СУ, аппаратура «нижнего» звена системы боевого управле-
ния, приборы системы прицеливания, источники питания, подстыко-
ваны ПАД’ы, проложены и подстыкованы к ракете заправоч-
но-сливные магистрали и соответствующая кабельная сеть.
11
Сборка комплекса ракеты без головной части осуществлялась на заво-
де-изготовителе ракет с проведением всего цикла контроль-
но-проверочных испытаний. Готовый комплекс ракеты поставлялся непо-
средственно на стартовую позицию для установки в ШПУ, минуя мон-
тажно-испытательный корпус.
Специфика минометного старта предъявила к объекту управления це-
лый ряд особых требований:
• полная автоматизация процесса подготовки и проведения пуска;
• обеспечение безударного отделения, сброса и увода поддона, буге-
лей и др. элементов в строго определенной последовательности;
• запуск маршевого ЖРД в условиях невесомости с проведением по-
следовательности операций по запуску с погрешностью по време-
ни - сотые доли с;
• необходимость выработки высоконадежной команды, фиксирую-
щей момент выхода из ТПК; эта команда являлась началом полет-
ной циклограммы.
Введение дополнительно к традиционной команде, соответствующей
фиксации момента начала полета ракеты - «контакт подъема (КП)» (по
которой начинала работать система наведения), еще одной - «контакт вы-
хода (КВ)» (от которой начинался отсчет циклограммы) вызвано острым
дефицитом времени на проведение целого ряда пусковых операций, воз-
никающим в результате существенного разброса параметров ПАД'ов,
а также необходимостью обеспечения безопасности (исключения катаст-
рофических последствий) в случае неисправности ПАД’ов, приводящей
к невыходу ракеты из ТПК (запуск маршевого двигателя внутри ТПК). На
начальном этапе реализации этого «революционного» способа старта тя-
желой жидкостной МБР команда «КВ» вырабатывалась с помощью элек-
тромеханического устройства, срабатывающего в момент прохождения
основанием ракеты верхнего среза ТПК. Решение вызывало определенные
трудности при изготовлении и было, по существу, местом ослабленного
контроля (отсутствие возможности прямой, непосредственной проверки
функционирования механизма за весь многолетний период нахождения
ракеты на боевом дежурстве). В дальнейшем команда «КВ» вырабатыва-
лась в результате решения навигационной задачи - вычислением «прой-
денного» ракетой пути с соответствующей подстраховкой.
3. Тип и класс ракеты - межконтинентальная баллистическая,
жидкостная, полностью ампулизированная.
Для обеспечения возможности удовлетворения этому и нижеследую-
щим тактико-техническим требованиям, вес головной части (ГЧ) этой ра-
кеты составлял ~8500 кгс и, соответственно, ее стартовый вес -
~210000 кгс, т. е., ракета принадлежит к тяжелому классу. В действитель-
12
ности, это самая мощная и совершенная боевая ракета, до настоящего
времени непревзойденная в практике мирового ракетостроения по своей
эффективности.
Как объект управления МБР этого класса представляет собой доста-
точно большую и весьма сложную техническую систему, при создании
которой было необходимо найти решение целого ряда науч-
но-технических проблем.
Основными факторами, определяющими сложность задачи, являлись:
• необходимость сохранения (не превышения) габаритов - длины и
диаметра модернизируемой ракеты 15А14, стоящей на боевом де-
журстве в ракетных войсках;
• наличие в баках ракеты более 188 тс жидкого топлива, колебания
которого вызывали значительные возмущения параметров движе-
ния ракеты (см. гл. 3);
• необходимость обеспечения весьма высокого уровня энерговесово-
го совершенства, характеризуемого коэффициентом
Кв. с. =Gnr/Go, кгс/тс.
Для данной ракеты этот коэффициент превышал 40 ед.
У базовой ракеты тяжелого класса (8К67) с газодинамическим спосо-
бом старта из ШПУ (комплекс второго поколения), созданной в середине
шестидесятых годов прошлого столетия, т. е., за пятнадцать лет до сдачи
на вооружение рассматриваемого комплекса МБР, этот коэффициент был
равен 31,8 кгс/тс при разнице в длине ракеты около двух метров, том же
диаметре (3 м) и весе топлива 167 тс. У ракеты 15А14 коэффициент Кв.с
был равен 36,7 при том же GT. Высокий уровень энерговесового совер-
шенства был достигнут, в том числе, за счет исключения внутрибаковых
механических устройств, демпфирующих колебания компонентов топлива
при полете ракеты.
• Использование в качестве органов управления I ступени четырех
поворотных маршевых двигателей. При отсутствии радиальных
продольных перегородок (см. выше) эффективность таких органов
управления в канале крена была существенно больше традицион-
ных значений за счет малого присоединенного момента инерции
относительно продольной оси ракеты.
• Организация разделения ступеней по «горячей» схеме, при которой
запуск рулевого двигателя II ступени проводился за ~1,5 с до вы-
ключения ДУ I ступени, почти за 4 с до разделения ступеней и за
более 7 с до команды на запуск маршевого двигателя II ступени.
4. Вид боевого оснащения - разделяющаяся головная часть (РГЧ)
с десятью боевыми блоками (ББ) мощностью 0,5 Мт и эффективным
13
комплексом средств противодействия противоракетной обороне
(КСП ПРО).
Созданная РГЧ обеспечивала поражение одной ракетой до десяти це-
лей, включая высокопрочные малоразмерные и особо крупные площадные
цели, расположенные на местности 300000 км2, в условиях эффективного
противодействия средств ПРО вероятного противника. Для разработчиков
эта РГЧ представляла собой принципиально новый объект управления
и потребовала решения целого ряда специфических задач динамики ракет,
в частности:
• выбор параметров универсальной высокоэнергетической жидкост-
ной ступени наведения с двигательной установкой, выполненной
по «тянущей» схеме, обеспечивающей оптимальное распределение
по целям десяти ББ на всех вероятных театрах военных действий;
• обеспечение возможности минимизации динамической «ошибки»
движения РГЧ в условиях изменяющейся конфигурации и, соответ-
ственно, положения центра масс объекта стабилизации;
• обеспечение практически полного отсутствия возмущений при от-
делении ББ как за счет выбора направления движения ГЧ при
«сбросе» блока, так и за счет создания безымпульсных устройств
отделения;
• создание ББ с оптимальными параметрами по баллистическому ко-
эффициенту, центровке, закрутке и т. д., обеспечивающими мини-
мальное рассеивание за счет возмущений на нисходящем атмо-
сферном участке траектории;
• создание КСП ПРО с ложными целями, имитирующими характери-
стики боевых блоков практически по всем селектирующим призна-
кам на внеатмосферном участке траектории и значительной части ат-
мосферного. На нисходящем атмосферном участке траектории дви-
жение ББ имитируется благодаря применению специального твердо-
топливного двигателя «разгона», не имеющего аналога в мировой
практике, прогрессивно (в 20 раз) возрастающая тяга которого ком-
пенсирует силы аэродинамического торможения ложной цели [149].
5. Тип системы управления - автономная, инерциальная, на базе
бортовой цифровой вычислительной машины (БЦВМ) и высокоточ-
ного комплекса командных приборов (ККП).
БЦВМ, в сочетании с цифровой «наземной» аппаратурой, размещае-
мой на ТПК, является центральным блоком управления, решающим все
математические и логические задачи с высокой точностью, надежностью
и быстродействием.
Применение цифрового вычислительного комплекса позволило обес-
печить:
14
• решение в процессе полета ракеты полной навигационной задачи
(терминальное наведение) и, соответственно, минимизацию методи-
ческой ошибки управления;
• обеспечение стабилизации ракеты на всем активном участке траек-
тории движения при «естественном» демпфировании колебаний то-
плива в баках (без ребер-перегородок);
• возможность повышения точности стрельбы за счет определения
и учета систематических инструментальных погрешностей ККП;
• оперативное дистанционное переприцеливание ракет в период бое-
вого дежурства, в том числе в процессе предстартовой подготовки,
по любой из заранее запланированных целей;
• повышение надежности комплекса за счет оперативного получения
информации о боевом состоянии ракеты, систем ТПК и пусковой
установки и, соответственно, обеспечения возможности своевре-
менного выявления и устранения неисправностей;
• полную автоматизацию управления всеми системами пусковой ус-
тановки, ТПК и ракеты при нахождении комплекса на боевом де-
журстве и пуске ракеты из заданной готовности.
6. Максимальная прицельная дальность стрельбы (МПД) -11000 км.
В самой общей постановке под МПД понимается наибольшее расстоя-
ние на «невращающейся» Земле от точки старта до точки цели, на которое
«полезный груз» доставляется ракетой с заданной вероятностью (напри-
мер, 0,997) при безусловном выполнении всех требований, оговоренных
ТТТ (в частности, по условиям эксплуатации, точности стрельбы, надеж-
ности и др.).
Классической схемой разработки «с нуля» ракетного комплекса и,
в частности, ракеты как объекта управления является:
- аванпроект,
- эскизный проект,
- разработка конструкции (КД),
- экспериментальная отработка (лабораторные, стендовые, статиче-
ские, динамические, функциональные и др. испытания),
- корректировка рабочей конструкторской и схемной документации,
- изготовление опытных образцов для огневых стендовых и летных
испытаний).
При этом в процессе динамического проектирования ракеты оценивае-
мое и рассчитываемое на соответствующем этапе разработки значение
МПД представляется критерием приемлемости исследуемого варианта со-
четания технических характеристик всех систем и агрегатов ракеты для со-
здания комплекса, полностью удовлетворяющего заданным требованиям.
15
В рассматриваемом случае, при модернизации стоявшего на БД ракет-
ного комплекса, МПД являлась инструментом определения технических
характеристик в основном модернизируемой части ракеты - ступени раз-
ведения и боевого оснащения (в пределах, заданных ТТТ), а также систе-
мы управления с новым программно-математическим обеспечением
(ПМО).
Применительно к ракете, оснащенной РГЧ, максимальная прицельная
дальность задавалась до середины условного прямоугольника разведения.
Площадь прямоугольника, с соотношением сторон (дальность - бок),
равном 2:1, при заданном составе и условном порядке разведения боевых
блоков и элементов комплекса средств противодействия по вершинам
этого прямоугольника (например, «цепочками» 3-3-2-2), однозначно оп-
ределяет параметры РГЧ (компоновку, конструкцию, энергетику и т. д.).
Таким образом, МПД, безусловно, одна из основных характеристик
ракеты, поскольку ее соответствие заданному значению интегрально под-
тверждало удовлетворение целому ряду требований к параметрам ракеты
(прочность, теплозащита, устойчивость и управляемость, точность
стрельбы, работоспособность спецзарядов и т. д.).
7. Точность стрельбы - ±0,65 км.
Точность стрельбы, так же как МПД, - основной параметр ракетного
комплекса в целом и ракеты в частности, поскольку характеризует сте-
пень их совершенства и является базовым для определения боевой эффек-
тивности комплекса.
Таким образом, точность стрельбы - одна из составляющих критерия
сравнительного анализа различных боевых комплексов и поэтому должна
приводиться к одинаковым условиям и в единой терминологии, основны-
ми из которых являются:
• «точность стрельбы» - полусумма предельных отклонений точки
падения от точки прицеливания по дальности и боковому направ-
лению в условной системе координат, начало которой расположено
в точке цели
2
• за предельное отклонение AL (AZ) обычно принимают такое значе-
ние, при котором вероятность получения больших по абсолютной
величине отклонений достаточно мала. Обычно вероятность при-
нимается равной 0,007. Это означает, что все случайные отклоне-
ния точек падения от соответствующих точек прицеливания с ве-
роятностью 0,993 не будут превышать заданных значений;
• отклонения от цели суть случайные величины, подчиненные дву-
мерному нормальному закону распределения и характеризуемые
16
средними квадратическими отклонениями ctl и ctz при нулевых
средних значениях. Предельное отклонение с уровнем вероятности
0,993 равно 2,7 ст.
Отклонения от точки прицеливания, или иначе рассеивание точек па-
дения боевых блоков, могут также характеризоваться вероятным (сред-
ним) отклонением В, связанным со средним квадратическим отклонением
соотношением
В = 0,6745 ст или AL (AZ) = 4ВД (4Вб).
• Еще одним критерием является: круговое вероятное отклонение
(КВО) - величина, равная радиусу круга, в котором находится по-
ловина всех точек падения испытываемой совокупности ББ.
Использование этого критерия стало возможным в результате:
- совершенствования законов управления по дальности стрельбы
и существенного уменьшения методической ошибки (в частности, при ис-
пользовании в системе управления БЦВМ);
- резкого улучшения параметров ББ и его характеристик, определяю-
щих рассеивание точек падения за счет возмущений, действующих на ат-
мосферном участке пассивного полета;
- повышение в несколько раз точности системы прицеливания;
- значительного уменьшения инструментальных погрешностей как за
счет качества приборов, так и за счет исключения влияния систематиче-
ских составляющих ошибок и т. п.
Реализация этих мероприятий не только повысила суммарную «точ-
ность стрельбы», но и приблизила эллипс рассеивания по форме к кругу,
т. е. AL ~ AZ ~ А.
КВО связано с СКО и вероятными отклонениями, как
А ~ 2,7 ст ~ 4В ~ 2,3 КВО.
Для оценки «точности стрельбы» в единых условиях расчет рассеива-
ния точек падения ББ производится для случая пуска ракет на контроль-
ную дальность - 10 000 км.
Для наглядного представления сложности удовлетворения требованию
по точности стрельбы ±0,65 км предположим, что величина отклонения
точки падения ББ от точки прицеливания вызвана одним-единственным
фактором - ошибкой определения продольной составляющей вектора
скорости в момент выработки «главной команды» на отделение ББ.
Ориентировочное значение этой составляющей при пуске на L = 10000 км
будет Vx «6500 м/с, а величина частной производной — при этом будет со-
dVx
ставлять «5000-^7 = 5000 с. Учитывая, что предельное отклонение
/с
17
Д=—— AVx=650 m,
dvx
допустимая ошибка определения значения Vx будет составлять AVX =
0,13 м/с или 210"5 от измеряемой величины. Поскольку эта ошибка далеко
не единственная, допустимая относительная погрешность определения
составляющей скорости на момент отделения ББ не должна превышать
1-Ю"5 во всех условиях эксплуатации объекта управления!
8. Обобщенный показатель надежности - 0,93.
В самом общем виде требование к надежности ракетного комплекса,
предъявленное в количественной форме, определяется как вероятность
доставки без повреждений кондиционного «полезного груза» в установ-
ленное время в заданный «квадрат» района цели, удаленного от старта на
расстояние, не превышающее максимальную прицельную дальность.
Надежность ракетного комплекса определяется вероятностью безот-
казной работы всех его агрегатов и систем при предстартовой подготовке,
при запуске и полете ракеты и ее головной части, а также надежностью
боевого оснащения при движении на нисходящем атмосферном участке
траектории.
Величина обобщенного показателя надежности является произведени-
ем значений показателей надежности выполнения указанных операций,
которые, в свою очередь, являются произведением вероятностей выпол-
нения своих функций элементами, от которых зависит безотказная работа
на соответствующем этапе.
Так, в укрупненном виде
Роб. =Рб. Г. *Рст* Рпр* Ррг* Рбб* Рд, где
РОб. - обобщенный показатель надежности - 0,93,
Рб. г. - вероятность выполнения требования по боеготовности, т. е. стар-
та через установленное время от момента получения команды - -0,997,
Рет - вероятность безотказной работы всех наземных и бортовых сис-
тем и агрегатов в процессе старта - -0,993,
Рпр - полетная надежность ракеты от запуска двигательной установки
I ступени до отделения головной части - -0,96,
Ррг - надежность работы головной части на безатмосферном участке
разведения элементов боевого оснащения - -0,99,
Рбб - вероятность преодоления ПРО и достижения работоспособными
боевыми блоками района цели - -0,997,
Рд - вероятность выполнения требования по точности стрельбы -
-0,993.
Значение одной из составляющих Роб., например, полетной надежности
ракеты является произведением вероятностей безотказной работы пнев-
18
могидравлической системы и двигательной установки I ступени (РдуО,
в целом системы управления (РСу), системы разделения ступеней (Ррс),
ПГС и двигательной установки II ступени (Рдуц), отделения головной час-
ти (Рог) и др.
Для достижения столь высоких показателей надежности ракеты как
объекта управления принимается по всем агрегатам и системам специаль-
ный комплекс проектных, конструктивных, технологических, экспери-
ментальных и производственных мер, определяемых планом обеспечения
надежности (ПОН). Например, для обеспечения задаваемого техническим
заданием на разработку системы управления показателя ее надежности,
реализация такого комплекса мероприятий приводит к увеличению
ее стоимости более чем на порядок, а габаритно-весовых характеристик
в 2-3 раза. Такое положение определяется: применением нескольких де-
сятков тысяч электрорадиоэлементов специальной серии, проходящих при
изготовлении тройной контроль, тренировку и отбор; троированием
каналов вычислительного комплекса с применением программно-
алгоритмических мер защиты от сбоев путем формирования результатов
вычисления по схеме «2 из 3» в каждом такте; дублированием электриче-
ских цепей и элементов в приборах и системе; троированием элементов
электроавтоматики (реле); проведением нескольких циклов лабораторно-
отработочных и стендовых испытаний с имитацией возможных неисправ-
ностей в крайних режимах эксплуатации и др.
Все это приводит к созданию системы управления, работоспособной
при возникновении в ней любой возможной неисправности!
9. Время пуска из полной боевой готовности - 62 с.
Боеготовность - весьма важная характеристика ракетного комплекса
и ракеты как объекта управления для обеспечения возможности проведе-
ния ответного пуска во время установленного системой раннего преду-
преждения факта полета боевых блоков противника в район стартовых
позиций.
В ТТТ, предъявленных к рассматриваемому комплексу, количественно
боеготовность была задана ~ в два раза хуже достигнутого в США ракет-
ными комплексами «Минитмен-Ш».
Но это комплексы твердотопливной ракеты, не требующей проведения
предстартовой подготовки пневмогидравлической системы, а главное,
с непрерывно работающей командной частью системы управления в про-
цессе всего времени нахождения ракеты на боевом дежурстве - с выте-
кающими отсюда последствиями (расходование ресурса командных при-
боров с их периодической заменой, повышенной опасностью несанкцио-
нированного пуска, расходом электроэнергии и т. д.).
19
Ракетный комплекс 15П018 находился в полной боевой готовности
с обесточенной системой управления. Это принципиально другое качест-
во комплекса было достигнуто благодаря применению уникального по
своим характеристикам комплекса командных приборов с форсированным
разгоном гироскопов, выводимых на тепловой (суть - точностный) режим
за несколько десятков секунд. При этом обеспечивалась прецизионная
стабильность определенных заранее систематических погрешностей, учи-
тываемых в установочных данных на пуск, т. е. не вызывающих отклоне-
ний точек падения боевых блоков от цели.
Высокая боеготовность комплекса при «холодном боевом дежурстве»
определялась также использованием:
• порохового аккумулятора давления для открытия за несколько се-
кунд многотонного защитного устройства («крыши») шахтной пус-
ковой установки;
• способа предварительного наддува баков путем впрыска основных
компонентов топлива на зеркало жидкости в баках ракеты.
10. Стойкость ракеты к поражающим факторам ЯВ в полете -
I уровень.
На ракету как объект управления требования полетной стойкости
к ПФ ЯВ I уровня в первую очередь относятся к системе управления. Удов-
летворение этому требованию было осуществлено путем использования
в приборах системы управления электрорадиоэлементов соответствующей
стойкости к рентгеновскому и гамма-нейтронному излучению, а также
программно-алгоритмической защиты бортового вычислительного ком-
плекса от сбоев в работе.
11. Гарантийный срок нахождения на боевом дежурстве - 10 лет
при регламенте один раз в три года.
12. Условие боевого дежурства ракеты - нахождение в полной бое-
вой готовности в ПУ.
Эти требования, предъявленные к ракете как объекту управления оп-
ределяют, в основном, необходимость:
• создания конструкции исполнительных элементов системы управ-
ления - рулевых приводов, электропневмоклапанов и т. д. - с ис-
пользованием рабочих элементов, деталей и уплотнений, гаранти-
рованно сохраняющих работоспособность заведомо больше задан-
ного срока;
• проведения с установленной периодичностью дистанционных пе-
риодических проверок, обеспечивающих контроль исправности
раздельно каждого из дублированных или троированных каналов,
а также их совместную работу в соответствии с заданным алго-
ритмом.
20
Первое обстоятельство определяется практической невозможностью
замены большинства исполнительных элементов на ракете, находящейся
в транспортно-пусковом контейнере в условиях ШПУ.
13. Боевое применение - в любых метеоусловиях при температуре
воздуха от -50 до +50°С и скорости ветра у поверхности Земли 25 м/с
до и после ядерного воздействия по боевому ракетному комплексу.
Это требование в большой степени определяет компоновку и конст-
рукцию ракеты в целом и ее ступеней, характеристики управляющих ор-
ганов и их приводов, управляемость ступеней и многие другие основные
характеристики ракеты как объекта управления (см. главу 3).
Такое положение объясняется в первую очередь тем, что ветровое воз-
действие на полет ракеты в плотных слоях атмосферы (I ступень - начало
II ступени) является основным возмущающим фактором (см. главу 2). За-
данное максимальное значение скорости ветра у поверхности Земли, рав-
ное 90 км/час, - однозначно, в соответствии с принятой методикой, уста-
навливает максимальное значение (2,7 о) случайной составляющей вели-
чины скорости ветра и закон ее изменения по высоте полета ракеты [104].
По этой методике на территории бывшего СССР максимальное значе-
ние («огибающая») скорости ветра на высотах 6-12 км, т. е. в районе мак-
симального скоростного напора, может достигать 70 м/с для большинства
районов Союза, и до 100 м/с - для районов «повышенных» ветров (на-
пример, Дальнего Востока).
* * *
Из приведенного выше экспресс-анализа примерного состава основных
тактико-технических требований, оказывающих радикальное влияние на
облик и параметры ракеты как объекта управления, видно, что создание
в семидесятые-восьмидесятые годы прошлого столетия ракетных боевого
или космического комплексов, отвечающих уровню требований, предъяв-
ляемых к перспективной на десятки лет технике, представляло весьма
сложную научно-техническую проблему.
Такое положение усугублялось, как указывалось в «Предисловии», от-
сутствием в то время теории и практики динамического проектирования
оригинальных ракетных и ракетно-космических комплексов. Таких, как
МБР с РГЧ группового и индивидуального наведения боевых блоков; гло-
бальной ракеты с высокой боевой эффективностью, оснащенной орби-
тальной головной частью; ракет-носителей, создаваемых на базе боевых
ракет средней и межконтинентальной дальности, для решения научных
(в том числе по программе «Интеркосмос») и военных задач, а также мно-
го других объектов управления, отличных по схеме построения от ранее
созданных.
21
Решение проблем, возникших при динамическом проектировании ра-
кет с «нетрадиционной схемой» построения, базировалось на фундамен-
тальных трудах по динамике «классических» ракет.
К таким работам относятся монографии (в порядке хронологии издания):
• [112] - Авторами рассмотрен целый ряд общих вопросов динами-
ки ракеты как твердого тела, с полостями, частично заполненны-
ми жидкостью.
Это одна из первых несекретных книг, изданных в СССР, - и в
этом также ее особая ценность.
• [14] - В книге излагаются теоретические основы и важнейшие
практические методы исследования и расчета движения центра
масс управляемых БРДД.
• [106] - Проведенные авторами теоретические и эксперименталь-
ные исследования доведены до результатов, которые могут быть
использованы в качестве справочных материалов в инженерной
практике динамического проектирования жидкостных ракет.
• [1] - Книга является учебным пособием, в котором в отличие от
более ранней учебной литературы значительное внимание уделено
учету упругости корпуса ракеты.
• [87] - В книге изложены методы исследования и проведен анализ
динамических свойств жидкостной ракеты как объекта регулиро-
вания. Рассмотрены поперечные колебания ракеты как замкнутой
системы, определены силы и моменты, действующие на ракету
при колебаниях жидкости в баках, приведен метод определения
динамических характеристик системы стабилизации.
• [95] - Монография является дальнейшим развитием и дополнени-
ем базовой книги [14]. Содержит разделы баллистики, которые
в [14] изложены кратко или вообще отсутствуют. Особое внима-
ние уделено взаимообусловленному решению задач баллистики,
динамики, управления и стрельбы.
• [Ю7] - Книга является основополагающей для практики динами-
ческого проектирования ракет-носителей и космических ступеней
с ЖРД, поскольку содержит приведенные к форме, удобной для
инженерных расчетов, уравнения возмущенного движения, учи-
тывающие все специфические особенности конструкции объектов.
Особое внимание уделено экспериментальным методам определе-
ния коэффициентов этих уравнений на конструктивно-подобных
моделях.
• [54] - Авторами рассмотрены динамические свойства ракеты как
объекта управления, структура дискретного автомата стабилиза-
ции, особенности построения бортовых цифровых вычислитель-
22
ных машин, согласующих и исполнительных устройств, входящих
в состав дискретных систем управления.
• [116] - Монография является обобщением целого ряда трудов,
опубликованных в пятидесятые-семидесятые годы в изданиях АН
СССР и АН УССР, издательстве «Наукова думка» и др., содержит
результаты теоретических исследований нелинейной динамики лета-
тельных аппаратов с жидкостью. Приведен вывод уравнений дви-
жения, учитывающих как немалые перемещения корпуса аппарата,
так и немалую деформацию свободной поверхности жидкости.
• [88] - Учебник для студентов высших технических учебных заве-
дений. Является развитием и дополнением [87], особенно в части
исследования продольных колебаний замкнутой системы, состоя-
щей из упругого корпуса с жидкостью в баках, системы подачи то-
плива и ЖРД.
Это далеко не полный перечень литературы, в которой изложено со-
стояние в начале семидесятых годов теории динамики ракет. Подробные
обзоры литературы по данному вопросу и обширная библиография име-
ются в работах [87], [106], [116] и, особенно, более четырехсот наимено-
ваний, в [107].
♦ * *
Настоящая книга состоит из семи частей со структурой, обычно приня-
той для книг по динамике ракет:
• Часть I. Динамика ракеты как твердого тела.
• Часть 2. Управление ракетой путем отклонения головного отсека.
• Часть 3. Динамика жесткой ракеты с учетом колебаний жидкости
в баках.
• Часть 4. Динамика ракеты с учетом упругости ее конструкции
и т. д. (см. «Оглавление»).
При этом в каждой части приводятся соответствующие основопола-
гающие материалы, описывающие физическую суть, без ранее опублико-
ванных выводов уравнений движения, но с добавлением в необходимом
объеме теоретического обоснования принятых оригинальных решений.
Например, в части 1 книги приведено обоснование вероятностного под-
хода к определению возмущающего воздействия на полет ракеты. Метод
расчета был доведен до межведомственной инструкции, необходимость
которой возникла при создании ракет-носителей на базе одноступенчатых
боевых ракет без увеличения эффективности их органов управления.
В части 1 книги отражены также вопросы обеспечения устойчивости
ракет с относительно большой степенью статический неустойчивости.
Там же проведен анализ технической устойчивости ракеты как стохасти-
23
ческой системы с разработкой вероятностной математической модели ра-
кеты [113].
Аналогично построены другие части книги, поскольку в каждой из них
есть решения проблем, возникших при динамическом проектировании ра-
кет как объектов управления, построенных по схеме, существенно отлич-
ной от «классической».
Так, в части 2, на базе анализа военно-политической обстановки, дает-
ся обоснование необходимости создания боевых ракетных комплексов IV
поколения и вынужденного поиска принципиально нового способа управ-
ления (глава 6).
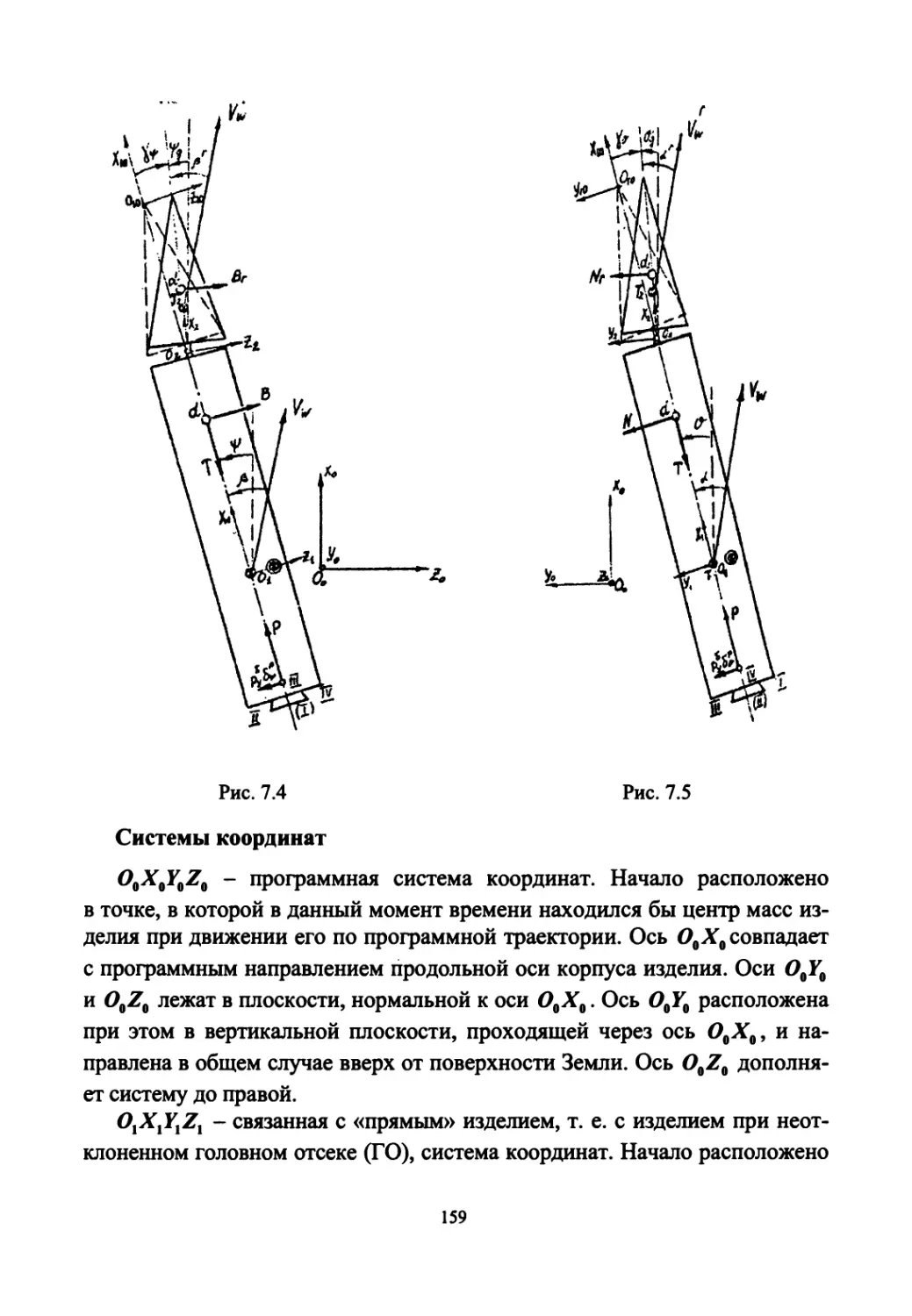
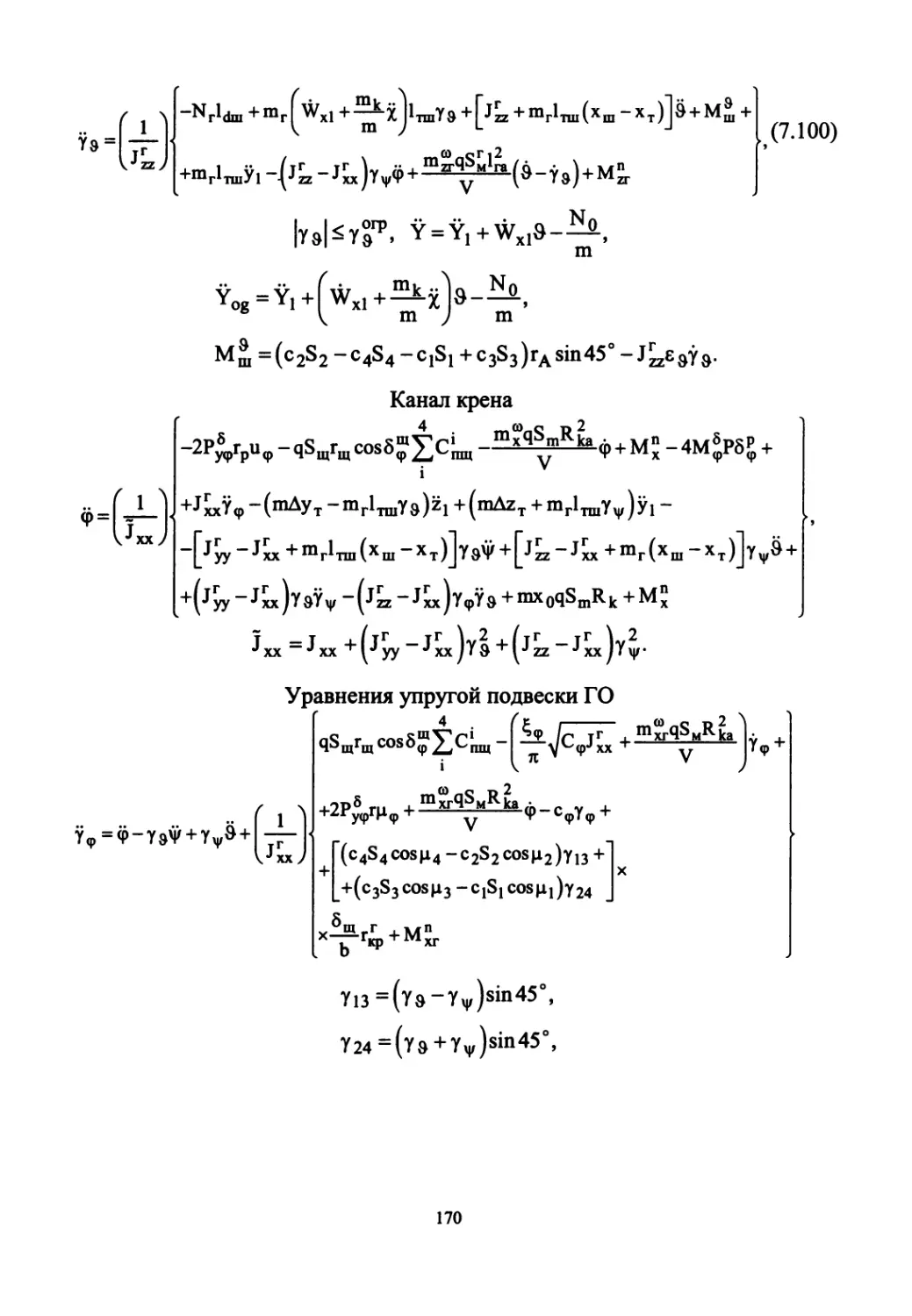
Глава 7 этой части содержит достаточно подробные материалы, вклю-
чая математическую модель движения ракеты с учетом аэроупругих коле-
баний конструкции, при управлении в каналах тангажа и рыскания путем
отклонения головного отсека.
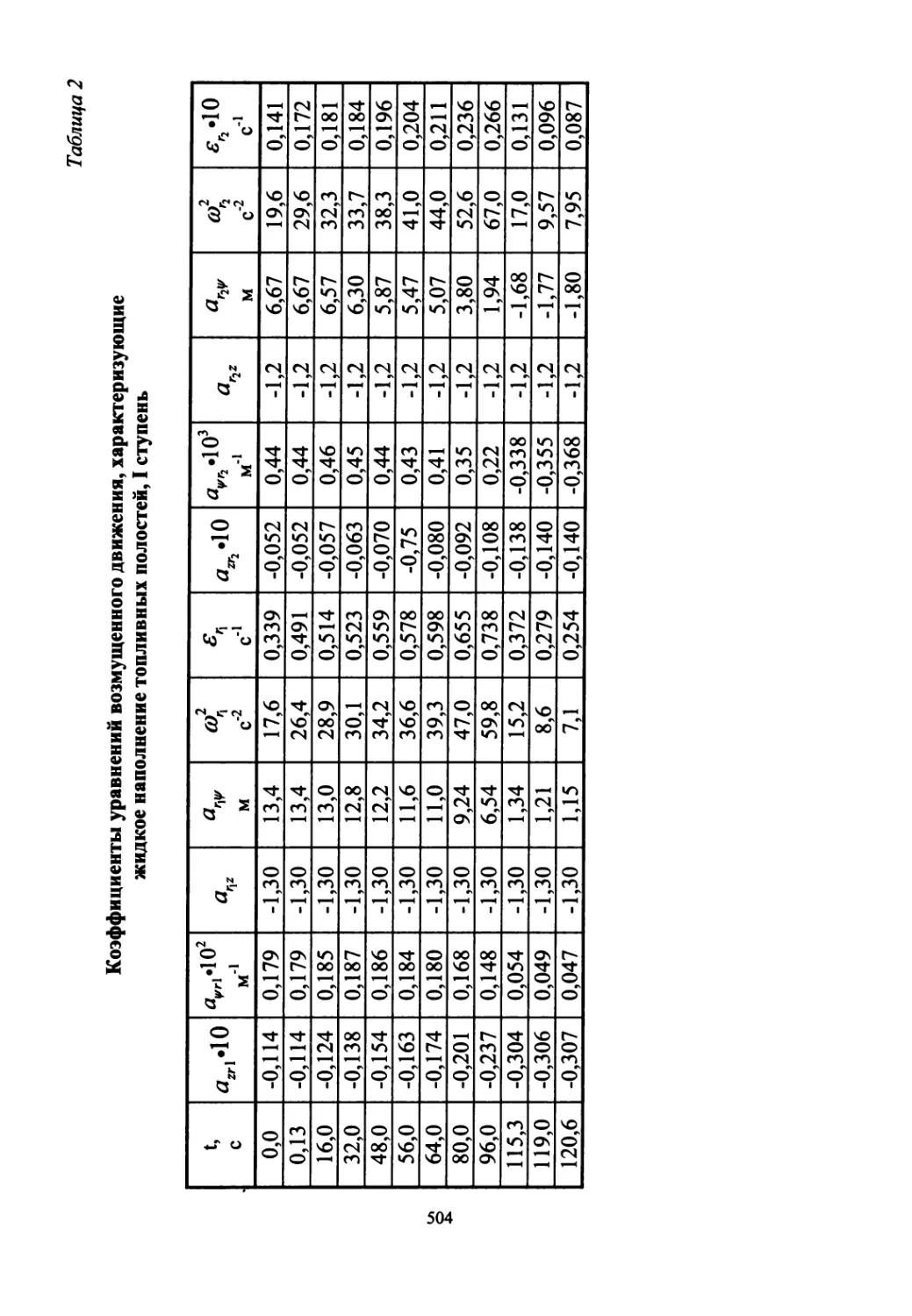
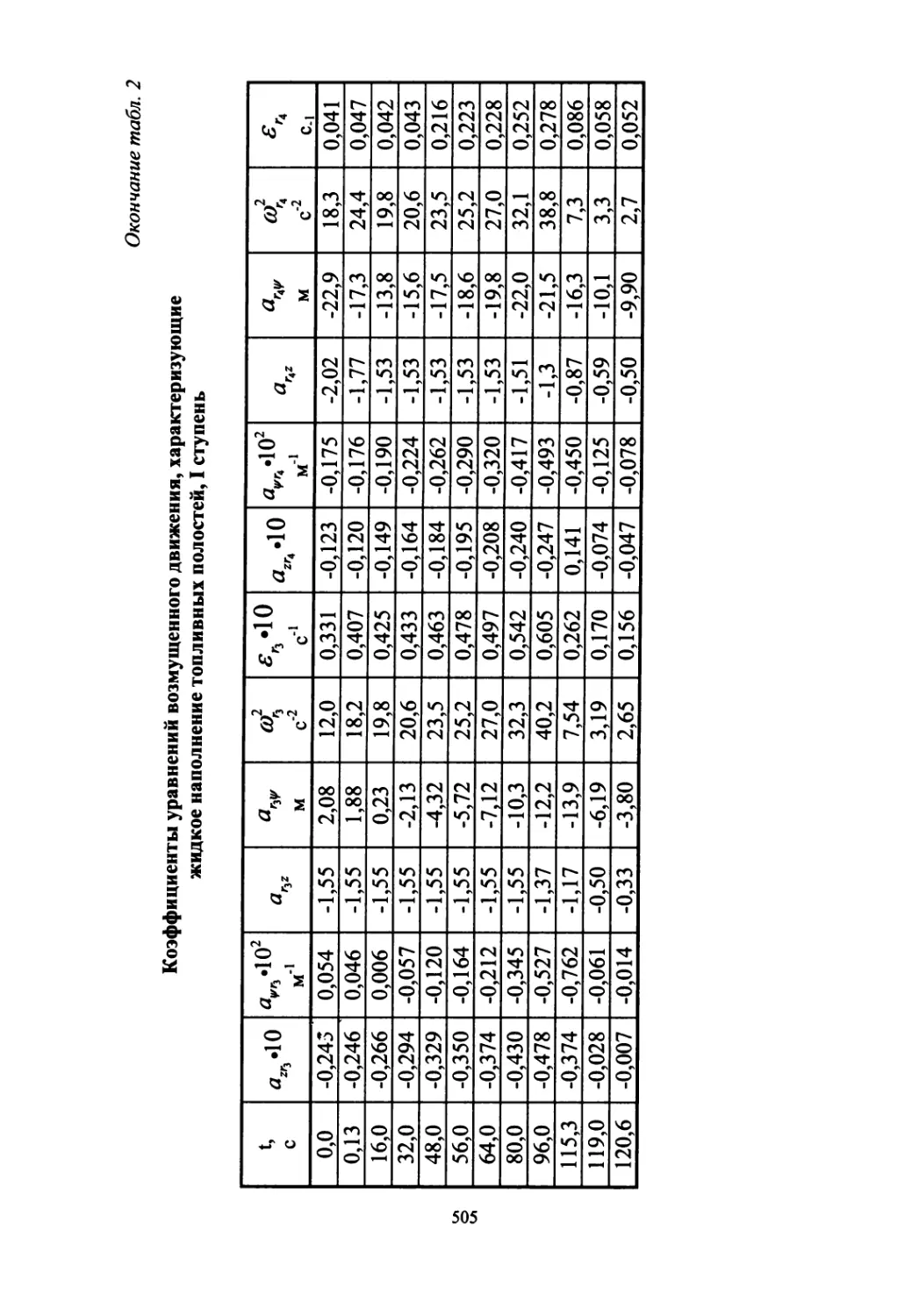
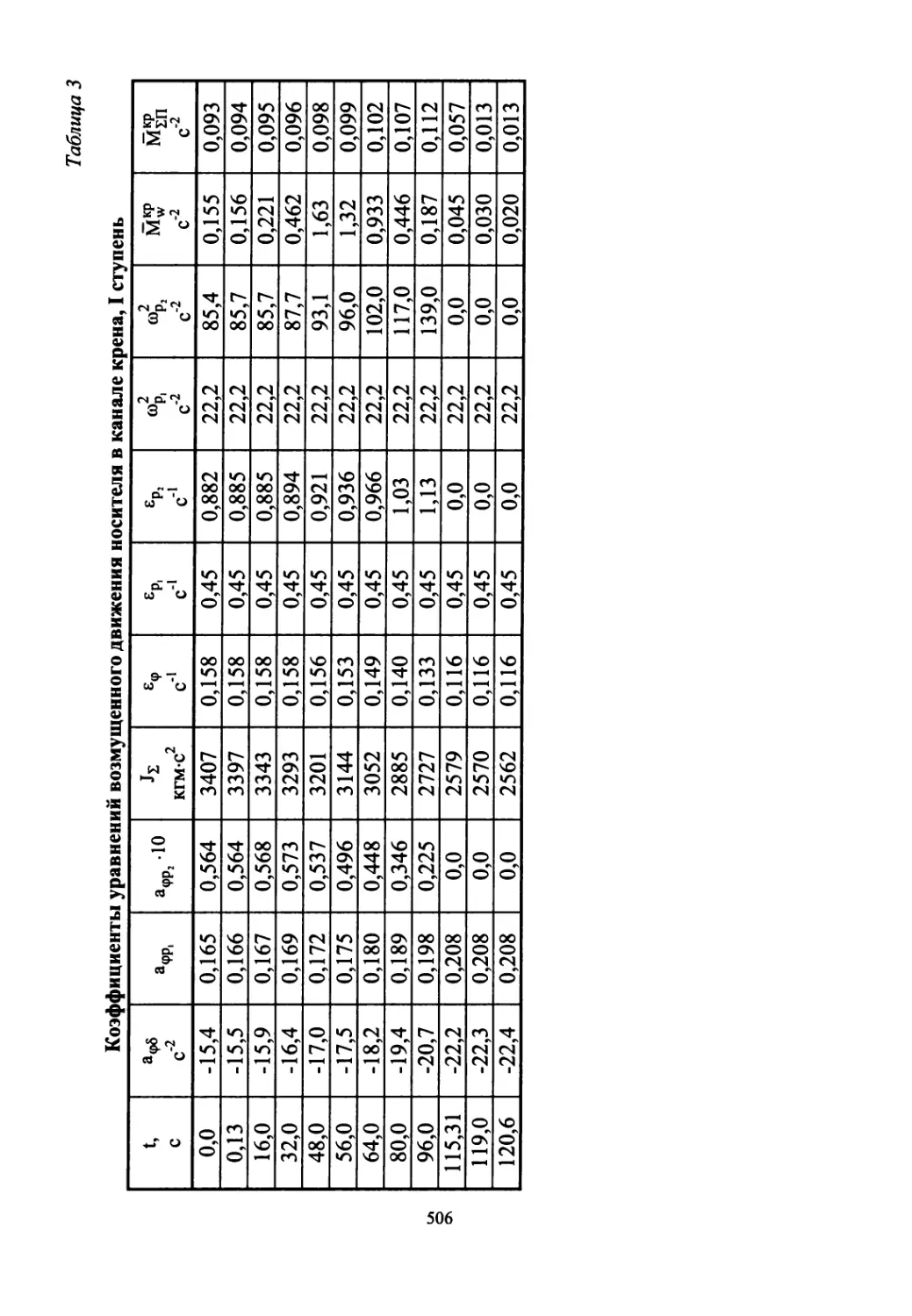
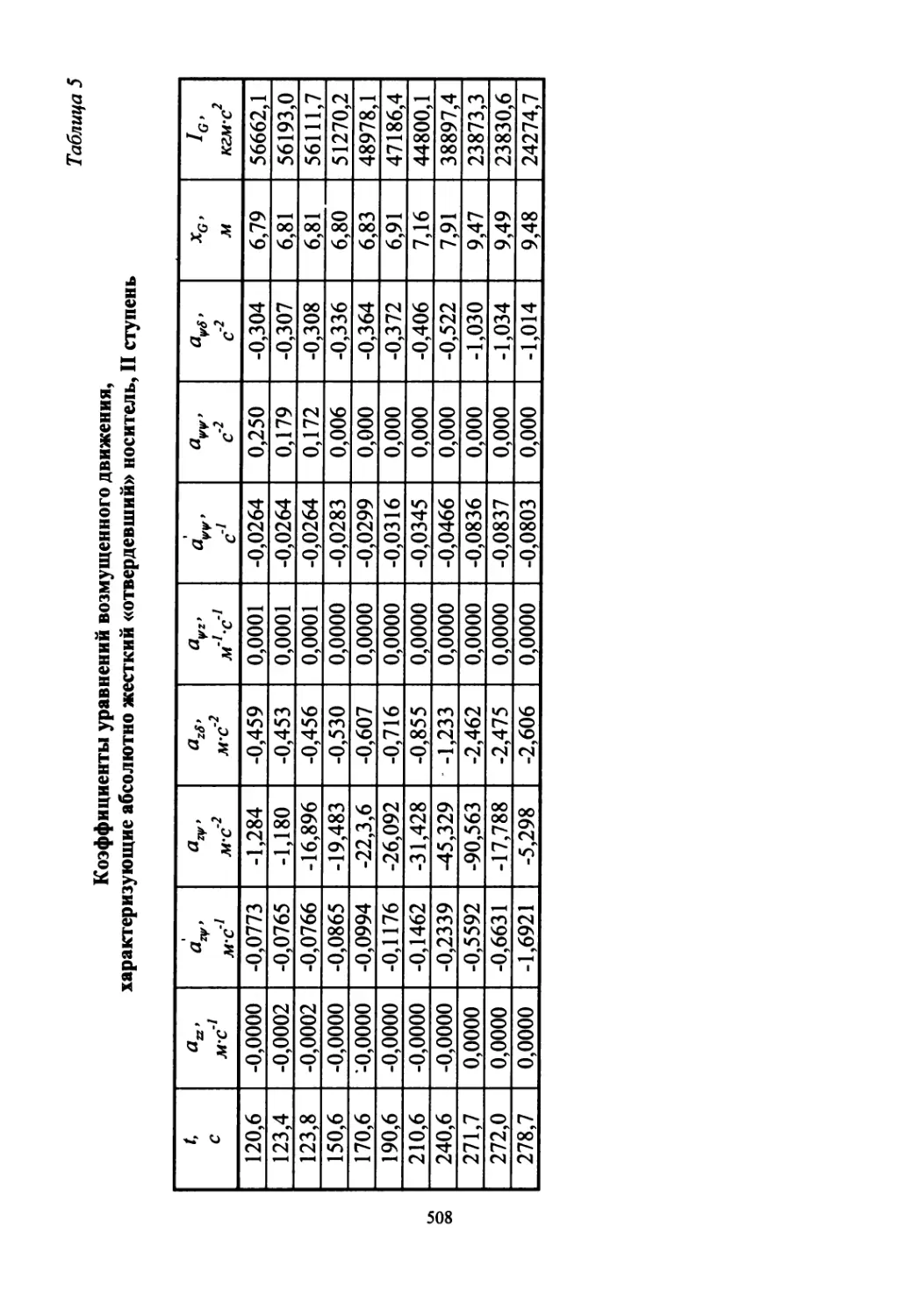
В части 3 приведена в качестве примера динамическая схема (матема-
тическая модель) «абсолютно жесткой» ракеты с баками, частично запол-
ненными компонентами топлива. В приложении даны численные значе-
ния коэффициентов динамической схемы конкретной трехступенчатой
ракеты-носителя 11К68 («Циклон-3»), созданной с использованием двух-
ступенчатой базовой ракеты тяжелого класса Р-36-«О» с автоматом ста-
билизации аналогового типа.
Часть 4 содержит материалы по динамике PH с учетом упругих
свойств ее корпуса, т. е. приведена «полная» динамическая схема (система
дифференциальных уравнений -50-го порядка). С целью придания цель-
ности этой главе, вывод уравнений с учетом упругости приведен в редак-
ции, принятой в [1]. Это избавит читателя от необходимости обращения
к источникам многолетней давности.
В части 5 изложены вопросы динамики таких космических объектов,
как боевая орбитальная часть и ступень разведения боевых блоков разде-
ляющейся головной части МБР, решение которых практически отсутству-
ет в открытой литературе. Приведены материалы по исследованию дви-
жения объектов с работающим и неработающим маршевым двигателем
как вне атмосферным, так и на участке спуска.
В части 6 приведены конкретные примеры использования возможно-
стей дискретных, цифровых систем управления, построенных на базе
БЦВМ, а также данные по конструкции и динамике РГЧ ракет II-IV поко-
лений.
Часть 7 книги посвящена вопросам работы систем и агрегатов ракеты
как объекта управления. В частности, приведены материалы по системе
управления расходования топлива, системе регулирования режима работы
ЖРД 11Д520идр.
24
Часть 1
ДИНАМИКА РАКЕТЫ КАК ТВЕРДОГО ТЕЛА
Настоящая часть книги содержит краткое изложение основополагаю-
щих материалов по динамике ракет. Таковыми материалами в основном
являются: уравнения невозмущенного и возмущенного движения; исполь-
зуемые системы координат; силы и моменты, действующие на ракету;
управляемость ракеты и устойчивость ее движения и др. Все основные
понятия проводятся применительно к исследованию динамики ракеты как
твердого тела. Математическая модель, т. е. адекватная система обыкно-
венных дифференциальных уравнений, описывающих движение «твер-
дой» ракеты, является базовой для изучения влияния жидкого наполнения
баков и упругости корпуса на динамику реальных МБР и PH КА.
Наряду с этим в части 1 излагаются результаты исследования управ-
ляемости и устойчивости ракет вероятностными методами.
Необходимость проведения подобных исследований возникла в про-
цессе динамического проектирования космических PH, построенных
путем установки дополнительных ступеней на штатные боевые ракеты,
без их доработки в части повышения эффективности их управляющих
органов.
Разработка вероятностного метода учета влияния возмущений, дейст-
вующих на ракету, а также построение ее вероятностной математической
модели, обеспечили возможность проведения пусков PH без существен-
ных ограничений условий эксплуатации.
25
Глава 1
УРАВНЕНИЯ НЕВОЗМУЩЕННОГО ДВИЖЕНИЯ
РАКЕТЫ
1.1. Системы координат
Для описания движения ракеты используем, как это обычно принято
разработчиками системы управления [54], стартовую, скоростную (поточ-
ную) и связанную системы координат*^
Стартовая система координат (рис. 1.1) используется для определе-
ния положения ракеты как твердого тела в пространстве. Начало старто-
вой системы координат совпадает с точкой старта О; ось Ох0 направлена
по касательной к дуге, соединяющей точку старта с целью; ось Оуо - по
нормали к поверхности Земли в точке старта; ось Ozo перпендикулярна
плоскости Ох0уо, называемой плоскостью стрельбы. За положительное
направление оси Оуо принято направление вверх от поверхности Земли;
положительное направление оси Ozo выбрано так, чтобы система коорди-
нат была правой.
Рис. 1.1
Поскольку стартовая система координат неподвижна относительно
Земли, ее в ряде случаев называют земной системой.
Вследствие вращения Земли траектория полета ракеты представляет
собой пространственную кривую, и для того, чтобы обеспечить попадание
ракеты в цель, прицеливание производят в плоскости, повернутой относи-
тельно плоскости стрельбы на некоторый угол. Величина этого угла опре-
В последующих главах, при описании специфических вопросов динамики ракет,
используются системы координат (СК), обеспечивающие возможность решения конкрет-
ных задач наиболее рациональным методом (в частности - инерциальные начальная стар-
товая и гироскопическая СК).
26
деляется из условия, чтобы в момент падения боевой блок (ББ) оказался
в плоскости стрельбы, и зависит от положения точки старта на Земле, на-
правления на цель и продолжительности полета ракеты. Если пренебречь
вращением Земли, то траекторию полета ракеты можно считать плоской,
а плоскость прицеливания - совпадающей с плоскостью стрельбы.
Система координат OxiyiZi, связанная с ракетой (рис. 1.2), имеет нача-
ло в центре масс ракеты; ось Oxi совпадает с продольной осью ракеты; ось
Oyi располагается в плоскости симметрии ракеты I—III, которая в момент
запуска при отсутствии послестартового разворота («прицеливание раке-
той») совпадает с плоскостью стрельбы; ось Ozi перпендикулярна плоско-
сти Oxiyi и направлена так, чтобы система координат была правой.
Рис. 1.2
Начало О скоростной системы координат Oxyz (см. рис. 1.2) располо-
жено в центре масс ракеты. Система координат называется скоростной,
так как ось Ох совпадает с направлением вектора скорости ракеты V от-
носительно воздушной среды. Поэтому эту систему координат называют
также поточной. Ось Ох является касательной к траектории полета раке-
ты; ось Оу направлена по нормали; ось Oz перпендикулярна плоскости
Оху. Положительное направление оси Оу совпадает с положительным на-
правлением оси Oyi связанной системы координат; положительное на-
правление оси Oz выбрано так, чтобы система координат была правой.
Для описания движения ракеты как твердого тела введем также угло-
вые координаты, характеризующие положение ракеты и вектора скорости
относительно стартовой системы координат.
Угол между проекцией оси Oxi на плоскость Охоуо и осью Ох0, или,
что то же самое, угол наклона продольной оси ракеты к горизонту точки
старта называют углом тангажа -3 (рис. 1.3). Угол между проекцией век-
тора скорости на плоскость Ох0уо и осью Ох0 обозначим через 0. За поло-
жительное направление отсчета углов 3 и 0 принимается направление
от оси Ох0 против часовой стрелки.
Угол между вектором скорости и продольной осью ракеты называется
углом атаки а:
а = £-0 (1.1)
27
За положительное направление отсчета угла а принимается направ-
ление от вектора скорости к продольной оси ракеты против часовой
стрелки.
Угол между вектором скорости и плоскостью Ох0уо обозначим через о
(рис. 1.4). Угол между продольной осью ракеты и плоскостью Ох0уо назы-
вается углом рыскания \|/. За положительное направление отсчета углов о
и \|/ принимается направление от оси Ох0 против часовой стрелки.
Рис. 1.4
28
Угол между проекцией вектора скорости на плоскость OxoZo и осью Oxi
называется углом скольжения 0:
0 = V-a (1.2)
Поворот ракеты относительно продольной оси задается углом крена
(вращения) ф между плоскостями Охоуо и Oxiyi при нулевом угле рыска-
ния. При этом за положительное принимается направление против часо-
вой стрелки, если смотреть с носка ракеты.
1.2. Силы, действующие на ракету
Основными силами, действующими на ракету в полете, являются:
• сила тяжести,
• тяга двигателя,
• аэродинамические силы,
• управляющие силы.
Схема действия сил в проекциях на плоскостях Охоуо и OxoZo показана
на рис. 1.3 и 1.4.
• При составлении уравнений движения ракеты как твердого тела бу-
дем рассматривать равнодействующую силы тяжести, приложенную
к центру масс ракеты и направленную по местной вертикали,
G(t) = m(t)g(h),
где m(t) - масса ракеты, изменяющаяся во времени; g(h) - ускорение силы
тяжести, зависящее от высоты полета.
Изменение массы происходит за счет выгорания топлива и значение ее
в каждый момент времени определяется выражением
m(t) = т0- (1.3)
о
где то - начальная масса ракеты; m(t) - массовый расход топлива, кото-
рый может быть переменным.
При постоянном расходе
• Направление силы тяги Р в расчетном случае совпадает с направле-
нием продольной оси ракеты. Величина ее определяется зависимостью
Р = Ро + ^(РО“А) (15)
где Ро - тяга двигателя у Земли; 8СОпл - площадь сопла в сечении среза;
рои р- атмосферное давление у поверхности Земли и на высоте Н.
Из формулы (1.5) видно, что по мере увеличения высоты полета и
уменьшения атмосферного давления тяга двигателя нарастает, достигая
максимального значения в пустоте.
29
• Аэродинамические силы возникают в результате обтекания корпуса
ракеты воздухом. Равнодействующая распределенных по поверхности
корпуса аэродинамических сил приложена в точке, называемой центром
давления. Вследствие симметрии ракеты относительно плоскостей Oxiyi
и OxiZi можно считать, что центр давления расположен на продольной
оси и характер перемещения его во время полета зависит от формы ракеты
и закона ее движения. Равнодействующая аэродинамических сил обычно
раскладывается по осям скоростной системы координат, и ее составляю-
щие обозначаются соответственно через X, Y, Z: составляющая X направ-
лена против вектора скорости ракеты и называется силой лобового сопро-
тивления', составляющая Y перпендикулярна вектору скорости и называ-
ется подъемной силой', составляющая Z перпендикулярна плоскости
стрельбы и называется боковой силой.
Величины составляющих аэродинамической силы подсчитываются по
формулам:
X = cx(M,a)qSM;
Y = cy(M,a)qSM',
Z = cz(M,P)qSM,
(1.6)
где <7 = ~-скоростной напор; р - плотность воздуха; V - скорость раке-
ты; SM - площадь миделева сечения корпуса ракеты; М - число Маха.
Безразмерные коэффициенты лобового сопротивления сх, подъемной
силы Су и боковой силы cz являются функциями числа М, угла атаки а
и формы ракеты. В силу симметрии ракеты су = cz. Для баллистических
ракет, полет которых происходит при малых углах атаки, можно считать
Из (1.6) следует, что аэродинамические силы существенно зависят от
параметров атмосферы - плотности, давления и температуры воздуха. Эти
параметры, в свою очередь, зависят от высоты полета, географической
широты места, времени года, суток и ряда других факторов, например от
степени активности Солнца.
Для определения конструктивных параметров ракеты, расчета траекто-
рий и других исследований, проводимых при динамическом проектирова-
нии, обычно используются таблицы стандартной атмосферы (СА), кото-
рые дают некоторые средние значения параметров спокойной атмосферы
в зависимости от высоты. Отклонения параметров атмосферы от стан-
дартных значений, а также ветер представляют собой атмосферные воз-
мущения, которые влияют на полет ракеты.
30
В СССР была принята стандартная атмосфера СА-64 для высот до
+200000 м (ГОСТ 4401-64). Для высот 200000-300000 м в этом же ГОСТе
приведены характеристики атмосферы, рекомендуемые координационной
комиссией при АН СССР по составлению ГОСТа на стандартную атмо-
сферу.
Для решения задач динамического проектирования, кроме стандарт-
ных значений параметров атмосферы, нужно знать также диапазоны воз-
можных отклонений этих параметров, соответствующие определенному
уровню вероятности, причем для различных условий как без учета време-
ни года и мест на земном шаре, так и с их учетом. Кроме того, для более
точных исследований требуется знание статистических зависимостей ме-
жду случайными отклонениями каждого параметра на разных высотах,
между отклонениями различных параметров на данной высоте и т. п.
Возможны различные методы описания возмущений параметров атмо-
сферы. Рассмотрим один из них. Температура Т и плотность атмосферы р
могут быть представлены в виде
T(h)=TCT(h)+AT(h) (1.8)
p(h)=PcT(h)[l+Ap/PcT(h)], (1.9)
где Tcr(h) и рст(Ь) - стандартные значения температуры и плотности;
AT(h) - отклонение температуры от стандартной;
Ap/pCT(h) - относительное отклонение плотности воздуха от стандартной.
Для задания случайных функций АТ и Ар/рст можно использовать ме-
тод канонических разложений.
Применительно к рассматриваемому случаю параметры атмосферы как
случайные функции высоты точки над поверхностью Земли представля-
ются в виде канонического разложения следующим образом:
ДТ = ДТ(Л) + £ ДТДЛ)*,; (1.10)
*=1
Рст Рст «=1 Р ст
где ДГ(Л), —(Л) - средние отклонения от значений С А, соответствующие
Рат
рассматриваемой точке;
А7](А), —(Л) - некоторые неслучайные отклонения от средних откло-
Рст
нений,
bi, Ci - случайные коэффициенты.
Такая запись параметров «случайной атмосферы» соответствует пред-
ставлению ее в виде суммы некоторого количества «атмосфер» со случай-
ными коэффициентами bi и сь Эти коэффициенты и координатные функ-
31
ции АТ;(А) и —(А) определяются на основе накопленных статистических
Рст
данных, характеризующих состояние атмосферы. Достаточно точное
представление случайных параметров атмосферы дает разложение, вклю-
чающее 10-11 членов.
Использование метода канонических разложений случайных парамет-
ров атмосферы позволяет решать различные задачи, возникающие при
проектировании ракет. Одной из наиболее часто встречающихся задач яв-
ляется задача оценки статистических характеристик параметров атмосфе-
ры с учетом случайного характера изменения координат и времени полета
ракеты (географические координаты движения ракеты и время полета за-
ранее неизвестны). Типичным примером такого рода задач является зада-
ча о рассеивании ракет. Построение канонического разложения в этом
случае сводится к определению неизвестных случайных величин и коор-
динатных функций для достаточно обширной области по данным метео-
зондирования атмосферы.
При проектировании ракет встречается и другая группа расчетов (на-
пример, при оценке управляемости или прочности аппарата), целью кото-
рых является изучение характеристик объекта для наихудших (крайних)
условий полета и оценка влияния предельных отклонений. Наиболее важ-
ными из расчетов этого типа являются расчеты в точках, соответствую-
щих наибольшим по величине отклонениям термодинамических парамет-
ров. Поскольку могут быть различные сочетания больших отклонений,
можно рекомендовать две системы функций: одна соответствует типич-
ным неблагоприятным зимним условиям, а вторая - летним. Зимней не-
благоприятной точке свойственны самые низкие температуры и самые
большие плотности у Земли и наименьшие плотности на больших высо-
тах. Летней неблагоприятной точке свойственны самые высокие темпера-
туры и малые плотности у Земли и большие плотности в стратосфере.
В некоторых случаях с целью упрощения расчетов вместо использова-
ния канонических разложений для крайних условий можно использовать
предельные значения температуры атмосферы по высоте. В качестве пре-
дельных распределений температуры при этом принимаются температуры
для так называемых стандартных дней - максимальные температуры теп-
лого дня и минимальные температуры холодного дня.
Соответствующие предельные значения относительной плотности воз-
духа определяются из уравнения состояния и дифференциального уравне-
ния равновесия.
При изучении движения ракеты'нужно определять момент Ма аэроди-
намических сил Y и X относительно поперечной оси, проходящей через
точку О - центр масс ракеты (рис. 1.3):
32
Ma =y(xrf -xc)cosa + X(xd-xc)sin«.
Для малых углов атаки cosa«l, sina«a, и
Ч =?»<«> <=ii7i(c"+c-)> <112)
где / - длина корпуса ракеты.
Момент Ма зависит, следовательно, как от аэродинамических характе-
ристик, так и от распределения масс ракеты, которое изменяется по мере
выгорания топлива. Взаимное расположение центра давления и центра
масс важно для стабилизации ракеты в полете.
Различаются:
• статически устойчивая ракета, когда xd>Xc, с^>0;
• статически неустойчивая ракета при xd<xc, с*<0;
• нейтральная ракета при ха= хс, С„ = 0.
Если центр давления находится впереди центра тяжести (С^<0), то при
отклонении оси ракеты от направления полета аэродинамические силы
создадут момент, отклоняющий ось ракеты на еще больший угол. Такая
ракета без автомата стабилизации летать не может.
Для обеспечения статической устойчивости или уменьшения степени
статической неустойчивости применяются специальные конструктивно-
компоновочные меры. Простейшей мерой является снабжение ракеты
хвостовым оперением. Однако для случая старта ракеты из ТПК такое
решение является практически неприемлемым (в крайнем случае исполь-
зуются складывающиеся стабилизаторы различных конструкций). Одним
из способов уменьшения статической неустойчивости является ввод в бак
окислителя промежуточного днища (см. главу 3).
Запас статической устойчивости определяется величиной
f^i.iooV/0-
I I )
Кроме момента Ма, который при С*>0 называется стабилизирующим
моментом, при вращении корпуса ракеты относительно поперечной оси
Ozi с угловой скоростью t9 возникает демпфирующий момент. Этот мо-
мент складывается из аэродинамического демпфирующего момента, обу-
словленного появлением дополнительных углов атаки
\а = —-----
V
33
и момента от кориолисовых сил. Координата х для произвольного попе-
речного сечения отсчитывается от вершины корпуса.
Аэродинамический демпфирующий момент всегда направлен в сторо-
ну, противоположную вращению корпуса ракеты:
К = ](х~хс)^-^ = ^12С^’ (1ЛЗ)
О сх к
где С&- вращательная производная от коэффициента аэродинамического
демпфирующего момента.
Демпфирующий момент от кориолисовых сил возникает при повороте
потока жидкости, движущейся в баках и трубопроводах ракеты, и потока
газов, движущихся по камере и соплу двигателя. Этот момент можно оп-
ределить, если принять, что указанные потоки вращаются так же, как и
корпус ракеты.
Величина и направление кориолисова ускорения определяются век-
торным произведением
ak=2$xVr,
где Vr - относительная скорость движущегося в ракете потока. Если, на-
пример, масса элемента движущегося по трубопроводу потока жидкости
равна pSndx, где Sn - площадь проходного сечения трубопровода, р -
плотность жидкости, то при sin ^<9 Л Vr) = 1 кориолисова сила будет равна
dYk=2pSnWrdx
и направлена в сторону, противоположную ускорению.
При полете ракеты в плотных слоях атмосферы момент от кориолисо-
вых сил Мк значительно меньше демпфирующего момента Мд от аэроди-
намических сил. За пределами атмосферы момент кориолисовых сил ста-
новится преобладающим. Таким образом,
Мп =МД+Мк. (1.14)
• Управляющие силы и моменты создаются органами управления ра-
кеты по командам системы управления. Управление полетом практически
осуществляется только изменением величины и направления равнодейст-
вующей N сил тяги двигателей и аэродинамических сил. Равнодействую-
щую N можно разложить на две составляющие Nt и Nn, направленные
соответственно вдоль вектора скорости V и перпендикулярно к нему.
Тангенциальная составляющая Nt, равная по величине
Nt=Pt-X, (1.15)
34
может служить для регулирования скорости полета. Изменение тангенциаль-
ной составляющей Nt у баллистических ракет достигается изменением тяги
основных двигателей (например, регулированием секундного расхода топли-
ва, если двигатель жидкостной) и включением или выключением различных
двигателей. Ту часть силы тяги ДР, которую можно использовать для регули-
рования скорости ракеты, назовем тангенциальной управляющей силой.
Нормальная сила Nn равна сумме проекций полной аэродинамической
силы и сил тяги на плоскость, нормальную к траектории:
Nn = R + Rn = R + F + Z. (1.16)
n n n n v 7
Ее составляющую в плоскости стрельбы N будем называть нормаль-
ной управляющей силой.
По аналогии с нормальной управляющей силой введем понятие боко-
вой управляющей силы дг, представляющей собой проекцию силы Nn на
перпендикуляр к плоскости полета.
Создавая требуемые по величине и направлению тангенциальную,
нормальную и боковую управляющие силы, можно обеспечить заданную
траекторию полета ракеты.
Возможны различные способы создания нормальной и боковой управ-
ляющих сил. У баллистических ракет, чтобы получить нормальную силу
различной величины, необходимо изменять угол атаки в плоскости поле-
та ау, поворачивая ракету вокруг центра масс. Когда ракета имеет угол
атаки ау, нормальная сила равна (рис. 1.5)
Ny=Psinay + Y*(P + cyqs)ay.
Рис. 1.5
35
Чтобы получить боковую управляющую силу, необходимо придать ра-
кете угол атаки az в плоскости, перпендикулярной к плоскости стрельбы.
Как было сказано выше, для получения требуемой по величине и на-
правлению нормальной силы необходимо определенным образом регули-
ровать ориентацию ракеты относительно вектора скорости. Эта задача
решается созданием управляющих моментов, которые вращают ракету
вокруг ее осей Охь Oyi и Ozi. Соответствующие движения обычно назы-
ваются движениями крена, рыскания и тангажа. Для образования управ-
ляющих моментов на ракете имеются органы управления. Последние соз-
дают сравнительно небольшие аэродинамические или реактивные силы,
моменты которых относительно центра масс ракеты являются достаточ-
ными для управления угловыми движениями ракеты.
Для изменения нормальной и боковой силы используется вращение
ракеты вокруг осей Oyi и Ozi с помощью органов управления рысканием
и тангажом. Эти же органы управления необходимы для стабилизации
требуемой ориентации ракеты в пространстве. Для стабилизации ракеты
по крену необходимы еще органы управления креном, создающие управ-
ляющий момент относительно продольной оси Охь И, наконец, необхо-
дим орган управления для изменения силы тяги основных двигателей, ес-
ли требуется регулировать величину скорости ракеты.
Используются следующие основные*) типы органов управления балли-
стическими ракетами:
1) воздушные рули;
2) газовые рули;
3) поворотные камеры сгорания основных двигателей (одна или не-
сколько);
4) поворотные сопла основных двигателей;
5) специальные насадки на срезе сопла (сферические, цилиндриче-
ские с косым срезом и др.);
6) разрезные сопла;
7) выдвижные щитки, работающие в струе двигателя перпендику-
лярно потоку;
8) вдув генераторного газа или впрыск жидкости в сверхзвуковую
часть сопла основного двигателя;
9) основной многокамерный двигатель, работающий в режиме фор-
сирования - дросселирования;
10) управляющие двигатели (неподвижные и поворотные);
11) управляющие сопла (поворотные и неподвижные);
*) Управление ракетой относительно поперечных осей (по углам i9 и I//) путем от-
клонения головного отсека рассматривается в главах 6 и 7 части 2.
36
12) комбинированные управляющие органы (например, воздушные
и газовые рули или воздушные рули с основными камерами, работающи-
ми в режиме форсирования - дросселирования).
Все перечисленные органы управления могут создавать управляющие
моменты рыскания и тангажа, однако не все из них пригодны для созда-
ния момента крена. Нельзя получить момент крена, если для управления
тангажом и рысканием используется, например, один поворотный двига-
тель или, если силы, создающие моменты тангажа и рыскания, направле-
ны вдоль продольной оси ракеты.
В этих случаях для управления креном приходится применять специ-
альные управляющие двигатели, тяга которых действует в поперечной
плоскости.
Во всех других случаях, когда имеется не меньше двух пар органов
управления тангажом и рысканием, создающих поперечные силы на неко-
тором расстоянии от продольной оси, для образования момента крена ис-
пользуется дифференциальное управление органами управления. Послед-
ние могут действовать симметрично (синхронно и синфазно), создавая
момент тангажа или рыскания, или асимметрично, создавая момент крена.
При сочетании указанных действий могут создаваться одновременно
и момент тангажа (рыскания) и момент крена.
Величина сил, создаваемых органами управления, зависит от переме-
щения этих органов (чаще всего углового) или от секундного расхода то-
плива, если для управления используется рассогласование тяг основных
двигателей.
Рассмотрим определение сил, создаваемых органами управления, и уп-
равляющих моментов на примере управления движением ракеты с помо-
щью четырех управляющих двигателей.
У многих современных ракет управление движением ракеты на актив-
ном участке осуществляется четырьмя управляющими двигателями. Распо-
ложение этих двигателей и направления их отклонения, принятые за поло-
жительные, показаны на рис. 1.6. Положительным отклонением управляю-
щего двигателя будем считать поворот его против часовой стрелки, если
смотреть со стороны соответствующей оси, т. е. на рис. 1.6 положительны-
ми будут отклонения двигателей II-IV вниз, а двигателей I-III вправо.
Принимая тяги Т всех четырех управляющих двигателей равными, запи-
шем проекции их равнодействующей на связанные оси координат в виде:
Txl =r(cos^ d-cost^ H-cos^, H-COSf^)
Tyl =7’(sin<52+sin<54)
Тг1 = —T (sin $ + sin )
(117)
37
где 5], 5г, 5з, 84 - соответственно углы отклонения управляющих камер I,
II, III и IV.
Очевидно, управляющие моменты в этом случае будут равны:
= Try (sin + sin 82 + sin 83 + sin 6^)
= -Tly (sin 8X + sin 83)
= -Tly (sin 82 + sin )
(1-18)
где гу - расстояние от продольной оси ракеты до продольных осей управ-
ляющих камер;
1У = Хс-Хда - расстояние от центра масс ракеты до оси вращения управ-
ляющих двигателей.
В этих выражениях сила тяги управляющего двигателя определяется
в зависимости от его параметров формулой (1.5).
Поскольку в жидкостных ракетах, созданных в конце пятидесятых го-
дов, применялись в качестве органов управления газоструйные рули, а эти
боевые ракеты затем использовались как база (I ступень) ракет-носителей
(см. главу 3), рассмотрим определение сил, создаваемых рулями такого
типа.
Подъемная сила воздушных и газоструйных рулей приложена к центру
давления плоскости руля: для воздушного руля подъемная сила Ув.р. пер-
пендикулярна вектору скорости потока воздуха, набегающего на руль, для
газоструйного руля подъемная сила Уг.р. перпендикулярна вектору скоро-
сти потока, истекающего из сопла двигателя:
YB.p = cy,p.(M,8)qSB.p.; (1.19)
УГф = ^.(5)^. (1.20)
38
Здесь Су в.р. - коэффициент подъемной силы воздушного руля; су г.р. -
коэффициент подъемной силы газоструйного руля; qr - скоростной напор
газовой струи двигателя; SB.P. - площадь воздушного руля; Sr p. - площадь
газоструйного руля; 8 - угол отклонения руля.
Если под SB.P. и Sr.p. понимать суммарную площадь воздушных и газо-
струйных рулей, то соответственно Yrp. и YB.P. определят суммарную
подъемную силу.
В случае, когда на ракете используются одновременно различные по
своему характеру управляющие органы, суммарная управляющая сила
определяется по формуле
(1.21)
где под Yi понимают управляющую силу каждого из используемых видов
органов управления. Аналогичным образом определяется и суммарный
управляющий момент Мр относительно центра масс:
Мр=£мр (1.22)
где под Mj подразумевается управляющий момент от каждого из исполь-
зуемых видов органов управления:
МВ.Р.=¥в.р.(хв.р. ~ хс); (1-23)
Мг.р. = \.р.(хг.р. ~ хс)> (1-24)
МУ«. = Yy.«.(xy.«.-xe)- (1.25)
Обозначения характерных размеров показаны на рис. 1.7: d — центр
давления; с - центр масс; хр - расстояние от носка до оси вращения
управляющего органа; хср - расстояние от носка до плоскости среза сопла.
1.3. Уравнения невозмущенного движения ракеты
При полете ракеты с работающим двигателем происходит отбрасы-
вание продуктов горения и ее состав непрерывно изменяется. Рассмат-
39
ривая движение ракеты, удобно в каждый момент времени включать
в ее состав только те материальные частицы, которые в этот момент на-
ходятся внутри определенного объема, занимаемого ракетой. При такой
постановке задачи ракета с работающим двигателем представляет собой
систему переменного состава, к которой непосредственно нельзя при-
менить теоремы динамики твердого тела. Однако, основываясь на этих
классических теоремах, можно доказать аналогичные теоремы для сис-
темы переменного состава и установить принцип составления уравне-
ний движения ракеты [95].
Уравнения движения реактивного летательного аппарата в произволь-
ный момент t можно записать в виде уравнений движения твердого тела,
получающегося в результате «затвердевания» реактивного аппарата в этот
момент времени, если в число внешних сил, приложенных к такому фик-
тивному твердому телу, включить реактивные силы.
Следовательно, векторное уравнение движения центра масс ракеты
можно записать в виде
Здесь m = m(t) - масса ракеты в момент времени t;
dV
—s- - ускорение центра масс в инерциальнои системе координат;
dt_
^F\ - сумма внешних сил, приложенных к ракете;
^Р. - сумма реактивных сил.
Под внешними силами, действующими на ракету, подразумевают та-
кие силы, как сила притяжения (7Г, полная аэродинамическая сила R, си-
ла взаимодействия ракеты с пусковой установкой или отбрасываемой сту-
пенью.
Как видно, составление уравнений движения тела переменного состава
сводится к определению реактивных сил, что является достаточно слож-
ной задачей. Основной из этих сил является реактивная сила w, которую
не удается непосредственно измерить. Поэтому принято определять силу
тяги ракетного двигателя по формуле (1.5), в которую входит сила, вы-
званная атмосферным давлением и давлением газа на срезе сопла (pa-p)Sa.
Хотя эта сила является внешней, ее объединяют с собственно реактивной
силой ш, поскольку при испытании двигателя на стенде измеряется си-
ла, действующая на опоры стенда. Соответственно сила (pa-p)Sa исключа-
ется из числа внешних сил ^Fr
Кроме силы тяги Р, определяемой формулой (1.5), в состав реактивных
сил входят:
40
1) силы, вызванные нестационарностью движения топлива и продук-
тов горения относительно корпуса ракеты;
2) кориолисовы силы, обусловленные движением топлива и продуктов
горения в ракете, вращающейся относительно инерциальной системы ко-
ординат;
3) силы, обусловленные перемещением центра масс ракеты относи-
тельно ее корпуса.
Перечисленные силы очень малы по сравнению с тягой, определяемой
формулой (1.5), причем непосредственное измерение их невозможно.
В зависимости от принятых допущений разные авторы получают для них
различные теоретические выражения. В баллистике обычно пренебрегают
указанными малыми реактивными силами.
Аналогичным образом составляется векторное уравнение вращатель-
ного движения ракеты относительно центра масс:
(L26)
Здесь к - главный момент (относительно центра масс ракеты) коли-
честв движения частиц «затвердевшей» ракеты относи-
тельно осей, проходящих через центр масс ракеты и дви-
жущихся поступательно со скоростью va относительно
инерциальной системы;
^MF - главный момент (относительно центра масс ракеты) всех
внешних сил, действующих на ракету, за исключением сил
атмосферного давления и давления газов в выходном сече-
нии сопла;
?МР - главный момент (относительно центра масс ракеты) силы тя-
ги ракетного двигателя, а также сил, вызванных движением
топлива и газов внутри вращающейся ракеты, нестационар-
ностью этого движения и перемещением центра масс ракеты
относительно ее корпуса.
В дальнейшем для упрощения уравнений вращательного движения ра-
кеты относительно ее центра масс будем пренебрегать моментами сил,
обусловленными нестационарностью движения топлива и газов внутри
ракеты и перемещением центра масс ракеты относительно ее корпуса, по-
скольку эти моменты достаточно малы.
Следует заметить, что обычно имеют место значительные по величине
моменты, обусловленные колебаниями жидкости в баках ракеты при на-
личии свободной поверхности. Однако при соответствующем выборе па-
раметров системы стабилизации колебания ракеты вследствие подвижно-
41
ста жидкости в баках оказываются малыми и их влияние на траекторию
ракеты несущественно.
Пространственное движение ракеты как твердого тела полностью оп-
ределяется шестью уравнениями: тремя уравнениями проекций сил на оси
ортогональной системы координат и тремя уравнениями моментов сил,
характеризующих движение относительно центра масс в трех взаимно
перпендикулярных плоскостях.
Для определения положения ракеты в пространстве примем стартовую
систему координат. В качестве угловых координат используем введенные
ранее углы 9, у, ф.
Обычно продольное и боковое движения ракеты, а также движение ра-
кеты вокруг продольной оси в первом приближении можно рассматривать
как независимые одно от другого.
Продольное движение ракеты, т. е. движение в плоскости стрельбы
Ох0уо, полностью определяется уравнениями проекций сил на оси Ох и Оу
скоростной системы координат и уравнениями моментов относительно
оси Oz. На основании рис. 1.3 эти уравнения имеют следующий вид:
уравнение проекций сил на ось Ох
ш— = Pcosa-X-mgsin0 + Fv(t); (1.27)
dt
уравнение проекций сил на ось Оу
mv-^ = Psina + Y-mgcos0 + Yp cosa + Fe(t); (1-28)
уравнение моментов относительно оси Oz
d24
Jz = Y(xd - хс) cos a - X sin a(xd - xc) - Mp& + Ma(t). (1.29)
Боковое движение ракеты, т. е. движение в плоскости Ox0zo, описыва-
ется:
уравнением проекций сил на ось Oz
m ^- = -Р sin р - Z - Zp + Fz (t); (1.30)
уравнением моментов относительно оси Оу
Jy = -Z cos P(xd - хс) - X sin P(xd - хс) - MPV (t) + Mv (t). (1.31)
Движение ракеты относительно оси Ох описывается уравнением
1хФ = МИ)(0 + Мф(0. (1.32)
В приведенных выше уравнениях через Fv(t), Fe(t), Fz(t), M&(t) обозна-
чены возмущающие силы и моменты, через Md$(t), Mpv(t), Mp^t), Yp, Zp —
управляющие силы и моменты, создаваемые рулевыми органами, через Jx,
Jy, Jz - моменты инерции.
42
Управляющими силами в уравнении (1.27) можно пренебречь ввиду их
малости. Значения Ур и Мр в каждом конкретном случае определяются со-
ставом управляющих органов по формулам (1.21) и (1.22). Для определе-
ния координат центра масс ракеты при движении ее по траектории доба-
вим к уравнениям (1.27), (1.28), (1.29) два кинематических уравнения:
xo=vcos0; yo=vsin0 (1.33)
и, используя соотношение (1.1), получим совокупность уравнений, харак-
теризующих движение ракеты в плоскости стрельбы. Эти шесть уравне-
ний связывают семь координат: х0, уо, У, 0, а, 8Р.
Для замыкания системы необходимо добавить уравнения, связываю-
щие координаты, определяющие движение ракеты, с координатами, опре-
деляющими положение управляющих органов. Зависимости эти доста-
точно сложны и будут рассмотрены ниже. Здесь же примем их упрощенно
в виде:
5.р, = f. р. (3); 5r.p. = fr р. (3); §у = fy О). (134)
Вследствие того, что движение ракеты принято плоским, параметры
бокового движения и движения вокруг продольной оси на невозмущенной
траектории имеют нулевые значения:
vz=0 = CT = y = \j/ = (p = (p = O. (1.35)
1.4. Расчетная траектория полета ракеты
Траектория полета ракеты от места пуска до цели разбивается на ак-
тивный участок (полет с работающим двигателем) и пассивный участок
(двигатель не работает).
На активном участке ракета выводится в заданную точку пространства
с заданной по величине и направлению скоростью. Конечные значения
координат и скорости выбираются так, чтобы после выключения двигате-
ля головная часть ракеты или отделившийся от нее боевой блок, совершая
свободный полет, достигли цели. Пассивный участок для ракет среднего
и большого радиуса действия находится на большей своей части в сильно
разреженных слоях атмосферы, и только вблизи точки падения ракета
вновь входит в плотные слои атмосферы.
После определения дальности стрельбы, тяги двигателя и массы раке-
ты производится выбор программы разворота вектора скорости при дви-
жении ракеты на активном участке траектории. Программа угла тангажа
должна быть выбрана так, чтобы к моменту выключения двигателя обес-
печить заданные значения координат и скорости. В книгах [14], [95] по
баллистике ракет рассмотрены требования к программе угла тангажа, ме-
тоды ее выбора и оптимизации, а также значимость формы программы
43
при определении основных тактико-технических характеристик ракет
в процессе их динамического проектирования. В результате выбора ос-
новных характеристик ракеты (тяги двигателя и веса) и программы угла
тангажа определяется невозмущенное движение ракеты, т. е. движение по
номинальной расчетной траектории.
При стрельбе на большие дальности влияние вращения Земли на дви-
жение ракеты на активном участке траектории значительно и расчетная
траектория имеет характер пространственной кривой. Поскольку для ана-
лиза вопросов динамики регулирования это изменение траектории не име-
ет существенного значения, далее будем считать номинальное (невозму-
щенное) движение плоским. Невозмущенное движение ракеты по расчет-
ной траектории описано ранее системой уравнений (1.27), (1.28), (1.29).
Боковое движение и движение вокруг продольной оси на расчетной тра-
ектории характеризуется нулевыми значениями параметров (1.35).
44
Глава 2
УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ РАКЕТЫ
2.1. Возмущения, действующие на ракету
Параметры номинальной траектории полета ракеты определяются рас-
четом в предположении, что ракета обладает номинальными тяговыми,
весовыми и аэродинамическими характеристиками и движется в атмосфе-
ре, характеризующейся расчетным распределением плотности и давления.
Фактическое движение ракеты происходит, как правило, при характе-
ристиках ракеты и атмосферных условиях, несколько отличных от номи-
нальных. Так как эти отклонения не могут быть предусмотрены и учтены
заранее, то следует считать, что ракета в полете находится под действием
возмущающих сил, искажающих расчетную траекторию.
Для того, чтобы оценить величину рассеивания точек падения ракеты,
т. е. точность стрельбы, и иметь возможность принять меры к ее повы-
шению, необходимо знать, как связаны отклонения фактических пара-
метров ракеты от номинальных и максимальные значения возможных
отклонений с возмущающими силами и моментами, действующими на
ракету в полете.
Возмущающие силы, действующие на ракету в полете, можно разбить
на группы, обусловленные:
1) воздействием внешней среды;
2) неточностью изготовления и монтажа ракеты и двигательной уста-
новки;
3) неточностью работы элементов и приборов системы управления.
К возмущениям первой группы следует отнести аэродинамическую
силу и момент от воздействия ветра. Если вектор скорости ветра W, обте-
кающего ракету в произвольном направлении, разложить на составляю-
щие по осям скоростной системы координат, то составляющая их изменит
величину модуля вектора скорости ракеты V, а составляющие Wy
и изменят его направление. В продольной плоскости появится допол-
нительный угол атаки CCW, который приближенно определится формулой
и; w
aw - —, в боковой плоскости соответственно pw = —.
Пренебрегая изменением скоростного напора, возмущающие силы,
обусловленные действием ветра, определим по формулам (1.6) с учетом
зависимостей (1.7):
45
Y = caqSK,a :
w ynM w’
Z =c“qSMP (21)
w y4 ^Mrw,
а соответствующие им возмущающие моменты:
Mwy=Yw(xd-xc);l
Мте =Zw(xd-xc).j (2’2)
Ко второй группе возмущений относятся возмущения, связанные
с неточностью установки двигателя на ракете, газодинамическим эксцен-
триситетом тяги двигателя и отклонением положения центра масс от
расчетного.
Параллельное смещение ц линии действия тяги относительно про-
дольной оси эквивалентно смещению pyi в направлении оси yi и смеще-
нию pzi в направлении оси zj:
Смещение вектора тяги относительно каждой из осей создает возму-
щающие моменты относительно центра тяжести:
Mu =P|ivl;l
у1 (2.3)
ч., =М
Аналогично перекос линии действия тяги относительно продольной
оси на угол е приводит к появлению сил и моментов в продольной и боко-
вой плоскостях:
Fs,=ps.;
MSi=Psyl(x,.-xc);
F£ji =Рег1;
Мс =Pe,.(x^-xY
Смещение положения центра масс от расчетного значения эквивалент-
но параллельному переносу линии действия тяги.
Возмущающий момент сил относительно продольной оси может воз-
никнуть за счет косой обдувки и неточности установки стабилизаторов.
Этот момент определяется формулой
Map = ca₽qSMap,
где сар - аэродинамический коэффициент, зависящий от формы ракеты и
числа М.
Момент относительно продольной оси может появиться также за счет
взаимного перекоса в установке камер в случае, когда двигатель имеет не
одну, а несколько камер сгорания. Так, например, если четыре камеры
сгорания двигателя установлены с перекосом на угол е, то момент от пе-
рекоса будет
46
M=4reP,
ф ф ’
где гф - расстояние от оси камеры до продольной оси ракеты.
К числу возмущений, определяющих вариацию модуля скорости и
значительно влияющих на ее направление, относятся отклонения пара-
метров двигателя Руд и т, а также массы ракеты и аэродинамического со-
противления от их расчетных значений.
Поскольку система управления использует в качестве регулируемого
параметра величину секундного расхода массы топлива (и, как следствие,
вариацию массы т), то в качестве возмущений, наряду с Руд, следует рас-
сматривать лишь начальные отклонения параметров m и т.
2.2. Уравнения возмущенного движения ракеты
Под действием возмущающих сил и моментов ракета движется не по
номинальной, а по возмущенной траектории. Основной задачей системы
управления является обеспечение устойчивого полета ракеты и получения
управляющих воздействий, удерживающих ракету вблизи номинальной
траектории.
Поскольку система управления удерживает ракету вблизи расчетной
траектории, чувствительные элементы системы должны реагировать на
отклонения регулируемых параметров движения ракеты от их расчетных
значений. Отсюда следует, что и теоретические исследования возмущен-
ного движения целесообразно производить по уравнениям, записанным
в отклонениях.
Выше указывалось, что уравнения возмущенного движения кроме чле-
нов, характеризующих действие расчетных сил, содержат члены, обуслов-
ленные действием возмущений. Параметры, характеризующие движение
ракеты, также будут возмущенными.
Если обозначить через iB параметр движения ракеты на возмущенной
траектории, iH - на номинальной, i - отклонение параметра от номиналь-
ного значения, то связь между ними определится соотношением iB = iH + i.
Для получения уравнений первого приближения, характеризующих
возмущенное движение ракеты, придадим приращение каждому парамет-
ру, входящему в уравнения движения. Исключим из полученных уравне-
ний члены, характеризующие номинальное движение, и пренебрежем
членами второго и высшего порядка малости. Это допустимо, так как от-
клонения возмущенных параметров движения от их номинальных значе-
ний при наличии системы управления достаточно малы.
К числу основных варьируемых параметров отнесем
И, Оу а, х0, т, ihy Ру G.
Для возмущенной траектории будем полагать
47
v, =vB+v; x0>=x0_+x0;
0,=0B+0; m, =m„+m;
G,=G„+G;
a, = aB+a; P, =P„+P;
Уо.=Уо.+У»; m,=mB+ih.
(2.5)
(2.6)
Для определения возмущений, связанных с отклонениями параметров дви-
гателя и ракеты, введем вариации параметров Руд и то, полагая
р =р +р ;
уд.в уд.н уд.’
iHq. = т0. 4- т0.
Вариациями остальных параметров, входящих в уравнения движения, как,
например, р, g, р, Суа, сД пренебрежем ввиду того, что влияние их на измене-
ние расчетной траектории невелико.
Преобразуем для примера уравнение (1.27) проекций сил на номинальное
направление вектора скорости ракеты. Используя формулы (1.5), (1.6), (1.27) и
соотношения (2.5), получим
(m„ +m)(v„ + v) = [-(Рув, +Pyl.)(G, +G)-SCOBp,(h,)]cos(aH + a)-
-(т, + m)g„ sin(0„ + 0) - c„ b-SM (v, + v)2 - Y,, sin(a, + a).
Если преобразовать это уравнение, полагая дополнительно, что а и 0
малы, т. е. при sin(a)»a, sin(0)«0, cos(a)»l, cos(0)«l, а также ¥р.нан»К8ан»0,
и исключить из уравнения а, то, используя соотношение (1.1), получим
+ ^-(V, +gBsin0.) Jihdt = —
CxhPhV.SM к/ I Л РН§1Пан1л lPHSinaHln I 1 т» I-
!Lj± V+ gHcos8H —*------8+ —--------3+ —Pv_HgHcosaH m+
I I 11 I I уд.н w и H I
j v л1„ ) V л1„ j л1н J
rhH \ F (t)
—g.cosa, PyB+-*—.
m„ )
Произведя аналогичные преобразования уравнения проекций сил на
ось Оу (1.28) и уравнения моментов относительно центра масс (1.29), по-
лучим
®4^^c°"p^N4^p"OT^+^c°-p"v-sM-v8"sine"')e+
кЧ ч J Ч )
—^соба^+с^ яД,) Э+|—— |5+|—!—Pysina, |m+|—+^*C°S^“| fmdt=
Л ' J I W J ЧЧ JoJ
(2.8)
^-4&sinaB]p).+.
F,(t).
ЧЧ’
48
t* 1
^(xp.H-x«) 8=
H
®+t[c“"P"V"Sm(x* -x«)cosaH +c™pHY,SMsinaH(x4, -X,
JH
+t[“cyHq"SM -^J-c^ASm cos“h(x* -x„)]o
Jh
+7-[c;HqHSM(x(h -Xjcosa,, +c„,q11SM cosajx^, -x„)]»4
H
^M8(t)
Jh
В последнем уравнении члены, содержащие вариации m, т0 и Руд,
(2.9)
отсутствуют, так как изменение массы и тяги влияет только на модуль
скорости и не создает моментов относительно центра массы. Величины
Fv(t), Fe(t) и Mg(t) характеризуют проекции суммарных возмущающих
сил на соответствующие оси и возмущающий момент относительно цен-
тра тяжести.
Уравнения (1.33), характеризующие изменение координат центра масс
ракеты, после варьирования имеют вид:
х0 = Vcos0H-уОн0;1
Уо = V sin 0Н + хОн0. J
Система уравнений (2.7) - (2.10) составляет полную систему уравне-
ний продольного движения ракеты в вариациях относительно параметров
V, 0, 3, Хо, Уо.
Для удобства проведения дальнейших исследований системы стабили-
зации продольного движения ракеты преобразуем эти уравнения, введя
в качестве независимых переменных вместо 0 и V составляющие Vx и zy
вектора скорости по осям Ох и Оу.
Проекции скорости V на оси Ох и Оу определяются по формулам:
Vy в = VB sin0; Vx в = VB cos0
Принимая во внимание, что на невозмущенной траектории Уун = 0, бу-
дем иметь
Vy > = Vy и + Vy = Vy = V.sin0 = (V„ + V)0« VH0;
V,,=(V,+V)co8esV,+V; V, =V. ' (2-11)
Дифференцируя выражение для Vy, получаем
Vy=V,e+V,ft (2.12)
Используя уравнение (1.27) проекций сил на ось Ох в виде
V, =—cosa, -g.sme, -i.,
mH mH
49
получаем
v,e=vy-^-ecosa,+ie+g,esme,. (2.13)
шн ГПН
Подставляя соотношения (2.11) - (2.13) в уравнения (2.7) - (2.9), при-
водим их к виду:
V, +cv.v.V« +cv,v,Vy +Cv,»9 + Cv.88 + Cv.*ril +
„ МО (2.14)
+cv,m Jmdt =cv,ra€m0+СуЛдРуд. ;
0 mn
vy +cv,v,Vx +cv,v,Vy +су,Л+Су/+су>йт+
•f.A Fv,(t) (2.15)
+cVm Jmdt ;
О
9+cs Vx+c« Vv+cs«9+css5 = ^^ (2.16)
<#v x <>v У «ю <x> т w/
У
Значения коэффициентов, входящих в уравнения (2.14)—(2.16), приве-
дены в табл. 2.1.
Для преобразования кинематических уравнений используем соотно-
шения между параметрами х0, уо, х и у. Так как скоростная система ко-
ординат повернута относительно стартовой в плоскости стрельбы на
угол 0Н, то
х = х0 cos0H +у0 sin0H;
у = -yosin0H+xocos0H.
Дифференцируя эти выражения, получаем
х = Ч+0ну;1
y = Vy + 0Hx;j
(2.17)
Система уравнений (2.14)—(2.16) представляет собой систему уравне-
ний первого приближения для продольного движения в параметрах 9,
Vx,Vy, х и у.
Перейдем теперь к выводу уравнений возмущенного движения в бо-
ковой плоскости. В разделе 1.3 было оговорено, что боковое движение
при полете ракеты по расчетной траектории отсутствует и параметры его
имеют нулевые значения (1.35). Поэтому боковое движение ракеты вы-
зывается только действием возмущающих сил и моментов, и уравнения
первого приближения, написанные для возмущенного движения ракеты,
имеют вид:
mV2 =-Psin0-Z-Zp;
JV = -Z cos 0(xd - хс) - X sin 0(xd - хс) - Mpv.
50
Таблица 2.1
Коэффициенты уравнения (2.14) Коэффициенты уравнения (2.15) Коэффициенты уравнения (2.16)
СхнР У М CVyVx А fl ун • h h м С9УЖ (сунам с о s а н + с х sin а н )х
J. х P.y.S и (ха, - хсн )
J.
CV„Vy ^sinc>0 „ &а»0, ГЛ Ч J СУуУу (< +с„)рЛ.^м 2m, CSVy (<+C»)gAM(x*-x»)°°S4 jyH
CV„9 ^sino; СУу9 PH cosaH+cyHqHSM СЭЭ <^+cJ^lJxA-Xa)C№Of, J.
CV,6 0 СУу6 m. C9S Л
CV„m P^g. cos а. СУут ^g.sina. С 9m 0
CVtm v.+g, sing, тн CVym У.е* + g„ COS0, СЭт 0
CVxm^ P»+g«sinfl, тн СУуЪ cos^ C9mv 0
СУХР^ mHgH cosaH т« CyyPyi mHgM sin^ С9РуЛ 0
Считая, что Т и 0 малы, ст = Т-р и что для малых ст Vz = -Vct, уравне-
ния бокового движения в вариациях можно переписать в виде:
или
* v V
Ч + CVzvY + CVZVZ Vz + Су65 = —
z г г г тн
е МП)
щ + с v V +с ш + сх5 = —-—
т yVz z уб -г
Ju
Если учесть, что ан мало (cosaH«l) и cf =с®, то коэффициенты уравне-
ний бокового движения могут быть выражены через коэффициенты урав-
нений продольного движения следующим образом:
CVZVZ =CVyVy; CVVZ =“ C3Vyi
^vzy ~~ ^vy3’ Cyy — C$9, ► (2 19)
CVZ8 = “CVy8> Cv8 = СЭ8* *
Принимая во внимание, что возмущающие силы и моменты с равной
вероятностью могут действовать как в продольной, так и в боковой плос-
костях, их можно считать одинаковыми для обоих видов движения. С уче-
том знаков они удовлетворяют следующим соотношениям:
F = -F • М = М
rvz FVy’ 1V1V lvla-
(2.20)
При этом предполагается, что ветровые возмущения, а также возмуще-
ния, связанные с неточностью изготовления ракеты и двигателя, одинако-
вы как для продольного, так и для бокового движений. Аналогия, полу-
ченная в записи уравнений продольного и бокового движения, весьма
удобна при проведении исследований.
52
Возмущенное движение ракеты вокруг оси Oxi описывается уравнени-
ем моментов сил, действующих на ракету относительно этой оси:
R®r мт
ф + ——5 = —t
j J
W Y Y
(2.21)
В заключение выразим через коэффициенты уравнений возмущенного
движения приложенные к ракете силу и момент от действия ветра. Для
этого, сопоставляя выражения (2.1) и (2.2) для силы и момента с табл. 2.1
коэффициентов, замечаем, что если пренебречь значением коэффициентов
лобового сопротивления Сх, приведенные силу и момент от действия ветра
можно представить в виде:
М
Ywy ~cVyvywy; -yL = c,VyWy.
2.3. Методы упрощения системы уравнений движения
ракеты
Система уравнений, описывающих возмущенное движение ракеты,
даже в предположении независимости трех плоских движений достаточно
сложна. Для упрощения исследований и выяснения физической сущности
процессов регулирования тех или иных параметров движения стараются
расчленить сложное движение на несколько простых, пренебрегая в каж-
дом отдельном случае теми факторами, которые не оказывают существен-
ного влияния на рассматриваемый вид движения. При упрощении исполь-
зуют обычно значительную разницу в частотах, которые характерны для
того или иного вида движения, специфические свойства траекторий бал-
листических ракет, различие в средствах, используемых для регулирова-
ния того или иного параметра.
Коэффициенты уравнений возмущенного движения ракеты зависят от
весовых, геометрических и тяговых характеристик ракеты, вида ее траек-
тории и параметров атмосферы. Они являются, таким образом, функция-
ми времени, определяемыми значениями всех этих характеристик на рас-
четной траектории. Если в уравнениях сил (2.14) и (2.15) все их члены от-
несены к массе ракеты, а в уравнении моментов (2.16) - к моменту инер-
ции, то уравнения оказываются записанными непосредственно в
ускорениях и каждый коэффициент определяет ускорение, которое при-
обретает ракета при единичном значении вариации. При такой форме за-
писи становится очевидным влияние вариации каждого параметра на ха-
рактеристики движения.
53
Физическая природа и закон изменения коэффициентов уравнений
возмущенного движения ракеты во времени наиболее наглядно выявляет-
ся при варьировании в отдельности каждым параметром.
При этом анализируется, под действием каких сил и по какому закону
меняются ускорения К , V , 19.
В качестве примера рассмотрим влияние вариации &.
Вариация угла тангажа есть результат отклонения оси ракеты от рас-
четного положения. При появлении вариации угла тангажа такое же при-
ращение получает угол атаки, так что а = Э. При этом появляется аэроди-
намическая сила и, как следствие, аэродинамический момент относитель-
но центра масс ракеты. Кроме того, из-за изменения направления оси ра-
кеты изменяются проекции силы тяги на оси Ох и Оу, что вызывает
появление ускорений в направлении этих осей.
Таким образом, при появлении вариации угла Э возникают ускорения,
определяемые в соответствии с уравнениями (2.14)-(2.16) и табл. 2.1 сле-
дующими формулами:
Vx = -cv 9Э = _P"Sina»,9 « 0;
' (2.22)
i9 = -c99& =
(< + CXH ) C0S aHQHSM (Xdn - Xcn )
Членом Cv && в уравнении проекций сил на ось Ох можно пренебречь,
так как из-за малости угла атаки на расчетной траектории он по существу
является членом второго порядка малости.
Коэффициент Су & складывается из двух составляющих. Основной яв-
Р cos а
ляется составляющая, определяемая величиной —-------которая ха-
растеризует перегрузку п, испытываемую ракетой при полете по расчет-
ной траектории: Пн =
GH
54
В момент отрыва ракеты от стартового стола Р = G и n = 1. Однако уже
за достаточно малый промежуток времени двигатель набирает расчетное
значение тяги и в дальнейшем за счет выгорания топлива перегрузка не-
прерывно растет. Составляющая, которая определяет величину ускорения
за счет подъемной силы, пропорциональна скоростному напору q и пото-
му от нулевого значения на Земле (при V = 0) она растет до тех пор, пока
приращение скоростного напора за счет увеличения скорости полета
больше, чем падение скоростного напора вследствие уменьшения плотно-
сти атмосферы. С того момента, когда падение плотности становится пре-
валирующим {q < 0), аэродинамическая сила начинает убывать, обраща-
ясь в нуль в пустоте.
Величина коэффициента так же, как и коэффициента Cv&9 про-
порциональна скоростному напору. Однако характер его изменения в зна-
чительной степени зависит от закона изменения расстояния (ха-Хс), опре-
деляющего плечо этой силы относительно центра тяжести. Здесь следует
повторить, что если центр тяжести ракеты расположен впереди центра
давления, то при появлении вариации i9 возникает момент кото-
рый стремится повернуть ось ракеты к расчетному положению. Такая ра-
кета называется статически устойчивой. Если центр тяжести расположен
позади центра давления, то в этом случае возникает дестабилизирующий
момент. Такая ракета называется статически неустойчивой. При Хс = Xd
коэффициент = 0, ракета нейтральна, и при появлении вариации i9
момента не возникает.
Необходимо отметить, что знак разности (Xd-Xc) может меняться по
траектории.
Аналогично можно проследить влияние остальных параметров (Vy, Vx,
8, m, т, Руд) на изменения ускорений Vx9V
На основании проведенного анализа и выяснения относительного
влияния того или иного члена уравнений на характер возмущенного дви-
жения ракеты система уравнений (2.14)-(2.16) упрощается и приводится
к виду:
Г . Fv
Vx + CVxVx^x + СУхт^ + CVxm — CVxmJnQ + CVxPydFyd ~ (2.23)
0 тн
Fv (0
Vy cvyvx Vx + cvyvy Vy + cvy&$ + cyys^ ~ ~ (2.24)
55
<9 + C9V И + C99& + CagS = . (2.25)
err У у crcr его j 4 z
* H
Уравнение (2.23), характеризующее движение ракеты вдоль траекто-
рии, может быть решено независимо от уравнений (2.24) и (2.25). Это зна-
чит, что возмущенное движение ракеты относительно центра масс и по
нормали к траектории практически не влияет на движение ракеты вдоль
траектории.
Стабилизация движения ракеты вдоль траектории осуществляется сис-
темой программного регулирования кажущейся скорости (РКС). Регули-
рование производится путем изменения тяги двигателя, которое осущест-
вляется изменением секундного расхода топлива или давления в камере
сгорания двигателя (см. часть 7).
Движение ракеты в плоскости стрельбы по нормали к траектории и от-
носительно оси Oz описывается системой уравнений (2.24) и (2.25). При
этом предполагается, что в случае анализа уравнений движения жидкост-
ной ракеты членом CvvVr в уравнении (2.24) можно пренебречь, так как
коэффициент Cvv мал, а значение вариации Vx сводится к минимуму
системой РКС. Для более аккуратной оценки влияния этого члена на дви-
жение ракеты по нормали к траектории следует учесть его в уравнении
(2.24) в виде возмущения, определив предварительно значение Vx в функ-
ции времени из уравнения (2.23). Анализируя далее систему уравнений
(2.24) и (2.25) в виде:
Vy + cvyvy Vy + + 9 (2.26)
м
<9 + C&v^ Vy + + с ^8 — —• , (2.27)
J н
отметим, что инерционность ракеты по отношению к управляющим воз-
действиям, изменяющим положение центра тяжести, значительно больше,
чем по отношению к управляющим воздействиям, вызывающим ее угло-
вые перемещения, т. е. уравнение (2.27) характеризует быстрые угловые
движения ракеты относительно центра масс, а уравнение (2.26) - относи-
тельно медленное изменение положения центра масс. Влияние движения
центра масс ракеты на угловое движение проявляется через член С&у Уу,
который является медленно меняющейся компонентой. Поэтому при ис-
56
следовании динамики углового движения им можно пренебречь и рас-
сматривать угловое движение независимо, в виде:
& + c99& + c9S8 = (2.28)
При рассмотрении стабилизации движения центра масс следует отме-
тить, что при наличии возмущающих сил необходимо поддерживать от-
личные от нуля углы отклонения ракеты, чтобы создавать составляющую
силы тяги, компенсирующую действие возмущений. Поэтому следует
также учитывать и уравнение моментов, в котором, однако, можно пре-
небречь членом <9, так как он характеризует быстрые изменения углового
положения оси ракеты и мало сказывается на движении центра масс. По-
этому движение центра масс можно описать следующими уравнениями:
Ру
Ру + CVyVy Vy + СУу9& + СУу8$ ~
С9Уу Vy + СЭ9& + С98$ = ~~у~ ‘
(2.29)
57
Глава 3
УПРАВЛЯЕМОСТЬ РАКЕТЫ
Обеспечение управляемости ракеты является одной из важнейших за-
дач динамического проектирования, которая сводится к выбору типа и
эффективности органов управления. Эффективность органов управления
оценивается максимальным управляющим моментом создавае-
мым органами управления при соответствующем их максимальном от-
клонении 3mav.
Эффективность органов управления характеризуется коэффициентами
усиления С^, и максимальными моментами. В плоскости
тангажа или рыскания коэффициенты соответственно равны:
I I
I ^zp(Xp~XJ
гИ - т
J У
в канале крена
I I
J X
Максимальный момент, который способны создать органы управления
в плоскости тангажа и рыскания, соответственно равен
(А/ )тях = (Хп ~ Хг )Зтях ,
х z/max yp х р cJ max’
~^п(Хп
х у/max zp\ р cJ max
в плоскости крена
(^)max =^i^nax-
х х/тах хр max
Момент, создаваемый органами управления, условно можно разделить
на три части
А/ „ = М„п + + м..
упр пр воз сто
Здесь Мпр - программный управляющий момент, необходимый для веде-
ния ракеты по программной траектории. Если i9np(t9H) и i9np(i9H) малы,
то Мпр также невелик; Мвоз - момент для парирования возмущений от вет-
ра, несоосности камеры двигателя, аэродинамической несимметрии и т. д.
Этот момент может быть значительным; М^ - момент, развиваемый ор-
58
ганами управления в процессе стабилизации, который определяется с уче-
том обеспечения требуемых качеств по быстродействию, точности, коле-
бательности переходных процессов.
В любой момент времени полета максимальный момент, который мо-
жет быть создан системой управления, должен быть больше потребного
момента управления
> (К1)+1м->1+1м-«1)-' <ЗЛ)
Например, для плоскости тангажа
Ryp(Xp > (\МпР\) + |Чо,| + |Ктб|)тах-
Так как правая часть неравенства может быть известна из анализа воз-
можных траекторий, условий полета, величин возмущений и т. д., а угол
<5тах определяется конструкцией устройств, ограничивающих поворот ор-
ганов управления, то из последнего неравенства можно определить мини-
мальный градиент управляющей силы
Л (l^nb + l^l + lK^bmax
v пР у I 8031 I c/ио |7 max
Kyp >------я—;--------------•
max x p c7
Это неравенство должно выполняться в любой момент полета.
Так как сигнал управления обычно «засорен» шумами, то на полезное
отклонение органов управления накладываются случайные отклонения.
Левая часть неравенства должна быть больше правой настолько, чтобы по-
ворот органов управления не доходил до уровня ограничения угла (5тах.
Таким образом, эффективность органов управления должна обеспечи-
вать парирование всех возмущений, а система стабилизации должна обес-
печить устойчивость движения ракеты относительно центра масс и стаби-
лизацию центра масс относительно заданной траектории.
При разработке первых боевых ракет дальнего действия вопрос об оп-
тимизации их удельных характеристик вообще не ставился, поскольку ос-
новной задачей была организация производства этих ракет в кратчайшие
сроки.
Для обеспечения «абсолютно» надежной управляемости руководство-
вались выражением (3.1).
В дальнейшем при динамическом проектировании ракет выбор типа
и эффективности органов управления производился с учетом возможно-
сти конструктивной реализации при условии минимальных энергетиче-
ских потерь. Потери энергетики при любом типе органов управления обу-
словлены соответствующим уменьшением удельной тяги двигательной
установки и увеличением «сухих» весов ступеней ракеты за счет весов ор-
59
ганов управления и конструкции их крепления, весов приводов и источ-
ников их питания.
Необходимость рассмотрения вопросов управляемости возникает не
только при проектировании и летных испытаниях ракет. Практика пока-
зывает, что динамические характеристики уже изготовленных ракет могут
претерпевать существенные изменения, вызываемые установкой дополни-
тельных ступеней, изменением весов, габаритов головных частей, спутни-
ков и т. д. В этом случае также возникает необходимость детального рас-
смотрения возмущений, с целью решения вопроса о рациональном ис-
пользовании готовых ракет без существенной их доработки.
Принятый в начале 60-х годов метод выбора потребной эффективности
управляющих органов не учитывал в полной мере случайный характер
возмущающих сил и моментов, и вероятность одновременной реализации
таких событий, как:
- действие на ракету максимальных возмущающих сил и моментов;
- максимальное отклонение конструктивных параметров ракеты, ав-
томата стабилизации и плотности атмосферы в худшую с точки зрения
управляемости сторону;
- максимальные начальные возмущения параметров движения на
участках разделения ступеней.
При определении начальных возмущений и возмущающих сил и мо-
ментов, обусловленных действием ветра, использовалась предельная оги-
бающая скорости ветра. Указанный метод не учитывал случайного харак-
тера изменения ветра и, естественно, давал оценку сверху.
В ходе решения вопросов оценки управляемости ряда ракет возникла
прямая необходимость пересмотра ранее принятого метода. Результаты
летных испытаний многих ракет показали, что при проведении расчетов
может и должен учитываться случайный характер возмущений, началь-
ных условий, разбросов параметров ракеты, автомата стабилизации и ха-
рактеристик атмосферы.
В такой постановке задача может быть решена методом Монте-Карло,
получившим широкое применение при решении задач, связанных с расче-
том кучности стрельбы. Однако этот метод в применении к задаче управ-
ляемости является довольно громоздким и требует для своего решения
больших затрат машинного времени. В связи с этим ставилась задача раз-
вития существующего метода при условии, что его практическое приме-
нение не будет слишком громоздким.
Эта задача сводится к решению двух вопросов:
- учет влияния случайных возмущений и начальных условий на
управляемость;
60
- оценка влияния случайного характера переменного оператора, опи-
сывающего систему «ракета — автомат стабилизации».
При решении первого вопроса использовалась методика задания вет-
ровых воздействий [104]. Воздействия, приложенные к ракете в полете,
представлялись в виде одной систематической и N случайных независи-
мых составляющих с нормальным законом распределения. Принималось,
что случайное воздействие является элементарной случайной функцией.
В результате была получена простая зависимость, которая дает возмож-
ность определить суммарную реакцию системы на случайные воздейст-
вия.
Содержание второго вопроса сводится к следующему. При проектиро-
вании ракет определяется потребная эффективность управляющих органов
для всей совокупности ракет данного типа. Производственные допуски на
изготовление и сборку ракеты и автомата стабилизации приводят к тому,
что параметры системы «ракета — автомат стабилизации» отличаются от
номинальных значений и носят случайный характер. Таким образом, опе-
ратор системы следует рассматривать как случайный.
В математической постановке задача может быть сформулирована сле-
дующим образом: случайная функция преобразовывается случайным не-
стационарным оператором; необходимо определить выходные переменные.
Решение такой задачи в общем виде является затруднительным. Для
приближенного решения вводилось предположение, что величины на вы-
ходе системы приобретают дополнительные отклонения, распределенные
по нормальному закону за счет случайности оператора. Получена простая
формула, дающая возможность в первом приближении определить влияние
случайных разбросов параметров системы на величину загрузки управ-
ляющих органов.
Рассматриваемая формула дает оценку сверху, но даже в этом случае
проведенный анализ показывает, что с точки зрения загрузки управляющих
органов влияние разбросов параметров системы и атмосферы является
пренебрежимо малым.
3.1. Вероятностный метод учета влияния возмущений,
действующих на ракету
Определение потребной эффективности управляющих органов, обеспечи-
вающей надежную управляемость ступеней ракеты, связано с необходимо-
стью объективной оценки влияния возмущений, действующих на ракету в по-
лете. В настоящей главе проводится анализ возмущений, а также метод опре-
деления параметров стабилизации и величин загрузки управляющих органов,
обусловленных как совокупным влиянием возмущений от целого ряда фак-
61
торов, так и разбросами параметров системы. При этом учитывается слу-
чайный характер всех факторов, влияющих на управляемость ракеты.
Ракета с автоматом стабилизации представляет собой сложную замк-
нутую систему, динамика которой в общем случае может быть описана
нелинейными дифференциальными уравнениями с переменными коэффи-
циентами (см. части 3 и 4). Эти уравнения должны учитывать наличие на
борту жидкого топлива и упругие колебания корпуса ракеты. Анализ та-
кой системы затруднителен. Однако практический опыт показал, что
оценка управляемости ракеты может быть произведена по упрощенной
системе, описывающей поведение ракеты как абсолютно твердого жест-
кого тела. В этом случае проведение анализа значительно упрощается,
а получаемые результаты дают достаточно точную количественную оцен-
ку. Поскольку наибольшее возмущающее воздействие от ветра на полет I -
начала II ступеней оказывается в канале рыскания, запишем выражения
(2.26)-(2.27) в упрощенном виде для этого канала
z = аа (t)z + (tty + azS (tty + Fz (t),
V = avz(t)z + (tty + avS (tty + My (t), (3-2)
8 = Nty)+Q(z).
В канале вращения уравнения будут иметь вид
(33)
8V = R(<P\
Здесь
(0 “ Функции независимой переменной t, выражающие закон изме-
нения параметров ракеты;
-/ ч -/ч M(t)
F(t) = ——, М (t) — —— - приведенные возмущающие силы и
т J
моменты в функции времени;
N(у<), С(^)> /?(ф) “ операторы, характеризующие идеальный ав-
томат стабилизации;
z - координата, характеризующая перемещение центра масс ракеты;
ф, у - координаты, характеризующие вращение ракеты вокруг центра
масс;
8 - угол поворота управляющих органов.
Коэффициенты ay (t) рассчитываются по следующим формулам:
62
CanqS
mV
P + C“qS
C°qS(xa-xc)
vz JV
<№(xa-xe)
vv J
_ nxR{l-xc)
avs - T
где ni - число управляющих органов, отрабатывающих возмущения.
Каждая система уравнений (3.2) и (3.3) может быть сведена к одному
уравнению более высокого порядка. Вид этого уравнения зависит от того,
относительно какой переменной система разрешена.
Для дальнейшего упрощения формы записи используем понятие опе-
ратора. С математической точки зрения не имеет значения физическая
природа той системы, при помощи которой осуществляется рассматри-
ваемое преобразование приложенного к системе воздействия. Имеет зна-
чение лишь тот закон, та совокупность математических операций, при
помощи которых данная система ставит в соответствие функциям на вхо-
де системы определенные функции на выходе системы.
Таким образом, при проведении анализа выражения (3.2) и (3.3) в опе-
раторном виде можно представить так:
l2 [P,t)z = 4 (p,t)F (t)+B2 (p,t)M(t),
Li(p,t)3 = A3(p,t)F(t) + B3(p,t)M(t), (34)
где Lm(p,t), An(p,t), Bm(p,t) - переменные линейные операторы, в которых
р = — - символ дифференцирования.
dt
Выражение для каждого из приведенных выше переменных операто-
ров, вообще говоря, может быть определено, однако это в дальнейшем не
потребуется, так как предполагается, что установление соответствия меж-
ду входом и выходом системы осуществляется с помощью численного ин-
63
тегрирования на ЭВЦМ или моделированием на машинах непрерывного
действия.
Для удобства рассмотрения материала данной главы еще раз отметим,
что возмущенное движение ракеты на активном участке траектории вы-
зывается целым рядом факторов. Основные из них следующие:
- возмущения, обусловленные наличием ветра;
- возмущения за счет технологических погрешностей изготовления
и монтажа ракеты и двигательной установки;
- аэродинамические возмущения, действующие на ракету при нали-
чии программного угла атаки;
- начальные возмущения на участке после разделения ступеней.
Проведенные многочисленные расчеты показывают, что для участка
полета ракеты, проходящего в плотных слоях атмосферы, аэродинами-
ческие возмущения являются основными. При полете вторых ступеней
ветер, как правило, оказывает существенное влияние только на началь-
ном участке, так как в дальнейшем полет проходит практически вне ат-
мосферы.
Возмущающие силы и моменты, вызванные наличием ветра, для плос-
костей рыскания и тангажа могут быть определены по формулам:
- qSCan (иЛ
=----—arctg\ - ;
т \У )
= qSC° (мЛ . / п \
F»y =----—arctg\ - Sin(5 );
- qSC“(xd-xc\ (иЛ
Мт =--------------arctg\ — ,
J W
^ = ~ g SC" Xc);
q'=±p(r2+*'2)-
В настоящее время накоплен большой статистический материал, ха-
рактеризующий ветровое поле Земли. Проведена обработка статистиче-
ских данных, включающих в себя около 95000 зондирований атмосферы
в различных точках Земли. Показано, что вектор скорости ветра w можно
рассматривать как векторную случайную величину с ненулевым средним.
Систематическая составляющая скорости ветра w0 над территорией
бывшего СССР направлена с Запада на Восток. Величина случайной со-
64
ставляющей скорости ветра, направление которой равновероятно, подчи-
няется нормальному закону распределения.
Разработана методика задания ветровых воздействий для различных
классов задач. Характеристика случайной составляющей скорости ветра
достаточно полно описывается каноническим разложением. Систематиче-
ская составляющая скорости ветра и составляющие канонического разло-
жения приведены в методике [104].
Огибающая случайной составляющей скорости ветра не дает полной
характеристики влияния ветра на движение ракеты, так как не в полной
мере учитывает вертикальный сдвиг скорости ветра. Известно, что на ха-
рактер переходного процесса в системе автоматического управления
влияет не только величина приложенного возмущения, но и скорость его
изменения (градиент). Поэтому для задач управляемости дополнительно
должно быть рассмотрено влияние ветра с градиентами, задаваемыми
в соответствии с методикой [104].
Сравнение расчетных величин возмущающих сил и моментов показы-
вает, что для ступеней ракеты, проходящих плотные слои атмосферы,
возмущения, обусловленные технологическими погрешностями, играют
несущественную роль по сравнению с аэродинамическими возмущения-
ми. Таким образом, возмущения за счет технологических погрешностей
в основном оказывают влияние на динамику II ступеней ракет. Эти воз-
мущения определяются целым рядом факторов. Основные из них сле-
дующие:
- смещение и перекос стыкующихся отсеков;
- смещение и перекос оси сопла относительно установочной базы;
- смещение и перекос установочной базы двигателя относительно ба-
зовой оси ракеты;
- упругая деформация рамы двигательной установки и т. д.
Возмущения, обусловленные технологическими погрешностями, мож-
но представить как сумму большого числа сравнительно малых слагае-
мых, каждое из которых связано с действием отдельной незначительной
причины, не зависящей от остальных, и играет относительно малую роль
в общей сумме. Каким бы законам распределения не были подчинены от-
дельные элементарные возмущения, особенности этих распределений
в сумме большого числа слагаемых нивелируется, и сумма оказывается
подчиненной закону, близкому к нормальному. Таким образом, можно
принять, что суммарные возмущения будут случайными величинами,
подчиняющимися нормальному закону. Кроме того, на ракетах проявля-
ется весовая асимметрия, которая носит систематический характер. Все
технологические возмущения, вообще говоря, могут быть сведены к двум
группам:
65
- возмущения, сводящиеся к силе и моменту,
- возмущения, сводящиеся только к моменту или только к силе.
Суммарная величина возмущения для каждой группы определяется как
геометрическая сумма случайных составляющих.
При выборе программы угла тангажа может оказаться, что на отдель-
ных участках траектории ракета летит с ненулевыми программными уг-
лами атаки. В этом случае на ракету действуют дополнительные аэроди-
намические возмущения, которые являются систематическими. Приве-
денные значения их могут быть определены по следующим формулам:
“ т пр
=-------—
О,-
пр
Кроме рассмотренных выше возмущений, на начальном участке полета
второй и последующих ступеней возникают начальные возмущения, ко-
торые вызваны двумя группами факторов:
- ошибками стабилизации в конце предыдущей ступени
(^о> АЛ
- процессом разделения ступеней ^0).
Каждой группе возмущений, действующих на предыдущей ступени,
соответствуют начальные возмущения последующей ступени с таким же
вероятностным законом распределения. Начальные возмущения за счет
процесса разделения ступеней можно считать случайными с нормальным
законом распределения.
Интегрирование системы уравнений возмущенного движения ракеты
удобно проводить, если правые части являются функциями времени. К та-
ким функциям могут быть сведены возмущения, обусловленные действи-
ем ветра и технологическими погрешностями.
Случайная составляющая скорости ветра является случайной функци-
ей координат точки пространства и времени. По сравнению с временем
полета ракеты, зависимостью скорости ветра от времени в данной точке
пространства можно пренебречь. Для ракет координаты точки простран-
ства можно считать однозначными функциями времени. Все остальные
характеристики, используемые при расчете возмущений, вызванных вет-
ром, также можно представить в функции времени полета ракеты.
Фактические положения центра масс относительно вектора тяги, опре-
деляющие возмущения за счет технологических погрешностей, также яв-
ляются функциями времени полета ракеты. Таким образом, правые части
66
системы уравнений могут быть представлены в виде случайных функций
времени полета ракеты.
При действии возмущений ракета получает случайные линейные и уг-
ловые ускорения. При этом все параметры движения ракеты оказываются
случайными функциями времени. Ракета и ее система управления в дан-
ном случае образуют динамическую систему, осуществляющую преобра-
зование случайной функции и дающую в результате другие случайные
функции: величину и скорость поперечного смещения центра масс; угол и
угловую скорость вращения ракеты вокруг центра масс; величину загруз-
ки управляющих органов. Ставится задача определения вероятностных
характеристик всех перечисленных параметров движения ракеты по дан-
ным вероятностным характеристикам возмущений.
Действие ветра вызывает одновременное появление возмущающих си-
лы и момента, которые связаны между собой соотношением
M(/) = F(Z)J(Z),
40=М')-*с(')]т^у-
За счет технологических погрешностей могут появляться возмущаю-
щие силы и моменты, как связанные между собой функциональной зави-
симостью, так и независимые.
Система (3.2) располагает двумя входами, так как возмущающие силы
и моменты преобразуются различными операторами. На систему дейст-
вуют следующие возмущения:
^W=^W+E^7,(<)+Ev,(z),
_ л (3.5)
У С
где_ _
Fq (f), MQ (/) - систематические составляющие;
- некоррелированные случайные коэффициенты с равны-
ми нулю математическими ожиданиями, обусловленные случайными со-
ставляющими скорости ветра и технологических погрешностей;
Л (О’ Л (О’ (0 ” неслучайные функции.
Рассматриваемая система «ракета — автомат стабилизации» может
быть представлена как многомерная система. При прохождении возмуще-
67
ний (3.5) через линейные операторы, на выходе системы получим парамет-
ры движения \|/, z, 5. Обозначим любой из них через Y(t). Тогда получим:
У 7 _
= (3.6)
у s
7
у C
На основании теории линейных преобразований случайных функций,
если входное случайное возмущение задано каноническим разложением
(3.5), выходная переменная выразится каноническим разложением:
y(')=y.(')+Z^W+L^(')+L^W. <37>
у 7 <
Y(t) является решением выражения (3.6).
Математическое ожидание выходной величины равно:
ту=м[г0(/)]+^^[кХ(')+1^ИуЛ')+2мИг<(')-
У 7 <
Все величины Vj центрированные, следовательно
ту ~ Ш
Дисперсия случайной функции Y(t) будет
(38>
У 7 <
Среднее квадратическое отклонение определится по формуле:
= frrfr? (0+(0+(О • (3-9)
V у 7 4 <
Принимая, что максимальное отклонение случайной величины, подчи-
ненной нормальному закону, не превосходит За, получаем, что максималь-
ное возможное значение выходной величины не превосходит значения
68
j'(')=n (')±,Ен.!-л2 (<)+XO;2 (<) <310’
У v 7 <
Полученная формула (3.10) дает возможность определить любой из
параметров стабилизации системы и загрузку управляющих органов
с учетом вероятностных характеристик входных сигналов.
В инженерной практике часто приходится рассматривать преобразова-
ние случайных функций случайными операторами. В совокупности оди-
наковых автоматических систем характеристики и значения параметров
отдельных систем всегда будут несколько различаться вследствие допус-
ков производства и неоднородности деталей, из которых системы соби-
раются. В результате операторы однотипных систем всегда получаются
в некоторых пределах различными. Оператор системы рассматриваемого
типа является случайным при рассмотрении всей совокупности данного
типа. Оператор конкретной системы этого типа является реализацией слу-
чайного оператора системы.
В применении к ракетам это выражается в том, что параметры ракеты,
автомата стабилизации и атмосферы в каждом конкретном случае отли-
чаются от их номинальных значений. Это приводит к отличию парамет-
ров движения и загрузки управляющих органов от значений, полученных
при номинальных параметрах системы. Таким образом, возникает целе-
сообразность рассмотрения влияния возмущений на линейную случай-
ную систему, какой в данном случае является система «ракета — автомат
стабилизации».
При оценке управляемости особенно важным является определение
запасов по загрузке управляющих органов. Опыт разработки ракет пока-
зывает, что для первых ступеней минимальные запасы соответствуют
району прохождения ракетой максимальных скоростных напоров; для
вторых ступеней таким участком является начальный участок после раз-
деления ступеней. Именно на этих участках и желательно определить
возможную максимальную загрузку управляющих органов, с учетом воз-
можных разбросов характеристик системы.
К системе приложена совокупность возмущений
/=1
Загрузка управляющих органов определяется как
<312)
1=1
69
Отклонения параметров системы приводят к тому, что оператор стано-
вится случайным, поэтому 80(t) и 8i(t) становятся случайными функциями.
Математическое ожидание выходной величины 8 равно
и соответствует номинальным параметрам системы. Дисперсия выходной
величины 8 равна
°. <314)
/=1
а среднеквадратическое отклонение
+ +<т2[3]}. (3.15)
V /=1
Случайная величина 8 вызвана совокупным влиянием большого числа
независимых случайных факторов, поэтому для нее можно принять нор-
мальный закон распределения. В этом случае диапазон возможных откло-
нений будет Зсг^ и максимальное возможное значение загрузки управ-
ляющих органов не превзойдет величины
/ п
Ъ ± 3 <т‘ [<?,]+£<7г [Г-]{S,1 + <Г! [й. ]}.
V /=1
Среднеквадратическое отклонение a[VJ принимаем равным
3
Определение величин a[8j] и а[8о] может быть проведено следующим
образом. Интегрируется система (3.2) при отклонении всех параметров
в худшую, с точки зрения управляемости, сторону на величину полного
допуска при действии возмущения Xj(t). Определяется разность
Д£ = 8 -8.
обусловленная отклонением параметров от номинальных значений. Сред-
неквадратическое отклонение принимается равным
4^1=^-
70
Значение q[8o] определяется аналогично. Вопрос выбора худшего со-
четания параметров ракеты и автомата стабилизации в настоящей главе не
рассматривается.
Расчетная формула для определения максимальной возможной загруз-
ки управляющих органов с учетом разбросов параметров динамической
схемы имеет вид
£ = £±/(Д£ )2 + Ук*
и 41 \ и max / I max
г max
з J
(3.16)
Здесь
^o(^max^i) ” загрузка управляющих органов при действии системати-
ческого (случайного) возмущения и номинальных параметрах динамиче-
ской схемы;
/ Д {У А
Азотах I ^/тах —1 - увеличение загрузки управляющих органов за
счет отклонений параметров динамической схемы от номинальных значе-
ний при действии систематического (случайного) возмущения.
Эта формула является оценкой сверху для загрузки управляющих ор-
ганов, т. к. при определении c[8i] и с[8о] принимается одновременное
максимальное отклонение всех параметров от расчетных значений, веро-
ятность которого ничтожно мала.
Ниже приводится некоторый численный анализ формулы (3.16). Оги-
бающая скорости ветра, используемая при оценке управляемости, состоит
из систематической (-33%) и случайной (-67%) составляющих [104].
Возмущения за счет технологических погрешностей в основном являются
случайными функциями. Таким образом, можно принять, что выполняет-
ся следующее соотношение между систематической (8о) и суммарной
случайной (8С) составляющими загрузки управляющих органов
Jc>2J0.
Наибольшим из рассматриваемых случайных разбросов параметров
ракеты, автомата стабилизации и плотности атмосферы для ракет со зна-
чительной статической неустойчивостью является разброс плотности ат-
мосферы, который может достигать 70 %. Все остальные возможные раз-
бросы значительно меньше в процентном отношении и играют меньшую
роль при оценке загрузки управляющих органов. Проведенные неодно-
кратные расчеты показывают, что можно принять
<<5,с, Д<50<^0.
71
Рассмотрим наиболее неблагоприятный случай, если
8С=^
^8С = 3Г
= 80.
С учетом разбросов параметров и приведенных выше соотношений
8 = 8. + ^02+4302+^02 = 3.34 (3.17)
Без учета разбросов параметров
3 = 380.
Погрешность определения загрузки управляющих органов без учета
случайных отклонений параметров ракеты, автомата стабилизации и
плотности атмосферы в этом случае составляет -10 %. Так как в действи-
тельности
8С >230, Ь8С<5С, Ь80<8й,
то учет отклонений параметров динамической схемы приведет к увеличе-
нию номинальной загрузки управляющих органов менее чем на 10 %.
Для ракет, близких к нейтральным, существенное влияние оказывает
разброс координат центра давления и центра тяжести. Это может привес-
ти к значениям A8j в несколько раз превосходящим 8i. В этом случае так-
же по формуле (3.16) может быть проведена оценка ожидаемого увеличе-
ния загрузки управляющих органов.
3.2. Оценка управляемости
Проведенные многократные расчеты показали, что максимальная за-
грузка управляющих органов получается при учете градиентов скорости
ветра по высоте. Таким образом, для оценки максимально возможной за-
грузки управляющих органов одноступенчатых ракет и I ступеней много-
ступенчатых ракет достаточно определить их загрузку в районе макси-
мального скоростного напора, за счет действия ветра, с учетом возмож-
ных градиентов скорости ветра, в соответствии с методикой [104]. Полу-
ченные значения следует геометрически суммировать с загрузкой*
управляющих органов, вызванной технологическими погрешностями.
При необходимости определения максимально возможных параметров
стабилизации в конце полета I ступени ракеты следует провести интегри-
рование системы (3.2) при условии действия систематических возмуще-
ний и каждого случайного независимого возмущения в отдельности.
Суммарные значения могут быть получены по формуле:
72
r(')=U0±J2J’(0- <ЗЛ8>
V у
Y(t)-z, z, ит. д.
С точки зрения максимально возможной загрузки управляющих орга-
нов на II ступени наиболее опасным является участок разделения ступе-
ней. Для определения параметров стабилизации и загрузки управляющих
органов на этом участке можно предложить следующий метод.
1) Интегрированием системы уравнений возмущенного движения
I ступени определяются начальные условия для II ступени у0,...уп за счет
систематической и каждой из случайных составляющих возмущающих
воздействий.
2) Интегрированием системы уравнений возмущенного движения
II ступени определяются параметры стабилизации и загрузка управляю-
щих органов:
- от действия систематической составляющей возмущающих сил
и моментов при систематических составляющих начальных воз-
мущений - y0(t);
- от действия каждой случайной составляющей возмущающих сил
и моментов при нулевых начальных условиях - yi(t);
- при отработке каждой группы начальных условий и нулевых
правых частях - yjn.
Суммарные возможные максимальные значения параметров стабили-
зации и загрузки управляющих органов II ступени могут определяться по
формуле
V /=1 7=1
Определенная таким образом загрузка управляющих органов не учи-
тывает возможные случайные разбросы параметров ракеты, автомата ста-
билизации и плотности атмосферы. Как показано выше, ожидаемое уве-
личение загрузки управляющих органов за счет этих факторов может
быть определено по формуле (3.16).
Предлагаемый метод может быть использован при оценке управляемо-
сти с помощью интегрирования системы уравнений возмущенного дви-
жения на цифровой вычислительной машине или моделирующей установ-
ке непрерывного действия.
Полученные результаты разработки вероятностного способа учета
влияния возмущающих факторов при оценке управляемости ракет яви-
лись базой для создания соответствующего межведомственного руково-
73
дящего документа. «Методика...» содержит алгоритм определения по-
требной эффективности управляющих органов всех ступеней ракет на ха-
рактерных этапах их полета (старт, участок максимальных скоростных
напоров, разделение ступеней, отделение ГЧ и др.).
При этом автомат стабилизации описывается приближенным уравне-
нием, достаточно точно соответствующим амплитудно-фазовой характе-
ристике АС в области низких частот.
В «Методике...» изложен следующий порядок проведения расчетов.
I ступень
1. Определяются параметры стабилизации и загрузка управляющих орга-
нов от действия суммарного ветра с градиентами, задаваемыми по ме-
тодике [104]. Строятся огибающие полученных решений - R .Где
/ w град
0 = f(v,faz,z,8,8,<р,ф,8^,8^).
2. Определяются параметры стабилизации и загрузка управляющих орга-
нов от действия систематической составляющей скорости ветра В .
3. Определяются параметры стабилизации и загрузка управляющих орга-
нов, обусловленные действием случайной составляющей скорости вет-
ра с градиентами, по формуле:
В = В -В .
4. Определяются параметры стабилизации и загрузка управляющих орга-
нов от действия возмущающих сил и моментов, обусловленных:
- весовой асимметрией ракеты - (5ас;
- технологическими погрешностями изготовления и монтажа ракеты
и двигательной установки - /Зп.
5. Суммарные максимальные значения параметров стабилизации и за-
грузки управляющих органов определяются по формуле:
^=|^+Л|+|7<9-.+Л
6. С учетом возможных случайных отклонений параметров ракеты, авто-
мата стабилизации и плотности атмосферы максимальные значения па-
раметров стабилизации и загрузки управляющих органов могут быть
определены по приближенной формуле:
। । Г~> "> '>
/<=|А, +A.I+ fa. •
74
где ДД = Д - Д.
Д’(Д) - значения параметров стабилизации и загрузки управляющих
органов при отклонении всех параметров изделия, автомата стабилиза-
ции и плотности атмосферы в худшую с точки зрения управляемости
сторону на величину полного допуска (при номинальных параметрах
динамической схемы).
II и последующие ступени ракеты
1. Составляющие начальных возмущений, определяемые как ошибки ста-
билизации в конце I ступени, следующие:
- систематическая Я? = Вк + Вк,
r'O Iwq г'ас^
- случайная BQ = Вк , BQ = Вк,
где Д*о? Д*с, Д* , ft* - ошибки стабилизации в конце I ступени,
обусловленные действием систематической составляющей ветра, мо-
мента от весовой асимметрии изделия, случайной составляющей скоро-
сти ветра с градиентами и возмущающих сил и моментов от техноло-
гических погрешностей соответственно.
Дополнительно учитываются случайные возмущения за счет процесса
« /эО
разделения ступеней - р.
2. Определяются составляющие параметров стабилизации и загрузки
управляющих органов:
До - от действия алгебраической суммы возмущающих сил и момен-
тов за счет систематической составляющей скорости ветра и
весовой асимметрии изделия при начальных возмущениях Д^;
Pw - от действия случайной составляющей скорости ветра при нуле-
вых начальных возмущениях;
Рп - от действия возмущающих сил и моментов, обусловленных тех-
нологическими погрешностями, при нулевых начальных возму-
щениях;
Ди» п > Рпп <>Рр ~ за счет начальных возмущений Д ° , Д °, Д °.
3. Суммарные максимальные значения параметров стабилизации и за-
грузки управляющих органов определяются по формуле:
а=|А| + #;.+а:"С-+А+А;.
75
4. С учетом возможных случайных отклонений параметров изделия, ав-
томата стабилизации и плотности атмосферы составляющие началь-
ных возмущений II ступени следующие:
- систематическая /3% = /3^ +
- случайные ДД° = Д/?*о + Д/?*с
/□00 _ nkQ лОО __ nkQ
rwa Р5 Рп Рп ’
где - ошибки стабилизации в конце I ступени, обусловлен-
ные действием систематической составляющей скорости ветра и мо-
мента от весовой асимметрии изделия при номинальных параметрах
I ступени;
Д/?*о, Д/7*с - увеличение pk^pkac за счет отклонений параметров I сту-
пени;
” ошибки стабилизации в конце I ступени, обусловленные
действием случайной составляющей скорости ветра с градиентами и
возмущающими силами и моментами от технологических погрешно-
стей при неблагоприятном сочетании параметров I ступени.
5. Суммарные максимальные значения параметров стабилизации и за-
грузки управляющих органов могут быть определены по приближен-
ной формуле:
Здесь:
Д, Д, , Д, Д “ с°ставляющие параметров стабилизации и загрузки
управляющих органов при номинальных параметрах II ступени;
ДД,ДД ,&/3n,&/3in - увеличение составляющих параметров стаби-
лизации и загрузки управляющих органов за счет неблагоприятного
сочетания параметров II ступени;
Рт— пъРпп^Ррп ~ составляющие параметров стабилизации
и загрузки управляющих органов за счет начальных возмущений
* * ♦
76
Необходимость разработки и выпуска соответствующего документа по
вероятностному способу учета влияния возмущающих факторов при
оценке управляемости ракет в начале шестидесятых годов прошлого сто-
летия определялась целым рядом обстоятельств, которые могут иллюст-
рироваться двумя примерами:
1. На базе боевой одноступенчатой баллистической ракеты среднего
радиуса действия (8К63) создавалась PH легкого класса 11К63 для за-
пусков КА на околоземные орбиты в интересах Академии наук - для
решения научных и Министерства обороны - прикладных задач.
Целесообразность выбора такого направления создания PH представ-
лялась очевидной как с экономической, так и с организационной позиций,
но только при условии использования боевой ракеты практически без из-
менений ее конструкции. Более того, первые несколько десятков пусков
PH должны были производиться из существующих ШПУ боевой ракеты.
Способ старта из шахты - свободный газодинамический, из пускового
стакана, на собственном двигателе.
Диаметр пускового стакана был выбран из условия обеспечения без-
ударного выхода боевой ракеты при действии на нее приземного ветра со
скоростью до 25 м/с. Соответственно зазор между «опасной» точкой, ко-
торой являлась наиболее удаленная от продольной оси ракеты точка кор-
пуса хвостовой части, и радиусом внутреннего стакана шахты составлял
1,4 м.
Длина PH 11К63 на 8,5 м (на 38 %) больше, чем длина ракеты и боль-
ше глубины ШПУ, т. е. воздействие приземного ветра на PH было уже
с нулевой секунды с соответственно большим возмущающим моментом.
Кроме того, продолжительность движения носителя в шахте (т. е. время
воздействия), из-за увеличения на ~ 20 % стартового веса, стала сущест-
венно больше времени выхода из шахты боевой ракеты.
В результате определенная по действовавшей методике допустимая
скорость приземного ветра сократилась практически вдвое, что не позво-
ляло обеспечить нормальную эксплуатацию. При вероятностном подходе
к решению данной задачи величина допустимого приземного ветра прак-
тически осталась на уровне, заданном для условий эксплуатации боевой
ракеты [131].
2. Для создания мобильного грунтового старта межконтинентальной
баллистической ракеты было необходимо разработать ракету сверх-
легкого класса со стартовым весом не более 30 тс. При этом конст-
рукция ракеты должна быть достаточно прочной при действии дли-
тельных вибрационных и ударных перегрузок, возникающих в процессе
транспортировки.
77
Очевидно, что оптимальным решением такой задачи являлось бы соз-
дание твердотопливной ракеты на высокоэнергетическом (Руд > 320 с)
смесевом топливе и легком композитном высокопрочном конструкцион-
ном материале. Но в то время ни того, ни другого в СССР и даже в мире
не было [51], [52]!
В связи с этим была разработана ракета по оригинальной схеме: I сту-
пень - твердотопливная, II - жидкостная, ампулизированная, с «задемп-
фированными» высококипящими компонентами топлива.
Поскольку реально в тот период был определенный задел только по
ТТРД со стальным корпусом и практическим удельным импульсом (без
учета потерь на управление) на Земле/в пустоте - 231/265 с, было необхо-
димо создание ЖРД с предельно высокими (для высококипящих компо-
нентов) удельными характеристиками как по импульсу, так и по весогаба-
ритным параметрам.
Реально создание ЖРД с предельно высокими удельными характери-
стиками было возможно только при минимально потребной эффективно-
сти управляющих органов, не требующих существенных весовых затрат
на их приводы, а также крепление и питание последних.
Такой двигатель был создан с тягой 14 тс, удельным пустотным им-
пульсом 327,5 с, с управлением по осям Т и Р путем вдува газогенератор-
ного газа в закритическую часть сопла, при максимальной потребной
управляющей силе < 300 кгс. Потери Руд на управление были менее 1 с.
♦ ♦ ♦
78
Глава 4
СИСТЕМА СТАБИЛИЗАЦИИ
Задачей системы стабилизации (СС) ракеты является обеспечение
устойчивого углового движения относительно ее центра масс, а также
управление движением центра масс в боковом и нормальном направ-
лениях.
В соответствии с этим, система стабилизации состоит из автомата уг-
ловой стабилизации (АУС) и автоматов боковой (БС) и нормальной (НС)
стабилизации.
В связи с малостью углов отклонения ракеты относительно их про-
граммных значений движения вокруг трех осей связанной системы коор-
динат принимаются независимыми - каналы тангажа (<9), рыскания (Iff) и
вращения (ф).
Ракета совместно с системой стабилизации образует замкнутую систе-
му автоматического регулирования. Динамические свойства этой системы
зависят как от свойств ракеты, так и от характеристик системы стабилиза-
ции. Главной частью замкнутой системы является ракета как объект
управления.
Система стабилизации должна обеспечивать устойчивость движения
ракеты, поэтому свойства СС зависят от динамических свойств объекта
управления.
4.1. Требования к параметрам системы стабилизации
Задачи, решаемые системой управления в целом и системой стабили-
зации в частности, а также способы и методы их решения, из-за ограни-
ченности объема книги приводятся в минимальном объеме.
Для преемственности со специальной литературой по СУ и с ранее
опубликованными трудами, материалы по существу вопроса в основном
изложим в редакции [87], [88], апробированной многолетней практикой со-
ответствующего вузовского курса.
Рассмотрим частотные характеристики абсолютно твердой ракеты
и требования, которые предъявляются к автоматам стабилизации, чтобы
замкнутая система была устойчива.
Проанализируем уравнения возмущенного движения в плоскости рыс-
кания. Вместо уравнений (2.26) рассмотрим уравнения движения, полу-
ченные в неподвижной системе координат. В силу симметрии ракеты они
будут такими же, как уравнения (2.27) для плоскости тангажа:
79
где
К + CVZVZ К + CVZ^ + CVZ8$ ~~
V + + cV4,y/ + V2 + с^З = О,
cvv = 1 PV* S(c^+cx),
гл mVH 2 ' 2 x>
cv =-—fp
’ 2 2 J’
cv,s=
г m
= 7 ^sllct+2Hmcj ](х~хм)<* >
* & r
\ /
. =-^-Slcfi,
¥¥ i 2 m
(4.1)
*0?
^¥¥
(4.2)
r H
c4>s =yRt(xp~xu)-
Боковое движение центра масс относительно номинальной траектории
более медленное, чем угловое движение относительно центра масс. По-
этому при исследовании углового движения в первом приближении мож-
но пренебречь смещениями центра масс, а при исследовании бокового
движения центра масс - пренебречь угловым ускорением у/ и угловой
скоростью \jf. Тогда вместо (4.1) получим две упрощенные независимые
системы уравнений:
уравнение углового движения относительно центра масс
¥ + Суу¥ + Суу¥ + cvs8 = °> <4-3)
и уравнения бокового движения центра масс
+ Сугуг Vz + + cvz8$ =
СууУ + СууУг+С^З^.
Передаточная функция по углу рыскания на основании упрощенного
уравнения (4.3) будет
80
к ~С^
Л ’ 8 рг + рс^+с„
(4.5)
Положив р = io, получим комплексное передаточное число
K(i(o) =---------------7 = U((o\ + iV(a>\ (4.6)
с + icoc — со
Знак коэффициента с определяется знаком коэффициента . Для
статически устойчивой ракеты С^>0, для статически неустойчивой
< 0, для нейтральной = 0.
Какими свойствами должен обладать автомат стабилизации, чтобы уг-
ловое движение относительно центра масс замкнутой системы было ус-
тойчивым? Чтобы ответить на этот вопрос, проведем анализ свойств ком-
плексного передаточного числа (ю) регулируемого объекта, опреде-
ленного уравнением (4.6). Для простоты рассуждений пренебрежем
демпфированием, т. е. примем С^- 0. Рассмотрим три разных случая.
1. Статически неустойчивая ракета, С& < 0.
Годограф комплексного передаточного числа К (ио) на плоскости
Z = U(a>)+iV(o>) показан на рис. 4.1. Это отрезок положительной вещест-
С X
венной полуоси
0,
, причем, как следует из сравнения коэффициен-
тов C^g и с на некоторых участках траектории, может быть С s!c <\9
81
Знаменатель комплексного передаточного числа K^ypj имеет один
положительный корень р = , поэтому согласно критерию Найквиста
для устойчивости замкнутой системы необходимо и достаточно, чтобы
годограф комплексного передаточного числа всей разомкнутой цепи
К(1ш) = К„ (,ш)КАС(/ш) = А, (а)ААС = A(a)elr<‘>
делал один положительный полупереход оси OU правее точки С(1ДО).
С учетом запаздывания автомата стабилизации на больших частотах такой
годограф представлен на рис. 4.2.
Рис. 4.2
Для обеспечения устойчивости движения амплитудно-фазовые ха-
рактеристики автомата стабилизации должны обладать следующими
свойствами.
Во-первых, на малых частотах, в том числе обязательно и при со = О,
автомат стабилизации должен усиливать сигнал, т. е. обладать коэффици-
ентом усиления k > 1. Это необходимо для того, чтобы точка А на оси U
была расположена правее точки С( 1 ДО).
Во-вторых, автомат стабилизации на малых частотах должен выраба-
тывать опережение по фазе, чтобы фаза разомкнутой цепи
на малых частотах была положительной. Это опережение по фазе должно
обеспечиваться корректирующим контуром АС.
В-третьих, для того чтобы годограф K(ico) делал один положительный
полупереход оси U правее точки С(1ДО), необходимо опережение по фазе
82
в диапазоне частот [0, со0]. Здесь со0 - частота, при которой опережение по
фазе автомата стабилизации переходит в запаздывание, флс(®о) = 0. Чем
больше коэффициент усиления к, тем до больших частот должно осуще-
ствляться опережение по фазе, чтобы точка В на оси U всегда была распо-
ложена левее точки С.
Следовательно, коэффициент усиления к должен быть не менее неко-
торой определенной величины (обозначим ее kmin), чтобы точка А (со = 0)
на оси U была правее точки С и не более кщах, чтобы точка В (со = ©о) была
левее точки С. Другими словами, коэффициент усиления должен быть ог-
раничен сверху и снизу
кmin < к < ктях . (4.7)
Если точка В будет совпадать с точкой С, то замкнутая система будет
находиться на границе устойчивости, малые возмущения будут вызывать
в системе незатухающие колебания. Так как фдс(й>о) = 0, то 8 = к((о0)ф
и для этого случая
<4-8>
-со
Из этого выражения можно найти частоту собственных колебаний
замкнутой системы
й) = А/Л(й)0)с^ + с(^.
Для устойчивости замкнутой системы точка В должна располагаться
левее точки С, поэтому автомат стабилизации должен обеспечивать опе-
режение по фазе до частот
> ^{(O^g+c^. (4.9)
При рассмотрении устойчивости замкнутых систем используются та-
кие условные понятия, как запас устойчивости по фазе, запас устойчиво-
сти по амплитуде, или, что то же самое, запас устойчивости по коэффици-
енту усиления. Запас устойчивости по фазе характеризуется углом опере-
жения ф*(со) при А(со) = 1, запас устойчивости по амплитуде - отношением
длины отрезка ВС (так же, как и длины отрезка АС) к длине отрезка ОС
равной единице. Чем больше отрезок ВС (АС), тем больше запас устойчи-
вости по амплитуде. Запас устойчивости дает возможность судить о до-
пустимых пределах изменения параметров системы без нарушения ее ус-
тойчивости.
Для того, чтобы замкнутая система имела запас устойчивости по ам-
плитуде, на основании соотношений (4.7) и (4.8) для статически неустой-
чивой ракеты (cvv<0) необходимо, чтобы выполнялись следующие нера-
венства:
83
CW8
(4.Ю)
Для того, чтобы замкнутая система имела запас устойчивости по фазе,
необходимо, чтобы автомат стабилизации по каналу у имел опережение
по фазе в диапазоне частот [0, соо]-
2. Статически устойчивая ракета, с > 0.
Годограф комплексного передаточного числа регулируемого объекта
показан на рис. 4.3. Он расположен на вещественной оси комплексной
плоскости Z. Там же пунктиром показан годограф с учетом коэффициента
демпфирования^. При с^=0 знаменатель комплексного передаточного
числа в (4.5) имеет два чисто мнимых корня, регулируемый объект нахо-
дится на границе устойчивости; при > 0 объект устойчив, но с малым
запасом устойчивости по фазе. Присоединение к регулируемому объекту
автомата стабилизации, обладающего запаздыванием на больших часто-
тах, приводит к появлению точки В (на рис. часть годографа разомкнутой
цепи изображена кривой а).
Для того, чтобы замкнутая система имела запас устойчивости по фазе,
необходимо, чтобы автомат стабилизации обладал опережением по фазе
до частот соо, определяемых неравенством (4.9). Величина соо является
важной характеристикой автомата стабилизации. Как будет показано
дальше, эта величина используется при оценке устойчивости движения
ракеты с учетом колебаний жидкости в баках.
Замкнутая система будет иметь запас устойчивости по амплитуде, если
коэффициент усиления автомата стабилизации будет ограничен сверху, т. е.
84
c^s
Ограничение коэффициента усиления снизу в рассматриваемом при-
мере не имеет места.
3. Нейтральная ракета, с =0.
Годограф комплексного передаточного числа объекта регулирования
при с = 0 совпадает с вещественной полуосью (рис. 4.4), знаменатель
комплексного передаточного числа в (4.5) имеет два нулевых корня.
Рис. 4.4
Если на малых частотах пренебречь динамическими свойствами авто-
мата стабилизации и принять
8 = ку,
то уравнение замкнутой системы будет иметь вид
p2y+kcvSy = 0.
При наличии возмущений замкнутая система будет совершать незату-
хающие колебания с собственной частотой
Эти колебания свидетельствуют о том, что замкнутая система нахо-
дится на границе устойчивости
О)
Годограф разомкнутой цепи на рис. 4.4 изображен кривой а. Вслед-
ствие запаздывания, обусловленного автоматом стабилизации на больших
частотах, появляется отрицательное пересечение вещественной оси - точ-
ка В. Для того чтобы замкнутая система обладала запасом устойчивости
85
по амплитуде, необходимо, чтобы автомат стабилизации обеспечивал
опережение по фазе в диапазоне частот [0, со0], где
Следовательно, коэффициент усиления здесь должен быть ограничен
только сверху, т. е.
г
*гаи(‘»о)<—•
Су8
Присоединение к нейтральной ракете автомата стабилизации, обла-
дающего указанными свойствами, приводит к тому, что замкнутая систе-
ма становится колебательным звеном с демпфированием.
Величина коэффициента с зависит от скоростного напора q, момен-
та инерции ракеты, взаимного расположения центра масс и центра давле-
ния, которые во время полета изменяются. Поэтому даже для одной и той
же ракеты в разные моменты времени могут иметь место ситуации, когда
> 0, с < 0, = 0. Во всех этих случаях автомат стабилизации дол-
жен обеспечить устойчивость движения.
Подводя итог, можно сформулировать два следующих основных тре-
бования к автомату угловой стабилизации:
1) автомат стабилизации должен обеспечивать опережение по фазе
в диапазоне частот [0, соо];
2) коэффициент усиления автомата стабилизации должен быть ог-
раничен и сверху и снизу.
Амплитудно-частотная и фазо-частотная характеристики автомата
стабилизации, отвечающие перечисленным требованиям и приведенной
ниже структуре, показаны на рис. 4.5. Увеличение коэффициента к(а>) =
Адс(со) по сравнению со статическим в некотором диапазоне частот обу-
словлено наличием в цепи АС корректирующего контура.
86
Чтобы решить, каким должен быть диапазон частот [0, соо] и какие ог-
раничения должны быть наложены на коэффициент усиления кпшх(<»о),
kmin, надо провести анализ комплексных передаточных чисел регулируе-
мого объекта и всей разомкнутой цепи для всех возможных моментов
времени полета.
Для примера на рис. 4.6 приведены типичные амплитудно-частотные
характеристики статически устойчивой ракеты для трех характерных мо-
ментов времени - непосредственно после старта, при малом и при боль-
шом скоростном напоре q. Для построения характеристик было использо-
вано комплексное передаточное число
к.W = , г г1 = 4,
1й)\ С +l<D\Cvl, 4- С • | — О)
|_ VV 1 / J (4 11)
— Cvl5
&L ~ СУгУг СрУг 9
соответствующее полной системе уравнений (4.1) с учетом, что
Рис. 4.6
Характеристики построены в логарифмическом масштабе, что очень
удобно при практическом расчете автоматических систем. Такие характе-
ристики называются логарифмическими амплитудно-частотными харак-
теристиками (ЛАХ). По оси ординат откладывается величина
Zr(o) = 201g4,(a>),
87
которая измеряется в децибелах (дб). Увеличение Lv(co) на каждые
20 дб соответствует возрастанию амплитуды в 10 раз. Нулевая точка
на оси ординат соответствует усилению амплитуды А0(о>) = 1. Ослаб-
лению амплитуды А0(а>)<1 соответствуют отрицательные значения ор-
динаты Lv(a>).
По оси абсцисс откладываются значения со в логарифмическом мас-
штабе. Единицами масштаба для оси абсцисс служат октава и декада. Ка-
ждой октаве соответствует увеличение частоты со в 2 раза, каждой дека-
де - в 10 раз. Частота, при которой логарифмическая характеристика пе-
ресекает ось абсцисс, называется частотой среза а>с-
При большом q на низких частотах логарифмическая характеристика
имеет такой же вид, как и характеристика интегрирующего звена; наклон
характеристики составляет - 20 дб/дек; наклон уменьшается до 0 дб/дек
при частоте cdl. При имеет место резонансный пик, величина ко-
торого зависит от общего демпфирования (сии +с^). Демпфирование
создастся угловым движением ракеты, а демпфирование cvv - попереч-
ным движением центра масс. При логарифмическая характери-
стика имеет такой же вид, как характеристика колебательного звена; на-
клон характеристики равен -40 дб/дек.
На начальном участке траектории и на больших высотах скорост-
ной напор уменьшается и амплитудно-частотная характеристика будет
такой, какая имеет место при малом q. Величины <dc, cdl
здесь значительно меньше, а резонансная амплитуда немного больше
по сравнению с соответствующими величинами при большом q.
За время полета в обычных условиях резонансная частота мо-
жет изменяться примерно от 0,2 до 10 1/с. Резонансная амплитуда мо-
жет изменяться в 3—4 раза при большом q и примерно в 100 раз при
малом q.
В момент непосредственно после старта ракеты аэродинамические си-
лы практически отсутствуют, поэтому на амплитудно-частотной характе-
ристике нельзя указать ни резонансной частоты, ни частоты <пь. Единст-
венной поперечной силой в этом случае является сила от управляющих
органов, и частота среза зависит от момента этой силы. На основании
(4.10) частота среза
Наклон амплитудно-частотной характеристики непосредственно после
запуска равен —40 дб/дек. В этом нетрудно убедиться, так как
88
Л И)
Л (10<ц)
201g Д, («ц)-201g Д, (10<ц ) = 201g
Су8
= 201g—— = 201gl00 = 40 дб/дек.
Су8
(10<ц)2
Более полную информацию для выбора коэффициентов усиления ав-
томата стабилизации можно получить путем построения областей устой-
чивости [87].
На основе рассмотрения семейства характеристик (см. рис. 4.6) и по-
строения соответствующей (например, в плоскости параметров К^-К^)
области устойчивости можно установить более конкретный диапазон час-
тот [0, <х>о] и верхнюю и нижнюю границы для коэффициента усиления ав-
томата стабилизации. Однако выбрать эти величины окончательно и назна-
чить запасы устойчивости по коэффициенту усиления (по амплитуде) и по
фазе на основании таких характеристик еще нельзя. Выбор запасов устой-
чивости - задача более сложная. Здесь нужно принимать во внимание воз-
можные разбросы параметров ракеты, отклонения параметров и характери-
стик автомата стабилизации, зависимость характеристик от температуры,
вибраций и других факторов. Величины этих параметров можно опреде-
лить на основе опыта эксплуатации ракет и систем их стабилизации.
В практике динамического проектирования ракет как объектов управ-
ления используют способ построения АФЧХ и областей устойчивости для
так называемых «крайних режимов», т. е. наихудшего сочетания парамет-
ров системы.
Рассмотрим теперь динамические свойства автономной системы стаби-
лизации бокового движения центра масс относительно заданной траектории.
Уравнения бокового движения центра масс (4.4) запишем с правой частью
+ Cv,v, К + СУл№ + CV.8$ ~ ’
m (4.12)
M
c vV + c w + c s8 = —
4fVz z y/8 у
Здесь ZB и Мув - длительно действующие возмущающие факторы, обу-
словленные ветром, несовпадением вектора силы тяги двигателей с про-
дольной осью корпуса и т. д.
Система стабилизации центра масс должна компенсировать действие
возмущающих факторов. Пусть, например, сила ZB и момент Мув возникли
в результате действия на ракету ветра. Тогда автомат угловой стабилиза-
89
ции повернет рули на некоторый угол 8, чтобы уравновесить возмущаю-
щий момент и держать корпус ракеты параллельно плоскости стрельбы
(\|/ = 0). Кроме поперечной силы, на корпус ракеты будет действовать еще
и поперечная управляющая сила Zp, причем в случае статически устойчи-
вой ракеты (сгг >0) силы ZB и Zp будут направлены в разные стороны,
а в случае статически неустойчивой ракеты эти силы будут направлены
в одну сторону. Под действием сил ZB и Zp центр масс ракеты будет пере-
мещаться в боковом направлении.
Чтобы компенсировать действие сил ZB и Zp, автомат стабилизации
центра масс должен повернуть корпус ракеты (вектор силы тяги двигате-
лей) так, чтобы сумма проекций на ось z сил ZB, Zp и Рэ была равна нулю,
или точнее, чтобы скорость Vz центра масс была равна нулю. Для стати-
чески неустойчивой ракеты угол поворота должен быть больше, чем для
статически устойчивой. Таким образом, система угловой стабилизации
стремится держать ось ракеты в плоскости стрельбы, а система стабили-
зации центра масс должна выводить эту ось из плоскости стрельбы.
Одним из возможных законов формирования сигнала в канале стаби-
лизации центра масс [87] будет
S = ky/-k{Vz -k2z9 (4.13)
где z - координата смещения центра масс. Так как стабилизация центра
масс и угловая стабилизация осуществляются одними и теми же исполни-
тельными органами, то структурная блок-схема автомата стабилизации
в плоскости рыскания будет иметь вид, показанный на рис. 4.7.
Рис. 4.7
Определим некоторые требования к выбору коэффициентов усиления
ki и кг, для чего из уравнений (4.12) и (4.13) установим зависимость меж-
ду координатой z смещения центра масс и возмущающей силой ZB. При-
няв Vz= pz, Мув= 0, получим
90
{p2(cw +kcvS)+ р[суЛ +Ц,« )
C¥Vz + kcv6 ) +
+^1 (CVzyCy8 ” C^CVZ8 )] + ^2 (CV^Cy5 — CYYCVZ6 )}^ =
~ +^5
При соответствующем выборе коэффициентов ki и кг можно обеспечить
хорошее качество переходного процесса. Чем больше коэффициент к2,
тем меньше статическое смещение центра масс, т. е.
„ _ + fays
т ^2 (CVzpCy8 ~~ CyyCVz8 )
и тем выше частота собственных колебаний центра масс
J^2 (CVzyCy8 ~ СугуСУг8 )
cw + kc^s
Но с увеличением коэффициента к2 может несколько уменьшиться за-
пас устойчивости по каналу \|/.
Как видно из уравнения смещения центра масс, коэффициент ki опре-
деляет затухание системы. Чем больше ki, тем быстрее затухают колеба-
ния центра масс.
Выбор значений коэффициентов усиления ki и к2 канала стабилизации
центра масс можно производить следующим образом: задаваясь возмуще-
ниями Zb и Мув, решить уравнения (4.11) и (4.13) для разных фиксирован-
ных моментов времени полета и найти зависимости Vz и z от коэффици-
ентов ki и к2, причем, если значения ki и к2 будут большйми, то в уравне-
нии моментов следует учитывать и ф. Руководствуясь требованиями
к точности полета, на основании полученных зависимостей можно выб-
рать приемлемые значения коэффициентов ki и к2.
Анализ уравнений с постоянными коэффициентами дает лишь качест-
венное представление о том, как будет осуществляться стабилизация цен-
тра масс. В реальных условиях коэффициенты уравнений и возмущающие
силы во время полета изменяются, и получить представление о макси-
мальной скорости Vz и максимальной накопленной ошибке в отклонении
координаты z можно из решения уравнений с переменными коэффициен-
тами на ЭЦВМ или на электронной моделирующей установке. Только по-
сле этого можно сделать окончательный выбор коэффициентов ki и к2.
Структура уравнений возмущенного движения в плоскости тангажа
такая же, как и в плоскости рыскания, поэтому требования к автоматам
угловой стабилизации и стабилизации центра масс практически такие же,
как и к автоматам стабилизации движения в плоскости рыскания.
91
Более простым является уравнение возмущенного движения относи-
тельно продольной оси
Ф + с^ф+с^б^О. (4.14)
Коэффициент обусловлен аэродинамическими силами, коэффици-
ент - управляющими силами.
Комплексное передаточное число по углу крена
Примеры амплитудных частотных характеристик в логарифмическом
масштабе приведены на рис. 4.8. При большом q на низких частотах на-
клон характеристики равен -20 дб/дек с изменением наклона до
-40дб/дек при частоте со = с^. Точка пересечения этой характеристики
с осью частот определяет частоту среза сос- С уменьшением q на больших
высотах амплитудная частотная характеристика изменяется в соответст-
вии с характеристикой для малого q. Характеристика «Старт» соответст-
вует условиям непосредственно после пуска ракеты: когда с^ = 09 а
не зависит от скоростного напора q и полностью определяется эффектив-
ностью рулевых органов.
Структура уравнения (4.14) аналогична структуре уравнения моментов
в плоскости рыскания при с^= 0. Поэтому и требования к автомату ста-
билизации по каналу крена аналогичны требованиям к каналу угловой
стабилизации при с = 0. Частота собственных колебаний ракеты с авто-
матом стабилизации относительно продольной оси
й> = ^(й>)с^, (4.15)
92
где к(со) - коэффициент усиления автомата стабилизации;
<ро хр X
Динамическая схема жидкостной ракеты в виде абсолютно твердого
тела является схемой первого приближения. На основании этой схемы
можно произвести расчет траектории полета и сформулировать основные
требования к системе управления и стабилизации. В некоторых случаях
такая схема является достаточной. Однако с увеличением удлинения раке-
ты допущение о жестком корпусе становится все более условным. При
поперечных возмущениях длинный корпус перемещается не как твердое
тело, а как гибкий стержень. Учет упругости корпуса позволяет выявить
дополнительные динамические свойства, которые существенны, напри-
мер, для угловой стабилизации ракеты. Кроме того, содержащиеся в баках
ракеты значительные массы жидкого топлива могут перемещаться отно-
сительно стенок и создавать дополнительные силы (см. части III и IV).
4.2. Структурная схема системы стабилизации
Типовая структурная схема аналоговой (непрерывной) системы стаби-
лизации показана на рис. 4.9.
Отличия структуры дискретной системы стабилизации, построенной
на базе бортовой цифровой вычислительной машины (БЦВМ), приведены
в [7], [54] и в части 6 книги.
На схеме обозначено:
ОУ Ракета как объект управления
ККП Комплекс командных приборов.
1. Измеряет углы отклонения ракеты относительно трех
взаимно перпендикулярных осей связанной системы ко-
ординат с началом в центре масс ракеты.
2. Интегрирует поперечные ускорения центра масс ракеты
в боковом (z) и нормальном (у Направлениях.
В качестве ККП в современных автономных инерциальных
системах управления, как правило, используется трехосный
гиростабилизатор с чувствительными элементами, установ-
ленными на его «неподвижной», не зависящей от вращения
Земли и эволюций ракеты, гиростабилизированной конст-
руктивной части («платформе»).
ДК Д$ Датчик команд, вырабатывающий электрические сигналы, про-
порциональные отклонению угла тангажа от его программного
значения ($лр), задаваемого системой управления в соответст-
вии с параметрами номинальной траектории полета ракеты.
93
ДК ф, ДК ф Датчики команд углов вращения (крена) и рыскания соот-
ветственно.
ДК у, Датчики команд, вырабатывающие электрические сигналы, про-
ДК z порциональные величинам нормальной и боковой скоростей.
)z Усилители сигналов у и z.
УП
кк
Z-
)l-IV
PMj.iv
POi.iv
flOCi.iv
ОС i-iv
Интегрирующие звенья, вырабатывающие электрические
сигналы, пропорциональные отклонению центра масс раке-
ты в нормальном и боковом направлениях.
Прибор усилитель-преобразователь (УПАС) или счетно-
решающий прибор (СРП-АС), выполняющий все логические
преобразования поступающих в него сигналов.
Корректирующие контуры, обеспечивающие коррекцию ди-
намических свойств системы стабилизации в каналах танга-
жа, рыскания и вращения (крена).
Входные каскады суммирования (без гальванической связи)
и усиления сигналов, сформированных корректирующими
контурами каналов тангажа и вращения, усилителями сигна-
лов >у и >у9 а также сигналов отрицательной обратной
связи II и IV рулевых машинок. В качестве усилителей-
сумматоров нашли широкое применение магнитные модуля-
торы или магнитные усилители, в которых каждый «слагае-
мый» сигнал подается на свою первичную обмотку.
Аналогично для каналов рыскания и вращения, >у и >у,
а также сигналов ОС каналов I и III рулевых машинок.
Выходные каскады усиления и формирования командных
сигналов в рулевые машинки.
Рулевые машинки (рулевые приводы), являющиеся испол-
нительными элементами системы стабилизации ракеты как
объекта управления.
Рулевые органы, в качестве которых условно показан способ
управления путем отклонения камер двигателей, являющиеся
исполнительными элементами объекта управления - ракеты.
Датчики отрицательной обратной связи.
В отличии от потенциометрических датчиков (ПОС'ов), приме-
няемых в системах управления ракет первого поколения, в на-
стоящее время, как правило, используются индукционные дат-
чики (ИДОС’ы) существенно более надежные в условиях воз-
действия значительных по величине вибрационных перегрузок.
Цепи жесткой обратной связи, охватывающие РМ и оба кас-
када усиления, образуя сервопривод.
94
Рис. 4.9
Назначение практически всех звеньев системы стабилизации и выпол-
няемые ими функции представляются очевидными из структурной схемы
рис. 4.9.
Считаем необходимым более подробно рассмотреть возможные вариан-
ты построения корректирующих контуров и цепей обратной связи, учиты-
вая их определяющее влияние на динамические свойства системы в целом.
4.2.1. Корректирующий контур
В качестве корректирующего контура (КК) можно использовать диф-
ференцирующие контуры первого или второго порядка с индукционной
и омическими нагрузками (обмотка усилителя).
На рис. 4.10 показан дифференцирующий контур первого порядка. За-
висимость выходного тока ii от входного напряжения uv выражается
дифференциальным уравнением
(а2р2 + ахр +1)^ = кд (Тдр + (4.16)
где
а2 =ЬТдкд,
= кд \Тд (К + г) + ’
Тд=ДС,
R, г - омическое сопротивление, С - емкость, L - индуктивность.
R
Рис. 4.10
На рис. 4.11 показан дифференцирующий контур второго порядка или
иначе - двухзвенный контур.
Рис. 4.11
96
Уравнения такого двухзвенного контура в общем виде могут быть за-
писаны как
?кк*\ + ^^kkh + А ~ &кк [Ткк\ + ^‘У/ккТкк^^ + )
или в упрощенном виде (для установившегося режима)
А = &кк (TkkUp + 'tykkfkkUyf + и¥ )•
С целью создания АС повышенной надежности, обеспечивающего не-
обходимые запасы устойчивости на всем активном участке траектории
полета ракеты, могут применяться различные варианты коррекции дина-
мических свойств системы стабилизации. Например:
- использование в качестве КК пассивного дифференцирующего кон-
тура второго порядка в сочетании с охватом жесткой отрицательной об-
ратной связью контура сервопривода с большим (близким к критическо-
му) круговым коэффициентом усиления;
- использование дифференцирующего контура второго порядка в со-
четании с вводом гибкой внешней отрицательной обратной связи в контур
сервопривода;
- использование корректирующего контура первого порядка в сочетании
с форсированным электронным усилителем каналов угловой стабилизации.
Возможно использование этого варианта при настройке параметров
АС по одной из границ области устойчивости.
Форсирование усилителя обеспечивается вводом в его цепь обратной
связи корректирующего контура в виде
Ri R2
С;
-0
UBx Cl * Q * U вых
0------X——-1—0
Передаточная функция корректирующего контура имеет вид
+Зтр+Г
Передаточную функцию всего тракта можно записать в виде
V ' l + /?r2T r2+3rTx ^ + 7^
\+ри \+р \+р
Использование последнего варианта коррекции динамических свойств
системы стабилизации позволили создать АС, обеспечивающий (в сочета-
нии с плавным изменением коэффициента усиления Ку) стабилизацию ра-
кеты, имеющей значение степени статической неустойчивости - коэффи-
циент с - равное-12 1/с2!
97
Глава 5
УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
Исследование устойчивости движения современных баллистических
ракет относительно программной траектории представляет сложную тех-
ническую задачу. Сложность задачи обусловлена тем, что, как показано
в главе III, возмущенное движение ракеты описывается системой диффе-
ренциальных уравнений высокого порядка с переменными коэффициен-
тами, а возмущающие воздействия являются нестационарными случай-
ными функциями.
Существуют два подхода к исследованию устойчивости движения. По-
становка задачи, сформулированная А. М. Ляпуновым [103], характеризу-
ется следующими особенностями:
- рассматривается бесконечный интервал времени,
- устойчивость рассматривается только по отношению к начальным
возмущениям,
- начальные и последующие возмущения считаются малыми.
В ракетной технике широкое применение нашло понятие технической
устойчивости движения, разработанное и введенное Н. Д. Моисеевым
[108], а именно:
- рассмотрение устойчивости на конечном интервале времени,
- устойчивость рассматривается по отношению к начальным возму-
щениям и постоянно действующим возмущающим силам и моментам.
Рассматривая в качестве критерия обеспечение движения ракеты по
траектории, близкой к программной, можно сказать, что устойчивость
в смысле Ляпунова не является ни необходимым, ни достаточным услови-
ем, а только техническая устойчивость дает необходимые и достаточные
условия выполнения задачи. Следует, однако, подчеркнуть, что если сис-
тема устойчива в смысле Ляпунова, то надлежащим выбором величины
управляющих воздействий ее всегда можно сделать технически устойчи-
вой по отношению к произвольным возмущающим воздействиям. В силу
этого существующий метод проектирования системы управления ракет
предусматривает обеспечение локальной динамической устойчивости
движения в смысле Ляпунова.
Таким образом, деление задачи на управляемость, стабилизацию и ус-
тойчивость является весьма условным, поскольку проблема обеспечения
динамической устойчивости современных баллистических ракет нераз-
рывно связана, и более того, включает в себя рассмотренные в предыду-
щих главах задачи:
98
- определение характеристик автомата стабилизации и связанные
с ним расчеты локальной динамической устойчивости движения в смысле
Ляпунова,
- определение потребной эффективности управляющих органов
и связанные с ним расчеты технической устойчивости движения с учетом
возмущающих воздействий.
Устойчивость в смысле Ляпунова определяется внутренними свойст-
вами системы, поэтому при ее исследовании стремятся как можно полнее
математически описать как ракету, так и автомат стабилизации, при этом
учитываются высокочастотные осцилляторы, определяемые колебаниями
жидкого наполнения топливных баков, упругими колебаниями корпуса
и их взаимным влиянием. Наиболее полная система дифференциальных
уравнений, описывающих возмущенное движение ракет, получена в рабо-
тах [106], [107] и обобщена в [143].
Методы исследования устойчивости возмущенного движения очень
многообразны, наибольшее распространение получили частотные и ал-
гебраические методы. Окончательная проверка динамической устойчиво-
сти движения ракеты проводится путем моделирования возмущенного
движения по полной динамической схеме с реальной аппаратурой автома-
та стабилизации.
При проектировании автомата стабилизации стремятся к тому, чтобы
надлежащим выбором его характеристик исключить из спектра собствен-
ных движений замкнутой системы составляющие, соответствующие коле-
баниям жидкости и упругим колебаниям корпуса. Благодаря этому, замк-
нутая система в возмущенном движении ведет себя как система «твердое
тело+автомат стабилизации», и для расчетов по определению потребной
эффективности управляющих органов можно пользоваться упрощенной
системой уравнений возмущенного движения, описывающей ракету как
абсолютно жесткое твердое тело, уделяя главное внимание вопросу пол-
ного учета возмущающих воздействий.
Одним из важных вопросов динамического проектирования является
определение и назначение запасов устойчивости движения, гарантирую-
щих работоспособность системы во всех эксплуатационных режимах.
Следует отметить, что обеспечение запасов устойчивости в смысле Ляпу-
нова во многих случаях может быть достигнуто без усложнения и утяже-
ления системы стабилизации. Что же касается запасов технической устой-
чивости, то они могут быть получены только за счет увеличения эффек-
тивности управляющих органов, что накладывает более жесткие требова-
ния к техническому обоснованию применяемых методов расчета. Эта
сторона менее всего освещена в специальной литературе.
99
Сложность задачи обусловлена тем, что, как показано в главе III, ха-
рактеристики ракеты и возмущающие воздействия описываются случай-
ными функциями. Наиболее корректным является вероятностный подход
к решению этой задачи, поскольку при создании совершенных по удель-
ным характеристикам ракетных систем недопустимы избыточность и «за-
пасы», приводящие к потере энергетики.
Известным способом решения сложных вероятностных задач является
метод статистических испытаний. Препятствием для его использования
в задачах исследования технической устойчивости движения ракет в шес-
тидесятые годы являлись большие затраты машинного времени, связан-
ные с численным интегрированием уравнений возмущенного движения.
Рассмотрим инженерные методы исследования технической устойчи-
вости ракет применительно к задаче динамического проектирования.
Основное внимание будет уделено рассмотрению приближенных ре-
шений, требующих минимальных затрат труда и времени и дающих в то
же время достаточно надежные оценки технической устойчивости движе-
ния. Анализ технической устойчивости ракеты как стохастической систе-
мы рассмотрим на примере решения задачи определения потребной эф-
фективности управляющих органов ракеты, описываемой нестационар-
ным случайным линейным оператором, находящейся под воздействием
случайных нестационарных возмущающих факторов.
5.1. Вероятностная математическая модель ракеты.
Постановка статистического эксперимента
Исходной системой уравнений при анализе технической устойчивости
ракет является система уравнений возмущённого движения (5.1), которая
в матричной форме имеет вид:
х = Ax + Bx + Q, (5.1)
где х - обобщенная координата системы,
А, В - матрицы коэффициентов,
Q - столбец возмущающих воздействий.
Элементы матриц А, В и столбца Q являются функциями параметров
атмосферы, движения ракеты и автомата стабилизации и с учетом воз-
можных эксплуатационных отклонений последних от номинальных зна-
чений должны рассматриваться как случайные функции времени.
Задача анализа динамики стохастической системы (5.1) частично рас-
смотрена в предыдущих главах. При этом был следующий подход: веро-
ятностный анализ устойчивости системы в смысле Ляпунова и независимо
от этой задачи рассмотрение вероятностных способов задания возму-
щающих воздействий.
100
Такой подход является недостаточно корректным, так как вероятност-
ные характеристики оператора системы (исследование устойчивости
в смысле Ляпунова) взаимосвязаны с вероятностными характеристиками
возмущающих воздействий (исследование технический устойчивости).
Неполный совместный учет вероятностных характеристик как оператора
системы, так и возмущающих воздействий проведен в главе III, в резуль-
тате получены оценки сверху управляемости ракет.
Наиболее общим методом решения сложных вероятностных задач яв-
ляется метод статистических испытаний, позволяющий учесть вероятно-
стные характеристики большого числа случайных величин.
Однако такой метод с использованием применяемого в настоящее вре-
мя численного интегрирования системы уравнений возмущенного движе-
ния был бы связан с большими затратами машинного времени (от 2 до
5 часов времени работы ЭВМ в зависимости от полноты постановки зада-
чи)*), что, безусловно, затрудняло его использование в практике проект-
ных организаций.
Затраты машинного времени можно сократить во много раз, если при
постановке статистического эксперимента воспользоваться приближен-
ным решением. При постановке статистического эксперимента необходи-
мо учитывать следующие вопросы:
- вероятностное описание случайных функций, определяющих мат-
рицы А, В и столбец Q;
- количество опытов, необходимое для надежного определения ста-
тистических характеристик загрузки управляющих органов;
- необходимая точность аппроксимации возмущающих воздействий;
- степень влияния отклонений отдельных параметров на статистиче-
ские характеристики загрузки управляющих органов.
Параметры, характеризующие ракету как стохастическую систему,
можно разбить на две группы: параметры, определяемые состоянием ат-
мосферы (плотность воздуха и скорость ветра), и параметры, определяе-
мые ракетой и автоматом стабилизации (массовые, инерционные, центро-
вочные, аэродинамические характеристики ракеты, тяга основных и
управляющих двигателей, коэффициенты усиления автомата стабилиза-
ции и т. д.).
Частичный анализ ветрового поля атмосферы проведен в главе I. Там
показано, что скорость ветра является случайной величиной с ненулевой
средней. Предложено несколько вариантов описания скорости ветра как
случайной функции высоты для различных задач проектирования ракет:
) Оценка соответствует состоянию вычислительной техники в шестидесятые годы
прошлого столетия.
101
огибающая предельных ветров, каноническое разложение, градиентное
задание скорости ветра.
Задача анализа технической устойчивости ракет относится к классу за-
дач, в которых существенную роль играет не только величина скорости
ветра в данный момент времени, но и вся предыстория изменения профи-
ля ветра по высоте. Этому требованию лучше всего отвечает задание ско-
рости ветра в виде канонического разложения. Но каноническое разложе-
ние в работе [104] составлено для узловых высот с шагом 3 км и в силу
этого не отражает свойства ветрового поля в слоях Ah < 3 км.
Кроме того, методика [104] рекомендует при оценке управляемости
ракет задавать скорость ветра по огибающей предельных скоростей ветра,
скорректированной градиентом скорости ветра. Однако такой способ не
учитывает высотную корреляцию ветра и исходит из условия одновре-
менной реализации максимальной скорости ветра, что ужесточает резуль-
таты.
Рассматриваемый ниже способ задания ветровых воздействий при ана-
лизе технической устойчивости ракет исходит из представления профиля
ветра в виде канонического разложения [104]:
W(h) = W0(h) + Y^(h), (5.2)
i
где Wo(h) - систематическая составляющая скорости ветра;
Wj(h) - неслучайные функции;
Vj - случайные числа, M[VJ = 0, avi = 1.
Задаваясь произвольным набором чисел Vj, независимых и распре-
деленных по нормальному закону, можно получать реализации профиля
ветра с учетом высотной корреляции его значений. Полученный таким
образом профиль ветра правильно отражает закономерности ветрового
поля атмосферы на узловых высотах с шагом 3 км. В интервалах между
узловыми высотами закон изменения скорости ветра принят линейным.
Такая модель ветра пригодна для задач динамики, в которых проявляет-
ся интегральный эффект влияния ветра, например, для оценки кучности
стрельбы.
При анализе технической устойчивости ракет такая детализация про-
филя ветра недостаточна. Процессы стабилизации ракеты в существенной
степени определяются характером изменения ветра в слое 3 км, зачастую
ракета критична к резкому изменению скорости ветра в слое до 0,5 км. За-
кономерности ветрового поля атмосферы в толщине слоя 0,5 км отража-
ются данными по вертикальному сдвигу ветра (градиенту скорости ветра).
В методике НИИ-88, разработанной в 1969 г., приведены значения гра-
диента скорости ветра для слоя Ah = 0,5; 1; 2; 3 км. Распространим эти
данные на произвольный слой действия градиента, аппроксимируя зави-
102
симость ломаной линией. На рис. 5.1 приведена полученная зависимость
вертикального сдвига ветра (AW) в функции толщины слоя (Ah) для раз-
личных высот полета (h).
Рис. 5.1
Скорректируем профиль ветра, полученный по каноническому разло-
жению (5.2) следующим образом. На высоте h^, соответствующей макси-
мальной скорости ветра, сформируем сдвиг ветра, выбрав толщину слоя
действия по равновероятному закону в диапазоне Ah = 0...3 км. Величину
сдвига ветра AW определим по формуле:
(5.3)
где к - случайное число, М[к] = 0, Зак= 1,
AWQixp, Ah) - величина сдвига ветра, определяемая по графикам рис. 5.1.
В зависимости от знака AW профиль ветра (5.2) корректируется в рай-
оне hxp либо вправо, если AW>0, либо влево, если AW<0 (см. рис. 5.2), при
этом максимальная величина скорости ветра увеличивается на величину
сдвига ветра и сдвигается по высоте на величину Ah. В случае, если полу-
ченное максимальное значение превышает огибающую предельных вет-
ров АУогиб, в качестве максимального значения скорости ветра принимает-
ся значение огибающей.
Сформированный профиль ветра полностью согласуется с данными
работы [104] и соответствует требованиям задачи анализа технической
устойчивости ракет.
юз
W, м/с
В настоящее время при анализе технической устойчивости ракет от-
клонения плотности воздуха от номинальных значений задаются по оги-
бающей максимальных значений в соответствии с ВСА-60. Это не обес-
печивает расчет в запас, так как не учитывается высотная корреляция из-
менения плотности воздуха, приводящая к градиентным нагрузкам. Наи-
более полно вероятностный характер изменения плотности воздуха
описывается каноническим разложением:
= (S.4)
L pAh) < a(a)J
где pH(h) - номинальное значение плотности;
Ар(й) „ „
—7^7 - среднее значение канонического разложения в случайной
А(Л)
точке;
Дд(й) .
—- координатные функции канонического разложения в случаи-
а(л)
ной точке;
Xi - случайные числа, M[Xi] = 0, axi = 1,
Отклонения параметров ракеты от номинальных значений, обуслов-
ленные рядом независимых факторов, можно считать распределенными
по нормальному закону, а их реализации определять по формулам:
104
5(/) = 5Д/)
1 + Jts
AS’(z)
W.
S = C^,Cay,Xd,Xm,P,P^,Jz, (5.5)
"’W=w-.(z)+^Aw’(0)>
где SH - номинальное значение,
Д5
—------максимальное случайное относительное отклонение,
тн - номинальная масса,
Дт(0) - максимальное случайное отклонение стартовой массы,
ks, km - случайные числа, M[ks, km] = 0,3<iks,km = 1.
При этом не представляет труда коррелированный учет отклонений
массы, центра масс и момента инерции.
Параметры AC к 9Т 9kt являются случайными величинами, подчинен-
ными нормальному закону распределения, их реализации можно опреде-
лять по формуле:
1 г, I
а = ан \ + ка— ,
аи )
(5.6)
где a = k¥,Tq,ki9
ан - номинальное значение параметра,
Да - максимальное случайное отклонение параметра;
ка - случайные числа. M[kJ = O,3cika= 1 •
Еще одну группу случайных величин составляют погрешности изго-
товления и монтажа ракеты и двигательной установки.
В главе I показано, что случайные составляющие являются независи-
мыми между собой и подчинены нормальному закону распределения.
Реализация составляющей перекоса (смещения) может быть определе-
на по формуле:
7 = Моих > (5-7)
Лтах - максимальное значение составляющей перекоса (смещения);
кл - случайное число, М[кл] = 0,ЗакЛ = 1.
Уравнения (5.2)-(5.7) позволяют в рамках статистического экспери-
мента сформировать реализации элементов матриц А, В и столбца Q.
Применив приближенное решение для загрузки управляющих органов,
можно определить реализацию последней. После проведения N опытов
статистические характеристики загрузки управляющих органов рассчиты-
ваются по формулам:
105
8k(t) - реализация загрузки управляющих органов в k-м опыте.
Таким образом, решается задача определения потребной эффективно-
сти управляющих органов ракеты как стохастической системы. Потреб-
ный управляющий момент определяется по формуле:
упр Рупр^тах. >
При решении задачи исходили из того, что управляющее усилие Рупр
задано, и требовалось определить угол отклонения управляющих органов.
Пересчет на другое Рупр очевиден. Выбор рационального соотношения
между тягой управляющих органов и углом их поворота проводится из
более общих условий проектирования ракеты.
Таким образом, рассмотренный метод статистических испытаний мо-
жет быть рекомендован как расчетный способ определения потребной
эффективности управляющих органов ракет.
В этом случае при малых затратах машинного времени (~ 15 мин.)
можно получить расчетные значения статистических характеристик за-
грузки управляющих органов ракеты с учетом случайного характера па-
раметров динамической схемы.
106
Часть 2
УПРАВЛЕНИЕ РАКЕТОЙ ПУТЕМ
ОТКЛОНЕНИЯ ГОЛОВНОГО ОТСЕКА
До изложения теоретических основ и описания конструктивно-
компоновочного решения нетрадиционного способа управления твердо-
топливной ракетой представляется целесообразным некоторое отступле-
ние («исторический экскурс») для обоснования необходимости ввода
в систему вооружения в восьмидесятые годы прошлого столетия еще од-
ной модели твердотопливной МБР наземного базирования.
Кроме того, необходим показ объективных причин поиска и реализа-
ции на этой модели нового способа управления в дополнение к многочис-
ленному ряду ранее созданных органов управления (глава 1), апробиро-
ванных при эксплуатации на ракетах США и СССР.
107
Глава 6
ПРИЧИНЫ СОЗДАНИЯ И ОСНОВНЫЕ ПОЛОЖЕНИЯ
НОВОГО СПОСОБА УПРАВЛЕНИЯ
6.1. Предыстория разработки IV поколения МБР
Во второй половине семидесятых годов XX века противостояние двух
великих ядерных держав и их «соревнование» в области создания меж-
континентальных баллистических ракет стратегического назначения на-
земного базирования можно характеризовать как патовую, или точнее,
цугцванговую шахматную позицию.
Такое положение определялось следующими обстоятельствами.
В США - завершено создание системы вооружения на базе твердотоп-
ливных МБР легкого класса типа «Минитмен» двух моделей:
• с моноблочной головной частью «Минитмен-П» - 450 МБР второ-
го поколения;
• с трехблочной РГЧ индивидуального наведения (РГЧ ИН) «Ми-
нитмен-Ш» - 550 МБР III поколения.
Все ракеты обладали достаточно высокой точностью попадания в цель
и располагались в одиночных рассредоточенных шахтных пусковых уста-
новках высокой прочности.
Уровень стойкости ракет к ПФ ЯВ не допускал проведения ответно-
встречного удара в условиях ядерного воздействия по БРК.
В СССР - завершено создание системы вооружения РВСН в основном
на базе жидкостных МБР III поколения [131], в том числе:
• модернизированных ракет Р-36 тяжелого класса типа 15А14 и
15А18, оснащенных десятиблочной РГЧ ИН при высокой точности
попадания. Более 300 ракет этого типа располагались в одиночных
ШПУ высокой степени защищенности,
• модернизированных ракет УР-100 легкого класса, включая:
- 15АЗО и 15А35 - всего 240 МБР, оснащенных шестиблочной
РГЧ индивидуального высокоточного наведения.
Стартовый вес этой модели -105 т (вес базовой модели -50 т), т. е. ра-
кета «переведена в средний класс».
- 15А15и15А16 - всего 150 МБР, оснащенных четырехблочной
РГЧ высокоточного индивидуального наведения. Стартовый
вес -72 т.
Кроме указанных ракетных комплексов III поколения в составе сис-
темы вооружения РВСН в этот период находились ракетные комплексы
II поколения с модернизированными ракетами УР-100К и УР-100У. Все-
108
го ~400 МБР этого типа могли оснащаться трехблочной кассет-
ной РГЧ.
Наряду с жидкостными ракетами в составе РВСН имелось по несколь-
ко десятков РК с моноблочными твердотопливными ракетами РТ-2П
II поколения и «Темп-2С» III поколения. Подробнее о ракетах этого типа
см. ниже.
В целом к концу семидесятых - началу восьмидесятых годов МБР на-
земного базирования были оснащены более чем 600(Р ядерных боезаря-
дов, но ни один из указанных типов ракет не допускал возможности про-
ведения ответно-встречного пуска в условиях ядерного воздействия про-
тивника по району боевого ракетного комплекса и даже по позиционному
району.
Таким образом, ни одна из сверхдержав, обладая колоссальным
ядерным потенциалом, исчисляемым миллиардами тонн тротилового
эквивалента и имея соответствующие средства их доставки на межкон-
тинентальные дальности, в здравом уме не могла рассчитывать на дос-
тижение каких-либо преимуществ ни в каком варианте применения это-
го вооружения.
Но в то же время, ни одна из стран не была застрахована от решения
какого-нибудь властного авантюриста-параноика нанести упреждающий
массированный удар всеми силами «ядерной триады» (МБР + БРПЛ +
МБ) по всей совокупности ракет противника с целью выведения их из
строя либо в ШПУ - действием ударной волны ЯВ, либо - в случае
встречного старта ракет - на начальном участке траектории под воздейст-
вием всех поражающих факторов ЯВ.
Именно эти два обстоятельства стали важнейшей причиной, во-пер-
вых, переговорного процесса об ограничении СНВ и, во-вторых, развер-
тывания работ по созданию еще более совершенных ракетных комплексов
МБР, обеспечивающих эффективный ответно-встречный удар в условиях
ядерного воздействия противника по боевому ракетному комплексу.
Такими ракетными комплексами четвертого поколения явились:
• В США - «Минитмен-Х» («МХ») с ТТРД и шахтным способом ба-
зирования;
• В СССР
- 15А18М («Сатана») с ЖРД и шахтным способом базирования;
РТ-23УТТХ с ТТРД с шахтным (15Ж60) и железнодорожным
(15Ж61) способами базирования;
> Разница в количестве боезарядов -4000 ББ, установленных на ракетах наземного
базирования США и СССР, компенсировалась соответствующим числом боеголовок
БРПЛ.
109
- РК «Тополь» с МБР РТ-2ПМ (15Ж58) - подвижный грунтовой
РК с твердотопливной ракетой.
Ракета 15А18М как объект управления практически не отличалась от ра-
кеты 15А18 (см. Введение), эффективность органов управления которой не
вызывала никаких нареканий за весь двадцатилетний срок ее эксплуатации.
Вместе с тем, ракета 15А18М должна удовлетворять дополнительному
требованию, вытекающему из ее основного назначения - обеспечение от-
ветно-встречного пуска в условиях ЯВ по району БРК. Применительно
к объекту управления решение такой задачи накладывает соответствую-
щее ужесточение требований к эффективности исполнительных органов
ракеты: обеспечение управляемости в условиях воздействия ударной вол-
ны (УВ) ядерного взрыва. Характеристики этого дополнительного возму-
щающего фактора задавались Заказчиком в виде документа «Модель ЯВ»
(по образу и подобию «Методики...» [104]).
Экспресс-анализ соответствия органов управления ракеты 15А18М ус-
ловиям эксплуатации при совместном воздействии ветра и УВ с парамет-
рами, задаваемыми указанными документами, в детерминированной по-
становке задачи дал отрицательные результаты. Однако вероятностный
подход к ее решению (метод Монте-Карло) подтвердил допустимость
эксплуатации ракеты с имеющимися органами управления с достаточным
уровнем надежности.
На ракете РТ-2ПМ были использованы традиционные типы органов
управления, исследование которых достаточно подробно проведено в мо-
нографии Н. Д. Коваленко [86].
Поэтому ниже остановимся только на особенностях процесса создания
и достигнутых тактико-технических характеристиках оригинальных твер-
дотопливных ракет СССР и США.
6.2. Исходные положения и ход работ
по созданию МБР IV поколения
6.2.1. США - МБР «Минитмен-Х»
В США с 1962 года после принятия на вооружение двухступенчатой
МБР «Титан-П», имевшей стартовую массу —148 т при массе моноблочной
полезной нагрузки ~3,2 т (Квс. = 21,6 кг/т) работы по созданию боевых
межконтинентальных ракет с ЖРД на высококипящих компонентах топ-
лива были прекращены.
Еще в 1956 году в США были начаты широкомасштабные исследова-
ния по использованию в этих целях ТТРД, как для ВВС - МБР наземного
базирования, так и для ВМФ - БРПЛ. Выбор этого направления опреде-
по
лялся высоким удельным импульсом смесевого топлива и технологией его
заливки в корпуса. Существенную роль сыграло подтверждение отрасля-
ми промышленности возможности достижения в ближайшей перспективе
существенного улучшения удельных характеристик ББ, СУ, конструкци-
онных материалов и других составляющих ракет.
В результате уже в 1960 году были завершены работы по созданию
БРПЛ «Поларис А1», а в 1962 году - МБР «Минитмен-I». Эта трехступен-
чатая МБР легкого класса имела стартовую массу ~32 т при массе полез-
ной нагрузки -0,7 т, коэффициент весового совершенства Кв.с. ~ 21,8 кг/т,
т. е. практически равный достигнутому в то же время Квх. двухступенчатой
жидкостной ракеты среднего класса.
К моменту начала работ над программой «МХ» в США имели бога-
тейший опыт боевой эксплуатации трех поколений МБР типа «Минит-
мен»: MI - с 1962 года; МП - с 1965 года; Mill - с 1970 года.
Только в период с июня 1963 года по сентябрь 1983 года с базы ВВС
Ванденберг было проведено 453 пуска ракет типа «Минитмен» (не считая
пусков, проведенных в рамках ЛКИ).
Управление вектором тяги обеспечивалось:
• на ракетах «Минитмен-П»
- на I и III ступенях - четырьмя качающимися соплами;
- на II ступени - впрыском жидкости в закритическую часть не-
подвижного сопла;
• на ракетах «Минитмен-Ш»
- на I ступени - четырьмя качающимися соплами с углом откло-
нения до ±7,5°;
- на II ступени - впрыском жидкости в закритическую часть не-
подвижного сопла;
- на III ступени - по тангажу и рысканию - впрыском жидкости
в закритическую часть сопла; управление по крену - реактив-
ными соплами, работающими на горячем газе.
Кроме опыта, накопленного США в процессе создания и эксплуатации
МБР «Минитмен», к моменту начала полномасштабной разработки ракет
«МХ» использовался в полной мере научно-технический потенциал, по-
лученный в результате работ по созданию и эксплуатации ТТРД трех по-
колений БРПЛ:
• I поколение - 1956-1962 гг. - «Поларис А1» и «Поларис А2» - бо-
лее 50 ракет с моноблочной ГЧ;
• II поколение - 1961-1964 гг. - «Поларис АЗ»,
1965-1971 гг. - «Посейдон СЗ»,
всего -650 ракет в основном с моноблочной ГЧ,
111
• III поколение - 1971-1979 гг. - «Трайдент С4»,
1981-1990 гг. - «Трайдент С5»,
-650 ракет с РГЧ ИН (-5000 ББ).
* * *
Целевая программа MX предусматривала создание МБР, которая по
своим энергетическим возможностям и точности стрельбы превзойдет
МБР «Минитмен» и позволит поражать малоразмерные и защищенные
цели.
Работы по программе MX были начаты в середине 1973 г. Этап перспек-
тивных исследований продолжался около шести лет - до октября 1979 г.
На этом этапе в период до марта 1976 г. было изучено около полутора де-
сятков альтернативных вариантов ракеты со стартовой массой от 27 до
143 т. Окончательно был выбран вариант со стартовой массой 88,4 т.
Период времени с 1976 г. по 1979 г. характеризовался эксперименталь-
ными исследованиями и разработками как по ракете, так и по способам ее
базирования.
Полномасштабная разработка началась в октябре 1979 г.
Фактически предварительное проектирование ракеты и ее главных
подсистем было начато еще на этапе демонстрации и подтверждения кон-
цепции, что позволило уже в апреле 1982 г. приступить к стендовым ис-
пытаниям РДТТI ступени.
Как известно, военно-политическое руководство и конгресс США мно-
гократно рассматривали вопрос о базировании МБР MX, и в 1983 г. было
принято решение о размещении первых пятидесяти ракет в модернизиро-
ванных шахтных пусковых установках МБР «Минитмен».
Летно-конструкторские испытания МБР MX начались в 1983 г. и
должны были закончиться в 1987 г. Однако в связи с задержкой поставок
инерциальных измерительных блоков (ИИБ) AIRS, ВВС США отложили
проведение трех последних испытаний МБР MX до 1988 г.
К середине 1988 г. было проведено 17 испытательных пусков. Всего
программой ЛКИ было предусмотрено проведение 20 пусков с АБ Ванден-
берг в сторону атолла Кваджелейн (Западный испытательный полигон).
По завершении ЛКИ планировалось начать контрольно-испытательные
пуски. В соответствии с нормами контрольно-испытательных пусков, оп-
ределенными из расчета 15-летнего периода пребывания МБР MX на бое-
вом дежурстве, для этих целей были предусмотрены 123 ракеты.
В декабре 1988 г. проводились работы по установке 50 МБР MX в пе-
реоборудованные шахты МБР «Минитмен» на базе ВВС США Уоррен
(шт. Вайоминг). К декабрю 1989 г. они были переданы в ведение коман-
дования материально-технического обеспечения ВВС США.
112
МБР «Минитмен-Х» как объект управления представляла собой
трехступенчатую баллистическую ракету среднего класса с тандемной
схемой построения, твердотопливными маршевыми двигателями и с раз-
деляющейся десятиблочной головной частью. РГЧ состояла из боевого
отсека и ступени разведения с жидкостной двигательной установкой.
Пуск МБР проводился из пускового контейнера с использованием
ПАД’а («холодный пуск»), при этом включение РДТТ I ступени происхо-
дило на высоте 15-20 м.
Основные характеристики «МХ»:
• Стартовая масса - 88400 кг, масса полезного груза - 3430 кг.
• Коэффициент весового совершенства ~38,8 кг/т.
• Удлинение (отношение общей длины к диаметру) 21,6/2,34 - 9,23.
• Точность стрельбы (предельное отклонение - 2,3 КВО) - 300 м.
• Конструкция двигателей всех трех маршевых ступеней выполнена
в виде моноблока с одиночным центральным отклоняемым (пово-
ротным) соплом. Рабочий угол - ±6 градусов (I и II ступени) и ±3
градуса (III ступень). Такой орган управления вектором тяги обес-
печивал создание круговой диаграммы Рупр. Скорость отклонения
сопла - 40 градусов/с.
• Тяга осевого двигателя РГЧ - 1360 кгс.
• Угол отклонения вектора тяги осевого двигателя - ±15 градусов.
• Система ориентации и стабилизации (СУОС) РГЧ - 8 двигателей
с тягой 30 кгс.
6.2.2. СССР - МБР РТ-23 (РТ-23 УТТХ)
Созданию окончательного варианта ракет РТ-23УТТХ предшествовал
многолетний этап проведения научно-исследовательских, проектно-
конструкторских и экспериментальных работ во многих специализиро-
ванных предприятиях бывшего Советского Союза.
Работы велись широким фронтом, в том числе с частичным дублиро-
ванием, в направлениях:
• разработки перспективных рецептур высокоэнергетического смесе-
вого топлива и технологии его заливки в корпуса двигателей [52];
• разработки конструкционных материалов корпусов двигателей
и формы зарядов с оптимальными удельными характеристиками [51];
• разработки наиболее эффективных органов управления, вызываю-
щих наименьшую потерю удельной тяги при приемлемой стоимо-
сти, технологичности, эрозионной стойкости и др.;
• создания энергетически наивыгоднейших конструкций двигателей;
• разработки оптимальных компоновочных схем МБР в целом, их
конструкции и способов базирования.
из
Первой опытно-конструкторской работой по созданию со сдачей на
вооружение была разработка РК 15П098 с ракетой РТ-2 [84].
Официально разработка была задана соответствующим постановлени-
ем в апреле 1961 года.
Работы проводились кооперацией предприятий, общее руководство
которыми возлагалось на ОКБ-1, возглавляемое академиком С. П. Коро-
левым. Заместителем Главного конструктора, непосредственно руково-
дившим работами по созданию МБР РТ-2, являлся И. Н. Садовский.
Межконтинентальная баллистическая ракета РТ-2 как объект управле-
ния представляла собой трехступенчатую твердотопливную МБР легкого
класса, построенную по тандемной схеме с моноблочной ГЧ.
Пуск РТ-2 производился за счет собственного двигателя I ступени из
глухого пускового стакана ШПУ типа «ОС» - «горячий» тип старта -
с частичным отводом газов через решетчатые окна в стакане.
Все РДТТ серийной ракеты РТ-2 снаряжались смесевым топливом,
в отличие от ее «предшественницы» - ракеты среднего радиуса действия
РТ-1, разработанной и испытанной под руководством И. Н. Садовского.
Первый успешный пуск ракеты РТ-2 состоялся в феврале 1966 года
с Государственного центрального полигона (ГЦП-4). Из-за невозможно-
сти пуска ракет на полную дальность, с этого полигона было проведено
только семь испытаний из 32, выделенных на ЛКИ. Дальнейшие испыта-
ния ракеты проводились с «северного» полигона - НИИП-53 в течение
двух лет - с ноября 1966 года по октябрь 1968 года.
В декабре 1968 года РК первой отечественной МБР с ТТРД, снаряжен-
ными смесевым топливом, был принят на вооружение.
К 1971 году было развернуто 60 ШПУ с РТ-2.
С 1972 года ракеты РТ-2 стали заменяться усовершенствованным ва-
риантом РТ-2П (процесс, аналогичный описанному выше, по замене «Ми-
нитмен-I» на «Минитмен-П»).
Основные характеристики ракеты РТ-2 как объекта управления:
• Стартовый вес -48 т. Вес «легкой» головной части -550 кг.
• Коэффициент весового совершенства -11,5 (при дальности стрель-
бы 9600 км).
• Органы управления - разрезные сопла двигателей всех ступеней.
• Стабилизаторы - решетчатые аэродинамические на I ступени.
• Длина полная - 21,27 м, максимальный диаметр корпуса - 1,84 м,
с «юбкой» - 2,0 м и размахом стабилизаторов -3,6 м.
• Точность стрельбы (предельное отклонение - 2,3 КВО) —5 км.
• Система управления - второе поколение (аналоговая с ГСП).
• Азимут прицеливания - ±45 градусов.
114
Дальнейшее развитие ракеты РТ-2 было проведено во исполнение по-
становления от декабря 1968 года, которым РК этой ракеты был принят на
вооружение. Основными отличиями ракеты РТ-2П от базового варианта
были: применение более совершенной ГЧ с весом, уменьшенным на 70 кг,
но большей мощности; комплектация новым двигателем III ступени
с двухслойным корпусом и модернизированным двигателем II ступени;
перевод всех трех ТТРД на однотипное смесевое пластичное твердое топ-
ливо; расширение сектора прицеливания до ±120 градусов; увеличение
максимальной прицельной дальности на 400 км и уменьшение минималь-
ной дальности до 1000 км.
* * *
Вторым, по времени начала работ, отечественным ракетным комплек-
сом с твердотопливной межконтинентальной ракетой был РК «Темп-2С»
с МБР 15Ж42.
Разработка комплекса МБР официально была задана НИИ-1 (МИТ) на
конкурсной основе с КБ «Южное» постановлением от марта 1966 года.
Предэскизные проработки РК в НИИ-1 были выполнены еще в 1965
году под индексом «Темп-С2», имея в виду дальнейшее развитие ранее
разработанной ракеты среднего радиуса действия комплекса «Темп-С».
В период 1965-1969 гг. был проработан ряд вариантов базирования
комплекса (ШПУ, грунтовой, ж/д) и, соответственно, ракет под эти вари-
анты. Стартовый вес МБР в процессе разработки изменялся от 37 до 44 т
в зависимости от базирования, комплектации полезной нагрузки и моде-
лей подвижных грунтовых средств (гусеничных, колесных).
Разработка комплекса «Темп-2С» конкретно с подвижной грунтовой
ПУ была задана НИИ-1 в июле 1969 года.
Летные испытания 35 ракет 15Ж42 начались в марте 1972 года и про-
должались до декабря 1974 года.
Первые два ракетных полка стали на боевое дежурство в феврале
1976 года. Всего было развернуто 7 ракетных полков (по данным, опубли-
кованным в США, в 1978-1985 гг. было развернуто под Плесецком от 50
до 100 МБР «Темп-2С»).
Основные характеристики ракеты 15Ж42 как объекта управления:
• Тип комплекса - подвижный грунтовой РК стратегического назна-
чения с твердотопливной трехступенчатой МБР III поколения (мо-
ноблочная боевая ступень; СУ с БЦВМ).
• Точность стрельбы (2,3 КВО) —3,5 км.
• Стартовый вес - ~44 т; вес головной части - 940 кг. Коэффициент
весового совершенства —21,4 кг/т (как указывалось выше, РТ-2П -
~11,5 кг/т, «Минитмен» —21,8 кг/т).
115
• Тип старта - минометный из ТПК с помощью ПАД.
• Длина -18,5 м, максимальный диаметр корпуса 1,79 м; решетчатые
стабилизаторы на I ступени.
• Органы управления - I ступень - газовые из тугоплавкого вольфра-
ма и аэродинамические решетчатые рули; II и III ступени - по крену
- газовые сопла с газогенератором; по тангажу и рысканию - вдув
в закритическую часть сопла горячих газов.
• Боевая ступень - четыре РДТТ малой тяги.
• Особенность - при разделении I и II ступеней введена пауза на за-
пуск двигателя в 10 с, что обеспечило, при соответствующей потере
энергетики (дальности стрельбы), управляемость II ступени мало-
мощными органами управления.
* * *
При создании ракетного комплекса с МБР РТ-23 (РТ-23 УТТХ) безус-
ловно учитывался также опыт разработки, испытаний и эксплуатации
РСРД 15Ж45 грунтового РК «Пионер». Двухступенчатая ракета, осна-
щаемая трехблочной РГЧ, создавалась на базе I и II ступеней ракеты
15Ж42. Разработка комплекса была задана постановлением от апреля
1973 года. ЛКИ с пуском 21 ракеты проводились в период с сентября 1974
года по март 1976 года. Комплекс сдан на вооружение в марте 1976 года.
Первый ракетный полк заступил на БД в августе 1976 года. Массовое раз-
вертывание комплекса началось с 1978 года. К 1986 году были разверну-
ты 441 ПУ.
На базе ракеты 15Ж45 в 1980 году был создан модернизированный ва-
риант с улучшенными ТТХ - ракета 15Ж53. Дальнейшее совершенствова-
ние ракеты в направлении увеличения «квадрата» разведения и повыше-
ния точности стрельбы проводилось в рамках работы «Пионер-3».
Ракетные комплексы «Пионер» ликвидированы по договору РСМД
в конце восьмидесятых годов прошлого века.
* * *
По аналогии с процессом создания в США комплекса ракеты «МХ»,
в бывшем Советском Союзе разработка РТ-23 (РТ-23 УТТХ) велась с уче-
том опыта проектирования, изготовления и эксплуатации твердотоплив-
ных ракет для ПЛ.
Значительным успехом в решении проблемы создания морских твер-
дотопливных ракет явилась разработка ГРЦ «КБ им. академика В. П. Ма-
кеева» ракеты РСМ-52 [18].
Разработка ТТРД I ступени ракеты РСМ-52 была осуществлена в пол-
ном объеме силами ГКБ «Южное» им. академика М. К. Янгеля. Более то-
го, I ступень ракеты РСМ-52 унифицирована с ТТРД I ступени ракеты
116
PT-23 (PT-23 УТТХ)! Характеристики этого двигателя приводятся в раз-
деле «ОХ РТ-23».
Разработка комплекса БРПЛ РСМ-52 велась в период 1973-1983 гг.
Ряд прогрессивных технических решений, реализованных в конструк-
ции ракеты РСМ-52, обеспечил впервые в бывшем СССР создание твер-
дотопливного РК для подводного флота, превосходящего по многим па-
раметрам зарубежный аналог III поколения БРПЛ.
Разработанный ранее - 1971-1980 гг. - в КБ Ленинградского произ-
водственного объединения «Арсенал» морской комплекс с твердотоплив-
ной ракетой РСМ-45 был доведен лишь до опытной эксплуатации, но
опыт создания этой БРПЛ также являлся определенной отправной базой
при разработке РТ-23.
* * *
Работы по твердотопливной тематике, т. е. по исследованию возмож-
ности создания ракетных комплексов с МБР на базе ТТРД были начаты
в КБ «Южное» в начале шестидесятых годов XX века.
В течение 1961-1962 гг. проводилась НИР, результаты которой пока-
зали, что разработка в ближайшие годы «чисто твердой» малогабаритной
МБР с требуемыми перспективными характеристиками нереальна.
Альтернатива была найдена в виде двухступенчатой комбинированной
ракеты легкого класса РТ-20П (8К99) с твердотопливной первой и ампу-
лизированной жидкостной II ступенями. МБР предназначалась для созда-
ния грунтового подвижного комплекса на конкурсной основе с НИИ-1
(см. «Темп-2С»).
В проектном плане в течение 1966-1974 гг. был выпущен целый ряд
соответствующих документов по ракетным комплексам с ракетами РТ-21
(15Ж41), РТ-22 (15Ж43) с различными типами старта.
По результатам проведенных работ были сформулированы достижи-
мые в то время характеристики комплекса с ракетой РТ-23 стационарного
базирования (15Ж44), предшествующей созданию РТ-23УТТХ.
Полномасштабная разработка комплекса ракеты 15Ж44 с моноблочной
ГЧ была задана в июне 1976 года.
К моменту выхода постановления у разработчиков комплекса имелся
вполне достаточный задел для создания как ТТРД, так и ракет на их базе.
На модельных и опытных двигателях отрабатывались новые топлива, спо-
собы снаряжения, формы зарядов, конструкционные, теплозащитные
и эрозионностойкие материалы, способы управления вектором тяги и др.
В составе ракеты 8К99 прошел летные испытания двадцатитонный ТТРД.
Полномасштабная разработка боевого железнодорожного ракетного
комплекса с ракетой 15Ж52 была задана в июне 1979 г. Этим же постанов-
лением моноблочная ГЧ на обоих вариантах ракет была заменена на РГЧ.
117
6.2.3. Управляемость PT-23
Как уже указывалось выше, исходя из технических, экономических и
организационных соображений на I ступени ракеты РТ-23 должен и мог
быть использован ТТРД разработки КБЮ для БРПЛ типа РСМ-52, созда-
ваемой в этот период времени Государственным ракетным центром «КБ
имени академика В. П. Макеева».
Для II и III ступеней на подходе были двигатели разработки КБЮ и КБ
ПО «Искра». Но ракета не версталась.
Дело в том, что для реализации энергетически оптимальной траекто-
рии, обеспечивающей выведение требуемого полезного груза, необходимо
было осуществить разделение I и II ступеней при значениях скоростного
напора, на порядок превышающих традиционные. Положение усугубля-
лось тем, что твердотопливный двигатель I ступени, работавший до выго-
рания, имел продолжительный участок спада тяги, на части которого
управляющие усилия, пропорциональные текущей тяге, недостаточны для
парирования ветровых воздействий. В результате отклонения I ступени
в каналах тангажа и рыскания могли достичь значительных величин, что
само по себе осложняло процесс разделения ступеней и исключало при
этом возможность введения паузы по аналогии с БР «Темп-2С». Но глав-
ная трудность заключалась в том, что для парирования этих отклонений
на участке полета II ступени потребные управляющие усилия составляли
>10 % от тяги двигателя, что принципиально недостижимо для исполь-
зуемого в создаваемом двигателе II ступени способа управления вектором
тяги путем вдува газа в закритическую часть сопла.
Такие управляющие усилия можно было получить на поворотном со-
пле, [92], [86] аналогичном используемому в «МХ», но технология пово-
ротного управляющего сопла ещё не была отработана, хотя американцы
однозначно приняли решение о внедрении такого органа управления. КБ
НПО «Искра» на двигателе III ступени меньшей размерности решило
применить аналог поворотного сопла, но испытывало принципиальные
затруднения в связи с повышенными упругими деформациями конструк-
ции, тем более опасными на большом сопле ДУ II ступени ракеты РТ-23.
Необходимо было найти такой способ управления ракетой [93], кото-
рый бы исключил неуправляемые участки полета при разделении ступеней.
Одним из таких способов является управление по схеме «утка», когда
управляющие органы - это может быть двигатель или аэродинамические по-
верхности - расположены в передней части ракеты. Однако проведенные
оценки показали, что управление по схеме «утка» недопустимо снижает энер-
гетические характеристики ракеты в случае использования двигателя и явля-
ется проблематичным для аэродинамических рулей по условиям минометно-
го старта и действия ударной волны от ЯВ на активном участке полета.
118
В 1967 г. группой проектантов КБ был запатентован принципиально
новый способ управления путем поворота головного отсека в двухстепен-
ном кардановом шарнире [69]. Этот способ использует две составляющие
возникающего управляющего усилия: аэродинамическую - в плотных
слоях атмосферы и массовую - на всём участке полета. В этом случае го-
ловной отсек задействовался на управление на конечном участке полета
I ступени, как раз там, где управляющих усилий от двигателя недостаточ-
но, исключался неуправляемый участок полёта при разделении ступеней,
дальнейшее управление II и III ступенями обеспечивалось за счет голов-
ного отсека, маршевые двигатели II и III ступеней были выполнены со
стационарными соплами без органов управления, что позволяло снизить
их вес, обеспечить оптимальную высотность и исключить потери Руд.
В декабре 1976 г. научно-технический Совет предприятия, проведен-
ный с привлечением ведущих специалистов отрасли, рекомендовал этот
вариант ракеты для эскизного проектирования, как единственно возмож-
ный в тех условиях.
Через год был разработан совместный отчет всех заинтересованных ор-
ганизаций: разработчиков ракеты, ТТРД, СУ и заряда с детальным сравне-
нием принятого варианта с классическим на основе твердотопливных дви-
гателей с перспективными поворотными соплами. Основной вывод: при-
нятый вариант имеет существенно лучшие технико-экономические показа-
тели по сравнению как с традиционными, так и с перспективными:
• упрощается конструкция двигателей, сокращаются объем и сроки
их отработки, повышается энергетика;
• исключаются неуправляемые переходные участки;
• могут быть использованы энергетически оптимальные траектории;
• ожидаемая экономия составляла 135 млн руб.
Основными проблемными вопросами при реализации этого варианта
были: адекватность динамической схемы; создание СУ при параметрах
ракеты, существенно отличных от традиционных, моделирование системы
стабилизации и ряд других.
КБЮ в сотрудничестве с ведущими специалистами страны - ЦНИИМаш,
днепропетровского Института технической механики АН УССР и Днепро-
петровского национального университета была разработана динамическая
схема (система дифференциальных уравнений) двухмассовой системы с пе-
ременными массами и конфигурацией (в том числе скачкообразно изме-
няющимися), с учетом упругости корпуса и карданного узла (см. главу 7).
Сложность создания системы управления вызвана тем, что масса и мо-
менты инерции управляющего органа - головного отсека, были несоизме-
римы с традиционными, что в сочетании с реально достижимой жест-
костью карданного узла обусловило его низкую собственную частоту
119
(~6 Гц). Это привело к усложнению структуры алгоритмов управления
и аппаратного состава: кроме обычного датчика обратной связи для орга-
низации контура сервопривода, был введен датчик угловой скорости на
корпусе ракеты и датчик угла в карданном шарнире.
Принимая во внимание сложность динамической схемы ракеты и сис-
темы стабилизации, был создан моделирующий комплекс, максимально
адекватный реальному полёту. С этой целью был спроектирован, изготов-
лен и поставлен разработчику СУ уникальный нагрузочный стенд [70],
[121], в котором был установлен штатный карданный узел с массово-
инерционным имитатором поворотного отсека, штатными рулевыми ма-
шинами и газодинамическим задатчиком нагрузочных шарнирных момен-
тов. В сочетании с аналого-цифровым комплексом и реальной аппарату-
рой системы стабилизации это обеспечило почти натурное моделирование
полёта с точностью до знания динамической схемы, которая могла быть
подтверждена только лётными испытаниями.
В связи с критичностью системы стабилизации к собственной частоте
подвески головного отсека в технологический процесс изготовления и
сборки ракеты была введена операция контроля этого параметра, для чего
была разработана методология и оборудовано рабочее место с аппарату-
рой контроля [57]. По мере набора статистики была подтверждена ста-
бильность собственной частоты, что позволило эту операцию исключить.
Предусмотренные методическим планом работы были завершены
в полном объёме и в заданные сроки. 26 октября 1982 года состоялся первый
пуск ракеты РТ-23 с новым способом управления. Его результаты не остав-
ляли сомнений: ракета с принятым способом управления будет летать.
А ещё через 7 лет уже модернизированная ракета с улучшенными так-
тико-техническими характеристиками РТ-23УТТХ была принята на воо-
ружение, внося свою лепту в обеспечение ракетно-ядерного паритета ме-
жду СССР и США.
♦ ♦ ♦
МБР «РТ-23 УТТХ» стационарного базирования - ракета 15Ж60 - как
объект управления представляла собой трехступенчатую баллистиче-
скую ракету среднего класса с тандемной схемой построения, твердотоп-
ливными маршевыми двигателями и с разделяющейся десятиблочной го-
ловной частью (РГЧ ИН), состоящей из боевого отсека и ступени разведе-
ния с жидкостной двигательной установкой.
Пуск МБР проводился из пускового контейнера с использованием
ПАД’а. Включение РДТТI ступени происходило на высоте ~25 м.
Основные характеристики ракеты 15Ж60 (в порядке перечисления
ТТХ «Минитмен-Х» (см. 6.2.1).
120
• Стартовая масса - 104,8 т, масса полезного груза - 4050 кг.
• Коэффициент весового совершенства - 38,65 кг/т.
• Удлинение (отношение общей длины к диаметру) 23 м/2,4 м - 9,58.
• Точность стрельбы (предельное отклонение - 2,3 КВО) - 500 м.
• Конструкция двигателей:
- I ступени - моноблочная, с частично утопленным в камеру сго-
рания поворотным управляющим соплом. Рабочий угол - ±6
градусов с круговой диаграммой Рупр.;
- II и III ступеней - моноблочная с частично утопленным в камеру
сгорания неподвижным соплом с выдвижным телескопическим
насадком;
- боевой ступени - маршевый двигатель большой тяги, установ-
ленный в кардановом подвесе, и 16 двигателей малой тяги
с многократными запусками в полете.
6.3. Физические основы управления путем отклонения
головного отсека
Моменты сил вокруг центра масс ракеты от аэродинамических и реак-
тивных сил, возникающие в результате относительного поворота отсеков
ракеты, обуславливаются несимметричным обтеканием ракеты воздуш-
ным потоком и смещением центра масс ракеты по перпендикуляру от ли-
нии действия силы тяги двигателя (рис. 6.1).
а) Рис. 6.1 б)
121
Если осесимметричная ракета движется с нулевым углом атаки, то
можно принять, что вектор Fa равнодействующей аэродинамических сил,
распределенных по поверхности ракеты, приложен в центре давления
и направлен по продольной оси ракеты в сторону, противоположную на-
правлению вектора V скорости ракеты.
На рис. 6.1а) показана плоскость AXZ (плоскость рыскания) инерци-
альной системы координат AXYZ и схема действия на ракету с соосно
расположенными головным и двигательным отсеками (/ = 0) аэродинами-
ческой Fa и реактивной Р сил при движении ракеты в плоскости с нуле-
выми углами атаки а и рыскания \у; а - угол между вектором скорости
и продольной осью головного отсека. Предполагается, что командные
приборы расположены в головном отсеке ракеты.
Линия действия сил аэродинамической Fa и реактивной Р проходят
через центр масс ракеты. Поэтому силы Fa, Р не создают момента сил
относительно центра масс ракеты.
На рис. 6.16) приведена схема действия сил на ракету с отсеками, по-
вернутыми друг относительно друга в шарнире Ш на угол у. На рисунке
показано положение ракеты, соответствующее значению у/ = 0. При / # 0
аэродинамическая сила Fa не проходит через центр масс ракеты и создает
вокруг центра масс ракеты момент сил, равный Ма = Fa*ha, где ha - плечо
действия силы Fa относительно центра масс (на рисунке ha не показано).
Сила тяги Р создает вокруг центра масс ракеты момент силы, равный
Мт = P*hm, где hm - плечо действия силы Р относительно центра масс ра-
кеты. Значение hm зависит от соотношения масс головного и двигательно-
го отсеков и может быть определено по формуле
=
к г
т + т
Здесь hm,h^ - расстояния от центра масс ракеты, центра масс голов-
ного отсека до линии действия силы тяги маршевого двигателя соответ-
ственно; тг,тк - масса головного и двигательного отсеков соответ-
ственно.
Очень важно, что моменты Ма,Мр всегда направлены в одну сторо-
ну, зависят от угла у и потому могут использоваться для управления уг-
ловым положением ракеты в пространстве. Градиент дМа/ду момента
Ма аэродинамических сил зависит от скоростного напора q и на участке
разделения I и II ступеней ракеты монотонно уменьшается от некоторого
122
значения (в начале участка) до нуля в связи с уменьшением q от некото-
рого значения до нуля. Градиент дМр1ду момента Мр от реактивной си-
лы Р на участке разделения ступеней монотонно возрастает в связи с уве-
личением плеча Лш, обусловленного уменьшением массы тпк вследствие
выгорания топлива. Таким образом, при малых значениях Мр значитель-
ным является Ма, при малых значениях Ма значительным является Мр.
Особенности изменения моментов Ма,Мр по времени полёта способст-
вуют обеспечению управляемости ракеты.
6.4. Общая характеристика ракеты
Твердотопливная ракета, управляемая относительным поворотом отсе-
ков, выполнена по тандемной схеме расположения ступеней (рис. 6.2).
Состоит из головного и двигательного отсеков (I, II и III ступеней), соеди-
ненных между собой с помощью цилиндрических шарниров, допускаю-
щих относительный поворот отсеков в двух взаимно перпендикулярных
плоскостях (см. раздел 6.2). Управление движением ракеты по тангажу
и рысканию осуществляется относительным поворотом отсеков с помо-
щью гидравлических приводов рулевого агрегата: при несоосном распо-
ложении отсеков действующие на ракету аэродинамические и реактивные
силы создают момент сил вокруг центра масс ракеты, который использу-
ется как управляющий момент. Управление движением ракеты по крену
реализуется с помощью обычных управляющих органов, реактивных со-
пел, двигателей и т. п.
Сравнение массово-инерционных, аэродинамических характеристик,
параметров приводов рулевых агрегатов ракеты, управляемой относи-
123
тельным поворотом отсеков, и ракеты с обычными управляющими орга-
нами (поворотными соплами, управляющими двигателями и т. п.) показы-
вает следующее.
1. Массы и одноименные моменты инерции головного и двигатель-
ного отсеков ракеты, управляемой относительным поворотом отсеков,
могут иметь близкие по величине значения, тогда как у ракеты с обыч-
ными органами управления масса и моменты инерции управляющих ор-
ганов намного меньше массы и соответствующих моментов инерции
корпуса ракеты.
В табл. 6.1 в качестве примера приведены типичные для ракеты,
управляемой поворотом отсеков, значения масс (т) и моментов инерции
(I) головного и двигательного отсеков. Моменты инерции отсеков опреде-
лены относительно оси шарнира, соединяющего отсеки, перпендикуляр-
ной продольным осям симметрии отсеков. В табл. 6.2 приведены массы
и моменты инерции поворотного управляющего сопла (ПУС) и корпуса
ракеты, управляемой обычным способом. Моменты инерции корпуса ра-
кеты и поворотного сопла определены относительно оси их взаимного
вращения, перпендикулярной продольным осям симметрии корпуса
и ПУС. Значения приведенных инерционных характеристик соответству-
ют моментам времени начала (/0) и конца (^) движения.
Таблица 6.1
Головной отсек Двигательный отсек
тго ^ГО I ступень II ступень III ступень
тдо 1до тдо 1до тдо 1до
кг кг-м2 кг кг-м2 кг кг-м2 кг кг-м2
*0 5-Ю3 0.24 105 105-103 28-105 55-103 4,8-105 18-Ю3 0,45-105
4 5-Ю3 0,24-105 55Ю3 9105 20-103 1,2105 6103 0.1105
Таблица 6.2
Поворотное управляющее сопло I ступень II ступень III ступень
mi m2(3i 1| Ъо) m I m I m I
кг кг кг-м2 кг-м2 кг кг-м2 кг кг-м2 кг кг-м2
^0 850 500 70 60 105-103 28-105 48-103 4,2-Ю5 19-103 0,46-105
4 850 500 70 60 55-Ю3 9-Ю5 24-103 1,4-105 5,5-103 0,12-Ю5
В табл, приняты обозначения: тцг, з) - масса управляющего сопла
I ступени (II, III ступеней); 1ц2, з) - момент инерции управляющего сопла
I ступени (II, III ступеней).
124
Анализ таблиц показывает следующее:
- диапазон изменения параметра ц, равного отношению массы голов-
ного отсека к массе двигательного отсека, есть
ц = 0,05+0,83;
- диапазон изменения параметра i, равного отношению момента
инерции головного отсека к моменту инерции двигательного отсека, есть
i = 0,9*10'2+2,4.
Значения ц = 0,83, i = 2,4 имеют место в момент времени tk\
- диапазоны изменения отношений массы и момента инерции пово-
ротного управляющего сопла (ПУС) к массе и моменту инерции корпуса
ракеты, управляемой с помощью ПУС, соответственно:
ц = 0,008+0,09;
i = 0,00018+0,04.
Значения ц и i, близкие к единице, свидетельствуют о соизмеримости
в течение некоторых отрезков времени полета масс и моментов инерции
отсеков ракеты, управляемой относительным поворотом отсеков.
2. Аэродинамические характеристики ракеты с шарнирно соединен-
ными отсеками существенно зависят от угла у относительного поворота
головного и двигательного отсеков, тогда как аэродинамические характе-
ристики ракеты с обычными управляющими органами практически не за-
висят от угла 8 поворота управляющих органов относительно корпуса
ракеты.
Запишем коэффициенты осевой и нормальной аэродинамических сил,
действующих на ракету, через их составляющие следующим образом:
Ст = сто + АСТ 4" ДСТ»
С — С 0 4- АС 4- АС_.
п пи л л
Здесь Сх, Сп, Схо, Спо - коэффициенты осевой и нормальной аэродина-
мических сил, при значениях у # 0, 5#0иу = 5 = 0 соответственно.
АСХ, АСп - приращения коэффициентов, обусловленные приращениями
углов у и 8 по отношению к нулевым значениям этих углов.
АСТ, АСП - приращения коэффициентов, обусловленные изменением
высоты полета и некоторыми другими неучтенными факторами.
В табл. 6.3 представлены значения составляющих аэродинамических
коэффициентов для ракеты, управляемой относительным поворотом отсе-
ков и ракеты, управляемой ПУС. Значения соответствуют величинам пло-
щади миделя Sm = 4,5 м2, числу Маха М = 2,5, у = = 10°, 8 = 5^ = 7°.
125
Таблица 6.3
Ракета с поворотными отсеками Ракета с ПУС
сг0 ДСГ (/=10°) С.0 АС„о (Г = ю°) Сг0 дсг (£ = 7°) С„о АС„о £ = 7°
I ступень 0,3 0,2 0,8 0,4 0,3 0,05 0,8 0,04
II ступень 0,4 0,1 0,9 о,1 0,3 0,05 0,8 0,04
Анализ таблицы показывает следующее:
- для I ступени ракеты с поворотными отсеками приращения ДСГ,
ДС„ составляют 66 % и 50 %; для II ступени - 25 % и ~10 % от соответст-
вующих значений Сг0, Сл0;
- для I и II ступеней ракеты с ПУС приращения ДСГ и ДС„ составля-
ют соответственно ~15 % и 5 % от Сг0, Сл0.
Таким образом, поворот отсеков на максимальный угол /, вызывает
в четыре раза большее относительное изменение ДСГ и в десять раз боль-
шее относительное изменение ДС„, чем при максимальном отклонении
управляющего сопла.
3. Распределение аэродинамической нагрузки по поверхности ракеты
с поворотными отсеками изменяется в процессе управления ракетой, что
влияет на упругие колебания ракеты.
6. 5. Конструктивное исполнение
Головной отсек крепится к ракете с помощью узла качания, представ-
ляющего собой карданный подвес с силовыми опорными переходниками.
Рулевой агрегат, расположенный внутри узла качания, отклоняя ГО от
продольной оси ракеты, обеспечивает управление полетом в каналах тан-
гажа и рыскания. Управление полетом ракеты по каналу вращения на ат-
мосферном участке траектории осуществляется аэродинамическими ру-
лями, установленными на головном обтекателе, а после сброса обтекателя
- жидкостными ракетными микродвигателями, входящими в состав дви-
гательной установки ступени разведения боевых блоков. Двигательная ус-
тановка ступени разведения жидкостная, работающая на двухкомпонент-
ном топливе. Один из компонентов этого топлива, а именно - горючее,
как менее агрессивный продукт, используется в качестве рабочей жидко-
сти рулевого агрегата отклоняемого ГО.
126
Узел качания ГО на основе карданного узла с центральным шарни-
ром показан на рис. 6.3. Он выполнен в виде большого конуса, уста-
новленного на переходнике 1 III ступени, и перевернутой усеченной
пирамиды 4, соединяющейся с отклоняемым ГО. Между ними в опорах
скольжения смонтирована крестовина центрального шарнира карда-
на 10. Особенностью такой схемы узла качания является наличие об-
щих баз крепления рулевых приводов 2 обеих плоскостей качания. Для
более равномерного распределения усилий на несущие элементы пере-
ходников в каждой плоскости качания установлено по два рулевых
привода.
5
1 - переходник III ступени; 2 - рулевой привод; 3 - пироклапан нагнетания;
4 -пирамида; 5 -пироклапоч слабо; 6 -термокомпенсатор;
7 -уравнительной трубопровод; 8 -метоллорукаб; 9 -дречажний клапан;
Ю - каодон; 11 -цечтральный узел подбода; 12 -зспрабочной клапан.
Рис. 6.3
Конструктивная схема карданного узла с центральным шарниром вы-
годно отличается от других схем карданных подвесов тем, что в ней ши-
роко используются в качестве силовых элементов тонкостенные оболоч-
ки, обладающие высокой жесткостью при минимальном весе. Расположе-
ние четырех РП по осям симметрии создает симметрию силовой схемы
карданного узла. Оси РП проходят через узлы, представляющие собой пе-
ресечение оболочек. При этом обеспечиваются благоприятные условия
для передачи усилий от рулевых приводов на силовые элементы узла ка-
чания. Существенно снижаются паразитные оболочечные моменты и из-
гибно-крутильные деформации элементов конструкции. Тем самым по-
вышается их жесткость.
127
Для задачи управления ракетой отклонением ГО, имеющего большой
момент инерции, предпочтительней непрерывный (аналоговый) принцип
управления РП по следующим причинам:
• он позволяет свести к минимуму перерегулирование в переходных
режимах и снизить тем самым колебательность процесса регулиро-
вания;
• реализуется аппаратно с минимальным числом связей с СУ;
• алгоритмы управления аналоговым приводом решаются с мини-
мальными затратами машинного времени БЦВМ;
• элементная база мощных аналоговых РП освоена в производстве,
а теория и практика их проектирования наиболее отработаны.
Требуемый коэффициент усиления по мощности РП порядка 2104 был
реализован двухкаскадным гидроусилителем, в первом каскаде которого
применен плоский золотниковый распределитель, а во втором - цилинд-
рический золотник. Для повышения надежности и улучшения стабильно-
сти характеристик РП в электрогидравлическом усилителе (ЭГУ) была
применена отрицательная механическая позиционная обратная связь меж-
ду каскадами.
Проблемным вопросом при проектировании РП отклоняемого ГО яв-
лялся выбор простых и надежных средств демпфирования колебаний
инерционной массы на упругом подвесе при большой жесткости нагру-
зочной характеристики рулевых приводов. Известно много различных ме-
тодов демпфирования, основанных:
• на разных принципах рассеивания энергии колебаний (вязкое или
сухое трение);
• введении в контур сервопривода обратных связей по ускорению
или производной от ускорения нагрузки (по перепаду давления
в полостях цилиндра или по динамическому давлению);
• организации перетечек рабочей жидкости между исполнительными
гидролиниями, соединяющими золотник ЭГУ с гидродвигателем.
Наиболее рациональным, требующим минимальных энергетических
затрат и наиболее просто реализуемым, является метод демпфирования за
счет организации перетечек рабочей жидкости между рабочими полостя-
ми гидроцилиндра с помощью небольших несимметричных начальных
отрицательных перекрытий по напорным и сливным кромкам цилиндри-
ческого золотника выходного каскада ЭГУ рулевого привода.
При таком методе демпфирующие качества рулевого привода наиболее
полно реализуются при малых открытиях окон золотника, т. е. именно
в том диапазоне рабочих перемещений золотника, в котором малого
скольжения механической характеристики рулевого привода не хватало
128
для демпфирования колебаний ГО. При больших открытиях золотник ве-
дет себя, как обычный отсечной, обеспечивая рулевому приводу высокое
быстродействие и приемистость. При этом максимальное развиваемое
усилие РП не уменьшается.
При наличии на ступени разведения ЖДУ создаются технические
предпосылки для применения системы питания рулевого агрегата гид-
равлической энергией от централизованного источника питания (ЦИП)
двигателя. Такая система является более совершенной в весовом и энер-
гетическом отношении, чем автономный бортовой источник мощности
РА. Пневмогидравлическая схема РА с питанием от ЦИП приведена на
рис. 6.4.
Рис. 6.4
ЦИП был выполнен в виде комбинации попеременно работающих вы-
теснительной и турбонасосной систем подачи компонентов топлива в ка-
меру сгорания ЖДУ. Он включал в себя питатели окислителя ПитОк и го-
рючего ПитГ, каждый из которых содержит дифференциальный поршень,
обеспечивающий вытеснение компонентов топлива, и блок управляющих
клапанов БУК, обеспечивающих подачу и сброс управляющего давления
на клапаны запуска газогенераторов ГГО и ГГГ турбонасосных агрегатов
ТНА Ок и ТНА Г. Питатели окислителя и горючего устроены и работают
аналогичным образом. Вытеснение компонентов топлива из питателей
при работе ЦИП обеспечивалось сжатым газом, поступающим из шаро-
баллона ШБ. После опорожнения питателей срабатывали клапаны БУК,
задействующие соответствующий ТНА для зарядки питателя, после чего
цикл вытеснения повторялся.
129
Подача питания от питателя горючего к РА в полете обеспечивалась
после срабатывания нормально закрытых пироклапанов ПКС и ПКН, со-
единяющих гидравлические магистрали РА с ЦИП. Отработанная жид-
кость после рулевого агрегата сливается в бак ЖДУ. Перед этим имев-
шаяся в рулевом агрегате консервирующая жидкость - минеральное мас-
ло марки РМ - предварительно сливается за борт ракеты через нормально
открытый пиропереключатель ППК. После завершения работы РДТТ
III ступени и перед отделением от нее ступени разведения срабатывают
открытые до этого пироклапаны разъемные ПКР1, ПКР2, которые отсе-
кают гидромагистрали РА от ЖДУ гидравлически и механически. Заряд-
ный клапан ЗК и дренажный клапан ДК служат для заправки РА консер-
вирующей жидкостью и подсоединения к нему технологической насосной
станции при наземных испытаниях. Температурные изменения объема
консервирующей жидкости при хранении РА в составе ракеты компенси-
руются термокомпенсатором ТК.
Такой схеме питания РА свойственна высокая экономичность, по-
скольку горючее после РА возвращается в бак. Безвозвратно расходует-
ся только та часть компонентов топлива, которая обеспечивает работу
ТНА в моменты подзарядки питателей. Безусловно, такое решение тре-
бует некоторого усложнения ПГС РА (введение дополнительных клапа-
нов ПКР и пиропереключателя ППК). Кроме того, для подвода рабочей
жидкости от ЖДУ, расположенной на головном отсеке, к рулевому аг-
регату, размещенному в переходнике III ступени ракеты, через цен-
тральный шарнир карданного подвеса требуется специальный узел под-
вода, состоящий из двух расположенных один в другом сильфонов
(см. рис. 6.3 поз. И). Однако вес рулевого агрегата получается меньше
по сравнению с вариантом питания РА от собственного бортового ис-
точника мощности.
Проблема исключения взаимовлияния рулевых приводов, установ-
ленных в одной плоскости качания, и влияния одной плоскости качания
на другую, обусловленные кинематическими особенностями узла кача-
ния с центральным шарниром, были решены введением уравнительных
трубопроводов между функционально идентичными полостями сило-
вых цилиндров.
130
Глава 7
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАКЕТЫ
С ШАРНИРНО СОЕДИНЕННЫМИ ОТСЕКАМИ
7.1. Постановка задачи
При создании ракеты с шарнирно соединенными корпусом (двигатель-
ной установкой) и головным отсеком (ГО) в среде разработчиков возник
и стал привычным термин «управление ракетой путем отклонения голов-
ного отсека» (см. главу 6).
Управление угловым движением ракеты предполагает поддержание
на активном участке траектории полета нулевых значений возмущений
программных величин углов тангажа, рыскания и вращения. Эти отклоне-
ния определяются относительно начальной стартовой инерциальной сис-
темы координат AXoYoZo (раздел 1.1), направления осей которой в полете
на борту ракеты формируется комплексом командных приборов (ККП).
Если ККП расположен в корпусе ракеты, то возмущения параметров угло-
вого движения ракеты определяются угловыми отклонениями корпуса ракеты
относительно системы координат AXoYoZo; система управления осуществля-
ет стабилизацию углового положения корпуса ракеты относительно этой сис-
темы координат путем отклонения ГО относительно корпуса ракеты.
Если ККП установлен в головном отсеке, то система управления ра-
кеты для стабилизации углового движения ГО осуществляет поворот кор-
пуса ракеты относительно ГО.
В этой связи термин «управление ракетой путем относительного по-
ворота отсеков», как обладающий большей общностью, особенно с уче-
том изменения в полете соотношения инерционных параметров системы
«корпус - ГО», представляется более удачным. В данной главе будем ис-
пользовать уточненный термин.
Ракета, управляемая относительным поворотом отсеков, - это шар-
нирная связка двух тел, движущаяся в поле массовых гравитационных сил
под действием поверхностных аэродинамических и сосредоточенных ре-
активных сил. Поскольку в нашем случае (РТ-23) ККП установлен в ГО,
то будем считать, что ГО совершает переносное движение, а корпус раке-
ты - относительное.
Математическая модель ракеты РТ-23 как объекта управления, имеющей
шарнирно соединенные отсеки, к началу проектных работ по ее созданию
разработана не была, хотя динамические особенности, присущие похожим
динамическим системам (ракетам с поворотным маршевым двигателем, со-
ставным космическим аппаратам и т. п.) изучались А. Ю. Ишлинским [77],
131
К. С. Колесниковым, В. Н. Суховым [87], [89], [90], Н. Ф. Герасютой,
И. М. Игдаловым, В. М. Морозовым, Н. Е. Зыковым [38], Г. А. Кононыхи-
ным, М. П. Харламовым, М. Е. Лесиной [91], [157], [158], М. Е. Литвином-
Седым [99], [100], Л. К. Лиловым, В. А. Чириковым [98], В. А. Сарычевым
[136], Л. Н. Рогачевой, Н. П. Степаненко [133], Ю. Н. Федосеевым [151] и др.
Анализ перечисленных работ показывает следующее.
Соотношения массово-инерционных характеристик корпуса и органа
управления, условия работы рулевого агрегата и характер аэродинамиче-
ского воздействия на корпус и ГО ракеты с шарнирно соединенными от-
секами существенно отличаются от соответствующих параметров бли-
жайшего аналога - ракеты, управляемой поворотом маршевого двигателя.
Поэтому исходные положения, упрощающие допущения, и, следова-
тельно, конечные результаты - математические модели динамики этих ра-
кет - априори нельзя принимать совпадающими.
С целью создания наиболее достоверной математической модели раке-
ты с шарнирно соединенными отсеками ее разработку проводили незави-
симо несколько организаций с последующим согласованием окончатель-
ного варианта как исходных данных на разработку системы управления.
Ниже излагаются результаты, полученные в Днепропетровском нацио-
нальном университете.
Рассмотрим возмущенное движение ракеты, управляемой относитель-
ным поворотом отсеков, с учетом ее динамических особенностей:
- соизмеримость массово-инерционных характеристик головного и
двигательного отсеков;
- конечная жесткость конструкции головного и двигательного отсеков;
- конечная жесткость элементов шарнирных кинематических связей
между отсеками;
- характер аэродинамического воздействия на ракету как шарнирную
связку двух тел.
Существуют разные методы вывода уравнений движения динамиче-
ских систем. В дальнейшем используются положения о движении свобод-
ной системы тел, изложенные А. И. Лурье [102]. Принимается, что факти-
ческое движение несущего тела неизвестно; оно определяется с учетом
влияния движения переносимого тела. Для описания движения ракеты ис-
пользовались следующие правые ортогональные системы координат.
AXoYqZo - инерциальная начальная стартовая система координат, точка «А»
которой совмещена с центром Земли. Оси координат этой систе-
мы колинеарны осям стартовой системы координат (раздел 1.1)
и в дальнейшем не изменяют своего положения в пространстве.
OXrYrZr - связанная система координат I. Начало отсчета совмещено
с центром масс ракеты. Оси параллельны главным централь-
132
ным осям инерции головного отсека. Ось ОХГ направлена
к носку ракеты.
LuxkYkZk - связанная система координат II. Начало отсчета совмещено
с точкой Ш (геометрическим центром шарнира). Оси парал-
лельны главным центральным осям инерции корпуса. Ось
ШХК совпадает с продольной осью симметрии корпуса и на-
правлена к носку ракеты.
UIXrYrZr - связанная система координат III. Начало отсчета совмещено
с точкой Ш. Оси параллельны соответствующим осям системы
координат I. Ось ШХГ направлена к носку ракеты. Оси систем
координат III и II совпадают при соосном расположении про-
дольных осей симметрии корпуса и головного отсека.
L(rXrYrZr - связанная система координат IV. Начало отсчета совмещено
с центром масс головного отсека. Оси параллельны соответст-
вующим осям системы координат I.
CXrYrZr - связанная система координат V. Начало отсчета помещено
в точку на продольной оси симметрии головного отсека, в ко-
торую проецируется центр масс ракеты. Оси параллельны
и сонаправлены соответствующим осям системы координат I.
Системы координат показаны на рис. 7.1 в). На этом рисунке точки
Цг, Цк, О - центры масс ГО, корпуса и ракеты в целом соответственно;
точка Ш - геометрический центр шарнира; точка С - проекция точки О на
продольную ось ГО. -к
Рис. 7.1
133
Ориентацию ракеты как системы двух тел в инерциальном пространстве
характеризует положение головного отсека относительно системы координат
AXoYoZo и положение двигательного отсека (корпуса) относительно системы
координат IIIXrYrZr. Принимается, что движение ракеты характеризуется
следующим:
- полет ракеты происходит в атмосфере, в гравитационном поле Земли
под действием силы тяги маршевого реактивного двигателя;
- угол у между осями продольной симметрии головного и двигательного
отсеков мал в том смысле, что sin у ~у и cos у ~ 1;
- аэродинамические нагрузки на ракету соответствуют гипотезе стацио-
нарности;
- поперечные упругие колебания ракеты таковы, что выполняются ги-
потеза о малости упругих деформаций и закон плоских сечений Навье [152].
7.2. Уравнения движения в векторной форме
7.2.1. Уравнение поступательного движения
Используя теорему о движении центра масс твердого тела, запишем
для головного отсека и корпуса
(7.D
at j=i
mK^-=iF*, (7.2)
dt v=i
где тг,mK - масса головного отсека и корпуса соответственно;
-г -к
го ,го - радиус-вектор центра масс головного отсека и корпуса относи-
тельно инерциальной системы координат соответственно;
XFp XFv ~ сумма внешних сил и сил в шарнире, действующих со-
У=1 v=l
ответственно на головной отсек и корпус, приведенные к их центрам масс.
Учитывая, что
-к _-г -г -к
г0 г0 +Рцц> Рцц Р цш ' Р шц 9
где рцц - радиус-вектор центра масс корпуса относительно центра масс
головного отсека (рис. 7.1 а, б);
—г
рцш - радиус-вектор шарнира относительно центра масс головного от-
сека;
—к
ршц - радиус-вектор центра масс корпуса относительно шарнира,
134
просуммируем выражения (7.1), (7.2) и получим
d2r[
dt2
л-т
d2р
dt2
(7.3)
т
J
где m - масса ракеты.
Принимая, что головной отсек движется относительно инерциальной
системы координат с угловой скоростью йу , а корпус относительно головно-
го отсека с угловой скоростью , выражение (7.3) запишем в виде:
J2ro к\3ш - dais К _ / к \ _ ( (7.4)
m~dtr+m ^xp*’+_/x^+£asx(^x^J+‘ax(^x^J+a'x('ux/’'<’)J=^F> 4 7
где — - оператор локальной производной в системе координат ЦГХГУГ2Г.
dt
Принимая во внимание, что (рис. 7.1 в)
_ —Г — к
Рцц РцЪ + Р$ц ’
где - - радиус-вектор центра масс ракеты относительно центра масс
головного отсека,
- ~р^ц - радиус-вектор центра масс корпуса относительно центра масс
ракеты,
запишем
тГ РцП=тК Роц- (7.5)
Подставим выражение (7.5) в (7.4) и, произведя преобразования, получим
т
+
(7.6)
л-т
х Ршу + <>$ х (<BS X р^)+ co X (©j X р^)+ co X (о X pw ) =
Проектируя вектор р^она оси системы координат ЦГХГУГ2Г (рис. 7.1 в) и
учитывая, что:
_г _ т _к _
Рсо~~ Ри^
где у - вектор угла поворота корпуса относительно головного отсека, пре-
образуем соотношение (7.6) к виду:
d2ro da) г . л —
т ^dP~^li~XXyo1 +т~^хР.
л-т
da)s _к
~dTXpua>
Kdo к _
• —хй xv +
dt Риа< Г
+ <os х X + о X X + ФХ (ox рт ) = £Fj
(7.7)
к
135
Выражение
d2ro ! da)
dt2 dt
ЦО
представляет собой линейное ускоре-
ние относительно инерциальной системы координат AXqYqZo проекции
центра масс ракеты на ось ЦГХГ; обозначая его Ус, запишем:
mV'+mK ^xp^xy+^xp^+®sx(cosxp^)+<ox(cosxp^)+®x(ffixp ) = £F’-(7.8)
at at j
Уравнение (7.8) является векторным уравнением движения проекции
центра масс ракеты с шарнирно соединенными отсеками, относительно
инерциальной системы координат AXoYoZo.
7.2.2. Уравнение углового движения
Для получения векторного уравнения углового движения ракеты вос-
пользуемся теоремой об изменении кинетического момента динамической
системы.
Для множества точек корпуса запишем:
(7.9)
at v=i
где Мк - главный вектор момента внешних сил и сил в шарнире, дейст-
вующих на корпус ракеты, относительно начала инерциальной системы
координат;
Fv - радиус-вектор v-й элементарной частицы корпуса относительно на-
чала инерциальной системы координат; т* - масса v-й элементарной
частицы корпуса; Kv - вектор линейной скорости v-й элементарной час-
тицы корпуса относительно начала инерциальной системы координат.
Принимая во внимание, что Fv = >о + Р*» где 'о ” радиус вектор точки
О относительно начала инерциальной системы координат; р* - радиус
вектор v-й элементарной частицы корпуса относительно точки О, запи-
шем выражение (7.9) в следующем виде:
iroxm‘^+itfxm*^ = MK. (7.10)
v=i at v=i at
На основании теоремы об изменении количества движения динами-
ческой системы имеем: — = FK> гДе FK - главный вектор внеш-
dt v=i
них сил и сил в шарнире, действующих на корпус ракеты. Принимая во
внимание, что
136
— _ - _ — - do K —
MK -rQxFK = Мо, Vv = к0 + Pv , где Ко - линейная скорость полюса О,
dt
Мо - момент внешних сил и сил в шарнире, действующих на корпус ра-
кеты относительно полюса О, запишем:
у —К' К * dVp . у — К К у Ру _ Г7К П 1 11
zL Р v 1^1 v X , q . у /. 11)
v=i dt „=1 dr
Для головного отсека:
“ d2 -г
<7Л2>
где м о - главный вектор момента внешних сил и сил в шарнире, дейст-
вующих на головной отсек относительно полюса О. Сложив (7.11) и
(7.12), получим
[ЬХ + Ztfx^+ ipjx<^ = ^o. (7.13)
(v=i y=i ) dt v=i dt y=i dt
Здесь Mo - момент внешних сил относительно полюса О. Совмес-
тим О с центром масс системы «корпус - головной отсек». Тогда
^Pvmv =0 как статический момент масс тк, тг относительно
v=l У=1 j J
центра масс ракеты и (7.13) принимает вид
. 2 — К j 2 —Г
щ —if v d р.. л __р г* Р / —
Хр*хт*—^+£ргхтг—J- = M0. (7.14)
V=1 dr j=i J dt1
Учтем, что р/ = рош +р^,, р/ = рош +pQ, где pmi,p^Vi prMj ~ радиусы-
векторы шарнира относительно точки О, элементарных масс корпуса и ГО
t/2p* d2 ру
относительно шарнира соответственно. Вычислим - 2 - , 2 .
= + = ^L = ^£ + ®sXp^ + ®Xpv’^Ti =
=—+ <в х+ .^ffixp“q) + cox(©sxp^,) + ^a*xpv) + ох(шхру).
dr dt dt dt
137
^=^+5хр;. ^=^+5хр;.
dt dt J dt dt J
d2pr, d2o -do ^(®xpf) _
—=—Vй + <°x Pout +-----—+®х(шхpf).
dt2 dt2 dt dt Kj
„ d d
Здесь —, —------символы локальных производных в системах коорди-
нат OXrYrZr, IIIXrYrZr соответственно. Теперь можно записать
+ pv х /и, ----------J-
v d2P0UI , -к„...к
хй (Ру 2 + Pv Xwv
, = i dt
dt2
dt
+ р* xm^x(fi)5 xp*v)]+ p*xm* ^(0}*Ру') + p*mf х [в х (® xp*)]}+
at
+ t{pj^^ ^ Р°ш + р^хт‘
,=1 J dt2 J
d(<oxpr)
+ p . xm‘----— 4
Pj J dt
+ Pjt»j xbx(®xPy)]} = Mo-
dt
(7.15)
Отметим, что
V Ту % „.К V Ту^ Р°ш — к
Pv ™v X P / X 0,
lv=i j=i dt
так как X pf ” статический момент масс относительно цен-
v=l ;=1 7
тра масс системы и преобразуем отдельные слагаемые выражения (7.15)
^Xpf) = ^^хСРош + Ршу)] = ^ХРОМ) + ^ХРш? = ^(№ХРоц) +
dt dt dt dt dt
do —r — d Рш] _______ —Г\ d(coxp ) d(£) —p — z_________ —Г\
—X pQ + co X (-^ + cos X p [.) =-+ —- X p Q + (0 X ( (OS X P;y),
138
d(jj>*py) = </[<»х(рош + р^)] = </(<вхрош) + d(a>xp*) = J((oxpo[u) +
dt dt dt dt dt
d(ii _/f — d d(®ХРОШ) t/tt) — % — d p —
+ ^-хр„ + шх^« = ^-^ + -хриу + шх(-^*т5хр_„).
= jkXp* + Xp^), так как ^-^= = 0. ^S = 0.
at at at at
^xp^)_^ -K - dPw-dtos xnK +m X
dt ~ dt *p™ + <°s* dt ~ dt Х^<*Х
dt
d PlUV I Tx yX/f
Л +(%XPbv
t/COc _// — .— _ jz ч
= -^TXP£v + C0SX(®SXPu/v)-
at
Учитывая результаты преобразований, перепишем (7.15) в виде
f Р*х m* {^-х Ршг +“7“х + % х fe х Ршг)+ йх (®x ру)} + (7.16)
v=i at at
я —Г р d ду у р _у у
+ Zpy xmf{—хр*+<ох(й)хрр} + 2£р*хт*
j=\ at v=l
*$ХРшу
о-
Введем обозначения: i = v(Jj, m.=m^\Jmj, РШ1=Ршу^Р^’
Pt =Ру\)рГг Pj = рош + ршу, Ру = рош + р*у, что позволяет записать
Рош х(^х2Хрш,) + рош х[®х(®х2ОТ(рш/)] + рош х(^-х Ът^р^у) +
dt i i dt v=i
+ Po»x[fflsx(casX Хт^р^)] + рошх[®х(й5х 1™*^)] +
V = 1 V=1
+ Ep^vxmv {~~xp^v + cosX(cosXp^v) + 2©x(©sxp^v)}+ (7.17)
v=i dt
.5?o _ _ z_ _X1 _
+ 2Рш, xm, {—X рш1. + (OX (ox p,)} = Mo.
i at
Учитывая, что Sm.p^ =трш0, lrnypKm=mKp^, где рш0 - радиус-
i v
вектор центра масс ракеты относительно шарнира, (ршо=”Рош)»
_ радиус-вектор центра масс корпуса ракеты относительно шарнира,
запишем векторное уравнение углового движения ракеты относительно
системы координат AXoYqZq
139
Рош Х(^ХтРош) + Рош х[й)х(йхтрои)] + рош х(^-хткр^ ) +
at at
+ Рош X[й5 X (Й5 X тк р*ч)] + рош X[йх (©sх тк р^)]+
+ fp^vxm5r{^7£xp^v + ©sx(c5sxp^v) + 2®x(©sxp^v)}+ (7.18)
v=l at
+ Z Рш, xm, {^7 X рИ1. + й x (й x P,.)} = J70.
7.2.3. Уравнение углового движения корпуса
относительно головного отсека
Используя выражение (7.9) и учитывая, что г у = rQ + рош + p*v, (7.19)
найдем
2Ххт<^=^> <7-20>
v at
где Мш - главный вектор момента внешних сил и сил в шарнире относи-
тельно точки Ш. Скорость v -й точки корпуса:
Vy = ^o+^%H!- + ®x(polu+p*v)+®5xpJfv. (7.21)
Дифференцируя (7.21), подставляя результат в (7.20) получим вектор-
ное уравнение углового движения корпуса ракеты относительно головно-
го отсека:
~2-
тК Р^ х Го + * Ршц Х х Рош) + 2 Wv {pL X [(^ + й5) X р^]} + +
v=i dt
+ Zwiv Р^хСй^йхр^ + Х^р^хЕйх^х
V=1 V=1
xP^v)]-— Хю*Р^х[йх(й5хр^)]-— 1т5гр^,х[йх(йхр^)] = л7ш.
m V=1 m V=1
(7.22)
+ тКРшц* юх
d Рош
dt
7.3. Уравнения движения в скалярной форме
Сравнивая линейные и нелинейные составляющие в уравнениях дви-
жения отметим, что нелинейные функции угловых скоростей, намного
меньше линейных и ими можно пренебречь как величинами второго по-
рядка малости. В результате уравнения движения можно записать в сле-
дующем виде:
140
wtV do)s y. -K __ v
7И r c 4"/И X Ршц j
at j
(7.23)
Рош
do)c k—k
X —±xmKp*
dt ц
Рош
da) -
x ~^~ХтРош
at
+ ЕРшу
V
к dtOg —к
x™v ~^-хршу
ткРшЧх^о + тКР^х(ахРош)+ f mv {P*v*№ +й)5)хР^В +
~2- V=‘ ( 7- \ (7-25)
_i_ X ~ X у d Р ош _|_>и^л^х О) X Р ош — -tr
+ т Ршцх dt2 +т Рищ тх dt
При выводе дифференциальных уравнений возмущенного движения
ракеты в качестве невозмущенного будем рассматривать программное
движение системы (у = (р = 0). Связь между проекциями на оси системы
координат OXrYrZr вектора угловой скорости ш устанавливается соот-
ношениями:
а)х = ф-ib Sira/f,
й)у =ф Costp + ihCosv Sirup,
(7.26)
a)z = Sirup+ & Cosy Costp.
На основе (7.26), получим с точностью до величин второго порядка
малости:
а* = a,'**?- = (7.27)
dt у dt dt v '
где со',, шу, со'» - проекции угловой скорости, соответствующие возму-
щенному движению, на возмущенные направления осей системы коорди-
нат OXrYrZr;
At>, Дф, Дуг - возмущения параметров движения.
Дифференцируем (7.27)
d(o'x’ _ J2Ay . da)'y’ _ J2Ayr da)'z' _ d2& d2k&
dt dt2 ’ dt dt1 ’ dt ~ dt2 + dt2
Для проекций возмущенной скорости точки С продольной оси голов-
ного отсека на оси системы ОХ^^Г с точностью до малых второго по-
рядка имеем
Vcx^ = ^сх+^х^ Vcy' = -Vex+ Vy ; V^ = Vcx^ + Vcz + ДVz, (7.29)
141
где V^., КсГ, VCY, Vcz — проекции возмущенного и невозму-
щенного векторов скорости точки С на оси системы OXrYrZr соответст-
венно; АКС — возмущение вектора скорости Vc. Из равенств, дифферен-
цируя, находим:
<&СХ =<&СХ t
dt dt dt
= ^. + ^CL + ^Lt (7.30)
dt dt сл dt dt dt '
dVCZ' = dVCX д ! r d^ j dVCZ ! d^VZ
dt dt * Cx dt dt dt
Длят, mr, Yy, y&> можно записать:
m' = m + Am,
m,r =mr +&mr,
(о$у = (D$y + Aco^y = Aco^y, (7.31)
coiz=cosz+A(Dsz»A(Dsz,
Yv=Yv+AYv=AYv,
7э=7э + а7э«а7э-
Учитывая (7.29-5-7.31), запишем уравнение (7.23) в проекциях на оси
системы координат OXrYrZr.
-согГст) + ^(^^ -^-УД) = ХГЯ. (7.32)
dt dt dt j
т^- + ^Усх+ =ZFly , (7.33)
dt dt j
m(^ + (SixVCY-(S>rVcx) + mK^-X^=T.FiZ, (7.34)
dt dt j
так как
Хк » -lK YK = -lK v ZK = -lK v
л ищ 1щц ’ * щц 1щц «3 » ^ЩЦ 11ЦЦ 'V ’
где — расстояние от центра масс корпуса ракеты до шарнира.
Принимая во внимание выражения (7.274-7.31), проводя линеариза-
цию уравнений (7.32-5-7.34) и отбрасывая члены второго порядка малости,
получим линеаризованные уравнения поступательного движения.
dNYX К tK f А d^SZ А \ AVP
т—^ + т 1шц(--------T^AYv-------V^-AYa) = AZ<x>
dt dt dt j
m^~mK (735>
142
X X 3A<°Sy =_^F дг + д^р
dt dt JX Ч’ Jz'
где YFjX, XZFjX, у ’ aXf z — суммы проекций и проекций
J J J J J J
приращений внешних сил на оси системы координат OXrYrZr соответст-
венно.
Записывая уравнение углового движения (7.24) в проекциях на оси
связанной системы координат OXrYrZr, принимая во внимание выраже-
ния (7.27-ь7.31), получим:
Уравнение в проекциях на ось ОХГ
,2 .72 \^Х у у у v ^zl .
ОШ ОШ J rft ЛОШ1ОШ dt ^ОШЛОШ dt
-т
, К
+ т
d®sx yk d®SY
dt Yuiy dt
YK |у d(OSZ
л шц £ош
vK —
dt Лшч
d®sx yk
dt £шц
+ £»»,
. ^2 \d<ox v daz
“r Z Ш1/ л Uli1 Uli dt ^uii^uii
(7.36)
к Z
ШЦ ^ош
+ у К (у*2.| YK1\^SX VK VK d®SY YK VK ^SZ
7" ТП v V MV T Z WV / . л ШУ I UlV . Zu/vAwV .
v dt dt dt
Уравнение в проекциях на ось ОУГ
\ d(Hy da)y — __ dtHy
~~М (Хош + Zoui) ХоиХош 3 ZouXoui +
dt dt dt
. к (d&SY ^sz VK X7 d®sx YK ^sy yk a r
~ v dt dt 1 шц)^ош dt 1 ШЧ dt л^*ц'лош
т~» /2 2 \ df^Y tr тг >~y tz d(i)z
+ X (X1Ш + Zwi) . ~7 ^uiXuii 1 *"
i I dt dt dt
( Yk2 + 7k2 VK VK 7K VK -
' £^ГПу \Л wv Z щу J dt Л. щу I щу dt Zjiuyluiy dt
Уравнение в проекциях на ось OZr
d<t>z у z ^X__7 v i
dt ОШ ОШ dt ош ОШ dt J
+ mK YK 7^\v (^ST 7K d<°SZ VK .
' \ dt Л-ШЧ dt dt dt * ШЧ' * 0,0 '
= МоХ;
+ (7.37)
(738)
— ^ОГ’
-т (TL +
143
ж-« z 9 ? \ dta? ry dtHy „ dtHy
+ 2mi (Xuii + YШ|) ~~T ^ua^uii ~~7 ^uti^iui .
i dt dt dt
+ (XKL
^SZ YK 7K d®SX VK 7K ^SY
A.un£un j IunZ^un ,
dt dt dt
= MqZ
Введем обозначения инерционных характеристик
^ШХ (Zuri + Yud)f шху ^^i^uii^tui 9 ox ~~ ua ~ ош 4" Zoiu) 9
i i
Iшу (^u + Zuii)f ^uua S’ ^oy ” шу ^^Xош Zow') *
=Zw/(X< + y<), ^=Z'”IYU,ZU,> Ц=/иа-т(Х2ош + У2ош),
jK уГ2 • 7Г2\
1 ШХ ~ Z^ITlj \I iuj т£ш] />
f _T ________my Y
oxy 1шху "t'*'OX1OUli
X^Yb,
I шу ~^1Пу (X UN +Ziuy)f
V
llL = 2mf(Y£+Y£),
V
..._ mX'Z'...«
иоа ош ош 1
rK -уКуК YK
uxyz Z^frlv ZjIUV 1 UN »
т _т _______mY 7
1 oyz 1uiyz ni 1 our*1 ОШ 1
7* - V 7K YK
1 uaz — £4iflv Zjiuv Л шу •
Запишем матрицу направляющих косинусов между осями систем ко-
ординат IIIXKYKZK и IIIXrYrZr. Взаимное положение осей координат ха-
рактеризуется углами yv, уд:
Cosy^Cosy^
-Sinye
+ Sitr^Cos^
+ Co^Sirq^ - Sirr(v
Cosrft 0
Siny4Sinyt Cosy^
(7.39)
Матричное уравнение перехода от системы координат IUXrYrZr к сис-
теме координат I1IXKYKZK имеет вид:
(7.40)
где
- матрица-столбец, элементами которой являются со-
ставляющие вектора p£v в системе координат IIIXKYKZK;
144
хк
ШУ
л
YK
ШУ
/
ZK
^ШУ
- матрица-столбец, элементами которой являются состав-
ляющие вектора p£v в системе координат IIIXrYrZr.
С учетом вышесказанного запишем выражение (7.40) в виде:
(7.41)
Здесь принято cosy^ « cosy^ «1, sin/у, « у^, sin/0 ® Уу, • у# = 0. Учиты-
вая (7.41), получим формулы для расчета осевых моментов инерции:
^шх = ^mi + Yuri )= SWV (%un Yun 1"*" f 1=
' v k J j \ J (7.42)
= I^+ILx+ ткХ^ц2 (yv2 +7^),
1шу = ZwiU«+zii) = Im? + Y%2v) + (xtf + Y^j) =
‘ V „ „ J « (7.43)
=1шу + Ituy + ^Wv (/фУшУ +YyZtuV +YwXuV )>
V
lux = 1ггц(х1, + Уш.) = lmf(x£ + y^v2) + (X^j + У^/) =
' V .. .. J „ <7-44>
= Ituz lua (’'iftYuiv YyZuiv YfyXiuv)>
IL = Zmf (У^ + ZS2), =Z<(y^ + Z^2), (7.45)
j V
1Гшу = T.mrj (x£ + z£), I^y = + Z«v2),
где 1^' - осевые моменты инерции динамической системы
«корпус - головной отсек» относительно осей системы координат
mxrYrzr.
При выводе формул (7.42)+(7.45) принято во внимание, что
X unY ШУ ~ ^1Иу XunZuN = ^ТПу YunZuN =
V V V
145
как центробежные моменты инерции относительно осей, параллельных
главным центральным осям корпуса ракеты.
Формулы для расчета центробежных моментов инерции имеют
вид:
/^ = Zт>Уш, = Zmv XLУ^ + XmjXQY^j = -(ly~I*)Ye-mKl£Ye, (7.46)
I = XmiX^='ZnhXLzL+llmjX^Z^=-(Ix-/z)rl,+mKl^ry . (7-47)
i V j
+Xm^Z^=-(mrr2 -1<Х;'2)ГЛ. (7.48)
где Z ^цш, Z - центробежные моменты инерции системы «корпус -
головной отсек» относительно осей системы координат IIIXrYrZr;
/*, If “ осевые моменты инерции корпуса ракеты относительно
главных центральных осей корпуса.
При получении выражений (7.46)+(7.48) учитывалось следующее:
1щху = I uixz ~ Iutyz = ®> Хщу = Хцу +Хшц„ Ущу = Yyy , Zwv = » (7.49)
р* =Хцу i +YKyj + Z^ к - радиус-вектор v-й точки корпуса ракеты
в проекциях на главные центральные оси корпуса, параллельные осям
системы координат IIIXrYrZr
2. Выражения
Imv X$'y%' = Zmv X$'z%' = Ъп* Y%'Z%' = О
V V V
как центробежные моменты инерции относительно главных центральных
осей корпуса ракеты.
3. Члены, содержащие 1*ц равны нулю, так как
V V
Emv Zgv - статические моменты масс относительно центра масс корпуса
v
ракеты;
Z , Z^, Z - центробежные моменты инерции системы «корпус - го-
ловной отсек» относительно осей системы координат
OXrYrZr.
Принимая во внимание соотношения (7.42)+(7.49), перепишем фор-
мулы (7.36) + (7.38) для случая, когда = 0 (отсутствует прокручивание
корпуса относительно головного отсека вокруг продольной оси отсека),
в виде:
146
т Я®* J J (тК >тКуКу
лох лоху лохх Vuay~rm лшц1ош/
-^+mKX^Z<>u^-=Mm,
d(tiY т d(tix d(toz ( х +mK(zK Z + XK X
£oy dt 1 oxy dt оуг dt ^Viay14'1 шц^ ош т л шц^ ош // '
Записывая векторные уравнения относительного движения корпуса
(7.25) в проекциях на оси связанной системы координат OXrYrZr, прини-
мая во внимание выражения (7.424-7.49) и считая скорость перемещения
центра масс системы относительно шарнира малой, получим:
jK d(OSY к dCQsz , к + К ZKZ +m*XKX
dt w dt +\шу m шц£ош ™ X^X^) Л v 5^
(7.50)
’5У
'* (7.51)
^SZ
dt (7.52)
rK d®SZ rK d(aSY . (тК . -KyK v .mKYKY \d<S>Z (rK , mK YK 7 V
1ua dt lu,yz dt ~r\UiZ~rm ЛЩЛошГГП 1шц1ош/ dt гшхг m ^шц^ош/^
d(^Y
x—
dt
-hK
vuiyz
~Y^V0X\nK
Мщг»
(7.54)
Используя выражения (7.27+7.31) и записывая их для возмущенного
и программного движений ракеты, отбросив члены второго порядка мало-
сти, получим линеаризованные уравнения углового движения в отклоне-
ниях.
147
л <*2д&
'л’““
( „к
к лК2\ т
™ ^шц1
dt
Z ) ДУу = A4>x>
(7.55)
ОШ
(7.56)
оу>
К,*)]. 32Л<р
ош / \ЛХ *Z }рУу/ 2
at
(7.57)
, З^Дг [г .к (.к
оу j 2 + Р* ил/ г ил/
at
32Л& Lx,x (fK
лог 2 i" шц у шц
at
4-\тк -ткек у PAa>sz _ лiz
+ |/шг т ^шц^ош] (ft —&М<
Уравнения относительного углового движения корпуса
(
„КлК2\ ! .
шц 1 +
к
г “Лг) Ду»
at at \ т J
(7.58)
/'+1U/J-/f К^“
at at \ m )
- ^oy + Vo^nVK = Mua- (7.59)
7.4. Силы и моменты, действующие на ракету
Рассмотрим движение ракеты вне атмосферы под действием силы тяже-
сти G, силы тяги Р, кориолисовой силы Fk9 возмущающих силы Fe и
момента Мв.
При получении структуры правых частей уравнений движения (7.35),
(7.55) -е- (7.59), величины кориолисовых сил определим для ракеты с твердо-
топливным двигателем. Кориолисовы силы, действующие на ракету с ЖРД,
рассматривались К. С. Колесниковым и К. А. Абгаряном, И. М. Рапопортом
[88], [1].
Упрощенная схема твердотопливного двигательного отсека приведена
на рис. 7.2.
148
Запишем выражения, определяющие величины проекций Fxr, F/, F/
кориолисовой силы FK на оси системы координат OXKYKZK (рис. 7.1).
FK = F*iK + Fy]K +F£kk ,
где iK, jK, кк - орты системы координат OXKYKZK.
Примем выполняющимися следующие допущения.
1. Течение частиц в канале А (рис. 7.2) имеет осевую симметрию и суммар-
ная радиальная скорость частиц равна нулю.
2. Относительные скорости частиц V? в направлении продольной оси корпу-
са ракеты в сечениях X = 0 (сечение В - плоскость верхнего днища твер-
дотопливной двигательной установки), X = 1Ш (сечение С - плоскость сре-
за сопла двигательной установки), равна соответственно: Q =0,
V I
ГХ\*=1Ш
3. Давление во всех точках любого поперечного сечения канала А сече-
ния, соответствующего xe[0,Zw] одинаковое, хотя по времени может
меняться.
4. Секундный расход массы топлива т через любое поперечное сечение ка-
нала А от верхнего днища до среза сопла, величина постоянная, изме-
няющаяся от сечения к сечению
pSV^ = т(х) - const. (7.60)
Здесь р - плотность продуктов сгорания; S - площадь поперечного
сечения канала А.
5. Образование движущихся в канале А частиц происходит равномерно по
поверхности канала и только на участке 0 < х < 1Ш.
149
6. Кориолисово ускорение равно: ак = 2ф'хКг, где (О - угловая скорость
поворота канала А: со' = ш + c5s.
На основе принятых допущений найдем, что секундное образование дви-
жущейся массы на длине х канала А равно
где----секундное образование массы на единице длины канала А.
1ш
Если 5ш(0)ЛИг) = 1, то проекции элементарной кориолисовой силы на
оси связанной системы координат ЦКХКУК2К равны:
на участке длины корпуса 0 < х < 1Ш
d Fy = 2pSvrx[#-ya]dx; dF^ = -2pSvrx[4'~Yv]dx; (7.62)
на участке длины корпуса 1Ш< х <1п
d Fy = 2pSyrx[&-ya]dx, d Fy = -2pSyrx[iif-Yv]dx. (7.63)
Используя (7.60), (7.61) перепишем выражения (7.62), (7.63) в виде:
при 0 < х < 1Ш
drf = 2тх[0 - Ye]dx = 2—[i? - y„]dx,
1ш
dpz = -2mxW - Yjdx = -2р[у< - yF]dx; (7.64)
при /ш < X < ln
dFr =2mI[^-Ye\dx, dFz=-2mx\\i-yjdr. (7.65)
Интегрируя выражения (7.64), (7.65) по x, получим:
Fy = [m[ij - Ya] 1ш + 2/й[0 - уД/„ - /ш)] = m(2 ln - Zj(tf - уД (7.66)
Проекции сил P, FB на оси системы координат OXKYKZK записыва-
ются следующим образом:
P = PIK\ FB =F*iK +Fy]k +FbzKk; G = -GJk. (7.67)
Моменты сил F*, P (рис. 7.2) равны:
Mp=RoaxP,
—к _
M =-2jrx(a)Xy r)dm. (7.68)
Запишем проекции радиус-векторов Rqa и г на оси системы коорди-
нат OXKYKZK, учитывая, ч?о
Roa = рош — XTiк, г = рош - (ХТ -ln+ X)iк,
150
Roa = -ХТ1К + + mKl^IK ( (7 69)
m m
r = ~(XT -ln+ X)iK + mKl^JK + mKl^rv^K
m m
Здесь XT— координата точки Ш, отсчитанная от плоскости С,
X — координата поперечного сечения корпуса, отсчитанная от
плоскости верхнего днища двигателя (рис. 7.2).
Получим
Мр = j* +>»К1^,РУ9 , (7 70)
тп тп
_ (ji _ / \тк 1к г • 1-
Мк =-"» \ ~+(.4'-r4f)Ys\'iK-’Щу'-Гу)*
\ Z J ТП
/ (^Т ~^п Л llfl _/ ~^П +А
“I 2 3 I 1" ш) 2
jK +2т(д-/а)х
(7.71)
* 1Ш
+У+(/„ - 1ш)2Хт 1п+1ш
2 3) 2
Кк.
Проведя линеаризацию выражений сил и моментов, действующих на
ракету с шарнирно соединенными отсеками, получим их линеаризованные
выражения в приращениях:
<?/ -1 А •
XLF'jy = Fy + m -a—Hi- Ь~Т»),
j \ 2 J
^FjZ=Fl-ni^^y^-Yv), (7.72)
м'ох= [(6> - у9 )yv +(щ-у¥ )у9 ]+ Мх + мупр.<р,
m m ‘
12п+1ш ^-Г^у,
(7.73)
(7-74)
(Хт-1„
Гэ~^ Ц-у-2-
(7.75)
X
yF+2w 1ш\
т^шц?
где — суммы проекций приращений внешних сил на оси
системы координат UIXKYKZK;
151
у 9 У&ч Y^ Yy, «9, \j/—возмущения параметров движения;
Л/оу, M'oz — проекции момента внешних сил на оси системы ко-
ординат OXKYKZK;
Мх, Му, Mz — проекции момента возмущающих сил на оси системы
координат OXKYKZK;
Мупр^ — проекции момента пары управляющих сил на ось систе-
мы координат OXKYKZK.
Запишем вектор F = Y.FjXiK + &£FjYjK + &^FjZKK в проекциях на
j j
программные направления осей системы координат СxrYrZr, вектор
М = MoxiK + MOYjK + MOZKK — в проекциях на оси системы координат
OXYZ.
Оси систем координат OXKYKZK, OXrYrZr параллельны соответствую-
щим осям системы координат LLIXKYKZK, LLIXrYrZr.
Поэтому, воспользовавшись выражением (7.39), получим
Frx 1 Yu Yy j ZFX + AZFr ys - A£FZ у J J j
Fr = -Yu 1 0 ^Fjr = “ SFjX Yd +
Fr rz Yy 0 1 £FjX Yy + ^FjZ
Mrox 1 Ys Yt ^ox ^OX + MqyId “ ^ozl4*
MrOY = “Ys 1 0 ' MOY = - ^oxld + MOY
Mroz Yt 0 1 MOZ Mqx7 T + Moz
= Р+
Проекции внешних сил на оси системы координат OXrYrZr
Frr = -Ру3 + F# +^2/”2
F/ = Лт + Fz ~ " Y<? )•
(7.77)
(7.78)
т
Проекции момента сил М на оси системы координат OXrYrZr.
152
М0Х “
2 I ~гп
г+ н \2ХТ 1п +1Ш
2 3 I ' 2
х[(4*-ГтЬ+(^-ъК1+^ +л/УЯЛф-
ШК1К
иГ 1 1ШЦ
Mqy ----
m
-2 Ц
(7.79)
Р?ч + 2m 1Ш
2Хт-1п^1ш
I
2 3
П
х
2
X
(7.80)
г _m 1щц р .• . (Хт-1п 1Ш А /. . \2ХТ-1п + 1Ш
Moz -------РУ«> -2m /ш —-—+— -(/„ -1Ш)—‘—— -------- х
m L I 3 ) 2
х(->-гЛ«?. (7'81)
Получим формулы для определения правых частей уравнения относи-
тельного движения. Движение корпуса относительно головного отсека
проходит под действием инерционных сил: -mK -mKYi9 -mKZx и
т
разностей управляющих сил (Р2-Л), (^1“^з)в шарнирном узле. Схема
действия инерционных сил, обуславливающих движение корпуса ракеты
относительно головного отсека в плоскости тангажа, показана на рис. 7.3.
Рис. 7.3
Здесь У] = Y -—0, Zj = Z - — у (7.82)
т т
в рамках принятых допущений составляющие ускорения системы «головной
отсек - корпус» в направлении осей OY, OZ соответственно.
Принимая во внимание (7.82), найдем проекции момента сил в шарнире.
153
Проекции момента сил в шарнире на оси системы координат IIIXrYrZr
М'шГ =-l^mK(Z+-Y)+—mKl^ yv - (Р2 - Pt)fj+, (7.83)
m m
M'uZ=l^mK(Y--^ + -тк1*цГа -(P4 -P3)r] + I&y,. (7.84)
m m
Здесь e - коэффициент демпфирования, ту - плечо управляющей силы
в шарнирном узле.
d(OKY do)?? d(Dcv
Принимая во внимание, что = -yz, = 0 и
используя выражения (7.35), (7.55X7-59), (7.71) (7.79Ж7.81), (7.83),
окончательно запишем уравнения движения ракеты, управляемой относи-
тельным поворотом отсеков.
Уравнения движения ракеты вне атмосферы
1. Уравнения поступательного движения
mZ = mKl^Yv -mfa- jv\11п -1Ш)-Р^~7у,)+ F”, (7.85)
mY = -тк1^7б + ~ To)&„ - /ш)+ P(t> - )+ Frn. (7.86)
2. Уравнения углового движения
-хм -ixV
xY^-[(lr -Iх)+тк1шЦ2
1-— 1ûÄ ~[mKl^2
m
X Го - 4^ln2 /a< К + - г До ] - 2т[/ш ^Г2 ln + у j-
_(/л -/ш)x2Хт ~^п + /ш][(у-+(^-7^]-(.т^ут + тк1^)х
x{Z~Y)-(mb.ZT + tnKl^Yv)(Y ~&) + Мпх +МупР^ (7.87)
154
= ~Хош)+^г + -mKl*4Xoa]Yv +
тк г (Хт-l I А / ЛХт-1 +1
+—Р1*цГу +2т[/шр—-(/„-/ш) г ш]х (7.88)
m 2 3 J 2
^~Yv)+my>
1о2^ = \тК1шц^шц-X0lu)+(lz ~Ix\w? + U*Y-тК1шЦХ0Ш1и +
+—Р1шЦГ6 -2^/Л^Р^+У-(/л-/№)2^Г ~/л +/ш]х (7-88)
m у 2 3 ) 2
x(ij-r„)+^.
3. Уравнения углового движения корпуса относительно ГО
/ к
'.М, = to -»to^> + [-"to’ > ~
+ (if - lx ir«» + "I ton + — V * Ml- ify^t,,
I m I m Y Y
(7.90)
toT.-fo-»to-f~)»-i”-to1fi+—
I m I
k 7 (7-91)
- тК1шц\У + ]-—Р1шЧУь + MZ -
\ m ) m
Уравнения движения ракеты в атмосфере
1. Уравнения поступательного движения
mZ = mKl^ -m(v-Yv)(2Z„-^-(P-Xa^-J^+Fz , (7.92)
mY = -mKl^yb +m^-uX2l„ -lM)+(P-Xa)(b-n)+FYn. (7.93)
155
2. Уравнения углового движения
х Wh fe - )+ (/f
к \ /
- m . _ KiK 2 m
1-----lYoYv-|> —
ТП
1оХ<Р = 1тк1^ц-Хош)+{^
XYeij-[^y-7х)+т^2
/OJ 1 \К}К .
к
т
-т\
х 2АГГ-Л+А«][(у _ )ув + (ft- ] _ (ОТД уТ + mKl^ Ye)(Z V) +
-(т^т+тЧ^У-^-^+М^ +MynPV+Maynf<f+Max. (7.94)
IoyW = -LmKl^ -xj+ftf -I$)№ + V»y+?-(P-xa)*
m
xZ* YV +2^/шр^ + ^-(/я -/ц)2уГг~2/л+/ц](¥--У¥)+А/? +M°y, (7.95)
IoZb=[mKl^-X^+tl*-I$\w + [I£y ~>”К1шЦХ0Ш]уь+— {P-Xa)*
m
X/* Ye -2^/шр^ + ^-(/я -U2Xr~2"+4M<>)+^ +M‘Z. (7.96)
3. Уравнения углового движения корпуса относительно ГО
I*Yiv = fc - )ч> + [тК1шц2 1 - ~ j+ (^ " ЬоФ +
+ mKl^4(z+P~Xa^}-—(P-Xatf^y + Ml- I&iy + BaKlKdut,
{ m I m
^Кф-
m
m
ik2
^шц
' A mK
-тЧЦ Y+—^0---------(Р-Ха)1шЦЪ+М^-^^ + Вак1^
l m ) m
(7.97)
(7.98)
156
В уравнениях (7.92-?7.98) приняты следующие обозначения:
Ха - колинеарная продольной оси корпуса составляющая равнодей-
ствующей аэродинамических сил, действующих на ракету;
1аш “ расстояние от центра давления корпуса до оси вращения шар-
нира;
Вак, №к - боковая и нормальная составляющие равнодействующей
аэродинамических сил, действующих на корпус ракеты;
Fr", Fz" - возмущающие силы, действующие на ракету в плоскостях
тангажа и рыскания;
М ш» М ш - моменты сил, создаваемые вокруг осей шарнира гидравли-
ческими приводами;
Мах, Му , Maz - моменты равнодействующей аэродинамических
сил вокруг главных центральных осей ракеты;
упР.(р “ моменты управляющих аэродинамических и реактив-
ных сил;
МХУ Му, Mnz - возмущающие моменты сил, действующие в соответ-
ствующих плоскостях;
ДУГ, AZr - составляющие весовой асимметрии ракеты.
Методы и формулы для определения перечисленных аэродинамиче-
ских и управляющих сил и моментов изложены в работах многих авторов
(см. часть 1).
7.5. Уравнение крутильных колебаний
Возмущенное относительное движение корпуса ракеты и головного от-
сека по координате обусловлено:
- переносным вращательным движением головного отсека ракеты от-
носительно продольной оси;
- демпфирующим моментом, обусловленным переносной угловой ско-
ростью головного отсека
мл = mxiq^m£ (ф-Ту);
- моментом от управляющих сил, создаваемых аэродинамическими
рулями, используемыми для управления по крену
МА.у =4qSpCy_p_(M,34,)rpCoS89-,
157
- моментами сил в двухстепенном карданном соединении головного
отсека и корпуса
Мш = [(с4 $4 Cos ц4 - с2 S2 Cosn2 )у13 + (Сз 5з Cos[i3 -
-CiSiCosiL^^-r^,.
Таким образом, движение корпуса ракеты по обобщенной координате
уф описывается следующим дифференциальным уравнением:
Г, = ф - // + C,r,Coj^ + ****** У» +
+[(C4S4Cos/i4 — CjSjCos Д2)/13 + (C3S3Cosfl3 — C1StCosfll )/14]_rLrJJJ. +
D
+ mx4SJ ф-С'Г, + м;г}. T,-(Yt+Y')sws*.
Здесь
5 , - упругие деформации конструкции в местах крепления приводов,
С, - коэффициенты жесткости,
Д - углы наклона линий действия приводов к продольной оси голов-
ного отсека, (/ = 1-4);
b - расстояние между корпусом и головным отсеком ракеты при их со-
осном расположении;
Ьш ~ расстояние от днища головного отсека до соответствующей оси
вращения карданного шарнира;
АПх » С ~ аэР°Динамические коэффициенты.
7.6. Исходные данные на разработку системы управления
Для обеспечения максимальной достоверности разработка математи-
ческой модели ракеты, управляемой путем отклонения головного отсека
(в терминологии ДНУ - «с шарнирно соединенными отсеками»), прово-
дилась также специалистами (см. главу 6) ЦНИИмаш, ИТМ АН Украины
иГКБЮ.
После рассмотрения и анализа всех полученных результатов была соз-
дана и согласована, в т. ч. с НИИ АП, динамическая схема как исходные
данные на проектирование СУ, в виде следующих основных систем диф-
ференциальных уравнений движения ракеты.
158
г
Рис. 7.4 Рис. 7.5
Системы координат
0oXoyoZo - программная система координат. Начало расположено
в точке, в которой в данный момент времени находился бы центр масс из-
делия при движении его по программной траектории. Ось 0ОХО совпадает
с программным направлением продольной оси корпуса изделия. Оси 0ОУО
и 0OZO лежат в плоскости, нормальной к оси OQXQ. Ось 0ОУО расположена
при этом в вертикальной плоскости, проходящей через ось OQXQ, и на-
правлена в общем случае вверх от поверхности Земли. Ось 0OZO дополня-
ет систему до правой.
OjXjZjZj - связанная с «прямым» изделием, т. е. с изделием при неот-
клоненном головном отсеке (ГО), система координат. Начало расположено
159
в центре масс «прямого» изделия. Ось - совпадает с продольной
осью корпуса и направлена в сторону носка головного отсека. Оси OtYt
и OtZt при программном движении изделия совпадают по направлению
с соответствующими осями O0Y0 и O0Z0 программной системы координат.
O2A\y2Z2 - связанная с ГО система координат. Начало расположено
в центре шарнирного соединения, связывающего корпус и головной отсек.
Оси О2Х2, O2Y2, О2%2 ПРИ заарретированном относительно корпуса го-
ловном отсеке параллельны соответствующим осям ОхХх, OXYX, (\ZX свя-
занной с «прямым» изделием системы координат.
O10A\0yi0Z10 - строительная система координат. Начало расположено
в геометрической вершине «прямого» изделия. Оси О10У10, О10У10, O29Z^
направлены параллельно соответствующим осям ОхХх, OXYX, OXZX свя-
занной с «прямым» изделием системы координат.
Направления отсчета углов между осями координат указаны на
рис. 7.4, 7.5.
OXYZ - поточная система координат. Начало расположено в центре
масс «прямого» изделия. Ось ОХ совпадает с продольной осью корпуса
и направлена в сторону носка головного отсека. Оси OY и OZ лежат
в плоскости, нормальной к оси ОХ. Ось OY расположена при этом в
плоскости пространственного угла атаки и направлена в сторону обдува
корпуса. Ось OZ дополняет систему до правой.
Массово-инерционные и центровочные характеристики изделия
т - масса изделия;
тг, тк - масса головного отсека, корпуса изделия;
т - секундный расход топлива через сопла реактивной двигательной
установки (ДУ);
7^, 7а - осевые моменты инерции «прямого» изделия относи-
тельно связанных осей O2X^Y2Z2;
- момент инерции изделия при отклоненном ГО относительно
оси ОхХх;
/£, 7£, /д - осевые моменты инерции ГО относительно связанных
осей O2X2Y2Z2;
ХТ (ЛГ*) - расстояние от плоскости среза сопел ДУ (от носка) до цен-
тра тяжести «прямого» изделия;
Ст - расстояние от носка до центра тяжести «прямого» изделия, отне-
сенное к длине ступени;
160
&yT, bzT - поперечные смещения центра тяжести «прямого» изделия
от продольной оси, обусловленные технологическими погрешностями из-
готовления изделия;
ДУгпп ^тш ~ поперечные смещения центра тяжести головного отсека
относительно центра шарнирного соединения, обусловленные технологи-
ческими погрешностями изготовления ступени;
Душ, Дгш - поперечные смещения центра шарнирного соединения
относительно продольной оси головного отсека;
х*г, стг - расстояние от носка до центра тяжести головного отсека
и то же расстояние, отнесенное к длине корпуса ГО.
Геометрические характеристики изделия
lK, RK - длина «прямого» изделия и радиус поперечного сечения из-
делия;
SM, - площади миделевых сечений изделия и ГО;
Хр - расстояние от плоскости среза сопел ДУ до точек приложения
реактивных управляющих и возмущающих воздействий;
Хщ ~ расстояние от плоскости среза сопел ДУ до оси вращения аэро-
динамических рулей при неотклоненном головном отсеке;
rF, гщ - расстояния от продольной оси «прямого» изделия до точек
приложения реактивных и аэродинамических управляющих усилий по
крену;
8Щ - площадь, к которой приведены аэродинамические характеристи-
ки руля;
1Г - длина корпуса головного отсека;
хш - расстояние от плоскости среза сопел ДУ до осей вращения голов-
ного отсека в плоскостях тангажа и рыскания;
- расстояние от центра тяжести головного отсека до тех же осей
вращения ГО;
Zdm - расстояние от центра давления головного отсека до тех же осей
вращения ГО;
Zgm - расстояние от точки установки датчиков системы управления до
тех же осей вращения ГО;
(Хкс /2) - расстояние от плоскости среза сопел ДУ до точки приложе-
ния кориолисовых сил, обусловленных движением продуктов сгорания
внутри корпуса ДУ,
161
Дур, &zP - смещения оси соплового блока ДУ относительно продоль-
ной оси корпуса изделия,
^га^ка ~ характерные размеры изделия, к которым приведены
аэродинамические характеристики.
Параметры движения изделия
t - текущее время;
Н - высота полета изделия над поверхностью Земли;
V, Vw - модули скоростей центра масс «прямого» изделия относи-
тельно Земли и относительно воздушного потока;
а, М - скорость звука, число Маха;
у, z - боковые отклонения центра касс «прямого» изделия от про-
граммной траектории в проекциях на оси программной системы координат;
ур z’i - проекции ускорений центра масс «прямого» изделия на свя-
занные оси OjXjKjZj ;
п*9 пгу9 nf - составляющие поперечной перегрузки в центре масс ГО;
Z^, У^, Zd9 Yd - параметры движения в боковых направлениях свя-
занной с ГО точки, в которой установлены датчики системы управления
(СУ);
Уа9 za - информация о движений изделия в боковых направлениях,
используемая для формирования алгоритмов управления;
уг9 <р - углы, определяющие ориентацию связанных с «прямым»
изделием осей относительно программной системы координат (углы рыс-
кания, тангажа и крена соответственно); индексы параметров изделия
в каналах Р, Т, В соответственно;
&д9 <рд - углы, определяющие ориентацию связанных с головным
отсеком осей относительно программной системы координат;
уа9 Фа ~ вычисленные на основе информации с датчиков СУ па-
раметры углового движения изделия, используемые для формирования
алгоритмов управления;
а9 ft - углы атаки и скольжения «прямого» изделия;
Oj. - пространственный угол атаки «прямого» изделия;
162
аг, fir - углы атаки и скольжения головного отсека;
алр, рнр - программные углы атаки и тангажа;
Фв - угол между плоскостью I-Ш и плоскостью угла атаки;
фг - угол между плоскостью I-Ш и плоскостью, в которой происходит
поворот головного отсека;
<ре - угол между плоскостью угла атаки и плоскостью, в которой про-
исходит поворот головного отсека.
Параметры управляющих органов, рулевых приводов
и автомата стабилизации
8?, 8^ 8у, Uy - координаты, характеризующие значения реактив-
ных управляющих усилий в каналах рыскания, тангажа и крена соот-
ветственно;
Руу9 Му - эффективность реактивных управляющих органов
в каналах тангажа (рыскания) и крена;
3* - угол поворота аэродинамических рулей от номинального положения;
ащо> ащ - местные углы атаки на поверхности аэродинамических
(/ = 1,2,3,4)
рулей при Оу =0 и а* #0;
- коэффициенты нормальных аэродинамических сил, дейст-
(/ = 1,2,3,4)
вующих на аэродинамические рули;
с„щ - производная коэффициентов нормальных аэродинамических
сил, действующих на аэродинамические рули;
Т/9 Т?9 Ту - постоянные времени приводов реактивных управ-
ляющих органов и аэродинамических рулей;
Т3, Т4 - постоянная времени автомата стабилизации в канале крена;
_ коэффициенты АС в каналах рыскания (тангажа)
К,, К.)
при управлении изделием с помощью реактивных управляющих органов;
163
b*, Ьф, Кф (аф, аф) - коэффициенты АС в канале крена при
управлении изделием с помощью реактивных (аэродинамических) управ-
ляющих органов;
а<ч’ % “ коэффициенты АС в канале крена, соответствующие тариро-
вочному скоростному напору qQ;
- углы отклонения головного отсека от номинального поло-
Г24, Г13
жения в плоскостях рыскании и тангажа и в плоскостях установки руле-
вых приводов;
у - пространственный угол отклонения ГО от номинального поло-
жения;
R. (i = 1,2,3,4) - усилия, развиваемые рулевыми приводами;
М ~ моменты, развиваемые рулевым агрегатом поворотов го-
ловного отсека относительно поперечных осей O2Y2 и O2Z2 связанной
с ГО системы координат;
Kv - коэффициент, характеризующий крутизну скоростной характе-
ристики рулевого привода (РП) при холостом ходе;
Кн - коэффициент линеаризации механической характеристики РП;
См - механическая жесткость силовой цепи РП;
- коэффициент обратной связи РП;
Ьш, b - номинальные расстояния от точки крепления РП на III ступе-
ни до поперечных плоскостей, проходящих через шарнирное соединение
и через точку крепления РП на ГО соответственно;
гА - плечо силы, создаваемой РП относительно центра шарнирного со-
единения;
- угол установки штока РП относительно продольной оси корпуса,
изделия;
- коэффициенты демпфирования колебаний головного отсека
относительно корпуса изделия конструктивными элементами шарнирного
соединения и демпфирующими устройствами;
аг9 ai
- коэффициенты АС в каналах рыскания (танга-
аЬ ау> ау}
жа) при управлении изделием с помощью поворотного отсека;
164
Гоф ^,огр Догр Догр С огр
у ’ /д ’ UVP ’ VP ’ U6P ’
- предельные значения координат, харак-
ёогр Догр Догр Догр Догр
теризующих значения управляющих усилий и их производных по вре-
мени;
R^\ , R“p, Rf - предельные значения усилий, развиваемых ру-
левым агрегатом, и их производных;
- расстояния от продольной оси ГО до точек крепления штоков РП
к головному отсеку;
х, (/ = 1,2,3,4) - линейные перемещения штоков РП относительно
корпуса изделия.
Внешние силы и моменты.
Коэффициенты аэродинамических сил и моментов
g - ускорение силы земного притяжения (9,81 м/с2);
Р - сила тяги реактивной двигательной установки;
Г, ТГ - осевые аэродинамические силы, действующие на изделие и на
головной отсек соответственно;
wx - продольное кажущееся ускорение изделия;
В, N - боковая и нормальная составляющие главного вектора аэроди-
намических сил, действующих на изделие;
No - нормальная аэродинамическая сила при а = апр, Р = = 0;
Вг, Nr - боковая и нормальная составляющие главного вектора аэроди-
намических сил, действующих на головной отсек;
ММ™р - проекций главного момента аэродинамических сил отно-
сительно осей OtYt и O1Z1 связанной с «прямым» изделием системы ко-
ординат;
т®, т*, т® - коэффициенты аэродинамического демпфирования из-
делия;
m®r, m®r, т°^ - коэффициенты аэродинамического демпфирования
головного отсека;
~ коэффициенты аэродинамических моментов относительно
строительных осей О10У10 и O10Zi0;
mJ, тТг - то же относительно связанных с «прямым» изделием осей
и OlZl;
165
Сп, Св, С*) С% - коэффициенты нормальной и боковой состав-
ляющих аэродинамических сил, действующих на изделие, и их произ-
водные;
Ст, Стг - коэффициенты осевых аэродинамических сил, действующих
на изделие и на ГО соответственно;
С* , Св - коэффициенты нормальной и боковой составляющих аэро-
динамических сил, действующих на головной отсек;
CJ, СТ - расстояние от носка до центра давления «прямого» из-
делия и головного отсека, отнесенные к длине изделия и ГО соответст-
венно;
X*, X* - расстояние от плоскости среза сопел ДУ до центра давления
«прямого» изделия в плоскостях Р, Т;
А» р(Н) - плотность атмосферы на уровне земной поверхности и на
произвольной высоте;
q - скоростной напор;
wy, wz - составляющие скорости ветра относительно Земли в продоль-
ной и боковой плоскостях;
w - модуль скорости ветра относительно Земли;
(А^-я/2) - угол между вектором скорости ветра и плоскостью
стрельбы изделия;
- составляющие перекоса вектора тяги ДУ в плоскостях танга-
жа и рыскания;
F”, М”, М”, М* - возмущающие силы и моменты, обуслов-
ленные технологическими погрешностями изготовления изделия
Ду,, Az,, Дуг, Дгг, vr, v„;
Л/"г, Mnv - возмущающие моменты, обусловленные технологиче-
скими погрешностями изготовления головного отсека и шарнирного со-
единения;
тх0 - коэффициент аэродинамической неосесимметричности «прямо-
го» изделия;
Л - поправочный коэффициент, учитывающий случайный характер
действующих на изделие возмущающих факторов;
166
c*x9 c'zv myi> m*zi ~ коэффициенты аэродинамических сил и моментов,
действующих на изделие, без учета влияния кабельных желобов в проек-
циях на связанные оси;
са =са ср =с?
ж я*» и* _ коэффициенты дополнительных аэродинамиче-
ских сил и моментов, обусловленных влиянием кабельных желобов,
в проекциях на связанные оси;
су9 сг9 ту9 тг - коэффициенты аэродинамических сил и моментов,
действующих на изделие, без учета кабельных желобов в проекциях на по-
точные оси OXYZ;
шх0, ~ коэффициенты аэродинамических моментов изделия
и управляющих органов по крену;
So. So. ту0< тг0< Sr. "IxZ. Cy0< mz0> m*>0 ~ КОЭффи-
циенты аппроксимации зависимости аэродинамических сил и моментов от
параметров движения изделия.
Параметры упругой подвески ГО
/и. (/ = 1,2,3,4) - массы штоков РП совместно с присоединенными
к ним массами поршней, цапф и конструктивных элементов креп-
ления PH;
5. (i = 1,2,3,4) - упругие деформации подвески ГО в районах поса-
дочных мест РП;
ct (i = 1,2,3,4) - жесткости подвески ГО в районах посадочных
мест РП;
- частота изгибных колебаний ГО относительно корпуса ступени
при «замороженном» рабочем теле РП;
£ - коэффициент демпфирования колебаний штоков РП совместно
с присоединенными к ним массами;
уф - угол поворотов головного отсека относительно корпуса за счет
крутильных колебаний ГО;
Д - частота крутильных колебаний ГО относительно корпуса
ступени;
- крутильная жесткость карданного узла ГО;
167
- декремент крутильных колебаний ГО;
% - продольные перемещения ГО относительно корпуса изделия за
счет податливости поворотного узла;
сх - осевая составляющая жесткости подвески ГО;
£х - коэффициент демпфирования продольных колебаний ГО;
fa - частота колебаний штоков РП с присоединенными к ним массами
относительно головного отсека без учета жесткости РМ;
Л» Ло - частота продольных колебаний ГО относительно ступени
при «замороженном» рабочем теле РП и при отсутствии РП соответст-
венно.
Параметры упругих колебаний корпуса
Р„ - обобщенные координаты для первых гармоник поперечных
(Л = 1,2)
колебаний корпуса изделия в плоскостях II-IV и I-III;
ая - приведенная масса поперечных колебаний корпуса изделия при
возбуждении n-й, гармоники;
” форма упругой линии корпуса изделия и ее производ-
ной при возбуждении n-й гармоники поперечных колебаний;
/ , fpn ~ частота n-й гармоники упругих поперечных колебаний кор-
пуса;
£?л, £рп ~ логарифмический декремент n-й гармоники упругих попе-
речных колебаний корпуса.
1. Уравнения движения системы «корпус и головной отсек» в исход-
ной координатной форме
Канал рыскания
В нМтшУу (тДут
Z’=(^) ~XT)‘1SM
V+F“
168
MyP -Pyv(XT -xp)5v -mJ WX1 + ^% hnnYy +
+1 Jyy + тг1тш(хш XT)JVy I Jyy JXx+mr1Trn(xrn хт)|т9Ф ’>
®r^dm + mr Wxi +
Yv-
1
Jr
\ yyj
-m,
уу4‘1Пр1тш(хш X.
, (7.99)
Z = Z1-Wxly>
20Д =Zj - WX1 +^Xk M* =(c2S2-C4S4 + CjSi -c3S3)rAsin45°-
k Hl J
Jyy^yY у
Канал тангажа
N + + т^пцУ з + (mAzT + тг1^цу )ф 4-
2mxkc-
3 + F°
M^p-P^(xT-xp)8^-m
'^®г^тш(хш хт)
_ m“qSml^ +rilXkc(2x
Jxx +тг^тш (хш x
-xkc) +
3 =
V
169
Nrldnj+mr^Wxi + m Xj^TrnYd+[jzz+ тг^тш(хш xt)J^*"Мш *"
+тг11шу| -(jTa - Jr„)rv<p+ (&-y9)+M^
(7.100)
|y9|^y7, y = y1+wx19-^o,
m
Yog=Y1+[wxl+^x]o-^(
6 V m ) m
мш =(C2S2 “C4S4 ~C1S1 + c3S3)rAsin45o - J^e3ys.
Канал крена
-2Р^Гриф -Ч8ЩГЩCOS5“£cShh-У-хЧ^каф + Mn _4M8p5p +
1Д +JixY<p-(mAyT-mrlTniYd)z1+(mAzT + mrlTOIYv)y1-
“[jyy ~ JXX _^тг^тш(хш ~~ XT)jYaV ~ Jxx +тг(хш “xt)]yvS +
+(jyy ~ Jxx)y»Yv “(^zz “ Jxx)y«pY3 + mxoQSmRk +MX
Уравнения упругой подвески ГО
Y<p=9-YaV + Yv3 +
Ч5щгщсо85“Х С'шц+
+2Р£рГиф + тхгЧ5мКкаф_ +
(c4S4cosp4 “C2S2 cospi2)Yi3 +
+ х
+(c3S3cosp3 -CjSjCospJy^
x^S-rr +Mn
Л b 1 кр 1V1 XT
713 =(Ys “ YN,)sin45°,
Y24 =(y® + Yv)sin45°,
170
= -M^Z- WX1 I Tr + cosgAf CjSj + Bryv -Nryэ
m n ymr mr mr^ "
"^TiuYv ? V ) ” " V » )
s2 =-(?v "V + Ys —S)rAsin45°-fwxl +^-Aosha«F^2 -
4 ' \ m ) л у m2
——(c2s2-R2),
m2
s4 = -(?<!, -У + У» -9)rAsin45° -fwxl +^x'|cosnA ~~ .F^4-
' ' V m ) п у
-—(c4s4-R4),
Шд
Si =-(yv -V-Ys + &)rAsin45°-fwx] +^- jflcosgA<p-Sl -
XT ' V m ) п у mj
—~_(C1S1-R1)’
ml
S3 =-(yv -W-Y& + 9)rAsin45° -fwxl +^-x1cosha ~~<F^S3 -
v ' \ m ) п у m3
——(C3S3-R3)-
2. Кинематические соотношения
Y13 =(y»-Yv)sm45o,
Y24=(-Y& + Yv)sin45°,
Wy =-WsinAwsin9np,
ww=A/v2 + wz2+wy2,
H1=Ha + Y13.
H3=Ma-Y13>
z-W
P = y + arctg—^-Z-,
a У-Wy
a = & - arctg v + ctnp,
Wz = WcosAw>
V
M=—
a
H2 = Ha-Y24>
M4 = Ha+Y24.
171
3. Аэродинамические силы и моменты
МГ -qSMlkaniy, mJ = myl-CTCB^^ B = qSMCB, No=qSMCn(a = anp)Yv=Y3=P = o), Br=qs;x, Tr=qSj.C?, M«P=qSMlkBmL Г i mZ=mzl+CTCn ~“ Vka 7 n=qSMcn, • T = qSMCx, Nr=qSrMCrn,
Mx-XqSMRkamx = ^dm(^гУу + BpYa) тх^(аУу РУз)*
4. Вспомогательные соотношения
q = (|W, р = р0 V" ’
U7 < Ро )
4=(1-c3f)1k. фс^м),
^=(1-C?)lk, Cd»=Cd»(a,M),
хт =(1-Ст)1к =1к-х*, С5 = С5(аг,м) = С5(рг,м),
^тш = -^тг’ ^dm — “ хш — ^d^ra»
172
mk = m-mr,
x =C 1
Атг '‘"гг1 г»
C|J2,ly.)3-(iM.2.3,4). <„ = (2rf.p)\,.
2tIa
сх=(2я^х) mr 2 Sci =(^я^хо) mr>
COS |1A j
m,= Ci .(i = 1,2,3,4),
(2Ttfs)2V
r^p=—------(b-bffl)tgnA.
P cosh A
[(c4s4cosg4-c2s2cosh2)yi3 +(C3S3COSH3-CjSjCOSgj^J^rJp
=(m»yv-mXyv)^-
5. Возмущающие силы и моменты
F“=-Pv¥, Fyn=-Pvs,
M“ =-Pv>v (хт - xp)-mWxiAzT + PAZp,
M z = -p° 3 ( x T - x P ) + mWx 1 Ay T + PAy p,
Мур — Шг§ПхА2тш ТгА2ш,
Mzr — — ^гб^хАУтш + ТгАуш,
Mx=-P(vvAyp + udAZp),
M XT ~ ТШ ~ А уА^тш j + NfAy пт В Г Az in
6. Учет упругих свойств корпуса
Для учета упругих свойств корпуса представленная выше система до-
полняется следующими уравнениями относительно обобщенных коорди-
нат qn, Рп(п = 1,2) для первых двух гармоник поперечных колебаний кор-
пуса изделия:
Qn +eqnQn *-a)qnQn =aqByv^v +ачву¥Уу (7.101)
Pn +epnPn +coqnPn =apnyeY3 +aPBY»7& +aPB59$3’ (7.102)
173
а уравнения (7.99), (7.100) записываются следующим образом:
2
+a3iZi +а32У+ a39x = b3 + ^(a’Mqn +a^qqn), (7.103)
n=l
2
?э + аб4У1+аб5» + а69Х = Ьб + £(аГ.рЛп + аГ.Р.Рп)> <7104)
П=1
2
'И8=¥ + УэФ-Уч,-£п'п(хш)Чп>
П=1
2
Zg =^og “(^gm + хт ~ xin)v — ^Лп(хш)Чп’
п=1
2
&8=Э-Уч,Ф-Т9 + £Пп(хш)Рп>
П=1
2
У g “Yog (igui + хт“хш)^~ Igm (y \|/Ф ~~ Yd) + Л П (х in )Рп •
п=1
Коэффициенты дополнительных уравнений (7.101), (7.102) и дополни-
тельных членов в уравнениях (7.103), (7.104) в соответствии с (7.99, 7.100,
7.101, 7.102) имеют при этом следующую структуру:
aqnyv аРпУэ Jyy(zz)Tl(xm)j,
аявУ¥ = —арпУэ ~^"а ^х^тшП (хщ),
ayvqn аУэРв
г Г ^тшЛп (Хш) + Л (хш) »
j yy(zz)
O)qB=27tfqB’
(CDa
Eq = — kq .
Чв П J Чв
PyVTln(xp)
ачА - -
ап
174
Часть 3
ДИНАМИКА ЖЕСТКОЙ РАКЕТЫ С БАКАМИ,
ЗАПОЛНЕННЫМИ КОМПОНЕНТАМИ
ТОПЛИВА
Исследование вопросов динамики ракеты, проведенное в части 1 на-
стоящего учебника, в представлении объекта управления как твердого те-
ла, является совершенно недостаточным и не отражает всей совокупности
проблем обеспечения устойчивости возмущенного движения жидкостной
ракеты.
Такое положение определяется значительным влиянием на устойчи-
вость ракеты как движения больших масс жидкости в баках, так и возник-
новением при этом сил, действующих на корпус объекта управления.
Задача изучения взаимодействия движущегося тела с жидкостью,
целиком заполняющей его полости, была рассмотрена еще в 1885 г.
Н. Е. Жуковским. Показано, что при исследованиях динамики реальное
тело с идеальной жидкостью в поле потенциальных сил можно заменить
эквивалентным телом с измененным тензором инерции. Таким образом,
хотя поведение жидкости в полости описывается уравнениями в частных
производных для сплошной среды, рассматриваемая механическая систе-
ма имеет то же число степеней свободы, что и твердое тело. Совсем иная
картина получается при отсутствии потенциальности течения жидкости.
Так, в случае однородного вихревого течения жидкости внутри полости
тела, совершающего ротационное движение, у системы «твердое тело
с полостью, полностью заполненной жидкостью» появляется бесконечное
число степеней свободы.
Наличие свободной поверхности жидкости при частичном заполнении
полости существенно осложняет задачу составления и исследования урав-
нений движения, поскольку также появляется еще бесконечное число до-
полнительных степеней свободы, связанных с волновыми движениями
жидкости.
175
Возрастающие потребности техники вызвали большой поток работ,
посвященных разработке линейной теории динамики тела с полостями,
частично заполненными жидкостью, находящегося в потенциальном поле
сил. Впервые линейные уравнения, вполне строго описывающие общий
случай возмущенного движения тела с цилиндрической полостью, час-
тично заполненной жидкостью, при заданной системе внешних сил были
получены Г. С. Наримановым в 1955 г. [115]. Затем независимо аналогич-
ные результаты получают Д. Е. Охоцимский, Б. И. Рабинович, Н. Н. Мои-
сеев [119], [127, [110]. Современное состояние линейной теории изложено
в ряде монографий Н. Н. Моисеева и В. В. Румянцева, Г. Н. Микишева и
Б. П. Рабиновича, К. С. Колесникова и др. [113], [106], [107], [87]. Краткий
обзор литературы по этому вопросу приведен в разделе «Введение».
Сложность вопросов, относящихся к изучению движения твердого те-
ла и жидкости, частично заполняющей его полость, требовала значительных
упрощений при формулировке условий задачи. Одним из существенных ус-
ловий, используемых при разработке указанной проблемы, является предпо-
ложение о малости параметров движения, позволяющее линеаризовать урав-
нения движения по величинам этих параметров. Движение можно считать
малым, если все параметры, его характеризующие, столь малы, что можно
пренебречь их произведениями, квадратами и более высокими степенями по
сравнению с членами, линейно зависящими от величин этих параметров.
В разработанной линейной теории эффект вязкости жидкости учиты-
вается лишь введением соответствующих диссипативных членов. При
этом предполагается, что рассеивание энергии колебаний в системе явля-
ется достаточно малым. Для полостей с гладкими стенками это предполо-
жение соответствует случаю движения жидкости относительно малой
вязкости. Таким образом, все гидродинамические коэффициенты уравне-
ний возмущенного движения, за исключением коэффициентов демпфиро-
вания, целиком определяются из решений задач гидродинамики, основан-
ных на концепции малых волновых движений идеальной жидкости. Ре-
зультаты сравнения многочисленных теоретических и экспериментальных
данных, полученных для различных форм полостей, полностью подтвер-
дили достоверность уравнений возмущенного движения при устойчивых
процессах, а следовательно, и правомерность сделанных при их выводе
допущений.
Обеспечение устойчивого полета и требуемой точности управления
современных жидкостных ракет тяжелого класса и ракет-носителей КА,
т. е. объектов управления с радиусом баков около одного метра и более,
невозможно без правильного описания динамических процессов, проис-
ходящих в деформируемой системе, которую представляет собой корпус
ракеты с большими массами жидкого топлива.
176
Глава 8
УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Разработка адекватной динамической схемы жидкостной ракеты, т. е.
составление системы дифференциальных уравнений, описывающих воз-
мущенное движение системы «тело — жидкость», а также выбор формы
записи коэффициентов этих уравнений, с доведением результатов иссле-
дований до возможности их использования в инженерной практике конст-
рукторских бюро в качестве справочных материалов, проведены Г. Н. Ми-
кишевым и Б. И. Рабиновичем [106].
В этой книге в наибольшей степени уделяется внимание прикладным
методам решения задач динамики, в частности, получению обозримых
механических аналогов и численных данных с достаточно обоснованной
оценкой точности. Полученные результаты проверены несколькими неза-
висимыми расчетными и экспериментальными методами.
Для всех боевых ракет стратегического назначения I и II поколений,
а также ракет-носителей на их базе (11К63, 11К65, «Циклон-2», «Цик-
лон-3»), созданных ОКБ-586 (ГКБ «Южное»), динамические схемы были
разработаны на базе и при непосредственном участии авторов труда [106].
Книга содержит вывод линеаризованных уравнений возмущенного дви-
жения жидкостной ракеты как в случае идеальной, так и в случае вязкой
жидкости и их приведение к канонической форме. Последнее сделано
в результате специального выбора обобщенных координат, характери-
зующих волны на свободной поверхности, и центра приведения системы
внешних сил, действующих на ракету.
Основными положениями созданной динамической схемы с позиций
разработчиков систем стабилизации являются следующие [54].
При полете жидкостной ракеты по возмущенной траектории ее баки
вместе с корпусом совершают малые колебания относительно как номи-
нальной траектории, так и приведенного центра масс. Из-за движения
стенок баков на свободных поверхностях находящихся в них компонентов
возникают волны, колебания которых описываются рядом функций Бес-
селя. Каждому члену ряда, который назван тоном колебаний, соответству-
ет своя обобщенная координата и своя собственная частота.
Наибольшую скорость имеют частицы жидкости, находящиеся в верх-
них слоях компонентов. С увеличением глубины скорость быстро умень-
шается. Поэтому приведенная масса жидкости, участвующая в колебани-
ях, меньше общей массы жидкости в баке, и она резко убывает с увеличе-
нием номера тона колебаний. Так, для первого тона колебаний приведен-
ная масса численно равна массе жидкости в объеме цилиндра высотой
177
0,45 радиуса бака, а для второго тона, по оценке, сделанной в [87], масса
в 30 раз меньше. Поэтому, как правило, учитывают лишь первый тон ко-
лебаний жидкости. Благодаря этим колебаниям возникают дополнитель-
ные силы и моменты, которые сказываются на движении ракеты.
В качестве характерного примера приведем динамическую схему
штатной трехступенчатой жидкостной ракеты-носителя 11К68 («Цик-
лон-3») с космическим аппаратом «Целина-Д». Общий вид PH и ее основ-
ные характеристики приведены на рис. 8.1 и в табл. 8.1.
Динамическая схема приводится по форме и с обозначениями, исполь-
зуемыми ОКБ-586 в семидесятых годах прошлого века при выдаче исход-
ных данных на разработку СУ в составе:
- системы уравнений возмущенного движения ступеней изделия в ка-
налах рыскания (тангажа) и крена;
- структуры коэффициентов и свободных членов этих уравнений (их
численные значения приведены в Приложении).
8.1. Уравнения возмущенного движения I ступени
в плоскости рыскания и структура коэффициентов
Система уравнений возмущенного движения I ступени в плоскости
рыскания составлена с учетом первой гармоники колебаний компонентов
топлива в баках и имеет вид:
4 _
z = aai + + а^у + azS3¥ + + Fz
Л=1
4 _
У = aVzz + а^у + а^у + avS8v + ^avr fn + Му,
Л=1
г + emrn + (oLrn = a 7z 4- arvw,
n m n m n гл z ’
где z - боковое отклонение центра масс изделия,
п (номер бака)=1, 2, 3, 4; i (номер ступени) = 1, 2;
у, - угол рыскания;
- угол отклонения управляющих органов по рысканию;
r„ (rn(s)) - обобщенная координата, соответствующая колебаниям жид-
кости в канале рыскания по первому тону на I и II ступенях (s-му тону на
III ступени);
Fz, М^, М™с - возмущающая сила и моменты на активных
и пассивных участках;
178
penrvtiKSi
Рис. 8.1
Основные технические характеристики PH 11К68
Таблица 8.1
Масса полезного груза, выводимого на круговые и эллиптические орбиты, кг До 4000
Тип старта Наземный, автоматизированный
Уровень автоматизации предстартовой подготовки и пуска PH 100%
Стартовый вес PH, тс 187
Количество ступеней 3
Общая длина, м 39,3
Диаметр, м: - I и II ступеней 3
- ГО 2,7
Топливо на всех ступенях Жидкое, самовоспламеняющееся с высоко- кипящими компонентами (АТ и НДМГ)
Характеристики ДУ I и II ступеней:
I ступень - тяга (на земле/в пустоте), тс 270,3/303,2
- удельный импульс (на земле/в пустоте), с 267,8/300,3
II ступень - тяга (на земле/в пустоте), тс -/101,5
- удельный импульс (на земле/в пустоте), с -/315,3
Характеристики ДУ III ступени:
- тяга, тс 7,96
- удельный импульс, с 344,4
- соотношение компонентов 2,1
Окончание табл. 8.1
Время работы, с:
- при однократном запуске 118
- при двукратном запуске 116
Система управления Автономная, инерциальная
Исполнительные органы СУ:
на I и II ступенях Четырехкамерный ЖРД с отклоняемыми камерами сгорания (КС)
на III ступени: - во время работы основного ЖРД 8 неподвижных рулевых газовых сопел
- после отделения III ступени до запуска основ- ного двигателя и во время полета перед его по- вторным запуском ЖРД малой тяги (8 камер) СУОС и 2 ка- меры для создания осевой перегрузки (все камеры неподвижные)
Точность выведения КА:
на круговую орбиту высотой 600 км: - по высоте орбиты, км +15
- по периоду обращения, с ±5
на круговую орбиту высотой 1500 км: - по высоте орбиты, км ±25
- по периоду обращения, с ±12
По сравнению с уравнениями жесткой ракеты здесь дополнительно
присутствует п уравнений относительно обобщенных координат гь г2, ...гп,
характеризующих колебания жидкости в соответствующих баках. В этих
уравнениях присутствуют члены az и ar^yi, характеризующие воздей-
ствия движений корпуса ракеты на колебания жидкости в баках. Коэффи-
циенты arz и arw характеризуют динамическое влияние линейных и угло-
вых ускорений корпуса ракеты на поведение жидкости.
В свою очередь влияние ускорений частиц жидкости на ускорение
центра масс ракеты и угловые ускорения ракеты вокруг центра масс ха-
рактеризуются величинами а г»и awrrn.
8.1.1. Формулы для расчета коэффициентов и свободных членов
1. Коэффициенты, характеризующие абсолютно жесткое «отвердевшее»
изделие в канале рыскания:
CaqS
а —----пЧ т .
а mV
aw~ mV^a^G + т^Х(} Xd^
_ C°qSm+P
т
2Р?
«а =---
т
а — ('*с ~
r‘ ICV
11 (xG -xd)2 (x„ +hn-x0)\
IV I 4 I
1GV 1G n=l *G
a — ~ ) .
j ’
*G
_ 2P„ (XG “ Xd ) .
Z ’
2G
где
C“, Cy - производные коэффициентов нормальной и подъемной сил;
q - скоростной напор;
St - площадь миделя;
Р - тяга двигательной установки;
V, т, wx - скорость, масса, кажущееся ускорение изделия;
181
xG - координата метацентра;
xd - координата центра давления;
Р& - градиент управляющей силы по рысканию, крену на I и II ступенях;
IG - момент инерции «жидконаполненного» изделия относительно
оси, проходящей через метацентр;
I - полная длина изделия;
/2, /1т - массовый суммарный секундный расход и расход из m-го бака;
- уровень компонентов топлива в m-й полости;
7?л, хт - характерный размер и координата точки m-й полости;
т™ - производная коэффициента аэродинамического демпфирующего
момента;
хр - координата точки приложения управляющей силы.
2. Коэффициенты, учитывающие влияние жидкого наполнения топлив-
ных полостей:
а, -_Pj&LXn
т "
А,
ar z =--
” Дл
<Ьг, = -^-[яДл - (Лл. - хс ) Д, ],
1g
ЗГ"[^лА)л “ (Хт ~ XG Ч ]»
Рп
2 И', -2
(О, = —<?,,
er
я
где
рп - массовая плотность компонента в n-м баке;
А>«’ Д«» А>л*> ДУ*> ~ безразмерные гидродинами-
ческие коэффициенты, характеризующие движение жидкости в n-й полос-
ти в канале рыскания, соответствующие первому тону на I и II ступенях
(s-му тону на III ступени);
R^n - радиус свободной поверхности в n-й полости;
182
£=1.8412 - первый корень уравнения = где А(Л) “ функция
Бесселя первого рода первого порядка;
5Л ) - логарифмический декремент колебаний жидкости в канале
рыскания (крена).
3. Свободные члены
_ F - M„
m Io
8.2. Система уравнений возмущенного движения
I ступени в канале крена и структура коэффициентов
Л=1
Р„ +£„ Рп +(Ор Р, +ф = 0,
где n = 1, 2 - номер бака;
Р (ри)) - обобщенная координата, соответствующая колебаниям жидко-
сти в канале крена по первому тону на I и П ступенях (s-му тону на Ш ступени);
ш* - экспериментальная частота n-го колебательного звена в канале крена.
Формулы для расчета коэффициентов и свободного члена:
I р. *
атР 4=Л + УЛ>
т ’ 2. X П ’
Л=1
(Dp 2 2
Ер =—-—(Dp = (Dn
р* л Р” п
4Pnsr _ Ма
----К>=—,
где 7Л, 1Рн - присоединенный и приведенный моменты инерции;
1Х - момент инерции «сухого» изделия относительно оси симметрии;
8* - логарифмический декремент вращательных колебаний в n-м баке
(экспериментальный);
(ор - собственная частота дополнительного n-го колебательного звена
в канале крена;
183
г* - расстояние от продольной оси изделия до точки приложения управ-
ляющей силы.
8.3. Уравнения возмущенного движения II ступени
и структура коэффициентов
Система уравнений возмущенного движения II ступени в канале рыс-
кания, составленная с учетом первой гармоники колебаний компонентов
топлива в баках, имеет вид:
z = azzz + azvyr + агм,у/ + azS8„ + £ azr rn + Fz;
п = 1
2 _
V = a¥zi + + a^sSv + У, + М * ;
п = 1
= a^z + аг^\
Система уравнений возмущенного движения в канале крена имеет вид:
<Р + е^ф + а9^Р„ = a,s8, + М~ , ;
лгф = лгу + м~:р
Р + ерР + а> 2рР+ф'= 0 \
П = 1 ,
- возмущающий момент, обусловленный действием ветра;
М? - возмущающий момент от погрешностей изготовления и монтажа
Формулы для расчета коэффициентов и свободных членов уравнений
для II ступени аналогичны соответствующим формулам для I ступени.
8.4. Уравнения возмущенного движения III ступени
и структура коэффициентов
С использованием носителя 11К68 реализуются две схемы выведения кос-
мических аппаратов (КА): с однократным и двукратным включением двигателя
Ш ступени.
Исследованию динамики космических ступеней на активном (с работаю-
щим маршевым двигателем) и пассивном (работа СУОС) участках движения
посвящены главы 12 и 11 соответственно.
Результаты расчета численных значений коэффициентов уравнений дви-
жения в характерные** «моменты» активных участков применительно к схеме
) Характерными «моментами» полета являются: старт, достижение числа Маха М=1, район
максимальных скоростных напоров, выключение ДУ-I, разделение ступеней, запуск ДУ-П, сброс
обтекателя и тому подобные «нестационарные» участки траектории.
184
выведения носителя с однократным включением двигателя
III ступени приведены в Приложении.
Для носителя с двукратным включением двигателя III ступени значе-
ния этих коэффициентов могут быть заимствованы из приведенных таб-
лиц для схемы с однократным включением. Например, на первом актив-
ном участке III ступени значения коэффициентов соответствуют приве-
денным в таблицах от момента включения двигателя (t^n.= 0) до его вы-
ключения (tjaa,. = tna).
После первого выключения двигателя следует участок охлаждения
ТНА длительностью —12,1 с, начиная с момента подачи команды ГК1. На
этом участке движения основные характеристики III ступени практически
постоянны, за исключением параметров, изменяющихся при выключении
двигателя: тяги маршевого двигателя P(t), разнотяговости управляющих
сопел AP(t), массового секундного расхода />(/) и ускорения wx(7), кото-
рые уменьшаются от номинальных значений до нуля, обуславливая суще-
ственное изменение коэффициентов уравнений движения.
Для определения этих коэффициентов их конечные значения на момент
выключения двигателя (^бл. = tnci) перемножаются на соотношения, харак-
теризующие изменения параметров движения ступени при охлаждении:
az8 дрЛК”! ’ azp(j) v) .ГК\ »
a (t^a™ Р^- а (/) = д'*1 •
av\‘) aw р > art\‘) ays лрпа ’
ГГК\
На пассивном участке движения, следующем после первого выключе-
ния двигателя, характеристики III ступени изменяются менее чем на 1 %.
Поэтому в начальный момент второго активного участка (t = tBKii) коэф-
фициенты уравнений движения равны нулю по аналогии с первым запус-
ком двигателя, а через 1,1с после подачи команды ВКП на второе включе-
185
ние двигателя (набор ~60 % тяги) эти коэффициенты равны их конечным
значениям на первом активном участке (tBKii + 1,1 с = tnci).
Последующие значения коэффициентов на втором активном участке
принимаются в соответствии с приведенными таблицами от = tnci до
tK = tnci+xz. Здесь приняты обозначения:
ВК5 - команда на первое включение маршевого двигателя III ступени
(соответствует времени t = 0 в таблицах коэффициентов);
tnci - время подачи команды на первое выключение двигателя, отсчи-
танное от команды ВК5;
Ibkii - время подачи команды на второе включение двигателя;
Т2 - длительность второго активного участка от момента появления тя-
ги двигателя (t = tBKii + 1,1 с) до его выключения.
8.4.1. Система уравнений возмущенного движения III ступени
1. Для активного участка
- в канале рыскания (тангажа):
3 2 _
z = + azS8y +
5=2 л=1
3 2 _
+ Ч
з=2 л=1
r„M + = <f'z +
л гп п г„ п rH гпФ'
и = 1, 2; 5 = 2,3.
- в канале крена:
ф + ajp + У У <£>’ Ря(,) = а „А + М~
* ФФ* 4>г„ п <рд <р др
5=1 л=1
и=1>2; j=i>2-
2. Для пассивного участка в канале рыскания (тангажа, крена):
^пас Q ।
W ~~ •
8.4.2. Структура коэффициентов систем уравнений
d
а. =—sin 35°,
zo е* ’
о¥т
186
• Z>(xc~xJ2 ЛА(хи+А,-хе)2
T т 9
1G л=1 lG
a„s =-^[sin350(xc-xc)+r₽cos350],
~ pl _ _ 1 (s)
r’n
ft—L-M;’ -к -^)л<',1 чад=2MW,
Lt^ *- ' G / л J ’ n R
Pn
g(,) = "
Л
0 (J)
_(J) _ n
QPnV Kn д(^) ’
Ig +1 n CO
°n n rn Pn
4 Pe П 9
" " " Л
где
- разнотяговость управляющих сопел по рысканию (крену)
на III ступени;
Р™ - управляющая сила по тангажу, рысканию и крену на пассивных
участках траектории;
- плечо управляющей силы по тангажу, рысканию, крену на пас-
сивных участках траектории;
/7^ “ безразмерные гидродинамические коэффициенты в канале
крена III ступени;
vx* VJ
> - кинематические параметры траектории на момент испол-
X, у, z J
нения главной команды на выключение двигателя III ступени (ГК1)
в стартовой системе координат.
187
Глава 9
КОЭФФИЦИЕНТЫ УРАВНЕНИЙ,
ХАРАКТЕРИЗУЮЩИЕ ЖИДКОЕ НАПОЛНЕНИЕ
ТОПЛИВНЫХ ПОЛОСТЕЙ
При исследовании динамики жидкостных ракет, топливо, частично за-
полняющее баки, отождествляется с механической системой, характери-
зующейся конечным числом степеней свободы. В случае плоского движе-
ния ракеты с баками цилиндрической формы - с одной степенью свободы,
а при наличии в баках радиальных перегородок (как в PH 11К68) - с двумя.
В нашем случае практический интерес представляет определение ко-
нечного числа коэффициентов уравнений возмущенного движения, соот-
ветствующих первым тонам колебаний жидкости.
Определяемые гидродинамические коэффициенты условно делятся на
три группы:
1. Коэффициенты при обобщенных координатах, описывающих волно-
вое движение топлива - квадраты частот собственных колебаний
жидкости.
2. Коэффициенты при вторых производных тех же обобщенных коорди-
нат - присоединенные массы и присоединенные моменты инерции
жидкости.
3. Коэффициенты при первых производных обобщенных координат - ко-
эффициенты демпфирования.
Определение гидродинамических коэффициентов производится в двух,
взаимно дополняющих друг друга, направлениях: расчетно-теоретическом
и экспериментальном.
Первое направление обеспечивает возможность определения коэффици-
ентов для баков относительно простой геометрической формы, а второе -
позволяет проверить корректность результатов теоретических расчетов
и дает возможность определять гидродинамические коэффициенты для
полостей любой конфигурации, не поддающейся теоретическому анализу.
Используемые в обоих направлениях методы исследования являются
в большей или меньшей мере приближенными. В каждом конкретном
случае используется тот метод, который дает результаты с необходимой
точностью при минимальных затратах времени и средств.
Требуемая в инженерной практике точность определения гидродина-
мических коэффициентов различных групп существенно отличается. Так,
допустимая погрешность определения частоты колебаний не превышает
2 %, а присоединенных масс и моментов инерции - 10 %. Коэффициенты
демпфирования могут определяться с еще меньшей точностью.
188
9.1. Расчетные методы определения гидродинамических
коэффициентов
Для получения достоверных результатов с требуемой точностью были
проведены многочисленные расчеты различными независимыми метода-
ми. При сравнительной оценке различных методов используются безраз-
мерные коэффициенты шп2, ш2, тп, тх, J, Z , обладающие по сво-
ему механическому смыслу инвариантностью относительно метода их оп-
ределения. Информация о коэффициентах Лп, ЛЛл, Дл, ДХп как не ин-
вариантных должна считаться промежуточной.
Один из первых расчетных способов определения гидродинамических
коэффициентов уравнений возмущенного движения ракет с баками ци-
линдрической формы (случай 11К68) основывался на решениях краевых
задач методом разделения переменных. Полные решения краевых задач
и выражения для всех гидродинамических коэффициентов для полостей
в форме прямого кругового цилиндра со сплошными радиальными пере-
городками и без них были получены Г. С. Наримановым в середине пяти-
десятых годов. В те же годы краевые задачи для полости, образованной
соосными круговыми цилиндрами (труба окислителя в баке горючего
I ступени PH 11К77 при отсутствии в нем перегородок) были решены
Д. Е. Охоцимским.
В начале шестидесятых годов Л. В. Докучаев получил решения крае-
вых задач для расчета гидродинамических коэффициентов методом раз-
деления переменных для соосных круговых цилиндров со сплошными
и разрывными ребрами (задачи, возникшие при проектировании PH
11К68).
В монографии [106] расчет гидродинамических коэффициентов мето-
дом разделения переменных проводится путем сведения краевых задач
для цилиндрических полостей к плоским задачам и преобразования выра-
жений для определяемых коэффициентов. В результате получены основ-
ные формулы для вычисления с дальнейшим их упрощением на основе
симметрии контура.
Наряду с основными формулами, полученными решением краевых за-
дач методом разделения переменных, в труде [106] приведен ряд прибли-
женных методов расчета гидродинамических коэффициентов для полос-
тей в форме тел вращения.
Наиболее распространенным в инженерной практике является вариа-
ционный метод решения краевых задач о колебаниях жидкости в полос-
тях, который считается классическим, поскольку обеспечивает получение
всей совокупности гидродинамических коэффициентов с необходимой
189
точностью. При массовых расчетах этот метод используется с двумя раз-
личными системами координатных функций - сферическими и цилиндри-
ческими, что обеспечивает получение достаточно надежных численных
результатов.
Остальные приближенные методы расчета коэффициентов использу-
ются, в основном, как средство независимого контроля и предварительной
оценки ожидаемых численных результатов. Ценность этих методов за-
ключается в том, что они позволяют при незначительной потере точности
рассчитать коэффициенты уравнений возмущенного движения со значи-
тельно меньшей затратой машинного времени, чем вариационный метод.
Одним из известных «грубых» приближенных методов решения крае-
вых задач является метод, основанный на приведении задач теории волно-
вых движений жидкости к интегральным уравнениям.
Другим известным методом является применение теории длинных
волн для решения однородной краевой задачи. При этом предполагается,
что длина волны велика по сравнению с глубиной жидкости и что ско-
рость частиц жидкости на свободной поверхности в направлении градиен-
та поля массовых сил невозмущенного движения мала по сравнению со
скоростью в перпендикулярном направлении. Таким образом, эта теория
дает положительные результаты, когда глубина жидкости относительно
мала (например, для баков в форме тора большого диаметра).
К этой категории относится также приближенный метод построения
собственных функций <ря однородной краевой задачи по известным зна-
чениям й)я. Предполагается, что каким-то образом, например, применени-
ем одного из расчетных приближенных методов или экспериментально,
найдены собственные значения шя, т. е. частоты собственных колебаний
жидкости в неподвижной полости. Определить во всех случаях значи-
тельно проще, чем собственные функции, в частности, применением ва-
риационного метода.
Следует указать также разработанный Л. И. Алексеевым, Г. А. Мои-
сеевым и В. И. Столбцовым метод достаточно простой оценки значений
собственных частот и присоединенных масс, соответствующих основному
тону колебания жидкости. Этот метод позволяет получить оценки инвари-
антных безразмерных коэффициентов, а также присоединенного момента
инерции при минимальной исходной информации.
Кроме перечисленных выше методов приближенного расчета гидроди-
намических коэффициентов в конце шестидесятых - начале семидесятых
годов рядом авторов были предложены достаточно оригинальные спосо-
бы получения достоверных результатов при минимизации затрат машин-
ного времени (например, «маятниковая» модель [87], [88] и др.).
190
9.2. Экспериментальные методы определения
гидродинамических коэффициентов
Наряду с теоретическими методами определения гидродинамических ко-
эффициентов уравнений возмущенного движения широко используются экс-
периментальные методы, основанные на измерении различных параметров
при свободных или вынужденных колебаниях системы «тело-жидкость»:
частот колебаний, амплитуд колебаний полости и жидкости, сил и момен-
тов, действующих на полость, и т. д. В отличие от теоретических методов,
которые дают возможность охватить класс полостей сравнительно простой
геометрической конфигурации, использование экспериментальных методов
позволяет определять гидродинамические коэффициенты для самых слож-
ных форм полостей, не поддающихся теоретическому анализу. Кроме того,
экспериментальные методы играют важную роль при оценке надежности
теоретических результатов, полученных приближенными методами расчета.
Вопросам экспериментального определения гидродинамических коэф-
фициентов посвящен ряд работ, в большинстве которых рассматривается
только частная задача - определение собственных частот колебаний жид-
кости и коэффициентов демпфирования. Экспериментальная методика,
позволяющая определять все гидродинамические коэффициенты уравне-
ний возмущенного движения, основанная на измерении главным образом
собственных частот парциальных систем, впервые в 1968 г. изложена
в работе [106]. Значения искомых коэффициентов для цилиндра, сферы,
тора и цилиндра с радиальными ребрами, полученные по этой методике,
приведены в работах [106], [107].
В этих работах для наиболее важного в практическом отношении слу-
чая, когда тело и полость обладают двумя плоскостями симметрии, линия
пересечения которых совпадает с продольной осью полости, рассмотрены
экспериментальные методы определения всех гидродинамических коэф-
фициентов. Основное внимание уделено определению собственных час-
тот, коэффициентов инерционных связей и присоединенных моментов
инерции, играющих главную роль в динамических исследованиях. Дана
оценка точности экспериментальных методов. Сформулированы требова-
ния к испытательному оборудованию. Приведены некоторые сведения
о возбудителях колебаний и датчиках для измерении колебаний жидкости.
В качестве основных методов определения собственных частот и форм
колебаний свободной поверхности жидкости рассматриваются методы
вынужденных и свободных колебаний.
Результаты аналогичных экспериментальных исследований колебаний
жидкости в баке ракеты, проведенных К. С. Колесниковым с целью опре-
деления всех гидродинамических коэффициентов, изложены в [87].
191
Экспериментальные исследования колебаний жидкости в полостях
различных форм остаются актуальными по сей день: результаты таких ра-
бот, проведенных Институтом технической механики АН УССР, опубли-
кованы в 2002 г. [26].
Ниже описывается методика и испытательное оборудование, исполь-
зуемые при экспериментальном определении всех гидродинамических ко-
эффициентов, по материалам [106]. Это представляется целесообразным,
поскольку при создании в ОКБ-586 (ГКБ «Южное») ракет первых поколе-
ний авторы труда [106] являлись соисполнителями по научному сопрово-
ждению разработок и, в частности, непосредственными участниками ди-
намического проектирования ракет, в том числе, по определению коэф-
фициентов динамической схемы указанными методами.
Более того, примененные в ОКБ методы и оборудование при разработ-
ке ракет и ракет-носителей последующих поколений были в принципе
аналогичны описываемым.
9.2.1. Определение коэффициентов инерционных связей
Определение коэффициентов инерционных связей проводится не-
сколькими методами.
Путем измерения собственных частот парциальных систем, соответст-
вующих поступательному движению тела и его вращению относительно
поперечной оси для случая, когда рассчитывается один первый тон коле-
баний жидкости, а также, когда учитываются два первых тона.
• Путем измерения параметров колебаний полости, возникающих под
действием гармонических сил или моментов. Этот метод рассматрива-
ется для случая поступательного движения полости. Механическая
система, к исследованию которой сводится задача, показана на рис. 9.1.
192
Вынужденные колебания этой системы описываются уравнениями
(9.1):
(т" + ти)(и + Рий + = Р;
Л=1
(9.1)
[и = 1, 2,... Й
В этих уравнениях необходимо положить P(/) = 7^cos<ar. Интересую-
щее частное решение системы уравнений (9.1) определяется в виде
и = мое,а*, sn = sQne,M, полагая при этом Р = PQe,03t.
• Путем измерения сил, действующих на полость в режиме гармони-
ческих колебаний для случая поступательного движения полости.
Система, к исследованию которой сводится задача, показана на
рис. 9.2. Дополнительная пружина введена для измерения силы, дейст-
вующей на полость, т. е. она является чувствительным элементом. Жест-
кость этой пружины cz подбирается с таким расчетом, чтобы собственная
частота колебаний полости была намного больше собственной частоты
колебаний жидкости. Колебания полости создаются заданием перемеще-
ния конца пружины по гармоническому закону.
Рис. 9.2
193
9.2.2. Определение присоединенного момента инерции
через суммарный момент инерции
Определение присоединенного момента инерции через суммарный
момент инерции производится, исходя из следующей зависимости:
Здесь
- собственная частота системы; с¥ - угловая жесткость пружины,
введенной в систему для создания восстанавливающего момента, причем
аг<бц, с¥-(т° + m)jxG>0.
Если ось вращения совпадает с метацентром системы, то
<т2[<Ц2-ст2(1-/01)]'
(93)
Жесткость следует подбирать таким образом, чтобы частота сгг бы-
ла бы много меньше частоты . При выполнении условия «: а\ выра-
жения (9.2) и (9.3) существенно упрощаются:
сш + т]хг
J° + J= Л г--------(9.4)
J‘ + J = ^-. (9.5)
Если параметры бц, /01, су и xG, входящие в формулы (9.2)-(9.5), за-
даны, то определение суммарного момента инерции сводится к определе-
нию собственной частоты системы .
9.2.3. Результаты исследований
Полученные результаты экспериментального определения гидродина-
мических коэффициентов для интересующего нас случая PH 11К68, при-
веденного в качестве конкретного примера в Приложении, показаны для
полостей в форме прямого кругового цилиндра с радиальными ребрами.
При условии, что К равноотстоящих ребер расположены на стенках до
глубины . Ширина каждого ребра равна Б.
В данном случае интерес представляли гидродинамические коэффици-
енты, соответствующие как движению цилиндра в плоскости Oxz, так и
вращению относительно продольной оси Ох. Так же, как в предыдущем
194
случае, за характерный линейный размер принят радиус цилиндра г0, а за
характерную точку - центр днища (рис. 9.3).
Искомые величины зависят от четырех безразмерных параметров:
г h -г . г b
h=—, hQ=—, kub=~.
го го го
Для случая движения цилиндра в плоскости Oxz искомые коэффици-
енты представлены в виде графических зависимостей от глубины жидко-
сти на рис. 9.4, 9.5. Эти коэффициенты получены экспериментально для
основного тона колебаний жидкости при различном числе и ширине ребер
с высотой =1.3г0 для уровней жидкости, расположенных как выше, так
и ниже верхнего края ребер.
На рис. 9.4 приведены значения квадрата собственной частоты коле-
баний жидкости <ц2. Каждая кривая соответствует определенной ширине
и определенному числу ребер. Как видно из графика, собственные часто-
ты первого тона колебаний жидкости в цилиндре с ребрами сильно зави-
сят от ширины и числа ребер. Так, например, для уровня h = г0 квадраты
3
собственных частот при b = 0 и при Z> = — r0, £ = 8 отличаются более чем
4
в два раза.
195
Рис. 9.5. Экспериментальная зависимость коэффициентов инерционных связей
гщ, mQl и присоединенного момента инерции J от глубины жидкости (= 1 .Зг0)
Зависимость частоты от ширины и числа ребер особенно сильно сказы-
вается при уровнях жидкости ниже верхнего края ребер. При уровнях, рас-
положенных выше ребер, зависимость частоты от их числа и ширины осла-
бевает и при h = 2г0 практически исчезает. При b = ~го собственная частота
колебаний жидкости близка к частоте колебаний в цилиндре без ребер.
На рис. 9.5 приведены величины т19 ти01, J в зависимости от глубины
жидкости, ширины и числа ребер. Как видно из графика, эти величины
изменяются значительно сильнее, чем собственные частоты. Так, при
к = 8, Ь =—га,
3 0
й = О.8го коэффициенты и w01 уменьшаются примерно на
30 %, а присоединенный момент инерции увеличивается в 1,5 раза, в то
время как квадрат собственной частоты изменяется всего на 12 %.
При вращении цилиндра с радиальными ребрами вокруг продольной
оси Ох часть жидкости вовлекается в движение вместе с полостью.
Кроме того, для достаточно широких ребер при вращательном движе-
нии цилиндра вокруг продольной оси возбуждаются также колебания
жидкости в незамкнутых полостях, образованных стенкой цилиндра
и ребрами. Эти колебания практически совпадают с колебаниями жидко-
сти в цилиндрических секторах.
196
9.2.4. Рассеяние энергии при колебаниях жидкости
В основу всех исследований [104], [106] была положена концепция
идеальной жидкости. Реальные жидкости обладают в той или иной степе-
ни вязкостью. Учет вязкости жидкости приводит к чрезвычайно сложным
задачам гидродинамики, решение которых в настоящее время наталкива-
ется на серьезные трудности.
Однако для больших чисел Рейнольдса задача значительно упрощает-
ся, так как в этом случае учет вязкости жидкости по существу сводится
к учету рассеяния энергии в системе при колебаниях жидкости или, дру-
гими словами, к учету демпфирующих свойств системы. При этом вслед-
ствие слабого рассеяния энергии колебаний жидкости в большинстве
практических задач демпфирующие свойства системы достаточно учесть
интегрально путем определения таких характеристик демпфирования, как
логарифмический декремент колебаний.
Различают два вида демпфирования: линейное (или вязкое) и нелинейное.
Линейное демпфирование обусловлено в основном рассеянием энер-
гии колебаний жидкости в тонком пограничном слое у стенок полости
и характерно для полостей с гладкими стенками. Соответствующие коэф-
фициенты демпфирования существенно зависят от числа Рейнольдса.
Нелинейное демпфирование возникает при колебаниях жидкости в полос-
тях, имеющих различные конструктивные элементы или устройства (стрин-
геры, шпангоуты, перегородки, сетки и т. д.; такие элементы имеются в баках
реальной PH, в том числе 11К68). Оно зависит от амплитуды колебаний и по
величине может значительно превосходить линейное демпфирование. Число
Рейнольдса в данном случае не играет существенной роли в достаточно ши-
роком диапазоне его изменения. Это обстоятельство имеет большое практи-
ческое значение, так как позволяет использовать для определения искомых
коэффициентов демпфирования сравнительно небольшие геометрически по-
добные модели полостей с соответствующими конструктивными элементами.
На практике обычно приходится иметь дело со слабым нелинейным
демпфированием, т. е. когда эффективная площадь конструктивных эле-
ментов невелика и амплитуды колебаний жидкости малы.
В этом случае нелинейное демпфирование можно в первом приближе-
нии учитывать так же, как и линейное, т. е. введением соответствующих
диссипативных сил в уравнения для обобщенных координат sn.
Таким образом, учет демпфирующих свойств реальной системы при
слабом демпфировании сводится к определению соответствующих коэф-
фициентов демпфирования.
Демпфирование колебаний жидкости является важным фактором в за-
дачах динамики твердого тела с жидким заполнением. Оно не только ог-
раничивает амплитуды колебаний, но и, как правило, расширяет границы
197
областей устойчивости. На практике для ограничения амплитуд колеба-
ний и расширения областей устойчивости нашли применение специаль-
ные демпферы колебаний жидкости, создающие дополнительное интен-
сивное рассеяние энергии колебаний. Демпфирование колебаний облегча-
ет постановку некоторых динамических задач на электронных модели-
рующих установках и ЭЦВМ.
Однако в ряде случаев демпфирование колебаний жидкости может
оказывать отрицательное влияние на динамические свойства системы
и должно быть по возможности уменьшено.
Характерным примером может служить процесс определения опти-
мальных значений коэффициентов демпфирования колебаний жидкости
в баках ракеты Р-36: баллистического варианта (8К67) и построенных на
ее базе ракет 8К67П (РГЧ), 8К69 (Р-36 орб) и ракет-носителей КА - «Ци-
клон-2» (11К69), «Циклон-3» (11К68).
На первом этапе разработки этой ракеты получение необходимых за-
пасов устойчивости во всех режимах эксплуатации обеспечивалось, в ча-
стности, установкой в баках II ступени демпферов колебаний жидкости по
схеме и с размерами, показанными на рис. 9.6.
При этом выбором соответствующих параметров автомата стабилиза-
ции была получена область устойчивости, показанная на рис. 9.8 сплош-
ными линиями.
В последующем, на этапе «борьбы за вес» была проведена оптимиза-
ция параметров АС с вводом их коммутации на 95 с полета, что позволило
уменьшить допустимую величину логарифмического декремента колеба-
ний жидкости и существенно снизить вес демпфирующих перегородок
(рис. 9.7). Полученная при этом область устойчивости показана на рис. 9.8
пунктирной линией.
Границы области устойчивости после коммутации параметров АС по-
казаны на рис. 9.9.
Несмотря на важность вопросов рассеяния энергии при колебаниях
жидкости исследования в этой области носят ограниченный характер.
Имеющиеся работы в основном посвящены определению коэффициентов
демпфирования.
В качестве одной из основных характеристик рассеяния энергии колеба-
ний наиболее часто употребляется логарифмический декремент колебаний.
Как известно, логарифмическим декрементом называют величину, равную
натуральному логарифму отношения двух последовательных амплитуд сво-
бодных затухающих колебаний системы с одной степенью свободы
<5 = 1п-^=- (9.6)
^т+1
и характеризующую темп затухания колебаний.
198
Рис. 9.7
199
Рис. 9.9
Определение логарифмического декремента (9.6) допускает его при-
менение как для линейных систем, описываемых уравнением
d s п ds 2 _ —ч
-T2- + ^ + <aS = 0> <9’7)
at at
так и для систем с нелинейными диссипативными силами, описываемых,
в частности, уравнением
d2s „(ds\ds 2 Л /лох
—г + Г— — + <s = 0. (9.8)
dt2 \dt)dt 0 k ’
200
В линейном случае логарифмический декремент является постоянной
величиной и связан с коэффициентом демпфирования Р и собственной
частотой й?0 соотношением
8 = -^—, (9.9)
или при слабом демпфировании (/7 «с й?0) соотношением
8=^-. (9.10)
В случае нелинейного демпфирования логарифмический декремент,
как правило, уже не является постоянной величиной для всего затухающе-
го процесса, а зависит от амплитуды колебаний.
Логарифмический декремент определяется по кривой процесса затуха-
ния свободных колебаний (рис. 9.10). При этом кривую обычно разбивают
на отдельные участки с практически допустимым числом периодов
и пользуются формулой
(9.П)
' ^+i
где i - число периодов, sm, sm+l - амплитуды начала и конца выбранного
участка.
Рис. 9.10
Вместо логарифмического декремента иногда используется безразмер-
ный коэффициент
g = A (9.12)
ч
Рассеяние энергии колебаний можно также характеризовать коэффи-
циентом поглощения, который равен отношению энергии, рассеянной за
период ДЕ, к максимальному значению энергии £, накопленной систе-
мой в начале рассматриваемого периода:
^0=^. (9.13)
Е
201
По существу этот коэффициент представляет собой относительное
рассеяние энергии колебаний. При слабом демпфировании коэффициент
поглощения связан с логарифмическим декрементом соотношением
^0=2^. (9.14)
Непосредственно коэффициент 'Pg можно определить при установив-
шихся вынужденных колебаниях системы путем прямого или косвенного
измерения энергии рассеяния ЛЕ и максимальной энергии Е.
Достаточно полную информацию о рассеянии энергии колебаний со-
держит так называемая петля гистерезиса, которая представляет собой за-
висимость между силой N, равной сумме диссипативной и восстанавли-
вающей сил, и перемещением s в режиме установившихся вынужденных
колебаний (рис. 9.11). Форма этой петли соответствует закону изменения
диссипативной силы, ее площадь равна энергии рассеяния за период ДЕ,
а площадь заштрихованного треугольника - максимальной энергии сис-
темы Е, Следовательно, петля гистерезиса может служить как для уста-
новления действительного закона диссипативных сил, так и для непосред-
ственного определения коэффициента поглощения. Для линейного демп-
фирования петлей гистерезиса является эллипс.
Рис. 9.11
Так же, как в предыдущем случае, экспериментальное определение ко-
эффициентов демпфирования проводится методами свободных и вынуж-
денных колебаний.
♦ ♦ ♦
Приведенные в Приложении в качестве характерного примера числен-
ные значения коэффициентов динамической схемы PH 11К68 определены
вышеописанными методами. Из таблиц видна тенденция изменения вели-
чин коэффициентов по времени полета и другие зависимости.
202
Часть 4
ДИНАМИКА РАКЕТЫ С УЧЕТОМ
УПРУГОСТИ ЕЕ КОНСТРУКЦИИ
Система дифференциальных уравнений возмущенного движения (адек-
ватная динамическая схема) ракеты, в представлении ее как твердого, абсо-
лютно жесткого тела, не отражает всех свойств ракеты как объекта управле-
ния. Это положение справедливо применительно как к твердотопливным ра-
кетам (или жидкостным - с «отвердевшей» жидкостью - см. часть 1), так и к
жидкостным ракетам, в т. ч. при учете подвижности компонентов топлива,
частично заполняющей баки (см. часть 2).
Неадекватность приведенных выше динамических схем объясняется тем,
что в процессе полета ракета под действием внешних сил подвергается уп-
ругим деформациям, которые необходимо учитывать при создании систем
стабилизации.
Исследования движения ракеты как упругого тела и расчет деформаций
различных элементов ее конструкции, возникающих под действием задан-
ных нагрузок, в общей постановке представляют собой весьма сложную за-
дачу механики.
В связи с этим при составлении уравнений движения ракеты, учиты-
вающих упругость ее конструкции, корпус ракеты обычно заменяют пря-
мым неоднородным упругим стержнем, с двумя плоскостями симметрии,
имеющим достаточное удлинение в направлении оси, лежащей на пересе-
чении плоскостей, т. е. длина I значительно больше г0 - характерного раз-
мера поперечного сечения. Стержень, работающий в основном на изгиб,
часто называют балкой [152]. Отсюда и упрощенную расчетную механи-
ческую модель именуют стержневой или балочной. Под изгибным пони-
мается такой вид нагружения, при котором в поперечных сечениях стерж-
ня возникают изгибающие моменты. Если изгибающий момент в сечении
является единственным силовым фактором, а поперечные нормальные си-
лы в данном сечении отсутствуют, изгиб называют чистым. В этом слу-
чае при выводе уравнений движения ракеты в любой плоскости симмет-
203
рии (рыскания или тангажа) пренебрегают взаимным влиянием деформаций
изгиба, сжатия, сдвига и кручения.
Исследования динамики ракеты с учетом упругости ее конструкции,
в частности, решение задачи об изгибных колебаниях корпуса ракеты, ба-
зируются на соответствующих уравнениях деформации стержня при чис-
том изгибе [152].
1. Зависимость величины поперечной силы от изгибающего момента.
Пусть стержень закреплен произвольным образом и нагружен распре-
деленной нагрузкой интенсивности q = /(х). Принятое направление для q
считается положительным.
Q=f(x)
Из стержня выделяется элемент длиной dx и в проведенных сечениях
прилагаются моменты М и M+dM, а также поперечные силы Q и Q+dQ.
Направления для этих силовых факторов приняты положительными в со-
ответствии с обусловленным правилом знаков. В пределах малого отрезка
dx нагрузку q можно считать распределенной равномерно.
Приравнивая к нулю сумму проекций всех сил на вертикальную ось и
сумму моментов относительно поперечной оси С, имеем:
Q + qdx-Q —dQ = 0,
М +Qdx+qdx~M-dM =0.
Производя упрощения и отбрасывая величину высшего порядка мало-
сти, получим:
dQ dM „
---— Q, = V-
dx-dx
204
Таким образом, поперечная сила представляет собой производную от
изгибающего момента по координате х, направленной по длине стержня.
Производная же по х от поперечной силы дает интенсивность внешней
распределенной нагрузки q.
Из соотношений для q и Q можно сделать некоторые общие выводы
о характере изгибающих моментов и поперечных сил для прямого стержня.
Если стержень нагружен только равномерно распределенной нагруз-
кой интенсивности q = const, очевидно, функция Q будет линейной, а М -
квадратичной.
Если стержень нагружен только сосредоточенными силами или мо-
ментами, то в промежутках между точками их приложения q = 0. Следо-
вательно Q = const, а М является линейной функцией х.
2. Напряжения в плоских сечениях.
Для тех участков стержня, где соблюдается условие чистого изгиба, из-
. dM а
гибающии момент, согласно выражению -^— = 0, остается постоянным
(М = const). Условия чистого изгиба могут возникать при различных внеш-
них нагрузках. Некоторые характерные примеры показаны на рис. а-е:
б)
Чистый.*
изгиб
205
Отвлекаясь от особенностей приложения внешних сил и условий
закрепления бруса в целом, рассмотрим только тот его участок, где
М = const и Q = 0. На границах этого участка действуют только моменты М
(рис. а).
Под воздействием моментов М стержень изогнется. Так как в любом
сечении возникает один и тот же изгибающий момент, то в случае одно-
родного стержня изменение кривизны для всех участков будет одним и
тем же. Следовательно, при чистом изгибе ось однородного стержня при-
нимает форму дуги окружности.
Легко обнаружить, что совокупность точек, расположенных до изгиба
в плоскости поперечного сечения стержня, после изгиба также образует
плоскость, но переместившуюся в пространстве. Действительно, рассмот-
рим среднее поперечное сечение АА (рис. г). Точки этого сечения по ус-
ловиям симметрии не могут получить преимущественных смещений ни
вправо, ни влево, поскольку и та и другая стороны полностью равноправ-
ны. Следовательно, это сечение остается плоским.
Разрезая стержень на две равные части сечением АА, получаем участ-
ки вдвое меньшие, находящиеся точно в тех же условиях, что и целый
участок (рис. д). Для каждой из полученных половин приведенные рассу-
ждения могут быть повторены (рис. е). Следовательно, средние сечения
этих половин остаются плоскими.
Этот процесс деления можно продолжать дальше. Тем самым будет
доказано, что в неограниченной близости от любого наперед заданного
сечения есть сколь угодно много таких сечений, для которых соблюдается
условие плоских сечений, т. е. все сечения однородного стержня при чис-
том изгибе не искривляются, а лишь поворачиваются. В общем случае из-
гиба это положение является приближенным и именуется гипотезой пло-
ских сечений.
Образование деформаций при чистом изгибе может рассматриваться
как результат поворота плоских поперечных сечений друг относительно
друга.
Применительно к ракете эта гипотеза исключает возможность волно-
образования на свободных поверхностях жидких компонентов топлива,
а также реальных деформаций элементов конструкции [1].
206
Глава 10
УРАВНЕНИЯ ДВИЖЕНИЯ УПРУГОЙ РАКЕТЫ
10.1. Уравнения поперечных колебаний
Вывод уравнений поперечных колебаний упругого стержня, с которым
отожествляется конструкция ракеты, базируется на указанных выше урав-
нениях деформации чистого изгиба. При этом в общем случае рассматри-
ваются стержни с меняющимися по длине площадью поперечного сече-
ния F, экваториальным моментом инерции сечения J и модулем упругости
при растяжении (сжатии) Е. Массовая плотность материала стержня обо-
значена через Q [107].
Используя известное соотношение элементарной теории изгиба, яв-
ляющееся следствием закона Гука для растяжения и гипотезы плоских се-
чений, устанавливающее связь между кривизной упругой линии и изги-
бающим моментом, получают основные уравнения изгиба стержня:
d2v
EJ^ = My. (10.1)
dx
d ( d2v\ dv „
— EJ—7 l = 7V----m-Q.
aJrl dx J dx y
d2 ( d2v\ d ( dv\ dm
dx I dx I dx) dx
(Ю.2)
(Ю.З)
где
N - продольная сила;
Q - поперечная сила;
M - изгибающий момент;
qz - погонная сила;
ту - погонный момент.
На рис. 10.1 показаны форма деформированного стержня и величина
его прогиба v(l) в системе координат Oxyz, ось Ох которой совпадает
с недеформированной осью стержня, а оси Оу и Oz параллельны главным
осям инерции недеформированного стержня. Начало координат находится
в плоскости левого среза стержня.
С помощью уравнения (10.3) легко получить уравнения поперечных
колебаний упругих стержней, выделив из внешних нагрузок в правой час-
ти силы инерции, а с помощью (10.1), (10.2) - динамические граничные
условия.
207
В соответствии с порядком уравнений должно быть по два граничных ус-
ловия на концах стержня. Дополнительно необходимо задать начальные ус-
ловия, заключающиеся в распределении перемещений и скоростей по длине
стержня при t = 0. В результате получают уравнение поперечных колебаний
(10.4), основные варианты граничных условий и начальные условия
(табл. 10.1).
|+pF^ = ^(x,0-^-m (х,Г). (10.4)
I Эг Эх
Таблица 10.1
Эх2^ Эх2 J Эх[ Эх J Эх^ ЭхЭг2
Характер закрепления конца x = Xj(xj = O, x2=Z) Граничное условие при X = X,
Свободен только в отношении поперечных перемещений (скользящая заделка) _^| =0; AIe/Mi = Эх|х=х' Эх[ Эх2 J |х=" ( dv d’v \ = Р^ +PJ-, ДЛ Эх ЭхЭг j '
Здесь qz(x,t), my(x,t) представляют собой погонные внешние нагрузки за
вычетом сил инерции, связанных с возмущенным движением, описываемым
введенными обобщенными координатами. Предпоследний член
в левой части (10.4) учитывает инерцию поворота сечений стержня. Через Р1
обозначены сосредоточенные продольные силы. Приложенные к концам
стержня, растягивающие, если Р1>0 и Р2>0, и сжимающие, если Р1<0 и
Р2<0, где:
P2 = Pi-jqx(x^dx.
О
Функция N(x,t) определяется (уравнение равновесия стержня в проек-
ции на ось Ох) следующим образом:
208
N{x,t) = Px-]qi{x,t)dx. (10.5)
о
В дальнейшем используются следующие дополнительные ограни-
чения:
/?=Р2=0; J(O) = J(Z) = O; m/0,0 = ^(/,0 = 0. (10.6)
Для практики представляет интерес случай, когда внешние нагрузки
включают как сосредоточенные силы, так и сосредоточенные пары (попе-
речные колебания).
В заключение приводят упрощенное уравнение поперечных колебаний,
которое получено из (10.4), если пренебречь продольными силами
и инерцией поворота поперечных сечений стержня и, кроме того, считать
ту = 0:
^EJ^\ + pF^ = qz{x,t). (10.7)
cbc2^ дх2) dt2 Чг
10.2. Уравнения сил и моментов
При заданных нагрузках qz и шу и при заданном движении подвижной
системы координат х, у, z определение прогиба корпуса v(x, t) сводится
к решению дифференциального уравнения изгибных колебаний (10.7)
с краевыми условиями (10.6).
Уравнения движения, совершаемого подвижной системой координат х, у,
z в начальной стартовой координатной системе Хо, уо, Zo, можно построить,
воспользовавшись теоремой о движении центра масс материальной системы
и теоремой об изменении момента количества движения, так как оси коор-
динат х, у, z совмещены с главными центральными осями инерции ракеты
[1]. Если к внешним силам, действующим на ракету, присоединить реактив-
ные силы и обозначить через Q главный вектор полученной системы сил и
через М - главный момент этих сил относительно начала подвижной систе-
мы координат х, у, z, имеют место равенства:
d
где
Jy - момент инерции ракеты относительно оси у (вращение ракеты
предполагается медленным).
При рассмотрении изгиба корпуса ракеты в плоскости рыскания обо-
значают через qz погонную поперечную силу, действующую на ракету,
и через ту - погонный момент внешних сил. Таким образом, внешние си-
лы, действующие в плоскости рыскания на участок ракеты, заключенный
209
между ее поперечными сечениями, имеющими абсциссы х и x+dx, будут
приводиться к силе qzdx и моменту mydx. Момент этой системы сил отно-
сительно оси у будет равен (qzx+my)dx. В соответствии с этим проекцию
главного вектора внешних сил Qz и проекцию главного момента Му опре-
деляют по формулам:
Q2 = м, = f(?z+т№- (10-9)
О о
Согласно (10.9) уравнениям (10.8) можно придать вид:
/
0 (10.10)
Jy~T= \^гХ + ту)^
dt 0
Уравнения сил и моментов (10.10) совместно с дифференциальным
уравнением изгибных колебаний (10.7) и краевыми условиями (10.6) оп-
ределяют движение подвижной координатной системы в плоскости рыс-
кания и изгибные колебания корпуса, возникающие в этой плоскости
в процессе движения ракеты.
В соответствии с уравнениями (10.10), определяющими ускорения WOz
da>
и —-, функция v(x,t), найденная из дифференциального уравнения (10.7)
dt
с краевыми условиями (10.6), всегда будет удовлетворять интегральным
условиям:
f '<( Ov \
jvpdx = 0, + —J l(& = 0, (10.11)
0 0\ J
где:
p=£pds; Jy = ^z2pds. (10.12)
Эти соотношения играют важную роль при исследовании изгибных
колебаний корпуса ракеты.
10.3. Дифференциальные уравнения движения ракеты
в плоскости рыскания, учитывающие упругость
корпуса ракеты
Для построения развернутых выражений погонной поперечной си-
лы qz и погонного момента ту, которые входят в уравнения сил и момен-
тов (10.10) и в уравнения изгибных колебаний в частных производных
210
(10.7), рассмотрим эти функции, порождаемые силой тяжести, аэроди-
намическими силами, реактивными силами и управляющими силами
и моментами.
1. Сила тяжести. В соответствии с первой из формул (10.12) функция ц(х)
представляет собой массу ракеты, приходящуюся на единицу ее длины в по-
перечном сечении S, имеющем абсциссу х. В связи с этим функцию ц(х)
принято называть погонной массой ракеты. Вектор погонной силы q, поро-
ждаемый силой тяжести, будет равен где g - вектор ускорения силы
тяжести. Проектируя вектор q на ось у, получим зависимость
$г=о. (Ю.13)
Центр масс любого поперечного сечения ракеты будет лежать на ее про-
дольной оси, так как ракета предполагается нами симметричной относитель-
но плоскостей у = 0 и z = 0. Таким образом, погонных моментов сила тяже-
сти порождать не может и в данном случае будет иметь место равенство
т=ГПу=^ (10.14)
2. Аэродинамические силы. В данном случае поперечную погонную
силу будем считать пропорциональной местному углу скольжения в соот-
ветствии с исходными предпосылками, сформулированными выше. Обо-
значая коэффициент пропорциональности через c(x,t), получим равенство
qz=cp\ (10.15)
где р* местный угол скольжения. Угол, на который поворачивается попе-
речное сечение ракеты в процессе изгиба, при малых изгибных колебани-
~ Эу
ях можно считать равным производной
Эх
В этом случае местный угол
скольжения /Г будет определяться равенством
Эу
/Г=д+^, (10.16)
Эх
где р - угол скольжения, соответствующий недеформированному состоя-
нию корпуса ракеты, т. е. угол между направлением вектора скорости
центра масс ракеты и положительным направлением оси х. Подставляя
(10.16) в (10.15), получим соотношение
( Эу А
(ЮЛ?)
В рассматриваемом случае можно положить
Шу=0, (10.18)
так как при исследовании устойчивости движения погонными аэродина-
мическими моментами практически можно пренебрегать.
211
3. Реактивные силы. Погонную поперечную силу qz, соответствующую
действию на упругий стержень сосредоточенной силы Qz, приложенной
в сечении стержня с абсциссой х=£, в сопротивлении материалов рассмат-
ривают, как предел, к которому стремится при е—>0 погонная поперечная
сила q*(x)9 определяемая равенствами:
при (10.19)
Е 2 2
* ЕЕ
<?*(*) = ПРИ И ПР11 £ + “<*</•
Формулам (10.19) можно придать вид
£(*)=Q,f(10.20)
где f(x,£) - функция, определяемая в интервале 0<х</ соотношениями
f(x^)=-upn^-^<x<^+^-, (10.21)
Е 2 2
/(х,£) = 0 при 0<х<£--| ипри £ + -|<х<7.
В случае действия на упругий стержень сосредоточенного момента Му,
приложенного в сечении стержня с абсциссой х = £, соответствующий по-
гонный момент шу(х) может быть выражен равенством
т/х) = Л//(х,£), (10.22)
где 8(х,£) - дельта-функция (предел f(x,£) при е->0).
Обозначим через хт абсциссу сечения ракеты, в котором к несущему
корпусу крепится двигательная установка. Суммарная сила тяги Р будет
иметь линию действия, показанную на рис. 10.2. Проекции вектора Р на
координатные оси х и z будут определяться равенствами:
Рх = Pcos0>, Pz = Psin0>, (10.23)
где ф - угол между направлением вектора Р и положительным направле-
нием оси х.
В соответствии с приближенными равенствами, установленными для
угла ф, формулам (10.23) можно придать вид
(
Р=Р, Р2=Р — • (10.24)
Как видно на рис. 10.2, реактивные силы, действующие на корпус ра-
кеты в его сечении, имеющем абсциссу х = хт, будут приводиться к попе-
речной сосредоточенной силе Qz и к сосредоточенному моменту Му, кото-
рые согласно (10.24) могут быть найдены по формулам:
212
(10.25)
Для погонной поперечной силы qz и погонного момента ту в рассмат-
риваемом случае будут иметь место соотношения:
\дх)х-хт
OT.=-p(vU/(x’xr)
(10.26)
В процессе вывода формул (10.26) в качестве точки приведения реак-
тивных сил пользовались точкой х = хт недеформированной оси ракеты
в соответствии с тем смыслом, который вкладывается обычно в погонную
силу qz и погонный момент ту в исходных уравнениях равновесия. Учет
влияния, которое оказывают на изгибные колебания корпуса ракеты из-
менения линии действия суммарной силы тяги Р посредством формул
(10.26), является весьма приближенным. Однако в задаче об устойчивости
изгибных колебаний данный эффект играет сравнительно несуществен-
ную роль и в связи с этим приближенный учет его посредством формул
(10.26) практически является вполне достаточным.
4. Управляющие силы и моменты. Обозначим через xz абсциссу по-
перечного сечения ракеты, в котором на ее корпус действуют управ-
ляющая сила, или управляющий момент. Если для движения ракеты
в плоскости рыскания система управления создает управляющую силу
Fzynp., соответствующая погонная поперечная сила qz может быть опре-
делена выражением
42=F^8{x,xy). (10.27)
213
Если система управления формирует сосредоточенный управляющий
момент Муупр (случай управления рассогласованием тяг), соответствующий
погонный момент ту может быть представлен соотношением
ту=М^8(х,ху). (10.28)
Для того, чтобы в дальнейшем не расчленять всякий раз указанные вы-
ше два случая управления движением ракеты, будем предполагать ниже,
что система управления порождает одновременно погонную поперечную
силу qz и погонный момент ту, выражаемые равенствами:
= F^Six.x^ ту = М™р8(х,ху). (10.29)
Условившись считать, что М(^р = 0 в том случае, когда система управ-
ления формирует управляющую силу, и полагая Fzynp =0, для
того случая, когда исполнительные органы системы управления создают
сосредоточенный управляющий момент.
Объединяя погонные поперечные силы, определяемые формулами
(10.17), (10.26) и (10.29), получим для поперечной погонной силы qz вы-
ражение
+ + 8{x,xT) + F 8(х,х). (10.30)
V дх) \дх)
4 Z X Z Х-ХТ
Полный погонный момент ту в общем случае может быть выражен со-
отношением
=_p(vLxr (10-31)
Подставляя (10.30) и (10.31) в уравнения сил и моментов, получим
уравнения:
thw0 = if Р + — \dx + р(—1 + F
Oz ov дх/ [дхЦ
Jv—^= f(p + — + 1 fj(x,xr)x<&- (10.32)
dt Д дх) \дх)х=Хт1
-P(v) +Р™,п \xdx +
\ /Х=ХГ zy”P- J \ ’ У} zynP-
0
(координата центра тяжести ракеты Хс всегда остается равной нулю).
Для любой функции f(x), заданной в интервале 0<х<7, при сколь угодно
малом положительном е соблюдается равенство
214
\8(x,^f{x)dx = /(£) + p(x,^)[/(x) - =
0 (+e 0 ° (10.33)
= /(^)+ p(x^)[/(x)-/(^)]A.
Если функция f(x) непрерывна в точке х = £, при любом сколь угодно
малом т| можно отыскать такое достаточно малое е.
Уравнениям (10.32) можно придать вид
mW0! = fl P +
(Д
<7 69 У
J^ = 0V + -
+х F +М™
у zynp. уупр.
zynp.
dv
дх
(10.34)
Введя обозначения
i i
F= В \cdx + F n; M = В [cxdx + xvFB + M
z 'J гУпР-1 z ' J У гУпР- УУпР-,
о 0
можно привести уравнения (10.34) к виду
(10.35)
mW°2 г$дх‘
da)„ 't
(10.36)
-V
Уравнения (10.36) представляют собой уравнения сил и моментов,
учитывающие упругость корпуса ракеты. В этих уравнениях согласно
(10.35) сила Fz представляет собой проекцию на ось z главного вектора
аэродинамических и управляющих сил, действующих на ракету при от-
сутствии изгибных колебаний ее корпуса, момент Му представляет собой
проекцию на ось у главного момента этих сил.
Непосредственная подстановка погонной силы qz и погонного момента
ту, в уравнение изгибных колебаний приводит к необходимости диффе-
ренцирования дельта-функции. Чтобы избежать этой операции, заменим
уравнение (10.7) системой двух дифференциальных уравнений в частных
производных для прогиба и(х, t) и перерезывающей силы 2(х, t). Получим
систему двух уравнений
215
d2v dQ dco
AfB AlL
dx I 2 dx1 J
. 3’v _ . da>
(10.37)
Краевые условия представляются в следующем виде
d2v
В2—f — 0, 0 = 0 при х = 0 иприх = /.
дх
(10.8)
Подставляя qz и ту из (10.30) и (10.31) в (10.37), получим систему
уравнений:
d2v dQ dco ( dvA
и—г + ——= uwn — их—- + с р +----- +
Р dt2 дх М Oz М dt Г дх)
8{x,xT) + Fzynp8{x,xy),
(10.39)
ох ох ) oxot at
-M^S^x,).
уупр. V ’ у/
Объединяя уравнения сил и моментов, дифференциальные уравнения
в частных производных и краевые условия, получим уравнения:
+ J
0
-V
о
d2v dQ dco
dt дх dt
( dv\ (dv\
+c \p + — +P — 8{x,xT) + F8{x,xv),
V dx) {dx),^ T w y
d (n 3^ . 3’v _ dm
77 \~Jy-^2~Q = Jy^+
ch^ dx ) y dxdt y dt
+P(y\^S{x,xT)-M^8{x,xy\
d2v
В—r = 0, 0 = 0 при x = 0 и при x = l.
дх
(10.40)
216
Уравнения (10.40) представляют собой уравнения движения ракеты
в плоскости рыскания, учитывающие упругость корпуса ракеты. Уравне-
ния определяют движение, совершаемое в этой плоскости подвижной сис-
темой координат х, у, z, и функции u(x,t), Q(x,t), характеризующие изгиб-
ные колебания корпуса ракеты.
В систему уравнений (10.40) входят дифференциальные уравнения
в частных производных. Уравнения движения ракеты в плоскости рыс-
кания можно преобразовать в бесконечную систему обыкновенных
дифференциальных уравнений. Это преобразование основывается на
исследовании так называемых собственных изгибных колебаний корпу-
са ракеты.
10.4. Собственные изгибные колебания корпуса ракеты
в плоскости рыскания
Изгибные колебания корпуса ракеты в плоскости рыскания, происхо-
дящие при отсутствии погонных поперечных сил qz и погонных моментов
ту, называют собственными колебаниями корпуса в плоскости рыскания.
dco
Согласно (10.10) в рассматриваемом случае ускорения woz и —- отсутст-
dt
вуют и, таким образом, дифференциальное уравнение изгибных колеба-
ний в данном случае принимает вид
д2 ( d2v^ д Г . d3v d2v
дх2 z дх2 J дх (У' dxdt2 J dt2
(10.41)
Краевые условия переходят при этом в краевые условия:
^-0
А(в -О
dxl z дх2 J у dxdt2
при х = 0 и при х = 7.
(10.42)
При рассмотрении дифференциального уравнения (10.41) с краевыми
условиями (10.42) предполагают, что функции ц и jy зависят от одной
лишь переменной х, пренебрегая медленным изменением вида этих функ-
ций, возникающим в рассматриваемом интервале времени за счет выгора-
ния топлива.
Однородное дифференциальное уравнение (10.41) с однородными
краевыми условиями (10.42) обладает очевидным решением u(x,t) = 0, ко-
торое принято называть тривиальным решением этой краевой задачи. Не-
217
тривиальные решения дифференциального уравнения (10.41), удовлетво-
ряющие краевым условиям (10.42), находят в виде произведения двух
функций [1]
v(x,0 = K(x)g(0, (10.43)
применяя в рассматриваемом случае метод, называемый методом Фурье,
или методом разделения переменных. Подставляя (10.43) в (10.41), полу-
чают равенство, приведенное к виду
z dx2)
d ( . d?} ..
-~T \jy^F +/zK
dxV dx J
d2g
dt2
g
(10.44)
Левая часть этого равенства не зависит от переменной t, а правая - не
зависит от переменной х. Таким образом, отношения, фигурирующие
в левой и в правой частях равенства (10.44), должны представлять собой
некоторую константу, которую обозначают через X. В соответствии с этим
функция V(x) должна удовлетворять дифференциальному уравнению
(10.45)
а функция g(t) - дифференциальному уравнению
d^g
^- + 2g = 0. (10.46)
При этом выполняются краевые условия:
d(„d2v\..dV .
— В,—г +л/,-- £ = 0.
z dx1 } Jz dx
при X = 0 и при X = I.
Для того, чтобы условия (10.47) выполнялись в любой момент време-
ни t, функция V(x) должна удовлетворять краевым условиям:
d ( d2Vy , dV
— л2—г +A/„—=o,
tfcl dx I y dx
при X = 0 и при X = I.
(10.48)
218
Дифференциальное уравнение (10.45) с краевыми условиями (10.48)
при любом значении числового параметра X имеет тривиальное решение
V(x) = 0. Те значения параметра X, при которых краевая задача, образуе-
мая дифференциальным уравнением (10.45) и краевыми условиями
(10.48), имеет нетривиальные решения, называют собственными значе-
ниями этой краевой задачи. Нетривиальные решения дифференциального
уравнения (10.45) с краевыми условиями (10.48), соответствующие собст-
венным значениям данной краевой задачи, называют ее собственными
функциями. Собственные значения краевой задачи, образуемые диффе-
ренциальным уравнением (10.45) и краевыми условиями (10.48) являются
вещественными и неотрицательными.
Собственные функции рассматриваемой краевой задачи V(x) и V*(x),
соответствующие различным ее собственным значениям X и X*, всегда
удовлетворяют условию
'/ . dV dV' .^.."1 , Л
у dx dx J
(10.49)
Свойство собственных функций, выражаемое этим интегральным со-
отношением, принято называть свойством их ортогональности.
При X = 0 дифференциальное уравнение (10.45) вырождается в урав-
нение
dx21 dx2 J
(10.50)
а краевые условия при X = 0 принимают вид
d2V d ( d2v\
В2^-г = 0, — =0 при x = 0 и при x =/. (10.51)
dx dx\ dx )
Согласно (10.50) имеет место равенство
d2V
Bz^ = Cx+C2x, (10.52)
dx
где Ci и С2 - произвольные постоянные. В соответствии с краевыми усло-
виями (10.51) обе постоянные Ci и С2 равны нулю. Получим дифференци-
альное уравнение, имеющее два линейно независимых решения:
V=1hV = x. (10.53)
Оба эти решения удовлетворяют краевым условиям и, таким образом,
краевая задача, образуемая дифференциальным уравнением (10.45) и
219
краевыми условиями (10.48), имеет собственное значение X, равное нулю.
Этому собственному значению соответствуют две собственные функции
краевой задачи, определяемые формулами (10.53), все остальные собствен-
ные значения рассматриваемой краевой задачи должны быть положитель-
ными. Эти положительные собственные значения обозначают через X,, j = 1,
2,..., условились нумеровать их в порядке возрастания, а соответствующие
им собственные функции - через Uj(x), j = 1,2,...
Первой из собственных функций соответствуют одинаковые перемеще-
ния поперечных сечений корпуса, второй из этих собственных функций -
перемещения, пропорциональные абсциссе поперечного сечения х.
В первом случае функция u(x,t) определяет поступательные перемещения
корпуса ракеты в плоскости рыскания, второму случаю соответствует вра-
щение корпуса вокруг оси у. Оба эти движения не сопровождаются дефор-
мациями корпуса и, таким образом, собственное значение рассматриваемой
краевой задачи, равное нулю, изгибных собственных колебаний корпуса ра-
кеты не определяет.
Положительному собственному значению краевой задачи X, будет соот-
ветствовать функция u(x,t), определяемая формулой
v(x,0 = K.(x)g.(0, (Ю.54)
где gj(t) - решение дифференциального уравнения
б/2р-.
-J^ + 2.g.=0. (10.55)
Полагая
^j=^j9 (10.56)
можно привести уравнение (10.55) к виду
-^ + ^£.=0. (10.57)
Общее решение дифференциального уравнения (10.57) может быть
представлено в виде
gy(Z) = Cycos(a>/ + pJ, (10.58)
где Cj и <pj - произвольные постоянные.
Подставляя, получают для прогиба корпуса ракеты u(x,t) выражение
v(x,Z) = CyKy(x)cos(fiy + (10.59)
Согласно (10.59) в рассматриваемом случае в любой момент времени t
перемещения поперечных сечений корпуса пропорциональны соответст-
220
вующим значениям функции Vj(x). Таким образом, функции Vj(x),
j = 1, 2,... определяют формы изгибных собственных колебаний корпуса
ракеты, а числа j = 1, 2,... - определяют частоты этих собственных
колебаний. Дифференциальное уравнение (10.57) принято называть диф-
ференциальным уравнением собственных колебаний.
При выводе дифференциального уравнения изгибных колебаний корпуса
ракеты не учитывалось рассеяние энергии, неизбежно сопровождающее
всякий реальный колебательный процесс. В соответствии с этим полученное
дифференциальное уравнение собственных колебаний (10.57) предопределя-
ет гармонический характер рассматриваемых собственных колебаний корпу-
са ракеты. Для того, чтобы учесть затухание собственных колебаний, надо
заменить это уравнение дифференциальным уравнением
. dg ,
Л + (1°-60)
Неоднократно проводившиеся натурные динамические испытания раз-
личных ракет, а также динамические испытания конструктивно подобных
ракетных моделей [107], свидетельствуют о том, что для упругих колебаний
корпуса ракеты логарифмический декремент собственных колебаний прак-
тически не зависит от номера их тона, обозначенного в уравнении (10.60)
через j. Логарифмический декремент собственных колебаний пропорциона-
лен отношению коэффициента демпфирования е, к частоте колебаний со j.
Таким образом, можно приближенно положить
Е
(10.61)
где Т| - безразмерный коэффициент, не зависящий от номера тона j. Ко-
эффициент Т| обычно лежит в пределах от 0,01 до 0,02. Согласно (10.61)
дифференциальному уравнению (10.60) можно придать вид
d2g dg. 0
«L+w «L + fl,2 0. (10.62)
at at
В заключение этого раздела необходимо отметить, что дифференци-
альное уравнение (10.45) с краевыми условиями (10.48) определяет функ-
ции Vj(x), j = 1, 2,... с точностью до произвольных постоянных множите-
лей. Для устранения этой неопределенности функции Vj(x), j = 1, 2,...
подчиняют всегда некоторому дополнительному условию. В качестве та-
кого дополнительного условия пользуются обычно начальным условием
Vj(x) = 1 при х = 0.
221
10.5. Дифференциальные уравнения возмущенного
движения упругой ракеты
Для получения системы дифференциальных уравнений возмущенного
движения упругой ракеты в виде, наиболее пригодном для использования
в инженерной практике, уравнения в частных производных (10.40) преоб-
разовываются в бесконечную систему обыкновенных дифференциальных
уравнений [1].
Используя свойство полноты последовательности собственных функ-
ций I, х, Vi(x), V2(x)..., выраженное в том, что любая функция f(x), непре-
рывная в интервале 0<х</, может быть разложена в ряд
f(x) = Cx +C2x + ^gkVk(x), сходящийся в любой точке интервала 0-ь/ к со-
к=\
ответствующему частному решению.
Вследствие выгорания топлива функции Ц и jy меняют свой вид, т. е.
различным моментам времени полета ракеты t будут соответствовать раз-
личные формы изгибных собственных колебаний корпуса ракеты.
Последовательность функций I, х, Vi(x,t), V2(x,t)... также обладает
свойством полноты, в результате прогиб корпуса V(x,t) может быть пред-
ставлен рядом v(x,0 = C1(r) + C2(0x + ^gjk(0Vt(x,r), сходящимся к соот-
*=1
ветствующему значению прогиба о.
Коэффициенты Ci(t) и C2(t) всегда будут тождественно равны нулю,
поскольку mCi = 0, JyC2 = 0. Отсюда прогиб надо искать в виде ряда:
vUr) = £^(OVt(x,r). (10.63)
к=\
Подставляя этот ряд в первые два уравнения (10.8), получим:
t=l_ (10.64)
J^ + lC^S=My.
Затем ряд (10.63) подставляется в уравнения в частных производных,
содержащиеся в (10.40). Учитывая медленные изменения формы изгиб-
ных собственных колебаний, пренебрегают зависимостью от времени t
функций Vk(x,t), k = 1, 2,...
После ряда последовательных преобразований, полученных таким об-
разом соотношений, получают дифференциальное уравнение вынужден-
ных колебаний корпуса ракеты, вызываемых аэродинамическими силами,
222
а также управляющими силами и нагрузками, возникающими вследствие
влияния изгиба корпуса на аэродинамические и реактивные силы.
С учетом рассеяния энергии, возникающего в процессе колебаний, пу-
тем замены уравнения собственных колебаний (10.57) дифференциальным
уравнением (10.62), получим
т, (1= pfycdx ~^Cjtgt +
dt > » (10.65)
pv. А
+(У) Р + -------2.1 Мт
'\rjJx=xy л г упр. I у упр.
\ )х-Ху
Объединяя уравнения (10.65) вынужденных колебаний корпуса ракеты,
соответствующие различным тонам этих колебаний, и присоединяя
к этой бесконечной системе дифференциальных уравнений уравнения сил и
моментов (10.64), получают систему уравнений, которая определяет движе-
ние координатной системы х, у, z, и бесконечную последовательность функ-
ций pi(t), p2(t).... Прогиб корпуса ракеты v(x,t), возникающий
в процессе изгибных колебаний в плоскости рыскания, определяют по функ-
циям pj(t), j = 1, 2,..., суммируя ряд (10.63).
Запишем уравнения возмущенного движения ракеты в плоскос-
ти рыскания в форме и с обозначениями, приведенными в части 3
(глава 8.1).
Для I ступени ракеты-носителя 11К68 с учетом первой гармоники коле-
баний компонентов топлива и первых двух тонов колебаний упругого корпу-
са (без учета их взаимного влияния - см. раздел 10.6) система уравнений бу-
дет иметь вид:
i = aui. + + azS3y + +Fz
Л=1
4 _
V = a^z++ a^gS^ + Xv/’+
n=l
r+En.r+c^r^a^z + a^
. 2 ” (Ю.66)
q; + £„sQi + Qs - a„A
’ll qi'h q^i qfi yr
2
1=1
n = 1,2,3,4; i = l,2.
Формулы для расчета коэффициентов и свободных членов, характери-
зующих абсолютно жесткую «отвердевшую» ракету и принятые при этом
обозначения, приведены в разделе 8.1.1а; соответственно коэффициенты,
223
учитывающие влияния жидкого наполнения - в разделе 8.1.16; свободные
члены - в разделе 8.1.1с.
Коэффициенты, учитывающие упругие свойства корпуса ракеты
2Р5П.(хп) ? / \2
В а>.
= ~~~ \ а8qi = П (ХГП )»
71
где:
Vm ~ уг°л рыскания, замеренный гироприборами;
qi - обобщенная координата, соответствующая i-му тону упругих коле-
баний корпуса;
Хщ - координата места установки чувствительных элементов гиропри-
боров;
Т|(х), Т|'(х) - форма и производная формы в сечении х, соответствую-
щие i-му тону колебаний корпуса в плоскости рыскания;
Pi - логарифмический декремент упругих колебаний корпуса i-ro тона;
ai - приведенная масса упругих колебаний i-ro тона;
fqi - собственная частота упругих колебаний i-ro тона.
Численные значения этих коэффициентов динамической схемы PH
11К68 приведены в табл. 19 и 20 Приложения.
10.6. Дифференциальные уравнения возмущенного
движения ракеты с учетом взаимного влияния
колебаний жидкости и упругости корпуса
Решение задачи учета взаимного влияния упругости корпуса ракеты
и колебаний компонентов жидкого топлива в ее баках проводится в рам-
ках исследований динамики тонкостенных конструкций с отсеками, со-
держащими жидкость.
В книге рассмотрен класс задач динамики упругих тел, содержащих
жидкость, выявлена общая структура уравнений возмущенного движения
и обоснована схема расчетов параметров конструкций ракет.
В монографии [107], содержащей список более четырехсот наименова-
ний использованной литературы, для решения прикладных задач, имею-
щих место в инженерной практике разработчиков ракетной техники, как
средство применяются методы исследования динамики деформируемых
систем и математической физики.
224
При выводе уравнений возмущенного движения упругой ракеты с ба-
ками, частично заполненными компонентами топлива, с учетом взаимного
влияния упругих колебаний корпуса и колебаний жидкого топлива в ба-
ках, вводятся практически все допущения и упрощения, принятые при ис-
следованиях, освещенных в предыдущих главах.
Так, для учета влияния жидкости на движение ракеты (часть вторая)
рассматриваются малые гравитационные волны в потенциальном поле
массовых сил, градиент j которого коллинеарен продольной оси ракеты.
Движение жидкости безвихревое. Жидкость идеальная и несжимаемая,
поверхностным натяжением пренебрегают. Возмущенное движение носит
характер малых колебаний, т. е. применяется линейная теория колебаний
систем - теория малых волновых движений.
В приведенном в разделах 10.3 + 10.5 (в качестве примера на базе [1])
выводе уравнений возмущенного движения упругой ракеты, сделанные
упрощения и принятые допущения также остаются в силе при иссле-
довании взаимного влияния колебаний жидкости и упругих колебаний
корпуса.
В основу исследований поперечных колебаний одномерных систем
с цилиндрическими отсеками принимают расчетную модель в виде упру-
гого стержня с отсеком, частично заполненным жидкостью, образованным
цилиндрической обечайкой и днищами в форме пологих сферических
оболочек. Цилиндрическая оболочка, образующая обечайку отсека, в свя-
зи с наличием силового набора обеспечивает геометрическую неизмен-
ность и нерастяжимость контура. Днища отсека при поперечных колеба-
ниях представляются абсолютно жесткими. Все деформации предполага-
ются упругими. Начальным статическим напряженным состоянием, свя-
занным с внутренним сжатием отсека и т. п., пренебрегают. При решении
гидродинамических задач пологую оболочку, образующую днище, отожде-
ствляют с плоской пластинкой.
Сделанные допущения позволяют в качестве объекта исследования
рассматривать механическую систему, в которой исключены «оболочеч-
ные» деформации с числом волн в окружном направлении, отличным от
единицы.
Используемая расчетная схема стержня с соответствующим отсеком и
основные обозначения приведены на рис. 10.3. Система координат
O*x*y*z* совершает некоторое невозмущенное движение в направлении
оси О*х* (или покоится); система координат Oxyz связана с недеформиро-
ванным стержнем - ее движение относительно O*x*y*z* описывает возму-
щенное движение стержня как жесткого тела. Начала координат обеих
систем расположены в плоскости нижнего торца стержня.
225
Поверхностная сила Р, приложенная в сечении х = хр, сохраняет при коле-
баниях стержня неизменное направление, будучи коллинеарна оси О*х*. Эту
силу можно считать аналогом силы тяги реактивного двигателя; основное от-
личие заключается в том, что последняя сила является следящей. Координаты
нижнего и верхнего днищ отсека обозначают через Хо
и хк, глубину жидкости - h, внутренний радиус цилиндра - г0, поверхность
нижнего днища - Sb боковую поверхность, смоченную жидкостью, - S2.
В дальнейшем предполагается, что колебания происходят в плоскости O*x*z*.
Не повторяя математическое описание процесса вывода уравнений
возмущенного движения, приведем лишь основную канву исследований.
10.6.1. Определение усилий, действующих на стенки
со стороны жидкости, при поперечных колебаниях
упругого отсека с жестким днищем
Предполагается, что известна функция u(x,t), характеризующая конфи-
гурацию упругой оси стержня в произвольный момент t. Определяют по-
тенциал смещений частиц жидкости.
Начальные условия для потенциала смещений заключаются в задании
формы свободной поверхности жидкости и распределения скоростей на
ней при t = 0. Граничные условия показывают, что в рассматриваемой за-
даче динамического взаимодействия колеблющейся жидкости и деформи-
рующегося отсека с геометрически неизменяемым контуром имеют зна-
226
чение только антисимметричные формы собственных колебаний жидко-
сти вида
p„(x,r,0) = £,(x,r)sin0.
Краевая задача для функции у, соответствующей изгибной деформа-
ции отсека при невозмущенной свободной поверхности жидкости, совпа-
дающей с поверхностью Z (рис. 10.3), сводится к двум более простым за-
дачам:
- найти решение уравнения Лапласа, удовлетворяющее неоднород-
ным граничным условиям при х = хо и х = xo+h и однородному ус-
ловию при г = г0;
- найти решение уравнения Пуассона, удовлетворяющее однородным
граничным условиям.
Затем переходят непосредственно к определению сил, действующих со
стороны жидкости на стенки отсека при его колебаниях. Эти силы можно
разделить на гидростатические, зависящие только от деформаций отсека
и его поворота как жесткого тела, и гидродинамические, определяемые
ускорениями стенок отсека в процессе его возмущенного движения. Те и
другие силы можно найти, если известно поле давлений в жидкости. Для
этого используют обозначение разности между давлением в некоторой
точке жидкости и давлением газа над свободной поверхностью. Послед-
нее определяется интегралом Лагранжа-Коши. Гидростатические и гид-
родинамические силы рассматриваются раздельно.
10.6.2. Составление уравнений возмущенного движения
рассматриваемой механической системы
По аналогии с процедурой, приведенной в разделе 10.4, выводят общие
уравнения поперечных колебаний с решением основной краевой задачи.
Рассматривается задача о колебаниях стержня со свободными концами
в потенциальном поле массовых сил с градиентом j, коллинеарным неде-
формированной продольной оси стержня, при наличии продольной си-
лы Р, антипараллельной j, приложенной в точке х = хр.
Уравнение возмущенного движения системы «стержень-жидкость»
получают, введя в правую часть уравнения (10.4) силы, действующие на
стенки отсека со стороны жидкости, и присоединив к нему уравнения
волновых движений жидкости, вытекающие из динамического граничного
условия на свободной поверхности.
Получают замкнутую систему интегро-дифференциальных уравне-
ний, определяющих полностью вместе с граничными и начальными ус-
ловиями поперечные колебания упругого стержня с цилиндрическим
отсеком, частично заполненным жидкостью. Эту сложную систему при-
водят к более удобному для приложений виду, построением некоторой
227
системы функций, удовлетворяющих граничным условиям на концах
стержня, а затем разложением функции прогибов u(x,t) и внешних на-
грузок в ряды по этим функциям. В качестве такой системы функций
в рассматриваемой задаче принимают формы собственных колебаний
стержня при отсутствии каких-либо внешних сил, кроме гидродинами-
ческих, а также связей между колебаниями стержня и волновыми дви-
жениями жидкости.
10.6.3. Приведение уравнений поперечных колебаний стержня
к системе обыкновенных дифференциальных уравнений
Преобразование общих интегро-дифференциальных уравнений попе-
речных колебаний стержня с отсеком, частично заполненным жидкостью,
начинают с приведения их к бесконечной системе обыкновенных диффе-
ренциальных уравнений при помощи метода Галеркина.
В результате система уравнений возмущенного движения (10.66)
с учетом всех факторов преобразуется к следующему виду.
Первые два и пятое уравнения системы дифференциальных уравнений
возмущенного движения ракеты в плоскости рыскания (10.66) остаются
неизменными.
В третье и четвертое уравнения системы (10.66) добавляются члены,
характеризующие взаимное влияние упругих колебаний корпуса ракеты
и колебаний компонентов топлива в ее баках.
В результате эти уравнения принимают вид:
2
'L + £rj + rfr,, = аг,Л ~
»=1
4
й+w+Еад
1=1
Структура коэффициентов, учитывающих взаимное влияние колебаний
жидкости в баках ракеты и упругих колебаний корпуса, имеет следующий
вид (численные значения этих коэффициентов динамической схемы PH
11К68 в качестве примера приведены в табл. 21 Приложения).
1. Для уровня компонентов в n-м баке hn<0,8^.H.n (радиус нижнего
сферического днища n-го бака):
о R3
а -С? -fto. (I я ( X ) - ГR I - (X. „ - Хшп )IЪ; (Хшп )},
qtrn I п *i \ шп / I сф.н.п on у сф.н.п шп у п I »t \ шп / i ’
ai
а =—— R.Mln-(AT. - AT )Alnf'(AT )|
гяд{ — I n •I \ tun f I сф.н.п on у сф.н.п tun J n J •I \ ШП /1
r*n
2. Для уровня hn>0.8^.H.n:
228
a - ?PXR . a - *th^R .
4iTn £-1 gin’ rn4i £3-l ?'"’
^qin ’
^=£7\(x>
^Ол x„
sh^hn) ^ + S^„)’
где
Хшп - координата шпангоута, к которому крепится нижнее днище бака;
Лл, Дл, ал - безразмерные гидродинамические коэффициенты,
соответствующие первому тону колебаний в n-м баке (см. часть 3);
^сф.н.п ~ координата центра нижнего сферического днища n-го бака;
7^л - радиус свободной поверхности в n-м баке;
£ = 1,8412 - первый корень уравнения ^- = 0, где А(^) ” функция
Бесселя I рода I порядка.
Остальные обозначения сохранены из раздела 8.1.1 и системы диффе-
ренциальных уравнений (10.66).
10.7. Определение основных динамических
характеристик ракеты как объекта управления
При создании современных конструкций ракет, в связи с резким увели-
чением их веса и размеров, значительным снижением относительной жест-
кости, существенным отличием компоновочных схем новых образцов от
разработанных ранее и рядом других факторов, становятся все более акту-
альными и занимают все больший удельный вес исследования динамиче-
ских свойств разрабатываемых конструкций. В результате исследований
должны быть определены с необходимой степенью точности их основные
динамические характеристики, в частности, собственные частоты, собст-
венные формы и коэффициенты демпфирования упругих колебаний [107].
Определение собственных частот, форм и коэффициентов демпфиро-
вания упругих колебаний в ряде случаев является наиболее трудным эта-
пом динамических исследований, так как рассматриваемые конструкции
представляют собой чрезвычайно сложные механические системы
с большим числом степеней свободы в узком частотном диапазоне.
Для каждой принципиально новой компоновки тяжелой ракеты этот
этап исследований, как правило, выливается в проведение обширных как
теоретических, так и экспериментальных работ.
Определение основных динамических характеристик чисто теоретиче-
ским путем возможно далеко не всегда. Даже использование сложных
229
расчетных схем, существенно отличных от обычной балочной идеализа-
ции, часто без дополнительного экспериментального обоснования не дает
уверенности в правильности полученных результатов. Кроме того, суще-
ствующие теоретические методы исследования, особенно в тех случаях,
когда необходимо учитывать эффекты тонкостенности конструкции, яв-
ляются ненадежными и требуют дальнейшего совершенствования. Коэф-
фициенты демпфирования могут быть определены только эксперимен-
тальным путем.
10.7.1. Теоретические методы определения форм и частот
изгибных собственных колебаний
Определение частот и форм собственных колебаний соответствующих
парциальных механических систем является центральным вопросом в со-
ставлении (раздел 10.6) удобных для инженерной практики уравнений
возмущенного движения эквивалентных упругих стержней в форме обык-
новенных дифференциальных уравнений.
Аналитические методы определения форм и частот собственных коле-
баний в полной мере являются приемлемыми только в случае однородно-
го стержня, т. е. когда EI(X) = const, т(Х) = const. В противном случае
используются различные приближенные методы расчета.
В настоящее время разработан целый ряд таких методов [1], [88], [107],
различающихся наглядностью физического процесса, экономичностью
вычислительных работ на ЭВМ, точностью расчетов и др.
Одним из наиболее распространенных методов является метод после-
довательных приближений, позволяющий решать задачу наиболее про-
стыми вычислительными средствами. Процедура расчета этим методом
подробно описана в монографии [1] и с некоторым отличием в учебнике
[88]. Для иллюстрации объема работы приведем основные этапы вычис-
лений.
Сущность метода заключается в построении процесса последователь-
ных приближений следующим образом.
В качестве нулевого приближения формы колебаний первого тона
принимают произвольную функцию /ю(х), причем /ю(0) = 1. Для быстроты
сходимости процесса вычислений эту функцию выбирают наиболее близ-
кой к искомой, например, принимают форму изгибных колебаний стержня
постоянного сечения.
Нулевое приближение/ю(х) удовлетворяет равенствам:
/ _ / _
Jm(x)fn (x)dx=0; Jm(x)fn (x)(x - xc )dx = 0,
0 0
230
где:
f (х) =
Для удовлетворения граничным условиям при х = I нулевое приближе-
ние выбирают в виде
Л О)=f' W+4о(* - *<)+До.
где:
/*(х) - форма собственных колебаний свободного стержня постоянно-
го поперечного сечения;
Аю, В ю - постоянные коэффициенты (константы интегрирования)
равные:
Jm(x)/*(x)(x-xc)A jm(x)ft'(x)dx
А 0_____________________• » 0___________
Л10 “ / ’ "10 — /
ри(х)(х - хс )2 dx
о о
Используя уравнения поперечных колебаний n-го тона свободного
стержня и граничные условия для концов стержня, дважды его проинтег-
рировав по х и учитывая граничные условия при х = 0, получают выра-
жение
EJ(x)/„'(x) = со2 jdc jm(x)/„ (x)dx.
о о
Разделив это уравнение на EJ(x) и дважды проинтегрировав по х, по-
лучают выражение для fn(x) в виде интегро-дифференциального уравне-
ния.
Подставив в полученное соотношение значения EJ(x), m(x), fio(x)
и проинтегрировав, находят первое приближение fn(x). Поскольку
/1(х) = //х)^2, первое приближение для собственной частоты колебаний
6уде1<,'=ж
После ряда преобразований вычисляют частоту и форму собственных
колебаний m-го приближения и в результате решения получают последо-
вательность собственных функций fim(x) и собственных частот a>im:
fio(x), fn(x), fi2(x).... fim(x);
(Oil, (012,(013.(01m-
Обе эти последовательности являются сходящимися и их пределы есть
собственная функция и собственная частота упругих поперечных колеба-
ний первого тона.
231
Для получения форм и частот собственных колебаний высших тонов
процесс последовательных приближений должен сопровождаться выпол-
нением условий ортогональности по всем низшим гармоникам, поэтому
метод последовательных приближений наиболее приемлем для определе-
ния первых двух тонов.
Расчет частот и форм собственных колебаний методом начальных па-
раметров, приведенный в [107], представляется весьма привлекательным
для реализации на ЭВМ, поскольку соответствующий алгоритм сводится
к решению задач линейной алгебры.
Метод начальных параметров, использованный А. Н. Крыловым для
расчета балок на упругом основании, получил широкое применение в за-
дачах статики и динамики сооружений. В последнее время в связи с раз-
витием машинных методов счета он успешно применяется для расчёта
частот и форм собственных колебаний упругих систем, в том числе и сис-
тем с параметрами, меняющимися по длине.
Этот метод оказался удобным для расчетов на ЭВМ и в случае боль-
шого количества присоединенных осцилляторов. Идея метода заключает-
ся в последовательном построении матриц переноса Н., связывающих
вектор перемещений и усилий Z. в конце i-ro участка стержня с анало-
гичным вектором Z._j в начале этого участка, так что Z. выражается
в виде произведения матрицы Ht на вектор Zt_x справа:
(i=l, 2,...Л),
где к - число участков, на которые разбит стержень (длина этих участков,
вообще говоря, совершенно произвольна).
Для вектора Zn последовательное применение соотношений для i = 1,
2,..., п приводит к равенству
Z. = »Z.,
я= П н.
i=n, л-1,...
С помощью матрицы перехода Н вектор Zm , соответствующий сече-
нию стержня х = I, выразим через вектор Zo, соответствующий сечению
х = 0. Наиболее целесообразно разбить стержень по длине на участки, на
которых погонные массовые и жесткостные характеристики можно счи-
тать постоянными; кроме того, присоединенные осцилляторы должны по-
падать на границы между участками. В этом случае можно получить ана-
литическое выражение матрицы Н.
232
Рассматривается задача о поперечных колебаниях упругого стержня,
разделенного на к участков, удовлетворяющих сформулированным выше
условиям.
В качестве методического примера рассмотрена конструкция с двумя
несущими цилиндрическими (как бы первая ступень) и двумя подвесными
сферическими отсеками с жидкостью. Стенки несущих баков считают уп-
ругими, а подвесных - абсолютно жесткими.
Расчет параметров собственных колебаний методом прогонки, изло-
женный в [88], по своей физической сути близок к предыдущему, по-
скольку используется тот же прием разбиения стержня на К участков, для
каждого из которых изгибную жесткость и погонную массу принимают
постоянными.
Преимуществом метода является возможность рассчитать форму и
частоту собственных колебаний любого тона, не определяя форму преды-
дущих тонов.
Расчет форм и частот собственных поперечных колебаний упругого
стержня методом прогонки в матричной форме, приведенный в [88], до-
веден до примера определения низших форм и частот собственных попе-
речных колебаний корпуса ракеты большого удлинения, схематизирован-
ного тонким неоднородным стержнем. В этом случае явлением сдвига
и инерцией вращения поперечных сечений пренебрегают.
По своей физической сути и по используемому математическому аппа-
рату метод весьма близок к методу начальных параметров.
10.7.2. Экспериментальные методы определения
основных динамических характеристик
Как уже указывалось выше (см. часть 3), экспериментальные исследо-
вания динамических свойств первых поколений ракет и ракет-носителей,
созданных ОКБ-586 в кооперации со специализированными предпри-
ятиями - разработчиками отдельных частей ракетных комплексов, прово-
дились силами НИИ-88 (ЦНИИМаш) под непосредственным научным ру-
ководством Г. Н. Микишева.
В книге [107], автором соответствующих разделов которой он являет-
ся, достаточно подробно освещены все аспекты проводимых исследова-
ний. Проведем изложение существа вопроса.
При определении основных динамических характеристик рассматри-
ваемых конструкций важную роль играют экспериментальные методы.
В основе этих методов лежат динамические испытания натурных конст-
233
рукций или специальных конструктивно подобных моделей, которые яв-
ляются почти точными уменьшенными копиями натурных конструкций.
В книге излагаются наиболее известные экспериментальные методы.
При этом главное внимание уделяется теоретическим основам этих ме-
тодов.
Содержание отдельной главы составляют методические материалы по
динамическим испытаниям натурных конструкций или их конструктивно
подобных моделей, в том числе описание типового вибрационного обору-
дования и измерительной аппаратуры.
Далее рассматриваются вопросы моделирования динамических
свойств тонкостенных конструкций, проектирования и изготовления
конструктивно подобных моделей, нашедших широкое практическое
применение.
При экспериментальном определении основных динамических харак-
теристик тонкостенных конструкций - собственных частот, форм коле-
баний и коэффициентов демпфирования - применяются различные мето-
ды. Наиболее известный и простой из них - резонансный - использовал-
ся при частотных испытаниях самолетов еще до Второй мировой войны.
В последующие годы он получил дальнейшее развитие и широкое рас-
пространение.
В резонансном методе собственные частоты колебаний определяются
по резонансным пикам амплитудных характеристик, а формы колебаний -
по соотношению амплитуд резонансных пиков в различных точках конст-
рукции. Таким образом, предполагается, что в окрестности того или иного
резонанса система ведет себя как система с одной степенью свободы, т. е.
влияние нерезонансных тонов колебаний не учитывается.
Для конструкций со слабым демпфированием и достаточно разнесен-
ными собственными частотами резонансный метод дает вполне удовле-
творительные результаты. Однако существуют такие конструкции, для
которых его применение наталкивается на серьезные трудности принци-
пиального характера. Эти трудности обусловлены рядом факторов: нали-
чием в системе близких собственных частот, сильного демпфирования,
а также демпфирования, связывающего главные колебания, т. е. во всех
тех случаях, когда реальная конструкция не может быть представлена
в окрестности рассматриваемого резонанса достаточно точно идеализиро-
ванной системой с одной степенью свободы.
Авторы Кеннеди и Пэнку предложили другой экспериментальный ме-
тод, основанный на использовании амплитудно-фазовых характеристик
системы, позволяющий определять собственные частоты, формы колеба-
234
ний и коэффициенты демпфирования даже в тех случаях, когда резонанс-
ный метод неприменим вообще из-за отсутствия явно выраженных резо-
нансных пиков. Однако метод Кеннеди-Пэнку также не лишен принципи-
альных недостатков и является громоздким.
В дальнейшем, по мере совершенствования испытательного вибраци-
онного оборудования и аппаратуры, предлагались различные эксперимен-
тальные методы.
Экспериментальные методы можно разделить на два принципиально
различных класса. К первому классу относятся методы, в которых возбу-
ждение колебаний конструкции производится простейшим способом, на-
пример, при помощи одного вибратора, а искомые величины находятся
путем анализа (иногда достаточно сложного) экспериментальных частот-
ных характеристик (или кривых свободных затухающих колебаний), по-
лученных для различных точек конструкции. Эти методы принято назы-
вать методами анализа. В частности, резонансный метод и метод Кенне-
ди-Пэнку являются методами анализа.
Ко второму классу относятся методы многоточечного возбуждения
колебаний. Конструкция возбуждается при помощи специальной многока-
нальной вибрационной установки, включающей целую систему вибрато-
ров, так, чтобы ее колебания происходили лишь по собственной форме
одного тона колебаний, представляющего интерес. В этом случае не тре-
буется больших усилий на анализ результатов, так как все необходимые
динамические характеристики определяются как для системы с одной
степенью свободы.
В книге [107] рассматриваются наиболее известные эксперименталь-
ные методы, нашедшие практическое применение. Главное внимание
уделяется теоретическим основам экспериментальных методов. Все ме-
тоды изложены применительно к упругой конструкции. Однако в прин-
ципе они могут использоваться для механической системы любой при-
роды, в частности, для определения гидродинамических коэффициентов
уравнений возмущенного движения объектов, идеализируемых как абсо-
лютно жесткое тело с полостями, частично заполненными жидкостью
[см. часть 3].
Во всех экспериментальных методах относительно физических свойств
испытываемой конструкции делаются определенные допущения. Обычно
предполагают, что конструкция является линейной, демпфирование сла-
бым, выполняется гипотеза Базиля, параметры конструкции не изменяют-
ся с течением времени, любая точка конструкции доступна для возбужде-
ния и измерения колебаний (последнее допущение практически не выпол-
няется, что несущественно).
235
10.8. Устойчивость движения упругой ракеты
Исследования влияния колебаний корпуса на устойчивость движения,
проводимые на ранних стадиях проектирования как ракет, так и систем
стабилизации, ведутся в рамках экспресс-анализа. Для обеспечения этого
необходимо максимально допустимое, с точки зрения достоверности по-
лучаемых результатов, упрощение математической модели при сохране-
нии наглядности физической сути задачи.
Учитывая, что спектры собственных частот упругих колебаний корпу-
са ракеты и колебаний компонентов топлива в ее баках в объектах управ-
ления с «приемлемыми» динамическими характеристиками не перекры-
ваются, исследование их влияния на движение ракеты проводится раз-
дельно и независимо.
Так, например, у ракеты-носителя 11К68 («Циклон-3») максимальное
значение частоты основного тона колебаний жидкости при движении
I ступени (96-я секунда полета) не превышает 1,3 гц (табл. 2 Приложе-
ния), а соответствующая минимальная частота упругих колебаний кор-
пуса не менее 3 гц (см. там же табл. 19).
Принятая в многолетней практике ГКБ «Южное» процедура исследо-
вания достаточности достигнутых динамических свойств ракет на ранней
стадии их проектирования, аналогична используемой КБ «Электропри-
бор» («Хартрон») - головным разработчиком систем управления этих ра-
кет [7] и сводится к следующему.
Для существенного упрощения выкладок используется простая модель,
учитывающая только первый тон упругих колебаний.
Полагают, что в некоторый момент времени за счет упругих колебаний
датчик команд кроме углового отклонения носителя как твердого тела (у)
замерит еще некоторый дополнительный угол, вызванный изгибом корпу-
са (Д\|/у). Иными словами, сигнал, снимаемый с датчика команд, равен
WK. = V+AVy-
Кроме того, за счет деформации корпуса появляются силы и моменты,
обусловленные изменением вектора тяги. Однако эти силы и моменты для
носителей настолько малы, что их влиянием можно пренебречь. Для про-
стоты пренебрегают также демпфирующим членом в уравнении упру-
гой линии.
Учитывая, что система стабилизации движения центра масс работает на
низких частотах, а упругие колебания корпуса имеют, как правило, частоты
(0>Ю с1, при анализе влияния упругости корпуса на устойчивость ракеты
влиянием системы стабилизации центра масс пренебрегают.
Таким образом, исследованию подлежит следующая система:
236
у/ = а^у/ + а^5,
Ч = a<<sS + a44q,
Ч'>.к=¥ + Ьуг, (10.67)
А^=<М’
а = -<ог.
ЯЯ У
В соответствии с системой (10.67) передаточная функция упругого но-
сителя может быть представлена в виде
^/7») = ^ = -^—+4^-- (Ю.68)
о р -а^ р -а
r W г ЯЯ
Характеристическое уравнение этой системы (р2 ~а^)(р2 -а^) = 0
распадается на два уравнения
р2-агг = 0,
Р2 “ ааа ~ 0*
Т' яя
Первое из них было подробно исследовано в части 1. Второе, если
учесть, что всегда aqq < 0, имеет два чисто мнимых корня. Это означает,
что полученные требования можно распространить и на рассматриваемый
случай. Однако наличие второго слагаемого в выражении (10.68) накла-
дывает некоторые дополнительные требования на систему стабилизации
в районе собственных частот упругих колебаний. Поскольку в этом рай-
оне значение частотного годографа, построенного по (10.68), практически
полностью определяется вторым слагаемым, рассмотрим частотный годо-
граф только этого слагаемого
или, учитывая, что aqq = -о2, получим
= (10.69)
Рассмотрим два случая.
!• а,Л,>°-
aaSttSa
При о = 0, FKW(O)= , . Затем при увеличении со годограф смещает-
а>
У
ся по вещественной оси вправо. При со = С0у устремляется к +оо и полуок-
ружностью радиуса R-юо переходит по направлению часовой стрелки к -оо.
При со—>оо годограф вдоль вещественной оси стремится к нулю (рис. 10.4 а).
237
Рис. 10.4. Частотный годограф упругой линии > 0:
а - объект; б - устойчивый случай; в - неустойчивый.
(10.70)
Поскольку для обеспечения устойчивости носителя как твердого тела
(первое слагаемое в (10.68) необходимо реализовать систему стабилиза-
ции с передаточной функцией
ка + Т-Р)
Wy с (Р) = —Y,
усл 1+Т,Р + Т2Р2
исследуем устойчивость системы «упругая линия плюс АС».
Передаточная функция этой разомкнутой системы может быть записа-
на в виде
(10.71)
к (1 + 7\р) aaSaSa
иг (п\— V______ч° °ч
рУГ)— 1 2 2 Л
1 + 71Р+Т2р р -аяя
Частотный годограф, построенный по (10.71), представляет собой произ-
ведение двух частотных годографов, построенных по (10.70) и на рис. 10.4 а.
По этим годографам строим годограф системы (10.71) (рис. 10.4 б). Харак-
теристическое уравнение (10.71) не имеет положительных корней, поэтому
необходимо, чтобы годограф рис. 10.4 б не охватывал точку (0j, +1).
Аналитически это условие можно записать Wp((d0)<1- После подста-
Т т т
новки в (10.71) значения а>1 = —---- и Re[FFK(fi?0)J = К* — - амплитуда
Тд • Т2 т\
АС на ©о, получим условие устойчивости по верхней границе:
238
2 _ ач^авч^тдТ1 < j
(10.72)
Рассмотрен случай, когда на частотах со—>соу система стабилизации
имеет фазовый сдвиг 2кл > уАС > -п, откуда следует соо < (Оу. Если это ус-
ловие не выполняется, то годограф, построенный по (10.71), будет иметь
вид, показанный на рис. 10.4 в, что свидетельствует о неустойчивости
замкнутой системы. Таким образом, помимо условия (10.72) необходимо
выполнение фазового условия устойчивости, изложенного выше.
2- <°-
В этом случае годограф (10.69) имеет вид, представленный на рис. 10.5 а.
Анализ этого годографа показывает, что для выполнения фазового условия
устойчивости необходимо, чтобы при со—>С0у 0 < уАС < п. Это условие озна-
чает, что соо > С0у. Если условие выполнено, то годограф разомкнутой систе-
мы (10.71) имеет вид, представленный на рис. 10.5 б. Условие устойчивости
(10.72) полностью распространяется на рассматриваемый случай, поскольку
при выполнении фазового условия знаменатель (10.72) отрицательный.
Рис. 10.5. Частотный годограф упругой линии, aqSaSq < 0:
а - объект; б - устойчивый случай; в - неустойчивый.
Годограф, представленный на рис. 10.5 в, соответствует случаю, когда
фазовое условие устойчивости не выполнено. Как видно из рисунка, ус-
тойчивость при этом нарушается.
239
10.9. Динамическая устойчивость упругой ракеты
с баками, частично заполненными компонен-
тами топлива
Методика исследований устойчивости движения ракеты с учетом вза-
имного влияния упругих колебаний корпуса и колебаний жидкости в ба-
ках путем построения и анализа АФЧХ (частотных годографов) достаточ-
но подробно изложена рядом авторов [1], [87], [107] и др.
В нашем случае ограничимся анализом членов системы дифференци-
альных уравнений, учитывающих взаимное влияние асцилляторов дина-
мической схемы ракеты-носителя 11К68. Из табл. 21 Приложения следует,
что коэффициенты, учитывающие взаимное влияние, на один-два порядка
меньше соответствующих величин, характеризующих раздельное воздей-
ствие упругих колебаний корпуса PH и колебаний компонентов
в баках носителя.
Очевидно, что в этом случае их взаимным влиянием можно пренебречь.
240
Часть 5
ДИНАМИКА КОСМИЧЕСКИХ
СТУПЕНЕЙ РАКЕТ
В 1960-1970 гг. в КБ «Южное» были созданы новые типы боевых ра-
кет и ракет-носителей космических аппаратов. К числу новых боевых от-
носился класс ракет с орбитальными головными частями; среди ракет-
носителей существенную часть составляли комплексы, созданные на ос-
нове баллистических ракет путем установки вместо головных частей спе-
циальных доразгонных блоков. Орбитальные головные части (ОГЧ) и до-
разгонные блоки представляли собой управляемые объекты, снабженные
реактивными двигательными установками. Конструктивно и по условиям
движения они имеют много общего, являются космическими летательны-
ми аппаратами и могут быть объединены общим названием - космические
ступени ракет.
Характерным для космических ступеней ракет является наличие уча-
стков движения двух типов:
- участков полета с работающим маршевым двигателем;
- участков управляемого полета с неработающим маршевым двигателем.
Значительная часть свободного полета космических ступеней прохо-
дит на высотах h > 80 км (на заключительном этапе возможно движение
ОГЧ в плотных слоях атмосферы). При движении с работающим двигате-
лем стабилизация осуществляется реактивными силами, создаваемыми
непрерывно; при движении с неработающим двигателем на больших вы-
сотах - с использованием релейной реактивной системы, исполнительны-
ми органами которой являлись реактивные двигатели малой тяги.
При больших отклонениях ступени от заданного направления двигатели
работают непрерывно. При малых отклонениях управление состоит в сле-
дующем: если величина отклонения не превышает допустимого значе-
ния, то управляющий сигнал находится в пределах зоны нечувст-
вительности системы стабилизации и исполнительные органы не вклю-
чаются; на границе зоны нечувствительности двигатели создают
241
одиночные управляющие импульсы постоянной величины и обеспечива-
ют автоколебательное движение ступени вокруг центра масс (автоколеба-
тельный режим стабилизации является наиболее экономичным). Такие ре-
активные системы получили название систем успокоения, ориентации,
стабилизации (СУОС); они способны создать большой управляющий мо-
мент вокруг центра масс, быстро устранить возмущения параметров угло-
вого движения ступени, произвести ее переориентацию.
Наличие длительных участков полета с неработающим двигателем
(участков свободного полета) является первой важной особенностью кос-
мических ступеней ракет. Характерна сложность программы движения:
предусматривается многократное включение и выключение маршевого
двигателя, выполнение программных поворотов вокруг центра масс,
обеспечение стабилизации в режиме автоколебаний, изменение точности
ориентации в заданные моменты времени полета, осуществление управ-
ления в плотных слоях атмосферы. Важная особенность космических сту-
пеней обуславливается их небольшим удлинением: как объекты регулиро-
вания они обладают значительной собственной и структурной неустойчи-
востью на участках полета с работающим маршевым двигателем. В связи
с указанными особенностями при проектировании космических ступеней
ракет возникла необходимость решения ряда научных и технических про-
блем, основные из которых следующие:
- проблема обеспечения стабилизации при минимальных затратах
энергии, точной ориентации и программного движения на участках сво-
бодного полета;
- проблема управления полетом ОГЧ с гиперзвуковыми скоростями
в условиях резко меняющихся скоростных напоров;
- проблема обеспечения устойчивости движения ОГЧ и доразгонных
ступеней на участках полета с работающим маршевым двигателем.
Ряд вопросов динамики летательных аппаратов рассматриваемого типа
к началу проектирования первых образцов таких аппаратов разработан не
был. В литературе отсутствовало сколько-нибудь достаточное освещение
автоколебательного движения космических ступеней ракет, их движения
после выключения двигателя, при выполнении программных поворотов
и обеспечении точной ориентации в заданные моменты времени полета.
Проблемы динамики космических аппаратов (КА) и ориентируемых
спутников Земли (ИСЗ) рассматривались. Основополагающие исследова-
ния были выполнены Б. В. Раушенбахом, К. Б. Алексеевым, Г. Г. Бебени-
ным [3], [9], [10]. Изучению колебательных движений КА посвящены ра-
боты [20], [33], [36], [37]. Возможность сложных периодических движе-
ний аппарата с релейной реактивной системой ориентации была отмечена
Э. В. Гаушусом [34]. Им же развиты теоретические вопросы исследования
242
таких движений, рассмотрена задача отыскания и исследования устойчи-
вости инвариантных точек преобразования отрезка, проведены исследо-
вания автоколебаний КА вне атмосферы, доказан ряд общих теорем суще-
ствования простых и кратных точек [35]. Колебания ИСЗ с пассивными
системами ориентации изучались В. В. Белецким [23]. В книге М. А. Пав-
ловского, В. П. Горбулина, О. М. Клименко [120] систематизированы во-
просы теории и практики исследования и синтеза систем ориентации КА;
методы расчета и анализа таких систем; анализируются энергозатраты
системы управления при использовании различных алгоритмов управле-
ния в переходных режимах движения и прецезионной ориентации.
Характерным для всех перечисленных исследований является рас-
смотрение задач динамики и управления КА длительного существования,
искусственных спутников Земли. При этом специфические особенности,
присущие космическим ступеням ракет и обусловленные принципами по-
строения систем управления ступеней, ограниченными углами прокачки
командных приборов, нюансами программного движения и т. д., не учи-
тывались. Решение ряда инженерных задач проводилось на основе весьма
приближенного представления о характере движения космических ступе-
ней в условиях орбитального полета, работа систем ориентации и стаби-
лизации предполагалась идеальной, влияние атмосферы и отклонений па-
раметров системы от их номинальных значений не учитывалось. Все это
приводило иногда к получению противоречивых рекомендаций, неблаго-
приятно отражалось на весовых и энергетических характеристиках кос-
мических ступеней. Результаты эксплуатации первых ракет с космиче-
скими ступенями поставили под сомнение правильность представлений
об их колебаниях в условиях невесомости. Данные телеметрии, получен-
ные при летных испытаниях, систематически указывали на наличие слож-
ных движений, не совпадающих с расчетными.
Одной из существенных технических проблем, возникающих при соз-
дании некоторых типов космических летательных аппаратов, является
обеспечение управляемого полета аппаратов при движении в плотных
слоях атмосферы с гиперзвуковыми скоростями. Трудности управления
обуславливаются большими скоростными напорами (q > 45 105 н/м2),
действующими на летательный аппарат, высокими температурами
(t > 3000°С), возникающими на поверхности летящего аппарата, сущест-
венными изменениями весовых, центровочных и аэродинамических ха-
рактеристик вследствие уноса массы и изменения скорости полета (чис-
ло М уменьшается от М = 25+20 до М = 1+0,7). Большие скоростные на-
поры и высокая температура чрезвычайно затрудняют использование
обычных управляющих органов - аэродинамических рулей, щитков, за-
крылков и т. п. Эти исполнительные органы без специальной термозащи-
243
ты (существенно увеличивающей вес конструкции) разрушаются при вхо-
де аппарата в плотные слои атмосферы. Использование в качестве управ-
ляющих органов реактивных двигателей также не всегда целесообразно:
из-за больших потребных тяг масса управляющих органов с системами
питания оказывается чрезмерно большой.
Задача оптимизации весовых и энергетических характеристик имеет для
ОГЧ и ступеней решающее значение. Решение этой задачи во многом оп-
ределяется полнотой исследования вопросов динамики и управления. Воз-
можности экспериментального исследования ограничены, так как проведе-
ние летных испытаний в необходимом объеме сопряжено со значительны-
ми трудностями из-за сложности постановки эксперимента, требует боль-
ших материальных затрат и т. д. В связи с этим проведение полного
теоретического анализа указанных вопросов приобретает особое значение.
Глава 11 книги посвящена оптимизации проектных параметров косми-
ческих ступеней ракет. В ней изложены методы выбора рациональной
эффективности управляющих органов СУОС с учетом случайного харак-
тера возмущений параметров движения и зависимости периода автоколе-
баний ступени от разности тяг диаметрально противоположных сопел;
улучшенной оценки необходимого запаса рабочего тела СУОС на основе
уточнения длительности скользящих режимов и изменений фазовых ко-
ординат по времени программных поворотов; изложены оригинальные
способы точной ориентации и управления ступенью при движении
в плотных слоях атмосферы с гиперзвуковой скоростью. В главе обобще-
ны материалы исследований, выполненных в Государственном конструк-
торском бюро «Южное» и Днепропетровском национальном университете
в течение ряда лет. Направления исследований подсказаны развитием ра-
кетной техники и уточнялись в ходе проектно-конструкторской разработ-
ки космических ступеней.
Исследования проводились по инициативе, под руководством и при не-
посредственном участии члена-корреспондента АН УССР Н. Ф. Герасюты.
244
Глава 11
ДИНАМИКА КОСМИЧЕСКИХ СТУПЕНЕЙ
С НЕРАБОТАЮЩИМ МАРШЕВЫМ ДВИГАТЕЛЕМ
11.1. Задачи динамики свободного полета
При рассмотрении углового движения космических ступеней с нерабо-
тающим маршевым двигателем используются следующие правые ортого-
нальные системы координат (раздел 1.1):
1. Гироскопическая система координат OX1Y1Z1 (система, начало ко-
торой точка О совпадает с центром масс летательного аппарата, а оси за-
даются гироскопическими приборами на борту аппарата).
2. Связанная система координат OX1Y1Z1 (точка О совпадает с центром
масс аппарата, а оси направлены по его главным центральным осям инерции).
3. Программная связанная система координат OXYZ (точка О совпада-
ет с центром масс аппарата, а оси системы - с программными положения-
ми осей 0X1, OYi, OZi).
4. Скоростная система координат OXcYcZc (точка О совпадает с цен-
тром масс аппарата, ось ОХс направлена по вектору скорости V , ось OYC
расположена в плоскости угла атаки и направлена в сторону внешней
нормали к траектории, ось OZc дополняет систему до правой).
Положение программной связанной системы координат относительно
гироскопической системы определим программными значениями углов
тангажа, рыскания и крена Х)пр, флр, флр; положение связанной системы -
углами о, ф, ф. Углы о, ф, ф при достаточно малых их значениях можно
считать расположенными в плоскостях тангажа, рыскания и крена.
Движение ступеней рассматриваемого вида на высотах h > 80 км
обычно происходит с небольшими угловыми скоростями при небольших
значениях угловых отклонений. Поэтому запишем уравнения движения
космической ступени вокруг центра масс в плоскости тангажа следующим
образом [40,178] (см. также, например, раздел 2.3, уравнение 2.28):
Ъ=ам8+ама+тг, (11.1)
di
- 8Х при j > Д или при тх А < j < Д и — < 0;
О при -т2Д < j' < тх&;
5 = | di di (И.2)
при mxA<j<&H или ПРИ _ А < j< ~т2^ и
di
+ 82 при j < —Д или при - Д < j < -т2 Д и — > 0.
dt
245
; = ТдО+Д а = алр +0.
Здесь а (апр.) - угол атаки (программный угол атаки) в плоскости тан-
гажа; 8 - управляющий параметр; а^, - коэффициенты управляю-
щих и аэродинамических моментов соответственно; mz- коэффициент
возмущающего момента; тх,т2 - параметры, определяющие величины
единичных управляющих импульсов, создаваемых диаметрально проти-
воположными управляющими двигателями малой тяги; А - параметр, оп-
ределяющий амплитуду автоколебаний ступени вокруг заданного направ-
ления продольной оси.
Уравнения в плоскостях рыскания и крена записываются аналогично.
С целью упрощения приведем уравнения к безразмерной форме. Вве-
дем новые переменные х и у следующим образом: t = xx О = Ду.
Тогда при апр = 0 получим
\|/ = 8+Ал|/ + 1,
8 =
di
- при i > 1 или при mx<i<\ и — < 0;
dr
0 при -m2<i<mx;
. , di . . di Л
при тх <i < 1 и — >0 или при -1 <i <-т2 и — <0;
dr dr
_ . 1 i . di'
+ £2 при/<-1 или при -1<i<-w2 и —>0.
dr
т7 . I к,
——, i = — = T\U4-w.
(11.3)
переменных
(И.4)
Здесь Х = Т = Тд
Преобразуем уравнения (11.3), осуществив замену
I . . „
у = \|/z--; у = У/. После подстановки получим
X
\j>z = 8 + Ал|Х/»
8 = <
е . I I Л I djx ~
— 81 при jj >1-F— или при тх+ — <у1<1 + — и—L<0;
X X X dx
I I
О при -m2+-<ji <mj+-;
Л л
I . , I dj, л , /
при ml+—< Ji<l+— и -^->0 или при -1 + —
X X dx X
+ 32 при у1^-1 + — или при -1 + — <j\ «
Л Л
I dh л
т? +— и — <0;
2 X dx
и — > 0.
X dx
246
J\=i + y = tVi + V/-
Уравнения (11.4) по форме записи совпадают с уравнениями (11.3), ес-
ли в последних I = 0.
Две проблемы неизменно привлекают внимание при проектировании
систем ориентации, стабилизации - проблема минимизации энергии, за-
трачиваемой при управлении летательным аппаратом, и проблема повы-
шения точности ориентации. Количество энергии, затрачиваемой на ста-
билизацию аппарата, существенно зависит от формы, амплитуды и часто-
ты его колебаний. Колебания аппарата в большинстве случаев являются
сложными, что обусловлено следующими причинами:
1. Наличием возмущающих моментов.
2. Влиянием атмосферы.
3. Неидеальностью элементов системы ориентации.
4. Неравенством импульсов управляющих моментов, формируемых
отдельными микродвигателями.
Неравенство импульсов управляющих моментов имеет место, если
различны эффективность отдельных двигателей или длительность их еди-
ничных включений. Оно может явиться следствием погрешности изготов-
ления исполнительных органов или системы управления в целом, а также
создаваться преднамеренно. В этом случае модули изменений угловых
скоростей летательного аппарата при включении диаметрально противо-
положных микродвигателей coj и со2 не равны между собой
((Oj й>2, А® = ©! - ©2 * 0) • Математически неравенство импульсов выра-
зим, приняв, что в уравнениях движения (11.3), (11.4) ЪхфЪ2,тх*т2. Для
определенности будем считать, что соответствует отрицательному уг-
ловому ускорению ступени, 0)2 _ положительному.
Точность ориентации характеризуется углом отклонения летательно-
го аппарата от программного направления и зависит от амплитуды ко-
лебаний аппарата вокруг центра масс. Для уменьшения стабилизацион-
ной ошибки ориентации амплитуду колебаний желательно выбрать
возможно меньшей, но уменьшение амплитуды сопровождается увели-
чением количества энергии, затрачиваемой на ориентацию (требования
точности и экономичности противоречивы). Уменьшение амплитуды
особенно нецелесообразно, если высокая точность ориентации требует-
ся не на всем протяжении полета, а только на отдельных незначитель-
ных по длительности участках. Важной задачей при проектировании
релейных реактивных систем ориентации и стабилизации является за-
дача выбора эффективности управляющих органов. Тяга управляющих
двигателей должна быть достаточно большой для того, чтобы отклоне-
247
ния ступени или космического аппарата от программного направления,
обусловленные начальными возмущениями, не превышали допустимых
значений. С другой стороны, желательно, чтобы тяга двигателей была
по возможности меньшей, так как в этом случае предъявляются менее
жесткие требования ко времени запаздывания в системе управления,
уменьшается импульс последствия, уменьшается расход энергии. На-
чальные возмущения летательного аппарата по углу (О0, Vo, Фо) и угло-
вой скорости (<>о, ф0, ф0) могут быть представлены как сумма система-
тической и случайной составляющих (см. главу 3). Наибольшие значе-
ния случайных составляющих обычно не менее чем на порядок превы-
шают систематические, что позволяет рассматривать начальные
возмущения как чисто случайные величины.
В свете изложенного представляется важным решение следующих
задач:
1. Исследование динамики колебаний и определение энергетических
затрат в случае движения аппарата вне атмосферы при действии возму-
щающего момента Мв и * со2, (Дсо= -со2 * 0).
2. Исследование динамики колебаний и определение энергетических
затрат в случае движения аппарата в атмосфере при действии возмущаю-
щего момента Мв и Cty со2, Aw 0.
3. Оценка влияния случайного характера начальных возмущений на
значение потребной тяги управляющих органов, выбор тяги двигателей и
определение запаса рабочего тела, необходимого для стабилизации ступе-
ни или космического аппарата.
4. Исследование и разработка методов точной ориентации при значи-
тельной амплитуде колебаний.
Допустимы предположения [33], [34]:
- при движении на большой высоте (h > 80 км) возмущающий момент
мал по сравнению с управляющим (Мв «Мупр.)\
- длительность импульсов управляющих двигателей мала и поэтому за
время их действия изменения угловой скорости космической ступени или
аппарата практически не сопровождаются изменением угловых координат.
Особое значение при проектировании специальных космических сту-
пеней ракет и спускаемых космических аппаратов имеют проблемы
управления свободным полетом летательных аппаратов, движущихся
в плотных слоях атмосферы с гиперзвуковыми скоростями. Все большее
внимание уделяется вопросам управления движением в канале крена.
Перспективным способом управления по тангажу и рысканию является
способ, основанный на радиальном смещении центра масс. Представляет-
ся целесообразным исследование возможности использования системы
248
перемещения центра масс для управления движением летательного аппа-
рата вокруг продольной оси.
При решении этой задачи используем следующие допущения:
1. Летательный аппарат имеет форму гладкого острого конуса и аэро-
динамически устойчив.
2. Перемещение масс внутри аппарата осуществляется в плоскостях
I-Ш, II-IV.
3. Изменения тензора инерции аппарата, связанные с перемещением
его центра масс относительно оболочки в поперечном направлении, неве-
лики и могут не учитываться.
11.2. Переходные режимы движения
Рассматривается движение космических ступеней на участках отработки
начальных возмущений, программных поворотов и скользящих режимов.
11.2.1. Обзор возможных движений
Движение космической ступени вокруг центра масс характеризуется
уравнением фазовой траектории, полученным на основе уравнений (11.1), (11.2)
ё2~ ёо = 2(а«8 • 8+mz) • (#- Ьо)~ам(Ь2~ Oq) • (11-5)
Уравнения фазовых траекторий в канонической форме приведены
в табл. 11.1/
Типичные траектории статически устойчивых космических ступеней
(Д =1 град) показаны на рис. 11.1, 11.2. Фазовая траектория статически ус-
тойчивой ступени состоит из сопряженных последовательно расположен-
ных эллипсов. Число витков траектории, а следовательно, и время уста-
новления периодических движений, существенно зависит от эффективно-
сти исполнительных органов. Типичные фазовые траектории статически
неустойчивых ступеней (я^<0) приведены на рис. 11.3, 11.4. Периоди-
ческие движения ступени под влиянием атмосферы могут устанавливать-
ся не вокруг нулевого положения (0=0), а вблизи нижнего (рис. 11.3) или
верхнего (рис. 11.4) амплитудных состояний [180]. Траектории состоят из
частей гипербол. Участки d-e соответствуют скользящему режиму движе-
ния. Траектории, соответствующие скользящему режиму, также состоят
из частей гипербол. Положение (нижнее или верхнее амплитудное), вбли-
зи которого устанавливается периодическое движение, зависит от значе-
ний коэффициентов а^, а&, а также параметров Т и Д.
Подготовлена В. А. Сизько
249
250
Таблица 11.1
ам а^8 + mz = М Значение знаменателя Каноническое уравнение траектории Вид тра- ектории
м=о - О = О0 = const Прямая
МФО - 62-^=2Л/(д-д0) Парабо- ла
м=о - & ! Д^2 Эллипс
МФО - & , д^2 2Л/(«-^0) + а^+^ 2M(iJ-iJ0) + aM^o+Oo Эллипс
<0 м=о ^0 ам<^ v0 О2 j Ь2 _ в»«?+«о Д^о + ^о Гипер- бола
м=о Oq ам>¥ и0 ам^2 , & _ j + *0 Гипер- бола
<0 МФО '2М(Ь-О0) + Ь20 М Л2 V0 & , Д^2 -! 2М(О-О0) + ам$о + до 2М(О-О0) + ам$1 + &% Гипер- бола
МФО 2A/(i)-1)0) + fl2 М Л2 vo ДррФ2 + = 1 2A/(i)-fl0) + амЬ1 + «о 2М(О-О0) + Гипер- бола
Рис. 11.1
7 ’ ( 1Д а
1 А 0. L град
-2
Рис. 11.2
251
Условием существования движения, фазовая траектория которого изо-
бражена на рис. 11.4, является отсутствие действительных решений у сис-
темы уравнений:
ё2-ё2=+ам(д2-д2); (П6)
тдё+е=+д,
что имеет место при выполнении неравенства Ь2 - 4ас < 0, где
b = -2Аа.^Тд&, а = (1 - а^Т2); с = я^(-Д2 + t>2) - Ь2;
0с, - координаты точки С. Граничное условие Ьс + а^ТдЬс = 0.
Учитывая, что Ьс = (Д-)/Тд, получим Тд = • (11.7)
В уравнениях (11.6) верхние знаки « + », « - » следует брать, если
начальная точка фазовой траектории находится справа от линии NN,
а нижние - если начальная точка находится слева от линии ММ.
Соотношение (11.7) позволяет осуществить разбиение плоскости
параметров на области существования фазовых траекторий,
представленных на рис. 11.3, 11.4. При Тд >^/1/^(1-Д/t>c) имеют ме-
сто траектории типа, показанного на рис. 11.4; при Тд <
траектории типа, показанного на рис. 11.3. На рис. 11.5, 11.6 показано
разбиение плоскости параметров на области траекторий указанных
типов.
Рис. 11.5
252
В дальнейшем движение, соответствующее фазовой траектории, пред-
ставленной на рис. 11.4, будем называть движением типа «а»; движение,
соответствующее траектории, представленной на рис. 11.3, - движением
типа «Ь».
Фазовая траектория изображающей точки может лежать как слева, так
и справа от линии включения независимо от того, имеет ли место движе-
ние типа «а» или «Ь».
Используя уравнения фазовых траекторий и прямых включения, запи-
шем условие, при выполнении которого вся траектория движения вдоль
1 ам Ь + алх.5
прямой включения лежит справа от линии включения: — < .
Наибольшие возможные значения координат 0с, 0с, 0d, 0d определяют-
ся уравнениями:
- в случае движения типа «а»
&с =-ам(Ь2с-&а) + 2а^с -0а); (11.8)
ТдЬс - 0с = А;
- в случае движения типа «Ь»
(п-9)
Уравнение — = |(^^+а^5)/0с| есть уравнение кривой, делящей
плоскость параметров на области существования скользящих режимов,
траектории которых расположены слева и справа от линии включения.
Если влиянием атмосферы можно пренебречь (л^ = 0), то из (11.9)
253
(11.10)
получаем условие —<1^8/1^ |,при выполнении которого фазовая тра-
тд
ектория скользящего режима полностью расположена справа от прямой
включения ГдО + О=-Д. Координата Ьагран определяется уравнениями
^-^=-2а^с-ЬаУ, ^а=^с;
тдЬс + = д; - 2д.
Уравнение граничной кривой имеет вид т/ =-2/3aj§|(Oa -Д)ао§6+0.50д j.
В качестве иллюстрации на рис. 11.7, 11.8 проведено разбиение плос-
кости параметров Тд,а^ на области, соответствующие траекториям, ле-
жащим слева и справа от прямой включения. На рис. 11.9-11.12 приведе-
ны траектории, соответствующие различным значениям постоянной вре-
мени системы Тд при следующих значениях остальных параметров:
= 0,024 с‘2; = 0,128 с’2; А = 1°, = 2°, = 2’5 град/с •
«05, с
254
Рис. 11.9
^град- г а Т( , =2с
4
о х' / >: 2 4 И
d ,град
-2 ч м
Рис. 11.10
дград 2 Тд = 2,5с
( А7
-4 *0 d 2 4 -
м' >,град
с''
-2 "м
Рис. 11.11
255
11.2.2. Выбор эффективности исполнительных органов
Эффективность исполнительных органов, определяемая тягой управ-
ляющего двигателя Рупр, должна быть достаточно большой для того, что-
бы отклонения регулируемой величины О от программных значений не
превышали допустимых Ъдоп. С другой стороны, желательно, чтобы рупр
было по возможности меньшим, так как в этом случае предъявляются ме-
нее жесткие требования ко времени запаздывания в системе регулирова-
ния, улучшается экономичность системы.
Отклонение регулируемой величины от программного значения, обу-
словленное начальными возмущениями параметров движения, определя-
ла
ется выражением 0 = ——+О0, где О0, О0 - начальные возмущения пара-
2а^§5
метров движения, которые будем рассматривать как чисто случайные ве-
личины с нормальным законом распределения (достаточно распростра-
ненный случай). Обычно из-за ограниченности углов прокачки
командных гироприборов необходимо выполнение условия
Н^дол., (11.11)
из которого следует требование, предъявляемое к тяге управляющих дви-
гателей
<11Л2)
Здесь I - момент инерции ступени относительно поперечной главной
центральной оси инерции; рупр - тяга управляющего двигателя и
плечо силы р относительно центра масс ступени соответственно.
Для практических целей важно знать значение тяги исполнительных
органов, обеспечивающее выполнение условия (11.11) с заданным уров-
нем надежности. В качестве одного из возможных способов решения та-
кой задачи можно предложить метод, основанный на использовании ре-
зультатов статистического эксперимента [29]. Статистический экспери-
256
мент проводится путем математического моделирования следующим об-
разом. Случайные величины О0 и О0 задаются формулами
О0 = |0ОЛ|•£; Оо = |оол|-Х , где Ъоп и Ьоп - предельные значения случайных
величин с заданным уровнем надежности; £ и X - случайные числа, реа-
лизуемые датчиком случайных чисел ЭВМ. Для каждой пары случайных
величин Ьоп и Ьоп по формуле (11.12) вычисляется значение рупр/> при
котором обеспечивается равенство 0тах = Ьдоп. При этом необходимо
учитывать, что если |т^^0 + $| < А, то включение исполнительных органов
в момент t = tQ не происходит. Включение происходит в момент t = tx, ког-
да |тдй0 + О0ц +1>0| = А. В результате N испытаний получается N значений
случайной величины рупр . По результатам расчетов строится гистограм-
ма, определяется закон распределения величины рупр и для заданной ве-
роятности Ро вычисляется такое значение Рупр, при котором выполняется
соотношение Р{0< Ро. Целесообразно ввести в рассмотрение неко-
торый условный эталон релейной системы, провести для него расчеты
и построить графики зависимости рупр = /(д0) для различных значений О0.
Пользуясь такими графиками, удобно решать частные задачи.
Примем следующие значения параметров эталонной ступени: /э =
1000 кгм с2, 1Э = 1 м. В качестве примера на рис. 11.14 приведены графи-
ки зависимости рэ = /(д0), построенные для нормальных законов распре-
деления случайных величин О0,О0 и соответствующие значениям Рупр,
Рис. 11.13
257
обеспечивающим Р{б<^дол} = 0,997. Предельные значения О0 и зада-
вались с уровнем надежности 0,997. Допустимое отклонение Ьдоп. прини-
малось = Ю°.
Расчеты показывают, что значение рупр/, определенное с использова-
нием метода статистических испытаний и обеспечивающее выполнение
условий (11.11) с уровнем надежности Р = 0,997, на 30-40 % меньше зна-
чения, определенного без учета случайного характера величин О0, О0.
11.2.3. Динамика программных поворотов
Движение космической ступени при выполнении программного пово-
рота вокруг центра масс рассмотрим, сначала не учитывая влияние атмо-
сферы в плоскости тангажа (а^=0) [180]. Подставим в уравнения движе-
ния вместо О и О значения $д и Ьд, соответствующие сигналам чувстви-
тельного элемента (датчика) системы управления, подчеркивая этим, что
включение исполнительных органов происходит по командам, снимае-
мым с датчика
i>=a«85(A ] = ТдЬд+Ъд. (11.13)
Для определенности будем считать, что в качестве датчика использу-
ется индукционный датчик углов и возмущающий момент отсутствует.
При отсутствии программного движения (программная связанная систе-
ма координат совпадает с гироскопической) статор индукционного дат-
чика углов жестко связан с корпусом космического аппарата. После по-
дачи команды на ускоренный программный поворот статор датчика на-
чинает вращаться с постоянной положительной угловой скоростью отно-
сительно корпуса аппарата (для определенности рассматривается
поворот ступени на отрицательный угол). С этого момента движение
статора в гироскопической системе координат не совпадает с движением
космического аппарата. Фазовые координаты статора датчика (t>d,ftd)
в гироскопической системе координат определяются соотношениями
i>d=i>dnp+fy -dd=bdnpt + b+^0; bdnp=bdnpt, (11.14)
где Ьдпр и Ьдпр - угол и угловая скорость программного поворота статора
датчика относительно корпуса аппарата (угол и угловая скорость поворо-
та программной связанной системы координат относительно гироскопи-
ческой системы координат); О и О - угол и угловая скорость поворота
258
летательного аппарата в гироскопической системе координат; О0 - на-
чальный угол поворота статора датчика относительно аппарата. Значения
угла О и угловой скорости О аппарата на участках движения с работаю-
щими двигателями (8^0) определяются выражениями (11.15), получен-
ными интегрированием уравнений (11.13):
О = + Og j = —ь о» (11.15)
~ Г 4-1 при •
ГДе§ = 1 1 Л J=Td^d+^d-
[-1 при j < -Д,
Подставляя О и О в уравнения (11.14), найдем (при 8 = -1)
^д=^дпр-а^ + Ьй,
а t2 (11.16)
^-+^ + ^0
и получим фазовую траекторию движения статора:
-(^дпр + V = -2а08 (ад -д0). (11.17)
Начало программного поворота может совпасть с любым фазовым по-
ложением космической ступени, находящейся в колебательном движении
вокруг центра масс. Для определенности в качестве точки, характеризую-
щей фазовое состояние ступени в момент начала программного поворота
Выбор точки соответствует максимальному времени включенного со-
стояния двигателя при выполнении программного поворота. Фазовое со-
стояние датчика в момент подачи команды на программное изменение уг-
ловой координаты О характеризуется точкой д0. При появлении положи-
тельной скорости Ьпр у статора датчика система управления производит
включение соответствующего двигателя и летательный аппарат приобре-
тает отрицательную угловую скорость. Фазовая траектория движения ста-
тора датчика (11.17) представляет собой параболу а0,а1,а2> симметрич-
259
ную относительно оси О (рис. 11.14). Участку а0,ара2 фазовой траекто-
рии статора датчика соответствует участок Aq, Alf Л2 фазовой траектории
движения космической ступени (рис. 11.14), уравнение которой:
(Н-18)
Координаты точки, в которой происходит выключение двигателя, по-
лучим, решая совместно уравнения:
“ (fy) пр + *0 J2 = - ^0 i
ТдЬд+Ьд=А.
Время движения изображающей точки на участке определяется
L I
выражением ta(m =taQai +taia2, где гвов( =^-, гв1в2 Используя со-
отношения (11.15), получим координаты Ф2,Ф2, определяющие положе-
ние точки Аг. Участку а2а3 траектории движения статора датчика с по-
стоянной скоростью соответствует участок Л2Л3 траектории движения
ступени. Координаты точек а3 и А3 определяются уравнениями
^ЭЗ = ^<)2, ^ЭЗ = ^Э2 “ 2А>
О3 = ^2; О3 = О2 + О2 • -—
^3
В точке а3 происходит включение исполнительного органа, который в
импульсном режиме работы уменьшает Оэз до значения, соответствую-
щего точке ап. Участку а3ап движения датчика соответствует участок
А3Ап движения аппарата. Координаты точек ап и Ап определяются по-
следовательным расчетом всех участков фазовой траектории. После дос-
тижения положения, соответствующего точке ап, статор датчика начинает
совершать автоколебания (участок тпрк на фазовой траектории статора).
Точкам фазовой траектории статора датчика тпрк соответствуют точки
MNPK фазовой траектории движения летательного аппарата. В момент
подачи команды на прекращение программного изменения О реализуется
значение пр = 0 и движение статора датчика относительно гироскопи-
ческой системы координат определяется выражениями
= 0; пр +0. Команда на прекращение программного поворота
может совпасть с любым фазовым положением статора датчика в его ав-
токолебательном движении. Для определенности принято, что в момент
подачи команды изображающая точка совпадает с точкой к фазовой тра-
ектории статора. Фазовое состояние статора после подачи команды
260
на прекращение программного изменения О изображается точкой к{, со-
стояние космической ступени в этот момент определяется точкой К.
По команде системы управления включается реактивный двигатель
и происходит уменьшение угловых скоростей аппарата (О) и статора дат-
чика (0э) относительно гироскопической системы координат. Уравнения
фазовых траекторий движения статора датчика и летательного аппарата
имеют соответственно вид:
= ~^д пр — )
Ь2-Ь2к=2а^-бк}
Фазовый портрет движения статора датчика команд и летательного ап-
парата после прекращения программного поворота подобен фазовому
портрету движения статора и аппарата после подачи команды на ускорен-
ный поворот (см. рис. 11.14).
Рассмотрим программное движение летательного аппарата вокруг цен-
тра масс в случае, когда влиянием атмосферы пренебречь нельзя (О^^О).
Будем считать, что в течение программного движения плотность атмо-
сферы остается постоянной = const). Тогда движение летательного
аппарата описывается уравнением с постоянными коэффициентами
i) + adoO = aos8 (11.19)
и фазовая траектория имеет вид
&-&0 =2a^-&0)-aM(b2 (11.20)
Если 5 * 0, то решения уравнения (11.20) имеют вид
1Х/)=С1е“'>'+С2е-“<>'+^> в(г)=С1Шое“0'-С2<Оое"“0', (Н-21)
Г7ТР г _ °0 . ty) г - °0 m - Г~п--
гдеС1-—+——- , с2-———— , ®о= V-Лой-
2 2(0о 2 2со0
Таким образом,
(ц.22)
©о 2со0С1
Уравнение фазовой траектории статора датчика получим, подставляя
уравнение связи фазовых координат (11.14) в уравнение фазовой траекто-
рии движения аппарата (11.20)
(й й У й2--’- Sfl ^дпр- In пр- пр- + 4<0°С1С2 й й
пр.) —— In vjo Vq
©0 2С00 С1
261
(л ^дпрх\п^д *>д ipF+4<о0С1С2 2 rt2
X In - — и^о) — ио
(Од °'Л п
2(OoCi
L J. (11.23)
В этом выражении O0,Od0 - начальные фазовые координаты аппарата
и статора датчика в гироскопической системе координат.
Построение фазовой траектории с использованием уравнения (11.23)
представляет значительные трудности. Можно предложить приближен-
ные методы построения фазовых траекторий.
Метод 1. Задаемся моментом времени t, для которого ищем фазовые
координаты статора датчика и аппарата. Фазовые координаты статора
датчика определяются из уравнений, полученных на основе (11.14)
и (11.21):
пр* - = —shdiQt + ГО0 - ch<№>
“О ( J
пр = ^QChGiQt + С00| fy) -I shG>Qt-
{ )
Точки включения и выключения исполнительных органов находим
графически как точки пересечения фазовой кривой статора датчика с ли-
ниями переключения. Моменты времени, которым соответствуют эти
точки, могут быть определены с достаточной точностью. Эта точность бу-
дет тем больше, чем меньше будет интервал между точками построения в
конце рассматриваемого участка движения. Зная t,$d,bd, легко постро-
ить фазовую траекторию, описывающую движение летательного аппара-
та, пользуясь уравнениями (11.14) или построив участки траектории
обычным способом (пользуясь уравнением фазовой траектории 11.20), за-
тем по уравнениям (11.14) нанести точку, соответствующую моменту пе-
реключения исполнительных органов. Эта точка будет начальной для сле-
дующего участка движения.
Метод 2. Задаваясь величиной скорости О (или ОД определим по
формуле (11.22) (если задавалось Од, то по формулам 11.14, 11.22) мо-
мент времени t, в который эта скорость достигается. Зная О, определим
соответствующую ей координату О - она должна удовлетворять уравне-
нию фазовой траектории аппарата (11.20); фазовые координаты статора
датчика определяются уравнениями связи (11.14). Конечная точка рас-
сматриваемого участка определяется графически для фазовой траектории
статора датчика. Ей соответствует точка, иллюстрирующая на фазовой
плоскости движение аппарата, координаты которой можно найти, пользу-
ясь равенствами (11.20), (11.21). Эти координаты должны удовлетворять
уравнению фазовой траектории аппарата.
262
Способ можно свести к аналитическому, решая одновременно уравне-
ния линий переключения, фазовой траектории аппарата, уравнения связи
между координатами статора датчика и координатами аппарата и уравне-
ние, выражающее зависимость времени t и скорости О на фазовой плос-
кости. Имеется пять уравнений, совместное решение которых дает коор-
динаты О, О, Ьд9 соответствующие моменту времени /, в который
происходит переключение исполнительных органов.
Метод 3. Воспользуемся методом вычисления времени движения
между двумя точками заданной фазовой траектории, разработанным
Дипрузом [151]. Для построения фазовой траектории программного
поворота зададимся величиной координаты аппарата , опреде-
лим соответствующую ей координату , пользуясь выражением
= ±^о + )") (Рис- H IS). Зная координаты
начальной точки Мо)- находим время 101 движения изображающей
точки от положения 0 до положения 1 с координатами по фор-
муле /01 =
2|<>1-<>о|
jOj-dol
Рис. 11.15
Фазовые координаты соответствующей точки фазовой траектории ста-
тора датчика (оЭ1, Од1) определяются уравнениями связи (11.14). Затем,
задаваясь величиной фазовой координаты релейной системы О2, анало-
263
гично определяем соответствующие ей величины ^32 и fy)2- Та-
ким образом, можно построить фазовую траекторию летательного аппара-
та, фазовую траекторию статора датчика и выполнить их временную
оцифровку (указать время движения от начальной до любой рассматри-
ваемой точки). Время движения между точками фазовой траектории j
и j +1 с координатами , О j, определяются формулой
tjj+i - 2 (11.24)
^y+1 ~$j
Результат определения времени по формуле (11.24) тем точнее, чем
меньше расстояние между точками j и j +1 на фазовой траектории. На
участках траектории, где переменная О меняется очень быстро, время оп-
ределим приближенно, поделив приращение скорости О на угловое уско-
рение аппарата О в средней точке такого участка (например, в случае, ко-
гда траектория пересекает ось О, на ускорение в точке О = 0).
Точки, соответствующие моментам переключения исполнительных ор-
ганов, определяем либо графически (как точки пересечения фазовой тра-
ектории статора датчика с линиями переключения), либо аналитически,
устанавливая момент равенства суммы + ЬдТд одной из величин
± A, ± mA (в соответствии с физическим смыслом задачи).
На рис. 11.15 приведены построенные с использованием метода 3 фа-
зовые траектории аппарата и статора датчика. Точки Aq, Ар..., фазовой
траектории летательного аппарата и точки а0, ах, ..., а9 - фазовой траек-
тории статора датчика, разделяющие отдельные участки траекторий на
рис. 11.15, соответствуют моментам изменения режима работы исполни-
тельных органов.
11.2.4. Расчет длительности скользящих режимов
Время движения летательного аппарата в скользящем режиме является
важной характеристикой, знание которой необходимо для правильного
выбора параметров системы ориентации. Ниже предлагается простой ин-
женерный метод расчета длительности скользящих режимов [82].
Длительность движения аппарата в скользящем режиме равна
(рис. 11.16)
m
= (И-25)
/=1
где ti,t2,...,tm - время движения изображающей точки фазовой траекто-
рии на участках 0-г1,1-г2, ...,m-l-rm соответственно.
264
Нахождение длительности скользящего режима сводится к определе-
нию времени движения изображающей точки вдоль этих участков. Так
как фазовая траектория движения космического аппарата состоит из уча-
стков движения с включенными исполнительными органами (участки ви-
да i-1+i', рис. 11.16) и участков свободного движения (участки вида
, ч (ОГ i 2(flp0-to]+(o2 Тд-^
i -i),w ti =T+----------------------------= —---—,
ftp .
co
где т - длительность движения аппарата при включенных исполнитель-
ных органах. Обычно Тд »-, поэтому
//=5>М (11.26)
^0
Подставляя полученное выражение в уравнение (11.25), находим
= (11.27)
/=1 и)
где m - число включений исполнительного органа на участке скользяще-
го режима. В качестве примера функция yL = /^—для различных m
представлена на рис. 11.17.
265
co
Рис. 11.17
Обозначим
(11.28)
fon — dm ) к
где т = ——е = vm - ордината точки, соответствующей концу
участка скользящего режима. Тогда
т 1 m-1 1
^=^1/---------~\ = Тд Е ’
/=1(т + е-и к=ок + г
(11.29)
где к = т - i.
Анализ рис. 11.17 и выражения (11.29) показывает следующее:
- при Ьт -> 0 длительность участка скользящего режима что
имеет место при — = т (е = 0), где т - целое число;
СО
- определение длительности скользящих режимов сводится к нахож-
дению суммы числовой последовательности, которую можно рас-
сматривать как частичную сумму бесконечного расходящегося ря-
да. При определении длительности скользящего режима принима-
ется, что 0 < Ьт < со (0 < е < 1).
Рассмотрим случай, когда определяется длительность неполного уча-
стка - случай, когда ордината конечной точки >со. Тогда, как следует
из выражения (11.28), величина е > 1, и выражение (11.27) можно предста-
вить следующим образом:
266
Чк^ТдЪ-т—^—Т = тд S1—!—.где k = l-i ие>1. (11.30)
/=1 (I + е -1) i=o к + е
Сумму числовой последовательности вычислим, пользуясь формулой
Эйлера-Маклорена [155], в которой частичная сумма расходящегося ряда
представлена в виде бесконечного ряда
If W= СJ/M* -1/W+%-hf'(i>)-... +
h- 2 2! 4! (11.31)
+('1Г (" -
Здесь f(x) - функция, которая рассматривается на конечном промежут-
ке (a,b) и может принимать значения /(а), /(а + й), /(&); А=
п
где п - число членов искомой числовой последовательности; В2,...»Вх -
числа Бернулли; С - постоянная Эйлера-Маклорена, для вычисления ко-
торой в выражении (11.31) необходимо выбрать какое-то Ь* > а, для кото-
рого вычисление суммы X f(x) не представляет трудностей. Тогда
а
C = Z/(x)-^J/(x>+14*)-^-A/^*)+^-A3r^)+... (11.32)
о * а
Формула Эйлера-Маклорена справедлива для тех бесконечных рядов,
которые в интервале (а, + «>) удовлетворяют следующим условиям:
- производные f^2k\x) четного порядка в интервале (а, + «>) знакопо-
стоянны;
- производные нечетного порядка при х—>°° стремятся
к нулю.
Числовая последовательность в выражении (11.29) удовлетворяет ука-
занным условиям, поэтому можно записать:
V-L--$ -с*+7—^____________
Д(*+е) ш + 2(/л + е)+2! |> + e)J
С + In би + е) тД г------ .
2(m+e) ^(т+е)2
Здесь
С = С*-1п£; /(х)=т-Ц И С= У у-!-^-1п(/ + е)+——;+--!—(11.34)
(к+£) Л(* + е) 2 (/ + е) п^+е)2’
^2 | 1
4! 6л+е)
267
где I < т (при вычислении Sm и С членами ряда, содержащими f”(k) и
производные более высоких порядков, можно пренебречь ввиду их мало-
сти). Значения коэффициента С для различных величин е при к = 4 при-
ведены в табл. 11.2. Погрешность определения частичных сумм по фор-
мулам (11.33), (11.34) иллюстрируется графиками функций а = а(т) (рис.
11.17) и при значениях А: = 3-5 не превышает 0,2 % (о - относительная
погрешность определения частичной суммы ряда по формуле Эйлера-
Маклорена).
Таблица 11.2
е 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
с 10,4 5,28 3,50 2,56 1,96 1,54 1,22 0,98 0,75 0,57
Рис. 11.18
Рис. 11.19
При определении длительности скользящих режимов удобно поль-
зоваться графиками функций —, построенными в логарифмической
Тд
системе координат. В качестве примера такие графики приведены на
рис. 11.19.
11.3. Колебания ступени вне атмосферы
11.3.1. Построение точечных преобразований
Рассмотрим колебательные движения космического аппарата, исполь-
зуя уравнения (11.3), при отсутствии возмущающего момента (L=0). Если
Ш1 = ©г, то фазовые траектории колебаний представляют собой замкнутые
циклы. Они могут быть смещены вдоль оси у. Это смещение носит слу-
чайный характер.
268
Пусть со2 >coi и со2 -ci>i = Дсо. Ограничимся случаем, когда Асхц. Вы-
берем в качестве отрезка без контакта отрезок прямой включения NN, для
точек которого выполняются условия 0 < К < ; К = у. Построим точеч-
ное преобразование этого отрезка в себя. Преобразование определяется
функцией последования:
а(И) = V + Дш при V < ,
д(У) = V - ©j при V > ©j.
/(И) =
Преобразования, определяемые функциями последования а(К) (соот-
ветствует двухимпульсному циклу) и ц(К) (соответствует одноимпульс-
ному циклу), обозначим через Та и Тц. Графики функций а(К), ц(К)
есть прямые, параллельные биссектрисе квадрантного угла, и поэтому
простые преобразования Та, не имеют неподвижных точек. Непо-
движные точки возможны у сложных n-кратных преобразований, напри-
мер у преобразований вида П^Т’цТд”1 с функцией последования
= an-i [Н(^)] = И 4- (л - 1)Дсо- ©j; п = 2, 3, ... . При этом неподвижной
точкой может являться любая точка отрезка без контакта (координаты не-
подвижных точек носят случайный характер). При выполнении условия
— = п -1 космический аппарат совершает автоколебательное движение;
Асо
в течение периода колебаний имеют место один одноимпульсный и (п-1)
двухимпульсных циклов. Ордината начальной точки первого двухим-
пульсного цикла, следующего за одноимпульсным, всегда удовлетворяет
условию 0 < Ко < Дсп Если при заданных и со2 имеем ci^ / Дсо=п -14- 8,
где 5<1 и л-1 = £(©!/Асо), то каждому рациональному о^/Дсо отвечают
неподвижные точки отображения соответствующих кратностей, иррацио-
нальному - незамкнутые траектории.
Ордината Ко непрерывно меняется в диапазоне 0 < Ко < Дсо; в процессе
регулирования возникают движения, характеризуемые преобразования-
ми 77“ 77“+1=TgT". Можно указать Кг=5Дсо такое, что при
Ко < Vr имеет место преобразование 77“+1, при Ко > Vr - преобразова-
ние 77“ (рис. 11.20).
Анализ движения космического аппарата вне атмосферы при действии
постоянного возмущающего момента будем проводить на фазовой плос-
кости (U, X), где U = 7\р4-у; Аг = у4-£Т. Тогда уравнение фазовой траек-
тории запишется в виде
X 2 - Х$ = 2L(U - Uo) 4- 28(С7 - UQ) - 2bT(X 2 - Х$).
(11.35)
269
Рис. 11.20
Рис. 11.21
Выберем в качестве отрезка без контакта отрезок прямой
t/ = l-co1T; -Т !2-TL<X <Т I2-TL. (11.36)
Получим следующие уравнения для функций последования:
/(Х) - = ^x2~2L(^t ~пРи х >
y(X) = ^[o2-^X2-Ei]2+E2 -(01 при Х<-/Ё-
Ех =2Z(2-co1T); Е2 =2L(2-g)2T).
Преобразования, определяемые функциями Р(|%|), у(|х|), будем обо-
значать через Тр и Ту соответственно. Вид функций последования
Р(|х|), у(|х|) представлен на рис. 11.21, на котором изображена диаграм-
ма Кенигса-Ламерея. Фазовая траектория, соответствующая ломаной ите-
рации 1-2-3-4, показана на рис. 11.22. Приведенная в качестве примера
траектория иллюстрирует сложное точечное преобразование типа
П3 = Т^Т2 с функцией последования f3(X) = у{у[Р(%)]}.
270
11.3.2. Зависимость колебаний от параметров системы
Рассмотрим процесс рождения сложных периодических движений при
изменении параметров и со2. Будем считать при этом, что параметр L
достаточно мал. При достаточно малых значениях максимальное зна-
чение |Р(А")|тах = |Р(0)| не превышает значения , и, следовательно,
функции fn(X) и преобразования Пп не определены, за исключением
преобразования Гр с функцией последования Р(А"). Очевидно, что это
имеет место до тех пор, пока 0(%) > При увеличении в момент А
в точке X = 0 рождается сложное точечное преобразование Пп, тип кото-
рого зависит от величин и со2. Область определения функции fn (X)
ограничена точками, в которых функция принимает значение
Р(Х)<-Т£Г. (11.37)
Решая неравенство (11.37) относительно X, получаем возможный ин-
тервал определения функции fn(X):
-7(7^-®1)2-2Z.CO1T <,X<.7(7£Г-<О1)2-2£(О1Т. (11.38)
С увеличением интервал (11.38) расширяется, а граничное значение
X = ПРИ этом увеличивается. Следовательно, можно указать такое
значение с^, при котором выполняется условие (11.37), соответствующее
случаю, когда функция 0(%) не имеет неподвижной точки. Из условия
(11.37) получаем
a>i> 2(2fi-LT). (11.39)
Дальнейшее исследование будем проводить при фиксированном зна-
чении cOj, удовлетворяющем условию (11.39). Параметр со2 по условиям
2
задачи может изменяться в пределах 0 < со2 - у •
Рассмотрим влияние на характер движения ступени параметра со2,
изменяя его от максимально возможного значения до нуля.
Пусть со2=у“а>>со1 (а “ малая величина). Тогда возможны сложные
движения, соответствующие точечным преобразованиям вида
7/Р =7р”"2Ту7р (т = 2,3,...) с функцией последования = 0{у[0(%)]}. При
уменьшении параметра со2 максимальное значение у=у(-у[Ё^) уменьша-
ется; сокращается число ступенек на участке фазовой траектории, соот-
ветствующей скользящему режиму; точечное преобразование после-
довательно переходит в преобразования л£_2, =Тр”"/"2ТуТр,
271
где I = 1,2,..., т - 2. При I = т - 2 имеет место преобразование П2 = ТуТ$,
которое с дальнейшим уменьшением со2 переходит в преобразования вида
773Y =Ту2Тр,77 Y =Тл"1ТрТу.
Рассмотрим процесс рождения и исчезновения сложных преобразова-
ний вида =ТрТу7р и П2 = ГрГу. Отметим бифуркационные моменты
этих преобразований.
Момент - момент рождения преобразования вида П3 =Т^ТуТ^ - на-
ступает при выполнении равенства (рис. 11.23)
MP{y[P(o)]}]=-V2^. (И.40)
Обозначим значение функции f3(X) в момент рождения преобразо-
вания 0 = Р{у[Р(О)]}- Подставляя в (11.40) значение 0, получаем равенство
p(0) = -7^i\ откуда 0 = Р(-Т£О. Функция ]?(%) соответствует точечному
преобразованию Гр’1, обратному по отношению к Гр;
)2 - ILa^T. Так как функция последования Р(%) не зависит
от со2 > то = const. Отметим, что 0 есть значение функции в момент рож-
дения любого преобразования вида =Грл"2ГуГр независимо от К = п-2
(К = 1, 2, 3, ...). Для любого преобразования П% при со2 = ©2Л можно за-
писать Л?=Р(0)=-7Ё;,где 0 = Рл-з{у[Р(О)]}.
Интервал определения функции последования {X) есть
supt-лР (-V^T),-< х < infi-лР 0]-
Момент - момент рождения неподвижной точки преобразова-
ния . Он определяется уравнением
РМР(Х)]} = х, (11.41)
которое в момент имеет кратные корни. С дальнейшим уменьшением
со2 из кратной неподвижной точки возникают две неподвижные точки ai и
аг (ai > ai). Неподвижные точки могут исчезнуть только при переходе че-
рез границы интервала определения функции ff.
Большая неподвижная точка ai исчезает в момент когда выполня-
ется равенство
P{Y[P(0)]} = 0. (И.42)
272
Момент А2 - момент рождения преобразования П2; наступает при
Р{у[Р(О)]} = -^Г- (11.43)
В этот момент в точке X = 0 рождается преобразование вида П2 = Ту7р
с функцией последования /2(Х) = vIPW]. Интервал определения функции
/2(Х) = ?[р(Аг)] такой же, как интервал определения функции последования
/3PW-
Момент Ff - момент исчезновения меньшей неподвижной точки пре-
образования п1 (преобразования, предшествующего преобразованию
П2)\ он определяется уравнением
₽{?[Р(-#Г)]}=-#Г- (11.44)
Уравнения бифуркационных кривых, соответствующие указанным
выше моментам, имеют одинаковую структуру. Действительно, уравнения
(11.40) - (11.44) можно записать в обобщенном виде
Р^{У[Р(Н]} = Л» (11.45)
где г и R принимают значения 0 и в уравнении (11.40), X и X
в уравнении (11.41) и т. д. Решая уравнение (11.45) относительно парамет-
ра со2, получим обобщенное уравнение бифуркационных кривых
©2 = (М + LT) + ^(AZ + LT)2+W-A/2-4Z , (11.46)
где М =VtP('-)]2 -Е1^ = [со1 + Р^(Л)]. Бифуркационные моменты преобразо-
вания П2 записываются аналогично моментам преобразования nf.
Обозначим значение функции /3Y в момент рождения преобразования
через ф03, т. е. ф03 = у{у[р(О)]}. Учитывая, что в этот момент справедли-
во равенство у[Р(0)] = -7^Г» получим
Фоз = = + 7ш2 +^2 • (11 -47)
Как следует из соотношения (11.47), значение функции в момент рож-
дения преобразования зависит от со2 и меняется с изменением со2.
Функция // определена для значений X, принадлежащих интервалу
SUp[-f2(-^)-4^\^X Если Фол > 0, то с уменьшением
со2 образуется кратная точка преобразования Пп, которая в последующем
разделится на две неподвижные точки а{, а2(б6лыпую и меньшую).
273
Бблыпая неподвижная точка исчезает при выполнении условия
ах =тЯ7л-1(“7^Г)’Ф]» которое эквивалентно условию одновременного вы-
полнения равенств fn (ах) - ах = 0, fn_x (а!) + = 0. Исключая значе-
ние at, получаем или/„(ф) = <р, где <р = у(-1/^’).
Если фол <0, то в преобразовании 77% не существует кратной и боль-
шей неподвижных точек. Меньшая неподвижная точка рождается в мо-
мент В% при выполнении равенства fn (ср) = ср. При дальнейшем уменьше-
нии со2 в момент Вх рождается кратная неподвижная точка простого пре-
образования Ту (рис. 11.23). Уравнение бифуркационной кривой, соответ-
ствующей моменту В19 может быть получено при решении системы
уравнений
у(С)-С = 0,
dy
= 1.
АХ х=с
Решая систему, получаем со2 + асо2 + + d = 0, где а = - 4LT,
b = 4Ex + 4L2T2 - со?, d = 4EJCD! + 4Zco? - co? - 4L2T2co1. Отсюда определяется
со2 - 1 • В дальнейшем кратная неподвижная точка расщепляется на
две (бблыпую и меньшую) неподвижные точки. Бблыпая неподвижная
точка исчезает при выполнении равенства (момент Д1) , от-
куда cof1 =ZT4-^Z2T2+(co1-7^)2-4Z . Координата меньшей неподвижной
точки с уменьшением со2 уменьшается до значения См = . Фазо-
вая траектория замкнутого цикла, соответствующая неподвижной точке с
координатой См, показана на рис. 11.24. Значение со2 =со21, при котором
См =7^2 , является бифуркационным (момент и определяется
уравнением y[V^7“coi] = Если со2 <uQ , то преобразование Ту не-
возможно (рис. 11.24). При со2 <со^ возникают движения, фазовые траек-
тории которых показаны на рис. 11.25. Последовательность анализа ука-
занных движений не отличается от последовательности анализа движе-
ний, рассмотренных выше.
На рис. 11.26 показаны бифуркационные кривые преобразований
77^, 772, Г7%. Кривые обозначены буквами, одноименными с обозначе-
ниями соответствующих бифуркационных моментов; приведены соотно-
шения, позволяющие определить уравнение каждой кривой.
274
Рис. 11.25
Рис. 11.26
Определим последовательность наступления бифуркационных момен-
тов преобразований 77*, (наряду с бифуркационными моментами пре-
образований 77*, 77^ указаны бифуркационные моменты предшествующе-
го и последующего преобразований):
- момента 4(4) - момента рождения преобразования 77^ (т7^)»
- момента F^tF^) - момента исчезновения меньшей неподвижной
точки предшествующего преобразования 77*_1(77Р+1);
275
- момента £„(£„) - момента рождения кратной неподвижной точки
преобразования 77Y(77^);
- момента Д*(д£) - момента исчезновения бблыпей неподвижной
точки преобразования 77j(77^);
- момента - момента рождения последующего преобразо-
вания 77nY+1(77^_1);
- момента Fj(F$) - момента исчезновения меньшей неподвижной
точки преобразования 77Y(77^).
Анализ последовательности наступления бифуркационных моментов
преобразования 77^ проведем с использованием диаграммы Кенигса-Ла-
мерея, построенной для преобразования 77^ (рис. 11.27). Применительно
к этому рисунку уравнения, соответствующие бифуркационным момен-
там, записываются следующим образом:
- для момента 4 ₽{y[P(o)]}=-V^; (11.48)
- для момента 4 рШ-Д>-А; (Ц-49)
- для момента 4 ^-{у[р(АГ)]}|х=с;=1, у[р(Сз )]= с’3; (11.50)
ал
- для момента у[₽(ф)]= ф • (11.51)
Пользуясь приведенными уравнениями и графиком функции P(Y), ко-
торая не зависит от изменяемого параметра со2, можно указать располо-
жение точек функции у(Аг), соответствующих бифуркационным моментам
(функция у(%) зависит от изменяемого параметра со2 и ПРИ уменьшении
его приближается к прямой X = X).
Действительно, уравнение (11.48) может быть записано в виде
у|р(о)]=р(-#Г), из которого следует, что точка А'3 (соответствующая мо-
менту ) определяется как точка пересечения ломаных 0-1-2-3 и 4-5-6-7.
Записывая уравнения (11.49) + (11.51) в виде у|р (-Т^Г)]=Р(“7^7)’
Р(Сз)=?(Сз); Р(ф)=?(ф), где <р=р(-7ЁГ), получим точки Г4',Вз,Дз (соот-
ветствующие моментам Ff, В%, Д3) как точки пересечения ломаных: 8-9-
10-13 и 4-5-6-7; 11-12-10-13 и 14-15; 18-5-16-17 и 4-5-6-7. Из рис. 11.27
следует, что при уменьшении параметра со2 бифуркационные моменты
наступают в такой последовательности:
276
yU)
Рис. 11.27
Рис. 11.28
Диаграмма Кенигса-Ламерея, характеризующая точечные преобразо-
вания 77Y, приведена на рис. 11.28. Для определенности построена диа-
грамма преобразования 77^. Уравнения, соответствующие бифуркацион-
ным моментам этого преобразования, имеют вид:
дЧ - для момента з y|p(O)]=-7£f. (11.52)
- для момента 4 (11.53)
- для момента 5з у№(Сз)]}=Сз; (11.54)
- для момента у{ у[Р(<Рз )1}= Фз
Учитывая, что = ; ; получим у{Иу(-Д')]}=-А . (11.55)
Записывая уравнения (11.52), (11.53) в виде ₽(O) = y[-#d,
Р(-Т£7) = 7[“7^Гь получим точки А3 и F3, принадлежащие кривым функ-
ции последования у(Х), как точки пересечения ломаных 0-1-2-3 и 4-5,
6-7-8-9и4-5.
Построение точки В3 на кривой у(Х) проводить не будем; отметим,
что момент В3 наступает перед моментом Д3. Для построения точки Д3
уравнение (11.55) запишем в виде Р[у(~7^)] = ?(“7^Г) • Точка Д3 находит-
ся как точка пересечения ломаной 6-<р3-10-11-12-13 и прямой 4-5. Выше
отмечалось, что значение ср3 есть значение f3 в момент рождения точеч-
277
ного преобразования 77j. Эта функция изменяется при изменении <о2. Ес-
ли со2 таково, что <р3 >-/£?» то (как следует из рисунка) Хд >XF >ХА,
так как Х9 >%12 >Х1. Если ф3<Л/^~, то ХА <ХД <XF. (На рис. 11.28
точки кривой у(%) для случая ф3 обозначены через ф3,Д3.) Таким
образом, последовательность наступления бифуркационных моментов за-
висит от интервала определения 773 (а значит, и 77^) и может быть
при <рл >7^7 ИЛИ 4, В^Д^Р^ при <р„ <7^. в послед-
нем случае возможно существование при одном и том же значении со2 не-
подвижных точек двух смежных преобразований П^Пп-х •
11.3.3. Устойчивость простых и сложных колебаний
Устойчивость простых неподвижных точек точечного преобразования
Гр следует из того, что для любых значений параметров системы и любых
значений X выполняется следующее условие:
_|<Ф(х)|
(11.56)
Следовательно, неподвижные точки преобразования Гр всегда ус-
тойчивы.
Преобразование Гу может иметь не более двух неподвижных точек.
Рождению неподвижных точек преобразования Ту соответствует бифур-
кационный момент В (рис. 11.23). При значениях параметров со2, соответ-
ствующих точкам, лежащим на бифуркационной кривой В, преобразова-
ние Ту имеет полуустойчивую неподвижную точку с характеристическим
корнем 1у = 1. При уменьшении параметра со2 эта точка расщепляется на
две неподвижные точки. Очевидно, что большая точка всегда неустойчи-
ва, так как ее характеристический корень 1у > 1. Характеристический ко-
рень меньшей неподвижной точки непрерывно уменьшается и, следова-
тельно, точка может стать неустойчивой только при 1у<-1. Характери-
стический корень 1у является монотонной функцией См и, следователь-
но, 1у принимает экстремальное значение на границе интервала
изменения См, Границе интервала изменения координаты См меньшей
неподвижной точки соответствует значение ш2 = со^ 1 • С целью определе-
ния устойчивости меньшей неподвижной точки найдем характеристиче-
ский корень в точке С = См = - coj:
278
[ш2 ”(“У(^2 -Ю1)2 “£1 )](^2 ” Ю1)
^ю2 -Т(7^Г”Ю1)2 j + “^1
ш2 - _£1 = 0 • Поэтому
Из уравнения неподвижной точки у(х) = х находим
= 0, и, следовательно, мень-
х=СЛ
шая неподвижная точка преобразования всегда устойчива.
Для сложных преобразований П^и функции определяются
формулами
v =^- = ^М-П2^[^₽(х)]; 1„ =^ = -® ffjkw]
dx dx i=1 dx dx dx i=idx
Здесь = P/-2{y13WH fl = Yi-i |Р«]. Производные функций последова-
ния Vn зависят от координаты неподвижной точки Х=С и параметра
ш2. Уравнение неподвижной точки уЛв1 [0(C)]= С не может быть разреше-
но относительно С и, следовательно, Хл, Х'л не могут быть выражены че-
рез параметр со2. Но уравнение можно разрешить относительно со2. Это
позволяет исключить параметр со2 и записать как функцию одного па-
раметра =1Л(С). Так, для преобразования П2 получим
LT + Jl2T2 -4£ + 20£Г + (С + (О1)2 0(С)С
(C+toi^Q + coiVp2^)-^!
где 0 = 7(С2 + - ©j )2 - Ех; 0(C) = —со) + ^С2 +2£со1Г. Преобразования
П^иП^ имеют по две неподвижные точки. Рождению этих точек соответст-
вует бифуркационный момент Вп, когда преобразования имеют по-
луустойчивую неподвижную точку С с характеристическим корнем Хл =+1.
Характеристический корень 1Л(С) является монотонной функцией С.
Анализ функции последования показывает, что характеристические
корни 1Л(С), А^(С) принимают экстремальные значения на границах обла-
сти изменения С. При уменьшении параметра ш2 координата неподвижной
точки уменьшается. Интервал изменения ш2 ограничен значением ш2 = 0 и,
следовательно, координата точки С ограничена значением Со, соответст-
вующим значению ш2 =0. Функция у(х)лриш2 =0 перерождается в функ-
279
цию Р(х) и, следовательно, характеристические корни для преобразований
П* и П% могут быть записаны в виде 1 n I _г =14 = П — IX (х)]. Здесь
IX-LO IX-LO
Л = Pi-i [Рл-i fQ )]• Так как сомножители d$/dx при любых значениях х
меньше единицы, что следует из неравенства (11.56), то
|1я|хв =1^п|х=с0 Э10 значит’ 470 ПРИ изменении параметра со2 непод-
вижные точки преобразования Я/, 77^ рождаются и исчезают, не изменяя
своей устойчивости. При этом большая точка всегда неустойчива, а мень-
шая всегда устойчива.
11.3.4. Анализ сложных автоколебаний
Выше показано, что в системах с 1 = 0 при L * 0 возможны сложные
периодические движения, характеризующиеся фазовой траекторией, со-
стоящей из одного одноимпульсного и п-1 двухимпульсных циклов, и ав-
токолебания, характеризующиеся фазовой траекторией, состоящей из од-
ного двухимпульсного и п-1 одноимпульсных циклов. Такие колебания
характеризуются устойчивыми точечными преобразованиями
Л„т = т;~% иnl = Tpn-2rY7p [40].
Рассмотрим вопрос о возможности существования других типов пе-
риодических движений. Совокупность всех возможных периодических
движений определяется множеством неподвижных точек преобразований
вида Пк = Тр 7р2 Ту3 7р4 [35]. Разобьем возможные виды преобразований на
несколько классов:
I - преобразования вида П% = Tfi~2TyT^,
П - преобразования вида 77J = Ту ;
Ш - преобразования, содержащие группы сомножителей II класса
Ф„Р+т =Г;-1Тр7’”-17р;
IV - преобразования, содержащие группы сомножителей II класса
= 7ря-2Г7рГр'и-27’уГр (л # т).
Рассмотрим отдельно вопросы о существовании различных видов пе-
риодических движений для значений параметра (02 е (со2, со22)
и со2 G (ю22, где ю2> ю22 ” бифуркационные значения парамет-
ра со2, соответствующие моментам рождения и исчезновения неподвиж-
ных точек преобразований, осуществляемых двухимпульсными циклами.
280
Значение со2 может быть определенно путем решения уравнений
dy(x)/dx\x=c = 1; у(С)-С = 0, а со22 ~ из равенства у|₽(О)]=-Л/Ё7. Пусть
имеем со22е (со2, со22). Для существования преобразований I класса
= Тр"_2ТуТр необходимо выполнение неравенства
rl₽(-V^’)]>P(-V^’)> (11.57)
где ]5(х) - функция, обратная функции последования Р(х). Неравенство
(11.57) для рассматриваемого диапазона изменений параметра со2 не вы-
полняется. Следовательно, преобразования I класса в рассматриваемом
диапазоне изменений параметра со2 не существуют. В этом диапазоне
значений параметра со2 существуют колебания, характеризуемые преоб-
разованиями П класса, свойства которых рассмотрены в разделах
11.3.14-11.3.3.
Рассмотрим преобразования Ш класса. Пусть |ти-и|>1. На рис. 11.29
изображена диаграмма соответствия бифуркационных моментов для пре-
образований П^. Анализ диаграммы позволяет заключить, что при раз-
личных значениях параметра со2 возможно существование при одном и
том же значении со2 неподвижных точек двух смежных преобразований
Пуп и 77J-J и ни при каких значениях параметров CDj и со2 не могут су-
ществовать одновременно преобразования Ту Тр и ТутТр, если \т - n| > 1.
Примем, что |ти-и| = 1. Рассмотрим преобразование T”TpTj~xTp.
Если при некоторых значениях параметров со2 и coj существуют
одновременно преобразования ТулТр и Г^Гр, то первое из них
определено в интервале (-v,+v), а второе - в интервалах
И (4-v,^), где v = fn^(~4^y, (Рис- 11-30). Для
существования преобразования Ту ТрТр необходимо существование в
интервале таких точек, которые преобразованием Т^Тр
преобразуются в точки интервала (-v,+v). В разделе 11.3.3 показано,
что характеристический корень меньшей неподвижной точки преобра-
зования Т^Гр не превосходит по модулю единицы, поэтому для любых
значений параметров в рассматриваемых диапазонах выполня-
ется неравенство
(11-58)
281
Рис. 11.29
Рис. 11.30
Равенство в (11.58) возможно только на бифуркационной границе. От-
сюда следует, что для любого хе (-^/Ё^,- v) функция fn_x(х)е (-^Ё^,- v).
Это означает, что преобразования Ш класса либо не существуют, либо не
имеют неподвижных точек.
Преобразования IV класса также не могут иметь места, так как не су-
ществуют преобразования I класса. Таким образом, совокупность всех
возможных периодических движений системы со значениями параметра
б^е(ю£, со22) полностью характеризуется преобразованиями вида
27J
2
Пусть теперь й)2е(со2,у). В этом интервале значений со2 возможны
колебания, характеризуемые преобразованиями I класса. На рис. 11.31 по-
казана диаграмма зависимости неподвижных точек преобразований
I класса от значения параметра со2. Анализ диаграммы показывает, что
неподвижные точки преобразований П% существуют не для всех значе-
ний (О2. Это объясняется очередностью наступления бифуркационных
моментов рождения и исчезновения неподвижных точек преобразований
77^. Момент исчезновения неподвижной точки преобразования П% на-
ступает раньше, чем рождается неподвижная точка преобразования л£+1.
Имеют место интервалы значений со2, где одновременно существуют
преобразования 77^и77^+1, но ни одно из них не имеет неподвижной точ-
ки. Для функций последования этих преобразований справедливо
/,Р(х)>х; fn+x(x)<x. Функция определена для значе-
ний X G [—^Ё|",—V j j а функция /лр+1(х) для хе ЬрРС-Т^Г)]- Здесь
282
vi = a Z>+i(x)> P(x) _ Функции, обратные функциям последо-
вания 4+1(х)> ₽(х)-
j Г* 5
4
0,1 0,2 0,3 0,4 0,5 0,6 ф2
Рис. 11.31
Диаграмма Кенигса-Ламерея для одного из значений параметра
2
со2 £ (ю22»у) имеет вид, изображенный на рис. 11.32. Анализ диаграммы по-
казывает, что преобразования могут переходить в 77^+1, поэтому возмож-
но существование преобразований Рт = П%+1 (т = 2,3,... п = 2,3,...)
с функциями последования Фт = Граница разрыва Vj функций
последования Фт(х) и зависит от значения со2; с увеличением со2
значение Vj уменьшается, расширяется область определения функции
fn+i(x) и преобразование Рт переходит в преобразование Рт+1.
Основные свойства преобразований Р$ рассмотрим на при-
мере преобразований с функциями последования
фт =f?(f2 Г-1 =р{г1₽ШхЯГ 1 ]}, которые возможны для значений
параметра со22е (ю23’ ю24)> где ю2з соответствует бифуркационному
моменту исчезновения кратной неподвижной точки преобразования
772. Оно может быть определено при решении системы уравнений
/2(С) = С; #2(х)/^|х=с=1, а со24 (соответствует бифуркационному
моменту рождения неподвижной точки преобразования П%) - из ра-
венства =
На рис. 11.33 иллюстрируются графики функций последования Ф(х)
ддя значения параметра со2е (со23,со24). Функции последования, для кото-
рых справедливо неравенство Фт(0) >, определены при
283
хе {мр[- д/яГ.-Фи,-!(-7^7) ]}• Если Фт(0) > -Jex,
то преобразования оп-
ределены при
и
хе М- (~4ЁХ) ]- Фт (-7ЁГ)}
хе К(-Х)’Фт-1(-Х)}
Для преобразований, область определения которых принадлежит от-
резку могут существовать неподвижные точки.
Рассмотрим устойчивость неподвижных точек преобразований Р$.
Как следует из 11.3.3, характеристический корень = \d(Pm(x)/dx\x=c за-
висит от произведения величин
df2(x)
Х2 —
df3(x)
dx
. Можно по-
и
казать, что если х = 0, то Aq =0; если х = ]Ь(-^Ё\), то А2 = °°- Поэтому Aq
может принимать любые значения от 0 до <». Неподвижные точки преоб-
разования Р% в зависимости от соотношений параметров (Ор со2 могут
быть как устойчивыми, если Хт <1, так и неустойчивыми. На рис. 11.33
показаны графики функций последования ф£(х), иллюстрирующие изме-
нения величины
d<Dj
dx
с изменением параметра со2.
-
Анализ очередности наступления бифуркационных моментов показы-
вает, что для одного значения со2 возможно существование неподвижных
точек нескольких преобразований Р^; поэтому если имеется хотя бы у
одного преобразования устойчивая неподвижная точка, то после оконча-
ния переходного процесса установятся автоколебательные движения, со-
284
ответствующие этой неподвижной точке. Если неподвижные точки всех
преобразований неустойчивы, то будут иметь место колебания слож-
ной формы, соответствующие преобразованиям, содержащим группы со-
множителей типа Р$. Анализ показывает, что неподвижные точки таких
преобразований либо не существуют, либо являются неустойчивыми.
11.3.5. Оценка расхода энергии
Сравним количество энергии, затрачиваемой исполнительными орга-
нами релейной системы при со1=со2 и (&i [42]. Рассмотрим движе-
ние при отсутствии возмущений (L = 0). Экономичность релейных систем
можно характеризовать числом включений исполнительных органов за
определенное время, поэтому представляет интерес задача, состоящая:
- в определении длительности (^) последовательности
m-l(m = n + l или т = п) двухимпульсных циклов и одного одноим-
пульсного, предшествующего двухимпульсным, при заданной величине
Ат-С град / с;
- в сравнении числа включений исполнительных органов при
Дсо=С град 1с за время с числом включений исполнительных органов
за это же время при установлении симметричных колебаний, которые
возможны, если Дсо=О. Длительность последовательности т-1 двухим-
пульсных циклов и одного одноимпульсного, предшествующего двухим-
пульсным, определяется выражением
ю-1 2Д-СО1Т 2Д-со27\ САГ
1 ° ж £ (Oj-Ko-G-l^co Ко+/Дсо' Ko
где Ко < Дсо - ордината начальной точки первого двухимпульсного цикла,
следующего за одноимпульсным. Представим ординату начальной точки
первого двухимпульсного цикла (0 < К < Дсо) в виде Ко = е • Дсо,
где 0 < е < 1 и будем считать, что с^ = Дсо- (п-1 + 6), где 0 < 6 < 1; тогда
----1----(И.59)
е Дсо z=i л-1 + (е-5) Дсо /=1 / + е
Рассмотрим отношение q= —, определяющее количество симметрич-
(с
ных колебательных циклов, общая длительность которых (tc - длитель-
ность одного симметричного двухимпульсного цикла).
Длительность симметричного двухимпульсного цикла, возникновение
которого возможно только при Дсо=0 (coj = со2 = со; Ко = со/2), равна
Д^д-с^т] (1160)
Ш1
285
Рассмотрим отношение
1
+-f'(11.61)
tc 4 f=i П-1+ (£-$) i-\ l+£ tc £ Z=1 / + Е
Зависимость q = /(e), рассчитанная для ряда значений п и 8, приведе-
на на рис. 11.29. Анализ выражений (11.58), (11.59) и зависимостей
q = /(£) позволяет заключить следующее:
- при со] = (п -1 + 8) • Дш и 8*0 можно указать ггр = 8 такое, что —> °°;
- существуют значения q <ггр и е2 >егр, при которых а следова-
тельно, и q будут наименьшими; значения q и е2 являются функциями
ординаты начальной точки первого двухимпульсного цикла Ко;
- если 8 = 0, то со] =(и-1)Дсо; ггр =0 и существует такое е3, при кото-
ром /р а следовательно, и q будут наименьшими;
- величины /£, q существенно зависят от ординаты начальной точки
первого двухимпульсного цикла, которая носит случайный характер;
- обычно tc > Т, поэтому в выражении (11.61) вторым слагаемым мож-
но пренебречь; это дает расчет в запас.
Экономичность релейных систем необходимо оценивать, принимая
длительность последовательности циклов равной ее наименьшему
значению (наихудший расчетный случай).
При 8*0 появление последовательностей циклов с начальными орди-
натами К01 =Е]Дш и К02 =е2Дш равновероятно, поэтому при оценке эконо-
мичности из двух величин q =/(£]) и ?=/(е2) необходимо выбирать
наименьшую {# = inf[q = f(t-i),q = f(е2 )]}. Величину Timin - наименьше-
го отношения расхода энергии в случае, когда релейная система соверша-
ет симметричные колебания (Дсо=О), к расходу энергии, когда движение
характеризуется несимметричными колебательными циклами (Дсо#0),
определим по формуле T|min =——-----, где 2(т -1) +1 - число включений
2(т -1) +1
исполнительных органов за время t™n, если Дсо*0; 2q' - число включе-
ний исполнительных органов за время при Дсо=0.
Зависимость Т|т/л = /(—) при 8 = 0 приведена на рис. 11.34. Она ха-
©1
растеризует экономичность системы с Дсо*0 по сравнению с системой,
для которой Дсо=О. Экономичность системы с Дш*0 иллюстрируется
также функцией Q, показанной на рис. 11.26. Здесь Q =—, где Q, Qc -
286
расход энергии за время т при со1^а)2 и со1=®2=со соответственно.
При определении Qc предполагалось, что co=inf(cDi, со2) и автоколебания
системы симметричны. Расчеты проведены для значений параметров
Д = 1; cdj =1,67; со2 =2,0; Т = 0,3; т = 810. Время т = 810 соответствует зна-
чению /«5400 с (время одного оборота спутника вокруг Земли) При вы-
бранных значениях ©j, со2 в течение т = 810 происходит «100 + 150
включений исполнительных органов; наблюдается 20 + 30 серий циклов
длительности =^(И0).
Кривые: 1-п=5,2-п=10
3-п=15,4-п=20
Рис. 11.34
Рис. 11.35
Приведенные материалы позволяют заключить, что если L = 0, то сис-
темы, у которых разность управляющих импульсов исполнительных орга-
нов Дсо составляет 5+10% от со, в 1,5+2,0 раза экономичнее систем,
у которых Дсо = 0.
Рассмотрим движение ступени при действии постоянного возмущаю-
щего момента (L #= 0). Интегрируя уравнения движения от t = 0 до t = Та,
получим формулу для определения периода автоколебаний:
Т;=7[Ю1+(«-1)А< (11-62)
где п - кратность цикла.
Если расход энергии за одно включение исполнительного органа обо-
значить ду (у =1,2-номер двигателя) и принять qx =rco1, q2 =г(02’ гДе г “
287
коэффициент пропорциональности, то расход энергии за время t (t»Ta)
определится формулой
Та
'* [исо1 + (и-1)СО2] tL
Учитывая соотношение (11.62), получим 0 = —11.
а»! + (п — 1)Дсо
Если (Dj = а>2, имеем Q = Qc = г • (2и0 -1) • t • L, п0- число импульсов в зам-
кнутом цикле. Тогда относительный расход энергии равен
д = 0_ = ^+(71-1)0)2
Qc [С01 + (w - 1)Асо](2п0 -1)
На рис. 11.37 показана зависимость относительного расхода от пара-
метра ш2 (cDj = const).
Рис. 11.36
Рис. 11.37
Функция 0(ш2) рассчитана для значения = 2; L = const > 0. Анализ
кривой, изображенной на рис. 11.37, позволяет заключить, что соответст-
вующим выбором параметра со2 с учетом возмущающего воздействия
можно снизить энергетические затраты на стабилизацию космического
летательного аппарата. Этот вывод является теоретической основой для
создания конструкции экономичной релейной системы ориентации и ста-
билизации КА. Система отличается тем, что ее исполнительные органы
создают при единичных включениях неравные по величине управляющие
импульсы, реализуя оптимальное значение Дсо=со2-cty #0, и признана
изобретением [115].
11.3.6. Выбор параметров экономичного регулятора
В [42] показано, что двухимпульсные автоколебания в системе
с Л = 0 и 1^0 являются экономически выгодными. В связи с этим целесо-
образна оценка возможности выбора параметров регулятора такими, что-
288
бы в процессе работы системы устанавливались именно эти автоколеба-
ния. Рассмотрим возможность разработки методов расчета областей су-
ществования двухимпульсных автоколебаний на плоскости параметров
системы со2, L. Границами областей существования несимметричных
двухимпульсных автоколебаний на плоскости являются бифуркационные
кривые, соответствующие моментам появления и исчезновения непод-
вижных точек простых точечных преобразований. Справа области суще-
ствования двухимпульсных колебаний ограничены значениями
£ = у(1-л/1-О,5Тсо1)2 и x = kld)l/2y[x-l.
Найдем расчетные формулы для построения границ областей существо-
вания двухимпульсных колебаний. Если 1 = 0, то двухимпульсные колеба-
ния характеризуются точечным преобразованием с функцией последования
YW = ^[ю2 “Vх2 ~^1]2 +^2 Как показывают расчеты, бифуркационные
значения параметра со2 ДДЯ моментов исчезновения большей и меньшей
неподвижных точек можно считать равными, поэтому для построения гра-
ницы области существования двухимпульсного цикла вполне допустимо
использовать формулу бифуркационного значения параметра, соответст-
вующего моменту исчезновения большей неподвижной точки
4 = LT + 7^2Г2+(®1-л/^)2-4А. (11.63)
Бифуркационный момент исчезновения меньшей устойчивой непод-
вижной точки наступает при меньших значениях со2, т. е. вычисления по
формуле (11.63) дают более узкую область существования двухимпульс-
ных циклов, чем она есть в действительности. Граница, соответствующая
бифуркационному моменту появления кратной неподвижной точки, мо-
жет быть определена путем решения системы уравнений:
Y(x*) = x* •
Приближенное значение координаты кратной неподвижной точки мож-
но определить по формуле хк = ^(Ст + 4^1)* где Ст =^2L(2-ay\T)-a\.
Тогда, используя второе уравнение системы, получим уравнение верхней
границы области существования в виде
со" = N + ^N2 + (С„ + (Dj - С2 + - 4Z, (11.64)
где N = ^C2 -Ei+LT.
289
На рис. 11.38 иллюстрируются области существования двухимпульс-
ных автоколебаний, построенные для различных значений со2 и т с ис-
пользованием предлагаемых формул. Области существования двухим-
пульсных циклов позволяют произвести выбор параметров со1,со2,Т из
условия обеспечения двухимпульсных автоколебаний, а также указать до-
пустимые отклонения этих параметров от их номинальных значений. Об-
ласти имеют достаточные размеры (допустимо отклонение параметров от
номинального значения на ±10%), что свидетельствует о возможности
практической реализации системы, в которых устанавливаются несиммет-
ричные двухимпульсные колебания.
Рассмотрим влияние начальных условий на характер установления
двухимпульсных автоколебаний. Рис. 11.39 иллюстрирует диаграмму Ке-
нигса-Ламерея, на которой показано, что независимо от координат на-
чальной изображающей точки после окончания переходного процесса
всегда устанавливаются двухимпульсные автоколебания, соответствую-
щие устойчивой неподвижной точке М. При этом, если координата на-
чальной изображающей точки Хо удовлетворяет условию Хо<Хб, то пере-
ходной процесс характеризуется фазовой траекторией, состоящей из по-
следовательности двухимпульсных циклов (ломаная итерации изображена
на рис. 11.39 пунктирной линией). Если Хо>Хб, то фазовая траектория пе-
реходного процесса содержит одноимпульсный цикл (ломаная итерации
изображена штрих-пунктирной линией).
Зависимость относительного расхода энергии Q, затрачиваемой сис-
темой при двухимпульсных автоколебаниях, от параметра со2 при разных
значениях возмущающего момента показана на рис. 11.40; Q - отношение
расхода энергии при установлении несимметричных колебаний к расходу
290
энергии, затрачиваемому на обеспечение симметричных автоколебаний
при со1=со2- Расчеты проведены для значений со2,Д соответствующих
области А на рис. 11.38. Анализ графиков показывает, что для всех значе-
ний параметров, соответствующих точкам области А, относительный рас-
ход энергии Q <1.
Рис. 11.40
11.4. Колебания ступени в атмосфере
11.4.1. Построение точечных преобразований
Фазовая траектория космического аппарата есть кусочно-
непрерывная функция, состоящая из элементов кривых второго поряд-
ка, уравнения которых -\ff2L0 =2§^ь -^£o)+^l ~Vlo\ J = U и
vi - vio = - vio )• точки сопряжения кривых располагаются на
линиях включения MM,NN и выключения (рис. 11.41).
Эти точки можно рассматривать как начальные и конечные точки от-
дельных участков траектории. Участки траектории, описываемые
уравнением -v£o = 28;(vz “Vlo)+^(vz “Viol есть элементы ги-
пербол, начинающиеся на прямых включения MM,NN и заканчи-
вающиеся на прямых выключения M'M'tN'N'. Участки траекторий,
описываемые уравнением = ^(vl _Vzo)> также есть элементы
гипербол. Гиперболы начинаются на прямых и заканчива-
ются в точках прямых MM,NN. Гиперболы, начинающиеся в точках,
координаты которых удовлетворяют условиям Vlm' < yL7, Vzjv' > Vl3»
симметричны относительно оси ординат. Конечные точки
291
удовлетворяют условиям Уш <У£4»Уш >У£8- Участки траек-
торий, начинающиеся в точках, удовлетворяющих условиям
Vli<Vln'<Vl39 Yl3 <Yln'<Ylu Wli<Wlm'<Wls> Yl5<Ylm'<Yl7, пред-
ставляют собой элементы ветвей гипербол, симметричных относитель-
но оси абсцисс. Траектории заканчиваются в точках отрезков линий
включения ММ, NN, для которых yL4 < у^ < yL10, yL9 < уш < yL8.
Траектории, начинающиеся в точках, имеющих у£1 < у£лГ < у£2 или
У£5 - Уш' — У£6» располагаются только в верхней или нижней коор-
динатным полуплоскостям соответственно.
Возможные колебательные движения космической ступени полностью
определяются фазовыми траекториями, состоящими из указанных выше
последовательно расположенных участков гипербол. Укажем абсциссы
характерных точек 1-10 фазовой плоскости у£,у£ :
Д1£ л Д1£ (Xi
= У£2=Д1£; ^£з=^; У£4 = ~;
До£ а ~’^2£ ~ (Хэ
У£5=-^; У£6=-Д2£; У£7=-тЛ-; У£8 = -„;
л । Л 2 Л 2
I 7 . х2 I 7 1 \2
0^2 Is-f л2 I 1 I I I j а2 I 1 1 |
V'i9=~ + }CL+A22Lll-~ ; У<Л1о=^-АМЛ+Дн 1-- .
Л у I Л. I Л. \ I Л. I
Здесь а,=1 + у; /С = 1-Л7’2; Кх=1 + Т-Д.; К2=1-т4Л.;
Л
С целью построения точечного преобразования выберем в качестве от-
резков без контакта отрезки прямых включения:
-i+y<v<£ <i+y; (11.65)
Л Л Л
TVi+Fi’-i+y; • (11.66)
Л Л Л
Построим точечное преобразование отрезков (11.65), (11.66) в себя.
Простейшие фазовые траектории, определяющие это точечное преобразо-
вание, изображены на рис. 11.41, 11.42. Показаны фазовая траектория, не
пересекающая ось ординат (траектория одноимпульсного цикла), и траек-
тория, пересекающая ось ординат (траектория двухимпульсного цикла).
Прямые FF',KK', уравнения которых y£=±y£Vl, есть асимптоты
292
гипербол фазовых траекторий. Эти прямые позволяют указать
на фазовой плоскости наибольшие изменения угловой скорости
2(Z + X) 2(X-Z)
= ^2Г ~Vx(i при которь1Х еще °беспечивается
одноимпульсный цикл. Если й)1Г<й)1; й)2Г<й)2, то возможен двухим-
пульсный цикл; если же хотя бы одно из указанных неравенств не выпол-
няется, то устанавливается одноимпульсный цикл; со1Г,со2Г являются би-
фуркационными значениями параметров ©.(/ = 1,2). Точечные преобразо-
\2
вания определяются следующими функциями последования:
Преобразование отрезка (11.65) в себя.
Если со, <®1Г,то £l(Wl)=^-Jal + Vz “
X i
Если cty > со1Г; со2 > ю2г; w2 > ^, то
Ei(vi) =
£z(Vz)=-y—iMz+fvz-^] при
A I I A J А2
T|z(Vz) = Y_llCi+ -(a2~^2l)
(11.67)
Преобразование отрезка (11.66) в себя.
Если ©2 <со2Г,то е* (Vi)=Z^2.+Jc£+|v£+-^
Если со2 > со2Г; > со1Г; > со2, то
/•;(vz)=
A2Z Y (а1 ~Alz)
К I К
(11.68)
— &2L
при Wl<-^-
К2
Преобразования, определяемые функциями последования
будем обозначать через и T^L соответственно.
293
Рис. 11.41
11.4.2. Зависимость колебаний от параметров системы
Множество возможных движений определяется преобразованиями:
Пк = ^1Т^2^37^4,где /C = 71+z2+z3+z4, (11.69)
являющимися всевозможными последовательностями преобразований
и Для нахождения всех кратных циклов точечного преобразо-
вания Пк необходимо исследовать все множество преобразований
(11.69). Рассмотрим сначала 7-кратные преобразования вида
Т
nl=T^T^i l = n + m (анализ проведем, считая £<—Хсо). Множество воз-
2
можных периодических движении рассмотрим, изменяя со2 от со2 = у - а
(а - малая величина) до со2 = 0, считая CDj = const > сог. При уменьшении
294
со2 изменяется вид части фазовой траектории, расположенной справа от
« Д] ♦)
прямой v = Vi = —L , и уменьшается число ступенек скользящего режи-
ма. Происходит переход от преобразований nf =Т^~2Т^Тг к преобразо-
ваниям =7g“3rT|7’e, П^_2 =Т^~4ТГуТг с функциями последования
//e(v)=e/-2{n[e(v)I}, //-i(v)=e/_3{n[e(v)]},...; /2e(v)='n[e(v)]- Подробно
последовательность перехода от одного преобразования к другому рас-
смотрим на примере преобразования П2. В табл. 11.2 указаны наименова-
ния бифуркационных моментов и уравнений функций последования
(в символической форме) для преобразования П2.
Диаграмма Кенигса-Ламерея для момента рождения преобразова-
ния П2 иллюстрируется рис. 11.43.
Рис. 11.43
Анализ диаграммы позволяет установить диапазон определения функ-
ции f2. Одной из границ диапазона является значение у = = —. Для
^2
♦ т
Здесь и далее для случаев L < —Х©! индекс L в формулах опущен, так как соот-
Т
ношения, соответствующие значениям L = 0 и L < — XcOj > записываются идентично.
295
нахождения второй границы запишем равенство, соответствующее мо-
менту рождения преобразования П2,
f Г (А1
ЕЛ £ —
I L
и обозначим значение функции
| = А1_
Ш *2
f2 в момент рождения через
(11.70)
к2 =п е
— . Тогда е(К2)=-^- или
К К2
11.43 ломаной
v2 =q
1-2-3 показано преобразование
и отмечена левая граница у = V2
диапазона определения функции. Функция f2 определена для значений
уе (У2> Уз)- Укажем бифуркационные моменты преобразования П2.
Момент Л2 - момент рождения преобразования П2. Процесс рождения
преобразования П2 заключается в следующем. При уменьшении со2
функция последования /Зе (\|/) увеличивается. При некотором значении со2
наибольшее значение функции последования /3е(\|/)| д “Липах
у=—L
К
границе разрыва преобразования
становится равным \|/3
=”!=^
(д.
£W £ —1
К
Момент В2 “ момент исчезновения неподвижной точки преобразования
; наступает при выполнении соотношения
ХЫ
. L }
AjL
^2
е
(11.71)
Момент - момент появления неподвижной точки преобразования.
Т df I
Отметим, что при всегда |хре(И2,х|/з)<ПОЭТОМУ преобразо-
вание П2 может иметь только одну неподвижную точку. Единственная
неподвижная точка преобразования П2 рождается, когда \|/ = V2 и спра-
ведливо равенство которое, учитывая, что \|/3 = е(К2), можно
записать в виде
(11.72)
296
Момент £? - момент изменения вида гиперболы преобразования Г .
t
2 .
В момент Е2 вторая производная —у в точках гиперболы преобразова-
dy1
ния Т£ меняет знак на обратный. Для момента Е2 справедливо соотношение
n[£(^i)]=^i; = (11.73)
Момент F? - момент появления вида гиперболы преобразования Г£
в области V < 0; наступает при выполнении равенства
V2 =д1- (11-74)
Момент К, - момент рождения преобразования 77? = Т2:Т ; соответст-
Т| с
вует значению со2, ПРИ котором /2
тах достигает значения у3.
При всех со2 > со22 имеет место /2(у)< у3.
В качестве примера определим момент рождения преобразования П3.
На диаграмме точечного преобразования цифрами Т-П-Ш-IV отмечена
(рис. 11.43) ломаная преобразования П2 = Т Т , цифрами 1-2-3-4-5-6 ло-
маная преобразования = Т^Т£. В момент У2 справедливо равенство
(11.75)
Момент ~ момент исчезновения неподвижной точки преобразова-
ния П2. Этому моменту соответствует соотношение
М£(ч'з)]=Ч'з- (11.76)
Уравнения бифуркационных кривых, соответствующие указан-
ным выше моментам, могут быть записаны на основе
(11.70) - (11.76), которые имеют одинаковую структуру.
тельно, если уравнения (11.70) и (11.71) записать
-Г Ai 1
= £ , то равенство
равенств
Действи-
в виде
(д,
77 Е —
К
а.
1^2
Tj[e(r)]=7?
(11.77)
будет обобщенной формой записи соотношений (11.70)-( 11.76). В равен-
п д| (Д11
R принимают значения — и —- для
/Г К2 J
стве (11.77) величины г и
А1
= е
А .
*2 Г
К
297
л ' д \
уравнения (11.70); —!- и £ —- для уравнения (11.71); V2 и V2 для урав-
К2 {К2 J
нения (11.72) и т. д.
Для получения обобщенного уравнения бифуркационных
кривых й)2=й)2(Л) решим уравнение (11.77) относительно со2:
со2 =“(а2 -Ф±д/ф2 + д), где
Д = («1 RK'f + (j _ _Иа2 _ ф2к к =
7Г I К I
При значении со2 < со^2 преобразование П2 не определено, но сущест-
вует преобразование 77^, момент возникновения которого был отмечен
выше как момент У2.
Укажем границы определения преобразования 77^. Так как преоб-
разование 77^ определяется соотношением то левая
граница диапазона определения 77^ есть координата точки пересече-
ния оси абсцисс ломаной a-b-c-d-e, соответствующей равенству
Vr3=4nf—1|-
Правая граница есть inf у/>3, —- I, где у^3 =^+р^_у'гз1=2^1-у'гз.
^2 ) К \К ) к
Для сохранения однообразия в обозначениях и следуя работе [33], назо-
вем момент возникновения преобразования 77^ моментом А3; момент
исчезновения неподвижной точки преобразования 772 - моментом В3.
Момент Y3 совпадает с моментом А3, момент Н2 - с моментом В3\
бифуркационные значения также совпадают:
= й)2 • Укажем остальные бифуркационные моменты
соответствующие
Га Н2
^2 = ^2 ’ ^2 2
преобразования П^.
298
Таблица 11.3
Обоз- на- чение Наименование бифуркационного момента Равенство, соответствующее бифуркационному моменту
^2 Рождение преобразования П2 £< 1 Г (М 7 £ — 11К ) 1=А J Кг
в2 Исчезновение неподвижной точки предыдущего преобразования £Т 1 £ ( А А Д1 <*2, ll=*L Jj Кг
с2 Рождение неподвижной точки преобразования П2 £ И .Kt). = А. Кг
г2 Изменения вида гиперболы преобразования TE £ Ч) Л11 = ^L Ki
ъ Появление гиперболы преобразования Т£ в области ф < 0 t][e(Ai)]=А,
G2 Рождение преобразования п3=т*те И 7=3. <1^ со 1 J = А К2
Я2 Исчезновение неподвижной точки предыдущего преобразования П2 И £ 42 J. _ Д1 Кг
Момент С3 - момент возникновения неподвижной точки преобразова-
ния . Бифуркационное значение со2 = ю23 может быть определено из
соотношения (рис. 11.43).
п{п[е(И3)]}=И3.
(11.78)
д
Здесь V3 = 7J — . Подставив в равенство (11.78) значение И3, получим
1*2 J
Г (Д1 )Т
Т] £1]
. L L
Д1
= Л —L илиП^Е 71 —L
к2 к2
Д1
Д1
К2
Бифуркационные моменты Е3 и F3 в преобразовании могут от-
сутствовать. Условием существования бифуркационного момента Е3 есть
соотношение
299
I Ai L
и ~
(Л2 J
(11.79)
(11.80)
условием существования момента F3 - соотношение
fAi Ъ
И ^2-
\К2 J
Оба условия следует определять при ш2 = (о^з .
Момент К - момент рождения преобразования = Т.1Т . Он насту-
Л Е
А1
( Д1_
пает при выполнении равенства Пр ч
L \ л. н л. 2
Момент 77? - момент исчезновения неподвижной точки преобразова-
Д.Г
к~ 1
ния . Он наступает при выполнении равенства Т]< 7] £
= Д1
к2
Дальнейшее уменьшение параметра о>2 вызовет последовательное появ-
ление преобразований 77^,77^,..., 77^. Характер наступления бифурка-
ционных моментов преобразований 77^, 77^,..., 77^ аналогичен характеру
наступления соответствующих моментов в преобразовании 77^. Анализ
соотношений (11.67) и диаграммы Кенигса-Ламерея (рис. 11.43) показы-
, (Д1 _
вает, что с уменьшением о>2 функция 7]\ — приближается к биссектрисе
квадрантного угла, и поэтому всегда, пользуясь условиями (11.79),
(11.80), можно указать преобразования 77^,77^ такие, после которых би-
фуркационные моменты , Е/+1 отсутствуют.
Значение со2 - , ПРИ котором выполняется условие
(А1
7? —L
*2
=А.
к2'
(11.81)
является бифуркационным значением появления неподвижной точки про-
стого преобразования Т^. Бифуркационное значение со^, соответствую-
щее моменту рождения неподвижной точки, определяется уравнением
300
1
z 1 1,1)
co, =— a, 1--+
T 2 K,
a2 1 л
к* к 1
>©!
T
(где Ф1 = ХТ2а2 +^2а2 ~(а1 -^Дг)2), полученным из равенства (11.81).
Бифуркационное значение cof7, соответствующее моменту
исчезновения неподвижной точки, определяется равенством
W2/Z =Г^1(«2+^2Ф2)<би1 (гДе ф2 =~+J3+(ir~тЙ >’ п^У4611'
17/ к V I Ki л ।
I a1 I al
ным из условия rd — = —.
Координата неподвижной точки преобразования 7^ определяется ра-
венством
. 2Д|Ф2^' + СО1Л] “ ^2Д |<о2Г + У — S^co2 ~ (о2)
V 27К(4-<О?) ’
где =К2(в + с)+Д2-а?+<о^Г2; S = 4Т2а^(к2В + Д2)-Л2.
Здесь и выше указаны корни, удовлетворяющие физическому смыслу
*
задачи V е
Д1 «1 _ * СО]
}Если ®‘ =“2" £=0,т° '•'«‘'Т7'-
При 6О2 < СО^ несимметричный замкнутый двухимпульсный цикл пе-
а1
реходит в m -импульсный замкнутый цикл, состоящий из m - 1 двухим-
пульсных и одного одноимпульсного замкнутого циклов. Одноимпульс-
ный цикл начинается и заканчивается на прямой ММ. Анализ возможных
движений при б02 < ^2 будем проводить с использованием функций по-
следования (11.68), соответствующих отрезку без контакта (11.66). Диа-
грамма Кенигса-Ламерея для 6О2 < показана на рис. 11.44. С умень-
шением со2 увеличивается по модулю абсцисса границы разрыва функции
последования и происходит перемещение кривых £*(у) и T|*(v) парал-
лельно оси абсцисс. Имеет место последовательный переход от
m -импульсного цикла к циклам m -1, m - 2, m - 3,..., m -1 = 1. Процесс ро-
ждения и исчезновения указанных циклов рассмотрим на примере трех-
импульсного цикла, который соответствует точечному преобразованию
#2=7^ с функцией последования р\ (у) = 7?* I?* О/7)]- В преобразова-
нии 772 могут иметь место следующие бифуркационные моменты изме-
нения его качественной структуры.
301
-v
Рис. 11.44
Момент А 2 - момент рождения неподвижной точки преобразования
♦ ♦
р2. Момент Д2 наступает при выполнении равенства
-Дг.
К2
т] е
_ Д2
К2
(11.82)
Подставив в функции е*(у), Т]*(у) значение ЦТ =——2-, получим
К2
_ oqTs/X -0-2
К2
£1 + ^2
к2 к
К
П
к I
( А х , :_____ (ц.83)
+ +(д1 _а1^г)2 =Va-
Анализ выражений (11.83) показывает, что с уменьшением со2 значе-
ние увеличивается, а е
Используя соотношение (11.83) для случая £ = 0, упростим уравнение
До Ло -г- 1
=----решая которое, можно получить со 2 . Графиче-
К2
ское решение показано на рис. 11.45. При получении его принималось во
внимание, что границей справа функции F2* является прямая ВВ', каждой
(11.83) 7)
-1
Кг
•* Д2
Л
.( Д2
Т?-----
Ч К2)
остаются постоянными.
302
точке этой прямой соответствует значение F2*, равное----и что
для абсциссы точки В справедливо соотношение
Заметим, что при со2 = ю22 наРяДУ с неподвижной точкой преобразо-
вания 772 существует неподвижная точка преобразования = 71? Т*.
т| t
Как правило, устанавливается пятиимпульсный цикл, соответствующий
преобразованию (ломаная 0-1-2-3-4-5-6 диаграммы точечных преобра-
зований на рис. 11.45). Трехимпульсный цикл преобразования 772 уста-
навливается только в случае Vo = Жя •
Рис. 11.45
Момент - момент исчезновения неподвижной точки преобразова-
_ ^2
ния 7?з; наступает при выполнении равенства т|* е* Т|
А2
. К2.
которое, учитывая соотношение (11.83), можно упростить
т|* |е* (- Va )]= . При со2 < со2 2 существует только преобразование 772.
К2
Момент С? - момент изменения вида гиперболы преобразования Г*.
Гипербола преобразования Г* вся расположена в области отрицательных
значений \j/(\j/<0). Уравнение бифуркационной кривой, соответствующее
моменту С*, может быть получено из равенства Т|* |е* (- Д 2 )]= -Д2.
зоз
при значении со2, удовлетворяющем равенству т]
Момент 2 - момент изменения знака второй производной —— в точ-
ках гиперболы преобразования на обратный. Момент е2 наступает при
выполнении равенства 7J* |е* )]= .
Момент F* - момент рождения неподвижной точки преобразования
773е =Т*2Т^ ; наступает при выполнении равенства .
Аналогично тому, как в момент j2 рождения неподвижной точки преоб-
разования 772 существовало преобразование 773, так и в момент F* рож-
дения преобразования 773 существует преобразование 772.
МоментУ* - момент исчезновения неподвижной точки преобразова-
ния 772; наступает при выполнении равенства Е* । 7J*l )[= -Д2.
L ' л 2 /J X 2
С дальнейшим уменьшением 6О2 преобразование 773е претерпевает изме-
нения, аналогичные указанным выше. При значении 6О2 =^2Г возникает
неподвижная точка простого преобразования Те*; наряду с простым пре-
образованием Т* может существовать сложное преобразование вида
Л*Е (п = 3,4,5,...), неподвижная точка которого исчезает в момент У*Е
~ А2
К2 ’
когда
-А2 .
К2 1
Исчезновение преобразования /7*е произойдет в момент Я*Е,
Д2 у - д2
[ К2 ) /С, '
Значение при рассмотрении принималось постоянным. Этим значе-
нием определяется возможность существования указанных выше бифур-
кационных моментов С*,Е*, так как условиями существования этих
Г1
моментов являются соответственно неравенства \|/а >-Д2Г;\|/а >—
где &2Г ~ а2 •
Отметим, что Кх > 1, и поэтому момент С* наступает раньше момен-
та £*. Подобное влияние оказывает величина у/а на возможность суще-
304
ствования преобразования типа 77*е = Т* 7^. Возможны такие значения
параметров, что при уменьшении со2 преобразование появляется вслед
за преобразованием 772*, а преобразования вида 77*е отсутствуют. Усло-
е г]
~^2
К2
(11.84)
вием существования преобразования 77^е = Т*2 7^ является
~^2
Аналогично неравенству (11.84) записываются условия существования
любого из преобразований вида 77 *е: е*
п-2
---Основные
*2
г]
~ А2
*2
фазы изменений точечных преобразований иллюстрируются рис. 11.46, на
котором представлены бифуркационные кривые в координатах Л,ш2. Все
кривые построены для значений =1,5; L = 0. Первая (I) группа кривых
соответствует преобразованию 772, вторая (П) - преобразованию 7^,
третья (Ш) - преобразованию 772*. Кривые А2 В2 С2 У2 Н2 иллюст-
рируют функции со2 = со2(Х), определяющие значения параметров Д, при
которых наступают описанные выше бифуркационные моменты. Обозначе-
ния кривых совпадают с обозначениями моментов. Кривые С^Я^С* со-
ответствуют бифуркационным моментам простых преобразований Т и Т*.
Л Е
Рис. 11.46
305
Моменты С , С* - моменты рождения неподвижных точек преобразо-
Т] Ь
ваний; момент - момент исчезновения неподвижной точки. Прямая
Sq (ю2 = const) характеризует зависимость <х>2 = <х>2 (X) в случае симмет-
ричного цикла (со2 = )• Анализ бифуркационных кривых позволяет за-
ключить следующее:
- с увеличением X уменьшается кратность сложных точечных преоб-
разований (уменьшается число импульсов в замкнутых циклах); сказанное
следует из того, что бифуркационные кривые групп I, II, III сближаются
с увеличением X;
- значение X влияет на последовательность наступления бифурка-
ционных моментов так же, как и значение параметра , что иллюст-
рируется характером кривых С* и К2*. Если Х<Х1? то неподвижная
точка преобразования Т* появляется при меньших значениях со2, чем
исчезает неподвижная точка преобразования
772 со2е <со22
Если
Х>ХИ то (&2£ >fi>22 • В области 0<X<Xj возможны преобразования
вида 77л**;
- если (Oj = со2 >сог(Дсо=0), то вид преобразований не зависит от зна-
чения X; независимо от высоты полета устанавливается только двухим-
пульсный симметричный цикл.
11.4.3. Устойчивость простых и сложных колебаний
Пусть возмущающий момент равен нулю: L = 0. Простые неподвижные
точки преобразования Пе находятся из уравнения е(\|/)-\|/ = 0, которое
w ♦ 1 + Ai
имеет единственный корень у =-----L. При любых значениях A i имеем
dz
(11.85)
Следовательно, неподвижная точка преобразования Те всегда устойчи-
ва независимо от значений параметров системы. Неподвижные точки пре-
образования Тл также всегда устойчивы, так как при любых X = 0
и уе (0,-—“д ) выполняется условие
306
(11.86)
Неподвижные точки преобразований П п = Т™Т* m находятся из урав-
нения Fn(\|/) - V = О, которое в общем случае не разрешается относитель-
но у в конечном виде. Для определения неподвижных точек могут быть
использованы численные или графические методы [42]. Неподвижные
точки сложных преобразований всегда устойчивы, так как производ-
ная функций последования
dy dy i=\dy
при всех значениях у по модулю не превышает единицы. Действительно,
<1 и
< 1, как было показано ранее.
Пусть возмущающий момент не равен 0 (1#0). Тогда
Условия устойчивости (11.85) неподвижной точки преобразования
удовлетворяются, если AL>0 или 2-со1Г>-2^(. Это неравенство выпол-
няется всегда, и поэтому одноимпульсный цикл устойчив. Условие устой-
чивости (11.86) неподвижной точки образования Тл удовлетворяется, если
• Поэтому в случае C0j > 2L/\r преобразование имеет единствен-
ную устойчивую неподвижную точку.
и
Если < —
1 ЛГ
то преобразование Тл имеет две неподвижные точки
(рис. 11.48), одна из которых всегда неустойчива. Доказательство устой-
чивости второй неподвижной точки аналогично доказательству устойчи-
307
вости неподвижной точки простого преобразования TY в задаче о движе-
нии ступени вне атмосферы при действии постоянного возмущения.
Неподвижные точки сложных преобразований Пп, соответствующих
сложным периодическим движениям системы при действии постоянного
момента, устойчивы. Доказательство устойчивости при cd, > 2I/kT анало-
гично доказательству устойчивости неподвижных точек сложных преоб-
разований для движения системы при отсутствии возмущения.
Доказательство устойчивости в случае со, < 2L/^T такое же, как доказа-
тельство устойчивости неподвижных точек сложных преобразований для
движения системы при действии возмущения. На рис. 11.49 иллюстриру-
ются функции последования преобразований Щ ='nz[£z(Vz)] для раз-
личных значений ш2, когда со, < 2L/^T.
11.4.4. Динамика простых колебаний
Рассмотрим характер переходных движений космической ступени при
установлении простых автоколебаний в случае <о1=со2=сои^ = 0 [ 179].
308
Проанализируем изменения фазовой траектории одноимпульсного
цикла. Пусть у/+1 * со/2. Тогда
AV(0 = V/+2-V/ = . • (П.87)
Разность Дф(/) является непрерывной ограниченной функцией
Можно показать, что для любых двух смежных одноимпульсных циклов
всегда выполняется неравенство Aij/,+2l < Aij/'l и lim Aij/’1 = O. От-
сюда следует, что последовательность несимметричных одноимпульсных
циклов монотонно сходится к симметричному циклу, координаты
точек фазовой траектории которого связаны соотношениями
Vi+2* =|v.+2*+i|=y; V/+2*=V/+2*+i=l-^-- Изменения ординат началь-
ных точек могут быть вычислены по формуле (11.87).
Рассмотрим изменения фазовой траектории двухимпульсного колеба-
тельного цикла. Отметим, что справедливо следующее (рис. 11.42):
1. Если
|v,+i|0у или V,+30y, то Ду/+2 =v/+2 -Vi+100 или Д yi+4 =у,+4 -у,+3<>0.
2. Если V,+1<0 и то Дуо)=у,.+4-у,.00.
Покажем, что для всякого несимметричного цикла |ф/+2| >|Аф/+4|. Ис-
пользуя уравнение фазовых траекторий, найдем
где а=т(2"ю7’)- (11-88)
Представим эти функции в виде рядов Тейлора в окрестностях точек
। । 0) (О
|V/+i| = —, Vi+3= — 9 что возможно, так как Дф/+2, Дф/+4-функции не-
прерывные, имеющие все производные при |ф/+1| = со/2 = ф1+3. Получим
д^/+2=4^+1 -Л*-.+...+(-1)и+1 4аг+1+^2+i)+...
1_а а а
д^+4=4--л« -4а«+-+(-i)n4v+3+^лз+,)+-
L а а а
, I. | со , со
; Л/+3=^+з--.
(11.89)
, (11.90)
СО
где а = — + ТХ;
2
Выражения остаточных членов ряда имеют вид:
309
п(л + 1)
Ki+4
в+1 2? + ТЛ
| z«\n+i____L 2___J _
2 ( } L‘ к^У+2’
где co>|v*+i|>(o/2, ®>|v*+3|>co/2.
Ряды (10.87), (10.88) сходятся абсолютно, так как Цщ |я,ч21)| = 0>‘
и—Ьоо I
= 0- Ряд ДуИ1+2-д¥/+4 = А —(hi+i +Л1+з)—y^f+i+л/+з)+’
и-»*» La Q
+“Т^+1 +А|3+з )*•••
а
является абсолютно сходящимся знакочередующимся
рядом. По теореме Лейбница для такого ряда соблюдаются условия
-(Л1+1 +Л(+з)>^-(л?+1 +лД3)>-^-(л,?+1 +Л,?+з )>..., из которых следует, что
а а а
в переходном процессе при установлении двухимпульсных автоколебаний
имеет место следующее:
|Ду
/+2 |>М+4|>|ДЖ 1+6 |>->|д¥ /+2л|>- •
Изменения Д^+2* ординат характерных точек циклов могут быть вы-
числены по формулам (11.88).
11.4.5. Анализ сложных автоколебаний
Выше показано, что при Дсо^О возможны сложные автоколебания,
соответствующие точечным преобразованиям вида
77^ =тп-\т^пг =T"-1T11. (11.91)
На рис. 11.49 иллюстрируются зависимости неподвижных точек пре-
образований вида (11.91) от параметра со2(со1 = const) для £^0. Анализ
рис. 11.49 показывает, что неподвижные точки преобразований сущест-
вуют не для всех значений параметра со2. Это обусловлено тем, что би-
фуркационный момент исчезновения неподвижной точки предыдущего
преобразования наступает раньше момента рождения последующего пре-
образования. Имеют место интервалы значений параметра со2, где непод-
вижные точки преобразования вида (11.91) отсутствуют. Назовем такие
интервалы интервалами типа «Г», а интервалы значений параметра со2,
зю
для которых существуют неподвижные точки преобразований (11.91), -
интервалами типа «Е» (рис. 11.49).
Рассмотрим вопрос о возможности существований видов периодических
движений и соответствующих им преобразований для интервалов «Г» и «Е».
Разобьем все возможные виды преобразований на несколько классов:
1 гтЕ _«рш—1<р
1. 1^.
Э — тт~1т
11 ™ v
3. Ф^т = T^TzT^-\(n * т). 4. Ф„е+И = Т^Т^Т^п * т).
Пусть со2 е (юг’Югг), где ^2^22 ~ бифуркационные значения парамет-
ра ©2 > соответствующие моментам рождения неподвижных точек преоб-
разований Т ,П2= Т Т
|| || с
соответственно. При рассматриваемых значениях
возможны сложные колебательные движения системы, соответствующие
точечным преобразованиям 77^ =Г”"1Г , т. е. преобразованиям П класса.
Т] ь
Как в случае L = 0, так и при L 0 каждое из преобразований имеет одну
неподвижную точку.
Можно показать, что совокупность всех возможных периодических
движений системы со значениями параметра со2> принадлежащими интер-
валами типа «Е», полностью характеризуется преобразованиями II класса.
Для интервалов типа «Г» характерно существование при одном значении
параметра со2 преобразований и П^+1, каждое из которых не имеет не-
подвижной точки. При этом преобразования 77^, определены для
значений координаты
(рис. 11.50). Здесь v2 = fn
J A,
е —- v2 ; у/е v2,—-
K2
/С2_
соответственно
4*2 J
есть граница разрыва преобразований 77^,
77^_j. Значение v2 зависит от величины co2. С увеличением параметра со2
у 2 возрастают, сокращается область определения функции /л+1. Диаграм-
ма Кенигса-Ламерея, построенная для значений со2, принадлежащих ин-
тервалу типа «Г», изображенная на рис. 11.50, иллюстрирует изменение
границы разрыва. Анализ диаграммы рис. 11.50 позволяет заключить, что
в рассматриваемом интервале возможны преобразования Ш класса типа
Ф^+т = 77^1| 77^ I . Действительно, если преобразования 77^ и су-
ществуют при одном значении со2 и не имеют неподвижных точек, то точ-
зи
ки у/е
>V2
преобразованием 77^ преобразуются в точки
А1
V* v2,-t
Л2_
ветствующей замкнутому циклу, характеризуемому преобразованием
= 77Рт72, иллюстрируется рис. 11.51. Функция fn (у)= Т]^ [е(у)] опре-
V
Кг)
дования ^(ж)=/Ж(ж)Г‘ , соответствующей преобразованию Ф^М,
координата может изменяться в пределах 3 —L < у < v2. Можно показать,
\К2 J
и обратно с помощью . Пример ломаной итерации, соот-
делена в интервале значений у/ е
, v2 , поэтому для функции после-
dfn+l
<Л|/
Отсюда = dFm
<Л|/
что в случае L = 0 =
< 1 и А. — <^п
ч 1 И Л2 — -----
< 1 для любых значений коор-
динаты у.
т
< 1. Следовательно, все неподвижные
у=С
точки преобразований при L = 0 устойчивы. Для любого со2, принад-
лежащего интервалу типа «Г», существует одна неподвижная устойчивая
точка. Координаты неподвижных точек могут принимать значения
y/e-hnf /„+i(v2);/n+1 -Л
►. В случае 7 = 0 совокупность всех
возможных периодических движений системы со значениями параметра
со2, принадлежащими интервалам типа «Г», полностью характеризуется
преобразованиями Ш класса.
312
2L df^M
Для случаев L * 0 и < -— производная • при изменении ко-
ЛТ dy
-/а,
ординаты в пределах е
Ai
<у<-^- может принимать значения как
К>
больше, так и меньше единицы.
Отсюда следует, что неподвижные точки сложных преобразований Ф„
могут быть устойчивы и неустойчивы. Особенности преобразований Ф%
для случаев L * 0 рассмотрим на примере преобразований, имеющих ме-
сто при значениях параметра со2 е (со3,со4), где со3,со4 - бифуркационные
значения параметра СО2, соответствующие моментам исчезновения и рож-
дения неподвижных точек преобразований и П2 соответственно.
Вид возможных функций последования изображен на рис. 11.52.
Здесь изображены графики функций последования
/з’С'И); F21(v)=/3nl/2(v)] и F3n(v)=У3’,{/'2ЕЛ(1и)]}» определенные для
( д. А
I Д1 I 4 Д1
значении v2,—- , у/е е —-
L 1*2
д
2| Aj ]
И же Л V р 2
I А у
ответственно. Анализ графиков, изображенных на рис. 11.52, показы-
вает, что при различных значениях со2 возможны неподвижные точки
преобразований различного вида. Так, при значениях параметра
2,6 < со2 - 2,28 возможны неподвижные точки преобразований вида
= &2 )• Пример ломаной итерации, соответствующей замкнуто-
му циклу, который характеризуется преобразованием = Ф2 J,
иллюстрируется на рис. 11.52.
К2)
; fi
\ 2 /J
со-
313
При значениях параметра 2,28 < со2 < 2,39 существуют неподвижные
точки преобразований Ф2 = П^П2, а для 2,4 < со2 < 2,43 возможны непод-
вижные точки преобразований (ф2)” 1.
Совокупности возможных колебательных движений ступени не исчер-
пываются рассмотренными. Поскольку неподвижные точки преобразований
могут быть неустойчивыми, возможны сколь угодно сложные колебания
системы. При значительной разности управляющих импульсов, создаваемых
исполнительными органами системы управления, возможны колебания, ха-
рактеризуемые преобразованиями вида Ф„+1 = . Свойства преобразо-
ваний этого вида аналогичны свойствам преобразований IV класса.
11.4.6. Оценка расхода энергии
Сравним количество энергии, затрачиваемой на обеспечение несим-
метричных колебаний ступени (Дсо^О), с количеством энергии, необхо-
димой для создания симметричных колебаний. Интегрируя уравнение
движения и производя преобразования, получим формулу для определе-
ния периода замкнутого двухимпульсного цикла (рис. 11.41):
т =j_ln
а Vx n(AT2|v,+2|-A2)-fcV,-Л1)’
Анализ ее показывает, что наименьший период имеют симметричные
колебания, для которых Tac=-jLln——, где ^=1- —Т. Период
VX i£2Yf-Ai 2
симметричных колебаний ступени при Дсо=0 определяется формулой
_ 4(2-соТ) и
Тс = —-----сложного л-импульсного цикла, состоящего из одного
одноимпульсного и m двухимпульсных циклов (л = 1 + 2?и), период авто-
колебаний можно определить по формуле Та =т^+ Е т®, где -
7=1
длительность одноимпульсного (двухимпульсного) незамкнутого цикла
(1) 1 т(2) = 1 1п (“2 + ^(-+2)) («1 - ^У(,+4))
' Vx cq-Aty, ’ J Jk (Д1 -V(l+i))(A2 + *V(/+2)) '
Здесь у(,+2) = ~—+ 7-S + (Vi -Д1/АГ)2. При ^=0 формулы для
К
упрощаются. Примем, как и выше, 5i=ro)i; #2=гсо2. Тогда
Q = ~ [(/n + l)-^ + ?иш2]. Для двухимпульсного замкнутого цикла имеем
314
rt ( \
Q =—(coj +cd2), а для симметричного цикла = ”—w- С целью сравне-
на Ндс
ния расхода энергии рассмотрим отношения Q = -Q-, Q* = @а-, где Qo "
Qac Qo
расход энергии при симметричных колебаниях.
На рис. 11.53 показана зависимость относительного расхода энергии от
параметра (02. График функции (Х^г) можно рассматривать состоящим
из отдельных участков, соответствующих периодическим движениям раз-
личного вида. Так, в рассматриваемом примере участок функции
Q (0 < со2 < 0,83) иллюстрирует расход энергии в случае установления од-
ноимпульсных периодических движений; участки б(0,8 < со2 < 1,14}-
(2,34 < со2 < 3,17) - расход энергии при установлении трехимпульсных
циклов. В диапазоне значений 1,34 < ш2 < V устанавливаются двухим-
пульсные циклы. Если 1,26 < со2 <1,34, то имеют место многоимпульсные
(семи-, девяти-, одиннадцатиимпульсные и т. д.) колебательные циклы.
Эти участки на рис. 11.53 не показаны. Кратность циклов возрастает
с увеличением со2 (со2 —»1,34). Функция относительного расхода Q имеет
экстремальные значения. Минимальные значения, равные нулю, достига-
ются в начальных и конечных точках, выделенных выше отдельных уча-
стков; максимальные значения - внутри участков. В начальных и конеч-
ных точках участков первая производная функции Q разрывна. Значения
функции Q -» 0 соответствуют замкнутым фазовым траекториям, в соста-
ве каждой из которых есть гипербола, проходящая вблизи начала коорди-
нат (Г ->©о).
315
Участок функции Q, характеризующий энергетические затраты при
установлении двухимпульсных циклов, делит график Q (со2) на две части.
Совокупность участков, находящихся слева от точки (со2 = t34; Q = 0),
соответствует периодическим движениям, фазовые траектории которых
содержат одноимпульсные циклы, расположенные в левой полуплоско-
сти; совокупность участков, находящихся справа от точки
В(со2 =1,7;б =0) - движениям, фазовые траектории которых имеют од-
ноимпульсные циклы в правой полуплоскости.
Анализируя зависимость Q от значения ш2 , можно отметить следующее:
- расход энергии существенно зависит от величины Дш=- со2;
- наименьшее количество энергии для обеспечения колебаний ступе-
ни необходимо при установлении одноимпульсных циклов;
- в случае двухимпульсного цикла наибольший расход будет, если
coj =со2;
- расход энергии при Дсо = 5-35% а>1 меньше, чем в случае
COi =(02 =со;
- реализовать колебания с расходом энергии, близким к нулю, за-
труднительно, так как в точках минимума Q производная
dQ
Jco2
11.4.7. Выбор параметров экономичного регулятора
Выше показано, что экономически выгодными движениями космиче-
ской ступени вокруг центра масс являются двухимпульсные несиммет-
ричные колебания. Рассмотрим вопрос выбора разности величины управ-
ляющих импульсов, при которой обеспечивается установление двухим-
пульсных несимметричных колебаний [171]. Определим область сущест-
вования двухимпульсных автоколебаний на плоскости параметров со2, /,
где
L
х-г
Границами области являются бифуркационные кривые, соот-
ветствующие моментам рождения и исчезновения неподвижных точек то-
чечного преобразования Тц. Бифуркационное значение со-
ответствующее моменту исчезновения устойчивой (большей) неподвиж-
ной точки, вычисляется по формуле
со“ =—(а2 + К2Ф2), Ф2 =-—+ JB+f—\
2 Tv 2 2 27 2 К \ К, К
316
полученной из равенства rj
*1
а1
—L. Фазовая траектория, соответст-
вующая моменту исчезновения устойчивой неподвижной точки преобра-
зования , показана на рис. 11.54 пунктиром.
Бифуркационное значение Ш2 = со^Сх) (вторая граница области сущест-
вования двухимпульсного цикла) определяется в зависимости от парамет-
ров системы. В случае, если выполняется неравенство > — (влияние
постоянного возмущающего момента на движение системы мало), момент
рождения неподвижной точки наступает при выполнении равенства
П(^-)=^-. (11.92)
А. 2 -К-2
Фазовая траектория, соответствующая этому моменту рождения не-
2L
подвижной точки, показана на рис. 11.54 сплошной линией. Если <-—,
то функция T|(V) имеет две неподвижные точки. Момент рождения не-
подвижных точек (кратная точка) наступает при выполнении равенств
=1-
Бифуркационное значение СО2 может быть вычислено по формуле
4=|[а2[1-^кН-|ф1 (11.93)
317
где = 1Г2а2 + J^2a2 ~(ai _^1д)2,
2L
полученной из равенства (11.92), либо, если <-—, определено решени-
ем системы уравнений
гд^г + - 7(2Д]®2г - М)2 - 5(°>2 - “2) , 11 „л \
Wi) = Vt; Vt = ——--------1---,---------Г---------------> (11 -94)
27K((O2-®i2)
где R = K2(B + C) + Д2-а2-со^Т2; S = 4Т2со^(^2В + Д2)-Я2. Заметим, что
если значение координаты неподвижной точки у*, найденное из (11.94),
не удовлетворяет неравенству — < у/*к < —, то и в случае L > /2 то-
К
чечное преобразование имеет одну неподвижную точку и поэтому значе-
ние ©2 должно вычисляться по формуле (11.93).
На рис. 11.55, 11.56 иллюстрируются области существования двух-
импульсных автоколебаний, построенные для различных значений па-
раметров системы с использованием предлагаемых формул. Области
существования двухимпульсных циклов позволяют произвести выбор
параметров системы , Ш2, Т из условия обеспечения экономичных
автоколебаний, а также указать допустимые отклонения этих парамет-
ров от их номинальных значений. Области имеют достаточные размеры
(допустимы отклонения параметров от номинальных значений в преде-
лах ±10%), что свидетельствует о возможности практической реализа-
ции систем, в которых устанавливаются несимметричные двухимпульс-
ные колебания.
318
©j = 2/ L=0,l
— — — ш2 (4
// i Jii .ULi —--
0,06 0,08 0.1 0,12 0,14
Рис. 11.56
Зависимость относительного расхода энергии Q, затрачиваемого на
стабилизацию космической ступени при установлении двухимпульсных
несимметричных колебаний, от параметра со2 при разных значениях воз-
мущающего момента, показана на рис. 11.57. Анализ графиков показыва-
ет, что при всех значениях параметров, соответствующих области сущест-
вования несимметричных двухимпульсных автоколебаний, относитель-
ный расход энергии Q < 1; следовательно, расход меньше, чем при уста-
новлении симметричных колебаний (L = 0, Дсо = 0).
Рис. 11.57
11.5. Методы точной ориентации
Рассматриваются методы повышения точности ориентации космиче-
ских ступеней, основанные на изменении амплитуды и фазы колебаний;
определяется зависимость точности ориентации от параметров СУОС, да-
ется сравнительная оценка рассматриваемых методов.
319
11.5.1. Изменение амплитуды колебаний
Метод предполагает уменьшение ошибки ориентации летательного
аппарата путем уменьшения амплитуды колебаний аппарата относительно
центра масс. Это достигается изменением коэффициентов усиления, вхо-
дящих в уравнение управления + ТдЬ)= ±Д.
Коммутация коэффициентов усиления производится с некоторым
упреждением по отношению к моменту времени, в который необходи-
ма повышенная точность ориентации. Введение упреждения вызвано
тем, что после коммутации коэффициентов усиления имеют место
участки переходного движения. Величина времени упреждения должна
быть не менее длительности переходного процесса. При заданной точ-
ности ориентации знание длительности переходных движений позво-
ляет осуществить правильный выбор времени упреждения (tynp >tnep.)
и обеспечить минимизацию расхода энергии на участке упреждения.
Рассмотрим возможные движения аппарата на участке упреждения и
оценим зависимость этих движений от параметров системы и требова-
ний к точности ориентации. Осциллограммы возможных движений ре-
лейной системы на участках упреждения представлены на рис. 11.58-
11.61. Они соответствуют случаям, когда ступень в момент
коммутации коэффициента усиления находится в крайнем
амплитудном положении.
Движение, представленное на рис. 11.61, не является рациональным,
так как на участках 2-3, 4-5 имеет место неоправданный расход энергии
вследствие перерегулирования по угловой скорости. Движения, показан-
ные на рис. 11.58, 11.59, более экономичны - благодаря реализации сколь-
зящих режимов (участок 2-3) длительность включенного состояния ис-
полнительных органов меньше.
320
Условием существования скользящего режима в точке 2 является не-
равенство где dj = а^Тд + 2ай5(д0 - Д])+ . Можно
г<> |д]|
считать, что О0 = Д; О0 = 0. Тогда зависимость граничного значения
Тд= ^гр. от параметров релейной системы выразится формулой
Тгр. =1/а<)872/За<)8(Д-Д1).
Определим длительность участка упреждения по формуле
tynp. = ^вк + *ск+*св> (11 *95)
где teK - время включенного состояния исполнительных органов (участок
0+1); tce - длительность участка свободного движения (участок 1 + 2);
tCK - длительность участка движения в скользящем режиме (участок 2+3).
Из рис. 11.58 следует Zw=j —; (11.96) (и.97> = (1L98)
где п + Е = — и со=ал8т; со т - длительность одного включения исполни-
тельного органа в импульсном режиме.
В выражении (11.98) будем учитывать л-1 включение исполнитель-
ных органов на участке скользящего режима и определять длительность
неполного участка скользящего движения. Это допустимо, так как точ-
ность регулирования по координате О при О=2Оак уже достигнута, хотя О
еще не уменьшилась до величины Ьак. Тогда
321
т 1
^ск = . с \ ~9
i=\(m + eJ-1
(11.99)
где т = п-1 и 1<ej<2, Ej=E+l. Подставляя (11.96 -г 10.98) в равенство
(11.95) и принимая й0 = 0, получим
, ^^2+2a08Ai , 1
УПР~ дЬ{т + £])—»'
(11.100)
На рис. 11.62 представлены зависимости tynp =tynp (j^) для ряда значе-
ний параметров а^,Тд и т. Показаны граничные значения времени упре-
ждения, соответствующие крайним значениям величины Ej = Ej (fy), кото-
рая может изменяться в диапазоне 1<ej <2. На рис. 11.62 верхняя граница
соответствует ej = 1, нижняя - е2 = 2.
Анализ выражения (11.100) и рис. 11.62 позволяют заключить сле-
дующее:
- с уменьшением коэффициента усиления К$ длительность участка
упреждения возрастает, что объясняется увеличением участка свободного
движения;
- с уменьшением значения время упреждения возрастает;
- с увеличением Тд время переходного процесса увеличивается, что
объясняется значительным уменьшением скорости свободного движения
релейной системы.
Рис. 11.62
Отметим, что при изменении амплитуды колебаний необходимо осу-
ществлять проверку условия существования автоколебательных движений
при заданном значении д j: со < —.
Тд
322
11.5.2. Изменение фазы колебаний
Метод изменения фазы колебаний предполагает такую программную
работу системы ориентации, которая обеспечивает переход аппарата в оп-
ределенный момент времени из любого фазового положения в колеба-
тельном движении в заданное и заключается в следующем [58], [177].
С некоторым упреждением tynp относительно заданного момента обеспе-
чения точной ориентации осуществляется программное включение одного
из исполнительных органов (обозначим его № 1). Выключение исполни-
тельного органа производится при включении исполнительного органа
№ 2 от уравнения управления = -А (возможно выключение ис-
полнительного органа № 1 по команде временного устройства). Вследст-
вие программной работы исполнительного органа № 1 летательный аппа-
рат из любого фазового положения (точки ^,^2’^з на Рис- 11*63) быстро
переходит в нижнее амплитудное положение (точки т19 т2, т3).
Случайный характер фазы колебаний в момент включения исполни-
тельного органа № 1 приводит к некоторому смещению по времени точек
т{,т2,т3. Наибольшее смещение, равное времени перехода летательного
аппарата из верхнего амплитудного положения в нижнее, характеризует
методическую ошибку перехода аппарата в нижнее амплитудное положе-
ние. Методическая ошибка вызвана случайным характером фазы колеба-
ний в момент программного включения исполнительного органа № 1 и
разбросом значения О после окончания переходного процесса.
Если включение произойдет в точке С фазовой траектории (рис. 11.64),
то через время tynp изображающая точка достигнет прямой пп (пусть
в точке п) и будет иметь скорость Ьп'. Включение может совпадать с
точкой d. Тогда выключение исполнительного органа № 1 произойдет
сразу же после включения (так как работает двигатель № 2) и через время
323
tynp + had. состояние космической ступени будет характеризоваться точкой
К, координата которой по углу равна = -^ак + йгП(г*пр+гор). Здесь top -
время, в течение которого необходима возможно более точная ориентация
космического аппарата.
Длина отрезка d\* зависит от координаты точки db которая
может иметь значение от 0 до 2^fljt=co. Таким образом, -О*| =
= 0^ - 2*&ак (t*ynp + top). Независимо от того, с какой фазой колебаний сов-
падает включение двигателя № 1, аппарат через время tynp будет иметь
угловую скорость О в пределах $„'<$< 2Ъак и угловое отклонение О от
амплитудного положения равное 0 < Д^ < ДФтах, где ДОтах - расстояние
между прямыми RQ, R'Q'. Наименьшее расстояние между прямыми бу-
дет в случае, когда обе точки п'и к' лежат на прямой R'Q'. В самом деле,
при опускании прямой пп уменьшается время tynp (за счет уменьшения
времени tck движения в скользящем режиме от точки S до точки п) и со-
ответственно уменьшается участок d\K- Длина участка d\* характеризует
методическую ошибку ДО ориентации аппарата при изменении фазы ко-
лебаний.
Если направление ориентируемой оси аппарата установить под углом
Ьзад -0,5(т\ -0^1) и программное включение исполнительного дви-
гателя произвести за время t = tупр до требуемого момента, обеспече-
ния $зад, то наибольшая методическая ошибка регулирования будет
Д^! = 0,5(Ок - ). Время от момента включения исполнительного органа
324
№ 1 до заданного момента точной ориентации равно tynp,=tas+tck;
где tck - время движения в скользящем режиме от точ-
ки S до ТОЧКИ Mj.
Инструментальные ошибки ориентации при использовании метода из-
менения фазы колебаний обусловлены: Д02 - допуском на постоянную
времени дифференцирующего контура Тд» ” допуском на приведен-
ную эффективность управляющих органов aos, ДО4 - допуском на ам-
плитуду колебаний Ьак.
Отклонение величины постоянной времени Тд от номинального зна-
чения вызывает поворот линии включения Ф+(Т± ДГ)й = ±Д. Поворот
линии включения, а также изменение приведенной эффективности
приводят к изменению амплитуды колебаний и времени движения изо-
бражающей точки на участках aS и Sn . К изменению амплитуды приво-
дит также разброс зоны нечувствительности Д. Изменение амплитуды
колебаний и времени переходного процесса вызывает перемещение пря-
мых RQ и R'Q' на фазовой плоскости вдоль оси О по отношению к их
номинальному положению. Максимальное смещение прямых и определя-
ет в каждом отдельном случае величину инструментальной ошибки.
Расчеты показывают, что использование метода управления фазой ко-
лебаний при ориентации летательного аппарата с параметрами
Д = 1°±6', п = (5±1,5>, а*8 = (0,195 ±0,039)^, Гор = 6с, 2^ = 0,004^
с с
позволяет получить точность ориентации ~ 1 О'.
11.5.3. Исследование движения при изменении фазы колебаний
В качестве основных характеристик движения примем величины: ДО -
точность ориентации; top - время, в течение которого необходима точная
ориентация; tynp - длительность участка упреждения, предшествующего
участку ориентации; Q - количество энергии, затрачиваемой на обеспе-
чение точной ориентации.
Рассмотрим возможные движения ступени, космического аппарата на
участке повышенной точности ориентации; оценим экономичность и точ-
ность систем при различных способах включения двигателя № 1. Осцил-
лограммы возможных движений представлены на рис. 11.65-11.68. Ос-
циллограмма, показанная на рис. 11.66, соответствует случаю, когда вы-
ключение двигателя № 1 осуществляется в момент включения двигателя
№ 2 от уравнения управления 7^О+О = -Д. Осциллограммы, приведен-
ные на рис. 11.65, 11.67, 11.68, соответствуют случаям, когда выключение
325
двигателя № 1 происходит по команде от временного механизма. При
включении двигателя № 1 по команде от временного механизма на участ-
ке упреждения имеет место движение летательного аппарата с выключен-
ным двигателем № 1, свободное движение и движение в скользящем ре-
жиме; длительность участка упреждения определяется выражением
%. ='™.+ (11-Ю1)
Рис. 11.65
-Л1 £ N
м"" п Л
7“ /О) _1 1
Здесь teKJl - длительность включённого состояния двигателя № 1; tce -
время свободного движения; tCK - длительность движения в скользящем
режиме.
326
При уменьшении 1вкл длительность участка скользящего режима
уменьшается и при некотором 1вкл = teKJl гр имеет место равенство
tynp. ~~ ^вкл. гр. + ^св. (11.102)
При выключении двигателя №1 от функционала управления на участке
упреждения свободное движение отсутствует и, следовательно,
tynp. = ^вкл. + (11.103)
Для исследования зависимости движения от параметров системы вос-
пользуемся уравнениями
, =АЫ_,
упр' со ор
^упр.
ad8 i=i n+e-i
— — ~— *о),
|*2
ТдЬх + О2 = -Д, К=L2------------21
со
|^1| АО
л + е=-—1, Д0=---------—1.
со 2
(11.104)
Будем считать, что top «tynp. и +top ~tynp_.
Рассмотрим несколько случаев.
1. Пусть = 1вкя гр (на участке упреждения движение в скользящем
режиме отсутствует); тогда система уравнений (11.104) может быть пред-
ставлена в виде:
, =AzM
со ’
О„=-ТД-Д;
^-^=-20^-00); (11.105)
|А |=а^вк;
0,=^; (0=0^1,
где Oj - угловая скорость аппарата в момент выключения двигателя № 1.
Так как наименьшая погрешность ориентации имеет место при = 0*.
(рис. 11.64), то
327
<о-(^+^) = ГдК1» тд-т t = t —— *св 'вк _ Т (11.106)
Учитывая, что О1~Ол “ ы (11.107)
и решая совместно (11.106) и (11.107), получим
а а f2 Т И ~а^вкл. т (11.108)
где O„=-A-Vd- (10.109)
Величина Oj определяется из уравнения =-2aos(t>1 -О0) и» ес-
ли О0 = 0, равна
^1=.2.^о_-Л?. (11.110)
Подставив (11.109), (11.110) в (11.106), получим
tlsKn/ a$b'~ + teKn/ д~( А-Оо) = 0- (11.111)
т
В уравнении (11.109) Тд»т, поэтому —. Уравнение позво-
2т т
ляет определить значение величины teKJl=teKJl2p ПРИ заданных
Т д’ ^9 A, Clffi
-авбТд + ЖаввТдУ+4ао5—(А-Оо)
teK,=---------*------=------1-------• (И-112)
2ао8^
т
При /вкл = 1вкл. гр. скользящий режим на участке упреждения отсутству-
ет и погрешность ориентации будет минимальной.
На участке ориентации при включении двигателя №2 могут иметь ме-
сто движения изображающей точки либо справа, либо слева от линии
включения Td&+O=-A. Для обеспечения движения справа (скользящий
режим движения) необходимо выполнение условия — <L^y = -^-. От-
|^л I ?гр
О
сюда <&п <а^Т ; так как teKJI =—то для определения граничного зна-
чения Тгр подставим (11.113) в (11.111), тогда
328
Т’^ + ф«8-(А + ^о)=О- (П-114)
Уравнение (11.114) может быть решено графически. Для решения за-
пишем его в виде
Х=У, (11.115)
Для примера на рис. 11.69, 11.70 представлено решение уравнений
(11.114) и (11.115) при А =10°, t>0 =10° и различных а^.
2. Пусть 1вКл.= tas • Тогда система уравнений (11.104) будет иметь вид:
гА-^=-Д;
=-2а^-Ы k = i------------1.
(О
Решение уравнений (11.116) получим графически, построив функции
= f^ynp) и ^k=^k dynp. + *ор) (Рис- 11-71). Точка пересечения кривых по-
зволяет определить fy. = $„, At>, tynp при top = 0 и при заданных параметрах
системы ориентации. Для определения Ък = f(top) и At> = f(top) необходи-
мо найти такие значения Ьк = , для которых выполняются соотношения:
^л = f (tупр.) > ^Л = $к ’
“ f (tynP' + top), top — const.
329
~ f(tynp) ^вкл ~ ?as
Зависимости Ad = f( teKJl ), tynp = f( teKJl ) при различных значениях
представленные на рис. 11.72, 11.73, являются решением системы уравне-
ний (11.116) (кривые ВВ”).
Jipn определения граничного значения Тгр запишем систему уравнений:
$ -&а =-2аМ -д0);
гД+^-Д; (11.117)
А = ~а&Тгр-
Решая систему (11.117), положив Ьа = 0, получим Тгр = .
V3
Для того чтобы на участке упреждения имел место скользящий режим
движения, необходимо выполнение условия Тд > Тгр, или teKJl < Тгр.
Зависимость =/(ао5) при А = 10° и Фа=10° иллюстрируется
табл. 11.4.
ззо
3. Пусть Твкл гР' <teKJl<t^ Тогда tynp. =teKJl+tce+tCK9 и для определения
основных показателей движения необходимо решить систему уравнений
(11.104). Эта система решается, как и в случае 2, графическим методом.
Таблица 11.4
[с 2] 0,5 1,0 1,5 2,0 2,5 3,0
^[с] 5,16 3,65 2,98 2,58 2,3 2,11
Зависимости Оп=/(г^р) и =f(tyv +top) при заданных Tg
и т, позволяющие определить основные показатели движения, представле-
ны на рис. 11.71. Результаты решения уравнений приведены на рис. 11.72,
11.73 (кривые АВ, А'В', Я'В').
Для определения количества энергии, необходимой для обеспечения
ориентации при использовании метода изменения фазы колебаний, можно
использовать приближенную формулу Q « 2PteKJl .
11.5.4. Возможности повышения точности ориентации
Рассмотренные выше методы изменения амплитуды и фазы колебаний
позволяют уменьшить стабилизационную погрешность ориентации до ве-
личины (0,2-0,5)А (А - зона нечувствительности исходной системы).
В отдельных случаях необходимо обеспечить более высокую точность
ориентации.
Рассмотрим один из методов, позволяющий обеспечить такую точность.
Этот метод, в отличие от описанного в разделе 11.6.2 метода, предполагает
многократное (через равные промежутки времени) программное включе-
ние одного из двигателей (например, № 1). Выключение двигателя № 1
может осуществляться двумя способами: либо от уравнения управления в
момент включения двигателя № 2, но не позднее, чем через t с после про-
граммного включения двигателя № 1 (если через t с не произошло включе-
ние двигателя № 2, двигатель № 1 выключается по команде от временного
механизма). Осциллограммы, иллюстрирующие движение аппарата при
реализации описанного метода ориентации, приведены на рис. 11.74, 11.75.
Рис. 11.74 соответствует случаю, когда выключение двигателя № 1
осуществляется от уравнения управления в момент включения двигателя
№ 2; рис. 11.75 - случаю, когда выключение осуществляется по времен-
ной команде.
На рисунках прямыми I-I, П-П ограничена область, соответствующая
повышенной точности ориентации аппарата. Цифрами 1, 2, 3 обозначены
точки, характеризующие фазовые состояния аппарата в моменты про-
граммных включений двигателя № 1. Независимо от того, с каким фазо-
331
вым состоянием аппарата совпадает первое программное включение дви-
гателя, после «п» программных включений изображающая точка будет
находиться в области, ограниченной прямыми I-I, П-IL Расстояние между
прямыми равно
2ДФ = соД/, (11.118)
где Дб - заданная точность ориентации; Дг - промежуток времени между
Время, необходимое на перемещение аппарата из верхнего амплитуд-
ного положения в положение, характеризуемое точками области повы-
шенной точности ориентации равно
^р.=Дгп, (11.119)
где п - число программных включений двигателя.
При выключении двигателя № 1 от уравнения управления длитель-
ность участка упреждения определяется выражением t = f01 + , где f01,
- длительность движения изображающей точки на участках 0-7, 1-п
соответственно (рис. 11.74).
Можно считать, что
*01 -
а&>
п
и <1Л=7эЕ
1
и + е = J—- и
со
е = -—
со
332
п 1 tvnn
Тогда t =-------- + ------ и л = -^- + а, где 0<а<1 - поправ-
ДЭ5 /=!« + £-/ М
ка, дополняющая отношение др целого числа.
Д/
При выключении двигателя №1 по временной команде длительность
участка упреждения определяется выражением =/01 +/12 + ... + /шл, где
zoi^i2^23> •• ^тп ~ длительность движения изображающей точки на участ-
ках 0+7,..., ш+п соответственно.
Анализ метода ориентации позволяет заключить следующее:
- метод обеспечивает высокую точность ориентации в течение дли-
тельного времени;
- величина стабилизационной погрешности ориентации не зависит от
способов включения двигателя № 1.
Таким образом, с использованием способа, являющегося предметом
изобретения [177], можно погрешность ориентации космической ступени
сделать в 2-5 раз меньше зоны нечувствительности системы ориентации.
11.5.5. Управление фазой колебаний в системе с ЦВМ
Рассмотрим задачу обеспечения заданных значений фазы колебаний
космической ступени в фиксированные моменты времени движения, если
управление ступенью осуществляется СУОС с логическим устройством
(ЦВМ); блок-схема СУОС представлена на рис. 11.76. Уравнение движе-
ния ступени описывается уравнением (И.3), в котором X = 0 и L = 0.
Рис. 11.76
БКП - блок командных приборов;
ЦВМ - цифровая вычислительная машина;
У - усилитель;
ИО - исполнительный орган;
ОР - объект регулирования.
Способ управления фазой колебаний, описанный в разделе 11.6.2, раз-
работан для систем, не имеющих логических устройств или ЦВМ. Если
в системе управления имеется ЦВМ, то возможно уменьшение методиче-
333
ской ошибки в управлении фазой колебаний путем сокращения интервала
возможных значений О в момент корректирующего включения двигателя
№ 1 и выбором в качестве заданного значения О не среднего, а одного из
амплитудных значений его в автоколебательном режиме.
Для сокращения интервала возможных значений фазы колебаний
в момент корректирующего включения двигателя № 1 можно использовать
логическое устройство, которое должно определить время, необходимое
для перехода системы из текущего фазового состояния в заданное, осуще-
ствить сравнение этого времени с временем Lct., оставшимся от текущего
значения до заданного, и выработать сигнал для корректирующего вклю-
чения исполнительных органов, когда указанные времена станут равны-
ми. В результате корректирующего включения исполнительных органов
ступень перейдет из текущего фазового состояния в заданное. Рассмотрим
алгоритм работы системы управления, выполняющей коррекцию фазово-
го положения ступени в заданный момент времени с высокой точностью.
Для определения времени упреждения tynP. воспользуемся фазовым порт-
ретом колебательного движения объекта на плоскости Ф, О (рис. 11.77).
На плоскости фазовых координат прямыми ММ, NN выделим область Р.
Примем, что фазовое состояние аппарата в момент t3ad. должно характе-
ризоваться координатами точек, принадлежащих области Р. Построим
графики зависимости времени движений изображающей точки из любого
положения на траектории a, b, с, d к границе (прямая ММ) области Р.
Будем рассматривать две фазовые траектории: траекторию О0, g, h, 1 под-
хода к ММ справа и траекторию О0, g, h, 1, к, г, s подхода к прямой ММ
334
слева. Обозначим время движения изображающей точки из точки ф0 до
точки 1 через ti; а из точки О0 до точки S через t2. На рис. 11.78 показаны
графики зависимостей Zi($o) и ^2(^0)- Скачкообразный характер кривых
объясняется наличием в фазовой траектории, соответствующей скользя-
щему режиму движения ступени, участков вида h-k. Число таких участков
в фазовой траектории, характеризующей движение изображающей точки
из состояния ($о,фо) к прямой ММ, зависит от начальных координат
(1?О’^о) точки- Число участков скачкообразно меняется на единицу при
изменении координат ($0, $0). Это приводит к скачкообразному измене-
нию функций ^(Оо) И z2(0o)-
Рис. 11.78
Весь интервал возможных значений ф0 разделим на п зон. Границами
зон будут прямые, определяемые скачками графиков Л(^о) и £2(^0)-
Примем, что время упреждения для каждой зоны есть постоянная величи-
на, которая может быть выбрана равной tynpл =0Л • (г' + t'2) - для первой
зоны, tVnn2 = 0’5 ^ + £)- второй зоны и t . =0,5-1 Л +Л . . 1 для
z г* X 2 3' ynp.J \ J j т 1 I
j-й зоны (j = 1, 2, 3,..., п). Такой выбор tj обеспечивает в момент времени
tK ддя фазовых координат объекта выполнения условия т?е Р.
В память ЦВМ должны быть занесены значения заданного момента
времени tk, граничные значения зон fy, Ф2, ...» &п и соответствующие
зонам значения времени упреждения.
Последовательность работы рассматриваемой системы обеспечения
требуемых фазовых координат ступени может быть следующая:
335
1. С целью определения момента корректирующего включения двига-
теля ЦВМ в момент времени = tK- tmeK < tn вычисляет signbmeK
и путем сравнения текущего значения $ = &тек с граничными значе-
ниями зон Оу определяет номер зоны j, в которой находится изо-
бражающая точка <1?^ Здесь обозначено:
значения фазовой координаты и скорости ступени в текущий мо-
мент времени f - наибольшее значение времени упрежде-
ния (соответствует зоне п). Если sign&meK <0, то с каждым шагом
квантования по времени вычисляется t . =t„m и, когда t <r,
дается команда на включение исполнительного органа № 1. Если
sigrr&meK >0, то корректирующее включение исполнительного орга-
на № 1 производится либо при выполнении равенства = t., либо
когда фазовая координата &тек изображающей точки совпадает с
граничным значением Фу+А. (; + &)-й зоны (&тек = и при этом
справедливо неравенство < tj+k.
2. Выключение исполнительного органа № 1 осуществляется при
включении исполнительного органа № 2 от функционала управле-
ния I.
Методическая ошибка обеспечения требуемого значения фазовой ко-
ординаты не будет превышать величину сот/2.
11 .6. Управление путем перемещения масс
Существо способа управления, основанного на использовании системы
перемещения центра масс, заключается в том, что центр масс летательно-
го аппарата в соответствии с командами системы управления перемещает-
ся (путем перемещения масс внутри аппарата [47]) в плоскостях 1-Ш,
П-IV. Возникающие при этом моменты аэродинамических сил использу-
ются в качестве управляющих моментов. Летательный аппарат может
быть выполнен в виде гладкого острого конуса.
11.6.1 . Оценка необходимых перемещений центра масс
Управление летательным аппаратом путем перемещения центра масс
существенно упрощается, если ввести самонастройку динамических ха-
рактеристик аппарата в процессе полета. Целью самонастройки должно
быть определение истинного значения плеча статической устойчивости
k = xd -хТи сведение его практически к нулю. В этом случае для управле-
ния потребуются малые поперечные перемещения центра масс.
336
В работе предложен новый способ регулирования величины к, при-
знанный изобретением и заключающийся в следующем.
Для дискретного регулирования величины к используется коническая
«юбка», состоящая из отдельных колец и являющаяся продолжением ко-
нуса аппарата [48]. При сбрасывании колец «юбки» равной ширины центр
давления аппарата смещается к носку дискретным образом.
Сброс колец «юбки» осуществляется по информации о поперечном
смещении центра масс аппарата в плоскостях тангажа и рыскания, необ-
ходимом для реализации заданного угла атаки.
Пусть, например, ширина одного кольца «юбки» составляет а,\ мм,
центр давления при сбросе одного кольца смещается к носку на Дхю мм
(дискретность «юбки» по xd есть Дхю) и наибольшее возможное попереч-
ное смещение центра масс равно ДУ[ тах =а2 мм- Если после ввода про-
граммного угла атаки перечное смещение центра масс ДУ1 = ДУ1тах> то это
означает, что £>Дхю, и по сигналу от системы управления сбрасывается
одно кольцо «юбки». Если через время Т (т - время переходного процесса)
после сброса кольца «юбки» поперечное смещение Д^ не уменьшается,
сбрасывается следующее кольцо «юбки» и т. д. Сброс колец осуществляет-
ся до тех пор, пока поперечное смещение центра масс Д^ не станет мень-
ше дг1тах5 так как это означает, что величина встала меньше дискретности
«юбки» по xd и сброс следующего кольца сделает летательный аппарат
неустойчивым. Дальнейшее уменьшение величины к возможно с исполь-
зованием системы перемещения центра масс в продольном направлении.
Перемещая массы внутри аппарата к носку, можно непрерывно увеличи-
вать к др величины дискретности «юбки», затем по сигналу системы
управления сбросить кольцо «юбки» и, таким образом, получить к = 0.
Рассмотрим характер движения летательного аппарата при изменении
величины к.
Уравнение возмущенного движения аппарата запишем в виде:
ДУ = ayy&Y 4-а^ДО+Гу,
О = а$укЛ Y + вфО + а$к(апр + ДО) + ДфДУ} + М
z^^z + a^v + ^z,
V = ayzkz + Яуф + +А7у (11.120)
Ф = аф(«лр + AO--^)Az, +аф(у--^-)ДГ1 +М^
ДУ1 =а0ДО + а1ДО, 5 = аофФ + а1фФ,
Az^aoY + ajV, ДО = О-Олр
337
Здесь ДУ (z) - смещения «нулевого» положения центра масс летатель-
ного аппарата в направлениях нормали к невозмущенной траектории и
перпендикуляра к плоскости стрельбы.
Точкой «нулевого» положения центра масс будем называть проекцию
центра масс на продольную ось аппарата; О, у, ф - углы тангажа, рыска-
ния, крена соответственно; апр - программный угол атаки в плоскости
тангажа; AXj, - управляющие смещения центра масс; S - координата,
характеризующая положение управляющих органов аппарата по крену;
Wy, Wz - скорость ветра в плоскостях тангажа, рыскания; Fy, Fz,My,Mz -
приведённые возмущающие сила и момент, действующие на аппарат в
плоскостях тангажа, рыскания.
Исследования проводились путём математического моделирования
движения аппарата на основе системы уравнений (11.120).
Скорость перемещения центра масс аппарата в продольном направле-
нии принималась равной Arj =50 мм/с; в поперечном направлении - не ог-
раничивалась. Коэффициенты автомата стабилизации принимались:
а0 =0,105м/град, =0,0525 М с/град, аОф = 4» «1ф =4С.
Моделирование переходных процессов проводилось для начальных
значений ха -хт =220, 170 и 150 мм. На рис. 11.79, 11.80 показано дви-
жение аппарата, если регулирование плеча аэродинамических сил осуще-
ствляется только дискретным образом с дискретностью «юбки» по xd,
равной Лхю = 25 мм.
Наибольшее располагаемое поперечное смещение центра масс прини-
малось равным ДГ1тах =25 мм. Как следует из осциллограмм, качество пе-
реходного процесса удовлетворительное. Сброс колец «юбки» прекраща-
ется при к = 20 мм и 25 мм. Максимальное значение A/j после сброса юб-
ки составляет 18 мм (рис. 11.79) и 22 мм (рис. 11.80); наибольшее значе-
ние статической ошибки ДО=0,5°.
На рис. 11.81 изображены переходные процессы при регулировании
величины к с помощью сбрасывания колец «юбки» по xd принята условно
равной &хю = 30 мм. Как видно из осциллограммы, дискретное умень-
шение к приводит к величине xd - хт = 20 мм (начальное значение
к = 170 мм). Затем происходит непрерывное увеличение к до величины
дискретности «юбки» Дхю = 30 мм, после чего сбрасывается ещё одно
кольцо. В результате к уменьшается практически до нуля. Это позволяет
осуществить управление движением аппарата вокруг продольной оси пу-
тём небольших поперечных смещений центра масс.
338
Рис. 11.81
339
11.6.2 . Способ управления движением вокруг продольной оси
Пусть начало движения летательного аппарата характеризуется нуле-
выми начальными условиями (апр = 0; A = i/0 = (pQ = 0; Д$о = у/0 = (pQ = О)
и значениями возмущающих сил и моментов Fy-Fz- 0; = Му = 0;
Мр > 0. Будем считать, что в начальный момент времени центр масс ап-
парата совпадает с точкой «нулевого» положения. Для компенсации дей-
ствия возмущающего момента М$ при t>to произведём следующие
операции [44].
1. Переместим центр масс аппарата из «нулевого» положения в поло-
жение 1 (рис. 11.82). Под действием момента сил лобового сопротивления
X на плече A/i возникает угол атаки Д0>0. Система стабилизации будет
перемещать центр масс вдоль оси в соответствии с уравнением
АУ1 =aoA^4-ajAO.
Координата центра масс в любой момент времени равна Kj = -ДГф + ДУ].
Обозначим время от момента перемещения центра масс в положение 1 до
момента достижения максимального угла атаки (рис. 11.83) через т.
давления масс
Рис. 11.83
2. В момент времени Z = T переместим центр масс на величину
AZg,||дгф| = |Д(рф|) в положении 2 (рис. 11.82). Сила лобового сопротивления
X на плече дгф создаёт момент =-Х • AZ^, поворачивающий аппарат
вокруг поперечной оси (рис. 11.84). Под действием этого момента
возникает угол атаки у<0, и система стабилизации аппарата в плоскости
рыскания будет перемещать центр масс аппарата в соответствии уравне-
нием AZX =aovКоордината центра масс по оси OjZj в любой момент
времени будет равна Zx =-Д2ф+Д71. Нормальная аэродинамическая сила
(обусловленная углом атаки ДА) на плече Zx (рис. 11.83) и нормаль-
ная аэродинамическая сила (обусловленная углом атаки у) на плече
340
Kj будут создавать вокруг продольной оси аппарата противоположно на-
правленные моменты и Л/фу. Суммарный момент будет равен
М9=М^ + М w = ЛЦ- AZ„ + AZj)- Nv (- ДУф + ДУ]).
Максимальное (по модулю) значение Л/ф будет иметь место в момент
времени / = Т, когда у = 0, Wv=0, AZ = 0 и Z^-AZ^. В дальнейшем,
вследствие увеличения (по модулю) угла у, плечо [zj будет уменьшаться,
а момент = -?/ф(-ДУф +ДУ1) - увеличиваться. При Z = 2t будет иметь
место ДО=|v| и Мф = 0.
3. В момент времени t = 2т исключим смещение центра масс от «нуле-
вой» точки по оси Oj/jj переместим центр масс из положения 2 в положе-
ние 3 (рис. 11.82). Тогда станет равным нулю и вновь возникает мо-
мент сил вокруг продольной оси, равный Л/ф = = N^(-AZ^ + AZX).
В течение Т с этот момент уменьшится до нуля в связи с уменьшением
до нуля величин ДО и N#.
4. В момент времени / = 3т переместим центр масс в положение 4
(рис. 11.82). Аэродинамическая сила Mg на плече ДУф создает момент
Л/ф, который при t = 3x с равен Л/ф=Л/фв=-^(Д¥1+Д¥ф), при
3T<Z<4T определяется формулой Л/Ф = -Л,\)(Д2-Д2ф)-ЛГф(Д¥1 +Д¥ф),
а при t = 4Т равен нулю М ф = 0.
5. В момент времени г = 4т переместим центр масс в положение 5,
вследствие чего опять возникает определяемый в диапазоне вре-
мени 4T<Z<5T формулой Л/ф = -мДА¥1 +АУф) и уменьшающийся
за Т с до нуля.
Дальнейшее перемещение центра масс производится аналогично при
Т = 5Т, 6Т, 7Т, 8Т в положения 6, 7, 8, 1 соответственно. В течение всего
времени перемещения центра масс в положения 1-2-3-4-5-6-7-8-1 и т. д.
вокруг продольной оси аппарата действует импульсный момент д/ф<0.
При необходимости направление действия момента можно изменить. Для
этого следует изменить направление перемещения центра масс на обрат-
ное (1-8-7-6-5-4-3-2-1).
Описанный вариант получения управляющего момента по крену пред-
полагает непосредственное перемещение центра масс на величины
± ДУф, ± А7ф, минуя цепи системы стабилизации.
341
Возможен также вариант ввода перемещений центра масс для управ-
ления по крену через цепи системы стабилизации. Он заключается в сле-
дующем.
1. Введем программный угол атаки в плоскости тангажа
>0 (а^ «0,5° +1,5°). В соответствии с командой системы управле-
ния центр масс аппарата из «нулевой» точки переместится в точку 1
(рис. 11.82) и через Т с угол атаки будет равен СЦ. Время переме-
щения будем считать малым по сравнению с Т.
2. В момент времени Т введем угол атаки в плоскости рыскания
av <0 |ja^| = |av|). Центр масс из точки 1 переместится в точку 2;
возникнет и начнет увеличиваться (по модулю) угол атаки в плоско-
сти рыскания. Нормальные аэродинамические силы , Ny, при-
ложенные в центре давления, расположенном на продольной оси
аппарата, будут создавать момент относительно точки 2, равный
Максимальное (по модулю) значение Л/ф будет достигнуто в момент
/ = Т, когда у = 0, Уф =0, =-y^AZ1.
При / = 2т будет иметь место |аф| = а^ и Мф=0. Изменяя в дальней-
шем программное значение углов атаки так, как показано на рис. 11.85,
получим управляющий момент по крену Л/ф <0. При изменении а0, аф
так, как показано на рис. 11.86, получим управляющий момент по крену
Л/ф>0.
Рис. 11.85
Рис. 11.86
Выше предполагалось, что перемещение масс внутри аппарата в попе-
речных направлениях осуществляется с большими скоростями и, следова-
тельно, перемещение центра масс аппарата относительно его оболочки
происходит бесконечно быстро. Рассмотрим возможность управления, ес-
ли скорость перемещения центра масс конечна.
Если подвижные массы внутри летательного аппарата перемещаются
вдоль осей 01 Yi, OiZi по гармоническому закону, то центр масс аппарата
в плоскости OiYiZi описывает окружность, показанную на рис. 10.87.
342
Примем программный угол атаки равным нулю (апр =0) и рассмотрим
упрощенную систему уравнений, описывающую движение аппарата во-
круг центра масс.
Рис. 11.87
i>+= ДУф60,
<р = (уДУф-0Д2ф)яф,
Д2ф = rcoscM,
ДУф = rsincof.
Здесь г - удаление центра масс аппарата от продольной оси аппарата;
со - угловая скорость перемещения центра масс по окружности вокруг
продольной оси. Коэффициенты уравнений (11.121) будем считать посто-
янными. Тогда решения уравнений, соответствующие установившемуся
движению, можно найти в виде:
О = А((о)5ш[со- t + у(со)],
V = A(co)cas[co-1 + у(со)],
^0 = = ’
rb
где
4»)= ,, „
^\a^k-(D2) + (О2а^2
(а)
(б)
(в)
(11.122)
, у(а))=arctg--------
. (11.123)
(11.121)
©4
где
(11.124)
Подставляя (11.123) в уравнение (10.121 в), находим
Ф = 4pSiny(cD),
_ a^b
ф " Г/--------й-------’
у(а^к-ш2) + (О2а$
Из уравнения (11.124) следует, что момент аэродинамических сил во-
круг продольной оси зависит от угловой скорости перемещения центра
масс. Значение со=со*, при котором Ф = Фтах, есть абсцисса максимума
343
функции Др (со). Оно определяется формулой со* = аък + (а^)2. Численные
значения величин, входящих в это равенство, таковы, что со* ))а$. По-
этому можно считать, что управляющий момент по крену будет наиболь-
шим (ср = ф^) при движении центра масс вокруг продольной оси аппара-
та с угловой скоростью, близкой к собственной частоте колебаний аппа-
рата в плоскостях тангажа (рыскания).
Пусть теперь программный угол атаки в плоскости тангажа
апр # 0 = const обеспечивается постоянным смещением центра масс д^
(при постоянных коэффициентах уравнений движения).
Для получения управляющего момента вокруг продольной оси центр
масс аппарата будем перемещать по окружности радиуса г вокруг точ-
ки А с координатами Zi = 0, (рис. 11.88). Тогда уравнения
(11.121) запишутся в виде:
$ += Z^(r sin 6# + ДУ;) = $0^0 а)
y/ + a\l,\fr + av\if = bv(rcos(iX) = S4,bv б) (11.125)
Рис. 11.88
Обозначая = Я|, ba = bv = b, aw = ам = а, получим решения
уравнений (11.125 а), б), соответствующие установившемуся движению,
в виде
i> = (ш) sin[<ttf + У|(<и)]+а, (11.126)
V = AX (ai) cosfftX + /j (®)],
где Aj(а) = у— £[, > Г1 (й>) = arctg, а = -ДГг
^(а-а2)2 + а2й)2 (О -а а
Найдем
<р = {- А{ (a)r sin (a) + Aj (®)ДУ; cosfax + (©)] - ar cos at}- (11.127)
344
Отсюда следует, что при движении центра масс по окружности вокруг
точки А возникают постоянные и гармонические составляющие момента
аэродинамических сил вокруг продольной оси. Постоянные составляющие
могут быть использованы для управления движением в канале крена.
11.6.3. Процессы стабилизации при управлении по крену
Проиллюстрируем возможность управления по крену путём переме-
щения центра масс. Используем вариант реализации способа получения
управляющего момента, основанный на введении программных углов ата-
ки a0,av. Графики управляющих функций а0 = а0(г) и а^=а^(г),
i' = aQ(p(p + показаны на рис. 10.86 (для случая sign /<0)« Амплитуды
импульсов управляющих функций примем = т? • /, = 1,5, т? = 0,25.
В соответствии с этим получим, что управляющий момент в канале
крена зависит от возмущений параметров движения аппарата по крену (от
угла ф и угловой скорости ф). Для простоты коэффициенты уравнений
(11.120) будем считать постоянными. Это предположение допустимо при
рассмотрении возможности получения управляющего момента по крену.
К тому же переменность скоростного напора (имеющая место в действи-
тельности) не влияет на соотношение возмущающего и управляющего
моментов, так как оба они линейно зависят от скоростного напора q.
Возмущающие моменты в каналах тангажа, рыскания примем равными
М$ = Мф = 100 кгм, возмущающий момент по крену равным мф = 50 кгм •
Процессы стабилизации, полученные при математическом моделиро-
вании движения, представлены на рис. 11.89; система перемещения цен-
тра масс обеспечивает стабилизацию по крену с достаточной точностью.
Рассмотрим движение аппарата при перемещении центра масс с ко-
нечными скоростями. Получим решение полной системы уравнений воз-
мущённого движения аппарата при перемещении центра масс так, как по-
казано на рис. 11.87, 11.88. Коэффициенты уравнений движения приведе-
ны в табл. 11.5.
345
Таблица 11.5
аУУ azz azy 4
с1 с1 м • с2 м • с2 м2 • с1 м2 • с1 с1 м'1 • с2 мЛ • с2
-0,318 0,318 1014 -1014 0,188 -0,188 0,467 -795 -795
ЬЛ К а, а1д
мА • с2 м'1 • с2 град м М X х град1 М X х град1 м • сх х град1 м • сх х град'1 м • С X х град1
-200 200 15 0,01 2385 4 • 10'3 6,8 • 10'3 4 • 10’3 6,8 • 10’3
Осциллограмма на рис. 11.90 иллюстрирует характер управляющего
момента по крену, полученного при г = 2,5 мм и бо2=12,5с“2 (алр=0)-
Колебательный характер объясняется погрешностями работы моде-
лирующей установки.
Рис. 11.90
Осциллограммы на рис. 11.91 + 11.93 иллюстрируют движение при
а = 15° и при перемещении центра масс по схеме, показанной на рис. 11.88.
Угловая скорость аппарата достигает при этом значении ф = б град/с
и практически знакопостоянна, что говорит о существовании постоянной
составляющей управляющего момента вокруг продольной оси. Анализ
представленных материалов позволяет заключить следующее:
1. При перемещении центра масс с постоянной скоростью в плоско-
сти, перпендикулярной продольной оси аппарата, по траектории,
представляющей собою окружность, возникает момент аэроди-
намических сил, действующих вокруг продольной оси.
2. Момент существенно зависит от угловой скорости перемеще-
ния центра масс. = Л/фтах при значении щ близком к собствен-
ной частоте колебаний аппарата по тангажу и рысканию.
346
3. В рассмотренном примере момент достигает величины ЛГф=18О кгм
при а = 0 и не превышает =20 + 30 кгм при алр=5°+15°
иг=1+2лш-
Рис. 11.93
Глава 12
ДИНАМИКА КОСМИЧЕСКИХ СТУПЕНЕЙ РАКЕТ
С РАБОТАЮЩИМ МАРШЕВЫМ ДВИГАТЕЛЕМ
(конструктивные методы обеспечения устойчивости движения)
Характерным примером космической ступени может служить III сту-
пень трехступенчатой жидкостной ракеты-носителя 11К68 («Цик-
лон-3») с космическим аппаратом «Целина-Д». Компоновочная схема
ступени представлена на рис. 8.1; основные технические характеристики
и математическая модель возмущенного движения приведены в главе 8.
Космическая ступень ракеты имеет существенно меньшее удлинение,
чем I и II ступени. Топливные баки ступени по условиям компоновки вы-
полнены торообразными (рис. 12.1); они характеризуются значительным
наружным диаметром (2,7 м) и сравнительно небольшой высотой.
Внутри каждого бака на 15—30 мм ниже уровня свободной поверхности
топлива, соответствующего полной заправке, установлена крышка (диа-
348
фрагма), отделяющая основной объем жидкости от объема газа над ее по-
верхностью; более 20 % площади каждой крышки - это закрытые сеткой
отверстия. Крышки не допускают прорыва газовых пузырей к заборным
устройствам баков и далее в двигатель при его запуске в условиях неве-
сомости.
Ячейки сетки имеют размеры, исключающие прорыв газовых пузырей
под крышки при отсутствии перегрузок, но допускают перетекание жид-
кости, обусловленное тепловыми расширениями и перегрузками от рабо-
ты двигателя.
Исследование динамических свойств космических ступеней как объек-
тов управления показало, что ступени характеризуются существенной
собственной и структурной неустойчивостью на частотах колебаний жид-
кости в баках. Неустойчивость движения предопределяется формой
и размерами топливных баков, которые обуславливают большую свобод-
ную поверхность и малую глубину жидкости. В цилиндрических баках
частицы жидкости, расположенные вблизи продольной оси ракеты, прак-
тически не участвуют в колебательном движении; в торообразных баках
вся жидкость удалена от продольной оси и вся участвует в колебательном
движении.
Расчеты показывают, что для обеспечения устойчивости движения на
частотах 1-го тона колебаний жидкости необходимо реализовать в баках
логарифмический декремент колебаний £ = 1.8-2 (в цилиндрических ба-
ках первых и вторых ступеней ракет без демпфирующих устройств
£< 0,005).
Для устранения дестабилизирующего влияния 1-го тона колебаний
жидкости на движение ступени в топливные баки III ступени ракеты-
носителя 11К68 было установлено по 12 радиальных перегородок, кото-
рые разделили внутреннюю полость каждого бака на 12 замкнутых отсе-
ков небольшого объема.
Этими конструктивными мерами 1-й тон колебаний жидкости был
полностью исключен, но возникло дестабилизирующее влияние колеба-
ний жидкости в каждом из 24 (по 12 в баке) замкнутых отсеков, которое
было устранено путем закрепления на каждой радиальной перегородке по
четыре ребра - демпфирующих элемента (рис. 12.1), обеспечивших значе-
ние 5 = 0.6.
Очевидно, что введение дополнительных конструкций в баки для
обеспечения устойчивости движения неблагоприятно отражается на весо-
вых и энергетических характеристиках ступени.
В связи с этим в Днепропетровском национальном университете были
проведены исследования возможности решения задачи более рациональ-
ными способами.
349
Как показано в части 3 книги (раздел 8.4.1), возмущенное движение
космической ступени с ЖРД на участках полета с работающим маршевым
двигателем описывается системой линейных дифференциальных уравне-
ний:
= az„¥ ^Zr^2
V = W + aVr^\ + aVr^2 + a^S, (12.1)
П = + a)2iri=^ + araZ + аг^’ U = !’2)»
A(P)8 = B(P)y + C(P)Z.
Коэффициенты системы (12.1) являются функциями физических пара-
метров ступени, гидродинамических характеристик жидкости и параметров
траектории движения ступени (раздел 8.4.2).
Основные из этих параметров следующие:
- конструктивные (геометрические) Ri9 SM, Хр, Iк, ;
- инерционные и центровочные ст, Iz, IG;
- параметры двигательной установки р, G, ;
- параметры жидкого наполнения р., vi9
- параметры траектории V, h9 W.
Гидродинамические характеристики жидкости описываются (глава 9):
- безразмерными коэффициентами гидродинамических сил и моментов
А» А/»
- присоединенными массой и моментом инерции жидкости m, I;
- безразмерной частотой и логарифмическим декрементом колебаний
жидкости ст,,
Ступень как объект управления с параметрами, выбранными из условий
удовлетворения тактико-техническим требованиям, зачастую оказывается соб-
ственно динамически и структурно неустойчивой [106] в интервалах времени
/г+1 - tK(r = 0, l,...w). Это в значительной мере обуславливается небольшим
удлинением космических ступеней и формой их топливных баков (возможные
схемы топливных баков иллюстрируются рис. 12.2). Совокупность требований
(тактико-технических, конструктивных, технологических и др.) определяет не-
которую область х» заданную системой неравенств |а. - б7?| < Да? (/ = 1,2,.. .,у),
где Да? - модули допустимых вариаций параметров ступени.
350
1175
Основная задача исследований формулировалась следующим образом:
определить совокупность вариаций независимых параметров 5а, <=х
таких, при которых объект управления с параметрами а? + 5а, характери-
зуется минимальными длительностью участков /г+1 ч- tr(r = 0, 1, ...т) и ве-
сом демпферов колебаний.
Решение задачи проводилось на основе варьирования физических па-
раметров ракеты: принималось утверждение о целесообразности измене-
ния гидродинамических характеристик жидкого наполнения топливных
баков (частот колебаний жидкости, гидродинамических сил и моментов,
присоединенных масс и моментов инерции) путем изменения формы
и конструкции топливного отсека.
12.1. Связь динамических характеристик ракеты
с конструктивными параметрами ступени
12.1.1. Собственная и структурная устойчивость ступеней
Устойчивость движения космических ступеней ракет на частотах
колебаний жидкости о, можно оценить без учета влияния канала бо-
ковой стабилизации, описывая объект управления передаточной функ-
цией вида
W(P) = ^1 = (12.2)
v / g(p) v /
М(Р)____
PN(P)
Р
1 az& azi\ Р azr2 ?
О a.pg -аЧГ}Р2 -aVr2P2
- ari2 О Р2 + 6]Р + ©2 О
- аГг2 О О Р2 + е2Р + ©2
1 -(а'2уР + -а^Р2 -а^Р2
О Р — — <2<рГ| Р ~ Р
~av -“r^P2 P2+6jP + ©? О
-аГ22 -аГ2уР2 0 Р2+е2Р + ©2
Здесь М(Р) = в0Р4 + в'Р3 + в[Р2 + в’Р + в2,
352
N(P) = aQP5 + a'P4 + a{P3 + a'P2 + a'2P + a",
e0 = a<¥8[l-Zll -Z22 + w(^zn +^z22)be2 =a'PS(0?G)2»
e, = aTS[ei(l-Z22+^22) + e2(l-Z11+^n)], (
ej = aTS[o)?(l - Z22 + n^Z22) + co2(l - Zn + w'PZn) + ],
в — б7кр§(£]й)2 "Ь $>2®! )>^0 = 1 — 1 — ^11 — ^22 ^22 — F *
a, = e1(l-Z22-T22) + e2(l-Z11-W11)-^(l-Z11-Z22)-^(WZii + 4^),
a{ = co?(1 - Z22 - ¥22) + o*(l - Zn - ¥п) - CPZn + 4Z22 ) - (1 - Z22) -
-£2a^4/ 0”^ll)”^Z4/(^/Z11e2 +'^Z22el) + ele2»
a” = -Ячлр (®? +0>2 + ele2 ”^22°)?)”aZr(X^Z11O)2 +'^Z22(O?)”
~ aZ^(e\^Z22 +е2^п ) + G)l2e2+(02el»
a2 = ®1 ®2 — aZ*¥ (®1 ^Z22 + ^h^Zn ) “ ^4^/(ei<02 + £2(£)2),a = —axjnj/CO^G)^.
7 _ _ P/^j ^1/ T7 .
Zij aZriarjZ ’r---
m Mj
Ai .
В формулах (12.3) использованы следующие обозначения
п d3____________________________________________________
'?z//=a<Fr(V=V-AfI/n/;
JG
п = Ozs = •
fl4<8 m(-^G
F° =Z12V21 +Z21T12 -Zh^ -Z22Tn =-Р12егУцР2^А/12(111 )2.
JGm
ni=X^XrR^h =
Нули POi и полюса P, передаточной функции W(P) обычно представля-
ется возможным записать в виде [106], [107]:
В этом случае Д, fioi можно определить, решая уравнения
ао0? “ а10? + а2 - 0,
^оРо/ “ Ро/ + Ьг - 0.
(12.5)
(12.6)
353
Область значений параметров объекта управления, которым соответст-
вуют комплексные корни уравнения (12.5) (область динамической неус-
тойчивости [140]), будем в дальнейшем обозначать через Л, в отличие от
области динамической устойчивости А, для точек которой корни уравне-
ния действительные.
Области структурной устойчивости и неустойчивости будем обозна-
чать через ф и ф соответственно. Известно [162], что Хеф и границы об-
ластей X, ф имеют общие точки. Структурную и собственную динамиче-
скую устойчивость ступеней ракет можно оценить, пользуясь критерием:
ступень как объект управления структурно устойчива, если выполня-
ется неравенство [106], [107]
Т = ОУ6СТ^ ~а^а^2 < 0 (12 7)
a^8aZi ""aZ5CT'PZ1Pl
Здесь vZi =(<»?-tf Х®2 -Р,2) + (®i -P,2)Z22P,2 + (®22 -P?)Znp?,
CT<PZ/ =<o?TZ22 +(0^Zii -рМ,, +4^), (f = l,2).
Обозначив [65] <^2 = к ; р2 = /| со?; Р2 = /2 <£>г > получим
т __ ^>(Л) _
*H/i)
/22(1-z11-z22+»>pZ|[ +^Z22)-/2(i+g-rz22-z11+W4>Zii
/,2(1-Zn -Z22 +»*PZ11 +»TZ22)-/,(! + k-kZ22 -Z„ +WTZ11 +n'¥Znk) + k'
Функция 4х есть отношение многочленов
=/2(l-zn-г22 +Wz„ +«Vza)-/(1 + *-^22-zll+«Vze + '»*Vz22) + *,
при значениях аргументов Р 9 являющихся корнями полинома
Fp =/2(l-zn -yn -z22 -фгг)-
-ЛЛ-^22-Лу22-211-\|/11+аЯ|/-1-(у211 +vZ22) + l]+[£-^-(£v222 +4%)].
©2 О>2
Отсюда следует сделанный в работе [65] вывод о том, что для струк-
турной устойчивости ступени необходимо и достаточно, чтобы корни
уравнений F^ = о и Fp = 0 перемежались. Перемежаемость корней свиде-
тельствует о наличии двух точек пересечения парабол Fy и Fp (в коорди-
натах F.9f)> поэтому условия структурной устойчивости могут быть запи-
саны в виде Fx > 0,F2 < 0 или Fx < 0,F2 > 0, где F[9F2 ~ ординаты первой
и второй точек пересечения парабол соответственно.
354
12.1.2. Влияние изменений конструктивных параметров ступени
на устойчивость невозмущенного движения
Влияние изменений конструктивных параметров ступеней на их дина-
мические характеристики можно определить на основе рассмотрения кор-
ней характеристических уравнений.
Характеристическое уравнение жёсткой «отвердевшей» ступени имеет
вид [63], [67]
Р3 + а'Р2 + а2Р + а3 = 0, (12.8)
здесь
ci\ kzdzs kip ciy/3>
Cl 2 ciygky 9
a$ ci ц/s ci zy ki 9
где kyciys » kzciz5'
Действительный корень уравнения (12.8) значительно меньше едини-
цы (Pi«l), что позволяет использовать для его вычисления приближен-
ное выражение
Pi = -4- <12.9)
Л2
Обычно поэтому действительная часть комплексных
корней уравнения (12.8) может быть вычислена по формуле
(12.10)
Уравнение частот получим из характеристического уравнения, поло-
жив Р = а± j’P и используя равенство (12.10)
2 куО^ь
Р + к у ci yz ci + ci ц/5 к ц/ + ~ kyCiyscizb'к i 0. (12.11)
Выражения (12.8)-(12.11) позволяют вычислить приближенные значе-
ния корней характеристического уравнения. Перемещение корней на
плоскости характеризует изменение динамических свойств ракеты. Так,
увеличение действительного корня (или действительных составляющих
комплексно-сопряженных корней) соответствует уменьшению запасов ус-
тойчивости; уменьшение собственной частоты «отвердевшей» ракеты
свидетельствует об ухудшении управляющей способности.
Раскладывая Р, а и Р в ряд Тейлора и ограничиваясь величинами пер-
вого порядка малости, получаем
8 Pl = Pi(x\ + Д Xi,-,x„ + Д т„)- Pitxi,-, Хп)= ~ 8. Xt+,...,+ ^- д х„-
355
°X\ vXn
8P = P(.Xx + &Xx,-,Xn + Ax„)-^(xp...,x„)= ^-AXi+,...,+^-Ax„.
°X\ ox„
Здесь
&X\... &X* - вариации независимых параметров;
5Pi, 5a, 5p - изменения корней характеристического уравнения.
Для оценки влияния изменений параметров на свойства ступени доста-
точно вычислить производные
8Р\ . . dP (/ = 1 2
dXt ’ dXt ’ dXt ’
n),
что позволяет:
- определить направления желаемых изменений параметров;
- вычислить изменения корней характеристического уравнения и, та-
ким образом, оценить изменения запасов управляемости, устойчивости.
Характеристическое уравнение ступени с учетом двух тонов колеба-
ний жидкости в баках имеет вид [63]:
Р~аГ¥ 0 рс№ рс№ Уг22 0 0 аТ,Р2 -(к^р) -<ъпр2 -ЪпР2 -(/Ae^+cd?) 0 0 0 0 -ЪъР2 -^ПР2 0 -(р2+е2р+соЗ) 0 0 0 -а^р2 -а*2),2 0 0 -(р2+е(2)р«о(2)2) 0 0 -а<2М -а^р2 0 0 0 ^р2+е(2)р+<о£2)2) 0 ~агъ -ОуЬ 0 0 0 0 (51P2+*2P+1) = 0
ИЛИ а13р13+а12р |2+.. ,.+А1Р+Ао=О. (12.12)
Коэффициенты Ав, Ап, ..., Ао представляют собой детерминантные
многочлены.
Например, А13 = BjA,
1 0
0 1
а а
Здесь д = и* nv
а Cl
r2z ЪУ
а® a(2)
rlz nv
a(2)
г22 r2V
Aj2 = B2 Д “ Bj A + Bj
a ci„ a<2) •)
^2 ZTi zr2
л... a(2)
vn yr2 vn W2
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
356
А5// =
b\jarxz ?)\jarxv
&2jar2z ^2jar2^
Я Л7<2) Я Л2)
^jarz °3jaZy
Я /7<2> Я л/2>
V4jar2z °4jaz^
&\jazrx
^jayrx
1
8? iCl 83
^2 J zr2 Zr^
(2)
8 2 j a\yr2 $3 J ^\|/r
1
1
Я Л7<2)
O4JaZr2
Я Л<2>
O4ja^fr2
1 о
О 1
Символы Sy имеют значения: Sy = 1 при i* j\ 8у = 0 при i = j.
Определитель Ai получается из А заменой второго столбца на столбец
Q igy
О
о
о
о
Решение характеристического уравнения (12.12) будем искать в виде
P=a±jp. Так как обычно на частотах колебаний жидкости имеет место не-
равенство |а|«1, в выражениях рп(п = 2,...,13) можно пренебречь члена-
ми, содержащими сГ.
Тогда
Pl = (aj+yp.Z » «aipf"-0/"'0* • (12.13)
Здесь: j = J-l .
Подставим равенство (12.13) в характеристическое уравнение (12.12)
и, разделяя действительную и мнимую части, получим
13 а/Р,12 А в + Р/2 Л12 ”П а/Р,10 Ап - Р/° Лю + 9а/Р,8 А9 + Р/As -
- 7а»Р/6 Ач ” Р,6Л6 + Sa/P,4 As + Р/Л4 ” За/P,2 Аз ~ Р,2 А2 ” а» Л1 + Ло = О,
Р/3 Л 1з ” 12 а/Р,11 Л12 ” Р/11 Лц + Юа/Р/ Лю + Р/ Л9 ” 8<х/Р/7 Лв ”
- Р,7 Л 7 + ба/Р/ Л6 + Pj5 As ” 4спР/ Л4 ” Р/ Аз + 2а/Р, Л 2 + Р/ А \ = 0.
Отсюда:
а _ Р)2А2 ” р;°4о + Р?4 - р^ + р?л4 - р?л2 + Лр = ц (1214)
' 13р;2Л13 -11р;0Лп +9р?Л9 -7Р?Л7 -5Р?Л5 -Зр?л3 + 4 01 ’
357
P/2^i3 ~P/°4i + РМ9 ~Р?^7 + Р?45 ~Р?^з + 4 _ _ £2 (12.15)
12р}°Л12 - Юр?Л10 + 8Р?Л8 - 6₽/Л6 + 4р?Л4 - 2Л2 Q2
Собственная частота pi вычисляется из уравнений (12.14), (12.15) ме-
тодом последовательных приближений. В качестве первого приближения
можно использовать
Влияние изменений параметров на устойчивость определяется произ-
водными
^_е,_£е_£1
aaf 8ХJ Vl дхJ 8Хj 8Xj (12.16)
ex, Ql e,
Здесь
^-= ^-(12 P!1 Л12 - 10 p’Л10 + 8P?Ag - 6р?л6 + 4P; A4 - 2р,.Л2) +
ОЛ j ОЛ j
+ zo 12 ЗЛ12 _ n 10 дЛю „8 dAt _ 6 dA6 4 dA4 _ 2 dA2 + SA0 _
Pi dXj ' dXj P/ dXj Pi dXj ' dX j ' dX j 8X/
= -^-P/02 + Fi>
dXj*2 1
|^ = |^(156А11Л13 -П0Д% +72ДЧ -42ДЧ +20ДЧ -6ДЛ3) +
+ (13 Д12 ^111 _ 11 д!» + 9Д? _ 7 дб Мт_ + 5д4 _ 3 д2 +
и' дх, 1 дХ, и‘ дх, дх. дХ, ' дХ, дХ,
= 5Д
dX,
= ^-(12 р*1 Л13 - 10 р’А}1 + 8р/Л9 - 6р(5Л7 + 4Р; А} - 2р,Л3) +
ОЛ j ОЛ J
, /о12 дЛ13 10 дАи g дА9 об J^7_+ »4 8А5 2 дА3 । ЭЛ|
к₽/ дХ} Pi dXj PidXj ‘ dXj ' dXj ' dXj дХ/
= rf~<120 " 80 + 48 " 24 + 8^<) +
ОЛ j иЛ j
+ (12 дю Э^2__ ю pi а^о_+ 8Д6 6Д4 9А^+ 4Д2 2
дХ j оХ j оХ j оХ j оХ j оХ j
358
гт ад
Производную найдем, приняв во внимание тождественность ра-
венств (12.14) и (12.15)
(^Р,22 + Fi + + F3a,)02 = (^-F4 + Fs + ^~Fbat + F7a,)e,.
Отсюда
dp, = (Г5 + F7a/)g1 - (Fx + F3af )g2 (12 17)
dXj (pe2 + Fa,.)e2 - (F2 + ’
При дифференцировании многочленов Л„(и = 0,1,...,13) используется
обычное правило дифференцирования детерминантов.
12.2. Выбор конструктивных параметров ступени
с учетом требования обеспечения устойчивости
Будем считать, что на начальной стадии проектирования определены
основные параметры ступени - весовые, инерционные, центровочные,
аэродинамические характеристики, характеристики двигательной уста-
новки, компонентов топлива и т. д. Выбрана форма и геометрические раз-
меры топливных емкостей. Если ступень с выбранными параметрами не-
устойчива на значительной части траектории, то для устранения неустой-
чивости необходимо:
- определить параметры, изменение которых оказывает наибольшее
влияние на собственную и структурную устойчивость ступени;
- определить целесообразные направления изменения этих параметров.
Используем критерий структурной устойчивости, сформулированный
в виде требования к перемежаемости корней уравнений = О, = О
(раздел 12.1.1) и приближенные формулы для определения вещественных
составляющих корней характеристического уравнения [144].
Направления целесообразных изменений параметров и степень их
влияния на структурную устойчивость ступени как объекта управления
определим по частным производным от корней fi9f! (/ = 1,2) полиномов
Fv,Гр по параметрам ступени; производные по некоторым параметрам
имеют, например, вид:
^ = ~2^{Па^2" +^22):F^L[^n + ^22 +2^(VZn +Vz22)] +
+ «(VZ11 + Vz22)(*l±4)h
359
2«1Т _
ri lk L d\
2к - by "I dt] kZy, _
------ , —— =---------т- 2ai ±
^^02 I
dfi . Zn
S-Vqi 4aj2/j
Sfj
dXT
df'i 1
a/G
+~^2~Уги -2C2(vn +W22)~2a2~^-(^Wz22 +Vz1I)]-(Vii +W22)(b2 ±d2)},
tt>2 ®2
<_ =^J-L(2/2 A± J-(^(2Z2 +-^)-^/2 -2o2 ^-21^ ±4)1
<2*01 2/w£ [ <25 “2 J
+^Г)±У (W +^y)-^2 ±4)1
0*02 2/1^5 [ «2 J
(2Г+3>г22 +(2+-j>„) +2(^,+^22)±
d\ J
-^MZn + Z22)±-J-[(6,(Z11 + kZn)-2k(Zn +Z22)t
4af ( 4 J
{о2[Гу22 +Vn +-T-(VZ11 + +H22 +~^-Vzn +
2(2 2*Q ®2 ^2 ®2
azw -LfO-L^SA./z A _i_O6/z _i_»/z A 4-
±^[^222(Ж2+>-^^и+|г,+^'+^^?<V+T,)
Здесь
=1-2ц -Z22 +«^z22 »
a 2 = 1 - - Z 22 ~W и - W22,
bi=K-Zn- Jcz22 - у n— Г y22 - (щ + щ ),
й)2
dt
Cj = Г,с2 = Г - ^-(р2п + 4SZ22 ),
G) 2
,2-4o,c,, i = l,2; 2-ch^^-)
A A f1 -11L f - _____________K°j
Rf1 r+x 2pX(l-8?) , A- h ,
• Rifu -X, + XT + Z-—-------, sh{^ -^-)
1 Koi
- корни уравнения I- =(8^i)N(Z>)-N((d^)I/(i>) = 0,
r .
di = —— отношение внутреннего и внешнего радиусов свободной по-
Roi
верхности жидкости в торовом баке.
360
Расчеты показывают, что основное влияние на структурную устойчи-
вость оказывают следующие параметры:
- момент инерции ступени относительно поперечной оси, проходящей
через метацентр ступени IG;
- координаты центра тяжести Хт и метацентра XG;
- радиусы свободных поверхностей жидкости в топливных баках Roi;
- координаты характерных точек Х,-.
Выделение параметров, оказывающих наибольшее влияние на собст-
венную динамическую неустойчивость, и определение целесообразных
направлений изменения этих параметров может быть проведено с исполь-
зованием приближенных формул для нахождения вещественных корней
характеристического уравнения [106]
а 1 Р?к{П)2 -Р?(1~^22 -У22))+СгН ~Р?<1 — -^11 -У11)}]~а^СТуг1Р,2
2 -P?(!-Z22 -V22)]+®2[®? -Pi?(1-Z11 -4'll)]+ezV°<rz> '
Значения Д2 определяются из биквадратного уравнения (12.5). Для оп-
ределения необходимых изменений параметров производится вычисление
dai тт
частных производных —-. Частные производные от а, по некоторым
дХу
параметрам имеют, например, вид:
- (4++ /• 71]+ Z4vZ11 (2Р1лХ + ЗА)},
= or V'zn ) + £1 (»22 - -^^22 + + DC},
О* q 21GB й?2 6У2
где
-Za-^n-^i)]; п=агг[(Г-Л)гг22 +(i-Z>qi];
6У2
Л2 =£i[l ~ Z’0“z22 4 ~ 4“ fi) + & “ C +
CO2
(? = Ai + f. • Л2 + В — C‘9
361
в = <Д(Г - Z)^z22 + (1 - Z)^n ];
С = - /)(1 - /) + (Г - /)г22/. + (1 - ZOzu/];
z2
Л2=Л1(/;-Г) + ВГ-СГ + //П; 5 = 4+E42+Z);
В качестве примера рассмотрим возможность улучшения динамиче-
ских свойств космической ступени одной из отечественных ракет, имею-
щей торообразные топливные ёмкости (рис. 12.3). Основные параметры
рассматриваемой ступени, выбранные на начальном этапе проектирова-
ния, следующие:
1. Плотность компонентов топлива-окислителя -148,7
м
-горючего-81,2 —’—
м
2. Рабочий запас компонентов топлива-окислителя - 1,9 т,
-горючего - 1,1 т.
3. Положение центра тяжести ступени:
- в начальный момент времени - 0,8 ik,
- в конечный момент времени - 0,68 ik.
Наружные размеры топливных баков соответствуют 7^ = Т?2 = 1,33 м.
Время движения ступени на активном участке траектории t = 114 с. Пред-
варительный анализ динамических характеристик ступени с указанными
выше параметрами показывает, что ступень структурно неустойчива в те-
чение 68 с. Численные значения частных производных, рассчитанные для
рассматриваемой ступени, приведены в табл. 12.1 и показывают, что ма-
лые изменения конструктивных параметров могут существенно повлиять
на структурную устойчивость ступени. Как следует из таблицы, наиболь-
362
шее влияние на структурную устойчивость оказывают изменения харак-
терных размеров топливных полостей и координат характерных точек.
Выбор наиболее рациональных с точки зрения структурной устойчивости
величин характерных размеров проводился путём проверки перемежаемо-
сти корней уравнений = 0, Fp = 0 для следующих сочетаний величин
характерных размеров топливных баков (направления изменений опреде-
лялись по знакам частных производных -^L):
dRi dR,
Вариант 1: Ri =1,13 м, Ri = 1,13 м; Вариант 3: Ri = 1,13 м, Ri = 1,16 м;
Вариант 2: R\ =1,13 м, Ri = 1,15 м; Вариант 4: Л =1,10 м, Ri = 1,16 м.
Таблица 12.1
t 8Rt 5/2 8R2 5/.' 8Rt 8R2 5/1 8R2 g/2 8R2 8R2 8R2
0 -2,04 -0,265 -1,77 -0,442 2,10 0,354 2,56 0,265
8 -1,68 -0,442 -1,24 -0,531 2,48 0,354 2,74 0,354
16 -1,59 -0,442 -1,86 -0,531 2,65 0,442 2,56 0,354
24 -1,42 -0,442 -1,86 -0,531 2,48 0,442 2,48 0,442
32 -1,15 -0,531 -1,59 -0,531 2,48 0,131 2,30 0,619
40 -0,973 -0,531 -1,59 -0,796 2,03 0,530 1,33 0,707
48 -0,885 -0,531 -1,59 -0,708 2,48 0,530 1,42 0,619
56 -1,15 -0,531 -1,86 -0,619 2,48 0,530 1,50 0,530
64 -1,24 -0,973 -1,86 -0,708 2,39 0,530 1,41 0,442
72 -1,15 -0,177 -0,620 -2,30 2,48 0,619 2,21 0,707
80 -0,973 -0,976 -0,350 -2,92 2,21 0,796 0,691 0,707
88 -0,885 -1,06 -0,260 -3,19 1,86 0,972 0,354 0,177
96 -0,175 -1,42 -0,440 -4,96 1,06 1,24 0,177 0,177
104 -0,175 -0,973 9,38 1,06 0,707 1,33 4,15 0,100
112 -0,175 -1,06 0,350 -0,265 0,442 1,33 1,59 0,088
t -^-10’ 8p, 3p2 ^10’ ap, <10’ -^10’ ^10’ Sp2 <10’ 5p2 ^10’ Sp2
0 0,202 0 0,403 0 0,123 0,123 0,370 0,123
8 0,202 -0,067 0,470 0 0,246 0 0,370 0,123
16 0,202 0 0,470 0 0,123 0,123 0,493 0,123
24 0,202 0 0,403 0 0,123 0 0,370 0,123
32 0,269 0 0,403 0 0,246 0 0,370 0
40 0,202 0 0,202 0 0,123 0 0,370 0
48 0,202 0 0,202 0 0,123 0 0,246 0
56 0,202 0 0,067 0 0,123 0 0 0
363
Окончание табл. 12.1
64 0,202 0 0,067 0 0,123 0 0 0
72 0,202 0,403 0 0 0,123 0,739 0 0
80 0,134 0 0 -0,067 0,123 0 0 0
88 0,134 0 0 -0,202 0,246 0 0 -0,123
96 0,067 0 0 -0,269 0,123 -0,123 -0,123 -0,123
104 0,067 0,067 1,55 0,134 45,8 0 0,735 0
112 -0,202 0 1,34 0,067 5,32 0 0,493 0
t & ^02 ы ^02 у; ^02 О ^10’ дт 'ж дт
0 0 0 -0,602 0 -0,480 0 -0,160 -0,016
8 0,301 0 -0,602 0,301 -0,500 0 -0,220 0
16 0 0 -0,602 0 -0,690 0 -0,220 -0,017
24 0 0 -0,602 0 -0,530 0 -0,210 0
32 0,301 0 -0,301 0,301 -0,370 0 -0,200 0
40 0,301 0 -0,301 0,301 -0,380 0 -0,170 0
48 0,301 0 -0,301 0 -0,400 0 -0,100 0
56 0,301 0 -0,301 0 -0,420 0 -0,063 0
64 0 0 -0,301 0 -0,660 0 -0,044 0
72 0,301 0 0 0 -0,230 0 0 0
80 0 0 0 0 -0,490 0 0 0,073
88 0 0 0 0 -0,260 0 0 0,180
96 0 0 0 0 -0,270 -0,270 0 0,330
104 0 0 0 0 -0,290 0 -1,13 0
112 0 0 0 0 -0,310 -0,310 -0,470 0,125
На рис. 12.4-12.7 приведены графики, иллюстрирующие перемежае-
мость корней для указанных выше вариантов. Анализ полученных резуль-
татов показывает следующее:
- при одновременном увеличении радиуса бака горючего и умень-
шении радиуса бака окислителя на 3 % по сравнению со значениями,
принятыми на начальном этапе проектирования, участок структурной
неустойчивости сокращается; его длительность составляет 6 с (18-24 с
на рис. 12.7) по сравнению с имевшими место 68 с (рис. 12.4);
- увеличение радиуса бака горючего при неизменном (r{ =ЦЗ м) ра-
диусе бака окислителя (рис. 12.5) является более эффективным. Увеличе-
ние радиуса бака горючего всего на 2 см по сравнению с принятым на на-
чальном этапе проектирования существенно сокращает участок структур-
ной неустойчивости - нестабилизируемость имеет место только на незна-
чительных участках траектории полёта ступени в районе 20 и 108 с полёта;
364
365
- для варианта ступени, имеющей внешние размеры по баку окислите-
ля, соответствующие Ri = 1,16 м и по баку горючего R2 =1,13 м, структур-
ная неустойчивость появляется только в течение 4 с (12-16 с на рис. 12.6).
Очевидно, что с точки зрения обеспечения структурной устойчивости ва-
рианты изменения параметров 2 и 3 (рис. 12.5, 12.6) являются равноцен-
ными. Так как минимальные изменения параметров соответствуют вари-
анту 2, то для рассматриваемой ступени наиболее рациональными явля-
ются следующие наружные радиусы топливных баков: бака окислителя
Ri = 1,13 м, бака горючего R2 = 1,15 м. Отметим, что анализ структурной
устойчивости ступени с выбранными наружными размерами топливных
баков необходимо проводить с учётом возможных отклонений параметров
ступени от их номинальных значений (разделы 12.R12.3).
12.3. Обеспечение устойчивости движения путем выбора
конструкции топливного отсека
12.3.1. Рациональная форма двусвязных топливных баков
Топливные отсеки ряда космических ступеней выполнены в виде торо-
образных баков, расположенных вдоль продольной оси. Такие баки обес-
печивают минимальное удлинение ступеней, но ухудшают их динамичес-
кие свойства - ступени с торообразными баками собственно и структурно
неустойчивы на длительных участках траектории. Причинами ухудшения
динамических характеристик являются:
- наличие больших свободных поверхностей жидкости, значительно
удаленных от продольной оси топливного отсека;
- малая глубина жидкости;
- неблагоприятная центровка ступени (для ступеней, имеющих малый
вес полезного груза сг>О,757к).
Ступеням с последовательно расположенными торообразными баками
5?
соответствуют большие коэффициенты инерционной связи —,
Ц
5? X2
Рис. 12.8, 12.9 иллюстрируют зависимость инвариантов —, от
Р Р
метрии топливных ёмкостей. Значения инвариантов рассчитаны для
ливных баков ступеней, имеющих одинаковый вес космических объектов
и одинаковые компоненты топлива; различия центровочных и инерцион-
ных характеристик обусловлены только геометрией топливных баков.
X2
Наибольшие величины безразмерных силовых коэффициентов связи —
Р
л0
Ц *
гео-
топ-
366
имеют место для торообразных и конусообразных топливных полостей,
z- z- 11 Го
наибольшее значение безразмерных моментных коэффициентов - для
М
торообразных топливных ёмкостей. Характерной особенностью ступеней
с двусвязными полостями является резкое увеличение влияния подвижной
жидкости на движение ступени в конце полёта за счёт быстрого возраста-
ния величин гидродинамических моментов.
1. сфера
2. сосн. цилиндр
3. конус
4. чечевица
1. сфера
2. сосн. цилиндр
3. конус
4. чечевица
Рис. 12.9
Анализ движения ступеней с торообразными баками необходимо про-
водить с учётом основного тона колебаний.
При установке в топливный бак ступени демпфирующих устройств
в виде кольцевых и радиальных перегородок силовое воздействие тонов
колебаний жидкости в ячейках, образованных кольцевыми и радиальными
перегородками, нередко оказывается очень существенным и сравнимым
с силовым воздействием основного первого тона колебаний жидкости,
возникающего в баке без демпфирующих устройств. Для примера на
367
тО)2
рис. 12.10 приведены графики инвариантов —для первого основного то-
е - х(2)2
на колебании жидкости и первого симметрического тона —т-т-, возникно-
вение которого обусловлено установкой кольцевых перегородок в баках.
Рис. 12.10
Улучшение динамических характеристик ступени может быть достиг-
нуто уменьшением площади свободной поверхности жидкости и увеличе-
нием её глубины, что конструктивно реализуется заменой последователь-
ного расположения торообразных топливных баков концентрическим
(поперечное разделительное днище А заменяется продольной раздели-
тельной обечайкой В, рис. 12.3).
Такое расположение баков при неизменной внешней конфигурации
ступени обеспечивает:
- практически в два раза меньшую свободную поверхность жидкости
в баках;
- существенное увеличение глубины жидкости;
- возможность широкого варьирования соотношением свободных по-
верхностей жидкости в баках, так как форма разделительной обечайки В
может быть выбрана только из условия получения удовлетворительных
динамических характеристик ступени.
Для одной из разработанных ГКБ «Южное» ступеней проведен анализ
эффективности замены последовательно расположенных торообразных
баков концентрическими [174]. Оценка устойчивости и определение вели-
чины потребного демпфирования проводились путём расчётов на ЭЦВМ
и моделирования возмущённого движения ступени с подключением ре-
ального автомата стабилизации. Результаты расчётов корней характери-
стического уравнения разомкнутой системы и амплитудно-фазовых час-
тотных характеристик объекта управления для ступеней с последователь-
368
ным и концентрическим расположением топливных баков показывают
следующее.
При естественном демпфировании (5 = 0,001-0,003) ступень с после-
довательно расположенными баками характеризуется значительной
собственной динамической и структурной неустойчивостью (табл. 12.2
и рис. 12.11). Противоречивые требования к фазовой характеристике ав-
томата стабилизации предъявляются в течение » 70 с полёта. Собственная
динамическая неустойчивость ступени с концентрическими баками про-
является только в течение «20 с полёта (с 80 с по 88 с и с 100 с по 115 с;
табл. 12.3). Длительность участка структурной неустойчивости также со-
кращается (43 с по сравнению с 68 с; рис. 12.12).
Рис. 12.12
Величина демпфирования, необходимого для устойчивого полёта сту-
пени, определялась путём моделирования возмущения движения ступени
с учётом первого и второго тонов колебаний жидкости в баках.
369
Таблица 12.2
t aplO2 a2102 Pi p2 Di d2 t arlO2 a2102 pl p2 Di d2
0 0,214 0,376 2,93 3,98 0,411 0,929 64 0,385 0,075 2,49 2,59 2,110 -14,90
4 0,207 0,400 2,99 3,90 0,324 0,998 68 0,391 0,092 2,42 2,51 -2,750 -12,80
8 0,201 0,427 2,95 3,81 0,226 1,070 72 - - - - - -
12 0,199 0,412 2,92 3,72 0,192 1,010 76 - - - - - -
16 0,197 0,398 2,89 3,63 0,156 0,936 80 - - - - - -
20 0,196 0,378 2,86 3,57 0,152 0,809 84 0,173 -0,263 1,96 2,06 9,30 1,16
24 0,196 0,358 2,24 3,50 0,147 0,673 88 0,186 -0,198 1,81 1,97 9,36 0,162
28 0,198 0,328 2,80 3,39 0,172 0,496 92 0,203 -0,182 1,66 1,87 9,46 -0,190
32 0,199 0,301 2,76 3,29 0,190 0,302 96 0,232 -0,131 1,42 1,78 -10,20 -1,970
36 0,204 0,253 2,72 3,20 0,286 -0,182 100 0,280 -0,093 1,11 1,70 -11,80 -4,53
40 0,210 0,209 2,69 3,11 0,413 -0,832 104 0,309 -0,079 1,08 1,53 -15,40 -6,5
44 0,214 0,159 2,65 3,01 0,472 -2,060 108 0,398 -0,041 0,98 1,36 -12,00 -17,3
48 0,218 0,112 2,61 2,91 0,546 -4,120 112 -0,172 -0,208 1,37 1,09 3,32 5
52 0,244 0,040 2,58 2,80 0,929 -15,300 114 -1,280 0,047 1,02 0,649 2,94 33,80
56 0,320 0,031 2,55 2,69 1,680 30,60 - -1,320 0,048 0,998 0,640 2,80 33,9
а - вещественная часть корня характеристического уравнения,
JP - комплексная часть корня характеристического уравнения,
D - проекция диаметра окружности АФЧХ на мнимую ось.
Таблица 12.3
t ai-102 a2102 Pl P2 D, d2 t a,102 a2102 pl P2 D, d2
0 -0,186 -0,135 3,32 4,25 0,596 1,75 60 -0,0092 -0,126 3,01 4,00 0,220 1,63
4 -0,186 -0,134 3,31 4,26 0,560 1,76 64 -0,085 -0,200 2,96 3,94 0,710 1,06
8 -0,184 -0,134 3,29 4,27 0,523 1,76 68 -0,139 -0,118 2,92 3,89 0,687 1,56
12 -0,182 -0,134 3,28 4,27 0,461 1,75 72 -0,130 -0,112 2,86 3,82 1,01 1,48
16 -0,180 -0,133 3,25 4,27 0,399 1,74 76 -0,116 -0,104 2,81 3,74 1,57 1,38
20 -0,181 -0,147 3,24 4,26 0,349 1,60 80 0,102 -0,096 2,76 3,66 2,29 1,27
24 -0,180 -0,162 3,21 4,26 0,301 1,48 84 -0,079 0,083 2,68 3,53 4,82 1,02
28 -0,178 -0,147 3,20 4,25 0,276 1,60 88 -0,057 -0,071 2,59 3,41 7,02 0,725
32 -0,174 -0,133 3,18 4,23 0,249 1,73 92 -0,022 -0,052 2,48 3,23 24,70 -0,229
36 -0,173 -0,133 3,17 4,20 0,226 1,72 96 -0,010 -0,035 2,38 3,05 66,70 1,78
40 -0,172 -0,133 3,15 4,17 0,202 1,70 100 0,052 -0,012 2,25 2,80 16,50 11,8
44 -0,172 -0,133 3,13 4,17 0,179 1,69 104 0,082 0,004 2,12 2,55 12,00 48,2
48 -0,170 -0,131 3,11 4,10 0,156 1,68 108 0,110 0,001 1,91 2,21 10,80 260
52 -0,166 -0,130 3,08 4,07 0,151 1,66 112 0,132 0,043 1,68 1,84 10,30 1,75
56 -0,161 -0,128 3,05 4,04 0,058 1,63 115 0,145 0,065 1,50 1,60 9,50 3,5
Моделирование проводилось при настройках автомата стабилизации,
соответствующих точкам А и Б области устойчивости (рис. 12.13) и вели-
Исследования устойчивости ступени с последовательным расположе-
нием топливных баков показало, что при естественном демпфировании
устойчивость не может быть обеспечена ни при каких настройках авто-
мата стабилизации. При декрементах колебаний жидкости 5 = 0,4 в пер-
вом баке и 5 = 0,8 во втором область устойчивости в плоскости парамет-
ров Тдк^ к у остаётся узкой (границы I-I на рис. 12.13) и запасы на изме-
нение параметров автомата стабилизации небольшими. В случае учёта
влияния только первого тона колебаний жидкости приемлемая ширина
области устойчивости может быть получена при декременте колебаний
жидкости 8 = 0,7 в первом баке и 8 = 1,4 - во втором (границы 2-2 на
рис. 12.13). С учётом влияния второго тона колебаний жидкости область
устойчивости сужается и смещается в сторону больших коэффициентов
усиления. Для обеспечения достаточных запасов устойчивости необхо-
димо увеличение декремента колебаний жидкости по 1-му тону до вели-
чины 8^ = 2,0 при декременте колебаний по 2-му тону 8^ = 0,6 (гра-
ницы 4-4 на рис. 12.13).
Для варианта ступени с концентрическим расположением топливных
баков, даже при естественном демпфировании с учётом влияния только
первого тона колебаний жидкости, область устойчивости является доста-
точно широкой, но лежит в районе больших коэффициентов усиления. При
учёте второго тона область устойчивости сужается, что выражается в пере-
мещении верхней и нижней границ. Эти перемещения обусловлены силь-
372
ной связанностью 1-го и 2-го тонов колебаний жидкости. Совмещение гра-
ниц области устойчивости с положением, определяемым влиянием только
1-го тона колебаний, возможно при декременте колебаний по первому тону
= 0,4 (границы 3-3 на рис. 12.13). Для уменьшения коэффициентов
усиления и обеспечения достаточных запасов устойчивости необходимо
иметь декремент колебаний жидкости по первому тону = 0,2-0,4; по
второму тону = 0,3*Н),4 (границы 4-4 на рис. 12.13) Указанные значе-
ния декрементов колебаний жидкости необходимы не по всей высоте ба-
ков, а только начиная с уровней, соответствующих 64 с полёта.
Моделирование переходных процессов для варианта ступени с концен-
трическим расположением топливных баков проведено при настройках
автомата стабилизации, соответствующих точке Б, естественном демпфи-
ровании по 1-му тону (j/0 = 0,001-Н),003) и декременте колебаний по 2-му
тону = 0,2 -Н),4.
Для получения приемлемых переходных процессов и достаточной
ширины области устойчивости в параметрах автомата стабилизации Тдк,
Ку для ступени с концентрическим расположением топливных баков
требуется практически в 10 раз меньшее демпфирование по 1-му тону
колебаний жидкости, в 1,5^-2 раза меньшее демпфирование по 2-му тону,
чем для ступени с последовательным расположением торообразных топ-
ливных баков.
Применительно к рассмотренной выше ступени проводился весовой
анализ торообразных топливных баков концентрической формы с цилин-
дрической разделительной обечайкой. Концентрические топливные баки
с цилиндрической разделительной обечайкой (без демпферов) тяжелее
последовательно расположенных торообразных баков (без демпферов)
примерно на 24 кг. Однако для обеспечения приемлемых динамических
характеристик ступени с последовательно расположенными баками в них
необходима установка демпфирующих устройств весом не менее 50-^60 кг.
Таким образом, «сухой» вес ступени с концентрическими баками на
25-*-30 кг меньше «сухого» веса ступени с последовательно расположен-
ными торообразными баками. Кроме того, с увеличением количества ус-
танавливаемых в баки демпфирующих устройств, особенно сетчатого ти-
па, резко возрастают неиспользуемые остатки компонентов топлива (ос-
татки незабора). Остатки незабора практически входят в «сухой» вес
ступени. Использование концентрических торообразных баков с профи-
лированной разделительной обечайкой позволяет уменьшить конечный
вес ступени за счет уменьшения веса демпфирующих устройств и умень-
шения остатков незабора компонентов топлива.
373
12.3.2. Использование профилированных разделительных
перегородок и обечаек
Применение топливных баков концентрической формы (введение ци-
линдрической продольной разделительной обечайки вместо поперечного
днища) уменьшает гидродинамические силы и моменты и является эф-
фективным способом устранения собственной динамической неустойчи-
вости. Структурная неустойчивость ступени при этом может оставаться
значительной (рис. 12.12). Возможность устранения (или существенного
уменьшения) структурной неустойчивости основывается на использова-
нии особенностей конструкции топливного отсека. При использовании
концентрических баков, благодаря наличию в них разделительной обе-
чайки, изменение радиусов поверхностей жидкости в топливных полостях
может быть проведено без изменения наружного контура бака - путем
профилирования разделительной обечайки.
Профиль обечайки рассчитывается в соответствии со знаками частных
5/. dff
производных —',-----Проиллюстрируем целесообразность использо-
dxj dXj
вания профилированных обечаек на примере ступени, рассмотренной
в разделе 12.3.1. При наличии в концентрических топливных баках ци-
линдрической разделительной обечайки ступень структурно неустойчива
в течение 43 с. Значения частных производных от корней полиномов
FynFp по независимым параметрам показывают, что для устранения
структурной неустойчивости ступени целесообразно изменить радиусы
свободных поверхностей жидкости, начиная с 60 с полета так, как показа-
но пунктиром на рис. 12.3. Результаты анализа структурной устойчивости
показывают, что введение профилированной разделительной обечайки
сокращает участок структурной неустойчивости почти вдвое. Струк-
турная неустойчивость имеет место в течение 26 с (с 54 с по 80 с полета;
рис. 12.14).
Собственная динамическая неустойчивость при замене цилиндриче-
ской обечайки профилированной практически не меняется (ступени
с концентрическими торообразными баками, как правило, собственно ус-
тойчивы).
Уменьшение влияния колебаний жидкости на движение ступеней мо-
жет быть достигнуто за счет выделения в топливных баках отдельных по-
лостей. Сущность деления баков на полости заключается в следующем:
- в каждом баке ступени (или в одном из баков, если этого достаточ-
но) выделяется полость I, которая заполняется жидкостью полностью
(рис. 12.15);
374
- компонент расходуется сначала из полости II; в течение времени опо-
рожнения полости II жидкость в полости I не совершает колебательного
движения вследствие отсутствия в этой полости свободной поверхности;
- перелив жидкости из полости I в II происходит после опорожнения
полости II.
Разделение бака на плоскости I и II может быть проведено с помощью
кольцевой перегородки (рис. 12.15). В верхней части перегородка имеет
несколько отверстий d, окруженных стаканами Д, которые играют роль
дренажно-запорных клапанов [175]. Через отверстия d обеспечивается
дренаж полости I при заправке бака жидкостью (предполагается, что сту-
пень заправляется в вертикальном положении), а также наддув полости
при ее опорожнении.
Стаканы обеспечивают запаздывание в опорожнении полости I по
сравнению с опорожнением полости II. Перегородка устанавливается на
таком уровне, что при заправке обеспечивается полное заполнение полос-
ти I (через кольцевое отверстие Е) и частичное заполнение стаканов (через
375
отверстия d). Во время работы двигателя жидкость расходуется сначала из
полости II. Одновременно, вследствие расхода через отверстие d, проис-
ходит уменьшение объема жидкости и понижение ее уровня в стаканах.
После полного опорожнения хотя бы одного из стаканов газы наддува
проникают в плоскость I через отверстие d и происходит перетекание
жидкости из полости I в полость II через кольцевое отверстие Е. Расход
жидкости из стакана через отверстие d определяется выражением
Q = f(2g-Ahnx -p-F)05dt, где F- площадь отверстия, ЛЛ - разность уровней
о
жидкости в стакане и в полости II (отсчет уровней ведется от нижнего по-
люса бака), пх - осевая перегрузка, // - коэффициент расхода (ртах = 1).
Расчеты показывают, что при начальном объеме жидкости в стакане рав-
ном *100 см3 и диаметре отверстия d = 1 мм обеспечивается запаздывание
5(Н60 с.
Для уменьшения колебаний жидкости при опорожнении полостей II
из-за периодических прорывов газов наддува под нижней кромкой разде-
лительных перегородок можно использовать дренажные трубки, соеди-
няющие верхние части дополнительных полостей I с основными полостя-
ми бака II (рис. 12.16); нижний срез трубок расположен выше нижних
кромок разделительных перегородок [176].
В качестве примера рассмотрим улучшение динамических характери-
стик ступени с последовательно расположенными баками, при установке
в бак окислителя перегородки (рис. 12.15), ограничивающей 40 % заправ-
ляемого компонента. Изменение динамических свойств ступени оценим
путем сравнения величин коэффициентов связи, проверки перемежаемо-
сти корней уравнений F^=0 и Fp=0 и путем моделирования возмущенного
движения ступени с использованием действующего макета автомата ста-
билизации. Сравнение коэффициентов Ziit Fa для ступени с перегородкой
376
в баке окислителя и без нее (рис. 12.17) показывает, что введение перего-
родки существенно уменьшает коэффициенты связи и, следовательно,
степень собственной динамической неустойчивости. Результаты расчетов
перемежаемости корней показывают, что установка в бак окислителя раз-
делительной перегородки сокращает также длительность участка струк-
турной неустойчивости ступени. Нарушение перемежаемости корнейfb ft'
имеет место только в районе 20 с (рис. 12.18).
Рис. 12.17
Рис. 12.18
Проводилось моделирование движения ступени с разделительной пе-
регородкой в баке окислителя и без нее. Результаты моделирования дви-
жения ступени без разделительной перегородки показывают, что для
обеспечения устойчивости в топливные емкости ступени необходимо ус-
тановить демпфирующие устройства, реализующие декременты колеба-
ний 8i(1)=2,0.
377
Необходимость повышения демпфирования для варианта ступени
с разделительной перегородкой в баке окислителя определялась путем
анализа переходных процессов при значениях коэффициентов усиления
автомата стабилизации, соответствующих нижней границе области устой-
чивости. При отсутствии дополнительного (по сравнению с естественным)
демпфирования в баках окислителя и горючего движение ступени неус-
тойчиво. Увеличение декрементов колебаний жидкости до значений д ~
0,2 приводит к появлению области устойчивости, обеспечивающей запасы
на увеличение и уменьшение коэффициентов усиления К^,К^ «±20%
(границы I-I на рис. 12.19).
При увеличении декрементов колебаний до значений 8 ~ 0,4 за счет
перемещения верхней границы обеспечивается приемлемая ширина об-
ласти устойчивости (запасы на увеличение и уменьшение значений пара-
метров автомата стабилизации составляют ~ ± 33 %; границы 2-2 на
рис. 12.19). Переходные процессы в системе при значениях коэффициен-
тов усиления автомата стабилизации, соответствующих рабочей точке А,
а также точкам В и С, принадлежащим верхней и нижней границам облас-
ти устойчивости 2-2, иллюстрируются рис. 12.20, 12.21, 12.22. Примене-
ние разделительных перегородок исключает необходимость установки
в топливные баки ступеней большого количества демпфирующих уст-
ройств и в большинстве случаев приводит к снижению «сухого» веса.
В тех случаях, когда вес разделительных перегородок сравним с весом
демпфирующих устройств, реализующих высокий декремент колебаний
жидкости (3 > 1,0), использование перегородок все-таки целесообразно.
Установка в баки большого количества демпфирующих устройств (коль-
цевых и радиальных перегородок) существенно усложняет ступени как
объекты управления - увеличивается число осцилляторов (до нескольких
десятков), расширяется диапазон собственных частот. Аналитическое оп-
ределение гидродинамических характеристик топлива становится затруд-
нительным, экспериментальное определение длительно по времени и тре-
378
бует больших экономических затрат. В связи с большим количеством
близких по частоте колебательных звеньев усложняется проектирование
автомата стабилизации. Применение разделительных перегородок позво-
ляет избежать перечисленных трудностей и обеспечить устойчивость
движения ступени с помощью автомата стабилизации апробированной
схемы.
Рис. 12.21
Рис. 12.22
379
12.3.3. Выбор размеров и формы разделительных перегородок
Эффективность разделительных перегородок может быть повышена
путем профилирования их боковой поверхности. Отметим, что возможно-
сти в выборе профиля перегородок достаточно широки, так как форма пе-
регородок может быть выбрана только из условий обеспечения структур-
ной устойчивости ступеней. Рассмотрим метод построения разделитель-
ных перегородок с использованием областей структурной устойчивости в
плоскости параметров Z>, Z2 [106] на примере разделительных перегоро-
док в полостях торообразной формы. Траектория движения отображаю-
щей точки для ступени с такими баками располагается, в основном, в об-
ласти структурной неустойчивости (область 1 на рис. 12.23). Наиболее
близкой к области 1 является область структурной устойчивости 2, харак-
теризующаяся тем, что в этой области малые изменения параметров могут
привести к существенному изменению координат отображающей точки.
Это объясняется характером изменения основных гидродинамических ха-
рактеристик баков при малых уровнях компонентов топлива (например,
параметр С, ->оо при А, -»0). В области 2 в качестве «желаемой» может
быть выбрана любая траектория отображаемой точки. Наиболее удобно
эту траекторию выбрать удовлетворяющей условию Zi = Z2, которое после
преобразования с использованием метода вписанных цилиндров приобре-
тает вид CxROi + Хх = C2R02 + Х2. Учитывая, что
Ло.А-^А) ( Ч 2-^,3)
СЛ,- = А/ +----. Л< =---------------------------,
&QI
^01/31 (£1 п ) ^02/32(^2 д
получим hx +--------------- + Хх = А2 +-----°— + Х2,
(12.18)
^2 - корни уравнения =
Из шести переменных Я0;,А(1 г0, (/ = 1, 2) независимыми являются четы-
ре Яо/, г0/ (/ = 1, 2). Задавая конечные или начальные значения уровней в ба-
ках, все остальные значения рассчитываем по формуле
Л7+|=Л”±ДЛ,., 1 = 1,2, (12.19)
где п - номер шага расчета, ДА,. - приращение уровня, определяемое по
формуле ДА, =---2 i-------. Знак «+» в формуле (12.19) соответствует
ft(R Qi - г Qi)pt
случаю, когда в качестве А° принят конечный уровень компонентов топ-
лива, знак «-» - когда А,0 - начальный уровень.
380
ZrZ2=0
Траектории отображающих точек:
_______ В случае гладких баков
_______В случае баков с профилир.
разделительн. перегородками
Область структурной
^устойчивости 2rZi-Z2=0
1-1 .
Область структурной
неустойчивости
Рис. 12.23
Определение размеров и формы перегородок производим следующим
образом. Пусть в момент времени tn уровни компонентов топлива в ба-
ках имеют значения h” и h” (рис. 12.24); считаем, что три радиуса сво-
бодной поверхности определяются заданным при проектировании кон-
туром баков. Тогда внешний радиус свободной поверхности в первом
баке Я"о1 находится из соотношения (12.18). При этом должно выпол-
няться условие
г1я<Го1<ЛЯ1, (12.20)
где Ля1,гя - параметры, определяющие контур бака. Для момента времени
(/„ ± Д/) уровень жидкости в первом баке h”+i рассчитывается по формуле
(12.19), во втором баке - равен заданному Ля+1. После определения h” на-
ходим значение Яо1, соответствующее уровню hn+l и удовлетворяющее
уравнению (12.18) и условию (12.20). Описанные операции повторяются
шраз. Полученный ряд значений Я01 (Яя01 ,Яя+1о1/Toi) определяет профиль
перегородки.
381
Координаты точек
й” Я 01
А 0,37 1,02
Б 0,33 0,94
В 0,14 0,82
hn2 г 01
Г 0,48 0,66
д 0,43 0,66
Е 0,3 0,52
Если для некоторого момента времени не удается выбором выпол-
нить одновременно уравнение (12.18) и условие (12.20), то следует удов-
летворения этих условий добиваться выбором другого параметра, напри-
мер, считать заданными r0l,R0l, R02 и определять г02. Смена параметра
предполагает введение еще одной разделительной перегородки. Шаг рас-
чета выбирается в зависимости от требуемой точности.
В качестве примера для ступени С5М ракеты IIK68 по предлагаемому
способу рассчитаны размеры и форма разделительных перегородок. Ре-
зультаты расчетов иллюстрируются рис. 12.24, на котором указан расчет-
ный и выбранный (из конструктивных и технологических соображений)
профиль разделительной перегородки. Проверка эффективности исполь-
зования таких перегородок проводилась путем построения траектории
отображающей точки М на плоскости параметров Zi,Z2. Результаты рас-
чета свидетельствуют о структурной устойчивости ступени с профилиро-
ванными разделительными перегородками в топливных баках в течение
всего времени полета (рис. 12.23).
С целью анализа качества процессов стабилизации проводилось моде-
лирование возмущенного движения ступени с разделительными перего-
родками выбранного профиля в топливных баках. Построение областей ус-
тойчивости показало, что при значениях декрементов колебаний жидкости
в полостях 1 и 2 бака окислителя = £2i =0.2 ив полостях 3, 4 бака горю-
чего д2 = &2 = ®-1 запасы на увеличение и уменьшение коэффициентов
усиления автомата стабилизации составляют ± 50%, что является достаточ-
382
ным. Осциллограммы рис. 12.26-42.28 иллюстрируют переходные процес-
сы, которые имели место при номинальных значениях коэффициентов уси-
ления автомата стабилизации (рис. 12.26), значениях, соответствующих
верхней (рис. 12.27) и нижней (рис. 12.28) границам области устойчивости.
Для сравнения на рис. 12.25 представлены процессы стабилизации сту-
пени при естественном демпфировании в основных и дополнительных
полостях.
Конструкторские проработки показывают, что суммарный вес внутри-
баковых устройств при использовании профилированных разделительных
перегородок уменьшается на 20 % по сравнению со случаем, когда устой-
чивость движения обеспечивается только демпферами.
383
12.4. Анализ эффективности использования
разделительных перегородок
по результатам натурного эксперимента
В разделе 12.3 предложены методы улучшения динамических свойств
космических ступеней, основанные на рациональном выборе размеров
и формы свободной поверхности жидкости в баках. Показана (с использо-
ванием теоретических значений гидродинамических характеристик жид-
кого наполнения топливных баков) эффективность методов, в частности,
эффективность использования разделительных перегородок. Ниже это
подтверждается на основе результатов эксперимента.
12.4.1. Описание экспериментальных емкостей
Емкости, предназначенные для экспериментального определения гид-
родинамических характеристик жидкости в полостях, содержащих разде-
лительные перегородки, были изготовлены на основе штатного топливно-
го отсека космической ступени изделия 11К68. Общий вид эксперимен-
тальных емкостей показан на рис. 12.29 (топливный бак окислителя) и на
рис. 12.30 (топливный бак горючего).
Теоретическая геометрия внутренних полостей, размеры полостей и
толщины оболочек экспериментальных емкостей выполнены такими же,
как и у штатных баков. Штатными являются также разделительные диа-
фрагмы (поз. 3, рис. 12.29, 12.30) и детали заборных устройств. Конструк-
тивные элементы топливного отсека, не относящиеся к конструкции внут-
ренних полостей, в состав экспериментальных узлов не включены.
Внутри экспериментальных емкостей вместо штатных демпферов коле-
баний жидкости установлены профилированные разделительные перего-
родки (поз. 6), с помощью которых в каждой емкости выделены основные
и дополнительные полости. Профиль разделительных перегородок, их тео-
ретические размеры выбирались по методу, описанному в разделе 12.3.
384
Бак окислителя
Рис. 12.29
7
корпус нижний
корпус верхний
диафрагма
заборное устройство
сетка
разделительная перегородка
дренажная трубка
Бак горючего
Рис. 12.30
1 корпус нижний
2 корпус верхний
3 диафрагма
4 заборное устройство
5 сетка
6 разделительная перегородка
7 дренажная трубка
8 ребро (демпфер)
9 ребро (демпфер)
Экспериментальные емкости окислителя и горючего изготовлены
в виде раздельных узлов, собранных независимо друг от друга, что обес-
печивает возможность их одновременного испытания на различных стен-
дах. Для удобства проведения работ корпуса ёмкостей сделаны разъём-
ными. Для обеспечения полного наполнения узлов жидкостью они уком-
плектованы дренажными штуцерами и трубопроводами. В нижних точках
ёмкостей имеются штуцера для слива жидкости при вертикальном и гори-
зонтальном положения узлов. Эти штуцера и заборные патрубки распола-
гаются в диаметрально противоположных точках ёмкостей. Дренажные
и сливные штуцера закрываются заглушками.
Экспериментальные ёмкости укомплектованы штуцерами для подсое-
динения указателей уровней. К штуцерам, расположенным в нижних точ-
ках ёмкостей окислителя и горючего, подсоединяются указатели уровней
в основных полостях. Эти указатели в верхней своей части сообщаются
с атмосферой. Для указателей уровней жидкости в дополнительных полос-
тях в каждой ёмкости имеется два штуцера: один - ниже нижней кромки
разделительной перегородки, второй - в верхней точке дополнительной
полости. Штуцера располагаются в вертикальных радиальных полостях
ёмкостей и позволяют удобное присоединение указателей уровней, кото-
рые для обеспечения условий эксперимента выполняются герметичными.
Для заполнения полостей топливом экспериментальные ёмкости снабжены
патрубками диаметрами 50 мм. Фланцы патрубков закрыты заглушками.
Измерение параметров колебаний жидкости в баках производится
струнными датчиками уровней: шесть датчиков (ДУ-1 -s- ДУ-6) установле-
ны в баке окислителя и восемь датчиков (ДУ-1 -s- ДУ-8) установлены в ба-
ке горючего. Расположение датчиков указано на рис. 12.31, 12.32. Струны
датчиков изолированы от корпуса и соединены с наружными контактами.
В местах прохода струн через диафрагму в последней предусмотрены ок-
на, закрытые пластинами из органического стекла с отверстиями для
струн.
Рис. 12.31
387
12.4.2. Постановка и результаты эксперимента
Экспериментально определялись следующие гидродинамические ха-
рактеристики жидкости в баках.
1. Собственные частоты колебаний жидкости в основных и дополни-
тельных полостях как функции уровня заправки.
2. Логарифмические декременты колебаний жидкости как функции
амплитуды колебаний и уровня заправки.
3. Положение метацентра системы «бак с жидкостью» для различных
уровней заправки.
4. Присоединённые моменты инерции жидкости при колебаниях бака
относительно поперечной оси, проходящей через метацентр системы.
5. Амплитудно-частотные характеристики (АЧХ) баков с жидкостью при
возбуждении колебаний в поступательном движении и вращательном дви-
жении относительно поперечной оси, проходящей через метацентр системы.
6. Зависимость силы реакции баков с жидкостью от частоты возбуждения.
Определялись также вспомогательные данные:
- веса «сухих» баков и оснастки для каждого вида испытаний;
- моменты инерции «сухих» баков с оснасткой относительно попереч-
ной оси, проходящей через метацентр системы.
Гидродинамические характеристики жидкости в основных полостях
определялись для следующих уровней заправки этих полостей:
- полости бака окислителя h =0,480 м; 0,330 м; 0,200 м;
- полости бака горючего h =0,480 м; 0,300 м;
- при полностью заполненных дополнительных полостях.
Характеристики жидкости в дополнительных полостях определялись
для уровней:
- в полости бака окислителя h =0,3 м; 0,25 м;
- в полости бака горючего h= 0,3 м; 0,48 м.
Уровни в основных полостях при этом поддерживались постоянными
и равными:
- в полости бака окислителя - 0,15 м,
- в полости бака горючего - 0,25 м.
388
Для определения собственных частот и логарифмических декрементов
поперечных колебаний свободной поверхности жидкости использовался
метод колебаний [106]. Баку, установленному на кинематическом стенде,
сообщались гармонические колебания в поперечном направлении. В резо-
нансном режиме проводилась остановка системы и струнными датчиками
уровня фиксировался процесс свободных затухающих колебаний иссле-
дуемого тона. Схема стенда и направления перемещений бака показаны на
рис. 12.33. Исследования проводились для первых и вторых тонов колеба-
ний жидкости в основных и дополнительных полостях, образованных раз-
делительными перегородками и стенками торообразных баков. Результа-
ты определения собственных частот колебаний (в поле силы земного тя-
готения) и логарифмических декрементов колебаний приведены на
рис. 12.34-^-12.36 и показывают, что экспериментальные значения частот
колебаний топлива меньше соответствующих расчётных значений. Экспе-
риментальные значения логарифмических декрементов колебаний жидко-
сти превышают расчетные в 2-3 раза.
389
Рис. 12.35
Положение метацентра системы «бак с жидкостью» для каждого уров-
ня заправки определялось по замерам опрокидывающих или восстанавли-
вающих моментов при разной высоте установки цапф подвески от нижних
полюсов баков. Координаты метацентра, соответствующие равенству ука-
занных моментов нулю, как функции уровней заправки, представлены на
рис. 12.37.
Присоединённый момент инерции жидкости находился как разность
между суммарным моментом инерции системы «бак с жидкостью» и мо-
ментом инерции «сухого» бака с оснасткой. Момент инерции системы
«бак с жидкостью» определялся путём возбуждения колебаний системы
относительно поперечной оси, проходящей через метацентр системы. Ес-
ли известны собственная частота системы (определяется методом сво-
бодных колебаний или по АЧХ системы) и угловая жёсткость пружины
390
Су, которая вводится в систему для создания восстанавливающего мо-
мента, то момент инерции системы равен
г и.
ст*[<ц2-стг(1-&01)]
При
/’+/«%
(12.21)
(12.22)
Аналогично находится момент инерции «сухого» бака с оснасткой.
Значения присоединенных моментов инерции жидкости в баках
окислителя и горючего для различных уровней заправки приведены на
рис. 12.37.
Испытания для построения амплитудно-частотных характеристик, со-
ответствующих поступательным и вращательным колебаниям системы
«бак с жидкостью», проводились при кинематическом и электродинами-
ческом возбуждении. Схемы испытаний приведены на рис. 12.33, 12.38.
Для построения амплитудно-частотных характеристик — = f (б»), — = f {со)
F F
колебания возбуждались с помощью вибратора при постоянной по ампли-
391
туде силе. В процессе установившихся вынужденных колебаний произво-
дилась запись перемещений баков и колебаний свободной поверхности.
Для каждого исследуемого уровня указанные параметры записывались
с помощью шлейфового осциллографа по показаниям струнных датчиков
уровня и датчика перемещений. Произведенные записи послужили осно-
вой для построения АЧХ системы в диапазоне исследуемых частот. На
рис. 12.39 в качестве примера приведены АЧХ бака окислителя с жидко-
стью; уровень заправки 0,330 м.
Определение зависимости силы реакции баков с жидкостью от частоты
возбуждения производилось при возбуждении гармонических колебаний
в поперечном направлении с помощью кинематического привода. Ампли-
туда перемещений обеспечивалась постоянной. В режиме установивших-
ся вынужденных колебаний производилась запись амплитуды силы реак-
ции бака с жидкостью, перемещений бака и колебаний свободных по-
верхностей с помощью датчиков сил, датчиков перемещений и датчиков
уровней. По произведенным записям были построены амплитудно-
частотные характеристики — = /(#)• На рис. 12.39 иллюстрируются АЧХ,
соответствующие линейным и угловым колебаниям бака.
Амплитудно-частотные характеристики имеют резонансные пики на
частотах, соответствующих собственным частотам системы «бак с жидко-
стью»; число пиков (три) соответствует числу колебательных звеньев, вы-
явленных в диапазоне частот колебаний жидкости. Минимумы амплитуд-
ной характеристики соответствуют собственным частотам колебаний
жидкости. Демпфирование колебаний оказывает сильное влияние только
на величину-резонансных пиков и минимумы амплитудно-частотной ха-
рактеристики. С ростом номера тона колебаний амплитуды резонансных
пиков существенно убывают.
392
-ч| €
Рис. 12.39
12.4.3. Обработка и анализ результатов эксперимента
Экспериментально определён момент инерции жидкости относительно
поперечной оси, проходящей через метацентр системы «бак с жидкостью»
(рис. 12.37). По результатам эксперимента определялись присоединённый
момент инерции жидкости относительно поперечной оси, проходящей че-
рез полюс бака, и инварианты % = % / .
Присоединённый момент инерции жидкости относительно полюса ба-
ка получен пересчётом по формуле
Ii=rGi-XfGi{XfGi-2XGi), (12.23)
где - присоединённый момент инерции жидкости относительно попе-
речной оси, проходящей через метацентр системы «бак окислителя с жид-
костью» («бак горючего с жидкостью»);
Xgi - координата метацентра системы «бак окислителя с жидкостью»
(«бак горючего с жидкостью»), отсчитанная от полюсов баков;
- координата метацентра бака окислителя (горючего).
^=^хр0,хЛ(5/Л05, (12.24)
1аа - присоединённый момент инерции, полученный для полости, за-
полненной водой, с характерным размером Ro = 0,764 м.
Координата метацентра бака окислителя (горючего) рассчитывалась
теоретически по методу вписанных цилиндров (рис. 12.40). Результаты
расчётов присоединённого момента инерции представлены на рис. 12.41.
Рис. 12.40
394
Сравнение присоединённых моментов инерции полученных по
экспериментальным данным и по методу вписанных цилиндров, показы-
вает существенное превышение экспериментальных значений над теоре-
тическими. Указанное расхождение может быть объяснено тем обстоя-
тельством, что при расходе топлива из дополнительной полости экспери-
ментально может быть определён лишь суммарный момент инерции, со-
ответствующий основной и дополнительной полостям. Разделение
результатов по полостям (основным и дополнительным) не представляет-
ся возможным.
Для определения с использованием данных эксперимента инвариантов
/. = —, характеризующих динамические свойства тела с жидкостью на
/Л*
частотах колебаний жидкости, использовался частотный метод, сущность
которого заключается в следующем [106].
Уравнения свободных колебаний системы «бак — жидкость» с учётом
двух тонов колебаний жидкости и упругости элементов крепления имеют
вид:
- для поступательного движения в поперечном направлении
(12.25)
- для вращательного движения относительно поперечной оси
(J° + J)(y + Буф + су* у) + ZX01ri = 0,
у=1
• М1(п +е/1 +<o*rl) + Zol(|/ = 0, (12.26)
Ц2О2 + е2г2 + <o2r2) + X02tj> = 0.
Здесь z»z»z - параметры поступательного движения системы «бак —
жидкость»,
г,г,г - параметры движения жидкости в баке,
°" - собственная частота колебаний системы, обусловленная упруго-
стью крепления,
395
_ коэффициенты, характеризующие присоединённую массу
жидкости.
Полагая в уравнениях (12.25), (12.26) демпфирование малым, будем
искать частное решение в виде:
z = zoeat, r}=rQiea\ r2=r02eat. (12.27)
Подставляя (12.27) в (12.25), получим
2 2 Л 2 Л 2 л
zoa +<t„z0+ о roi« + о f02a =0,
т + т т + т
j
z01a2 +®i2r0i +—z0a2 =0,
Ai
Z02#2 +^2г02 + —=0,
А2
отсюда
zQa2 _ ^2 zQa2
Г01 Ai а2 + cd2 ’ °2 ^2 а2 + а>22
Если
Предположим,
а «-^/2 4-/ет. Подставляя это значение а в (12.28) и отделяя действи-
тельную и мнимую часть, а также пренебрегая членами второго порядка
малости, получим уравнения:
1 + Z1 2+Х2 2=0’ f'
-ах ^-ах (1229)
^2 . v_п
396
Уравнения использовались для вычисления коэффициентов инерцион-
ных связей. При этом собственные частоты колебаний системы и жидко-
сти определялись по провалу и пику экспериментальной амплитудно-
частотной характеристики.
о2 /
Графики инвариантов полученные описанным способом, приве-
дены на рис. 12.42, 12.43. На графиках контурными линиями указаны зна-
чения, построенные по данным эксперимента; пунктирными - получен-
ные путём экстраполяции. При экстраполяции учитывались конструктив-
ные особенности полостей - наличие рёбер, сеток и т. д., а также величи-
ны предельных значений при минимальном и максимальном возможных
уровнях топлива в баках.
Рис. 12.43
12.4.4. Расчёт коэффициентов уравнений движения
Для анализа устойчивости ступени С5М IIK68, имеющей разделитель-
ные перегородки в топливных баках, использовалась динамическая схема
в виде (глава 8):
397
Z = alvW + £ alrfi + azS8,
1=1
V = a„V + S a„r,n + avs5> ‘ = 1 > 2- (12.30)
i=l
rt + Ef. 4- бу/г = az 4- aryij/.
Коэффициенты уравнений возмущённого движения рассчитывались
с использованием экспериментальных значений гидродинамических ха-
рактеристик по формулам, приведенным в главе 9. Момент инерции сту-
пени относительно поперечной оси, проходящей через метацентр ступени,
и положение метацентра рассчитывалось по формулам:
2
JG=JZ- m(XG - Хт )2 + Z(-L - Л) - т- PoiRoi О - - Хт),
/=1 w, 2
2
XG=XT+^----------, 5,= -^. (12.31)
4/И Л;
При расчёте коэффициентов предполагалось, что основные и дополни-
тельные полости баков опорожняются последовательно. Расход топлива
проводится сначала из основных полостей (в течение 83 с из полости бака
окислителя и 61 с из полости бака горючего), а затем из дополнительных.
Во время опорожнения основных полостей дополнительные заполнены
жидкостью полностью. При опорожнении дополнительных полостей уро-
вень жидкости в основных полостях остаётся неизменным.
Соответствие уровней жидкости в топливных ёмкостях моментам вре-
мени полёта устанавливалось с помощью тарировочных характеристик ба-
ков (рис. 12.44) и графиков изменения объёмов жидкости в баках по време-
ни полёта. Изменение уровня по времени полёта для описанной
выше последовательности опорожнения иллюстрируется кривыми I
(рис. 12.45, 12.46). Для сравнения показаны также кривые II, характери-
зующие изменение уровней в баках в случае быстрого перетекания жидко-
сти из дополнительных полостей в основные (до выравнивания уровней) в
моменты опорожнения основных полостей до уровней hk.
398
Рис. 12.45
Величины безразмерных гидродинамических коэффициентов рас-
считывались по экспериментально полученным значениям инвариантов
—. При этом значение X, принималось равным единице.
А;
Значение безразмерного гидродинамического коэффициента Х& рас-
считывалось по формуле
/7 । 2-ch^)
. 1 .
Значения собственных частот и коэффициентов демпфирования коле-
баний жидкости в топливных баках, соответствующие различным момен-
там времени полёта, определялись по формулам
2 Л 2 /-2
Roi ' *
с использованием экспериментальных данных, представленных
на рис. 12.34-42.36. Здесь W - кажущееся ускорение ступени. Результаты
расчётов коэффициентов уравнений возмущённого движения приведены
в табл. 12.4.
399
12.4.5. Анализ устойчивости
Исследование устойчивости движения ступени проводилось с исполь-
зованием экспериментальных значений гидродинамических характери-
стик путём расчёта корней характеристического уравнения ступени как
объекта регулирования в диапазоне частот колебаний топлива, функции у,
диаметров АФХ объекта и траектории отображающей точки на плоскости
параметров Zi и Z2. Результаты расчётов представлены в табл. 12.5, на
рис. 12.47 и показывают, что ступень в течение всего времени полёта соб-
ственно динамически устойчива, причём модули корней характеристиче-
ского уравнения существенно меньше, чем при расчётах с использованием
теоретических значений безразмерных коэффициентов. Существенно
меньше стали и диаметры окружностей амплитудно-фазовых характери-
стик объекта. Объясняется это тем, что, во-первых, экспериментальные
значения логарифмических декрементов колебаний жидкости оказались
выше расчётных и, во-вторых, более рациональным стало соотношение
частот колебаний жидкости в баках.
Рис. 12.47
Траектория отображающей точки на плоскости параметров Zi и Z2
находится в течение всего рабочего времени полёта ступени в области
структурной устойчивости. В целом проведенные расчёты свидетельст-
вуют о целесообразности использования разделительных перегородок
для устранения дестабилизирующего воздействия подвижности топли-
ва. Оценка устойчивости ступени С5М ракеты IIK68, выполненная с ис-
пользованием характеристик жидкости, определённых эксперименталь-
но, показывает, что установка разделительных перегородок обеспечива-
ет собственную и структурную устойчивость ступени как объекта
управления.
400
Таблица 12.4
t ~a'ir Ю azy/ -<•10 ^^<5
с м • с"1 м • с~2 м • с2 с' с2
0 0,196 16,2 0,309 0,119 0,643
4 0,196 16,4 0,316 0,107 0,594
8 0,201 16,9 0,323 0,107 0,600
12 0,207 17,3 0,331 0,108 0,606
16 0,213 17,7 0,338 0,110 0,612
20 0,220 18,2 0,347 0,111 0,620
24 0,228 18,6 0,355 0,113 0,626
28 0,236 19,1 0,364 0,115 0,634
32 0,245 19,6 0,374 0,116 0,640
36 0,254 20,1 0,384 0,116 0,643
40 0,263 20,7 0,395 0,116 0,644
44 0,274 21,3 0,406 0,115 0,643
48 0,285 21,9 0,418 0,114 0,640
52 0,296 22,5 0,430 0,114 0,641
56 0,306 23,2 0,444 0,112 0,643
60 0,317 24,0 0,458 0,110 0,638
64 0,334 24,8 0,473 0,131 0,694
68 0,335 25,6 0,489 0,128 0,706
72 0,337 26,5 0,506 0,124 0,721
76 0,344 27,5 0,525 0,121 0,737
80 0,355 28,6 0,550 0,117 0,744
84 0,394 29,7 0,566 0,123 0,716
88 0,448 30,9 0,589 0,094 0,531
92 0,448 32,2 0,615 0,094 0,530
96 0,525 33,7 0,643 0,089 0,505
100 0,559 35,3 0,673 0,093 0,479
104 0,593 40,0 0,706 0,087 0,507
108 0,633 38,9 0,743 0,084 0,487
112 0,678 41,02 0,783 0,080 0,468
114 0,701 42,2 0,805 0,077 0,455
401
Продолжение табл. 12.4
t "°-, ~av й)2 л
с I лГ1 I лГ1 с-2 м • с1
0 0,335 0,054 0,001 0,15 10 14,8 0,172
4 0,342 0,066 0,001 0,19 10 14,8 0,181
8 0,350 0,067 0,001 0,21 10 14,9 0,190
12 0,356 0,071 0,001 0,27 10 14,9 0,199
16 0,366 0,075 0,001 0,37 10 14,9 0,208
20 0,375 0,078 0,002 0,55 10 14,9 0,217
24 0,385 0,081 0,002 0,11 10 14,9 0,225
28 0,394 0,085 1,34 0,485 14,8 0,234
32 0,405 0,089 1,32 0,496 14,8 0,244
36 0,415 0,093 1,18 0,477 14,7 0,255
40 0,427 0,098 1,06 0,444 14,7 0,265
44 0,439 0,103 0,957 0,426 14,6 0,275
48 0,452 0,108 0,866 0,411 14,5 0,284
52 0,456 0,113 0,786 0,398 14,5 0,295
56 0,450 0,116 0,716 0,389 14,5 0,306
60 0,445 0,119 0,652 0,382 14,5 0,316
64 0,411 0,107 0,600 0,331 14,9 0,331
68 0,363 0,110 0,495 0,315 15,3 0,346
72 0,308 0,107 0,409 0,297 15,4 0,359
76 0,256 0,105 0,350 0,302 15,0 0,366
80 0,221 0,126 0,311 0,382 13,1 0,352
84 0,613 0,509 0,389 0,785 9,57 0,660
88 0,636 0,353 0,697 1,40 9,41 0,490
92 0,653 0,380 0,518 1,17 8,85 0,398
96 0,667 0,430 0,389 1,100 7,90 0,338
100 0,670 0,476 0,238 0,821 7,13 0,285
104 0,683 0,388 0,253 0,700 8,64 0,330
108 0,701 0,413 0,240 0,764 8,20 0,357
112 0,717 0,446 0,226 0,843 7,72 0,380
114 0,723 0,464 0,231 0,942 7,42 0,390
402
Окончание табл. 12.4
t azr2 ^2 -ar2z ar2V
с I I c-2 м • c~!
0 0,183 -0,046 0,66 10 -0,23 10 14,2 0,468
4 0,187 0,026 0,61 10 0,13 10 9,93 0,380
8 0,191 0,029 0,85 10 0,2 10 9,94 0,369
12 0,195 0,028 0,001 0,34 10 10,1 0,362
16 0,200 0,023 0,008 0,001 10,6 0,358
20 0,205 0,017 1,20 0,164 11,0 0,353
24 0,210 0,012 1,20 0,109 11,5 0,348
28 0,215 0,006 1,28 0,485 12,0 0,343
32 0,221 0,005 1,12 0,044 12,2 0,333
36 0,227 0,001 1,02 0,082 12,1 0,319
40 0,233 0,017 0,896 0,117 11,9 0,304
44 0,240 0,024 0,788 0,149 11,7 0,289
48 0,247 0,033 0,691 0,184 11,4 0,273
52 0,254 0,046 0,590 0,219 11,0 0,255
56 0,262 0,065 0,497 0,259 10,6 0,236
60 0,270 0,088 0,417 0,288 9,99 0,217
64 0,129 -0,047 0,721 -0,556 26,5 0,444
68 0,095 -0,035 1,08 -0,842 29,8 0,579
72 0,066 -0,024 1,08 -0,813 31,6 0,690
76 +0,053 -0,017 1,010 -0,665 30,2 0,766
80 +0,042 -0,010 0,884 -0,455 27,1 0,835
84 0,329 0,104 0,362 0,280 12,0 0,258
88 0,337 0,074 0,302 0,285 11,5 0,311
92 0,347 0,083 0,253 0,236 11,0 0,311
96 0,359 0,092 0,215 0,240 10,6 0,336
100 0,373 0,106 0,182 0,252 10,1 0,359
104 0,381 0,135 0,158 0,273 9,6 0,380
108 0,390 0,156 0,138 0,296 9,02 0,397
112 0,397 0,182 0,117 0,321 8,29 0,408
114 0,400 0,198 0,107 0,335 7,87 0,411
403
Таблица 12.5
t, с т «1 а2 Р> Р2 D1 D2
0 0,884 -0,234 -0,088 3,77 3,85 0,217*10"* 0,491*10"*
4 5,89 -0,209 -0,093 3,47 3,85 0,520*10’5 0,521*10"*
8 2,03 -0,185 -0,098 3,15 3,85 0,254*10"* -0,547*10"*
12 -0,599 -0,182 -0,103 3,21 3,84 0,115* 10'3 0,724*10"*
16 -0,480 -0,179 -0,112 3,26 3,84 0,183*10'3 0,915*10"*
20 -0,216 -0,207 -0,155 3,75 3,85 0,014 0,506* 10’2
24 -9,64 -0,142 -0,199 3,82 3,92 0,191*10’2 0,116*10'
28 84,4 -0,166 -0,576 3,59 8,36 0,016 0,021
32 62 -0,163 -0,508 3,63 7,85 0,018 0,024
36 50,6 -0,158 -0,392 3,60 6,89 0,016 0,031
40 48,8 -0,152 -0,321 3,57 6,23 0,013 0,038
44 63,6 -0,146 -0,273 3,53 5,72 0,842*10'2 0,045
48 133 -0,139 -0,243 3,48 5,36 0,36*10’2 0,051
52 -47,2 -0,129 -0,216 3,40 5,01 0,962* 10’2 0,059
56 -17,1 -0,118 -0,199 3,31 4,76 0,025 0,062
72 0,42 -0,179 -0,381 4,09 5,83 0,033 0,275*10'2
76 0,373 -0,181 -0,415 4,02 5,57 0,029 0,207*10'2
80 0,124 0,165 -0,440 3,93 5,33 0,046 0,107*10’2
84 16,3 -0,167 -0,342 3,49 4,13 0,010 0,037
92 -1042 -0,159 -2,26 3,46 14,0 1,018 0,023
96 -251 -0,174 -1,03 3,23 7,14 0,016 0,060
100 -1,56 -0,158 -0,228 2,87 5,57 0,041 0,023
104 -5,73 -0,175 -0,246 3,02 3,64 0,996* 10’2 0,023
108 -6,66 -0,188 -0,272 2,94 3,58 0,912*10'2 0,023
112 -8,22 -0,196 -0,294 2,83 3,50 0,756*10’2 0,022
404
Часть 6
РАКЕТА КАК ОБЪЕКТ УПРАВЛЕНИЯ
БОРТОВОЙ ЦВМ
В части 6 настоящей книги проведен краткий сравнительный анализ
сложившегося к середине 70-х годов XX века состояния в США и СССР
стратегических ракетно-ядерных сил наземного базирования. Показана
необходимость разработки в Советском Союзе новых ракетных комплек-
сов четвертого поколения как адекватная реакция на создание США ком-
плекса «М-Х».
Аналогичная весьма напряженная обстановка была и раньше - в конце
60-х - начале 70-х годов - когда, несмотря на меньшую численность раз-
вернутых пусковых установок МБР «Минитмен» (см. главу 6), они пред-
ставляли серьезную угрозу стратегической группировке ракет наземного
базирования СССР и, соответственно, обороне страны в целом.
Такое положение в основном определялось следующими обстоятель-
ствами:
1. В два-три раза более высокой точностью попадания боевых блоков
в цель.
2. Значительно меньшим временем боеготовности - 32 с вместо 4-5 мин.
3. Наличием примерно на половине группировки ракет «Минитмен»
(на «М-Ш») трехблочной разделяющейся головной части с индивидуаль-
ным наведением ББ на цель (РГЧ ИН). В результате число боеголовок
в американской группировке превосходило количество (но не мощность)
ББ, установленных на советских ракетах.
Достижение всех этих, определяющих боевую эффективность, качеств
стало возможным в первую очередь благодаря применению в системе
управления ракет бортовой цифровой вычислительной машины (БЦВМ),
а именно:
1. Существенное повышение точности стрельбы получено за счет реа-
лизации полетных алгоритмов с практически нулевой методической
ошибкой наведения на цель, а также в результате значительного умень-
405
шения влияния инструментальных погрешностей, путем выработки по-
правок в «полетное задание», рассчитанных БЦВМ по результатам систе-
матического масштабирования командных приборов в процессе боевого
дежурства в «нулевой» готовности.
2. Сокращение времени пуска ракеты из полной боевой готовности
достигнуто за счет боевого дежурства в «горячем» состоянии, т. е. с не-
прерывно работающим командным «ядром» - комплексом командных ги-
роскопических приборов и БЦВМ. (Эксплуатационные, энергетические,
экономические и др. характеристики ракетного комплекса при этом зна-
чительно ухудшаются).
3. Возможность индивидуального высокоточного наведения ББ на
цель обеспечивалась работой систем стабилизации, наведения и навига-
ции по достаточно сложным («гибким») алгоритмам, реализация которых
требовала высокого быстродействия и больших объемов долговременной
и оперативной памяти вычислительной машины.
Для достижения паритета и, более того, превосходства в ракетно-
ядерном соревновании двух сверхдержав (точнее, в гонке вооружения в
разгар «холодной войны») была разработана по результатам проведенно-
го ряда научно-исследовательских работ (НИР) концепция и программа
создания ракетных комплексов МБР третьего поколения. Реализация
этой программы обеспечила резкое повышение боевой эффективности
группировки комплексов МБР, поскольку в результате их модернизации,
кроме существенного улучшения трех вышеуказанных основных ТТХ
(см. главу 6), была значительно повышена степень защищенности ракет в
ПУ, а также увеличена вероятность прохождения ББ к цели в условиях
действия противоракетной обороны противника, за счет применения в
составе боевого оснащения развитого комплекса средств преодоления
(КСП ПРО).
Наряду с этим:
• значительно повышена надежность;
• улучшены эксплуатационные характеристики;
• оптимизированы стоимостно-временные затраты на модерниза-
цию РК;
• улучшены многие другие параметры, за счет применения миномет-
ного старта жидкостных ракет из транспортно-пускового контейне-
ра (ТПК), с установкой на нем проверочно-пусковой аппаратуры и
сборкой ТПК в условиях ракетного завода (см. «Введение»).
Как уже указывалось, многие из этих достижений стали возможны
благодаря использованию в составе системы управления бортового циф-
рового вычислительного комплекса (БЦВК) в сочетании с наземным
(НЦВК), устанавливаемым на ТПК.
406
Особенности построения систем управления на базе цифрового вычис-
лительного комплекса в настоящее время опубликованы в достаточно
большом количестве специальной и общетехнической литературы. Наи-
более полный материал с освещением всех аспектов проблемы содержит-
ся в [54].
В монографии Я. Е. Айзенберга, В. Г. Сухореброго [7] в основном рас-
смотрен круг задач проектирования систем стабилизации (СС) ракет, сис-
темы управления которых построены на базе БЦВМ. В этом труде особое
внимание уделено синтезу корректирующих алгоритмов и инженерным
методам проектирования СС носителей КА с учетом действия на них всей
совокупности возмущений.
В настоящей книге ограничимся приведением нескольких характерных
примеров использования возможностей БЦВМ для решения конкретных
нетрадиционных задач, возникших в ГКБ «Южное» при динамическом
проектировании боевых ракет и ракет-носителей.
407
Раздел 6.1
РГЧ И БЦВМ НА РАКЕТАХ ГКБ «ЮЖНОЕ»
До изложения материала, соответствующего в полной мере заглавию
настоящего раздела книги, считаем целесообразным для «полноты карти-
ны» допустить некоторое отступление от главной темы («исторический
экскурс»), изложив предпосылки создания и техническую сущность кон-
струкции первой советской разделяющейся головной части, разработан-
ной без использования БЦВМ.
Глава 13
РГЧ КАК БОЕВОЕ ОСНАЩЕНИЕ РАКЕТ
II-IV ПОКОЛЕНИЙ
13.1. Разделяющаяся головная часть МБР 8К67П
Для создания РГЧ без использования в составе системы управления
БЦВМ было реализовано техническое решение, не имеющее аналогов
в мировой практике ракетостроения.
13.1.1. Основные положения
Основная и главная особенность разработки первой РГЧ определялась
сложностью поставленной в декабре 1967 г. военно-политическим руко-
водством СССР задачи срочного ее создания и летной демонстрации до
проведения пусков РГЧ ракетой «Минитмен-Ш».
В такой жесткой постановке проблема могла быть решена только пу-
тем оснащения разделяющейся головной частью штатной ракеты Р-36
баллистического варианта (ракета 8К67).
При этом условии, как следствие «основной» особенности, возникала не
менее сложная инженерная задача: конструкция РГЧ должна обеспечивать
возможность замены штатного боевого оснащения ракеты 8К67 (монобло-
ки - «тяжелый», 20 мгт, и «легкий», 8,0 мгг, - с комплексом средств преодо-
ления ПРО) в процессе ее боевого дежурства (заправленная ракета, стоя-
щая в ШПУ) с минимальными, в случае крайней необходимости, доработ-
ками бортового и наземного проверочно-пускового оборудования без слива
компонентов топлива и выемки ракеты из шахтной пусковой установки.
Но, как известно, системы управления ракет II поколения были анало-
говыми, Это было вызвано, в основном, отсутствием в СССР во время на-
чала работы над созданием этого поколения самых мощных в мире бое-
408
вых ракет Р-36 бортовых вычислительных машин, годных по своим тех-
ническим и эксплуатационным характеристикам для установки на боевые
ракеты. При этом учитывался «горький» опыт США по внедрению БЦВМ
в СУ ракеты «Минитмен». По имевшейся достоверной информации [180],
[181], в 1959 г., когда началась установка на боевое дежурство МБР «Ми-
нитмен-I», отказы оборудования в системе наведения ракет имели место
примерно каждые 600 часов работы. Блок системы наведения на каждой
ракете приходилось заменять примерно 15 раз в год. Извлечение неис-
правного блока, установка нового, его калибровка после достижения тем-
пературной готовности требовали 7 суток. Таким образом, каждая ракета
снималась с боевого дежурства в среднем на 105 суток в году.
В 1963 г. на повышение надежности оборудования системы наведения
МБР «Минитмен» было ассигновано 150 млн долларов США, в результате
чего среднее время наработки на отказ было увеличено и замена блока
системы наведения на каждой ракете производилась в среднем реже чем
один раз в год. Экономия составила примерно 1,5 млрд долларов.
* * *
Поставленная задача Конструкторским бюро «Южное» в кооперации
соисполнителей-разработчиков: системы управления (КБЭ), наземного
оборудования (КБСМ) и др., была успешно решена - первый демонстра-
ционный пуск экспериментальной полномасштабной 3-блочной РГЧ был
осуществлен в августе 1968 г., т. е. через 8 месяцев с момента начала раз-
работки! До конца этого же года было проведено еще 4 успешных пуска.
Разработка штатного варианта разделяющейся головной части в соста-
ве трех блоков, снаряжаемых зарядами мощностью 2,3 мгт (во много раз
превосходящей мощность ББ «Минитмен-Ш») и 401-килограммового
КСП, была проведена, включая ЛКИ, в 1969-1970 гг. В этот же период
была создана вся инфраструктура (корпус сборки, изотермический транс-
портный агрегат и др.).
Комплекс ракеты Р-36 с разделяющейся головной частью был принят на
вооружение в 1970 году, повысив боевую эффективность ракеты в 2 раза.
13.1.2. Способ разведения ББ РГЧ
За основу реализованного технического решения был принят запатен-
тованный [28] группой специалистов ОКБ-586 в 1968 г. способ разведения
блоков, принципиальная схема которого приведена на рис. 13.1.
Подобно тому, как лыжник, скатываясь с трамплина, приобретает ско-
рость, позволяющую ему прыгать на расстояния свыше 100 м, так и боевой
блок, отпущенный с ракеты при работающем двигателе, приобретает ско-
рость в направлении, перпендикулярном продольной оси ракеты. Величина
этой скорости пропорциональна перегрузке пх, действующей на ракету
409
в момент сброса блока. Приращения дальности и боковой координаты явля-
ются функциями также угла наклона направляющих, по которым скатыва-
ются блоки а, и угла разворота РГЧ относительно продольной оси ракеты (р:
dL ATZ
dV~'у'
Ы = Ы(пх,а, р) = —ЛУх+—ЛУ
V х 44 dVx х dVy у
дг = дг(п1,а,р)=-^-дгг,
дух,дуу,ду,=/(Пх,а,р)
Рис. 13.1
Теоретические исследования по динамике разделяющейся головной
части такого типа изложены в соответствующих томах эскизного проекта
и кандидатской диссертации В. А. Гонтаровского. Основные технические
решения по конструкции РГЧ ракеты 8К67, которая была реализована
в трёхблочном варианте, предложены Г. А. Кожевниковым, В. В. Лазаря-
ном, В. А. Сиренко, Ю. П. Панкратовым и др. [94].
Отметим основные принципиальные вопросы, связанные с решением
этой технической проблемы.
Инерционный способ отделения блоков путём скатывания их по на-
клонным направляющим под действием осевой перегрузки, обусловлен-
ной работой ДУ, является одним из наиболее простых, надёжных и доста-
точно эффективных способов отделения блоков и их разведения по задан-
но
ным целям, удалённым друг от друга в боковом направлении на расстоя-
ния до 30 км. Достоинством этого способа является также возможность
отделения блоков без выключения маршевого двигателя, что особенно
важно для твердотопливных ракет, выключение двигателей которых со-
пряжено с большими трудностями.
13.1.3. Конструкция РГЧ
Основным силовым узлом РГЧ являлась платформа, устанавливаемая
на штатный приборный отсек ракеты, находящейся в шахтной пусковой
установке. Для крепления ББ на силовой платформе и последующего их
разведения использовались установочные кольца с каретками, опираю-
щимися на направляющие платформы. Разведение ББ осуществлялось
«скатываением» их по наклонным направляющим при работе двигатель-
ной установки II ступени ракеты на основном режиме. При пуске на мак-
симальную прицельную дальность перегрузки в момент начала скатыва-
ния превышали 11 раз.
При движении блока по направляющим конструкция РГЧ обеспечивала:
- свободное движение без заклинивания, но с минимальным люфтом;
- минимальные угловые возмущения блока при отделении;
- минимальные реакции в опорных катках.
Выполнение этих требований достигнуто применением коробчатых
направляющих и опорных катков, как это показано на рис. 13.2.
Мх1
\ ч \ Х| ц.м. \ \ G, = Wxtn6 \ rzl R, cR2 Рис. 13.2
411
Передние катки установлены в районе пересечения линии действия
осевой инерционной силы блока с направляющей и воспринимают на-
грузку от блока на активном участке. Задние катки располагаются в рай-
оне пересечения нормали из центра масс блока с направляющей и воспри-
нимают, в основном, инерционную силу при движении блока по направ-
ляющей. Эта группа катков препятствует также вращению блока после
схода передних катков с направляющей.
Отделение блоков осуществляется одновременно или последовательно
по команде от автомата управления дальностью. По этой команде сраба-
тывают разрывные болты крепления кареток с блоками к платформе и на-
чинается их свободное движение по направляющим. Сообщаемые блокам
продольная и боковая составляющие скорости учитываются в полётном
задании при расчете настроечного значения функционала на выдачу глав-
ной команды.
Для уменьшения аэродинамического сопротивления и исключения
взаимодействия набегающего потока с элементами конструкции, в резуль-
тате которого возникали акустические колебания на звуковых частотах
(«свист»), боевые блоки устанавливались с наклоном к продольной оси
ракеты на 11°, а на вершины ББ устанавливался обтекатель в виде трехко-
нусного наконечника.
Внешний вид РГЧ при установке ее на ракету 8К67П показан на рис. 13.3.
Рис. 13.3
13.1.4. «Прямоугольник» разведения
Предельные возможности инерционного способа отделения блоков по
ширине прямоугольника разведения ограничены величиной продольной
412
перегрузки ракеты. Боковая скорость блока в зависимости от пройденного
пути может быть определена по формуле:
JP (cos a-sina + f sina)
ly-----Д—7---------- -XV »
тк + sin а + fmp- cos а • sin ai / , ms
i
где у - боковое перемещение блока при движении по направляющей;
Р - тяга двигателя;
тк- масса корпуса ракеты;
ms- масса боевого блока;
Д- коэффициент трения;
а - угол наклона направляющей к продольной оси ракеты.
Исследуя на экстремум функцию боковой скорости, можно определить
оптимальное значение угла наклона направляющих, которое при Д = О
составляет:
I Д
а = arctg -.
Для ракеты 8К67 оптимальное значение угла а составляет ~ 36°, а мак-
симальная боковая скорость блока при разгоне по направляющим, не вы-
ходящим за габариты ракеты, составляет ~15л</с. При стрельбе на макси-
мальную дальность ширина прямоугольника разведения составляет
~30км.
Что касается длины прямоугольника разведения, то она практически не
ограничена. В многоблочной РГЧ, в которой блоки сбрасываются попар-
но, чтобы исключить возмущающие воздействия в системе стабилизации
из-за асимметрии конструкции, выбором интервала между сбросами бло-
ков длину прямоугольника разведения можно довести до нескольких ты-
сяч километров.
13.1.5. Точность стрельбы
Рассеивание точек падения боевых блоков разделяющейся головной
части ракеты 8К67П определялось кроме совокупности возмущающих
факторов, воздействующих на моноблоки, еще рядом специфических воз-
мущений, присущих принятому способу «инерционного» разведения.
13.1.5.1. Возмущения участка разведения ББ
При расчете рассеивания точек падения боевых блоков РГЧ учитыва-
лись все факторы, в принципе приводящие к отклонению (в том числе
минимальному) параметров движения ББ от их номинальных значений,
принятых в баллистических расчетах.
Приведем перечень этих возмущений и их величины.
413
Погрешность угловой стабилизации ракеты в момент схода ББ с на-
правляющих:
по тангажу - Д19 - 0,4 градуса,
по рысканию - Ау, - 0,3 градуса,
по вращению - &<р - 2,0 градуса.
Погрешность угла установки направляющих схода ББ относительно
продольной оси платформы РГЧ - 10 дуг. мин.
Погрешность угла установки направляющих схода ББ в плоскости
опорного шпангоута платформы РГЧ
ДД, ДД, ДД - 0,7 градуса.
Разброс рабочей длины направляющих схода ББ
Д/П Д/2, Л/3 — 3 мм.
Погрешность ориентации платформы РГЧ относительно линии дейст-
вия суммарной тяги двигательной установки II ступени ракеты:
по тангажу - Рт ~ 10 дуг. мин.,
по рысканию - РР ~ 10 дуг. мин.
Отклонение тяги двигателя II ступени на момент схода ББ с направ-
ляющих (ошибка системы регулирования кажущейся скорости) - 2,8 %.
Разброс задержки исполнения команды на разведение ББ
Дту - 0,002 с.
Отклонение выдачи ГК за счет методической ошибки СУ
Д/ГА. - 0,1 с.
13.1.5.2. Отклонения параметров движения ББ в результате
воздействия возмущающих факторов на участке разведения
Ддя значительного упрощения формул зависимости параметров дви-
жения ракеты от измеряемых составляющих кажущегося ускорения и об-
легчения анализа влияния возмущений на эти параметры целесообразно
движение ракеты рассматривать относительно инерциальной (начальной
стартовой) системы координат.
Начало инерциальной системы координат OXqYoZo помещено в центр
Земли, а координатные оси направлены параллельно соответствующим
осям стартовой (земной) системы координат.
Между параметрами движения ракеты, определенными относительно
инерциальной и стартовой систем координат, имеют место следующие
соотношения:
414
rc = r-R„, У = Уа-а>3хг,
где rc, 7 - радиусы-векторы, определяющие положение центра масс ра-
кеты относительно точки старта и относительно центра Земли соответст-
венно;
- радиус-вектор, определяющий положение точки старта относи-
тельно центра Земли;
К, Va - векторы скорости центра масс ракеты, определяемые относи-
тельно стартовой и инерциальной систем координат соответственно;
а>з - вектор угловой скорости суточного вращения Земли.
Номинальные и возмущенные значения параметров движения боевых
блоков в процессе разведения определяются путем интегрирования сис-
темы дифференциальных уравнений вида:
Ху = bnXj + Л12Уу + bnZj
Y^b2lX^b22Y^b23Z}
%j = ^31^G + ^32^; + ^33^j
где Xj9 YJ9 Zj - составляющие ускорения j-го ББ в связанной системе
координат;
^11» ^12 » ^13
^21’ ^22’ ^23
^31 > ^32» ^33
направляющие косинусы между осями
связанной и начальной стартовой
системами координат
В табл. 13.1 приведены выражения косинусов углов между осями свя-
занной и начальной стартовой (инерциальной) системами координат.
Таблица 13.1
Оси ОХо OY0 OZ0
ОХ' cos^/cosi9 sini9 -siny,-COS19
ОУ -cos^f- sin 19- cos0> cos <9-cos cos0<sin0? + +sin i/r- sin Э- cos <p
OZ' cosy<sini9sin^ + +siny/rcosp -cosi9-sin0> COS0< -COS07- -siny, sin <9-sin 0?
415
Параметры движения Х}9 YJ9 Zj определяются решением системы
линейных дифференциальных уравнений
«1/
Х,+^Л,=0,
7 mj 7
Y.+-^- Л. = 0,
7 mj
Z.+^-R. = 0,
7 ntj 7
Xya4y + YjOsj + Zjaij + = 0,
/И у=1 Ш
3
где m - mrK - ^my: тГк - масса ракеты в момент tnc, mj - масса j-ro ББ;
aiy = -flp sinxy • cosay + sinay - flT cos/y • cosay9
a2J = -sin/y • cosay - flp sinay9
a3y = -flT sinay + cos/y • cosay9
ач=рт ^Yj - Pp sin/y ~ *g<*P
aSj = Pptgaj-smrJ9
aj = tgaj - PT cosyj + 0p sin/y.
P - суммарная сила тяги двигательной установки II ступени;
а} - угол между направляющей схода j-ro ББ и продольной осью
платформы РГЧ;
у} - угол установки направляющей схода j-ro ББ в проекции на плос-
кость опорного шпангоута платформы РГЧ;
Х 9 Rj - кажущееся ускорение ракеты (без ББ) и силы реакции, дейст-
вующей на ББ (определяются решением системы дифференциальных
уравнений).
При проведении расчетов величин отклонений параметров движения
ББ в результате возмущений на участке разведения рассматривались сле-
дующие два варианта расположения ББ на платформе РГЧ - рис. 13.4.
416
ББ "А’
Рис. 13.4
Результаты расчетов величин отклонений параметров движения ББ
приведены в табл. 13.2, 13.3.
13.1.5.3. Отклонения точек падения ББ
Составляющие отклонений точек падения ББ от точек целей, обуслов-
ленные возмущающими факторами участка разведения, определялись по
формулам:
3 ЯЛ
У=1»2»3;
3 Я7
/-W.
где AqJik - отклонения параметров движения (ДКХ, &Vy9 ДКг) j-ro ББ за
счет i-ro возмущающего фактора в момент схода ББ с направляющих;
дБ dZ.
—-9 —- частные производные дальности и направления по па-
дЯа дял
раметрам ДКХ, ДИ,, ДИ j-ro ББ в момент времени его схода с направ-
ляющих.
Расчеты проводились для различных геофизических условий стрельбы
при использовании одной и той же программы тангажа.
В табл. 13.4 сведены результаты расчета отклонений точек падения ББ
от целей за счет действия всей совокупности возмущений, действующих
на активном и пассивном участках и при сходе ББ с направляющих.
417
Таблица 13.2. Отклонения параметров движения ББ (вариант 13.4 а)
№ п/п Возму- щения Величина и размер- ность ББ «А» ББ «Б» ББ «В»
AVX AVy AVZ AVX AVy AVZ AVX AVy AVZ
м/с м/с м/с м/с м/с м/с м/с м/с м/с
1. Аф 0,4 град -0,10 0,15 0 -0,10 0,15 0 -0,02 0,19 0
2. £ 0,3 град 0,04 о, -0,11 -0,04 0 -0,11 0 0 -0,14
3. п 2,0 град 0,10 -0,23 0,14 -0,10 0,23 0,14 0 0 -0,29
4. Аси 10 дуг. мин. 0,20 0,08 -0,01 0,00 0,00 0,00 0,00 0,00 0
5. А(*2 10 дуг. мин. 0,00 0,0 0,00 0,20 0,08 0,01 0,00 0,00 0
6. Аа3 10 дуг. мин. 0,00 0,0 0,00 0,00 0,00 0,00 0,19 0,10 0
7. р> 0,7 град 0,04 -0,08 0,05 0 0 0 0 0 0
8. р2 0,7 град 0 0 0 -0,04 0,08 0,05 0 0 0
9. Рз 0,7 град 0 0 0 0 0 0 0,00 0,00 -0,10
10. All 3 мм 0,04 0,03 0,01 0 0 0 0 0 0
11. Д12 3 мм 0 0 0 0,03 0,03 -0,01 0 0 0
12. А1з 3 мм 0 0 0 0 0 0 0,05 0,00 0
13. Рт 10 дуг. мин. -0,10 0,02 -0,02 -0,10 0,02 0,02 0,21 0,10 0
14. р0 10 дуг. мин. 0,17 0,10 -0,02 -0,12 -0,07 -0,04 0,02 0,00 -0,07
15. АР 2,8 % 0,33 0,21 0,11 0,33 0,21 -0,11 0,40 0,04 0
16. Дт3 0,002 с 0,13 0,08 0 0 0 0 0 0 0
17. АТ4 0,002 с 0 0 0 0,18 0,08 0 0 0 0
18. Атз 0,002 с 0 0 0 0 0 0 0,18 0,08 0
19. AtM 0,1 с 0,04 0,03 0,01 0,04 0,03 -0,01 0,05 0,01 0
419
Таблица 13.3. Отклонения параметров движения ББ (вариант 13.4 б)
№ п/п Возму- щения Величина и размер- ность ББ «А» ББ «Б» ББ «В»
AVX ДУу AV2 ДУХ ДУу AVZ ДУХ ДУу av2
м/с м/с м/с м/с м/с м/с м/с м/с м/с
1. Дф 0,4 град -0,12 0,14 0 -0,02 0,18 0 -0,07 0,16 0
2. 0,3 град 0,02 0 -0,11 0,02 0 -0,14 -0,04 0 -0,12
3. п 2,0 град 0,06 -0,13 0,25 0,06 -0,13 -0,25 -0,11 0,26 0
4. Дои 10 дуг. мин. 0,20 0,07 -0,01 0,00 0,00 0,00 0,00 0,00 0
5. Да2 10 дуг. мин. 0,00 0,00 0,00 0,19 0,09 -0,01 0,00 0,00 0
6. Даз 10 дуг. мин. 0,00 0,0 0,00 0,00 0,00 0,00 0,19 -0,08 0,01
7. Pl 0,7 град 0,02 -0,05 0,09 0 0 0 0 0 0
8. р2 0,7 град 0 0 0 0,02 -0,05 -0,09 0 0 0
9. Рз 0,7 град 0 0 0 0 0 0 -0,04 0,10 0,00
10. Ah 3 мм 0,03 0,02 0,01 0 0 0 0 0 0
И. А12 3 мм 0 0 0 0,03 0,00 0,01 0 0 0
12. А1з 3 мм 0 0 0 0 0 0 0,03 0,01 -0,01
13. Рт 10 дуг. мин. -0,14 -0,02 -0,02 0,17 0,10 0,03 -0,01 0,07 -0,06
14. Рп 10 дуг. мин. 0,09 0,07 -0,06 0,11 0,02 -0,06 -0,15 -0,06 -0,03
15. ДР 2,8 % 0,31 0,25 0,06 0,40 0,05 0,06 0,36 0,15 -0,13
16. Ат3 0,002 с 0,18 0,08 0 0 0 0 0 0 0
17. Дт4 0,002 с 0 0 0 0,18 0,08 0 0 0 0
18. Ат5 0,002 с 0 0 0 0 0 0 0,18 0,08 0
19. AtM 0,1с 0,04 0,03 0,01 0,05 0,01 0,01 0,04 0,02 -0,02
Таблица 13.4
Азимут Даль- ность Отклонения ББ «А», «Б», «В»
А£вюи AZeKlw AZ рви AZ разе А£ ^^пас AZ пас AL^ + AZ,.
2
А=0° L-Lrohtp 4,5 4,0 3,7 0,3 2,9 1,4 5,4
А=90° L-Lmax 3,8 3,9 3,2 0,3 3,1 1,5 5,1
Из табл. 13.4 следует, что полусумма предельных (2.7а) отклонений
точек падения каждого ББ по дальности (А^) и направлению (AZz) от
своих расчетных точек прицеливания не превышает ±5,4 км при пусках на
контрольную дальность (10000 км) с азимутом стрельбы 0°.
Тактико-технические требования Министерства обороны (ТТТ МО)
в части точности стрельбы - ±6,0 км выполнялись с достаточным запасом.
* * *
В порядке примечания к табл. 13.4 необходимо отметить, что относи-
тельно большие величины отклонений точек падения ББ от точек прице-
ливания за счет возмущающих факторов, действующих на нисходящем
атмосферном участке траектории, определялись в основном двумя факто-
рами:
1. Применением боевых блоков с относительно большим в 2-3 раза по
сравнению с ББ III и IV поколений баллистическим коэффициентом
6 = Сх—=0.38 10’3 —,
G кгс
Сх - аэродинамический коэффициент лобового сопротивления;
S - площадь наибольшего поперечного сечения («юбки») ББ - м2;
G - вес боевого блока - кгс.
Очевидно, что при прочих равных условиях величина коэффициента 6
определялась значением Сх, т. е. величиной угла полураствора конуса
корпуса ББ и степенью его «затупления» (соотношением угла и длины об-
разующей конуса).
При одних и тех же величинах разброса коэффициента <5, т. е. одина-
ковых отклонениях габаритно-весовых параметров от их номиналов, зна-
чения отклонений точек падения блоков от точек целей за счет возмуще-
ний атмосферного участка траектории будут различны и являться функ-
цией скорости и, соответственно, времени движения ББ в атмосфере.
2. Отсутствие в конструкции ББ каких-либо устройств или систем
обеспечения ориентированного входа в атмосферу с углами атаки
а с 90°.
420
Чем больше угол атаки при подходе к границе атмосферы, принимаемой
в расчетах рассеивания Н «80 ч-100 км, тем больше амплитуды угловых
колебаний ББ относительно его поперечных осей в процессе движения и
больше время стабилизации угла атаки.
В результате - возрастание «эффективного» аэродинамического сопро-
тивления и, соответственно, величины недолета, т. е. отрицательного откло-
нения блока по дальности.
С целью минимизации отклонений точек падения ББ от точек прицелива-
ния, на боевых блоках ракет КБ «Южное», требования к точности стрельбы
которых были значительно выше, были применены специальные системы и
конструктивные элементы для обеспечения организованного входа в атмо-
сферу и вращения при движении в ней.
Так, на торце «легкого» моноблока ракеты Р-36 была установлена конст-
рукция системы ориентации и стабилизации (СОС), обеспечивающая разво-
рот ББ после его отделения от II ступени на угол, соответствующий углу
входа в атмосферу [73].
Исполнительные органы системы - ПРД заклона, ПРД останова, пара со-
пел закрутки относительно продольной оси, элементы крепления и сброса
конструкции СОС - работали по циклограмме прибора управления, установ-
ленного на сбрасываемой раме системы. Вес всей системы
с источником питания, задействуемым при отделении ББ, не превышал
20 кг при весе «легкого» моноблока - 4000 кг.
На ББ ИН, ориентация которых была обеспечена ступенью разведения,
устанавливались специальные аэродинамические пилоны («крылышки»),
создающие вращающий момент относительно продольной оси.
Вращение вокруг продольной оси с оптимальной угловой скоростью
практически сводило к нулю отклонения точек падения ББ из-за действия
возмущения, возникающего за счет поперечного смещения центра масс ББ
относительно геометрической оси симметрии.
13 .2. Оснащение Р-36М разделяющейся головной частью
Работы в ГКБ «Южное» по созданию первой в СССР разделяющейся
головной части с индивидуальным высокоточным наведением каждого
боевого блока в соответствующую точку прицеливания были начаты
в конце шестидесятых годов для боевого оснащения ракеты Р-36М
(15А14).
Поскольку модернизация ракеты Р-36 должна была обеспечить суще-
ственное (во много раз) повышение ее эффективности в любых условиях
боевых действий, в том числе при вводе в строй американской перспек-
тивной системы противоракетной обороны, к боевому оснащению ракеты
были предъявлены весьма жесткие тактико-технические требования.
421
Сложность поставленной задачи в основном определялась следующи-
ми требованиями:
- комплектации РГЧ десятью боевыми блоками, т. е. в 3,33 раза
большим количеством ББ, чем на ракете «Минитмен-Ш»;
- создания РГЧ с тремя вариантами комплектации, в том числе
с «разнокалиберными» ББ;
- укомплектования РГЧ развитым комплексом средств противодейст-
вия ПРО, обеспечивающим «защиту» всех ББ как на внеатмосферной час-
ти траектории, так и в атмосфере;
- обеспечения «гибкости» боевого применения, в том числе пуск не-
скольких (от 1 до 10) ББ в одну точку прицеливания с необходимым ин-
тервалом времени, либо их «развоз» в любой комбинации по точкам при-
целивания, расположенным произвольным образом на площади, размером
в десятки тысяч квадратных километров;
- конструктивного исполнения РГЧ, обеспечивающего возможность
замены БО на ракете, стоящей на боевом дежурстве в ШПУ (моноблоки
на РГЧ и обратно);
- ограниченности габаритов конструкции РГЧ: внешний диаметр го-
ловного обтекателя не должен превышать 3 м при длине не более 5 м.
Для удовлетворения этим, во многом противоречивым, требованиям
было необходимо решение ряда первоочередных задач, основными из ко-
торых являлись:
- разработка схемы полета, обеспечивающей минимизацию времени
разведения при оптимальных энергомассовых характеристиках двига-
тельной установки (ЖРД - ТТРД, тяга, рулевые органы, управляющие
усилия и др.);
- разработка максимально уплотненной компоновки РГЧ с мини-
мальными габаритно-весовыми характеристиками конструкции (рамы,
опоры, силовой набор и пр.).
Как указывалось выше, ближайшим и единственным аналогом разра-
батываемой в конце шестидесятых годов РГЧ ракеты 15А14 была созда-
ваемая в то время РГЧ ракеты «Минитмен-Ш», наиболее полная и досто-
верная информация по характеристикам которой была опубликована в от-
крытой печати лишь в 1984 году и сводилась к следующему [180], [181].
«Головная часть Мк-12 несет три боеголовки W-62 с тротиловым экви-
валентом по 170 кт, ГЧ Мк-12А - три боеголовки W-78 с тротиловым эк-
вивалентом по 335 кт.
На вооружении находились 300 ракет «Минитмен-Ш», оснащенных
ГЧ Мк-12А, и 250 ракет с ГЧ Мк-12. Согласно данным, представленным
Конгрессу, 300 ракет с ГЧ Мк-12А должны находиться на боевом дежур-
422
стве и в 2000 г., а число ракет с ГЧ Мк-12 к 2000 г. должно быть сокра-
щено до 96.
Ступень разведения использует основной ЖРД, расположенный по
продольной оси и обеспечивающий приращение скорости, а также десять
ЖРД ориентации, расположенных по периферии. Основной ЖРД (фирма
Rocketdyne), изготовленный из бериллия, имеет тягу 136 кг и смонтирован
в шарнирном подвесе. ЖРД ориентации фирмы Bell Aerospace изготов-
лены из ниобия с силицидным покрытием. Шесть ЖРД, обеспечивающих
ориентацию по тангажу и рысканию, имеют тягу по 10,4 кг, остальные че-
тыре ЖРД, обеспечивающие ориентацию по крену, - по 8,2 кг. Основной
ЖРД и ЖРД ориентации работают на монометилгидразине и четырехоки-
си азота. В системе подачи компонентов топлива предусмотрены пиро-
клапаны. Компоненты топлива хранятся в двух идентичных цилиндриче-
ских двустенных баках из нержавеющей стали и вытесняются из бака гиб-
кой диафрагмой, растягивающейся под давлением сжатого гелия, который
хранится в сферическом баллоне из титанового сплава. Баки и баллон по-
сле заправки запаиваются. Двигательная установка ступени разведения
рассчитана на хранение в течение 10 лет.
На ступени разведения установлена автономная система управления
PBCS (Post Boost Control System - система управления для работы по
окончании активного участка). Электронное оборудование этой системы
защищено от поражающих факторов ядерного взрыва. Система использу-
ет три гироскопа, акселерометры и БЦВМ, команды от которой поступают
на двигательную установку ступени разведения, которая обеспечивает по-
требное приращение скорости и заданную ориентацию ГЧ перед отделе-
нием каждой боеголовки. Система PBCS снабжена средствами для обна-
ружения и противодействия помехам.
Все три боеголовки отделяются от ГЧ Мк-12 (МК-12А) в течение
1 мин, после чего срабатывает система самоликвидации, разрывающая
корпус ГЧ на несколько десятков осколков, дезориентирующих радиоло-
каторы системы ПРО.
Боеголовка W-78 ГЧ Мк-12А внешне идентична боеголовке W-62 ГЧ
Мк-12. Она имеет такие же габариты, но использует миниатюризованные
предохранительное устройство и взрыватель. В результате три боеголовки
W-78 с тротиловым эквивалентом по 335 кт размещаются в ГЧ Мк-12А
в таком же объеме, как боеголовки W-62 с тротиловым эквивалентом
по 170 кт в ГЧ Мк-12».
Результаты анализа отрывочной информации о ходе работ по РГЧ ракеты
«Минитмен-Ш» практически не могли быть использованы КБЮ
в должной мере, поскольку существенное «количественное» отличие требовало
поиска новых «качественных» решений.
423
Исследования, проводимые с целью решения перечисленных проблем
создания разделяющейся головной части, велись в КБЮ и ДГУ широким
фронтом, с учетом анализа поступающей информации по работам в США.
1. Первым бесспорным решением явился выбор схемы полета - траекто-
рии движения РГЧ, - состоящей из участка наведения головной части в за-
данную точку прицеливания и участка отделения элементов боевого осна-
щения.
Движение РГЧ рассматривается в баллистической системе координат
О Лор, оси которой ориентированы по следующим направлениям:
Л - градиентное направление дальности полета РГЧ;
Р - градиентное направление бокового движения РГЧ;
и - нейтральное (инвариантное) направление движения РГЧ, вдоль ко-
торого приращение скорости головной части не влияет на отклонения точек
падения отделяемых элементов БО от точек прицеливания, т. е.
— = —= 0
dVjdVj
На участке наведения движение осуществляется в плоскости Хр, при от-
делении ЭБО - в v-направлении.
Градиентные направления X и р называют также оптимальными балли-
стическими направлениями, поскольку приращение скорости вдоль этих на-
правлений максимально влияет на изменение по дальности и боковому на-
правлению соответственно.
Подробно схема полета РГЧ с учетом переходных участков движения из
одного характерного баллистического направления в другое рассмотрена в
разделе 13.5 на примере «последней модели» РГЧ как наиболее характерно-
го объекта управления.
2. Значительно более сложной и трудоемкой задачей был выбор типа
двигательной установки в части: вида топлива (ЖРД - ТТРД); типа и эффек-
тивности управляющих органов; величины силы тяги и схемы ее приложе-
ния (тянущая - толкающая); закона изменения тяги в процессе полета, а так-
же на различных участках движения; компонуемое™ при наличии сущест-
венной «разнокалиберное™» элементов боевого оснащения и др.
Принятые решения были настолько неоднозначны ввиду сложное™ их
реализации, что вызвали достаточно глубокую проработку ряда альтерна-
тивных технических решений, вплоть до разработки этой РГЧ с жидкостаой
двигательной установкой (вариант 15Ф143УЖ).
Штатаая разделяющаяся головная часть ракеты Р-36М, получившая ин-
декс 15Ф143У, была создана унифицированной под три варианта комплек-
тации ее боевым оснащением и соответствующим комплексом средств про-
таводействия ПРО.
424
В качестве двигательной установки был применен твердотопливный
реактивный двигатель, в наибольшей степени удовлетворяющий требова-
ниям по энергомассовым параметрам, компонуемости и эксплуатации
при переоснащении ракеты в условиях ШПУ еще двумя видами головных
частей.
Движение РГЧ осуществлялось по толкающей схеме с плавно изменяю-
щейся величиной тяги двигателя (см. табл. 13.5).
В качестве органов управления использовались высокоэффективные
(Рупр.^О.ДЗРосевой) маломоментные вращающиеся управляемые сопла, не тре-
бующие рулевого агрегата с чрезмерной массой.
В качестве примера оценки РГЧ как объекта управления рассмотрим во-
просы обеспечения управляемости и устойчивости движения одного из вари-
антов комплектации - «РГЧ-5», в составе: четырех боевых блоков весом 658
кг; одного ББ весом 348 кг; трех ложных блоков весом 190 кг.
В качестве расчетного случая выбран вариант стрельбы ракетой с РГЧ-5 на
максимальную дальность как наиболее тяжелый с точки зрения управляемо-
сти.
Управляемость РГЧ-5 на участке разведения оценена для варианта по-
строения боевого порядка «цепочка», так как в этом случае время между мо-
ментами отделения боевых блоков минимально.
Все блоки, за исключением ЛБ2 и ЛБЗ, отделяются с помощью четырех-
звенного механизма (рис. 13.5). Расчёт управляемости проведен последова-
тельно для участков отделения блоков и участков успокоения РГЧ после их
отделения.
Использование в системе управления БЦВМ и высокие требования
к стабилизации РГЧ по линейной скорости её центра масс обусловили необ-
ходимость введении нелинейного закона регулирования этой скорости.
Управление движением РГЧ осуществляется четырьмя поворотными со-
плами ТТРД. Максимальный угол поворота сопел ±90 град, максимальная
скорость поворота сопел ±300 град/с.
При оценке управляемости учтены следующие возмущающие факторы:
- погрешности изготовления и монтажа двигательной установки,
- поперечное смещение центра тяжести, возникающее при отделении
элементов РГЧ.
Формулы для расчёта возмущающих сил и моментов аналогичны соответ-
ствующим выражениям, приведенным в части 1 книги для абсолютно твердой
ракеты.
Исходные данные, использованные при расчётах управляемости РГЧ, при-
ведены в табл. 13.5, в которой помещены данные по ТТРД системы разведе-
ния, центровочные и массово-инерционные характеристики, порядок сброса
блоков, а также параметры четырехзвенного механизма.
425
426
Таблица 13.5. Параметры РГЧ-5 при стрельбе по одной цели
Наименование блоков ББ1 ЛБЗ ББЗ ББ5 ББ2 ЛБ2 ЛБ1 ББ4
Наименование параметра и его размерность
t, с 3.0 14.2 17.9 24.3 30.3 32.7 37.2 42.6
G, кг 6262 5604 5406 5216 5191 4533 4443 4095 4008 3350 3300 3110 3030 2840 2750 2092
m, м 638 571 551 532 529 462 453 417 408 341 336 317 309 290 208 213
I» 538 486 457 423 420 378 361 328 311 260 258 226 206 189 160 122
1у, 1127 1067 1011 947 940 882 856 794 769 697 686 632 610 567 542 452
Iz, 1173 1093 1012 981 972 897 855 824 783 685 676 652 610 583 530 427
Хт, м 2.043 1.974 2.001 2.043 2.041 1.955 1.968 1.902 1.916 1.776 1.784 1.841 1.861 1.792 1.816 1.560
Ут,м -0.001 0.078 0.078 0.081 0.084 -0.001 -0.016 -0.017 -0.001 0.130 0.129 0.137 0.114 0.122 0.160 0.000
Zr, м 0.023 -0.027 -0.026 -0.072 -0.073 -0.018 -0.017 -0.093 -0.093 -0.023 -0.031 0.043 0.046 0.105 0.100 0.000
Р, кг 1250 1250 1220 1180 ИЗО 1110 1080 1050
Y. градусы 304 0 124 0 236 180 180 56
bl, м -0.556 - -0.575 -0.628 -0.754 - -0.738 -0.970
С1,м -0.956 - -0.975 -1.028 -1.154 - -1.138 -1.370
г, м 1.040 - 1.040 0.730 1.040 0.730 1.040
Ivon, М 1.926 - 1.945 1.998 2.124 - 2.208 2.340
Lit, М -0.606 - -0.625 - -0.804 - 1.010
L2iim 0.060 - 0.060 0.060 0.060 - 0.060 0.060
Уравнения движения РГЧ на участках отделения блоков получены
в свободнопадающей системе координат OXYZ, начало которой (точка О)
совпадает с центром тяжести РГЧ, а оси в момент начала отделения бло-
ков ориентированы по связанным с РГЧ осям координат (в не-
возмущенном движении);
- ось 0X1 совпадает с продольной осью РГЧ и направлена сторону
приборного отсека;
- ось OZi расположена в плоскости сброса блока (составляет угол у
с плоскостью стабилизации IV);
- ось ОY1 дополняет систему до правой ортогональной.
Схема работы механизма отделения приведена на рис. 13.5, схема рас-
положения блоков в плоскости XiOZi - на рис. 13.6. Система уравнений
движения имеет вид:
+ ^п^к + + ^14^ = к1 5
+ dilZk + + <*24* = кГ>
d^ Xk + <*32^4 + <*330* + <*34* = к3 5
+ d^ik + = к4.
Рис. 13.5
427
Рис. 13.6
Параметры движения блоков могут быть получены с помощью урав-
нений связи:
<рк =(Рг=(Р^ хг = хк + (^ -^2)cos^ + (e1 + a2)sinp + rcos(p-a),
zr = zk +(«! +e2)cos^-(^1 “£2)sinp-rcos(p-a).
Системы уравнений движения РГЧ на участках успокоения после
сброса блоков и на участках программных разворотов получены в системе
координат 0‘X‘y/Z*:
- ось ОХ* ориентирована по v-направлению;
- ось OY* - по ^-направлению;
- ось OZ\ - дополняет систему до правой ортогональной.
Начало координат (точка О) совмещено с программным положением
центра тяжести РГЧ.
Система уравнений возмущенного движения на участках успокоения
по каналам тангажа и рыскания имеет вид:
l9 = dag Sa + Ма + Мд.
dVj & el el
Система уравнений возмущенного движения на участках программных
поворотов имеет вид:
428
у = а^&+ау15а + Ру,
z = + a ^8* + a.^p+Ft,
l9 = fliM Sa + Ma + Ma9
у/ + а^ф = a^Sy + a^Ss + a^S* + Л/* + M”9
Ф = a*rS' + aTt,S» +я^у + М' + М'.
При проектировании систем управления, в которых в качестве основ-
ного счетно-решающего устройства используется бортовая цифровая вы-
числительная машина, важным является правильный выбор типа серво-
привода. Основными требованиями, предъявляемыми к сервоприводу, яв-
ляются:
- принципиальная возможность решения задачи стабилизации изде-
лия с учетом требуемой точности и качества регулирования;
- простота и надежность;
- минимальный вес и габариты;
- минимальное количество связей с аппаратурой системы управления;
- простота и надежность согласующих устройств и усилителей мощ-
ности.
С учетом этих требований были рассмотрены два варианта построения
сервопривода с использованием:
- рулевого привода с релейной скоростной характеристикой;
- рулевого привода с шаговым двигателем.
Основными преимуществами рулевого привода с релейной скоростной
характеристикой являются;
- простота и надежность конструкции в силу отсутствия жесткой об-
ратной связи;
- технологичность в изготовлении, вытекающая из релейности скоро-
стной характеристики и отсутствия золотников;
- минимальное количество связей с аппаратурой системы управления;
- простота, надежность и малый вес согласующих устройств.
Наряду с отмеченными достоинствами данный тип привода обладает
рядом недостатков,
В силу отсутствия местной обратной связи привод с релейной скорост-
ной характеристикой обладает так называемым естественным самоходом
исполнительного механизма. Помимо этого, при подаче на вход управ-
ляющего механизма РМ сигналов различной полярности, привод также
будет характеризоваться «самоходом» исполнительного механизма, что
приводит к неконтролируемому, постоянно увеличивающемуся отклоне-
нию управляющих органов.
429
Причиной такого «самохода» является отличие максимальной скоро-
сти привода при различных полярностях входного сигнала, которое обу-
словлено технологическими разбросами. При этом скорость «самохода»
определяется величиной максимальной скорости и разницей между мак-
симальными скоростями РМ при обеих полярностях входного сигнала.
В замкнутой системе «изделие+АС» «самоход» приводит к постоянно-
му увеличению координат, характеризующих отклонение пространствен-
ного положения от программного.
«Самоход» управляющих органов приводит также к ухудшению точ-
ности регулирования скорости центра масс, что является одним из суще-
ственных недостатков такого типа привода для стабилизации РГЧ, где
требуется высокая точность стабилизации.
Для компенсации имеющегося самохода и увеличения точности регу-
лирования возможно введение в систему стабилизации центра масс па-
раллельно работающих с основным алгоритмом, так называемых интегри-
рующих алгоритмов системы стабилизации, что приводит к усложнению
алгоритмов и к дополнительной загрузке БЦВМ. Введение в систему ста-
билизации интегрирующих алгоритмов приводит к ухудшению качества
переходных процессов и ухудшению точности регулирования на участках
разворотов РГЧ и участках разведения, характеризующихся скачкообраз-
ным изменением параметров изделия и возмущений.
Одной из основных характеристик любого привода является потребная
максимальная скорость перемещения управляющих органов.
Исходя из требований устойчивости системы и качества регулирова-
ния, на участках ускоренных разворотов РГЧ и в моменты сбросов боевых
блоков потребная максимальная скорость отклонения управляющих орга-
нов составляет <У = 200°/с (при располагаемой 300°/с), поскольку смена
информации на выходе БЦВМ происходит с тактом по времени То = 0,05 с,
минимальная длительность импульсов, поступающих на вход управляю-
щего механизма РМ, равна т=0,05 с.
Таким образом, с учетом выбранной максимальной скорости привода,
дискретность по уровню отработки входной информации приводом со-
ставляет Д<? = 10°.
Максимальная эффективность управляющих органов РГЧ
= 7 -ь 8 и для обеспечения устойчивости системы необходимо
с
выбирать статические коэффициенты усиления угловой системы стабили-
зации к* = к& «1.5-г-2. В связи с этим, при дискретности отклонения
управляющих органов Д5 = 10° обеспечить заданную точность регулиро-
вания скорости центра масс весьма затруднительно.
430
3. Другим недостатком РМ с релейной скоростной характеристикой
является нестабильность коэффициентов усиления системы стабилизации,
обусловленная разбросами максимальной скорости привода, что приводит
к некачественной компенсации систематических возмущений, вызванных
смещением центра тяжести РГЧ за счет отделения элементов. Нарушение
компенсации также приводит к недопустимому ухудшению точности ста-
билизации скорости центра масс РГЧ.
Указанных недостатков лишены приводы, в которых в качестве управ-
ляющего механизма используется шаговый двигатель.
Сигнал с БЦВМ выдается в виде «пачек» импульсов. Частота выдачи
«пачек» определяется частотой смены информации f° = 20 Гц. Размер
«пачки» определяется величиной приращения хода, пропорционального
углу отклонения управляющих органов. Максимальный размер «пачки»
равен 6 импульсам, что соответствует приращению угла отклонения
управляющих органов А8 = 9°. Частота следования импульсов в «пачке»
выбрана f = 125 Гц. Отклонение управляющих органов, соответствующее
одному импульсу входной информации, равно 1,5°.
Учитывая вышеизложенное, построение системы стабилизации РГЧ
проведено с использованием рулевой машинки с шаговым двигателем.
Основные технические характеристики шагового двигателя следующие:
- напряжение питания - 27^ В,
- число фаз управляющего сигнала - 4,
- частота отработки шагов - f = 125 Гц,
- число шагов на один оборот - 24,
- момент инерции нагрузки, приведенной к валу двигателя -
10"3 4-10"2гсм/с2,
- момент нагрузки на валу двигатели 80 гем,
- потребляемая мощность не превышает 8 Ватт.
Моделирование переходных процессов стабилизации РГЧ проводи-
лось с РМ с релейной скоростной характеристикой и РМ с шаговым дви-
гателем.
13.3. Разделяющаяся головная часть ракеты МР-УР100
Созданная практически одновременно с РГЧ ракеты 15А14, разделяю-
щаяся головная часть для ракеты МР-УРЮО (МР-УР100 УТТХ) была ос-
нащена четырьмя однотипными боевыми блоками и соответствующим
комплексом средств противодействия. Для разведения ББ использовалась
твердотопливная ДУ, конструктивно-компоновочная схема которой ана-
логична схеме двигательной установки РГЧ 15Ф143У ракеты 15А14.
431
Различие основных характеристик этих ДУ (рабочий запас топлива,
суммарный импульс тяги, время работы) обусловлено меньшим числом
элементов БО и, соответственно, в 3,7 раза меньшим весом РГЧ.
В связи с одноярусной компоновкой РГЧ и работой ДУ по толкающей
схеме, эта головная часть как объект управления отличалась от РГЧ
15Ф143У упрощением ее динамической схемы движения на всех участках
траектории.
Рис. 13.7
13.4. Разделяющаяся головная часть ракеты Р-36М УТТХ
Комплекс ракеты Р-36М УТТХ (15А18) разработан в плане дальнейше-
го совершенствования и повышения в 2-3 раза боевой эффективности на-
ходящегося на вооружении комплекса ракеты Р-36М (15А14).
Основные тактико-технические характеристики ракетного комплекса,
ракеты 15А18 и ее боевого оснащения достаточно подробно представлены
во «Введении» книги в качестве примера, наглядно иллюстрирующего
сложность современных систем вооружения.
При использовании в составе ракеты 15А18 конструк-
ции первых двух ступеней ракеты 15А14 без их доработки,
основным различием этих ракет является применение
в составе ракеты 15А18 принципиально новой конструк-
тивной схемы разделяющейся головной части и системы
управления с улучшенными ТТХ.
РГЧ ракеты 15А18 состоит из двух основных частей:
- универсальной высокоэнергетической жидкостной
ступени наведения (СН) с двигательной установкой, вы-
полненной по «тянущей» схеме и работающей на основ-
ных компонентах топлива;
- головной части (ГЧ) с десятью однотипными бое-
выми блоками повышенной мощности и соответствующим
комплексом средств противодействия ПРО.
Конструктивно ГЧ выполнена по двухъярусной схе-
ме с единым аэродинамическим обтекателем. Компо-
новка верхней части (II ступень) ракеты 15А18 показана
на рис. 13.7.
Двигательной установкой СН является четырехкамер-
ный двухрежимный ЖРД, отклонения качающихся камер
которого создают управляющие усилия.
Тяга ДУ на основном режиме - при переприцеливании
- 4S500 кгс, на режиме дросселирования - при разведении и отделении
элементов БО - 4x200 кгс.
432
Во время полета первых двух ступеней ракеты камеры ДУ РГЧ зафик-
сированы в «транспортировочном» исходном положении, при котором они
полностью вписываются во внутренний габарит головного обтекателя:
камеры установлены соплами в сторону приборного отсека с углом -190°
относительно оси Xi присоединенной системы координат (см. рис. 13.8).
Установка камер ДУ СН в рабочее положение осуществляется их поворо-
том относительно оси, перпендикулярной оси качания камер на угол
-170°. Поворот производится механизмом, расфиксируемым по команде
после отделения РГЧ с ПО от II ступени. Камеры ЖРД устанавливаются
в рабочее положение, при котором угол между продольной осью камеры
и осью Xi равен 18°. Максимально допустимый рабочий угол качания ка-
мер составляет ±50 град с угловой скоростью 8 = 100 град/с.
На упрощенной схеме управления движением РГЧ - рис. 13.9 - пока-
заны отклонения камер, соответствующие подаче команды на отработку
угла тангажа +Ai9. При этом срезы сопел камер 2, 3 поворачиваются
к плоскости III, а камеры 1,4 - от плоскости I.
Сборка «ГЧ+СН+ПО» как объект управления обладает динамическими
свойствами абсолютно твердого летательного аппарата, поскольку компо-
ненты топлива задемпфированы конструктивными средствами (гибкая
мембрана), а частоты упругих колебаний более чем на порядок выше ра-
бочей частоты угловой стабилизации.
Специфические вопросы динамики РГЧ ракеты 15А18, связанные с со-
вершаемыми в процессе разведения ББ эволюциями, подробно рассматри-
ваются в разделе 13.5 на примере наиболее общего, в смысле решаемых
задач, случая.
13.5. Разделяющаяся головная часть ракет
РТ-23 (РТ-23 УТТХ)
Основные тактико-технические характеристики разделяющейся голов-
ной части, идентичной для шахтного и железнодорожного варианта бази-
рования ракет РТ-23, приведены в разделе 6.2 книги. Там же для сравне-
ния даны соответствующие параметры РГЧ ракеты «Минитмен-Х», схема
построения которой во многом аналогична головной части РТ-23.
Как уже указывалось в предыдущих разделах, эта РГЧ стала последней
модификацией разделяющейся головной части, созданной в СССР.
Ее основным отличием от описанных выше является применение
многофункциональной жидкостной двигательной установки, состоя-
щей из реактивных двигателей большой и малой тяг многократного
включения [76].
433
Рис. 13.8
435
По своей сути РГЧ РТ-23 является «классическим» примером космиче-
ского летательного аппарата (ЛА), анализ достаточно сложной схемы
движения которого позволяет рассмотреть все специфические вопросы
динамики полета такого типа объектов управления.
Конструктивно РГЧ ракет РТ-23, как и ранее описанные модификации
разделяющихся головных частей с индивидуальным наведением элемен-
тов боевого оснащения в соответствующие точки прицеливания, состоит
из ступени наведения (в ряде источников - ступени разведения - «СР») и
отсека боевого оснащения. Отделение РГЧ от последней ступени проис-
ходит с присоединенным к ней приборным отсеком ракеты с универсаль-
ной системой управления полетом всех ступеней, включая РГЧ.
Как объект управления РГЧ рассматривается как абсолютно твердое тело,
поскольку влияние колебаний топлива в баках и упругих колебаний корпуса
на динамику движения исключено конструктивными мерами. Упрощенная
конструктивная схема РГЧ представлена рис. 13.10, на котором обозначено:
/ крем
Рис. 13.10
OXYZ - строительная система координат;
OjXjYjZj - связанная система координат (Oj - центр масс РГЧ);
I-Ш, II-IV - плоскости нормальной и боковой стабилизации движения
РГЧ соответственно.
Двигательная установка РГЧ РТ-23 состоит из двигателя большой тяги
(ДБТ) величиной 500 кгс, установленного в кардановом подвесе по «толкаю-
щей» схеме, и шестнадцати релейных управляющих двигателей малой тяги
(ДМТ), установленных стационарно, которые можно поделить на три группы:
первая группа включает четыре маршевых ДМТ 5...8, установленных
по «тянущей» схеме под углом а к продольной оси X;
вторая группа включает четыре управляющих ДМТ 1...4, установлен-
ных по «тянущей» схеме, и четыре управляющих ДМТ 13... 16, установ-
ленных по «толкающей» схеме параллельно продольной оси X;
436
третья группа включает четыре управляющих ДМТ 9... 12, установлен-
ных по «моментной» схеме перпендикулярно продольной оси X.
Все релейные ДМТ имеют одинаковый уровень номинальной тяги
Рн=11.2 кгс. Диаграммы изменения тяги ДМТ при его включении (выклю-
чении) представлены на рис. 13.11.
На рис. 13.11 обозначено:
Р - тяга управляющего двигателя;
t - текущее время полета;
to - момент подачи управляющей команды на включение (выключение)
двигателя;
xz - запаздывания моментов срабатывания двигателя, i=l.. .4.
Величины tz обусловлены характеристиками электрогидроклапанов
ДМТ и могут принимать значения Ti = Т2« 0,020 с; тз = Т4 « 0,040 с.
В процессе полета РГЧ, по мере израсходования запасов топлива и от-
деления элементов оснащения, изменяются ее массово-инерционные
и центровочные характеристики.
В табл. 13.7 приведены номинальные значения углового и кажущегося
линейного ускорений РГЧ, соответствующие началу и концу участка раз-
ведения элементов боевого оснащения.
Таблица 13.7
Величина Значение
начало разведения конец разведения
Угловое ускорение РГЧ: соXi, град/с2 ±10 ±25
соУ1, град/с2 ±10 ±25
<bZi, град/с2 ±5 ±15
Кажущееся ускорение РГЧ: , м/с2 -0,2 -1,0
437
Приведенные значения соответствуют включенному состоянию сле-
дующих двигателей:
<ЬХ1 -ДМТ9, 11 или 10, 12;
<ЬУ1 - ДМТ 5, 6 или 7,8;
cbZi - ДМТ 1, 4 или 2, 3;
WXi -ДМТ1...8.
Система управления РГЧ построена на базе бортовой цифровой вычис-
лительной машины (БЦВМ), с помощью которой формируются по опреде-
ленным алгоритмам управляющие сигналы на двигательную установку. При
этом используется информация с датчиков параметров движения центра
масс и углового движения РГЧ вокруг центра масс. Наличие БЦВМ в конту-
ре системы управления вводит дискретность в процесс управления движе-
нием.
Следовательно, систему управления движением следует рассматривать
как релейную, дискретную систему с временным запаздыванием.
13.5.1. Схема движения
Введем следующие системы координат:
- гироскопическая система координат (инерциальная), оси кото-
рой направлены по осям чувствительности гиростабилизированной плат-
формы (ГСП), установленной на РГЧ (Ог - центр ГСП; - оси отсчета уг-
лов рыскания, крена, тангажа соответственно);
ОДур - баллистическая система координат (см. раздел 13.2);
Оси v, 2, р баллистической системы координат являются программ-
ными направлениями ориентации осей XJ9 YJ9 Z; связанной системы ко-
ординат.
Полет РГЧ проходит вне условной границы атмосферы и может быть
представлен, начиная с момента отделения ее от ракеты-носителя, в виде по-
вторяющихся типовых участков движения (рис. 13.12).
1. Участок наведения РГЧ в заданную точку прицеливания.
Движение осуществляется в Хр - плоскости с помощью ДБТ (возможно
движение с помощью ДМТ), управляющие моменты вокруг связанных осей
РГЧ создаются следующим образом:
вокруг оси Xi - путем попарного включения двигателей 9... 12 по «мо-
ментной» схеме;
вокруг осей Yi, Zi - путем поворота камеры ДБТ в двух взаимно-
перпендикулярных плоскостях.
После набора РГЧ требуемого приращения кажущейся скорости в Хр -
плоскости, по команде от системы управления ДБТ выключается, РГЧ
438
Схема
Движения РГЧ
элементов
на участке
оснащения
разведения
Рис, 13.12
разворачивается в нейтральное направление, вдоль которого осуществ-
ляется отделение элементов оснащения. Так как ДБТ обладает разбро-
сом импульса тяги при выключении, то возможны после его выключе-
ния возмущения кажущейся скорости центра масс РГЧ и ее угловой
скорости.
В табл. 13.8 приведены диапазоны возможных значений возмущений
поперечных составляющих кажущейся скорости рассматриваемой РГЧ по
мере разведения элементов оснащения.
Таблица 13.8
Величина Значение
начало разведения конец разведения
Приращение кажущейся скорости РГЧ: АИ\, м/с AFKp,M/c ±0,2 ±0,1 ±0,5 ±0,2
2. Участок поворота РГЧ в нейтральное направление.
Поворот в v-направлении осуществляется по «моментной» схеме
с помощью двигателей 1...4, 9... 16, при этом управляющие моменты во-
круг связанных осей создаются следующим образом:
вокруг оси Xi - путем попарного включения двигателей 9... 12 по «мо-
ментной» схеме;
вокруг осей Yi, Zi - путем попарного включения двигателей 1...4,
13... 16 по «моментной» схеме.
В результате поворота продольная ось РГЧ ориентируется по (-v)-
направлению (рис. 13.13).
На рис. 13.13 обозначено:
упр9впр ~ программные углы ориентации (рыскание, тангаж) балли-
стической системы координат относительно гироскопической, которые
определяются с помощью направляющих косинусов v-направления, по-
лученных в процессе наведения (<рлр =0).
При повороте РГЧ по «моментной» схеме практически не возникает
дополнительных приращений кажущихся скоростей AH\,AFKp, однако
по окончании поворота возможны возмущения углового движения
осей связанной системы координат относительно баллистической
(рис. 13.14). Рассматриваемые диапазоны значений возмущений приве-
дены в табл. 13.9.
440
Рис. 13.14
441
Таблица 13.9
Величина Значение
Угловая скорость РГЧ д<р, д^, д0,град/с ±5
Угол ориентации РГЧ д^?, д^, Д0, град ±5
3. Участок отделения элементов оснащения.
На этом участке осуществляется отработка до допустимых величин
возникших возмущений параметров движения с последующей стабили-
зацией:
приращений поперечных составляющих кажущейся скорости ц. м.
ди;, ди;;
углов д^, Д|/, Д0 относительно программных направлений v, Л, р\
угловых скоростей д<р, д^, д#.
Движение РГЧ реализуется по «тянущей» схеме с помощью двигателей
1.. .8, при этом управляющие моменты вокруг связанных осей создаются сле-
дующим образом:
вокруг оси Xi - путем попарного включения двигателей 9... 12 по «мо-
ментной» схеме;
вокруг оси Yj - путем попарного включения двигателей 5.. .8;
вокруг оси Zi - путем попарного включения двигателей 1.. .4.
При полете РГЧ в v-направлении после окончания процесса стабилиза-
ции параметров движения и набора требуемого приращения AWO, по коман-
де от СУ происходит отделение очередного элемента БО. Затем выполняется
отход РГЧ на заданное относительное расстояние от отделившегося элемен-
та и ее поворот в Хр-плоскость для движения в следующую точку прицели-
вания.
Уровни допустимых значений возмущений параметров движения
в момент отделения элемента оснащения приведены в табл. 13.10.
Таблица 13.10
Величина Значение
Угловая скорость РГЧ: Д^, Ду>, Д0,град/с Угол ориентации РГЧ Др, Др\ Д0,град Кажущаяся скорость РГЧ: ди;, ди;, м/с ±1 ±2 ±0,02
442
13.5.2. Состав возмущающих факторов
Возмущающие факторы, обусловленные технологическими погрешно-
стями изготовления и монтажа, которые приводят к возмущению движе-
ния РГЧ на участке отделения ЭО, можно разделить на две группы:
- первая группа содержит возмущающие факторы, которые вызыва-
ют только возмущающий момент относительно связанных осей;
- вторая группа содержит возмущающие факторы, которые вызывают
возмущающие силу и момент.
Предельные значения возмущающих факторов приведены в табл.
13.11, 13.12 соответственно.
Таблица 13.11
Наименование возмущающего фактора Значение
Систематическая составляющая поперечного смещения центра масс РГЧ Случайная составляющая поперечного смещения центра масс РГЧ Линейное смещение ДУ относительно осей строительной системы координат РГЧ Разнотяговость управляющих ДМТ 1.. .4 Разброс запаздываний моментов срабатывания ДМТ 1.. .4 ±50 мм ±5 мм ±5 мм ±10% ±0,020 с
Таблица 13.12
Наименование возмущающего фактора Значение
Разнотяговость управляющих ДМТ 5... 12 Перекос осей сопел управляющих ДМТ 1... 12 ±10 %
относительно номинального положения 50 угл. мин
Разброс запаздываний моментов срабатывания ДМТ 5... 12 ±0,020 с
При этом также возможен разброс номинального значения суммарной
тяги ДУ РГЧ, который может достигать ± 20%.
13.5.3. Уравнения движения
Запишем систему дифференциальных уравнений, которая описывает
пространственное движение центра масс РГЧ при ориентации оси Xi свя-
занной системы координат в нейтральном направлении - v и ее угловое
движение вокруг центра масс.
Не нарушая общности рассуждений, совместим оси баллистической
системы координат O7Xvp с осями гироскопической системы координат
Ог^т|д (рис. 13.15). Тогда ориентация осей связанной системы координат
443
относительно гироскопической будет характеризоваться программными
углами:
Флр=0; Флр=0; 0лр=-90град;
а также углами крена, рыскания, тангажа и соответствующими угловыми
скоростями:
ф = Дф; ф = Дф; 6 = &пр + Д9;
ф = Дф; ф = Дф; 0 = Д9.
Уравнение движения центра масс РГЧ в векторной форме имеет вид:
диг=—Ар; (13.1)
т
где AW = (AW^, AW*, AWp) - вектор приращения кажущейся скорости
ц. м. РГЧ в проекциях на оси баллистической системы координат;
F = (Fxl, F , F2 ) - вектор силы тяги ДУ РГЧ в проекциях на оси свя-
занной системы координат;
m - масса РГЧ;
А - матрица направляющих косинусов осей связанной системы коор-
динат относительно баллистической системы координат:
Л=Ы=
«11
а21
а12 °13
а22 а13
а32 а33
z = 1...3;у = 1...3;
°31
444
ап =-Cos Ду Cos ДО; а21 =-SinA(p SinAy CosAG + CosAcp SinAG;
a12 = СозДу5тД&, a22=SinAcp SinAvg SinAO + CosAcp CosAG;
a13 =-5’шАф; a23=SinA(p cos Ay;
a31 = -Cos Ду Sin Ду CosAG - 5z>iA(pSzwAG;
a32 = Cos Ду Sin Ду Sin AG - 57иАф CosAG;
a33 = Cos Acp Cos Ay.
Составляющие вектора силы F без учета запаздываний моментов сра-
батывания ДМТ и возмущающих факторов, приведенных в разделе 13.5.2,
можно записать в виде:
Fxt =-[P1 + P2 + P3 + P4 + (P5 + P6 + P7 + P8)C,osa];
FYt = F9 “ " Fll + ^12’
FZj = (Р5 + Р6 - Р7 - PJSina;
где Р'=РН - номинальное значение тяги ДМТ, i=l... 12.
Уравнение движения РГЧ вокруг центра масс в векторной форме имеет вид
Й = Ф; (13.2)
где со = (соХ1 ,<оУ1 ,<о21) - вектор угловой скорости в проекциях на оси свя-
занной системы координат;
Ф = (ФХ ,Ф^ ,Фг ) - вектор углового ускорения в проекциях на оси
связанной системы координат;
Фх, =((/У1 -VV’i +Л/х1)/Л1;
ФГ1=((/21-711)(оХ|(о21+Л/?1)//?1;
ф21 =((Л, +A/Z1)//Z,;
7Х1 J ,IZ^ - осевые моменты инерции;
М = (МХ , MYi, Mz ) - вектор-момент силы тяги ДУ в проекциях на
оси связанной системы координат.
Составляющие вектора-момента М без учета возмущающих факторов
можно записать в виде:
^Х1 = (~Л +^6 “Л + М^па + (^9 “ До +^П ~F\2)zK9
MYi= (Р1 + Р2 -Рз -P4)zy + (Р5 + Р6 - Р7 -P*)(zMCosa + (хм -xT)Sina);
Мд = (~Р+ Л + Л “?4)Уу + ("А + ^6 + Л "Ря)УмС°5а +
+ (~Р) + Р\0 + 1 “ ^12 )(хх “ ХТ )»
где уу, zyi хм, ум, zM, хК9 zK - координаты центров мест установки
соответствующих двигателей в строительной системе координат;
445
хт - продольная координата центра масс в строительной системе ко-
ординат.
Кинематические соотношения Эйлера между угловыми скоростями
^zi вокруг связанных осей Хи Yn Zl и угловыми скоростями
Др, Др, Д0 вокруг осей баллистической системы координат запишем
в виде:
Дф = (со 5шД0 - соХ1 СоуДО) / СауДц/;
Дф = coyi CostsQ - соХ1 &иД0; (13.3)
Д0 = со21 +Дф&’иД\|/.
Уравнения (13.1)-(13.3) описывают пространственное движение РГЧ
в баллистической системе координат O7vXp на участке отделения элемен-
тов оснащения.
13.5.4. Минимизация времени разведения элементов оснащения
В разделе 13.5.1 описаны типовые участки движения РГЧ при разведе-
нии элементов оснащения РГЧ в заданные точки прицеливания. Возмож-
ны различные схемы разведения, а следовательно, различное количество
типовых участков движения, последовательность их чередования, количе-
ство отделяемых элементов оснащения.
Одним из основных требований, предъявляемых к системе управления,
является минимизация суммарного времени разведения элементов осна-
щения.
Удовлетворить это требование можно путем уменьшения времени
процессов стабилизации на каждом из типовых участков движения.
Минимизация времени переходных процессов стабилизации парамет-
ров движения на участках отделения элементов оснащения должна осу-
ществляться при одновременном обеспечении заданной точности регули-
рования параметров движения на момент их отделения:
по поперечным составляющим вектора ошибки кажущейся скорости
центра масс ДИ^, \Wp в проекциях на оси баллистической системы коор-
динат;
по ошибкам угловой ориентации Др, Др, Д0 и угловым скоростям
Др, Др, Д0.
Задача минимизации времени переходного процесса стабилизации на
участке отделения может быть сформулирована в общем виде:
синтез закона управления, обеспечивающего за минимальное время
после поворота РГЧ в v-направление отработку возмущений параметров
движения до допустимых величин.
446
Как следует из математической модели (13.1)-(13.3) пространственного
движения, управляющими параметрами системы являются тяги двигателей Р>,
i=1...12, величины которых ограничены, т. е. |^|<Рн. Количество регули-
руемых параметров равно восьми: Д^, Д0, Д#>, Ду>, Д0, ДИ^, &Wp.
Учитывая большую размерность системы дифференциальных уравнений
движения и вектора управления l7 = (P15 Р2,..., Р12), применение известных
методов оптимального управления для решения поставленной задачи практи-
чески невозможно, тем более в реальном масштабе времени полета РГЧ.
В связи с этим использован следующий порядок работы:
1. Проведено максимально допустимое из условий точности регулирова-
ния упрощение уравнений движения.
2. На основе упрощенной по п. 1 системы решена задача синтеза закона
оптимального по быстродействию управления.
3. Полученный по п. 2 закон управления скорректирован применительно
к исходной системе уравнений движения (13.1)—(13.3).
13.5.5. Упрощение уравнений движения
Для решения поставленной задачи (раздел 13.5.4) сделан ряд предполо-
жений, упрощающих полученные уравнения движения (13.1)-(13.3) на уча-
стке отделения элементов оснащения.
1. Учитывая, что угловые скорости Д^>, Д^, Д0 достаточно малы, пре-
небрегая величинами второго порядка малости, получаем следующие выра-
жения для угловых ускорений:
Фу/ =MYi! IYi',
®zi ~ Мд /1д-
При этом, если углы ориентации Д^>, Д^, Д0 по вращению, рыска-
нию, тангажу таковы, что допустимы соотношения SinX = X, CosX = l,
Х = Дф, Дф, ДО, то матрица А направляющих косинусов записывается
следующим образом:
-1
ДО
-Дф
ДО -Дф
1 Дф
-Дф 1
а кинематические соотношения Эйлера принимают вид:
Дф = -а>Х1;
Дф = %;
Д0 = шг1.
447
Учитывая полученные соотношения, уравнения движения (13.1)-(1.3)
запишем в виде:
+F?iA0-FZiAV);
A^=-(F A0 + F +F Д<р);
т 1 '11
A^p=l(-FXiAV-FJ,iA<p + FZi); (13.4)
\=мХхиХх-
®У1 = МУХ ^У\ ’
<bZi=A/Zi //Z];
A<p = -<oJi;
AV = <oyi;
A0 = <oZj.
Как следует из полученных уравнений, угловое движение в одном из
каналов управления не влияет на угловое движение в двух других каналах
и оказывает влияние только на линейное движение центра масс.
2. Введем следующий порядок работы двигателей для управления
движением:
управляющие двигатели 1...4 выключаются попарно (1,4 или 2,3) для
создания управляющего момента вокруг оси Zi или постоянно включены;
управляющие двигатели 5...8 выключаются попарно (5,6 или 7,8) для
создания управляющего момента вокруг оси Yj или постоянно включены;
управляющие двигатели 9... 12 выключаются попарно (9,11 или 10,12) для
создания управляющего момента вокруг оси Xi или постоянно включены.
Выражения для составляющих векторов F,M принимают вид:
Fx = -(Pi +1*2 + Рз + ^4 + (Р5 + Рб + Р7 + Ре) Gosa);
Fv =0;
У1
fz = (Р5+p6 - р7 - рв) Sina;
(13.5)
MXi=(P9 + Pio-Pii-Pi2)zK;
МУ1 =(Р5+Р6-Р7-Р8) (zMCosa + (xM-хт) Sina);
MZj = (-Pi + Р2 + Р3 "Р4)Уу
448
3. Учитывая, что угловое движение РГЧ в канале управления по вра-
щению несущественно влияет на ее движение в каналах управления по
тангажу и рысканию, поскольку управляющие двигатели 9... 12 не созда-
ют управляющих сил и моментов в этих каналах, уравнения движения
ц. м. и углового движения РГЧ вокруг центра масс (13.4) принимают вид:
=—(—F -F Д^);
т 1 1
Д1К =—(F A0 + F2Ap);
т 1 1
A1F =—(-F Д^ + F ); (13.6)
т ч 1
Ыр = -МJI '
'Г *1 V
Д0 = Л/ //.
Z1 21
где Fx , Fv , Fz , Мх , Mv , Mz
X1 yl Z1 1 У1 1
определяются по формулам (13.5).
4. Пренебрегая углом а установки управляющих двигателей 5...8 и
учитывая соотношения (13.5), а также равенство Fyi=Fxi=0, уравнения
движения (13.6) принимают вид:
AWV = Fx = -(Pi + Р2 + Р3 + Р4 + Р5 + Р6 + Р7 + Р8);
m 1 m
AWX =-Fx Д0 = (Pj + P2 + P3 + P4 + P5 + P6 + P7 + Р8)Д0;
m 1 m
AWp = Fx^ Ay = ~(Pj + p2 + рз + p4 + P5 + p6 + p7 + Pe)AVJ (13.7)
Аф = -Мх^ /Ц = (-p9 + P10-Pll + P12)ZK/IX1;
Ау = МУ1/1У1 =(P5+P6-P7-P8) zM/Iy^;
A6 = MZi/IZi=(-P1 + P2 + P3.P4)yy/IZi.
Как следует из полученных уравнений движения, канал управления по
вращению можно рассматривать независимо от каналов управления по
тангажу и рысканию; взаимосвязь последних обусловлена только работой
управляющих двигателей 1...4 и 5...8, тяги которых создают продольное
ускорение в нейтральном направлении v.
5. Введем в рассмотрение управляющие параметры UQ,UW для урав-
нений движения РГЧ в плоскостях нормальной и боковой стабилизации
соответственно, приняв следующие обозначения:
449
_P1+P2+7^+7^+P5+P6+P7+7^
1- ’ 1 Iyx ’ 2~
Тогда UQ = ~ + P2 + ^3 ~ Л jyv = P5 + P6 ~ P7 ~ P8 .
2РЯ 2PH
и уравнения движения в плоскостях нормальной и боковой стабилизации
соответственно можно записать в виде:
Дё = АГ1еС7е;
ДИ\ = -АГ2Д0;
(13.8)
ДИ^^Ду;
(13.9)
где т, / I Iz, уу9 zM, zK, Рн - массово-инерционные, геометрические
и тяговые характеристики, приведенные в разделе 13.5;
К* - величины номинальных угловых ускорений по тангажу и
рысканию соответственно (табл. 13.7);
ив\ и* - управляющие параметры для каналов управления, по тангажу
и рысканию соответственно, принимающие значения -1; 0; +1;
К 2 - величина номинального продольного ускорения, принимающая
4Ри 6РН 8РН ~ тт6 ттш
значения——, ——, —— в зависимости от значении U и Uv.
m m m
Таким образом, через величину К2, угловое движение в канале танга-
жа влияет на движение ц. м. в канале рыскания, а угловое движение в ка-
нале рыскания влияет на движение ц. м. в канале тангажа.
Если пренебречь этой зависимостью, т. е. зафиксировать значения К2,
то движение в плоскостях нормальной и боковой стабилизации соответст-
венно описывается следующими упрощенными уравнениями:
А0 = /С1еС7е;
А^=-А'2Д0;
(13.10)
значение из интервала
Д(/ = K*UV\
Ы¥р=К2Ьу,
Кг - фиксированная величина продольного ускорения, принимающая
___________________Г 4^ 8РЯ~|
т т
(13.11)
450
13.5.6. Принципы формирования дискретного оптимального
управления
На рис. 13.16 представлена функциональная схема системы стабилизации
углового движения и движения центра масс РГЧ в плоскости нормальной
стабилизации (канал управления по тангажу).
Рис. 13.16
На рис. 13.16 обозначено:
БЦВМ - бортовая цифровая вычислительная машина, которая по опреде-
ленным алгоритмам формирует дискретный цифровой сигнал
U [пТ0], п = 0,1,2... (значение управляющей функции U в дискретный момент
времени пТо);
Н-Д - преобразователь непрерывных сигналов S(f) = (Si9 S29 S3) (Si -
угол тангажа, Si - угловая скорость, S3 - кажущаяся скорость ц. м.), посту-
пающих с датчиков параметров движения, в дискретные цифровые сигналы
Г [лТ0] = (гр г2, г3), необходимые для расчетов в БЦВМ;
Д-Н - преобразователь дискретного цифрового сигнала С/[лГ0] БЦВМ
в непрерывный управляющий сигнал L(t) на двигатели 1.. .4;
y(t) - вектор значений фактических параметров движения в плоскости
стабилизации, F = (У,, У2, У3);
S(t) - вектор значений фактических параметров движения в плоскости
стабилизации, измеренных датчиками, s = (Sp S2, S3);
г[иТ0] - вектор значений фактических параметров движения в плоскости
стабилизации в дискретный момент времени t = nT0, п = 0, 1, 2, ...,
r=(rXi г2, г3);
С/[иТ0] - дискретные значения управляющей функции U;
TQ - период дискретности формирования управляющих сигналов;
L(f) - непрерывный управляющий сигнал на двигатели 1.. .4;
Р(/)-вектор значений тяг двигателей 1... 4, Р = (7^, Р2, Р3, р4);
451
гтр [иТ0] - вектор значений требуемых параметров движения.
Наличие в системе стабилизации БЦВМ и преобразователей приводит
к квантованию входных и выходных сигналов по уровню и по времени
[54].
Таким образом, рассматриваемая система стабилизации является дис-
кретной, нелинейной.
Сделаем ряд допущений, упрощающих математическую модель систе-
мы стабилизации:
а) инерционность и погрешность измерений датчиков отсутствуют,
т. е. S(t) = y(t);
б) разрядность преобразователей Н-Д, Д-Н достаточно велика,
поэтому можно пренебречь квантованием сигнала по уровню, т. е.
wi=s«U0
в) электрогидроклапаны двигателей являются безынерционными
звеньями системы стабилизации с коэффициентом передачи, равным еди-
нице, т. е. запаздывания моментов срабатывания двигателей т, равны ну-
лю, i= 1...4 (раздел 13.5);
г) формирующий элемент преобразователя Д-Н является экстраполято-
ром нулевого порядка, т. е. управляющий сигнал L(t) на приводы двигате-
лей 1...4 представляет собой кусочно-постоянную функцию (рис. 13.17);
ЩО
t/[3T0]
G-------
С/[иТ0]
Ф
СД(н+1)Т0]
------
С/[2Т0]
^о]
Ф---
^+2)Г0]
<3---
С/[(и+3)Т0]
<)------
^+4)Г0]
<5---1
।
।
О То 2Т0 ЗТ0 4Т0
иТ0 (л + 1)т0 (п + 2)Т0 (п + 3)Т0 (п + 4)Т0
Рис. 13.17
(На рис. 13.17 точками U[0], U[To], U[2To], ... обозначены дискретные значения
управляющей функции U).
452
д) движение в плоскости стабилизации описывается уравнениями, анало-
гичными уравнениям (13.10):
A0 = ^t/;
=-£2Д0; (13.12)
где U - управляющая функция, М “ ’
Для упрощенной модели системы стабилизации сформулируем принципы
формирования управления L(t) с целью минимизации времени переходного
процесса стабилизации движения:
а) в каждый конкретный момент времени t = nT0, n = 0, 1, 2,... измеряют-
ся с помощью датчиков параметры движения центра масс и углового движе-
ния в гироскопической системе координат Ог£т]д (угол тангажа, угловая
скорость, кажущаяся скорость ц. м.), т. е. измеряется вектор
г[пТ0] = (г1, г2, г3):
Г]=0, г2=0, r3 = W?; (13.13)
б) с помощью БЦВМ, по разработанному НПО АП (головным предпри-
ятием по СУ) алгоритму Ф1(*) определяются рассогласования параметров
движения с требуемыми значениями Гф[пТ0] в баллистической системе ко-
ординат, т. е. определяется вектор Х[пТ0] = (Хр Х2, Х3):
Х = Ф1(г-^р) = (А0, А0, AWX); (13.14)
в) по полученным рассогласованиям параметров движения РГЧ,
в БЦВМ по определенному алгоритму Ф2(*) формируется программная оп-
тимальная по быстродействию управляющая функция Unp(t), nT0<t<
<nT0 + T(n), удовлетворяющая условию ^^(t)] <1 и обеспечивающая от-
работку рассогласований в «нуль» с заданной точностью е2, е3 за ми-
нимальное время Т(п):
и = ипр(1) = Ф2(х[пТ0], t); (13.15)
г) БЦВМ формирует дискретный цифровой сигнал U[nT0] в соответ-
ствии с полученной управляющей функцией Unp(t), который затем преобра-
зуется в непрерывный управляющий сигнал L(t) на двигатели 1...4, соз-
дающие тяги Р|(0 = Р|(1, L(t)), t = 1...4.
Поскольку Ф1(») известен, синтез закона управления движением заклю-
чается в разработке алгоритма Ф2(*) формирования программной управ-
ляющей функции Unp(t).
453
13.5.7. Синтез закона управления
При синтезе законов управления дискретно-непрерывными системами
возможны следующие подходы [54]:
1) синтезируют непрерывный закон управления, пренебрегая дискрет-
ностью системы, а затем, введя дискретность в закон управления, анали-
зируют динамику системы в целом;
2) синтезируют дискретный закон управления, описав динамику сис-
темы конечно-разностными уравнениями с учетом дискретности.
Первый подход позволяет воспользоваться достаточно хорошо разра-
ботанными методами синтеза непрерывных систем управления, однако
требуется дополнительный анализ динамики системы, а возможно,
и коррекция полученного закона управления. Второй подход может при-
вести к значительным математическим трудностям при синтезе закона
управления.
Для решения поставленной задачи синтеза управления используем
первый подход.
Предлагаемый ниже закон управления основан на предположении, что
с помощью БЦВМ имеется возможность определять в каждый дискретный
момент времени t = nT0 (за время т<Т0) по фазовому состоянию системы
Х[пТ0] и номинальным значениям параметров РГЧ и ДУ программную
управляющую функцию Unp(t), nT0<t<nT0 + T(n), n = 0,1,2,..., обеспе-
чивающую перевод системы из начального фазового состояния Х[пТ0]
в начало координат О за минимальное время Т(п).
В этом случае в соответствии с функцией Unp(t) формируется дис-
кретный цифровой сигнал U[nT]:
U[nT] = Unp(t)| ; (13.16)
и соответствующий управляющий сигнал L(t) (рис. 13.18):
Д0 = ФЦ nT0 < t < (п + 1)Т0. (13.17)
В соответствии с сигналом L(t) формируются тяги двигателей 1...4
и РГЧ осуществляет движение в течение времени То. Так как
L(t) * Unp(t), nT0 < t < (п + 1)Т0, то движение не будет расчетным, а сле-
довательно, пользоваться функцией Unp(t) при (n + l)T0 <t<nT0 + T(n)
и значением сигнала U[(n + 1)TO] при формировании управляющего сиг-
нала L(t), (п + 1)Т0 < t < (п + 2)Т0, на следующем такте работы БЦВМ уже
нельзя.
454
Поэтому на следующем такте (п + 1)Т0 < t < (п + 2)Т0 работы БЦВМ
значения возмущений параметров движения РП! Х[(п + 1)Т0] рассматри-
ваются как величины, соответствующие новому начальному фазовому со-
стоянию системы стабилизации и снова определяется программная управ-
ляющая функция Unp(t), (п + 1)Т0 < t < (п + 1)Т0 + T(n +1), а следовательно,
дискретный цифровой сигнал U[(n + 1)Т0 ]:
U[(n + l)To] = Unp(t)|t=(n+i)To (13.18)
и соответствующий управляющий сигнал L(t) (рис. 13.19):
L(t) = U[(n + 1)Т0], (п + 1)Т0 < t < (п + 2)Т0. (13.19)
Таким образом, определяя в каждый дискретный момент времени
t = nT0, n = 0, 1, 2,... программную оптимальную по быстродействию
управляющую функцию U пр (t), nT0 < t < пТ0 + Т(п), по значениям реаль-
ных рассогласований параметров движения Х[пТ0] в этот момент време-
ни, формируем оптимальное управление L(t), nt 0 < t < (п + 1)Т0:
L(t) = L(x[nT0]) , n = 0, 1, 2,... (13.20)
455
Формирование управления движением описанным способом поз-
воляет:
- определенным образом учитывать дискретность То БЦВМ;
- использовать хорошо разработанные методы решения задачи опти-
мального быстродействия.
Для решения задач поиска непрерывного оптимального по быстродей-
ствию управления разработано много численных методов, основанных на
применении принципа максимума Л. С. Понтрягина [125].
В основном, в этих методах используются процедуры интегрирования
системы уравнений движения и сопряженной системы дифференциальных
уравнений, что требует достаточно больших затрат вычислительного вре-
мени и ресурсов.
Для решения поставленной задачи в реальном масштабе времени ис-
пользуется метод определения программной оптимальной по быстродей-
ствию управляющей функции, который не использует указанные проце-
дуры и который обеспечивает возможность решения задачи оптимизации
за время, меньшее периода дискретности То.
В основу метода определения программного управления движением
РГЧ в плоскости стабилизации, позволяющего отработать возмущения
параметров движения после ее поворота в «нуль» за минимальное время,
положено использование теоремы о числе переключений А. А. Фельд-
баума [27].
456
Согласно этой теореме, искомым управлением является кусочно-
постоянная функция U(t), 0<t<T, имеющая не более трех интервалов
знакопостоянства (две точки переключения ti, t2), принимающая, в зави-
симости от начальных условий, значения на границе области управления
U:|U(t)|< 1, с начальным значением U(t), равным +1 или -1, т. е.
U(t) = Um(t), ш = 1, 2, 3; 0<t<T,
где: Uj(t) = ±l, 0<t<T, tj=t2=T;
U2(t) =
0<t<tb t2=tb
+1, tj <t<T;
±1, 0<t<tb
U3(t) = <kl, ti<t<t2;
±1, t2<t<T.
Входной информацией для алгоритма поиска программного оптимально-
го по быстродействию управления движением РГЧ в плоскости стабилиза-
ции являются следующие величины:
X?, Х2, Х3 - значения возмущений параметров движения после пово-
рота в плоскости стабилизации;
еь е3 - допустимые значения возмущений по углу ориентации и кажу-
щейся скорости ц. м. на момент отделения элемента оснащения;
Н - шаг итерации для поиска первого момента переключения ti искомой
управляющей функции U(t);
Ki, К2 - номинальные значения углового и продольного ускорений РГЧ.
Выходной информацией алгоритма являются следующие величины:
U(0) - значение искомой управляющей функции U(t), определенной на
интервале времени [О, Т];
Т - программное время перевода системы из начальной в конечную точ-
ку;
tj, t2 - значения моментов переключений функции U(t), которые могут
быть определены при конечном числе итераций.
Используя материал, приведенный в разделах 13.5.1-13.5.7, имеется воз-
можность сформулировать искомый алгоритм управления движением в
плоскости стабилизации в следующем виде:
1) по известному алгоритму Ф1( ) в баллистической системе координат
vXp определяются возмущения параметров движения Д0, Д0, соот-
ветствующие дискретным моментам времени t = nTc,n = 0, 1, 2,...;
457
2) по алгоритму Ф2() определяется программная оптимальная по быст-
родействию управляющая функция:
u=unp(t)=unp^t, де, де, aw^; птс<^пто+т(п);
при реализации которой динамическая система (13.12) переводится за мини-
мальное время Т(п) из точки ^А0, А0, AW^ в точку (0,0, 0);
3) формируется дискретный цифровой сигнал:
^Ы=^(г)|г=пГ((.
>
равный +1 (или -1) в момент времени t = лТ0;
4) формируется непрерывный управляющий сигнал:
£(/) = С7[иГ0] , ИГ0<Г<(И + 1)Т0;
равный +1 (или -1) на интервале времени лТ0, (л + 1)Т0 , который опре-
деляет знак управляющего момента в плоскости стабилизации;
5) формируются управляющие команды на двигатели (включить, выклю-
чить) таким образом, чтобы с помощью их был обеспечен управляющий мо-
мент нужного знака;
6) указанные операции осуществляются на каждом такте работы БЦВМ
иТ0, (и + 1)Т0 , и = 0, 1, 2,...
Необходимо при этом отметить следующее: так как программная опти-
мальная управляющая функция является кусочно-постоянной, то формируе-
мый управляющий сигнал
L(t) = U[nTQ] , иТ0 <Z<(и + 1)Г0
не вносит погрешность по величине программного управляющего сиг-
нала (рис. 13.20), а может вносить погрешность по продолжи-
тельности своего действия, т. е. если момент переключения г, функции
(г) находится на интервале
лТ0, (л + 1)Т0 , то продолжительность
458
действия сигнала £(/) превышает требуемую на величину
Дт = (л + 1)Т0 -rt, если момент переключения tx находится вне интерва-
то погрешность не вносится в пределах данного так-
та работы БЦВМ.
Погрешность по продолжительности действия сигнала £(/) опреде-
ленным образом влияет на динамику системы стабилизации. Однако кор-
рекция программной управляющей функции на каждом такте работы
БЦВМ отслеживает это влияние, учитывает реальное движение РГЧ.
Результаты анализа телеметрической информации, полученной в про-
цессе летных испытаний нескольких десятков ракет РТ-23 (РТ-23 УТТХ),
а также достигнутая точность попаданий ББ в заданные точки прицелива-
ния полностью подтвердили правильность используемых методов управ-
ления РГЧ.
459
Раздел 6.2
БЦВМ КАК СРЕДСТВО ДЛЯ РЕШЕНИЯ
НЕТРАДИЦИОННЫХ ЗАДАЧ ДИНАМИКИ РАКЕТ
По мере предъявления к ракетным комплексам и ракетам все более
жестких тактико-технических требований возросла «идеологическая» на-
грузка на их системы управления. Расширялся круг задач, решаемых СУ
при подготовке к пуску, старте и полете, в том числе по обеспечению воз-
можности оптимизации характеристик «смежных» систем и агрегатов.
Особенно это проявилось после появления в ее составе БЦВМ.
Система управления, построенная на базе цифрового вычислительного
комплекса в составе бортовой (бортовых) и наземной (наземных) цифро-
вых вычислительных машин, действительно стала наиболее интеллекту-
ально развитой составной частью ракетных комплексов и способной при-
нять на себя решение ряда нетрадиционных задач динамики.
Приведем способы решения некоторых задач, возникших в ГКБ «Юж-
ное» в процессе динамического проектирования.
Глава 14
НЕТРАДИЦИОННЫЕ ЗАДАЧИ ДИНАМИКИ РАКЕТ
14.1. Обеспечение безопасности БЖРК
Одним из революционных технических решений по обеспечению пус-
ка боевых ракет наземного базирования, в том числе жидкостных МБР
тяжелого класса, явилась разработка идеологии и практическая реализа-
ция минометного старта из транспортно-пускового контейнера, ставшего
единственным видом старта всех ракет III и IV поколений, созданных КБ
«Южное» в 70-80-е годы прошлого столетия.
Не вдаваясь в комплексный анализ преимуществ этого вида старта (см.
«Введение») отметим, что он обеспечил существенное снижение тепло-
вых, газодинамических и акустических нагрузок как на элементы старто-
вого комплекса, так и ракеты, поскольку запуск маршевого двигателя
осуществляется на высоте ~20 м над стартовым сооружением (срезом
ТПК). Тем не менее для БЖРК этого оказалось недостаточно. Для обеспе-
чения безопасности пускового модуля и снижения нагрузки на его оси и
полотно железной дороги необходимо было обеспечить такую ориента-
цию оси ракеты в момент запуска двигателя, чтобы факел ДУ не попадал
на модуль (см. рис. 14.1).
460
Рис. 14.1
Для удовлетворения этому требованию в поддоне ракеты, который
обеспечивал герметичность подракетного объема при движении ракеты
в контейнере, установлен специальный пороховой ракетный двигатель
(ПРД) заклона. Момент выхода ракеты из ТПК фиксируется специальным
датчиком (КВ), по команде которого осуществляется запуск полетной
циклограммы. По одной из первых временных команд включается ПРД
заклона, обеспечивающий создание угловой скорости ракеты в плоскости,
перпендикулярной продольной оси пускового модуля. После этого поддон
отделялся от ракеты, а время подачи команды на запуск маршевого двига-
теля выбиралось из условия гарантированного набора требуемого угла за-
клона ракеты (уо) при появлении тяги ДУ. Гашение приобретенной угло-
вой скорости и возвращение ракеты в вертикальную плоскость произво-
дилось с помощью штатных управляющих органов по алгоритмам СУ.
Основные события проиллюстрированы диаграммой на рис. 14.2.
Определяющими параметрами рассмотренной схемы старта явились
время включения ДУ Оду), угол заклона ракеты в момент включения
ДУ(уо) и максимальный угол заклона на стартовом участке полета (ушах)-
Значение 1ду определяется энергетическими возможностями миномет-
ного старта и должно быть минимальным, при этом должно обеспечи-
ваться следующее условие: вертикальная скорость ракеты Vy > 0, высота
461
Импульс тяги ПРД заклона определялся, исходя из обеспечения непо-
падания факела ДУ на пусковой модуль (у0 - 15 град) в момент появле-
ния тяги ДУ.
Максимальный допустимый угол разворота ракеты ограничивался
сверху кинематикой гиростабилизированной платформы комплекса ко-
мандных приборов СУ и не должен был превышать 45 град.
Выбор алгоритмов управления ракетой на участке гашения угловой
скорости и возвращения ракеты в вертикальную плоскость произведен из
условий обеспечения попадания факела ДУ на пусковой модуль с макси-
мально возможной высоты.
При столь больших начальных условиях возможна раскачка в системе
стабилизации ракеты. Эта проблема решалась реализацией так называемо-
го алгоритма компенсации начальных условий (КНУ):
Укну
5 = KV
при t < т
5 = Kv • у + • ф при t > т.
В начальный момент при t = 0 рули не реагируют на угловое отклоне-
ние ракеты (\|/ = \|/о, Укну = 0), но обеспечивают гашение угловой скоро-
462
сти. К моменту t = т накопленный угол у полностью вводится в алгоритм
(Укну = v(t)), т- е- осуществляется переход на обычный алгоритм стаби-
лизации.
Примечание.
Необходимо отметить, что в практике морского ракетостроения
подобные задачи решались, уже начиная с середины пятидесятых годов,
в том числе средствами аналоговых систем управления [18]. Сложность
этих задач усугублялась их решением в детерминированной постановке.
При старте баллистических ракет (БР) как с надводного положения
подводной лодки (ПЛ), так и при старте из ПЛ, движущейся с доста-
точно большой скоростью на глубине несколько десятков метров, вели-
чины начальных условий полета ракеты определялись действием только
«естественных» возмущающих факторов при отсутствии принудитель-
ных программных воздействий. Поэтому устойчивость на начальном
участке полета первых советских БРПЛ (Р-11ФМ, Р-13, Р-21) обеспечи-
валась, наряду с ограниченными возможностями аналоговых систем
управления, путем уменьшения величин возмущающих факторов (волне-
ние моря, параметры качки ПЛ, скорость хода ПЛ, глубина погружения
при пуске БР и т. д.) за счет ограничений условий боевой эксплуатации.
Кроме того, предъявлялись достаточно жесткие требования к конст-
руктивно-компоновочной схеме ракеты в части ограничения степени
статической неустойчивости, характеризуемой величиной коэффициен-
та в уравнении моментов и потребной эффективности управляющих
органов (соотношение коэффициентов и ).
Так, на первой советской БРПЛ, стартующей из-под воды (Р-21), не-
смотря на жесткие ограничения диаметра шахты, были установлены
стабилизаторы, а органами управления являлись все четыре поворотные
камеры маршевого двигателя. На ракете Р-13, стартующей из надводно-
го положения ПЛ, наряду со стабилизаторами, смещающими центр
аэродинамического давления в направлении повышения статической ус-
тойчивости (от носка) ракеты, при остром дефиците энергетики в бак
окислителя было введено промежуточное днище, «удерживающее»
центр масс ракеты в наиболее возможном «переднем» положении.
* * *
Задача обеспечения безопасности пускового модуля во всех (без огра-
ничений) условиях эксплуатации, а именно, в любое время года и суток,
при любых погодных условиях, была решена в вероятностной постановке
с учетом следующих возмущающих факторов:
• действие ветра и технологических погрешностей изготовления
и монтажа ракеты и двигателей;
463
• отклонения от номинальных значений:
- параметров минометного старта;
- массово-инерционных характеристик ракеты;
- импульса тяги ПРД заклона;
- тяги двигателя;
- параметров системы стабилизации.
Задача решалась численным интегрированием уравнений возмущенно-
го движения ракеты как абсолютно жесткого твердого тела.
В ходе ЛКИ и штатных пусков ракет БЖРК полностью подтвердилась
правильность принятых решений и выполнение всех предъявленных тре-
бований. А при пусках в зимних условиях даже снег на элементах конст-
рукции пускового модуля оставался нетронутым.
* * *
При создании БЖРК, используя широкие возможности цифрового вы-
числительного комплекса, была решена еще одна оригинальная задача -
обеспечение возможности пуска ракет с любой точки разрешенных участ-
ков маршрута боевого патрулирования. Запрещенными для пуска участ-
ками маршрута в основном являлись станционные пути, тоннели, мосты
и тому подобные непригодные места старта ракет.
Пуск с любой точки позиционного района обеспечивался в весьма ог-
раниченное ТТТ [131] время боевой готовности, которое определялось
в основном длительностью и последовательностью технологических опе-
раций: обесточивание контактной сети; открытие крыши стартового ваго-
на; подъем ТПК с ракетой; набор готовности СУ, включая ввод в БЦВМ
уставок полетного задания.
Задание на пуск, кроме параметров точки цели, получаемых в составе
боевой кодограммы по линиям системы боевого управления, включало
также параметры точки старта (координаты, высоту, ускорение силы тя-
жести на поверхности Земли и др.).
Эти параметры с использованием НЦВМ определялись автоматически
системой навигации [72] с суммарной погрешностью, вызывающей от-
клонение точки падения ББ от цели, не превышающее 150 м (доля в пре-
дельном отклонении, равном 700 м не более 16 м).
Для реализации возможности автоматического определения геодезиче-
ских параметров системой навигации была создана специальная геодези-
ческая железнодорожная лаборатория (ГЖДЛ), осуществляющая заблаго-
временную геодезическую подготовку позиционного района [71].
Результаты работы ГЖДЛ в виде электронного носителя информации
(дискеты) соответствующего маршрута патрулирования, использовались
НЦВМ системы навигации для выработки установок задания на пуск.
464
14.2. Обеспечение безударности старта PH «Зенит»
Ракета-носитель «Зенит» (11К77) стар-
тует с пускового устройства (ПУ), разме-
ры которого в плане предельно сокраще-
ны. Это, наряду с уменьшением затрат
времени и стоимости строительства, упро-
стило решение вопросов по созданию под-
вижных частей наземных заправочных
коммуникаций и поворотных опорных
устройств.
Общий вид пускового стола с уста-
новленной на нем ракетой представлен на
рис. 14.3.
Схема пускового устройства показана
на рис. 14.4.
До высоты подъема ~4 м хвостовой
отсек ракеты находится в цилиндрическом заглублении. После выхода из
заглубления до высоты ~8 м опасной точкой стартового сооружения явля-
ется кабель-мачта (точка К). Исходная величина зазора между движущей-
ся ракетой и стартовым сооружением на
этих участках полета составляет ~1 м.
Длительное движение PH в непо-
средственной близости от элементов
стартового сооружения при малых за-
зорах между ними обусловило жесткие
требования к точности стабилизации
из условий обеспечения безударности
старта. Вместе с тем, как показывает
анализ, использование традиционного
алгоритма стабилизации движения PH,
содержащего контур угловой стабили-
зации и стабилизации центра масс, не
позволяло обеспечить выполнение
предъявляемых требований на рас-
сматриваемом участке движения. Это
схема на рис. 14.5.
При реализовавшихся показанных на схеме сочетаниях отклонения
центра масс Z и углового отклонения PH \|/ традиционный алгоритм ста-
билизации создает управляющее усилие Рупр на их отработку, при этом
Рис. 14.4
обстоятельство иллюстрирует
465
движение хвостового отсека PH приводит к уменьшению зазора Д между
PH и стаканом стартового сооружения.
При расчете динамики старта необходимо было учитывать:
- несоосность PH и ПУ;
- разность подпорных усилий опорных устройств;
- перекос и смещение вектора тяги двигательной установки;
- усилие за счет процесса расстыковки кабель-мачты;
- атмосферный ветер;
- отклонения параметров системы от номинальных значений.
Из общих соображений ясно, что коль скоро ограничения задаются по
определенным координатам (в данном случае перемещение хвостового
отсека должно быть минимальным), то и максимальный эффект может
быть достигнут при организации управления по этим координатам. Так
родилась идея управления на стартовом участке полета до прохождения
опасных точек стартового сооружения по отклонению хвостового отсека
от исходного положения. При наличии на борту ракеты БЦВМ расчет та-
ких управляемых координат не представлял труда. Так в канале рыскания
координата, характеризующая отклонение хвостового отсека, определяет-
ся по формуле:
zx. =zu.m. +v(L-xUM),
где zu м - отклонение центра масс ракеты в возмущенном движении;
у - угол рыскания;
L - длина ракеты;
хц м - координата центра масс ракеты.
Соответствующий алгоритм управления
л в канале рыскания был принят в виде:
ч, /Д 3„=К1|,ги + К'¥г„,при 0<Ь<4м.
Tjl В канале тангажа алгоритм стабилизации
/ / / аналогичен, но время его работы соответству-
I ет 0 < h < 8 м. Переход на традиционный алго-
лу 4 /цм ритм угловой стабилизации и стабилизации
/ / / центра масс в каналах рыскания и тангажа
I / / осуществлялся после прохождения отметок 4 м
I и 8 м соответственно.
/ / / В процессе летных испытаний и штатной
-----а I------------ эксплуатации были подтверждены правиль-
I ” I ность предложенного решения и уточнены ко-
" '*•’ личественные оценки динамики старта.
Рис. 14.5
466
14.3. Обеспечение безопасности старта РКН «Зенит-38Ь»
Ракета-носитель «Зенит» взята за основу при разработке международ-
ной программы «Морской старт» и совместно с разгонным блоком ДМ,
разработки РКК «Энергия», составила ракету космического назначения
(РКН) «Зенит-38Ь».
Схема старта РКН «Зенит-З SL» идентична схеме для PH «Зенит», но
старт осуществляется с плавучей платформы, находящейся в свободном
движении в окрестности заданной точки Тихого океана вблизи экватора
(рис. 14.6).
В этом случае к комплексу возмущений, перечисленных выше, добав-
ляются возмущающие воздействия, обусловленные качкой платформы,
вызванной атмосферным ветром и волнением океана. Условия старта за
счет качки существенно ужесточаются. Вместе с тем, возникает проблема
информационного обеспечения использования существующих на PH «Зе-
нит» алгоритмов стабилизации на начальном участке полета, т. к. после
разрыва связей ракеты со стартовым сооружением на борту ракеты отсут-
ствует информация о движении платформы и расчет взаимного положе-
ния платформы и ракеты невозможен.
Одновременно ужесточаются требования по ограничению воздействия
стартующей РКН на платформу: кроме обеспечения безударности старта
накладываются ограничения на положение следов струй двигательной ус-
тановки на палубе платформы из условий обеспечения допустимых уров-
ней акустического, газодинамического и теплового воздействия.
467
Эти требования формулируются следующим образом:
- до высоты подъема 30 м оси струй не должны выходить за
круг радиусом R от центра ПУ;
- на высотах от 30 до 200 м оси струй не должны пересекать па-
лубу на расстоянии дальше L,
где R и L - функции высоты полета РКН (рис. 14.7).
Рис. 14.7
Указанное обстоятельство привело к необходимости проведения ком-
плекса теоретических исследований, направленных на поиск идеологии
управления ракетой и определение количественных характеристик дина-
мики старта.
По результатам статистического анализа около 30 пусков PH «Зенит»
уточнены возмущающие воздействия на начальном участке полета в сто-
рону их существенного уменьшения. С учетом этого проведено математи-
ческое моделирование совместного движения качающейся стартовой
платформы и стартующей с нее РКН «Зенит-З SL». Исследовался началь-
ный участок полета в зоне непосредственной близости ракеты и элемен-
тов стартового сооружения.
Доказано, что при скорости ветра, параметрах движения платформы и
высоте волны, имеющих место в районе старта, возможна реализация во-
обще неуправляемого движения ракеты в канале рыскания до высоты по-
лета 4 м и в канале тангажа до высоты 8 м. При этом вероятность старта
без соударения близка к 1 (0,999999).
В целом циклограмма работы алгоритмов управления ракетой на уча-
стке полета до высоты ~200 м характеризуется следующим.
После разрыва связей РКН с опорами стартового сооружения управле-
ние ракетой осуществляется только в канале крена (относительно про-
дольной оси) для обеспечения в полете симметричного расположения ка-
468
мер двигательной установки и их факелов относительно кабель-мачты
Управление в канале рыскания начинается после выхода ракеты из за-
глубления ПУ (Н = 4 м), а в канале тангажа после прохождения опасной
точки кабель-мачты (Н = 8 м). Алгоритм стабилизации был выбран, исхо-
дя из обеспечения ограничений по следам струй двигательной установки
на палубе платформы.
Как показал анализ, обычные алгоритмы угловой стабилизации и ста-
билизации центра масс не обеспечивали выполнение предъявленных тре-
бований. Поставленная задача была решена с помощью алгоритма, фор-
мульная запись которого совпадает с классической, но коэффициенты
управления в каналах стабилизации центра масс имеют обратные знаки:
5д = Кд • Ф+ Кф • Ф- Ку • у - Ку • у - тангаж,
5у = Ку • v + K^• V_KZ z-K^ z -рыскание.
Следует отметить, что такие алгоритмы неустойчивы (корни характе-
ристического уравнения имеют положительные действительные части),
однако техническая устойчивость до высоты полета 200 м обеспечивается.
Дополнительное уменьшение отклонения следов факела ДУ от центра
ПУ получено введением в алгоритм отклонения камер ДУ программного
сигнала на синхронное сведение всех 4-х камер ДУ к плоскости II-IV
в пределах рабочих углов отклонения, без создания поперечного воздей-
ствия на РКН.
На рис. 14.9 приведены графики следов струй ДУ на палубе СП, полу-
ченные по данным реальных пусков РКН «Зенит-З SL», которые подтвер-
ждают выполнение всех предъявленных требований.
469
Рис. 14.9
14.4. Минимизация нагрузки на корпус ракеты
Поиски алгоритмов стабилизации, минимизирующих потребные
управляющие усилия для обеспечения устойчивого полета ракеты по тра-
ектории, близкой к программной, и одновременно уменьшающих аэроди-
намические нагрузки на корпус ракеты при полете в плотных слоях атмо-
сферы, сопровождают всю историю ракетной техники. Особенно актуаль-
но решение этой задачи при модернизации ракет и ракет-носителей (ха-
рактерный пример приведен в части 1 книги).
В начале 60-х годов перед ОКБ-586 была поставлена задача создания
двухступенчатой PH легкого класса на базе стоящей на вооружении бое-
вой одноступенчатой ракеты Р-12 - первенца КБ. Эта ракета-носитель по-
лучила впоследствии наименование «Космос» и, в основном, обеспечила
выполнение космических программ «Космос» и «Интеркосмос».
В качестве управляющих органов на этой ракете использовались газо-
струйные рули - поворотные аэродинамические поверхности из графита,
установленные в раструбах сопел маршевых двигателей, которые обеспе-
470
чивали создание управляющих усилий в каналах тангажа, рыскания и
крепа. Эффективность этих органов управления была невелика и уже при
создании Р-12 проектантам-ракетчикам и управленцам пришлось прило-
жить немало усилий, чтобы обеспечить управляемость ракеты. В те же го-
ды, как и в случае создания первых морских ракет (раздел 14.1), в перво-
начальном варианте ракета Р-12 имела аэродинамические стабилизаторы,
что уменьшало аэродинамическую неустойчивость благодаря смещению
центра давления к хвосту ракеты. Для обеспечения благоприятной массо-
вой центровки бак окислителя имел промежуточное днище, разделяющее
бак на две части: сначала вырабатывался компонент из нижней части ба-
ка, а затем из верхней. Совместное действие этих конструктивных реше-
ний (аэродинамического и массового) позволило существенно уменьшить
степень неустойчивости боевой ракеты и обеспечить её управляемость
располагаемыми управляющими усилиями.
На эту ракету, с минимальными её доработками, было необходимо ус-
тановить II ступень, длина которой из условий обеспечения требуемой
энергетики (количества топлива) оказалась соизмеримой с длиной ракеты
Р-12, что существенно усложняло обеспечение управляемости (см. главу 3).
Из газоструйных рулей уже на ракете Р-12 было «выжато» всё, а приме-
нение более мощных органов управления (например, поворотных управ-
ляющих двигателей) привело бы к коренной переделке существующей
ракеты.
Необходимость решения сложной практической проблемы всегда сти-
мулирует развитие прикладной науки. В данной ситуации это подтолкну-
ло начало системных исследований по динамике ракет. В НИИ-88 разви-
вается направление по изучению внешних атмосферных факторов, в част-
ности, исследования по систематизации данных, описывающих ветровое
поле Земли. Работы через годы завершились созданием отраслевого стан-
дарта, нормирующего задание ветра в задачах динамики ракет [104].
В это же время, в ОКБ-586 разрабатывались инженерные методы ис-
следования технической устойчивости ракет как объектов управления
с вероятностными характеристиками [112]. Эти исследования заверши-
лись созданием межотраслевой методики учета влияния возмущающих
факторов при оценке управляемости (см. главу 3).
Таким образом, уже к середине 60-х годов была в основном завершена
разработка методологии выбора потребных управляющих усилий, позво-
ляющая обоснованно выбирать управляющие органы ракет при их проек-
тировании и модернизации с учетом всех вероятностных характеристик
как динамической схемы ракеты, так и возмущающих воздействий.
Наиболее сложным является решение задачи выбора управляющих ор-
ганов первых ступеней, полет которых происходит в атмосфере. Возму-
471
щенное движение, например I ступени трехступенчатой жидкостной раке-
ты в канале рыскания описывается системой из 12 дифференциальных
уравнений второго порядка (см. главу 10):
- 2 уравнения движения твердого тела;
- 6 уравнений колебаний компонентов топлива в баках;
- 3 уравнения упругих колебаний корпуса;
- 1 уравнение движения упругой подвески управляющих органов.
Однако благодаря тому, что спектры собственных частот достаточно
разнесены, после решения разработчиком системы стабилизации задачи
обеспечения устойчивости высокочастотные осцилляторы оказываются
задемпфированы и задача определения потребной эффективности управ-
ляющих органов может решаться в рамках модели ракеты как твердого
тела. Уравнения системы стабилизации при этом также были упрощены.
И, наконец, возмущающими воздействиями от технологических погреш-
ностей изготовления и монтажа ракеты и двигательной установки, кото-
рые достаточно велики (до 20 % от ветрового воздействия), в рамках ве-
роятностной методологии их учета можно пренебречь.
Таким образом, задача сводится к выбору алгоритмов управления ра-
кетой, как твердым телом, минимизирующих загрузку управляющих ор-
ганов при действии атмосферного ветра. Расчетным случаем является
действие в районе максимальных скоростных напоров ветра с градиента-
ми скорости ветра в соответствии с отраслевыми стандартами.
Рассмотрим особенности стабилизации аэродинамически неустойчи-
вой ракеты при действии ветра в зависимости от вида закона управления.
1. Закон управления 5 = Kv • у + • ф, где
5 - угол отклонения управляющих органов,
\|/ - угол рыскания.
При действии на ракету ветра со скоростью W (рис. 14.10), возникает
о W W
угол скольжения pw=arctg—«— и в силу неустойчивости ракеты она
начинает разворачиваться таким образом, что угол скольжения возрастает
до величины PL = Pw + V.
В соответствии с законом управления рули поворачиваются, создавая
управляющий момент, направленный на компенсацию аэродинамического
возмущающего момента. После завершения переходного процесса уста-
навливается равновесное состояние, при котором суммарный угол сколь-
жения больше угла скольжения от ветра на величину у:
Pi = Pw + V > Pw •
472
X
________________ z
Рис. 14.10
Таким образом, в системе стабилизации, реализующей управление
только по углу отклонения ракеты от программного положения, суммар-
ный аэродинамический момент, действующий на ракету, всегда больше
аэродинамического момента от ветра. Для его уменьшения необходимо
уменьшать ошибку стабилизации у, т. е. увеличивать коэффициенты Ку,
в законе управления, но такое увеличение ограничено реально суще-
ствующей областью устойчивости.
2. Закон управления 8 = Kv • у + К^, • ф - Kz • z - К* • z, где
z - отклонение центра масс от программного значения.
В этом случае при рациональном выборе коэффициентов управле-
ния Kv, Kv, Kz, Ki переходный процесс характеризуется схемой, приве-
денной на рис. 14.11, для которой Pz = Pw - |v| < Pw.
Таким образом, в системе стабилизации, реализующей управление по
угловому отклонению ракеты и отклонению центра масс, может быть дос-
тигнуто уменьшение суммарного аэродинамического возмущающего мо-
мента, обусловленного действием атмосферного ветра.
Рассмотренные алгоритмы управления могут быть реализованы в ана-
логовом виде, без использования БЦВМ, что и обусловило их широкое
использование в первых поколениях баллистических ракет. Возможности
473
кардинального уменьшения нагрузок, действующих на ракету в полете,
при их применении ограничены.
Рис. 14.11
Из общей теории известно, что эффективность управления может быть
существенно повышена при введении в закон управления информации
о возмущающих воздействиях, в нашем случае - о скорости ветра или об
угле атаки. К сожалению, надежного прибора, позволяющего определить
угол атаки набегающего потока на движущейся ракете и пригодного для
использования в системе стабилизации, не было создано. Однако с введе-
нием в состав системы управления ракеты БЦВМ появилась возможность
по имеющейся информации о движении ракеты рассчитать угол атаки,
ввести эту информацию в закон управления и тем самым существенно по-
высить эффективность управления и снизить аэродинамические нагрузки
на корпус и потребные управляющие усилия.
Принципиальная схема решения задачи достаточно проста: на борту
ракеты в реальном масштабе времени, с использованием информации
с командных приборов о фактическом движении ракеты рассчитывается
текущее значение угла атаки. Для этого система уравнений возмущенного
движения ракеты как абсолютно жесткого твердого тела (см. часть 1), ко-
торую для наглядности (в канале рыскания) запишем в следующем виде:
474
z = a2SP + aZ4,v|/ + a26-8
v|/ = a>„p-p + a1(,6-8
разрешается относительно 0,
z-W
где p = v + ——---искомая функция, суммарный угол скольжения в кана-
ле рыскания,
z - отклонение центра масс ракеты от плоскости стрельбы,
V - угол рыскания ракеты,
8 - угол отклонения управляющих органов,
аш, azy ’ azs» aVa> aV8 ~ переменные во времени коэффициенты, номи-
нальные значения которых содержатся в памяти БЦВМ.
Естественно, что при решении этой задачи возникают вопросы, свя-
занные с фильтрацией информации, получаемой численным дифференци-
рованием показаний датчиков комплекса командных приборов. Мы не ос-
танавливаемся на этом, отсылая желающих глубже познакомиться с этими
проблемами к статье коллектива авторов под руководством Я. Е. Айзен-
берга, главного конструктора систем управления многих ракет разработки
ГКБ «Южное» [6].
Возможны несколько путей дальнейшего использования полученной
информации об угле скольжения 0:
1. Непосредственное введение в алгоритм стабилизации значения 0
с определенным весовым коэффициентом, и выбор всех коэффици-
ентов уравнений управления из условий обеспечения устойчивости
замкнутой системы стабилизации. Так поступили в НПО «Хартрон»
г. Харьков при разработке системы стабилизации PH «Энергия»
с космическим кораблем «Буран» [6].
2. Введение специальной программы угловой ориентации PH в кана-
лах тангажа и рыскания
Vnp(t) = -₽(t)
так, что стабилизация ракеты осуществляется относительно этой
программы, оперативно рассчитываемой на борту летящей ракеты.
Так поступили в НПО АП г. Москва при создании системы стаби-
лизации PH «Зенит» и её модификации по международной про-
грамме «Морской старт» (авторский коллектив под руководством
М. С. Хитрика, И. М. Баскакова, В. И. Садовского и др.).
Не вдаваясь в сравнительный анализ этих двух основных технологий,
многие детали и тонкости которых являются ноу-хау авторов, отметим
основные результаты от их внедрения на примере PH «Зенит».
475
PH «Зенит», проектирование которой вело ГКБ «Южное» в 70-е годы
прошлого века, была одной из первых отечественных ракет, на которой
реализован алгоритм минимизации аэродинамических нагрузок на корпус:
система стабилизации должна обеспечить непревышение величиной про-
изведения скоростного напора на пространственный угол атаки (<? а) оп-
ределенного значения. Для PH «Зенит» это значение составляло
~ 20000 гРад. Алгоритм прошел апробацию пусками двухступенчато-
м
го носителя «Зенит» с космодрома Байконур, показав свою работоспособ-
ность и приемлемое качество переходных процессов в системе стабилиза-
ции, и обеспечил выполнение требований по ограничению Алго-
ритм обладал возможностью оперативной перенастройки благодаря вве-
дению через полетное задание специального массива настроечных
констант (НКАС), что позволяло обеспечивать пуски в широком диапазо-
не массы полезных нагрузок (от 3 до 12 т) и траекторий их выведения.
Особенно ярко преимущества нового подхода к проектированию сис-
темы стабилизации проявились в процессе адаптации PH «Зенит» к меж-
дународной программе «Морской старт». Установкой разгонного блока
разработки РКК «Энергия» «Зенит» превращался в трехступенчатую ра-
кету космического назначения, при этом существенно увеличивались мас-
са и длина ракеты, к тому же блок полезного груза разработки «Боинга»
имел больший диаметр. Это привело к существенному увеличению степе-
ни аэродинамической неустойчивости РКН и соответственно аэродинами-
ческих нагрузок на корпус.
В этих условиях судьба программы «Морской старт» во многом опре-
делялась возможностью системы управления реализовывать существенно
более жесткие требования по ограничению произведения (<? а). Это было
необходимо, чтобы не подвергать коренной переделке конструкции I и II
ступеней PH «Зенит». Задача была успешно решена в ходе проектных ис-
следований по системе стабилизации. Достигнутые результаты позволили
внести в Документ контроля интерфейсов (ДКИ) ограничение по величи-
не произведения скоростного напора на пространственный угол атаки,
обеспечиваемого системой стабилизации
q • а < 13500-— •
м
По результатам анализа свыше 10 пусков РКН «Зенит-З SL» с морской
платформы, проведенных на момент написания этой книги, максимальное
значение (<?-а) не превысило 10000КГС ^ад.
476
Часть 7
СИСТЕМЫ И АГРЕГАТЫ РАКЕТЫ
КАК ОБЪЕКТА УПРАВЛЕНИЯ
Основными ракетными объектами регулирования являются жидкост-
ный реактивный двигатель (ЖРД) и система его питания.
Управление работой ЖРД обычно выполняется системами: поддержа-
ния давления в камерах сгорания (СПД), регулирования кажущейся ско-
рости (РКС) и управления расходованием топлива (СУРТ).
Учебник [88] содержит достаточные материалы по теории и практике
регулирования ЖРД, включая динамические схемы двигателя, в которых
он рассматривается как силовой и нагрузочный агрегаты. В связи с этим,
учитывая ограниченный объем настоящей книги, в ней проблема про-
дольных упругих колебаний ракеты вообще не рассматривается. Ограни-
чимся описанием отличий системы регулирования двигателя РКН «Зенит»
от приведенных в [88] и более подробным рассмотрением принципов по-
строения и работы СУРТ.
Раздел 7.1
СИСТЕМА РЕГУЛИРОВАНИЯ 11Д520
Двигатель 11Д520 является на мировом уровне самым мощным по тяге
и лучшим по своим удельным характеристикам ЖРД в своем классе. Дос-
тижение двигателем 11Д520 столь высоких параметров определялось
(в том числе) применением принципиально новой автоматики, на базе ко-
торой создана система программного запуска и выхода двигателя на ос-
новной режим работы. Кроме того, эта система обеспечила возможность
высокоточного поддержания задаваемых с учетом конкретного образца
режимов по тяге и соотношению компонентов топлива.
В двигателе 11Д520 используется замкнутая электрогидромеханиче-
ская схема регулирования по двум каналам (рис. 7.1):
477
• давлению в камерах (Рк);
• массовому соотношению компонентов топлива в камерах (Км) с ис-
пользованием внутридвигательных обратных связей.
Исполнительным органом при регулировании двигателя по каналу Рк яв-
ляется регулятор расхода горючего со следящим приводом (МРГ), который
установлен в магистрали питания горючим газогенераторов.
Исполнительными органами при регулировании двигателя по каналу Км
являются: механизм дросселя горючего со следящим приводом МДГ, уста-
новленного в магистрали питания горючим камер, и механизма дросселя
окислителя с приводами МДО 1,2.
В состав следящих приводов МДГ и МРГ входят сравнивающие устрой-
ства, формирующие сигналы рассогласования по отклонению текущих зна-
чений величин параметров от значений, задаваемых регулятором
командного давления (РКД).
РКД, установленный в малорасходной магистрали перепуска параллельно
первой ступени насоса горючего, формирует с помощью дросселей-
задатчиков значения командных давлений параметров, поступающих на вхо-
ды сравнивающих устройств.
Текущие значения величин параметров поступают к штуцеру сравниваю-
щего устройства от смесительной головки второй камеры (канал Рк) и к шту-
церу сравнивающего устройства от суженой части трубы Вентури (канал Км).
Возникшие рассогласования приводят к перемещению чувствительных эле-
ментов сравнивающих устройств и связанных с ними командных золотников
следящих приводов, что приводит к перекладке приводами исполнительных
органов и к изменению режима работы двигателя.
Изменение режима работы двигателя по внутридвигательным обратным
связям вызывает изменение контролируемых сравнивающими устройствами
параметров и, как следствие, перемещение командных золотников и пере-
кладку исполнительных элементов следящими приводами до тех пор, пока
сигнал рассогласования не уменьшится до зоны нечувствительности сравни-
вающих устройств.
Регулирование режима работы двигателя по каналу Рк осуществляется по
командам СУ, подаваемым на привод МРКД1, в результате чего дросселем-
задатчиком РКД формируется значение командного давления, эквивалентно-
го программному значению Рк. Сформированные новые программные зна-
чения Рк отрабатываются следящим приводом МРГ.
Регулирование двигателя по каналу Км осуществляется по командам СУРТ,
подаваемым на привод МРКД2, связанный с дросселем-задатчиком Км, что
вызывает на выходе дросселя-задатчика формирование нового значения ве-
личины командного давления и перекладку исполнительного элемента дрос-
селя следящим приводом МДГ для парирования возникшего рассогла-
сования.
478
479
От II ступ, насоса ”Г"
Рис. 7.1
При отсутствии командных сигналов СУ и СУРТ системой регулирова-
ния с помощью внутридвигательных обратных связей обеспечивается под-
держание основного режима работы двигателя.
Работа двигателя.
Во время предстартовой подготовки с наземной вычислительной машины
в бортовую ЦВМ переписываются индивидуальные коэффициенты двигате-
ля, включающие:
К1 - угловое положение МРКД1 для главной ступени тяги (ГСТ);
К2 - угловое положение МРКД1 для конечной ступени тяги (КСТ);
КЗ - угловое положение МРКД1, соответствующее концу плавного дрос-
селирования;
К4 - угловое положение МРКД2 при номинальной температуре горючего
в баке на ГСТ;
К5 - коэффициент связи между углом МРКД2 и величиной Км;
Кб - угловая поправка на положение МРКД2, вводимая в момент начала
плавного дросселирования;
К7 - угловое положение МРКД2 на КСТ при номинальной температуре
горючего и ряд других коэффициентов.
Данные коэффициенты определяются при испытаниях двигателя на заво-
де-изготовителе.
Для обеспечения точной настройки ДУ измеряется температура горючего
в баках ракеты и передается в БЦВМ для учета в регулировании режимами
работы.
Подготовке двигателя к запуску предшествует заправка баллонов двига-
теля гелием, баков топливом, вакуумирование полостей горючего двигателя,
продувка магистралей двигателя азотом, установка регулирующих органов
в исходное положение и обогрев двигателя теплым воздухом от системы
термостатирования хвостового отсека.
В процессе подготовки двигателя к запуску подается питание на моторы
вспомогательного агрегата питания. После выхода их на стационарный ре-
жим подаются команды на установку приводов агрегатов регулирования
в исходное для запуска положение.
Привод МРКД-1 устанавливается в положение, соответствующее на-
стройке РКД по давлению в камерах (Рк) на режим главной ступени; привод
МРКД-2 устанавливается в положение, соответствующее настройке на но-
минальное соотношение компонентов в камерах (Км), при этом вводится по-
правка, учитывающая фактическую температуру горючего в баке. По коман-
дам системы управления пневмопривод и приводы МРГ (регулятор расхода
горючего), МДГ (дроссель горючего), МДО1 и МДО2 (дроссели окислителя)
устанавливаются в положение, соответствующее начальной настройке пред-
варительной ступени тяги.
480
Затем производится открытие разделительного клапана горючего и начи-
нается заполнение двигателя горючим.
Запуск двигателя осуществляется посредством подачи в определенной
последовательности команд системой управления на ЭПК, по которым про-
изводится:
- поступление окислителя в газогенераторы и в тракты охлаждения га-
зоводов, турбины и узлов качания;
- горючее начинает поступать к форсункам и поясам завесы камер сго-
рания;
- самовоспламеняющееся пусковое горючее начинает поступать в газо-
генераторы и камеры сгорания где, соприкасаясь с окислителем, происходит
его воспламенение.
Перевод двигателя на режим предварительной ступени производится по-
средством подачи команды на ЭПК ВОР, обеспечивающего перекладку
пневмопривода и на открытие регулятора расхода.
Через определенное время от первой команды на запуск производится ав-
томатический контроль достижения двигателем режима предварительной
ступени по четырем сигнализаторам давления. При положительном резуль-
тате контроля по команде СУ начинается перевод двигателя на режим глав-
ной ступени - привод МРГ открывает регулятор расхода.
В процессе выхода на главную ступень включаются внутридвигательная
обратная связь системы регулирования по каналу Рк и внутридвигательная
обратная связь системы регулирования по каналу Км.
Штатный останов двигателя - двухступенчатый. Сначала двигатель пере-
водится на режим конечной ступени. Перед переводом на конечную ступень
производится его плавное дросселирование. Дросселирование производится
посредством подачи команд на приводы МРКД1,2 и МДО1,2, скорость пере-
кладки которых определяется и задается СУ. Останов двигателя с режима
конечной ступени производится закрытием ЭПК ВОР11, при этом пневмо-
привод закрывает регулятор расхода, обеспечивая уменьшение по опреде-
ленному закону расход горючего в газогенераторы и, следовательно, тяги
двигателя.
Глава 15
СИСТЕМА УПРАВЛЕНИЯ РАСХОДОВАНИЕМ
ТОПЛИВА
15.1. Основные технические требования,
предъявляемые к системе
Система управления расходованием топлива (СУРТ) предназначена для
оптимизации использования располагаемого запаса топлива в полете ракеты.
481
Объектом регулирования СУРТ является динамическая система, со-
стоящая из двигательной установки ступени, топливных баков и связы-
вающих их трубопроводов.
Оптимизация использования располагаемых запасов топлива обеспе-
чивается синхронизацией выработки окислителя и горючего, а также про-
гнозированием момента окончания компонентов топлива.
Синхронизация выработки окислителя и горючего на ступени реализует-
ся путем автоматического изменения коэффициента соотношения расходов
компонентов топлива через ЖРД в допустимом диапазоне регулирования.
Прогнозирование момента окончания компонентов топлива осуществ-
ляется на основе измерительной информации системы о фактическом рас-
ходовании компонентов топлива в процессе полета ракеты.
Система управления расходованием топлива должна обеспечивать
следующие динамические и точностные характеристики:
- отклонение коэффициента соотношения расходов компонентов топ-
лива от номинального значения в процессе реализации управления не
больше величины, допустимой для данного ЖРД - порядка (7... 10) %;
- минимальные разбросы остатков компонентов топлива (в % от но-
минального рабочего запаса компонента) на момент выключения ЖРД -
для современных ракет ~ 0,3 %.
15.2. Принципы построения и алгоритм
функционирования СУРТ
Управлением расходования топлива ракеты с ЖРД можно, не увеличи-
вая заправленной массы топлива, существенно повысить энергетику раке-
ты, т. е. выводить на орбиту значительно больший груз, или тот же груз на
более высокие орбиты.
Повышение эффективности использования располагаемого запаса топ-
лива достигается применением специальной системы управления, воздей-
ствующей на режим расходования топлива.
Своего рода ключевым понятием, характеризующим общие потери
в энергетике ракеты, является понятие гарантийных запасов топлива,
смысл которого состоит в следующем.
В каждый из баков ракеты дополнительно к рабочему запасу топли-
ва, полностью израсходуемому в расчетно-номинальных условиях вы-
ведения, необходимо резервировать некий дополнительный запас топ-
лива, предназначенный для компенсации случайных возмущений, дей-
ствующих на процесс расходования топлива и на траекторные коорди-
наты ракеты. Это возмущения типа погрешностей заправки баков,
настройки двигателей по параметру К, отклонений удельного импульса
тяги двигателей, давления наддува баков, температуры компонентов
482
топлива, аэродинамических характеристик ракеты и т. д. Выделение та-
ких запасов топлива из общего заправляемого в баки ракеты количества
топлива возможно лишь за счет соответствующего сокращения рабочих
запасов, что приводит к снижению номинальной энерговооруженности
ракеты.
Поэтому действие специальных систем, получивших общее название
«Система управления расходованием топлива», должно приводить,
прежде всего, к парированию комплекса названных возмущений и, следо-
вательно, минимизации потерь рабочих запасов топлива.
При приближении к моменту выключения двигателя масса ракеты
уменьшается до «сухого» веса конструкции, которая составляет малую
долю от взлетной массы. Неиспользованное топливо на этом фоне будет
сказываться неблагоприятно как в виде недополученного импульса, так и
в увеличении конечной массы ракеты.
Уменьшение неиспользуемого топлива достигается решением систе-
мой СУРТ двух задач управления:
- управление режимом расходования топлива,
- обеспечение наиболее полной выработки топлива.
Управление режимом расходования топлива осуществляется, главным
образом, для снижения гарантийных запасов топлива, а это можно осуще-
ствить, если к моменту выключения ЖРД с высокой точностью синхрони-
зировать количества окислителя и горючего. В подавляющем большинст-
ве проектных условий эксплуатации необходима жесткая (независимая от
возмущений, действующих на траекторные параметры) синхронизация
опорожнения баков окислителя и горючего. Для этого измеряются теку-
щие количества компонентов, сравниваются их относительные количества
и по результатам сравнения изменяется соотношение расходов окислителя
и горючего в такую сторону и в такой мере, чтобы рассогласование стало
равным нулю. С позиций минимизации динамической составляющей -
разбросов параметра К, а следовательно, и минимизации потерь в удель-
ной тяге, СУРТ строят по терминальному принципу - обеспечение наи-
лучших конечных характеристик, т. е. в идеальном случае нулевого рассо-
гласования к моменту выключения ЖРД.
Дополнительное повышение энергетических характеристик ракеты да-
ет так называемая «полная» выработка топлива. Под «полной» выработ-
кой топлива понимается такой способ его расходования, при котором не-
использованное топливо в конце работы ступени сводится к минимально
потребным величинам, определяемым только условиями безаварийного
выключения двигателей.
483
Управление «полной» выработкой топлива заключается в организации
выключения двигателей не по набору заданного функционала, а при мак-
симально возможном использовании запасов топлива.
При этом двигатели нижних ступеней ракеты выключаются по инфор-
мации о количестве топлива в баках ступени так, чтобы обеспечить «ну-
левой» остаток топлива. Это позволяет использовать практически весь га-
рантийный запас топлива нижних ступеней в качестве рабочих запасов.
Двигатель же последней ступени выключается по функциональному или
терминальному способу управления.
Эффект повышения энергетических характеристик здесь определяется
тем обстоятельством, что в большей своей части резервирование гаран-
тийных запасов производится из условия компенсации на последней сту-
пени суммарного по ступеням воздействия случайных возмущений - то-
гда как при выключении ЖРД ступеней по функционалу эти возмущения
парируются парциальным образом на каждой ступени.
Для управления полной выработкой топлива СУРТ по информации
о текущих запасах топлива в баках прогнозирует момент окончания рабо-
чих запасов. Принцип работы системы заключается в нахождении осред-
ненного на интервалах времени расхода топлива и прогнозирования по
этой информации момента окончания рабочих запасов. Указанный способ
определения момента окончания запасов эффективен при условии работы
ЖРД с постоянным суммарным расходом топлива.
Построение СУРТ ведется на основе принципа высокоточного порого-
во-дискретного измерения запасов компонентов топлива, терминального
управления расходованием этих запасов и формирование моментов их
полной выработки.
Рассмотрим принципы построения СУРТ на примере структурной схе-
мы (рис. 15.1).
В баках окислителя (БО) и горючего (БГ) установлены датчики уров-
ня окислителя (ДУО) и горючего (ДУГ) с набором равного числа изме-
рительных точек (ИТ), которые реагируют на факт пересечения зеркалом
компонента уровня, на котором ИТ установлены. При опорожнении ба-
ков в номинальных условиях пересечение ИТ одинаковых номеров в ба-
ках О и Г происходит одновременно, разность времен их пересечения
to~t2 и рассогласования запасов компонентов равны нулю. При наличии
возмущений истинные процессы опорожнения отличаются от номиналь-
ных, и возникает неодновременность пересечения ИТ одинаковых номе-
ров в баках О и Г. Это приводит к появлению временного рассогласова-
ния А/ = to -t2 * 0, характеризующего рассогласования запасов окислите-
ля и горючего. Результаты измерений преобразуются в усилителе-
484
преобразователе и являются входными сигналами вычислительного уст-
ройства (ВУ). ВУ может быть реализовано аппаратно в виде прибора или
программно в БЦВМ. В ВУ реализуется алгоритм СУРТ. С выхода ВУ
сигнал j поступает в устройство управления приводом, далее команда
А« поступает на привод дросселя. Дроссель, установленный в магистра-
ли горючего, поворачивается на угол Дог, осуществляя изменение расхо-
да горючего и, соответственно, коэффициента соотношения компонентов
8 К через ЖРД. Описанная схема повторяет свое действие при срабаты-
вании каждых из последующих пар ИТ, вплоть до последних перед тер-
минальным моментом.
Рис. 15.1. Структурная схема СУРТ
485
Вычисление управляющей команды, определяющей отклонение расхо-
да горючего, а следовательно, и величины параметра К, решается путем
последовательных вычислений Ж по данным дискретных измерений
временных рассогласований. Для этого ВУ по двум смежным измерениям
величины А/ формирует сигнал на перекладку дросселя адр9 (рис. 15.2)
• At-At
CL = ---!1
U* др
КДРДТ1 ’
где Atи At। - временные рассогласования объемов топлива в баках со-
ответственно, при (i - 1)-м и i -м измерениях,
ATi - интервал времени между (i -1) — м и i - м измерениями,
„ 55К ЖЖ
Кдо =-------коэффициент, учитывающий характеристики дросселя.
5ад₽
Кроме того, ВУ формирует сигнал на перекладку дросселя, пропор-
Рис. 15.2
Таким образом, суммарный сигнал на перекладку дросселя, форми-
руемый ВУ, определяется по соотношению
486
a (At, - At,_,) + !> At,
адр v ’
кдр
где а = -i-, ь =__-_“ коэффициенты, определяющие терминальный мо-
ATj tk - tj
мент системы,
tj - момент времени i-ro измерения;
tk - момент времени выключения ЖРД.
„ А » а + Ь
Принимая А = а и В =-------, выражение для ало преобразуется
а н
к двучленному виду:
кдр
которое и является основным соотношением алгоритма СУРТ по каналу
синхронизации опорожнения баков.
Интервалы времени между измерениями и оптимальные значения ко-
эффициентов алгоритма управления определяются математическим мо-
делированием работы системы совместно с моделью объекта регулиро-
вания с учетом действующего состава возмущающих факторов, ошибок
измерения и разброса характеристик исполнительных механизмов (при-
вода, дросселя).
Рассмотрим некоторые особенности построения алгоритма канала про-
гнозирования момента окончания запасов топлива.
Прогнозирование момента окончания рабочих запасов топлива осуще-
ствляется алгоритмически на основе обработки текущей информации
с датчиков уровней.
Простейший алгоритм прогнозирования момента окончания компо-
нентов топлива использует информацию двух измерительных точек дат-
чика уровня, максимально разнесенных по времени срабатывания (по всей
высоте бака).
На основании измеренных моментов времени прохождения компонен-
том одной из измерительных точек датчиков уровня в верхней части бака
и одной из измерительных точек в нижней части бака определяется сред-
ний расход компонента из бака.
Если принять, что расход компонента на интервале между прохожде-
нием нижней точки и моментом окончания компонента равен среднему
значению, то можно записать соотношение для вычисления момента
окончания компонента tk:
хИЗМ _ аИЗМ
tk = + Ок”1 - С") • -——
к v z А НОМ _ А ном
1Н 1в
487
где t"3M,t"3M - моменты времени прохождения уровнем компонента верх-
ней и нижней измерительных точек датчика,
tJJ0M,t"0M - номинальные (программные) моменты времени, опреде-
ляемые из условия номинального расхода,
t£0M - номинальный момент времени окончания компонента.
В этом соотношении для вычисления момента окончания компонента
используется минимальное количество измерительной информации.
Для повышения точности определения момента окончания компонента
в алгоритме системы обычно используется весь объем имеющихся изме-
рений. Для этого в алгоритме строится модель процесса расходования
компонента в виде прогнозируемых моментов времени срабатывания из-
мерительных точек датчика уровня.
Рассогласование между прогнозируемыми моментами и фактически-
ми моментами времени срабатывания измерительных точек используется
для формирования корректирующей поправки, учитывающей реальный
расход компонентов топлива, при помощи которой модель перестраива-
ется таким образом, чтобы свести это рассогласование к нулю к концу
процесса опорожнения баков. После прохождения последней измери-
тельной точки в алгоритме формируется момент времени окончания
компонента в баке.
Учитывая, что в процессе регулирования по каналу синхронизации
опорожнения баков рассогласование текущих запасов компонентов
уменьшается в идеальном случае до нулевого значения к концу процесса
опорожнения, в основу канала прогнозирования положен следующий
принцип работы. Первоначально на основе раздельной обработки уровне-
мерной информации прогнозируются процессы расходования и моменты
окончания каждого из компонентов. Затем путем осреднения результатов
раздельного прогноза формируется прогноз процесса расходования и мо-
мента окончания суммарных запасов топлива.
Такой принцип построения обеспечивает высокую точность прогнози-
рования и обладает определенной гибкостью, позволяя использовать ре-
зультаты раздельного прогнозирования в нерасчетных режимах работы.
Так, например, в случае отказа одного из измерительных каналов не-
возможно использовать информацию, поступающую с другого работоспо-
собного канала. Кроме того, при возникновении отказов в цепях исполне-
ния вычисленной команды СУРТ или воздействии нерасчетных возмуще-
ний, для компенсации которых не хватает эффективности регулирующего
органа СУРТ, моменты окончания окислителя и горючего могут сущест-
венно отличаться.
488
В качестве признака перехода канала прогноза на раздельное про-
гнозирование можно принять превышение рассогласованием прогнози-
руемых моментов окончания окислителя и горючего заданного порого-
вого значения. При этом для формирования команды на выключение
двигательной установки используется прогнозируемый момент вре-
мени, соответствующий тому компоненту, который вырабатывается
первым.
Базовый алгоритм СУРТ
Базовый алгоритм системы управления расходованием топлива разра-
ботан на основе изложенных принципов построения системы.
Вычисление алгоритма СУРТ осуществляется в ВУ во время полета
ступеней ракеты.
Алгоритм системы условно разделен на функциональные блоки:
- блок формирования начальных состояний;
- блок обработки входной информации;
- блок прогнозирования момента окончания топлива;
- блок вычисления управляющих команд;
- блок формирования управляющих команд.
1. Блок формирования начальных состояний.
В этом блоке формируются начальные состояния переменных значе-
ний алгоритма СУРТ.
2. Блок обработки входной информации.
Формирование информации о прохождении уровнями компонентов
измерительных точек:
а) информация о прохождении зеркалом жидкости заданных измери-
тельных точек поступает по каналам Онечет(Гнечет) и Очет(Гчет) и харак-
теризуется появлением 1 в соответствующих разрядах входного слова вы-
числительного устройства. Правильной последовательностью чередова-
ния сигналов по любому из датчиков (окислителя или горючего) считает-
ся: НЕЧЕТ, ЧЕТ, НЕЧЕТ и т. д.;
б) формирование номера измерительной точки j0(r) и формирование
момента времени 11 при прохождении уровнем компонента j -й точки
Jo(r) [ io(r) ]+ 1 ’
tj(r)=t;
в) если зафиксированы одноименные точки окислителя и горючего,
формируется номер пары точек i
i=Jo=jr
489
Примечание. В процессе нормального расходования топлива выпол-
няется условие
> t*r> > t*?.
3. Блок прогнозирования момента окончания топлива.
Вычисления в блоке производятся при приеме сигналов с измеритель-
ных точек каждого датчика:
а) вычисление временного рассогласования At °между измеряемым
и прогнозируемым моментами прохождения уровнями компонента топли-
ва j -й измерительной точки
At^)=to(r)_to(r)nporii) причем
tj проги t j проги (l-Tj)-Tj npHj = l,
v° vr
Тт jnom T jnom « „ c
» = —1---= — --------номинальный относительный объем запасов то-
J vrOHOM жтГНОМ
*запр *запр
плива на j-й измерительной точке, определяется расстановкой измери-
тельных точек,
Vj°,Vjr - номинальный объем компонента под измерительными
точками,
V™„pM, V™™ - номинальный заправляемый объем компонентов топлива,
Т, - номинальное время работы ЖРД;
б) вычисление приращения корректирующей поправки ДХ*Г), учиты-
вающей реальный процесс выработки компонентов топлива
АХ°/г) = Aj • (Вj • Atj(r) - At*?), причем
АХ*г) = 0 при j = 1;
в) вычисление корректирующей поправки 1*г), учитывающей реаль-
ный процесс выработки компонентов топлива
1*г) ^Z+AA*0;
г) вычисление прогнозируемого момента времени прохождения уров-
нями компонентов топлива (j +1) -й измерительной точки
fO(r) __ fO(r) । /1 1 1°(г)\. /т —T \.T«
l(j+l) проги ” lj ПрОГН ' ' ''J ) Mj Ij + l/ 1I5
д) прогнозирование среднего по окислителю и горючему момента про-
хождения уровнями (j +1) -й измерительной точки t(j+1) прогн
490
f — t° . K*° -L tr . K*r
l(j+i) ПРОГН l(j + 1) проги “ l(j+1) проги 9
где К0 = , Кг = 1 1 - весовые коэффициенты, зависящие от ко-
эффициента соотношения расходов компонентов из бака;
е) вычисление времени суммарной выработки топлива.
ЕСЛИ | tj+1 проги ““ t j+1 проги | , ТО
Тк = t(j+l) проги ’К + t(j+i) проги К ,
еСЛИ | t j+j проги — t j+1 проги | ) 9 ТО
T|j = ШШ( tj+i проги 9 tj + 1 проги ),
где £ - допустимое рассогласование моментов времени tj+lnporn, tj+i проги,
определяемое на (j +1) -й измерительной точке.
4. Блок вычисления управляющих команд:
а) вычисление временного рассогласования Atj на i-й паре измери-
тельных точек
б) вычисление управляющего воздействия ASKj др на i -й паре измери-
тельных точек
А5К|др = Aj • (Вj *Atj — Atj_j);
в) вычисление отклонения коэффициента соотношения весовых расхо-
дов ЖРД от номинала
5KiJq>=| ЗК1др | + ДЗК,др.;
5. Блок формирования управляющих команд:
а) управляющие команды формируются в виде времени отработки т|0Тр
(времени поворота выходного вала привода) и признаков на закрытие (от-
крытие) дросселя иза1ф(от1ф), соответствующих потребной величине и
знаку вычисленного изменения коэффициента соотношения расходов
компонентов топлива ASKj др :
Ti отр = 6’1 АЗК । др |,
где 0 - коэффициент, учитывающий скорость отработки приводом управ-
ляющего воздействия.
Признак U откр, формируемый при &8К. др ( 0 , приводит к уменьше-
нию коэффициента соотношения расходов компонентов путем увеличе-
491
ния расхода горючего. Признак U , формируемый при &5К.др > О,
приводит к увеличению коэффициента соотношения расходов компонен-
тов путем уменьшения расхода горючего. Признаки U 0Ткр и U закр реали-
зуются в виде электрических управляющих сигналов;
б) формирование признака VK на выключение ЖРД
VK= 1, если (Tk -t) < ДТВК,
где t - текущее бортовое время,
ДТВК - временной интервал выдачи команды на выключение ЖРД, оп-
ределяемый от момента полной выработки топлива.
Здесь приведены основные соотношения, которые используются на
всех ракетах для решения задачи управления расходованием компонентов
топлива. Однако в зависимости от конструктивных особенностей ракеты,
циклограммы работы, количества и характеристик ЖРД на ступени, обес-
печения отказоустойчивости системы и т. д. алгоритм СУРТ может суще-
ственно развиваться и дополняться.
Так, например, в условиях переменных циклограмм работы ЖРД
с участками плавного дросселирования появляются переменные по вре-
мени отклонения суммарного расхода топлива, которые существенно
влияют на точность прогнозирования текущих запасов топлива. В этом
случае оценку текущих запасов топлива в системе и его расход можно
формировать с использованием оценки расхода топлива, формируемой
в системе наведения по инерциальной информации, что позволяет учиты-
вать отклонение суммарного расхода на интервалах между измерениями
и обеспечить приемлемое качество прогнозирования.
15.3. Аппаратная реализация СУРТ
Состав системы
Учитывая опыт разработок СУРТ, наиболее целесообразным путем
минимизации весовых характеристик аппаратуры системы является функ-
ционально-конструктивная реализация преобразовательной части системы
в составе системы управления ракеты и использования в качестве вычис-
лительной части функционального тракта бортовой цифровой вычисли-
тельной машины (БЦВМ).
Поэтому в состав современной СУРТ входят:
- датчики уровня, устанавливаемые в баках компонентов топлива,
- преобразовательно-вычислительная часть, функционально входя-
щая в аппаратуру системы управления,
- электропривод,
492
- исполнительное устройство (дроссель), размещенный в магистрали
горючего ЖРД и являющийся его принадлежностью.
Датчики уровня
Наиболее сложными и ответственными моментами при построении
аппаратуры СУРТ являются создание высокоточных уровнемеров, спо-
собных работать в бортовых условиях в компонентах с агрессивными или
криогенными свойствами, а также обеспечение высокой надежности этих
уровнемеров, так как отказ их в предельных случаях может привести
к аварийной ситуации для ракеты в целом.
Задачи, подобные этой, никогда ранее не ставились в измерительной
технике. Требовалось измерять запасы компонентов в баках (или, пра-
вильнее, рассинхронизацию запасов окислителя и горючего) с погрешно-
стью, не превышающей десятых долей процента. Проведенные исследо-
вания и экспериментальные работы по выбору принципа измерения уров-
ней на борту ракеты показали, что реализация таких точностей непрерыв-
ными уровнемерами невозможна. Решение было найдено на основе
порогово-дискретного принципа программного управления и вылилось
в создание ряда уникальных по своим характеристикам дискретных ши-
рокобазных уровнемеров с различными по своей физической основе то-
чечными чувствительными элементами, с эффективными гидромеханиче-
ской и электрической системами фильтрации сигналов, резко снижающи-
ми уровень помех при измерениях.
Поскольку определение среднего уровня компонента в нужный момент
времени производится по результатам измерения уровня в одной точке
поверхности в условиях значительных деформаций зеркала жидкости под
действием возмущающих сил, при разработке дискретных уровнемеров
пришлось решать две самостоятельные задачи:
- разработка устройств, обеспечивающих получение на небольшом
участке колеблющейся поверхности жидкости невозмущенного среднего
уровня (эти устройства названы успокоителями датчиков уровня);
- разработка средств индикации границы раздела жидкой и газовой
среды (чувствительных элементов).
Успокоительные устройства датчиков уровня по своим принципиаль-
ным и конструктивным решениям являются едиными для различных ра-
кет и компонентов, и лишь конкретные значения их параметров опреде-
ляются индивидуальными особенностями данной ракеты и физическими
свойствами компонента. Однако, как будет показано ниже, значительные
различия в физико-химических свойствах компонентов и газовых сред
наддува не позволили создать единого чувствительного элемента для всех
используемых в настоящее время ракетных топлив.
493
Успокоительные устройства
Изучение поведения поверхности жидкости в баках ракеты на ак-
тивном участке полета и разработка теории успокоительных устройств
вылились в сложную самостоятельную задачу. Теоретические исследова-
ния, стендовые и летные эксперименты, выполненные в ОПМ АН СССР,
РКК «Энергия» и ГКБ «Южное», заложили основу для разработки мето-
дики инженерных расчетов успокоительных устройств и их эксперимен-
тальной отработки, показали, что отклонения свободной поверхности то-
плива в баках от равновесного положения при полете ракеты весьма зна-
чительны. Амплитуда колебаний жидкости у стенок бака может достигать
±(200-300) мм при заданной точности измерения в несколько мм.
Принцип работы успокоительного устройства основан на измерении
среднего уровня по методу сообщающихся сосудов. Успокоитель пред-
ставляет собой цилиндрическую трубу, размещаемую внутри бака парал-
лельно его продольной оси по возможности ближе к центру, открытую
сверху и сообщающуюся с нижней частью бака через две тонкие трубы
(удлинители).
Успокоительная труба позволяет изолировать чувствительные эле-
менты датчика от поверхностных волнений. Поскольку эти волнения за-
тухают с глубиной, то у входа в удлинители давление осредняется до ве-
личины приблизительно равной гидростатическому давлению столба со
средним уровнем, который и устанавливается в измерительной трубе ус-
покоителя.
Наряду с этим имеется группа возмущений, распространяющихся
в глубину бака и создающих в районе расположения удлинителей пульса-
ции давления. При этом частоты этих пульсаций имеют широкий спектр
с нижним граничным значением порядка 1 Гц. В области резонанса эти
возмущения способны вызвать колебания в измерительной трубе с ампли-
тудами, достигающими сотен миллиметров.
Для частот, отличных от резонансной, коэффициент успокоения
Ку~«1,
а2
где G) - частота возмущающих колебаний,
Q - собственная частота столба жидкости в успокоителе.
В свою очередь Q является функцией продольной перегрузки gnx
и приведенной гидравлической длины успокоителя
1 Ч
1 _ УД^тр
П₽ ™sy/
Л gnx
£2 = J—*•;
V
494
где 1пр - приведенная длина успокоителя,
1уд, 8уд - длина и площадь поперечного сечения удлинителей,
STp - площадь поперечного сечения трубы успокоителя,
m - количество удлинителей.
Таким образом, задача успокоения жидкости и получения среднего
уровня внутри успокоительной трубы решается путем создания необхо-
димой приведенной гидравлической длины успокоителя выбором конст-
руктивных параметров успокоителя при известных (рассчитанных) внут-
рибаковых возмущениях.
Использование удлинителей для снижения собственной частоты стол-
ба жидкости в успокоителе приводит к возникновению новых вредных
явлений - разгонных колебаний, увеличению разброса статического от-
ставания зеркала жидкости в успокоителе, обусловленного гидравличе-
скими сопротивлениями. Для уменьшения влияния разгонных колебаний
на точность измерения используется специальный гаситель, названный
перфорационным. Перфорационный гаситель разгонных колебаний пред-
ставляет собой отрезок трубы того же диаметра, что и успокоитель, с ря-
дом перфорированных отверстий определенной площади, расположенных
на расчетном расстоянии от верхнего среза гасителя. За время движения
зеркала жидкости по длине гасителя происходит его разгон до номиналь-
ной величины, при этом устанавливается разность уровней жидкости
в успокоителе и в баке, равная по величине статическому отставанию из-
за гидросопротивлений успокоителя.
Чувствительные элементы датчиков уровня
Индикаторами границы жидкости и парогазовой среды наддува явля-
ются чувствительные элементы датчиков, расположенные внутри успо-
коительной трубы. Существенные различия в свойствах используемых
компонентов и парогазовых сред наддува не позволяют создать единого
высоконадежного чувствительного элемента, удовлетворяющего задан-
ным требованиям по точности измерения для всех компонентов и различ-
ных условий эксплуатации.
Анализ физических свойств наиболее распространенных компонентов
ракетных топлив показывает, что АТ, ТГ-02, РГ-1, О и Н являются хоро-
шими диэлектриками, АК-27И - электролитом с относительно высокой
проводимостью, а НДМГ в диапазоне заданных условий на несколько по-
рядков меняет проводимость и может рассматриваться и как проводник,
и как диэлектрик.
495
Контактные датчики
Для дискретного измерения уровня компонентов-электролитов (АК-
27И) был разработан контактный чувствительный элемент, работающий
на принципе разрыва электрической цепи, образуемой двумя металличе-
скими электродами и электропроводным компонентом. При этом метал-
лическими электродами являются измерительная труба и специальные
Г-образные контакты, расположенные внутри измерительной трубы на
расчетных уровнях. Датчик с такими чувствительными элементами при-
менен на ракете 8К64 для измерений уровня окислителя АК-27И.
Качество работы контактного датчика определяется отношением со-
противления цепи, предшествующего моменту отрыва компонента от
торца Г-образного электрода, к сопротивлению утечки между электро-
дами. Величины указанных сопротивлений определяются эксперимен-
тально.
Контактные датчики, несмотря на целый ряд положительных качеств
(простота конструкции, отсутствие подвижных частей, высокий уровень
сигнала полезной информации, простота электрической схемы, не тре-
бующей специальных источников питания и др.), применимы только для
компонентов топлива с относительно высокой электропроводимостью.
Такое ограниченное применение контактных датчиков существенно сни-
жает ценность их положительных качеств.
Емкостные датчики
Проведенные исследования по выбору чувствительного элемента
датчика для замера уровня компонентов-диэлектриков показали, что
наиболее полно всем требованиям работы в бортовых условиях отвеча-
ют емкостные чувствительные элементы, принцип работы которых ос-
нован на изменении величины электрической емкости воздушного кон-
денсатора при заполнении межэлектродных промежутков компонентом-
диэлектриком.
Изменение емкости при сливе компонента определяется
dt ан 5t
где е - диэлектрическая проницаемость измеряемой среды,
Со - емкость чувствительного элемента в воздухе.
Конструктивно чувствительный элемент представляет набор концен-
трично расположенных металлических колец высотой около 6 мм. Эле-
менты жестко, через изоляторы, крепятся в трубе успокоителя, что обес-
печивает необходимую жесткость и виброустойчивость.
Значение емкости такого элемента в воздухе составляет Со «30 пкФ.
496
Пластины конденсатора через специальные стеклометаллические гер-
мовыводы соединяются с токонесущими коаксиальными проводами, за-
ключенными в металлическую трубу.
Измерительная электрическая схема на емкостных чувствительных
элементах представляет собой симметричный электрический мост пере-
менного тока, два плеча которого образуют параллельно соединенные
чувствительные элементы (нечетных и четных номеров соответственно),
а два другие плеча - электрические конденсаторы постоянной емкости,
встроенные в усилитель-преобразователь. Питание моста осуществляется
от специального статического преобразователя напряжением 50В с часто-
той 50 кГц. Такие датчики, отличающиеся конструктивной простотой, от-
сутствием подвижных элементов, высокой точностью и надежностью
применяются в системе опорожнения на ракетах с холодным газобаллон-
ным наддувом (8К64).
Однако на ракетах с горячим газогенераторным наддувом применение
емкостных датчиков для измерения объемов компонентов типа НДМГ
и АТ потребовало коренного пересмотра измерительной схемы со значи-
тельным ухудшением весовых характеристик системы. Это было вызвано
изменением диэлектрических свойств верхнего слоя НДМГ под действием
рабочего тела системы газогенераторного наддува, выявленным на этапе
стендовых и летных испытаний ракеты (8К67).
Таким образом, емкостные датчики для измерения уровня компонен-
тов-диэлектриков в условиях горячего газогенераторного наддува баков
оказались не работоспособными, что вызвало необходимость проведения
работ по созданию новых чувствительных элементов, основанных на
принципах, не использующих электрические свойства компонентов и не
уступающих емкостным датчикам по точности, надежности, агрессивной
стойкости и простоте измерительной схемы.
Этим условиям в полной мере удовлетворяют разработанные индук-
тивные поплавковые датчики.
Индуктивные датчики
Индуктивный поплавковый датчик был разработан по принципиально
новой конструктивной схеме, несмотря на то, что в основу разработки
был положен широко используемый в ракетной технике, в частности
в системах контроля заправки, поплавковый датчик с индуктивным инди-
катором координат поплавка. Однако известные конструкции таких дат-
чиков, используемых в стационарных условиях, имеют ряд недостатков,
исключающих возможность их применения для целей систем управления
расходованием топлива.
497
Индуктивный датчик СУРТ представляет собой дискретный измери-
тель уровня с системой чувствительных элементов (катушек индуктивно-
сти), расположенных вдоль вертикальной оси датчика на расстояниях, со-
ответствующих расчетным объемам компонента топлива в баке. В сочета-
нии со свободно плавающими на поверхности жидкости пустотелыми по-
плавками чувствительные элементы обеспечивают выдачу информации
о положении уровня компонента.
Восемь катушек индуктивности включены в мостовую схему (рис.
15.3). В каждое плечо моста включены последовательно два чувствитель-
ных элемента. Количество катушек индуктивности в схеме может быть
и иным, но кратным четырем. В исходном состоянии мост сбалансирован
и выходное напряжение моста практически равно нулю.
Принцип действия датчика основан на изменении индуктивности чув-
ствительного элемента при приближении к нему магнитопроводящих по-
плавков, в результате чего баланс моста нарушается и на измерительной
диагонали моста появляется напряжение разбаланса. Форма выходного
сигнала приведена на рис. 15.4. Сигналы с нечетных и четных чувстви-
тельных элементов противофазны.
Информацией о моменте прохождения компонентом расчетного уров-
ня является появление напряжения разбаланса, которое при достижении
определенной величины вызывает срабатывание порогового устройства
усилителя-преобразователя.
498
Основные технические характеристики датчика:
- напряжение питания - (25±3) В,
- частота питающего напряжения - (1000± 10) Гц,
- потребляемый ток - < 0,7 А,
- максимальное выходное напряжение —>170 мВ,
- порог срабатывания - (90.. .120) мВ,
- крутизна выходного сигнала на уровне
порога срабатывания - > ЮмВ/мм.
Конструктивно датчик представляет собой герметичный корпус в виде
тонкостенной трубы из нержавеющей и немагнитной стали. Внутри кор-
пуса по его оси размещены чувствительные элементы, отстоящие друг от
друга на расчетных расстояниях. Корпус датчика вставлен в успокоитель.
В кольцевом зазоре между корпусом датчика и успокоителем находится
система сферических поплавков, которая при работе датчика отслеживает
положение зеркала жидкости. Поплавки выполнены из магнитопроводя-
щей стали, устойчивой против коррозии.
Электрические цепи из корпуса датчика выводятся на наружную по-
верхность бака через специальный гермовывод.
Индуктивный датчик по сравнению с контактными и емкостными дат-
чиками имеет ряд преимуществ, которые позволили использовать его при
разработке СУРТ для целого поколения боевых и космических ракет, раз-
работанных в ГКБ «Южное», начиная с ракеты 8К69.
Эти преимущества:
- высокая универсальность датчика, т. е. индифферентность выход-
ных характеристик датчика к физико-химическим свойствам ком-
499
понентов топлива (кроме жидкого водорода) и среды рабочего тела
наддува;
- высокая коррозионная стойкость;
- высокие показатели надежности;
- высокий уровень полезного сигнала;
- некритичность к параметрам бортовой кабельной сети;
- не требуется специальный высокочастотный источник питания;
- возможность проведения технологической тарировки баков на
штатных датчиках.
Преобразовательно-вычислительная часть
Преобразовательно-вычислительная часть системы строится на базе
бортового цифрового вычислительного комплекса системы управления
и включает в свой состав бортовую цифровую вычислительную машину,
усилитель-преобразователь, устройство управления приводами. А также
общую аппаратуру системы управления, обеспечивающую в том числе
функционирование тракта системы.
Электропривод и исполнительное устройство
Электропривод системы предназначен для преобразования электриче-
ских управляющих команд, поступающих с выхода устройства управле-
ния приводами, в механические управляющие воздействия на исполни-
тельное устройство (дроссель), и представляет собой агрегат электроме-
ханического типа на базе электродвигателей постоянного тока.
Управляющие воздействия на электропривод подаются в виде импуль-
сов напряжения бортового источника постоянного тока требуемой дли-
тельности и полярности. Механические управляющие воздействия элек-
тропривода реализуются в виде поворота выходного вала электропривода.
Электропривод оснащен телеметрическим потенциометром угла поворота
выходного вала и контактно-ламельным устройством для контроля и при-
ведения выходного вала в исходное положение по командам системы
управления. На выходной вал электропривода жестко посажена подвиж-
ная заслонка дросселя, при перемещении которой изменяется коэффици-
ент соотношения расходов. Дроссель устанавливается в магистрали горю-
чего и является принадлежностью ЖРД.
500
Заключение части 7
В ходе развития ракетной техники комплексная структура бортовой
и наземной аппаратуры системы управления претерпела существенные
изменения, в первую очередь, связанные с применением цифровых вы-
числительных машин.
Комплексная структура современных ракет-носителей имеет следую-
щие преимущества:
- универсальность структуры, заключающаяся в возможности ее
применения на различных ракетах и с выполнением ряда вариантов
функциональных задач, решаемых этими носителями. Универсаль-
ность достигается унификацией комплексных структур отдельных
блоков изделия с одинаковым приборным составом, введением
идентичных уплотненных каналов передачи информации между
БЦВМ и аппаратурой блоков изделия и стандартизацией формы
представления информации в сечениях сопряжения с БЦВМ;
- контейнеризация аппаратуры функционально сопряженных при-
боров.
При применении современных комплексных структур СУ достигается
положительный эффект, определяющийся:
- возможностью использования одного командного и вычислитель-
ного комплексов на последней ступени во всех модификациях сис-
темы;
- существенным сокращением связей между бортовой и наземной
аппаратурой;
- уменьшением веса бортовой кабельной сети;
- технологичностью, достигнутой группированием функционально
сопряженных приборов в контейнеры;
- адаптивностью системы, способной при изменении задач быстро
приспосабливаться заменой минимального числа блоков.
В схемах включения пиротехнических устройств, электро-, гидро-
и пневмоклапанов используются электромагнитные реле совместно с по-
лупроводниковыми элементами, обеспечивающими «щадящий» режим
работы коммутационных устройств, уменьшающими потребляемый ток
501
и вес бортовой кабельной сети и обеспечивающими многоразовую комму-
тацию. Кроме того, схема защищена от попадания ложной полярности на
нити пирозапалов со стороны корпуса и не требует отстыковки штепсель-
ных разъемов при испытаниях.
С целью уменьшения токо-
вых нагрузок применена после-
довательная схема включения
пиротехники с использованием
стабилизатора тока, выполнен-
ного на германиевом транзи-
сторе. Для исключения обрыва
цепи при сгорании нити, после-
довательно включенного пиро-
запала, последняя зашунтиро-
вана цепью из стабилизатора и
диода, включенных последова-
тельно (рис. 15.5).
Система контроля автомати-
ки PH построена с использова-
нием встроенного устройства
параметрического уплотнения
на полевых транзисторах и
микросхемах. Такая система по-
зволяет осуществлять контроль
автоматики двигательной уста-
новки (АДУ) с соблюдением
необходимых мер безопасности
и минимальным количеством
связей с наземной аппаратурой.
Кроме того, схема позволяет
рис is проверять автоматику на техни-
ческом комплексе и контроли-
ровать ее работу в полете ракеты с использованием БЦВМ. В сравнении
со схемами, примененными в более ранних разработках, данное решение
имеет следующие преимущества: меньший вес, уменьшение количества
связей в десятки раз, меньшее время проверок вследствие совмещения
контроля сопротивления изоляции с контролем целостности цепей, про-
стоту изменения количества и выбора контрольных цепей.
502
Приложение
ЧИСЛЕННЫЕ ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ УРАВНЕНИЙ
ВОЗМУЩЕННОГО ДВИЖЕНИЯ
Таблица 1
Коэффициенты уравнений возмущенного движения,
характеризующие абсолютно жесткий «отвердевший» носитель, I ступень
t, с м-с'1 2 а °. S В °. N) - м-с'2 awz ’ м^-с’1 с’1 с2 * с-2 XG ’ М 2 кгмс
0,0 0,0000 -0,0695 -9,820 -0,766 0,0000 -0,0077 0,000 -0,178 15,62 1239779,8
0,1 0,0000 -0,0704 -14,796 -0,767 0,0000 -0,0078 0,000 -0,178 15,62 1239088,8
4,0 -0,0014 -0,1295 -14,807 -0,787 0,0003 -0,0180 0,006 -0,181 15,65 1226793,7
16,0 -0,0058 -0,3140 -16,066 -0,856 0,0012 -0,0284 0,100 -0,191 15,72 1181228,5
28,0 -0,0106 -0,5146 -18,756 -0,935 0,0020 -0,0465 0,333 -0,206 15,89 1142446,8
32,0 -0,0122 -0,5765 -19,840 -0,965 0,0021 -0,0476 0,428 -0,207 15,95 1129109,2
48,0 -0,0195 -0,7441 -25,419 -1,098 0,0024 -0,0576 0,849 -0,225 16,30 1086093,9
56,0 -0,0179 -0,7011 -28,296 -1,177 0,0025 -0,0523 1,099 -0,240 16,62 1046969,7
64,0 -0,0152 -0,5746 -30,784 -1,267 0,0023 -0,0411 1,221 -0,256 16,97 1011094,4
80,0 -0,0081 -0,3572 -32,654 -1,498 0,0012 -0,0266 0,965 -0,312 18,01 898665,0
96,0 -0,0024 -0,2467 -34,429 -1,791 0,0003 -0,0189 0,362 -0,424 19,57 762271,0
112,0 -0,0006 -0,2660 -41,293 -2,227 0,0001 -0,0254 0,118 -0,752 21,95 472856,7
115,3 -0,0004 -0,2811 -9,254 -2,339 0,0001 -0,0292 0,093 -0,896 22,59 410290,5
116,0 -0,0004 -0,2809 -5,987 -2,344 0,0000 -0,0290 0,087 -0,896 22,60 410632,1
119,0 -0,0003 -0,2792 -5,271 -2,366 0,0000 -0,0284 0,058 -0,908 22,66 407720,1
120,6 -0,0002 -0,2790 -4,380 -2,376 0,0000 -0,0282 0,048 -0,916 22,69 406446,6
504
Таблица 2
Коэффициенты уравнений возмущенного движения, характеризующие
жидкое наполнение топливных полостей, I ступень
t, с ^•10 W10' м'1 % м Q О с’ <V1O м'1 аг2¥ М § О е «10 г2 с'1
0,0 -0,114 0,179 -1,30 13,4 17,6 0,339 -0,052 0,44 -1,2 6,67 19,6 0,141
0,13 -0Д14 0,179 -1,30 13,4 26,4 0,491 -0,052 0,44 -1,2 6,67 29,6 0,172
16,0 -0,124 0,185 -1,30 13,0 28,9 0,514 -0,057 0,46 -1,2 6,57 32,3 0,181
32,0 -0,138 0,187 -1,30 12,8 30,1 0,523 -0,063 0,45 -1,2 6,30 33,7 0,184
48,0 -0,154 0,186 -1,30 12,2 34,2 0,559 -0,070 0,44 -1,2 5,87 38,3 0,196
56,0 -0,163 0,184 -1,30 11,6 36,6 0,578 -0,75 0,43 -1,2 5,47 41,0 0,204
64,0 -0,174 0,180 -1,30 11,0 39,3 0,598 -0,080 0,41 -1,2 5,07 44,0 0,211
80,0 -0,201 0,168 -1,30 9,24 47,0 0,655 -0,092 0,35 -1,2 3,80 52,6 0,236
96,0 -0,237 0,148 -1,30 6,54 59,8 0,738 -0,108 0,22 -1,2 1,94 67,0 0,266
115,3 -0,304 0,054 -1,30 1,34 15,2 0,372 -0,138 -0,338 -1,2 -1,68 17,0 0,131
119,0 -0,306 0,049 -1,30 1,21 8,6 0,279 -0,140 -0,355 -1,2 -1,77 9,57 0,096
120,6 -0,307 0,047 -1,30 1,15 7,1 0,254 -0,140 -0,368 -1,2 -1,80 7,95 0,087
Окончание табл. 2
Коэффициенты уравнений возмущенного движения, характеризующие
жидкое наполнение топливных полостей, I ступень
t, с %-Ю2 м'1 aV а w м г3 с’2 £•10 г3 с'1 <4-10 ^•ю2 м’1 М (N ГЧ S 'о £rt С-1
0,0 -0,245 0,054 -1,55 2,08 12,0 0,331 -0,123 -0,175 -2,02 -22,9 18,3 0,041
0,13 -0,246 0,046 -1,55 1,88 18,2 0,407 -0,120 -0,176 -1,77 -17,3 24,4 0,047
16,0 -0,266 0,006 -1,55 0,23 19,8 0,425 -0,149 -0,190 -1,53 -13,8 19,8 0,042
32,0 -0,294 -0,057 -1,55 -2,13 20,6 0,433 -0,164 -0,224 -1,53 -15,6 20,6 0,043
48,0 -0,329 -0,120 -1,55 -4,32 23,5 0,463 -0,184 -0,262 -1,53 -17,5 23,5 0,216
56,0 -0,350 -0,164 -1,55 -5,72 25,2 0,478 -0,195 -0,290 -1,53 -18,6 25,2 0,223
64,0 -0,374 -0,212 -1,55 -7,12 27,0 0,497 -0,208 -0,320 -1,53 -19,8 27,0 0,228
80,0 -0,430 -0,345 -1,55 -10,3 32,3 0,542 -0,240 -0,417 -1,51 -22,0 32,1 0,252
96,0 -0,478 -0,527 -1,37 -12,2 40,2 0,605 -0,247 -0,493 -1,3 -21,5 38,8 0,278
115,3 -0,374 -0,762 -1,17 -13,9 7,54 0,262 0,141 -0,450 -0,87 -16,3 7,3 0,086
119,0 -0,028 -0,061 -0,50 -6,19 3,19 0,170 -0,074 -0,125 -0,59 -10,1 з,з 0,058
120,6 -0,007 -0,014 -0,33 -3,80 2,65 0,156 -0,047 -0,078 -0,50 -9,90 2,7 0,052
Таблица 3
506
Коэффициенты уравнений возмущенного движения носителя в канале крена, I ступень
t, с а<Р« с2 аФР| аФР, -10 кгмс2 еч> с1 Ер. с'1 ер. с'1 о © “р, с2 му с’2 МЫ1 с'2
0,0 -15,4 0,165 0,564 3407 0,158 0,45 0,882 22,2 85,4 0,155 0,093
0,13 -15,5 0,166 0,564 3397 0,158 0,45 0,885 22,2 85,7 0,156 0,094
16,0 -15,9 0,167 0,568 3343 0,158 0,45 0,885 22,2 85,7 0,221 0,095
32,0 -16,4 0,169 0,573 3293 0,158 0,45 0,894 22,2 87,7 0,462 0,096
48,0 -17,0 0,172 0,537 3201 0,156 0,45 0,921 22,2 93,1 1,63 0,098
56,0 -17,5 0,175 0,496 3144 0,153 0,45 0,936 22,2 96,0 1,32 0,099
64,0 -18,2 0,180 0,448 3052 0,149 0,45 0,966 22,2 102,0 0,933 0,102
80,0 -19,4 0,189 0,346 2885 0,140 0,45 1,03 22,2 117,0 0,446 0,107
96,0 -20,7 0,198 0,225 2727 0,133 0,45 1,13 22,2 139,0 0,187 0,112
115,31 -22,2 0,208 0,0 2579 0,116 0,45 0,0 22,2 0,0 0,045 0,057
119,0 -22,3 0,208 0,0 2570 0,116 0,45 0,0 22,2 0,0 0,030 0,013
120,6 -22,4 0,208 0,0 2562 0,116 0,45 0,0 22,2 0,0 0,020 0,013
Таблица 4
Правые части уравнений возмущенного движения в канале рыскания (тангажа), I ступень
t с ЪпЮ м-с'2 М£П10 м-с'2
0,0 0,244 0,037
0,13 0,410 0,096
16,0 0,438 0,102
32,0 0,495 0,111
48,0 0,568 0,122
56,0 0,609 0,129
64,0 0,653 0,139
80,0 0,763 0,172
96,0 0,908 0,235
115,3 0,922 0,316
120,6 0,105 0,036
Таблица 5
Коэффициенты уравнений возмущенного движения,
характеризующие абсолютно жесткий «отвердевший» носитель, II ступень
А с «=• м-с'1 ° 3 м-с2 azs- м-с2 Qpz- м'-с' с1 aw’ с2 ау8> с2 XG> М Ig> кгм-с2
120,6 -0,0000 -0,0773 -1,284 -0,459 0,0001 -0,0264 0,250 -0,304 6,79 56662,1
123,4 -0,0002 -0,0765 -1,180 -0,453 0,0001 -0,0264 0,179 -0,307 6,81 56193,0
123,8 -0,0002 -0,0766 -16,896 -0,456 0,0001 -0,0264 0,172 -0,308 6,81 56111,7
150,6 -0,0000 -0,0865 -19,483 -0,530 0,0000 -0,0283 0,006 -0,336 6,80 51270,2
170,6 -0,0000 -0,0994 -22,3,6 -0,607 0,0000 -0,0299 0,000 -0,364 6,83 48978,1
190,6 -0,0000 -0,1176 -26,092 -0,716 0,0000 -0,0316 0,000 -0,372 6,91 47186,4
210,6 -0,0000 -0,1462 -31,428 -0,855 0,0000 -0,0345 0,000 -0,406 7,16 44800,1
240,6 -0,0000 -0,2339 -45,329 -1,233 0,0000 -0,0466 0,000 -0,522 7,91 38897,4
271,7 0,0000 -0,5592 -90,563 -2,462 0,0000 -0,0836 0,000 -1,030 9,47 23873,3
272,0 0,0000 -0,6631 -17,788 -2,475 0,0000 -0,0837 0,000 -1,034 9,49 23830,6
278,7 0,0000 -1,6921 -5,298 -2,606 0,0000 -0,0803 0,000 -1,014 9,48 24274,7
Таблица 6
Коэффициенты уравнений возмущенного движения,
характеризующие жидкое наполнение топливных полостей, II ступень
t, с °-, агН.1О2 м'1 av М >3 о Со* 'о ^•10 а *10 ¥"2 м'1 aV аг2^ М °, „е Мм» К) £ .10 г2 с'1
120,6 -0,035 0,434 -1,26 1,44 1,59 0,120 -0,162 -0,067 -1,2 -4,64 1,78 0,042
123,4 -0,036 0,430 -1,26 1,41 1,63 0,120 -0,162 -0,068 -1,2 -4,64 1,82 0,043
123,7 -0,037 0,455 -1,32 1,50 27,7 0,513 -0,167 -0,07 -1,23 -4,73 32,1 0,180
150,0 -0,089 0,352 -1,53 0,60 23,5 0,015 -0,479 -0,136 -1,5 -4,25 23,5 0,155
170,0 -0,101 0,031 -1,53 0,05 26,5 0,016 -0,536 -0,155 -1,46 -4,62 26,5 0,164
190,0 -0,117 -0,468 -1,52 -0,733 31,9 0,018 -0,605 -0,170 -1,36 -4,48 31,2 0,177
240,0 -0,159 -1,60 -1,25 -2,17 46,7 0,305 -0,694 -0,168 -1,16 -4,86 41,4 0,204
271,7 -0,040 -0,69 -0,50 -1,83 63,3 0,253 -0,196 -0,049 -0,571 -3,07 63,3 0,253
278,7 -0,005 -0,08 -0,34 -2,12 3,58 0,004 0,0 0,0 0,0 0,0 0,0 0,0
Таблица 7
Коэффициенты уравнений возмущенного движения в канале крена, II ступень
t, с м, с’2 с1 § о афр> е<р с1 с'2 с2 кгм с2
120,6 -6,20 0,45 22,1 0,348 0,194 0,0145 0,005 1542
123,4 -6,20 0,45 22,1 0,348 0,194 0,014 0,005 1542
123,7 -6,20 0,45 22,1 0,348 0,194 0,011 0,099 1542
150,0 -6,20 0,45 22,1 0,348 0,194 0,0015 0,099 1539
190,0 -6,20 0,45 22,1 0,348 0,194 0,0 0,099 1535
240,0 -8,56 0,0 0,0 0,0 0,105 0,0 0,136 1108
271,7 -11,1 0,0 0,0 0,0 0,052 0,0 0,178 849
278,7 -11,1 0,0 0,0 0,0 0,050 0,0 0,01 847
Таблица 8
510
Правые части уравнений возмущенного движения
в канале рыскания (тангажа), II ступень
t, с Ъп™ м-с’2 м1П10 с-2 F^-10 мс'2 Mw10 с-2
120,6 0,018 0,039 0,628 -0,585
123,4 0,023 0,044 0,558 -0,495
123,7 0,430 0,815 0,555 -0,490
150,0 0,491 0,859 0,097 -0,086
190,0 0,662 1,01 0,013 -0,006
240,0 1,17 1,40 0,0 0,0
271,7 2,28 2,74 0,0 0,0
278,7 0,156 0,220 0,0 0,0
Таблица 9
Активный участок траектории III ступени
Коэффициенты уравнений возмущенного движения, характеризующие абсолютно жесткий
«отвердевший» носитель, III ступень
t, с мс1 Л > ° 3 alS. м-с2 а с'1 с2
1,10 -0,0122 0,000 -0,149 -0,0036 -0,152
1,12 -0,0117 -8,530 -0,170 -0,0035 -0,173
1,65 -0,0193 -14,074 -0,336 -0,0057 -0,341
14,0 -0,0180 -12,832 -0,309 -0,0052 -0,306
28,0 -0,0195 -13,614 -0,327 -0,0054 -0,319
48,0 -0,0223 -14,914 -0,359 -0,0058 -0,343
60,0 -0,0244 -15,819 -0,380 -0,0061 -0,361
80,0 -0,0288 -17,601 -0,423 -0,0068 -0,404
100,0 -0,0349 -19,835 -0,477 -0,0080 -0,469
116,24 -0,0420 -22,114 -0,532 -0,0094 -0,555
Таблица 10
Коэффициенты уравнений возмущенного движения, характеризующие жидкое наполнение
топливных полостей, III ступень, II и III тона
t, с <’•10 а<2>.ю2 гп м’1 а<2) а<2).10 м ®2(2) г ^2) с'- <’•10 а(2).ю2 V"2 м’1 а™ Л10 м ®2(2> '2 с2 <2) с*
0,0 0,306 1,13 1,15 13,3 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0
1,1 0,306 1,13 1,15 13,3 149,0 0,385 0,0 0,0 0,0 0,0 149,0 0,265
8,0 0,185 0,67 0,688 7,94 157,0 0,289 0,0 0,0 0,0 0,0 157,0 0,199
20,0 0,358 0,54 1,37 6,78 165,0 0,176 -0,197 -0,162 -1,39 -3,72 170,0 0,103
40,0 0,424 0,46 1,49 5,30 204,0 0,114 -0,228 -0,175 -1,47 -3,98 205,0 0,114
60,0 0,389 0,26 1,25 3,09 230,0 0,121 -0,207 -0,168 -1,21 -3,67 232,0 0,121
80,0 0,269 -0,037 0,773 -0,428 247,0 0,300 -0,158 -0,136 -0,834 -2,87 245,0 0,280
100,0 0,133 0,11 0,343 1,18 251,0 0,993 -0,081 -0,073 -0,383 -1,44 251,0 0,857
108,0 0,051 0,074 0,115 0,704 259,0 1,58 -0,068 -0,055 -0,300 -1,03 259,0 1,21
112,0 0,0 0,0 0,0 0,0 263,0 1,86 -0,063 -0,045 -0,256 -0,766 263,0 1,54
116,24 0,0 0,0 0,0 0,0 268,0 1,16 -0,056 -0,033 -0,188 -0,305 269,0 1,94
Окончание табл. 10
Коэффициенты уравнений возмущенного движения, характеризующие жидкое наполнение
топливных полостей, III ступень, II и III тона
t, с ^>•10 а<3,.102 Ц/Г] м'1 ат Г?! <’•10 м й>2(3> п с'2 с"1 а£>.10 а(3> »102 Г г2 м’1 а? а<3)»10 г2уг М 6У2(3) г2 с'2 с 1
0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0
1,1 0,0 0,0 0,0 0,0 242,0 0,324 0,0 0,0 0,0 0,0 240,0 0,257
8,0 0,0 0,0 0,0 0,0 255,0 0,276 0,0 0,0 0,0 0,0 253,0 0,222
20,0 0,372 0,998 1,43 1,25 275,0 0,210 -0,201 -0,172 -1,41 -3,96 272,0 0,155
40,0 0,413 0,191 1,45 0,236 305,0 0,131 -0,225 -0,189 -1,45 -4,28 305,0 0,125
60,0 0,438 0,290 1,41 0,350 348,0 0,158 -0,239 -0,190 -1,40 -4,17 350,0 0,162
80,0 0,446 0,534 1,28 0,614 374,0 0,209 -0,248 -0,185 -1,31 -3,90 376,0 0,207
100,0 0,308 0,423 0,795 0,454 403,0 0,460 -0,203 -0,139 -0,959 -2,72 403,0 0,383
108,0 0,121 -0,022 0,289 -0,022 416,0 0,792 -0,157 -0,098 -0,701 -1,84 416,0 0,583
112,0 0,011 -0,306 0,025 -0,289 423,0 0,954 -0,118 -0,081 -0,501 -1,46 423,0 0,768
116,24 0,0 -0,168 0,012 -0,124 430,0 0,600 -0,059 -0,052 -0,285 -0,985 430,0 1,07
Таблица 11
Коэффициенты уравнений возмущенного движения в канале крена, III ступень
t, с Q Q Л кгм с2 aw с'1 <РР\ Р\ с-2 Р\ с'1 Р\<Р ®2(,) Р1 с-2 Р1 с1 а<‘> Р1<Р «2»40 <РР1 о<2>.ю <РР\
0,3 0,0 320,0 0,048 0,281 0,0 0,0 0,662 0,0 0,0 0,0 0,0 0,0
1,1 -0,047 320,0 0,177 0,275 140,0 0,363 0,640 166,0 0,270 0,0 0,0 0,0
8,0 -0,105 320,0 0,181 0,185 158,0 0,290 0,476 172,0 0,208 0,0 0,0 0,0
20,0 -0,105 320,0 0,166 0,196 180,0 0,182 0,546 180,0 0,107 0,664 0,130 0,295
40,0 -0,107 312,0 0,162 0,302 196,0 0,112 0,760 196,0 0,112 0,793 0,172 0,276
60,0 -0,125 269,0 0,157 0,366 216,0 0,117 0,823 212,0 0,116 0,844 0,203 0,231
80,0 -0,150 223,0 0,132 0,404 239,0 0,296 0,757 230,0 0,272 0,768 0,224 0,263
100,0 -0,182 185,0 0,089 0,326 268,0 1,03 0,509 253,0 0,861 0,574 0,203 0,232
108,0 -0Д99 170,0 0,063 0,225 282,0 1,65 0,299 264,0 1,22 0,439 0,168 0,167
112,0 -0,207 162,0 0,047 0,108 290,0 1,97 0,125 269,0 1,55 0,327 0,136 0,103
116,24 -0,215 156,0 0,033 0,112 298,0 1,52 0,094 275,0 1,95 0,130 0,070 0,103
Окончание табл. 11
Коэффициенты уравнений возмущенного движения в канале крена, III ступень
t, с й>2(2) Р1 с2 42> Р\ с1 а<2! Р\<Р о2<2) Рг с'2 ?2> Р1 с'1 ат а*2>»10 <РР1
0,3 0,0 0,0 0,0 0,0 0,0 0,0 0,0
1,1 234,0 0,160 0,0 223,0 0,157 0,0 0,0
8,0 241,0 0,163 0,0 230,0 0,160 0,0 0,0
20,0 253,0 0,168 0,804 242,0 0,165 0,855 0,167
40,0 269,0 0,175 0,693 263,0 0,173 0,589 0,128
60,0 271,0 0,177 0,522 268,0 0,176 0,515 0,124
80,0 298,0 0,187 0,512 292,0 0,185 0,491 0,138
100,0 332,0 0,418 0,385 323,0 0,344 0,360 0,119
108,0 348,0 0,725 0,242 338,0 0,526 0,227 0,080
112,0 357,0 0,887 0,132 345,0 0,695 0,125 0,047
116,24 365,0 0,685 0,102 353,0 0,900 0,025 0,010
Таблица 12
Правые части уравнений возмущенного движения
в канале рыскания (тангажа), III ступень
t, с ЪпЮ м с2 МЕ„ с2
1,1 0,0 0,0
1,55 0,51 0,074
4,8 0,46 0,066
16,0 0,48 0,070
40,0 0,54 0,076
64,0 0,61 0,087
88,0 0,69 0,102
116,0 0,834 0,133
Таблица 13
Приведенный возмущающий момент в канале крена, III ступень
t, с с2
1,1 0,074
1,55 0,187
4,8 0,167
16,0 0,152
40,0 0,157
64,0 0,192
88,0 0,242
116,0 0,330
516
ПАССИВНЫЙ УЧАСТОК ТРАЕКТОРИИ III СТУПЕНИ
Номинальные значения приведенной эффективности исполнительных
органов СУОС.
Таблица 14
Номер пассивного участка Длительность рабо- ты ДУ на преды- дущем активном участке, с Приведенная эффективность, град/с2
по тангажу (рысканию) по крену
I 0 0,535 1,06
П 5 0,540 1,06
П 15 0,552 1,06
II 112 0,850 2,04
ш 117 0,992 2,14
Примечания:
1. Нумерация пассивных участков начинается с момента отделения
III ступени от II, т. е. I пассивный участок соответствует отрезку траекто-
рии от момента отделения III ступени до момента первого запуска ДУ, II -
от момента первого выключения ДУ до момента ее второго включения,
III - от момента второго выключения ДУ до момента отделения КА.
2. Приведенная эффективность исполнительных органов СУОС по тан-
гажу (рысканию) рассчитана для случая работы одного УБ.
517
Таблица 15
Максимальные значения приведенных возмущающих моментов от импульса
последействия после первого выключения ДУ III ступени
t, с Приведенный возмущающий момент (град/с2) после первого активного участка длительностью:
tiy 5 с tiy=15c *ду 112 с
по Т(Р) по К по Т(Р) по К по Т(Р) по К
12,0 0,408 0,144 0,417 0,144 0,705 0,285
12,2 0,0366 0,0126 0,0370 0,0126 0,0637 0,0249
29,4 0,0366 0,0126 0,0370 0,0126 0,0637 0,0249
50,9 0,0361 0,0125 0,0366 0,0125 0,0625 0,0248
51,0 0,00456 0,00957 0,00461 0,00957 0,00785 0,00189
88,1 0,00456 0,00957 0,00461 0,00957 0,00785 0,00189
88,2 0,0 0,0 0,0 0,0 0,0 0,0
Примечания:
1. Нуль времени соответствует моменту подачи команды на выключе-
ние двигателя.
2. В расчетах использовались следующие значения углов отклонения
заслонок газораспределителей:
- по тангажу (рысканию) 5V=13±3°;
- по крену 5(р=13±6°.
518
Таблица 16
Максимальные значения приведенных возмущающих моментов
от импульса последействия после второго выключения ДУ III ступени
t, с Приведенный возмущающий момент (град/с2) после второго активного участка
по Т(Р) по К
0,0 13,7 2,57
0,052 14,0 2,65
0,065 7,45 1,39
0,10 1,41 0,386
0,35 0,358 0,0598
0,70 0,195 0,0361
27,4 0,157 0,0323
27,5 0,0206 0,00382
50,0 0,0 0,0
Примечания:
1. Нуль времени соответствует моменту подачи команды на выключе-
ние двигателя.
2. В расчетах использовались следующие значения углов отклонения
заслонок газораспределителей
- по тангажу (рысканию) 8V=22±3°;
- по крену 5ф=10±6°.
Таблица 17
Приведенный возмущающий момент от разнотяговости УБ СО39
действующий на ступень в течение 100 с перед вторым включением
Длительность работы ДУ на первом ак- тивном участке, с Величина момента по тангажу (рыс- канию), град/с2
5 0,00063
15 0,00122
112 0,0140
Примечание: Величина возмущающего момента от разнотяговости УБ
СОЗ в канале крена пренебрежимо мала.
519
Таблица 18
Величины отклонений коэффициентов уравнений возмущенного движения
от номинальных значений, %
Коэффици- ент I ступень II ступень III ступень
активный участок пассивный участок
a zz ±25 ±70 - -
±5 ±5 ±5 -
a zw ±5 ±5 ±5 -
az5 ±5 ±5 ±5 -
^zrm ±5 ±5 ±5 -
avz ±30 ±70 - -
aw ±30 ±70 - -
а цду ±10 ±10 ±10 -
avs ±10 ±10 ±10 ±23
^vnn ±10 ±10 ±10 -
£rm ±5 ±5 ±5 -
®2nn ±10 ±10 ±10 -
&rmz ±10 ±10 ±10 -
Этшш ±10 ±10 ±10 -
6qi ±15 - - -
±20 - - -
<02ai ±35 - - -
<£»2<12 ±45 - - -
BqiS ±10 - - -
a®5 ±10 ±10 ±10 ±23
Примечание: Отклонения остальных коэффициентов равны нулю.
520
Таблица 19
Коэффициенты уравнений возмущенного движения, характеризующие
упругие свойства корпуса носителя, I ступень, I тон
t с м м с <О2„1 с2 a&ii м'1
0 -6,07 0,224 197,0 0,163
10 -6,39 0,229 208,0 0,164
20 -6,73 0,235 218,0 0,165
30 -7,П 0,243 233,0 0,170
40 -7,48 0,251 248,0 0,174
50 -7,94 0,261 268,0 0,184
60 -8,38 0,271 289,0 0,194
70 -8,67 0,283 315,0 0,213
80 -8,97 0,295 341,0 0,232
90 -8,75 0,308 373,0 0,267
100 -8,52 0,321 405,0 0,302
ПО -9,84 0,333 436,0 0,288
120 -11,6 0,344 468,0 0,275
120,59 -Н,9 0,345 470,0 0,274
Таблица 20
Коэффициенты уравнений возмущенного движения,
характеризующие упругие свойства корпуса носителя, I ступень, II тон
t с 3q26 м с'2 и>292 с’2 а&г м’1
0 -1,210 0,485 929,0 -0,626
10 -1,078 0,486 935,0 -0,654
20 -0,964 0,488 942,0 -0,683
30 . -1,015 0,489 946,0 -0,670
40 -1,075 0,490 950,0 -0,658
50 -1,345 0,494 965,0 -0,607
60 -1,715 0,498 980,0 -0,556
70 -2,390 0,511 1030,0 -0,488
80 -3,410 0,524 1080,0 -0,420
90 -4,660 0,565 1265,0 -0,372
100 -6,550 0,606 1450,0 -0,324
НО -3,670 0,710 2038,0 -0,511
120 -2,430 0,814 2626,0 -0,699
120,59 -2,390 0,821 2660,0 -0,710
521
Таблица 21
Коэффициенты уравнений возмущенного движения, учитывающие взаимное влияние колебаний
жидкости и упругости корпуса, I ступень, I и II тона
t с а,г -10 Я\г\ аг\Я\ О -Ю ?1г2 ^2<?1 ааг 10 ЯМ аъя\ О Ю ям
0 -0Д69 -0,273 0,094 0,240 0,674 0,622 -0,079 -0,167
10 -0,182 -0,243 0,109 0,266 0,732 0,647 -0,153 -0,248
20 -0,167 -0,212 0,126 0,292 0,782 0,659 -0,208 -0,323
30 -0,143 -0,175 0,149 0,331 0,836 0,674 -0,266 -0,394
40 -0,118 -0,117 0,174 0,370 0,878 0,676 -0,332 -0,469
50 -0,098 -0,110 0,198 0,405 0,889 0,660 -0,403 -0,550
60 -0,077 -0,083 0,224 0,441 0,885 0,632 -0,481 -0,631
70 -0,039 -0,041 0,262 0,503 0,865 0,601 -0,557 -0,710
80 0,002 0,002 0,303 0,561 0,831 0,561 -0,632 -0,778
90 0,040 0,042 0,343 0,642 0,730 0,490 -0,686 -0,825
100 0,080 0,082 0,382 0,719 0,618 0,463 -0,509 -0,802
по 0,116 0,098 0,418 0,685 0,325 0,245 -0,245 -0,425
115,03 0,122 0,104 0,436 0,677 0,145 0,132 -0,150 -0,245
120,6 0,142 0,112 0,464 0,665 0,112 0,100 -0,140 -0,240
Окончание табл. 21
Коэффициенты уравнений возмущенного движения, учитывающие взаимное влияние колебаний
жидкости и упругости корпуса, I ступень, I и II тона
t с а 10 Ог\Ч2 а Ю Я2Г2 °Г2Ч2 аог Ю2 ЯгЪ аГЗ,Я2 а Ю2 ?2Г4 а^Я2
0 0,285 0,660 -0,221 -0,935 -0,364 0,056 0,817 0,288
10 0,284 0,693 -0,219 -0,976 0,514 0,083 0,714 0,212
20 0,283 0,725 -0,218 -1,02 1,31 0,221 0,430 0,134
30 0,284 0,720 -0,216 -1,01 2,18 0,366 0,109 0,033
40 0,285 0,715 -0,215 -0,954 2,95 0,490 -0,247 -0,075
50 0,295 0,657 -0,220 -0,891 4,08 0,600 -0,683 -0,185
60 0,309 0,597 -0,225 -0,797 5,29 0,680 -1,26 -0,289
70 0,331 0,528 -0,227 -0,658 7,15 0,752 -2,07 -0,399
80 0,366 0,456 -0,229 -0,518 9,69 0,795 -3,28 -0,491
90 0,415 0,395 -0,203 -0,350 13,8 0,858 -4,72 -0,526
100 0,506 0,335 -0,151 -0,182 19,3 0,927 -4,38 -0,441
по 0,572 0,491 0,083 0,131 18,8 0,676 -0,512 -0,039
115,03 0,585 0,545 0,155 0,300 4,70 0,480 0,034 0,007
120,6 0,605 0,620 0,215 0,410 3,90 0,480 0,130 0,029
СПИСОК ЛИТЕРАТУРЫ
1. Абгарян К. А., Рапопорт И. М. Динамика ракет. - М.: Машинострое-
ние, 1969.-378 с.
2. Авдеев В. В., Полякова Н. М,, Шептун Ю. Д. К определению харак-
теристик колебаний жидкости в двусвязных полостях: Материалы
Всесоюзной конференции по колебаниям механических систем. -
К.: Наукова думка, 1971.
3. Авдеев В. В., Шептун Ю. Д. Анализ условий фазовой стабилизации
твердого тела с жидкостью И Механика твердого тела. - № 3. - 1971.
4. Авдеев В. В., Шептун Ю. Д. Приближенный метод исследования
структурной устойчивости механических систем: Сб. статей
«Вопросы теории и техники автоматических систем». ДГУ. -
Д., 1972.
5. Авдеев В. В., Шептун Ю. Д. Учет требований динамики при выборе
параметров последних ступеней ракет и космических аппаратов:
Сб. статей; МОМ, РКТ. - Серия 1, вып. 3. - 1972.
6. Айзенберг Я. Е., Златкин Ю. М., Калногуз А. Н., Батаев В. А., Кузь-
мин А. И. Управление по углам атаки и скольжения первых ступеней
PH И Косм1чна наука i технолога. - 2002. - Т. 8. - № 1. - С. 61-80.
7. Айзенберг Я. Е., Сухоребрый В. Г. Проектирование систем стабили-
зации носителей космических аппаратов. - М.: Машиностроение,
1986.-224 с.
8. Алексеев К. Б., Бебенин Г. Г. Управление космическим летательным
аппаратом. - М.: Машиностроение, 1964.
9. Алексеев К. Б., Бебенин Г, Г., Ярошевский В. А. Маневрирование
космических аппаратов. - М.: Машиностроение, 1970. - 416 с.
10. Алексеев К. Б., Бебенин Г. Г., Ярошевский В. А. Экстенсивное управ-
ление космическими ЛА. - М.: Машиностроение, 1977. - 120 с.
11. Андреев Н. Н., Брикер В. В., Игдалов И. М. Некоторые вопросы про-
ектирования объектов, управляемых с помощью систем регулирова-
ния центровки; РКТ. - Серия 1, вып. 4. - ЦНТИ «Поиск», 1980.
12. Андронов А. С., Брикер В. В., Игдалов И. М. Теоретические основы
управляемости одного типа КА. Проблемы навигации и автоматиче-
ского управления. - М.: АН СССР, 1972.
13. Андронов А. А., Хайкин С. Э. Теория колебаний. - Гостехиздат, 1954.
14. Аппазов Р. Ф., Лавров С. С., Мишин В. П. Баллистика управляемых
ракет дальнего действия. - М.: Наука, 1966.
524
15. Асриев В. И., Герасюта Н. Ф., Игдалов И. М., Морозов В. М. О ста-
билизации изделия с поворотным УО большой массы; РКТ. -
Серия 1, вып. 3. - ЦНТИ «Поиск», 1981.
16. Атлас гидродинамических коэффициентов уравнений возмущенного
движения твёрдого абсолютно жёсткого тела с жидким наполнени-
ем.-НИИ-88, 1965.
17. Баева Н. И., Горяченков А. Г., Колозезный Э. А. и др. Об одном спо-
собе ликвидации структурной динамической неустойчивости ракет
при наличии жидкого наполнителя баков. - ЦНИИмаш, 1965.
18. Баллистические ракеты подводных лодок России / Под общей ред.
И. И. Величко; ГРЦ «КБ им. академика В. П. Макеева». - Миасс,
1994.
19. Баскаков И. М., Дишель В. Д, Игдалов И. М. Способ обеспечения
минимальной дальности многоступенчатой ракеты с ТТРД; Автор-
ское свидетельство № 113216, 1978.
20. Беленький А. Д., Гаушус Э. В. Исследование релейной системы вто-
рого порядка с неустойчивой линейной частью // Автоматика и те-
лемеханика. - № 10. - 1970.
21. Белецкая Н. Г., Липицкий С. Г. Динамика упругих колебаний с под-
вижными отсеками И Проблемы динамики, управления и системного
анализа летательных аппаратов. - М.: Из-во МАИ, 1982. - С. 62.
22. Белецкая Н. Г., Липицкий С. Г. Математическая модель движения
системы упругих тел И Пятая Всесоюзная конференция по управле-
нию в математических системах. 1985 г. - Казань: Из-во Казанского
авиационного института, 1985. - С. 63.
23. Белецкий В. В. Движение искусственного спутника относительно
центра масс. - М.: Наука, 1965.
24. Бермант А. Ф. Отображения. Криволинейные координаты. Формулы
Грина. - М.: Физматгиз, 1958.
25. Бессекерский В. А., Попов Е. П. Теория систем автоматического ре-
гулирования. - М.: Наука, 1966.
26. Богомаз Г. И, Сирота С. А. Колебания жидкости в баках. - Д.: ИТМ
НАНУ, 2002.
27. Болтянский В. Г. Математические методы оптимального управле-
ния. - М.: Наука, 1966.
28. Будник В. С., Гонтаровский В. А., Игдалов И. М., Лазарян В. В., Ха-
нин И Г. и др. Способ разведения ББ РГЧ скатыванием по направ-
ляющим. Авторское свидетельство № 51088, 1968.
29. Бусленко Н. П., Голенко Д. Н. Метод статистических испытаний. -
М.: Физматгиз, 1962.
525
30. Вильямсон, Лакинз. Применение метода фазовой плоскости к опро-
кидыванию приземляющегося корабля // Ракетная техника и космо-
навтика. - Т. 7. - № 1. - 1969.
31. Гаррард У. Л. Метод квазиоптимальной стабилизации угловой ско-
рости космического корабля // Мир, механика. - № 4 (116). - 1969.
32. Гатаулин Н. Г, Столбецов В. И. О некоторых оценках коэффициен-
тов уравнений возмущённого движения тела с жидкостью И Меха-
ника твёрдого тела. - № 3. - 1966.
33. Гаушус Э. В. Исследование автоколебаний космических аппаратов,
I, IIИ Автоматика и телемеханика. - № 9, 10. - 1968.
34. Гаушус Э. В. Исследование одного типа автоколебаний космическо-
го аппарата; ИСЗ. - Вып. 16. - АН СССР, 1963.
35. Гаушус Э. В. К теории точечных преобразований // Автоматика и те-
лемеханика. - № 2. - 1966.
36. Гаушус Э. В. Динамика релейной системы управления ориентацией
космического аппарата. Космические исследования. - Т. 7. - Вып. 3. -
1969.
37. Гаушус Э. В., Смольянинов Н. Д. Исследование релейной динамиче-
ской системы третьего порядка // Автоматика и телемеханика. -
Вып. 3.- 1970.
38. Герасюта Н. Ф., Игдалов И. М., Морозов В. М., Зыков Н. Е. и др.
О стабилизации ракеты с поворотным управляющим органом боль-
шой массы // Ракетная и космическая техника. - Сер. 1: Теория рас-
чета, проектирования и конструирования ракетно-космической тех-
ники. - ГОНТИ-3. - 1981. - Вып. 3. - С. 18-32.
39. Герасюта Н. Ф., Шептун Ю. Д., Ярошевич С. В. Влияние неравенст-
ва управляющих импульсов на автоколебания релейной системы:
Материалы Всесоюзной конференции по колебаниям механических
систем. - К.: Паукова думка, 1971.
40. Герасюта Н. Ф., Шептун Ю. Д., Ярошевич С. В. Исследование авто-
колебаний космического аппарата // Космические исследования на
Украине. - К.: Паукова думка, 1973. - Вып. 2. - С. 57-70.
41. Герасюта Н. Ф., Шептун Ю. Д., Ярошевич С. В. Исследование
влияния неравенства управляющих импульсов на колебания релей-
ной системы с неустойчивым объектом регулирования: Материалы
пятого Всесоюзного совещания по проблемам управления, 1971.
42. Герасюта Н. Ф., Шептун Ю. Д., Ярошевич С. В. Об экономичности
систем стабилизации космических аппаратов // Космические иссле-
дования на Украине. - К.: Паукова думка, 1973. - Вып. 2 - С. 38-46.
43. Герасюта Н. Ф„ Шептун Ю. Д., Ярошевич С. В. Об экономичности
сложных автоколебаний: Материалы Всесоюзной конференции по
колебаниям механических систем. - К.: Паукова думка, 1971.
526
44. Герасюта Н. Ф., Зыков Н. Е., Игдалов И. М., Шептун Ю. Д., Яроше-
вич С. В. Способ управления по крену МГЧ и космическими аппара-
тами, движущимися в атмосфере. Авторское свидетельство № 45393,
1969.
45. Герасюта Н. Ф., Калищук В. В., Шептун Ю. Д., Ярошевич С. В. Ре-
лейная реактивная система стабилизации последних ступеней носи-
телей и космических аппаратов. Авторское свидетельство № 51654,
1970.
46. Горская Н. С., Крутова И. Н., Рутковский В. Ю. Динамика линей-
ных сервомеханизмов. - М.: АН СССР, 1959.
47. Гордиенко А. Д., Зыков Н. Е., Мороз Ю. А., Шептун Ю. Д. Способ
управления МГЧ с использованием ртути. Авторское свидетельство
№42302, 1968.
48. Гордиенко А. Д., Зыков Н. Е., Копорулин Л. В., Морозов В. М., Мороз
В. Н., Шептун Ю. Д. Способ регулирования расстояния между цен-
тром давления и центром тяжести МГЧ в полете. Авторское свиде-
тельство № 46733, 1968.
49. Гурман В. И., Лавровский Э. К, Сергеев С. И. Оптимальное управле-
ние ориентацией симметрического вращающегося КА И Космиче-
ские исследования. - Т. 8. - Вып. 3. - 1970.
50. Депри А. Изучение свободного вращения твёрдого тела около непод-
вижной точки с помощью фазовой плоскости // Мир, Механика. -
№2(108).- 1968.
51. Джур Е. О., Кучма Л. Д., Манъко Т. А., Санш Ф. П., Санш А. Ф., Ci-
тало В. Г. Гкшмерш композицшш матер!али в ракетно-косм!чнш
техшщ: Пщручник. - К.: Вища осв!та, 2002. - С. 399.
52. Джур Е. О., Кучма Л. Д., Санш Ф. П., Санш А. Ф. Твердопаливш ра-
кетш двигуни: матер!али й технологи: Пщручник. - Д.: Вид-во Дш-
пропетр. ун-ту, 1999. - С. 320.
53. Дикшатулу Б. Л., Баласубраманъян Р. Линии равного времени на фа-
зовой плоскости нелинейных систем И Мир, механика, № 5(99). -
1966.
54. Динамика систем управления с бортовыми цифровыми вычисли-
тельными машинами / Под ред. М. С. Хитрика и С. М. Федорова. -
М.: Машиностроение, 1972.-231 с.
55. Драйнер И. С., Регли У. и др. Навигация, наведение и стабилизация
в космосе. - М.: Машиностроение, 1970.
56. Загускин В. Л. Справочник по численным методам решения уравне-
ний. - М.: Физматгиз, 1960.
57. Зайцев В. А„ Игдалов И. М., Кочерга Г. Ф. Стенд контроля характе-
ристики узла качания. Авторское свидетельство. № 196390, 1983.
527
58. Зыков Н. Е., Игдалов И. М., Мадатов Г, Л., Шептун Ю. Д. Повыше-
ние точности автономного измерения высоты полета ориентирован-
ного спутника // Оборонная техника. - № 9. - 1965.
59. Зыков Н. Е., Игдалов И М., Морозов В. М., Серый Е. А. Определение
реакции ракеты на ветровые воздействия И Оборонная техника. -
№8.-1967.
60. Зыков Н. Е., Игдалов И. М., Полякова Н. М., Шептун Ю. Д. Концен-
трические топливные баки с профилированными разделительными
перегородками: Материалы Всесоюзной конференции. - ЛМИ, 1967.
61. Зыков Н. Е., Игдалов И. М., Полякова Н. М., Шептун Ю. Д. О форме
топливных баков последних ступеней носителей и КА с ЖРД: Мате-
риалы Всесоюзной конференции. - ЛМИ, 1967.
62. Зыков Н. Е., Игдалов И. М., Полякова Н. М., Шептун Ю. Д. Концен-
трические топливные баки с профилированной разделительной пере-
городкой: Труды НИИ-88 7(100); Материалы Всесоюзной конферен-
ции. - ГОНТИ. - № 1. - 1967.
63. Зыков Н. Е., Макаров Г. Д., Серый Е. А., Шептун Ю. Д. Влияние от-
клонений параметров на устойчивость движения ракеты с ЖРД:
Труды ДГУ. - Вып. I. - 1967.
64. Зыков Н. Е., Полякова Н. М., Панфилова В. Н., Шептун Ю. Д. Выбор
основных характеристик системы успокоения, ориентации и стаби-
лизации И Оборонная техника. - № 11. - 1967.
65. Зыков Н. Е., Полякова Н. М., Шептун Ю. Д. О структурной неустой-
чивости последних ступеней носителей и космических аппаратов
с ЖРД И Оборонная техника. - № 9. - 1967.
66. Зыков Н. Е., Игдалов И, М., Полякова Н. М., Шептун Ю. Д. О форме
топливных баков последних ступеней носителей и КА с ЖРД // Обо-
ронная техника. - № 7. - 1967.
67. Зыков Н. Е., Серый Е. А., Шептун Ю. Д. Влияние малых отклонений
параметров на управляемость и устойчивость «отвердевшей» ракеты
// Оборонная техника. - № 11. - 1965.
68. Зыков Н. Е., Серый Е. А., Шептун Ю. Д. Влияние отклонений пара-
метров на устойчивость ракеты с полостями, частично заполненны-
ми жидкостью И Оборонная техника. - № 6. - 1966.
69. Игдалов И. М., Кашанов Э. М., Кожевников Г. А. Способ управления
ракетой поворотом Г. О. Авторское свидетельство № 40584, 1968.
70. Игдалов И. М., Ковтун С. Ф., Копорулин Л. В., Паппо-Корыстин В. И.,
Шуба И. Н. Нагрузочный стенд узла качания Г. О. Авторское свиде-
тельство № 210418, 1984.
71. Игдалов И. М., Ладонкин О. М., Шубин С. В. Геодезическая Ж. Д. ла-
боратория РКТ. - Серия 1, вып. 2. - ЦНТН «Поиск», 1991.
528
72. Игдалов И. М., Матюшенков С. А. Устройство для измерения геоде-
зических параметров. Авторское свидетельство № 1394960, 1988.
73. Игдалов И. М., Ханин И. Г., Якупов Р. С. Системы ориентации и ста-
билизации ББ. Авторское свидетельство № 40591, 1968.
74. Игдалов И. М., Морозов В. М. Об одном методе оценки управляемо-
сти ракет: Труды VIII НТК, предприятие п/п В-2969, 1968.
75. Игдалов И. М„ Корях В. И., Ханин И. Г. Устройство закрутки ББ при
отделении от ГЧ. Авторское свидетельство № 83524, 1974.
76. Игдалов И. М., Карамян А. А., Красовский А. А., Лепескин И, Б., Ло-
бачев А. И. Устройство РГЧ с моментальным управлением. Автор-
ское свидетельство № 65736, 1972.
77. Ишлинский А. Ю. Механика относительного движения и силы инер-
ции. - М.: Наука, 1981. - 192 с.
78. Калищук В. В., Шептун Ю. Д., Ярошевич С. В. Исследование релей-
ных систем одного типа: Сб. статей «Вопросы теории и техники ав-
томатических систем»; ДГУ. - Д., 1972.
79. Калищук В. В., Шептун Ю. Д„ Ярошевич С. В. Колебания космиче-
ского аппарата: Материалы Всесоюзной конференции. - ЛМИ, 1969.
80. Калищук В. В., Шептун Ю. Д., Ярошевич С. В. Колебания релейной
системы при действии постоянного возмущения: Сб. статей «Вопро-
сы теории и техники автоматических систем»; ДГУ. - Д., 1972.
81. Калищук В. В., Шептун Ю. Д., Ярошевич С. В. Определение дли-
тельности переходных процессов; Сб. статей «Вопросы теории и
техники автоматических систем»; ДГУ. - Д., 1972.
82. Калищук В. В., Шептун Ю. Д., Ярошевич С. В. Скользящие режимы
движения - вопросы теории и техники автоматических систем. -
Д., ДГУ, 1971.-С. 30-39.
83. Карачаров К А., Пилютик А. Г. Введение в техническую теорию ус-
тойчивости движения. - М.: Физматгиз, 1962.
84. Карпенко Л. В., Уткин А. Ф., Попов А. Д. Отечественные стратегиче-
ские ракетные комплексы (справочник). - СПб.: Невский бастион,
1999.
85. Киняпин С. Д. Простейшая релейная система регулирования неус-
тойчивого объекта И Изв. вузов, радиофизика. - Т. 1. - № 1. - 1958.
86. Коваленко Н. Д. Ракетный двигатель как исполнительный орган сис-
темы управления полетом ракет (термогазодинамическое управле-
ние вектором тяги). - Д.: ИТМ НАНУ, 2004. - 412 с.
87. Колесников К С. Жидкостная ракета как объект регулирования. -
М.: Машиностроение, 1969. - 298 с.
88. Колесников К С. Динамика ракет. - М.: Машиностроение, 1980. -
376 с.
529
89. Колесников К. С. О колебаниях управляемых систем с жидкостью //
Машиностроение. - 1982. - № 2. - 32-39.
90. Колесников К С., Сухов В. Н. Упругий летательный аппарат как объ-
ект автоматического управления. - М.: Машиностроение, 1974. -
268 с.
91. Кононыхин Г. А., Харламов М. П. Об уравнении движения системы
двух тел, связанных упругим сферическим шарниром: Доклады
АН УССР. - 1979. - т. А. - № 1. - С. 275-279.
92. Конюхов С. Н., Близниченко В. В., Алдошин В. Ф. и др. Выбор ор-
ганов управления твердотопливных ракет И Ракетная и космиче-
ская техника. Сер. I. Теория расчета, проектирования и конструиро-
вания ракетно-космической техники. - ГОНТИ-3. - 1981. - Вып. 3. -
С.136-142.
93. Конюхов С. Н. Об одном примере достижения рациональной цели
эффективным и экономическим способом: 2-ая международная
НТК «Космонавтика». Радиоэлектроника. Геоинформатика. - Ря-
зань, 1998.
94. Лазарян В. В., Панкратов Ю. П., Серенко В. А., Филипенко Т. П.
и др. Конструкция РГЧ с инерционным разведением ББ. Авторское
свидетельство № 99592, 1968.
95. Лебедев А. А., Герасюта Н. Ф. Баллистика ракет. - М.: Машино-
строение, 1970. - 224 с.
96. Лебедев А. А., Чернобровкин Л. С. Динамика полета беспилотных ле-
тательных аппаратов. - М.: Машиностроение, 1973. - 616 с.
97. Леонов Н. Н. О точечном преобразовании прямой в прямую И Изв.
вузов, радиофизика. - Т. 2. - № 6. - 1959.
98. Лилов Л. К, Чириков В. А. Об уравнениях динамики систем взаимо-
связанных тел // Прикладная математика и механика. - 1981. - Т. 45. -
№3.-С. 525-534.
99. Литвин-Седой М. 3. Механика систем связанных твердых тел И Ито-
ги науки и техники: Сер. Общая механика. - М.: ВИНИТИ, 1982. -
Т. 5.-С. 3-61.
100. Литвин-Седой М. 3. Уравнение движений основного тела системы
твердых тел переменного состава: Доклады АН УССР. - 1962. -
Т. 142.-№2.-С. 289-291.
101. Локк А. С. Управление снарядами. - М.: Госиздат техн.-теор. лит.,
1957.-775 с.
102. Лурьев А. И. Аналитическая механика. - М.: Физматгиз, 1961. -
824 с.
103. Ляпунов А. М. Общая задача об устойчивости движения. - М.: Гос-
техиздат, 1950.
530
104. Методика № 1 (№ 2) задания ветровых воздействий при проектиро-
вании ракет. - М.: НИИ-88, 1963.
105. Микишев Г. Н. Демпферы колебаний жидкости: Труды НИИ-88. -
№8.-1961.
106. Микишев Г. Н, Рабинович Б. И. Динамика твёрдого тела с полостя-
ми, частично заполненными жидкостью. - М.: Машиностроение,
1968.
107. Микишев Г. Н, Рабинович Б. И. Динамика тонкостенных конструк-
ций с отсеками, содержащими жидкость. - М.: Машиностроение,
1971.-563 с.
108. Моисеев Н Д. О некоторых методах теории технической устойчиво-
сти. - ВВИА им. Н. Е. Жуковского, 1945.
109. Моисеев Н. Н. Движение твёрдого тела, имеющего полость, частич-
но заполненную идеальной капельной жидкостью И ДАН СССР. -
№4.-1952.
110. Моисеев Н Н. Задача о движении твёрдого тела, содержащего жид-
кие массы, имеющие свободную поверхность // Вестник АН СССР. -
№5.- 1956.
111. Моисеев Н. Н, Румянцев В. В. Динамика тела с полостями, частично
заполненными жидкостью И ДАН СССР. - Т. 124. - № 2. - 1959.
112. Моисеев Н. Н, Румянцев В. В. Динамика тела с полостями, содержа-
щими жидкость. - М.: Наука, 1965. - 440 с.
ИЗ. Морозов В. М. Инженерные методы исследования технической ус-
тойчивости ракет. - Д.: ДГУ-КБЮ, 1968. - 118 с.
114. Нариманов Г. С. О движении твёрдого тела, полость которого час-
тично заполнена жидкостью // ПММ. - Т. 20. - Вып. 1. - 1956.
115. Нариманов Г. С. О колебаниях жидкости в подвижных полостях //
ИАН СССР, ОНТ. - № 10. - 1957.
116. Нариманов Г. С., Докучаев Л. В., Луковский И. А. Нелинейная дина-
мика летательного аппарата. - М.: Машиностроение, 1977. - 208 с.
117. Неймарк Н И. Метод точечных преобразований в теории нелиней-
ных колебаний И Изв. вузов, радиофизика. - Т. 1. - № 1, 2, 5, 6, 19. -
1958.
118. Некоторые проблемы автоматической стабилизации и навигации;
ИСЗ: Сб. статей. - ВВИА им. Н. Е. Жуковского, 1959.
119. ОхоцимскийД. Е. К теории движения тела с полостями, частично за-
полненными жидкостью И ПММ. - Т. 20. - Вып. 1. - 1956.
120. Павловський М. А., Горбулш В. П., Клименко А. Н Системи керуван-
ня обертальним рухом КА. - К.: Наукова думка, 1997. - 200 с.
121. Паппо-Корыстин В. М., Иванов С. А. Стенд для отработки систем
качания отсека ракеты И Некоторые проблемы теории, конструкции
531
и проектирования ракет и ракетных двигателей. - Саратов, 1986. -
Вып. 18.-С. 67-68.
122. Пеня В. Н., Карнаух А. В. Влияние момента Мангуса на устойчивость
движения асимметричного летательного аппарата И Проектирование
летательных аппаратов и их систем. - К.: Паукова думка, 1985. -
С. 90-97.
123. Пилютик А. Г. Анализ динамических свойств и устойчивости дви-
жения баллистических ракет: Доклад о научно-исследовательских
работах. - ЦНИИмаш, 1965.
124. Пономарёв В. М. Теория управления движением космических аппа-
ратов. - М.: Наука, 1965.
125. Понтрягин М. С. Математическая теория оптимальных процессов. -
М.: Наука, 1976.
126. Порцелли Дж., Конноли А. Оптимальное управление ориентацией
быстровращающегося космического объекта // Мир, механика. -
№ 1(113).- 1969.
127. Рабинович Б. И. Об уравнениях возмущенного движения твердого
тела с цилиндрической полостью, частично заполненной жидкостью
И ПММ. - Т. 20. - Вып. 1. - 1956. - 39-50 с.
128. Рабинович Б. И., Черёмных С. В. К задаче оптимизации некоторых
динамических характеристик объектов регулирования: Труды 3(90). -
ЦНИИмаш, 1967.
129. Рабинович Л. В. Метод фазовой плоскости в теории и практике ре-
лейных следящих систем. - М.: Энергия, 1965.
130. Рапопорт И. М. Динамика упругого тела, частично заполненного
жидкостью. - М.: Машиностроение, 1967.
131. Ракеты и космические аппараты Конструкторского бюро «Южное»
/ Под общей ред. С. Н. Конюхова. - Д., ГКБЮ, 2000.
132. Роберсон Р. Е. Методы управления спутниками и космическими ко-
раблями: Технический доклад 60-643, 1960.
133. Рогачева Л. Н., Степаненко Н. П О движении двух твердых тел, со-
единенных сферическим шарниром И Вестник МГУ. - Сер. 1: Мате-
матика, механика. - 1971. - № 6. - С. 106-111.
134. Румянцев В. В. Об устойчивости равновесий твёрдого тела с полос-
тями, частично заполненными жидкостью И ДАН СССР. - Т. 124. -
№2.- 1959.
135. Савчук В. С., Сашн. Ф. П та iH. «Секретний» пщроздш галузг -
Д.: Вид-во Дншропетр. ун-ту, 2001. - 374 с.
136. Сарычев В. А. Положение относительного равновесия двух тел, со-
единенных сферическим шарниром, на круговой орбите И Космиче-
ские исследования. - 1967. - Т. 5 - № 3. - С. 360-364.
532
137. Святодух В. К. Динамика пространственного движения управляе-
мых ракет. - М.: Машиностроение, 1969.
138. Сидоров И. М., Коротаева И. П. Об устойчивости механических
систем со многими степенями свободы при наличии корректирую-
щего устройства И АН СССР, Техническая кибернетика. - № 4. -
1965.
139. Сидоров И. М., Коротаева И. П., Черёмных С. В. Исследование
структурной устойчивости колебательных систем со многими степе-
нями свободы: Труды 6(74). - НИИ-88, 1965.
140. Сидоров И. М., Черёмных С. В. Об одном методе исследования
устойчивости регулируемых систем И Механика твёрдого тела. -
№2.-1967.
141. Сизько В. А., Игдалов И. М., Шептун Ю. Д. Анализ процессов стаби-
лизации последних ступеней ракет на участках полета с неработаю-
щим маршевым двигателем: Материалы VIII научно-технической
конференции. - Кн. 3. - П/я В-2969. - 1968.
142. Синяков А. Н. Системы управления упругими подвижными объекта-
ми. - Л.: Из-во ЛГУ, 1981. - 200 с.
143. Справочные материалы для конструкторов по динамике баллистиче-
ских ракет и носителей космических аппаратов. - ГОНТИ, ЦНИИ-
маш, 1967.
144. Сухов В. Н. Некоторые особенности стабилизации баллистических
ракет с помощью сигнала по перегрузке. - ЦАГИ, 1965.
145. Тихонова 3. И., Борохова Н. В. О методике составления уравнений
малых колебаний сложных механических систем И Изв. вузов. Ма-
шиностроение. - 1978. - № 12. - С. 17-21.
146. Тихонравов М. К, Яцунский И. М. и др. Теория космических полётов.
- Ч. 1. - ИСЗ. АН СССР, 1963.
147. Товстик П. Е., Улитин М. И., Филиппов С. Б. Колебания твердого
тела, закрепленного на тонких упругих криволинейных стержнях
И Прикладная механика - Л.: Из-во ЛГУ, 1981. - № 5. - С. 119-130.
148. Трифоненко Б. В. Движение твердого тела с управляющими связями
И Прикладная механика. - Л.: Из-во ЛГУ, 1981. - № 5. - С. 100-106.
149. УрьевН. И., Половой И. А., МеланченкоГ. А. и др. Квазитяжелая
ложная цель. Авторское свидетельство № 168210, 1982.
150. Уэбб К. Р. Анализ нелинейных систем управления И Мир, механика. -
№ 1 (113).- 1969.
151. Федосеев Ю. Н. К составлению уравнений движения многомассовых
пространственных механических систем И Машиноведение. - 1969. -
№6.-С. 36-39.
152. Феодосьев В. И. Сопротивление материалов. - Издание 9. - М.: Нау-
ка, 1968.-512 с.
533
153. Феодосьев В. И., Синярев Г. Б. Введение в ракетную технику. -
М.: Оборонгиз, 1960. - 506 с.
154. Фихтенгольц Г. М. Курс дифференциального и интегрального ис-
числения. - Т. 2. - М.: Наука, 1966.
155. Флюге-Лотц И. Метод фазовой плоскости в теории релейных сис-
тем. М.: Физматгиз, 1959.
156. Харламов М. П., Кононыхин Г. А. О движении по инерции тел, свя-
занных сферическим шарниром И Механика твердого тела. -
К., 1980.-№ 12.-С. 52-62.
157. Харламов П. В. Об уравнениях движения системы твердых тел И Ме-
ханика твердого тела. - К., 1972. - № 4. - С. 52-73.
158. Харламова Е. И., Лесина М. Е. Об уравнениях движения двух свя-
занных тел // Механика твердого тела. - К., 1980. - № 12. - С. 26-44.
159. Цыпкин Я. 3. Теория нелинейных импульсных систем. - М.: Наука,
1973.
160. Черёмных С. В. О некоторых задачах устойчивости твёрдого тела
с жидким заполнением // Механика твёрдого тела. - № 3. - 1966.
161. Черёмных С. В. О собственной и структурной устойчивости твёрдого
тела с жидким заполнением при действии следящей силы: Труды
6(74).-НИИ-88, 1965.
162. Черноусенко Ф. Л. О движении твердого тела с подвижными внут-
ренними массами И Изв. АН УССР. - Сер.: Механика твердого тела. -
1973.-№4.-С. 33-34.
163. Черноусько Ф. Л. О движении твердого тела с упругими и диссипа-
тивными элементами И Прикладная математика и механика. - 1978. -
Т. 42. -№ 1.-С. 34—42.
164. Шаталов А. С., Топчеев Ю. И., Кондратьев В. С. Летательные аппа-
раты как объекты управления. - М.: Машиностроение, 1972. - 240 с.
165. Шептун Ю. Д., Авдеев В. В. Обеспечение устойчивости ступеней
малого удлинения и космических аппаратов с ЖРД: Материалы Все-
союзной конференции. - ЛМИ, 1969.
166. Шептун Ю. Д., Авдеев В. В. Приближенный метод оценки устойчи-
вости летательных аппаратов с ЖРД как объектов регулирования:
Материалы Всесоюзной конференции. - ЛМИ, 1969.
167. Шептун Ю. Д., Белецкая Н. Г., Липицкий С. Г. Динамика упругого ЛА
// Гагаринские научные течения в космонавтике и авиации. 1988. -
М.: Наука, 1989.-С. 118.
168. Шептун Ю. Д., Белецкая Н. Г., Липицкий С. Г. Динамическая систе-
ма упругих колебаний системы двух тел II Гагаринские научные те-
чения в космонавтике и авиации. 1985. - М.: Наука, 1986. - С. 89.
169. Шептун Ю. Д., Герасюта Н. Ф., Зыков Н. Е., Игдалов И. М., Яроше-
вич С. В. Способ управления по крену МГЧ и космическими аппара-
534
тами, движущимися в атмосфере. Авторское свидетельство № 45393,
1969.
170. Шептун Ю. Д., Герасюта Н. Ф., Калищук В. В., Ярошевич С. В. Ре-
лейная реактивная система стабилизации последних ступеней носи-
телей и космических аппаратов. Авторское свидетельство № 51654,
1970.
171. Шептун Ю. Д., Зыков Н. Е., Игдалов И. М., Полякова Н. М., Ката-
нов Э. М. Концентрические топливные баки с профилированной раз-
делительной перегородкой, обеспечивающие устойчивость движе-
ния ракеты. Авторское свидетельство № 37960, 1966.
172. Шептун Ю. Д., Зыков Н. Е., Игдалов И. М., Полякова Н. М. Торооб-
разный бак последней ступени ракеты-носителя с ЖРД, содержащий
разделительную цилиндрическую перегородку. Авторское свиде-
тельство № 40420, 1967.
173. Шептун Ю. Д., Зыков Н. Е., Полякова Н. М., Шевченко Б. А., Семе-
нов Е. А., Кудерский В. Н. Торообразный топливный бак окислителя
и горючего, содержащий перегородки в виде конусов и дренажные
трубки. Авторское свидетельство № 56933, 1970.
174. Шептун Ю. Д., Зыков Н. Е. Способ повышения точности автономно-
го измерения спутником высоты его орбиты. Авторское свидетель-
ство № 30084, 1964.
175. Шептун Ю. Д, Система шарнирно соединенных отсеков как объект
управления И Ракетная и космическая техника. - Сер. 1: Теория рас-
чета, проектирования и конструирования ракетно-космической тех-
ники. - ГОНТИ-3. - 1981. - Вып. 4. - С. 81-95.
176. Шептун Ю. Д., Ярошевич С. В. Влияние атмосферы на колебательное
движение космического аппарата И Космические исследования. -
Т. 6.-Вып. 4.- 1968.
177. Шептун Ю. Д., Ярошевич С. В. Динамика релейных систем: Учебное
пособие. - Д.: ДГУ, 1985. - 84 с.
178. Шептун Ю, Д., Ярошевич С. В. К вопросу о колебаниях космических
аппаратов, I, II И Космические исследования. - Т. 10. - Вып. 2, 3. -
1972.
179. Шилов А. А., Васильев А. Ф. Динамическая устойчивость простран-
ственного движения летательных аппаратов на больших углах атаки
при некоторых видах инерционно-аэродинамической асимметрии:
Труды ЦАГИ. - 1971. - Вып. 1345. - С. 68.
180. Aviation Week Space Technology, 1984, Smarch, V. 120, n 10, p. 55-58.
181. Defense Electronics, 1984, dec., V. 16, n 17, p. 54-56.
535
ОГЛАВЛЕНИЕ
Список сокращений........................................3
Предисловие..............................................4
Введение.................................................9
Часть 1. ДИНАМИКА РАКЕТЫ КАК ТВЕРДОГО ТЕЛА..............25
Глава 1. УРАВНЕНИЯ НЕВОЗМУЩЕННОГО
ДВИЖЕНИЯ РАКЕТЫ.....................................26
1.1. Системы координат..................................26
1.2. Силы, действующие на ракету........................29
1.3. Уравнения невозмущенного движения ракеты...........39
1.4. Расчетная траектория полета ракеты.................43
Глава 2. УРАВНЕНИЯ ВОЗМУЩЕННОГО
ДВИЖЕНИЯ РАКЕТЫ.....................................45
2.1. Возмущения, действующие на ракету..................45
2.2. Уравнения возмущенного движения ракеты.............47
2.3. Методы упрощения системы уравнений движения ракеты.53
Глава 3. УПРАВЛЯЕМОСТЬ РАКЕТЫ...........................58
3.1. Вероятностный метод учета влияния возмущений,
действующих на ракету............................61
3.2. Оценка управляемости...............................72
Глава 4. СИСТЕМА СТАБИЛИЗАЦИИ...........................79
4.1. Требования к параметрам системы стабилизации.......79
4.2. Структурная схема системы стабилизации.............93
4.2.1. Корректирующий контур.........................96
Глава 5. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ..........................98
5.1. Вероятностная математическая модель ракеты.
Постановка статистического эксперимента.........100
Часть 2. УПРАВЛЕНИЕ РАКЕТОЙ ПУТЕМ ОТКЛОНЕНИЯ
ГОЛОВНОГО ОТСЕКА.............................107
Глава 6. ПРИЧИНЫ СОЗДАНИЯ
И ОСНОВНЫЕ ПОЛОЖЕНИЯ НОВОГО
СПОСОБА УПРАВЛЕНИЯ_________________________________108
6.1. Предыстория разработки IV поколения МБР...........108
6.2. Исходные положения и ход работ по созданию МБР
IV поколения........................................НО
536
6.2.1. США-МБР «Минитмен-Х»........................110
6.2.2. СССР-МБР РТ-23 (РТ-23 УТТХ).................113
6.2.3. Управляемость РТ-23.........................118
6.3. Физические основы управления путем отклонения
головного отсека.......................................121
6.4. Общая характеристика ракеты......................123
6.5. Конструктивное исполнение........................126
Глава 7. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАКЕТЫ
С ШАРНИРНО СОЕДИНЕННЫМИ ОТСЕКАМИ...............131
7.1. Постановка задачи................................131
7.2. Уравнения движения в векторной форме.............134
7.2.1. Уравнение поступательного движения..........134
7.2.2. Уравнение углового движения.................136
7.2.3. Уравнение углового движения корпуса
относительно головного отсека......................140
7.3. Уравнения движения в скалярной форме.............140
7.4. Силы и моменты, действующие на ракету............148
7.5. Уравнение крутильных колебаний...................157
7.6. Исходные данные на разработку системы управления.158
Часть 3. ДИНАМИКА ЖЕСТКОЙ РАКЕТЫ С БАКАМИ,
ЗАПОЛНЕННЫМИ КОМПОНЕНТАМИ ТОПЛИВА______________________175
Глава 8. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ....................177
8.1. Уравнения возмущенного движения I ступени
в плоскости рыскания и структура коэффициентов..........178
8.1.1. Формулы для расчета коэффициентов
и свободных членов..................................181
8.2. Система уравнений возмущенного движения
I ступени в канале крена и структура коэффициентов.....183
8.3. Уравнения возмущенного движения
II ступени и структура коэффициентов...............184
8.4. Уравнения возмущенного движения
III ступени и структура коэффициентов..............184
8.4.1. Система уравнений возмущенного движения Ш ступени.186
8.4.2. Структура коэффициентов систем уравнений....186
Глава 9. КОЭФФИЦИЕНТЫ УРАВНЕНИЙ,
ХАРАКТЕРИЗУЮЩИЕ ЖИДКОЕ
НАПОЛНЕНИЕ ТОПЛИВНЫХ ПОЛОСТЕЙ...................188
9.1. Расчетные методы определения
гидродинамических коэффициентов.........................189
537
9.2. Экспериментальные методы определения
гидродинамических коэффициентов...........................191
9.2.1. Определение коэффициентов инерционных связей...192
9.2.2. Определение присоединенного момента инерции
через суммарный момент инерции.......................194
9.2.3. Результаты исследований.......................194
9.2.4. Рассеяние энергии при колебаниях жидкости.....197
Часть 4. ДИНАМИКА РАКЕТЫ С УЧЕТОМ
УПРУГОСТИ ЕЕ КОНСТРУКЦИИ.................................203
Глава 10. УРАВНЕНИЯ ДВИЖЕНИЯ УПРУГОЙ РАКЕТЫ______________207
10.1. Уравнения поперечных колебаний.....................207
10.2. Уравнения сил и моментов...........................209
10.3. Дифференциальные уравнения движения ракеты
в плоскости рыскания, учитывающие упругость
корпуса ракеты...........................................210
10.4. Собственные изгибные колебания корпуса ракеты
в плоскости рыскания......................................217
10.5. Дифференциальные уравнения возмущенного
движения упругой ракеты...................................222
10.6. Дифференциальные уравнения возмущенного
движения ракеты с учетом взаимного влияния
колебаний жидкости и упругости корпуса...................224
10.6.1. Определение усилий, действующих на стенки
со стороны жидкости, при поперечных колебаниях
упругого отсека с жестким днищем..............226
10.6.2. Составление уравнений возмущенного движения
рассматриваемой механической системы.................227
10.6.3. Приведение уравнений поперечных колебаний
стержня к системе обыкновенных
дифференциальных уравнений....................228
10.7. Определение основных динамических
характеристик ракеты как объекта управления..............229
10.7.1. Теоретические методы определения форм
и частот изгибных собственных колебаний.......230
10.7.2. Экспериментальные методы определения
основных динамических характеристик.................233
10.8. Устойчивость движения упругой ракеты...............236
10.9. Динамическая устойчивость упругой ракеты с баками,
частично заполненными компонентами топлива...............240
538
Часть 5. ДИНАМИКА КОСМИЧЕСКИХ СТУПЕНЕЙ РАКЕТ________________241
Глава 11. ДИНАМИКА КОСМИЧЕСКИХ СТУПЕНЕЙ
С НЕРАБОТАЮЩИМ МАРШЕВЫМ ДВИГАТЕЛЕМ....245
11.1. Задачи динамики свободного полета....................245
11.2. Переходные режимы движения...........................249
11.2.1. Обзор возможных движений.......................249
11.2.2. Выбор эффективности исполнительных органов.....256
11.2.3. Динамика программных поворотов.................258
11.2.4. Расчет длительности скользящих режимов.........264
11.3. Колебания ступени вне атмосферы......................268
11.3.1. Построение точечных преобразований.............268
11.3.2. Зависимость колебаний от параметров системы....271
11.3.3. Устойчивость простых и сложных колебаний.......278
11.3.4. Анализ сложных автоколебаний....................280
11.3.5. Оценка расхода энергии..........................285
11.3.6. Выбор параметров экономичного регулятора.......288
11.4. Колебания ступени в атмосфере........................291
11.4.1. Построение точечных преобразований.............291
11.4.2. Зависимость колебаний от параметров системы....294
11.4.3. Устойчивость простых и сложных колебаний.......306
11.4.4. Динамика простых колебаний......................308
11.4.5. Анализ сложных автоколебаний....................310
11.4.6. Оценка расхода энергии.........................314
11.4.7. Выбор параметров экономичного регулятора.......316
11.5. Методы точной ориентации.............................319
11.5.1. Изменение амплитуды колебаний..................320
11.5.2. Изменение фазы колебаний.......................323
11.5.3. Исследование движения
при изменении фазы колебаний...........................325
11.5.4. Возможности повышения точности ориентации......331
11.5.5. Управление фазой колебаний в системе с ЦВМ.....333
11.6. Управление путем перемещения масс....................336
11.6.1. Оценка необходимых перемещений центра масс....336
11.6.2. Способ управления движением
вокруг продольной оси..................................340
11.6.3. Процессы стабилизации при управлении по крену...345
Глава 12. ДИНАМИКА КОСМИЧЕСКИХ СТУПЕНЕЙ РАКЕТ
С РАБОТАЮЩИМ МАРШЕВЫМ ДВИГАТЕЛЕМ
(конструктивные методы обеспечения
устойчивости движения).....................................348
539
12.1. Связь динамических характеристик ракеты
с конструктивными параметрами ступени....................352
12.1.1. Собственная и структурная устойчивость ступеней...352
12.1.2. Влияние изменений конструктивных параметров
ступени на устойчивость невозмущенного движения.....355
12.2. Выбор конструктивных параметров ступени
с учетом требования обеспечения устойчивости........359
12.3. Обеспечение устойчивости движения путем выбора
конструкции топливного отсека............................366
12.3.1. Рациональная форма двусвязных топливных баков.366
12.3.2. Использование профилированных разделительных
перегородок и обечаек...........................374
12.3.3. Выбор размеров и формы разделительных перегородок.380
12.4. Анализ эффективности использования разделительных
перегородок по результатам натурного эксперимента........384
12.4.1. Описание экспериментальных емкостей...........384
12.4.2. Постановка и результаты эксперимента..........388
12.4.3. Обработка и анализ результатов эксперимента...394
12.4.4. Расчет коэффициентов уравнений движения.......397
12.4.5. Анализ устойчивости...........................400
Часть 6. РАКЕТА КАК ОБЪЕКТ УПРАВЛЕНИЯ
БОРТОВОЙ ЦВМ.............................................405
Раздел 6.1. РГЧ И БЦВМ НА РАКЕТАХ ГКБ «ЮЖНОЕ»__________________408
Глава 13. РГЧ КАК БОЕВОЕ ОСНАЩЕНИЕ РАКЕТ
II-IV ПОКОЛЕНИЙ__________________________________408
13.1. Разделяющаяся головная часть МБР 8К67П...................408
13.1.1. Основные положения............................408
13.1.2. Способ разведения ББ РГЧ......................409
13.1.3. Конструкция РГЧ...............................411
13.1.4. «Прямоугольник» разведения....................412
13.1.5. Точность стрельбы.............................413
13.2. Оснащение Р-36М разделяющейся головной частью........421
13.3. Разделяющаяся головная часть ракеты МР-УР100.............431
13.4. Разделяющаяся головная часть ракеты Р-36М УТТХ...........432
13.5. Разделяющаяся головная часть ракет РТ-23 (РТ-23 УТТХ)....433
13.5.1. Схема движения................................438
13.5.2. Состав возмущающих факторов...................443
13.5.3. Уравнения движения............................443
13.5.4. Минимизация времени разведения
элементов оснащения.................................446
540
13.5.5. Упрощение уравнений движения...............447
13.5.6. Принципы формирования дискретного
оптимального управления........................451
13.5.7. Синтез закона управления...................454
Раздел 6.2. БЦВМ КАК СРЕДСТВО ДЛЯ РЕШЕНИЯ
НЕТРАДИЦИОННЫХ ЗАДАЧ
ДИНАМИКИ РАКЕТ......................................460
Глава 14. НЕТРАДИЦИОННЫЕ ЗАДАЧИ
ДИНАМИКИ РАКЕТ......................................460
14.1. Обеспечение безопасности БЖРК....................460
14.2. Обеспечение безударности старта PH «Зенит».......465
14.3. Обеспечение безопасности старта РКН «Зенит-З SL».467
14.4. Минимизация нагрузки на корпус ракеты............470
Часть 7. СИСТЕМЫ И АГРЕГАТЫ РАКЕТЫ
КАК ОБЪЕКТА УПРАВЛЕНИЯ......................477
Раздел 7.1. СИСТЕМА РЕГУЛИРОВАНИЯ 11Д520...................477
Глава 15. СИСТЕМЫ УПРАВЛЕНИЯ
РАСХОДОВАНИЕМ ТОПЛИВА...............................481
15.1. Основные технические требования,
предъявляемые к системе.............................481
15.2. Принципы построения и алгоритм функционирования СУРТ.482
15.3. Аппаратная реализация СУРТ.......................492
Заключение части 7.....................................501
Приложение.............................................503
Список литературы......................................524
541
Навчальне видання
1гдалов Йосип Менделевии
Кучма Леошд Данилович
Поляков Микола В1кторович
Шептун Юрш Дмитрович
РАКЕТА
ЯК ОБ’СКТ КЕРУВАННЯ
П1ДРУЧНИК
Допущено MwicmepcmeoM oceimu i науки Украгни
Росшською мовою
Вщповщальний за випуск А. С. Стпков
Техшчний редактор В. А. Усенко
Корекгор В. А. Нечай
Комп'ютерна верстка Т. В. Карпенко
Подписано до друку 15.03.2004. Формат 60x84^/ . Llanip офсетний. Друк офсетний.
Умов. друк. арк. 32,62. Умов, фарбовщб. 32,62. Обл.-вид. арк. 35,06.
Тираж 1000 прим. Замовлення № 436.
Видавництво ТОВ «Виробничо-комерщйна ф!рма «АРТ-ПРЕС»
49050, м. Дшпропетровськ, вул. Козакова, 3
Свщоцтво ДК № 1042 вщ 17.09.2002 р.
Друкарня ТОВ «Виробничо-комерщйна ф!рма «АРТ-ПРЕС»
49050, м. Дшпропетровськ, вул. Козакова, 3
Телефакс (056) 370-20-27
ISBN 966-7985-81-4