Author: Орлова И.В.
Tags: теория статистики статистические методы учебники и учебные пособия по статистике статистика экономический анализ статистический анализ
ISBN: 978-5-9558-0108-7
Year: 2009
Text
> < л .-И I,
МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ
АНАЛИЗ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ:
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
В SPSS
УЧЕБНОЕ ПОСОБИЕ
Под ред. И. В. Орловой
Рекомендовано
Учебно-методическим объединением по образованию
в области статистики в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по специальности «Статистика»
и другим экономическим специальностям
Москва
Вузовский учебник
2009
ОГЛАВЛЕНИЕ
Предисловие...................................................3
Глава 1. Введение в многомерный статистический анализ.........5
1.1. Предмет и задачи многомерного статистического анализа .... 5
1.2. Методы многомерного статистического анализа..........7
1.3. Применение MCA в экономических исследованиях.........9
Глава 2. Множественный регрессионный анализ.................16
2.1. Линейная модель множественной регрессии.............16
2.1.1. Математический аппарат модели множественной
линейной регрессии.................................. 16
2.1.2. Особенности практического применения
регрессионных моделей................................23
2.1.3. Использование SPSS для построения модели
множественной линейной регрессии.....................26
2.2. Нелинейные регрессионные модели в SPSS..............42
2.3. Логистическая регрессия.............................57
2.3.1. Математическое описание логистической
регрессии............................................57
2.3.2. Реализация логистической регрессии в SPSS.
ROC-анализ...........................................60
Задачи для самостоятельного решения......................78
Гпава 3. Кластерный анализ..................................91
3.1. Общая характеристика процедур кластеризации.........91
3.1.1. Кластерный анализ и его роль в социально-
экономических исследованиях..........................91
3.1.2. Расстояния между объектами и кластерами.......93
3.1.3. Анализ качества классификации.................99
3.1.4. Методы кластерного анализа...................103
3.2. Реализация кластерного анализа в SPSS..............112
3.2.1. Иерархическая кластеризация..................112
3.2.2. Кластеризация ^-средними.....................123
3.2.3. Двухэтапный кластерный анализ................126
3.2.4. Комплексный пример использования методов
кластерного анализа................................ 138
Задачи для самостоятельного решения.................... 143
20’ 307
Diaea 4. Факторный анализ...............................154
4.1. Факторный анализ как метод выявления латентной
структуры и скрытых закономерностей................. 154
4.1.1. Основные понятия факторного анализа...... 154
4.1.2. Методика факторного анализа в случае одного
объясняющего фактора....................... 156
4.1.3. Методика факторного анализа в случае нескольких
объясняющих факторов............................. 158
4.2. Реализация факторного анализа в SPSS........... 162
Задачи для самостоятельного решения................. 192
Глава 5. Дискриминантный анализ.........................194
5.1. Теоретические предпосылки дискриминантного
анализа............................................. 194
5.1.1. Области применения и методы дискриминантного
анализа.......................................... 194
5.1.2. Постановка задачи на исследование методами
дискриминантного анализа......................... 196
5.1.3. Геометрическая интерпретация дискриминантных
функций.......................................... 198
5.1.4. Критерии сравнения выборок по нескольким
признакам........................................ 201
5.2. Алгоритм выполнения дискриминантного анализа....204
5.3. Методы оценки информативности показателей.......208
5.4. Реализация дискриминантного анализа.............211
5.4.1. Пример применения дискриминантного анализа
при наличии двух обучающих выборок................211
5.4.2. Пошаговый алгоритм дискриминантного анализа >
в SPSS.......................................216 >
5.4.3. Дискриминантный анализ в SPSS при наличии t;
двух обучающих выборок ..................... 225 <
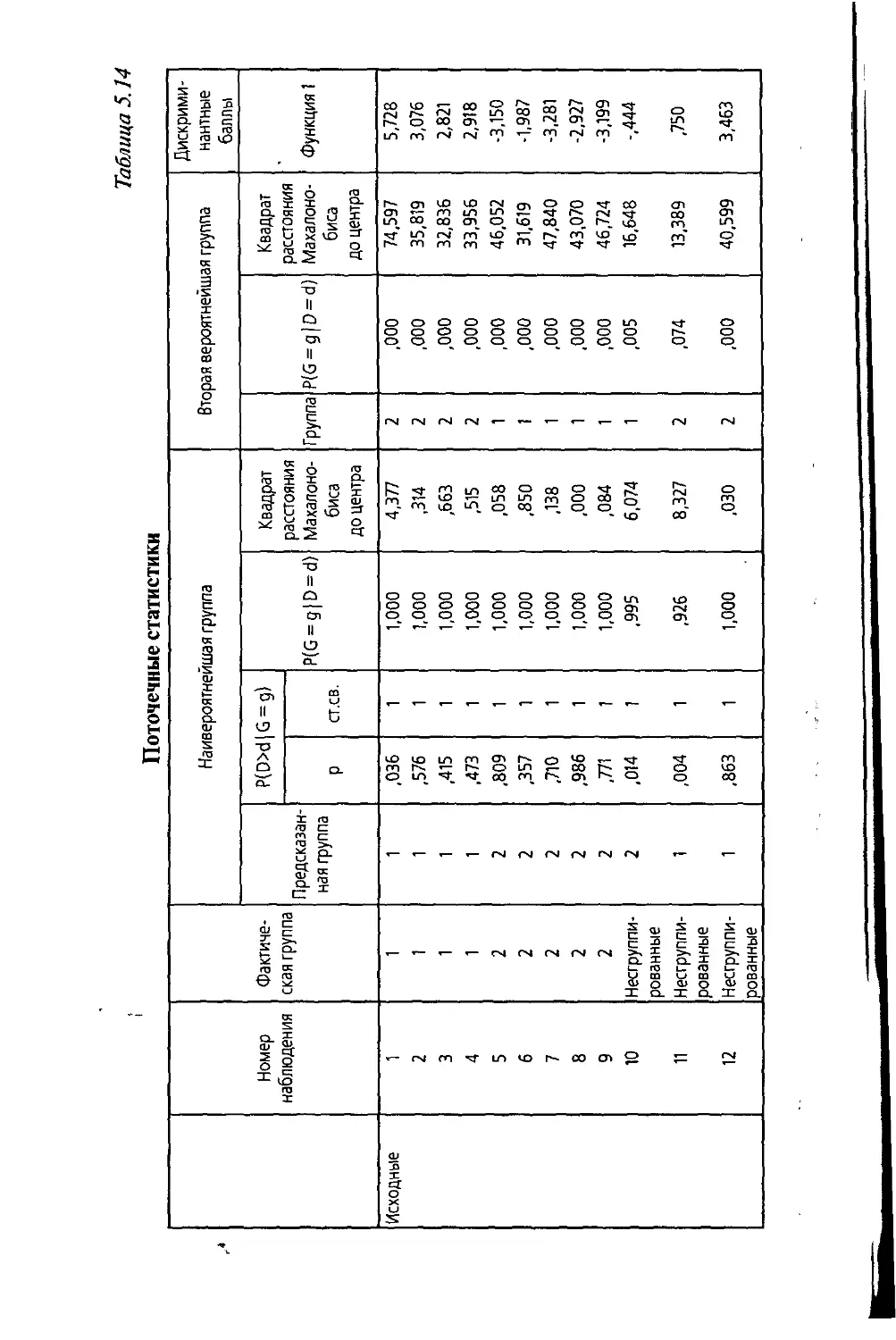
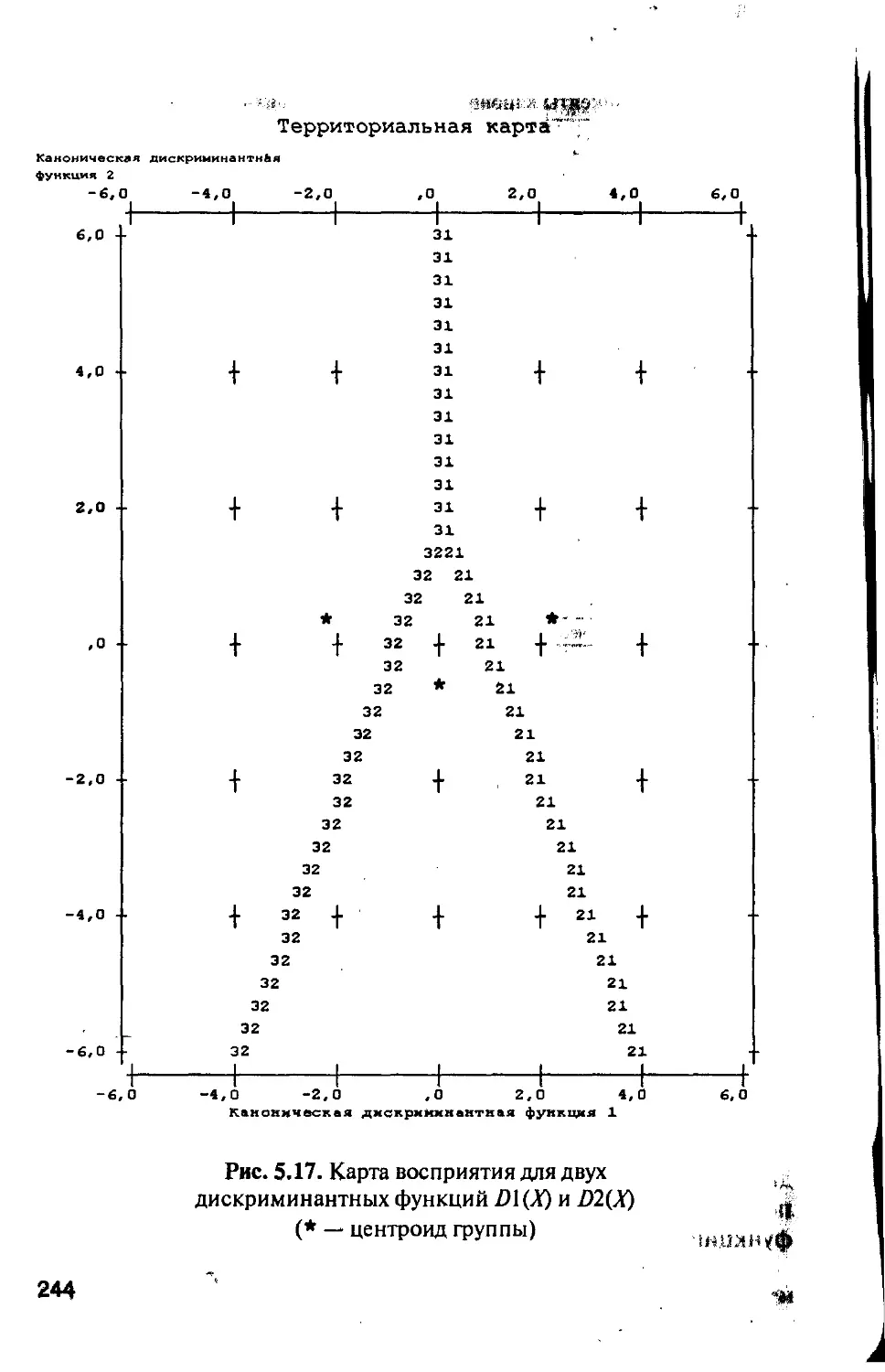
5.4.4. Дискриминантный анализ в SPSS при наличии
трех обучающих выборок............................234
Задачи для самостоятельного решения..................248
Глава 6. Дисперсионный анализ...........................255
6.1. Общие понятия и применение дисперсионного анализа.... 255
6.1.1. Виды дисперсионного анализа............... 255 *
6.1.2. Проверяемые гипотезы и требования
к анализируемым данным............................257
6.1.3. Идея дисперсионного анализа и ее графическая
интерпретация.....................................259
308
1
6.2. Модели дисперсионного анализа...................262
6.2.1. Однофакторный дисперсионный анализ........262
6.2.2. Двухфакторный дисперсионный анализ........263
6.2.3. Многофакторный дисперсионный анализ.......266
6.3. Реализация дисперсионного анализа в SPSS........267
6.3.1. Пошаговые алгоритмы однофакторного
дисперсионного анализа в SPSS.....................267
6.3.2. Однофакторный дисперсионный анализ в SPSS
при наличии несвязанных выборок...................269
6.3.3. Однофакторный дисперсионный анализ в SPSS
при наличии связанных выборок с повторными
измерениями...................................... 276
6.3.4. Двухфакторный дисперсионный анализ в SPSS
без повторных измерений...........................281
6.3.5. Двухфакторный дисперсионный анализ в SPSS
с повторными измерениями..........................292
Рекомендации по выполнению самостоятельного задания..303
Список использованной литературы........................304
Глава 1
ВВЕДЕНИЕ В МНОГОМЕРНЫЙ
СТАТИСТИЧЕСКИЙ АНАЛИЗ
. кг
1.1. ПРЕДМЕТ И ЗАДАЧИ
МНОГОМЕРНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА
Исходная информация в социально-экономических исследова-
ниях чаще всего представляется в виде набора объектов, каждый
из которых характеризуется рядом признаков (показателей). В ка-
честве объектов могут выступать страны, регионы, предпри-
ятия, респонденты и т.д., а в качестве признаков — различные
показатели социально-экономической структуры изучаемых объ-
ектов.
В настоящее время вычислительные системы и компьютерные
сети позволяют накапливать большие массивы данных для реше-
ния задач обработки и анализа данных.
Как показывает опыт анализа массовых явлений, число объек-
тов может достигать многих десятков и сотен; число признаков
также может исчисляться десятками. Очевидно, что непосред-
ственный (визуальный) анализ исходных данных при большом
количестве объектов и признаков практически малоэффективен —
можно лишь выявить отдельные особенности изучаемой структу-
ры, извлечь иллюстративные частные примеры.
В реальных исследованиях возникают задачи уменьшения, кон-
центрации исходных данных, выявления структуры и взаимосвязей
между ними на основе построения обобщенных характеристик мно-
жества признаков и множества объектов. Такие задачи могут решать-
ся методами многомерного статистического анализа (MCA).
Многомерный статистический анализ — раздел математической
статистики, развивающий математические методы выявления ха-
рактера и структуры взаимосвязей явлений, характеризующихся
большим количеством различных свойств.
Обычно для проведения анализа используются результаты из-
мерения компонент многомерного признака для каждого объекта
из исследуемой совокупности.
Механизм анализа данных и прогнозирования, который еще
принято называть Data Mining, т.е. «извлечение информации»,
«добыча данных», «добыча знаний», позволяет использовать в при-
5
кладных решениях инструменты для выявления закономерностей,
которые обычно скрываются за большими объемами информации.
Математической основой инструментария анализа данных явля-
ется многомерный статистический анализ, бурное развитие кото-
рого началось в конце XX века в период массового распростране-
ния компьютеров.
В настоящее время методы и модели MCA используются в со-
ставе новых информационных технологий, называемых интеллек-
туальным анализом данных.
Можно выделить три основные задачи, решаемые в рамках MCA:
1) исследование характера явных и неявных зависимостей меж-
ду объектами или признаками;
2) классификация объектов или признаков как при задании
профиля групп, так и при его отсутствии;
3) снижение размерности пространства признаков за счет вы-
явления внутренней структуры в заданной совокупности.
Развитие вычислительной техники и программного обеспече-
ния способствует широкому внедрению методов MCA в практику.
Однако если исследователь применяет программы без понимания
математической сущности используемых алгоритмов, это может
привести к неверным или необоснованным результатам. Значимые
практические результаты могут быть получены только на основе
профессиональных знаний в предметной области, подкрепленных
владением математическими методами и пакетами прикладных
программ, в которых эти методы реализованы.
Сущность MCA состоит в том, что многомерные исходные дан-
ные обрабатываются математико-статистическими методами с
привлечением вычислительной техники, в результате чего об изу-
чаемом объекте появляется новая информация (в том числе скры-
тая, ненаблюдаемая непосредственно — латентная) в табличной
или графической форме, которая впоследствии анализируется и
интерпретируется в интересах принятия решений.
Выделим основные этапы проведения многомерного анализа
методами MCA [35]:
• постановка задачи на исследование, определение объемов ис-
ходной и выходной информации, выбор формы представления
данных;
• определение последовательности обработки исходной инфор-
мации и выбор методов ее обработки из арсенала методов
MCA;
6
• сбор и систематизация исходных данных для их обработки;
• предварительный анализ данных: по критериям однородности,
• соответствию данных статистической гипотезе, подчинению
’ закону распределения и отсутствию в них грубых ошибок;
• уточнение математической постановки задачи и оценка воз-
;;; можности применения методов MCA (при необходимости уточ-
няется набор методов анализа);
• проведение вычислительного эксперимента с помощью вычис-
лительной техники;
• оценка результатов по статистическим критериям качества, не-
противоречивости полученных результатов экономическим вы-
водам и по степени их интерпретируемости;
• обобщение результатов исследования в табличной или графи-
ческой форме, интерпретация, выводы, предложения и практи-
ческие рекомендации по результатам проведенного анализа.
Организуя поэтапное проведение исследований с применением
методов MCA, можно повысить их эффективность.
1.2. МЕТОДЫ МНОГОМЕРНОГО
СТАТИСТИЧЕСКОГО АНАЛИЗА
К методам многомерного статистического анализа относятся
пошаговая линейная и нелинейная регрессия, логистическая ре-
грессия, кластерный анализ, компонентный, факторный, диспер-
сионный, дискриминантный анализ и др.
В учебном пособии будут рассмотрены наиболее часто приме-
няемые методы.
Множественный регрессионный анализ предназначен для по-
строения модели, позволяющей по значениям независимых пере-
менных получать оценки значений зависимой переменной. Мно-
гие потребности анализа данных можно так или иначе свести к
задачам регрессии. В частности, регрессия применяется для таких
задач, как прогнозирование, оценка рисков, анализ эластичности
спроса.
Логистическая регрессия — инструмент для решения задачи
классификации. Логистическая регрессия — это разновидность
множественной регрессии, назначение которой состоит в анализе
связи между несколькими независимыми переменными и зависи-
мой переменной, которая является бинарной (т.е. может прини-
мать только два значения).
7
Методы снижения размерности многомерного пространства объ-
единяют в себе компонентный и факторный анализ.
Метод главных компонент состоит в том, чтобы среди всех ли-
нейных комбинаций множества признаков наблюдаемых объектов
выделить гораздо меньшее число таких, изменчивость которых в
значительной степени описывает изменчивость первоначального
набора признаков в целом. В дальнейшем можно использовать эти
найденные комбинации (которые и называются главными компо-
нентами) для классификации и других задач, связанных с изуча-
емыми объектами.
Можно привести также пример, когда измеряемые по разным
методикам коэффициенты экономической активности сводят пу-
тем их комбинирования к одному (интегральному) показателю. За
этим стоит мысль о том, что, хотя каждый из предлагаемых коэф-
фициентов по-разному учитывает экономические факторы, все
они призваны объяснять одно и то же явление, и, значит, это яв-
ление наилучшим образом должно описываться какой-то их ли-
нейной комбинацией, являющейся как бы результатом «компро-
мисса» между различными методиками.
Факторный анализ занимается определением относительно не-
большого числа скрытых (латентных) факторов, изменчивостью
которых объясняется изменчивость всех наблюдаемых показате-
лей, связанных с каждым из подвергающихся изучению объектов.
В этом смысле оцениваемые латентные факторы можно считать
причинами, а наблюдаемые признаки — следствиями. Результаты
факторного анализа будут успешными, если большое число при-
знаков удается достаточно точно объяснить малым количеством
причин.
Итак, факторный анализ направлен на снижение размерности
рассматриваемой задачи.
Метод главных компонент и факторный анализ часто дают
близкие результаты. Именно поэтому метод главных компонент
иногда считают частью факторного анализа. Однако это не так.
Математические модели факторного и компонентного анализа
различны.
Методы многомерной классификации, к которым относятся клас-
терный и дискриминантный анализ, предназначены для разделения
совокупностей объектов на классы, в каждый из которых должны
входить объекты в определенном смысле однородные или близкие.
При кластерном анализе заранее неизвестно, сколько получится
8
групп объектов и какого они будут объема. Дискриминантный анализ
разделяет объекты по уже существующим классам.
Пусть при изучении объектов у каждого из них измеряется боль-
шое количество показателей. Если число измеряемых показателей
достаточно велико, то с ростом количества объектов возникает ряд
проблем: объем информации очень велик, а нужно ли хранить ее
всю? И как наглядно представить себе всю информацию, чтобы
извлечь из нее некую суть, необходимую для принятия решения?
Задачу классификации, т.е. объединения данных в некоторые
группы, можно рассматривать как частный случай задачи сниже-
ния размерности. Дело в том, что индивидуальное (большое) раз-
нообразие данных после успешного решения задачи классифика-
ции переходит в групповое разнообразие с некоторыми усреднен-
ными показателями данных в пределах одного класса.
Многомерный дисперсионный анализ предназначен для оценки и
исследования дисперсий комплексов признаков.
Рассмотрим для примера зависимость урожая Y от внесения в
почву определенного вещества (удобрения). Это и будет фактор X,
который в данном случае является нечисловой величиной. В про-
стейшем случае имеется два уровня фактора X:
1) удобрение было внесено (фактору присваивается значение 1);
2) удобрение не было внесено (фактору присваивается значе-
ние 0).
Пусть нам заранее известна дисперсия величины Y в случае,
когда фактор Xне действовал. Далее оценивается дисперсия Yпод
воздействием фактора X. Если фактор X не оказывал влияния на
изменчивость Y, то новая дисперсия несильно отличается от преж-
ней. Если же дисперсия стала значительно больше, то вклад фак-
тора в изменчивость наблюдаемой случайной величины следует
признать значительным.
Идея дисперсионного анализа заключается в оценке степени
влияния факторов на исследуемую величину. В основе этого раз-
дела MCA лежит изучение доли той дисперсии, которая объясня-
ется через изучаемый фактор, в полной дисперсии.
1.3. ПРИМЕНЕНИЕ MCA
В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ
< ,:Ж
В этом параграфе представлены наиболее часто встречающиеся
на практике задачи анализа данных. 4 „ ,п
Фактически любой экономический процесс описывается набо-
ром многомерных статистических данных. Качество и полнота
информации о его структуре и развитии зависят от совершенства
методов исследования этих эмпирических данных. В связи с этим
MCA обладает наиболее широким спектром методов анализа,
направленных на выявление структуры и взаимосвязей экономи-
ческих переменных, причин и последствий протекания экономи-
ческих процессов. Все это, при высоком уровне стохастичности
финансово-экономических процессов, дает возможность плани-
рования и предсказания их протекания с определенной вероят-
ностью.
В экономическом анализе применимо большинство методов
MCA. Например, важнейшей составной частью экономических
исследований оказывается задача выявления и анализа силы, харак-
тера и формы взаимосвязей показателей, выбранных для описания
того или иного процесса. При наличии количественной информа-
ции, записанной в виде матрицы исходных данных, для решения
указанных задач может быть привлечен корреляционный анализ,
затем он подкрепляется множественным регрессионным анализом.
В определении структуры взаимосвязей, а также в выявлении
причин наличия связей вообще наиболее подходящим оказывает-
ся факторный анализ. Известно, что взаимосвязь двух или более
экономических показателей объясняется либо тем, что они обу-
словливают друг друга, либо тем, что на каждый из них воздей-
ствует некий скрытый, не входящий в данную группу признак.
Факторный анализ как раз и позволяет определить эти неявные,
скрытые факторы. Сложную структуру взаимосвязей экономиче-
ских показателей в каком-либо явлении факторный анализ объяс-
няет наличием у этого явления небольшого числа скрытых, обоб-
щенных характеристик («общих факторов»), каждая из которых в
той или иной мере воздействует на все исходные показатели. Те из
показателей, чьи изменения в наибольшей степени определяются
каким-то фактором, оказываются тесно связанными между со-
бой.
В экономических исследованиях актуальными являются также
различные процедуры классификации объектов. При этом наблюда-
ется тенденция к комплексному использованию методов фактор-
ного анализа и автоматической классификации. Сначала с по-
мощью методов классификации получают группировку объектов в
исходном многомерном пространстве признаков. Затем с помощью
10
факторного анализа выявляют небольшое количество основных
факторов (лучше, если их будет два). В результате каждый объект
представляется точкой в пространстве главных факторов, а каждый
кластер — группой точек. Расположение этих групп на плоскости
факторов определяет «статус» каждой из них, а также дает нагляд-
ную интерпретацию компактности полученных групп, их объема,
относительной удаленности друг от друга и т.п.
В ситуации, когда имеется большое число равноправных при-
знаков, многие из которых взаимосвязаны и в значительной мере
дублируют друг друга, лучше вначале применить один из методов
факторного анализа, а затем, исходя из полученных значений фак-
торных весов для каждого из объектов, построить автоматическую
классификацию объектов в пространстве уже меньшей размерно-
сти, определяемой числом факторов.
Основными направлениями применения методов MCA в экономике
являются банковское дело, финансы, страхование, производство,
управление отношениями с клиентами, коммерция, маркетинг,
фондовый рынок и др.
Применение MCA для решения задач государственного и ре-
гионального уровня оправдывает себя, например, при оценке ин-
вестиционной привлекательности регионов, классификации реги-
онов по социально-экономическим показателям или уровню жиз-
ни населения и пр.
В качестве примеров можно привести следующие постановки
задач, для решения которых используются методы MCA [6, 32]:
• оценка эффективности рекламы;
• прогнозирование объема продаж;
• эконометрические технологии в управлении клиентами;
• прогноз денежных поступлений от продажи полисов; ъ1
• определение кредитоспособности клиента банка; ';ч
• проведение маркетинговых исследований в банке; i l-t
• выявление групп клиентов, выгодных страховой компании; ш
• выявление мошенничества в страховой деятельности.
Оценка эффективности рекламы. При оценке влияния рекламы
на спрос продукции проводятся маркетинговые исследования,
основанные на опросе потенциальных покупателей и на статисти-
ке покупок в динамике. При этом часто представляется возможным
непосредственно измерить величины, определяющие поведение
покупателя (факторы), а иногда неизвестны даже число и содер-
жательный смысл факторов. Для измерений могут быть доступны
11
другие величины, тем или иным способом зависящие от этих фак-
торов. При этом, когда влияние неизвестных факторов проявляет-
ся в нескольких измеряемых признаках, последние могут обнару-
живать тесную связь между собой (например, корреляционную),
поэтому общее число факторов может быть гораздо меньше, чем
число измеряемых переменных, которое обычно выбирается ис-
следователем в той или иной мере произвольно. Для обнаружения
влияющих на измеряемые переменные факторов используются
методы факторного анализа.
Для оценки влияния прироста объемов покупок в зависимости
от затрат на рекламу естественно воспользоваться регрессионной
моделью с распределенными лагами, поскольку объемы закупок
зависят от затрат на рекламу не только (и не столько) в данный
момент, но и в предыдущие периоды времени. Для построения
модели достаточно иметь информацию о продажах и затратах на
рекламу в течение некоторого времени. Построенная модель по-
зволяет получить прогноз объема продаж и выбрать стратегию за-
трат на рекламу в динамике.
Оценить эффективность рекламы достаточно сложно, так как
она зависит от многих внутренних и внешних факторов (уровень
доходов населения, его изменение, поведение конкурентов, из-
менение политической и экономической ситуации и др.). Для
оценки эффективности рекламы применяют корреляционный и
регрессионный анализ на основе кластерного и факторного ана-
лиза.
Прогнозирование объема продаж. Объем продаж — один из клю-
чевых показателей, характеризующих деятельность коммерческой
фирмы. Поэтому задача прогнозирования объема продаж представ-
ляет большой интерес, например, для компаний, которые занима-
ются оптовой торговлей. Товароведам необходимо знать примерное
количество продукции, которое они смогут реализовать в ближай-
шее время, для того чтобы, с одной стороны, иметь достаточное
количество товаров на складе, а с другой — не перегрузить склады
продукцией, что особенно актуально для продукции с небольшим
сроком хранения.
В большинстве случаев объем продаж того или иного товара
поддается прогнозу. Например, многие товары продаются в соот-
ветствии с ярко выраженной сезонной составляющей, что легко
определяется с помощью аналитических технологий. Применяя
эти технологии, можно прогнозировать объемы продаж по всем
12
товарным позициям, что особенно актуально в случае их большо-
го количества. При необходимости можно также учитывать и до-
полнительные факторы, например рекламную кампанию, конъ-
юнктуру рынка, действия конкурентов и т.п. Комплексный учет
всех факторов может значительно повысить качество прогноза.
Эконометрические технологии в управлении клиентами. Изучение
поведения клиента — важная задача маркетологов, продавцов,
сервис-менеджеров, аналитиков во многих отраслях экономики.
Действительно, клиент — это основной источник прибыли любой
организации; от количества клиентов напрямую зависит ее доход.
В последнее время в Интернете появилось большое количество
ресурсов, связанных с технологиями управления клиентами, по-
стоянно проводятся исследования рынка и презентации новых
продуктов по анализу поведения клиента.
Проанализировав данные с помощью MCA, можно прогнози-
ровать поведение клиентов, планировать маркетинговые кампа-
нии, всесторонне изучать причины потери клиентов, выполнять
сегментацию клиентов. Имея перед глазами готовую модель раз-
деления клиентов по группам, можно без труда разработать наибо-
лее эффективную стратегию компании. Предоставляя скидки раз-
личным группам клиентов и позиционируя новый товар, можно
добиться увеличения прибыли организации.
Прогноз денежных поступлений от продажи полисов. Множест-
венный регрессионный анализ позволяет найти зависимость про-
даж полисов от различных показателей. Используя построенные
уравнения, можно прогнозировать изменения выбранных показа-
телей в зависимости от изменения других показателей. С помощью
того или иного программного продукта получают уравнение зави-
симости в явном виде, а также доверительные интервалы, оценку
точности решения и оценку адекватности модели.
Определение кредитоспособности клиента банка. Решением такой
задачи является ответ на вопрос: выдавать ли кредит клиенту? Без
применения методов MCA эта задача решается сотрудниками бан-
ка на основе их опыта, интуиции и субъективных представлений о
том, какой клиент является благонадежным.
Применяя кластерный анализ или логистическую регрессию (из
арсенала методов MCA) к ретроспективной информации, можно
провести классификацию клиентов по совокупности признаков и
выделить среди них две группы: клиенты, вернувшие кредит, и кли-
енты, не вернувшие кредит. В дальнейшем на основе анализа группы
13
клиентов, не вернувших кредит, по совокупности признаков состав-
ляется образ потенциального неплательщика. Затем при поступле-
нии сведений о новом клиенте определяется его принадлежность к
той или иной группе («вернет кредит», «не вернет кредит»).
Проведение маркетинговых исследований в банке. Эта задача ре-
шается в целях привлечения выгодных клиентов банка.
1. С помощью методов MCA можно провести классификацию
(сегментирование) клиентов банка на «более выгодных» и «менее
выгодных». После выявления сегмента «более выгодных» клиентов
банк может активизировать свою маркетинговую политику среди
клиентов этого сегмента.
2. Методами классификации MCA клиенты банка по совокуп-
ности признаков делятся на различные группы. С учетом этого
банк может сделать свою маркетинговую политику более эффек-
тивной за счет предложения различным группам клиентов тех ви-
дов услуг, в которых они нуждаются.
Выявление групп клиентов, выгодных страховой компании. По
совокупности характерных признаков с помощью методов класси-
фикации проводится сегментация клиентов компании на группы.
Далее, используя информацию, полученную в результате сегмен-
тации клиентов, страховая компания может с наибольшей выгодой
и наименьшим риском предлагать определенный перечень услуг
некоторым группам в соответствии с их потребностями.
Выявление мошенничества в страховой деятельности. Эта задача
решается на основе формирования общего стереотипа поведения
клиентов-мошенников, подобно задаче «определения кредитоспо-
собности заемщика», рассмотренной ранее.
Методы MCA находят применение в различных областях дея-
тельности, например в таких, как промышленное производство,
маркетинг, торговля и т.п.
Специфика промышленного производства и технологических про-
цессов позволяет использовать методы MCA для решения ряда
производственных задач, например:
• комплексный системный анализ производственных ситуаций;
• оценка зависимости от параметров технологического процесса;
• выявление скрытых (латентных) факторов, влияющих на каче-
ство изделий;
• обнаружение и идентификация ранее неизвестных взаимосвя-
зей между производственными параметрами и факторами, влия-
ющими на них.
14
Маркетинговая деятельность многих компаний связана с обра-
боткой результатов исследований методами MCA. В этой сфере
применяются практически все методы многомерного анализа, на-
пример, при решении следующих задач:
• сегментация потребителей по спросу, доходу, месту житель-
ства;
• сегментации торговых предприятий по качеству работы;
• оценка конкурентоспособности товара по совокупности фак-
торов;
• психографическая сегментация рынка; , ,
• изучение продукта и бенчмаркинг продукта;
• исследование имиджа торгового предприятия; . 1
• оценка качества работы интервьюеров; |f ,t,
• создание карты брендов и др.
Торговля, интернет-технологии, телекоммуникации также ис-
пользуют MCA для решения своих многообразных задач.
Приведенные примеры подтверждают, что возможности мето-
дов MCA очень широкие и они находят применение как в теоре-
тических исследованиях, так и при решении практических задач.
В заключение заметим, что эффективность методов MCA давно
доказана. Его огромные возможности в анализе многомерных дан-
ных, проверке различных теорий и гипотез не заставят ждать своих
результатов. Поэтому хороший экономист в современной Рос-
сии — это экономист, не только знающий основы MCA, но и уме-
ющий применять на практике его основные методы и алгоритмы.
Глава 2
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
В главе будет рассмотрено построение с помощью программы
SPSS наиболее распространенных моделей регрессии: линейной,
нелинейной и логистической, а также использование этих моделей
при решении экономических задач. В учебное пособие не вошли
более сложные модели, реализованные в программе SPSS.
2.1. ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
2.1.1. Математический аппарат модели множественной
линейной регрессии
Задача регрессионного анализа состоит в построении модели,
позволяющей по значениям независимых переменных получать
оценки значений зависимой переменной.
Переменные, участвующие при построении модели, можно раз-
делить на следующие типы:
• результирующая (зависимая, эндогенная) переменная Y — харак-
теризует результат или эффективность функционирования эко-
номической системы. Значения ее формируются под воздей-
ствием ряда других переменных и факторов, часть из которых
поддается регистрации, управлению и планированию. В регрес-
сионном анализе результирующая переменная играет роль
функции, значение которой определяется значениями объ-
ясняющих переменных, выполняющих роль аргументов. По
своей природе результирующая переменная всегда случайна
(стохастична);
• объясняющие (независимые, экзогенные) переменные X — это
переменные, которые поддаются регистрации и описывают
условия функционирования реальной экономической системы.
Они в большой мере определяют значения результирующих
переменных. Обычно часть из них поддается регулированию и
управлению. Еще их называют факторными признаками. В ре-
грессионном анализе это аргументы результирующей функ-
ции Y. По своей природе они могут быть как случайными, так
и неслучайными.
В то время как зависимая переменная должна быть непрерыв-
ной (за исключением логистической регрессии), независимые пе-
16
ременные могут быть как дискретными, так и категориальными,
такими как «пол» или «тип применяемого препарата». Если все
независимые переменные (или большинство из них) являются
категориальными, то в этом случае лучше использовать дисперси-
онный анализ.
Функция f(X{, Х2,..., Хк), описывающая зависимость показате-
ля от параметров, называется уравнением (функцией) регрессии*.
Уравнение регрессии показывает ожидаемое значение зависимой
переменной Упри определенных значениях независимых перемен-
ных X.
По количеству включенных в модель факторов Xмодели делят-
ся на однофакторные (парная модель регрессии) и многофакторные
(модель множественной регрессии), а по виду функции /(%,,
Х2,..., Л).) — нелинейные и нелинейные.
Модель множественной линейной регрессии имеет вид
у,-= а0+ «!%,! + а2х/2 + ... + akxjk + Ej, i = \,n, (2.1)
где п — количество наблюдений.
Коэффициент регрессии показывает, на какую величину в
среднем изменится результативный признак у,-, если переменную
Xj увеличить на одну единицу измерения при фиксированных зна-
чениях остальных переменных, входящих в модель, т.е. ау. является
нормативным коэффициентом. Коэффициент а0 может быть как
положительным, так и отрицательным.
Анализ уравнения (2.1) и методика определения параметров
становятся более наглядными, а расчетные процедуры существенно
упрощаются, если воспользоваться матричной формой записи:
У=Ха + Е, (2.2)
’ Термин «регрессия» (лат. regression — отступление, возврат к чему-либо)
ввел английский статистик Ф. Гальтон. Он исследовал влияние роста
родителей и более отдаленных предков на рост детей. По его модели
рост ребенка определяется наполовину родителями, на четверть — де-
дом с бабкой, на одну восьмую — прадедом и прабабкой и т.д. Другими
словами, такая модель характеризует движение назад по генеалогичес-
кому древу. Ф. Гальтон назвал это явление регрессией как противопо-
ложное движению вперед — прогрессу. В настоящее время термин
«регрессия» применяется в более широком плане — для описания
статистической связи между случайными величинами.
2-1591
17
где У— вектор зависимой переменной размерности п х 1, пред-
ставляющий собой п наблюдений значений у-,
X— матрица п наблюдений независимых переменных Х\,
г Х2,Хк, размерность матрицы ЛГравна п х (к + 1) (& — ко-
личество факторов, включенных в модель). Дополнитель-
ный фактор XQ, состоящий из единиц, вводится для вычис-
ления свободного члена. В качестве исходных данных
могут быть использованы временные ряды или простран-
ственная выборка;
а — подлежащий оцениванию вектор неизвестных параметров
г размерности {к + 1) х 1;
л; е — вектор случайных отклонений (возмущений) размерности
1 п х 1; е отражает тот факт, что изменение у, будет неточно
описываться изменением объясняющих переменных X,
так как существуют и другие факторы, не учтенные в дан-
ной модели.
Таким образом,
хи
*21
*„1
Уравнение (2.2) содержит значения неизвестных параметров oCq,
ОС], а2, ..., ак. Эти величины оцениваются на основе выборочных
наблюдений, поэтому полученные расчетные показатели не явля-
ются истинными, а представляют собой лишь их статистические
оценки. Модель линейной регрессии, в которой вместо истинных
значений параметров подставлены их оценки (а именно такие ре-
грессии и применяются на практике), имеет вид
y = = f+ е,
(2.3)
где А — вектор оценок параметров;
е = Y - ХА — вектор «оцененных» отклонений регрессии, ос-
татки регрессии;
У — оценка значений Y, равная ХА.
Построение уравнения регрессии осуществляется, как правило,
методом наименьших квадратов (МНК), суть которого состоит в
минимизации суммы квадратов отклонений фактических значений
результативного признака от его расчетных значений, т.е.
18
Xu-Л) -»min- r,
/=i
Формулу для вычисления параметров регрессионного уравне-
ния по методу наименьших квадратов приведем без вывода:
А = (УХ)-итГ (2.4)
Для того чтобы регрессионный анализ, основанный на обычном
методе наименьших квадратов, давал наилучшие из всех возмож-
ных результаты, должны выполняться следующие условия, извест-
ные как условия Гаусса — Маркова.
Первое условие — математическое ожидание случайной состав-
ляющей в любом наблюдении должно быть равно нулю'.
= 0 для всех i = 1, п.
Иногда случайная составляющая будет положительной, ино-
гда — отрицательной, но она не должна иметь систематического
смещения ни в одном из двух возможных направлений.
Фактически если уравнение регрессии включает свободный
член, то обычно это условие выполняется автоматически, так как
роль константы состоит в определении любой систематической
составляющей Y, которую не учитывают объясняющие перемен-
ные, включенные в уравнение регрессии.
Второе условие состоит в том, что дисперсия случайной составля-
ющей должна быть постоянна для всех наблюдений. Иногда случай-
ная составляющая будет больше, иногда меньше, однако не долж-
но быть априорной причины для того, чтобы в одних наблюдениях
она порождала большую ошибку, чем в других.
Эта постоянная дисперсия обычно обозначается о2(е), или час-
то в более краткой форме с2, а условие записывается следующим
образом:
£>(е,) = £>(е,) = с2 для любых наблюдений i и J.
1 J ь
Выполнимость данного условия называется гомоскедастично-
стью (постоянством дисперсии отклонений). Невыполни-
мость данной предпосылки называется гетероскедастичностью
(непостоянством дисперсии отклонений).
Третье условие (условие независимости) предполагает отсут-
ствие систематической связи между значениями случайной состав-
ляющей в любых двух наблюдениях. Например, если случайная со-
ставляющая велика и положительна в одном наблюдении, это
2
19
не должно обусловливать систематическую тенденцию к тому, что
она будет большой и положительной в следующем наблюдении.
Случайные составляющие должны быть независимы друг от
друга. Это условие можно записать следующим образом:
M(ez, еу) = 0 (/ # J).
Данное условие означает, что отклонения регрессии (а значит,
и сама зависимая переменная) не коррелируют. Для временного
ряда yt это означает отсутствие автокорреляции ряда е;.
Четвертое условие состоит в том, что в модели (2.1) возмущение г,-
(или зависимая переменная yt) есть величина случайная, а объясня-
ющая переменная — неслучайная.
Если это условие выполнено, то теоретическая ковариация меж-
ду независимой переменной и случайным членом равна нулю.
Наряду с условиями Гаусса — Маркова обычно также предпола-
гается нормальность распределения случайного члена.
В тех случаях, когда выполняются предпосылки, оценки, полу-
ченные по МН К, будут обладать свойствами несмещенности, со-
стоятельности и эффективности.
Качество модели регрессии связывают с адекватностью модели
наблюдаемым (эмпирическим) данным. Проверка адекватности
(или соответствия) модели регрессии наблюдаемым данным прово-
дится на основе анализа остатков е,- = у, - yt.
Анализ остатков позволяет получить представление, насколько
хорошо подобрана сама модель и насколько правильно выбран
метод оценки коэффициентов. Согласно общим предположениям
регрессионного анализа остатки должны вести себя как независи-
мые (в действительности — почти независимые) одинаково рас-
пределенные случайные величины.
При анализе качества модели регрессии в первую очередь ис-
пользуется коэффициент детерминации, который определяется сле-
дующим образом:
п п
Ж-я2 Z*2
А2 = 11-------= 1 _ -Л------, (Ц
/=1 /=1
где у,- — предсказанное (рассчитанное по уравнению регрессии^
значение зависимой переменной;
у — среднее значение зависимой переменной.
20
Коэффициент детерминации показывает долю вариации резуль-
тативного признака, находящегося под воздействием изучаемых
факторов, т.е. определяет, какая доля вариации признака Кучтена
в модели и обусловлена влиянием на него факторов, включенных
в модель.
Чем ближе R2 к единице, тем выше качество модели.
Для оценки качества регрессионных моделей целесообразно
также использовать коэффициент множественной корреляции (ин-
декс корреляции)
R =
Шу-у)2
/=1
£(У,-У)2
/=|
(2.6)
Данный коэффициент универсален, так как отражает тесноту свя-
зи и точность модели, а также может использоваться при любой
форме связи переменных.
Важным моментом является проверка значимости построенного
уравнения в целом и отдельных параметров. Оценить значимость
уравнения регрессии — значит установить, соответствует ли мате-
матическая модель, выражающая зависимость между Yи X, факти-
ческим данным и достаточно ли включенных в уравнение объяс-
няющих переменных Хдля описания зависимой переменной Y.
Оценка значимости уравнения регрессии проводится для того,
чтобы узнать, пригодно уравнение регрессии для практического
использования (например, для прогноза) или нет.
• Для проверки значимости модели регрессии используется
/-критерий Фишера:
F__ R2/k
(y-Rhfa-k-Y)
(2.7)
Если расчетное значение cV|=&hv2 = «- A: - 1 степенями сво-
боды, где к — количество факторов, включенных в модель, больше
табличного при заданном уровне значимости, то модель считается
значимой.
В качестве меры точности применяют несмещенную оценку
дисперсии остаточной компоненты, которая представляет собой
21
отношение суммы квадратов уровней остаточной компоненты к
величине п- к - 1. Квадратный корень из этой величины (ое) на*
зывается стандартной ошибкой:
---------— w
«Л
• Значимость отдельных коэффициентов регрессии проверяется
по /-статистике путем проверки гипотезы о равенстве нулю у-го
параметра уравнения (кроме свободного члена):
<2-9)
гдеоа — стандартное (среднеквадратическое) отклонение коэф-
фициента уравнения регрессии Oj.
Величина о., представляет собой квадратный корень из произ-
> >
ведения несмещенной оценки дисперсии иу-го диагонального
элемента матрицы, обратной матрице Xх X.
Caj=Ge\[bjj’ ф
где bjj — диагональный элемент матрицы (XLY)-1.
Если расчетное значение /-критерия с п - к - 1 степенями сво-
боды превосходит его табличное значение при заданном уровне
значимости, коэффициент регрессии считается значимым.
В противном случае фактор, соответствующий этому коэффици-
енту, исключают из модели (при этом ее качество не ухудшится).
Уравнение регрессии применяют для расчета значений показа-
теля в заданном диапазоне изменения параметров. Оно ограни-
ченно пригодно для расчета вне этого диапазона, т.е. его можно
применять для решения задач интерполяции и в ограниченной
степени для экстраполяции.
Прогноз, полученный подстановкой в уравнение регрессии
ожидаемого значения параметра, является точечным. Вероятность
реализации такого прогноза ничтожна мала. Целесообразно опре-
делить доверительный интервал прогноза.
Для того чтобы определить область возможных значений ре-
зультативного показателя при рассчитанных значениях факторов,
следует учитывать два возможных источника ошибок:
• рассеивание наблюдений относительно линии регрессии;
♦ ошибки, обусловленные математическим аппаратом построения
самой линии регрессии.
22
Ошибки первого типа измеряются с помощью характеристик
точности, в частности величиной ое. Ошибки второго типа обу-
словлены фиксацией численного значения коэффициентов регрес-
сии, вто время как они в действительности являются случайными,
нормально распределенными.
Для линейной модели регрессии при прогнозировании инди-
видуальных значений границы доверительного интервала рассчиты-
ваются по формуле Y iU(X ). Величина отклонения от линии
регрессии U(X вычисляется по формуле
Опроси) = ОЛ71 + ^пТрогн(^Т^Г'^прогн, (2. 10)
Где ^прогн — (1, Лчпрогн, ^2прогн> Лшрогн)’
ta — табличное значение /"-статистики Стьюдента при заданном
уровне значимости а.
2.1.2. Особенности практического применения
регрессионных моделей
Одним из условий регрессионной модели является предполо-
жение о линейной независимости объясняющих переменных, т.е. ре-
шение задачи возможно лишь тогда, когда столбцы и строки мат-
рицы исходных данных линейно независимы. Для экономических
показателей это условие выполняется не всегда.
Под мультиколлинеарностью понимается высокая взаимная кор-
релированность объясняющих переменных, которая приводит к ли-
нейной зависимости нормальных уравнений. Мультиколлинеар-
ность может возникать в силу разных причин, например: не-
сколько независимых переменных могут иметь одинаковый
временной тренд, относительно которого они совершают малые
колебания.
Существуют различные способы для определения наличия или
отсутствия мультиколлинеарности:
• анализ матрицы коэффициентов парной корреляции. Явление
мультиколлинеарности в исходных данных считают установлен-
ным, если коэффициент парной корреляции между двумя пе-
ременными больше 0,8;
• исследование матрицы ХУХ. Если определитель матрицы Х^Х
близок к нулю, это свидетельствует о наличии мультиколлине-
арности.
23
Для устранения или уменьшения мультиколлинеарности исполь-
зуется ряд методов:
• исключение одного из двух сильно связанных факторов. Это самый
простой, но не всегда самый эффективный метод. Он состоит в
том, что из двух объясняющих переменных, имеющих высокий
-и коэффициент корреляции (больше 0,8), одну переменную ис-
ключают из рассмотрения. При этом какую переменную оста-
t вить, а какую удалить из анализа, решают в первую очередь на
основании экономических соображений. Если с экономической
точки зрения ни одной из переменных нельзя отдать предпоч-
,г тение, то оставляют ту, которая имеет больший коэффициент
корреляции с зависимой переменной;
S: переход от первоначальных факторов к их главным компонентам,
ш число которых может быть меньше, затем возвращение к перво-
начальным факторам',
; использование стратегии шагового отбора, реализованной в ряде
алгоритмов пошаговой регрессии.
Наиболее широкое применение получили следующие схемы
построения уравнения множественной регрессии:
• метод включения факторов;
• метод исключения — отсев факторов из полного его набора.
В соответствии с первой схемой признак включается в
уравнение в том случае, если его включение существенно увеличи-
вает значение коэффициента множественной корреляции, что по-
зволяет последовательно отбирать факторы, оказывающие суще-
ственное влияние на результирующий признак даже в условиях
мультиколлинеарности системы признаков, отобранных в качестве
аргументов из содержательных соображений. При этом первым в
уравнение включается фактор, наиболее тесно коррелирующий с Y,
вторым — тот фактор, который в паре с первым из отобранных дает
максимальное значение коэффициента множественной корреля-
ции, и т.д. Существенно, что на каждом шаге получают новое зна-
чение коэффициента множественной корреляции (большее, чем
на предыдущем шаге); тем самым определяется вклад каждого
отобранного фактора в объясненную дисперсию Y.
Вторая схема пошаговой регрессии основана на последователь-
ном исключении факторов с помощью /-критерия. Она заклю-
чается в том, что после построения уравнения регрессии и оценки
значимости всех коэффициентов регрессии из модели исключают
тот фактор, коэффициент при котором незначим и имеет наимень-
24
шее значение /-статистики по абсолютной величине. После этого
получают новое уравнение множественной регрессии и снова про-
водят оценку значимости всех оставшихся коэффициентов регрес-
сии. Если и среди них окажутся незначимые, то опять исключают
фактор с наименьшим значением /-критерия. Процесс исключения
факторов останавливается на том шаге, при котором все регресси-
онные коэффициенты значимы.
Ни одна из этих процедур не гарантирует получения оптималь-
ного набора переменных. Однако при практическом применении
они позволяют получить достаточно хорошие наборы существенно
влияющих факторов.
При отборе факторов также рекомендуется пользоваться сле-
дующим правилом: число включаемых факторов обычно в 6—7раз
меньше объема совокупности, по которой строится регрессия. Если
это соотношение нарушено, то число степеней свободы остаточ-
ной дисперсии очень мало. Это приводит к тому, что параметры
уравнения регрессии оказываются статистически незначимыми,
а F-критерий меньше табличного значения.
Особым случаем мультиколлинеарности при использовании
временных выборок является наличие в составе переменных ли-
нейных или нелинейных трендов. В этом случае рекомендуется сна-
чала выделить и исключить тренды, а затем определить параметры
регрессии по остаткам. Игнорирование наличия трендов в зависи-
мой и независимой переменных ведет к завышению степени вли-
яния независимых переменных на результирующий признак, что
получило название ложной корреляции.
Наиболее часто в практических исследованиях возникает вопрос:
сколько надо наблюдений для надежного определения параметров
регрессии? Выбор числа наблюдений определяется требованиями к
точности и надежности оценок параметров. Достижение желаемой
точности определяется как объемом выборки, так и расположением
прогностических значений факторов. Чем более разнесены послед-
ние от средних выборочных значений, тем меньше точность прогно-
за. Минимальный необходимый объем выборки обычно считают
равным 6—8 наблюдениям на каждую переменную при прогнозиро-
вании около средних значений факторов. При удалении прогнозных
значений факторов от средних минимальный объем выборки растет
пропорционально квадрату отклонения от них [20].
Большим препятствием к применению регрессии является
ограниченность исходной информации, при этом ценность ин-
25
формации может снижаться не только вследствие указанных за-
трудняющих обстоятельств (мультиколлинеарности, зависимости
остатков, небольшого объема выборки и т.п.), но и за счет ее «за-
соренности», т.е. проявления новых обстоятельств, которые ранее
не были учтены.
Резко отклоняющиеся наблюдения могут быть результатом либо
действия большого числа сравнительно малых случайных факто-
ров, которые в редких случаях приводят к большим отклонениям,
либо это действительно случайные один или несколько выбросов,
которые можно исключить как аномальные. Однако если на не-
сколько десятков наблюдений приходится не менее трех аномаль-
ных отклонений, их приписывают наличию одного или нескольких
неучтенных факторов, которые проявляются только в виде ано-
мальных наблюдений.
*i! 2.1.3. Использование SPSS для построения
модели множественной линейной регрессии
Рассмотрим применение программы SPSS на примере задачи,
приведенной в [30] и решенной в Excel.
Пример 2.1. Построить модель для предсказания объема реали-
зации одного из продуктов кондитерской фабрики по данным,
приведенным в табл. 2.1.
Принятые в таблице обозначения:
• зависимая переменная
У— объем реализации, млн руб.;
• независимые, объясняющие переменные:
Х} — время, мес.;
Х2 — расходы на рекламу, тыс. руб.;
Х3 — цена товара, руб.;
Х4 — средняя цена товара у конкурентов, руб.;
Х5 — индекс потребительских расходов, %.
Требуется:
1) обосновать выбор факторных признаков для построения
регрессионной модели на основе анализа матрицы коэффициентов
корреляции;
2) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить линейную регресси-
онную модель, включающую значимые факторы. Дать экономиче-
скую интерпретацию коэффициентов модели регрессии;
26
Таблица 2.1
Исходные данные
У А. %2 Аз а4 а5
126 . 1 4 15 17 100
137 2 4,8 14,8 17,3 98,4
148 4 3 3,8 15,2 16,8 101,2
364 15 5,8 16 17,7 112,3
384 16 5,7 15,1 16,2 112,9
3) для оценки качества всего уравнения регрессии определить
линейный коэффициент множественной корреляции и коэффи-
циент детерминации. Оценить значимость уравнения регрессии;
4) построить точечный и интервальный прогноз результиру-
ющего показателя на один месяц вперед (а = 0,1), если известны
следующие прогнозные значения объясняющих переменных:
Х2 = 5,75; Х3 = 17,24; = 15,32; Х5 = 112,468.
Решение.
Подготовка данных для использования пакета SPSS
Данные могут быть введены непосредственно в SPSS или им-
портированы из текстовых файлов, файлов формата Excel, ACCESS
и т.п. В нашем случае имеется файл данных в формате Excel
(рис. 2.1). Приступим к импорту данных в файл SPSS.
Для импорта данных из файла формата Excel в SPSS выполним
следующие действия:
1. После запуска программы SPSS и появления на экране пус-
того файла SPSS, подобного изображенному на рис. 2.2, выберем
в строке меню Файл -» Открыть -» Данные и зададим имя Excel-
файла с нашими данными, его тип, после чего нажмем кнопку
Открыть (Open) (рис. 2.3).
2. В новом диалоговом окне (рис. 2.4) зададим диапазон ячеек
(например, A1:F17). Если в первой строке Excel-файла находятся
имена переменных, следует установить флажок Читать имена пере-
менных из первой строки данных. Щелкнем на кнопке ОК.
3. На экране появятся импортированные данные в формате
SPSS (рис. 2.5).
4. Для редактирования данных с использованием пакета SPSS
нажмем в нижней строке меню кнопку Переменные. Это позволит
27
j А ”1Т у"' __J3 Х1 _ с Х2 D ____ хз ___ Е Х4 __ F Х5 _,_G
2 1 126 1 4 15 17 100
3 ! 137 2 4.8 14.8 17.3 98.4
148 3 3.8 15.2 16.8 101.2
191 4 8.7 15.5 16.2 103.5
6 274 5 8.2 15.5 16 104.1
7 ‘ 370 6 9.7 16 18 107
з: 432 7 14.7 18.1 20.2 107.4
'Pt! 445 8 18.7 13 15.8 108.5
10 367 9 19.8 15.8 18.2 108.3
11 i 367 10 10.6 16.9 16.8 109.2
12 | 321 11 8.6 16.3 17 110.1
13 307 12 6.5 16.1 18.3 110.7 ,,.v.
14 i 331 13 12.6 15.4 16.4 110.3 ‘ .1 . V.
1 15 i 345 14 6.5 15.7 16.2 111.8 \ ; ЛТ
16 ! 364 15 5.8 16 17.7 112.3 . ХИ; -
17 384 16 5,7 15.1 16.2 112.9 ХП . ..ПО;
18 J..„, , „ 11,Ш И . 'UU
V
Рис. 2.1. Файл исходных данных в формате Excel
28
1 Рис. 2.3. Импорт данных в SPSS
Опсрыгие <|ыи.юв Ixcel
D:\n римеры\лин_регр.х!$.
р Читать именапеременных из первой строки данных.
Лист: р1ист1 [А1 F17]
Диапазон gjAlJFI 7
Отмена. Справка
Рис. 2.4. Диалоговое окно Открытие файлов Excel
просмотреть всю информацию о переменных, импортированных в
SPSS-файл, и внести нужные изменения и дополнения. В столбце
«Метка» (рис. 2.6) введем расширенное имя переменной (до 256 сим-
волов). Эта информация будет использована при создании отчетов.
5. Каждой переменной в файле данных SPSS будет соответство-
вать отдельная колонка. Используя меню Файл —> Сохранить как,
сохраним данный файл с расширением <name>.sav (рис. 2.7).
Решение задачи в SPSS
1. Выбор факторных признаков для построения регрессионной
модели на основе анализа матрицы коэффициентов корреляции. Для
построения матрицы парной корреляции всех переменных с по-
мощью пакета SPSS выполним следующие действия:
29
1 t Без имени - SPSS Редактор Данных s®®1
Файл Дзавка Вид Данные Преобразовать Анализ ^Графика Сервис Окно Справка
к~>| 1 Y ' d fc| C? | M| ~ 126 •Fid
xi I X2 ;«X3IS1: X4 X5
126 1 4.0 15.0 17.0 100.0
2 137 2i 4.8 14.8 17.3 98.4
3 148 31 3.8 15.2 16.8 101.2
4 191 4 8.7 15.5 16.2 103,5
5 274 5 8.2 155 16.0 104.1
6 370 6 9.7 16.0 18.0 107.0
1 432 7| 14.7 18.1 20.2 107.4
8 445 8 18.7 13.0 15.8 108.5
9 367 9 19.8 15.8 18.2 108.3
10 367 101 10.6 16.9 16.8 109.2
11 321 11] 8.6 163 17.0 110.1
12 307 12 6.5 16.1 18.3 110.7
13 331 13 12.6 15.4 16.4 110.3
W 14 345 141 6.5 15.7 16.2 111.8
15 364 151 5.8 16.0 17.7 112.3
; 1 6 384 16 5.7 15.1 16.2 112.9
з | > j\ Данные ЛПеременны- / < j .. J
;SPSS Процесс op готов
Рис. 2.5. Данные задачи представлены в формате SPSS
“ Гм.н имени SPSS Релли тор hinitiix
Файл Правка|:: Вид Данные Преобразовать Анализ ГрафикаСерв>«Окно<Справка
»| -;.|rd П1Ж1 Ш
Имя ||:!!ЬТИП Ширина Десятин Метка
'*1 Y Числовая 11 0 Объём реализации (млн. руб.)
2 XI Числовая 11 0 Время (мес.)
3 X2 Числовая 11 1 Расходы на рекламу (тыс. руб.)
4 X3 Числовая 11 1 Цена товара (руб.)
5 X4 Числовая 111 1 Средняя цена товара у конкурентов (руб.)
6 X5 Числовая 11 1 Индекс потребительских расходов (%)
Рис. 2.6. Редактирование данных SPSS
• Выберем в верхней строке меню Анализ —> Корреляция —> Пар-
ные.
• Переменные, относительно которых проверяется степень кор-
реляционной связи, поочередно переместим в поле тестируемых
переменных справа (рис. 2.8).
• Для начала расчета нажмем кнопку ОК.
30
Рис. 2.7. Сохранение данных
В результате в выходной области появится матрица парной кор-
реляции всех переменных (табл. 2.2). Полученные результаты со-
держат коэффициент корреляции Пирсона, вероятность ошибки,
соответствующую предположению о ненулевой корреляции, и ко-
личество использованных пар значений (в нашем случае оно рав-
но 16).
Коэффициент корреляции R между двумя переменными ука-
зывает силу связи между ними и принимает значения от -1 до +1:
если значение находится ближе к единице, это означает наличие
сильной связи, а если ближе к нулю, то слабой.
Анализ матрицы коэффициентов парной корреляции показы-
вает, что зависимая переменная, т.е. объем реализации имеет тес-
ную связь с индексом потребительских расходов (г = 0,816),
с расходами на рекламу (гу = 0,646) и со временем (гуХ} = 0,678).
Однако факторы Х{ и Х5 тесно связаны между собой (гХ| = 0,96),
что свидетельствует о наличии мультиколлинеарности. Из этих
двух переменных оставим в модели Х5 — индекс потребительских
расходов.
На основе анализа матрицы коэффициентов парной корреля-
ции делаем вывод о целесообразности построения двухфакторно-
го регрессионного уравнения Y - f(X2, Х5).
31
a)
М Парные корреляции
|£м^&мреалгм.ацииУ
Переменные:
$ Время (мес.)[Х1]
$ Расходы на рекламу
: & средняя цена товара,
$ Индекс потребитель!.
Односторонний
0 Метить значимые корреляции
Коэффициенты корреляции
И Пирсона О Тау-b Кендалла Г"! Спирмена
Крит ерий значимости;
<*,’ Двухсторонний
Рис. 2.8. Построение матрицы парной корреляции в SPSS
2. Построение линейного уравнения регрессии. По заданию необ-
ходимо построить регрессионную модель со значимыми фактора-
ми в линейной форме.
Оценка параметров регрессии осуществляется методом наи-
меньших квадратов. Для проведения регрессионного анализа с по-
мощью пакета SPSS выполним следующие действия:
• Выберем в верхней строке меню Анализ -> Регрессия Линей-
ная.
32
Таблица 2.2
Корреляции
Объем реализа- Время Расходы на Цена Средняя цена товара Индекс потреби-
ЦП и (млн руб.) (мес.) рекламу (тыс. руб.) 1Ubdpd (руб.) у конкурен- тов (руб.) тельских расходов (%)
Объем реализации (млн руб.) Корреляция Пирсона Знч. (2-сторон) 1 ,678(**) ,646(**) .233 .385 .226 .399 ,816(“)
.004
.007 .000
N 16 16 16 16 16 16
Время (мес.) Корреляция Пирсона ,678(“) 1 .106 .174 -.051 ,960(“)
Знч. (2-сторон) .004 .695 .520 .851 .000
N 16 16 16 16 16 16
Расходы на рекламу (тыс. руб.) Корреляция Пирсона Знч. ,64б(**) .106 1 -.003 .204 .273
.007 .695 .990 .448 .306
(2-сторон)
N 16 16 16 16 16 16
Цена товара Корреляция .233 .174 -.003 1 .698(**) .235
(руб.) Пирсона
Знч. (2-сторон) .385 .520 1990 .003 .380
N 16 16 16 16 16 16
Средняя цена Корреляция .226 -.051 .204 ,698(**) 1 .031
товара Пирсона
у конкурентов Знч. .399 .851 .448 .003 .910
(руб.) (2-сторон)
N 16 16 16 16 16 16
Индекс потребитель- Корреляция Пирсона .816(**) ,960(**) .273 .235 .031 1
ских расходов .306
(%)' (2-сторон) .000 .000 .380 .910
N 16 16 16 16 16 16
** Корреляция значима на уровне 0.01 (2-сторон.).
• Поместим переменную У в поле для зависимых переменных,
объявив переменные Xt, Х2, Х3, Х4, Х5 независимыми (рис. 2.9).
Линейная регрессия
[ $ Время (мес.) [Х1] I
j Расходы на рекламу^
j Цена товара (руб.) р
I $ Средняя цена товару
$ Индекс потребитель
.; у переменная:
j ‘ | $ Объем реализации
Блок!
Метон:
: Независимые переменные:
$ Время (мес.) (XI)
j $ Расходы на ^ла^(тьО;',;':;’|
' ^Цена jroB^pa(py6.)P<31 v'
1 Принудительное включение v >
(Вставка ]
| Сброс ]
[Отмена ]
| Справка |
Переменная отбора наблюдений
Метки наблюдении
Веса
[Статистики—| Графики. ["Сохраниты,. 1 (Параметры... |
Рис. 2.9. Диалоговое окно Линейная регрессия
М-
Ц1’!
Используем метод исключения, установленный по умолчанию
в поле Метод.
• В полях панели Статистики отметим флажками Оценки, Согласие
модели и Дурбин — Уотсон (в нашей литературе это критерий Дар-
бина — Уотсона) (рис. 2.10), затем нажмем Продолжить.
}• В полях панели Сохранить отметим флажками необходимые поля
! (рис. 2.11) и нажмем Продолжить.
I» Значения, установленные по умолчанию в полях панели Пара-
метры, не меняем; они будут использованы для определения
критерия Фишера с доверительной вероятностью 0,95.
• Начнем вычисления нажатием ОК.
Результаты регрессионного анализа выводятся в табличном
виде.
При последовательном подборе переменных в SPSS предусмот-
рена автоматизация, основанная на значимости включения и ис-
ключения переменных.
34
t.l 'ЛЦ
Линейная регрессия; Статистики
г Коэффициенты регрессии
j Р Оценки
• Г” Доверительные интервалы
|.Г”-Матрица ковариаций
7 Согласие модели
Изменение R-квадрат
Описательные статистики
Частичные и частные корреляции
П Диагностики коллинеарности
[Продолжить |
<Отмена J
Справка j
Остатки
%? Дурбин-Уотсон
Г” Диагностика по наблюдениям
Рис. 2.10. Диалоговое окно Линейная регрессия: Статистики
1ин(‘ин.11| ]>р г pet 4 ин- ( охрп
Предсказанные значения
!** Нестандартизованные
Г* Стандартизованные
Г Скорректированные
I Стандартные ошибки для средних
?- Остатки
17
.Г
ф-Расстояния
........
Нестандартизованные
Стандартизованные
Стьюдентизированные
Удаленные
Стьюдентизированные удаленные
| Продолжить |
Отмена |
Справка|
Махаланобис
Кук
Разбалансировка
Статистики влияния
г Интервалы предсказания......
Н.П Среднее П Отдельное значение
1 Доверительный интервал: f* :
DfBeta
Стандартизованные ОШ eta
DfFit
Стандартизованные DtFit
Ковариацонное отношение
р Сохранить в новом файле • •• ••
i Г~ Статистические коэффициенты
Экспортировать модель в Формате XML
Обзор [
С*
п
5й!
Рис. 2.11. Диалоговое окно Линейная регрессия: Сохранить
'Ж
В таблице «Включенные/исключенные переменные» (табл. 2.3)
перечислены переменные, которые были последовательно исклю-
чены на каждом шаге.
Таблица 2.3
Включенные/исключенные переменные
Модель Включенные переменные Исключенные переменные Метод
1 Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время(а) Принудительное включение
2 Цена товара (руб.) Исключение (критерий: вероят- ность F-исключения > = .100)
3 Средняя цена товара у конкурен- тов (руб.) Исключение (критерий: вероят- ность F-исключения > = .100)
4 Время Исключение (критерий: вероят- ность F-исключения > = .100)
а Включены все запрошенные переменные Ь Зависимая переменная: Объем реализации (млн руб.) и
В таблице «Сводка для модели» (табл. 2.4) приведены значения
коэффициента детерминации, коэффициента множественной кор-
реляции, стандартной ошибки, коэффициента Дарбина — Уотсона
последовательно для всех моделей. В последней строке приводят-
ся данные для окончательной модели.
Таблица 2.4
Сводка для модели
Модель R R квадрат Скорректированный R квадрат Стд. ошибка оценки Дурбин - Уотсон
1 .944(a) .891 .836 41.649
2 .943(b) .889 .848 40.044
3 .939(c) .882 .852 39.537
4 .927(d) .859 .837 41.473 1.357
а Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время Ь Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Время с Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.), Время d Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.) е Зависимая переменная: Объем реализации (млн руб.)
36
В табл. 2.5 приведены результаты дисперсионного анализа и
значения /•’-критерия, полученные на каждом шаге (здесь СТ.СВ. —
число степеней свободы, Знч. — значимость).
Дисперсионный анализ
Таблица 2.5
Модель Сумма квадратов СТ.СВ. Средний квадрат F Знч.
1 Регрессия Остаток Итого 141371.778 17346.660 158718.437 5 10 15 28274.356 1734.666 16.300 .000(a)
2 Регрессия Остаток Итого 141079.525 17638.912 158718.437 4 11 15 35269.881 1603.537 21.995 .000(b)
3 Регрессия Остаток Итого 139960.250 18758.188 158718.437 3 12 15 46653.417 1563.182 29.845 .000(c)
4 Регрессия Остаток Итого 136358.334 22360.104 158718.437 2 13 15 68179.167 1720.008 39.639 .000(d)
а Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время b Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Время с Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.), Время d Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.) е Зависимая переменная: Объем реализации (млн руб.)
Таблица 2.6 содержит следующие данные:
• первый столбец — номер модели;
• второй — используемые в модели независимые переменные;
• третий — коэффициенты уравнения регрессии;
• четвертый — стандартные ошибки коэффициентов уравнения
регрессии;
• пятый — стандартизованные коэффициенты;
• шестой — /-статистика, используемая для проверки значимости
коэффициентов уравнения регрессии.
Уравнение регрессии зависимости объема реализации от затрат
на рекламу и индекса потребительских расходов, полученное на
последнем шаге, можно записать в следующем виде:
... Y= -1471,314 + 9,568Х,+ 15,754^.
Таблица 2.6
Коэффициенты (а)
Модель Нестандартизованные коэффициенты Стандартизо- ванные коэффициенты t Знч.
В Стд. ошибка Бета
1 (Константа) -3017.396 1094.485 •2.757 .020
Время -13.419 10.378 -.621 -1.293 .225
Расходы на рекламу (тыс. руб.) 6.672 3.009 .319 2.218 .051
Цена товара (руб.) -6.477 15.779 -.067 -.410 .690
Средняя цена товара у конкурентов (руб.) 12.238 14.410 .136 .849 .416
Индекс потреби- тельских расходов (%) 30.476 11.525 1.337 2.644 .025
2 (Константа) -2914.326 1024.234 -2.845 .016
Время -12.569 9.778 -.582 •1.285 .225
Расходы на рекламу (тыс. руб.) 7.125 2.691 .340 2.648 .023
Средняя цена товара у конкурентов (руб.) 7.930 9.492 .088 .835 .421
Индекс потреби- тельских расходов (%) 29.151 10.637 1.279 2.740 .019
3 (Константа) -2957.613 1009.969 -2.928 .013
Время -14.316 9.431 -.663 -1.518 .155
Расходы на рекламу (тыс. руб.) 7.229 2.654 .345 2.724 .018
Индекс потреби- тельских расходов (%) 30.951 10.285 1.358 3.009 .011
4 (Константа) -1471.314 259.766 -5.664 .000
Расходы на рекламу (тыс. руб.) 9.568 2.266 .457 4.223 .001
Индекс потреби- тельских расходов (%) 15.754 2.467 .691 6.386 .000
а Зависимая переменная: Объем реализации (млн руб.)
38
Коэффициенты уравнения регрессии показывают, что при уве-
личении затрат на рекламу на 1 тыс. руб. объем реализации увели-
чится на 9,568 млн руб., а при увеличении индекса потребительских
расходов на 1% — на 15,754 млн руб.
3. Оценка качества модели. Оценка качества всего уравнения
регрессии производится с помощью коэффициентов детерминации
R2 и множественной корреляции R. Их значения можно найти в
табл. 2.4 «Сводка для модели».
Коэффициент детерминации R2 = 0,859 показывает долю ва-
риации результативного признака под воздействием изучаемых
факторов. Следовательно, около 86% вариации зависимой пере-
менной учтено в модели и обусловлено влиянием включенных
факторов.
Коэффициент множественной корреляции R - 0,927 показы-
вает тесноту связи зависимой переменной У со всеми включенны-
ми в модель объясняющими факторами.
Проверку значимости уравнения регрессии проведем на основе
/’-критерия Фишера. Значение критерия Фишера F = 39,639 мож-
но найти в табл. 2.5 «Дисперсионный анализ».
Вероятность, соответствующая расчетному значению F-крите-
рия, выводится в правой колонке табл. 2.5 под заголовком «Знч.» —
значимость. Ее величина свидетельствует о значимости уравнения
регрессии (Знч. < 0,001).
Уравнение регрессии следует признать адекватным, модель
считается значимой.
4. Построение прогноза по модели регрессии. Для построения
прогноза вначале введем прогнозные значения выбранных факто-
ров Х2 = 5,75 и = 112,468 (рис. 2.12).
Затем запускаем процедуру Анализ —> Регрессия —> Линейная, в ка-
честве независимых переменных указываем «Расходы на рекламу»
и «Индекс потребительских расходов» (рис. 2.13).
В полях панели Сохранить следует обязательно отметить необхо-
димость сохранения интервалов предсказания для отдельных зна-
чений с вероятностью 90% (рис. 2.14) и нажать Продолжить.
На рис. 2.15 приведены результаты прогнозирования по модели
регрессии: точечный прогноз, верхняя и нижняя границы.
С вероятностью 90% объем реализации в прогнозируемом ме-
сяце составит от 273,94 до 436,85 млн руб.
39
XI Х2 ХЗ „„........
1 126 1 4.00 15.0 17.0 100.000
2 137 2 4.80 14.8 17.3 98.400
3 148 3 3.80 15.2 16.8 101.200
4 191 4 8.70 15.5 16.2 103.500
5 274 5 8.20 15.5 16.0 104.100
6 370 6 9.70 16.0 18.0 107.000
7 432 7 14.70 18.1 20.2 107.400
8 445 8 18.70 13.0 15.8 108.500
9 367 9 19.80 15.8 18.2 108.300
10 367 10 10.60 16.9 16.8 109.200
И 321 11 8.60 16.3 17.0 110.100
12 307 12 6.50 16.1 18.3 110.700
13 331 13 12.60 15.4 16.4 110.300
14 345 14 6.50 15.7 16.2 111.800
15 364 15 5.80 16.0 17.7 112.300
16 384 16 5.70 15.1 16.2 112.900
17 5.75 112.468
Рис. 2.12. Введены прогнозные значения объясняющих факторов
В 1ИН0И1МЯ ня
: 4^ Время (мес.) [XI ]
: 4^ Расходы на рекламу
: 4^ Цена товара (руб.) [>
4^ Средняя цена товаре]
; 4^ Индекс потребитель:
Зависимая переменная:
Блок1 из!
Независимые переменные:
: Расходы на рекламу (тыс. на
[ Вставка"]
[Сброс [
[ Отмена ]
[ Справка ]
Метод: ! Принуд i-гтельное включение
Переменная отбора наблюдения
Метки наблюдении
Веса:
[Статистики... ] [ Г рафики.. - ] | Сохранить... j [Параметры... |
Рис. 2.13. Заполнение диалогового окна Линейная регрессия
/1инейная регрессия: Сохранить
1
Предсказанные значения ........
жр Нестандартизованные
||П Ст&шартизованные
|!П!Скбдоектированные ' '
f Г Стандартные ошибки для средних
Остатки 1
р"
Расстояния
i I™ Махаланобис
Г Кук
Г Разбалансировка
Н естандартизованьые
Стандартизованные ?
Стьюдентизированные
Удаленные
Стьюдентизированные удаленно
Статистики влияния •
| Продолжить |
Отмена j
Справка
• Интервалы предсказания.
Г Среднее Р Отдельное значение
Доверительный интервал: | 1 !
DfBeta
Стандартизованные DfBeia
DR
Стандартизованные 0 FFit
Ковариацонное отношение
Г
- Софанить в новом файле...
Г” Статистические коэффициен ы
г Экспортировать модель в ФорматеХМ1
Обзор;;-^
Рис. 2.14. Заполнение поля Линейная регрессия: Сохранить
PRE 1 •liiRESJ- - : IfEicr lillfc Mi UICFl *
1 142.24674 -16.246'4 59.70119 224.79229
2 124.69687 12.30313 40.05231 209.34143
3 159.23651 -11.23651 78.03246 240.44055
' 4 242.35334 -51.35334 165.01260 319.69408 J
Bills 247.02086 26.97914 170.17685 323.86487
6 307.05682 62.94318 231.32030 382.79333
7 361.20003 70.79997 282.49880 439.90127
8 416.80185 28.19815 332.70365 500.90006
9 424.17653 -57.17653 338.01935 510.33371
10 350.32471 16.67529 274.11289 426.53653
345.36547 -24.36547 268.45428 422.27666
12 334.72353 -27.72353 256.11282 413.33424 JG
13 386.78970 -55.78970 309.39496 464.18444 :r
14 352.05169 -7.05169 272.19034 431.91303
15 353.23023 10.76977 272.06331 434.39716
16 361.72512 22.27488 279.57913 443.87110 'lb
17 355.39830 273.94332 436.85327 i
Рис. 2.15. Результаты прогнозирования
2.2. НЕЛИНЕЙНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ В SPSS
Хотя во многих практических случаях моделирование экономи-
ческих зависимостей линейными уравнениями дает вполне удов-
летворительный результат, однако ограничиться рассмотрением
лишь линейных регрессионных моделей невозможно. Поэтому
рассмотрим построение и анализ нелинейных регрессий в SPSS.
Если между экономическими явлениями существуют нели-
нейные соотношения, то они выражаются с помощью соответ-
ствующих нелинейных функций.
Различают два класса нелинейных регрессий:
1. Нелинейные регрессии по включаемым в них объясняющим пере-
менным, но линейные по оцениваемым параметрам. Данный класс
нелинейных регрессий включает уравнения, в которых зависимая
переменная линейно связана с параметрами. Примеры:
• полиномы разных степеней (например, А-й степени)
У; = а0 + alxi + arf + а^ + ... + а^ + е/,
• равносторонняя гипербола (
b
y.=a + — + ei.
xi
2. Регрессии, нелинейные по оцениваемым параметрам. К данно-
му классу регрессий относятся уравнения, в которых зависимая
переменная нелинейно связана с параметрами. Примеры:
• степенная функция
* ь
• показательная (экспоненциальная) функция
yt=abx'.
Если нелинейная модель внутренне нелинейна, то она не может
быть сведена к линейной функции и для оценки ее параметров
используются итеративные процедуры, успешность которых зави-
сит от вида уравнений и особенностей применяемого итеративно-
го подхода (см. пример 2.4).
При оценке параметров регрессий, нелинейных по объясня-
ющим переменным, используется подход линеаризации (см. при-
мер 2.2), именуемый еще «замена переменных». Суть его состоит в
замене «нелинейных» объясняющих переменных новыми «линей-
ными» переменными и сведении нелинейной регрессии к линей-
42
ной. К новой, «преобразованной» регрессии может быть применен
обычный МНК [4,43]. Если необходимо применять прямой метод
вычисления параметров, т.е. находить минимум функции потерь
и
- у,)2 численным методом, то следует иметь в виду, что оцен-
/=|
ки, найденные по линеаризированному уравнению, могут заметно
отличаться от оценок, найденных первым способом (см. при-
мер 2.3).
Возможность перевода в линейную модель нужно использовать
всегда, так как в этом случае параметры регрессии вычисляются
непосредственно, а не определяются с помощью итераций.
Пример 2.2. Имеются данные об объеме выпускаемой продук-
ции и температуре (табл. 2.7). Требуется построить модель зави-
симости объема выпускаемой продукции от температуры при тех-
нологическом процессе с помощью полинома второй степени
у,- = ай + a]xi + а2х? + е? Исходные данные и результаты расчетов
отобразить на графике.
Таблица 2.7
Исходные данные
Объем выпуска продукции Y Температура^
127 600
139 625
147 650
147 675
155 700
154 725
153 750 ,
148 775
146 800
136 825
129 850
Решение. Пример может быть решен двумя способами.
Способ 1. Использование замены переменных. Приведенные в
таблице данные находятся в файле obprod. Если введем новую пе-
ременную Z(zt=х]), получим двухфакторное уравнение линейной
регрессии: у,- = а0 + + a2zt + £,, для оценки параметров которого
43
используется обычный МНК. В результате с помощью линейной,
регрессии получаем модель/ = -712,105 + 2,391^-0,002Х2.
Способ 2. Использование нелинейной регрессии. Последователь-
ность действий такова:
1. Введем исходные данные (рис. 2.16).
obprod SPSS Родах гор Данных
Фа^ 1^«вкаВиДлДаннь1еПреобра>овать Анализ Графика Сервис Окно Справка
sg|H|S| JSjj о | о? ’ll Л-Г | Li В|ф|Пь|1У<^1
Имя Тип Ширина ДесЯ Метка —|
1 Y Чпс левая 8 ij Объем выпуска продукции
2 X Чис левая 8 2 Температура
< 1 ► 1\ Данные ^Переменные / „r'SS Процессор готов
Рис. 2.16. Переменные в файле obprod
Г 2. Выберем в меню АнализРегрессияНелинейная.
Г 3. Поместим переменную «Объем выпуска продукции» в поле
для зависимых переменных (рис. 2.17).
Рис. 2.17. Диалоговое окно Нелинейная регрессия
44
4. Щелкнем по кнопке Параметры в левой части окна. Получим
диалоговое окно, в котором можно задавать начальные значения
параметров модели (рис. 2.18). ;
Рис. 2.18. Диалоговое окно Нелинейная регрессия: Параметры
В SPSS в русифицированном варианте кнопка Параметры встре-
чается дважды (см. рис. 2.17): кнопка слева отвечает за начальные
параметры модели, а кнопка справа — за параметры, связанные с
выбором метода.
Укажем в поле имен имя первого параметра, например а0, а за- '
тем щелкнем в поле Начальное значение, введем значение 0 и щелк-
нем на Добавить.
Общего универсального метода определения параметров нели-
нейной связи, к сожалению, не существует.
5. Щелкнем на поле Выражение, задающее модель и внесем в
него следующую формулу: аО+а1*Х+а2*Х**2. При вводе формулы
можно использовать клавиатуру, находящуюся в диалоговом окне.
Диалоговое окно будет выглядеть так, как на рис. 2.17.
6. Щелкнем на кнопке Сохранить... и отметим нужные типы
сохраняемых данных (рис. 2.19):
Нелинейная регрессия: Сохранить нояые не...
Предсказанные значения
Остатки;
Производные
| Продолжить I
Отмена |
Справка |
Рис. 2.19. Сохранение новых переменных ’ '
45
* Предсказанные значения — сохраняет предсказываемые значения
в виде переменной с именем PRED_;
• Остатки — сохраняет остатки в виде переменной с именем RESID;
• Производные — одна производная сохраняется для каждого па-
раметра модели. Имена производных создаются путем добавле-
ния префикса ‘d.’ к первым шести символам имени параметра;
• Значения функции потерь — этот параметр доступен, если задавать
свою собственную функцию потерь. Имя переменной loss_ при-
писывается значениям функции потерь.
7. Щелкнем на кнопке Параметры в правой части окна — по-
явится следующее диалоговое окно (рис. 2.20).
Не/1инейндя репрессия: Параметры
:ОБутстреп оценки стаадаргкойоимбки
/Метод оценивания .. .................. ..........
Г Последовательное квадратичное программирование Левенберг-Марквардт
. . . Лееенберг-Марквардт
’ Максимум итераций
,: н Сходимость суммы квадратов:-1Е-8 * *]
' ’ ; • Сходимость параметров; ИЕ-8 j
-...= ...................................
I —: | Продолжить I Отмена J,
ЙР
sn
ла
Рис. 2.20. Диалоговое окно Нелинейная регрессия: Параметры
W Выбираем используемые методы оценивания:
Последовательное квадратичное программирование. Этот метод при-
меним к моделям с ограничениями и без них. Последовательное
и квадратичное программирование используется автоматически,
если пользователь задает модель с ограничениями, функцию
потерь или бутстреп-процедуру. Можно ввести новые значения
в полях Максимум итераций и Ограничение шага, а также изменить
выбор в выпадающих списках Точность поиска, Точность функции
и Бесконечный шаг;
• Левенберг—Марквардт. Алгоритм, задаваемый по умолчанию для
моделей без ограничений. Метод Левенберга — Марквардта
недоступен, если пользователь задает модель с ограничениями,
функцию потерь или бутстреп-процедуру. Можно ввести новое
значение в поле Максимум итераций, а также изменить выбор в
46
выпадающих списках Сходимость суммы квадратов и Сходимость
параметров;
• Бутстреп — это метод оценивания параметров генеральной со-
j. вокупности, основанный на многократном извлечении одной
и той же выборки, расчете статистик по каждой выборке и оце-
нивании распределения этих статистик по выборкам. Каждая
L - выборка формируется путем случайного отбора наблюдений с
... возвращением. Как правило, каждая очередная извлекаемая
. выборка содержит то же самое число наблюдений, что и исход-
u ная, однако некоторые наблюдения могут случайно отбираться
несколько раз, а другие не отбираться вовсе.
8. Для начала вычислений нажмем ОК.
Представление результатов нелинейной регрессии. Сначала про-
токолируется процесс итераций. В рассматриваемом примере для
достижения заданного уровня точности понадобилось восемь ите-
рационных шагов (табл. 2.8).
Таблица 2.8
История итераций
Номер итерации Сумма квадратов остатков Параметр
аО а1 а2
1.0 228175.000 .000 .000 .000
1.1 94282.367 17.719 .024 3.14Е-005
2.0 94282.367 17.719 .024 3.14Е-005
2.1 2156.789 71.989 .066 4.08Е-005
3.0 2156.789 71.989 .066 4.08Е-005
3.1 805.464 80.257 .182 .000
4.0 805.464 80.257 .182 .000
4.1 620.192 -19.944 .463 .000
5.0 620.192 -19.944 .463 .000
5.1 325.646 -221.846 1.026 -.001
6.0 325.646 -221.846 1.026 -.001
6.1 38.325 -625.657 2.150 -.001
7.0 38.325 -625.657 2.150 -.001
7.1 29.105 -712.105 2.391 -.002
8.0 29.105 -712.105 2.391 -.002
8.1 29.105 -712.105 2.391 -.002
Затем следует распечатка конечных значений всех трех парамет-
ров вместе с соответствующей стандартной ошибкой и доверитель-
ным интервалом (табл. 2.9).
47
Оценки параметров
Таблица 2.9
Параметр Оценка Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
аО -712.105 54.372 -837.486 -5 86.724
al 2.391 .151 2.042 2.740
а2 -.002 .000 -.002 -.001
В результате итерационных вычислений получаем такую же
модель, что и ранее при вычислениях первым способом: Y =
= -712,105 + 2,39IX- 0,002Х2. График модели, расчетные значения
которой представлены на рис. 2.21, приведен на рис. 2.22.
Ш obprod - SPSS Редактор Данных
Файл Правка Вид Данные Преобразовать Анализ Графика Сервис Окно Справка
511 I J М &J «М *Г
11 :Y “ Y ’ И 27 X PRED_ RESH)
I 1 127.00 600.00 625.00 128.48 -1.48 1
2 139.00 137.72 1.28 ; j
3 147.00 650.00 144.90 2.10
147.00 155.00 675.00 150.01 -3.01
5 700.66 153.06 1.94
б 154.00 725.00 154.04 -.04
7 153.00 750.00 152.97 .03
8 148.00 775.00 149.83 -1.83
9 146.00 800.00 144.62 1.38
10 136.00 825.00 137.36 -1.36
11 129.00 850.00 128.03 .97
< | г |\Данные /Переменные / 1 < 1 1 jJ 5PS5 ГЙэоцессор готов
Рис. 2.21. Вычисленные значения переменной Y (графа PRED_)
Пример 2.3. По данным табл. 2.10 требуется построить произ-
водственную функцию, описывающую зависимость объема про-
мышленного выпуска черной металлургии Красноярского края от
факторов «труд» и «капитал»:
Y = a0Ka'L“2,
48
160
Рис. 2.22. График исходных данных и результатов моделирования
иОДД'
Таблица 2.10
Исходные данные
Год Объем промышленного выпуска черной металлургии, млн руб. Y Основной капитал, млрд руб. К Численность ППМ, чел. L
1985 94,7 0,2 5636
1990 112,4 0,3 5520
1995 224500 1160,6 4502
1996 302000 1160,6 4515
1997 486900 1159,3 5454
1998 283 2,4 4109
1999 392,2 2,4 3897
2000 493,9 2,5 3958
2001 696,4 1,6 4086
Источник: Злобин Д.А. Производственная функция отрасли «черная ме-
таллургия» (http://seeurban.ru/Text/zl .htm).
где Y— объем промышленного выпуска черной металлургии в
денежном выражении;
К— основные фонды в денежном выражении;
Z — трудовой фактор, численность промышленно-производ-
ственного персонала в отрасли «черная металлургия»
(ППМ), чел.
4 - 1591
49
Решение. Рассмотрим два способа решения задачи.
Способ 1. Использование замены переменных. Для построения
этой модели необходима линеаризация модели по параметрам. Для
этого прологарифмируем обе части уравнения:
In Y= lna0 + a,ln Х"+ a2lnZ.
В SPSS для логарифмирования используем функцию LN. Для
этого в редакторе данных указываем Преобразовать —> Вычислить
переменную (рис. 2.23).
Г Рис. 2.23. Вычисление новых переменных
На этапе моделирования свободный член In а0 исключен как
параметр, ухудшающий статистические свойства модели. В исход-
ной мультипликативной модели ай принимается, соответственно, за
единицу. Параметр а0 в экономической литературе интерпретирует-
ся как коэффициент нейтрального технического прогресса [42].
Заполним диалоговое окно Линейная регрессия (рис. 2.24), указав
на необходимость сохранения предсказанных значений. В окне
вывода SPSS получим результаты (табл. 2.11). Уравнение регрессии
будет иметь вид
In Y = 0,985 In К + 0,666 In L.
Перейдем к исходным переменным от предсказанных (перемен-
ная PRE_1) с помощью функции ЕХР (рис. 2.25) и получим следу-
ющую производственную функцию:
у = j^0,985£0,666
50
I Линейная регрессия
; Объем промышлемнЬ
I Основной капитал, ър
Численность ППМ,
/Чик
^LNL
.... Зависимая временная:
Г~П # LW ~' 1
Блок! из 1
•! - | След, |
. Независимые переменные:
J_^f|/>LNK М.
t| Д|Д /* LNL' ДД
ЕЮ)
| Вставка ]
[сброс I
[ Отмена |
[ Справка]
Метод: ) Принудительное включение
Переменная отбора наблюдений
Метки наблюдений:
Веса:
Статистики .. ] [ Графики... | [ Сохранить... j [ Параметры...
Рис. 2.24. Ввод данных для построения линейной модели примера 2.3
Таблица 2.11
Коэффициенты(а, Ь)
Модель Нестандартизованные коэффициенты Стандартизо- ванные коэффициенты t Знч.
В Стд. ошибка Бета
1 (пК .985 .045 .474 21.844 .000
InL .666 .022 .649 29.900 .000
а Зависимая переменная: InY
b Линия регрессии через начало координат
Способ 2. Использование нелинейной регрессии. Выбрав в меню
Анализ -> Регрессия -> Нелинейная, выполним необходимые действия
по построению нелинейной модели (рис. 2.26).
Представление результатов нелинейной регрессии. Сначала про-
токолируется процесс итераций. В рассматриваемом примере для
достижения заданного уровня точности понадобилось 19 итераци-
онных шагов. Потом выводятся статистические характеристики.
В таблице «Оценки параметров» (табл. 2.12) приводятся оценки
параметров модели вместе с соответствующей стандартной ошиб-
кой и доверительным интервалом. - .
А
51
I Вычислить переменную
Вычисляемая переменная: Числовое выражением
EXP(PREJ)
Тип и метка...
'i£> Объем промышление
•^> Основной капитал, м
<£> Численность ППМ, ч
' _d .Mid
АВ5(числвыр)
1 i ~ W 1 ! ?! oi АМУ(кригерий,знач,знач,...)
ARSIN[4HC/iBbip)
•$> Unstandardized Predic
;_d _11 jj _o_lj
..cl jJjjJ мд.а.™4
, ЕСЛИ... ।
'I 1 ;Вс^^а'ф||^^С:|^|^Ртмена^
ART АМ(числвыр)
CDFN0RM(z3Ha4)
CDF.BERNOULLI(q,p)
Рис. 2.25. Переход к исходным переменным
Ж Нелинейная регрессия
,£> Основной калил ,
ф Численность ПП
InY
4>lnL
м$> Unstandardized Р ;
—) -Зависимая переменная
А I ( промышленнг
И Выражение, задающее модель:
11ДК ” а1 ‘ L “ а2 ..... ”..
Вставка^
Сброс|
; Отмена |
Параметры... |
— ““
а2(2)
Г ?-И^=1' 1 I 2Рз W АВЗ(числвыр) :а: .
Ж:1 ji —1—АНУ(критерий.знач.знач....)
/1 I j 0 1.1. АВ31М(числвыр)
..I «I и I АПТАМ(числвыр)
11Д!Д1Ц;.аа1 СОРМОВМ(гзнач) ЯШЯ/Ш
Щ; -Фк}№Щ,ия nOTepb.^|f":0rpaHM4evw.Wg|-WB:l^p^<Tb.,.^ П араметръ»^,.|
Рис. 2.26. Заполнение диалогового окна Нелинейная регрессия
примера 2.3
Оценки параметров
Таблица 2.12
Параметр Оценка Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
al .474 .256 -.131 1.079
а2 1.109 .212 .607 1.610
-.ZlSlJj Финки»:
52
Получили следующую производственную функцию с коэффи-
циентами а{ и а2, отличающимися от полученных ранее:
Y = j^o,474£i,io9
Далее выводятся результаты дисперсионного анализа. Здесь ин-
терес может представлять член, обозначенный Я-квадрат; его сле-
дует понимать как часть суммарной дисперсии, которая обуслов-
лена построенной моделью. Вычисленное значение этого парамет-
ра (0,92920) указывает на очень хорошую степень приближения.
Сравним визуально значения, рассчитанные по двум получен-
ным моделям, с исходными данными (рис. 2.27).
-<-0бъем выпуска черной
металлургии, млн руб., У
-•—Способ 1
-•--Способ 2
550 000
500 000
450 000
400 000
350 000
300 000
250 000
200 000
150 000
100 000
50 000
123456789
Рис. 2.27. Графики исходных данных и расчетных значений
(способ 1 и способ 2)
Из приведенного рисунка видно, что модель, полученная спо-
собом 2, лучше аппроксимирует исходные данные (по алгоритму в
модели 2 минимизируется отклонение модели от исходных данных,
а не от их логарифмов).
Пример 2.4. На основании информации о норме безработицы и
темпах инфляции (табл. 2.13) требуется: 1) построить диаграмму
рассеяния; 2) построить модель регрессии зависимости темпов
инфляции от нормы безработицы; 3) отобразить на графике ре-
зультаты расчетов.
53
Исходные данные
Таблица 2.13
Темпы инфляции Y 1 1,1 1,2 1,3 1,7 2,9 2,9 4,2 5,4
Норма безработицы X 6,5 5,4 5,5 5 4,4 3,7 3,7 3,5 3,4
Решение. Построим диаграмму рассеяния для переменных X
(процент безработных в общей численности рабочей силы) и Y
(темп инфляции) на основании данных табл. 2.13.
Характер диаграммы рассеяния (рис. 2.28) явно указывает на
наличие нелинейной связи между рассматриваемыми переменны-
ми. Изображенная на диаграмме прямая у( = 7,95 - 1,21х(, подоб-
ранная методом наименьших квадратов, очевидным образом не
соответствует характеру статистических данных, хотя значение
коэффициента детерминации А2 = 0,7184 и представляется доста-
точно высоким.
3 3,5 4 4,5 5 5,5 6 6,5 7
Норма безработицы (X)
Рис. 2.28. Диаграмма рассеяния
В связи с этим при подборе моделей к реальным статистическим
данным следует обращать внимание не только на коэффициент
детерминации, но и (обязательно!) на соответствие подобранной
модели характеру статистических данных.
На практике подбор наилучшей модели регрессии выполняют
с помощью специальных программных продуктов, таких как
STATISTICA, SPSS, СТАТЭКСПЕРТи др.
Построение нелинейной модели темпов инфляции в SPSS:
1. Введем исходные данные (рис. 2.29).
2. Выберем в меню Анализ -> Регрессия Нелинейная.
54
Фа^1 Правка Вид С|Данные
Tempi - SPSS Редактор Данных
с£|Я|^В| Ej|:Ро| d “=!&| <л
Имя Тип Ши Деся Метка
1 Y Числовая 8 2 Темпы пнфлящш (Y)
2 X Числовая 8 2 Норма безработицы (X)
Нет
|Нет
*|»[\Данныё~ХПеременные /
^55 Процессор готов
Рис. 2.29. Исходные данные введены
3. Поместим переменную «Темпы инфляции» в поле для зави-
симых переменных и введем начальные значения параметров мо-
дели (рис. 2.30).
в Нелинейная регрессия
[Темпы инфляции 6
___
Норма безработиц
Зависимая перемени аяс В W
' Twa
Выражение, задающее модель:
XI (al + а2" х)
Вставка
Сброс I
Отмена j
Справка I
Параметры.
а1(0)
а2(2)
Функции: I... 1
АВБ^числвыр) а
AN ¥(Критерий,знач,знач„.
ARSIN(4ncnBbip)
ДПТАМ(числвыр)
CDFN0RM(z3Ha4) v<;
Функция потерь... ^z Ограничения... j Сохранить... | Параметры.
jJjJ „o_LT
Рис. 2.30. Диалоговое окно Нелинейная регрессия примера 2.4
4. Задав сохранение предсказанных результатов, в окне полу-
чим следующие результаты (рис. 2.31).
Используя программный продукт SPSS, получаем модель с
большим коэффициентом детерминации R2 - 0,998 (табл. 2.14):
„ х,-
1 У‘ -6,321 + 2,045х,.’
График модели свидетельствует о хорошем соответствии подобран-
ной модели характеру статистических данных (рис. 2.32).
Оценки параметров
Таблица 2.14
Параметр Оценка Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
al -6.321 .149 -6.673 -5.969
а2 2.045 .043 1.943 2.147
»ые феобрвзомть Анализ Графисв Сервис Окно Ставке
[ felOfl «I BfelGl <»|<з>|
. . * PRED_1 RESID_1 пьр
1 1.00 6.50 .93 .07
2 1.10 5.40! 1.14 -.04
3 1.20 5.50 1.12 .08
1 । т И 1.30 5.00 1.28: .02 1.70! 4.40! 1.641 .06 2.90! 3.70 2.971 -.07
2.9Ui J.fU Z.Vf •Mf
8 4.20 3.50 4.18 .02
9 5.401 3.40 5.38 .02
10
Рис. 2.31. Вычисленные значения переменной Y(графа PRED_1)
56
2.3. ЛОГИСТИЧЕСКАЯ РЕГРЕССИЯ Т
л 2.3.1. Математическое описание -s . < ь
логистической регрессии
В регрессионном анализе обычно предполагается, что резуль-
тирующий показатель у: является количественной величиной,
которая может принимать любые значения на множестве действи-
тельных чисел. Однако в экономических и социальных исследова-
ниях часто приходится сталкиваться с задачами, в которых зави-
симая переменная может принимать только целочисленные зна-
чения: 0, 1, 2,....
В зависимости от типа переменных модели с дискретными за-
висимыми переменными разделяются на модели выбора среди ко-
нечного числа альтернативных вариантов и модели счетных данных.
К числу последних относятся модели, где Y — это, например, ко-
личество предприятий, обанкротившихся в текущем году, или чис-
ло аварий, совершенных водителем за исследуемый период.
В зависимости от числа конечных вариантов, среди которых
осуществляется выбор, различают модели бинарного выбора и моде-
ли множественного выбора.
В моделях бинарного выбора результирующий показатель может
принимать только два значения: 0 и 1. Например, результаты голо-
сования (за, против), решение о выдаче кредита (кредит выдан,
в кредите отказано), решение о покупке товара (0 — нет, 1 — да),
результат трудоустройства (примут на работу или нет), состояние
обследуемого пациента (заболел, чувствует себя хорошо).
К моделям множественного выбора относятся модели с неупо-
рядоченными и упорядоченными альтернативными вариантами.
Рассмотрим более подробно бинарную логистическую регрессию.
В этом случае исследуется зависимость дихотомической (имеющей
всего два значения) переменной от одной или нескольких незави-
симых переменных, имеющих любой тип шкалы.
При решении задачи классификации на основе логистической
регрессии применяют ROC-анализ (подробнее о нем см. в подпа-
раграфе 2.3.2). В последние годы логистическая регрессия получи-
ла распространение, например, для расчета рейтинга заемщиков,
при управлении кредитными рисками и в ряде других прикладных
задач [5, 6]. Поэтому логистическую регрессию и ROC-анализ по-
чти всегда можно увидеть в наборе алгоритмов программы Data
Mining [16].
57
Логистическая регрессия выражает статистическую связь в виде
зависимости P{Y = 1 | X} - f(X), т.е. прогнозируется вероятность
события {У= 1}, обусловленная значениями независимых перемен-
ных Х{, Х2, Хк. Задача регрессии может быть сформулирована
следующим образом: вместо предсказания бинарной переменной
мы предсказываем непрерывную переменную со значениями на
отрезке [0, 1] при любых значениях независимых переменных.
Логистическая регрессия выражает связь между откликом и
переменными в виде формулы
P{Y = l\Xl,X2,...,Xk} = -——T- = —(2.11)
1 + еу 1 + е’у
где /*{•} — вероятность того, что произойдет интересующее собы-
тие;
е_= 2,718... — основание натуральных логарифмов;
Y = а0 + atXt + а2Х2 + ... + — линейное уравнение регрес-
сии.
Название «логистическая регрессия» происходит от названия
логистического распределения, имеющего функцию распределе-
ния
ж>=-4-
1 + е
Таким образом, модель, представленная этим видом регрессии,
по сути является функцией распределения этого закона, в которой
в качестве аргумента используется линейная комбинация незави-
симых переменных.
Отношение вероятности того, что событие произойдет, к веро-
ятности того, что оно не произойдет, Р/(\ - Р) называется отноше-
нием шансов (ОШ).
С этим отношением связано еще одно представление логисти-
ческой регрессии. Разрешив (2.11) относительно У, получаем
У = 1п(Р/(1 - Р)), где Р- P{Y = 1 | А), Х2, ..., Хк}. Тогда отношение
шансов может быть записано в виде
p/Q_p)_e«o+^l+^2+-+«A — Q°OQaXlQa2^2 .. .Qak^h = I.
= еа°(еа|)У| •••(е°*)А‘.
Отсюда получается, что, если модель верна, при независимых
Хр Х2, ..., Хк изменение Х^ на единицу вызывает изменение отно-
шения шансов в е0> раз.
58
График зависимости, связывающей вероятность события
/
P{Y - 11 Х},Х2,...,Хк} = F(Y) =-у и величину Y, показан на
1 + ег
рис. 2.33. Эта зависимость носит нелинейный характер, причем Р
не может выходить за пределы диапазона 0—1.
Если вместо функции распределения F(Y) =------п- выбрать
1 + е г
у
функцию распределения нормального закона F(Y) = —j= f е~х ^2dx,
л/2л Д
то вместо логит-модели получим близкую ей пробит-модель.
Различить, когда следует применять логит-модель, а когда —
пробит-модель, в случае малых выборок невозможно, поскольку
оценки коэффициентов модели Y - а0 + ауХ{ +... + а)Хк отличаются
множителем, который практически постоянен.
Существует несколько способов нахождения коэффициентов
логистической регрессии. На практике часто используют метод
максимального правдоподобия. Он применяется в математической
статистике для получения оценок параметров генеральной сово-
купности по данным выборки. Основу метода составляет функция
правдоподобия, выражающая плотность вероятности (вероятность)
совместного появления результатов выборки YJr Y2,..., Yk:
цу, y2, ..., Yk, G)=xKi;e)-p(^; 0).
Согласно методу максимального правдоподобия в качестве
оценки 0 неизвестного параметра 0 принимается такое значение
0 = ©(Ур ..., Yk), которое максимизирует функцию L.
59
Множественный логит- или пробит-анализ является
естественным продолжением бинарного и возникает, когда
рассматривается выбор между более чем двумя альтернативами.
Упорядоченный логит имеет дело с альтернативами, которые мож-
но расположить в определенном порядке.
Мультиномиальная логистическая регрессия является вариантом
логистической регрессии, при которой зависимая переменная не
является дихотомической, как при бинарной логистической ре-
грессии, а имеет больше двух категорий. В то время как при бинар-
ной логистической регрессии независимая переменная может
иметь интервальную шкалу, мультиномиальная логистическая ре-
грессия пригодна только для категориальных независимых перемен-
ных, причем имеет значение, относятся ли они к шкале наимено-
ваний или к порядковой шкале. Конечно же не исключается воз-
можность задания в качестве ковариат независимых переменных,
имеющих интервальную шкалу.
В то время как мультиномиальная регрессия предназначена для
зависимой переменной, относящейся к номинальной шкале,
порядковая регрессия предназначена для целевой переменной, при-
надлежащей к порядковой шкале. Независимые переменные и здесь
должны быть категориальными (т.е. иметь номинальную или по-
рядковую шкалу), однако в качестве ковариат допускается приме-
нение переменных с интервальной шкалой.
2.3.2. Реализация логистической регрессии в SPSS.
ROC-анализ
Система SPSS позволяет решать задачи с бинарным откликом
с помощью логистической регрессии. Ввод исходных данных вы-
полняется аналогично множественной линейной регрессии. Рас-
смотрим несколько способов анализа логистической регрессии со
следующим набором данных.
Пример 2.5. По 50 водителям были зарегистрированы возраст
(переменная Х,), состояние зрения (имеются проблемы со зрени-
ем — значение переменной Х2 равно единице, нет проблем —
нулю), уровень подготовки водителя (если прошел курсы для во-
дителей, Х3 - 1, если нет, Ху - 0) и наличие дорожно-транспортных
происшествий (ДТП) в последний год (0 — нет; 1 — да)
(табл. 2.15). ’' 1 '! ’ '
60
Таблица 2.15
Статистика по ДТП с учетом возраста,
результатов проверки зрения и подготовки водителя
№ п/п ДТП в прошлом году Y Возраст *1 Зрение Т2 Прошел курсы для водителей *3
1 1 19 1 1
2 0 44 0 1
3 1 48 1 0
50 0 19 0 1
Требуется выяснить, могут ли выбранные переменные (возраст,
состояние зрения и подготовка водителя) использоваться для того,
чтобы предсказать, были ли у водителя ДТП в прошедшем году.
Решение. Приведенные в таблице данные находятся в файле ДТП.
sav (рис. 2.34), откроем его.
"ДТП - SPSS Редактор Данных
Файл Правка Вид Данные Преобразовать Анализ Графика Сервис Окно Справка
i^|h|s[ 5] ц]_Д *=1М фIfrl cldjlnl ГТо>!
Имя Тип Ширина Десят Метка —
1 ¥ Чис левая 8 •> ДТП в прошлом года-
2 Xi Чис левая 8 2 Возраст
3 Х2 Числовая 8 •> Зрение
; 4 хз Чис левая ©0 2 Прошел курсы для водителей
; ~ Л)
< | > |\ Данные ^Переменные / 1- 4 | |
•SPSS Процессорготов
Рис. 2.34. Переменные в файле ДТП
1. Выберем в меню Анализ -» Регрессия -» Логистическая (Ana-
lyze -» Regression -»logistic). Открывается диалоговое окно Логисти-
ческая регрессия (рис. 2.35).
2. Поместим переменную «ДТП в прошлом году», содержащую
информацию о дорожно-транспортном происшествии в прошед-
шем году, в поле для зависимых переменных, а остальные перемен-
ные — в поле ковариат.
3. В процедуре логистической регрессии в SPSS предусмотрены
средства для автоматического включения в уравнение переменных
взаимодействий. Для этого в диалоговом окне в списке исходных
61
Рис. 2.35. Диалоговое окно Логистическая регрессия
переменных выделим имена переменных, взаимодействия которых
предполагается рассмотреть, затем перенесем выделенные имена
в окно независимых переменных, нажав кнопку >а*Ь>.
4. Используя кнопку Категориальные... (Categorical...), можно
подготовить для расчета категориальные (т.е. принадлежащие к
номинальной шкале) переменные. Если в обычной линейной ре-
грессии для работы с неколичественными величинами необходимо
подготавливать специальные индикаторные переменные, то при
реализации логистической регрессии в SPSS это делается автома-
тически.
5. С помощью кнопки Сохранить... (Save...) можно добавить в
файл дополнительные переменные; в разделе Предсказанные значе-
ния (Predicted Values) отметим Вероятности (Probabilities) и Принадлеж-
ность к группе (рис. 2.36).
6. Нажав на кнопку Параметры..., можно организовать вывод
дополнительных статистических характеристик и графиков. В дан-
ном расчете делать этого не будем.
7. Начнем расчет нажатием ОК.
Результаты расчетов приведены в таблицах вывода SPSS. После
таблиц «Сводка обработки наблюдений» и «Кодировка зависимой
переменной» приведена «Таблица классификации» (табл. 2.16). На
нулевом шаге, пока модель еще не построена, все «предсказанные»
значения Yравны единице, и потому все наблюдения, в которых
Y = 1, «предсказаны» верно, а наблюдения, где Y - 0, — неверно.
62
/кинетическая регрессия: Сохранить поеме переменные ГХ;
г Предсказанные значения......... - Остатки.---ВЯсП ' | Продопжить |
Т?^Вероятности , 1 Нестандаотизован»ые i ,
fgS3:! ' PT— „ I
; I** Принадлежность к .группе : I Логит ......и...., -. ,,, ,..,1
'''ВЯШЖв'' \ Г" Стыоденгизироваьмые - Справка I
«'Влияние- •--- >
I Стандартизованные .......
/ П Кука':Ввв^В-<в; : <
в : : < I .Уклонение <в--ссВВ'.:1>
I Значения разбалансировок ;
:;Г” s D f Beta( s] Г
Рис. 2.36. Сохранение новых переменных
Поэтому из этой таблицы (шаг 0) можно лишь узнать, сколько
наблюдений имеют значения У, равные единице, и сколько — рав-
ные нулю. Логистическая модель на следующих шагах будет пред-
сказывать шансы и вероятности попадания в ДТП, базируясь на
интересующих нас переменных.
Таблица классификации^, Ь)
Таблица 2.16
Наблюденное Предсказанное
Y Процент корректных
.00 1.00
ШагО Y .00 0 25 .0
1.00 0 25 100.0
Общий процент 50.0
а Модель включает константу, b Разделяющее значение = .500
Качество приближения регрессионной модели оценивается с
помощью функции правдоподобия. Мерой правдоподобия служит
отрицательное удвоенное значение логарифма этой функции
(-2 Log(L)), отображаемое в таблице «Сводка для модели» (табл. 2.17).
Чем меньше это значение, тем лучше сформированная модель.
Сводка для модели
Таблица 2.17
Шаг -2 Log Правдоподобие R квадрат Кокса и Снелла R квадрат Нэйджелкерка
1 46.587(a) .365 .487
а Оценивание закончено на итерации номер 5, потому что оценки параметра изменились менее чем на .001.
63
В качестве начального значения для -2Log применяется значе-
ние, которое получается для регрессионной модели, содержащей
только константы. После добавления переменных влияния зна-
чение -2Log равно 46,587; это значение на 22,727 меньше, чем на-
чальное. Подобное снижение величины означает улучшение; раз-
ность обозначается как величина хи-квадрат и является значимой
(табл. 2.18). Это означает, что начальная модель после добавления
переменных влияния стала значительно лучше.
Таблица 2.18
Объединенные тесты для коэффициентов модели
Хи-Квадрат ст.св. Знч.
Шаг1 Шаг 22.727 3 .000
Блок 22.727 3 .000
Модель 22.727 3 .000
R квадрат Кокса и Снелла и R квадрат Нэйджелкерка — псевдокоэф-
фициенты детерминации, полученные на основе отношения функ-
ций правдоподобия моделей только с константой и со всеми коэф-
фициентами. Эти коэффициенты редко используются при сравне-
нии моделей, поэтому мы не будем на них останавливаться.
На основе модели логистической регрессии можно строить
предсказание — произойдет или не произойдет событие {У = 1}.
Правило предсказания, по умолчанию заложенное в процедуру
логистической регрессии, таково; если предсказанная вероятность
события больше 0,5, считаем, что событие произойдет; если
меньше или равно 0,5, считаем, что событие не произойдет.
На основании данных «Таблицы классификации» (табл. 2.19)
(шаг не равен нулю) можно определить число верно и неверно пред-
сказанных наблюдений в каждой из категорий анализируемой пе-
ременной откликов и общий процент корректных предсказаний.
Проанализируем таблицу «Переменные в уравнении»
(табл. 2.20), полученную методом принудительного включения.
В таблице используются следующие обозначения;
• В — коэффициенты а- регрессионного уравнения;
• Стд.Ошибка — мера изменчивости коэффициентов о,.;
; • Вальд — критерий значимости коэффициентов регрессии. Чем
выше его значение (вместе с числом степеней свободы), тем
выше значимость коэффициента регрессии;
64
Таблица 2.19
Таблица классификации^)
Наблюденное Предсказанное
Y- зависимая переменная Процент корректных
.00 1.00
Шаг1 Y - зависимая переменная .00 20 5 80.0
1.00 5 20 80.0
Общий процент 80.0
а Разделяющее значение = .500
Таблица 2.20
Переменные в уравнении (модель 1)
В Стд.Ошибка Вальд СТ.СВ. Знч. Ехр(В)
Шаг1(а) XI .014 .019 .557 1 .455 1.014
Х2 2.173 .763 8.115 1 .004 8.788
ХЗ -2.170 .763 8.092 1 .004 .114
Константа -.747 1.038 .518 1 .472 .474
а Переменная(ые), включенная на шаге1: XI, Х2, ХЗ.
• ст.св — число степеней свободы;
• Знч. — значимость по критерию Вальда (при гипотезе а = 0);
• Ехр(В) — величина, используемая для интерпретации результа-
тов, отношение шансов (е°')-
Наблюдаемая значимость коэффициентов вычисляется на ос-
нове статистики Вальда. Универсальность статистики Вальда по-
зволяет оценить значимость не только отдельных переменных, но
и в целом категориальных переменных, несмотря на то, что они
дезагрегированы на индексные переменные. Статистика Вальда
имеет распределение хи-квадрат. Число степеней свободы равно
единице, если проверяется гипотеза о равенстве нулю коэффици-
ента при обычной или индексной переменной, и для категориаль-
ной переменной равно числу значений без единицы (числу соот-
ветствующих индексных переменных). Квадратный корень из
статистики Вальда приближенно равен отношению величины ко-
эффициента к его стандартной ошибке — так же выражается (-ста-
тистика в обычной линейной модели регрессии.
В нашей таблице коэффициентов «Переменные в уравнении»
(см. табл. 2.20) значимы переменные Х2 и Х3. Переменная Х{ (воз-
раст) не вошла в уравнение.
5 - I 591
65
Анализируя данные, можно обратить внимание, что в группе
водителей, которые не попадали в ДТП, значительно больше лю-
дей среднего возраста, а в группе попадавших в ДТП, кажется, есть
некоторый избыток самых молодых и самых пожилых индивиду-
умов. Базируясь на этих результатах, создаем новую дихотомичес-
кую переменную Х4, равную нулю для водителей, возраст которых
от 21 года до 65 лет, и единице в других случаях (рис. 2.37).
К Логистическая регрессия
\#> Возраст |Х1]
<£> Зрение [Х2]
ф Прошел курсы для вег
ф Вне 21-65 |Х4]
'*,ет^й.р1ринудительное включение
... Переменная отбора наблюдений?
Категориальные... j Сохранить.. | Параметры., j
Рис. 2.37. Ввод переменных
Построим уравнение логистической регрессии (модель 2), ис-
пользуя новую переменную сначала методом принудительного
включения, потом методами включения и исключения.
Выбор метода осуществляется с помощью окна Метод, включа-
ющего в себя следующие процедуры:
X Принудительное включение (Enter) — процедура отбора, при
которой все переменные блока вводятся за один шаг;
X Отбор включением — шаговый метод отбора переменных,
в котором проверка включения основана на значимости статис-
тики критерия множителей Лагранжа. Критерии исключения мо-
гут быть различны:
• значимость условного отношения правдоподобия (Условный);
• вероятность отношения правдоподобия статистики, основанной
на оценках максимального частного правдоподобия (Отношение
правдоподобия);
• вероятность статистики Вальда (Статистика Вальда); ;
66
V Отбор исключением — шаговый отбор исключением. Провер-
ка на исключение может быть основана на использовании:
• критической статистики, представляющей собой условное от-
ношение правдоподобия (Условный);
• вероятности статистики отношения правдоподобия, основан-
ной, в свою очередь, на оценках максимального частного прав-
доподобия (Отношение правдоподобия);
• статистики Вальда в качестве критической (Вальд).
Для построения уравнения логарифмической регрессии, вклю-
чающего JQ, выполним следующие действия:
1. Выберем в меню Анализ Регрессия Логистическая (Ana-
lyze -» Regression logistic).
2. Поместим переменную «ДТП в прошлом году», содержащую
информацию о дорожно-транспортном происшествии в прошед-
шем году, в поле для зависимых переменных. В качестве независи-
мых переменных укажем все остальные переменные за исключе-
нием переменной А", (возраст).
3. С помощью кнопки Сохранить (Save) добавим в файл допол-
нительные переменные; в разделе Предсказанные значения (Pre-
dicted Values) отметим Вероятности (Probabilities) и Принадлежность к
группе.
4. Нажав на кнопку Параметры, можно организовать вывод до-
полнительных статистических характеристик и графиков (рис. 2.38).
5. Начнем расчет нажатием ОК.
Логистическая регрессия: Параметры [X
Статистики и графики----------- -------— : ~ -.......\ | Продолжить
Р Графики классифькацкм : F** Корреляции оценок
;Г~ Критерий согласияХосмера-Лемешоеа Г~ История итераций : 2........
Р Л ст очечный вывод остатков Г" ДИдляекр(В): р~ %\ Справка
...It "Ю
Г > - .. ..< О ж
г Вывести..... ....... ........................
’• На каждом шаге На последнем шаге
Критерии шагового отбора.. ; Порог классификации [б ~
: Включение: [.05 Исключение: 10 г-—
Максимум итераций: ;2С
Г** Включить в модель константу
Рис. 2.38. Диалоговое окно Параметры
Проанализируем теперь результаты расчетов. По всем трем ме-
тодам были получены аналогичные модели. Все переменные в
уравнении значимы.
Качество модели 2 заметно улучшилось, значение -2Log, которое
отражается в таблице «Сводка для модели», теперь равно 38,099.
В «Таблице классификации» (табл. 2.21) тоже произошли измене-
ния к лучшему. Так, процент корректно предсказанных событий
увеличился с 80 до 86.
Таблица 2.21
Таблица классификации(а)
Наблюденное Предсказанное
ДТП в прошлом году Процент корректных
.00 1.00
Шаг! ДТП а прошлом году .00 21 4 84.0
1.00 3 22 88.0
Общий процент 86.0
а Разделяющее значение = .500
Приведем также таблицу «Переменные в уравнении»
(табл. 2.22), полученную методом включения.
Таблица 2.22
Переменные в уравнении
В Стд.Ошибка Вальд ст.св. Знч. Ехр(В)
Шаг1 Х2 2.097 .646 10.529 1 .001 8.143
Константа -1.099 .471 5.431 1 .020 .333
Шаг 2 Х2 2.565 .849 9.120 1 .003 13.000
Х4 2.565 .849 9.120 1 .003 13.000
Константа -2.565 .822 9.743 1 .002 .077
ШагЗ Х2 2.657 .931 8.136 1 .004 14.250
ХЗ -2.055 .843 5.943 1 .015 .128
Х4 2.421 .907 7.120 1 .008 11.259
Константа -1.598 .904 3.124 1 .077 .202
Уравнение регрессии будет выглядеть следующим образом:
Y = -1,598 + 2,657Х2 - 2,055Xj + 2,421Х4.
Если подставить соответствующие значения независимых пе-
ременных в это уравнение, результатом будет логарифм шансов
68
попадания в ДТП. Для того чтобы определить сами шансы, необ-
ходимо возвести число е (основание натуральных логарифмов) в
эту степень. Рассчитать вероятность того, что человек попадет в
аварию, на основе информации о его зрении, уровне подготовки и
возрастной группе можно с помощью следующего соотношения:
ОШ = Р/{\ — Р), .............. ;..,
где ОШ — отношение шансов; 7
Р — вероятность попадания в ДТП. i
Разрешив это уравнение относительно Р, получаем
Р=ОШ/(1+ОШ). ! <
! Используем это уравнение для того, чтобы предсказать шансы
и вероятность попадания в ДТП для человека, у которого нет ни-
каких проблем со зрением (Х2 = 0), никогда не учившегося на кур-
сах для водителей (Х3 - 0) и относящегося к возрастной группе от
21 года до 65 лет (%4 = 0). Расчеты будут следующими:
Log(OLIlnonM вдтп) = Y = -1,598 + 2,657%, - 2,055%3 + 2,421%4 =
= -1,598 + 2,657-0-2,055-0 +2,421-0 =-1,598; ; .
ОШпопад. вдтп = ехр(-1,598) = 0,2023,
а соответствующая вероятность попадания в ДТП : (
Лопад. ВДТП = 0,2023/(1 + 0,2023) = 0,1683.
Взяв аналогичного человека, но имеющего проблемы со зрени-
ем (%2 = 1), снова рассчитываем шансы и вероятность:
Ьоё(ОШпопад вдтп) = Y = -1,598 + 2,657%2 - 2,055%3 + 2,421%4 =
= -1,598 + 2,657 • 1 - 2,055 • 0 + 2,421 • 0 = 1,059;
ОШпопадвДТП = ехр(1,059) = 2,8842; “
впопад. ВДТП = 2,8842/(1 + 2,8842) = 0,7425.
Итак, шансы попадания в ДТП у человека с проблемами со
зрением резко увеличиваются от 0,2023 до 2,8842, почти в 14 раз
(2,8842/0,2023 = 14,25). Как было отмечено, изменение Xj на еди-
ницу вызывает изменение отношения шансов в еа' раз. Эту инфор-
мацию можно получить из последнего столбца Ехр(В) таблицы
«Переменные в уравнении» (см. табл. 2.22).
Прокомментируем некоторые другие таблицы результатов.
69
Корреляционная матрица (табл. 2.23) включается в протокол
выводимых данных при установке флажка Корреляции оценок в поле
Статистики и графики диалогового окна Параметры (см. рис. 2.38).
Таблица 2.23
Матрица корреляций
Константа Х2 Х4 ХЗ
Шаг1 Константа Х2 1.000 -.729 -.729 1.000
Шаг 2 Константа Х2 Х4 1.000 -.789 -.754 -.789 1.000 .493 -.754 .493 1.000
ШагЗ Константа Х2 ХЗ Х4 1.000 -.663 -.240 -.678 -.663 1.000 -.241 .438 -.678 .438 -.109 1.000 -.240 -.241 1.000 -.109
Если независимые переменные Хх, Х2, Хк слишком тесно
связаны между собой, т.е. нарушается условие их независимости,
то построенное уравнение регрессии может быть некорректным.
Диаграмма, приведенная на рис. 2.39, появляется в окне вывода
при установке флажка Графики классификации в поле Статистики и
графики (см. рис. 2.38). В диаграмме для обозначения прогнозиру-
емой вероятности используются два значения: 1 — «ДТП произой-
дет» и 0 — «ДТП не произойдет». По горизонтальной оси отложены
значения прогнозируемой вероятности, а по вертикальной оси —
частоты. Как видно из диаграммы, некоторые столбики включают
и 0, и 1, что говорит об ошибках в предсказании. Цифрам 1 в пра-
вой части диаграммы и цифрам 0 в левой ее части соответствуют
правильные предсказания относительно ДТП. Количество пра-
вильных и неправильных предсказаний приведено в «Таблице
классификации» (см. табл. 2.21).
С помощью логистической регрессии мы прогнозируем только
вероятность совершения ДТП конкретным водителем в зависимо-
сти от значений (для этого водителя) включенных в модель пере-
менных. Далее надо определить разделяющее значение — порог ве-
роятности для прогнозирования принадлежности водителя к груп-
пе совершивших или не совершивших ДТП. Как отмечалось, по
умолчанию этот порог принимается равным 0,5. Выбрать порог
можно с использованием аппарата ROC-анализа.
70
Step number: 1
Observed Groups and Predicted Probabilities
16
Predicted
1
0
0
0
0 1
0 0
0 10 0
0 0 0 0
0 0 0 0
0 0 0 0
1
1
1 1
1 1
0 1
0 1
1
1
1
1
1
1
1
1
1
1
Prob: 0 .25
.5 .75
Group:000000000000000000000000000000111111111111111111111111111111
Predicted Probability is of Membership for 1.00
The Cut Value is .50
Symbols: 0 - .00
1-1.00
Each Symbol Represents 1 Case.
Рис. 2.39. Фактическая группировка и прогнозируемые вероятности
Процедура ROC-анализа полезна для оценки эффективности
схем классификации, имеющих одну переменную с двумя катего-
риями, по которым классифицируются объекты.
ROC-кривая (Receiver Operator Characteristic) — кривая, которая
используется для представления результатов бинарной классифика-
ции. Построение ROC-кривой осуществляется с помощью диалого-
вого окна ROC Кривые в режиме построения графиков (рис. 2.40).
Поскольку классов два, один из них назовем классом с поло-
жительными исходами, второй — с отрицательными исходами.
ROC-кривая показывает зависимость количества верно классифи-
цированных положительных исходов от количества неверно клас-
сифицированных отрицательных исходов. В терминологии ROC-
анализа первые называются истинно положительными, вторые —
ложно отрицательными. При этом предполагается, что у
классификатора имеется некоторый параметр, варьируя который,
получают то или иное разбиение на два класса. Этот параметр час-
то называют порогом или точкой отсечения. В зависимости от него
будут получаться различные величины ошибок I и II рода. В логис-
тической регрессии в качестве параметра для разбиения на классы
71
M ROC Кривые
; $ Возраст [XI] 1
1 $ Зрение [Х2]
i $ Прошел курсы для в:
V# Вне 21-65 [Х4]
1 Предсказанная груН
Проверяемые переменные:
Предсказанная вере?
Переменная состояния:
/ ДТП в прошлом годм
Значение переменной 'Т
состояния:
Выводить
Ej ROC КрйваяЖл^М-
WF: 0 С диагональной опорной линией
0 Стандартная ошибка и доверительный интервал
Е Координатные точки ROC Кривой
Рис. 2.40. Построение ROC-кривой в программе SPSS
выбирается расчетное значение уравнения регрессии (см. подпа-
раграф 2.3.1). При этом порог отсечения изменяется от 0 до 1.
Основные понятия и применение ROC-анализа рассмотрим на
данных примера 2.5.
Для понимания сути ошибок I и II рода рассмотрим «Таблицу
классификации» (табл. 2.24), которая строится на основе результатов
классификации по модели (порог отсечения равен 0,5) и по факти-
ческой (объективной) принадлежности водителей к классам совер-
шивших ДТП в прошлом году (1,00) или не совершивших (0,00).
Таблица 2.24
Таблица классификации(а)
Наблюденное Предсказанное
ДТП в прошлом году Процент корректных
.00 1.00
Шаг1 ДТП в прошлом году .00 21 (ТР) 4 (FN) 84.0
1.00 3 (FP) 22(TN) 88.0
Общий процент 86.0
|Э Разделяющее значение = .500
Поясним обозначения, приведенные в табл. 2.24:
• TP (True Positives) — верно классифицированные положительные
примеры (так называемые истинно положительные случаи)',
72
• TN {True Negatives) — верно классифицированные отрицатель-
ные примеры {истинно отрицательные случаи)',
• FN {False Negatives) — положительные примеры, классифициро-
ванные как отрицательные (ошибка I рода). Это так называемый
ложный пропуск — интересующее нас событие ошибочно не
обнаруживается {ложно отрицательные случаи)',
• FP {False Positives) — отрицательные примеры, классифициро-
ванные как положительные (ошибка II рода). Это ложное обна-
ружение, так как при отсутствии события ошибочно выносится
решение о его присутствии {ложно положительные случаи).
Что является положительным событием, а что — отрицатель-
ным, зависит от конкретной задачи. В нашем примере мы прогно-
зируем вероятность совершения ДТП, поэтому положитель-
ным исходом будет класс «ДТП произошло», отрицатель-
ным— «ДТП не произошло».
При анализе чаще оперируют не абсолютными показателями,
а относительными — долями {rates), выраженными в процентах. *
Доля истинно положительных случаев {True Positives Rate)'.
TP
TPR =--------100%.
TP + FN
Доля ложно положительных случаев {False Positives Rate) '.
FP
FPR = ——-----100%.
TN + FP
Введем еще два определения: чувствительность и специфич-
ность модели. Ими определяется объективная ценность любого
бинарного классификатора.
Чувствительность {Sensitivity) — это и есть доля истинно поло-
жительных случаев:
TP
Se = TPR = ——----100%.
TP + FN
Специфичность {Specificity) — доля истинно отрицательных слу-
чаев, которые были правильно идентифицированы моделью:
TN
Sp = —^-----100%.
TN+ FP
Заметим, что FPR = 100% - Sp.
В нашем примере
Se = TPR= ТР/{ТР+ FN) 100% = 21/(21 +4) 100%= 84%;
73
Sp = TN/(TN+ FP) 100% = 22/(22 + 3) • 100% = 88%.
Модель с высокой чувствительностью часто дает истинный ре-
зультат при наличии положительного исхода (обнаруживает поло-
жительные примеры), а модель с высокой специфичностью — при
наличии отрицательного исхода (обнаруживает отрицательные
примеры).
Построение ROC-кривой:
1. Для каждого значения порога отсечения, которое меняется
от 0 до 1, с шагом dx (например, 0,01) рассчитываются значения
чувствительности Se и специфичности Sp. В качестве альтернативы
порогом может являться каждое последующее значение примера в
выборке.
2. Строится график зависимости: по оси У откладывается чув-
ствительность Se, по оси X — величина 100% - Sp (сто процентов
минус специфичность), или, что то же самое, FPR — доля ложно
положительных случаев (рис. 2.41).
Для идеального классификатора график ROC-кривой проходит
через верхний левый угол, где доля истинно положительных слу-
чаев TPR составляет 100% или 1 (идеальная чувствительность),
а доля ложно положительных примеров FPR - 0. Поэтому чем бли-
74
же кривая к верхнему левому углу, тем выше предсказательная
способность модели. И наоборот, чем меньше изгиб кривой и чем
ближе она расположена к диагональной прямой, тем менее эффек-
тивна модель. Диагональная линия соответствует «бесполезному»
классификатору, т.е. полной неразличимости двух классов.
Сравнение ROC-кривых:
• визуальная оценка расположения ROC-кривых относительно друг
друга. Кривая, расположенная выше и левее, свидетельствует
о большей предсказательной способности модели. Так, на
рис. 2.42 две ROC-кривые совмещены на одном графике. Вид-
но, что модель 2 лучше.
Однако визуальное сравнение ROC-кривых не всегда позволяет
выявить наиболее эффективную модель;
• оценка площади под ROC-кривыми. Теоретически площадь изме-
няется от 0 до 1, но, поскольку модель всегда характеризуется
кривой, расположенной выше положительной диагонали, обыч-
но говорят об изменениях от 0,5 («бесполезный» классифика-
тор) до 1 («идеальная» модель). Эта оценка может быть получе-
на непосредственно вычислением площади многоугольника под
экспериментально полученной ROC-кривой. Численный пока-
затель площади под кривой называется AUC (Area Under Curve)
(рис. 2.43).
75
Рис. 2.43. Площадь под ROC-кривой (модель 2)
В нашем примере площадь под ROC-кривой у модели 2 больше,
чем у модели 1 (табл. 2.25 и 2.26).
Таблица 2.25
Площадь под кривой (модель 1)
Площадь Стд. ошибка Асимптотическая Знч. Асимптотический 95% Доверительный интервал
Нижняя граница Верхняя граница
.859 .054 .000 .754 .964
Таблица 2.26
Площадь под кривой (модель 2)
Площадь Стд. ошибка Асимптотическая Знч. Асимптотический 95% Доверительный интервал
Нижняя граница Верхняя граница
.908 .044 .000 .822 .994
Можно считать, что чем больше показатель AUC, тем большей
прогностической силой обладает модель. Однако следует знать, что
AUC предназначен скорее для сравнительного анализа нескольких
моделей и не содержит никакой информации о чувствительности
и специфичности модели.
76
В литературе иногда приводится следующая экспертная шкала
для значений ALJC, по которой можно судить о качестве модели
(табл. 2.27).
""" Таблица 2.27
Оценка качества модели по значению AUC
Интервал AUC Качество модели
0,9-1,0 Отличное
; 0,8-0,9 Очень хорошее
0,7-0,8 Хорошее
0,6-0,7 Среднее
0,5-0,6 Неудовлетворительное
Идеальная модель обладает 100%-й чувствительностью и спе-
цифичностью. Однако на практике добиться этого невозможно,
более того, невозможно одновременно повысить и чувствитель-
ность, и специфичность модели. Компромисс находится с по-
мощью порога отсечения, так как пороговое значение влияет на
соотношение Se и Sp. Можно говорить о задаче нахождения опти-
мального порога отсечения.
Порог отсечения нужен для того, чтобы относить новые приме-
ры к одному из двух классов. Для определения оптимального по-
рога нужно задать критерий, так как в разных задачах различная
оптимальная стратегия.
Критериями выбора порога отсечения могут выступать:
• требование минимальной чувствительности (специфичности)
модели. Например, нужно обеспечить чувствительность теста
не менее 80%. В этом случае оптимальным порогом будет мак-
симальная специфичность (чувствительность), которая дости-
гается при 80% (или значение, близкое к нему «справа» из-за
дискретности ряда) чувствительности (специфичности);
• требование максимальной суммарной чувствительности и специ-
фичности модели. Данное значение порога обычно предлагается
пользователю по умолчанию;
• требование баланса между чувствительностью и специфичнос-
тью, т.е. Se ~ Sp. В этом случае порог есть точка пересечения
двух кривых, когда по оси X откладывается порог отсечения,
а по оси Y — чувствительность или специфичность модели
(рис. 2.44).
77
. Рис. 2.44. «Точка баланса» между чувствительностью
, ..... и специфичностью (модель 2)
1 ,'HU
: I
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ*
й?
„I Задача 2.1. Построение линейной модели цены колготок
Построить линейную модель зависимости цены колготок от их
плотности, состава и фирмы-производителя в торговых точках
Москвы и Московской области весной 2006 г.
Цена колготок — это зависимая переменная Y(руб.). В качестве
независимых, объясняющих переменных были выбраны: —
плотность (DEN), Х2, Х3 — соответственно содержание полиамида
и лайкры (%); Х4 — фирма-производитель (0 — Sanpellegrino; 1 —
Грация) (табл. 2.28).
Таблица 2.28
Исходные данные
№ п/п У %2 %4
1 49,36 20 86 14 0
2 22,51 20 97 3 1
44 90 50 76 24 0
45 120 70 74 26 0
В полном объеме числовые данные для задач приведены на CD.
78
Требуется:
1) рассчитать матрицу парных коэффициентов корреляции;
оценить статистическую значимость коэффициентов корреляции.
Пояснить выбор факторов для включения в модель;
2) построить уравнение регрессии. Оценить статистическую
значимость параметров регрессионной модели с помощью /-кри-
терия, проверить нулевую гипотезу о значимости уравнения с по-
мощью Л-критерия (а = 0,05), оценить качество уравнения регрес-
сии с помощью коэффициента детерминации Л2;
3) построить уравнение множественной регрессии только со
статистически значимыми факторами. Рассчитать доверительный
интервал для каждого наблюдения (уровень значимости принять
равным 5%). Указать торговые точки, в которых цены завышены;
4) результаты п. 3 отобразить графически (исходные данные,
предсказанные значения, доверительный интервал).
Задача 2.2. Исследование рынка жилья в Москве в районе станции
метро «Крылатское»
Имеются данные (табл. 2.29) о продаже квартир на вторичном
рынке жилья в Москве в районе станции метро «Крылатское» в
марте 2006 г.
Таблица 2.29
Исходные данные
№ п/п Y Х1 Х2 х« Х7
1 139 40 20 8 1 0 0 7
2 130 37,5 18 7 1 0 0 10
3 ПО 32 17,2 7,2 1 0 0 10
42 200 73,5 47,6 12,3 3 0 1 15
43 83 49 29,5 5,1 3 0 0 20
44 430 160 75,5 19,5 4 1 0 5
Источник'. Из рук в руки. 2006.
Принятые в таблице обозначения:
Y— цена квартиры, тыс. долл.;
Xt — общая площадь квартиры, м2;
Х2 — жилая площадь квартиры, м2;
Х3 — площадь кухни, м2;
79
Х4 — число комнат в квартире; *
Х5 — тип дома (1 — кирпичный, монолит; 0 — другой);
Х6 — расстояние относительно Рублевского шоссе (1 — близко
к Рублевскому шоссе; 0 — далеко от него);
Х7 — расстояние до метро, минут пешком.
Определить факторы, формировавшие цену квартир на вторич-
ном рынке жилья в Москве весной 2006 г., и построить линейную
модель зависимости цены от влияющих факторов.
Требуется:
1) составить матрицу парных коэффициентов корреляции.
Установить, какие факторы коллинеарны;
2) построить уравнение регрессии, характеризующее зависи-
мость цены от всех факторов;
3) оценить значимость полученного уравнения. Определить,
какие факторы значимо воздействуют на формирование цены
квартиры в этой модели;
4) определить, значима ли разница в ценах квартир, располо-
женных на Рублевском шоссе и в других районах;
5) определить, значима ли разница в ценах квартир разных
типов домов;
6) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить модель формирования
цены квартиры за счет значимых факторов. Дать экономическую
интерпретацию коэффициентов модели регрессии;
7) оценить качество построенной модели. Дать оценку влияния
значимых факторов на результат с помощью коэффициентов элас-
тичности, р- и Д-коэффициентов.
Задача 2.3. Исследование рынка жилья в Московской области
По данным о рынке жилья в Московской области, представлен-
ным в табл. 2.30, исследуется зависимость между ценой квартиры
Y(тыс. долл.) и следующими основными факторами:
Xt — город области (1 — Подольск, 2 — Люберцы);
Х2 — число комнат в квартире;
Х3 — общая площадь квартиры, м2;
Х4 — жилая площадь квартиры, м2; !
Х3 — этаж квартиры;
‘ Х6 — площадь кухни, м2.
Определить факторы, формировавшие цену квартир на рынке
жилья в Московской области весной 2006 г.
80
Таблица 2.30
Исходные данные
№ п/п У *1 Х2 *6
1 115 2 4 70,4 51,4 9 7
2 85 1 3 82,8 46 5 10
3 69 1 2 64,5 34 6 10
79 280 1 4 155 85 5 21
80 200 1 4 108,4 60 4 10
Источник’. Недвижимость и цены. 2006. 1—7 мая.
Требуется:
1) составить матрицу парных коэффициентов корреляции.
Установить, какие факторы коллинеарны;
2) построить уравнение регрессии, характеризующее зависи-
мость цены от всех факторов;
3) оценить значимость полученного уравнения. Определить,
какие факторы значимо воздействуют на формирование цены
квартиры в этой модели;
4) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить модель формирования
цены квартиры за счет значимых факторов. Дать экономическую
интерпретацию коэффициентов модели регрессии. Определить,
существует ли разница в ценах квартир, расположенных в Подоль-
ске и Люберцах;
5) оценить качество построенной модели.
Задача 2.4. Анализ деятельности аудиторско-консалтинговых
групп «Российский аудит»
Имеются данные рейтинга аудиторско-консалтинговых групп
«Российский аудит» по итогам 2004 г. (табл. 2.31).
Принятые в таблице обозначения: i ;
Y — совокупная выручка за 2004 г., тыс. руб.;
Х} — выручка по аудиторским проверкам, тыс. руб.;
Х2 — среднее число специалистов; fi
Х3 — выручка на одного специалиста*, тыс. руб.;
Х4 — число аттестованных аудиторов.
* Выручка на одного специалиста не является результатом деления со-
вокупной выручки на общее число специалистов, т.е. не связана функ-
6—1591
81
Таблица 2.31
Исходные данные
Группа Г . .А *3
Deloitte 1 709 721 922 797 589 2563 150
«БДО Юникон» 1 074 836 501 656 584 1969 181
ФБК 735 656 287 642 390 1886 90
«Балт-Аудит- Эксперт» 64 822 15 178 93 697 34
«Финансы» 64 706 13 251 78 830 25
«ПрофКонсалт- Холдинг» 63 660 20 510 7 9094 4
Построить модель зависимости совокупной выручки от приве-
денных факторов.
Требуется:
1) составить матрицу парных коэффициентов корреляции.
Установить, какие факторы коллинеарны;
2) построить уравнение регрессии, характеризующее зависи-
мость Yот значимых факторов;
3) определить, какие факторы значимо воздействуют на фор-
мирование совокупной выручки в этой модели. Дать экономиче-
скую интерпретацию коэффициентов модели регрессии. Оценить
качество построенной модели;
4) ранжировать аудиторско-консалтинговые группы по степени
их эффективности;
5) рассчитать доверительный интервал для каждого наблюдения
(уровень значимости принять равным 5%). Указать консалтинго-
вые группы, в которых фактические значения показателя «Сово-
купная выручка» превышают граничные значения.
Задача 2.5. Анализ деятельности предприятий одной отрасли
РФ-1
Имеются данные об экономической деятельности 25 предпри-
ятий одной отрасли Российской Федерации в 1997 г. (табл. 2.32).
ционально, так как часть работ может передаваться на выполнение
субподрядчикам, которые не попадают в число заявленных специа-
листов. Таким образом, вся выручка идет на меньшее число сотрудни-
ков.
82
Таблица 2.32
Исходные данные
№ п/п Y *1 *3 Л
1 7960 864 16 144 4,9 3,2
2 42 392 8212 336 472 60,5 20,4
3 9948 1866 39 208 24,9 9,5
23 6612 3801 169 995 75,9 27,2
24 16 3420 46 142 972 349 27,5 10,8
25 2948 2535 163 695 65,5 19,9
Принятые в таблице обозначения:
Y — прибыль от реализации продукции, млн руб.;
Х} — численность промышленно-производственного персона-
ла, чел.; '
Х2 — среднегодовая стоимость основных фондов, млн руб.; •
Х3 — электровооруженность, кВт • ч;
Х4 — техническая вооруженность одного рабочего, млн руб. ‘Ц
Требуется:
1) рассчитать параметры линейного уравнения множественной
регрессии с полным перечнем факторов;
2) оценить статистическую значимость параметров регресси-
онной модели с помощью /-критерия, проверить нулевую гипоте-
зу о значимости уравнения с помощью F-критерия (а - 0,05), оце-
нить качество уравнения регрессии с помощью коэффициента
детерминации Я2;
3) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить модель формирования
прибыли от реализации за счет значимых факторов;
4) дать оценку влияния значимых факторов на результат с по-
мощью коэффициентов эластичности, [3- и Д-коэффициентов;
5) рассчитать прогнозные значения результата, если прогноз-
ные значения факторов составляют 80% от их максимальных зна-
чений.
Задача 2.6. Анализ деятельности предприятий одной отрасли
РФ-2
По данным, представленным в табл. 2.33 (п = 25), изучается
зависимость объема выпуска продукции Y(млн руб.) от следующих
факторов (переменных):
83
Jf] — численность промышленно-производственного персона-
ла, чел.;
Х2 — среднегодовая стоимость основных фондов, млн руб.;
Х3 — износ основных фондов, %;
ХА — электровооруженность, кВт • ч; :
Х$ — техническая вооруженность одного рабочего, млн руб.; j
Xh — выработка товарной продукции на одного работающего,
руб.
Таблица 2.33
Исходные данные
№ п/п Y *2 *3 *4 *5 *6
1 32 900 864 16 144 39,5 4,9 3,2 36 354
2 203 456 8212 336 472 46,4 60,5 20,4 23 486
3 41 138 1866 39 208 43,7 24,9 9,5 20 866
23 98 010 3801 169 995 60,4 75,9 27,2 26 756
24 1 087 322 46 142 972 349 50,0 27,5 10,8 23 176
25 55 004 2535 163 695 25,5 65,5 19,9 21 698
Требуется:
1) построить матрицу парных коэффициентов корреляции.
Установить, какие факторы мультиколлинеарны;
2) построить уравнение множественной регрессии в линейной
форме с полным набором факторов;
3) оценить статистическую значимость уравнения регрессии и
его параметров с помощью критериев Фишера и Стьюдента;
4) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить модель регрессии за
счет значимых факторов. Оценить качество уравнения регрессии
с помощью коэффициента детерминации;
5) рассчитать прогнозные значения результата, если прогноз-
ные значения факторов составляют 80% от их максимальных зна-
чений.
Задача 2.7. Анализ накладных расходов-1
По данным, представленным в табл. 2.34, исследуется зависи-
мость между величиной накладных расходов 40 строительных орга-
низаций Y(млн руб.) и следующими тремя основными факторами:
84
X] — объем выполненных работ, млн руб.;
Х2 — численность рабочих, чел.;
Х3 — фонд заработной платы рабочих, млн руб.
Таблица 2.34
Исходные данные
№ п/п У *2 *3
1 5,7 26,9 1276 12,250
2 5,0 24,5 975 10,627
3 4,5 18,4 869 6,865
39 2,4 13,9 488 5,856
40 2,5 10,6 740 7,326
Требуется:
1) построить уравнение множественной регрессии в линейной
форме с полным набором факторов. Отобрать в модель информа-
тивные факторы по /-критерию для коэффициентов регрессии;
2) построить уравнение множественной регрессии только со
значимыми факторами. Рассчитать индекс корреляции R и оценить
качество полученного уравнения регрессии с помощью коэффи-
циента детерминации Л2;
3) оценить статистическую значимость уравнения регрессии,
используя критерий Фишера F(a = 0,05), и статистическую значи-
мость параметров регрессии, используя критерий Стьюдента;
4) дать сравнительную оценку силы связи между факторами и
результатом с помощью коэффициентов эластичности, [3- и Д-ко-
эффициентов;
5) рассчитать прогнозное значение результата, если прогнозные
значения факторов составляют 70% от их максимальных значений.
Задача 2.8. Анализ накладных расходов-2
По данным, представленным в табл. 2.35, исследуется зависи-
мость между величиной накладных расходов 40 строительных
организаций У (млн руб.) и следующими тремя основными факто-
рами:
Xt — объем выполненных работ, млн руб.;
Х2 — численность рабочих, чел.;
Х3 — фонд заработной платы рабочих, млн руб. 11 ’•-Mf
ОС
с®
Таблица 2.35
Исходные данные
№ п/п Y %2 *3
1 3,5 11,9 980 5,754
2 4,0 12,1 675 5,820
3 3,1 11,2 1020 4,267
38 1,6 7,4 159 1,570
39 1,2 2,2 162 1,142
40 1,5 2,6 101 0,429
Требуется:
1) используя пошаговую множественную регрессию (метод ис-
ключения или метод включения), построить модель для зависимой
переменной «Накладные расходы» за счет значимых факторов.
Рассчитать индекс корреляции R и оценить качество полученного
уравнения регрессии с помощью коэффициента детермина-
ции 7?2;
2) оценить статистическую значимость уравнения регрессии,
используя критерий Фишера F(a = 0,05);
3) дать сравнительную оценку силы связи между факторами и
результатом с помощью коэффициентов эластичности, Р- и Д-ко-
эффициентов;
4) ранжировать организации по степени их эффективности.
г Задача 2.9. Исследование взаимосвязей показателей финансовых
' рынков
В табл. 2.36 представлены среднемесячные данные за 2002—
2004 гг. для следующих показателей:
• курс американского доллара, руб.;
• процентная ставка по депозитам физических лиц в кредитных
организациях;
• сальдо торгового баланса (ТБ) — разница между экспортом и
импортом), млн долл. США;
• прирост золотовалютных резервов (ЗВР) Банка России (сред-
немесячные приросты), млн долл. США;
• индекс потребительских цен (ИПЦ) на товары и платные услуги
населению, %. ,
88<
- -.t-иг Таблица 2.36
Исходные данные
Год Месяц Курс доллара Процентная ставка Сальдо ТБ Прирост ЗВР ИПЦ
2002 1 30,473 10,1 3850 284 103,1
2002 2 30,806 10 3504 -214 101,2
2004 36 27,904 9,6 10 467 10 096 101,1
Требуется:
1) проанализировать связи между данными пятью показателя-
ми по следующей схеме:
а) оценить тесноту и направление связи для каждой пары вели-
чин;
б) выделить мультиколлинеарные факторы;
в) выбрать два ведущих фактора для показателя «Курс дол-
лара»;
2) построить линейную модель регрессии с ведущими факто-
рами, пояснить экономический смысл ее параметров;
3) оценить качественные характеристики модели по следующей
схеме:
а) проверить статистическую значимость уравнения и его па-
раметров;
б) проверить предпосылки МНК, определив математическое
ожидание остатков и исследовав их на гомоскедастичность;
в) оценить уровень точности модели на основе средней отно-
сительной ошибки;
г) оценить, какая доля вариации показателя «Курс доллара»
учтена в построенной модели и обусловлена включенными в нее
факторами;
4) выполнить прогноз показателя «Курс доллара» на январь,
февраль и март 2005 г., определить ошибку прогнозирования с
доверительной вероятностью 95%. Сравнить полученные резуль-
таты с фактическими данными за 2005 г.:
январь — 28,009; февраль — 27,995; март — 27,626.
Задача 2AQ. Исследование рынка жилья в Орле (районы Железно-
дорожный и Заводской)
В табл. 2.37 приведены данные по цене квартир в Орле и по
различным факторам, ее обусловливающим.
87
Таблица 2.37
Исходные данные
№ п/п Цена Общая площадь Пло- щадь кухни Жилая площадь Район Этаж Тип дома Коли- чество ком- нат
1 520 33 6 19,5 1 4 1 1
2 435 28,7 6,1 15,8 1 2 1 1
3 800 52 7 32 1 7 1 2
49 670 54,3 9 38,8 2 2 1 3
50 970 62 8,5 38 2 5 1 3
В графе «Район» использованы обозначения:
1 — Железнодорожный (элитный, относится к центральным
районам);
2 — Заводской.
В графе «Тип дома»:
1—кирпичный;
( 0 — панельный.
Требуется:
1) проанализировать связь всех факторов с показателем «Цена»
и между собой. Отобрать факторы, наиболее подходящие для по-
строения регрессионной модели;
2) сконструировать фиктивную переменную, отображающую
принадлежность квартиры к центральным и периферийным рай-
онам города;
3) построить линейную модель регрессии для всех факторов,
включив в нее фиктивную переменную. Пояснить экономический
смысл параметров уравнения;
4) распределить факторы (кроме фиктивной переменной) по
степени влияния на показатель «Цена»;
5) построить линейную модель регрессии для наиболее влия-
тельных факторов, оставив в уравнении фиктивную переменную.
Оценить качество и статистическую значимость уравнения и его
параметров;
6) обосновать целесообразность или нецелесообразность вклю-
чения в уравнения п. 3 и 5 фиктивной переменной;
7) определить, сколько будет стоить квартира общей площадью
74,5 м2 в элитном (периферийном) районе.
88
Задача 2.11. Исследование рынка жилья в Орле (Советский и Се-
верный районы)
В табл. 2.38 приведены данные по цене квартир в Орле и по
различным факторам, ее обусловливающим.
Таблица 2.38
Исходные данные
№ п/п Цена Общая площадь Площадь кухни Жилая пло- щадь Район Этаж Тип дома Количе- ство комнат
1 440 29,1 5,8 15,7 3 1 1 1
2 535 36,1 9,8 14,8 3 9 1 1
...
33 770 62,8 8,4 38,7 4 8 0 3
34 870 62,8 13 38,9 4 5 0 3
В графе «Район» использованы обозначения:
3 — Советский (элитный, относится к центральным районам);
4 —Северный.
В графе «Тип дома»: . .
1 — кирпичный; :
О — панельный.
Требуется:
1) проанализировать связь всех факторов с показателем «Цена»
и между собой. Отобрать факторы, наиболее подходящие для по-
строения регрессионной модели;
2) сконструировать фиктивную переменную, отображающую
принадлежность квартиры к центральным и периферийным рай-
онам города;
3) построить линейную модель регрессии для всех факторов,
включив в нее фиктивную переменную. Пояснить экономический
смысл параметров уравнения. Оценить качество модели, статис-
тическую значимость уравнения и его параметров;
4) распределить факторы (кроме фиктивной переменной) по
степени влияния на показатель «Цена»;
5) построить линейную модель регрессии для наиболее влия-
тельных факторов, оставив в уравнении фиктивную переменную.
Оценить качество и статистическую значимость уравнения и его
параметров;
89
6) обосновать целесообразность или нецелесообразность вклю-
чения в уравнения п. 3 и 5 фиктивной переменной;
7) оценить интервальные оценки параметров уравнения с ве-
роятностью 95%;
8) определить, сколько будет стоить квартира общей площадью
74,5 м2 в элитном (периферийном) районе.
Глава 3 Л-
« КЛАСТЕРНЫЙ АНАЛИЗ
3.1. ОБЩАЯ ХАРАКТЕРИСТИКА
ПРОЦЕДУР КЛАСТЕРИЗАЦИИ
3.1.1. Кластерный анализ и его роль
в социально-экономических исследованиях
При анализе и прогнозировании социально-экономических
явлений исследователь довольно часто сталкивается с много-
мерностью их описания. Это происходит, например, при ре-
шении задач сегментирования рынка, построения типологии стран
по достаточно большому числу показателей, прогнозирования
конъюнктуры рынка отдельных товаров, изучения и прогнозиро-
вания экономической депрессии и многих других проблем.
Кластерный анализ — один из методов многомерной статисти-
ки — наиболее ярко отражает черты многомерности в процедуре
классификации объектов. Название «кластерный анализ» проис-
ходит от английского слова «.cluster» — гроздь, скопление. Впервые
определил предмет кластерного анализа и дал его описание иссле-
дователь Трион (Tryon) в 1939 г. [3].
Главное назначение кластерного анализа — разбиение множе-
ства исследуемых объектов, характеризуемых совокупностью при-
знаков*, на однородные в соответствующем понимании группы
(кластеры). Это означает, что решается задача классификации дан-
ных и выявления соответствующей структуры в ней. Иными сло-
вами, предполагается выделение компактных, удаленных друг от
друга групп объектов или отыскание «естественного» разбиения
совокупности на области скопления.
Кластерный анализ является одним из направлений статисти-
ческого исследования социально-экономических процессов, ко-
торые связаны с изучением массовых явлений.
Пример 3.1. Некая фирма собирается начать выпуск нового
стирального порошка. Разработана анкета, содержащая ряд вопро-
сов, характеризующих отношение респондентов к свойствам про-
дукта. Респонденты должны проранжировать факторы по степени
их значимости, начиная с самого важного, — от 1 до 8.
Строгое определение понятий «объект» и «признак» будет дано в под-
параграфе 3.1.2.
91
Результаты классификации объектов (респондентов) по пере-
менным (свойствам продукта) представлены в табл. 3.1.
Таблица 3.1
Результаты классификации респондентов по предпочтениям
Свойство продукта Ранги свойств по сегментам
1 (18%) 2(7%) 3 (60%) 4(15%)
Моющая способность 3 8 2 7
Отдушка 5 5 7 1
Цена 8 7 1 Н 2
j-ч ’ О > ’ , Безвредность 1 4 8 ж-з
Эффект отбеливания 2 6 3 6
Подсинивание 4 3 6 8
Быстрое растворение 7 1 4 '(1 5
Отсутствие пыления t. 6 2 5 -
'8i
Получилось четыре сегмента, существенно различающиеся
между собой по наиболее важным признакам продукта. Эти при-
знаки выделены в таблице. Их можно назвать «сегментообразу-
ющими». Легко видеть, что сегмент 3 — самый крупный (60% от
выборки). Это прагматики, для которых важнейшей характерис-
тикой продукта является его цена, а также такие качества, как
моющая способность и эффект отбеливания. В следующем по ве-
личине сегменте 1, напротив, на первом месте стоит безвредность
порошка, цена же занимает последнее место.
Далее может проводиться сегментация по вопросам, касающим-
ся, например, стиля поведения респондентов («покупаю дешевые»,
«пользуюсь новинками» и т.п.).
Таким образом, результаты кластерного анализа фактически
опишут портрет потребителя с рациональной (свойства стираль-
ного порошка) и эмоциональной (оценка степени согласия с ут-
верждениями) точек зрения. На основе их можно определить це-
левую группу качеств, расставить акценты в рекламном сообще-
нии, избавиться от иллюзий относительно исключительности
своего товара по какому-либо определенному свойству и т.д.
Большое достоинство кластерного анализа в том, что он
позволяет выполнить разбиение объектов не по одному параметру,
а по целому набору признаков. Кроме того, кластерный анализ,
в отличие от большинства математико-статистических методов,
92
не накладывает никаких ограничений на вид изучаемых объектов
и позволяет рассматривать множество исходных данных практи-
чески произвольной природы. Это имеет большое значение, на-
пример, для прогнозирования конъюнктуры рынка, когда показа-
тели весьма разнообразны и затруднительно применение традици-
онных эконометрических подходов.
Кластерный анализ играет важную роль и для совокупностей
временных рядов, характеризующих экономическое развитие.
В частности, можно выделить периоды, когда значения соответ-
ствующих показателей были достаточно близкими, а также опре-
делить группы показателей, динамика которых во времени наибо-
лее схожа.
Необходимость развития и использования методов кластерного
анализа продиктована прежде всего тем, что они помогают постро-
ить научно обоснованные классификации, выявить внутренние
связи между единицами наблюдаемой совокупности. Построение
классификаций особенно актуально для слабоизученных явлений,
когда необходимо установить наличие связей внутри совокупности
и попытаться привнести в нее структуру.
Методы кластерного анализа могут применяться с целью сжатия
информации, в условиях постоянного увеличения и усложнения
потоков статистических данных. При этом в задачах социально-
экономического прогнозирования весьма перспективно сочетание
кластерного анализа с другими количественными методами (с кор-
реляционно-регрессионным, факторным анализом и т.п.).
Как и любой другой метод, кластерный анализ имеет опреде-
ленные недостатки и ограничения. Так, состав и количество
кластеров зависит от выбираемых критериев разбиения. При све-
дении исходного массива данных к более компактному виду могут
возникнуть определенные искажения, а также потеряться индиви-
дуальные черты отдельных объектов за счет замены их характерис-
тик обобщенными значениями параметров кластера.
3.1.2. Расстояния между объектами и кластерами
Различия между схемами решения задач классификации во
многом определяются тем, что понимают под сходством, однород-
ностью объектов.
Введем вначале такие ключевые для данной главы понятия, как
объект и признак.
93
Под объектами будем подразумевать конкретные предметы ис-
следования, нуждающиеся в классификации. Такими объектами
могут быть, например, потребители продукции, отличающиеся
своими предпочтениями, различные регионы или страны, пред-
приятия, их продукция и т.п.
Признак (синонимы: свойство, переменная, характеристика)
представляет собой конкретное свойство объекта.
Различные свойства могут выражаться как числовыми, так и
нечисловыми значениями. Например, объем производства может
измеряться в килограммах или тоннах, цена жилья — в тысячах
рублей (долларов) и т.п. Такие признаки называются количествен-
ными (непрерывными). Над ними можно производить арифметиче-
ские операции.
В отличие от числовых характеристик ряд признаков может иметь
дискретные, прерывистые значения. В свою очередь, дискретные
признаки делятся на две группы. Первая группа — порядковые (ран-
говые) переменные. Таким признакам присуще свойство упорядо-
ченности значений. К ним можно отнести возраст, этаж дома, год
выпуска и др. Значения ранговых переменных представляются на-
туральными числами. Вторая группа дискретных признаков не име-
ет такой упорядоченности и носит название номинальных перемен-
ных. Это переменные, принимающие два значения (дихотомичес-
кие) или более. Этим значениям можно поставить в соответствие
некоторые числа, которые, однако, не будут отражать какой-либо
упорядоченности значений переменной. Примером таких признаков
может быть пол респондента, тип дома, вид транспортного средства
и т.п. Эти признаки относятся к шкале наименований. Их можно
считать качественными характеристиками объектов.
Обычной формой представления исходных данных в задачах
кластерного анализа служит прямоугольная таблица «объект —
признак»
% - XIJ ... X,/
Х = хц ••• ху xim , !
... Xnj ... Хпт
каждая строка которой представляет результат измерений т рас-
сматриваемых признаков на одном из п обследованных объектов.
94
Пример 3.2. Пусть имеется 13 объектов, у которых измерено два
признака Хи У (табл. 3.2).
Таблица 3.2
Совокупность объектов с двумя признаками
Испытуемый Признак X Признак Y
А 27 19
В 11 46
С 25 15
D 36 27
Е 35 25
F 10 . ' ‘ 43
G 11 44
Н 36 :'м 24
I 26 14
J 9 --« 45
К 33 23
L 27 16
М 10 47
Непосредственная инспекция таблицы данных не позволяет
увидеть то, что является очевидным, но после построения диаграм-
мы рассеяния (рис. 3.1) совокупность объектов распадается на три
хорошо различимые группы.
Рис. 3.1. Диаграмма рассеяния
Объекты внутри кластера более «похожи» друг на друга, чем на
объекты из других групп. Таким образом, кластерный анализ ори-
ентирован на выделение некоторых геометрически удаленных
групп, внутри которых объекты близки.
В кластерном анализе для количественной оценки сходства
вводится понятие «расстояние между объектами». Кроме термина
«расстояние» в литературе часто встречаются и другие термины —
«метрика», «мера», которые подразумевают метод вычисления того
или иного конкретного расстояния.
Если каждый объект описывается т признаками, то он может
быть представлен как точка в /и-мерном пространстве, и сходство
с другими объектами будет определяться как соответствующее
расстояние.
Расстоянием между i-м и j-м объектами в пространстве призна-
ков называется такая величина dy, которая удовлетворяет следу-
ющим аксиомам:
1)
2)
3)
dy = dj<
dij + dJo *
4)
5)
(неотрицательность);
(симметрия);
(неравенство треугольника, здесь q —
номер объекта);
если dy Ф 0, то i j (различимость нетождественных объ-
ектов);
если dy - 0, то i - j (неразличимость тождественных объ-
ектов).
Меру близости (сходства) объектов удобно представить как ве-
личину, обратную расстоянию между объектами.
В многочисленных изданиях, посвященных кластерному анали-
зу, описано более 50 различных способов вычисления расстояния
между объектами. Выбор расстояния является узловым моментом
исследования. От него во многом зависит окончательный вариант
разбиения объектов на классы при данном алгоритме. Чаще других
используются следующие меры расстояния между объектами:
1) евклидово расстояние
I т
\к=1
2) взвешенное евклидово расстояние
(3.1)
т
diJ = JEwk(xik - xJk)2'-
U=1
(3.2)
96
к- 3) расстояние Минковского
< m \'/Р
dj ~ |'Л7А — Xjk |
U=1 7
(3.3^
4) расстояние city-block (расстояние городских кварталов) '
т
diJ = Y\xik - xJk[ (3-4)
Ar=J
где cig — расстояние между i-м и/-м объектами;
т — число переменных (признаков), которыми описываются
объекты;
хЛ, Xjk — значения Л-й переменной соответственно у z-ro и/-го
объектов;
wk — вес, приписываемый А>й переменной, пропорциональный
степени важности признака в задаче классификации;
р — показатель степени, определяемый исследователем.
Дадим несколько комментариев к приведенным выше мерам
расстояний между объектами.
Евклидово расстояние — одно из наиболее известных расстоя-
ний, которое доступно для восприятия и понимания в случае ко-
личественных признаков. Часто применяется также квадратичное
евклидово расстояние, равное квадрату dt-.
В ряде случаев используется взвешенное евклидово расстояние,
при вычислении которого учитываются весовые коэффициенты
wk, придающие отдельным слагаемым в сумме большую значи-
мость.
Весьма напоминает выражение для евклидова расстояния так
называемое обобщенное степенное расстояние Минковского, в кото-
ром в степенях вместо двойки используется другая величина. В об-
щем случае эта величина обозначается символом р. При р = 2
получаем обычное евклидово расстояние. Выбор конкретного зна-
чения степенного показателя р осуществляется самим исследова-
телем.
Частным случаем расстояния Минковского является так назы-
ваемое Хеммингово расстояние, или расстояние городских кварталов
(city-block), соответствующеер = 1. Это расстояние широко исполь-
зуется для дихотомических (имеющих всего два значения) каче-
ственных признаков, относящихся к номинальной шкале. В этом
случае оно равно числу несовпадений значений соответствующих
признаков для рассматриваемых z-ro и /-го объектов.
- 1591
97
Как видно, метрика Минковского фактически представляет
собой большое семейство метрик, включающее и наиболее попу-
лярные.
Однако существуют и принципиально отличающиеся от метрик
Минковского методы вычисления расстояния между объектами.
Так, расстояние Махаланобиса имеет достаточно специфические
свойства. Оно связано с корреляциями переменных. Когда корре-
ляции между переменными равны нулю, расстояние Махаланоби-
са эквивалентно квадрату евклидова расстояния.
В более широком смысле под объектами можно понимать не
только исходные предметы исследования, представленные в мат-
рице «объект — признак» в виде отдельной строки или отдельными
точками в многомерном признаковом пространстве, но и отдель-
ные группы таких точек, объединенные тем или иным алгоритмом
в кластер. В этом случае возникает вопрос: что понимать под рас-
стоянием между такими скоплениями точек (кластерами) и как его
вычислять? Иными словами, необходимо определить правила вы-
числения расстояния между группами объектов или меры близости
(сходства) двух групп объектов (в отличие от меры расстояния меж-
ду объектами), которые будут важны при объединении кластеров.
Отметим, что для определения расстояний между кластерами
разнообразных возможностей еще больше, нежели при вычисле-
нии расстояния между двумя наблюдениями в многомерном про-
странстве. Эта процедура осложняется тем, что в отличие отточек
кластеры занимают определенный объем многомерного простран-
ства, имеют протяженность и состоят из многих точек.
Мера сходства для объединения кластеров может быть опреде-
лена различными методами (рис. 3.2):
Рис. 3.2. Меры сходства для объединения кластеров
98
• методом «ближнего соседа» — степень сходства оценивается по
расстоянию между ближайшими объектами кластеров (а);
• методом «дальнего соседа» — степень сходства оценивается по
расстоянию между наиболее отдаленными объектами класте-
ров (б)’,
• центроидным методом — расстояние между кластерами опре-
деляется расстоянием между их центрами тяжести (с);
• методом средней связи — расстояние определяется как среднее
арифметическое всех попарных расстояний между представи-
телями рассматриваемых групп.
Использование различных мер сходства для объединения объ-
ектов (кластеров) приводит к различным кластерным структурам
и влияет на качество кластеризации. Поэтому соответствующая
мера должна выбираться с учетом имеющихся сведений о суще-
ствующей структуре совокупности объектов.
3.1.3. Анализ качества классификации ib
Кластерный анализ приводит к разбиению на кластеры с учетом
всех группировочных признаков одновременно. При этом, как
правило, не указаны четкие границы каждой группы, а также не-
известно заранее, сколько групп целесообразно выделить в иссле-
дуемой совокупности.
С целью сравнительного анализа качества различных способов
разбиения в кластерном анализе вводится понятие функционала
качества разбиения Q(S). Многие методы кластеризации различа-
ются тем, что их алгоритмы на каждом шаге вычисляют разнооб-
разные функционалы качества разбиения. Решение экстремальных
задач позволяет определить количественный критерий, следуя ко-
торому можно было бы предпочесть одно разбиение другому. При
выборе количественного показателя качества разбиения исходят
подчас из эмпирических соображений.
Под наилучшим разбиением понимают то, на котором достигает-
ся экстремум (минимум или максимум) выбранного функционала
качества.
Пусть исследователем выбрана метрика d в пространстве X на-
блюдений (объектов) Xt, Х2,..., и 5= (5И 52,..., Sp) — некоторое
фиксированное разбиение объектов на заданное число р классов
.У|, S2,..., Sp. . r,(Ji <j ’j, < ( ' i, < > i
7*
99
Наиболее распространены следующие характеристики функци-
онала качества:
• сумма внутриклассовых дисперсий расстояний
р
Ql(S) = ^Yd (х^ (3.5)
/=1 л,е5,
• сумма попарных внутриклассовых расстояний между внутриклас-
; терными элементами
р
02<S) = X X d2(Xj,Xj), (3.6)
Z=1 x^jeS/
Й
pie Х/, Xj — многомерные переменные, характеризующие соответ-
;. ственно объекты A), Xj,
S/ — некоторый фиксированный кластер;
X/ — среднее значение многомерной переменной X;, вычислен-
ное по наблюдениям /-го кластера (центр /-го кластера).
Судить о качестве разбиения позволяют и некоторые простей-
шие приемы. Например, сравнение средних значений признаков
в отдельных группах со средними значениями в целом по всей
совокупности объектов. Если отличие групповых средних от обще-
го среднего значения существенное (для проверки существенности
применяется /-критерий Стьюдента), то это является признаком
хорошего разбиения.
Перечисленные способы оценки качества разбиения предпола-
гают формальный подход и являются для исследователя только
вспомогательными средствами. Основная роль принадлежит со-
держательному анализу результатов классификации.
Выбрать лучший вариант разбиения легче, если провести под-
готовительную работу. К подготовительному этапу относят, прежде
всего, выбор признаков, характеризующих классифицируемые объ-
екты. На начальном этапе желательно также определить критерии
качества, отвечающие условию задачи, или целевую функцию, зна-
чения которой позволят сопоставить различные схемы классифи-
кации. В экономических исследованиях целевая функция, как
правило, должна оптимизировать некий параметр, определенный
на множестве объектов (например, максимизировать прибыль,
минимизировать затраты и т.п.).
В тех случаях, когда формализовать цель задачи не удается,
критерием качества классификации может служить возможность
100
содержательной интерпретации найденных групп, например, в ре-
зультате определения кластерных профилей.
Пример 3.3. Допустим, проведено анкетирование сотрудников
некой компании и нужно определить, каким образом можно наи-
более эффективно управлять персоналом, т.е. необходимо разде-
лить сотрудников на группы и для каждой из них выделить наибо-
лее эффективные рычаги управления. При этом различия между
группами должны быть очевидными, а респонденты внутри группы
будут максимально похожи. Не вдаваясь пока в подробности про-
цедуры кластеризации, рассмотрим результирующую таблицу клас-
терных профилей (табл. 3.3).
Таблица 3.3
Кластерные профили
(%)
Кластер Муж. 30-50 лет Более 50 лет Руково- дящие работ- ники Мед. обслу- живание Льготы 3/п Стаж Образо- вание
1 80 90 5 70 10 12 95 30 30
2 50 70 45 13 60 70 60 40 20
3 90 35 10 5 30 20 70 20 50
В первом столбце таблицы находится номер кластера, данные
по которому отражены в строке. Например, первый кластер на 80%
составляют мужчины, 90% попадают в возрастную категорию от 30
до 50 лет, а 12% респондентов считают, что льготы очень важны.
Составим теперь портреты респондентов каждого кластера.
Первая группа — в основном мужчины зрелого возраста, зани-
мающие руководящие позиции. Соцпакет (медицинское обслужи-
вание и льготы) их не интересует. Они предпочитают получать
хорошую зарплату, а не помощь от работодателя.
Вторая группа, наоборот, отдает предпочтение соцпакету. Со-
стоит она в основном из людей в возрасте, занимающих невысокие
посты. Зарплата для них, безусловно, важна, но есть и другие при-
оритеты.
Третья группа наиболее «молодая». Здесь очевиден интерес к
возможностям обучения и профессионального роста. У этой кате-
гории есть хороший шанс в скором времени пополнить первую
группу. ; ' В * * 11 ’ г*|им
101
Таким образом, планируя кампанию по внедрению эффектив-
ных методов управления персоналом, можно увеличить соцпакет
у второй группы в ущерб зарплате. Специалистам из третьей груп-
пы можно рекомендовать пройти обучение.
В зависимости от количества признаков, их взаимосвязи, вы-
бранного критерия качества определяется наиболее подходящий
алгоритм классификации. Все это облегчает последующую интер-
претацию результатов разбиения и позволяет судить о его качестве
с точки зрения поставленной задачи.
В целом различают три подхода к проблеме кластерного анализа:
• эвристический — характеризуется отсутствием формальной мо-
дели для сравнения различных решений; алгоритм строится,
исходя из интуитивных соображений;
• экстремальный — задается критерий, определяющий качество
разбиения на кластеры;
• статистический — задача кластерного анализа решается на
' основе вероятностной модели исследуемого процесса.
J Существуют визуальные способы исследования результатов
^Кластеризации. Они связаны прежде всего со свойствами кластеров.
Обсудим наиболее важные из них.
i 1. Плотность распределения наблюдений внутри кластера. Это
свойство дает нам возможность определить, насколько данный
кластер является «заполненным», или же наоборот — разрежен-
ным. Несмотря на очевидность этого свойства, однозначного спо-
соба вычисления плотности кластера не существует. Наиболее
удачным показателем, характеризующим компактность, плотность
«упаковки» многомерных наблюдений, является дисперсия рассто-
яния от центра кластера до отдельных его точек. Чем меньше дис-
персия этого расстояния, тем ближе к центру кластера находятся
наблюдения, тем больше плотность кластера. И наоборот, чем
больше дисперсия расстояния, тем более разрежен данный кластер
и, следовательно, есть точки, находящиеся как вблизи центра клас-
тера, так и достаточно далеко от его центра.
2. Размер кластера. Основным показателем размера кластера
является его «радиус». Это свойство наиболее полно отражает фак-
тический размер кластера, если рассматриваемый кластер имеет
круглую форму или является гиперсферой в многомерном про-
странстве. Однако если кластеры имеют удлиненные формы, ради-
ус или диаметр уже не отражает их истинного размера.
102
3. Локальность, отделимость кластеров. Это свойство характе-
ризует степень перекрытия и взаимной удаленности кластеров друг
от друга в многомерном пространстве. В частности, используя
данное свойство, можно в дальнейшем рассмотреть вопросы о
целесообразности объединения наиболее близких кластеров или
их перекрывающихся частей, об отделении от кластера элементов,
больше других удаленных от его центра, и пр.
Таким образом, кластерный анализ — это не только формали-
зуемая процедура; в нем всегда есть место наблюдению, интуиции,
искусству и творчеству исследователя.
3.1.4. Методы кластерного анализа
Классификацию методов кластерного анализа можно предста-
вить в виде следующей схемы (рис. 3.3).
Рис. 3.3. Схема классификации методов кластерного анализа
Из всех методов кластерного анализа наиболее распространен-
ными являются иерархические агломеративные методы. Сущность
их заключается в следующем. На первом шаге каждый объект вы-
борки рассматривается как отдельный кластер. Процесс объеди-
нения кластеров происходит последовательно: на основе матрицы
расстояний (или матрицы сходства) R = (d^), где d^ — расстояние
между /-м иJ-м объектами, объединяются наиболее близкие объ-
екты. ..
103
Последовательность объединения легко поддается геометричес-
кой интерпретации и может быть представлена в виде дендрограм-
мы (рис. 3.4). На вертикальной оси отмечается расстояние, на ко-
тором объединялись объекты или кластеры. Процесс прекращают,
когда объединяются кластеры, находящиеся на большом расстоя-
нии друг от друга.
< Рис. 3.4. Пример дендрограммы иерархического
агломеративного кластерного анализа
Методы иерархического агломеративного кластерного анализа
различаются не только используемыми мерами сходства (см. под-
параграф 3.1.2), но и алгоритмами классификации. Наиболее рас-
пространенными из них являются следующие методы:
• одиночной связи;
• полных связей;
• средней связи;
• Уорда.
В методе одиночной связи объект будет присоединен к уже су-
ществующему кластеру, если хотя бы один из элементов кластера
имеет тот же уровень сходства, что и присоединяемый объект.
Отсюда и название метода — «одиночная (или единственная)
связь».
Для метода полных связей присоединение объекта к кластеру
происходит лишь в том случае, когда сходство между кандидатом
на включение и любым из элементов кластера не меньше некото-
рого порога.
104
Метод средней связи имеет несколько модификаций, которые
являются некоторым компромиссом между одиночной и полной
связью. В них вычисляется среднее значение сходства кандидата
на включение со всеми объектами существующего кластера. При-
соединение происходит в том случае, когда найденное среднее
значение сходства достигает или превышает некоторый порог. Наи-
более часто используют среднее арифметическое сходство между
объектами кластера и кандидата на включение в кластер.
Популярный метод Уорда построен таким образом, чтобы оп-
тимизировать минимальную дисперсию внутрикластерных рассто-
яний. На первом шаге каждый кластер состоит из одного объекта,
в силу чего внутри кластерная дисперсия расстояний равна нулю.
Объединяются те объекты, которые дают минимальное прираще-
ние дисперсии, вследствие чего данный метод имеет тенденцию
к порождению гиперсферических кластеров.
Приведем пример агломеративного иерархического алгоритма.
Пример 3.4. Требуется провести классификацию шести регионов
по двум заданным признакам. Исходные данные по материалам
Российского статистического ежегодника [33], раздел «Отраслевая
структура промышленного производства по регионам Российской
Федерации в 2003 году», представлены в табл. 3.4.
Таблица 3.4
Отраслевая структура промышленного производства (фрагмент)
№ п/п Область Объем промышленного производства, %
электроэнергетика машиностроение
1 Липецкая 6,9 11,5
2 Тульская ПД 20,1
3 Тамбовская 21,3 34,2
4 Воронежская 20,5 22,1
5 Белгородская 9,7 13,4
6 Брянская 18,2 29,4
Решение. Воспользуемся меню графиков в SPSS и представим
две заданные переменные в виде простой диаграммы рассеяния
(рис. 3.5), на которой отчетливо видны две группы точек. Следо-
вательно, шесть данных областей явно распадаются на два различ-
ных кластера.
Воспользуемся теперь агломеративным иерархическим алгорит-
мом классификации. В качестве расстояния между объектами возь-
105
0Воронвжская Там6ов°ая
оБрянская
оТульская
о Белгородская ;
о Липецкая if
10 15 20 25 30 35
Машиностроение
Рис. 3.5. Диаграмма рассеяния
мем обычное евклидово расстояние. Тогда, согласно формуле (3.1),
расстояние между первым и вторым объектами
</12 = 7(Н,1 -6,9)2 + (20,1- 11,5)2 = 9,57,
между первым и третьим
</13 = 7(21,3-6,9)2 + (34,2 -11,5)2 = 26,88. ,,j
Очевидно, что d{ j = d22 =... = d66 = 0. j
Аналогично находим все остальные расстояния между шестью
объектами и строим матрицу расстояний: 1
(3) (4) (5) (6)
26,88 17,24 3,38 21,17) '
17,4 9,61 6,85 11,7
0 12,13 23,82 5,71
12,13 0 13,87 7,65 '
23,82 13,87 0 18,12
5,71 7,65 18,12 0 ,
(1) (2)
0 9,57
9,57 0
Я = 26,88 17,4
1 17,24 9,61
3,38 6,85
ч21,17 11,7
106
Из матрицы расстояний следует, что первый и пятый объекты
наиболее близки (г/15 = 3,38), поэтому они объединяются в один
кластер.
После первого объединения имеем пять кластеров:
*^(2)> ^(3)’ ^(4)’ ^(1,5)’ *5(6)-
Расстояние между кластерами определим по принципу «бли-
жайшего соседа». Так, расстояние между кластерами 5(2) и *$<15)
определяется равенством [15]
^2,(1,5) ~ ^(*$2>^(1,5)) ~ 2^21 + 2^25 ~ 2^21 ~ ^251 =
= 1(9,57 + 6,85) - -|9,57 - 6,85] = 6,85.
Таким образом, расстояние d2 (] 5> равно расстоянию от второго
объекта до ближайшего к нему объекта, входящего в кластер 5(15),
т.е. d2 (|5) = d25 = 6,85. Тогда матрица расстояний примет вид
,'Й
#2 =
(2) (3) (4) (1,5) (6)
0 17,4 9,61 6,85 11,7 Л
17,4 0 12,13 23,82 5,71
9,61 12,13 0 13,87 7,65
6,85 23,82 13,87 0 18,12
11,7 5,71 7,65 18,12 0 )
Объединяем теперь третий и шестой объекты, имеющие наи-
меньшее расстояние d36 = 5,71. После объединения имеем четыре
кластера:
^(2)> *^(4)’ ^(1,5)’
Вновь найдем матрицу расстояний. Для того чтобы рассчитать
расстояние до кластера 5), воспользуемся матрицей расстоя-
ний R2. Например, расстояние между кластерами 5(1 5) и S(3 6)
^(1,5),(3,6) = ^(^(1,5), %)) = 2 ^О,5),3 + 2 ^(1,5),6 ~ ~ ^0.5),б| =
= 1(23,82 + 18,12) -1|23,82 -18,12] = 18,12. И*’
В результате получим новую матрицу расстояний > • ‘
107
(2) (4) (1,5) (3,6)
i 1г1' ' 0 9,61 6,85 11,7'
9,61 0 13,87 7,65 Г I " : Г ;.? ..
6,85 13,87 0 18,12
Jl,7 7,65 18,12 0
Теперь объединяем кластеры 5(15) и (d(l 5) 2 = 6,^^ наи-
меньшее). В результате получим три кластера:
*^(2,1,5)’ S(4)’ S(3,6y ,, t j SI
Так как j
^(2,1,5),(3,6) = ^(2,1,5)> *\з,6)) = ’ ’’ ,
= 2 ^,(3,6) + 2 4x5),(3,6) “ 2 р2,(з,б) _ 4i,5),(«d *1 I
•>&
то новая матрица расстояний будет иметь вид
(2,1,5) (4) (3,6)
' 0 9,61 11,7'
^4 = 9,61 0 7,65
111,7 7,65 0 ,
Объединяем теперь кластеры 5(4) и 5(3 6) (</(3>6)4 = 7,65 — наи-
меньшее). В результате получаем два кластера *У(2>1>5), S(4 3 ^,
расстояние между которыми, найденное по принципу «ближайше-
го соседа»,
^(2,1,5),(4,3,6) = ^(^(2,1,5)> ^(4,3,6)) =
= 2 42,1,5),4 + 2 4г,1,5),(3,6) ~ 21^2,1,5),4 “ 42,1,5),(3,6)| = 9,61.
Тогда
" (2,1,5)(4,3,6) ,1‘4' '
1 ' 1, , r Hh t
d ( 0 9,6П
.5 г 1^9,61 oj ,и. >’
Таким образом, последнее объединение произойдет на рассто-
янии 9,61.
Результаты иерархической классификации объектов представ-
лены в виде дендрограммы на рис. 3.6.
108
Рис. 3.6. Дендрограмма кластеризации шести регионов
Из рисунка видно, что предпочтение следует отдать предпослед-
нему этапу классификации, когда все области были разбиты на два
класса 5(2>1>5), *$(4Д6)-
Иерархические дивизимные методы противоположны агломера-
тивным по логическому построению процедур классификации.
Исходной посылкой дивизимных методов является то, что перво-
начально все объекты принадлежат одному кластеру. В процессе
классификации от этого кластера отделяются группы схожих меж-
ду собой объектов. Таким образом, на каждом шаге количество
кластеров возрастает, а мера расстояния между ними уменьшается
(рис. 3.7).
Рис. 3.7. Дендрограмма иерархического дивизимного алгоритма
109
Пример 3.5. Пусть дана матрица расстояний между пятью объ-
ектами X],Х5
Требуется провести классификацию по дивизимному алго-
ритму.
Решение. Наиболее удаленными являются объекты Х1 и Х2
(dl2 = 4,49); оценим расстояния оставшихся объектов до первого и
второго:
*/31 < ^32 —объект Х3 ближе к Xf, н-.р
^41 > ^42 ~~ объект Х4 ближе к Х2;
Д51 > ^52 ~ объект Х5 ближе к Х2.
Таким образом, получаем два кластера: 5Д1, 3} и S2{2, 4, 5}.
В каждом из них анализируем расстояния между объектами, и на
очередном шаге происходит разделение того кластера, где дости-
гается максимум расстояния между объектами:
d}3 = 2,16; d25 = 1,93; d24 = 1,92; d45 = 0,71.
Наибольшее расстояние di3 = 2,16, следовательно, объекты Х} и
Х3 выделяем в отдельные кластеры. В кластере S2{2, 4, 5} ищем
максимальное расстояние max{^24, d23, d43} = 1,93. На следующем
шаге из этого кластера выделяем объект^ и, наконец, на послед-
нем шаге разделяем кластер <S'4{4, 5} на два кластера на расстоя-
нии 0,71.
Дендрограмма последовательности разбиений представлена на
рис. 3.8.
Из этого примера видно, что дивизимный алгоритм не требует
пересчета матрицы расстояний на каждом шаге классификации,
в отличие от агломеративных методов.
Сущность итеративных методов кластерного анализа заключа-
ется в том, что процесс классификации начинается с задания не-
которых начальных условий (количество образуемых кластеров,
110
порог завершения процесса классификации и др.). Итеративные
методы в большей степени, чем иерархические, требуют от поль-
зователя интуиции при выборе типа классификационных процедур
и задании начальных условий разбиения, так как большинство этих
методов очень чувствительны к изменению задаваемых парамет-
ров. В отличие от иерархических методов итеративные алгоритмы
могут привести к образованию пересекающихся кластеров, когда
один объект может одновременно принадлежать нескольким клас-
терам.
Примером итеративной кластеризации может служить метод
к-средних [35]. Алгоритм метода ^-средних (впрочем, как и иерар-
хический агломеративный метод Уорда) основан на принципе ми-
нимизации внутрикластерной дисперсии (см. подпараграф 3.1.3).
Метод ^-средних принадлежит к группе итеративных методов
эталонного типа. Название метода было предложено Дж. Мак-
Куином в 1967 г. [18]. Этот метод удобен для обработки больших
статистических совокупностей.
После того как принято волевое решение о числе разбиений,
алгоритм ^-средних начинает свою работу с того, что случайным
образом в пространстве назначает центры будущих кластеров. За-
тем вычисляется расстояние между центрами кластеров и каждым
объектом, и объект приписывается к тому кластеру, к которому он
ближе всего. Завершив приписывание, алгоритм вычисляет сред-
ние значения для каждого кластера. Набор средних представляет
собой координаты нового положения центра кластера. Алгоритм
вычисляет расстояние от каждого объекта до центров кластеров и
111
приписывает объекты к ближайшему кластеру. Вновь вычисляют-
ся центры тяжести, и этот процесс повторяется до тех пор, пока
центры тяжести не перестанут «мигрировать» в пространстве.
Процедуры кластеризации почти всегда сопряжены с трудоем-
кими расчетами, поэтому для реализации соответствующих алго-
ритмов применяются пакеты специальных прикладных про-
грамм.
3.2. РЕАЛИЗАЦИЯ КЛАСТЕРНОГО АНАЛИЗА В SPSS
Программы кластерного анализа являются составной частью
многих пакетов статистической обработки данных, в том числе и
SPSS. В части кластеризации программа SPSS дает возможность
проведения двухэтапного кластерного анализа, иерархической
кластеризации и кластеризации ^-средними. Это хорошо видно
после выбора в строке меню команды Анализ -> Классификация
(Analyze —> Classify) (рис. 3.9).
Рис. 3.9. Меню статистики
3.2.1. Иерархическая кластеризация
В следующем примере рассмотрим возможности программы
SPSS при решении задачи иерархической кластеризации объектов
по нескольким группировочным признакам одновременно.
Пример 3.6. В табл. 3.5 приведены индексы цен в секторах эко-
номики по ряду регионов Российской Федерации в 2003 г. [33].
112
Таблица 3.5
Индексы цен, %, в секторах экономики в 2003 г.
№ п/п Область Индекс потре- битель- ских цен Индекс цен произво- дителей промыш- ленной продукции Индекс цен произво- дителей на реализо- ванную с.-х. продук- цию Индекс цен производи- телей в строитель- стве Индекс тари- фов на грузо- вые пере- возки
1 Белгородская 112 115,8 124,5 110,3 108,3
2 Брянская 112,9 132,1 106,1 109,9 107,3
3 Владимирская 115,3 115,5 113,3 113,9 113,5
4 Воронежская 111,7 115,4 126,8 117,7 109,7
5 Ивановская 114,7 115,1 115 115,2 100
6 Калужская 114,3 124,8 114,5 119,6 104,6
7 Костромская 113,5 115,1 101,4 111,3 116,7
8 Курская 116,2 116,1 142 113,7 116
9 Липецкая 113,4 118,1 121,8 112,7 140,5
10 Московская 111,7 129,5 108 105,8 134,7
11 Орловская 112,2 114,9 150 111,7 114
12 Рязанская 114,9 113,5 125,7 114,7 139,6
13 Смоленская 112,9 116,1 107,5 119,6 103
14 Тамбовская 110,5 115,6 123 115,5 118,9
15 Тверская 112,8 109,4 110,1 117,4 122,1
16 Тульская 116,7 118,3 121 117,2 105,9
17 Ярославская 111,9 113,3 111 109,6 132
Требуется:
1) определить наиболее подходящее количество кластеров для
разбиения областей на группы по всем пяти признакам;
2) провести классификацию регионов иерархическим мето-
дом;
3) дать графическое представление процесса объединения об-
ластей в виде дендрограммы;
4) для каждого из полученных кластеров дать содержательную
интерпретацию, определив кластерные профили.
Решение. В редакторе данных создадим таблицу, в которой будет
одна текстовая переменная и пять числовых (рис. 3.10).
8 - 1591
113
А- *Ииденсы иен [Набор, .данных?] - SPSS Редан гор Данных
Файл Правка Вид Данные Преобразовать Ана^з Графика: ЗДвис Oioio Справка
&HQ В * ™ О? М ‘Г Гт Нлё 1И:,^ г
:20: Области
Области Потребители Промышленность СХ Строительство Перевозки!
> I Белгород 112,00 115,80 124,50 110,30 108,30]
2 Брянск 112,90 132,10 106,10 109,90 107,30]
3 Владимир 115,30 11550 113,30 113,90 113,50!
i 4 Воронеж 111,70 115,40 126,80 117.70 109,70]
i 5 Иваново 114,70 115,10 115,00 115,20 100,001
6 Калуга 114,30 124,80 114,50 119,60 104,60’
! 7 Кострома 113,50 115,10 101,40 111,30 116,70|
I 8 Курск 115,20 116,10 142,00 113,70 116,00]
i 9 Липецк 113,40 118,10 121,80 112,70 140,50]
! ю Москва 111,70 129,50 108,00 105,80 134,701
! 11 Орел 112,20 114,90 150,00 111,70 114,00!
। 12 Рязань 114,90 11350 125,70 114,70 139,601
13 Смоленск 112,90 116,10 107,50 119,60 103,00]
14 Тамбов 110,50 115Д) 123,00 115,50 118,9б1
15 Тверь 112,80 109,40 110,10 117,40 122,10
1Б Тула 116,70 118,30 121,00 117Д0 105,90]
17 Ярославль 111,90 113,30 111,00 109,60 132,00]
1? i I"
Рис. 3.10. Индексы цен в редакторе данных
Для начала проведем предварительную классификацию, кото-
рая позволит определить наиболее целесообразное количество
кластеров. Для этого выберем в меню Анализ -> Классификация ->
Иерархическая кластеризация... (Analyze —> Classify —> Hierarchical Clus-
ter Analysis...).
Появится диалоговое окно Иерархический кластерный анализ
(рис. 3.11).
Поместим числовые переменные, соответствующие индексам
цен, в поле тестируемых переменных, а текстовую переменную
«Области» будем использовать для обозначения (маркировки) на-
блюдений.
Для начала должно быть достаточно только вывода обзорной
таблицы порядка агломерации. Для этого в окне Иерархический
кластерный анализ (Hierarchical Cluster Analysis) активизируем кноп-
ку Статистики... (Statistics...). Откроется диалоговое окно Иерархичес-
кий кластерный анализ: Статистики (Hierarchical Cluster Analysis: Statis-
tics), в котором активизируем вывод последовательности слияния,
опция Порядок агломерации (Agglomeration schedule) (рис. 3.12).
114
Рис. 3.11. Диалоговое окно Иерархический кластерный анализ
Рис. 3.12. Диалоговое окно Иерархический кластерный анализ: Статистики
В результате в окне просмотра (табл. 3.6) будет приведен обзор
принадлежности, из которого можно определить очередность по-
строения кластеров, а также их оптимальное количество.
Для определения того, какое количество кластеров следовало
бы считать оптимальным, решающее значение имеет показатель,
выводимый под заголовком «Коэффициент» (Coefficient). Под этим
коэффициентом подразумевается расстояние между двумя класте-
рами, определенное на основании выбранной дистанционной меры
(в нашем случае это квадрат евклидова расстояния). На том этапе,
когда мера расстояния между двумя кластерами увеличивается
скачкообразно, процесс объединения в новые кластеры необходи-
мо остановить, так как в противном случае были бы объединены
уже кластеры, находящиеся на относительно большом расстоянии
8*
115
Таблица 3.6
Шаги агломерации
Этап Кластер объединен с Коэффициент Этап первого появления кластера Следующий этап
Кластер 1 Кластер 2 Кластер 1 Кластер 2
1 9 12 43,430 0 0 10
2 1 4 62,260 0 0 3
3 1 16 87,850 2 0 8
4 5 13 88,850 0 0 6
5 8 11 89,440 0 0 16
6 5 6 132,115 4 0 11
7 3 15 139,910 0 0 9
8 1 14 156,987 3 0 11
9 3 7 168,525 7 0 12
10 9 17 266,345 1 0 13
11 1 5 298,305 8 6 12
12 1 3 386,649 11 9 14
13 9 10 460,167 10 0 15
14 1 2 523,984 12 0 15
15 1 9 1012,915 14 13 16
16 1 8 1265,510 15 5 0
друг от друга. Оптимальным считается число кластеров, рав-
ное разности количества наблюдений (17) и номера шага (14),
после которого коэффициент увеличивается скачкообразно. Таким
образом, в нашем примере оптимальное количество кластеров
равно 3.
Теперь организуем для каждого наблюдения вывод информации
о принадлежности к кластеру. Для этого вновь откроем диалоговое
окно Иерархический кластерный анализ (Hierarchical Cluster Analysis) и
щелкнем по выключателю Статистики... (Statistics...) (см. рис. 3.11).
В разделе Принадлежность к кластерам (Clusters Membership) активи-
зируем опцию Одно решение (Single solution) и укажем желаемое
количество кластеров 3 (рис. 3.13). В этом же окне можно заказать
вывод матрицы расстояний между объектами исследования, опция
Матрица близостей (Proximity matrix).
Замечание: программа дает возможность получения диапа-
зона кластеров, который задается с помощью опции Диапазон ре-
шений (Range of solutions).
Информацию о принадлежности каждого наблюдения к опре-
деленному кластеру можно сохранить в новой переменной. Ис-
пользуя выключатель главного диалогового окна Сохранить...
116 ч
Рис. 3.13. Заполнение опций
Принадлежность к кластерам и Матрица близостей
(Save...), активизируем опцию Одно решение (Single solution) и для
указания желаемого количества кластеров введем 3 (рис. 3.14).
Теперь помимо таблицы порядка агломерации для каждого наблю-
дения будет выводиться также информация о принадлежности к
кластеру.
Рис. 3.14. Диалоговое окно
Иерархический кластерный анализ: Сохранить новые...
Вернувшись в главное диалоговое окно, щелкнем по выключа-
телю Графики... (Plots...) (см. рис. 3.11). Активизируем опцию выво-
да древовидной диаграммы Дендрограмма (Dendrogram) и посред-
ством опции Не надо (None) отменим вывод накопительной диа-
граммы (рис. 3.15).
С помощью кнопки Метод... (Method...) (см. рис. 3.11) получим
возможность выбрать метод образования кластеров, а также метод
расчета дистанционной меры и меры подобия. Программа SPSS
предлагает в общей сложности семь различных методов объедине-
117
Рис. 3.15. Диалоговое окно Иерархический кластерный анализ: Графики
ния. Метод Межгрупповые связи (Between-groups linkage) устанавли-
вается по умолчанию (рис. 3.16).
Рис. 3.16. Диалоговое окно Иерархический кластерный анализ: Метод
Дистанционные меры и меры подобия зависят от вида перемен-
ных, участвующих в анализе. По умолчанию в качестве дистанци-
онной меры для интервальных переменных устанавливается Квад-
рат расстояния Евклида (Squared Euclidean distance).
Программа SPSS дает возможность стандартизировать значе-
ния, если это необходимо. Соответствующие установки можно
118
сделать в поле Стандартизация (Transform Values'). На практике чаще
всего применяют ^-стандартизацию.
Приведем результаты затребованных нами процедур.
Дендрограмма (рис. 3.17) визуализирует процесс слияния, при-
веденный в обзорной таблице порядка агломерации (см. табл. 3.6).
Она идентифицирует объединенные кластеры и значения коэффи-
циентов на каждом шаге. При этом отображаются не исходные
значения коэффициентов, а значения, приведенные к шкале от О
до 25. Кластеры, полученные в результате слияния, отображаются
горизонтальными линиями.
Rescaled Distance Cluster Combine
CASE 0 5 10 15 20 25
Label Num +-------+------+-------+-------+------+
Липецкая
Рязанская
Ярославская
Московская
Владимирская
Тверская
Костромская
Ивановская
Смоленская
Калужская
Белгородская
Воронежская
Тульская
Тамбовская
Брянская
Курская
Орловская
Рис. 3.17. Дендрограмма кластеризации
Из табл. 3.7 видно, что в первый кластер попали 11 областей
Центрального региона (этот кластер получился самым большим),
во второй — 2 области (Орловская и Курская), в третий — 4 облас-
ти (Ярославская, Рязанская, Московская, Липецкая).
Матрица близостей (табл. 3.8) позволяет увидеть, например, что
наиболее близкими характеристиками (индексами цен) обладают
в первом кластере Белгородская и Воронежская области, во вто-
ром — Липецкая и Рязанская.
119
Таблица 3.7
tb
Принадлежность к кластерам
Наблюдение 3 кластера
1:Белгородская 1
2:Брянская 1 /1 S'./
3: Владимирская 1
4: Воронежская 1
5:Ивановская 1 а ’ л 1 .> s»s.
6:Калужская 1 Н-М" р ж
7: Костромская 1 XkOJ
8:Курская 2 . A'io f >
9:Липецкая 3
10:Московская 3
11:Орловская 2
12:Рязанская 3 Шь
13:Смоленская , 1
14:Тамбовская - ’ ' Л 1
15:Тверская 1 .. .
16:Тульская 1 .... ,
17:Ярославская 3
Однако пока неясно, что означают полученные три кластера.
Разобраться в этом нам помогут кластерные профили. Они пред-
ставляют собой распределенные по кластерной принадлежности
средние значения переменных, которые включены в анализ.
Если рассмотреть содержимое таблицы в редакторе данных, то
заметно, что там добавилась переменная clu3_1 (рис. 3.18). Эта пере-
менная указывает на кластерную принадлежность каждого наблюде-
ния и может быть использована для расчета кластерного профиля.
Выберем в меню Анализ -» Сравнение средних -» Средние (Ana-
lyze -> Compare Means -> Means...).
Переменным задачи присвоим статус зависимых, переменной
clu3_1 — статус независимой (рис. 3.19) и начнем расчет.
В качестве результатов выводятся средние значения (или стан-
дартные отклонения) переменных (табл. 3.9).
Видим, что в первый кластер попали области, имеющие при-
мерно одинаковый уровень цен по всем пяти секторам (правда,
немного выше индекс цен производителей промышленной про-
дукции), области из второго кластера отличаются высоким индек-
сом цен производителей на реализованную сельскохозяйственную
продукцию и, наконец, области из третьего кластера характеризу-
ются высоким индексом тарифов на грузовые перевозки.
120
Таблица 3.8
Матрица близостей
Регион Квадраты евклидовых расстояний
Белго- род Брянск Вла- димир Воро- неж Ива- ново Калуга i Кост- рома Курск Ли- пецк Моск- ва Орел Рязань . Смо- ленск Там- бов Тверь Тула Яро- славль
Белгород ,00 606,22 176,42 62,26 190,93 286,47 607,91 394,83 1057,14 1177,24 685,55 1014,19 404,48 143,94 489,81 93,96 750,69
Брянск 606,22 ,00 387,60 775,42 452,83 227,19 401,77 1645,83 1552,82 779,38 2271,67 1800,45 370,54 729,54 806,59 482,14 988,63
Владимир 176,42 387,60 ,00 224,10 187,35 200,63 162,01 831,15 813,06 752,10 1361,95 839,77 182,50 148,86 139,91 137,74 382,43
Воронеж 62,26 775,42 224,10 ,00 248,67 276,03 738,45 307,47 1008,82 1318,86 593,23 918,07 422,92 105,40 469,95 81,74 816,99
Иваново 190,93 452,83 187,35 248,67 ,00 135,02 480,50 990,50 1703,43 1557,81 1439,54 1685,50 88,85 439,19 553,36 89,05 1082,44
Калуга 286,47 227,19 200,63 276,03 135,02 ,00 481,64 1000,32 1435,41 1167,55 1513,44 1502,50 129,21 392,63 569,86 97,71 1001,02
Кострома 607,91 401,77 162,01 738,45 480,50 481,64 ,00 1662,90 993,57 608,41 2371,14 1130,98 295,15 498,29 175,04 556,09 334,94
Курск 394,83 1645,83 831,15 307,47 990,50 1000,32 1662,90 ,00 1021,13 1767,91 89,44 832,10 1404,95 405,39 1124,96 560,35 1260,14
Липецк 1057,14 1552,82 813,06 1008,82 1703,43 1435,41 993,57 1021,13 ,00 404,54 1510,17 43,43 1662,60 490,50 573,59 1228,98 223,79
Москва 1177,24 779,38 752,10 1318,86 1557,81 1167,55 608,41 1767,91 404,54 ,00 2440,71 682,75 1376,58 763,38 702,95 1278,84 293,21
Орел 685,55 2271,67 1361,95 593,23 1439,54 1513,44 2371,14 89,44 1510,17 2440,71 ,00 1264,10 1991,59 770,83 1720,72 968,67 1852,06
Рязань 1014,19 1800,45 839,77 918,07 1685,50 1502,50 1130,98 832,10 43,43 682,75 1264,10 ,00 1705,57 460,19 578,12 1190,31 308,90
Смоленск 404,48 370,54 182,50 422,92 88,85 129,21 295,15 1404,95 1662,60 1376,58 1991,59 1705,57 ,00 515,88 421,31 215,70 962,09
Тамбов 143,94 729,54 148,86 105,40 439,19 392,63 498,29 405,39 490,50 763,38 770,83 460,19 515,88 ,00 223,99 221,62 357,67
Тверь 489,81 806,59 139,91 469,95 553,36 569,86 175,04 1124,96 573,59 702,95 1720,72 578,12 421,31 223,99 ,00 475,71 175,68
Тула 93,96 482,14 137,74 81,74 89,05 97,71 556,09 560,35 1228,98 1278,84 968,67 1190,31 215,70 221,62 475,71 ,00 887,01
Яро- славль 750,69 988,63 382,43 816,99 1082,44 1001,02 334,94 1260,14 223,79 293,21 1852,06 308,90 962,09 357,67 175,68 887,01 ,00
Йй *Индексы цен [Набор_данных2] - SPSS .Редактор Данных
Файл Правка Вид Данные Преобразовать Анализ Графика Сервис Окно Справка
& а а е * 'at G> М -F S £ П <4>
20: Области — _ — _ — .. — -
Области Потребители ] Промышленность | СХ | Строительство | Перевозки сшзП Г
1 Белгород 112,00 115,80i 124.501 110,30 108,30 11
2 Брянск 112,901 132,10! 106.10! 109,90 107,30 —
3 Владимир 115,30! 11550! 113,301 113,90 11350 ii
4 Воронеж 111,70! 115,401 126,80! 117,70 109,70 ii
5 Иваново 114,70! 115,10! 115.00! 115,20 100,00 ii
6 Калуга 114,30! 124,80! 114,50! 119,60 104,60 и
7 Кострома 113,50! 115,10! 101,40! 111,30 116,70 1!
8 Курск 116,20! 116,10! 142,001 113,70 116,00 21
9 Липецк 113,40! 118,101 121,80! 112,70 140,50 3!
10 Москва 111,70! 129,5о1 108.00! 105,80 134,70 3!
11 Орел 112,20! 114,90Г 150,00! 111,70 ' 114,00 2*
12 Рязань 114,90! 113,50! 125,70! 114,70 139,60 3
13 Смоленск 112,901 116,10! 107,50! 119,60 103,00 1
14 Тамбов 110,50! 115.60! 123,00! 115,50 118,90 1
15 Тверь __ 112,801 109,40 110,101 117,40 122,10 1
Рис. 3.18. Исходная таблица в редакторе данных
вместе с переменной кластерной принадлежности Clu3_1
Рис. 3.19. Диалоговое окно Средние
Средние значения переменных
Таблица 3.9
Average Linkage (Between Groups) Потребители Промышлен- ность Сельское хозяйство Строительство Перевозки
1 113,39 117,56 114,84 115,24 110,00
2 114,20 115,50 146,00 112,70 115,00
3 112,98 118,60 116,63 110,70 136,70
Итого 113,39 117,56 118,92 113,87 116,87
122
3.2.2. Кластеризация It-средними । ‘
Метод к-средних, как было отмечено (см. подпараграф 3.1.4),
относят к итеративным методам классификации. Недостаток
их заключается в том, что необходимо заранее задать количество
кластеров, а не получить его в качестве результата, как в иерархи-
ческом анализе.
Программа SPSS предлагает довольно простую реализацию ме-
тода k-средних. Если количество кластеров к, которое необходимо
получить в результате объединения, задано заранее, то первые к
наблюдений используются как первые кластеры. На последующих
шагах кластерный центр заменяется наблюдением, наименьшее
расстояние от которого до кластерного центра больше расстояния
между двумя ближайшими кластерами. По этому правилу заменя-
ется тот кластерный центр, который находится ближе всего к дан-
ному наблюдению. Так получается новый набор исходных кластер-
ных центров. Для завершения шага процедуры рассчитывается
новое положение центров кластеров, а наблюдения перераспреде-
ляются между кластерами с измененными центрами. Этот итера-
ционный процесс продолжается до тех пор, пока кластерные
центры не перестанут изменять свое положение или пока не будет
достигнуто максимальное число итераций.
Пример 3.7. Требуется выполнить методом k-средних кластери-
зацию данных, приведенных в табл. 3.5.
Решение. Выберем в меню Анализ -> Классификация -> Кластери-
зация Передними (Analyze Classify К-Means Cluster...).
Откроется диалоговое окно Кластерный анализ методом к-средних
(К-Means Cluster Analysis') (рис. 3.20).
Переменные помещаем в поле тестируемых переменных. Теперь
нужно указать количество кластеров. Предварительно проведенный
для этих данных иерархический кластерный анализ (см. пример 3.6
в подпараграфе 3.2.1) позволил определить оптимальное количество
кластеров, равное 3. Это значение и вводим в поле Число кластеров
(Number of Clusters). Через выключатель Итерации... (Iterate...) укажем
число итераций, равное 99 (рис. 3.21); установленного по умолчанию
количества итераций 10 будет недостаточно. Как и ранее, восполь-
зуемся выключателем Сохранить... (Save...), чтобы с помощью допол-
нительных переменных зафиксировать принадлежность наблюдений
к кластеру. Для начала расчетов нажимаем ОК.
123
Рис. 3.20. Диалоговое окно Кластерный анализ методом /(-средних
Рис. 3.21. Диалоговое окно
Кластерный анализ методом i-средних: Итерации...
В отчете (табл. 3.10—3.15) могутбыть представлены первичные
кластерные центры, история итераций (т.е. как изменялись коор-
динаты кластерных центров с каждым шагом и на какой итерации
это изменение прекратилось), окончательные центры кластеров,
расстояние между конечными центрами, информация о принад-
лежности к кластерам, расстоянии объектов до кластерных цент-
ров, числе наблюдений в каждом кластере и т.п.
Как видно, эти результаты совпадают с результатами, получен-
ными ранее (см. табл. 3.7), за исключением нумерации кластеров.
Отчет позволяет установить, например, что из трех кластеров
наиболее близкими являются второй и третий, первый же кластер
занимает обособленное положение по отношению к двум другим
(см. табл. 3.13). В табл. 3.15 кроме кластерной принадлежности
выводится расстояние объектов (областей) до кластерных центров.
Например, во втором кластере ближе всего к центру Владимирская
область (ее характеристики будут определяющими в этой группе),
124
' Таблица 3.10
Начальные центры кластеров
Кластер
1 2 3
Потребители 112,2 112,9 113,4
Промышленность 114,9 116,1 118,1
Сельское хозяйство . 150,0 107,5 121,8
Строительство 111,7 119,6 112,7
Перевозки 114,0 103,0 140,5
Таблица 3.11
История итераций
Итерация Изменения центров кластеров
1 2 3
1 4,729 10,123 8,445
2 ,000 1,258 3,978
3 ,000 ,000 ,000
Таблица 3.12
Конечные центры кластеров
Кластер
1 2 3
Потребители 114,20 113,39 112,98
Промышленность 115,50 117,56 118,60
Сельское хозяйство 146,00 114,84 116,63
Строительство 112,70 115,24 110,70
Перевозки 115,00 110,00 136,70
Таблица 3.13
Расстояния между конечными центрами кластеров
Кластер 1 2 3
1 31,741 36,727
2 31,741 27,165
3 36,727 27,165
Таблица 3.14
Число наблюдений в каждом кластере
1 2
Кластер 2 11
3 4
Валидные 17
Пропущенные значения 0
125
Таблица 3.15
Принадлежность к кластерам
Номер наблюдения Область Кластер Расстояние
1 Белгородская 2 11,211
2 Брянская 2 17,990
3 Владимирская 2 4,929
4 Воронежская 2 12,523
5 Ивановская 2 10,383
6 Калужская 2 10,075 -
7 Костромская 2 15,716
8 Курская 1 4,729
9 Липецкая 3 6,757
10 Московская 3 14,928
11 Орловская 1 4,729
12 Рязанская 3 11,683
13 Смоленская 2 11,147
14 Тамбовская 2 12,575
15 Тверская 2 15,509
16 Тульская 2 8,375
17 Ярославская 3 9,175
а Брянская — занимает обособленное положение по отношению к
другим элементам кластера (в дальнейшем можно рассматривать
вопрос об отделении этого региона от второго кластера). Пример-
но на одинаковом расстоянии от центра второго кластера Иванов-
ская и Калужская области. Это означает не то, что они близки по
своим характеристикам, а то, что их геометрическое положение в
кластере примерно одинаково.
В заключение отметим, что для содержательной интерпретации
групп объектов, полученных при использовании метода ^-средних,
нет необходимости определять дополнительно кластерные профили,
так как ими фактически являются конечные центры кластеров.
3.2.3. Двухэтапный кластерный анализ
Процедура «двухэтапный кластерный анализ» представляет собой
средство разведочного анализа для выявления естественного раз-
биения на группы (или кластеры), которое без ее применения труд-
но обнаружить. В методе используется иерархическая агломера-
тивная процедура кластеризации. Алгоритм специально разработан
для классификации большого количества наблюдений. Про-
цесс осуществляется в два этапа. Вначале обнаруживаются центры
126
кластеров, а затем наблюдения приписываются кластерам на
основе построения специального дерева параметров кластериза-
ции, включающего в себя центры кластеров.
Алгоритм, используемый этой процедурой, имеет несколько
привлекательных особенностей, которые отличают его от
традиционных методов кластерного анализа:
• работа с категориальными (порядковыми, номинальными) и непре-
рывными переменными',
• автоматический выбор числа кластеров', сравнивая значения
критерия отбора модели для различных кластерных решений,
процедура может автоматически определить оптимальное чис-
ло кластеров;
• масштабируемость’, формируя дерево свойств кластеров (СК),
которое является компактным представлением информации о
наблюдениях, двухэтапный алгоритм позволяет анализировать
большие файлы данных.
Пример 3.8. В ходе исследования определены 12 характеристик
151 модели автомобилей, производимых 28 компаниями. Фрагмент
данных представлен в табл. 3.16.
Требуется провести сегментацию производителей по характе-
ристикам выпускаемых ими автомобилей.
Решение. Вначале проведем классификацию автомобилей по
однородным группам и выявим профили полученных сегментов.
Выберем в меню Анализ —> Классификация —> Двухэтапный кластер-
ный анализ... (Analyze Classify Two-Step Cluster Analysis...).
Откроется диалоговое окно Двухэтапный кластерный анализ (Two-
Step Cluster Analysis) (рис. 3.22).
На рис. 3.22—3.25 представлена последовательность заполнен-
ных диалоговых окон, необходимых для реализации поставленной
задачи.
Сделаем некоторые пояснения по заполнению диалоговых окон.
J Мера расстояния (Distance Measure) (см. рис. 3.22). Выбор в
этой группе определяет, как вычисляется сходство между двумя
кластерами:
• Log-правдоподобия (Log-likelihood). Мера правдоподобия при-
писывает переменным вероятностное распределение. Предпо-
лагается, что непрерывные переменные имеют нормальное
распределение, а категориальные — мультиномиальное. Все
переменные предполагаются независимыми;
127
Buick BMW 1 Audi Acura i Производитель
Century Regal L/1 LU LU NJ NJ NJ OO OO LU A4 A6 A8 Integra TL RL‘ Модель
91,561 39,350 19,747 9,231 17,527 20,397 18,780 1,380 16,919 39,384 8,588 Продажи
1 1 1 1 1 1 1 1 1 1 1 Легковой To же Тип транспорт- ного средства (легковой, грузовой)
21,975 25,300 26,990 33,400 38,900 23,990 33,950 62,000 NJ NJ N) QC — О b/1 ООО ООО Цена
3,1 3,8 NJ NJ NJ bo bo V» 1,8 2,8 4,2 1,8 3,2 3,5 Объем двигателя
175 240 40 40 *-J LU LU О 150 200 310 140 225 210 Мощность
О о 40 40 о о 107,3 107,3 111,4 102,6 108,7 113,0 *— о О Ji. 00 ~ 04 b- NJ Колесная база
NJ NJ 'J 04 04 О OO 00 ЧО LO Д 68,2 76,1 74,0 67,3 70,3 71,4 Ширина
194,6 196,2 176,0 176,0 188,0 178,0 192,0 198,1 172,4 192,9 196,6] Длина
3,368 3,543 3,179 3,197 3,472 2,998 3,561 3,902 2,639 3,517 3,850 Снаряженная масса
L/1 OO 04 04 1л 04 04 NJ — — LJ OO 04 bj Ixi 4^ 13,2 17,2 18,0 Объем бака
NJ NJ Ы V» NJ NJ NJ Ui Д 04 NJ NJ NJ — NJ '-J NJ NJ NJ N) Ln ОС Расход топлива
LU 04 V» *-J NJ NJ NJ NJ bo NJ 40 04 NJ OO О NJ LU lu 40 lo NJ LU NJ NJ LU NJ b- Q4 ОО Ln -J LJ Логарифм продаж
Данные об автомобилях различных производящих компаний
Двухэтапный кластерный анализ
Производитель^.. г
^Модель [Модель]
►
►
Мера расстояния • •
. Log-прзаюподобия
Число кластеров
С;) Определять автоматически
Максимум: J15 в
Категориальные переменные: .........
j Тип транспортное... [ {--------->
| Н'' < ( Вставка j
[' :;>Э> [ Сброс ]
------------ ..----} I Отмена ]
Непрерывные переменные; ; [ Справка ]
Продажи в тыс... О;
; ^Цена втысяча...
Объем двигате...
J ^Мощность (л.С.... .
: л., .....,....
Количест во непрерывных переменны»
Подлежат стандартизации; <w1f
Считаются стандартизованными О
Критерий кластеризации
0 Байесовский информационный критерий (BIC)
0 Информационный критерий Акаике (AIC)
j Задеть
[Параметры..] [ Графики... ] | Вь1вод.. ]
Рис. 3.22. Диалоговое окно Двухзтапный кластерный анализ
Лпух.напный KiidciepiihiH аноди»; 11с1р<эмс1ры
^Обработка выбросов
П Применить фильтрацию шумов
К Выделение памяти -- -
Г Максимум (Мб); р4
Продолжить^
W: Отмена :н1|-
Стандартизация непрерывных переменных
^шаются стандартизованными;
:i Справка__|
I
Л
4
Псцдежет стандартизации:
^Продажи в тысяч
^Цена в тысячах!..
Объем двигателя
$ Мощность (л.с.)[ Д
i<< Д°™лмиге-!1^0)
Критерии настройки дерева свойств кластеров (СК)
Максимальная глубина дерева (уровней). |3
Максимально возможное
число узлов;
585
; Обновление модели кластеров.
:: : Г’ Импорт XML-Файла дерева свойств кластеров
Рис. 3.23. Диалоговое окно Двухэтапный кластерный анализ: Параметры }1
9-1591
129
Рис. 3.24. Диалоговое окно Двухэтапный кластерный анализ: Графики
Рис. 3.25. Диалоговое окно Двухзтапный кластерный анализ: Вывод
• Евклидова (Euclidean). Евклидова мера — это расстояние «по
прямой линии» между двумя кластерами. Она может быть ис-
пользована, только когда все переменные являются непрерыв-
ными (см. подпараграф 3.1.2).
J Число кластеров (Number of Clusters). Выбор в этой группе по-
зволяет задать, как будет определяться число классов:
130
• Определять автоматически {Determine automatically). Процедура
автоматически определит наилучшее число классов, используя
критерий, заданный в группе Критерий кластеризации (Clustering
Criterion). Дополнительно можно ввести положительное целое
число, задающее максимальное количество кластеров, которое
должна рассмотреть процедура;
• Задать {Specifyfixed). Позволяет зафиксировать количество клас-
теров в решении, определив его положительным целым чис-
лом.
V Количество непрерывных переменных {Count of Continuous Vari-
ables). Эта группа дает сводную информацию об установках, каса-
ющихся стандартизации непрерывных переменных, заданных в
диалоговом окне Параметры {Options).
V Критерий кластеризации {Clustering Criterion). Выбор в этой груп-
пе задает способ, которым автоматический алгоритм кластериза-
ции определяет число кластеров. Можно задать либо Байесовский
информационный критерий (Schwarz’s Bayesian Information Criterion,
BIC), либо Информационный критерий Акаике (Akaike’s Information
Criterion, AIC).
V Параметры... (Options...). В данном окне можно определить
переменные, подлежащие стандартизации, а также установить кри-
терии настройки дерева свойств кластеров.
V Графики... (Plots...). Процедура выводит столбиковые диаграм-
мы частот в кластерах, круговые диаграммы частот в кластерах,
а также диаграммы важности переменных.
V Вывод... (Output...). Процедура выдает значения информаци-
онных критериев (AIC или BIC) по числу кластеров в решении,
частоты в кластерах, а также описательные статистики по класте-
рам для окончательного разбиения на кластеры.
Структура отчета, который дает в нашем случае программа, бу-
дет иметь следующий вид:
1) таблица, позволяющая определить оптимальное число клас-
теров, которому соответствует наименьшее значение BIC и наи-
большее значение отношения мер расстояния (табл. 3.17). В нашем
примере оптимальное число кластеров равно 3;
2) частота распределения автомобилей по трем полученным
кластерам (табл. 3.18); .>:.«
3) профили кластеров (табл. 3.19); : i g
: 4) частоты для категориальной переменной (табл. 3.20);
5) круговая диаграмма распределения по кластерам (рис. 3.26);
9»
131
Таблица 3.17
Автоматическая кластеризация
Число кластеров Байесовский информа- ционный критерий Шварца (BIC) Изменение В1С(а) Отношение изменений В1С(Ь) Отношение мер расстояния(с)
1 2 пК 3 У ' 4 5 тЙ 6 Жй7 ;и 8 9 10 11 12 13 14 15 1435,798 1228,254 1132,272 1164,910 1211,522 1265,544 1335,742 1408,874 1492,557 1578,410 1670,273 1763,152 1857,778 1956,753 2055,803 -207,544 -95,981 32,637 46,613 54,022 70,197 73,132 83,683 85,853 91,864 92,878 94,627 98,974 99,050 1,000 ,462 -,157 -,225 -,260 -,338 -,352 -,403 -,414 -,443 -,448 -,456 -,477 -.477 1,528 ' 2,554 1,203 1,121 . 1,358 1,069 ьззз ;а( ’-о73 вн 1,255 1,045 1,084 $ 1,265 1,005 1,034
а Изменения по отношению к предыдущему числу кластеров в таблице. Ь Отношения изменений оцениваются относительно решения из двух кластеров. с Отношения мер расстояний основываются на сравнении решения для текущего количества клас- теров с предшествующим количеством кластеров.
Распределение по кластерам
Таблица 3.18
Число объектов % объединенных % от итога
Кластер 1 60 39,7% 39,7%
2 52 34,4% 34,4%
3 39 25,8% 25,8%
Объединенный 151 100,0% 100,0%
Итого 151 100,0%
6) процент наблюдений в кластере для категориальной пере-
менной (рис. 3.27);
7) по каждой переменной приводится дисперсия внутри клас-
тера с контрольной линией для общего среднего (рис. 3.28). Так,
в нашем примере наибольшая дисперсия переменной «Продажи
в тысячах» в третьей группе автомобилей;
8) важность непрерывных переменных для каждого кластера
(рис. 3.29-3.31).
132
Таблица 3.19
Центроиды (средние)
Кластер
1 2 3 Объединенный
Продажи в тыс. Среднее 54,76910 30,43875 82,74174 53,61516
Цена в тыс. Среднее 18,76068 37,62800 26,56182 27,27290
Объем двигателя Среднее 2,168 3,665 3,559 3,043
Мощность Среднее 140,72 232,10 187,92 184,38
Колесная база Среднее 102,852 108,387 112,972 107,372
Ширина Среднее 68,535 72,731 72,744 71,067
Длина Среднее 178,610 193,417 191,110 186,938
Снаряженная масса Среднее 2,83610 3,54444 3,96759 3,37227
Объем бака Среднее 14,858 18,448 22,064 17,956
Расход топлива Среднее 27,40 23,02 19,51 23,85
Логарифм продаж Среднее 3,3887 2,7155 3,9157 3,2930
Таблица 3.20
Частоты для переменной «Тйп транспортного средства»
Автомобиль Грузовик
Частота Процент Частота Процент
Кластер 1 59 53,2% 1 2,5%
2 52 46,8% 0 ,0%
3 0 ,0% 39 97,5%
Объединенный 111 100,0% 40 100,0%
Размер кластера
Номер кластера
Рис. 3.26. Круговая диаграмма распределения по кластерам
133
Процент внутри кластера «Тип транспортного средства’
Рис. 3.27. Процент наблюдений в кластерах
для категориальной переменной
Одновременные 95% доверительные интервалы
для средних значений
Продажи в тысячах
Контрольная пиния для общего среднего значения = 53,615
Рис. 3.28. Дисперсия внутри кластера для переменной
«Продажи в тысячах»
Номер кластера = 1
Применена поправка Бонферрони
Переменная Переменная
Объем двигателя -
Объем бака -
Снаряженная... -
Мощность (л.с.) -
Цена в тысячах -
Ширина -
Колесная база -
Расход топлива -
Длина -
Логарифм продаж -
Продажи в... -
-20 -15
]
-10 -5 0 5 10
Г Стьюдента
_____Критическое значение
[~| Тестовая статистика
Важность непрерывных переменных для первого кластера
Номер кластера = 2
Применена поправка Бонферрони
Мощность (л.с.) -
Продажи в... _
Ширина -
Объем двигателя _
Цена в тысячах -
Длина -
Снаряженная... _
Расход топлива _
Логарифм продаж -
Объем бака _
Колесная база _
Критическое значение
Тестовая статистика
-6
-2 0 2
ГСтьюдента
4 6 8
Рис. 3.30. Важность непрерывных переменных ДЛЯ второго кластера
135
Критическое значение
Тестовая статистика
в S
t
йнжД
жад/Ж мфвдтмй
t Стьюдента
Рис. 3.31. Важность непрерывных переменных для третьего кластера
Характеристика, для которой /-статистика находится левее ле-
вого критического значения, проявляется в данном кластере менее
всего. Соответственно, переменные, /-значение у которых правее
правого критического, — наиболее важны в данной группе.
Анализ отчета позволяет установить наличие трех сегментов,
в каждом из которых автомобили характеризуются следующим
образом:
1 — неэкономичные малой мощности;
2 — мощные, крупногабаритные, дорогие, непопулярные;
3 — самые экономичные, скорее популярные.
Принадлежность производителей к полученным кластерам
можно определить, используя Описательные статистики (Descriptive
Statistics) [9]. Для этого строим перекрестное распределение пе-
ременной «Производитель» и кластеризующей переменной
(табл. 3.21).
Из таблицы отчета видно, например, что самые экономичные
автомобили производят компании Dodge, Ford, Nissan, Toyota.
’ Таблица 3.21
Таблицдсруряженностн «Производитель — Номер кластера»_____
Производитель % по категории переменной «Номер кластера»
Профиль и номер кластера Итого
Неэкономичные малой мощности (1) Мощные непопулярные дорогие(2) Экономичные, скорее популярные(3)
Acura 1,7% 3,8% 2,0%
Audi 1,7% 3,8% 2,0%
BMW 3,3% 1,9% 2,0%
Buick 7,7% 2,6%
Cadillac । 5,8% 2,6% 2,6%
Chevrolet 6,7% 9,6% 6,0%
Chrysler c ; OBfe 5,0% 5,8% 4,0%
Dodge I 5,0% 1,9% 15,4% 6,6%
Ford 1 6,7% 3,8% 12,8% 7,3%
Honda 3,3% 7,7% 3,3%
Hyundai M 5,0% 2,0%
Infiniti !. 1,9% ,7%
Jaguar ; 1,9% ,7%
jeep - । 7,7% 2,0%
Lexus 7,7% 5,1% 4,0%
Lincoln 3,8% 2,6% 2,0%
Mercedes 5,0% 9,6% 2,6% 6,0%
Mercury 3,3% 3,8% 5,1% 4,0%
Mitsubishi 5,0% 3,8% 5,1% 4,6%
Nissan 3,3% 1,9% 10,3% 4,6%
Oldsmobile 3,3% 5,1% 2,6%
Plymouth 3,3% 1,9% 2,6% 2,6%
Pontiac [ 3,3% 5,8% 2,6% 4,0%
Porsche 1 I t 5,8% 2,0%
Saab ,. 1,7% 1,9% 1,3%
Saturn ' I '''° 8,3% 3,3%
Subaru | 1,7% 2,6% 1,3%
Toyota >r 6,7% 1,9% 10,3% 6,0%
Volkswagen 10,0% 4,0%
Volvo 6,7% 3,8% 4,0%
Итого 100,0% 100,0% 100,0% 100,0%
137
3.2.4. Комплексный пример использования
методов кластерного анализа
Пример 3.9. Имеются отдельные показатели социально-эконо-
мического положения Орловской области за период с 2000 по
2004 г. (табл. 3.22).
Таблица 3.22
Показатели социально-экономического положения Орловской области
в 2000-2004 гг.
№ п/п Показатель развития 2000 2001 2002 2003 2004
1 Объем промышленного производства (ОПП), млн руб. 15 078 17314 18 665 24 980 30 096
2 Инвестиции в основной капитал (ИОК), млн руб. 3305 6100 5730 5400 6900
3 Оборот розничной торгов- ли (ОРТ), млн руб. 9339 12 092 15 655 18 087 21 357
4 Объем выпуска сельско- хозяйственной продукции (ОВСХП), млн руб. 14016 12 068 14 032 15 227 15 409
5 Доходы консолидирован- ного бюджета (ДК.Б), млн руб. 4480 5123 7033 7656 8643
6 Дефицит (профицит) консолидированного бюджета (ДП), млн руб. 51,6 -438 -232 250 -34
7 Количество предприятий и организаций (КПиО) 3910 3918 4344 3905 4443
8 Сальдированный финан- совый результат деятельно- сти предприятий и органи- заций (СФР), млн руб. 10 052,5 2188,1 1920 3610 3998
9 Численность официально зарегистрированных безработных (ЧОЗБ), тыс. чел. 4 4,1 6,6 6,9 11,8
10 Среднедушевой денежный доход населения (СДД), РУб. 1330,8 1818,8 2567 3265 3845
Источник: http://www.cbr.ru.
138
Требуется:
1) используя процедуры кластерного анализа, сформировать
группы показателей с аналогичной динамикой за рассматриваемый
период времени;
2) дать содержательную интерпретацию полученных групп;
3) используя результаты кластеризации и корреляционный ана-
лиз, осуществить выбор факторов, наиболее подходящих для ана-
лиза среднедушевого денежного дохода;
4) подобрать уравнение регрессии, позволяющее получить до-
стоверный прогноз среднедушевого денежного дохода;
5) оценить прогнозные значения среднедушевого денежного
дохода на 2005—2006 гг. (для сравнения: по данным Орловского
регионального комитета государственной статистики, среднеду-
шевой доход населения Орловского региона в 2005 г. составил
4578 руб.).
Решение.
1. Для выбора оптимального количества кластеров воспользу-
емся таблицей порядка агломерации (табл. 3.23).
Таблица 3.23
Шаги агломерации
Этап Кластер объединен с Коэффициент Этап первого появления кластера Следующий этап
Кластер 1 Кластер 2 Кластер 1 Кластер 2
1 6 9 315 843,380 0 0 7
2 2 5 12160 548,000 0 0 4
3 7 10 14 983 846,280 0 0 4
4 2 7 46 310 415,840 2 3 6
5 3 4 68 067338,000 0 0 8
6 2 8 78 594497,190 4 0
7 2 6 130 830394,544 6 1
8 1 3 277 045 551,000 0 5 9
9 1 2 1083 089 015,855 8 7 0
Значительный скачок коэффициента наблюдается после шес-
того шага; как указано в подпараграфе 3.2.1, это означает, что для
данных, включающих 10 наблюдений, оптимальным является ре-
шение с четырьмя (10-6 = 4) кластерами.
Организуем теперь для каждого наблюдения вывод информации
о принадлежности к кластеру. Независимо от выбора процедуры
139
кластеризации исследуемые показатели классифицируются оди-
наково (табл. 3.24).
Таблица 3.24
Принадлежность к кластерам
Наблюдение 4 кластера
1:0ПП 1
2:И0К 2
3:0РТ 3
4:0ВСХП 3
5:ДКБ 2
6:ДП 4
7:КПиО 2
8:СФР 2
9:ЧОЗБ 4
Ю:СДД 2
По результатам кластеризации единственным представителем
первого кластера является показатель «Объем промышленного
производства». Второй кластер включает пять показателей, среди
которых «Инвестиции в основной капитал», «Доходы консолиди-
рованного бюджета», «Количество предприятий и организаций»,
«Сальдированный финансовый результат деятельности предпри-
ятий и организаций», «Среднедушевой денежный доход населе-
ния». Третий и четвертый кластеры представлены двумя показате-
лями: соответственно «Оборот розничной торговли» и «Объем
выпуска сельскохозяйственной продукции» относятся к третьему
кластеру, а «Дефицит (профицит) консолидированного бюджета»
и «Численность официально зарегистрированных безработных» —
к четвертому.
2. Разобраться в значении кластеров нам помогут кластерные
профили (табл. 3.25).
- ' Таблица 3.25
Кластерные профили
Кластер Среднее
2000 2001 2002 2003 2004
1 15078,00 17314,00 18 665,00 24980,00 30 096,00
2 4615,66 3829,58 4318,80 4767,20 5565,80
3 11677,50 12080,00 14 843,50 16 657,00 18 383,00
4 27,80 -216,95 -112,70 128,45 -11,10
Итого 6156,69 6018,80 6972,06 8238,69 9466,88
140
Показатель, представляющий первый кластер, характеризуется
устойчивым ростом средних значений в течение рассматриваемых
пяти лет (ускорение роста наблюдается в 2003 и 2004 гг.). Величины
из третьего кластера, имея тренд, схожий с тенденцией объема
промышленного производства, тем не менее характеризуются бо-
лее равномерными изменениями во времени. Индикаторы второ-
го кластера отличает самый низкий по сравнению с представите-
лями уже рассмотренных групп уровень средних значений, которые
больше соответствуют параболической тенденции. Интерпретация
четвертого кластера затруднительна в силу специфики представ-
ляющих его величин.
3. В дальнейшем рассмотрении больше других нас будет инте-
ресовать показатель «Среднедушевой денежный доход населения»
(СДД). В результате классификации СДД попал во второй кластер,
состав которого представлен в табл. 3.26.
Таблица 3.26
Состав второго кластера
Год СДД, руб. иок, млн руб. ДКБ, млн руб. КПиО СФР, млн руб.
2000 1330,8 3305 4480 3910 10 052,5
2001 1818,8 6100 5123 3918 2188,1
2002 2567 5730 7033 4344 1920
2003 3265 5400 7656 3905 3610
2004 3845 6900 8643 4443 3998
Анализ направления и силы связи для каждой пары переменных
в полученной группе проведем с помощью матрицы коэффици-
ентов парной корреляции [43], рассчитанных по Пирсону
(табл. 3.27).
Таблица 3.27
Матрица коэффициентов парной корреляции
СДД ИОК ДКБ КПиО СФР
СДД 1 ,724 ,9890) ,616 -,471
иок .724 1 ,708 ,604 -,8330
ДКБ ,989(**) ,708 1 ,684 -,496
КПиО ,616 ,604 ,684 1 -,357
СФР -,471 -,8330 -,49б -.357 1
♦* Корреляция значима на уровне 0.01 (1-сторон.). * Корреляция значима на уровне 0.05 (1-сторон.).
141
Прямая тесная связь показателя СДД наблюдается с величина-
ми «Инвестиции в основной капитал» (коэффициент корреляции
равен 0,724) и «Доходы консолидированного бюджета» (корреля-
ция составляет 0,989). Причем из отчета программы SPSS видно,
что статистически значима с вероятностью 99% корреляция с по-
казателем «Доходы консолидированного бюджета».
4. Подберем теперь уравнение парной регрессии [43], позволя-
ющее получить достоверный прогноз показателя СДД.
В табл. 3.28 представлен фрагмент регрессионного анализа в
SPSS.
Таблица 3.28
Фрагмент регрессионного анализа в SPSS
Модель Ненормированные коэффициенты Нормированные коэффициенты t Знч.
В Стд. ошибка Бета
1 Константа ДКБ -1269,160 .582 337,498 ,050 ,989 -3,761 11,675 ,033 ,001
И Наиболее подходящим оказалось линейное уравнение вида
f СДД = -1269,16 + 0,582 ДКБ,
так как оно обладает хорошими качественными характеристиками
(Етн = 4,2%, Л2 = 0,978), статистически значимо вместе со свои-
ми параметрами.
5. Прогноз СДД на 2005—2006 гг. (с вероятностью 80%) пред-
ставим в виде точечных и интервальных оценок. Результаты соот-
ветствующих расчетов приведены в табл. 3.29.
Л
л Таблица 3.29
Результаты прогнозирования
Год ДКБ СДД (фактическое) СДД (предсказанное) Нижняя граница Верхняя граница
2005 9844,698 4578 4460,459 4032,85 4888,07
2006 10 930,598 - 5092,608 4631,23 5553,99
График аппроксимации и прогноза (рис. 3.32) демонстрирует удач-
ное соответствие полученных результатов и фактических данных.
Завершая обзор процедур кластеризации, хотелось бы отметить,
что методы кластерного анализа заслуживают внимания, так как
142
Рис. 3.32. График аппроксимации и прогноза
по линейному уравнению парной регрессии
облегчают понимание интереснейших статистических методов и
взаимосвязей. Это, в свою очередь, расширяет возможности ана-
лиза, планирования и прогнозирования производственно-хозяй-
ственных ситуаций.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ*
Задача 3.1. Исследование структуры денежных расходов и сбере-
жений населения
В табл. 3.30 представлена структура денежных расходов и сбе-
режений населения по регионам Центрального федерального
округа Российской Федерации в 2003 г. [33].
Требуется:
1) определить оптимальное количество кластеров для разбие-
ния регионов на однородные группы по всем группировочным
признакам одновременно;
2) провести классификацию областей иерархическим методом
с алгоритмом межгрупповых связей и отобразить результаты в виде
дендрограммы;
3) проанализировать основные приоритеты денежных расходов
и сбережений в полученных кластерах;
* В полном объеме числовые данные для задач приведены на CD.
143
Г'Таблица 3.30
i Структура денежных расходов и сбережений населения
(%)
№ п/п Область ПТиОУ ОПиВ ПН ПФА ДР
1 Белгородская 62,3 7,9 1,5 28,3 8,4
2 Брянская 66,5 6,3 0,8 26,4 5,2
3 Владимирская 56,5 9,7 1,1 32,7 -0,7
18 г. Москва 76,8 9,4 3,6 10,2 -6,0
Обозначения:
ПТиОУ — покупка товаров и оплата услуг; ОПиВ — обязательные платежи
и взносы; ПН — приобретение недвижимости; ПФА— прирост финансо-
вых активов; ДР — прирост (уменьшение) денег на руках у населения.
4) сравнить полученную классификацию с результатами при-
менения алгоритма внутригрупповых связей.
Задача 3.2. Исследование показателей промышленности
В табл. 3.31 приведены основные показатели и фонды промыш-
ленности России за 2000—2004 гг.
Таблица 3.31
Основные показатели и фонды промышленности России за 2000—2004 гг.
Показатель 2000 2001 2002 2003 2004
ЧДО 161 155 151 145 151
ОПП 4763 5881 6868 8498 11 209
ЧПП 13 294 13 282 12 886 12 384 11 800
кв 1,2 1,1 1 1,1 1,1
Источник: http://www.gks.ru
Обозначения:
ЧДО — число действующих организаций, тыс.; ОПП — объем промыш-
ленной продукции, млрд руб.; ЧПП — среднегодовая численность про-
мышленно-производственного персонала, тыс. чел.; ФР — сальдирован-
ный финансовый результат, млн руб.; РПТ — рентабельность проданных
товаров; ОФ — наличие основных фондов, млрд руб.; ИОФ — степень
износа основных фондов, %; КО — коэффициент обновления; КВ — ко-
эффициент выбытия.
144
Требуется:
1) определить группы показателей, имеющих аналогичную ди-
намику во времени, обосновать выбор количества кластеров;
2) проанализировать специфику изменений во времени пока-
зателей каждого кластера, используя кластерные профили;
3) выяснить, какие показатели имеют тенденцию, соответству-
ющую динамике рентабельности проданных товаров;
4) используя результаты п. 3 и матрицу коэффициентов парной
корреляции, выбрать ведущие факторы для показателя РПТ;
5) провести регрессионный анализ с выбранными факторами.
На основе построенной модели дать точечные и интервальные
оценки рентабельности на 2005, 2006 гг.
Задача 3.3. Анализ рентабельности предприятий
В табл. 3.32 представлены значения показателей производствен-
но-хозяйственной деятельности предприятий машиностроения
[15].
Таблица 3.32
Показатели производственно-хозяйственной деятельности
предприятий машиностроения
Номер предприятия У2 *3 Л *5 Y
1 1,23 1,45 166,32 10,08 17,72 13,26
2 1,04 1,30 92,88 14,76 18,39 10,16
3 1,80 1,37 158,04 6,48 26,46 13,72
20 1,46 2,22 50,40 7,56 13,69 25,17
Обозначения:
Xt — премии и вознаграждения на одного работника; Х2 — фондоотдача;
Х2 — оборачиваемость нормируемых оборотных средств; Х4 — оборачива-
емость ненормируемых оборотных средств; Х5 — непроизводственные
расходы; Y — рентабельность.
Требуется;
1) провести классификацию предприятий на оптимальное ко-
личество кластеров, используя алгоритм, минимизирующий внут-
рикластерную дисперсию. Результаты представить в виде дендро-
граммы; J
10- 1591
145
2) выбрать факторы, более других влияющие на рентабель-
ность. Подтвердить полученные выводы методами корреляцион-
ного анализа;
3) подобрать уравнение регрессии, достоверно отображающее
зависимость рентабельности от выбранных факторов;
4) выяснить, как будет изменяться уровень рентабельности с
каждой единицей изменения ведущих факторов.
Задача 3.4. Анализ деятельности кредитных организаций
В табл. 3.33 и 3.34 представлены показатели деятельности кре-
дитных организаций, зарегистрированных соответственно в Ор-
ловской и Курской областях Центрального региона Российской
Федерации, за 2005 г.
Требуется:
1) определить оптимальное количество кластеров для показа-
телей каждой области. Осуществить классификацию показателей
поданным их изменений во времени. Сравнить результаты разби-
ения для двух областей;
2) провести иерархическую кластеризацию для каждой области
в диапазоне от 3 до 7 кластеров. Найти классификацию, в которой
группы показателей д ля Курской и Орловской областей полностью
совпадают;
3) используя результаты п. 2 и корреляционный анализ, ото-
брать факторы, более всего подходящие для анализа показателей
«Активы в рублях» и «Активы в валюте». Одинаков ли набор фак-
торов, полученный для каждой области?
4) провести регрессионный анализ ДЛЯ каждой области с целью
получения прогнозных оценок показателей «Активы в рублях» и
«Активы в валюте» на два ближайших месяца вперед. Результаты
исследований представить графически-
Задача 3.5. Классификация регионов по уровню социально-эконо-
мического развития
В табл. 3.35 приведены отдельные показатели социально-эко-
номического положения регионов Центрального округа России в
2004 г.
Требуется:
1) подобрать оптимальное количество кластеров для разбиения
регионов на однородные группы по всем группировочным призна-
кам одновременно;
146
Таблица 3.33
Показатели деятельности кредитных организаций в Орловской области, тыс. руб.
Показатель Январь Февраль Март Апрель Май Июнь Июль Август Сен- тябрь Октябрь Ноябрь
Активы в рублях 877 047 891 701 862 008 889 053 851 416 872 165 847 854 870 087 878 006 861 885 878 167
Активы в валюте 669 897 837 1464 1885 1914 2099 2823 2746 2247 3101
Пассивы в рублях 877 690 892 583 862 808 890 507 853 296 874 074 849 838 872 895 880 721 864 127 881 195
Вклады физиче- ских лиц 137 743 138 339 146158 153 597 159 065 163 578 172 887 178 790 192 389 200 115 209 708
Источник: http://www.cbr.ru
Таблица 3.34
Показатели деятельности кредитных организаций в Курской области, млн руб.
Показатель Январь Фев- раль Март Апрель Май Июнь Июль Август Сен- тябрь Ок- тябрь Ноябрь
Активы в рублях 2679,557 2760,339 2811,828 3014,000 3112,249 3194,933 3339,352 3388,981 3447,429 3678,745 3702,359
Активы в валюте 170,983 173,117 173,312 168,596 193,905 188,597 197,803 198,743 202,612 205,949 205,913
Пассивы в рублях 2694,022 2784,762 2825,321 3031,701 3153,905 3235,233 3777,690 3432,732 3488,840 3716,036 3739,184
Вклады физиче- ских лиц 132,612 133,924 136,669 135,904 132,837 135,261 135,682 138,850 139,135 141,394 141,175
Источник: http://www.cbr.ru 7’ / ..
Таблица 3.35
Показатели социально-экономического положения регионов Центрального округа России в 2004 г.
Область ОПП ИОК ОРТ ОВПСХ ДКБ ДП КПиО СФР ЧОЗБ СДД ИПЦ ИЦП
Белгородская 120018,8 19956,8 36559,8 29300,0 16690,0 962,1 24943,0 27139,2 11,186 4015,8 101,1 103,5
Брянская 32448,4 6994,0 30896,5 14482,7 14236,2 -468,1 12057,0 6366,9 12,700 3692,0 112,9 114,4
Ивановская 30655,1 8518,7 17137,1 6626,0 10527,8 33,7 27536,0 898,8 13,700 2604,5 112,0 107,8
... ...
Ярославская 93715,6 20535,1 31028,2 4084,2 17484,4 -1958,6 38417,0 6824,5 12,000 4986,0 111,7 109,1
Источник: http://www.gks.ru.
Таблица 3.36
Показатели социально-экономического положения регионов Центрального округа России в 2005 г.
Область ИОК ОРТ ОВПСХ ДКБ ДП КПиО СФР ЧОЗБ СДД ИПЦ ИЦП
Белгородская 12568,5 32794,2 25600,0 18506,1 1996,1 25713,0 33024,0 9,567 4955,0 110,9 99,4
Брянская 3997,5 26963,8 13459,7 13391,1 283,8 12685,0 4169,8 11,600 4353,5 109,3 105,0
Ивановская 7113,0 14382,7 5870,6 9456,2 869,1 28500,0 848,9 12,700 2998,2 107,1 105,9
...
Ярославская 12349,8 23 538,3 3896,0 16 583,4 626,7 40 255,0 5931,9 11,600 5613,0 109,3 111,1
Источник: http://www.gks.ru.
Обозначения:
ОПП — объем промышленного производства, млн руб.; ИОК — инвестиции в основной капитал, млн руб.; ОРТ —
• оборот розничной торговли, млн руб.; ОВПСХ — объем выпуска продукции сельского хозяйства, млн руб.; ДКБ —
доходы консолидированного бюджета, млн руб.; ДП — дефицит (профицит) консолидированного бюджета, млн руб.;
КПиО — количество предприятий и организаций; СФР — сальдированный финансовый результат деятельности
предприятий и организаций, млн руб.; ЧОЗБ — численность официально зарегистрированных безработных, тыс. чел.;
СДД — среднедушевой денежный доход населения, руб.; ИПЦ — индекс потребительских цен, %; ИЦП — индекс
цен производителей, %.
2) выполнить классификацию, применив метод ^-средних;
’ 3) используя сравнение средних, определить кластерные про-
фили для каждой группы;
4) провести сравнительный анализ социально-экономического
положения областей, представляющих различные кластеры. Какое
положение в полученной классификации занимает ваш регион?
5) используя аналогичные данные за 2005 г. (показатели за пе-
риод с января по сентябрь 2005 г. приведены в табл. 3.36), оценить
основные тенденции социально-экономического развития регио-
нов Центрального округа Российской Федерации.
Замечание. Перед выполнением данного задания целесооб-
разно провести факторный анализ имеющихся показателей с целью
сжатия информации и выделения главных факторов [9].
Задача 3.6. Исследование показателей социально-экономического
развития г. Москвы
Известны отдельные показатели социально-экономического
положения г. Москвы за период с 2000 по 2004 г. (табл. 3.37).
Таблица 3.37
Показатели социально-экономического положения г. Москвы
за период с 2000 по 2004 г.
№ п/п Показатель развития 2000 2001 2002 2003 2004
1 Объем про- мышленного производства, млн руб. 229085,8 287 038,2 346694,7 389 091,5 483 489,9
2 Инвестиции в основной капитал, млн руб. 156 215,2 188 258,5 205 363,6 263 797,4 317 944,9
3 Оборот розничной торговли, млн руб. 682 337,3 886 389,8 1 034 743 1 178 970,3 1 370 135,1
... ...
9 Среднедуше- вой денежный доход населе- ния, руб. 8530,1 16 666,4 13 675,1 19 693,4 20 617,7
Источник: http://www.cbr.ru.
149
Требуется:
1) используя процедуры кластерного анализа, сформировать
группы показателей с аналогичной динамикой за рассматриваемый
период времени;
2) дать содержательную интерпретацию полученных групп;
3) используя результаты кластеризации и корреляционный ана-
лиз, осуществить выбор факторов, наиболее подходящих для ана-
лиза доходов консолидированного бюджета (ДКБ);
4) подобрать уравнение регрессии, позволяющее получить до-
стоверный прогноз ДКБ;
5) выполнить точечный и интервальный прогноз показателя на
2005 и 2006 гг. ;
Задача 3.7. Исследование рынка жилья
В табл. 3.38 представлены данные по рынку жилья в городе N.
Таблица 3.38
Данные по рынку жилья в городе N
№ п/п Район Стоимость при продаже, тыс. долл. Оценочная стоимость, тыс. долл. Время от послед- ней оценки,лет
I Северный 110,6 107,0 1
2 Южный 171,4 104,8 4
3 Восточный 276,5 209,0 3
1000 Южный 247,9 181,1 3
Требуется: !
1) распределить квартиры на оптимальное количество групп; «
2) определить профиль каждого кластера; ।
3) определить принадлежность районов города к выделенным
сегментам (на основе построения перекрестного распределения
переменной «Район» и кластеризующей переменной).
Задача 3.8. Классификация сотрудников i
В табл. 3.39 представлены данные о сотрудниках некоего пред-;
приятия.
Требуется:
1) определить оптимальное количество групп сотрудников; *
150
Таблица 3.39
Данные о сотрудниках предприятия
№ п/п Воз- раст Доход, тыс. руб. Цена транс- портного средства, тыс. руб. Уровень образования Стаж Удовлетво- ренность работой Пол
1 55 72 36,2 Неполное среднее 23 Удовл. Ж
2 56 153 76,9 Неполное среднее 35 Скорее удовл. М
3 28 28 13,7 Незакончен- ное высшее 4 И да и нет Ж
6400 28 22 П,1 Неполное среднее 2 И да и нет м
2) распределить сотрудников по группам, дать содержательную
интерпретацию полученных сегментов;
3) определить процентное соотношение мужчин и женщин в
найденных сегментах.
Задача 3.9. Сегментация сотрудников предприятия
Проведено анкетирование сотрудников в целях определения
характерных особенностей трех категорий занятых на предприя-
тии: сотрудник секретариата, сотрудник среднего звена и менеджер
(табл. 3.40).
Таблица 3.40
Результаты анкетирования сотрудников
№ п/п Пол Образование КЗ ЗП НЗП Стаж Опыт НМ Возраст
1 М 15 3 57 000 27 000 98 144 0 55
2 м 16 1 40 200 18 750 98 36 0 49
3 ж 12 1 21450 12 000 98 381 0 78
474 ж 12 1 29 400 14 250 63 9 0 43
Обозначения:
Образование — количество лет, потраченных на образование; КЗ — кате-
гория занятости (1 — сотрудник секретариата, 2 — сотрудник среднего
звена, 3 — менеджер); ЗП — заработная плата в настоящее время, руб.;
НЗП — начальная заработная плата, руб.; Стаж — время работы с момента
поступления, месяцы; Опыт — предыдущий опыт работы, месяцы; НМ —
принадлежность к национальному меньшинству (0 — нет, 1 — да).
151
Требуется:
1) определить оптимальное количество групп сотрудников. Вы-
яснить, не будет ли целесообразным уменьшить число кластеров,
г^ябранное программой;
i 2) распределить сотрудников на группы, различия между кото-
рыми очевидны, а внутри групп респонденты максимально похо-
жи. Описать профили полученных сегментов;
3) определить принадлежность трех категорий сотрудников к
полученным сегментам, построив перекрестное распределение
переменной КЗ и кластеризующей переменной.
Задача 3.10. Классификация государств по социально-экономичес-
p'j ким и демографическим признакам
Имеются социально-экономические и демографические пока-
затели, характеризующие 106 государств мира, принадлежащих к
определенной экономической группе (табл. 3.41).
Таблица 3.41
Социально-экономические и демографические показатели государств
№ п/п Страна ЧН ПН ГН СПЖЖ СПЖМ ДС ВВП ЭГ СКД
1 Афгани- стан 20 500 25 18 44 45 168 205 3 6,9
2 Аргентина 33 900 12 86 75 68 25,6 3408 6 2,8
3 Армения 3700 126 68 75 68 27 5000 5 3,2
106 Замбия 9100 11 42 45 44 85 573 4 6,7
Обозначения:
ЧН — численность населения страны, тыс. чел.; ПН — плотность населе-
ния на 1 км2; ГН — доля городского населения, %; СПЖЖ — средняя
продолжительность жизни женщин; СПЖМ — средняя продолжитель-
ность жизни мужчин; ДС — детская смертность на 1000 новорожденных;
ВВП — валовой внутренний продукт надушу населения; ЭГ — регион или
экономическая группа (1 — страны с развитой экономикой, 2 — Восточ-
ная Европа, 3 — Тихоокеанский регион/Азия, 4 — Африка, 5 — Ближний
Восток, 6 — Латинская Америка); СКД — среднее количество детей в
семье.
152
Требуется:
1) провести кластеризацию государств на оптимальное число
кластеров;
2) дать содержательную интерпретацию полученных сегментов
на основе исследования кластерных профилей;
3) определить характерные особенности экономических групп
по их принадлежности к полученным сегментам.
Глава 4
ФАКТОРНЫЙ АНАЛИЗ
’ • ...
г
4.1. ФАКТОРНЫЙ АНАЛИЗ КАК МЕТОД ВЫЯВЛЕНИЯ
ЛАТЕНТНОЙ СТРУКТУРЫ И СКРЫТЫХ ЗАКОНОМЕРНОСТЕЙ
4.1.1. Основные понятия факторного анализа
Факторный анализ (ФА) — это совокупность методов, которые
на основе реально существующих связей объектов (признаков)
позволяют выявить латентные (неявные) обобщающие характерис-
тики организационной структуры. При этом предполагается, что
наблюдаемые переменные являются линейной комбинацией фак-
торов. Под фактором понимается гипотетическая непосредственно
не измеряемая, скрытая (латентная) переменная, в той или иной
мере связанная с исходными наблюдаемыми переменными. К фак-
торному анализу относятся: метод главных компонент; методы
многомерного шкалирования, применяемые для формирования
факторного пространства по информации о близости объектов;
методы кластерного анализа, применяемые для описания неколи-
чественных факторов.
Основные цели факторного анализа:
• сокращение числа переменных (редукция данных);
• определение структуры взаимосвязей между переменными
(классификация переменных);
• косвенные оценки признаков, неподдающихся непосредствен-
ному измерению;
• преобразование исходных переменных к более удобному для
интерпретации виду.
Если кратко охарактеризовать факторный анализ, то наиболее
важными являются следующие моменты:
1) в противоположность контролируемому эксперименту фак-
торный анализ опирается в основном на наблюдения над естествен-
ным варьированием переменных;
2) при использовании факторного анализа совокупность пере-
менных, изучаемых с точки зрения связей между ними, не выбирается
произвольно: сам метод позволит выявить основные факторы, ока-
зывающие существенное влияние в данной области;
3) факторный анализ не требует предварительных гипотез, на-
оборот, он сам может служить методом выдвижения гипотез, а так-
154
же выступать критерием гипотез, опирающихся на данные, полу-
ченные другими методами;
4) факторный анализ не требует априорных предположений от-
носительно того, какие переменные независимы, а какие зависимы,
метод не преувеличивает причинно-следственные связи и решает
вопрос об их мере в процессе дальнейших исследований.
Метод факторного анализа первоначально был разработан в
психологии с целью выделения отдельных компонентов человече-
ского интеллекта из многомерных данных по измерению различ-
ных проявлений умственных способностей. Однако очень быстро
этот метод завоевал и такие области применения, как социология,
экономика, география и др. [27].
Переменные, значения которых можно измерить, нередко име-
ют для исследуемого объекта достаточно условный характер, лишь
опосредованно отражая его внутреннюю структуру, движущие
механизмы или факторы. Например, исследователь ставит цель:
провести сравнительный анализ темпов экономического роста
отдельных регионов. Закономерен вопрос: чем измерить эконо-
мическое развитие и какие показатели следует включить в иссле-
дование?
Когда неизвестный фактор проявляется в изменении несколь-
ких переменных, в процессе анализа можно наблюдать существен-
ную корреляцию между переменными. Тем самым факторов может
быть существенно меньше, чем измеряемых переменных, число
которых исследователь выбирает достаточно субъективно.
Степень влияния фактора на некоторый показатель (перемен-
ную) статистически характеризуется величиной дисперсии этого
показателя при изменении значений фактора. Если расположить
оси исходных переменных ортогонально друг к другу, то можно
обнаружить, что в этом многомерном пространстве объекты груп-
пируются в виде эллипса рассеяния, более вытянутого в одних
направлениях и почти плоского в других. Если теперь провести
новые оси соответственно осям эллипса рассеяния, то можно го-
ворить о выделении скрытых факторов и оценивать их сравнитель-
ную значимость в терминах дисперсии. При этом оказывается, что
толщина такого эллипса по некоторым осям настолько мала, что
можно исключить эти факторы из исследования.
Как правило, применение методов факторного анализа вклю-
чает три этапа:
1) выделение первоначальных факторов;
155
2) вращение выделенных факторов в целях облегчения их ин-
терпретации в терминах исходных переменных (в частности, для
исключения отрицательных значений);
3) содержательная интерпретация новых факторов в предмет-
ных терминах, что является творческой задачей исследователя,
выходящей за рамки предлагаемого формального метода.
Наиболее часто факторный анализ используется для выявления
в наблюдаемых признаках хр ..., хк некоторых латентных (скры-
тых) переменных fm, называемых факторами. Гипотеза о наличии
этих факторов основана на предположении о существовании чего-
то общего в наблюдаемых признаках. Выводимые гипотетические
факторы обладают следующими свойствами:
1. Они образуют линейно независимый набор переменных,
т.е. ни один из факторов (компонент) не выводится как линейная
комбинация остальных.
2. Переменные, являющиеся гипотетическими факторами,
можно разделить на два основных вида — общие и характерные
факторы. Они отличаются структурой весов в линейном уравне-
нии, которое выводит значение наблюдаемой переменной из ги-
потетических факторов. Общий фактор имеет несколько пере-
менных с ненулевым весом, или факторной нагрузкой, соответ-
ствующей этому фактору. При этом фактор называется общим,
если хотя бы две его нагрузки значительно отличаются от нуля.
Характерный фактор имеет только одну переменную с ненуле-
вым весом (т.е. только одна переменная от него зависит).
3. Всегда предполагается, что общие факторы не коррелируют
с характерным фактором, также и характерные факторы не корре-
лированы между собой.
4. Обычно предполагается, что общих факторов меньше, чем
наблюдаемых переменных, однако число характерных факторов
принимают равным числу наблюдаемых переменных.
4. 1.2. Методика факторного анализа в случае
одного объясняющего фактора
В случае существования только одного фактора суть ФА состо-
ит в объяснении корреляции между наблюдаемыми признаками с
помощью корреляции этих признаков с фактором г(х/, /), i = 1, к.
В общем случае может быть несколько факторовт < к.
Корреляцию между наблюдаемыми признаками и факторами обо-
156
значают r(xz, jJ) = ajjf i = 1, k; j = 1, m. Величины йу называются
факторными нагрузками, они образуют матрицу факторных нагру-
зок
А = (ау), i = \,k\j = \,т.
Как правило, основная цель факторного анализа состоит в объ-
яснении корреляционной матрицы признаков R ее матрицей фак-
торных нагрузок А. Матрицу А находят численными методами,
определяя собственные числа и векторы матрицы R при выполне-
нии условия т < к.
Предположим, существует один объясняющий фактор. На пер-
вом этапе формируют матрицу наблюдений (исходных данных) X],
'Ио
где п — количество наблюдений признаках,.
Вычисленная корреляционная матрица наблюдений Xравна
Целью факторного анализа является нахождение латентной
переменной (так называемого фактора), которая бы позволила вос-
произвести наблюдаемую корреляционную матрицу с использова-
нием соответствующей процедуры вычислений. Редуцированную
(преобразованную) корреляционную матрицу R+ можно воспроизвес-
ти с помощью вектора а факторной нагрузки по уравнению
R+ = aa\ (4.1)
Ч2 12 ' • л/ 'аС
'21 • • r2k — (°1 а2 — ak) а2 (4.2)
Л1 Пс2 • / :: Ч
157
Вектора = (аха2... ак) представляет собой факторную нагрузку
ненаблюдаемого фактора. В результате умножения ааТ получим
матрицу R+, принципиально отличающуюся от R диагональными
элементами. Диагональные элементы матрицы R+ называются
общностями. Общность /-го элемента будем обозначать через А?.
Величина /? = 1 - А? называется характерностью. Диагональные
элементы исходной и редуцированной корреляционных матриц
связаны соотношением
г, = г/ + /2. (4.3)
Таким образом, значения компонент вектора а, называемых
факторными нагрузками, воспроизводят все коэффициенты кор-
реляции для всех переменных. Фактор f непосредственно для из-
мерения не доступен — он гипотетичен. Для установления таких
гипотетических факторов и применяется факторный анализ.
Из приведенного алгоритма ясно, что, прежде чем определить
фактор, нужно построить редуцированную корреляционную мат-
рицу R+ по значениям общностей. Оценка общностей составляет
первую проблему факторного анализа, проблему общности. Второй
проблемой является определение фактора. Это так называемая
проблема факторов.
4. 1.3. Методика факторного анализа
в случае нескольких объясняющих факторов
В общем случае для объяснения корреляционной матрицы по-
требуется не один, а несколько факторов. Каждый фактор харак-
теризуется столбцом, каждая переменная — строкой матрицы А.
Фактор называется генеральным, если все его нагрузки значитель-
но отличаются от нуля и он имеет нагрузки от всех переменных.
Схематически такой фактор изображен на рис. 4.1 столбцомfx.
Фактор называется общим, если хотя бы две его нагрузки значи-
тельно отличаются от нуля. Столбцы/j,/2,/3 на Рис- 4.1 представ-
ляют такие общие факторы. Они имеют нагрузки от более чем двух
переменных. Если у фактора только одна нагрузка, значительно
отличающаяся от нуля, то он называется характерным (см. столбцы
их—и6 на рис. 4.1). Каждый такой фактор представляет только одну
переменную. Решающее значение в факторном анализе имеют
общие факторы. Если общие факторы установлены, то характер-
ные получаются автоматически.
158
Число высоких нагрузок переменной на общие факторы назы-
вается сложностью. Например, переменная %! на рис. 4.1 имеет
сложность 2, а переменная х3 — сложность 3.
A f2 f3 щ и2 и3 U4 и5 и6
;iV 'я Н
* 1 X X X
* 2 X X X
'h . '}>' 'li '* '
* 3 X X X X .. , ..Л. . :
* 4 X X X
* 5 XX X
Х6 X X X
Генеральный
фактор
•Ч’, ’ . t! !
Общие факторы Характерные факторы
Рис. 4.1. Схематическое изображение факторного отображения t ;
(крестик означает высокую факторную нагрузку)
Построим модель
т ___ ______
xi = X aijfj + ei’ i = l,k’, j = 1, rn, (4.4)
J=1
гдех(. — наблюдаемые переменные (исходные признаки);
fj— ненаблюдаемые факторы т < к\
йу — факторные нагрузки;
<?z — случайная ошибка.
Здесь fj и е, не коррелированы, причем et связана только с хр
нулевым средним и дисперсией /?•:
М(ееу) = Е, М(е) = 0, M(ef) = О,
&fj — некоррелированные случайные величины с нулевым средним
и единичной дисперсией:
M(f) = О, М(#т) = Е
(Е — единичная матрица).
Тогда
т
<4-5)
;=1 »
159
т
где а? _ -_я общНОСТЬ) представляющая собой часть диспер-
7=1 сии х,., обусловленная факторами; ,
/? — часть дисперсии х,., обусловленная ошибкой.
В матричной записи факторная модель примет вид
X - AF + е, (4.6)
где А — матрица нагрузок (размерности к х /и);
F— вектор факторов (размерности т х 1); i?i
е — вектор ошибок.
Корреляции между переменными, выраженные факторами,
можно вывести следующим образом:
R = М(ХХ^) = MiAFFW) + M(LIX) =
= A4T + Z2 = /?+ + Z2, (4.7)
где Z2 = (/?) — диагональная матрица порядка к, содержащая дис-
персии ошибок [15].
Основное условие: Z2 — диагональная, а разность R - L2 — не-
отрицательно определенная матрица. Дополнительным условием
единственности решения является диагональность матрицы
A{L2)~XA\
Имеется множество методов решения факторного уравнения.
Наиболее ранним методом факторного анализа является метод
главных факторов, в котором методика анализа главных компонент
используется применительно к редуцированной корреляционной
матрице R+ с общностями на главной диагонали. Для оценки общ-
ностей обычно пользуются коэффициентом множественной кор-
реляции между соответствующей переменной и совокупностью
остальных переменных.
Факторный анализ проводится исходя из характеристического
уравнения, как и в анализе главных компонент:
\R+ - Х£| = 0. (4.8)
решая которое, получают собственные числа X,- и матрицу норми-
рованных (характеристических) векторов V, и затем находят мат-
рицу факторного отображения:
А = ГЛ"1/2.
Для получения оценок общностей и факторных нагрузок исполь-
зуется эмпирический итеративный алгоритм, который сходится к
160
истинным оценкам параметров. Сущность алгоритма сводится к
следующему: первоначальные оценки факторных нагрузок опре-
деляются методом главных факторов. На основании корреляцион-
ной матрицы R формально определяются оценки главных компо-
нент и общих факторов:
к
Yauxi
(4.9)
где fj — главные компоненты (вектор-столбцы);
ау — коэффициенты при общих факторах;
X/ — исходные данные (вектор-столбцы);
Ху — соответствующее собственное значение матрицы R.
Оценками факторных нагрузок служат величины
1„ - i = 1, X; j - \,т.
У и V I ’ ’ ’ J ’
(4.Ш)
Оценки общностей получаются как
«id
/=|
На следующей итерации модифицируется матрица R: вместо
элементов главной диагонали подставляются оценки общностей,
полученные на предыдущей итерации. На основании модифици-
рованной матрицы R с помощью вычислительной схемы компо-
нентного анализа повторяется расчет главных компонент (которые
не являются таковыми с точки зрения компонентного анализа),
определяются оценки главных факторов, факторных нагрузок,
общностей, специфичностей. Факторный анализ можно считать
законченным, когда на двух соседних итерациях оценки общностей
меняются слабо.
Примечание. Преобразования матрицы R могут нарушать
положительную определенность матрицы R+ и, как следствие, не-
которые собственные значения R+ могут быть отрицательными.
Для лучшей интерпретации полученных общих факторов к ним
применяется процедура вращения. Если факторный анализ ведется
в терминах главных компонент, то значения факторов могут быть
вычислены непосредственно. В случае вращения главных компо-
нент соотношения, связывающие исходные переменные и значе-
ния факторов, несколько усложняются. Приведем в матричном
11-1591
161
виде соотношение, оптимальное по скорости вычисления и неза-
висимое от метода вращения факторов:
F =
(4.12)
где F — матрица т повернутых факторов;
А — матрица коэффициентов при общих факторах;
5Т — повернутая матрица Л; *
Ат — диагональная матрица т собственных членов;
X — матрица исходных данных.
При определении числа общих факторов руководствуются следу-
ющими критериями: число существенных факторов можно оце-
нить из содержательных соображений, в качестве числа общих
факторов т берется число собственных значений, больших либо
равных единице (по умолчанию), выбирается число факторов,
объясняющих определенную часть общей дисперсии или суммар-
ной мощности.
4.2. РЕАЛИЗАЦИЯ ФАКТОРНОГО АНАЛИЗА В SPSS
Рассмотрим различные задачи факторного анализа, решения
которых были получены с использованием SPSS — комплекса
программ статистической обработки и анализа данных.
Пример 4.1. Имеется следующая информация по крупнейшим
банкам России за 199* год (табл. 4.1).
Требуется:
1) выявить в структуре исходных данных скрытые факторы и
дать их содержательную интерпретацию;
2) представить результаты вычислений в графическом виде;
3) упорядочить структуру исходных данных в соответствии со
значениями выявленных факторов.
Решение. Выявим скрытые факторы и проведем классификацию
банков, используя факторный анализ. Группируя данные по пока-
зателям (по колонкам), сформируем матрицу наблюдений, описы-
вающую данные измерений 27 объектов по 8 соответствующим
переменным %], ...,х8:
*1,1 ‘ ‘ *1,8
х =
VX27,l х27,8,
162
Таблица 4.1
Характеристика крупнейших банков России за 199* год
Название банка Соб- ствен- ный капитал, руб. Привлеченные ресурсы, руб. Ссудная задолженность Средства в банках, руб. Полу- ченная балансо- вая прибыль, руб. Объем вложений в государ- ственные ценные бумаги, руб. .
исключая банки банков рубли валюта
Сбербанк РФ 6 099 889 61 067 494 2 693 209 12 245 033 3 506 209 8 494 017 3 010 424 27482031
Внешторгбанк 3 764 350 9 635 474 11 392 991 31 323 4 629442 12 580 665 876 083 2 778 819
ОНЭКСИМбанк 1 370 596 8 090 357 4 822 784 3 138 452 7159184 4 992 534 260 727 600 883
Инкомбанк 1 052 618 7 597 614 1 952 306 1 749462 3 329 294 3 115018 806 354 722 440
Мосбизнесбанк 640 478 3 121 342 874 474 1 177 193 1 793 015 1 636 690 482 539 969496
Роскредит 557 032 1 669 324 2 897 602 809 268 1 360 040 1 275 028 400 351 889 704
МФК 1 120 847 1 880 688 7 513 267 317 719 4 393 383 5 096 594 207 889 753 993
Империал 996 003 1 257 359 2 909 163 772 401 2 055 202 3 429 889 395 220 626 085
Моск, индустриальный 572 385 2 305 445 11424 1 234 517 222 695 208 384 609 219 185 066
Менатэп 625 027 2 155 954 621010 3 049 381 2 921 867 1 227 582 285 677 191631
Уникомбанк 469 496 6 009 677 155 665 1 381 584 406 261 106 505 463 639 86 559
Промстройбанк 487 892 3 617 644 1 056 781 1009 361 613 389 543 725 435 813 587 507
Банк «С.-Петербург» 139 342 80 577 60 209 465 825 142 151 115 487 131 294 21 885
Межд. Моск, банк 731 741 3 578 276 2 079 819 1883 1 067 004 4 379 298 206 038 485 507
Окончание табл. 4.1
Название банка Соб- ствен- ный капитал, руб. Привлеченные ресурсы, руб. Ссудная задолженность Средства в банках, руб. Полу- ченная балансо- вая прибыль, руб. Объем вложений в государ- ственные ценные бумаги, руб.
исключая банки банков рубли валюта
Стол, банк сбереж. 867 715 1 810 844 1 148 687 368 887 1413719 776 843 36 162 135 611
Тверьуниверс. банк 262 228 1 766 648 2 046 477 760 565 423 275 1 933 104 81 604 129 307
Автобанк 615 759 2 337 665 2 262 400 517 422 798 883 368 165 331 008 535 557
Возрождение 376 954 448 769 477 209 1 118 207 486 884 240 858 171 132 191 528
Стройпромбанк 349 026 1 591 390 126 045 516 400 129 389 239 225 348 931 285 697
Альфа-банк 278 098 1 613 021 495 630 310 688 1 134 677 342 809 85 612 60 312
Токобанк 1 032 806 922 507 1010 895 262 494 1 659 435 800 967 120 516 43 653
Мостбанк 375 585 525 904 1 459 773 1 378 033 1 168 135 516 771 109 647 4235
Якиманка 24 304 12 930 4665 27 838 76 350 24 058 17 708 13 571
Межкомбанк 413 497 981 672 687 848 119 884 812 640 620 219 187 428 488 873
Енисей 116210 469 296 4712 448 470 77 762 65 551 154 143 4170
Башкредитбанк 575 268 46 866 43 277 359 810 160 614 284 218 454 708 77 159
Мосстройэк. банк 246 722 909 856 219 163 1 115 686 87 453 61 600 136 567 12 864
Для описания данных используем редактор данных в SPSS,
т.е. рабочий лист, каждый столбец которого соответствует отдель-
ной переменной, а каждая строка — отдельному наблюдению,
в каждой ячейке хранится одно наблюдаемое значение переменной
(рис. 4.2).
- 0«пк 1 ий.н! 1 Р'Ф» I gss.bura
Сбербанк РФ 6099889 61067494 2693209,0 12245033 3506209.0 8494017,00: 3010424 27482031
Внешторгбанк 3764350 9635474 11392991 31323ХЮ 4629442.0 12580665 Д-: 876083Д 2778819
3 ОНЭКСИМбанк 1370596 8090357 4822784Д 3138452.0 7159184.0 4992534.00 i 260727Д 600883.0
Инкомбанк 1052618 7597614 1952306.0 1749462Д 3329294Д 311501800; 806354Д 722440,0
F Мосбизнесбанк Г64О478Д 3121342 874474.00 1177193,0 1793015.0 1636690.00 ! 482539Д 969496,0
6 Роскредит 557032Д 1669324 2897602,0 809268Д0 1360040.0 1276028.00! 400351Д 889704,0
7 МФК 1120847 1880688 7513267.0 317719Д0 4393383Д 5096594.00! 207889Д 753993.0
а Империал 996003,0 1257359 2909163.0 772401,00 2055202Д 3429889.00! 395220.0 626085,0
9 Моск, индустриальный 572385,0 2305445 11424,00 1234517.0 222695.00 203384.00Г 609219.0 185066,0
10 Менатэп 625027Д 2155954 621010.00 3049381Д 2921867Д 1227582.00! 285677Д 191631,0
и Уникомбанк 469496,0 6009677 155665,00 1381584Д 406261,00 106505.00! 463639.0 86559.00
12 Промстройбанк 487892.0 3617644 1056781.0 1009361,0 613389.00 543725 ДО; 435813.0 587507.0
13 Банк "С-Петербург" 139342,6 80577,00 60209,00 465825ДО 142151,00 115467.00* 131294.0 21885,00
Межд. Моск, банк 731741Д 3578276 2079619.0 1883ДО 1067004Д 4379298 ДО! 206038Д 485507Д
Рис. 4.2. Представление исходной информации в редакторе данных
Переменные в SPSS можно определить следующим образом:
щелкнуть по ярлычку Переменные (Variable view) в левой нижней
части таблицы. Так осуществляется переход в режим просмотра
переменных, где последовательно, строка за строкой описываются
необходимые переменные. При выборе имени переменной руковод-
ствуются следующими правилами:
1. Имена переменных могут содержать буквы латинского алфа-
вита и цифры, также допускаются некоторые специальные симво-
лы (без пробелов).
2. Имя переменной должно начинаться с буквы.
3. Последний символ имени не может быть точкой или знаком
подчеркивания.
4. Длина имени не должна превышать 8 символов.
Затем задаем тип переменной (численная, строковая и др.) и
форматы ввода, вывода переменной (рис. 4.3).
Созданный файл сохраняется с помощью стандартного диало-
гового окна.
Порядок выполнения факторного анализа
На первом шаге процедуры проводится нормализация заданных
значений переменных (т.е. из каждого значения вычитается выбо-
165
;]£) задача»ф
Dank
kaprtal
resursjb
resurs
.-tf _rub
zad_val
sredstva
pnbil
gos_bum
_2
3
_5
J
_8
9
[Hr
;HeT
Нет
Нет
Нет
Нет
Нет
•Нет
[Нет
:НбТ
Нет"
Нет
Нет
Нет
Тнет
|Нет
И 9
Ж"
э_
9
L
10‘
9"
.....
Текст
Числовая
Числовая
Числовая
Числовая
Числовая
Числовая
Числовая
Числовая
Пралущенны^Ш^на} Выравнивание^
[По левому краю i
IПо правому краю;
По правому краю;
По правому краю;
По правому краю:
Поправому краю|
По правому краю;
По правому краю'
По правому краю'
название банка
[Собственный капитал
Привл.ресурсы. иски. банки
Привлеченные ресурсы _____
Ссудная задолжен, (рубли)
Ссудная эадолж. (валюта)
Средства в банках_________
Полученная баланс, прибыль
Объем вложений в гос.бум.
Рис. 4.3. Описание переменных
рочное среднее и полученный результат соотносится со средним
отклонением по выборке), затем рассчитываются корреляционные
коэффициенты Пирсона между рассматриваемыми переменны-
ми [9].
Исходным элементом для дальнейших расчетов является кор-
реляционная матрица. Для построенной матрицы вычисляются
собственные значения и соответствующие им собственные векто-
ры, для определения которых используются оценочные значения
диагональных элементов матрицы (относительные дисперсии
простых факторов).
Собственные значения сортируются в порядке убывания, для
чего обычно отбирается столько факторов, сколько имеется соб-
ственных значений, превосходящих по величине единицу. Соб-
ственные векторы, соответствующие этим собственным значе-
ниям, образуют факторы, а их собственные значения получают
название факторных нагрузок, т.е. коэффициентов корреляции
между соответствующими переменными и факторами.
Для соответствующих вычислений выберем в меню Анализ —>
Снижение размерности (Сокращение данных) -э Факторный анализ
(Analyze —> Data Reduction —> Factor) (рис. 4.4). Откроется диалоговое
окно Факторный анализ (рис. 4.5).
Отметим все переменные слева и перенесем их в окно справа
Переменные (Variables). Щелкнем по кнопке Описательные... (Descrip-
tive statistics...) и оставим по умолчанию вывод первичных результа-
тов, включающий: первичные относительные дисперсии простых фак-
торов, собственные значения и процентные доли объясненной дисперсии.
Дополнительно можно вывести одномерные статистики (Начальное
решение (Initialsolution)) и корреляционную матрицу (рис. 4.6).
С помощью кнопки Извлечение... (Extraction...) (см. рис. 4.5)
можно выбрать различные методы отбора факторов. Наиболее
166
['1 задача1ф.а. - SPSS Редактор Данным
‘Файл Главка Вид Данные Преобразовать , Анагиз Графика Сервис Окно Справка
££|аЙ1 ва| »!.-•! ь=|с?| д| >г °тчет* '; ~
...1 J — ! —-J Описательные статистики ►
1: bank * 4 Сбербанк РФ Таблицы ►
ка Сравнение средних
gg Общая огненная модель
У Сметам*» модели
Корреляции
регрессия
1 О Лсглинейный анализ
64G> Классификация
>
>
>
►
ilij
12245033
| 31323.00
: 138452.0
749462,0"
? 177193,0
3506209,0
4629442.0
7159184'6
3329294,0
1793015.6
849401
125806
499253
311501
163669
11 Анализ «жал
ggg Непараметричеекие критерии
Временные ряды
Выживаемость
о2:
.., Множественные отклики
465 *
... Анализ пролущеньодх значенкв»,.,
/О'4 Сложные выборки
^чгДУЧ'Г...ffrw7rr<rr-..Н7Л'1Ч IЯ Г"
‘ 234517,0; _222695,00^__20838
049381,0 ’'292'1867.0 122758
38'1584.0* 406261‘бо’ 10650
: 009361 ji)t.613389,66|."54372
Ж5Я75ЛП1 UWiTinl ' 1154Я
Рис. 4.4. Выбор факторного анализа в процедуре
Снижение размерности в меню SPSS
Рис. 4.5. Диалоговое окно Факторный анализ
2SJ
Статистики ' •
Р Одномаряяв описэтельные
Р Начальное решение
• Корреляционная матрица--------
Г" Коэффициенты Г“ Обратная
Г" Уровни значимости Г" Восг$хэизведег<ная
Г“ Детерминант Г Ангиобраз
’ Г* КМО и критерий сферичности Бартлетта
Рис. 4.6. Выбор вида выводимых результатов в окне
Факторный анализ: Описательные
167
распространенным является предлагаемый по умолчанию метод
главных компонент (рис. 4.7).
Рис. 4.7. Выбор метода отбора главных факторов
Количество отобранных факторов в этом случае приравнивает-
ся к числу собственных значений, превосходящих единицу. Допол-
нительно можно указать нужное количество факторов, вывести
график собственных значений. Так как неповернутое факторное
решение предоставляет малозначимую информацию, можно
предотвратить его появление щелчком на соответствующей опции
Неповернутое решение (Not turned decision).
Кнопка Вращение... (Rotation...) (см. рис. 4.5) позволяет выбрать
метод вращения. При вращении факторов желательно, чтобы каж-
дый фактор имел ненулевые или значимые нагрузки (коэффици-
енты) только для небольшого количества переменных. Кроме того,
желательно, чтобы каждая переменная имела ненулевые или зна-
чимые нагрузки с небольшим числом факторов (если можно, то с
одним). Если несколько факторов имеют высокие значения фак-
торных нагрузок с одной и той же переменной, то их трудно интер-
претировать. Вращение не влияет на общности и процент объяс-
ненной полной дисперсии. Однако процент дисперсии, обуслов-
ленный влиянием отдельного фактора, меняется. Следовательно,
различные методы вращения позволяют интерпретировать различ-
ные факторы.
Если при вращении сохраняется прямоугольная система коор-
динат, оно называется ортогональным.
Существуют следующие методы вращения:
• варимакс (varimax) — вращение, максимизирующее дисперсию;
минимизирует число переменных с высокими значениями на-
грузок, увеличивая тем самым интерпретируемость факторов;
это самый распространенный метод;
168
• квартимакс (quartimax) — ортогональное вращение, при кото-
ром происходит минимизация количества факторов, необходи-
мых для объяснения переменной. Используется крайне редко и
не рекомендуется для применения;
• эквимакс (equamax) — ортогональное вращение: компромисс
между предыдущими методами;
• прямой облимин (direct oblimin) — косоугольное вращение;
• промакс (рготах) — комбинация ортогонального и косоуголь-
ного вращений.
Активизируем метод варимакса (рис. 4.8) и оставляем активи-
зированным вывод повернутой матрицы факторов.
Рис. 4.8. Выбор метода вращения отобранных факторов
Дополнительно можно организовать вывод факторных нагрузок
в графическом виде, в котором первые три фактора будут представ-
лены в трехмерном пространстве; при наличии двух факторов при-
водится изображение в одном слое.
Также можно сохранить найденные значения факторов в виде
дополнительных переменных. Для этого следует задействовать
выключатель Значения факторов... (Scores of factors...) (см. рис. 4.5)
и отметить Сохранить как переменные (Save as variables) (рис. 4.9).
По умолчанию установлен регрессионный метод.
Рис. 4.9. Выбор метода расчета выделенных факторов
169
Выключатель Параметры... (Options...) (см. рис. 4.5) предназначен
для обработки пропущенных значений. Здесь обеспечивается воз-
можность заменить пропущенные значения средними значениями
соответствующих переменных (рис. 4.10).
Рис. 4.10. Организация проверки пропущенных значений
Для проведения расчетов щелкнем ОК (см. рис. 4.5), в окне об-
зора появятся результаты (рис. 4.11).
Файл ГЬдска вид Данньи- Преебражхмтъ Встаем Формат
Г. Вывод I SPSS Viewer
Описательные статиспам
АнализN
4648318
11555619
1815833
2555681
1284733
2329968
1556606
1739808
2963373
1980585
400238,3
565890,8
1420894
5238168
Среднее
894884,0
Собственный капитал
Приьл.ресурсы. /сил.
банки
Привлеченные ресурсы
Ссудная задолжен.
(рубли)
Ссудная задолж.
(валюта)
Средства в банках
Полненная баланс,
прибыль
Объем вложений в гос.
&УМ. ______________
Стд откл
1252238
еы>0А
Журнал
Факторный анатмэ
Заголовок
Примечания
Описате/ым статистики
Обя/юсти
Полная объясненная дисперсия
Граф»* собственных значений
Матрица компонент
Матрица повернутых компонент
Матрица преобразования компонент
График компонент факторов 1,2
Рис. 4.11. Вывод результатов факторного анализа:
описательные статистики
* Факторный анализ
Из табл. 4.2, где представлена полная объясненная дисперсия,
видно, что только два фактора имеют собственные значения боль-
ше единицы и два отобранных фактора (компоненты 1 и 2) объяс-
няют 92,9% совокупной дисперсии.
170
.. -".г-;.г Таблица 4.2
Полная объясненная дисперсия
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % диспер- сии Кумулятив- ный % Всего % диспер- сии Кумулятив- ный %
1 5,512 68,906 68,906 4,569 57,110 57,110
2 1,921 24,016 92,921 2,865 35,812 90,921
3 ,395 4,939 97,860
4 ,063 ,791 98,651
' 5 ,050 ,624 99,275
6 ,032 ,394 99,669
7 ,019 ,240 99,909
8 ,007 ,091 100,000
Метод выделения: Анализ главных компонент.
Кроме того, можно организовать графический вывод результатов
для самостоятельного отбора необходимого количества скрытых
факторов. Например, критерий «каменистой осыпи» рекомендует
оставлять последним отобранным тот фактор, который показывает
начало «осыпи», т.е. плавной хвостовой части кривой (рис. 4.12).
Рис. 4.12. Вывод результатов факторного анализа:
собственные значения выделенных факторов
Дополнительно, в графическом виде можно представить фак-
торные нагрузки в системе координат выделенных соответству-
ющих факторов (рис. 4.13).
171
График компонент в повернутом пространстве
< ) Приел, рес. банков о ° Средства Задолж. в ранках в валюте о Капитал Прибыль Привл. pec. Q без банков о
Задолж. в рублях
$
чр
«о
Хк..
-1,0 -0,5 0,0 0,5 1,0
Компонента 1
Рис. 4.13. Вывод результатов факторного анализа:
графическое представление факторных нагрузок
Теперь начинается наиболее творческая часть факторного ана-
лиза. Необходимо попытаться объяснить отобранные факторы.
Воспользуемся матрицей повернутых компонент (табл. 4.3).
Таблица 4.3
Матрица повернутых компонент(а)
Компонента
1 2
Собственный капитал .811 ,548
Привл. ресурсы без банков ,973 ,207
Привл. ресурсы банков -,001 ,972
Ссудная задолж. (рубли) .955 ,079
Ссудная задолж. (валюта) ,193 ,850
Средства в банках ,396 ,884
Балансовая прибыль ,949 ,215
Вложения в гос. бумаги ,978 .145
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера,
а Вращение сошлось за 3 итерации.
Во-первых, можно взять в руку карандаш и в каждой строке
повернутой факторной матрицы отметить те факторные нагрузки,
которые имеют наибольшие абсолютные значения. Как уже было
сказано, эти факторные нагрузки следует понимать как корреля-
ционные коэффициенты между переменными и факторами.
172
Во-вторых, можно воспользоваться встроенными процедурами
ранжирования (сортировки) как в SPSS, так и в Excel.
Итак, для каждого выделенного фактора проведем сортировку
исходных переменных в порядке убывания их взаимосвязи с дан-
ным фактором. Можно предположить, что фактор 1, в первую
очередь связанный с низкорискованными инвестициями, уровнем
собственного капитала и нормой прибыли, характеризует надеж-
ность (стабильность) банков, тогда как фактор 2 — показатель
активности по привлечению средств (рискованности) банков.
Поскольку в ходе вычислений был проведен расчет значений фак-
торов, это означает, что к списку исходных переменных были до-
бавлены две новые переменные, названные fac1_1, fac2_1
(рис. 4.14).
» Мии» Грвфию* Уттпм окт Лммм»
ili
[Сбербанк РФ (
Вмацлоргбан I
I ОНЭКСИМбанк
Инкомбанк J
Мосбкзнасба
=_5
_•
то
МФК
Империал
Моск индустр
Манатэп
609988900] 61067494 Д
3764350 ДО' 9635474ДО
137^"доГ'авоэ57да
105261800! 7597614.00
640478ДО] 3121342ДО
К7032ДЬ|1689324Д0
1120847 ДО4 1880688,00
“»ШЭДбГ1257Э89Д0
" 572ЭЮДб|_ 230^5Дб]
Йбд27Дб| 215аюрй
26932О9Д0
113929910
4822784 ДО
1952306ДО
874474Д0
2897602 Л0
7513267 Д0
2909163 ДО
11424Д0
£2101000
»I MI-11
12245033ДХО6ХВ0О1_8/в«ПГрО 3010424Д27462031 4.9234
3138452 00 7159184 ДО
174946200' 332929400
__809268 001 136004080
31771900 4393383 00
_ 772401 ДО*" 2056202 00
2ЙИ6Д0
ХИ9381Л01 2921867 ДО
12580665 Д; 87608300
4992534.00*' 260727 ДО
_Э11Й18ДЬ| 806354 ДО
1636690 ДО* 482539 ДО
1275028 ДО ‘ 40035100
5096594 ДО! 207889 ДО
3429089 00 395220,00
208384.00* 609219Д0
™^2275ЮДОГ 285677 ДО4
2778819; -2304
600663.0* .2122
722440Д| .16135
9684960* Д120
" 6897040! -.2192
753993Д' -.7123
626065.0! -2459
185066Д' .11248
191631 Д' .02029
2872
3,657
1Д75
"Л447
..'157
Д764
ТДЗ!
.4965
“-.Л52
Рис. 4.14. Представление результатов расчета выделенных факторов
Используя вычисленные значения факторов для каждой пере-
менной, можно выполнить сортировку банков по степени убыва-
ния каждого отдельного фактора и таким образом составить рей-
тинг ведущих российских банков по уровню надежности и актив-
ности. В табл. 4.4 представлены пятерки лидеров каждого
рейтинга.
Рейтинги банков по надежности и активности
Таблица 4.4
Фактор 1 (надежность) Фактор 2 (активность)
Сбербанк РФ 4,92 Внешторгбанк 3,56
Инкомбанк 0,16 МФК 1,93
Уникомбанк 0,11 ОНЭКСИМбанк 1,87
Моск, индустриальный 0,11 Империал 0,50
Менатэп 0,02 Инкомбанк 0,44
173
Таким образом, в результате проведенного факторного анализа
были выявлены латентные факторы, характеризующие стабиль-
ность и активность российских банков, и проведена соответству-
ющая классификация банков. Полученные данные позволяют
сделать вывод, что только небольшую часть банков России в 199* г.
можно было считать надежными. Наиболее активные банки мож-
но охарактеризовать как рискованные, поскольку они не вошли в
число наиболее надежных. Единственным исключением стал Ин-
комбанк, занимающий высокие позиции в обоих рейтингах.
Пример 4.2. Имеются официальные статистические данные за
2003 г. по всем административным субъектам Российской Федера-
ции (табл. 4.5).
Таблица 4.5
Основные показатели социально-экономического положения
регионов Российской Федерации в 2003 г.
№ п/п Область Индекс промышленного производства, % к 2002 г. Строительство жилых домов, % к 2002 г. Продукция сельского хозяйства, % к 2002 г. Оборот розничной торговли, % к 2002 г. Объем платных услуг населению, % к 2002 г. Инвестиции в основной капитал, млрд руб. Иностранные инвести- ции, тыс. долл. США
1 Белгородская 105,4 101,2 104,5 107,4 104,2 14,7 23 339,00
2 Брянская 103,7 91,2 111,4 107,6 102,5 6,0 6402,00
3 Владимирская 105,2 108,2 100,1 108,6 103,2 9,3 85 179,00
80 Еврейская авт. 107,0 62,5 108,3 103,9 100,8 1,4 533,00
Источник', http://www.gks.ru
Требуется:
1) выделить и интерпретировать главные факторы по месторас-
положению и по экономическим показателям отдельных облас-
тей;
2) выполнить ранжирование областей по выделенным призна-
кам (факторам).
174
Решение. Первая задача — выявить скрытую структуру по рас-
положению областей (т.е. по географическому фактору). Для этого
сначала необходимо перегруппировать исходные данные на рабо-
чем листе. Воспользуемся инструментом Транспонирование (Trans-
posing) (в меню Данные) для транспонирования исходных перемен-
ных. Затем запускаем надстройку Анализ —> Снижение размерности —>
Факторный анализ (Analyze -» Data Reduction —> Factor), совершая те
же действия, что и в предыдущем примере.
В результате вычислений выделено два ведущих фактора, объ-
ясняющих 98,7% совокупной дисперсии (табл. 4.6). В данном ана-
лизе можно было оставить и один ведущий фактор, поскольку он
объясняет более 90% совокупной дисперсии, и интерпретировать
его как экономический рост.
Таблица 4.6
Полная объясненная дисперсия
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % дисперсии Кумулятив- ный % Всего % дисперсии Кумулятив- ный %
1 72,672 90,840 90,840 63,304 79,129 79,129
2 6,317 7,896 98,736 15,685 19,606 98,736
3 ,873 1,091 99,827
Попробуем объяснить два ведущих фактора. Для облегчения их
интерпретации проведем сортировку в порядке убывания значений
отдельных факторов по всем экономическим показателям (можно
средствами SPSS, можно средствами Excel) (табл. 4.7).
Таблица 4.7
Сортировка показателей по двум ведущим факторам
Фактор 1 Фактор 2
Иностр, инвестиции 2,14 Инвестиции 1,97
Оборот торговли -0,16 Иностр, инвестиции 0,76
Платные услуги -0,18 Сельское хоз-во -0,45
Пром, производство -0,22 Строительство -0,48
Строительство -0,23 Пром, производство -0,51
Сельское хоз-во -0,24 Платные услуги -0,64
Инвестиции -1,11 Оборот торговли -0,66
175
Фактор 1 характерен для активно развивающихся экономиче-
ских зон, перспективных с точки зрения вложения иностранных
инвестиций, фактор 2 — для областей со стабильным уровнем
экономического развития. Таким образом, можно предположить,
что двумя основными признаками скрытой структуры являются,
во-первых, благоприятные перспективы экономического развития
(фактор 1) и, во-вторых, стабильная экономическая инфраструкту-
ра, обусловленная географическими факторами (фактор 2).
Анализ матрицы факторных нагрузок подтверждает предвари-
тельные выводы. В табл. 4.8 приведены пятерки областей-лидеров
в рейтинге областей в порядке убывания зависимости от выделен-
ных признаков (перспективности и стабильности). Полученные
результаты анализа можно представить графически (рис. 4.15).
Здесь особенно наглядно представлено деление административных
субъектов на два лагеря.
Таблица 4.8
Рейтинги областей по перспективности и стабильности
Факт. нагр. 1 (перспективность) Факт. нагр. 2 (стабильность)
Пензенская область 0,999 Ямало-Ненецкий авт. округ 0,338
Ивановская область 0,998 Тюменская область 0,337
Курганская область 0,995 г. Москва 0,337
Еврейская авт. область 0,987 Московская область 0,337
Республика Бурятия 0,966 Сахалинская область 0,337
График компонент в повернутом пространстве
1,0-1
Московская область Белгородская область Орловская область а Курганская область 7. Пензенская область у
Эвенкийский авт. округ о Республика Дагестан Республика <Й?Респу( Ингушетия Карачаево 0 Ивановская область Читинская область . о лика Алтай Черкесская Республика
-1,0 -0,5 0,0 0,5 1,0
Компонента 1
Рис. 4.15. Вывод результатов факторного анализа:
графическое представление факторных нагрузок
176
Вторая задача анализа — выявить факторные признаки среди
экономических показателей. Берем данные из условия задачи (без
транспонирования). Запускаем факторный анализ и анализируем
полученные результаты (отобрано три фактора) (табл. 4.9).
Матрица повернутых компонент/а)
Таблица 4.9
Компонента
1 2 3
Индекс промышленного производства, % к 2002 г. ,199 -.695 -.004
Строительство жилых домов, % к 2002 г. ,035 .621 -,314
Продукция сельского хозяйства, % к 2002 г. -.025 ,018 ,926
Оборот розничной торговли, % к 2002 г. ,209 -,450 ,418
Объем платных услуг населению, % к 2002 г. ,056 ,769 ,100
Инвестиции в основной капитал, млрд руб. ,904 -,154 ,073
Иностранные инвестиции, тыс. долл. США ,905 ,025 -,024
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.
,а Вращение сошлось за 4 итерации.
Учитывая оценку общностей, исключим несколько показателей
как несущественные: строительство, промышленное производство
и оборот розничной торговли. Повторный анализ дает результаты,
приведенные в табл. 4.10.
Полная объясненная дисперсия
Таблица 4.10
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % диспер- сии Кумулятив- ный % Всего % диспер- сии Кумулятив- ный %
1 1,692 42,290 42,290 1,683 42,081 42,081
2 1,034 25,853 68,144 1,043 26,063 68,144
3 ,959 23,967 92,111
4 ,316 7,889 100,000
Метод выделения: Анализ главных компонент.
Имеем два выявленных фактора (в первоначальном варианте их
было три), которые подлежат интерпретации (табл. 4.11).
Фактор 1 — экономический подъем, т.е. перспективы экономиче-
ского ускорения, фактор 2 — неразвитая экономическая инфра-
структура, обусловленная географическими факторами и мало-
12 - 1591
177
Таблица 4.11
Матрица повернутых компонент(а)
Компонента
1 2
Продукция сельского хозяйства, % к 2002 г. Объем платных услуг населению, % к 2002 г. Инвестиции в основной капитал, млрд руб. Иностранные инвестиции, тыс. долл. США -.020 -.059 .916 ,917 ,739 -.703 ,053 -.001
Метод выделения: Анализ методом главных компонент. Метод вращения: Варимакс с нормализацией Кайзера, а Вращение сошлось за 3 итерации.
численностью населения, характерная для аграрных регионов.
Посмотрим пятерку лидеров (табл. 4.12).
Таблица 4.12
Сортировка областей по факторам
Фактор 1 Фактор 2
г. Москва 7,02 Камчатский край 1,95
Тюменская область 4,34 Приморский край 1.83
Ямало-Ненецкий авт. округ 1,32 Томская область 1.82
Сахалинская область 0,97 Тульская область 1.54
Московская область 0,94 Воронежская область 1,44
Окончательные выводы: по итогам 2003 г. наилучшее экономи-
ческое положение сложилось в Москве, Тюменской области и
Ямало-Ненецком автономном округе.
Пример 4.3. Имеются условные данные о среднедушевом по-
треблении товаров и услуг в некоторых странах за 199* г.
(табл. 4.13).
Требуется выделить и интерпретировать главные факторы.
Решение. Сначала рассмотрим потребление по странам. Для это-
го необходимо перегруппировать исходные данные на рабочем
листе. Воспользуемся инструментом Транспонирование (Transposing)
(в меню Данные) для транспонирования исходных переменных.
Запускаем надстройку Анализ ->Снижение размерности -> Факторный
анализ (Analyze -» Data Reduction -» Factor) и выявляем два фактор-
ных признака. В зависимости от их значений ранжируем показа-
тели расходов (табл. 4.14).
Выделено два фактора, объясняющие 90,5% вариаций перемен-
ных. Для их интерпретации проведем сортировку переменных
178
Таблица 4.13
Среднедушевое потребление товаров и услуг в 199* г.
Страна Про- дукты Кварт- плата Обуст- рой- ство дома Транс- порт Лече- ние Обуче- ние Одеж- да Про- чее
Россия 1200 475 210 280 525 800 210 35
Украина 1000 500 230 245 500 760 195 35
Белорус- сия 1250 500 220 225 475 815 220 35
Эстония 1685 660 285 400 525 1120 310 40
Казах- стан 925 370 160 205 475 570 165 30
Таджики- стан 450 240 100 140 315 415 115 25
США 2600 2825 1225 2025 2415 2025 1100 1360
Япония 1725 1550 800 1275 2200 1275 525 1000
Германия 2370 2150 1550 1000 2475 1000 700 500
Турция 1000 475 170 265 575 265 275 120
Таиланд 850 115 150 225 675 225 265 145
Таблица 4.14
Полная объясненная дисперсия
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % дисперсии Кумулятив- ный % Всего % дисперсии Кумулятив- ный %
1 8,758 79,619 79,619 6,098 55,437 55,437
2 1,202 10,928 90,547 3,862 35,110 90,547
3 ,604 5,492 96,039
по степени влияния отдельных факторов, учитывая факторные
нагрузки (левая часть таблицы — первый фактор, правая — второй)
(табл. 4.15), а также рассмотрим графическое представление ре-
зультатов (рис. 4.16).
Чтобы лучше понять смысл выявленных факторов, рассмотрим,
как зависят от них различные показатели расходов (табл. 4.16).
Обобщив все полученные результаты, можно сделать следу-
ющие выводы: фактор 1 характеризует развивающиеся страны
(основная статья расходов — продукты и учеба, т.е. инвестиции в
будущее); фактор 2 — богатство (благополучие). Проведенный
12*
179
Таблица 4.15
Сортировка стран по факторным нагрузкам
Факт. нагр. 1 Факт. нагр. 2
Эстония 0,96 Япония 0,92
Белоруссия 0,94 Германия 0,87
Россия 0,93 США 0,80
Украина 0,91 Турция 0,65
Казахстан 0,89 Таиланд 0,58
Таджикистан 0,86 Казахстан 0,45
Турция 0,66 Таджикистан 0,42
Таиланд 0,56 Украина 0,39
США 0,40 Россия 0,37
Германия 0,31 Белоруссия 0,33
Япония 0,25 Эстония 0,27
График компонент в повернутом пространстве
Япония оо Германия °СШАоТурция Таиланде Казахстан Россия^ Таджикистан^, Белоруссия
~I-----------1----------------------1----------Г-
-1,0 -0,5 0,0 0,5 1,0
Компонента 1
Рис. 4.16. Вывод результатов факторного анализа:
графическое представление факторных нагрузок
анализ позволяет утверждать, что наиболее благополучными и
здоровыми нациями из перечисленных являются японцы и
немцы, а в наиболее бедственном положении пребывают гражда-
не бывшего СССР.
Если искать скрытые факторы в структуре расходов (данные до
транспонирования), то получим графические результаты, приве-
денные на рис. 4.17.
180
Таблица 4.16
Сортировка показателей расходов по двум факторам
Фактор 1 Фактор 2
Продукты 1,85 Лечение 1,73
Обучение 1,26 Квартплата 0,88
Одежда -0,17 Продукты 0,63
Квартплата -0,34 Транспорт -0,03
Лечение -0,50 Обустройство дома -0,55
Обустройство дома -0,53 Прочее -0,60
Транспорт -0,57 Обучение -0,89
Прочее -1,00 Одежда -1,17
Рис. 4.17. Вывод результатов факторного анализа:
собственные значения выделенных факторов
Таким образом, отобран один фактор, объясняющий 89,7% ва-
риаций переменных (табл. 4.17).
Таблица 4.17
Полная объясненная дисперсия
Компонента Начальные собственные значения
Всего % дисперсии Кумулятивный %
1 7,180 89,748 89,748
2 ,401 5,015 94,763
3 ,295 3,682 ! ’ 98,445
181
Проведем сортировку показателей расходов по степени корре-
лированности с выявленным фактором и рассмотрим страны в
порядке убывания значения этого фактора (табл. 4.18).
Таблица 4.18
Сортировка показателей расходов и сортировка стран
по уровню жизни населения
Факт. нагр. Значение фактора
Квартплата 0,99 США 2,19
Транспорт 0,98 Германия 1,24
Одежда 0,98 Япония 0,97
Лечение 0,95 Эстония -0,17
Продукты 0,94 Белоруссия -0,46
Прочее 0,93 Россия -0,46
Обустройство дома 0,93 Украина -0,52
Обучение 0,88 Турция -0,58
Казахстан -0,65
Таиланд -0,67
Таджикистан -0,88
Данный фактор можно интерпретировать как уровень жизни
населения. Здесь лидирующее положение занимают США, в конце
списка — страны СНГ и Таиланд.
Рассмотрим постановку задачи, включающую нечисловую ин-
формацию.
Пример 4.4. Требуется выявить скрытые факторы, влияющие на
характеристики вкладчиков банка (табл. 4.19).
Решение. Сначала с помощью встроенных инструментов SPSS
перекодируем нечисловую информацию в числовую. Для этого
воспользуемся функцией меню Преобразовать —> Перекодировать —>
В те же переменные... (Recode into Same Variables). Исходные данные
(пол: женский (1), мужской (-1); образование: начальное (1), сред-
нее (2) и т.д.) теперь выглядят так, как показано на рис. 4.18.
Затем запустим факторный анализ и попробуем интерпретиро-
вать два выделенных фактора (рис. 4.19).
Фактор 1 можно охарактеризовать как богатство, фактор 2 —
как информированность (или опыт). Сравнение лидеров рейтингов
(табл. 4.20) подтверждает данную классификацию.
$82
Таблица 4.19
Характеристика вкладчиков банка
№ п/п Пол Образование Вклад, ден. ед. Возраст
1 М Высшее 300 30
2 Ж Высшее 350 35
3 Ж Незаконченное высшее 1000 21
4 М Среднее 250 42
5 М Среднее 200 20
6 Ж Высшее 400 38
7 Ж Незаконченное высшее 350 34
8 М Начальное 800 19
9 м Высшее 3000 54
10 ж Среднее 1800 48
11 м Высшее 250 63
12 ж Высшее 350 69
13 ж Незаконченное высшее 1600 53
14 м Среднее 350 28
15 м Среднее 200 42
16 ж Высшее 750 55
17 ж Незаконченное высшее 350 51
18 м Начальное 900 33
19 м Высшее 2500 53
20 ж Среднее 2000 69
Н] зад. 1.фа. SPSS Редактор Данных
«Яй» Лж» ВП4. Д«м«1ч>жймэм*» 'М»»/'гр»фим.«;й,в*: с*1’3 -4
5 Ч||| 1| 1 л 1 , Вычислить, у. Визуальная кап >г аризация... Йлюдвия... ' 2bs-' . В другие переменные...
номер — по. Подсчитать;.. асг
1 1.00 Ранжировать на 0.00
-2 2.00 е,оо
нрйряд.;. емыхнисол...
ХмЗ 3.00 Создать вренен !1.00
4.00 1 ^вменить оролп 2.00
5.00 - Г^.4 0.00
6.00 В .00
7.00 3SO.0O 34,00
8,00 If 1 800,00 19,00
9,00 -1 4 3000,00 54,00
10 10,00 1 2^ 1800,00 48,00
Рис. 4.18. Представление нечисловой информации в SPSS
183
График компонент в повернутом пространстве
Вкладо ^Возраст Образование о
° Пол
-1,0 -0,5 0,0 0,5 1,0 !
Компонента 1 1
Рис. 4.19. Вывод результатов факторного анализа: 1
графическое представление факторных нагрузок I
Таблица 4.20
Сортировка вкладчиков банка по двум факторам
№ Пол Образ. Вклад Возраст Фактор 1
20 Ж Среднее 2000 69 2,01
19 м Высшее 2500 53 1.67
9 м Высшее 3000 54 1,06
13 ж Незак.выс. 1600 53 0,74
18 м Начальное 900 33 0,65
№ Пол Образ. Вклад Возраст Фактор 2
12 Ж Высшее 350 69 1,49
2 Ж Высшее 350 35 1,23
6 ж Высшее 400 38 1,14
16 ж Высшее 750 55 1,09
13 ж Незак.выс. 1600 53 0,57
Пример 4.5. Требуется исследовать официальные статистические
данные по Владимирской области, приведенные на сайте http://
www.fira.ru (рис. 4.20).
Решение. Возьмем, например, данные по 4-му кварталу 2004 г.
(рис. 4.21).
Эти данные необходимо конвертировать в SPSS: убираем пока-
затель «Все отрасли экономики», сортируем, например, по убыва-
нию первого показателя (рис. 4.22).
Описание переменных выглядит так, как показано на рис. 4.23.
Запускаем факторный анализ, выделяя два значимых фактора в
структуре переменных. Получаем отчет: статистические характе-
ристики, коэффициенты парных корреляций (рис. 4.24).
Анализируем два выделенных фактора до и после вращения
(правая часть таблицы суммарной дисперсии (табл. 4.21)).
184
[Anal СТО
1 Зквартеп, Рентабельность прода», ПРОц. Влад>ымроея область (1 Г)
1 .
/ОСтекогежая и фарфоро-фатссвая промыв лемюсть (без прадгуиятий по производс _
5 I Маи иное троежяе и металлообработка (без прсмыелекеюсти медм^нсжой техники)
Б 'ГЫ|девая промышленность (1 BOPP)
ЯШ Элегтрознергетмса (11100)
. 10 ; Ле псе я промыв пенноеть (17000)_____
11 Транспорт (51000)_______________________
;12;Жигенфю-ко**»унепьное хозяйство(90000)
13 'Сесъекое хозяйство (20000)
зш
1TI й" № J з-.К'к-.'кПГТ
?D1
8,8
10,7
2.9
5,7
-0,9
j£g
3 »
2003
2004
•18,7
-16. £
13,7
ЭД
4,6
-12
3,6
-4.8
'
_°1
4,2
Н2
И18
□*21
15 квартал, Обеспеченностьсобственнымиобороттаявии средстве**, ПРОЦ. Владимирская область(17)
Iii________________________________________________________________________;
18 Стекосуная и фарфоро-фачговая громы в пеннхть (без гредсриятий по прсмзводс _
19 .Cery.CMoe хозяйство (20000)_____________________________________________
23 ГЫклвая громы и ленное ть (18000)______________________________________
21..;Мавинострое»*е и металлообработка (без промыв ленное ти медицтктой техгмки)
32
8,7
2002
13
13,5
11,9
$а
10,4
6,9
3
5,5
2,5
Я1
-11
-11
435
12,7
Л
4,8
03
45
16,1
64
7,5
Л1
2,2
2Й1
-73
ЛИ
_iil
6,3
63
245
-;oj
_35
22
33
_п
-13,1
_11
2003
.
m
4,5
6,6
5
6,1
Л
•10,3
-2,6
-2,1
-13
Электроэнергетика (11100)_____________
Sj Ле пса я промы в леность (17000)_______
|Жилиа/<о-коммунальмое хозяйство (90000)
У Транспорт(51000)________________________
-3,7
-1Б4
-88,8
•29.3
-6.6
-59,8
211
25
2-
1-1163
250600;...
28,8
J2J
-69,8
_02
12,3
•18,2
-59,8
623,2
-102,7
J2£
75
__Z1
-202
-75,9
-92
_л!
___0
2а
В£
-12
Т52
-32,9
3 кв
128
10,4
14,2
_Z£
J18
-38,4
252
103
_zi
126
23
•78
200,3
_^8
73,3
-98,8
___9,3
____42
_85
169,4
72,4
_2ВЗ
-56
___36
•37,3
•118,5
2034
2 кв
383
15,7
___5,1
•12,7
_И2
-58,7
-1353
37,7
ИЗ
_12
-0,5
-33
•34,6
-393
-40,6
-1122
Рис. 4.20. Исходная информация, представленная в Excel
Рис. 4.21. Отобранная для факторного анализа информация
за 4-й квартал 2004 г.
Рис.
Представление исходной информации для анализа в SPSS
185
Срок оборота кредиторской задолженности
None i8
Владимир
реитабел
собста ср
Right
RigM
Right
Numeric
Numeric
Stnng
Scali
Scato
Scale
Scale
None”l§"
None 9
P) Владимирская область 4 квартал 2004 r
|2_J Рентабельность продаж
[2 .Обеспеченность собственными оборотными средствами
|2 । Текущ эя ликвидность (общее покрытие) ____
|2 I Срок оборота дебиторской вадоякчоюсти___________
Майна Графики Утилиты Окно I*
Рис. 4.23. Описание переменных в редакторе данных
я
Факторный анализ
й-
Фаггорный анализ
Журнал
Факторный анализ
Журнал
Факторный анализ
I Заголовок
Примечания
Описательные ст л
Общности
Полная объяснены
Г рафик собственш:
Матрица ксмпонен
Матрица повернут
Матрица пресбразс
График компонент
Описательны* статистики
Среднее Стд откл АнализN
Рентабельность продаж Обеспеченность 1,4778 5,22489 9
собственными оборотными средствами -37,0222 75,68325 9
Текущая ликвидность (общее локрьп'ие) ,9889 ,48581 9
Срок оборота
дебиторской задолженности Срок оборота 52,1111 28,82466 9
94,1111 47,80284 9
кредиторской
задолженности
Рис. 4.24. Вывод результатов факторного анализа:
описательные статистики
Таблица 4.21
Полная объясненная дисперсия
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % дисперсии Кумулятив- ный % Всего % дисперсии Кумулятив- ный %
1 4,552 91,046 91,046 2,952 59,047 59,047
2 ,312 6,246 97,292 1,912 38,246 97,292
3 ,106 2,119 99,411
4 ,028 ,560 99,972
5 ,001 ,028 100,000
Метод выделения: Анализ главных компонент.
186
Попытаемся интерпретировать выделенные факторы, анализи-
руя матрицу повернутых компонент (табл. 4.22).
Таблица 4.22
Матрица повернутых компонент(а)
Компонента
1 2
Рентабельность продаж .771 .615
Обеспеченность собственными оборотными средствами ,909 .342
Текущая ликвидность (общее покрытие) .411 ,905
Срок оборота дебиторской задолженности -.852 -,507
Срок оборота кредиторской задолженности -.799 -,584
Метод выделения: Анализ методом главных компонент. Метод вращения: Варимакс с нормализацией Кайзера, а Вращение сошлось за 3 итерации.
Фактор 1 наиболее тесно напрямую связан с уровнем обеспе-
ченности собственными оборотными средствами и имеет обратную
зависимость от сроков оборота задолженностей (назовем условно
«достаточность собственных денежных средств»). Упорядочим от-
расли экономики Владимирской отрасли по состоянию на 4-й квар-
тал 2004 г. по убыванию значения фактора 1 (рис. 4.25, а).
Из приведенного рейтинга следует, что наиболее благополуч-
ными отраслями можно считать пищевую промышленность, ма-
шиностроение, легкую и химическую промышленность.
Фактор 2 в большей степени зависит от текущей ликвидности
и слабо связан с рентабельностью (условно интерпретируем как
востребованность данной отрасли). Упорядочим отрасли по убыва-
нию фактора 2 (рис. 4.25, б).
Наилучшая ситуация в стекольной и фарфоро-фаянсовой про-
мышленности, машиностроении и жилищно-коммунальном хо-
зяйстве.
Наиболее слабые отрасли по состоянию обоих факторов на
анализируемый период времени — сельское хозяйство и транс-
порт.
Пример 4.6. Известна динамика основных показателей целлю-
лозно-бумажной промышленности по некоторым областям (сайт
http://www.fira.ru) (рис. 4.26).
Требуется выявить скрытые факторы в структуре показателей
отрасли, интерпретировать их и определить передовые и отста-
ющие области.
187
a)
Рис. 4.25. Представление результатов расчета выделенных факторов:
о — по убыванию значений фактора 1;
б — по убыванию значений фактора 2
Заедите ослих
Рентабельность
>К»арт*л, Целлюлозно-бумажная промышленность (15300), Динамика выручки от продажи товаров, работ, услуг (к соответствующему периоду пре/
........................I........;........ .................I тпт I тлгм
Рис. 4.26. Исходная информация, представленная в Excel
188
Решение. Возьмем, например, данные за 3-й квартал 2004 г. По-
скольку области перечислены в разном порядке, необходимо
сгруппировать строки в каждой таблице и упорядочить данные по
областям. Затем выбираем по всем показателям информацию за
интересующий нас квартал (рис. 4.27).
Рис. 4.27. Отобранная для факторного анализа информация
за 3-й квартал 2004 г.
Далее копируем эти данные в SPSS (рис. 4.28).
Рис. 4.28. Представление исходной информации для анализа в SPSS
Запускаем факторный анализ, изучаем полученные результаты
(табл. 4.23).
Удаляем два статистически незначимых фактора: рентабель-
ность и срок оборота дебиторской задолженности. Опять запуска-
ем факторный анализ (табл. 4.24).
Два выявленных фактора объясняют 91% суммарной диспер-
сии, попробуем их интерпретировать (табл. 4.25).
Фактор 1 тем больше, чем выше затраты и срок кредиторской
задолженности и чем меньше собственных средств, поэтому можем
интерпретировать его как кризисное состояние отрасли. Упорядо-
чим области по возрастанию этого фактора (рис. 4.29, а).
189
ад: ’Н Таблица 4.23
1 ’ *? Матрица компоиент(а)
Компонента
1 2
Рентабельность продаж ,362 ,571
Обеспеченность оборотными средствами -.936 -,100
Динамика выручки от продажи товаров, работ -,095 ,811
Динамика затрат на оплату труда по основному виду деятельности ,986 -,080
Текущая ликвидность (общее покрытие) -,890 -,395
Срок оборота дебиторской задолженности ,646 -,687
Срок оборота кредиторской задолженности ,871 -.059
Метод выделения: Анализ методом главных компонент, а Извлеченных компонент: 2
Таблица 4.24
Полная объясненная дисперсия
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения
Всего % диспер- сии Кумулятив- ный % Всего % дисперсии Кумулятив- ный %
1 3,485 69,698 69,698 3,485 69,698 69,698
2 1,061 21,211 90,909 1,061 21,211 90,909
3 .257 5,137 96,046
4 ,198 3,953 100,000
5 9.01Е-06 ,000 100,000
Метод выделения: Анализ главных компонент.
Матрица компоненте а)
Таблица 4.25
Компонента
1 2
Обеспеченность оборотными средствами -,959 -.143
Динамика выручки от продажи товаров, работ ,037 ,996
Динамика затрат на оплату труда по основному виду деятельности ,975 -,122
Текущая ликвидность (общее покрытие) -,896 -,097
Срок оборота кредиторской задолженности ,901 -.157
Метод выделения: Анализ методом главных компонент, а Извлеченных компонент: 2
a)
Рис. 4.29. Представление результатов расчета выделенных факторов:
а — по возрастанию значений фактора 1;
б — по убыванию значений фактора 2
Результат: наилучшая ситуация с целлюлозно-бумажной про-
мышленностью в Нижегородской и Ленинградской областях. Наи-
более высока вероятность кризисной ситуации в Республике Ка-
релии.
Фактор 2 тем больше, чем больше выручка от продаж, назовем
его эффективностью работы данной отрасли. Ранжируем области
по значению этого фактора (рис. 4.29, б).
Результат: наиболее эффективна данная отрасль в Пермской
области и Республике Коми. Наихудшая ситуация в Архангельской
области.
Таким образом, подводя окончательные итоги, можно сделать
вывод: в 3-м квартале 2004 г. Ленинградская область заняла ли-
дирующие позиции в производстве и реализации целлюлозно-
бумажной продукции (ведущие места в двух последних таблицах
(см. рис. 4.29)). Для Республики Карелии, наоборот, характерны
наименьшая эффективность данной отрасли экономики и высокий
риск кризисного состояния.
191
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ*
Задача 4.1. Анализ деятельности предприятий легкой промыш-
ленности
Имеются данные обследования 20 предприятий легкой про-
мышленности (табл. 4.26) по следующим характерным призна-
кам:
Л", — уровень фондоотдачи;
Хг — трудоемкость единицы продукции;
Ху — удельный вес закупочных материалов в общих расходах;
Х4 — коэффициент сменности оборудования;
Х5 — премии и вознаграждения на одного работника;
Х6 — удельный вес потерь от брака;
Х7 — среднегодовая стоимость основных производственных
фондов;
Xs — среднегодовой фонд заработной платы;
Х9 — уровень реализуемости продукции;
Лю — индекс постоянного актива (отношение основных средств
и прочих внеоборотных активов к собственным сред-
ствам);
Х}, — оборачиваемость оборотных средств;
Л12 — непроизводственные расходы.
Таблица 4.26
Исходные данные
Номер пред- при- ятия Х2 А %4 *7 Л ^11 ^12
1 1,44 0,26 0,27 1,46 0,68 0,75 58,42 19 074,00 0,74 0,73 82,44 18,29
2 1,75 0,31 0,45 1,36 0,78 0,87 63,99 27404,00 0,73 0,85 137,52 18,28
3 1,75 0,29 0,40 1,28 0,99 0,89 91,43 34 873,00 0,78 0,80 76,32 16,83
20 1,22 0,42 0,26 1,09 0,54 0,10 48,41 20 122,00 0,69 0,67 138,24 22,26
В соответствии с номером варианта (табл. 4.27) выбрать наблю-
дения нужных переменных, провести факторный анализ, выявить
и интерпретировать факторные признаки, указать наиболее благо-
получные и перспективные предприятия.
В полном объеме числовые данные для задач приведены на CD.
192
Варианты заданий
Таблица 4.27
Вариант Номера переменных для анализа Вариант Номера переменных для анализа
1 1,3, 5-7, 9, 11, 12 6 2-4, 7,8, 10-12
2 1-3, 7,8, 10-12 7 1-3, 5, 8,9, 11, 12
3 2, 3,5,6,9-12 8 1,2, 6-11
4 1-5,7, 9, 10 9 1-5, 10-12
5 1,3,4, 6, 7,9, 10,12 10 1,3-6, 8-10
13- 1591
Глава 5
ДИСКРИМИНАНТНЫЙ АНАЛИЗ
5.1. ТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ
ДИСКРИМИНАНТНОГО АНАЛИЗА
5.1.1. Области применения
и методы дискриминантного анализа
Теория дискриминантного анализа* начала разрабатываться с
конца 50-х годов XX в. такими известными учеными, как Р. Фишер,
П.Ч. Махаланобис, Г. Хотеллинг и др. В настоящее время эта тео-
рия продолжает развиваться (например, появилась теория кано-
нических дискриминантных функций) и применяется в экономи-
ке, психологии, социологии и других науках [15, 35].
Дискриминантный анализ (ДА) является разделом многомерно-
го статистического анализа, включающим в себя методы класси-
фикации многомерных наблюдений по принципу максимального
сходства при наличии обучающих признаков.
В отличие от кластерного анализа здесь новые кластеры не
образуются, а лишь формулируется правило, по которому объек-
ты, подлежащие классификации, относятся к одному из уже су-
ществующих (обучающих) подмножеств (классов) на основе срав-
нения величины дискриминантной функции классифицируемого
объекта с некоторой константой дискриминации. Например,
в изучаемой системе появляется новый объект, характеризующий-
ся той же совокупностью изучаемых признаков, и необходимо
выяснить, к какому классу его следует отнести с наибольшей ве-
роятностью.
Дискриминантная функция в общем случае составляется в виде
линейной комбинации исходных показателей, коэффициенты ко-
торой подбирают из условия наибольших различий функции меж-
ду известными классами.
Области применения дискриминантного анализа:
• статистический анализ и моделирование зависимостей между
отдельными признаками с учетом разделения неоднородных
статистических совокупностей на однородные группы (клас-
сы);
Здесь под дискриминацией понимается различие.
194
• выбор переменных, которые наилучшим образом различают (дис-
криминируют) возникающие совокупности (две или более);
• классификация новых объектов на основе выявленных зависи-
мостей;
• составление карты восприятия;
• прогнозирование поведения новых объектов наблюдения путем
их сопоставления с поведением объектов обучающих подмно-
жеств;
• уточнение результатов классификации, полученных в кластер-
ном анализе, и т.п.
Например, банк при выдаче кредитов классифицирует своих
клиентов по ряду признаков на надежных и ненадежных, тогда с
помощью ДА можно определить, к какой из ранее выявленных
совокупностей (обучающих выборок) следует отнести новых кли-
ентов. Другой пример: при проведении маркетинговых исследова-
ний можно выявить отличительные характеристики потребителей
товаров, реагирующих на тот или иной вид рекламы.
Дискриминантный анализ может проводиться несколькими
методами.
В зависимости от реализованного алгоритма различают две груп-
пы методов ДА:
* методы интерпретации межгрупповых различий по дискрими-
нантным переменным, позволяющие установить отличия одно-
го класса от другого;
* методы классификации на основе дискриминантных функций,
с помощью которых по выбранным признакам новые объекты
распределяются по существующим классам.
По количеству обучающих выборок различают два вида мето-
дов ДА:
• для двух групп (two-group descriminant analysis) — строится толь-
ко одна дискриминантная функция с одной переменной;
• для трех и более групп применяется множественный дискрими-
нантный анализ (multiple descriminant analysis) — строится
несколько дискриминантных функций (по количеству групп
минус единица).
Кроме того, в зависимости от правил дискриминации в литерату-
ре рассматривается три вида ДА [10]:
* линейный дискриминантный анализ Фишера (предложен Фише-
ром) — правила дискриминации представлены в виде линейной
комбинации дискриминантных переменных;
195
• канонический дискриминантный анализ — правила дискримина-
ции представлены в виде дискриминантных функций;
• линейный дискриминантный анализ — правила дискриминации
представлены совокупностью характеристик (групповая кова-
риационная матрица, групповой вектор средних, определитель
ковариационной матрицы).
5.1.2. Постановка задачи на исследование
методами дискриминантного анализа
Пусть имеется множество М, состоящее из п объектов наблю-
дения, каждый /-й объект которого описывается совокупностью
р значений дискриминантных переменных (признаков) xzy (i = 1, л;
J = 1, р). Причем все множество М объектов включает q (q > 2)
обучающих подмножеств Мк размером пк каждое и подмноже-
ство Л/о объектов, подлежащих дискриминации. Здесь к — номер
подмножества (к = 1, q).
Требуется установить правило (линейную или нелинейную дис-
криминантную функцию f (х)) распределения т объектов подмно-
жества Мо с соответствующими признаками по подмножествам Мк.
Выбор вида дискриминантной функции f (х) зависит от геометри-
ческого расположения разделяемых классов в пространстве дис-
криминантных переменных. Геометрическая интерпретация по-
становки задачи ДА на примере двух обучающих подмножеств
(<7 = 2) тИ| и Мг представлена на рис. 5.1.
Наиболее часто используется линейная форма дискриминантной
функции, которая представляется в виде скалярного произведения
вектора дискриминантных множителей Л = (at, а2,..., ар) и векто-
ра дискриминантных переменныхX1 = (хп, хд,..., х1р):
Е- = АХУ, (5.1)
или
/;. = «1х/1+а2х,.2 + ... + аЛ,
где Xх — транспонированный вектор дискриминантных перемен-
ных Ху (значений у-х признаков у /-го объекта наблюде-
ния).
Основные предположения в теории дискриминантного анализа:
* множество Мобъектов разбито на несколько (q > 2) обучающих
подмножеств (классов) Мк, которые от других групп отличают-
ся переменными ху;
196
Рис. 5.1. Геометрическая иллюстрация постановки задачи ДА (q = 2)
в каждом подмножестве Мк находится по крайней мере два
объекта наблюдения (пк > 2), причем все объекты множества М
должны принадлежать одному из подмножеств (классов) Мк,
число п объектов наблюдения должно превышать числор дис-
криминантных переменных (0 < р < п - 2) не менее чем на две
единицы. Число р обычно выбирается на основании логиче-
ского анализа исходной информации;
дискриминантные переменные Ху должны измеряться по интер-
вальной шкале или шкале отношений. Интервальная шкала
используется для количественного описания различий между
свойствами объектов. Она задается точкой отсчета (например,
средняя величина, мода и медиана) и единицей измерения.
Шкала отношений (частный случай интервальной шкалы) по-
зволяет соотнести количественные характеристики какого-либо
свойства у разных объектов;
между дискриминантными переменными существует линейная
независимость (отсутствует мультиколлинеарность), т.е. ни одна
переменная не должна быть линейной комбинацией других пере-
менных, в противном случае они не несут новой информации;
все подмножества гомоскедастичны, т.е. выполняется прибли-
зительное равенство между собой ковариационных матриц
для каждого подмножества (класса) Мк,
197
• внутри каждого подмножества Мк выполняется нормальный
закон распределения дискриминантных переменных Ху при
фиксированных остальных переменных.
Если данные условия не выполняются, то рассматривается во-
прос о целесообразности использования дискриминантного ана-
лиза для классификации новых наблюдений.
Основные проблемы ДА — отбор дискриминантных перемен-
ных и выбор вида дискриминантной функции. Для получения
наилучших различий обучающих подмножеств могут использо-
ваться критерии последовательного отбора переменных [40] или
пошаговый дискриминантный анализ. После определения набора
дискриминантных переменных решается вопрос о выборе вида
дискриминантной функции (линейной или нелинейной).
В качестве дискриминантных переменных могут выступать
не только исходные (наблюдаемые) признаки, но и главные
компоненты или главные факторы, выделенные в факторном
анализе.
Алгоритмы методов дискриминантного анализа реализованы во
многих пакетах статистической обработки информации типа SPSS,
STATGRAPHICS, STAT1ST1CA, VSTAT, ОЛИМП, СтатЭксперт,
STADIA 6.0 и др.
5.1.3. Геометрическая интерпретация
дискриминантных функций
Геометрически дискриминантные переменные представляются
в виде осей р-мерного евклидова пространства, в котором каждый
z-й объект наблюдения является точкой этого пространства с ко-
ординатами Ху. Скопления точек в пространстве образуют q обуча-
ющих подмножеств (классов), различия и взаимное положение
которых можно определить с помощью их центроидов.
Центроид — воображаемая точка подмножества, координаты
которой определяются средними значениями переменных внутри
данного подмножества. Используется для описания различий меж-
ду подмножествами и определения принадлежности к ним новых
объектов.
Центроиды характеризуют положение к-го подмножества в про-
странстве размерностью q - 1, т.е. на единицу меньшей числа под-
множеств (классов).
198
На рис. 5.2 в координатах двух дискриминантных переменных
л,, х2 изображены два подмножества Mt и М2 (обучающие выборки)
множества М, внутри которых точками обозначены принадлежа-
щие им объекты.
Рис. 5.2. Геометрическое представление
дискриминантных переменных х|э х2
Положение каждого z-го объекта к-го подмножества характери-
зуется двумя дискриминантными переменными х^и х$\ Подмно-
жества М} и М2 разделены линейной комбинацией дискриминант-
ных переменных л, их2 вида
Дх) = о|х| +а^с2. (5.2)
Дискриминантные множители а,, а2 канонической дискрими-
нантной функции (5.2) для к-го подмножества позволяют перейти
от двухмерного пространства первичных показателей к одномер-
ному, обеспечивая при этом минимальную ошибку классифика-
ции.
Поворот осей до совпадения оси х, с линией, разделяющей под-
множества, позволяет перейти к новой системе координат (рис. 5.3).
Новая система координат с осями x't и х2 разделяет проекции объ-
ектов, принадлежащих разным подмножествам, на ось х2 таким
образом, что подмножества М( и М2 находятся по разные стороны
от оси х('. Граница, разделяющаяподмножества Мх и_М2, совпадает
с осью х,', она задана функцией f(x) = 0,5(/(|)(х) + /(2)(х)), равно-
удаленной от /(|)(х) и /(2)(х).
199
Рис. 5.3. Геометрическая интерпретация центров (центроидов)
двух обучающих подмножеств и М2
Величина /(х) называется константой дискриминации. Из
рис. 5.2 и 5.3 видно, что объекты, расположенные над прямой 7(х),
находятся ближе к центру подмножества М{, и поэтому их относят*
к первой группе, а объекты, расположенные ниже этой прямой, —
ближе к центру подмножества М2, поэтому их относят ко второй
группе. Такой выбор границы /(х) обеспечивает минимальную
вероятность ошибки классификации.
Линейная функция (5.2) представляет собой проекцию /-го объ-
екта на некоторую (одномерную) дискриминантную ось. Если
среднее значениеу-го признака у объектов к-го подмножества обо-
значить через Xjk\ то средние значения функций /(1)(х) и /<2)(х)
в подмножествах определяются по формулам
/(1)(х) = atxt(I) + о2^2(1)’
/(2)(х) = aiX](2) + а2х^2).
Геометрически функции /(1>(х)и /(2)(х) представляют собой две
параллельные прямые, проходящие через центры (центроиды)
подмножеств (см. рис. 5.3).
Линейную дискриминантную функцию не всегда можно ис-
пользовать для описания разделяющей прямой (поверхности) меж-
ду подмножествами. Например, если обучающие подмножества
не являются выпуклыми, то линейная дискриминантная функция
не обеспечивает минимальные ошибки классификации.
200
Если обучающие подмножества близко расположены друг к
другу, вероятность ошибочной классификации новых объектов
возрастает по мере их удаления от центров обоих множеств. В этом
случае пересматривается набор дискриминантных переменных.
Для графического отображения центроидов и отдельных объ-
ектов наблюдения в пространстве дискриминантных функций
строятся карты восприятия. Они визуализируют количественные
данные о сходстве объектов наблюдения в форме графиков (одно-
или двухкоординатных) [9, 10].
Если используется одна дискриминантная функция, то точки,
соответствующие объектам, вычисленным по этой функции,
располагаются вдоль некоторой прямой в однокоординатной сис-
теме. В этом случае точки характеризуют долю функции, которая
относится к данному наблюдению. Недостаток такого способа ото-
бражения в том, что при большом количестве точек «растворяется»
информация о плотности их распределения, и тогда строятся
гистограммы для каждой группы. Это позволяет проводить отно-
сительное сравнение распределения групп.
Когда строится несколько дискриминантных функций,
центроиды и объекты отображаются на графиках в двухкоординат-
ной системе, в пространстве значений двух функций. Если функ-
ций более двух, такой график весьма информативен, поскольку
первые две функции остаются наиболее важными по сравнению с
остальными. Групповые центроиды выделяются символами (звез-
дочками и т.п.) на фоне других объектов наблюдений.
Карты восприятия позволяют визуально оценить степень раз-
личимости групп и взаимное расположение их центроидов. Пря-
мые линии в поле графика разделяют собой «территории» соответ-
ствующих групп. Графическое представление карты восприятия
двух функций при трех обучающих выборках можно увидеть на
рис. 5.17.
5.1.4. Критерии сравнения выборок
по нескольким признакам
Первым критерием сравнения выборок [17] является коэф-
фициент детерминации. Для нескольких групп общую дисперсию
признака можно представить в виде суммы межгрупповой и внут-
ригрупповой дисперсий, тогда мерой изменчивости будут суммы
квадратов отклонений наблюдений от соответствующих средних:
201
55* = 55„ + 55е,
где 55* — сумма квадратов отклонений наблюдений от общего
среднего, она характеризует общую изменчивость;
55и — межгрупповая дисперсия, т.е. сумма квадратов отклоне-
ний групповых средних от общего среднего, она харак-
теризует изменчивость между группами;
55е — внутригрупповая дисперсия, т.е. сумма квадратов откло-
нений наблюдений от групповых средних, она характе-
ризует изменчивость внутри групп.
Разделив обе части уравнения на 55*, получим
। _ + 55е
55* 55* ‘
55 хх
Отношение —- называется коэффициентом детерминации, его
55*
обозначают Т)2; он показывает, во сколько раз изменчивость наблю-
дений между группами превышает полную изменчивость:
п2=^_ = 1_^
55* 55*'
Известно, что значение этого коэффициента может находиться
в пределах 0 < r|2< 1. Если все групповые средние равны общему
среднему, то SSU = 0, и тогда т]2 = 0, т.е. разницы между группами по
среднегрупповым значениям показателя х нет. Если внутри групп
нет никакой изменчивости, то 55е = 0, и тогда r|2 = 1, а это значит,
что разным значениям переменной х соответствуют разные классы.
Чем ближе т|2 к единице, тем лучше дискриминационная способ-
ность переменной х.
Квадратный корень из коэффициента детерминации т]2 назы-
вается эмпирическим корреляционным отношением.
Вторым критерием является характеристика X (собственное
значение)', она показывает, во сколько раз изменчивость между
группами превышает изменчивость внутри групп:
Лямбда характеризует долю дисперсии оценок дискриминант-
ной функции, которая не обусловлена различиями между группа-
ми. Если средние для всех групп равны, то X = 1, и она уменьшает-
ся с ростом разностей средних значений. Чем больше X, тем лучше
подобрана дискриминантная функция. J
202
Оба критерия связаны соотношением
м
-
Качество классификации в каноническом дискриминантном
анализе может оцениваться по одной из следующих характерис-
тик:
* относительное процентное содержание
-^-•100%
р
показывает, на сколько процентов данная функция слабее дру-
гих;
коэффициент канонической корреляции
К
показывает, какая часть полной изменчивости дискриминант-
ной функции объясняется разницей между группами;
критерий Фишера рассчитывается по формуле
<7-1
и затем сравнивается с табличными значениями Fa h при
выбранном уровне значимости а (обычно а = 0,01 или 0,05) и
числе степеней свободы q - 1 и п - q либо оценивается по уров-
ню значимости а.
Уровни значимости характеризуют вероятность того, что разли-
чия между группами являются случайными. Дискриминантная
функция считается значимой при заданном уровне значи-
мости а и числе степеней свободы v, если для нее фактические
значения критериях2будут превышать табличные%* v-
Вместо этого можно использовать уровень значимости (Sig.) —
вероятность того, что статистика х2 при нулевой гипотезе
(незначимости дискриминантной функции) случайно достигнет
вычисленного уровня. Если для функции а < 0,01, то найденная
дискриминантная функция значима;
статистика Уилкса подробно рассмотрена в параграфе 5.3.
203
5.2. АЛГОРИТМ ВЫПОЛНЕНИЯ
ДИСКРИМИНАНТНОГО АНАЛИЗА
Рассмотрим основные этапы алгоритма ДА при нормальном за-
коне распределения показателей применительно к линейной дис-
криминантной функции вида (5.1) на примере, когда q = 2. Это
позволит лучше понять его сущность.
1. Исходные данные представляются либо в табличной форме,
в виде q подмножеств обучающих выборок Мк и подмножества Мо
объектов, подлежащих дискриминации (табл. 5.1), либо сразу в виде
матриц %(1), Х(Г>,Х^ размерности пк хр;
< Y(i) *11 Y(l) *12 Y(l)> - X\p fY(2) *11 Y(2) *12 Y(2)A " *!/>
xw = Y(l) *21 Y(l) *22 • Y(l) " x2p , %(2) = Y(2) *21 Y(2) *22 Y(2) " X2p
Y(l> <*«,! Y(l) *«;2 • Y(l) " Xn,Pj Y(2) <*„21 Y(2) *n22 • Y(2) " XwJ
X(4} = ( Y(?) *11 y(9) *21 Y(?) *12 Y(?) *22 Y(?)) " X\p x(4) •• x2p , X^ = W Y(0) *21 Y(0) *12 Y(0) *22 • Y(°)> Xlp Y(0) • x2p
Y(?) <\1 x(n2 n,2 Y(4) \p) Y(0) <*ml Y(0) *m2 • Y(°) • Лтр J
где Х^ — матрицы с обучающими признаками (к = 1, q)-,
%(°) _ матрица новых т объектов, подлежащих дискримина-
ции (размерности т хр);
р — количество свойств, которыми характеризуется каждый
z-й объект.
Здесь должно выполняться следующее условие: общее количе-
ство объектов п множества Мдолжно быть равно сумме количества
объектов/и (в подмножестве Л/о), подлежащих дискриминации, и
ч
общего количества объектов \ пк в обучающих подмножествах, где
а=|
q — количество обучающих подмножеств (q > 2):
ч
п = т + ^пк.
к=1
204
Таблица 5.1
Табличная форма задания исходных данных
Подмножество Мк (к = 1,9) Номер объектаi (J = l,nk) Свойство (показатель) Xj (J = Kp)
xi x2 XP
1 „(1) *12 r(l)
Mt (£=1) 2 r(D x22 Y(l) X2p
И1 r(D Хл,2 ... r(D Xn,P
1 r(2) x12 ... r(2) Xtp
М2(к = 2) 2 r(2) *21 r(2) x22 v(2) X2p
«2 r(2) лл21 r(2) Si, 2 r(2) >hp
... ... „(4) xv
1 x<?> „(«) X)2 Y(«)
Mq(k = q) 2 „(«) X2| „(?) x22 Y(«) X2p
Y(?) *л,1 Xn2 ««2 ... ",P
1 r(0) X|2 ... Xip
Мо(к = О), подлежащее 2 „(0) *21 Y(°) x22 ... r(0) X2p
дискриминации т r(0) Лт1 r(0) xm2 r(0) Лтр
Примечание. Здесь пк — объем обучающей выборки в к-м подмножестве.
2. Определяются Xjk) — средние значения по каждомуJ-му при-
знаку для i объектов внутри к-го подмножества (к= 1, 2):
1 ___
i=<• р-
Пк ,=1
Результаты расчета по каждому подмножеству представляются
В виде вектор-столбцов Xw:
205
xw =
Х1
?(Л)
х2
7(Л)
л
3. Для каждого обучающего подмножества рассчитываются ко- ;
вариационные матрицы (размерности р хр). Элементы каждой
матрицы вычисляются по формуле
1 я* __
w=-LsM‘> -
пк ,=|
4. Рассчитывается объединенная ковариационная матрица S по
формуле
г г
5 =---------(njS^ + л25(2)).
П| + «2 - 2
5. Рассчитывается матрица 5'1, обратная к объединенной ко-
вариационной матрице S, по формуле
5-1=ш5,
где |5| — определитель матрицы S (причем |s| 0);
S — присоединенная матрица, элементы которой являются
алгебраическими дополнениями элементов матрицы S'.
6. Рассчитывается вектор-столбец А =
А
дискриминантных
множителей с учетом всех элементов обучающих подмножеств по
формуле
А = S~\Xm - Х(2)).
Последняя формула получена методом наименьших квадратов
из условия обеспечения наибольшего различия между дискри-
минантными функциями. Наилучшее разделение двух обучаю-
щих подмножеств обеспечивается сочетанием минимальной
внутригрупповой вариации и максимальной межгрупповой ва-
риации.
206
7. По каждому /-му объекту (/ = 1, я) множества М определяется
соответствующее значение дискриминантной функции:
^> = 44> + ^4>+...+v^
8. По совокупности найденных значений FW рассчитываются
средние значения F(k) для каждого подмножества Мк:
^=±7^), где* = 1,2.
9. Определяется общее среднее (константа дискриминации) для
дискриминантных функций:
10. Выполняется распределение (дискриминация) объектов под-
множества Мо, подлежащих дискриминации, по обучающим вы-
боркам и М2. С этой целью рассчитанные в п. 7 по каждому /-му
объекту значения дискриминантных функций
F/0) = + А2х$ +... + Арх$}, i = \,m
сравниваются с величиной F общего среднего. По результатам
сравнения каждый объект относят к одному из обучающих под-
множеств:
• если F(V} > Г(2), то /-й объект подмножества Мо относят к под-
множеству Afj при /J(0) - F > 0 и к подмножеству М2 при
F^} - F < 0;
• если F(r> < F(2\ то заданный объект относят к подмножеству Мх
при - F < 0 и к подмножеству М2 в противном случае.
11. Качество распределения новых объектов можно оценивать
по степени вклада переменных в дискриминантную функцию на
основе стандартизованных канонических коэффициентов дискри-
минантной функции.
Влияние признаков на значение дискриминантной функции и
результаты классификации может оцениваться по таким показате-
лям, как:
• дискриминантные множители (коэффициенты дискримина-
ции);
• дискриминантные нагрузки признаков;
• дискриминантная матрица.
207
Дискриминантные множители зависят от масштабов единиц
измерения признаков, поэтому не всегда удобны для оценки.
Дискриминантные нагрузки вычисляются как парные линейные
коэффициенты корреляции между рассчитанными уровнями дис-
криминантной функции и значениями признаков, взятых для ее
построения. Они более надежны в оценке признаков.
Дискриминантная матрица характеризует меру соответствия
результатов классификации фактическому распределению объек-
тов по подмножествам и используется для оценки качества анали-
за. В этом случае дискриминантная функция формируется по объ-
ектам (с измеренными р признаками) обучающих подмножеств,
а затем проверяется качество этой функции путем сопоставления
фактической классовой принадлежности объектов с той, что по-
лучена в результате формальной дискриминации.
5.3. МЕТОДЫ ОЦЕНКИ ИНФОРМАТИВНОСТИ ПОКАЗАТЕЛЕЙ
После построения дискриминантных функций и проверки их
качества сокращают число показателей. Если средние значе-
ния переменных в выборках (подмножествах) различаются слабо,
это означает, что одна или несколько переменных являются пло-
хими дискриминаторами. Коррелированные переменные в ДА !'
могут нести одинаковую информацию, и каждая из них может быть
хорошим дискриминатором. При этом остальные переменные
могут оказаться лишними, поскольку содержат мало новой ин-
формации. Наличие избыточных переменных увеличивает число
неправильных классификаций. Для отбора показателей по крите-
рию их информативности применяется ряд методов.
Метод последовательных подключений', вначале отбирается пе-
ременная с наилучшим одномерным различием; затем анализи-
руются все пары с этой переменной, и по наилучшей паре отби-
рается вторая переменная; далее анализируются все тройки с
двумя уже отобранными переменными. Процесс продолжается до
тех пор, пока оставшиеся переменные не перестанут улучшать
различия.
Метод последовательных исключений', на каждом шаге отбрасы-
вается по очереди одна из переменных и определяется наихудшая,
которая отбрасывается окончательно. Процесс исключений закан-
чивается, когда очередное исключение ухудшает различие между
классами.
».
208
Метод полного перебора всех комбинаций переменных требует
значительных затрат времени и отличается высокой стоимостью
расчета.
Метод подключения-исключения является альтернативой методу
полного перебора. Здесь перед подключением очередного показа-
теля исключается самая малоинформативная из ранее подключен-
ных переменных. Процесс заканчивается, когда уже нечего исклю-
чать и нечего подключать.
Статистика Уилкса (Л-статистика): в анализ включается та
переменная, которая на данном шаге имеет наименьшую
Л-статистику. Данный критерий считается наилучшим критерием
отбора, он оценивает относительный вклад остаточной дисперсии.
Его преимущество в том, что он учитывает не только различия
между классами, но и однородность каждого класса (степень скоп-
ления объектов вокруг центроидов).
Оценка информативности показателя по статистике Уилкса ана-
логична оценке значимости членов регрессионной модели с по-
мощью коэффициентов частной корреляции.
Если I — общее число дискриминантных функций с ненулевы-
ми Х(., то
Л _1 1 1 1
1 + Xj 1 + Х2 1 1 + X/
есть мера остаточной изменчивости с учетом всех дискриминантных
функций, т.е. Ло оценивает дискриминационную способность всей
системы функций.
Далее оценивается дискриминационная способность системы
без первой, наиболее важной функции:
Л =1 1 1
1 + А>2 1 + Xj 1 + X/
Эта величина уже больше, чем Ло. Чем ближе Л( к единице, тем
слабее дискриминационная способность оставшейся системы
функций.
Затем вычисляется
1 + Xj 1 + X;
итак до Лм.
14 - 1591
209
Значимость Лу. оценивается последовательно по критерию Пир-
сона
X? = _Гп_1_£±£\пд
к 2 7
который сравнивается с табличным значением %2 v. Здесь п — число
наблюдений, р — число переменных, q — число классов,
v = (р-J )(<? -j - 1) — число степеней свободы.
Для расчета Л-статистики (без перехода в пространство кано-
нических функций) используется формула [17]:
1И
\B+W\'
где |И/| — определитель матрицы внутригрупповых ковариаций В
(при условии равенства ковариационных матриц по груп-
пам);
|Z?+ H^l — определитель общей матрицы ковариаций.
Находится значение Лр для полного набора показателей и Л,для
меньшего их числа.
Затем рассчитывается характеристика %2 (распределенная по
закону Пирсона для числа степеней свободы »=pq-р)‘.
2 ( 1 ЛР
X =~ п-1~-—- In—,
I 2 J Л/
где I — общее число дискриминантных функций (/ = q - 1).
Если вычисленное значение %2 меньше табличного %2 v, то ис-
ключение части показателей не вызывает потерю информации.
Последовательный отбор переменных позволяет найти опти-
мальное количество показателей, которое обладает такими же
(или лучшими) дискриминантными возможностями, что и полный
набор исходных переменных. Чем меньше показателей, тем легче
интерпретировать результаты анализа.
Поскольку переменные, отобранные в модель, являются силь-
ными дискриминаторами и могут коррелировать между собой
(нести одну и ту же информацию), то после каждого исключения
(подключения) пересчитывается Л-статистика Уилкса и оценива-
ется значимость изменений в этой характеристике. В связи с тем
что Л-статистика Уилкса является мерой остатка модели (мерой
неопределенности), желательно, чтобы она принимала наи-
меньшее значение.
210
5.4. РЕАЛИЗАЦИЯ ДИСКРИМИНАНТНОГО АНАЛИЗА
5.4.1. Пример применения дискриминантного анализа
при наличии двух обучающих выборок
Пример 5.1. Имеются данные по двум группам промышленных
предприятий отрасли (табл. 5.2):
%! — среднегодовая стоимость основных производственных
фондов, млн ден. ед.;
х2 — среднесписочная численность персонала, тыс. чел.;
х3 — балансовая прибыль, млн ден. ед.
Исходные данные взяты из [15] и дополнены тремя предпри-
ятиями, подлежащими дискриминации.
Таблица 5.2
Показатели деятельности промышленных предприятий отрасли
Группа предприятий Мк(к=0, 1,2) Номер предприятия i (1=1, 2,..., пк) Показатель Xj (/=1,2,3)
х2 х3
Группа передовых 1 (1) 224,228 17,115 22,981
предприятий Л/, 2 (2) 151,827 14,904 21,481
(*=1) 3 (3) 147,313 13,627 18,669
4 (4) 152,253 10,545 10,199
Группа отстающих 1 (5) 46,757 4,428 11,124
предприятий М2 2 (6) 29,033 5,510 6,091
(к = 2) 3 (7) 52,134 4,214 11,842
4 (8) 37,050 5,527 11,873
5 (9) 63,979 4,211 12,860
Группа предприятий 1 (Ю) 55,451 9,592 12,840
MQ, подлежащих 2 (П) 78,575 11,727 15,535
дискриминации 3 (12) 98,353 17,572 20,458
(Л = 0)
Примечание. Цифры в скобках соответствуют общей нумерации всех пред-
приятий множества М.
Требуется провести классификацию (дискриминацию) трех но-
вых предприятий (по табл. 5.2 это предприятия 10—12), образу-
ющих группу Мо с известными значениями исходных перемен-
ных.
14*
211
Решение. Воспользуемся алгоритмом, представленным в пара-
графе 5.2.
1. Значения исходных переменных для обучающих подмно-
жеств и М2 (групп предприятий) записываются в виде матриц
ХО и Л
'224,228 151,827 17,115 14,904 22,98 Г 21,481 '46,757 29,033 4,428 5,510 11,124' 6,091
х(|) = ; Ха> = 52,134 4,214 11,842
147,313 13,627 18,669
37,050 5,527 11,873
152,253 10,545 10,199
к63,979 4,211 12,860,
а для подмножества Мо — группы предприятий, подлежащих клас-
сификации, в виде матрицы Х(0):
<55,451 9,592
Х(0)= 78,575 11,727
98,353 17,572
12,840'
15,535
20,458,
Общее количество предприятий, составляющих множество М,
будет равно п = 4 + 5 + 3 = 12.
2. Определяются элементы векторов (координаты центро-
идов в обучающих подмножествах и Л/2) как средние значения
по каждому признаку для пк предприятий в каждой выборке:
(168,9053'1
Х(1) = 14,04775 , Х(2) =
г45,790б'
4,778
. 10,758 ,
18,3325 J
3. Для каждого обучающего подмножества М} и М2 рассчиты- ваются ковариационные матрицы S<k> (размерностир хр):
<1023,949 55,61977 82,89305'
55,61977 5,646869 11,32551 >
к82,89305 11,32551 24,44716,
145,8412 -6,6084 22,78478'
5<2> = -6,6084 0,371782 -0,90248
22,78478 -0,90248 5,750306 i:U
212
4. Рассчитывается объединенная ковариационная матрица
(1023,949 55,61977 82,89305'
11,32551 +
S =------
4 + 5-2
5,646869
4- 55,61977
82,89305 11,32551 24,44716?
145,8412
+ 5- -6,6084
^22,78478
' 689,286 :
= 27,06244
63,64230
-6,6084 22,78478V
0,371782
1 -0,90248
27,06244 I
3,492341
5,82709
: -0,90248 =
! 5,750306J
63,64230'
5,82709 .
18,07717^
5. Рассчитывается матрица S-1, обратная к объединенной ко-
вариационной матрице 5:
5_|
'0,0022780 -0,009248 -0,005045')
-0,009248
-0,005045
0,657093
-0,179253
-0,179253 .
0,130860
6. Рассчитываются дискриминантные множители (коэффици-
енты дискриминантной функции) по всем элементам обучающих
подмножеств:
0,657093
-0,179253
<45,790бЛ'
4,778
10,758 I
А =
X
0,0022780 -0,009248 -0,005045']
-0,009248
-0,005045
V 168,9053'
14,04775
18,3325
х
-0,179253
0,130860
' 0,156720 '
3,594781 .
-1,291500
Тогда дискриминантная функция примет следующий вид:
F= 0,156720%, + 3,594781%2 - 1,291500%3.
7. Для каждого /-го объекта к-го обучающего подмножества Мк
определяется значение дискриминантной функции (i = 1,пк;
£=1,2):
= 0,156720-224,228+ 3,594781 17,115 +
+ (-1,291500) • 22,981 = 66,98581;
213
Ер = 0,156720 - 151,827 + 3,594781 14,904 +
+ (-1,291500) -21,481 =49,69829;
Е/1) = 0,156720- 147,313 + 3,594781 • 13,627 +
+ (-1,291500)- 18,669 = 47,96202;
Ер = 0,156720- 152,253 + 3,594781 • 10,545 +
+ (-1,291500)- 10,199 = 48,59610;
F/2> = 0,156720 - 46,757 + 3,594781 • 4,428 +
+ (-1,291500) - 11,124 = 8,878822;
Ер = 0,156720 • 63,979 + 3,594781 -4,211 +
+ (-1,291500)- 12,860 = 8,555749.
8. По совокупности найденных значений FW в каждом подмно-
жестве Мк рассчитываются средние значения Ё(Р
Ё(|) = 53,29306, Ё(2) = 10,45823.
9. Определяется общее среднее (константа дискриминации) для
дискриминантных функций:
Ё = |(53,29306 +10,45823) = 31,87564.
10. Выполняется распределение трех объектов подмножества
Мо по обучающим подмножествам М1 и М2, для чего по каждому
объекту (/ = 1, 2, 3) рассчитываются значения дискриминантных
функций:
Ер = 0,156720 • 55,451 + 3,594781 - 9,592 +
+ (-1,291500)- 12,840 = 26,58859;
Ер = 0,156720-78,575+ 3,594781 • 11,727 +
+ (-1,291500) - 15,535 = 34,40685;
Е3(0> = 0,156720 • 98,353 + 3,594781 • 17,572 +
+ (-1,291500) - 20,458 = 52,15991,
которые затем сравниваются с общей средней Е = 31,87564.
Поскольку Ё(|) > Ё(2) (т.е. 53,29306 > 10,45823) и дискрими-
нантная функция по первому объекту меньше общей средней,
т.е. Е](0) - Ё < 0 (26,58859 - 31,87564 < 0), то предприятие 1 подмно-
жества MQ относится к подмножеству М2.
214
Учитывая, что разности Г2(0) - F > 0 (34,40685 - 31,87564 > 0) и
Г3<°> - F > 0(52,15991 - 31,87564 >0), предприятия 2 и 3 подмноже-
ства Л/о относятся к подмножеству Мх.
Если бы выполнялось условие F(V> < F(1\ то объекты Мо отно-
сились бы к подмножеству при /J(0) - F < 0 и к подмножеству
М2 в противном случае.
11. Оценка качества распределения новых объектов выполня-
ется путем сравнения с константой дискриминации F значений
дискриминантных функций Fp> обучающих подмножеств Мх и М2.
Поскольку для всех найденных значений выполняются неравен-
ства FW>F и Fp^< F, можно предположить, что новые предпри-
ятия подмножества Л/о распределены по обучающим подмноже-
ствам верно.
Графическая интерпретация результатов дискриминации в сис-
теме координат «отклонение (удаленность) объектов от общей
средней — порядковый номер объекта» представлена на рис. 5.4.
Как видно, в положительной области графика находятся предпри-
ятия подмножества с высоким уровнем показателей, а в отри-
цательной — предприятия подмножества М2. В результате дискри-
минации предприятие 1 подмножества Л/о отнесено к подмноже-
ству М2, а предприятия 2 и 3 — к подмножеству М{, т.е. объекты
подмножества Мо с положительными координатами (верхняя
Рис. 5.4. Распределение объектов подмножества Мо
по обучающим подмножествам Л/, и М2
21S
полуплоскость графика) отнесены к подмножеству Мх, а объекты
с отрицательными координатами (нижняя полуплоскость) — к под-
множеству М2.
Следует заметить,' что практически все предприятия подмноже-
ства М2 удалены от среднего значения на одинаковом расстоянии,
в то же время предприятия первой обучающей выборки М{ имеют
существенный разброс внутри своей группы. Координаты центро-
идов равны по абсолютной величине, но имеют разные знаки.
Замечание. Расчеты и рис. 5.4 выполнены в среде Excel с
использованием встроенных функций.
5.4.2. Пошаговый алгоритм
дискриминантного анализа в SPSS
Обработка исходных данных, приведенных в табл. 5.2 (см. под-
параграф 5.4.1), в системе SPSS ведется в диалоговом режиме в
такой последовательности [9, 26, 36, 39]:
1. Запустить программу SPSS с помощью пиктограммы на ра-
бочем столе или в главном меню Windows с помощью команды
Пуск Программы SPSS для Windows.
После запуска SPSS в открывшемся диалоговом окне SPSS для
Windows щелкнуть кнопкой Отмена (Cancel).
2. В окне редактора Данные (Data View) (см. рис. 2.2) ввести
числовые данные для рассмотренного примера 5.1 (см. табл. 5.2).
Общий вид экрана с введенными данными приведен на рис. 5.5.
рЛ пример [Набор данных! ] - SPSS Редактор Данных
файл Л дмя J- a QJ <з Л- ВИД л Данные преобразовать Анализ В * <♦ Ь & И Г Г- В Ф R > Срафи<а С$ репс фно £пр te.
Q
х1 х2 хз гр ' пер .-.□р' I пер ГТ
1 224,228 17,115 22,981 1
2 151,827 14,904 21,481 1
3 147,313 13,627 18,669 1
4 152,253 10,545 10,199 1
S 46,757 4,428 11,124’ 2
6 29,033 5,510 6,091 2
7 52,134 4,214 11,842 2
8 37,050 5,527 11,873 2
9 03,979 4,211 12,860 2
10 55,451 9,592 12,840 9
11 78,575 11,727 15,535 9
12 98,353 17,572 20,458 9 —
Рис. 5.5. Введенные данные в режиме Данные
216
Здесь в четвертом столбце указана принадлежность объектов к тому
или иному множеству. Объектам, подлежащим дискриминации,
присвоена цифра 9.
Перейти в режим Переменные (Variable View) и задать структуру
исходных данных (рис. 5.6). Для каждой переменной определяются
Имя (Name), Тип (Туре), Ширина (Width), Знаки после запятой
(Decimals), Метка (Label), Значения (Values), Пропущенные (Missing),
Ширина столбца (Columns), Выравнивание (Align) и Шкала (Measure)
(подробно о вводе параметров переменных см. в главе 2).
Без имени - SPSS Редактор Данных
Файл Пмвка Вид Данные Греобравоеатъ Анапе Графика Серене Оно Справка
Имя) Тил ) Ширина|змаки после запятой)
х1 ;Числовая8
х2 Числовая 8
хЗ Числовая 8
гр ^Числовая 8
Метка
Стоимость ОПФ
Персонал
Прибыль
Группы
Значения) Пропущенные) Ширина столбца) ВыраеЛ
Нет
Нет
Нет
Нет
Нет
Нет
Нет
Нет
По прав
По прав
По прав
:По прав
2
3
8
Рис. 5.6. Режим Переменные окна редактора данных
Введенные данные целесообразно сохранить в файле
(Файл -> Сохранить как...), задав имя файла и папку. Если исходные
данные уже были набраны в Excel и строки соответствуют объек-
там, а столбцы переменным, то их можно перенести в SPSS. Для
этого в SPSS необходимо подготовить структуру файла исходных
данных. После чего открывается файл данных в Excel (подготов-
ленный файл при этом не закрывается), копируется блок данных,
подлежащих переносу, и вставляется в файл SPSS.
3. В строке меню SPSS выбрать Анализ -»Классификация -»Дис-
криминантный анализ... (рис. 5.7).
Г 10.545 т
Т 4?428 Г
Т’5.510 '
Г 4.214
8
9
10
12
224,23 ! 17.115
151,83 = 14,904
147,31 : 13,627
152.25
46.757
29.033
52.134
37,0W”T 5,527
63,979 I 4,211
55,451 ‘ 9.592
78,575 f 11,727
98,353* : 17,572
22.981.
21,481
18,669
10.198
11,124
6,091
11.842
11,873
12,860
12,840
15,536
20.458
кластеризация к-среддои
Иерархическая кластеризация...
Снижение размерности
Анализ шкал
Негираметрические критерии
бременчые ряды
Выживаемость
Множественные откл*и
Анализ гропущеьньк значений...
Сложные выборки
Отчеты
Сосательные статистики
Таблицы
Сравнение средних
Общая линейная модель
Смешанные модели
Корреляции
Регрессия
"2
2
' ejj
2
5
6
Рис. 5.7. Порядок выбора в меню дискриминантного анализа
217
После этого откроется диалоговое окно Дискриминантный анализ
{Discriminant Analysis) (рис. 5.8), в котором находятся:
• область со списком доступных для анализа переменных;
• поле Группирующая переменная {Grouping Variable) — используется
для задания зависимой переменной (рис. 5.9). Диапазон изме-
I Дискриминантный анализ
Группирующая переменная:
Стайность ОПФ [>1]
♦I___________
Персонал [х2]
<$> Прибыль [хЗ]
Независимые:
(S вводить независимые вместе
С Использовать шаговый метод
Переменная отбора
Статистики... Мецзд, I Классифицировать... <: Сохранить...
Рис. 5.8. Диалоговое окно Дискриминантный анализ
М Г&ЭфИМ c-toim
mi rid bi&l Ml С П*
1
2
2
4
~5
6
7
8
224.23 i 17.115 22.981 1
«W........! 143Ю4 ' 21 431* 1
147,31 | 13,627 18.669i 1 ИфГруппмМ
152,».....Г'10.545 г 10.199Г ijg
46.757 i 4.428 11,124' ~2"Я
29.033 : 5.510 5,091 ‘ “2 В
52.134 4.214 • 11.942* 2 j|
37,050 . 5,527 11,873 . 2 !
63,979” I 4,211 I 12.8воТ” 2 |
56.451’ i 9,592 I 12.840! 9 *
78.575 "* 11,727 15,536 9
98.353 I 17.572 20.4581 '9
Группирующая переменная .!
Ш 1МИИМИММИМИ
Задать диапазон I —— »
□
□
□временная отбора
1^1 1
Махш.
J Пластифицировать,. I » Сохранить-
Рис. 5.9. Задание минимального и максимального значений
группирующей переменной -
$18
нения этой переменной вводится после нажатия кнопки Задать
диапазон... (Define Range...), затем в открывшемся диалоговом
окне задаются минимальные и максимальные значения груп-
пирующей переменной и подтверждаются нажатием кнопки
Продолжить (Continue)-,
• область Независимые (Independents) (см. рис. 5.8) для выделения
независимых переменных;
• переключатели выбора вида дискриминантного анализа:
а) Вводить независимые вместе (Enter independents together) — вы-
бирается по умолчанию;
б) Использовать шаговый метод (Use stepwise method)-,
• поле Переменная отбора (Selection Variable) — указывается имя тех
переменных из списка доступных, которые могут принимать
заданное значение. С помощью кнопки Значение... (Value...) в
диалоговом окне Установка значения (Set Value) вводится числен-
ное значение переменной (рис. 5.10). С учетом этого в анализе
будут участвовать только те объекты, которые принимают за-
данное значение;
Рис. 5.10. Задание уровня значений переменной отбора
• четыре кнопки управления параметрами ДА, расположенные в
нижней части окна (см. рис. 5.10):
1) кнопка Статистики... (Statistics...) — используется для выявле-
ния зависимостей между предикторами перед началом дискрими-
нантного анализа (рис. 5.11).
219
Дискриминантный анализ: Статистики
; Описательные статистики Матрицы —-............
F Средние! : Г Внутригрупповая корреляция
| Однофакторный дисперсионный анализ | Внутригрупповая ковариация
: Г М Бокса Г" Групповые ковариации
' Г~ Общая ковариация
Коэффициенты функции
Г Фишера
I Нестандартизованные ГТ! : I _ I
I _ «“н Продолжить Отмена Справка
Рис. 5.11. Общий вид диалогового окна Статистики
s Флажки в группе Описательные статистики (Descriptives) озна-
чают:
• Средние (Means) — средние значения и стандартные отклонения
для каждой переменной каждой группы и выборки в целом;
* Однофакторный дисперсионный анализ (Univariate ANOVAs) — если
число уровней зависимой переменной равно двум, то это /-кри-
терий для сравнения между собой двух средних значений для
групп по каждой переменной;
• М Бокса (Box’s М) — критерий проверки многомерной нормаль-
ности исходных данных на основе близости значений опреде-
лителей ковариационных матриц для уровней зависимой пере-
менной (нулевая гипотеза Яо). Результаты теста оценивают по
статистической значимости Знч. (Sig.). Если Знч. > 0,05, то дан-
ные характеризуются многомерным нормальным распределе-
нием, в противном случае (при Знч. < 0,05) такая нормальность
распределения не обеспечена.
J Флажки в группе Коэффициенты функции (Function Coefficients)
означают:
• Фишера (Fisher's) — канонические коэффициенты уравнения
регрессии;
• Нестандартизованные (Unstandardized) — нестандартизованные
коэффициенты уравнения регрессии, вычисляются для исход-
ных значений предикторов.
J Флажки в группе Матрицы (Matrices) означают:
• Внутригрупповая корреляция (Within-groups correlation) — матрица,
состоящая из соответствующих средних значений корреляци-
онных матриц для уровней зависимой переменной;
220
• Внутригрупповая ковариация (Within-groups covariance) — матрица,
состоящая из соответствующих значений ковариационных мат-
риц для уровней зависимой переменной;
• Групповые ковариации (Separate-groups covariance) — отдельные
ковариационные матрицы для каждого уровня зависимой пере-
менной;
• Общая ковариация (Total covariance) — ковариационная матрица
для всей выборки;
2) кнопка Метод... (Method...) — диалоговое окно Шаговый метод
(Stepwise method) (рис. 5.12) доступно, когда в диалоговом окне
Дискриминантный анализ (Discriminant Analysis) переключатель уста-
новлен в положении Использовать пошаговый метод (Use stepwise
method) (см. рис. 5.8).
Рис. 5.12. Общий вид диалогового окна Шаговый метод
У В группе Метод (Method) можно выбрать метод составления
дискриминантного уравнения:
• Лямбда Уилкса (Wilks’ lambda) — метод основан на минимизации
коэффициента Уилкса (X) после включения в уравнение регрес-
сии каждого нового предиктора. Коэффициент Уилкса характе-
ризует долю дисперсии оценок дискриминантной функции,
которая не обусловлена различиями между группами. Он равен
единице, когда средние значения для всех групп равны, и умень-
шается с ростом разностей средних значений. Уровни значи-
мости характеризуют вероятность того, что различия между
' группами случайны. Например, при Знч. < 0,001 имеют место
221
существенные различия между средними значениями дискри-
минантной функции в исследуемых группах;
• Необъясненная дисперсия (Unexplained variance) — на каждом шаге
вводится переменная, минимизирующая сумму необъясненной
изменчивости между группами;
• Расстояние Махаланобиса (Mahalanobis distance) — измеряется
удаленность наблюдений для данной независимой переменной
от среднего по всем наблюдениям;
• Наименьшее F отношение (Smallest F ratio) — отбор переменных
основан на максимизации F-отношения, вычисленного по рас-
стоянию Махаланобиса между группами;
• V Рао (Rao’s V) — позволяет определить минимальное увеличе-
ние Кдля переменной. После выбора этой опции вводится ми-
нимальное значение переменной в дополнительном окне
V-ввода (V-to-enter), которое используется в анализе.
S В области Критерии (Criteria) задаются значения критериев для
включения в дискриминантное уравнение и исключения из него
предикторов:
• Использовать F-значение (Use Fvalue) — если флажок стоит в этой
строке, то по умолчанию используются критические значения
F-критерия: FKp = 3,84 — в окне Включение (Entry) при уровне
значимости 0,05 и F =2,71 — в окне Удаление (Removal) при
уровне значимости 0,10. Переменная включается в модель,
если для нее F> FKp = 3,84, и удаляется, если F< FKp = 2,71.
Значение включения всегда должно быть больше значения уда-
ления. Чтобы включить большее количество переменных в мо-
дель, необходимо понизить верхнее критическое значение FKp,
а чтобы исключить большее количество переменных из модели,
необходимо увеличить нижнее критическое значение FKp;
• Использовать вероятность F (Use probability of F) — флажок ставит-
ся, когда задается уровень значимости для F-критерия. По умол-
чанию введены значения 0,05 и 0,10.
У В группе Вывести (Display) задается вывод величин:
• Отчет о шагах (Summary of steps) — пошаговый вывод основных
результатов обеспечивается по умолчанию;
• F для попарных расстояний (Ffor pairwise distances) — выбирается
установкой флажка, когда используется метод Расстояние Маха-
ланобиса (Mahalanobis distance)',
3) кнопка Классифицировать... (Classify...) — позволяет управлять
вычислением вероятностей, итоговыми результатами классифика-
ции и выводом графиков в диалоговом окне (рис. 5.13).
222
Рис. 5.13. Диалоговое окно в режиме Классификация
J Априорные вероятности {Prior Probabilities) — в классификации
используются два переключателя:
• Все группы равны {Allgroups equal) — вероятности принадлежно-
сти объектов к каждой из групп полагаются равными;
• Вычислить по размерам групп {Compute from group sizes) — вероят-
ности принадлежности объекта к каждой из групп пропорцио-
нальны размерам групп.
J В группе Вывести {Display) расположены опции для вывода
результатов анализа:
• Поточечные результаты {Casewise results) — используются, когда
файл данных не слишком велик, тогда в результат включается
список объектов и для каждого объекта указываются фактическая
группа, прогнозируемая группа, вероятность попадания в про-
гнозируемую группу и значения дискриминантных функций;
• Итоговая таблица {Summary table) — включает в результат число и
процент корректных и некорректных классификаций для каж-
дой группы;
• Скользящий контроль {Leave-one-out) — каждый объект класси-
фицируется с помощью функций, входными значениями для
которых являются все объекты, в том числе и те, для которых
классификация неизвестна.
Опция Заменить пропущенные значения средним {Replace missing
values with mean) используется, чтобы при классификации отсут-
ствующие значения независимой переменной заменить сред-
ним.
J Ковариационная матрица {Use Covariance Matrix) имеет два пе-
реключателя:
223
• Внутригрупповая (Within-groups) — по умолчанию классифициру-
ет объекты с помощью общей внутригрупповой матрицы кова-
риаций;
• Отдельно по группам {Separate-groups) — объекты классифициру-
ются с помощью матриц ковариаций, отдельных для каждой
группы.
J В группе Графики {Plots) доступны следующие графические
опции:
• Объединенные группы {Combined-groups) — в вывод включается
гистограмма (если число групп равно двум) или диаграмма раз-
броса (если число групп более двух);
• Для отдельных групп {Separate-groups) — выводится несколько
диаграмм, каждая из которых соответствует одной группе;
• Территориальная карта {Territorialтар) — используется, когда за-
висимая переменная имеет три уровня и более. Здесь числа
(номера) соответствуют группам, в которые объекты классифи-
цированы. Среднее в каждой группе обозначено звездочкой в
пределах ее границ. Карта не отображается, если имеется толь-
ко одна дискриминантная функция;
4) кнопка Сохранить... {Save...) — позволяет сохранять новые
переменные для каждого объекта (в том числе «неизвестного»),
В открывшемся диалоговом окне (рис. 5.14) заказывается следу-
ющая информация:
• Предсказанная принадлежность к группе {Predicted group member-
ship)',
• Дискриминантные баллы {Discriminant scores) — соответствуют
оценкам дискриминантных функций;
Рис. 5.14. Диалоговое окно в режиме Сохранить
224
• Вероятности принадлежности К группам {Probabilities of group member-
ship).
Кроме того, здесь имеется поле Экспортировать модель в формате
XML {Export model information to XML file).
Введенная информация подтверждается кнопкой Продолжить
{Continue).
4. Для начала выполнения расчетов необходимо в диалоговом
окне Дискриминантный анализ {Discriminant Analysis) щелкнуть по
кнопке ОК (см. рис. 5.8).
5.4.3. Дискриминантный анализ в SPSS
при наличии двух обучающих выборок
Пример 5.2. Возьмем исходные данные примера 5.1, рассмот-
ренного в подпараграфе 5.4.1. Напомним, что здесь обучающие
выборки представлены двумя группами предприятий: к первой
группе относятся передовые предприятия, образующие подмно-
жество Л/|, а ко второй — отстающие, составляющие подмноже-
ство Л/2.
Требуется провести классификацию (дискриминацию) трех но-
вых предприятий, образующих группу Л/о, с известными значени-
ями я, (среднегодовой стоимости основных производственных
фондов, млн ден. ед.), х2 (среднесписочной численности персона-
ла, тыс. чел.) и х3 (балансовой прибыли, млн ден. ед.).
Решение. Согласно рассмотренному в подпараграфе 5.4.2 алго-
ритму последовательность действий такова:
1. Запустить программу SPSS, в открывшемся после запуска
окне щелкнуть по кнопке Отмена {Cancel). После этого активизи-
руется редактор данных Данные {Data View).
2. Щелкнуть мышкой по ярлычку Переменные {Variable View) и
в открывшемся окне задать структуру исходных данных по каждой
переменной: определить Имя {Name) — х1, х2, хЗ и гр, Тип {Туре)
переменной оставить по умолчанию Числовая {Numeric), Ширина
{Width) устанавливается равной 8 (по умолчанию), Знаки после
запятой {Decimals) и другие параметры ввести такими, как на
рис. 5.6.
3. Вернуться в окно Данные {Data View) и ввести значения для
всех переменных. Подлежащим дискриминации переменным при-
своить номер, отличный от 1 и 2, например 9.
15 - 1591
225
4. Выбрать в строке меню Анализ -> Классификация -> Дис-
криминантный анализ... (Analyze —> Classify —> Discriminant...) и в
открывшемся диалоговом окне Дискриминантный анализ (Discrimi-
nant Analysis) (см. рис. 5.8), поместить переменную «Группа» [гр]
в поле Группирующая переменная (Grouping Variable). Затем после !
щелчка по кнопке Задать диапазон... (Define Range...) ввести ми-
нимальное и максимальное значения этой переменной: 1 и 2
(см. рис. 5.9).
Независимые переменные «Стоимость ОПФ» [х1 ], «Персонал»
[х2] и «Прибыль» [хЗ] ввести в список Независимые (Independents).
5. Выбрать вариант дискриминантного анализа Вводить незави-
симые вместе (Enter independents together) в этом же диалоговом
окне.
6. Щелкнуть по кнопке Статистики... (Statistics...) и в открывшем-
ся диалоговом окне (см. рис. 5.11) активизировать опции: Средние
(Means), Однофакторный дисперсионный анализ (Univariate ANOVAs),
Нестандартизованные (Unstandardized), Внутригрупповая корреляция
(Within-groups correlation) и подтвердить кнопкой Продолжить (Con-
tinue).
7. Щелкнуть по кнопке Классифицировать (Classify...)
(см. рис. 5.8), чтобы в открывшемся диалоговом окне (см. рис. 5.13)
в группе Вывести (Display) установить опции для вывода результатов
анализа: Поточечные результаты (Casewise results) и Итоговая таблица
(Summary table), после чего щелкнуть по кнопке Продолжить (Con-
tinue).
8. Щелкнуть по кнопке Сохранить... (Save...) (см. рис. 5.8) и в
открывшемся диалоговом окне (см. рис. 5.14) установить флажки
напротив: Предсказанная принадлежность к группе (Predicted group
membership), Дискриминантные баллы (Discriminantscores), Вероятности
принадлежности к группам (Probabilities of group membership), затем
щелкнуть по кнопке Продолжить (Continue).
9. Чтобы выполнить расчеты по алгоритму дискриминантного
анализа и открыть окно вывода, необходимо щелкнуть по кнопке
ОК (см. рис. 5.8). Вычисления и вывод результатов осуществляются
автоматически.
Результаты расчета представлены в виде таблиц, рассмотрим
основные из них.
Вначале выводится таблица с комментариями по новым пере-
менным, которые появляются дополнительно к исходным в резуль- *
тате проведения ДА (табл. 5.3).
226
Таблица 5.3
Примечания
Комментарии
Созданные или измененные переменные Dis_1 DislJ Dis1_2 Dis2_2 Предсказанная группа для анализа 1 Значения дискриминантной функции 1 для анализа 1 Вероятность принадлежности к группе 1 для анализа 1 Вероятность принадлежности к группе 2 для анализа 1
В таблице «Сводка результатов обработки наблюдений»
(табл. 5.4) представлены результаты анализа действительных и
пропущенных значений.
Таблица 5.4
Сводка результатов обработки наблюдений
Невзвешенные наблюдения N Процент
Валидные 9 75,0
Исключенные Пропущенные или лежащие вне диапазона коды группирующей переменной 3 25,0
По крайней мере одна пропущенная дискриминантная переменная 0 ,0
Оба групповых кода пропущены или лежат вне диапазона, и отсутствует по крайней мере одна дискриминантная переменная 0 ,0
Итого искл. 3 25,0
Всего набл. 12 100,0
Общее количество наблюдений составило 12 единиц, в том чис-
ле 9 действительных и 3 подлежащих дискриминации. В последней
графе табл. 5.4 приведены эти же данные в процентном соотноше-
нии.
В следующей таблице «Групповые статистики» (табл. 5.5) при-
водятся средние значения, стандартные отклонения и количество
наблюдений для всех переменных из обеих групп и для каждой
группы в отдельности.
По средним значениям заметен более высокий уровень пере-
менных в первой группе предприятий, чем во второй (стоимость
ОПФ составляет 168,90525 по сравнению с 45,79060 млн ден. ед.,
численность персонала — 14,04775 и 4,77800 тыс. чел., прибыль
18,33250 и 10,75800 млн ден. ед.). Здесь же приведены и общие
средние значения по каждой переменной.
Результаты теста на значимость различий между переменными,
находящимися в разных группах, приведены в таблице «Критерий
15*
227
Таблица 5.S:
Групповые статистики
Группы Среднее Стд. отклонение Кол-во валидных (искл. целиком)
Невзве- шенные Взвешенные
1 Стоимость ОПФ 168,90525 36,949497 4 4,000
Персонал 14,04775 2,743931 4 4,000
Прибыль 18,33250 5,709310 4 4,000
2 Стоимость ОПФ 45,79060 13,501905 5 5,000
Персонал 4,77800 ,681709 5 5,000
Прибыль 10,75800 2,681023 5 5,000
Итого Стоимость ОПФ 100,50822 69,379127 9 9,000
Персонал 8,89789 5,188907 9 9,000
Прибыль 14,12444 5,635112 9 9,000
равенства групповых средних» (табл. 5.6). С помощью этих данных
выясняется существенность различий (т.е. присутствуют ли разде-
ляющие (дискриминирующие) особенности).
Таблица 5.6
Критерий равенства групповых средних
Лямбда Уилкса F СТ.СВ1 СТ.СВ2 Знч.
Стоимость ОПФ ,125 48,866 1 7 ,000
Персонал ,113 54,677 1 7 ,000
Прибыль ,498 7,053 1 7 ,033
В данном примере получены весьма значимые различия
между группами, поскольку для всех переменных Знч. < 0,05. Если
бы уровень значимости для некоторых переменных превысил зна-
чение 0,05, их можно было бы исключить из списка независимых
переменных без ухудшения качества классификации.
Таблица «Объединенные внутригрупповые матрицы» объеди-
ненных коэффициентов корреляции (табл. 5.7) используется для
анализа взаимосвязи между отдельными переменными. Здесь за-
Таблица 5.7
Объедииениые внутригрупповые матрицы
Стоимость ОПФ Персонал Прибыль
Корреляция Стоимость ОПФ 1,000 ,552 ,570
Персонал ,552 1,000 ,733
Прибыль ,570 ,733 1,000
228
метна существенная корреляция между размером прибыли и чис-
ленностью персонала, поэтому целесообразно было бы сделать
проверку на возможное присутствие мультиколлинеарности. При
наличии мультиколлинеарности отдельные коэффициенты дис-
криминантной функции окажутся незначимыми.
Результаты анализа коэффициентов дискриминантной функции
приведены в таблице «Собственные значения» (табл. 5.8).
Таблица 5.8
Собственные значения
Функция Собственное значение % объясненной дисперсии Кумулятивный % Каноническая корреляция
1 13.598(a) 100,0 100,0 ,965
а В анализе использовались первые 1 канонические дискриминантные функции.
Большое собственное значение 13,598 подтверждает высокую
точность подобранной дискриминантной функции. Две группы
J дискриминируются одной функцией, которая учитывает 100% дис-
персии, корреляция между исходными данными и полученными
на основе модели очень сильная и составляет 0,965.
По критерию «Лямбда Уилкса» проверяется значимость дискри-
минантной функции; он показывает, значимо ли различаются меж-
ду собой средние значения дискриминантной функции в обеих
группах (табл. 5.9).
Таблица 5.9
Лямбда Уилкса
Проверка функции(й) Лямбда Уилкса Хи-квадрат ст.св. Знч.
1 ,069 14,745 3 ,002
Поскольку дискриминантная функция значима на уровне
Знч. = 0,002, то имеет смысл использовать ее для дальнейшей клас-
сификации.
В таблице «Нормированные коэффициенты канонической дис-
криминантной функции» (табл. 5.10) приведены стандартизован-
ные канонические коэффициенты дискриминантной функции,
полученные из коэффициентов дискриминантной функции для
переменных, к которым применены ^-преобразования (вычтены
средние значения и разделены на дисперсию). Стандартизованные
коэффициенты позволяют непосредственно сравнивать вклад каж-
дой независимой переменной в различение двух групп.
229
Таблица 5.10
Нормированные коэффициенты канонической дискриминантной функции
Функция
1
Стоимость ОПФ ,629
Персонал 1,026
Прибыль -,839
Например, на включение новых предприятий в ту или иную
группу сильнее всего оказывает влияние (в порядке убывания):
численность персонала, стоимость ОПФ и прибыль.
В структурной матрице (табл. 5.11) приведены коэффициенты
корреляции между каждой независимой переменной и значением
дискриминантной функции. Здесь переменные проранжированы
по степени их влияния; о силе связи можно судить по значениям
этих коэффициентов.
Таблица 5.11
Структурная матрица
Функция
1
Персонал Стоимость ОПФ Прибыль ,758 ,716 ,272
Объединенные внутригрупповые корреляции между дискриминантными переменными и нормированными каноническими дискриминантными функциями. Переменные упорядочены по абсолютной величине корреляций внутри функции.
Ненормированные (нестандартизованные) канонические ко-
эффициенты дискриминантных функций приведены в табл. 5.12.
Они используются для построения уравнения дискриминантной
функции:
£>(%) = -4,507 + 0,024xt + 0,549х2 - 0,197х3.
Таблица 5.12
Коэффициенты канонической дискриминантной функции
Функция
1
Стоимость ОПФ ,024
Персонал ,549
Прибыль -.197
(Константа) -4,507
Ненормированные коэффициенты
230
С помощью данного уравнения можно рассчитать принадлеж-
ность предприятия из множества Мо к той или иной обучающей
группе. Для этого необходимо подставить значения показателей xt,
х2 и х3 («Стоимость ОПФ», «Персонал», «Прибыль») по каждому
предприятию, вычислить значения D(X) и сравнить их со значени-
ями функции, вычисленными для центроидов. Значения функции
для центроидов приведены в табл. 5.13.
Таблица 5.13
Функции в центроидах групп
Группы Функция
1
1 3,636
2 -2,909
Ненормированные канонические дискриминантные функции вычислены в центроидах групп.
Информация о фактических (Actual Group) и предсказанных
(Predicted Group) группах для каждого предприятия и дискрими-
нантные баллы (Discriminant Scores), полученные при подстановке
значений переменных в уравнение D(X), приведены в таблице «По-
точечные статистики» (табл. 5.14). Здесь же даны P(D > d I G = g) —
вероятности принадлежности предприятия к группе (G) при данной
величине дискриминантной функции (D) и P(G = g I D = d) — веро-
ятности наблюдаемого значения дискриминантной функции (D),
если задана принадлежность объекта к группе (G).
В результате дискриминантного анализа с высокой вероятностью
определена принадлежность дискриминируемых предприятий к
обучающим подмножествам Мх и М2. первое предприятие (поряд-
ковый номер 10) отнесено к подмножеству М2 с вероятностью 0,995,
второе и третье (порядковые номера И и 12) отнесены к подмно-
жеству М} с соответствующими вероятностями 0,926 и 1,0.
Если классификация проведена неудачно, т.е. предсказанные
значения не совпадают с истинными, то этот объект помечается
двумя звездочками и под таблицей выводится сообщение: «“ Невер-
но классифицированный случай» (Misclassified case).
Окончательные результаты дискриминантного анализа приве-
дены в таблице «Результаты классификации» (табл. 5.15). Здесь в
последней строке содержится информация о точности построен-
ной модели. В данном случае все три дискриминируемых предпри-
ятия корректно отнесены к первой и второй группе, из них два
предприятия — к первой и одно — ко второй группе.
231
Таблица 5.14
Поточечные статистики
Номер наблюдения Фактиче- ская группа Наивероятнейшая группа Вторая вероятнейшая группа Дискрими- нантные баллы
Предсказан- наягруппа P(D>d|G = g) P(G = g|D = d> Квадрат расстояния Махалоно- биса до центра Группа P(G = g|D = d) Квадрат расстояния Махалоно- биса до центра Функция 1
Р ст.св.
Исходные 1 1 1 ,036 1 1,000 4,377 2 ,000 74,597 5,728
2 1 1 ,576 1 1,000 ,314 2 ,000 35,819 3,076
3 1 1 .415 1 1,000 ,663 2 ,000 32,836 2,821
4 1 1 ,473 1 1,000 ,515 2 ,000 33,956 2,918
5 2 2 ,809 1 1,000 ,058 1 ,000 46,052 -3,150
6 2 2 ,357 1 1,000 ,850 1 ,000 31,619 -1,987
7 2 2 ,710 1 1,000 ,138 1 ,000 47,840 -3,281
8 2 2 ,986 1 1,000 ,000 1 ,000 43,070 -2,927
9 2 2 ,771 1 1,000 ,084 1 ,000 46,724 -3,199
10 Несгруппи- рованные 2 ,014 1 ,995 6,074 1 ,005 16,648 -,444
11 Несгруппи- рованные 1 ,004 1 ,926 8,327 2 ,074 13,389 ,750
12 Несгруппи- рованные 1 ,863 1 1,000 ,030 2 ,000 40,599 3,463
Таблица 5.15
Результаты классификаций а)
гр Предсказанная принад- лежность к группе Итого
1 2
Исходные Частота 1 4 0 4
2 0 5 5
Несгруппирован- ные наблюдения 2 1 3
% 1 100,0 .0 100,0
2 ,0 100,0 100,0
Несгруппирован- ные наблюдения 66,7 33,3 100,0
а 100,0% исходных сгруппированных наблюдений классифицировано правильно.
Окончательные результаты классификации в SPSS совпадают с
результатами, полученными в примере 5.1 (см. подпараграф 5.4.1),
несмотря на то, что алгоритмы реализации ДА и вывод промежу-
точных результатов в обоих случаях несколько различаются.
После проведения дискриминантного анализа к файлу исход-
ных данных добавятся четыре новые переменные (на рис. 5.15 они
выделены темным фоном):
Г" Пример - SPSS Data Editor
Hie E<it View Data Transform Analyze Graphs Utitles Wnclow Нф
kSrld
jl; DisJ л
х1 х2 хЗ гр Dis_ 1 I Dis1_1 J Dis1_1 I Dis2_2
1 224,228 17,115 22,981 1 | 5.72317 1.00000: . ,00000
2 151,827 14,904 21,481 1 1 ; 3,07607 1.00000* “”,00000
3 147,313 13,627 18,669 1 1 "Т 2.82148 1,0000бГ .00000
4 152,253 10,545 10,199 1 1 2.91836 1.00000! ,00000
5 46,757 4,428 11,124 2 2 -3.1501 .00000 1,00000
6 29,033 5,510 6,091 2 2 -1,9871 ,00000 1,00000
1 52,134 4,214 11,842 2 2 J -3.2806 ,00000 1,00000
8 37,050 5,527 11,873 2 2 -2,9267* .00000 1,00000
9 63,979 4,211 12.860 2 2 -3.1995* ,00000 1,00000
10 55,451 9,592 12,840! 9 2 -.44422 ,00503 ,99497
11 78,575 11,727 15,535 9 1 1 .75035 .92630 ,07370
12 98,353 17,572 20,458 9 1 Г 3.46288 1,00000 ,00000
-1г
Рис. 5.15. Общий вид файла исходных данных
с новыми переменными в режиме Данные
’< Dis_1 — номер предсказанной группы;
Dis1_1 — значение дискриминантной функции;
Г Dis1_2 — вероятность принадлежности к группе 1;
| Dis2_2 — вероятность принадлежности к группе 2.
5.4.4. Дискриминантный анализ в SPSS ’
при наличии трех обучающих выборок
Пример 5.3. Кредитный отдел коммерческого банка провел вы-
борочное обследование своих заемщиков. Общий размер выборки
составил 30 наблюдений, отобранных случайным образом для по-
строения дискриминантной функции. По каждому заемщику была
собрана информация по следующим показателям:
Х| — брал ли заемщик кредит в коммерческих банках ранее;
х2 — среднемесячный доход семьи заемщика, тыс. руб.;
х3 — срок (период) погашения кредита, лет;
х4 — размер выданного кредита, тыс. руб.;
х5 — состав семьи заемщика, чел.;
х6 — возраст заемщика, лет;
у — вероятность своевременного погашения выданного кре-
дита: низкая (Н), средняя (С) и высокая (В).
Результаты выборочного обследования приведены в сводной
таблице исходных данных (табл. 5.16).
Требуется построить дискриминантные функции с использова- .•
нием пакета SPSS, оценить значимость дискриминантной функции |
по коэффициенту Уилкса (А,), построить карту восприятия и диа- ?
граммы взаимного расположения наблюдений в пространстве двух
функций, интерпретировать результаты анализа.
Решение. В качестве зависимой переменной выберем вероят-
ность своевременного погашения кредита заемщиком. Учитывая,
что она может быть низкой (Н), средней (С) и высокой (В), каждой
категории присвоим соответствующую оценку 1, 2 и 3. Количество
заемщиков в каждой категории распределено поровну, и последние
составляют три обучающие выборки.
Для первой независимой переменной — брался ли заемщиком
кредит в коммерческих банках ранее, введем две оценки: 1 — кре-
дит ранее брался и 2 — не брался.
'.И1 Ь -
234
Таблица 5.16
Результаты выборочного обследования заемщиков банка
№ п/п Брался ли кредит ранее (1 — да, 2 — нет) Средне- месяч- ный доход семьи заемщи- ка, тыс. руб. Период погаше- ния кредита, лет Размер кредита, тыс. руб. Состав семьи заемщи- ка, чел. Воз- раст заем- щика, лет Вероят- ность погаше- ния кредита
1 1 25,20 5 180,0 3 43 С(2)
2 1 35,25 6 270,0 4 51 В(3)
3 1 31,50 7 150,0 6 42 В(3)
4 1 24,35 7 170,0 5 56 Н(1)
5 1 26,35 6 120,0 4 45 В(3)
6 1 37,50 8 370,0 5 48 В(3)
7 1 23,10 5 130,0 3 52 С(2)
8 1 28,50 2 180,0 6 51 С(2)
9 1 32,00 7 250,0 4 53 В(3)
10 1 34,05 7 160,0 5 45 С(2)
11 1 36,70 6 170,0 5 44 В(3)
12 1 35,90 5 200,0 4 41 В(3)
13 1 28,15 3 180,0 6 54 С(2)
14 1 24,65 4 120,0 3 56 В(3)
15 1 31,00 5 160,0 2 48 В(3)
16 2 16,05 5 140,0 3 58 Н(1)
17 2 18,10 3 130,0 2 55 Н(1)
18 2 21,65 2 150,0 2 37 С(2)
19 2 25,20 5 220,0 4 33 С(2)
20 2 22,05 6 360,0 3 42 С(2)
21 2 19,15 3 160,0 2 45 Н(1)
22 2 27,50 1 120,0 2 57 С(2)
23 2 23,05 3 150,0 3 51 Н(1)
24 2 17,50 10 400,0 5 44 Н(1)
25 2 18,65 2 90,0 4 54 Н(1)
26 2 20,90 5 310,0 3 36 С(2)
27 2 28,50 8 480,0 2 36 В(3)
28 2 16,70 6 280,0 2 26 Н(1)
29 2 18,35 3 220,0 3 28 Н(1)
30 2 20,65 3 250,0 2 42 н<1)
235
Построение дискриминантной функции
Выполним дискриминантный анализ по данным для 30 заем-
щиков в такой последовательности:
1. Запустить программу SPSS и ввести исходные данные по
обучающей выборке, используя окна задания структуры перемен-
ных и редактора данных: Переменные (Variable View) (названия пе-
ременных см. в п. 2), Данные (Data View) по описанному алгоритму
(см. подпараграф 5.4.2). Фрагмент окна редактора с введенными
данными представлен на рис. 5.16.
5FSS Пхмсар гаг» : . ДНЯМ*
Вйа»{^БАШ-11 SPSS-
Рис. 5.16. Окно редактора с фрагментом введенных данных
В строке меню (см. рис. 5.7) выбрать Анализ —> Классификация —>
Дискриминантный анализ... (Analyze -> Classify —> Discriminant...), в от-
крывшемся диалоговом окне Дискриминантный анализ (см. рис. 5.8)
поместить переменную «Погашение кредита» [Вероятн] в поле Груп-
пирующая переменная (Grouping Variable). После этого щелчком по
кнопке Задать диапазон... (Define Range...) открыть новое диалоговое
окно (см. рис. 5.9) и ввести минимальное (1) и максимальное (3)
значения этой переменной.
236
2. Далее в список Независимые (Independents) ввести шесть не-
зависимых переменных (см. рис. 5.8): «Кредитная история» [Исто-
рия], «Доход семьи заемщика» [Доход], «Срок погашения кредита»
[Срок], «Размер кредита» [Кредит], «Состав семьи заемщика» [Семья],
«Возраст заемщика» [Возраст].
3. Оставить по умолчанию прямой метод дискриминантного
анализа Вводить независимые вместе (Enter independents together).
4. Щелкнуть по кнопке Статистики... (Statistics...) и в открывшем-
ся диалоговом окне (см. рис. 5.11) активизировать опции: Средние
(Means), Однофакторный дисперсионный анализ (Univariate ANOKAs),
Нестандартизованные (Unstandardized), Внутригрупповая корреляция
(Within-groups correlation) и подтвердить кнопкой Продолжить (Con-
tinue).
5. Щелкнуть по кнопке Классифицировать... (Classify...)
(см. рис. 5.8). В открывшемся диалоговом окне (см. рис. 5.13) в
группе Априорные вероятности (Prior Probabilities) заказать вариант
Вычислить по размерам групп (Compute from group sizes), в группе Вы-
вести (Display) включить все опции для вывода результатов анализа,
в группе Графики (Plots) включить все опции, после чего щелкнуть
по кнопке Продолжить (Continue).
6. Щелкнуть по кнопке Сохранить... (Save...) (см. рис. 5.9) и в
открывшемся диалоговом окне (см. рис. 5.14) установить флажки
напротив: Предсказанная принадлежность к группе (Predicted group
membership), Дискриминантные баллы (Discriminant scores), Вероятности
принадлежности к группам (Probabilities of group membership), затем
щелкнуть по кнопке Продолжить (Continue).
7. Для реализации алгоритма дискриминантного анализа и от-
крытия окна вывода щелкнуть по кнопке ОК (см. рис. 5.8). Вывод
результатов осуществляется в автоматическом режиме.
Рассмотрим более подробно вывод результатов дискриминантно-
го анализа. Вначале выводится табл. 5.17 с комментариями по вновь
созданным переменным (Dis_1, Dis1_1, Dis2_1, Dis1_2, Dis2_2,
Dis3_2).
Подробный анализ информации в форматах табл. 5.18—5.31
проводится подобно примеру 5.2.
Из данных таблицы «Критерий равенства групповых средних»
(см. табл. 5.20) следует, что переменные «Срок погашения креди-
та», «Размер кредита», «Состав семьи заемщика», «Возраст заем-
щика» незначимо различаются по группам, поскольку для них
уровень значимости Знч. > 0,05, поэтому классификацию заемщи-
237
Таблица 5.17
Примечания
Комментарии
Созданные или измененные' переменные Dis_1 Dis1_1 Dis2_1 Dis1_2 Dis2_2 Dis3_2 Предсказанная группа для анализа 1 Значения дискриминантной функции 1 для анализа 1 Значения дискриминантной функции 2 для анализа 1 Вероятность принадлежности к группе 1 для анализа 1 Вероятность принадлежности к группе 2 для анализа 1 Вероятность принадлежности к группе 3 для анализа 1
Число невзвешенных наблюдений, записанных в рабочий файл данных после классификации 30
Сводка результатов обработки наблюдений
Таблица 5.18 '
Невзвешенные наблюдения N Процент
Валидные 30 100,0
Исключенные Пропущенные или лежащие вне диапазона коды группирующей переменной 0 ,0
По крайней мере одна пропущенная дискриминант- ная переменная 0 ,0
Оба групповых кода пропущены или лежат вне диапазона, и отсутствует по крайней мере одна дискриминантная переменная 0 ,0
Итого искл. 0 ,0
Всего набл. 30 100,0
ков целесообразно проводить по первым двум переменным: «Кре-
дитная история» и «Доход семьи заемщика».
Анализ матрицы коэффициентов в табл. 5.21 свидетельствует об
отсутствии мультиколлинеарности, поскольку коэффициенты кор-
реляции малы.
Результаты теста многомерной нормальности приводятся в двух
таблицах: «Логарифмический определитель» (см. табл. 5.22) и
«Результаты тестов» (см. табл. 5.23). В табл. 5.22 приведены следу-
ющие значения:
• Ранг — размерность ковариационной матрицы (6 х 6), число 6
показывает количество переменных, включенных в дискрими-
нантное уравнение;
• Лог. определитель — отражает логарифмы определителей каждой
ковариационной матрицы;
238
Таблица 5.19
Групповые статистики
Вероятн. погаш. кредита Среднее Стд.отклонение Кол-во валидных (искл.целиком)
Невзвешенные Взвешенные
1 Кредитная история 1,9000 ,31623 10 10,000
Доход семьи заемщика 19,1550 2,64212 10 10,000
Срок погаш. кредита 4,5000 2,50555 10 10,000
Размер кредита 199,000 91,22012 10 10,000
Состав семьи заемщика 3,3000 1,15950 10 10,000
Возраст заемщика 48,9000 9,97163 10 10,000
2 Кредитная история 1,5000 ,52705 10 10,000
Доход семьи заемщика 25,6300 4,03844 10 10,000
Срок погаш. кредита 4,1000 1,96921 10 10,000
Размер кредита 199,000 77,95298 10 10,000
Состав семьи заемщика 3,7000 1,49443 10 10,000
Возраст заемщика 45,0000 8,24621 10 10,000
3 Кредитная история 1,1000 ,31623 10 10,000
Доход семьи заемщика 31,9350 4,44116 10 10,000
Срок погаш. кредита 6,2000 1,31656 10 10,000
Размер кредита 229,000 117,42137 10 10,000
Состав семьи заемщика 3,9000 1,28668 10 10,000
Возраст заемщика 46,4000 6,02218 10 10,000
Итого Кредитная история 1,5000 ,50855 30 30,000
Доход семьи заемщика 25,5733 6,44289 30 30,000
Срок погаш. кредита 4,9333 2,13240 30 30,000
Размер кредита 209,000 94,62631 30 30,000
Состав семьи заемщика 3,6333 1,29943 30 30,000
Возраст заемщика 46,7667 8,11845 30 30,000
Критерий равенства групповых средних
Таблица 5.20
Лямбда Уилкса F СТ.СВ1 ст.св2 Знч.
Кредитная история ,573 10,047 2 27 .001
Доход семьи заемщика ,322 28,480 2 27 ,000
Срок погаш. кредита .811 3,137 2 27 ,060
Размер кредита ,977 ,319 2 27 ,729
Состав семьи заемщика ,962 ,535 2 27 ,592
Возраст заемщика ,959 ,575 2 27 ,570
239
Таблица 5.21
Объединенные внутригрупповые матрицы
Кредитная история Доход семьи заемщика Срок погаш. кредита Размер кредита Состав семьи заем- щика Возраст заем- щика
Корре- Кредитная история 1,000 -,477 -,103 ,426 -,569 -,422
ляция Доход семьи заемщика -.477 1,000 ,077 -.071 ,524 ,193
Срок погаш. кредита -,103 ,077 1,000 ,616 .282 -.351
Размер кредита ,426 -,071 ,616 1,000 -,018 -.469
Состав семьи заемщика -,569 ,524 ,282 -,018 1,000 .173
Возраст заемщика -,422 ,193 -.351 -,469 ,173 1,000
Таблица 5.22
Логарифмический определитель
Погашения кредита Ранг Лог. определитель
1 6 11,709
2 6 12,898
3 6 9,371
Объединенные внутри групп 6 13,815
Напечатаны ранги и натуральные логарифмы определителей групповых ковариационных матриц.
• Объединенные внутри групп — матрица из средних значений кова-
риационных матриц, построенных для каждого уровня зависи-
мой переменной.
В табл. 5.23 приведено следующее:
• М Бокса — значения критерия равенства ковариационных мат-
риц, который используется для проверки многомерной нор-
мальности распределения;
• Приблизительно — приближенные значения F-критерия, харак-
теризующего близость определителей;
Таблица 5.23 '
Результаты тестов
М Бокса 67,205
F Приблизительно ct.cbI СТ.СВ2 Знч. 1,067 42 2164,247 ,357
Проверка нулевой гипотезы о равенстве ковариационных матриц. Box's М (Критерий М Бокса) - критерий многомерной нормальности.
240
• ст.св1, ст.св2 — числа степеней свободы, используемые для опре-
деления уровня значимости;
• Знч. — значимость. Если Знч. > 0,05, то данные характеризуются
многомерным нормальным распределением, в противном слу-
чае (при Знч. < 0,05) такая нормальность считается нарушен-
ной.
Поскольку фактическая значимость Знч. = 0,357, что больше
0,05, то данные характеризуются многомерной нормальностью,
при отсутствии которой не все переменные имели бы нормальное
распределение.
Данные таблицы «Собственные значения» (см. табл. 5.24) по-
казывают, что первая функция учитывает 92,5% дисперсии, а кор-
реляция между исходными данными и данными, полученными по
модели, довольно высокая и составляет 0,878. Для второй функции
эти значения намного меньше.
Таблица 5.24
Собственные значения
Функция Собственное % объясненной Кумулятивный Каноническая
значение дисперсии % корреляция
1 3.376(a) 92,5 92,5 ,878
2 .275(a) 7,5 100,0 ,465
а В анализе использовались первые 2 канонические дискриминантные функции.
Оценка значимости дискриминантных функций проводится по
коэффициенту Уилкса (X). Из данных таблицы «Лямбда Уилкса»
(см. табл. 5.25) видно, что для первой функции значимость
Знч. < 0,001, следовательно, она позволяет значимо и надежно
дискриминировать наблюдения. В то же время значимость второй
функции составляет лишь 0,310. Поэтому в дальнейшем для клас-
сификации целесообразно использовать только первую дискрими-
нантную функцию.
Таблица 5.25
Лямбда Уилкса
Проверка функции(й) Лямбда Уилкса Хи-квадрат СТ.СВ. Знч.
от 1 до 2 ,179 42,122 12 ,000
2 ,784 5,958 5 ,310
16 - 1591
241
Таблица 5.26
Нормированные коэффициенты канонической дискриминантной функции
Функция
1 2
Кредитная история ,683 ,579
Доход семьи заемщика -,907 ,171
Срок погаш. кредита ,031 1,378
Размер кредита -,300 -,569
Состав семьи заемщика ,694 -,364
Возраст заемщика ,286 ,793
Таблица 5.27
Структурная матрица
Функция
1 2
Доход семьи заемщика Кредитная история Состав семьи заемщика Срок погаш. кредита Возраст заемщика Размер кредита -,7910 ,4700 -,1070 -,199 ,072 -.072 ,003 -,015 -,068 ,6010 ,3020 .1490
Объединенные внутригрупповые корреляции между дискриминантными переменными и нормированными каноническими дискриминантными функциями. Переменные упорядочены по абсолютной величине корреляций внутри функции. * Максимальная по абсолютной величине корреляция между переменными и дискриминантными функциями.
Формально по данным таблицы «Коэффициенты канонической
дискриминантной функции» (см. табл. 5.28) можно построить две
дискриминантные функции:
D\(X) = 0,591 + 1,71 Зх( - 0,240х2 + 0,015х3 - 0,003х4 +
+ 0,526х5 + 0,035х6;
D2(X) =-9,016+1,450Х] + 0,045х2 + 0,692х3 - 0,006х4 -
- 0,275х5 + 0,096х6.
Однако поскольку значимость второй функции более 0,001, ее
для дискриминации использовать нецелесообразно.
Координаты центроидов по группам приведены в таблице
«Функции в центроидах групп» (см. табл. 5.29). Они используются
для нанесения центроидов на карту восприятия.
л
242
Таблица 5.28
Коэффициенты канонической дискриминантной функции
Функция
1 2
Кредитная история 1,713 1,450
Доход семьи заемщика -,240 ,045
Срок погаш. кредита ,015 ,692
Размер кредита -,003 -,006
Состав семьи заемщика ,526 -,275
Возраст заемщика ,035 ,096
(Константа) ,591 -9,016
Ненормированные коэффициенты
Таблица 5.29
Функции в центроидах групп
Вероятн. погаш. кредита Функция
1 2
1 2,146 ,347
2 -,022 -,704
3 -2,124 ,357
Ненормированные канонические дискриминантные функции вычислены в центроидах групп.
Построение корты восприятия (территориальной карты)
Карта восприятия строится автоматически при задании условий
в диалоговом окне Классифицировать -> Графики -> Территориальная
карта {Classification -> Plots —> Territorial тар). Она визуализирует
разделение наблюдений функциями. Так, первая функция D\{X)
делит наблюдения на две группы: 1,2 и 2, 3, вторая функция D2{X)
отделяет наблюдения 2 от всех остальных (рис. 5.17).
Поле графика разделено дискриминантными функциями на три
области: в левой части находятся преимущественно наблюдения
третьей группы с высокой вероятностью своевременного погаше-
ния кредита; в правой части — первой группы с малой вероят-
ностью и в нижней части — второй группы со средней вероят-
ностью.
В таблице «Поточечные статистики» (см. табл. 5.30) размещена
информация о фактических {Actual Group) и предсказанных
{Predicted Group) группах для каждого заемщика и соответствующие
дискриминантные баллы {Discriminant Scores), полученные при
подстановке значений переменных в уравнения дискриминантных
функций .О1(Л) и D2{X).
16*.
243
Каноническая функция 2 -6,0 Территориальная карта "’ “
дискриминантная *' 4,0|
-4,0 -2,0 I 1 ,0 2,0
6,о 4- 1 1 31 31 31 31 31 31
4,0 •• + + 31 + 31 31 31 31 31 +
2,0 + + * 31 + 31 3221 32 21 32 21 32 21 *“ - +
,0 - J- -(- 32 -|- 21 -|- - 32 21 32 * 21 32 21 32 21 32 21 +
-2,0 - 32 32 32 32 32 32 + 21 21 21 21 21 21 +
-4,0 -- -6,0 -- + 32 + 32 32 32 32 32 32 + + 21 + 21 21 21 21 21 21
-6,о" -4,0 -2,0 Каноническая ,0 2,0 дискриминантная функция 4,0 1
6,0
6,0
Рис. 5.17. Карта восприятия для двух
дискриминантных функций D\(X) и D2(X)
(* — центроид группы)
IH.UXH
244
Таблица 5.30
Поточечные статистики
Номер наблюде- ния Фактиче- ская группа Наивероятнейшая группа Вторая вероятнейшая группа Дискриминантные баллы
Предска- занная группа P(D>d G = g) P(G = g|O = d) Квадрат расстояния Махалоно- биса до центра Группа P(G = g|O = d) Квадрат расстояния Махалоно- биса до центра Функция 1 Функция 2
Р ст.св.
Исходные 1 2 2 ,535 2 ,605 1,251 3 ,392 2,115 -1,140 -.714
2 3 3 ,677 2 ,991 ,781 2 ,009 10,122 -3,006 ,398
3 3 3 ,516 2 ,550 1,323 2 ,442 1,757 -,983 ,209
4 1 1 ,183 2 ,639 3,394 2 ,314 4,814 ,628 1,392
5 3 2(**) ,505 2 ,595 1,364 3 ,379 2,266 -.619 ,300
6 3 3 ,412 2 ,997 1,776 2 ,003 13,492 -3,402 .733
7 2 2 ,567 2 ,723 1,135 3 ,189 3,818 -.170 ,351
8 2 2 ,136 2 ,985 3,983 3 ,009 13,341 -.121 -2,697
9 3 3 ,669 2 ,974 ,805 2 ,026 8,072 -2,081 1,253
10 2 3(”) ,892 2 ,957 .228 2 ,043 6,449 -2,046 ,829
11 3 3 ,789 2 ,979 .473 2 ,021 8,158 -2,762 .101
12 3 3 ,249 2 ,982 2,782 2 ,018 10,816 -3,309 -,817
13 2 2 ,586 2 .961 1,068 1 ,022 8,579 ,082 -1,732
14 3 2(«) ,637 2 ,712 ,901 3 ,243 3,053 -,386 ,173
15 3 3 ,783 2 ,987 ,488 2 ,013 9,094 -2,820 ,421
16 1 1 ,114 2 ,999 4,338 2 ,001 19,095 3,409 2,002
17 1 1 ,910 2 ,974 ,188 2 ,026 7,467 2,288 .756
18 2 2 ,491 2 ,899 1,424 1 ,097 5,880 ,735 -1,626
19 2 2 ,810 2 ,811 ,422 1 ,176 3,478 ,627 -.736
Окончание табл. 5.30
Номер наблюде- ния Фактиче- ская группа Наивероятнейшая группа Вторая вероятнейшая группа Дискриминантные баллы
Предска- занная группа P(D>d G = g) P(G = g|D = d) Квадрат расстояния Махалоно- биса до центра Группа P(G = g|D = d) Квадрат расстояния Махалоно- биса до центра Функция 1 .Функция 2
Р СТ.СВ.
20 2 2 ,522 2 ,575 1,299 1 ,407 1,990 ,751 ,134
21 1 1 ,682 2 ,729 ,767 2 ,270 2,755 1,597 -,335
22 2 2 ,749 2 ,790 ,579 1 ,126 4,248 ,107 ,046
23 1 1 ,765 2 ,766 ,537 2 ,233 2,920 1,428 ,201
24 1 1 ,160 2 ,998 3,659 2 ,002 16,423 2,900 2,105
25 1 1 ,419 2 ,991 1,740 2 ,009 11,058 3,282 -,324
26 2 2 ,608 2 ,723 ,995 1 ,272 2,951 ,957 -,894
27 3 3 ,877 2 ,937 ,263 2 ,062 5,679 -1,868 ,802
28 1 2С») ,466 2 ,613 1,527 1 ,385 2,457 1,198 -,902
29 1 1 ,906 2 ,977 ,198 2 ,023 7,685 2,580 ,252
30 1 1 ,128 2 ,684 4,108 2 ,316 5,652 2,146 -1,680
Для исходных данных квадрат расстояния Махалонобиса вычисляется по канонической функции. Для кросс-проверяемых данных квадрат расстояния
Махалонобиса вычисляется по наблюдениям.
** Неправильно классифицированное наблюдение
Данные таблицы «Результаты классификации» (см. табл. 5.31)
свидетельствуют о том, что для 86,7% наблюдений классификация
проведена корректно, высокая точность достигнута в первой и
второй группах (90%), в третьей группе она несколько ниже
(80%).
Таблица 5.31
Результаты классификации (а)
Вероятн. погаш. кредита Предсказанная принадлежность к группе Итого
1 2 3
Исходные Частота 1 9 1 0 10
2 0 9 1 10
3 0 2 8 10
% 1 90,0 10,0 .0 100,0
2 ,0 90,0 10,0 100,0
3 ,0 20,0 80,0 100,0
а 86,7% исходных сгруппированных наблюдений классифицировано правильно.
На рис. 5.18, а—в отражено расположение заемщиков каждой из
трех групп на плоскости двух дискриминантных функций 7)1 (А) и
D2(X). По этим графикам можно проводить детальный анализ ве-
роятности погашения кредита внутри каждой группы, судить о
характере распределения заемщиков и оценивать степень их уда-
ленности от соответствующего центроида.
Кроме того, на рис. 5.18, г в той же системе координат приведен
объединенный график распределения всех групп заемщиков вмес-
те со своими центроидами; его можно использовать для проведе-
ния сравнительного визуального анализа характера взаимного
расположения групп заемщиков банка с разными вероятностями
погашения кредита. В левой части графика расположены заемщи-
ки с высокой вероятностью погашения кредита, в правой — с низ-
кой, а в средней части — со средней вероятностью. Поскольку по
результатам расчета вторая дискриминантная функция D2(X) ока-
залась незначима, то различия координат центроидов по этой
оси незначительны. Этот факт подтверждается картой восприятия
(см. рис. 5.17).
ж«.<
'1гг.
247
б) Канонические
дискриминантные функции
Вероятн. погаш. кредита = 2
а) Канонические
дискриминантные функции
Вероятн. погаш. кредита = 1
Центроид
группы
*1 В
1 -
0 -
е
Центроид
группы
м2
0,5 1,0 1,5 2,0 2,5 3,0 3,5
-2-10 1
Функция 1
Функция 1
в) Канонические
дискриминантные функции
г) Канонические
дискриминантные функции
Функция 1
Рис. 5.18. Расположение наблюдений на плоскости
двух дискриминантных функций для групп с низкой (а), средней (б),
высокой (с) вероятностью погашения кредита и для всех групп (г)
а &
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ*
Задача 5.1. Оценка качества классификации областей Централь-
ного федерального округа, полученной методом клас-
терного анализа
По результатам предварительно проведенного кластерного ана-
лиза (см. задачу 3.1) выбрать одну-две области из каждого выде-
ленного класса (обучающего подмножества) и методом ДА прове-
рить принадлежность выбранных областей к своим группам (клас-
В полном объеме числовые данные для задач приведены на CD.
248
терам). Задание выполнить по алгоритму дискриминантного
анализа в SPSS подобно примеру 5.2 (см. подпараграф 5.4.3).
Задача 5.2. Проверка правильности отнесения региона к опреде-
ленной группе ВРП по видам экономической деятель-
ности
Администрация региона решила уточнить принадлежность сво-
его региона по структуре ВРП (валового регионального продукта)
по видам экономической деятельности (по ОК.ВЭД) именно к той
группе регионов, в которую он был отнесен на основе официально
опубликованных данных, полученных с помощью кластерного
анализа. Используя исходные данные и результаты классификации
регионов Российской Федерации, фрагмент которых приведен на
рис. 5.19, с помощью дискриминантного анализа убедиться в пра-
вильности отнесения рассматриваемого региона к данной группе
(последняя графа таблицы исходных данных) и проверить качество
классификации остальных регионов по вероятностным показате-
лям принадлежности регионов, приведенным в таблице поточеч-
ной статистики, полученной в выводе результатов дискриминант-
ного анализа. Номер региона соответствует варианту задания.
Задача 5.3. Оценка кредитоспособности юридических лиц в ком-
мерческом банке
В качестве значимых показателей, характеризующих финансо-
вое состояние организаций-заемщиков, банком выбраны шесть
показателей:
QR — коэффициент срочной ликвидности;
CR — коэффициент текущей ликвидности;
EQ/ТА — коэффициент финансовой независимости;
TD/EQ — суммарные обязательства к собственному капиталу;
ROS — рентабельность продаж;
FAT — оборачиваемость основных средств,
которые предварительно оцениваются с помощью пакета Audit
Expert. Нормативные показатели приведены в табл. 5.32. По этим
данным выделены четыре группы заемщиков, составляющие обу-
чающие подмножества: с отличными финансовыми показателя-
ми — группа 1, с хорошими — 2, с плохими — 3 и очень плохими —
группа 4 (табл. 5.33).
На основе дискриминантного анализа с использованием паке-
та SPSS определить, к какой из четырех категорий относятся три
заемщика (юридических лица), желающие получить кредит
249
ЙгЖ.»дь«г| *i.....* Jf . £? ~z .
j3 CWI
LA. L .... В " С .. 0 .. . е _ F G Н 1 L J 1 К -J 1« М N 0 р : R. •
1 Отраслевая структура ВРП по видам экономической деятельности (по ОКВЭД)
2 за 2006 год (в процентах)
А. < Регион (соответствует Добавленная стоимость по видам экономической деятельности (в основны ценах.
NB п.п. номеру варианта) Раздел А Раздел В Раздел С Раздел D Раздел “~в Раздел F Раздел G Раздел Н Раздел 1 Раздел J Раздел К Раздел L Раздел М Раздел N Раздел 0 .DBSSh. ровочная
Jj Сельско Рыболо вство. Добьма полезных Обрабат ывающи Проиэво дство и Строите льство Оптовая и рознич- Гостини цы и Транспо рти Финанс овая Операц ИИ с Государ ственно Образов ание Здравоох ранение Предост авление перемен- ная
7 хозяйст рыбоео ископаем е распреде мая рестора связь деятель недвиж е и прочих
« 1 Российская Федерация 6,4 0,3 12,8 20,4 3.9 5,8 19,4 0,9 10,7 1.1 8,5 3,2 2,8 3,2 1,6 1
9 2 Белгородская область 12,6 0 21,6 22,7 3.8 6,4 13,4 0,4 6,4 0 4,1 2,8 2,6 2,6 0.8 1
10 3 Брянская область 13,8 0 0,1 21,8 4,8 4,3 16 0,9 16,2 0 6,4 5,9 4,6 6,3 1 2
11 4 Владимирская область 11.8 0 о,з 34 5,7 4,6 10,6 1 10,2 2,2 6,8 5,1 3,6 3,7 1,6 3
12 5 Воронежская область 10,4 0 0,4 21,5 4,6 5,8 21,1 1,2 10,2 о,з »,1 4,9 4,4 4,4 1,7 2
13 6 Ивановская область 9,4 0 о,з 21,3 9,1 11.5 12,9 1,2 9,4 0 6,4 6,7 4.9 в м 2
14 7 Калужская область 11,6 0 0,4 29,2 3,6 6,2 16,8 0,4 9,4 0 7,3 5,4 4,1 4,6 1,2 3
15 8 Костромская область 17,6 0 0,1 20,8 10 11,6 9,9 0,4 10,6 0 3,4 5,9 4,2 4,2 1,4 2
18 9 Курская область 16,2 0 17,8 11,8 17,7 4,3 8,3 о,з 8,5 0,2 4 4,6 3,5 2,9 0,9 1
17 10 Липецкая область 7,5 0 0,6 66 2,8 6.8 Ю,4 0,4 5,2 0,2 2,9 2,5 2,2 2,7 0.8 3
18 11 Московская область 4,9 0 0,2 24,9 5,9 7,8 20,1 1,7 8,2 1.9 11,6 4,1 3,2 4,1 1,4 3
19 12 Орловская область 14,2 0 0,1 23,7 3,6 6,3 13,7 0,7 19,9 0 3,8 4,6 4,9 3,6 1,1 2
20 13 Рязанская область 12,8 0,1 о,з 22,6 5,9 5,9 19,7 0,7 12,3 0 5,3 6,3 4,2 4 0.9 2
21 14 Смоленская область 11 0 0,4 22,6 8,9 6 17,9 2.6 Ю,1 0 4.1 6.2 4,1 4,1 1 2
22 15 Тамбовская область 16,3 0 0 14,7 6,2 8,4 22,8 0,3 13,7 0 4,2 6,3 4,7 1.1 2
23 16 Тверская область 8,1 0 0,1 22,4 7,5 9 16,8 1.2 13,9 0 6,2 4,9 4,1 4,6 1,3 2
24 17 Тульская область 8,8 0 0,5 32 6,5 4,3 17.3 0,6 8,6 0,1 8,2 4,1 3,4 4 1.6 3
25 18 Ярославская область 6,9 0 0,1 32,2 4,7 8 16,6 1,6 13,9 0,2 5,9 3,7 3,8 з.з 1.3 3
28 19 г Москва 0 0 0,1 15,4 2,5 3,9 40,6 1,3 8,6 3,6 14,5 2,7 1.6 2 3,3 3
27 20 Республика Карелия 6,1 0,7 19.6 17,8 4,3 5,1 10,5 0,8 15.6 0 6 5.2 3,8 4,5 1,1 1
28 21 Республика Коми 3,2 0 34,4 10,1 3,6 7,6 9,1 0,4 12,6 0 9,1 3,4 2.6 3,3 0.7 1
29 22 Архангельская область 5,4 1 20,1 18,5 2,7 6,7 12 2 13,8 0 6,7 3,8 3,3 4,1 0,9 1
30 23 Вологодская область 7,5 0 0 46,4 3,5 10,3 6,6 0,6 11,7 0,6 3,2 3.4 2,2 3,3 0,8 3
31 24 Калининградская область 6,7 2,3 14,8 16,3 2,7 5,8 17,2 1,5 11,8 0,3 6,6 6,6 3,5 4,1 1 1
32 25 Ленинградская область 9 0 0,8 28 4,6 9,4 11.5 0.6 20,8 0,1 6,1 3 2,4 3,1 0,7 2
33 26 Мурманская область 0,6 7 7 14,1 24,9 6 2,4 Ю,7 0,7 12,7 0 6,8 4.7 3,1 4,3 1,3 3
34 27 Новгородская область 9,8 0 0 36,2 6,7 6,8 15,2 U 8.8 0,1 4,2 3,9 3 4,2 0,9 3
35 28 Псковская область _Ц2_ 0,1 0,1 17,9 5,2 4,1 21,6 1 16,6 0 4 6,6 4,3 4.9 2,6 2
1 ПУСК й Л -5 а» Нэткивто. э ГлтЬ-М?.. Bhtao^Ex-
Рис. 5.19. Результаты классификации регионов России
и исходные данные к задаче 5.2
Таблица 5.32
Нормативные показатели состояния заемщика
Состояние заемщика QR CR EQ/TA TD/EQ ROS, % FAT, раз
Отличное >0,68 > 1 >0,57 0-0,4 >4,95 >0,73
Хорошее 0,41-0,68 0,6-1,0 0,34-0,57 0,4-0,8 2,97-4,95 0,44-0,73
Плохое 0,2-0,41 0,3-0,6 0,17-0,34 0,8-1,11 1,49-2,97 0,22-0,44
Очень плохое 0-0,2 0-0,3 0-0,17 >1,11 <1,49 <0,22
Таблица 5.33
Обучающие подмножества к задаче 5.3
Пока- затели заем- щика Обуча- ющие под- мно- жества QR CR EQ/TA TD/EQ ROS, % FAT, раз Группа
Отличные 1 1,690 2,210 0,670 0,392 5,216 7,15 1
2 0,930 1,530 0,590 0,231 21,425 12,71 1
10 2,400 1,150 0,570 0,010 14,233 16,84 1
Хорошие 11 0,578 0,644 0,428 0,700 3,197 0,543 2
12 0,619 0,696 0,539 0,494 4,495 0,700 2
20 0,421 0,723 0,372 0,426 3,121 0,669 2
Плохие 21 0,262 0,391 0,337 0,840 2,418 0,405 3
22 0,371 0,435 0,268 1,052 2,940 0,318 3
30 0,285 0,498 0,174 0,943 1,793 0,370 3
Очень плохие 31 0,112 0,175 0,153 1,310 -2,658 0,127 4
32 0,149 0,070 0,036 7,951 -3,932 0,056 4
...
40 0,041 0,050 0,119 136,321 1,361 0,100 4
251
в коммерческом банке. Данные по трем заемщикам выбираются
согласно номеру варианта в табл. 5.34. При этом показатели пер-
вого заемщика соответствуют номеру варианта, а для двух других
заемщиков показатели находятся в следующих двух строках.
По результатам расчета построить дискриминантные функции;
оценить их значимость по коэффициенту Уилкса (X). Построить
карту восприятия и диаграммы взаимного расположения наблю-
дений в пространстве трех функций. Выполнить интерпретацию
результатов проведенного анализа.
Задача 5.4. Оценка кредитоспособности физических лиц в ком-
мерческом банке
Кредитный отдел коммерческого банка провел выборочное об-
следование 30 своих клиентов (физических лиц). На основе пред-
варительного анализа данных, заемщики оценивались по шести
показателям:
X] — заемщик брал кредит в коммерческих банках ранее;
х2 — среднемесячный доход семьи заемщика, тыс. руб.;
х3 — срок (период) погашения кредита, лет;
х4 — размер выданного кредита, тыс. руб.;
х5 — состав семьи заемщика, чел.;
х6 — возраст заемщика, лет.
При этом по вероятности возврата кредита выявлены три груп-
пы заемщиков (обучающие подмножества): группа 1 — с низкой,
группа 2 — со средней и группа 3 — с высокой вероятностью пога-
шения кредита (группирующая переменная). Результаты выбороч-
ного обследования заемщиков приведены в табл. 5.35.
На основе дискриминантного анализа с использованием пакета
SPSS необходимо классифицировать трех клиентов банка (по веро-
ятности погашения кредита), т.е. оценить принадлежность каждого
из них к одной из трех групп. Данные по первому заемщику выби-
раются согласно номеру варианта в табл. 5.36. Показатели по второ-
му й третьему заемщикам находятся в двух строках, следующих за
выбранным вариантом. По результатам расчета построить значимые
дискриминантные функции, их значимость оценить по коэффици-
енту Уилкса (X). В пространстве двух дискриминантных функций
для каждой группы построить диаграммы взаимного расположения
наблюдений и объединенную диаграмму. Оценить место располо-
жения каждого заемщика на этих диаграммах. Выполнить интерпре-
тацию результатов проведенного анализа.
252
Таблица 5.34
Варианты для расчета к задаче 5.3
Вариант QR CR EQ/TA TD/EQ ROS, % FAT, раз
1 6,337 1,910 0,441 0,196 7,521 0,255
2 1,028 0,503 0,452 0,186 22,510 0,280
3 0,614 2,982 0,592 0,303 13,179 2,712
4 8,604 4,496 0,284 0,109 17,181 10,115
5 6,207 4,423 0,366 0,228 15,385 2,151
6 8,250 4,792 0,023 0,480 10,418 2,932
7 3,868 0,072 0,473 0,476 6,571 0,564
8 7,864 2,037 0,244 0,255 14,791 2,593
9 0,060 4,316 0,789 0,311 13,786 1,671
10 5,715 0,693 0,488 0,138 3,749 2,632
11 2,617 1,225 0,650 0,398 20,280 16,043
12 3,516 0,227 0,421 0,455 4,632 2,291
13 1,405 0,162 0,280 0,337 3,142 2,398
14 4,762 0,821 0,143 0,095 3,708 0,145
15 2,263 1,098 0,771 0,178 10,311 0,491
16 6,102 0,085 0,308 0,399 8,823 2,807
17 3,389 1,425 0,877 0,450 15,678 1,941
18 6,637 1,715 0,046 0,033 24,885 2,374
19 2,009 2,768 0,522 0,168 6,124 2,841
20 4,209 1,787 0,113 0,073 -3,346 2,830
21 6,659 1,859 0,048 0,298 1,586 1,130
22 5,165 1,778 0,196 5,228 -2,631 2,638
23 8,079 4,552 0,141 0,547 -10,375 0,758
24 1,067 2,330 0,681 0,637 5,004 0,350
25 0,831 2,131 0,215 0,750 -9,417 0,566
26 8,589 1,520 0,063 0,596 -4,635 1,906
27 9,455 4,879 0,818 0,754 10,531 25,179
28 3,577 4,033 0,136 0,684 12,435 1,498
29 8,640 4,956 0,567 0,446 -10,219 1,489
30 3,382 1,281 0,704 0,453 -8,563 2,071
31 7,700 4,758 0,270 0,446 -4,876 2,111
32 9,106 0,267 0,348 0,514 -7,597 2,786
33 6,820 3,525 0,757 0,662 -10,360 2,425
60 0,389 0,661 0,157 250,214 0,769 2,481
253
Таблица 5.35
Обучающие подмножества к задаче 5.4
№ п/п Брался ли кредит ранее (1 — Да, 2 — нет) Среднеме- сячный ДОХОД семьи заемщика, тыс. руб. Период погаше- ния кредита, лет Размер креди- та, тыс. руб. Состав семьи заем- щика, чел. Возраст заемщи- ка, лет Вероят- ность погаше- ния кредита
1 1 27,6 7 140 4 46 2
2 1 25,6 8 190 5 37 2
3 1 32,75 8 170 6 43 2
... ... ... ... ...
30 1 29,4 4 200 6 55 2
Таблица 5.36
Варианты для расчета к задаче 5.4
Вари- ант Брался ли кредит ранее (1 — Да, 2 — нет) Среднеме- сячный ДОХОД семьи заемщика, тыс. руб. Период погаше- ния кредита, лет Размер кредита, тыс. руб. Состав семьи заемщи- ка, чел. Возраст заемщика, лет
1 1 28,75 6 370 4 42
2 1 18,62 4 230 5 35
3 1 36,47 10 450 6 43
...
60 1 34,34 4 130 4 31
Глава 6
ДИСПЕРСИОННЫЙ АНАЛИЗ
6.1. ОБЩИЕ ПОНЯТИЯ И ПРИМЕНЕНИЕ
ДИСПЕРСИОННОГО АНАЛИЗА
>
6.1.1. Виды дисперсионного анализа
При моделировании социально-экономических явлений и про-
цессов часто возникает необходимость исследовать влияние одной
или нескольких независимых переменных (факторов) на одну или
несколько зависимых переменных (результативных признаков).
Подобные задачи можно решать методами дисперсионного анали-
за, автором которого является Р. Фишер.
Широкое применение дисперсионный анализ находит в эконо-
мике, например, при изучении сегментов рынка с точки зрения
объема потребляемого товара, при проведении маркетинговых
исследований и пр.
Дисперсионный анализ — совокупность статистических методов
обработки данных, позволяющих анализировать изменчивость
одного или нескольких результативных признаков под влиянием
контролируемых факторов (независимых переменных), качествен-
ных или количественных.
Обычно с помощью данного метода исследуют влияние каче-
ственных факторов. Количественные факторы для де-
тального исследования зависимости результативного признака от
факторного обычно предварительно группируются, и затем к ним
применяются методы регрессионного анализа. При проведении
такого дисперсионного анализа важно правильно выбрать источ-
ник и объект влияния, т.е. определить зависимые и независимые
переменные. Здесь под фактором понимается некоторая величина,
определяющая свойства исследуемого объекта или системы, т.е. при-
чина, влияющая на конечный результат.
В зависимости от признаков классификации различают не-
сколько категорий дисперсионного анализа [35].
По количеству учитываемых факторов выделяют:
однофакторный анализ — исследуется влияние одного фактора;
,многофакторный анализ — изучается одновременное воздей-
ствие двух или более факторов.
255
По наличию связи между выборками значений (количеству по-
вторных измерений) одно- и многофакторный дисперсионный
анализ разделяется на два типа:
• анализ несвязанных (различных) выборок — проводится, когда
имеется несколько групп объектов исследования, находящихся
в разных условиях. (Проверяется нулевая гипотеза Но: среднее
значение зависимой переменной одинаково в разных условиях
замера, т.е. не зависит от исследуемого фактора.);
• анализ связанных (одних и тех же) выборок — проводится для
двух и более замеров, проведенных на одной и той же группе
исследуемых объектов в разных условиях. Здесь возможно вли-
яние неучтенного фактора, которое можно ошибочно приписать
изменению условий.
По количеству зависимых переменных, подверженных воздей-
ствию факторов, т.е. по количеству результативных признаков, '
различают:
• одномерный анализ (ANOVA или ANCOVA — ковариационный ;
анализ) — воздействию факторов подвержена одна зависимая ?
переменная;
• многомерный анализ (MANOVA — многомерный дисперсионный '
анализ или MANCOVA — многомерный ковариационный ана-
лиз) — воздействию факторов подвержено несколько зависимых
переменных.
Многомерный дисперсионный анализ используется в тех слу-
чаях, когда необходимо одновременно исследовать влияние фак-
торов и возможных ковариаций (независимых переменных) на
несколько зависимых переменных. Кроме того, многомерный
дисперсионный анализ может проводиться вместо одномерного,
когда зависимые переменные коррелируют между собой.
Многомерные методы, реализованные в SPSS, открывают ши-
рокие возможности в области применения дисперсионного анали-
за. Для этого могут использоваться разнообразные процедуры
MANOVA, которые позволяют проводить регрессионный анализ
(простой и множественный), дискриминантный, канонический
анализ, анализ главных компонент и др.
По цели исследования выделяются следующие модели дисперси-
онного анализа:
• детерминированные — уровни всех факторов заранее фиксиро-
ваны и проверяется именно их влияние (проверяется гипотеза
Но об отсутствии различий между средними уровнями);
256
• случайные — уровни каждого фактора получены как случайная
выборка из генеральной совокупности уровней фактора (про-
веряется гипотеза Но о том, что дисперсия средних значений
отклика, вычисленная для различных уровней фактора, не от-
лична от нуля);
• смешанные — здесь уровни одних факторов заранее фиксирова-
ны, а уровни других получены случайной выборкой.
По виду зависимой переменной различают:
• обычный дисперсионный анализ — категориальная переменная;
• ковариационный анализ (ANCOVA) — интервальная или метри-
ческая переменная.
6.1.2. Проверяемые гипотезы и требования
к анализируемым данным
Методы дисперсионного анализа используются для проверки
гипотез о наличии связи между результативными признаками (од-
ним или несколькими) и исследуемыми факторами, а также для
установления силы влияния факторов и их взаимодействий.
В задаче дисперсионного анализа выделяются три составляющие
общей вариативности признака:
• вариативность, вызванная действием каждой независимой пе-
ременной;
• вариативность, вызванная взаимодействием независимых пе-
ременных;
• вариативность случайная, обусловленная всеми неучтенными
причинами.
Оценка значимости вариативностей, обусловленных отдельным
действием каждой исследуемой переменной и их взаимодействием,
по отношению к случайной вариативности проводится по
/"-критерию Фишера.
Например, для двух независимых переменных (факторов) А и В
рассчитываются соответствующие значения /"-критерия:
• для вариативности, обусловленной действием фактора Л,
„ Вариативность, обусловленная действием переменной А
Л А — ,
Случайная вариативность
• для вариативности, обусловленной действием фактора В,
Вариативность, обусловленная действием переменной В
Го — -----------------------------------------------\
Случайная вариативность
17- 1591
257
• для вариативности, обусловленной взаимодействием факторов
А и В,
„ Вариативность, обусловленная действием переменных ДиВ
----------------- :------------------------------•
Случайная вариативность
Здесь в числителе находятся оценки дисперсий, поэтому дан-
ный метод считается параметрическим. Ббльшим значениям вари-
ативности отдельных признаков или их взаимодействия соответ-
ствуют более высокие эмпирические значения F-критерия.
В дисперсионном анализе проводится проверка статистической
значимости различий выборочных средних двух или более совокупно-
стей. Для этого предварительно формулируются гипотезы:
• нулевая гипотеза Но: средние величины результативного при-
знака во всех условиях действия фактора (или градациях фак-
тора) одинаковы;
• альтернативная гипотеза : средние величины результативно-
го признака в разных условиях действия фактора р а зл и ч -
н ы.
Методы дисперсионного анализа могут применяться для нор-
мально распределенных совокупностей (многомерные аналоги
параметрических тестов) и для совокупностей, не имеющих опре-
деленных распределений (многомерные аналоги непараметриче-
ских тестов) [10, 40].
В первом случае необходимо предварительно установить, что
распределение результативного признака является нормальным.
Для проверки нормальности распределения признака можно ис-
пользовать показатели асимметрии А
j (•*/ ~ Х'Ср) [б
А = —-----тА = J-
ло V п
и эксцесса Е
V,(x.-Xcn)4 [б
Е = ' epL-з, тЕ = 2J-,
П<5 Ун
гдех(, хср — значение результативного признака и его среднее
значение;
о — среднеквадратическое отклонение результативного
признака;
п — число наблюдений;
тА, тЕ ~ ошибки репрезентативности для показателей А и Е.
258
Если показатели асимметрии и эксцесса не превышают более
чем в 3 раза свои ошибки репрезентативности, т.е. А < ЗтА и
Е < ЗтЕ, то распределение можно считать нормальным. Для
нормальных распределений показатели А и Е равны нулю.
Данные, относящиеся к одному условию действия фактора
(к одной градации), называют дисперсионным комплексом. При про-
ведении дисперсионного анализа должно соблюдаться равенство
дисперсий между комплексами. Для выполнения данного требова-
ния необходимо уравнивать число значений в каждом из комплек-
сов, при этом отбор значений должен осуществляться случайным
образом. (В SPSS это реализуется так: Данные Отбор наблюде-
ний -> Отбор наблюдений (диалоговое окно) -> Случайная подвыбор-
ка -> Подвыборка... (кнопка) -> Отобрать наблюдения: Случайная под-
выборка (диалоговое окно).)
Во втором случае, когда выборочные совокупности имеют
произвольные распределения, используются непараметрические (ран-
говые) методы однофакторного (критерии Крускала — Уоллиса,
Джонкхира) и двухфакторного (критерии Фридмана, Пейджа) дис-
персионного анализа [22]. (В SPSS: Анализ -> Непараметрические
критерии ->...)
Если независимые переменные принимают только дискретные
значения, измеренные по номинальной или порядковой шкале, то
проводится факторный анализ. Если же независимые переменные
принадлежат к интервальной шкале или шкале отношений (в этом
случае их называют ковариациями), то проводится ковариационный
анализ.
6.1.3. Идея дисперсионного анализа
и ее графическая интерпретация
Рассмотрим графическую иллюстрацию зависимости ставки до-
ходности акций от положения дел в экономике страны (рис. 6.1, а).
Здесь исследуемым фактором является уровень состояния эконо-
мики (точнее, три уровня ее состояния), а результативным призна-
ком — ставка доходности. Приведенное распределение показывает,
что данный фактор оказывает существенное влияние на доход-
ность, т.е. с улучшением дел в экономике растет и доходность ак-
ций, что не противоречит здравому смыслу.
Заметим, что выбранный фактор имеет градации, т.е. его вели-
чина изменялась при переходе от одной градации к другой (от
17*
259
a)
Доходность
акций, %.
30,0--
«---------ж------------ж-----------►
Спад Нормальное Подъем
Состояние
экономики
W 6)
Доходность
акций, % 4
А
м
А------м-------—ж---------►
Спад Нормальное Подъем
Состояние
экономики
Рис. 6.1. Соотношение влияния фактора и внутригруппового разброса:
а — существенное влияние фактора; б — незначимое влияние
фактора (значителен внутригрупповой разброс)
одного состояния экономики к другому). Количественная градация
фактора является лишь частным случаем, кроме того, фактор мо-
жет иметь градации, представленные даже в номинальной шкале.
Потому чаще говорят не о градациях фактора, а о различных усло-
виях его действия.
Рассмотрим теперь идею дисперсионного анализа, в основе
которой лежит правило сложения дисперсий: общая дисперсия равна
сумме межгрупповой и средней из внутригрупповых дисперсий '.
_2 _ =2 , с2
О — СУ,- + ох,
где а2 — общая дисперсия, возникающая под влиянием всех фак-
торов ХУ,
а? — межгрупповая дисперсия, обусловленная влиянием всех
прочих факторов;
82 — средняя внутригрупповая дисперсия, вызванная влиянием
группировочного признака.
260
I Влияние группировочного признака хорошо видно на рис. 6.1.
I Так, на рис. 6.1, а влияние фактора существенно по сравнению с
внутригрупповым разбросом, следовательно, межгрупповая дис-
персия будет больше внутригрупповой (о? > 8J), а на рис. 6.1, б
I наблюдается обратная картина: здесь преобладает внутригрупповой
I разброс и практически отсутствует влияние фактора.
। На этом же принципе построен и дисперсионный анализ, толь-
I ко в нем используются не дисперсии, а средние квадратов откло-
I нений (MSX, MSBH, Л/5меж), являющиеся несмещенными оценками
соответствующих дисперсий. Их получают делением сумм квадра-
I тов отклонений на соответствующее число степеней свободы
I (п - 1), (п -т) и (т - 1). Здесьп - ^tij — общее количество наблю-
дений, nj — число измерений в у-й градации фактора, т — число
градаций фактора. С учетом этого имеем:
1 т 4j
М$х = - X)
•I 1 /=»
(для совокупности в целом);
MSBH
ин
1 w nj
—zs>f-*,>2 *
(для внутригрупповой средней);
А/*5*ме,|.
Меж
1 т
----" *)2
т -1 J
(для межгрупповой средней),
1
n
। т ni
где х = -^хц — общая средняя по всем измерениям (по всем
7=1'=| группам);
1
Xj = —^х& — групповая средняя для j-Й градации фактора.
nj i=i
Математические ожидания соответственно для внутригруппо-
вой и межгрупповой суммы квадратов отклонений
£(М5вн) = а2;
£(Л/5Меж) =
1 22, _ _ , 7 (модель с фиксированным
т-1 7“ 7 фактором),
2 2
nffi + сг
(модель со случайным
фактором).
261
Если E(MSm) = £(Л/5меж) = а2, то нулевая гипотеза Но об отсут-
ствии различий между средними подтверждается, следова-
тельно, исследуемый фактор не оказывает существенного влияния
(см. рис. 6.1, б). Если фактическое значение F-критерия Фишера
F = E(MSU^/окажется больше критического Fa т_1 п_т,
то нулевая гипотезаНо при уровне значимости а отвергается
и принимается альтернативная гипотеза Я, — о существенном воз-
действии фактора (см. рис. 6.1, а).
6.2. МОДЕЛИ ДИСПЕРСИОННОГО АНАЛИЗА
6.2.1. Однофакторный дисперсионный анализ
Постановка задачи. Имеется группа из п объектов наблюдения
с измеренными значениями некоторой исследуемой перемен-
ной Ху. На переменную Ху оказывает воздействие некоторый каче- :
ственный фактор Л с несколькими т уровнями (градациями) воз-
действия. Измеренные значения переменной Ху при различных
уровнях фактора А приведены в табл. 6.1 (они также могут быть
представлены в матричном виде).
Таблица б. 1 <
Табличная форма задания исходных данных для однофакторного анализа '
Номер объекта Значения переменной Ху при уровне (градации) фактора Aj (j = 1, т)
наблюдения i Л2 Ат
(самый (низкий) (самый
низкий) высокий)
1 хн Х,2
2 Х2| х22 XJ Х2т
п *„1 Хп2 Хпт
Примечание. Здесь каждый уровень может содержать разное количество
откликов, измеренных при одном уровне фактора, тогда каждому столбцу
будет соответствовать свое значение tij.
Требуется оценить значимость влияния данного фактора на
исследуемую переменную.
Для решения этой задачи может использоваться однофакторная
модель дисперсионного анализа.
262
J
Однофакторная модель дисперсионного анализа аддитивного типа
имеет следующий вид [39]:
хи = xj + Fj + е<7’
где Ху — значения исследуемой переменной (отклики) д ля /-го объ-
екта наблюдения при/-м уровне фактора;
Xj — групповая средняя для /-го уровня фактора;
Fj — эффект, обусловленный влияниемJ-го уровня фактора;
Еу — случайная компонента, обусловленная влиянием неконт-
ролируемых факторов.
Основные предпосылки для использования дисперсионного
анализа:
1. Равенство нулю математического ожидания случайной ком-
поненты: М(Еу) = 0.
2. Дисперсия случайной компоненты постоянна: D(Ey) = а2.
3. Случайная компонента Еу, а следовательно, и Ху имеют нор-
мальный закон распределения.
4. Число градаций факторов должно быть не менее трех.
5. Случайные компоненты взаимно независимы: cov(e^., Ек1) = 0
(/ к). При невыполнении последнего условия (т.е. при наличии
взаимосвязей) отношение дисперсий может оказаться сильно ис-
каженным.
Данная модель в зависимости от уровней фактора с помощью
F-критерия Фишера позволяет проверить одну из нулевых гипо-
тез Яо:
• средние значения для групп откликов, измеренных при различ-
ных уровнях фактора, не имеют существенных различий между
собой (случай с фиксированными эффектами);
• дисперсия средних значений для групп откликов, измеренных
при различных уровнях факторов, не отлична от нуля (для слу-
чайных эффектов).
При выполнении дисперсионного анализа для связанных вы-
борок возможна проверка еще одной нулевой гипотезы //0(и) — ин-
дивидуальные различия между объектами наблюдения выражены
не более, чем различия, обусловленные случайными причинами.
6.2.2. Двухфакторный дисперсионный анализ
Постановка задачи для несвязанных выборок. Пусть имеются
выборочные данные из п объектов наблюдения с измеренными
263
значениями переменной Хд, на которую оказывают воздействие два
качественных фактора А и В с несколькими уровнями (не менее
Двух).
Измеренные значения переменной Хд при различных уровнях
воздействия факторов приведены в табл. 6.2, в каждой ячейке ко-
торой находится один отклик, полученный при соответствующем
сочетании уровней исследуемых факторов. При этом все уровни
фактора В соответствуют только одной выборке.
Таблица 6.2
Табличная форма задания исходных данных для несвязанных выборок
Номер объектаi (i = 1, п) Уровень (града- ция) фактора Вк (к = 1, р) Значения переменной Хд при уровне (градации) фактора Лу (J = 1, т)
Л2
1 В> *п *12 *1т
2 В2 *21 *22 хи *2т
п вп *„1 *п2 *«я>
Примечание. В данном случае номер объекта совпадает с номером уровня
фактора В. Число наблюдений в столбцах может быть различным.
Требуется для каждого отдельно взятого фактора и в их взаимо-
связи оценить значимость влияния факторов Л и В на исследуемую
перемен нуюх^..
Постановка задачи для связанных выборок. Для одной и той же
группы из п объектов наблюдения известны измеренные значения
некоторой исследуемой переменной Хдк в различных условиях воз-
действия двух качественных факторов Л и В (не менее двух уровней
воздействия для каждого фактора) (табл. 6.3). В каждой ячейке
таблицы находится один отклик, измеренный при соответству-
ющем сочетании уровней исследуемых факторов Л и В.
Требуется оценить значимость влияния факторов Л и В на ис-
следуемую переменную х^, каждого отдельно и во взаимосвязи.
Для решения данной задачи может использоваться двухфактор-
ная модель дисперсионного анализа.
Требования к исходным данным для связанных выборок: и
1. Исследуемые факторы должны быть независимыми.
2. Каждый фактор должен иметь не менее двух уровней.
3. Количество значений в ячейках комплекса должно быть оди-
наковым и содержать не менее двух наблюдений. 18
264
Таблица 6.3
Табличная форма задания исходных данных для связанных выборок
Номер объекта/ в группе (/ = 1, пк) Уровень (градация) фактора Вк (к - 1, р) Значения переменной xjjk при уровне (градации) фактора Aj (J = 1, т)
А1 л2 Ат
1 2 хш Х211 Х121 Х221 Е Е и и'
пк Хи.П X»,2I %nkmi
1 2 *112 Х212 Х122 Х222 * • it
пк Хи,12 х«,22 хпкт2
Xijk
1 2 ВР *11/, х21/> Х12р Х22р Х1тр Х2тр
пк хи,1/> хпк2р ^пктр
Примечание. Здесь каждый уровень фактора А может содержать разное
количество откликов, измеренных при одном уровне фактора В, тогда
каждому столбцу будет соответствовать свое значение пк.
4. Каждой градации фактора В должно соответствовать одина-
ковое количество градаций фактора Л.
5. Все объекты наблюдения должны пройти всевозможные со-
четания градаций двух факторов.
6. Результативный признак должен иметь нормальное распре-
деление, иначе нарушается корректность выводов.
Модель двухфакторного дисперсионного анализа учитывает вли-
яние двух факторов: А и В. Она описывается уравнением
xijk ~ xj *" Fj + Gfc + 1jfc + £yk,
где xiJk — исследуемая переменная (для несвязанной задачи i ис-
ключается);
ху- — групповая средняя;
Fj— эффект, обусловленный влиянием J-го уровня факто-
ра Л;
Gk— эффект, обусловленный влиянием к-го уровня факто-
ра В\
265
Ijk— эффект, обусловленный взаимодействием двух факторов,
он отражает отклонение средней от суммы слагаемых
Xy + ^.+ G^;
£ijk ~ случайная компонента, учитывающая влияние некон-
тролируемых факторов. ,
Здесь проверяются три нулевые гипотезы:
а) для фиксированных факторов
• при проверке Н0А сравниваются соотношения MSA/MSBH',
• при проверке Яов — соотношения MSg/MS^',
• при проверке Нмв— соотношения MSAB/MSm(,
б) для случайных факторов с распределением Фишера —
Снедекора
• при проверке Н0А сравниваются соотношения MSA/MSAB,
* при проверке НйВ — соотношения MSB/MSAB,
• при проверке НйАВ— соотношения MSAB/MSBH. ;
Кроме названных трех гипотез, по соотношению MSH/MSBU ,
может проверяться еще одна нулевая гипотеза Я0(и) — индивиду-
альные различия между объектами наблюдения выражены не бо- [
лее, чем различия, обусловленные случайными причинами. 4
6.2.3. Многофакторный дисперсионный анализ
Если число воздействующих факторов более двух, то использу-
ется многофакторная модель дисперсионного анализа вида
Xij...q — х + Fj + Gk + ... + Zq +
где Ху — исследуемая переменная (отклики);
х — общая средняя;
Fj — средний эффект, обусловленный влияниему-го уровня
первого фактора;
Gk — средний эффект, обусловленный влиянием £-го уровня
второго фактора;
Zg — средний эффект, обусловленный влиянием </-го уровня
последнего фактора;
Е/; — случайная компонента.
Замечание. В данную модель не включены межфакторные
взаимодействия, поскольку число их сочетаний значительно воз-
растает с увеличением числа факторов, включенных в модель. По-
скольку интерпретация таких взаимодействий затруднена, обычно
останавливаются на оценке лишь главных факторов и только при
266
необходимости парные эффекты взаимодействия между выделен-
ными значимыми факторами проверяются методом двухфактор-
ного анализа.
6.3. РЕАЛИЗАЦИЯ ДИСПЕРСИОННОГО АНАЛИЗА В SPSS
6.3.1. Пошаговые алгоритмы
однофакторного дисперсионного анализа в SPSS
Дисперсионный анализ в среде SPSS можно проводить по не-
скольким направлениям [9, 26]:
• традиционным «классическим» методом по Фишеру {Fisher),
когда совокупная дисперсия всех наблюдаемых значений рас-
кладывается на дисперсию внутри отдельных групп и диспер-
сию между группами. В SPSS это процедура ANOVA;
• новым методом «общей линейной модели» (GLM — General Linear
Model). Здесь «общая линейная модель» строится на основе кор-
реляционного или регрессионного анализа. В SPSS эта процеду-
ра реализована в GLM и многомерном дисперсионном анализе
MANOVA {Multivariate Analysis of Variances). В GLM используется
линейная модель неполного ранга {non full rank linear model). После
проведения дисперсионного анализа в GLM проводится тест на
сравнение средних значений отдельных слоев (градаций). Слои
(градации) определяются различными уровнями исследуемого
фактора. В MANOVA используется линейная модель полного ранга
(full rank linear model). Здесь же включен ряд дополнительных
видов анализа (регрессионный, дискриминантный, каноничес-
кий, анализ главных компонент и др.), которых нет в GLM.
На основе процедуры Общая линейная модель можно выполнить
следующие расчеты:
• ОЛМ-одномерная... — одномерный дисперсионный анализ
(Univariate...)',
• ОЛМ-многомерная... — многомерный дисперсионный анализ
(Multivariate...)',
• ОЛМ-повторные измерения... — многомерный дисперсионный
анализ с учетом повторных измерений (Repeated Measures...)',
• Компоненты дисперсии... — расчет компонент дисперсии (Variance
Components...).
Для выбора вида дисперсионного анализа на основе процедуры
Общая линейная модель используется вспомогательное меню, пред-
ставленное на рис. 6.2.
267
” Вез имени - SPSS Редактор Данных
Графика Сервис Ою-ю
Отчеты
Описательные статистики
Таблицы
Сравнение средних
А ил ли*,
Сграека
Обща-ч ш н^йчая модель
Смешанные модели
Корреляции
Регрессия
Лог линейный анализ
Классификация
Омжеьме размерности
Анализ икал
Непараметрические критерии
Временные ряды
Выживаемость
Множественные отклики
Анализ пропущенных значений...
Сложные выборки
'Р.. I I пе':’
ОЛИ-одномерная...
ОЛМ-многомеркая...
ОЛМ-повторные измерения...
Котюненты дисперсии,,,
Рис. 6.2. Вспомогательное меню Общая линейная модель
Известно, что для сравнения средних значений двух выборок
(как зависимых, так и независимых) используется /-критерий
Стьюдента. Дисперсионный анализ позволяет проводить сравнение,
средних значений более чем двух выборок. Напомним, что общая
вариативность переменной раскладывается на две составляющие:
межгрупповую (факторную), обусловленную различием групп по
их средним значениям, и внутригрупповую, обусловленную влия-
нием неучтенных факторов. Чем больше отношение межгрупповой
изменчивости к внутригрупповой, тем больше различаются сред-
ние значения выборок, тем выше статистическая значимость раз-
личий (проверяется по /'’-критерию Фишера).
Обработка исходных данных методом однофакторного дисперси-
онного анализа в системе SPSS ведется в диалоговом режиме в та-
кой последовательности:
1 . С помощью пиктограммы на рабочем столе или в главном
меню Windows с помощью команды Пуск —> Программы —> SPSS для
Windows запустить программу SPSS. После ее запуска в открывшем-
ся диалоговом окне (SPSS для Windows) щелкнуть кнопкой Отмена
(Cancel).
2 . Перейти в режим Переменные (Variable View) и задать структу-
ру исходных данных. Для каждой переменной определяются Имя
(Name), Тип (Туре), Ширина (Width), Знаки после запятой (Decimals),
Метка (Label), Значения (Values), Пропущенные (Missing), Ширина,
столбца (Columns), Выравнивание (Align) и Шкала (Measure).
268
3 . В окне редактора Данные {Data View) ввести числовые данные
для рассматриваемого примера и сохранить их в файле. Для этого
используются следующие команды: Файл -»Сохранить (или Сохра-
нить как) —» ... Далее указываются папка, в которой сохраняется
файл, и имя файла.
6.3.2. Однофакторный дисперсионный анализ в SPSS
К при наличии несвязанных выборок
Пример 6.1. Имеются выборочные данные по результатам об-
следования средней стоимости 1 м2 жилой площади на рынке вто-
ричного жилья в четырех районах города за 10 месяцев (табл. 6.4),
причем за 9-й и 10-й месяцы данные неполные.
Таблица 6.4
Стоимость 1 м2 жилой площади, тыс. ден. ед.
Номер района Месяц
1 2 3 4 5 6 7 8 9 10
1 19,5 18,9 19,1 19,0 19,2 19,3 19,2 19,4 20,1 —
2 18,7 19,3 18,9 19,1 18,8 18,7 18,7 19,0 19,1 19,7
3 19,9 19,2 18,8 19,0 19,1 19,0 18,9 19,2 — —
4 18,8 18,6 19,0 18,8 18,5 18,4 18,3 18,6 18,9 19,1
Требуется установить, различается ли средняя стоимость 1 м2
жилой площади в различных районах города.
Решение. Исходные данные здесь представляют собой несвя-
занные выборки. В качестве исследуемого фактора выберем
район города, тогда роль зависимой переменной будет выполнять
средняя стоимость 1м2 жилой площади.
Выдвинем нулевую гипотезу Но: средние цены на 1 м2 жилой
площади во всех районах одинаковы, т.е. они не зависят от выбран-
ного района.
Решение проведем в среде SPSS по следующему алгоритму.
1. Активизируем программу SPSS.
2. В окне Переменные опишем все исходные данные, согласно
условию задачи (рис. 6.3).
3. Введем значения переменных в окне Данные, причем пере-
менной «Фактор» — factor присвоим номера соответствующих ад-
министративных районов города (рис. 6.4).
269
। •fr./’jbC (Надорванных! ] - tfeSS Ред»иф Данн-чх
Файл фжа Вид Д«ы Греэбраэоыть Анализ Грфюйр(^|1Р^::;ррав<а.Ж ...........
ъна в *1» uu г- вд-п
111 ^Числовая 8 2 ^Стоимость 1 кв. Нет Нет 8 По центру КаЯичвепонная
2 factor ^Числовая 8 0 {Район ™₽°А’..Н»т |Нет 8............ |По цмору ^Количественная
Рис. 6.3. Фрагмент окна Переменные
с заданной структурой исходных данных
и Жилье - SPSS Редактор Данных
Файл Правка Вид Данные Преобразовать Анализ Графика Сервис Окно Справка
EJI =|&| м| -rid I Й fef.
:14: factor Х1 ~'z factor пер пер Г.&Р пер » пер
1 19,50 1
2 18.90 1
3 19,10 1
4 19,00 1
5 19,20 1
< 6 19.30 1
7 19,20 1 !
8 19,40 1
9 20.10 1
10 18,70 2
11 19,30 2
12 18,90 2
13 19.10 2
14 18,80 2
Рис. 6.4. Фрагмент окна Данные с введенными переменными
4. Сохраним файл с исходными данными, например, под име-
нем «Жилье» с использованием в командной строке меню Файл
{File) и функции Сохранить как... (Save as...).
5. В окне Данные закажем однофакторный дисперсионный ана-
лиз с помощью меню Анализ -» Сравнение средних -» Однофакторный
дисперсионный анализ... (Analyze —> Compare Means —> One Way ANOVA)
(рис. 6.5).
6. В открывшемся диалоговом окне Однофакторный дисперсион-
ный анализ (One Way ANOVA) выделим зависимую переменную х1 и
внесем ее в поле Слисок зависимых (Dependent List), а переменную
factor — в окно Фактор (Factor) (рис. 6.6).
7. Щелчком по кнопке Параметры... (Options...) откроем диало-
говое окно Однофакторный дисперсионный анализ: Параметры. В об-
ласти Статистики (Statistics) выделим Описательные (Descriptive)
и Проверка однородности дисперсии (Homogeneity of variance test)
(рис. 6.7).
270
Рис. 6.5. Выбор однофакторного дисперсионного анализа
в процедуре Сравнение средних в окне Данные
Рис. 6.6. Диалоговое окно Однофакторный дисперсионный анализ
с введенными переменными
Выделенные статистики подтверждаются кнопкой Продолжить
(Continue), в результате возвращаемся в режим Однофакторный дис-
персионный анализ (One Way ANOVA).
8. Щелчком по кнопке Апостериорные... (Post Нос...) (см. рис. 6.6)
откроем новое диалоговое окно Однофакторный дисперсионный ана-
лиз: Апостериорные множественные сра... (One Way ANOVA: Post Hoc
Multiple Comparisons) и в области При равенстве дисперсий (Equal Vari-
ances Assumed) выделим критерий Дункан (Duncan) (рис. 6.8).
Априорные контрасты задаются, когда рассматриваются множест-
венные сравнения (например, если бы в данном случае проводилось
сравнение одного района с комбинацией из трех остальных).
271
Однофакторный дисперсионный анализ: Параметры
Статистики —----—~~—
| р- Описательны^
] Г" Фиксированные и случайные эффекты
j (7 (Проверка однородности дисперсии
I Г" Брауна-Форсайта
I Г Уэлч
..............—.....................
Р [рафик средних
-Пропущенные значения-------_____
(• Исключать по отдельности
С Исключать целиком наблюдения
Продолжить
Отмена
Справка
Рис. 6.7. Диалоговое окно Однофакторный дисперсионный анализ:
Параметры с заданными статистиками
Рис. 6.8. Диалоговое окно Однофакторный дисперсионный анализ:
Апостериорные множественные сра... с введенными условиями
9. Вычисления по выбранному алгоритму однофакторного
дисперсионного анализа начинаются после щелчка по кнопке ОК
(см. рис. 6.6).
По окончании вычислений в окно просмотра выводятся резуль-
таты расчета (табл. 6.5—6.8).
В таблице «Описательные статистики» (см. табл. 6.5) приведены
основные показатели по районам и их итоговые значения:
272
Таблица 6.5
1. Описательные статистики
Стоимость 1 кв. м
N Среднее Стд. отклонение Стд. ошибка 95% доверительный интервал для среднего Минимум Максимум
Нижняя граница Верхняя граница
1 9 19,3000 ,35355 ,11785 19,0282 19,5718 18,90 20,10
2 10 19,0000 ,31972 ,10111 18,7713 19,2287 18,70 19,70
3 8 19,1375 ,33780 ,11943 18,8551 19,4199 18,80 19,90
4 10 18,7000 ,26247 ,08300 18,5122 18,8878 18,30 19,10
Итого 37 19,0216 ,37943 ,06238 18,8951 19,1481 18,30 20,10
• N — количество наблюдений по каждому району и суммарное;
• Среднее — среднее арифметическое значение стоимости 1 м2
жилой площади по каждому району и по всем районам вместе;
• Стд. отклонение, Стд. ошибка — стандартные отклонения и стан-
дартные ошибки;
• 95% доверительный интервал для среднего;
• Минимум, Максимум — минимальные и максимальные значения
средней цены для каждого района.
Критерий однородности Ливиня (см. табл. 6.6) используется для
проверки дисперсий на гомогенность (однородность). В данном
случае он подтверждает незначимость различий между дис-
персиями для средней цены в различных районах, поскольку
Знч. = 0,991, т.е. существенно больше 0,05. Поэтому результаты,
полученные с помощью дисперсионного анализа (ANOVA), при-
знаются корректными, и для дальнейшего анализа можно исполь-
зовать тест Шеффе (Scheffe) — при равенстве дисперсий.
В противном случае (когда проявляется значимость различий)
рекомендуется использовать тест Т2 Тамхейна (Tamhane's Т2) — для
неравных дисперсий.
Таблица 6.6
2. Критерий однородности дисперсий
Стоимость 1 кв.м
Статистика Ливиня ст.св.1 ст.св.2 Знч.
,035 3 33 ,991
В таблице ANOVA (см. табл. 6.7) приведены результаты одно-
факторного дисперсионного анализа.
18 - 1591
273
Таблица 6.7
ANOVA
Стоимость 1 кв.м
Сумма квадратов СТ.СВ. Средний квадрат F Знч.
Между группами 1,844 3 ,615 6,075 ,002
Внутри групп 3,339 33 ,101
Итого 5,183 36
Первый элемент, стоящий на пересечении столбца «Сумма
квадратов» и строки «Между группами», представляет собой сумму
квадратов разностей между общим средним значением и средними
значениями каждой группы с учетом весовых коэффициентов,
равных числу объектов в группе. Второй элемент этого столбца
представляет собой сумму квадратов разностей среднего значения
каждой группы и каждого значения этой группы.
Столбец «ст.св.» содержит число степеней свободы v:
• межгрупповое (v = Число групп —1);
• внутригрупповое (v = Число объектов - Число групп - 1).
Столбец «Средний квадрат» содержит отношение суммы квад-
ратов к числу степеней свободы.
В столбце «F» приведено отношение среднего квадрата между
группами к среднему квадрату внутри групп.
В столбце «Знч.» содержится значение вероятности того, что
наблюдаемые различия случайны, и если величина значимости мала,
это свидетельствует о статистически достоверных различиях. Здесь
уровень значимости Знч. = 0,002 указывает, что различия между
средними значениями переменной Х1, т.е. стоимости 1 м2 жилой
площади, для четырех районов города статистически достоверны.
В таблице «Однородные подпоследовательности» (см. табл. 6.8)
представлены различия по средней цене стоимости 1 м2 жилой
площади между двумя группами районов. В первую группу входят
районы 4 и 2, во вторую — районы 2, 3 и 1. Следует обратить вни-
мание,-что район 2 может быть отнесен как в первую, так и во
вторую группу. Если бы различий не было, то все районы состав-
ляли бы одну группу.
В ряде случаев для наглядности представления различий в сред-
них значениях по градациям фактора строятся графики средних
значений. Такой график приведен на рис. 6.9, и он визуально под-
тверждает наличие двух групп районов, наиболее близких по сред-
ним ценам; эти же группы были выделены в табл. 6.8.
274
Таблица 6.8
Однородные подпоследовательности
Стоимость 1 кв.м
Дункан
Район города N Подмножество для альфа = .05
1 2
4 10 18,7000
2 10 19,0000 19,0000
3 8 19,1375
1 9 19,3000
Знч. ,052 ,064
Рис. 6.9. График средних значений цен
за 1 м2 жилой площади по районам города
Таким образом, возвращаясь к условию задачи, можно сделать
следующий вывод: нулевая гипотеза Но о том, что средние цены на
1 м2 жилой площади во всех районах одинаковы (не зависят от
выбранного района), отвергается и принимается альтернатив-
ная гипотеза Нх о существенном различии средних цен.
Наиболее низкие средние значения цен за период наблюде-
ния продолжительностью 10 месяцев отмечались в районе 4
(см. рис. 6.9), а наиболее высокие цены — в районах 1 и 3, район 2
по средним ценам занимает промежуточное положение.
18*
275
•%; 6.3.3. Однофакторный дисперсионный анализ в SPSS
при наличии связанных выборок с повторными
измерениями
Пример 6.2. Требуется проверить, является ли значимым влия-
ние фактора сезонности на среднеквартальный размер потреби-
тельских кредитов, выдаваемых коммерческим банком в течение
последних пяти лет (табл. 6.9). При этом влияние других факторов
не учитывалось (хотя такая возможность имеется).
Таблица 6.9
Среднеквартальный размер кредита, млн руб.
Год Квартал
1 2 3 4
1-й 12,40 23,65 20,90 21,50
2-й 12,98 24,41 22,67 22,50
3-й 13,32 25,13 29,86 24,82
4-й 14,45 . 27,35 33,52 25,24
5-й 15,75 28,68 38,82 26,29
Решение. Здесь выборки являются связанными, поскольку
все поквартальные данные относятся к одному и тому же объекту
наблюдения (коммерческому банку).
Согласно условию задачи исследуемым фактором является
сезонность (ей соответствует номер квартала), тогда зависимой
переменной будет среднеквартальная сумма выдаваемых кредитов.
Выдвинем нулевую гипотезу Яо: среднеквартальные суммы кре-
дитов, выдаваемых банком, не зависят от фактора сезонности.
Решение проведем в среде SPSS по следующему алгоритму.
1. Запустим программу SPSS.
2. В окне Переменные опишем все исходные данные. Номер
строки соответствует году, а каждый столбец — одному из кварта-
лов: кв1, кв2, квЗ, кв4. На пересечении строк и столбцов находятся
среднеквартальные размеры выдаваемых кредитов.
3. Значения переменных введем в окне Данные (рис. 6.10).
4. Вызовем дисперсионный анализ: Анализ -> Общая линейная
модель -> ОЛМ-повторные измерения... (см. рис. 6.10).
5. В открывшемся диалоговом окне ОЛМ-повторные измерения:
Задать факторы в поле Имя внутригруппового фактора вместо установ-
ленного по умолчанию имени фактора factor! введем новое имя:
квартал, а в поле Число уровней зададим значение 4 и подтвердим
кнопкой Добавить (рис. 6.11).
276
одноф с поот - SPSS Редактор Данных
Графика Сервис окно Сграека
Файл Главка Вид Данные Преобразовать
Отчеты
Описатегьные статистики
Табл-цы
Сравнение средних
Смешанные модели
Корреляции
Регрессия
Лог линейный анализ
Классификация
Снижение размерности
Анализ шкал
Непараметрические критерии
Временные ряды
Выживаемость
Мзожествеьные отклики
Анализ пропущенных значений...
Сложные выборки
п&цая л-^+чкая «лзд-зль
Рис. 6.10. Введенные данные и вспомогательное меню
Общая линейная модель для проведения дисперсионного анализа
с повторными измерениями
Рис. 6.11. Диалоговое окно
ОЛМ-повторные измерения: Задать факторы
277
Поскольку других факторов с повторными измерениями нет, то
выходим из этого диалогового окна посредством нажатия кнопки
Задать.
6. В открывшемся диалоговом окне ОЛМ-повторные измерения...
перенесем переменные кв1, кв2, квЗ, кв4 из левого поля в правое
поле Внутригрупповые переменные с помощью вспомогательных кла-
виш со стрелками (рис. 6.12). Поля Межгрупповые факторы и Кова-
риаты задействовать не будем.
Рис. 6.12. Диалоговое окно ОЛМ-повторные измерения...
7. После нажатия кнопки ОК (см. рис. 6.12) программа реализу-
ет алгоритм дисперсионного анализа с повторениями, и в окне
просмотра появляются результаты расчета (табл. 6.10—6.15).
Сначала выдается сводная таблица для внутригрупповых фак-
торов (см. табл. 6.10).
Далее следуют результаты расчета для фактора «квартал» (см.
табл. 6.11). Здесь же приведены различные тестовые величины:
След Пиллая (Pillai's Trace), Лямбда Уилкса (Wilks'Lambda), След
Хотеллинга (Hotelling's Trace) и Наибольший корень Роя (Roy's
Largest Root). С помощью преобразований по данным тестовым
величинам восстанавливается значение F, по которому затем опре-
деляется значимость Знач. (Sig). След Пиллая является наиболее
сильным и устойчивым (робастным) тестом.
278
Таблица 6.10
Внутригрупповые факторы
Измерение: ИЗМЕРЕНИЕ-1
квартал Зависимая переменная
1 кв1
2 кв2
3 квЗ
4 кв4
Таблица 6.11
Многомерные критерии(Ь)
Эффект Значение F Ст.св. гипотезы Ст.св. ошибки Знач.
квартал След Пиллая 1,000 2170,415(a) 3,000 2,000 ,000
Лямбда Уипкса ,000 2170.415(a) 3,000 2,000 ,000
След Хотеллинга 3255,622 2170.415(a) 3,000 2,000 ,000
Наибольший корень Роя 3255,622 2170.415(a) 3,000 2,000 ,000
а Точная статистика
Ь План: Intercept
Внутригрупповой план: квартал
Таблица 6.12
Критерий сферичности Моучли(Ь)
Измерение: ИЗМЕРЕНИЕ-1
Внутригрупповой эффект W Моучли Прибл. хи-квадрат СТ.СВ. Знач. Эпсилон(а)
Гринхауз- Гайссер Юнх- Фельдт Ограниченный снизу
квартал ,000 21,200 5 ,001 ,344 ,356 ,333
Проверка нулевой гипотезы о том, что ковариационная матрица ошибок ортонормированного преобразования зависимых переменных пропорциональна единичной матрице. а Может использоваться, чтобы корректировать степени свободы для усредненных тестов значимости. Скорректированные тесты отображены в таблице «Проверка внутригрупповых эффектов». Ь План: Intercept Внутригрупповой план: квартал
Результаты тестов, судя по уровню значимости, подтверждают
существенное влияние сезонного фактора (квартала).
После этого приводятся результаты проверки нулевой гипотезы
о пропорциональности ковариационной матрицы ошибок орто-
нормированного преобразования зависимых переменных единич-
ной матрице по критерию сферичности Моучли (Mauchly’s Test of
Sphericity) (см. табл. 6.12).
Проверка сезонного фактора проводится также традиционным
«классическим» методом Фишера. Результаты расчета приведены
279
в табл. 6.13, в строке «Предполагая сферичность». Они также под-
тверждают значимость влияния фактора сезонности, поскольку
вероятность ошибки (значимость) практически равна нулю.
Далее в табл. 6.14 и 6.15 приводятся результаты расчетов для
проверки внутригрупповых контрастов и оценки эффектов
межгрупповых факторов.
Проверка внутригрупповых эффектов
Таблица 6.13
Измерение: ИЗМЕРЕНИЕ-1
Источник Сумма квадратов типа III СТ.СВ. Средний квадрат F Знач.
квартал Предполагая сферич- ность Гринхауз-Гайссер Юнх-Фельдт Ограниченный снизу 659,668 659,668 659,668 659,668 3 1,033 1,067 1,000 219,889 638,493 618,205 659,668 26,116 26,116 26,116 26,116 ,000 .006 ,006 ,007
Ошибка (квартал) Предполагая сферич- ность Гринхауз-Гайссер Юнх-Фельдт Ограниченный снизу 101,038 101,038 101,038 101,038 12 4,133 4,268 4,000 8,420 24,449 23,672 25,260
Проверка внутригрупповых контрастов
Таблица 6.14
Измерение: ИЗМЕРЕНИЕ-1
Источник квартал Сумма квадратов типа III СТ.СВ. Средний квадрат F Знач.
квартал Линейный 292,068 1 292,068 93,884 ,001
Квадратичный 367,567 1 367,567 37,119 ,004
Кубический ,032 1 ,032 ,003 ,961
Ошибка Линейный 12,444 4 3,111
(квартал) Квадратичный 39,610 4 9,902 •
Кубический 48,985 4 12,246
Оценка эффектов межгрупповых факторов
Таблица 6.15
Измерение: ИЗМЕРЕНИЕ-1 Преобразуемая переменная: Среднее
Источник Сумма квадратов типа III СТ.СВ. Средний квадрат F Знач.
Свободный член Ошибка 10775,939 162,831 1 4 10775,939 40,708 264,715 ,000
280
Таким образом, в результате решения данной задачи в среде
SPSS установлено, что нулевая гипотеза Но о независимости сред-
неквартальных сумм кредитов, выдаваемых банком, от фактора
сезонности отвергается и принимается альтернативная ей
гипотеза Нх о существенном влиянии данного фактора на размер
выдаваемых потребительских кредитов.
6.3.4. Двухфакторный дисперсионный анализ в SPSS
без повторных измерений
Пример 6.3. На шести участках (одинаковой площади) опытной
станции испытывались пять новых сортов пшеницы, причем на
каждом участке применялся свой тип удобрения. Данные по уро-
жайности приведены в табл. 6.16.
Таблица 6.16
Урожайность сортов пшеницы по участкам, ц/га
Номер участка Сорт
1 2 3 4 5
1 16,50 24,75 16,50 5,50 16,50
2 11,00 19,25 22,00 8,25 13,75
3 24,75 8,25 27,50 19,25 11,00
4 22,00 11,00 38,50 11,00 27,50
5 41,25 30,25 35,75 24,75 38,50
6 33,00 38,50 41,25 30,25 24,75
По результатам испытаний требуется выяснить:
а) значимы ли различия в средней урожайности различных
сортов пшеницы независимо от типа удобрения;
б) значимо ли влияние типа применяемого удобрения на уро-
жайность независимо от сорта.
Решение. Согласно условию задачи исследуется влияние на уро-
жайность (зависимую переменную) двух факторов — типа удобре-
ния и сорта пшеницы.
Выдвинем две нулевые гипотезы:
• Н0А: различия в средней урожайности пшеницы, вызванные
влиянием типа удобрения (фактора Л), выражены не более, чем
различия, обусловленные случайными причинами;
281
• HQB: различия в средней урожайности пшеницы, вызванные
влиянием сорта (фактора В), выражены не более, чем различия,
обусловленные случайными причинами.
Решение проведем в среде SPSS по следующему алгоритму:
1. Запустим программу SPSS.
2. В окне Переменные опишем все исходные данные (рис. 6.13).
доухфакт 6еэ1 - SPSS Редактор Данных
Файл Главка Вид....Да-ные преобразовать Анализ Графика Сервис Окно' Сгржа
с# и(в] ч| 11-j _•> цг-j di л.гч • Метка | Значения j Пропущенные! Ширина столбца
Имя Тип | Щирина| Знаки после запятой ।
1 Урожайность Числовая 8 2 Нет Нет •7 По пр(
2 Удобрение Числовая :2 ;0 Нет 7 По цее
3 Сорт Числовая 1 0 {1, сорт 1). .Нет 5 По цен 1
Рис. 6.13. Фрагмент окна Переменные
с заданной структурой исходных данных
3. В окне Данные введем значения переменных согласно усло-
вию задачи. Первый столбец исходных данных отведем для значе-
ний урожайности пшеницы, второй — для типа удобрения, тре-
тий — для сорта пшеницы (рис. 6.14).
4. Вызовем дисперсионный анализ: Анализ -> Общая линейная
модель -> О Л М-о дно мерная... (см. рис. 6.14).
5. В открывшемся диалоговом окне ОЛМ-одномерная из списка
доступных переменных, расположенных в левой части диалогово-
го окна, перенесем переменную «Урожайность» в поле Зависимая
переменная, а переменные «Удобрение» и «Сорт» — в поле Фиксиро-
ванные факторы (рис. 6.15).
6. Нажав кнопку Модель... (см. рис. 6.15), откроем диалоговое
окно ОЛМ-одномерная: Модель (рис. 6.16). Здесь закажем настраива-
емую модель и выберем исследуемые факторы; по умолчанию стро-
ится полнофакторная модель, которая учитывает все варианты
взаимодействий независимых переменных. Выход из этого диало-
гового окна подтверждаем кнопкой Продолжить.
7. Для интерпретации результатов анализа выведем графики с
помощью кнопки Графики... (см. рис. 6.15). В диалоговом окне ОЛМ-
одномерная: Графики профилей по горизонтальной оси закажем
«Удобрение», а сорта пшеницы выведем в виде отдельных линий
графика (рис. 6.17). Далее необходимо нажать кнопку Добавить,
после чего можно выйти из диалогового окна с помощью кнопки
Продолжить.
282
' даухфакт 6«э1 - SPSS Редактор Данных
и»
Файл Правка Вид данные Преобразовать
15:Сорт
8
9
10
12
13
14
15
16
17
16
19
20
21
22
Урожайно] удобрени! Сорт
сть | в I
16.50
11,00:
24,751
22.00'|''
....41,'28|—в
33.0©“" о
24,7<Г" 1
19,20?
8.26!
11,00!
30.26 !
38,50:
16,50!
22.00!
27.50!
38,50:
35,70?
41,25?
6.50!
8,26*
19.25
...11.00
1нные/Переменные /"
Графим Сервис окно
Отчеты
Олисате/ьные статистики
Таблицы
Сгтмвка
2
2
2
2
2
2
Смешанные моде/м
Корре ляци4
Регрессия
Лсггрней-ьм анагмэ
Классификация
Слежение размерности
Анализ икал
Непараметрические критерии
Временные ряды
Выживаемость
ЬЗ-южестэежые отклики
Анализ гропущегьых значений...
Сложные выборки
О/м-кмогсмерная...
ОЛМ-повтсрные измерения.
Компоненты дисперсии.
yj
Обобщенная факторная SPSS Грсцессор готов
<<щзя линЧ'ная ww*
| 0ЯГ4<>днг^*<м
2
3
2
5
6
2
б
2
3
3
7
б
б
2
3
; пуск * В 3».
К Г"-'*'К J| Д'О'Мен-г ‘Н..
. ITT
Рис. 6.14. Общий вид редактора с введенными данными
и меню Общая линейная модель для проведения
двухфакторного дисперсионного анализа
8. Нажатием кнопки Параметры... в диалоговом окне ОЛМ-одно-
мерная (см. рис. 6.15) зададим необходимые для анализа параметры,
которые следует вывести в результатах расчета (рис. 6.18).
9. Откроем диалоговое окно ОЛМ-одномерная: Апостериорные
множественные сравнения для набл... нажатием кнопки Апостериори...
(см. рис. 6.15) и среди 18 тестов выберем один — тест Шеффе
(рис. 6.19). Выход из диалогового окна подтверждаем кнопкой
Продолжить.
10. После нажатия кнопки 0К (см. рис. 6.15) начинается вычис-
лительный процесс по алгоритму дисперсионного анализа с учетом
выбранных условий.
Результаты расчета в выводе представляются в виде таблиц и
графиков. Вначале выводится сводная таблица «Межгрупповые
факторы» (табл. 6.17), в которой приведены общие сведения об
изучаемых факторах, присвоенных метках и о количестве наблю-
дений (N) по каждому фактору.
283
ОЛМ-одиомерная
Фиксированные факторы:
Случайные факторы:
Ко^ариаты:
[Удобрение]
•4> [Сорт]
Зависимая переменная:
-^Урожайность
Взвешенный МНК:
Вставка j Cfipoc | Отмена j Справка |
Рис. 6.15. Диалоговое окно ОЛМ-одиомерная
с введенными переменными
Рис. 6.16. Диалоговое окно ОЛМ-одномерная: Модель
284
ОЛМ-одномерная: Графики профилей
; факторы:
Удобрение
Сорт
Горизонтальная ось:
|Удобрение
Продолжить
Отмена
Отдельные линии:
Сорт
Справка
Отдельные графики:
Добавить
Графики:
Рис. 6.17. Диалоговое окно ОЛМ-одномерная: Графики профилей
OSIM-одномерная: Параметры
____ ' м
Оцененные маргинальные средние
Фактор(ы) и ихезаинодействия:
(OVERALL)
Удобрение
Сорт
Вывести средние для:
(OVERALL)
.' I ", I Удобрение
> til_Сорт
Сравнить главные эффекты
Вывести ..................
(V Списательные статистики
R Оценки силы эффекта
Г Наблюденная мощность
Г Оценки параметров
Г" Матрица коэфф, контрастов
Г” Критерии однородности
Г График разброса по уровням
Г” График остатков
Г Отсутствие согласия
Г" Орщая функция, допускающая оценку
Доверительные интервалы на ур. знач. 95%
Отмена | Справка I
Продолжить
Рис. 6.18. Диалоговое окно ОЛМ-одномерная: Параметры
285
Рис. 6.19. Диалоговое окно
ОЛМ-одномерная: Апостериорные множественные сравнения для набл...
Таблица 6.17
Межгрупповые факторы
Метка значения N
1 А 5
2 В 5
3 С 5
4 D 5
5 Е 5
6 F 5
1 сорт 1 6
2 сорт 2 6
“3 сортЗ 6
4 сорт 4 6
5 сорт 5 б
В таблице «Описательные статистики» (табл. 6.18) содержатся
средние значения и стандартные отклонения всех выборок, а так-
же итоговые значения по всем данным.
286
Таблица 6.18
Описательные статистики
Зависимая переменная: Урожайность
Среднее Стд.отклонение N
А сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 16,5000 24,7500 16,5000 5,5000 16,5000 15,9500 6,84744 1 1 1 1 1 5
В сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 11,0000 19,2500 22,0000 8,2500 13,7500 14,8500 5,70252 1 1 1 1 1 5
D сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 22,0000 11,0000 38,5000 11,0000 27,5000 22,0000 11,66726 1 1 1 1 1 5
Е сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 41,2500 30,2500 35,7500 24,7500 38,5000 34,1000 6,62288 1 1 1 1 1 5
F сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 33,0000 38,5000 41,2500 30,2500 24,7500 33,5500 6,56554 1 1 1 1 1 5
Итог сорт 1 сорт 2 сортЗ сорт 4 сорт 5 Итог 24,7500 22,0000 30,2500 16,5000 22,0000 23,1000 11,00000 11,53690 9,83870 9,83870 10,28956 10,77485 6 6 6 6 6 30
287
Таблица 6.19
Оценка эффектов межгрупповых факторов
Зависимая переменная: Урожайность
Источник Сумма квадратов типа III СТ.СВ. Средний квадрат F Знач. Частная Эта в Квадрате
Скорректированная 2474.450(a) 9 274,939 6,162 ,000 ,735
модель
Свободный член 16008,300 1 16008,300 358,780 ,000 ,947
Удобрение 1875,500 5 375,100 8,407 ,000 ,678
Сорт 598,950 4 149,737 3,356 ,030 ,402
Ошибка 892,375 20 44,619
Итог 19375,125 30
Скорректированный 3366,825 29
ИТОГ
a R квадрат = ,735 (Скорректированный R квадрат = ,616)
Таблица «Оценки эффектов межгрупповых факторов»
(табл. 6.19) содержит результаты проверки основных гипотез двух-
факторного дисперсионного анализа.
В данном случае имеем следующее:
1. Переменная «Удобрение» оказывает статистически достовер-
ное влияние на распределение зависимой переменной «Урожай-
ность», поскольку F- 8,407 при Знач. = 0,000 (средние значения
урожайности по типам удобрений составили: 15,95; 14,85; 18,15;
22,00; 34,10 и 33,55).
2. Переменная «Сорт» также оказывает статистически значимое
влияние на распределение зависимой переменной «Урожайность»,
поскольку F= 3,356, а Знач. =0,030 (средние значения урожайности
по сортам: 24,75; 22,00; 30,25; 16,50 и 22,00).
В следующих трех таблицах (табл. 6.20-6.22) выводятся описа-
тельные статистики для совокупности всех данных и для каждого
из исследуемых факторов.
Далее в табл. 6.23 выведены результаты расчета апостериор-
ных критериев, в частности теста Шеффе, по сравнению отдель-
ных типов удобрений. По результатам расчета можно видеть, что
удобрения Е и F наиболее значимы по своему воздействию на
урожайность пшеницы и отличаются от других типов удобре-
ний.
Факт различного воздействия удобрений подтверждается и при-
веденными в табл. 6.24 результатами сравнения средних по одно-
288
Таблица 6.20
1. Среднее средних
Зависимая переменная: Урожайность
Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
23,100 1,220 20,556 25,644
Таблица 6.21
2. Удобрение
Зависимая переменная: Урожайность
Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
А 15,950 2,987 9,719 22,181
В 14,850 2,987 8,619 21,081
С 18,150 2,987 11,919 24,381
D 22,000 2,987 15,769 28,231
Е 34,100 2,987 27,869 40,331
F 33,550 2,987 27,319 39,781
Таблица 6.22
3. Сорт
Зависимая переменная: Урожайность
Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
сорт 1 24,750 2,727 19,062 30,438
сорт 2 22,000 2,727 16,312 27,688
сортЗ 30,250 2,727 24,562 35,938
сорт 4 16,500 2,727 10,812 22,188
сорт 5 22,000 2,727 16,312 27,688
родным подмножествам. В зависимости от своей эффективности
выделены три подмножества удобрений.
Вывод результатов заканчивается графиками профилей
(рис. 6.20), на которых представлены зависимости средней урожай-
ности пшеницы от типа удобрения и от сорта.
Из данного графика видно, что наиболее эффективно на сред-
нюю урожайность оказывает влияние удобрение Е и наименее
эффективно — удобрение В. Если рассматривать влияние сорта,
можно заметить, что наиболее урожайным является сорт 3 и наи-
менее урожайным — сорт 4. Поскольку сорта 2 и 5 имеют одина-
ковые средние значения урожайности, то соответствующие две
линии на графике слились в одну.
19 - 1591
Таблица 6.23
Множественные сравнения
Зависимая переменная: Урожайность
Шеффе
(1) (J) (1-П-я разность средних Стд. ошибка Знач. 95% доверительный интервал
Нижняя граница Верхняя граница
А В 1,1000 4,22463 1,000 -14,4536 16,6536
С -2,2000 4,22463 ,998 -17,7536 13,3536
D -6,0500 4,22463 ,836 -21,6036 9,5036
Е -18,1500(») 4,22463 ,016 •33,7036 -2,5964
F -17,60000 4,22463 ,020 -33,1536 -2,0464
В А -1,1000 4,22463 1,000 16,6536 14,4536
С -3,3000 4,22463 ,986 -18,8536 12,2536
D -7,1500 4,22463 ,720 -22,7036 8,4036
Е -19,2500(*) 4,22463 ,009 -34,8036 -3,6964
F -18,7000(‘) 4,22463 .012 -34,2536 -3,1464
С А 2,2000 4,22463 ,998 -13,3536 17,7536
В 3,3000 4,22463 ,986 -12,2536 18,8536
D -3,8500 4,22463 ,972 -19,4036 11,7036
Е -15,9500(‘) 4,22463 ,042 -31,5036 -,3964
F -15,4000 4,22463 .053 -30,9536 ,1536
D А 6,0500 4,22463 ,836 -9,5036 21,6036
В 7,1500 4,22463 ,720 -8,4036 22,7036
С 3,8500 4,22463 ,972 -11,7036 19,4036
Е -12,1000 4,22463 .195 -27,6536 3,4536
F -11,5500 4,22463 ,236 -27,1036 4,0036
Е А 18,1500(*) 4,22463 ,016 2,5964 33,7036
В 19,25000 4,22463 ,009 3,6964 34,8036
С 15,9500(‘) 4,22463 ,042 ,3964 31,5036
D 12,1000 4,22463 .195 -3,4536 27,6536
F ,5500 4,22463 1,000 -15,0036 16,1036
F А 17,6000(‘) 4,22463 ,020 2,0464 33,1536
В 18,70000 4,22463 .012 3,1464 34,2536
С 15,4000 4,22463 .053 -,1536 30,9536
D 11,5500 4,22463 ,236 -4,0036 27,1036
Е -,5500 4,22463 1,000 -16,1036 15,0036
Основано на наблюденных средних.
* Разность средних значима на уровне ,05.
Количество значений, заданных для специального контраста (SPECIAL), должно быть кратным
количеству уровней данного фактора. Критерии для проверки гипотезы вычислить невозможно.
290
Таблица 6.24
Урожайность
Шеффе
N Подмножество
1 2 3
В А С D F Е 5 5 5 5 5 5 14,8500 15,9500 18,1500 22,0000 18,1500 22,0000 33,5500 22,0000 33,5500 34,1000
Знач. ,720 ,053 ,195
Представлены средние по однородным подгруппам. Основанный на суммах квадратов типа III член, содержащий ошибку, - это средний квадрат (ошибка) = 44,619.
Оцененные маргинальные средние
Сорт
— сорт 1
— сорт 2
-— сортЗ
... сорт 4
— сорт 5
Рис. 6.20. Зависимость средней урожайности пшеницы
от ее сорта и типа удобрения
Таким образом, в результате решения данной задачи методом
дисперсионного анализа, реализованного в алгоритме одномерной
линейной модели, нулевые гипотезы Н0А и Ново незначимом вли-
янии типа удобрения и сорта пшеницы на ее среднюю урожайность
отвергнуты и приняты альтернативные гипотезы о существен-
ном влиянии названных факторов на урожайность.
19’
291
6.3.5. Двухфакторный дисперсионный анализ в SPSS
с повторными измерениями
Пример 6.4. На опытной станции проводилось испытание че-
тырех типов удобрений и четырех новых технологий выращивания
одной зерновой культуры. Данные об урожайности этой культуры
приведены в табл. 6.25.
Таблица 6.25
Урожайность зерновой культуры на опытных участках, ц/га
Номер участка Уровень фактора А (тип удобрения) Уровень фактора В (технология выращивания)
1 2 3 4
1 22,60 21,80 20,60 18,70
2 1 22,20 21,40 19,70 17,60
3 1 21,20 20,80 17,40 18,40
4 20,20 19,90 16,80 17,00
1 13,10 14,60 14,00 14,20
2 15,20 14,30 14,70 15,10
3 Z 13,20 12,70 13,10 14,90
4 12,40 12,30 12,80 13,80
1 14,60 15,30 13,70 14,40
2 7 12,80 16,60 13,90 15,50
3 э 14,70 14,80 13,30 15,00
4 13,60 15,10 13,15 15,50
1 14,80 14,90 15,10 13,00
2 Л 15,80 14,20 14,60 15,70
3 4 15,70 15,30 14,30 15,00
4 15,50 15,60 14,20 14,80
По приведенным результатам испытаний требуется установить,
влияют ли на урожайность типы удобрений и новые технологии
выращивания.
Решение. Поскольку условия задачи соответствуют требованиям
к исходным данным для проведения двухфакторного дисперсион-
ного анализа с повторениями (см. подпараграф 6.2.2), то восполь-
зуемся его алгоритмом. Здесь рассматривается воздействие двух
факторов: типа удобрения и технологии выращивания. Роль зависи-
мой переменной выполняет урожайность зерновой культуры. В от-
личие от примера 6.3 здесь каждому типу удобрений соответствуют
292
не один, а четыре опытных участка земли, в этом и заключается
требование повторения измерений при одном и том же условии.
Выдвинем нулевые гипотезы:
• Нол: различия в урожайности зерновой культуры, вызванные
влиянием типа удобрения (фактора Л), выражены не более, чем
различия, обусловленные случайными причинами;
• Нов: различия в урожайности зерновой культуры, вызванные
влиянием технологии выращивания (фактора В), выражены не
более, чем различия, обусловленные случайными причинами.
Для решения используем пакет SPSS и реализуем следующий
алгоритм:
1. Запустим программу SPSS.
2. В окне Переменные последовательно опишем исходные дан-
ные (рис. 6.21).
двух повтори - SPSS Редактор Данных
Файл Пмвю Вид График Сервис Окно Справка "
i| чЭнаим после запятой | Метка | Значения [ Пропущенные [ширина столбца |
• • •
.....
"2
.....
2
...
2
.....
....
2
'2
2
....
• 2
.....
2
О
J Тип [ширина
1Числовая 8
8
9
10
12
13
14
15
16
17
Имя |___________
урожаи!11 Числовая 8
урожай12 Числовая 8
урожай13 Числовая 8
урожаи14 Числовая :8
урожай21 Числовая 8
урожай22 Числовая 8
урожай23
урожай24
урожай31
урожаи32
урожаиЗЗ .Числовая#
урожаиЗЛ Числовая :8
урожаи41 Числовая#
урожай42 Числовая 8
урожай43 Числовая 8
урожай44^Числовая 8
участок
Числовая 8
Числовая#
Числовая °8
Числовая#
Числовая 8
Нет
Нет
Нет
Нет
...Нет
Нет
Нет
'Нет
Тнет
"=Нат
Тнет
ЧНет
!Нет
1Нгг
:Нет
~~1нот
-"]нат...
BbipaaJL
Нот
Нет
Нет
Нет
Нот
‘Нет
Нет
Нет
Нот
Нет
Нот
Нет
Нот
SHOT
iHOT
^Нет
'‘Нот
S
б
V
б
б
5
1б"
1б"
5
б
5
5
5
Б
.По правом |
По правом
По правом
;По правом
По правом
По правом
По правом
•По правом I
По правом
*По правом
•По правом
,'По правом
По правом
;По правом
*По правом
1По правом
;По правом :
2
5
6
5
5
Рис, 6.21. Фрагмент окна Переменные
с заданной структурой исходных данных
3. Согласно условию задачи в окне Данные введем значения
переменных (рис. 6.22). По четыре столбца исходных данных от-
ведем под соответствующие варианты технологий выращивания
зерновой культуры и в четырех строках укажем номера опытных
участков. Матрицы данных для каждого уровня фактора В распо-
лагаются в четырех строках, соответствующих номеру участка.
4. Вызовем дисперсионный анализ: Анализ —> Общая линейная
модель -> ОЛМ-повторные измерения... (см. рис. 6.22).
293
Рис. 6.22. Фрагмент окна Данные с введенными значениями
переменных и меню Общая линейная модель для проведения
двухфакторного дисперсионного анализа с повторными измерениями
5. В открывшемся диалоговом окне ОЛМ-повторные измерения:
Задать факторы в поле строки Имя внутригруппового фактора вначале
зададим тип удобрения (тип_уд) и число уровней, равное 4, что
подтверждается клавишей Добавить, аналогично поступим с зада-
нием вариантов технологий выращивания (технол) и соответству-
ющего им числа уровней — 4. Для выхода из этого диалогового
окна щелкнем по кнопке Задать (рис. 6.23).
Рис. 6.23. Диалоговое окно ОЛМ-повторные измерения: Задать факторы
294
6. В новом диалоговом окне ОЛМ-повторные измерения...
(рис. 6.24) в левом поле выделим необходимые переменные и с
помощью кнопки с указателем перенесем их в правое поле Внутри-
групповые переменные.
Рис. 6.24. Диалоговое окно ОЛМ-повторные измерения...
для задания переменных
7. Нажатием кнопки Параметры... (см. рис. 6.24) откроем диа-
логовое окно ОЛМ-повторные измерения: Параметры и закажем вывод
следующих результатов: Описательные статистики и Оценки размера
эффекта (рис. 6.25). Выход изданного режима подтвердим кнопкой
Продолжить.
8. В окне ОЛМ-повторные измерения... (см. рис. 6.24) щелкнув по
кнопке Модель..., в открывшемся диалоговом окне ОЛМ-повторные
измерения: Модель в области Задать модель выберем режим Настраи-
ваемая (рис. 6.26). Из левого поля Внутригрупповые перенесем в
правое поле Внутригрупповая модель переменные тип_уд и технол. Для
выхода из диалогового окна нажмем на кнопку Продолжить.
9. Чтобы вывести графики профилей в диалоговом окне ОЛМ-
повторные измерения... (см. рис. 6.24), щелкнем по кнопке Графики...,
и тогда откроется диалоговое окно ОЛМ-повторные измерения:
295
Рис. 6.25. Диалоговое окно ОЛМ-повторные измерения: Параметры
Рис. 6.26. Диалоговое окно ОЛМ-повторные измерения: Модель
296
Графики профилей (рис. 6.27). Здесь зададим по горизонтальной оси
переменную тип_уд и в качестве отдельных линий — переменную
технол, что подтверждаем кнопкой Добавить. Для выхода из окна
щелкнем по кнопке Продолжить.
Рис. 6.27. Диалоговое окно ОЛМ-повторные измерения: Графики профилей
10. Для выполнения расчетов в диалоговом окне ОЛМ-повторные
измерения... щелкнем по кнопке ОК (см. рис. 6.24).
Вывод результатов расчета по алгоритму двухфакторного дис-
персионного анализа с повторными измерениями содержит следу-
ющую информацию.
Вначале выводится сводная таблица «Внутригрупповые факто-
ры» (табл. 6.26), в которой приведены перечень изучаемых факто-
ров и сведения о зависимой переменной.
Далее приводятся результаты расчета показателей (табл. 6.27),
которые составляют описательную статистику (среднее значение,
стандартное отклонение, количество наблюдений N).
Затем для исследуемых факторов следуют результаты расчета
различных многомерных тестов (табл. 6.28): След Пиллая, Лямбда
Уилкса, След Хотеллинга, Наибольший корень Роя, по которым
восстанавливается значение F для последующего определения зна-
чимости.
Таблица 6.26
Внутригрупповые факторы
Измерение: ИЗМЕРЕНИЕ-1
тип_уд технол Зависимая переменная
1 1 урожай11
2 урожай12
3 урожай13
4 урожай14
2 1 урожай21
2 урожай22
3 урожай23
4 урожай24
3 1 урожай31
2 урожай32
3 урожайЗЗ
4 урожай34
4 1 урожай41
2 урожай42
3 урожай43
4 урожай44
Таблица 6.27
Описательные статистики
Среднее Стд. отклонение N
урожайП 21,5500 1,07548 4
урожай12 20,9750 ,82614 4
урожай13 18,6250 1,81544 4
урожайМ 17,9250 ,77190 4
урожай21 13,4750 1,20381 4
урожай22 13,4750 1,14419 4
урожай23 13,6500 ,86603 4
урожай24 14,5000 ,60553 4
урожай31 13,9250 ,89954 4
урожай32 15,4500 ,79373 4
урожайЗЗ 13,5125 ,34731 4
урожай34 15,1000 ,52281 4
урожай41 15,4500 ,45092 4
урожай42 15,0000 ,60553 4
урожай43 14,5500 ,40415 4
урожай44 14,6250 1,15000 4
298
Таблица 6.28
Многомерные критерий b)
Эффект Значение F Ст.св. гипотезы Ст.св. ошибки Знач. Частная Эта в Квадрате
тип_уд След Пиллая ,999 347.170(a) 3,000 1,000 ,039 ,999
Лямбда Уилкса ,001 347.170(a) 3,000 1,000 ,039 ,999
След Хотеллинга 1041,509 347.170(a) 3,000 1,000 ,039 ,999
Наибольший корень Роя 1041,509 347.170(a) 3,000 1,000 ,039 ,999
технол След Пиллая ,990 32.892(a) 3,000 1,000 ,127 ,990
Лямбда Уилкса ,010 32.892(a) 3,000 1,000 ,127 ,990
След Хотеллинга 98,676 32.892(a) 3,000 1,000 ,127 .990
Наибольший корень Роя 98,676 32.892(a) 3,000 1,000 .127 ,990
а Точная статистика
b План: Intercept
Внутригрупповой план: тип уд+технол
Результаты всех тестов свидетельствуют о том, что значимым
является фактор «Тип удобрения», а влияние фактора «Технология»
несущественно.
В следующих четырех таблицах (табл. 6.29—6.32) приводятся
оценки значимости исследуемых факторов на основе «классиче-
ского» метода Фишера.
Таблица 6.29
Критерий сферичности Моучли(Ь)
Измерение: ИЗМЕРЕНИЕ-1
Внутригрупповой эффект W Моучли Прибл. хи-квадрат ст.св. Знач. Эпсилон(а)
Гринхауз- Гайссер Юнх- Фельдт Ограни- ченный снизу
тип _уд ,010 8,013 5 ,214 ,448 ,680 ,333
технол ,027 6,222 5 ,352 ,385 ,475 ,333
Проверка нулевой гипотезы о том, что ковариационная матрица ошибок ортонормированного
преобразования зависимых переменных пропорциональна единичной матрице.
а Может использоваться, чтобы корректировать степени свободы для усредненных тестов
значимости. Скорректированные тесты отображены в таблице «Проверка внутригрупповых эффектов». b План: Intercept Внутригрупповой план: тип уд+технол
299
Результаты проверки, приведенные в таблице «Проверка внут-
ригрупповых эффектов» (см. табл. 6.30) в строке «Предполагая
сферичность», подтверждают значимость влияния обоих факторов.
Однако данный метод менее точен, чем другие, поэтому будем
считать, что влияние фактора «Технология» не значимо, о чем
свидетельствует большинство тестов.
Таблица 6.30
Проверка внутригрупповых эффектов
Измерение: ИЗМЕРЕНИЕ-1
Источник Сумма квадратов СТ.СВ. Средний F Знач. Частная Эта
типа III ьвсщрсн в Квадрате
тип_уд Предполагая сферичность 357,320 3 119,107 79,961 ,000 ,964
Гринхауз- 357,320 1,344 265,819 79,961 ,001 ,964
Гайссер Юнх-Фельдт 357,320 2,039 175,203 79,961 ,000 ,964
Ограниченный снизу 357,320 1,000 357,320 79,961 ,003 ,964
Ошибка Предполагая 13,406 9 1,490
(тип_уд) сферичность Гринхауз- 13,406 4,033 3,324
Гайссер Юнх-Фельдт 13,406 6,118 2,191
Ограниченный снизу 13,406 3,000 4,469
технол Предполагая сферичность 13,370 3 4,457 6,757 ,011 ,693
Гринхауз- 13,370 1,156 11,564 6,757 ,068 ,693
Гайссер Юнх-Фельдт 13,370 1,424 9,392 6,757 ,052 ,693
Ограниченный снизу 13,370 1,000 13,370 6,757 ,080 ,693
Ошибка Предполагая 5,936 9 ,660
(технол)_ сферичность Гринхауз- 5,936 3,469 1,711
Гайссер Юнх-Фельдт 5,936 4,271 1,390
Ограниченный снизу 5,936 3,000 1,979
3$)
Таблица 6.31
Проверка внутригрупповых контрастов
Измерение: ИЗМЕРЕНИЕ-1
Источник ТИП-УД технол Сумма квадратов типа III СТ.СВ. Средний квадрат F Знач. Частная Эта в Квадрате
тип_уд Линейный Квадратич- ный Кубический 153,804 164,000 39,516 1 1 1 153,804 164,000 39,516 40,839 718,781 83,306 ,008 ,000 ,003 ,932 ,996 ,965
Ошибка (тип_уд) Линейный Квадратич- ный Кубический 11,298 ,684 1,423 3 3 3 3,766 ,228 ,474
технол Линейный Квадратич- ный Кубический 6,399 .431 6,541 1 1 1 6,399 ,431 6,541 27,451 .322 16,014 ,014 ,610 ,028 ,901 ,097 ,842
Ошибка (технол) Линейный Квадратич- ный Кубический ,699 4,011 1,225 3 3 3 .233 1,337 ,408
Таблица 6.32
Оценка эффектов межгрупповых факторов
Измерение: ИЗМЕРЕНИЕ-1 Преобразуемая переменная: Среднее
Источник Сумма квадратов типа III ст.св. Средний квадрат F Знач. Частная Эта в Квадрате
Свободный член Ошибка 15849,236 9,808 1 3 15849,236 3,269 4847,730 ,000 ,999
В следующих четырех таблицах (табл. 6.33—6.36) выводятся опи-
сательные статистики для всех уровней исследуемых факторов
(средние и стандартные отклонения).
Таблица 6.33
1. Среднее средних
Измерение: ИЗМЕРЕНИЕ-1
Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
15,737 ,226 15,017 16,456
301
Таблица 6.34
2. тип_уд
Измерение: ИЗМЕРЕНИЕ-1
тип_уд Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
1 19,769 ,526 18,095 21,443
2 13,775 ,422 12,433 15,117
3 14,497 ,076 14,256 14,738
4 14,906 ,153 14,421 15,392
Таблица 6.35
3. технол
Измерение: ИЗМЕРЕНИЕ-1
технол Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
1 16,100 ,234 15,356 16,844
2 16,225 ,241 15,458 16,992
3 15,084 ,411 13,777 16,392
4 15,538 ,215 14,852 16,223
Таблица 6.36
4. тип_уд * технол
Измерение: ИЗМЕРЕНИЕ-1
тип_уд технол Среднее Стд. ошибка 95% доверительный интервал
Нижняя граница Верхняя граница
1 1 21,550 ,538 19,839 23,261
2 20,975 ,413 19,660 22,290
3 18,625 ,908 15,736 21,514
4 17,925 ,386 16,697 19,153
2 1 13,475 ,602 11,559 15,391
2 13,475 ,572 11,654 15,296
3 13,650 ,433 12,272 15,028
4 14,500 ,303 13,536 15,464
3 1 13,925 ,450 12,494 15,356
— 2 15,450 ,397 14,187 16,713
3 13,513 ,174 12,960 14,065
4 15,100 ,261 14,268 15,932
4 1 15,450 ,225 14,732 16,168
2 15,000 ,303 14,036 15,964
3 14,550 ,202 13,907 15,193
4 14,625 ,575 12,795 16,455
302
Вывод результатов двухфакторного дисперсионного анализа
заканчивается графиком профилей (рис. 6.28).
технол
— 1
— 2
.... з
.... 4
Рис. 6.28. Зависимость урожайности культуры
от типа удобрения и технологии
Вид графиков свидетельствует о существенном воздействии
первого типа удобрения и менее значимом влиянии других типов
на урожайность зерновой культуры. В то же время фактор «Техно-
логия» не позволяет выявить закономерность, поскольку взаимное
пересечение линий свидетельствует о случайности влияния данно-
го фактора.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
САМОСТОЯТЕЛЬНОГО ЗАДАНИЯ
По аналогии с примерами 6.1—6.4 составить задачи с экономи-
ческим содержанием и своими исходными данными, с соблюде-
нием необходимых ограничений. Сформулировать проверяемые
нулевую и альтернативную гипотезы. Провести решение состав-
ленных задач в среде SPSS. Представить результаты расчета и их
графическую интерпретацию с соответствующим анализом в рам-
ках дисперсионного анализа. Сделать вывод о результатах провер-
ки принятых гипотез.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Cody R., Smith J.. Applied statistics and the SAS programming Language,
Pretence Hall, 1991 http://pubhealth.spb.ru/SASDIST/MLR.htm
2. Fawcett T. ROC Graphs: Notes and Practical Considerations for
Researchers// 2004 Kluwer Academic Publishers.
3. Tryon R.C. Cluster Analysis //Ann. Arb., Edw. Brothers. 1939.
4. Айвазян C.A., Мхитарян B.C. Прикладная статистика. Основы эконо-
метрики: Учебник: В 2 т. — М.: ЮНИТИ-ДАНА, 2001.
5. Андреева Г.В. Скоринг как метод оценки кредитного риска // Банков-
ские технологии. 2000. № 6.
6. Барсегян А.А. и др. Технология анализа данных: Data Mining, Visual
Mining, Text Mining, OLAP/А.А. Барсегян, M.C. Куприянов, B.B. Сте-
паненко, И.И. Холод. — 2-е изд., перераб. и доп.— СПб.: БХВ-Пе-
тербург, 2007.
7. Болч Б., Хуань КДж. Многомерные статистические методы для эко-
номики. — М.: Статистика, 1979.
8. Большаков А.А., Каримов Р.Н. Методы обработки многомерных дан-
ных и временных рядов: Учеб, пособие для вузов. — Горячая линия —
Телеком, 2007.
9. БююльА., Цефель П. SPSS: искусство обработки информации. Анализ
статистических данных и восстановление скрытых закономерностей:
Пер. с нем. — СПб.: ООО «ДиаСофтЮП», 2005.
10. Гайдышев И. Анализ и обработка данных: специальный справоч-
ник. — СПб.: Питер, 2001.
11. Доугерти К. Введение в эконометрику: Учебник: Пер. с англ. — М.:
ИНФРА-М, 1999, 2001.
12. Дронов В.С. Основы математики (избранные главы). — Барнаул:
Изд-во Алт. гос. ун-та, 1998.
13. Дронов С.В. Многомерный статистический анализ: Учеб, пособие. —
Барнаул.: Изд-во Алт. гос. ун-та, 2003.
14. Дубров А.М. Компонентный анализ и эффективность в экономике:
Учеб, пособие. — М.: Финансы и статистика, 2002.
15. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистиче-
ские методы. — М.: Финансы и статистика, 2003.
16. Дюк В., Самойленко A. Data Mining: учебный курс. — СПб.: Питер,
2'001.
17. Егоршин А.А. Многомерные методы статистического анализа: Учеб,
пособие. — Харьков: ХГЭУ, 1997.
18. Елкина В.Н., Загоруйко Н.Г. Количественные критерии качества так-
сономии и их использование в процессе принятия решений // Тр.
ИМ СО РАН. Серия «Вычислительные системы», 1969, вып. 36, Но-
восибирск.
х
304
19. Калинина В.Н., Соловьев В.И. Введение в многомерный статистиче-
ский анализ: Учеб, пособие. — М.: Изд-во ГУУ, 2003.
20. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятно-
стей и математическая статистика: Учеб, пособие. — М.: Высшая
школа, 1991.
21. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. — М.:
ЮНИТИ-ДАНА, 2002.
22. Кулаичев А.П. Методы и средства анализа данных в среде Windows.
STADIA 6.0. — М.: Информатика и компьютеры, 1998.
23. Магнус Я. Р, Катышев П.К, Пересецкий А.А. Эконометрика. Началь-
ный курс: Учебник. — 6-е изд., перераб. и доп. — М.: Дело, 2004.
24. Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб, пособие. —
М.: Финансы и статистика, 2002.
25. Наследов А.Д. Математические методы психологического исследова-
ния: Учеб, пособие. — 2-е изд., испр. и доп. — СПб.: Речь, 2006.
26. Наследов А.Д. SPSS: Компьютерный анализ данных в психологии и
социальных науках. — СПб.: Питер, 2005.
27. Окунь Я. Факторный анализ: Пер. с польск. — М.: Статистика, 1974.
28. Орлова И.В. Экономико-математические методы и модели. Выпол-
нение расчетов в среде EXCEL. Практикум: Учеб, пособие для ву-
зов. — М.: ЗАО «Финстатинформ», 2000.
29. Орлова И.В. Экономико-математическое моделирование: Практиче-
ское пособие по решению задач / ВЗФЭИ. — М.: Вузовский учебник,
2004.
30. Орлова И.В., Половников В.А. Экономико-математическое методы и
модели: компьютерное моделирование: Учеб, пособие. — М.: Вузов-
ский учебник, 2007.
31. Паклин Н. BaseGroup Labs: Логистическая регрессия и ROC-анализ —
математический аппарат http://www.basegroup.ru/labs/
32. Практика применения — Лаборатория BaseGroup Labs http://www.
basegroup.ru/practice/
33. Российский статистический ежегодник. 2004: Стат. сб. / Росстат. —
М., 2004.
34. Россия в цифрах. 2004 / Госкомстат России. — М., 2004.
35. Сошникова Л.А. и др. Многомерный статистический анализ в эконо-
мике / Л.А. Сошникова, В.Н. Тамашевич, Г. Уебе, М. Шефер; Под
ред. проф. В.Н. Тамашевича. — М.: ЮНИТИ-ДАНА, 1999.
36. Таганов Д.Н. SPSS: Статистический анализ данных в маркетинговых
исследованиях. — СПб.: Питер, 2005.
37. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: Учебник. — М.: Эк-
замен, 2003.
38. Толстова Ю.Н. Измерение в социологии. — М.: ИНФРА-М, 2003.
39. Туркин В.С. Методы обработки маркетинговой информации: Учебно-
методическое пособие. — М.: МГУЭСИ 2004.
29- 1591
305
40. Факторный, дискриминантный и кластерный анализ / Дж.-О. Ким,
Ч.У. Мюллер, У.Р. Клекка и др. — М.: Финансы и статистика, 1989.
41. Харман Г. Современный факторный анализ: Пер. с англ. — М.: Ста-
тистика, 1972.
42. Шелобаев С.И. Математические методы и модели. — М.: ЮНИТИ,
2001.
43. Эконометрика: Учебник /И.И. Елисеева, С.В. Курышева, ТВ. Касте-
ева', Под ред. И.И. Елисеевой. — 2-е изд., перераб. и доп. — М.: Фи-
нансы и статистика, 2005.
УДК 311(075.8)
ББК 60.6я73
М73
Авторы: Н.А. Концевая (гл. 4); И.В. Орлова (гл. 1 совместно
с В.Н. Уродовских и Е.С. Филоновой; § 2.1 и 2.2;
§ 2.3 совместно с В.Б. Турундаевским); В.Б. Турун-
даевский (§ 2.3 совместно с И.В. Орловой); В.Н. Уро-
„ довских (гл. 1 совместно с И.В. Орловой и Е.С. Фи-
лоновой; гл. 5 и 6); Е.С. Филонова (гл. 1 совместно
с И.В. Орловой и В.Н. Уродовских; гл. 3)
к Рецензенты кафедра математической статистики и экономет-
рики МЭСИ (зав. кафедрой — д-р экон, наук, проф.
В.С. Мхитарян) и зав. кафедрой прикладной мате-
, матики ГУУ д-р экон, наук, проф. В.А. Колемаев
Многомерный статистический анализ в экономических
М73 задачах: компьютерное моделирование в SPSS: Учеб, по-
собие / Под ред. И.В. Орловой. — М.; Вузовский учебник,
2009.- 310 с.
ISBN 978-5-9558-0108-7
Книга посвящена многомерному статистическому анализу
(MCA) и организации вычислений по MCA. Для реализации
методов многомерной статистики используется программа об-
работки статистической информации — SPSS версии 14. Дано
исчерпывающее описание среды организации вычислительных
работ в системе SPSS. Помимо теоретической части приведены
практические рекомендации по решению задач MCA, а также
1 задачи для самостоятельной работы.
Для студентов и аспирантов всех экономических специаль-
ностей университетов и вузов, а также для работников, зани-
мающихся анализом финансово-экономического состояния
фирм и предприятий.
ББК 60.6я73
ISBN 978-5-9558-0108-7
© Вузовский учебник, 2009
Ji" fili A A -Ы ;i фОЙ.и'Й,!’ p » 1 ’'I
. , - }l;i Xi-' • ' -
ПРЕДИСЛОВИЕ
Учебное пособие посвящено методам многомерного статисти-
ческого анализа (MCA) и организации вычислений по MCA. Оно
продолжает серию учебных изданий, предназначенных для разви-
тия у студентов практических навыков применения методов MCA
при решении конкретных экономических и финансовых задач с
использованием компьютерных технологий. В книге представлена
практическая технология компьютерного моделирования эконо-
мических систем, необходимая для понимания причинно-след-
ственных связей в экономике, для прогнозирования, планирования
и принятия решений менеджерами.
Работа подготовлена в соответствии с программой по дисцип-
лине «Эконометрика», учитывающей требования Государственных
стандартов подготовки специалистов по специальностям «Бухгал-
терский учет, анализ и аудит», «Финансы и кредит» и «Экономика
труда».
Необходимость создания данного учебного пособия следует из
того, что изучение ряда тем курсов «Эконометрика» и «Статистика»
требует применения современного программного обеспечения для
решения реальных экономических задач, вытекающих из типовых
хозяйственных ситуаций.
В качестве инструментального средства для реализации методов
многомерной статистики используется распространенная програм-
ма обработки статистической информации — SPSS (аббревиатура
от Statistical Package for the Social Science) версии 14. Существуют и
другие пакеты, однако этот продукт наиболее доступен, поэтому
его применяют при решении многих прикладных задач и в качестве
вспомогательного средства в дисциплинах, читаемых на кафедре
экономико-математических методов и моделей.
SPSS содержит хорошее аналитическое программное обеспече-
ние, предоставляет решения в области «добычи знаний» (Data
Mining), позволяет выявить скрытые связи данных, находящихся
в базах и хранилищах данных. Программные продукты SPSS по-
могают решать прикладные задачи в различных областях, от клас-
сификации и профилирования клиентов до анализа кредитного
риска, управления контролем качества и повышения производи-
тельности персонала, занимающегося продажами.
3
Изучение и практическое применение методов MCA на базе
современных программных продуктов, к которым относится SPSS,
поможет сделать первые шаги в этом направлении.
Пособие состоит из шести глав, в которых рассмотрены методы
прикладной статистики: регрессионный, кластерный, факторный,
дискриминантный и дисперсионный анализ, а также изложены
основные требования к сбору и представлению исходных данных.
В работе раскрывается методология решения задач с применением
всех перечисленных методов, с последующим анализом, выводами
и предложениями по результатам моделирования.
Каждая глава состоит из трех частей: теоретическая часть, прак-
тикум, задачи для самостоятельного решения. Теоретическая ин-
формация приведена в виде краткого обзора. Основная часть ма-
териала представляет собой иллюстрацию использования модулей
программы SPSS для проведения разного рода эконометрических
исследований. Книга содержит большое количество примеров,
характеризующих реальное состояние современной российской
экономики.
Отличительной особенностью пособия является наличие задач
для самостоятельного решения по каждой теме. В целях сокраще-
ния объема книги числовые данные для задач размещены на CD.
Учебное пособие является практическим руководством по ис-
пользованию методов MCA, которое поможет студентам, аспиран-
там, менеджерам овладеть этими методами и применять их в вы-
пускных квалификационных работах и при решении практических
задач.
Учебное издание
МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ
АНАЛИЗ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ:
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В SPSS
Учебное пособие
Редактор И.В. Мартынова
Корректор М.В. Литвинова
Компьютерная верстка А. И. Паркани
Подписано в печать 19.12.2008.
Формат 60 х 90/16. Печать офсетная. Гарнитура Newton.
Усл. печ. л. 20,0. Уч.-изд. л. 18,8.
Доп. тираж 2000 экз. Заказ № 1591.
Издательский Дом «Вузовский учебник»
127247, Москва, ул. С. Ковалевской, д. 1, стр. 52
Отпечатано с готовых диапозитивов в ОАО ордена «Знак Почета»
«Смоленская областная типография им. В. И. Смирнова».
— 214000, г. Смоленск, проспект им. Ю. Гагарина, 2.