Author: Матасов В.Ф. Ульянцев В.П.
Tags: оружие вооружение артиллерийско-техническое имущество бронированные машины и специальные средства транспорта стрелковое оружие личное оружие боеприпасы и боевые отравляющие вещества управляемые и неуправляемые ракеты и реактивные снаряды автоматика военное оборудование военное дело
ISBN: 5-7679-0219-4
Year: 2001
Министерство образования Российской Федерации
Тульский государственный университет
В.Ф. Матасов, В.П. Ульянцев
ПРОЕКТИРОВАНИЕ АВТОМАТИКИ ОРУЖИЯ
Учебное пособие
Рекомендовано учебно-методическим объединением вузов
по университетскому политехническому образованию
в качестве учебного пособия для студентов технических университетов,
обучающихся по специальности 171300
“Стрелково-пушечное артиллерийское и ракетное оружие”
Тула 2001
УДК 623.422.4.001.63 ( 075 )
Проектирование автоматики оружия. Учеб, пособие / В.Ф. Матасов, В.П.
Ульянцев; Тул. гос. ун-т. Тула, 2001. 160 с.
ISBN 5-7679-0219-4
Рассматриваются вопросы расчета и проектирования механизмов
автоматики оружия. Особое внимание уделено ППМ, ПДМ, запирающим
механизмам, а также системам с различными принципами работы
автоматики.
Предназначено для студентов высших учебных заведений,
обучающихся на специальности 171300, а также может быть полезно
инженерно-техническим работникам, занимающимся проектированием
автоматического оружия.
Табл. 4. Ил. 53. Библиогр.; 9 назв.
Печатается по решению библиотечно-издательского совета Тульского
государственного университета.
Под общей редакцией д-ра техн, наук, проф. В.Л. Баранова.
Рецензенты: кафедра Мб МГТУ им. Н.Э. Баумана, д-р техн, наук, проф.
А.А. Королев;
технический директор АК “Туламашзавод” канд. экон,
наук, доц. Е.А. Дронов;
начальник отдела КБ приборостроения канд. техн, наук,
доц. А.В. Игнатов.
ISBN 5-7679-0219-4
© В.Ф. Матасов, В.П. Ульянцев, 2001
© Тульский государственный
университет, 2001
ПРЕДИСЛОВИЕ
Стрелково-пушечное вооружение (СПВ) в настоящее время является
миболее распространенным видом боевой техники, предназначенным для
’сшения различных задач, возникающих в результате проведения боевых
псраций. Создание высокоэффективных образцов СПВ является сложной
лдачей. Выбор основных параметров автоматики оружия обуславливает-
I областью его применения, условиями эксплуатации.
Автоматическое оружие относится к классу машин-автоматов, в
(руктуре которых имеются различные механизмы, выполняющие опера-
пн в определенной последовательности без участия стрелка. От надежнос-
11 работы механизмов автоматики полностью зависит и надежность рабо-
1 и всей системы в целом.
В главе 1 приведены методики расчёта и проектирования запираю-
I иIX узлов автоматического оружия. Рассматриваются вопросы жесткости
I прочности этих узлов.
В главе 2 даны общие сведения о проектировании цилиндрических
। пнтовых пружин сжатия, цилиндрических винтовых пружин кручения,
11'। нматических пружин.
Глава 3 посвящена вопросам проектирования патроноподающих ме-
111 измов ленточного и магазинного типов. Анализируются законы движе-
п1| патронной ленты, работа патроноподающих механизмов с двумя и
। . мя кинематически связанными звеньями, даётся методика проверки
: ^временности подачи патронов на линию досылания для патронопода-
1 || и lx механизмов магазинного питания.
В главе 4 представлены методики проектирования ударных механиз-
> г- куркового и ударникового типов, приведены характеристики серий-
« ' капсюлей-воспламенителей.
В главе 5 рассматриваются вопросы проектирования ускорительных
। '..ншзмов рычажного, кулачкового, копирного и пружинного типов.
В главе 6 даётся анализ функционирования запирающих механизмов
1 рекосом затвора и поворотом затвора относительно оси, параллельной
и канала ствола.
3
В главах 7-9 представлены методики проектирования различных схем
автоматики, а также механизмов досылания патронов.
В главе 10 рассматриваются вопросы проектирования стволов стрел-
ково-пушечного вооружения, даётся оценка мощности тепловых источни-
ков при производстве выстрела и нагрев ствола, приводится методика рас-
чёта прочности ствола ио упругому сопротивлению. Заканчивается глава
краткими сведениями о живучести стволов СПВ с рассмотрением процес-
сов, определяющих износ ствола.
Глава И посвящена вопросам расчёта и проектирования спусковых
механизмов.
Все главы заканчиваются рассмотрением примеров по материалам
данной главы.
Данное учебное пособие является продолжением учебного пособия
“Расчет автоматического оружия”, авторы В.Ф. Матасов, В.П. Ульянцев,
под общей редакцией В.Л. Баранова.
При изложении материала авторы стремились рассматривать наибо-
лее типичные и часто встречающиеся на практике вопросы расчета и про-
ектирования механизмов и узлов автоматики оружия.
Авторы выражают глубокую благодарность представителям отрасли
за ценные советы по написанию настоящего учебного пособия, рецензен-
там А.А. Королёву, Е.А. Дронову, А.В. Игнатову, а также П.В. Полозюку
за помощь в подготовке рукописи к изданию.
РАСЧЕТ И ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ
АВТОМАТИЧЕСКОГО ОРУЖИЯ
1. РАСЧЕТ И ПРОЕКТИРОВАНИЕ ЗАПИРАЮЩИХ УЗЛОВ
При проектировании запирающих узлов производится расчет узла
тирания (рис.1) на прочность сцепления затвора со ствольной коробкой
;щ выстреле, на упругую деформацию при выстреле и на температурную
формацию в процессе интенсивной стрельбы.
Рис. 1. Принципиальная схема узла запирания:
l-ствольная коробка. 2-ствол, 3-затвор. I- длина участка ствола,
воспринимающего нагрузку при выстреле. I-длина узла запирания.
1,и1г- длины участков затвора с различными поперечными сечениями
Прочность сцепления затвора со ствольной коробкой определяется по
пае, действующей на это сцепление, методами расчета сопротивления мате-
риалов. Сила, действующая па опорные поверхности, может быть различ-
ч >й в зависимости от условий крепления оружия на станке или установке.
* 'штывая, что оружие должно нормально функционировать во всех случаях
« « крепления на сганке или установке, необходимо принимать во внимание
наибольшую возможную силу, определяемую по следующей зависимости:
N =Р S
ЧП 1 tn°n ’
i ;е Рт - максимальное давление порохового газа в канале ствола;
Sn - площадь поперечного сечения патронника у казенного среза.
По этой силе и допускаемому напряжению [ст] находим необходимую
i-мцадь опоры запертого затвора на ствольную коробку F:
5
р ч
IT _ А Ш П
И’
Упругая деформация узла запирания определяется силой N,,,. действу-
ющей на узел, и жесткое чью узла Су:
или размерами 1, и Fj деталей, составляющих узел
“1 1.
Ax = praSnZ—-
где пд - количество деталей, входящих в узел:
] - длина детали узла или участка ее с площадью поперечного сече-
ния (см. рис. 1);
Е - модуль упругости материала узла запирания.
Упругая деформация узла запирания во избежание поперечного об-
рыва гильзы при выстреле для каждого типа патрона не должна превы-
шать некоторого заранее заданного значения Дх. Тогда последнее выра-
жение можно записать в виде условия, которое необходимо выполнять при
проектировании:
Ц = Дх
itlEFi " PmSn ‘
Из данного выражения следует, что в целях надежности функциони-
рования оружия узел запирания следует проектировать как можно короче.
Как показывает опыт, деформация узла запирания не может быть до-
пущена более 1 мм для 14,5-мм патрона и более 0,43 мм для винтовочного
патрона.
При равномерном нагреве узел запирания как замкнутая система
стальных деталей не изменяет своих параметров и функционирует нор-
мально. При разных условиях нагрева отдельных звеньев узла его функци-
онирование может быть нарушено. Эго нарушение обычно связано с нагре-
вом участка ствола позади крепления его в ствольной коробке (см. рис. 1).
Нагрев этого участка ствола в процессе стрельбы сопровождается его уд-
линением Д1с, при этом происходит уменьшение зазора между казенным
срезом ствола и зеркалом (дном чашечки) затвора. При фиксации патрона
выступающим фланцем или цилиндрическим выступом на корпусе гильзы
возможны случаи незапирания ствола. Во избежание этого приходится
6
благоврсменно увеличивать указанный зазор на величину температур-
ой деформации ствола, что обычно неблагоприятно отражается на попе-
чной прочности гильзы.
Температурная деформация определяется температурой нагрева
вола Т и длиной участка 1с:
Д1С - аТ1с,
ос а- коэффициент линейного расширения (для стали порядка 12-Ю'6 град1).
При проектировании оружия необходимо максимально приближать
.сто крепления ствола в ствольной коробке к казенному срезу ствола.
1 ри расчете деталей узла запирания действующая на них сила давления
фохового газа принимается статической и осевое сопротивление гильзы
• учитывается. В зависимости от способа запирания ствола расчет нор-
,1льных реакций опоры имеет некоторые особенности.
Рис. 2. Расчетная схема запирающего механизма:
а - поворотом затвора, б - перекосом затвора. 1-боевой упор затвора,
2- затвор. 3-опорная плоскость коробки автоматики. 4-затворная рама
Для систем с запиранием поворотом затвора или муфты (рис. 2, а),
. оецируя все силы на продольную ось, получим выражение для сил реак-
> ii. действующих на каждую опорную поверхность боевых выступов зат-
ра и боевых упоров ствольной коробки в общем виде :
Р Я
R ___________д ш^п_______
m kHnB(cosa + fsina)’
где nB - количество боевых выступов затвора;
к„ = 0.6-0.7 - коэффициент неравномерности работы боевых выступов;
f - коэффициент трения;
а - угол наклона винтовой линии опорных поверхностей боевых вы
сгупов затвора.
Для обеспечения самоторможения затвора под действием приложен-
ных сил должно выполняться условие tga < f или а < р, i де р = arctg f
угол трения.
Для оценки прочности элементов деталей необходимо проверить на
смятие, изгиб и срез боевые выступы затвора и боевые упоры ствольной
коробки:
гг = Кщ т - ~ RnJ
°см t ’ 1ср „ ’°и W > (1)
^ср ^ср
где SCM - площадь смятия боевого выступа затвора;
Scp - площадь среза;
1 - расстояние от основания опорной поверхности до ее центра тяжести
W - момент сопротивления изгибу боевого выступа.
Для обеспечения прочности элементов запирающего узла необходи-
мо, чтобы расчетные напряжения были меньше допускаемых. Допускае-
мые напряжения определяются по следующим зависимостям:
г т 1.2...1.3
Рем J_ ств - для неподвижных соединений;
псм
г 1 0.6...0.8
PcmJ= ав - для малоподвижных соединений; (2)
псм
г 1 0.5...0.6 г 1 ое
[5 ср то ТО изг ТО ,
®ср ®изг
где псм = 1,2...1,5; пср = 1,5...1,7; пиз, = 1,3...1,5.
Для систем с перекосом затвора (см. рис. 2) величина реакций связс!
определяется по следующим зависимостям:
Р S
RM ~ —7-----——------<, R = Rm (sin а + f cos а)
kH(cosa + fsina) ш л
Из выражения для силы реакции Rm следует, что с увеличением утла с
реакция Rn( увеличивается. При этом возрастает и реакция R. Поэтому дл.
обеспечения прочности деталей узла запирания целесообразно угол а де
дать возможно меньшим, но достаточным для обеспечения свободной
движения затвора при отпирании.
По значению реакции ИП]для узлов с запиранием перекосом затвора
щовсряется прочность опорных поверхностен затвора и ствольной короб-
I! только по напряжениям смятия.
Для систем с запиранием двумя боевыми упорами величина реакций
вязи определяется по следующей зависимости:
2kH (cos а + f sin а)'
Коэффициент кн принимается равным 0,8-0,9. Если боевые упоры при
• •ыстреле работают на сжатие, то их прочность проверяется по напряжени-
;м сжатия. При запирании защелками они обычно работают на растяже-
"ие, поэтому следует произвести проверку прочности затвора по напряже-
нии растяжения и напряжениям смятия:
тс Sp - минимальная площадь поперечного сечения защелки.
В системах с запиранием роликами контакт последних с боевыми
норами ствольной коробки при выстреле осуществляется по линии. В мес-
контакта цилиндра с плоскостью возникают сжимающие напряжения,
< и (большая величина которых определяется ио формуле
(3)
1р = kjfp к! = 0,8...0,9,
в- Рр - сила, приложенная к ролику, Н;
1р - длина линии контакта ролика с опорой, м;
гр - радиус ролика, м;
Йо- радиус опорной поверхности.
Допускаемое контактное напряжение определяется по зависимости
0.557пк ’
в, - 1,5 - коэффициент запаса прочности.
Расчет соединения ствола со ствольной коробкой на прочность пронз-
ит я гак же, как сочленения затвора со ствольной коробкой. При этом
।11; io возникает необходимость расчета напряжений смятия и среза.
2. РАСЧЕТ И ПРОЕКТИРОВАНИЕ ПРУЖИН
В автоматическом оружии получили широкое применение пружины
разнообразного устройства и назначения. В зависимости от назначения их
можно разделить ini следующие виды: возвратные, боевые, буферные и
пружины деталей автоматики, механизмов и устройств (извлекателей,
спусковых механизмов, магазинов, амортизаторов и т.д.).
По характеру устройства пружины автоматического оружия делятся
па четыре типа: винтовые, спиральные, пластинчатые и специальные. Вин-
товые пружины в зависимости от формы бывают цилиндрическими, при-
зматическими и коническими. Чаще всего в автоматическом оружии при-
меняются винтовые цилиндрические пружины круглого или прямоуголь-
ного сечения. Как правило, эти пружины рабо тают на сжатие или круче-
ние. Пружины круглого сечения могут изготавливаться из одной или не-
скольких жил. В последнем случае их называют многожильными и обычно
используют в качестве возвратно-боевых.
Винтовые призматические пружины применяют в коробчатых мага-
зинах для подачи патронов. Работают они обычно иа сжатие. Спиральные
пружины прямоугольного или круглого сечения применяют в дисковых и
барабанных магазинах для подачи па тронов и в других устройствах. Плас-
тинчатые пружины применяют для извлекателей, спусковых механизмов,
различного рода фиксаторов и устройств. К специальным пружинам отно-
сятся тарельчатые пружины, кольцевые пружины трения, пружины с ото-
гнутыми витками различной формы, пружинящие детали.
Условия работы пружин автоматического оружия характеризуются
цикличностью и большими скоростями их нагружения. Однако время их
деформации значительно больше периода собственных колебаний витков,
поэтому при расчете пружин используют статические методы с введением
соответствующих допущений по максимальной скорости нагружения пру-
жин (например, для возвратных пружин максимальная скорость их нагру-
жения не более 11 м/с) и коэффициентов запаса прочности.
Выбор материала пружин производится с учетом конкретных усло-
вии их работы, степени динамичности их нагружения и важности предпо-
лагаемого места их использования. Для пружин сжатия и кручения, изго-
товляемых холодной навивкой, рекомендуется использовать стальную уг-
леродистую проволоку 1-го класса. Промышленность выпускает ее с раз-
мерами диаметра (dp от 0,14 мм до 8 мм). Для одножильных пружин ис-
пользуется весь диапазон размеров, а для многожильных - диаметры dp от
0.3 до 2,8 мм. После изготовления такие пружины подвергаются только
отпуску для снятия вну греннпх (остаточных) напряжений. Для пружин ди-
аметром dp более 3 мм применяются стали 60С2А. 65С2ВА. 60С2ФА. Пру-
• и।и, изготовленные из этих сталей, подвергаются термообработке в го-
гчм виде и могут работать в интервале температур - 40...-250 °C.
Важной характеристикой цилиндрических и призматических пружин
крутым сечением, работающих па сжатие и кручение, является отноше-
ie среднего диаметра пружины к диаметру проволоки, называемое индек-
•м пружины Ср. Для многожильных пружин величина индекса определя-
।ся как отношение среднего диаметра пружины к диаметру троса, а для
1>>жин прямоугольного сечения - к стороне витка пружины, перпендику-
.|рпой оси пружины. При расчете указанных пружин принимается Ср > 4.
орать значение Ср < 4 нежелательно, так как в этом случае сильно увеличи-
1ю гея напряжения на внутренних волокнах и затрудняется навивка пру-
. ины. При расчете и проектировании пружин рекомендуется принимать:
। ношение стрелы рабочего поджатия к стреле максимального поджатия
> более 0.9, величину максимального зазора между витками 5р при рабо-
« м поджатии пружины не менее 0.2 мм на виток.
Целью расчета и проектирования пружин автоматического оружия
ч шется определение их геометрических размеров, обеспечивающих дос-
.: очную прочность и силовые характеристики, необходимые для работы
ч юматики.
Известные зависимости теории сопротивления материалов позволя-
I получить основные формулы, применяемые для расчета цилиндричес-
• их винтовых пружин. Эти формулы выведены в предположении, что
и юскосгь витка перпендикулярна оси пружины, перерезывающие силы
и не учитываются, а взаимные удары витков отсутствуют.
2.1. Цилиндрические винтовые пружины сжатия
При расчете винтовых цилиндрических пружин с круглым сечением
ьюволоки используются следующие зависимости:
Но ~ (пр + 1)^р + §рпр +
Hi = Но -F],
H2 = H0-Fi-X,
Н3 = (пр+1.5>р, <4)
_н2-н3
°р ’
ПР
ПР, = пр + (!-5-2),
8kpDon3
Т’=-^Г’
Л-Н, !!,.
t = ~ 1,5<*р. <4,
пр
n^-b-L,
8npD^
п2=п,на-Ь,
*1
П3-П2Н;*“Нз, 0)
Н0-Нг’
_ 8крРрпз
к|’ " 4(СР-1) ‘ 'с15' Lp"hP1V(7rD0? + t\
где Hft, НР н2, н3 - высота пружины соответственно в свободном со-
стоянии, при предварительном поджатии, при рабо-
чем поджатии, при полном соприкосновении витков, м;
пр - число рабочих витков пружины;
пр1 - полное число витков пружины;
X - рабочий ход пружины, м;
tp - шаг навивки пружины, м;
Пр П2, Пэ - усилие соответственно предварительного, рабочего под-
жатия пружины и при соприкосновении витков, Н;
G - модуль упругости второго рода, Н/м2;
- напряжение при соприкосновении витков. Н/м2;
Кр - коэффициент концентрации напряжений в пружине;
F] - стрела предварительного поджатия пруж’ины. м;
Lp - длина проволоки пружины, м.
Пружины прямоугольною сечения витков обладают большей массой
ио сравнению с пружинами крут лого сечения ви тков, но при тех же габари-
тах они позволяют получить большую жесткость и допускаю г большие на
"яжения Методика их расчета аналогична вышеприведенной. Имеется
инь нек < >рая разница в рабочих зависимостях:
Do - DH - ар,
Hj — (йр + 1.5^>р,
Н0-1.5Ьр
tp »
пр
SFja^G
"1 =------зП----2\’
^p^pDolap+bp)
(6)
_ n3Dokp
,p“W m
ар, 1>р соответственно высота и ширина сечения вшка пружины, м;
Др,Ср - коэффициенты, определяемые в зависимости от отношения
ар^р >
Для пи шндрических винтовых пружин G - 810,0Н/м2. а значения па-
не ।ров приведены в табл. 1.
Таблица 1
Значение параметров Др,Е,р
1.00 1.25 1.50 1.75 2.00 2.25 2.50 2.75 3.00
._± 8.05 7.98 7.90 7.82 7.75 7.68 7.60 7.52 7.45
0.208 0.221 0.231 0.239 0.246 0.252 0.258 0.262 0.267
1 Три проектировании пружин необходимо, исходя из заданных сило-
\ характеристик пружины или величины работы, совершаемой пружи-
|| на участке рабочего поджатия Z, определить ее геометрические пара-
ды основными из которых являются размеры поперечного сечения
। га и количество рабочих витков. Для определения последних необходи-
мей ги количество расчетов силовых характеристик пружины и напря-
iinii с целью получения заданных посадочных размеров пружины, число
. >рых зависит от опыта расчетчика.
Задачу проектирования пружин из тестированной проволоки, воз-
I.HO реализовать на ЭВМ. Для этого необходимо представить значение
11км о усилия пружины Пс на участке рабочего хода X в виде функции
nc f (dp ,Ср, dp ,Тр).
а значение количества рабочих витков пружины в виде функции
Ир =f(dp’Cp’X’nc’ap)'
Поступим следующим образом. Примем расчетное напряжение кру-
чения
ъ = 1дЫ-
тде [т] ’ допускаемое напряжение кручения для заданного диаметра про-
волоки, Н/м2.
Расчетное напряжение кручения согласно формуле (5)
8n3D0kp
1ПП
г , 8n3D0k„
1,1[т]=—
Ttdp
Учитывая, что
п3=1,1п2, п2=арп15 D0=Cpdp,
Пт + П7 П1(1 + ар)
п = —----=. =------.
2 2
после соответствующих преобразований получим
_ л(ср дфддфр W-
4%1^7ы)ср+2,4б7с;-11 <s
Расчетное усилие предварительного поджатия согласно формуле (4)
^GdJ
П1 =----Ji
8npD03
Учитывая, что
к ic соответствующих преобразований получим
n = (l + <Xp)dpGX
Пр 16пс(ар-1)ср
(9)
В приведенных зависимостях ар > 1 - коэффициент, характсризую-
'и величину отношения усилия рабочего поджатия к усилию прсдвари-
i.Horo поджатия пружины.
Усилие предвари тельного поджатия пружины обычно определяется
’ависимости
nj=Knmg, (Ю)
К„ = 4...6 - коэффициент перегрузки;
ш - масса подвижных звеньев в крайнем переднем положении:
g - ускорение свободного падения, м/с2.
Расчет остальных геометрических параметров пружины проводится
• вышеприведенным зависимостям.
2.2. Цилиндрические винтовые пружины кручения
Пружины кручения рассчитываются на сопротивление изгибу. При
. чеге винтовых цилиндрических пружин кручения с круглым сечением
в.июлоки используются следующие зависимости:
н,=(»р+1)1р. 1=5^,
Пр
Ф?хЕ<
Mi =-*-1—
57.3 64L
M2=Mi-% М3=1,1М2, ар=
Ф1 Mi
4с -1
''-’дУ-Л l«”D-
При закручивании пружины на максимальный угол ф^ длина умень-
шится на величину
ч. :lbd
360пр
где 103 — 10 - А10- длина одного вилка после закручивания пружины на
угол (Д.
Внутренний диаметр пружины D„ назначается так, чтобы при работе
витки пружины мот ли свободно вращаться на стержне, служащем осью
пружины:
DBJ=b*-dp, DB>DB3.
л F
В вышеприведенных зависимостях:
М3 - крутящий момент соответственно при предвари-
тельном, рабочем и максимальном закручивании
пружины. Нм:
Ф1»Ф2,ФЗ - угловая деформация пружины соответственно при
предварительном, рабочем и максимальном закру-
чивании пружины, т рад.
Ргнвернутая длина рабочих витков
Ср = npy/(7d)o)2+t2.
Длина проволоки
С, = !.р - длина двух концов пружины, м.
Для реализации задачи проектирования пружин кручения предста-
вим значение среднего момента Ме. на участке рабочего хода ф в виде
функции
Me = f(dp,cp.ap.CTp)-
тт значение количества рабочих витков пружины в виде функции
ПР - f(dp5p/-%Medp).
Поступим следующим образом. Примем расчетное напряжение изгиба
°Р =С1[Д.
тде [ст] - допускаемое напряжение изгиба для заданного диаметр -
проволоки, Н/м2.
Расчетное напряжение изгиба согласно формуле (12)
32М3К
СТР =
7Tdp
32М3Крк
rtdp3
Учитывая, что
M2 = apMlt D0=cpdp,
Мс
Р
(13)
2
к- соответствующих преобразований получим
^dfo](cp-l)(
16-ap(4-cp
Расче тный крутящий момент предварительного закручивания пружи-
а. lacno формуле (11)
м =
Ф1°ДЕдр
57.3 • 64Lp
(учётом
Ф
Ф1 = .
ар-Г
п _________фМ^ар^др___________
Р 128 • 57.з(ар - 1)мс ^ср J2 +t2 ’
11ри плотной навивке витков пружины, т.е. когда t = dp,
n =________________(p°n(l + ap)Edp____
Р 128 • 57.3(ap - 1)мс ^'(пСр)2 +1
(14)
В приведенных зависимостях а - коэффициент, характеризующий
величину отношения крутящего момента рабочего закручивания пружины
М2 к крутящему моменту предварительного закручивания пружины Мр
Е = 2,1-10 Н/м2.
Для тестированных диаметров проволоки величина допускаемых на-
пряжений определяется следующим образом:
dp = О,3-1О"3 м... 1,210-3 = 160-107Н/м2;
dp = 1,3-10-Зм... 2.8 10 з [о = 140-107 Н/м2;
dp = 0,3-Ю-3 м ... 0,63-10-3 [т] = 159-Ю7 Н/м2:
dp = 0,7-10-з м ... 2,8-Ю-3 [т] =175-107 - 26.84-10117 ар.
Наиболее рациональные геометрические параметры пружины, обес-
печивающие нормальное их функционирование при циклическом нагруже-
нии. могут- быть получены при сср = 2.
2.3. Призматические пружины сжатия
При расчете призматических пружин сжатия с круглым сечением про-
волоки используются следующие зависимости:
г - Яв dp t _ но ~3~dp h = Ьв -ав
F2=H0-H2, F3=H0-H3, npi = np + 2,
LP=пр. Л2кгр+4ьр)2+t2’
ni =
-9 nr hp
20 p p
(15)
f2 f3
П, = n, —, n3 n2 -
- 4 2 F2 ’
t =ilnAihJ. Ii6
где F3. F2 - стрела поджатия пружины соответственно при рабочем ходе и
при соприкосновении витков, м;
np - число рабочих витков пружины;
пр1 - полное число витков пружины;
гр - средний радиус закругления витка, м;
hp - расстояние между горизонтальной осью симметрии и центром
закругления витка, м;
Ь„ - соответственно ширина и дайна витка пружины, м.
Пример:
Рассчитать силовые характеристики призматической пружины мага-
АКМ.
Исходные данные
Диаметр проволоки dp ..........................1,6-10-3м
Средний радиус закругления витка гр............. 6,3-КУ3 м
Расстояние между горизонтальной осью
симметрии пружины и центром
закругления витка hp...........................20-10'3 м
Высота пружины при предварительном
поджатии Н].................................... 0,210 м
Высота пружины в свободном состоянии Но........ 0,525 м
Высота пружины при рабочем поджатии Н2.........0,040 м
Высота пружины при полном
соприкосновении витков Н3......................0,037 м
Модуль упругости второго рода G................8- 10,п Н/м2
Число рабочих витков пружины пр................21
Полное число витков пружины пр1................23
1) Определяем стрелы поджатия пружины:
I-, = Но - Hi = 0.525 - 0.210 = 0.315м
F2 = Но - Н2 = 0.525 - 0.040 = 0.485м
F3 = Но - Н3 = 0.525 - 0.037 = 0.488м
2) Определяем усилие поджатия пружины:
П1 =
12.8пр
FjGTtdJ
7 9 7
р +3hDr„ +—rarDh„
2 Р Р 20 р р
_________________0.315 8 1010 3.14(1.6 10~3 У_____________________
; 213.14(б.3 1О+3.2о 1о~3(б.З IO-3? + — 3.14 6.3 10-3(20 10 3
2 3 ’ 20 х
II2 = П1 = 14 °’4S5 = 21.5H, П3 = П2 — = 21.5
2 F, 0.315 F,
0.488
0.485
21.6Н.
3) Определяем шаг навивки пружины:
t = Но^зар = (1525 -3 101 = 4 77 10_3 м
пр 21
4) Определяем напряжение при соприкосновении витков :
= 16п3(гр+ЬР) = 16 21.б(б.3 1(Г3 + 20 10~3) = 70 7 107 Н
KdP 3.14 (1.6 10'3)3 м2
Допускаемое напряжение кручения для dp = 1,6 1(F3m, [т] = 132-Ю7 Н/м2.
5) Определяем развернутую длину проволоки:
Lp = npi /2пгр + 4hp J2 +12 . 2.81м.
3. РАСЧЕТ И ПРОЕКТИРОВАНИЕ ПАТРОНОПОДАЮЩИХ
МЕХАНИЗМОВ
Механизмы подачи патронов разделяются на механизмы ленточной
подачи и механизмы подачи патронов в магазине.
Механизмы подачи патронов предназначены для продвижения ленты
с патронами (патронов в магазине) в течение одного цикла работы автома-]
тики к приемному окну ствольной коробки, откуда происходит его досыл-1
ка в патронник ствола.
3.1. Механизмы ленточного типа
Механизмы ленточного типа широко применяются при создании еди-1
ных и ручных пулеметов, а также автоматических пушек. Применение по-
дающих механизмов ленточного типа позволяет при небольшом измене-
нии массы образца значительно упростить конструкцию системы питания
и увеличить скорострельность за счет использования патронных лент.
В то же время механизмы ленточного типа в автоматическом оружий
являются наиболее трудоемкими при проектировании и требуют отладки
на опытном образце.
Подача патрона требует относительно большой затраты энергии]
Для работы патроноподггющего механизма (ППМ) используется энергия
чжпых частей автоматики (ствола, затвора, затворной рамы). Необ-
ычность расходования энергии подвижных частей на подачу патронов
i n : темп стрельбы в определенную зависимость от конструкции патро-
|" тающего механизма. Проектирование механизмов ленточного типа
инея, в основном, к определению профиля кулачков, исходя из опреде-
шл о закона движения патронной ленты. При проектировании подаю-
мсханизмов необходимо исходить из условий получения минималь-
- \ силий в ленте и минимальных затрат кинетической .энергии ведущего
। автоматики на работу механизма.
3.1.1. Законы движения патронной ленты
Прямоугольный закон движения патронной ленты. Схема прямоу-
। пого закона движения патронной ленты изображена на рис. 3.
Рис 3. Схема движения патронной ленты по прямоугольному закону
(S - полный путь подачи патронной ленты )
Величину хода ползуна подачи определим как
®П ~ V1M ’ •
<) [ сюда
хлм ~ .
1п
У силия, возникающие в патронной ленте, определим по зависимости
| Руднева:
Рл = х/тлслхл+О
Щачение Q мало зависит от значения хл, поэтому определим усилие
ИШСНМОСТИ
Р, \т.Л'.|*.|
Подставляя значениехлм, получим значение
-----с
Рлм = Дтлс.з-. . (17)
•П
Работу, расходуемую на перемещение ленты на один шаг, можно он
ределить по следующей зависимости:
_____q2
А = 7галсл .П .
*•11
Треугольный закон движения ленты. Схема треугольного закона дви|
жения патронной ленты изображена на рис. 4.
Рис. 4. Схема движения патронной ленты по треугольному закону
Определим для треугольного закона перемещение ползуна подачи и)
зависимости
S — ' ^лм^п
откуда максимальная скорость движка подачи
2Sn
Y = ----—
Алм .
Максимальное значение усилия протягивания ленты
_____24
РЛМ = ОП1СЛ (is;
*п
< ] отпивая зависимости (17) и (18), можно сделать вывод, что усилия,
акающие в ленте, перемещающейся по треугольному закону, в два
и п,шс усилий в ленте при применении прямоугольного закона.
1‘айоту, расходуемую на протягивание лент для данного случая, опре-
> по формуле
А = f-x/mTc^x^dx = f,/mllcn—xdt = fJm^c^x^dt.
J V I J1 JI j у JI JI £ J v J1JIJ1
J,iкон изменения скорости патронной ленты выразим через значение
имачьной скорости ленты. На участке разгона
dx>.2x,'\ dXjl= —,Mdt
dt t t
ln/2 ln
Y — 2Хдм f
АЛ 1 .
< ответственно работу определим по следующей зависимости:
А — Ар + Ат,
• 11 Ат - работы, затрачиваемые на перемещение патронной лен-
ты на участках разгона и торможения соответственно.
1 ели Ар — Ат, то А = 2Ар, т. е.
ф,
2 -------
А = 2 f л/пъТГ —dt,
О
-----4х t3
Л_ Т I", „ лм1
— ^д)тлсл 2
tn
4х2 t3
= 2д/и^с7 2 ,м " =
t„ -3 8
(-----4
А = д/mлсл
*п
Из данной зависимости следует, что работа, совершаемая при движе-
: 1снты по треугольному закону, больше работы, совершаемой по пря-
ольному закону в 4/3 раза.
Синусоидальный закон движения ленты. Схема синусоидального за-
кона движения патронной ленты изображена на рис. 5.
Рис. 5. Схема движения патронной ленты по синусоидальному закону
Перемещение движка подачи можно определить по следующей фор-
муле:
8П = f*n(t)dt
Определим скорость движения ленты через значение
*л
. ( Ttt I
= х,м sm — ,
тогда
t
8П
J лм
О
• I I,
sin — dt
Un J
или
с _ In
п 4АЛМ
TC
откуда
nSn
v _-----
JIM -
Значение максимального усилия протягивания ленты можно опреде-
лить по формуле
.1 работа для синусоидального закона
. ‘г I--------• , ‘г /----- •
А KmnC.TXndt= _НтЛСЛхЛм81П — dt =
о о \1п7
_‘"Г '-----2 1
/л/тЛслхЛм -
О 2
a I 2nt
1 - cos----
I tn
dt.
----я Sntn я г---------S„
А = Jm сл----= —Jm c —
v л л 4 4-2 8* л л .
1П 1п
Грапецеидальный закон движения лепты. Схема трапецеидального
н на движения патронной ленты изображена на рис. 6.
Рис. 6. Схема движения патронной ленты по трапецеидальному закону
Для этого закона подачи патронной ленты полный его путь
— + Sn0CT + Sn
। выраженный через максимальную скорость
пост
S --х2
°п 2 лм
где S„ocr - участок движения ленты с постоянной скоростью.
Откуда
„2 _ 2Sn__________
Алм
1р ^ПОСТ *т
Максимальное значение усилия протягивания ленты определим по
формуле
р _ rm c 2Sn
р “ пост ~ 1т
Работа, совершаемая патроноподающим механизмов при подаче лен-
ты на один шаг, в данном случае
А — А -4- А 1 А
р ^пост лп
Для периода разгона и торможения работу можно определить по сле-
дующим зависимостям (см. треугольный закон):
____*2
АР = л/тЛл
л
____х2
Ат = tT .
Для периода движения ленты с постоянной скоростью работа (см.
прямоугольный закон):
I------— 2
АПОСТ — дСл ^ЛМ^ПОСТ ’
тогда
Ш лсл \зм
tn t
— +1 + —
3 пост 3 '
Выражая максимальную скорость через перемещение движка подачгж
получим
A / 4Sn | ^p
А = 7тлсл 7—.--------— T + t
Ip *пост + It k. *
3J
йот закон подачи является промежуточным между прямоугольным
•,! ольными законами, т. е. при tp = t, = 0 и tnuci = tn
!---- 4S^ /--— S*
A = лС Л-------ytn =^шлсл —
(2tn)
(’.тедователыю,
P.1M — "\/*®ЛСЛ ~ .
Ml
В этом случае трапецеидальный закон превращается в прямоуголь-
и 11 ри t = tT и tn<xr) - 0 получаем
. /----4S^ 1/ а ,------------4S„
А = л/тлса2 +М=Чтлсл~ —.
1П п
Таким образом,
Р = /т с 2§п
*ЛМ УШЛ1Л
*п
Следовательно, трапецеидальный закон превратился в треугольный
.1 н подачи патронной ленты.
Таким образом, из рассмотренных законов движения патронной лен-
1 исходя из минимальной работы, расходуемой на перемещение ленты
н.п подачи, целесообразно при проектировании патроноподающих ме-
чи ;мов ленточного типа использовать прямоугольный закон.
5.1.2. Проектирование патроноподающих механизмов ленточного типа
При проектировании патроноподающих механизмов ленточного
и и (ППМЛТ) принимаем прямоугольный закон подачи ленты. При этом
• и । зсм, что передаточное отношение от основного звена механизма авто-
"Ч1КИ к подающим близко к постоянной величине. Перемещение подаю-
>п'. пальцев определяется по следующей зависимости:
~ Sл + ^заб ^пер >
" ^заб ' забег подающих пальцев за очередной патрон;
Snep - перебег подающих пальцев в конце подачи очередного патрона.
Запас хода подающих пальцев по сравнению с шагом ленты S, необ-
-1 iM для того, чтобы удерживающие пальцы могли надежно зайти за зве-
। г щаиного на линию досылания патрона, а подающие пальцы могли
I hi за очередное звено ленты.
При проектировании патроноподающих механизмов данного типа
необходимо иметь в виду, что скорость перемещения ведущего конца лен-
ты должна быть х,, < 5 м/с исходя из сохранения прочности звена ленты и
отсутствия ее растряски (смещение патронов относительно звена).
При передаточном отношении от основного звена механизма автома-
тики к подающим пальцам патроноподающего механизма близком к по-
стоянной величине.
где хл - перемещение основного звена механизма автоматики на участке
работы патроноподающего механизма.
Для штатных образцов автоматического оружия характерен момент1
включения в работу патроноподающего механизма ленточного типа с нача-
ла открывания канала ствола и его выключения из работы при положений
основного звена механизма автоматики за шепталом автоматического огня.
Рассмотрим вопрос проектирования патрононодающих механизмов
применительно к их наиболее распространенным схемам.
3.1.3. ППМЛТ с двумя кинематически связанными звеньями
Основное звено и подающие пальцы совершают поступательное пе-
ремещение. Принципиальная схема ППМЛТ приведена на рис. 7.
Рис. 7. Принципиальная {.\сма 111171 копирно-ползункового типа:
1-заты>рная рама. 2-ползуп >ки)ачи
Применительно к данной схеме ранее [10] была получена аналитичес-
, .ависимость для передаточного отношения Z2 = tga.
Гак как Z2 = , то
Sn
— = tga
X,
1 л
Откуда
Sn
a = arctg-
Х1Л
После определения угла наклона паза подающего механизма можно
итп к построению рабочего профиля кулачка. Для этого проводим две
'.отельные прямые на расстоянии, равном величине хода ползуна пода-
чу. Затем проводим прямую линию под углом а к последним. Таким об-
> 'М, получим теоретический профиль паза на основном звене. Проведя
1 но окружностей радиусом, равным радиусу выступа на ползуне пода-
с центром на теоретическом профиле и строя огибающую, получаем
'чий профиль паза подающего механизма.
Основное звено перемещае тся поступательно, а подающие пальцы со-
, ыают вращательное движение. Принципиальная схема ППМЛТ приве-
: । на рис. 8.
Рис. 8. Принципиальная схема ППМ рычажного типа:
1 - затворная рама. 2 - рычаг подачи, 3 - патрон в ленте
Величины геометрических параметров данного тана подающих меха-
низмов h и Н обычно известны и являются результатом эскизной прора-
ботки компоновки патроноподающего механизма. Неизвестными являют-
ся параметры аир. которые и необходимо определить. С этой целью
надо получить аналитические зависимости для передаточных функций
применительно к рассматриваемой схеме механизма. Для получения ана-
литических зависимостей передаточных функций используем расчетную
схему, приведенную на рис. 9.
Рис. 9. Расчетная схема ППМ рычажного типа
Уравнения равновесия сил, приложенных к подвижным звеньям:
- для 1-го звена
Р = N(sinpsina + f cosa)+ fjNj + f2N2;
N = N(sinp cos a - f sin a);
= N(cosa - f sina)cosp;
- для 2-го звена
P2 = Nh(cosa - f sin a) - N3H;
- для 3-го звена
p3 = N3-
Из уравнений равновесия исключаются реакции связей (N, N2.
N3), выражается Pt через Р2 и Р3:
sinafsinp - f(f2 + f2)cosp]+cosa(f + fj sinp + f2cosp)
I ] — ' 2---------------~—-------------------------------Ь
h(cosa - f sin a)
Hsina[sinp - f(ft + f2)cosp] + cosa(f + f) sinP + f2cosp)
h(cosa - f since)
I Pi полученных уравнений следует
_ sin a[sinp - f (f) + f2)cosp] + cosa(f + fj sin P + f2 cosp).
1 1 —--------------------------------------------------J
h(cosa - f since)
_ Hsincefsinp-f(fj + f2)cosp]+cosa(f + f) sinp + f2 cosp)
n(cosa -1 sin a)
_ since sin p _ tgee • sin p
Zj — I?/ , —---------— — ----;
hcosce h
Z = T = tgasinpH
3 3^=°) h
Гак как Z2 — Z3, то
Sn * *4 • n
—У- = — tgee sin p
*1л h
I \ w
. Snh
a = arctg---M.
x^Hsinp
При проектировании подающих механизмов данного типа стремятся
му. чтобы при его работе угол р был близок к 90°. тогда в первом при-
п гении можно принять
f Snh
се = arctg 1.
Х1«Н
3.1.4. ППМЛТстремя кинематически связанными звеньями
Механизм, в котором профиль кулачка выполнен на основном звене
ннематическая связь с ползуном подачи осуществляется с помощью
межуточного звена.
Принципиальная схема данного механизма приведена на рис. 10.
Рис. К). Принципиальная схема ППМ с копиром на затворной раме:
1-затворная рама: 2-передаточный рычаг: 3-ползун подачи
Величины геометрических параметров данного типа подающего ме-
ханизма г, Г; и Н (характеризующего начало теоретического профиля ку-
лачка на основном звене механизма автоматики! обычно известны из эс-
кизной проработки компоновки механизма. Неизвестным является закон
изменения угла О. профиля кулачка. Для решения данной задачи необхо-
димо получить аналитические зависимости для передаточных функций
рассматриваемого механизма. С этой целью используем расчетную схему,
приведенную на рис. 11.
Рис 1J. Расчетная схема ППМ с копнро.м па затворит'! раме
' равнения равновесия сил, приложенных к подвижным звеньям:
in 1 -Iо звена
Р; = N(sina + fcosa) + fiNj:
N1 = N(cosa -f sin a).
|,ля 2-го звена
1*2 - N[f sin(a + p - <p)- cos(a + P - (p)^ - N2(cos<p + f2sin <p)r.
1..1 Я 3-го звена
P2 = N2+f3N3;
N3=f2N2.
i I i указанных уравнений равновесия исключаются реакции связей (N,
-, \3) и выражается Р1 через Р2 и Р3.
р _ sin a(l - ff3) + (f + f\ Jcosa p
q [f sin(a + |3 - <p) - cos(a + [3 - <p)]
[sina(l - ffi)+ (f + fi)cosa]r(cos(p + f2sin<p)
rjfsinfu.1 p- (p)-cos(a-*-P~ip)](l-f2f3) 3
I h полученных уравнений следует
_ sina(l - ff]) + (f + f3)cosa
2 rj[f sin(a + p-(p)-cos(a + p-<p)]
_ [sin a(1 - ffj) + (f + f3 )cos a]r(cos ф + f2 sin ф).
3 q [f sin(a + P~ ф)-сов(а + p - ф)](1 - f2f3 )
7 _ш _ sina
*Ф-°) j-j cos(a + p - ф) ’
7 __ _ r sin a cos ф
"3 3(fj’“) q cos(a + p - ф)'
Гак как Z3 = Z3, то
Sn _ r sin a cos ф
Х1Л г1со8(а + р-ф)'
Из последней зависимости после соответствующих преобразований
’ I им
--------------------
Sn rising -<р)-Х1л cos <p-
В связи с тем, что угол сх изменяется при перемещении осповног
звена механизма автоматики, запишем данную зависимость в виде
(X, = arctg
_____Эпг1С<>8(0-Ф1)
Snrisin(p-(Pi)-Xiflcos(Pi ’
Рассмотрим геометрическую сторону задачи применительно к cipyi
турной схеме механизма, приведенной на рис, 12.
Рис. 12. Схема построения профиля копира на затворной раме для ППМ
Структурная схема механизма строится следующим образом. Из т.
радиусом г проводим дугу окружности. От горизонтального луча О вве]
и вниз откладываем отрезки величиной Sn/2, через концы которых пр
водим горизонтальные прямые до пересечения с построенной дугой о
ружности в точках S, и Sn. Проводим горизонтальный луч на расстоян!
Н от точки О. Из т. О радиусом Г] проводим дугу окружности, точка пер
сечения которой с горизонтальным лучом хи. Далее разбиваем величи:
параметров Sn и х1л на определенное количество участков nv. Величи!
участков будут
пу ПУ
Тогда текущие значения геометрических параметров, необходим!
для графического построения теоретического профиля кулачка, будут с
ределяться по зависимостям
<Pi = arctg
Sn-2ASni
xu=iAxi, Sni=iASn,
i = 1,2,...,.
Графическое построение теоретического профиля кулачка проводит-
ледующим образом. Вычерчивается i-e количество положений рычага
OSp Из т. хп дуги окружности радиуса rt в направлении, противопо-
। ном движению основного звена механизма автоматики, откладывают-
оответствующие горизонтальные отрезки хн, в правом конце которых
водится луч под соответствующим углом ар Затем вычерчивается кри-
касательная к данным наклонным лучам, которая и будет теоретичсс-
; профилем кулачка.
Механизм, в котором кинематическая связь основного звена с ползу-
ч подачи осуществляется с помощью промежуточного звена, на кото-
1 выполнен профиль кулачка.
Принципиальная схема данного механизма приведена на рис. 13.
Рис. 13. Принципиальная схема ППМ с копиром на передаточном рычаге:
1 -затворная рама. 2-передаточный рычаг, 3-ползун подачи
Величины геометрических параметров данного типа подающего ме-
шзма г. Н и г, (характеризующего начало теоретического профиля ку-
н<а на промежуточном звене механизма) известны из эскизной прора-
!ки компоновки механизма. Неизвестным является закон изменения
угла a j, профиля кулачка и параметра гп. Аналитическая зависимость дл
а, будет аналогична выше рассмотренному случаю, т.е.
8пгп cos(B- ф)
cq = arctg----------------------
8пгп8т(р-ф)-х1лгсо8ф-
Рассмотрим геометрическую сторону задачи применительно к струн
турной схеме механизма, приведенной на рис. 14.
Структурная схема механизма и аналитические зависимости для от
ределения геометрических параметров, необходимых для графического нс
строения теоретического профиля кулачка аналогичны выше рассмотрев
ному случаю.
Рис. 14. Схема построения профиля копира на передаточном рычаге для ППМ
С учетом специфики структурной схемы данного подающего меха
низма необходимо дополнительно связать аналитические параметры гн
хп. Исходя из геометрических соображений
rli
sin(p-91)
8ш(ф! - (Pi)
Графическое построение теоретического профиля кулачка проводит
ся следующим образом. Вычерчивается исходное положение рычаг
XjiOSj. Затем из т. О проводим лучи под углом ф| к отрезку Охи на коте
рых откладываем отрезки, равные соответствующему значению ги, из коь
цов которых под углом у = 180 — р - о.; — <р; проводим лучи, а за тем, пре
ведя к ним касательную кривую, получаем теоретический профиль копира
3.2. Механизмы магазинного типа
Механизмы подачи патронов магазинного типа предназначены для
, |едоватеньного перемещения патронов, находящихся в магазине, к
'емнику. Перемещение очередного патрона к приемнику должно осуще-
• !яться за определенное время цикла работы автоматики, которое долж-
ч>1ть меньше времени движения затвора от фланца гильзы до крайнего
пего положения затвора и обратно; т.е. механизм подачи патронов дол-
* обеспечивать своевременность подачи патронов к приемнику (на ли-
’ досылки).
При проектировании механизмов магазинного типа в первую
редь необходимо определить значения перемещения патрона X и У
т . 15). Перемещение патрона определяется следующими условиями: ис-
:ным положением патрона (пули), который должен находиться возмож-
ыиже к патроннику, исходным положением оси патрона, которая дол-
। находиться как можно ближе к оси канала ствола.
Рис. 15. Схема перемещения патрона из магазина в патронник:
1-патрон, 2-патронник ствола
В идеальном случае оси патрона и канала ствола должны совпадать.
Магазин имеет три основных элемента: корпус (собственно магазин),
.1 нагель и подающую пружину (рис. 16).
Подаватель отделяет патроны от пружины, передает усилие пружины
,ы троны и обеспечивает' плотность скольжения для досылки последнего
юна в однорядном магазине и двух последних патронов в двухрядном
l а «ине.
Подаватель фиксирует патроны в строго определенном положении в
а «ине. Размеры патрона и требуемая емкость магазина определяют раз-
•!.1 мат азина. Форма и размеры магазина должны обеспечивать опреде-
леиность порядка движения патронов, а емкость магазина в пределах до-
пустимых размеров должна быть возможно большей.
Рис. 16. Схема коробчатого магазина: а - однорядного, б-двухрядного;
1-подающая пружина магазина. 2-подаватель, 3-корпус магазина. 4-патрон,
5-досылатель
Для однорядных магазинов ширина внутренней часта магазина hj
равна диаметру патрона плюс величина зазора между гильзой и внутрен-
ней стенкой магазина:
hi - Dr + (0.15...0.20),
где Dr - диаметр гильзы; 0,15-0,20 - зазор между сгенками корпуса.
Для двухрядного магазина
h2 = 1.866Dr + (0.15...0.20).
Глубина полезного объема, т.е. объема, занимаемого патронами, для
однорядного магазина
W!=Drn.
Для двухрядного магазина глубину полезного объема можно вычис-
лить по формуле
W2 '(n l)I)r.
где п - число патронов в магазине.
Двухрядные магазины проектируются так, что отрезки прямых, соеди-
няющих центры патронов, образуют равносторонний треугольник, а пода-
ватель контактирует сразу с двумя последними патронами (см. рис. 16).
В этом случае при перемещении патронов на линию досылки можно избе-
жать заклинивания в магазине.
Досылаемый патрон удерживается за счет силы трения между гиль-
и загибами магазина. Форма загибов магазина существенно влияет на
актер подачи патронов. Для надежной фиксации патрона загибами ма-
> на необходимо, чтобы радиус загибов R3 был меньше радиуса гильзы
рис. 17).
Рис. 17. Схема для определения радиуса загибов магазина
I-корпус магазина. 2-патрон, 3-досылатель
В противном случае положение патрона при подаче его будет изме-
на я. что отражается на площадке контакта затвора с фланцем гильзы, а
। с на траектории движения патрона при досылке. При досылке патро-
/ вор своей передней частью (досылателем) касается дна гильзы, что
п-1 привести к преждевременному воспламенению капсюля, поэтому
ч'ходимо предусмотреть расстояние а между капсюлем-воспламените-
i и нижней кромкой досылателя (рис. 18).
Рис 18. Положение досылателя относительно капсюля цитрона
и расстояние между капсюле и патрона и нижней кромкой досылателя.
/-досылатель, 2-дно гильзы. З-кстсюль-воспламетипель/
Загибы магазина, ограничивая выход патрона в ствольную коробку,
направляют его при досылке. Правильно выбранная длина загибов корпу-
са магазина обеспечивает надежную досылку патрона в патронник. Заги-
бы магазина совместно с усилием подающей пружины контролируют по-
ложение патрона при его движении в патронник.
Загибы магазина определяют направление патрона до тех пор, пока
усилие подающей пружины действует в пределах границ загибов (см. рис
17). Если усилие пружины смещается за пределы загибов магазина, то пат)
рон может повернуться пулей вверх, что приводит к утыканию патрона fl
верхнюю часть казенного среза ствола. Слишком длинные загибы долг<^
удерживают патрон при досылке, что также приводит к утыканию патрон^
в казенный срез ствола (рис. 19).
Рис. 19. Схема для определения длины загибов корпуса магазина:
а - короткие загибы, б- длинные загибы
(1-корпус магазин». 2-патрон. 3-патронник ствола)
Значения X и Y (см. рис. 15) определяются по трафарету патрона пре
черкиванием его движения из магазина в патронник, для того чтобы гз
было утыкания патрона в казенный срез ствола и чтобы фланец гильзы вы
ходил из загибов магазина в тот момент, когда пуля вошла в патронил
ствола. Загибы магазина должны быть такой длины, чтобы центр масс:
(ЦМ) патрона находился бы в пределах загибов до тех пор, пока пуля ы
войдет в патронник.
3.2.1. Определение времени подачи патронов
При движении в откате затвор проходит фланец гильзы, доходит до
.мьника, ударяется о него и начинает двигаться в крайнее переднее по-
ение. Время подачи патрона па линию досылки t„ должно быть меньше
лени t,a- движения досылателя от фланпа патрона, находящегося в при-
нте, в крайнее заднее положение и обратно к фланцу патрона, т.е.
ija6 (рис. 20).
Рис. 20. Схема для определения времени подачи патронов:
1-подаватель магазина. 2-патрон. 3-досылатель, 4-пружина .магазина
Для надежности обеспечения своевременности подачи патрона с уче-
; 1>а шичиых непредвиденных сил сопротивления примем время подачи
। ’< и ia
ln 2 1заб'
Среднюю скорость движения патрона за время его подачи обозначим
1огда1п . , где дх-значение перемещения патрона в магазине.
хпс
Положив, чго
v — Хпм
Апс ' _
НИМ
2 Ax
Хпм
где хпм - максимальная скорость патрона за время его подачи.
Определим максимальную скорость патрона из равенства кинетиче
кой энергии патрона в конце подачи и работы сил, приложенных к нему:
|тхпм = ("с + Q)4x,
1
где m - тпят + т|1од + -тпр;
тПЯТ - масса патрона;
тпод ‘ масса подавателя;
- масса пружины магазина;
Пс - средняя сила поджатия пружины магазина на участке;
Q - сила тяжести патронов и подавателя.
Максимальная скорость подачи определяется выражением
или
t„ V m
откуда
_ 2Дхл/ш _ [2тДх
x/2(nc-Q)Ax Vnc-Q'
(19)
Примем
пс - Q = п = сх,
тогда
^2шЛх
*П ~ 1 •
V сх
Значения тих зависят от количества патронов в магазине.
Для дисковых и барабанных магазинов время подачи патрона на ли
нию досылки можно определить по следующей зависимости:
f _ А(Р _ А(Р
1П ,
С9с С0т
\<р - угол поворота подавателя при движении его на один шаг;
<ос - средняя угловая скорость подавателя;
то максимальная угловая скорость подавателя.
Максимальную угловую скорость подавателя можно определить ана-
1ным образом:
1 2
~Jn®m — МДф,
1„ - момент инерции подавателя относительно оси вращения;
М - момент силы пружины магазина, равный произведению силы
пружины на наибольший радиус закручивания пружины.
Очевидно, что
I- модуль упругости первого рода;
J - момент инерции сечения пружины;
Ф - угол закручивания пружин магазина.
Тогда
__ l2EJA<p
ф
!2JnM(p
} Е Jtp
(20)
Время движения затвора t3a6 определяется при расчете велограммы
ля (см. рис. 20).
Пример 1. Определить угол наклона профиля кулачка основного зве-
ханизма автоматики применительно к схеме механизма, приведенной
1с. 8.
Исходные данные
Калибр d............................... 7.62 мм
Рабочий ход подающих пальцев Sn........ 25 10 "3 м
Величина плеча рычага подачи h......... 36-10 ’3 м
Величина плеча рычага подачи Н......... 60-10"3 м
Рабочих ход основного звена на участке
работы ППМ xlq......................... 0,125 м.
Определяем величину угла наклона профиля кулачка;
Snh 25 10’3 36 10’3
а = arctg—44— = arctg---------------у-;
х1лН 0.125 60 10’3
а = arctg0.12 = 7°.
Пример 2. Определить время подачи очередного патрона на линик
досылания при наличии в магазине 30 патронов и 1 патрона.
Исходные данные
Сила тяжести 30 патронов и подавателя Q.............. 3.2 Н ,
Сила тяжести 1 патрона и подавателя Qj............... 0,3 Н
Перемещение патрона в магазине при подаче дх ........... 0,005 м
Среднее усилие поджатия пружины магазина
при 30 патронах Пс....................................... 21,5 Н j
Среднее усилие поддатня пружины магазина
при 1 патроне П1с........................................ 14,0 Н
Масса 30 патронов и подавателя с пружиной ш.........0.32 кг j
Масса 1 патрона и подавателя с пружиной nij.............. 0,03 кг '
1) Определяем время подачи патрона па линию досылания при нали^
чип в магазине 30 патронов:
. 2mAx [2 0.32 0.005 3
= ------= J-----------= 13.2 10 с.
ync-Q V 21.5 3.2
2) Определяем время подачи патрона на линию досылания при нали|
чин в магазине 1 патрона:
I 2т1Дх
^nic-Qi
t
п
,'2 0.03 0.005
V 14 - 0.3
= 4.6 10“3с
4. РАСЧЕТ И ПРОЕКТИРОВАНИЕ УДАРНЫХ МЕХАНИЗМОВ
При исследовании и проектировании ударных механизмов возникав^
необходимость определения следующих характеристик:
величины кинетической энергии бойка, необходимой для гарантиро!
ванного воспламенения капсюлей-воспламенителей (К-В);
величины массы бойка при условии исключения инерционного накола!
диаметра отверстия в зеркале затвора для выхода бойка при условия^
обеспечения прочности колпачка капсюля-воспламенителя;
времени работы ударного механизма.
При проектировании ударных механизмов стрелкового оружия необ-
,м<> обеспечить 100%-ное воспламенение капсюля-воспламенителя с
чмальной энергоемкостью боевой пружины. Это особенно важно для
1'твного, охотничьего и снайперского оружия с целью уменьшения
лущений, воспринимаемых оружием при срабатывании ударного меха-
ма и для улучшения меткости оружия при одиночной стрельбе.
Существующие конструкции ударных механизмов (куркового и удар-
ного типов) в зависимости от способа передачи энергии от курка
рника) к бойку можно раздели ть на три группы (рис. 21,22):
Рис. 21 Принципиалы/ые схемы курковых ударных механизмов:
курок и боек движутся совместно после их соударения, б - курок после удара по бойку
'.‘анавливается. а бое/: по инерции движется дальше, в -курок и боек жестко соединены
Рис. 22. Принципиальные схемы ударных .механизмов ударникового типа:
а - курок и боек движутся совместно пос не их соударения, б - курок после удара по бойку !
останавливается, а боек по инерции движется дальше, в -курок и боек жестко соединены]
1
в конце рабочего хода курок (ударник) ударяет по бойку. После удара|
курок (ударник) и боек движутся совместно, расходуя кинетическую энер-1
гию на деформацию колпачка капсюля-воспламенителя (см. рис. 21,а и 22,а);
в конце рабочего хода курок (ударник) ударяет по бойку. После уда-|
ра курок (ударник) останавливается, а боек движется, расходуя кинетичес-
кую энергию на деформацию колпачка капсюля-воспламенителя (см. рис.
21,6 и 22,6);
в конце рабочего хода курок (ударник), выполненный как одно целое
с бойком, расходует кинетическую энергию на деформацию колпачка кап-
сюля-воспламенителя (см. рис. 21,в и 22,в).
Кинетическая энергия курка (ударника) в конце его.рабочего хода (в
момент удара по бойку) определяется по следующей зависимости:
Е = Арр
(21)
\ =
М, +М2
2
I - кинетическая энергия (ударника), курка;
к - работа боевой пружины;
[3] - коэффициент, учитывающий суммарные потери энергии при де-
формации боевой пружины;
Mj - момент при закручивании на угод предварительного поджатия
боевой пружины:
М2 - момент при закручивании на полный рабочий угол боевой пружины;
Ф - рабочий угол закручивания боевой пружины;
111 - усилие предварительного поджатия боевой пружины;
Г12 - усилие в конце рабочего хода боевой пружины;
д - рабочий ход боевой пружины.
Значение коэффициента р1 рекомендуется принимать равным 1,2-1,4 -
жатии пружины и 0,7-0,8 - при разжатии пружины.
В результате ударного подключения боек приобретает скорость, оп-
.немую по зависимостям, применительно к конструкциям ударных ме-
мов:
।руппаа
b .
vibV
руина б
xb =b(l + kb);
1руппа в
ХЬ = Ч,
I2E , „ ,
= t— - скорость курка (ударника) в точке удара по бойку (в кон-
\ ш
це рабочего хода):
m = —
H
2 и m — mv - масса ударника, приведенная к точке удара соот-
ветственно для куркового и ударникового удар-
ных механизмов;
kb- коэффициент восстановления скорости при ударе, равный 0,4;
_ m
° - относительное значение масс;
шб
nig- масса бойка;
J - момент инерции курка относительно оси вращения;
Е - кинетическая энергия курка (ударника) в момент удара по бойку, j
При определении положения оси курка в процессе проектирования^
следует обеспечивать условие се — р2, так как при этом ударные реакции
не передаются на ось курка. Здесь р - радиус инерции курка; с - расстояние
от центра масс курка до оси вращения; е - расстояние от центра масс курка
до линии удара.
Кинетическая энергия, передаваемая на воспламенение капсюля-вос-
пламенителя, определяется по зависимостям применительно к конструкци-
ям ударных механизмов:
групп а
1 руина б
Ы1+к„)2
,23)
группа в
Еб=Е. (24),
Для обеспечения 100%-ного воспламенения необходимо выполнить
следующее условие:
Еб>ЕкЬ,
1 де Екь - энергия, обеспечивающая 100%-ное воспламенение капсюля-вос-
пламенителя.
Энергию ЕкЬ, характеризующую чувствительное гь каш-юля-воспла-
менителя к удару, получают при испытаниях капсюия-восп намспп геля на
прах в соответствии с техническими условиями. Значения энергии Ekb
|Я серийных капсюлей-воспламенителей приведены в табл. 2.
Таблица 2
Характеристики некоторых капсюлей-воспламенителей
Наименование патрона Тип капсюля Ега, Дж Б, Дж ЕКВ’ Дж Б,, Дж me 103 Дж
5.45-мм пистолетный па- трон КВ-10 0.275 0.326 0.059 0.065 1.62
5,45-мм патрон КВ-16 0.589 0.763 0.196 0.181 4.59
7,62-мм патрон обр. 1943 г 57-К-210 0.54 0.69 0.245 0.218 5.53
7.62-мм винтовочный патрон 57-к-ОИ 1.053 1.46 0.301 0.268 6.8
7,62-мм целевой винтовоч- ный патрон 7.62-мм целевой винтовоч- ный патрон «Экстра» 9-мм патрон охотничий 57-к-Ш 0.382 0.492 0.078 0.081 2.05
Изделие ВГ-12 квм-з 0.24 0.258 0.015 0.022 0.55
12.7-мм и 14-мм патроны 57-К-501 1.354 1.95 0.301 0.268 6.8
Патрон целевой винтовоч- ный «Экстра» кольцевого воспламенения 5,6-мм — 0.242 0.261 0.09 0.099 2.48
5,6-мм спортивно- охотничий патрон со стальной гильзой — 0.361 0-416 0.09 0.099 2.48
11атрон целевой винтовоч- ;ый кольцевого воспламе- нения калибра 5,6-мм — 0.332 0.377 0.09 0.099 2.48
Патроны охотничьи 12,16,20 калибра с бумаж- ной гильзой Центральн. воспламен. 0.783 1.025 0.09 0.099 2.48
«жевело» 0.301 0.377 0.09 0.099 2.48
Примечание. Ек„ - минимальная кинетическая энергия курка или ударника, обеспечиваю- щая 100%-ное воспламенение капсюлей; Екв - максимальная кинетическая энергия курка или ударника, обеспе- чивающая 100%-ное воспламенение капсюлей
Безотказность действия ударных механизмов зависит от энергетичсс-
•ю запаса ударного механизма. Энергетический запас ударного механиз-
.. предо[авляет собой отношение энериги бойка к энергии, обеспечиваю-
cii 100%-ное воспламенение капсюля-воспламенителя:
Eg
а = —
Ekb
Для обеспечения безотказной работы ударного механизма энергети-
ческий запас а должен быть не менее 1,00.
Однако известно, что большое влияние на чувствительность капсю-
ля-воспламенителя оказывает скорость бойка в момент удара по капсюлю.
Экспериментальные исследования показывают, что энергия бойка, необхо-
димая для 100%-ного воспламенения капсюля-воспламенителя, уменьшает-
ся с увеличением скорости бойка и может быть определена по следующей
эмпирической зависимости:
Еб=Бхбп,
где Б - постоянное значение, которое определяется типом капсюля-воспла-
менителя;
п = 1/3 - показатель степени.
Для определения параметра Б в первом приближении использовались
результаты копровых испытаний серийных капсюлей-воспламенителей
(см. табл. 2).
Параметр Б определяется по зависимости
где хг = - скорость груза в момент удара по капсюлю-воспламенителю;
g - ускорение свободного падения;
h - высота падения груза.
Полученные значения параметра Б для серийных капсюлей-воспла-
менителей приведены в табл. 2.
С учетом приведенной эмпирической зависимости далее приводится
анализ работоспособности ударных механизмов с точки зрения выяснения
величины соотношения инерционных характеристик ударного механизма,
обеспечивающих минимальную энергоемкость боевой пружины, т.е. опре-
деление оптимальной величины параметра Ь.
Кинетическая энергия бойка, обеспечивающая 100%-ное воспламене-
ние капсюля-воспламенителя, при определенном энергетическом запасе
ударного механизма с учетом скоростного фактора
Eg=aBXg.
Из заданной зависимости можно определить скорость бойка приме-
нительно к конструкциям ударных механизмов:
Iруппа а
1
Г 2аБ
ХЬ lm6(l + b)J
группа б
1
. _ f 2аБ^2-п
хб= — ;
I m6 J
группа в
1
. _ С 2aBV-n
хб = -----I
I тб J
С учетом полученных зависимостей для скорости бойка можно опре-
1нгь необходимую кинетическую энергию бойка применительно к кон-
векциям ударных механизмов:
группа а
_2 1-п
шб ("гаБЪ-п (b + l)22Zn
Еб - -Н--------------к----’
2 I п’67 Ь
группа б
2 1_п
_ шб (2аБ |2-n (b+l)22-n.
6 2 mg J b
группа в
2
_ m6 f 2аБ ]2-п
2 к тб J
Используя полученные выражения для кинетической энергии бойка,
ткже соотношения (22)-(24), из зависимости (21) получим следующие
политические выражения работы боевой пружины применительно к кон-
। рукциям ударных механизмов:
группа а
v 2 2^П
_ mg Г 2аБ 2-п (1 + b) 2-п .
2рД m6 J b
группа б
2
5А _ mg f 2аБ^2-п 1 2b(b + l)b-(b + l)2
5b 2рДтб; (1 + кб)2 Ь2
откуда b = 1;
группа в
Данная функция монотонно возрастает и не имеет экстремума.
С учетом полученных зависимостей для оптимальной величины пара-
метров минимальная энергоемкость боевой пружины применительно к
конструкциям ударных механизмов равна:
группа а
2 2~—
ЗА _ шб | 2аБ |2-п п Г2п-2А 2-п
3b 2pj <m6J п - 2 п )
группа б
А .
П1Ш
2
шб (2aE^2-n 4
2₽11 тб J (l + kb)2
(25)
(26)
При падении оружия и приходе подвижных частей автоматики в пе-
реднее положение подвижные детали испытывают действие инерционных
ударных импульсов, условно приложенных в центрах масс этих деталей. В
связи с этим необходимо определить минимальную массу бойка, обеспечи-
вающую 100%-ное невоспламенение капсюля-воспламенителя при его
инерционном наколе. Максимальная кинетическая энергия бойка
шбхб1
*•61 - —»
где хб1 = хн - скорость бойка при приходе подвижных частей в переднее
положение
или хб1 = -x/^ghj (1 - kb ) - скорость бойка при падении оружия;
g- ускорение свободного падения;
hj - высота падения оружия, принимается равной 1,5 м;
kb - коэффициент восстановления скорости при падении оружия.
Коэффициент восстановления скорости следует определить опытным
путем на изделиях, аналогичных проектируемым. При этом коэффициент
восст ановления скорости определяется как отношение высоты отскока из-
дсипя к высоте бросания. При отсутствии опытных данных значение коэф-
фициента восстановления скорости рекомендуется принимать kb = 0,2.
, (ля обеспечения 100%-ного невоспламенсния необходимо выполнять
ющее условие:
Eg Ejcb,
I kb - энергия, обеспечивающая 100%-ное невоспламенение.
)пергию , характеризующую чувствительность капсюля-воспла-
- юля к удару, получают при испытаниях капсюля-воспламенителя на
। .г х в соответствии с техническими условиями. Значения энергии Ekb
грийных капсюлей-воспламенителей приведены в табл. 2.
Невоспламенение капсюля-воспламенителя при инерционном наколе
и. и г от коэффициента запаса а, характеризующего отклонение энергии
I, .1 от энергии, обеспечивающей 100%-ное невоспламенение капсюля-
глменителя, т.е.
Еб
а1
Ekb
Для обеспечения 100%-ного невосплвменения капсюля-воспламените-
- >ффициент запаса сц должен быть менее 1,00.
(’ учетом коэффициента запаса сд и влияния скоростного фактора
< \ иствительность капсюля-воспламенителя к удару получим следующее
1 ношение:
Тогда минимальная масса бойка, обеспечивающая 100%-ное невосп-
в пение капсюля-воспламенителя при инерционном наколе,
шб ’ (27)
Для определения параметра Б1 в первом приближении использова-
I । результаты копровых испытаний серийных капсюлей-воспламените-
| (см. табл. 2).
Параметр Б1 определили по зависимости
Полученные значения Б1 и расчетные значения минимальной массы
ика для случая падения оружия при коэффициенте запаса сд = 1 приме-
। |ьно к серийным капсюлям-воспламенителям приведены в табл. 2.
Зависимость (27) позволяет определить оптимальное значение мас-
сы бойка, а (25), (26) -минимальную энергоемкость боевой пружины для
рассматриваемых групп ударных механизмов.
Диаметр отверстия в зеркале затвора и диаметр бойка определяются
из условия обеспечения прочности колпачка капсюля
или
43^ср]
где dfl - диаметр бойка (отверстия в зеркале затвора);
8 - толщина дна колпачка капсюля;
[тср ] - допускаемое напряжение на срез материала колпачка капсюля;
Рш - максимальное давление порохового газа в канале ствола.
Например, при [xcpJ = 0,35-105 Па, 5 = 0,7-10 3 м, Рт = 0,45-105 Па
получим d6 < 2,2 мм.
Для обеспечения надежности воспламенения капсюлей выход бойка
из отверстия в затворе для ударных механизмов, работающих от боевых
пружин, не должен быть менее определенного предела (предел приблизи-
тельно равен 1,5 мм).
Выход бойка из отверстия в затворе для ударных механизмов, рабо-
тающих от возвратных пружин, должен находиться в определенных преде-
лах, из которых нижний обеспечивает отсутствие осечек, а верхний - отсут-
ствие пробивания капсюлей. Для капсюлей винтовочных патронов эти
пределы составляют 1 и 1,8 мм.
Указанные пределы выходов бойка могут рассматриваться как ори-
ентировочные, так как целесообразные выходы бойков из отверстия в зат-
воре определяются для каждого конкретного типа оружия. При этом учи-
тываются тип гильзы (упор скатом или фланцем), тип ударного механизма
и формы бойка, тип и размеры узла запирания, а также величины зазора
между дном гильзы и зеркалом затвора.
Пример 1. Определить коэффициент энергетического запаса ударно-
го механизма куркового типа группы а.
Исходные данные
Тип капсюля-воспламенителя
Масса бойка mg...........
57-к-ОН
0,0051 кг
Момент инерции курка относительно
оси вращения!.................................. 0,0935-10'4кгм"2
Расстояние от оси вращения курка до
линии удара Н.................................. 25,5-10'3м
Коэффициент, учитывающий потери
кинетической энергии боевой
пружины при ее работе (разжатии) .............. 0,8
Момент, развиваемый пружиной
при ударе курка по бойку Mj.................... (490-637)-10-3 Н-м
Момент, развиваемый боевой
пружиной при постановке
курка на боевой взвод М2 ......................(843-1225)-10-3Н-м.
Постоянная капсюля воспламенителя Б............ 1,46 Дж
Угол поворота курка (закручивания
боевой пружины) ф
innOf 100
100 ------рад
(57.3
Скорость бойка в момент удара Хд..........(3-4) м/с
1. Определяем относительную величину Ь:
Н2шб
0.935 10 5
(25.5-10"3)2- 0.0051
2.82.
2. Определяем минимальную величину работы боевой пружины:
А — Mlmin + -^2min ф _
min 2 57.3
(490 + 843) 10' 100 , п
= 2---------------------= 1.16 Дж.
2 57.3
3. Определяем работу боевой пружины с учетом скоростного фактора:
, - А. 21 П
А = m6 f 2аБ1 12-п (l + b)z2-n =
2Р1 ( mg J b
6
5.1 Ю 3< 2 1.46 >7 3.828 ,, „
=------------------- I--------= 1.2 Дж.
2 0.8 (5.I 10'3J 2.82
4. Определяем коэффициент энергетического запаса
А 2
т.е. при работе ударного механизма возможны случаи иевоспламене-
ния капсюля-воспламенителя.
Пример 2. Спроектировать ударный механизм группы а.
Исходные данные
Тип капсюля-воспламенителя...................57 - К - 011
Рассеяние от оси вращения курка
до линии удара Н.............................25,5-10-3 м
Коэффициент, учитывающий потери
механической энергии боевой
пружины при ее работе (разжатии) р* .........0,8
Постоянная капсюля-воспламенителя Б.......... 1,46 Дж
Минимальная масса бойка mg...................6,8Т0’3 кг
1. Определяем величину параметра Ь:
- 1 -2
. и - 2 3 _
b = ---= , = 7
п _ 1
3
2. Определяем величину массы бойка при коэффициенте запаса а = 0,9:
П1д - СХШд = 0.9 6.8 • 10 3=6 -10 Зкг.
3. Определяем момент инерции курка
J = m6H = 6 10~3(25.5 -10-3Г = 0.39 10 5 кг м.
4. Определяем минимальную энергоемкость боевой пружины при
а = 1.25 по зависимости (25):
z ч-2 . ,2' "
. шй [ 2осБ |2-n п ( 2п - 2 ) 2 и
^тт ло ~
2pi V тб ) n- 2< п )
2
6 10 3 Г 2 1.25 1.46 V j.
1 О.зЧ 6.1(Г3 ) 3
1 Z 6
6 10“У2 1.25 1.46> 7
1.6 V 6 10' J
1 8
- 8 7 = 1.4Дж.
5. Определяем силовые характеристики боевой пружины при <хр = 2.
м = ^Amin = = 0.93 н м;
1 1 + ар 1 + 2
М2 = ctpMi = 2 0.93 = 1.86 Н м.
5. РАСЧЕТ И ПРОЕКТИРОВАНИЕ
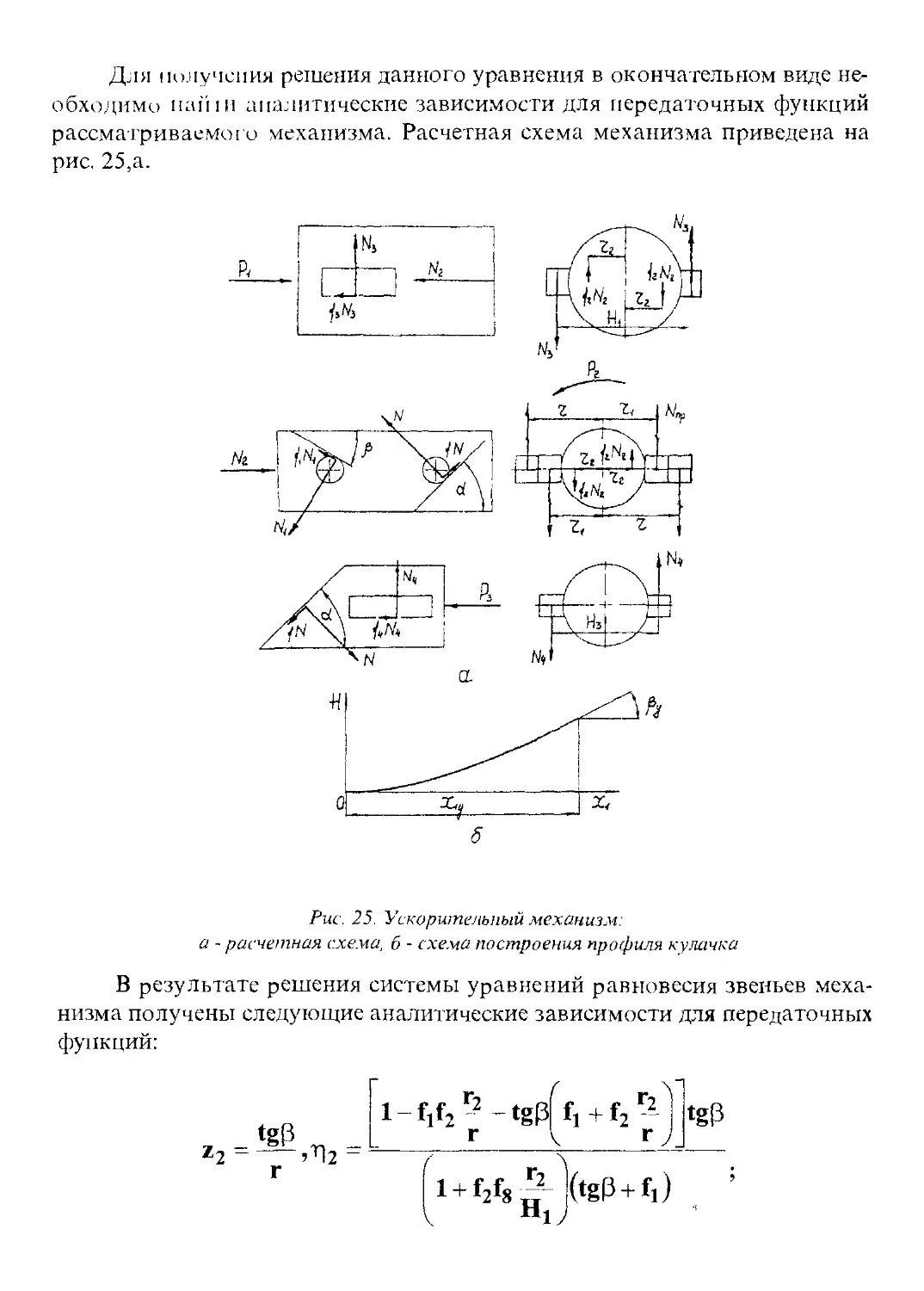
УСКОРИТЕЛЬНЫХ МЕХАНИЗМОВ
В автоматическом оружии, действие автоматики которого основано
> принципе использования отдачи ствола при его коротком ходе, для ра-
। ы механизмов открывания канала ствола используется кинетическая
I ргия ствола, полученная им в результате действия давления порохового
1 1 .а на дно канала ствола. К концу отпирания канала ствола в данных сис-
мах оружия подвижные части (затвор, затворная рама) обычно не при-
• •рс1ают достаточного запаса кинетической энергии для обеспечения на-
- кпой работы механизма автоматики и требуемого темпа стрельбы. По-
>му в системах с отдачей ствола при его коротком ходе применяются
- пениальные механизмы, сообщающие дополнительную кинетическую
пергию подвижным частям за счет кинетической энергии ствола. Меха-
UII (мы эти называются ускорительными, так как, перераспределяя кинети-
ь скую энергию, они ускоряют движение подвижных частей. Ускоритель-
"4с механизмы в зависимости от принципа их действия и конструкции сле-
о и г разделить на рычажные, кулачковые, копирные и пружинные.
5.1. Ускорительные механизмы рычажного типа
Действие ускорительных механизмов рычажного типа заключается в
ытуюшем. После отпирания канала ствола рычаг ускорителя, закреплен-
ный в коробке автоматики или на стволе, в результате удара передает
часть кинетический энергии ствола подвижным частям. При этом во время
удара часть кинетической энергии теряется.
Ускорительные механизмы этого типа имеют наиболее простое уст-
ройство и не требуют высокой точности изготовления деталей, однако
ударная работа этих механизмов снижает срок службы деталей механизма.
Принципиальные схемы ускорительных механизмов приведены на рис. 23.
Рис. 23. Принципиальные схемы рычажных ускорительных механизмов:
a-ось вращения рычага закреплена на коробке автоматики,
б-ось вращения рычага закреплена на стволе; 1-ствол, 2-рычаг, 3-затвор
При определении параметров движения звеньев ускорительного меха-
низма ударного действия можно использовать зависимости разрывного изме-
нения скоростей звеньев исполнительных механизмов при ударах, а именно:
mi +тз г- 11 + кв(1- гз)]
х“ =---------Из-------------хТ;
ИЦ + Шз -Z—
Пз
*3 = z3*l + кв(гз -1>1-
При проектировании ускорительного механизма ударного действия
задача заключается в рациональном выборе геометрических размеров рыча-
га ускорителя а и ap которые определяются передаточным отношением z3.
Скоростью подвижных частей после работы ускорительного меха-
низма можно задаться, руководствуясь обеспечением нормальной работы
механизма автоматики. Зная скорость подвижных частей и ствола до рабо-
ты ускорительного механизма X] и желаемую скорость подвижных частей
после работы ускорительного механизма Х3 , воспользовавшись приведен-
1.1 ми выше формулами, найдем зависимость для передаточных функций
П3:
*3 =
mi +шз—[1 + кв(1“гз)]
„ ПЗ _
~ ~ z>
Го] + П13
ПЗ
z3 + kB(z3
। куда получим следующее уравнение:
~т3(хз - хг)- лзт1(1ткв)х| + тДкв^ + X3U 0.
Т13
Получив аналитические зависимости для передаточных функций z3,
, 3 и подставив их в приведенное уравнение, получим зависимость, позво-
тощую определить значение геометрических параметров ускорителя а и
.1,. задавшись значением одного из них.
5.2. Ускорительные механизмы кулачкового типа
Для обеспечения безударной работы ускорительных механизмов при-
еняются ускорительные механизмы кулачкового типа. Механизмы этого
. нпа по конструкции аналогичны рычажным механизмам. Они также име-
. н рычаг, па котором выполнен кулачок, профиль которого определяет
1Кон движения ствола и подвижных частей во время работы ускоритель-
ного механизма. Кулачковые механизмы требуют высокой точности изго-
. овления деталей и обработки сложных профилей кулачков, что усложняет
и удорожает их производство. Однако обеспечиваемая ими плавность pa-
к. гы позволяет получить хорошую живучесть деталей и надежность рабо-
i.i ускорительного механизма.
При проектировании ускорительных механизмов задаются законом
л шенения скорости подвижных частей, который обеспечивает к концу ра-
югы ускорительного механизма достаточный запас кинетической энергии
о. щвижных частей для нормального функционирования механизма авто-
матики и требуемого темпа стрельбы. Если в первом приближении пренеб-
речь действием пружины, сил трения и моментом инерции ускорителя, то
о время работы ускорительного механизма потерь кинетической энергии
не будет. Это можно выразить следующим уравнением:
2 -2
mi +m3 2 mjxj m3x3
2 x10 2 " г >
или
где mb m3 - соответственно масса ствола и подвижных частей,
Хщ - скорость ствола и подвижных частей к началу работы ускори-
тельного механизма,
ХрХз - соответственно скорость ствола и подвижных частей во вре-
мя работы ускорительного механизма.
Задаваясь законом изменения скорости подвижных частей х3 — f(t)
и используя приведенную выше формулу (28), можно определить закон из-
менении скорости ствола Xj = f (t).
При линейном законе возрастания скорости подвижных частей в
функции времени обеспечивается постоянство ускорения подвижных час-
тей, при котором инерционные силы, действующие на подвижные части,
будут наименьшими.
В данном случае
*3=X1O + X3t. (29)
Подставив данную зависимость в уравнение (28), получим
*1 = J[1 + + *3*)2
К mi
ИЛИ
_ D 2x10m3 m3 2
xl~Ax10----------x3l ----x3r •
]/ nil ml
Найдем закон изменения перемещения ствола Xj(t) и подвижных час-
гей x3(t). Введем обозначения
с~ х10’
ъ = - 2тзхюхз
mi
т3 .
а=----~х3,
mi
тогда
Ё51 = у/at2 + bt + с.
dt
Проинтегрировав данное выражение, получим
Xi =
+ bt + c
4а
А . 2at + b
~7= arc sin —т=~
-A i°-
С учетом пределов интегрирования
2at x/at^+lbt - с + by/at2 + bt + с - э/с
Xj =
4а
А ( . 2at + b b
-/=--= arcsin—7===—arcsin^
A = 4ac - b2.
При линейном законе изменения скорости подвижных частей
v _X3k-X10
3 7Г~,
с х3к- скорость подвижных частей в конце работы ускорительного ме-
ханизма,
ty - время работы ускорительного механизма.
С учетом этого параметра последние зависимости будут иметь вид
а = -5j-(x3k - хю>
mity
Ь = -^ЩЧо(х3к-Х1О>
Hljty
c = *io;
Л=11П3^10(кзк_х10)|1 + .
mi L mi
Перемещение подвижных частей в функции времени-определим, нро-
тегрировав формулу (29):
2
v„ ,t + ХЗк“хЮ 1
x3 -x10t +------- ~-
ly Z
Тогда перемещение подвижных частей относительно ствола будет оп-
ределяться по следующей зависимости:
Хз1 =хз-хт
При известной величине х3к , определяющей необходимый запас ки-
нетической энергии подвижных частей, задаваясь временем работы уско-
рительного механизма t = ty или величиной перемещения подвижных час-
тей относительно ствола на участке его работы xv, представляется воз-
можным графическим методом построить профиль кулачка ускорителя.
Построение профиля кулачка ускорителя можно выполнить в последова-
тельности, предложенной А.А. Благонравовым:
- выбираем схему ускорительного механизма;
- вычерчиваем на листе бумаги опорные поверхности ствола и под-
вижных частей, взаимодействующих с ускорителем, а также отмечаем на-
чальное положение оси ускорителя, т.О.;
- рассматривая движение подвижных частей относительно ствола (при
неподвижном стволе и движущейся навстречу коробке автоматики) наметим
ряд точек xo,xi ,xv ’ соответствующих расчетным значением х31;
- наложим на полученную схему чистый лист кальки и нанесем на
него положение оси ускорителя (т. О), опорную поверхность ускорителя
А-А, взаимодействующую со стволом, и линию, соответствующую опор-
ной поверхности подвижных частей:
- переместим точку О кальки в точку х, схемы так, чтобы линия опор-
ной поверхности ускорителя (на кальке) касалась опорной поверхности
ствола на схеме и проведем на кальке линию вдоль линии I-I схемы;
- переместим точку О кальки в точку х2 схемы, повернем кальку до |
совмещения опорной линии ускорителя (на кальке) с опорной поверхпос- i
тыо ствола (на схеме) и вдоль линии П-П проведем на кальке линию.
Повторяя последний прием для положений оси ускорителя в точках
х3,х4,..., получаем на кальке серию пересекающихся прямых. Кривая,
вписанная касательно к пересекающимся прямым, и будет профилем ку-
лачка ускорителя.
5.3. Ускорительные механизмы копирного типа
Ускорительные механизмы копирного типа представляют собой раз-
новидности кулачковых механизмов. Кулачок закреплен неподвижно и иг-
। роль копира, с которым взаимодействую! подвижные детали обычно
е! ролик. Механизмы копирного типа позволяют использовать ускори-
л.ный механизм для отпирания канала ствола и этим сократить количе-
исполнительных механизмов автоматического оружия. Ускоритещ,-
< механизмы копирного типа обычно содержат два подвижных звена;
। вор и затворную раму. В этом случае во время работы ускорительного
j чанизма осуществляется ускорение затворной рамы относительно затво-
ири одновременном отпирании канала ствола. Конструкция ускори-
п.ных механизмов существенно зависит от способа запирания канала
вода. Копирные ускорительные механизмы имеют относительно слож-
- устройство, детали изготавливаются с большой степенью точности.
! ,нако они обеспечивают плавность работы.
Рис. 24. Ускорительный механизм копирного типа:
а - расчетная схема. 6 схема построения профиля кулачка
Расчет характеристик движения звеньев ускорительного механизма
ширного типа проводи гея аналогично ускорительным механизмам ку-
ркового типа. Некоторую специфическую особенность представляет
.ишь построение теоретического профиля копира. Рассмотрим построение
нофиля копира ускорительного механизма, принципиальная схема кото-
1 то приведена на рис. 24,а.
Для построения профиля копира ускорительного механизма с враща-
щимся затвором (муфтой) следует реальную схему механизма упростить.
। вернув его рабочие поверхности на плоскоеib по среднему радиусу ко-
пра. Построение теоретического профиля копира при заданной зависи-
мости за i норной рамы x3 от перемещения с тола Х| можно осуществить
следующим образом (см. рис. 24,6).
Проведем из т. О горизонтальный луч и, отложив на нем отрезки, со-
ответствующие Дх^, приведем из их концов ряд вертикальных прямых лу-
чей. Затем на этом же горизонтальном луче отложим отрезки, соответству-
ющие Лх3, и из концов их проведем лучи, наклонные под углом а, к гори-
зонтальному лучу. Точки пересечения соответствующих вертикальных и
наклонных лучей дадут точки теоретического профиля копира, соединив
которые плавной кривой получим сам профиль, который затем свертыва-
ется по среднему радиусу реального копира.
Проектирование ускорительного механизма копирного типа с учетом
реальных условий его работы может быть проведено и аналитическим мето-
дом. Рассмотрим этот вопрос применительно к принципиальной схеме меха-
низма, приведенный на рис. 24,а. Ускорительный механизм обычно включа-
ет в себя три подвижных звена: ствол, затвор и затворную раму. Задаемся
инерционными характеристиками этих звеньев по величине, близкими к од-
ноименным характеристикам аналогичного по назначению образца оружия.
Определяем характеристики движения ствола и связанных с ним под-
вижных частей к моменту начала работы ускорительного механизма
(обычно соответствующему моменту вылета пули из канала ствола)
xlg,xlg и t2- Время t2 берем из результатов расчета внутренней баллис-
тики, а перемещение и скорость ствола определяем расчетным путем.
Уравнение движения ствола на участке работы ускорительного механизма
ш(х1>1 =PSk,
где
2 „2
/ \ z2 z3
m(xj) - ni] + m2 — + m3 + m4
Л2 Пз
Для аналитического решения приведенного дифференциального урав-
нения заменим переменную во времени движущую силу средней величиной
Р Q _ U ПЛ
гс°кн
ц
или, преобразуя, получим
Р Ч
рс8кн = = const.
1п| *8 |
Запишем исходное уравнение в виде
<Ьц _ PgSRH
’ ЛРГ
In ь
. умножив и разделив левую часть уравнения на dxj получим
intx^dx! = P^udX)
Откуда
•2 _k2 _2PgSKHX? dxl
ly lg ln|'pso m(xi)’
'Л)
• /- ирхянизма и ско
т *ir х1у - величина участка работы ускорительного меллп
рость ствола к концу его работы.
гг ,,честна величина
При проектировании ускорительного механизма извесю
г т. о а ча лается исходя
; . рос ги затворной рамы к концу его работы х3у, которая •
। Tov если ствол ки-
=. \словия нормального функционирования автоматики. 1dK- L
. ма гически связан с затворной рамой до конца работы механизма,
XJ т 9
z3y
- передаточное отношение в конце работы ускорительного механизма
С учетом этого последнее уравнение примет вид
(30)
Для получения решения данного уравнения в окончательном виде не-
обходимо naiiin аналитические зависимости для передаточных функций
рассматриваемого механизма. Расчетная схема механизма приведена на
рис. 25,а.
Рис. 25. Ускорительный механизм:
а - расчетная схема, б - схема построения профиля кулачка
В результате решения системы уравнений равновесия звеньев меха-
низма получены следующие аналитические зависимости для передаточных
функций:
7 - tgP Г -
z2 “ 542 “
г
tgp
1 м/2
г
-tgp f] +f2
Z3 = Z2 —-,Т|з = T|2 "-----^7------Ч------'
2 tga tga(l + ftga)
Согласно принципиальной схеме механизма угол р есть переменная
личина, меняющаяся от0° до величины, соответствующей концу работы
корительного механизма р, а следовательно, и г2,Г|2тоже величины пе-
менные. Зададимся линейным законом изменения z2, т.е. z2 = АхР В кон-
. работы ускорительного механизма х, = xlv и передаточное отношение
_ tgPy _ .
z2y —----— Axjy,
е Ру - угол наклона копира в конце работы ускорительного механизма.
Тогда можно получить следующую зависимость:
tgPy
А =
ГХ1у
Введем обозначение постоянных величин, входящих в вышепривс-
нные зависимости:
(31)
!ег.г1,г2,Н1.Н3 - геометрические параметры ^механизма, известные из его
эскизной проработки;
f, fb f2, f3, f4 - коэффициен ты трения, значения которых соответствуют
рассматриваемым условиям работы механизма.
Выразим tga через хь т.е. tga = Агх,. Тогда для приведенной массы
'.лучим следующую зависимость:
m(xj)= Ш) +
Ax^rAx; + ft)
r(Aj -rAXjA2)
+ m4
tn.обозначая
В = гщ + ш4;
В] = m2 + m3
nCl + ftgg)
tga(A4tga-A5)’
получим
mfv i R^R AA3X1(Arx1 +fj
m(xj) - В + Bi —r---— r-
r(Ai - rAA2Xi)
X7
Найдем решение интеграла J / д . После интегрирования и соот-
О m\xlJ
вегствующих преобразований получим следующую зависимость:
Х1гУ dxj 1 f BAi B]A3f4 - Br2A2 I
0 m(xi) a|^2A2 t3Aj r3Aj J
X JУгД±ЧМ fВ]ДЛ _ д . Wili
I A! J I 1 A2 Jr2A2
B1AA3 2
2rA2 Х!У'
Подставив полученную зависимость и выражение для
z3 = Axi -'L,
J tga
будем иметь
x3ytg2a
A2ri2xly
2PgS^. 1J BAi BiA3ft-Br2A2 BxA2A3^
A^2A2 r3A2 r3A3 j
w
( rAA^Xiy । f у
• In -1-----LIL + BxA3fi - Br2A2 -
I Ai И
АхАзВИ xiy
A2 Jr2A2
B1AA3
xly
2
В полученной зависимости неизвестными являются параметры А
Х1у И (X.
Сократим число неизвестных, используя уравнение (31). Получим
Xly
Xjy
rtgax3y
ntgpy
In -
I Pa J
2Ре8кн(В4ГвЛ
(32)
B4=B
Для определения угла а используем зависимость для Т)3. Как пока-
..1вает опыт эксплуатации современных образцов автоматического ору-
< ия величина к.п.д. механизма в затрудненных условиях работы, т.е. при
'эффициенте трения скольжения равном 0,25 должна быть > 0,4. С уче-
>м ранее принятых обозначений получим
_ (Ai~A2tgpXA4tga - A5)tgp
3 А3 (tgP + fj Xl + ftga)tga
Из последнего выражения
/в,± Jb^-4bJ
a = arctg------------- , (33)
IС
в _ _ А4(а3 - A2tgpy )- A3T|3(tgpy + fl)
A^3fri3{tgPy + f, J
B = A5tgPy(A! -A2tgpy)
3 "A^fePy+ffT ’
где Ру - значение угла р копира в конце работы ускорительного механизма.
Задаваясь значением угла ру в диапазоне от 10° до 60°, получим ряд
значений а = а(Ру . Реальные значения углов а используем для решения
уравнения (32) применительно к нормальным условиям эксплуатации ме-
ханизма (коэффициент трения скольжения равен 0,15), в результате кото-
рого получаем значение участка работы ускорительного механизма х1г
Далее находим значение параметра А по формуле (31). Используя аппрок-
симационную зависимость и аналитическую зависимость для передаточно-
го отношения, получим
. tgP
Axj
г
откуда
Р = arctg(Axjr). (34)
Для построения теоретического профиля копира разбиваем величи-
ны xlv и Н= г(р2 на определенное количество участков и рассматриваем
соответствующие значения Hj, pj в конце каждого участка. Затем прово-
дим горизонтальный луч из т.О., на котором откладываем величину участ-
ка х1у, из конца которого на вертикальном луче откладываем вверх отре-
зок, соответствующий величине Нь из конца которого проводим луч под
углом pj. Получим ряд пересекающихся наклонных лучей, проведенная
плавная касательная кривая к которым и будет теоретическим профилем
копира, свернув который по среднему радиусу г с учетом радиуса ролика
получим реальный профиль копира. Схема построения теоретического
профиля копира приведена на рис. 25,6.
5.4. Ускорительные механизмы пружинного типа
Рассмотрим принципиальную схему пружинного ускорительного ме-
ханизма, приведенную на рис. 26.
Для перераспределения кинетической энергии затвора и ствола здесь
используется пружина, которая взводится в период совместного движения
ствола и затвора под действием силы давления порохового газа на дно ка-
нала ствола и после отпирания канала ствола разжимается, ускоряя затвор
и замедляя ствол. Ускорительные механизмы пружинного типа имеют не-
которые преимущества по сравнению с рассмотренными ускорительными
механизмами, обеспечивая плавность работы. Надежность работы этих
механизмов зависит от качества пружины ускорителя. Кроме того, общие
; ирмления конструкции механизмов этого типа получаются сложными и
(Ывают трудности при ручном перезаряжании без взведения пружины
корителя. Вследствие этих недостатков ускорительные механизмы яру-
сного типа в ав томатическом оружии распространения не получили.
!‘ис. 26. Принципиальная схема работы ускорительного механизма пружинного типа.
I-ствол, 2-затвор. 3-клин
Пример. Спроектировать ускорительный механизм копирного тина к
лемету ПК.
Исходные данные
Калибр d.........................................7,62-10 Зм
Масса пули mq....................................9,6-103 кг
Масса заряда шй1 ................................3,1-10’Зкг
Путь пули по каналу ствола 1д ...................0,56 м
Начальная скорость пули v0 ...................... 840 м/с
Площадь канала ствола SKH........................ 0,476-10’4 м
Коэффициент фиктивности массы пули ф ............1,09
Дульное давление Рл.............................. 650-105 Па
Атмосферное давление Ра.......................... 10 5 Па
Масса ствола ш,..................................2,2 кг
Масса затворной рамы ш3..........................0,9 кг
Масса затвора т4.................................0,1 кг
Момсш инерции затвора m2........................6,0-10"6 кгм2
Радиус взаимодействия ролика затвора
с копирами г.................................... 16,6-10 3 м
Рабочий угол поворота затвора
при запирании <р2...............................^0 °
Радиус взаимодействия ролика затвора
с затворной рамой г3............................ 11,910*3 м
Средний радиус площади контакта
затвора с дном гильзы г2........................3,6-10~3 м
Ширина направляющей базы ствола Н3..............20-10 -3 м
Ширина направляющей базы
затворной рамы Н3...............................26-10’3 м
Скорость затворной рамы в конце
работы ускорительного механизма х3у.............8 м/с.
1. Определяем диапазон изменения угла а при значении коэффици-
ента трения скольжения 0,25 и к.п.д. механизма Т]з = 0,4 по формуле (33).
Вычисляем значения постоянных коэффициентов при f2 = f3 = f4 =
= 0,25:
f=f = i 27-f2 0,5 0,25-0,16.
rp
a.=1 - № p=1 - °’16 °’25^;64f>=15
A = f +f2*1 = 0,16 + 0,25-,6 10- =0,21-
2 1 r 16,6 IO 3
A = 1 + f2f3 = 1 + 0,25 0,25 3,6 1 ° = 1.
Аз 23Ht 20 10 3 ’
r 119 10-3
A4= 1 - ff4 — = 1 - 0,25~-------. = 0,98
4 4H3 26 103
r 119-10-3
A = f + f4 -й- = 0,16 + 0,25 = 0,27,
5 H3 26-IO-3
jтем определяем параметры В2 и В3 для значений угла ру — 15 °, 30 °. 45 °
io зависимостям
в Ад(А1 ~ A2tgPy)tgpy - A3r|3(tgpy + ft)
2 A3fr]3(tgpy +fj)
в - A5tgPy(Ai~A2tgP )
3 А3Гт1зЙ^+fl)
при
Py =20°, a = 65 и 52°;
Py =30°, a = 73 и 42°;
py =45°, a = 72 и 43°.
2. Определим характеристики движения подвижных частей до начала
работы ускорительного механизма (момент вылета пули из канала ствола):
(pm + 0,5m10 (1,09 9,6 10“3 +0,5 3,1 10“3В40 , „ ,
х -----*--------Vn = а---;--------------------l— = 3,2 м/с;
g m1 + m3+m4 2,2+ 0,1+ 0,9
(pm 0,5m „ 1,09 9,6 10-3 +0,5-3,1 IO-3
xlo =-------------1 =--------------—------------0,56=2,1 10 M
” mt + m3 + m4 6 3,2
3. Определяем перемещение ствола на участке работы ускорительно-
। о механизма xlv по формуле (32) для нормальных условий работы. Прини-
маем следующее сочетание значений сочетания углов:
ру = 30°,a = 73°,42°;
.2 frtga*3yA , fpg
I ritgPy j j LPa
2pgSKH(B4 + B5)
Вычисляем значения параметров B4 и В5 по зависимостям
В4 = В
------L——1-1
2A2tgpy
в-в'^
fjA2 + Aj _ А2*ёРу + f-[A2 Ai
А2*ёРу I A1 J A2 2
где
В = mj + m4;
Bl
- m2 +m3
^(l + ftga)
(A4tga- A5)tga
При
f2 = f3 = f4 = 0,15;
f = fl = 1,27-f2 = l’27 °’5 °’15 = °Д;
rP
A! = 1, A2 = 0,13, A3 = 1, A4 = 0,17;
В = 2,2 + 0,1 = 2,3 кг.
При a = 73°
В^б-Ю22,7-Ю-‘
tg73°(l tg73° -0,17)
При a = 42°
Bi = 6 10 6 + 0,9 = 217,4 106
tg42°(ltg42°-0,17)
При a = 73°
Bs = 22.7 10 6 ------- ----
16,62 10-6
0,1 0,13 + 1, L 0,13 0.58
0,132 0,58 V 1
0,1 0,13-1 0,58
0,13 + 2
= 1.26.
При a = 42°
B5 = 217,4 10 6(- 55,7 103 )= -12,11
(1.16,6.10-3-2Ul-0’130’58
V ’ I 1
- 0,06.
При py = 30°,a = 73°
xb =
(16,6 10“3 3,27 8^ , f 650 105
------------------|n
4 11,9 10“30,58 ) ( 105 )
2 650 105 0,476 10 4(0,06-1,26)
= 3,44м.
При p = 30°,a. = 42°
3,2 2
16,6 10 3 0,98
11,9 10“3 0,58 ,
/ с \
, 650 1О5
In
I Ю5
25,1 10 3m.
Х1У 2 650 IO5 0,476 10 4 (0,06 - 12,11)
Таким образом, из двух значений реальным является последнее, т.е.
а =42«, ру = 300 и х1у = 25,1-Ю-з м.
4. Определяем значение угла Р в функции перемещения ствола ио
формуле (34):
P = arctg(ArXj).
Из формулы (31)
Ч₽,=_0377
хь 25,1 103
Разобьем величину xlv, например, на 5 участков, тогда для каждого
участка получим
Х1 = 0; Ро=О°;
Xi = 5-10-3M; 31=6,6°;
xi 10 10“3м; р2 =13°;
Xi =15 10"3м; р3 =19°;
xi = 20 10“3м; р4 =24,7°;
Xi = 25 10 3м; р5 = 30°.
5. Определим высоту развертки копира на плоскость по радиусу г:
Н = Гф2 = 16,6 10“3 --= 8,7 10“3м.
2 180
Полученную величину также разобьем на 5 участков:
xi =О;Но =0;
xi = 5 10 3м;Н1 = 1,74 10 Зм;
Xi = 10 10-3м;Н2 = 3,48 10"3м;
xi = 15 10“3м;Н3 = 5,22 10 Зм;
Х1 = 20 10 3м;Н4 = 6,96 10“3м;
Xi = 25 • 10-3м;Н5 = 8,7 • 10“3м.
6. Строим профиль копира, используя значения р; и Н,. К серии на-
клонных пересекающихся лучей проводим плавную касательную кривую,
которая будет теоретическим профилем копира. Свернув его по радиусу г с
учетом радиуса ролика получим реальный профиль копира.
6. РАСЧЕТ И ПРОЕКТИРОВАНИЕ
ЗАПИРАЮЩИХ МЕХАНИЗМОВ
Механизмы отпирания и запирания канала ствола служат для сцепле-
.г.! ствола с затвором перед выстрелом и для их расцепления после выстре-
: Особенность работы этих механизмов в том, что они работают при
этствии на их детали силы давления порохового газа. Это приводит к
. > (ьшим давлениям в парах механизма, что при наличии относительного
помещения звеньев механизма заставляет обращать особое внимание на
енмнение износа их рабочих поверхностей. При работе механизма дей-
вуют относительно большие и нестабильные силы трения, в связи с чем
грата энергии на их преодоление может изменяться в больших пределах,
. о существенно сказывается на работе автоматики в различных условиях
'.силуатации. Поэтому желательно при их проектировании предусмотреть
нструктивные решения, обеспечивающие минимальную затрату энергии
> ! их работу и стабильность этой энергии.
В зависимости от способа запирания канала ствола запирающие ме-
• шизмы можно разделить на механизмы с самозапирающимся затвором
ле гемы с отдачей свободного и полусвободного затвора) с полупринуди-
• 1ьным и принудительным отпиранием канала ствола.
Наиболее широкое распространение в практике проектирования ав-
• .магического оружия получили запирающие механизмы с принудитель-
ым запиранием (отпиранием) канала ствола. Особенностью их работы
и-, тяется то, что отпирание канала ствола осуществляется принудительно
счет кинетической энергии основного звена механизма ав томатики. Усг-
। liicTBo этих механизмов не допускает самоотпирания при любой величи-
к- давления порохового газа в канале ствола. Данные механизмы следует
мзделить на механизмы, обеспечивающие раннее и позднее отпирание ка-
па та ствола. В первом случае отпирание канала ствола заканчивается при
1ЛЛИЧИИ в нем значительного давления пороховою газа, действие которо-
. । через гильзу на затвор используется для работы автоматики. Во втором
(учае отпирание канала ствола заканчивается при незначительном давле-
нии в канале ст вола, действие которого через гильзу на затвор не оказыва-
! । существенного влияния на работу автоматики. При позднем отпирании
> .шала ствола сила экстракции гильзы оказывает наименьшее влияние на
1>аботу автоматики и кинетическая энергия сообщается затвору в резулыа-
е удара затворной рамы или в результате работы ускорительного меха-
шзма. При таком способе сообщения киншической энергии затвору обыч-
но возникают большие силы в парах механизма, что приводит к снижению
рока службы деталей. При раннем отпирании значительная часть кинети-
1ССКОЙ эпертии сообщается затвору давлением порохового газа, что зна-
чи1слы||> уменьшает силы, действующие в парах механизма, сообщающего
за твору лишь час и. кинетической энергии. В этом отношении применение
раннего отирания выгодно. Однако при раннем отпирании работа автома-
тики зависти о । условий экстракции гильзы, что ухудшает надежность работы
автоматики. Раннее отпирание может также приводить к разрывам гильз.
Эти недостатки раннего отпирания сильно ограничивают его приме-
нение. Позднее, как и раннее отпирание канала ствола обычно определяет-
ся величиной свободного хода основного звена механизма. Свободным хо-
дом называется перемещение основного звена механизма автоматики под
действием давления порохового газа до начала отпирания канала ствола.
Рассмотрим вопросы расчета и проектирования запирающих механизмов с
принудительным запиранием (отпиранием) канала ствола.
6.1. Запирающие механизмы с перекосом затвора
Принципиальная схема запирающего механизма приведена на рис. 27.
Рис. 27. Принципиальная схема запирающего механизма с перекосом затвора.
* 1 -затворная рама; 2-затвор
Затворная рама совершает возвратно-поступательное перемещение.
При запирании канала ствола она действует наклонной под углом а рабо-
чей гранью на ответные элементы затвора, а при отпирании канала ствола
элемент затворной рамы действует на ответную поверхность наклонной
под углом р рабочей грани затвора. Основная задача при проектировании
механизма состоит в обеспечении минимальной и стабильной энергии,
идущей на его работу. При определенных инерционных характеристиках
подвижных звеньев механизма и линейных геометрических размерах по-
ставленная задача должна решаться путем анализа аналитических зависи-
мостей его передаточных функций.
В связи с тем, что в процессе отпирания и запирания канала ствола
работают различные наклонные рабочие грани затворной рамы и затвора,
i оведем указанный анализ для процесса отпирания и запирания канала
вола.
При отпирании канала ствола рассмотрим расчетную схему запираю-
л о механизма, приведенную на рис. 28.
[‘ас. 28. Расчетная схема запирающего .механизма с перекосом затвора при запирании
Из условия равновесия звеньев запирающего механизма под действи-
м заданных сил получим после соответствующих преобразований следу-
>. ндис зависимости:
_ sin(P + y)
Z 2 — ~ ' “ *!
xcos(P + у) Jsin(P + у) -sinP(Jj - xi siny)
ZiA
П2 =-------------2--------------
sin(p + y)(l - f z) -г 2f cos(P + y)
зри
A = cos(p + y)(x - fy) - sin(p + y)(y + fx) -
2
- sinp(yi cosy - X] siny) - f cos(yj sin у + Xj + x j cosy) -
- f[y] cos(p + y) + Xi sin(P + у)}
Величина угла у выбирается из условия самоторможения затвора при
выстреле для минимального значения коэффициента трения скольжения
11ары сталь-сталь:
g = aretgf.
Величина этого угла для запирающих механизмов с принудительным
(апираннем у = 5...6°,
В приведенных зависимостях неизвестной является величина угла Р,
которую можем найти из зависимости для к.п.д. при f = 0,25 (затрудненные
. словия эксплуатации) и щ = 0,4.
Ana ini пчпым образом поступим с расчетом механизма запирания
капала с i ы>ла Расчсшая схема механизма запирания канала ствола приве-
дена па рис. 20.
Рис. 29. Расчетная схема запирающего механизма с перекосом затвора при отпирании
Из условия равновесия звеньев запирающего механизма под действи-
ем .заданных сил получим после соответствующих преобразований следую-
щие аналитические зависимости:
г2=^-;
x-ytga
1 + fJ-xtga
x-ytgq
2 1 - f1 2 + 2fctgq
Из последней зависимости, полагая f = 0,25 и ~ 0,4, определяем
значение угла а.
При полученных значениях углов аир необходимо опенить работу
сил трения, обусловленную возможным расклиниванием подвижных час-
тей в направляющих при их возвратно-поступательном движении, т.к. зат-
вор взаимодействует с затворной рамой при совместном движении рабо-
чими гранями соответствующих наклонных поверхностей. Рассмотрим
этот случай применительно к расчетной схеме, приведенной на рис. 30.
Дифференциальное уравнение движения подвижных частей
(ш, + m2)xj = П - f(Nj + N2);
Nj = N2 = N(cosa - fsina).
Рис. 30 Расчетная схема движения подвижных частей
при наличии их расклинивания в направляющих
Тогда
(П1]+П12)х1 = п - 2fN(cosa - fsina).
Для нахождения неизвестной реакции поступим следующим образом:
m2Xj = Nsina(l + Р);
т, Xj = П - N[sin(l - Р) + 2fcosa],
Найдем из уравнения движения затвора X] и, подставив его в уравне-
nie движения затворной рамы, получим
+ 2f cos а
Тогда окончательно будем иметь
(raj +т2)*1 = Щ1 -
Вгл им -.иачение
2f(1 - ftga)__
m.
tga 1 mi f2 1 “,| -• 2f
m2
Toi да
(mi +m2)xi = n(l-aT),
г.е. силы трения будут уменьшать движущую силу.
Как видно из зависимости для а,, величина последней может быть
уменьшена в основном за счет увеличения отношения
т1
ш2
6.2. Запирающий механизм с поворотом затвора
Определенный интерес при проектировании запирающих механизмов
представляет запирающий механизм с поворотом затвора, принципиаль-
ная схема которото приведена на рис. 31.
Рис. 31. Принципиальная схема запирающего механизма с поворотом затвора.
I-затворнаярама. 2-затвор во вращательном движении относительно продольной оси
Согласно приведенной схеме, затворная рама, действуя рабочей гранью
наклонного паза под углом а на ведущий выступ затвора, поворачивает ет о
относительно продольной осн при запирании и отпирании канала ствола.
Исходя из требований, предъявляемых к механизмам с принудитель-
ным отпиранием канала ствола, проведем анализ передаточных функций.
я получения аналитических зависимое гей передаточных функций рас-
1 >трим расчетную схему механизма, приведенную на рис. 32.
Рис. 32. Расчетная схема запирающего механизма
с поворотом затвора при отпирании
Из условия равновесия звеньев под действием заданных сил после со-
тгетвующих преобразований, получим
z .
2 r[l+ p(A2tga~ A3)]’
[1- ftga + pAj(Atgq - A ])] tga
[1 + p(A2tga-A3)](tga(l - f2) + 2f)
p = —, A = cosy + fsiny, Ai = siny - fcosy,
r
. . . 2
A2-smycosy, A3=sm y.
Найдем экстремальное значение функции = r|2(a)’ Д;1Я че1 ° 1Ю ч.мем
ную производную по а и приравняем ее нулю:
дт|2 = tg2a(BB3 -BiB2) -2BB4tga -BiB4 = Q
да (tg2aB2 +B3tga-B4)
: ы получим алгебраическое уравнение
tg2a-
2ВВ4
BB3-BiB2
. В1В4
tga-----:
BB3-BjB4
= 0
9
В цАА1 -f, Bl = 1-цА2, B2 = (l-f2)uA2;
В, (1 - f2)(l - piA3) + 2fuA2;
B4 2fuA3 - 2f.
Решим это алгебраическое уравнение:
а = arctg
вв4 ± I_______В2В2_____
ВВ3 - В1В2 ' (ВВ3 - BjB2)2
___вгв4
вв3 — в4в2
(35;
Далее находим действительные корни уравнения (35). Затем каждый
из найденных корней исследуем способом сравнения знаков производной
г|2 дня а4-Ааи для cq + Да. Если знак г)(а) переходит +к-. то при
а = otj имеем для Ц2(а) максимум, а если от наоборот - то минимум.
Полученное значение а в случае максимального значения функции
т|2(а) будет оптимальным для рассматриваемого условия эксплуатации (со-
ответствующего значения коэффициента трения скольжения).
Пример. Определить величину утла а и значение к.п.д. ц2 для запира-
ющего механизма автомата АК. принципиальная и расчетная схемы кото-
рого приведены на рис. 31 и 32.
Исходные данные
Коэффициент трения скольжения f................... 0,25
Угол самоторможения у.............................6 0
Средний радиус площади контакта
боевых упоров Г( ................................. 10.7-10'3 м
Средний радиус площади контакта ведущего
выступа затвора г................................. 14,4-10'3 м
1. Определяем значения постоянных параметров:
А = cos у + f sin у = 0,99 + 0,25 0,1 = 1;
Al = sin у + f cosy = 0,1 + 0,25 0,99 = -0,15;
A2 = sin у cos у = 0,99 0,1 = 0,1;
A3 = sin2 у = 0, pi = — = 0,74;
r
B = MAi - f = 0,74(-0,15) - 0,25 = -0,36;
Bi = 1 - p.A2 1 0,74(-0,15)2 = 1;
В2 = (1 - f2l‘A2 = (1 - 0,252)- 0,74 • 0,1 = 0,07;
В3 = 1 - f2 + 2fpA2 = 1 - 0,252 + 2 • 0,25 0,74 0,1 = 0,97;
В4 = 2fp-A3 - 2f = 2 0,25 0,74 • 0 - 2 • 0,25 = -0,5.
2. Определяем значения угла а по формуле (35):
а = arctg
(- 0,ЗбХ- 0,5)_
(-0,36)-0.97-1 0,07
± If °’18У 1 °>5
\ f 0,42 J + 0,42
= arctg0,75 = 36,9°.
Принимаем а = 37°.
Исследуем полученное значение корня способом сравнения знаков
;•> ягзводной T]j(сх) при
Аа = -10°,а = 27° :
, / \ .2 2ВВ4 О]В4
l2V BB3-B1B2 BB3-BjB2
= 0,512 + 0,86 0,51 -1,19 = -0,49;
Aa=10°,a = 47°;
p'(a) = 1,07 2 + 0,86 1,07 - 1,19 = 0,87.
Таким образам, полученное значение угла а соответствует минимуму
. икции Г)2(а).
4. Определим величину к.п.д. тр:
, I1 ~ ftga + цАд (Alga - A3)]tga
2 [1 + u(A2tga - А3)] -[(1 -7^(7+2f]
_ [1-0>25-0,75-0,74 0 15(1 • 0,75 - ОД5)]0,75 = $
[1 + 0,74(0,1 • 0,75 - О^^оТ^Х^ТгХгз]
Так как полученное значение к.п.д. меньше 0,4, то для определения
ia а необходимо, используя данную функцию, получить алгебраическое
1внение при = 0,4.
7 ( IИ ТЕМЫ С ОТКАТОМ СТВОЛА И ЗАТВОРА
PaccMoipHM вопрос расчета и проектирования систем с откатом ство-
ла и затвора. Фу пкпию движущего механизма выполняет баллистический
двигатель - ствол.
Основное назначение движущих механизмов - сообщить основному
звену к концу отпирания канала ствола (на активном участке) определен-
ный запас кинетической энергии, необходимый для надежного функциони-
рования механизма автоматики в естественных условиях эксплуатации. За
критерий надежности функционирования автоматики может быть принят
приведенный запас кинетической энергии подвижных частей в конце отката
Еь, который для шта тных образцов автоматического оружия составляет:
для пистолета Еь 3,5 Дж при Л = 0,04 м,
для автомата Еь = 5,5 Дж при X = 0,135 м,
для пулемета Еь = 8,5 Дж при X -' 0,154 м.
При изменении рабочего хода основного звена механизма автомати-
ки приведенный запас кинетической энергии в конце отката будет опреде-
ляться по зависимости
Е’ь=Е^-,
Л
где X - принятое значение рабочего хода основного звена механизма авто
матики.
Кинетическая энергия основного звена в конце активного участка ра
боты движущего механизма Ео при определенном значении его массы пц
будет определяться величиной необходимой скорости Xjq. Величину пос-
ледней можно на этапе проектирования образца оружия определить исхо-
дя из баланса кинетической энергии подвижных частей с начала открыва-
ния канала ствола Ej до конца отката:
Ei=Eb + £Ah
j=i
N
где X Aj _ суммарная работа сил сопротивления исполнительных меха
j=l
низмов в откате, с использованием соответствующих зависи-
мостей теории удара.
Рассмотрим зависимости для определения работы силы сопротивлс
ния исполнительных механизмов.
Работа силы сопротивления возвратной пружины
Ар
Л 'j
ПА + -- Ро
г Ро = 13
Работа силы сопротивления боевой пружины
А = А • X. -г-К.
Фк
ie vK. <[>к - соответственно коэффициент приведения сил от курка к основ-
ному звену механизма автоматики и его рабочий угол поворота;
Хк - рабочий ход основного звена механизма автоматики на участке
взведения курка.
Работа силы сопротивления буферной пружины
к -)
ic - рабочий ход основного звена механизма автоматики на учасгке ра-
боты буферного устройства.
Работа силы сопротивления пружины ствола
А = пАс+ 7^ Ро.
I 2 ) '
с 1С - рабочий ход ствола на участке деформации его пружины.
Работа силы сопротивления патронной ленты
Ал = + <2л)фл^л>
!С z.v Фл " передаточное отношение и коэффициент приведения сил от лен-
ты к основному звену механизма автоматики,
- перемещение основного звена механизма автоматики на участ-
ке работы патроноподающего механизма ленточного типа;
х1с - средняя скорость основного звена механизма автоматики на
рассматриваемом участке.
Из опыта расчета характеристики движения основного звена меха-
1 ',ма автоматики на учасгке работы патроноподающего механизма лен-
• iHoro типа можно принять
х1с « 1,4х1б = 2 J—
iде них,) • приведенная масса основного звена механизма автоматики на
рассма । риваемом участке ei о перемещения.
Рассмо 1рнм вопрос расчета и проектирования движущих механизмов
применительно к системам автоматического оружия с различными схема-
ми автоматики.
7.1. Системы с откатом ствола
При проектировании автоматического оружия с откатом ствола ис-
пользуются схемы автоматики с длинным и коротким ходом ствола.
7.1.1. Системы с длинным ходом ствола
В данном случае вопрос проектирования сводится к определению
массы подвижных частей П1п . Согласно закону сохранения энергии мо-
жем записать следующее уравнение:
т2 N
Е1 = ^’—Еб + SAj.
2mur j=l
Из данного уравнения получим
m
(36)
7.1.2. Системы с коротким ходом ствола
В системах с коротким ходом ствола затвор жестко связан со стволом
iiHini, на некотором пути отката (свободный ход). После отпирания затво-
ра ciboji в течение некоторого времени движется назад, а затем с помощью
сгпольной пружины возвращается в исходное положение. Затвор продол-
жает откатываться за счет энергии, ко торую он получил при движении до
момента отпирания, и дополнительной энергии, полученной им от ствола с
помощью ускорительного механизма.
Свободный ход ствола вместе с затвором (путь до момента отпира-
ния затвора) приближенно можно определить следующим образом: если
начало отпирания затвора будет совпадать с дульным моментом, то рас-
цепление затвора со стволом произойдет в период последействия газон,
когда давление в канале ствола, как известно, быстро падает. В этом слу-
чае экстракция гильзы будет происходить в благоприятных условиях и
возникновение поперечных обрывов 1ильзы маловероятно.
Если пренебречь сопротивлением ствольной и возвратной пружин, то
юбодный ход системы
m + 0.5ши
1 =------------1Д, (37)
®*ств + ®*затв
io шста - масса ствола.
В большинстве систем с коротким ходом ствола исполнительные ме-
- П1ИЗМЫ автоматики используют для своей работы энергию подвижных
। юней автоматики (затворной рамы). Поэтому в подобных системах энер-
пя затвора пополняется за счет энергии ствола с помощью ускорительно-
>> механизма. Перед началом работы ускорительного механизма (начало
эботы совпадает с моментом отпирания затвора) скорость ствола и зат-
, >ра
шп + 0.5шю
v =—S----------
тн *0
тств + тзатв
и- VH - скорость ствола и затвора в начальный момент работы ускори-
тельного механизма.
Кинетическая энергия ствола и затвора определяется соответственно
, > зависимостям
m V2
р _ Ц1СТВ тн .
^ств — 2 ’
m V2
р _ затв и
*ОТат 2
Очевидно, что только в идеальном случае - без потерь энергии на
г.т гие пружин и в ускорительном механизме - максимальная кинетическая
юргия затворной рамы могла бы быть равна сумме Еств и Езат, а макси-
' । льная скорость затвора
V - I__________-___(Е +Е У2| 1 + П^ств- |
Тзатвшах , ' ств затв/ Г'н| (ЗУ)
у Шзатв у \ ®Цатв)
Увеличение передаточного отношения с помощью ускорительного ме-
V
лшзма z - —не приводит к возрастанию скорости затвора, а только
^затв
.сныпает время работы ускорительного механизма, при этом увеличива-
ся нагрузки, действующие на элементы ускорительного механизма.
( дрмчи сюропы, скорость затворной рамы должна обеспечивать
запас iiicpi iiii i с.
Е
1 =
V2
затв т затвмах
п
= Ez + EAj.
j=i
2
7.2. Системы с откатом затвора
В практике проектирования автоматического оружия находят приме-
нение схемы автоматики с откатом свободного и полусвободного затво-
ров. Функцию движущего механизма в данных системах выполняет также
баллистический двигатель - ствол. Особенности работы рассматриваемых
схем автоматики - наличие сил трения между гильзой и патронником, дей-
ствие давления порохового газа через дно гильзы на затвор.
7.2.1. Системы со свободным затвором
В данном случае вопрос проектирования сводится к определению массы
затвора. Согласно закону' сохранения энер! ин запишем следующее уравнение:
I«S2 N
2Фзт18кн j=i
Из данного уравнения получим
mi =
2(Рз$кн
t2q2
__________
( N
Еб + ZAj
< j=i
(40)
7.2.2. Системы с полусвободным затвором
В процессе проектирования запирающих механизмов с откатом полу-
свободного затвора необходимо определить величину приведенной массы
затвора ni(xr) и скорость подвижных частей к копну работы механизма
Рассмотрим решение поставленной задачи применительно к механиз-
му. включающему три кинетически связанных подвижных звена при по-
стоянном значении приведенной массы затвора, т.е.
m(xt) = const.
Уравнение баланса энергии подвижных частей с момента ударного
подсоединения к затвору кинематически связанных с ним звеньев в конце
работы запирающего механизма до конца отката будет
EJ"4+"2^fcLE6+£Ai;
2 j=l
_(rn1+rn2)xlm+m3x3m
xi - ;
ni] + m2 + ni3
ми, учитывая то, что x3m = z3xlm, получим
_ m, +m2 + m3z3
X1 xlm,
ni]+ni2 + m3
де mI; m2, m3 - соответственно масса затвора, промежуточного звена
и затворной рамы;
z3 - передаточное отношение от затвора к затворной раме;
х1ш - максимальная скорость затвора к концу работы движущего ме-
ханизма.
Подставив выражение для в уравнение баланса энергии, получим
I / N А
2(mj + m2 + m3l Еб + JA,
4 Л__________________\ Н ).
х1т
Ш] + т2 + m3z3
С другой стороны, к концу активного участка работы движущего ме-
ханизма
= ^б$дн______
lm m(x1>p3SKH
Приравнивая правые части последних уравнений, получим
/ \ (i»i+m2 + m3z3)l6S ди
m\xi)- । ' " - ;
1 I N
<P3SKHJ2(ml + nl2 + I»3 J Еб + £ Aj •
V I j=i J
(42)
В формуле (42) неизвестны передаточные отношения механизма. Для
их определения необходимо получить соответствующие аналитические за-
висимости применительно к конкретной схеме механизма-. Затем провести
анализ аналитической зависимости для к.п.д. механизма применительно к
;aiрудне-i11!।.1 м \ч ц>виям работы, в результате которото получаем соотно-
шения для со । соме грических параметров. Определив закономерность из-
менения 1 соме 1 рнчсских параметров в определенном диапазоне и рассмат-
ривая нормальные условия работы механизма, рассчитываем закономер-
ность изменения приведенной массы ш(х1) функции одного из них. По ре-
зультатам расчета строим график. Рассчитываем, а затем строим i рафик
изменения правой части уравнения (42) в функции принятого геометричес-
кого параметра механизма. Точка пересечения указанных графиков дает
величину необходимой приведенной массы затвора m(Xj) на участке рабо-
ты запирающего механизма. Построив график изменения передаточного
отношения z3 функции принятого геометрического параметра механизма и
проведя через точку пересечения предыдущих графиков вертикальную ли-
нию, получим соответствующее значение z3. Далее по формуле (41) опреде-
лим скорость подвижных частей к концу работы механизма х^.
Пример. Спроектировать запирающий механизм с полусвободным
затвором для автомата калибра d - 5,45 мм, принципиальная схема кото-
рого приведена на рис. 33.
Рис. 33. Принципиальная схема полусвободного затвора:
1-затвор. 2-ролики. 3-затворная рама
Исходные данные
Усилие предварительного поджатия
возвратной пружины П,........................25 Н
Жесткость возвратной пружины с...............185,2 Н/м
Рабочий ход X ...............................0,135 м
Минимальная энергоемкость боевой
пружины Amin ................................0,82 Дж
Угол поворота курка срк .....................1,39 рад
Коэффициент приведения сил от
курка к затвору v|/k ........................33,2 1/м
Перемещение затвора на участке
взведения курка Лк .......................... 0.06 м
Приведенная кинематическая энергия
подвижных частей в конце отката Еб...........5,5 Дж
Площадь поперечного сечения
дна гильзы S.IH.............................. 0,785 10'4 м2
Площадь поперечного сечения
капала ствола SKH............................ 0,245 10“4 м2
Масса пули mq................................ 3,410'3 кг
Масса порохового заряда ши...................1,35 10~3 кг
Коэффициент фиктивности массы пули ф.........1,1
Начальная скорость пули vn...................910 м/с
Масса затвора ш,.............................0,07 кг
Масса двух роликов т2........................0,03 кг
Масса затворной рамы ш3......................0,4 кг
Коэффициент фиктивности массы затвора ф .....1,64
Диаметр ролика dp............................8- 10~3 м
1. Определяем работу возвратной пружины:
а а r 185,2 0,135; ,ЛТТ
Ар = н---------Ро = 25 0,135 н-------------1,3 = 6,6Дж.
I 2 J I 2 J
2. Определяем работу боевой пружины курка:
Ак = A mi _ХК = о,82 • 0,06 33,2 = 1,2Дж.
к ш*“ фк 1,39
3. Применительно к расчетной схеме механизма, приведенной на рис.
34,а определяем аналитические зависимости для передаточных функций.
Из условия равновесия звеньев механизма под деме гнием заданных сил по-
лучим следующие аналитические зависимости для передаточных функций:
z2 = —-Ц- ,Т)2 = 1 ~ f 2 + 2ftgp;
cosp
z -sin(P + Y) = (tgy - f/1 - f2 - 2ftgp)
3 sinycosp’ 3 (l + f^tgy
Puc. 34. Полусвободный затвор:
a - pin читая i хема, б - схема графического определения
основных параметров запирающего механизма
4. Из зависимости г|3 представим зависимость для угла у:
y = y(f >Р);
у - arctg i
2f 2tgP - f(l - f 2)
Tf^ + ^ + ZftgP-l’
Из условия заклинивания механизма 1 - f2 - 2ftgp - 0, откуда мини-
мальное значение утла
о l f2
2f '
В рассматриваемом механизме имеет место трение качения, т.с.
f.aL
dp
d2 - 4f 2
|3<агсГ«|, к
dp4fK ’
। де fк = 0,0004 м - для затрудненных условий работы механизма;
fK = 0,0003 м - для нормальных условий работы механизма.
Применительно к нормальным условиям работы
Р < 81,5.
Задаваясь изменением угла р в диапазоне от 5 до 45°, определяем со-
। >тветствующие значения угла у.
5. Определяем при f = fK величину и закономерность изменения пере-
ыточных функций z2 = z(p),T|2 = r|(p),z3 = z(p),т|з = T|(p), а затем вели-
чину и закономерность изменения приведенной массы. По результатам
расчета строим графики m(xj ) ~ m (р) И z3 = z(p).
6. Проводим расчет правой части уравнения (42), обозначив ее через
А =
Фз$кн
(™1 + m2 -ип3г3)1б8дн '
I / n у
2(mi +m2 + m3) Еб+ XAj
j=1 )
-—- = 1,43;
910
т ( о Y о 1300
Хб = VPmq +РтШЛ0’Р =---
V0
I6 = (1,1 3,4 10’3 +1,43 1,35 10“3)910 = 5,16H c;
A =_______5ДФ^ = 0?274 1д
1,64 0,245 10-4^2(0,07 + 0Д)3 + 0.4X5.5 + 6,6 1,2)
По результатам расчета строим график А = А(р).
7. И i графиков, приведенных на рис. 34.6. получаем
m(Xj) = Зкг, z3 = 2,2.
8. Определяем максимальную скорость затвора к концу активного
участка работы движущего механизма:
1б8дн 5,16 0,785 10 4 . . ,
х = — ----=------------------- = 3,4м/с
т(х3)ф38кн 3 1,64 0,245 10 4
9. Определяем скорость подвижных частей к концу работы запираю-
щего механизма по формуле (41):
m, + m2 + m3z3 . 0,07 + 0,03 + 0,4 2,2 . ,
xt = -1---------xim =-----------------’----3,4 = 6,7 м/с
rnl+m2 + m3 0,07 + 0,03 + 0,4
8. РАСЧЕТ И ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ ДОСЫЛАНИЯ
ПАТРОНОВ В ПАТРОННИК
Досылание патрона в патронник в автоматическом оружии осуще-
ствляется при безударном воздействии на патрон и наличии ударного воз-
действия на патрон в начале и в конце его досылки.
При проектировании досылающего механизма необходимо выпол-
нить следующее условие: силы, действующие на элементы патрона в про-
цессе его досылки, не должны превосходить усилия, извлекающего пулю
(снаряд) из гильзы для данного па трона.
При безударной досылке патрона величина и закономерность изме-
нения сил инерции, действующих на элементы патрона, могут быть опре-
делены в результате решения дифференциального уравнения движения ос-
новного звена автоматики.
Особый интерес представляет расчет инерционных сил, возникающих
в элементах патрона при извлечении его из звена ленты в механизмах с не-
прямой досылкой.
В образцах оружия, где извлекатель патронов жестко связан с веду-
щим звеном автоматики, например, в пулеметах ПК, ПКМ, КПВ, можно
считать, что извлечение патронов из ленты осуществляется безударно,
плавно. Ускорения, возникающие в элементах патронов, в этом случае
можно определить по значению максимального ускорения основного зве-
на автоматики на участке извлечения патронов. По значению Xjm на этом
участке можно определить силу инерции, действующую на соединение
нули с дульцем гильзы:
Ри
Данное значение Ри < Рц не должно превышать пулеизвлекающего
\силия для досылаемого патрона.
В системах оружия, где извлечение патронов из звена ленты сопро-
вождается ударом извлекателя по фланцу гильзы (пулеметы РП-46, СГМ,
ДС-39), и в других системах, где извлечение патронов из магазинов сопро-
вождается ударом досылателя по дну гильзы (в автоматах, пистолетах), а
1 акже при фиксации патронов в патроннике возникают значительно боль-
шие ускорения, чем при безударной работе и соответственно большие
инерционные усилия в элементах патронов.
Найдем зависимость для расчета допустимой скорости досылателя
при ударном досылании патрона.
Для расчета инерционной силы в этом случае можно воспользоваться
’.ависимостями теории удара при допущении о том, что между поверхнос-
i ями дульца гильзы и запрессованной в нем пули при ударе возникает де-
формация сдвига.
В начале досылания патрона потенциальная энергия деформации
с. щита при ударе выражается через потерю кинетической энергии подвиж-
иых частей автоматики по следующей зависимости:
Шпг Шпа 2
11 ~ -----------
2(тпг *" тпа )
тогда
РЛг _ Шпг '"па *2.
2СиГдг 2(тпг + тпа )
। ie Ри - инерционная сила при ударе;
тпг - масса подвижных частей;
шпа - масса патрона;
1Д1 - длина дульца гильзы;
ГД1. - площадь сопряжения пули и дульца гильзы;
f - коэффициент трения скольжения пары пуля-дульце гильзы;
GH - условное напряжение сдвига в соединении пули с дульцем гильзы;
Р„ - пулеизвлекающее усилие.
Из условия отсутствия смещения пули относительно дульца гильзы
Р < Рп- Тогда при Ри = Рп, после соответствующих преобразований, по-
лучим сгс lx югн\ io '.авнсимость для предельной скорости подвижных час-
тей:
[х2 ] = I ^тнч + т"а >ДГ«>п (43)
V тпч ' тпа
Пример. Определить предельную скорость подвижных частей при
ударном досылании патрона.
Исходные данные
Масса подвижных частей тпч................. 0,5 кг
Масса патрона mna.......................... 0,015 кг
Длина дульца гильзы 1дг.................... 0,008 м
Коэффициент трения пары пуля-дульце
гильзы f.................................. 0,1
Пулеизвлекающее усилие Рп................. 1200 Н
1. Определяем предельную скорость подвижных частей по формуле
(36):
- ] _ /(®пч тпа Kr^n
X1J- I —
V тпч тпч
Яо?5 + 0ДИ5У0,008 0,1 1200
]! 0,5 0,015
= 8,9 м/с.
9. РАСЧЕТ И ПРОЕКТИРОВАНИЕ
ГАЗООТВОДНОГО ПРИВОДА АВТОМАТИКИ
В автоматическом оружии широко используются системы с отводом
порохового газа из канала ствола в боковое газоотводное устройство
(БГУ),что объясняется широкими энергетическими возможностями такого
привода механизма, обеспечивающего надежную работу механизма авто-
матики в естественных условиях эксплуатации.
Один из вариантов проектирования БГУ состоит в определении по-
требного импульса БГУ и диаметра газоотводного отверстия в стволе по
следующим конструкт ивным параметрам, назначаемым проектировщиком:
nij - масса затворной рамы, dn - диаметр поршня;
wOK - начальный объем газовой камеры; Adn - диаметральный зазор;
L10 - расстояние or казенного среза ствола до газоотводного отверстия.
Необходимую эффективную величину импульса БГУ определим ис-
ходя из количества движения приведенной массы затворной рамы к концу
участка отпирания:
m(xi)xio =
В приведенном выражении Xjq - неизвестная скорость затворной
рамы в конце участка отпирания. Для определения ее, используем уравне-
ние баланса энергии подвижных частей с начала открывания канала ство-
ла до конца отката
Е1 = 1111±^(11о)2 = Еб + ^А.
2 j=l
и соответствующую зависимость при ударном подсоединении затвора к
затворной раме
хю =------------ хю.
П1( +ш2
Используя приведенную систему уравнений, получим
N
2(mi+m3)(E6 + XAj)
± _ V j=i .
хю ~
Тогда импульс БГУ определится по следующей зависимости
JK3 ~ -1) J2(mi + ш3)(Еб + £Aj)
mi \ j=i
где Ш], т3 - соответственно масса затворной рамы и затвора.
Величина удельного импульса БГУ к концу отпирания канала ствола
: ^кэ
’ Sr
Эффективная величина импульса БГУ обусловлена сбросом порохо-
вого газа в атмосферу после отпирания канала ствола и составляет часть
удельного импульса порохового газа, поступившего в газовую камеру за
период выстрела.
Для определения диаметра газоотводного отверстия необходимо
знать величину удельного импульса порохового газа i,.
()п|ч чс icmie величины подведенного удельного импульса порохово-
го lain рассмофспо ранее. Неизвестными параметрами для определения
величины ik являю юя Ркт и tkm.
Как ука и.тадось ранее,
7...10’
fk = + *з)
ИЛИ
Максимальное давление порохового газа в газовой камере с учетом
величины удельного импульса порохового газа к концу выстрела
тогда, исходя из известной эффективной величины удельного импульса,
получим
р _ ____ г 1кэ__________,
Рк“’е<Ьт^7Ы1 + гф]- 1471
где tk, - время эффективной работы БГУ или время движения затворной
рамы к концу отпирания канала ствола.
Время эффективной работы БГУ определим в первом приближении,
исходя из следующих соображений. Примем допущение о том, что ско-
рость движения затворной рамы на участке отпирания постоянна и равна
Xjq. Затем определим скорость затворной рамы к концу участка свободно-
го хода Xjo, используя формулу удара в Начале отпирания канала ствола
т1
±10 = т(х10)Х1с’
откуда
^m(xioh
х1с - х10,
1111
где m(\Ih) - приведенная масса затворной рамы па участке о тпирания.
При линейном законе изменения скорости затворной рамы на участ-
ке свободного хода, получим следующую зависимость для определения
времени эффективной работы БГУ:
t _ 2х1с , х10
‘кэ - ~--+ ----
х1с х10
или
_ 2m1xlc + m(x10)x10
‘кэ ---------, (48)
т(хю)х10
> те х1с, х]0 - длина участков свободного хода и отпирания канала ствола.
Далее, используя полученные формулы (44...46) и (48), находим зна-
1сние параметров, входящих в уравнение (47), и определяем величину мак-
симального давления порохового газа в БГУ по уравнению (47). Величину
v тельного импульса порохового газа в БГУ за период выстрела определим
но ранее полученной зависимости:
Jk = Pkmetkm-
Определение диаметра газоотводного отверстия d0, обеспечивающего
.аданную величину удельного импульса порохового газа, проводим, ис-
пользуя табличный метод, предложенный профессором М.А. Мамонтовым.
Определяем величину относительного удельного импульса:
Входными величинами табличного метода являются значения отно-
сительных параметров сг0, оп. оЛ], стД, для определения которых задаемся
величиной геометрических размеров БГУ: в первом приближении в соот-
ветствии с величинами dp, wuk = (8...10) 10-3Sn. Adn = 0,1 103м. образца ору-
дия аналогичного назначения; (d > 210-3 м - диаметр газоотводного отвер-
гия в стволе).
Далее, варьируя величину d0 и используя табличный метод [10, табл.
4-7]. Искомая величина d0 будет получена при условии равенства расчетно-
о и табличного значений относительного удельного импульса с погреш-
ностью 2 %, т.е.
hk » hb.
Пример. Спроектировать БГУ для пулемета калибра d=7,62 мм
(обр. 1930 г.).
Исходные данные
Подведенный удельный импульс i, ...............0,7-105 Нс/м2
Масса >а торной рамы гщ........................0,9 кг
Масса затвора т3................................0.1 кг
Момен т инерции затвора относительно
продольной оси т2...............................6- 10“й кгм2
Коэффициент приведения сил па участке
отпирания ц/2...................................1/м
Передаточное отношение на участке
отпирания z2....................................54 1/м
Диаметр поршня dn............................... 14-Ю’3 м
Диаметральный зазор AdH........................0.1-10'3 м
Усилие предварительного поджатия
возвратной пружины П] ..........................40 Н
Жесткость возвратной пружины с..................260 Н/м
Рабочий ход X...................................0,154 м
Масса патрона со звеном т,,.....................0,03 кг
Жесткость ленты с,..............................15104 Н/м
Перемещение затворной рамы на участке
подачи патронной ленты на шаг X,..............0,1 м
Коэффициент приведения сил от
ленты к затворной раме д/л.....................0,65
Передаточное отношение от
ленты к затворной раме гл......................0,23
Момент инерции рычага подачи
относи т ельно оси вращения т4..................0,6-10-4 кгм2
Коэффициент приведения сил о г
рычага подачи к затворной рамс у/4..............55 1/м
Передаточное отношение от рычага
подачи к затворной раме z4......................2.0 1/м
Перемещение затворной рамы на
участке свободного хода х]с.....................8-10’3 м
Перемещение за творной рамы на
участке о тирания х)0.............................10-10-3 м
Время движения пули по каналу
ствола к дульному моменту twl...................1,29м 10-3 с
Дульное давление Рл.............................667-105 Па
Начальная скорость пули v0......................840 м/с
Масса порохового заряда то......................3,15-10’3 кг
Площадь поперечного сечения
канала ствола S,.H..............................0.476-10-4 м2
Атмосферное давление Ря..........................105 Па
Приведенный запас кинетической
энергии подвижных частей в конце отката Е6.......8,5 Дж
1. Определяем работу возвратной пружины:
Л Z 3 А1СЛ 260 0,1542\
АР ~ (п1^-+ п^)Ро ~ ^40 • 0,154 +--------- 1,3 - 12 дж
Находим работу силы сопротивления патронной ленты при ее подаче
на шаг при
Q„ - 5тл8 = 5 0,03 10 = 1,5Н;
m(xj) = inj + m3 = 1,0кг;
xlc
2SZ = 2®5 =
\'m(xi) \ 1,0
5,8м/с,
огда
Ал =(7тлслгл±1срл)ч/лХл = (д/0,03-15-104 0,23 5,8 +1,5) 0,65 0,1 = 5,9 Дж.
3. Определяем эффективную величину полного и удельного импуль-
>в по формулам (44) и (45):
rn(xj) = Ш[ + m3 + тдгдц/д = 0,9 + 0,1 + 0,6 10 4 55 - 20 = 1,07 кг;
= 1П(Х1) п2(т1 + т3)[ Еб + £ аХ . 72(Oj7o;i)(8,5 +127^9) =
т1 I j=l ) °’9
8.6 Нс;
Sn = 0,785d2 = 0,785 142 1 0~6 = 1,54 10“4м2;
iK3 = Z- = = 5,6 10 4
sn 1,54 10~4 и2
4. Определяем время, соответствующее максимальному давлению по-
’хового газа в газовой камере, по формуле (46):
. о 1300 1300
^од ~ 1,2910 с, р —1,55;
840
v0
ь = рА" = -667 10 5 М76 10-4 = 1143v
(p-O,5)rnmvo (1,55-0,5) 3,15 10'3 840
,э = 1,„ Б =_u„
b (PaJ 1143
667 1О5
105 ,
= 5,7-10 3 c;
l,l(tOfl + t3) 1,1(1,29 10 3 + 5,7 IO'3) з
1401 8,5 8,5 ’
5. Определяем время эффективной работы БГУ по формуле (48):
m(x10) = nij + m2z2i|/2 = 0,9 + 6 10 6 -54-81 = 0,93кг;
I I N
Шт!+ш3) Еб + £А- _____________________
* I j=i J _ #40,9+ 0,l)(8,5 + 12+ 5,9)
— —--—----------------—--------------------------aJM i CJ
m j 0.9
2m1xlc+m(x10)x10 2 0,9 8 10 3 +0,93 10 10’3 3
lr--> - "" - ------------------------------ «3 4-1 J. V C.
m(x10)x10 0,93-8,1
6. Определяем максимальное давление порохового газа в газовой ка-
мере по формуле (47):
— ^кз
'э
tkm
3,1 10~3
0,9 10 3
= 3,44;
etkm[l -e Z’ (1 + Z3)J
__________5,6 104_______
2,72 • 0,9 103[1е 3’44(1 + 3,44)]
= 266,7 105Па.
7. Определяем величину удельного импульса порохового газа БГУ и
относительного удельного импульса
ik = 266,7 105 2,72 0,9 10 3 = 0,65 105Нс/м2;
ik 0,65 105 ,,,
pk = ? = -------= 0,93.
ir 0,7-105
8. Определяем величину относительных параметров <з0, <зА, оп, от:
w0K = 9 10 3Sn = 9 io 3 1,54 10~4 = 13,86 107m3;
\d„ = 0,1103m, d0 = 2 10 3m, So =3,14 10’6m2;
ASn = 0,785 • (14,l2 -142) • 10"6 = 2,2 • 10 62;
13,86 НТ7 л ,, та. 0,9 кг
— ок s0 = — г- = 0,44м, 3,14 10б = ? j = 5844—у; 1,54 10 4 м2
AS„ 2,2 106 s„ 1,54 10"4 _
Од = —п- = — т = 0,014, °п =— = -7 7 = 49.
sn 1,54 10 4 So 3,14 10’6
9. Определяем диаметр газоотводного отверстия в стволе при
d„ = 2 10'3м:
Лкт 3lKOV0vmvm0 •
Из табл. 4...7 [10] приложения находим
Лко = 0,78, v0 = 0,89; vm = 1,19, vm0 = 1,0;
цкт = 0,78 0,89 1,19 1,0 = 0,83,
1 Лк > Лкт’
Делаем второе приближение. При d0 = 310-3 м,
So = 7,06 10-6 м2.
13,86 10 " 1,54 Ю 4
о ------------ = о,2м, оп =------------г = 21,8.
7,06 10-6 7,06 10 6
Из табл. 4...7 [10] приложения находим
Лио = 0,9, v0 = 0,94; vnl = 1,1, vm0 = 0,98;
Лкт = 0,9 0,94 1,10,98 = 0,91.
Так как п1;, отличается от рт на 2%, то принимаем окончательно
d0 = 3 10-3 м.
10. РАСЧЕТ И ПРОЕКТИРОВАНИЕ СТВОЛОВ СИВ
Известно, что ствольный узел является основным узлом СПВ, обеспе-
н тающим высокоскоростное стабилизированное движение пуль или сна-
рядов (он) к цели. Он является резервуаром, в котором сгорает пороховой
яряд. Давление образующихся при горении пороховых газов использует-
। для сообщения пуле (сн) поступательного движения с определенной ско-
росши и oiipc.ic'ieuiio.M направлении. Ствол выполняет также функцию со-
общения нуле (сп) вращательного движения вокруг ее продольной оси, не-
обходимого для обеспечения устойчивого иолета за пределами ствола.
Высокое давление пороховых газов используется, кроме того, для ав-
томатизации процесса перезаряжания оружия, и ствол, таким образом, явля-
ется в автоматическом оружии основным элементом двигателя автоматики.
Как часть оружия ствол работает в особых условиях. Его внутренняя
поверхность подвергается непосредственному воздействию порохового
газа, обладающего высоким давлением и высокой температурой, а также
трения ведущих элементов пуль (сн) при их движении в канале Эти обстоя-
тельства с неизбежностью приводят к интенсивному нагреву ствола при
автоматической стрельбе.
Интенсивный нагрев конструктивных элементов ствольного узла су-
щественно снижает функциональную надежность как самого узла, так и
всего оружия, вызывая падение дальности, кучности и меткости стрельбы,
ухудшая условия работы автоматики, эксплуатации оружия.
Именно поэтому разработчикам современного СИВ приходится ре-
шать наряду с другими вопросами важнейшие проблемы обеспечения тер-
мостойкости, прочности и живучести ствольного узла.
10.1. Нагрев стволов СПВ
При стрельбе автоматическим огнем стволы СПВ вследствие горения
порохового заряда и воздействия ведущих элементов пуль (сн) нагреваются
до весьма высоких температур, в значительной степени снижающих функци-
ональную надежность ствольного узла и образца СПВ в целом. Среди ос-
новных отрицательных последствий такого нагрева можно отмстить:
1) возможность самопроизвольного выстрела, разрушения ствольно-
го узла и задержек в стрельбе при самовоспламенении элементов снаряже-
ния патрона, находящегося в разогретом интенсивной стрельбой оружии;
2) снижение механических характеристик материала ствола и умень-
шение сопротивления его стенок действию выстрела;
3) снижение живучести ствола, так как износ его канала быстро воз-
растает с ростом температур;
4) ухудшение условий эксплуатации СПВ (увеличение трения в под-
вижных частях автоматики, рассеивание выстрелов, трудности обслужива-
ния и т.п.).
Инженерный анализ этого явления эребует математического описа-
ния процессов теплообмена в ствольном узле при автоматической стрельбе
и количественной оценки его последствий.
10.1.1. Оценка мощности тепловых источников
Многочисленные экспериментальные и теоретические исследования
нагрева стволов СПВ при стрельбе позволили установить, что основными
источниками тепла, определяющими уровень их нагрева являются:
1) работа сил врезания и трения пули (сн) при ее движении по капа-
iy ствола;
2) теплоотдача горящего порохового газа из-за непосредственного
его соприкосновения с поверхностью канала ствола,
3) теплоотдача от порохового газа стенке ствола вследствие тепло-
вого излучения.
10.1.2. Теплообразование при трении пули (снаряда)
Приближенную оценку теплового потока от работы сил трения мож-
но получить, если найти мощность трения на единице площади контакти-
рования
q = fokv,
1 де Чт" плотность теплового потока, образующегося в результате трения
пули (сн) о ствол, Вт/м;
f - коэффициент трения, определяемый эмпирической зависимостью
вида
1 + av
I — 1Л-----.
° 1 + pv ’
f0 = 0,24 - значение коэффициента трения при v = 0;
а = 0,0217, р = 0,132 - эмпирические коэффициенты;
- давление в зоне контакта между пулей (сн) и стволом, Па;
v - скорость скольжения, м/с.
Очевидно, что тепловой поток от работы сил трения распределяется
в основном между стволом ( qc„,) и пулей (сн) ( qn ), т.е.
Чт=Чст+Чп’
причем
Чп ~ атпЧтп’
Чет ~ ~ О' тп )Чт ’
I де атп - коэффициент распределения теплового потока;
А.„, ХсТ - коэффициенты теплопроводности контактирующих материа-
лов пули (сн) и ствола, Вт/(м-к);
р =Hv
ге - число Пекле;
аС1
Н - длина зоны контакта пули (сн) со стволом, м;
аст - коэффициент температуропроводности материала ствола, м2/с.
10,1.3. Теплоотдача пороховых газов
Интенсивность такого теплообмена рассмотрим на основе элемен-
тарной модели явления, предложенной профессором М. А. Мамонтовым.
Предположим (рис. 35), что каждая частица порохового газа, имею-
щая температуру, равную средней температуре газа в ядре его потока Т,,
при ударе о стенку ствола принимает температуру стенки Тст. т.е. ее темпе-
ратура понижается на величину (Тг - Тет).
Рис. 35. Принципиальная схема взаимодействия порохового газа со стволом
При этом допущении количество тепла, которое отдадут за время dt
час тицы газа массой dmfj.
dQ = crdmffl(Tc - Тст) (49)
где С, - удельная массовая теплоемкость газа.
Если представить последовательные удары частиц газа о некоторый
участок поверхности как поток газа, то объем газа, приходящий в сопри-
косновение с поверхностью dF за время dt.
do = dFV"dt,
где V" - средняя скорость удара частиц газа в направлении нормали к по-
верхности.
Тогда их масса составит
dmQ) = prV“dFdt, (50)
где рг - плотность порохового газа.
Подставляя выражение (50) в соотношение (49), найдем
dQ = crprV“(Tr - TCT)dFdt
или
Ч,=^“ = «гРгуг"(Тг-Т„).
С другой стороны, плотность теплового потока по закону Ньютона
выражается зависимостью
- Чг = аг(Тг-Тст), (51)
откуда непосредственно следует соотношение для коэффициента теплоот-
дачи в виде
аг = аорг, (52)
де а0 = crV“ - постоянная коэффициента теплоотдачи, определяемая
обычно по экспериментальным данным.
Таким образом, интенсивность теплоотдачи порохового газа зависит
первую очередь от его плотности.
Экспериментальные исследования показывают, что другими факто-
рами, также существенно влияющими на интенсивность теплоотдачи, яв-
1ЯЮТСЯ скорость газового потока вдоль омываемой им поверхности, диа-
метр канала ствола и др. Это нашло свое отражение в используемых в на-
। оящее время для численных расчетов на ЭВМ зависимостях, рекомендуе-
шь руководящими техническими материалами.
10.1.4. Тепловое излучение пороховых газов
Интенсивность теплообмена между пороховым газом и стенкой ство-
1 । посредством теплового излучения может быть оценена в соответствии с
" лестным законом Стефана-Больцмана. В общем случае плотность тепло-
го потока, воспринимаемого стволом, определяется зависимостью
Чиз
1 4- Ест
2
с0£г
т У
А сг
iooj
(53)
Со - коэффициент излучения абсолютно черного тела, Вт/м;
ЕСТ,8Г - степень черноты газа и ствола.
Пример. Определить мощность тепловых источников в 12,7-мм стволе.
Исходные данные
Коэффициент теплопроводности:
- материала ствола '/.ст......................25 Вт/(м-к)
- материала пули А.г.........................150 Вт/(м-к)
Ко эффициент температур опр ов о дности
материала ствола агг..........................6,4-КГ6 м2/с
Длина зоны контакта пули со стволом Н.........30-10-3 м
Скорость пули V............................... 300 м/с
Давление в зоне контакта между пулей
и стволом <зк.................................200 МПа
Давление порохового газа Рг..............’.... 300 МПа
Температура порохового газа Тг................ 3000 К
Газовая постоянная R.......................... 370 Дж/(кг-К)
Постоянная коэффициента теплоотдачи ..........600 Вг-м/(кг-К)
Температура поверхности канала ствола ТС1.....900 К
Коэффициент излучения сО......................5,77 Вт/м2
Степень черноты:
- порохового газа ег.........................0,8
- стенки ствола ест..........................0,8
1. Определяем коэффициент трения пули о ствол:
f = f0
1 + aV
I+pv
= 0,044-
2. Определяем коэффициент распределения теплового потока:
CL
^ТП
______А_________
лп + 0,57ХстР°’5
= 0,182.
3. Определяем плотность теплового потока, образующегося в рсзуль
тате трения пули о ствол:
qT = faKV = 2,64 109Вт/м2
4. Определяем плотность теплового потока в ствол:
Ост = 0 “атп)Чт ~ 2,16109Вт/м2-
5. Определяем плотность порохового газа:
р = 270 кг/м3
RTr
6. Определяем коэффициент теплоотдачи порохового газа:
ar =aopr =1,62 IO5 ВТ/(м2 Ю-
7. Определяем плотность теплового потока;
qr =аг(Тг-Тст)-3,4 108Вт/м2.
8. Определяем плотность теплового потока, передаваемого стволу
посредством теплового излучения:
1 + Нет
Чиз = - “~ с0Ег
&
ГМ4
liooj
Гт )4
г ст
U00 )
3,33 106Вт/м2
9. Определяем условную мощность тепловых источников, выделяе-
мую на участке ствола длиной Дх = 0,01 м:
NT = qCIndAx = 862кВт;
Nr = qritdAx = 135кВт;
NH3 = qH37tdAx = 1,33кВт.
Таким образом, плотность теплового потока qH3 мала по сравнению с
величиной qr и этим источником тепла можно пренебречь при анализе на-
. рева стволов.
10.1.5. Количество тепла, поступающего в ствол при выстреле
Приведенные в предыдущем разделе зависимости для оценки тепло-
вых источников показывают, что их интенсивность не одинакова по длине
тола. Поэтому и количество тепла, поступающего в ствол за период выс-
1 рела, будет разным для различных участков ствола.
Рассмотрим поперечное сечение ствола (рис. 36), расположенное на
: -эсстоянии х от дна снаряда перед выстрелом.
Очевидно, что количество тепла Q^x, поступающего в ствол при вы-
। реле через небольшой участок боковой поверхности канала, длиной Ах,
рнлегающий к рассматриваемому сечению, может быть определено сле-
. ющим соотношением:
QEx
' tx t2+t3 1
JqCTXdt + Jqrxdt rcdAx
Пх~А‘х ‘x J
tx - время движения пули до рассматриваемого сечения ствола;
Atx - время воздействия трения пули о рассматриваемый участок.
Рис. 36. Расчетная схема ствола
Интегралы, входящие в соотношение, представляют собой количе-
ство тепла, поступающее в ствол от грения пули п воздействия пороховых
газов через единицу площади боковой поверхности канала:
К
qt = jqCTxdt.
ц-дц
*2 +t3
Qrs= fanA
В первом приближении можно допустить, что
Qtx — Чст^х ’
где At «----.
V
’ X
Н - длина зоны контакта пули со стволом;
qc, - плотность теплово!о потока в ствол от трения пули.
10.1.6. Количество тепла от теплоотдачи пороховых газов
По формуле Ньютона имеем
Чгх = «г(Тг -Тх)
или
t-T
Qrx = ’ |аг(Тг-Тх)ск5
К
Тх - температура поверхности ствола на рассматриваемом участке.
Воспользовавшись теоремой о среднем, получим
*2^*3
Qrx = v farTrdt
*х
где v = 1 -
“ - средний относительный перепад температур порохо-
г А
вых газов и стенки ствола.
Учитывая также, что в первом приближении
0Сг — <Х()Рг ’
и принимая во внимание уравнение состояния порохового газа
Р
1<ТГ-
Рг
найдем
Qrx = ^t2fPdt,
где СЦ) - постоянная коэффициента теплоотдачи;
R - газовая постоянная,
Р,рг - давление и плотность газа.
Разобьем весь промежуток интегрирования на два, соответствующих
пиродинамическому периоду и периоду последействия
Qrx = Qi + Q2,
где
Q1=-V^‘jpdt;
к t.
tj + t,
q2 = v^- JPdt.
Используя уравнение движения пули, для первого периода получим
dV рс
<pmq — = PSK„
или
*? t2 фШа dV <pmQ 'г'
fPdt = —1 — dt =---------dV =
J J S dt S J
t t u’kh Ul кЭкн у
(рта , ,
= ^-i(Vo-Vx),
^кн
так что
Qi
R sKH
В периоде последействия давление порохового газа изменяется по за-
кону
Р = Рде-Ь ‘
где Рд - давление в начале периода последействия;
t - время, отсчи тываемое от начала периода последействия.
В соответствии с этим законом длительность периода последействия
составляет
1.
t, = In
3 b
Р 1
д
PaJ
Для интеграла в зависимости нетрудно установить следующую це-
почку равенств:
Таким образом,
q, = TToA
2 R b ’
или, учитывая, ч то для параметра b показательного закона существует за-
висимость.
Р ч
Ь ~ - д ки ____
(p-O,5)mfflvo ’
Q2 = -“~(P-°,5)mfflVo.
Ко ки
В результате имеем
Qrx
^-[<pmq(vo-vx)+(p-O,5)mfflvo .
(54)
Пример. Найти количество тепла, поступающего в 12,7-мм ствол че-
рез участки длиной Ах = 0,01 м, расположенные в начале нарезной части и
\ дульного среза.
Исходные данные
Калибр d.......................................12,7 10'3м
Длина зоны контакта пули и ствола Н............30 10-3 м
Площадь поперечного сечения канала ствола SKH..127 10'6 м2
Газовая постоянная R...........................70 Дж/кг К
Постоянная коэффициента теплоотдачи а0.........600 Вт м/кг-К
Относительный перепад температур v.............0,7
Коэффициент фиктивности ф .....................1,08
Масса пули mq..................................48,210'3 кг
Масса порохового заряда mffl ..................16,5 10'3 кг
Дульная скорость пули v0 ......................800 м/с
Коэффициент полного действия пороховых газов Р.1,625
Скорость пули
- на участке 1 ................................300 м/с
- на участке 2 ...............................800 м/с
Плотность теплового потока от трения пули,
- на участке 1 ................................2,16 Ю9 Вт/м2
- на участке 2................................5,22 109 Вт/м2
1. Определяем количество тепла, поступающее в ствол от трения пули
. воздействия пороховых газов через единицу площади поверхности кана-
.1 ствола на участке 1:
<k,
„ va
Qrx =
' RS
2. Определ:
участке 1:
3. Определ;!
Qtx Чет;
Qrx “ RS
Qvx = (Qj
Таким об$
тепла, поступав]
срезу в связи с
ствола тспловы.^
.»!
В предыду!
лучают различи!
перь задачу опр]
по всей его длщ
величины позво)
вого заряда,a cj
нагрева сiвола, j
Указанное]
где
Qi.,
Для первого из интегралов по соотношению (54) имеем
Q£r = 71(1 j[(Pmq (vo - vx)+ (₽- O,5)mfflvo}lx
или, учитывая, что x = —у vx,
Vo
Qxr = + (p-0,5)mto]v0 jdx-
К\н 0
1,
- Tmq Jvx dx} = 7rd{[(pmq + (p - 0,5)mffl ]v0^ -
_2(Pm51;. j y2dy j = vetoed ! jepm +(р-0,5)шю]-
Vo о RSKH
- j Фгач v0} = rcd• 1Д |cpmq + (p - 0,5)mffl v0 =
з kskh J
(55)
Оценку количества тепла, поступающего в ствол от трения пули (сн),
можно получить на основе соотношений
'« к
QvT = jQTX7tddx - TtdH j(l-arn)fcKdx.
о о
Элементарный анализ соотношений, определяющих значения атп и
f. показывает, что в связи с быстрым ростом скорости пули (сн) в функции
перемещения на большей части ствола может быть с достаточной точнос-
тью принято:
1 - атп = 0,9...1;
Р
I Io ному ini ici рал ( Qy ) приводится к виду
QvT « O,957tdHf0 — ckl,
u P K A ’
где пк - среднее по длине ствола контактное давление между пулей (сн)
и стволом.
Пример. Найти количество тепла, поступающего в 12,7-мм ствол при
одиночном выстреле. Принять в дополнение к исходным данным предыду-
щего примера 1Д = 1 м. = 180 МПа.
1. Определяем количество тепла от трения пули:
QIt = O,95ndHf0 | ок1 д = 8Д9 • 103 Дж.
Определяем количество тепла от действия порохового газа:
_ Н va0
Q11 I R ’
3 mq_
mq vo = 10,3 103 Дж.
3. Общее количество тепла, поступающего в ствол при одиночном
выстреле:
QE =QSr +QSt =18,49 Ю3 Дж.
Таким образом, на нагрев стенок ствола расходуется приблизи тельно
такая же часть энергии порохового заряда, что и на сообщение пуле запаса
кинетической anepi пн поступательного движения
2 Л
mqV(j
2
= 15,3 Ю3Дж.
10.!.8. Численные методы оценки уровня нагрева стволов
Практика инженерного анализа образцов СПВ требует оценки уров-
ня нагрева стволов при решении разнообразных вопросов, связанных, на-
пример, с возможностью самопроизвольного выстрела из нагретых ство-
лов, снижением механической прочности ствола, падением его баллисти-
ческих характеристик, ухудшением условий эксплуатации и проч.
Для этих целей в НИИ и КБ исследуются соответствующие числен-
ные методики расчета на ЭВМ температурных полей стволов как при оди-
ночной, так и при автоматической стрельбах.
Основная идея численных методов решения состоит в том, что исход-
ная математическая задача, сформулированная в дифференциальных опе-
раторах, с гюмошыо некоторых приемов трансформируется к более про-
стому виду, например, к системе алгебраических уравнений.
Ранее мы уже отмечали, что оценка уровня нагрева стволов может быть
дана численным решением уравнения теплопроводности при соответствую-
щих условиях однозначности. Рассмотрим теперь эти решения подробно.
На рис. 37...39 показаны типовые расчетные схемы и соответствую-
щие формулировки, наиболее часто использующиеся в инженерном анали-
зе нагрева стволов СПВ. Из приведенных рисунков видно, что любая раз-
новидность расчетной схемы предусматривает решение уравнения тепло-
проводности, записанного лишь в той или иной форме.
Рис. 37. Принципиальная схема распределения количества тепла по длине ствола
Рис. 38. Одномерная расчетная схема (поперечное сечение ствола)
изотермы
Рис. 39. Двумерная расчетная схема (поперечное сечение ствола)
Теплопроводность при одномерной расчетной схеме определяют по
следующим зависимостям:
ат 'а2т ют)
— = а —аг +---;
at v ar2 г Sr}
Т = То при t - 0;
ат
/ сх, (1,1) 0 при г = гв;
Sr
5Т
г + «в(Т - тв) = 0 при г = гн.
Sr
Поперечное сечение ствола (двумерная расчетная схема) находят по
следующим зависимостям:
ат _ f а2т 1 ат i аМ.
St dr2” г Зг г2 Эф2 J
Т = То при t = 0;
/. ^ + а, (Т Т.) = 0 при r^eTi;
Sn
л^ + ав(Т~Тв) = 0 при г,феГ2.
Sn
Продольное сечение ствола (двумерная расчетная схема) рассчитыва-
ют по выражениям
ат f с2т 1 ат аМ
at ar2 г ar az2 J
Т = То при t = 0;
+ <xr(T-Tr) - 0 при nzeE;
ап
/ „ + «в(Т Тв) = 0 при r,zeT2
ап
10.1.9. Дискретизация решения в пространстве и времени
Рассмотрим теперь задачу о нагреве ствола (рис. 40) более подробно.
Допустим, что с внутренней поверхности ствол, имеющий первоначальную
температуру То, нагревается потоком газа с температурой Тг > То. Причем ин-
тенсивность конвективного теплообмена здесь характеризуется коэффициен-
том теплоотдачи а,.. Пусть также рассматриваемый ствол с наружной поверх-
ности отдает тепло в окружающую среду, имеющую температуру Тв > Тг с ин-
тенсивностью, характеризуемой коэффициентом теплоотдачи ав.
Рис. 40. Двумерная расчетная схема (продольное сечение ствола)
Допустим, наконец, что температурное поле стенки ствола таково,
что температура в ней меняется лишь во времени и по толщине, т.е.
Т = T(r,t). В этом случае необходимо решить уравнение теплопроводности
при следующих краевых условиях:
ат Га2т i ат i а2т^
at 1^ аг2 г аг г2 а<р2 ?
rB <r<rH,t>t0;
(56)
T To при гв < г < rH, t = t0; (57)
ат X н ar(Tr - 1) = 0 при r = rB, t)0; or (58)
ат X— + ав(Т - Тв) = 0 при r = rH, t)0. or (59)
Приведенные уравнения образуют исходную систему уравнений, для
которой ниже рассматривается алгоритм решения методом конечных раз-
ностей.
Рис. 41. Пространственно-временная сетка
Будем искать решение уравнения теплопроводности (56) для момен-
тов времени tk, k = 1, 2. 3 . .. в точках с координатами Г;, i = 0,1, 2, 3, ..., т.е.
будем искать значения температур Т, удовлетворяющих уравнению (56),
только для указанных времен и точек исследуемой стенки (узлов простран-
ственно-временной сетки (рис. 41).
Обозначим через Tik значение температуры в точке с координатой г =
Г; в момент времени t - tk. Будем для простоты считать, что вся толщина
г — г
стенки ствола разбита на N равных интервалов Дг = —---------, называемых
N
шагом интегрирования по координате г, так что
Го = г», Б = Гв + iAr.
rN=rH, i=0,l,2,...N.
Считаем также, ч го значения температур находятся в последователь-
ные моменты времени, отстоящие друг от друга на одну и ту же величину
At. называемую шагом интегрирования по времени, так что
tk = t„ + kAt k = 1.2,3,....
Заменим первую и вторую производные по радиусу в уравнении (56)
разностными отношениями
дт = Ti+lk -
аг ~ 2Аг ’ (60)
d2T ~ Ti+lk ~ 2Tik + Ti-lk
аг2 - 2Ar2 (61)
Первую производную по времени в уравнении теплопроводности (56)
можно заменить одним из следующих отношений:
ат ~\+1-т-
at ‘J? At
1T ~VL.
at At
ат ~ ткт1 - тк
at 2At
(62)
(63)
Очевидно, что здесь возможны и другие расчетные схемы. Поэтому
для краткости ограничимся схемами решения, полученными в соответ-
ствии с (62) и (63).
“Явная” схема решения
Подставляя (60), (61), (62) в уравнение теплопроводности (56), полу-
чим тай называемую “явную” схему решения:
^k+i Tik ~ ГTi+lk - 2Tik + Т;_1к 1 Ti+lk - Т;_1к
= Д----------------------------------------------
At дг2 Fj 2Ar
или
К, Tik ~ ГTi+lk “ 2Tik + Tj-ik 1 Ti+lk “ Ti-lk
At дг2 Fj 2Ar
(64)
Характерной особенностью такой схемы решения является возмож-
ность “явно" выразить из соотношения (64) величину Tik+]
Tj + 1 VAtTi-ik -4 1 - + Цг2 2r-Ar J ' 1К Ar2 J ( 1 1 Кт + . 2 а л (Ar2 2r,Ar)
ИЛИ Tj =aiTi+lk + biTik + ciTi Ik? (65) i = l,2,...,N-l; k = 1,2,3,...,
где ( 1 1 Kt a, = —- + aAt; I^Ar2 2i-ArJ К 1 Кт с'=и?ГЩгГ‘; <661 bi =1-(а, +£,).
Алгоритм расчета температур по разрешающему уравнению (65) зак-
лючается в следующем:
1. По начальному условию (57) находятся значения температур ТН1,
соответствующие первой строке расчетной сетки:
Ti0 = То, i = 1,2,...,N. 2. По уравнению (55), записанному для к = 0, находятся значения тем
ператур Тп, соответствующие второй строке расчетной сетки:
Tj] — ajTi+]0 + Ь(Т;о + С;Т;_]0: (67) i = 1,2,3,...,N-1,
т.е. для всех узловых точек второй строки, кроме двух крайних (Т0], TN,).
Последние определяются из граничных условий (58) и (59), записанных и
виде
XIllKoi + (Xr(T То1)=о; Ar (T Tc) = o Ar
или
Тп + ?гЛг Тг
'Р _________Л____
01 а Дг
1 + - С-
X
(68)
(69)
«ПДГ^
Tn-!, +-г~тв
гг __ _____Л______
N1 авДг
1 + -8---------
X
Таким образом, будет заполнена вся вторая строка расчетной сетки.
3. По уравнению (65), записанному для k = 1, находятся значения тем-
ператур Т12, соответствующие третьей строке расчетной сетки, кроме То2 и
TN2, которые в свою очередь определяются из граничных условий (58) и
(59) и т.д.
Иными словами, если известны значения температур Tik, соответству-
ющие k-й строке расчетной сетки, то по соотношению (65) находятся зна-
чения Tj для всех i, кроме i = 0 и i = N. Остающиеся два значения нахо-
дятся в соответствии с граничными условиями (58) и (59) по зависимостям
Т, +
т , "*' >-
°k+1 . агДг
1+ _г-----_
X
(70)
(71)
TNk+l -
,aji4_rT
N~1к+1 в
t । авЛг
X
Нетрудно установить, что расчет по “явной” схеме решения очень
прост и легко реализуется на ЭВМ по рекуррентным зависимостям (65)-
(71). Однако для него характерна жесткая взаимосвязь между шагами ни-
трирования
Дг2
At<——,
2a
нарушение которой приводит к неверным результатам. Это ограничение
о многих случаях становится чрезмерно жестким и требует значительных
затрат машинного времени ЭВМ на решение сравнительно несложных за-
дач. Поэтому в таких случаях переходят к несколько более сложной, но не
имеющей указанного ограничения “неявной” схеме решения.
“Неявная” схема решения
Если частную производную по времени в уравнении (56) заменить
приближенным соотношением (63), то получим так называемую “неяв-
ную” схему решения уравнения теплопроводности:
At
•+1 -2Т= +TU Т:+1 -Т,
I^Ik_________1 1k । 1 *k
Ar2 2г;Аг
или
1
Аг2
f 1
I^Ar, 2г-Ar
1 (, 2aAt
----- aAtTj_j — 1 н----r-
2r,Ar J k у Дг2
1 aAtT =-Tj
‘k Jk-J
ИЛИ
CiTi lk aiTik +aTi+lk Tk l (72)
i = 2, 3, ..., N-l; k = l,2, 3, ...,
где
f 1
ai “ . 2
I Ar
—-— aAt;
2r;Ar)
Ci
—-— aAt;
2nAr J
1 У
1
Ar
CZj = Э] + Cj + 1.
Если считать, что по некоторым соображениям значения температур
Tj^ ! известны, то для нахождения температур Tj следующей строки рас-
четной сетки необходимо решить систему уравнений специального вида
(72). Для этого разработан эффективный вычислительный алгоритм, нося-
щий название метода прогонки.
Будем искать решение системы алгебраических уравнений (72) в виде
Tik = FjTi+lk +Gi; i = 0,-1. (73)
Если записать данное соотношение для индекса i-1
Ti-1K ~ ‘ TiK + Gi-1
и поставить выражение П1К в уравнение (72), то можно получить
ciFi-lTi + ciGi-1 “ diTiK + aiTi+lK = ~TiK_i
ИЛИ
Из сопоставления (73) и (74) следует, что коэффициенты F,- и Gj мож-
но вычислить по рекуррентным формулам
F: =------!-----,G: = ---——
Из граничных условий можно найти также, что
(76)
(77)
Зависимостей (73), (75), (77) достаточно, чтобы на каждом шаге ин-
тегрирования по времени определять значения температур TiK в соответ-
ствии с алгоритмом:
1) по формулам (76) находятся значения коэффициентов Fo и Go;
2) по рекуррентным соотношениям (75) осуществляется так называе-
мая прямая прогонка, в ходе которой для последовательно возрастающего
индекса i = 1; i = 2 ... определяются значения коэффициентов Ff и Gj вплоть
до Fn.j и Gn.i;
3) по соотношению (77) вычисляется значение температуры TNk на-
ружной поверхности ствола;
4) по рекуррентным соотношениям (73) осуществляется обратная
прогонка, в ходе которой для последовательно убывающего индекса i = N-1,
i - N-2,... определяются значения искомых температур TiK вплоть до Ток;
5) делается новый шаг интегрирования по времени, для которого пос-
ледовательность вычислений повторяется, начиная с п.1.
Можно легко подсчитать, что “неявная" схема решения на каждом
шаге интегрирования требует в 2 раза большего числа арифметических
действий, чем "явная’'. В то же время такая схема не имеет ограничений на
шаги интегрирования и оказывается эффективной для расчета периодов
сравнительно медленного изменения условий теплообмена.
10,1.10. Температурные поля стволов СПВ
Температура является одним из важнейших контролируемых пара-
метров работы стволов автоматического оружия. Круг задач, возникаю-
щих при исследовании нагрева стволов, весьма широк и занимает значи-
тельное место в деятельности инженеров-разработчиков СПВ.
Многочисленные теоретические и экспериментальные исследования по-
зволили выявить многие закономерности трансформации температурного
поля стволов при автоматической стрельбе. Рассмотрим некоторые из них.
Как мы уже отмечали, процесс нагрева стенок ствола при выстреле
о отчается гой особенностью, что промежуток времени, в течение когоро-
I о ствол получает тепло от порохового газа и снаряда, исчисляется сотыми
долями секунды. Из-за кратковременности действия выстрела это тепло
воспринимается лишь очень тонким слоем металла, прилегающим к повер-
хности канала ствола и имеющим толщину не более 0,5 мм.
В этом слое температура при выстреле изменяется чрезвычайно ин-
тенсивно (рис. 42), достигая на поверхности ствола максимальных значе-
ний (1300-1500 К), близких к температуре плавления.
\ /
Рис. 42. Температурное поле при одиночном выстреле
Легко установить. что максимальные температуры определяются
двумя основными факторами: интенсивностью подвода тепла к поверхнос-
ти канала ствола и способностью металла ствола отводить его в глубь
стенки. В начальные моменты действия газа (до tm) металл ствола не успе-
вает справляться с отводом тепла и температура на его поверхности рас-
тет . С течением времени интенсивность подвода тепла от порохового газа
падает из-за уменьшения сто плотности, в го время как созданный в повер-
хностном слое ствола градиент температур еще весьма велик. Процессы
отвода тепла начинают превалировать над процессами его подвода, и тем-
пература в указанном слое снижается.
Однако снижение температуры происходит сравнительно медленно и
продолжается после окончания действия порохового газа (t,). В промежут-
ках между выстрелами (до 1Ц) происходит дальнейшее выравнивание тем-
ператур по толщине стенки-ствола.
Исследования показывают, что выравнивание температур не успева-
ет закончиться к началу очередного выстрела в очереди (рис. 43) и новый
выс трел происходит при более высокой темпера гуре.
Рис. 43. Изменение температуры внутренней поверхности ствола
при автоматической стрельбе
Температура поверхности канала ствола, соответствующая началу
очередного выстрела, носит название температуры, устанавливающейся к
началу очередного выстрела, или просто устанавливающейся температу-
ры. Рост устанавливающихся температур с числом выстрелов в очереди яв-
ляется важнейшей характеристикой ствольного узла (рис. 44).
Рис. 44. Рост устанавливающихся температур с числом выстрелов в очереди
Легко установить, что кривая устанавливающихся температур тесно
связана с темпом стрельбы Тс или, в более общем случае, с режимом
стрельбы.
Из приведенных графиков видно, что устанавливающиеся температу-
ры интенсивно растут с числом выстрелов в очереди. Исследования пока-
зывают, например, что для высокотемпных систем (—1000 -:-1500 в/мип Hit
1 ствол) эта температуры уже к 50 ... 75 выстрелу достигают значений ~ 850
... 900 К, ограничивая, как будет показано ниже, дальнейшую стрельбу.
Интенсивность теплового воздействия пороховых газов и снарядов
различна для различных сечений по длине канала ствола. При патронном
заряжании поверхность патронника теплоизолируется от непосредствен-
ного соприкосновения с нагретыми газами гильзой, уносящей при экстрак-
ции полученный ею при выстреле запас тепла.
Наиболее интенсивно и наибольшее время пороховые тазы воздей-
ствуют на участок канала ствола, прилегающий к началу нарезов. Кроме
того, здесь же происходит наиболее интенсивное деформирование ведущих
элементов снаряда, сопровождающееся значительным тепло выделением.
Очевидно также, что количество тепла, передаваемого стволу при
выстреле, постепенно уменьшается для сечений, находящихся ближе и
дульному срезу. Это связано как с меньшей интенсивностью воздействия
пороховых газов, давление и плотность которых падают но мере движения
снаряда по каналу ствола, так и с меньшей продолжительностью такого
воздействия.
Отмеченное указывает на то, что наибольшего уровня температурь!
достигают на начальном участие движения снаряда по стволу. Именно в
этих сечениях наиболее быстро с числом выстрелов растут и температуры,
устанавливающиеся к началу очередного выстрела.
При перерыв.-! \ в с.'рельбе сначала происходит быстрое (~ за 10 с) вы-
равнивание ।см,iep.-i ।\ р 1 ц> толщине ствола (здесь наибольшие градиенты)
! рис. 45), а за i см w ice медленное по ei о длине.
Рис. 45. Температурное поле ствола при перерывах в стрельбе
Легко установить, что уровень температур в различных сечениях
ствола в первые момент ы после прекрашения стрельбы определяется не
I олько количеством полученного при с трельбе тепла, но и толщиной сте-
нок или массой ствола в этих сечениях.
Может оказаться, например, что участки ствола, расположенные
ближе к дульному срезу и получающие при стрельбе меньше тепла, будут в
первые моменты иметь благодаря меньшей толщине стенок большую тем-
пературу на наружной поверхности, чем какие-либо другие участки. По-
этому дальнейшее выравнивание температур по стволу и ствольному узлу
во многом определяется его геометрией и конструктивным исполнением.
10.2. Прочность стволов СПВ
Стволы СПВ при стрельбе находятся иод действием системы сил, вы-
зывающих сложное напряженно-деформированное состояние (НДС) мате-
риалов их конструктивных элементов.
При выстреле давление пороховых т азов выталкивает снаряд из ство-
ла. При этом давление .в стволе сначала быстро возрастает, достигая вели-
чины Р1П~(35ОО ... 4000)-10? Па. По мере дальнейшего продвижения снаряда
давление пороховых газов из-за увеличения объема заснарядного про-
странства надает до дульного значения Р -500 10s Па.
Веледе гипс тако! о характера изменения давления внутри ствола на-
ружные ею очертания в большинстве случаев представляют собой либо
коническую пнбо с i упепчатую цилиндрическую поверхность с уменьше-
нием диаметральных |>и гмеров к дульному срезу.
Очевидно, что стенки ствола должны быть рассчитаны таким обра-
зом, чтобы они обеспечивали прочнос ть ствола в первую очередь от дей-
ствия давления пороховых газов. Однако при этом необходимо учитывать,
что давление пороховых газов приводит в движение снаряд и ствол, в ре-
зультате чего возникает еще ряд сил. дейс твующих на стенки ствола, силы
взаимодействия снаряда со стволом, силы сопротивления откату ствола,
инерционные силы и проч.
При обжатии и врезании ведущих элементов снаряда в нарезы ствола
происходит пластическое деформирование материала ведущих элементов,
и величина усилия взаимодействия со стволом очень быстро возрастает,
достигая максимальных значений, зачастую превышающих давление поро-
ховых газов. После врезания, сопровождающегося значительным тепловы-
делением. температура поверхности ведущих элементов снаряда возраста-
ет практически до температуры плавления их материала (меди), и при
дальнейшем движении снаряда по стволу происходит интенсивный износ
ведущих элементов.
Этот процесс приводит к быстрому уменьшению радиальных и осе-
вых воздействий на ствол со стороны снаряда по мере продвижения его к
дульному срезу.
При движении по каналу ствола снаряд приобретает определенный
запас кинетической энергии, вращения, необходимых для его устойчивою
полета на траектории. При этом в результате взаимодействия снаряда с бо-
евыми гранями нарезов возникают силы, стремящиеся вызвать поворо г
ствола и его движение вперед. Величина этих сил меняется при движении
снаряда по стволу в зависимости от напряженно-деформированного состо-
яния ведущих элементов снаряда.
Следует отметить также силовые воздействия снаряда на ствол, воз-
никающие в результате колебательного движения снаряда в стволе и неиз-
бежной кривизны оси ствола.
Отдача оружия при выстреле, характер его движения при стрельбе
привозят к возникновению инерционных нагрузок, оказывающих в ряде
случаев (длинные стволы, вращающийся блок стволов и проч.) существен-
ное влияние на напряженно-деформированное состояние и прочность эле-
ментов ствольного узла.
Суммируя изложенное, можно установить, что стволы СПВ при
стрельбе находятся иод действием системы сил, вызывающих сложное на-
пряженное состояние материала их стенок. Очевидными поэтому становят-
ся трудности решения задачи о расчете ствола на прочность при точном
учете всех перечисленных силовых факторов, а также особенностей нагру-
жения ствола при автоматической стрельбе.
Большое разнообразие конструктивною исполнения стволов и усло-
вий их жсплуатации предопределяет сравнительно широкий круг задач
расчетов на прочность. Тем не менее, среди них можно выделить типичные
или основные задачи, т.е. те, которые определяют эффективность и надеж-
ность работы образца СПВ.
Поскольку основным силовым фактором, действующим на ствол, яв-
ляется давление пороховых газов, первой типичной задачей прочностного
расчета можно считать задачу оценки напряженно-деформированного со-
стояния для случаев:
- конструктивного исполнения стволов с различной геометрией внеш-
ней поверхности;
- конструктивного исполнения стволов с различной геометрией кана-
ла ствола;
- наличия концентраторов напряжений;
- действия, помимо механических нагрузок, теплового фактора и т.п.
Другой типичной задачей прочностного расчета является оценка
НДС нарезной части ствола при взаимодействии с ведущими элементами
пуль (сн).
Учитывая сложность анализа процессов нагружения материалов
ствольного узла, в данном разделе рассматриваются лишь некоторые из них.
10.2.J. Упругое деформирование стволов давлением пороховых газов
Стволы СПВ при стрельбе находятся под действием системы сил,
приводящих к работе ствольных материалов в условиях сложного напря-
женно-деформированного состояния. Для простейшей оценки этого состо-
яния примем следующие основные допущения:
допускаем, что ствол можно представить как трубу постоянного по-
перечного сечения, сохраняющую до и после деформации цилиндрическую
форму и всякое поперечное сечение плоским;
пренебрегаем всеми силовыми факторами, кроме давления порохо-
вых газов;
считаем, что давление пороховых газов приложено статически по
нормали и внутренней поверхности ствола и распределено равномерно и
симметрично относительно оси канала ствола;
предполагаем, что материал ствола однороден и изотропен, т.е. свой-
ства материала считаются одинаковыми во всех точках и по всем направ-
лениям.
В этом случае задача сводится к расчету толстостенной трубы, нагру-
женной равномерно распределенным внутренним давлением (рис. 46).
В такой постановке задача была решена в середине XIX века независимо
друг от друга Ламе и Гадолиным.
Рис. 46. Расчетная схема нагруженного ствола
Как известно из курса сопротивления материалов, напряженно-де-
формированное состояние толстостенной трубы, нагруженной внутренним
давлением, характеризуют семь величин (рис. 47):
ог,ат,аг - радиальное, тангенциальное и осевое нормальные напря-
жения;
er,sT,sz - радиальная, тангенциальная и осевая нормальные дефор-
мации; и - радиальное перемещение.
Рис. 47. Компоненты напряженного состояния ствола
Указанные величины связаны между собой:
- уравнениями равновесия
«Ь г + Gr ~ gt _ 0.
dr г
гп
2л Jczrdr = Rz;
г.
- геометрическими уравнениями
du u
gr = —,r, = const •
dr r
- физическими уравнениями
£Г -v(aT +GZ)];
E
4 = “lCTr ~v(ar + CTz)}
E
ez =|k-v(cr
E
где Rz - осевая нагрузка на ствол;
Е, v - модуль Юнга и коэффициент Пуассона ствольного материала.
Решение приведенной системы уравнений с учетом граничных условий
ст г = - Р при г - гв;
пг=0 при г = гн;
Rz =0
позволяет получить следующие зависимости для определения напряжении:
(78)
г( 2 г')
с =_рГв\Гн Ц
г »-2С2
Г V Н ГВ /
cz=0. (80)
Из приведенных зависимостей (78) и (79) следует (рис. 48):
1. Распределение напряжений в стенке ствола неравномерное.
2. Максимальные уровни напряжений достигаются на внутренней по-
верхности ствола:
2 2
сг =-Р<0,ст=рЦ^2к>0.
гн - 'в
Рис. 48. Эпюры напряжений в стенке ствола
3. Сумма радиальных и тангенциальных напряжений одинакова по
толщине стенки ствола:
cr + = idem.
За счет увеличения толщины стенкой невозможно достичь величины
тангенциальных напряжений, меньших, чем давление пороховых газов:
а2 +1
=Р-~-----при г = гЕ;
а2 1
f 2 'l
1|та^да Р 1 + ----= Р,
I a2-lj
~ _ н
1 де а - — - относительный радиус наружной поверхности ствола, харак-
гв
геризующий толщину стенки ствола.
Таким образом, решение задачи о распределении напряжений по тол-
щине стенки ствола позволяет установить, что наибольшие напряжения
достигаются на внутренней поверхности. Однако само по себе знание на-
пряженно-деформированного состояния в наиболее нагруженном месте нс
дает еще количественной оценки прочности ствола. Для получения ее необ-
ходимо ответить на вопросы:
1. Что сравнивать, т.е. какие величины или совокупность величин
взять в качестве критерия оценки прочности?
2. С чем сравнивать, т.е. с характеристиками какого состояния (упру-
гость, пластичность, разрушение) сравнивать такой критерий?
Ответ на второй вопрос кажется достаточно проспим и очевидным -
с свод должен работать в условиях упругости, поскольку только в этом слу-
чае можно ожидать одинаковости условий ведения снаряда по каналу
сI вола. Более поздние исследования показали однако, что сравнительно
тонкий (менее 0,5 мм) поверхностный слой канала ствола неизбежно рабо-
тает в условиях циклического пластического деформирования, вызванного
действием нагрева и связанного с появлением температурных напряжений.
Учитывая, что толщина такого слоя мала по сравнению с толщиной стен-
ки ствола, обычно считают допустимым предположение об упругом де-
формировании.
Ответ на первый вопрос дается теориями (условиями) прочности, г.е. ги-
потезами о причинах перехода деформирования из одного состояния в другое.
Эти теории дают возможность судить о состоянии деформирования
при многообразных сложных нагружениях реальной конструкции на осно-
вании особенностей деформирования ее материала в существенно более
простых условиях (например, на основе диаграммы одноосного растяже-
ния цилиндрического образца).
Известен ряд теорий прочности, которые связывают изменение состо-
яния деформирования:
1) с наибольшими нормальными напряжениями;
2) с наибольшими относительными деформациями;
3) с наибольшими касательными напряжениями;
4) с величиной энергии формоизменения и т.д.
Очевидно, что каждая последующая теория является более совершен-
ной. чем предыдущая, но не идеальной и требует при ее использовании для
расчета конструкций введения соответствующего коэффициента запаса
прочности.
10.2.2. Предел упругого сопротивления ствола
При расчете стволов СПВ обычно применяется вторая теория проч-
ности. для которой на основе многочисленных экспериментальных иссле-
дований найдены определенные коэффициенты запаса прочности.
По этой теории предельное упругое состояние наступает тогда, когда
наибольшая относительная деформация становится равной максимальной
упругой деформации при одноосном растяжении. В рассматриваемом слу-
чае условие прочности запишется в виде
где - предел упругости материала ствола.
Учитывая, что по закону Гука
Ч = - v(or + az)],
Jb
и принимая = 0, v = 1/3. условие прочности
GT-1/3 Gr < Ge,
на внутренней поверхности ствола запишем следующим образом;
2 2а2 +1 „
----->---Р- ае-
За2-1
В инженерных расчетах стволов СПВ максимальное расчетное давле-
ние, которое может выдержать ствол, не получив при этом остаточных де-
формаций, принято называть пределом упругого сопротивления ствола Pv:
3 а2 -1 г
РУ а = —
У 2 2а2 +1 гв
Из полученной формулы видно, что увеличить предел упругого со-
противления можно либо за счет характеристик материала ое, либо за счет
толщины стенок ствола а.
(81)
i 0.2.3. Методика расчета прочности стволов по упругому сопротивлению
Проверочный расчет
Целью проверочного расчета является определение коэффициентов
запаса прочности по различным сечениям ствола и сравнение их со значе-
ниями, рекомендуемыми нормалями и руководящими материалами.
При таком расчете считаются известными кривая давления пороховых
газов в функции пути снаряда по стволу, конструкция и материал ствола.
Расчет проводится в следующем порядке;
1. Выбирается ряд сечений, в которых производится проверочный
расчет.
2. Наносятся кривые давления порохового газа для различной темпе-
ратуры порохового заряда (-50, +20, +50 °C).
3. Строится огибающая кривая давлений Рр. При этом положение
точки максимума давления смещается на 1,5...2 калибра к дульному срезу.
На участке от дна канала ствола до точки максимума давление принимает-
ся равным от РКП1 до РП1, где РК1П = ^КРШ.
4. В выбранных сечениях ствола по формуле
Р =3 а21
Ру - 2 ,
2 2а -ь 1
определяются значения ynpyi <>i о сопротивления ствола и строится соот-
ветствующая кривая.
5. Определяются коэффициенты запаса прочности в расчетных сече-
ниях:
_Pv
пр (82)
ГР
где Рр - значение давления по кривой, п. 3.
6. Строится график изменения запасов прочности по длине ствола.
Расчетные значения сравниваются с рекомендуемыми.
При расчете стволов, имеющих специфические, конструктивные от-
личия от рассмотренного случая, предел упругого сопротивления вычисля-
ется по зависимостям, приведенным в табл. 3.
Таблица 3
Расчетные зависимости для предела упругого сопротивления
Предел упругого сопротивления
Схема ствола
Т9-1
Т9-2
К5 - а—(К1 + 3), к3 = сД(К] +1)
L L
-э 2 2 2
К,=
г2 - и Г3 - r2 L
3
2
3a* 2(at2 - 1)
^а2 +1)(2а12+1)
Т9-3
'az
3 al — 1
РУ = ДГТф,
2а i+l
Расчет при проектировании
Целью расчета является предварительный выбор наружной конфигу-
рации ствола н (или) материала ствола по пределу упругости. При этом
считается, что в результате решения задачи внутренней баллистики полу-
чены все необходимые данные для конструктивного оформления внутрен-
ней поверхности ствола (d, 1Д, Wo, 10 и т.д.).
Расчет проводят в следующей последовательности:
1. Выбираются сечения по длине ствола, в которых производится расчет.
2. Определяются кривые давлений при различной температуре поро-
хового заряда и по известным правилам строится огибающая результиру-
ющая кривая.
3. Учитывая рекомендации по выбору коэффициентов запаса прочно-
сти, строят кривую желаемого упругого сопротивления ствола:
Ру = пРр.
4. По полученным результатам выбирают:
а) материал ствола при заданной его геометрии
б) геометрию наружной поверхности при заданном материале ствола
Гз^еТ2Р7
Гн~Гв^ЗаГ-7]^-
После конструктивного оформления наружной поверхности и выбо-
ра материала проводится проверочный расчет.
10.2.4. Рекомендуемые материалы и коэффициенты запаса прочности
При выборе коэффициента запаса прочности следует учитывать, что
запас прочности неравномерен по длине ствола и может колебаться в зави-
симости от конструктивных, технологических и эксплуатационных факто-
ров в широких пределах. Например, в современных образцах СПВ в связи
со стремлением снизить уровень нагрева стволов реализуются конструк-
ции с существенно более массивными стенками, чем это требуется из сооб-
ражений прочности. Поэтому ниже приведены значения минимальных за-
пасов прочности, апробированные практикой отработки систем СПВ.
В районе максимума давления пороховых газов принимают
п = 1,3...1,5. Такая величина запаса прочности обусловлена как неточнос-
тями рассмотренной выше теории сопротивления трубы, так и возможны-
ми отклонениями действующих величин давлений от расчетных, разбро-
сом механических свойств материала и т.п.
В сечениях ствола в области патронника запас прочности берется
ниже n = 1,0-1,1. Причинами такого снижения являются;
а) наличие казенника и гильзы, воспринимающих часть действующих
нагрузок;
б) отсутствие не учитываемых при расчете силовых факторов, дей-
ствующих со стороны снаряда;
в) высокая точность обработки, отсутствие нарезов и др. У дульного
среза запас прочности берется не менее двух, так как условия работы мате-
риала в концевой части трубы даже при прочих равных условиях являются
более тяжелыми, чем в сечениях, удаленных от торца трубы. Кроме того,
силовые воздействия со стороны снаряда, надульных устройств и т.п. ока-
зывают здесь существенное влияние на напряженное состояние материала
ствола. Однако зачастую даже при п = 2 стенки ствола получаются весьма
тонкими, не обеспечивающими эксплуатационной надежности. Поэтому
обычно принимают п > 2...5.
Для изготовления стволов обычно применяются следующие марки стали:
50А ГОСТ 5160-49, ое = (55...80) 10? Па;
50РА НО 2338-57, СТе = (55...80) 107 Па;
ЗОХРА НО 2774-58, ае = (60. ..90)- 107 Па;
ЗОХН2МФА ГОСТ 5160-49, ае = (70...95) 107 Па.
Выбор марки стали определяется условиями работы ствола. Для
стволов охотничьих ружей, самозарядных и спортивных винтовок, писто-
летов и автоматов рекомендуется применять марки 50А, 50РА, ЗОХРА.
Для пулеметных стволов с целью обеспечения их живучести обычно
используют сталь ЗОХН2МФА, которая сохраняет высокие механические
свойства до температур 850-950 К. Кроме того, в высокотемпных образцах
СПВ для поддержания живучести стволов на требуемом уровне применя-
ются специальные жаропрочные материалы.
Пример. Рассчитать параметры упругого сопротивления 12.7-мм
ствола пулемета “Утес’’.
Исходные данные
Материал ствола.......................... ЗОХН2МФА
Предел упругости СТе .................. 800 МПа
Масса порохового заряда тС) ........... 0,016 кг
Масса пули т(|......................... 0,048 кг
Коэффициент фиктивности ф ............. 1,076
1. Выбираем 15 поперечных сечений по длине ствола, в которых про-
водим проверочный расчет (рис. 49).
2. По результатам внутрибаллистического расчета строим огибаю-
щую кривую Р(1) давлений порохового газа в канале ствола (рис. 49).
В выбранных поперечных сечениях по формуле (81) определяем пре-
дел упругого сопротивления ствола (табл. 4) и строим соответствующую
кривую Pv(l) (рис. 49).
4. В расчетных сечениях по формулы (82) находим значения коэффи-
циента запаса прочности, которые представляем на графике (рис. 49) в
виде кривой п(1).
Рис. 49. Результаты расчета ствола на прочность
5. Сравниваем значения коэффициента запаса с рекомендуемыми. Из
сравнения следует, что расчетная величина п существенно выше минималь-
но необходимых значений по всей длине ствола.
Примечание. Указанный вывод соответствует оценке упругого со-
противления ненагретого стрельбой ствола. В случае автоматической
стрельбы можно считать, что в соответствии с ростом температуры будет
происходить неуклонное снижение запасов прочности.
Таблица 4
Результаты расчета прочности 12,7-мм ствола
Номер сечения а гв Р р , М П а Р д , М П а N
1 2.0 2 3 8 2 5 1 6 1.3 5
2 2.2 9 3 7 5 5 3 7 1.4 3
3 3.0 8 3 7 3 5 6 7 1.52
4 3.4 6 3 6 5 5 7 4 1.5 7
4.0 9 3 6 5 5 8 2 1.5 9
5 4.0 9 3 5 0 5 8 2 1.6 6
3.46 3 5 0 5 7 4 1.6 4
6 3.15 2 2 0 5 6 8 2.5 8
7 2.8 3 1 4 0 5 6 0 4.0 0
2.3 6 1 4 0 5 4 1 3.8 6
8 2.3 6 1 3 0 5 4 1 4.16
2.8 3 1 3 0 5 6 0 4.3 1
9 2.83 1 2 5 5 6 0 4.4 8
2.3 6 1 2 5 5 4 1 4.3 3
1 0 2.2 8 1 0 5 5 3 6 5.10
1 1 2.2 0 9 0 5 3 1 5.9 0
2.3 6 9 0 5 4 1 6.0 1
1 2 2.3 6 8 7 5 4 1 6.2 2
2.2 0 8 7 5 3 1 6.10
1 3 2.0 4 8 0 5 1 8 6.4 8
2.5 2 8 0 5 4 9 6.8 6
1 4 2.52 7 8 5 4 9 7.0 4
2.3 6 7 8 5 4 1 6.9 4
1 5 2.3 6 7 5 5 4 1 7.2 1
10.2.5. Влииние температуры на прочность ствольных материалов
Одним из непосредственных следствий интенсивного нагрева стволов
при напряженных режимах стрельбы является снижение прочности харак-
теристик ствольных материалов. На рис. 50 приведены зависимости меха-
нических характеристик (пределы прочности <Уе, пределы текучести cs.
модуль Юнга Е и коэффициент Пуассона v) от температуры для типичных
ствольных сталей.
Как следует из приведенных графиков, прочностные.характерце гики
ствольных сталей монотонно снижаются с ростом температуры. При этом
наиболее интенсивное снижение этих свойств наблюдается в интервале
температур от 550 до 650 °C. Указанный температурный интервал ограни-
чивает возможность использования ствольных сталей при стрельбе боль-
шими боекомплектами по целому ряду критериев термопрочности, износо-
стойкости и живучести.
Рис. 50. Качественная зависимость механических характеристик ствольных сталей
от температуры: 1-ст. 30ХН2МФА, 2-ст.50РА, З-ст.ЗОХРА
Другим следствием нагрева ствола является возникновение значи-
тельных по величине температурных напряжений. Эти напряжения непос-
редственно связаны с разной нестационарностью и неравномерностью
температурного поля по толщине стенки ствола.
Рассмотрим нагрев приповерхностного слоя металла ствола. Нагре-
вание этого слоя должно сопровождаться его температурным расширени-
ем, которому, однако, препятствует основная толща стенок трубы. Рас-
сматриваемый процесс легко представить состоящим из:
1) беспрепятственного температурного расширения слоя;
2) сжатия слоя практически до исходных размеров. В результате, в
рассматриваемом слое возникнут напряжения сжатия. Очевидно также,
что равномерный нагрев всей стопки не вызовет появления температурных
напряжений, так как в этом случае температурные деформации не встреча-
ют каких-либо препятствий.
Таким образом, можно ожидать, что резкие температурные градиен-
ты, возникающие в стенке ствола при выстреле, должны приводить к появ-
лению температурных напряжений, в значительной мере искажающих на-
пряженное состояние от действия механических нагрузок.
Если в системе уравнений напряженно-деформированного состояния
толстостенной трубы учесть в законе Гука температурные деформации
£Г = ik ~V(°T +oz)] + aT;
Jb
et = - [с?г - v(gf + gJJ-u.T:
го при ранее принятых допущениях температурные напряжения в стенке
трубы определятся зависимостями
(83)
(84)
(85)
где а - коэффициент линейного расширения материала ствола;
Т - температура ствола.
Дадим приближенную оценку температурных напряжений на поверх-
ности каналгт ствола, считая температуру распределенной по толщине
стенки в соответствии с рис. 51.
Рис. 51. Распреде.юшс температуры в поверхнт пишм с.юс егтю.’ш
Из соотношений (83)-( 85) следует, что при г = г„
о
т
г
= 0:
о
т
т
т
= cz
аЕТп, 2аЕ
1-V +(1Т^)[Г2_Г2
rH
fTrdr
(86)
Для принятого закона распределения температур зависимость (86)
принимает вид
Д = Д = --^-(тш-т0Х1-А>
1 - v
=-------=-------,
1 + *к гн ~ гв
гв
где Т,„, То - значения температур на границах поверхностного слоя.
Ранее было установлено, что толщина прогретого слоя при выстреле
не превышает 0,5 мм. Тогда
3«гн - гвД«1
и, таким образом,
т т CtE / \
----(Тш-Т0). (87)
1 - V
Сопоставим в качестве примера напряжения на поверхности канала
ствола от механического и теплового воздействий порохового газа. В ка-
честве исходных данных примем следующие:
dB = 2 гв - 30 мм; dH = 2 г„ = 60 мм;
Р = 3000 105 Па, Тт = 1293 К, То = 293 К;
Е = 2 10” Па: = 1/3; а = 10 5 1/К;
dp
гн
а = — =2
гв
Тогда напряжения оглавления порохового газа
= 0;Ог =-3000 105Па;
2 ।
м = = 5000 105Па
а2-1
1 смпершурпыс напряжения в лом же случае соснавя! 0^-0;
= и,1 = --аЕ- (тш - То)= -30000 105 Па.
1 - v
Из полученных результатов следует, что температурные напряжения
значительно превосходя ! по абсолютной величине напряжения от механи-
ческих воздействий, существенно меняя при этом распределение напряже-
ний в узком поверхностном слое ствола (рис. 52).
Рис. 52. Эпюра напряжений по толщине стенки ствола
Таким образом, при больших перепадах температур, имеющих место
в стенке при выстреле, можно ожидать появления на поверхности ствола
знакопеременных напряжений и пластических деформаций, величина ко-
торых не зависит от толщины стенки ствола.
На этот факт обращал внимание еще в начале XX века выдающийся
русский ученый-металлург Д. К. Чернов. Он считал, что последовательный
интенсивный нагрев и охлаждение поверхности капала ствола в ходе каж-
дого выстрела приводит к циклическим напряжениям сжат ия-растяжения,
образованию трещин и разрушению поверхностного слоя.
10.3. Краткие сведения о живучести стволов СПВ
Непрерывный рост мощности образцов СПВ сопровождает ся повы-
шением начальной скорости пуль (си), максимально! о давления порохо-
вых газов, увеличением скорострельности, размеров отстреливаемого бое-
комплект и ужесточением режимов его отогрела. Все это приводит к более
интенсивному нагреву стволов при стрельбе и, как следствие, к ухудшению
условий работы их материалов.
Повышенный нагрев в значительной степени влияет на изменение ме-
ханических характеристик материала, его способность сопротивляться из-
носу. В результате химического, теплового и механического воздействий
пуль (сн) и пороховых газов происходит по степенное разрушение канала
ствола и снижение его баллистических характеристик.
Свойство стволов противостоять износу при стрельбе в условиях
нормальной эксплуатации принято называть живучестью.
Показателем живучести ствола является технический ресурс -количе-
ство выстрелов до предельного состояния ствола. Для конкретных образ-
цов СПВ, исходя из их функционального назначения, предельное состоя-
ние обычно указывается в ТТЗ.
Например, состояние ствола считают предельным при появлении хо тя
бы одного из следующих признаков исчерпания технического ресурса:
- при увеличении характеристик рассеивания более чем в два раза:
- при отклонении начальной скорости пуль (сн) на К) %;
- при появлении 50 %-овальных или боковых пробоин, для которых
максимальный размер.
При .этом за номинальные значения соответствующих характеристик
принимаются значения, указанные в ТТЗ, или среднестатистические значе-
ния, полученные стрельбой из нового, неизношенного ствола.
Опыт показывает, что для современных образцов СПВ, имеющих на-
пряженные режимы стрельбы, живучесть стволов в зависимости от их ка-
либра составляет в среднем:
- для d = 5.45...7,62 мм N - 12000...25000 выстр.;
- для d = 12,7...14,5 мм N- 5.000... 10.000 выстр.;
- для d = 23...30 мм N- 1.500...6.000 выстр.
Иными словами, длительность активной жизни стволов, определяе-
мая движением пули (сн) по каналу ствола (~0,001...0,003 с), практически
оценивается величинами порядка ~ 1...10 с.
В связи с тем, что продолжительность и интенсивность стрельбы ав-
томатического оружия определяются, прежде всего, живучестью его ство-
лов, а сами стволы являются в технологическом и экономическом отноше-
ниях сложными, дорогостоящими узлами, проблема поддержания живуче-
сти па необходимом уровне считается одной из важнейших проблем повы-
шения эффективности СПВ.
f
10.3.1. Общая характеристика процессов, определяющих износ стволов
При автоматической стрельбе из образцов СПВ в ствольном узле в
ходе каждого выстрела осуществляются следующие основные процессы.
В начале выстрела происходит воспламенение порохового заряда.
Нарастающее вследствие горения пороха давление пороховых газов при-
водит в движение пулю (сн). Пройдя сравнительно небольшой, зависящий
от износа канала ствола участок нуги, на котором возможен прорыв поро-
л о вых газов из запульного (заспарядного) пространства, пуля (сн) начина-
взаимодействовать своей оболочкой (ведущим пояском) с поверхностью
канала ствола. Последующее обжатие и врезание в нарезы ствола приво-
дит к нарастанию радиального и осевого усилий взаимодействия, которые
достигают максимальных значений к концу врезания и постепенно падают
лри дальнейшем движении пули (сн).
На поверхности контакта пули (сн) со стволом возникают значитель-
ные силы трения, работа которых приводит к существенному возрастанию
температуры контакта и определенному тепловому потоку, идущему на
нагрев ствола.
Воздействие пули дополняе тся тепловым, механическим и химичес-
ким воздействиями на поверхность канала ствола пороховых газов, имею-
щих высокую температуру, плотность и концентрацию агрессивных ком-
понентов.
Таким образом, каждый участок поверхности ствола подвергается
более или менее продолжительному и интенсивному нагружению, вызыва-
ющему возникновение в материале ствола соответствующего теплового,
напряженно-деформированного и структурно-фазового состояний и при-
водящему к его постепенному износу и разрушению.
Последующие выстрелы при автоматической стрельбе дополняют и
интенсифицируют отмеченные процессы, которые находятся во взаимосвя-
зи и взаимно влияют друг на друга. В процессе стрельбы общий уровень
нагрева элементов ствольного узла неуклонно повышается и достигает к
концу работы значительных величин, во многом определяющих износ и
живучесть образцов СПВ.
В первом приближении можно считать, что износ определяется двумя
главными факторами: действующими на поверхность ствола нагрузками и
“несущей способностью" ствольного материала, т.е. способностью сопро-
тивляться действию таких нагрузок.
В стволах СПВ износ реализуется либо в виде отрыва частиц металла
с его поверхности, либо в виде формоизменения, деформирования нарез-
ной части. Очевидно поэтому, что и в том, и в другом случаях "несущая
способность” может быть охарактеризована прочностью связей между от-
дельными частицами металла, т.е. с помощью известных механических ха-
рактеристик типа предела текучести, прочности и т.п.
Учитывая это обстоятельство, а также известный факт роста темпера-
туры с числом произведенных выстрелов, можно констатировать посте-
пенное снижение "несущей способности” в ходе стрельбы.
В то же время поверхностные нагрузки на ствол, определяемые бал-
листикой выстрела, меняются с настрелом сравнительно слабо. Итогом ме-
няющегося соотношения "нагрузки - несущая способность" и является
рост износа и соответствующее снижение живучести стволов с увеличени-
ем размеров огшреливаемо! о боекомплект (рис. 53).
N
Рис. 53. Зависимость живучести стволов и их износа от размеров
отстреливаемого боекомплекта
10.3.2. Основные механизмы изнашивания стволов и их причины
Исследования показывают, что с увеличением числа произведенных
выстрелов происходит увеличение диаметральных размеров канала ствола
и искажение его первоначальной формы. Этот процесс, характеризуемый
общим термином износ ствола, может в зависимости от большого числа
конструктивных, технологических, баллистических и эксплуатационных
факторов принимать разнообразные формы: развитие и разгар сетки тре-
щин, отрыв хромового покрытия, сколы, смятие полей нарезов, образова-
ние и разрушение химически и структурно измененного материала в повер-
хностном слое и т.д.
Однако внешний признак износа -(изменение геометрии канала ство-
ла), имеет постоянно наблюдаемую закономерность - существование трех
характерных зон износа:
1) зоны наибольшего износа, прилегающей к началу нарезов;
2) зоны умеренного износа в средней части ствола;
3) зоны повышенного износа вблизи дульного среза.
Поскольку причинами износа являются тепловые, механические и хи-
мические воздействия ведущих элементов пуль (сн) и пороховых газов, не-
трудно установить, что наибольший износ в первой зоне связан с наиболь-
шей интенсивностью и продолжительностью таких нагрузок по сравнению
с другими участками ствола.
Механизмы износа на этом и ji.pvi их участках ствола, а также длина
он износа могу г быть различны гая различных образцов СПВ. Известны
етырс основных, наиболее ярко проявляющихся механизма износа стволов:
рибомеханический, термоштастичсскнй. >розионнъш и термохимический.
Первый из них определяется процессами, сопровождающими трение
;едущих элементов пуль (сн). Трение ведущих элементов пуль (сн) о ствол
отличается той особенностью, что взаимодействие контактирующих мате-
шалов здесь происходит при высоких давлениях (~ 200...400 МПа) и ско-
юстях (до 1000 м/с). Ранее мы уже отмечали, чт о столь высокие параметры
(заимодействия неизбежно ведут к большим значениям температур в зоне
с онта ктирования.
В подобных условиях взаимодействия необходимо так подобрать
сон тактирующие материалы, чтобы один из материалов пары трения
трактически не изнашивался. Естественно, что речь здесь идет о материале
:твола. Для этого необходимо, чтобы другой контактирующий материал
эыл значительно слабее, мягче, податливее, чем первый. В то же время
тельзя, очевидно, допускать и существенного износа ведущих элементов
гули (сн), поскольку терялось бы такое цепное качество ствольного балли-
стического двигателя, как кучность стрельбы.
Исходя из этих соображений, уже давно эмпирическим путем подо-
брана и до настоящего времени используется пара трения “медь-сталь”
тли ее разновидность “томпак-хром”, В таких парах выделяющееся тепло
‘размягчае т” поверхностный слой пули (сн) вплоть до оплавления и обра-
зования своего рода высокотемпературной смазки, снижающей коэффици-
ент трения в системе “пуля-отвод”.
Этот процесс для определенного диапазона параметров трения безус-
ловно выгоден с т очки зрения износа. Но при повышении скорости сколь-
жения все более начинает проявлят ься и отрицательный фактор - расплав-
ленная медь переносится на поверхность ствола, причем давление, оказы-
аемое сю на выступы шероховатостей ствола, пропорционально скорост -
V2
ному напору р —. Последняя величина, пропорциональная квадрату ско-
12
рости скольжения, растет в направлении дульного среза.
Таким образом, физические процессы, реализуемые при трении пули
(сн) о ствол, предопределяют рост грибомеханического износа. Очевидно, что
при прочих равных условиях величина такого износа будет тем больше, чем
больше длина участка контакта пули (сн) со стволом. Для примера отметим,
что в 12,7-мм пуле Н = 30 мри. в т о время как ширина ведущего пояска 30-мм
снаряда Н = 10 мм. Поэтому трибомеханический износ ствола пулями более
ярко выражен, чем такой же механизм износа в стволах большего калибра.
Напротив, механизм термопластического износа является превалиру-
ющим в малокалиберных пушках. Основные закономерности энно износа
состоят в следующем.
С ростом числа выстрелов в очереди температура поверхности ство-
ла к каждому новому выстрелу непрерывно повышается. Интенсивность
повышения 'температуры при этом определяется в первую очередь темпом
стрельбы, гак как материал ствола с уменьшением промежутков времени
между очередными выстрелами все более и более не успевает справляться с
о тводом тепла от внутренней поверхности.
В результате каждый последующий выстрел в очереди начинается
при температуре поверхности канала ствола большей, чем на предыдущем
выстреле. Если же учесть непрерывное снижение прочностных характерис-
тик металла ствола с ростом температуры, то оказывается, что каждый но-
вый снаряд, имеющий практически неизменную прочность его ведущих
элементов, будет врезаться в нарезную часть ствола, все более ослабляе-
мую предыдущими выстрелами.
Таким образом, можно полагать, что на некотором выстреле в очере-
ди температура поверхности канала ствола достигнет такого уровня, при
котором механические характеристики материалов ствола и ведущих эле-
ментов снаряда будут близки по величине. Очевидно, что дальнейшая
стрельба приведет в этом случае к смятию (выглаживанию) нарезной части
ствола. Ствол исчерпает свою живучесть из-за неправильного, дестабили-
зированного вращением полета снарядов на траектории.
Указанный вид износа, связанный с пластическим деформированием
нарезной части ствола в условиях высоких температур, и принято назы-
вать термопластическим износом. В стволах малокалиберных пушек такой
механизм износа устанавливает существование предельных или критичес-
ких режимов стрельбы, при которых ствол выходит из строя при произ-
ведете одной непрерывной очереди выстрелов или серии очередей с ко-
ре i коми перерывами.
Вполне понятно, что чем меньше темп стрельбы и размеры отстрели-
ваемого боекомплекта, тем в большей степени будет ослаблен термоплас-
। пчсский износ, тем меньше его воздействие на ресурс ствола. В таких ус-
повпях на первый план выдвигаются механизмы эрозионного и термохи-
мического износа.
Явление эрозии, или поверхностного разрушения твердых тел под
действием жидкой или газообразной среды, хорошо изучено, поскольку
встречается в разнообразных технических устройствах: двигателях, турби-
нах и т.п.
В самом грубом представлении можно считать, что при эрозии мель-
чайшие частицы потока газа разрушают поверхностный слой металла
вследствие ударов о его поверхность. По лому эрозия заметно возрастает с
увеличением кинетической энер: ни чействующих частиц, а также с повы-
шением шероховатости поверхности.
Если частицы или изделие, на которое они воздействуют, находятся
при высоких температурах, то процесс эрозии значительно усиливается
термическим влиянием в связи со снижением прочностных свойств метал-
ла. При наличии агрессивной среды возникает дополнительное химическое
взаимодействие между частицами и поверхностью металла, что приводит к
еще более сильному эрозионному разрушению.
Характер разрушения поверхности при эрозии бывает весьма разно-
образным. На поверхности металла появляются трещины, продольные бо-
роздки различной формы и размеров, но ориентированные, как правило, в
направлении потока. В зависимости от характеристик металла и парамет-
ров воздействующего потока может происходить или равномерное “сдува-
ние” часгиц о поверхности, или явно выраженное локальное разрушение
поверхности.
Наиболее четко суть явления эрозии с тволов горящими пороховыми
газами раскрыл еще в начале XX века выдающийся русский ученый-метал-
лург Дмитрий Константинович Чернов.
В своей работе “О выгорании каналов в стальных орудиях” Д. К.
Чернов отмечал: “...при воспламенении заряда в канале орудия образуется
чрезвычайно сгущенная газовая атмосфера, которую можно назвать ог-
ненною жидкостью, принимая во внимание ее большую плотность, близ-
кую к плотности самого пороха, и очень высокую температуру. Падая,
раскаленная жидкость, при давлении в несколько тысяч атмосфер, плотно
прилегающая к стенкам канала, быстро нагревает поверхностный слой ме-
талла до высокой температуры, причем толщина такого слоя, вследствие
кратковременности нагревающего действия газов, будет очень незначи-
тельна и выразится в десятых или сотых долях миллиметра”, и далее “...
поверхностный слой металла нагревается выше точки плавления и бук-
вально смывается быстродвижущимися пороховыми газами. Раскаленный
канал представляется тогда в виде изборожденной гладкими продольными
морщинами поверхности ...”.
Подводя итог краткому описанию процессов поверхностного изна-
шивания стволов, отметим, что в стволах любого образца СПВ в процессе
стрельбы реализуются все рассмотренные механизмы износа и живучесть
определяется их совокупным влиянием.
К настоящему времени предложен целый ряд теоретических и экспе-
риментальных зависимостей, описывающих основные закономерности
того или иного вида износа. Однако ввиду исключительной сложности
процессов, происходящих при стрельбе, эти зависимости имеют ограни-
ченное применение и не позволяют во многих случаях с достаточной степе-
нью точности рассчита н- количество выстрелов, приводящие ствол в не-
годное состояние.
11. РАСЧЕТ И ПРОЕКТИРОВАНИЕ СПУСКОВЫХ МЕХАНИЗМОВ
При проектировании спусковых механизмов необходимы проверки
прочности деталей, величины усилия спуска и времени подъема шептала
после, его расцепления со спуском в конструкциях, имеющих отрывники.
При проверке прочности деталей проводится расчет напряжений,
возникающих в них при остановке на шептало ударника, курка или основ-
ного звена автоматики. Для определения напряжений в деталях можно
воспользоваться зависимостями теории удара.
Рассмотрим спусковой механизм для ведения непрерывной стрельбы,
схема которого приведена на рис. 54. При ударе боевого взвода основного
звена автоматики (затворной рамы или затвора) 3 по шепталу 2 происхо-
дят деформации среза и сжатия шептала и боевого взвода.
Рис. 54. Принципиальная схема спускового механизма непрерывной стрельбы:
I-корпус механизма. 2-шептало, 3-боевой взвод затворной рамы (затвора).
4-пружина, 5- спусковой крючок
Приравнивая потерю кинетической энергии основного звена автома-
шин сумме потенциальной энергии деформации шептала и боевого взво-
да. получим
п* + П2 -
mlm2
2(mj + т2)
(88)
П Tnh Pnb
i де II, _ - поюнциальная лнер1ия деформации сжатия
ZEjFj 2G2F3
и сдвига шептала:
Ш] - масса основного звена автома тики и связанных с ним деталей;
т2 - масса короба оружия (ствольной коробки)
п _ Гп12 + РпЬ
* *2 ~ г + - потенциальная энергия деформации сжатия
21.2Г1 2Ь2Гз
и сдвига боевого взвода;
Р„ - сила, возникающая при ударном взаимодействии звеньев;
Е] и Е2 - модули упругости материала шептала и боевого взвода соот-
ветственно;
G] и G2 - модули сдвига материала шептала и боевого взвода соответ-
ственно;
I] - длина линии сдвига шептала;
F] - контактная площадь сжатия;
F2 - площадь плоскости сдвига шептала;
12 - длина линии сдвига боевого взвода;
F3 -площадь плоскости сдвига боевого взвода,
Подщавив выражения для определения касательных напряжений и
потенциальной энергии в зависимость (88), получим
(89)
Используя выражение (89), можно определить силу Ри и по ее величине
произвести расчет напряжений сжатия и сдвига шептала и боевого взвода:
G = — Т = Т = Р? •
см F/1 F2’2 F3
Для обеспечения прочности рассматриваемых деталей расчетные зна-
чения напряжений должны быть меньше соответствующих допускаемых
напряжений.
Усилие спуска (см. рис. 54), необходимое для приведения в действие
спускового механизма, может быть определено по зависимости
рЛ'
Н1П
р _ 2LZ
или Гс - -
Л
где П. М - соответственно сила или момент силы, действующие на звено
механизма, удерживаемое шедшим;
Н[ - плечо действия усилия спуска относительно его оси вращения;
Z
~ - коэффициент приведения сил от звена удерживаемою шепталом
к спуску.
Время движения шептала Atm отрывного устройства на величину
полном' выхода должно быть меньше времени движения основного звена
At3 от момента воздействия его на отрывник до постановки на шептало
Atm <At3.
Значение At3 может быть определено после расчета характеристик
движения основного звена (по велограмме).
Время выхода шептала можно определить приближенно по зависи-
мости
Хс
где хс = -— - средняя скорость движения шептала под действием своей
2
пружины;
хш - максимальная скорость движения шептала к концу его выхода.
Скорость хш можно определить из равенства кинетической энергии
шептала и работы силы пружины шептала па участке его перемещения А11П1:
2
тш^ = П1±Д2ДЬшР1,
огкуда
t
АШ л ,
V т Ш
где р = 0,7-0,8 - коэффициент потерь механической энергии пружины
шептала.
Подставляя Х| в выражение для AtUJ, получим
Например, при тш
Pl = 0,8 получим
= 0,04 кг, АЬШ = 0,006 м, П, = 10 Н. П, - 14 Н,
Д*Ш =
Ц-'Ч МОО _7 о7.1О-3с
(10 +14)0,8
СПИСОК ЛИТЕРАТУРЫ
1. Расчет и проектирование автоматического оружия / А.М. Богоро-
дицкий, Е.Н. Коротков, В.Ф. Матасов, В.Л. Чернопятов. - М.: ЦНИИ ин-
формации, 1983. 4.1. - 86 с.
2. Расчет и проектирование автоматического оружия / А.М. Богоро-
дицкий, Е.Н. Коротков, В.Ф. Матасов, Л.А. Кичаков - М.: ЦНИИ инфор-
мации, 1984. Ч. 2. - 127 с.
3. Проектирование ракетных и ствольных систем / Под ред. Б.В. Ор-
лова. - М.: Машиностроение, 1974. - 828 с.
4. Чуев Ю.В. Проектирование ствольных комплексов. - М.: Машино-
строение, 1976. - 240 с.
5. Орлов Б.В.. Ларман Э.К., Маликов В.Г. Устройство и проектирова-
ние стволов артиллерийских орудий. - М.: Машиностроение, 1976. - 432 с.
6. Мамонтов М.А. Некоторые случаи течения газа. - М.: Оборопгиз,
1951.- 490 с.
7. Михеев М.А., Михеева И.М. Основы теплоотдачи. - М.: Энергия,
1973.- 220 с.
8. Руководящий технический материал РТМ ВЗ-71-70. Пистолеты, пу-
леметы, автоматы, винтовки. Методы расчета кинематики и динамики ис-
полнительных механизмов. - 170 с.
9. Отраслевой стандарт OCT B3-3478-76. Оружие стрелковое. Мето-
ды расчета на прочность. - 173 с.
10. Матасов В.Ф.. Ульянцев.В.П. Расчет автоматики оружия. Учеб,
пособие. - Тула: Изд-во ТулГУ, 2001. - 164 с.
Содержание
Предисловие...................................................3
Расчет и проектирование механизмов автоматического оружия.........5
1. Расчет и проектирование запирающих узлов...................5
2. Расчет и проектирование пружин........................... 10
2.1. Цилиндрические винтовые пружины сжатия......... 11
2.2. Цилиндрические винтовые пружины кручения....... 15
2.3. Призматические пружины сжатия.................. 18
3. Расчет и проектирование патроноподающих механизмов........20
3.1. Механизмы ленточного типа.......................20
3.1.1. Законы движения патронной ленты............21
3.1.2. Проектирование патроноподающих механизмов
ленточного типа...................................27
3.1.3. ППМЛТ с двумя кинематически связанными звеньями.28
3.1.4. ППМЛТ стремя кинематически связанными звеньями..31
3.2, Механизмы магазинного типа......................37
4. Расчет и проектирование ударных механизмов................44
5. Расчет и проектирование ускорительных механизмов..........57
5.1. Ускорительные механизмы рычажного типа......... 57
5.2. Ускорительные механизмы кулачкового типа....... 59
5.3. Ускорительные механизмы копириого типа..........62
5.4. Ускорительные механизмы пружинного типа....... 70
6. Расчет и проектирование запирающих механизмов.............77
6.1. Запирающие механизмы с перекосом затвора .......78
6.2. Запирающий механизм с поворотом затвора.........82
2. Системы с откатом ствола и затвора........................86
7.1. Системы с откатом ствола........................88
7.1.1. Системы с длинным ходом ствола.............88
7.1.2. Системы с коротким ходом ствола ...........88
7.2. Системы с откатом затвора.......................90
7.2.1. Системы со свободным затвором .............90
7.2.2. Системы с полусвободным затвором................90
8. Расчет и проектирование механизмов досылания патронов
в патронник............................................... 96
9. Расчет и проектирование газоотводного привода автоматики.........98
10. Расчет и проектирование стволов спв..........................105
10.1. Нагрев стволов СПВ.................................106
10.1.1. Оценка мощности тепловых источников..........107
10.1.2. Теплообразование при трении пули (снаряда)...107
10.1.3. Теплоотдача пороховых газов..................108
10.1.4. Тепловое излучение пороховых газов...........109
10.1.5. Количество тепла, поступающего в ствол при выстреле. 111
10.1.6. Количество тепла от теплоотдачи пороховых газов.112
10.1.7. Суммарные потери энергии на нагрев ствола....116
10.1.8. Численные методы оценки уровня нагрева стволов..118
10.1.9. Дискретизация решения в пространстве и времени..121
10.1.10. Температурные поля стволов СПВ.................128
10.2. Прочность стволов СПВ.................................131
10.2.1. Упругое деформирование стволов давлением пороховых
газов .............................................133
10.2.2. Предел упругого сопротивления ствола.........137
10.2.3. Методика расчета прочности стволов по упругому
сопротивлению......................................138
10.2.4. Рекомендуемые материалы и коэффициенты запаса
прочности..........................................140
10.2.5. Влияние температуры на прочность ствольных
материалов.........................................143
10.3. Краткие сведения о живучести стволов СПВ...........147
10.3.1. Общая характеристика процессов, определяющих износ
стволов............................................148
10.3.2. Основные механизмы изнашивания стволов и их
причины............................................150
11. Расчет и проектирование спусковых механизмов.................154
Список литературы................................................157
МАТАСОВ Василий Федорович
УЛЬЯНЦЕВ Виктор Петрович
ПРОЕКТИРОВАНИЕ АВТОМАТИКИ ОРУЖИЯ
Учебное пособие
Редактор И. А. Есаян
Компьютерная верстка Л.М. Мухановой
Изд. лиц. ЛР № 020300 от 12.02.97. Подписано в печать 5.07.200
Формат бумаги 60x84 '/16. Бумага офсетная.
Усл. печ. л. 9,3. Уч.-изд. л. 8,0.
Тираж 100 экз. Заказ Й Я.
Тульский государственный университет.
300600, г. Тула, просп. Ленина, 92.
Отпечатано в редакционно-издательском центре
Тульского государственного университета.
300600, г. Тула, ул. Болдина, 151