Г. Л. КОТКИН, В. Г. СЕРБО
СБОРНИК ЗАДАЧ ПО КЛАССИЧЕСКОЙ МЕХАНИКЕ
ИЗДАНИЕ 2-Е, ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего
специальное’' образования СССР в качестве учебного пособия для студентов физических специальностей университетов
@
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1977
СОДЕРЖАНИЕ
Предисловие ко второму изданию .	4
Из предисловия к первому изданию .	.	4
ЗАДАЧИ ОТВЕТЫ
И РЕШЕНИЯ
§ 1.	Интегрирование уравнений движения систем с одной степенью свободы	. .	5	71
§ 2.	Движение частиц в полях . ,	7	82
§ 3.	Сечение рассеяния в заданном поле. Столкновение частиц.....................13	118
§ 4.	Уравнения движения. Законы сохранения . . . ............................16	132
§ 5.	Малые колебания систем с одной степенью свободы...........................24	148
§ 6.	Малые колебания систем с несколькими степенями свободы	....	28	162
§	7.	Колебания линейных цепочек	.	39	214
§	8.	Нелинейные колебания........... 42	232
§ 9.	Движение твердого тела. Неинерциальные системы отсчета ....	45	245
§ 10.	Уравнения Гамильтона. Скобки Пуассона .................................. 51	267
§ 11.	Канонические преобразования .	56	277
§ 12.	Уравнение Гамильтона ~ Якоби	62	293
§ 13.	Адиабатические инварианты .	.	65	305
Литература.......................318
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Настоящее издание существенно дополнено и переработано. Наибольшей переработке подверглись §§ 6 и S В § 6 для исследования колебаний сложных систем более широко используются свойства симметрии и методы теории возмущений. Значительно расширен § 9 (о движении твердого тела)
Мы рады случаю выразить глубокую благодарность редактору английского перевода задачника профессору Д. тер Хаару. многочисленные замечания которого способствовали устранению ряда неточностей и опечаток.
Мы признательны А. В. Михайлову за полезные обсуждения некоторых новых задач.
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Предлагаемый сборник задач предназначен для студентов-физиков. По охватываемому материала ан примерно соответствует книгам «Механика» Л Д. Ландау и Е. М. Лифшица и «Классическая механика» Г Голдстейно
Мы надеемся, что чтение сборника будет интересным не только для студентов, изучающих механику, но и для лиц, знающих ее Порядок расположения задач в основном такой же, как и в курсе Ландау и Лифшица, за тем исключением, что систематическое использование уравнений Лагранжа начинается здесь с § 4. Задачи же первых трех параграфов можно решать, используя лишь уравнения Ньютона и законы сохранения знергии, импульса и момента импульса За редкими исключениями обозначения в сборнике совпадают с обозначениями «Механики» Л. Д Ландау и Е М Лифшица и часто даже специально не оговариваются. В задачах об электрических цепях используется Международная система единиц СИ, а в задачах о движении частиц в электромагнитных полях — гауссова система.
Мы глубоко благодарны Ю И Кулакову за постоянную помощь. Нам особо хотелось бы подчеркнуть его роль в составлении и обсуждении большого числа задач. Мы считаем приятным долгом поблагодарить И Ф Гинзбурга за целый ряд полезных советов и указаний, которые были нами приняты к сведению Мы весьма благодарны В Д. Кривченкову, живое участив и советы которого укрепили нас в решимости довести до конца эту работу.
§ 1.	Интегрирование уравнений движения систем с одной степенью свободы
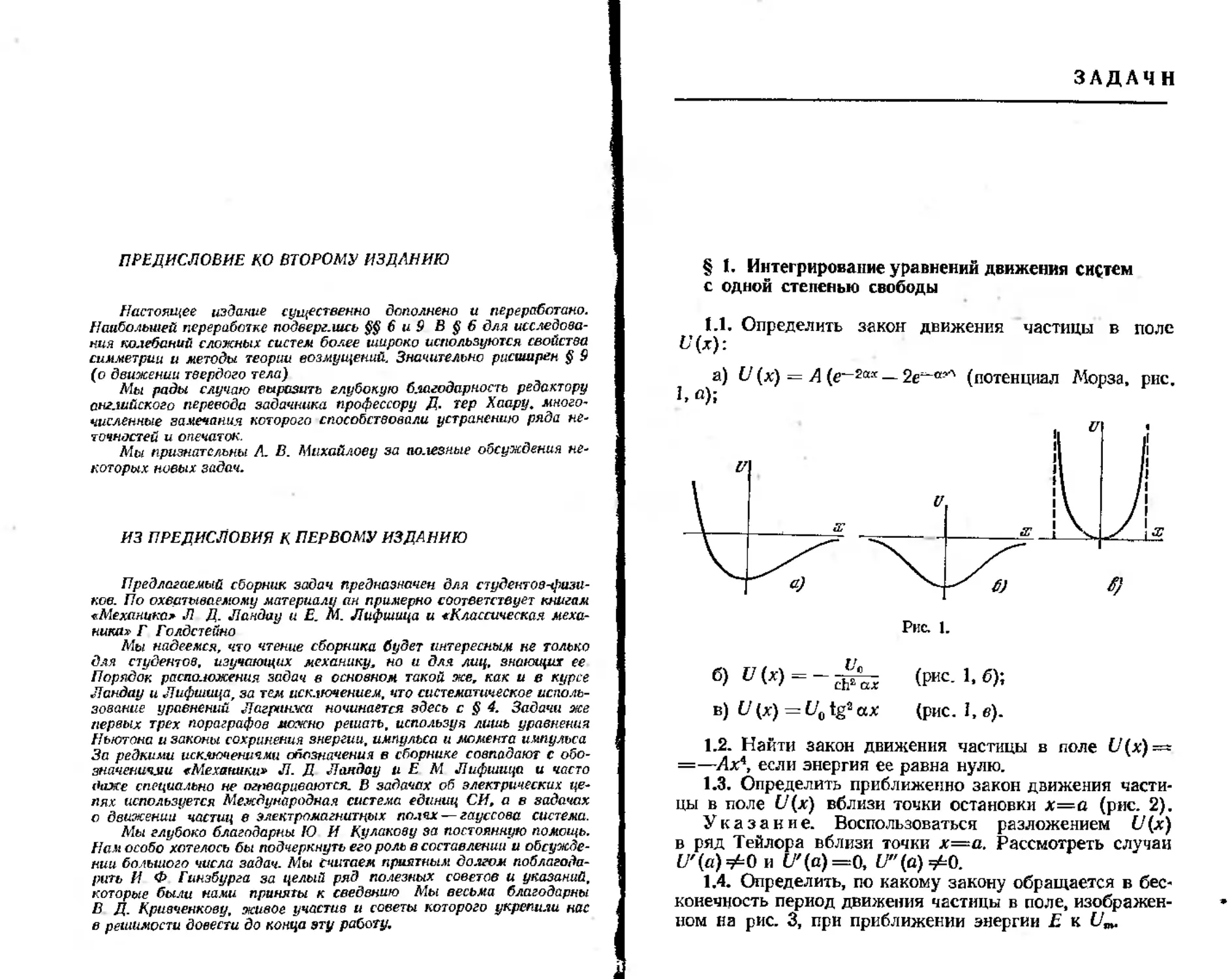
1.1.	Определить закон движения частицы в поле Г(х):
a)	U (к) = А (е~2ах — 2е^“?Л (потенциал Морза, рис. 1,«);
(л
Рис. I.
О	(Р«с. 1.6);
В) и (х) = Ц> tg2 ах (рис. 1. в).
1.2.	Найти закон движения частицы в поле (/(x) = =—Ах\ если энергия ее равна нулю.
1.3.	Определить приближенно закон движения частицы в поле U(x) вблизи точки остановки х=а (рис. 2).
Указание. Воспользоваться разложением U (х) в ряд Тейлора вблизи точки х=а. Рассмотреть случаи £/'(а)^0 и СГ(а)=0, U"(a)^O.
1.4.	Определить, по какому закону обращается в бесконечность период движения частицы в поле, изображенном на рис. 3, при приближении энергии £ к Um.
ЗАДТЧП
1.5.	а) Оценить период движения частицу в поле £'(х) (рис. 4), если ее энергия близка к U,„ (т. е.
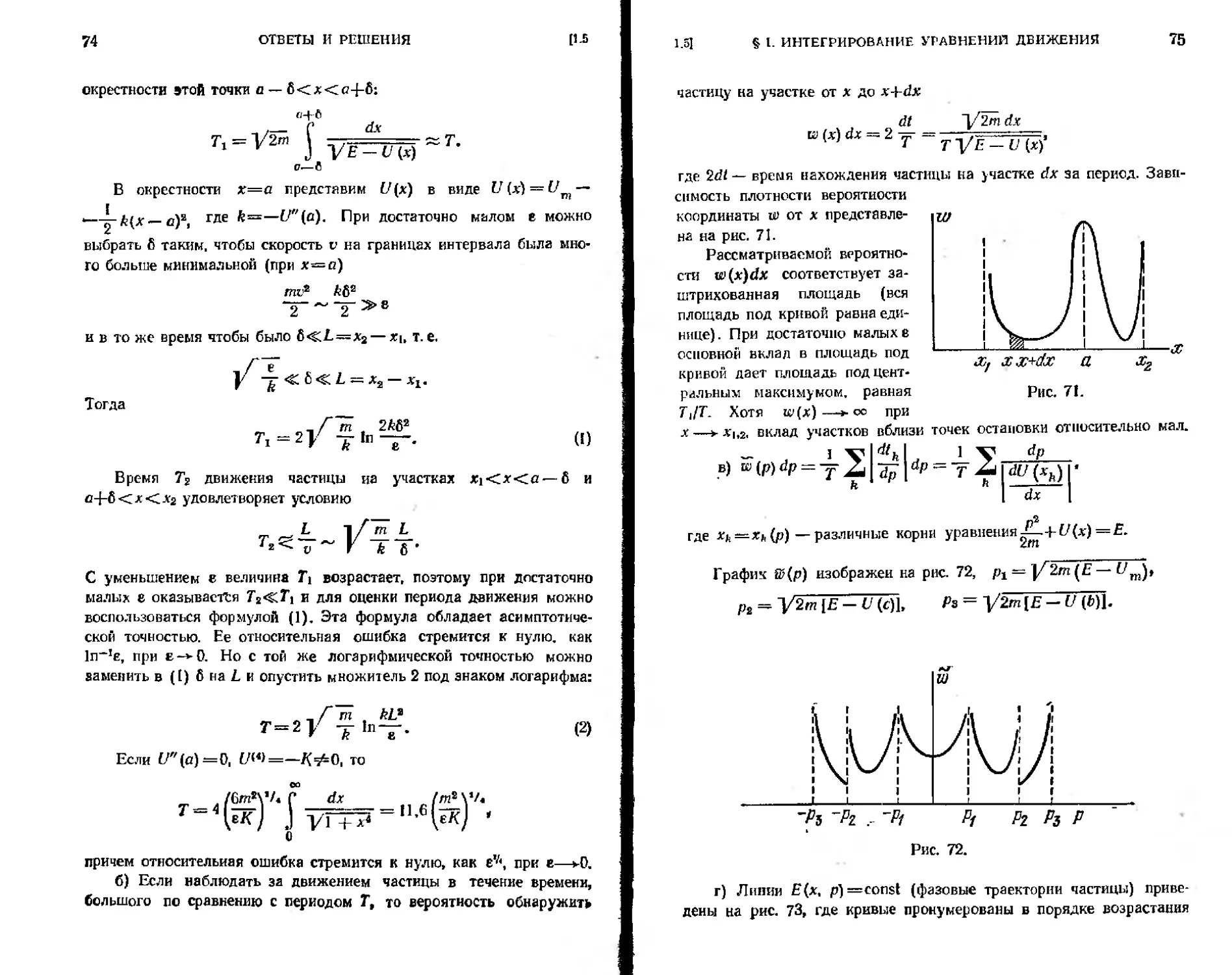
б)	Определить, в течение какой части периода частица находится на участке от х до x-±dx.
"I
Рис. 2.
в)	Определить, в течение какой части периода частица имеет импульс mi в интервале от р до p+dp.
г)	На плоскости х, р=тх изобразить качественно линии Е(х, p)=eonst для случаев E<Urp.E=ll,n, Е>11„.
1.6. Частица массы т может двигаться по окружности радиуса 1 в вертикальной плоскости в поле тяжести
и
Ркс 3	Гис 4.
(математический маятник). Найти закон ее движения, если кинетическая энергия в нижней точке £ равна
Оценить период обращения маятника в случае, когда £ — 2mg/<g;2nig/.
1.7. Определить закон движения математического маятника при произвольном значении энергии.
Указание. Зависимость утла отклонения маятника от времени выражается через эллиптические функции (см., например, [1],стр. 150).
§ 2 HBWKFflHE ЧАСТИЦ В ПОЛЯХ
1.8.	Определить изменение закона движения частицы на участке, не содержащем точек остановки, вызванное добавлением к полю Е(х) малой добавки 6L'(x).
Исследовать применимость полученных результатов вблизи точки остановки.
1.9.	Найти изменение закона движения частицы, вызванное добавлением к полю U(x) малой добавки ЬЪ'(х):
a)
б) L’(x)=™—",
, «'ZXS t>U(x)
ММЧ=Ф‘;
1.10.	Определить изменение периода финитного движения частицы, вызванное добавлением к полю U(x) малой добавки б(7(х).
1.11.	Найти изменение периода движения частицы, вызванное добавлением к полю Ъ'(х) малой добавки 6U(x).
a)	U (х) = 2' (гармонический осциллятор), ЬИ (х) ==
I' t л л*”2*8	Е . «ах3
б)	U (х) = ~2—,	6U (х) =
в)	V (х) = А (е~2-“ — 2е-г«), 6L' (х)=—Ve™ (У<Л).
1.12.	Частица движется в поле U(x) — cha°R^ с энергией Е > L'o. Найти время задержки частицы при движении от х = — <х> до х = + <х> по сравнению со временем свободного движения с той же энергией.
§ 2.	Движение частив в полях
2.1.	Описать качественно характер движения частицы в поле L' (г) = — —----у при различных значе-
ниях момента импульса и энергии.
2.2.	Найти траектории и законы движения частицы в поле
и =
(— V при r<zRt 1 0 при r>R
(рис. 5, «сферическая прямоугольная потенциальная яма») при различных значениях момента и энергии.
2.3.	Определить траекторию частицы в поле U(r) = Выразить изменение направления ее скорости
при рассеянии через энергию и момент.
2.4.	Определить траекторию частицы в поле U(r)~ =~-—Найти время падения частицы в центр поля
с расстояния г. Сколько оборотов
V
вокруг центра сделает при этом ча-________р стица?-
’”"1 г 2.5. Определить траекторию час-,^v	тицы в поле t7(r)=—у* Най-
ти угловое расстояние Д<р между двумя последовательными прохож-Рис. 5. деииями перигелия (точки г=гП11п), период радиальных колебаний Тг и период обращения 7V При каком условии траектория окажется замкнутой?
2.6.	Определить траекторию частицы в поле V(г) = — _Л— Р
г Г2 *
2.7.	При каких значениях момента импульса М возможно финитное движение частицы в поле U (г) ?
a) U (г) « — ае~хг/г; б) U (г) = — Ve—y-'r\
2.8.	Частица падает в центр поля С7(г) =—аг~п с конечного расстояния. Будет лн число оборотов вокруг центра, сделанных при этом частицей, конечным? Будет ли конечным время падения? Найти уравнение траектории для малых г.
2.9.	Частица в поле U(r) уходит на бесконечность с расстояния г=/=0. Будет лн число оборотов, сделанных ею вокруг центра, конечным?
а) и=аг-п; 6) 17(г)=—аг~я.
2.10.	Определить время падения частицы с расстояния в центр поля U(г) =—а/г, рассматривая траекторию как вырожденный эллипс. Начальная скорость частицы равна нулю.
2.11.	Определить наименьшее расстояние, на которое приблизится частица, излетающая из бесконечности со скоростью v и прицельным параметром р на другую, первоначально покоившуюся. Массы частиц mi, т2, закон взаимодействия U(r)—а/гп.
2.12.	В системе центра масс определить траектории финитного движения двух частиц, массы которых т\ и т2, а закон взаимодействия U (г) = — а/г.
2.13.	Определить положение фокуса пучка частиц, близких к оси пучка, при рассеянии в центральном поле U(г), предполагая, что частица, летящая вдоль оси, поворачивает назад.
2.14.	Найти область, недостижимую для пучка частиц, летящих из бесконечности со скоростью v параллельно оси z н рассеиваемых полем U(r)=a/r.
2.15.	Найти область, недостижимую для частиц, вылетающих со скоростью и в различных направлениях из одной точки А в поле U(r) = —а/г.
2.16.	Найтн траекторию частицы в поле 17(f) =—а/г, используя интеграл движения А = [vM] — ~ .
2.17.	Определить изменение зависимости периода Т радиальных колебаний точки в центральном поле U(r) от энергии и момента, вызванное изменением поля на малую величину 6i7(r).
2.18.	Показать, что траектория частицы в поле U(r) = — ae~r,D/r при условии	представляет
собой медленно прецессирующий эллипс, и найти угловую скорость его прецессии.
2.19.	Найти скорость прецессии орбиты в поле U(г) — — a/ri+t, где |е| «С 1.
2.20.	Найти угловую скорость прецессии орбиты частицы в поле U ~	-Ь— прн р «с wiw2a6, та>2Ь6, где а
и b — параметры невозмущеиной траектории:

2.21.	Показать, что потенциальная энергия системы Земля— Луна в поле Солнца, усредненная за месяц, имеет вид t7(r)=— “----Д (г —расстояние от центра
масс системы Земля — Луиа до Солнца; принять для простоты, что плоскость орбиты Луны совпадает с плоскостью орбиты Земли). Определить происходящее из-за этого смещение перигелия за сто лет. Масса Луны в 81 раз меньше массы Земли, расстояние до Луны а= =•= 380 тыс. км, среднее расстояние до Солнца равно 150 млн. км.
2.22.	Определить угловую скорость прецессии орбиты в поле U (г) = — — 4- &U(r), если эксцентриситет орбиты е -С 1, полагая
6П (г) = 6U (д) 4 (г - a) ЫГ (а) 4 4* (г - й)2 W (*)>
где а = Г|Дах~^Гт1п— средний радиус орбиты.
2.23.	Определить угловую скорость прецессии орбиты частицы в поле U (г) = —— 4- 6U (г) (6U(r) — малая добавка) с точностью до второго порядка включительно по бП(г).
2.24.	Найти уравнение траектории частицы, движущейся в поле U (г) = —— 4- -у» рассматривая как малую добавку к кулоновскому полю.
2.25.	Показать, что задача о движении двух заряженных частиц в однородном электрическом поле 8 сводится к задачам о движении центра масс и о движении частицы в заданном поле.
2.26.	При каком условии разделяются задачи о движении центра масс и об относительном движении для двух заряженных частиц в однородном магнитном поле?
Векторный потенциал магнитного поля удобно выбрать в виде
А = 4-
2.27.	Выразить кинетическую энергию, импульс и момент импульса системы N частиц через координаты
Якоби:
<"=’...
я^Г,	. • 4- тугг?
^ + ...4^ •
2.28.	На первоначально покоившуюся частицу налетает частица такой же массы т, имевшая на бесконечности скорость v и взаимодействующая с первой по закону U (г) = а/г”. Удар центральный. Найти точку остановки налетевшей частицы.
2.29.	Доказать, что для заряженной частицы в однородном магнитном поле Зъ интегралом движения является MJC + Yc кЭД*, где М = m[rv].
2.30.	Найти траекторию н закон движения заряженной частицы в магнитном поле Зъ = gr/r3 (поле магнитного монополя).
Подобный вид имеет магнитное поле тонкого длинного соленоида вне его в точках, удаленных от его торца на расстоиние, большое по сравнению с диаметром соленоида, но малое по сравнению с его длиной.
2.31.	Описать качественно характер движения и внд траектории заряженной частицы в поле магнитного диполя т, движущейся в плоскости, перпендикулярной к вектору т. Векторный потенциал магнитного диполя А = [иг]/г3.
2.32.	а) Описать качественно движение заряженной частицы в поле V = ~^т%г2, где г—расстояние от оси z (поле равномерно заряженного цилиндра), прн наличии однородного магнитного поля JC, параллельного ОСИ 2.
б)	Найти закон движения н траекторию заряженной частицы, движущейся в поле V — air2 в плоскости, перпендикулярной постоянному однородному магнитному полю JC
2.33.	Заряженная частица движется в кулоновском поле V(г) = —а/r в плоскости, перпендикулярной к однородному магнитному полю -К. Описать траекторию частицы. Исследовать случай, когда JC мало, и случай, когда поле U(r) является малым возмущением.
2.34.	Найти законы движения двух одинаковых заряженных частиц в однородном магнитном поле ЭС в случае, когда траектории их лежат в одной плоскости, перпендикулярной к JC, а энергию их взаимодействия U(г) — е2/г можно считать малой поправкой.
2.35.	Показать, что в поле V (г) — — — — Fr сохраняется величина F [vM] _ 2^1 + 2- [Fr]2. Истолковать этот интеграл движения при очень малых F.
2.36.	Исследовать влияние малой добавки 6(7(г) = = — Fr к кулоновскому полю на финитное движение частицы.
а)	Найти среднюю (за период) скорость изменения момента импульса.
б)	Определить зависимость от времени момента импульса, размеров и ориентации орбиты, если сила F лежит в плоскости орбиты.
в)	Тот же вопрос при произвольной ориентации силы.
Указание. Составить и решить усредненные по периоду уравиеиия движения для векторов M = m[rv] н А = [vM] - V- .
2.37.	Найти систематическое изменение траектории финитного движения заряженной частицы в поле U(г) —а/r под влиянием слабых постоянных однородных электрического н магнитного полей g н К.
а)	Ограничиться случаем, когда магнитное поле пер« пендикулярио плоскости орбиты, а электрическое поле лежит в ней.	• •
б)	Рассмотреть общий случай.
2.38.	Найтн систематическое изменение эллиптической орбиты частицы в поле U(r) — ~а/г под влиянием малой добавки 6E/=^r2(3cos20— 1). (Таково, например, усредненное за месяц поле тяготения Луны в околоземном пространстве — поле «приливных сил».) Ограничиться случаем, когда плоскость орбиты проходит через ось г.
2.39.	Найти систематическое смещение траектории финитного движения частицы, движущейся в поле U = — —а/r и в поле магнитного диполя т, если влияние магнитного диполя можно рассматривать как
малое возмущение. Векторный потенциал выбрать в ви-
[шг|	к
де ^тг-
2.40.	Определить среднюю скорость прецессии орбиты частицы в поле U(r) =—ct/r под действием малой добавочной силы F = pv (такой вид имеет сила тормо-о 2
жения излучением, в этом случае р = гДе Ц~~ заряд частицы,— см. [2], § 75).
§ 3.	Сечение рассеяния в заданном поле. Столкновение частиц
3.1.	Найти дифференциальное эффективное сечеиие рассеяния частнц, скорость которых до рассеяния параллельна оси г, на гладкой упругой поверхности вращения р(г):
a) p = b‘£in-^-,
б)р=Лхп, 0<л<1;
.	, с2 с2
В) р = Ь-_,	—<2<оо.
3.2.	Найти поверхность вращения, сечеиие упругого рассеяния на которой совпадает с резерфордовским.
3.3.	Найти дифференциальное эффективное сечеиие рассеяния частиц сферическим «потенциальным горбом»:
t/(r) = |V "₽*' г<а-
(О при г>а.
3.4.	Найти сечение падения частиц в центр поля: а)У(г)=^-А; б)£/(г) = |-£.
3.5.	Найти сечение падения частиц на шарик радиуса R, находящийся в центре поля U(r):
3.6.	Найти дифференциальное эффективное рассеяния частиц в поле U(r): '
сечение
a) </(г) =
Т 'R
О
б) 1/(г) =
|-L ты2 (г2 -/?2)
О
при г < R, прн r>R.
3.7.	Найти дифференциальное эффективное сечение рассеяния быстрых частиц (£^> !/) в поле U(r):
a) £/(r) = Vln(l +£);
при г < R, прн r>R.
3.8.	Найтн дифференциальное эффективное сечение рассеяния частип на малые углы в полеСг (г)—-Д-—
3.9.	Найтн дифференциальное эффективное сечение рассеяния частиц в поле U = — а/г2,
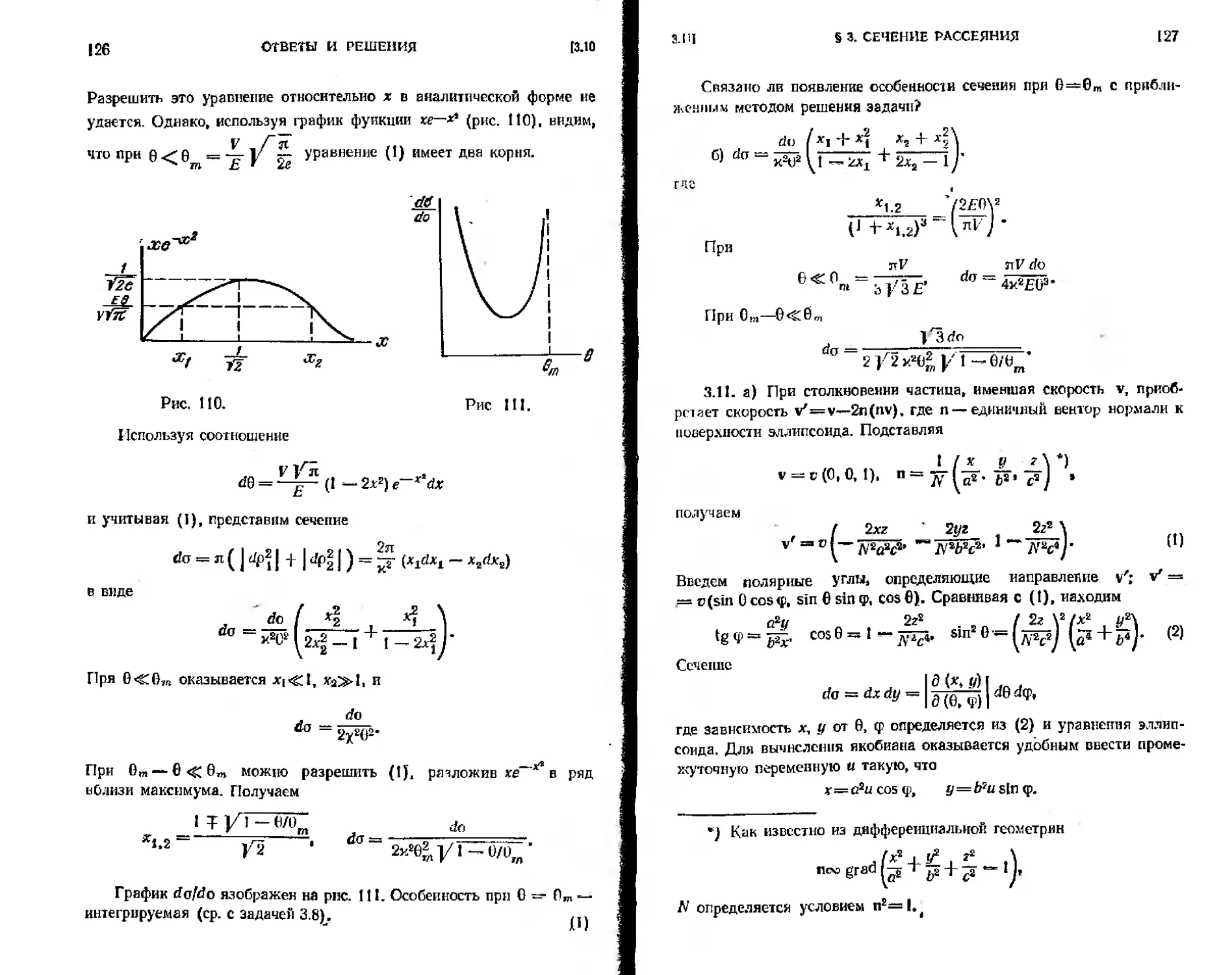
3.10.	Найти дифференциальное эффективное сечение рассеяния быстрых частиц	в поле U(r). Иссле-
довать подробнее предельные случаи, когда угол отклонения близок к своему минимальному или максимальному значению:
a) t/(r) = Ve-’M; б)
3.11.	Поток частиц, скорости которых первоначально параллельны оси z, рассеивается на неподвижном эллипсоиде
Найти дифференциальное эффективное сечение рассеяния, если эллипсоид:
а) гладкий упругий, б) гладкий неупругий, в) шероховатый упругий.
3.12.	Найти дифференциальное эффективное сечение рассеяния на малые углы в нецентральном поле £/(г):
а>	6)U(r) = H
. 3.13. Найтн поправку к дифференциальному эффективному сечению рассеяния частиц в поле U(г), вызванную изменением поля на малую величину 6t/(r):
а)У(г) = у, 81/(г) = Ь
6)f/(r) = v- 6l/W = ^;
в)С/(г) = А 6£/(,)=£.
3.14.	Определить усредненное по времени дифференциальное эффективное сечение рассеяния как функцию приобретаемой частицами энергии при рассеянии в поле U (г, t) ~ (Vt + V2sin ю0 е~к*г'быстрых частиц (Е Vi 2).
3.15.	Частица, летящая со скоростью V, распадается на две одинаковые частицы. Определить распределение по углу разлета распадных частиц (угол между направлениями вылета обеих частиц). Распад в системе центра масс изотропен, скорость распадных частиц в с. ц. м. равна Vo.
3.16.	Найти распределение распадных частиц по энергиям в лабораторной системе, если в системе центра
2
масс угловое распределение имеет вид sin2 0odoo, где 0О— угол между скоростью V первичной частицы и направлением вылета распадной частицы в с. Ц. м. Скорость распадных частиц вс. ц. м. v0.
3.17.	Электрон, имевший иа бесконечности скорость v, налетает на другой электрон, первоначально неподвижный (прицельный параметр р). Найти скорости электронов после рассеяния.
3.18.	Определить интервал значений, которые может иметь угол между направлениями скоростей после столкновения движущейся частицы (масса mi) с первоначально покоившейся (масса m2).
3.19.	Найтн дифференциальное эффективное сечение рассеяния гладких иеупругих шариков на таких же шариках, первоначально покоившихся.
3.20.	Найти закон, по которому/Изменяется интенсивность пучка частиц при прохождении им области, заполненной поглощающими центрами. Плотность распределения центров п, сечеиие поглбщения о.
3.21.	Найти число актрв реакции, происходящих в объеме dV за время dt прн столкиовеиин двух пучков частиц со скоростями vb у2 и плотностями гц, п2. Сечение реакции равно о.
3.22.	Частица массы М движется в области, заполненной частицами массы т М (первоначально неподвижными). Сеченне рассеяния частиц т иа частице М есть de = f(0)do. Столкновения упругие. Найтн:
а)	«силу трения», действующую на частицу 7И;
б)	средний квадрат угла отклонения 0 частицы М.
§ 4.	Уравнения движения. Законы сохранения
4.1.	Частица в поле U (х) = — Fx за время т перемещается из точки х = 0 в точку х = а. Найти закон движения частицы, предполагая, что он имеет внд x(t) = = At2 4- Bt -f- С, н подбирая параметры А, В, С так,. чтобы действие имело наименьшее значение.
4.2.	Частица движется в плоскости хОу в поле
и (х,у) = |° при х<0-(V при х > О,
перемещаясь за время т из точки (—а, 0) в точку (а, а). Найти закон движения частицы, предполагая, что он имеет вид
*1,2 (0 == ^1.2^ + #1.2>
У 1,2 (0 = ^1,2^ -J" ^1.2-
Значки 1, 2 относятся к левой (х < 0) и правой (х > 0)' полуплоскостям.
4.3.	С помощью непосредственного вычисления доказать ковариантность уравнений Лагранжа относительно преобразований координат
Q2, ..., Q„ t), i= 1, 2, ..., s.
4.4.	Каким образом должна преобразовываться функ-ция Лагранжа при переходе к новым координатам
н «времени»
<h=q*(Qi, Q2. -Х-, Q«. т), i=l, 2,..., s, t = t(Qi, Qs, Qa, t),
чтобы уравнения Лагранжа сохранили свой вид?
4.5.	Записать функцию Лагранжа н уравнения движения частицы в поле U(x), введя «местное время» т=/—Хх.
4.6.	Как преобразуется функция Лагранжа
при переходе к координатам q и «времени» т:
х = q ch X + т sh X, t = q sh X + т ch X?
4.7.	Найти законы преобразования энергии и обобщенных импульсов при преобразовании координат
9i=A(Qi... . Q., О,‘=1..... s.
4.8.	Найти законы преобразования энергии и обобщенных импульсов, сопряженных полярным и декартовым координатам, при переходе к системе отсчета, вращающейся вокруг оси г:
а)	<р=ф'+Ш, г=г';
б)	x=x'cos£tf— г/sin Qf, £=x'sin RZ-f-^cos Qt
4.9.	Найти законы преобразования энергии и импульсов при переходе к системе отсчета, движущейся со скоростью V. Функцию Лагранжа U в движущейся системе выбрать в виде
a)	L\ — L (г' + V/, К 4- V, /), где L (г, г, /) — функция Лагранжа в неподвижной системе;
б)	L'2 = -V (г* -|- V/, t). Здесь отличается от
Lt иа полную производную по времени от функции Vmr'4-i \Ч.
2 Г. Л. Коткин, В Г. Сербо
4.10.	Пусть бесконечно малое7преобразоваиие координат и времени имеет вид ? 7
=
f = t Д- еХ (q, t), е -> О,
и пусть ствия:
при этом преобразовании сохраняется вид дей-
Доказать, что величина
У (д.Х - Ч'|) - LX
Г до.
является интегралом движения.
4.11.	Обобщить теорему предыдущей задачи иа случай, когда вид действия при преобразовании координат и времени меняется следующим образом:
*
4.12.	Найти интегралы движения, если вид действия не меняется при:
а) пространственном сдвиге, б) повороте, в) сдвиге начала отсчета времени, г) винтовом сдвиге, д) преобразовании задачи 4.6.
4.13.	Найти интегралы движения для частицы, движущейся:
а)	в однородном поле 1/(г) = — Fr;
б)	в поле U(г), где U(r) — однородная функция:
i7(czr) = a"t7(r)
(уточнить, прн каком п преобразование подобия не меняет вид действия);
в)	в поле бегущей волны £/(г, /) = U(r— VI), где V — постоянный вектор;
г)	в магнитном поле, заданном векторным потенциалом А (г), где А (г) — однородная функция.
д)	в электромагнитном поле, вращающемся с постоянной угловой скоростью Q вокруг оси z.
4.14.	Найти интеграл движения, отвечающий преобразованию Галилея.
Указание. Использовать результат задачи 4.11.
4.15.	Найти интегралы движения для частицы в однородном магнитном поле И‘, если векторный потенциал задан в виде:
а) А = 4- [№1; б) А:, = А, = 0, Ау =
4.16.	Найти интегралы движения для частицы в поле:
а)	магнитного диполя А= [шг]/г3, n = const;
б)	А9 = ц/г, Аг = Аг = 0.
4.17.	Составить уравнения движения системы, функция Лагранжа которой:
a)	L (х, х) — е~^~& 4- 2хе~^ f e~v'dy;
о
б)	L (х, х, t) «	(х2 - <о«х4).
4.18.	а) Записать компоненты вектора ускорения частицы в сферической системе координат.
б)	Найти составляющие ускорения в ортогональной системе координат qf, если элемент длины задан соотношением
ds2 =	+	+ hjdql,
где q2, q3) —коэффициенты Ламэ.
4.19.	Записать уравнения движения частицы в произвольных координатах qt, связанных с декартовыми координатами Xi соотношениями:
a)	xt = xf(qb q2, qz), 1=1, 2, 3;
6)	Xi = x{(qit q2, ?3, 0. l=h 2. 3.
4.20.	Показать, что функция Лагранжа [31]
L = -^ (г2 + г202 + г2<р2 sin2 6) - ф cos 6
описывает движение заряженной частицы в магнитном поле = gr/r3 (см. задачу 2.30).
Найти интегралы движения.
4.21.	Проверить, что функции Лагранжа ql
= ~2---^71» ^ 2— — 2С “Ь ^2
а)	б)
Рис. 6.
приводят к правильным «уравнениям движения» для Ф и q2 и правильным значениям энергии. Здесь qi=i— ток, идущий по индуктивности S? в иаправлении от А к В (рис. 6, a), q2 — заряд на верхней пластине конденсатора (рис. 6, б), a U — напряжение между точками А и В (U = <рв—<рл).
4.22.	Используя ад
дитивность функции Лагранжа и результат предыдущей задачи, составить функции Лагранжа н уравнения Лагранжа для цепей, изображенных на рнс. 7 (а, б н в).
а)	б)
Рис. 7.
е)
4.23.	Найти функции Лагранжа следующих систем: а) цепь с переменным конденсатором, подвижные пластины которого соединены с маятником т (рис. 8, а). Зависимость емкости от угла поворота С(<р) известна, массой пластни конденсатора пренебречь;
б) сердечник на пружинке жесткости k, втягиваемый внутрь соленоида, индуктивность которого есть заданная функция смещения сердечника &(х) (рис. 8, б).
4.24.	Квадратная идеально проводящая рамка может вращаться вокруг закрепленной стороны АВ = а (рис. 9). Рамка находится в постоянном однородном магнитном поле Jt, перпендикулярном к оси АВ. Индук
тивность рамкн масса стороны CD равна т, массами других сторон можно пренебречь.
Описать качественно характер движения рамки.
4.25.	Пользуясь методом неопределенных множителей Лагранжа, получить уравнения движения частицы
в поле тяжести, если оиа может двигаться по заданной кривой:
а)	параболе, лежащей в вертикальной плоскости;
б)	окружности радиуса г = I, расположенной в вертикальной плоскости.
Выразить силы реакции связи.
4.26.	Частица движется в поле тяжести вдоль прямой, равномерно вращающейся в вертикальной плоскости. Составить уравнения движения частицы и найти момент силы реакции.
4.27.	Влияние связей и треиия иа движение системы можно описать, вводя в уравнен ня движения обобщенные силы реакции связей н трения:
dL _ р
а)	Как изменяется со временем энергия системы?
б)	Как должны преобразовываться силы R, при переходе к новым обобщенным координатам
4< = q<(Qi...<?., 0.
чтобы уравнения движения сохраняли свой вид?
4.28.	Пусть уравнения связей имеют вид
<?₽ = 2 bpnqn, ₽ = 1................г,
п—г4-1
причем функция Лагранжа Г(дг+ь ...» 9». 9ь .... 9- О и коэффициенты Ьеп не зависят от координат
Показать, что уравнения движения могут быть представлены в виде
где Г(?г+ь -	9», 9н-ь .... 9«» 0—Функния, получае-
мая исключением скоростей .... дг из L с помощью уравнений связей.
4.29.	Струну можно прёдставить как предельный слу-’ чай системы N частиц (рис. 10), соединенных упругой
7
а 2а	па
Рис. 10.
нитью, при /V—> ос, а—>-0, Na=const. Функция Лагранжа дискретной системы имеет вид
L (91» 9г» —»9а» 91» 9г« • • ♦»9а» О =
А-Н
"	(9л» 9п	9?'—1» 9п« 0»
гг=1
где 9« — отклонение n-й частицы от положения равновесия.
а)	Получить уравнение движения непрерывной системы как предельный случай уравнений Лагранжа дискретной системы.
б)	Получить выражение энергии непрерывной системы как предел выражения энергии дискретной системы.
Указание. Ввести координату точки струны х, а также величины, получаемые при предельном переходе а—>0, п=х[а—* ос:
Ч (х, 0 = lim <?„ (0,	= lim	,
<?(х. q, %. * А = дх dt ’ /	а
4.30.	Заряженная частица движется в потенциальном поле U(г) и в постоянном магнитном поле 3£(г), причем U(г) и JC(r) являются однородными функциями координат степени k и п соответственно, т. е. U (аг) == = ай£/(г), ЗС(аг) = апЗС(г). Вывести для данной системы принцип подобия, уточнив, при каком значении п он имеет место.
4.31.	Обобщить теорему вирнала для системы заряженных частиц в однородном магнитном поле J£- Потенциальная энергия системы U является однородной функцией координат (/(агь ..., агв) = c?L/(r1, ..., г8), а движение системы происходит в ограниченной области пространства и с ограниченными скоростями.
4.32.	Три одинаковых частицы движутся по одной прямой н попарно взаимодействуют друг с другом по закону Uih — U(xx—Л'л), где Xt — координата i-й частицы. Проверить, что кроме очевидных интегралов движения
Р = П1(Л| + х2 +х3).
Е = ~ (i? + 4 + х|) +	+ иг1
существует дополнительный интеграл движения [28]
Л=тт,х2хз—x\U2i—x2U3l—
в случае, если функция Ч(х) имеет вид: a)t/(x)=^,	б)1/(х) = ^.
4.33.	Рассмотреть столкновение трех частиц, описанных в предыдущей задаче. Пусть х} > х2 >х3 н при .—оо расстояния между частицами бесконечно велики, а их скорости о(=х,(/=—оо) таковы, что г'з>т'2>Щ. Найти v't =Х((/=+оо).
§ 5.	Малые колебания систем с одной степенью свободы
5.1.	Найти частоту <в малых колебаний частицы в поле U(x)'.
a)	U(х) = V cos ах—Fx\
б)	U (х) =з V (А2—sin2ax).
5.2.	Найти частоту малых колебаний системы, изображенной на рис. 11. Система вращается в поле тяжести вокруг вертикальной оси с угловой скоростью Q.

Рис. 11.	Рис. 12.
5.3.	Частица массы т, несущая заряд q, может двигаться в поле тяжести по вертикальной окружности радиуса 7?. В ннжнен части окружности закреплен заряд q. Найти положение равновесия н частоту малых колебаний частицы (рис. 12).
5.4.	Найти закон движения частицы в центральном поле U (г) — — а/г* (0 < п < 2) по траектории, близкой к окружности.
5.5.	Найти частоту малых колебаний сферического маятника (частица массы т подвешена на нити длины 0, прн которых угол отклонения нити от вертикали 0 осциллирует аблизи значения 0О.
5.6.	Найти поправку к частоте малых колебаний двухатомной молекулы, вызванную наличием у нее момента импульса М.
5.7.	Найтн свободные колебания системы (рис. 13), если частица может двигаться:
а)	вдоль прямой АВ;
б)	перпендикулярно АВ.
Как зависит частота от натяжения пружинок в поло-женнн равновесия?
5.8.	Найти свободные колебания системы (рис. 14), если она находится в однородном поле тяжести и частица может двигаться только вертикально.
5.9. Найти установившиеся малые колебания плоского маятника, точка под-
Рис. 15.
Рис. 13.
Рис. 14.
веса которого равномерно движется по окружности радиуса а с частотойQ (рис. 15). Длина маятника I
5.10. Найти установившиеся колебания напряжения
па конденсаторе в ток в контуре с источником напряжения U(t) = U1)sin bit (рис. 16).
5.11.	Найти закон движения осциллятора с трением, первоначально покоившегося, под действием силы F(t) =Fcosyt.
5.12.	Определить энергию Е, приобретенную осциллятором под действием си-
(0 «= Fe~(г/т) за все время ее действия, если при t——оо:
а)	осциллятор покоился;
б)	амплитуда колебаний была равна а.
5.13. Найти движение под действием силы F(t):
а)	неустойчивой системы, описываемой уравнением
б)	осциллятора с трением
X 4- 2Хх 4- <ojx — — F (t).
5.14.	Найти дифференциальное эффективное сечение возбуждения изотропного осциллятора до энергии в быстрой частицей (£	V), взаимодействующей с ним
по закону
U(r) = Ve~xM.
Начальная энергия осциллятора равна нулю.
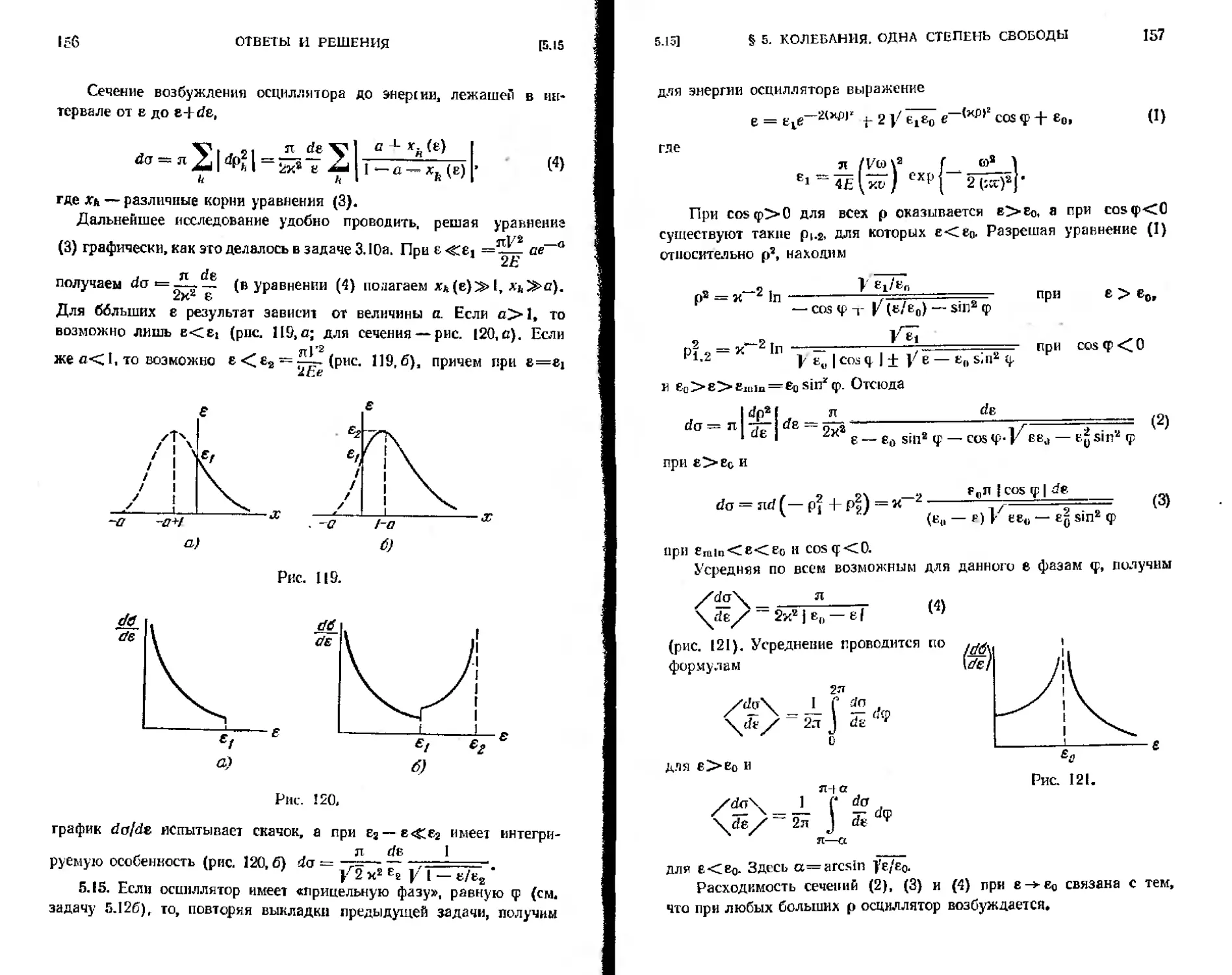
5.15.	Осциллятор может колебаться только вдоль оси г. Найтн дифференциальное эффективное сечение возбуждения осциллятора до энергии в быстрой частицей, взаимодействующей с ним по закону U (г) = Ve~K!lr*. Скорость частицы параллельна осн г, ее энергия
Начальная энергия осциллятора во-
5.16.	На гармонический осциллятор действует сила F(i), причем F(—ос)=0, F(-f-oo)=F0. Найти энергию E(-f-oo), приобретенную осциллятором за все время действия силы, н амплитуду колебаний его при t—>+<», если при t—>—оо осциллятор покоился.
5.17.	Найти энергию, прибретенную осциллятором под действием силы
F (0 =
Y<;’J ^(2-е-м)
при I <. 0.
при t > 0.
Энергия осциллятора при t—>—оо равна £0-
5.18.	Оценить изменение амплитуды колебаний осциллятора, если сила F(/) включается медленно и плавно за большой промежуток времени т, такой что сот^>1. Прн t < 0 сила F(t) = 0, при t > т сила F(t) = Fo, при 0</<т справедлива оценка F(**(0 ~ А>/т* (k= = 0,1. ..., п-f- 1); причем F<B> (0) = F00 (т) = 0 ($ = = 1,2, ..., п — 1), а n-я производная силы при /=0 и t ~ т испытывает скачок.
5.19.	Найтн установившиеся колебания осциллятора под действием периодической силы F(t) :
a)	F(/) = F - (t/т—п) при nT^t<Z(n 4- 1)т (рис. 17);
6)	F (/) = F- (1 — £“w*), /' — t — пт при «т^и<(п-Н)т (рис. 18).
Оценить время установления колебаний, если декремент затухания равен б.
в)	Найтн установившийся ток в контуре (см. рнс. 16) с источником пилообразного напряжения U (/) — = (//т—л)Г при лт</<(л4-1)т.
Рис. 17.	Рис. 18.
5.20.	На осциллятор с трением (собственная частота соо, сила трен ня fT₽=—21mx) действует вынуждающая сила F(t).
а)	Найти среднюю работу Д этой силы при установившихся колебаниях, если F(t) — fjcos at -j- fecos 2at.
б)	To же для F(t)= 2 aneinat, a^„ = a!l.'
n=~ca
в)	Найти среднюю за большой промежуток времени работу силы F (/) = Дсоб coi£ -f- f2cos co2J при установившихся колебаниях.
г)	Найти полную работу силы F(t)— f ф(и)
ф(—<й) =1)?*(со), если осциллятор прн t—* — оо покоился.
5.21.	Гармонический осциллятор находится в поле бегущей волны, которая действует на него с силой /•(х, t) = f(t— x/V), где х— отклонение осциллятора от положения равновесия, V — скорость волны. Предполагая х достаточно малым, найти связь между переданными осциллятору энергией А£ и импульсом
Др = f F(x (/),/) dt.
ограничившись приближением, квадратичным по F, и считая /(± ©о) — 0.
§ 6. Малые колебания систем с несколькими степенями свободы
В задачах 6.1—6.21 с помощью общих методов рассматриваются свободные и вынужденные колебания относительно несложных систем (с двумя-тремя степенями свободы). В задачах 6.18 — 6.21 приведены системы с вырожденными собственными частотами.
Для исследования более сложных систем полезно использовать ортогональность собственных колебаний и свойства симметрии системы. Соответствующие теоремы приведены в задачах 6.22 и 6.39, а иллюстрации их применения, например, в задачах 6.26 — 6.33 и 6.40 — 6.45, 6.47, а также в задачах о колебаниях молекул 6.46, 6.48 — 6.52.
Влияние малого изменения системы на ее движение можно исследовать с помощью метода последовательных приближений — теории возмущений. Общей форме теории возмущений в задачах о малых колебаниях посвящена задача 6.34, конкретным примерам — задачи 6.35, 6.37, 6.41, 6.42, 6.506. Полезно отметить, что подобным же образом строится теория возмущений в квантовой механике.
В задачах 6.36 — 6.38 изучаются колебания систем, в которых действуют «гироскопические» силы (см. также задачи 9.24 — 9.27).
6.1. Найти свободные колебания системы, изображенной на рис. 19, при которых частицы движутся вертикально. Найти нормальные координаты и выразить через них функцию Лагранжа.
6.2. Найтн установившиеся колебания системы, описанной в предыдущей задаче, если точка подвеса движется в вертикальном направлении по закону a(t), где
а)	а (/) = a cos у/,
б)	а(1) =а(-^--и}
при t<{n 4- 1)т.
6.3.	Найти свободные малые колебания плоского двойного маятника (рис. 20).
6.4.	Найти свободные колебания системы, функция Лагранжа которой
г _ 4 у* + “I*,2 2
Как выглядит траектория точки с декартовыми координатами (х, у)?
6.5.	Найти нормальные колебания системы, функция Лагранжа которой:
a)L = ±+i!_^+^ + axJ/;
б)	L =	+	+
6.6.	Найти нормальные колебания в системах связанных контуров: а) рнс. 21, а; б) рис. 21, б.
Я, '%г	^2
а)	б)
Рис. 21.’
6.7.	Найти нормальные колебания системы частиц, соединенных пружинками (рис. 22). Частицы могу г
Я> mt к2 т2 к3	к т kf т к
Рис. 22.	Рис. 23.
двигаться только вдоль прямой ZB. Найтн свободные колебания системы.
6.8.	Найтн свободные колебания системы (рис. 23), если в начальный момент:
а)	одна нз частиц имеет скорость v, скорость другой и отклонения обеих частиц от положения равновесия равны нулю;
б)	одна из частиц отклонена от положения равновесия на расстояние а, отклонение другой и скорости обеих равны нулю.
Частицы могут двигаться только вдоль прямой АВ.
6.9.	Определить поток энергии от одной частицы к другой, используя условия предыдущей задачи.
6.10.	Найти свободные колебания системы (см. рнс. 23), если на каждую из частиц действует сила трения, пропорциональная ее скорости.
6.11.	Найти свободные малые колебания двойного маятника (рис. 24), если в начальный момент верхний маятник вертикален, нижний отклонен на угол р I, а скорости их равны нулю. Массы маятников '///////,	Мкт, причем М т.
Y	в.12. Найти установившиеся колебания сн-
Ь	стемы (см. рис. 23), если точка А, в которой
\	закреплен левый конец пружины, движется
дА по закону acosff в направлении прямой АВ.
\	6.13. Найти установившиеся колебания си-
у стемы двух частиц на кольце*) (рис. 25, а), \ если точка А движется по кольцу по закону л?* a cos yt. Исследовать зависимость амплитуд Рис 24. колебаний от частоты вынуждающей силы.
6.14.	Три частицы, каждая массы т, связанные пружинками, могут двигаться по кольцу (рис. 25, б). Найти установившиеся колебания системы, если точка А движется по кольцу по закону a cos 7/.
Л	А
а)	б)
Рис. 25.
6.15.	Нантн установившиеся колебания системы, изображенной на рис. 23, если точка А движется по закону dcosf/. На частицы действует сила трения, пропорциональная скорости.
6.16.	Найти движение системы рис. 22, если в начальный момент частицы покоились в положениях равнове
*) В этой и подобных задачах кольцо предполагается гладким и неподвижным.
сия, а точка А движется по закону a cos у!. Массы частиц равны (гп[ = т2 = т).
6.17.	Найти установившиеся колебания частицы (рис. 26) под действием однородного переменного поля
Рис. 26.	Рис. 27.
(7(г) =—F(/)r, где вектор F(f) лежит рисунка, в случаях:
a) F(£) = F0cosб) F(0 вращается с оставаясь постоянным по величине.
в плоскости
частотой 7,
одинаковых
6.18. Найти нормальные колебания трех
частиц, связанных одинаковыми пружинками и могущих двигаться по кольцу (рис. 27).
Определить нормальные координаты, приводящие функцию Лагранжа к сумме квадратов.
Рис. 28.
Рис. 29.
6.19.	Найти свободные колебания системы, рассмотренной в предыдущей задаче, если в начальный момент одна из частиц отклонена из положения равновесия. Начальные скорости равны нулю.
6.20.	Найти нормальные колебания системы трех частиц, которые могут двигаться по кольцу (рис. 28).
6.21.	Найтн нормальные координаты системы четырех частиц на кольце (рис. 29).
6.22.	Пусть нормальные колебания системы, описываемой функцией Лагранжа
= ~2~ 2
имеют ВИД
х"1 (t) = 4',)cos(«Ii + <pI).
Доказать, что амплитуды, соответствующие колебаниям с различными частотами coj и to,, удовлетворяют соотношениям
i.3	i.i
6.23.	На систему, описываемую функцией Лагранжа Ь = 4- S (trii jXiXj — ktjXtXj),
наложена линейная связь
2 «1*1 = 0,	= const.
i
Пусть все собственные частоты системы без связи различны Qi<ПгДоказать, что все собственные частоты системы со связью <oz лежат в промежутках между Qf:
Qi toj	(й2 ^ ... ^	1 Рд-.
6.24.	Установившиеся колебания системы, описывае-, мой функцией Лагранжа
Ь - 4- 2 (fWi — kijXiXi) + S xifi cos yl,
можно представить в виде xt (t) — cos yt. (Почему?) (обозначения задачи 6.22).
Выразить коэффициенты Х(,) через ft и
Исследовать зависимость Х(,) от
Показать, что если для s-ro нормального колебания SMP-O.toV’jeO,
6.25.	Система частиц, связанных пружинками, может совершать малые колебания. Пусть к одной из них — частице А — вдоль направления х приложена сила F=FGcosft, а другая — частица В — при этом совершает установившиеся колебания, при которых проекция ее отклонения на направление хг имеет вид Хв = Ccosyt.
Показать, что прн действии силы F на частицу В вдоль осн х' возникают такие колебания частицы А, что хл = — Ccosyt (теорема взаимности).
6.26.	Найтн нормальные колебания системы частиц, которые могут двигаться по кольцу (рнс. 30).
6.27-	Найтн нормальные колебания системы четырех частиц на кольце (рнс. 31).
6.28.	а) Найти нормальные колебания системы, изображенной на рнс. 32. Все частицы в пружинки одинаковы. Натяжение пружинок в положении равновесия
3 Г. Л. Коткин. в. г. Сербо
f = H где /—равновесное расстояние между частицами.
Указание. Некоторые из нормальных колебаний очевидны. Определение остальных можно упростить, используя соотношения задачи 6.22.
б) Найти нормальные колебания системы четырех одинаковых частиц, изображенных на рис. 32 (пятая частица отсутствует, а пружннкн в этом месте соединены). Коэффициенты жесткости и натяжения всех пружинок одинаковы.
6.29.	Три частицы, имеющие различные массы (I = 1,2,3), могут двигаться по кольцу (рис. 33). Прн каких значениях коэффициентов жесткости пружинок kt в данной системе наступит вырождение частот?
6.30.	Какие из нормальных колебаний системы рис. 27 мало изменяются прн малом измеиенин системы, состоящем в следующем:
а)	жесткость пружины 1—2 изменена на малую величину bk-
б)	к частице 3 добавлен малый перегрузок 6m;
в)	к частице 1 добавлен перегрузок 6ть а к частице 2 — 6т2?
6.31.	Для случаев а) н б) предыдущей задачи описать свободные колебания, если в начальный момент частицы 1 и 3 смешены навстречу друг другу иа одинаковые расстояния. Начальные скорости частиц равны нулю.
6.32.	Система рис. 29 имеет вырожденные частоты, поэтому ее нормальные колебания не определены однозначно. Даже малое изменение масс частиц или жесткостей пружинок может привести к снятию вырождения.
Найти нормальные колебания системы рис. 29, близкие к нормальным колебаниям системы, которая получится, если:
а)	к первой н второй частицам добавить одинаковые перегрузки;
б)	изменить одинаково жесткость пружинок 1—2 и 3-4-
в)	добавить перегрузок к первой частице.
6.33.	Частицы 1 и 3 системы, описанной в задаче 6.326, в начальный момент отклонены от положения равновесия на одинаковое расстояние навстречу друг другу;
начальные скорости всех частиц равны нулю. Описать свободные колебания системы.
6.34.	Определить, насколько изменяются собственные частоты системы, описываемой функцией Лагранжа
ь0 = 4~ 5 (m4xixi — Ьнхм)
при небольшом ее изменении:
6L = у 2	— ftkijXiXj).
Все собственные частоты исходной системы невырождены.
6.35.	Найти изменение собственных частот системы рнс. 31, если к первой частице добавлен малый перегрузок 6m, так что е = 6m/m «с 1.
6.36.	Определить свободные колебания анизотропного заряженного осциллятора с потенциальной энергией U (Г) = Y («1Х2 4- (all/ 4- <o|z2) в однородном магнитном поле ЭС, параллельном оси г. Рассмотреть, в частности, подробнее предельные случав:
a)	б)
в) ©1 = 0)2»|о^|
(здесь (djg = eSftfmc).
6.37.	Определить свободные колебания анизотропного гармонического осциллятора с потенциальной энергией 1У (г) =-у (©iX® + ofy® + mfz®) в слабом маг-витном поле JC—(Же, о, Ж), рассматривая влияние магнит^ «н_____________
кого поля как малое возмуще- /	|
ние.	I
6.38.	Математический маят- /	у—:--------'
ннк является частью электрн- ?
ческой цепи (рис. 34). Перпен-
дикулярно к плоскости рисунка	Рис. 34:
приложено постоянное одно-
родное магнитное поле К. Найти нормальные колебания системы.
3*
6.39.	Пусть система, совершающая малые колебания (а следовательно, и ее функция Лагранжа L(x, х)) не изменяет своего вида при замене
х,/=1,2.....N,
3	3
причем постоянные коэффициенты Sy = удовлетворяют условию*)
^s,A6 = 6iM.
Доказать, что:
а)	если нормальное колебание xt = cos(toZ + <р) невырожденное, то амплитуды At симметричны или антисимметричны относительно данного преобразования, т. е.
или У SijA, = 4- At, или У SijAj = — А/, i	i
б)	если частота вырождена, то можно выбрать нормальные колебания симметричными или антисимметричными;
в)	если на систему действует внешняя сила, симметричная (антисимметричная) относительно данного преобразования, то антисимметричные (симметричные) нормальные колебания не возбуждаются. (Это один нз примеров так называемых правил отбора.)
6.40.	Используя соображения симметрии, найти нормальные колебания системы рис. 35.
6.41.	Описать свободные колебания системы (см. рнс. 32), если в начальный момент частицы 1 н 4 смещены навстречу друг другу на одинаковые расстояния в горизонтальном направлении, а начальные скорости всех частиц равны нулю. Натяжение пружинок I—где I—равновесное расстояние между частицами (ср. с задачей 6.31).
6.42.	Найтн поправки к частотам нормальных колебаний системы четырех частнЦ на кольце (рнс. 29), возникающие при малых изменениях масс — на Ьгщ для первой и на 6/л2 для второй частицы.
*) Это условие означает, что при двукратном преобразовании система возвращается в исходное состояние. Таким свойством обладают, например, отражения относительно плоскости симметрии системы или повороты на 180° относительно оси симметрии.
6.43. Используя соображения симметрии, определить векторы нормальных колебаний системы частиц (рис. 36). Все массы частиц н пружинки одинаковы.
6.44. Найти нормальные колебания системы восьми масс, прикрепленных пружинками к неподвижной рамке
(рис. 37). Жесткости kt натяжения f и длины I всех пружинок одинаковы.
6.45.	Рамка, изображенная на рнс. 37, колеблется вдоль направления ДД по закону a cos-у Л При каких значениях частоты 7 возможна резонансная раскачка колебаний?
6.46-	Найти нормальные колебания линейной симметричной молекулы ацетилена С2Н2 (рнс. 38), предпо
Рнс. 37.
лагая, что потенциальная энергия молекулы зависит как от расстояния межд) соседними атомами, так и от углов НСС.
6.47-	Две одинаковые частицы прикреплены пру-
•---•---> —♦
неси
Рис. 38.
жннками к неподвижной рамке (рис. 39). Система симметрична относительно оси CF. Какие сведения о
нормальных колебаниях можно получить, не зная жесткостей н натяжений пружинок?
6.48.	Классифицировать собственные колебания молекулы этилена С2Н4 по их свойствам симметрии относительно осей АВ и CD (рис. 40). В положении равновесия все атомы молекулы расположены в одной плоскости.
6.49.	Найти нормальные колебания молекулы, имеющей форму равностороннего треугольника. Считать, что потенциальная энергия зависит только от расстояний между атомами (все атомы одинаковы). Момент с точностью до малых первого порядка включительно по амплитуде колебаний равен пулю.
6.50.	Молекула АВ3 имеет форму правильного треугольника, в центре которого находится атом А, а в вершинах—атомы В (такова, например, молекула хлорида бора ВС13).
а)	Используя соображения симметрии, определить кратность вырождения собственных частот молекулы.
б)	Определить, насколько изменятся частоты колебаний, оставляющих молекулу равносторонним треугольником, и колебаний, выводящих атомы из плоскости, если одни из атомов В (его масса т) заменить его изотопом, близким по массе Ьт). Масса атома Л равна тА.
6.51.	Используя соображения симметрии, определить кратность вырождения различных собственных частот «молекулы», состоящей из четырех одинаковых «атомов» н имеющей в положении равновесия форму правильного тетраэдра.
6.52.	Молекула метана СН< имеет форму правильного тетраэдра, в вершинах которого расположены атомы водорода, а в центре — атом углерода.
а	) Определить кратности вырождения собственных частот молекулы.
б	) На скольких различных частотах происходит резонансное возбуждение собственных колебаний молекулы СН4, если на нее действует однородное переменное электрическое поле? (Речь идет фактически об электромагнитных волнах инфракрасного диапазона, длина волны которых на несколько порядков больше размеров молекулы.) Учесть, что атомы водорода и углерода имеют заряды противоположных знаков.
Как зависит амплитуда колебаний атома углерода от ориентации молекулы по отношению к электрическому полю?
§	7. Колебания линейных цепочек
Рассматриваемые в задачах этого параграфа цепочки частиц, соединенных пружинками, представляют собой простейшие модели, используемые в теории твердого тела (см., например, [18]). Электрические аналоги таких цепочек — искусственные линии, находящие применение в радиотехнике (см., например, [16]).
7.1.	Определить нормальные колебания системы .¥ одинаковых частиц массы т, связанных одинаковыми пружинками жесткости k и могущих двигаться по прямой (рис. 41).
Л	Л
Рнс. 41.	Рис. 42.
Указание. Удобно искать нормальные колебания в виде суперпозиции бегущих волн.
7.2.	То же'для системы (рис. 42), один из концов которой свободен.
7.3.	Найти свободные колебания N частиц, соединенных пружинками в могущих двигаться по кольцу (рис. 43), Массы всех частиц и жесткости пружинок одинаковы. Пусть движение представляет собой бегущую
по кольцу волну. Проверить, что поток энергии равен произведению линейной плотности энергии на групповую скорость.
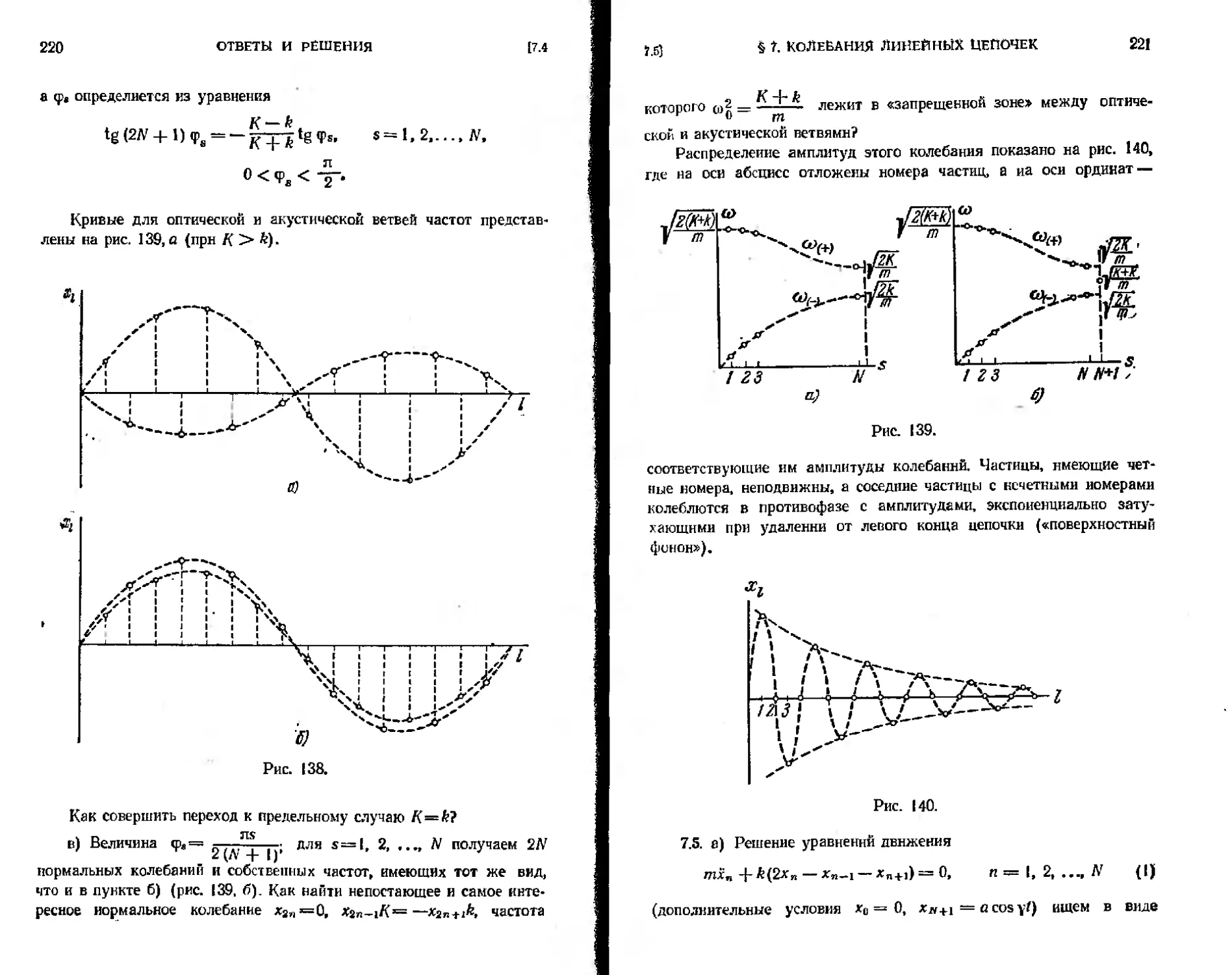
7.4.	Определить свободные колебания системы частиц, могущих двигаться по прямой:
a)	2/V частиц с массами tn и М, соединенных одинаковыми пружинками жесткости k (рис. 44);
б)	2N частиц с массами tn, соеди-Оиенных пружинками жесткости k н /( (рис. 45);
в)	2N -|-1 частиц с массами т, соединенных пружинками жесткости k и К (рнс. 46).
См. указание к задаче 7.1.
г 7-5. а) Найти установившиеся колебания системы, описанной в задаче Рис. 43.	7.1, если точка А движется по закону
a cos yt (рнс. 41).
б)	То же для системы, изображенной на рнс. 42.
7.6.	То же для системы рнс. 44.
7.7.	Найтн нормальные колебания системы частиц, могущих двигаться по прямой и соединенных пружинками, если
a)	1=1, 2, .... /V—1, жесткости пру-
жинок одинаковы (рис. 47); исследовать случаи tnN т и тк с т\

Рнс. 44.
Рис. 45.
б)	ki = k йк+ь /=1, 2, .... N, все частицы одинаковы (рис. 48); исследовать случаи kK+i >> k и ЛЛ-+1 С k.
7.8.	a) N маятников связа-к К * Ь К & ны пружинками, и могут дви--гаться лишь в вертикальной плоскости, проходящей через
Рис. 46.	горизонтальную линию подве-
са (рнс. 49). Найти нормальные колебания системы, если все маятники и пружинкн одинаковы и в положении равновесия длина пружинки
равна расстоянию между точками подвеса соседних маятников.
б) 27V одинаковых маятников связаны одинаковыми пружинками и могут двигаться лишь в вертикальных плоскостях, перпендикулярных круговой линии подвеса
/77	/77	к к \ /л А Л &
jwAWA......
Рис. 47.
Рнс. 48.
г(рнс. 50). Расстояние между соседними точками подвеса равно а. Длина каждой нз пружинок в нерастянутом состоянии равна Ь. Исследовать, как зависит устойчивость малых колебаний вблизи вертикали от значения параметра Ъ — а. Радиус окружности линии подвеса /? считать достаточно большим, так чтобы малыми величинами ///?, а/А‘, ОД можно было пренебречь.
Рис. 51.
7.9.	а) К одному концу искусственной линии рнс. 51 подключен источник переменного напряжения U cos ft Какое комплексное сопротивление Z(*y) следует подключить к другому концу линии, чтобы колебания в ией
представляли собой бегущую волну, т. е. чтобы напряжение па каждом из конденсаторов отличалось от напряжения па соседнем только определенным сдвигом фазы?
б)	То же для искусственной линии рис. 52.
Рис. 52.
7.10.	Упругий стержень можно представить как предельный случай системы N частиц (см. рис. 41) при условии N—► оо, а—>0, причем Nm = const и Na = == const, где т — масса частицы, а — расстояние между соседними частицами в положении равновесия. Получить уравнения колебаний стержня как предел уравнений движения дискретной системы.
Указание» Ввести координату точки стержня | = = па, а также величины, получаемые прн предельном переходе а —> 0
х(&, 0 = limx„ (/),
dt,	a
7.11.	Получить уравнение колебаний стержня предыдущей задачи с учетом первой неисчезающей поправки, связанной с конечностью расстояния а между соседними частицами.
§ 8.	Нелинейные колебания
8.1.	Определить искажение гармонического колеба* ния осциллятора, вызванное наличием ангармонических поправок к потенциальной энергии:
б)бУ(х) = ^’.
8.2.	Определить искажение гармонического колебания осциллятора, вызванное ангармонической поправкой к кинетической энергии
_____тухх"2 02 — 2 '
8.3.	Найтн ангармонические поправки к колебаниям маятника, точка подвеса которого движется по окружности (рис. 15).
8.4.	Найти колебания осциллятора под действием силы ficos с»1/ 4- fzcos (02/ с учетом ангармонической по-
Е.	i. max* правки ос/ (х) = —g—.
8.5.	Маятник представляет собой грузик массы подвешенный на пружннке жесткости k. Длина ненапряженной пружинки /о. Найти ангармонические поправки к колебаниям маятника.
Воспользоваться декартовыми координатами отклонения грузика от положения равновесия.
8.6.	Найти амплитуду установившихся колебаний а нга рмони чес кого осцилл я тор а
( х + 2>.i 4- со ох 4-	= f cos со/
а)	в области резонанса | со — ©о] -С сад
б)	в области резонанса иа утроенной частоте вынуждающей силы |3со— (1)01 С «о.
8.7.	а) Определять амплитуду и фазу установившегося колебания осциллятора при параметрическом резонансе:
х 4- 2Хх + ©о (1 4- h cos 2<о/) х 4- ₽х3 = 0
(л«1,	—
б)	Определить амплитуду третьей гармоники установившегося колебания.
8.8.	Определить колебание осциллятора
x + (0o(l 4-Acos2w/)x = 0	| (о — (о01С ©D)
а)	в области неустойчивости относительно параметрического резонанса;
б)	вблизи области неустойчивости.
8.9.	Частота гармонического'осциллятора (о(0 меняется по закону, изображенному на рис. 53. Найти
области неустойчивости относительно параметрического резонанса.
8.10.	Определить, как изменяются со временем амплитуды слабо связанных осцилляторов, функция Лагранжа которых
£ = у (i* 4- у2 - co2x2 - 4(dV + 2ах2//).
8.11.	Найти частоту малых свободных колебаний маятника, точка подвеса которого совершает вертикальные колебания с большой частотой 7(7
8.12.	Определить эффективную потенциальную энергию:
а)	частицы массы т, находящейся в поле
| г — a cos со/ |	| г 4- a cos со/ j (г с)>
б)	осциллятора, находящегося в поле ,, о ar cos со/ Щг) = 2а —Гя—.
8.13.	Определить движение быстрой частицы, влетающей в поле 1/=Л(х2—у2)sin kz под малым углом к оси г(й2£»Л).
8.14.	Определить скорость смещения центра орбиты заряженной частицы в слабо неоднородном магнитном паче ==	— О, Ж = причем
3^' (х)	,	mvc
С — 2Н*) Г ’ ГС= еув (л)» где г — радиус орбиты.
8.15.	Задача представляет собой механическую модель фазовых переходов второго рода.
Железный шарик массы т может колебаться вдоль оси у на пружинке, потенциальная энергия которой имеет вид U(y) =—Су2-^-Ву* *). С помощью электромагнита возбуждают колебания шарика по закону i/ocos^/, причем 7 много больше частоты его собственных колебаний**).
Найтн частоту малых собственных колебаний шарика в зависимости от параметра Т — у%.
§ 9.	Движение твердого тела. Неииерциальиые системы отсчета
9.1. В вершинах квадрата со стороной 2а расположены массы m и М (рис. 54, а). Найти компоненты тензора
инерции относительно; а) осей х, у, z\ б) осей х', у', совпадающих с диагоналями квадрата, и z.
9.2.	Найтн главные оси инерции и главные моменты инерции следующих систем:
а)	массы m и М расположены в вершинах прямоугольника со сторонами 2а и 2Ь (рнс. 54,б).
б)	массы пг и 2/л
расположены в вершинах прямоугольного треугольника с катетами 2а н 4а (рис. 54, в). х •
•)	Такова, например, потенциальная энергия системы, изображенной на рис. 13, если шарик может двигаться лишь в направлении осн у, перпендикулярной к линии АВ, и длина нерастянутой пружинки /0 больше /. В этом случае при |у| С I имеем
с = ^(4—/)//, в = ад/3.
•*	) При действии высокочастотной силы f(i)=—(fifo72/m)cos 7/ в пределе: у -*• <», амплитуда вынужденных колебаний стремится к уо, поправки к амплитуде и высшие грамоники имеют малость
г’?
9.3.	Выразить момент инерции /и относительно осп, параллельной единичному вектору п и проходящей через центр инерции тела, через компоненты тензора инерции.
9.4.	Найти главные моменты ниерцин шара радиуса R, имеющего внутри полость в форме шара радиуса г (рнс. 55).
9.5.	Выразить компоненты тензора квадруполыгого момента масс
D,, = J (Зхл — г!6м) pdV
(р — плотность) через компоненты тензора инерции Iik.
9.6.	Найтн частоту малых коле-баннй однородного полушара, нахо-/	/ \ дящегося на гладкой горизонталь-
/	£	ной поверхности в поле тяжести.
	1—г-^т--На покоившуюся гантельку, \-----------------—7	состоящую из пары касающихся
\	/	одинаковых шариков, налетает тре-
тий такой же. Скорость его V перпендикулярна линии центров ган-
Рис. 55.	тельки и направлена к центру одно-
го из ее шариков. Найти скорость шарика и гантельки после столкновения. Удар упругий.
9.8.	Какова станет продолжительность суток, когда они сравняются (за счет действия приливных сил) с месяцем (т. е. период обращения Земли вокруг оси станет равным периоду обращения Луны вокруг Земли). Припять для простоты, что ось вращения Земли перпендикулярна плоскости орбит Земли и Луны. Для численных оценок считать Землю однородным шаром радиусом а ~ 6,4 тыс. км и массой Л1, в 81 раз большей массы Луны т\ расстояние от Земли до Луны == 380 тыс. км.
9.9.	Два одинаковых однородных шара, вращающихся с одинаковыми по величине угловыми скоростями <о, медленно сблизившись, жестко состыковываются друг с другом. Определить движение образовавшегося тела. Найти, какая часть начальной кинетической энергии переходит в тепло. До состыковки угловые скорости шаров были направлены:
а) перпендикулярно ливни центров и параллельно друг другу; б) одна — вдоль лннни центров, другая — пер п енд и кул яр но.
9.10.	Однородный шар радиуса г и массы т катится, не проскальзывая, по горизонтальной плоскости со скоростью V. В момент, когда он касается другого такого же шара, лежавшего неподвижно, шары жестко скрепля-еотся (рис. 56). Плоскость абсолЕОтно гладкая (после скрепления шары свободно скользят по ней).
Рис. 56,
Рис. 57.
С какими силами действуют на плоскость шары? Ускорение свободного падения достаточно велико, так что шары все время касаются плоскости.
9.11.	На однородный эллипсоид вращения (полуоси а = Ь, с) налетает частица, движущаяся параллельно осн Оу со скоростью v и прицельными параметрами ръ р2 (рнс. 57), и прилипает к нему. Описать движение
Рис. 58.
эллипсоида, предполаЕая, что его масса много больше массы налетающей частицы.
9.12.	Гирокомпас представляет собой быстро вращающийся диск, ось которого может свободно поворачиваться в горизонтальной плоскости (рнс. 58). Иссле
довать движение гирокомпаса на широте ct. Угловая скорость вращения Земли Q.
9.13.	Волчок с неподвижной точкой опоры- О, вращавшийся с угловой скоростью Q вокруг своей оси (скорость прецессии считаем малой), касается горизонтальной плоскости краем диска (рис. 59).
Найтн угловую скорость волчка, когда проскальзывание диска прекратится. В момент касания нутаций не было.
9.14.	В поле тяготения неподвижной точечной массы движется однородное тело массы имеющее форму эллипсоида вращения. Найти функцию Лагранжа системы, выбрав в качестве переменных сферические координаты центра тяжести и углы Эйлера. Размеры тела малы по сравнению с расстоянием до центра поля.
Указание. Потенциальная энергия системы приближенно равна 
«
где R = (Xh Х2, Х3) — радиус-вектор центра эллипсоида, Dih — тензор квадрупольного момента масс (см. задачу 9.5), <р(Я) ~ — yM/R — потенциал поля тяготения (ср. [2], §42).
9.15.	Определить угловую скорость прецессии земной оси под влиянием притяжения Солнца и Луны. Наклон земной оси к плоскости орбит Земли и Луны равен 67°. Для простоты Землю считать однородным эллипсоидом вращения, полярная полуось которого с меньше, эквато--	..	с —- с _ I
рнальнои полуоси а, причем —”^зоо‘
9.16.	Составить уравнения движения для проекций момента на подвижные оси координат, выбранные по осям инерции. Проинтегрировать эти уравнения для свободного движения симметрического волчка.
9.17.	Исследовать устойчивость вращения асснмет-рического волчка относительно главных осей инерции с помощью уравнений Эйлера.
9.18.	Однородный шар радиуса а движется по внутренней поверхности вертикального цилиндра радиуса bt не проскальзывая. Найти закон движения шара.
9.19.	а) Плоский симметричный относительно своей осн диск катится по гладкой горизонтальной плоскости (трение отсутствует). Определить закон движения диска (в квадратурах).
Исследовать подробнее закон движения в следующих случаях.
Определить, при каких условиях угол наклона диска к плоскости остается постоянным.
Диск катится так, что его ось сохраняет определенное. (горизонтальное) направление. Определить, при какой угловой скорости вращения вокруг этой оси такое движение устойчиво.
б)	Диск катится без проскальзывания по горизонтальной плоскости. Найти уравнения движения и ответить на те же вопросы, что и в пункте а).
в)	То же для диска, который катится по горизонтальной плоскости, не проскальзывая и не проворачиваясь вокруг вертикальной оси *).
г)	Находящийся на наклонной плоскости диск вращается без проскальзывания вокруг своего диаметра, перпендикулярного этой плоскости. Найти смещение диска за большое время. Наклонная плоскость составляет малый угол ct с горизонтальной.
9.20,	а) Найти в квадратурах закон движения неоднородного шара, который движется без трения по горизонтальной плоскости. Распределение плотности симметрично относительно оси, проходящей через центр масс и геометрический центр шара.
Исследовать влияние малых снл трення на движение шара в случае, когда в отсутствие трения шар двигался бы так, что угол между осью симметрии и вертикалью был бы постоянным.
б)	Найти уравнения движения описанного шара, если он катится без проскальзывания по горизонтальной плоскости.
9.21.	Найти отклонения к востоку и к югу от вертикали свободно падающего с высоты h тела. Начальная скорость тела равна нулю.
*) Это означает, что сцепление диска с плоскостью в «точке» соприкосновения таково, что площадка в месте контакта не скользит по плоскости и ие проворачивается. Потерями энергии иа трение качения пренебречь.
4 Г. Л. Коткин, В. Г, Сербо -
9.22	*). Сосуд, частично заполненный постепенно затвердевающей эпоксидной смолой, приводят во вращение С угловой скоростью 0)2 вокруг оси АВ, которая в свою очередь вращается вокруг неподвижной оси CD с угловой скоростью*он (рис. 60). Какую форму примет, затвердев, поверхность смолы?
Рис. 61.
9.23.	Частица движется в центральном поле t/(r). Найти уравнение траектории и закон движения в системе координат, равномерно вращающейся с угловой скоростью £2, параллельной моменту импульса М.
9.24.	Найти малые колебания частицы т, прикрепленной пружинками жесткости kv и /г2 к рамке, вращающейся в своей плоскости с угловой скоростью ft (рис. 61). Частица может двигаться в плоскости рамки.
д-u
9.25.	Гладкий параболоид 2г = — 4--у вращается вокруг вертикальной оси z с угловой скоростью со. При каком значении cd нижнее положение неустойчиво для частицы, находящейся внутри параболоида? Ускорение силы тяжести g = (0, 0, —g).
9.26.	Рамка с частицей массы т, закрепленной на пружинках (длины которых /, коэффициенты жесткости k и натяжения при -неподвижной рамке f) вращается с угловой скоростью 7 вокруг оси г, смещенной на расстояние а от центра рамки (рнс. 62).
Определить равновесное расстояние частицы от оси и исследовать его устойчивость.
"} Задача Б. С. Кузьмина и М. П. Перельройзена,
Рассмотреть следующие случаи:
а) частица может двигаться только вдоль пружин; б) возможны любые смещения частицы.
9.27.	Две звезды движутся по окружностям вокруг их центра масс. В системе отсчета, в которой звезды неподвижны, найтн такие точки, в которых помещенное там легкое тело также остается неподвижным. Исследовать устойчивость этих «положений равновесия». (Ограничиться точками, не лежащими на прямой, соединяющей звезды.)
9.28.	Определить нормальные колебания трехатомной молекулы, описан
ной в задаче 6.49, если ее момент импульса М ие равен нулю. Угловая скорость вращения молекулы Q
здесь /г — коэффициент жесткости связи. Момент импульса перпендикулярен к плоскости молекулы.
Рис. 62.
§ 10. Уравнения Гамильтона. Скобки Пуассона
10.1.	Пусть функция Гамильтона 7/ системы частиц не изменяется при бесконечно малом переносе (повороте). Вывести отсюда закон сохранения импульса (момента импульса).
10.2.	Найти функцию Гамильтона свободно движущегося Симметрического волчка, выбрав в качестве координат эйлеровы углы 0, <р, ip.
10.3.	Определить функцию Гамильтона ангармонического осциллятора, функция Лагранжа которого
т А'2 Сй2.Г2	з . р * о
L = — — -------ах8-)- рхх2.
10.4.	Найти закон движения частицы, функция Гамильтона которой
10.5.	Найти уравнения движения частицы, функция Гамильтона которой Н (р, г) = ^рр(луч света).
Найти траекторию, если п(г) = ах.

10.6.	Найти функцию Лагранжа, если функция Гамильтона равна
а) Н (р, г) = £ - pa (а = const); б) Н (р, г) =
10.7.	Найти закон движения заряженной частицы в однородном постоянном магнитном поле JC, решая уравнения Гамильтона. Векторный потенциал выбрать в виде
Ау — Жх, Ax — At = 0.
10.8.	Исследовать качественно движение заряженной частицы в неоднородном магнитном поле, описываемом векторным потенциалом А — (0, 1гх2, 0). Сравнить с дрейфовым приближением.
10.9.	Показать, что задача о движении двух частиц с противоположными зарядами (е и —е) в однородном магнитном поле приводится к задаче о движении одной частицы в заданных потенциальном и магнитном полях [30].
В задачах 10.9—10.13 идет речь о движении электронов в металле или полупроводнике. Электроны в твердом теле представляют собой систему частиц, взаимодействующих как друг с другом, так н с ионами, образующими кристаллическую решетку. Их движение описывается квантовой механикой. В теории твердого тела часто удается привести задачу о движении многих взаимодействующих частиц, составляющих тело, к задачам о движении отдельных свободных частиц (называемых квазнчастицами — электронами или дырками в зависимости от знака заряда), имеющих, однако, сложную зависимость энергии от импульса Е(р) («закон дисперсии»)*). Во
*) Например, для дырок в кристаллах германия и кремния
Е <р) = 2m [Лр! ±	+ с" (р«Р? + Р«4 + Р,Р?)]-
где оси координат выбраны в соответствии с симметрией кристаллов, т — масса электрона, а константы А, В, С имеют следующие значения:
	А	В	с
Ge	-13,1	8,3	12,5
Si	-4,0	1.1	4,1
многих случаях оказывается возможным рассматривать движение квазичастиц с помощью классической механики. Функция Е(р) является периодической функцией с периодом, равным периоду так называемой обратной решетки *). В остальном рассматриваемые далее зависимости е(р) можно считать произвольными.
10.10.	Известно, что е(р) является периодической функцией р с периодом, равным периоду обратной решетки, умноженным иа 2лИ (например, для кубической решетки с периодом а период е(р) равен 2лй/а).
Определить закон движения электрона в однородном электрическом поле 8.
Указание к задачам 10.11—10.13. В этих задачах удобно, кроме обобщенного импульса Р, ввести кинематический импульс р=Р—^-А, где А — векторный потенциал магнитного поля.
10.11.	Полагая функцию Гамильтона
Д(Р,г) = е(р-^А) + гФ,
получить уравнения движения (заряд электрона е < 0)\
10.12.	а) Найти интегралы движения электрона в твердом теле в однородном магнитном поле. Как выглядит «траектория» в импульсном пространстве?
б) Доказать, что проекция траектории электрона в однородном магнитном поле на плоскость, перпендикулярную к J€, в обычном пространстве получается из траектории в импульсном пространстве поворотом и изменением масштаба.
10.13.	Выразить период обращения электрона в однородном магнитном поле через площадь 5(£, р^) сечения поверхности е(р) =Е в импульсном пространстве плоскостью р^ = р = const.
10.14.	Вычислить скобки Пауссона:
а)	{Л4<, Xj}, {A!*, pj, {Mit MJ;
♦) Например, для кристалла, решетка которого обладает в направлении оси х наименьшим периодом а, имеем е(р«, pv, Pz)=* / 2лЛ \
= в1рж + -у, ри, pk где Л —постоянная Планка.
б)	{ар, Ьг), {аМ, Ьг}, {аМ, ЬМ} ;
В)	{м. гр}, {р, г”}, (р, (аг)2}.
Здесь xh pit Mt — декартовы компоненты векторов, а, b — постоянные векторы.
10.15.	Вычислить (Л,-, ЛД, где
=	+	= т Iх» +
ла = 4 (хРу — УРх). Л4 = х! + У2 + р2 4- р=.
10.16.	Вычислить {И, Ай}, {Ал, Лй}, где Л,л = == xtxh + p<ph.
10.17.	Показать, что {Mz, <р} = 0, где <р— любая скалярная функция координат и импульсов частицы.
Показать, что {MXt 1} = [nf], где f—векторная функция координат и импульсов частицы, п— единичный вектор в направлении оси г.
10,18.	Вычислить скобки Пуассона {f, аМ), {fM, 1М), где а = const, f, 1 — векторные функции г, р.
10.19.	Найти {Мс, MJ, где Л1С, МЕ — проекции момента импульса на оси £, | декартовых координат, жестко связанных с вращаЕОЩИМся твердым телом.
(0.20. Составить уравнения движения проекции Мп момента импульса на оси, связанные со свободно вращающимся телом. Функция Гамильтона
<х.₽
10.21.	В этой задаче рассматривается модель электронного и ядерного парамагнитного резонанса (см [18], гл. IX). Функция Гамильтона намагниченного шара в однородном магнитном поле J€ имеет внд
где I — момент инерции, y — гиромагнитное отношение.
Составить уравнения движения вектора момента импульса М и найти закон его движения в случаях:
а)	3£= (0, 0, Ж),
б)	JC = Cos ot, sin со/, <л?0) н в начальный момент М = (0, 0, Мо).
10.22.	Найти {vh uj для частицы в магнитном поле.
10.23.	Доказать, что значение любой функции координат и импульсов системы f(p(/), </(/)) выражается через значения р н q в момент /=0 формулой
f(P(/).9(/))=f + p{«J} \	....
где
/ = МР(0),<7(0))» а //-//(р(0)><?(0))
— функция Гамильтона. (Ряд предполагается сходящимся.)
Вычислить с помощью этой формулы p(t), q(t), Р2(/), <?2(0 Для:
а)	частицы в однородном поле;
б)	осциллятора.
10.24.	Доказать равенства
a)	{f (Р1.91).Ф(Ч'(Р1.«1).Р2.«2. •••)} = Ц {f. <rf:
б)	{f (Р,. <7i, Р2, 92). ® (<Р (Pi. 91 Р2. 9г), Ра. 9з. •)) =
0Ф (С »,
В) {/ (Р. 9), ф (<Р1 (Р, 9), <Г, (р. Ч) • - -} = 2	<?• f <}•
10.25.	а) Пусть функция Гамильтона зависит от переменных Qi, Pi лишь через посредство функции f(qi, pj
Н = Н(f(qh Р1), Чг, р2..q„, р„).
Доказать, что f(qi, Pi) есть интеграл движения.
б) Найти интегралы движения частицы в поле (использовать сферические координаты).
10-26. Как известно, для частицы в поле 1/ = «=- —а/г существует интеграл движения
A- (»М]-Н.
а)	Вычислить скобки Пуассона {А,, Д], {A,
б)	В случае финитного движения (£ < 0) для векторов J12 =	± j/_!^Aj вычислить скобки
Пуассона
{H,JIt2}, {Ль-М, P1U1J, {/й,ы
и сравнить их со скобками Пуассона для компонент момента импульса М. Выразить функцию Гамильтона И через Ji и J2-
§ 11.	Канонические преобразования
11.1,	Найти каноническое преобразование, задаваемое производящей функцией:
a)	F (<?, Q, /) = y та (?) <?’ ctg Q.
Записать уравнения движения в переменных Q и Р для гармонического осциллятора с частотой о(ф
б)	f(?,Q.0 = y™(>[|7-^]’ctgQ.
Записать уравнения движения в переменных Q и Р для гармонического осциллятора, на который действует внешняя сила F(t).
П.2. Найти производящую функцию вида V (р, Q), приводящую к тому же каноническому преобразованию, что и F(q, Р) = q2ep.
11.3.	Какому условию должна удовлетворять функция Ф(д, Р), чтобы ее можно было использовать в качестве производящей функция канонического преобразования?
Рассмотреть, в частности, пример
Ф(<7, Р) =?2 + Р2.
11.4.	Показать, что для системы с одной степенью свободы поворот в фазовом пространстве (q, р) является каноническим преобразованием.
11.5.	Рассматриваются малые колебания ангармонического осциллятора, функция Гамильтона которого
н ах <Ссо2, рх-С 1. В каноническом преобразовании, задаваемом производящей функцией Ф = хР -|- ах2Р ЬР*,
подобрать параметры а и Ь так, чтобы новая функция Гамильтона с точностью до членов первого порядка по cc<d—2Q, pQ включительно не содержала ангармонических членов, и найти х(/).
11.6.	В каноническом преобразовании, задаваемом производящей функцией Ф — хР -Г ах3Р 4- ЬхР3, подобрать параметры а и b так, чтобы малые колебания ан-
д8 ll)2X2
гармонического осциллятора Н — у 4——Г ₽х*в новых переменных Q, Р сводились к гармоническим. Членами второго порядка по pco-2Q2 в новой функции Гамильтона пренебречь.
11.7.	Показать, что преобразование
Р	Р
х = Xcosl 4- ^sinl, у = Vcosl 4- ~ sink,
pv = — sin X 4- Py cos X, px = — ттУ sinl— PxcosX является каноническим. Найти новую функцию Гамильтона, Н'(Р, Q), если
W(p.9)=^ + ^(*2 + </!)
(ср. с задачей 11.17). Описать движение двумерного осциллятора при У = Pv == 0.
11.8.	Используя преобразование предыдущей задачи, привести функцию Гамильтона изотропного гармонического осциллятора в магнитном поле, заданном векторным потенциалом А= (0, 3@х, 0), к сумме квадратов и найти закон его движения.
11.9.	С помощьео канонического преобразования привести к диагональному виду функцию Гамильтона анизотропного заряженного осциллятора с потенциальной энергией t/ (г) = у- (со?х2 4-	+ cofz2), находящегося
в однородном постоянном магнитном поле, заданном векторным потенциалом А= (0, Жх, 0).
11.10.	Применяя каноническое преобразование задачи 11.7 к парам нормальных координат, соответствующих стоячим волнам системы частиц на кольце (см. задачу 7.3), получить координаты, соответствующие бегущим волнам.
11.11.	Показать, что преобразование
Pl = Xp5?(j/27\ cos
S = t!=(K2P;cos<2, + Q.,).
I/WICU
Р(,=^(-Г27\5!п<2, +Р2)
является каноническим. Найтн уравнения Гамильтона частицы в магнитном поле, заданном векторным потенциалом А = (—g-J/Ж у*$,о)в новых переменных.
11.12.	Каков смысл канонического преобразования, задаваемого производящей функцией Ф(д, P)=aqP?
11.13.	Показать, что градиентное преобразование потенциалов электромагнитного поля является каноническим преобразованием для координат и импульсов заряженных частиц, и найти соответствующую производящую функцию.
11.14.	Как известно, замена функции Лагранжа /.(в, q, 0 иа V (q, q,t) = L (q, q, I) +	’ где f (q, 0 —
произвольная функция, не изменяет уравнений Лагранжа. Показать, что это преобразование является каноническим, и найти его производящую функцию.
11.15.	Найти производящую функцию канонического преобразования, состоящего в переходе от q(l)t p(t) к Q(0 =9(* + т)» ^(0 == P(t + т), т = const для:
а)	свободного движения,
б)	движения в однородном поле, U(q) =—fg;
в)	осциллятора.
11.16.	Выяснить смысл канонических преобразований, задаваемых производящими функциями:
а)	Ф(г, Р) = гР -|- 6аР;
б)	Ф(г, Р) = гР-|-6<р[гР];
в)	Ф(«у, Р, /) = qP-\- faH(q, Pt 0;
г)	Ф(г, Р) =гР + 6а(г24-Р2),
где г —декартовы координаты, а ба, б<р, бт, ба—бесконечно малые параметры.
11.17.	Показать, что каноническое преобразование, задаваемое производящей функцией
Ф (х, у, Рх, Pv) = хРх + уРУ + ъ (ху + РХРЬ),
где е->0, представляет собой поворот в фазовом пространстве.
11.18.	Указать производящие функции для бесконечно малых канонических преобразований, представляющих собой:
а)	винтовое движение;
б)	преобразование Галилея;
в)	переход к вращающейся системе отсчета.
11.15*. Каноническое преобразование задано производящей функцией Ф (<?. Р) = qP -]-hW(q, Р), где
Для произвольной функции f(q, р) найти с точностью до первого порядка малости изменения ее величины, связанное с изменением аргументов
11.20. Найти {//, гр}, где функция Гамильтона и . ч р2 , аг
п (г, Р) — gm + 73 ’ и получить, исходя из результата,
интеграл уравнений движения. Для вычисления удобно воспользоваться результатами предыдущей задачи и задачи 11.12.
11,21.	Найти изменение вида зависимости М, р2, рг, Н(г, р, t) от г, р при преобразованиях задачи 11.16.
11.22.	Показать, что результат последовательного выполнения двух бесконечно малых канонических преобразований, заданных производящими функциями
ФДд, р) ^qP-^kiW^q, Р), Х^О, i = 1, 2,
пе зависит от порядка их выполнения (с точностью до второго порядка малости включительно), если
{^(q, р), Wt(q, р)}=0.
11.23.	Найти каноническое преобразование, представляющее собой результат последовательного выполнения бесконечно большого числа N бесконечно малых канонических преобразований, заданных функцией
Ф (<7. Р) ~ qP 4- -£ № Р)> & = const, Л/ -> оо;
а)	Ш'(г, Р) — frP] а, а ~ const;
б)	W(x, у, Рх, Ру) = At,
где At определены в задаче 10.15.
Указание. Составить и решить для конкретных дифференциальные уравнения для Q (X), Р(Х).
11.24.	а) Как изменяется со временем объем, объем в импульсном пространстве и фазовый объем, занимаемые группой свободно движущихся вдоль оси х частиц? В начальный момент координаты частиц заключены в интервале х0 < х < х0 + Дх0, а импульсы —в интервале Pq <2 р <2 Ро + Дро-
б)	Тот же вопрос для частиц, движущихся вдоль осн х между двумя стенками. Соударения со стенками абсолютно упругие. Друг с другом частицы не взаимодействуют.
в)	Тот же вопрос для группы гармонических осцилляторов.
г)	Тот же вопрос для группы гармонических осцилляторов с трением.
д)	Тот же вопрос для группы ангармонических осцилляторов.
е)	Будем описывать распределение частиц в фазовом пространстве в момент i функцией распределения w(x, р, t) такой, что число частиц с координатами в интервале от х до х dx и импульсами в интервале от р до p + rfp есть р, t)dxdp. Определить функции распределения группы свободных частиц н группы гармонических осцилляторов, если в начальный момент
' 'Р' ' 2пЛр„Ах0 Р| 2A.tg 2Лр§ /'
11.25.	Введем переменную
mcojt-r-tp
а = —е'Ч
а)	Найти скобки Пуассона {а*, о}. Выразить через а и а* функцию Гамильтона гармонического осциллятора
„ _ Р3 I
“ 2т + 2 •
б)	Показать, что Q = с и Р = 1а*— кононические переменные. Найтн новую функцию Гамильтона H'dQ, Р).
в)	Для осциллятора с ангармонической добавкой к потенциальной энергии bU= трх4 усреднить функцию Гамильтона H'(Q, Р) по периоду быстрых осцилляций 2 л/со.
Используя усредненную функцию Гамильтона, найти медленные изменения переменных Q и Р.
г)	Исследовать закон изменения амплитуды колебаний осциллятора под действием нелинейной резонансной силы	/
Я === ^ +	*” /л2°)2ах4 cos 4t0^-
11.26.	Исследовать изменение амплитуды колебаний системы трех осцилляторов со слабой нелинейной связью: и =	(Р2 + Р2 + Р2) + у (и?х2 + «2Р!.+ <&' + ахуг),
если |	—©8 («С©!, J ах | << cof. Рассмотреть под-
робнее случай, когда в начальный момент |#|-<|х|, z = 0, у — z = 0.
Воспользоваться тем же методом, что и в предыдущей задаче.
11.27.	Функция Гамильтона ангармонического осциллятора, испытывающего параметрическое воздействие, имеет вид
и р* гт/сд2	с . 2 mfix1
Н = 2^ + Т" С -rhcosZyt) х2 + -у--
Введем канонические переменные
тюх Ч-ip	n Л
а = -- ew, Р = ia*.
[/2тю
а)	Найти новую функцию Гамильтона //' (д, Р, t) и усреднить ее по периоду быстрых осцилляций 2л/т.
б)	Исследовать изменение амплитуды колебаний в области резонанса И— <в| С ho, если в начальный момент величина а близка к нулю.
11.28. а) Проверить, что преобразование
х = Q cos yt + ~ р sin у/,
р = — moQ sin yt + Р cos у/.
является каноническим. Получить новую функцию Гамильтона H'(Q, Р, i) для осциллятора с параметрическим возбуждением:
,, Р2 > то2х2,1	, о ..
# =	—(l-fccos2T/).
б) Усреднить //'(Q, Р, t) по периоду 2л/у и исследовать качественно движение точки на фазовой плоскости Q, Р. Принять А < 1, с = 1 —у/со С 1.
§ 12.	Уравнение Гамильтона—Якоби
12.1.	Найти траекторию и закон движения частицы в поле 17(г) с помощью уравнения Гамильтона — Якоби:
a)U(r) = -Fx; б) U(г) = -Л- + -/L.
12.2.	Определить траекторию и закон движения частицы, рассеиваемой в поле 17(г) — аг/r3. Траекторию выразить через квадратуры, а при Ер2^>а — и аналитически. Скорость частиц до рассеяния направлена противоположно вектору а.
12.3.	Найти сечение рассеяния на малые углы частиц, скорость которых до рассеяния направлена противоположно оси z, в поле U(г);
. j j ( ь л cos 0 gt. г 7 f \	& cos2 G i j 1 в % Ъ (0)
а)17(г) = —; б)С/(г) = -^—; в) и (г) =
12.4.	Найти сечение падения частиц в центр поля U (г):	- -
а)	б) t/(r)=£+7S
в) =	r)l/(r)=^.
Усреднить сечение, предполагая все направления а равновероятными,
12.5.	Найти сечеиие падения частиц на шарик радиуса R, являющийся центром поля U(г) s= аг/г3.
12.6.	Определить траектории и законы движения частиц, рассеиваемых и падающих в центр поля 17(г). Траекторию выразить через квадратуры, а при Ер2^а— и аналитически.
Для первого поля найти аналитическое выражение траектории частицы падающей в центр при Ep2<g.a. Скорость частиц до рассеяния параллельна оси г.
а) (/ (г) =	6) I/ (г) = - a(1 + sinfi).
12.7.	Найти траекторию и закон движения частицы, падающей в центр поля U(г) = аг/г3. На бесконечности частица летит вдоль прямой у — р, х = —ztga, где р — прицельный параметр (вектор а параллелен оси z, начальные сферические координаты частицы г = со, 0 = л — а, = 0). Траекторию выразить через квадра-
2£р2
туры, а при сс2< ~и аналитически.
12.8.	а) Определить траекторию (выразить через квадратуры) финитного движения частицы в поле
=	приМ. = 0.
711 \ и cos G . у
б)	То же для поля 17 (г) =—----Р-у.
12.9.	При каком условии траектория, найденная в предыдущей задаче, окажется замкнутой?
12.10.	Описать качественно характер движения частицы и вид траекторий в поле
12.11.	При каких значениях момента импульса А1, частицы возможно финитное движение в поле V (г) ?
. .т/ . Т bcos2fi	. bcos2G а
a)l/(r) = 7T---—i б)С7(г) = —-2--------
Как выглядит при этом траектория?
12.12.	Найти уравнение траектории и закон движения частицы в поле U(r) в параболических координатах:
a)U(r) = -y-; б) !7(r) = -^--Fr.
шая из начала координат
т
Рис. 63.
В случае б) ограничиться рассмотрением финитного движения, траекторию и закон движения выразить в квадратурах.
12.13.	Внутри гладкого упругого эллипсоида вра-ifl
щения ~	= 1 движется частица, вылетев-
под углом а к оси г. Найти области эллипсоида, недоступные для частицы.
12.14.	Найти траекторию частицы (выразить через квадратуры) в поле двух кулоновских центров U (г) ~ " а а . ГГ}.
(рис. 63), если скорость частицы на бесконечности параллельна оси
O2OiZ- Описать движение частицы, «падающей», иа «диполь», образованный данными центрами.
12.15.	Короткая магнитная линза образована полем, определяемым векторным потенциалом Ар =	(*)»
дг = Дг = 0 (Ж (г) отлично от нуля в области |z|<a). Из точки (О, О, z0) иа линзу падает пучок электронов, близких к оси г. Найти точку (0, 0, Zi), где пучок будет сфокусирован. Предполагается, что г0, Zi а.
Указание. Интеграл уравнения Г амильтона — Якоби искать в виде разложения по степеням г
S (г, <р, г, () = — £/ + Р»ч> + /(г) + гф(г) + у C(z) 4- ...
12.16.	Магнитная лнзна образована полем, определяемым векторным потенциалом Av = -^- гЗвг (г). А, — = Лг = о, где (z) = [	Из точки (0, 0, гс)
на линзу падает пучок электронов, близких к оси г. Найти точки, в которых он будет сфокусирован.
Указание. Полный интеграл уравнения Гамильтона — Якоби искать в виде разложения по г.
12.17.	Каким образом можно иайти действие как функцию координат и времени, зная полный интеграл уравнения Гамильтона — Якоби?
12.18.	Сформулировать и доказать теорему об интегрировании уравнений движения с помощью полного интеграла уравнения
ё+ р. А = о,
dt \ fy )
где H(q, р, /) — функция Гамильтона. (Уравнение Гамильтона — Якоби в р-представлении.)
12.19.	С помощью уравнения Гамильтона — Якоби в р-представлении найти траекторию и закон движения частицы в однородном поле.
§ 13.	Адиабатические инварианты
13.1.	На нити, пропущенной через (рис. 64), подвешена частица массы tn. среднюю силу, действующую на колечко А нити при малых колебаниях маятника. Найти изменение энергии маятника при медленном вертикальном перемещении колечка.
13.2.	Частица движется в прямоугольной потенциальной яме ширины t. Найти, как изменяется энергия частицы при медленном изменении /, рассматривая столкновения частицы со «стенкой» ямы.
13.3.	Шарик, находящийся в лифте, подскакивает над упругой плитой. Как изменяется максимальная высота, иа которую поднимается шарик, когда ускорение лифта медленно изменяется? Как меняется высота, если плита медленно поднимается?
колечко А Определить со стороны
Рис. 64.
13.4. Как изменяется энергия частицы в поле (7 при
медленном изменении параметров поля?
5 Г. Л. Коткин, В. Г. Сербо
а) Ч = А	6) I/ = - з^_;
в) t/ = l/„tg!ax;	r)t/=A|x|".
Указание. Может оказаться удобным использовать формулу ([1], § 49)
7=2«^.
оЕ
13.5.	Частица движется по наклонной плоскости АВ (рис. 65), упруго отражаясь от стенки в точке А. Найти, как изменяется максимальная высота подъема частицы при медленном изменении угла а.
13.6.	Как изменяется амплитуда колебаний маятника О А (рис. 66), находящегося в наклонной плоскости, при медленном изменении угла а?
13.7.	Найти адиабатический ин-
вариант для математического маят- /\ иика, не	предполагая	колебания /	\	D
малыми.	/
/X \
в	\	X
__________ \
Рис. 65.	Рис. 66.
13.8.	Вдоль прямой ОА (рис. 67) могут двигаться две частицы, представляющие собой упругие шарики малого радиуса, массы которых соответственно т и М, причем т С М. В точке О частина т отражается от
_______________т______________М	I_,	,	, я}?________________________________________*	4 Н т ' М
Рис. 67.	Рис. 68.
упругой стенки. Предполагая, что в начальный момент скорость легкой частицы гораздо больше скорости тя
желой, определить закон движения тяжелой частицы, усредненный по «периоду» движения легкой.
13.9.	В этой задаче рассматривается модель иона Hf. Две частицы массы М и находящаяся между ними частица массы т С М могут двигаться только вдоль прямой АВ (рис. 68). Легкая частица притягивается к каждой из тяжелых с постоянными силами f, а при столиовениях отражается упруго. Определить частоту малых колебаний расстояния между тяжелыми частицами (усреднив по движению легкой).
13.10.	Решить методом последовательных приближений уравнения задачи 11.1,а для Р и Q в случае, когда частота изменяется медленно (со со2, со «С coco), с точностью до первого порядка по <о/со2 включительно.
В чем преимущество переменных Р, Q перед р, q в этом случае?
13.11.	Убедиться, что <7=со_1/2ехр if odi удовлетворяет уравнению ty-f-co2 (/) *7=0 с точностью, до первого порядка по со/со2 включительно.
13.12.	На осциллятор действует сила F(t). Найти зависимость адиабатического инварианта I — от времени.
13.13.	Найти связь между объемом и давлением «газа», состоящего из частиц, которые движутся параллельно ребрам внутри куба, размер которого медленно изменяется.
13.14.	Частица движется внутри упругого параллелепипеда. Как изменяется энергия частиц, если:
а) размеры параллелепипеда медленно изменяются, б) параллелепипед медленно поворачивается?
13.15.	Частица движется в сфере с упругими стенками, радиус которой медленно изменяется. Как изменяется при этом энергия частицы и угол, под которым она налетает на стенку?
13.16.	Как изменяется энергия и траектория частицы, совершающей финитное движение в поле (7(г) при медленном изменении коэффициента 7?
(0<л<2); 5)V = ^ + ^-
13.17.	Найти изменение энергии частицы в центральном поле при медленном «включении» малой добавки к полю 6С7(г).
13.18.	Найти зависимость от времени энергив системы двух связанных осцилляторов, функция Лагранжа которой имеет вид
L = У (х2 + у2 — е>1Ха —	+ 2axj0
при медленном изменении О|. Как изменяется траектория точки (х, у)?
13.19.	Пусть связь осцилляторов в предыдущей задаче мала: a<C«i,2* Показать, что адиабатические инварианты, вычисленные в пренебрежении связью, сохраняются вдали от области вырождения (иц = (02) и резко изменяются при медленном прохождении этой области.
13.20.	В какой области oi(0 будут сильно меняться адиабатические инварианты осцилляторов, если связь имеет вид Ш == $х2у?
13.21.	Определить минимальное расстояние, на которое приблизится к ребру двугранного угла а частица, упруго отражающаяся от его граней. На расстоянии I от ребра угол падения частицы на грань равен <р0.
Задачу решить двумя способами: методом отражений (точно) и с помощью адиабатического инварианта — в случае малых а и <р0.
13.22.	Определить границы области, в которой движется между двумя упругими поверхностями у = 0 и ,<jch ах
у =	частица, вылетевшая из начала координат
под углом <р к оси у в плоскости ху(а, ф« 1), н период колебаний вдоль оси х.
13.23.	Как изменятся радиус и положение центра орбиты заряженной частицы при движении в однородном магнитном поле, медленно изменяющемся по величине? Векторный потенциал выбрать в виде
а) А = (0,Ж,0); б) Д=Аг = 0. А^ = ~Жг.
Объяснить, почему результат зависит от выбора А.
13.24.	Вычислить адиабатические инварианты для заряженного осциллятора в однородном магнитном поле.
13.25.	а) Определить адиабатические инварианты для заряженного анизотропного гармонического осциллятора с потенциальной энергией V (г) =	(со!*2 4-
4- ®2У2 + ®з2а) в однородном магнитном поле JC, параллельном оси z. Векторный потенциал выбрать в виде А = (0, Жх; 0).
б) Пусть вначале J£=0 и траектория осциллятора заполняет прямоугольник |х| a,	Каким
станет его движение, если магнитное поле медленно возрастает до большой величины (такой, что
в) Пусть магнитное поле слабое
и вначале осциллятор колеблется почти вдоль оси к. Каким станет его движение, если величина <оь медленно уменьшаясь, достигнет значения cd' < &>я такого, что «jg	— toj?
13.26.	Частица совершает финитное движение в плоскости, перпендикулярной магнитному диполю ш. Как меняется энергия частицы при медленном изменении величины го?
13.27.	Найти период колебаний электрона вдоль оси в магнитной ловушке. Магнитное поле ловушки симметрично относительно оси 2, причем = 0,	= 3@г (г),
^г=-уЖ(г).
а)	ЯМг)=Ж,(1+>Л112-^];
б)	3?г(г) = ж(1 + £)
13.28.	Как изменяются энергия электрона и период его колебаний вдоль оси z в магнитной ловушке, описанной в предыдущей задаче при медленном изменении параметров поля 3@q, К, а?
13.29.	Найти изменение энергии частицы в центральном поле U (г) при медленном включении слабого однородного магнитного поля JC.
13.30.	Как известно, при наличии вырождения движения увеличивается число однозначных интегралов движения. Указать интегралы движения в поле
=	+ V).
13.31.	Найти переменные действие — угол для следующих систем:
а)	осциллятор;
„	и, к ПРИ
б)	частица в поле с/ (х) = {
(гх при х>0.
13.32.	Для частицы а периодическом поле
О
V
1/(х) =
при па < х <\п -г -у) а,
при (п + -i-j а <х <_ (п + 1) а,
п = 0, ±I, ±2, ...
в случае Е > V провести каноническое преобразование с производящей функцией
S(x,P) = V2m If — (x)J dx,
»
где E(P) выражается из равенства
Р = f / 2m[£ - (7 (л)| dx.
6
ОТВЕТЫ И РЕШЕНИЯ
§ 1 Интегрирование уравнении движения с одной степенью свободы
1.1. а) По начальным значениям х(0) и х(0) определяется энергия частицы Е. Дальнейшее ее движение находится из закона сохранения энергии
/пл1 2
-2- + (/(х)=£.	(1)
При £^0 частица может двигаться в области — движение инфинитно (£=£' на рис. 69). При £<0 (Е—Е") частица движется в области х2^л^Л’з, движение финитно. Точки Поворота определяются из формулы (I) U(x,) Е:
при £ > О,
при £ — О,
(2)
1 , л + VA (А - | Е I)
Г2.3 = ^1П-------ТЁ1-------
при £<.0.
Из (1) получаем
dx
V'£ - (/ W
(3)
Отсюда
I Л ~ УЛ (4-Ч £ |) cos (а/V21 £ |//п-р С)
8 W = а ln	--------------
при £ < 0,	(4)
1 Г 1 Ла2 1
ж(0 = —1п[у + —(*+С)2] при £=а	(5)
1 , VА (Л + £) ch (at 1/2ЁМ7 + С) - Л
х W “ а 1п-------------Ё---------------
при Е > 0.	(6)
Постоянные С определяются начальными значениями х(0), например,
в (4) при х(0)>0
С — arccos
Л - | £ | г'-*1”1
I Л - (Л - |£| ) ’
Точки поворота (2) также легко найтн из (4)—(6).
Движение при £<0, согласно (4), периодическое с периодом = — J/ Если Е близко к минимальному значению U(x), равному t/min = U (0) — —А (т. е.
слабо зависит от Е. В этом случае (4) можно записать в виде
Частица при этом совершает гармонические колебания вблизи точка х=0 с амплитудой определяемой разностью Е— (/mm, в с частотой, не зависящей от энергии. Такой характер движения при Е, близком к (/min, имеет место почти в любом поле б7(х). (Подробнее об этом см. в § 5.)
При Е^О частица, движущаяся справа, доходит до точки поворота Xi (см. (2)), поворачивает назад и уходит на бесконечность. При этом скорость ее со временем стремится к У2Е/т сверху.
б)	* (0 = ~ Arsh |	' £|£ 1^" SU1 V2 I Е l-'™ -г с)]
при Е < 0,
х (t) = + — Arsh j/"—- sh (а/ 2Е1т С)| при Е > 0,
х(0 = ± ~ Arsh (а/ 1/2Ув/ш + С)	при Е = 0*).
‘) Arsh х = In(х -f- |/х« -pl).
1 51
в)	* (0 = -i- arcsin [ ЁТй; sin («< У ----- £|) + с].
Почему в некоторых формулах приведенных ответов знаки двойные?
1.2.	x(h =-------*° Хп — Знак в знаменателе
I+tx01/2A/m'	'
противоположен знаку х(0). Пусть для определенности х(0)>0. При х(0)>0 частица уходит на бесконечность за время}/ Разумеется, реально речь может идти только о большом, но конечном расстоянии, до которого простирается заданное поле f/(x).
При х(0)<0 частица асимптотически приближается к точке х=0.
1.3.	Вблизи точки остановки „
U(x)—E—(х— а)Г, где F —
=—U'(a), т. е. можно считать, что ____________
движение частицы происходит под *	S'" i
действием постоянной силы F. Счи-	/	| 'ч
тая. что х(0) — а, получаем	/	]
।
Ft2	*
X (/) = а +	 i-----------л
Точность этой формулы	убывает	Рис.	70.
при удалении от точки х=а.
Маленький отрезок пути з вдали от точки остановки частица проходит за время toos. Если же отрезок пути примыкает к точке остановки, то для его прохождения необходимо время r=V2rns/|F|, т. е. Тсо|/в.
Если £/'(а)=0 (рис. 70), то разложение U(x). необходимо продолжить до следующего члена:
l/(x)= £: у(,"'(а)(х-с)’.
В этом случае x(0=o+sc±M, где $=х(0) — а, Х®=------а знак
в показателе определяется направлением скорости в начальный момент. Для прохождения участка пути до точки остановки частице необходимо бесконечно большое время.
1.4.	Если U" (п)=#0, то 7 coin в, где е== Um — E. Если и—2
L'"(n)=...=l/<"-1>(<!)=0, l«"l(n)=^0, то £эВ Z“ .
1.5.	а) При малом е=Е — Um частица движется медленнее всего вблизи точки х=а. Поэтому и весь период движения Т можно оценить по времени 7i прохождения (туда и обратно) малой
окрестности этой точки а — б<х<с-{-б:
?! = У 2т
dx
]/E — U(x) ~Т‘
В окрестности х=а представим U(л) в виде U(x) = UTn~-где k=—U"(a). При достаточно малом е можно выбрать 6 таким, чтобы скорость v на границах интервала была много больше минимальной (при х=о)
/по2 Лб2 "2" >8
и в то же время чтобы было б«:£=х2— Х|, т. е.
Тогда
„ mA m . 2Л62 Л=2Т vln—.
(I)
Время Т2 движения частицы иа участках «1<х<о— б и о-Н$<л<Л2 удовлетворяет условию
г г —~ 1/—
'«< V Г к 6‘
С уменьшением в величина 7\ возрастает, поэтому при достаточно малых 8 оказывается 72<^Т] и для оценки периода движения можно воспользоваться формулой (1). Эта формула обладает асимптотической точностью. Ее относительная ошибка стремится к нулю, как 1п“’е, при е-*-0. Но с той же логарифмической точностью можно заменить в (I) б на L и опустить множитель 2 под знаком логарифма:
Л,/*ГИ kl* т=гУ т in—.	(2)
Если U" (с) = 0, (/<*> =—7(^=0, то
_ л /WVA f dx	л /л?2 \>/«
W j угт? _,1-6(ек) '
причем относительная ошибка стремится к нулю, как е%, при е—>0. б) Если наблюдать за движением частицы в течение времени, большого по сравнению с периодом Г, то вероятность обнаружить
частицу на участке от х до x+dx
tn (х) dx = 2-^-
2т dx tVe — litf
где 2dt — время нахождения частицы на участке dx за период. Зави-
симость плотности вероятности координаты w от х представлена на рис. 71.
Рассматриваемой вероятности w(x)dx соответствует заштрихованная площадь (вся площадь под кривой равна единице). При достаточно малых е основной вклад в площадь под кривой дает площадь под центральным максимумом, равная TJT. Хотя ш(х)—»-со при х —► Х|,2. вклад участков вблизи
Рис. 71. точек остановки относительно мал.
в) й(р)Нр = у^|^|<1р = у2р^)Т-
где гЛ(р)—различные корни уравненияU(x) =Е.
График й?(р) изображен на рис. 72, р1 — ]/г2т^Е—^т)г
рй = У2т [E — U(c)\, Рз = У2т\E-U (*)j.
г)	Линии Е(х, p)=const (фазовые траектории частицы) приведены на рис. 73, где кривые пронумерованы в порядке возрастания
энергии. При U(c)^E<Um фазовая траектория 2 двусвязна. Стрелки указывают направление движения точки, изображающей состояние частицы.
1.6.	За начало отсчета потенциальной энергии принимаем нижнюю точку. При E=2mgl имеем
Ч> «) = — п + 4 arctg (е±",®'г tg	——j
(ср — угол отклонения маятника от нижнего положения). Знак в по
казателе совпадает со знаком ф(0). Маятник асимптотически приближается к верхнему положению.
При 0<Е— 2mgl^2mgl маятник вращается, медленно «переваливая» через верхнее положение. Период обращения можно оценить, используя результат (2) предыдущей задачи:
Т = VТ ln E-2mel :
е0 = WmgZ.
1.7.	Угол отклонения маятника отсчитываем от нижнего положения. Энергия £ =-^-ml2 * *<p2+/ngZ(l —cos<p). Пусть в момент £оугол ф (Zo) = 0 и для определенности ф (Zo) > 0. Введя k=имеем
2 У g L/---------------Ф “Н<”	(0
При А<1 маятник колеблется в пределах —фтСфСфи» и fe=sin^. Подстановкой sin I = -£• sin-у интеграл (1) лриводит-
ж	Г- -
ся к виду ♦) t = J/ - F (с, k) t0.
*) Функция
ПМ)=|
ft
1/1 — 4s sin* g
—так называемый не-
полный эллиптический интеграл первого рода. Если к=£($, k},
Отсюда
Ф — 2 arcsin [Л sn {и, Л)],
и — (? — /п)
Период колебаний

В предельных случаях (ср. с задачей 1.4)
Г = 2п|/’у(ц-^] при <рт«1. /—у g
Т = 41/ у1п--_ф- при п-<гт«1-
При маятник не колеблется, а вращается. Из (1) получаем
ф =2 Arcsin sn у), и = k (t — t0) J/ у.
Период обращения
В частности, при £ — 2mgl^2mgl получаем
У-Г g E-imgl’
то | выражается через одну из эллиптических функций Якоби — эллиптический синус: sin£—sn(a, k). Полным эллиптическим интегралом первого рода называется функция K(fe)=£^-2", Приведем также формулы для двух предельных случаев:
П /	*8\
К(Ь) =-yll +-4 I при *<!,
1	16
К W “ у In ПР” 1 ~	* 1 
Таблицы и формулы этих функций можно найти, например, в [10].
где ео=32 mgl. Этот результат отличается от довольно грубой оценки, сделанной в предыдущей задаче, значением постоянной е0, т. е. на число, не зависящее от Е — 2 mgl.
1.8.	Закон движения в поле U (х) -{-fit/ (х) определяется равенством
лГ Р_________dx________
<=’ 2 J у £ - I/ (х) - 6С'(х)
а
(х=а при f=0). Разлагая подынтегральное выражение в (() ио степеням fit/(x), получаем
t=t0(x)+6f(x).	Д2)
где
‘3)
а
_ ± С 60 <*>dx	/А
WW- 2 У 2	(4)
а
Пусть закон движения в отсутствие поправки б(/(х). определяемый из уравнения t=to(x), есть x=Xo(t). Тогда из (2) находим
x=x0(t —fit(x)),	(5)
причем в малой поправке fit(x) можно положить х—x0(t), а также провести разложение (5) по fit. Окончательно
х = х0 (t) - х’ (0 fit (х0 (f)).	(6)
Вблизи точки остановки х=х> разложение (2) становится неприменимым. так как поправка fit(x) ->ос при х
Замечательно, однако, что формула (6) оказывается справедлива вплоть до точки остановки, если
|6(."(x)|«|F|, F=-tr(I,J.	(7)
Этот факт связан с тем, что хотя с приближением к точке остановки fit возрастает, зависимость x(t) вблизи экстремума оказывается слабой
Очевидно, что вблизи Xj невозмущеннос движение имеет вид «o(n = *i + ^(t-G)a.	(В)
Добавление fit/ смещает точку остановки на Sxlf согласно уравнению
(7(xi+6xi)+6(7(x1+6xi)=£. Отсюда 6хх —	, С учетом возму-
щения 6(7 аналогично (8) имеем /
х (/) = Х1 + 6^ 4-	- 6/х)»	(9)
(в силу (7) поправкой к F пренебрегаем). Убедимся, что расчет по формуле (6) приводит и (9).
Область интегрирования в (4) разобьем на две части: от а до b и от b до х, где b лежит вблизи хь Во второй области можно положить SU=6U(xi) и U (х) =Е — (х — Xi)F. Тогда
у7п 6(7 (X,) /z£3 (x-xj
6/ =
(W)
4- 6(0,
1 -I / т Г 6(7 (х) dx 1/~т &U (х*) Wo = Т F 2 J (Е _ f/)3/2 - YFUb—xJ ь
Подставляя (10) в (В) в (6) я пренебрегая получим (9) с бЛ=&о.
1.9.	а) Воспользуемся результатами предыдущей задачи. Невоз-мущешюе движение
х0 (I) = a sin to/, Е «	m<o2d9.
При этом J SU/U | С е = — I. Поправка
«<w- Д (V0”-*2+-2а)-
и, согласно формуле (6), предыдущей задачи
х (/) = a sin (dt — у (cos® <i>( 4-1 —2 cos о/).
С точностью до членов первого порядка по е включительно х(() = a sin (ш/ 4-	— -|-а — — д cos 2cof
(ср. с задачей 8.1 б).
б) Действуя так же, как и в предыдущем пункте, получаем
/ 3	7	I \
х (Q = a sin сй1 де I "jf cos — _g'.s5n — “g- sin Зсо/1,
рд2
E=fe«l-
Этот результат имеет относительную точность -~е2 в течение одного периода, а через в-1 периодов формула (1) становится полностью неприменима. Учитывая периодический характер движения, можно распространить результат (1) на бблыпнй промежуток времени. С точностью до членов порядка е включительно формула (1) преобразуется к явно периодическому виду
I
о
Не учтенные нами в (1) поправки приводят к изменению частоты порядка е2со. так что (2) сохраняет относительную точность ~ е в течение е-1 периодов (ср. с задачей 8.1а).
1.10.	Искомое изменение периода
хе	п
f	dx	Г dx
J yE-U(x)-fiU(X) J ] Е-U(x)
Xi	J
Разлагать подынтегральное выражение (1) по бС/(х) нельзя: условие применимости теоремы о дифференцировании несобственного интеграла по параметру нарушено, так как полученный при дифференцировании интеграл расходится. Разложение подынтегрального выражения по 6(7 (х) до линейного члена включительно можно провести, если представить 67" в виде
67 = 2 У 2m [ f F £ - U (x)-6U (*) dx -
L«i+6x,
- j VE-U(X) dx . (2) Xi	J
Отсюда
6T “ - Я j	13)
где
Т
<«/> = у [	(4)
О
- среднее по времени значение 6 (Л
Время движения вблизи точек остановки составляет малый
вклад в период (разумеется, если Ur(xi, s) ¥=0); по этому поводу см задачу 1 3. Именно поэтому формула (3) может давать хорошее приближение.
В некоторых случаях даже малая добавка 6U(х) может существенно изменить характер движения частицы (см. например, задачу 1.11 б, в).
Действуя аналогично, можно получить следующие члены разложения 6Т по 61/;
т _ уз= V ЫГ	f IK'W!^.
1 п! a£”J ГЕ-I'M »г-0	к,
Формальное выражение (5) может оказаться асимптотическим или даже сходящимся рядом.
I.II. а) Поправка к периоду 2л/о, полученная по формуле (5) предыдущей задачи, равна —Злр£/2ты5 и мала при достаточно малых Е.
б) Г рафики потенциальной энергии U (х) и (/ (х) 4-61/ (х) изображены на рис. 74. Видно, что при E>L/rn—mta6/6a2 добавка делает движение инфинитным. При значениях £, близких к Um, период колебаний неограниченно возрастает (как |ln((/m —Е)|; см. задачу 1.4); поэтому нельзя рассчитывать, что в этом случае он определяется небольшим числом членов ряда (5) задачи 1.10. Если же EcUM, то поправка к периоду 67—5д£/18иС.''„,.
в) 6т = J m • формула применима, если J ЕI »| U I а» ’ 2alE\hy2
(£<0).
6 г. Л, Коткнн, В. Г. Сербо
Е
с решением за-
где v =
дачи 1.16).
E-Ut
§ 2. Движение частиц в полях
2.1. Для исследования движения частицы используем законы сохранения энергии и момента импульса;
П7Г2
— +(J{r)^E,	(1)
т[гг]=»М.	(2)
Согласно (2) траектория является плоской кривой. Введя в ее плоскости полярные координаты (рис. 75), получаем
тг2 тг2®2
—(r) = Et
mrz(p = M.	(4)
Исключая из (3) <р с помощью (4), находим
гиг2
—+%ф(г) = Е. (б) • где
г„ л;з _____л	(r} ~ U (r) + 2m'2'
О	Таким образом, радиальное движе-
Рис. 75.	ние можно рассматривать как одно-
мерное движение в поле 14фф(г). Для качественного исследования характера движения используем графики
а V ЛР
!7а.М,М“ Т -	+SmT’	(6)
при различных значениях Л1 (рис. 76),
Если 12cxfr22<jM4, то 1/8фф имеет два экстремума (при Гш— Л1а { V М* — 12аут2 \
=-------~2~а-------:— I. Максимальное значение С'8фф (ri) =Отлл
положительно при М4> 16сфп2 (рис. 76, а) и отрицательно при 12сфя2<Л44< 16офп2 (рис. 76,6); в обоих этих случаях иафф(г2) = S2=dmln <0.
Рис. 76,
Если же Л4*< 12сфп2. то функция {7эфф(г) монотонна (рис. 76, в).
Рассмотрим подробнее случай а). Если Е>игаая, то частица, летящая из бесконечности, падает в центр поля. При этом величина <р, согласно (4), возрастает. Этих соображений достаточно для того, чтобы грубо изобразить траекторию частицы (рис. 77, а).
На больших расстояниях, таких, что , главную роль
сс
в U(r) играет член — — и траектория мало отличается от гиперболы.
(О виде траектории при г->0 см. задачу 2.8.)
ЕСЛИ ЭНерГИЯ Е близка К Umax, то интервал значений г, близких к и, частица проходит очень медленно. Вращение же радиуса-вектора продолжается своим чередом со
М
скоростью <Р ~ ^2 , так ЧТ0 части‘
а)	6)
Рис. 77.
да может сделать много оборотов вокруг центра, прежде чем пройдет этот интервал (рис. 77, б). Если E«Umax, то частица в своем
6*
радиальном движении асимптотически приближается из бесконечности к точке r=fj (ср. с задачей 1.3). Траектория же представляет собой спираль, приближающуюся к окружности радиуса Л с центром в О (рнс. 78, кривая а). Если частица с такой энергией удаляется от центра в области г<гь то ее траектория также приближается к этой окружности, но изнутри (рис. 78, кривая Ь). Наконец, при E=Umax возможно движение по окружности г=г>.
Любое изменение величин Е или Л-f переводит частицу на траекторию, удаляющуюся от этой окружности, т. е. движение с неустойчиво.
Если 0<E<fAnax, то частица, летевшая из бесконечности, отражается от потенциального барьера иЭфф(г) и вновь удаляется на бесконечность. Примерный вид траекторий в этом
Рис. 78. случае показан на рис. 79 (кривые а и Ь). Если энергия близка к Una-*., то частица сделает много оборотов вокруг центра, прежде чем радиальная скорость г изменит знак. Чем ближе энергия к нулю (при фиксированном М это соответствует увеличению прицельного параметра), тем менее искривлена траектория частицы. При £<Umas возможно также падение в центр поля частицы, которая движется в области г<а. Траектория в этом случае изображена на рис. 80.
При t/min<E<0 частица может также совершать радиальные колебания в области c^r^d (рис. 81). Если энергия близка к нулю.
Рис. 79.	Рис. 80.	Рис- 81.
то размах радиальных колебаний велик, период их тоже может стать большим. При энергии, близкой к <7 min. траектория близка к окружности радиуса г2, причем угол поворота радиуса-вектора за период радиального колебания зависит от величин а, у, М (ср. с задачей 5.4). При Е«t/вив частица движется по указанной окружности,
Подобным же образом можно исследовать движение частицы в остальных случаях.
Какими особенностями может обладать траектория, если /И*= = I2cqm2?
Закон движения и уравнение траектории можно найти, используя уравнения (4), (5). Из (5) получаем
;=+(?) откуда
Исключив dt из (7) с помощью (4), найдем уравнение траектории , М Г dr
<₽ - ± )2Й J г* ]/£-Ц,фф(/) + С ’	<9)
Рассмотрим случай Af4>l2cc7m®. Если частица движется к центру, то в (7) (а значит, и в (8)) следует выбрать знак «минус». Пусть г=г0 при тогда (8) можно переписать в виде
/~пг Г dr
Равенство. (10) определяет в неявном виде зависимость г от времени. Если траектория проходит через точку r=r0, <р=фс, то уравнение траектории (с учетом выбранного знака) приобретает вид
V = - М J + То,	(Ч)
т» где
В частности, для частицы, скорость которой на бесконечности составляет С ОСЬЮ X угол нужно ПОЛОЖИТЬ Г0=ОО, <ро=Л— ф.
Если £>Пп1Их, то уравнения (|0) и (II) полностью определяют закон движения и траекторию частицы.
Если же 0<.E<l7niaz, то вти уравнения отвечают только участку АВ траектории (рис. 79, кривая с). В точке В радиальная компонента скорости А обращается в нуль, а затем меняет знак. Поэтому участок траектории ВС описывается уравнением (9) со знаком «плюс», причем
постоянную нужно определять заново. Удобно записать (9) в виде f dr
<г = м J ^КТ+С'’	(,2)
rmin
Нижний предел интеграла мы могли выбрать произвольно, пока не определена постоянная С'. Согласно (12) имеем
С,=<р(г щ)п)-	(13)
Определяя <p(fmin) из (II), получаем уравнение участка траектории ВС:
Подобным же образом определяем закон движения на участке ВС
(г rmin\ —
( - f	dr	(15)
rmin r0 )	Ц)фф(г)
Если	/(0)<0, <p|t=o=<pa, то уравнение
(II)	описывает участок траектории АВ (рис. 81). Участок ВС описывается уравнением
С dr
<р = м ) ;2 |р । + <й.	(16)
где угол можно получить, положив в (И) г=а. Уравнение участка CD
Г dr
*₽ — — Л/ J г-2 | р | +	О')
ъ
где фз определяется из (16) при г=Ь и т. д. Подставляя в (16) и (17) значения tpi и <р2, представим уравнения участков траектории в виде
Нетрудно убедиться, что уравнение участка траектории, отвечающего n-му радиальному колебанию (считая участок АВ первым),
имеет вид *)
ф = М
dr +’’»•
(20)
В приведенных формулах предполагается, что угол ф изменяется непрерывно, ограничения 0^<р<2л не вводится. Данному значению г соответствует бесконечно много значений ф (при различных п и знаках в формуле (20)); (₽ есть многозначная функция г. Наоборот, зависимость г(<р) однозначна.
Аналогично можно выразить законы движения и уравнения траектории и в других случаях.
2.2.	Вне сферы радиуса R частица движется со скоростью | 2Ejm, а внутри — со скоростью у 2(£Ц- V)/m. В зависимости от соотношения Е и М получаются различные виды траекторий.
При 2^ ~ V < Е< 2^ частииа лкб° Движется внутри сферы, испытывая отражения на границе (рис. 82, с), либо (если, кроме
♦) Уравнение траектории (20) можно представить в виде
где
того, Е>0) может двигаться и вне сферы (траектория прямая,
п
При -—— г имеет место 2iw?
рис. 82,6).
(рис. 82,6).
преломление траектории
Как выглядит траектория при Е — 2т/^ ~~
2.8.	Для определения уравнения траектории используем формулы
f Mdr	„	,,	, ЛР
’“ J	офф^ М +2rnr‘- О
В результате вычисления *) получаем
Траектория представляет собой кривую, получаемую из гипербо-лы с помощью уменьшения полярных углов в 7 раз (рис. 83). Постоянная ф определяет ориентацию траектории.
*) Интеграл, записанный в виде
М __ Г____________Mdr____________
Л 9 J r‘ / 2m (Е - Мг/2тг‘ — а/г) ’
где Ф=ЛР+2ггр, сводится к соответствующему интегралу в задаче Кеплера (см. [ПЛ 15).
Направление асимптот определяется условием г -* го, или ecos(q)112— ф) =1. Скорость отклоняется на угол
2 I 2	/ 41: I , Л1”|
я-(<р,-<р,) = п- у arccos — = п - у arclg |/	+
2.4.	Полезно прежде всего исследовать характер движения с помощью графика иаыь(г). Для случая р<Л42/2т этот графин изображен на рис. 84. В этом случае возможно только инфинитное движение в области г^гт, причем £>0. Уравнение траектории такое же.

Рис. 85.
Рис. 86.
как в задаче 2.3 (уравнение (2)), а в равенствах (3) нужно заменить Р на —р. Основное отличие от траектории, найденной в задаче 2.3. возникает вследствие того, что ус I. Примерный вид траектории показан на рис. 85. (Точка перегиба Л определяется условием dU/dr—O, т.е. r=2p/ct.)
Для случая p>Afz/2/n график Us$<t>(r) приведен иа рис. 86.
„2
рГпИ [J — —х--------------г-;-- то частица, летящая из беско-
Если с > итах - 4 (р _ м212ту
нечности, падает в центр поля. Уравнение траектории и в этом случае можно получить из уравнения задачи 2.3. Для этого, кроме замены Р на — р, нужно заменить ф на ф а затем воспользоваться формулами
sin ix — i sh x, У —л = i Ух,
В результате получим
Траектория для этого случая изображена на рис. 87,а. Заметим, что при г->0 оказывается <р-> <ю. Это значит, что частица, падая виентр поля, делает вокруг него бесконечное число оборотов.
Если E<t7maX, то, согласно рис. 86, возможно движение либо в области Ь^.г<со (рассеяние), либо в области 0<г^п (падение
а)	б)
Рис. 87.
иа центр). Уравнение траектории получаем, используя равенство cosix=chx (а во втором случае еще и замену ф на ф+л/к):
__________//_______ п _	/	4£ / Ж
r ~ 1 + e"ch /(ф ~ фр е ~ 1/ 1 —	®
В случае Е~Ьюа, воспользоваться формулой (2) задачи 2.3 нельзя (так как при ее выводе предполагалось е^О) и нужно вновь брать интеграл (I). Получаем
__ р'______________
т 1 + сехр (— у'ф)‘ т.е.
' = I ± ехр[-Т' (<Р~ *)1 “’™ ' = Р
в зависимости от начального значения г. Траектория представляет собой либо спираль, начинающуюся на бесконечности или вблизи от центра и асимптотически приближающуюся к окружности радиуса /==//, либо саму эту окружность (рис. 87,6).
Наконец, в случае p=M2/2rz также проще вновь взять интеграл.
В этом случае происходит рассеяние, а уравнение траектории aJE
r ~ I — лпсс2 (ф — ф)2/2.М«£-
Время падения частицы в центр поля определяем с помощью формулы
Например, для случая, когда траектория имеет вид (2), время падения с расстояния г	•	*	
1= { У f (V^-ar-p- М’/гт - Ур-Мфт) +
, а	. 2Er/a-1	I '
+ 2ЁГ 2Ё^““т-----?-----агсяп-^
2.5.	Уравнение траектории
___________Р_____________
1 -{- е cos у (<р — ф)
Jp, е> 7 определены в задаче 2 3). При £<0 движение фицитное*)
ла Ут	2п	_
г~ (2|Е|)3'2’	Д’ =у	ТФ тГг-
Траектория замкнутая, если у — рациональное число. На рис. 88 изображена траектория для 7 «5.
2.6.	При §<АР/2л1
Рис. 88.
Р
1 — е cos у (ф — ф) *
т-=/1-
2/пр /И8’
если Е<0, то Дф=2п/7, Tv=yTr (ТТ то же, что в задаче 2.5). При р>Л12/2/п (в обозначениях задачи 2.4)
' ~ е' sh у' (ф — ф) — I • если £> r = e"cli у’(ф-ф) —I • «ли
♦) Период тот же. что и в поле U0=—alr. Для определения Тг достаточно заметить, что добавление к полю Uq добавки р/г3 сказывается на радиальном движении так же, как увеличение М. Период же Тт в кулоновском поле 1)й от М не зависит.
формулу (1) задачи 2.3) при Е (при п—2), а при л >2— членом М2/2тг*. Получаем
Рис. 89.
при л >2.
2.7.	а) Финитное движение возможно, если функция 1/8ф*(г) имеет минимум. Уравнение П'фф (г) = 0 приводится к виду f(х) = =-=Мъи1ат, где f(x)=x(x+l)e-*, x=xr. С помощью графика f(x) легко убедиться, что это уравнение имеет корни только при условии, что хЛ-Р/шп меньше максимального (при х>0) значения f(x).
Последнее равно (2 -|- Уб)ехр	0,84 Итак, финит-
ное движение возможно, если ЛР<0,84ап2/>с.
б)	Финитное движение возможно, при ЛР<8л1 V/e2x2.
2.8.	В уравнении траектории (см. малых г можем пренебречь величиной также и (рис. 89)
Mln (г/г.)
Г2й«^ЛР + ф“ ПРН " = 2-2>лг—1+";г Ч> = /2та (п — 2)
Число оборотов оказывается бесконечным только при л=2.
Время падения в центр конечно, поскольку радиальная скорость прн приближении к центру возрастает.
2.9.	Число оборотов частицы вокруг центра бесконечно только в случае б) при Е=»0, л=2.
2.10.	Время падения равно л /8сх.
2.11.	Относительное движение характеризуется моментом Л1 = /ПО2	ГП1 /п2
= mvp и энергиейЕ — -g-, где т = — -_ц"" — приведенная масса. Искомое расстояние определяется условием (/-ш,и) = Е. Простой ответ может быть получен при л = 1,2,4.
2.12.	Траектории частиц;
~;— = 1 ± е cos q>, ''*1,2'1,2
где
-j- т2‘
М2 та'
Е и М — полные энергия и момент системы. Частицы движутся по подобным коническим сечениям с общим фокусом, причем радиусы-векторы частиц в любой момент направлены противоположно (рис. 90).
2.13.	Как легко видеть на рис. 91, 03 = р (cig фо — ctg 2фо).
Здесь
При р -> О
dr________
-U(z)/E-p»/r»
Фо =Р
оо	оо
Г ---dr -_ррзрЗ/гА С -
.1 ^Vl-C/.E Г ОЕ J ,, rmin	rinin
(ср. с задачей 2.23), так что
(со	\	1
f dr I
Р J л!УП^ИЁ I + 0 >   
fniin	/
Точка S — мнимый фокус пучка рассеянных частиц, гак как с точностью до первого порядка по р включительно положение точки пересечения асимптоты траектории с осью пучка не зависит от р.
Рис. 90.
2.14.	Уравнение траектории р
— = a cos (ф — ф0) — If
АР 1/ 2£Л1£	„	-
где р = —t е — у ।  — г а фо определяется из условия ф->0 при г-> оо : cos фо= lie. Область, недостижимая для частиц, ограничена огибающей семейства траекторий,
Для определения ее продифференцируем уравнение траектории
М*	Mi [IE
— 4-1-сяЧ,--у-sinif = 0	ft)
по параметру М:
2Л! т/2Е
— - | —sin<p = 0,	(2)
И исключим М из (I) и (2):
2olEr = I 4- cos q>.
Итак, недостижимая для частиц область г £ ([ -j- cos (р) огРани’ чена параболоидом вращения (рис. 92).
2а6
2-IS- Р< । -б-2_ (j _6)*cosy ’
2.16.	Умножим равенство
таи*
rAefi = '2cT’ GA=a-
[vM] - — = А
скалярно на г. Обозначив через у угол между г и А, получаем
/И2
—— ar=Ar cos <р
р	Afa IАI
или — = 1 4- е cos <р, где р е =
рис д2	Отметим, что вектор А направлен от
центра поля к точке г=гШ1П.
ах/
2.17.	&Г = — где
г < Г~т Г &U(t)dr
(ср. с задачей 1.10). Подобным же образом изменение углового расстояния между последовательными прохождениями точек г ~
66/
= гша можно представить в виде6Д<р = ^ (ср. [1], § 15, задача 3; § 49).
2.18.	В области г D поле U(r) мало отличается от кулоновского U0(r} = —а[г. Поэтому траектория финитного движения близка к эллипсу, параметр р и эксцентриситет е которого, определяемые постоянными Е и М, сохраняются, а ориентация изменяется. Скорость
поворота эллипса Q определяется смещением перигелия за период
£2 = CAij/Го, где 6Дф вычисляем по формуле предыдущей задачи а аг
coU=-^-—а Го — период в кулоновском поле*). В результате вычисления получаем Q = M{2mD2. Уравнение траектории можно представить в виде
у-= I + ecosrqi,	(I)
Отклонение кривой (!) от истинной траектории — первого порядка малости по f>U, т. е. в течение одного периода уравнение (!) описывает траекторию с такой же точностью, как уравнение неподвижного эллипса. Однако уравнение (I) сохраняет ту же точность в течение многих периодов. Поэтому именно это уравнение можно назвать «правильным нулевым приближением».
Иначе говоря, в уравнении (!) учтены только накапливающиеся
эффекты первого порядка.
2.19. Поле U(г} = — а/г,+е мало отличается от кулоновского, поэтому орбита частицы в этом поле представляет собой медленно прецессирующий эллипс. Разлагая U(r) по в, представим его в виде a	ъа т
U(г) «= и0(г) 4- &U, где t/0 (г) =	= у In -q, а = a/?~et
£ — постоянная, равная характерному размеру орбиты.
Смещение перигелия за период 6A<j> = -^LJ6U dt (см. задачу 2.17)
вычисляем, сделав замену
' - - ГЕ'=£ <Е- а. ‘ = уЛ +
Т — ясс 2 |£~]з (см [П. § 15). Получаем
__ 2л _______
бАф _ есс д С сс (I — ecosj) _ ь-яа Т ~ 2л дМ J 1п 2|£|/?
О
2л
в |£| де Г cosEdg ~~ я дА! J ! — a cos с о
2л 1 -У| -е2
Г е2 81
*) Удобно перейти к интегрированию по £, причем (см. fl], § 15)
= 5jEj(1 -£С“Э-
При е>0 направление прецессии орбиты совпадает с направлением
движения частицы по орбите, а при е<0 — противоположно ему. Л Л	3 3 о24-^2 М
2.20.	Й-----2 т<о в,ь, । Л11.
2.21.	Пусть расстояния от Земли и Луны до Солнца равны п
н Гв, а до нх центра масс— соответственно aY н а2 (рис. 93). Потенциальная энергия
_ Ут()тх _ утптъ
П2
Рис. 93.

гд.е /Л|, ны,

7 — гравитационная постоянная, т0, т2 — массы Солнца, Земли и Лу-причем mtai =т2а2- Подставляя
rt,2 =V г* + °1,2 + 2ГаЬ2 C0S W — УГ0Л между направлениями от центра масс на Солнце и Землю) и разлагая по малым па-
раметрам
L7 (г, ф) =
получим
(3 cos2 1),
где а — ут,„ (тх -г т2) «= утоти ₽=f Tmo + m!a!) =tT
При усреднении за месяц cos2i|) заменяется на */г и потенциал
принимает вид. указанный в условии.
Смещение перигелия за год (см. [I], задача 3 к § 15) блр Зл 1 а \2
Смещение перигелия за столетие
100^=7,7".
Следует заметить, что полное смешение перигелия Земли за столетие 1158" обусловлено главным образом влиянием Юпитера и Венеры.
Интересно, что оценка релятивистской поправки дает величину ~100-2л(—j ~ 1", с «30 км/сек (см. [2], § 39 и § 101).
2.22.	Аналогично задаче 2.18 имеем
д - a dez Г	(а 1
Q == дМ ~~2дМ [6t//	+ Т ^U" (о)] ~
=	[»(«) -l4 №"(“)]гтгг
^стсладующцг членов разложения 6U по (г-а) даст в Q вклад
2.23.	Смещение перигелия за период можно представить в виде 4 а« Г“+Л!
Дф = _-Г2и__ j (E-l/^-K/f.*, 714-Сп
С точностью до второго порядка по 61/ имеем
Д<р = 2л + 6,<р + 6а<р,
, д
, а2
a-’’“-2M!0£lJ'«ei')%
где <f>-среднее значение функции /(г) за период Т кого движения (ср. с задачей 2.17). Скорость прецессии
невозмущен-
о -= .^+ ^29 __ Йй<р 6х<р 67
T-iHT - т

2.24.	Представим уравнение траектории т== Г Mdr
разлагая подынтегральное выражение по 6U = в виде
где
Ч> = Фо(г)+Мг).
Пренебрегая в (2) поправкой 6ф(г), получим, разумеется, уравнение траектории в кулоновском поле (см. [1], § 15)
р
~ = I 4-е cos <р,	(5)
(2)
(3)
(4)
7 Г. Л. Боткин, В. Г. Сербо
где р_ в_ у/1	Учитывая же в (2) поправку бф (г),
получим вместо (5)
~~ = I 4 е cos (q — ftp (г)).	(6)
В правой части (6) можно провести разложение по бф(г), а также подставить в Ctp(r) зависимость г«=го(ф)> определяемую, согласно (5),
“ = I 4 е cos ф 4 еВф (г0 (ф)) sin ф.	(7)
Вычисляя*) интеграл (4), находим
_	т2ау ( Л 2еа 41 .
6ф (г0 (Ф)) = -др-1 - Зф - ~— sin ф -
1 4 е cos ф	J
-	<2й + -М)cos <Plj- (8)
Подставляя (8) в (7), с точностью до первого порядка по
получаем
—- = 1 + ecos[(l + 3£)о>| k I 2е- * ' sin= ч —
_ 1 4 е cos ф
— Е----j-------[2е + (е! + I) cos <р] (9а)
*] Удобно представить (4) в виде
дС	V 2 т у dr
J '’V е~2^ + т
и перейти к интегрированию по ф согласно (5);
„ д rn^va f	4 ,
6’’= дм~/¥~ J u+<;«’s'rt‘J<f=
Зт2\>а	т2уа де т^уа Зф
= --лр-<<р + С5|П,й + -л}Гад)51п<|>+-мЗ_дЛ7(| +ccos <й-
(8')
Находя из (5)
2М де	Зф .	де е2 — 1
тагг = д/Й cos ‘Р “ е ей sln f 	ЙЙ = еМ
к подставляя в (8'), получаем (8),
или
у =s 1 -J- е' cos Хф -ь f cos 2ф,
X == I J- ЗС>
L .	- 2е» + 5е - I \
Р -Д|+С-----------2е-------}
{	„ е« - 2е3 - е2 - 2 \
е ~ е 4- £	2е2	J,
,	.е” + 2е8 + *+1
'	” * 2й
(96)
Вблизи ф = 0, я разложение (2) становится неприменимым, так как 6ф неограниченно возрастает. Однако уравнение траектории (9) справедливо и в этих областях (ср. с задачей (1.8)).
В случае инфинитного движения (Е 0) уравнение (9) решает задачу. Если же Е < 0, то (9) есть уравнение траектории лишь на нескольких оборотах*), пока остается З^ф 1. Сохраняя в (8) только накапливающуюся часть Сер—,— 3£ф, получаем уравнения
~ — 1 4- е cos 1ф,
X = I + Я,
(10)
описывающие траекторию на большом участке («правильное», в отличие от (5), нулевое приближение; ср. с задачей 2.18). Нетрудно также видоизменить уравнение (9) так, чтобы оно описывало траекторию на большом участке с точностью до первого порядка включительно:
— = I 4- е' cos Хф 4“ / cos 2Atp.	(11)
2.25 Достаточно убедиться, что выраженная через координаты
центра масс R = -1 1 Т—~	н относительного движения г =
r	m-i 4-
— г2 —г> функция Лагранжа разбивается на две части:
L = Li (R, R) 4- L2 (г, г),
Ь (R, R) = ~'4 "'г R2 +• (е, + е,) gR, Ь(г,г)=^г»--LJ + m(j._^gr.
*) В частности, радиус-вектор г должен быть периодической функцией <р.
Функция Li(R, R) определяет движение центра масс, происходящее так же, как движение частицы с массой гтц 4* и зарядом щ 4- е2
в однородном поле. Относительное движение, определяемое Z.2(r, г), происходит так же. как движение частицы с массой т =	...
mj 4- д?2 (приведенная масса) в кулоновском и однородном полях.
Такой же результат можно получить, конечно, и исходя из уравнений движения частиц.
m,rl + m2r? е, . е- .
2.26.	L ==---g-------+ J Л (г,) r,+ f Л (г2) гв. Функция
Лаграпжа разбивается на две части, содержащие только R, R и г, г (обозначения задачи 2.25), если — =-^-/п2*
т< 4-	. fi 4- e-> . , л ,n *.
*2 Ra + “4“ A (R) R + vr
4"	»
c(m, + mtF A(r) r-
N	N
2.27.	T — 2 Pt&p p e llwKv» M ~ 2 ^ib ГДе n= 1	n= J
.. ....A--.).p„=2^.
2.28.	Обозначим координаты летевшей и покоившейся вначале частиц через xi н х2. Пусть в начальный момент %i = —/?. х2 = 0.
₽ rt
Центр масс системы движется по закону X = —	4- у. Относи-
тельное движение с координатой х = л'2~-Х1 происходит по закону
Закон движения первой частицы
«X— -д-
______dx
У I — 4а./тигхп
х
“ т-
Расстояние между частицами уменьшается до величины «=
/№2\1/п
= 1-^—I , а затем вновь возрастает. Когда оно вновь станет
равно /?, первая частица окажется в точке
Точка остановки налетевшей частицы есть предел Х\/ при Р-»-оо.
Если то хп^-оо при /?-►<», т. е. обе частицы после столкновения уходят на бесконечность.
2 30 Уравнение движения
СР ™ = —s (1 г]	(О
имеет интегралы	
mv2	
~2~ = Е>	(2)
ев г — = J.	(3)
 n	d г2	
Умножив (I) скалярно на г, получаем rv = 0 или	—	— = 0,
откуда	
r2 = iT»!(«-	И)
Умножив (3) скалярно на r/г, получаем
— “ = J cos 0,	(5)
где 0 — полярный угол в сферической системе координат с осью г, параллельной вектору J. Проекция (3) на ось г
► *?£
mr\' sin2 0 — ~ cos 0 = J
совместно с (5) даст
Ч> = ^.	(6)
При t = to имеем v = и с учетом (5) *g Интегрируя уравнение <р <Р = То +	r0<j> sin 0 и из (6) следует: J = в-™	(Л ГпО —.	ц	пол viaсм sin 0т2 (О’ 1	. V (t — to) staearcte	•	<8>
Таким образом, частица движется с постоянной скоростью о по поверхности конуса (J — const. Введя
Ф = (ср—<р0)sin 0,	(9)
перепишем (8) в виде
Равенства (4), (9) и (10) можно интерпретировать следующим образом: движение точки по развертке конуса оказывается равномерным и прямолинейным, причем г и ф—полярные координаты в плоскости развертки.
2,31. Движение заряженной частицы в электромагнитном иоле определяется функцией Лагранжа
r;vs	е
L = ~2~ — eq> -J — vA,	(1)
где ф и А —скалярный и векторный потенциалы (см [2], § 16, 17). .Используя цилиндрические координаты, имеем
L = T(;, + ^ + ^4-T(^v-'-	(2)
Из уравнения движения для г
- „ лпгф mz 4- «7 7-
= 0
видно, что при г — 0 компонента силы, параллельная оси z, обращается в нуль. Поэтому, если г(0) = г(0) = 0, то траектория частицы лежит в плоскости г — 0. Так как <р является циклической координатой, имеем	.
-4-;= mr'<p + 77 “ р„= const.	(4)
am	с' v
Отсюда видно, что в случае инфинитного движения есть значение Mt при г—><х>. Кроме того, выполняется закон сохранения энергии (так как dLfdl = 0):
~ (h + ,«<>) = J?.	(5)
Исключая кз (5) ф с помощью (4), находим
Т^ + ^эфф ('> = ₽.	(Ч
где
^афф (r) 2mr2 (РЧ сг
Таким образом, движение вдоль радиуса происходит так же, как одномерное в поле С7Эфф(г).
Графики £4фф(г) для случаев рФ < 0 и > 0 изображены на рис, 94, а и б соответственно.
Рис. 94,
В случае pv < 0 для любой энергии Е > 0 движение инфинитно. Для того чтобы качественно изобразить траекторию, полезно выразить из (4)
| Р<р | ей пгт3	тег3'
(8)
Скорость поворота радиуса-вектора частицы имеет все время одно и то же направление и возрастает с приближением к диполю.
Рис. 95.
Примерный вид траектории показан на рис. 95 (кривая /). Траектория симметрична относительно прямой, соединяющей центр поля с ТОЧКОЙ Г == Г 1п[ц.
В случае Рч > 0 возможно рассеяние частиц любой энергии
Е>0, а при E<t/m = 32^2^2 (Е—Et на рис. 94, б) возможно также финитное движение. Из равенства
’ _ Р(р fm
“ tnr3 ~ тсг'л
следует, что ф >0 при г^> г, — — и ф < 0 при г < гь При r=rt ^Pip
частица имеет «точки остановки» ио ф.
Частица с энергией Е > Um (Е = Е2) на рнс. 94. б рассеивается, причем в двух точках г = и ее скорость параллельна радиусу-вектору (рис. 95, кривая 2).
При Е < Um возможно рассеяние без точек остановки по ф (рис. 95, кривая 3) или финитное движение в кольце a г Ь (рис. 96). В последнем случае частица в течение периода совершает как прямое (участок АВ), так и «понятное» (участок ВС) движение по ф.
2.32. а) Удобно использовать цилиндрические координаты, а векторный потенциал выбрать в виде А^ =	r3@, Аг = Аг ~ 0. Дви-
жение в направлении оси г равномерное, а в плоскости, перпендикулярной к оси г,-—финитное. Проекция траектории на эту плоскость изображена на рис. 97. Траектории а, б, в отвечают условию pv > 0 * •*)) и соответственно IA <	< ^2, Е± — U2, 14 < Е±, где е, & е______
D=is? й=Гй5тг. Л,я Рч < 0 траектория приведена на рис. 97, г, для р9 = 0 — на рис. 97, д.
Закон движения частицы в этой плоскости легко найтн. зная движение свободного изотропного осциллятора с частотой £2 (см. [1], § 23, аадача 3)
—	—	/ b ~ V)
Г8 fl2 cos2 Qf _J_ £,2 sJn2	ф s= — fi/ -|- ArCtg ( ” tg £2/ J
Здесь минимальный (b) и максимальный (а) радиусы определяются
*) Для определенности считаем З'ё > 0, р9 — обобщенный импульс, соответствующий координате ф.
•*) Ветви Arctg tgfiA нужно выбирать так, чтобы угол <р был непрерывной функцией /,
энергией Е =	(a2 -J- 62) — р^Й и импульсом рф = m£iabt
а начала отсчета t и <р выбраны так, что ф(0)= 0, г(0)= а. Интересно, что период радиальных колебаний Т = л/й не зависит от Е н pv. Угол поворота радиуса-вектора за этот период Дер = зт(± 1 — •—Й/Й) для рФ^ О и Д<р = —fi/й для рФ = 0 не зависит от £*).
Как изменится движение частицы, если 1 < О?
Интересно сопоставить движение частицы в этой задаче с движением в скрещенных электрическом н магнитном полях (см.
[3], § 22).
2.33. Уравнение траектории
Ф =
Й = 2^?

°яфф (г) г + 2 v ~	*
") Другой способ решения приведен в задаче 6.36.
Качественно характер движения можно исследовать, используя графики 1Л)фф(г). При этом нужно обращать внимание на то, что ср меняет знак, когда г проходит через значение r0 ~ 1 / В резуль-I/ Г7?й‘
тате получаем траектории, приведенные на рис. 97, а — д*). Различные траектории на рисунках соответствуют следующим условиям:
с) > 0, t/min < Е < 170, где Umia — минимальное значение ^афф(г), ^0 “ ^8фф(^о)>
б)	р9 > 0, Е » L'c;
в)	р9 > 0, Е > С/с;
г)	Рч> < 0;
<5) рф «= 0. В последнем случае частица падает в центр на первом же витке.
Рассмотрим подробнее два предельных случая.
Уравнение (1) представим в виде
mQ2r2
2
-QL (2)
Таким образом, можно считать, что влияние магнитного поля сводится к замене энергии на Е* = Е -f- p^Q, добавлении к полю
_ а х _
с/  ---—• дооавкн	= —-— (которая приводит к процессия
орбиты) и к добавочной прецессии с угловой скоростью £1 При достаточно малых значениях магнитного поля Зё поле <5U может
оказаться малой добавкой к (7п == ~~ — — Для этого доста-2тг г *
точно, чтобы во всей области движения частицы выполнялось условие
ви««|1/.(л)|.	'	(3)
Скорость прецессии, вызванной 617, можно определить как л бДф 1 д
а= Т =TSF„(J'<61'»-	<’)
*) Качественный характер исследования с помощью графиков позволяет воспользоваться тем же приближенным изображением тра-
екторий, что и в задаче 2.32. Разумеется, точные траектории частиц в обеих задачах различны.
где усреднение 617 производится по движению частицы в поле Uo с энергией Е' и моментом рР, а Т — период этого движении (ср, с задачами 2.17, 2.18). Вычисление*) приводит к значению
°-----2| £' г	(S>
причем 617 действительно можно считать малой поправкой, если кроме (3) выполнено также условие 6Д<р <£ 2л, т. е.
й!₽<1а/т|£'Г"/!«1.	(6)
Разумеется, 617 нельзя считать малой поправкой, если Е'^С, так как в этом случае удаление 617 качественно меняет характер движения.
Величина Q' может оказаться как малой по сравнению с Q, так и большой. Знак £У противоположен знаку т. е. направление этой скорости противоположно направлению движения частицы по орбите. Направление же скорости Q определяется магнитным нолем.
Итак, траектория представляет собой эллипс, прецессирующий с угловой скоростью
Qnp = - G +	(7)
точнее говоря, поскольку может оказаться ОТ I, в системе отсчета, вращающейся с угловой скоростью Qn₽, траектория представляет собой неподвижный эллипс.
Интересно сопоставить полученные результаты с теоремой Лармора (см. [3], § 45, см. также задачу 9 23).
Возможен ли случай, когда 6(7 можно считать малой поправкой, если энергия частицы Е положительна?
Далее рассмотрим случай, когда малой поправкой можно считать поле 17 — — а/r. Движение без учета 17 происходит по окружности. Ее радиус а и расстояние b от ее центра до центра поля можно выразить через максимальное и минимальное расстояния частицы от центра поля
2 £ + +
г1.2 -	т£2г		<“>
Возможны два варианта расположения окружности, изображенные на рис. 98. Если pwO < 0, то осуществляется случай а), если
> 0, то осуществляется случай б). В обоих случаях
.. + . £
b ~ 2тЦ» • п “2тО2-	<9)
*) Для вычисления <б(7> удобно использовать переменные, примененные в задачах 2.18, 2.19. Так как период в поле 170 не зависит от р<р, в (4) можно вынести Т из-под знака производной.
ОТВЕТЫ И РЕШЕНИЯ
Учет полк V приводит к систематическому смешению этой окружности (называемому дрейфом), причем ее радиус и расстояние от центра поля, определяемые постоянными а и Ь, не изменяются, т. е. центр ее перемещается по окружности радиуса Ь. Угловая скорость смещения центра окружности
д
где усреднение V производится по равномерному движению по
Рис. 93.

окружности. Ограничимся случаем, когда а Ь. В этом случае можно считать просто
<^>=-т«	о°)
а
так что	Заметим, что в этом
случае линейная скорость дрейфа равна где е& = а/Ь2 — сила, действующая на частицу на расстоянии b (ср. [3], §22).
2.34. Задача о движении двух одинаковых заряженных частиц
в однородном магнитном поле сводится к задачам о движении центра масс и об относительном движении (см. задачу 2.26).
Координаты центра масс
X — R cos cof,	|
Y = — R sin cat, J где a=e3fSltnc.
Относительное движение совпадает с движением частицы с массой zn/2 и зарядом е/2 в поле U—e~/r и в однородном магнитном поле Э%. Это движение подобно рассмотренному в предыдущей задаче, только в формулах следует заменить т на zn/2, е на е/2 н а на —е2. Ограничимся случаем, когда радиус орбиты а мал по сравнению с расстоянием до центра поля (см. рнс. 98,6). Частоту радиальных колебаний с большей, чем в предыдущей задаче, точностью легко определить, разлагая (г) = ~	± ш в ряд
вблизи r=b (см. [1], § 21) Из условия ^дфф(Ь) = ° находим
1/zn2	7п т / (й \	2е2
V пт01164—-4 ’,=^- <2>
Отсюда для а =1/ 26,°ФФ(Ь> получаем окончательно а,—и—X т » m	*
а расстояние между частицами
r= b+a cos («йгН-оф	'(3)
Для нахождения ф(/) воспользуемся сохранением обобщенного нм-m I •	ы \ ~	/о,
пульса pw = — г2 I ф — ) С учетом (2}, (3) получаем
<р(/)^_у(_Х8|11(Юг<+а^_|_ч)[|.	(4)
Воспользовавшись (3) и (4), можно представить координаты относительного движения в виде
f У?
x=r cos <р=& cos (у/ — <р0)4- a cos I tot -|- у -J- Р I,
у = г sin <р — — b sin (у/ — фо) — a sin -|- у 4~ Р Р = а — фо.
Здесь первые слагаемые отвечают движению центра окружности с дрейфовой скоростью Ьу, а вторые — движению по этой окружности с угловой скоростью to 4-
Координаты частиц xI2 = j + A, t/12 = Y ± А удобно пред-
ставить в виде
*1.2 = ± Т C0S (V/ “ Ф») + Pf ,2008 (W/	^1.2>*
_ b
yi,2 “ + ~2 dn W “ Фв> Pl.2 sin (w/ l‘ ‘•ht»2)’
i де
Pl. 2 = yf R* + T ± aR C0S (т I" Py’
± a sin (y 4- pj
1бФ1,2=	lyt V
2R ± a cos (у 4- pl
(6)
Итак, центры окружностей, по которым движутся частицы, вра-щаюгся вокруг начала координат с угловой скоростью у (дрейфуют
со скоростью 67/2), а радиусы этих окружностей пульсируют с частотой 7/2 (рис. 99).	•'
Механизм «перекачки» энергии проще всего понять в другом предельном случае; аЗ>6 (расстояние между центрами орбит частиц мало по сравнению с радиусами орбит (рис. 100)). Очевидно, работа,
Рнс. 99.
Рис. 100.
совершаемая силами взаимодействия, иад второй частицей положительна, а над первой — отрицательна в течение многих периодов.
2.35. Убедиться в постоянстве данной величины несложно, используя уравнения движения (ср. [I], § 15), причем удобно представлять ее в виде AF + -- [FrP, где А = [vIH] — 21. Прн малых значениях F траектория близка к эллипсу, большая полуось которого направлена по вектору А, а эксцентриситет е = | А| /а. В этом случае AF « const, или е cos if = const, где if — угол между А и F.
2.36. Появление малой добавки к потенциальной энергии 617 (г) приводит к изменению величин, характеризующих движение частицы (момент, положение перигелия и т.д.), причем за небольшой промежуток времени (несколько периодов невозмущенного движения) они также изменяются мало. Однако за длительное время изменения накапливаются, так что некоторые величины могут измениться во много раз.
В частности, орбита в течение малого промежутка времени остается эллипсом. Большая полуось этого эллипса а = определя-2| с I
ется энергией и не изменяется за длительное время. Эксцентриситет
1/.	/И»
же е" J/ 1 — н ориентация подвержены накапливающимся изменениям,
а) Изменение момента определяется уравнением
м- [rF],

Усредним это уравнение но периоду
<M>=[<r>F],
(2)
где
(3)
Зав
О
Для усреднения используем систему координат с осью Oz, параллельной М, н осью Ох, параллельной А (рис. 101). (Здесь А = [vM] — 21 — дополнительный интеграл в задаче Кеплера; напомним, что вектор А направлен от центра поля к перигелию, а |А| = ае.) Очевидно, что — <г> параллелен Ох. Подставляя х = ==a(cos| — е), t = —(£ — еsin £). /Л получаем
2л
<*>=;£( J —«)(1-
го
Таким образом.
, ч	Зае А _ За
<0-----Ч | А I 2а А-
б) Если сила F перпендикулярна к М, то из соображений метрик ясно, что орбита — плоская кривая, а вектор М сохраняет свое
направление (с точностью до знака). Перепишем (2), (5), опуская знак усреднения, в виде
• Здй
М = -г- г sin
(5)
СИМ-
(6)
где — угол между А и F. Учитывая, что
е cos ip=е=const
(7)
(см. задачу 2.35), и исключая из (6) е и находим
М2 таа'
(8)
Интегрируя уравнение (8), получаем
Af=Af0cos(Q/+P),
(9)
где
а также
Зг 1 / а	
D = T К W. = v ">oa(l-es), е = Fl — (1 — е2) cos2 (Й/ + р).
Итак, траектория представляет собой эллипс, покачивающийся
Рис. 102. >
около направления F и меняющий в такт покачиваниям эксцентриситет (рис. 102). Направление движения частицы по эллипсу также изменяется (вместе со знаком М). Период колебания эллипса 2л/Й гораздо больше периода обращения частицы по эллипсу Т.
в) В общем случае рассматриваем также изменение вектора А. Используя уравнения движения, легко получить
A = ~[FM]4-[v(rFn.	(Ю)
Для усреднения (10) используем равенства /dx2\	)
, \	/А	п
\^2/	= °-	I
•	•	/d \	п	I
<хуу <ух; =-- ху/ = 0, At
<Ж|/>_<ух> = -. J
Получаем
3
<A> = g-[FM).
(Н)
(12)
Итак, для М и А, усредненных по периоду (знак усреднения далее опускаем), имеем систему уравнений
•	3
М = Й[РА].
Компоненты этих векторов, параллельные F, сохраняются:
MF == const,	AF=const
(14)
2.36J
§ 2. ДВИЖЕНИЕ ЧАСТИН В ПОЛЯХ
— результат, который легко получить и из других соображений. Для поперечной компоненты М
Мд. — М —
из (13) получаем уравнение
Мд. + Q’Mi = 0.
’(15)
(16)
Его решение запишем, введя систему координат OXjXjXj с осью Xs, параллельной F:
Mt == Вг cos Qt 4- C\ sin Qt, 1
Afa = Ba cos Qi -|- Ca sin Qt. J ‘
Теперь из (13) находим
Ai = — (Bs sin at — C, cos fi().
3F
A, = (Bi sin tit — С, cos G/).
(1«)
Постоянные B|,E, C;,2 определяются, как и следовало ожидать.
начальными значениями векторов М и А.
Конец вектора М описывает эллипс с центром на оси А'з в плоскости ц, параллельной OXiX2 (рис. 103). Конец вектора А также описывает эллипс с центром на оси Х3 в
плоскости о, параллельной ц, подобный первому и повернутый на п/2. При этом А все время перпендикулярен к М. Плоскость траектории перпендикулярна к М, вектор А определяет направление на перигелий орбиты.
Итак, плоскость траектории поворачивается («прецессирует») вокруг F. Угол, составляемый плоскостью орбиты р с F, колеблется при этом около некоторого среднего значения. Колеблются около среднего значения эксцентриситет и угол между проекцией F на плоскость р в направлением на перигелий. Все эти движения происходят с частотой Q.

Рнс. 103.
Напомним, что мы пренебрегали поправками первою порядка по F, если они не приводили к накапливающимся эффектам. Решение справедливо для отрезка времени порядка нескольких периодов прецессии орбиты.
6 Г. Л. Котки и. В. Г. СерОо
Не приведет ли учет следующих приближений к качественному изменению характера движения (например, к уходу частицы на бесконечность)? Точное решение задачи о движении частицы в поле U = -Л —Ft, возможное в параболических координатах (см. задачу 12Л26), показывает, что при заданном £<0 и достаточно малых F подобных эффектов не возникает.
Подчеркнем, что появление накапливающихся изменений орбиты под действием сколь угодно малого возмущения связано с вырожде
нием невозмущенного движения.
В [5], § 7.3 можно найти решение этой задачи с использованием канонической теории возмущений.
2.37.	Согласно теореме Лармора (см. (2], § 45) орбита частицы в однородном магнитном поле вращается вокруг центра кулонов-ского поля с угловой скоростью fi = —	* где q— заряд частицы.
При этом векторы М и А изменяются со скоростями
М( = [ЙМ].	А>—[£А].	(I)
Усредненные за период скорости изменения векторов М и А под влиянием постоянной силы F = <?8 определены в предыдущей задаче (см. формулу (13));
M, = |^[FA1.	А,= Д(ЕМ].	И
Усредненные скорости изменения векторов М н А под влиянием обоих полей равны
М=МН-М2. А^К+Аа.	(3)
а)	Направим ось х по электрическому, а ось у по магнитному полю. Тогда уравнения (3) принимают вид
Л» = -ЙЛ' Л = ЙЛ«~2^Л<1 *Г=2ТЛВ-
Решение этой системы:
С,
Й
Да == - — В cos (со/ + 3) +
'AV=B sin (tof-J-p), п 2mQ
М ~ 2aw В sin № + в + С>
где со^уй^+ЭоГ^/^а, а постоянные В, р, С определяются начальными значениями А и М.
Итак, конец вектора А движется по эллипсу с осями, параллельными осям х и у (рнс. 104) в центром на оси х, Орбита при этом покачивается (или вращается при	причем периодически
У
Рис. 104.
изменяется эксцентриситет. При 9аРВ>4/паЙоС эллиптическая орбита периодически вытягивается в отрезок.
3F -\Г а .. т/’та
б)	Обозначив Qf — *2 у N = А у запишем (3) в виде М = [ЙМ] [DpN], N == [ON] -}- Складывая и вычитая эти уравнения, находим
*1,2 ~ 1^1,2*1.21*
где	*1,2 e Va(M±N), со12 = Й+ (1р.
Таким образом, векторы J|,a вращаются с постоянными угловыми скоростями Wi.j:
JIt2 (0 = *1,2 (°) cos “1.2* +
Г м1.2 I	*12 (®)	2 I
<r\^Jl,2(0)|	+M1'2 '^2 ’ (1~COS °1.20’
п векторы M J, + J2, A =	~ (Jj — J2) полностью опреде-
ляются через свои начальные значения.
Мы не будем подробно анализировать этот ответ. Заметим только, что Ю| = со2» если электрическое и магнитное поля взаимно перпендикулярны.
2.38.	Пусть частица движется в плоскости xz. Уравнения для вектора А (см. формулу (10) из задачи 2.36) можно привести к виду
А х — — 2₽ (5хг? — 2х?®) = гМ — 2р & хг2,
• г. •	'.	48	d
Az = 2Р (4xxz - г#) = — хМ + 20 xz’, где М=лг(хх—xz) — медленно меняющаяся функция времени. 8*
После усреднения этих уравнений получаем
;г = 4₽Л1<х>=-6^Ла[М, где а — большая полуось эллипса. Отсюда
Ах 3/2
т. е.. в отличие от аалами 2.366, конец вектора А колеблется не вдоль прямой, а вдоль гиперболы
3 А^ — А% 4- const.
Зависимость А от времени можно найти из уравнения та С < = -9₽с J МАг*
в котором М и At должны быть выражены как функции А»,
Например, для случая, когда в начальный момент/1,(0) = О, Дя(0)=аео (е0 — начальное значение эксцентриситета), имеем
Д
таа (с2 — хг)
а
С течением времени орбита медленно поворачивается в плоскости xz и превращается в отрезок, составляющий с осью х угол
Входящий сюда интеграл приводится к полному эллиптическому
интегралу первого рода (см. примечание к задаче 1.7 и [10), стр. 96—97)
I = -----7^=----А' (*).
6 л У Wc {За3
где Т — период невозмущенного движения.
2.39. Функция Лагранжа системы (q — заряд частицы)
птиг а q [и
“-2- + -+-Т —
лишь обозначениями отличается от рассмотренной в [2] (задача 2 к § 105). Уравнения движения
М = ^[МП.|,
;	<7	. , Зу(Мт)
А =	[АИ 1 +	ИМ
при усреднении по периоду Т невозмущенпого движения дают уравнения, описывающие систематическое изменение векторов М и А:
•	от
<M> = [G-MJ. У =	(!)
<А> = [ЙА),	Й = С'-ЗМ^Р,	(2)
где а н е —большая полуось и эксцентриситет иевозмущенной орбиты. Уравнение (I) можно переписать также в виде
<М>=[ЙМ],	(3)
так как вектор £2 — ft' параллелен М.
Из (2) и (3) видно, что эллипс, по которому движется частица, прецессирует «как целое» с угловой частотой £2. Другая интерпретация может быть дана на основе уравнений (1) и (2): в системе координат. вращающейся с частотой £2', вектор М, а с ним и плоскость движения частицы, неподвижен, вектор же А, а с ним и перигелий орбиты, вращается с постоянной частотой £2 — £2' вокруг направления М.
Укажем еще, что усреднение величин If г3 и г/г5 удобно проводить, перейдя от переменной t К углу <р;
Т	2п	2Л
/1 \ I С <и _ m С d<t> _ m С	_ 2пт
г3(/)-ТМ ) r(<p)~rMpJ <’ +fcos,l-)*l-ТМр' 0	i>	<1
Т	2Л
1 С Ar __ m Г cos <р 2лте
Р = АгТ J г® dt “ ATM J г» d<P = 0	0
2.40. При усреднении уравнений (см. формулу (10) задачи 2.36)
A = ~[FMH-(v[rFH
учтем, что <F>=0 и что, согласно уравнениям невозмущенвого движения,
d t г \ czv Зсхг (rv)
mv = aFmv^5?(-a^J = -‘^ + ”7r--
Это дает (см. предыдущую задачу)
<а>__Е₽Ж1\_Н₽/£ . ^£\_„ w “ т2 \ г* / - т2 \г» + г4 /-
Злсф
2m2as (I — (")"' ’
Отсюда видно, что скорость изменения вектора А направлена в сторону, противоположную самому вектору А. Как известно, вектор А направлен к перигелию орбиты и по величине равен Л = сиг. Таким образом, добавочная сила не вызывает прецессию орбиты, а приводит к уменьшению эксцентриситета
Можно также показать (см. [2], § 75. задача I), что вследствие потери энергии и момента частица за конечное время упадет па центр.
§ 3- Сечение рассеяния в заданном поле. Столкновение частиц
3.1. а) Как легко видеть на рис. 105, угол отклонения частицы 0 равен удвоенному углу наклона касательной к поверхности в точке столкновения. Поэтому
6 dp b г ‘8Т = л=ТсозТ-
Отсюда
р2 =	— й2 tg2 Д
И
.	,	fi dG efido
dc = n|dp2|=n04gT-C0s2(f)/2 =-------g-.
4 cos4 ~2~
Возможно отклонение частицы па углы от пулевого (при р->Ь) до
"m = 2arcl8— (при р-»0).
™ а
рис. 105.
Итак,
о<е<е„.
при
do —
б) do —
asdo
, 0
4 cos4 ~2~
(1 — п) sm 0 cos*3 у
При л —*1 приведенное сечение равно
do ( 0 при 0 > 60 — 2 arctg /, do (и при 6<6о.
Этот результат ошибочен. Почему?
в) do =
do
- 2 6	• О
Sin*3-у- sin 6
При 0 < е < 0т = 2 arctg
О при его<6-
3.2. Параболоид вращения р2 = ~ г
с.
Сближаются ли траектории частиц, рассеянных в поле и на пара-
йж=У1 - ViE.
Чем вызвано отличие этого сечения от сечения рассеяния на потенциальной яме (см. [1], § 19, задача 2)? .
3.4.	а)
I р	а2 \	а2
я (Е	4Ег) "₽и £'>4Р'
О =	2
о	при Е<^-
Как изменится сечеиие при изменении знака а?
б) а =
SL-ИГ
£ 4’<
3.5.	а) Рассмотрим движение пучка частиц в поле U{r) = а	Ер2 а
=------Графики иэфф (л) =— пр» различных значениях
прицельного параметра р приведены иа рис. 106.
га = (п - 2)1/п
При больших значениях р (кривая /) частица рассеивается, приближаясь к центру поля на расстояние Пп1п(р), определяемое условием' ПЭфф(Гт1п)=£. При уменьшении р уменьшается и rmlll вплоть до значения г0, достигаемого при р=р0 (кривая 2). При еще меньших р частица падает в центр (кривая 3).
Величины Го и р0 определяются условиями f
^зфф ~ ^вфф (Го) “ ®
п Пп - 2) a I1'» ₽» “ ' и - 2 L 2Е J *
Если R>ro, то па шарик падают частицы с гаЛи^Я, в сечение падения
— ЯР2 (ruiln — Я) — л^2 ’1 ER2]'
Если то на шарик падают частицы, которые упали бы в центр, к сечение падения
9 ля Г(л — 2) а 12/п
<’ = "₽? = ^2	2Ё— ] '
6)	а = п (г ]/-£- — "!) если 2ЙЁ >₽,£/?*< у.
Если же хотя бы одно из этих неравенств не выполняется, то
с - л/г» (i + £R4 - £д2).
.	*г(1 +МЛ>
3.6.	а) ас — ------------g-гу где
4 u + Asin2-g-j ’
. 4RE (RE + а) ?>= _ .
Как объяснить результат, получаемый при сх-|-2/?Е—-О?
б)	В плоскости траектории частицы введем декартовы координаты с осью х, направленной вдоль оси пучка, н осью у — вдоль прицельного параметра. Движение частицы в области	есть
гармоническое колебание по каждой из коордииат, причем в начальный момент этого колебания (при t = 0) yQ = р, у0 = о, хс =
~ — У R2 — р2, х0 = v, так что _______________________— v'
х = — 1 R2 — р2 cos о/ + “ sin tot, у = р cos tot. (I)
Момент выхода частицы из области действия сил определяется условием
x2+y2=Z?\	(2)
а угол 0 между скоростью частицы в этот момент и осью х— условием
У pw .
Sine =	—sin cof.	(3)
Подставив (1) н (3) в (2), получаем уравнение
p*-p2fl2(l +>.sin2e) + -j-Д4 (1 + Z)= sin’0 >-0,
122
ОТВЕТЫ И РЕШЕНИЯ
где X = ^2^8- Отсюда
р| 2 = ^* (14- X sin2 0 + У cos2 0 — X2 sin3 6 cos® 0),
в сечение
.	/ г , 91 . । . 91 \	. / ?	9\ П ~Ь X2 cos 20) do
Лт = n ( | dp* | + | dp| | ) - nd (рГ - p|) = 2yl-V51n,fl- 
Если X > 1, то возможно рассеяние только на углы, меньшие
Л . RW Л Л do
Bpl = arcsin ~^2—• а при 0 -> 0» сечение неограниченно возрастает. Такая особенность сечения называется радужным рассеянием (см. [11], гл. 5, § 5). Подобного типа особенность сечения приводит к образованию радуги при рассеянии света каплями воды.
Примеры радужного рассеяния см. также в задачах 3.8, ЗЛО.
3.7.	а)

do
do- е3(2^-6)2 О
V при 0c9m=nj
при 0>6т.
б) Прн вычислении угла рассеяния (см. [I], § 20)
С F«dx  v pV^-p'
J 2£ -2 E K‘
учтем, что сила
12Vy 2I'p fs = |	~ A'2
lo
прн	<: X < Д/А2 — Р2,
ори |x[ > У/?2 —p2.
Отсюда находимp^2 = -у T?2 (I 4- I—G3/U^J, где Om=V/E, поэтому <*° == л (|dp21-{-|dp||) = ad(P| — р|). Окончательно
№
о
do =
при 0<U<0m, при е>е„.
Сравните этот ответ с ответом задачи 3.66, в которой рассматривался потенциал, отличающийся знаком от данного.
3.8.	Угол отклонения частицы
„ |3л₽ яп I ®“|4£р’~2£р!|
W
легко вычисляется по общей формуле*). Зависимость 0(р2) изображена на рис. 107. Из (I) находим
<,Ь=4и(| 1 |./Л|~<)
ла2
Г;|Р W Ссчи1,,е
do = л ( | dp’ | + | dp| | + | dp’ | ) = nd (- р^ + р| - р|) =.
ал / 1+е/2а 2-e/em \
Для справедливости полученного результата достаточно, чтобы каждое слагаемое в (1) было много меньше единицы. Оценка показывает.
Рис. 108.
что для этого достаточно выполнения условия Выражение (2) получено для 0<0«. Если 6„, I, то для G,n<6«S 1 сечение
„я / 1 4-В/26	\
Зависимость ~ от 0 изображена на рнс. J08. При 0~*О и при
О -> 0„ сечение — неограниченно возрастает. Сечение рассеяния
*) Проше всего взять оба слагаемых (1) из задачи 2 к § 20 работы [1].
124
ОТВЕТЫ И РЕШЕНИЯ
в интервал углов, прилегающий к 6 = 0, бесконечно, так как рассеяние на малые углы отвечают большим прицельным параметрам.
Сечение рассеяния в интервал углов 0,п—6<0<(Jm
С

конечно и стремится к нулю при 6 -> 0.
Как зависит количество рассеянных частиц, попавших на счетчик, от размеров счетчика, если он расположен под углом 0,„?
Рис. 109.
3.8.	Скорость частицы после рассеяния ко сравнению с первоначальным направлением оказывается повернутой на угол
Счетчик рассеянных частиц регистрирует имеете с частицами, отклоненными на угол |0| < л, также и частицы, сделавшие предварительно несколько оборотов вокруг центра (рис. 109, а) Наблюдаемый угол отклонения / лежит в пределах 0<Х<л и связан с 0 соотношением	.
-0^2л/±х.	(2)
где верхнему знаку соответствует Z = 0, I,..., а нижнему — 1~ 1, 2,... (рис. 109,6). Из (1) и (2) имеем
₽’ (X. Л ±) = в* + у (2л/ ± -х - 2л! + 2п ± X
Сечение
<!а = п 2 | ф (х, I, Ч ) | J- я § | rfp’ (•/„ 2=0	2-1
v..,™,a „,м dP2 <%» 1> +) . ~ Ф2 (X. I. ~) s. л
«читывай, что-----—----<0, ------—------>0, находим
ds = nd [- У Р2 (X. I. +) + У, P'(Z. I, -)J =
л2о3 / 1	1 \	по2 (2 л2 — 2л^ 4- х2)
• ~ ~2~ d (2л — х — х /	2х2 (2л — у)2sin х d°’
Сечение — обращается в бесконечность при 0->л В данном случае это приводит к тому, что сечение рассеяния в малый конечет
ный телесный угол д0 = J 2л sin х dX “ л7.о рав,1°
Л—Хо
Л	,____
с® f do „	„ 1/ До
Д" = 2Й J 7=“’х»=«2 Ут-
Л—/о
Появление особенности дифференциального сечения обусловлено тем, что угол отклонения, равный л, достигается при значениях прицельного параметра р(л, I, ±), отличных от нуля. В телесный угол До, пропорциональный квадрату малой величины Дх^Хо* попадают частицы, летевшие до рассеяния через площадки 2лрДр, площади которых пропорциональны первой степени Др оо Хо- Такую особенность рассеяния называют сиянием (см. [11], гл. 5, § 5).
Такая же особенность есть и в рассеянии па угол х=0, но в данном случае опа маскируется бесконечным сечением из-за рассеяния частиц со сколь угодно большими прицельными параметрами. Сияние при рассеянии вперед могло бы проявиться, например, при ограничения диаметра налетающего на центр пучка частиц,
3,10. а) Условие £?> V приводит, как легко видеть, к малости угла отклонения частицы при рассеянии. Изменение нмпульса
<“ —
Др==— J l/(|p + v(|)« = ^-i-ixe-,’>
где х=хр.
Угол отклонения
Др УУл ,
Разрешить это уравнение относительно х в аналитической форме не
удается. Однако, используя график функции хе—** (рис. 110), видим,
V ,/~Л ™"Р"е<ет=£ Г й
уравнение (1) имеет два корня.
Рис 111.
V V л	,
dQ == —|г- (1 — 2x2) e-x*dx
и учитывая (I), представим сечение
da = я( | Цр*| + |*||) = у (xjdx, - x,dx,)
в виде
.	' <?О / *2	,
Й<,=^2х|-1 + 1-2х^-
Г1ря 0<g:GJn оказывается Х|С 1, Ха;»1, и
. do do - 2з(8О2.
При Gm — G 6m можно разрешить (1), рачложив хе А'в ряд вблизи максимума. Получаем
*1.2 -	,<2
do =
do
WCfl-W,’
График do/do изображен на рис. 111. Особенность при 0 =- 0™ —
интегрируемая (ср. с Задачей 3.8).	pj
Связано ли появление особенности сечения при G=6m с приближенным методом решения задачи?
du /*1 + А к, +
б) do = Л!	+ 2Xj _ ! J.
гче	(
*1.? '/глпу
(' i-W
При л V	nV do
е<°™ = ь7П’ dO = 4^£b>-
При 0m—
П*» О(У =--г=--о  	—.
2Гг><Чк '-е-Ч,
3.11. а) При столкновении частица, имевшая скорость v, приобретает скорость v,=v—2n(nv), где п— единичный вектор нормали к поверхности эллипсоида. Подставляя
1 ! х у ? \ *)
v = c(0,0.1), n = jy^T. js. 75J  получаем
г ( 2хг 2t/z 2г2
v = о NW, — Л1 - Л,»с J •	U)
Введем полярные углы, определяющие направление v'r Vх = .== o(sin 0 cos<₽, sin 6 sin q>, cos 6). Сравнивая c (1), находим
Л 2z2	. » „	/ 2z \2 /л2	p2\
= cose^i-^. «n’e^pvvj	(2)
Сечение
rfo = dxdi/ = ||^pe!i<p.
где зависимость x, у от 8, <p определяется из (2) и уравнения эллипсоида. Для вычисления якобиана оказывается удобным ввести промежуточную переменную и такую, что
х=айи cos ф, у=Ьги sin <р.
Как известно из дифференциальной геометрии поо grad Т 4-	— 11,
N определяется условием п2==|.
Из (2) получаем 2zu	2za 6 z
eln 6 — д,8с2, I — cos 0 = Л,2с4, tg 2 — ucii
и из уравнения эллипсоида находим
u~z == ст сад2 ф -J- Ьъ sin2 Ф 4- с2 tg2
Далее,
д (х, у) _ д(х,у)д(и, ф) д2&8 ди*
д (0. ф) ~ 0 («I Ф) d_(G. ф) — 2 сЮ * Окончательно
fl’feVdo
«О —	Q /	Q \ 2 •
4 cos4 “g- I с2 cos2 ф 4* 62 sin2 ф 4- c8 tg2 j
С помощью какого предельного перехода можно получить из этого результата сечение рассеяния на параболоиде?
fl2fe2cs do
dc ~ cos3 0 (a8 cos2 ф 4- b* sin8 <р,+ с2 1g2 6)а ’ cos Gost2c2 do
Е) da “ sin4 6 (o’ cos’ ф + f Sill’ Ф + c’ ctg’ 6)’-
3.12. а) Изменение импульса при рассеянии,
Др = _|^,
При рассеянии на малые углы в правую часть (I) можно подставить г (/) = Р 4- v/. где р -L v:
й₽ = “£ J + й
Пусть ось z параллельна v, ось у перпендикулярна к а. Тогда
Направление скорости после рассеяния характеризуем углами в
♦) Замена в (2) дифференцирования по г дифференцированием по р (при условии р -L vco) приводит к тому, что полученная формула определяет только компоненты Др, перпендикулярные к vw.
сферической системе координат Др»
‘8’ = 5Г/
0 = ^. р
(4)
Из (3) ясно, что рассеяние происходит только в интервал углов
Из (3) в (4) находим
л Зя
у<?< 2
, ”“x sin <Г cos <р	т по» cos2 <р
Р« - - 2Е е ' Ри ~	2£ О 	®
Сечение
VI	хч I а (₽а- Р») 1	/™.Уав!«р
dn = 2 dp А = i | 7(6. -<й I d0 = (т)	d0- (6)
(Суммирование в (6) проводится по двум возможным, согласно (5), значениям р)
| а. f do
б) do = 	, аь*“ компонента а, перпендикулярная к v«,
Сечение оказывается симметричным относительно vM (хотя поле отнюдь не симметрично относительно этого направления).
3,13.	Изменение угла отклонения частицы (ср. с задачей 2.17)
Из уравнения 0 —0е(р) + £>6(р) находим
Р = Р„(в)-«е(р,(е))^Э
(ср. с задачей I 8). Здесь зависимость Gc(p) соответственно ро(6), определяется при б(/(г)=0. Отсюда сечение
do	1 dp21 I Фо (G) d	Л dp0	(0) I
dfT = n	| dO I	= я] ~5W	- do ЗР» (0) 66 (Po	(6)) —I	=
don dr	don]
= do + jo [60 (p0 (0)> do]-
Знак перед d/dG противоположен знаку dpo(0)/d6.
do л₽ d "-6 + 2cos0/2
E> 8 do E dl) sin 0	;
, do _ 2f (я — 0)2
“ de “ n“ )' ft d0 J 0(2.1 — 0) ’
9 Г. Л Котики. В. Г. Сербо
3.14.	Приобретаемая частицей энергия
(Р — Ар)2 Р2
е= "2И.......
определяется в первом порядке лишь изменением продольной компоненты импульса. Так как отклонение частицы можно считать малым, в выражении для силы
dU (г, I) дг ’
действующей на частицу, положим (после дифференцирования) г= = р + v(/ —- т). Здесь р — прицельный параметр, ат — момент времени, в который частица находится на минимальном расстоянии от центра. Тогда
e = v [ F(0 dt — e^e-^cosq),
to*
em = T nls— e . T = cor,
а сечение рассеяния для частиц с данным т при cosq)>0 (сояф<0) есть
при 0 < е < е cos ф
РР» I е 1 > ет | cosij. |.
(0> » > «„ cos <f),
В падающем пучке есть частицы с различными т. Усредняя се-
чение по фазе ф (например, ддя &>0 по формуле
С 7’., \Л/ - 2п J do d4>.
а — arccos
получим
ECCCCS^J при |е|<₽ , \Л / -	m
[°	nP“ I p I > >,„
_ 4V X’sinOdO	I'2-11®
3* IO* ' П Г  	—, 7. = lit- ,
Л cos® (J ] 1 — X2 tg2 fi	L’o
0^0^ arctg ?~t, если V < vUt
(n —arctg [Л|	если V<v0.
3.16.
dN
N
ЧЛпах~ПГ~ W (Лпах-^йп)3
т . < т	т
‘ mtn	1 шах*
П1ЙП £ (°0 t )2>
3.17.	tg f), = ctg 0, =
Тш„ = ^ («о+О2.
rm2
£рр	а.у
V1 = Уа» + &t>2'	1’2 = T«2-t2P2 ’
3.18.	“гр < 6 «£ л при m-f < пг21 л
G = ~2 при тг — тг;
„	„ Л
О «£ 0 С при > m2.
3.19.	В системе центра масс в результате столкновения составля юшая скорости, нормальная к поверхности шариков в точке сопри кос повели я, обратится в нуль, а тан
генциальная &<) сохранится (рис. 112). Сечение рассеяния, выраженное через угол % отклонения частицы в системе центра масс,
de = зт | dp2) =
= 4n2n|dcossyJ = 4a2cosydo.
Для перехода к лабораторной системе из равенства
и'о sin X tgO = ----------
ро cos х + Ц» находим
3	„	1
COSE Xli2 — •— cos2 0 — 1 + -
Рис. 112.
sin у cos x 1 4- cos® x
cos 0 p 9 cos2 6 — 8.
Учитывая обе возможные связи % с G, получаем
do = 4л«2 (| d cos2 X! | |- | d cos® y2 |) = 4na2d (cos2 x8 ~ cos® Xi) —
5 — 9 sin2 6
= 4“8 f 1-9 sin’0 d0’
. 1
причем O<0<arcsin-y.
У*
Если налетающие шарики тождественны с первоначально покоившимся, так что не имеет смысла различать их после рассеяния, то к полученному сечению следует добавить сечение вылета первоначально покоившихся шариков в телесный угол do:
do' — 4а2cos 6 do (0 < 0 < л/2).
3.20.	/(х) = /(0)е-КО1.
3.21,	dN—оП1Пг | Vj—v?1 d Vdt.
8.22.
а)	Етр = 2лтп2п J / (0) (I — cos 0) sin 0 d0 *); о
I m \2 ?
б)	<©2> = 2л I jj- 1 nt \ f (0) sin10 d0;
здесь I — путь, пройденный частицей массы М, и — ее скорость, ап — концентрация легких частиц.
§ 4. Уравнения движения. Законы сохранения
4.1. Полагая х=0 при f=0, находим С=0, а из условия х—а при t=i находим В = — — Ат. Используя функцию x(t) — At2 |-4-^——Axjt, вычисляем действие
S = j L (л-, л) dt = л2 -]- ExJ di =
0	ii
п?Л2т3 md2 FAt3 Fax
= “6“ + TF”~ + ~2~-
dS _n
Из условия — u’ определяющего минимум действия, находим
F
л — — Ясно, что закон движения
2пГ
*) Величина (1 — cosO) do называется транспортным
(	f do
ем в отличие от полного сечения j do
сеченн-
в данном случае оказывается точным. Однако приведенное решение задачи позволяет только утверждать, что этот закон является в определенном смысле наилучшим среди всех мыслимых законов предложенного вида.
Чтобы убедиться, что найденный закон движения дает значение S меньшее, чем любой другой закон х(/),т. е. является истинным, н^жно проверить, что он удовлетворяет уравнению Лагранжа.
f о/ — а	прн 0 < t < /0,
4 2. х (t} = < t-----------
1 г — WJtm (i — t) 4- а при tc. < i < т,
«/(/) == at/r.
где vx = (2aUfmT)'ft, t0 = a/vx.
4.3. Из соотношения
„	•	.	/ да • dq '
L (Q, Q.t) = L [q (Q, t), q(Q, Q, t), t) = L\q, 4- t.
находим
d dL dq d dL dL d dq
ay d^ + a«e<i'
..	do d dq
Учитывая, что = -j- ~ получаем dQ dt dQ’
d_dL_ dL_~ ‘ dt OQ
dq / d dL dt\
= dQ\di~^-^y
d dL dL n
Таким образом, справедливость уравнения —— зт-= 0 при-
1 dq 4
водит к справедливости аналогичного уравнения
tn
d dL dL
В случае нескольких степеней свободы вместо (1) получим
Здесь dq dqdz 9 =	d/=^d7-
dr ~ dQ аг дг' dr ~~ dQ dx dx‘ m x3	• r, • dx
4,s’	л=-уГП7“(Н } m‘ x=s‘
4.6.	L = --|/ .-(4j.
Предложенная задача поставлена чисто формально. Однако, как данная функция Лагранжа, так и рассматриваемое преобразование («исправленные» введением размерных множителей) имеют простой физический смысл в теории относительности (см. [3], § 4, 8).
Er =^jElQl — L находим
б)
(1)
4.7.	Для Р, = д®1
Р	Г, р
Pl = ZidQlPK‘ Е =Е~2^-и-k	k
4.8.	Используя формулы предыдущей задачи, получаем
г, р'ф = тГ (</ + Q) = Рф, £' = £-йрф;
Рх = рх cos Ql — ру sin Q/, ] Py = px sin Q/ -J- py cos Qi. j
Из (1) следует p'=p, а сами эти равенства представляют собой закон преобразования компонент вектора при переходе к системе координат, повернутой па угол Qt. Подчеркнем, что р'=£ту' (ср. [I], § 39).
4.9.	а) Е'—Е—Vp, р'=р;
mV3
б)	£ — £ —- Vp-g—, р' — р — /nV.
Два выражения энергии отличаются на постоянную Обычио используется второе выражение, так как именно оно согласуется с определением энергии в теории относительности.
4.10.	Пусть ?i = fi(t) описывает движение системы (траектория АВ на рис. 113). Так как вид действия не изменяется при переходе к переменным qit f, равенства qi = fAt') также описывают действи-
те льное движение системы. Выраженные в переменных «у,, t с точностью до первого порядка по е, эти равенства имеют вид
Ф(г-бО=Л(О-б9ь
где
d^=eYf(f(0n, fir=eX(f(/),0
(траектория А'В' на рис. 113).
Малые изменения координат и времени начала и конца движения при переходе от траектории
ДВ к траектории А'В' приводят к „	f
изменению действия:
[05 в	/ SR
SA-B- ~ SAB =[5 (- во +	ti/S
i *	J а	—
Здесь (см. [1], § 43)
5Г = /--2-т-«, = -£(0.	t
i d(h
ле лг	Рис- 113-
С другой стороны, согласно условию задачи, = 8д,&, так что
С (<л)lX («Л. ‘л) - С а) (0 а- ‘л) =
= £(^)вХ(?в- (B)-2<’i(Gi)e4'i (?в- 'в), или
EX—SptYi — const.
Доказанная теорема представляет собой, в сущности, единый вывод различных законов сохранения. Важность ее возрастает в связи с тем, что подобная же теорема имеет место и в теории поля (теорема Нетер, см. [12, 13]).
4.11.	V ~ (?tX — V.) — LX — / = const.
fin
4.12.	а) Импульс;
б)	момент импульса;
в)	энергия;
h
г)	Pt ~ cons^» « шаг винта;
д)	Ех — pxt — const — интеграл движения центра инерции системы (см. [2], § 14).
4.13.	а) Потенциальная энергия U(г) ——Fr, а с ней вместе и действие, нс изменяются при сдвигах п направлении, перпендикулярном к F, и при поворотах относительно оси, параллельной F. Поэтому интегралами движения являются компоненты импульса, перпендикулярные к F, и компонента момента импульса, параллельная F. Так как функция Лагранжа не зависит от времени, интегралом движения является энергия
Утверждение, что различные точки в некоторой области «равноправны», означает, что во всех этих точках равны значения потенциальной энергии (а не силы!).
б)	Преобразование подобия г'=аг может сохранять вид действия, еси одновременно преобразуется время /'=0/. Вклад в действие кинетической энергии
Г лга'* a8 f т&
остается неизменным при ₽=а!, а вклад потенциальной энергии — J U (г') dt' ~ — ccn₽ J U (г) dt ж» —- an+2 J U (г) dt при п~— 2.
Чтобы воспользоваться теоремой, сформулированной в задаче 1.10, записываем бесконечно малое преобразование подобия, положив а= 1-|-е, е->0:
.	^(J+eJr, Г=(1+2е)Г.
гак что W = г, X — 21 н интервал движения
dL
(vX - Чг) — LX = гтх - 2£Г = С.	(Q
1 Л’
Из (1) можно найтн /(/), учитывая, что rv ==	>
2£
Г2=-_Г2+С/ I а.	(2)
Если Е<0, то частица падает на центр (при этом г-»-оо). Если Г>0, удобнее ввести вместо С, CL другие константы т, В и записать (2) в виде
2Е
(t- т)« 4- В.
Прн В>0 зависимость /(/) такая же. как для свободного движения частицы со скоростью Оо — у 2Е'т и прицельным параметром р В. При В<0 частица падает на центр.
Поля, для которых выполняется условие этой задачи, приведены, например, в задачах 12.6, 12.7»и см. [1, задача к § 15].
в)	Е—Vp== const;
г)	гр—2£/=const, гре p = mv-f-— А, если А(аг)=а~’А(г);
д)	Е—faQ=const.
4.14.	mr—pf—const (ср. с задачей 4.12д).
Является ли этот интеграл движения для замкнутой системы восьмым независимым интегралом (кроме Е, М, р)?
4.15.	а) Пусть ось г параллельна Сдвиг вдоль оси z и поворот вокруг нее не изменяют вида А, а следовательно, и вида дейст-dL
вия. Поэтому интегралами движения являются pz =	— тг и
дг
Mz^xpy—урх=т(ху—ух) 4"2^-(^я + У2)- Кроме того, интегралом
т .
движения является энергия Е = -у (х“ ~Ь Уъ + г2).
т •	•	•	,	• г ,	•
б)	Е — 2	+ У2 + г2), Ру =тУ~\-~^х, рг=тхс задачей 10.7).
Соображения симметрии позволяют определять различные интегралы движения в зависимости от выбора векторного потенциала данного воляЗ£. Но все величины: £. pt=p'z, Мл ру—являются интегралами движения независимо от выбора А.
т •		• ет
4.16.	а) Е = -j- (х! + IP + z’). Mt = т (ху — ух) +
(здесь ось z выбрана параллельной вектору ш). Ср. с задачей 2.31.
б)	Из свойств симметрии данного поля можно получить следующие интегралы движения:
Mt = p^ = mr^ + ^. Е =-J-(А + r'i’+ И).
Однако движение в этом «поле» есть свободное движение. Действительно, функция Лагранжа
mva «и • ^ = -2-+Т”
отличается от функции Лагранжа свободной частицы только на полную производную по времени функции (разумеется, в этом случае ЭД=го1 А—0).
Заметим, что в случае, когда р есть функция времени, рг и М, остаются интегралами движения.
J38
4.17.	а) х-}-х=0. Такое же уравнение может быть получено из функции Лагранжа Lt(x, х) —&— х2. Кек известно, если две функции Лагранжа отличаются на полную производную функции координат и времени, то опи приводят к одинаковым уравнениям Лагранжа. Обратное утверждение неверно.
б)	%4-ах+п>2х=0.
4.18.	а) Уравнения Лагранжа для частицы в поле U в сферических координатах
т (г — гцй sin® 6 — /б2) -J-	= О,
т (г«6 + 2гг6 — r*i2 s:n 6 cos (J) +	= 0,
dU
m (r2<p sin2 fi 4- 2rz qj sin® 6 -f- 2г28ф sin 6 cos 0) 4-	= 0
легко привести к виду
m(v)f=(F) f, где компоненты силы есть компоненты — grad U:
„ г _Z L<M F _ 1 W
* dr ’	0 г дJ * ф г sin 0 дф‘
Отсюда
(у)г = Г — Гф2ЬН12 0 — г б2, (v)o=r64-2r6 — гф2 cos 6 sin б, (у)ф=гф$т 64-2/ф sin 04-2гбфсоз 8.
/ . . Ы. 2q.q. х— 4‘l,tdqk
= + 2
ft-1
4.19.	а) Функция Лагранжа

3 т жт •  L = ~2 Л i.k^i
где
•Л, dxt
{Xx = X,Xi~y. xa=2).
приводит к уравнениям
т2®.Л-!-т 2 г<лАЛ=-|т (S = 1.2,3). (t) где
Г	1 (дв'Ь ,
‘•*1	2 dqt + dqk dq* )
б)	Введя обозначение qt(x, t) = t, можем сохранить все выклад-
ки и формулы предыдущего пункта, лишь заменив У на
1	"Т’
Какой смысл имеют в уравнениях (1) члены, содержащие Г|,ы (fe—1,2,3,4), если qt— декартовы координаты во вращающейся системе отсчета (см. задачу 4.8)?
4.20.	Так как предложенная функция Лагранжа только слагаемым г = —= — Ф cos 6 отличается от функции Лагранжа свободной ча-1 с *
стицы, го компоненты силы в сферической системе координат (см. задачу 4.18а) имеют вид
F, =0,
1 dt-i е^ф sin 0
F0“ г дВ = сг • _ 1 d dl.f ego ч ~ г sin 0 di ~ сг
и действительно совпадают с компонентами силы Лоренца
V|vMI=^|vrl.
8L	г. /псл
Поскольку —=0	интегралом движения является энергияЕ—-------#
Разберемся, каким образом возникает интеграл движения
, eg г
J = m[rv]-f
Функция Лагранжа не изменяется при поворотах вокруг оси г, поэтому интегралом движения является
• eg
= /пл2<р sin2 0 — — cos 0 = Jz.
Другие же повороты системы приводят к изменению функции Лагранжа на полную производную функции координат по времени, которая
нижет быть отброшена •). Поэтому интегралом движения является и проекция /г. на любую другую ось. а значит, и вектор J.
Действие, соответствующее данной функции Лагранжа, не изменяется при преобразовании подобия. Поэтому интегралом движения является
prr — 2Е1 = тгг — 2Et
(ср с задачей 4 !3б).
4.2!. Уравнения движения
- 27 = <РЛ-<!>„.	^ = <РВ-Ч>Л-
Будем считать, что источник напряжения представляет собой конденсатор очень большой емкости Со, а заряд его в момент, когда fli=0, есть Q. Энергия системы, включающей источник и индуктивность, £0 =	-г 92. Смещая начало отсчета энергии и рассматри-
вая предел Со->оо, a QJCo—U, получаем
Q2
Е = Е° ~~ 2Q = U(h + ~-
Именно к такому значению энергии приводит предложенная функция Лагранжа.
Подобно этому энергия частицы т в однородном поле силы nix2 _	'''
—F (0 есть ~2~ Ч- Fx.
К такой же функции Лагранжа можно прийти от функции Лагранжа электромагнитного поля и взаиыодейс]вня поля с зарядами (см. И. 27.28):
L = У Л' + 4 Jajov-J	(I)
(в гауссовой системе единиц).
Вообще говоря, электромагнитное поле есть система с бесконечным числом степеней свободы. Но поля в конденсаторе и в соленоиде определяются зарядом д2 и током qi. Используя уравнения
с rot JC=4nj, divg=4np
(и учитывая, что поля сосредоточены в ограниченном объеме},
♦) Например, при повороте вокруг оси х на малый угол 6а к £ eg d
добавляется 6L = 6а — (etg U cos у).
получаем
f ФР dV = J ф div 8 dv =
« 4л j div((J 5)dV^4^i J 8 grad q = и аналогично
так что
t=s;
Поэтому функция Лагранжа может быть выражена через энергии
I С ?2
электрического поля в конденсаторе | &*dV = я магнитного—в индуктивности J 3%2dV = -2’S’?2(c.m [3], § 2. 32),
При наличии внешнего поля <JCd, создаваемого токами ]е, следует заменить в (1) JC, A, j на ЭС—Э£с, A-HV, j+je. Добавка к функции Лагран?ка (1) с учетом уравнения с rot 3te=4nje легко приводится к виду
Отбрасывая слагаемые, зависящие лишь от внешнего поля, и учитывая, что для тонкого провода jrfV—gidl, где tfl— элемент длины провода, получаем
т J A.ldv = V J V = 7~ Jrot Vs = Т- J К'dS-
При наличии внешнего электрического поля 8е (или сторонних полей) получаем
- Sv«.
'(9о и фое — заряд и потенциал во внешнем поле а-го проводника).
Варьированию <71,2 соответствует, таким образом, произвольное варьирование зарядов и токов, сопровождаемое определенным варьированием потенциалов. Легко видеть, что при таком варьировании должен быть справедлив принцип наименьшего действия.
S’?? <ll	л ,	g? 1'
4.22.	a) L=-^- — -^+V(q, — qxY,	б) L~ 2 “ 2С-
, ,	_L О. •’J.-L да-2	+ 9»1*
«) L~ 2 gl9i+ 2 г»92~ 2С,_2C,~	X •
„ t т ml2®2 Zq2 ,	q2
4.23.	a) L = —— 4-	-r mgl cos q — 2сТф);
t mx* 2(х)<р kx*	q*
6) L — 2 ~	2	2 ~	~ '2C~
4.24.	Пусть <p—угол поворота рамки вокруг оси АВ, отсчитываемый от направления магнитного поля, q —ток в рамке (для него положительным считается направление от А к О). Функция Лагранжа системы
U)
L =-£’ я?а2ф2 + Zq2 + sin ф.
Интегралы движения — энергия
Е = -у- maty 4- ~тг Zq2
и импульс, сопряженный циклической координате q и имеющий смысл полного магнитного потока через рамку,
~ = ^<7 т- sin ф = Фо.
Поэтому ток в рамке однозначно определяется ее положением q = (Фо — 3%ая sin tpJ/S’.
Подставляя это значение д в (I), получаем
гш V +	4 (ч). 1’ад ('Й = (Ф» - Жа2 sin <р)2/г<?.	(2)
Таким образом, задача о движении системы сводится к одномерной Рассмотрим подробнее случай 0<Фо<5^а2. График £70фф(ф) для этого случая приведен на рис. 114. Видно, что при £>Стах= — (Фс-'г^^)2^^ движение рамки представляет собой вращение,
Рис. 114
причем является периодической функцией временя с периодом л/2
; *,ф— J„/2l
При	Фо —	=
— Um рамка совершает периодиче-
ские колебания ______в_ интервале углов ф| < ф < я — фь где
ф ___ 1 / О<2>Р
<p1=arcsin	1 причем при £-> l/щах период движения воз-
о а стает до бесконечности (см. задачу 1.5). При 0<£< tJm возможны юлсбапия либо в интервале ф| < ф < Ч2> либо в интервале л — фг < ф < л — <р5, где
. Фо--Г2/-£
<pa=arCSin---.
Как изменится по сравнению с описанным характер движения рамки, если она обладает малым сопротивлением?
4,25.	а) Уравнения движения системы можцо получить из функции Лагранжа с добавкой, учитывающей связь (см. [4], § 2.4)
t’ = -у- (л* + z') — mgy I X (г — «=),
где л — зависящий от времени множитель Лагранжа. Уравнения движения
тх——2"ках,
rnz — nig=K
(1)
(2)
вместе с уравнением связи z=ax5 полностью определяют движение частицы. В правой стороне уравнений (1), (2) стоят компоненты силы реакции по соответствующим осям Rx=—2Хох и RZ=X. Воспользовавшись уравнением связи, легко выразить их через координату и скорость частицы:
(2ах2 — mg) т
Rx = -2axRv Rz=
б)
гпг — nig COS ф — ЩГф2 = X,
mr’tp |-2;иггф mgr sin ф = О, г = I.
Сила реакции направлена вдоль г и равна
7. =—mg cos ф — /п/фа.
4.26.
L* = -у- (гаф® г2) -J- mgr cos ф Ь X (ф — Qf)j
%=2rnrrQ-j-nigr sin Q/ — обобщенная сила, отвечающего координате <р (момент силы).
4.2?. а) е = -^+2«Л-
б) Закон преобразования левых частей уравнений движения приведен в задаче 4.3:
<11 SQI ~ ft d<< \ d( */,,
Таким же должен быть и закон преобразования правых частей:
*<=2^4-	о»
ft «
Если в закон преобразования координат не входит явно время, то скорости преобразуются по закону
У д
обратному (I).
Иначе говоря, компоненты силы Я* образуют ковариантный вектор, в то время как компоненты скорости — коптравариантный вектор в s-мерном пространстве (см. [2], § 83).
Таким образом, зная силы реакции связей и трения в декартовых координатах, можно определить силы Ri в любых обобщенных координатах. В частности, если силы трения выражаются через диссипа-dF	s	г
тивную функцию R. =------—, то преобразование г сводится к замене
* dqt переменных.
4.28.	Указанные в условии уравнения получаем, исключая Хр из уравнений
d_ dL dL defy
j_£L_dL _ v -
dl dqn	~< P4»"’
0=1
n —'4 I..s,
и учитывая, что
— =dL+S'dkb д'Ч« 4.
0=lin=r+idfy 4u
Таким образом, уравнения движения системы с неголономными связями отнюдь не совпадают с уравнениями Лагранжа, хотя уравнения связи и позволяют исключить из функции Лагранжа некоторые координаты и скорости.
4.29.	а) Учитывая, что входит в Ln и Ln+i, получаем уравнения Лагранжа
d dLn dLn dLv ^n+i
<U +	— й('Ч. + 1)	C*7» = fn (I)
При a->0
i din ##	। ay
a dqn~^ 0 idqidi}' а dqn~" dq ’
t [ SL„ dLn+i 1_____________a ag
° [0(ДМ 0 СЧ.+1)J dx 0W0X)’ так что уравнения (I) переходят в уравнение
д д? , д d& dT
di д (dq-'dl)-г dx д (dq/Ох) ~ dq'	(2)
Здесь производные d!Ot и d[dx относятся к функции q(x, /) и ее производным.
Система /V обыкновенных дифференциальных уравнений (1) переходит в одно уравнение в частных производных (2). Для непрерывной системы переменная х играет роль «номера» точки.
Мы не будем останавливаться на физических следствиях уравнения (2), так как изучение систем с бесконечным числом степеней свободы является предметом не механики, а теории поля (см. [4], гл. II; [2]. § 32).
Яд!? dq г)
4.30.	Функция Лагранжа L —	— U (г) 4- A (г) v, - где
А (г) —векторный потенциал магнитного поля, J£=rot А (разумеется, А (г) всегда можно выбрать в виде однородной функции координат 1—5 степени п+1). Если при преобразовании подобия г-> аг, / -• а Ц, векторный потенциал преобразуется так же, как и скорость, т. е. если п _ то L -*• akL. Поэтому уравнения движения остаются неизменными при таком преобразовании и выполняется принцип механического подобия (см. [I], § 10)-*
10 г. Л. Дочкин. В. г. Сербо
Из приведенного вывода ясно, что принцип механического подобия справедлив также для магнитного поля, постоянного и в пространстве. если только при преобразовании подобия его величина
изменяется в с/л раз (см., например, задачи 2.30—2.33, 6.36).
'К т rn
4.31.	Кинетическая энергия системы Г— / —- поэтому
2 ’
=4-(v-"vr')-yrm;“
jmI c?Vfi a at I «• a a /	a a a
При усреднении sa большой промежуток времени слагаемое
У	представляющее собой полную производную по вре-
мени от ограниченной функции, обратится в нуль (см. [1], § 10).
. dU ,
Подставляя во второе слагаемое w?t;vo = —[v^JC] 11 усред-а
няя по времени, получаем
\27- + Я2-т-[гЛ1^ = ^>.
Здесь скобки < > означают усреднение по времени. В частности, если е е
магнитное поле З-Г постоянно и во времени и	. то
т
2<’">|£и<М> = *Ж
где М=JfflofieVe] —момент импульса системы.
4.32.	а) Запишем в виде двух слагаемых dt
[т (А |Л'2А'а -}- ХуХ2хЗ 4“ ^Лй^э)	13	X3^1S1 *
(*1^23 Т х2^‘13 V Х3^12).	(1)
Используя уравнения движения
= ^12 4“ ^13. tnxs = ^21 4* ^23» Г?1Л'з = Г31	/^32,	(2)
duih
---лр= (*,-^)3	(3)
и введя относительные расстояния
х, — х2=х, х2 — х3=у, Xi—Х3=2,
запишем второе слагаемое из (I) в виде
Собирая слагаемые с одинаковыми степенями г, перепишем (4)
2ga (х-у}{ I х8 + *У -1 У2 х±У\ т [х*ул~~ zWtf i3x^J-
Подставляя сюда 2=^+{А легко убедиться, что это выражение обращается в пуль.
Первое слагаемое из (I) обращается в нуль для произвольных сил. Чтобы показать это, достаточно использовать уравнения движения в форме (2) и подставить
^lh “ Й(*1 ~Ъ|)	~	=~^l~x^ Flh-
Укажем, наконец, что в данном поле преобразование подобия не меняет вида действия, и потому кроме трех указанных есть еще и четвертый интеграл движения (см. задачу 4.136)
m (л1Х14-х2х2+^з) — 2EL	(5)
4.33.	При сближении любой пары частиц энергия их взаимодействия неограниченно возрастает, поэтому частицы не могут пройти «одна сквозь другую» и порядок их расположения на прямой сохраняется.
При столкновении двух частиц равной массы, но с произвольной энергией взаимодействия (обеспечивающей лишь непроницаемость частиц) эти частицы просто обмениваются скоростями. (Это следует из законов сохранения энергии и импульса). Если столкновения трех частиц происходят поочередно, так что во время сближения двух частиц третья находится далеко от них, то будет происходить просто обмен скоростями, причем соударения закончатся, когда впереди будет находиться самая быстрая, а позади — самая медленная из частиц, т. е. в этом случае
°1 = :'з’ v2 ~ у2* с3=	(О
В общем же случае, когда сближаются все три частицы одновременно, величины скоростей отнюдь не будут сохраняться.
Тем удивительнее, что для указанных в предыдущей задаче сил сохраняется ответ (I). Это можно показать, используя все три интеграла движения: Р, Е, А. Учитывая, что при t->-±оо функции
и сравнивая Р, Е, А при -] оо и при /->—со, получим
три уравнения:
Решая эту систему относительно мы получим, вообще говоря, шесть различных решений. Однако все эти решения можно угадать.
Легко проверить, что решение (I) удовлетворяет системе (2). Далее, так как уравнении (2), очевидно, симметричны относительно всех шести возможных перестановок частиц, то ясно, что остальные корни системы (2) могут быть получены простыми перестановками из (I).
После этого нетрудно убедиться, что только ответ (1) может осуществиться при 4-оо, ибо любой другой вариант предполагает (в силу указанных неравенств v3>O2>vi) возможность дальнейших столкновений частиц.
§ 5. Малые колебания систем с одной степенью свободы
5.1. а) (О’ ==
mint/ (х) существует при
в) ~ 3 m о (г (1/4)/ ’
где амплитуда х0 определена равенством
£=лг+4" va,x>=4" Va**o-
5.2. функция Лагранжа системы (см. (I], § 5, задача 4)
L = та* [6s (I -J-2 sin2 0) -f- Й£ sin2 О -J- 2fc'§ cosOj , где введено обозначение Йу — 2gla.
При й>й0 потенциальная энергия системы
U (0) « —* та2 (й2 sin2 О 4- 2Й^ cosG) имеем минимум при cos 0о=й^>'йа. Разлагаем 1/(0) вблизи 0О, а в кинетической энергии полагаем
I | 2 sin5 0 = 1 + 2 sin5 0, = 3- 2	= 2^5,
тогда
L
—-g-b:2,
где k = U" (6o), x=0 — 60 Отсюда
co2 == — == Q2 —--"
•	3J—2Й*
(£2 >Q0>-
При частота колебаний пропорциональна угловой скорости вращения со = —— й, а 0О = -Д В случае £2 -> Йо малые колебания ‘
совершаются с частотой со -> 0, а 0О -* 0.
Если й<£20. то можно рассматривать колебания вблизи Во—0 прн упругих соударениях боковых масс
<о« = £’2 —fis (Й<Й0).
При П = £20 потенциальная энергия V имеет минимум при 6о=0 н представима вблизи него в виде
1/ = ио=С*(- 2
т. е. колебания существенно нелинейны. Оставляя и в кинетической энергии члены до четвертого порядка, получим
2я _ т = 8 (' Vi I 202d0
Здесь 0« — амплитуда колебаний (ср. [I], § II, задача 2а|.
При х0> 1 точка А — положение устойчивого равновесия, а при х.,<1 — неустойчивого. Положение устойчивого равновесия фо при
>о< 1 определяется условием sin -у- == дС1.
5.4.
f = fo+a COS СО (f — /о).
2дй
<Р = <Ро + П ~ 'о) ~ sin [со (t — /0)],
где ГС1 Фо. я. *о— константы интегрирования (а<^г0),
О
со = Q У2 — п.
5.5.	В точке 0 — 0о эффективная потенциальная энергия Дэфф(0) = м*
= 2тр sjnl! g —mgl cos fl (см. [1]. § 14, задача I) имеет минимум, поэтому (^8фф (во) = 0, Отсюда находим
sin4 в0 cos-3 6„,
а частота малых колебаний
I [ ^афф W 1/g 1 +3cos20, “(Во)— |/ тр ~ Г I cost).
Для применимости этого расчета необходимо, чтобы
Т ‘''и» (0«> (Л0>! > 4 I ^вфф <"<’> I
где ДО — амплитуда колебаний. Если 0о~1, это условие выполняется при A0<gC I. Однако при Оо< I оказывается <7'фф (0о) и колебания по 0 можно рассматривать как малые, только если Л0<^Оо. Тем не менее в этом случае полученный результат <o=2)fg// справедлив и для Д6~0о, когда колебания по 0 перестают быть гармоническими. Действительно, по осям х и у в этом случае происходят малые гармонические колебания с частотой j/^y/д. е. маятник движется по эллипсу, совершая за один оборот два колебания по углу 0 (см [1], § 23, задача 3).
5.6.	Эффективная потенциальная энергия для радиальных колебании молекулы
1	Л12
И = У (Л ~ го)2 то
где г — расстояние между атомами, а т — приведенная масса. Добавление второго члена, предполагаемого малой поправкой, приводит к малому смешению положения равновесия
г ЛР , , 3-
Изменение частоты определим, разлагая £/эфф(^) в ряд вблизи точки го+йго:
,,	।	9	с „ ЛР ?М*
^вфф (') = т '"“о	&»)г I ^2 +	(' - 'ч ~ ^>г-
Отсюда поправка к частоте
_ 3448 „ 3Q8
6м 2,^-4 = W
где О = М/тг^ — средняя скорость вращения молекулы.
5.7.	а) Смещение из положения равновесия
х	т /	Х$
x = x„coso; + -^sin<a(= у	cos(o/ + ф),
б) Пусть натяжение одной пружинки f. Для малых смещений колебания гармонические у=А cos((oi+(f), <i)2=2f/nil.
При f—kl частота колебаний та же, что и в пункте а). Если пружинки не натянуты (f=0). колебания нелинейны, возвращающая сила F—~ky3/i2; частота (см. задачу 5.16)
r У* г (3/4) l/2OTO Г(1;4) V т I
(у„,— амплитуда колебаний).
Если частица может двигаться в плоскости ху, то ее движение при /=/=0 и малых смещениях представляет собой гармонические колебания вдоль осей х и у с частотами = 2k/т и = 2f-ml соответственно (см. задачу 6.3).
5.8.	Пусть у — координата частицы, отсчитанная от точки верхнего подвеса. Функция Лагранжа системы
L = -j- — k (у — /)2 -р mgy =	— k\y — l — -2k] + const
2k соответствует осциллятору с частотой ю2 _ —. и положением равно-
весия у.э — I -п поэтому у=уа+А cos (cot+q>).
Заметим, что, выбирая в качестве координаты отклонение от положения равновесия, мы исключаем из функции Лагранжа поле тяжести.
5.9. Угол отклонения маятника от вертикали аЗ*	I ой8 1 t
ф — g —. ZQ2 C0S й<«
(см. также задачу 8.3).
Возможны также колебания маятника вблизи направления ра-S	S
диуса-вектора ф = Qt 4- s'n ^^~а‘
Б.10. Ток в контуре
dq _ Un sin (tof — <p)
= Л “ Угя!+(иу>—l,w>
to?—* 1/toC
tg4> =-----jj-----
можно получить, решая уравнения Лагранжа для q. Функция Лагран-
жа системы
?9а q±
L~ 2 ^2С
(см. задачу 4.22) диссипативная функция
равна '/г/^ (с.м. [3], § 48).
»
б)
 Рнс. 115.
5.11. Общее решение уравнения движения (см. [1], § 26; см. также [14])
...	F
х + 21х -f- wjx = ~ cos у/
при условии to® = cog — X2 > 0 имеет вит
х (/) — е (a cos to/ b sin «/) 4-
F[(“n —•y,)cosyf+2?.-y sinyr]
—t*)2 + ^2v!1
где а и b — константы, определяемые из начальных условий. Полагая
х(0) ==х(0) «=0. найдем окончательно
х w = Н - (с“v/ " cos w) +
/	tog -J- у2	\ 1
4- 2Ху I sin yt — —2?Ь[ - e~w sin ©/ j I. (1)
Исследуем полученное решение вблизи резонанса у —to-f e. ]е|<<о. Если трение полностью отсутствует, т. е. Х=0, то в окрестности резонанса движение осциллятора представляет собой биения;
F F.t
x = S^sin7-5in“-'-	<2>
причем величина амплитуды и частота биений определяются степенью близости к резонансу (рис. 115, а). Когда же у=«0 (т. е. имеет место полный резонанс) ври е -» 0 получим
*=i2^;/sinu'>,‘
т. с колебания, амплитуда л(0 которых неограниченно возрастает по закону а(1)=П/2ть)0 (рис. 115.6).
При наличии даже малого трения (Х<^Мо) картина движения качественно меняется. Так, при Х«:|е| из (I) легко получить вместо (2)
р _________________________
* (0 =	' 1 “ 2e~U т е1 + '-2Л* С“ (О»' + 4,1 (О)• И)
Здесь <pj (/) — некоторая медленно меняющаяся во времени фаза колебаний. Амплитуда колебаний медленно осциллирует с частотой |е| около значения F/2mioo|e|, постепенно приближаясь к нему 1рис. 116, а). Замечательно, что во время переходного процесса амплитуда может достигать значений, почти вдвое больших амплитуды установившихся колебаний. При соотношениях ]е|	получаем
р
* = ~е-М) с“(%' + ф2 (/)>-
В этом случае происходит переходный процесс с плавно растущей
х
8)\
Рис. 116.
амплитудой, асимптотически приближающейся к значению определяемому коэффициентом трения X (рис. 116, б). И, наконец,
если е и X— величины одного порядка малости, | е | ~ X <С о0, то осцилляции амплитуды вокруг значения, отвечающего установившимся колебаниям F/2 pz2 пдоп | е |, весьма неглубоки (для случая е« X, см. рис. 116, в).
Таким образом, система приходит к установившимся колебаниям для этих трех случаев (рис. 116) за время I порядка 1/Х (это, впрочем, очевидно и из (1)).
Качественное исследование процесса установления колебаний (переходного процесса) при Х«:о0 удобно проводить с помощью
Рис. II7.
Рис. 118.
векторных диаграмм (рис. 117). Вынужденное колебание изображается проекцией на ось х вектора ОА, вращающегося с угловой скоростью Y. Вектор свободного колебания АВ вращается с угловой скоростью (о, и длина его убывает пропорционально е-и. В начальный момент АВ+ОЛе&О.
Каков характер переходного процесса, если х(0)=0, х(0)=/=6?
5.12.	а) Энергия, приобретенная осциллятором.
Г-^Т^схр
—4
существенно зависит от того, как быстро включается сила (от параметра от). При мгновенном ударе (а>т<1) или при очень медленном включении силы (от> I) передачи энергии малы, максимум передачи nF2
энергии Етл* = достигается при тт=1/2/<я (рис. 118).
б) Если x-»-acos(ot-Hp) при /->оо *), то
nF2	— |(wi)»	— £(<0Т)«
Д£=£ (-г со) —£(—<») = <j~' т2е — У nataxFe sin ф.
*) q> имеет смысл «прицельной фазы», т. е. той фазы, которую осциллятор имел бы при /=0, если бы не было вынуждающей силы.
В зависимости от величины ф осциллятор приобретает или теряет энергию. Это изменение энергии подобно поглощению или вынужденному испусканию света атомом.
При усреднении по фазе ф получим тот же ответ, что и в пункте а).
5.13.	а) х (/) = jjJ [Si (/) + Е, (01. да
Е,	2 = e±u' J i- F (t) «**" Л + *0 Т Р*о  Lo	J
6)^(d=-in,f(г,+;0 + ' о
+(/®Х) х0||, где to = jAwg — X2.
5.14.	На осциллятор действует сила
F(0=~3ft/(|r-r„(/)l),	О)
где г(/)—отклонение осцилллятора, а го(О — радиус-вектор налетающей частицы. Предполагая отклонение частицы малым, полагаем гс(/) = р-1vt (р — прицельный параметр, векторы р и v взаимно ортогональны). Считая также малой амплитуду колебаний осциллятора, полагаем в (I) (после дифференцирования) г—0; тогда F(l) = = —2za V' (р + v/) -exp (—х2р2 — Hsv2f).
Колебания ио направлениям р и v независимы и возбуждаются до энергий
<2)
соответственно. Здесь Fw и /Р — компоненты силы по направлениям v и р. Полная энергия возбуждения осциллятора *)
л Vs
е = “2£ <* + °> е ’ °*	(3>
где
1	„	1 Zto\a
C=Ymt-	х=2(кр)2.
*) Интересно отметить, что зависимость е(со) такая же, как в зависимость спектральной плотности излучения быстрого электрона
в поле U (г) (см. [2], § 67),
Сечение возбуждения осциллятора до энерсии, лежашей в интервале от в до e-J-de,
dty — л
2hi=
к
л de у 1 Д х (fe) 2ха в J1 — а — хк (в)
(4)
где Xh — различные корни уравнения (3).
Дальнейшее исследование удобно проводить, решая уравнение
(3) графически, как это делалось в задаче 3. 10а. При в «CBj =^- ае~а
2с
получаем da	(в уравнении (4) полагаем хк(е)>I, х^^а}.
Для ббльших в результат зависит от величины а. Если 1, то возможно лишь e<et (рис, 119»а- для сечения — рис. [20, с). Если л Г2
же a< 1, то возможно е < в2 = —~~ (рис. 119,6), причем при e=8j 2he
Рис. И 9.
скачок.
график da/de. испытывает
а при Bs — 8<£вг имеет интегри-л de 1
руемую особенность (рис. 120,6) аа = ~7тг~ ; 7~
у 2 х2 Ч У I — в/е2
5.15.	Если осциллятор имеет «прицельную фазу», равную ф (см, задачу 5.126), то, повторяя выкладки предыдущей задачи, получим
для энергии осциллятора выражение
е = е1е~2(хрг г 2 У	е~(ир,г cos <р + е0,	(I)
где
л /Vox2 f аа } ex''|~2Wj-
При costp>0 для всех р оказывается е>е0, а при cos(p<0 существуют такие р».®. для которых Е<е0. Разрешая уравнение (I) относительно р2, находим
л	f' Ei/Ef)
р» = и 2 In----------,	^=г при е > е0,
— COS ф т у (е/б0) — Sin2 ф
р2 = х*“2 In ---=----- в*— .........	- при COS <Р < О
Н1’2	у в„ I cos ф | ± У е — 8„ sin2 ф
и е0>е>Е1[11п=Со 81пгф. Отсюда
I dp21 , я	de
da — л I . I de — „ 8	1 г------------- (2)
*	1	e — e0 sin2 Ф — cos Ф-P £e,t — eg sin2 ф
при 8> Ес И
da = nd(— p, 4-pf)=« 2
в цл I cos ф | de
(eu —₽)]• ee0“£gsin2<p
при Cmin<e<eo и cos<p<0.
Усредняя по всем возможным для данного е фазам ф, получим
i//’do\____п
\de/ ~ 2х2 j еп — еI
(4)
для 8<е0. Здесь a=arcsin 1!е/е0.
Расходимость сечений (2), (3) и (4) при в -> в0 связана с тем,
что при любых больших р осциллятор возбуждается.
С чем связала дополнительная особенность в (3) и почему ее нет в (4)?
5.16.	Для функции Лагранжа L —	тх2 — -g- "г(о2х2 -)• xF(/)
энергия системы
/и _ я? » F (/) л
О)!1 Л (Q
2 |ь т(о I 2ти)2'
где
| = х км = е™' | e-^—F(i)dz	(1)
(см. [I], § 22). Хотя выражение для энергии имеет определенный предел при /-»«•, интеграл, определяющий ^(1) при /-*-<», не имеет предела (так как F(t)->F0 при т->оо). Интегрируя (I) по частям, получим
iF(h	Г
(2)
где F'(t)-»0 ври т -> со а интеграл сходится при /-><». Из (2) видно, что движение осциллятора при /->-со представляет собой гармонические колебания (второе слагаемое в (2)) около нового р
положения равновесия*» = (первое слагаемое в (2)). Передан-пая осциллятору энергия в соответствии с этим имеет вид
*<1 “> = ~2^ + 2^| f
I —00	I
5.17.	Л£ = £<-|-с») — Е (— со) =
^0 ,	fi?b2F0cos<p
“	2/пю2 ~ 2/nto2 (Xs - со2)2	1» -р (о8 *
£{) ™- -у- m(i)2a?, ф — «прицельная фаза» (см. сноску к задаче 5.126}.
Б. 18. Проводя в формуле^ (т)=5(0) е’"’ + j F (/) е~^'<я (см. [1], § 22) л-кратнос интегрирование по частям, получаем
выражение
£(v) = E(O)ei<K
+ m«’ '	т(<и),"+1>
____e—------(
Здесь | £ (0) | =оо(£>, где а0—амплитуда колебаний до момента включения силы. Предпоследний член в этой формуле по порядку величины равен	—п( а последний, вообще говоря, гораздо
меньше (если Г< ”+*)(/) изменяемся плавно). Квадрат амплитуды колебания <о~21 g _ j при по порядку величины равен
r - J •
Таким образом, если сила включается медленно и плавно, передача энергии очень мала.
5.19.	а) В промежуток времени 0^/^т колебания имеют вид л‘=Л?/гпсо2т4-В sin cos bit.
Движение окажется установившимся, если
л(т)=х(0), х(т)=л(0).
Эти условия приводят к системе уравнений
F
4- Bsin сот С (cos гот — I) — 0,
В (cos сот — 1) — С sin сот = 0,
(О
определяющей постоянные В и С. Таким образом, при 0^/г^т
F х <‘> = тш‘
t sin (wt — сот'2)] Т “ 2sin (сот/2) j‘
Если же t лежит в промежутке пт^(С(«+1)т (где п— целое), то в правой части (2) следует заменить t на f=t— пт(О^Г^т).
При сот, близком к целому кратному 2л, второй член в (2) оказывается очень большим—случай, близкий к резонансу. При <от= ,=-2л/ (/ — целое) установившихся колебаний быть не может
(система (I) противоречива *)).
1	F	• 1
б)	X (0 = - 11'1	+ -„(Х + ш) е~" +
для	здесь
т (X -j- to) J__ei<ot ’
для	(п-|-1)т в правой части следует заменить / иа tr=t~~нт.
в)	При <оо — (ЯС)—1/» > X = /?/2^ установившийся ток
t	I V [ eal I \
/(>	1тЬ-е“‘ + атЛ
а = — X -j- i ]/Лс>§ — X2	(i)
для 0=^«Ст. Для л < — «5 л + I нужно в формуле для тока заменить I на t'=t — т.
Можно ли, используя (I), получить выражение для установившегося тока при too< X или при top—X?
т
5.20.	а) А = у J F (t) х (f) dt = о
Хсо2 т
fl , Vl
(о“ — ®o)z+ 4/Au2 T — 4o!)2 + 16Хго8
t. e. каждая из двух гармоник силы передает энергию независимо
- / 2л\
от другой (здесь период Т ~ ~г~ I.
*) Представив силу в виде ряда Фурье
P/А F V F  2П1 i
i=i
видим, что резонансную раскачку колебаний может вызывать каждая гармоника вынуждающей силы. При т=2л//со для достаючно больших t (каких именно?)
Ft
й А ==^ у । ° I8 п*
т Zi (ш2_.n^c>^)2-(.4X^to^n^
)1. Г	/?<“i	/рг»|	"I
Е> <Л>" т	+	+ (to2-to2)2-)- 4/Ао2 ]-
При усреднении за большой промежуток времени
Ю,.в оказывается, что каждая из сил ficoschf и f2coscj2f передает энергию осциллятору независимо. Это связано с тем, .что лишь средние квадраты тригонометрических функций отличны от нуля. При Г -# сю
Т
‘•р sin2 (dj/ dt — "g-	(1 “ sin 2(OjT) a
0
а средние значения перекрестных произведений типа sin иц/ • cos o>|f, sin «t/ • cos Oaf и т. д. исчезают. Например, при Т-> оо
О
1 — cos (©i — cog) T 1 — cos (G>j 0);) T =	2 (to, — to,) T +	2 (oj, + to,) T
г)	Смещение осциллятора *
_ Г ф (со) dto
* J coj — (D« 4- 2iW
отсюда полная работа силы F(t) равна
Л==
о
о21 ф (co) I2
----— > A-------------- Cftl).
_ (u2)2)- «.2o,2
0.
(D
При доказательстве последнего равенства использовано обратное преобразование Фурье J F (/)£*“'Д = 2лф« (о).
При Х<£(Оо основной вклад в интеграл (I) дает окрестность вблизи собственной частоты осциллятора © = ©о>
Поэтому
л _ 4я | ф (ю„) Р to,, Г Г	_______1
~	[ J (о2 — в>2)2 )- 4/А>2 Г
И Г. Л. Котыш, В. Г. Сербо
При этом сомножитель, стоящий в квадратных скобках, легко вычисляется и оказывается ие зависящим от К» Л=	I.
2т (ср. с формулой (22, 12) из (!]).
5.21. Учитывая, что отклонение осциллятора х есть малая величина первого порядка по F, получим
Л£= J	f 7(0*1».
—00	—ОС
ео	со
ДР= J F(x.t)dl^ J р(О-Н<)у]л. -------ОС	—ОС
Интегрируя второе слагаемое по частям, найдем
Г	А£
др= j /(Orff-l-y
В частности, если [ f (/) dt = 0, то ДЕ= УДР.
Поясним условие малости х на примере действия иа осциллятор группы волн f (0 = cos у/.- Малым параметром в разложении F(x, t) является х/?., где Х=2я1//'(—характерная длина волны, т. е.
1*1 h
_2лл1|ю5~уЧ
§ 6.	Малые колебания систем с несколькими степенями свободы
6.1.	Пусть х, — отклонение i-й частицы от положения равновесия (1=1, 2). Функции Лагранжа системы
t=-у (*i *|)—v 1'1+*«>“]•	0)
Уравнения движения
mx.-j-k (2xi — х2) =0,
mx-2+k(x2 — Xj) =0
подстановкой xf=Z,-cos (co/-|-q') сводятся к системе алгебраических
уравнений
<—/я<о=+-2А)Л, —
—ЛД,+ (—тсо24-А)Лг=О.	(2)
Эта система имеет нетривиальное решение, если ее определитель равен нулю:
(—znw2+2*) (—rnw’+A) — ks—0.	(3)
Отсюда получаем собственные частоты
•>	3 + /б k
®1.2 “	2	' т *
Из лвух уравнений (2) станляя значения coj и со2 в гулами
в силу (3) лишь одно независимо. Пол-(2), получим соотношения между ампли-
2
А,
Аг = А
ДЛЯ 10—(£),,
2
/11 ~
—~= В для о — 15—1
Таким образом, свободные колебания системы суть
Xi = A cos (ш(/+ф1)+Всо$ (<i)2/+<p2), /5+1 л	/5 — [	(4)
х9 =---2— А С03 ^1* + Vi) — —2— 6 С03	+ •₽)•
Постоянные А, В, <рь <f2 определяются начальными условиями.
Свободные колебания (4) полностью описывают движение системы. Однако при решении многих задач удобнее пользоваться нормальными координатами, например в задачах с вынуждающей силой (см. задачи 6.26 и 6.24), при построении теории возмущений (см. задачу 6.34), при переходе к квантовой механике. Это связано с тем, что нормальные координаты Qt, определенные равенствами
Xi = ?i + ?s,
Уб^- ।
(5)
?2»
приводят функцию Лагранжа (I) к сумме квадратов
L = т ft - оЭД + т (% -а уравнения движения для и д3 разделяются:
il +	= 0.
Подобным же образом задача о движении двух взаимодействующих тел сводится к задачам о движении центра инерции и о движении частицы с приведенной массой в заданном силовом поле.
Отметим, наконец, что более общий случай системы N частиц с одной точкой подвеса рассмотрен в задаче 7.2.
6.2.	Функция Лагранжа системы	*
1 = -F (*? + ^) - 4- [(^1 “ ° ('))’ + (*1 ~ *«)Т
Если отбросить член —	ka2 (/), представляющий собой полную про-
изводную по времени, то L можно переписать в виде
L^LML. ^L=Xika(t}t	(1)
где Lo — функция Лагранжа системы с неподвижной точкой подвеса (см. формулу (1) из предыдущей задачи). Такая запись удобнее тем, что сразу позволяет выписать «вектор» внешней силы
и -т
а)	Уравнения движения
znji4fe(2*. — л‘г) =ka cos \t,
Л1Г2 +* (л-2 — к i) — 0	(2)
подстановкой *)
Я|=.4 cos^t x2=-Bcos7/	(3)
приводятся к линейной неоднородной системе двух уравнений относительно /1 и В. Отсюда
ak (—	4- k) в =________________fife2_______
m2 (у2 —	(у2 — tor;) ’ ша (у2 — <й})(т2 — <°1) *
о 3 = p's k		'
где o>| q — —2----лГ '*** П0РМЯЛ1,ные частоты системы.
Зависимость амплитуд А и В от частоты у изображена на рнс. 122, а.
*) Общее решение системы (2) является суперпозицией свобод-
ных и вынужденных колебаний При наличии даже малою трения свободные колебания затухают, поэтому после большого промежутка
времени решение системы (2) не зависит от начальных условий и представляет собой вынужденные колебания (3),
При переходе через точки резонанса амплитуды А и В меняют знак, что отвечает изменению фазы колебаний на л. При частоте у = Vk/m колебания верхней массы полностью демпфируются: /1=0.
На рис, 122, б изображен примерный вид зависимости |Л| от частоты вынуждающей силы при наличии трепня.
На каких частотах будут демпфироваться колебания верхней частицы, если к нижней подвесить еще одну частицу на такой же пружинке?
б)	Вводя нормальные координаты t/ьв (см. формулу (5) из предыдущей задачи), представим функцию Лагранжа (I) в виде
L=Li(<7i, <7i)+L2,(<72, <7я), г 5 ±	/*2
£12 =----------т (<71.2 «
(ср. с формулой (6) предыдущей задачи).
Таким образом, задача сводится к отысканию установившихся колебаний двух независимых осцилляторов, па каждый из которых действует пилообразная сила (см. задачу 5.19а)
Разумеется, и в пункте а) можно было ронять задачу, переходя к нормальным координатам (ср с задачей 6 24).
6.3.	Вводим систему координат с началом в точке подвеса и осью у, направленной по вертикали вниз. В качестве обобщенных координат выберем координаты Xi п Ха точек .4 и В. В выражение для потенциальной энергии С = — tngyi — tngy2 подставляем f7i(-*i) и Уа(Х1, ха} с точностью до второго порядка по хь2//:
Уа ~ У1 +	" Х()2 % 31 — 	2[	•
а в выражение для кинетической энергии
~ т ,•<,	-9	’9	-„к
г = ”Т + *2 + У$)
— О-
L —
подставляем j/i и ys с точностью до первого порядка:
•	•	•	(^2	*1) (хй
Ь’1 ==— n~2i~	~	I
После этого функция Лагранжа
х 1 ~ "2? <х« “ Х1'2 + Smgl
совпадает с функцией Лагранжа системы, рассмотренной в задаче 6.1, если принять k=mgll и отбросить несущественную постоянную 5mgl. Поэтому найденная в задаче 6.1 зависимость Xj(f) и х2(/) справедлива и для двойного маятника.
Если точка подвеса маятника движется по закону Хо = о (/)<£(, то, как ле1ко убедиться, мы возвращаемся к функции Лагранжа, рассмотренной в задаче 6.2.
6.4.	Закон движения
X—a cos (cV+ф),	р=6со$ (ызН-ф)-
Постоянные а. Ь, ф, ф определяются начальными условиями. Траектория расположена внутри прямоугольника (рис. 123):
—а^х^п,	—b^y^b.
Вообше говоря, траектория «заполняет» весь прямоугольник. Точнее, если со1 и ь>2 несоизмеримы, она проходит как угодно близко
к любой точке этого прямоугольника. Движение точки в этом случае не является периодическим (хотя движение ее проекций на оси координат периодическое) Если же Ы| и (о8 соизмеримы (/cot=nco2, где I и п — целые числа), то траектория представляет собой замкнутую кривую, называемую фигурой Лисса -жу. Движение в этом случае периодическое, период равен 2яп/с0|, 6.5. а) Для данной системы переход к нормальным координатам есть просто поворот в плоскости (х, у) (рис. 124):
к=Qj cos ф — Q2 sin ф.	у=Qi sin tp-f-Qa cos <p.
(1)
Действительно, кинетическая энергия при повороте не меняет своего вида, а в потенциальной энергии коэффициент при Qj • Q2> равный
"У" (W1 = ^г) s’n 2<р '—acos 2Ф«
можно обратить в нуль, если определить параметр ф из условия
ctg 2ф =
Зависимость <р от <0| показана па рис. 125, ширина области частот, в которой происходит переход от ф=0 к ф=л/2 порядка а/<о2.
Рис. 124.
При слабой связи,а <С |	нормальные колебания локали-
зованы. т. е. при ot< w2 оказывается ф«0 и xajQi, y~Qz, а при
coj>Q)S получаем ф^-~ и х»— Q3l
При |	— <о|| <а нормальные колебания перестают быть лока-
л 1	. I
лизованными: ф . х (Qi — Qz), F »= y~ (Qi + Q2) (cm. [1], § 23, задача 1).
Нормальные частоты
^1.2 = 4" [“1 + °2 +1/Г(ш2 — “1)2+ *«»]	(2)
лежат вне интервала парциальных частот*), т. е. fii<coj и й2>о2 (для определенности считаем И]<<о2). Соотношения подобного рода для систем со многими степенями свободы известны под названием «теорем Рэлея» (см. [15] и задачу 6.23).
Зависимость Р|.2 от со( показана на рис. 126. Видно, что отличие нормальных частот ft112 от парциальных coi* (равно как и нормальных
*) Следуя Мандельштаму [7], парциальной частотой мы называем частоту колебаний системы, которая получается из исходной при
(или при j/sO). -
координат Qi, Q2 от координат х, у) при малых а несущественно всюду, за исключением области вырождения ] о| — со||^ а. При достаточно малых о, одна из нормальных частот становится мнимой —система
перестает быть устойчивой.
В координатах Qi и Q2 закон движения и траектория такие же, как в предыдущей задаче.
б) Нормальные координаты можно получить в этом случае из результатов предыдущей задачи простой замепой
2	2> причем нормальные частоты
данной задачи обратны нормальным частотам Q>t8 предыдущей задачи. Почему?
Можно ли обнаружить факт незави-
симости нормальных частот от знака а
(или р) из вида функции Лагранжа, не находя Qi,2 в явном виде? -6.6. а) Функция Лафанжа системы (см задачу 4.22)

1 Г«1 ,	(у, + е,).]
2 !<+€,+ с ]•
где и — заряды на верхних пластинах конденсаторов С| и Сг.
Введя новые переменные — х и V 2?2 — у, функцию Лагранжа задачи 6.5а с параметрами
мы получим

1
сУХ#’,'
б)	Замепой переменных qx — х, д9 = l/Ct у можно функцию Лагранжа данной системы свести к функции Лагранжа задачи 6.56 с параметрами
W1.2 — (& + ^1,2) С1,2»
Р=27УС1СВ.
Могут ли данные системы стать неустойчивыми?
6.7.	Пусть Xi и Х2 — отклонения частиц ГИ| и т2 от положения равновесия. Сделав замену Улц х^<=х и х2—у, получим для системы функцию Лагранжа, рассмотренную в задаче 6.5а.
В различных предельных случаях ответ может быть получен без решения уравнений. Например, если все kt=k и	то возможно
нормальное колебание очень низкой частоты q2 =-—	=~тг х9 (ча-
1 zm2 *	2 8
стица mi является как бы элементом пружинки, а частица ms колеб
лется между пружинками жесткости -L-й слева и k справа) и очень 2й
высокой частоты ~ (когда частица т2 почти покоится). Амплитуду колебаний второй частицы можно найти, рассматривая ее движение как вынужденное под действием вынуждающей силы kxt высокой частоты (см. [1], формула (22.4)): х _
® 2тг 1 *
Подобным же образом интересно рассмотреть случаи
а)	гп1=^т2, ki=k2<&ka;
б)	все жесткости различные, но одного порядка, а
в)	А-г>&1=£з, а массы nt] и т2 одного порядка.
6.8.	а) х, 2 = имеют форму биений;
о
хх = - cos е/ • sin to/,
sin to./ + -—siiico2/]; при ki<£k колебания I
— — sin e/«cos со/.
, — “ту- (cos + cos ws/); при k^k jq = rr cos cf-cos <nt, x2=a sin ef-sin co/.
, k o 2*, + k k.
Всюду -“= “> c2 “ ni * 6 — ‘2k <i°t’ ° ~ 2 (°l	C,>2'
6.9.	Энергия, переданная от первой частицы ко второй за время dt, -равна работе силы F~k(Xi— xs)
dE ~k(xt — ха)с1х2=к(Х1 — x2)x2dt,
а поток энергии = k (xt—x2)xa. Для предельного случая k^k в задаче 6.8а поток энергии, усреднсипый по периоду быстрых колебаний, равен о», sin 2г/ и меняет знак с частотой, равной удвоенной частоте биений.
6.10.	Уравнения движения
/n.rr|-fe,(xi — х2) +/fexi+axi =0,
(Х2 — Х[) -J-AXj-j-ClX2== Oj
при замене xi 2 ~ 7^5	- ?8)Рвс,,алЬ10,,ся на два уравнения для
I 2
нормальных координат
+ W?<71 -I- 21^ = о.
i* + j-2iia=o.
ОТВЕТЫ И РЕШЕНИЯ
16.11
n k гле^ = -, §25).

fe -fi у)/'	гу
>| = ———2Х = — . Поэтому при X<toi,2 (см. (1],
*1.2 = e M [a (Ti« + Ti) ± b cos (?,( 4-44)1.
где Т1,2=И “1.2—x2'
Для системы рис. 22 при наличии трения характеристическое уравнение нс биквадратное, а четвертой степени, поэтому найти свободные колебания гораздо сложнее.
6.11.	Функция Лагранжа двойного маятника
f _ — 'х2 > ~ *2 _	д-2 _ J 2 < /	— у >2]
L~~ 2 j ' 2 *2	21 Л1 21 1*1 “•"’** хи ]»
где Xi и х? — отклонения точек М и т от вертикали, проходящей через точку подвеса (ср. с задачей 6.3). Заменой
_ X	у
’ Х'~Ум'
функция Лагранжа сводится к виду, рассмотренному в задаче 65а, причем
2	2 2tng
ш1~ш1=-мГ<а
В этом случае
* = ^(C.-QS). y = ^(Qi + Qt). где Qi—a, cos Q,sin Q,t,
“1.2
I + 2-
V
С учетом начальных условий получаем
Л /р -
Qi.2(0)=0
Xi = /р у sin у/ sin у -j I,
Хя = /р COS у/ COS у- t.
Таким образом, маятники колеблются «по очереди» и амплитуда верхнего маятника в yMfm раз меньше, чем нижнего.
6.12.
—да?1)
-----"7”---ЪЧ / <-5V cos ТЛ
/п8(у* — ^1)(т8 —и1)
akkj
Xj=V«(T=-Mf)(T’~<0|) C“lA
2
И2 = ——•
6.13. xt
ak х*~ А —/иуа
cos yt,где Xi — смешение вдоль кольца
из
положения равновесия i-й частицы. Резонанс возможен только на одной из нормальных частот при ^—klm (см. задачу 6-24).
6.14.	Пусть Xi—смещение вдоль кольца из положения равновесия i-й частицы, тогда
ал(а| — у!)
2оЛ«
С“Т '
k	2k
где собственные частоты со, равны о? - — (2 +	—	со? = —.
1,а	' 1 » • т 	2 т
Обратим внимание на то, что при т=*<ог смешения Х1=Хз=0, а х^= —a cos yt Почему число резонансов в системе меньше числа нормальных частот?
6.15.	Уравнения движения (ср. с задачей 6.12)
mxj+ax. (х, — х2) —ka Re m£2+ar2-j-fex2-j-fei (х2 —	=0.
Ишем решение в виде *i = Re Ле*'*, xs=ReBe’vl. Для Л и В получаем уравнения
(—mys-|-2 itn Ay+fc-t-fej)/! — k{B—ka.
—+ (—лг(2-}-2 im Xy+A-{-fc|)fi=O, 2шХ = с,
откуда
ak (fe At — my8 -j- 2/Amy)_______
л/2 ( y2 — 2iXy —	( y2 — 2tAy — (o|y
________________akki________________ tn1 ( ys — 2/Ay — ( у8 — 2iA? cogj’
ah	(у2 •—“1 ~ Т “1) + 4^!Т2 cos (Tz + Ti + Ts + Ф)
“ |/ l(vs - и?)2 + 4Vy2] [(у2 — и2)2 + 4Zav2j
____________gkkt cos (vt + ?i I qig)____________
m2 \/ [(y2 „ a2)2 4- 4Л“т“] [(у2 — о2)2 +
, k ,	_ 2<T	. .	«.У
“=»• “! = -S—	« = И2+Ю|_2у.-
Между колебаниями двух частиц возникает сдвиг фаз ф; полного демпфирования колебаний первой частицы нет. Амплитуда колебаний как функция частоты вынуждающей силы у имеет один или два максимума в зависимости от соотношения параметров ыц сог и А (см. [16], §1).
6.16.	Функция Лагранжа системы (х и у — смещения из положения равновесия первой и второй частиц)
т	+ К	. 2^? \
L =	(л2 + S2 - х2 - -^-а у2 + -J + *lOx ccs у/
отличается от функции Лагранжа, рассмотренной в задаче 6.5а, лишь слагаемым xkxa cos 7^ отвечающим силе ki a cos 7/, действующей на первую частицу. Ниже ми будем пользоваться обозначениями задачи
6.5а. Парциальная частота <о1>2 = Г —--------- соответствует нор-
мальной частоте системы, которая получится, если закрепить вторую (первую) частицу в положении равновесия, т. е. положить #=0 (соответственно х— 0). При переходе к нормальным координатам Qb Qs функция Лагранжа приводится к виду
L = -у (01 - OjQi + Qi - QfCf) + (f 1Q1 г FE<W COS yf, где Fi~ki «cos q> и F2=—fej a sin q> — проекции амплитуды силы f=felacosyf на нормальные координаты Q1 и Q2 (рис. 127). Для координаты Qb2 мы получаем уравнение движения осциллятора с частотой £2 ьз под действием вынуждающей силы F\ Начальные условия Qi(0) =С*»(0) =0. Получаем
Fi (cos yt — cos 2Z)
Q‘-2=	'"(Ча-Т1)’ Л
У данной системы в приближении слабой связи
(для определенности &1<Лз) интересно рассмотреть резонанс па второй нормальной частоте. Полагая 'y=Q2(I-J-€)), имеем
4 &1а
Qi — k — k (cos — cos ®10»
„	AjtjB /	°£ \
= —-----5— Sin I Bl -0- Н sin <М ири 81 [< 1,
лга}^! V 2 /
г»
Qs = — 2т(^ ®Z sin °3»1	при 61 = °*
Таким образом, даже при слабой связи амплитуда Q2 может быть
большой или расти со временем, одиако скорость ее изменения при
этом будет мала. Поскольку угол поворота мал (sin<p=8), для смещений имеем: x=Qi — 8Q2 и y=Q2.
Какова скорость роста амплитуды колебаний при резонансе на первой частоте y-Di?
Как изменится характер колебаний, если на обе частицы будет действовать малая сила трения, пропорциональная скорости (ср. с задачей 5.11)?
Рис. 127.
Fn cos ф
°-17- а’* = тМ-?ГС“Т''
FffS’nq)
—---------— cos -vt.
т(й)| —у2)
где ы|= —, со, =	—угол между направлением сил& и осью
АВ. а х и у— смещения из положения равновесия вдоль осей АВ и CD. Частица колеблется вдоль прямой, проходящей через центр.
Интересно, что при у® = ®|sin’ ф + cos2 Ф эта прямая перпендикулярна к вектору Fo. В атом случае работа вынуждающей силы равна пулю. Поэтому, казалось бы, наличие даже малого трения должно привести к затуханию колебаний. Так ли это?
F	F
б) *=~Г*2----ГГ cos Yt ₽=~7-2-----Траектория —
'	т(°2“"У)
млипс с полуосями а = т[и2_т„| » = и|и|_т.|-	Если
величины — у2) и («of—’Т2) противоположны по знаку, то движение частицы по эллипсу происходит по часовой стрелке, а вектор силы вращается против часовой стрелки.
Как изменятся описанные выше картины движения частицы, если натяжение пружинок в положепии равновесия не равно пулю?
Рис. 128.
6.18. Пусть xt — смешение i-й частицы вдоль кольца из положения равновесия. Три частицы могут врашаться по кольцу с постоянной угловой скоростью, при этом
Xi=x2=xa=Cf-|-Cl=fli(/). toi=O.	(1)
Колебания же частиц 1 и 2 навстречу друг другу с равной амплитудой
*1= — х, = А cos (и,< + а) = ?,(/), ч-О, в,= |/ — Й происходят, очевидно, с той же частотой, что и колебания частиц 2 и 3 навстречу друг другу
*1=0, *2= —*3 = BcOS (С0з<+?)=9з(Л, <»3=Ь>2.	(3)
Введем «вектор смещения»
xs *з
тогда колебания (1) — (3) можно представить в виде (рис. 128)'.
Л\	/ 1\	( о\
Г1=[1|<7ь г2= (“1ft. гз —I 4ft. '	(4)
\1/	\ 0J	\—1/
Любая линейная комбинация векторов г2 н г3 также представляет собой колебания с частотой Ыг- Таким образом, в пространстве с декартовыми координатами xh xs, xs совокупность решений, отвечающих колебаниям с дважды вырожденной частотой со2= (о8, определяет пло
скость, проходящую через векторы г2 и гз*). Как легко видеть из (4), оба эти вектора (а. следовательно, и все векторы, лежащие в этой плоскости) ортогональны вектору И (общее соотношение ортогональности см. в задаче 6,22}.
Функция Лагранжа системы
= "2*	2~ [(*1 “ Я-а)2 "Ь (*2	*з)2 4“ (*з	*i)21 •
(5)
Нормальные координаты должны диагонализовать одновременно обе квадратичные формы — для кинетической и для потенциальной энергии. Поскольку в (5) кинетическая энергия уже пропорциональна сумме квадратов скоростей, то преобразование от х,- к нормальным координатам, не меняющее ее вида, должно быть ортогональным, а векторы соответствующих нормальных колебаний — взаимно ортогональными. Векторы г< независимы, но не ортогональны друг другу: Г1Г2= =Г1Г3—0, ио г2Гзт^0. Чтобы получить нормальные координаты, достаточно в плоскости векторов г2 и г3 выбрать два взаимно ортогональных вектора. Это могут быть, например, вектор г2 и ортогональный ему вектор e<fy где единичный вектор е найден из условия eri=era=0. В итоге набор нормированных векторов **)
. г, , г, ,	1 [ П
г'-|з’ ’’"у? г“ е’а~иЦ_’у’“	(6)
позволяет определить нормальные координаты:
1 ! 1
= J. 5 91 + , г, 9а + , г 9з»
13	| 2 J 6
*2 уз’1 уг’, + | с’3' 1	2
1з~уз’1“1 б’”
•) Отметим, что в этой плоскости линейная комбинация вида an(Z)-J-fer2(0 представляет собой либо колебания по прямой (при а=р, р+л), либо движение по эллипсу (при а¥=Р).
•♦) Множители l/УЗ и 1/У2 введены для того, чтобы нормировать векторы г£.условием = при этом условии преобразование (7) ортогональное.
которые приводят функцию Лагранжа (5) к виду
* = £(?? +«2 ~ш2?2 + ?3 7	<8)
/
Разумеется, любые координаты, полученные из qir q3 ортогональным преобразованием (т. е. простым поворотом вокруг г(), также являются нормальными координатами.
8.19. Начальные условия для смещения Xt вдоль кольца
Xi (0) = а и х2(0) =х8(0) =х<(0) =0.
Отсюда для нормальных координат Qi (см. формулу (7) предыдущей задачи) найдем начальные условия-.
’(0) = Й’ *’(0) = Й’ ,а (0’= й <0) = °'
Поэтому с	й	а
с, =	Qo = -7=. cos®2r. оа = -7=. cos
} 3 V2	3 У 6
и с учетом того, что со2=о)3, получаем окончательно а 2а	а а
= -g- —g cos toaf, xB =	= -g- -J- -3- cos (£»й/.
6.20.	Пользуемся обозначениями задачи 6.18. Функция Лагранжа системы
L = V (*1 + 2*2 + 3j,D ~ Т (2 (Х1 ~ *•>’ + 6 — ’»>’ |"
+ 3(Х,-Х,1’]. (1)
Уравнения движения подстановкой X£=4»cos (со^4-ф) сводятся к системе трех алгебраических уравнений:
(—шеи» 4- 5й) Ai — 2kA2 —ЗМ3 = 0, |
— 2kAi 4- (— 2/жо» 4- 8А) At — 6М8 = 0.1	(2)
— 3M| —	4- (— З/псо’ 4- Ы) Л3 = 0.)
Эта система имеет нетривиальное решение, если се определитель равен нулю;
й)2 (то2 — 6А) ®=0.
Отсюда находим собственные частоты системы:
®1 = 0, <OS=MS = J/
Значению coj = O ртвечает очевидное решение — вращение по кольцу с постоянной угловой скоростью
1 hi. ?t(0 = c/+Ct.
(3)
Для совпадающих частот ws=cd3 в системе (2) лишь одно уравнение является независимым:
Л1 -{-2/4 2-[“3/1 з=0.
Любые наборы величин At, удовлетворяющие условию (4), дают колебания с частотой ы2. В частности, можно выбрать такие колебания, чтобы первая, или вторая, или третья частица покоилась:
I 0\	Г 3\	/ 2\
= I 3 U, г3 = I 0 j?s, = I — 1 hi» (5) \—2/	\-1/	\ 0/
^i=C, cos (со2/Ч-фО, /=2, 3, 4.
Согласно (4) любая линейная комбинация векторов (5) ортогональна вектору
- (1\
2 .
\3/
Легко убедиться, что набор векторов
Г1- Г4, Г3
позволяет, как и в задаче 6.18, определить нормальные координаты, которые приводят функцию Лагранжа (1) к диагональному виду. Векторы (6) удовлетворяют не простому соотношению ортогональности (как в задаче 6.18), а соотношению «ортогональности с весом» (см. задачу 6.22).
6.21.	Векторы нормальных колебаний
12 г. л Когкнн. В. Г. Серба
9i=Acos (co//+<pi), 1=1. 2, 3; q^Ad+As.
I'
Функция Лагранжа системы
L = Т (’ + «2 + 'is + И - “1?1 - “М - “з«з)-
Это, конечно, не единственный выбор. Любые векторы, полученные из данных поворотом в плоскости, определяемой векторами п в г2, также будут векторами нормальных колебаний, например;
(поворот на л/4). Но векторы rlt г2, г3, г4 хотя и независимы, но не приводят функцию Лагранжа к сумме квадратов.
6.22.	Амплитуды нормальных колебаний удовлетворяют уравнениям
-и52т,/">+2*ол",=0-	с>
-^2'",Л,) +2 М',=о-	<2>
Умножим уравнение (I) на Л,6*, а уравнение (2) — на Взяв в обоих уравнениях сумму по I, получим
-	2	+ 2	= о. Pi
у	а
-	2 ^иА^А^ + X ktJAPAt} = °-	0)
V	U
Вычтем уравнение (4) из уравнения (3), учитывая, что и kij=kji; получим
—of) 2 тцл =°.
V
т. е, при o.^oj
2'”,И'*,^П = 0.	(5)
W
п одновременно из (3)
2^/-’Цп=о.	(6)
Удобно воспользоваться терминологией, принятой в линейной алгебре. Набор амплитуд данного колебания будем называть вектором амплитуды	Л^,	Доказанные соотношения
(5)	и (6) означают, что амплитуды А<*> и ДСП взаимно ортогональны, если скалнрное произведение определять с помощью метрических тензоров Wij, ИЛИ kjj.
В случае вырождения (если соа = ю/) амплитуды А(,) и A<z> не обязаны удовлетворять соотношениям (5) и (6). Но в этом случае всегда можно выбрать, и притом не единственным способом, такие амплитуды, которые удовлетворяли бы (5) и (6) и приводили бы функцию Лагранжа к сумме квадратов.
6.23. Переходя к нормальным координатам
xt=2 i
преобразуем уравнение связи 2М1=0’	=
I	i
Уравнения движения с неопределенным множителем Лагранжа Z
“Ь
можно решить, полагая
qi~Ct cos l=Acos (cof-J-ф).
Выразив Ci из уравнения
М, (cf - o’) ct = 6,4
и подставив в уравнение связи, получаем для новых частот уравнение
у
2<Л1,(0|-а») ”0,
Для исследования этого уравнения удобно представить график (рис. 129)
* (“*) = Xi Л1 Дй® — а») •
Обратим внимание, что функция ^(to2) меняет знак, проходя через
6.24. Подставив ТхЮдС*)
После этого расположение корней О/ становится очевидным. Если какой-нибудь из коэффициентов Ь( равен нулю, то соответствующее нормальное - колебание (и его частота) (р2 не изменяются при наложении связи.
Рассмотренному в этой задаче факту можно дать простую геометрическую интерпретацию (см. [6], §24). cos^f в уравнения движения
2	+ 2	= /|cosVf.
3	3
получим следующую систему уравнений для определения коэффициентов ХЮ;
3,1	3,1
Ее проще всего решить, используя соотношения ортогональности (5), (6) задачи 6.22.
Для этого умножим уравнения (2) на и, просуммировав по г, получим окончательно
F
k<S) — _____®_____
A'.W-V2)’
где
Fe = J] A Pf., Мв jA\s} А{?\ Ks = ^k.fA^A <-s>, *	1,3	iJ
а величина	является s-й нормальной частотой системы
в соответствии с формулой (4) задачи 6.22*). Зависимость от 7 имеет резонансный характер.
Для нормальных колебаний q., введенных по формуле *,=5^'Ч(0.	(3)
*) Если некоторые нормальные частоты вырождены, то соответствующие нм амплитуды нормальных колебаний мы считаем выбранными так, чтобы они удовлетворяли соотношениям ортогональности (5) и (6) задачи 6.22.
будем иметь вместо (1) следующие уравнения движения:
+ К А Fecos vZ-
(4)
Отсюда, если вектор силы /< ортогонален к амплитуде некоторого s-ro нормального колебания 2	= 0, то соответствующая нормаль-
ная координата удовлетворяет уравнению свободных колебаний, и резонанс на данной частоте при о = о, не проявляется.
Отметим, что работа внешней силы в этом случае равна нулю
Пусть вектор силы параллелен какому-либо нормальному колеба-ншо:
= const (/ = 1,2,..., Д').Может ли такая сила возбудить
другие нормальные колебания?
6.25.	Вынужденные установившиеся колебания можно представить в виде (см предыдущую задачу)
Х1 “*	f’ljfр
где
₽«/=2
I
(/о* — у2) ’
Теорема взаимности отражает тот факт, что
Как изменится формулировка Xi и Xj имеют разные размерности ской системы)?
6.26.	Нормальные колебания
этой теоремы, если координаты (например, для электромехаииче-
' 1 \
— т/Л-1 |
1 I
Ч— т/М/
где (?1 = At В, q. == А} cos (to./ -{- i = 2, 3, 4; to| = —, to| =*
2ft м- “4
2ft (M + т) т	-
 -	. 1ри первых колебания легко угадываются,
а последнее находится из условия ортогональности к первым трем По-скольку массы частиц различны, условие ортогональности двух
нормальных колебаний А и В имеет вид тЛ1В14-Л1/!52В24-/лЛзВз4-< +Л1/14В4=0 (см. задачу 6.22).
6.27.	Пусть х, — смещение 1-й частицы вдоль кольца. Два нормальных колебания легко угадываются:
/	9 2й
+	(0 = COS (<021 + ф2), «2 = —.
Два других вектора должны быть ортогональны к векторам (1) в метрике, определяемой коэффициентами квадратичной формы кинетической энергии (см. задачу 6.22), т. с. иметь вид
Подставляя (2) в уравнения движения первой и второй частиц /п%1 -f-A (2*!—х4—х2) —0,	mx2-\-k (2хг—х4—х3) = О,
получаем уравнения для определения величин а, b в частот k
•	(— /л(о* -f- ЗА) а--2" b ~ О»
(3)
— 2ka + (— Щ<о2 + 2А) b = 0.
Из (3) находим и>|5 =	6з,4 = 0 ± /З) а3или
(I \
1 + /5 \
1	На.4^0»
3 V5 /
~ 2 + 2 /
03,4 — ^3,4 Cos (ю3.4^ + Чз.О*
6.28. а) Пусть xj, yf, zi — отклонение i-й частицы от положения равновесия. Функция Лагранжа системы имеет вид (см. задачу 5.7)
L=L!(x, х)-f-£i(y, j/)+£i(2, г),
£> (х. 1) = у- (xf + if + xj + if + if) —
~ "Г [Л1 + <*• —	+ <*S — *.)’ + xf + х| _|_
+ (х, — х5)« + (xs - х4)> + xf ], поэтому колебания по х. у и г происходят независимо. Легко угадать три нормальных колебания по х;
Два остальных нормальных колебания должны быть ортогональны к векторам (1) и потому иметь вид*)
(2)
Подставляя этот вектор в уравнения движения для первой п пятой частиц
тх] +А (2X1—х5) —О,
tfix5+fc(4x5—X]—х2—х3—х4) =0,
получим два уравнения для определения a, d и частот х (—сАп+2Л)а—М=0,	(3)
——m<o2-f-4^)d=0.
Решив (3), найдем о|5 — (3 + F5) ~ и d4>5 = (— 1 ± У5) й4,5.
•) Пусть г4<5=(а, Ь, с, е, d)ssr, тогда условия ортогональности (г, г!) = (г, Г2) = (г, г3)=0 дают соотношения а=Ь=с=е.
Окончательно
*4Л‘
(4)
1 + 1'5/
Для колебаний по осям у и г получаются такие же результаты, что и по оси х. Таким образом, в системе имеется всего три различ-2k
ные частоты: <о2 = ---девятикратно вырожденная и две трехкратно
1 т
вырожденные “Jt5 - (3 + /5) (о святив вырождения см. зада-
где f— натяжение пружинок, а I— длина одной пружинки н положе-нии равновесия.
Если f=kl, то колебания в направлении оси х (или у) имеют такой же вид, как в направлении оси г, если считать г= (льх2, х3, х4) (или г =(уъ yi, у* i/з)). Если же f^kl, то вырождение снимается. Два
1/1^ ,Л2Г
нормальных колебания с частотами <0х = у — и (о9 = у 7л7 С°В' падают с Г| и г2. Два других по условию ортогональности должны иметь вид
Для их нахождения достаточно уравнений дннжения двух частиц
mxj 4- k (2xx лБ) == 0, тхя + ~(2ха— х&) = 0.
Здесь
*5 в [Л (*1 + X») + “7“ (*» + ««)]/(2Л + "7")
— координата точки соединения пружинок, определяемая из условия максимальности потенциальной энергии при заданных х1,2,з,4.
Решая уравнения, получаем
г f + kl t	,
“а ml  *• ” — kl
, 2kf , kl m tf + нг b^ra*-
6.29.	В данном случае ответ может быть получен простым обобщением результатов задачи 6.20 без явного вычисления собственных частот «о*.
Пусть в системе имеется вырождение: <о1=0, а <о2=(Оз- Частоте (О[=0 отвечает вращение частиц по кольцу
(|\
1	h^+Ci).
1	/
Из-за вырождения частоты <о2 любой вектор
(лД
Л, I cos (со/ + ф),	(1)
Л,/
удовлетворяющий условию
m1/l1-f-m2Z2-f-rns.43=0,	(2)
представляет собой нормальное колебание с частотой о=ы2. (Равенство (2) есть условие ортогональности вектору п в метрике, определяемой коэффициентами квадратичной формы кинетической энергии—см. задачу 6.22). В частности, можно выбрать такое нормальное колебание (1), чтобы первая частица покоилась:
/4i=0,	0«	(3)
Подставляя (3) в уравнения движения
(mjtD2—fe2—&з) А1 -]- й3Л g-f-fejHg=0.
Аз-41+ (ш2(ог—ki—fe3) Л г4"^1^з=0,
Л2Д1+А|Лг4- (гпцы2—fei—kg) Л3=0,
мы немедленно получаем, что они имеют решение лишь при
== 0.
Сравнивая (3) и (4), находим, что ш2йг=т3йа. Повторяя подобные рассуждения для случаев, когда покоится вторая или третья частица, получаем, что при вырождении частот коэффициенты А а с необходимостью удовлетворяют условию
mlki=mik2—mik3.	(5)
С другой стороны, из приведенных рассуждений видно, что (5) является и достаточным условием вырождения частот. В самом деле, если выполнено условие (5), то в системе существуют три различных нормальных колебания с частотами, отличными от нуля. Из этих трех колебаний в силу (2) лишь два линейно независимы. Отсюда однозначно следует, что эти три колебания имеют одну и ту же частоту.
Таким образом, (5) является необходимым и достаточным условием вырождения частот.
6.30.	Для решения удобно воспользоваться методом, изложенным в задаче 6.27.
а)	Нормальные колебания
I |(С^ -! С8),
1 Ы2 cos (o>2f + <j2), О/
1 M8cos(<d3/+ <р8), — 2/
(1)'
- (3 + 2е) k 9 3k 6А
=-----“----,	= ТГ, С = ~Т~
2 т *	т * к
близки при малых е к колебаниям (6) задачи 6.18 —амплитуды векторов колебаний совпадают, однако частоты различны. Поэтому, если в задаче 6.18 любая суперпозиция векторов г2 и Г3давала также нормальные колебания, теперь выбор вектора г2 и г3 вполне однозначен.
б)	Нормальные колебания
/А
Г1=[ I \1 /
' Л
— 1 I Аа cos (си2/ + ф2), О/
(1 \
2 IА3 cos (со3/ + <ра),	(2)
«ЗА „ 34-е А 6m w2 = ^r-	е=т
близки при малых е к колебаниям (6) задачи 6.18. Если перегрузок был добавлен к частице 2, то нормальные колебания
/1\ / 1\
гх = I Ч (G/ -г С2), г8 = I 0 ] Д2 cos (<о8/ 4- <Р8), W	1/
(I \
2 I
__±_ 1 Д3 cos (оа/+ <f>s)
l+« I
1 )
близки к суперпозиции нормальных колебаний (6) задачи 6.18.
fc2.s	®, — Ei ± V в? -г в| —е,е,
“2.3	f, 4-es Т 1 t'j —е,!-, '
“2.3 к -й" (3 - В, — «. + V + бт
ei =
I а\
6.31.	а) Вектор начального смещения г (0) =1 0 I представляем \—а/
в виде суперпозиции векторов г{ (см. формулу (1) предыдущей задачи), взятых в начальный момент времени /=0:
г(0)~Г!(0)4-г2(0)4-Гз(0)л
(1)
Аналогично представим вектор начальной скорости
г(0) ='п (0) +’г2(0) +г8(0).	(2)
Из системы уравнений (1) и (2) получим следующие значения констант; А2=Аэ=а/2, Cj = C2=(T2=<P3=0 или
cos 6 cos ь>8/ еы3/
sin —sin о,/
— COS (i\t
Таким образом, движение частив 1 и 2 имеет характер биений, частота которых определяется возмущением бй, а частица 3 участвует в простом колебании с частотой wg. Подчеркнем, что далее очень малая добавка бй приводит к накапливающимся изменениям, которые для достаточно больших времен становятся существенными (ср. с задачей 2.36).
6.32.	а), б)
в) то же, что и в задаче 6.21, формула (1).
6.33.
*1,2 —	*3,4 —
а
+ cos
I /2k 4- 26fe , a	i / 2k
I ~' + ТС“ V
колебания частиц имеют характер биений (см. по этому поводу задачу 6.31).
6.34.	Можно ожидать, что изменения частот и векторов нормальных колебаний окажутся малыми, и воспользоваться методом последовательных приближений. Удобно перейти к нормальным координатам исходной системы (см. задачу «6.24)
i
При этом 61 принимает вид
б£=4 2
io
где
6Л1.=	-У	(2)
18	И • J	to	1Л * Л
i,j	i>i
а уравнения движения
Л1, («, + ofo) = - 2 (6Л|| А + в*;А)-	(3>
Предполагая, что в нулевом приближении возбуждено только колебание <7„. можем оставить в правых частях уравнения (3) только слагаемые с s=n.
Для определения добавки к частоте Ь)п достаточно выписать одно уравнение (с 1=п):
(«„ + «•«„„) «„ + («»»“«+вк„„) ?„ - о.
откуда
(“»
I 6юп)! =
м„„<°5 + вк„п
М»+М4ПП '
так что
г.	'пп п ПТ»	...
“ ”2Л1^'	<4>
Уравнения с 1=£п позволяют пайти поправки к вектору нормального колебания. При этом правые части уравнений можно рассматривать как заданные силы частоты оп. Возбуждение колебаний qt, как мы и ожидали, оказывается слабым, так как эти «силы» малы.
Можно получить и следующие приближения, уточняющие поправки к <оп и векторам нормальных колебаний (см., например, [13], гл. I, § 5).
Полезно заметить, что величина 6Л1ИИ в (2) представляет собой добавку к удвоенной кинетической энергии системы при условии, что скорости х* =л!п). Отсюда следует, в частности, что при увеличении масс частиц 6Л1пп>0 и, согласно (4),быи^0. Подобным же образом легко видеть, что при увеличении коэффициентов жесткости пружинок собственные частоты Могут только возрастать (ср. [6], § 24; [15])-
Важно понять, что изменится когда мы ищем поправку к вырожденной частоте (пусть <о₽ = о>п). В этом случае «сила» в правой части уравнений (3) оказывается резонансной. Поэтому координата возрастает со временем, и ее тоже нужно учитывать в правых
частях уравнений (3). Таким образом, в этом случае нужно использовать уравнения (3) совместно с l—п, р, оставив в правых частях только слагаемые с s=n, р
М (q	= о — ЛД1 п 6/Г о •—ЬК G
п\1 п '	ПгРЛ ‘ ‘прчр 'ппУп nPVp’
(5)
(? Р + Шр’р) = - М,рЛ - 6Л1Р,.% - в/<рп«п - Wpp’p-
Ясно, что сказанное относится н к случаю <i)j>«wn.
Итак, для определения поправок ко всем собственным частотам (включая и вырождение) в добавке (I) к функции Лагранжа можно отбросить все члены, содержащие произведения нормальных координат, относящихся к различным частотам исходной системы.
6.35.	Используем обозначения и результаты задач 6.27 н 6.34. Ясно заранее, что 6tOi=0. Для остальных частот
ю ЗМЛЛЬ
6<о	, п = 2, 3, 4.	(1)
Матрица кинетической энергии тц диагональна, причем
tnn=m22=mi3=m,	тц—2т.	(2)
Матрица &nif имеет единственный отличный от пуля элемент
бтп«=б/п.	(3)
Подставляя в (I) выражения (2) и (3), а также компоненты векторов нормальных колебаний г„, найденные в задаче 6.27, получим
6ю2 — — есоя, *<°з_4 — од е£0з,4*
6.36.	Векторный потенциал выбираем в виде
0).
функция Лагранжа
1 =	+ ? + *2) - -у -I- <&’ -I- <ф2) i a-^ixy - ух).
где =т~. 3$ тс	Для х и у получаем уравнения х -f- <ofx *—	= 0, У +	= °*
Удобно искать колебания в виде
х=Ке(Яе’О‘), y=Re(Beioe).
Система уравнений
(<о, — й*) А — ОВ - О, + (со* — РЛ) В = О
приводит к колебаниям
х = Ке(л(е'£1',,)=
Ль = ake Фй, k— 1, 2,
с частотами
С1.2 = V + “2 + “Х ± /(“1 + “! +	4шМ1-
Пусть для определенности 0)i>Ct>2, <о^>0. Тогда первое из найденных колебаний представляет собой движение по эллипсу с большой осью, направленной вдоль оси х, по часовой стрелке, а второе — по эллипсу с большой осью, лежащей вдоль оси у, в обратном направлении.
Движение вдоль осн г оказывается гармоническим колебанием, не зависящим от магнитного поля,
Z— Сз COS (ы3*4-<рз)-
Свободное движение осциллятора представляет собой суперпозицию найденных колебаний. Эти колебания можно назвать нормальными, обобщая тем самым понятие нормального колебания: движения в направлениях осей х и у происходят с одной и той же частотой, ио со сдвигом фаз. Привести функцию Лагранжа к
диагональному виду с помощью линейного преобразования только координат невозможно, так как переход к нормальным координатам связан в этом случае с каноническим преобразованием (см. задачи 11.7—11.9).
а)	Если магнитное поле малб,и^<®1 — то эллипсы нормаль-
*°ЖЮ1.2 •
ных колебаний сильно вытянуты, а частоты	----5Т
близки к <01,2. траектория осциллятора без магнитного поля запол-
няет прямоугольник со сторонами, параллельными осям координат (см. задачу 6.4); влияние слабого магнитного поля приводит только к небольшой деформации области, заполняемой траекторией. (Теорема Лармора здесь неприменима, так как поле U не обладает симметрией относительно оси г.)
б)	В сильном магнитном поле > ©1,2 нормальное колебание с частотой	происходит по окружности, а нормальное коле-
банке с частотой »-я ~ ~—1 — по эллипсу, у которого отношение осей, параллельных х и у, равно ©2/^1- Таким образом, происходит движение по окружности, центр которой относительно медленно движется по эллипсу.
Известно, что при движении заряженной частицы в сильном однородном магнитном поле в плоскости, перпендикулярной к полю, появление слабого квазиоднородного поля £/(г) (т. е. такого, что сила F = —* мало изменяется в пределах круговой орбиты) приводит к медленному смещению (дрейфу) центра орбиты в направлении, перпендикулярном к F (т. с. по линии уровня С7(г)) (см. [2], § 22). Заметим, что в нашем случае подобный же дрейф происходит и в сильно неоднородном осцилляториом поле.
в)	Если ©|=©2. то в плоскости (х, у) нормальные колебания представляют собой движения по окружностям в противоположные стороны с частотами П1<2 = © ±	где © =
Поэтому в системе, вращающейся с частотой °°®е частоты этих движений оказываются равными <о. Такие движения суть нормальные колебания изотропного осцилляюра с частотой <о. Действительно, сумма и разность таких колебаний с равными амплитудами
представляют собой линейные колебания по осям х или у. (Мы отвлекаемся от смешения вдоль магнитного поля).
Если магнитное поле ыалб, <ojg < то ылсоь и все влияние поля на движение осциллятора сводится к появлению вращения («прецессии») вокруг оси z с частотой — ® jg/2 (теорема Лармора, ср. [2], § 45). Если же	то использование вращающейся
системы теряет наглядность.
6.37. Уравнения движения
У + 4%) = — <%*’ + Шхг, где
о =	. со = ------.
ж тс z тс *
решаем с помощью последовательных приближении. Ищем координаты в виде x=x‘”-f-x<2», у=у{|>4-^2), z=z«’-f-z<2>, где х‘2>, l/(2>, z<2> малы по сравнению с х(1), у(,). 2{,). В первом приближении пренебрегаем малыми членами, стоящими в правых частях уравнений:
х<ч=Д cos (сМ+а), yW=B cos (cozH-P)» 2(0=3 с cos (cos^+y)-
Поправки x<’>, #(2), z(2) определяются из уравнений
;-<2>4-и2х<г> = игй">.
у(2)	(o|i/(2) = — <й2х(11 + <ояг(1Ь	(1)
г<э + а2г<2> = _Юз1Ч1>.
Получаем
(	— sin +з >
* =
со,® A sin (<0i£ + ct)	sin (в>37 4- у)
4/^)=z	ч ч	5	?	*
L2 ~	^2 ~ W3
<ажтаВ sin (ый/ -|- р)
13 р. л. Котики. В. Г. СерСо
Поправки оказываются малыми, если |<oz|	w2|, |cojt| |соа—
—to3|. Нормальные колебания суть колебания по эллипсам, сильно вытянутым вдоль осей координат.
Если же, например, |o2^|(Di—к>2], |й)х||<>)г—«оз!. то и у<2\ согласно (2), уже не малы. Это связано с тем, что частоты «сил» <ozy{n и —<ozx<*) в (I) оказываются близкими к собственным частотам осциллятора. В этом случае в уравнениях первого приближения следует сохранить резонансные члены;
?1> + ю2х<‘>-ог;<1>=0;
?ч+и|у|1> + ‘>г;<1,=о,	(3)
*	«в2	—и»
т. е. влияние -9^z на движение необходимо учесть точно Система (3) рассмотрена в задаче 6.36. Для поправок второго порядка имеем уравнения
?2> + ®2х<2»=0, ?2, + <»fy<2> = <0«?1».
?2> + <о|г(2)=-«х ?*>.
Выпишем свободные колебания, во избежание громоздкости ограничившись случаем й)1=ш2«<й:
<о
Нормальные колебания (4) с частотами о £ -JL происходят (в принятом приближении) по окружностям, плоскости которых составля-
ют с плоскостью (х, у) углы + ------------- (поворот вокруг оси у),
G>3 — <i>2
& колебание с частотой ws — по сильно вытянутому вдоль оси z эллипсу, лежащему в плоскости (у, г).
6.38.	Колебания маятника предполагаем малыми, угол отсчитываем от вертикали против часовой стрелки, в качестве второй координаты возьмем заряд q ка правой пластине. При отклонении маятника на угол <р магнитный поток через контур равен Ф —const—-g-2<р, поэтому функция Лагранжа (см. задачу 4,21)
L = -L \тР у* + S? - mgltp “	” ^аФ <7
Если ввести координаты х = /<р и у — у <£fmq,т0 функция Лагранжа нашей системы отличается от рассмотренной в задаче 6.36 (С параметрам,. = X, и| =	= _ -_^L пр„ , = oj
лишь на полную производную по времени: <о^ ху. Поэтому уравнения движения я их решения в задаче 6.36 справедливы и для нашего случая.
6.39.	Пусть
r=Acos (шН-ф), А=(Д|, Да .... A/у)	(1)
— какое-либо нормальное колебание. Поскольку замена
не меняет вида функции Лагранжа, то наряду с (1) должно существовать нормальное колебание вида
Sr = SA cos (art + <p), (SA). = 2 StfAr	(2)
Здесь S — матрица с элементами Sfj, которая по условию обладает свойствами (£ — единичная матрица, ST — транспонированная матрица S);
S’=S, SS=E.	(3)
а)	Если данная частота со не вырождена, то решение (2) может отличаться от (1) разве лишь общим множителем:
Sr=cr»
Аналогично
SSr=cSr=c2r.
Поскольку SS—E, то из (4) немедленно следует, что г=с2г, или с2=»
«= 1 и с=±1. Поэтому для невырожденной частоты
или Sr«=-f-r» или Sr=—г.
б)	Если частота со вырождена, то колебания (I) и (2) могут и не совпадать. Но их сумма и разность
r±Srt=(A±SA) cos (<о/+<р)
также являются нормальными колебаниями с той же частотой, обладающими необходимыми свойствами симметрии.
в)	Добавка к функции Лагранжа имеет вид	где
1 = (Ь./2. ...W
— внешняя сила, действующая на систему.
Пусть сила f симметрична, а нормальное колебание га вида (1) — антисимметрично относительно преобразования S, т. е.
Sf = -f-f,	Sra = —re.	(5)
Данная сила не влияет на колебание га, если факторы f и го взаимно ортогональны (см. задачу 6.24):
(f,ro) = 0.	(6)
Из (5) следует, что
(Sf, Sro)= —(f, re).	(7)
С другой стороны, левую часть (7) можно переписать в виде
($t$re) = (f,S'Sr0).	(8)
Из (3) очевидно, что STS=£. Сравнивая тогда (7) и (8), получим немедленно (6),
Остаются ли неизменными пункты а) — в) задачи, если заранее не требовать условия ST=S?
6.40.	Пусть Xi — смещение i-й частицы вдоль кольца из положения равновесия, для определенности считаем положительным смещение против часовой стрелки Система явно симметрична относительно поворота на угол 180° вокруг оси АВ, проходящей через положение равновесия второй частицы и центр кольца. Поэтому и функция Лагранжа системы
— 4 [ 2 (ч ~ хн 0’ I’ (*» — ri>' j
не изменяет своего вида при соответствующей такому повороту замене
х2->—х2. х,-> —Хз. *8->—х4->—х& х6->—х4.	(1)
Использование соображений симметрии (см. предыдущую задачу) и ортогональности позволяет очень просто свести эту задачу с пятью степенями свободы к двум независимым задачам с двумя степенями свободы каждая.
Действительно, векторы нормальных колебаний, симметричные я антисимметричные относительно преобразования (1), имеют вид
Кроме того, одно антисимметричное «колебание» легко угадывается — это вращение всех частиц по кольцу
Два других (помимо rai) антисимметричных колебания должны быть ортогональны к га1 с метрическим тензором, определяемым коэффициентами кинетической энергии, т. е.
m(2c+tf)+2Alf=0.	(2)
В итоге в г0 и гв остаются неопределенными всего по два коэффициента. Для определения их достаточно использовать всего лишь два уравнения движения из пяти, например для первой и пятой частиц:
mxi 4-fe (2xi — ха — х5) = О,
(3)
ALc5-f- k (2x5—х< — Х|) = 0.
Подставляя сюда явный вид гл, найдем для двух симметричных колебаний
ь1.г = ("У “<1.2 - 2) “1.2'
“<1 2 = гЛп <2Л1 + Зт +
Аналогично, подставляя в (3) вектор гв и учитывая (2), найдем
С2.3 = (-у1 ®?2.3 — 1 j *2,3’	rf2.3 = 2с2.3 “ ^2,3»
<s=ass (4Л1+m+/4-(4Л,~т)2+4-т2)-
6.41.	Рассматриваемая система близка к изученной в задаче 6 28а. функция Лагранжа в нашей задаче отличается на малую величину
fit=6Lj (х, х) +6L2(«/- У) +6L3(e, z),
6Li (х, х) = -у- [х| 4- (х2 — х5)а + (х4 — х6)3 + х|],
1.
И в этом случае колебания по х, у, г происходят независимо Нас интересуют только колебания по х.
Для определения частот колебаний удобно воспользоваться методом последовательных приближений (см. задачу 6.34). Частоты (оа,4 невырожденные, так что к этим колебаниям непосредственно применима формула (4) из задачи 6.34.
Частота <0i исходном задачи (6.28а) трехкратно вырождена, поэтому, казалось бы, для определения поправок к частоте и векторов нормальных колебаний придется рассматривать систему уравнений типа (5) из задачи 6.34. Однако свойства симметрии системы позволяют сразу же указать те векторы нормальных колебаний исходной системы, которые мало изменяются при добавлении 6L. Это как раз векторы (I) из задачи 6.28, потому что именно они обладают определенными свойствами симметрии; колебание г3 симметрично относительно оси АВ и антисимметрично относительно CD, Г| — симметрично, а г2 — антисимметрично относительно обеих осей. Поправки к частотам этих колебаний тоже можно вычислять по формуле (4) из задачи 6 34.
Подставляя Х|= —ха=1, Хг=х4=Хз=0, находим
6Ац = — 26/-!=О,
так что 6<Oi=0. Аналогично
6Я22= —26£i(Xi«=X3=x5=0, х2= —х4—1) «= — 4f'i, Af3 — 2Z-! («1=хз =xg= 0, х2— —it = I, х*=0) = 2m,
/ ь-
так что o<os — —el/ ' 2tn
6Кзз= — 4efe, М3=4пт 6<j>3 = — — ~ 1/" —. 2 r 2tn
Представляя вектор начального смещения Г (0)
тор начальной скорости г(0) =0 в виде г (0) = £
== 2 г £ (0) соответственно, найдем, что £
а
Ay ~ As = Л8=	~ А ь = <Р| ~0.
Таким образом, в данном приближении четвертое и пятое нормальные колебания не возбуждаются, и колебания частиц
xi3 — “g- (+ cos toji -f- cos <o3Q,
a x2 4 =	(± cos<o2i—cos<o30, xR—0
носят характер биений (см. по этому поводу задачу 6,31).
6.42.	В этой задаче удобно воспользоваться методом последовательных приближений (см. задачу 6.34). Изменение масс приводит к появлению добавки к функции Лагранжа
66 =	(6m, if + 6m,
Ее следует выразить через нормальные координаты исходной системы (см. задачу 6.21). При этом коэффициент при произведении обобщенных скоростей qiqz отвечающих вырожденной частоте, оказывается равным нулю. Остальные произведения qtq, (для	можно опу-
стить, как это отмечено в задаче 6.34. Получаем
6ti=-f- 6m, ?, + 4“ 6m, + -g- (6m, + 6m,) (	+ Ц).
Функция Лагранжа L-f-6^i, как и функция Лагранжа исходной системы, разделяется насшаемые, каждое из которых содержит только одну из координат qi. Координаты остаются, тдким образом^
нормальными, а для вычисления поправок к частотам можно восполь-зоваться формулой (4) из задачи 6.34;
fOj == •— tOj, 6<Оа = — "д (Og, 6(0s = — g «Од,
Все собственные частоты системы стали различными, исчезла неоднозначность выбора векторов нормальных колебаний: с точностью до Bi это векторы (I) из задачи 6.21.
Интересно, что при 6гЦ[=6я22 частоты (Oj-f-Croj и <о2-}-6(о2 вновь совпадают друг с другом (с точностью до поправок второго порядка I ficoj >— 6(й21 ~ «1 (Oj). В этом случае функция Лагранжа Z.4-6L1 снова приводит к неоднозначному выбору векторов нормальных колебаний. Однако в точном решении задачи прн 6nzi=6m2 векторы нормальных колебаний имеют вид
1 — 1
+ /1 + е +	± Зе
+ Г1 + е + Эе» + Зе
и при малых е близки к векторам (2) задачи 6.21 (с точностью до опущенных здесь нормировочных множителей). Резкое изменение вида нормальных колебаний происходит в очень узком интервале изменения масс |6mj —6т2| ^е2т (ср. с задачей 6.5а). Для определения векторов нормальных колебаний в этом интервале значений 6т2 можно было бы воспользоваться следующим приближением в методе последовательных приближений.
6.43.	Очевидно, движения частиц в направлении осей АА и ВВ независимы. Будем рассматривать движение в направлении оси АА.
Для первой и четвертой частиц положительными считаем отклонения влево, для второй и третьей — вправо. Согласно результату задачи 6.39 нормальные колебания r= (хц х2, Хэ, х4) могут быть выбраны симметричными или антисимметричными относительно осей АА и ВВ. Для симметричного относительно оси АА колебания Х|— х2»=х3. Если к тому же это колебание симметрично относительно оси ВВ, то xl=xz, х$=х4, так что для этого дважды симметричного колебания имеем г„=(1, 1, 1,
Для колебания, симметричного относительно оси АА и антисимметричного относительно оси В В, имеем xj=x4, xz—xs и Х|= —х2,
х4= —.Xi, так что
г*о=(1, —I, —— 1, 1) Не-
подобным же образом находим
Го«=(1, 1, —1, —1)9ао Гав = (11 —К I» —1)9ов«
Аналогично находятся векторы нормальных колебаний в вертикальном направлении.
Частоты колебаний можно найти, подставив найденные векторы в уравнения движения.
При наличии вырождения, кроме найденных нормальных колебаний, существует множество нормальных колебаний, не обладающих указанными свойствами симметрии. Нетрудно сообразить, например, что частоты ss и аа колебаний совпадают о1в—ипо«=2)'А/т, если натяжение пружинок не произвольно, а равной/ (где/ —длина каждой из пружинок в положении равновесия). Но тогда нормальным колебанием будет любая суперпозиция векторов гво и ги, например вектор (1,0, 1, 0)«7„.
Аналогично можно найтн векторы нормальных колебаний в направлении оси ВВ.
6.44.	Очевидно, колебания в направлениях АА, ВВ и в направлении, перпендикулярном плоскости рамки, независимы. Рассмотрим, например, первые.
Компоненты вектора колебания удобно размещать в таблице, соответствующей форме рамки. Для частиц, расположенных слева от оси ВВ, положительными считаем отклонения влево, для частиц, расположенных справа — вправо. Колебание ss, симметричное относительно обеих осей АА и ВВ, имеет вид
lx X X х\
\х X X хТ
Колебания х, X сводятся к колебаниям системы, рассмотренной в задаче 6.7 с m2=M, где следует положить	А2—
«Ц As=2A-J-A', k'=ffl. Таким образом, имеется два ss колебания.
Колебания sa, симметричные относительно осн АА и антисимметричные относительно оси ВВ, имеют вид
х X —X — х\
х X -X — xj*
причем теперь k3—k', ki=k-\-k’.
Аналогично для as- и аа-колебаний:
/	х	X	X	х\	t	г
г х у „J *i=* + 3V. Л3=2Л + 2Аг',
\	Л	Л	*“ ZA	Л]
I	х	X	— X	—	х\
U -х X J = 4 + ъ =
Подобным же образом можно найти остальные шестнадцать нор-мальных колебаний.
6.45.	В обозначениях предыдущей задачи вектор силы
r-k—k't ~-k'.
k', k + k'\ k', k + k')
a cos yt.
Он ортогонален всем нормальным колебаниям, кроме симметрнчно-антнсимметричных (so). Поэтому резонанс возникает лишь при двух частотах у — где
(<2)2 = 2^{k{2М + т)+ "Г±
р/"(2.М — т) -г- -L- (М — т) р-Ь W.Mm
6.46.	Линейная молекула С2Н2 имеет всею семь нормальных колебаний: три продольных колебания н по два изгибных колебания в двух взаимно перпендикулярных плоскостях (см., например [!],§ 24).
Задача об определении двух симметричных продольных колебаний Xi=—х^ л2= —Хз сводится к задаче 6.7 с параметрами
fes=2ftcc. ki=G, где &нс и & сс ~ жесткости связей НС и СС.
Антисимметричное продольное колебание xi=x4, х2—хз, / ЛНг (тн -г тг)
4-тсХг=0 имеет частоту w — I/	v———- ---А (такую же,
.  у Vc
как и «молекула» СН). Заметим, что продольное смещение молекулы как целого xi=x2=xa=x4 можно рассматривать как второе антисимметричное колебание, причем условие ортогональности к нему первого антисимметричного колебания совпадает с условием равенства нулю полною импульса молекулы.
Поперечное симметричное колебание yi = yt, у^—уз,
^НУ1 + тсу2 =0,
_ ^НСС (тН ~Г Wc) .
“<3 - /гнстнтс
Здесь ^нсс — жесткость молекулы при изгМбе: при изгибе связи НСС на угол б потенциальная энергия возрастает на ftHCC62/2.
Поперечное антисимметричное колебание у\~ ~У\, у2— —Уз,
mGlCdh + mIi (lCC + 2iHc) ~ 01
2 _ *HCc[mCZCC + (2tHC ~b zcc)a]
“°2-	mHmcZ2c/2c
где /нс и /сс ~~ равновесное расстояние между атомами Н—С и С—С соответственно. Отметим, что соотношение между смещениями атомов этого колебания может быть найдено из условия равенства нулю полного момента импульса молекулы (или ортогональности вектору чистого вращения молекулы как целого yi~ —уа~—-уя. Уг *нс "Ь ^сс) — ^сс» которое можно рассматривать как второе антисимметричное колебание).
6.47.	Обозначим отклонения частиц от положения равновесия в направлении BD через х, и х2, а в направлении CF — через у, и у2. Поворот вокруг оси симметрии CF на 180° приводит к заменам:
Xi st —Х2.	yt у2,
т. е. преобразование S поворота вектора колебания г— (xj, Уъ х2, у2) имеет вид
Sr=(—х2, й, —х,, <л).
Вследствие симметрии системы в ней возможны нормальные колебания двух видов: г« — симметричные относительно оси CF, для которых Sr, = r«, и антисимметричные го, для которых Sra — —га. Для симметричного колебания (—х2, у2, —хц yi)~ (*i У1 х2, Уз), откуда
г,= (х, у, —X, у).
Аналогично
ГО=(Х, у, X, — у).
(Для антисимметричного колебания поворот вокруг оси симметрии равносилен изменению фазы колебания на л.)
Возможны два симметричных и два антисимметричных колебания; для определения частот н векторов каждой пары колебаний достаточно использовать два уравнения движения.
Можно получить еще некоторые сведения о виде нормальных колебаний, не зная жесткостей пружинок. Условие ортогональности векторов колебаний гЛ| и r1S сводится к равенству
2m{x,lx,1+y,iy,1') =0,
показывающему, что векторы отклонений, например, частицы I при каждом из двух симметричных колебаний взаимно перпендикулярны (рнс. 130, а). То же самое относится и к антисимметричным колебаниям (рис. 130, б).
Рис. 130.
Направление, в котором отклоняется частица при каждом из нормальных колебаний, нельзя определить, не зная жесткостей пружинок. Действительно, если жесткость и натяжения пружинок АС и СЕ малы, то отклонения частиц при нормальных колебаниях направлены почти вдоль илн поперек пружинок BD, и, наоборот, при малой жесткости пружинок BD нормальные колебания происходят почти вдоль илн поперек пружинок АС и СЕ.
Разумеется, при вырождении частот можно выбрать и другие векторы нормальных колебаний, не обладающие свойствами симметрии. Например, при «выключенной» пружинке BD это могут быть колебания каждой из частиц вдоль или поперек пружинок АС н СЕ.
6.48.	Обозначим отклонения каждого из атомов от положения равновесия в направлениях OD через ОА — через yi, перпендикулярно плоскости молекулы — г,-.
Колебания молекулы С2Н4 разделяются на сохраняющие молекулу плоской и выводящие атомы из плоскости. Рассмотрим последние колебания.
Вектор отклонения атомов удобно записывать в форме
(zj	гЛ
г5 I.
*8	гв/
Для колебания, симметричного относительно оси АВ.
24=2!, zs=z2, г6=г3.
Если колебание к тому же антисимметрично относительно оси CD, то
га— —zi, z2= —г2, zs= —zs, z6— —z4.
Итак,
Это «колебание» оказалось вращением вокруг оси CD.
Аналогично симметричные относительно обеих осей колебания
Одно из них
Это поступательное движение. Амплитуды другого можно определить, учтя его ортогональность вектору гмд:
4mzI+2Afz2—О,
т — масса атома водорода, М — углерода.
Антисимметричное относительно обеих осей колебание
аа
есть крутильное колебание вокруг оси CD. Наконец,
Здесь для вращения вокруг оси АВ (ras,i) ai=loc/lGH —отношение расстояниГ| атомов углерода и водорода от оси АВ в положении равновесия; для нзгибного колебания (гв*,2)
2т *он
Аналогично могут быть рассмотрены и колебания, ие выводящие атомы из плоскости молекулы Вектор отклонения запишем в виде
S/1	*4 У4\
Г =	f/S *6 УЪ I.
Vs Ул	хе yj
Общий вид колебания as
/*1 У1	Xj — j/A
roe = I	0 *s 0	L
V1 “1/1	У1/
В число as-вколебаний» входит поступательное движение молекулы в направлении оси х (xi=x2, ^=0) Два других as-колебания изображены на рис. 131, а, б.
ж)
Рис. 131.
Чтобы представить себе вид отклонений атомов прн этих колебаниях, заметим, что расстояние между атомами углерода не изменяется — связь С—С «не работает» Если пренебречь взаимодействием относительно далеких атомов (например, 1—4, 1—5 на рис. 40), а также жесткостью углов вида 1—2—5, то рассматриваемые колебания совпадут с симметричными относительно оси CD колебаниями двух .«молекул» Н2С, происходящими в противофазе (ср. с задачей 6.46;
колебания молекулы вида Д2В рассмотрены в [I], § 24, задача 2).
Общий вид sa колебания
/ *1 У1	— уЛ
rea = I 0 уЛ 0 у2 I.
\~ «1 Ух	*1 yj
Кроме поступательного движения в направлении оси у, вектору г,о соответствуют два колебания (рис. 131, в, г). Одно из них (в) можно представить себе как колебания двух «молекул» НаС, антисимметричные относительно осн CD и происходящие в фазе. Другое (г) —это вращения «молекул» НгС в разные стороны. Если бы можно было полностью пренебречь связями удаленных атомов и жесткостью углов вида 1—2—5, то частота этого колебания оказалась бы равна нулю.
Среди аа-колебаний есть вращение молекулы как целого в плоскости ху, антисимметричные колебания «молекул» НгС в противофазе (рис. 131, д) и их вращения в одну сторону (рис. 131, е).
Возможны также три ss-колебания (полносимметричиые), они изображены иа рис. 131, ж, з, и (подробнее о колебаниях молекулы этилена см., например, в [17].)
6.49.	Функция Лагранжа
L = -^-(u? + u|+u^)—-|-{| г{„ — гм+ и, —11,1 — 0е +
— ( I — ги + U, — | — I)1 + ( I rso — г1о + “а — ”1 I — 0“).
где /=|г10 — г2с,| = |г2о — Гзо| = |гзо — Г10|; ио — смещение д-го атома из положения равновесия, определяемого радиусом вектором го0- Поскольку | и„ | С/, имеем
t = ‘f’(ul + u2 + ui) — V ((е1г(“1 —«.))“ +
+ (<Чз (“S “ пз))’ + (еа1 (Из — И,))’},	(1)
где
гю ц Гер _______ГрЦ j гяп _____г3п — г14)
с12 — i • еаз — i . езт — i *
В системе отсчета, где полный импульс «(щ+игфиз) =0, выполняется условие
ui+us+u4=0.	, (2)
Кроме того, накладываем на ио условие
[г joUild- [fgoUs] + [г 3t)U3] =0,	(3)
равносильное требованию, чтобы момент импульса молекулы
м=т 2 [г«>+%>“«]	и)
обращался в нуль с точностью до первого порядка по uu включительно.
208 .
ОТВЕТЫ И РЕШЕНИЯ
TG.49
Оказывается удобным выбрать для описания движения каждого атома свою систему декартовых координат (рис. 132), сохраняя
таким образом симметрию в описании системы. Равенства (2), (3)
в этих координатах дают *)
«•+(~4’йз+У’Х8)+(_’т!/,“1тХ1)=0, (6)
Уг + Уч + Уз = 0, откуда
£ = х? + -»2-Ь*з)—-у( *1Ха +	+ зд) —
—2" *(*? + *? +*з)-
*) Например, умножая обе стороны равенства (2) на е2а, получим (5). При этом нужно учесть, что вектор е23 в различных системах имеет координаты
еаз = (0, Di = (П,

3 Ид—(Хо, У а) а-
Равенство (6) получается из (5) круговой перестановкой индексов^
Одно нормальное колебание (полносимметричное) очевидно:
Р)
Два других колебания ортогональны первому, что приводит к условию*)
*18> + *23> + «з° = °’	« = 2.3.	(8)
Одно из этих колебаний симметрично относительно осн xj :	= х^2\-
другое — антисимметрично : Xj3> = 0, х^ ~ — *з3>-
Учитывая (8), имеем
^> = -242,=-^г, = /4’»-
,	' 3	19)
у(3)_____(3) = -1 в
х2 — л3 J/293*
Замена
*®	у3 91	p<6 ?8 + р.^-93»
приводит функцию Лагранжа к виду
L=_T’ (’< + 2«!+2«f)—t'Gi+»!+«!)•	<10>
Нормальные колебания, соответствующие этим координатам, приведены на рис. 133, Их частоты
°> = /34’ и*=ш»=/йг
Вид функции Лагранжа (10) сохраняется при повороте в плоскости gs. 7э-	_
*) Использована метрика fe<j. В (7), (9) множители перед q выбраны так, что + Xg,2 4- х|Г)2 = gf.
Г. Л Кот кин, В. Г. Сербо
Момент импульса с учетом квадратичных по иа членов
|М| = т|£[поио]| = т|ад3 —Ме|
может быть отличным от пуля, если колебания q% и q3 происходят со сдвигом фаз.
Рис. 133.
А
Интересно разобраться, какие изменения может внести в эту картину зависимость потенциальной энергии от углов, образуемых связями. Очевидно, на частоту колебаний qt такая зависимость не повлияет. Частота колебаний и q-t изменится, но двукратное вырождение сохранится. Действительно, наряду с некоторым колебанием q возможно также колебание, полученное из q поворотом на 2л/3. Его частота должна быть такой же, как и частота колебаний q. С другой стороны, оно отличается от q (при повороте на 2я/3 само с собой совпадает только колебание q\). Таким образом, мы обнаруживаем два независимых колебания с одной частотой. Нормальные координаты в этом случае должны удовлетворять только одному условию: быть ортогональными qi\ в частности, q% и q$ остаются нормальными координатами.
6-50. а) Вводим координаты атомов В так же, как в предыдущей задаче, для атома А — координаты х4, у4, z4 с осями, параллельными xlt Уь z, и началом в центре треугольника.
Есть четыре степени свободы движений, выводящих атомы из плоскости ху. Три из них отвечают поступательному движению вдоль оси z и вращениям вокруг осей х4 и $*, а одно — колебанию (при котором, очевидно, zt=zz=zs, wAz44-/n(z1+z24-zs) =0). Частота этого колебания со, невырожденная, она лишь случайно могла бы совпасть с частотой какого-нибудь другого колебания.
Рассмотрим колебание атомов в плоскости ху, симметричное относительно оси х4. Общий вид такого колебания:
4/1=0, х8=ха, «/2=—4/з,	£/*=0.
Вектор смещения содержит четыре независимых параметра: xb xs, у?, х4,
т. е. на такие движения приходится четыре степени свободы. Одна из них отвечает поступательному движению молекулы вдоль осн хь одна — подносим метрнчному колебанию

с частотой w2 (рис. !34, с), а две остальные —колебаниям, нарушающим симметрию молекулы. Частоты этих колебаний со» и со* (рис. 134, б, в).
Рнс. 134,
Из четырех оставшихся степеней свободы одна приходится на поступательное движение в направлении оси yt, одна — иа вращение вокруг оси х*. а две — на колебания. Это колебания, которые могут быть получены из уже указанных с частотами <в3, поворотом на 2л/3 вокруг оси zt (ср. с предыдущей задачей).
Итак, частоты (й1, ы2—невырожденные, частоты со» и вц —двукратно вырождены.
Заметим, что векторы колебания, антисимметричного относительно оси х4, можно получить, зная вектор симметричного. Для этого достаточно взять определенную суперпозицию колебаний, полученных из последнего поворотами вокруг оси г< на углы ±2л/3, а именно — их разность (см. рис. 134, г).
б) Изменения собственных частот можно определит^ используя теорию возмущений (см. задачу 6.34):
„ о б/И
Для полносимметричного колебания в качестве нормальной координаты выберем Xj. Тогда величины М и 6А4 определяются как 14*
коэффициенты в выражениях кинетической энергии и добавки к ней: dm -й ДЛ/ -2
2 *1= 2 *1'
3m -2 _ Л? -2
2 Х1 “ 2 *1’
так что
dm
6Й-
Для колебания вдоль оси z кинетическая энергия и добавка к ней равны
И»— и.
1 2 1’
так что
dmm
6ы1	2 3m(3m + mA)
Например, для хлорида бора замена одного атома хлора с атомным весом 35 на изотоп с атомным весом 37 уменьшает частоты u>i и на 0,1 % и I % соответственно.
6.51. Пусть колебание, при котором молекула остается подобной сама себе (рис. 135, а), происходит с частотой й)ь
Частота колебания, сохраняющего свой вид при поворотах вокруг осн OD на угол 2я/3 (рис. 135, б), вообще говоря, отлична
Рис. 135.
от wi. Иное распределение смещений атомов можно получить, производя отражение смещений в плоскости ВСО, получится колебание, отличающееся от второю лишь тем, что атомы А и D поменялись ролями. Частота этого колебания ci)3=(j)2 Подобным же образом отражение в плоскости АОС меняет местами атомы В и D, сохраняя частоту о4=со2. Это четвертое колебание не сводится к суперпозиции преды
дущих, так как, в отличие от них, несимметрично относительно плоскости AOD.
Колебание, симметричное относительно плоскости АОВ и DOC (рис. 135, е), имеет частоту ь)5, отличную от 0), и ci)2. Поворот на угол 2л/3 вокруг осн OD, равносильный круговой перестановке А, В и С, приводит к колебанию, симметричному относительно плоскостей СОА и DOB, а его частота tug—сс*.
Итак, молекула обладает тремя собственными частотами одно-, дву- я трехкратно вырожденными.
В заключение заметим, что молекул, рассмотренных в задачах 6.49 н 6.51, по-видимому, не существует в природе. Однако подобный же метод исследования может быть применен н к реальным молекулам.
6.52. а) Прн полносимметричных и дважды вырожденных колебаниях, указанных в предыдущей задаче (см. рис. 135, а, в), атом углерода остается неподвижным. Есть еще две трехкратно вырожденные частоты. Соответствующие колебания похожи на колебания, изображенные на рис. 135, б, только атом углерода колеблется либо в том же направлении, что атом D, либо в противоположном.
б) Добавка к функции Лагранжа, описывающая действие электрического поля g (/), есть
а
где еа — заряд, иа — смещение д-го атома.
4
В любом колебании и + wcu^ = так что а=1 а
2 ейиа = 'М —+ 4 р-
С=1	V т I
При подносим метричном и дважды вырожденных колебаниях 2^оио = 0 н эти колебания не возбуждаются. При колебании рис. 135, б, напротив,2есио =/= 0 и подобные колебании возбуждаются.
Итак, резонанс возможен на двух частотах.
Вектор g можно разложить на три слагаемых gj, параллельных осям симметрии каждою из трех колебаний молекулы с вырожденной частотой. Каждое из слагаемых g> приведет к колебанию атома углерода с амплитудой, пропорциональной g>, и одним и тем же коэффициентом пропорциональности к. Поэтому u5=Hg и |и5| не зависит от ориентации молекулы. Можно убедиться, что амплитуды колебаний атомов водорода |П|.2,з,*| тоже не зависят от ориентации молекулы и параллельны вектору g.
§ 7. Колебания линейных цепочек
7.1. Функция Лагранжа системы
N
ч+2
п— 1
(I)
где хп — смещение n-й частицы из положения равновесия. Введем также координату положения равновесия n-й частицы Хп = па, где а—равновесная длина одной пружинки. Система уравнений Лагранжа
/ИХ] 4- £(2х, ""	~ О,
“„ + *(2х„“хп-1-х»+1) = °. л = 2.3.....N~
mxjv+ (2xN ~~ XN-1)= °
эквивалентна системе
тхп + Л(2хп — х,
(2)
(3):
при дополнительном условии
Хо = Хдг+1 =- 0.	(4)
Из физических соображений можно предвидеть, что нормальными колебаниями должны быть стоячие волны. Удобнее, однако, выбрать
xn=Zei(<ot±n’J.	(5)
При таком выборе система N уравнений сводится к одному уравнению
k <р ш!=4 — яп>у,
(6)
которым определяется связь частоты с разностью фаз колебаний соседних частиц ф. Смысл подстановки (5) заключается в выборе для Хп решения в виде бегущей волны с волновым вектором р — q/а, так как nq = nap = pXn. Уравнение (6) устанавливает, таким образом, связь между частотой и волновым вектором.
Условиям (4) можно удовлетворить, подбирая суперпозицию бегущих в обе стороны волн xfi =	’Пф)4-
Условие х0 = 0 дает А = — В или хп ~ 2iSsin(n<p)ei“1, т. е. стоячую волну. Из условия на другом конце хл+1 = 0 определяются возможные значения частот («спектр частот»),
7-11
2|6
Уравнение sin (W-H) ф=0 приводит к N независимым решениям
ns	„
ч’.-jv+T-	s=l-2 к- т
В самом деле, $ = 0, s = JV-f-l дают s = N + I фаза = —<p.v_(+2 + 2л, т. е. решения, отвечающие s=A’+Z,
нулевые решения, а для
выражаются через решения, отвечающие s «. АГ-/4-2.
Из (6) и (7) находим А' различных частот
2flV+ I)’
Рис. 136.
На рнс. 136 различные частоты’укладываются дискретными точками на синусоиду. Вектор нормального колебания
отвечающего $-й частоте,
где
sin <pe 'J siu2<ps | sin /V(fe J

qt (/) = Re (21В5е<ог') = C* cos (aj + aj
-s-я нормальная координата, а множитель
г------ Г N Т"1*
/Нл-=[28Ь,ги<р.]
введен для нормировки: (rg, rg,) == б^,^. Общее решение есть суперпозиция всех нормальных колебаний
W ________
*n=2 V ArTTT’.Wsmn^.
8~1	‘
Матрица перехода от хп к qa

 11/15 sin---------
A' J I
является ортогональной матрицей, приводящей функцию Лагранжа к сумме квадратов, отвечающих набору ДО различных осцилляторов:
L- 2ч(?,. ?.)• Ч(«.-
в=1
7.2. Уравнения движения для данной системы те же, что и уравнения (3) предыдущей задачи, при дополнительном условии х0 «= О, = *л+|. Поэтому
(2s-1) л	„
% = 2.V-I-1 ' s~
sin*25-')”.
2(2Л'-|- 1)
хп = 2sin п<ра • cos (т/+°,)* п
Частный случай при ДО = 2 см. в задаче 6.1,
7.3. Уравнения движения совпадают с уравнениями (3) задачи
7.1 при дополнительном условии х0 = хя и x\v+i = *1. Поэтому
ф,“дГ. 8 = 0.1».ДО—1,
о *=2т/~Asin—,
* V т N
причем частоты со, и Qw-> совпадают, а соответствующие им волновые векторы отличаются знаком ips = 2л — срN_s, Частоте ы0 = О отвечает движение всех частиц по кольцу с постоянной скоростью. В системе возможны колебания вида
= Re Л(1)
т. е. бегущие по кольцу волны. Упомянутое выше двукратное вырождение частот соответствует волнам, бегущим в разные стороны Наложение двух таких волн с ранными амплитудами дает стоячую волну
,(.)±xW-s) = 2|^|
[cos n<ps cos (cogf -J- ag), [sin n<pg sin (tog/ 4- ag).
(2)
Это и есть нормальные колебания (все точки движутси в фазе или противофазе)«
В соответствующих нормальных координатах
в
х„ “ S (’,1 С05 «ф, + Чп ™ "’») + »»•
i—1
N—\
R = —J-, N — нечетное,	(3)
функция Лагранжа приводится к диагональному виду:
L = V { ’ ° + 2 [ ’ •'+ 4 ‘2 ~ “•(’»< +	<4>
(Если число частиц четное, то формулы (3), (4) следует несколько видоизменить в связи с тем, что частота шЯ/з невырожденная; формула (1) при s = N/2 сразу же определяет стоячую волну.)
Интересно заметить, что повороты в плоскостях qai,
<Msta₽s.
?K = ^l™₽, + «'s2cosf,.
сохраняющие вид функции Лагранжа (4), соответствуют смещению узлов стоячих волн:
R
х„ =«»+ 5 Kicos (п<р. - ₽«) + я” ("т. “₽.)]• 6—1
Для бегущих волн (1) средний поток энергии по кольцу (см. за« дачу 6.9) *)
2л/®
Scp = ^- j к (xn-l “xn)^d' = V *MI2“slnlr-и
а групповая скорость
♦) Ниже для краткости мы всюду опускаем индекс s. Вычисление потока Sep и энергии Е удобно производить в комплексной форме, воспользовавшись формулами из [2J, § 48.
где а—равновесная длина одной пружинки, р = <р/д — волновой вектор. Энергии
N	N
£ = v2 *" + 42 (xn-xn-l)* = 2.V|41’*sin’-| = n=i	n=l
= 4 NrnnA | A I2,
и потому
£	e
Na % e
7.4.	а) Уравнения движения
**2n-i + k (2x2n-l ~ *2n-2 - M ~ °’	(|)
^*Sn *4 (2x8n " x2n-l x2»4-l) ~ °’
причем Xo — «2w+i = 0, n = I, 2, ..N.
Ищем решение в виде бегущих волн разной амплитуды
,	. =» дЛ®>*±<2я-1)ф]
(2)
- ==:ВД®1±2Пф1
*171	•
Для определения Л и В получаем систему однородных уравнений
(=	+ 2k) А — k (е-|ф 4- ?ф) В = 0,
—	+ е*’) А + (— Ma1 + 2)i)fi = 0.
имеющих нетривиальные решения, только если детерминант обращается в нуль. Это условие определяет связь частоты с разностью «раз колебаний соседних частиц
g \ г тМ г
тМ
Ц=т+Ти'
Дополнительным условиям удовлетворяют только определенные линейные комбинации бегущих волн (2). а именно:
«гп-i = sin (2п — 1) Ч , cos (ш / + ав), x;n=",slrl 2,1 г< «с“("7+ "-.)
у которых <р„ = ^г—у. так
как «Pg/v-j.j_# = л то различные
7-4]
§ 7 колебания Линейных Цепочек
219
частоты при выборе определенного знака в (4) мы получим лишь для $ — 1, 2, ,JV. На рис. 137 (для случаи А1 > т) они укладываются
дискретными точками на две различные кривые, одну из них («•<_)) принято называть акустической, /фугую оптической.
Общее решение имеет вид
JV
*2п-1= S sln <2" - о Т£ I Л+)е X
8=1
KCos(m(+),< + as)-|-
+ А-),СС8(И<-Р/ + ₽31.
Рве. 137.
N
Х-2П = 231П 2П% [В(+). COS (Ш(+ st + Gs) + В(_„ COS (М(_,/+₽,)], 8=1
где Л (±)в 11 ^(±s) связаны, согласно (3), соотношением
Ш’ “ -24^ч>.	ш’’
Замечательно, что В(_)8 и Л(_)8, отвечающие акустическим частотам, имеют одинаковые знаки, а и А+)® для оптических частот имеют противоположные знаки (т. е. соседние частицы с массами т и М колеблются в противофазе). Распределение амплитуд колебаний для случая W = 10, s — 2 показано на рис. 138, где на оси ординат отложены номера частиц, а на оси абсцисс — соответствующие им амплитуды (о —для акустических и б—для оптических колебаний) .
Каким образом можно получить из результатов данной задачи предельный случай tn = Л| (см. задачу 7.1)?
б) Нормальные колебания
*8! = Ае Shl 2,1C0S (“«* + “<)
К sin 2л® + A’ sin (2п — 2) (р
1 — 71 о------;	------_____—_cos /м t а \
2п-1 s	Д-— „„,,2	I « т •>’
где
>2 =	[«-I- k q у (К - 4“ +	cos’<P, ],
a определяется из уравнения
K — k tg (2N + 1)	tg <ps.
л
®<<P,< V
$=!, 2,..., N,
Кривые для оптической и акустической ветвей частот представлены на рис. 139, а (при К > k).
Как совершить переход к предельному случаю K=k?
Ч)
Величина <ps=
ns
2(Л' + If
для s=l, 2,
,N получаем 2ЛГ
нормальных колебаний и собственных частот, имеющих тот же вид,
что и в пункте б) (рис. 139, б). Как найти недостающее и самое инте-
ресное нормальное колебание х2„=0,	—*2я+Д частота
у.5)	§ t колебания Линейных цепочек
которого ©2 = —-hA лежит в «запрещенной зоне» между оптиче-” т
ской и акустической ветвями?
Распределение амплитуд этого колебания показано на рнс. 140, где на осн абсцисс отложены номера частиц, а иа оси ординат —
Рис. 139.
соответствующие им амплитуды колебаний. Частицы, имеющие четные номера, неподвижны, а соседние частицы с нечетными номерами колеблются в противофазе с амплитудами, экспоненциально затухающими при удалении от левого конца цепочки («поверхностный фонон»).
7.5. а) Решение уравнений движения
тхп 4-Л(2х„ —	— xn+i) = 0,	п=|, 2,..., W (I)
(дополнительные условия х0 = 0, х«+1 == a cos \1) ищем в виде
стоячих волн хп = Д sin пф cos yt так, чтобы сразу удовлетворить первому дополнительному условию. Тогда из второго условия находим константу Д — c/sin(jV1)ф, а нз уравнений (I)—«волновой вектор» стоячей волны
<р ту2
2"= 1k'
sin2
При Т2 < -^установившиеся колебания
Oill /if
x» = 0Sta(1v + i)<pC0Si’'
(2)
имеют большую амплитуду, если знаменатель sin(W + 1)ф близок к нулю. Но именно это условие и определяет спектр собственных частот со, (см. задачу 7.1), т. е. при этом мы имеем случай, близкий к резонансу, у « <оя. При yC®i =2 8‘П 2 (ЛН- 1) коле^ания
(2) соответствуют медленному растяжению и сжатию всех пружипок как целого:
4k
Если у2 > — то- сделав в (2) замену ф — л — пр, получаем
х =(—ijK+>+”0——cosW
*п '	1	°sh(.V+ nv1,
где ch’	Амплитуды колебаний частиц убывают (прн «ф» I
— экспоненциально) к левому концу цепочки. Естественность зто-4Ь
го результата особенно очевидна для уя когда частота вынуждающей силы лежит гораздо выше спектра нормальных частот. В этом случае крайняя правая частица колеблется с малой амплитудой в противофазе с вынуждающей силой, a (N—1)-я частица в первом приближении покоится. Затем можно движение pV—1)-й частицы рассматривать как вынужденное колебание, вызванное вынуждающей силой большой частоты со стороны xV-й частицы, и т. д. Отметим, что в явлениях полного внутреннего отражения имеет место аналогичное затухание волны (например, при отражении коротких радиоволн от ионосферы).
4k
Какой внд имеет установившееся колебание прн у8 == —?
cos (W — п 4- И) <Р
б) х„ = а —, лг ,—гтт---cos yt,
' n cos (Л -J-
<p tnyz	4k
sm V=4T "P"
.	«h(,v—Л + И)1|;
*n = (-1)a dKJV+^t 'ros
, „ 4 _ wy® „ 4k np" v>-m~'
7.6.	Если частота вынуждающей силы лежит в области акустических собственных частот о < у2 <2klM или в области оптических 2k 2k
собственных частот — < у2 < —- (см. задачу 7.4а), то установившиеся колебания
sin (2г; - |)<р
*2п-1 - ° sin (2jV + I) <р cos > '
_ .и ~|/2fr —nrfa „ sir! 2 n<[
2" “Г 2k — Aly2 sin (2jV + l)<pCOST/’
где cos2 tp = — —m4*’ ), a верхний (нижний) знак от-всчает частоте у, лежащей в области акустических (оптических) собственных частот.
2k 2k
Для частот < -у» < —t лежащих в «запрещенной зоне», w„ cb (2я — 1)4
*гп-1 = (—1)‘ а (2 у + |) ф cos \1,
х =(_()"+"„ г/~2^-"Va sti 2п-ф MS f
SB 1	° Г Л1у! — 2frch(2<v+ 1)Ф
(24-т?>)(Л1уа-2Ч sh2 ф =-------фр----------.
и для частот у2 > k/ц, лежащих выше границы оптической ветви, sb (2п — 1)у_
x2n-l - а sb (2Л + 1)х 05 г/’
Л 1 /2k — ту2 sb 2пу „ t
Чп ° Т 2Л—Л1Тл s'; (2.V -1-1) Z “ Т ’
(Aly2 — 24)(my2 — 2k)
ch’ X =--------фр-------,
колебания затухают к левому концу цепочки.
7.7.	а) Решение уравнений движения
mx„ + *(2xn—х„_, —х„+1) = О, п = 1. 2...., N — 1,	(1)
тл‘хк+4(2хл—Хл_1)=0	(2)
(дополнительное условие «о — 0) ищем в виде стоячих волн: = Д sin ntf cosа), п = I, 2, .iV — 1,
(3) хк ~ Z?cos(<d( 4- а).
Из (1) находим связь 4k . , <р в — ЯП«-г- = <А
Из уравнений (1) и (2), с учетом (3) и (4), получаем систему
A sin JV<p — В = 0,
•- Л sin (.¥ — 1) <Р +	siT]2_^’ + 2^ = 0.
Отсюда В = A sin Мр, а параметр <р определяется как решение трансцендентного уравнения
sin Л'<р (—- sin8	— 2 —cos <р ] = cos Лгф sin ip. (5)
\ т 2	)
При тц >> т, кроме очевидных нормальных колебаний, когда частица гпц почти неподвижна (sin
~ ^8 Sln С05 “Ь аа)’ П ~ ’ 2...........jV*
т %
teA4K=2S-cos~r- s = 1-2...........л'-1-
имеется нормальное колебание, при котором амплитуды частиц линейно убывают к левому концу цепочки,
*!.'” = B-^cos(V + aJ,.), “n“^(1+4)'
Частина при этом колеблется между пружинками жесткости k (справа) и жесткости k/N (слева). Тот факт, что уравнение (5) имеет подобное решение, устанавливается следующим рассуждением. Предполагая ф малым и сохраняя лишь главные члены, получим из (5) т /	1 \
<ра = ——11 4-у )в полном согласии со сделанным предположением.
При Шд, т имеются обычные колебания, характерные для системы из (/V—1)-й частицы с пружинкой жесткостью fe/2 на правом
конце (параметр фв н частоты определяются из уравнения tg Мр =* Sin ф ..
~ ~~ 2 — созср^ Креме них, существует нормальное колебание, при котором амплитуды частиц убывают к левому концу цепочки
,« ib т	о 2k
ch “2" = Sn^S>1, “n=«n‘
Формально значение параметра ф можно получить из уравнения (5), сделав замену <р = л — £ф и предполагая ф болыуим. Это нормальное колебание можно рассматривать в первом приближении как простое колебание Частицы малой массы при покоящихся остальных частицах, а затем рассмотреть движение остальных частиц как вынужденные колебания под действием высокочастотной силы kxK == — Абсо5(сол?+ ал). приложенной к правому концу цепочки из Л;—J одинаковых частиц (см. задачу 7.5а).
б) При fe,v+1 k решение совпадает с решением задачи 7.2. При e.v+i k имеются нормальные колебания, при которых jV-я частица почти неподвижна:
«П1 = А. s-" "Ф. С,В (“.< + «.)	ЬП’ -у •
Ч,	s=l,2...JF-1.
Параметр <рв определяется из уравнения
^2 sin8 -5- —	* j sin /V(f = cos А’ф sin <p,
которое в рассматриваемом приближении имеет вид
k
tg Л7ф = — £---sin ф.
(6)
Уравнение (6) допускает еще одно решение, которое можно получить, положив <р = п — 1ф и предполагая ф большим. В этом случае имеем
- (- ч'4 'вк СОЗ (шЛ.( + а„), cii«A = ^, 4 = ^11,
2 4Л Л т
т. е. амплитуды частиц убывают к левому концу цепочки. (5 Г. Л. Цоткин. В. Г. Сербо
226
ОТВЕТЫ И РЕШЕНИЯ
[7.8
Каким образом можно получить это последнее колебание, используя результаты задачи 7.5?
7.8.	Пусть <рп — угол отклонения и-го маятника от вертикали, а) s-е нормальное колебание
<р„=cos (п - 4*) 4's cos w+“,)
где спектр частот (рис. 141) начинается со значения <оо = j/g/I:
<Pfi= s=0, 1,2.............-V —I.
б) Ясно, что при b — а = 0 все маятники (в линейном приближении) колеблются независимо друг от друга с частотой Ц> = y'~gTl.
С ростом параметра Ъ — а пружинки сначала ослабляют возвращающую в положение равновесия силу тяжести, а затем начинают «расталкивать» соседние маятники, так что малые колебания маятников вблизи вертикали становятся неустойчивыми.
Функция Лагранжа системы
2W
'fn-u. n—i
n—l \	‘
где удлинение п-й Пружинки (принимаем /|АП | <Сп)

Дп	1 •
С точностью до членов ф* включительно
2 (rfi *“ аЛ« " ^2 + РЛ*) + const>
_ (fr —д) kl _ 1	_«£_
а ~ amg ’ Р — 12 а ~ ±mgdA'
Уравнения движения в линейном по <рл приближении
ё
Фп + ~Г I^b - а (2% “ <₽nH “ %-1) 1 = 0
(1)
имеют решения в виде бегущих воли
<рп =
с частотами (см. рис. 142)
“s2 = -f-('-fa«n2-^). *- = тг
J2)
8 = 0,1,...,Я,
причем частоты Ио и <о« невырождены, а остальные частоты двукратно вырождены.
Отсюда видно, что при
4а — 1 >0, или b — а >	,
колебания неустойчивы — некоторые становятся отрицательными. Раньше всех обращается в нуль частота <oN. Ей соответствует i]\v = = л, т. е. нормальное колебание типа «гармошки», при котором соседние частицы колеблются в противофазе: <р„ s= — фп-ь Естественно поэтому и новое положение равновесия <ря0 искать в виде «гармошки»:
фю — — Фео = фзо = — фю = ... = — ф2.уо — ф-	(4)
Значение ф найдем из условия равновесия —— — о или •
%. - “ (2<Р« “ «W1 - tn-i) - "Г Ч1’ + 2р (Тл - Тл+ 1)S 4-
+ W„ -%-)’= о. (6)
что дает
ф= ±
Г 6 (4а — I) 192₽ — 1 '
Рассмотрим теперь малые колебания вблизи нового положения равновесия (4). Введем малые смещения
тогда с точностью до включительно потенциальная энергия (I) равна
и = 4- те12 [(1 “ 4- 4 - (“ - 24₽<р=> х
х (xn-x„ + 1)3j-:-const. (6)
Сравнивая (1) и (6), легко увидеть, что хи имеет решение такого же вида, как и <рп (2) с частотами
ш; = -у- [1----Г <f ° - 4 (“ ~ 24plf2> 511,2 v]’
„	а	I	9
Однако теперь для малых	- Ьсс of положительны
	24].'	2	3
(см. (3)):
ш» > л- [* “ лг ~4 ,а “2W)]=¥<4к - *» °>
т. е. малые колебания вблизи нового положения равновесия (4) устойчивы.
Таким образом, с ростом параметра а первоначальная конфигурация вертикальных маятников сменяется «гармошкой». Такое изменение симметрии подобно изменению симметрии термодинамических систем прн фазовых переходах второго рода. Аналогом а при этом является внешний параметр типа температуры, магнитного поля и т. д. (см., например, [23]).
Конечно, уравнение (5) может иметь и другие ненулевые решения, кроме найденного (4). Например, ему удовлетворяет значение <рл = которое, однако, не является физическим, так как отвечает большим углам отклонения, а само разложение (I) справедливо лишь при малых <р.
7.9.	а) Ток в n-й катушке обозначим qn. Функция Лагранжа
t=-г 2	—г (’»~ ’п+1)г ]+cos
(ток через сопротивление Zобозначен <?.v^i). Комплексное сопротивление Z(y) можно ввести в уравнения движения с помощью
диссипативной функции *)
f = 4-z^.+1.
Уравнения движения
2V1 +	(?1 — Vs) = и COS 'it,
+ 4- ^п~Чп-1 -«„+,) = 0.	"“2.3.......N, (2)
~С~ (^N+ 1 ~ ^A’) = Z^N+f	(3)
Решение ищем в виде
V„ = Re (Лг*'”-"”).
причем можем считать, не ограничивая общности, что — л/2 ф <; л/2. Из (2), (3) получаем
± v/^C=2sin(cp/2),	(4)
=4- ± у 4- (/ - тscr)- <я
Поскольку в сопротивлении Z происходит диссипация энергии, должно быть ReZ >0, т. е. в (5). а следовательно, и в (4) нужно выбрать знак плюс. При этом 0 <р С л/2. Амплитуда может быть определена иэ уравнения (1).
При 72 > 2?С/4 распространение бегущих волн по искусственной линии невозможно (ср. с задачей 7.5а).
*) Заметим, что уравнения движения для цепи с гармоническим напряжением частоты w можно получить и из одной лишь «диссипативной функции»
Уравнения имеют вид ной нулю).
f=“r2z„ <“>«>?
J?
SF
з= о (функция Лагранжа принята рав-«V»
б) Уравнения движения
^'<„-1 + Т" (г’2п-> - ’2п-2- «гл) =»•	"=2- 3.  • • > N-
S’^Sn + 4’(2‘’i„“’I"-l“?8-+l)==0-" = '-2’....... ,V1 (6)
с точностью до обозначений совпадают с уравнениями (I) в задаче 7.4. Кроме того,
&i<in + "с* («71 - <7а) e U cos yf>	(7)
~С~ (^22V+1 “ ^2^) ~ “ Z<^2N+i*	(8)
Решение ищем в виде
о	= а№~ ,(2п— 1)ф»
Я!-1	(9)
q№ = Be’VI-'2W.
Не ограничивая общности, считаем — л/2^ф^л/2. Из (1)
(1 — Y*/Y?) А — cos (f • В = 0,	9
Vi.2 = F7’	<10>
cos <р А — (I — Т2/т|) В = 0,	1,2
откуда
cos’ <р = (I - Т’/’4) (1 -
Пусть, например, у, <уг- Условия 0 cos 2<р I выполняются при 0 < Y Yi (область «акустических» волн, ср. с задачей 7.4) и при	(область «оптических» волн). Вне этой
области распространение бегущих воли невозможно (ср. с задачей 7.6).
Из формулы (8)
t i В i ( В \ В sin <р Zz=^C~~yC~e =уС (1- A" cos f) + Т'уС-'	(1|>
Здесь, как и в пункте а), должно быть ReZ > О, т.е. -^-sinq>>0. В области y^Tfi амплитуды А и В имеют одинаковые знаки, так что <р > 0. В области у2 < у< Vyi + Т^’ наобоРот’ < 0 и q; < 0. Подставив в (II) значения В/A, costp и sinq, получаем окончательно
У - 1 /	/.	Уе\2-^1Су»
23	+	2 У 2-а>2С’,-2 ' 2 Т1'
231
Отрицательное значение <р в области «оптических» колебаний означает, что фазовая скорость бегущей по линии волны направлена от сопротивления Z к источнику напряжения. Групповая же скорость, определяющая поток энергии (ср. с задачей 7.3), естественно имеет противоположное направление (см., например, рнс. 137, где dt0< I)
7.10.	Уравнения колебаний дискретной системы (см. формулу (3) задачи 7.1) преобразуем к виду
g /*гг+1 Хп т \ а
1
а
= 0.

(1)
Величина----== 4г— в пределе имеет смысл линейной плотности стерж-
а Iva
—х , ня р. Относительное удлинение отрезка а, т. е. величина —--2—1
а ’
х — к
пропорционально действующей на него силе г — ka —-----—1 по-
а *
этому в пределе ka имеет смысл модуля упруюсти стержня х. Таким образом, уравнение (I) в пределе переходит в волновое уравнение
<я*(Е.О .а8*(Е,<) „ ер ~' ое» -и-
(2)
где v = Ух/р имеет смысл фазовой скорости волны.
Вместо системы N обыкновенных дифференциальных уравнений мы получили одно уравнение в частных производных (ср. с задачей 4.29).
Отметим, что для данного вывода необходимо важное предположение о том. что функция хп (0 стремится к определенному пределу х(|, /), являющемуся достаточно гладкой функцией.
7.11.	При малых а можно приближенно представить смещения в виде	0. *n±i=*(t±0, 0=^(1.
дх{1.1) а8 /)	fl»№(L0 п
± а —5^-’	Т —± V +   • • ПР" этом УРага,е-
ние (2) задачи 7.10 переходит в уравнение
д2х и д2х на2 д}х др~~р'
В то время, как каждое из уравнений (1) задачи 7.10 содержит смещения трех соседних точек (дальнодействие), уравнение (1)
содержит лишь смещение х в данной точке £ (близкодействие). Член —	в уравнении (1) соответствует приближенному учету ма-
лого отличия системы от непрерывной.
Подробнее об учете пространственной дисперсии и исследовании уравнения (I) см. [19], гл. 4, § 4.
§ 8.	Нелинейные колебания
8.1.	а) Уравнение движения
А' +	— рА'я	(1)
решаем методом последовательных приближений (ср. с задачей 6.34): x = x,-&t = Aew + X»e-“l‘' -| Ьх.	(2)
«Сила»
-	= - рдзс3"“"’ _ зрлм«еи»' — Зрлл*2е_’“"' — (М’3?-'”'1"'
содержит резонансные слагаемые
—	— ЗрАА«2е-!в»' = - ЗР | А |Е к,
которые удобнее присоединить к слагаемому co<jx в левой части (I). Это приводит к замене
ю2 - М2 =ю2 + ЗР I А [=.
Для 8х получаем уравнение
б.г -р <оабх — — р (д3е3ш{ -| ко мп л. сопряж.), откуда
рЛ3
&Х ~ &03 e3tWr +комвл- СОНрЯЖ.
Итак,
х = a cos -[ ср) -| cos (3°* + 3<^ & = ~2~ ае^ (ср- с [1], § 28). На рис. 143 изображены графики x(f)
При р > 0 происходит ограничение колебаний, при р < 0 максимумы становятся более острыми. Эти особенности колебаний н знак поправки к частоте нетрудно усмотреть из графика L'(x). Другие способы решения см. в задачах 1,9 и 11.25в.
б) Решая задачу тем же способом, что и в пункте а), получаем:
г/Д Я
2а | Л |3 а/1‘* “о + е
учитывать слагаемое — 2ахсбх, содержащее резонансные члены
З05	3uj
^х=^|Д|3
“о 3“о
Это приводит к замене
5asfla
82.
к = a cos tat — — у<за cos 2о/ уда.
, t Y g
“ =>= cofi 4- де .
8.3.
“ g — IQ2 C0S Q/ + 12 (g — IQ2) (g — 41Q2) Sin 2Qt (обозначения задачи 5.9).
8.4.	х = л<014-х<*>+..ч
<0) _ fl COS Wi *	1 Cos
?4 = _______________________________Kfi _
— <0j)2	2m<02 (coj-— <!>|)2
af| cos 2(0^	cos 2a)2t
2m (tog — 4tOj) (lOg — <of )2	2m — 4o|) (co2 — co2)2
____________«fib cos (io, — <og) /____________
- (u, - в,)»] (ш2 ~ Bi) (‘“о “ “D
__________cf jfg COS (<01 + co,,) t____ m[<u2-(o>, |- ы!)а](ю2-ю2](ш2- m2) 
Какие комбинационные частоты возникают при учете ангармо-rriRx^ нической поправки — —!—?
4
8.5.	Функция «Лагранжа
£ = -j- й“ + уг) —	(/(/—^)’ + х2 — U2 — msv =
= ~Т (**+ — “i^ — “г^2 — ~г + 2а1“И + ....
ш? = #
___
а- 2тР-
„г____L
h ’ tt2 in 1
r mt
Действуя далее так же, как и в задаче 8.1, получаем a.ab
X = u COS (Ш,/ + <й — гк,8 (г,.ъ +	) cos (к,;! + шв( + <р + ф) +
2S, (25, - BJ с“ (“1г ~	+ Ф ~
ОС2 _ R&2	Rft2
У = ь COS (<o2f + if) ]--—2--+ —, cos (2coef 4- 24)) 4-
Z<°2	00)"
СШ2
+ ЧК-М) “8<г“*' + г<й-
Ангармонические поправки резко возрастают при 2(£>1£»б)2- Случай 2О|— о2 рассмотрен в задаче 8.10.
8.6.	а) Решение уравнения ищем в виде
х — Aeiiat 4- А *е-,ие.
Приравнивая коэффициенты при eital, получаем
(ы2 — оя 4- 2Лш+ЗР | Л Iя) Л = 4" f.
откуда
[(и?- <>’ + зр I Л Iя)2 + А«ш«] | 4 Iя =
Исследование этого уравнения, кубического относительно |Л|2, можно провести подобно исследованию аналогичного уравнения (29.4) в [I], 8.7. а) Решение уравнения колебаний
х4- 2Хх 4-	4-Л cos Serf) *4- рх3 = 0	(1)
ищем в виде
х = Ае‘ы +	(2)
причем сохраняем только члены, содержащие е ^'"'*). Приравнивая нулю коэффициенты при . находим
ы2Л + (и2 -	-2ЛЖ — ЗР | Л Is) Л* = О,
Л	(3>
у- ы2Л> 4- (<ия - ш2 Г 21О)Л - ЗР | Л Iя) А = 0.
Не равное нулю А возможно при условии
-у «2	- (й2 - 2iG)X - зр I А |а
ш2 —	4- 2/6)1 — зр I АI2 -у (1)2
*) Предполагаем, что члены с е*84"*, значительно меныпие, будут компенсированы вкладом в (2) третьей (армоники, как это видно из дальнейшего.
откуда
1 л |! = гр [“*-“§ ± V	“Sj2 - (2<А)*].
Из (3) получаем *)
. А 4Х s,n2<p=im
см 2’ = + Д V (“Г “о)' ~ '2ы>->2 •
Итак,
х = a cos (со/ -J-cp),
(5)
(6)
(7)
где 4 = -j-®4
Зависимость |А|2 от ш2 изображена на рис. 145 (для определенности считаем £ > 0). В некоторых областях частот возможны две
или трн (считая нулевую) различные амплитуды установившихся колебаний.
Амплитуды, соответствующие участкам AD и CD, реально не осуществляются, так как такие колебания неустойчивы (доказательство этого относительного участка AD см. в следующей задаче, а исследование устойчивости колебаний на участках ABC, CD и D£ см. в [8]).
б) С учетом третьей гармоники
х имеет вид
х — Л'1"1 4- /!•«—*“'+ Ве5‘“'+	(8)
Мы предполагаем, что |В| <£. |А|, что будет подтверждено результатом. Подставляя (8) в (1), выделим члены, содержащие еэ,ы(; при этом опускаем произведения В на малые параметры. Оказывается,
„ / Л МЕ\ „
В=[1б + ^)А	И
и, действительно, |В| <£. |А|.
•) Формулы (6) определяют фазу с точностью до слагаемого мл. Определение фазы с большей точностью не имеет смысла, так как изменение фазы на л соответствует просто сдвигу начала отсчета времени.
Таким образом,
х — a cos(co/-f- ср)-f- cos(3urf 4- if),	(IC)
где fe—2|CJ, ip=argB.
Нетрудно заметить, что пятая гармоника окажется малой второго порядка №А), седьмая—третьего (~ №А) и т. д. Эю служит обоснованием используемого способа вычисления амплитуд. Четные гармоники не возникают.
8.8.	а) Ищем решение уравнения в виде
x(f) = a(t)cos mt 4- 6(0sin mt,	(I)
где a(t) и b(t)—медленно изменяющиеся функции времен!. Длч определения a(t) и b(t) получаем систему уравнений (см. [1], § 27)
• / ЛцА.
ар|о— <оо11) = 0,
V	(2)
• /	А
Ъ — I со — с% — ~4~)а== °-
Если |«)| — <ос| < ft«0/4. то ее решение
а(0=	4- С2^'),
b(t) = а2( Cte-’' — C2es'),	(3)
где
S = -i- /(Лш„)2 — 16 (О — о,,)2.	о,.2 =	±	" Ч).
Отсюда
х = C'est cos(cof — <р)4- C"e~et cos(cof 4- q:),	(4)
где tg<p=ai/a2 (рис. 146).
Таким образом, колебания, вообще говоря, неограниченно возрастают. Скорость их роста, характеризуемая величиной s, действительно мала. В реальных условиях возрастание амплитуды колебаний прекращается, например, если становится существенной роль ангармонических поправок (см. задачу 8.7) нли обратное влияние колебаний иа устройство, периодически изменяющее частоту.
Полезно обратить внимание на аналогию между полученным результатом и особым решением задачи о нормальных колебаниях цепочки частиц, соединенных пружинками различной жесткости (задача 7.4в). Неоднородность с периодом 2a вдоль цепочки приводит к нарастанию вдоль цепочки амплитуды установившегося колебания.
причем «длина волны» равна 4а (рис. 140), подобно тому как периодическое изменение со временем частоты осциллятора приводит к возрастанию со временем амплитуды.
Рнс. 146.
Рис. 147.
Еще более полную аналогию можно обнаружить с задачей 7.6. Области неустойчивости относительно параметрического резонанса соответствует запрещенная зона спектра колебаний цепочки.
К подобным же уравнениям приводит в квантовой механике задача о движении частицы в периодическом поле. В этой задаче также появляются «запрещенные зоны» и «поверхностные состояния».
б) Если [со — (Оо| >Л^о/4, то
х = С₽! sin (flf + ф) cos — Сря cos (fif 4- ip) sin <of, где Й == -|- V16 fro — %)2 —	,
P I V4(° — “<) ± при (0> (00l
2 I + 1 4 ((00— 0J) i; Л(00 При <0<(0j.
Колебания представляют собой биения:
х = С |/41 <0 —	1 “ Л(й0 cos (2£М4~ф) cos (cof 4- 6),
где 6 — медленно меняющаяся фаза (см. рис. 147). Если частота приближается к границе области неустойчивости, то глубина модуляции колебаний приближается к полной, а период их неограниченно растет.
Каков внд колебаний при [со — 0)с[ = йо0/4?
8.9. Пусть при 0 < i < т колебание х = f. Тогда на отрезке т < t < 2т,
х = aei(i>tt 4- be~i(0st,
где а и 6 определяются условием «сшивания» при t = т:
л (т -0)»т|т 1 0), х(т — 0) = а (т 4- 0),
откуда
ei<(Oi—ю*)т

Аналогично находим, что при 2т < t <z Зт
*=аг,'°'1+
где
+«>1 .
а = е W,T I cos <овт 4- i —-------— sin <о2т
I	2(o1cd2
Ясно, что колебание вида
4- Ве~™*'	(1)
при 0 < t < т переходит через период 2т в колебание
А (<«*“' + ₽£“”•') + В	+ ₽•?’“') =
= (аЛ + р«В) «?*"' + (0Л + а«В) е-!в>*.
Найдем такую линейную комбинацию (I), чтобы через период 2т колебание сохраняло свой вид с точностью до постоянного множителя:
(аЛ -I- p«fi) f™1' + (РЛ + а’В) e_iM1’ = Ц (Аг1"'1' + Ве~'“''), (2) здесь t' = t — 2т,
аЛ J- р«В = |И-г*“‘тЛ, PA+a*B = ji?2i“'TB.
Система (2) имеет нетривиальное решение при условии (а - рг-2'“л) («• - рг2™-1) - ₽₽• = О,
откуда
Н.2 = Т ± /Vя ~ 1.
где
(1)2 | (0^
у = Re (cte2’1011) = cos с^т cos соат — —1-------sin (i)xt sin <оат.
Через п периодов колебание
= л1.2 (fkM +	° <' < t.
переходит з
х, 2 («) = р? 2А J £ (?“'' +	), 0 < Г = « - 2пт < т.
Любое колебание представляет собой суперпозицию колебаний вида Xi,а, в частности действительное колебание (только и имеющее непосредственный физический смысл)
*(/) = Ле<ш<'+0<(<т,
есть сумма Х|(0 + *г(0 с
А’-М . М-А« Л1= К-К ’ М-ч '
Если 7 < 1, то |Ц|,2] “ 1 и колебания хь2(/) (а с ними и *(/))' остаются ограниченными.
Если же у > 1, то щ > 1, и амплитуда колебаний неограниченно возрастает. Это и есть случай возникновения параметрического резонанса. Нетрудно убедиться, что при малой разности частот
Рис. 148.
| «01 — соа| <£ вл это условие выполняется, если частоты близки к лп/т:
| (И; + И.) 1 - 2ЛП | < - "ц~ “Т 
На рис. 148 (взятом из [20]) показаны области неустойчивости О1носительно параметрического резонанса.
8.10.	Уравнения движения
у frt’r — g*y*-y — ot
и 4- 4ч,°? — сх< => О.
Решение ищем в виде
у---/pfrnt-|-Л*р-*<0» । gr
у == /?£«<’» f_ £j*p_7,,u' -p бу, принимая, что А и В — медленно меняющиеся амплитуды колебаний, и более быстро осциллирующими слагаемыми бх н бу можпо пренебречь: |А| с й)|Л | с (1)2|А|, |В| с ш|В| <1>2|Я|, бх бу |А|. Сохраняя только слагаемые с eiblt (соответственно e2i(at) и пренебрегая |А|, |В[, получаем
wA — faHA* — а
(П
4<1>В-”=Л’ = 0.
Легко видеть, что из (1) следует |А|2-5-4|В|г= С = const	(2)
(это чакон сохранения энергии) п
Д«2В + ЛаВ* = О = cons'..	(3)
Используя (I), находим
и 4 I'll’-to U'2c-/I2»*)-	«)
Возведем (4) в квадрат и учтем (2), (3):
(4 I А 1г'Г = - ^ 1<Л’2й + /-=-В’)2 - 4 И I51 в |21 =
\ut ] СО*
=-^Sll д I1 <с —I д |«) — О«1. О)
Уравнение (5), аналогичное закону сохранения энергии для задачи об одномерном движении частицы с координатой |А|2, удобно исследовать с помощью графика t/flAf2) = ()А|2 — С) |А|* (рис. 149).
Таким образом, амплитуда |А| испытывает колебания — происходят биения. Зависимость амплитуд ]А| и |В| от времени может быть выражена через эллиптические функции (мы не будем этого делать). 16 Г. Л. Коткин, В. Г. Сербо
|А|2
Рис. 149.
Отметим, что, в отличие от колебаний осцилляторов с линейной связью (задача 6.8), в данном случае от начальных амплитуд н фаз зависит не только глубина биений, по и период.
Эта задача имеет отношение, например, к связи продольных низ-гибиых колебаний молекулы СО2 (так называемый резонанс Ферми, см. [21]) и к удвоению и делению частоты света в нелинейной оптике (см. [22]).
8.11.
а2у2
8.12. а)
б)
(ср. [11. § 30 задача 1).
С/афф
^ефф
0)
где (1>0 — собственная частота осциллятора.
Обратим внимание на то. что зависимость Vai^ со г~6 характерна для меж молекулярных сил. Если подставить в (1) значения величин*): а ~ е2 ~ (5 • ]0-1° ед. СГСЭ)2, т ~ 10~27 г, а ~ 10-8 сл, о»10м сек~1, типичные для атомов, то получим 6'Эфф~ ~ 10-59 эрг-см^г*, что по порядку величины близко к правильному значению для ваи-дер-ваальсова взаимодействия. Такой результат может служить указанием на физическую природу этого взаимодействия. Полный же расчет ван-дер-ваальсовых сил возможен лишь в квантовой механике.
8.13.	Движение вдоль оси z почти равномерное, z = vt. В плоскости (х, у) на частицу действует быстро осциллирующая сила fx = 2Ах sin kvt, fv ~2Ау sin kvt. Соответствующий эффективный
потенциал	(ха + J/a), где Q =
Офф 2	tn.RU
е2 (l0~t!\)2
’)Б системеСИ: °-~
а ~ 10-*° л. 1/эфф ~ Ю-18 [Л-]"
т ~ Ю~30кг,
Согласно условию частота колебаний силы kv Q, так что сила действительно быстро осциллирующая. Итак, в плоскости (х, у) частица совершает гармонические колебания с частотой Q около оси г. Эта задача иллюстрирует принцип жесткой фокусировки пучков частиц в ускорителях.
8.14.	Уравнения движения
тх = Ж (х) у,
ту = — —3№(х) х. с
Ищем закон движения в виде
х = *4-£.	+	(1)
где слагаемые t) описывают быстрое движение по почти круговой орбите, а X, У —медленное смещение ее центра (сравните с [1],§ 30).
Подставляя (!) в уравнения движения, разлагаем 5£?(Х-]-£) по степеням
х+Ё=в,У+ оч + — тс дх
У + Ч = -шХ-ш|------'-'1* HX+i)
тс их
и разделяем быстро осциллирующие и медленно меняющиеся слагаемые. Для осциллирующих слагаемых
t = w]> t) = — (i)5, о =	(X),
тс
откуда
| = г cos of, t] = —г sin (of.
Для медленно меняющихся членов имеем
Х= шУ+-£. ?*<!&, тс дх
 е ш
У = —шХ —ДЕ> где	тс дх '
ф'|> = — г!и <cos“	<Е Ё> = о.
Поскольку X, У*'- выХ, 8(оУ, то левые части (2) можно положить равным» нулю.
16*
Итак»
y = J±" =-1_ЕС,Х = 0.
2тс дх 2
(Скорость смещения центра орбиты (скорость дрейфа) в более общем случае рассмотрена в [2], задача 3 к § 22 и [8], § 25.)
8.15.	Уравнение движения шарика
т? = -^Й + /(0-
Собственное движение шарика под действием пружинки описывается «низкочастотным» смещением х = у — у0 cos yt, для которого
mJ = - dV (* + Со5 Tt>
dx
Усредняя по периоду 2я/у высокочастотного движения
(<cos2n+1 уО = 0, <cos2yf> = -L, <cos* yty = JL), получим эффективную силу и соответствующую эффективную потенциальную энергию
W = Лх‘ -г11*'- А = — с + 4" е®0’
График функции £/»ф$(х) изображен на рис. 150.
При А > 0, пли Т =у^> Тс — 4С/9В шарик колеблется
вблизи точки х=0с частотой си = у2Almcoy ТТ . При
А < 0, или Т <Г Ге, минимумы ^вфф(х) расположены в точках ± *0 == ± У—Л/2В и шарик колеблется вблизи одного из них с частотой со = д/__ ~Утс~т.
Возникающая картина весьма близка к картине фазовых пере-
ходов второго рода, описываемых
Рис. 150.	феноменологической теорией Лан-
дау [23]. Быстрые вынужденные колебания являются аналогом теплового движения (соответствующего оптическим модам колебаний системы, не связанным с переходом), а величина Г	аналог температуры. При больших Т систе-
ка колеблется вокруг положения равновесия х ~ 0. При этом имеется симметрия относительно замены х->— х. При уменьшении температуры до значения Т< Тс шарик начинает колебаться вокруг одного из новых положений равновесия: х0 или —хо. При этом симметрия х->-—х, очевидно, разрушается. Значение Те — аналог температуры фазового перехода второго рода. В окрестности точки Т=Те величина Хо мала, x0 cjoJ/ 7'с —Т, и мала частота собственных колебаний <о.
§ 9.	Движение твердого тела. Неинерциальиые системы отсчета
9.1.
а)	/2а2 (ш| М) 2а*(т-М) | 2аа (л? — Al) 2а2 (т -J- М) \	0	0
б)	14а2 т	0	0	\
( 0	4о«А1	0
\ 0	0	4д2 (т Af) J
0
о
4аа (гп -}- AI),
9.2.	Для обеих фигур одной из главных осей является ось, перпендикулярная к плоскости рисунка и проходящая через центр инерции фигуры (ось z). Главная ось х повернута на угол <р к стороне (Ул/ каждой из фигур. Главная ось у перпендикулярна к оси х. Обе эти осн проходят через центр тяжести фигур.
а)	Координаты центра в осях О'х'у' (х' = b, if = сг):
= 2 (а2 + Ь2) (АЦ-/Я),
ZXJt = (аа + Р) (Af -J- m) + Mb* a2)2 (Af + m)» + 4aa63 (Af — m)2, lyu = (a2 4- ba) (M + m) 1 f(b2 - a2)2 (M -f- ш)2 ,- 4aaba (A] m)af
.	— J rr.i„ 2ab (Af — m}
при a a b, <f - -y arctg
б)	В осях O'x'ifz' (рис. 15]) координаты центра масс О: х* = у' = a, z' = 0. В системе координат Ох"у"г" с осями, параллельными осям х', у', г', тензор	инерции
/3	1	0\
/’.k = 4та2	1	1	0 .
\0	0	4/
При переходе к системе Oxyz, повернутой иа угол <р вокруг z".
координаты преобразуются следующим образом:
х — х" cos ф + у" sin ф, у = — х" sin ф 4- у" cos ф, z = z", а компоненты тензора инерции — как произведения координат: 'хх = 4х с“2 Ф + '2,'ху sin Ф cos Ф + 'т sin2 Ф =
— 4та2 (3 cos8 ф -f- sin 2ф + sin8 ф),
Ivv = 4/nfi2(3cos2 ф — sin 2ф 4- sin® ф),
Ilz — I6ma2,
lxv — 4maz{— sin 2tp 4- cos 2ф), ^XZ ~ IyZ — 0.
Угол ф выбираем так, чтобы выполнялось условие 1хи — 0, например Ф = л/8. Тогда
'хх = 4"мг(2+У2 ). 1т = «™“(2 - |Т).
9-3- /п= 2
i.k
9.4. Центр масс: точка на оси симметрии (/? — г) г3 на расстоянии	—с__ от центра тара
влево. Тело ~ симметрический волчок. Отно-т 2
/, = /,=
сительне оси симметрии г = ——--------- -— у
3	/<3 — г° 5
Х(/?6 — г5);относительно перпендикулярных осей, проходящих через центр масс,
[-|-(£s
т
R3 - г3
№-r)sfSffq (Я3-г») Г
О-5- О,й= (2М 3/ib (см. [2|,§ 99).
\ п /
9.6.	Центр масс расположен на оси полушара на расстоянии
R от центра шара (/? —радиус шара). Момент инерции относи-
тельно любой из осей, перпендикулярных к оси симметрии (т — масса полушара)
/ = — т/?2 - т (А /?Г = А т/?8. 5	\ 8 /	320
При колебаниях центр масс может двигаться только по вертикали.
Пусть ф—угол поворота полушара, z— высота центра масс над 3
плоскостью z — R — -g- Z?cos ф. Функция Лагранжа системы
1 • 1 ] •
L ~ "2~ /ф2 4- -~2~ тгъ- mgz, или при малых ф L ~ -ту- /фв —
3
'	Отсюда частота малых колебаний
<0=1/122. JL.
Г 83 я
9.7.	Очевидно, скорость шарика после столкновения v может быть направлена только вдоль или против V, т. е. v=vV/V. Скорость гантельки после удара и направлена вдоль V, ее угловая скорость <о.
Законы сохранения импульса, энергии и момента импульса (относительно центра гантельки):
mV = то 4- 2ти,
1 1 1
mV2 — то* + mu* +	/ ю8*
mVг = ш 4- /о,
где т — масса
ции гантельки.
Отсюда
14
шарика, г — его радиус, / — тг* — момент инер-о
_LV _?	__L.L
---13 V' u“ 13 V’ ш~ 13 г
9.8.	В настоящее время расстояния от центра инерции системы
Земля — Луна до Земли и Луны равны —~—р и — р соот-М + т М -г т
ветственно, а момент импульса системы
Мт _
^ = м+тг**. (»
где Qji и Од —угловые скорости вращения Луны вокруг Земли и Земли вокруг собственной оси (й3 /£2Л«28). При записи (1) мы считали Луну материальной точкой, а у Земли учитывали вращение вокруг центра инерции и вокруг собственной оси (с моментом инер« ции I = 2- Ata‘).
5
В момент, koi да сутки сравняются с месяцем, угловая скорость вращения Земли ю совладает с угловой скоростью Луны, расстояние от Земли до Луны (по третьему закону Кеплера) станет равным R \ а момент импульса
(2)
(3)
где
Из (!) и (2) найдем уравнение для х = -щ: Ол X (1 + k — Л)8 == ks -g-,
|2__ m Q-n-- 3S
Уравнение (3), или х{4,8 —x)s — 2,01, имеет два действительных корня: Х|« 1/55 и х2«4. Первый из них отвечает будущему, второй — прошлому. Соответственно в первом случае месяц станет равным 55 современным суткам, во втором— был равен 6 часам. Расстояние от Земли до Луны станет равным 1,6/?, а было—2,6а.
(О более реалистических, чем рассмотренная, моделях эволюции системы Земля — Луна см., например, [24], гл. 2.)
2
8.9. а) Тело вращается с угловой скоростью — (о; в тепло пере-
5	'
шло — начальной кинетической энергии.
‘	1/2
б) Линия центров вращается с угловой скоростью	® вокруг
направления момента М, составляющего с ией угол 45°; при этом 5 тело вращается вокруг линии центров с угловой скоростью -^-(0.
19
В тепло перешло начальной кинетической энергии.
2о
0.10.
9.11.	Момент инерции эллипсоида (см. [I]. § 32, задача 2е) от-2Л1
носительно оси вращения/а“ —— а2; относительно любой перпенди-5
кулярной ей оси, проходящей через центр масс, /1 = —-J—-J1
5
(Л! — масса эллипсоида).
Налетающая частица массы tn-^М передает эллипсоиду импульс Р= (Рх,pv,ps} —1,0) и момент импульса М=/лц(р,],0,—р2).
В системе, движущейся со скоростью » найдем (см. [1], § 33), что эллипсоид будет вращаться вокруг полуоси с с угловой
М 5т-рг
скоростью ь23 ~ -г=- = “ одновременно прецессируя вокруг /3
правления М с угловой скоростью
Й_|М| _ 5™К₽i + ₽2
/, М (с2 4- с8)
9.12.	Обозначим угловую скорость вращения диска вокруг его оси ф, Угол между этой осью и направлением на север <р. Угловая скорость диска в инерциальной системе «>=£24-4?+it > ее проекции: на ось диска w3—ф+£2 cos a cos ср, па вертикаль <<>i = q>4-<2 sin а, на горизонтальную ось, перпендикулярную оси диска, cos a sin ф.
Функция Лагранжа равна кинетической энергии (учтем, что Л=/2):
L = Д (ф 4- £2 sin а)2 4- ~2 i^s cos® а s‘n® Ф +
4-	ту /3 (ф Q crs <х cos ф)2.
Исследовать движение удобно, используя интегралы движения pv и £ = рм>ф+ pv4 — £'
— /3 (ф 4- Q cos a ccs ф),
£ = у Л (Ф® — Q2 sin2 а) — -g-	8 cos2 a sin2 cp +
I
+ *2 /3 (Ф2 fi2 cos2 a cos2 <p).
Исключив ф, находим
£ = J W + Р0фф (ф) + const, где
С'0фф ф) — — cos а cos ф 4- -g-/jfi2 cos2 а cos2 ф.
Ограничимся случаем ф»й. Тогда p^fvls^, и<яю (Ф) cos а cos «Г*
Функция [У9фф (<р) имеет минимум при <р=0 (т. е. в направлении на север). Ось гирокомпаса колеблется около этого направления. Для малых колебаний
] .
^Эфф («Й = У /8г«>Й C0S « • ?8 + Const
полминуты /для-уЗ-сояа.
и частота колебаний осн равна )/ ~ £2фcos а. Например, для гироскопа, делающего около 10 тысяч оборотов в минуту, период колебаний приблизительно
Каким образом можно учесть момент инерции рамки?
9.13.	Удобно использовать подвижную систему координат с осью х, проходящей через точку касания диска с поверхностью стола. В этой системе
d'M
д- + |<р, М1=К.
где М — момент импульса волчка относительно неподвижной точки О, К—момент действующих на него сил (ср. [I], § 36). Проекция (I) на ось х
—	= Кх,
Очевидно, Кх—С, так что M3C=const.
Пусть /1 = /г^=/з — главные моменты инерции волчка относительно точки О. В начальный момент
M — Q/з, Mx = £/3cose.
Когда проскальзывание прекратится, ось х станет мгновенной осью вращения, т. е. угловая скорость волчка w будет направлена вдоль оси х, а А1х=/з(о cos2 6+/1W sin2 6. Таким образом,
_	а/, с<» е
/я cos2 0 -f- /1 sin® 6 ’
Отметим, что после прекращения проскальзывания (р=—cd tg 6-
9.14.	Пусть а=Ь^с—полуоси эллипсоида, R, 6, Ф— сферические координат центра инерции эллипсоида, 0, <р, ф— эйлеровы углы, причем ось х3 движущейся системы направлена вдоль полуоси с. Кинетическая энер1ия гела (см. [1]. § 35)
г = у (R* + Я2ё> - sin2 в) + у (1р« Йп« 0 + в2) +
+ у (<f cos е + 4)*, (1)
где ц = /2 = ~ (с2 4- с2) и /3 = ~£~а2—моменты инерции эллипсоида относительно осей Xi, Xs, х$.
Предложенная потенциальная энергия взаимодействия эллипсоида с кулоновским центром может быть преобразована к виду
утМ yMD 3cos2tz— I
и-~~ R - 4	’ Я3 ’	w
где D==2(/j—/3), а а —угол между радиусом-вектором R и осьюхз-Единичный вектор ехз» задающий направление оси, имеет компоненты еяз= (sin © sin <р, —sin 0 cos <р, cos 6). Отсюда
Rex
cos a =	8 = cos 6 cos 0 + sin 6 sin в sin (ср — Ф).	(3)
Из (]), (2) и (3) получается окончательное выражение для функции Лагранжа L=T —V.
9.15.	Рассмотрим вначале влияние только Солнца. Начало системы координат совместим с Солнцем, ось Х8 (см. обозначения предыдущей задачи) направим перпендикулярно к плоскости орбиты Земли, ось х3 — на север.
Можно ожидать, что угловая скорость прецессии земной оси <р мала по сравнению со скоростями суточного ф и годичного Ф вращения Земли. Поэтому в функции Лагранжа сохраним лишь члены первого порядка по ср. Кроме того, положим постоянными величины R, 6=я/2 и Ф, причем
у = 2яУ1й='г°л.	(И
и усредним cos2 сс за год: <cos2a>=V2 sin2 6 После этого
£ = 1 /,0s + | /, ГО* + 2W cos 6)-	stns 0.
Из сохранения Ри>=/з(Ф+<рсо5 0) и pv=/8ф cos 0 следует, что 4 и 0=23° сохраняются (с точностью до величин порядка ср). Уравнения движения по углу 0
/1*0 + /зфф sin 0+	---— sin 0 cos 0 = 0
с учетом того, что 0 ~ 02 ср2, дает
а2 — с« _ 2 (а — с) Подставляя соотношение (I) и —----------------» получим
г;д= — А —---£ Al cos 6 дь — 16" в год,
2 “ ф
Скорость прецессии, вызываемой Лупой, получается из (2) заменой массы Солнца М иа массу Луны и R — расстоянием от Земли до Луны и оказывается рапиой — 31" в год. Полная скорость <р= =—48" в год. Наблюдаемая величина (рэкси =—50,2" в год (см [24], гл. 2).
Таким образом, земная ось вращается вокруг оси Xs с периодом около 26 тысяч лет в направлении, противоположном вращению Земли вокруг Солнца (так называемое предварение равноденствий).
9.IC.	Al, +	Л1.А1, = Кй
при /[ = /2
/И1 — В сез ((о/ - - ф), Л12 = В sin (со/ -f- ф), М3 = const,
<й = ^7^ ~ 7?') (см- 14» § 36» а также СР- с задачей 10.20).
9.17.	Рассмотрим движение вокруг оси, близкой к оси инерции
Xi. Из уравнений Эйлера (см. [1], формула (36.5))
61+^=Аад, = о fl
получаем £?i~const с точностью до членов, пропорциональных Й2,з/£i*Cl. Два других уравнения при этом условии становятся линейными относительно Й2 и ®з- Предполагая
й2.3~А
получаем для s уравнение
(1)
(2)
При /2<Л-</з или /з<Л</2 уравнение (2) имеет действительные корни, что. согласно (I), соответствует неустойчивости вращения относительно оси Xj.
Если же момент инерции /1 является наибольшим или наименьшим, то уравнение (2) имеет мнимые корни, т. е изменение fiz и йз имеет характер осцилляций и вращение вокруг оси х( устойчиво.
9.18.	Движение шара определяется уравнениями
w?v=mg-{-f,	(1)
/о = [at ],	(2)
v+[(oa] =0.	(3)
о
где т—масса шара, / — —та2 —его момент инерции, а — радиус
шара, проведенный в точку его касания с цилиндром, f — сила, приложенная к шару в этой точке (сумма сил реакции и трения), v — скорость и <!> — угловая скорость шара.
Удобно воспользоваться цилиндрическими координатами с осью z, направленной по оси цилиндра. При этом необходимо учитывать, что проекция скорости изменения любого вектора А на подвижные оси определяется формулами
(А)Ф=А,+ИЧ = А» - ^лг>
(А),= Лг + 1И1г=Л,-<рИф	(4)
(г = b — a,q,Z — координаты центра шара, <p=vc/r), Из уравнений
rq4-a(i)i=0
получаем
ov= const, (i>t = const, fv = o.
Из уравнений
tnvz = —tng+fz, Vt — ato?.==0,
/	) =---аД, / (tor - фШд) =0
следует
(/-{-ma2) to^-J-Z^Wo:=0,
откуда	________
ш =Cca>(C«Fa), »=!/' ;= lZ4-.
v	' / + mcr r 7 r
tof = —• 2av^	Ts’n a^’
z = z0 ~ a sin (Qt + a).
Таким образом, шар совершает гармонические колебания по высоте, и в такт этим колебаниям изменяется радиальная компонента угловой скорости.
9.19.	а) В качестве обобщенных координат выбираем координаты X, ¥ центра и эйлеровы углы ф, 6, ф ([1]. § 35). Ось Z вертикальна, подвижная ось х3 направлена по оси диска. Линия пересечения плоскости диска с плоскостью XY (линия узлов) составляет угол ср с осью X. Функция Лагранжа
£ =	(Х« + У« 4- с262 cos2 6) + .1 Л (02 4- ф2 sin2 6) 4-
4- 2. /3 (ф cos 0 + ^)2 — mga sin 6,
где /[=/2 и /а—моменты инерции диска относительно осей Xi, х2, х3, а — радиус, т — масса диска (высота центра диска над плоскостью Z=a sin в).
Интегралами движения являются обобщенные импульсы
тХ = рх, mY = ру,
/jср sin2 64-/3Cos 6 (ф cos 6 4- ф) = рф = Mz,	(1)
/3 (ф cos е + ц’; =	= Л(а
и энергия, В системе координат, движущейся с постоянной скоростью (X, У, 0), центр диска движется только в вертикальном направлении. Из (1) находим
• Му — Мя cos 0	«	д.« М7 — Л1« cos 0
^=—/,3.^-е	 ^4; —We -cose- й
и, подставляя в интеграл энергии, получаем
1	„ „ „ • Alq (Му — ALcosO)2
£ = 1 (/, + ma! cos" 0) 0" +	-I- 1 -	> + mga sin 6.
£1Я	Z/j Sill и
(3) Отсюда через квадратуры определяется зависимость 6(f), а затем с помощью (2) зависимость ф(/), х]>(0-
Угол наклона диска совершает колебания, и в такт с ними изменяются скорости прецессии ф и вращения вокруг оси ф. Уравнения (2), (3) подобны уравнениям движения тяжелого симметрического волчка (см., например, уравнения (4)—(7) из [I], § 35, задача I).
Качение диска устойчиво при mga IiH# верчение—при
б)	В отсутствие проскальзывания на диск, кроме сил тяжести mg и реакции опоры R, действует еше сила трения f.
Уравнение
М — [aR] = [af]
удобно записать в проекциях на оси Z, Хз и £ (ось £ — линия узлов)*):
= fip cos Л1з - ha' d dL dL .	. л
л 7^^ = fs“s '	(5)
Здесь а — вектор, проведенный из центра диска в точку его соприкосновения с плоскостью.
Запишем уравнение
mV=f-{-R-|-mg
в проекциях на оси £ и т), где ось т] горизонтальна в перпендикулярна оси £ (см. формулу (4) предыдущей задачи):
ft=m(V)t=m(VE+<fVn),
Условие качения без проскальзывания V+[fia]=0 приводит к равенствам
V5=—c(4'-hpcos 0), Vn=a0.	(7)
Подставляя (I). (6), (7) в (4). (5). получим систему уравнений относительно углов Эйлера. Движение без проскальзывания и без отрыва диска от плоскости возможно, если
g+Z^O
(р—коэффициент трения).
Полагая 6=0, получаем <р=ф=О, причем 6, ф и ф связаны соотношением
/д Ф (ф cos 6 4- ф) sin 6 — sin 6 cos 6 + mga cos 6 — 0	(8)
(здесь и далее з = Л з +zkq2)- Центр диска, двигаясь с постоянной по величине скоростью У=о|йз|=а|ф-Ьфсо8 0|, описывает окруж
*) В отсутствие силы трения эти уравнения представляют собой уравнения Лагранжа для углов Эйлера.
ность р<адн\са R = V/|<p|. Условия (8) можно представить также в виде
= | li0 V2 cos 6 + mga2R2 etg 0
В частности, если масса диска сосредоточена в его центре (/[=/3== =0), то получаем элементарное соотношение: l/2=g/?|ctg 0|.
Гироскопические эффекты, возникающие при отличных от нуля /1,3. могут оказаться весьма значительными. Например, для одно-
R^>a получаем ~ V2 — в том же счучае 2V2=
родного диска^2/м = !3 — ~ та2 ) в случае = g7?|ctg0|; для обруча (2Л — /3=/на2) = g/?|ctgO|.
При качении диска s вертикальном положении
0 = ~, <р = 0, ф = £23 — const.
Для исследования устойчивости такого движения положим в уравнениях (1), (4) — (7)
0=Л--₽, ₽<С1, 4>~₽~₽fis«fi3,
и сохраним только члены первого порядка малости. Получаем
Л4г = /[ф4-/з^з^=const,	Qs—const,
+	— mgi.P =• О,	(10)
откуда
4 ₽ +	—,n№ J f = j-3 Л1
Если
й2>дт?п,	(|1)
ltl3
то при отклонении угла 6 от л/2 возникают малые колебания р и q?:
Р =	—£ -г ₽0 cos (wt + d),
/xwa
»	тр.аМг	/3Q..R0 . , . , A.
Ф = ~----5—~ — 3 J10 sm + 6),
2	n2
где co2 — —~г
'I't	'l
Направление движения диска также испытывает малые колебания, причем диск движется не вблизи прямой, а вблизи окружности ради уса oQ3 /|<d8/mgaM z.
Таким образом, наличие малого отклонения начальных условий от (9) может привести либо к малым колебаниям вблизи «равновесного» движения по прямой (если Mz — 0, ₽о^О) либо к новому «равновесному» движению (если A4z#sO, ро^О).
Если неравенство (11) не выполнено, то движение неустойчиво.
Можно сказать, что движение происходит с 6~const, если в «пространстве» 0, ф, ф точка лежит на поверхности, определяемой уравнением (8). Нетрудно убедиться, что прн условии (И) движение устойчиво относительно возмущений, выводящих точку (0, ф, ф) с поверхности (8) и безразлично относительно ее перемещений по этой поверхности. Аналогично обстоит дело и с устойчивостью движения диска на гладкой плоскости (нужно только заменить/^ 3 на/1,3)-
Верчение диска вокруг вертикального диаметра устойчиво, если
в)	Отсутствие вращения вокруг вертикальной оси (верчения) приводит к условию
= Ф 4- ф cos 6 = 0.	(12)
На диск в этом случае действует добавочный «момент треиия верчения» N, направленный вертикально, и вместо (4) получаем
Alz = cos 0 N, M3 ==> f^a 4- A’ cos 0.	(13)
Интегрирование уравнений движения относительно легко сводится к квадратурам (в отличне от уравнений пункта б)).
Движение с постоянным углом наклона возможно, если, кроме условия (8), выполняется й условие (12). т.е. ф и ф определяются углом 6. В этом случае
R= а | sinO tgOI,	slrl0—
l3 — etg2 0
Качение диска в вертикальном положении устойчиво при Яз >
г)	При наличии малого наклона плоскости к функции Лагранжа следует добавить член mguX (ось X направлена вверх вдоль плоскости, ось У горизонтальна, ось Z перпендикулярна плоскости). Полагая в (1), (4)—(7)
е=Д~Р, ₽«1,	~ ₽« £3Z> ф~₽~ЙгС^г
17 Г. Л. Коткии, В. Г. Сербо
И, добавляя вклад CL, получаем
l\ S + 01 “ 4)	“ "igop “ mgaa sin-&zf,
ф + (^a 4- 2/na8) &zp “ — mgaa Соз
откуда ’
ф « « /2 +	4- a cos Oz/. p = -2a sin Qz/.
Z8 1Л j
Подставляя (7) и 6, (pQSz<, ф в
X и cos <p — Vn sin ср, У = V^sin Ф +Vn cos q>
и усредняя по периоду вращения, находим
<х> = 0, <у> = _(1+^ + Ш^\а1г£3
I /3 2Isti‘z I z
т. е. диск смещается, не теряя высоты.
9.20.	а) Положение шара определяется координатами его центра масс X, У, Z и углами Эйлера 0, <р, ф (см. [1], § 35), которые задают положения главных осей инерции. Ось Z направлена вверх, ось х3 — от центра масс к геометрическому центру шара, для которого Хз=6, радиус ;шара а. Исследование движения шара проводится так же, как и в предыдущей задаче.
Если Мг=£Мз, то С/эфф(6) имеет минимум при Оот^О, Л и при энергии Ь'=1/Эфф(0о) происходит устойчивое вращение шара с постоянным углом 6 = 0о. при этом Z=a—icosOo- Точка шара, которая в данный момент соприкасается с плоскостью, имеет скорость п = = (&<р4"0ф) sin 6о. направленную вдоль линии узлов.
Учтем теперь малую силу сухого трения t Она направлена н сторону, противоположную v, и приведет к изменению угла Во-При
Mz = sin 6о,	sin Go.	(1)
откуда
Afza — Л'13& = С=соп51.	(2)
Для быстро вращающегося шара Л1а?Л1з, М/яМcos 6о. или с учетом (2)
Mfacos 0О — Ь) — С.	(3)
Отсюда видно, что при уменьшении момента импульса из-за трения
угол 0о должен уменьшаться, если acos0D— 6>0, и увеличиваться, если с cos 0о—6<0. При этом в силу (1), (3) 0D=— fb/aC (a cos 0О— ~Ь)2-
Центр масс медленно движется вдоль оси Z, а в плоскости ХУ переменная сила трения fx =—/соэф, fy«=a—fsinqp вызывает вра
щение центра масс по малой окружности с угловой скоростью <р. Конечно, даже малая сила трения приведет со временем к тому, что проскальзывание исчезнет и скорость ннжией точки шара станет равной нулю.
б) Пусть R4= (Х+6 sin 0 sin ф, У — b sin 0 cos <р, с)— координаты геометрического центра шара; £2= (fix, £2Г, □2)=(6созф+ +Ф sin 6 sin ф, 0 sin ф — ф sin 0 cos ф, ф+ф cos 0)— угловая скорость вращения шара и а= (0, 0, —л) — радиус, проведенный из геометрического центра шара в точку касания. Тогда условие качения шара без проскальзывания йц+[^а]—О представляет собой неголономную связь:
Х=0(а— 6 cos 0)я1пф— (аф+Ьф)81п 0совф,
(4)
У=—0 (а — b cos 0)cos ф — (сф4-йф)зш 0 sin ф.
Уравнения движения
тХ = М, тУ = ?,2,
Мг = (7.1 cos ф-Н-а sin ф) b sin 0,
Ais= (?.i cos фЧ-Т.2 sin ф)п sin 0,
d dL dL . .
— = (_ sin ф cos ф) (a — b cos 0) с/ ()Э ou
(5)
(6)
(7)
(8>
содержат в правых частях силы трения и моменты этих сил. Множители Лагранжа Хд, Х2 с помощью условий связи (4) могут быть
выражены через углы Эйлера. Так, проекции силы трения на линию узлов /ц и на перпендикулярное направление fj_ равны
f । == ф (fl — b cos 0) — т [(оф Ьф) sin 0J,	(9)
= — т Л- [0 (а — b cos 0)] — т<р (оф -[- ^ф) sin 0.	(10)
Заметим, что (6), (7) совпадут с (1), если в уравнениях (1) заменить силу сухого трения =Ff на силу трения покоя /и (9). Как и раньше, М2а — М3Ь=С является интегралом движения (2).
17*
0.21. При решении задачи необходимо учесть, что высота тела над землей ft мала ио сравнению с радиусом Земли и центробежное ускорение RQ2 (Q — угловая скорость Земли) малб по сравнению с ускорением свободного падения на поверхности Земли g. Таким образом, в задаче есть два малых параметра:
ei^h/R^=RQa/g ~ 0,01.
В уравнении движения (f — гравитационная постоянная, М — масса Земли)
г - -	□?+.' + 2 [vO] + [О [R + г, CJ] (I)
I R + <Т
разложим первое слагаемое в ряд по малому параметру
=e+2lv0]+g,+ [0[r0]], r(0)=h,	v(0) = 0,	(2)
g = - VAf «, + [O(ROJI, g, = J" (3R	_ Д.) [I + O(e,)J.
Кориолисово ускорение 2[vO] ~ gtti ~ и ~ Big имеют первый порядок малости, а [Я[гП]] ~ 8|Cag—второй.
Вертикаль h аитипараллельна вектору g и составляет малый угол a=e2slnlcosX с направлением вектора R (здесь X— северная широта (геоцентрическая) — угол между плоскостью экватора и вектором R). Выбираем ось z по вертикали вверх, ось к — по меридиану к югу, ось у — по широте к востоку, тогда
g=(0,0,— g), R=/?(sina,0,coscQ, fl=R(—cos(a-hA), 0, sin(a-hX)).
В нулевом приближении частица движется с ускорением — g вдоль оси 2, В первом приближении кориолисово ускорение приводит лишь к отклонению иа восток, причем величина смещения у ~
е3	Ускорение gi имеет вдоль z составляющие
~£1g, а вдоль к и у — лишь второго порядка, поэтому в первом приближении влияние gi приведет лишь к увеличению времени падения с высоты ft на величину ~ Е1 y^h/g. Отклонение к югу, таким образом, возникает лишь во втором порядке. Запишем уравнение (2) в проекциях иа выбранные оси, удерживая для компонент 2, у, х слагаемые нулевого, первого и второго порядков малости соответственно:
*«=—£, У~— 2zficos Xi
x=2$/Q sin X+g(3z sin a — x)//?4-fi2z sin X cos X.
Решая методом последовательных приближений, найдем
г = Л — -у gt\ у = -у gt*£l cos "Kt х = 2Л/*йв sin Л cos 1.
Подставляя время падения/ =y2h/g,найдем отклонение к востоку и югу
у = *у A cos Ji. х « 2ej ваА sin 2Х.
9.22.	Воспользуемся системой отсчета, вращающейся вместе с сосудом; ось х направим вдоль АВ, начало координат поместим в неподвижной точке — пересечении осей АВ и CD. Угловая скорость системы 0=<di-]-©s= (о2, <at cos (ог1,—(Oi sin (о2О- На каждую частицу жидкости массы т в этой системе отсчета наряду с силой тяжести nzg действуют силы инерции (см. [1], § 39): сила Кориолиса 2m[vflJ, центробежная сила	и сила /п[г6], где Й—
скорость изменения вектора Q в неподвижной системе отсчета.
При затвердевании смолы скорости частиц (относительно сосуда) обращаются в нуль и сила Кориолиса исчезает. Остальные три слагаемые нужно усреднить по периодам вращения:
<mg> «== — mg «cos (OiO, <sin	sin (o2/>, <sin o>if cos (o2/>) =0,
если
<m[rfi]>=m[r<0>], <Q>^< [<DiO2] >= [<coi>(d2] =0.
Наконец,
/Д |Orl»\ = m
\ cJr 2 1	/	2 dr '
где
U = <[OrP> =	- (Or)») =
= I 0>|) Г1 — <(*&*, 4- j/G), COS G»,( — 2G>, sin 0>,Г)»> =.
= <4-«s + l^-+“,i) (!''+«’) o)
Поверхность жидкости расположится по линии уровня 1/(г) «= F=const Смола затвердеет в форме эллипсоида вращения.
Что изменится в этом результате при 0)i=w2?
При g=0 и <о2->0 из (1) получается, очевидно, неправильное решение. Почему?
9.23.	I = 1/Z С Лг
’ 2 J )/£ + ЛЮ-1/ефф г— Г («_ U <,,= 1Л?.. I'» I Г 2 J |/£тМЙ-1/аМ
где Е—энергия, Л! — момент импульса во вращающейся системе Л18
отсчета, £7^ = U (г) 4	-2-. Напомним, что Е=Е0— AIQ, №=№&
где Ео и М©— энергия и момент импульса в инерциальной системе.
Интересно, что центробежная потенциальная энергия — m£2sr!/2 не входит в £78фф.
9.24.	В системе координат, связанной с рамкой, функция Лагранжа данной задачи совпадает с рассмотренной в задаче 6.36 (при 2=0 и с параметрами d)^ = — 2fi, =-£-4-	— ^2).
ПрИ <q2 > о движение частицы совпадает с движением анизотропного осциллятора в магнитном поле 2# = —2тс£2/е. Траектория частицы для случая ец = а2 изображена на рис. 97 к задаче 2.32. В частности, если о| = и2 = 0, движение частицы совпадает с движением свободной частицы в магнитном поле х = х0 + й cos у=у0—ASinWjgC т е. частица равномерно движется по окружности радиуса а с центром в точке (л'о, у0). Интересно разобраться, какому движению частиц в неподвижной системе координат соответствует последний случай, в частности при а = 0 или при х0 — Уо = 0.
Если центробежная сила превысит силы возвращающие, действующие сс стороны обеих пружинок, <о j>2 < 0, то частица по-прежнему совершает малые колебания. Хотя потенциальная энергия имеет при x=y=Q максимум, устойчивость этого положения равновесия обеспечивается силой Кориолиса.
Если же «I и иршекл разные знаки (т. е. х*=у=0 — седловая точка для потенциальной энергии), то это положение равновесия неустойчиво.
Интересно сопоставить Эти результаты с ответом задачи 5.4. В системе отсчета, вращающейся с угловой скоростью EJ, точка го, фо лежит иа гребне «потенциальногоцирка»; потенциальная энергия a mQ2rs
U = — —— — —g— имеет максимум относительно смещения в на
правлении радиуса-вектора и не изменяется при смещении в азимутальном направлении. В этом случае одно из нормальных колебаний происходит с частотой <о, частота же другого обращается в нуль: положение равновесия безразлично относительно некоторых возмущений (например, изменения <р0).
9.26. Функция Лагранжа
t = -у (V + [юг|)а + mgr =
= -у ((* — »«/)“ + (У + <«)’ 4- г'а — g\^- +	j] -
Для малых колебаний можно опустить z, тогда уравнения движения
х — 2оу 4- —• оз2) х = О, у 4- 2<ад 4-	----to8) у = 0.
Ищем решение в виде
X = у — BejQt
(1)
н для й8 получаем уравнение
Q« — ^X4- Х4-2Ш»
Легко убедиться, что кории его действительны. Однако при
м (3я j	—* ы>
<0
один из корней Of < 0, так что соответствующее движение
приводит к уходу частицы от начала координат. Это и означает, что нижнее положение частицы неустойчиво. Считая для определенности Об, получаем область неустойчивости
Обратим внимание на то, что при	движение устойчиво,
хотя потенциальная энергия во вращающейся системе отсчета
(<*—T-V
2 к а )	2\ b )
представляет не потенциальную яму, а потенциальный горб. Устойчивость в этом случае обеспечивается действием сил Кориолиса,
9.26.	а) Потенциальная энергия (включая центробежную) тта№
U (х) = k (х = а)1	—g—.
Условие U'(xc) =0 определяет положение равновесия
2Ло х° _ 2k —ту1’
Интересно, что при частоте вращения 7, большей частоты собственных колебаний частицы V2A/rn, оказывается х0<0, а при положение равновесия близко к осн вращения.
Знак U"(x0)=2k — iwf определяет устойчивость положения равновесия: при mi2<2k равновесие устойчиво; при m^Z>2k — неустойчиво.
б)	Очевидно, положение равновесия такое же, как в пункте а). Для исследования устойчивости рассмотрим потенциальную энергию при малых смещениях из положения равновесия:
и (х, у. г) = I/ (х„ о, 0) + *4 +	+
где
ki = 2k —
.	/+*(х0—fl)
f — fe (%Q — fl) I Xq -J- g
— my* = — my2 + £3.
Сравнение с задачей 9.24 приводит к заключению, что равновесие неустойчиво лишь в том случае, если kt и k2 имеют разные знаки. В частности, при nrf^Sk+if/l равновесие устойчиво, в отличие от результатов пункта а). Если же kfa < 0, то отклонение частицы от точки (х0, 0, 0) нарастает со временем (пока не станет существенным воздействие стенок рамки, которое мы не рассматриваем).
9.27.	Воспользуемся декартовыми координатами во вращающейся системе отсчета. Начало координат поместим в центр масс, система вращается с угловой скоростью ю вокруг оси г, а звезды расгкн ложены иа оси х (рис, 152),
„	__ ZZto
Пусть расстояния от звезд до центра масс о, 9 = + ------------.
mi 4- те
где /7ii,s — массы звезд, а — расстояние между ними. Из равенства
„ Т/тцт8 ----; ой' = г— ml +W2	О8
(Y — гравитационная постоянная) получаем
Потенциальная энергия тела массы т (включая центробежную энергию)
,,	vmmi vmms m<o* m
t/(x. p. z) = --L—L-i—2 | -9-(x’4-^)<
'1	' в x
где <1,в — расстояние до звезд, г= (х, у, г) — радиус-вектор тела, n	dU
Положение равновесия тела определяется условием= Q, или
Отсюда z=0 и (при у=£С) ц*=гъ=а.
Таким образом, звезды и точка равновесия находятся в вершинах правильного треугольника. Есть две такие точки, так называемые °	। а 1'3 п
точки Лагранжа,	— о2 х0 = Уо~ _l_ —z0 — и.
Вблизи точек Лагранжа
t/ (х0 -|- Xi, !/0 4- yi, Zq -|- ) = 3	9	1
= v (*о. tu. г») — ~ ти>’л1 — 2та>г,й---g- ma’yj +
а = ± Vlmi-ra2).
zG6
ответы и Решения
(129
Движение в направлении z, очевидно, устойчиво. Уравнения движения, в плоскости х, у
3 .
*1 "4”	‘	= °*
9
&I ~ w’f/t — 2axi + 2uxt = 0.
Подстановка x=Aei(lt, y~BetClt приводит к уравнению для £2:
27
£24 _ (jjSQt Д- —— <о« — 4a2 = 0.
10
Его корни действительны при 64а’>23ю\ т.е. при
^27т1Шя. Это условие выполняется, если масса одной звезды больше другой не менее чем в 25 раз. В этом случае движение тел в окрестности точек Лагранжа устойчиво. Устойчивость движения
обеспечивается силами Кориолиса (ср. с задачей 9.25).
„	dU
На оси х есть еще три точки, в которых = 0w однако движение вблизи них неустойчиво.
Для системы Солнце — Юпитер в точках Лагранжа наблюдают
ся астероиды.
9.28.	Будем рассматривать колебания в системе отсчета, вращающейся вместе с молекулой. Функция Лагранжа получается из (1) задачи 6.49 заменой иа на ua+[£2, rn0+uo], а угловая скорость вращения системы отсчета 12 выбирается равной угловой скорости вращения молекулы в отсутствие колебаний 12m У = Условие (3) задачи 6.49, эквивалентное требованию $/|+^2+£/з=0. отсутствует.
Введя qa = (yt + & + уя} и пренебрегая квадратичными по £2 членами*), можем представить функцию Лагранжа в виде
L~ 2 ( ff2i+ 2<72 +2^3 + ^4)“ 2 (91 + 92 + ?з) +
•	•	4.	«	«
mfi (?1?, — Wl) + -g-тО (?t?s - ад,).
•) Учет этих поправок привел бы к заменам:
1->1 (|	Я-.п(| -
Уравнения движения приводят к нормальным колебаниям
fl’l11 = A] COS {Ш.? + <Г1), ,4° = 2 Л1sin (“1‘ + ’ !>•
^2,3) “ л2,з cos (“г.s' + Ч’г.з). 42,3) = ± Л2.з sin (и2.з( + Тг.з).
=	?l4,=« + D.
Вместо условия (3) задачи 6.49 получаем
2а<%1+2в(г«л»==0-о
или (?4 — 2£2gi=O, что соответствует выбору С=0 Постоянную D, определяющую начальный поворот молекулы относительно вращающейся системы отсчета, также удобно положить ранной нулю.
Как выглядят колебания, если во вращающейся системе отклонения в начальный момент имеют вид, изображенный на рис. 133, а начальные скорости равны нулю?
§ 10.	Уравнения Гамильтона. Скобки Пуассона
10.1.	Пусть в—вектор бесконечно малого смещения; прн этом
Га Га ~ Га + Е’ Ра ~* Ра Ра1 Н {Та' Ра) ~ Н (Га’ Ра)'
Отсюда = 0- Используя уравнение Гамильтона, получасу:
₽-2^“-2гг =о. P«const. а	а а
Прн бесконечно малом повороте
г. -» г» = r. + Is» го1- Ра - р= = ро + [4 Р J.
" Со- р«) = н (г«. ₽«) l^f Г«1 +	14 Р„| - о =
в I a	rG
“ 2 {- Ра 14 rJ t' 14 p„l} = - 4 2 -di lr«P«I-а	а
ИЛИ
10.2.
M=S[rap<.l=c«is'-
а
. Ре , (Рф~Густа0)г,4
2/,	2/, sin* е	гЦ
юл. я-.____£L_+^
2(1+2₽х)	2
колебаний (Jewel < со2, |0х] < 1)
В частности, для малых
рЗ (i)2Jf2
Я = -g- + —g- ф «А- — ₽хр2 + 2₽sx2ps — ..
и с точностью до линейных по а, р членов добавка к функции Гамильтона гармонического осциллятора связана с добавкой к функции Лагранжа соотношением 6/7=—В£ (ср. [I], § 401.
10,4.	x=acos (со(+ф),р=—ь)00 8ш(<о(-Кр),где ш=(1+2Х£'о)<Ос, £0 = “j- w|a8.
10.5.
_£И—£E*L. £ = .£₽ р = 1р|. пр n* dp v n* dt'* 1H1
Предложенная функция Гамильтона описывает распространение света в прозрачной среде с показателем преломления п в приближении геометрической оптики (см. [3], § 65). «Частицей» является волновой пакет, г(/) есть закон именно его движения; г —это групповая скорость, а вектор р, перпендикулярный к волновому фронту, определяет волновой вектор.
Траектория при л(г)=ах
x-C1cb(jL + C,).
где Ci, С2 определяются начальной и конечной точками траектории, , т (v — а)2
10.6.	а) £ = —б) L = 0;
подобные «частицы» нельзя описывать с помощью функции Лагранжа (см. [2], § 53).
10.7.	Данный векторный потенциал определяет магнитное поле направленное параллельно оси z,
Функция Гамильтона
" (X. V, г. Рх. PJ = -L 5±
Так как Н не зависит от у и г, имеем p^^const, рг=const. Пред-
ставив Н в виде Н “ ~ 4- (х — х0)* -|- £1., где св = —, х0 = 2m 2	2т	тс
— видим, что для х, рх получается такая же функция Гамильтона, как для гармонического осциллятора. Поэтому
х=а cos(cdf+<p)4-xo, рхsin (о/+ф).
Для определения у и г используем уравнения
У =
дН дру
m" (fy 4“	= "" “fl cos(to/ + *Й’
откуда
у = — asin (св/ -|- ф) 4- у0, z=* E*-t + Zorn
Частица движется по винтовой линии с осью, параллельной Обобщенный импульс pv определяет расстояние этой оси от плоскости yz.
10.8.	Магнитное поле направлено по оси z в равно 2hx. Движение по оси z равномерное. Отвлекаясь от него, рассмотрим движение в плоскости ху. Функция Гамильтона
я=Д+* L z»x«Y 2m 2m \у с /
не зависит от у и /, Поэтому интегралами движения являются обобщенный импульс pv и энергия Е:
р„ = ту + — х*.
E =	+ (Л	(х) = ± (р9 - £ х’У.
Для ря^С график Ь'эфф(^) изображен на рис. 153, а примерный внд траектории — на рис. 154. Следует учесть, что скорость
т тс
всюду отрицательна и колеблется вблизи значения pvjm.
Для pv>0 график
изображен на рис. 155. Скорость
при любом значении Е принимает как положительные, так и отрицательные значения. Примерный вид траекторий изображен на рис. 156f случаям а — О соответствуют уменьшающиеся значения энергии.
При больших энергиях Е » Um — ^(2т размах колебаний по оси х велик и среднее за период значение <х2> больше Поэтому среднее значение
<j>= — (xj-<x®>) тс 4	1
отрицательно (см. рис. 156, а). При уменьшении энергии <р> возрастает до нуля (рис. 156 б), а за-тем становится положительным (рис. 156, в). При энергии Е = Um частица, \	/ имеющая в начальный момент
\	Um / х>хъ и х<0, асимптотически при-
\ т'	/ ближается к оси у (рис. 156, г).
— Х-Z..	Наконец, при Е < Um частица
~хо	я	движется либо в области вблизи (—хэ),
рие |55	либо в области вблизи х0 (рис. 156, д).
Можно показать, что <р> при этом больше пуля. При [х— Хс| <;х0 частица движется по окружности, центр которой медленно дрейфует вдоль оси у. Чтобы найти скорость
дрейфа, необходимо при вычислении учитывать первые ангармонические поправки
к = х0 a cos ь>/	(3 — cos 2©Г),
что дает
• сЕ
(ср. с задачей 8.14).
10.9. Введя координаты центра масс R и относительного движения г (ср. с задачами 2.25 и 2 26), представляем функцию Лагранжа в виде
L - Т «*+ £ |Э<г] R I L, (г. О + ~ [Ни] Т.
Л1 = rnt 4- wjj, (I)
где функция Лагранжа
4 ?+' допг+л (к=мя)
2 2с	г \ ms 4- т4 /
соответствует частице с приведенной массой т, движущейся в магнитном полеЭД' и кулоновском поле.
Последнее слагаемое в (1) перепишем в виде
£№i;=£№iR+4^iKR1r.
Отбрасывая полную производную по времени, имеем
L = 4r R‘+ — [Jfr] R + L, (г, 2 с
Эта функций Лагранжа не зависит явно от R, поэтому сохраняется обобщенный импульс
P«=»|g — A1R 4- у = const,	(2)
Функция Гамильтона системы имеет вид
« = 24(₽-7-1№1У + ^(₽-й[К'г1)а“^
Отсюда с учетом (2) видно, что частица массы т движется в однородном магнитном поле ЭД' в силовом поле с потенциальной энергией
У = ~7 + ^(Р~Т№)’-
Если направить ось z по ЭД, то
U = — у 4- 4" тф4 Кх — о)2 + (</ — Ь)г14- const,
__cLs к сР»
“ r.l'X W ‘X-
После нахождения г(/) закон движения центра масс определяется из уравнения (2)
е Г 1	1
«<') = м-лд Крюл +R».
10.10. '
p=po+eg/, Е(р)—egr=E0, (г — г0)е £=е(Рв+е£7) — е(р0).
10.11.
10	.12. а} в (р) = Е, р^ = const, где р^— проекция импульса па направление магнитного поля J£’. Траектория в импульсном пространстве определяется линией пересечения двух поверхностей: е(Р) = Е и P^ = const-
б)	Из уравнения движения Р =“ [гJ{] видно, что проекция
траектории электрона иа плоскость, перпендикулярную к магнитному полю получается нэ траектории в импульсном пространстве поворотом на угол л/2 вокруг и изменением масштаба в раз.
10.13.
<3е
ер-
где Kb — ортогональная к составляющая вектора
10.14.	а) -2	-2	'llM-
h	кН
б)	аЬ.
{аМ, Ьг]	2bjxj} = ^aibj{Mv А'/И
I i 3 J У
=—= —[‘Ь1Г. — [аЬ]Л1.
в) 0. пгг"”2. 2а (аг).
10.15.	{Af, АЛ = — Sef?-ftAfe, {Ар А4} = 0. здесь i, j, k прини-h
мают значения I, 2, 3 (ср. с задачей 10.14а).
10.16.	{Л4р Л/ь} — —	— X eikl^ip {ЛА’ Л«Л =
»	+ ^1кМи + т ^kiMИ' где	— Р-л>-
*) Подробнее о движении электронов в металле (задачи 10.9— 10.13) см., например, [18], [25], § 4.
• *) е(jа — полностью антиси мметричный тензор, С|23 = 6231 = £ЗГ2 = U *1«2 в е321 = ^2>Я = ~-1»
остальные компоненты eiift равны нулю.
18 Г. Л. Коткин, В. Г. Сербо
10.17.	При повороте сисюмы как целого на бесконечно малый угол е вокруг оси z изменение 6ф любой функции координат и импульсов в первом порядке по е равно
*Ч> = Ч-’ (х - W, У + “. г, рх — tpy, р* + ерг. pt) —
-4>(x.S,x.px. Рг Р,) =
/ d<p дф d$ ftp \	,
= 1 (- ЗГ» +	~W,P« + рх) = е <"»' ’’>•
Если ф — скаляр, то его изменение при повороте равно нулю. Поэтому {ф, Л'2}—0. Если ф=^х—компонента векторной функции, то ее изменение при повороте &fx = —efv, значит,
{Mt,fx)=-fv ИЛИ Иг, f) = [nf]
{ср. [1], § 42, задачи 3,4). Чему равны скобки Пуассона {/И„ Тхх}, где Тхх — компонента тензорной функции?
10.18.
(1. а/М| =[1. al.fl/M, IM)	+5Л1.Л1 (f Z*}.
ik ‘
10.19.	Полагая во второй формуле предыдущей задачи f = е» и 1=ej, где е; и cs —орты осей £ и £ в подвижной системе координат, получим
{/Vlt. W = +Afn.	(1)
Это равенство отличается знаком правой части от аналогичного соотношения для проекций момента на оси неподвижной системы координат
{Л1„ЛМ==-М».	(2)
Как было показано в задаче 10.17 (см, также [4], § 8.7). скобки Пуассона (2) характеризуют изменение компоненты Л1Х при повороте системы как целого па бесконечно малый угол £ (рис. 157. а) 6Л1Ж= =е{Л!п Л!х}=—eA-fv. Скобки Пуассона (1). равные
{есМ, еЕМ} = {Л/ье.}М,
характеризуют изменение проекции неподвижного вектора М на ось при бесконечно малом повороте подвижной системы координат вокруг оси £ (рис 157, б, на рисунке оси т] £ совпадают до поворота с осями х, у, г).
юло. Ма=Х^у
в частности, если выбрать подвижную систему так, чтобы тензор инерции М был диагоналей, получим уравнения Эйлера (см. [1], § 36 с учетом соотношения А1а«=/айа).
Рис. 157,
10.21. Уравнения движения
Mi = {//, A1J	или М =-ЯдаЪ
т. е. вектор М вращается с угловой скоростью — у J£. а) Вектор М прецессирует вокруг направления
А1Х «=А1* (0) cos у Ж*4-Мv (0> sin y^cZ,
Л1„=— Mx(0)sin у W+Al^(0)cos уЖХ
А1,=-А1,(0).
б) Вектор ЛА вращается С угловой скоростью —yj£, которая в свою очередь вращается вокруг оси z с угловой скоростью со. Удобно воспользоваться вращающейся системой отсчета, в которой вектор неподвижен. В этой системе компоненты угловой скорости вектора М равны
<о'х = —У5?*. % = 0. «о, = —Ж, —<о = е.
При заданном начальном условии компоненты М во вращающейся системе
Л1’ = — а у- Af0 (1 « cos X/), Му = аМ0 sin X/, Л1’ =	+ о2 cos "ktj Af0.
где 7. = р'ге2 _|_ а = 8я +	•
18»
В неподвижной системе
М* =« Мх cos art — M'v sin <о/, Му = Мх sin cat + M'v cos cat, м’г = мх.
При Ж «Ж зависимость амплитуд MXtV от to носит резонансный характер: вообще говоря, эти амплитуды малы	но
при |e| = |to+7^oKTf^i они резко возрастают, достигая значений ~М0 В частности, при w—
А1х=—Mo sin 4%it sin
MU=MD sin cos
AL=Af0cos Y^i/-
10.22.
k pt F/a
10.23.	a)p(/)=p+H. r(/) = r + “ + ^;
6) p(/)=pcos co/— mcaq sin cat,
p
?(0=?cosorf+ — sin Mi.
Разумеется, эти величины проще вычислить, не используя скобок Пуассона. Но предложенный метод легко может быть перенесен в квантовую механику (см. [26], § 34).
10.25.	а) Согласно предыдущей задаче
df , дН
-2 = {//,/) = -{Л/;=0.
б) Функция Гамильтона
Рг 1
Н = 2т + 2W5 С6, р6' М’ где
Р2
I (в. ₽e- М = 4 т Sih т 2me cos 6.
Интегралы движения: Е, рч и, согласно предыдущему, f.
10.2в. г){А,Л;} = -—
/1=1
{И.,Лу=-2 eukAk-. k=l
б) {Я. М=0, {Ль ы=о,
3	3
{Лг Jlj} 2j ZlJk\k' {Лг *^2/} ~ ~ S ®Ufc/2fc*
A=i	А=1
maJ ФМ >!)
Векторы J| и J2 — независимые интегралы движения. Каждый из них имеет такие же скобки Пуассона для своих компонент, как и обычный момент импульса. Наличие двух таких «моментов» тесно связано с так называемой «скрытой симметрией» атома водорода (см. [27], гл. I, § 5).
§ 11.	Канонические преобразования
- /'2Р*	г_______
11.1.	а) д = у — sinQ, Р = I 2шсоР cos Q,
•	(Л	•	<0
Q = w -Ь g^sin 2(2, Р = —Р —cos2Q.
В данном случае Р и Q — переменные действие — угол. Эти переменные удобнее, чем р и д для решения задачи методом теории возмущений, если частота и меняется медленно: со<Сь>2 (см. задачу 13.9).
F /~2Р	._______
=	^sinQ, р = Т 2m<oPcosQf
Q = ы -J- F I/"cos Q, P = F у 2m©P sin Q.
П.2. т(р,<э--<г(1 + 1п^).
11.3.	Функция Ф(^|,	Pj, Рг,Р«) определяет кано-
д«Ф
ническое преобразование, если Get др' 0.
11.4.	Пусть Q = 0cosa — psina, P=?sina+pcosa. Тогда {Л Q}p. q e —{?. р}т. ч sin2а 4- {р, </} р, ч cos2 а = I. Для системы с одной степенью свободы этого достаточно, чтобы преобразование было каноническим.
11.6.	Нетрудно сообразить (и это подтверждается последующими вычислениями), что каноническое преобразование должно быть близко к тождественному, и члены ох2Р и ЬР3 в производящей функции малы. Чтобы разрешить соотношения
р==Р+2ахР, Q=x-|-ax2+3bPa
определяющие каноническое преобразование, относительно х и р, заменяем в малых членах х на Q и р на Р:
p=P+2aQP, х = Q—aQz— ЗЬР*.	(1)
Подобным же образом поступаем, выражая функцию Гамильтона в новых переменных:
Н' (Q, Р) = -у +	4- а(? + PQP’ 4- -OTO2Q3
— 3bw2QP2 члены четвертой степени по Q, Р.
Полагая а —по2=0, 0+2о —36е>г=0, обратим в нуль и члены третьей степени. Таким образом, в указанном в условии задачи приближении 3=Дсо5ш/, Р=—о>Я sin о/ и согласно (!) х = =A costal— at)-2A2— (p+acd-2)A2sinaa>l (ср. [1], § 28).
11.6.	Приведя функцию Гамильтона к виду, рассмотренному в задаче 10.4, получаем х = Q — Q3 — QP2, где Q=Acoscol» Р=_Шо,1 sin at, ш = <а0 -р i л» (ср. [1]. § 28).
11.7.	f/'(P, Q)=tf(P. <2).
При Х=А sin (си/4-ф), У=0 —осциллятор совершает движение по эллипсу
х=А cos X sin (о Л-(р), у=А sin X cos(ci)f+<p)<
11.8. Для того чтобы сделать запись менее громоздкой, удобно временно положить т=ш=<«с=1. В окончательных выражениях эти множители легко будет восстановить. Преобразование задачи (11.7) представляет собой поворот в плоскости хри и урх, поэтому
оно сохраняет вид части функции Гамильтона, равной
4^+^+p^+pd-
Добавка же, возникающая от членов
£Зв*х*~Яхру . Равна
~ ар (X1 cos® X + р| sin1 X + 2ХРу sin X cos X) +
+ Ж (Х> — Р|)sin X cos X — X (cos1 X — sin1 X) XP?.
Недиагональный член ХРГ исчезнет, если положить
sina 1—• cos’14~ 5£sinlcosl = О, т. е. tg2Z = ^.
После несложных преобразований функция Гамильтона приводится к виду
Н -	(Р1 + ₽i ctg1 X) + ~ (X1 tg1 X + YS). (1)
Таким образом, переменные X, У испытывают гармонические колебания с частотами, равными соответственно
(ср. [2]» § 2L задача). Каждой из координат X, Y соответствует движение по эллипсу; произвольное колебание — суперпозиция двух таких движений (ср. задачи 6.36, 117).
Интересно, что при ^->0 оказывается Л=л/4 (а отнюдь не /.=0). Это значит, что даже при очень слабом поле % «нормальными» оказываются колебания, «поляризованные по кругу». Колебания же, отвечающие координатам X(Y) при 1=0, которые в отсутствие поля <?£ были бы линейными, при наличии поля Ж медленно изменяют направление поляризации.
Если магнитное поле переменное, то к функции Гамильтона (1) следует добавить частную производную по времени производящей функции
PXPY
Ф = - тшу etg X----— tg X +	----
(выразив ее через X, У, Рх, Ру) {см. также сноску к решению задачи 13.25).
11.9.	Полагая в каноническом преобразовании предыдущей за-
дачи о = <0s, tg 2Х-а----------тт, получим
Н’ = к -I ₽Г + + Т ( ?*’ +
\	2 J
где £2j,s определены в задаче 6.23.
11.10.	Преобразование (К«я/4)
сохраняет вид функции Гамильтона (ср. с задачей 11.7)
Колебание, соответствующее Xt=*A cos(<i)8f-bp), есть
Л
^.== j7]sin(%' + ЯФ.+Р),
а соответствующее YS=B cos(<i)s/+p) — есть колебание
х"==Й5!п(_“'' + '‘<р,₽Р)’
11.11.	Новая функция Гамильтона H'^aPi. Уравнения движения в новых переменных имеют вид
р|==Р2=(22=0. <2»=©.
Как изменится вид функции Гамильтона ff, если зависит от времени?
11.12.	Предложенное преобразование p—aJ\ r^Qja. есть преобразование подобия.
11.13.	Градиентное преобразование A/=A + Vf(r, 0>Ф/;=Ф —’ — -L — можно представить как каноническое преобразование
г'=г, Р'==Р—~ помощью производящей функции
0>(r.P) = rP--j-/(r,Z).
11.14.	Ф(с, P)=-qP-f(q, ZJ.
11.15.	б) f, (,,<?) = ^(<? + Q) + ^(o-Q)’l
в> Ft ® = Яй12’0 “ + <2*> сот мт] •
II.	16. а) О = г+ба, Р«р —сдвиг системы как целого иа 6а (или сдвиг системы координат на —ба).
б) С точностью до бесконечно малых первого порядка включительно
Q—г+[6ф, г], Р=р + [6ф, р].
Преобразование представляет собой поворот системы координат на угол — б«р.
В) Q(t)=q(i+Srt), P(0=p(f+61), Н'(Р, Q, q, H-ftr). Преобразование представляет собой сдвиг во времени на 6т (ср. П].§45).
г) Q=r+2p6a, Р—р —2гба.
Преобразование представляет собой поворот на угол 2ба в каждой паре плоскостей Xipt (i= 1,2,3) в фазовом пространстве.
11.18. а) Ф(г, Р)=гР4-пРба-т-п[гР]6ф, где ба—смещение вдоль
направления п, а 6ф=-^Яд-_ угол поворота вокруг п(й —шаг винта); п
б) Ф(г. Р, /)=гР — VPf+mrVj
в) Ф(г, Р, /)=гР — /6£2[гР].
11.19.	bf(q, p)=l{W,f}P,q.
В самом деле, подставляя значения новых переменных Р =* =	и Q =	в f (Q. Р) н разлагая полученное выра-
жение по степеням Л, получим с точностью до первого порядка
включительно
А..	.	а/Ж(<7.р) .df dW{q,p)
W(<l.p)=bgq—fy-------a-q~ •
11.20.	Полагая в предыдущей задаче Ф=гР + ХгР получим преобразование подобия с а=1+Х (см. задачу 11.12) Предложенная функция Гамильтона такова, что H'(Pr Q)=a2//(P, Q), и поэтому
ЦЯ, гр}=сЯ'— Я=2Х,Я(Л-*0). С другой стороны, {Я, гр} = = jj(rp). Отсюда гр — 2£/==const (ср. с задачей 4.136).
11.22,	Пусть dig и б]Р •)—изменения координат и импульсов, связанные с преобразованием, задаваемым <Dj. Тогда
f (1 + м. р + 61Р) =
= I (Я. Р) + ’! (В7, to. Р). Г (?. Р» + ^Т1 to, р). (1)
К каждому из слагаемых правой части (1) применим далее преобразование, задаваемое функцией Фа,
1 to + 5,1». р + вир) - f + х, {в?,, 1} +{в?!, л +
+ м. (*'„ {г„ /)) +	. (2)
Преобразование (9. р) дает добавку выше второго порядка ма-лести. Результат применения этих преобразований в обратном порядке
I (? + 61,9. р + sJ2p) = Г + X, (ИТ, п + х, {»„ fl +
+ М. {1Г,. {№„/))+ Цф, + Л|ф, (S) отличается от (2) только членами второго порядка, пропорциональными ЛД2. Вычитая (3) из (2), получим
{ТГЬ Ш - {W'j, {I72, Ш)-*М w, ед.
Поэтому, в частности, сдвиги 1№=баР (см. задачу 11.16) перестановочны, а повороты вокруг разных осей Х17=6<р[гР] —нет.
Справедливо ли утверждение, обратное сформулированному в задаче?
11.23.	Каноническое преобразование с переменным параметром X, можно рассматривать как «движение», причем Л играет роль времени, a Kz(g, р)—функция Гамильтона (ср. с задачей 11.16в). Уравнения «движения»
dQ dW(Q, Р)	dP	dW(Q.P)
dk~ дР •	<fX----dQ ’
*) Укажем, например, изменение импульса с точностью до второго порядка:
61Р = р _ р =
, ЖТ to' Р) , 8ВТ to. Р) , .20®В7, fe, ₽) авт (7. р)
°"	S?	Л*	+Л1 dpdq дц
Эти уравнения легко получить и формально из результата задачи 11.19.
а)	Бесконечно малое изменение координат и импульсов при данном каноническом преобразовании имеет вид
I	К
~ дГ {«7. г) = -у {Л1а,г)=- [п, г] бф.
бр = — [п, р] бф,
где М = [г, р], п =~» бф =	' ^т0 пРеобР0Зование представ-
ляет собой поворот системы координат иа угол бф вокруг направления п. Направив ось z по а, получаем окончательно
Х=хсо5ф — у sin ф, У—у cos ф+х sin ф, Z>=z
в аналогичные формулы для компонент импульса.
б)	Бесконечно малое изменение координат и импульсов при каноническом преобразовании, задаваемом Ль имеет вид
бл —/здбф, by = —р^бф, 6ра=хбф, бру »= £/бф,
где бф =	. Это преобразование представляет собой поворот на
угол 4-бф в плоскости хр* и на угол —бф в плоскости ypv. Поэтому
Х=хсо5ф+ра sin ф,	У=р cos ф •—ру sin ф,
РХ — —х Sin ф-}-ра COS ф,	Ру—у sin фЧ-ру COS ф.
Аналогично Aa(As) задает поворот на угол ф (—ф) в плоскостях XPv И УР*(ХУ И pxPv) и ^4 — поворот на угол 4ф в плоскостях хрх и УРи-
Отнюдь не любой поворот в фазовом пространстве является каноническим преобразованием. Например, поворот в плоскости xpv — ие каноническое преобразование.
Интересно сравнить движение двумерного изотропного гармонического осциллятора (функция Гамильтона Н =s'~2~ Ла) и движение частицы в плоскости ху в произвольном поле, обладающем осевой симметрией, t/(x2+j/2). В обоих случаях интегралами является момент импульса 2А3, сохранение которого связано с инвариантностью системы по отношению к поворотам вокруг оси 2. Для осциллятора, кроме того, есть интегралы движения А и Аа сохранение которых связано со «скрытой» симметрией — инвариантностью функции Гамильтона относительно определенных поворотов в фазовом простран
стве. В этом смысле осциллятор подобен частице в трехмерном центральном поле, для которой есть три интеграла движения Мх, v, t.
Наличие дополнительных интегралов движения у осциллятора приводит к тому, что точка (х, у. рх. pv) в фазовом пространстве движется по замкнутой линии, в то время как для частицы в поле t7(x2+p2) фазовая траектория «заполняет» двумерную поверхность (см. [1}, § 52).
11.24.	а) В импульсном и фазовом пространстве выделенный объем с течением времени не меняется, в координатном пространстве происходит его «расплывание». Так, если в начальный момент состояние системы изображалось прямоугольником ABCD (рнс. 158),
то через время t, он перейдет в параллелограмм A'B'C'D’ (AD= =A'D']t причем расстояние по оси х между точками А* и С' равно Дх = Дх0-f-Со временем этот параллелограмм вырождается в узкую полоску большой длины.
б)	Если в точке x=L расположена стенка, то выделенный фазовый объем уже не будет параллелограммом A’B'C’D', а будет иметь вид, изображенный на рнс. 159, а. С течением времени первоначальный фазовый объем ABCD превратится в ряд очень узких параллельных полосок, которые почти равномерно распределятся внутри двух прямоугольников 0=^х<^£, р0<р</?о+Дро и 0^х<£, —ро~Дро^рС —ро (рис. 159, б).
в)	Фазовая траектория для осциллятора с энергией Е и частотой <о — эллипс 4- vs = 1 с полуосями а = 1/ л — 1/ —
l	*	Г ты21 ° — Г т •
Все точки выделенного фазового объема движутся по таким эллипсам 2л
к через период Т=— возвращаются в исходное состояние. Размеры
выделенного «объема» по координатам Дх и импульсам Др пульсируют с частотой 2 со. В отличие от предыдущего пункта, здесь ие происходит расплывания выделенного фазового объема по всей доступной области фазового пространства.
Рис. 159.
г)	Для осциллятора с трением (сила трения fTP=—2т/.х)
х = ае м cos {tot q?),
p = mx = —sin w/ + qp)+ lcos(cof + q?)].
и колебания co временем затухают, поэтому фазовая траектория представляет собой спираль
, -iU
а2 mato )
Выделенный фазовый объем с течением времени уменьшается до нуля. Несохранение фазового объема здесь связано с тем. что система не является канонической — для полного ее описания необходимо
задавать не только функцию Лагранжа
Ь = у-(х8~сф2). но
и диссипативную функцию F —-^-гпУ.х2 (см. [1], § 25).
Если же для данной системы выбрать «функцию Лагранжа» в
виде

(ср. с задачей 4.17), то для соответствующих канонических перемен-
, dL'
них х	выделенный фазовый объем будет сохраниться, од-
нако в этом случае обобщенный импульс р'—тхе^* не имеет, как прежде, простого физического смысла.
д)	Так как период движения в этом случае зависит от энергии, выделенная область фазового пространства с течением времени растягивается, сзаполняя» всю доступную область фазового пространства (ср. с пунктом б)).
Пусть вначале выделена область х0<х<х0+Дл, ра<р<ро+Др. Нетрудно оценить время, через которое самые быстрее частицы сделают па одно колебание больше^или меньше), чем самые медленные:
А^ + |^.
е)	Пусть имеется N частиц таких, что точки фазового пространства, изображающие их состояние, распределены в начальный момент с плотностью А’о>(хо, ри, 0) и перемещаются согласно уравнениям
X=f(x~, Ро, О.
(I) Р = Ч(х,:, Ро, <)•
Здесь
f (ч. р,. /) = ч + — t, Фр=. Q =Ро для свободного движения и
I (*,. Ро. <) = *0 cosИ/ + sta W/.
<р(лГо, ро, тсйх0 sin (Df-bpoCos ©/
для гармонических осцилляторов. Тогда количество частиц в выделенной области фазового пространства, все точки которой движутся по такому же закону, остается постоянным; в частности, для бесконечно малого фазового объема dxdp имеем
Nw(x, р, t)dxdp=^Nw(xo, рл, G)dxodpo.
Согласно теореме Лвувплля (см. [1], § 46) ^х’ р) = 1, поэтому Р ио. Ро)
w{x, Р, tl=w(x» Ра, 0),	(2)
Выражая из (1) Хо и р»
X0=f(X, р, —0. ро = ф(х. Р. —t)
в подставляя в (2), получаем
и(*, р. о = и(/(х, р, —о,	<р(х, р, —I), 0),
или
ехр|-а(х-ЛТ-Р(х-Х)(р-Р)-Т(р-Р)а1
® (*. Р, ») -	2лДр0Л.г,
где X — f(X0, Ро, t), Р = ц.(Х0, Ро, /), а коэффициенты а, р,'( длясво-бедных частии
_____1	t _________1 fl
а 2Дх^’ /лДх^’ 2Др| 2/п2Дх|’
и для осцилляторов
COS2 <ot /П8(02 sin2 со/ cos2 со/ sin2 со/
а 2Axq 2Дрд * 2Л₽о
(ты 1 \ —------------5 I-
лРо	таЛх;)
На рис. 160, 161 показано, как перемещаются области фазового пространства, в которых 2лДхоДро и {х, pt I) -g- (для свободных
частиц и осцилляторов соответственно). Эти области представляют собой эллипсы, деформирующиеся со временем*). Центры их
*) Если масштабы по осям р и х в фазовом пространстве гармонических осцилляторов выбраны так, что гпы=* 1, то фазовые траектории представляют собой окружности, а выделенная область в фазовом пространстве вращается вокруг начала координат, не деформируясь.
перемещаются по такому же закону (1), как и частицы. В случае свободного движения этот эллипс неограниченно растягивается, в случае же движения осцилляторов —лишь пульсирует. Заметим, что распределения по координатам и по импульсам уже не являются независимыми (а)(х, р, t) не разбивается на два множителя вида »|(х,	<))
Представляет интерес рассмотреть функции распределения по координатам (независимо от значений импульса)
К>(х, t)= J Ш(х, Р, t) Ар
и по импульсам
w(p,t) = [ tu(x, p,t)dx. — 30
Эти распределения оказываются гауссовскими с максимумами в X и Р соответственно;
и(х, /) = -т=г— Г 2ЛЛ' ,
)2лДх
I <Р~И»
Mp,f) = Z7=r-e 2Л₽’ •
У 2лДр
где для свободного движения
Др?
Лх’ =	ЛР* = м.
а для осцилляторов
Др2
Дх3 = Дх§ cos2 со/ 4- ^7^2 sin2 со/,
Др2 = Др2 cos2 <ot -I- ^2(02Axgsin2 со/.
11.25. а) {о*, a}=—i, H0=(Mi*a.
б) Переменные P и Q канонические, поскольку {P. Q} = 1. Из равенства dF=p{x, Q)dx— P(x, Q)dQ определяется производящая функция	<r
f (X, Q, /) - 4" /ПИХ’ -I Y Q2^-2^ -1 у 2^xQe-,<0<.
Новая функция 1	Гамильтона И-го Р1-И ,aF <?<?<) п «о (Q>	“о "Г 'QI	— 0.
в) Выделив	в (Qe~^ „ (ре’му Л Д	У 2^	)
слагаемое — 3Q2! ненную функцию	D3/2mib^, не содержащее времени, получаем усред-Га мильтона <*'«?. р»»-»^3-
В дальнейшем с* Очевидно, 41 Уравнения Г	юбки < >, обозначающие усреднение, опускаем, о —iQP= [Qo|2“ |а|2—интеграл движения, амильтона
Q	..ту.
откуда	<2 = 0^4 Р=«&'*,
так что
1 Х“Г2	— (Qoe“iffl'' +	cos (и'( + <р). ты v	г
Влияние доб	явки W сводится к изменению частоты .	, 3PIQJ3 и = ю+ ИтчУ =И+ 8ш
(ср. с задачей 8Л).
г) Новая функция Гамильтона
4 eM&t । е—4i<o/
2
Н' (Q, S, t) = г№а(
]/2т(о	}
после усреднения сводится к
19 Г. Л. Котики, В. Г. Сербо
Для переменной £=—iQP=|n]2, пропорциональной квадрату амплитуды колебаний, уравнение движения
,	1а
I ={<Н'>Л} =—2-(Р'- Q’).
Учитывая, что
(Q4 -j- Р5) = Л = const.
находим
V = -4A» + c^\
Таким образом, g изменяется так же, как координата частицы (с массой, равной единице) в поле {/(£) = при энергии—2Л2 (ср. с задачей 1.2). Амплитуда за конечное время возрастает до бесконечной величины (так называемый взрывной рост амплитуды).
Разумеется, использование усредненной функции Гамильтона справедливо только при т. е. при £<£св/а.
11.26. Вводим новые переменные:
а =
тш+у, е„	ь=e,w
V 2т<й	*	1/2/п®®	'
_ .тоу4-<Р, ,и-, У 2mws
(со=6124-®з) и канонические сопряженные им импульсы ia*, ib\ ic*. Новая функция Гамильтона, усредненная по периодам 2л/о)2,8,
<//*>= е [ а 12-И) (a*6c-|-ob*c*),
а
в = со. — со, п = —г	; —.
4 у 2тоы2(о3
Уравнения движения	с=—iea — —h}ac*.
имеют интегралы *) <ЯХ>=А	с=—ii]ab* lol2+[fe|2=B, |с|»+|Ср-С.
Интегралы В и С называют интегралами Мэнли —Роу,
11.27]
Уравнение
1 а |2 = it; (flb*c* — с* fee)
можно представить в виде, удобном для качественного исследования:

где | = [«|2,
V(6) = (Z-e£)*-4tft(B-4) (С-1).
В начальный момент с=0, поэтому
А — еС, В<С и
V 1г<!ц*с
т)=(с-Е)’(е’-4а-
-4Ч»(С-В)(С-|).
Графики У(£) для случаев с2<4г(2С и е2> >4>]2С приведены на рис. 162, а и б.
В первом случае £ испытывает колебания, так что происходят биения. Энергия
Рис. 162.
периодически перекачивается от осциллятора к к осцилляторам у, z и обратно. Во втором случае (т. е. при большой «расстройке» 8 и малых начальных амплитудах) колебания у и г не возбуждаются. Подробно об этой задаче см. [22].
11.27. а) <Я'>=е|о|2+р[о|4+т](с2+й*2)> гДе
б) Уравнения движения
—-а=i (е -]-2ц | а |2) a -}-2it]o •,
а *= —i(£-f 2p|flj2)а *Ц-2п]О
имеют постоянные решения
„ 2п — 8 ao = 0’ 1°11 = ~2|1“ ‘
Для £=]а]2 получаем уравнение
I =•— 2«т)(й *2~
Учитывая, что <//,>=е|+|л|84-7](о2+й*5) =C=const, получаем
V+V(E)=O,
is*
где V(^)=4?]2[(a«+a2)s —4]аР]=4(С-е^—16i]V В интересующем нас случае, согласно начальным условиям, величина С мала. В области резонанса |g[<2i] график V(g) (рис. 163) позволяет заметить, что £ испытывает колебания в пределах от нуля до £»п«2|а1|а.
Таким образом, переход к установившемуся режиму колебаний g = |ai|2 (ср. с задачей 8.7) может быть обеспечен лишь каким-то неучтенным нами механизмом, например трением, и быть весьма длительным. Подчеркнем, что этот переходной процесс имеет характер биений даже при нулевой «расстройке», е—О, в отличие от переходного процесса в линейных колебаниях (см. задачу 5.11). гнкцня Гамильтона <Я' (<2, Р, t))—
?)=•	---<2“ + е + “5") р2- Величина
VQ2 4- Р2/т2(о2 представляет собой амплитуду колебания. Переменные
Рис. 163.
11.28. Усредненная
Рис. 164. .
Q н Р мало изменяются за период 2л/у. Это легко видеть из уравнений Гамильтона, содержащих малые параметры в и h.
На плоскости Q, Р точка, изображающая состояние системы, движется по линии H'(Q, P) = C=const. На рие. 164, а и б приведе
ны семейства таких линий для области параметрического резонанса |«|<й/2 и ее окрестности |е1>й/2. В первом случае амплитуда в конечном счете неограниченно растет, во втором — испытывает биения (ср. с задачей 8.8).
§ 12. Уравнение Гамильтона —Якоби
12.2. Очевидно, что траектория — плоская кривая. Переменные в уравнении Гамильтона — Якоби разделяются, если воспользоваться полярными координатами, направив полярную ось z вдоль а. Полный интеграл уравнения Гамильтона — Якоби
s = — Et ± f УР —SmccosO М + [ У 2тЕ — fl/rs dr. (1) Для уточнения знаков в (1) воспользуемся соотношениями
pr=^mr—^r — ±j/^2mE^‘^‘e	(2)
. dS г__________________
ре = тг28 = -^0 = ± У$ — 2та cos 0.
(3)
11а начальном участке траектории г < 0, 6 > 0 (мы предполагаем, что траектория расположена над осью z, рис. 165). Поэтому перед первым радикалом в (1) нужно сохранить нижиий знак, а перед вторым — верхний. Равенство — = в — 310 уравнение др траектории 6

J Р — 2та cos О
л® У2тЕ — Р/г»
Нижние пределы интегралов можно выбрать произвольно, пока не определена постоянная В. При нашем выборе из условия 6->0 при г-*-со следует В=0.
Постоянная ₽ есть интеграл движения нашей задачи и из (3) ₽ = pl 4- 2та cos 0. Она выражается через параметры частицы при г-э-со и б -* 0, т. е. до столкновения, когда ре=мор (р прицельный параметр), 0»2м(Ер24-а)у
При изменении г от со до = |/ 2тЁ =	’ опре'
делаемого условием рг=0, 6 изменяется ог нуля до 0W такого, что
г?и
de________+ f dr
) р — Цта cos О J г2 У 2тЕ — р/г*
(5)
Дальнейший рост 0 сопровождается ростом г. При этом р, знак. Уравнение участка траектории LM е	т
меняет
de
J — 2/KflcosO вт
Удобнее переписать, сложив 6	со
dG
. ггУ2тЕ— ₽№ °" гт
(5) и (6):
(6)
dr
dr
r« V2mE — p/r2
-=0.
При г —> со траектория асимптотически параллельной ON. Угол 6тах можно найтн из равенства ®тах
f dQ _
J У р —’ 2та cos 0
J ггУ2тЕ~р/гг гт
(7)
приближается к прямой,
K‘
,2 Г-____- dr- . --Л-
J ^У2гпЕ-$1г‘ Т₽ г?п
„ cls
Равенство А определяет зависимость r(t). Выбирая А так, чтобы г(0)=гт, получаем
(8)
Vfi •~-2ma cos©
M
L

К
'=1^+4
----------•-------------Z =1/Лр1 + 4- + оа<а. (9)
Интеграл по г в (4) и (7) вычисляется Рис. 160.	элементарно, а по 0 сводится к эл-
липтическому.
При Ер2»с можно разложить подынтегральное выражение в (4)
и (7J по степеням	С точностью до первого порядка
Г sin 0 = г (1 — cos ©I m 2Ер2 J
(10)
(рис. 166).
В этом приближении угол отклонения скорости частицы после рассеяния равен нулю. Объясняется это тем, что действие силы на разных участках траектории (в нулевом приближении это прямая К'М') частично, а в первом приближении полностью компенсируется.
12.3. а) Для определения угла отклонения частицы нужно провести разложение по а/Ер3 в (8) задачи 12.2 до второго порядка. Получаем уравнение
бг,Ях+'-уоиа,+4-(	+4-sin 2М=" (,)
Решая его с точностью	• нах°лим *) угол отклонения
х = п-етах = Ая(^у=зя(5^5)2. и
Сечение рассеяния
Зависимость от х получается такой же, как при рассеянии на малые углы в поле у/r4, убывающем гораздо быстрее, чем U(г).
jib do
б) da = 8£х8,
в) При условии £р2>1Ь(6) | для всех 0 имеем вместо (10) задачи 12.2 с точностью до второго порядка
е	е
t = “	fb(e)do +	( Иб)®	=
р J	р J
о	о
arcsin—22 при О<0<0т,
л — arcsin ^2 при 0m < 0 < 0гаая
•) Ищем 0roai в виде 0max = Oo+6i + 02-|----. где 0i ~ ^^J0O. Уравнение (!) в нулевом приближении 0о=л; в первом приближении 0х + jsin 0О = 0, откуда 01=О; во втором приближении
е, + у- е, со, в,+.1 (у )2(о„ + -L sin 26.) = о, откуда следует (2).
л
Если J Ъ (0) 40 = л =f= 0» то </а=
do.
(1)
Если же <Ь>=0. то da —
12.4. а) Переменные в уравнении Гамильтона — Якоби разделяются, если выбрать сферические координаты с осью г, параллельной а. Обобщенные импульсы
рг = т г — — ]/ЪпЕ — р/г2, р = тг2 6 = ± ]Zp — 2ma cos 6 — p^/sin2 6,
рф = mr2q sin8 0 = const.
Постоянную В = pl. 4* —	4- 2ma cos 0 легко найти, заметив, что
' sin2 0
л? 4-	= Л12, где М — полный момент частицы; его удобно вы-
D sin2 6
числить при г-*-со, 0-»-л— а (а — угол между vTO и а), т. е. до столкновения. Согласно (1) цадение в центр возможно при условии р<0, или
Pz< (a/B)cos а.
(2)
Таким образом, падение возможно, если а < л/2; в этом случае сечение падения о= (na/E)cos а Усреднение по возможным ваправле-п/2
ниям а дает <о> = — I cos а • 2л sin ada =	. Интересно, что
4л J Е	4Е
О
площадка, определяемая условием (2), представляет собой круг с пентром иа оси пучка частиц (хотя поле не обладает симметрией относительно этой оси).
12.5. о =
л/?2 4- -g COS а, О,
a cos а > — ER2,
a cos а < — ER2,
где а — угол между vTO и а.
12.6. а) Используем те же обозначения, что и в задаче 12.2, Уравнение начального участка траектории (г-*-со, 0-»-л)
f rfn = f - _А_________________________	(!)
J р — Ъпа cos 0 J г2 V 2тЕ — tyr2
причем
р = 2т (Ер® — а).
В случае Р > 0 угол 6 убывает при изменении г от со до гт и дальнейшем возрастании до со. Уравнение участка траектории после прохождения минимального расстояния до центра
р________dO____________л , Р______________dr______
J Vp 2та cos 0 ~ 2 У р + J г2 ]/2/?1Е —р/г2* О	гт
Очевидно, что прн Ер2»в падает с уравнением (11) задачи 12.2.	А
При р<0 возможно падение в центр поля (заметим, что, согласно (2), допустимы только значения р^ —2та). При этом г монотонно убывает о г со до 0.
Угол 0 убывает от л
до 0j, при котором ре	"с
обращается в нуль (уча-
сюк траектории АВ; рис. 167). При этом р—2та cos Gi=0. Затем угол возрастает до значения 2л — 6| (участок траектории ВС)
со	п	0
f dr = С de + С de
J г2 2тЕ pr~2 q У Р “ 2me cos 0 g V Р " %та cos 0
(4)
В точке С импульс ре вновь меняет знак и 0 убывает до значения б| в точке D, затем вновь возрастает и т. д.
Уравнение всей траектории можно представить в виде
со	Я
f------ dr =(-[)"( ~Tde  ~ +
4- 2П С d0 _	(5)
J У Р — 2та cos 6
(п = 0, 1,2,...).
Одному значению 6 (0| < 6 < 2л — 0д) соответствует бесконечно много значений г (п может принимать любое целое неотрицательное значение, так как интеграл в левой части (5) при r-^Q неограниченно возрастает). Таким образом, частица совершает бесконечно много колебаний между прямыми BD и СЕ прежде, чем упасть
в центр.
В случае малых прицельных параметров Ер2<Сй оказывается л— О «С 1, так что в (5) можно заменить cos 6 на — 1-}—L. (л =- 0)8. В результате получаем *)
6 — л — р
•= Arsh
(6)
Закон движения /(/) определяется так же, как в задаче 12.2. Если р > О, то справедлив закон, определяемый формулой (9) из задачи 12.2. Если р < 0, то
г(0 = 1>У/г —т2, v = V2Elm, — о> </<r= VIPI/2E, (7)
причем падение происходит в момент времени т.
б) Если р > О (Ер2 > а), то
Г	,;0	aresinL», ет<е<л,
е ]/l+^(U sin0) „-aresinZ™, е„й<0<0га.
Если р < О (Ер2 <а), то
/Л 6	оо
( [ + [ + 2( (] —	46	.. . = С_____ dr
J jy V₽T2™(l + sine) J r2 T/2mE -
где I— число полных колебаний no углу (от 6| до 0? и обратно), совершенных частицей, знаки (±) для движения против (по) часовой стрелке (рнс. 168, а)
л	Ер8	Ер3
65 = — arcsin ——, fl2 = л 4- arcsin-.
а	а
Если р = О (Ер2 = а),
г = -Е=1л
У2

‘в 4г
— -2- < 0 < л.
•) Arsh х = 111 (х + У1 I х2).
Частица движется по траектории рис. 168, б, причем закон движения г = —• Д/	t (I < 0, падение происходит при 0).
г т
12.7.	Полный интеграл уравнения Гамильтона — Якоби см. в [1], § 48. Обобщенные импульсы те же, что и в задаче 12.4а. Падение в центр возможно, если ₽=2zn(£p2 — a cos а) <0 (что заведомо выполняется грк а2<2Ер2/аС1),
Рнс. 168.
Уравнения траектории
С___________________________
ф j Л	р2
siu’oj/ ₽ — 2macosB—
_т >, С KiTidB
r- с J “7Г
fg=IPI/2mE
в общем случае не могут быть проинтегрированы в элементарных функциях. Но качественное описание движения легко дать, если заметить, что уравнение (1), связывающее между собой углы 0 и <р, с точностью до обозначений совпадает с уравнением траектории сферического маятника (см. [1], § 14, задача 1). Поэтому частица
движется так, что точка пересечения ее радиуса-вектора с поверхностью сферы радиуса I описывает такую же кривую, как н сфериче-
„	,	г - Р
скин маятник длины I с энергией, равной и моментом импульса,
равным pv в поле тяжести g	Эта кривая заключена между
двумя «параллельными» окружностями на сфере 0 = 0j и 6 = 62.
При условии а2<2£р2/а<^1 уравнения (1) и (2) легко проинтегрировать:
у 2е ая -г (2е — a*) cos 2«р и
Из (3) видно, что частица, падая на центр, движется в области между двумя коническими поверхностями 0|	6	02. вращаясь
вокруг оси z, причем один полный оборот вокруг оси z приходитси на два полных колебания по углу 6. Для сферического маятника
Рис 170.
Рнс. 169.
в этом приближении траектория замкнута (представляет собой эллипс).
12.8.	а) Уравнение траектории финитного движения (при котором нет падения в центр)
р/г= 1-|-е cos f(0).
(1)
где
Р та'
__________
2ina ~
- ~р-- cos 6
а константы Е и £ удовлетворяют неравенствам Е<0, р>0.
Если 0 < £ < 2та, то орбита «заполняет» область ABCDEF (рис. 169); Г1<г^Г2, г* g ==_£_, 0^0 < 0а, 0Х — arcsin JL-, 62 — 2л — С\, т. е. проходит сколь угодно близко к любой точке этой области.
Если р = 2та, то
f(G) = /21ntg(0/4) 4-Q	(2)
и траектория расположена внутри кольца л г ^г2 (рис. 170) Если р > 2та, то траектория заполняет кольцо г± г г2.
В частности, если р » 2та, то
3	3
f (6) = е ч- Csin о + т + - рч-с2,	(3)
где t==ma{$. Это — слабо деформированный прецессирующий эллипс, характер деформации которого связан с его ориентацией. Уравне-ние (3) применимо и при 0^£~2. Интересно сравнить его с результатами задачи 2.24.
12.10. Переменные в уравнении Гамильтона — Якоби разделяются. если выбрать ось г вдоль вектора а (см. [1], § 48, форму-
ла (489)). Движение по радиусу /
_ Р 2гпга при 3^=0 такое же, как н движение частицы в кулоновом поле — а/г с моментом р и энергией £. При р < 0 происходит падение частицы as ds
Уравнения траектории = const, = const. Первое
на центр, из них
,, sin» в у/ ₽ —2macos в —gjjjj
совпадает с уравнением траектории сферического маятника с энергией р/2т/2 и моментом Afz = fc в поле тяжести g— —а/ml3 (см [1], § 14, задача 1). Второе уравнение связывает г и 0. При анализе этого уравнения можно также воспользоваться аналогией со сфери-
ческим маятником.
12.11.	а) |Л1.1< V'nWZ.
б)	Финитное движение возможно при любом Мг.
12.12.	б) Полный интеграл уравнения Гамильтона — Якоби (см. [1], § 48, задача 1)
S=~ В -|-р,ф+р, (?) d? + [ рч (1)) di), где	=
=	₽ + ТЧ-
Траектория и закон движения определяются уравнениями
3S
= В,
dS
= С,
dS дЕ
= А
f --------С <?ч м <4	Рф f tfn r
J	J ЧРП(Ч) - B’ 4 - 2 J s»p, (I) “ 2 J n!P4('D ' c’
Для исследования характера движения нужно определить области допустимых при данных Е, £ значений | и tj. Графики эффек-
тивных потенциальных энергий (4(£) и С7Л(^) изображены на рис, 171.
Если Д=0, то при — та<$<та (см. кривые а) и £<0 движение как по %, так и по т) финитно, при Е 2> 0 — инфинитно. С по-
Рис. 172.
гуры ABCD вокруг оси г (см. движение инфинитно.
явлением малой силы £>0 на графике £/|(g) появляется максимум (см. кривые Ь)\ При U^id<ZE<Z t^gmax ДНИ" жение по-прежнему финитно В «плоскости pz» движение ограничено областью
Ч1<ЧО|г
(рис, 17ф; сама же плоскость рг вращается вокруг оси z с угловой ско-
ростью Траектория заполняет область пространства, образуемую вращением фи-
задачу 2,36), При Uita^<E
С ростом F величина уменьшается, a 1/чпцп растет. Когда окажется l/gma» < tfqmin, финитное движение станет невозможным (при ₽<-ma + ^-(FmpJ)’z> экстремумы вообще отсут-ствуют).
12.13.	В эллиптических координатах, р=О)'(£2 — U(1—tflt г—a£i). с=}'62 — а2, потенциал
и =
СО при В > ?D = Ь/а, 0 при Н <
зависит только от и переменные в уравнении Гамильтона — Якоби разделяются (см. [1], § 48).
Область недостижимых значений t] определяется условием
2/ло2Е—р/(1 —t]s)< 0 или |г)| > |cos а|.
Итак, движение происходит в области |т|| < |cosa|, 1 < £ < £0 (заштрихованная на рнс. 173 область).
12.14.	Переменные в уравнении Гамильтона — Якоби разделяются в эллиптических координатах (см. [1], § 48, задача 2 при cci = — а2 ==а). Дли частицы, летящей из бесконечности вдоль оси г, постоянная ₽ = — 2тЕр2 -4- 4macr, где р— прицельный параметр.
При р < 0 траектория качественно не отличается от траектории частицы, рассеиваемой в поле точечного диполя (см. задачу 12.66).
При р > 0 частица «падает» на диполь (т. fe. проходит в своем движении через отрезок OjOa) и вновь уходит на бесконечность. Если
Рис. 173.
Рис. 174.
дополнительно ру](1]|)=0 при t)i <0, то частица движется в области, ограниченной гиперболой т) = >] (Рис- ^4),
12.15.	В уравнении Гамильтона — Якоби

отделяются время и угол <р:
S « - Ei + дир + S(r. г).	(2)
Рассматривая далее только траектории, пересекающие ось г, положим рф = 0. Разделить переменные т и z в уравнении не удается, и мы будем искать интеграл его приближенно, в виде разложения по г.
$(',г) = $0(2) + лНг)4-7ОЮ+ ...	(3)
Так как радиальный импульс
₽, = 57 = 4'М +'<’(z) + 	(4)
для частицы, летящей вдоль оси z (при г — 0), равен нулю, то для рассматриваемого пучка частиц ф(2)=*0. Подставляя (3) в ([) и приравнивая коэффициенты ври одинаковых степенях г, получаем (ср. [2], § 56, задача 2)
So(z)=pz,	(5)
ра' (г) + а2 + Ж2 (г) = 0.	(6)
Вне линзы (при |г|>а. 2^(г) = 0) из (6) следует, что р
“(г)=7|^ пРи г<— а,	(7)
р
=	при z>a.	(8)
Уравнения траекторий
as
*4.2 = 2(г + сЫ’“ 'л	(8)
— уравнения прямых, пересекающих ось г в точках — С112 *), т. е. z0 == — Ci, zt ——Cg. Из (6) получаем я	я
ро (а) - ро (- а) + f o2<fe + Ж2 (г) Л = 0.	(10)
*-а	Да
*) При г, близких к С1Л оо так что разложение (3) неприменим. Однако уравнения траекторий (9) остаются справедливыми и в этой области.
Поскольку |zUri| > а, из (7), (8) получаем
о(± О)	(П)
г1,0
а
Оценим [ о2<!г. Согласно (6) о (г)—монотонная функция. Поэтому —а
С	2а р^
1 o2da -п— С ра (+ а).
Л	zl,0
Таким образом, из (10)
Ж!(г)<'2=7'-	.(12)
Условие |z0,i] а действительно соблюдается, если а<&
12.16. Точки
фокусировки
ИГп = *в(етс*е,<го + Т1
В зависимости от величины ?.2=1 + (^JC/2cxp)2 имеется одна или несколько точек фокусировки.
12.17.
S(q, Q0. t, «o)=f(fc a,(q, q0, t. t0), f) —f(qo, a[q, ?o, t, to), t0),
где f(q, a, 7)—полный интеграл уравнения Гамильтона — Якоби, а зависимость a(q, q0, t, f0) определяется уравнением (системой уравнений для случая многих степеней свободы)
Sf(q,a,l) _дЦд„а,(,) да	да
§ 13.	Адиабатические инварианты
13.1.	ЕЧ = const
13.2.	График I ~vl представлен на рис. 175, в. Величина vl колеблется около приблизительно постоянного значения причем
А/ 7
амплитуда колебаний имеет относительную величину —•~ _е
* v
20 Г. Л. Коткив, В. Г, Сербо
Отклонение <oZ> от постоянной имеет высший порядок малости
-at
13.3.	ftcog“4
13.5.	h е= sin2/3“*
13-6.	а сс sin
8ml
13.7.	/ =-----;
2 I’ cos2 -у К
13.8.	Обозначим через х и X координаты частиц m и М, отсчитываемые от точки О. Движение легкой частицы можно приближенно рассматривать как движение между двумя стенками, одна из которых перемещается. Поскольку выполняется условие
ы » Mi,
Рпс. 175.
(I)
сохраняется усредненное по периоду произведение |х|X = С (см. задачу 13.2). Исключая х из закона сохранения энергии
mx* , MX* _ p 2 ‘	2
находим, что влияние легкой частицы на движение тяжелой равносильно появлению потении-
гпС2
альной энергии у (X) =
МХ2 ( Т,{У. Р
Уравнение —— с
приводит к закону движения
1/ mC* 2Е
X =* у ~2£~	~М~^—T)s Постоянные Е, С и т могут быть
определены по начальным значениям X, X и х (не зависят от х(0)).
После того как условие (I) будет нарушено, предлагаемый способ решения задачи будет неприменим.
Подобное приближение (называемое адиабатическим) находит широкое применение, иапример, в теории молекул.
13.9.	Обозначим координаты тяжелых частиц ХЬ2, а легкой х. При Xi < х < Х2 потенциальная энергия
(7= (x-X,)f+(X,-x)f ^(Xs-X,)f.
Поэтому легкая частица свободно движется между тяжелыми, и |х| (Ха— Xi)== С = const (см. предыдущую задачу). С учетом этого из закона сохранения энергии для относительного движения тяжелых частиц (X = Х2 — Xi) получаем
М Г2 J mC’ I- IV С ~4~	+ 2Х* ‘¥fX=E.
Разлагая (X) =	вблизи минимума Хо= (тС2{[),/а.
находим частоту малых колебаний «иона»
2(7” (Хо) 6/ “ = М - мх„ 
13.10.	В уравнениях для Р и Q
0=<о+ J?_sui2Q, P = — P“cos2Q 2со	о
разложим частоту в ряд по L Ограничиваясь поправками первого порядка, получим ,
t
Q = (<ооГ + ф) 4- 2* 4/® + I sin 2Q dt* W
2ы0 n
где «о и Wo — значения частоты и ее производной в момент времени t0 = 0, причем ©о = и в С1.
-/"Ip"
Фаза Q и амплитуда Д = у тЬ)~ возмущенного движения относительно мало отличаются от своих невозмущенных значений 20»
/2Р даже для промежутков времени, много больших периода колебаний 2л/© (рис. 176).
Так, для моментов времени /^1/е©а второй член в (I) порядка едипицы, а третий — порядка е, и поэтому
Q = <»,( + <р + 2.	Р = Ро.
Но такое изменение фазы приведет к тому, что в переменных р, q
возмущенное движение
Рис. 176.
q 7) =г Лъ cosf ©0/	<р + -L ®0Г«
будет существенно отличаться от невозмущенного
<7с(0 =А) cos (®0Г + <р), так что разница
9(0 — 9о(0 ~ ?о(О.
При попытке строить теорию возмущений для переменных q и р мы получим для поправки первого порядка (0 уравнение
•• . 2
51 -г <^51 =“
— — 2©0©flMo cos (®0/ -|- <p) с растущей во времени резонансной силой. Поэтому полученное
в такой теории решение справедливо лишь для малых промежутков времени порядка нескольких периодов колебаний
2л I
©о с е©0 *
13.I2J (0 = 1 (0) 4- j F (0 sin ы/ di -о t
_ — L (0) — i F (/) cos и/ dl 4- _1_
и	m©2 J	2m®
L	J 0
e1a1dl
Таким образом, если сила изменяется медленно, то /(0 осциллирует вблизи /(0). Если F(/)->const при ?-*-«», то полное изменение адиабатического инварианта /(со)—/(Q) может быть очень малым (см. задачу 5.18),
13.13.	PV‘f‘ = const.
лч I 7?	7?	7? \
13.14.	a) £=2^1 jr+fcr + Tr 1.гда °- Ь- с-л™ ребер
параллелепипеда, a const. Сохраняются абсолютные величины проекций скорости па каждое из ребер.
13.15.	Переменные разделяются в сферических координатах. Момент импульса М сохраняется строго (Мл является, кроме того, адиабатическим инвариантом, соответствующим углу <р). Адиабатический инвариант для радиального движения
rmin
О)
Зависимость Е(₽) можно выяснить, не вычисляя интеграла (I). Замена г = Rx даёТ
/г=-^ j }/A2mE№~^^=/r(W.AI).	(2)
хпйп
откуда ERZ = const Поэтому для угла падения а
ztnin М
^^ = - = ^7=-= Const.
2
13.16. а) Есоу2’"; б) Е~у-'.
гыах
13.17. CE = <W> = -1 (
rmin
&Jdr_______
? м5 Гл
Л 2^-и)
13.18.	Е—/iQi+Z^a (обозначения задачи 6.5а). Траектория заполняет прямоугольник JQil <	| Qs К ]/'/в^Г*
Условия применимости теории адиабатических инвариантов:
fljCCj, Я,«СД (> = 1,2).
Вие области вырождения эти условия сводятся к таким же условиям, наложенным иа В области вырождения ({ tti	а)
второе условие оказывается более жестким я дает <Oj с а (область вырождения проходится за время, гораздо большее периода биений).
13.19.	В отсутствие связи аху система распадается иа два неза-
висимых осциллятора с координатами х и у.
ЕХ	Еу
батические инварианты/* = “, этих осцилляторов.
Соответствующие адиа-где Ех и Ev—энергии
При учете связи система состоит нз двух независимых осцилляторов с координатами Qi и Если частота изменяется достаточно
медленно, то сохраняются
Вне области вырождения нормальные колебания сильно локализованы, а именно при О|«йа оказывается Qj==x, Qs~y< а при W) > <i)E Qi = у, Qa =— х. Таким образом, яри <t>i < о2 оказывается 7Х == /ь lv = /2, при со2 < (Щ,—наоборот, 1Х = /2, lu = /t (рис. 177).
Рис. 178.
Проиллюстрируем это следующим примером. Два маятника, длина одного из которых может медленно изменяться, связаны пружинкой малой жесткости (рис. 178). При значительной разнице длин маятников I и L нормальные колебания почти совпадают с колебаниями одного или другого маятинка.
Пусть вначале маятник АВ колеблется с амплитудой фо. а маятник CD—с очень малой. При уменьшении L амплитуда колебаний
маятника CD остается малой, пока длина его не станет почти равна I. При LkI амплитуда его возрастает (а при 1= L оба маятника будут колебаться с амплитудами, равными в противофазе). С дальнейшим убыванием L почти вся энергия перейдет к маятнику CD, и амплитуда его станет равной = *р0 ^”77j ’ как для отйель-ного маятника.
При сравнительно быстром прохождении области вырождения <щ а подобной перекачки энергии между осцилляторами не происходит. Если, кроме того,to] wf, <0j «Дог.то сохраняются 1Х и 1У.
13.20,	Из уравнений движения
х 4-	20X0 = 0,	(I)
У + ®fsz + ₽Х“ = 0	(2)
легко обнаружить, что связь осцилляторов приводит к большой передаче энергии при 2qi « id2.
Пусть х = a(J)-cos(<i>]f 4* <?)» У — b(t)cos(Gbt 4- Ф). Если Ь, то член ₽х2=	+ 4"₽°2 cos В играет ₽оль вынуж-
дающей силы, приводящей к резонансному росту у. Если же а Ь, то член 2$ху = 2fibx cos(co2f 4-ф) в (1) приводит к параметрической раскачке колебаний х. Подробное исследование системы (1) и (2) можно найти в задаче 8.10.
। Область резонансного взаимодействия:	— со21 < р&шу*.
Сильное резонансное взаимодействие осцилляторов имеет место, вообще говоря, при условиях nv>i = rn<o2, где пит — целые числа. Однако ширины областей частот, в которых осуществляются эти резонансы, при не очень малых п и т чрезвычайно малы (см. [1], § 29). Поэтому их влиянием на движение осцилляторов можно пренебречь при о>| не слишком малых (хотя и достаточно малых для того, чтобы можно было использовать теорию адиабатических инвариантов).
13.21.	Пусть частица, движущаяся в плоскости ху под малым углом к оси у (|xj С | г/|), отражается от оси х и от кривой £/и(*) (рис. 179).
Если считать закон движения в направлении оси х известным, то можно исследовать движение в направлении оси у, рассматривая х(0 как медленно изменяющийся параметр. Сохраняется адиабатический инвариант ^p^di/=2|pj,|^o(x) =2п/, и это равенство определяет зависимость ру(х).
Для определения же x(t) можно использовать закон сохранения энергии ntsx2 -f- Ру (х) == 2тЕ. Минимальное расстояние хгащ определяется условием р‘у (xmin) = 2tnE. Подставляя УсДл) — х tg а, 2л/=2~[/2гтгЕ1 tg а cos <р0» получаем xwiD = I cos <pu.
Решение задачи методом отражений очевидно из рис. 180 Этот метод дает точное решение, применимое при любых углах а и
по не может быть обобщен па случаи, когда £/o(-v) не является прямой.
2л
13.22.	tg ах = tg <р, Т =-----77--'	.
6 m	ao^/cos2(p
13.23.	а) Задача о движении частицы в магнитном поле при указанном выборе векторного потенциала сводится к задаче о движении гармонического осциллятора (см. задачу 10.7). Адиабатический инвариант
Е -* p^l2m t.«®
1 =--------« — т?К,
сто, где а —	— радиус орбиты частицы (см. [2], § 21J.
Соотношение /сола2^ допускает простую интерпретацию: радиус орбиты изменяется так, что поток магнитного поля через площадку, охватываемую ею, остается постоянным. Расстояние центра cpj, орбиты от плоскости yz, равное	с ростом уменьшается.
Возникновение дрейфа орбит связано с появлением электрнче-~	1 ЙА Г I • \
ского поля g = — ~	— 10,	— хз^, 01 при изменении магнит-
ного поля (ср. [2], § 22).
Векторы электрического поля g и скорости для различных положений орбиты частицы показаны иа рис. 181.
б)	Функция Гамильтона в линдрических координатах
р?
Н ~ 2т + 2m +
 2тгг — 2с г
Интегралами движения являются	Рис. 181,
pt и рч.
Адиабатический инвариант для радиального движения
rmax
после замены г = принимает вид
£тах __________________________
J V2тЕ1К-' —- i- Р)’ « = «/, (рф.
tmln
Поэтому Ej-fStf = const, т. е. энергия поперечного движения изменяется так же, как в пункте а). Расстояние центра орбиты от начала координат
Gnax ~1~ *тИ1 ^тпах £min 1
2	“ 2УЖ
С ростом 3S центр орбиты приближается к началу координат (рис. 182).
*) Интересно, что /, фактически не зависит от ру при р, > 0. Действительно, г представляет собой изменение угла Дф за вре-мя одного радиального колебания, а при рф > 0 начало координат лежит вне траектории (см. рис. 98, б), и потому Дф = 0.
При изменении 2S появляется электрическое поле
=	#r = #t = 0.
силовые линии которого представляют собой замкнутые окружности. В реальных условиях однородное магнитное поле может существовать только в ограниченной области про* странства. Электрическое поле, иоявля----------------„ ющееся при изменении магнитного, очень Л сильно зависит от формы этой области
EZ/^уЧ	и условий на ее границе (см. [2], § 21).
Например, поле, рассмотренное в случае •	а), осуществляется вблизи проводящей
рис 122	плоскости с током, в случае б) — в со-
леноиде *).
Сильная зависимость характера дви-
жения частицы от слабого поля g даже в случае предельно малых объясняется наличием вырождения (при = const периоды движения по двум координатам х, у или г, <р совпадают).
Заметим, что величина оказалась адиабатическим инвариантом в обоих случаях. Можно показать, что этот результат не зависит от выбора А (см. [2], § 21; [8], § 25).
13.24.	Выбрав векторный потенциал в виде
=	Лг=Лг = °«	0)
получаем адиабатические инварианты
Z (О »	'q> — Pyr
£гпах
=	V J	= /,(Рф,С),	(2)
5min
где
~ V®» + (e/<S/ /nc)s ‘
*) Изменения электрического воля, связанного с изменением выбора А, не было бы, если бы одновременно был изменен скалярный
1 .
потенциал на величину ^{/(градиентное преобразование).
Таким образом,

Векторный потенциал (1) задает магнитное поле, симметричное относительно оси г, проходящей через центр осциллятора.
При другом выборе А
А* = Д» = О,
Аи =» хЯ(Г)
(4)
получаем фактически другую физическую задачу. Функции Лагранжа в этих двух задачах отличаются иа
. Ate \ е • б£ = ^- f 2З Wxyj 23 Э^ху,
т. е. отличие их, если отбросить в (5) несущественную полную производную по времени, очень мало.
В предыдущей задаче, где движение было вырождено, именно появление этой добавки приводило к полному изменению направления и скорости дрейфа орбиты. В нашем же случае движение осциллятора при JC = const невырожденное, И добавка может быть отброшена (ср. с задачей i3.19). Поэтому соотношения (3) справедливы и при другом выборе А. При прохождении области вырождения (J£=0) соотношения (3) сохраняются только для аксиально-симметричного поля (1). Поведение же осциллятора, например, в поле (4) при прохождении через нуль требует дополнительного исследования.
13.25.	а) С помощью канонического преобразования можно привести функцию Гамильтона к сумме двух независимых осцилляторов (для X, Y; см. здачу 11.9). Адиабатическимв инвариантами являются отношения энергии каждого из этих осцилляторов к его частоте.
Напомним, что колебания каждого из них представляют собой движение по эллипсу (см. задачу 6.36). Выраженные, например, через амплитуду с* колебаний вдоль осв х, адиабатические инварианты равны
то? Й£
1,2- <„1	(*-1.2).
Прн изменении параметров системы к новой функции Гамильтона добавляется также частная производная производящей функции по времени, равная*) ЦгпсоаХУ + РхРу/тыя). Эта добавка мала
(Л « Ок), и ее можно ие учитывать, если только собственные частоты не совпадают (ср. с задачей 13.19). Случай вырождения при W1 = <о2 и магнитном поле, проходящем через нуль, требует отдель-
ного рассмотрения.
При другом выборе векторного потенциала, приводящего к тому
же магнитному полю, но другому электрическому, £ = — ~ адиабатические инварианты оказываются прежними (опять за исключением случая <oi == co2)JC = 0).
Если ы1 = <п2, то возможен и другой инвариантов (см. предыдущую задачу).
б) Пусть для определенности Wi > а>2.
выбор адиабатических
Движение происходит
. центр же окруж-
по окружности радиуса а
2© с частотой
ности перемещается по эллипсу с полуосями, параллельными осям к и у и равными
6 У®1®#
с частотой
в) Колебание будет происходить почти вдоль оси у, амплитуда его увеличится в |/'<о1/(ов раз (ср. с задачей 13.19).
13.27.	а) Движение частицы в плоскости ху происходит под действием медленно изменяющегося (из-за смещения вдоль оси z) магнитного поля Прн этом сохраняется адиабатический инвариант /. д Е । Iе(см- задачу 13.23). Из закона сохранения энергии х Ч тс
*) Вычисление частной производной производящей функции можно упростить, используя следующие соображения.
При переходе от момента t к t + fit необходимо совершить дополнительно каноническое преобразование, соответствующее переходу от X к К 4- 6k Такое преобразование задается производящей функ-шюй Ф (х, Y, р'х, Ру) - ХР'х 4- ГРу+ Й. (тМ,ХУ + Р^Ру/тга,) (см. задачу 11.17). Поэтому 55 |	= X (тагХГ +Рх'\/т<‘>,').
имеем
тг>2 , . e^(z) г
2
Частица движется в направлении оси г так, как двигалась бы в потенциальном поле U (г) = /.	Период колебаний (ср. с зада-
че ‘
чей 26 из [1]. §П)
2ла
Т =----/-	 — •»
v р Л sin2 а — cos2 а где а — угол между скоростью частицы v и осью г в начале координат. Частицы, для которых ctg’cc > К, не удерживаются в ловушке. Условие применимости теории адиабатических инвариантов заключается в том, чтобы изменение магнитного поля за один оборот частицы было мало. Это дает mcKvt -С M'5g0,
Примером магнитной ловушки могут служить радиационные пояса Земли (подробнее о ловушках см. [29]).
б)	Т= 2na/osin<z.
13.28.	а) — Ez) az = const, E^X0=CQnst, E — £x + £z;
6)	= const, ЕгУГ 3fSja= const.
13.29.	Пренебрегая в функции Гамильтона
_£l J__d_ .	sin* 0
Н ~ 2m 2mr2 “г 2mr2 sin2 0 2cm 8mca последним членом, квадратичным no 5g, можем разделить переменные в уравнении Гамильтона — Якоби,
При медленном изменении 5g величины в в £ ч” н 2тс остаются постоянными.
Рх мА’	„
13-30.	+	= £.. 2^+2moV = £E.
- р^)у + хрхру = А, (m'fA* - ру-	= ~ {£„ Л).
ЛИТЕРАТУРА
I.	Л. Д. Ландау, Е. М. Лифшиц, Механика, «Наука», 1973.
2.	Л. Д. Ландау. Е, М. Лифшиц, Теория поля, «Наука», 1973.
3.	Л. Д. Ландау, Е. М. Лифшиц, Электродинамика сплошных сред, Гостехнздат, 1957.
4.	Г. Голдстейн, Классическая механика, «Наука», 1975.
5.	Д. тер Хаар, Основы гамильтоновой механики, «Наука», 1974.
6.	В. Г1. Арнольд, Математические методы классической механики, «Наука», 1974.
7.	Л. И. Мандельштам, Лекции по теории колебаний, «Наука», 1972.
8.	Н. И. Боголюбов, Ю. А. Митропольский, Асимптотические метол ы в теории нелинейных колебаний, Физматгиз, 1958.
9.	Ю. И. Неймарк, Н. А. Фуфаев, Динамика неголопомных систем, «Наука», 1967.
10	Е. Янке, Ф. Эмде, Ф. Лёш, Специальные функции, «Наука», 1964.
II.	Н. Мотт. Г. Месси, Теория атомных столкновений, «Мир», 1969.
12.	Н. fl. Боголюбов, Д. В. Ширков, Введение в теорию квантованных полей, «Наука», 1976.
13	Р. Курант, Д. Гильберт, Методы математической физики, Гостех-издат, 1951.
14.	Г. С. Горелик, Колебания и волны, Физматгиз, 1959.
15	Дж. В. Стрэтт (лорд Рэлей), Теория звука, т. I. гл 1V. Гостехнздат, 1940.
16.	Л. М Бонч-Бруевич, Радиоэлектроника в экспериментальной физике, «Наука», 1966.
17.	М. В. Волькенштейн, Л. А. Грибов, М. А. Ельяшевич, Б. И. Сте-панов, Колебания молекул, «Наука», 1972,
18.	Я. Киттелъ, Введение в физик)' твердого тела, Физматгиз, 1962.
19.	И. Л. Кукин, Теория упругих сред с микроструктурой, «Наука», 1975.
20.	Дж. П. Ден-Гартог. Механические колебания. Физматгиз, 1960.
21.	Э, Ферми, Научные труды, т. 1, стр. 440, «Паука», 1971.
ЛИТЕРАТУРА	----- bi«
22.	Н. Бломберген, Нелинейная оптика, Приложение 1, §§ 5, 6, «Мир», 1966.
23.	Л. Д. Ландау, Е. М. Лифшиц, Статистическая физика, гл. XIV, «Наука», 1976.
24.	Ф. Стейси, Физика Земли, «Мир», 1972.
25.	И. М. Лифшиц, М. Я. Азбелъ, М. И. Каганов, Электронная теория металлов, «Наука», 1971.
26.	Д. И. Блохинцев, Основы квантовой механики. «Высшая школа», 1961.
27.	А. И. Базе, Я. Б. Зельдович, А. М. Переломов, Рассеяния, реакции и распады в нерелятивистской квантовой механике, «Наука», 1971.
28.	Р. Calogero, О. Ragnisco, Lettere al Nuovo Cimento 13, 383 (1975).
29.	Л. А. Арцимович, С. Ю. Лукьянов, Движение заряженных частиц в электрических и магнитных полях, «Наука», 1972.
30.	М. Ш. Рывкин, Доклады Академии наук, 221, № 1 (1975).
31.	Б. В. Соколов, Ядериая физика, 23, 628 (1976); 26, 427 (1977).