Author: Гоноровский И.С. Галустов Г.Г. Демин М.П. Прозоровский В.Е. Рыжов В.П. Федосов В.П.
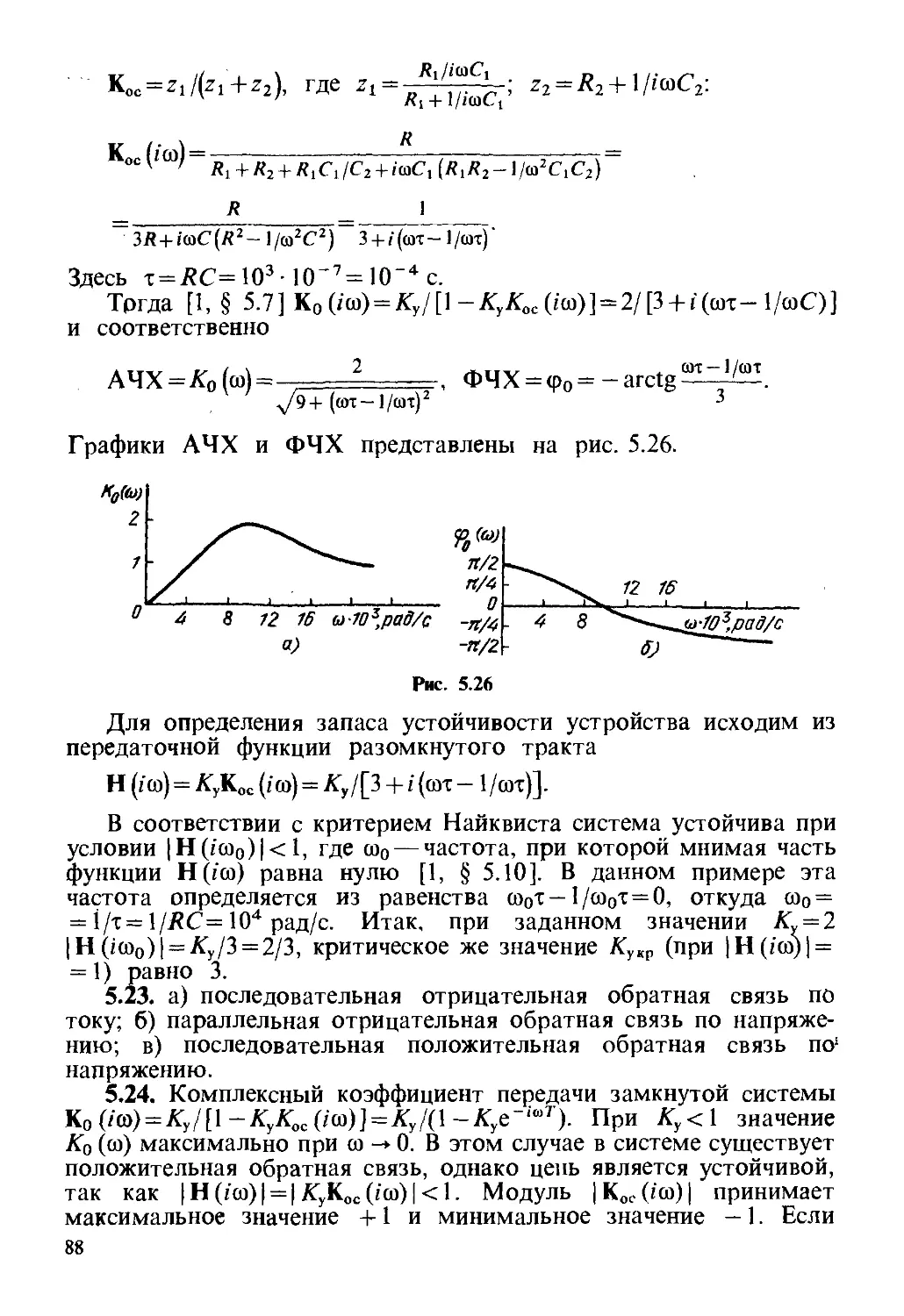
Tags: электротехника общая радиотехника радиотехника
ISBN: 5-256-00344-5
Year: 1989
Text
РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ И СИГНАЛЫ.
ПРИМЕРЫ
И ЗАДАЧИ
Под редакцией И. С. Гоноровского
Допущено Государственным комитетом СССР по
народному образованию в качестве учебного пособия для
студентов радиотехнических специальностей вузов
Москва
но и связь»
1989
^-^ MOCt
(Ε)«Рад
ББК 32.841
Ρ 15
УДК 621.372 + 621.351(075)
Авторы:
Г. Г. ГАЛУСТОВ, И. С. ГОНОРОВСКИЙ, М. П. ДЕМИН, В. Е. ПРОЗОРОВСКИЙ,
В. П. РЫЖОВ, В. П. ФЕДОСОВ
Рецензенты: кафедра «Теория цепей и сигналов» Горьковского политехнического
института, доктор техн. наук, профессор С. И. Баскаков
Редакция литературы по вычислительной технике
Радиотехнические цепи и сигналы. Примеры и задачи:
Ρ 15 Учеб. пособие для вузов/Г. Г. Галустов, И. С. Гоноровский,
М. П. Демин и др.; Под ред. И. С. Гоноровского.— М.:
Радио и связь, 1989.— 248 с: ил.
ISBN 5-256-00344-5.
Пособие охватывает все разделы курса «Радиотехнические цепи и сигналы»: общую теорию
детерминированных и случайных сигналов, методы анализа воздействия сигналов на линейные,
нелинейные и параметрические цепи, а также синтез цифровых цепей, обобщенную линейную
фильтрацию и кецегральный анализ. Приводятся методические указании к решению задач.
Данное пособие ориентировано на 4-е издание учебника И. С Гоноровского «Радиотехнические
цепи и сигналы». Может быть также использовано при самостоятельном изучении курса.
Для студентов вузов радиотехнических специальностей.
2302020000-114
Р 046(01)-89 »* ББК 32Ш
Учебное издание
ГАЛУСТОВ ГЕННАДИЙ ГРИГОРЬЕВИЧ, ГОНОРОВСКИЙ ИОСИФ СЕМЕНОВИЧ, ДЕМИН МИХАИЛ
ПЕТРОВИЧ. ПРОЗОРОВСКИЙ ВИКТОР ЕВГЕНЬЕВИЧ, РЫЖОВ ВЛАДИМИР ПЕТРОВИЧ, ФЕДОСОВ
ВАЛЕНТИН ПЕТРОВИЧ
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ. ПРИМЕРЫ И ЗАДАЧИ
Учебное пособие
Заведующая редакцией Г. И. Козырева, редактор издательства Т. М. Бердичевская, переплет
художника С. Ю. Архангельского, художественный редактор Н. С Шеин, технический редактор
И. Л. Ткаченко, Корректор Т. СВласкина
ИБ № 2004
Сдано в набор 9.1.89. Подписано в печать 21.04.89 Формат 60x88/16. Бумага офсетная №2
Гарнитура Тайме. Печать офсет. Усл. печ. л. 15,19. Усл. кр.-отт 15,19. Уч.-изд. л. 14,16. Тираж 20 000 экз.
Изд. № 22697. Зак. № 687 Цена 80 к.
Издательство «Радио и связь». 101000 Москва, Почтамт, а/я 693
Ордена Октябрьской Революции и ордена Трудового Красного Знамени МПО «Первая Образцовая
типография» Союзнолиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и
книжной торговли. ΙΠ054, Москва, Валовая, 28
ISBN S-256-00344-5 © Издательство «Радио и связь», 1989
Предисловие
Настоящее пособие содержит большое число примеров и задач,
иллюстрирующих физическую и количественную стороны
процессов и явлений, изучаемых в дисциплине «Радиотехнические цепи и
сигналы». Решение этих задач способствует также освоению
математического аппарата, необходимого для применения теории
к анализу конкретных радиотехнических устройств.
Тематика пособия охватывает все основные разделы курса
«Радиотехнические цепи и сигналы». Оно рассчитано на
совместное использование с одноименным учебником И. С. Гоноровского
(изд. 4-е), поэтому не содержит выводов расчетных формул.
Названия глав пособия совпадают с названием глав указанного
учебника. Разделам, посвященным статистическим методам
радиоэлектроники, а также методам цифровой обработки сигналов,
выделено относительно большее число примеров и задач, нежели
«старым», более установившимся разделам.
К задачам, для решения которых требуется материал,
выходящий за пределы учебника И. С. Гоноровского, рекомендована
дополнительная литература. Довольно подробные указания по
решению задач позволяют использовать книгу в качестве пособия
на практических занятиях по курсу РТЦ и С. Потребность в
подобном пособии особенно возрастает в связи с современной
тенденцией увеличения объема семинарских и лабораторных
занятий, а также внеаудиторной самостоятельной работы
студентов.
Главы 4, 5 и 10 пособия написаны Г. Г. Галустовым, гл. 1, 14 и
15—И. С. Гоноровским, гл. 12—М. П. Деминым, гл. 2 и 8—
В. Е. Прозоровским, гл. 7 и 11—В. П. Рыжовым, гл. 3, 6 и 13—
В. П. Федосовым, гл. 9—Г. Г. Галустовым и В. П. Рыжовым.
Глава 1. ОБЩИЕ ХАРАКТЕРИСТИКИ
РАДИОТЕХНИЧЕСКИХ ПРОЦЕССОВ
И ЦЕПЕЙ
1.1. В антенне радиопередающего устройства возбуждаются
колебания с частотой /=1000 МГц. Определить длину
электромагнитной волны в свободном пространстве (вакууме), излучаемой
антенной передатчика.
1.2. Прием радиосигналов с несущей частотой f0 = 300 кГц
осуществляется в четырех пунктах, удаленных от передающей
антенны на расстояние соответственно г0, г0 + 250, г0 + 500 и
г0+ 1000 м. Определить разность фаз между напряжениями на
входах приемников 1—2, 1—3 и 1—4.
1.3. Полоса пропускания приемника радиовещательного
диапазона составляет примерно 5 кГц. Определить относительную
стабильность частоты передатчика, работающего на волне λ =
= 1000 м, чтобы уход частоты Δ/ не превышал 1% от полосы
пропускания приемника. То же при рабочей волне λ = 25 м.
1.4. Полоса пропускания радиолокационного приемника
составляет примерно I МГц. Определить требуемую относительную
стабильность частоты передатчика при рабочей волне λ=10ΰΜ,
чтобы уход частоты не превышал 1% от полосы пропускания.
1.5. На колебательный контур с параметрами L, С и г
воздействует периодическая последовательность коротких
импульсов напряжения с периодом Τ (рис. 1.1, а). Возбуждаемые в
I I I I
-Г 0 Г 2Т t
а)
Д/1^/\/\Л;/\/\л4/У·;
Рис. 1.1
Рис. 1.2
контуре колебания изображены на рис. 1.1,6. Каковы возможные
частоты в спектре этого колебания?
1.6. На колебательный контур из предыдущей задачи
воздействуют одновременно две периодические последовательности: одна с
периодом Тх (совпадающим с Г) и вторая с периодом Т2фТх. Каковы
структура и спектральный состав возбуждаемых в контуре колебаний?
1.7. На конденсатор, емкость которого изменяется по закону
C(t) = C0(\+ms'mQt), воздействует напряжение u(t) = Ui sincot ί,
— οο<ί<οο. Определить ток, отбираемый от источника
напряжения, и проанализировать спектральный состав тока.
1.8. На конденсатор переменной емкости из задачи 1.7
действуют одновременно два напряжения: и{ (i)= U1 sincu! ί,
u2 (0= ί>J2 sin ω2 t. Определить ток в цепи конденсатора и
проанализировать его спектр.
1.9. На диод с
нелинейной вольт-амперной
характеристикой (рис. 1.2)
воздействует
гармоническое колебание u1(t) =
= U1cos(u1 t. В пределах
| «ι (ί) | < U0
характеристику можно
аппроксимировать выражением /=
= i(U0) +aiul+a2ui.
Определить ток i(t) и
проанализировать его спектр.
1.10. На диод из задачи 1.9 воздействует сумма напряжений
u(t) = u1 (t) + и2 (0= Ui coscoi t+ i/2cosco21 при ω1φω2. Определить
ток i(t) и проанализировать его спектр.
1.11. Прием радиосигнала осуществляется приемником,
собственный шум которого (дробовой эффект в электронном приборе,
тепловой шум во входной цепи) имеет мощность Рш=10~4Вт,
равномерно распределенную в полосе частот Af= 1 МГц. Какой
должна быть мощность сигнала на входе приемника, чтобы при
полосе пропускания Af2 = \0 кГц обеспечивалось отношение
сигнал— помеха не менее 10 дБ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
1.1. λΟΜ = ί:Γ=3·1010/109 = 30ΰΜ.
1.2. При разности хода Δ г задержка сигнала во времени Αί =
= Аг/с и фазовый сдвиг <p = (u0At = 2nf0Ar/c = 2nAr/X.
Следовательно, φ!_2 = π/2, φ1_3 = π, φ!_4 = 2π.
1.3. Допустимый уход частоты Δ/=10 2 5 103 = 50Гц.
Несущая частота/о = 3 · 108/103 = 3 · 105 Гц, и на волге λ=1000Μ
требуемая стабильность частоты Δ///0«1,7· Ю-4. На волне λ = 25 м
требуется Af/f0 ά 4 · 10 " 6.
5
1.4. А/<1(Г2'106=104Гц; при /0 = 3 109Гц Δ/7/0< 1,5 · ί(Γ5.
1.5. Собственные колебания (затухающие) в контуре имеют
период Т0~2пу/ЬС и частоту/о = 1/Г0, однако эти колебания есть не что
иное, как сумма спектральных составляющих (гармоник) с частотами
fn = n/T, и = 0, 1, 2, ..., содержащихся во входном воздействии (в
импульсном напряжении) [1, § 2.3 ]. В линейной системе с постоянными
параметрами возникновение новых частот невозможно [1, п. 1.4.2].
1.6. Рассматриваемая система является линейной, и в
соответствии с принципом суперпозиции отклики на воздействие двух
импульсных последовательностей можно определять независимо
один от другого [1, п. 1.4.2]. Колебание в контуре, изображенное
на рис. 1.1,6, должно быть дополнено аналогичным колебанием в
виде затухающих серий, повторяющихся с периодом Т2. Спектр
суммарного колебания содержит гармоники с частотами fn = nlT1,
и = 0, 1, 2, ..., и гармоники fm — m/T2, m = Q, l, 2, .'.'.·.
Взаимодействия между спектрами /„ и /т нет.
1.7. Заряд конденсатора q(t) = u(t)C(t) и ток
i (t) = dq/dt = d-^ С (ή + и (1)^ = (и1Ш1 cos ω, ή χ
at at y '
x [C0(\+m sin Ω ή] +U1 sin ωι t[mC0Q cos Ω t] =
= Uγ α>! C0 cos «ι t+ — (ωι+Ω)ύη(ωι+Ω) t — — (ω1— Ω) χ
χ C0 sin (ο)!— Ω) ί
Первое слагаемое с частотой rot определяет ток, посылаемый в
конденсатор постоянной емкости С0 источником напряжения
υι5ΐηωίί. Остальные слагаемые с частотами ojj+Ω,
отсутствующими в спектре воздействия, являются результатом вариации
емкости [1, п. 1.4.3 и формулы (10.6)—(10.8)].
1.8. Конденсатор С (ή является линейным элементом, и в
соответствии с принципом суперпозиции токи it (t) и /2 (ή,
создаваемые напряжениями мх (ή и и2 (ή, можно определять
независимо один от другого. Повторяя решение, приведенное в
задаче 1.7, получаем гармонические колебания в спектре
суммарного тока со следующими частотами: ω1? α>ι±Ω и ω2, ω2±Ω [1,
§ 1.4.4 и формулы (10.6)—(10.8)].
1.9. В соответствии с [1, п. 1.4.4 и формулой (8.15)]
i(t) = i(U0) +a1Ux cosgoj t-\-a2V\ cos^j t =
= ιψ0) + *Ηί + aiUicosait + ^cosl^t.
Постоянная Первая Вторая
составляющая гармоника гармоника
6
1.10. По аналогии с предыдущим примером
i(t) = i(Uo) +tfi {Ui cosro! t+ U2cosm2 ή + a2(U! coso»! t +
+ U2cosa2t)2= i^i/0) + ^l + a^i +
Постоянная составляющая
+ aiUi cosgoi t + агUi cos 002 t +
Первые гармоники ω ι и α>2
Η Lcos2ro1 И——-cos2co2 t +
Вторые гармоники 2ωι и 2шг
+ яг ί/i Ui cos (шг + ω ι) t + a2 Ui Ui cos (ω2 — ωι) t.
Комбинационные частоты гог + ωι и а>2 —ωι
Наряду с гармониками 2а>х и 2ω2 в спектре тока возникают
комбинационные частоты |ω2+ω,|, являющиеся результатом
взаимодействия гармонических колебаний их (ή и и2 (t) в
нелинейном элементе (диоде).
1.11. Мощность шума на выходе фильтра пропорциональна
полосе пропускания Δ/2. Таким образом,
Λ«»« = (Δ/2/Δ./'ι)Λ«=10-6Βτ.
Для получения на выходе С/П=10дБ (10 раз) требуется сигнал
мощностью Рс= 10РШВЫХ = 10~5 Вт.
Глава 2. ХАРАКТЕРИСТИКИ
ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
2.1. ОБОБЩЕННАЯ СПЕКТРАЛЬНАЯ ТЕОРИЯ
СИГНАЛОВ
2.1. Определить нормы функций на интервалах
ортогональности, указанных в квадратных скобках справа от функции:
a) sign[sin(2n7rf/:T)], [0, Т\; б) -L sign [sin (2"πί/Γ)], [0, Τ];
7
S(t)\ Рис. 2.1
A
-Т/2 -Т/4 О 7/4 Т/2 t
в) y/2cos2nnt, [О, 1]; г) sm2nnt, [О, 1];
д) exp (i2nni/T), [О, Г]; е) -Uexp (UnntjT), [О, Г]
(здесь и — целые положительные числа).
Какие из приведенных функций ортонормированы?
2.2. Написать обобщенный ряд Фурье по системе функций 1,
cos — t, cos 2— t, ..., cosn — t, ... для импульса прямоугольной
формы с амплитудой А (рис. 2.1), определенного на промежутке
времени [—Т/2, Т/2]. Длительность импульса т„ = Т/2. Определить
относительную среднеквадратическую ошибку при аппроксимации
функции s(t) двумя, тремя и четырьмя слагаемыми обобщенного
ряда Фурье.
2.3. Один период синусоидального колебания с амплитудой
1 В в базисе ортонормированных на интервале [0, 1 ]
функций Уолша wal(l,0), wal(2, θ), ..., wal(n, θ) аппроксимируется
четырьмя членами обобщенного ряда Фурье [1, § 14.5]:
м(0) = 0,636 wal(l, θ) -0,265 wal (5, θ) -0,052 wal (9, θ) -
-0,128 wal(13, θ), Β.
Определить норму функции и (Θ). Больше или меньше полученной
величины норма исходного колебания? Определить энергию
колебания и (Θ), выделяемую на сопротивлении 1 Ом. Сравнить полученное
значение с энергией исходного колебания в том же сопротивлении.
2.4. Аппроксимировать симметричный импульс s(t)
прямоугольной формы с амплитудой А и длительностью τ„, заданный на
интервале (— Т/2, Т/2), тремя слагаемыми обобщенного ряда
Фурье по системе ортогональных полиномов Лежандра первого
рода. Построить зависимость аппроксимирующей функции s.d (ί) от
ί/Τ при A=l и —Τ/2<ί<Τ/2. Определить среднеквадратическую
ошибку аппроксимации.
2.5. Аппроксимировать на интервале (0, оо) импульс s(t) = l,
0<ί<τ„, тремя слагаемыми обобщенного ряда Фурье по системе
ортонормированных функций Лагерра. Определить относительную
среднеквадратическую ошибку аппроксимации.
2.6. Аппроксимировать импульс
s(t) = e\p(-at) -εχρ(-βί), 0<ί<οο,
8
где а=103с-1; β = 2 · ΙΟ3 с-1, тремя слагаемыми обобщенного
ряда Фурье по системе ортонормированных функций Лагерра.
Определить нормы исходного и аппроксимирующего
импульсов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
2.1. а) у/Т; б) 1; в) 1; г) Ι/λ/2; д) у/Т; е) 1. Ортонормированы
функции б), в), е) [1, § 2.2].
2.2. Определяем квадраты норм функций [1, § 2.2]:
Г/2
г
фоИ =
Г/2
г
l2dt=T, ||φ„||2 =
cos22nn-dt = -.
Τ 2
- Γ/2 - Γ/2
Определяем коэффициенты обобщенного ряда Фурье [1, § 2.2]:
Т/4
Г
с0 = :
Г/4
Г
Adt = A/2, c„ = '-t
A cos 2nn-dt = A mLUJlL
Т л π/2
- 7'/4 - Г/4
Обобщенный ряд Фурье по заданной системе функций
/ \ А 2 2π 2 - 2π , 2 с 2π
s\t)=— + -cos — t cos 3 —1+ —cos 5 — t— ... —
w 2 π Τ 3π Τ 5π Τ
2Λ(-\Υ (2η-\)2π
^ ^-COS- '-—t... .
π(2л-I) Τ
Относительная среднеквадратическая ошибка определяется по
формуле
Г/4 N \ , Т/4
/ 1/4- η \ ι 1/ц.
М„= J *2(/)Λ- Σ^ΙΙφ.ΙΙ2 / ί ί2(*)Α·
\ -Γ/4 η = 0 /' -774
■Τ/4 η = 0 /' -774
Подставив найденные значения с„ и || φ„ ||2
М2 = 1-
;0,095, Μ3=\---~-
,, ι I 22 22 22
Ml = 1 — - — -г — г =^
9π2
25π2
2
0,033.
22
9Ϊ2
получим
0,049,
2.3. Норма функции μ(Θ) определяется в соответствии с
равенством [1, § 2.2]
|| и(θ)||= [(0,636)2+ (0,265)2+ (0,052)2+ (0,128)2]1/2^0,703 В.
Из неравенства Бесселя [1, § 2.2] следует, что норма исходного
колебания больше полученного значения.
9
Энергия электрического колебания, выделяемая на
сопротивлении 1 Ом, определяется квадратом нормы соответствующей
функции [1, § 2.2]:
|| и {ή ||2 = 0,493 В2 -с;
энергия одного периода синусоидального колебания с амплитудой
1 В на том же сопротивлении равна 0,5 В2 · с.
2.4. После замены переменной x = t)T
ι \ ) А, — хИ<х<хИ,
(0, х< -хИ, х>хИ,
где χ„ = τ„/Τ.
Квадрат нормы полиномов Лежандра Р„(х) [1, § 14.2] равен
|| Р„(х) || =2/(2и+ 1). Коэффициенты обобщенного ряда Фурье для
импульса заданной формы определяются по формуле
с» = -
2п+)
APn(x)dx.
При нечетных и полиномы Лежандра — нечетные функции и
соответствующие коэффициенты равны нулю. Аппроксимирующая
функция 5а (х) запишется так:
5а (х)= С0Р0 (х) + С2Р2 (х) + С4.Р4. (х),
где Р0(х)=1; Р2(х)=\(Зх2-\); Р4(х)=^(35х4-30х2 + 3); с0 =
2·0+]
А ■ \dx=Ax„; c2 =
2·2+1
Α-(3χ2— \)άχ = -Αχ„{χ% — Ι);
с4 = -
2·4+]
"Χ
и
г
А-(35х*-30х2 + 3)ах = -АхИ(7х^-\0х% + 3).
Подставив значение χ„ = τ„/Τ= 1/2, получим с0 = 1/2; с2 =
= — 15/16; с4= 135/256. После подстановки переменной t
аппроксимирующая функция примет вид
5a(i) = co + c2^12(^2-l]+c4^560(^4-120(^2 + 3
Зависимости аппроксимирующей функции sa (t) (штриховая) и
исходной s(t) (сплошная) от отношения t/T изображены на
рис. 2.2. Среднеквадратическая ошибка [1, § 2.2]
М= °'{ 52Л-[со2||РоН112 + с221|Р2Н112 + с4211Л(х)112]^0,086.
-0,5
10
Рис. 2.2
s(t),3
W=/i
V
-0,5~0,25 0 0,25^ t/Τ
2.5. Заменив переменную χ = ί/τΗ, запишем сумму первых трех
слагаемых обобщенного ряда Фурье по системе функций Лагерра
[1, § 14,2]:
5а (х) = с0/0 (х) + сi/j (х) + с212 (х),
где /0(х) = е-*/2; /, (х) = (-х+ 1)е"^2; 12(х)=(~ -2х+ 1V^2.
Коэффициенты обобщенного ряда Фурье:
c0 = Je-*/2i& = 2(l -e"1/2)^0,786;
о
1
Ci = \(\~x)e-X'2dx = 4(e~1/2- 1)^0,426;
с2 =
(\-2x+^)e-x/2dx=(2-3e-1'2)*0,\8.
Подставив значения коэффициентов и функции Лагерра в
исходную формулу, после приведения подобных членов и замены
переменной получим
^(f)=(l,392-0,786f/TH + 0,09fVT2)e~'/2\
Относительная среднеквадратическая ошибка Μ = 0,168.
2.6. После замены переменной χ = 2αί форма напряжения
запишется так:
i(x) = exp(-i)-exp(-^
Определим коэффициенты обобщенного ряда Фурье в базисе
функций Лагерра [1, § 14.2]:
с0 =
βχ
(е-*/2_е *2)e-x/2dx=l_
1+β/α'
И
oo
г
Cl =
β*
(e-*/2-e °2){-x+\)e-xl2dx=
(1+β/α)2 1+β/α'
С 2 =
0U
Г _Ef
(e-*/2_e «2)(^_2x+i)e-*/2ii!C=-A-+ 8
1+β/α (1+β/α)2
(1+β/α)3'
Подставив в последние формулы β/α = 2, получим с0 = 1/3; с ι =
= -2/9, с2=-2/27.
После обратной замены переменной аппроксимирующую
функцию получим в виде
^w=[b^,-2ai)-|(,-4ar+2a2i2)]e"a,=?7x
x(l+20af-4a2f2)e~°".
Норма исходного импульса
00
г- Г
s =
(е-*/2-е «2)2 ^
о
1/2
1+?- 4
η 1/2
Ρ 1+β/α.
ί 0,4082.
Норма аппроксимирующей функции
II 5а II = [СО + С\ + С}]1'2*0,4074.
2.2. ГАРМОНИЧЕСКИЙ АНАЛИЗ
ПЕРИОДИЧЕСКИХ КОЛЕБАНИЙ
2.7. Построить амплитудную и фазовую спектральные
диаграммы напряжения
2
"(ΉΣ
1
■cos
и=1
2πη·106ί+-(-1)
и+1
В.
Изобразить зависимость напряжения от времени.
2.8. Выполнить спектральный анализ колебания
и = 0
1+2"
Определить его период.
2.9. На вход приемника, настроенного на частоту /0 = 500 кГц,
воздействует помеха в виде периодической последовательности
12
u(t)\
U
u(t)i
rvm* π π ъ π
or* τ t
δ)
Рис. 2.3
прямоугольных импульсов с амплитудой А = 10 мВ, следующих с
периодом Т= 50 мкс. В полосу пропускания приемника попадает
одна из гармоник периодической последовательности. Определить
номер этой гармоники и выявить зависимость амплитуды помехи
на выходе приемника от длительности импульсов τ„ при
скважности Γ/τ„, равной 20, 15, 10 и 5.
2.10. Построить амплитудную спектральную диаграмму
четной периодической последовательности прямоугольных импульсов
(рис. 2.3, а) с длительностью τ„ = 1 мкс и амплитудой 11= 1 В при
периодах Т, равных 3 и 4 мкс. Как изменится спектр
рассматриваемой последовательности при совмещении начала отсчета
времени с фронтом одного из импульсов (рис. 2.3,6)1
2.11. Представить в виде ряда Фурье периодическую
последовательность треугольных импульсов напряжения (рис. 2.4, а).
Построить амплитудную спектральную диаграмму, приняв U= 1 В,
τ„ = 0,5 мс, Т= 1 мс.
иЩ
uz(t)
Л.А.Л Л УЖУУ
2 2 2 2
а)
-г _т* о и
2 2
ю
Рис. 2.4
2.12. Чем отличаются спектры напряжений их (ή и u2(i),
временные диаграммы которых изображены на рис. 2.4, а и
61 Как отличаются средние мощности, выделяемые напряжениями
u1(t) и и2 (/) на сопротивлении 1 Ом при τ„ = 0,5 мс, Г=1мс
и £/=1 В?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
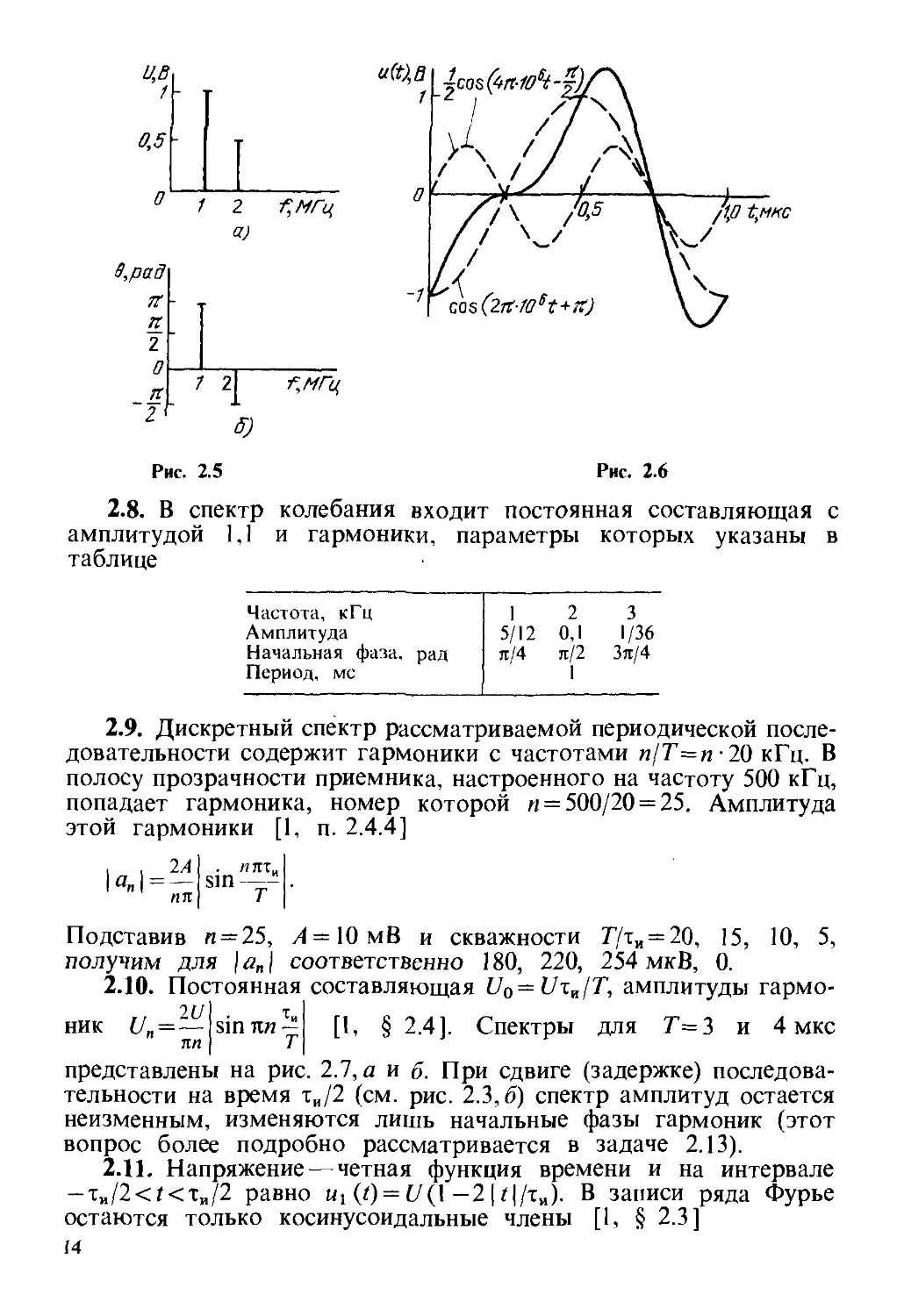
2.7. Напряжение представляет собой сумму двух
гармонических колебаний, частоты которых 10б Гц и 2 106Гц, амплитуды
1В и 0,5 В, а начальные фазы π и —π/2. Амплитудная
спектральная диаграмма напряжения изображена на рис. 2.5, а,
фазовая — на рис. 2.5,6. На рис. 2.6 изображены каждое
гармоническое колебание и их сумма (сплошная кривая).
13
0,5
О
в,рад\
π
п_
2
О
u(t),B
1 2 Г,МГц
а)
Τ'
/1,0 t,MKC
1 2| Г,МГц
δ)
Рис. 2.5
Рис. 2.6
2.8. В спектр колебания входит постоянная составляющая с
амплитудой 1,1 и гармоники, параметры которых указаны в
таблице
Частота, кГц
Амплитуда
Начальная фаза, рад
Период, мс
1
5/12
π/4
2
0,1
π/2
I
3
1/36
3π/4
2.9. Дискретный спектр рассматриваемой периодической
последовательности содержит гармоники с частотами п/Т=п -20 кГц. В
полосу прозрачности приемника, настроенного на частоту 500 кГц,
попадает гармоника, номер которой « = 500/20 = 25. Амплитуда
этой гармоники [1, п. 2.4.4]
\а„ = —
ηπ
sin
nwi.
Подставив гс = 25, Л=10мВ и скважности Г/ти = 20, 15, 10, 5,
получим для I а„ \ соответственно 180, 220, 254 мкВ, 0.
2.10. Постоянная составляющая U0=Uz„(T, амплитуды
гармоник U„ =
2U
sin пп
[I, § 2.4]. Спектры для Т=3 и 4 мкс
представлены на рис. 2.7, а и б. При сдвиге (задержке)
последовательности на время τ„/2 (см. рис. 2.3, б) спектр амплитуд остается
неизменным, изменяются лишь начальные фазы гармоник (этот
вопрос более подробно рассматривается в задаче 2.13).
2.П. Напряжение — четная функция времени и на интервале
— ти/2<Г<ти/2 равно ux {t) = U(\ — 2|ί|/τ„). В записи ряда Фурье
остаются только косинусоидальные члены [1, § 2.3]
14
υ,Β
°Λ
0,2
о
-
I.Тт.τ
/ 2
и,в
0,6-
0,4-
0,1-
т . τ τ
Li J J Τ ι ΤΤτ . ΤΤΤ
3 ПМГц u 1 2 3 f,Mru,
Ю
Рис. 2.7
M(')=T+ Σ a» cos и у ί.
η=1
Коэффициенты ряда
τ /2
Я„=:
U( 1 ) cos и -^ ГЛ = / λ. (1 — cos nn \ ).
(ял) τ,,
Для заданных параметров импульса постоянная составляющая
напряжения
t/0=f£ = ^b = 0,25 В.
Амплитуды гармоник
2 -10 3
Un = an =
(лл)20,5-10_3
1 — cos пп
0,5-10"
Ю~3
лл
4 / , лл
т 1 —cos —
Частоты и амплитуды первых семи гармоник приведены в
таблице
L· кГц
и., в
1
0,405
2
0,202
3
0,045
4
0
5
0,016
6
0,022
7
0,008
На рис. 2.8 изображена амплитудная спектральная диаграмма
заданной последовательности треугольных импульсов напряжения.
υ,β
0,2-
0,1 -
О
1 2 3 4 5 Г,кГц
Рис. 2.8
15
2.12. Напряжение и2 (t) связано с напряжением щ (t) следующим
образом: u2(t)=U—ul(t) (см. рис. 2.4). Следовательно, постоянная
составляющая трапецеидальных импульсов и2 (t) равна разности U и
постоянной составляющей последовательности ut (t). Начальные
фазы спектральных составляющих обеих последовательностей
отличаются на π. Амплитуды спектральных составляющих напряжений
«2 (0 и «! (О совпадают. Средние мощности, выделяемые
напряжениями ut (ί) и u2(t) на сопротивлении 1 Ом, различаются на 0,5 Вт.
2.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ
НЕПЕРИОДИЧЕСКИХ КОЛЕБАНИЙ
2.13. Определить спектральную плотность униполярного
прямоугольного импульса, изображенного на рис. 2.9. Построить
АЧХ и ФЧХ спектральной плотности при длительности импульса
т„=1мс и амплитуде U=\ В. Используя полученные графики,
построить аналогичные зависимости для импульсов вдвое
меньшей длительности. Отобразить на графиках влияние задержки
импульса на время τ„/2.
uit)k
и
~Г„/2 0tj2 t Рис. 2.9
2.14. Определить спектральную плотность, эффективную
длительность, эффективную ширину спектра и произведение
эффективных длительности и. ширины спектра сигнала s(t) = Ae~"^' при
а=Ю3с-1. Найти частоту, при которой спектральная плотность
равна 1/10 от своего максимального значения.
2.15. Колоколообразный (гауссовский) импульс задан в виде
s(t) = A exp ( — 2t2\xi\ |/|>0. Приравняв ти=1 мс, определить
частоту /гр, ограничивающую полосу, в пределах которой содержится
90% энергии импульса.
2.16. Найти сигнал s(t), соответствующий спектру S((o),
представленному на рис. 2.10, я. Аргумент спектральной плотности
θ (ω) на всех частотах равен нулю.
5,В/Гц\
0,5-W'3
О ГГ,хГц
а)
Рис. 2.10
16
2.17. Переходная характеристика цепи1 первого порядка s(t) =
= 1 — е т°, где τ0 — постоянная времени. Определить ее
спектральную плотность S (ω).
2.18. Определить спектральную плотность колебания s(t) =
= (1 —e_c")cosro0i, заданного при ί^Ο.
2.19. Найти спектральную плотность трапецеидального
импульса s (ή, показанного на рис. 2.11, а, и его производной s' (t)
(рис. 2.11,6).
2.20. Найти спектральную плотность треугольного импульса
(рис. 2.12).
sftU
А
s(t){
А
А
,
N.
А
-f-f*
а)
у-Гф
Σ t
2
-tJZ 0tJ2 t
Рис. 2.12
Гф
4—*
s'CtJ
0
-А/Ц
А/Гу
Гф
(че—-»
_ т
t
ю
Рис. 2.11
2.21. Определить АЧХ и ФЧХ спектральной плотности
сигнала в виде суммы двух смещенных во времени δ-функций: s(t) =
= δ(/)+δ(/-/0).
Построить соответствующие характеристики.
2.22. Сигнал задан в виде s(t) = A [δ(/ + τ„/2) -δ(ί-τ„/2)].
Определить его спектральную плотность S (ω). Как изменится
форма сигнала и его спектр при интегрировании? Определить
спектр при повторном интегрировании.
2.23. Определить спектральные плотности первой S! (ω) и
второй S2 (ω) производных сигнала s (t) = А ехр (— α | /1). Каков
закон убывания спектра сигнала и его производных при частотах,
отвечающих условию ω/α»1? Объяснить результат.
2.24. Экспоненциальный импульс напряжения и(/)=е~°", />0,
u(t) = 0, t<0, действует на цепь, подавляющую все частоты,
превышающие граничное значение /гр, при которой АЧХ спектра
снижается до одной десятой максимального значения U(0).
1 Переходная характеристика цепи -отклик на воздействие в виде единичного
скачка.
17
Определить долю энергии в отсекаемой части спектра и разность
напряжений на выходе и входе (изменение фаз цепью не
учитывать). Построить зависимость напряжения на выходе цепи
от времени.
2.25. На входе радиотехнического устройства действует
прямоугольный импульс напряжения с амплитудой U длительностью τ„,
а также гармоническое колебание с амплитудой Um, частотой / и
начальной фазой θ0. Определить спектральную плотность U(gj)
суммарного напряжения при совмещении начала отсчета времени
с серединой импульса.
2.26. Определить спектральные плотности пачек импульсов
прямоугольной и треугольной формы, изображенных на рис. 2.13.
u,(t)
uz(t)
U
ти τ
NT
а)
0 г„ τ
Рис. 2.13
UuUL
NT
δ)
2.Π. Полуволновый косинусоидальный импульс
длительностью ти задан в виде s (ή = A cosπί/τ„ при — τ„/2<ί<τ„/2.
Определить его спектральную плотность S (ω). Построить АЧХ
спектра в координатах ωτ„, S/(Az„).
2.28. Определить спектральную плотность импульса s(t) =
= А ехр (— α | /1) sine (at).
2.29. Определить спектр и форму сигнала s(i) = sl (t)s2(t), если
известны спектральные плотности сомножителей S1 (ω) = 2ос/(ос2 +
+ ω2) и 82(ω) = πδ(ω) +1/(/ω).
2.30. Спектральная плотность импульса в диапазоне частот от
/=0 до |/|^10 МГц практически равномерна и составляет
10 мкВ/Гц. Определить амплитуды первых десяти гармоник
периодических последовательностей подобных импульсов с
периодами 1 мс и 1 мкс.
2.31. Построить АЧХ спектральной плотности униполярного
прямоугольного импульса длительностью 1 мкс. Используя
полученный график, построить амплитудные спектральные диаграммы
периодической последовательности импульсов с периодом Т,
равным 1,5τ„.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
2.13. Спектральная плотность прямоугольного импульса [1,
п. 2.10.1] Щш) = — sin — = ί/τ„ sine | —|. Зависимости АЧХ и
ω 2 \ 2 /
ФЧХ спектральной плотности от частоты / при заданных
длительности импульса 1 мс и амплитуде 1 В определяются по
формулам
ω
sin
10"
--1 sin π/· ΙΟ"31;
π/
9=-тш, n\03^f<{n+l)\0\ n = 0, 1, 2, ....
АЧХ показана на рис. 2.14, α, а ФЧХ —на рис. 2.14,6. При
уменьшении длительности импульса в два раза, значения АЧХ и
ФЧХ можно найти из тех.же рисунков, изменив соответственно
масштабы координат. На рис. 2.14, г показана новая АЧХ, а на
рис. 2.14, Э—новая ФЧХ. При сдвиге импульса на τ„/2 АЧХ не
изменяются, а ординаты ФЧХ уменьшаются на ωτ„/2. ФЧХ
сдвинутых импульсов изображены при τ„=1 мс на рис. 2.14, β и
при ти = 0,5мс на рис. 2.14, е.
а,в/гцх
0,5-10
1
1
1
1
I
-
2
2
3
г)
|
з
#Г,кГц
\ψ*Γ,ι
I
2 3
в)
4\Г,кГц
Рис. 2.14
2.14. Спектральная плотность симметричного
экспоненциального импульса [1, § 2.12]
„, \__2Ла__2л__[__
α Ι + ω^/α2
Эффективная длительность импульса [1, § 2.12]
1/2
A\-2mdt
I J
о
Тэф —
]A2t4'2mdt
,00
/j
' О
1
"ν^"α
= 0,707 мс.
Эффективная ширина спектра импульса [1, § 2.12]
19
-ω
о
П 1/2
= ос=103 рад/с;
/3φ=Ω3φ/2π*159Γ4.
Произведение полосы на длительность
0*7*= 1/,Д «0,707.
Максимальное значение спектральной плотности S(0) = 2A/(x.
Спектральная плотность уменьшается в 10 раз на частотах ωΓρ,
определяемых из уравнений 1/(1 + ШгР/ос2) = 0,1. Эти частоты равны
ωΓρ= ±Зос= ±3 ■ 103 рад/с, соответственно /гр«477 Гц.
2.15. Искомая частота определяется из уравнения [1, § 2.12]
0,9=-
π
ехр( — x2)dx.
Используя численные методы решения трансцендентных
уравнений и вычисления интегралов или табулированные значения
интеграла вероятности, находим frp = 370 Гц.
2.16. В соответствии с рис. 2.10, а спектральная плотность
(0,5-Ю-3 Гц"1, -2π·103<ω<2π103,
^ [ 0, ω<-2π!03, ω>2π103.
Обратное фурье-преобразование [1, § 2.6]
2я103
*(/) = -
0,5-10-3е^Ю = 81п(2я1з03?)
-2я-103
Раскрыв неопределенность при / = 0, получим s (0) = 1; s (t)
обращается в нуль в точках ±пп, т. е. в моменты /„=±0,5· 10~3л.
Форма сигнала s(t) представлена на рис. 2.10, б.
2.17. Искомая спектральная плотность равна разности
спектральных плотностей единичного скачка [1, приложение 1 ] и
экспоненты [1, § 2.12]:
β(ω) = πδ(ω) +1/(/'ω) -τ0/(1+/ωτ0).
2.18. Спектральная плотность
8(ω) = ΐ[πδ(ω-ωο)+πδ(ω + ω0) + 7^ + 7^-
! _J 1.
α+('(ω-ω0) a+/(o)+(D0)J
20
2.19. Представленный на рис. 2.11,6 сигнал является суммой
двух прямоугольных импульсов разной полярности. Спектральная
плотность положительного импульса, середина которого
смещена влево на (Τ—τφ)/2 относительно начала координат, равна
2А . ωτφ -"»-—ί
— sin —" е l , соответственно спектральная плотность отрица-
ωτφ 4
тельного импульса равна ——sin—-ехр( — /ω—— 1 [1, §2.8].
ωτφ 4 \ 2 /
Искомая спектральная плотность
с1 х 2Л . ωτφ/ ''ω-y^ -/ω—-*\ . 4/( . ωτφ . Γ-τφ
S(go) =—sin—(e 2 -e 2 = *— sin—isinoo -.
v ' ωτφ 4 \ / ωτφ 2 2
Вместо вычисления фурье-преобразования трапецеидального
импульса (рис. 2.11, а) целесообразно воспользоваться готовой
формулой для спектральной плотности его производной, разделив
последнюю на /ω [1, § 2.8]:
S/ \ 4/1 . ωτφ . Τ— τφ
(ω =—5— sin—2sin ω -.
V ' ω2τφ 2 2
2.20. Треугольный импульс на рис. 2.12 совпадает с
изображенным на рис. 2.11, а, если принять τφ = τ„/2 и Τ=τ„. Методика
решения, аналогичная использованной в задаче 2.19, приводит к
следующему результату:
V ' ω2τ„ 4 2 (ωτ,,/4)2
2.21. Значение спектральной плотности функции δ(/) равно 1
[1, § 2.11]. Смещение во времени на t0 учитывается
множителем e~"°V Таким образом, спектральная плотность суммы
двух δ-функций S(a))=l+exp( — /ω/0). Вынося за скобку
множитель ехр (— /ω/0/2), получаем S (ω) = [ехр (/ω/0/2) + ехр (— /ω/0/2)1 χ
χ exp (— /ω/0/2), откуда модуль спектральной плотности 5(ώ) =
= 2|cosgj/0/2|. Аргумент спектральной плотности θ(ω) = πη — ω/0/2.
Зависимость модуля спектральной плотности от ω/0/2 изображена
на рис. 2.15.
гт\
Рис. 2.15 -**-§**-£ *£ *&2**t,/2
2.22. Спектральная плотность сигнала в виде суммы двух
смещенных во времени δ-функций
21
S (ω) = A (eimJ2 - e "im»'2) = 2 A i sin
ωτ„
При интегрировании получается симметричный униполярный
импульс прямоугольной формы с амплитудой А и длительностью
τ„. Его спектральная плотность [1, § 2.8]
s ι (ω) = S (ω)/(/ω) = -£- sin °ψ.
При определении спектра после повторного интегрирования
необходимо учесть, что прямоугольный импульс имеет ненулевую
площадь Ξι[0) = ΑτΗ, поэтому [1, § 2.8 и приложение 2)
δ2(ω) = ^+π81(0)δ(ω) = ^δΙη^ + π^τΗδ(ω).
2.23. Спектр сигнала s(i) (см. задачу 2.14) 8(ω) = 2αΛ/(α2 + ω2).
При ω» α 8κΰ) = 2αΛ/ω2. В знаменателе показатель степени ω
равен двум (ω" + 1 = ω2). Следовательно, производная первого
порядка s'(t) имеет разрыв непрерывности [1, § 2.13]. При
дифференцировании сигнала [1, § 2.8] спектр 81(ω) = /ω8(ω) =
= 2/αΛω/(α2 + ω2). При ω»α Sl(m) = 2iJ;A/(o, что указывает на
наличие в производной сигнала s'(t) скачка величиной 2а.А [1,
§ 2.12]. При повторном дифференцировании спектральная
плотность становится равной S2(co) = (/ro)2S(ro)=—2ω2α/ί/(α2+'ω2). При
ω»a S2(go)=— 2αΛ, что говорит о наличии во второй
производной s"(/) δ-функции отрицательной полярности с
коэффициентом 2<хА.
2.24. Спектральная плотность экспоненциального импульса [1,
§2.12]
Шш)= = — expl —/arete-I.
Максимальное значение спектральной плотности ί/(0)=1/α.
Спектральная плотность уменьшается в десять раз при выполнении
условия (1 +ω2ρ/α2)1/ = 10, откуда ωΓρ= + 9,95α. Энергия колебания
гр
на входе цепи
Э =
]
'вх
ехр (— 2а/) dt =
2а'
о
Энергия отсекаемой части спектра
дэ=!
π
а Ч1 · ♦ опП ЗЛ9Ю"2
2 2 dm = - [ - — - arctg 9,95 ] =
α+ω α\2 π / α
9,95a
22
так что относительная величина АЭ/ЭВХ = 6,37 10 2. Напряжение
на выходе цепи
9,95а 9,95а / оЛ
. Г . , со . Г cos ωί-arctg-
U2(t) = - - , ' e-'afc'8«eitt>tAn = l —W_ */<&,;
-9,95a 0
9,95а
«2(0)= [ ^ = ^rctg^[95a = 0,468.
α
При ί#0 интеграл нельзя представить элемен ι арными функциями.
Сделав подстановку л: = со/а, приведем его к виду, удобному для
численного интегрирования:
9,95
. Г /
/ ч 1 cos [xctt — arctg χ) ,
Μ2(ί) = - ν , -=-!■ αχ.
w π J УТТ^
о
На рис. 2.16, α показаны экспоненциальный импульс u1(t) и
импульс, полученный при усечении спектра u2(t), на рис. 2.16,б
зависимость Au = u1(t) — u2(t) от параметра at.
2.25. Определив спектральную плотность прямоугольного
импульса [1, § 2.9] и спектральную плотность гармонического
колебания [1, § 2.13], получим
U (ω)=—sin —" + Ш[е1Ч (ω - 2nf) + е " ίθοδ (ω + 2π/)].
2.26. Спектральные плотности
υ^ω)^—e-i<eV2sin^ £ с-^1^т;
U2(M)=-^e-toV2sin2^ X exp [-/(«-1)ωΓ].
ω τ» 4 и = 1
2.27. Представив заданный сигнал в виде произведения
прямоугольного импульса и coso)0i, где ω0 = π/τ„, искомый спектр можно
определить с помощью теоремы о смещении спектра [1, § 2.8, 3.3]:
S ^ = Ц^кsm ^ω ~ π/τ^ Ти/21+^К s'n ^ω+π/τ^ τ"/2^} =
ωτ„ — π ωτ„ + π ωτ„
/sin sin \ cos—
.2 2 \ 2ϋτΜ 2
= Ατ
ωτ„— π ωτΜ + π
23
S/(Ar»)
0,64
Рис. 2.16
Рис. 2.17
На рис. 2.17 изображена зависимость 5(ω)/(Λτ„) от ωτ„.
2.28. Импульс можно представить в виде произведения Ае
и sinc(oci). Спектры сомножителей:
г( \-]π/α ПРИ ~α<ω<α'
ЬИ~|0 при ω<-α, ω>α;
π(ω) = 2αΛ/(α2+ω2)
(см. [1, § 2.10.] и задачу 2.14).
Искомый спектр определяется сверткой Ο(ω) и * (ω) [1, § ζ.» J.
SH=5
π 2/ίαί/.ϊ
αα2+(ω-χ)2 α
= - arctg 2
2.29. Спектральная плотность определяется сверткой исходных
спектров
8(ш) = :
2а
πδ(χ) + -
~2π J α2+(ω-.ν):
— no
форма сигнала (см. задачу 2.24)
„/f4_J"exp( —at/), t>0;
AW-|o, *<о.
2.30. 0,02 В; 20 В [1, § 2.7].
24
dx=-
οι 4-' ω
Рис. 2.18 Ап
1,34 -1,0
Οβ7 -Οβ-
О О
1 2 J Г,МГц
2
2.31. АЧХ импульса заданной формы 5(ω)=-
на рис. 2.18 штриховой линией. Частоты гармоник /п = п/Т=
= 0,66и МГц. На этих частотах определяются по графику значения
спектральной плотности. Умножив эти значения на 2/Г=1,33 106,
определим амплитуды гармоник Ап. Постоянная составляющая
равна 5(0)/ Т.
2.4. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ
РЯДОМ КОТЕЛЬНИКОВА
2.32. По заданной совокупности отсчетов {s(nAt)}, взятых с
шагом At из континуального сигнала s(t), требуется восстановить
исходный сигнал. Один из возможных способов основан на
использовании специального фильтра. Каковы должны быть
характеристики фильтра — импульсная, АЧХ и ФЧХ?
Исходить из условия, что отсчеты s(nAt) представляют собой
достаточно короткие импульсы, близкие к дельта-функции δ (г].
2.33. Определить шаг дискретизации единичного скачка s(i)=l,
ί>0, при котором обеспечивается воспроизведение перепада с
длительностью фронта τφ не больше заданной.
2.34. Определить шаг дискретизации экспоненциального
импульса s(t) = e~al, ί>0, при котором обеспечивается
воспроизведение фронта с длительностью τφ, не большей 10% от постоянной
времени τ=1/α=1 Мс. Определить приближенно требуемое число
отсчетов.
2.35. Определить число отсчетов, необходимое для
представления прямоугольного импульса с длительностью τ„ = 1 мс, при
условии, чтобы длительность перепадов восстановленного
импульса не превышала 5% от τ„.
2.36. Спектральная плотность S(co) импульса s(t) с
длительностью τ„=1 мкс представлена совокупностью отсчетов (S(nAro)}.
Определить максимальный интервал Δω между отсчетами, при
котором возможно восстановление спектральной плотности S(go).
Зависит ли этот интервал от формы импульса s(t) (при неизменной
длительности τ„)?
2.37. Вычислить отсчеты S(nAco) спектральной плотности
прямоугольного импульса s (ή с длительностью ти = 1 мкс и ампли-
25
3-Ю,7/ГЦ
\
\
1
ν1"~Ν^->^-.~
sin
ωτ„
показана
тудой Е~Ю В. Изобразить линейчатый спектр графически.
Каковы должны быть интервалы Δω между отсчетами, чтобы
исключить возможность потери информации о спектре.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
2.32. Импульсная характеристика фильтра g(i) должна
совпадать с базисной функцией ряда Котельникова:
фЛФ
sin(o„,(/-n/2/J
wm(i-«/2/J
ζ ν sin ω_/ „ r
Учитывая, что импульсная характеристика фильтра должна
отвечать условию g(t)=0 при ί<0, запишем ее в форме
где t3- задержка (рис. 2.19, а), обусловленная инерционностью
фильтра.
*ъ гг„ 4zfm
а) б)
Рис. 2.19
Тогда искомая передаточная функция фильтра
К(«о) =
sinu)m{t-i,)Q-iiat
dt.
Спектральная плотность функции
sincum<
равна π/ω„, — ωΜ<ω<
<шт, а с учетом задержки ί, [1, § 2.15]
ω„
О при |ш|^шт.
26
Таким образом, АЧХ и ФЧХ, равная ωί3, должны иметь вид,
показанный *н'а рис. 2.19, б.
АЧХ Должна быть максимально близкой к прямоугольной, а
ФЧХ — к линейной.
2.33. На рис. 2.20 представлена последовательность отсчетов,
взятых из единичного скачка, а на рис. 2.21—соответствующие
эти1\* отсчётам базисные функции φ0('), Φι('), ··· и их сумма.
Задержка этих функций во времени, обусловленная
инерционностью формирующего фильтра (см. рис. 2.19, а), здесь не
учитывается. При учете задержки получается график
восстановленного сигнала, представленный на рис. 2.21. Длительность
перепада τφ, отсчитываемая между точками «а» и «б» (рис. 2.21),
практически равна 1,5Δί. При этом следует учитывать, что
положение точки «а» на оси времени может не совпадать с
истинным моментом1 скачка исходного сигнала. Ошибка, ε может
достигать величиНь! Δί (см. рис. 2.20).
sCt)
At
\/ \/
л л Χ X л
Рис. 2.20
Рис. 2.21
2.34. Используя результаты решения предыдущей задачи,
нетрудно построить график, представленный на рис. 2.22.
В данном случае первый отсчет будет е-"', длительность фронта,
как и ранее, τφ=1,5Δί.
Рис. 2.22
at
27
Тогда τ/τφ = τ/(1,5Δί) = 10, откуда Δί = τ/15.
Задаваясь условием, чтобы уровень отсчетов к концу импульса
не превышал примерно 2% от первого отсчета, получаем е~ ,/т =
= е /15 = 1/50, откуда требуемое число отсчетов Ν^. 15 In 50^58.
В зависимости от случайной величины ε, наибольшее значение
которой может достигать At, разброс пика импульса заключен в
пределах от 6_<ϊΔ' = 0,95 до единицы.
2.35. Как и в двух предыдущих задачах, длительность
перепадов τφ«1,5Δί, следовательно, τ„/(1,5Δ?) должно быть не менее 20,
а общее число отсчетов Ν=τ„/Δί^30.
2.36. Максимальный интервал между отсчетами спектра [1,§ 2.16]
Δω^2π/Γο = 2π·106 рад/с.
2.37. Основываясь на выражении
S(ro)=10T„sinci^j [1, формула (2.69)],
построить график спектра, определить частоты, на которых S(ot)J
обращается в нуль, и рекомендовать интервал Δω, исключающий
возможность обращения в нуль всех отсчетов S(nAro) [кроме
отсчета S(0)].
2.5. СПЕКТРАЛЬНЫЙ АНАЛИЗ
ДИСКРЕТИЗОВАННЫХ СИГНАЛОВ
2.38. Сигнал s(t) = cos2nf0t, —cc<t<cc, подвергнут
дискретизации с шагом Г=1/2/0. Найти спектральную плотность дискрети-
зованного сигнала. При каких других значениях частоты сигнала f
s(t) спектр дискретизованного сигнала будет таким же?
2.39. Сигнал .y(f) = [2cos(27rl03? + 0,5) + 6cos(37rl03? + 0,8)], мВ,
— οο<ί<οο, подвергнут дискретизации с шагом Г=0,2 мс.
Построить амплитудный спектр дискретизованного сигнала.
2.40. Сигнал s(t)=Aехр (— ί2/2τ }, — oo<t<oo, (гауссовский
импульс) подвергнут дискретизации с шагом Γ=1,4τ. Найти и
построить спектральную плотность дискретизованного сигнала.
2.41. Шаг дискретизации сигнала из предыдущего примера
уменьшен в два раза. Построить новый спектр.
2.42. Сигнал s\t) из примера 2.40 ограничен по спектру на
уровне \ω\ = κ/Τ, Γ=1,4τ, что привело к новому сигналу a-j (ί). Шаг
дискретизации сигнала st(t) выбран Т1 = Т/2. Сравнить спектры
Sr(ai) и STi (ω) дискретизованных сигналов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
2.38. Используя выражение для спектральной плотности
гармонического сигнала [1, § 2.13] и связь между спектрами
28
дискретизованного и исходного сигналов [1, § 2.17], получаем
(рис. 2.23)
SH = f Σ δ[ω-(2«±1)ω0].
и= — αο
Штриховой линией на рис. 2.23 показан модуль передаточной
функции ФНЧ, с помощью которого сигнал s(t) может быть
восстановлен по своим отсчетам s(kT)=cos2nf0KT, k=0, ±\,
±2, ... .
ST(u)
Zrt\
ψ<?(ο>-6>ΰ)
> Zrt\ 4rt_
'У\ Τ
Рис. 2.23 ~^ωο ~^®ο ~ωο ° ωο 3ω0 5ω0 ω
Такой же спектр получится при замене частоты f0 в s(t) на
(2/+1)/0, /=1, 2, ... . Однако в этих случаях восстановление
аналогового сигнала с помощью ФНЧ невозможно (на выходе
ФНЧ будет косинусоида частоты f0).
2.39. Спектр изображен на рис. 2.24.
2.40. Спектральная плотность дискретизованного сигнала [1,
§2.17]
ι °°
Sr(oj)=- £ S(<d-/i2ji/7),
где S(a)) = /i у/2п,тсхр { — τ2ω2/2} — спектральная плотность
исходного аналогового сигнала s(i) [1, п. 2.10.3].
Спектр ST(m) изображен на рис. 2.25. На этом же рисунке
штриховой линией показан спектр 5(ω) сигнала s(t).
Sj-to)
L_L
ST,6/c
т 30
ι
ι
J ι L
-5
0 11β 3,54 5 Βξ5 ЪкГц
Рис. 2.24
Рис. 2.25
2.41. Новый спектр представлен на рис. 2.26. В данном
примере отдельные спектры, соответствующие различным
значениям п, не перекрываются.
2.42. В полосе частот |ω|^π/Γ заключено 99,85% энергии
гауссовского импульса s(t) [2, п. 2.9.2]. Отсюда можно сделать
29
4to,s(krt)
s(t)^sr(t)
-4Γ, -ЗГ, -2T, -Tj 0 T, 2Tf ΙΓ, 4ГГ t
Рис. 2.26
Рис. 2.27
вывод о том, что сигналы s,(i) и s(t) практически неразличимы
(рис. 2.27). Таким образом, наиденные в примерах 2.40 и 2.41
спектры являются соответственно спектрами Sr(co) и Sr,(co).
2.6. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
2.43. Найти корреляционную функцию 2?8(τ) треугольного
импульса длительностью ти с амплитудой А (рис. 2.28, а).
Определить энергию импульса, выделяемую на сопротивлении 1 Ом.
Построить график функции.
sCt)i
*t
-0,5 О 0,5 t/r№
а)
Bs(T)/Bs(0)
а)
es(r),Bzc
-1 -0,5 0 0,5 1 г/ги
6)
Рис. 2.28
-0,5 0 0,5 1 %мс
Рис. 2.29
2.44. Найти взаимную корреляционную функцию двух
прямоугольных импульсов с параметрами £/, = I мВ, ти, = I мс и
£/2=2мВ, ти2=0,5мс (рис. 2.29, а). Определить интервал
корреляции.
зо
S&)\
-Τ, Ο
Bs(t)/6s(0)
s(t)k
тчи
г
2
И^
а)
Bs пер(W|
'-Г
Рис. 2.30
0
Рис. 2.31
2.45. Найти корреляционную функцию Β3{ή импульса,
изображенного на рис. 2.30, а. Определить энергию импульса,
выделяемую на сопротивлении 1 Ом. Построить график
зависимости отношения Β%(τ)(Β%(0) и определить интервал
корреляции.
2.46. Найти корреляционную функцию колебания s(t) =
= s\n{2nf0t + %).
2.47. Найти корреляционную функцию сигнала пилообразной
формы с периодом Τ и амплитудой А (рис. 2.31, я). Изобразить
график Bs(t). Определить среднюю мощность, выделяемую в
сопротивлении 1 Ом.
2.48. Найти модуль спектральной плотности импульса,
корреляционная функция которого изображена на рис. 2.32.
Ba(rh
Рис. 2.32
2.49. Определить корреляционную функцию сигнала,
спектральная плотность которого
ЬИ- о, м>шт.
2.50. Определить корреляционную функцию экспоненциального
импульса s(t) = e\p( — ш), 0<ί<οο.
31
2.51. Определить корреляционную функцию и интервал
корреляции колебания
/л 1/4 sin ωί, — π/ωίζίίζπ/ω,
5"' (О, ί<-π/ω, ί>π/ω.
2.52. Определить взаимные корреляционные функции:
а) двух экспоненциальных импульсов s1(t) = AQ~"', .v2(i) = /4e~p',
0<ί<οο;
б) произвольного сигнала s{t) и дельта-функции δ(ί);
в) экспоненциального si(t) = Ae~al, 0<ί<οο, и прямоугольного
s2(t) = A, 0<ί<τΗ, импульсов. Построить зависимость Β2\{τ) при
значениях параметров А = \ В, а=103с-1, ти = 0,2 мс.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
2.43. Рассматриваемый сигнал определяется условиями
,л Ы1-2И/ти), -ти/2^ти/2,
5W-jo, ,<-ти/2,,>ти/2.
Его корреляционная функция
*,М=
ι 2 τ» Ι * τ
wT!"5+rr· τΗ/2<τ^τ„,
τ;
0, τ>τΗ.
В области τ<0
Β,(τ) = Β,(-τ).
Нормированная по максимальному значению Bs{0)
корреляционная функция представлена на рис. 2.28, б.
Энергия импульса, выделяемая в сопротивлении Л=10м,
Э = В5(0)=Л\/3.
2.44. Взаимная корреляционная функция [1, § 2.18] двух
прямоугольных импульсов напряжения при сдвиге импульса
длительностью 0,5 мс на время τ представляется отрезками
прямых, определяемых формулами
£21(τ) = 0, т<-0,51(Г3с;
т+0,5-10"3
B2l(z)= J 21(Γ31(Γ3Λ = 2·1(Γ6(τ + 0,5·1(Γ3), В2с,
о
-0,510"3^τ<0;
32
ι + 0,5·10 J
Β2ί(τ) = J 2-10~310~3А = 1(Г9В2-с, (Κτ<0,5·10-3;
τ
ΙΟ"3
Β21(τ)= J 21(Г31(Г3<# = 21(Г6(10-3—с), B2c,
τ
0,5·1(Γ3:ζτ<1(Γ3;
Β21(τ) = 0, τ^ΚΓ3 с
График функции Β21(τ) показан на рис. 2.29, б. Интервал
корреляции 1,5 мс.
2.45. Корреляционная функция на интервале |τ|^τΗ
Bs{z)= J A2dt-)A2dt + ]A2dt = A2{2xa-^x).
-τ„ + τ 0 τ
На интервале 2τ„ > | τ | > ти
*,(τ)=- ) Α2ώ = Α2{τ-2τΆ).
При |τ|>2τΗ
Энергия импульса, выделяемая на сопротивлении 1 Ом,
Э = В5{0) = 2А\.
График функции Bs(z)/Bs(0) показан на рис. 2.30,б. Интервал
корреляции равен 4ти.
2.46. Bs(z) = 0,5cos2nf0T. Корреляционная функция не зависит
от начальной фазы.
2.47. Корреляционная функция периодического колебания [1,
§ 2.18] пилообразной формы определяется выражением
Г/2+τ Г/2
-Т/2 -Γ/2 + τ
= 2Л>(*2-1+1\
\т2 т б)
Рассчитанная по этой формуле корреляционная функция показана
на рис. 2.31,6. Средняя мощность, выделяемая на сопротивлении
Юм [1, § 2.18], P = Bsnep(0) = A2p.
2.48. Корреляционная функция
, γ ΓΛ?(τΗ + τ), -τΗ<τ<0,
Ва(х) = и2(хи-х), (Κτ^τΗ;
(О, |τ|>τΗ.
33
Квадрат модуля спектральной плотности определяется по
формуле [1, § 2.19]
ее ее τ„
S2(oo) = J Bs(x)eimdx = J A2{xa + x)emdx + \ A2{x„-x)emdx.
Вычислив интегралы, получим
S N=-^r(1-Cost0T")=-Tsin2-=rl
sin-
ωτ,,
Как и следовало ожидать, S(m) соответствует прямоугольному
импульсу s(l), корреляционная функция которого показана на
рис. 2.32.
2.49. Bs{x) = ^smc(<»mx) [1, § 2.19].
2.50. Z?s(T)=le-«l*l.
2.51. Корреляционная функция
Bs(x)=<
,2/π τ \ , Α2 . . . 2π, ,2π
ΑΔ\-—-^ coscoiH—sin ωτ , <τ< —,
\ω 2 / 4ω ω ω
η 2π 2π
0, τ< -—, τ> —.
Ο) Ο)
2.52. Взаимные корреляционные функции:
а) *'2^=^е~РТ' τ>0; Β^=&^> τ<0;
со
б) Ζ?δ5(τ) = J δ(ί)ί(ί+τ)Λ=ί(τ) [1, § 2.18];
D
0, τ<-τΗ,
в) #2ι(τΗ
τΗ + τ
A2 e"0l/Λ = ^(l-e-0l(τ-+τ,), -τΗ^τ<0,
о
τ +τ
V
е-0"^—е~"т(1-е~аЧ τ>0.
α ν
На рис. 2.33 изображена зависимость Β2ί{χ) при заданных
параметрах.
34
Рис. 2.33
0,2
о,Ч
О 1 2 Г,мс
Глава 3. МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
3.1. АМПЛИТУДНО-МОДУЛИРОВАННЫЕ
КОЛЕБАНИЯ
3.1. Определить число радиовещательных, радиотелефонных,
телевизионных, телеграфных каналов, которые могут работать без
взаимных помех в диапазоне длин волн λ=2 —5 м, при следующих
данных: максимальные частоты в спектрах передаваемых
сообщений для телеграфных каналов 300 Гц, радиотелефонных 3 кГц,
радиовещательных 5 кГц, телевизионных 6 МГц; передача
телевизионного сигнала ведется на одной боковой полосе частот АМК;
для устранения перекрестных помех между каналами связи
предусмотреть защитные интервалы шириной 10% от
максимальной частоты спектра сообщения. Оценить относительную полосу
частот АМК при λ=2 и 5 м.
3.2. На рис. 3.1 представлена диаграмма АМК. Записать
аналитическое выражение подобного сигнала и изобразить его
спектрограмму. Определить среднюю за период модуляции
мощность, выделяемую на сопротивлении 1 Ом.
u(t),B
4
2
О
-2
-4
Рис. 3.1
3.3. Задано аналитическое выражение АМК
!/(/) = 20 [1+0,3 cos(l04f + 7r/6)+0,5cos(5-103f + 7r/4)]-cos(106f +
+ π/3), Β.
35
5Вл
10Βλ
roz
ZOB,
г -45°
Z-103
<so°
10 В,
2-10z
1/16
г225
50-,
10 z
0
г/80°
Г,Гц
Рис. 3.2
Построить спектральную и
векторную (при ί = 0)
диаграммы, определить ширину
спектра и среднюю мощность,
выделяемую на сопротивлении
1 Ом.
3.4. На рис. 3.2
приведена спектрограмма напряжения.
На основании этой
спектрограммы определить
парциальные коэффициенты модуляции,
составить аналитическое выражение данного колебания и
изобразить его векторную диаграмму для момента времени t = 0.
Определить, во сколько раз мощность АМК, средняя за период
модуляции, больше мощности несущего колебания.
3.5. Задано аналитическое выражение для АМК
u(t)=U[\+0,5cos(2nl02t + 30°) + 0,5cos(2n75t+y)]cos(2n\05t +
Определить начальную фазу γ, при которой коэффициент
модуляции вниз Ми равен единице.
3.6. Изобразить векторные диаграммы АМК, аналитическое
выражение для которого дано в задаче 3.5, при γ = 60° для
следующих моментов времени: ^=0, ?2 = ^25мс, /3 = 2,5мс,
ί4 = 5 мс.
tyfHC
Рис. 3.3
3.7. Задано АМК в виде периодической
последовательности радиоимпульсов с прямоугольной огибающей (рис. 3.3)
при следующих данных: длительность импульса ти=10мкс,
период повторения rt = 20MKC, частота заполнения ω0 = 2π/Τ0,
причем ти/Г0»1; амплитуда импульсов £/т=10В. Составить
аналитическое выражение для АМК и построить
спектрограмму.
3.8. На рис. 3.4 представлено колебание, отличающееся от
сигнала из предыдущего примера (см. рис. 3.3) добавлением
синфазного (немодулированного) напряжения с амплитудой Δ = 2Β.
36
Рис. 3.4
tMKC
В чем отличие спектра нового сигнала от спектра
предыдущего?
3.9. Задано аналитическое выражение однотонального АМК
i/(i)=5[l+0,8cos(2nl03i + 30°)]cos(2nl05i + 90°), В.
После разложения на спектральные составляющие заменить в
несущем колебании начальную фазу 90° на 0°. Определить
максимальное изменение фазы результирующего колебания за
период модуляции.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
3.1. Ширина спектра АМК зависит от максимальной
частоты Fmaji в спектре модулирующего колебания следующим
образом: A/=2Fmax. Следовательно, ширина спектра сигнала
с учетом защитного интервала для радиовещательного
канала составляет 11 кГц, радиотелефонного 6,6 кГц;
телевизионного при передаче на одной боковой полосе АМК 6,6 МГц;
телеграфного 0,66 кГц. Частотный диапазон, предназначенный
для работы перечисленных каналов, составляет 90 МГц,
поэтому число телевизионных каналов 13, радиовещательных 8182,
радиотелефонных 13 636, телеграфных 136363. Относительная
полоса частот АМК при λ=2 м составляет для
телевизионного канала 4-Ю-2, радиовещательного 6,7-10~5,
радиотелефонного 410~5, телеграфного 410~6. При λ=5Μ
соответственно 0,1; 1,7-10"*; 10~4; Ю-5.
3.2. По приведенному графику определяем параметры АМК:
Г0 = 4 мс, Гмод = 20 мс, U0 = 3 В, MJ=2 В, θ0= -90°, γ = 0°,
коэффициент модуляции Μ = 2/3. Тогда аналитическое выражение
заданного АМК принимает вид
i/(/) = 3(l+-cos2n50ijcos(2n250i-90°), В.
Спектральная диаграмма представлена на рис. 3.5.
Средняя мощность, выделяемая на сопротивлении 1 Ом,
составляет 5,5 Вт.
37
Звт-М
Ряс. 3.5
1вл~90
1вт-90
200 250 500 Г,Гц
3.3. Преобразуем заданное выражение в сумму гармонических
колебаний:
i/(i) = 20cos(l06i + V3) + 3cos[(106-l04)r+n/6] + 3cos[(106 +
+ 104)f + n/2] + 5cos[(106-5l04)f + 7r/l2] + 5cos[(l06 + 5l04)f +
+ 7π/12], Β.
Анализ полученного выражения показывает, что в спектре
этого колебания содержатся пять составляющих: несущее
колебание с частотой Ю6 рад/с и две пары боковых частот
(106±104) рад/с и (106 + 5·104) рад/с; парциальные коэффициенты
модуляции составляют 2-3/20=0,3 и 25/20 = 0,5. Спектральная
диаграмма колебания показана на рис. 3.6, векторная при ί = 0—
на рис. 3.7. Так как в приведенном АМК Qmax = 5■ 104 рад/с,
ширина спектра Aw==2Qmax= 105 рад/с. Среднюю мощность
колебания можно рассчитать по формуле [1, § 3.2]
Pcp = 0,5t/2(l+0,5 £мА,
где η—число гармонических составляющих в спектре
модулирующего колебания.
Следовательно, -Рср = 234 Вт.
20β-r π/3
5в
П/Г2 π/6
4/0'
ИГ
и%5г
4it/2
10
se-
4-W
77Г/Г2
ω,ραδ/c
Рис. 3.6
иыг
^ЪЫ
Ж
и«ы
υ
Рис. 3.7
Рис. 3.8
3.4. Амплитуда г'-й боковой составляющей спектра AM К равна
UMJ2, где М( — парциальный коэффициент модуляции,
U—амплитуда несущего колебания (в данном примере. [/=30 В).
Поэтому при /=1 UM1/2 = 10, откуда М, =2-10/30 = 0,67, при г = 2
А/2 = 2 5/30 = 0,33. Аналитическое выражение принимает вид
M(f) = 30[l+0,67cos(2nl03f + 3n/4) + 0,33-cos(2n2-103f + 7r/2)] x
xcos(27rl06f + 7r/2), В.
38
Векторная диаграмма при ί = 0 показана на рис. 3.8. Средняя
мощность заданного АМК в 1,28 раз больше мощности несущего
колебания.
3.5. γ = 67,5°.
3.6. Векторные диаграммы для моментов времени ^=0,
12 = 1,25 мс, ?3 == 2,5 мс и ί4 = 5 мс представлены соответственно на
рис. 3.9, а, б, в, г.
-2п-101рад/с
1,5jt-Wrрад/с
^-2я-10град/с
Х^г \-1,5пГ0град/с
UbSZ
-/ \-гпю5рад/с °
и а)
)-2тг-705рад/с
S)
Рис. 3.9
у2я-105рад/с -L yznw5pad/c
3.7. Огибающая АМК, представленного на рис. 3.3
(периодическая последовательность униполярных прямоугольных
импульсов), определяется рядом Фурье:
г τ ι л U- , 2π. , . 2π . 2π
U{t)=-f+a1cos-t+a3cos3-t+a5cos5-t+ ...,
i. 1 \ J j J i
где коэффициенты
2ί/_ · τ„
αη = —- sin ηκ —
ηη
Τχ
[1, π. 2.4.4].
При xJT^l/2, a^lujn, a3=-2UJ3n, a5 = 2UJ5n,.,
искомое аналитическое выражение
w(i)=t/(i)cos(rooi+eo)=^<5cos(av+6o)+J
cos
L0t+pj + Q0)
+
39
+cos[m0i-~i + d0
+cosl(o0t-3yt + Q0
cosiro0i + 3pi + eoj +
+ ...
Спектр AMK представлен на рис. 3.10. Парциальные
коэффициенты модуляции определяются из равенства 2/ηπ = Μη/2; таким
образом, Λ/Ί=4/π=1,27, Μ3 = 4/3π = 0,42 и т. д.
ит/гт
ι
ко
+
^
'ό
ξ?
ι
fa
ιό
+
ιό
+
Ч?
Рис. 3.10
Хотя Μγ > 1, перемодуляции в данном случае нет,
поскольку третья, седьмая и т. д. гармоники модулирующей
функции U(t) складываются с первой гармоникой в противо-
фазе.
3.8. Амплитуда спектральной составляющей с частотой ω0
увеличится в 1 +A/Um = 1,2 раза, амплитуды колебаний боковых
частот останутся прежними, а парциальные коэффициенты
модуляции уменьшатся в 1,2 раза.
3 9 θ =77 3°
3.2. КОЛЕБАНИЯ С УГЛОВОЙ МОДУЛЯЦИЕЙ
3.10. Изобразить спектральную диаграмму
частотно-модулированного колебания (ЧМК), у которого частота несущего
колебания равна 2 МГц, девиация частоты 2 кГц, частота
модуляции 20 кГц, амплитуда несущего колебания 10 В, начальная фаза
0°. Построить векторную диаграмму для ll = T/8. Сравнить со
спектром АМК, заданного аналитически:
s (t)= 10 [1+0,1 cos (2π2·103ί)] cos (2π2 106ί).
3.11. Задано аналитическое выражение ЧМК
s(f) = 5cos[27rl05f + 6cos(27rl02?) + 60G].
Определить индекс модуляции, практическую ширину
спектра и число гармонических составляющих в пределах этой
ширины.
40
3.12. Девиация частоты ЧМК равна 5 кГц. Определить
минимальную частоту модуляции, при которой амплитуда
спектральной составляющей с частотой несущей равна нулю.
3.13. Найти максимальную и минимальную мгновенные
частоты, а также девиацию частоты для ЧМК, заданных следующими
аналитическими выражениями:
а) s(/)=10cos[2n-108? + 5sin(2n3 105?) + 7sin(2n6-106f)];
б) s(/) = 40cos[2nl07f + 2sin(2n5105/) + 4sin(2n2105f)];
в) s(/) = 50cos[27rl07f-4cos(27rl05f) + 6cos(2n3 105/)].
3.14. Мгновенная частота ЧМК изменяется по закону f{i) =
= 5 cos (271/^ +30°), кГц. Частота F принимает значения в пределах
200 Гц... 2,5 кГц. Определить значения частот F, при которых в
спектре ЧМК будет отсутствовать составляющая с частотой f0.
3.15. Вычислить спектры ФМК и ЧМК при одинаковых
несущих частотах 100 МГц и амплитудах 10 В.
При ФМК задан индекс модуляции 5, а при ЧМК задана
девиация частоты/д = 50 кГц. Сравнение спектров ФМК и ЧМК
провести для модулирующих частот Ft = 10 кГц и F2 = 5 кГц.
3.16. Для канала радиосвязи с применением фазовой модуляции
отведена полоса частот 100 кГц при несущей частоте f0= 10 МГц.
Какова наивысшая возможная частота модуляции F при условии,
что индекс угловой модуляции т должен быть не меньше 5.
3.17. На вход фазового модулятора поступает сигнал s(t),
показанный на рис. 3.11. Каковы законы изменения фазы θ(/) и
мгновенной частоты модулированного колебания?
s(tj
Рис. 3.11
3.18. Рассчитать суммарную мощность спектральных
составляющих в пределах практической ширины спектра и сравнить со
средней мощностью ЧМК u(t)=l0cos[2n-\06t + mcos(2n-W*t +
+ π/2)], В, выделяемой на сопротивлении 1 Ом. Индекс модуляции
принимает значения: а) т = 0,4', б) т = 5; в) т=10.
3.19. Оценить коэффициент паразитной амплитудной
модуляции в колебании, рассмотренном в задаче 3.18, при т = 0,4 и
удержании в спектре только трех составляющих.
3.20. Частотно-модулированный радиоимпульс с
прямоугольной огибающей имеет длительность 1 мс. амплитуду 5 В при
изменении мгновенной частоты по закону o)(i) = (omin + p/, 0^/^
ίζ 1 мс, где Gomin = 2n5-104 рад/с—начальное значение частоты;
β = 2π2· 107 рад/с2 — скорость изменения частоты.
41
Определить базу этого радиосигнала и записать его
аналитическое выражение, если начальная фаза колебания π/6.
3.21. Частота ФМК изменяется по закону ω(/) = 2π·106(1 +
+0,1 cos 2π 104/), рад/с. Найти аналитическое выражение этого
колебания, если его амплитуда равна 20 В.
3.22. Задано аналитическое выражение
линейно-частотно-модулированного (ЛЧМ) радиоимпульса с колоколообразной
огибающей:
a(t) = Ae'"2'2cos(ω0/ +β/2), -οο<ί<οο.
Определить энергию и базу этого сигнала при А = 10 В,
/0 = 1 МГц, ос = 104с-1, β=109 раде-2. Построить зависимость
эффективной ширины спектра от β при заданном α и при
изменении β в пределах 0...108 1/с2.
Примечание. База сигнала ΛΓ=Δί3φΔ/3φ, где Δί3φ=-χ
со
χ |ί(ί)|2ί#—эффективная длительность сигнала; Δ/3φ =
52(ω)ί/ω—эффективная ширина спектра.
2nS2mix((o)
3.23. Для колебания с амплитудно-фазовой модуляцией,
заданного аналитическим выражением
s(t) = 5 [1+0,8 cos (2π·103/)] cos [2π·106ί+0,2<κ>8(2π·103/)],
рассчитать и построить спектральную диаграмму.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
3.10. При индексе угловой модуляции Ηΐ = ω./Ω = 0,1
учитываются только три спектральные составляющие [1, § 3.6].
Амплитуды боковых составляющих спектра UJ2 = 0,5 В. Спектральная
диаграмма представлена на рис. 3.12, а, а векторная при / = 0—
на рис. 3.12, б для момента времени t1 = Г/8 = 6,25 мкс.
Для сравнения на рис. 3.12, в и г построены спектральная и
векторная диаграммы для АМК, которое отличается от колебания
с угловой модуляцией только фазой нижней боковой
составляющей спектра.
3.11. Индекс модуляции т = 6 рад, практическая ширина
спектра Δω = 8,8-103 рад/с, число спектральных составляющих в
пределах Δω не превышает η = 14.
3.12. При угловой модуляции А0 = U0J0(m), a J0(m) обращается
в нуль при m=fJF= 2,405; 5,52 и т. д. Следовательно, первый
42
Рис. 3.12
10В-к ΰ
180°\S^-*
015Вт О
2-70'
Urn*
, ПГЦ- ^n-W*рад/с
(ΐιϊ^3^7ζΤΛ 4η· Μ * рад/с
щрЬп· 10ерад/с
2-70°
а)
10By 0е
Ю
0,5'Вт О
2-10'
0,5В г О
2-10*
Г,Гц
2-Ю1
в)
10В
-4П-Ю*рад/с
471-10 и рад/с
и-AH(t,) = 10,7В
3)
нуль амплитуды А0 получается при т = 2,405, откуда Fmin=fJ2,A =
= 2,08 кГц.
3.13. а) /т„ = .14,35:107Гц, /„,„ = 5,65-107 Гц; б) /т„=11,8х
χ 106 Гц, /min = 8,2-106 Гц; в) /т„= 12,2·106 Гц, /т1п = 7,8-106Гц.
3.14. F=2,08; 0,91; 0,58; 0,42; 0,33; 0,28; 0,24; 0,21 кГц.
3.15. Число гармонических составляющих в пределах
практической ширины спектра при угловой модуляции, как ФМ, так
и ЧМ, равно N=2(w+1)+1 (независимо от модулирующей
частоты).
Амплитуды боковых частот Un=UJ„(m), где J„(m) — функции
Бесселя, для т = 5 приведены в табл. 3.1, а спектры ФМК
представлены на рис. 3,13, α для Ft =± 10 кГц и на рис. 3.13,6 для
F2 = 5 кГц. Единственное различие этих спектров в интервалах
между соседними спектральными линиями (10 и 5 кГц).
Таблица 3.1
η
Л (5)
0
—0,18
1
-0,33
2
0,047
. 3
0,37
4
0,39
5
0,26
6
0,13
При ЧМК с девиацией/д = 50 кГц и модулирующей частотой
Fj' —10 кГц индекс модуляции fJF1 = 5. Поэтому спектр ЧМК,
представленный на рис. 3.14, а, не отличается от спектра ФМК,
показанного на рис. 3.13, а.
При F2 = 5 кГц индекс модуляции /n/.F2 = 10. Значения JM0)
приведены в табл. 3.2, а спектр ЧМК представлен на рис. 3.14,6.
43
S,6
2,88rrt
5,96-ru
3,66
/,δδτ'σ" Τ
1,8&тП \ff47S
3#ΒΎ0
0,478„
10«\10
■*—»+*
ш'Ча'
ч5-
10,4\Ю*
W
Що
а)
Гг=5-103Гц
А
10
η = 10"Гц
3,96-0
3,6'ВтТГ
1,8В-
2,8ВтП
0Λ7ΒΎ0
5-10 sГц
Ю
Рис. 3.13
1,8В jTC
3,6В
3,9 В^О
W
* И
W
■* ^f* 9
0,478^0
tO* \10А
70'
2,86-гО
1,8 ΒΊ О
АГЦ
Гг~6-10*Гц
ю
3,2В 0 328 О
2>#Т01?7^В/72мв2гя2,6ва 2,3 Я ' Ί29 0
f,nf
Видно, что с понижением модулирующей частоты (и ростом
индекса модуляции) число спектральных составляющих в полосе,
определяемой девиацией частоты /д, растет.
Таблица 3.2
2 3 4 5
9 10 II
Λ (Ю)
-0,25 0,044 0,26 0,06 -0,22 -0,23 -0,014 0,22 0,32 0,29 0,21 0,12
44
3.16. Фазомодулированное колебание определяется
выражением
и [t) = Um cos [2π/01 + т cos (2nFt)],
где m=fJF, а /д — девиация частоты.
При полосе частот канала 100 кГц девиация не может
превышать 50 кГц, следовательно, должно выполняться условие
Fmax^fjm= 10 кГц.
3.17. Фаза θ(/) изменяется по закону, совпадающему с
изменением сигнала s(t), а мгновенная частота (o(t) = (o0 + dQ/dt
изменяется относительно среднего значения со0 по форме
меандра.
3.18. При средней мощности ЧМК Рср = 50Вт: а)Р=54Вт;
б) Р=49,68 Вт; в) Р = 49,5 Вт. Следовательно, при т = 0,4
приближенное вычисление мощности исходного колебания по трем
спектральным составляющим (дя«: 1) приводит к завышению
результата, а при т = 5 и 10 отбрасывание боковых составляющих
в спектре, номер которых больше т +1, приводит к
систематической погрешности со знаком минус.
3.19. Μ=0,4.
3.20. Полная мгновенная фаза колебания
ψ(/) = 2π·50·103/ + 2π·107ί2 + π/6.
Девиация частоты /а= 10 кГц; база колебания N = Af3$zn = m =
= 2/дти = 20. Формула, описывающая данное колебание,
(5cos(27r-5-104f + 27r-10V + 7r/6), 0<ί<τ„,
и(')-{0, /<0, />τ„.
3.21. i/(/) = 20cos(27r-106/+10sin27r-104/), В.
3.22. Определим энергию узкополосного сигнала
ос ос
Э,= J s2{t)dt = A2 J e-2a2(2cos2(co0/ + P/2)^«
о — ос
- = 6,25 10~3В2с.
:— /- = 6.25·10~3°2
2α-
1 /π,„_4
Отсюда эффективная длительность сигнала А/Эф = - /-10 с,
или Δί3φ = 62,65 мкс.
Для определения Δ/3φ необходимо найти спектральную
плотность заданного сигнала
г.2,2
S(co)= J A-e~at ε^°ί + ^ώ =
45
_n/5 1
Тогда Δ/3φ =
(ω-ω0)2
е 4(α2-/β)5 -οο<ω<οο
2,/2π
, следовательно, база сигнала
w
= А/эфА/эф=^7а4 + Р2 = 1,26.
График зависимости А/эф от β приведен на рис. 3.15.
А%-Ю*,гц
58
7,5в-
8 β·109ε-'
0,258 Л
10ί
2,5В-
fOs f°StOs
щ »f* 9
/о3У>гц
Рис. 3.15 Рис. 3.16
3.23. Преобразуем заданное выражение к виду
s(/) = 5cos(2n-106f + 0,2cos2n-103/)+2cos[2n(106+103)f +
+0,2cos2n-103f] + 2cos[27r(106-103)/ + 0,2cos27r-103/].
В правой части равенства содержатся три слагаемых, каждое из
которых является колебанием с угловой модуляцией. Индексы
модуляции этих колебаний одинаковы (дя = 0,2), а несущие частоты
различны: 106; 106 + 103 и 106-103. Учитывая, что т<1, можно
рассчитать и построить спектральную диаграмму колебания,
представленную на рис. 3.16.
3.3. АНАЛИТИЧЕСКИЙ СИГНАЛ
3.24. Для заданного радиосигнала
i/(r)= Ucos(o)0t+eo + msmClt), —оо <ί<οο,
при Ω«:ω0 составить выражение для огибающей амплитуд,
полной мгновенной фазы, средней частоты, начальной фазы и
комплексной огибающей амплитуд.
3.25. Комплексная огибающая амплитуд аналитического
сигнала имеет спектральную плотность
а)^'И=1Й^Г; 6)^2Η=Τ^-' *^M«>)=j—e ,ω'°·
46
Определить исходные физические сигналы, имея в виду, что
ω0»β.
3.26. Исходный сигнал является радиоимпульсом с
прямоугольной огибающей амплитуд:
, xf^cosoV, -τ„/2^ί^τ„/2,
U[) [О, /<-τ„/2, />τ„/2.
Найти спектральную плотность комплексной огибающей
амплитуд аналитического сигнала.
3.27. Определить огибающую функции a(t) = Asinro0i/(ro0/),
построить ее и сравнить с исходным сигналом. Сделать выводы из
сравнения.
3.28. Определить и построить график модуля
спектральной плотности когерентного сигнала, фазоманипулированно-
го по коду Баркера с базой N=5 и представленного на
рис. 3.17. Длительность элемента кода Баркера ти=10мкс,
амплитуда А = 10 В.
ffCtJi
Рис. 3.17
3.29. Определить комплексную огибающую пачки из 10
радиоимпульсов с частотой заполнения ω1=ω0+Ω, где Ω—допле-
ровское приращение частоты, /=100 Гц. Период повторения
импульсов Т=\ мс, амплитуда 10 В. Изменением фазы колебания
внутри радиоимпульса пренебречь.
3.30. Рассчитать и построить корреляционную функцию
линейно-частотно-модулированного (ЛЧМ) радиоимпульса и
радиоимпульса с неизменной частотой заполнения ω0, соответствующей
средней частоте ЛЧМ радиоимпульса. Огибающие
радиоимпульсов прямоугольные, длительность (τ„ = 5 мс) и амплитуды
одинаковы. Исследовать зависимость ширины основного лепестка
корреляционной функции от девиации частоты и сравнить ее
при f =5 кГц и /д = 0.
3.31. Определить и построить корреляционную функцию фазо-
манипулированного по коду Баркера сигнала, заданного в
примере 3.28. Выяснить зависимость уровня боковых лепестков от
базы сигнала.
3.32. При настройке фортепиано настройщик одновременно
слушает звучащую струну и камертон. Определить и построить
огибающую суммарного сигнала в предположении, что оба
колебания узкополосные и имеют одинаковые экспоненциальные
47
огибающие, равные максимальные значения, а частоты заполнения
отличаются на 2 Гц. Выражение для огибающей каждого сигнала
А(п = Ае-°-Ъ(.
3.33. Определить минимально необходимую частоту
дискретизации колебания
a(t) = A(l+0,Scos2n-l03t)cos2nl06t, -οο<ί<οο,
из условия последующего полного восстановления. Рассчитать
АЧХ идеального восстанавливающего фильтра.
3.34. Решить задачу 3.33 для ЛЧМ радиоимпульса с
прямоугольной огибающей, частотой заполнения /0 = 100 кГц, девиацией
частоты 5 кГц, длительностью 10 мс.
3.35. Рассчитать потери в мощности ЧМК, заданного
выражением в примере 3.18, при восстановлении в идеальном фильтре,
рассчитанном исходя из практической ширины спектра заданного
ЧМК. Определить период циклической дискретизации Т0 в этих
условиях, в 3 раза меньший периода дискретизации по Котель-
никову.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
3.24. Применив преобразование Гильберта к исходному
сигналу, получим сопряженный сигнал
u1(t)=Usm(o30t + Q0 + ms\nQt), — оо</<оо.
Огибающая определяется по формуле [1, § 3.10]
полная мгновенная фаза
ψ (ί) = arctg [mj (ί) / и (t)] = ω01 + θ0 + m sin Ωί;
мгновенная частота
ω (ί) = d v|/ (t) j dt = ω0 + mQ cos Ωί;
средняя частота ω0,
начальная фаза
Ψ(0) = θο;
комплексная огибающая
U(t)= Uexp[i(% + msinQt)].
3.25. Комплексная огибающая Al(t) аналитического сигнала
определяется обратным преобразованием Фурье спектральной
плотности
48
А1(0=100е(л/4е-р', ί>0.
Остальные комплексные огибающие аналитических сигналов
можно получить из At(i), используя соответствующие свойства
преобразования Фурье:
Α2(ί)=100είπ/ν, ί^Ο;
Α3(ί)=100είπ/4εβ('~4 t^t0.
Исходные физические сигналы [1, § ЗЛО]:
a)a(f)=100e~p'cos((u0f + 7r/4), ί^Ο;
6)a(/)-100ep'cos(ro0i + n/4), f^O;
в) <z(/)=100eP('-'o>cos(av + 7r/4), t^t0.
3.26. Поскольку сигнал и (ή определен как четная функция
времени, огибающая амплитуд является действительной функцией:
'U, -τ„/2^^τ„/2,
О, *<-τΗ/2, ί>τΗ/2,
а ее спектральная плотность
£/(ro)=£/THsin(a)TH/2)/((DTH/2).
3.27. Определим сопряженный по Гильберту сигнал по
известной формуле [1,§ 3.9]
U(t) = .
МО —7
sin ω0τ
ω0τ(τ-/)
dx.
Произведя замену переменной χ = ω0τ, можно свести этот
интеграл к табличному [13, 3.723.12]:
smxdx
х(х—г)
= —(1 —cosz).
Тогда al(i) = A(l— cosco0/)/((u0i), а огибающая
sin ω01/2
A(t) = y/a2(t) + a21(t) = A
ω0//2
Графики ait) и A(t) представлены на рис. 3.18, из которых
следует, что A[t) не является огибающей для a(t) в обычном
смысле, т. е. не проходит вблизи максимумов a(t) и не является
касательной [I, § 3.9]. Это объясняется тем, что заданный сигнал
не является узкополосным.
49
Рис. 3.18
3.28. Представим первый радиоимпульс последовательности
рис. 3.17 в виде четной функции
ι \_ίAcos(o0t при -τ„/2^/<τ„/2,
M'J-jo при Μ>τ„/2.
Спектральная плотность подобного сигнала [1, §3.3]
8» = :
_А\ fsin[(u)-co0)T,,/2] | 8Ϊη[(ω+ω0)τ„/2]
(ω-ω0)τ„/2
(ω+ω0)τ,,/2
В области частот ω>0 второе слагаемое в фигурных скобках
пренебрежимо мало, поэтому
S>) = S>0+fl)*^!^3, Ω=ω-ω0
Ωτ„/2
Спектральная плотность последовательности радиоимпульсов,
представленной на рис. 3.17,
S(ro) = S1(ro0 + Q) + S2(ro0+Q) + S3(ro0+Q)-
-S4(Mo + n) + S5(ro0 + n) = S1(Mo+Q)[l+e-,'(tt,o+«K+
В случае когерентной последовательности радиоимпульсов (оо0ги =
= η2π, η—целое число) последнее выражение упрощается:
S(ro) = S(«0 + n)=:^^^(l+e-^ + e
-ί2Ωτ
2 Ωτ,/2
-e-i3£lTH + e-i4iiT.)
й модуль спектральной плотности
ΩτΗ/2
График SA(2nF) при N=5 показан на рис. 3.19.
3.29. Комплексная огибающая аналитического сигнала,
соответствующего первому радиоимпульсу, A(t) = A, — τ„/2<ί^τ„/2, а
50
Рис. 3.19
7
2
и 20 40 60 80 100 120 140 t60 180~Г,кГц
набег фазы, обусловленный доплеровским смещением частоты за
время Т, равен Ω Г. Следовательно, набег фазы для и-го
радиоимпульса будет ηΩΤ и комплексная огибающая A„(t) =
= е'"ат. Физическое же колебание внутри и-го радиоимпульса будет
an(t) = Acos(oi0t+nQT).
3.30. Корреляционная функция ЛЧМ радиоимпульса [1, § 3.11]
имеет вид
Βα{τ)=-^ βτΜ/2 cos03oT> -τκ<τ<τΗ,
где использованы обозначения, принятые в примере 3.22.
При β = 0
*-(τ) = ^(1-|τ|/τ.)«>8ω0τ, |τ|<τ„,
что совпадает с корреляционной функцией прямоугольного
импульса с смодулированным высокочастотным заполнением.
Отметим, что при достаточно большой базе сигнала ширина
основного лепестка функции Ва(х) равна 2//д [1, рис. 3.32], а в
отсутствие частотной модуляции (β = 0) протяженность
корреляционной функции равна 2τ„. При ти = 5мс и /д = 5кГц ширина
основного лепестка Βα(τ) для ЛЧМ импульса в 25 раз меньше
длительности Βα{τ) при /д=0.
3.31. Для построения корреляционной функции
радиоимпульса, фазоманипулированного по коду Баркера, можно
воспользоваться графическим методом, переходя к огибающей
A(t), как и в примере 3.28. Особенностью Alt) таких
сигналов является возможность представления огибающей
последовательностью действительных чисел с соответствующими коду
Баркера знаками. Смещая последовательности относительно
исходной 5 раз (по числу элементов кода) и складывая
смещенные последовательности, можно получить огибающую
искомой корреляционной функции. Уровень ее боковых
лепестков составляет l/N=0,2 от максимального значения при
τ=0.
S^ZrtFHO ■'.в/гц
51
3.32. С учетом исходных данных физический сигнал можно
определить выражением
a (t) = А е" °'3' (cos ω11+cos ω21),
которое можно преобразовать, применив известные
тригонометрические формулы:
я(П = 2Ле u,3'cos ——ifcos ——-t = 2Ae u,3,cos — tcos(ont =
ν / 2 2 2 °
= 2 A e~ 0,3( cos 2πί cos ω01.
Анализ полученного после преобразований выражения
показывает, что огибающая исходного физического сигнала
A{t) = 2Ae'°'M\cos2nt\.
График A (t) представлен на рис. 3.20. Из этого графика следует,
что при несовпадении частот rot и ω2 возникают биения с разностной
частотой. Такой метод измерения частоты носит название метода
акустических биений и применяется также в электроизмерениях.
A(t)
2А
А
Рис. 3.20 ° 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 t,c
3.33. Частота дискретизаций для заданного сигнала должна
быть Fa^2 кГц, восстанавливающий фильтр должен иметь полосу
пропускания 2 кГц, среднюю частоту АЧХ 1 МГц.
3.34. F.^10 кГц, П*=10кГц, /ср=100кГц.
3.35. /> 10 кГц, п1 = 5кГц, /ср = 2,5 кГц.
Глава 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ СИГНАЛОВ
4.1. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ПРОЦЕССОВ
4.1. Дано колебание ξ(ί) = χ(ί)ψ(ί), где x(t)—случайный
стационарный процесс; ψ(ί) — неслучайная функция времени. Определить,
является ли это колебание стационарным процессом.
52
4.2. Случайный процесс представлен в виде ξ(/) = ψ(/)+7, где
ψ(ί)—стационарный эргодический процесс; Υ—случайная
величина. Определить, является ли процесс ξ(ί) эргодическим.
4.3. Задан сигнал в виде постоянного напряжения случайного
уровня ξ (/)=£/. Можно ли процесс ξ(ί) назвать стационарным и
эргодическим.
4.4. Случайное колебание ξ(ί) в любом сечении представляет
собой непрерывную случайную величину с одномерной
плотностью вероятности р(х, t). Определить в общем виде выражение
для математического ожидания m^(t) и дисперсии D^(t) колебания
ξ(ί). Изобразить примерный вид реализации случайных процессов:
а) нестационарных по математическому ожиданию; б)
нестационарных по дисперсии; в) нестационарных по математическому
ожиданию и по дисперсии одновременно.
4.5. По заданной графически функции распределения Р{х)
стационарного случайного колебания (рис. 4.1) определить
плотность вероятности и изобразить примерный вид реализации этого-
процесса.
Рис. 4.1 -5-4 -5 -2-1 0 1 2 3 4 5 6 χβ
4.6. Сопротивление цепи r(t) (линейный элемент) и
протекающий по ней ток /(/) представляют собой некоррелированные
стационарные случайные колебания. Определить среднее значение
электродвижущей силы Е, создающей ток в цепи, если известно,
что гаг=Ю0Ом, а гаг=1А.
4.7. По заданной плотности вероятности стационарного
случайного процесса (электрического тока) р(/) = ос/2ехр( — ki), к>0.
05ζ/<οο, определить коэффициент а, функцию распределения Р(/)
и вероятность пребывания значения / в интервале (0,1 /к).
Построить графики функций /?(/) и P{i) для частного случая
4.8. Определить математическое ожидание, дисперсию, средний
квадрат и среднеквадратическое значение стационарного
случайного напряжения, заданного одномерной плотностью вероятности
. . Г0,1 В-1, 0:ζΜ5ζ10 В,
^"'~{θ, и<0, и>\0В.
Указать размерности найденных величин.
4.9. Плотность вероятности огибающей узкополосного гаус-
совского процесса определяется выражением [1, с. 129]
53
{ 0, и<0.
Определить математическое ожидание этого колебания.
4.10. Задано, что функция распределения стационарного
случайного напряжения u\t) имеет вид
„, ч f 1 - ехр'{ - ки% -и > 0, к > 0, В ~~ι,
Определить математическое ожидание, средний квадрат и
дисперсию этого процесса. Пояснить физический смысл этих
параметров."
4.11. Напряжение на, выходе измерительного усилителя
представляет собой нормальный стационарный случайный
процесс с математическим ожиданием ти= — 50 мВ и
дисперсией, D.^ — 0,01 В2. Определить вероятность того, что
мгновенное , значение напряжения не превысит по абсолютной
величине 150 мВ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
4.1. Для проверки стационарности колебания ξ(ί) определим
его математическое ожидание и дисперсию:
Λζ[ξ(/)]=Λ[*(/)Ψ(/)] = Ψ2(/)Λ[*(/)1
Поскольку статистические характеристики функций ξ(ί) зависят от
времени, процесс ξ(ί) является нестационарным.
4.2. Из условия, что Μ [У] от времени не зависит, а ψ(ί)
является стационарным процессом, вытекает, что ξ(ί) также
является стационарным процессом. Для эргодичности процесса
ξ(ί) требуется, чтобы и случайный процесс y(t), в сечении
которого в момент времени t = t0 получена случайная величина Y,
был эргодическим.
4.3. Случайный процесс ξ(ί)=£/ стационарен, поскольку при
усреднении по множеству все статистические характеристики не
зависят от времени; процесс ξ(ί) не эргодичёский, поскольку при
усреднении по времени результат будет зависеть от выбранной
реализации.
4.4. Математическое ожидание и дисперсия случайного
колебания ξ(ί) могут быть записаны в виде
OO QO
mt(t)= J xp(x, t)dx; D^(t)= j" [x-m%(tj]2jp(x, t)dx.
— oo — oo
54
Реализации процессов, γ которых от времени зависит только
/ηξ(ί), только D^[t) или m^t) и D^(t), показаны соответственно на
рис. 4.2, а, б, в.
Рис. 4.2
4.5. Функцию распределения Р(х) представим в виде прямой,
проходящей через две точки с координатами (χι, yi) и (х2, у2):
(х-х1)1(х2-х1)={у-у1)1{у2~уЛ
При Χι=— 3, >ί=0, х2 = 4 и у2 = \ получаем у = Р(х) = (х+3)/7.
Функция распределения и плотность вероятности связаны
соотношением p(x) = dP(x)/dx, следовательно,
при -3«ξχ«ξ4,
р(х)=< '
О при х< -3, х>4.
00 4·
Убеждаемся, что условие нормировки p(x)dx= -dx=\
выполняется. График плотности распределения и изображение одной
из возможных реализаций процесса показаны на рис. 4.3.
Лх(Р
1ч
1
чэ
*·*
«3
-и*
-^
Ζ 0 Ζ-
II III
Рис. 4.3
4.6. Исходя из очевидного соотношения e(t)=r(t)i(t) и
учитывая независимость линейной функции r(t) от тока i(t), получаем
e{t) = r{t)i(t)=mrmi=m В.
55
4.7. Из условия нормировки J p(i)di=\ следует
a=l/ ji2e~kidi=k3l2
о
[13, 2.322.2].
Функция распределения
P(i) =
izQ-Kldi=\-
k2i2 + 2ki+2 -ki
при i>0,
О при /<0
[13, 2.322.2].
Вероятность попадания значения i{t) в интервал (0,1 /&)
P(0^i^llk)= 1-0,914 = 0,086.
Графики функций p(i) = (k3/2)i2e~kt, A~l и P(i) при к = Ъ
показаны на рис. 4.4, а и 6.
О 2/к 1 2 3 С,А
а)
1 2 3 i,A
Ю
Рис. 4.4
4.8. Математическое ожидание стационарного напряжения
определим по формуле
10
M[u(t)] = mu= J up(u)du=5 В.
о
Средний квадрат случайного колебания
10
M[u2(t)] = J u2p(u)du = 33,3 В2.
о
Дисперсия случайного колебания
ю
Du= J (u-mu)2p(u)du = M[u2(i)]-m2 = S,33 В2.
о
Среднеквадратическое значение
56
σ„ = 7^=2,88 В.
4.9. Математическое ожидание огибающей узкополосного гаус-
совского процесса определим из выражения
00
г
т =
и -u^l)du_
G1
Произведя замену переменной u/{y/2a) = t, найдем
00 00
ти = аУ2 J 2ί2εχρ(-ί2)Λ^σ4/2 J t2texp(-t2)dt.
о о
Интегрируя по частям, окончательно получаем
Λΐ„ = σ>/2ν/π/2 = σν/π/2!»1,26σ, Β.
4.10. Вначале определяем плотность вероятности
ζ ν dPiu) \ke~ku при м^О,
р{и) = ^--'
<1и
О
при м<0.
Размерность ρ (и) — В 1.
Математическое ожидание
т =
00
г
up{u)du =
Средний квадрат
uke~kudu^-, В.
M[u2(t)]= u2p(u)du=^, В2
Дисперсия
Du = M[u2(t)]-m2 = l/k2, В2.
Математическое ожидание mu=U0 имеет смысл постоянной
составляющей стационарного случайного колебания, М[м2(/)] —
средней мощности (полной) колебания, выделяемой в
сопротивлении 1 Ом, a Du—средней мощности, выделяемой флуктуацион-
ной составляющей колебания.
4.11. Задача сводится к определению вероятности того, что
положительное отклонение случайной величины U от. среднего
значения ти= — 50 мВ остается в пределах 0...200мВ, а
отрицательное отклонение — в пределах 0... — 100 мВ.
57
Вероятности этих двух событий равны соответственно
0.2
P(0<[/<0,2) = --L= е-и2/(2°и»Л = ф(-^=) = Ф(2),
y/2nD„ J \y/Dj
P(0<\U\<0,1) =
ο,ι
V^A.
е-»2/(2Дц,
,л—Ш-{1)·
И/νΌ
где Ф
(—)' —
\JdJ sfa J
-»2/2
<ft— функция Лапласа [5, с. 532].
Совместная вероятность указанных двух событий
/»(|ί/|^0,15) = Φ(2)+Φ(ΐ) = 0,8185,
т. е. вероятность того, что напряжение на выходе усилителя не
выходит из полосы -100...+200 мВ, составляет 0,8185.
4.2. КОРРЕЛЯЦИОННЫЕ И СПЕКТРАЛЬНЫЕ
ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ
ПРОЦЕССОВ
4.12. Задана ковариационная функция случайного колебания
W·
^(ί.ί)=ι/Ρ-(ί-ί)2].
где t—безразмерное время.
Определить ковариационную функцию случайного колебания
η(/)=β"'ξ(0+^2ί·
4.13. Показать, что модуль корреляционной функции \R(i{tl, t2)\
случайного процесса ξ(ί) меньше или равен половине суммы
дисперсий процесса в моменты времени t=t1 и t = t2.
4.14. Спектральная плотность мощности W((o) стационарного
процесса x(t) задана графически (рис. 4.5). Определить дисперсию
и корреляционную функцию процесса, указать их размерности.
58
-ω, 0 ut 0
Рис. 4.5
u(t)
L
Рис. 4.6
4.15. Напряжение с выхода электронного коммутатора
представляет собой стационарный случайный процесс u(t) (рис. 4.6),
описываемый двумерной плотностью вероятностей
ри{и1, и2; τ) = 0,5Ρ1(τ)δ(«1-1)δ(Μ2-ΐ) +
+0,5Ρ2(τ)δ(Μι-1)δ(Μ2)+0,5Ρ2(τ)δ(Μι)δ(Μ2-1) +
+0,5Р1(х)Ци1)Ци2), Β-1,
η / ч 1+οχρ(-2λτ) η , ν 1-εχρ(-2λτ) .
где Λ(τ)= 4 '? ^Μτ) = j ■> λ—параметр
процесса U(t).
Определить корреляционную функцию процесса U{t)^
спектральную плотность мощности Ή полную мощность процесса U(t);
изобразить графики корреляционной функции и спектральной
плотности мощности указанного процесса.
4.16. Дан стационарный случайный процесс (рис. 4.7)
M(i)=£/0cos((u0i + (p), В,
где амплитуда U0 и частота ω0—детерминированные величины;
φ — случайная величина, равномерно распределенная в
интервале · —π^φ<π. Найти его ковариационную и корреляционную
функции.
и(Цвк
Рис. 4.7
4.17. Ковариационная функция случайного тока i(t),
представленная на рис/4„8, описывается . выражением
^(т)=0,8ехр(-102|т|)+0,9, А2.
Определить и изобразить на графике спектральную плотность
мощности процесса i(t), полагая закон распределения
нормальным, качественно изобразить на графике реализацию случайного
тока i(t).
4.18. Даны корреляционные функции трех случайных
процессов: а) /?(τ) = Α/(1+α2τ2); б) Д(т) = Аехр(-ос2т2); в) R(x) =
= AsinoLx/((x.x). Определить интервал корреляции τ, = - \r(x)\dx,
— αο
где г (τ) — нормированная корреляционная функция процесса.
59
4.19. Определить корреляционную функцию случайного
процесса χ(ί) = ξ(ί)η(ί), где ξ(ζ) и г\(()— стационарные случайные
некоррелированные нормальные процессы с корреляционными
функциями /?ξ(τ) = σ2εχρ( — α2τ2) и )?η(τ) = σ2/(1 +огт2) и
математическими ожиданиями га^гап = 0.
4.20. Известны математические ожидания и корреляционные
функции двух случайных колебаний ξ(ί) и η(ί). Определить
(математическое ожидание и корреляционную функцию случайной
функции χ(ί) = ξ(ί) + η(ί) в общем виде.
4.21. Определить взаимные спектральные плотности Ю^п(ш) и
Μ/ηξ(ω) процессов ξ(ί) и η(ί) = ύ?ξ(ί)/ dt. Корреляционная функция
процесса ξ(ί) задана: /?ξ(τ) = σ2εχρ( — α2τ2).
4.22. Определить спектральную плотность ^(ω)
процесса χ(ί) = ξ(ί)η(ί), где ξ(ί) и r\{t)—независимые нормальные
случайные процессы с известными математическими ожиданиями
т% и тц и корреляционными функциями /?ξ(τ)=σ2εχρ( — at |т|),,и
/?η(τ) = σηεΧΡ(-α2ΐτΐ)·
4.23. Определить спектральные плотности средней
мощности стационарных случайных колебаний по известным
корреляционным функциям: а) /?(τ)=σ2εχρ( — a|x|)cosro0r, 6) RM =
= σ2εχρ( —β2τ )cosgo0-c. Построить графики полученных W((o).
4.24. По заданной графически спектральной плотности средней
мощности (рис. 4.9) определить корреляционную функцию R(x)
стационарного случайного процесса.
..weut),e2/rn
Wo
_l_l 1 LU ^
-u^-utf 0 ω)ωΰωζ ω рис_ 4.9
4.25. Вычислить эффективную ширину спектра
стационарных процессов по заданным их корреляционным функциям:
а) R(z) = Ae-«W; б) R(x) = Ae-a^cos(o0v, в) R(x) = Ae-a2'2/2cos(o0x.
4.26. Определить корреляционную функцию и дисперсию
стационарного случайного процесса, имеющего спектральную
плотность средней мощности И^(ш) = 2Лос/(ш2 + ос2), А>0, ос>0.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
4.12. Прибавление неслучайного слагаемого не оказывает
влияния на ковариационную функцию случайного процесса. При
умножении же случайной функции на неслучайную функцию φ(ί)
ковариационную функцию нужно умножить на φ(ίι)φ(ί2)· Таким
образом,
60
KnCi^He-W/Cl-^-^)2].
4.13. В задаче требуется показать, что
Ι^(Ί, '2)Ι<0,5[σ|(^) + σ|(ί2)].
Для доказательства воспользуемся соотношением
^{Ι[ξ(Ί)-^(0]±Κ('2)-«ξ('2)]Ι2}>ο.
При переходе к центрированным значениям случайной функции
£(ί) = ξ — Ήξ(') получим
^{ι4(ί)±4('2)ι2}>ο.
Учитывая, что математическое ожидание модуля суммы равно
модулю суммы математических ожиданий слагаемых, записываем
|л/[|а(/1)]±ш[|(/1)|(/а)]+л/[|а(/)]|>о,
откуда следует
или,учитывая, чтоM[^(tl)^(t2)] = R(tl, t2),окончательно получаем
\R{h,t2)\^[_vl{h) + *l{h)\
4.14. Корреляционная функция
*v ; 2π ν ; 2π υ π ω, τ
График корреляционной функции показан на рис. 4.10.
ν/0ω,/η
Рис. 4.10
Дисперсия процесса x(t)
Dx = Rx(0)=Wo(oJn.
Ее можно определить и непосредственно по спектральной
плотности мощности:
D=.
2π
W(<o)d<o =
2π
W0d<a=1^=W02fx.
61
Размерности корреляционной функции и дисперсии процесса χ(ί)
совпадают и могут быть либо [А2], либо [B2J, в зависимости от
того, что описывает функция x(t)—ток или напряжение.
4.15. Корреляционную функцию процесса, заданного
двумерной плотностью вероятности, найдем из выражения
00 00
R«(x)= ί ί {ui-mu)(u2-mu)pu(ui,u2;x)duldu2.
Для определения математического ожидания ти найдем
одномерную плотность вероятности р(и), проинтегрировав pu(ui, и2\ τ)
по их:
00
г
Р{"г)= Pu("i, "2; *)dui= -Р1(х)+-Р2(х) 8(м2-1) +
+[^Λ(τ)+^2(τ)]δ(Μ2).
Учитывая, что Pt =0,5(1 -be 2λτ), Р2 = 0,5(\-е 2λτ), получаем
р(и2)=р(и1)=р(и) = 0,5Ци-1)+0,5Ци).
Определим математическое ожидание и корреляционную
функцию процесса:
00 00
гаи= J up(u)du = J г/[0,5 6(г/-1) + 0,56(г/)]Л/ = 0,5 В;
Μτ)= ί ί {ul-mu){u2-mu)pu(ui,u2;x)duidu2 =
— oo - oo
= 0,25ε-2λ|τ|, Β2.
Спектральная плотность средней мощности
00 00
Wu(a)= Ru(x)c~i°"dx = 2 Ru(x)cos2nfxdx = 4x2+X £
Полная мощность процесса U(t)
Ри = RJ0)+тги =Du+m2u= 0,5 В2/Ом.
Такую мощность выделяет процесс U(t) в сопротивлении 1 Ом.
Графики Ru(x) и ^„(ω) изображены на рис. 4.11,а, б.
4.16. Ковариационная функция стационарного эргодического
ι
τ
Г
процесса определяется с помощью выражения Ки(х)= Hm - u(t) x
T-oo^J
О
62
Рис. 4.11
-ffZA) О Ιί(2λ)
а)
-Ζλ
О 2λ 2rtf
xu(t + x)dt, следовательно, для U(t)= £/0cos(a)0i4-cp) будем иметь
]
τ
г
Ки(τ) = Hm - U0 cos (ω0ί + φ) U0 cos(ω0 /4-ω0τ 4- φ)dt =
T-<x>TJ
О
Τ
= lim —
Γ-αο *
ul Γι
[cos ω0τ + cos (2ω0ί 4- 2φ 4- ω0τ)] dt.
После несложных преобразований получаем
Κ„(τ) = ^οο$ω0τ, Β2.
Так как в общем случае ковариационную функцию молено
представить в форме Ku(x) = R (х) + т^, то очевидно, что в
рассматриваемом примере Ku(x) = Ru(x). Важно отметить, что
корреляционная функция гармонического колебания со случайной
фазой φ является также гармоническим колебанием с той же
частотой Шд; независимо от начальной фазы φ корреляционная
функция Ru\x) является косинусоидальным колебанием (рис. 4.12).
_U±/2
Ри
\ J2nAig τ
с. 4.12
Щ(2яГХАг/Гц
8-ГСГ1
А
s ι
-200 L
I
•^M-2irf(Zrtf)
ι >— u
> 200 2rtf,pad/c
Рис. 4.13
4.17. Для случайного процесса с ненулевым средним значением
спектральная плотность мощности Η^(ω)= \Усо(оз)-\-т2 ·2πδ(ω)
[1,§ 4.3], где И^да(ш)—сплошная часть спектра, соответствующая
флуктуационной составляющей тока /.
При заданной корреляционной функции /?((т) = 0,8ехр(-102|τ|)
получим [1, § 4.4]
63
00
г
3,2· ΙΟ2
»»= Ri(xy^dx + m2-2n^)=j:^~^1 + 0,9-2nb(2nf).
График Wfibif) изображен на рис. 4.13.
Полная мощность (средняя) процесса i(t), выделяемая в
сопротивлении 1 Ом, Pi = Ri(0) + mJ = 1,7 А2 Ом. Примерный вид
одной из реализаций i(t) изображен на рис. 4.14.
Рис. 4.14
4.18. Для заданных корреляционных функций:
aWT)=^r=r-^n; \=
a* 1+aV к
r-r=-arctg(Ta)
1+aV α ьу '
π
б)ф) = е-Л2; τκ =
ιΙτ = - "
π 2
αν 2ν π
е " τ dx =
J 2α '°°' α\/2' J π
e-'A=l
00
sinai , 1
— ят=-
ατ α
sin λ: , _ 1 π
λ: α 2'
4.19. Для любых двух нормальных стационарных процессов
корреляционная функция их произведения определяется
выражением [5, с. 149]
Rx (τ) = *ξ (τ) Д„ (τ) + Λξη (τ) /?ηξ (τ) + т2Д„ (τ) +
+ ™2/?ξ(τ) + ™ξ™η[/?ξη(τ) + /?ηξ(τ)].
Учитывая, что процессы ξ(ί) и η(ί) некоррелированные
(/?ξη(τ) = /?ηξ(τ) = 0), с математическими ожиданиями т^ = тц = 0,
получаем
Rx(x) = R,(t)Rn(t).
64
Подставляя значения корреляционных функций, находим
Дх(т) = а2а2ехр(-ос2т2)/(1+ос2т2).
4.20. тх = тг + тп, Rx(tlt t2) = Rl(ti, t2) + Rn{i1, t2) + R^(tl, t2) +
+ *ηξ('ΐ,'2)·
4.21. Вначале определим спектральную плотность мощности
процесса ξ (t)
И^(оо) = Λξ(τ)ε"ίωντ=
ίωτ^_ σ4 »-<ο2/(4,»2)
2α уπ
Взаимная корреляционная функция стационарного процесса
ξ(ί) и его производной η(ί) = <ίξ/ύ?ί определяется выражением
[5, с. 149]
00 00
Λςη(τ) = ^ = £ Ws((o)eiaTda = /ооИ^(оо)е"""Ло.
— αο ~οο
Из этого выражения следует, что взаимной корреляционной
функции Λξη(τ) соответствует взаимная спектральная плотность
W^ (оо) = /оо Wξ (ω) = /ω
-ω2/4«2
7α. J π
Учитывая, что Ληξ(τ) = Λξη(-τ) и ΡΓηξ(ω)= ΡΓξη(ω) [1, с 125],
получаем
И^(оо)=-/ооИ^(оо),
т. е. взаимные спектральные плотности Η/ηξ(ω) и И^л(оо)— чисто
мнимые функции. Из этого вытекает важное следствие:
/?ξη(τ = 0) = /?ηξ(τ = 0) = - /ооЖ4.(оо)Ло = 0,
7π
т. е. взаимная корреляционная функция стационарного случайного
процесса ξ(ί) и его производной r\(t) = d<£,(t)/dt в совпадающие
моменты времени (т. е. при τ = 0) равна нулю.
4.22. Корреляционная функция произведения двух независимых
случайных процессов с нормальным законом распределения
определялась в примере 4.19. Учитывая, что математические
ожидания не равны нулю, записываем
Rx(x) = R,(x)Rn(x) + miRn(x) + m*R,(x).
Применив прямое преобразование Фурье, после подстановки функ-
65
ций /?ξ (τ) и /?η (τ) получим выражение для спектральной плотности:
ψχ(ω)= f^ + ^+.«l°33L.
/w2o2oti
π[ω2+(α! + α2)2] π(ω2 + α!) π(ω2 + α2)'
4.23. Учитывая, что R(x)— функция четная, спектральные
плотности средней мощности определим с помощью выражения
W(m) = 2 j R(x)cosmxdx;
о
00
а) Ψ(ω) = 2 J a2e_e<|T|cos(u0-ccos(u-cdT =
о
_ϊ + ? 1.
+ (ω+ω0)2 a2 + ((D-co0)2J
= σ2
Корреляционная функция и соответствующая ей спектральная
плотность для ω0»α изображены на рис. 4.15, а, б:
°° 2 2
б) \¥(ω) = 2 J a2e βτ cosGo0-ccosGra/T =
о
2 (ω-ω0)2 (ω+ω0)2
4β^
ρ2 + е Ψ ].
Wiuj
(7
ZL
ω„ ω
Рис. 4.15
Гауссовское распределение огибающей корреляционной функции
приводит к гауссовскому энергетическому спектру. Для ω0 = 0
(видеосигнал) спектральная плотность запишется в виде
Ж(ш) = а2ехр{-ш2/(4р2)}/(2ру^).
Корреляционные функции и соответствующие им спектральные
плотности при ω0 = 0 и Шд^О приведены на рис. 4.16, а, б.
4.24. Корреляционная функция по заданной спектральной
плотности W(<s>) определится из выражения
R(x) = - W(o3)cosa)xdo3 = -
W0 cos ωτί/ω =
66
Рис. 4.16
*fr;ter,V*Vcos«,r
WTutJ
•^^^шш-тшШшатт''''ттт^^^^^ш*^^^ш^~шшш*^Л1ш1Дш*^^^^/*
-ωβ
ω» ω
/Pi
W((u)\
Τ ί)
ω
W0Sis> sin Δωτ/2
cosro0x,
π Δωτ/2
где Δω = ω2 — ο^; ω0 = (ω!+ω2)/2.
График R{x) представлен на рис. 4.17.
/\
Рис. 4.17
4.25. Эффективная (энергетическая) ширина спектра, который
группируется вблизи частоты ω = 0 («низкочастотный спектр»),
определяется выражением [3, с. 199]
(Δω)3φ =
W{Q) W(oy
где R(0)—корреляционная функция при τ = 0;
00 00
W(0)= J R{x)e-ie"dx\a = 0 = 2l R(x)dx.
-oo 0
Таким образом,
00
(Δω)3φ = Λ(0)/2|Λ(τ)ύ?τ.
о
67
В случае узкополосного шума с центральной частотой
эффективная ширина определяется выражением
со
(Δω)3φ=—-Ц, где \¥(ω0)=2 R(x)cos(o0xdi.
0
При заданных корреляционных функциях получаем:
со
a)R(x) = Ae~°M; R{0) = A; 2 R(x)dx = ^; (Δω),ψ = ?;
ο
6)R{x) = Ae-*^cos<u0x; R(0) = A; W(a>0) =
со
Λ С Л
=2А ίε~α|τ|οθ82ω0τύ?τ=-+/4 e-a|T|cos2(u0T</T»-
о а J α
о
со
(при α«:ω0 интеграл J e~"|T|cos2(o0T</T стремится к нулю).
о
Таким образом,
(Δω)3φ = R (0) / W(m0) = А а./А = ос;
в) R{x) = Ae-*2'2'2cos(o0x; R(0) = A; Щщ) =
ου αυ
= 2А \e-*2*2l2cos2 n0xdx = A $ e-'2*2l2dx +
э о
е_а τ/2cos2(fl0Ti/t«- /-,
ot γ 2
о
со
+ А
при этом
(Δω)3φ = Ν/2/πα.
4.26. Основываясь на выражении
т=:
W(o3)cosund<o,
получаем
68
Rh) = -2Aa
v π
αω = — —е βτ = /4ε " при τ>0;
α24-ω2 π 2α
Λ(τ) = ΛεβΤ при τ<0
или
R(x) = Ae~aW, -oc<t<cc.
4.3. УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ
ПРОЦЕССЫ
4.27. Корреляционная функция стационарного узкополосного
случайного процесса л(; )=/l(?)cos[o)0i+9(i J] имеет вид Rx(x) =
= σ2εχρ( — a2T2/2)cosa)0t. Определить условия, при которых
функцию A(t) можно считать медленной по сравнению с cos(o0t.
4.28. Определить корреляционную функцию узкополосного
случайного колебания x{t) = A(t)cos[o30t+Q(t)\ где A{t) и θ(ί) —
случайные, медленно меняющиеся функции. Спектральная
плотность средней мощности случайного процесса представлена на
рис. 4.9. Изобразить (качественно) реализацию процесса и
отметить на ней средний период огибающей.
4.29. Для узкополосного случайного процесса x(i) = /l(i)cos x
χ[ω0ί + θ(ί)] с заданной корреляционной функцией Rx{t) получить
приближенную формулу для корреляционной функции -Κη(τ)
производной r\{t) = dx{t)j dt. Исходить из условия медленности
изменения амплитуды A{t) и фазы 0(f).
4.30. Определить связь между математическим ожиданием
огибающей тА стационарного узкополосного шума и его средне-
квадратическим значением σχ.
4.31. Показать, что дисперсия огибающей σ\ стационарного
узкополосного гауссовского шума связана с квадратом его
среднеквадратического значения σ2 выражением σ\ = [2 — π/2]σ2.
4.32. Задан нормальный узкополосный случайный процесс
x(t) = A(t)cos[(a0t + Q(t)], где A[t) и θ(ί) — медленно меняющиеся
случайные функции времени; ω0 — средняя частота узкополосного
процесса. Определить, является ли этот процесс эргодическим
относительно математического ожидания тх.
4.33. Узкополосный нормальный случайный процесс x{t) имеет
энергетический спектр, изображенный на рис. 4.9, причем WQ =
= 0,5· 10_3 В2/Гц; Δω = |ω2— ω, | = 2· ΙΟ3 рад/с. Определить
вероятность того, что огибающая этого процесса превысит уровень
Α0 = 3σχ, где σχ — среднеквадратическое значение процесса x[t).
4.34. Задан узкополосный нормальный шум с
корреляционной функцией /?x(t)=16exp( — 4- 104t2)cos27i· 106t, В2. Определить
среднее значение, дисперсию и среднеквадратическое значение
69
огибающей шума. Изобразить (качественно) реализацию
узкополосного шума и отметить на ней вычисленные параметры.
4.35. Задан узкополосный нормальный процесс х(п с
корреляционной функцией Rx[x) = A exp( — p2t2/2)coso)0t. Определить
энергетический спектр огибающей этого процесса. Для А =0,25 В2
построить график спектральной плотности огибающей.
4.36. Реализации узкополосного процесса представлены в виде
суммы квадратурных колебаний:
χ (ή = Ас (i) cos ω0ί — As (t) sin ω0ί,
где Ас (t) = A (t) cos Q(t); As(t) = A (с) sin θ(ί); ω0 = (ωt+ω2)/2
—центральная частота энергетического спектра (см. рис. 4.9).
Определить корреляционные функции RAc (τ), RAs (τ)
квадратурных колебаний.
4.37. Задана двумерная плотность стационарного
узкополосного колебания x(t): р(А, 0) = Лехр [ — Λ2/(2σ2)]/(2πσ2), где А и Θ —
случайные амплитуда и фаза; σ2 — дисперсия процесса χ (ή.
Определить математическое ожидание гав и дисперсию σβ фазы
колебания θ(ί).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
4.27. Условие медленности изменения огибающей Α (ή
узкополосного стационарного процесса x(t) по сравнению с cosa)0i
можно записать в виде [7, с. 358]
(Аш)э«гш0.
Эффективная ширина спектра (Δω)3φ процесса, имеющего
корреляционную функцию /?х (τ) = σ2 ехр ( — g2T2/2)cosro0T,
определялась в задаче 4.25 и равна (Δω)3φ = 4/2/π α. При этом условие
медленности огибающей Α (ή сводится к выполнению неравенства
ω0^>^/2/π ос.
4.28. Коррелированная функция процесса при заданной
спектральной плотности Wx (ω) рассматривалась в задаче 4.24 и
проиллюстрирована рис. 4.17. Средний период огибающей
приближенно можно определить выражением Тср= -, где (Δω)3φ =
(Δω) эф/2
= |ω2 — ah I — энергетическая (эффективная) полоса (см. рис. 4.9).
Примерный вид реализации узкополосного случайного процесса
x(t) показан на рис. 4.18.
4.29. Дифференцируя x(t) по времени, получаем
η(0 = ^(ί)/^=-ωοΛ5ίη[ωοί + θ(ί)] + f^cos [ω0ί + θ(ή] -
-Λ(/)^ίη[ωο/ + θ(/)].
70
Рис. 4.18
x(t)i
Τ0=Ζτί/ω„
Так как по условию· Α (ή и θ(ί)— медленно меняющиеся
функции, то вторым и третьим слагаемыми можно пренебречь по
сравнению с первым. Таким образом,
η(/)=^«-ω0Λ(/)8ΐη[οΜ + θ(ί)].
Нетрудно видеть, что y(t) = A (t) sin [ω0ί + θ(ί)] есть процесс,
сопряженный по Гильберту процессу л: (/), поэтому [1, § 4.7] их
корреляционные функции равны, т. е. Rx (τ) = Ry (τ), и
корреляционная функция /?η (τ) отличается от Rx (τ) = Ry (τ) только множителем
ωό:
Д„(т)*ш^(4
4.30. В задаче 4.9 было найдено соотношение, которое
отвечает и на вопрос, поставленный в данной задаче: тА =
4.31. Средний квадрат огибающей шума [1, § 4.6]А2 = 2σ*, т. е.
средняя мощность огибающей равна удвоенной дисперсии шума.
Дисперсия огибающей определяется как разность между полной
средней мощностью огибающей и мощностью, выделяемой
постоянной составляющей огибающей тА, т. е.
<52Л = М[А2] -т\ = 2<52х- (σχν^/2)2 = σχ2(2-π/2),
что и требовалось доказать по условию задачи.
4.32. Представим процесс x(t) в форме
χ {ή = A (t) cos θ (ί) cos ω0ί - Α (ί) sin θ (ί) sin ω0ί =
= AC (ή cos ω0ί— As (ί) sin ω0ί,
где Ac(t) = A(t)cosQ(t); As(t) = Α (ή sin θ (ή.
В узкополосных нормальных стационарных процессах
огибающая Α (ή подчиняется распределению Рэлея, а θ (ί) равномерно
распределена в интервале [—π, π]. Кроме того, функции Α (ή и
θ (ί) в совпадающие моменты времени не коррелированы [1,
п. 4.6.2], поэтому
71
M[Ac{t)] = M[A{t)]M[cosQ(t)]=m*
2π
cos0u?0 = O;
Μ [Α, [ή] = Μ[Α (ί)] Μ [sin θ [ή] = mA
2π
sin0u?0 = O.
Отсюда следует, что Μ [x(t)]=mx = 0.
Вычислим теперь среднее за конечный промежуток времени по
одной реализации процесса x(t):
τ
ι*
:χ7(ή = ί А, cos[ω0ί + θ,]dt = ^[ύη(ω0Τ+θг)-sinθ,].
*
о
Отсюда вытекает, что
lim xt (t) = mx = 0.
Г—да
Так как усреднение по ансамблю и по времени дает совпадающие
результаты, можно утверждать, что процесс χ (ή эргодичен
относительно математического ожидания.
4.33. Дисперсия рассматриваемого процесса χ (ή
2 1
σ2 = -
W0{<o)d<o = 2{f2-f1)lV0 = l Β2; σ,= 1 Β.
Тогда искомая вероятность
Р{А>А0) =
рА (A) dA =
4е A2l2dA=e~9'2«0,011 (-1%).
Таким образом, вероятность пребывания χ (ή в пределах ±А0 =
= ±3σχ составляет ~99%. Поэтому ширину «шумовой дорожки»
(наблюдаемой, например, на экране осциллографа) принято
считать равной ~6σΛ.
4.34. Учитывая, что σ2 = /?χ(0), находим
σ2 = 16 Β2, σχ = 4 Β.
Среднее значение огибающей узкополосного процесса
определяется через σχ соотношением [1, § 4.6]
M[A\=mA = <5xs/nl2 «5 В.
72
Дисперсия огибающей связана с σ2 выражением
DA = o2A=(2-n/2)o2x=0A29o2x = 6,86 В2,
следовательно,
σΛ = ,/Ζ)7«2,6 Β·
Реализация процесса показана на рис. 4.19.
Рис. 4.19
4.35. Энергетический спектр огибающей узкополосного
процесса можно записать в виде [1, п. 4.6.1]
^(Ω) = ^2πδ(Ω) + ^Ι
Ό2(τ)<
ίΩτ
dx,
где r0(x)—огибающая нормированной корреляционной функции
процесса χ (ί).
При заданной функции Rx(x) очевидно, что огибающая
нормированной функции имеет вид
Α·0(τ)=εχρ(-β2τ2/2).
Подставляя г0 (τ) в выражение для WA (Ω) и учитывая, что σ2 =
= Rx(0) = A, находим
ΐνΑ(^) = γ2πδ(α) + ψ-
-βν
е cosQxdx =
= ^2πδ(Ω) +
πσ2χ 1 JH -Ω2/(4β2
—- - bi—e
2 2 2β
Отсюда видно, что энергетический спектр огибающей примыкает к
нулевой частоте. Первое слагаемое в правой части выражения для
WА (Ω) соответствует постоянной составляющей огибающей, а
второе—сплошной части спектра. Если дисперсия процесса
σ2 = А =0,25 В2, то спектральная плотность огибающей
73
Η^(Ω) = ^^^2πδ(Ω) + ^^Lexp {-Ω2/(4β2)} =
8β
1,74
= 3,92·2πδ(Ω) + ^εχρ{-Ω2/(4β2)}, В2/Гц.
График спектральной плотности WA(Cl) для β=102 изображен на
рис. 4.20.
ЫАШ0-г,в2/Гц
■ Z,92-2rtff(Si)
-240 -160 -80 0 80 160 Qj>ad/c Рис. 4.20
4.36. Сопоставим случайную функцию Ac(t) с функцией χ (ι):
χ (ή = Α (ή cos [ω0ί+θ(ί)]; Ac (t) = A (t) cos θ (t).
Отличие Ac(t) от χ (ή состоит в исключении слагаемого ω0ί из
аргумента косинуса cos [ω0ί + θ(ί)]. Энергетический спектр WAc(Cl)
случайной функции Ac(t) можно получить из энергетического
спектра функции χ (ή сдвигом на ω0 левого лепестка и на — ω0
правого лепестка спектра Wx(<si) процесса χ (ή (см. рис. 4.9). В
результате получаем энергетический спектр WАс (Ω) = 2 Wх (ω0 -ί- Ω),
группирующийся вблизи нулевой частоты. Обозначив Δω = |ω2 —
— ω1\ (рис. 4.9), запишем
w (Q)J2W°> -Δω/2^Ω^Δω/2,
0, Ω<-Δω/2, Ω>Δω/2.
Тогда
Rac{i) =
Δω/2
2π
WAc{Q)eia4Q =
in/ ~ гл лл ^οΔω sin Δωτ/2
π Δωτ/2
Аналогичные рассуждения можно привести и для функции
As(t) и получить корреляционную функцию
п , s 1¥0Δω sin Δωτ/2 п , ·.
Ras (τ) = ir-~ = Rac (τ).
Δωτ/2
Δω/2
W0d(o, т. е. дисперсии
При этом RAc (0) = RAs (0) = -^ = σ2 = -
π π
-Δω/2
квадратурных колебаний процесса х (ή одинаковы и равны
дисперсии σ2 самого узкополосного процесса.
74
4.37. Интегрируя двумерную плотность ρ (Α, Θ) по переменной
А, определяем одномерную плотность распределения фазы Θ:
Α>(θ)= p(A,Q)dA =
2πσχ
1 -·42/(2σί)
d{A2) = ^-, -π^θ^π,
2π
т. е. начальная фаза θ распределена равномерно в интервале
[-π, π].
Используя одномерную плотность рй (Θ), находим
т6= θ — ύ?θ = 0; σθ2 =
2π
θ2Α)(θ)ύ?θ = π2/3.
Глава 5. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ С ПОСТОЯННЫМИ
ПАРАМЕТРАМИ
5.1. АКТИВНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
5.1. Составить матрицу А -параметров для триода — активного
четырехполюсника (рис. 5.1). Параметры триода: статический
коэффициент усиления μ = 40, крутизна анодно-сеточной характеристики
5=10 мА/В; внутреннее сопротивление /?( = 4кОм; сопротивление
в цепи сетки г = 0,3 МОм. Межэлектродные емкости не учитывать.
5.2. Используя условия задачи 5.1, определить матрицу Z-na-
раметров активного четырехполюсника.
ί*
)е* )е, ГЬ *1' |е2*е'Ф Dip Ь
с'\ъ
Рис. 5.1
Рис. 5.2
Рис. 5.3
5.3. На рис. 5.2 приведена одна из возможных схем замещения
транзистора типа ρ—и—р. Параметры схемы: гэ = 50Ом, гк =
= 2 МОм, г6 = 500 Ом, гт = 1,9 МОм. Составить матрицу Ζ и найти
численное значение ее определителя Δζ.
75
5.4. Каскад транзисторного апериодического усилителя задан
схемой замещения коллекторной цепи (рис. 5.3). Определить
проводимость нагрузки GH, необходимой для получения коэффициента
усиления K(2nf)= 14 на частоте/= 1 МГц. Крутизна проходной
характеристики транзистора S= 50 мА/В, суммарная паразитная емкость
С0 = 40 пФ, выходная проводимость транзистора G, = l,5· 10~4 См.
5.5. Транзисторный каскад резонансного усилителя с общим
эмиттером задан схемой замещения коллекторной цепи (рйс. 5.4).
Контур в коллекторной цепи настроен на частоту входного
сигнала /0 = 500 кГц, индуктивность контура £ = 0,65 · 10~4 Гн,
выходная проводимость транзистора Сг = 2,5 · 10~4 См, крутизна
5=50 мА/В. Определить добротность контура, необходимую для
получения на выходе амплитуды £/вых = 3 В при амплитуде на
входе £, = 0,03 В.
Рнс. 5.4 Рис. 5.5 Рис. 5.6
5.6. Эмиттерный повторитель на транзисторе КТ 324 (рис. 5.5)
нагружен на RH = 300 Ом и возбуждается источником сигнала с
внутренним сопротивлением /?; = /?„. Параметры транзистора:
Л21э=120, гк = 3-106 Ом, гэ=14 0м, г6 = 75 0м. Определить
коэффициент усиления эмиттерного повторителя по напряжению, его
входное и выходное сопротивления.
5.7. Определить напряжение на выходе эмиттерного
повторителя (рис. 5.6) в отсутствие сигнала (при £с = 0), если падение
напряжения на резисторе /? = 50 кОм составляет 2,5 В. Известны
сопротивление Лн=1 кОм, h2i3-S0.
5.8. На рис. 5.7 представлена схема замещения транзистора
для низких частот (без учета межэлектродных емкостей).
Определить матрицы Z- и Я-параметров схемы при следующих значениях
элементов схемы замещения: гб=200 Ом, г, = 30 Ом, гк = 400 кОм,
а=0,995.
Рис. 5.7 Рис. 5.8 Рис. 5.9
76
5.9. Для простого каскада усиления по рис. 5.8 составить
матрицу У-параметров, считая известными параметры триода μ,
S, R-, и емкость С между анодом и сеткой (остальными
межэлектродными емкостями можно пренебречь).
5.10. Определить амплитуду входного сигнала, необходимую
для получения на выходе каскада (рис. 5.9) сигнала с амплитудой
£^»ых = 4В. Сопротивление Rs=4,5 кОм; параметры транзистора:
гб = 125 Ом, гэ = 25 Ом, Л21Э = 4,0; сопротивлением разделительных
емкостей С\ и С2 пренебречь.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
5.1. При линейном режиме работы триода для определения
синусоидальных составляющих токов и напряжений можно
использовать схемы замещения (рис. 5.10), из которых следует, что
rI,=Ei; 12 + Е2/Д(=-5Е,.
Рис. 5.10
о
о
Умножив правую и левую части второго уравнения на Rt и
учитывая, что для триода справедливо равенство μ = 57?,-, получаем
Λ(Ι2 + Ε2=-μΕ1 или Е! = --Е2--12,
μ μ
а учитывая, что It = Е4 /г, имеем
Ιι = Е2— —12.
μτ μτ
Этому уравнению соответствует матрица
[А] =
-1/μ -Rt/μ
-1/(μτ) -R,far)
-0,025 -100 Ом
-0,83 10~7См -3,33-НГ4
5.2. Матрица Z-параметров
т-
■2^21 -^22
г 0
-цг -Ri
3-10s Ом 0
-1,2Ю70м -4Ю30м
5.3. В соответствии со вторым законом Кирхгофа можно
записать
E,=I1r3+(I1+I2)r6 = I1(r3+r6)+I2/-6;
Εί-Ε,,^Ι, +I2)r6 + I2r1;
K2 = h{r6 + rm) +12{г6 + гж),
77
откуда находим
^ц=гэ + г6; Z12 = r6; Z2l=r6 + rm; Z22 = r6+rK;
Az = Z11Z22-Z12Z2l=(r3 + r6)(r6 + rK) -r6(r6 + rK)&\50-106 Ом.
5.4. Модуль передаточной функции можно записать в виде [1,
§ 5.4]
Возведя обе части выражения в квадрат и сделав
соответствующие преобразования, получим
(G,.+GH)2 = S2/*2M-Ko)2;
GZ + 2GtGH + G?-S2/K2((o) + (шоС)2 = 0.
Разрешив это уравнение относительно G„ и отбросив
отрицательное значение GH, для Κ(ω)=\4 и ω = 2π/= 2π ■ 106 рад/с получим
Gh = 34-1(T4Cm.
5.5. Максимальный коэффициент усиления каскада с
резонансным контуром определяется по формуле
tfma* = S/(G, + Gm)= 1/вых/Е1 = 100,
откуда
Gm = S/tfmax-G,. = 2,5-10-4CM.
Характеристическое сопротивление контура
p = mpL = 2nfpL = 6,2Z ■ 500-103 0,65 ■ 10~4«200 Ом.
Искомая добротность контура
e=l/Gmp = 20.
5.6. Коэффициент усиления по напряжению, входное и
выходное сопротивления эмиттерного повторителя как активного
четырехполюсника выразим через его Z-параметры [1, § 5.2]:
ΑΓ£ = £2/£1=Ζ21ΖΗ/[(Ζ11+Ζ,·)(Ζ22 + Ζ„)-Ζ12Ζ2)];
ΖΒΧ = Ζ11 — Ζ12Ζ21/(Ζ22 + ΖΗ); ΖΒΗΧ = Ζ22 —Ζ12Ζ2ι\\Ζ\\ +Ζι);
Z-параметры в схеме с общим коллектором связаны с
параметрами транзистора соотношениями [2, § 5.4]
Z1i = r6 + rK; Z12=rK-rm; Z2lxrK; Z22 = rK-rm + r3; rm = arK =
= Α2ιΛ/0+Α2ΐ3).
Подставляя заданные значения параметров, получаем Zt ι ~
^ЗЮ6 + 72 0м; Ζ12«3 104Ομ; Ζ21«3 106Ομ; Ζ22 = 3 104 +
+ 14 Ом.
Коэффициент усиления по напряжению с учетом равенств
Ζ, = /?; = ΖΗ = /?Η = 300 Ом, КЕ& 0,946; входное и выходное
сопротивления повторителя ΖΒΧ = 31 кОм; Ζβηχ«18 0μ.
78
5.7. Um = 4B.
5.8. С учетом условия г,«;(1 — а>) гк матрицы [Z] и
[^-параметров равны
230 Ом 30 Ом
-394Ю30м 6Ю30м
2,21 103 Ом 5,025 ■ 103
66 1,67-10~*См
И =
[Я] =
5.9. Уп =
ι
Yl2=-
1
γ _J £.
21 /юс л,'
J 2 2— ~
1
_ 1
кос" ~" <coC" ""' /соС Л,·' ~" /соС Л/
5.10. Так как незаданный параметр транзистора гк обычно
составляет сотни килоом, то можно считать, что выполняется
неравенство GH= l/RK^>h22 = (l +h21)/rK. Тогда коэффициент
усиления каскада приближенно равен [1, § 5.2] KE^SRK, где S=
=h2l3/ZBli— крутизна проходной характеристики транзистора в
рабочей точке.
Входное сопротивление каскада ΖΒΧ = Ζη—(Ζ12Ζ2ι)/(Ζ22+ΖΗ)
после несложных преобразований можно выразить через
параметры транзистора: ZBX = RBX = r6 + (1 +Л21э) гэ:
Подставляя заданные значения параметров, находим S=
= h2l3/[r6+(\+h2l3)r3] = 0,35- ΙΟ"3 Α/Β;
Ke = SRkk 156.
Необходимая амплитуда на входе каскада определяется
соотношением
;2,56 10~2
и„ = ил
,/Ая«:
В «26 мВ.
5.2. СВОЙСТВА ЛИНЕЙНЫХ ЦЕПЕЙ
С ОБРАТНОЙ СВЯЗЬЮ
5.11. Определить вид обратной связи, если известно, что
коэффициент усиления основного четырехполюсника Ку=\03 от
частоты не зависит, а передаточная функция четырехполюсника
обратной связи Кос (гш) = 0,5 ■ 10_3e-in/* (рис. 5.11).
5.12. Усилитель, коэффициент усиления которого не зависит от
частоты, подвержен влиянию температурных изменений, в резуль-
>Лн
<кос(м —ι
Рис. 5.11
Рис. 5.12
79
тате чего номинальное усиление АГУ = 104 может изменяться в
пределах ±20%. Найти коэффициент отрицательной обратной
связи Кос, введение которой снизит нестабильность усиления до
±2%. Каков будет коэффициент усиления К0 в целом?
5.13. В цепь эмиттера однокаскадного резистивного усилителя
введен резистор Лос = 30 Ом. Сопротивление нагрузки усилителя в
коллекторной цепи (рис. 5.12) RH=\,5 кОм, паразитная емкость
Сп = 50пФ, крутизна проходной характеристики транзистора S=
= 20 мА/В, а его выходное сопротивление /?,= 15 кОм. Определить
частоты, при которых АЧХ усилителя упадет до 1Д/2 от своего
максимального значения при наличии и отсутствии обратной
связи.
5.14. Амплитуда третьей гармоники на выходе усилителя
составляет 5% от амплитуды первой гармоники. Каков должен
быть коэффициент обратной связи, чтобы амплитуда третьей
гармоники снизилась до 0,5% амплитуды первой гармоники?
Каково будет усиление, если до введения отрицательной обратной
связи коэффициент усиления был /Гу=103?
5.15. Определить комплексный коэффициент передачи
активного четырехполюсника (рис. 5.13,а, 6, в, г), охваченного обратной
связью.
г) Рис. 5.13
5.16. Дан усилитель с параметрами: коэффициент
усиления Ку = 400, коэффициент гармоник /Гг=10%, входное и
выходное сопротивления соответственно 10 и 5 кОм.
Определить те же параметры усилителя после введения в него
последовательной отрицательной обратной связи по
напряжению с АГ0С = 0,05.
5.17. Комплексный коэффициент передачи усилителя Ку(г'ш) =
= — 103/(1 +/ω ■ τ). Рассчитать и построить АЧХ и ФЧХ усилителя
после введения в него частотно-зависимой обратной связи. Схема
четырехполюсника обратной связи дана на рис. 5.14. Считать, что
его Двх = оо, Двых = 0, t = /?C=10-3c-1.
80
5.18. Как изменится импульсная характеристика
транзисторного усилителя, изображенного на рис. 5.15, если его охватить
частотно-независимой отрицательной обратной связью с Кос =
= 0,08? Параметры элементов усилителя: выходное сопротивление
o+<fn,
R OJMOm
о CZ3 f о
ЩнФ
X
5ых
Рис. 5.14 Рис. 5.15
транзистора /?; = 20 кОм, сопротивление нагрузки R„ = 2 кОм,
емкость, шунтирующая нагрузку, Сн=100 пФ, крутизна проходной
характеристики транзистора S=15mA/B (межэлектродными
емкостями транзистора пренебречь).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
5.11. В данной задаче модуль знаменателя передаточной
функции замкнутой системы
11 - Ку (ίω) Кос (ίω) | = | 1 - 103 0,5 ■ 10- 3 cos π/4 + i0,5 sin π/41 =
= 0,74<1.
Следовательно, передаточная функция К0 (ω) > Ку (ω) и обратная
связь положительна (на данной частоте) [1, § 5.7].
5.12. При отрицательной обратной связи [1, § 5.8]
АК0 1 АКУ
Ко 1+| КуКос | К.
у"ос I **-у
В данной задаче относительная нестабильность ДА"У/АГУ = 0,2,
а допустимая нестабильность ΔΚ0/Κ0 = 0,02, следовательно,
должно выполняться условие \КуКос\ = 9 и АОС = 9-10-4. При этом
коэффициент усиления системы, охваченной обратной связью,
а:0=а:у/(1+|^^ос|)=103.
5.13. В отсутствие обратной связи АЧХ усилителя,
представленного на схеме рис. 5.12, Ку (ω) = SR3 j^Jl + ш2/?э2С„ , где R3 =
= RiRH/(Ri + RH) [1, § 5.4]. Граничная частота, соответствующая
снижению АЧХ на 3 дБ, определяется из условия шгр/?эСп=1,
откуда шгр= 14,7 · 106 рад/с, /гр = 2,34 МГц.
При введении в цепь эмиттера (см. рис. 5.12) резистора Roc,
отвечающего условию R0C<s:RH<s:Ri, коэффициент обратной связи
^ос = "~ ^ос /Rh = ~ 0,02.
81
Новый коэффициент усиления
„ ,. \ К,М SR3/(\+i(nR3Ca)
Λ0^ω)=
1 -Ky(i(a) Koc 1 + S7?,(-0,02)/(l + mR3C„)
= SR3/[{\ +0,02SR3) +г'шЛэСп];
K0 (ω)=SRjJ{l + 0,02SR3)2+ (а>ЯэСп)2.
Трехдецибельному ослаблению АЧХ в данном случае
соответствует граничная частота шгр = (1+0,0257гэ)/(ЛэСп) = 2,27 ■ Ю7 рад/с,
/vp = 3,61 МГц. Как видим, введение отрицательной обратной связи
значительно расширило полосу пропускания усилителя.
5.14. Требуемый коэффициент обратной связи легко находится
из соотношения 0,005/0,05= 1/(1 + \КУК0С\), \КУК0С\ = 9 и )А^С) =
= 9 10 3. Новый коэффициент усиления К0 = Ку){\ + | КуК0С |) = 100.
5.15. а) *И~5; б) Μ,ω)= - 7Щ^-Щ;
з) K0{ie>y
Ro
R0(\+i(j>rC)
R{]+i<aR0C0y } °[ ' л[1+,ъс0(л+г)]
5.16. лВХОс~
190 кОм, #ГОС = 0,48%, Двыхос«240кОм.
5.17. После введения обратной связи комплексный
коэффициент передачи системы будет
К0 (ιω) = Ку (ίω)/[1 - Ку (ιω) Кос (ίω)].
Коэффициент передачи цепи обратной связи в данной задаче
Кос(1ш)=1/[1шС(/г+1/(ггоС))]=1/(1 + 1ГОт), т = ДС=НГ3 с.
Подставляя Кос (/со) в выражение для К0 (ίсо), получаем
К0 (ico) = - (1 + ιωτ)/( 1 - 10"3ω2τ2 + i2 ■ 10"3ωτ).
Амплитудно-частотная характеристика усилителя (рис. 5.16, а)
принимает вид
К (со) = 4/ΐ + ω2τ2/ν/(ϊ_-103ων)2 + 4·10-6ω2τ2,
а ФЧХ (рис. 5.16,6) определится из выражения
500
400
300
Ζ0Ο
WO
φ(ω)-α,
рад
'20 ЪО 40 ω-ίθ^ραβ/c
а)
20 30 40 й)Ю3,рад/с
0J Ряс. 5.16
82
φ (ω) = π + arctg (ωτ) — arctg
2·1(Γ3ωτ
I-coV-lO-3
5.18. Эквивалентную схему замещения выходной цепи
усилителя можно представить в виде рис. 5.17. Комплексный коэффициент
передачи напряжения
КЕ (ιω) =-SRJ{\ + 1шСп/гэ) = - Ку тах /(1 + ίωτχ),
где
Лита» — ^Лч
кутах
S _ ς, RiRH
Gn+G,
Ri + R„
:27; т, = /г,Сп=1,8-10"7 с.
Этому коэффициенту передачи соответствует импульсная
характеристика
*(')=-
к,
у плах '/ту .
15-10-Vlo7,/1·8.
Введение в усилитель отрицательной обратной связи приводит
к уменьшению ту в 1+ | К0СКутях | раз, т. е.
Хэкв = ту/(1+ |^осАГутах|) = 5,7Ю-8 с.
Новая импульсная характеристика
go{t)=-Kyatlle ™/τ.
уэкв
■4,75-107е
-(/5,7-10"
Графики нормированных импульсных характеристик g (t) и g0 (t)
представлены на рис. 5.18. Как и следовало ожидать, введение
max
Рис. 5.17
0,2 0,й 0,6. 0,8 ί,Ο 1,2 t-107C
Рис. 5.18
отрицательной обратной связи приводит к более быстрому
убыванию импульсной характеристики, что соответствует
расширению полосы пропускания цепи.
5.3. КРИТЕРИИ УСТОЙЧИВОСТИ АКТИВНЫХ
ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮ
5.19. Оценить устойчивость активного четырехполюсника с
обратной связью (рис. 5.19) на основе анализа поведения его
передаточной функции К0 (г'со) на ^-плоскости для двух случаев;
83
Рис. 5.19
Рис. 5.20
Ку<\ и Ку>\. Построить АЧХ и ФЧХ разомкнутой системы при
/Гу=-1000 и RC=0,00\ с. При анализе полага.ь, что входное
сопротивление активного четырехполюсника бесконечно велико, а
выходное—равно нулю.
5.20. Комплексный коэффициент передачи усилителя Kj (ίω),
охваченного обратной связью (рис. 5.20), выражается как
отношение [3, с. 436]: Ку (ίω)= —Ζ2/Ζι. Вычислить коэффициент передачи
замкнутой системы, состоящей из трех идентичных усилительных
каскадов (рис. 5.21). Оценить устойчивость этой системы на основе
Ряс. 5.21
критерия Рауса — Гурвица и на основе критерия Найквиста.
При каком отношении резисторов R2/Ri данная система
устойчива?
5.21. Используя критерий Рауса—Гурвица, проверить,
является ли устойчивой линейная система, описываемая
характеристическим уравнением р*-\-2р3-\-Зр2+р+\ =0.
5.22. На рис. 5.22 представлена схема усилителя с
отрицательной обратной связью при следующих параметрах: Ci = C2 = C =
= 0,1 мкФ, Rl = R2 = R=l кОм, Ку(/ω) = Ку = 2. Входное
сопротивление сумматора RBr -* оо, выходное сопротивление усилителя Ку
£®Е®1
Сг
■CZH
ϋδβιχ
ι
Рис. 5.22
близко к нулю. Рассчитать АЧХ К0 (ω) и ФЧХ φ0 (ω) устройства в
целом. Определить критическое значение Кукр, при котором
устройство теряет устойчивость.
84
o + /fm
ο+^ηι
5.23. Определить виды и указать цепи обратной связи в
следующих схемах усилителей (рис. 5.23, а, б, в).
5.24. Комплексные коэффициенты передачи прямой и обратной
ветвей замкнутой системы (рис. 5.24) соответственно равны
Ку (ια>) = Ку (Ку > 0); Кос (/ω) = ехр (- /ωΤ).
При каких значениях Ку данная система устойчива? Какой вид
имеет АЧХ устойчивой замкнутой системы при различных
значениях ΚγΊ
иЛх
?
<?>
t
1
Ри
КуС/оу
Кос/ί'ω;
с. 5.24
—J
UBhix
1
5.25. Амплитудно-фазовая характеристика (годограф) двух кас-
кадно соединенных четырехполюсников может быть
аппроксимирована уравнением в полярных координатах Л=ос(1 + cos ос).
Определить критическое значение акр, при котором замкнутая
система, составленная из этих четырехполюсников, теряет
устойчивость. Построить для ос = 0,5оскр годограф разомкнутой системы
Η (/ω).
5.26. Электрическая цепь описывается дифференциальным
уравнением 3-го порядка
bod3u/dt3 + b1d2u/dt2 + b2du/dt+b3u = 0,
b0=l, bi=A, Ьг=\, b3 = 2.
Используя критерий Рауса—Гурвица, определить, является ли
данная цепь устойчивой, а также определить размерность
коэффициентов bo, by, b2, b^, если размерность переменной и [В], а
слагаемых в уравнении [В2/А].
85
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
5.19. Передаточная функция замкнутой системы
К0{р)=Ку/[\-КуКос(р)1
где Кос(/>)=1/0+яО; z = RC.
Таким образом,
К0(р) = Ку/[1-Ку/(\+рх)] = Ку(]+рх)/{1+рх-Ку).
Эта функция обладает единственным полюсом ри= — (1 — Ку)/х.
При Ку < 1 этот полюс расположен в левой полуплоскости, что
указывает на устойчивость замкнутой системы. При Ку>\ полюс
расположен в правой полуплоскости — система неустойчива.
Передаточная функция разомкнутой системы определяется как
произведение: Н(г'ш) = Ку(гш)К0С(1ш), и при Ку(/ш)= -1000, τ = 0,001 с
Н(г'ш)= — -—;—=- , —ехр {г'Гтг — arctgtat)]}.
Следовательно, АЧХ
Η(ω)=103/^/ΐ+(ωτ)2
и ФЧХ
φ„ (ω) = φ, (ω) + φ00 (ω) = π - arctg (ω · τ).
Графики АЧХ и ФЧХ разомкнутой системы представлены на
рис. 5.25, а,
δ.
ны-ю*
1,0
Οβ
0,6
0,4
0,2
0
/. ■
δ
W
2й
а)
,,, J
ω-ίΟζ, рад/с
φΗ(ω),ραό
3,0
2,0
1,0
0
8 16 2й ы-10г,рад/с
Рис. 5.25
5.20. Передаточная функция одного каскада на /^-плоскости
К (п)= - ΖΛή- _ ЫрС) I _ _ Яг I
Zi(p) Rz + \/(pC)Rl Rl]+pR2C
саскадного
К(/>) = К?(/>)=(- 0
Для трехкаскадного усилителя
3 ι
(i+pRzC)3
86
Учитывая, что коэффициент обратной связи Кос— 1, запишем
передаточную функцию замкнутой системы в форме
КоЫ =
_ *(/>) _
(-
и
1 -К {р)Кас (1 +pR2cy [1 + (*2/*t)3/(l +PR2CfY
Характеристическое уравнение системы
{R2jRl)3+{\+pR2C)3 = 0 или (l+PR2cyR?+Rl = 0,
R3 + 3pR2CR3 + 3p2C2RiR3+p3C3RiR3 + Ri = 0.
Для составления определителей выпишем все коэффициенты
характеристического уравнения:
6o = (C/?,/?2)3; b, = 3RlR\C2; b2 = 3CR2Rf; b3 = R? + Rl
Для того чтобы цепь была устойчива, необходимо, чтобы
Ьо>0, а также были положительны все определители:
A1=b1=3R$RlCz>0\
bi Ьъ О
Δ2 =
b\ Ьъ
bo b2
3R£R{C2 Rf + Ri
(CR1R2)3 3CR2Rf
>0; Δ,=
b0 b2 0
0 br Ьъ
>0.
Нетрудно убедиться, что в данном случае Δ3 = Δ^, Δ2 =
= 9R32C^RfR3-R31R3C3R23-RiC3Rf>0, откуда RiC3Ri(8Rf-
-Rf)>0 или, если R2/R1<2, Δ2>0, bo = (CR1R2)3>0.
Таким образом, система устойчива при R2/R1<2.
Для определения устойчивости цепи с помощью критерия
Найквиста запишем
(]+(СоЛ2С)3
_(-R2/RiY +3(u2RJC(R2/Riy .3o>R2C{Rl/R2)3
(1 + со2Л22С2)3
a3RiC3(H2IRi)3
(]+со2Л22С2)3
(]+со2Л22С2)
?Г2\1
Для того чтобы цепь была устойчивой, необходимо
выполнение одновременно двух условий:
1т[Н(/ш)] = 0; Re [Η (ίω)] < 1.
Из первого условия получаем (R2/Rl)3 (Зш/?2С—ш3/?2С3) = 0,
откуда находим rot=0, ш2 = ч/3/(/?2С). Из второго условия
находим, подставляя ω = ω2, (Л2/Л1)3(Зш2Л|С|- 1)/(1+ш2/?1С2)3< 1,
S(R2/R1)3<64 или R2/R1<2; последнее условие совпадает с
результатом, полученным при решении с применением критерия
Рауса — Гурвица.
5.21. Система устойчива.
5.22. Сначала находим передаточную функцию цепи обратной
связи
87
Ri/iaCi
Koc=z1/(z1+z2), где zt = ^ly.J^-1 zz = R2 + \li(aCz:
Кос(г'со) = -
R
Rl+R2 + RlCl/C2 + io>C1{RlR2-]l(j>2ClC2)
R 1
ЗЯ + 1СоС(Л2-1/со2С2) 3 + ((ωτ-1/ωτ)"
Здесь т = ДС=1031(Г7=1(Г4с.
Тргда [1, § 5.7]К0(ш) = Ау/[1-АуАос(/Ш)] = 2/[3 + |((Пт-1/гоС)]
и соответственно
АЧХ^^о(ш)^— 2 ФЧХ = ф0=-агс1ё^е1^1.
4/9+(ωτ-]/ωτ)2 3
Графики АЧХ и ФЧХ представлены на рис. 5.26.
12 16 ы-ю\рад/с
а)
Рис. 5.26
Для определения запаса устойчивости устройства исходим из
передаточной функции разомкнутого тракта
Η (гсо) = КУК0С (гсо) = Ку/[3 + i (ωτ - Ι/ωτ)].
В соответствии с критерием Найквиста система устойчива при
условии |Н(г'со0)|<1, где ω0 — частота, при которой мнимая часть
функции Н(г'со) равна нулю [1, § 5.10]. В данном примере эта
частота определяется из равенства ω0τ— 1/ωοτ=0, откуда со0 =
= 1/т=1//?С= Ю4 рад/с. Итак, при заданном значении Ку = 2
|Н(гсо0)| = -Ку/3 = 2/3, критическое же значение Кукр (при |Н(г'со)| =
= 1) равно 3.
5.23. а) последовательная отрицательная обратная связь по
току; б) параллельная отрицательная обратная связь по
напряжению; в) последовательная положительная обратная связь по*
напряжению.
5.24. Комплексный коэффициент передачи замкнутой системы
K0(i(o) = Ky/[l-KyKoc(ioi)]=Ky/(l-Kye-imr). При Ку<\ значение
К0 (со) максимально при ω -♦ 0. В этом случае в системе существует
положительная обратная связь, однако цепь является устойчивой,
так как | Η (г'со) | = | АГУК0С (г'со) | < 1. Модуль |Кос(г'со)| принимает
максимальное значение +1 и минимальное значение — 1. Если
Koc = — 1, то в системе существует отрицательная обратная связь:
Re{exp ( — i(oT)}=cos(oT. Поэтому, если ωΤ=2πη, то при и = 0, 1,
2, ... , ω = 2ηπ/Τ К0 = Ку/(\—Ку), т. е. обратная связь
положительная. Если ωΓ=(2η-1)π, и=1, 2, 3, ... , ω = (2η-1)π/Γ, K0 = Ky/(l +
+ Ау), то обратная связь отрицательна.
В результате можно заключить: если Ку < 1, то цепь устойчива
независимо от частоты ω. При положительной обратной связи
К0 -* оо при Ку->\; при отрицательной обратной связи Ко-+0,5
при Ку -* 1.
АЧХ замкнутой системы для двух значений Ку представлена на
рис. 5.27.
5.25. В соответствии с критерием Найквиста система
неустойчива, если годограф системы охватывает точку с координатами
(1,0). В полярных координатах это соответствует случаю, когда
А^\, φ=0. В критическом случае А = \, φ = 0, при этом αιρ =
= 4/(1+cosO) = 0,5.
Годограф устойчивой системы при α=0,5αΙρ=0,25 показан на
рис. 5.28.
Ка(ь»
4
2
0
\ А Л (Х'ы §
ι ι ι ι ι ι ι 1
η Ζτΐ 3rt 4я Sir 6rt 7it 8rt ω
TTTTTTTT
Рис. 5.27
.1т[НСшЛ
-0,2 J\
W?£ 0,4/ 0,6 йе[И(ЗД]
-Ц^у/
Рис. 5.28
5.26. Характеристическое уравнение исходного
дифференциального уравнения запишется в виде
В соответствии с критерием Рауса — Гурвица система будет
устойчивой, если b0>0 и все определители, составленные из
коэффициентов характеристического уравнения, будут
положительными:
Д, = г>г = 4>0; Δ2 =
bi h
b0 b2
= b1b2-bob3 = 2>0;
A,=
bi b3 0
b0 b2 0
0 fei Ьъ
= b1b2b3-bjb0 = 4>0.
89
Так как b0 = 1 > 0 и все определители положительны, можно
сделать вывод, что система, описываемая дифференциальным
уравнением, устойчива.
С учетом указанных условий размерности коэффициентов
следующие: Ь0 — Вс3/А; Ьх — Вс2/А; Ь2 — Вс/А; Ь3 — В/А.
Глава 6. ПРОХОЖДЕНИЕ
ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ
С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
6.1. ВОЗДЕЙСТВИЕ ШИРОКОПОЛОСНЫХ
СИГНАЛОВ НА АПЕРИОДИЧЕСКИЕ ЦЕПИ
6.1. На дифференцирующую цепь (рис. 6. Π подается импульс
s(t) = A ехр ( —αί), ί^Ο; Α = 10 В; α = 4·106 с . Постоянная
времени цепи RC=0,5 мкс. Вычислить спектральную плотность сигнала
на выходе и найти сигнал sB
:(')·
С
Рис. 6.1
Рис. 6.2
6.2. На интегрирующую цепь (рис. 6.2) подается тот же сигнал,
что и в предыдущей задаче. Постоянная времени цепи RC=
= 0,5 мкс. Вычислить спектральную плотность сигнала на выходе
и найти 5ВЫХ(0·
6.3. На дифференцирующую цепь (см. рис. 6.1) подается
импульс s(t) = Atexp(-at), t>0; 4 = 10* В-с , а=103с-1 (рис.
6.3). Постоянная времени цепи RC=2 мс. Вычислить
спектральную плотность сигнала на выходе и найти 5ВЫХ(0·
6.4. На интегрирующую цепь (см. рис. 6.2) подается тот же
сигнал, что и в предыдущей задаче. Постоянная времени цепи
RC=2 мс. Вычислить спектральную плотность сигнала на выходе
и найти s
90
:(/)·
6.5. На дифференцирующую цепь (см. рис. 6.1) в момент t = 0
подается положительный прямоугольный импульс с амплитудой
£=10 В длительностью τ„ = 3 мс. Постоянная времени цепи
RC=\ мс. Найти сигнал на выходе цепи.
6.6. На интегрирующую цепь (см. рис. 6.2) в момент ί = 0
подается тот же сигнал, что и в предыдущей задаче. Постоянная
времени цепи RC = 5 мс. Найти сигнал на выходе цепи.
6.7. На дифференцирующую цепь (см. рис. 6.1) воздействует
периодическая последовательность прямоугольных импульсов с
амплитудой £=10 В, длительностью τ„ = 0,5 мс, с периодом
Г=1мс. Начало отсчета времени ί = 0 совпадает с фронтом
одного из импульсов. Постоянная времени цепи RC=0,159 мс.
Основываясь на спектральной плотности одиночного импульса,
найти спектр входной импульсной последовательности.
Основываясь далее на передаточной функции цепи, найти спектр
выходного сигнала.
6.8. На интегрирующую цепь (см. рис. 6.2) воздействует то же
колебание, что и в предыдущей задаче. Постоянная времени цепи
RC = 0,159 мс. Найти спектр на выходе цепи.
6.9. На цепь, представленную на рис. 6.4, в момент ί = 0
подается импульс e(t) = Eexp(-a.t), t^O. Определить в общей
форме ток iL{t).
Рис. 6.4
6.10. Решить задачу 6.9 для входного импульса e{t) =
= E(t-t1)exp [-ot(f-fi)], t>tu Ί>0·
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
6.1. Умножив передаточную функцию заданной цепи Κ(/ω) =
= imRCI(l+i(oRC) на спектральную плотность входного сигнала
S (ω) = 4/(α + ί"ω), получим спектральную плотность SBUX (ω). АЧХ и
ФЧХ спектра выходного сигнала представлены на рис. 6.5 и рис. 6.6
ω-gSewx (/«>, г/wtf
δ ωίΰ,ραΰ/ο
Рис. 6.5
Рис. 6.6
91
соответственно. Штриховыми линиями показаны АЧХ и ФЧХ
спектра входного сигнала. Применив обратное преобразование
Фурье к SBhlx (ω), получим выходной сигнал, график которого
представлен на рис 6.7.
6.2. Спектральная плотность сигнала на выходе
8вы^ш)=10/[(1+ш5 1(Г7)(4 1()6 + *ш)], Be;
^('НЮ^^-е-4'06'), В.
въыхФуВ s(f)tB
Рис. 6.7
Рис. 6.8
6.3. Применив к входному сигналу преобразование Фурье,
получим спектральную плотность 8(ω) = ^/(α + /ω)2, — οο<ω<οο;
умножив ее на К (/ω), найдем SBblx (ω) = iaARCj [(ос + /ω)2 (1 +
+ ui)/?C)] и выходной сигнал
показанный на рис. 6.8.
6.4. 8ΒΗΧ(ω) = 5-106/[(103 + ίω)2(5-102 + ίω)], Be;
w(i) = 20[(l + 103i)e-,()3'-e-5-1()V), В (рис. 6.9).
6.5. Выходной сигнал можно определить, используя метод
интеграла свертки
s СО, в
5ъь,х(*),В
s ъх (Ό, Sftmx (t), $г βοιχ, Β
sbx(t)
SifteixW
t,MC
Рис. 6.9
Рнс. 6.10
92
*1вых(')=·
10е-|0\ В, 0<ί<3 мс,
_95е_10з(,_з.,о-Ч в, ,>3мс.
6.6.
,,)£(1-е-'/<яс>), (К^ти,
На рис. 6.10 представлены входной сигнал к задачам 6.5 и 6.6 и
выходные сигналы .ViBblx(0 и 52вых(0·
6.7. Комплексные амплитуды гармоник входного сигнала
[1, § 2.7]
где S (ω) = Ετ„ sine (ωτ„/2) exp (— /ωτ,,/2) — спектральная плотность
одиночного импульса при отсчете времени от фронта импульса.
Определим амплитуды гармоник входного сигнала:
Α„ = -Ετ„ sine
ν 2 ;■
Умножив А„ на передаточную функцию цепи К(/иш!), получим
формулу для определения амплитуд дискретного спектра на
выходе:
2
U„ = /i„K(/nro1) = -£THsinc(nro1T„/2)K(/nroi)exp ( —/ηωιτ„/2).
Амплитуды гармоник выходного сигнала
,т 2 г. /ηω,τΗ\ n<o,RC
t/n=-£T„sinc —ρ '
Γ V 2 /у1+(пю,ЛС)2
Результаты вычислений амплитуд /ί„ гармоник входного и
выходного сигналов представлены в табл. 6.1 и 6.2.
Таблица 6.1
η
А„ В
0
5
]
6,37
2
0
3
2.12
4
0
5
1,27
6
0
7
0,91
Таблица 6.2
η
и„. в
0
0
]
4,5
2
0
3
2,0
4
0
5
1.25
6
0
7
0,9
93
An,B
10
Κ(ω) Κ(ω)
G$C
Ι
1 1 1 1 , τ
10
JL
2 3 4
Рис. 6.11
5 6 -е,кГц
2 3 4 5 бГ^Гщ
Рис. 6.12
Спектральные диаграммы показаны на рис. 6.11 и 6.12; кроме
того, на рис. 6.11 представлена штриховой линией зависимость
модуля передаточной функции от частоты.
6.8. Умножив выражение для амплитуд А„ (см. решение задачи
6.7) на передаточную функцию заданной цепи Κ(/ηωι)= 1/(1 +
+ in(OiRC), получим формулу для расчета амплитуд дискретного
спектра на ее выходе:
. _2 ExKsinc(n(olTla/2)exp( — in(ulxtL/2)
п~Т 1 + ш(о,ЛС '
Амплитуды гармоник входного сигнала определяются так же, как
в задаче 6.7. Амплитуды гармоник выходного сигнала
1
.. 2 г ■ (η<ϋιτκ\
Ун- (пщясу
Результаты вычислений приведены в табл. 6.3, а спектральная
диаграмма — на рис. 6.13.
Таблица 6.3
η
и„ в
0
5
]
4,5
2
0
3
0,67
4
0
5
0,25
6
0
7
0,13
6.9. То/с
6.10. Ток
Ί>0,
и„,в
10
5
О
Η(ω)
Ш
ч
0,5.
ч
Κ(ω)
J . 1 . .—. : ,
12 3 4 5 ^кГц
Рис. 6.13
94
где β = /?,/?2/[Ζ.(/?ι+/?2)].
6.2. ПРОХОЖДЕНИЕ ИМПУЛЬСНЫХ
СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЙ
УСИЛИТЕЛЬ
6.11. На вход транзисторного усилителя (рис. 6.14) поступает
прямоугольный положительный импульс длительностью τ„ =
= 200 мкс. Параметры усилителя: Ср = 0,1 мкФ, Rp = 20 кОм, С0 =
= 20 пФ, R= 10 кОм. Внутреннее сопротивление источника сигнала
равно нулю. Входное сопротивление транзистора в линейном
режиме 50 кОм, выходное 200 кОм. Определить длительность
фронта выходного импульса, отсчитываемую от 0,Штах до
0,9£/тах, а также относительный спад вершины к моменту ί = τ
и·
6.12. На дифференцирующую цепь (см. рис. 6.1) поступает
прямоугольный импульс с амплитудой £ длительностью 50 мкс.
Внутреннее сопротивление источника сигнала Я,-= 50 Ом. Найти
параметры Λ и С из условия получения на выходе укороченного
импульса (первого, положительного) длительностью 10 мкс,
определяемой на уровне 0,5£/выхтах, где £/выхтах — пик импульса,
который должен быть не менее чем 0,95£.
6.13. На вход цепи (рис. 6.15) с постоянной времени τ„ = 2 мс в
момент времени ί = 0 подается прямоугольный импульс
длительностью ти = 2 мс, амплитудой £=1 В. Определить сигнал на
выходе цепи. Выяснить, как изменится форма выходного сигнала, если:
а) существенно увеличить постоянную времени цепи; б)
существенно ее уменьшить. Изобразить соответствующие временные
диаграммы и объяснить их с временной и спектральной точек зрения.
Рис. 6.16
6.14. Используя переходную характеристику резистивного
усилителя с параметрами схемы замещения (рис. 6.16): /?=10кОм,
/?, = 50кОм, С0=1 нФ, S=5 мА/В, найти и построить сигнал на
его выходе, если на входе действует сигнал s(r) = £exp( — αί), ί#*0,
где £=1 В, а = 2-105с-1.
6.15. На входе пятикаскадного апериодического усилителя,
составленного из идентичных звеньев (см. рис. 6.16), действует
95
сигнал s(t) = \0cos2n- I03t + 20s'm2nl,5■ W3t, В. Определить
соотношение амплитуд гармонических составляющих с частотами
103 Гц и 1,5· Ю^Гц на выходе цепи при z1 = C0/(\/Ri+\/R) =
= 0,2 мс. Сравнить с однокаскадным усилителем.
6.16. На входе цепи (см. рис. 6.14) действует сигнал e{t) =
= £ехр(—αί), t^O. Определить и построить выходной сигнал при
я=кгс-\ тр=ср/(1//гр+1//г1В)=10мс, т1 = с0/(1//г+1//г,-)=5х
χ 10 5 с, используя метод интеграла наложения.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
6.11. Выходное напряжение можно определить выражением
[1, § 6.4]
"вы*(>)=-*тах£(е~'Л|,-е~'/Т1), 0<ί<τ„,
где Ктах— максимальное значение передаточной функции
усилителя; Ε—амплитуда импульса на входе; тр = Ср/(1//?р + 1//?вх); τι =
= C0/(\/R+l/Ri). Для расчета τφ (от уровня 0,1 до уровня 0,9 от
[/вшта1) необходимо определить максимальное значение £/вых в
интервале [0, ти ]. Продифференцируем ивых (ή по времени и
приравняем производную нулю:
d-^S= -Κ^ε( —U -'W + J-e-'^-Vo.
Л тах \ τρ τ, J
Отсюда получается критический момент времени ίκρ=1,8 мкс и
^выхтах = 1^тах£|· Таким образом, формирование фронта импульса
в данном случае определяется вторым слагаемым в исходной
формуле ивых{1) и, следовательно, τφ=4,6· Ю-7 —2,1 · Ю-8 =437 не.
Выходное напряжение при / = ти = 200мкс "вых(ти) = 0,87 \КтахЕ\.
Тогда спад вершины выходного импульса составляет 13%.
6.12. Сопротивление R дифференцирующей цепи можно найти
из условия С/выхтах/£=Д/(Л+Л;) = 0,95, откуда Д = 0,95Д;/0,05 =
= 950 Ом. Длительность выходного импульса должна быть 10 мкс,
следовательно, подставив /,=10 мкс, u(ti) = 0,5Umax, R = 950 Ом и
R, = 50 Ом в выражение u(i)=£/maxexp { —i/[C (R+-K,·)]}, получим
С=14,4 нФ.
6.13. Передаточная функция заданной цепи К (/ω) = 1/(1 +/ωτ„).
С помощью преобразования Лапласа можно получить выражение
для выходного сигнала:
1-е-0·5·10'', 0<^τΗ,
0,6е-°·5103', ί>τ„.
Сигнал мвых(/) изображен на рис. 6.17 под номером 1. Там же под
номером 2 показан выходной сигнал при постоянной времени цепи
Тц>тц, а под номером 3—т„«:тц.
96
(<) =
иШ,в
20 50 t,Mxc
2. J 4 5 t,MC
Рис. 6.17
Рис. 6.18
Уменьшение крутизны спада при τ„>τ4 (кривая 2) объясняется
ослаблением высокочастотных составляющих спектра сигнала при
АЧХ фильтра /Γ(ω)=[ΐ +(сотц)2]~1/2. При τ„<τ„, наоборот,
крутизна спада возрастает (кривая 3).
6.14. Используя метод интеграла Дюамеля, находим выходной
сигнал
ESRR,
uM=^^(e-«'-e-'/M-^—, t>
у ' Λ+Λ,-ν ;ατ,-1
о,
временная диаграмма которого показана на рис. 6.18.
6.15. Модуль передаточной функции и-каскадного усилителя
[1, §5.5]
*» =
**· 1 max
Р+К)2]"'2'
Отношение амплитуд колебаний с частотами а^ и ω2 на
выходе составит
^1
Ι+ίω,τ?)2
η/2
= 0,5-4,14 = 2,07.
Для однокаскадного усилителя это отношение равно 0,66.
6.16. Используя интеграл наложения [1, §6.3]
и (ή = \е(х)g{t — x) dx,
где g(t)=-KmaxE^e-^-U^)j
импульсная характеристика цепи, получаем
"(')=-*-*£
-•1ч
-'/*п
(ΐ-ατΟΚ-ΐ) 1-ост! ατρ-1_
t>0.
97
Рис. 6.19
График выходного сигнала
представлен на рис. 6.19.
6.3. ПРОХОЖДЕНИЕ МОДУЛИРОВАННЫХ
КОЛЕБАНИЙ ЧЕРЕЗ УЗКОПОЛОСНЫЕ
ИЗБИРАТЕЛЬНЫЕ ЦЕПИ
6.17. Коэффициент амплитудной модуляции напряжения на входе
резонансного усилителя равен 100%, а на выходе 71%. Параметры
контура, настроенного на частоту несущего
колебания: С=500 пФ, Q = l50,fp = l МГц, а сопротивление нагрузки
/?н = 50кОм. Определить частоту модуляции.
6.18. На последовательный колебательный контур воздействует
ЭДС e(i)=(10+10cos27r· 103i)cos2n- 105ί, В. Частота несущего
колебания ЭДС равна резонансной частоте контура. Найти
добротность контура, при которой амплитуды боковых
составляющих спектра тока равны 40% амплитуды несущего колебания.
6.19. На последовательный колебательный контур воздействует
ЭДС e(t) = E(l+0,Scos2n- 104i)cos2n- 106ί. Резонансная частота
контура равна 1 МГц, емкость контура 200 пФ, коэффициент
модуляции тока в контуре 0,6. Определить добротность,
индуктивность и сопротивление потерь контура.
6.20. Последовательный контур возбуждается
частотно-модулированной ЭДС со следующими параметрами:/0 = 16 МГц, частота
модуляции /^ = 8 кГц, индекс угловой модуляции тчм =
= 20 рад. Емкость контура 100 пФ. Найти остальные параметры
контура из условия пропускания «крайних» боковых частот спектра
колебания1 с ослаблением не более 3 дБ.
6.21. Ток в цепи коллектора транзисторного усилителя
определяется выражением /к (/)=/(! +0,8cos2n · 103/1) cos2n · 105/, a
создаваемое этим током на нагрузочном колебательном контуре
напряжение промодулировано по амплитуде с глубиной, на 30%
меньшей, чем ток iK(t). Сопротивление нагрузки /?н = 50 кОм,
выходное сопротивление транзистора /?; = 100 кОм, коэффициент
1 Из расчета полной ширины спектра частотно-модулированного колебания
&f*2mFu [1, § 3.6].
S6b!X (t)/U
98
Рис. 6.20
о+^п,
включения со стороны транзистора p1=LJL = 0,5 (рис. 6.20), со
стороны нагрузки p2=L2/L = 0,25. Емкость контура 400 пФ.
Определить добротность контура, индуктивность и сопротивление
потерь.
6.22. Радиостанция работает на волне 4,25 м с использованием
частотной модуляции. Наивысшая частота модуляции FM =
= 100 кГц, индекс угловой модуляции т = 0,1. Какова должна быть
добротность контура в тюнере, настроенном на эту станцию,
чтобы индекс модуляции уменьшался не более чем на 3 дБ?
6.23. На вход резонансного усилителя с передаточной функцией
Κ(/ω] = 2ζ?/[ΐ +/'(ω — ωρ)/Δω0] поступает импульсный сигнал с
линейной частотной модуляцией s(i) = £cos(o)0i + 6i2/2), 0^ί^τ„.
Параметры контура: Q = 50, ωρ = 10'5 рад/с Δω0 = 104 рад/с;
параметры сигнала: £ = 0,1 В, ω0=ωρ, β = 10 рад/с2, τ„ = 4 мс.
Проверить применимость метода мгновенной частоты в
условиях данной задачи [I, §6.11].
6.24. Определить закон изменения огибающей выходного
импульса в предыдущей задаче.
6.25. Найти закон изменения мгновенной частоты колебания в
контуре (к задаче 6.23) и сопоставить его с входным сигналом.
Рис. 6.21
6.26. На вход цепи, представленной на рис. 6.21, в
момент времени 1 = 0 подключается ЭДС e{t) = E(\ +McosOMi) x
xcos(rooi + 0o). Вычислить методом (приближенным) интеграла
свертки напряжение на выходе цепи при ω0=ωρ, ΩΜ = 2/τ„ где
τκ = 2ρ/ω
6.27. На входе цепи, представленной на рис. 6.21, действует
ЭДС e(f)=£exp(-ocf)cos(ov + 0), '^°> гДе E=1Q, a=104 с-1,
ω0 = 2π · 106 рад/с, θ = π/4. Пользуясь приближенным спектральным
методом, определить напряжение на выходе цепи при ωρ = ω0.
Полоса пропускания 2Δω0 = 2π·104 рад/с. Построить график
выходного напряжения.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
6.17. F=6,5 кГц.
6.18. Q = 36,2.
99
6.19. 0 = 44,1, £ = 130 мкГн, R=IS Ом.
6.20. Q = 50, L=\ мкГн, R = 20 Ом.
6.21. ρ =197, L = 6,3 мГн, /? = 20,2 Ом.
6.22. При заданном индексе модуляции т = 0,1 в спектре ЧМК
можно учитывать лишь три спектральные составляющие [1, § 3.6]:
/о и /о±^> причем индекс угловой модуляции пропорционален
амплитуде первой боковой частоты. Для того чтобы уменьшение
индекса модуляции в контуре не превышало 3 дБ, должно
выполняться условие [1+(2%р)2]1/2=1, т.е. Q=fp/(2F).
В данном случае fp=fo = c/i. = 70,6 МГц, /^ = 100 кГц и
ρ = 70,6 106/100 103 = 353.
6.23. Условия применимости метода мгновенной частоты:
Ω/Δω«;1 и год/Аш<1 [1, § 6.11 ]. Для ЛЧМ импульса под Ω можно
подразумевать величину 2π/τ„, а под сод — величину βτ„/2. Таким
образом, приведенные выше условия дают
Ω/Δω = 2π/(τ„Δω)«0,075; ωΛ/Δω = βτ„/(2Δω)= Ι.
Следовательно, для анализа применим метод мгновенной частоты.
6.24. При точной настройке контура на среднюю частоту
сигнала (ωρ = ωρ) и линейном изменении частоты ЭДС в пределах
от /0—/д до /0+/д огибающая амплитуд на выходе
υΒί,χ(ή = 2ρ/^1 + {2[ω(ί)-ωρ]/Αω0^}\ ш0-шд<ш(*)<ш0 +
ω„
Огибающая £/вЫХ (ή (рис. 6.22) воспроизводит форму АЧХ усилителя.
dt),B
ыы%Ц)-105,рад/с
6*25. В соответствии с методом мгновенной частоты [I, § 6.П]
выходную частоту колебаний определяем выражением
швых (t) = di\i/dt+dq)/dt,
где d\\i/dt—мгновенная частота входного колебания (в данном
случае изменяющаяся линейно);
dip
It'
d
"It
arctg
ω(')~ωΡ
Δωη7
— ωΛ<ω(ί)<
ω„
Таким образом, поправка d<$\dt (рис. 6.23) не превышает 5%, и
с нею можно не считаться.
6.26. Напряжение на выходе цепи определим выражением
[1, §6.6, п. 2]
100
:(/)-Re
-e'V
A(x)G(t-x)dx
где A(t) = E(l+McosQt)el6« — комплексная огибающая входного
напряжения, a G(i)=-e~''n/2e~i/T«, t^0, — импульсной характе-
ристики узкополосной цепи (при ω = ω0).
Вычислив интеграл, придем к следующему результату
[2, § 6.9]:
u^(t)=-\QEY+-j==^cos{to-4>)-
— е
+-
м
:cos9cos(ro0i + 90)
где φ = arctg Ωτκ = arctg 2 = 63,4°.
В стационарном режиме (ί->οο)
«■«(')=-,6Я
1+--ρ cos (Ω ί - φ) cos (ω0ί+θ0)
Инерционность контура при Ωτκ = 2 приводит к уменьшению
глубины модуляции в у/5 раз и отставанию огибающей по фазе на
63,4° относительно огибающей входного колебания.
6.27. Комплексная огибающая заданной ЭДС имеет вид
A(i) = £exp( — at + iQ), t^O, а изображение по Лапласу этой
функции S(p) = Eeief(<x+p).
Упрощенная передаточная функция цепи (низкочастотного
эквивалента) Ki(p) = Q/(l+pxK) [1, §6.6].
Следовательно,
С + 100 С+ 100
1 ; 2л/
S(p)Kl{p)e'»dp = EQei«
2πί
ep,dp
(α+ρ)(\+ρτ.
с —loo
EQe"
-ατ.
(е-в-е-'/т.)
:(<) =
EQ(c~
ψΛ
cos(oooi+0).
l-ατ,
При заданных параметрах
"вых(')=14,7(е-1о4,-е-я1°4,)со5(2Л-106/+Л/4), В.
101
Ubb\x(t),B
Рис. 6.24
3 t,MC
График ΜΒΜΧ(ί) показан на рис. 6.24.
Для облегчения построения диаграммы период
высокочастотного заполнения увеличен в 10 раз.
Глава 7. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ
СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ
7.1. СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ
МОЩНОСТИ И КОРРЕЛЯЦИОННЫЕ
ФУНКЦИИ СЛУЧАЙНОГО ПРОЦЕССА
НА ВЫХОДЕ ЦЕПИ
7.1. На интегрирующую RC-цепь с параметрами R=10 кОм,
С=0,5 мкФ подается шум с равномерным энергетическим
спектром в полосе Δ/=104 Гц и дисперсией 0,5 В2. Найти дисперсию
выходного процесса.
7.2. На последовательный колебательный контур с
добротностью β = 20 и резонансной частотой/р= 160 кГц воздействует
случайный процесс с корреляционной функцией /?вх(т)=авХе~а'т',
где σ2χ = 4Β2; ос=106 с . Определить корреляционную функцию
процесса на выходе контура (при съеме напряжения с емкости).
7.3. Спектральная плотность шума моря на выходе гидро-
фона аппроксимируется функцией 1Υ(ω)= 10~6/[(104+ 102ω2)χ/|ω|],
В2/Гц. Во сколько раз отличаются среднеквадратические значения
напряжения на выходах фильтров анализатора спектра с
практически прямоугольной характеристикой и с полосами пропускания
1 ... 2 Гц и 2 ... 3 Гц при одинаковом коэффициенте усиления
тракта анализатора?
7.4. На дифференцирующую RC-цепь с параметрами R =
= 10 кОм, С=5 нФ подается шум с равномерным в полосе 800 Гц
102
2
энергетическим спектром Wo=\0~6 В2/Гц и равным нулю вне
этой полосы. Определить среднеквадратическое значение
выходного напряжения.
7.5. На идеальный ФНЧ с коэффициентом передачи Ко = 0,5 и
частотой среза F= 16 кГц подается шум со спектральной
плотностью мощности 1ΥΒΧ(ω)= Ю^0е"р|<а| при W^IO'* В2/Гц,
β=10~5 с. Найти дисперсию и интервал корреляции выходного
процесса.
7.6. Шум со спектральной плотностью мощности W((o) = al(o
я = 4 10 В2/с, подается через разделительную RC-цепъ (R =
= 100 кОм, С=1 мкФ) на усилитель с коэффициентом усиления
К=\03. Определить среднеквадратическое значение выходного
напряжения усилителя.
7.7. На вход устройства (рис. 7.1) с идеальной линией задержки
(ЛЗ) на время Т= 1 мс подается случайный процесс с
корреляционной функцией ΛΒΧ(τ) = σ2χ -, где σ2χ = 0,1 В2; Q = 2nF, F= 1 кГц.
Определить корреляционную функцию выходного процесса.
R
ЛЗ-
Σ -~ —сз—II'
-J sbx(V- |>4в»ыхФ
-1
I
IZ
Рис. 7.1 Рис. 7.2
7.8. На интегрирующую RC-цепь (R=l кОм, С=0,1 мкФ)
действует процесс с энергетическим спектром вида Wm((o) =
= ИУр+Н)2], И^0=10"6 В2/Гц, β=10^5 с. Найти
корреляционную функцию выходного напряжения.
7.9. На электрическую цепь (рис. 7.2) действует стационарный
случайный процесс с математическим ожиданием 0,5 В и
корреляционной функцией /?вх(т) = 4е~10 |τ|, В2. Найти суммарную
мощность процесса на выходе цепи при i?= 500 Ом, С ==10 мкФ.
7.10. Найти взаимную корреляционную функцию между
входным и выходным процессами для интегрирующей цепи первого
порядка с постоянной времени 2 мс при действии на входе белого
шума со спектральной плотностью мощности W0=№~6 В2/Гц.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
7.1. Энергетический спектр шума на входе цепи
*Μω)=σ2χ/(2Δ.Α - 2πΔ/^ ω ^ 2πΔ/,
а на выходе цепи, модуль передаточной функции которой
Α^(ω)= 1/λ/1 +(ωτ)2 Π, § 5.4 и § 6.5], энергетический спектр
юз
Следовательно, дисперсия выходного процесса
σ2 =
1
2π
2πΔ/
^ΒΗχΝύ?ω =
2πΛ/
σΛ 1 <Λϋ
2Δ/π
l+o>V
■2«Δ/
arctg (2πΔ/τ).
2Δ/πτ
При t = /?C=5-10~3 с, 2πΔ/τ = π102»1 arctg (2πΔ/τ) * π/2 и
σ2ΗΧ = 2,5·1(Γ3 Β2.
7.2. Сначала находим энергетический спектр входного процесса
[1, §7.3]:
^„(ω) = σ
е a|t'cosan:i/r =
2<χσ2
α2 + ω2'
Квадрат модуля передаточной функции при β»1 [1, §5.6]
β2
*» = -
1+4β2
ω„
Ww;, ι
Рис. 7.3
В пределах полосы пропускания контура, т. е. при ω^ωρ,
энергетический спектр можно считать равномерным (рис. 7.3):
Тогда энергетический спектр на выходе
КЫ*П-
2ασ2ρ2
(α2 + ω2)
+ 4ζ>:
и корреляционная функция выходного процесса
104
со
г
Κ»Λτ):
2π
1УВЫХ (ω) cos ωτάω = 12 5, бе
5 10 |τ|
cos ΙΟ6 τ, Β'
7.3. Использовав табличное значение интеграла [13, 2.211]
dx A b /~
=arctg - J x,
при заданных параметрах а, Ь и с находим σ2 = 2·10~3 В2,
σ! = 10-3 в2; тогда о,/о2 = ^=1,41.
7.4. авЫХ = 0,79 мВ.
7.5. Дисперсию определим спектральным методом:
2 1
σ = —
w ВЫХ г.
2Л
2nF
Г
2nF
Г
W0e-^^Kl<ka=- W0t~^Kldm=
■2nF
w0l
= 2^^(l-e-P2"F)^lB2.
Интервал корреляции для процессов с неотрицательной
корреляционной функцией можно получить в виде [8, с. 127]
00
г
τ* л[о)
R (τ) dx
(рис. 7.4).
Из теоремы Винера — Хинчина следует, что
00 00
с с
Д(0) = ! ψ(ω)άω, a R(x)dx=-W(0);
отсюда
_π W(Q) _π 1
f IV {ω) dm эф
о
где Δω3ψ — эффективная ширина энергетического спектра, равная
при заданных условиях
2nF
Δω3φ =
Q-^d(o=Ul-e-^"F) = ^^6,2-lO* рад/с.
105
Тогда Чж = 2,53 10~3 с=2,53 мс.
7.6. авых=14,1 мВ.
7.7. Спектральная плотность мощности входного процесса
равномерна в пределах +Ω и равна
оо
г
и/иИ=
2 «ηΩτ ^ < „
вх Ωτ
σ2χ, |ω|^Ω,
0, |ω|>Ω,
^0=£σ2χ-0,5·1(Γ4 В2/Гц.
Передаточная функция цепи Κ(/ω) = 1 — e_ie>r, соответственно
A:2(ro) = (l-cosro7)2'+sin2ro7'=4sin2(ro7'/2).
Спектральная плотность мощности процесса на выходе
V ' B V ; V ; [θ, |ω|>Ω.
Корреляционная функция выходного процесса
Явь,* (τ) = — №вых (ω) cos ωτάω =
2π
- σ2χ2 (1 — cos ω 7) cos ωτί/ω =
= σ:
Ω
cos ωτύ?ω —
Ω
cos (ωΓ— ωτ) dm — —
ν ' Ω
cos{(oT+(oz)d(o
= σ2χ [2sincQx- sincQ (Τ-τ)-sincQ (74- τ)].
7.8. Квадрат модуля передаточной функции цепи Κ2(ω)=
= 1/[1 +(ш/?С)2], а спектральная плотность мощности
^вы»=^»хИ*>Н
wn
[|+(Ш^][1+(шЛС)2]·
По теореме Винера — Хинчина
00
. г
Д-ы,(х)=
^οΰοβωχί/ω
[1+(шЙг][1+(шЛС)2]·
106
По таблицам интегральных преобразований [9, с. 243]
находим
= 10-4[0,le-lo5|Tl-e-lo4lTl], В2.
7.9. Суммарная мощность процесса на выходе определяется
суммой мощностей постоянной и переменной составляющих:
Квадрат модуля передаточной функции /С (ш) = [4+(ш/?С) ] ,
поэтому твых = тшК(0) = 0,25 В, а дисперсия с учетом результатов
задачи 7.8
2 _W0*{*-RC)_ W0a _ σξ% _.. r2
вых n[a2-(RC)2] n(a + RC) a + RC ' "
Таким образом, Р = 0,46 В2.
7.10. Так как выходной и входной процессы связаны
интегралом Дюамеля
ос
y(t)= x(t-z)g(z)dz,
о
по определению взаимной корреляционной функции
00 00
г
Rxy{x) = M{x(t-z) x(t-z)g{z)dz}= Rx(x-z)g(z)dz.
о о
Для белого шума Rx(z)= W0b{z) [1, § 4.4], поэтому при импульсной
характеристике цепи первого порядка g{z) = — ехр I — — I получим
RC \ RC1
00
R М= |^0δ(τ-ζ) —е-г«яс>^=-^е-^(ЯС> =
ху\ ) о \ ) RC RC
О
= 5-I0-4e-5-lo2|t|, В2, τ^Ο.
7.2. ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ
ЛИНЕЙНОЙ ЦЕПИ
7.11. Найти математическое ожидание и дисперсию процесса на
выходе интегрирующей ΛΖ,-цепи в переходном режиме при
1П7
τ
лз
ι_
Σ
YW
«fix»
ι—ή ■ » <· Μ
Rz
д-(Г2
включении на ее входе в момент ί=0 белого шума со
спектральной плотностью И/0 = 10-8 В2/Гц и постоянной
составляющей /ивх = 0,1 В. Параметры цепи: L=\ мГн, R=l кОм.
7.12. В момент времени ί = 0 на вход интегрирующей цепи
первого порядка с постоянной времени 0,2 мс подается
широкополосный шум. Через какое время дисперсия выходного
напряжения достигнет половины установившегося значения?
7.13. На колебательный контур с параметрами j„=\ МГц,
β = 20, коэффициентом передачи при резонансе К0 = 0,2 ь момент
t=0 подается белый шум со спектральной плотносгью W0=№~*
В2/Гц. Определить закон изменения во времени и установившееся
значение дисперсии на выходе контура.
7.14. Случайный процесс с корреляционной функцией RBX(x)
подается на вход цепи, структурная схема которой приведена на
рис. 7.5. Выразить корреляционную функцию выходного процесса
КыЛт) чеРез RbAt)·
X(t)
Рис. 7.5 Рис. 7.6
7.15. Определить отношение сигнал/шум на выходе
интегрирующей RL-цехт (Д=500 Ом, L=5 мГн) при подаче на ее вход
сигнала .vBJ[(i) = 0,5cos 105ί, В, и шума с равномерным спектром и
дисперсией σΒΧ = 0,4 В2 в полосе Δ/=160 кГц.
7.16. К генератору шума подключены параллельно две
интегрирующие RC-цепи (рис. 7.6); Rl=2 кОм = 2R2, Сх = 2С2 =
= 1 нФ. Шум имеет равномерный спектр в полосе Δ/== 1,6 МГц и
дисперсию σ2χ = 400 мВ2 (^0 = 0 вне полосы Δ/). Найти взаимную
корреляционную функцию для выходных напряжений.
7.17. Белый шум со спектральной плотностью мощности
^0=10-10 В2/Гц подается на два параллельно включенных
резонансных усилителя с одинаковыми коэффициентами усиления
ΛΌ = 20 и резонансными частотами соответственно ωρ1 = 107 рад/с,
ωρ2=1,1·107 рад/с и одинаковыми полосами пропускания
Δω = 2·106 рад/с. АЧХ усилителей практически прямоугольные,
ФЧХ — линейные в полосе пропускания. Определить взаимную
корреляционную функцию выходных напряжений усилителей.
7.18. На идеальное дифференцирующее устройство с
постоянной времени τ0 = 1 мкс подается случайный процесс с
прямоугольным в полосе Δ/= 16 кГц энергетическим спектром W0=\u~b
В2/Гц. Определить дисперсию процесса на выходе устройства.
7.19. На входе дифференцирующей цепи с постоянной времени
τ0 = 1 мс действует случайный процесс с корреляционной функцией
108
ΛΒΧ(τ) = 4βχρ(-α2τ2), В2, где а=10 с-1'. Найти дисперсию
процесса на выходе.
7.20. Напряжение с выхода генератора шума с
равномерной спектральной плотностью мощности W0= 10~8 В2/Тц
подается через разделительную ЛС-цепь (Лр=10 кОм, Ср = 0,1 мкФ)
на интегратор, выполненный на основе операционного
усилителя (рис. 7.7) с параметрами R„=\0 ком, Си= 10 нФ.
Определить корреляционную функцию выходного процесса.
Рис. 7.7
7.21. Случайный процесс с плотностью вероятности
равномерной в пределах от — я до +а (я = 2В) и нормированной
корреляционной функцией гвх(т)=ехр( —α|τ|), α=104 с-1, подается на
интегрирующую цепь с постоянной времени τ0 = 1 мс. Оценить
характер плотности вероятности выходного процесса.
7.22. Как изменяются коэффициенты асимметрии и эксцесса
процесса с экспоненциальным распределением при его прохождении через
высокодобротный колебательный контур? Изобразить временные
диаграммы и плотности вероятности входного и выходного процессов.
7.23. Обобщенный телеграфный сигнал, т. е. процесс,
принимающий фиксированные значения (±5В) случайным образом
(рис. 7.8) при пуассоновском законе распределения моментов
перемен знака (среднее число перемен знака за 1 с равно и),
подается на интегрирующую цепь. Изобразить вид плотности
вероятности выходного процесса для различных значений
постоянной времени цепи: т0 = 0,3/и, τ0 = 3/η.
x(tj
-iff
Рис. 7.8
Рис. 7.9
7.24. Случайный процесс представляет собой совокупность
отрезков линейно изменяющегося напряжения с одинаковой
крутизной 5"=104 В/с, случайным знаком крутизны и случайной
длительностью (рис. 7.9). Вероятности положительных и
отрицательных знаков одинаковы. Определить плотность вероятности
заданного процесса после его дифференцирования.
7.25. Для моделирования случайного процесса на ЭВМ
генерируются случайные числа с равномерным распределением на интер-
109
вале (О, 1) и в каждый дискретный момент времени складываются
пять таких чисел. Записать приближенное выражение для
одномерной плотности вероятности генерируемого процесса.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ. РЕШЕНИЯ И ОТВЕТЫ
7.11. Вероятностные характеристики процесса на выходе
линейной цепи в переходном режиме можно определить с
помощью импульсных характеристик. Для рассматриваемой цепи
импульсная характеристика g(/) = oce~°", /^0, где a = R/L=\0b с-1.
Математическое ожидание выходного процесса определяется
выражением
I I
™»ыхМЧг('-*К*М^^ае~а('~*Чх^=™вх(1-е-а(), /^о.
о о
Дисперсия выходного процесса определяется через двойной
интеграл
Овых(0 = ШЫ£(*2)Явх(*1-*2)^1^2
о о
Для белого шума корреляционная функция Rm(xl—x2) =
= ^„δ^χ — х2), поэтому с учетом фильтрующего свойства
δ-функции получим
ов2ых(0= g(xi)
о
g{x2)W0b(xi-x2)dx2
dxt =
= W0
g(xl)g(xl)dxl = W0
α2α"2α*·ί&, =-^0α(1-αΓ2βί).
В установившемся режиме (/->oo) σΒ2Μχ = 5·10 3 Β:
36ых
Gftbix (*)
Рис. 7.10 α) δ)
На рис. 7.10 изображены примерный вид реализаций выход
ного процесса {а) и зависимости математического ожидания
«««(/) и дисперсии а2ых(0 (б).
но
7.12. Δ/ = 0,07 мс.
7.13. Дисперсия на выходе контура
ав2ых(/) = ав2Ых(1-е-2^) = ав2Ых(1-е-2^П
где авых определяется по методике, изложенной в примере 7.2:
^=\У0К1-2^ - = 0,314 В2.
7.14· Корреляционная функция выходного процесса
х[^(/-1)ищ(/-г-1)]Н2/ги(1)|/ги(1-1)|/гк(н1].
7.15. Используя определение отношения сигнал/шум в виде
отношения амплитуды сигнала к среднеквадратическому значению
шума и учитывая, что модуль передаточной функции
интегрирующей цепи K((o)=[\+((oL/R)2]~^12, получаем для выходного
процесса
qtux = AMlatha = K(Cl)AjJalRI(2afL) = 2,\3,
что в 2,7 раз больше отношения сигнал/шум на входе.
7.16. Выражая реакцию цепи на входное воздействие через
интеграл Дюамеля, получаем по определению взаимной
корреляционной функции [1, § 4.5]
{00 00 ")
ί ί Si^{xi)s2bAx2)s(xi-tl)g(x2-t2)dxldx2y
-αο-οο J
Поскольку в данном примере полоса шума на входе
значительно шире, чем полоса пропускания каждой из цепей
(а1 = 1/Л1С1 = 5· 10s с-1, a2 = \/R2C2 = 2\06 с-1, Δω»αΐ5
Δω»α2, можно считать входной шум практически
некоррелированным. Тогда
00 00
Д12»ых(>1, >2)= ί ί W06(x2-xl)gi(xl-tl)g2(x2-t2)dxldx2 =
— оо — оо
00
= W0 \ gl{x-tl)g2(x-t2)dx = ^^[e-^^-t^-e-^+a^].
— oo
Взаимная корреляционная функция в отличие от
корреляционной в общем случае несимметрична (не является четной). В
данном случае при t{>t2
R It t \W°a^e,-«\ (H-12)·
л12вых1'1' h) L, " e
при t2 > tt
in
R it t иУоа1а2е-';.«7.-||)
Л12вьИ'1' l2) „ , „ e
Д. j -г ОС 2
При стационарном входном шуме /2 — /t можно заменить на τ
(в установившемся режиме). Тогда окончательно получаем при
Л12вЫх(т)=^^е»>^1,6-10-5е°'5-10\ В2;
Oil "г0£2
при τ^Ο
И>1<*2
Л1амв(т) = -^ге-^=1,б-10-5е-а-10!, В2.
а( -fa 2
7.17. Для фильтров с прямоугольными АЧХ задачу удобно
решать спектральным методом:
*12.ых(т)=^ j ^(ω)Κ1(/ω)Κ·2(/ω)β^ω =
йр2
2π
И^о/^о cos [ωτ + φι (ω)— φ2 (ω)] άω,
ωρ1
где φ!(ω)=-^(ω-ωρ1); φ2(ω)=-^(ω-ωρ2) —ФЧХ фильтров.
Δω
Тогда
βρ2
&ΐ2№*{τ)=Ζ ^ο*ο cos
Δω
ωτ--^(ω-ω_1)+--^(ω-ωρ2)
Δων ρ1/ Δων ρζ'
d(o =
ωρί
ωρ2
w0Kl
πτ
sinon
-^ο^ο25ίη(ωρ2-ωρ1)τ^ί(ωρ2 + ωρ1)τ_
2 2
πτ
<»pl
1
= 2,54 · ΙΟ"8 -sin 106tcos 1,05 10 7τ, Β2.
τ
7.18. σ2Μχ=13,3·10-4 Β2.
7.19. Передаточная функция дифференцирующей цепи
описывается выражением Κ(ίω) = ίωτ0/(\ +/ωτ0). Поскольку входной
корреляционной функции /?вх(т) = е~а τ соответствует спектраль-
I 2 2
ная плотность мощности №,(ω)=λ/ι/α е **/4а [1, табл. 2.1],
112
ширина спектра входного процесса имеет порядок а, что
позволяет пренебречь в знаменателе передаточной функции
слагаемым /ωτ0, и тогда Κ(ίω)^ίωτ0.
Последнее выражение соответствует идеальному
дифференцирующему устройству, корреляционная функция на выходе
которого
Кых{Т)-Ч
-£Л»м
= xl(2a2a4-^2 -2a\2Q-^2).
Отсюда ав2ых = Двых(0) = 8-10-4 В2.
7.20. Спектральная плотность мощности шума на выходе
разделительной цепи определяется выражением
^»= W0{vRpCp)2l[\ +ИРСР)2].
Коэффициент передачи интегратора на операционном
усилителе с обратной связью через емкость Ки(ш)= 1/(/ш/?„Си) (при ωτ«:1).
Отсюда спектральная плотность мощности выходного процесса
»ыЛ) "'Wows (/гиси)2(1+ш/грср)'
По теореме Винера - Хинчина
W
— αο
= 10-4 ехр (— 5 ■ 1031 τ |), В2.
7.21. Выходной и входной процессы связаны интегралом
Дюамеля:
О
Чтобы воспользоваться методом характеристических функций,
заменим входной процесс совокупностью дискретных отсчетов,
взятых в соответствии с теоремой Котельникова через интервал
Δ/=π/Ω = τκ, где τκ — интервал корреляции [8, с. 127], и
представим интеграл Дюамеля в виде суммы:
N
к=1
Число слагаемых в сумме ./V определяется скоростью затухания
импульсной реакции, и для заданных исходных данных можно
считать Ν^ Τ/τκ = 4.
При равномерном распределении входного процесса
характеристическая функция
113
a
e-M-Js
e*xdx-
I 8Ϊηοη_ I sin 2η
la ar\ 4 2η
Поскольку отсчеты входного процесса, взятые через интервал
корреляции, практически независимы, совместная плотность
вероятности суммы слагаемых
Θ,ν(η) = Θ1(η)Θ2(η)...Θ;ν(η) = [Θ1(η)]Λί.
Плотность вероятности выходного процесса определим,
применив преобразование Фурье к характеристической функции
[8, с. 32]:
P{y)-h в,(л)е-^А,-1Г1
δΐηοη
ат\
cosr\ydr\.
На основе табличного значения интеграла
косинус-преобразования !
{-\)>"2-2mnm{{m\)-2u2m~l +
■2"» ■ £ (-\)m[(2a» + u)2m-1+(\2an-U\)2m-1]\
s\n at
cos utdt= \ ~,
ι η — 1
и ^ 2am,
0, u^2am,
[m + n)\[m—n)\
p(y)
Л
w
рассчитаны плотности вероятности для
N=l, 2, 4, приведенные на рис. 7.11.
Очевидно, что при ,/V>4 происходит
нормализация выходного процесса.
L
υ У Рис. 7.11
7.22. Как известно, отклонение закона распределения от
нормального характеризуется коэффициентами асимметрии к± и
эксцесса ке. Для экспоненциального распределения р(х) = ае~"х,
х>0,
1 Диткин В. Α., Прудников А. П. Интегральные преобразования и
операционное исчисление, СМБ.— М.: Физматгиз, 1961.
114
μ3_ 1
00
\(x-mx)3OLe~axdx = 2;
.μ*.
00
•3 = ^4 \(x~mx)*<xe-*xdx-3 = 6,
где
σ'
т
l = \(x-mx)2oiQ^xdx=l/a2;
о
со
.= Jxae~a*i/x=l/oc.
Такие большие значения ка и ке свидетельствуют о
существенном отличии рассматриваемого распределения от нормального.
Действительно, негауссовская плотность вероятности может быть
представлена рядом Эджворта [8, с. 286]
р(х)~-
φ(ΐ) (х~т\ _ К ф(4) (*-т\ + *« ф(Д) Л"^
где Ф(,[,(·)—Л>я производная от интеграла вероятности, а при
полученных значениях ка и &е роль второго и третьего членов ряда
значительна.
Ч*(*>\
»вых'
||Ц^
о
Рис. 7.12
Рис. 7.13
После прохождения через высокодобротный колебательный
контур выходной процесс в любой момент времени будет являться
суммой многих соизмеримых по величине составляющих. В силу
центральной предельной теоремы теории вероятностей
распределение суммы станет весьма близким к нормальному (рис. 7.12, 7.13).
Поэтому коэффициенты асимметрии и эксцесса выходного
процесса будут близки к нулю.
115
X(t),
Рис. 7.14
7.23. Отклик интегрирующей цепи на обобщенный телеграфный
сигнал при τ0 = 0,3/« приведен на рис. 7.14, а при τ0 = 3/η—на
рис. 7.15. В соответствии с этими рисунками плотности
вероятности выходных процессов, характеризующие частоту встречаемости
различных мгновенных значений, приведены на рис. 7.16. Из
рисунков видно, что при τ0>τκ происходит нормализация процесса.
p(X)\r„=Z/nlr„=0,3/n
χ(ϋΐ
^***^ ^- ^**^ .а.- _»- I ar и ... _
О 5 х,в
Рис. 7.15 Рис. 7Л6
7.24. Вследствие одинаковости наклона отрезков входного
будет принимать только два
dx(t
процесса производная ν = τ0—-
dt
значения: + Sz0, где τ0 — постоянная времени дифференцирующего
устройства, причем значения вероятности положительных и
отрицательных знаков производной одинаковы и равны 1/2.
Следовательно, плотность вероятности производной
p{y) = (l/2)b{y-Sz0) + {\/2)6(y+ST0).
Плотности вероятности входного р(х) и выходного ρ (у)
процессов представлены на рис. 7.17.
i*Q/+Stu
j<r(</Sre)
Sre *,У Рис. 7.17
В данном случае очевиден эффект денормализации случайного
процесса на выходе линейной цепи, объясняемый тем, что при
дифференцировании процесса подчеркиваются высокочастотные
составляющие процесса и нарушаются условия центральной
предельной теоремы теории вероятностей.
7.25. р(х)'
-(х-т)2/2а2 т_
, т = 0,5; σ = 0,645.
116
7.3. СОБСТВЕННЫЕ ШУМЫ
В РАДИОЭЛЕКТРОННЫХ ЦЕПЯХ
7.26. В коллекторной цепи транзисторного усилителя с
нагрузкой в виде параллельно соединенных резистора R = 5 кОм и
емкости С=20 пФ протекает ток с постоянной составляющей
/0=1 мА. Определить напряжение шума, создаваемое дробовым
эффектом, а также минимальное напряжение входного сигнала,
при котором сигнал/шум на выходе не менее 10 дБ. Коэффициент
усиления усилителя Ку = 50.
7.27. Фото датчик с сопротивлением Ra = 1 МОм, удельной
чувствительностью γ=103 мкА/лм · В, постоянной времени τ= 10 мс
включен между источником постоянной ЭДС £=10 В и
нагрузочным резистором R=\00 кОм. Определить порог
чувствительности датчика в данной схеме (минимальный световой поток, при
котором отношение сигнал/шум равно 20 дБ), считая, что шум
является тепловым, а измерение производится при комнатной
температуре.
7.28. Параметры усилителя, схема замещения которого
приведена на рис. 7.18: /0 = 2 мА, Яг = 10 кОм, Сг = 50 пФ, R= 100 кОм,
С=10 нФ. Определить дисперсию дробового шума на выходе
усилителя и найти его корреляционную функцию.
buix
ш
Ги Цлз\-
^
вых
Σ —
(t)
Рис. 7.18
Рис. 7.19
7.29. Определить дисперсию напряжения на выходе цепи
с импульсной характеристикой g (ή=Ω sin Ω//'(Ω/), Ω = 103 рад/с,
при воздействии белого шума со спектральной плотностью
W0 = l(r6 В2/Гц.
7.30. Микровольтметр построен на основе гальванометра с
постоянной времени τ = 1 с и усилителя со спектральной
плотностью собственных шумов Wo = \0~12 В2/Гц. Каково минимальное
значение напряжения, которое можно измерять этим
микровольтметром с погрешностью не более 10%?
7.31. Определить корреляционную функцию дробового шума
на выходе резонансного усилителя с сопротивлением
коллекторного перехода 50 кОм и нагрузкой в виде колебательного контура
с Q = 20, L=100 мкГн, С=100 пФ, коэффициентом включения
контура в цепь коллектора /? = 0,33. Постоянная составляющая
коллекторного тока /0 = 2 мА.
7.32. Найти спектральную плотность мощности и
корреляционную функцию процесса на выходе цепи (рис. 7.19) при воздействии
белого шума со спектральной плотностью ^=10 В2/Гц. Время
117
запаздывания сигнала в идеальной линии задержки τ3 = 1 мс,
постоянная времени интегратора τ„ = 5τ3.
7.33. /?С-фильтр построен в виде трех идентичных
интегрирующих RC-цепей, разделенных операционными усилителями с
квэффициентами усиления Ку = \0, R=\00 кОм, С=10 нФ.
Определить спектральную плотность мощности и корреляционную
функцию шумов на выходе фильтра, считая, что шум в основном
обусловлен входным резистором при Г=300 К.
7.34. Прямоугольный импульс длительностью ти = 50 мкс с
пиковым значением 20 мВ подается на интегрирующую цепь на фоне
белого шума со спектральной плотностью Wo = \0~10 В /Гц.
Найти постоянную времени цепи τ, при которой обеспечивается
максимум отношения сигнала к шуму. Определить отношение
сигнал/шум.
7.35. Радиоимпульс с прямоугольной огибающей
длительностью ти = 10 мкс, с частотой заполнения 5 МГц и амплитудой
1 мВ подается на резонансный усилитель, настроенный на частоту
заполнения импульса. Дисперсия шума на входе усилителя σ2 =
= 10~6 В2 в полосе 10 МГц. Определить добротность контура
резонансного усилителя, при которой обеспечивается максимум
отношения сигнал/шум, и вычислить это отношение при заданных
параметрах.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
7.26. Исходя из выражения для дисперсии дробового шума
[1, § 7.3] получаем
σ"=ί>/οέ=2'10~6 β2; σ-=ι'4 μΒ·
Среднеквадратическое значение приведенного ко входу шума
σΒΧ = ojKy = 28 мкВ. Отсюда t/Bxmin^3aBX^ 100 мкВ.
7.27. Спектральная плотность мощности шума датчика
И/0 = 4Шг = 8,28-10-14 В2/Гц.
Полосу пропускания датчика как инерционной цепи первого
порядка определим выражением Δ/=1/τ=100 Гц. Тогда
дисперсия шума σ2= W0Af= WJ(2z), а пороговая чувствительность
Φηίη = 10σΛΛ/?γ£/?)= 1,4-Ю-* лм.
7.28. При ЯгС; = 5-10 7с«:ЛС=10 Зс при определении
дисперсии можно пренебречь влиянием разделительной цепи.
Тогда
^0 = е/0Дг = 3,2-10-18 В2/Гц;
ав2ых^о/(2ад) = 3,2-10-12 В2;
/г(т)^а2е^|т|/(К^> = 3,2-10-12е-21°61т1, В2.
118
7.29. Так как импульсная характеристика и передаточная
функция линейной цепи связаны преобразованием Фурье,
00
Κ(/ω) = ί Ω^^ώ = fa Γ?4^Ω'
• Ι Ωί [Ο, |ω|>Ω;
a2=V0
π
Ω
Г
π2ύ?ω = π^0Ω = 3,14·10-3 Β'
7.30. Считая гальванометр системой первого порядка,
определим дисперсию собственных шумов:
a2=W0\g2(t)dt = ^ = 0,5-lO-i2 B:
Действительно, так как WBm ίω) = W0K2 (ω) = W0K (/ω) Κ * (/ω), то
произведению К(да>)К*(/ш) будет соответствовать свертка
g(t)*g( — t) = Rg(t). Следовательно, при белом шуме
°Lx = Двых(0)= WoRg(0)= W0]g2 (t)dt.
о
Тогда чувствительность гальванометра при заданной
погрешности измерений £/min = 10 σ = 7 мкВ. Решение может быть
получено также спектральным методом.
7.31. Корреляционная функция [1, § 7.3]
2С
где Rm=p2pQ = 2,2 кОм; ακ = ^ = 2,5 · 105 с-1; σ2 = 0,35·1(Γ8 В2.
7.32. Передаточная функция цепи
КУ=-(1-е"'Ч
Квадрат модуля коэффициента передачи
Κ2(ω)=Λ-4$\ή2^.
ν ; ω2τ; 2
При этом спектральная плотность мощности определяется
выражением
M/Bbix(o3) = 4224sin2^=^sin20,5-10-4 В2/Гц.
выху / ω2τ2 2 О)2 '
119
*ыЩ
>W^
Рис. 7.20
Корреляционная функция по теореме Винера — Хинчина:
R*M =
ι
4fV0
2π 25ω2τ„
sin
2^е-^ = 0,04^(1-Я1
В'
τ|^τ„
Графики ffBblx(co) и ЛВЬ|Х(т) приведены на рис. 7.20.
7.33. Сначала определим спектральную плотность
тепловых шумов, создаваемых первым резистором: W0=2kTR =
= 4,14· 1(Г6 В2/Гц.
Квадрат модуля коэффициента передачи каждого звена
определяется выражением К\ (ш) = #2/[1+(ш/?С)2], а результирующий
квадрат модуля коэффициента передачи Л^2(ш) = Л^/[1+(ш/?С)2]3.
По теореме Винера — Хинчина (с использованием таблиц
преобразования Фурье [5, с. 290])
Явых(т)- —
00
г
W0K6yeiaxda> W0K
[1+((оЛС)2]3 RC
1+^;+
,-ΙτΙ/RC.
RC 3 (RC)2
σ2 = 4·10~7 Β2.
7.34. При воздействии на ЛС-цепь прямоугольного импульса
где a=l/RC.
Максимальное значение сигнала достигается при ί = τ„:
^выхтах-" ^вых (τκ) ~ " \1 е ")·
Дисперсия шума на выходе цепи σ2ΜΧ= W0/2RC=l/2(x.W0.
Отношение сигнал/шум определим через пиковое значение сигнала и
среднёквадратическое значение шума. Тогда
q = j2U[l-exp(-*Tn)]/y/oW0.
Приравнивая к нулю производную dq/da., получаем
da
U
I _з
τ„αοπ2е~а°птТи + е_2 (1 —е-"оп^и)] = о.
120
Отсюда
αοπττΗ=1η(2αοπττ„+1); осопт=1,25/ти=1/ДС; ДС=0,8ти=40 мкс.
При этом
qmax = 0,9yJU2T/W0=\2,7.
7.35. Воспользуемся методом огибающих, т. е. опишем
заданную высокочастотную цепь эквивалентной для огибающей
низкочастотной цепью [1, § 6.6]. Тогда оптимальные параметры
контура можно определить следующим образом:
«опт = 1,25/ти = ωρ/2β = π/ρ/ρ; ^foπτ =fp/QonT = 0,4/τ„;
β«πτ=/ΡΧ./0,4 = 2,5/ρτΗ=125.
Максимальное отношение сигнал/шум на выходе контура
qmax=0,9y/U4bfj2^) = 6,3S.
Глава 8. НЕЛИНЕЙНЫЕ ЦЕПИ
И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
СИГНАЛОВ
8.1. ГАРМОНИЧЕСКИЙ АНАЛИЗ ТОКА
В НЕЛИНЕЙНОЙ БЕЗЫНЕРЦИОННОЙ ЦЕПИ
8.1. Вольт-амперная характеристика нелинейного сопротивления
описывается уравнением i=I0(el"~ir),'f— 1), где /0 = 500 мкА;
г=Ю Ом; φ = 0,03 В. Построить зависимость тока / от напряжения
и при изменении и в пределах —1...+ 1 В. Определить
дифференциальное сопротивление и сопротивление постоянному току;
построить соответствующие зависимости от напряжения и.
8.2. Аппроксимировать характеристику нелинейного
сопротивления, заданного в предыдущей задаче, двумя отрезками прямых,
потребовав совпадения крутизны характеристик в окрестности
точки и=\ В. Аппроксимировать эту же характеристику
полиномом второго порядка, потребовав совпадения токов при
напряжениях, близких к — 1; 0; 1 В. Построить соответствующие
зависимости.
8.3. К нелинейному сопротивлению, параметры которого
указаны в задаче 8.1, приложено напряжение и[{)=со%Ш, В,
— со <t<cc. Пользуясь аппроксимациями характеристик,
полученными в предыдущей задаче, определить постоянную
составляющую, амплитуды первой и второй гармоник тока и среднюю
121
Таблица 8.1
и6, В
('„, мА
0,2
0,1
0,24
0,6
0,28
1,9
0,32
8,0
крутизну. Сравнить результаты, полученные при разных
аппроксимациях.
8.4. Рабочий участок проходной характеристики iK(u&)
биполярного транзистора задан значениями тока, приведенными в
табл. 8.1. Задавая смещение на базе U0 на середине рабочего
участка, аппроксимировать характеристику транзистора
полиномом третьей степени.
8.5. Проходная характеристика биполярного транзистора в
окрестности рабочей точки U0 представлена полиномом третьей
степени /к = 0,9 + 28,3 (и6- U0) + 875(и6- U0)2+ 10 400(и6- U0)*, мА.
Переменная составляющая напряжения на базе транзистора равна
сумме двух гармонических колебаний с амплитудами 60 и 10 мВ и
частотами 1 и 0,8 МГц. Выполнить спектральный анализ
коллекторного тока и построить спектр.
8.6. Аппроксимировать проходную характеристику, заданную ρ
предыдущей задаче, полиномом второй степени, потребовав;
совпадения тока при напряжениях 0,2; 0,26; 0,32 В. Выполнить
спектральный анализ коллекторного тока при воздействии,
указанном в задаче 8.5. Сравнить результаты.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
8.1. При определении данных, необходимых для построения
графиков, нецелесообразно задавать значения напряжения и, так
как при этом оказывается необходимым для вычисления тока
решать трансцендентное уравнение. Разрешив данное уравнение
относительно напряжения и, получим
« = φ1η(1+///0) + ί>.
Сопротивление постоянному току
*-Г>(1+Й+'·
Дифференциальное сопротивление
_du_ φ
R"-di-J^T0+r
Для определения тока на границах заданного интервала
напряжения можно воспользоваться методом дихотомии (половинного
122
Таблица 8.2
w, В
ι. м.Л
R, Ом
К„, Ом
Окончание та
и, В
i", мА
R, Ом
Д,, Ом
-1
-0,5
2000
-0,5
-0,5
1000
5л. 8.2
0,19
10
19
13
0,31
20
16
11
-0,1
-0,5
200
0,53
40
13
11
-0,052
-0,4
130
310
0,64
50
13
11
-0,03
-0,3
100
160
0,74
60
12
10
-0,017
-0,2
85
109
0,85
70
12
10
-0,008
-0,1
80
85
0,95
80
12
10
0
0
70
70
1,06
90
12
10
деления). Для построения графика достаточно, чтобы границы
интервала при расчете отличались менее чем на 0,1 от заданных.
Результаты расчета приведены в табл. 8.2.
Зависимость тока / от напряжения и показана на рис. 8.1, α
сплошной линией. На рис. 8.1,5 изображена зависимость
сопротивления постоянному току R и дифференциального
сопротивления Rd от напряжения и.
ι',μΑ
R,kOm
'''·:'£*..··' \° °>* °>& <*>В
а)
-1,0 -0,6 -0,2 0 0,2 0,6 и,В
Рис. 8.1
8.2. Крутизна характеристики 5"—величина, обратная
дифференциальному сопротивлению. Из табл. 8.2. видно, что
дифференциальное сопротивление при напряжении примерно 1 В равно
10 Ом, следовательно,
123
S=0,l A/B=100 мА/В.
Уравнение прямой, имеющей такую крутизну, i=S{u— ϋγ), где
Ul — напряжение, соответствующее изгибу характеристики. Это
напряжение можно найти по формуле Ul=ul — ilIS, где их и
г\ — координаты точки, в которой задана крутизна 5". Так как при
напряжении 1 В значение тока в таблице не задано, воспользуемся
значениями г/, =0,95 В и i^—-80 мА. При этом i/i =0,15 В.
Таким образом, уравнение аппроксимирующей функции
■_ J® ПРИ — оо<"<0,15 В,
'~ (100(м-0,15), мА, при 0,15 Βζικοο.
Этому уравнению соответствует штриховая линия на рис. 8.1, я.
При аппроксимации степенным полиномом 1 = а0 + ахи-\-а2и2.
Коэффициент я0 равен нулю, поскольку при напряжении м = 0 ток
/=0. Коэффициенты «, и а2 определяются из системы уравнений
-0,5·10-3=-α, + «2; 80 · 10~ 3=0,95fll+0,95я2,
откуда α, =43,4 мА/В; я2 = 42,9 мА/В2.
Второе уравнение системы в связи с тем, что значение тока при
напряжении 1 В не задано, справедливо для м = 0,95 В, /=80 мА.
Кривая изображена на рис. 8.1, я точками.
8.3. Из условия задачи следует, что амплитуда управляющего
напряжения £=1 В, а постоянная составляющая Uo = 0. При
аппроксимации характеристики отрезками прямых угол отсечки
[1,§ 8.3]
0 = arccos-^^ = 81,4°;
постоянная составляющая тока [1,§8.3]
/0=—(sin0-0cos0) = 25 мА;
π
амплитуда первой гармоники тока [1, с. 228, 231]
/t=—(G-sin0cos0) = 4O мА;
амплитуда второй гармоники тока [1, с. 228]
/2=—(sin0cos0-2cos20sin0) = 21 мА;
средняя крутизна Scp = ΐ1/Ε= 40 мА/В.
При аппроксимации той же характеристики степенным
полиномом
/0 = й0+1/2д2£2 = 21 мА; /t = aL£=43,4 мА;
124
/2 = 1/2я2£2 = 21 мА; Scp = /1/£=43,4 мА/В.
25 — 21
Расхождение при определении 10 составляет δ = 100= 16%;
43 4—40
при определении Ι1 δ = -' 100= —7,8%; при определении /2 6 = 0.
8.4. В соответствии с табл. 8.1 напряжение на базе,
соответствующее заданному положению рабочей точки,
U0 = 0,2 + (0,32 -0,2) /2 = 0,26 В.
Аппроксимирующий характеристику полином
it = a0 + a1(u6-U0) + a2(ue-U0)2 + a3{u6-U0)3.
Подставив в это выражение значения тока и напряжения из
табл. 8.1, получим четыре уравнения для определения неизвестных
коэффициентов а0, о,, а2, я3:
0,1=я0-я10,06+я2(0,06)2-я3(0,06)3;
0,6 = fl0-fll 0,02+ я2(0,02)2-я3(0,02)3;
1,9 = я0 + «10,02 + а2 (0,02)2 -д3(0,02)3;
8 = α0 + α,0,06+α2(0,06)2-α3(0,06)3.
Решив эту систему относительно неизвестных параметров,
найдем я0 = 0,9мА, а, = 28,ЗмА/В, я2 = 875мА/В2, «3= 10400 мА/В3.
Таким образом, формула, аппроксимирующая проходную
характеристику транзистора, принимает следующий вид:
гк = 0,9 + 28,3 (щ- 0,26) + 875 (и6- 0,26)2 + 10 400 (мб-0,26)3
(размерность тока мА, напряжения В).
8.5. Для определения амплитуд и частот спектральных
составляющих тока положим
u=U0+ Uacos(uat+Ubcos(uht,
где £/а = 60мВ, С/ь=10мВ, ωα = 2π/α, шь = 2тг/ь, /а=Ю6Гц, fb =
= 0,8-106 Гц.
Ток коллектора
4 = a0 + al(Ua cos ωαί + Ubcos ω,,ί) + я2 ((/„ cos ωαί + Ubcos oy )2 +
+ a3(Uacos(aat+ Ubcos(obt)3.
Используя известные тригонометрические формулы для
квадрата и куба суммы двух гармонических колебаний, приходим к
следующим составляющим в спектре коллекторного тока:
постоянная составляющая
/0 = я0 + (я2£/в2)/2 + (я2£/ь2)/2 = 2,51мА;
гармоники колебания с частотой /а=106Гц, амплитуды
которых
125
ial=aiUa + a3^U2bUa + 3~U3^ = 3A7 ыА,
le2 = a2U*/2 = 1,57 мА, la3 = a3U3a/4 = 0,56 мА;
гармоники колебания с частотой/ь = 0,8 · Ю6 Гц и амплитудами
rbl=aiUb + aJ^UbU3a + 3-Ui) = 0,S5MA,
Ib2 = a2Ul/2 = 0,044 мА, Ib3 = a3Ul/4 = 0,0026 мА
и комбинационные колебания с частотами fa+fb = 1,8 · 106 Гц и
/0—/ь=0,2· 106 Гц, амплитуды которых
/u=ytW = 0,26MA;
комбинационные колебания с частотами 2/а+/ь = 2,8· 106 Гц и
2/0—/ь= 1,2· 106 Гц, амплитуды которых
/21=я3^£/в2£/6 = 0,28мА;
комбинационные колебания с частотами 2/6+/0 = 2,6· 106 Гц
и 2/ь—/0 = 0,6· 106 Гц, амплитуды которых
/12=д3^£/в£/2 = 0,047мА.
Амплитудная спектральная диаграмма коллекторного тока
изображена на рис. 8.2.
J,mA
Τ.Ϊ
Τ л
..тТ
" 0,4 0,8 1,2 1,6 2,0 2,4 Ψ,ΜΓυ, Рис. 8.2
8.6. Полином, аппроксимирующий проходную характеристику,
запишем так:
iK = а0 + а, (и6-0,26) + а2(и&-0,26)2.
Определив значения тока, соответствующие заданным
напряжениям на базе, и подставив их в записанное выражение, получим
систему трех уравнений
0,1 = а0- а10,06 + а2 (0,06)2;
126
0,9 = a0;
8 = α0 + α10,06 + α2(0,06)2.
Решив эту систему, получим я0 = 0,9 мА, Я!=65,8мА/В, а2 =
= 875мА/В2.
Спектральный анализ тока в данном случае позволяет
определить постоянную составляющую тока /0, амплитуды первой и
второй гармоник обоих колебаний и амплитуды комбинационных
колебаний первого порядка. При этом можно воспользоваться
формулами, приведенными в методических указаниях к
предыдущей задаче, при а3 = 0. Постоянная составляющая тока,
амплитуды вторых гармоник колебаний и амплитуды комбинационных
колебаний первого порядка получаются одинаковыми при
представлении характеристики полиномами второй и третьей степени.
Амплитуды первых гармоник при аппроксимации полиномом
второй степени получаются такими:
lai=al Ua = 3,95 мА; hi=al Ub = 0,66 мА.
Погрешности соответственно равны
δ„ = 3'95:3'47100=12%, 5b = i°'66:0'851100 = 22%.
3,95
0,85
8.2. НЕЛИНЕЙНОЕ РЕЗОНАНСНОЕ
УСИЛЕНИЕ И УМНОЖЕНИЕ ЧАСТОТЫ
8.7. Кусочно-линейная аппроксимация проходной
характеристики транзистора (рис. 8.3) определяется параметрами: крутизна
линейной части 5"=400 мА/В, напряжение, соответствующее точке
излома, U, =0,5 В. Вывести уравнение колебательной
характеристики /к1(£), где 1ж1—амплитуда первой гармоники коллекторного
тока; Ε—амплитуда гармонического напряжения на базе.
Построить колебательные характеристики в диапазоне амплитуд
05ζ£ίζ0,4 В для двух положений рабочей точки (£/0): 0,4 и 0,6 В.
(ft <Ί>
Рис. 8.3
Рис. 8.4
8.8. В цепь коллектора резонансного усилителя включен
параллельный колебательный контур (рис. 8.4). Частота колебаний
на входе усилителя равна резонансной частоте контура. Ампли-
127
туда £=0,3 В. Сопротивление контура при резонансе /?=100Ом
(при неполном включении контура). Постоянная составляющая
напряжения на коллекторе £0=10В. При кусочно-линейной
аппроксимации характеристики транзистора его параметры:
крутизна характеристики 5=400 мА/В, напряжение нижнего сгиба
U1=0,5 В. Определить коэффициент усиления и КПД усилителя
при напряжении £/0 = 0,6 В.
8.9. Параметры транзистора и колебательного контура в схеме
резонансного усилителя указаны в предыдущем примере. Выбрать
положение рабочей точки U0, обеспечивающее линейность
колебательной характеристики при нелинейном режиме усилителя.
Найти амплитуду напряжения на базе, при которой амплитуда
напряжения на контуре достигает 8,5 В. Определить коэффициент
усиления и КПД усилителя. Как изменится КПД при уменьшении
амплитуды напряжения на базе вдвое?
8.10. При умножении частоты используется транзистор,
проходная характеристика которого аппроксимируется выражением
. _ ί0 при и6^иг,
^'{S^-U^ при ub>Uv
Параметры транзистора: 5=50 мА/В, £/, =0,5 В. Приняв
максимальное значение тока в импульсе 1т равным 12,5 мА, определить
положение рабочей точки U0 и амплитуду напряжения на базе £,
при которых имеют место наилучшие условия для удвоения
частоты.
8.11. В схеме резонансного удвоителя частоты использован
транзистор, параметры и режим работы которого заданы
в условии предыдущей задачи. Резонансная частота контура
/р=1 МГц, емкость С=250 пФ, добротность 2 = 50. Коэффициент
включения контура в коллекторную цепь /; = 0,2. Найти амплитуду
напряжения на коллекторе транзистора и мощность в контуре.
8Л2. Какова должна быть характеристика нелинейного
элемента, чтобы обеспечить линейность колебательной характеристики?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ
И ОТВЕТЫ
8.7. Амплитуда первой гармоники тока [1,§ 8.5] Il=alIm, где
a, = [0-sin0cos0]/[Tt(l — cos0)] — коэффициент Берга.
Целесообразно выразить 7, непосредственно через (У, — U0 с помощью
I Г Г J
соотношения 0 = arccos — -. То1да можно прийти к следующему
Ε
результату:
arccos—— ! I ■ '
128
Таблица 8.3
(/„. В
0,4
0,6
/,. мА. при Е. В, равном
0,05
0
20
0.1
0
40
0.15
6,6
53,4
0.2
15,6
64,3
0.25
25,2
74,7
о.з
35,0
84,9
0.35
44,8
95,1
0.4
55
105,2
Если E<UY — U0, то коллекторный ток равен нулю. Если
£<£/0—£/,, то изменения управляющего напряжения не выходят
за пределы линейного участка проходной характеристики и
амплитуда первой гармоники тока I1 = SE. В табл. 8.3 приведены
результаты расчета ΐ1, соответствующие значениям Ε и U0. На
рис. 8.5 изображены колебательные характеристики,
соответствующие напряжениям смещения 0,4 и 0,6 В.
8.8. Амплитуда первой гармоники коллекторного тока при
указанных значениях Ε и U0 равна /\=85мА (см.
методические указания к задаче 2.1). Средняя крутизна [1, § 8.6] Scp =
= /j/£=283 мА/В. Коэффициент усиления К =ScpR — 28,3.
Амплитуда напряжения на коллекторе UK = EKy = 8,5 В. Угол отсечки тока
0=arccos^4^=l,91 рад=109°.
Ε
Коэффициент полезного действия [1, § 8.5]
ot 1/1 e-sinGcosG U.
КПД;
2а0 Е0 2 sin θ — θ cos θ E0
= 0,59.
Ι,,μΑ
8.9. Линейность колебательной
характеристики обеспечивается выбором напряжения
смещения U0 равным напряжению нижнего
сгиба характеристики транзистора U0=Ul=0,5 В
(угол отсечки θ=π/2). При этом средняя
крутизна не зависит от амплитуды колебаний
на базе и равна' Scp = S/2 = 200 мА/В.
Коэффициент усиления K=ScpR = 20.
Амплитуда входного напряжения £=8,5/20 = 0,43 В;
КПД = 0,67. При уменьшении амплитуды
напряжения на базе вдвое пропорционально
уменьшается амплитуда напряжения на
коллекторе и вдвое уменьшится КПД усилителя.
8.10. Наилучшие условия для удвоения частоты с точки зрения
обеспечения максимального отношения амплитуды второй
гармоники (и = 2) коллекторного тока к максимальному значению тока в
импульсе [1, § 8.6] будут при угле отсечки θ= 120ο/" = 60°. Макси-
129
ΰ,ί 0,2 0,3 ε,8
Рис. 8.5
малыше значение тока в импульсе [1, § 8.3] Im = SE{\ — oos0),
откуда E=Iml\S{\ — cos0)] = O,5 В. Угол отсечки связан с
напряжением на базе транзистора соотношением cos0 = (£/, — U0)/E,
из которого определяется положение рабочей точки U0=l/1 —
-£cos0 = O,25 В.
8.11. Коэффициент второй гармоники [1, § 8.3]
_2(sin2ecos6-2cos29sine)_2sin2e(cose-2cos2e)
2 27r(22-1)(l-cos6) 67r(l-cosG) '
Подставив в формулу значение 0 = 60°, получим ос2 = 0,275.
Амплитуда второй гармоники тока /2 = /та2 = 3,44 мА.
Сопротивление контура при резонансе R=p2Qp, где р=1/(2тс/рС)—
характеристическое сопротивление контура. Следовательно, R =
=p2Q/(2nfpC)=\270 Ом. Амплитуда напряжения на коллекторе
транзистора равна амплитуде напряжения на контуре:
UK = I2R = 4,37 В.
Мощность в контуре
Р=/2С/к/2 = 7,5· 10~3 Вт.
8.12. Характеристика должна иметь вид, показанный на рис.
8.3. Напряжение смещения U0 должно совпадать с £/х. Угол
отсечки при этом будет 90° независимо от амплитуды
гармонического сигнала, что и обеспечивает пропорциональность
(линейность) между амплитудой первой гармоники тока и
амплитудой входного напряжения.
8.3. ПОЛУЧЕНИЕ
АМПЛИТУДНО-МОДУЛИРОВАННЫХ
КОЛЕБАНИЙ
8.13. На базу транзистора с вольт-амперной характеристикой,
представленной на рис. 8.3 (при 5=50 мА/В и ί7χ = 0,5 В), подается
высокочастотное напряжение с постоянной амплитудой и
регулируемое напряжение смещения U0. Найти зависимость амплитуды
первой гармоники коллекторного тока /х от U0 (так называемую
статическую модуляционную характеристику). Построить
характеристики I^Uq) для £=0,4 В и £=0,2 В.
8.14. Параметры нелинейного элемента, работающего в
схеме амплитудного модулятора, приведены в задаче 8.13.
Напряжение смещения £/0 = 0,5 В. Определить коэффициент
модуляции первой гармоники тока при амплитуде
высокочастотного напряжения £=0,4 В и амплитуде модулирующего
напряжения Un=0,2 В.
130
8.15. На вход амплитудного модулятора, рассмотренного
в задаче 8.14, подается напряжение и = 0,5 + 0,2 cos 2π 104ί +
+ 0,4cos2n· 106i, В. Модулированное напряжение снимается с
колебательного контура в цепи коллектора; контур настроен на
частоту 1 МГц, добротность контура Q = 50. Найти коэффициент
модуляции колебания на выходе модулятора.
8.16. На базу транзистора с вольт-амперной характеристикой,
аппроксимируемой полиномом i=a0 + alu+a2u2, при я0 = 0,9 мА,
а^бОмА/В и а2 = 900 мА/В2 подается напряжение
u(t)~ U0+ UacosQt+ Uwcos(o0t = 0fi2 + 0fi4cosQt+
+ 0,02 cos ω0ί, Β.
Определить коэффициент модуляции Μ первой гармоники
коллекторного тока и зависимость Μ от соотношения амплитуд
8.17. Какой должна быть характеристика нелинейного
элемента модулятора, чтобы получить модуляцию с подавлением
несущей частоты? Как при этом обеспечить неискаженную
модуляцию?
Uа и
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
8.13. Если U1 — E<U0<Ul + E, то уравнение статической
модуляционной характеристики совпадает с уравнением
колебательной характеристики (см. методические указания к
задаче 8.7). При расчете следует учесть, что аргументом
является величина U0, a Ut и Ε заданы. При U0^U1—E ток
равен нулю, при JJ^U^-VE значения /х не изменяются. В
табл. 8.4 приведены результаты расчета /х, соответствующие
значениям U0 и Е. На рис. 8.6 изображены модуляционные
характеристики.
Таблица 8.4
£, В
0,4
0,2
/,, мА, при U„, равном
0,1
0
0
0,2
1,4
0
0,3
3,9
0
0,4
6,9
1,95
0,5
10
5
0,6
13,1
8,04
0,7
16,1
10
0,8
18,5
10
0,9
20
10
0,2 0,4 0,6 0,81/0,ϋ
Рис. 8.6
8.14. Напряжение смещения в процессе модуляции
изменяется от £/0-£/Ω = 0,3Β до U0+Un = 0,7 В. Этим
предельным напряжениям соответствуют амплитуды первой гармони-
131
ки тока /1т!п = 3,9мА и /1тая=16,1мА (при Ε = 0,4 В). Тогда
M = (Il max- A min)./(A max + h min) = 0,61.
8.15. Мът = М [ΐ+(2ρΩ/ωρ)2]*=:0,43 [Ι,δ 6.8].
8.16. Подставив заданное напряжение u\t) в полином i=a0 +
+а.{и+а2и2 и выделив слагаемое с частотой ω0, найдем
амплитуду первой гармоники Il=(al + 2a2u)Um. Минимальное значение
Ληίη = [αι+2α2(£/0- un)]Um· a максимальное /max = [a1+2a2(t/0 +
+ иа))ит.
Тогда
^ = (Am«-Al-fa)/(A-« + /imto)-^n/(0»5fl1/fl2-l-i/o)=0»14.
Как видим, в том случае, когда характеристика нелинейного
элемента имеет вид полинома второй степени, коэффициент
модуляции не зависит от амплитуды Ua и пропорционален
амплитуде модулирующего напряжения Un.
8.17. Вольт-амперная характеристика должна быть четной
функцией аргумента u—U0, т.е. i{u—U0) = i(U0 — u), где U0—
постоянная составляющая управляющего напряжения. В этом
случае при представлении ее рядом Тейлора в последнем
будут отсутствовать члены с нечетными степенями
аргумента. При воздействии совокупности гармонических колебаний
на нелинейный элемент с такой характеристикой в спектре
отклика будут отсутствовать нечетные гармоники, в том
числе первая гармоника колебания с несущей частотой. Для
неискаженной модуляции характеристика должна быть
квадратичной.
8.4. ДЕТЕКТИРОВАНИЕ
АМПЛИТУДНО-МОДУЛИРОВАННЫХ
КОЛЕБАНИЙ
8.18. Схема детектора амплитудно-модулированных
колебаний изображена на рис. 8.7. Внутреннее сопротивление диода
Л;=ЮОм. Сопротивление /?=10 Ом. На входе действует
напряжение e{t) = E[\ +McosQi)coscu0/ = (l +0,5cos2n· 104/)cos2nx
χ 106r, В. Определить емкость С, обеспечивающую
удовлетворительное сглаживание высокочастотной пульсации выходного
напряжения и неискаженное воспроизведение модулирующего
колебания. Определить амплитуду сигнала на выходе.
с
о Рис. 8.7
132
8.19. Рассмотренный в предыдущей задаче амплитудный
детектор (см. рис. 8.7) является нагрузкой резонансного усилителя.
Емкость контура С=1000пФ, резонансная частота /р=106Гц.
Определить полосу пропускания контура (собственными потерями
в контуре можно пренебречь).
8.20. При детектировании слабых сигналов вольт-амперная
характеристика диода в схеме детектора (см. рис. 8.7)
аппроксимируется полиномом второй степени: i=a0 + aiu+a2u2. Вывести
уравнение характеристики детектирования.
8.21. На детектор с квадратичной характеристикой
детектирования действует напряжение с коэффициентом модуляции
Μ =0,5. Определить коэффициент гармоник выходного
напряжения.
8.22. Определить напряжение на диоде детектора (см. рис. 8.7).
Параметры элементов схемы и входное напряжение заданы в
условии задачи 8.18.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
8.18. Постоянная времени нагрузочной цепи должна
удовлетворять неравенствам 1/ш0С-КСО/П. При заданном R приходим к
неравенствам ]/(u0R^C<tl/QR. Емкость целесообразно определять
как среднее геометрическое величин 1/(ω0/ϊ) и ]/(flR):
С=1/(ДУш^)=160-1(Г12 Ф=160пФ.
Напряжение на выходе амплитудного детектора, работающего
в режиме больших амплитуд с отсечкой тока (линейное
детектирование), можно определить простым выражением
uBM(t) = E(t)cosQ=(\+0,5cos2n\0*t)cosQ,
где угол отсечки θ связан с параметром RifR соотношением
Ri/R=(tgQ-Q)/n [1,§ 8.8]. При R{/R= 1(Г3 θ=10° [1, график на
рис. 8.26].
Таким образом, cos θ = 0,98 и
w»«x(')=:(1+0'5cos2T,tl04i)'0'98'
откуда следует, что амплитуда сигнала на выходе детектора
0,5 0,98 = 0,49 В.
8.19. Схема замещения контура, шунтированного детектором,
представлена на рис. 8.8, где R„ — входное сопротивление
детектора, отнесенное к току первой гармоники It. Известно, что в
режиме работы с отсечкой тока Rn = R/2, где R — нагрузочное
133
"к,
Ь>0
сопротивление в цепи детектора [1,§ 8.9]. Относительная полоса
пропускания контура, шунтированного сопротивлением, 2Δ///ρ =
= 1/(2 = 1/(ωрС/?д), а абсолютная полоса 2Л/=1/(2тсС7?д). В данной
задаче при Дд = Д/2 = 5·103 Ом и С=103пФ
2Д/=3,2 104Гц.
8.20. Напряжение, приложенное непосредственно к диоду,
un(t) = Ecoso)t— U0, где Ε—амплитуда входной ЭДС; U0 = I0R —
выпрямленное напряжение, создаваемое на нагрузочной цепи RC.
Подставив Ид(') в полином, аппроксимирующий вольт-амперную
характеристику
i(t) = a0 + a1(Ecosa)t — I0R)-\-a2(Ecosa)t — I0R)2 и выделив
слагаемые, не зависящие от времени, придем к выражению
I0 = a0-a1I0R + a2E2/2 + a2IoR2-
Как правило, выполняется условие a1I0R»a2(I0R)2. Поэтому
зависимость постоянной составляющей тока от амплитуды
напряжения на входе можно привести к виду
10 = а0/(]+а^) + а2Е2/[2{]+а^)].
Таким образом, характеристика детектирования получается
квадратичной.
8.21. ЯГ = 0,5М2/(2М) = 0,125.
8.22. и- =ί?-мвыx=(l+0,5cos2π■104/)cos2π■106/-0,98-
— 0,49 cos 2π · 1О4/, В. Выходное напряжение детектора ивых
определено в задаче 8.18.
8.5. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКИХ
КОЛЕБАНИЙ НА ЦЕПИ С НЕЛИНЕЙНЫМИ
РЕАКТИВНЫМИ ЭЛЕМЕНТАМИ
8.23. В последовательный колебательный контур с нелинейной
емкостью включены источники: смещения £0 = 5 В и
гармонической ЭДС с амплитудой Е. При заданном смещении
дифференциальная емкость равна С0=100пФ, емкость C=q/u = S0 пФ,
резонансная частота в режиме малых амплитуд /0=10МГц,
добротность контура Q = 40. Параметр, учитывающий
нелинейность вольт-амперной характеристики [1,§ 8.14],
*з = [1^С-(2Л/0)2]/(С£0)2 = 6,16 1033Кл-2с-2.
134
&>п
ω0
Риг Я 8
Определить частоту, при которой амплитуда заряда на емкости
максимальна, если £=0,1 В. Чему равны амплитуды тока в
контуре и. напряжения на индуктивности при этой частоте?
Определить частоты, соответствующие уровню 0,7 максимальной
амплитуды. Выяснить вопрос об устойчивости контура.
8.24. Дифференциальная емкость варикапа, используемого в
удвоителе частоты, схема замещения которого изображена на
рис. 8.9, равна С0 = С/у/\+ки, где С=30пФ; к=2 В-1;
ц—напряжение на варикапе. Напряжение источника e(/) = 5 + 0,2cos2nx
χ 50-106/. Эквивалентное сопротивление контура при резонансе
/?=50кОм. Определить колебательную' мощность источника и
амплитуду напряжения на контуре, если резонансная частота
контура вдвое больше частоты воздействующих колебаний. Как
изменится амплитуда напряжения на контуре при уменьшении
амплитуды источника вдвое?
8.25. Схема замещения утроителя частоты изображена на
рис. 8.9. Резонансная частота контура /р = 50 МГц, добротность
Q = 50, емкость С=20 пФ. Определить амплитуду напряжения на
контуре Е2 при частоте подводимых колебаний /, = 16,5 МГц, если
мощность, отбираемая от генератора, Р=10 Вт.
Рис. 8.9 Рис. 8.10
8.26. Напряжение источника в схеме, изображенной на рис. 8.9,
равно сумме гармонических колебаний e(t)=cos2n- 107?+cos2n4x
xlO7/, В. Мощность источника Р=10_4Вт. На резонансной
частоте /р=50МГц сопротивление высоко добротного контура
/?=50кОм. Определить амплитуду напряжения на контуре и
мощность воздействующих колебаний.
8.27. Преобразователь частоты образован системой двух
высокодобротных контуров с резонансными частотами fi = 10 МГц и
/2 = 50 МГц, связанных нелинейной емкостью (рис. 8.10).
Сопротивление контуров при резонансе R = R1 = R2= 10 кОм. Частота
гармонической ЭДС источника/= 60 МГц. Определить мощность
источника, необходимую для возбуждения колебания с частотой
10 МГц и амплитудой Е1 = \ В. Чему равна при этом
амплитуда £2?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
8.23. Индуктивность контура
135
1=1/(С0(2я/0)2) = 2,53-1(Г6Гн,
сопротивление
r = 2nf0L/Q = 3,9SOM,
затухание
a = r/(2L) = 0,785-l06c-1.
Задаваясь амплитудой заряда А, соответствующие значения
частоты можно определить по формуле [1,§ 8.14]
ω2 = ω§-2α2+-63Λ2±
^-4a2Mg + 2a2(2a2-^2*3
1/2
Максимальное значение А=Ат получается, когда подкоренное
выражение равно нулю, т. е.
Е2
Ji m ι ~ Ji m
4 , 2 юо-a2
3a2b,L2
= 0.
Решив это уравнение относительно Ат, получим
Am=i-lat*+
2 ωο — α2
+
3a2b,L2
1/2") 1/2
= 3,71 10
■ю
Кл.
Соответствующая частота
J m
2π
■J
ωΙ-2α2 + -ϋ3Αΐ
1/2
= 10,77 МГц.
Амплитуда тока при этой частоте
/=Лт2я/т = 2,51-10-2А.
Амплитуда напряжения на индуктивности
EL = 2nfJL = A,7>\ В.
Частоты, соответствующие амплитудам заряда 0,7Лт, равны 10,24
и 10,52 МГц. Поскольку большая из этих частот меньше fm,
можно сделать вывод, что при заданной амплитуде входного
напряжения возможны неустойчивые состояния.
8.24. Амплитуда напряжения источника Ε=0,2 В мала по
сравнению с напряжением смещения Е0 = 5 В. В этом случае
вольт-кулонную характеристику варикапа можно
аппроксимировать полиномом второй степени [1, § 8.15]. Поскольку
коэффициент bl = C0 + dq/du, коэффициент
Ь,=;
d2q I d2Cn
С
2du2 2 du2
VO+M3
При напряжении w = £0 = 5B b2= -0,411 10
136
-12
Кл/В2.
Колебательная мощность источника [1, § 8.15] Pl=blu)lE*R/2.
Подставив ωχ = 2π· 50 · 106 рад/с, £=0,2 В и значения других
параметров, получим
/^ = 6,67-ΙΟ-7 Вт.
Мощность, выделяемая в сопротивлении R, равна мощности
генератора Р2 = Р1. Амплитуда напряжения на контуре
E2 = ^2P2R = 0,258 В.
При уменьшении амплитуды источника вдвое амплитуда Е2
уменьшится в 22 = 4раза.
8.25. Полное сопротивление контура на частоте 3/^=49,5 МГц
[1, § 5.6]
Ζκ = =£==== =5,62-103 Ом.
Сдвиг фаз тока и напряжения в контуре
φ^-arctg 2β^! = 450.
Мощность, отдаваемая источником, и мощность, выделяемая в
контуре, одинаковы [1, § 8.15]:
Ρ^Ρ2=(Ε22/2Ζκ)οο$φζ, откуда Е2 = ^/2PlZK/cosZK= 1,26 В.
8.26. Падение напряжения на контуре создает колебание с
частотой f=fi+f2 = 10 +4-107 = 5 ■ 107 Гц. Мощности колебаний с
частотами fi и /2 (соответственно Ρί и Р2) в сумме равны
Р=Р1 + Р2. Справедливы пропорции [1, § 8.17]
Pxlh=Pilfi= -Poll· откуда Ρ, =flP/{fl +f2) = 2-\0~5 Вт; Р2 =
=Λ*7(/ι+/2) = 8·1<Γ5Βτ; Ρ0=-10-4Βτ.
Знак «минус» указывает, что контуром потребляется энергия.
Амплитуда напряжения на контуре
£2-У2ЛР=3,1бВ.
8.27. При амплитуде колебания на контуре Εί выделяемая
мощность P1 = El/(2R) = 5 · Ю-5 Вт. Для определения отбираемой
от источника мощности Ρ воспользуемся пропорцией [1, § 8.17]
PJA=-P/l· откуда Р=-(//Л)Л = -ЗЮ-4Вт.
Здесь знак «минус» указывает, что мощность отбирается от
источника. Из пропорции P2/.f2=~P/l· находим мощность в
другом контуре
137
P2=-Pf2lf=2-ΙΟ'* Вт
и амплитуду
E2 = j2RP2 = 2,23 В.
Глава 9. ГЕНЕРИРОВАНИЕ ГАРМОНИЧЕСКИХ
КОЛЕБАНИЙ
9.1. LC-ГЕНЕРАТОРЫ С ВНЕШНЕЙ ОБРАТНОЙ
СВЯЗЬЮ
9.1. Составив дифференциальное уравнение для автогенератора на
полевом транзисторе (рис. 9.1, а) в режиме запуска при малых
амплитудах колебания (источники питания и смещающих
напряжений на схеме не показаны), определить условие
самовозбуждения генератора.
VT
Рис. 9.1 a) S)
9.2. Найти минимальную взаимную индуктивность М, при
которой наступает самовозбуждение автогенератора,
представленного на рис. 9.1, а. Параметры контура: L = 500 мкГ, С=2000 пФ,
г=5 0м. Параметры транзистора: 5=5 мА/В, μ=20.
9.3. Определить напряжение смещения на затворе и3,
соответствующее границе самовозбуждения генератора (рис. 9.1, а),
при вольт-амперной характеристике транзистора 1с^ = а0+а1щ+
+аги\, мА, где а0 = 2 мА, ах = Ъ мА/В и а2 = 0,\5 мА/В2. Заданы
параметры: /?эк=12кОм, АГОС = 0,05, μ=100.
9.4. Генератор с контуром в цепи сетки и индуктивной связью
(рис. 9.2) генерирует колебания с частотой /0=1 МГц.
Добротность контура β = 50, взаимная индуктивность М=5 мкГ.
Характеристика лампы аппроксимируется полиномом третьей степени
га = 25 + 6мс — 0,1ис, мА. Смещение на сетке U0= — 4 В. Определить
стационарную амплитуду напряжения на сетке.
138
и*
г° \lA
L
-1—o +
=?£"
Tfgy+yg
Τ—F13-*
КГ Jf
©—Τ Τ U
-j—'
Рнс. 9.2
Phc. 9.3
9.5. Составить дифференциальное уравнение и вывести условие
самовозбуждения трехточечной схемы автогенератора,
изображенной на рис. 9.3. Проходную характеристику транзистора
аппроксимировать линейной функцией г'ст = 5,г/3.
9.6. Определить, насколько частота колебаний
транзисторного генератора отклоняется от резонансной частоты контура
(рис. 9.1, а), если аргумент комплексной крутизны cps = 25°.
Параметры контура: L=80 мкГ, С=320 пФ, Q = 50. Влиянием
выходного сопротивления транзистора пренебречь.
9.7. Определить полосу частот, в которой происходит
захватывание частоты генератора с контуром в цепи коллектора, если
контур имеет параметры: Q = 50, ρ = 200 Ом, /р = 1 МГц,
коэффициент обратной связи АГ0С = 0,1; характеристика транзистора
аппроксимируется выражением гк = 10 + 2(мб— U0) — 0,5(цб— U0)3, мА, а
синхронизирующее напряжение вводится в цепь базы и имеет
амплитуду £=0,16 В.
9.8. В катушке контура генератора (в цепи базы) наводится ЭДС
10 мВ. Определить, в какой полосе генератор может
синхронизироваться этой ЭДС, если/р=1 МГц, Q = 50, ρ = 200 Ом, Μ=3,2 мкГ.
9.9. Для повышения добротности контура используется его
регенерация по схеме на рис. 9.4; при этом Qo = 20, /p = 200 кГц,
VT
Рис. 9.4
-1 „Аса г /γ\
\ии ±
ч
-£
to
Ь1Х
£=1мГ, крутизна характеристики транзистора в рабочей точке
2 мА/В. При каком значении взаимной индуктивности Μ полоса
пропускания регенерированного контура будет равна 1 кГц?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
9.1. Для упрощения решения перейдем к параллельной схеме
замещения колебательного контура (рис. 9.1,6), где R3K = L/(rC).
139
Тогда, исходя из уравнений Кирхгофа для токов в цепи
коллектора
1я + 1,
а также выразив ток ικ в виде линейной функции (при малых
амплитудах) iK = s(Koc—\ик, где Koc = M/L—коэффициент
обратной связи; 5'=μ//?,·, приходим к следующему дифференциальному
уравнению генератора (в линейном режиме):
dt1 \CR„ СЛ, LC) dt LC "
ИЛИ
d2ll, , » du% , ι η
^+ 3κΐ+ω°"κ '
где обозначено аэк = (1/2С)(1/Дэк+1/Д,-.Ш/£) [1, § 9.2].
Для возбуждения колебаний необходимо, чтобы коэффициент
при первой производной был отрицателен. Таким образом,
условие самовозбуждения сводится к неравенству
Ml 111
— > = μ-.
L R3XS SRt RJXS μ
9.2. Критическое значение М, соответствующее порогу
устойчивости системы (т. е. возникновению колебаний),
\R„S μ/ S μ
При заданных параметрах г, С, L, S и μ находим Мкр =
= 4,5 1(Г6Гн.
9.3. Сначала найдем крутизну S, необходимую для
возбуждения генератора:
S=—-—!—, = 2,08 мА/В
*„(*«-1/μ) '
(см. примеры 9.1 и 9.2).
Исходя из определения дифференциальной крутизны
S=-—=—- (α0 + α^3 + аги\ ) = а1 + 2а2щ
ащ ащν '
найдем искомое напряжение смещения
и3=(5'-а1)/(2л2)=-3,06 В.
140
9.4. Для генератора на электронной лампе с контуром в цепи
г MSC.
сетки в установившемся режиме выполняется равенство —:—-=
= 0 [2, с. 441], где Scp = Iul/Ue—средняя крутизна;
/а1—амплитуда первой гармоники анодного тока; Uc — искомая амплитуда
напряжения на сетке. Таким образом, ис= — 4+Uccosmpt.
Подставив ис в уравнение вольт-амперной характеристики и выделив
слагаемые с множителем cosa)_i, придем к следующему
выражению для амплитуды первой гармоники тока:
h ι = 6 Uc - 4,8 Uc - 0,075 Ul = 1,2 Uc - 0,075 U 3.
Следовательно, Scp = /,t/Uc = 1,2-0,075V\ и Uc = y/([,2-Sep)/0,075.
С другой стороны, из условия r/L — MScp/(LC) = 0 вытекает
равенство
_гС _ ' - ι ι ι
•Jen Г7 —
ср Μ io2pLM ω.Ζ, Λ/ω. Q Μω.
При Q = 50, ωρ = 2π-10 рад/с и Л/= 5 - Ю- Гн получаем Scp =
= 0,64 мА/В. Таким образом, окончательно £/с = 2,74 В.
9.5. По схеме рис. 9.3 составляем уравнения iCT=i1— /,
L^-L-'+ri+i |/Л=0.
1 <// ώ С
С учетом /^iCT + i запишем
Так как icx = Su^ = SLdildt; dicr /dt = SLd2i/dt2, то, подставив в
предыдущее уравнение iCT, выраженное через ток i, и
продифференцировав его по времени, получим
CLiSLe^+(L+L))C^2 + rC^+i=0.
1 dt3 v ' ' Л2 dt
или
bod3i/dt3 + b1d2i/dtz + b2di/dt+b3i=0.
Для самовозбуждения цепи, описываемой уравнением третьего
порядка, на основании критерия Рауса — Гурвица необходимо
выполнение неравенств [1, § 5.9] ^t>0; b1b2>b3b0; b3>0, где
b0 = L1LCS; bi^L + L^C; b? = rC; b3 = l.
Подставляя значения коэффициентов, получаем
rC(L1+L)C-LiLCS>0,
откуда условие самовозбуждения
141
S<rC/L3K,
где Ь^Ь^ЩЬ^ + Ь).
9.6. Учитывая, что влиянием выходного сопротивления
транзисторного каскада можно пренебречь, уравнение фазовой
характеристики контура вблизи резонансной частоты приближенно
можно определить выражением
или tg<pK~2QAm/Q)p = 2QAf/fp, где Δ/=/-/ρ.
Отсюда отклонение частоты
Δ/=7^ι§Φκ = 4,7·103 Гц = 4,7 кГц.
9.7. Вначале определим амплитуду установившихся колебаний
из условия Scp = rC/M. При кубической аппроксимации
вольт-амперной характеристики транзистора
3 3
•S,cP = «i+-«3t/ycT = 2--0,5t/^T, мА/В;
-=1 мА/В;
пст= /"' "сру" = 1,57 В.
ус V 0,75α3
Из (9.68) [1] находим 2Af=fpj- — = 2 кГц.
9.8. 2Д/=10кГц.
9.9. Определим эквивалентную добротность контура
Q3K=fp/2Af=200.
Для достижения такой добротности в контур необходимо
ввести отрицательное сопротивление, определяемое из соотношения
[1,§ 9.12]
&*/&>= 1/(1-WH1^
откуда гОТр=0,9г, где r = p/Q0 = 63 Ом. Тогда готр = 57 0м; однако
'Ότρ = MS/C=K0C p2S. Отсюда
Koc = rOTp/(p2S) = 0,02; Μ= K0CL = 20 мкГн.
9.2. ГЕНЕРАТОРЫ С ВНУТРЕННЕЙ
ОБРАТНОЙ СВЯЗЬЮ И ГЕНЕРАТОРЫ
С ЗАПАЗДЫВАЮЩЕЙ ОБРАТНОЙ СВЯЗЬЮ
9.10. Автогенератор с внутренней обратной связью
представлен схемой замещения (рис. 9.5). Рабочая точка выбрана посредине
142
Г5*
Itf.l
О
*<г
Рнс. 9.5
падающего участка вольт-амперной
характеристики нелинейного элемента; при этом
отрицательное дифференциальное
сопротивление в рабочей точке | /?_ | = 50 Ом.
Индуктивность контура £=5мкГн, сопротивление
потерь г= 10 Ом. Определить максимальную
емкость контура С, при которой в схеме
будут возбуждаться автоколебания.
9.11. Определить сопротивления резисторов R1 и R2 в схеме
автогенератора на туннельном диоде (рис. 9.6), при которых
выполняется условие самовозбуждения и обеспечивается
устойчивость стационарного режима генератора. Заданы параметры:
С=50 пФ, (2=100, L=0,2 мкГ, £=1,5 В. Характеристика
туннельного диода приведена на рис. 9.7.
Рнс. 9.6
0,1 0,2 0,3 0,4 и,в
Рис. 9.7
9.12. Определить установившуюся амплитуду напряжения на
контуре генератора с туннельным диодом (см. рис. 9.6) с
параметрами, приведенными в примере 9.11.
9.13. Для генератора на туннельном диоде с вольт-амперной
характеристикой, приведенной на рис. 9.7, построить фазовый
портрет при условии, что рабочая точка выбрана при напряжении
смещения 0,15 В, а эквивалентное сопротивление колебательного
контура равно 150 Ом. Пользуясь фазовым портретом, нарисовать
временные диаграммы напряжения на контуре при возбуждении и
установлении колебаний.
9.14. Релаксационный генератор собран по схеме, приведенной
на рис. 9.8, с использованием неоновой лампы; /?=10кОм,
ί,ΜΑ
25
20
15
10
5
-
у
/
fL·
-vr
A SO
Οχ
150 UJ3
Рис. 9.8
Рис. 9.9
143
С=10нФ, £=200 В. Вольт-амперная характеристика лампы
приведена на рис. 9.9. Определить частоту колебаний и
ориентировочно изобразить временную диаграмму напряжения на емкости и
фазовый портрет генератора.
9.15. Резонансный усилитель с резонансной частотой 10 МГц и
полосой пропускания 2 МГц охвачен обратной связью через
линию задержки с временем запаздывания τ3=0,475 мкс. Рабочая
точка усилителя выбрана на участке с наибольшей крутизной.
Определить частоту генерируемых колебаний.
9.16. Определить частоты, на которых происходит
возбуждение генератора с запаздывающей обратной связью (τ3=1 мкс) и
ориентировочно изобразить временную диаграмму генерируемых
колебаний. Колебательная система резонансного усилителя
выполнена в виде связанных идентичных колебательных контуров,
настроенных на частоту 10 МГц при Q = 20 и коэффициенте связи
к = 0,22.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
9.10. Из условия возникновения колебаний в автогенераторе с
внутренней обратной связью R3>\R_ | находим C<Lj{r\R_ |), или
С<10_8Ф. Емкость должна быть не более 10 нФ.
9.11. Для устойчивой работы генератора, изображенного на
рис. 9.6, необходимо выполнение условия /?э>|/?_|. Из
вольт-амперной характеристики диода находим
| Д_ | = (0,2/5)· 103 = 40 Ом; R3 = pQ = 64 ■ 103 Ом.
На практике обычно принимается \R_ | = (0,3 ...0,5) R3. В
рассматриваемом случае /?э»|/?_|, поэтому для согласования R3 с
\R-\ требуется неполное включение. Определим коэффициент
включения контура р='-ч/31 R- |/Лэ«0,14. Схема генератора
примет вид, изображенный на рис. 9.10. Учитывая, что суммарная
емкость контура измениться не должна, находим С1С2/(С1+С2) =
= 50 пФ, откуда
Cj = 360 пФ; С2 = 58 пФ.
Для обеспечения устойчивого положения рабочей точки на
падающем участке характеристики диода необходимо выполнение
условия \R_\>Ri3, где Ri3 — внутреннее сопротивление
эквивалентного источника.
Рис. 9.10 Рис. 9.11
144
Для выбора сопротивлений R1 w R2 заменим схему делителя с
источником питания эквивалентной схемой на рис. 9.11. Если
выбрать рабочую точку посредине падающего участка
вольт-амперной характеристики, то статическое сопротивление туннельного
диода в рабочей точке будет
гст = 0,15/5 1(Г3 = 30 Ом.
При выполнении условия гст»/?;э напряжение на диоде будет
близко к напряжению источника:
UCM^E3 = 0,\5B.
Задаваясь R2 = 2 0m, находим
Я, = Д2 (£-£,)/£, = 20 Ом.
Для определения индуктивности дросселя Ьдр можно
воспользоваться условием ШрЬцр»R'^=p2pQ-
9.12. Найдем зависимость амплитуды первой гармоники тока
через туннельный диод от амплитуды напряжения методом трех
ординат, для чего зададимся различными значениями
амплитуд относительно рабочей точки (рис. 9.12). При этом /t =
= l/2(/max-/min). По найденным значениям /t построим зависи-
100 и,мв
Рис. 9.12
Рис. 9.13
мость среднего сопротивления диода /?ср = ц//1 от амплитуды
напряжения (рис. 9.13). Точке пересечения этой кривой прямой
R=R3=\24 Ом соответствует стационарная амплитуда колебаний,
равная 40 мВ.
9.13. Используем дифференциальное уравнение генератора на
туннельном диоде [1, § 9.9]:
dt2 \L CR.
di>- f l+r>lR- i =o
dt
LC
145
Для того чтобы ΒΑΧ диода вошла в уравнение в явном виде,
целесообразно записать уравнение через напряжение на контуре,
которое связано с током через индуктивность выражением
u=L~. Тогда
at
] du /r 1 λ 1 1 1
Ldt \L CR-) LU LC L
udt = 0
(пренебрегаем rK/R~ по сравнению с единицей).
Дифференцируя это выражение по времени и введя
обозначения
ί» = 2α; J—ω2.; J_e*e*>M,
L LC R- du du
где <р(и) = г'д—вольт-амперная характеристика туннельного диода,
получаем
d2u , Г_ , 1 d<v(u)~~\du , 2 η
^ + 12«+с-^\7,+(0°и = °-
Для построения фазового портрета генератора введем переменную
du d2u do do du dv ™ ■ ,
v =—, при этом -—-=—= = v—. Тогда дифференциальное
dt * dr dt du dt du
уравнение принимает вид
.* + [*+1йИ].+*-о.
Фазовый портрет для генератора, описываемого данным
уравнением, удобно строить методом Льенара [8, с. 544]. Для
этого выделим производную —=—< 2<х-\ ZX1 u+tOou> и
du ρ у_ С du J J
построим характеристическую кривую
*-[-*-ω·]*
Для ее построения аппроксимируем вольт-амперную
характеристику туннельного диода выражением in = a0 + al(u—U0) +а3{и —
-U0)3, где а0 = ЗмА; а1=-5· КГ2 А/В; а3 = \0А/В3.
Уравнение характеристической кривой принимает вид
или для заданных параметров
flu
ω0 3 1-10м2
146
ν/ωα,Β
0.4
(рис. 9.14, штриховая линия).
Для построения фазовой
траектории из произвольной точки т,
соответствующей начальным условиям,
проводится горизонтальная прямая до
пересечения с характеристической
кривой и из точки пересечения —
перпендикуляр на горизонтальную ось. Из
этой точки на горизонтальной оси (/)
циркулем проводится дуга 1т
достаточно малой длины, а далее
процедура повторяется.
Из построенной фазовой
траектории следует, что начало координат
является особой точкой типа
«неустойчивый фокус», а предельный цикл
близок к эллиптическому, что свидетельствует о близости
колебаний к синусоидальным (за счет фильтрации высших гармоник
контуром).
Для построения временной диаграммы по фазовой траектории
последняя разбивается на ряд участков по напряжению: Аць
Аи2, ... , Ащ; при этом на каждом участке определяется средняя
скорость ν< и Δί. = -Δί/(.
Vi
Последовательное применение этой процедуры дает
изображение нарастающего по амплитуде колебания (рис. 9.15).
Рис. 9.14
6 t,MKC
Рис. 9.15
0,6 0,8 1,2 1,6 2,0 %мС
Рис. 9.16
9.14. При включении ЭДС емкость заряжается через резистор
до тех пор, пока нагрузочная прямая не достигнет точки В (см.
рис. 9.9). При этом
uc{t) = E-{E-Un)e-"(RC\
Максимальное напряжение на емкости uc(fi) равно напряжению
зажигания газового разряда в лампе U3, поэтому
U^E-(E~Un)e~''l(RC\
откуда
147
*Д RCj £-[/э E-U,
Рабочая точка при зажигании разряда неустойчива и скачком
переходит в положение D, после чего происходит разряд емкости
— t/(R С)
до достижения точки F. При разряде uc(t)=U3e ' , где R{ —
внутреннее сопротивление неоновой лампы в зажженном
состоянии. Разряд продолжается до напряжения потухания uc=Un,
откуда время разряда
t2 = R(CIn (Uз/V„).
Период колебаний T=ti + t2. По вольт-амперной
характеристике лампы определяем £/3 = 100В, £/п = 25 В, Ле=500 Ом, отсюда
Г=0,63 мс, следовательно, частота колебаний
F=l/r=l,59 кГц.
Временная диаграмма напряжения на емкости приведена на
рис. 9.16.
Для построения фазового портрета найдем ток через емкость
ic = C— и отображение /с=/("с)» являющееся фазовым портретом
генератора.
На стадии заряда емкости ток ic = {E — uc)/R (прямая АВ на
рис. 9.17). При разряде емкости ic=—uc/Ri (прямая DF на
рис. 9.17). Если же учесть нелинейность лампы, т. е. зависимость
Ri от напряжения, то этот участок отображается кривой DF.
и\
«(f)/
1
Рис. 9.17
0 2 4 6 8 10fT ЪМГц
Рис. 9.18
9.15. При постоянном значении коэффициента усиления в
широкой полосе частот возможно генерирование колебаний на
частотах fk=k/x3. В полосе пропускания резонансного усилителя
размещаются составляющие с частотами 8,4; 10,5; 12,6 МГц
(рис. 9.18). Так как генератор работает в мягком режиме (рабочая
точка на участке с максимальной крутизной), то более слабые
составляющие будут подавлены в нелинейном элементе и
установятся колебания с частотой 10,5 МГц.
148
9.16. Так как kQ = 4,4>h АЧХ резонансного усилителя
горбая, с частотами максимумов [8, с. 195]
/1=/ρ(1-0,5ν/Λ2-1/ρ2) = 0,914/ρ«9 МГц;
Λ=/Ρ(1+0,5ν/Λ2-1/ρ2)=1,086/ρ*11 МГц.
u(t)k
-дву-
t,MKC
Рис. 9.19
При такой АЧХ возможны одновременно колебания с частотами
f\ и /2 и колебание генератора имеет вид биений (рис. 9.19).
9.3. ДС-ГЕНЕРАТОРЫ
КОЛЕБАНИЙ
ГАРМОНИЧЕСКИХ
9.17. В замкнутой системе, состоящей из усилителя и
четырехполюсника обратной связи (рис. 9.20), заданы: Rt = 100 кОм,
R2=l МОм, C\ = 10 пФ, С2=1 пФ. Коэффициент усиления А, = 1,3;
при этом аргумент комплексного коэффициента передачи равен 2π
во всем частотном диапазоне. Составить уравнение для
комплексной передаточной функции цепи и определить, возможно ли в ней
самовозбуждение колебаний.
Л
гС=Н
I
._i_*j° ' 1 L-j *j °
Рис. 9.20
Рис. 9.21
Рис. 9.22
9.18. Четырехполюсник обратной связи в автогенераторе
представляет собой цепочку из резисторов R и конденсаторов С= 170 пФ
(рис. 9.21). Выходное сопротивление активного четырехполюсника
Rt = 6,5 кОм. Частота генерируемого колебания должна быть
/г = 6 кГц. Определить сопротивление R и коэффициент усиления
активного четырехполюсника Ку, при котором в автогенераторе
возникнут колебания. Что изменится, если R и С поменять местами?
9.19. Для ограничения амплитуды автоколебания при
сохранении синусоидальной формы в ЯС-генератор (рис. 9.22) введен
149
терморезистор R„ характеристика которого представлена на
рис. 9.23. Параметры транзистора: S=2 мА/В, /?f=40 кОм;
коэффициент передачи четырехполюсника обратной связи на частоте
генерации Кос=1/29; сопротивления отвечают условию /?,·//?<с 1.
Определить сопротивление /?ст резистора в стоковой цепи,
обеспечивающее стабильный режим генерации при расположении
рабочей точки на характеристике терморезистора вблизи значения
Дср = 200Ом (17=0,1 В).
0J 0,2 0,3 U.B
Рис. 9.23
Рис. 9.25
9.20. Определить условия возбуждения замкнутой системы,
состоящей из активного четырехполюсника и четырехполюсника
обратной связи (рис. 9.24), считая, что активный четырехполюсник
имеет RB
оо и R„
0).
9.21. В ЛС-генераторе на операционном усилителе (рис. 9.25)
сопротивление резистора /?3=ЮкОм. Определить минимально
возможное сопротивление R2 для обеспечения устойчивой
генерации.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
9.17. Коэффициент передачи четырехполюсника обратной
связи (см. рис. 9.20) в операторной форме
k(d\^vi(p)- R2[R2 + \/(pC2)]
\Р> U, (p) PCl[Rl + \/{pCl)+R2/(pR2C2+\)Y
Подставляя очевидное соотношение Ui=kyU2 и заменяя оператор
ρ символом дифференцирования, приходим к дифференциальному
уравнению
d2u2 / 1 1 1-*Л</„2 1 _0
clt2 \RxCy R2C2 RlC2) dt RlR2ClC2
Коэффициенты этого уравнения
b0 = Ubl=^- +
R2C2 + Л,С2 ° ' 2 RyR2ClC2
= 106c~2.
В соответствии с критерием Рауса — Гурвица для устойчивости
системы необходимо, чтобы выполнялись условия &i>0, b2>0
150
[1, § 5.9]. Так как bt<0, то система неустойчива, т. е.
возбуждаются колебания на частоте ωΓ = 4/ό7=103 с-1 [1, § 9.11].
Ri С С С
о Ф^кшр^2
Рис. 9.26
9.18. Заменим активный элемент эквивалентным источником
ЭДС с внутренним сопротивлением Rt (рис. 9.26). Составим
уравнения Кирхгофа для данной цепи:
/1(Л, + Л-/х)-/2Л=С/;
-hR+h(2R-ix) -/3Л=0;
-I2R+h{2R-ix)=0,
где х=1/соС.
Решив систему относительно тока 1Ъ, найдем
/3 = С/Л2/[Л3-5Лд:2 + Лг(ЗЛ2-х2)+г(х3-6Л2х-4ЯКгх)].
Так как выходное напряжение U2=hR, то коэффициент
передачи
-£/2/£/=1/(α+/β),
™-'-Κϊ)2+?[3-(ϊ)2]:|,-(ϊ)'-6ϊ-4?ί·
На частоте генерации β = 0, учитывая, что х=1/(соС), находим
nT=l![RCJ6+4R~/R].
Если %/R<$zl, то (uT = l/(RCy/6) и при заданном С
R=65 кОм. По известным ωΓ и R находим коэффициент усиления
усилителя, необходимый для возникновения колебаний:
Ку= -а=29 + 23Лг/Л+4(Лг/Л)2 = 31,4.
Таким образом, для возбуждения колебания необходимо, чтобы
Ку>31,4.
При замене в четырехполюснике обратной связи С на R и R на
С частота генерации будет определяться выражением сог^
—\fbl(RC), улучшится фильтрация высших гармоник, вследствие
чего форма колебаний станет ближе к синусоидальной. Однако
потребуется дополнительный разделительный конденсатор для
отделения постоянной составляющей с выхода четырехполюсника
обратной связи на вход усилителя.
9.19. Коэффициент усиления линейного активного
четырехполюсника (без учета обратных связей) равен SR3K, где Дэк =
= RiR„/(Ri+R„), а коэффициент отрицательной обратной связи,
обусловленной терморезистором, равен R,/R3K.
151
В стационарном режиме выполняется условие
5/гм= 1/(1/29 -Λ,//?,.),'
откуда /?э1« 2 · 104 Ом.
Таким образом, искомое сопротивление
Rc^R^RJiRi-R3S) = 4,1 ■ 104 Ом.
Амплитуда напряжения на терморезисторе равна 0,1 В, а на
выходе автогенератора
ивых = 0,1 Л,./Л, «Ю В.
9.20. Условия возбуждения для замкнутой системы, состоящей
из активного четырехполюсника с RBX->оо и /?чых->0 н
четырехполюсника обратной связи (см. рис. 9.24), выглядит следующим
образом:
КУК0С>1; сру + срос = 2тш, /7=1, 2, 3,
где Ку, фу — коэффициент усиления и фазовый сдвиг активного
четырехполюсника; Кос, срос—коэффициент передачи и фазовый
сдвиг четырехполюсника обратной связи.
Условия возбуждения для данной цепи выполняются на
частоте [1, § 9.11] шгр = у/в/(RC), при этом коэффициент усиления
должен быть Ку>29.
9.21. Исходя из общего положения
АГУЛ:0С> 1; сру + срос = 2тш, л=1, 2, ... ,
и учитывая, что для четырехполюсника обратной связи в схеме на
рис. 9.25 на частоте генерации [1, § 9.11] /Toc(cor)= 1/3, находим,
что Ку(олг)>3. А так как для масштабного усилителя на базе
операционного усилителя Ky = R2/R3, то искомое минимально
возможное значение R2 будет
ЛГуЛ3 = 30кОм.
Глава 10. ПРИНЦИП ПАРАМЕТРИЧЕСКОГО
УСИЛЕНИЯ
10.1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ЛИНЕЙНЫХ ПАРАМЕТРИЧЕСКИХ ЦЕПЕЙ
10.1. Вольт-кулонная характеристика нелинейной емкости
(варикапа) аппроксимирована полиномом q(u) = q(0) +30- 10~9м +
+ 10-10~9м2, к. Управляющее напряжение, приложенное к
варикапу, изменяется по закону еу = Еу cos ωγί. Какова должна быть
152
амплитуда Еу для осуществления модуляции емкости на 50%
(л? = 0,5).
10.2. На цепь, состоящую из последовательно соединенных
резистора г и параметрического резистора R(t), сопротивление
которого изменяется по закону R(i) = R0[(l-\-McosUt),
воздействует высокочастотное напряжение e(t) = Ecos (ω0ί + φ). Выявить
структуру тока в цепи при условии r<tzR0 и Ω«:ω0.
10.3. В замкнутой цепи (рис. 10.1), образованной постоянным
резистором Л =10 Ом и параметрическим конденсатором C{t) =
= C0 + at, С0 = 20пФ, а = 0,1 пФ/с. Напряжение на конденсаторе в
начальный момент мс(0)=10 В. Определить закон изменения uc(t)
при ί>0.
Ш я
-о о
cm
q(t)
Рис. 10.1
Рис. Ю.2
Рис. 10.3
10.4. В схеме, представленной на рис. 10.2, сопротивление
переменного резистора изменяется по закону R(t) = R0(l+smQt),
Ω = 2π/Τ, а входное напряжение—по закону е (t) = U sin Ωί, причем
известно, что /?»/?(ί). Определить постоянную составляющую
напряжения на выходе цепи.
10.5. В цепи г, С (ή (рис. 10.3) емкость конденсатора
изменяется по закону C(t) = C0 [1+е ,/τ1(ί)], т = гС0. Определить
импульсную характеристику цепи, использовав в качестве воздействия
ЭДС e{t) = b(t), а в качестве отклика — заряд конденсатора.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
10.1. Дифференциальная емкость определяется выражением
С(еу) =
% =30·10-9 + 2·10·10-9Μ, пФ,
du »=*„+*,
где 30-10~9 = С0—емкость в рабочей точке и = Е0.
При заданном управляющем напряжении еу дифференциальная
емкость изменяется по закону
2-10
C(f) = 30-10-9 + 2-10-10-9£yCosM¥f = 30-10-9(l + ~
' * У у 30
χ £у cos оу = 30 · 10~9(l+mcosoy), где т=—-£, = 0,5, откуда
£у = 0,75 В.
10.2. Ток в цепи г, R(t)
153
i (t) = e (t)/[r + R(t)] = E cos ((o0t + q>)/[r + R0/(1+Μ cos Ωή].
При r<z:R0
i(t)&(E/Ro){l + Mcosnt)cos(u>0t + q>)
представляет собой амплитудно-модулированное колебание.
Глубина модуляции определяется глубиной модуляции параметра
R(t).
10.3. Для замкнутой цепи R, С (ή при линейно изменяющейся
емкости C(t) = C0 + at напряжение на конденсаторе определяется
выражением [2, с. 378]
uc{t)=U0(\+at/Coy(1+aR)l(aR\
где С/„ = МО) =10 В.
Подставляя заданные значения параметров, получаем
ис(*)= 10/(1+5-КГ3*)2.
10.4. Напряжение на выходе цепи
um(t) = R(t)e(t)/[R + R(t)l
При R^R(t)
"вых(')~— (1 +S'n Ωί) Usm Ωί = — Usin Ω' + у V*™* Ω' =
=^υ
sinQt+ -- -cos20i
2 2
Постоянная составляющая на выходе цепи
U0 = [R0/(2R)]U.
Таким образом, постоянное напряжение на выходе такой цепи
пропорционально амплитуде входного сигнала.
10.5. По определению импульсная характеристика является
откликом цепи на единичный импульс δ(ί — χ), подаваемый в
момент t = x. Дифференциальное уравнение, описывающее
рассматриваемую цепь,
ai{i)d^+a0{t)q{t,x) = b{t-x),
где M0 = r, flo(0 = {Co[l+e-'/tl(0]}"1·
Решение уравнения можно записать в виде
I
*(/,*)=' ехр{- Шаг).
λ:
Подставляя коэффициенты at (ί) и а0 (ί), получаем
154
q(t, x)=-exp|-
dz
rCo[l+exp(-z/T)]j'
При гС0 = т интеграл в квадратных скобках является
табличным [14, № 569]:
dz
τ I +exp(-z/r)
= _ίΖί_ [Ιη(1+ε-'/τ)-1η(1+ε-χ/τ)] =
~ln
+ e
-ι/t
+ e
-Φ
Введя обозначения a = t — x, запишем
l+e-'/T
τ \ 1+e
q(t, x) = ~exp] - - -In
-d-«vt
Из этого выражения следует, что в момент ί = χ, α = 0, q(t,x)
образует скачок, равный \jr. Из выражения для q(t, x) видно, как
изменение емкости во времени влияет на характер разряда: в
аргументе экспоненты кроме —α/τ (как и при постоянной емкости
+ ехр(-//т)
С0) появляется слагаемое In
]+ехр(—xjt)
Закон изменения
V-
0 1 2 J 4 5 6 t/t
Рис. 10.4
КО 2,0 3,0 4,0 t/r
Рис. 10.5
С(0/Со показан на рис. 10.4, а график функции rq(t, χ) при х = 0 —
на рис. 10.5. Отсчет времени t на рис. 10.5 ведется от момента
х=0, соответствующего максимальному значению C(t)/C0.
Штриховой линией на рис. 10.5 показана зависимость е~°'т,
соответствующая импульсной характеристике цепи при постоянной емкости С0.
10.2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ
КОЛЕБАНИЙ
10.6. Характеристика нелинейной емкости параметрического
усилителя представлена на рис. 10.6. Напряжение смещения,
155
С(и),пФ
φ
/6>c
*
К
-7 ~6 S -4 -Ζ -2-1 О 1 и,В
Рис. 10.6
Рис. 10.7
определяющее положение рабочей точки на характеристике,
Ес= — 2 В, амплитуда напряжения накачки {/„= 1 В. Данные
колебательного контура: резонансная частота /р= 107 Гц,
индуктивность L = 2,5 МкГн, внутренняя проводимость источника
сигнала G; = 3,75- 10~2 См. Проверить устойчивость усилителя при
шунтировании контура нагрузочной проводимостью G„ = Gli.
10.7. Определить полосу пропускания контура
параметрического усилителя при наличии и отсутствии напряжения накачки.
Коэффициент модуляции емкости шс = 0,05, общая проводимость
потерь контура G„ = Gi = 2 ■ Ю-3 См, резонансная частота контура
а>0=109рад/с, емкость контура в отсутствие напряжения накачки
С0 = 50пФ. Усилитель работает в синхронном режиме.
10.8. Определить коэффициент усиления параметрического
усилителя при следующих данных: проводимость нагрузки в сумме с
проводимостью потерь контура составляют '1,7-Ю-3 См, контур
настроен на частоту ω0 = 2 ■ 1 (г рад/с, емкость контура С0 = 300 пФ,
а коэффициент модуляции емкости тс = 0,05.
10.9. Одноконтурный параметрический усилитель представлен
эквивалентной схемой (рис. 10.7), G,*— проводимость,
учитывающая влияние накачки. Частота усиливаемого сигнала /с = 1.0 МГц,
внутренняя проводимость источника сигнала и проводимость
нагрузки равны Gi = G„ = \0~3 См. Емкость контура в отсутствие
напряжения накачки Со = 500 пФ.
Найти критическое значение коэффициента модуляции емкости,
при достижении которого усилитель переходит в режим генерации.
10.10. Емкость колебательного контура параметрического
усилителя изменяется по закону C(/) = 600+10cosooHi, пФ;
добротность контура в отсутствие накачки Q = 80, контур
настроен на частоту ωρ = ω„/2. Определить коэффициент усиления
напряжения.
10.11. Параметры колебательного контура параметрического
усилителя следующие: добротность Q = 90, емкость С0 = 250 пФ,
индуктивность £ = 150мкГн. Частота накачки /н = 2/р, где /„ —
резонансная частота контура.
Определить максимально допустимую амплитуду АС вариации
емкости, при которой усилитель сохраняет устойчивость.
156
10.12. Определить, во сколько раз увеличится ток в
параметрическом контуре при включении генератора накачки, если известно,
что характеристическое сопротивление контура ρ =100 Ом,
сопротивление потерь г = 3 Ом, а коэффициент модуляции гас = 0,05.
Рис. 10.8
с, ν.
10.13. В двухконтурном параметрическом усилителе (рис. 10.8)
первый контур с резонансной частотой /j = 30 МГц при
характеристическом сопротивлении pi = 160Om, внутренней
проводимости источника сигнала G, = 0,2 ■ 10~3 См и нагрузочной
проводимости G„y = Gi = 0,2' Ю-3 См должен за счет использования
накачки обладать полосой пропускания 80 кГц. Частота накачки
/н = 90МГц, постоянная составляющая параметрической емкости
С0 = 50пФ. Нагрузочная проводимость второго контура (7и2 =
= G„i=0,2· 10"3 См. Определить коэффициент модуляции
емкости.
10.14. В двухконтурном параметрическом усилителе из
предыдущей задачи определить коэффициент усиления мощности Кр.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
10.6. Из рис. 10.6 следует, что амплитуда изменения емкости
под воздействием напряжения накачки при Ес = ~ 2 В равна
ДС=4 пФ. Среднее значение емкости контура (включая среднюю
емкость варикапа)
Со-
KL
0,110~9Ф=100пФ.
Таким образом, глубина модуляции емкости тс=АС/С0 =
=0,04, а отрицательная проводимость G3K, учитывающая влияние
накачки [1, § 9.5],
|СЭ1[| = тсшрСо/2=1,25-10-4См.
Поскольку суммарная проводимость Gf + GH = 2GH = 7,5 · 10~2 См>
>|G31|, приходим к выводу об устойчивости рассматриваемого
усилителя.
10.7. В отсутствие модуляции емкости ширина полосы контура
на уровне 0,707 определяется из выражения [1, § 5.6]
Δω0ι707 = ω0/β.
Добротность контура
157
g = <D0C0/(G1I + Gi) = 25.
Таким образом,
Δω0,707=4· 107 рад/с; Δ/0,707~6,35 МГц.
При модуляции емкости в контур вносится отрицательная
проводимость
|6эк| = тсш0Со/2=1,25-10"3 См.
Добротность контура при модуляции емкости
ρ' = ρ·2·1(Γ3/(2·1(Γ3-1,25·1(Γ3)*67.
Ширина полосы на уровне 0,707
ΔωΌ,707 = ω0/β' = 1,49· 107 рад/с; Δ/ό,7θ7~2,37 МГц,
т. е. ширина полосы пропускания регенерированного контура
уменьшилась примерно в 2,6 раза.
10.8. Коэффициент усиления напряжения параметрического
усилителя, работающего в синхронном режиме, можно выразить
через эквивалентные добротности [1, § 10.6]:
(ОоСо (G„ + G,) _ G„ + Gi
Q™ (G„ + G,-- mc coo Со/2) сооСо G„ + Gi-mcCDoCo/2'
где QL и Q3K—эквивалентные добротности колебательного
контура усилителя при наличии и отсутствии модуляции емкости.
Проводимость, учитывающая влияние накачки,
|Сэк| = тсш0Со/2=1,5-10-3См.
Следовательно, коэффициент усиления напряжения
ЛГ£ = (СИ+С()/(СН + С(-СЭ1[)~8,5.
10.9. Критическое значение коэффициента модуляции емкости
[1, § Ю.6]
i»ic«p = 2((?i + G1I)/(rocCo)«0,064.
10.10. Коэффициент усиления при ωρ=ω„/2
KE = {Ga + Gi)/{GH + Gi-mc(o0C0/2) = {l-mc/mCsp)-1,
где mc%p = 2{Gi + G„)l{(i)QCQ) = 2IQ^·, Q3K—добротность контура с
учетом Gi и Ga — в отсутствие модуляции емкости, т. е. в данной
задаче
тс,ф=1/40, а тс = АС/С0=1/60.
Таким образом,
КЕ = 3.
10.11. Резонансная частота /р = 0,82 МГц, АС<5,5 пФ.
10.12. Результирующее активное сопротивление гэ = г— \гя„\ =
= г — гаср/2 = 0,5 Ом. Ток в контуре возрастет в г/гэ = 6раз.
158
Рис. 10.9
10.13. Схема замещения усилителя представлена на рис. 10.9.
Эквивалентная отрицательная проводимость, учитывающая
влияние накачки, определяется выражением [1, § 10.7]
\G3S\ = (mcC0/2)2(o1(o2/Gti2.
В данной задаче ш2 = ши-шь а требуемое значение \G3K\ находим
из условия
C( + G„i-|G,.I=- ' -2Δ/· '
CiPi /ι Ρι'
откуда
\G3K\ = Gi + GHl-
2Δ/, 1 2ΔΛ 1
~7 = 20и1- — .
.ft Р( /ι Ρι
Подставив заданные параметры, получим
|Сзк| = 3,83-1(Г4См.
Тогда коэффициент модуляции емкости
т2 /jGJb,
<-oV ω(ω2
10.14. Коэффициент усиления мощности определяется по
формуле [1, § 10.7]
KP=(l+G3K/2Gnl)-2 = 553.
10.3. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ
КОЛЕБАНИЙ
10.15. В колебательном контуре параметрического генератора
емкость С (ή изменяется по гармоническому закону с частотой
/н = 2-107Гц при среднем значении С0 = 100пФ. Сопротивление
потерь контура г = 2 0м. Определить необходимые для генерации
значения тс при правильной настройке контура и при расстройке
его на 50 кГц относительно частоты /и/2.
10.16. Определить коэффициенты модуляции параметра
реактивного элемента, при которых возможно возбуждение
колебаний в параметрическом контуре, настроенном на
частоты ω„/2, ωρ, 3ωΗ/2. Задана добротность контура на
частоте ωι=ωΗ/2: β=100.
159
24-
/ -
«»Τ ι ι
.,1 .. ..
c(u),r?c
28
20
16
12
β
* 1
ι
10.17. В одноконтурном
параметрическом генераторе, работающем на
варикапе, характеристика которого приведена
на рис. 10.10, напряжение смещения
равно Есм= — 2 В. Параметры
колебательного контура: L = 2 10~6 Гн, С=190 пФ,
сопротивление потерь гк = 1 Ом.
Определить критическое значение коэффициента
модуляции емкости тСкр и амплитуду
-5 -4 -з -2 -1 О и,В напряжения генератора накачки.
10.18. Контур параметрического ге-
с- ' нератора, работающего в синхронном
режиме, настроен на частоту ωρ = ω„/2 и состоит из индуктивности
L= \00 ■ UT 6 Vvl,гараметр^чесъ-зйэдлъоста С {1)= Ш3 {\ + тсcas<&„(),
пФ, и активного сопротивления потерь г, = 2 0м. Определить
критическое значение коэффициента модуляции емкости.
10.19. Определить время установления колебаний в параметро-
не, если известно, что отношение начальной амплитуды к
стационарной Ао/АСТ=0,001. Контур параметрона настроен на
частоту /р=/„/2. Коэффициент модуляции емкости контура гас в
два раза больше критического т„, емкость контура изменяется по
закону C(i)=100(l+mccos2u· 120· 106/), пФ, проводимость
нагрузки контура GH = 5 ■ 10"4 См.
10.20. В параметроие емкость контура изменяется по закону
С(/) = 30 (1+0,13 cos 2π· 80 · 106/), пФ. Время установления
стационарной амплитуды 10 мКс при добротности контура Q = 80.
Определить стационарную амплитуду колебаний параметрона,
если начальная амплитуда Ао=\0~5 В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
10.15. Критическое значение коэффициента модуляции емкости
определяется выражением
тс кр = 2Λ/ΐ + (2Δωρ/ωρ)2"/β,
где Δω = ωΗ/2—ωρ^ расстройка контура относительно частоты
ωΗ/2; добротность контура Q= l/(2n/pCor)~80.
При ωρ=ωΗ/2 критическое значение
mCsp = 2/Q = 0,025.
При настройке на частоту ωρ — Δω
ю£1р=0,032.
Таким образом, для возбуждения колебаний в контуре,
расстроенном относительно /„/2 на 50 кГц, требуется коэффициент
модуляции емкости т'Скр=*0,0Ъ2.
160
10.16. Критическое значение коэффициента модуляции емкости
в параметрическом генераторе, работающем в синхронном
режиме, определяется соотношением между частотой накачки ω„ и
частотой собственных колебаний контура ω0. При наиболее
благоприятном для генерации соотношении ω„ = 2ω0 mCKp = 2JQ =
= 0,02. При ω„ = ω0 значение тСкр возрастает до
т'сшр= 1,41/Уё = 0,141,
при ω„ = 2/(3ω0)
Wc.P = 1,28 \[Q =0,276.
10.17. При смещении Еси= — 2 В из графика на рис. 10.10
определяем емкость варикапа в рабочей точке Св = 8 пФ. Емкость
контура (с учетом емкости варикапа)
С0 = С+СВ= 198 пФ.
Частота настройки контура
ω0 = 1/^1^=5,025-107 рад/с.
Добротность контура
Q=moL/r*\00.
Критическое значение вариации емкости
гоС1р = 2/β = 0,01.
Амплитуда изменения емкости на варикапе
АС=тСжрС0к4пФ.
По графику на рис. 10.10 находим, что при Еси= — 2 В и
Св = 8 пФ изменению АС=4 пФ соответствует изменение
напряжения в 1 В. Следовательно, необходимая амплитуда напряжения
генератора накачки U= 1 В.
10.18. Критическое значение коэффициента модуляции емкости
при ωρ = ωΗ/2, г = 2 0м определим по формуле
>ncKP = 2/Q = 2r/^/L/C0,
где С0=1000пФ—емкость контура в отсутствие напряжения
накачки.
Следовательно, тСкр = 0,013.
10.19. Время установления колебаний в параметрическом
генераторе определяется выражением [1, § 10.8]
'max = 4 In (A„/A0)l[(m - 2d) ωρ],
где d=\/Q = GJ(<upC0y, ωρ = ωΗ/2.
В соответствии с аналитическим выражением для С (ή,
приведенным в формулировке задачи 10.19, Со = 100 пФ=10-10 Φ
и ωΗ = 2π· 120· 106 рад/с. Поэтому d= 1,325 · 10~2 и критическое
161
значение тСк„ = 2а=2,65 · Ю-2 [1, § 10.8]. Кроме того, по условию
тс = 2тСкр=4а, так что разность mc — 2d=2d=2,65\0~2. Таким
образом,
>тах=41п(1000)/(2,65-10"22п-60-106)*2,8-1(Г5 с.
10.20. Используя выражение [1, § 10.8]
In (ACT/A0) = (га - 2/Q) оутах/4
и учитывая, что ωρ = ω„/2=40· 106, получаем
АСТ = А0 exp [(га - 2d) оутах/4].
Подставляя значения т в выражение для С (ή, находим АСТжО,22 В.
Глава 11. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ НА НЕЛИНЕЙНЫЕ
И ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
11.1. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ В НЕЛИНЕЙНЫХ
БЕЗЫНЕРЦИОННЫХ ЦЕПЯХ
11.1. На нелинейный элемент с характеристикой у = ах2, а = 0,2 1/В,
действует процесс χ (ή с равномерной в пределах — 1... +1 В
плотностью вероятности. Определить плотность вероятности
выходного процесса.
11.2. Нормальный процесс с нулевым математическим
ожиданием и дисперсией 2 В2 подается на нелинейный элемент с
характеристикой у=у0еах, ^0 = 0,5 В, а = 0,1 1/В. Найти плотность
вероятности выходного процесса.
11.3. Найти плотность вероятности квадрата огибающей
нормального случайного процесса.
11.4. Нормальный процесс с нулевым математическим
ожиданием и дисперсией 9 В2 подается на нелинейный элемент с
характеристикой
{ах2, х^0,
0, х<0; а = 0,5 1/В.
Найти плотность вероятности и математическое ожидание
выходного процесса.
11.5. На двухсторонний ограничитель с характеристикой,
приведенной на рис. 11.1 (а = 0,5 В, Ь=\ В), действует нормальный
162
случайный процесс с нулевым математическим ожиданием и
дисперсией 1 В2. Найти математическое ожидание и дисперсию
процесса на выходе ограничителя.
11.6. Найти математическое ожидание и дисперсию процесса
на выходе нелинейного четырехполюсника с характеристикой,
изображенной на рис. 11.2, при входном воздействии в виде
синусоиды со случайной фазой; амплитуда постоянная, равная 2 В.
11.7. На идеальный двухсторонний ограничитель с выходным
напряжением ±2 В подается нормальный случайный процесс с
нулевым математическим ожиданием. Определить
характеристическую функцию выходного процесса.
11.8. На нелинейный элемент с характеристикой у = ах2
подается нестационарный процесс вида χ(ί) = ξ(0 +6cosOi, где ξ(ί) —
стационарный нормальный случайный процесс с нулевым
математическим ожиданием и дисперсией σ2. Записать выражение для
одномерной плотности вероятности выходного процесса.
11.9. Процесс χ (ή с равномерной плотностью вероятности в
пределах ± 1 В и независимыми значениями подается на
нелинейный элемент с характеристикой у = ахъ, а = 2 В-2. Определить
двумерную плотность вероятности процесса на выходе.
11.10. На квадратор с характеристикой у—ах1 (а = 0,2 1/В)
воздействует гауссовский случайный процесс с корреляционной
функцией /?х(τ) = σ*ехр ( — α|τ|), где σχ = 0,5 В; ос = 104 1/с.
Определить спектральную плотность мощности выходного процесса.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
11.1. Вначале запишем плотность вероятности входного
процесса
c/2b, — b^x^b,
0, \х\>Ь; Ь=\ В.
Величину с определим из условия нормировки
р{х) = -
υ
p(x)dx= j ^dx = ^{b + b)=l,
-ь
163
т. е. с=\ и р(х)=\/(2Ь).
Обратная функция для характеристики у = ах2 двузначна:
х=±л/у/а, а у'(х) = 2ах и
. . Γθ,5 В-1, -1 B^x^l В,
'(*Ho,M>ib.
Поэтому
При у ->0 u(v/u6c -»0, чем и объясняется обращение ρ (у) в
бесконечность в этой точке.
11.2. Плотность вероятности выходного процесса
^w=-4f7«p{-sb[ln(£",a
auyjln у
11.3. Огибающая нормального случайного процесса
распределена по закону Рэлея
ρ(Α) = <σ V **V
[О, Λ<0,
из чего следует, что
ρ(Α>)=ρ(ή = \α° V ΰσ
(θ, ζ<0,
, ζ^Ο,
т. е. распределение экспоненциальное.
11.4. Плотность вероятности
/ΌΗ
,5(у) +
2 2σ^/2παγ
о, ^<о.
Математическое ожидание
ι [у
-,/(W)
е , у>0,
ту =
yp(y)dy =
lu^Jbi Vя
α2σ3
<fy.
164
Обозначая л/у/а =ги используя табличное значение интеграла
[13, 3.461.2]
x2e\p(-b2x2)dx = ~T при Ь>0,
получаем ту = а<з2/4=1,12 В.
11.5. Вследствие симметрии входного распределения и
нечетности характеристики ограничителя очевидно, что математическое
ожидание выходного процесса равно нулю. Линейной части
характеристики ограничителя соответствует усеченное гауссовское
распределение в пределах ±Ь, а горизонтальным участкам —
дельта-функции с коэффициентами, определяемыми площадями
входного распределения при \х\>а. Таким образом, плотность
вероятности выходного процесса
ехр(-^гл)> -Ь<у<Ь,
р(у) = \ S(a)6(y-b), y = b,
S(a)6(y + b), y=-b,
. 0, \y\>b,
где S(a) =
ρ(χ)άχ = Φ(ςο) - Φ (a/b); Φ (ζ) =
-χ2 β
e dx —
интеграл вероятности.
Второй начальный момент при ту = 0 равен дисперсии
™2у= y2p(y)dy= J S(a)6(y + b)y2dy + S(a)6(y-b)y2dy +
— оо — оо b
b b
+
2 a
У ;—exP
bawln
a2y2
2b2 σ2
dy = 2S{a)b2 + 2
2 a
у =exp χ
/>σ4/2π
-ь
*'-££)*·
165
Интеграл в формуле для т2у не выражается через элементарные
функции. Однако, учитывая, что нормальное распределение
достаточно полого вблизи нуля, можно аппроксимировать ρ {у) при \у\<Ь
равномерным распределением (это допустимо при а<а). Тогда
p(y)=lb[l-S(a)], -b^y^b;
ь
о
Окончательно получаем
m2y = <52y=2S(a)b2+j[l-2S(a)] = 0,73 В2.
Интересно отметить, что большая часть мощности процесса в
данном случае обусловлена значениями ±Ь, а не промежуточными
значениями.
11.6. Так как выходной процесс представлен только двумя
1 2
значениями: 0 и 2 В, то р(у) = -&(у) + -δ(у-2); ту=1,33 В;
т2у = 2,66 В2; σ2=1,33 В2.
11.7. Для идеального двухстороннего ограничителя
Г 2, х>0,
^ = 2S'gnn-2,*<0.
Плотность вероятности
р(у) = ]-Цу-2)+]-6(у+2).
Характеристическая функция распределения процесса у (t)
определяется выражением [1, § 7.6]
θ(η) =
p(y)e™dy= U(y-2)e^ydy+ Х-Ь{у + 2)ё*Чу.
Используя фильтрующее свойство δ-функции [1, формула
(2.91)], получаем
9(r|) = ie"-i2,,+ -ei2,, = cos2r|.
11.8. Функция bcosClt является математическим ожиданием
заданного процесса, поэтому его плотность вероятности
выражается в виде
166
p(x, t)=—= exp } - —jlx-bcosQtyl.
Используя (11.6) [1, § 11.1], получаем
""· ή=Ί^[αρ{- Mfi -*cos£2')}+exp {■
X -
— b cos Ωί
2σ2
Таким образом, выходной процесс является негауссовским и
нестационарным.
11.9. При независимых значениях хи х2 двумерная плотность
вероятности р(уи y2)=Pb>i)p(y2)-
Для у = ах плотность вероятности
]
Р(У) =
р(х)
dx
= J 2b-3ay2'3/a
О, М>2В,
—, -2В^2В,
где Ь = \ В (см. задачу 11.1).
Тогда
ν iw^5' ~2В^2В'
<(УиУ2 Ы
(О, \у\>2В.
11.10. ^(ω) = α2σ42πδ(ω)+α2σ44α/(4α2 + ω2)=10"32πδ(ω) +
+ 1(Γ3·4·1(Γ4/(4·1(Γ8 + ω2), В2/Гц [1, § 11.3].
11.2. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО
ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
11.11. На диодный однополупериодный детектор подается
нормальный случайный процесс χ (ή с корреляционной функцией
^*(t) = 9e~103|T|cos Ι06τ, В2. Диод имеет линейно-ломаную вольт-
амперную характеристику, внутреннее сопротивление диода /?< =
= 100 Ом. Параметры нагрузки детектора: /? = 100кОм, С=
= 1000пФ. Найти математическое ожидание и дисперсию
выходного процесса ζ (ή.
11.12. Пользуясь данными предыдущего примера, найти
плотность вероятности выходного напряжения детектора при
квадратичной вольт-амперной характеристике диода у = ах2, а = 2 мА/В2.
167
11.13. На вход тракта, состоящего из идеального
одностороннего ограничителя и идеального ФНЧ с частотой среза
Ω = 2· 103 рад/с, подается нормальный процесс χ (ή с
корреляционной функцией Rx(x) = 4e\p ( — p2t2)cos 105τ, где β = 10 М/с.
Определить математическое ожидание выходного процесса ζ (ή
и построить графики плотностей вероятности и энергетических
спектров на входе и выходе ограничителя у (ή, а также на
выходе ФНЧ.
р(х).
Wx{b))\
О
Г
щ
ω
ΙΔίΛ
Ζω0 (ο
Рис. И.З
11.14. Решить пример 11.13 при замене одностороннего
ограничителя устройством с характеристикой ^ = |х|.
11.15. На вход линейного детектора подается узкополосный
гауссовский процесс χ (ή с равномерным в полосе Л/=10кГц
спектром W0 = 10~* В2/Гц при центральной частоте /0 = 10 МГц.
Постоянная времени нагрузки детектора ЛС=20мкс. Определить
плотность вероятности процесса на выходе детектора ζ (ή и его
спектральную плотность мощности.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
11.11. Так как R/R^IO5 ■ 10_2:»1, то угол отсечки θ близок
к нулю и cosG^l; следовательно, при выполнении условия
2π/ω0«:RC«;2π/Ω [Ι, § 8.9] на выходе детектора воспроизводится
огибающая входного процесса ζ (ή. Поскольку огибающая имеет
рэлеевское распределение, то mz = l,26ax = 2,52 В, σ2 = 0,43σ2 =
= 0,86 В2 (см. решение задачи 4.9).
11.12. При квадратичной характеристике диода и выполнении
остальных условий задачи выходное напряжение пропорционально
168
квадрату огибающей [1, § 11.4]. В этом случае mz = aaxR = S В;
a2z=a2a$R2 = 64B2.
11.13. Так как частота среза ФНЧ удовлетворяет
условию β«:Ω«;ω0, то на выходе фильтра выделяется
постоянная составляющая ограниченного сигнала,
пропорциональная огибающей: Ζ (ί) = Κ0α0Α (ή, где ос0 — коэффициент
Берга. Для идеального ограничителя без смещения угол
отсечки θ = π/2, следовательно, ос« = 0,32. При этом т2=1,26<зх<х0 =
= 0,57 В; af = 0,43a^oco = 0,88 В . Графики плотностей
вероятности и энергетических спектров процессов приведены на
рис. 11.3.
11.14. По сравнению с однополупериодным при двухполупе-
риодном выпрямлении удваиваются постоянная составляющая и
среднеквадратическое значение, а в спектре остаются только
полосы с центральными частотами, кратными четным значениям
несущей частоты.
11.15. При выполнении неравенства 2π/103:»/?(?:»2π/107
огибающая процесса, выделяемая детектором, распределена по закону
Рэлея [1, § 4.6]
Ρ(ή = ·
iexp -±_), z>0,
0, ζ<0,
где σ2=Ψ0Α/=\ В2.
Ковариационная функция процесса ζ (ή приближенно
описывается выражением [1, формула (4.77)]
λ,(δ) =
πσ
Τ"
i+b2W
где rx(x)— огибающая корреляционной функции χ (ή.
Для процесса с равномерным в полосе Δ/ спектром
[1, табл. 2.1]
rx(t) = (sinnAfx)/nAfx.
Выполняя преобразование Фурье для Κζ (δ), получаем следующее
выражение для спектральной плотности мощности [5]:
/К
-άω
Δω ω
Рис. 11.4
169
(l+£J), |ω|<Δω,
ζ (_0, |ω|>Δω,
График спектральной плотности мощности Wz (ω) приведен на
рис. 11.4.
11.3. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ
ГАРМОНИЧЕСКОГО СИГНАЛА
И ГАУССОВСКОГО ШУМА
НА АМПЛИТУДНЫЙ И ЧАСТОТНЫЙ
ДЕТЕКТОРЫ
11.16. На вход тракта полосовой фильтр — детектор — ФНЧ
подаются гармонический сигнал А^ cos2nf0t и помеха в виде шума
с равномерным спектром в полосе Δ/= 1 МГц при центральной
частоте f0 = 0,5 МГц. В качестве полосового фильтра используется
резонансный усилитель, настроенный на частоту сигнала, с
полосой пропускания 5 кГц. ФНЧ реализован в виде
интегрирующей цепи с параметрами /?=10кОм, С=0,01 мкФ. Отношение
сигнал/шум на входе тракта Αι/σι=0,5. Найти отношение
сигнал/шум на выходе.
11.17. Решить задачу 11.16 при замене квадратора
односторонним ограничителем (линейное детектирование).
11.18. На вход тракта из идеального ограничителя с
характеристикой y = asignx; a = 2 В, и узкополосного фильтра,
настроенного на частоту сигнала, подается гармонический сигнал с
амплитудой 0,2 В и помеха с дисперсией 0,01 В2. Определить
амплитуду сигнала и отношение сигнал/помеха на выходе тракта.
11.19. На вход каскадно-соединенных двухстороннего
ограничителя с характеристикой j; = signx, частотного детектора с
крутизной характеристики детектирования 5"=10~4 В/Гц и ФНЧ с
полосой пропускания 0,5 кГц подается сумма гармонического
сигнала с амплитудой 1 В и шума с дисперсией σ2 = 0,05 В2 в
полосе Δ/=10 кГц. Найти дисперсию шума на выходе частотного
детектора.
11.20. По данным задачи 11.19 определить отношение
сигнал/шум на выходе частотного детектора при действии на входе
ЧМ сигнала с девиацией частоты А/гд=10Гц.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
11.16. На выходе полосового фильтра амплитуда сигнала А2 =
2
= А1КУ, а дисперсия al= W0Af3Kf = — -Afo.jKf, следовательно,
отношение сигнал/шум по напряжению на выходе фильтра
170
η Al
41
σ2
σι
AlKy ~<7ι
/π Δ/ Ν
J 2 AF У
/2 Af
/ π Δ/ο. 7
При выполнении условия l/Af0<1?s>RC^l/f0 можно
воспользоваться формулой (11.47) [1, § 11.5], откуда 9з~-^<72=4.
>2
11.17. ?3*V2?2 = 79 [1, § 11.5].
11.18. Согласно [1, § 11.7] As=l,06B, /гвых = 2,4.
11.19. Согласно (11.55) [1, § 11.6]
Отсюда дисперсия помехи на выходе частотного детектора
п;,=1 wv{a,ja-' ls--'v'i>'
Ω
45Ч2ДИ^
Ωί,Ίχ. J /\ j
m
2π 4Λν ' 2π
Γ2
Спектральная плотность мощности 1¥0 = σ /(2nAF).
Следовательно, σ2„ = 0,52 10~4 В2.
11.20. Лвых = 4,6.
11.4. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ НА ЛИНЕЙНЫЕ
ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
11.21. На идеальный перемножитель подартся процессы с
корреляционными функциями /?х(т) = 0,1е~"10 '^ в2; r (τ) =
= 0,5е~2 |т|, В2. Определить ширину спектра процесса на выходе
перемножителя.
11.22. В линии дальней связи уровень сигнала вследствие
замираний изменяется во времени по закону Α(ί)=Α0 [\+Μξ(ή],
где ξ(/)—случайный процесс с функцией корреляции е °,
τ0 = 0,1 с. Сигнал представляет собой случайный процесс с
равномерным спектром W0 в полосе 2500 Гц. Найти среднюю
мощность процесса на выходе линии связи.
11.23. Белый шум действует на одноконтурный резонансный
усилитель, емкость контура которого изменяется по закону
C(t) = C0k2t2, ίι5ζί5ζί2· Выявить характер изменения мгновенного
энергетического спектра шума на выходе усилителя.
11.24. На линию задержки с равномерной АЧХ, время
запаздывания которой изменяется по закону z3=z0 + kt, действует
171
случайный процесс с корреляционной функцией Rx (τ) = σ2 ехр χ
χ (— α Ι τ I). Определить корреляционную функцию выходного
процесса.
11.25. Радиотелескоп принимает излучение объекта,
удаляющегося от Солнечной системы со скоростью 0,5 ■ 108 м/с и имеющего
корреляционную функцию излучения гх(т) = е cos2nf0z, β =
= 104 с-1; /о=1010 Гц. Найти корреляционную функцию процесса
на выходе радиотелескопа.
*ЮЛ77}№,
ФНЧ
z(t)
u(t)
Гетеродин
Рис. И.5
11.26. На вход синхронного детектора^ (рис. 11.5) подается
процесс с равномерным в полосе 1 кГц спектром с центральной
частотой 2 МГц и дисперсией 16 мВ2. Гетеродин дает колебание
м(i)=0,5cos(2π2· 106ί+φ), а ФНЧ имеет полосу 1 кГц.
Определить дисперсию выходного процесса.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
11.21. В соответствии с [I, § 11.8] корреляционная функция
процесса на выходе перемножителя определяется в виде
Д(т) = едЗД=0,05е-3'°2|т|.
Интервал корреляции по определению (см. задачу 7.5)
Используя соотношение между интервалом корреляции и шириной
спектра (см. задачу 7.5) τκ=π/(2Δω), получаем
Д/=1/4тж = 80Гц.
11.22. Корреляционные функции случайного сигнала с нулевым
средним и канала связи определяются выражениями
ЗД = ^?^; *η(τ)=1+^ν|ΐ|/τ°; Δω = 2π/<
откуда R(x) = Rx(z)R„(x) = A
- Л2
1+-MV
2
hi/to
sin Δωτ/2
Δωτ/2
. Таким
образом, средняя мощность (при сопротивлении 1 Ом) выходного
процесса
а2 = Д(0) = 0,273 В2.
172
11.23. Резонансная частота и добротность контура изменяются
во времени по закону
PW у/ЕсЩ Jlclkt ki w '\/c(') *'
Используем соотношение WBKX (ω) = WBX (ω) /Γ2 (ω), где /Γ (ω) —
модуль передаточной функции цепи.
Передаточная функция резонансного усилителя [1, § 5.6]
К(гш) = АГтах/
1 + ίβ
ω
ω
О ω.
ρπιη
ρ mar
Рис. 11.6
С увеличением емкости С (ή
резонансная частота ωρ (ή уменьшается и
соответственно полоса частот
мгновенного спектра процесса,
выделяемого контуром, смещается в область
низких частот. Добротность контура
во времени снижается, что
сопровождается расширением полосы
частот (рис. 11.6).
11.24. Поскольку линия задержки
имеет равномерную АЧХ, выходной и входной процессы
связаны соотношением y(t) = x [t—τ3(ή]. Тогда импульсная
характеристика линии задержки может быть записана в
виде g(t,z) = 6 [τ3(ή -ζ].
Используя интеграл свертки и определение корреляционной
функции, получаем
00 00
Ry{ti,t2)=i J δ[τ3(ίι) -zj δ [τ3(ί2) -z1\Rx{zl -z2)dzldz2 =
— ao — ao
= Rxb,(ti)-T,{h)+ti-ti]·
Отсюда при z3 = x0 + kt корреляционная функция
Ry(t2-ti) = Rxbo + kti-T0-kt2 + t2-ti] =
= Rx[k{tl-t2)+t2-tl] = Rx[T{l-k)] = a2xe-*lx{l-k)l.
Из полученного выражения видно, что при линейном
изменении времени запаздывания изменяется масштаб времени для
корреляционной функции (она растягивается в (1—&) раз), а
энергетический спектр сжимается во столько же раз.
11.25. Так как ω0»β (узкополосный процесс), то за счет
эффекта Доплера происходит смещение спектра вниз на величину
Ω = νω0/ο= 1,66 ■ ΙΟ9 рад/с. В соответствии с теоремой смещения
спектра [1, § 2.8] временная функция должна быть умножена на
множитель еш', следовательно, корреляционная функция примет
вид
173
Ry(τ) = Rx(τ)cosΩτ=-σ2ε τ [cos(go0 —Ω)τ+οο5(ω0 + Ω)τ].
11.26. Корреляционные функции сигнала и гетеродина
определяются выражениями
Rx(z)=a2^~^-cos π/οτ; Ru(τ) = -Λ2 cos2π/0τ;
На выходе ФНЧ будет выделяться низкочастотная
составляющая процесса с корреляционной функцией Rz (τ)=-Α2σ2 χ
χ sine (nFz/2). Дисперсия этого процесса
σ2 = Λζ(0)=10-3Β4
Глава 12. ДИСКРЕТНАЯ ОБРАБОТКА
СИГНАЛОВ. ЦИФРОВЫЕ ФИЛЬТРЫ
12.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ
СИГНАЛОВ. СПЕКТР ДИСКРЕТИЗОВАННОГО
СИГНАЛА
12.1. Аналоговый сигнал s(ί) = A sin — t, 0^t^Tc = 20 мке, А = \ В,
' с
подвергнут дискретизации путем умножения его на периодическую
последовательность прямоугольных отсчетных импульсов. Шаг
дискретизации Г=2мкс, длительность импульсов т0 = 0,5мкс,
амплитуда U0. Найти спектральную плотность дискретизованного
сигнала и его амплитудный спектр (рис. 12.1).
12.2. Сигнал s(t) = e~M, ί>0, α=5·103 1/с, подвергнут
дискретизации с шагом Г=10 мке при длительности отсчетных
импульсов τ0 = 100 не (рис. 12.2, а). По спектральной плотности 5"Γ(ω)
дискретизованного сигнала sT(t) оценить долю энергии
сигнала s(t), содержащуюся в основном (центральном) лепестке
спектра.
12.3. Определить полную энергию, содержащуюся в спектре
ΞΤ(ω) сигнала из предыдущего примера, и сопоставить ее с
энергией, определенной непосредственно по дискретизованному
сигналу sT(t).
174
1,0
0,5
s(t)-e-at
ΓΤτ<.
~ГГТт>
οτπ
А
о т^
/
ζ
/\
?4
τ
"*"*
ч
N
1
rB t
Рис. 12.1
12.4. Отсчетный импульс s {kT) запоминается в интегрирующей
ЛС-цепи на время Тср, необходимое для срабатывания АЦП. Это
время должно быть менее шага дискретизации Г= 10 мкс.
Синтезировать запоминающее устройство, обеспечивающее требуемую
точность измерения s(kT) за время то=Ю0нс (ошибка в
пределах 1%) и удержание измеренного напряжения в течение
времени Гср = 8мкс на уровне не ниже 95% от первоначального
значения.
А
1 —
—
St
It)
ι
6
(t)
i '
I
1
1 '
On
Рис. 12.3
MT
-τ ο. τ
ΜΤλ
Г с А
12.5. Прямоугольный импульс s (ή подвергнут дискретизации с
шагом Τ (рис. 12.3). Найти спектральную плотность Sr((o)
дискретизованного сигнала.
12.6. Экспоненциальный импульс s(t) = e~at, t^O, α = 2·104 1/с,
подвергнут дискретизации с шагом Г=10мкс. Найти
спектральную плотность дискретизованного сигнала.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
12.1. Спектральную плотность дискретизованного сигнала
определим по формуле [1, § 2.17]
SrH=tf0y Σ sinc(^)s(W-«Ml),
n= - оо \ /
где спектральная плотность исходного (континуального) сигнала
175
С/ \_^4^с COS((o7*c/2) -ίωΓ/2
о (СО) ; гяг С
ν 7 π 1 - (ωΓ./π)2
Положив для упрощения U0 = 1 В, получим
S (Ш) = ^-^- У sinc^""T°^ cos[((°-'1(')i)7W23 е-'"[(«»-иШ1)Гс/2]
После подстановки исходных данных модуль этого выражения
принимает вид
5Γ(ω)«3,18·1(Γ6 У smc(nn/4) ^^Z__, в/Гц.
sT(b))/sT(0) График 5V(oj) представлен
f . на рис. 12.4. В данном примере
ω! /2 = π/Γ превышает
максимальную частоту спектра 5" (ω) и
отдельные спектры,
соответствующие различным значениям и, не
перекрываются. В полосе частот
от — со ^2 до шг/2 спектр ST((o)
практически точно
воспроизводит спектр 5" (ω) (с
коэффициентом τ0/Γ при £/0 = 1).
12.2. Спектральная плотность
S((a) исходного сигнала s(t) в
полосе частот от — шт до сот
Рис· 12·4 изображена на рис. 12.2,6.
Пренебрегая энергией, содержащейся
вне этой полосы, находим энергию дискретизованного сигнала в
центральном лепестке спектра 5Υ(ω) (и = 0):
00
— оо
где Э5—полная энергия континуального сигнала s(t).
В рассматриваемом примере
Э,=
ν ' 2α
и, следовательно, при U0= 1 В
3ο = (τ0/Γ)2·1/2α=1(Γ4/104=1(Γ8 в2-с.
12.3. Основываясь на выражении для ST(m) [1, § 2.17] и
применяя равенство Парсеваля, энергию в и-м лепестке спектра
176
можно привести к виду 3„=30sinc2 (ηπτ0/Τ). Тогда суммарная
энергия спектра 5Υ(ω) дискретизованного сигнала Эу = Э0
00
χ Σ sine2 (ηπτ0/Τ)].
С помощью выражений [13]
1+2х
sine2 (χ) =
1 1—cos2x
ΣΙ π γ-ι
cos л* _ π πχ χ
~Τ2 Τ ~ Τ +Τ
выражение для суммарной энергии спектра приводится к простому
результату
Э^=(т0/Г)Э5.
Определим теперь энергию того же дискретизованного сигнала
sT (t), представленного не в спектральной, а во временной области.
Энергия к-го отсчета s(kT) при длительности τ0 равна x0s2 (кТ)
[изменением s(t) в интервале τ0 пренебрегаем]. Тогда
Э =1^2(кТ)=-^.
^ 1, — Л 1С
к = 0
При осГ«:1
Эу = τ о /2а Г=(τ0 / Τ) Э5,
где 3s = l/2oc— полная энергия сигнала s(t) (см. пример 12.2).
Как и следовало ожидать, энергия полного спектра Эу
совпадает с энергией дискретизованного сигнала sT(t). В пределе,
при скважности (Τ/τ0)-*\, Эу-► Э5 и эффект дискретизации
пропадает [отсчетные импульсы вписываются в сигнал s(t) без
пропусков ].
кТ-гд кТ кТ+Тср (к+1)Т
δ)
Рис. 12.5
12.4. Структурная схема устройства выборки и хранения
отсчетов представлена на рис. 12.5, а. Внутреннее сопротивление
177
источника сигнала η в сумме с прямым сопротивлением замкнутого
электронного ключа (ЭК) составляет десятки ом, например п + г„р =
= 20 Ом. Обратное сопротивление разомкнутых ключей R06P и
входное сопротивление операционного усилителя (ОУ) Rm составляют от
сотен килоом до единиц мегаом. Диаграмма напряжения сигнала s (t)
и напряжения на конденсаторе uc{i) представлены на рис. 12.5,5.
При замкнутом 3Κι (ЭКг разомкнут) постоянная времени
цепи заряда конденсатора т3 = {п + г„р)С должна отвечать условию
1-е */т'>0,99, откуда τ3/τ0^ 1 /In 100и0,2. Отсюда С^0,2т0/(г/+
+ г™)«1 нФ (изменением s(t) на интервале τ0 пренебрегаем).
При размыкании 3Kt (ЭК2 также разомкнут) постоянная
времени цепи разряда конденсатора τρ = (Яобр || Ro6p || Rm) C^RyC
должна отвечать условию е τ*»Ιτ',^0,95, откуда Гср/тр«0,05.
Следовательно, Ry должно отвечать неравенству Ry^tp/C=
= Гср/0,05С* 160 ком. Время срабатывания 3Kt при включении и
выключении не учитывалось.
При замкнутом ЭК2 напряжение uc(t) обнуляется.
12.5. Применяя преобразование Фурье [1, § 2.6] к заданному
дискретизованному сигналу и учитывая, что спектральная
плотность функции δ(ί-&Γ) равна e~i<akT, находим
м и
SrH= [U0 Σ b{t-kT)]c-^dt=U0 X e
J k=-M t=-M
iakT
= TJ ып1<й{2М + 1)Т/2]
~ ° sm(aT/2)
Графики 5Γ(ω) при iV=2M + 1=9 и S((o) при TC=NT
представлены соответственно на рис. 12.6, α и б. Вид полученной £Γ(ω)
ST(to)k
Рис. 12.6
-100 -50 0 50 /00 Г,кГц
а) ±
7 а
-100 0 100 Г, кГц
Рис. 12.7
178
объясняется тем, что спектр дискретизованного сигнала равен
сумме (с коэффициентом 1/1) смещенных спектров S(gj — π2π/Τ)
исходного сигнала s(t) [1, формула (2.123)].
12.6. Спектральная плотность заданного дискретизованного
сигнала определяется выражением [1, § 2.17]
Sr(M)= £ s(kT)e-l,*T,
к = 0
и в данной задаче (с учетом формулы геометрической прогрессии [13 ])
к = 0 ' °е
Модуль этого выражения Sr (ω) =1/^/1 — 26cosa)r+62 и модуль
спектральной плотности исходного экспоненциального импульса
5'(ω)=1/ν/α2+ω2 [1, табл. 2.1] представлены на рис. 12.7 (см.
также обсуждение результата решения задачи 12.5)
12.2. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
12.7. Дискретизованный сигнал, рассмотренный в предыдущей
задаче, ограничен длительностью TC = NT:
/V — 1
М')= Σ e_etr8(i-ifc7), O^k^N-l, oc = 2-104l/c, Г=10мкс,
к=0
Гс = 80мкс.
Найти спектральную плотность Sr(co) сигнала sT(t) и
дискретное преобразование Фурье (ДПФ) S(n) последовательности отсче-
/V — 1 /V — 1
тов s(k)= ^ e~atr= Σ bk, b = e~aT. Полученные результаты
4=0 к=0
сравнить. Как изменится S(n) при уменьшении шага дискретизации
Τ исходного континуального сигнала вдвое?
12.8. Показать, что при непериодическом сигнале s(i), заданном
на конечном интервале TC = NT, ОДПФ определяет отсчеты
сигнала {s(kT)=s(k)}, £=0,1, ..., N—l, периодически
повторяющиеся с периодом N
12.9. Найти ДПФ сигнала s(k) = Asin(—к), А = \, 0^k<N=S.
12.10. Вычислить ДПФ S(n) последовательности отсчетов
отрезка гармонического сигнала s(k) = AsinhoTk), 0^k<N, N=S,
A = \, ωΤ=(2-2π/Ν=π/2; π; 5 -2π/Ν= 1,25π; 1,5; π/Λ^π/8).
12.11. Найти ДПФ сигнала s(£) = 7 + 6cos(—/t—0,8 ] +
' +2cosfe& + 0,5j, 0<k<N=9.
179
12.12. Найти ДПФ сигнала, рассмотренного в задаче 12.5.
Число отсчетов сигнала N=2M+l=9, нумерация отсчетов: к = 0,
1, 2, ..., JV-1 (рис. 12.8,я).
12.13. Сигнал из предыдущей задачи дополнен N нулевыми
отсчетами (рис. 12.8,6):
,.ft/0 при 0:^8,
^ ' {θ при9^А:^17.
Найти ДПФ этого сигнала и сравнить его с результатом,
полученным в предыдущей задаче.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
12.7. ДПФ заданного сигнала s(k) определяется выражением
П, § 12-4]
N- 1 .Лс
S(")= Σ *(*)е~'* ,
к = 0
и в данном примере (с учетом формулы геометрической
прогрессии [13])
/V — 1
2п
~1—П
S(n)= χ Ьке~^"к = {\-Ь")/(\-Ье~'»").
1с=0 V
Сопоставим S(n) со сплошным спектром Sr(ro)
Sr(a>)= X ^*e-itofcr = (l -^Лге-;<йЛ'г)/(1 -^~ίωΓ).
к = 0
На частотах ω„ = η2π/Τ0 значения спектра Sr(a>„) тождественно
совпадают с соответствующими значениями S (и).
"о]
а)
01Z3
Щ f
0123
ви0
В)
0 1
щ
0/23
Рис. 1
180
1 f
s(k)
/\/=9
8 к
• ·
s(k)
N=■78
8 '7
SC/2)
/V=9
г з 6
. t.i. t, ι ι,!, Ι
9 П
2.8
к
» η
3 η
-100 -50 0, „ 50 100
5)
11 ГГт r 11111 г
■200
-100
г,*гц
15
β-Σ*ν*
rriit mi
jL
100
Рис. 12.9
ZOO Г,*Гц
Уменьшение шага дискретизации Τ при Тс = const приводит к
увеличению вдвое числа N как временных отсчетов сигнала sT(t),
так и отсчетов его спектра Sr(co„)=S(n) (рис. 12.9). Форма ST((o)
при уменьшении Τ несколько изменяется за счет меньшего
перекрытия отдельных спектров SJa>—η2π/Τ) исходного
континуального сигнала длительности Г„.
нуального сигнала длительности
12.8. Вследствие периодичности функции
,2п ,2п . .
ι — пк ι — ηΙκ±ΙΝ) _ __ _
е" =е Λί обратное ДПФ
Аналогично, ДПФ
£ s(k)e~'~NkH = S(n±lN).
к=0
Таким образом, ОДПФ определяет периодически
повторяющуюся с периодом Ν совокупность ограниченного числа Ν
отсчетов {s(k)} исходного непериодического сигнала.
Напомним, что дискретизация с шагом Τ ограниченного по
длительности непериодического сигнала s(t) приводит к
периодической структуре сплошного спектра Sr(ro) с периодом (на оси
частот) 2π/Τ. В свою очередь, повторение этого дискретизованного
сигнала sT(t) с периодом TC = NT приводит к дискретизации
спектра Sr(ro) с интервалом Аоз = 2п/Тс.
12.9. Основываясь на выражении для ДПФ, получаем
IV-1 /„ \ .2п , ,N-1
к=о V / " к=о
e-''^-,)A-e-'i("+,)A"
Модуль этого выражения
„, , \ΝΑ/2 при η = ΙΝ±\, 1=0, 1, ...,
v ' /О при других п.
Как и следовало ожидать, полученный результат является
периодическим повторением линейчатого спектра гармонического
сигнала.
12.10. Представим алгоритм ДПФ в виде
S(n)= Σ s(k)e"Nnk= I s(k)Cos(^nk }-i Σ s(k)x
k = 0 k = 0 Vv / k = 0
181
xsin(~nk) = a„-ibn, \S{n)\ = S{n)=\/at + bt; argS(«) = -arctg£.
При четном N и действительных отсчетах s{k) S(n) = S *( — η),
и = 0, 1, ..., Ν/2 [1, § 12.4]. Это позволяет упростить вычисления
S(n) путем расчета коэффициентов ап и Ь„, п = 0, 1, ..., N/2, с
помощью алгоритма БПФ. Сигнальный граф алгоритма БПФ с
прореживанием по времени [1, рис. 12.39] изображен на рис. 12.10.
Вычисления выполнены с помощью микрокалькулятора
«Электроника МК-61» по программе:
П-хО
П->х2
П->х1
П-хЗ
П->х8
П->хс
П->х2
Π->χί/
+
+
П->х4
П->х6
П->х5
П->х7
П->ха
П->х<?
П-х5
П->х6
х->П1
2
+
+
+
+
+
+
+
—
П->х9
FV
х->П8
х->Пя
дс-»Пе
х->П<?
х-П2
х-П5
х->П0
2
П-х2
-г
П->х0
П->х2
П->х1
П-хЗ
П-х8
П->хс
П->х2
FV
—
х->П8
П->х4
П->х6
П->х5
П-х7
П->ха
П->х<?
П-х5
+
х-П5
Π-χί>
—
—
—
—
—
—
—
х->
П2
Π-xrf
+
х->П9
х->П2>
χ->Πί/
х->П6
х->ПЗ
х->П4
х-П7
П->х9
П->х6
х->П2
П->х8 Π->χί>
х->П6 с/п
Указания. Исходные данные s(&) (вычисляемые перед счетом
с помощью калькулятора) вводятся в регистры памяти RG0...RG7
в соответствии с номером отсчета к = 0...7. В этих же регистрах
после счета запоминаются выходные данные: а0 в RG0, ах в RG1,
bi в RG2, а2 в RG3, Ь2 в RG4, аъ в RG5, Ь3 в RG6, я4 в RG7.
Хранение выходных данных позволяет вычислить (с помощью
того же калькулятора) значения S(n) и argS(n). При повторном
счете исходные данные s(k) вводят заново.
S(0k ж А
s(V\\ /Об
sCJ,oX///v
8β1ινννγ
yfck(x-y)
Рис.
.——•02'
12.10
I
1
a) 1
1
-6-4-
5
ί [
1
δ) Ι
1
-5-J
4
2 <
4
i
12
7
St
I I
1 6) I
Ι λ, ι
4
1
4 6 η -6-4-2 0
S(n)
1 3
.1.. l!fitll
Ъ 5 η
Рис. 12.11
i
±
9
f гт I !
2 4 6 rt
Ιΐΐιϋ!
112
J4 /г
Результаты вычислений ДПФ S(n) представлены на рис. 12.11.
Штриховыми линиями показано периодическое повторение
182
спектров ДПФ. Полученные результаты наглядно иллюстрируют
частотную характеристику устройства ДПФ [1, § 12.15].
При ωΓ=π/2 составляющие спектра S(п) (рис. 12.11,а)
попадают на максимумы АЧХ 2-го частотного канала (и =±2) и нули
остальных каналов (отсчеты s(k) соответствуют дискретизации
ровно двух периодов отрезка синусоиды).
При ωΤ=π все отсчеты s(k) = 0 (два отсчета на период
синусоиды) и, следовательно, спектр ДПФ равен нулю. При
замене в выражении s(k)=A sin (ωΓΑ;) функции sin на cos
спектральная составляющая (только при ω>0) попадает на максимум
АЧХ 4-го частотного канала [S(4) = NA = 8]. Указанная замена
эквивалентна представлению отрезка дискретизованной гармоники
в комплексной форме e,<etr=cos(a)7jfc) + isin(a) Tk).
При ωΓ=1,25π шаг дискретизации Τ (8 отсчетов на 5 периодов
синусоиды) превышает максимально допустимое значение π/ω.
Устройство ДПФ выделяет в этом случае ложные (зеркальные
относительно η=±Ν/2) составляющие S(±3) = AN/2. Истинные
составляющие спектра (ω = ±5·2π/ΝΤ) возникают в результате
периодического повторения вычисленного ДПФ (рис. 12.11,6).
При незначительной расстройке частоты сигнала
относительно максимума АЧХ того или иного частотного канала (в
данном примере η = 2, (ύΤ=1,5φη2π/Ν = π/2ζζΙ,57) составляющая
S(±n) = S(±2) несколько уменьшается, а на других частотах
спектр не, равен нулю (рис. 12.11, в).
При ωΤ=π/8 дискретизации подвергается полпериода
синусоиды и ДПФ S(n) представляет собой отсчеты спектра Ξτ(ω)
дискретизованного синусоидального импульса (рис. 12.11, г).
Число отсчетов N=8 в данном случае недостаточно и ДПФ не
дает полной информации о спектре. При недостаточном числе
отсчетов N это положение справедливо во всех других случаях
большого отклонения ω Γ от центральных частот η2π/Ν, а также
при дискретизации импульсных сигналов другой формы.
12.11. ДПФ суммы двух гармонических колебаний
представлено на рис. 12.12.
S(n) 63
L
1,!..1.1
ΙίΛ
Л.
-/V-8 -6 -3 -101 5 6 8/V
ι ι 1—1—1 ι ι ν
Рис. 12.12 -Ζη/Τ -3ω0-ω00ωΰΖω0 2rt/T ω
12.12. Подставляя s(k) в выражение для ДПФ, получаем
« \-п V -'■£"*-п 1-е"'2'и _iuoNnpHn = 0, ±N, ±2N, .
[П)~ \ioe ~ U°T^^-\ 0 при других п.
183
Результат (см. рис. 12.8, в) представляет собой значения
сплошного спектра ST(a>) дискретизованного сигнала sT(t) на
частотах ωη = η2π/Τι. = η2π/ΝΤ=ηω1/Ν, и в данном примере при п,
не кратных Ν, эти значения равны нулю (см. также рис. 12.6, а и
[1, § 12.15]). Таким образом, в пределах периода N лишь одна
спектральная составляющая с амплитудой NU0 отлична от нуля.
12.13. При увеличении числа временных отсчетов с N до N{ =
= 2N добавлением N нулевых отсчетов интервал между соседними
дискретными частотами сокращается вдвое. Заменив в ДПФ
предыдущего примера период N на Nl = IN, придем к ДПФ, которое
определяет большее число спектральных коэффициентов (рис. 12.8,г):
S{n)=U0{\-e-im)l{\-e~imiN).
Модуль этого выражения S(n)= U0sin(nn/2)/sin(rm/2N)
представлен на рис. 12.8,г.
12.3. z-ПРЕОБРАЗОВАНИЕ
12.14. Найти z-преобразование §(z) сигнала s(t) = e"1' = e''l+"°)\
/^0, дискретизованного с шагом Т. Определить полюсы функции
§(г) в трех частных случаях:
р1=0, ρί = σί<0 и ρι=ΐωι.
12.15. Установить, как изменится z-преобразование
произвольного дискретного сигнала s(k) в результате умножения его на
к. Используя установленную связь, найти z-преобразование
дискретного сигнала s1 (к)=к-1 {к), где
](k\ = il пРик>0'
[> (0при£<0
— последовательность отсчетов из единичного скачка s(t)=\, ί^Ο.
12.16. Используя результат, полученный в предыдущем
примере, найти z-преобразование дискретного сигнала
s2(k)=k2-\{k).
12.17. Найти z-преобразование дискретного сигнала s [к),
представленного на рис. 12.13.
rafir) sz(k) 4t 4r5
Jftff ZS
il
s(k)
0/23 к 0/234 к 0123 к Рис. 12.13
12.18. Найти z-преобразование дискретного сигнала Si(/c) =
= kbk-\(k), используя известное z-преобразование сигнала s[k) =
= bkl(k) (см. п. 2 решения примера 12.14).
184
12.19. Установить, как изменится равенство, определяющее
z-преобразование дискретного сигнала s(k) = bk· 1 (к), в результате
его дифференцирования по Ь.
12.20. Дискретный сигнал s{k)=\{k), & = 0,1, 2, ..., оо прорежен
Μ—1 нулевыми отсчетами, в результате чего получен сигнал
(рис. 12.14) для М = 4
. ._Гу(/и)=1 при к = тМ,
1 * ' (0 при других к.
Выразить !§! (ζ) через z-преобразование непрореженного
сигнала s(k)=\(k).
y1111111IIHfIITIIff1IIT1—
0f2S*5 φ) *
JmU'4''4" 4" :#''''' к
_ι ι 1 ι ι ι ».
Рис. 12.14 0 12 3 4 5т
12.21. Найти z-преобразование последовательности отсчетов из
прямоугольного импульса s(k)=U0, к = 0, 1, ..., iV —1, N=9.
Сопоставить ДПФ этого же сигнала (см. задачу 12.12) с
найденным z-преобразованием.
12.22. Последовательность отсчетов из прямоугольного
импульса s(k)=U0, к = 0, 1, ..., Ν—\, N=9, прорежена нулевыми
отсчетами с нечетными номерами, в результате чего получена
последовательность 2N отсчетов
|£/опри/с = 0, 2, ..., 2(N-l),
5^ ' {0прик=\, 3, ..., 2/V-1.
Найти z-преобразование прореженной последовательности
отсчетов. Сопоставить полученный результат с ДПФ сигнала,
рассмотренного в задаче 12.12.
12.23. Найти z-преобразование последовательности конечного
числа отсчетов sl(k) = s(k)-k, где s(k) = l (к = 0,\, ..., Ν—1) —
сигнал, рассмотренный в примере 12.21 (при U0 = \).
12.24. Найти отсчеты s(k) сигнала, z-преобразование которого
S(z) = 2-z-2 + 3z-5.
12.25. Найти обратное z-преобразование функции S(z) =
= z_3/(z + 0,8) разложением ее в степенной ряд.
12.26. Найти обратное z-преобразование функции S(z)=
= (2z2 + 3z)/(z—1)2 путем использования табличных
преобразований.
12.27. Решить предыдущий пример вычислением
интеграла обратного z-преобразования с использованием теоремы о
вычетах.
185
12.28. Найти обратное z-преобразование дробно-рациональной
функции S(z) = (z+0,2)/(z2 — l,8z+0,8) путем разложения ее на
простые дроби и использования табличных преобразований.
12.29. Найти дискретный сигнал, z-преобразование которого:
а) S(z) = 0 2z/(z-0,8)(z-l)2;
б) §(z) = (2zi + 3z)/(z-l)2 (сопоставить с примерами 12.26,
12.27);
в) S(z) = (2z2 + 4z)/(4z2-5z+l).
12.30. Решить предыдущий пример при
§(z) = (5z2-l,35z+2,25)/(z2-l,26z + 0,81).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
12.14. Основываясь на выражении для прямого z-преобразова-
ния [1, § 12.6], находим.
00 СО
Щ= Σ s{kT)z~k = X ePlVk=l-fe'''rz-1+e'''2rz-2 + ...=
k = 0 k=0
= l/(l-eP'V')=z/(z-eP'').
Полюс функции S (ζ) расположен в дочке ζπ = еР' .
1. При pt=0 ζπ = 1, сигнал 5(/)=еР'=|, /JsO, последовательность
отсчетов s(kT)=\, к—О, I, 2, ..., и z-преобразование S(z) = z/(z—I).
2. При р1=<51 rot=0, zn= ea>'=b, где 0<6<1 (при о(<0).
Соответственно j(i)=e°·', /3*0, s(kT)=ea^T-b\ fc = 0, 1, 2, ..., и S(z) = z/(zri>).
3. При ρ^κΰ! at=0, ζπ = ε'ωι7". Соответственно s(/) = e,(0'', /^0,
s(ikr) = eft0·*7', £ = 0, 1, 2, ..., и S(z) = z/(z-e'(0·7").
Положение найденных полюсов ζπ на z-плоскости
иллюстрируется рис. 12.15.
Рис. 12.15
12.15. Дифференцируя по ζ выражение, определяющее
z-преобразование сигнала s(&), получаем
S'(Z)=
dz
00
Σ *(*Κ
.Jc=0
= £ (-Λ)5(Λ)ζ-'[-1 = -ζ-1 Σ ks(k)z-\
k=0 k=0
откуда
£ Jb(*)z-* =
)с=0
ί/ζ
Σ *(*)Η(-
k=0 J
186
В рассматриваемом примере s(k)=\(k), S(z) = z/(z— 1) (см. п. 1
примера 12.14) и для sl(k) = l(k)-k
Si(*) =
d
dz
ζ
z-\
м=
-I
{-ζ)=ζΐ{ζ-\γ
12.16. Представим заданный сигнал в виде s2(k) = [\(k)-k]k=
=s1(k)-k (z-преобразование сигнала st (к) найдено в примере
12.15). Тогда, используя методику, рассмотренную в предыдущем
примере, находим
'Г z ](-z) = z(z+l)/(z-l)3.
S2(z) =
dz
О2
12.17. Представляя заданный сигнал в виде суммы (см.
рис. 12.13) s(k) = s1(k) + s2(k) = 3l(k)+l(k)-k и используя
результаты примеров 12.14 (п. 1) и 12.15, находим
S(z) = S1(z) + S2(z) =
3z
3z2-2z
(ζ-\γ (ζ-ιγ
Этот же результат получается при использовании z-преобра-
зования только сигнала s2(k)=\(k)-k. Из рис. 12.13 видно, что
сигнал s(k) получается из s2(k), если в нем «уничтожить» два
отсчета: s(l)=l, s(2) = 2, а все остальные сдвинуть на три шага
влево. Для z-изображения находим
S(z) =
,-l
[z-\f
■2z'
z3 =
3z2-2z
12.18. Используя результат, получаемый при
дифференцировании §(z) по ζ (см. пример 12.15), находим
$Λή=
d
~dz
ζ
z-b
("*) =
-b
м=
bz
(z-bf
12.19. Дифференцируя обе части равенства У bkz k=-. г
к=о (z~b)
получаем
по Ь,
ΚΛ*)=ΣΜ
k-iz-k =
к=0
(z-bf
(сравни это соотношение с результатом предыдущего примера).
Дифференцируя второй раз по Ь, получаем
UHIM*-i)*
k-2z-k =
2z
\з'
При b = 1 это выражение приводится к виду
187
уЦк-ή k = _z__
L· 2 (ζ-1)'
Дифференцирование первого равенства по b I раз дает
Σ k{k-\)...{k-l+\)b- -z ~ =
*-!„-*_ "*
12.20. Основываясь на выражении для z-преобразования,
получаемое оо ОО
§ι(ζ) = Σ Μ*)ζ"*= Σ 5(m)z-mM= Σ z-mM=l/(l-z-M) =
)c=0 m = 0 m=0
= zM/(zM-l) = S(zM),
где S(z) = z/(z — 1)—z-преобразование сигнала s(&)=l(A;).
Соотношение S t (z) = § (zM) справедливо при прореживании
произвольных дискретных сигналов. Справедливо и обратное
утверждение: если St (z) = S(zM), то их обратные z-преобразования
связаны соотношением
ilr\_js{m) ПРИ к = упМ,
' (О при других к.
12.21. Основываясь на выражении для z-преобразования,
получаем
к=0
Первое слагаемое в правой части полученного выражения есть
z-преобразование отсчетов из сигнала s(t) = UQ, t^O, а
второе— z-преобразование отсчетов из того же сигнала, задержанного
на ./V шагов дискретизации.
Из сопоставления ДПФ последовательности конечного числа
отсчетов прямоугольного импульса
| α ~ί2πη
S (η) = Un .,, ιν.
(см. задачу 12.12) с найденным z-преобразованием !§(ζ) видно, что
S (и) есть значения 1§(ζ), равномерно расположенные в Ν точках
2_е1(2д/лг)п единичной окружности на плоскости ζ. Этот вывод
справедлив для любых последовательностей с конечной длиной в
N отсчетов.
12.22. Основываясь на свойстве z-преобразования сигнала,
прореженного нулевыми отсчетами (см. пример 12.20), и используя
z-преобразование непроцеженного сигнала (см. пример 12.21),
находим §(z)=l/0(l-z ")/(1-2~2)·
Из сопоставления ДПФ S (и) сигнала, рассмотренного в задаче
12.12, с найденным S(z) следует, что значения S(z), равномерно
расположенные в 2N точках ζ = е'("/ЛГ)и единичной окружности на
плоскости ζ, соответствуют двум периодам ДПФ S(и).
Отметим, что для увеличения числа отсчетов одного периода
спектра ДПФ S (и) необходимо добавлять нулевые отсчеты в конце
(или в начале) последовательности s(k) (как, например в задаче
12.13). Прореживание последовательности s(k) нулевыми
отсчетами не дает такого увеличения числа отсчетов спектра.
12.23. Используя методику нахождения z-преобразования при
умножении последовательности отсчетов на к, рассмотренную в
примере 12.15, находим
s,w-^(-«)-
dz
dz
-^-^-ζ'Ν
-1 z-\
M =
(z-1)-
(z-lf
(z-l)(\-N)z-"-z-z~"
("Φ
Nz~
(ζ-ΐγ
1
Основные результаты z-преобразований дискретных
последовательностей, полученные в данном параграфе, приведены в
табл. 12.1. Здесь же (пи. 8—10) приведены z-преобразования
других дискретных функций [12], часто встречающиеся в
практических задачах.
Таблица 12.1
Номер
1
2
3
4
5
6
7
9
10
s(k), k>0
к
к2
Ьк
kbk~l
2
*(*-1)...(*-/+1)
/.'
Abk sin ak
Abk cos ak
а-Ь {аФЬ)
k = o
ζ
{z-bf
i'-ьГ1
Abz sin a
z2-2bzcosa+b2
Az(z — bcosa)
z2—2bzcosa + b2
ζ
(z-a)(z-b)
12.24. 5(0) = 2, 5(2)=-1, 5(5) = 3. При других к s(k) = 0.
189
12.25. Представляем заданную функцию !§(z) в виде ряда по
отрицательным степеням ζ:
S(Z)=:Z-4
■Σ (-ο,8ζ-γ,
k=0
_(ζ + 0,8)_
откуда (с учетом задержки на четыре шага)
[ > X 0 при£<4.
Однако эту же функцию S(z) можно разложить в ряд по
положительным степеням ζ:
., , [1,25(- 1,25)3-Л при к^З,
откуда s(k) = < '
v ; (0 при к>Ъ.
Таким образом, если функция S(z) задана алгебраическим
выражением, то ее обратное z-преобразование в общем случае не
является единственным. Вид последовательности s[k) зависит от
области сходимости ряда.
В первом из полученных в данном примере разложений ряд
сходится при |zl>0,8, а во втором — при |z|<0,8 (z/0).
Последовательность s{k), соответствующая второму разложению S(z), в
практических задачах не встречается. Поэтому в дальнейших
примерах область сходимости определяется как внешняя область
круга \z\ = r0, содержащего все полюсы функции S(z) (обычно
12.26. Представим заданную функцию S(z) в виде
Используя табличное z-преобразование (см. п. 2 табл. 12.1) с
учетом опережения на один шаг дискретизации первого
слагаемого, получаем
s(k) = 2(k+iy\(k+\) + 3k-l(k) = [2(k+l)+3k]-l(k)=(2+5ky\(k).
Замена здесь функции 1(А;+1) на 1Ш объясняется тем, что
2(к+\)\к=_1=0.
12.27. Основываясь на формуле обращения [1, § 12.6], находим
Ul = l
Вычисление вычета в двукратном полюсе ζπ = 1
подынтегральной функции дает
190
;(£) = Res
z= 1
2z*+1+3z
\2
-]=!(^+1 + 3z')
(z_()2 j rfzV.„ ,.._, s2(*+l) + 3Jfc=2 + 5*,
k=0, 1, 2,..., при k<0 s(k)=0.
12.28. Представляем заданную дробно-рациональную функцию
: §(z) в виде суммы двух^ простых дробей, соответствующих
корням Zj 2 знаменателя S(z) = c1/(z — z1) + c2/(z — z2), z12 = 0,9±
±VO,81 -0,8 = 0,9 + 0,1. Коэффициенты разложения находим с
помощью ci=S(z){z — zi)\z=z.:cl=6, с2=—5.
Таким образом,
S(z) = -^ "— = 6
-Z
z-1 z-0,8 z-1 z-0,8
(множитель ζ-1 соответствует задержке на один шаг
дискретизации). Используя табличные преобразования (см. пп. 1 и 4
табл. 12.1), получаем (с учетом задержки на один шаг)
ί(^) = [6-5·(0,8)*-1]·Ι(Α:-Ι).
12.29. Представляя заданные дробно-рациональные функции в
виде суммы простых дробей, находим
я\ Я(7\= °'2г - с' ι С2 4- Сз = 4 4- ] - 4
' { ' (z-0,8)(z-l)2 z-0,8 >-l)2 z-1 z-0,8>-l)2 z-1
(коэффициенты разложения с; найдены путем приведения дробей к
общему знаменателю и приравнивания коэффициентов при
одинаковых степенях ζ в числителях разложения), откуда (см. пп. 1, 2, 4
табл. 12.1) с учетом задержки на один шаг
s(k) = [4-{0,S)k-1+{k-l)-4]-l(k-\) = [3,2-{0,8)k~2+k-5]x
х\(к-2).
Замена 1(к— 1) на I (А: — 2) объясняется тем, что s[k)\k=l=Q;
' v ; (z-1)2 z-1 (z-1)2 z-1
откуда (см. пп. 1 и 2 табл. 12.1) s(k)=(5k+2)-\ (к);
CyZ c2z 2z l,5z
ϊ) S(Z):
-0,25 z-1 z-0,25'
откуда (см. пп. 1 и 4 табл. 12.1) s(k) = [2-1,5 (0,25)*]· l(Jfc).
12.30. Знаменатель B(z) = z2 — l,26z + 0,81 заданной функции
S(z) имеет комплексно-сопряженные корни и соответствует
знаменателю табличных z-преобразований (см. пп. 8 и 9 табл. 12.1).
Сопоставляя коэффициенты в знаменателях: 2b cos a = 1,26 и
б2 = 0,81, получаем 6 = 0,9; cos a = 0,7; а = 0,7954.
191
Выделим в числителе функции S(z) члены,
соответствующие числителям табличных z-преобразований. После выделения
A1z(z-bcosa) = 5z(z-0,9-0,7) = 5z2-3,\5z (см. п. 9 табл. 12.1) в
числителе остается l,8z + 2,25. После выделения A2bzs'ma=l,8z
(см. п. 8 табл. 12.1) в числителе остается свободный член 2,25 (при
^42 = 1,8/6 sin uf = 2,8). Свободный член (с учетом задержки на один
шаг) приводим к виду [A3bz sin a) z'1 =2,25, откуда А3 =
= 2,25/£ sin я = 3,5.
Таким образом,
S(z) = 5z(z-0,9cos0,7954)/£(z) + 2,8(0,9zsin0,7954)/.8(z) + 3,5x
χ [(0,9 ζ sin 0,7954)/Л (ζ)] ζ" *,
откуда
s(k) = [5 -(0,9)kcos(0,7954Jk) + 2,8 (0,9)* sin (0,79 54*)] · I (Jk) + 3,5 χ
χ (0,9)*" * sin [0,7954(£ - I)]· I (Jk- 1 ) = [5,73-(0,9)"cos(0,7954£-
-0,5105)]· l(ik) + 3,5 -(0,9)t-1 -sin [0,7954 (ik-1)]· 1 (к-1).
12.4. ПРИНЦИП ДИСКРЕТНОЙ ФИЛЬТРАЦИИ
12.31. Алгоритм работы заданного дискретного фильтра
описывается разностным уравнением sBMX(kf)=s(kT) — s[[k— 1) Г].
Схема фильтра представлена на рис. 12.16. Найти импульсную-
характеристику фильтра g1 (kT).
Примечание. В данной главе под gt (kT)
подразумевается отклик дискретного фильтра на воздействие в виде
единичного отсчета
Μ*η=
(1 при к = 0,
[0 при к /0.
Не смешивать 51{кТ) с дельта-функцией δ(/)!
ftOrT) *~х1Г,(кТ)-<Гкк-1)1~\
s(kT)
Ζ
КЖ\\х]
fs
Рис. 12.16
-2Т-Т О Τ 2Τ
Рис. 12.17
12.32. На вход дискретного фильтра с импульсной
характеристикой из предыдущего примера поступают отсчеты
периодического треугольного колебания, представленные на рис. 12.17.
Найти сигнал на выходе фильтра.
12.33. Дискретный сигнал, состоящий из трех отсчетов (iV=3):
s(kT) = 0,5b1(kT)-b1[(k-\)T] + 2b1[(k-2)T], поступает на вход
фильтра, импульсная характеристика которого g1(kT) = 2bl(kT)+
192
+ 6t [(к-1) Τ] + 0,5 δι [{к -2) Τ] + 0,256! [(к-3) Γ] содержит четыре
отсчета (Я=4). Найти сигнал на выходе фильтра.
12.34. Найти сигнал на выходе дискретного фильтра ъ виде
свертки входного сигнала s( " * " ""
и импульсной характеристики
(рис. 12.18,6).
выходе дискретного фильтра в виде
г(*Г)=1 (^П-'Ш-4)й(Ρ-· '2.18 «
ки фильтра £t (£Т) = 1 (Л;Т) - 1 [(к - 7) 7]
U_L
«f*7?'
о г
AT
\\\\\
а)
0 Τ
LU
4
3
2
«
7/"
О Τ
ът вт
6)
-L
9Т
Рис. 12.18
12.35. Составить разностное уравнение, определяющее
алгоритм работы фильтра, импульсная характеристика которого
задана в примере 12.33. Построить структурную схему фильтра.
12.36. Найти импульсную характеристику рекурсивного
фильтра, заданного разностным уравнением sbMli{kT) = s(kT) + bls1ltlKx
х[{к-1)Т\, \Ь1\<1. Построить структурную схему фильтра.
12.37. На вход рекурсивного фильтра первого порядка с
параметрами, обозначенными на рис. 12.19, а поступает сигнал
Найти сигнал sBhIX(&7) в два фиксированных момента времени:
2Т и 5Г.
f'(nTLgMO gt(nT)
1
0,5\
а)
ЬГ0,5
ς(ηΤ)-ψΤ)
3 S6wx
(ηΌ
Iff-ι 2\ Ζ\
Hit. ут ι r r . /il II In..
От t ο τ 3T t от t
B) a) ff)
Рис. 12.19
Рис. 12.20
12.38. На фильтр из предыдущего примера поступает сигнал
j(fcr) = 28, (*Γ) + δ, [(к- 1) Τ] -δ,[(*-2) Γ]. Найти сигнал *ЯЪ1х(кТ)
для всех к.
12.39. На вход трансверсального фильтра поступает сигнал
s(kT) совпадающий с импульсной характеристикой фильтра
g\(kT)=l{kT)-l[{k-4)T]=s(kT) (рис. 12.20, а). Найти сигнал на
выходе фильтра.
193
12.40. На вход рекурсивного фильтра, рассмотренного в
примере 12.36, поступает сигнал s[kT) = bk, b = 0,5, к—О, 1,
2, ..., έ1=0,8. Найти сигнал на выходе фильтра.
12.41. На вход рекурсивного фильтра из предыдущего примера
поступает периодическая последовательность единичных отсчетов
со
s{kT\ — £ 6j [(k+lN) Г]. Найти отсчеты сигнала на выходе
|=-оо
фильтра в интервале одного периода {0^k<N). Полученный
результат сравнить с импульсной характеристикой фильтра (N=8,
Ьх =0,8).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
12.31. Подставив в заданный алгоритм Ъх (кТ) вместо s(kT),
получим
Л (Α:3Γ) = δ1 (*3Γ)-δ1 [(*:- 1) Г].
Очевидно, g1{0)=\, gl(T)=-l, g^kT^O при к>1.
Зд(пТ)
О
2д\[п±1)Т]
Г
а)
1
-то τ Ι
-2 I
д[(п±2)т]
-2Т Ι-/
δ)
Рис. 12.22
3,15
U
tu
Π
в)
Рис. 12.21
-1,5
IT
°6ых
1,625
0,75
JLt
Гля
45
5Т
12.32. Основываясь на принципе суперпозиции, просуммируем
отклики фильтра на каждый отсчет входного сигнала. На
рис. 12.21.а, б, в показаны отклики на отсчеты ..., s( — 2Т), s(—Г),
s(0), s(T), s(2T), .... Каждый из этих откликов является
импульсной характеристикой фильтра g1 (кТ), смещенной на
соответствующее число тактов и умноженной на значение s(kT).
Результирующая последовательность sbblli(kT) показана на
рис. 12.21, г. Сопоставление огибающих последовательностей
ότι 94
счетов на рис. 12.17 и 12.21, г показывает, что рассматриваемый
фильтр осуществляет дифференцирование входного сигнала.
12.33. Как и в предыдущем примере, находим отклики на
каждый отсчет входного сигнала: 5(0) = 0,5 дает на выходе
0,5g1 (kT); s(T)= — 1 дает на выходе — gl [(& — 1) Г]; 5(2Г)=1 дает
на выходе 2gl [(&— 2) Г].
Сумму откликов в данном примере можно записать в виде
*ш*Лкт)= Σ s{mT)gl[{k-m)T\, k = 0, 1,..., 5.
m = 0
Сигнал на выходе представлен на рис. 12.22.
Обобщая полученное выражение на Η отсчетов импульсной
характеристики и Ν отсчетов входного сигнала, приходим к
алгоритму дискретной свертки
s.m{kT) = Σ s(mT)gl[{k-m)T\, k = 0, \,...,N+H-1.
m=0
Это же выражение заменой переменных можно преобразовать
к виду
s.m{kT) = Σ s[{k-m)T]gl{mT), k = 0, 1, ...,Η+Ν-2.
m = 0
12.34. Основываясь на выражении
W^H Σ s[(k-m)T]gl{mT), k=0, I, ..., H+N-2,
получаем
*»Ых{кТ)=<
£ \=\+knpn0^k^N-\=3,
m=0
к
£ 1=4 при N-l=3<k^H-l=6,
m = k-3
Н-\
£ 1 = 10-УсприЯ-1=:6<А:^Я+Л^-2=:9.
ш = к- 3
Результирующий сигнал представлен на рис. 12.18, в.
12.35. Подставляя в выражение
*вых(кТ) = Н£ s[(k-m)T]gl(mT)
m = 0
отсчеты заданной импульсной характеристики, получаем
sm{kT) = 2s{kT) + s[{k-l)T\ + 0,5s[(k-2)T] + 0,25s[{k-3)T].
195
Структурная схема трансверсального фильтра, реализующего
этот алгоритм, представлена на рис. 12.23.
%25
Рис. 12.23
12.36. Подставим в заданное разностное уравнение вместо
s{kT) единичный отсчет 6t (kT):
?1(ΛΓ) = δ1(ΛΓ) + ^1[(Α:-Ι)Γΐ.
Задавая к = 0,1,... и учитывая, что gi(—T) = 0, получаем
*ι(0) = Ι, 8χ{Τ) = ^, gl{2T) = bl...,gl{kT) = b\,
т.е. gl(kT) = b\-l(kT). Структурная схема и импульсная
характеристика фильтра представлены соответственно на рис. 12.19, а и б.
12.37. Используя полученную в задаче 12.36 импульсную
характеристику gt [кТ) = Ь\ -1 (кТ), сигнал на выходе фильтра
находим с помощью дискретной свертки:
'.-Л*7')- Σ s(mT)gl[(k-m)T].
m = 0
Для нахождения 5ВЫХ(2Г) умножаем s(mT) на g1\jl — m)Tj и
суммируем по всем m (рис. 12.24, а):
sbMX(2T) = s(0)g1(2T) + s(T)g1(T) + s(2T)gl(0) = l-(0,5)2+\-0,5 +
+ 1-1=1,75.
Аналогично (рис. 12.24, б)
s(kr)
ΦΌ
2 afar)
\1
0 ΤΖΤΖΤ4Γ t 0T2T3T4T5rt
1
in
11
J.W8
ш 321 I F
11
12
\\
0T\ t
Λ ι'ίί
Ζ s(0)gf(kT)
1 j ll 1
О Т2Т
7 8JB
ι f t .
sCDgftk-DT]
ill 1
2· * » iff
it? i-1 1
О Т2Т
Ο Τ
a)
S)
5T t
or
О 2Т
'вых
(kT)
О Г
s(2T)gf[(k-2)f\
t
t
Рис. 12.24
Рис. 12.25
*«,(5Г) = *(0)*, (5T) + s{T)gx (4T) + s(2T)gl (3T) + s(3T)gl (2T) +
+ s{4T)gl{T) = 0,9687 5.
196
12.38. Основываясь, как и в предыдущем примере, на
выражении
*»,(*Γ)=Σ s(mT)gl[(k-m)Tl
т = 0
получаем (рис. 12.25)
%(0)g,(0) = 2npHfc = 0,
s(0)gi(T) + s(T)gl(0) = 2 при к=1,
S{Q)gi{2T)-yS{T)g1{T) + s{lT)g1{0) = 0w?^k=l,
О при к^З.
№)■■
Как видно из рис. 12.25, отклик на каждый отсчет входного
сигнала представляет собой за счет рекурсии последовательность
затухающих отсчетов. Однако в данном примере начиная с
момента t — ΙΤ эти отклики взаимно компенсируют друг друга.
Этот же результат непосредственно следует из разностного
уравнения фильтра (см. условие задачи 12.36), так как при к>2
sm{kT) = Smux[{k-\)T\ = Q.
12.39. Ответ представлен на рис. 12.20, б (см. также решение
задачи 12.34)
12.40. Подставляя в выражение
*«,(*ΓΗΣ s(mT)gl[{k-m)T]
m = 0
отсчеты входного сигнала и импульсной характеристики фильтра
gt [kT) из задачи 12.36, получаем
m= 0 m= 0 /li
=^-3{0,Sk + 1-0,5k+l\ Л = 0, 1,2
12.41. Отклик фильтра на единичный отсчет δι (кТ) равен
gl(kT) = b\·1 (кТ) (см. решение задачи 12.36). При воздействии на
входе периодической последовательности единичных отсчетов
выходной сигнал на основании принципа суперпозиции
00 00
W*n= Σ *i[(*+w)7]= Σ ьгМ)-\[(к+ш)т]=
I = — со Ι = — со
=g[(k + N)T].
Для одного периода этого сигнала (0^k<N)
00
g{kT) = b\YjbiiN=b\l{\-bIi).
1=0
197
Сравнение полученного результата с импульсной
характеристикой фильтра (см. задачу 12.36 и рис. 12.19) показывает, что
при любом к в пределах 0^k<N отсчет сигнала на выходе при
заданном периодическом воздействии в (1 — Ь^)"1 «1,2 раза
больше соответствующего отсчета импульсной характеристики, что
объясняется наложением «хвостов» от откликов на предыдущие
единичные отсчеты.
12.5. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ
ФИЛЬТРОВ. ПЕРЕДАЧА СИГНАЛОВ
12.42. На вход дискретного фильтра с импульсной
характеристикой gi(kT) = 6l[kT) — 6l[_[k—\)T\ (см. рис. 12.16) поступают
отсчеты, взятые с шагом Г=1 мкс из сигнала s(t) = e~at, ί^Ο,
α = 5·10 1/с. Найти сигнал на выходе фильтра с помощью
z-преобразования.
12.43. На трансверсальный фильтр первого порядка (см.
рис. 12.16) поступает шумовая помеха χ [ή (эргодический
случайный процесс) с корреляционной функцией /?χ(τ) = σ^_("τ/α)2,
Μ [*(/)] = 0, дискретизованная с шагом Т. Найти корреляционную
функцию Ry{kT) и дисперсию σ2 отсчетов помехи на выходе
фильтра. Определить коэффициент ослабления помехи в фильтре.
Параметры помехи: ос = 20 мс, σ* = 10-4Β2, шаг дискретизации
Т— 2 мс.
12.44. Решить предыдущий пример при спектральном
представлении передаточной функции и входного шума.
12.45. На трансверсальный фильтр второго порядка с
импульсной характеристикой gt {кТ) = Ъ^ (кТ)-2Ь1 [(к- 1) Γ] + δ! [{к-2) Т]
поступают отсчеты шумовой помехи, заданной в двух предыдущих
примерах. Определить коэффициент ослабления помехи в фильтре
и сопоставить с найденным в примере 12.43.
12.46. Определить передаточную функцию фильтра,
структурная схема которого изображена на рис. 12.19. Найти сигнал
на выходе фильтра при входном сигнале s(k)=e~',kT = bk,
е-аГ=:6<1, к^О.
12.47. Найти с помощью z-преобразования сумму целых чисел
до нуля до к sk (к) и сумму их квадратов s 2 (&).
12.48. Сигнал на выходе фильтра при воздействии s(k)=\(k)
равен sBbIX(k)=(l—bk)-l(k), 0<b<\. С помощью метода
z-преобразования найти передаточную функцию фильтра и построить его
структурную схему.
12.49. На вход трансверсального фильтра, передаточная
функция которого Κ(ζ) = 2—ζ-1 + 2ζ-2, подан сигнал s[k) = bk-l (к),
£ = 0,8. Найти сигнал на выходе фильтра.
12.50. Алгоритм работы трансверсального фильтра
описывается разностным уравнением sbblx(k) = 0,5s(k) + s(k—\) + 0,5s(k — 2).
198
Найти импульсную характеристику и передаточную функцию
фильтра. Построить АЧХ фильтра.
12.51. Найти и построить АЧХ трансверсального фильтра,
алгоритм работы которого описывается разностным уравнением
5»ых (*) = - 0,55 (к) + s{k-2)- 0,55 (к - 4).
12.52. Передаточная функция цифрового фильтра задана
своими нулями и полюсами на ζ-плоскости: ζ01
= 0,
-02,3'
±0,5/,
ζπ1=0,8, zn2)3=0,6exp{ + m/3}. Построить структурную схему
фильтра в прямой, последовательной и параллельной формах.
12.53. Выбрать параметры цифрового резонатора
(рекурсивного фильтра второго порядка), резонансная частота которого
ωρ = 2π/5Γ, а относительная полоса пропускания по уровню
половинной мощности 2Δω/ωρ = 0,01.
12.54. Найти передаточную функцию цифрового фильтра,
структурная схема которого представлена на рис. 12.26.
£*£*
?Ьъхх(г) S(z)
bf~0,5X(z)af=2,5
Рис. 12.26
{>i^Z;
6,-0,8
Рис. 12.27
12.55. Найти передаточную функцию рекурсивного фильтра,
структурная схема которого представлена на рис. 12.27. Построить
структурную схему заданного фильтра в канонической форме и
составить его разностное уравнение.
12.56. Структурная схема фильтра, состоящего из
последовательного соединения двух фильтров первого порядка
(трансверсального и рекурсивного), представлена на рис. 12.28. Составить
sOrrj
Рис. 12.28
а,ж3
Pf~0,5
разностное уравнение фильтра, найти его передаточную функцию
и представить структурную схему фильтра в канонической форме.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
12.42. Передаточная функция фильтра К(г)= £ g1 {kT)z
к=0
-к.
199
= 1 — ζ 1 =(ζ—\)/ζ, z-преобразование входного сигнала S(z) =
=z/(z-e~aT)=z/(z-b), где b=e~aT (см. п. 2 в примере 12.14).
Таким образом,
SBMX(z)=S(z)K(z)=(z-\)/(z-b).
Отсчеты сигнала на выходе фильтра находим с помощью
обратного z-преобразования. Представляя SBhIX(z) в виде
и используя табличное преобразование (п. 4 табл. 12.1), получаем
ί.„(*η=*'·ι(*)-*'"1·ι(*-ΐ)=[0+*')-*'"1]·4*-ί)=ί-
-{l-b)bk-1-l(k-l)=l-(l-e-''^e-''(k-1)T-l(k-l).
При осГ«:1 1 —е_аГ«1 —(1 —αΓ) = αΓ. Таким образом, при
аГ«:1 отсчеты 5вых(Л;Г)й:1 —аГе_а( )Г,1 (&—1) являются
отсчетами производной сигнала s(i). Как и в примере 12.32, убеждаемся,
что фильтр с импульсной характеристикой g1(kT) =
= δ1 (кТ) — δ1 [(к— 1) Г] по существу является дифференцирующим
устройством.
12.43. Основываясь на алгоритме работы фильтра у{пТ) —
—х{пТ)—*[(" — 1) Г] и на стационарности процесса χ (ή, находим
корреляционную функцию отсчетов помехи на выходе фильт-
ра Ry(kT) = {x(nT)-x[(n-l)T\}{x[(n + k)T\-x[(n + k-\)T]} =
= х(пТ) х[(п + к)Т] + х[(п-\)Т]х[(п + к-\)Т]-х(пТ)х
xxUn + k-\)T]-x[(n-\)T]x[(n + k)T\=Rx(kT) + Rx(kT)-
-RMk-l) T]-Rx[{k+ 1) Τ] = 2Rx(kT)-2Rx[{k+ 1) Τ].
Дисперсия отсчетов помехи на выходе фильтра (к=0) σΐ —
=Ry{0)==2Rx(0)-2Rx(T) = 2<,x[l-rx(T)l где Γ,(Γ)-Λ,(Γ)/σ2-
_е-(лГ'а) ~о,906. Окончательно
σ2 = 2σ2(1 -0,906)=0,188σ2=0,188 10"4 Β2.
Мощность помехи ослабляется в фильтре приближенно в 5,3
раза. Заметим, что в случае белого шума χ(ή имело бы место не
ослабление, а увеличение дисперсии в два раза.
12.44. Сначала находим спектральную плотность входного
шума
00 00
Wx(<o) = J Rx{z)e-im4T = 2o2x$ e-(ml'x)2cosG)TdT=W0e-'x2F2,
- αο 0
где 1¥0 = аох/у/к; F=m/2K [13, с. 494].
АЧХ фильтра получаем из передаточной функции K(z)=l — ζ-1
(см. пример 12.42) после подстановки z=e"*r:
200
I к (eltt,r) I = 11 - e"ίωΓ | = 21 sin (ωΤ/ 2) |.
Дисперсия шума на выходе фильтра
•V2 оо
σι
ι
Ψχ(ω)\Κέ°τ\2άω=^
ea2f2 sin2 (nFT)d(2nF)
(предел интегрирования ω1/2 заменен на оо, так как Wx(u>J2)?aO).
Используя табличный интеграл [13, 3.896.4]
00
$e-Vx2cosbxdx = ^Tt/4pexp{-b2/4p},
о
находим
a^^J^l-e-W*)2)
откуда после подстановки числовых данных
а2 = 0,188а2=0,188-1(Г4 В2.
Полученный результат, как и следовало ожидать, совпадает с
дисперсией σ2, найденной в предыдущем примере по
корреляционной функции отсчетов выходного шума.
12.45. Заданный фильтр может быть представлен каскадным
соединением двух трансверсальных фильтров первого порядка [1,
п. 12.8.3]. Таким образом,
| К (е'<°г) | = [21 sin (ωΓ/2) |]2=4 sin2 (ωΤ/2).
Дисперсия шума на выходе фильтра
•V2 оо
г
σ;
ι
i»r\|2j •бИ'о
Иуа>)|К(е'тГ)|2Ло
-a2F2
sin4 (nFT)d(2nF).
Подставив sin4x=- —-cos2x— sin2 2x и вычислив табличные
интегралы [13], получим
-(πΓ/α}2 ·
<sl = %W0-
1
-О
.-(2пГ/а)
0,0995σ2«10"5 Β2
Ослабление шума в рассмотренном фильтре примерно 10, т. е.
вдвое больше, чем в фильтре первого порядка.
12.46. Передаточная функция фильтра
00
к=0
201
На выходе фильтра z-преобразование сигнала SHhII(z) =
= [z/(z-b)][z/(Z-bl)l
Сигнал на выходе находим с помощью табличного
преобразования (см. п. 10 табл. 12.1). С учетом опережения на один шаг
получаем
(см. также решение примера 12.40).
Особый интерес представляет частный случай b=b1. Раскрывая
получающуюся в этом случае неопределенность, находим 5ВЫХ(А;) =
={k+l)bk-l (к). Для получения сигнала на выходе фильтра в виде
sBbiX(k)=kbk-l (k — l) требуется введение задержки Τ и умножение на
b = bx (точка / в схеме на рис. 12.19). При b — \ \bx<\)
а при съеме выходного сигнала в точке 2 (см. рис. 12.19)
w(*)=b£i(*-i).
При b1-^\ (b = l) звы*(к)=к\ {к — 1) (в точке 2, совпадающей с
точкой 1).
Таким образом, рассмотренный фильтр реализует умножение
заданной последовательности входных отсчетов s{k) — b ·1 (к) на к.
12.47. Представляя сумму целых чисел от 0 до А; в виде
дискретной свертки функций s(k)=k-\(k) и g(k) = l(k):
к к
sk{k)= Σ m = s(k)*g(k) = £ m-\{k-m)
m=0 m=0
и переходя к z-преобразованию, имеем (см. пп. 1 и 2 табл. 12.1)
St(z) = S(z)fi(z)-(-^jI-lT-(-^nsz.
Используя табличное преобразование (см. п. 6 табл. 12.1 при
Ъ = 1), получаем
sk(k)J^-l(k+l)J^-l(k-l).
Аналогично сумма квадратов целых чисел s 2(к) = [к2 χ
χ 1 (£)]*1 {к). Для z-преобразования имеем (см. пп. 1 и 3 табл. 12.1)
S M-Z(z+1) z - г 72 , z 7
akAz)-{z_ly ζ_\-{ζ-\γ +(ζ-ι)* '
202
откуда, используя табличное преобразование (см. п. 7 табл. 12.1
при Ь=\ и 1=3), получаем
V(*) =
{к + 2){к+\)к {к+Щк-1)
3! 3!
l{k-l)J^±}f±M-l{k-l).
12.48. Используя табличные z-преобразования заданных
входного и выходного сигналов (см. пример 12.14) S(z)=z/(z—1) и
K*x{z)=z/(z-\)-z/(z-l)), определяем
k(z)=SBUX(z)/S(z)=l-(z-l)/(z-b)=(l-b)/(z-b).
Структурная схема фильтра представлена на рис. 12.29.
Рис. 12.29
•1) + 2йк-2-1(*-2) = 25,(*) +
12.50. gM^oJbl'fa + bTk-Yj+OJbAk-l), k{z) = 0,5 + z~l +
График АЧХ фильтра представлен на рис. 12.30.
12.49. s.m[k) = 2bk-Hk)-bk-1-\{k-
+ 0,6δ1 (к- lJ+2,48 (0,8)*"*;1 (Jfc-2).
jKfe'"*">|
|К(е»тЛ
12
7"
Г
Рис. 12.30
л
τ
2jt ω
Τ
2Л _П_П_ 0 J£ rt 2л ω
Τ Τ 27 2Τ Τ Τ
Рис. 12.31
12.51. |К(ег**г)|=251'п2(ш7). График АЧХ фильтра представлен
на рис. 12.31.
12.52. Заданную передаточную функцию К (ζ) записываем в
форме [1, § 12.7]
К (z) = z(z-0,5«)(z + 0,Si)
* ' (z-0,8)(z-0,6e,,"3)(z-0,6e"i"'3)'
Для построения прямой структуры фильтра представляем
числитель и знаменатель в виде полиномов по отрицательным
степеням ζ:
Κ(ζ) =
ζ (ζ2+ 0,25)
ζ3+0,25ζ
(z-0,8)(z2-2-0,6cosji/3-z + 0,36) ζ3- 1,4ζ2 + 0,84ζ-0,288'
1+0,25ζ~2
1 —1,4ζ_1 + 0,84ζ~
-0,288ζ~
203
Рис. 12.32
Прямая структурная схема фильтра, соответствующая
полученной записи К (ζ), представлена на рис. 12.32, а.
Для построения последовательной (каскадной) структуры
фильтра представляем К (ζ) в виде произведения двух
передаточных функций: К (ζ) = К, (ζ) К 2 (ζ), где К, (ζ) =1/(1 -0,8z-1); K2(z) =
=(1+0,25ζ"2)/(1-0,6ζ_1+0,36ζ"2).
Последовательная структурная схема фильтра представлена на
рис. 12.32,6.
Параллельная структура фильтра получается при
представлении К (ζ) в виде суммы простых дробей. Так как два полюса К (ζ)
являются комплексно-сопряженными, разложение ft (z) ищем в
форме
К (ζ)-
C2Z +C3Z
ζ-0,8
-0,6ζ + 0,36
Приводя выражение для К (ζ) к общему знаменателю и
приравнивая коэффициенты при одинаковых степенях ζ в
числителях, получаем систему уравнений
с,+с2 = 1,
c3-0,6cl-0,Sc2 = 0,
0,36с,-0,8с3 = 0,25,
откуда
с, и 1,712; с2« -0,712; с3%0,458.
Окончательно выражение для К (ζ) приводится к виду
1,712 0,712-0,458ζ_1
Κ(ζ) =
1-0,8ζ_1 1-0,6ζ_Ι+0,36ζ'
204
Параллельная структурная схема фильтра представлена на
рис. 12.32, е.
12.53. Передаточная функция рассматриваемого фильтра [1,
п. 12.8.4]
щ-
l-ft.r-'-M"2 (ζ-ζπ1)(ζ-ζπ2)'
\b2\>bll4); by
где znU2=b1/2±iyf\b2\-bi/4 = rne±i*"(b2<0,
=2rncoscpn, b2=-r*.
Тогда АЧХ
|К(е*^| = 1/|(е*г-гпе^)(е*г-гпе-*»)|.
Форму обычной резонансной кривой
в диапазоне малых расстроек
относительно резонансной частоты ωρ = φπ/Γ АЧХ
приобретает при расположении полюсов
ζπΐ,2 вблизи окружности |ζ| = 1. Из
диаграммы, представленной на рис. 12.33,
следует
Рис. 12.33
{е™7 - ra е**-)=е< (ef (ω " %> т - га) * е*· [1 - rn + i (ω - ωρ) Γ],
(е"*г — гае ~ ίφή « 2гп sin φπ « 2 sin φπ.
При этих условиях АЧХ
*у-
1 °
znf/
Ί
Г
ад
ζίωΤ
\ \
1\
X
|&(е-г)|*1/(25тФпЛ/(1-гп)2 + [(ш-Юр)Г]2) и |&(е
= l/2sin9n(l-rn).
ΐωΓι
Ослабление АЧХ в у/2 раз получается при (ω—ωρ)Τ= ±(1 — /■„).
Тогда из условия 2Δω/ω =2(1—гп)/(рп = 0,01 находим гп =
= 1-0,01φπ/2*0,994; φπ = ωρΓ=2π/5.
Параметры фильтра: b1=2rncosq>nzzO,6l4, b2 = —rl^ —0,987.
12.54. Как видно из рис. 12.26,
§ΒΜ^) = 2§(ζ) + 0,5·2Χ(ζ) + 2,5Χ(ζ) = 2§(ζ) + 3,5Χ(ζ),
где X(z) определяется в промежуточной точке схемы из
выражения X(z) = §(z)z-1+0,5X(z)z-1: X(z) = § (ф-1/0 -0,5z-1).
205
Следовательно,
S-«(*) = S(z) 2 + -^ =S(*)
3,5z_I \ a/ v2 + 2,5z
ι
l-0,5z-1 / v Ί-Ο,δζ-1'
откуда fi(z)=(2+2,5z-1)/(l-0,5z-1).
Полученный результат является частным случаем общего
выражения передаточной функции цифрового фильтра с прямыми
и обратными связями [1, § 12.7].
12.55. Используя методику решения предыдущего примера,
получаем S№X{z)=k1S(z) + k2Y-^-LrT=S(zy ,^Υ
откуда
/Cj +/с2~ ^ι^ι2"1 4 —],6z_I
„-1
K(z) =
]-ί»ιΖ_1 1-0,8ζ"
Структурная схема фильтра в канонической форме совпадает
со схемой фильтра, рассмотренного в предыдущем примере (см.
рис. 12.26), при а0 = к1+к2 = 4, ах = — к1Ь1 = — 1,6, ^^ =0,8.
Разностное уравнение рассмотренного фильтра
*«.(*3Γ)-(*ι+*2Μ*^-Μι*[(*-ί)3Γ]+*ι*-«·[(*-ί)3ΐ·
12.56. 2s{kT) + 3s[{k-\)T]=x{kr) = snm{kr)-0,5stm[{k-l)Tl
Κ(ζ) = (2 + 3ζ-1)/(1-0,5ζ-1).
Структурная схема фильтра в канонической форме имеет такой
же вид, как и в двух предыдущих примерах (см. рис. 12.26).
Глава 13. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
СИГНАЛОВ НА ФОНЕ ПОМЕХ
13.1. Синтезировать фильтр, согласованный с видеоимпульсом
прямоугольной формы, действующим на фоне белого шума (с
нормальным распределением). Амплитуда видеоимпульса £=5 В,
длительность ти = 2 мс, спектральная плотность мощности шума
ψ0(υή = 5 · 10~2 В2/Гц. Вычислить отношение пикового значения
сигнала к среднеквадратическому значению помехи на выходе
фильтра.
13.2. Сигнал и помеха из предыдущей задачи пропускаются
через интегрирующую RC-цепь. Вычислить отношение сигнал/шум
206
на выходе цепи в зависимости от постоянной времени цепи τ„.
Найти это отношение и при τ„ = τ„0ΠΤ. Оценить потери (в
децибелах) в отношении сигнал/помеха по сравнению с
результатом предыдущей задачи.
13.3. Рассчитать и построить АЧХ и ФЧХ фильтра,
согласованного с видеоимпульсом
S(t):
С Aea(t~T\ t^T,
Ιο , t>T.
Проверить по критерию Пэли-Винера реализуемость фильтра,
определив его параметры.
13.4. Определить минимально необходимую амплитуду
радиоимпульса с прямоугольной огибающей на входе согласованного с
ним'фильтра для достижения на выходе отношения сигнал/шум,
равного единице. Длительность импульса 1 мкс, спектральная
плотность мощности белого шума 4 мВ2/Гц.
13.5. Задан сигнал в виде последовательности видеоимпульсов
с различными пиковыми значениями (рис. 13.1). Определить
импульсную характеристику согласованного фильтра,
синтезировать фильтр. Изобразить сигнал на выходе и вычислить
отношение сигнал/шум. Спектральная плотность мощности белого шума
на входе 10^мВ2/Гц.
s(t),e
4
Ζ
О
-Ζ
ТТ.
s3(t)
I
I
\.
Рис. 13.1
Рис. 13.2
13.6. Заданы четыре сигнала (рис. 13.2). Указать, для каких
сигналов можно построить согласованные фильтры, а для
каких — нет, объяснить почему.
13.7. Радиоимпульсы sl(t) = El cos(o0i и s2(t)=E2cos{o30t+—)
длительностью ти1 =ти2=ти=100 мкс с прямоугольной формой
огибающей и одинаковыми амплитудами Е1 — Е2 — Е—\0 В
подвергаются согласованной фильтрации на фоне белого шума со
спектральной плотностью мощности И^0 = 10 ~4 В2/Гц.
Высокочастотное заполнение первого импульса не модулировано, а
частота заполнения второго изменяется по закону ω(ί)=ω0 + βί,
где ω0 = 2π/0 = 2π·108 рад/с; β = 2π·2/Λ/τΗ; /д = 50 кГц—девиация
207
частоты. Определить длительности импульсов на выходе
согласованных фильтров, пиковые значения импульсов £1вых, £2вых и
отношения £ΐΒΗΧ/σ„ Е2вых/а2.
13.8. Синтезировать согласованный фильтр для фазоманипули-
рованного по коду Баркера радиоимпульса s(t) с числом
элементов N=1 (см. рис. 13.9, а). Синтез провести двумя способами: по
передаточной функции К(ш) и по импульсной характеристике g(t).
Определить выходной сигнал sBbIX(0 и относительный уровень
боковых лепестков сигнала.
13.9. Определить коэффициент сжатия ЛЧМ радиоимпульса с
прямоугольной огибающей в согласованном фильтре.
Длительность импульса 10 мс, девиация частоты 5 кГц.
13.10. Определить параметры гребенчатого фильтра для
сигнала в виде пачки видеоимпульсов, оценить отношение сигнал/шум
на выходе в зависимости от числа импульсов N. Огибающая пачки
прямоугольная, период повторения импульсов Τ =2 мкс.
13.11. Синтезировать согласованный фильтр для пачки из Ν
радиоимпульсов, повторяющихся с периодом Т, если: а)
начальные фазы высокочастотного заполнения всех импульсов
одинаковы; б) начальные фазы флуктуируют от импульса к импульсу.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
13.1. Исходя из спектральной плотности заданного сигнала
S(o>)=:£(l-e-,tt,TH)/(iG>) и формулы K(i(u) = AS*((u)e~i,A,o [1, § 13.2]
при t0 = ти находим передаточную функцию согласованного
фильтра [1, п. 13.5.1]
Κ(ίω)=—(1-е ""Ή
V ' (О) V '
Структурная схема фильтра представлена на рис. 13.3.
Множитель 5Α/(ϊω) реализуется интегратором, вычитаемое
е~"*т«—линией задержки ти.
Отношение сигнал/шум (по напряжению) на выходе фильтра
[1, формула (13.9)] при £=5 В, ти = 2 мс и И^0 = 5 · 1(Г2 В2/Гц
r\=j3iW~o = y/E2tJWo=l-
-> Интегратор
I ^ Линия задер- _|
жки на ги ~
1,0
0 0,5 1,0 1,5 2,0 2,5 3 tjt^
Рис. 13.3
208
Рис. 13.4
13.2. Максимальное значение сигнала на выходе фильтра будет
в момент ί = τΆ
*вьЖ) = £(1-е-и/<4
Спектральная плотность мощности шума на выходе
^™,(ω)= W0K2H= W0/[l +(ωτ„)2]
и среднеквадратическое значение шума
„ _fe f_*_l",_foYB
"" 12. J ι+KPJ W)
— oo
Таким образом, отношение сигнал/шум
'M(0_.g(i-e--"'L [Σ &i_e-V^„)
Как видно из рис. 13.4, оптимальное значение (см. задачу 7.34)
тцжти. При этом коэффициент
У2тц/ти(1-е-^„)=:^(1-е-1)=:0,9«1 дБ
характеризует уменьшение отношения сигнал/помеха в
«квазиоптимальном» фильтре по сравнению с согласованным.
13.3. Спектральная плотность заданного сигнала
8(ю) = £е-"*г/(а-/ю).
Передаточная функция согласованного фильтра при ί0 = Τ [1,
§ 13.2]
KH = /lS*He-iffiO = ^£—e-™r=^/(l + ™
v ' v ' α + ι'ω α ' γ α
Модуль функции Κ(/ω) отвечает условию [1, § 13.3]
00 00
;<оо.
Кроме того, найденная функция Λ^ω) стремится к нулю
лишь в одной точке (при ω-юо), следовательно, искомый
согласованный фильтр не противоречит критерию Пэли-Ви-
нера.
АЧХ и ФЧХ фильтра показаны на рис. 13.5. Из выражения для
К (/ω) следует, что в рассматриваемом случае согласованным
209
αΚ(ω)
ΑΕ 1
1,0
0,5
0
-45°
-90°
иг$К(ш)
><^
ι
2
^АЧХ
3 4 ω/α
ФЧХ
д®,с-'
ц —
-г ν
Ά
2 4 5
tt
δ t,MC
Рис. 13.5
Рис. 13.6
фильтром является ЛС-фильтр нижних частот с постоянной
времени τ = /?С=1/ос.
13.4. Е=2 В [U формула (13,9)1.
13.5. Импульсная характеристика согласованного фильтра
связана с исходным сигналом соотношением [1, § 13.3] g(t) =
= As(t0-t), /0 = 9мс, и представлена на рис. 13.6 при А =
= 1 (В-с)-1.
Согласованный фильтр может быть реализован в виде
каскадного соединения фильтра К^гсо), согласованного с одиночным
импульсом, линии задержки с отводами, весовыми усилителями и
сумматора (рис. 13.7) при
ι \_Л В' O^'^l мс>
5l^~(0, /<0, />1 мс.
Отклик подобного фильтра может быть рассчитан тремя
способами: сверткой функций s(t) и g(t); вычислением
корреляционной функции входного сигнала 5(0; рассмотрением
прохождения через фильтр каждого из импульсов по отдельности с
суммированием их на выходе.
Мв
sftj
,(ω)
—»»
1
-1
1
Линия задержки
мо 5мс
rh г2
2
1мс
г. *
2 А
1мс
L _i
• ι
, 1
ί
Сумматор
Рис. 13.7
Рис. 13.8
Выходной сигнал 5ВЫХ(0 показан на рис. 13.8 при А =
=0,1 (В-с)-1. Отношение сигнал/шум на выходе синтезированного
фильтра [1, формула (13.9)]
П = У^о = 28,6.
210
13.6. Согласованные фильтры могут быть реализованы
только для сигналов s2(t) и s3(/), так как для сигналов it (t)
и 54(0 импульсные характеристики фильтров g(0^0 при t<0,
a t0 = cd.
13.7. Учитывая, что сигнал на выходе согласованного фильтра
по форме совпадает с корреляционной функцией входного сигнала,
получаем: длительность первого импульса т1вых = 2тя=200 мкс [1,
§ 2.18]; пиковое значение £1вых =
8,7 В [1, п. 13.5.1],
отношение £ΐΒΜ^σ, =v/3^=v/£^/^=10 [l, §13.4].
Соответственно для ЛЧМ импульса: т2вых= 1//д = 20 мкс [1,
п. 13.5.2]; Е2ъых = ^У^яЕ=Ъ2Ъ [1, п. 13.5.2], E2bJo2 =
Итак, хотя £2вых в 3,7 раз больше, чем £1вь1Х, отношение
сигнал/шум на выходе согласованного фильтра одинаково для
обоих сигналов st (t) и s2 (0 (при одной и той же энергии сигнала и
спектральной плотности шума W0). Это объясняется тем, что для
сжатия сигнала требуется расширение полосы пропускания
фильтра, что соответственно увеличивает σ2.
13.8. Для определения передаточной функции согласованного
фильтра воспользуемся выражением [1, § 13.2] KonT(to) =
= AS*((o)e шо, где S(a>) — спектральная плотность входного
сигнала, a t0^Tc. В данном случае ί0=ΊΤ.
f
ттттмь,
Ьп*+1
1 , .
0,-+/ | Ь-+/ | 6,—Г | h—t | Os~+r I bg'-f ι
τ гт
s(t)
37" 4T
a)
ST
6T
7T
Щш)
~
1» Линия задержки ·\
Τ
1
1 ,
Г
* ,!
- >
τ
Кг
1 -
τ
'—
1
τ
г У
τ
I \f
Сумматор
Кы,Ю
Рис. 13.9 ff)
Спектральную плотность первого элемента сигнала обозначим
Sj (ω). Тогда с учетом знаков bk (рис. 13.9, а) получим
S(a>)=S,(o>)[l+e
- ΐωΤ
+е
- i(02T _ g -i(o3T _ е - ί<*4Γ , е - ίο»5 Τ _ g
йлбГ
]■
211
Искомая передаточная функция приводится к виду (при t0 = lT)
KmT(m)==AS\(i(u)e-i,uT[- \ +е~™т-е~шт + е~ш*т+e-i,A5T +
где K1(/ra) = >iS*i(ra)e~"*r — передаточная функция фильтра,
согласованного с первым элементом сигнала, а К2(ш) — передаточная
функция многоотводной линии задержки с весовыми
коэффициентами Ьк=±\, чередующимися в порядке, зеркальном по
отношению к сигналу s(t).
Функция Κοπτ(/ω) реализуется схемой, представленной на
рис. 13.9,6.
К этой же схеме можно прийти исходя из соотношения [1,
§ 13.3] gonT(t) = As(t0-t), согласно которому импульсная
характеристика по своей форме должна совпадать с зеркальным
отражением входного сигнала.
вых
Рис. 13.10
Сигнал sBblx(t), с точностью до постоянного
коэффициента равный корреляционной функции сигнала s(t),
изображен на рис. 13.10. Относительный уровень боковых лепестков
равен 1/7.
sCt)
5 вых
(t)
*-β
ЕЪых>&Ъъ
Ч
Рис. 13.11
13.9. Общая длительность сигнала на выходе
согласованного фильтра равна 2т„ (см. методические указания к
примеру 3.30), а его основного лепестка \Ц'Л [1, рис. 13.11].
212
Следовательно, основной лепесток выходного сигнала в Хи/Д = 50 раз
короче входного импульса. Коэффициент сжатия длительности на
уровне 0,707 от пикового значения равен ПО [1, с. 410].
13.10. Гребенчатый фильтр, выполненный в виде
согласованного с одиночным импульсом фильтра и рециркулятора, в состав
которого входят сумматор и линия задержки с передаточной
функцией βεχρ( — /ω/3), где β<1 (см. рис. 13.11), должен иметь
время задержки в линии t, = Т= 2 мкс.
Амплитуда импульсов на выходе рециркулятора накапливается
в геометрической прогрессии и после прохождения всей пачки
равна £ΒΗΧ = £ΒΧ(1 + β + β2 + ... + βΛΓ). Отношение максимального
значения амплитуды импульса на выходе к входной амплитуде
можно определить по известной формуле суммы геометрической
прогрессии
^/^(ι-βΊ/Ο-β)·
Дисперсия шума на выходе рециркулятора (см. рис. 13.11)
σ
2^2
; = σ2χ + β2σ
вых —^вх ι н ^вых, откуда отношение среднеквадратических
значений шума на выходе и входе σΒΜΧ/σΒΧ = (1 — β2) /2, а выигрыш в
отношении сигнал/помеха, обусловленный применением
рециркулятора,
Лвы,/Лвх = £вых°м/(£вхавыхН1 -β")^ +β)/0 "β)·
Следовательно, если β = 0,9, а N=100, то отношение
сигнал/помеха на выходе увеличится по сравнению с входным в 4,4
раза (или на 13 дБ).
13.11. Если начальные фазы всех импульсов одинаковы
(когерентная пачка), то фильтр может быть реализован в
виде каскадного соединения фильтра, согласованного с
одиночным импульсом, линии задержки с отводами через t3 =
= Т и сумматора [1 § 13.5.3]. Выигрыш в отношении
сигнал/шум будет в yJN раз выше, чем для одиночного
импульса.
. 13.12
s(t)
ρ-> /7 —»| СФ,
t
■— sintyflfr;
г-COS <ue(t)
I—> /7 —» СФг -
-*кв
с
t
-*кв
'Вых
ft)
В случае некогерентной пачки согласованный фильтр должен
содержать два квадратурных канала (рис. 13.12) [1, с. 419]. На
рисунке: Π — перемножитель; СФ1 и СФ2 — согласованные с
квадратурными составляющими сигнала фильтры; KB —
квадратор; С — сумматор.
213
Глава 14. ЭЛЕМЕНТЫ СИНТЕЗА
РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ
14.1. СИНТЕЗ АНАЛОГОВЫХ
ЧЕТЫРЕХПОЛЮСНИКОВ
14.1. Задана передаточная функция четырехполюсника К(р>) =
= А/(р-рп1)(р-ра2), где Ра1= - l/(RiCt); рп2= - l/(R2C2) —
полюсы функции К(р») на плоскости ρ = σ + ΐω; А — постоянный
коэффициент, с-2. Определить структуру четырехполюсника в
виде каскадного соединения двух взаимно независимых
простейших четырехполюсников (развязанных с помощью эмиттерного
повторителя).
14.2. Решить пример, аналогичный 14.1, при передаточной
функции четырехполюсника Κ(ρ)=ρ2/(ρ-ρηί)(ρ-ρ„2), Ρ„ι =
= -l/(/?1C1), Pn2=-l/(R2C2).
14.3. Задана передаточная функция четырехполюсника К(р) =
= Bj{p-Pnl){p-Pn2) с полюсами Pni=-RljLi и Pa2=-R2jL2.
Построить схему четырехполюсника в виде каскадного соединения
двух взаимно независимых элементарных четырехполюсников.
14.4. Составить передаточную функцию четырехполюсника,
аналогичного четырехполюснику из предыдущего примера, при
съеме напряжений с индуктивностей Lt и L2.
14.5. Определить параметры фильтра нижних частот Бат-
терворта второго порядка. Частота среза /с=104Гц,
нагрузочное сопротивление /?=104Ом. Сопряжение фильтра с
выходной цепью транзистора (источник тока Ii = SEi) показано
на рис. 14.1.
,,-sf, J, ϋΙΔ "^L
φ»,2 ψ,Ζ |W
I
I
* I
ε,
Рис. 14.1 Рис. 14.2
14.6. Синтезировать ФНЧ Баттерворта второго порядка с
частотой среза /с=104 Гц на основе активной /?С-цепи. Один из
возможных вариантов цепи приведен на рис. 14.2 [1, § 15.3].
Входное сопротивление операционного усилителя бесконечно
велико, выходное сопротивление близко к нулю. Заданные
параметры: постоянная времени R2C2=\ja>c, C2/Cl = 0,4-
14.7. Синтезировать фильтр нижних частот Баттерворта
третьего порядка с частотой среза /с=104Гц на основе активной
ЯС-цепи.
214
14.8. Синтезировать на основе активной RC-цепи ФНЧ Чебы-
шева второго порядка с частотой среза /с=104 Гц и
неравномерностью АЧХ в полосе пропускания не более 3 дБ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
14.1. Условие развязки элементарных четырехполюсников
позволяет представить К(р») в виде произведения Kt (р)К2(р), где
Ki(p)- Al
к2(р)=
At
P-P.i P+l/R^!
-A1R,Ci
A2R2C2
Ri+\lCip
]/C2p
P-Pa2 P+i/R2C2 "'"' ' R2+VC2p
Последние множители в правых частях есть не что иное, как
безразмерные передаточные функции RC-цепи при съеме
напряжения с конденсатора. Поскольку и К(р) — безразмерная функция,
то Al = l/RlCl, A2=\jR2C2. Искомая схема принимает вид,
показанный на рис. 14.3.
14.2. В данном примере
ρ «,
К2(р) =
Р-Р.1 P+V*iCi Ri + VCtP
R2
R2+]/C2p
и схема синтезируемого четырехполюсника отличается от
схемы на рис. 14.3 только тем, что напряжения снимаются с
резисторов.
эп
Ъ
Рис. 14.3 Рис. 14.4
14.3. По аналогии с примерами 14.1 и 14.2
в,
Κ^-Κ^Κ^)--
в,
p+R1/L1p+R2/L2
Приравняв Bi = R1/Li и B2 = R2/L2, получим
K1(p) = /?1/(/?1 + Ll/>), K2(p) = R2/{R2 + L2p).
Схема четырехполюсника представлена на рис. 14.4 (съем
напряжений с резисторов Ri и R2).
14.4. При съеме напряжений с индуктивностей передаточная
функция одного звена равна Ll2pj{Rl2 + Li2p), а всего
четырехполюсника
215
Κ (ρ) = LiL2P2
ψ> [b + LrfXRt + Ljpf
14.5. Передаточная функция ФНЧ Баттерворта второго
порядка определяется выражением
К(р) = \Рпи2\21(р-Рм)(р-Рт\
где полюсы
pnl=(-lly/2 + ilj2)o>c, Pnl=p*ni={-\lj2-ilj2)ac
[1, § 15.5].
После приведения знаменателя К(р») к виду
{ρ-Ρηΐ){ρ-Ρηΐ)=Ρ2-2^{Ρηΐ,2)Ρ + \Ρηΐ,2\2=Ρ2 + \βω*Ρ + ωϊ
запишем передаточную функцию фильтра в форме
К (р) = ω 11{р2 + Jlv>cp + ω с2).
Непосредственно из схемы (см. рис. 14.1) вытекает
соотношение
K{p) = SRZ12{p)/[Zi2{p) + Z2(p) + R].
Таким образом, приходим к равенству
«с CJ? Zl2(p)
SR
р2 + ^2<оср+<о2с Z12(p)+Z2(p) + R
Это равенство может быть удовлетворено только при
Zl2{p)=l/Cp, Z2(p) = Lp и SR=l.
При этом
Ψ} p2 + (R/L)p+\/LC
Сопоставление приведенных двух форм функции К(р>) позволяет
определить параметры синтезируемого фильтра: l/LC=(2nfc)2,
L=Rj{yft.ac\ C=1/(gjc2L).
При /"с = 104Гц и Д=104Ом получаем L = 0,ll Гн, С=
= 71(Г9'Ф.
14.6. Передаточная функция фильтра, представленного на
рис. 14.2 [1, § 15.6],
KQjRiR2ClC2
К(р) =
Ρ2+ΊΓ7τ(^ + 7^+1-Κο )Ρ + -,
Как и в предыдущем примере (фильтр Баттерворта второго
порядка), полюсы этой функции />п12 = (—1/х/2 + г'/х/2)шс и
передаточная функция должна иметь вид
216
Κ (ρ)=ω Ι /{ρ2 + ^2<йср + ω2).
Приравнивая знаменатели в приведенных двух выражениях для
К(р>), получаем следующие условия для определения основных
параметров схемы:
l/^C^C^
2
-ω;
^(^+|+1-*о)=^·
При наложенных условиях /?2С2«1/шс и С2/С1 = 0,4 из первого
равенства находим RiCimR2C2 = \jiuc, а из второго К0=\ +
+ C2/Ct + 1-^/2» 1.
Как видим, в данном устройстве назначение операционного
усилителя заключается лишь в осуществлении глубокой
отрицательной обратной связи.
В частном случае при С2 = 0,01 мкФ получаем
С1 = С2/0,4 = 0,025 мкФ, Ri = 1/шс С1 = 636 Ом, R2 = 2,5i?t =
= 1270 Ом.
При р = 0 (т.е. на нулевой частоте ω) Κ(ρ»)=1.
14.7. Передаточную функцию ФНЧ Баттерворта третьего
порядка сначала запишем в общей форме
(P-Pni)ip-Pn2)ip-P*3)'
где Рп ι = - «>с; Рп2 = (- 0,5 + /х/3/2)шс; рп3 =/7*п2 = (- 0,5 - |\/3/2)а>с [1,
§15.5].
Переписав затем эту функцию в виде произведения
будем трактовать К (ρ») как передаточную функцию каскадного
соединения двух развязанных звеньев с передаточными функциями
Ki(p) = ^i/(p-A.i) = ^i/(p+<dc) и К2(р) =
= ^2/(p2-2Re(pn2,3)/> + |pn2|2).
При Al = l/RlCl и RlCl = l/o3c первая функция реализуется
звеном первого порядка Ru Cv При съеме напряжения с
конденсатора Сх
p+\iR,Cy Ry + \IClP
Вторая передаточная функция К2(р) = А2/(р2 + а)ср + оз2) при
полюсах рп2,з = ( — 0,5 + г'ч/з/2)(ос реализуется звеном второго
порядка, схема которого и параметры совпадают с приведенными на
217
рис. 14.2, однако параметр операционного усилителя К0 должен
быть примерно 1,4 (а не 1).
При А2 = ч>1 К2(0)=1, а также K(0) = Kt (0)К2(0) = 1.
14.8. По своей структуре фильтры Чебышева и Баттерворта
совпадают. Для перехода от фильтра Баттерворта к фильтру
Чебышева требуется лишь изменить сопротивления резисторов Rl
и R2 (или емкости конденсаторов Ct и С2) в схеме рис. 14.2, а
также несколько изменить коэффициент усиления К0
(операционного усилителя) в соответствии с новыми полюсами передаточной
функции. Для фильтра Чебышева второго порядка при заданной
неравномерности АЧХ (не более 3 дБ) полюсы рп1=( —0,322-f
+ Ю,777)сос, рп2=р*п1 = (-0,322-Ю,777)сос [1, § 15.7]. При этом
К [р) = 0,708/(р2 + 0,645/)+0,708).
Приравнивая, как и в примере 14.6, соответствующие
коэффициенты полиномов в знаменателях передаточных функций,
получаем следующие условия для определения параметров активной
ЛС-цепи:
1/(/г.с1/г2с2)=о,708шс2,
Сохранив соотношения, принятые в примере 14.6 для фильтра
Баттерворта (Л2С2«1/шс, C2/Ct = 0,4), получим RlCi = y/2/(oc,
K0=l/^2 + C2/Cl + 1 -0,645« 1,46.
При С2 = 0,01 мкФ и Сх =0,025 мкФ
R2 = 1 /шс С2 = 1600 Ом, R ι = Уг/ω, Ct * 900 Ом.
14.2. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ПО
АНАЛОГОВОМУ ПРОТОТИПУ
14.9. Задан аналоговый фильтр нижних частот в виде простой
RC-цеии со съемом напряжения с конденсатора. Передаточная
функция цепи Ка(р)= 1/(1+-φ), постоянная времени τ=4 мс.
Основываясь на дифференциальном уравнении цепи, определить
структуру дискретного фильтра при шаге дискретизации Т= 1 мс.
Оценить отклонение АЧХ Κτ(ω) от ΚΆ(ω) на частоте/=500 Гц и
расхождение импульсных характеристик gT(kT) и ga(t) к моменту
времени t = τ.
14.10. Синтезировать цифровой фильтр с импульсной
характеристикой gT(kT), точно совпадающей с отсчетами ga(kT)
импульсной характеристики из предыдущего примера. Сопоставить
АЧХ цифрового и аналогового фильтров.
14.11. Синтезировать цифровой фильтр, инвариантный
относительно импульсной характеристики аналогового ФНЧ
Баттерворта второго порядка с частотой среза /с=104Гц. Частота
218
дискретизации 1/Г=104Гц. Сопоставить АЧХ цифрового и
аналогового фильтров.
14.12. Синтезировать цифровой фильтр, инвариантный
относительно АЧХ аналогового ФНЧ Баттерворта второго порядка с
частотой среза /с=104Гц. Частота дискретизации 1/Г=104Гц.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
14.9. Дискретизация уравнения
dt +RCU™*V> RCC[t)
с шагом Т приводит к разностному уравнению [1, § 15.12J
ивыЛ^Т)=^ще{^Т)+^ивык{тТ-Т), z = RC.
e(mT) ^^
U
e(t) £ч| Рис. 14.5
Этому уравнению соответствует рекурсивный фильтр первого
порядка с передаточной функцией Кт(р) = а0/(1 — Ьхе~рТ)
(рис. 14.5) и импульсной характеристикой gT(kT) = b\, где
Γ/τ , 1
l + T/τ ι ] + Τ/τ
Амплитудно-частотная характеристика дискретного фильтра
приводится к виду
Кт (ω) = Γ/τ ,
Vl+(] + r/T)2-2(] + r/T)cosror
а импульсная характеристика — к виду gT(kT) = 1/(1 + Τ/τΫ [1,
§15.12].
Соответствующие характеристики аналогового прототипа:
^а(ш)=1/ч/1+(шт)2; ga(t)=l-c-"\
При ω = 2π·500 рад/с КткО,\\, а АГа«0,08.
В момент / = τ = 4ãà = 0,41, a xga = e '«(U?.
14.10. Импульсная характеристика данной аналоговой цепи
ga(t) — -e </τ· По условию импульсная характеристика цифрового
фильтра должна представлять собой последовательность 1, е_г/\
е~2Г/т,... (постоянный коэффициент l/τ опущен). Применив к этой
219
последовательности z-преобразование, получим передаточную
функцию
Й(г)=1+е-г"г-Че-2Г/'г-2 + ...=
= l/(l-e-r/Tz-1)=z/(z-e-r/T),
имеющую полюс zn = e~T,z = ep"T.
Как и в предыдущем примере, полученной функции К (ζ)
соответствует рекурсивный фильтр первого порядка, однако
полюс ζπ связан с полюсом рп = — Τ/τ аналоговой цепи
стандартным z-преобразованием: zn = ep"T.
При этом импульсные характеристики gT(kT) и ga(t)
совпадают при любом шаге дискретизации Т. Амплитудно-частотные
характеристики ΚΤ(ωΤ)= 1/^/1+е_2Г/т— 2e_r/Tcosror и АТа(ш) =
= Ι/λ/1 +(ωτ)2 существенно различаются.
14.11. Как и в предыдущем примере, решение основывается на
методе стандартного ^-преобразования. При заданной
передаточной функции аналогового прототипа Κ(ρ>) = ω2 /(р»2 + х/2шс/7 + Шс) с
полюсами pni4z = {^ly/2±ijy/2)uic (см. пример 14.6), импульсная
характеристика фильтра
К(р)е"А5р=-^(е'н1'-е*п1') =
c — iao
= v^ce--c'/^sin(<Dci/>/2).
По условию импульсная характеристика цифрового фильтра
должна удовлетворять требованию, чтобы gT(kT)=ga(kT) =
= (1/2г)(ерпгк — epnirk) (постоянный коэффициент Л/2шс опущен).
Применив z-преобразование к последовательности gT(kT), к = 0,
1, 2, ..., получим передаточную функцию искомого
фильтра
Л , Г 00 00 ,
ziLk = 0 k = 0
ii'Vl-e'-'V1 \-/"тг-*
Ho ep"' = zni и ер"' = z*ni есть не что иное, как отображения точек
Pni и /7„! из р-плоскости на z-плоскость. Очевидны следующие
выражения:
220
ζ„ι.2 = е"в'Т/Л [cos (шсГ/У2) ±ίsin (а>сГЛ/2)].
Подставив в последнее выражение значения рп1 и />„ь после
несложных преобразований получим
K(z)=a1z-l/{l-b1zl-b2z-2),
где я^е"**'7' 2sin(сосГ,\/Т); й1 = 2е"'*':Г/ 2cos(ω,-Τ/^/ϊ); b2 =
= — e
Λ
Данной передаточной функции К (ζ) соответствует структурная
схема фильтра, приведенная на рис. 14.6. Для построения АЧХ
ι
τ
Рис. 14.6
следует положить z = e"°r и определить |К(е"°г)|. Прямое вычисле-
Λ
ние модуля приведенной выше функции К (ζ) связано с
громоздкими вычислениями. Задача упрощается при представлении
передаточной функции в форме
Κ(ζ) = α
ι(2-ζ.ι)(-'--;,)'
Ч^Т) = ^ййг
■(e'-T-z.1)(e'-r-z;1)'
Λ
когда \К(ешТ)\ = \а1 \l(R„iRn2)- При этом вычисление АЧХ
сводится к измерению расстояний /?nl = |eitt,r — ζπ1| и Rtl2 = \ei'AT — z*nl \ от
точки е (на окружности |ζ| = 1), соответствующей углу ωΤ, до
полюсов ζπί и гор На рис. 14.7 показано положение полюсов
znli2 = c ° I cos—= + mn —^ I на z-плоскости при (осТ/у/2 =
= 0,1 2п/у/2 и проиллюстрирован смысл /?п1 и Rn2.
Λ
Результаты вычисления |К(е'юГ)| = АГг(шГ) приведены на
рис. 14.8. На том же рисунке представлена АЧХ аналогового
221
I I I I 1 1
0 1 2 J 4 5<u/at
Рис. 14.7 Рис. 14.8
фильтра ΑΓ,(ω/ω0)=1/>/ΐ+ (ω/ωβ)τ=1/>/ΐ+ (1/ω0Γ)4(ωΓ)4.
Можно отметить значительное уменьшение крутизны спада |Кг(со7)|
по сравнению с | Ка (ωΤ) |.
14.12. Для приближения формы АЧХ цифрового фильтра к
форме АГа(ш/шс) используется дробно-линейное преобразование
z = {l+p)/{l-p), p = (z-l)/(z+l),
в результате которого АЧХ ЛГа(со/шс), сохраняя масштаб на оси
ординат, сжимается в пределах -π<ωΓ<π,
Связь между абсциссой шцГ функции АГ(шц7) и абсциссой ш/сос
функции АГа(ш/шс) определяется соотношением [1, § 15.13]
ro„r=2arctg(ro/n0),
где Ω0 — нормирующая частота, обеспечивающая требуемое
соответствие между какими-либо характерными частотами
передаточных функций аналоговой и цифровой цепей. В данной задаче
такими частотами являются частоты среза сосц и (оса
цифрового и аналогового фильтров. Для указанных частот сосцГ=
= 2arctg((oca/n0).
По условию задачи соСц = 0,1 ·2π/Γ, шсцГ/2=18° и,
следовательно, coca/n0 = tg(coCI1 Г/2) = 0,3249, а О0 = шса/0,3249. Таким
образом, искомое соотношение между соцГ и ш/шса имеет вид
соцГ= 2 arctg (ω/Ω0)=2 arctg (0,3249ш/соса).
Построение АЧХ Кт((оцТ) по заданной АЧХ ЛГа(со/соса) для
фильтра Баттерворта 2-го порядка показано на рис. 14.9.
Структурная схема фильтра Баттерворта 2-го порядка,
инвариантного относительно АЧХ, может быть определена по
передаточной функции
222
О 30 60 90 120 150 180 ς^Γ
Рис. 14.9
Κ(ζ) =
Α0(ζ+ή2 _Α0(]+2ζ-ι + ζ-2)
{z-zni){z-z'Ki) \-biZ 1-b2z'
2 >
которая получается при подстановке p = (z— l)/(z+l) в
передаточную функцию аналогового фильтра К (/?) [1, § 15.13]. В последней
формуле bi = 2Rt{zai) и b2=-\zni\2.
Л
Полюсы функции К (ζ) на плоскости ζ связаны с полюсами
Pni,2/mca = (— 1/\/2 ±'7ν2), нормированными относительно
частоты среза шса, соотношениями
■+WM.(-./^+^)_
1 -0,3249 (-1/V2+ iljl)
Ζη2 = ζ*πί= 0,57 -/0,294.
Структурная схема фильтра приведена на рис. 14.10. Трансвер-
Л
сальная часть схемы обусловлена наличием в функции К (ζ)
двукратного нуля в точке г= — 1. Этим и объясняется подавление
хвоста АЧХ в центральной части диапазона частот от 0...2π.
14.3. ЦИФРОВАЯ ФИЛЬТРАЦИЯ
КОМПЛЕКСНЫХ СИГНАЛОВ
14.13. Радиосигнал a (t) = A0 cos (ω0 + ΰ>α) ί, где ωη = 2π/η—доп-
леровское смещение частоты, которое может быть как
положительным, так и отрицательным, в результате квадратурной
обработки [1, § 13.9] преобразуется в комплексный сигнал s (ί) =
= sc (ί) + is, (ή = Α0 cos ωαί + iA0 sin ωΛί. Синтезировать узкополос-
223
ный цифровой фильтр для определения знака шд. Абсолютное
значение частоты /д= Ю3 Гц. Частота дискретизации 1/Г=104Гц.
Полоса пропускания фильтра должна быть порядка 150 Гц.
14.14. Синтезировать гребенчатый режекторный фильтр с
управляемой частотой режекции на основе трансверсального
фильтра 1-го порядка.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
14.13. В качестве узкополосного цифрового фильтра
реагирующего либо только на положительную, либо только на
отрицательную доплеровскую частоту, может быть использован рекурсивный
фильтр первого порядка с комплексным весовым коэффициентом
в цепи обратной связи. Передаточная функция подобного фильтра
Λ
Κ(ζ) = 1/(1— Βγζ"1) имеет единственный полюс в точке ζα = 6ί =
let T r-r ι'ω Τ r-r n
= rt α . Приравняв ωπ частоте шд, получим za = rt л . При шд>0
полюс расположен выше оси х, при шд<0 — ниже оси х.
Амплитудно-частотная характеристика подобного фильтра
| к (είωΓ)| = 1/| 1 - ,·6ί(ω~ω«)Γ| = 1/^/1+г2-2гсо&((о-<од)Т.
Л ι Τ
При резонансе (со = шд) максимальное значение |К(е**д )| =
= 1/(1-г).
Полосу пропускания резонатора (по ослаблению на 3 дБ)
можно определить из условия
l + r2-2rcos(2nAfT) = 2{l-r)2, cos(2nAfT)= 1 - (l-r)2/2r.
При 2πΔ/Γ<ί:1 cos(2nAfT)*l - (2πΔ/Γ)2/2, откуда
По соображениям устойчивости фильтра радиус г
нежелательно задавать близким к единице. Положив г = 0,95, получим
д/= 1 -^L 104 * 80 Гц, 2Δ/= 160 Гц.
Структурная схема фильтра приведена на рис. 14.11. Весовые
коэффициенты Ьх и Ьу определяются выражениями
61 = ζ„ = ге"*д ; bx = r cos содΓ= 0,768; £> = rsincoar=0,559.
14.14. Трансверсальный фильтр первого порядка с
действительным весовым коэффициентом at позволяет осуществить
полную режекцию только на частотах ωΓ=π или 0 [I, § 12.9]. При
224
Ss вых (">)
Sc(m)
£е6ых0Ч>
SsC">)
sftbixW
Рис. 14. Π
Рис. 14.12
комплексном коэффициенте αγ = ах + iay = — е
функция фильтра
ίωΤ
передаточная
if» „Г
i(c*-t* )Г
K(z)=l-e · ζ"1, К(е,вТ)=1-е'
где ω0—частота, на которой требуется осуществить режекцию
колебания, т.е. К (е ° ) = 0.
Амплитудно-частотная характеристика фильтра
|K(eitt,r)| = |l-cos(ro-ro0)r+/sin(ro-roo)r| = 2
. (ω-ω0) Τ
sm-—~—
Структурная схема фильтра приведена на рис. 14.12.
Задавая весовые коэффициенты ах= —соьщТ, ау= — sma>0T,
можно перемещать нуль АЧХ по оси соГ во всем частотном
диапазоне 0... 2π.
Глава 15. ОБОБЩЕННАЯ ЛИНЕЙНАЯ
ФИЛЬТРАЦИЯ. КЕПСТРАЛЬНЫЙ
АНАЛИЗ
15.1. ОБРАБОТКА МУЛЬТИПЛИКАТИВНОГО
СИГНАЛА
15.1. Заданный мультипликативный сигнал s(t) = sl(t)s2(t)
преобразовать в сумму χ(ί) = χ1 (ή +χ2(ή так, чтобы функция xt (ή
зависела только от si(t), a x2(t)—только от s2(t).
Сформулировать требования к st (t) и s2 (t), обеспечивающие реализуемость
заданного преобразования.
225
15.2. Мультипликативный сигнал s(t) = s1 (t) s2 (ή = Α (1 +kt χ
xsinni)(l+/t2sincooO> 0</<Гс, с параметрами А=\, к1=0,25,
А:2 = 0,05, Q = 2n/T=2nF, Т=ТС/Ю, ω0 = 2π/0 = 10Ω преобразовать в
сумму χ(ή = Χί (ή + х2 (ή. Исходные сигналы Si (t)= 1 + 0,25 sin Ωί и
si (t)= 1+0,05 sin ω0ί представлены на рис. 15.1, α, результирующий
сигнал s(t)—на рис. 15.1,6. Найти функции xt (t), x2(t) и
построить графики их спектральных плотностей Xt (ω), Χ2 (ω).
sr,sz
f,0 =</ν\/\^^\/\/\/χ<
Τ/4
Τ/2 ST/4
α)
Рис. 15.1
15.3. Преобразовать сумму >" (0=>Ί (0 +^2 (0 в
мультипликативный сигнал $»ых(0 = 51вых(052выЛ0 τ&κ> чтобы сомножитель
■У1вых(0 зависел только от yt (ή, а сомножитель i2BbIX—только от
Уг
(ΟΙ 5.4. В мультипликативном сигнале, рассмотренном в примере
15.2, требуется изменить соотношение между сомножителями sx (ή
и s2 (t): именно второй сомножитель должен иметь вид (1 + 5Л;2х
χ sin ΰ>0ή, т. е. амплитуда колебания с частотой ω0 должна быть
усилена в 5 раз. Построить функциональную схему обработки
сигнала.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.1. Единственным оператором, позволяющим осуществить
подобное преобразование, является логарифмический. Поэтому
необходимо прологарифмировать заданный мультипликативный
сигнал
x{t) = ln s(t)=ln si(i) +ln s2(t),
откуда следуют равенства
χ1(/)=1ηί1 (ί), x2(t)=\ns2(t).
Сигналы Si (t) и s2 (t) должны быть больше нуля на интервале
своего определения.
15.2. Применительно к заданному сигналу s(t) приведенные в
предыдущем примере результаты позволяют написать
xi(t) = ln(l-\-ki sinOi), x2(i) = ln(l+&2sin(uof).
Спектральные плотности этих функций
226
Χι (ω)= J In (1 + ki sin nt)e-im,dt,
о
X2 (ω) = J In (1 + k2 sin co0f) e~ imdt.
Основываясь на разложении
ln(l + a) = a-a2j2 + a3/3- ... при |α|<1,
получаем
x1(i) = 0,25sinQi-^^sin2ni+... = 0,25sinnr-
-0,016 (1-cos Щ+ ... ,
x2{t)=0,05sm(o0t- * ' ' sm2o30t+ ... = 0,05 sin ш0Г-
- 6,25-10~4(1-cos 2ω0ί) + ... .
При заданных значениях А:! = 0,25 и А;2 = 0,05 можно пренебречь
слагаемыми с высшими степенями в разложении 1п(1+я) и
подставить xt (t) = 0,25 sin Ωί, χ2 (ί)«0,05 sin ω0ί. Таким образом, в
рассматриваемом примере функции χ ι (ή и х2 (Г) представляют
собой отрезки гармонических колебаний длительностью Тс с
частотами соответственно Ω и со0. Спектральные плотности Χχ (ω)
и Х2 (со) подобных функций легко определяются [1, с. 81 ]. Графики
функций Xi(2nf) и X2(2nf) при ТС = Ю Τ и F=\jT, /0=10F
изображены на рис. 15.2. Спектры Хх (со) и Х2 (со) в данном случае
не перекрываются.
,с rX,(2ftf)
1
Рис. 15.2
" г Ас
L
F'7/Τ
ψ—κ^ζϋ**)
15.3. Сумму y(t)=yl (t) +y2(t) можно трактовать как
логарифм искомого мультипликативного сигнала snax (t), т. е.
у (i)=ln sBM (ί) = 1η ίΐΒΗΧ (ί) +1η 52вых (ή.
Отсюда следует, что для определения ίΒΗΧ(ί) к функции у (ή
нужно применить преобразование, обратное операции
логарифмирования. Таким преобразованием является потенцирование
227
ехР [У (')] = exP [ln J™ {ή] = w (')·
Таким образом,
ίι.»«(ί) = βχρ|>ι(ί)]=β,,<0,
*2».х(0=ехР[)'2(0]вае,2<')·
15.4. Поставленная задача может быть осуществлена в три
этапа:
преобразование мультипликативного сигнала s(i)=Si(t)s2(i) в
сумму x(t) = xi(t)+x2{t);
разделение сигналов хх (7) и х2 (0 с помощью частотных
(линейных) фильтров Lt и L2 [при условии неперекрытия спектров
Χι (ω) и Х2 (со) ] и относительное усиление в 5 раз сигнала у2 (ή на
выходе линейного фильтра L2\
преобразование сигнала у (ή с выхода фильтров в
мультипликативный сигнал ίΒΗΧ (0 = s 1вых (0 ί2»Ηχ (О-
j-T-L_^
Рис. 15.3
Функциональная схема обработки должна иметь вид,
показанный на рис. 15.3. Сигнал на выходе
■W (0 = е>1 " ^ =ί1»Ηχ (0 Л'2вых (О-
Полагая коэффициенты передачи фильтров Lt и L2 равными
единице, получаем
y1(t) = x1(t) = 0,25smQt, y2(t)=5x2(t)=0,25smo3Ot.
Поскольку величина 5Л;2 = 0,25 достаточно мала по сравнению с
единицей, можно считать
■w(')=exP [°>25 sin Ωί] ехР [°>25 sin ω0ί]«(1 + 0,25 sin Ω,ή χ
χ (1 + 0,25 sin co0f), 0<t<Te.
8 вых'
Τ/2 ЗТ/4
Рис. 15.4
Новый мультипликативный сигнал с измененным
соотношением между амплитудами Αί = 0,25 и 5&2 = 0,25 изображен на
рис. 15.4 (сравнить с рис. 15.1).
228
15.2. ОБРАБОТКА СВЕРНУТОГО СИГНАЛА
15.5. Сигнал s(t) = sl(t)*s2(t) (свертку) преобразовать в сумму
x(t) = xi(t) +x2(t) так, чтобы xt (ή зависело только от si(t), a
χ2(ή—только от s2(t). Построить функциональную схему
обработки сигнала.
J5.6. Дискретный сигнал s(m)=si {m)® s2{m) (свертку)
преобразовать в сумму х(т)=х1{т) +х2{т). Построить
функциональную схему обработки сигнала.
15.7. Сумму y(t)=yl (ή +y2{t) преобразовать в свертку
■ϊΒΗχ(0 = ίΐΒΗχ(0*·ϊ2ΒΗχ(0· Построить функциональную схему
обработки.
15.8. Объяснить суть обобщенного принципа суперпозиции.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.5. Первый шаг—применение к s(t) преобразования Фурье, в
результате чего временная свертка переходит в произведение
спектров [1, § 2.8 и § 16.2]:
P[s{t)] = P[sl{t)*s2{tj] = Sl{a)S2{<o) = S{(»).
Второй шаг—логарифмирование полученного произведения:
In [S (ω)] = In St (ω) + In S2 (ω).
Третий шаг — переход из спектральной области во временную
с помощью обратного преобразования Фурье:
00
откуда следуют равенства
Xl (t)=& [In St (ω)], x2{t) = F [In S2 (ω)].
Функциональная схема обработки показана на рис. 15*5.
s(t)
ЧЕТзЬ^ШтжйЕИ
хЮ-
s,(f)*sz(t) =s/M-s2fui) "ins^+ins/w; -xf(t)+xz(0
Рис. 15.5
15.6. Первый шаг — применение к дискретному сигналу s(m)
z-преобразования:
^[s{m)] = S(z) = Sl{z)S2{z).
229
Таким образом, свертка s(m) преобразуется в произведение
S^zJS^z) [1, § 16.2].
Второй шаг — логарифмирование полученного произведения:
lnS(z) = ln§1(z)+ln§2(z).
Третий шаг — обратное z-преобразование:
ξ-1[1η§(ζ)] = —.Ф1пЩ ^-4ζ = χ(τη)
[1, с. 364], откуда следуют равенства
χ1Η = ξ-1[ΐη§1(ζ)], χ2Η = ξ-1[1η§2(ζ)].
Функциональная схема обработки сигнала представлена на
рис. 15.6.
зт*
?[]
%(ζ)-
^ites^Oi
х(т) =
=Sf(m)9>s2(m) =Sj(z)Sz(z) -lnS,G0+lnS2(z) =x1(m)+хг(т)
Рис. 15.6
15.7. Первый шаг — применение к функции y[t) преобразования
Фурье:
^Ι>(')]= ϊ >'(0ε"ίω,Λ = Υ(ω)=Υ1(ω)+Υ2(ω).
Второй шаг—потенцирование функции Υ (ω):
ехр [Υ (ω)] = exp [Υι (ω)] exp [Y2 (ω)].
Третий шаг — обратное преобразование Фурье, в результате
которого произведение спектральных функций переходит во
временную свертку [1, § 16.2]:
i»«(0=f Ϊ eY.He^He^ffl=ilBUX(/)«2.Ux(i).
— αο
Функциональная схема обработки показана на рис. 15.7.
yft)·
■**·[]
ехр[ ]
-y,(t)+y2(t)
=Yt(tu)+Yz(<u»
eY<*» =
*"'[]
Рис. 15.7
15.8. Принцип суперпозиции, справедливый для линейных
систем, предусматривает только операцию сложения сигналов на
входе системы. Обобщенный принцип суперпозиции
предусматривает также и операции умножения или свертки сигналов. Для
осуществления систем, подчиняющихся обобщенному принципу
230
суперпозиции, требуется сочетание нелинейных и линейных
преобразований сигнала (гомоморфная обработка). Между сигналами
si(t) и s2(t), образующими произведение или свертку, в
гомоморфной системе (как и в линейной системе) отсутствует
взаимодействие.
15.3. КЕПСТР МОЩНОСТИ СИГНАЛА
15.9. Вычислить кепстр мощности Cs(ra) дискретного сигнала
s{m), представленного на рис. 15.8, при следующих параметрах:
А = \ В, Т~\ мкс, 6 = 5· 104 с-1. Составить функциональную схему
обработки сигнала.
s
A i
■■ * Д » ш*
TvrNT fhlm
Рис. 15.8 Рис. 15.9
15.10. Вычислить корреляционную функцию Bs(m) и
сопоставить ее с кепстром Cs(ra) для сигнала s(m) из предыдущего примера.
15.11. Вычислить кепстр мощности импульса прямоугольной
формы, дискретизованного с шагом Τ (рис. 15.9), при следующих
параметрах: А = \ В, Ν=τ„/Τ.
15.12. Построить функциональную схему вычисления кепстра
мощности сигнала s(t)=sl(t)*s2(t) (свертка), который дискретизован
с шагом Т, основанную на использовании БПФ и ОБПф.
15.13. Задан сигнал в виде суммы s(t) = s1(t) + as1(t—t0), где
ouj (t — t0)—сигнал, задержанный на время t0 относительно
исходного сигнала st (t): ос— постоянный коэффициент. Привести s(t) к виду
свертки s (ί )=s ι (t )*ί2 ('), где s2(t)—подлежащая определению функция.
15.14. Вычислить функцию In | S2 (ешт) |2 и кепстр мощности
сигнала s2(m) = b(m) + ab(m — m0) при m0=10, α = 0,8.
15.15. Вычислить кепстр мощности сигнала s{m) = s1(m) +
+ as1(m — m0) для случая, когда Si(m) соответствует сигналу,
представленному на рис. 15.8, при N=56. Совместить на одном
рисунке графики Csl(ra) и Cs2(m) для т0=10, ос = 0,8.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.9. Кепстр мощности дискретного сигнала s(m) определяется
выражением
231
50 60 N-f m
Cs{m) = ~ ln|S(eimr)|2cos(mcor)u?(cor),
2π
где S(e"°r)—z-преобразование сигнала s(t), дискретизованного с
шагом Г [1, § 16.5].
В данном примере
S{ei<aT) = A £ e-ftmre
— im<aT_
m = 0
l-e_"e
-ί>Γ„-ίωΓ '
ЬТ=0,05.
Находим квадрат модуля функции S(e"°r):
А* А2
1 -2е-"гео8ю7Ч-е-2*г_ 1 -2dcosaT+d2'
ISfe^l^
где обозначено d=exp( — ЬТ)хО,95.
Тогда
In | S (е'тГ) |2 = In Л 2 - In (1 - 2rfcos со7Ч ^2).
Графики функций |S(e,<or)| и In |S (ε'ωΓ) |2 при А = \ В и ЬТ=0,05
представлены на рис. 15.10.
360°
Рис. 15.10
Выражение для кепстра мощности приводится к виду
Cs(m) = \nA2- J cos(m(oT)d(G)T)-~ ln(l-2dcos(oT+d2) χ
2π
2π
χ cos (m(oT)d((oT).
При га = 0 первый интеграл равен 2π, а второй обращается в
нуль [13, 4.224.14] и
π
С8(0) = 1пЛ2-^ 1п(1-2^со8(оГ+й?2)й?(соГ)=1пЛ2.
232
При m/Ο первый интеграл обращается в нуль, а второй равен
\~2^d) Ε13' 4'397-6] и
Cs(m) = dm/m, га=1, 2, ....
График Cs(m) при d=e О,05%0,95 представлен на рис. 15.11, а
функциональная схема — на рис. 15.12.
с*
1,0
0,8
0,6
W
а 2
0
-
'
-
>
I ! ϊ τ t . . .
/ 23456789 Ют
Рис. 15.11
S(m)
S(z) \S(z)\z In ISfzjl2 CsCm)
Рис. 15.12
15.10. Корреляционная функция дискретного сигнала
определяется выражением
Bs {т) = у | S (είωΓ) |2 cos (тсоГ) d(a>T),
которое отличается от Cs(m) только отсутствием операции
логарифмирования под знаком интеграла. Подставив
\S(eimT)\2 = A2/(l-2dcos(uT+d2)
(см. решение предыдущей задачи) и вычислив последний интеграл
[14, 859.122], получим
Bs{m) = A
2π
С08(тшТ)с1(шТ) =А2 2ndm _ 2,m (] _ ,2ч
{\-2dcosioT+J2) 2n{\~d2) l{ >'
Функции Bs{m) и Cs(m) при /1 = 1 В и й?=0,95 представлены на
рис. 15.13. Отметим более быстрое убывание кепстра.
15.11. Для сигнала в виде импульса прямоугольной формы
z-преобразование
\-1
sin-
ΝωΤ
S(eimT) = A X e-imaT = A
m = 0
ωΤ
sin-
cosi ωΤ )-/'sin( ωΤ
233
ва
10
8
6
4
Ζ
о
%
0,8
0,6
0,U
0,2
О
π
r \ Ζ 4 6 8/0 12 14 16 18 ΖΟ m
<js t
a)
\\\\lt,.
Ζ 4 6 8 10 m
δ)
Рис. 15.13
ifl
0,8
0,6
0,Z
0
^^^^тМшшштЛшштяМшт
яЛштттМшттЛ^^
/ Ζ Ζ 4 5 6 7 8 3/0 M-f m
Рис. 15.14
|S(e-)| = ^|sin^j|/|sin^j|,
In IS (είωΓ) |2 = In A 2 + 21n | sin (~\ | —21n/ sin (ψ) |.
Кепстр мощности
Cs(m)=lnA2— cos(m(oT)d((oT)+2±-
In I sin —— 11 cos χ
π
x (mo>T)d(<oT)-2± ln|sin(^]|cos(mco7)d(cor).
При т = 0 первый интеграл равен 2π, а второй и третий равны
-2π1η2 [13, 4.224.3]. Таким образом,
С8(0) = 1пЛ2.
При т/0 первый интеграл равен нулю, а второй обращается в
нуль ввиду ортогональности функций In | sin 1 и cos (moo Г) на
интервале —π, π, третий же интеграл равен ( —π/m) [13, 4.384.7].
Таким образом,
C»=-2-L(-*V
m=l, 2, ..., Ν-\.
Полученный результат представлен на рис. 15.14.
234
15.12. Все преобразования сигнала, предусмотренные
функциональной схемой на рис. 15.12, остаются в силе. Необходимо лишь
отобразить, во-первых, то, что входной сигнал является сверткой,
и, во-вторых, что вычисление S (е"*П на ЭВМ производится по
алгоритму ДПФ. Из определения ДПФ
\-1
s(n)= £ i(m)expl —i
m = 0
.In
'—1
N
-mn
n=\, 2,
N-L
видно, что каждый из комплексных спектральных коэффициентов
S(n) = ReSin) + /Im|S(n)| есть не что иное, как значение S(z) в
точке z=e /ЛГ, лежащей на окружности единичного радиуса:
S (и)=Re S (и)+/ Im S (и) = S (ei2,tn/Ar).
Переходя к квадратам модулей |S(n)|2 = [ReS(nV]2 + [ImS(n)]2
и логарифмируя, получаем N чисел вида In|S(и)| , т.е. набор
дискретных значений функции ln|S(e"*r)|2.
Применив, наконец, ОБПФ, найдем кепстр мощности
cjw)=^iollnlsWl2«p(^«w)=cilH+cl2(w),
m = 0, l, ..., 2JV-1.
Алгоритм перечисленных преобразований представлен на
рис. 15.15.
Re S(n)
S(/77>
/Re S(n))
»S, (m) β s2(m) lm Sr^TnC 3 |—0«n S(n)) z
Рис. 15.15
\S(n)\2
Ml
ln|SM2
•АОБПФ
C(m)=
•zsjm)+zs2m
15.13. Составим выражение для спектральной плотности
сигнала s[t):
S(ro)=S1(ro)+aS1(ro)e-''(0'° = S1(ro)(H-ae-''(0'»)=
= S1(a>)S2(a>),
где 82(ω)=1+αε-'ω'0.
Получилось произведение двух спектральных плотностей, из
чего следует, что s(t) является сверткой s^t^s^t), где s2{t) —
функция времени со спектральной плотностью S2(a>). Очевидно,
что 52(ί) = δ(ί) + αδ(ί-ί0) (рис. 15.16). Переходя к дискретному
сигналу s(m)=sl(m) + <xsl(m — m0), получаем аналогичные
соотношения:
§ (eitt,r) = S (е/тГ) (1+ е " ,Μ»ω7) = S x (eiaT) S2 (eitt,r);
235
s2(t)
№
a<r(t-t0)
0 t0=mBT t p„c< 15<16
S2 (eitt,r) = 1+ α exp (- im0(oT);
s (m) = sj (m)®52 (m); s2 (m) = δ (га) = αδ (га — m0).
В данном случае задержка t0=mT, где т0 — целое число.
Существенно, что множитель S2((o) = l-f осе_,0)'с или S2(e"oT) =
= 1 + осе~"и°(оГ, учитывающий задержку сигнала на время i0, a
также постоянный коэффициент а, от структуры спектра
исходного сигнала sl{t) не зависит.
15.14. Сигналу s2(m) = oc6(ra —га0) соответствует z-преобразова-
ние
S2(e,'<ftr)=l+ae-,>r'°(o:r.
Запишем |S2(eitt,r)|2 в форме
|1+<хе
-imniuT 12 .
+ 2а cos (т0(йТ)+а2
={\+ae-imo<s>T)(l+ae + imomT).
Тогда
ln|S2(e,'tt,r)|2=:ln(H-ae-,'mo<ftr) + ln(H-ae + imo<ftr).
Так как |ае " ""°ωΓ | < 1, можно написать
1пП+ае~(тотГ) = ае~,'тотГ--е~'"2то0)Г+—е~'3т^
у ' 2 3
овг —.
ln(l+ae + imo'°r) = ae + imou" e
Г a Q + i2m0<ft7' ι 5Le-i3m0mT.
3
Тогда
ln|S2(e''mr)|2 = a2cos(m0ro7^--2cos(2ra0a>r) +
a3
-\—2cos(3ra0a>r)—...,
и общее выражение для кепстра
Cs2 {m) = ~ In |S2 (efar )|2 <χ>*{ηι0ωΊ)ά{ωΤ)
2π
236
приводит к следующим результатам:"
Cs2(0) = 0, Cs2(±m0)=:a, Cs2(±2m0)= -£
Cs2(±3m0)= "3
a
"Τ
Графики функции ln|S2(e"*r)(2 (а) и кепстра Cs2(m) (б) при
ос=0,8, т0 = Ю представлены на рис. 15.17.
1,0
m|S2(e!";|
гь>, |2
as/3
■ ί ,-у.
ft ιωΤ -3ϊ-30-Ζ5
-aV2
Рис. 15.17
\-15-10-
I -да,
a*/Z
я ■ I ■
-5" 0 5" Л7/5 \25Z0Z5m
Щ *
-аг/2
15.15. Кепстр мощности исходного сигнала вычисляется по
формуле Csl(m) = dmim (см. решение 15.9 и рис. 15.11), а кепстр
Q.2(m) следует перенести с рис. 15.17,6.
15.4. ОТНОШЕНИЕ СИГНАЛ/ШУМ НА ВХОДЕ
ЛОГАРИФМИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ
ПРИ КЕПСТРАЛЬНОЙ ОБРАБОТКЕ СИГНАЛА
15.16. Сигнал s(t)—At"bt, ί>0 (см. рис. 15.8), действующий на
фоне белого шума x(t) со спектральнойнплотностью мощности
Wx(o))=const, подвергается дискретизации с шагом Т. Вычислить
отношение η (ω Г) спектральной плотности энергии сигнала к
спектральной плотности энергии шума после дискретизации.
Отметить значение η (ωГ) в точке ωΓ=π. Данные сигнала и
помехи: Λ = 10 В, Т=\ мкс, & = 5-104с-1, число отсчетов сигнала
N=64; Wx(.(o)^l0~6 В2/Гц.
15.17. Исходя из условия, что единственной помехой при
кепстральной обработке является шум квантования, определить
требуемую разрядность АЦП для сигнала из предыдущего
примера. Для ослабления взаимодействия сигнала и помехи в
логарифмической нелинейности обеспечить выполнение
неравенства η(π)>10.
15.18. Определить величину η (π) для сигнала s(t) = Bte~bt
(рис. 15.18) при использовании 10-разрядного АЦП. Парамет-
237
20 40 60 80 /00 1201 m
N4
Рис. 15.18
ры сигнала: Ь = 1,25 · 106 с-1, Г=40 не, JV=128. Максимальное
значение сигнала smox на входе АЦП Не должно
превышать 10 В.
15.19. Сопоставить результаты решения примеров 15.17 и
15.18; объяснить необходимость повышения разрядности АЦП при
переходе от сигнала sl(t) — Ae~bt к сигналу s2(t) = Bte~bt.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.16. Спектральная плотность энергии континуального
сигнала 5(0 равна 5"5(ω) [1, с 36]. а после его дискретизации с шагом
Τ—соответственно S (со)/Г (при условии, что спектр сигнала
ограничен полосой — 1/2Г...+1/2Г [1, с. 65]). Переходя к z-преоб-
разованию S (е'тТ)/Т, получаем [1, с. 362]
m=0 m=0
k-m ■ 0,05„-ί»Η»Γ
Поскольку е-63 0,05 = 0,04, замена верхнего индекса
суммирования га = 63 на оо не приводит к существенной
погрешности. Тогда в соответствии с вычислениями примера 15.9
получаем
|S(eimr)J2^2/(l-2i/coscor+u?2),
^=ехр(-6Г)*0,95.
Определим теперь спектральную плотность энергии помехи,
действующей на отрезке времени TC = NT, совпадающем с
длительностью обрабатываемого сигнала 5(0- Заметим, что при заданной
спектральной плотности мощности Wx((u) спектральная
плотность энергии равна Тс\Ух((й). После дискретизации с
шагом Г спектральная плотность энергии помехи TcWx(u>)/T2 = NgI,
где σΙ=1Υχ(ϋή/Τ—средняя мощность помехи в полосе
частот -Ι/2Γ...+ 1/2Γ.
Итак, искомое отношение [1, § 16.8]
η(ω7) =
β(ε*°τ)]2
ΝσΙ
I
κσχ/ N(\-2dcosiuT+d2)'
В данном примере σ2= Η^(ω)/Γ=1(Γ6/1(Γ6 = 1 В2, (Α/σχ)2 = 100 и
238
ν,Αβ
Рис. 15.19
300 360
ωΤ, град
η(ωΓ) = 100/[Λ^(1-2ί/οο8ωΓ+ί/2)]. График функции η(ωΓ)
приведен на рис. 15.19.
Находим значения У)(юТ) в характерных точках m оси юТ:
η(0)= 100/JV(I -d}2 = 100/64 (0,05)2 = 104/16-^(40 дБ— 12 дБ) =
28 дБ,
η(π)= №/N(1 +d)2= 100/64 ·3,8->(20 дБ —23,8 дБ)= -3,8 дБ.
15.17. Из предыдущего примера видно, что для обеспечения
η (π) ^10 требуется отношение мощностей сигнала и помехи на
входе АЦП
(Л/а^2^л(п)Лф+^2 = 10-б4-3,8 = 10-243-^(10дБ + 23,8дБ)=:
= 33,8 дБ; '
Α/σχ>50.
Это означает, что динамический диапазон АЦП должен быть
не меньше 34 дБ, т. е. число разрядов должно быть не меньше 6
(6 дБ на разряд).
Графики функции η (ω Г) для Λ/σ =10 и 50 представлены на
рис. 15.19.
15.18. Для сигнала s(t) = Btt~bt, b>0, t^0, z-преобразование
\-ι
8(е™т)=ВТ£ те~ЬТте-
imTm
\-l
m=0
ВТ X me
m = 0
-(bT+ia>T)m
имеет вид арифметико-геометрической прогрессии. При N=128 и
£>Г=0,05 слагаемое (N- 1)ебГтз»0,2 и замена верхнего индекса
суммирования N—1 на оо не Приводит к существенной
погрешности. Поэтому [13, 0,113]
S{eiaT)*BTe-bTe-iaT/{l
-bT0-ia>T/ίλ а-Ьте-шТ\2
и спектральная плотность энергии сигнала
|§(е*г)|2=(Д7У)2Д1 -2dcosG>T+d2)2, d=e'bT.
Нетрудно убедиться, что 5(0 достигает максимума s„
момент t=\jb = 20 Т.
Таким образом,
■B/eb в
239
,2
'max
(BTd)2=(besm^)2=(0,05)2(ed)2sl
и
\S{eiaT)\2 = 25 ■ W-*e2d2s2max/{l -2dcosG>T+d2).
Спектральная плотность энергии помехи (шум
квантования), как и в двух предыдущих задачах, равна Νσχ. Искомое
отношение
''max
ΝσΙ N(\-2dcosioT+d2)\ax
Ho (smilx/ax)2 есть не что иное, как динамический диапазон
АЦП, в данном примере 10-разрядного.
Таким образом, (smax/ax)2rj = 60 дБ (6 дБ на разряд).
В точке (йТ—п
Л(Я)=Ы№^У=Ю1И^. ΙΟβ«9-9,6 дБ.
,у ' N{\+d)*\axJ 128(1+0,95)4
Итак, вблизи точки ωΤ=π, где спектральная плотность энергии
сигнала минимальна, обеспечивается превышение на ~10дБ
спектральной плотности энергии помехи. Исследования
показывают, что такого превышения достаточно для удовлетворительного
определения кепстра сигнала.
15.19. Для сигнала sl(t) = Ae~ln, ί>0>
Άί(π)=Α2/(\+ά)2
(см. пример 15.17), а для сигнала s2{t)=Bte~bt, ί>0,
η2(π) =
с2
0тах
(см. пример 15.18).
При одинаковых значениях ЬТ (в данных примерах ЬТ =0,05;
й?=0,95) имеет место соотношение
η2(π) ег{ЬТ)гаЧзта
η,(π) {\+d)2 \ A
Приравнивая амплитуды импульсов smax=A, получаем η2(π)/
/η^π^Ι,δ-10-3. Столь резкое снижение η2(π) объясняется
более быстрым убыванием спектральной плотности сигнала
s2(0; Действительно, 5Ί ((S>) = A/yJb2 + (S>2, S2 (ω) = Bj(b2 + ω2 ). При
ω»6 5Ί(ω) убывает со скоростью 1/со, a S2(g>) — со
скоростью 1/ω .
15.5. КОМПЛЕКСНЫЙ КЕПСТР
15.20. Определить кепстр испытательного сигнала sl(t) = b(t), a
также s2(t) = a6(t) при а>0.
240
15.21. Найти комплексный кепстр Cs(m) сигнала s(m),
представленного на рис. 15.8. Неоднозначность, обусловленную
комплексным логарифмом функции S(z), устранить с помощью
метода логарифмической производной. В чем различие между
Cs(m) и кепстром мощности Cs(m) для данного сигнала?
15.22. Составить алгоритм определения комплексного кеп-
стра на основе логарифмической производной с
использованием БПФ.
15.23. Составить алгоритм определения кепстра, основанный
на прямом вычислении комплексного логарифма, с
использованием ОБПФ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.20. В этих простейших примерах общее выражение для
комплексного кепстра [1, § 16.9]
00
Л
Cs{q) = ~ lnSHe^co
приводит к следующим результатам:
1. 5ι(ί) = δ(ί), S»^, lnS.H^O, Csl{q)=0;
2. s2(t) = a6(t), S2(co) = tf, In S2 (ω) = In a,
^W-s
lnaeittMJ d(o = lnab(q).
При a< 1 весовой коэффициент In α отрицателен, при а> 1
—положителен.
15.21. Определение комплексного кепстра сигнала, не
требующее знания его ФЧХ, имеет вид [1, § 16.10]
С4.(т)=—LJ_ φ [S'(z)~\zmdz, m/0.
4 ' mini J *- v /J
При т = 0
cM=i
\n\S(eiaT)\d{(uT)
[1, с 491].
Для сигнала s(m), представленного на рис. 15.8,
241
ν / г_е ьт ^ > dz z{z-e bT)
Поэтому
с.И=
-&T(m-l)_
m 2πί Τ (ζ—е ьг) m
Ы = 1
-, тЗИ;
С5(0)=1 ln[^(l-2e-6rcosror+e-26r)1/2] x
χί/(ωΓ)=1ηΛ
[13, 4.224.14].
При Λ = 1, Cs(0) = 0 Cs(m) = e-6rm/m, m=\, 2, 3,....
При ra^l комплексный кепстр Cs(w) рассматриваемого
сигнала совпадает с кепстром мощности С(гп) («минимально-фазовый»
сигнал). (См. решение примера 15.9 и рис. 15.11.)
15.22. Предварительно необходимо представить S(e"*r) и
S'(e"*r) в виде z-преобразований:
S{eiaT)= X 5(m)e-itt,mr,
m = 0
N-1
S'(etor)=:-/ X т5(т)е-(|
-ίωιηΓ
пл I'" It;
m = 0
Следующий шаг — использование соотношения между ДПФ и
^-преобразованием [1, § 12.6]:
Ν 1 -Ί-Γ 1ят
/2я\
I — и
S(n)= Σ *Не ™ =S(emTKT^n
m = 0 \ ,
S'(n)=-i Σ ^(m)e"Vb=:s'(ei,',r)|(((7,_2!.n
N-1
'Σ'
m = 0
Тогда приведенные в предыдущем примере 15.21 выражения
для кепстр а принимают вид
242
Cs{m)= - —VГ^]е«2^)-, Кша- 1;
^(oj-iYmiSiii)!.
iv n = 0
15.23. Алгоритм обратного ДПФ записывается в виде
<»=/ς 1п8(й)е^",)-1 Υ 0η5(ω)+
лп = 0 л = 0
+ /[θ5ΓΛ(ω) + £2π]}εί(2π/Λ,)'"", га = 0, I, ..., JV-1.
Главное значение аргумента 05ГЛ(со) вычисляется на ЭВМ
непосредственно с помощью стандартной программы. Это
значение затем дополняется корректирующей последовательностью [1,
§ 16.10].
15.6. ИЗМЕНЕНИЕ КЕПСТРА ПРИ
НЕКОТОРЫХ ПРЕОБРАЗОВАНИЯХ СИГНАЛА
15.24. Определить кепстр сигнала st (га), задержанного на га0
тактов.
15.25. Сигнал st(t), дискретизованный с шагом 7\ = 5мкс,
подвергается сжатию в η = 5 раз при неизменном числе отсчетов
(что необходимо для сохранения формы сигнала). Выявить
влияние сжатия сигнала на его кепстр.
15.26. Сигнал st (t) со спектральной плотностью Si (ω)
подвергается дифференцированию. Определить кепстр производной
dsi (t)/dt.
15.27. Определить кепстр сигнала s(t)=$sl(t)dt.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ
15.24.^ Если исходному сигналу sl(m) соответствует z-преобра-
зование S(e"°r), то задержанному на т0 тактов сигналу s2(m) =
=5j (га — га0) соответствует
S2(ei<or)=:e"imo<ftrS(ei<or)
и
lnS2 (еШТ)= -/га0шГ+1п Sx (eiaT).
Применив к этому выражению обратное z-преобразование,
получим
Cs2(ra)=-/ra0 —
(oTeime>Td(u>T) + Csl(m).
243
Первое слагаемое в правой части, учитывающее эффект
задержки, не зависит от структуры сигнала ^(/я). Назовем его
«кепстром задержки» и обозначим Ст (т):
С*» =
/га0 —
xeimx dx.
При га = 0 интеграл J xdx=0, так что Cm (0) = 0.
-я
При га/О
imx j л · sin (»»π)—»»π cos (тл) „. π / ч
xeimxdx=2i—-—-—5 -—-= —2i-cos[nm)
[1, § 16.11] и
с*0Н=
' 2π
2/—cos(mn)
т
При задержке сигнала на один такт (w0 = l) кепстр задержки с
возрастанием га убывает по закону 1, —1/2, +1/3 и т.д. С
возрастанием задержки масштаб Ст (т) увеличивается
пропорционально величине га0.
15.25. Из условия задачи очевидно, что преобразование
сигнала заключается в уменьшении шага дискретизации в η раз, так что
Тг—Тх\п—\ мкс. Отсчеты функции s2(t) совпадают по величине с
отсчетами функции sl (t). Следовательно,
S^^S^e^i/"^ X 5l(m)e-,tt,7Vn
m = 0
и кепстр сжатого сигнала будет
InSJe'^/'-kos—d№
* ' и \ и
С-2И=^
Изменение шага дискретизации (7\ /η вместо 7\) не оказывает
влияния на структуру кепстра. Изменяется лишь масштаб кепст-
рального времени: интервалы между отсчетами кепстра на оси
будут Г2 = Г, /5 = 1 мкс.
15.26. Функции s(t) = -~-^ соответствуют спектральная
плотность S (ω) = i(oSl (ω) и логарифм lnS(ro)=ln(/ro) + lnS1(ro). Второе
244
слагаемое определяет кепстр исходного сигнала st (t), из чего
следует, что при дифференцировании сигнала к его кепстру Csl (q)
добавляется кепстр
со
Можно показать [1, § 16.11], что последнее выражение приводится
к виду
где γ = 0,577 — постоянная Эйлера, a u(q)—единичный скачок в
момент q = 0.
При q>0 C^{q)^-\lq.
15.27. Исходим из условия S1(0) = 0, так что спектральную
плотность интеграла можно записать в форме S2(ro) = S1(ro)/(/ro)
[1, приложение 2]. Тогда In S2(co)= — lni/a^+lnS! (ω). Повторяя
рассуждения, приведенные при решении предыдущей задачи,
приходим к следующему результату:
С„итfa) =-Сдиф(?) = !/? при q>0.
СПИСОК ЛИТЕРАТУРЫ
1. Гоиоровский И. С. Радиотехнические цепи и сигналы. Учебник для вузов.— 4-е
изд., перераб. и доп.—М.: Радио и связь, 1986.
2. Гоиоровский И. С. Радиотехнические цепи и сигналы: Учебник для вузов.— 3-е
изд., перераб. и доп.— М.: Сов. радио, 1977.
3. Баскаков С. И. Радиотехнические цепи и сигналы: Учебник для вузов.— М.:
Высшая школа, 1983.
4. Баскаков С. И. Радиотехнические цепи и сигналы. Руководство к
решению задач: Учеб. пособие для радиотехн. спец. вузов.— М.: Высшая
школа, 1987.
5. Горяинов В. Т., Журавлев А. Г., Тихонов В. И. Статистическая радиотехника:
Примеры и задачи: Учеб. пособие для вузов.— 2-е изд., перераб. и доп.— М.:
Сов. радио, 1980.
6. Лёзии Ю. С. Введение в теорию и технику радиотехнических систем: Учеб.
пособие для вузов.— М.: Радио и связь, 1986.
7. Левин Б. Р. Теоретические основы статистической радиотехники. Кн.1.— М.:
Сов. радио, 1974.
8. Тихонов В. И. Статистическая радиотехника.— 2-е изд., перераб. и доп.— М.:
Радио и связь, 1982.
9. Хемминг Р. В. Цифровые фильтры: Пер. с англ./Под ред. А. М. Трахтма-
на.— М.: Сов. радио, 1980.
10. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов: Пер.
с англ./Под ред. Ю. Н. Александрова.— М.: Мир, 1978.
11. Цифровые фильтры и их применение: Пер. с англ./В. Каппелини, А. Дж. Кон-
стантинидис, П. Эмилиани.— М.: Энергоатомиздат, 1983.
245
12. Корн Г., Кори Т. Справочник по математике для научных работников и
инженеров.— М.: Наука, 1970.
13. Градштейи И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений.—М.: ГИФМЛ, 1963.
14. Двайт Г. Б. Таблицы интегралов и другие математические формулы.— М.:
Наука, 1983.
ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. общие характеристики радиотехнических процессов и
ЦЕПЕЙ 4
Методические указания, решения и ответы 5
Глава 2. характеристики детерминированных сигналов 7
2.1. Обобщенная спектральная теория сигналов 7
Методические указания, решения и ответы 9
2.2. Гармонический анализ периодических колебаний 12
Методические указания, решения и ответы 13
2.3. Гармонический анализ непериодических колебаний 16
Методические указания, решения и ответы 18
2.4. Представление сигналов с ограниченной полосой частот рядом
Котельникова 25
Методические указания, решения и ответы 26
2.5. Спектральный анализ дискретизованных сигналов 28
Методические указания, решения и ответы 28
2.6. Корреляционный анализ детерминированных сигналов 30
Методические указания, решения и ответы 32
Глава 3. модулированные колебания 35
3.1. Амплитудно-модулированные колебания 35
Методические указания, решения и ответы 37
3.2. Колебания с угловой модуляцией 40
Методические указания, решения и ответы 42
3.3. Аналитический сигнал 46
Методические указания, решения и ответы , , 48
Глава 4. основные характеристики случайных сигналов 52
4.1. Вероятностные характеристики случайных процессов 52
Методические указания, решения и ответы 54
4.2. Корреляционные и спектральные характеристики случайных
процессов 58
Методические указания, решения и ответы 60
4.3. Узкополосные случайные процессы 69
Методические указания, решения и ответы 70
Глава 5. линейные радиотехнические цепи с постоянными
ПАРАМЕТРАМИ 75
5.1. Активные четырехполюсники 75
Методические указания, решения и ответы 77
5.2. Свойства линейных цепей с обратной связью 79
Методические указания, решения и ответы 81
5.3. Критерии устойчивости активных цепей с обратной связью 83
Методические указания, решения и ответы 86
Глава 6. прохождение детерминированных сигналов через
ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ 90
6.1. Воздействие широкополосных сигналов на апериодические цепи 90
246
Методические указания, решения и ответы 91
6.2. Прохождение импульсных сигналов через апериодический
усилитель 95
Методические указания, решения и ответы 96
6.3. Прохождение модулированных колебаний через узкополосные
избирательные цепи 98
Методические указания, решения и ответы ; 99
Глава 7. прохождение случайных сигналов через линейные
цепи 102
7.1. Спектральные плотности мощности и корреляционные функции
случайного процесса на выходе цепи 102
Методические указания, решения и ответы 103
7.2. Параметры распределения случайного процесса на выходе
линейной цепи 107
Методические указания, решения и ответы ПО
7.3. Собственные шумы в радиоэлектронных цепях 117
Методические указания, решения и ответы 118
Глава 8. нелинейные цепи и нелинейные преобразования
сигналов 121
8.1. Гармонический анализ тока в нелинейной безынерционной цепи 121
Методические указания, решения и ответы 122
8.2. Нелинейное резонансное усиление и умножение частоты 127
Методические указания, решения и ответы 128
8.3. Получение амплитудно-модулированных колебаний 130
Методические указания, решения и ответы 131
8.4. Детектирование амплитудно-модулированных колебаний 132
Методические указания, решения и ответы 133
8.5. Воздействие гармонических колебаний на цепи с нелинейными
реактивными элементами 134
Методические указания, решения и ответы 135
Глава 9. генерирование гармонических колебаний 138
9.1. Z-C-генераторы с внешней обратной связью 138
Методические указания, решения и ответы 139
9.2. Генераторы с внутренней обратной связью и генераторы с
запаздывающей обратной связью 142
Методические указания, решения и ответы 144
9.3. ДС-генераторы гармонических колебаний 149
Методические указания, решения и ответы 150
Глава 10. прицип параметрического усиления 152
10.1. Основные характеристики линейных параметрических цепей 152
Методические указания, решения и ответы :. 153
10.2. Параметрическое усиление колебаний 155
Методические указания, решения и ответы 157
10.3. Параметрическое возбуждение колебаний 159
Методические указания, решения и ответы 160
Глава 11. воздействие случайных процессов на нелинейные и
ПАРАМЕТРИЧЕСКИЕ ЦЕПИ 162
11.1. Преобразование случайных процессов в нелинейных
безынерционных цепях 162
Методические указания, решения и ответы 163
11.2. Воздействие узкополосного шума на амплитудный детектор 167
Методические указания, решения и ответы 168
11.3. Совместное воздействие гармонического сигнала и гауссовского
шума на амплитудный и частотный детекторы 170
247
Методические указания, решения и ответы 170
11.4. Воздействие случайных процессов на линейные параметрические
цепи 171
Методические указания, решения и ответы 172
Глава 12. дискретная обработка сигналов, цифровые фильтры.... 174
12.1. Дискретизация непрерывных сигналов. Спектр дискретизованного
сигнала 174
Методические указания, решения и ответы 175
12.2. Дискретное преобразование Фурье 179
Методические указания, решения и ответы 180
12.3. z-преобразование 184
Методические указания, решения и ответы 186
12.4. Принцип дискретной фильтрации 192
Методические указания, решения и ответы 194
12.5. Характеристики цифровых фильтров. Передача сигналов 198
Методические указания, решения и ответы 199
Глава 13. оптимальная фильтрация сигналов на фоне
ПОМЕХ 206
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, РЕШЕНИЯ И ОТВЕТЫ 208
Глава 14. элементы синтеза радиоэлектронных цепей 214
14.1. Синтез аналоговых четырехполюсников 214
Методические указания, решения и ответы 215
14.2. Синтез цифровых фильтров по аналоговому прототипу 218
Методические указания, решения и ответы 219
14.3. Цифровая фильтрация комплексных сигналов 223
Методические указания, решения и ответы 224
Глава 15. обобщенная линейная фильтрация, кепстральный
анализ 225
15.1. Обработка мультипликативного сигнала 225
Методические указания, решения и ответы 226
15.2. Обработка свернутого сигнала 229
Методические указания, решения и ответы 229
15.3. Кепетр мощности сигнала 231
Методические указания, решения и ответы 231
15.4. Отношение сигнал/шум на входе логарифмического преобразователя
при кепетральной обработке сигнала 237
Методические указания, решения и ответы 238
15.5. Комплексный кепетр 240
Методические указания, решения и ответы 241
15.6. Изменение кепстра при некоторых преобразованиях сигнала 243
Методические указания, решения и ответы 243
Список литературы 245