Author: Карташов Э.М.
Tags: теплопроводность теплопередача физика теплофизика теплотехника
ISBN: 5-06-004091-7
Year: 2001
Text
Э.М. КАРТАШОВ
Аналитические
МЕТОДЫ В ТЕОРИИ
ТЕПЛОПРОВОДНОСТИ
ТВЕРДЫХ ТЕЛ
Издание третье, переработанное
и дополненное
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебного пособия
для студентов высших
технических учебных заведений
Москва
«Высшая школа» 2001
УДК 536.2
ББК 22.37
К 27
Федеральная целевая программа книгоиздания России
Рецензент: проф. С. 77. Рудобашта (зав. кафедрой теплотехники
Московского государственного агроинженерного университета
им. В. П. Горячкина)
ISBN 5-06-004091-7 © ГУП «Издательство «Высшая школа», 2001
Оригинал-макет данного издания является собственностью издательства «Вы¬
сшая* школа», и его репродуцирование (воспроизведение) любым способом без
согласия издательства запрещается.
ПРЕДИСЛОВИЕ
Аналитическое изучение процессов теплопроводности является
одним из основных разделов современных инженерных исследова¬
ний в машиностроительной, энергетической, атомной промышлен¬
ности, в технологических процессах химической, строительной, тек¬
стильной, пищевой, геологической и других отраслях промышлен¬
ности. Это представляется совершенно естественным, если учесть,
что тепловые явления в природе играют особую роль. Достаточно
указать, что практически все процессы в той или иной степени
связаны с изменением температурного состояния и переносом теп¬
лоты. Следует также отметить, что инженерные исследования кине¬
тики целого ряда физических и химико-технологических процессов
аналогичны задачам стационарной и нестационарной теплопровод¬
ности. К ним можно отнести процессы диффузий, седиментации,
вязкого течения, замедления нейтронов, течения жидкостей через
пористую среду, электрические колебания, сорбции, сушки, горения
и др.
Именно этими обстоятельствами объясняется бурное развитие
теории теплообмена в последние десятилетия и то исключительное
внимание, которое ей уделяется как в физической теплотехнике, так
и в других областях науки, в частности, в дифференциальных урав¬
нениях математической физики в связи с созданием и развитием
аналитических методов решения краевых задач уравнения тепло¬
проводности и ему родственных. Даже поверхностное изучение
соответствующей научной и учебной литературы показывает, что
краевые задачи для уравнений параболического (и эллиптического)
типа — предмет практически необозримого числа исследований.
С годами их поток не уменьшается, охватывая все новые содер¬
жательные математические объекты, и все большее число самых
разнообразных приложений.
Классические краевые задачи для дифференциальных уравнений
математической физики в силу их чрезвычайно широкого приме¬
нения исторически привлекали внимание ученых разных направ¬
лений: математиков, механиков, физиков, химиков, теплофизиков
и т. д. Создавались новые, более общие и более корректные фи¬
зические и соответствующие им математические модели процессов,
разрабатывались новые аналитические, графические, численные (с
помощью метода конечных разностей) методы, методы аналогий
и другие подходы для решения целых классов задач; необычайно
высокого уровня развития достигла качественная теория диффе¬
ренциальных уравнений в частных производных. Применение чи¬
сленных методов на базе ЭВМ существенно расширило класс ма¬
тематических моделей, допускающих исчерпывающий анализ. На
основе точного решения задачи даже громоздкого вида можно
3
было проследить влияние любого параметра на кинетику процесса.
Разностные схемы приближенного вычисления решения задачи по¬
зволили при построении исходной математической модели процесса
не стремиться к сильным упрощениям, необходимым для получения
точного аналитического решения. А. Н. Тихонов и А. А. Самарский
разработали теорию создания разностных схем для дифференциаль¬
ных уравнений обыкновенных и в частных производных с гладкими
и разрывными коэффициентами в виде эффективных алгоритмов,
чрезвычайно приспособленных для реализации на вычислительных
машинах. Качественная теория дифференциальных уравнений
в частных производных позволяла, не решая самих дифференциаль¬
ных уравнений (с заданными краевыми условиями), получать необ¬
ходимые сведения о тех или иных свойствах решения. Аналитичес¬
кие методы теории нестационарного переноса позволяют получать
решение большого числа краевых задач. Результаты таких решений
предоставляют возможность наглядного и удобного анализа явле¬
ний, позволяют отразить влияние всех факторов, оценить их значи¬
мость и выделить главные из них, т. е. провести аналитический
анализ решения исходной задачи. Наличие аналитических решений
определенного класса краевых задач представляет интерес и для
построения разностных схем приближенного вычисления решений
достаточно сложных задач, плохо поддающихся исследованию дру¬
гими методами. Уверенность в том, что решение вычислено прави¬
льно, достигается применением той же вычислительной схемы для
расчета тех модельных задач, точные аналитические решения кото¬
рых заранее известны.
Несмотря на наличие обширной литературы по математической
физике, студенты и аспиранты высших технических учебных заведе¬
ний, специализирующиеся в области теплофизики, так же как и на¬
учные работники и инженеры, работающие в этой области, испыты¬
вают серьезные затруднения в подборе руководства по аналитичес¬
ким методам теории теплопроводности. Особенно это относится
к задачам нестационарной теплопроводности в областях с граница¬
ми, движущимися во времени; с переменным во времени относи¬
тельным коэффициентом теплообмена на границе области; при
фазовых превращениях — задачи Стефана (прямые и обратные)
и более общие для уравнений параболического типа со свободной
границей, а также задачи в гидромеханике с более сложными (чем
классические) граничными условиями; с разнородными граничными
условиями на линиях на плоскости и в пространстве; краевые задачи
линейного сопряжения граничных условий (или задачи Гильберга).
В этих случаях классические аналитические методы математической
физики становятся неприменимыми, так как оставаясь в рамках
этих методов, не удается согласовать решение уравнения теплоп¬
роводности с наличием дополнительных факторов, усложняющих
постановку соответствующей краевой задачи. Возникает необходи¬
мость в создании специального математического аппарата, кото¬
рый оказывается эффективным при нахождении точного анали¬
тического решения задачи только в определенной ситуации. В то же
4
время и для областей канонического типа вызывают определенные
трудности многомерные задачи теплопереноса (особенно в ци¬
линдрической и сферической системах координат); тепловые задачи
в слоистых телах и с нестационарными граничными условиями
при сопряжении сред, обладающих существенно разной теплопро¬
водностью, либо случаи, когда граничные условия сопряжения зада¬
ются на поверхностях, являющихся координатными в различных
координатных системах. Несмотря на хорошо развитую аналити¬
ческую теорию нестационарного теплопереноса при решении про¬
стейших одномерных задач для бесконечной пластины, бесконеч¬
ного сплошного и полого цилиндра (радиальный поток тепла),
сплошного и полого шара (центральная симметрия), и для этих
случаев имеется обширное поле деятельности. Один из важных
вопросов — улучшение сходимости рядов типа Фурье — Бесселя
в аналитических решениях краевых задач до абсолютной и равно¬
мерной вплоть до границы области, когда в постановке краевой
задачи не выполняются условия сопряжения краевых функций (на¬
чальной и граничной) в угловых точках фазовой области определе¬
ния уравнения нестационарной теплопроводности. Такие улучшен¬
ные решения представляют собой функциональные конструкции
нового вида, отличные от известных (классических) и являются
весьма удобными при рассмотрении многих практических вопросов
теплофизики: расчеты теплофизических постоянных на основе реше¬
ния обратных задач; определение времени прогрева детали канони¬
ческой формы; расчет времени выхода процесса на стационарную
фазу и т. д.
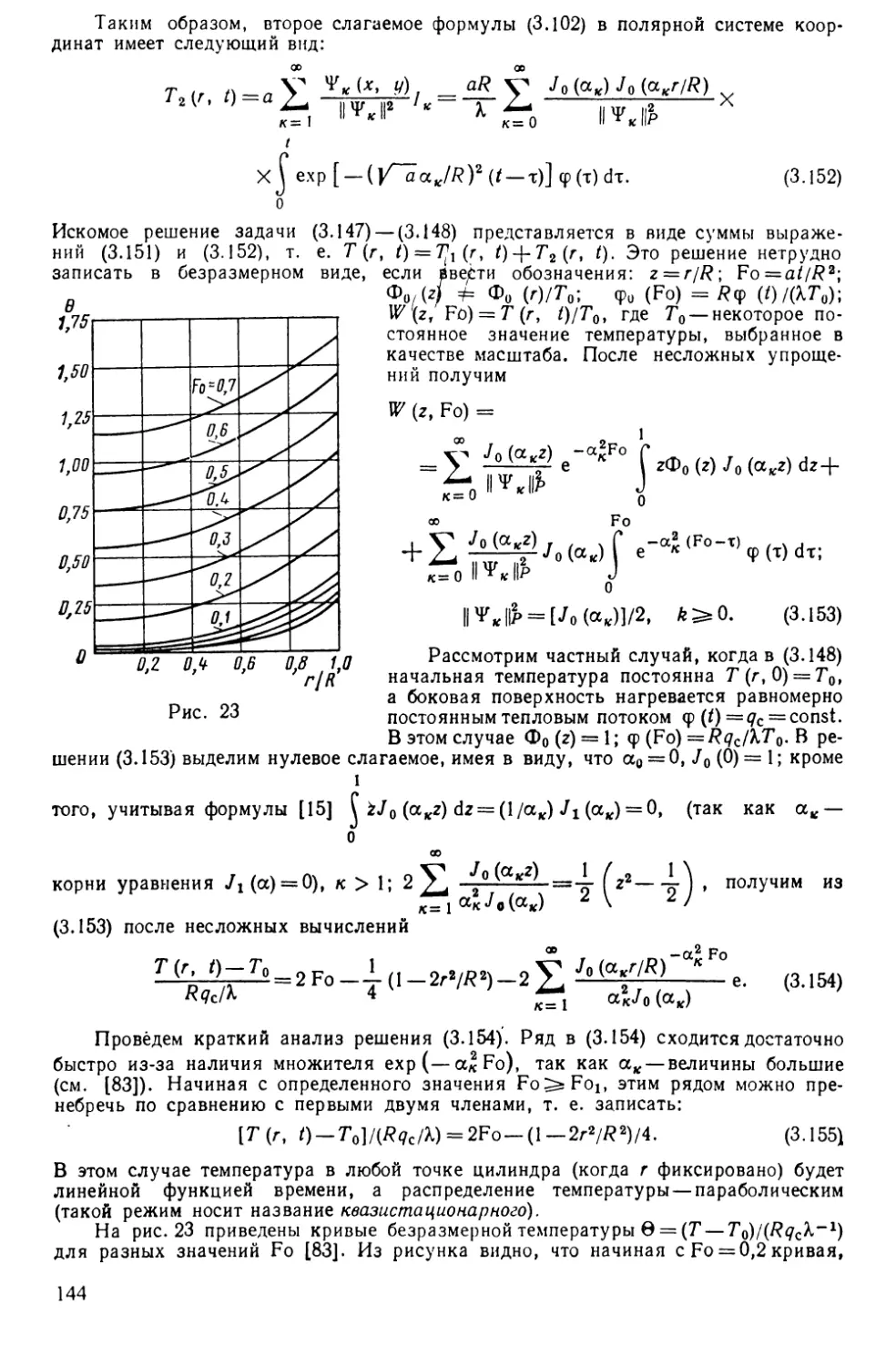
Все вопросы, отмеченные выше, рассмотрены в настоящей книге.
Основная задача, которую поставил перед собой автор, состояла
в том, чтобы отобрать, обобщить и представить в удобной для
изучения форме тот обширный материал, составляющий содержа¬
ние аналитической теории теплопроводности и разбросанный в ори¬
гинальных и обзорных специальных работах по теории теплопрово¬
дности (и других разделах прикладной математики и физики), а так¬
же в многочисленных монографиях по математической физике
и специальным функциям, в которых изучаются классические ана¬
литические методы решения дифференциальных уравнений с част¬
ными производными, указываются различные искусственные при¬
емы, конкретные подставки, преобразования, приближения и т. п.
Все это необходимо было изложить применительно к решению
краевых задач уравнения теплопроводности, сохранив при этом
основные преимущества метода, его обзорность и возможности
качественного анализа.
При этом оказалось, что число литературных ссылок намного
превысило тот объем, который возможен в рамках данной книги.
Поскольку невозможно перечислить всю литературу по аналитичес¬
кой теории теплопроводности (причем число публикаций в этой
области непрерывно растет), автор ограничился в ссылках только
теми работами, которые, по его мнению, представляют для студен¬
тов и других заинтересованных читателей первостепенный материал
для более детального изучения рассматриваемых проблем. Автор
исходил из опыта преподавания курса «Аналитическая теория теп¬
лопроводности», а также участия в совместных исследованиях с раз¬
личного рода научно-исследовательскими институтами и промыш¬
ленными предприятиями.
В настоящем учебном пособии излагаются основные аналити¬
ческие методы решения краевых задач стационарной и нестационар¬
ной теплопроводности (и родственных явлений), классических
и обобщенного типа, апробированные на широком классе тепловых
задач: 1) метод разделения переменных (метод Фурье); 2) метод
продолжений; 3) метод произведения решений; 4) метод Дюамеля;
5) метод интегральных преобразований (с конечными и бесконеч¬
ными пределами в декартовой, цилиндрической и сферической си¬
стемах координат) с улучшением сходимости рядов типа Фурье
в аналитических решениях краевых задач нестационарной теплопро¬
водности в ограниченных областях; 6) операционный метод; 7)
метод функции Грина (для нестационарной и стационарной тепло¬
проводности); 8) метод отражения (метод источников). Рассмот¬
рены новые разделы аналитической теории теплопроводности, в ча¬
стности: 1) методы решения краевых задач нестационарной тепло¬
проводности в области с движущимися границами (метод тепловых
потенциалов, метод функции Грина, метод рядов, метод функци¬
ональных преобразований); 2) методы решения краевых задач сте-
фановского типа, с переменным во времени относительным коэф¬
фициентом теплообмена, с разнородными граничными условиями
на линиях на плоскости и в пространстве (метод сопряжения, метод
дуальных интегральных уравнений, метод Винера — Хопфа, метод
тепловых потенциалов).
Каждому методу отводится самостоятельная глава или параг¬
раф, если предполагается объединить группу методов, предназна¬
ченных для решения одного класса задач; по этому принципу по¬
строена, например, гл. VIII. В начале каждой главы излагаются
теоретические основы метода, и после того, как читатель познако¬
мится с самим методом, он сможет посмотреть применение данного
метода при решении конкретных тепловых задач с подробным
ходом решения, с основными преобразованиями и расчетами.
В тексте пособия приводятся в качестве самостоятельных упра¬
жнений задачи (с ответами), позволяющие читателю проверить
усвоение того или иного метода. Наряду с ними формулируются
задачи, решение которых может составить содержание курсовой
работы, а во многих случаях и студенческого научного исследова¬
ния.
Предполагается, что читатель знаком с основами дифференци¬
ального и интегрального исчисления и решением обыкновенных
линейных дифференциальных уравнений в объеме высших техничес¬
ких учебных заведений, а также имеет представление о тригономет¬
рических рядах и интеграле Фурье. В некоторых случаях более
сложный математический аппарат излагается в самом тексте и од¬
6
новременно даются соответствующие ссылки на учебную математи¬
ческую литературу.
Автор учитывал, что читатель может заинтересоваться не всеми
методами, рассмотренными в книге, а только теми, которые его
интересуют в настоящий момент времени. В соответствии с этим
книга построена так, что отдельные ее главы могут изучаться
независимо друг от друга. В то же время, исходя из практических
соображений, читателю рекомендуется ознакомиться со всем содер¬
жанием книги, так как все задачи теории теплопроводности не
могут быть успешно решены каким-либо одним из названных мето¬
дов. Кроме того, знакомя учащегося с возможностями и пределами
применимости каждого аналитического метода, мы внушаем ему
мысль о том, что для каждой задачи (и даже в пределах одной
задачи) имеется свой наиболее рациональный метод решения с точ¬
ки зрения экономии времени, труда и достижения наибольшей
точности.
Основное внимание в книге уделено изложению методов и связи
между ними, вопросам функционального конструирования аналити¬
ческих решений тепловых задач (классических и обобщенного типа),
построению рабочих (расчетных) формул записи аналитических ре¬
шений и методике пользования найденными решениями. Значитель¬
но меньше внимания в книге уделяется физическому анализу най¬
денного решения. Читатель, интересующийся вопросами такого
рода, может обратиться к известному учебному пособию А. В.
Лыкова «Теория теплопроводности», в котором на многочисленных
примерах дано детальное изложение методики физического анализа
аналитического решения задачи. В данной книге этими вопросами
мы не будем заниматься, с тем чтобы сосредоточить основное
внимание на аналитических методах решения краевых задач для
уравнений теплопроводности.
Настоящее издание подготовлено на основе предыдущей книги
автора аналогичного названия (М.: Высшая школа, 1985, 480 с.).
В книге сохранены ее общее содержание, распределение материала
и характер изложения с упором на выбор рационального подхода
при нахождении аналитического решения той или иной краевой
задачи для уравнения теплопроводности, его наглядности и оп¬
тимальной формы функционального конструирования, возможно¬
сти представления одного и того же решения в различных (эк¬
вивалентных) функциональных формах.
В предлагаемое издание внесены ряд изменений и дополнений по
новым разделам аналитической теории теплопроводности твердых
тел; отметим наиболее существенные из них. В главе I дается
постановка динамических задач термоупругости. Этот класс задач
описывает проблему теплового удара, актуальность которой воз¬
росла особенно в последние десятилетия в связи с созданием мощ¬
ных излучателей энергии и их использованием в технологических
операциях. Рассмотрены также гиперболическая модель теплопро¬
водности на основе классической феноменологии Максвелла —
Каттенео — Лыкова о конечной скорости распространения тепла
в твердых телах и модели теплопроводности в средах с тепловой
памятью. В главе V расширены таблицы интегральных преобразо¬
ваний Фурье — Ханкеля с улучшением сходимости соответствую¬
щих рядов в аналитических решениях краевых задач нестационар¬
ной теплопроводности. В главе VII переработаны параграфы, по¬
священные методу функций Грина для областей с движущимися
границами. В главе IX предложены обширные таблицы аналитичес¬
ких решений дуальных интегральных уравнений и парных сумма-
торных рядов, используемых при изучении процессов переноса теп¬
ла и массы в твердых телах с трещинами.
Автор с благодарностью примет замечания и пожелания
по настоящему пособию, которые можно направить по адресу:
Москва, ГСП-4, Неглинная ул., 29/14, издательство «Высшая шко¬
ла».
Автор
ВВЕДЕНИЕ
Основы математической теории теплопроводности были заложены еще
трудами Ломоносова, Ньютона, Ламберта, Био, Фурье, Лапласа,
Пуассона, Ламе, Томсона (лорда Кельвина), Римана и других вы¬
дающихся ученых. Длительное время эта теория оставалась достоя¬
нием теоретиков и только в простейших случаях находила практи¬
ческое применение. Однако за последние десятилетия положение рез¬
ко изменилось. Появление мощной вычислительной техники открыло
новые возможности применения теории для практических целей
и фактически привело ее к новому расцвету. Инженеры, применяв¬
шие ранее эту теорию почти исключительно к стационарным состоя¬
ниям, разработали много полезных таблиц и графиков, позволяющих
решать более общие задачи. Новыми методами для объяснения мно¬
гих тепловых явлений заинтересовались геологи и географы. Боль¬
шой вклад в теорию теплопроводности внесли математики; ими бы¬
ла создана качественная теория дифференциальных уравнений пара¬
болического типа, к которому относится уравнение теплопроводности,
дано строгое математическое обоснование аналитическим методам
решения краевых задач теплопроводности.
Круг задач теории теплопроводности исключительно обширен
и непрерывно пополняется большим количеством новых результатов,
которые должны найти свое отражение в учебной литературе. Прин¬
ципиальной стороной аналитической теории теплопроводности явля¬
ется возможность варьирования классическими методами дифферен¬
циальных уравнений математической физики при решении рассмат¬
риваемой краевой задачи. Это объясняется тем, что решение одной
и той же тепловой задачи можно искать в различных классах функций.
Эти функции должны быть таковыми, чтобы они, во-первых, доста¬
точно легко находились и, во-вторых, обеспечивали сходимость про¬
цесса настолько хорошо, чтобы можно было сделать требуемые в
задаче заключения о свойствах полученного решения. Представление
аналитического решения одной и той же задачи в различных экви¬
валентных функциональных формах (тождественных в смысле числа)
имеет большую практическую ценность, так как позволяет варьиро¬
вать решением в зависимости от постановки задачи: например, пред¬
ставление решения тепловой задачи в форме ряда Фурье, удобной
для больших времен от начала процесса, или в виде формулы сум¬
мирования Пуассона, более подходящей для малых времен от на¬
чального состояния и используемой, например, в теории закалки.
Здесь и в других случаях немаловажную роль при дальнейшей
работе с найденным решением задачи играет эффективное использо-
9
вание дискретной вычислительной техники. Благодаря этому заметно
усилилось влияние аналитического подхода при решении краевых
задач (классических и обобщенного типа) для уравнения теплопро¬
водности.
При расчете температурных полей можно указать в основном
четыре группы методов: а) аналитические (сюда относятся и при¬
ближенные методы, в том числе асимптотические); б) графические;
в) численные (основанные на применении разностных схем); г) экс¬
периментальные (включающие и методы моделирования).
Аналитический метод дает возможность получить решение тепло¬
вой задачи в виде математического выражения для температуры как
функции пространственных координат и времени. Решение должно
удовлетворять определенному дифференциальному уравнению, из ко¬
торого оно получено, и определенным начальному и граничным ус¬
ловиям, налагаемым самим конкретным процессом. Однако при этом
почти во всех случаях приходится математически упрощать рассмат¬
риваемый процесс, для того чтобы этот метод мог дать желаемые
результаты; и хотя решения, полученные при этих условиях, вовсе
не являются физически «точными», все же предпочтительным мето¬
дом вычисления температурного поля следует (где это возможно)
считать формальный аналитический метод.
Асимптотические методы решения тепловых задач представляют
несомненный интерес, ибо в ряде случаев они позволяют получить
решение более простыми средствами. Однако асимптотика сама по
себе рассматривает предельные случаи и в этом смысле является ог¬
раниченной.
За последние годы в практику аналитической теории теплопро¬
водности стали входить приближенные методы расчета температур¬
ных полей, основанные на совместном применении интегральных
преобразований и вариационного исчисления [149], пока этот под¬
ход находится еще в стадии развития.
Графические методы основаны на свойствах дифференциального
уравнения теплопроводности и численных принципах. Они быстро
дают первое приближение к действительному распределению темпе¬
ратуры [181].
Большими потенциальными возможностями обладают численные
методы решения тепловых задач, основанные на методике конечных
разностей (или методе сеток). Дифференциальное уравнение тепло¬
проводности при этом заменяется системой алгебраических уравне¬
ний (разностным уравнением), начальное и граничные условия так¬
же заменяются разностными начальным и граничными условиями для
сеточной функции и дальнейшее решение задачи сводится к выпол¬
нению простых алгебраических операций. Повторяемость однотипных
операций в этом методе представляет большие удобства для исполь¬
зования современной вычислительной техники. Этим методом могут
быть решены любые задачи для тел произвольной геометрической
формы, линейные и нелинейные [18, 37, 127]. Недостатком метода
является необходимость выполнения очень большого количества вы¬
числительных операций, особенно для трехмерных и даже для дву-
10
ных задач, и его ограниченные возможности для аналитических
исследований. Здесь, как и в графическом методе, параметризация
задачи связана с необходимостью решения ее заново.
Последние методы — экспериментальные — играют большую роль
в исследовании явлений теплопроводности. Электрическое моделиро¬
вание основывается на формальном сходстве дифференциального
уравнения теплопроводности с уравнением электрических колебаний
в проводнике и также является распространенным методом при ре¬
шении тепловых задач — линейных и нелинейных [7, 79].
В заключение остановимся кратко на истории развития теории
теплообмена.
Основоположником учения о теплоте был великий русский уче¬
ный акад. М. В. Ломоносов. В середине XVIII в., опередив на сто
с лишним лет науку Западной Европы, Ломоносов создал единую
теорию теплоты и строения вещества, изложив основы ее в работе
«Размышление о причине теплоты и холода» (1744). Эта теория теп¬
лоты содержала в себе все основные элементы современной теории,
а именно: закон сохранения массы и энергии; представление о теп¬
лоте как результате движения элементарных частиц тела; о степени
нагрева как мере интенсивности движения этих частиц; о механизме
теплопроводности как обмене энергии движения между отдельными
частицами; об абсолютном нуле температуры и др.
В 1807 г. французский ученый Ж- Фурье сформулировал основ¬
ную гипотезу теплопроводности, положившую начало развитию ма¬
тематической теории теплопроводности. Им же в 1822 г. изложена
теория распространения теплоты в твердых телах в труде «Анали¬
тическая теория тепла».
В 1831 г. знаменитый русский математик акад. М. Б. Остроград¬
ский опубликовал свою работу «Замечания по теории теплоты», в
которой дал общее решение уравнения теплопроводности для твер¬
дого, однородного и изотропного тела.
С развитием техники роль процессов переноса теплоты в различ¬
ных тепловых устройствах и машинах стала возрастать и тепловым
процессам стало уделяться значительно больше внимания, особенно
со второй половины XIX в. В литературе тех времен имеется много
работ по вопросам теплопереноса и некоторые из них сохранили
значимость до наших дней.
В научных исследованиях все шире используются методы мате¬
матического анализа. В 1881 —1882 гг. в Москве проф. А. Г Столетов
прочел свои известные лекции по теории теплопроводности,- состоя¬
ние из двух разделов: 1) теория теплопроводности; 2) механическая
теория теплоты, или термодинамика. В книге «Теория теплоты»
(М., 1882 г.) проф. Столетов писал: «С исторической точки зрения
Учение о теплопроводности есть начало теории теплоты и вообще
математической физики; сюда впервые в 1807 г. Фурье в своей
«Iheorie de la chaleur» приложил математический анализ». Здесь
Столетов указывает на громадное прикладное значение матема¬
тической теории теплоты.
И'
Проф. А. Г. Столетова считают первым создателем курса современ¬
ной теплофизики, которая выделяется в самостоятельную науку
в конце XIX — начале XX в.
Из работ зарубежных ученых, посвященных теории теплоты,
кроме уже названных широко известны труды Кирхгофа, Пуассона,
Вебера, Томсона, Планка, Ляме, Пуанкаре, Карслоу, Егера, Эккер¬
та, Дрейка, Гребера, Эрка, Григуль, Якоба и др.
Большой вклад в развитие учения о теплоте сделан советскими
теплофизиками и представителями близких направлений: М. В. Кир-
пичевым, М. А. Михеевым, А. А. Гухманом создана теория подобия
теплофизических процессов; А. С. Предводителевым и его ученика¬
ми выполнены глубокие исследования по теории переноса вещества
и теплоты в процессах горения; Н. Н. Рыкалиным, Б. Я. Любовым,
С. А. Шестериковым — при воздействии на твердые тела концент¬
рированными потоками энергии; А. Г. Шишковым — при изучении
процесса термодиффузии в газовых смесях; О. Г. Мартыненко — в
теории свободноконвективного теплообмена; Н. В. Павлюкеви-
чем — в физической кинетике и процессах переноса при фазовых
превращениях. Крупный вклад в теорию конвективного теплооб¬
мена и общие вопросы теплоты внесли работы С. С. Кутателадзе,
В. С. Авдуевского, В. М. Иевлева, А. В. Лыкова, Б. С. Петухова,
Д. А. Лабунцова, А. И. Леонтьева, А. А. Жукаускаса и др. Матема¬
тиками В. А. Стекловым, И. Г Петровским, С. Л. Соболевым,
A. Н. Тихоновым, А. А. Самарским, В. С. Владимировым,
B. А. Ильиным, Н. С. Кошляковым, Г А. Гринбергом и другими
выполнены фундаментальные работы по развитию аналитических
методов дифференциальных уравнений математической физики
и решению краевых задач для уравнения теплопроводности (и род¬
ственны^ явлений). Основные достижения в этой области за послед¬
ние годы изложены в обзоре автора книги, посвященном 275-летию
Российской академии наук (Известия АН, серия Энергетика, 1999.
№ 5. С. 3 — 34).
Математическая теория теплопроводности непрерывно обо
гащается новыми аналитическими, численными (разностными)
методами (работы А. А. Самарского, С. К. Годунова, Л. А. Коз-
добы и др.), широкое развитие получила качественная теория диф¬
ференциальных уравнений параболического типа. В настоящее вре¬
мя исследования по теплообмену интенсивно развиваются как в
академических учреждениях и специализированных отраслевых ин¬
ститутах, так и во многих высших учебных заведениях нашей
страны.
ГЛАВА I
ОСНОВЫ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ
§ 1. ОБЩИЕ ВОПРОСЫ ТЕОРИИ ТЕПЛООБМЕНА
При соприкосновении отдельных частей тела или отдельных взаимо¬
действующих тел, имеющих различную температуру, происходит об¬
мен кинетической энергией между движущимися структурными ча¬
стицами (молекул, атомов, свободных электронов), вследствие чего
интенсивность движения частиц тела с меньшей температурой увели¬
чивается, а частиц тела с большей температурой — уменьшается. Та¬
кой энергетический обмен между взаимодействующими телами или
их отдельными частями с неодинаковой температурой называется теп-
лообменом или теплопередачей. В результате одно из соприкасающихся
тел нагревается, а другое остывает. Количество энергии, переданной
частицами более горячего тела частицам более холодного, называется
количеством теплоты или просто теплотой. При эгом теплота пере¬
ходит от точек с более высокой температурой к точкам с более низкой
температурой, если процесс протекает в одном теле. При теплообмене
между различными телами это положение также сохраняется, т. е. теп¬
лота переходит от более нагретых к более холодным телам. Таким об¬
разом, конечный результат теплообмена между ограниченными тела¬
ми или частями одного и того же тела заключается в уравнивании их
температур, после чего процесс прекращается.
Такую форму передачи средней кинетической энергии от частицы
к частице называют микрофизической формой передачи энергии, так
как передача энергии происходит на молекулярном уровне, без види¬
мого движения тел. Микрофизическая трактовка процессов передачи
теплоты дается в курсах теоретической физики. В курсах теплотех¬
ники эта проблема излагается в рамках макрофизики, поскольку
указанный вид энергетического обмена обусловливается лишь темпера¬
турным состоянием его участников, а температура с молекулярно¬
кинетической точки зрения является величиной статистического ха¬
рактера, т. е. приобретает смысл только применительно к макроско¬
пическим телам.
Понятие «теплообмен» охватывает совокупность всех явлений, при
которых имеет место перенос некоторого количества теплоты из одной
части пространства в другую в твердых, жидких и газообразных те¬
лах. Эти процессы по своей физико-механической природе весьма
многообразны, отличаются большой сложностью и обычно развиваются
в виде целого комплекса разнородных явлений. Для удобства принято
13
делить перенос теплоты на простейшие виды: теплопровод¬
ность, конвекцию, теплообмен излучением,
или радиацией. Эти процессы глубоко различны по своей при¬
роде и характеризуются различными законами. Соответственно этому
и строится математическая теория описания каждой формы тепло¬
обмена, со своими уравнениями, своими математическими методами,
аналитическими (точными и приближенными) или разностными (чис¬
ленными), или методами аналогий.
Теплопроводность (кондукция) характеризуется тем,
что ее действие связано с наличием вещественной среды и что тепло¬
обмен может происходить только между такими частицами тела (мо¬
лекулами и атомами), которые находятся в непосредственной близо¬
сти друг от друга. Явление это можно представить себе так, что тепло¬
та переходит от одной частицы к другой, однако при этом сами частицы
не перемещаются. В чистом виде процесс теплопроводности наблюдает¬
ся в твердых телах, для которых к настоящему времени наиболее пол¬
но разработана и аналитическая теория (т. е. теория, описывающая
процесс в терминах дифференциальных уравнений математической
физики). В металлах передача теплоты происходит вследствие движе¬
ния свободных электронов. В жидкостях и твердых телах — диэлект¬
риках теплопроводность осуществляется упругими, акустическими
волнами, образуемыми согласованными смещениями всех молекул и
всех атомов из их равновесных положений. Взаимодействие волн
приводит к энергетическому обмену между частицами и слоями тела.
Теплопроводность как молекулярный процесс передачи теплоты на¬
блюдается и в газах, где молекулы не занимают фиксированного по¬
ложения, а постоянно меняют свое место, даже если вещество в целом
находится в состоянии покоя.
Учение о теплопроводности основано на простых количественных
законах и располагает хорошо разработанным математическим аппа¬
ратом, особенно для однородных и изотропных тел. Тем не менее бы¬
стро развивающаяся техника постоянно ставит новые задачи в теории
теплопроводности, которые способствуют развитию новых математи¬
ческих методов для их решения, так что эта область математики на¬
ходится в непрерывном движении и не может считаться окончательно
завершенной.
Конвекция наблюдается тогда, когда материальные частицы
какого-нибудь тела изменяют свое положение в пространстве и при
этом переносят содержащуюся в них теплоту. Это явление имеет место
в жидкостях и газах и всегда сопровождается теплопроводностью,
т. е. передачей те.плоты от одной частицы к соседней, если только во
всей текущей массе нет полного равенства температур.
Рассматривая области, расположенные внутри потока (т. е. не
обращаясь к процессам, происходящим на твердых поверхностях,
которые ограничивают поток) или на его поверхности, можно обе
формы переноса теплоты охватить одним понятием — теплопровод¬
ность в движущихся средах. Если учесть, кроме этого, влияние огра¬
ничивающих твердых стенок, то будет наблюдаться более общий случай
теплообмена между стенками и движущейся жидкостью: этот обмен
14
обусловлен тем, что частицы среды, находящиеся вблизи стенки,
отнимают от нее теплоту и уносят ее с собой. При этом перемещающие¬
ся частицы жидкости контактируют не только со стенками, но и между
собой. Теплообмен между средой и стенкой называют теплоотда-
ч е й.
Особый вид теплообмена наблюдается в тех случаях, когда на гра¬
нице между стенкой и потоком происходит изменение агрегатного со¬
стояния тела. Это имеет место при переходе теплоты от поверхности
нагрева к испаряющейся жидкости, от конденсирующихся паров
к поверхностям охлаждения, при таянии и при замерзании. Соответ¬
ствующие этому процессу математические модели относятся к числу
наиболее сложных, описываемых дифференциальными уравнениями
математической физики.
Теплообмен излучением характеризуется отсутстви¬
ем контакта между телами, обменивающихся теплотой. Примером мо¬
жет служить излучение Солнцем теплоты на Землю через космическое
пространство, в котором, как известно, плотность вещества ничтожна.
Явление теплового излучения возникает у поверхности или внутри
тела в результате сложных молекулярных и атомных возмущений.
При этом некоторая часть внутренней энергии тела преобразуется
в электромагнитные волны (или в другом представлении в фотоны —
кванты энергии) и уже в такой форме передается через пространство.
Все эти различные формы переноса теплоты не обособлены и в чи¬
стом виде встречаются лишь на отдельных участках пути прохожде¬
ния теплоты. В большинстве случаев один вид теплообмена сопутству¬
ет другому и разделить их между собой очень трудно. При этом может
создаться впечатление о некоем едином процессе теплопереноса.
В практических расчетах такие сложные сочетания элементарных
видов теплообмена расчленяются и весь процесс сводится к простому.
При этом, если возможно, указываются условия, когда выделенный
один какой-либо вид теплообмена существенно доминирует над осталь¬
ными. Практически все процессы, рассматриваемые в теории тепло¬
обмена, протекают при взаимодействии твердых тел с жидкими или
газообразными средами, размеры которых много больше размеров
составляющих их структурных частиц. Поэтому такие статистические
понятия, как температура, давление, плотность, теплоемкость, вяз¬
кость и др., могут быть приписаны даже таким малым элементам си¬
стемы, которые с физико-математической точки зрения могут рассмат¬
риваться как дифференциалы ее объема. Это означает, что изучаемая
среда может рассматриваться не как совокупность отдельных мате¬
риальных частей, а как непрерывное, сплошное пространство, и эго
обстоятельство позволяет при аналитическом описании процесса пере¬
носа теплоты в данной среде использовать методы математического
анализа, привлекая такие понятия, как непрерывность и дифференци¬
руемость. Именно с этих позиций и строится аналитическая теория
•теплопроводности. Исключение приходится делать только при взаимо¬
действии тел с весьма разреженным газом, когда размеры тела стано¬
вятся соизмеримыми с длиной пути свободного пробега молекул. Со¬
ответственно этому меняется и математическая модель процесса.
15
В книге рассматривается перенос теплоты только теплопроводностью,
что найдет свое отражение в последующих параграфах в соответствую¬
щих математических моделях.
Перенос теплоты теплопроводностью, как и любой другой физиче¬
ский процесс, может быть выражен математическим языком.
Одним из законов, лежащих в основе аналитической теории тепло¬
проводности, является гипотеза Фурье *, связывающая перенос теп¬
лоты внутри тела с температурным состоянием в непосредственной
близости от рассматриваемого места. Поэтому при изучении теории
теплопроводности прежде всего необходимо установить основные по¬
нятия, такие, как температурное поле, градиент
температуры, вектор теплового потока.
§ 2. ТЕМПЕРАТУРНОЕ ПОЛЕ
Температурным полем называется совокупность значений температу¬
ры во всех точках рассматриваемого пространства (тела) в каждый
фиксированный момент времени.
Температура является скалярной величиной, так как она характе¬
ризует тепловое состояние в любой точке тела, определяя степень его
нагретости. Температуре нельзя приписать какое-либо направление и
поэтому температурное поле является скалярным. Математическим
выражением распределения температуры в теле является выражение,
содержащее в качестве независимых переменных пространственные
координаты и время:
в декартовой системе координат
Г = Т (х, у, г, t);
в цилиндрической системе координат
Т = Т (г, ф, г, t)\ (1Л)
в сферической системе координат
Т = Т (г, ф, 0, t).
Основной задачей аналитической теории теплопроводности являет¬
ся изучение пространственно-временного изменения температуры,
т. е. нахождение зависимости (1.1). Уравнение (1.1) является записью
наиболее общего вида температурного,поля, когда температура в теле
изменяется с течением времени и от одной точки к другой. Такое поле
соответствует неустановившемуся тепловому режиму теплопроводно¬
сти и называется нестационарным температурным полем. Если теп¬
ловой режим является установившимся, то температура в каждой
точке тела с течением времени остается неизменной, меняясь лишь от
точки к точке. Такое температурное поле называется стационарным
и температура является функцией только координат, например в де-
* Многочисленные экспериментальные проверки гипотезы Фурье дали осно¬
вание считать эту гипотезу законом теории теплопроводности.
16
картовых координатах
Т=Т(ху уу г), dT/dt=0.
(1.2)
Примером нестационарного температурного поля может служить
поле нагревающейся в печи стальной заготовки или поле стеклянной
пластины, нагретой до высокой температуры и быстро охлаждаемой
потоком воздуха. А в прогревшейся стенке здания, где температура
каждой точки не меняется во времени, температурное поле будет ста¬
ционарным.
Температурное поле, соответствующее уравнениям (1.1) или (1.2),
является пространственным, или трехмерным, так как температура
является функцией трех координат.
Если вдоль одной из координат температура остается постоянной, то
математически это условие записывается (например, для координа¬
ты г) следующим образом: dT/dz=0. В этом случае поле называется
двумерным и записывается: для нестационарного режима Т=Т(ху уу t)\
для стационарного режима Т=Т(ху у).
Если температура остается постоянной вдоль двух координат
(например, у и z), то дТ/ду=дТ/дг=0 и поле называется одномерным.
В этом случае можно записать: для нестационарного режима Т=Т(ху t);
для стационарного Т=Т(х). Примером одномерного температурного
поля может служить поле неограниченной пластины, у которой длина
и ширина бесконечно велики по сравнению с толщиной; теплота в дан¬
ном случае распространяется перпендикулярно поверхности пластины.
Переменные ху уу z, фигурирующие в уравнении (1.1), определяют
положение любой точки рассматриваемого тела, являясь координата¬
ми этой точки в выбранной системе координат. Эти переменные могут
принимать бесконечное множество числовых значений, как и перемен¬
ная /, характеризующая время течения процесса теплопроводности.
Совокупность всевозможных числовых значений переменных ху уу z, /,
каждому из которых соответствует вполне определенное значение тем¬
пературы Т—Т(х, уу z, /), называется областью определения функции
Т(ху уу z, t). Функция Т(х, уу z, t) в своей области определения считает¬
ся обычно непрерывной, дважды непрерывно дифференцируемой по
пространственным координатам (ху уу z) и непрерывно дифференци¬
руемой по времени t.
В аналитической теории теплопроводности распределение темпе¬
ратуры в рассматриваемой области описывается функцией Т(ху уу z, /),
относящейся к так называемому классу функций С2 (за исключением
тех случаев, о которых будет сказано особо). Этот факт используется
при выводе дифференциального уравнения, описывающего процесс
теплопроводности в изучаемом теле. В теле, имеющем температуру
Т(ху у} z, /), можно выделить поверхность, во всех точках которой в не¬
который момент времени температура одинакова. Такая поверхность
называется изотермической поверхностью или поверхностью уровня.
Уравнение поверхности уровня имеет следующий вид:
Т(Ху уу z, t)=C или Т=С, где С=const.
В отличие от стационарных в нестационарных полях форма и распо¬
ложение изотермических поверхностей с течением времени изменяют¬
17
ся. Изотермические поверхности характеризуются следующими ос¬
новными свойствами:
а) две изотермические поверхности, имеющие различные темпера¬
туры, никогда не пересекаются друг с другом, так как в одной и той же
точке тела одновременно не может быть двух различных температур;
б) изотермические поверхности не имеют границ внутри тела. Они
или кончаются на поверхности, или замыкаются на себя, располагаясь
внутри тела;
в) теплота не распространяется вдоль изотермической поверхности,
а направляется от одной изотермической поверхности к другой. Это
следует из положения о том, что тепло¬
вая энергия распространяется от более
нагретого участка к менее нагретому.
Таким образом, можно считать, что
изотермические поверхности разделяют
твердое тело на тонкие «слои» — изотер¬
мические оболочки, отделяющие часть
тела с температурой, большей, чем Т=
= С, от части тела с температурой,
меньшей, чем Т=С. Пересечение изо¬
термических поверхностей плоскостью
дает на этой плоскости семейство изо¬
терм (линии, соответствующие одинако¬
вой температуре). Они обладают теми же свойствами, что и изотерми¬
ческие поверхности, т. е. не пересекаются, не обрываются внутри те¬
ла, оканчиваются на поверхности либо целиком располагаются внутри
самого тела. На рис. 1 представлен участок двумерного температурного
поля с изотермами 7\ 71±2АТ' и т. д.
Задание температурного поля соотношением Т=Т(х, у, z, t) не все¬
гда дает достаточно ясное представление о поведении этого поля, а за¬
дание изотермических поверхностей (поверхностей уровня) с отметкой
на них соответствующих значений температуры Т=С равносильно за¬
данию самого поля Т=Т(х, у% г, /), при этом взаимное расположение
18
поверхностей уровня даст наглядное представление о соответствующем
поле температур. Указанный способ изображения поля особенно удо¬
бен, когда речь идет о двумерном поле.
Равенство вида Т(х, у> t)=C (всюду время t фиксировано) опреде¬
ляет на плоскости (х, у) некоторую кривую у=ф(*, с, t). Такие кривые
называются линиями уровня (изотермами) плоского (двумерного)
температурного поля Т=Т(х, у, t) (рис. 2, 3). На практике приходит¬
ся иметь дело с температурными полями, обладающими специальными
свойствами симметрии, облегчающими изучение таких полей. Рассмот¬
рим некоторые частные случаи (для стационарных полей).
Поле Т называется плоскопараллельным, если в пространстве суще¬
ствует направление, при сдвигах вдоль которого поле Т переходит
само в себя. Плоскопараллельное, или двумерное, поле задается, как
указывалось, равенством Т=(х, у). Изотермические поверхности та¬
кого поля — это семейство цилиндрических поверхностей Т(х, у)=С.
Поле Т называется осесимметрическим, если оно переходит само
в себя при повороте пространства на произвольный угол вокруг не¬
которой фиксированной прямой — оси симметрии этого поля. Осесим¬
метрическое температурное поле задается соотношением (в цилиндри¬
ческой системе) T=T(r, z), т. е. изображается функцией, зависящей
только от переменных г и z (но не от угла). Изотермические поверхно¬
сти такого поля представляют собой поверхности вращения.
Если температурное поле Т задается функцией, зависящей лишь от
одной координаты г, т. е. 71=71(г), то поле называется цилиндрическим.
Изотермические поверхности такого поля — круглые цилиндры.
Если значение функции Т (в сферической системе координат) за¬
висит лишь от переменной г (но не зависит от углов <р и 0), где г — рас¬
стояние от некоторой фиксированной точки М0 (начала координат),
то такое температурное поле называется сферическим. Изотермические
поверхности сферического поля — семейство концентрических сфер.
§ 3. ТЕМПЕРАТУРНЫЙ ГРАДИЕНТ
Рассмотрим две бесконечно близкие изотермические поверхности
с температурами Т и 7,+Д7,(Д7,>0) и какую-либо точку М, лежащую
на одной из них (рис. 4). Перемещаясь из точки М вдоль любых на¬
правлений, можно обнаружить, что интенсивность изменения темпе¬
ратуры по различным направлениям неодинакова. В предыдущем па¬
раграфе рассматривалось направле¬
ние перемещения по изотермиче¬
ской поверхности, вдоль которого
температура не изменялась. Если
же перемещаться вдоль какого-
либо направления /, пересекающе¬
го изотермические поверхности, то
наблюдается изменение темпера¬
туры. Используя понятие произ¬
водной скалярного поля по задан¬
ному направлению, можно описать Рис. 4
19
его локальные свойства, т. е. изменение температуры Т при пере¬
ходе от точки М к близкой точке ЛГ по направлению I. Скорость изме¬
нения температуры Т в точке М в направлении I характеризуется
производной функции Т
дТ/д1 = lim [Т (М') — Т (М)]/А/. (1.3)
Л/ -*■ о
Производная функции Т(М) по направлению /=(cos a, cosp, cosy)
вычисляется по формуле
дТ/д1 = (дТ!дх) cos а+ (дТ/ду) cos р + (дТIdz) cos у.
Наибольшая разность температуры на единицу длины вектора пере¬
мещения [Т(М' ) — Т(Л4)]/Д/ наблюдается в направлении нормали я
к изотермической поверхности (рис. 4). В Соответствии с (1.3) макси¬
мальная скорость изменения температуры при этом равна пределу
отношения изменения температуры АТ к расстоянию между изотерми¬
ческими поверхностями по нормали Ля, когда Ля стремится к нулю:
дТ/дп= lim [Т (АГ)— Г(М)]/Ля = lim ЛТ/Дя. (1.4)
Ап -► 0 Ап -+ О
Итак, в любой точке М изотермической поверхности можно по¬
строить некоторый вектор, направленный по нормали к этой поверх¬
ности в сторону увеличения температуры. Абсолютная величина этого
вектора равна изменению температуры на единицу длины перемещения
в рассматриваемом направлении — скорости возрастания температу¬
ры в этом направлении (т. е. производной от температурной функции
Т по направлению нормали я). Такой вектор называют градиентом
температуры в точке М или градиентом температурного поля и запи¬
сывают в виде символа grad Т: <.
в декартовых координатах (х> у, z)
. ~ дТ . , дТ . . дТ - /t Cv
gradr = 17I+l7/+HTk’ <L5>
в цилиндрических координатах (г, <р, г)
. гр дТ , 1 дТ , дТ .
gradr = ire' + 7__e«+ir*: (1.6)
в сферических координатах (г, ф, 0)
* гр дТ . 1 дТ , 1 ЭГ
gradT— df er+ r 50 + r sin е еч> • (1-7)
Для обозначения вектора (1.5) в теории поля иногда приме¬
няют символ grad Т = vТ.
Согласно сказанному выше, можно записать
| grad Т \ = дТ/дп (1.8)
длина вектора grad Т равна скорости возрастания Т в этом направле¬
нии. Здесь и всюду далее я — единичный вектор нормали.
Температурный градиент показывает, насколько интенсивно (рез¬
ко) меняется температура внутри тела. Он является важной величи-
ной, определяющей многие физические явления (появление трещин
в хрупком теле от неравномерного нагрева вследствие возникновения
термических напряжений и деформаций и т. п.).
Производная от функции Т по направлению нормали it и вектор
grad Т связаны соотношением
дТ1дп=п grad Т. (1.9)
Вектор нормали п к поверхности T=const в точке М может иметь два
противоположных направления, одно из которых можно считать внеш¬
ним по отношению к данной поверхности, а другое внутренним. По¬
кажем, что независимо от того, как выбрано направление нормали п,
вектор (1.5) при всех обстоятельствах направлен в сторону возрастаю¬
щей температуры.
Если нормаль п направить в сторону больших температур, то
дТ!дп>0 и, как следует из (1.9), градиент температуры будет направ¬
лен в ту же сторону (угол между векторами п и grad Т равен нулю).
Если нормаль направить в сторону убывающей температуры, то про¬
изводные дТ/дп<0 и grad Т окажутся направленными противоположно
этому направлению, т. е. опять в сторону возрастающей температуры
[в (1.9) угол между векторами п и grad Т равен 180°]. Эти рассуждения
будут использованы в последующих параграфах.
§ 4. ТЕПЛОВОЙ ПОТОК. ВЕКТОРНАЯ И СКАЛЯРНАЯ
ФОРМЫ ЗАКОНА ФУРЬЕ
В теле, не находящемся в полном тепловом равновесии (т. е. обладаю¬
щим неравномерным распределением температуры), всегда происхо¬
дит перенос теплоты. Отсюда следует, что для передачи теплоты тепло¬
проводностью необходимо неравенство нулю температурного градиента
в различных точках тела. В этом смысле температурный градиент яв¬
ляется основным физическим параметром, определяющим условие
возникновения теплового процесса, и можно сказать, что соотношение
grad ТФ0 является необходимым условием возникновения внутри
тела теплового потока. Тепловой поток в отличие от температуры —
величины скалярной — имеет вполне определенное направление,
а именно: от точек тела с более высокой к точкам с более низкой темпе¬
ратурой. Таким образом, тепловой поток можно рассматривать как
вектор, направленный в сторону уменьшения температур, а поле теп¬
ловых потоков — векторным. Для математического описания поля
тепловых потоков вводится вектор q, называемый вектором плотности
теплового потока. Под вектором плотности теплового потока в точке М
температурного поля понимают вектор, направление которого совпа¬
дает с направлением переноса теплоты, а абсолютная величина вы¬
ражает тепловой поток или интенсивность переноса теплоты, изме¬
ряемую количеством теплоты, проходящей в единицу времени через
единицу площади поверхности, перпендикулярной направлению пото¬
ка в рассматриваемой точке. Обозначим через dQ количество теплоты,
проходящее через изотермическую поверхность площади da за время
dt. Тогда, по определению, абсолютное значение вектора плотности
21
теплового потока можно записать в виде
q=dQ/(dodf). (1.10)
Формула (1.10) характеризует плотность теплового потока единично¬
го элемента изотермической поверхности. Понятие плотности теплово¬
го потока, как будет показано ниже, применимо к любой, а не только
к изотермической поверхности.
Опыт показывает, что передача теплоты теплопроводностью про¬
исходит по нормали к изотермической поверхности от мест с большей
температурой к' местам с меньшей температурой. Следовательно, век¬
тор плотности теплового потока направлен по нормали к изотермиче¬
ской поверхности в направлении падения температуры. Можно го¬
ворить о плотности теплового потока и вдоль любого другого направ¬
ления /, отличного от направления нормали rt. В этом случае плотность
теплового потока в направлении / есть проекция вектора q на это на¬
правление, т. е. величина <7 cos (я, /).
Идея о существовании органической связи между вектором плот¬
ности теплового потока и температурным градиентом легла в основу
учения, созданного Фурье. Сущность гипотезы Фурье состоит в том,
что тепловой поток через элемент изотермической поверхности вполне
определяется значением температурного градиента в рассматривае¬
мой точке М. Действительный смысл этой связи заключается в том,
что тепловые потоки в среде всегда определенно направлены. Возник¬
новение тепловых потоков вдоль изотер¬
мических поверхностей невозможно, так
как по всей изотермической поверхности
составляющая градиента температуры рав¬
на нулю. Следовательно, векторы плотно¬
сти теплового потока q и grad Т направлены
по нормали к изотермической поверхности,
но в противоположные стороны (рис. 5).
С увеличением перепада температур,
т. е. с возрастанием температурного гради¬
ента, увеличивается и плотность теплового
потока. Опыты показали, что плотность
теплового потока можно считать пропорци¬
ональной первой степени удельного пере¬
пада температуры. Это и явилось основой
гипотезы Фурье о наличии простейшей количественной зависимости
между абсолютными значениями векторов плотности теплового потока
и температурного градиента. На основе этих данных, а также сообра¬
жений о противоположном направлении этих векторов закон
Фурье в векторном виде записывается следующим обра¬
зом:
q=—К grad Т. (1.11)
Этот закон, сформулированный в виде гипотезы, был подтвержден
многочисленными опытами. Выражение (1.11) описывает механизм
теплопроводности и используется при выводе уравнения теплопровод-
22
ности, лежащего в основе всех теоретических исследований процессов
теплопроводности.
Наглядное представление о мгновенном распределении потоков
теплоты могут дать линии, касательные к которым в каждой точке
температурного поля совпадают с соответствующими нормалями к изо¬
термическим поверхностям. Такие линии называются линиями теп¬
лового потока (рис. 5).
Коэффициент пропорциональности А называется теплопроводностью
и является физической константой, характеризующей теплопроводя¬
щие свойства материала данного тела. Подставляя в уравнение (1.11)
единицы q и температурного градиента, найдем для А единицу
Вт/(м-град).
Числовое значение теплопроводности определяет количество теп¬
лоты, проходящее через единицу площади изотермической поверхности
в единицу времени при градиенте температуры, равном единице. По¬
добно другим величинам этого ряда (удельная теплоемкость, электри¬
ческое сопротивление, плотность, модуль упругости и т. п.), значение
теплопроводности в общем случае зависит от природы вещества, его
структуры, влажности, давления, температуры и других факторов.
В большинстве случаев теплопроводность А для различных материа¬
лов определяется опытным путем, а при технических расчетах значе¬
ние А берется из справочных таблиц.
С повышением температуры А возрастает (что связано с увеличением
скорости движения молекул и их учащенным соударением), от давле¬
ния же А практически не зависит.
Зависимость теплопроводности от температуры в общем случае
довольно сложная, однако для большинства твердых тел, жидкостей
и газов при умеренных температурах она оказывается почти линей¬
ной, т. е. Х=Х0[1±:Ь(Т—Го)], где А0 — теплопроводность при темпера¬
туре Т0‘, b — постоянная, определяемая опытным путем. В силу того,
что эта зависимость не резко выражена, в аналитической теории теп¬
лопроводности величина А для облегчения выводов считается постоян¬
ной, т. е. dA/dr=0; допускаемая при этом ошибка во многих практи¬
ческих расчетах не превышает 1—2%.
Выражение (1.10) запишем в виде
dQ=q da d/. (1.12)
Как отмечалось, нормаль п к элементу da изотермической поверх¬
ности может иметь два направления (направляющие косинусы этих
направлений отличаются только знаками). Условимся считать тепло¬
вой поток положительным, если направление потока совпадает с вы¬
бранным направлением нормали, и отрицательным, если оно ему про¬
тивоположно. Для абсолютных значений векторов, входящих в ра¬
венство (1.11), следует, что q=X\gradT\. Теперь в равенстве (1.8) не¬
обходимо поставить знак минус, т. е. jgrad Т\=—дТ/дп и
я=—ХдТ!дп. (1.13)
Действительно, для нормали, совпадающей с направлением гра¬
диента, имеем дТ!дп>0; перенос же теплоты происходит всегда в на¬
23
правлении падения температуры, т. е. как раз в противоположную
сторону и, следовательно, по договоренности выше, должно быть
AQ<0, или, что то же самое, </<0, что и объясняет знак минус в форму¬
ле (1.13). Изменив направление нормали на противоположное, имеем
дТ/дп<.0, но тогда AQ>0 и опять-таки знак минус сохраняется. Под¬
ставляя теперь в (1.12) вместо q правую часть равенства (1.13), можно
записать закон Фурье в скалярной форме:
рез малый участок da изотермической поверхности за время At по
направлению нормали п к площадке dd (рис. 6). В общем случае тем¬
пературный градиент у разных точек изотермической поверхности раз¬
личный и изменяется с течением времени. Поэтому количество тепло¬
ты, прошедшее за время t через изотермическую поверхность конеч¬
ных размеров площадью a
Тепловой поток может быть определен вдоль любого направления
через площадь, перпендикулярную этому направлению (в практике
часто встречаются случаи, когда площадка ориентирована в поле
произвольным образом). Покажем, что равенство (1.14) справедливо
для любых поверхностей, а не только для изотермических.
Выберем произвольную элементарную площадку dF так, чтобы
угол между нормалью I к ней и вектором плотности теплового потока
qn в рассматриваемой точке был равен ф (рис. 7). Поток теплоты по
нормали п ив направлении / можно вычислить, используя (1.10) и
dQ=—ЦдТ!дп)Ш1
(1.14)
Выражение (1.14) определяет количество теплоты, проходящее че-
л
I
(Яп>0)
Рис. 6
Рис. 7
Q = — $ Я (дТ/дп) d/ da.
(1.15)
0 a
(1.14):
_dQ_ , дТ_ .
da d/ ' дп '
так как п = / cos ф.
24
Отсюда находим, что
dQ = -k-^-dFdt. (1.16)
Общее количество теплоты, протекающее за время i через конеч¬
ную площадь поверхности F,
с-17)
О F
В частном случае, когда тепловой режим стационарный и тем¬
пературный градиент одинаков по всей площади поверхности F,
можно записать
Таким образом, для определения количества теплоты, проходя¬
щего через какую-либо площадь поверхности твердого тела, нужно
знать температурное поле внутри данного тела, что составляет
главную задачу аналитической теории теплопроводности.
Так как qt является составляющей вектора плотности теплового
потока qny т. е. qL = qnzosqp, то из этого уравнения следует, что
самым большим тепловым потоком, отнесенным к единице площади
поверхности, будет тот, который рассчитан вдоль нормали п к изо¬
термической поверхности [dacos(cp = 0) = l].
В этом параграфе не затрагиваются усложненные анизотропией
случаи теплопроводности. Для таких веществ, как древесина, слю¬
да и т. п., теплопроводность X зависит от направления, поэтому про¬
стое правило косинусов для получения составляющей qt несправед¬
ливо.
Если спроектировать вектор плотности теплового потока на коор¬
динатные оси, то в соответствии с его определением (1.11) можно за¬
писать:
qx — — ^ (дТ/дх); \
Чу = -ЦдГ1ду)-, (1.18)
qz= — Х фТ/дг). )
Тепловые потоки, выраженные уравнением (1.18), являются состав¬
ляющими вектора плотности теплового потока.
§ 5. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Изучение любого физического процесса методами математики сводит¬
ся к установлению аналитических зависимостей между величинами,
характеризующими это явление. Для сложных физических процессов,
в которых определяющие величины изменяются в пространстве и
времени, установить зависимость между этими величинами иногда
невозможно. В этих случаях на помощь приходят методы математиче¬
ской физики, которая рассматривает протекание процесса не во всем
25
изучаемом пространстве, а в некотором объеме вещества и в течение
элементарного промежутка времени.
В пределах выбранного объема и элементарного промежутка вре¬
мени становится возможным пренебречь изменением некоторых вели¬
чин, характеризующих процесс. Это дает возможность на основе са¬
мых общих принципов природы вывести дифференциальное уравнение
рассматриваемого процесса, которое представляет собой наиболее
общую связь между существенными для исследуемых процессов вели¬
чинами и характеризует свойства, присущие всем физическим явлени¬
ям, в основе которых лежат одни и те же закономерности.
Интегрируя далее дифференциальное уравнение, можно получить
аналитическую зависимость между величинами для всего пространства
и всего рассматриваемого промежутка времени.
Связь между величинами, участвующими в передаче теплоты тепло¬
проводностью, устанавливается в этом случае так называемым диф¬
ференциальным уравнением теплопроводности, на основе которого
строится математическая теория теплопроводности. В основу вывода
дифференциального уравнения теплопроводности положен закон со¬
хранения энергии, сочетаемый с законом Фурье. С законом Фурье
мы познакомились выше, а закон сохранения энергии в рассматривае¬
мом случае может быть сформулирован следующим образом.
Выделим в теле некоторую часть объема К, ограниченную замкну¬
той поверхностью S, через которую происходит тепловое взаимодей¬
ствие выделенной части с окружающей ее средой — остальной частью
тела. Имеет место следующее утверждение: количество теплоты Q,
полученное выделенным объемом за время dt вследствие теплопровод¬
ности, а также от внутренних источников теплоты, равно изменению
внутренней энергии вещества, содержащегося в выделенном объеме:
Q=Qi+Q2, f (1.19)
где Q — изменение внутренней энергии вещества, содержащегося
в выделенном объеме V за время dt, Дж; Qx — количество теплоты,
введенное в выделенный объем путем теплопроводности за время dt,
Дж; Q2 — количество теплоты, которое выделилось в объеме V за
время dt вследствие внутренних источ¬
ников теплоты, Дж.
Это утверждение вместе с законом
Фурье (1.14) положено в основу вывода
дифференциального уравнения тепло¬
проводности — основного уравнения
аналитической теории теплопроводно¬
сти. Для облегчения вывода примем с
самого начала некоторые упрощения,
которые так или иначе пришлось бы сде¬
лать в дальнейшем в связи с возникшими
математическими трудностями при ре¬
шении задач аналитической теории те¬
плопроводности. Принимаемые упроще-
Рис. 8 ния сводятся к следующим:
26
1. Деформация рассматриваемого объема, связанная с изменением
температуры, является очень малой по сравнению с самим объемом.
2. Макроскопические частицы тела неподвижны относительно
друг друга.
Пусть V — выделенный объем произвольной формы части тела,
ограниченный замкнутой поверхностью S (не обязательно изотерми¬
ческой); п — единичный вектор внешней нормали к точкам поверх¬
ности S (рис. 8); Т(х, у, z, t) — температура тела в точке (л:, у, г) в мо¬
мент времени t. Вычислим общее количество теплоты Q, полученное
выделенным объемом за малый промежуток времени dt, имея в виду,
что Q=Qi+Q2. Для вычисления Qi воспользуемся законом Фурье
в скалярной форме (1.14). Количество теплоты, подведенное в выделен¬
ный объем через элементарную площадку da за время d/, равно (с уче¬
том того, что направление потока теплоты противоположно направле¬
нию нормали)
dQ1 = ^*^-dad/ = Xngradr dodt = — qndodt, (1.20)
где q = — X grad Т — вектор плотности теплового потока.
Количество теплоты, протекающее за время dt через
поверхности S, выразится интегралом
<?! = — df $$ qndo = — d/J J qndo,
s s
где qn — проекция вектора q на нормаль п.
Поверхностный интеграл (1.21) можно преобразовать в объемный
по формуле Остроградского — Гаусса, связывающей двойной инте¬
грал по поверхности S с тройным интегралом по объему К, ограничен¬
ному этой поверхностью:
Sb«da== SSSdiv?dy- (L22)
s v
Таким образом,
Q, = —d/JJJdivflrdK (1.23)
V
Выделение или поглощение теплоты внутри объема V удобно ха¬
рактеризовать с помощью плотности (мощности) тепловых источников.
Под плотностью тепловых источников понимают такую функцию
F(x, у, г, 0» когда в элементарном объеме dV за промежуток времени
dt выделяется количество теплоты, равное
dQ2=F(x, у, z, t)dVdt=F{My t)dVdt. (1.24)
Тогда за промежуток времени dt в теле объемом V выделится количе¬
ство теплоты
Qt = d/5SJF(M,/)dV. (1.25)
V
Здесь F(M, t)>0; если F(M, /)<0, то теплота не выделяется, а погло¬
щается; функция F(M, t) считается непрерывной и ограниченной..
площадь
(1.21)
27
Общее количество теплоты Q, полученное выделенным объемом V,
Q = dt$§§F(M, t)dV—dt JJJdivqdV. (1.26)
V V
С другой стороны, согласно формуле (1.19), это количество теплоты
равно изменению внутренней энергии вещества, содержащегося в вы¬
деленном объеме. Указанное изменение на основании первого закона
термодинамики может быть выражено формулой
Q—CdT, (1.27)
где С — теплоемкость выделенного объема; dТ — изменение его тем¬
пературы.
Таким образом, Q может быть вычислено двумя способами, с одной
стороны, по формуле (1.26), с другой — путем учета изменения тем¬
пературы в точках объема У, ограниченного поверхностью S. В точке
(лс, у% г) за промежуток времени dt температура Т(х, у, г, t) изменится
на
Т(х, у, z, /+d/)—Т(х, у, г, t)=(dT/dt)dt.
Элементу объема dV массой pdK для такого изменения температуры
потребуется количество теплоты, равное cp(dT/dt)dVdt, а всему объему
CdT = dt 5 { 5 ср (dT/dt) dV, (1.28)
V
где с—удельная теплоемкость, Дж/(кг-град); р — плотность вещества,
кг/м3; ф, Дж/(м3-град).
Принимая во внимание (1.27) с учетом (1.26) и (1.28), находим
ф-gl + divflf—F(M, ol dV = 0. (1.29)
ш
Равенство (1.29) должно выполняться для любой части тела
объемом V. Это возможно только тогда, когда в каждой точке
внутри тела
Н-div q — F (М, /) = 0. (1.30)
Это заключение справедливо, если левая часть в равенстве (1.30) —
непрерывная функция. Предположим, что в точке М(х, у, z) равенство
нарушается, т. е., например, [cpd77d/+div<7—F(M, Тогда, ин¬
тегрируя обе части неравенства по некоторой области 1/, содержащей
точку М, получим противоречие с условием (1.29).
Так как д==—Xgrad7\ то равенство (1.30) можно записать следую¬
щим образом:
Cp(dT/dt)=div(hgradT)+F(M, t). (1.31)
Получено уравнение, которому должна удовлетворять функция
Т(х> у, z, /), представляющая собой температуру некоторого тела. Это
уравнение называется дифференциальным уравнением теплопровод¬
ности или уравнением Фурье.
28
Для изотропного гомогенного тела параметры с, р, Я постоянные;
далее, так как div (grad Т)=Л7\ где Л —оператор Лапласа, то оконча¬
тельно запишем (если разделить обе части (1.31) на ср)
<?77д/=аДГ(М, t)+[\Kcp)]F(M, t), (1.32)
где д=Я/(ф) — коэффициент пропорциональности, называемый
температуропроводностью, м2/ч.
В декартовых координатах уравнение (1.32) имеет вид
dTldt=a{d*Tldx*+d*Tldy*+d*Tldz2)+[\{cp)\F(x, у, г, t). (1.33)
В цилиндрических координатах (г, ф, z), связанных с декартовыми
коодинатами соотношениями:
x=rcos ф, y=rsin ф, z=z;
0^г<оо, 0^ф<2л, —оо<г<+оо,
уравнение (1.32) принимает вид
дТ (дП , I дТ , 1 дП . дП\ , I ,ч
^ = Ч^+“^Г+7Г^Ф5' + ^Г] + Ф (Л г- О-
В сферических координатах (г, ф, 0), связанных с декартовыми ко¬
ординатами соотношениями:
x=r cos ф sin 0, у—г sin ф sin 0, z=r cos 0,
0<><оо, 0^фС2л, О^0^л,
уравнение (1.32) записывается в виде
дТ Г д%Т , 2 дТ . I д ( . Q дТ \ .
<Э< “ a [ дг* г dr "*"/-2sin0de (Sm 50 j “*■
Ф-0- о-
В частном случае, когда температурное поле обладает сфериче¬
ской симметрией, последнее уравнение (при F = 0) принимает вид
ОТ __ ( д2Т 2 дТ \
dt ~~~ й \ дг2 г дг )•
Если вместо T(ry t) ввести новую функцию £/(r, t) с помощью подста¬
новки U(r, t)=rT(ry t)y то вместо уравнения относительно T(r, t) по¬
лучим после несложных преобразований следующее:.
dUldt=a(d4Jldr%
напоминающее уравнение теплопроводности для неограниченной пла¬
стины (или тонкого стержня с теплоизолированной боковой поверх¬
ностью). Указанная подстановка является исключительно важной
в аналитической теории теплопроводности; ее применение позволяет
использовать найденные аналитические решения тепловых задач для
бесконечной пластины при описании соответствующих температур¬
ных полей в сферических телах (сплошной или полый шар).
В отличие от Я, которая характеризует теплопроводящую способ¬
ность тела, а характеризует теплоинерционные свойства тела и являет¬
29
ся мерой скорости выравнивания температурного поля в рассматривае¬
мой среде. Действительно, по определению, а=Х/(ф)=Я/с', где с' —
объемная изобарная теплоемкость. Отсюда температуропроводность а
прямо пропорциональна теплопроводности X и обратно пропорцио¬
нальна аккумуляционной способности с' вещества. Особенно нагляд¬
ным становится физический смысл а в уравнении теплопроводности,
когда отсутствует внутреннее тепловыделение и dT!dt=akT{M, t).
Зная вблизи точки М(х, у, z) зависимость температуры от координат,
можно предсказать, как быстро будет нарастать (или спадать) темпера¬
тура в этой точке при переходе к следующему моменту времени. При
этом чем больше а (т. е. чем меньше с'), тем пропорционально быстрее
меняется во времени температура. Таким образом, а характеризует
способность вещества изменять с большей или меньшей скоростью свою
температуру во времени.
А. В. Лыковым показано [83], что температуропроводность прямо
пропорциональна скорости распространения изотермической поверх¬
ности.
Оператор Лапласа в правой части (1.32) характеризует изменение
теплового потока в точке М и (в геометрическом смысле) является ме¬
рой кривизны изотермической поверхности в этой точке. Этим и обу¬
словлено изменение температуры в данной точке, так как наибольшая
быстрота перестройки температурного поля отвечает участкам боль¬
шей кривизны, и наоборот. Для иллюстрации этих соображений на
рис. 9 рассмотрим две температурные кривые, соответствующие одно¬
мерному температурному полю dTldt=ad2T/dx2 (без источников теп¬
лоты F=0), для момента времени tx (кривая 1) и t2=ti-\-dt (кривая 2).
Из рисунка видно, что за время dt температура сильнее всего изме¬
нилась на участках а и Ь, где температурная кривая обладает боль¬
шей кривизной.
В то же время знак оператора Лапласа в данной точке показывает,
в каких случаях температура этой точки при переходе от момента вре¬
мени t к tx+dt возрастает (нагревание) и в каких случаях убывает
(остывание).
30
Возрастание температуры в данной точке обусловливается тем,
что в слой материала, охватывающий эту точку, подводится теплоты
больше, чем за тот же промежуток времени отводится (величина
д2Т/дх2 положительна). При убывании температуры, наоборот, отво¬
дится теплоты больше, чем за время dt подводится (величина д2Т/дх2
отрицательна) (рис. 10).
Уравнение (1.33) является основой аналитической теории тепло¬
проводности, которую создал Фурье в начале XIX в., одновременно
положив начало разработке многих родственных задач математиче¬
ской физики. Интересно отметить, что Фурье объяснял механизм пере¬
дачи теплоты, основываясь на теплородной теории, тогда как уже за
полвека до него Ломоносов в своей диссертации «Размышление о при¬
чине теплоты и холода» решительно отверг такой метафизический
взгляд.
Уравнение (1.32) выведено при условии некоторой идеализации
процесса и в этом смысле является феноменологическим (описатель¬
ным) уравнением аналитической теории теплопроводности. Вопрос
о том, насколько точно это уравнение описывает реальный физиче¬
ский процесс теплопроводности, может быть решен только сравнением
результатов, полученных при решении уравнения и эксперименталь¬
ным путем. В абсолютном большинстве случаев феноменологическое
описание процесса теплопроводности находится в весьма удовлетво¬
рительном согласии с экспериментом. Некоторое несоответствие, об¬
наруженное за последнее время и касающееся поведения материалов
при повышенных температурах, не меняет существа вопроса.
Уравнение (1.32) представляет собой дифференциальное уравнение
в частных производных, в котором независимыми переменными яв¬
ляются время и три пространственные координаты, а зависимой пере¬
менной— функция Т (температура). Это уравнение первой степени
(линейное), поскольку зависимая переменная Т входит в него только
в первой степени. Но вместе с тем оно является уравнением второго'
порядка, так как дифференциальный оператор Т содержит производ¬
ные второго порядка от Т по пространственным переменным. Функция
F считается заданной функцией, в общем случае функцией координат
и времени.
Уравнение теплопроводности (1.32) в курсах математической физи¬
ки относится к дифференциальным уравнениям
параболического типа и согласно этому типу уравнений
для него выбираются соответствующие аналитические методы реше¬
ния.
Может, в частности, оказаться, что температура рассматриваемого
тела в любой его точке не изменяется во времени, т. е. является функ¬
цией только координат (установившееся состояние). Тогда dT/dt=0
и уравнение (1.32) принимает вид
АГ(М) + (1/Х)/г(М)=0, (1.34)
где плотность тепловых источников F(M) уже не зависит от вре¬
мени.
Уравнение (1.34) называется уравнением Пуассона.
31
Если внутри тела отсутствуют тепловые источники и температур¬
ное поле стационарно, то имеем уравнение (в декартовых координатах)
№(М)=д*Т1дх*+д*Т1ду*+д*Т1дг*=0, (1.35)
которое называется уравнением Лапласа.
Функции, удовлетворяющие уравнению Лапласа, называются
гармоническими. Уравнение Лапласа принадлежит к дифферен¬
циальным уравнениям эллиптического типа
и согласно этому типу уравнений для него выбираются соответствую¬
щие аналитические методы решения.
Стационарное температурное поле в некоторых задачах можно
получить из нестационарного путем предельного перехода
ГСТ(М) = lirn Г(М, t). (1.36)
t -+ 00
На практике такой переход осуществить, как правило, не удается;
в некоторых случаях на помощь приходит операционное исчисление
с его теоремой о конечном значении
(см. гл. VI).
Уравнение Лапласа (1.35) не только
описывает стационарное температурное
поле, но и играет первостепенную роль
при описании других установившихся
процессов, например, равновесного ра¬
спределения зарядов по поверхности проводника.
Задача. Выведите уравнение линейной теплопроводности для тонкого стерж¬
ня с теплоизолированной боковой поверхностью и внутренними источниками теп¬
лоты в виде
dT/dt=ad2T/dx2+[\/(cp)]F(x, t). (1.37)
Замечание. Ось стержня следует принять за ось абсцисс (рис. 11); в этом
случае изотермическими поверхностями для линейной теплопроводности будут
сечения стержня, перпендикулярные оси Ох, нормаль к ним совпадает с осью Ох
и дТ/дп = дТ/дх,если направление нормали п совпадает с положительным направ¬
лением оси Ох.
Закон Фурье в скалярной форме для рассматриваемого случая
имеет вид
dQx=—k(dT/dx)Sdt
(где S — площадь поперечного сечения стержня с абсциссой х)\ при
этом количество теплоты, сообщенное выбранному малому участку
стержня (х, x+dx) и равное разности входящей и выходящей теплот,
dQx—dQx+dx=X(d2T/dx2) Sd* dt. (1.38)
§ 6. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
ДЛЯ АНИЗОТРОПНЫХ ТВЕРДЫХ ТЕЛ
Анизотропия — явление, которое состоит в том, что физические свой¬
ства тела различны по разным направлениям. Анизотропия тепловых
свойств наиболее резко проявляется в кристаллических и волокни¬
32
стых структурах. В указанных телах вектор плотности теплового по¬
тока q в какой-либо точке М не направлен по нормали к изотерми¬
ческой поверхности, проходящей через эту точку. Поэтому вместо
соотношения q=—XgradT в точке М имеет место более общая зависи¬
мость, заключающаяся в том, что каждый компонент вектора q яв¬
ляется линейной функцией компонентов градиента температуры в этой
точке:
— Я* = Кх (дт!дх) + Ку (дТ>дУ) + Kz (дТ/дг), \
— Я у = \х (дТ !дх) + Ку (дТ Ш + \z (дТ/дг), V (1.39)*
— Яг = Кх (дТ!дх) + Ку (дт/ду) + Kz (дТ/дг). )
В (1.39) величины kiK(i,K = x,y, z) являются компонентами тен¬
зора второго ранга—тензора теплопроводности X
(1.40)
ч^г* К у ^zz .
причем X—симметричный тензор hiK = XKi.
Уравнение теплопроводности (1.31) остается справедливым для
случая, когда X есть тензор (1.40). Отсюда, используя операцию
умножения тензора на вектор, можно записать (1.31) в' следующем
виде:
fКх Ку Кж\
К* Ку Кг ) grad Г +F(M, 0 =
у'Кх Ку Кг/
“div [(l“T7 + x*> + +
+\.^)j+K^r+K%-+K.,?P)i>}+FW, О- (I-H)
В случае однородной (анизотропной) среды Х{К = const и урав¬
нение (1.41) примет вид
™ дТ __1 д2Т .1 д*Т х \ д*Т , ,1ч д2Т ,
Ф dt kxx дх2 ~Tkyy ду2 + kzz dz2 Ку +kyx) dxdy^~
+ (Kz + Kx)j^ + {K* + Ky)fyjz + F(M> 0- (1-42)
Если воспользоваться симметричностью тензора X, то уравне¬
ние (1.42) (при F = 0) можно записать
дТ _ 1 64 , 1 д*Т II &Т , 01 дп ,
cPW-A**~W+Ky-fyr + Ky 'д*+2К*1>Шу г
+ 2^S + 2VS- (1-43)
дТ
cp_aT = dlv
Выражения (1.39) представляют собой компоненты вектора, полученного
при перемножении тензора (1.40) на вектор grad Г справа [см. (1.41)].
2-339 33
Уравнение (1.43) можно преобразовать к новой системе прямоуголь¬
ных координат (*', у', г') таким образом, чтобы освободиться от
смешанных производных и перейти к виду
Новые оси координат (л', у', г') называются главными осями
теплопроводности у а коэффициенты (Xlf Х3)—главными коэффи¬
циентами теплопроводности. На практике указанное преобразова¬
ние можно произвести различными способами, в частности путем
предварительного приведения матрицы (1.40) к диагональному виду
с помощью соответствующего поворота системы координатных
осей (Ху уу г):
coscxf, cosPj, cosy, — направляющие косинусы новых координатных
осей (новых переменных) (*', у'у г') в старой системе координат
(Ху уу г).
В новых координатах матрица (1.40) имеет вид
Отсюда нетрудно записать и преобразованное уравнение теплопро¬
водности, которое в случае kt = const (i = 1, 2, 3) имеет вид, совпа¬
дающий с (1.44)*
Для отыскания коэффициентов преобразования (1.45) необходимо
найти последовательно три нормированных решения (/,, пр
* Подробно о теории указанного преобразования можно прочитать, напри¬
мер, в книге Н. В. Ефимова «Квадратичные формы и матрицы». Наука, 1972.
(1.44)
где W (*', у', z\ t) = T (х, у, г, t).
где /, = cosa,, m, = cosP(, n, = cosY, (t= 1, 2, 3), а l\m]-\-n} — 1;
(1.46)
(1.47)
системы
(t = 1.2,3), (1.48)
34
где Xt— корни характеристического уравнения
Кх \
XV
VX
-К
"'у г
Кг — ^Ч
(1.49)
Заметим, что уравнение (1.49) имеет только вещественные корни
(это утверждение доказывается в теории квадратичных форм). Обо¬
значим отличные от нуля решения системы (1.48) через (/(/), ти\
пи)), причем эти неизвестные определяются с точностью до произ¬
вольного множителя пропорциональности d. Возьмем d =
= l(i)* + mU)i + nU)i> тогда l{ = dl{i)t m, = d/n(/)f n{ = dnU).
Рассмотрим пример. Пусть коэффициент X есть тензор второго
ранга вида
/4 2 0\
Ь = ( 2 5 2 ), (1 50)
\0 2 6/
а соответствующее уравнение теплопроводности, согласно (1.43),
имеет вид
дТ л . с д2Т а д2Т дЧ . А д*Т п С1.
ф dt ~ дх2 + ду2 + дг2 + дхду+ дидг ’ ^ 51)
Приведем это уравнение к виду (1.44). Прежде всего составим ха¬
рактеристическое уравнение (1.49)
4—X 2 0
2 5—X 2 = о,
0 2 6—Х
откуда = 5, = 2, X;
перейдет в следующее:
dW к d2W , 0 d2W
сР~й = 5^тт + 2
8. Согласно (1.44), уравнение (1.51)
d2W
дх'2
ду'2
■8
дг'2 ’
(1.52)
где (х\ у'> г') — новые переменные, связанные со старыми перемен¬
ными (Ху уу г) формулами преобразования (1.45).
Для вычисления коэффициентов. (/f, mt, nt) в этих формулах
составляем систему (1.48)
(4 — X;) 1{ + 2га, = 0, \
2/j + (5—Xt)m^ + 2«, = 0, > (i = 1, 2, 3). (1.53)
2ш, + (6 — /,) •), = 0 J
Полагая здесь >^ = 5, переходим к системе
— 1Л + 2/71 j =0, |
2lx + 2/1, =0, > (1.54)
2тх + пх = 0. J
35
В качестве ненулевого решения этой системы можно взять, на¬
пример, /(1) =— 2, /пш =— 1, А2(1) = 2; так как при этом d =
= — 2/3; = —1/3, nl — 2/3. Аналогичным образом, полагая в
(1.53) Хг2 = 2 и Ха = 8, находим следующие два нормированных ре¬
шения—единичные векторы второго и третьего главного направле¬
ний: (2/3, —2/3, 1/3); (1/3, 2/3, 2/3). Таким образом, искомые
формулы преобразования и преобразованная матрица (1.50) имеют
соответственно вид:
После нахождения температурной функции W (х\ у', г', /), удов¬
летворяющей уравнению (1.52), можно возвратиться к искомой
функции Т (х, у, z, /), используя формулы преобразования (1.55)
[разрешенные относительно (*', у\ г')]. Уравнение (1.44) можно
упростить дальнейшей заменой переменных, полагая*:
где X выбирается произвольным.
Так как по правилу дифференцирования сложной функции имеем
т. е. примет тот же вид, что и уравнение теплопроводности для изо¬
тропного твердого тела.
Создается впечатление, что преобразованиями уравнений (1.45)
и (1.56) удается снять серьезные математические трудности, связан¬
ные с анизотропией среды. Однако в конкретных случаях дело обсто¬
ит гораздо сложнее. В новой системе координат (х/ уz') происхо¬
дит искажение границ рассматриваемого тела, а именно: в уравнения
новых граничных поверхностей начинают входить пространственные
переменные. В связи с этим усложняются граничные условия рассмат¬
риваемой задачи (см. §3 гл. II), так как теперь они оказываются за¬
данными на переменных граничных поверхностях. Это обстоятельство
затрудняет применение классических аналитических методов при ре¬
шении новой тепловой задачи, а в большинстве случаев теряется и
0 При переходе к новым переменным целесообразно ввести и новое обозна¬
чение функции. Это удобно при вычислении частных производных по новым пере¬
менным в процессе преобразования уравнения (1.44).
= 1 lV4+1+4= 1/3, то искомое первое главное направление будет:
2 / , 2 / , 1 ,
з * + з Г/ + 3 г
1 , 2,2,
У ~~ 3 Х зУ f 3Z
(1.55)
2 , , 1 , . 2 ,
г = У* +jy +У2 ’
g=*'(W'2; ti = */'(W/2;
t = z'(XA3)I/2; U(l, T], t, t)=W(x\ y\ z\ 0, (1.56)
dx' “ d\ dx' “
то уравнение (1.44) перейдет в следующее:
dW __ди d% _
(1.57)
36
принципиальная возможность их использования. Таким образом,
выигрывая в упрощении записи основного уравнения теплопровод¬
ности (1.43), проигрывают в усложнении граничных условий задачи.
Исключение составляют некоторые простейшие случаи, когда тело
не ограничено по всем пространственным переменным либо оно огра¬
ничено плоскостями, перпендикулярными главным осям теплопро¬
водности (в новой системе координат уравнение таких плоскостей
x'=const, у'=const, z/== const), или в случае, когда тело ограничено
плоскостями, перпендикулярными одному из главных направлений,
и круговыми цилиндрами с осью симметрии, направленной вдоль
данного направления. Во всех указанных случаях целесообразно
предварительно упростить исходное уравнение (а вместе с ним и ис¬
ходную тепловую задачу).
Рассмотрим теперь в уравнении (1.39) частный случай, когда ани¬
зотропная среда является ортотропной — теплопроводность различ¬
на в трех взаимно перпендикулярных направлениях:
<7* = — К(дТ/дхУ> Я„ = — ч (дТ 1ду)\ Яг = — К (дТ/дг). (1.58)
Если среда к тому же однородна (Х, = const, i = x, у, г), то урав¬
нение (1.31) имеет вид (при F = 0)
дТ№ = ах (д'Т/дх*) + аИ (д*Т/ду*) +
+ аг (д*Т/дг*), (а, = >.,/(ср); i = x,y,z) (1.59)
и может быть приведено к виду (1.57) с помощью преобразований
| = х(а/ах)1/2\ ц = у (а/ау),/2; £ = г(а/аг)‘/2,
где а можно выбрать произвольным.
В цилиндрической системе координат уравнение теплопровод¬
ности для ортотропного однородного тела имеет вид
дТ fd*T.idT\L яф дЧ . дч
Здесь
ar = V(cP)> = К/(ф); а2 = К/(ср)’
Заменой переменных г' = г(а/аг){/2, ф'=ф (а/аф)1/2, г' = z (a/az)[f2
уравнение (1.60) приводится к виду
dW__„(d*W , 1 dW , 1 d*W , d*W \ n fll4
HT~~a \ dr'* + r' dr' + r'* dtp'2 + dz'* /* I1-**1)
В монографии [55] излагается физическая теория теплопроводно¬
сти анизотропных твердых тел. Следует отметить, что вследствие
трудности измерения теплопроводности анизотропных тел практика
располагает весьма малым количеством экспериментальных данных
и поэтому к настоящему времени в аналитической теории теплопро¬
водности решено ограниченное число специальных задач.
37
§ 7. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
В ДВИЖУЩЕЙСЯ СИСТЕМЕ КООРДИНАТ И В ДВИЖУЩЕЙСЯ
СРЕДЕ
Уравнению
dT/dt=a№ (М, t) (1.62)
подчиняется распределение температуры Т(М, t) в однородном изот¬
ропном твердом теле, отнесенном к неподвижной связан¬
ной с телом системе координат.
Рассмотрим теперь, как изменяется это уравнение, если система
координат испытывает трансляционное перемещение по отношению
к телу. В этом случае изменение
температуры (dT!dt)dt за интервал
времени d/, которое наблюдается в
точке М этой подвижной системы,
складывается из двух составляю¬
щих. Первая составляющая — изме¬
нение температуры с течением време¬
ни в неподвижной точке простран¬
ства; вторая — перемещение наблю¬
дателя, жестко связанного с под¬
вижной системой координат, за вре¬
мя dt на определенное расстояние
ds=fldt, в результате чего наблю¬
датель попадает в точку с другим
значением температуры. Эта вторая составляющая имеет значение
dsyT=vyTdt, где v — вектор скорости подвижной координатной си¬
стемы по отношению к телу; уТ — локальный температурный гра¬
диент. При выводе уравнения теплопроводности, основанном на со¬
ставлении теплового баланса, для элемента объема тела учитывается
только первая составляющая, поэтому из наблюдаемого изменения
температуры (д77д£)д/вточке М нужно вычесть перемещение (vyTdt),
возникшее в результате движения системы координат.
В системе координат, совершающей трансляционное перемещение
со скоростью V, уравнение теплопроводности (1.62) принимает сле¬
дующий вид:
дТ/dt—vyT = аДТ, или dT/dt = аДГ (М, /) + г>у7\ (1.63)
где ДТ—оператор Лапласа; уТ —вектор-градиент функции Т.
Рис. 12 поясняет эти рассуждения для одномерного температур¬
ного поля. Если v = v1i, где ^ = const, то можно записать
дТ/dt = а (д2Т/дх2) + (дТ/дх). (1.64)
С помощью подстановки
Т (х, t) = U (х, t) exp ^—-jj^x—(1.65)
уравнение (1.64) приводится к виду dU/dt — a(d*U/dx2).
38
Если внутри твердого тела имеется источник теплоты мощностью
F (М, /), то к правой части уравнения (1.63) нужно добавить произ¬
ведение (1 /cp)F(M, t).
Уравнение
дТ /д2Т , д*Т . д*Т\ . ( дТ , дТ . дТ \ . 1 DiAA
а/ — а[дхг + дуг ^ дга ) + a* +Ua ду дг ) + ср ^ ^
нетрудно упростить с помощью подстановки
Т(х, у, г, t) — U (х, у, г, t)exp( — ^rv—(1.66)
V <= i /
в которой г = xl + yj + zk, v = vj + vj + v3k, a rv = xv1-\-yvi-\- zva —
скалярное произведение.
Получим
dU/dt = a&U{x, у, г, t) + (l/cp) Fit
( I
= fexP^i™+45l>’
Подстановка (1.65) является частным случаем (1.66).
Пусть теперь в (164) v1 = vl(t)1 т. е.
дТ/dt = ад2Т/дх2 + vl(t)dT /дх. (1-67)
Здесь может быть полезной следующая подстановка:
Т (х, t) = U (х, /)ехр [-^x-^joUOd/]. (1.68)
переводящая уравнение (1.67) в следующее:
dU d2U х ' / х\ г 1 ( ' dv \ п
аГ = а -M+2-av'WV [v' = di)- <169)
Если S, = a1/ + a2(a/ = const), то уравнение (1.69) переходит в
простейшее
dU/dt = a (d2U/dx2) (v\ = d2S/dt2).
Если Sj = («,/2) P-fa2/ + a, (a, = const), то имеем
dU/dt =^a(d2U/dx2) + (aj2a) xU. (1 70)
В более общем случае в декартовой системе координат урав¬
нение
dT/dt =а&Т (М, 0 + ®(0 V7, + (l/cp)/=,(Ml 0» (1 -71)
где ©(0 = М0< + М0У + ^ (t)k, целесообразно упростить подста¬
новкой
г- з
Т(М, t) = U (М, /)ехр
ill d<] . (1-72)
39
переводящей уравнение (1.71) в уравнение вида
dU/dt=aMJ(M, t) + (\l2a)rv' (t)U + (\/ср) Ft(M, t), (1.73)
Ft(M, t) = F (M, /)exp
jo?(0 df.
Здесь также представляет интерес случай S{(t) = aut + аи, где
at/ = const (/ = 1, 2; i= 1, 2, 3).
Рассмотрим далее случай, когда система координат совершает
не только трансляционное (поступательное), но и вращательное
перемещение, характеризующееся вектором угловой скорости <о.
Если V — вектор скорости рассматриваемой точки системы, то по
известной формуле кинематики (см.: Тарг С. М. Краткий курс теоре¬
тической механики, § 74. М., Наука, 1967) можно записать
v = v0 + <dxr1 (1.74)
где v0—вектор скорости мгновенно поступательного перемещения
начала координат; г—радиус-вектор точки М в подвижной системе;
[о) -г] = (о>yz—ы2у) I + ((ozx—о>хг)У+ (о)ху—сo^z) k—векторное произ¬
ведение.
Уравнение теплопроводности (1.63), которое остается справед¬
ливым и в этом случае, принимает следующий вид:
дТIdt — akT (М, t) + v,sjT(My 0 + [©-г] уГ(М, t). (1.75)
Если внутри тела имеется источник теплоты F (М, /), то в пра¬
вой части уравнения (1.75) появляется еще одно слагаемое (1/ф)/7.
Рассмотрим частный случай (1.74), когда начало координат совер¬
шает сложное перемещение в плоскости (поступательное с одновре¬
менным вращением по окружности), описываемое в полярной системе
координат x = rcos(p, y = r sin ф вектором скорости вида
v = vrer + v(peqn (1.76)
где vr = dr/dt = г—радиальная скорость прямолинейного движения
начала координат вдоль радиуса; иф = гю = /’ dcp/d/ = гср—переносная
скорость вращательного движения с угловой скоростью о, направ¬
ленная перпендикулярно радиусу в сторону возрастания угла ф.
Запишем далее вектор grad Т в полярной системе координат,
используя (1.6):
grad Т = (дТ/дг) ег + (1/г) (дТ/<5ф) еф. (1.77)
Если Т (г, ф, г, t)—температурное поле, то уравнение (1.75) для
этого случая примет следующий вид:
дТ (дП . 1 дТ , 1 , д*Т . д2Г\ • дТ . дТ
dt ~ а ( дг* + Л дг + г2 + дсп* + д7* ) +Г дг "^0) дсп • (1-78)
dt ~ \дг* 1 Г дг 1 г* ^ дер2 ^ dz2 J ^ дг 1 дц>
В частном случае вращательного движения системы координат
с угловой скоростью со, если ифеф = согеф—линейная скорость вра¬
щательного движения в окружном направлении, (1/г) (дТ/ду) *>ф —
градиент температуры в этом направлении, то уравнение (1.78) при
40
Т — Т (г, ф, t) запишется следующим образом:
дТ (дгТ , 1 дТ . 1 дгТ\ , дТ .. 7„.
dt ~ 0 [ дгг т дт + г* Зфг j + W dq> ' ^ 9)
Рассмотрим теперь дифференциальное уравнение теплопроводности
для движущейся среды, т. е. допустим, что происходит движение от¬
дельных частей тела относительно друг друга, как это имеет место
в случае жидкостей и газов. Благодаря этому к тепловому потоку
вследствие теплопроводности добавится еще другой поток теплоты,
происходящий от того, что движущаяся материя перенесет с собой
вследствие своей теплоемкости некоторое конечное количество теп¬
лоты.
В специальном выводе этого уравнения нет необходимости, так
как можно воспользоваться уравнением (1.63). Действительно, пусть
v (М, /) — вектор скорости движущейся среды. Уравнение теплопро¬
водности в движущейся среде сводится к уравнению (1.63), если «оста¬
новить» среду, но заставить двигаться систему координат со скоростью
[—v{My /)]. В этом случае имеем
dTldt=aAT(M, t)—v grad 7 (М, t)+(\/cp)F (М, t). (1.80)
К уравнению (1.80) применимы все упрощающие его подстановки,
указанные выше. В декартовой системе координат уравнение (1.80)
можно записать в несколько ином виде, если воспользоваться поняти¬
ем полной или материальной производной: пусть координаты точки
М(х, у, г) изменяются с течением времени, тогда при дифференцирова¬
нии функции Т(М, /) как сложной функции от t получим
^_дТ дТ^дх д_]^йу_ дТ^дг__
d/ dt ‘ дх d/ ' ду d/ ‘ dz dt
дТ , дТ , дТ i дТ дТ . ^ АТ
= dt+v^ + vyW + V^==df + VgTadT-
Таким образом, уравнение (1.80) можно переписать в другом виде
dr/d/ = а ДГ (М, /) + (1/ср) F (7W, /). (1.81)
В случае стационарного температурного поля из (1.80) имеем
а АТ (М) — я grad Г (М) + (1/ф)Г(М) = 0
или (учитывая, что а = Х/ф)
АТ (М)—via grad Г + (1 /X) F (М) = 0. (1.82)
К уравнению вида (1.80) сводится уравнение теплопроводности в неоднородной
(анизотропной) среде в одномерном случае. Укажем для этого случая ряд полез¬
ных подстановок.
Уравнение вида
с(*>е(*>?=^[Мдг)£] (1,83)
преобразуем последовательно с помощью подстановок:
Т (X, 0 = [с (X) р (*) Я (дс)]“1/2/сое (дс, 0: j
*'=*oJ |^C(t(^Tdjc; i <l 84)
Хд /
41
где /Со, *о — постоянные, выбранные надлежащим образом для сохранения размер¬
ности. При этом необходимо предположить, что в рассматриваемой области функ¬
ция Ус (х) р (х)/К (х) непрерывна, а х' (х) монотонно возрастает (или убывает) и
непрерывно дифференцируема, так что существует обратная функция х = х(х'),
также обладающая этими свойствами. С учетом (1.84) получим, преобразуя (1.83):
где f (х') — новая (известная) функция. Введем далее
х'
U (х', т) = W(x\ /) exp ^ / (ot) d ос; т = x\t, (1.86)
о
В новых переменных уравнение (1.83) окончательно принимает вид
3U d*U . , dU п
-W=^-f(x)W (1-87)
Аналогичным образом могут быть рассмотрены цилиндрическая (осесиммет¬
ричный случай) и сферическая (центральная симметрия) системы координат.
§ 8. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
В ДЕФОРМИРУЕМОМ ТВЕРДОМ ТЕЛЕ
Рассмотрим вопрос о связи процесса теплопроводности и упругого
деформирования твердого тела при наличии в нем градиента темпера¬
туры. При выводе уравнения теплопроводности (1.32) предполага¬
лось, что температурное поле не зависит от вызываемых этим полем
деформаций. Строго говоря, это не совсем верно, поскольку при де¬
формировании выделяется или поглощается теплота, которая влияет
на распределение температуры. Излагаемый в этом параграфе вопрос
принадлежит к числу достаточно трудных в аналитической теории
теплопроводности и примыкающей к ней теории термоупругости и
в то же время чрезвычайно важных для многих прикладных задач
теории прочности твердых тел [66—68]. Следует также учесть, что
изложение данного вопроса в разнообразной литературе по тепло¬
проводности и механике сплошных сред далеко не элементарно и не
однозначно. Вследствие этого возникает необходимость рассмотрения
указанного вопроса в компактном виде, достаточно приемлемом для
изучения.
Рассмотрим тело, свободное от внешних нагрузок, с неравномер¬
ным распределением температуры. Если тело изотропно и однородно
и все элементарные объемы тела одновременно и в одинаковой степени
изменяют свою температуру, то возникающая в нем деформация не
вызывает появления напряжений. В этом случае деформации (удли¬
нения) по трем осям координат (х, у, z) равны ехх еуу ezz——Т о),
где а — коэффициент линейного расширения; Т(М, t) — температура
точки М тела в момент времени t\ 7,0=const — начальная (исходная)
температура, при которой тело находится в недеформированном и
ненапряженном состоянии (все напряжения и деформации равны
нулю).
42
В действительности, изменение температуры тела, а следовательно,
и тепловое расширение (сжатие) элементарных объемов происходит
неравномерно, вследствие чего в теле возникают внутренние напря¬
жения j=xt у, г), обусловливающие добавочные удлинения и
сдвиги. Величины вц являются компонентами тензора напряжения а,
определяющего напряженное состояние в любой точке М внутри тела
и по любой площадке, проведенной через точку М
/QXX ®Ху
°= °«х °уу °иг • (1 88)
^XX
°*U
ax,
V
°yy
V
°zx
%
°zz
При этом aij=Oji (тензор а— есть симметричный тензор второго ран¬
га). По аналогии с обозначением вектора в тензорном исчислении
(см., например: Кочин Н. Е. Векторное исчисление и начало тензор¬
ного исчисления. М., изд. АН СССР, 1951) вводится следующее ус¬
ловное обозначение для тензора:
o = oxJ+oyJ+ozkt (1.99)
где векторы ах, о^, ог имеют следующее разложение по ортам i9
Ъ k:
°p=c’px-i + apy-i + apz k (Р = Х, у, г). (1.90)
Деформированное состояние в точке М определяется тензором
деформации е
/еXX гху ехг
е = ( V %У I■ О-91)
\егх ezy
При этом также е,у =
Напряжения и деформации связаны между собой следующими
соотношениями линейной термоупругости (закон Дюамеля — Ней¬
мана):
оц = + 2|ле/у —(ЗА. + 2р) ат (Т-Т0) 6„, (1.92)
где к, jn—постоянные Ламе для изотермической деформации, свя¬
занные с техническими упругими модулем сдвига G, коэффициентом
Пуассона v, модулем упругости Е (модулем Юнга) соотношениями:
X = 2Gv/(\—2v); p = G; 2p = £'/(l+v); ат — коэффициент линейного
термического расширения (ат = а/3); б/;—символ Кронекера
б _ I0’ *'=*'■
6"~ I 1. •■* = /;
е = (ехх + гуу + ezz) — объемное расширение, при этом ди *= de/de,у.
Возникающие в теле вследствие деформирования перемещения
(Uх, U", U:) связаны с компонентами ги тензора деформации гео¬
метрическими соотношениями
1 /ди( dU/\
*u~Asr+-Sr)- <193>
43
Перечисленные величины(/*, ei]t ои являются функциями координат
(х, у, г) и времени t.
В классической теории теплопроводности считается, что единствен¬
ной причиной возникновения в теле теплового потока является нали¬
чие grad Т=0. Однако при тепловом деформировании тела в случае
большой скорости теплового потока возникает так называемый эф¬
фект связности, состоящий во взаимодействии полей деформации и
температуры. Выведем дифференциальное уравнение теплопровод¬
ности для рассматриваемого случая, привлекая для этого необходи¬
мые законы механики сплошных сред и термодинамики необратимых
процессов.
Рассмотрим упругое тело, внутри которого выделим объем V, огра¬
ниченный замкнутой поверхностью s. Вследствие явления термоупру¬
гого деформирования на каждый элемент da этой поверхности дей¬
ствует сила со стороны частиц тела, лежащих вне объема V. Эта сила
пропорциональна величине площадки da и зависит от направления
вектора единичной нормали к рассматриваемому элементу; обозна¬
чим ее через Pnda, где вектор Рп называется напряжением на площад¬
ку da с нормалью п (сила, отнесенная к единице площади). Отметим,
что напряжение Рп> вообще говоря, не будет перпендикулярно площад¬
ке da. Пусть cos (п, х), cos (п, у), cos (я, z) — компоненты вектора
внешней нормали п к поверхности s. Согласно теории упругости, век¬
тор напряжения Рп может быть выражен через компоненты тензора
напряжения а следующим образом:
Pn = oxcos(nt x) + avcos(n, y) + ozcos (я, г)=а-я, (1.94)
где векторы ох> ау, oz определяются выражениями (1.90).
Суммарная сила, действующая на выделенный объем по поверх¬
ности s, вычисляется интегралом
з s V V
(1.95)
Здесь использована формула Остроградского — Гаусса (1,22).
Пусть далее на каждый элемент массы объема V действует объем¬
ная нагрузка /(М, t) (сила, отнесенная к единице массы), вклю¬
чающая инерционные силы; пусть также ц(М, t) — вектор скорости
частицы тела в точке М; р—плотность вещества (р = const). В соот¬
ветствии с законами механики можно записать:
(1-96)
s V V
Так как рассматриваются малые деформации (малые перемещения
или скорости) в рамках линейной термоупругости, то в правой
части равенства (1.96) можно пренебречь изменением пределов интег¬
рирования с течением времени и выполнить дифференцирование под
44
знаком интеграла. Учитывая, кроме того, выражение (1.95), получим
J55[divo + p/—р£Г] dV = 0. (1.97)
V
Так как уравнение (1.97) применимо к любому произвольному объему
V, то подынтегральное выражение должно быть равно нулю в любой
точке рассматриваемого тела
div o-f-р/— pv = 0. (1.98)
Выражение (1.98) является основным уравнением механики сплошных
сред.
Для удобства дальнейших рассуждений условимся относить такие
термодинамические величины, как внутренняя энергия U, энтро¬
пия S, а также мощность тепловыделения F, ■ к единице объема
тела (а не к единице массы). Пусть U (М, t) — внутренняя энергия
элемента тела, расположенного в точке М в момент времени /;
тогда внутренняя энергия выделенного объема V в момент времени t
равна U (My t)dV. Результирующая поверхностная нагрузка
г
(поверхностное напряжение), действующая на объем V, совершает
в единицу времени работу ^Pn-f-da. Точно так же объемная
S
сила / совершает в единицу времени работу, равную $ $ $ / • г;-dK.
v
Пусть F(M, t)—мощность теплового источника, действующего
в выделенном объеме; ~q— вектор плотности теплового потока. Сум¬
марное количество теплоты, полученное объемом V за единицу вре¬
мени (см. § 5, гл. 1)
-Sb-.do+Sn/r-d'/=HSdiv^grad7’)dV+SH/rdV/-
V V г
где qn — проекция вектора q на направление внешней нормали п к s.
По закону сохранения энергии следует: работа, совершенная
в единицу времени поверхностными и объемными силами, действую¬
щими на выделенную часть тела, плюс энергия, полученная этой
частью тела в единицу времени путем теплопередачи и действия
источников, равны скорости возрастания суммы кинетической и'внут-
ренней энергии
JJPn.0.da+ $S$7-u-dl/-$$ </„do+$jJf.dK =
“■9!"
Рассмотрим подробнее первое слагаемое в левой части (1.99)
5 5 ^ • do = J J a,i;,rt,(l0=:5SJ div (°,у) dV.
в я v
45
Можно показать, используя правило_умножения тензора а на век¬
тор v, что div (а-и) = и-div о + ^ах-^ + ау-^- + а2-^У Переходя в
(1.99) к объемному интегралу по формуле Остроградского—Гаусса
и используя (1.98), получим для произвольной точки М (jc, у у г):
div (Я,т grad Т) + F -\-(^ох + оу + о2 = U. (1.100)
Преобразуем далее третье слагаемое в левой части (1.100), исполь¬
зуя симметричность тензора напряжения а, геометрические соотно¬
шения (1.93) и тот факт, что vi = Ul\
— dv , — dv , — dv • ,
x ~dx ° у ~dy °z ~dz ~ °xx'Bxx °*У X
X exy + °xz ' exz + °ax ' Eyx + °yy ' eyy +
+ °yz ' Zyz + °zx • &zx + °z,' Ezy + °zz ' Ezz• = GiJEt/-
Мы обозначили расписанную сумму для краткости произведением
°ij Etj (1» / = *» У» г) с повторяющимися индексами i, /. Повторение
индексов означает, как это принято в тензорном исчислении, сум¬
мирование по этим индексам. Таким образом, окончательно будем
иметь следующее уравнение, связывающее между собой скорость
изменения плотности внутренней энергии, количество полученной
теплоты и скорость работы деформации, произведенной силами
внутренних напряжений:
О = div (Хт grad Т) F (1.101)
Перейдем теперь к рассмотрению внутренней энергии выделенного
объема. Запишем в дифференциальной форме первый закон термо¬
динамики, полагая, что бесконечно малое перемещение единицы
объема тела состоит только из деформации
dU = dez-y -j- T dS. (1.102)
Это соотношение гласит: малое изменение внутренней энергии равно
элементарной работе деформации-и количеству полученной теплоты.
Здесь dS—дифференциал энтропии S, причем внутренняя энергия
и энтропия — функции, зависящие от U = U(ei/t S); S = S(e/y, Т).
Находим
dS=(^)rdt-/+(5D.dT С-103)
и подставляем (1.103) и (1.102). Это дает
dU- [т (^)г + Ч d'» + 7'(f)tdT'
Так как dU есть полный дифференциал, то должно выполняться
равенство
46
Отсюда следует, что
(^)г+(ж)«-°- <||05>
В законе Дюамеля — Неймана (1.92) независимыми переменными
являются ги и 7\ так как o{J = <ji/(e{Jy Г), отсюда (дои/дТ)в =
= — (ЗА,+ 2p)aT6t/. Подставляя в (1.105), находим
(j|-) г +зд ^ - <31+ад■
С учетом этого соотношения выражение (1.104) запишется следующим
образом:
dU = <зи ■ &ги + (ЗХ + 2ц) ат • Т ■ de + Т dТ. (1.106)
С другой стороны, сравнивая соотношение
с (1.106), получаем (dU/dT)e=zT (dS/dT)e. Но (dU/dT)e = CEi где
Ct—объемная теплоемкость при постоянной деформации (постоян¬
ном объеме). Таким образом, Т (dS/dT)e = CB можно записать в виде
dU = ou-dEU + (3X + 2\i)aT-T-de + Ce-dT. (1.107)
Подставив в (1.107) закон Дюамеля — Неймана (1.92), получим
d U =■ 2ре I j • d ztJ -)- Ае • de -f- (ЗА, -f- 2 р) ост de -}- Се • dT.
Интегрируя полученное выражение и предполагая, что U = 0 в на¬
чальный момент времени, найдем
U = е*/ + (1/2) Я• еа + (3A,-f- 2р) ат-Т0-е + Се (Т — Т0). (1.108)
Подставляя в левую часть выражения (1.101) выражение (1.108) и
учитывая при этом (1.92), а также равенство е/у-е-8/у = е-е (точка
означает дифференцирование по /), найдем (при А,т = const)
ee74(3^ + 2p)aT.7Ve {l + [(7-Г0)/Г0]} = ХТ AT + F. (1.109)
Согласно предположению о малости деформаций рассматривается
случай, когда [{Т—T0)/TQ] 1, что приводит к линеаризации вто¬
рого слагаемого в левой части равенства (1.109). Если ввести, кро¬
ме того, удельную теплоемкость се и плотность материала р так,
что Се = рсе, то окончательно получаем уточненное или связанное
уравнение теплопроводности в следующем виде:
рСе 6Т(м’ ° +(ЗХ + 2ц)«т-Г0-е(М. 0 = ХТДГ(М, 0 + f(M, 0-
(1.110)
В отличие от классического уравнения теплопроводности (1.32)
уравнение (1.110) содержит слагаемое, связывающее приращение
температуры со скоростью изменения объема деформируемого тела.
Использование уравнения (1.110) показывает на необходимость од¬
47
новременного определения полей температуры и деформации, что
связано с определенными математическими трудностями при рас¬
смотрении конкретных случаев.
Перейдем теперь к анализу связной части в уравнении (1.110).
Перепишем уравнение (1.110) в следующем виде (при F = 0):
Здесь 60 = (ЗХ+ 2р)а а; • Т0/р2 cv • v\ —безразмерный параметр; ve =
= К(^ + 2р)/р—скорость распространения в упругой среде волн
расширения; cv — удельная теплоемкость при постоянном объеме
(<cv и се в линейной теории упругости взаимозаменяемы). В уравне¬
нии (1.111) член, пропорциональный 60, отражает влияние связан¬
ности, и им можно пренебречь по сравнению с единицей, если
(1.112)
аТ Ь + бо
Чтобы провести числовые сравнения, нужно оценить значения пара¬
метра 60. Так, для стекла марки С-90-1: Я = 2,48 -1010 Н/м2; р =
= 2550 кг/м3; р = 2,9-1010 Н/м2; cv = 8,33-102 Дж/(кг-град); ат = 2,7х
х 10"5 1/град. Если взять для примера Т0 = 200°С, то получим
60 = 0,0016, а из (1.112) следует, что в этом случае связанность
будет малой, если приближенно [e/(aT)J <^370. Для стали: р =
= 7,7 кг/м3; Л=1,26-1011 Н/м2; р,=8,4-1010 Н/м2; cv=4,6-102 Дж/(кгх
х град); ат = 3,5-10”^ 1/град и если взять для примера Т0 = 90°С,
то получим б0 = 0,014, а из (1.112) найдем, что [е/(аГ)] <^20.
Из приведенных примеров видно, что возможность пренебречь
членом связанности зависит не только от выполнения требования
60<^1, но и от условия, чтобы скорости изменения деформации и
температуры имели значения одного и того же порядка. Это условие
предполагает, что изменение перемещений во времени происходит
непосредственно вслед за изменением температуры. Это имеет место,
если поле температур с течением времени не испытывает резких изме¬
нений или внезапных скачков. Расчеты показывают, что в кристалли¬
ческих телах эффект связанности полей деформации и температуры
обычно мал. Однако подобное положение не сохраняется для новых
материалов (например, поливинилбутираля), обладающих большим
параметром связности. Для такого рода материалов расчет температур¬
ного поля предполагает решение связанной линейной динамической
задачи термоупругости. Для этого далее необходимо рассмотреть (ко¬
ротко) вывод полной системы уравнений.
Присоединим к уравнениям (1.92), (1.93) и (1.110) (при F=0)
три уравнения движения без объемных сил
°1/./ = Р^< ('. /' = *. У> *)• (1.113)
Здесь запятая на уровне индексов означает дифференцирование по
координате, отделенной запятой, т. е.
_ dOjj _ д°хх_ foxy foxz
“ сЦ ~~ Ох ** оу ' Ог '
48
Аналогично, Г, и V/t кк означают: Т { = dT/di (i = x, у, г);
,, d*Ui . d*Ui , d*Ui ... ..
^1, КК~ Qx2 “b Qy* Qz2 &U I (l, К X, у у z).
Выразим в уравнениях (1.113) напряжения о/у через деформации
ги по формуле (1.92), учитывая, что члены, содержащие ей Г,
сохраняются только при * = /:
2|xei/y у + ^е,/ — (ЗХ + 2р) ат Т 1==р0{.
В этом уравнении заменим деформации е/у перемещениями по фор¬
муле (1.93), внеся вместо / повторяющийся индекс к и учитывая,
что UKtiK = UKM. Получим
рД(У/ + (Х, + р) UКч к{ — (ЗЛ + 2р)ат*Т { = рО{. (1.114)
Три уравнения (1.113) совместно с четвертым уравнением (1.114)
при определенных начальных и граничных условиях описывают из¬
менение в пространстве и во времени связанных между собой полей
деформации и температуры. Запишем уравнения в векторной форме:
( pA(/-t-(A, + |Li)grad(div U) — (3^-f-2p)aT-gradr = p{7; (1.115)
I dT/dt + (ЗХ+2\х) [aT/(cep)] Г0 div £7 = а ДГ, (1.116)
где е= div U\ а=Хт/(сер). Из уравнения (1.115) может быть прин¬
ципиально определена деформация (перемещение) тела при произ¬
вольно заданной температуре тела. Подстановка в уравнение (1.116)
полученного таким образом выражения для div U приведет к уравне¬
нию, определяющему распределение температуры, в котором неизве¬
стной функцией является только Г(х, yt г, t). В случае, когда скорость
изменения температуры во времени мала, в уравнении (1.116) можно
пренебречь инерционным членом р{7; задача термоупругости, описы¬
ваемая уравнением (1.115) без инерционного члена (р£/=0) и уравне¬
нием (1.116), называется связанной квазиспгатинеской задачей термо-
упругости.
Соотношения (1.115) — (1.116) дают постановку связанной ди¬
намической задачи термоупругости в перемещениях. Этот класс
задач описывает проблему теплового удара, когда создаются усло¬
вия скачкообразного изменения температуры поверхности твердо¬
го тела или граничащей с ней среды, а также объемного температур¬
ного удара при скачкообразном повышении температуры объ¬
ема тела от начальной Г0 до значения Г, > Г0. В частном случае
цилиндрического температурного поля T=T(r, t) уравнения
(1.115) — (1.116) упрощаются. Так как для этого случая U2 = 0,
Ur=U(r, /), то (1.115) — (1.116) дают (с учетом внутренних источ¬
ников):
49
дг2 г дг г2 v2 dt2 (I — v) дг
1 d2U (l+v)ocтдТ
(1.117)
- = а —+-— -
дТ (д2Т 1 дТ\
dt
(д2Т 1 дТ\
\ дг2 г дг)
(1-2 v)c,p dt с,р
+ ~F(r, t)
где v„= у/(Х+2 fi)/p — скорость звука в материале упругого тела.
Важным в практическом отношении является также случай сфери^
ческой симметрии, когда температурное поле Т=Т(г, /), где (г, ср,
в) — сферическая симметрия координат. Для этого случая С/ф =
= Ue=0, Ur= U (г, 0 и основные соотношения будут:
Соотношения (1.117) — (1.118) используются при исследовании
проблемы теплового удара в телах, ограниченных, соответственно,
цилиндрической или сферической поверхностью. Из этих соотноше¬
ний могут быть определены функции перемещения U (г, /), тем¬
пературы Г(г, t) и далее искомые напряжения (Ту(г, t) и деформации
Еу (г, t) (что и требуется в конечном счете для описания напряженно-
деформированного состояния твердого тела во внутренних точках)
по формулам (1.113), (1.92). В ряде случаев (массивные твердые
тела; тонкие пластины) в декартовой системе координат более
удобной аналитической формой для исследования является поста¬
новка динамической задачи термоупругости непосредственно в на¬
пряжениях, вытекающая из общих уравнений (1.92), (1.93), (1.113)
и уравнений совместности в деформациях
где yijk — альтернативный (антисимметричный) тензор третьего
ранга, q, р, m, п, z, j=x, у, z. Если выразить из (1.92) деформации
Еу через напряжения подставить в (1.119) и произвести преоб¬
разования, учитывая (1.113), (1.93) и свойства тензорной алгебры, то
в результате получим следующее основное уравнение динамической
термоупругости в напряжениях:
(1.118)
Уqni7mpj^ij/пл (-^> О О*
(1.119)
50
(1 + V)A<T,(M, 0 + aV^-) + «г£р27^ °+^-V AT(M, 0^1 =
OlOJ [_ OlOJ 1—V J
t)-~a(M, t)5iJ+2?^«T(T(M, 0-mJ-
(1.120)
ti частном случае температурного поля T=T(z, t), возникающие
вследствие наличия температурного градиента напряжения будут
зависеть только от z и t, то есть t)\ при этом перемещения
Ux= Uy = 0, Uz=Uz(z, t). Из (1.120) для напряжения o2Z{z, t) с учетом
того, что cr(z, t) = [(1 + v)/(l - v)](jzz (z, t) - [2<xTE(1 - v)] [T(z, t) - TQ] и из
(1.116) следует
'd2azz i d2ozz (I+v)arp d2T(z, t)
dz2 v2 dt2 (1 — v) dt2
(1.121)
где
8T д2Т (ЗЯ+2р)а тТ0де
— = а — , (1.122)
dt dz2 Cgp dt
e(z, 0= ^ Ozz(z, 0 + 0 + V)gr[T(z, /)-Г0] =
2G(1 — v) (1—v)
=-3-aa(z, t) + (V^2~~ [T(z, 0 -U (1.123)
Х + 2ц (Я + 2/j)
Соотношения (1.122) и (1.123) приводят к следующему уравне¬
нию теплопроводности с учетом связанности полей температуры
и напряжения (более удобная форма для исследования)
(1 + <5i) — — Д — — S2
dt dz2 dt
где
(3;. + 2/i)24 Г0 (l+v)ar r0
d\ — 1 Ui —
Cep2 t'2p (1 -V)
Уравнения (1.121) — (1.122) (без учета эффекта связанности) яви¬
лись предметом многочисленных исследований в зависимости от
51
условий нагрева твердого тела (температурный нагрев; нагрев сре¬
дой; тепловой нагрев тепловым потоком однородным, импульс¬
ным, пульсирующим, периодическим и т. д.), его геометрической
формы и особенностей физико-механических характеристик матери¬
ала [176; 179].
Что касается динамических задач термоупругости на осно¬
ве соотношений (1.117) — (1.122) с учетом связанности, то эти воп¬
росы еще не получили своего развития в термомеханике. В отдель¬
ных работах, выполненных в этом направлении (ссылки в [201; 203])
установлено существенное отличие решений динамических за¬
дач термоупругости о тепловом ударе на поверхности полуограни-
ченного массива (упругое полупространство) без учета связи полей
деформации и температуры и с учетом этой связи: в случае несвя¬
занного решения (при температурном нагреве) на фронте термоуп¬
ругой волны, распространяющейся с поверхности внутрь тела со
скоростью звука в данной среде, имеет место разрыв напряженийсо
скачком ЕатТ01(1 — 2v), неизменный во времени, тогда как при
связанном решении разрыв с течением времени быстро умень¬
шается.
Развитие указанного класса задач по тепловому удару про¬
исходило по мере изменения (и усложнения) модельных представле¬
ний теории теплопроводности: классическая феноменология Фурье
при бесконечной скорости распространения теплоты; теория Макс¬
велла — Каттанео — Лыкова, учитывающая конечную скорость
тепловой волны; среды с тепловой памятью и, наконец, пере¬
ход к упруговязким телам в рамках линейных реологических мо¬
делей.
Остановимся на этих вопросах коротко и основное внимание
уделим соотношениям, лежащим в основе модельных представле¬
ний теории теплового удара при резко нестационарных процессах
нагрева и охлаждения границы твердого тела. Тело при этом счита¬
ется однородным и изотропным и физико-механические характери¬
стики тела (упругие и теплофизические коэффициенты) не зависят от
температуры, являясь постоянными величинами (учитывая микро-
секундные времена длительности динамических эффектов). Отме¬
тим также, что динамические задачи термоупругости формулиру¬
ются на стыке теории теплопроводности и механики деформиру¬
емого твердого тела и представляют собой перспективное направле¬
ние для научных исследований в области термомеханики. Читателя,
заинтересовавшегося этими вопросами, отсылаем к обзорам автора
[201; 203].
А. В. Лыковым в [83] был предложен обобщенный закон тепло¬
проводности для изотропных тел, учитывающий инерцию теплово¬
го потока,
52
-* да
q = — Argrad Т— т*—,
dt
(1.124)
где г* — время релаксации теплового потока, связанное со скоро¬
стью распространения теплоты vT соотношением ьт=л/а/х*. Для
металлов т* = 10“11 с; для стали vT= 1800 м/с; для аллюминия
vr=2930 м/с, для аморфных тел типа стекол и полимеров, имеющих
сложную структуру, время релаксации достигает значений (10"7 —
10"5), при этом гг может превышать скорость распространения
звука vp. Если записать уравнение энергии (1.110) в виде (1.30),
т. е. как
рсГ{М' ° = '-divq(M, t)+F(M, t) — (32+2fi)aT • Т0ё (M, t)
dt
(1.125)
и учесть (1.124), то в результате получим следующее уравнение
теплопроводности гиперболического типа с учетом конечной скоро¬
сти распространения теплоты:
1дТ{М, 0 , 1 д2Т(М, 0 ч, п ^ [де(М} 0 ^д2е(М, f)"|
(1.126)
а без учета связанности и при отсутствии источников
—— = аАТ(М, г) -х*— (1.127)
dt dt1
Гиперболическая модель теплопроводности широко применя¬
ется на практике. Так уравнение (1.127) используется для описа¬
ния температурных полей при высокоинтенсивном теплообмене
в устройствах импульсной и лазерной техники; при лазерной об¬
работке металлов; в процессах плазменного напыления; в энер¬
гетических каналах ядерных реакторов; для описания процес¬
сов переноса теплоты в псевдоожиженном слое; в дисперсных сис¬
темах и зернистых материалах; в слоистых полупроводниковых
структурах; при описании процесса электронной теплопроводности
в высокотемпературной плазме; при математическом модели¬
ровании фронтовых процессов терморазложения; для описания
температурных полей в кристаллах катализатора и при выращива-
53
= Д Т(М, 0 + (1Дг) \F(M, 0 + т
нии гомоэпитаксиальных пленок германия, возникающих в ходе
экзотермических химических реакций. Уравнения (1.126) — (1.127)
и основные соотношения термомеханики приводят к иному клас¬
су моделей теории теплового удара, отличному от (1.115) —
Следующий класс указанных моделей основан на теплопровод¬
ности в средах с тепловой памятью. Описание процессов переноса
теплоты при интенсивном кратковременном нагреве и в диапазоне
низких температур, а при обычных условиях в средах со сложной
структурой (поликристаллические материалы; полимеры) привело
в последние десятилетия к построению теории теплопроводности (и
термоупругости) с тепловой памятью. Под памятью здесь понима¬
ется учет зависимости текущего состояния материала от предысто¬
рии изменения термомеханических величин, а именно: тепловой
поток q(M, t) и внутренняя энергия С/Э(А/, t) определяются не
только текущими значениями температуры и градиента температу¬
ры, но в отличии от (1.11) и (1.124) и предысторией их изменения
где а (/), Р (t) — соответственно функции релаксации теплового по¬
тока и внутренней энергии (дифференцируемые скалярные функции
/е(0, оо) с а(оо) = /?(оо) = 0). Функции релаксации заменяют коэф¬
фициенты переноса и являются функциями тепловой памяти. Для
небольших изменений температуры Гуртин М. Е. и Пипкин А. С.
получили линеаризованное уравнение теплопроводности с учетом
тепловой памяти [215]:
(1.116).
[215]:
00
(1.128)
о
00
из(М, 0= U0+c,p[T(M, 0 — 7о] + P(s)[T(M, t—s) — T0]ds,
о
(1.129)
=а(0)ДТ(М, <)+J af(s)AT(M, t-s)ds. (1.130)
о
При определенном виде функций релаксации уравнение (1.130) пере¬
ходит в гиперболическое уравнение теплопроводности (1.127). Для
больших времен решение уравнения (1.130) совпадает с классичес¬
ким для уравнения Фурье. Что касается динамической задачи тер¬
моупругости, то в случае упругого полупространства температуры
T(z, t) соотношение (1.115) теперь имеет вид
00
дг11Лг, 0 d*U. ВТ Г
0*+2д)—— р—= аг(ЗА+2р) —- I y(s)T(z, t-s)ds,
О
(1.131)
где у (0 — температурная релаксация напряжения. Искомые напря¬
жения находятся с помощью соотношений
оо
duz Г
<t„(z, 0 = (А + 2р)—- аг (3 А+2ц)Т(z, t)+ y(s)T(z, t-s)ds;
о
axx(z, t) = oyy(z, t) = -^—a„(z, 0“т~~ T(z, /) +
Л + 2 fi Л + 2/i
oo
+7^T fy(s)T(z,t-s)ds.
X + 2ftj
0
На практике в качестве функций релаксации выбирают, например,
экспоненциальные
<*(0 = (2г/т,)ехр(-//т,);
0(О = (с«р/т,)ехр(-//тэ);
7(0 = [«г (ЗА + 2ц)/т„] exp (- t/zj,
где гр = 10 11 с — время релаксации теплового потока, тэ=
= 10“13 с — время релаксации внутренней энергии, г„= 10 с —
55
время температурной релаксации напряжения [215]. Если подста¬
вить выбранную а (0 в (1.125), то придем к (1.121).
Следующим обобщением теории теплового удара является пере¬
ход к упруговязким телам [178]. Полимерные материалы по реоло¬
гическим свойствам удобно разделить на упруговязкие и вязкоуп¬
ругие. Например, каучуки (или их растворы) относят к упруговяз¬
ким материалам, так как они характеризуются вязким течением,
а сшитые эластомеры — к вязкоупругим, поскольку у них вязкое
течение практически не наблюдается. Простейшая реологическая
модель вязкого материала, сочетающего упругие и вязкие свойства,
предложена Максвеллом: напряжение c(t) и деформация e(t) при
одноосном растяжении связаны соотношением
\ dtr <т de
— + (1.132)
Edt г] dt
где rj — вязкость. Для формулировки реологических законов, свя¬
зывающих напряжения t) и деформации ву(М, t), необходимо
ввести девиатор напряжений 5,У(М, t) и девиатор деформаций еи(М,
t) с помощью соотношений
Sy(M, t) = Oij(M, t)-o*(M, t)8y
(1 133)
ey(M, t) = Ey(M, t) — e(M, t)5y
*
где а* и e — среднее нормальное напряжение и среднее удлине¬
ние
о*{М, t) = -You{M, t); в(М, 0, 0=х,у, г)
i ^ i
В рамках среды Максвелла (1.132) зависимость между напряжени¬
ями и деформациями для упруговязкого тела в девиаторной форме
имеет вид
dSiAM, 0 1 deJM, t)
- + ~ Sy (М, t) = 2G , (1.134)
dt xp dt
где постоянная ^ = 77/(7 — время релаксации материала.
Соотношения (1.93), (1.113) и (1.134) приводят к следующе¬
му уравнению динамической термовязкоупругости для упруговяз-
56
кого полупространства (полуограниченный массив) температуры
T(z, t):
d2azz 1 d2azz (1+v) а2Т
= a Tp h
dz2 v2 dt2 (1 —v) dt2
d2
taa(z, z) + oc2[T(z, z)-T0]}dz, (1.135)
32 +2/i 4 \ip 4/ipar(32+2/i)
где p = ; a«= ; a2 = . В случае упругой
3?p (X + 2/i) 3^(2 +2/i)2 3x^(2 +2/i)2
среды время релаксации хр = оо (у = оо), при этом а! = а2 = 0 и уравне¬
ние (1.135) переходит в уравнение (1.121), обобщая, таким образом,
(1.121) на упруговязкие тела. К уравнению (1.135) необходимо при¬
соединить уравнение теплопроводности (1.122) с учетом связанно¬
сти полей деформации и температуры и в такой постановке соот¬
ношения (1.122), (1.135) представляют собой практически не изучен¬
ные проблемы современной теории теплопроводности и термомеха¬
ники.
Задача. Покажите, что уравнение теплопроводности с внутрен¬
ним тепловым источником F(x, t) с учетом конечной скорости
распространения теплоты (1.124) для тонкого стержня (рис. 11)
имеет вид:
dt дх2 dt2 dt
dT(x, t) d2T .d2T /л t ЧГ ч “ ^(jc, О"
= a--z* — + (l/cp)\ F(x, t) + z*
(1.136)
ГЛАВА II
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА КРАЕВЫХ
ЗАДАЧ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
§ 1. УСЛОВИЯ ОДНОЗНАЧНОСТИ
Дифференциальное уравнение теплопроводности (1.31) является ма-
тематической моделью целого класса явлений теплопро¬
водности и само по себе ничего не говорит о развитии процесса тепло¬
переноса в рассматриваемом теле. Математически это объясняется
неединственностью решения дифференциальных уравнений в частных
производных, к которым относится и уравнение теплопроводности.
57
Действительно, даже для обыкновенного дифференциального уравне¬
ния я-го порядка F (х, у, у\ у", . . ., у{п))= 0 общее решение у=
= f(x,Ci,C2, . . С„) ЗаВИСИТ ОТ Я ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ 6’i,C2, . . .,сп.
Для уравнений же в частных производных общее решение зависит
от произвольных функций, для нахождения которых необходимо знать
некоторые дополнительные особенности процесса, чтобы выделить
его из множества других. Например, общее решение уравнения
д2Т!{дхду)=0 имеет вид Т(х, y)=f\{x)+fi(y), где fx(x) и f2(y) — произ¬
вольные функции класса С2*. Таким образом, при интегрировании
дифференциального уравнения в частных производных получаем бес¬
численное множество различных решений. Чтобы получить из этого
множества одно частное решение, соответствующее определённой
конкретной задаче, необходимо иметь дополнительные данные, не
содержащиеся в исходном дифференциальном уравнении теплопро¬
водности. Эти дополнительные условия, которые в совокупности с диф¬
ференциальным уравнением (или его решением) однозначно опреде¬
ляют конкретную задачу теплопроводности, называются условиями
однозначности.
В условия однозначности входят:
1. Геометрические условия, характеризующие
форму и размеры тела, в котором протекает процесс теплообмена. На¬
пример, если рассматривается стержень, то, поместив систему коорди¬
нат так, как это показано на рис. 13, а, можно математически описать
данное тело неравенством —форма и размеры тела (рис. 13, б)
в виде прямоугольника опишутся неравенствами 00*Q/i</a;
в случае круга радиусом R или его части (рис. 13, в, г), или кругового
сектора (рис. 13, 5) соответственно запишем: 0^/^/?;
0<<£<а.
* Множество функций /(*, у, г) образует класс функций С2 в некоторой
области изменения переменных ху у, г, если в этой области функции f (х, у, г)
непрерывны вместе с частными производными по любым переменным до второго
порядка включительно.
58
2. Физические условия, характеризующие физические
свойства тела (тепло- и температуропроводность), а также закон рас¬
пределения внутренних источников теплоты.
3. Граничные условия, характеризующие особенности
теплового взаимодействия граничной поверхности тела с окружающей
средой.
4. Временные, или начальные, условия, харак¬
теризующие состояние тела в исходный момент времени, или, иначе,
определяющие распределение температуры в любой точке тела в не*
который момент времени, который для исследуемого процесса тепло¬
обмена принимается за начальный.
Перечисленные условия в совокупности определяют одно (конкрет¬
ное) явление теплопроводности и в этом смысле могут быть также на¬
званы условиями единственности.
Для тела определенной геометрической формы с определенными
(известными) физическими свойствами условия однозначности сводят-'
ся к заданию начального и граничного условий. Эти условия в сово¬
купности называются краевыми условиями. Итак, начальное условие
является временным краевым условием, а гранич¬
ные условия — пространственным краевым усло¬
вием. Дифференциальное уравнение теплопроводности вместе
с краевыми условиями составляет краевую задачу урав¬
нения теплопроводности (или короче — тепловую
задачу). Разумеется, для установившегося процесса теплопровод¬
ности необходимость задавать начальное условие отпадает, и в этом
случае краевая задача будет состоять из уравнения теплопроводности
и граничных условий.
§ 2. КРАЕВЫЕ УСЛОВИЯ
Перейдем к формулировке начального и граничного условий, которым
должна удовлетворять функция Т(х, у, г, /)=71(М, t), описывающая
распределение температуры в некотором теле.
Пусть G—конечная область трехмерного пространства, где про¬
исходит процесс теплопроводности (т. е. G — область изменения
пространственных переменных х, у, г), и S — граница области, кото¬
рую будем считать кусочно-гладкой поверхно¬
стью (т. е. поверхностью, состоящей из конеч¬
ного числа гладких кусков). Пусть далеей—
цилиндрическая область в четырехмерном
пространстве (й=Сх(0, /0), т. е. совокупность
точек (М, /) с М g G, t£ (0, t0)> где /0>0. Осно¬
ванием цилиндра й с образующими, парал¬
лельными оси t (рис. 14), служит область G
(при £=0), высота цилиндра /0, а граница со¬
стоит из боковой поверхности S6=Sx[0, t0]
и двух оснований: нижнего М £ G, /=0, и
верхнего М £ G, t=t0. Таким образом, ци¬
линдрическая область Й является обл а-
59
стью задания уравнения теплопроводности
(1. 31), область G, соответствующая геометрической форме и размеру
тела, в котором изучается процесс теплопроводности, есть область
задания начального условия, a S — область
задания граничных условий (в точках области S
происходит взаимодействие тела с окружающей средой, которое и
описывается граничными условиями); G — есть объединение множе¬
ства G и его границы S. Например, если G=(a<*<b), то G=(a<
x^b).
Начальное .условие для уравнения теплопроводности
состоит в задании температуры во всех точках области G в момент
t—О, от которого и ведется отсчет времени
Т(МШ 0|/=о = Ф0(М), MS С, (2.1)
где данная функция Ф0(М) непрерывна в точках G (т. е. во всех точ¬
ках тела). В случае равномерного распределения температуры в теле
начальное условие упрощается:
Т (М9 О'=о = 710 = const, M£G. (2.2)
Условие (2.1) означает, что следует найти такое решение Т(М, t)
тепловой задачи, которое по мере приближения времени к начальному
значению стремилось бы во всех точках области G к заданной величи¬
не Ф0(М):
lim Т (Му 0 = Фо(М), М S G. (2.3)
/->о
Понимание начального условия (2.1) в предельном смысле (2.3)
объясняется исключительно теми классами конкретных функций,
которыми описываются решения краевых задач уравнения тепло¬
проводности. Эти функции во многих случаях не имеют смысла при
/=0, однако допускают предельный переход при /->-0. Например,
функция
Т {х, t) = 1-р==- J Ф0 (5) е" dg (2.4)
0
является решением уравнения теплопроводности dTldt=ad2T/dx*
с начальным условием Г(х, 0)=Ф0(*), х>0. Как видно из самого пред¬
ставления (2.4), выражение, записанное в правой части, не определе¬
но при t=0, однако если Ф0(*) — непрерывная функция, то можно по¬
казать (см. § 5 гл. III), что
, г (Х~*)Я
lim - Ф0(Е)е dg = Ф0(лг).
t-+ о 2 у nat J
о
Если начальное распределение температуры Ф0(М) разрывно в не¬
которых точках области G (или поверхности S), то решение Т(М, t)
тепловой задачи будет обладать таким свойством, что эти разрывы
должны исчезнуть начиная с момента времени t^tz> 0 (te — очень
60
короткое время) и тогда полученное решение должно стремиться к за¬
данной начальной температуре во всех точках тела, где начальное
распределение непрерывно. Этим замечательным свойством обладают
именно решения уравнения теплопроводности.
Граничные условия — условия теплового взаимодей¬
ствия тела с окружающей средой — могут быть заданы в различной
форме в зависимости от характера процесса. В тех случаях, когда на
границе тела не происходит никаких процессов с поглощением или
выделением теплоты и отсутствует теплообмен излучением, граничные
условия на поверхности соприкосновения двух сред в самом общем
виде заключаются в равенствах температур и тепловых потоков:
Тт = Тс\ Ят[дТт(М, t)/dn] = Xc [<?ГС(М, t)/dn],
где Тт, Тс — температуры тела и среды; Хт, — теплопроводности
тела и среды; п — нормаль к граничной поверхности тела — среда.
Однако в практических задачах такая форма граничных условий
чрезвычайно неудобна, так как для расчета температуры твердого
тела необходимо решать сопряженную задачу, т. е. отыскивать тем¬
пературное поле и в окружающей среде. Поэтому в ряде практически
важных задач желательно перейти к более простым граничным усло¬
виям. В математической теории теплопроводности в большинстве
случаев используются четыре основных условия, представляющих
собой идеализацию действительных физических процессов.
Граничное условие I рода состоит в задании поверхностного распре¬
деления температуры для любого момента времени
Т(М, t)=0(M, t), £>0, (2.5)
где М — точка, находящаяся на поверхности S; Ф(уИ, t) — заданная
непрерывная функция (по пространственным переменным и време¬
ни t) в точках области S.
В частном случае может оказаться, что температура на поверхно¬
сти одинакова на протяжении всего процесса теплообмена и с тече¬
нием времени не меняется, т. е. Т(М, t)M€S=Tn, С>0. Это может
быть осуществлено при искусственном поддержании постоянной тем¬
пературы или при особых условиях теплообмена между поверх¬
ностью тела и окружающей средой, например, в таких интенсивных
процессах, как кипение, конденсация, вынужденное движение жид¬
ких металлов и др., когда температура поверхности тела близка к тем¬
пературе окружающей среды.
Граничное условие II рода состоит в задании плотности теплового
потока для каждой точки поверхности тела как функции координат
и времени
—к[дТ(Му t)/dn] = G)(M, 0. *>0, (2-6)
где (М, t) — заданная непрерывная функция точки М и времени t
в области 5; п* — нормаль к поверхности S в точке М.
• Будем считать, что всюду при формулировке граничных условий п — внеш¬
няя. нормаль к точкам граничной поверхности 5 рассматриваемого тела.
61
Здесь следует различать процессы охлаждения и нагревания.
Для процесса охлаждения дТ/дп < 0; тепловой поток при этом счи¬
тается положительным, так что условие (2.6) относится к процессу
охлаждения. Для процесса нагревания дТ/дпУ 0, тепловой поток
отрицательный и мы должны записать (если считать, что Ф(Л4, t)^0)
—к[дТ(М, t)/dn] = — Ф(М, t),
или
к [дТ (М, t)/dn] = Ф (Af, t)9 М е s, t > 0. (2.7)
>
В простейшем случае плотность теплового потока через поверх¬
ность может быть постоянной по поверхности и во времени
—к [дТ (М, t)/dn] |Mqs =qn = const, t > 0
(например, при нагревании различных металлических изделий в вы¬
сокотемпературных печах [74]).'
Выражение (2.6), когда Ф(М, /) = 0, дает условие тепловой изо¬
ляции граничной поверхности тела. По определению, теплоизолиро¬
ванной поверхностью называется поверхность, через которую не
проходит поток теплоты. В этом случае (2.6) имеет вид
[дТ (Af, t)/dn] |m€S = 0, t > 0. (2.8)
Граничное условие III рода. При этом условии задаются температура
окружающей среды Тс и закон конвективного теплообмена между
поверхностью тела и окружающей средой. Для описания процесса
теплообмена используется закон Ньютона—Рихмана (или просто
Ньютона). Согласно этому закону, количество теплоты, отдаваемое
единицей площади поверхности S с температурой Тп в единицу вре¬
мени в окружающую среду с температурой Тс в процессе охлажде¬
ния (Тп > Тс)у пропорционально разности температур поверхности
тела Тп и окружающей среды Тс:
q = a[Tn — Тс] =а[Т (М, OUes-TJ. (2.9)
где а — коэффициент пропорциональности, называемой коэффициен¬
том теплоотдачи.
Для процесса нагревания тела можно написать аналогичное со¬
отношение, поменяв в (2.9) местами Тп и Тс. Коэффициент теплоотда¬
чи а характеризует интенсивность теплообмена между поверхностью
тела и окружающей средой. Численно он равен количеству теплоты,
отдаваемому (или воспринимаемому) единицей площади поверхности
в единицу времени при разности температур между поверхностью
тела и окружающей средой в один градус. В отличие от теплопровод¬
ности к коэффициент теплоотдачи а не является физической констан¬
той, характерной для того или иного вещества. В общем случае он
отражает совместное действие конвекции и излучения и поэтому за¬
висит от многих факторов: геометрической формы и размеров тела,
физических свойств среды, омывающей тело, направления и скорости
омывания, теплоемкости, плотности, вязкости среды, температуры
62
поверхности нагрева Тп и др. Поэтому простота закона (2.9) обманчи¬
ва; вся сложность вопроса о теплообмене между телом и окружающей
средой сосредоточивается на методе определения а при конкретных
условиях задачи.
Таким образом, в общем случае а может изменяться заданным об¬
разом по координатам и времени. Для упрощения задачи в расчет¬
ных схемах в качестве первого приближения принимают а постоянным.
Согласно закону сохранения энергии, теплота, которая отводится
с единицы площади поверхности тела в единицу времени вследствие
теплоотдачи [см. уравнение (2.9)], равна теплоте, подводимой к едини¬
це площади поверхности в единицу времени вследствие теплопровод¬
ности из внутренних объемов тела, и равна согласно закону Фурье,—
[ЦдТ/дп)]. Приравнивая эти выражения, придем к условию на грани¬
це тела:
при охлаждении тела
—к [дТ(М, t)/dn]=a[T(M, t)—Ф(М, /)]. M€s> t > 0; (2.10)
при нагревании тела через его поверхность окружающей средой,
температура которой ГС = Ф(М, /), (учитывая, что дТ/дп > 0),
— ЦдТ/дп] = — а[Ф(М, t)—T(M, /)]> M£St t > 0, (2.11)
или
— I [дГ (М, /)/Зл] = а[Г(М, 0—Ф(М, f)], M£S, t> 0,
т. е. опять условие (2.10).
Таким образом, условие (2.10) справедливо как для процесса
охлаждения, так и для процесса нагревания. Здесь Ф(М, t) и а —
заданные непрерывные функ¬
ции точки М и времени t на
поверхности S при 0 < t
t0 < оо.
В конкретных задачах при
записи граничных условий III
(или И) рода приходится вы¬
числять производную по нор¬
мали дТ/дп, что в некото¬
рых случаях вызывает опре¬
деленные трудности (особен¬
но в цилиндрической и сфе¬
рической системах коорди¬
нат). Поясним эти вычисле¬
ния на примерах. Рассмотрим
стержень (рис. 15) и вычис¬
лим производную по направлению нормали к торцам стержня в
граничном условии (2.40) при его охлаждении. Так как температу¬
ра Т стержня зависит только от одной пространственной перемен¬
ной х (температурное поле одномерное), то формула производной
функции Т по нормали (см. § 2 гл. I) в данном случае имеет вид
дТ/дп = (дТ/дх) cos а, где а—угол, образуемый нормалью п с поло¬
жительным направлением оси х. На левом конце стержня направле¬
63
ние вектора нормали п противоположно положительному направле¬
нию оси х и
дТ/дп \x=-i = дТ/дх \Xm-i cos л = — дТ/дх .
На правом конце стержня эти направления совпадают и
дТ/дп |Xzzi = дТ/дх |*=/ cos 0 = дТ/дх |х=/.
Таким образом, граничные условия III рода для стержня при его
охлаждении (и нагревании) с торцов в окружающую среду темпера¬
туры Тс имеют вид:
Я((?Г/(?^)|,=_/ = а[Г|х==_/ — Тс], t > 0 \
[(3770*) !„_,>(>]; I
-к(дТ/дх)\х^ = а[Т\х^-Тс], t> Of (2.12)
[(дТ/дх) \x=i < 0]. J
Рассмотрим теперь круг и вычислим дТ/дп в любой точке М,
лежащей на окружности этого круга. Прежде всего запишем в по¬
лярной системе координат формулу для производной функции Т (г, ф)
по направлению нормали п, учитывая, что дТ/дп = п grad Т:
grad Т (г, ф, t) = (dT/dr)er + (\/r)(dT/dy)e<p, (2.13)
где ег и еф— единичные векторы ортогонального базиса (вг, еф)*.
Пусть вектор п образует углы а и р соответственно с направле¬
ниями векторов ег и еф. Тогда л = cos а ег + cos 0 еф. Так как ска¬
лярное произведение двух векторов п и gгаdф равно сумме парных
произведений одноименных координат, то окончательно получим
дТ (г, ф, t)/dn = (дТ/дг) cos а+ /г) (dT/dy)cos$. (2.14)
Запишем теперь граничные условия III ряда для круга радиуса
R (рис. 16) при его охлаждении через граничную окружность. На¬
правление нормали в точке М совпадает с направлением вектора ег
* Напомним, что всегда вектор ег направлен вдоль радиуса от полярного
начала 0, а вектор е<р—против часовой стрелки.
64
Так как a = 0(coscc=l), а 0 = (л/2)(cos0 = 0), то
(дТ/дп) \rm R = (дТ/дг) \гя R cos 0 = (дТ/дг) \гя я,
и в соответствии с (2.11) можно записать
—Х[дТ(г, ф, t)/dr]\r=R = a[T (г, ф, /) —Гс] [(дТ/дг) |Л=Я < 0].
(2.15)
С учетом (2.14) рассмотрим более интересный пример охлажде¬
ния или нагревания кругового сектора (или клина) (рис. 17) через
его граничные поверхности <p = ±Y- На поверхности ф=±у соот¬
ветственно имеем:
дТ/дп\ ф= +Y = дТ/дг |ф= +Y cos л/2 + V
+ (1/г)(<ЗГ/<?ф)|ф=+усозО = (1//-)(аГ/аф)|ф=+у; I
дТ/дп |Ф=_У = дТ/дг |ф=_у cos л/2 + (1/г) х | (2‘6)
х (дТ/дф) |,,=_vcos л = — (1/г) (дТ/дф) |ф=_у. j
Таким образом, можно записать:
^ (I/O (дТ/ду) |ф== + v = a (Т |ф= + 7 Тс)у (дТ/ду) |ф= + Y < 0; 1
Х(1/г)(а7,/аф)|фг=_у=-а(Г|ф=_у — Гс), (дТ/ду |ф:—Y > 0). р ‘ }
Уравнение (2.10), выражающее в аналитической форме граничное
условие III рода, называется дифференциальным уравнением тепло-
обмена и по существу является частным выражением закона сохра¬
нения энергии для поверхности тела. Это уравнение справедливо
в самом общем случае и сохраняет силу в условиях стационарного и
нестационарного режимов, так как вытекает из соображений, что тон¬
кий поверхностный слой, для которого составляется баланс подвода
и отвода теплоты, не может аккумулировать или выделять теплоту.
Из граничного условия III рода как частный случай можно полу¬
чить граничное условие I рода. Запишем это условие в виде
—(К1а)[дТ{М, t)/dn]\M es = T (М, T)\M6S—TC.
Если коэффициент теплообмена а имеет очень большое значение
(а—► оо) или теплопроводность к мала (X—►()), то
Т(М, 0|м MS—Te= lim [—(tya )дТ(М, Т)/дп]м«s = 0,
a -►»
откуда Т (М, t)M€S = Tct t> 0, т. е. температура поверхности тела
равна температуре окружающей среды. Если коэффициент теплооб¬
мена а очень мал (а—►О), то из (2.10) получим условие тепловой
изоляции граничной поверхности — равенство нулю потока теплоты
через поверхность тела дТ(М> t)/dn = 0> M£S, £ > 0. Заметим, что
математическое решение задачи в случае а/к > 0 недействительно
для случая а/к = 0, и здесь нужно проявлять осторожность, чтобы
не получить ошибочный результат.
Если ввести коэффициент h = a/k—относительный коэффициент
теплообмена ([Л] = м”1, причем всегда h > 0), то условие (2.10)
3-339
65
можно записать в следующем виде:
дТ (Му t)/dn = — h[T (М, /) — ср(М, *)],
М € Sf t > 0.
(2.18)
В такой форме его можно использовать в соответствующих тепловых
задачах.
Граничные условия сопряжения * применяются в случае контакта
двух твердых тел. Если между граничными поверхностями тел SH
имеется идеальный тепловой контакт (тела очень тесно прижаты, на¬
пример в спаях), то их температуры на поверхности контакта долж¬
ны быть одинаковыми. Кроме того, тепловой поток, выходящий из
одного тела через контактную поверхность, должен быть равен теп¬
ловому потоку, входящему в другое тело. Таким образом, если Г,
и Т2 — температуры тел, находящихся в условиях плотного, тепло¬
вого контакта, то для точки М контактной поверхности граничные
условия сопряжения имеют следующий вид:
где индексы 1 и 2 относятся к двум телам; п— общая нормаль к кон¬
тактной поверхности SK в точке М.
В случае неидеального теплового контакта между двумя телами
(контактные поверхности разделены тонкой прослойкой) обычно
вводится понятие контактного сопротивления R (или контактной
проводимости MR). Равенство тепловых потоков здесь имеет место,
но появляется пропорциональная им разность между двумя поверх¬
ностными температурами. Соответствующие граничные условия име¬
ют вид:
где п—внешняя нормаль к контактной поверхности SK в точке М
относительно тела /. (В работе [7] исследуются различные виды
соединений, включая как плотный контакт, так и случай разделе¬
ния контактных поверхностей прослойками хорошей и плохой про¬
водимости.)
Граничные условия сопряжения могут быть использованы при
нахождении приближенного решения уравнения теплопроводности
в неоднородной среде. Пусть, например, Т (ху t) описывает темпера¬
турное поле стержня 0, являясь решением уравнения
где б (х), р(х), Х(х) — непрерывные функции в области л ^ [0, /].
* В литературе встречается и другой термин: граничные условия сопряжения
называют граничными условиями IV рода.
Тг(М, 01*к =тг(м, 0|5к;
К [дТ, (М. 0/dn]|Sll = M<?7\(M, /)/<5л]|5к.
(2.19)
(2.20)
(2.21)
с(д:)р(лг) (дТ/dt) — div [А,(х) (дТ/дх)\,
(2.22)
66
Уравнение (2.22) не может быть сведено к уравнению с постоян¬
ными коэффициентами и его приходится решать приближенно (за
исключением некоторых специальных случаев задания теплофизичес¬
ких коэффициентов). Одним из простых методов приближенного ре¬
шения является замена с(х), р(х), Х(х) кусочно-постоянными функ¬
циями. Для этого разобьем интервал (0, /) на частичные интервалы
(/Л_г, 1п) и в каждом таком интервале будем считать коэффициенты
уравнения (2.22) постоянными: с(х) = сп\ р(*) = р„; Х(х) = Хп (в ка¬
честве сп, р„, Хп можно взять значения функций с(х), р(х), >,(*)
в любой точке частичного интервала). Потребуем далее, чтобы функ¬
ция Т (х, t)=*Tn(x, t), х€(1и_г, 1п), в каждом частичном интерва¬
ле удовлетворяла уравнению теплопроводности
dTjdt = ап (дгТп1дхг) [ап -= Хп/(спр„)],
а в точках деления 1п—условиям сопряжения. В простейшем слу¬
чае эти условия заключаются в непрерывности температуры и непре¬
рывности теплового потока:
t) \x = ln-0 = Tn+1(xy t)\x=ln + 0,
К[дТп(х, t)/dx]\xssln-o = kn+l[dTn+i(x, t)/dx]\x=in+0.
Практически важным является и несколько более простой слу¬
чай, когда процесс теплопроводности происходит в конечном числе
сред, но с разными (постоянными) коэффициентами в уравнении (2.22)
(т. е. в кусочно-однородной среде), или, иными словами, когда коэф¬
фициенты уравнения (2.22) в среде (0, /) терпят разрывы — скачки.
Если 1п — точки разрыва коэффициентов, то промежуток (0, /), в ко¬
тором ищется решение задачи, разбивается точками разрыва коэф¬
фициентов на несколько частей, внутри которых функция Т(х, t)
удовлетворяет уравнению теплопроводности, а на границах (т. е. в точ¬
ках 1п) — условиям сопряжения (2.23).
Следует заметить, что тепловые задачи с граничными условиями
сопряжения приобрели большое значение в последние годы в связи
с развитием высокотемпературной теплофизики — расчет многослой¬
ных покрытий головок ракет, элементов преобразователей энер¬
гии и т.д. Графический смысл граничных условий I, II, III родов и со¬
пряжения рассмотрен в монографии [83]. В случае контакта с идеаль¬
ным проводником или с хорошо перемешиваемой жидкостью гранич¬
ные условия, возникающие в контактных задачах, могут быть
заменены на более простые, заменяющие в некотором смысле гранич¬
ные условия сопряжения.
Пусть тело /, у которого теплопроводность Хх и температура Т на¬
ходятся в условиях совершенного теплового контакта по поверхности
SK с телом 2, имеющим физические параметры Х%у с2, р2; пусть также
граничная поверхность (свободная от контакта) тела 2 взаимодей¬
ствует со средой, у которой температура Т0 и коэффициент теплообме¬
на а2. Предположим, что X2^>Xlt т. е. тело 2 по отношению к телу /
считается идеальным проводником теплоты, вследствие чего темпера¬
туру тела 2 по всему объему можно считать постоянной (по простран¬
(2.23)
67
ственной переменной) и равной температуре контактной поверхности
ТК-
Рассмотрим систему составных цилиндрических труб достаточно
большой длины (где температура не зависит от длины): внутренняя
(тело /) — стеклянная (#i<r</?2), а внешняя (тело 2) — металличе¬
ская (R2^^Rs)- Таким образом, цилиндрическая поверхность r=R2
является контактной поверхностью. Так как теплопроводность металла
в 50—60 раз больше теплопроводности стекла, то металлическая тру¬
ба может считаться идеальным проводником теплоты и теплопровод¬
ность металла принимается бе¬
сконечно большой.
Выведем граничные условия
для указанного случая, исходя
из следующего уравнения ба¬
ланса теплоты: теплота, посту¬
пающая в тело 2 через контакт¬
ную поверхность, расходуется
на увеличение температуры те¬
ла 2 и на теплообмен тела 2 со
средой заданной температуры.
Выделим элемент объема
dl/(ABCDA^iCiDJ, как пока¬
зано на рис. 18, и составим для
него уравнение баланса тепло¬
ты, имея в виду, что в выделен¬
ном объеме при поглощении те¬
плоты не создается градиента температуры, так как Х2 считается бе¬
сконечно большим. Согласно закону Фурье (1.14), количество те¬
плоты, поступающее в объем dV через элемент контактной поверх¬
ности A BCD площадью dSlt
dQ = -K[dT(r, tydr^^dS^t.
За время dt температура объема dV, равная Т (/?2, /), изменит¬
ся на Т (/?2, t + dt)—Т (R2t t) = [dT (R2, t)/dt]dt, на это потребует¬
ся сообщить объему количество теплоты, равное dQ^c^^dT /dt)dV dt.
За это же время потеря теплоты в окружающую среду с элемента¬
ми граничной поверхности А1ВхСхОл площадью dS2 вследствие тепло¬
обмена составит dQ2 = а2 [Т(R2, t) — Tc] dS2 df. Так как dQ =
= dQ! + dQ2, то, приравнивая соответствующие выражения, можно
записать уравнение баланса теплоты
(дТ/дг) |re Ri dS1 dt = с2р2 (дТ/dt) |г=*bdV dt + а2 (Т \Тс) х
*dS2df.
Рис. 18
Вычислим далее элементы площадей dSly dS2 и элемент объема dl^:
dSx *= R2 d(p dz\ dS2 *= R3 d(p dr,
Подставив найденные значения в уравнение баланса теплоты, после
сокращения на одинаковые множители окончательно получим иско¬
мые граничные условия в следующем виде:
-ltR% [дТ (г, t)/dr] = (1/2) с2р2 (RI-
-Rl)[dT(r, + t)-Tс]. (2.24)
Если ввести толщину трубы d = /?3 — /?а, то это условие можно
переписать в следующем виде:
дТ(г, t) 1 c2p2d Л d \ дТ (г, t)
дг |г=я, V ' 2#а) dt
x[T(tf2, t)-Tс]. (2.25)
В частности, если граничная поверхность г = /?8 теплоизолирована
(а2 = 0), то условие (2.25) переходит в следующее:
[,дТ(г, 0/^1 |г=/?г = — (^Р^А,) [1 + ^/(2/?я)] [<ЗГ (г, t)/dt]\r-RM. (2.26)
Аналогичным образом можно получить соответствующее гранич¬
ное условие для стержня (0<jc^/), на конце (х=0) которого помещено
тело с бесконечно большой теплопроводностью [вследствие чего тем¬
пературу по всему объему этого тела можно считать постоянной и
равной 7X0, 01 и происходит теплообмен с внешней средой. Если а —
коэффициент теплоотдачи, С — теплоемкость тела, i — теплопровод¬
ность стержня, Тс — температура окружающей среды, то можно
записать
).[дТ(х, t)ldx]\^0 = C[dT(x, 0/ЭД Uo + aU(°> t) — Tc], t>0. (2.27)
Здесь также может быть рассмотрен* случай, аналогичный (2.26).
К условиям, аналогичным (2.24), приводит контакт твердо¬
го тела с хорошо перемешиваемой жидкостью. Пусть
твердое тело имеет теплопроводность Я, площадь контайной поверх¬
ности S и температуру на поверхности Т (Л4, t)Mes = TUf причем Тп
сохраняет постоянное значение на всей поверхности. Хорошо пере¬
мешиваемая жидкость, соприкасающаяся по поверхности S с твер¬
дым телом, имеет массу Мт и удельную теплоемкость сх\ темпера¬
туру жидкости в любой ее точке при всех t > 0 считаем одинако¬
вой и равной Tn(t) (при t = 0 температура жидкости может быть
не равна Тп). Кроме того, имеет место теплообмен жидкости с окру¬
жающей средой, так что потеря теплоты в среду с температурой Тс
с единицы площади за единицу времени составляет а, (Тп— Тс), где
оц — коэффициент теплоотдачи. При этих условиях на поверхности
раздела твердого тела и жидкости имеет место следующее гранич¬
ное условие:
дТ (М, t)
дп
do = MTCl^+a1(7’n-re). (2.28)
M6S т 1 dt
Если внутри жидкости имеется источник теплоты, выделяющий
в единице объема в единицу времени количество теплоты, равное
Q, то к левой части уравнения (2.28) нужно прибавить член Q.
69
Существенная разница между использованием граничных условий
(2.19) — (2.20) и (2.25), как видно, заключается в том, что вместо ре¬
шения двух задач по определению температур Тг и Г2 (в составных об¬
ластях — тело 1 и тело 2), связанных между собой условиями (2.19) —
(2.20), решается одна задача (что значительно проще), одним из гра¬
ничных условий в которой является условие типа (2.25). Здесь, прав¬
да, появляется член дТ/dt, что вносит определенные трудности в при¬
менении к такому классу задач классических, аналитических методов
решения. Однако можно указать один метод, а именно — операцион¬
ный (см. гл. VI), который одинаково пригоден для обоих случаев.
Упрощения граничных условий сопряжения (2.19) — (2.20) до¬
пускают также задачи стационарной теплопроводности в тех случаях,
когда в некоторых средах мала вариация температурного поля по
определенным направлениям. В частности, если рассматривается мас¬
сивное твердое тело, на поверхности которого имеется совершенный
тепловой контакт с тонкой оболочкой из другого материала, не содер¬
жащей источников теплоты, и граничные условия заданы на внешней
поверхности оболочки, то можно приближенно ввести эффективные
граничные условия непосредственно на поверхности массивного твер¬
дого тела [121]. При формулировке граничных условий теплового
контакта (2.19) — (2.20) предполагается, что контактирующие тела
разделены идеальной (математической) поверхностью, причем каж¬
дое из тел является однородным вплоть до поверхности раздела.
В действительности между телами может иметь место некоторый пере¬
ходный слой, свойства которого отличаются от свойств контактирую¬
щих тел (например, сопряжение тел через прослойки конструктивного
происхождения; система тел, соединенных с помощью сварочных швов,
ребер жесткости, и т. д.). Сказанное относится и к телам с инород¬
ными включениями, в том числе и пустотами (например, металлы, со¬
держащие неоднородности в виде неметаллических макровключений,
вторичных фаз, или различного рода макродефекты в виде пор, тре¬
щин). При расчете температурного поля в системе таких тел при¬
шлось бы задавать граничные условия сопряжения на всех контакт¬
ных поверхностях, что, естественно, усложняло бы соответствующую
задачу теплопроводности.
Действительно, рассмотрим твердое тело, содержащее инородное
включение (либо систему двух тел), и предположим, что тело и вклю¬
чение разделяются некоторым промежуточным слоем толщиной 26, на
поверхностях Si и S2; которого осуществляется идеальный тепловой
контакт с телом и включением. Тогда в соответствии с (2.20) можно
записать:
К (дТ'/дп,) |s, = ki (dTjdnJ Iv Т0 \s< = 7\ |,t; 1
M<^o/^L = M<?7Vdn2)U, T0\,=Tt\,t, f * •
где r0, Гь Г а — температуры; Х,0, Х2 — теплопроводности соот¬
ветственно слоя, тела и включения; пх и п2 — единичные векторы нор¬
мали к поверхностям S, и S2.
Возможна замена точных граничных условий (2.29) приближенны¬
ми, которые получены в работе [112], исходя из следующей расчетной
70
модели: считая толщину переходного слоя 26 малой по сравнению
с другими размерами, можно рассматривать его как тонкую оболочку
с определенными теплофизическими характеристиками. Сохраняя
эти характеристики постоянными и устремляя толщину оболочки к
нулю, можно получить некоторую физическую поверхность раздела
между телом и включением с присущими ей определенными значения¬
ми физических характеристик, а также граничные условия, которым
должны удовлетворять на этой поверхности величины, характеризу¬
ющие тепловое состояние системы.
Перечисленные выше граничные условия в большинстве практиче¬
ских случаев задаются в каждой точке поверхности S — граничной
поверхности рассматриваемого тела. Однако возможны случаи, когда
то или иное граничное условие имеет место не на всей поверхности S,
а на каком-либо кусочно-гладком ее участке. В этом случае приходим
к так называемым разнородным граничным условиям (часто втречаю-
щимся в задачах дифракции, селективной диффузии [113]) (см. гл. IX).
Рассмотрим несколько примеров.
1. В полуплоскости 0, — оо < х < +оо, задаются произвольные вели¬
чины: на одной части граничной поверхности (х > 0) — нестационарная темпера¬
тура, на другой (дг < 0) — тепловой поток. Если Т (х} у, t)—температурное поле
в этой полуплоскости, то на поверхности (у = 0) имеем разнородные граничные
условия вида:
т (*. У» 0 |у = о = ф1 (*, t), х > 0, t > 0;
— К [дТ (х, у, t]/dy] l^o = Фг {х, t), х< 0, t> 0.
2. Пусть бесконечный однородный цилиндр вращается с постоянной угловой
скоростью со и на поверхности цилиндра r = R происходит теплообмен с двумя
различными средами, температура которых произвольным образом изменяется по
окружности у поверхности цилиндра и не зависит от времени. В этом случае
[если ввести неподвижную в пространстве и, следовательно вращающуюся по
отношению к диску систему координат (см. § 7 гл. I)] температурная функция
Т (г, (р) удовлетворяет уравнению теплопроводности во внутренних точках ци¬
линдра
— о (дТ/ду) =а [д2Т/дг2-}-(\/г) дТ/дг-\-(\/г2) (д2Т/ду2)], 0<r< R,
а на поверхности r = R — разнородным граничным условиям вида:
—к (дТ/dr) \r=R = al[T \r=R—М<р)], Фо < ф < 2я—ф0;
3. Рассмотрим бесконечное пространство (х, у, г) с нулевой начальной тем¬
пературой, в плоскости хОу которого во все моменты времени t > 0 действует
круговой тепловой источник (х2 + у2< R2) постоянной температуры Т0 в каждой
точке круга, а остальная часть плоскости хОу (х2 + у2 > R2) теплоизолирована.
Если Т (х, у, г, t) — нестационарное температурное поле, симметричное относи¬
тельно плоскости г — 0, то, рассматривая процесс теплопроводности только в верх¬
ней части пространства (г > 0), имеем на граничной поверхности z = 0 разнород¬
ные граничные условия вида:
т (х, Уу z, t)\z=o = T0t x2 + y*<.R2; 1
[дТ (х, у, z, t)ldz]2=0 =0, *2 + у2 > R2. f
Аналитические методы решения краевых задач теплопроводности
с разнородными граничными условиями используют аппарат теории
функций комплексного переменного и являются довольно сложными
(2.30)
71
по своей структуре. Одним из немногих методов решения этого класса
задач является метод Винера — Хопфа [110], основы которого будут
изложены в гл. IX. Следует также указать работу [151], в которой
описываются краевые задачи теплопроводности с разнородными
граничными условиями и формальная техника их решения более про¬
стая, чем в [1101. Из других подходов следует отметить методы дуаль¬
ных интегральных уравнений [143] и тепловых потенциалов [114]
(см. гл. IX).
Задача 1. Используя закон Ньютона (2.18), показать, что дифференциаль¬
ное уравнение теплопроводности для стержня при наличии теплообмена через
боковую поверхность имеет вид
дТ/dt — a (д2Т/дх2)—т2 (Г— Гс), 0 < х < /, / > 0, (2.32)
где т2 = Ph/(cpS) (Р — периметр поперечного сечения стержня; S — площадь по¬
перечного сечения; 7^ —температура окружающей среды).
Указание. Воспользоваться рассуждениями § 5 гл. I.
Задача 2. Используя тот же закон (2.18), показать, что дифференциальное
уравнение теплопроводности для пластины толщиной 6 при теплоотдаче на на¬
ружных поверхностях, параллельных плоскостям симметрии, имеет вид г.
dT/dt = a (д2Т/дх2 + д2Т/ду2)-т2 (Т — Тс), (2.33)
где
та = 2а/(6ср).
§ 3. ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ
Как отмечалось, дифференциальное уравнение теплопроводности (1.31)
связывает временное и пространственное распределения температуры
внутри тела в любой момент времени />0. Для того чтобы найти
это температурное поле, надо знать распределение температуры внутри
тела в начальный момент времени (начальное условие), геометриче¬
скую форму и размеры тела и закон теплового взаимодействия между
поверхностью тела и окружающей средой (граничное условие). Иными
словами, необходимо решить краевую задачу уравнения теплопровод¬
ности, к постановке которой и перейдем в данном параграфе. Напомним,
что через G обозначена область изменения пространственных перемен¬
ных соответственно геометрии и размерам тела, в котором изучается
процесс теплопроводности, через S — граница области G (т. е. гранич¬
ная поверхность тела), через Q — цилиндрическая область измене¬
ния пространственных переменных и времени t (не включая сюда точки
границы S и значения времени /=0); таким образом, Q есть область
определения дифференциального уравнения теплопроводности.
Основные краевые задачи для уравнения теплопроводности фор¬
мулируются так:
требуется найти в цилиндрической области Q дважды непрерывно
дифференцируемое по пространственным координатам, непрерывно
дифференцируемое по времени t и непрерывное вплоть до границы
решение Т (М, /), уравнение теплопроводности
dT/dt = а АТ (М, /) + /(М, t), М ^ G, / g (0, /0), [/ = /7(ср)], (2.34)
где Л — оператор Лапласа по координатам точки М.
72
Это решение в области G при t *= 0 непрерывно изнутри и удов¬
летворяет начальному условию
Т{М9 01*-о = Ф.(М). MgG(=G + S), (2.35)
а на границе S—какому-либо одному из следующих граничных
условий:
1. Решение Т (М, t) непрерывно на боковой поверхности SB =
= (Sxt^Q)
Т(М, /) = ф(М, /), MgS, />0. (2.36)
2. Решение Т (Л4, /) в каждой точке на боковой поверхности SB
имеет предельное значение нормальной производной
—к[дТ(М, t)/dn\ = q>(M9 t)9 t^O. (2.37)
3. Решение Т (М, /) непрерывно на боковой поверхности SB в каж¬
дой точке этой поверхности имеет определенное значение нормаль¬
ной производной и
—Х[дТ(М9 t)/dn]=a[T(M% t) — ф (Af. t)]9 M$S9 0, (2.38)
или
dT(M9 t)/dn = — h[T (M, i)—ff(M9 0], M$S9 0. (2.39)
Здесь Ф0(Л4) — заданная функция точки М, непрерывная в замкну¬
той области G + S; ф(Л4, t)—заданная непрерывная функция точ¬
ки М и времени t на поверхности SBi т. е. в точках MgS для
значений времени t € [0, /0]; /(Л4, t) — заданная функция точки М
и времени /, непрерывная по всем переменным в области опреде¬
ления уравнения теплопроводности.
Предполагается также выполнение условий согласования
Ф0 (М) |м €s = ф (Л4> 0 |/=о, м в s (2.40)
в случае граничных условий I рода (2.36);
-Х[ЗФ0(М)/ал]|м€5=Ф(Л4, 01/=0, mbs (2.41)
в случае граничных условий II рода (2.37);
дФ0 (М)/дп \м es = - h [Ф0 (М)-ф (М, 01/*о. м es (2.42)
в случае граничных условий III рода (2.39).
Без выполнения условий согласования нельзя было бы построить
непрерывную функцию Т(М, t), удовлетворяющую соответствующему
граничному условию в замкнутой области й. Таким образом, для урав¬
нения теплопроводности имеем согласно заданию граничных условий:
первую краевую задачу (2.34), (2.35), (2.36);
вторую краевую задачу (2.34), (2.35), (2.37);
третью краевую задачу (2.34), (2.35), (2.39).
Обозначим через А П В — пересечение множеств А и В (совокуп¬
ность точек, принадлежащих одновременно множеству А и множеству
В). Тогда в случае первой краевой задачи (2.34) — (2.36) отыскивается
73
функция Т(М, t), удовлетворяющая уравнению теплопроводности
(2.34) в й и принадлежащая классу функции C2(Q) П С°(й), если крае¬
вые функции задачи принадлежат классу функций:
0O(M)6C°(G); Ф(М, 0€C°(Sx[Of Q); (2.43)
f(M, I) €С°(Я).
В случае второй краевой задачи (2.34), (2.35), (2.37) или тре¬
тьей краевой задачи (2.34), (2.35), (2.39) отыскивается функция
Г(М, t)9 удовлетворяющая уравнению теплопроводности (2.34) вЙ
и принадлежащая классу функций
_ С2(Й)nC°(Q), gradM Т £ С0 (й),
Ф0 (M)€Cl(G); Ф (М, 0 6 С0 (S х [0, /0]), /(М, 0€C°(Q). (2.44)
При этом должны выполняться соответствующие условия согласова¬
ния.
В качестве первого обобщения основных краевых задач можно
указать смешанную краевую задачу для уравнения теп¬
лопроводности (2.34), когда на части границы
S области G выполняются краевые условия
первой краевой задачи, на другой ее части —
краевые условия’второй или третьей краевой
задачи *. Здесь также для отыскания реше¬
ния Т(М, t), непрерывного вплоть до гра¬
ницы области Й, необходимо следить за вы¬
полнением соответствующих условий согласо-
Рис. 19 вания.
Поясним приведенные выше рассуждения
на примере третьей краевой задачи для стержня О^.х^.1 с тепло¬
изолированной боковой поверхностью. Требуется найти функцию
Т(х, t), определенную и непрерывную в замкнутой области 0
O^t^to, удовлетворяющую в открытой области уравнению тепло¬
проводности,
dT/dt=a(d2T/dx2), 0<*</, £>0; (2.45)
начальному условию
Т(х, 0)=Ф0(х), 0<*</ (2.46)
и граничным условиям
дГ[х, t)ldx\xz=« = hx[T(0, 0—<Pi(0L t'S* 0; (2.47)
дТ(х> t)/dx\x=l = — h2[T(l, 0—Ф.(0]. *>° (2.48)
(здесь Ф0(*) и ф^(0 (/ = 1, 2) — непрерывные функции, удовлетво¬
ряющие условиям согласования),
d®0(x)/dx|*=0== ^[ФДО)—фЦО)]; \ q
dO0 (x)/dx |*=| = — h2 [Ф0 (/)—ф, (0)]. j
* Постановка краевых задач с граничными условиями сопряжения, а также
с разнородными граничными условиями будет рассмотрена позже.
74
Ъ *
Итак, решением третьей краевой задачи для стержня называется
функция Т(х, t)f удовлетворяющая условиям (2.45) — (2.49); она
определена в прямоугольнике ABCD (рис. 19). Предполагается, что
Т(ху t) удовлетворяет уравнению теплопроводности только при
О0<С^/0 но не при £=0 (сторона А В) и не при х=0 (сторона
AD) и х=1 (сторона ВС), где имеют место начальное и граничные усло¬
вия. Если бы потребовали, чтобы уравнение (2.45) удовлетворялось,
например, при /=0 (т. е. в точках отрезка АВ), то пришли бы к сле¬
дующему условию:
д2Т _1 дТ
дх2 г»о a dt
й2Ф0(х)
или —= (1/а) т; (х, 0) (2.50)
/=о dx2
Равенство (2.50) показывает, что в этом случае на начальное рас¬
пределение температуры Ф0(х:) накладывается жесткое ограничение,
вторая производная в нуле равна (1/а) Tftx, 0) (помимо того,
что при этом начальная функция должна быть дважды непрерывно
дифференцируемой). Этим требованием ограничилась бы область
изучаемых физических явлений, исключив из рассмотрения те функции
Ф0(х), для которых требование (2.50) не выполняется.
Равенства (2.49) необходимы для непрерывности решения Т(х, t)
в замкнутой области, так как непрерывность функции Т(ху t) во внут¬
ренних точках прямоугольника (О^х^.1, O^t^to) следует из того,
что в этих точках эта функция удовлетворяет уравнению (2.45) (в
этом смысле и понимается фраза «непрерывность решения вплоть до
границы»). Таким образом, требование непрерывности Т(х, t) при 0^
по существу относится только к тем точкам, где задают¬
ся начальное и граничные условия (заметим, что граница t=t0 в поста¬
новке краевой задачи не участвует; предполагается лишь, что при
t=U решение ограничено).
Все сказанное сохраняет силу и для задач с несколькими незави¬
симыми геометрическими переменными.
Рассмотрим далее постановку третьей краевой задачи для цилиндра
радиусом r=R и длиной /. Если длина цилиндра значительно больше
его диаметра 2R (t^>2R), то его можно считать неограниченным цилинд¬
ром, у которого длина бесконечно велика по сравнению с диаметром.
Предположим, что теплообмен между поверхностью цилиндра и окру¬
жающей средой происходит одинаково по всей поверхности. Тогда
температура цилиндра будет зависеть только от времени и радиуса
(осесимметричное поле).
Пусть T(r, t) — температурная функция. Тогда в области 00
(O^rCR) функция T(r, t) удовлетворяет:
уравнению теплопроводности
J = a (*£ + 1£) + /(г, 0, <><'<«. '>0; (2.51)
начальному условию
Г (г, 0) = ФДг), (2.52)
75
(2.53)
(2.54)
Условий (2.52) и (2.53) еще недостаточно для постановки краевой
задачи уравнения теплопроводности (2.51). В случае сплошных цилинд¬
ров (а этот случай и рассматривается здесь) точка л=0, соответствую¬
щая оси цилиндра, является особой точкой для дифференциального
уравнения (2.51) [второе слагаемое в правой части равенства (2.52)
при г=0 теряет смысл]. Для ликвидации этого недостатка потребуем,
чтобы выражение (\1х)дТ1дг имело конечное значение при г=0; по¬
следнее возможно, если выполняется равенство
К этому же условию можно прийти и из следующего сообра¬
жения. Умножая обе части равенства (2.51) на г, получим
Точка г=0 является внутренней точкой цилиндра и в этой точке, как
и в любой другой внутренней точке области 0функция T(r, t)
должна быть дважды непрерывно дифференцируема по г и непрерывно
дифференцируема по /, откуда при г->0 равенство (2.56) даст условие
(2.55). Это условие фактически означает, что температура Т(г, t) на
оси цилиндра (г=0) должна быть конечной на протяжении
всего процесса теплообмена (часто это условие записывается в виде
Таким образом, краевыми условиями в рассматриваемой задаче
будут (2.52) — (2.55). Эти условия вместе с уравнением (2.51) позволят
найти функцию Г(г, t), описывающую распределение температуры в
сплошном цилиндре при теплообмене на его боковой поверхности.
Для уравнения (2.34) вовсе не обязательно рассматривать краевые
задачи лишь в ограниченных областях. Очень часто важно решить его
для неограниченной области. Это бывает, например, в случаях, когда
размеры рассматриваемой области очень велики по сравнению с мас¬
штабом изучаемого явления. Тогда приходят к предельным случаям
краевых задач.
Так, например, рассмотрим процесс теплопроводности в очень длин¬
ном стержне, теплоизолированном с боковой поверхности. В течение
небольшого промежутка времени влияние теплового режима, заданно¬
го на торцовых граничных сечениях стержня в его центральной части,
оказывается весьма слабым и температурное поле на этом участке
определяется в основном начальным распределением температуры в
стержне. В этом случае точный учет длины стержня не имеет значения,
так как изменение длины стержня не оказывает существенного влия¬
ния на температуру интересующего нас участка. В задачах подобного
типа считается, что стержень имеет неограниченную длину |х|<!+оо.
дТ(г, t)/dr\rmt — 0.
(2.55)
| Т(г, *)|<+оо, г>0).
76
Аналогичным образом можно рассмотреть и бесконечную плоскость
(двумерное температурное поле) или неограниченное пространство
(трехмерное температурное поле), когда влиянием граничных условий
можно пренебречь при изучении температурного поля где-то в сред¬
ней части области. В некоторых случаях возникает необходимость
рассмотреть температурное поле для полуограниченной области, на¬
пример в полуограниченном стержне или в полубесконечном цилиндре,
и т. п., когда интересующий нас участок находится вблизи одной
границы и далеко от другой границы. В этом случае необходимо учи¬
тывать тепловое влияние ближнего граничного участка и начальное
распределение температуры.
Отметим следующее важное обстоятельство. При рассмотрении
бесконечных областей далеко не безразлично, как ведет себя решение
в далеких точках рассматриваемой области. Во многих случаях только
при известных предположениях об этом поведении задача становится
определенной, а именно: необходимо наложить на решение дополни¬
тельное ограничение — решение должно обращаться в нуль на бес¬
конечности или быть ограниченным на бесконечности. Иначе решение
остается неопределенным.
Обозначим через Е3 — трехмерное пространство, т. е. совокупность
точек М, координаты которых определяются тремя действительными
числами, и сформулируем в качестве одной из основных предельных
краевых задач для уравнения теплопроводности задачу Коши.
Требуется найти ограниченное решение уравнения теплопровод¬
ности
дТ1д1=аЬТ(М9 t)+f(M, 0, М€Е3у t>О, (2.57)
дважды непрерывно дифференцируемое по пространственным коорди¬
натам и непрерывно дифференцируемое по времени / во всех точках
пространства Е3 при С>0, непрерывное при £=0, удовлетворяющее:
начальному условию
Т(М, 01,=о = Ф.(М). М£Е3 (2.58)
и условию ограниченности на бесконечности, записанному в виде
Ига Т(М, 0 = 0, или |Т(М, 0|< + °°, |М|.—► оо. (2.59)
| М | —► оо
Здесь Ф0(М) — заданная непрерывная, ограниченная функция,
ФобС0^); функция f(M, 1)€С°(М£ЕЯ, I > 0).
При этих условиях решение задачи Коши (2.57) — (2.59) является
функцией класса
Т (М, 0 € С2 (М е £*, / > 0) п С° (М € ЕЯ9 t > 0). (2.60)
Заметим, что вместо условия ограниченности на Ф0(М) могут быть
наложены другие менее ограничительные условия. В частности,
Ф0(М) может неограниченно возрастать; в этом случае и решение
задачи будет обладать тем же свойством, имея тот же порядок роста
на бесконечности (см. §5 гл. III).
Для полуограниченного стержня с начальной температурой Ф0(х)
и теплообменом на торце температурная функция Т(х, /), принадле-
77
жащая классу функций (2.60), удовлетворяет следующим уравнениям:
dT/dt— а(д2Т/дх2), х > 0, / > 0; (2.61)
Т(х, 0) = Фо(ж), х>0; \
дТ(х, t)/dx\x=0 = h[T (0, /)—Ф(0]. 0; 1 (2.62)
\Т(х, /| < + оо, х>0. J
При этом имеют место условия согласования Фо (л:) \X = Q = h [Ф0 (0) —
—ф (0)].
Кроме рассмотренных возможны предельные случаи и другого
типа, когда пренебрегают точным учетом начальных условий. Крае¬
вые условия здесь остаются неизменными, а начальные отсутствуют.
В каждом из таких случаев вырождения можно говорить соответ¬
ственно о первой, второй и третьей краевых задачах без начальных
условий для одномерного полупространства:
dT/dt=a(d2T/dx*), *>0, — оо</<+оо; (2.63)
[р1(д77дх) + р„7,|я=, = рзф(0> НК + оо, Р^ = const; 1
YimT (х, t) = 0, л:—* оо; limТ (х, /) = 0, t —► +00. )
Здесь ф (0 — заданная непрерывная ограниченная функция.
Последнее краевое условие заменяет отсутствовавшее начальное.
Рассмотрим далее несколько примеров постановки краевых задач
теплопроводности с граничными условиями сопряжения.
Возьмем простейшую систему, состоящую из двух полуограниченных стерж¬
ней с теплоизолированной боковой поверхностью. Начальные температуры и теп¬
лофизические характеристики тел различные. В начальный момент времени тела
приведены в соприкосновение в точке х = 0. Если Тх(х, t) и Т2{х, t) — темпера¬
тура соответственно левого (х < 0) и правого (х > 0) стержней, то имеем следую¬
щую краевую задачу:
dTl/dt = ald2Tl/dх2, х < 0, t > 0; dT2/dt = а2 д2Т2/дх2, х > 0, * > 0; (2.65)
Т1 (х, 0) = Ф1г; (х), * < 0; Т2 (х, 0) = Ф20 (х), х > 0; (2.66)
Тх (0, t) = T2 (0, 0, / > 0; ^ [дТ1 (х, t)/dx]x=0 = X2 [дТ2 (х, t)/dx]x=0, t > 0. (2.67)
lim Тг(х, 0=0, lim T2(x,t)= 0, t > 0.
— CD + CD
Здесь Ф/о (x) (i = 1, 2) — заданные ограниченные непрерывные функции в своей
области определения Ф10 (х)£.С° (х < 0), Ф2о М6С°(х > 0); при этом Тх (х, /)£
gC2(x< 0, / > 0), 7\>(х,
(х > 0, t > 0). В этой задаче не
выполняются условия согласова¬
ния; о решении такого рода задач
будет сказано позже.
Рассмотрим более слож¬
ный пример, когда гранич-
— ные условия сопряжения за-
У даются на поверхностях, яв¬
ляющихся координатными, в
различных координатных си¬
стемах.
Пусть требуется определить
температурное поле Тх (/•, 0) в по¬
лусфере г < г0, 0^0 ^ я/2, из
Рис. 20 материала с теплопроводностью Я*
78
и коэффициентом теплоотдачи Нъ находящейся на поверхности большого круга
0 = я/2 в совершенном тепловом контакте с бесконечной плоскопараллельной
пластиной — l^z<* 0 из материала с коэффициентами Х2, h2t температурой
Т2 (р, г). Здесь (г, 0) — сферические координаты; (р, г) — цилиндрические коорди¬
наты, причем полярный угол 0 отсчитывается от положительного направления оси
2, значению 0 = л/2 соответствует значение 2 = 0 (рис. 20). Функции Тг(г, 0) и
Т2 (р, г) удовлетворяют следующим уравнениям:
В левую часть второго из граничных условий (2.70) входит про¬
изводная по нормали (по направлению оси г) к контактному кругу
0^г<г0, 0 = л/2. В сферической системе для 7\, зависящей лишь
от г и 0, имеем (см. § 3 гл. I) grad Тг = (dTjdr) er + (dTjdQ) (1/г) во.
На контактной поверхности п = — е0, и так как dTvfdn = rt-gvad ТХУ
то, перемножая два вектора скалярно, найдем, что dTjdn =
= —(1 /г)дТг1д& при 0 = я/2, 0^г<г0. Остальные выражения,
входящие в граничные условия задачи, в разъяснении не нуждаются.
Заметим, что тепловые задачи, аналогичные рассмотренной, воз¬
никают при исследовании кинетики кристаллизации из расплава
микромонокристаллов полупроводников на инородных подложках,
когда кристаллизуемые капли расплава близки по форме к полусфере
В теории теплопроводности еще недостаточно отработаны аналити¬
ческие методы решения такого класса задач; приближенный метод ре¬
шения сформулированной задачи (2.68) — (2.71) изложен в [1101.
Обратимся вновь к краевым условиям (2.35) — (2.38) для уравне¬
ния теплопроводности (2.34). Как отмечалось, для того чтобы решение
задачи имело гладкость С0 в случае граничных условий I рода или С1
в случае граничных условий II и III родов вплоть до границы области
задания дифференциального уравнения теплопроводности, необходимо
накладывать на краевые функции задачи дополнительные условия,
т. е. условия согласования (2.40) для первой краевой задачи, (2.41) —
для второй и (2.42) — для третьей.
Однако эти условия непрерывности являются весьма ограничи¬
тельными и не всегда соответствуют реальным условиям задачи. В са¬
Xi дТ j |
г дО (0 = л/2
|о<г<г(
г- о
0<р<л0
(2.69)
(2.68)
дТ\
дг г=г0
0<9<Л/2
(2.70)
^’./*U_t=Al(7’1|,= _l-7’c);
lira Г, (р, г) — 0; дТг/дг |,,=0 = 0.
(2.71)
\Z = О
[1221.
79
мом деле, рассмотрим простейшую задачу об остывании равномерно
нагретого стержня, теплоизолированного по боковой поверхности,
с температурой на торцах 7\ меньше начальной Г0:
dT/dt=a(d2T/dx2), 0<х<1, t>0;
Т(ху 0) = Г0, 0<х</, 740, t) = T(ly t) = Tt, ОО.
Если ТгфТ0, то решение этой задачи должно быть разрывным в
точках (0, 0) и (/, 0).
Этот пример (как и некоторые предыдущие) показывает, что по¬
ставленные выше условия непрерывности начального значения и ус¬
ловия сопряжения его с граничными условиями исключают из рас¬
смотрения практически важные случаи. Краевые задачи теплопровод¬
ности, в которых начальная функция не сопряжена с граничными
функциями, являются достаточно многочисленными для потребностей
практики и могут быть решены теми же аналитическими методами,
что и сформулированные выше. Более того, решения краевых задач
с указанными начальными условиями будут иметь ту же аналитическую
форму, что и соответствующие краевые задачи с условиями согласо¬
вания краевых функций.
Таким образом, не принимая во внимание выполнение условий
согласования (если они специально не заданы), можно говорить о
краевых задачах следующего вида:
первая краевая задача
дT/dt = aAT(My t) + f(M,t)y M£Gt f>0;
Т (УИ, 0) = Ф0(М), MgG; Т(М,0 = Ф(М,0, M£S,t> 0;
вторая краевая задача
dT/dt=aAT(Mt t) + f(M, t)y MgG, t > 0; )
Т(М,0) = Ф,(М),М^; I
— X [дТ (M, t)/dn} = ф (М, t), М € s, t > 0; J
третья краевая задача
<ЗТ/^ = аДГ(М, /) + /(М, t), M£G, t > 0;
Т(М, 0) = Ф0(М), M£G;
дТ/(М, t)ldn = — h[T(M, t)—ф(М, 01, <>0,
а также смешанная краевая вадача и краевые задачи с граничными
условиями сопряжения.
Здесь /(М, 0 € С° (Q); Ф0 (М) £ (G); Ф(М, 0 € (Sx f > 0).
Решение Т(М, t) принадлежит классу функций С2(Q) и не является
в общем случае непрерывным вплоть до границы области определения
уравнения теплопроводности. Возможно также, что начальная функ¬
ция Ф0(Л4) и функция источника/(М, <) не являются непрерывными,
допуская в области G конечное число точек разрыва 1 рода (ступен¬
(2.72)
(2.73)
(2.74)
80
чатые функции). Однако структура решения задачи такова, что это не
скажется на принадлежности решения классу C2(Q).
В качестве второго обобщения краевых задач теплопроводности
можно рассмотреть случай, когда область определения пространствен¬
ных переменных G с границей S
зависит от времени /, т. е. когда
G=G(t)=Gt. В этом случае Qt—не¬
цилиндрическая область, так как се¬
чение этой области плоскостью t =
= const представляет собой прост¬
ранственную область Gt с границей St,
зависящей от времени t (рис. 21). В та¬
ких случаях говорят о краевых за¬
дачах теплопроводности в области с
подвижными границами или краевых
задач теплопроводности обобщенного
типа. Для таких задач граничные ус¬
ловия имеют ту же форму и можно говорить о первой, второй,
третьей или смешанной краевой задаче обобщенного типа (краевой
задаче обобщенного типа с граничными условиями IV рода). Кра¬
евым задачам обобщенного типа посвящена гл. VIII.
Следует, однако, заметить, что наличие движущейся границы
может изменить вид граничного условия, характеризующего определен¬
ный тепловой режим на данной границе. Остановимся сейчас на фор¬
мулировке условия тепловой изоляции движущейся границы и пока¬
жем, что это условие отлично от классического (2.8). Рассмотрим про¬
цесс теплопроводности в теплоизолированном с боковой поверхности
стержне 0<Оc<.y(t)> t>0, и выведем условие теплоизоляции правого
торца х=у (/), предполагая наличие некоторого начального распреде¬
ления температуры и некоторого граничного условия на левом торце
х=0.
Пусть Т(х, t) — температурное поле стержня, в котором к тому же
действует непрерывно распределенный нестационарный источник теп¬
лоты
dT/dt=a(d*T/dx2)+f()с, /);
О<*<*/(/), *>0 [а=Х/(ф)],
(2.75)
a v(t)=dy/dt — скорость перемещения границы x=y(t).
Запишем уравнение теплового баланса в момент времени' (/+Д/)в
считая границу x=y(t) теплоизолированной:
y{t) + by y(t)
— a dTfx*'" &t + cp А/ ^ /(*, t) dх = ср j [Т (х, / + ДО —
о о
у (/) +
— т (X,t)\dx+cp ^ Т (xt /+A/)dx.
у it)
81
Ко второму из интегралов справа применим теорему о среднем
</ (О + Д/У
— а д- .*1 At + Л/ j* /(а:, /) dx =
о
y(t)
= $ [Т (х, t + &t) — T(x, l)]dx + T(x, t + At)\x=!/+eay^y,
О
где 0 < 0 < 1.
Разделив обе части равенства на и перейдя к пределу при
Д/ —► 0, получим
y{t) y(t)
~а д'Тдх’ 0 + j /)djC= j %-dx + v(t)T (X, 0 !*=.„«)•
n 0
Подставим под знак интеграла вместо дТ/dt правую часть урав¬
нения теплопроводности (2.75), произведем интегрирование и при¬
ведем подобные члены. В результате окончательно получим условие
--j,*’ 0 1 +vJ*lT(x,t) I =0, (2.76)
дх \x=y(t) a v ' \x-y(ty v '
которое и представляет собой условие тепловой изоляции для под¬
вижной границы. Если скорость движения границы v(t) = 0, то при¬
ходим к условию (dT/dn)s = 0, означающему теплоизоляцию непод¬
вижной граничной поверхности.
Задача. Показать, чго условие тепловой изоляции цилиндрической поверх¬
ности r — y(t) при аналогично, как и в случае (2.76), имеет вид
дТ (г, t)/dr + [v(t)/a]T (г, /)=0 при r = y(t), если Т (г, () удовлетворяет уравне¬
нию дТ/dt=a ДГ (г, t).
Рассмотрим постановку еще одного класса температурных задач в области
с подвижной границей, отличающихся от рассмотренных выше своеобразным
граничным условием.
При изменении температуры тела (нагревании или охлаждении) может проис¬
ходить изменение его физического состояния, в частности при переходе через
точку плавления —переход из жидкой фазы в твердую (распространение застыва¬
ния в расплавленную металлическую массу при охлаждении или проникновении
холода в стоячую массу воды или в сырую землю) или обратный переход. При
этом на поверхности фазового перехода все время сохраняется постоянная тем¬
пература.
Рассмотрим жидкую массу, ограниченную с одной стороны плоскостью х = 0
и неограниченно простирающуюся в другую сторону. Пусть в начальный момент
времени / = 0 температура в жидкой массе всюду постоянная Т{). Граничная по¬
верхность длительно поддерживается при некоторой постоянной температуре Т ^
ниже точки затвердевания жидкой массы Тп. В таком случае прилегающий слой
быстро затвердевает и граница затвердевания будет со временем все дальше i.
дальше проникать внутрь жидкой массы. Поставим краевую задачу о распреде¬
лении температуры (как функции места и времени) и о скорости продвижения
поверхности раздела фаз (жидкой и твердой).
Рассмотрим плоскую задачу, когда поверхностью раздела является плоскость
x — y(t). Сформулируем граничные условия, которые должны выполняться на
поверхности затвердевания: пусть Тг(х, t) и Т2(х, /)— температуры соответственно
твердой н жидкой фаз. Переход из одной фазы в другую сопровождается погло¬
щением или выделением определенного количества теплоты, которое называется
теплотой перехода. Для перехода вещества из твердого состояния в жидкое
необходимо сообщить ему количество теплоты Q = Xnmt где т—масса расплавив-
82
шегося *тела; Хп — удельная теплота плавления (А,п — количество теплоты, которое
нужно сообщить единице массы твердого тела, находящегося при температуре
плавления, чтобы перевести его в жидкое состояние). При затвердевании (кри¬
сталлизации) жидкой массы происходит выделение теплоты. При этом теплота
кристаллизации равна теплоте плавления.
На границе затвердевания x = y(t) имеем следующий тепловой баланс. К твер¬
дому веществу в направлении убывающих х за время At через квадратный санти¬
метр утекает, согласно закону Фурье, количество теплоты Qi=hi{dTlldx)x=y(t) At.
Эта теплота слагается из выделяющейся при затвердевании некоторой массы
жидкости за время А/ теплоты и теплоты, отданной жидкостью твердому веще¬
ству. За время At граница затвердевания передвинется на отрезок А у и, следо¬
вательно, затвердеет количество вещества рАу, где р — плотность образующейся
фазы; при этом выделится количество теплоты Q2 = AnpA*/, которое должно быть
отведено в результате теплопроводности. За это же время со стороны ^жидкой
массы в твердую фазу приходит количество теплоты Q3 = ?v2 (дТ2/дх)х_у (У) + Д< Atr
Так как Qi = Q2 + Qs. получим - * - - 7
t)/dx]x=yiUM = \np Ay+T^ldTvix, t)/dx]x= у«) + \у Л/.
Разделив обе части равенства на А/ и перейдя к пределу при At —► 0, полу¬
чим граничное условие на поверхности раздела фаз
[KidTi(x, t)/dx—1гдТг(х, t)/dx]x=y (t) = lnp (dy/dt). (2.77)
Это условие имеет место как для процесса затвердевания (когда Ау > 0 и
(dy/dt) > 0), так и для процесса плавления (когда Ау < 0 и (dy/dt) < 0); направле¬
ние процесса определяется знаком левой части. Таким образом, для определения
закона движения поверхности раздела твердой и жидкой фаз и температуры
в каждой из них имеем следующую краевую задачу:
dT1/dt==ai (d2Tf/dx2), 0 < х < y(t), t > 0;
дТ2/dt = а2 (д2Т2/дх2), х > y(t), t > 0; (2.78)
Tf (0, /) = Tit t > 0;
T2 {.x, 0) = 7V x > 0, lim T2 (x, t) = TQ; (2.79)
Л'->00
Ti (y (t), () = Т2(у(1),() = Т„, t>0; (2.80)
(kidTi/dx—K2 дТ2/дх)х=уА) = %пр (dy/dt), t > 0.
Задачу (2.78) — (2.80) называют задачей Стефана (или задачей
о фазовом переходе, или задачей о промерзании) в честь австрийского
ученого И. Стефана, который в 1889 г. поставил и решил задачу о фа¬
зовом переходе. В постановке рассмотренной задачи функция x=y(t)—
свободная граница, которая не задана (в отличие от рассмотренных
выше случаев) и подлежит определению вместе с функциями 7\(лс, t).
Задачи Стефана подробно излучаются в работах [94; 95; 98—1001.
Следует заметить, что краевые задачи теплопроводности в области
с подвижной границей за последние годы приобретают все большее
значение в различных прикладных разделах физики и* математики.
С математической точки зрения эти задачи принципиально отличны
от классических, так как к ним неприменимы классические методы
разделения переменных и интегральных преобразований. Аналитиче¬
ским методом решения такого класса задач посвящена специальная
глава (см. гл. VIII).
Что касается уравнения теплопроводности гиперболического
типа
то для него пбстановка краевых условий имеет следующий вид:
начальные условия
Т(х, /)|«-о=Фо(*), 0 *£*</;
ЗТ(Х, о
dt
= Ф1 (х), 0
/=0
граничные условия первого рода
т(х, Ol*-o=<pi(0, о 0;
Т(рс, t)\x=i=<p2(t), 0;
граничные условия второго рода
дТ{х, I)
дх
х*»0
= ( l+r*-J<Pi (0, t>0;
X
8Т(х, 0
дх
= -[ 1 + т*-)<p2(t), 0;
граничные условия третьего рода
дТ(х, 0
дх
аг(х, о
5*
:=1
= -й2( 1+т*-1[Г(х, 01*-/-ЫО], ^0.
Для уравнения теплопроводности в средах с тепловой памятью,
например, в области х>0, /^0
«щ*, о г2г(х, о
£(0) + с£1о . +
dt dt2
ет(х, t-s)
Р (s) , ds--
dt
84
начальное условие записывается в виде
Т(х, /)1<-о=Фо(*), х^О;
дТ{х, О
dt
=Ф|(х), х^О.
Г = О
Граничные условия имеют вид:
первого рода (температурный нагрев)
Т(х, t)\xss0 = cp(t), t^O;
второго рода (тепловой нагрев)
00
J.W
дТ(х, t-s)
дх
ds=cp(t), 0;
х=0
третьего рода (нагрев средой)
00
{«и
дТ(х, t-s)
дх
ds=h[T(x, 01*=о-<р(0],
|Г(х, 01 < + °°, х^О, 0.
В заключение этого параграфа рассмотрим постановку основных
краевых задач для уравнения стационарной теплопроводности.
Пусть по-прежнему G — область, лежащая в конечной части про¬
странства (х, у, z), S — кусочно-гладкая поверхность, ее ограничива¬
ющая, п — нормаль к S, М(х, у, г) — пространственная точка.
Для уравнения Пуассона (1.34) постановка основных краевых задач
теплопроводности следующая:
требуется найти решение Т (М) уравнения
ДГ(М)+/(М)=0, М 6 G(/=(1/X)F), (2.81)
дважды непрерывно дифференцируемое в области G и удовлетворяющее
каким-либо из следующих граничных условий (начальное условие
здесь отсутствует, так как процесс стационарный).
1. Решение Т (М) непрерывно в замкнутой области G + S( = G)h
и удовлетворяет условию
Г(М) = ф(М), M£S. (2.82)
2. Решение Т (М) в каждой точке на поверхности S имеет пре¬
дельное значение нормальной производной и удовлетворяет условию
—Х[дТ(М)/дп]=<р(М), MgS. (2.83)
3. Решение Т (М) непрерывно в замкнутой области G + S, в каж¬
дой точке поверхности S имеет предельное значение нормальной
производной и удовлетворяет условию
— Х[дТ (М)!дп] = а[Т {М) — <p(M)], (2.84)
где ф(М) — заданная на S непрерывная функция; f(M)—функция,
непрерывная в G.
Каждая из перечисленных краевых задач называется внутренней
краевой задачей. Первая краевая задача (2.81), (2.82) называется
задачей Дирихле, вторая краевая задача (2.81), (2.83)—задачей
Неймана, задача (2.82), (2.84)—третьей краевой задачей. В задаче
Дирихле отыскивается функция Т (М) класса С2 (G) П С0 (G); в задаче
Неймана, третьей краевой задаче или краевой задаче со смешанными
граничными условиями отыскивается решение класса (^(GJnC^G).
Для уравнения Лапласа или Пуассона могут быть рассмотрены
и краевые задачи для системы сред с граничными условиями сопря¬
жения (2.19) —(2.20).
Аналогично ставятся краевые задачи для уравнения (2.81) и в
бесконечной области G*, внешней по отношению к поверхности S и
содержащей бесконечно удаленную точку; эти задачи называются
внешними краевыми задачами. Отличие их от внутренних краевых задач
состоит в том, что помимо граничных условий на S задается еще усло¬
вие на бесконечности. Однако этот вопрос решается различно для
плоскости и для пространства, т. е. для двух и трех независимых пере¬
менных внешние краевые задачи ставятся по-разному.
Для случая трех переменных решение Т(М) должно равномерно
стремиться к нулю при стремлении точки М к бесконечности. Послед¬
нее (при постановке всех внешних краевых задач) обеспечивает одно¬
значную определенность соответствующих им физических процессов
или, что все равно, единственность решения краевых задач (см. § 5
данной главы). Для случая двух переменных решение Т(ху у) должно
быть ограничено на бесконечности, т. е. должно выполняться нера¬
86
венство | Т (х, у) | <УУ=const (N — некоторое число) всюду в области
решения задачи. Требование обращения решения в нуль на бесконеч¬
ности и здесь оказывается достаточным, чтобы решение задачи было
единственным, но оно является слишком сильным, так как при нем
задача может оказаться вообще неразрешима.
В качестве примера рассмотрим постановку задачи Дирихле для
уравнения Лапласа в области G{ (х, у)у 0<.х<1и 0 <f/</2}:
д*Т/дх* + д'Т/ду* = 0, 0 < х < /*, 0 < у < /2; (2.85)
т (0, у) = ф! (у) ) т {х, 0) = ф9 (*) )
} 0(2.86)
т У) = %(У)) т (х, /г) = ф4 (•*) )
Здесь q>t (у) € С0([0, /,]); Ф( (х) £ С° (Ю, /,]).
Для того чтобы решение Т (х, у) было непрерывным вплоть до гра¬
ницы области определения дифференциального уравнения (2.85),
необходимо потребовать выполнения условий согласования: cpi(0) =
= фз(0), ф! (/Я)=ф4(0); ф 2 (0) ==ф8 (^l) » ф2(/2)=ф4(/1).
Заметим следующее обстоятельство. В постановке задачи предпо¬
лагали всюду непрерывность граничных функций <pf(i = l, 2, 3, 4);
между тем иногда бывает необходимо рассматривать такие случаи,
когда в какой-либо граничной точке М0 краевая функция имеет разрыв
первого рода ф(УИ0+0)—ф(М0—0)=Ь(Ф0), где b — заданное число,
ф(М0+0) и ф(А1о—0) — предельные значения ср (М) при подходе к
точке М0 по граничному контуру с разных сторон.
Покажем, что с помощью несложных преобразований можно уст¬
ранить это обстоятельство. Пусть (для определенности) точка разры¬
ва лежит на правой стороне x=lf прямоугольника G(0<^/i, 0
т. е. MQ(lu d0)t где 0<d0</a и граничная функция ф2(у) имеем в этой
точке разрыв первого рода: ф2(^0+0)—ф2(^о—10)=Ь(Ьф0).
Введем новую температурную функцию 7\ (х, у) с помощью подста¬
новки
Tt(x, у)=*Т(х, у)— (b/л) arctg(2/*—х)!(у—d0).
Функция (х, у) в области G является дважды непрерывно диф¬
ференцируемым решением уравнения Лапласа; действительно, непо¬
средственным дифференцированием можно проверить, что таковым
является функция ©(*, y)=(b/n) arctg(2/х—х)/(у—d0). При этом имеет
место равенство Tt (/i, d0+0)—Tx(lu d0—:0)=0, так как 0(/b d0+0)—
~©(/i, d0—0)=b. Таким образом, на граничном отрезке x=lt функция
Тх{х, у) непрерывна. Поэтому, решая для определения задачу
Дирихле в смысле сделанной выше постановки при непрерывной крае¬
вой функции Ф21 (у) ==ф2(.у)—ф!л) arctg lj(y—do) и полагая Т(х, у) =
(х, у)+&(х, у), получим решение задачи при разрывной краевой
функции ф2(у). В дальнейшем, без ограничения общности можно рас¬
сматривать задачу Дирихле (а также и другие задачи стационарной
теплопроводности) в том смысле, как она была поставлена выше при
непрерывных краевых функциях (если противное специально не ого¬
ворено), требуя, чтобы искомое решение было непрерывным в замкну¬
87
той области, т. е. вплоть до границы области определения уравнения
Лапласа (или Пуассона).
Перейдем теперь к математической интерпретации начальных и
граничных условий. Как отмечалось, при классической постановке
краевых задач теплопроводности требуется, чтобы решение Т(М, t)
было непрерывным в Й, имело непрерывные производные Т\, Т’х, Т"хх,
удовлетворяло во всех точках Q уравнению (2.34), а при t=0 и (М, t) £
£SB— условиям (2.35) и (2.36). При этом для второй и третьей крае¬
вых задач требуется дополнительно, чтобы и частные производные по
пространственным переменным функции Г(М, t) существовали и были
непрерывны в Q.
Если G — неограниченная область, то к этим требованиям добавля¬
ется еще условие о поведении решения на бесконечности. Однако
имеется достаточно большой класс практически важных краевых задач
теплопроводности, решение которых с гладкостью С0 или С1 вплоть
до границы области определения дифференциального уравнения теп¬
лопроводности существует не всегда (например, взаимодействие равно¬
мерно нагретого тела со средой постоянной температуры, отличной от
начальной температуры тела, также постоянной). При этом имеет
место и другая особенность функциональных конструкций решения,
когда в ряде случаев решение в точках граничной поверхности не опре¬
делено, но допускает операцию предельного перехода при приближении
к границе (или при £->0). Поэтому при математическом рассмотрении
задачи теплопроводности краевые условия не следует рассматривать
как условия, которым искомая температура обязана удовлетворять
на поверхности S или в начальный момент времени /=0. Краевые
условия следует считать предельными усло¬
виями.
Граничные условия нужно понимать в том смысле, что для любого
фиксированного значения времени £>Э температура или ее производная
по нормали, или комбинация температуры и ее производной стремятся
к заданному значению при приближении точки к поверхности.
Начальное условие следует понимать в том смысле, что для фиксиро¬
ванной точки внутри области G температура должна стремиться к за¬
данному значению по мере того, как t стремится к нулю.
Поясним сказанное на следующем примере.
Пусть Т (х, 0 — распределение температуры в стержне 0^х«^/, теплоизоли¬
рованном с боковой поверхности; Ф0 (х) — начальная температура стержня, имеет
переменное значение; на левом торце х = 0 задано значение теплового потока
ф! (t) для t > 0, на правом торце х — 1 при t > 0 происходит теплообмен со сре¬
дой, температура которой <р2 (/)•
Согласно сказанному выше, следует записать для Т (х, t) уравнения:
дТ/dt — a (д2Т/дх2), 0 < х < I, t > 0;
lim Т (х, t) = O0 (х) для фиксированного х в области 0 < х < /; (2.87)
t-+ о
lim X (дТ/дх) = у1 (/) для фиксированного t > 0; (2.88)
*-*о
lim (дТjdx-\-hT) = /i<p2 (t) для фиксированного t > 0. (2.89)
x-+l
88
Выше мы записали бы эту задачу в виде:
dT'/dt = a (д2Т/дх2), 0 < х < I, О 0;
Т(х, 0) = Ф0(х), 0< х< /; Х[дТ(х, t)/dx]x=0 = фх (0, * > 0; (2.90)
дТ(х, t)/dx \x-t — h [Т (/, /) — фа (/)], t > 0, (2.91)
имея в виду теперь, что краевые условия (2.90) — (2.91) нужно понимать в смысле
(2.87) — (2.89). Если к тому же ФоМ^С1^» Ф» ф|(0€£°(*^0) и выполнены
условия согласования ХФ'0 (х) |х = о = ф1 (0); Ф^ (х) \x = i = h [Фо (0 — фг (0)]. то ре¬
шение Т(х, t) £С2 (Q) П^0 (Q), Т\ £С°(&), где Q= [(х; t)\0 < х < ly t > 0]. В слу¬
чае невыполнения последних условий решение дается в виде Т (х, /)б^2(^)*
§ 4. БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ
Как было показано выше (см. § 3 гл. II), аналитическое описание про¬
цесса теплопроводности включает в себя дифференциальное уравнение
(2.34) и условия однозначности в виде физических параметров (К, р, 6’),
геометрических размеров (/ь /2,...), начальной температуры тела
Т0=Ф(Л4), граничных условий дТ/дп—р27"=—<р(М, /), М £ S.
В результате решения поставленной краевой задачи находится
функция, математически описывающая температурное поле тела в
любой момент времени t>0 (если процесс нестационарный). В аналити¬
ческое выражение этой функции входят независимые переменные
х, уу г, /, начальная и граничная функции, физические параметры,
геометрические размеры тела, т. е.
Т=Т(х, уу 2, /, X, р, с, а, /,, /2, ..., Го, Тс). (2.92)
Аналитическое описание процесса теплопроводности было пред¬
ставлено в размерных единицах; отсюда и решение краевой задачи
получается в тех же единицах. Выражение (2.92) показывает, что
температура тела зависит от большого числа переменных и постоянных
параметров. Это обстоятельство затрудняет числовые расчеты, прово¬
димые по формуле (2.92). Становится весьма сложным привести ре¬
зультаты расчета в определенную систему, уловить влияние отдель¬
ных факторов на течение процесса.
Задача значительно облагчается, когда размерные переменные объ¬
единяются в безразмерные комплексы (критерии). Эти безразмерные
комплексы, или числа подобия, состоят из разноименных величин,
объединение которых осуществляется разными способами: методом
масштабных преобразований, путем анализа
размерностей и др. При этом происходит уменьшение числа
определяющих параметров в аналитическом решении задачи, что и об¬
легчает его числовую обработку. .
Безразмерные комплексы, являющиеся как в постановке задачи,
так и в ее решении по существу новыми переменными, называют иначе
обобщенными переменными. Замещение обычных переменных обобщен
ными является основной задачей теории подобия (или теории обобщен¬
ных переменных), получившей в нашей стране свое развитие в работе
[19].
Обобщенные переменные можно получить для любого физического
процесса. Для этого нужно иметь его математическое описание в виде
некоторых уравнений. Анализ этих уравнений в модельной задаче
89
позволяет установить, какие факторы общего вида влияют на искомую
величину, т. е. отыскать эти обобщенные переменные. Метод преоб¬
разования исходной краевой задачи теплопроводности к задаче отно¬
сительно безразмерных (обобщенных) переменных широко использу¬
ется в аналитической теории теплопроводности. Безразмерные решения
обладают большей познавательной ценностью, так как позволяют уста¬
новить внутренние связи между переменными и параметрами задачи,
более глубоко изучить физический смысл полученного решения (осо¬
бенно это важно для краевых задач с большим числом определяющих
параметров и независимых переменных).
В то же время можно пойти и по другому пути. Каково бы ни было
аналитическое выражение, представляющее решение той или иной
краевой задачи теплопроводности, все входящие в него размерные
величины оказываются либо уже сгруппированными в безразмерные
комплексы, либо их без труда можно в них сгруппировать. Рассмотрим
простой пример.
Пусть Т (х)— стационарное температурное поле плоской пластины 0
толщина которой много меньше по сравнению с наименьшей протяженностью
поверхностей, на которых заданы равномерные, но не равные между собой тем¬
пературы: 7^ (0) = 7^!; Т(1) = Т2 (Т{>Т2)- Найдем температурное поле пластины
Т (х) как решение краевой задачи
d277dx2 = 0, 0 <*</; Т(0) = Ти Т{1) = Т2. (2.93)
Интегрируя это несложное уравнение, получим
Т (дг) = 7"! — (7"! — Т2) (х/1). (2.94)
Температура пластины, как видно из (2.94), зависит от четырех определяю¬
щих параметров Т = Т (х, I, Ти Т2). Однако (2.94) легко преобразовать в выра¬
жение вида
[Тх — Т (х)]/(Г1-Г2)=х//. (2.95)
Если теперь ввести вместо независимой переменной х новую (безразмерную)
переменную г = х/1, а вместо искомой температуры пластины Т (х) новую (безраз¬
мерную) функцию W (z) = ITi — Т (х)]1(Т\ — Г2), то (2.95) примет вид W(z)=z,
при этом 0 W (z) 1.
Преимущества безразмерной температурной функции W (z) по срав¬
нению с первоначальной (2.92) Т=Т(х, /, Ти Т2) очевидны. Действи¬
тельно, вместо пяти размерных величин в данном случае оказываются
только две — безразмерная температура и безразмерная координата.
Количественное соотношение между ними — соотношение прямой
пропорциональной зависимости — является совершенно универсаль¬
ным, т. е. присуще искомому множеству явлений, а именно: плоским
пластинам любых толщин, при любых температурах на поверхностях,
для любого материала, из которого сделана пластина (дерево, железо,
камень, стекло), лишь бы процесс теплопроводности был стационарным
и. одномерным.
Как отмечалось, для установления безразмерных величин, специ¬
фических для данной краевой задачи, нет необходимости в наличии
ее аналитического решения; достаточно располагать уравнением теп
лопроводности и соответствующими для него краевыми условиями.
Рассмотрим уравнение (1.33) с внутренним (постоянным) истом
90
ником теплоты, удельная мощность которого равна ^(Вт/м3):
дТ/dt = а (д2Т/дх2 + д2Т/ду2 + д2Т/дг2) + qv/(cp). (2.96)
Заметим, что в (2.96) температура входит под знаком производной,
поэтому ее можно отсчитывать от любого постоянного значения,
например от начальной температуры Г0 (если она имеет постоянное
значение). Если помимо постоянной начальной температуры в усло¬
вие задачи входит еще другая постоянная температура, например
температура среды Тс, то за масштабную разность температур
естественно принять (Т0 — Тс) или (Тс — Т0). Тогда безразмерная
температура определится выражением W = (T — Т0)/(ГС — Т0). Урав¬
нение (2.96), которое можно переписать следующим образом:
теперь запишем в виде
™ = W М_\ (2 97)
dt а\ дх2 ^ ду2 ^ дг2 / ф (Тс — Т0)'
Для приведения к безразмерному виду независимых переменных
(х, у, z) в качестве линейного масштаба выберем характерный раз¬
мер рассматриваемого тела, например размер /0, и введем новые
переменные
х' = х//0; y’=y/l0\ г' — zJlQ. (2.98)
По правилу дифференцирования сложной функции,
dW/dx = (dW/dx') (dx'/dx) = (1//0) (dW/dx'y,
d2W/dx2 = (l/ll) (d2W/dx,%) и т. д.
Подставим новые переменные в уравнение (2.97)
dW _ а / d2W d2W d2W \ qv
М “ ll V дх'2 + dy'2 + dz'2 ) Ф(ГС-Г0)
или
dW = d2W . d2W d2W ЯуЧ (<2qq
d(atHl) dx'2 ^ dy'2 dz'2 ^ X(TC-T0)' [ ' ]
В уравнении (2.99) выражения at III и qJl/[k(Tc — TQj] являются
безразмерными; первое из них называют числом Фурье F0 = at/ll\
второе же обозначим через Qv = qvlo/[h(Tc—Т0)].
Число Фурье заняло в дифференциальном уравнении (2.99) место
времени и может рассматриваться как безразмерное время.
Оно характеризует протекание процесса во времени и является
независимой переменной. Безразмерный комплекс Qv является пара¬
метром, так как предполагается, что в условии задачи Тс и Т0
заданы (вообще параметром будем называть безразмерный комплексу
в котором все размерные составляющие считаются заданными по
условию задачи).
91
Окончательно, уравнение (2.99) в безраз!мерном виде запишется
следующим образом:
dW_ _ . q 2]00
dFo dx'* + Qy* + d2’* 1
где
W(x', y', z‘, Fo) = [T(*, y, z, t) — Tv\/{Tt — T0). (2.101)
Заметим, что если нестационарный процесс периодический, то
в качестве масштаба времени можно взять продолжительность од¬
ного периода /пер. Тогда безразмерное время, отсчитываемое от
начала периода, можно выразить / = ///пер, a Fo — а/пер//о и в этом
случае этот комплекс становится уже параметром задачи. В апе
риодическом процессе теплопроводности не существует характерного
промежутка времени, имеющего смысл естественной масштабной
единицы, поэтому в такого рода процессах в качестве безразмер¬
ного переменного времени и выбирается число Фурье Vo = at/II.
Для стационарного процесса гз уравнение теплопроводности
д2Т/дх2 + д2Т/ду2 + д2Т/дг2 + qv/X = 0 (2.102)
начальная температура Т0 не входит в условие задачи и критерий
Qv использован быть не может. За начало отсчета температуры
тела может служить температура среды, в качестве масштаба тем¬
пературы можно использовать параметр qJl/K, имеющий размер¬
ность температуры. Таким образом, в случае (2.102) вводим размер
ные переменные по формулам (2.98) и безразмерную температуру
по формуле
W(x\ у\ г') = [Т(х, у% г)—Тc]/(qvll/X). (2.103)
Уравнение (2.102) в новых переменных имеет вид
д 2Wtdx'2 + d2W/dy'z + д 2Wldz'2 +1=0. (2.104)
Заметим следующее: подстановка (2.101) для уравнения (2.96)
введена при условии постоянной начальной температуры. Если
начальная температура тела переменная, то безразмерная темпера¬
тура- может быть введена и для нестационарного процесса с помощью
подстановки (2.103). Например, рассмотрим краевую задачу
{х> у’ г)€°’ t>0; (2Л05'
т (*, у, г, 0) = Ф0(Х, У, г), (ху Уу z)gG; (2.106)
(дТ/дп) \Si = -h(T\Sl-Tc)y t > 0; (2.107)
— А, (дТ/дп) \Si = q9 t > 0; (2.108)
Q= const, q = const, Tc = const, S = Si+S2.
Запишем (2.105) —(2.108) в безразмерных переменных. Введем последовательно:
1 х'=х/10у yf = у!Iq\ г =z//0; Fo = a*//jj; 2) W (x'f y't г', Fo) = [r(*, y} z, t)—
-Tc]/(Ql$-i).
Уравнение (2.105) запишется в виде
dW d2W , d2W , d2W
Начальное условие (2.106) имеет вид
№(*', У’, 2'. Fo)|fo-o = ®0(*', У', г'), (х', у', z')£G\ (2.110)
где
ф,', (*\ у'< *') = №<>(•*. у, г)—T’cl/(QioA)> (0'=o/W-
Граничное условие (2.107) преобразуется следующим образом. Обозначив через
/г' = /г//0 и записав (2.107) в виде
(дГГ-Ге. 1 =_h\J~T с 1
W QW . к . W к
найдем, учитывая, что д/дп — {д/дп') {дп'/дп) = (1//0) (д/дп'),
1 cWI MV71
—j 5—г с ' = — Л lv к ' ИЛИ -3-7-
/0 pi ^
В граничном условии появился еще один безразмерный параметр — число Био
Bi—hl0 или Bi=a/0A. Таким образом, граничное условие (2.107) в безразмерных
переменных окончательно имеет следующий вид:
61 "'к- вЛ|"
Аналогичным образом преобразуем граничное условие (2.108). Перепишем
его в виде
( д [Т{х, у, z, 0 — I _ №А)к
\дп' [ qw J/s; *
откуда получим
где qi=q/Ql0 — безразмерная величина.
Сравним между собой решения краевых задач (2.105) — (2.108)
и (2.109) — (2.112) в случае, когда область G, например параллелепипед
0<х</о, O^Q/^/i, 0^г^/2. Для задачи (2.105) — (2.108) решение
Т(х, у, z, t) есть функция, зависящая от следующих переменных и па¬
раметров:
Т=Т(х, у, z, U Тс, Q, q, К с# р, а, /0, /ь /2). (2.113)
Для решения W(x', у\ 2', Fo) задачи (2.109) — (2.112) можно
записать
W=W(x'y у\ 2', Fo, Bi, qu IJU, /2//0). (2.114)
Если сравнить выражение (2.113) с (2.114), то видно, что последнее
содержит значительно меньше определяющих параметров. Если в
решение задачи (2.105) — (2.108) параметры с, р, X, /0, /ь /2, а, 7С,
qt Q входили как отдельные величины, каждая из которых по-своему
влияла на температурное поле 7\ то в решение задачи (2.109) — (2.112)
эти величины входят в состав немногих комплексов Fo, Bi, qly lJlQy
IJIq и безразмерная температура определяется лишь восемью без¬
размерными независимыми переменными и параметрами против четыр¬
надцати для размерной температуры. При этом важно изменение самих
безразмерных комплексов и не имеет значения, как изменяются сами
93
размерные величины, из которых составлены эти комплексы. Таким
образом, если найдено аналитическое решение задачи (2.109) — (2.112),
то полуденный результат автоматически распространяется на бесчис¬
ленное множество тепловых явлений, которые объединяются в одну
группу вместе с исходным (2.109) — (2.112) при выполнении ряда тре¬
бований, заключающихся в том, чтобы одинаковым значениям безраз¬
мерных величин действительно отвечали подобные явления. Для этого
необходимо: а) геометрическое подобие тел; б) подобие их физической
структуры; в) подобие начальных состояний; г) подобие граничных
условий, т. е. условий теплового взаимодействия тела на граничных
поверхностях с окружающей средой.
Безразмерные комплексы, появляющиеся при переводе исходной
краевой задачи теплопроводности к безразмерному виду, конструиру¬
ются на основе соответствующих аналитических зависимостей, имею¬
щих место в математической модели процесса. Следует отметить, что
способ их образования при этом не единственный и одна и та же исход¬
ная задача может иметь различное представление в безразмерном виде.
Все зависит от содержания конкретной задачи, от той цели, которая
ставится перед ее решением.
Рассмотрим в качестве примера задачу на нагревание конечного сплошного
цилиндра О^г < R, с постоянной температурой Г0, помещенного
в среду с постоянной температурой Тс (Тс > Т0). На поверхностях r = R, z — 0
выполняется закон теплообмена Ньютона; на поверхности z = / задан тепловой
поток ^ = const; во внутренних точках тела имеется тепловой источник, выделяю¬
щий в единице объема в единицу времени количество теплоты Q= const; предпо¬
лагается также, что твердое тело движется с постоянной скоростью в направле¬
нии оси z. Запишем соответствующую краевую задачу теплопроводности (имея
в виду осевую симметрию процесса):
'+£
дТ { дЧ , \ дТ . дЧ \ дТ
dt ~а \ дг3 г дг dz2 J V dz
0<r < R, 0 < z < /, t > 0; (2.115)
T\tmо=П; -|£-|f=R=—M7’lr=/?—т’с); IT(r, z, oi< + co, r^o- (2.lie)
(dT/dz)z=o = h (T |г_0 — Tc); -X(dT/dr)z=l = q. (2.117)
Вводим безразмерные переменные: r' =^r/R\ z' = zJR\Fo = at/R2; W (r',z't Fo) =
= (Tc — T)l(Tc—Го).
Преобразуем вначале уравнение (2,115)
dW лп7/ , / с x *>R dW , QR2
= \W(r\ z't Fo)—— “згг + тТт1 т~\ • (2118)
dFo v, , , w a dz, -r X(Tc_Tq) •
В правой части уравнения (2.118) выделились два безразмерных комплекса
и0 = 1)Rla и Q'v = Q#2/[X (Тс — Т0)]. В процессе преобразования граничных усло¬
вий (2.116) и (2.117) выделяются еще два безразмерных комплекса: число Bi —hR
и q'v = qRl{K(TQ — Т0)]. Окончательно получим следующее представление задачи
(2.115) —(2.117) в безразмерном виде:
dWidFo = bW {r't z*, Fo) — v0 (5 W/dz') + Q'v,
0 <,r' < 1, 0 < z' < l/R; Fo > 0; (2.119)
U?|fo = o= 1; dWfdr' |r,= l=-Bi W \г,_л\ (2.120)
dWldz' |2- = „ = Bi W |z.= 0; dWldz’\2,^:R = -q'v-,
W (r, z', Fo)/< + oc, r' 5= 0. (2.121)
94
Как видно из задачи, tF=tt7(r', г', Fo, v0, Q'v, Bi, q' , l/R).
Рассмотрим еще одну безразмерную форму задачи (2.115) — (2.117). Введем,
как и выше, безразмерные переменные л', z', Fo и безразмерную температуру
вида W (г', г', Fo) = (rc — T)/(QR*/X). Преобразуя исходную задачу, получим:
dW/dFo = Д W7 (г', г', Fo) — v0(dW/d2') + l,
О < 1, 0 < z' < ///?, Fo > 0;
tf|Fo-o“ W. dW'dr' = , =—Bi V^|r. = 1.
dW!dz' |z' = 0 = Bi W\z' = o’> |г' = //Я = Я1*
lQi = q/(RQ)]\ I W(r', z', Fo) | < + oo, r'^0.
Решение этой задачи зависит от следующих переменных и па¬
раметров:
W = W(r\ г', Fo, b0f Qv, Bi, ql9 l/R).
§ 5. КОРРЕКТНОСТЬ ПОСТАНОВОК КРАЕВЫХ ЗАДАЧ
Выше отмечалось, что постановка краевых задач теплопроводности
содержит некоторые (краевые) функции, входящие в начальное и
граничные условия задачи. Очевидно, что решение задачи также зави¬
сит от этих функций, так как распределение температуры в теле в
конечном счете определяется его начальной температурой, тепловым
состоянием граничной поверхности тела (граничные функции) и на¬
личием в теле тепловых источников (или ctokqb). Краевые функции
задачи обычно определяются из опыта и поэтому не могут быть найде¬
ны абсолютно точно. Всегда неизбежна некоторая погрешность в
определении начальных или граничных условий. Эта погрешность
будет сказываться и на решении задачи, а так как краевая задача опи¬
сывает реальный физический процесс, то решение этой задачи должно
характеризоваться функциями, непрерывно зависящими
от краевых функций задачи. Если бы не было этой
непрерывной зависимости, то два существенно различных процесса
теплопроводности могли бы соответствовать практически одинаковым
системам краевых функций задачи (различие которых лежит в пре¬
делах точности измерений), т. е. решение задачи существенно зависело
бы от погрешностей измерения. В этом случае процесс теплопроводнос¬
ти (как, впрочем, и любой другой процесс, описываемый соответству¬
ющими краевыми задачами) нельзя было бы считать физически опре¬
деленным такими исходными данными задачи.
Решение той или иной краевой задачи для какого-либо дифферен¬
циального уравнения или системы уравнений является у с т о й-
ч и в ы м (относительно краевых функций задачи) или непрерывно
зависит от краевых условий, если каким бы ни было положительным
число е, найдется положительное число б, когда при изменении крае¬
вых функций задачи на величину, не превосходящую по абсолютному
значению числа б, решение получает в каждой точке рассматриваемой
области и ее границы приращение, по абсолютной величине не превос¬
ходящее е. В этом случае соответствующий процесс называется физи¬
чески определенным. •
95
Краевая задача для какого-либо уравнения или системы уравнений
в рассматриваемой области поставлена корректно, если
решение этой краевой задачи в указанной области существует,
единственно и является устойчивы м.
Приведем пример некорректной постановки задачи. Как показал
Адамар, задача Коши для уравнения Лапласа д2Т/дх2-{-д2Т/ду2=0 в
области |х|<Соо, 0<г/<1, при условиях Т(ху 0) = 1; дТ(х, 0)idy = (l/k) х
X sin kx поставлена некорректно. Действительно, решение этой задачи
есть Т(х, y) = (\/k2) sh kysin kx. При k-+oo краевая функция
(Mk) sin равномерна относительно x; однако решение задачи в
указанной области прил^тя (т=0, ±1, ±2, ...) не стремится к нулю,
т. е. (l/k2) sh kysin кхфО при хфтп и &->оо.
Если поставленная краевая задача теплопроводности имеет не¬
сколько решений, то слова «решение задачи» теряют смысл. Поэтому
прежде чем говорить о решении задачи, необходимо доказать его
единственность. Мы покажем ниже, что решение каждой из поставлен¬
ных краевых задач единственно. Для практики наиболее существенным
является вопрос 2), так как нахождение решения тем или иным ана¬
литическим методом фактически означает доказательство существова¬
ния решения. Нахождению решений разнообразных краевых задач
теплопроводности, собственно, и посвящена эта книга. Что касается
устойчивости решения краевой задачи, то, как будет показано, процесс
распространения теплоты физически определяется своими начальной
функцией Ф0(Л4), граничными функциями ф(М, t) и функцией теплово¬
го источника /(М, t) в правой части уравнения теплопроводности.
Перейдем к рассмотрению вопроса единственности решения краевых
задач (2.34) — (2.38), записав их для краткости в следующем виде:
dT/dt =аАТ (М, t) + f(M, t), М £ G, / > 0; (2.122)
Т(М, 0|/-о=Ф0(М). MeG( = G + S)- (2.123)
$,[дТ(М, /)/<?п]—р2Г(М, t) = — <p(M, t), M£S, />0, (2.124)
где Р1 + Р2 > 0.
Если Pi = 0, Р2 = 1» то имеем первую краевую задачу; если
Р2 = 0, р! = ^ (I—теплопроводность), имеем вторую краевую задачу;
если pt = — X, Р2 = а[ф(Д4, t) = aТср, а—коэффициент теплоотдачи],
имеем третью краевую задачу.
Пусть Tt(M, t) и Т2(М, t)—два различных решения задачи
(2.122) —(2.124) и U (М, t) = T1 — Т2. Функция U (М, t) является
решением однородной задачи
dU/dt =а (Му /), M^G, t> 0; (2.125)
(/(М, 0) = 0, M€G; [?>AdU/dn)-P2U]Mts = Q, 0. (2.126)
Рассмотрим интеграл
•/(о=тШ(/,(Л1,
96
имеем
<2127)
G G
Запишем формулу Остроградского
$$$div[£(M, 0]dK=5j£-«dCT (2.128)
G S
и положим в ней E=UyU. Так как
div (U VU) = U div VU + (\Uy = U VU + (VU)\ ttVU = dU/dn, (2.129)
то получим из (2.127), (2.128), (2.129)
4f4Sw|>-‘1.ro<Wdl'- (2.130)
S G
Из (2.130) находим для первой и второй краевых задач, учиты-
вая, что t/|5 = 0 или (dU/dn) |5 = 0,
4f-=-»SW<Wdl/'
G
В случае третьей краевой задачи в (2.124) должно быть
— ХдТ/дп = а [Т — Тср]; отсюда имеем для U (М, /);
dUldn = — (a/X)U, M£S, t^O
и
S G
Для всех трех краевых задач 0. Это означает, что J (t)
все время убывает. Но У (0) = 0, следовательно, J(t)^ 0. Однако
согласно определению, J (0^0. Единственным выходом из этого
противоречия является J (t) = 0, а значит, и U (/) = 0, т. е. Тх = Т2.
Таким образом, решение каждой из трех краевых задач_ в классе
функций, непрерывно дифференцируемых в области един¬
ственно.
Такой же вывод получается для двумерных краевых задач в
классе функций, удовлетворяющих условиям применимости формулы
Грина (см.: Фихтенгольц Г. М. Курс дифференциального и ин¬
тегрального исчисления, т. 3. Наука, 1969). Для этого достаточно,
пользуясь формулой Грина, рассмотреть интеграл ./ = (1/2) U2\[x,
G
у, t)do. В случае одномерных краевых задач следует рассмотреть
i
интеграл J = (1/2) {j U (х, /) dx. Несколько сложнее доказать един-
о
ственность решения для краевых задач обобщенного типа. Впрочем,
4-339 97
для первой краевой задачи
Т(х, 0) = Ф0(х), 0<*<</(0);
Т(0, t) = (Pi(t)> т[{/(0> *] = Ф*(0*
можно по-прежнему рассмотреть интеграл
У И)
J (0 = у j* иг(х> Od*-
о
Так как
«и.. 4+Tut**—<
то опять приходим к утверждению, что Т1 = Т2.
В случае второй или третьей краевой задачи обобщенного вида
доказательство единственности решения меняется. Действительно,
рассмотрим для определенности третью краевую задачу:
dTidt=a(d*Tidx2) + f{x> /), 0 <x<y(t), 0 'j
Т(х, 0)=ФДдс), 0<*<i/(0) = #0; I
а7'/^|яии = л1[Г|,ж,-ф1(0]. t>b f K }
dT/dx\x=uit) = -h2[T\x=u(t) — ф2(<)]. t> 0 J
и докажем единственность ее решения. Пусть по-прежнему функция
U (х, /) = Т,(х, t) — Т 2(х, t) является решением однородной задачи
для (2.131). Используя формулу
div рЕ = pdiv £-f £V/7, (2.132)
положим в ней p = U(x, /), £ = grad{/(x, 0» тогда получим
(У div (grad (У) = div (U grad U) — (VU)2.
Проинтегрируем обе-части этого равенства по области 0 ^x^y(t)
у ф y(t) y{t)
0 0 о
или
У (О УФ y(t)
0 0 0
Используя однородные граничные условия для (У, получим
уф y(t)
J -£-(l/*)d* =-2а [МУ* (*,(/), П+^иц0, Oj-e J (4г)2(1л:-
и о
(2.133)
Проинтегрируем равенство (2.133) по t на промежутке [0, С]>
где 0 < t"0 ^ /0 — некоторое произвольное значение t. Получим,
98
учитывая, что (л:, 0) = 0:
У (О Г *о
j U*(x,t;)dx = —2a h2§ и* ({/((), t)dt +
о L о
fo 1 *0 у (О
+ ft1>’(0, 0 dt -fl J j (^ydxdt.
О J о о
Так как правая часть неположительна, а левая — неотрицательна,
то отсюда следует, что
y(t)
J U2(x, /J)dx = 0,
о
откуда U(х, t*0) = 0 для произвольного t*0 > 0, т. е. Тг (х, t) == Т2 (х} t).
Подобным образом можно было бы рассмотреть единственность
решения краевых задач с граничными условиями сопряжения,
а также и сложные случаи граничных условий.
Желающих ознакомиться с более общими теоремами существования
и единственности решения краевых задач уравнения теплопроводности
с гладкими и разрывными коэффициентами (система сред), имеющего
достаточно общую форму записи, можно отослать к специальной лите¬
ратуре [81, 82, 126, 147]. Мы не останавливаемся также на вопросах
непрерывной зависимости решения одномерных краевых задач тепло¬
проводности обобщенного типа от границы, т. е. от изменения кривой
x=y(t) (0^^/о), задающей боковую границу. Эти вопросы для урав¬
нения теплопроводности с гладкими и разрывными коэффициентами
рассматриваются в работе [52].
Заметим далее следующее. В постановке задачи (2.122) — (2.124)
предлагается выполнение условий согласования начальной и
граничной функций и непрерывность краевых функций задачи. Этим
самым автоматически определяется класс функций Т(М, /), для кото¬
рых справедлива теорема единственности. Можно, однако, отказаться
от выполнения этих условий и сформулировать теорему единственно¬
сти при более слабых предположениях. Так, например, для случая
кусочно-непрерывных, не сопряженных на¬
чальной функции Ф0(М) и граничной ф(М, /) в
первой краевой задаче
dT/dt = aAT(M,t), Mg 0, * > 0; (2.134)
Г(Л1, 0) = Ф0(М), М £ G; Т{М9 /) = ф(М, 0. / >0(2.135)
функция Т (М, /), удовлетворяющая (2.134) — (2.135), определяется
однозначно начальной и граничной функциями, если: а) Т (М, t)
непрерывна в точках непрерывности функций Ф0(М) и ф(М, /);
б) Т (М, t) ограничена в замкнутой области Q(MgG, 0^/^/0),
где /0—произвольное положительное число.
Перейдем к рассмотрению единственности решения краевых задач
стационарной теплопроводности. Рассмотрим сначала внутренние
краевые задачи для конечных областей (для определенности про¬
99
цесса нагревания для второй и третьей краевых задач)
ДГ (Af) + (1 A) F (М) = О, М € G; (2.136)
pjarowj/dn] —р2Г(М) = — ф(М), m^s. (2.137)
Справедлива следующая теорема: решение первой и третьей
внутренних задач (2.136) — (2.137) единственно в классе функций Т (М)
непрерывных в G + S ( = G) вместе с частными производными первого
порядка по координатам точки М.
Пусть Тt(M) и Т2(М)—два различных решения задачи (2.136) —
(2.137) и 0 (М) = ТХ — Г2, где U (М) удовлетворяет однородным
уравнениям Д£/ = 0 в G и ^^dU/dn)—13 (/ = 0 на S. Покажем, что
U = 0.
Для доказательства положим в формуле (2.132) E = VU и p = U,
тогда [см. (2.129)]
U AU == div (UvU)-(vU)*. (2.138)
Проинтегрируем обе части этого равенства по области G и восполь¬
зуемся формулой Остроградского для первого интеграла в правой
части равенства. В результате получим
Ш('АУ“к=П1'^МП(ти)’111'' <2|39)
G 3 G
Так как в GMJ — 0, а на S выполняются однородные условия
первой, второй или третьей краевых задач, то из формулы (2.139)
получаем в случае первой (и второй) краевой задачи
5$$(Vt/)W = 0 (2.140)
G
и в случае третьей краевой задачи
55 J(Vt/)*dK + (oA) 55 и*йо = 0. (2.141)
G S
Из этого вытекает, что в G градиент равен нулю 4U = 0, откуда
следует, что U (М) — const в G. А так как решение U (М) непре¬
рывно в замкнутой области G и t/(A4) = 0, MgS, то всюду в G
выполняется U (М) = 0, т. е. Т1 = Т2.
В случае третьей краевой задачи из (2.141) следует, что каждый
интеграл равен нулю, откуда £/(М)е=0 в G и Тг = Т2.
Для второй краевой задачи (задачи Неймана) из (2.141) выте¬
кает следствие: решение внутренней задачи Неймана определяется
с точностью до произвольной постоянной. Действительно, из (2.139)
следует, что yU == 0, М £ G или U (М) = const, т. е. 7\(М) =
==Г2(М) + const. К задаче Неймана обычно приводят физические
проблемы, для которых появление постоянного слагаемою в реше¬
нии либо несущественно (если выбор начала отсчета значений
функции может быть произвольным), либо это постоянное слагаемое
определяется из дополнительных требований к поведению функций Т
на границе. Остановимся сейчас на этом вопросе и одновременно
100
получим условие существования решения внутренней краевой задачи
Неймана.
В формуле (2.132) положим вначале p=U(M), £ = grad Т (М),
а затем р = Т (УИ), E = gradU (М) и проинтегрируем обе части этого
равенства по области G, преобразуя затем по формуле Остроград¬
ского интеграл в левой части равенства. Получим в обоих случаях:
G S G
Вычитая из верхнего равенства нижнее, получим формулу
Грина для оператора Лапласа:
Щ(идг_гдс/,ак=^(«4|-г »)<!,, ,2.142)
G S
Положим теперь в формуле (2.142) U = —1, а в качестве Т (М)
возьмем решение уравнения стационарной теплопроводности (2.136),
непрерывное вместе с частными производными первого порядка
в (G + S):
<2N3>
S G
Рассмотрим теперь’внутреннюю задачу Неймана: —ХдТ (М)/дп =
= ф(М), MgS. При произвольных функциях ф(М) и F (М) (даже
непрерывных) вторая краевая задача может не иметь решения. Так
как на поверхности S известно значение дТ/дп, то для разреши¬
мости задачи Неймана должно выполняться условие (2.143) или
$5<p(M)da=$$$/:’(M)dV. (2.144)
S G
Легко понять физический смысл соотношения (2.144). Для существо¬
вания решения второй краевой задачи уравнения Пуассона в огра¬
ниченной области G(=G+S) при стационарной теплопроводности не¬
обходимо, чтобы количество теплоты, образующееся в области G за
время М от действия внутренних источников теплоты, было равно
суммарному тепловому потоку, уходящему через границу области
S за тот же промежуток времени.
В частности, если F(M)=0, то из (2.143) найдем условие существо¬
вания решения второй краевой задачи для уравнения Лапласа
(2.145)
S S
Заметим, что для первой краевой задачи единственность решения
справедлива при непрерывности решения в G, но не требуется непрерыв¬
ности его первых частных производных в замкнутой области.
Часто встречается также первая краевая задача с разрывными гра¬
ничными условиями. Очевидно, функция, непрерывная в замкнутой об¬
101
ласти G, не может быть решением этой задачи, поэтому выше была
уточнена постановка краевых задач применительно к данному случаю.
Можно показать [137], что если функция Т(М) удовлетворяет в области
G уравнению Лапласа ДГ=0, непрерывно примыкает к граничным
значениям в точках непрерывности кусочно-непрерывной граничной
функции ц>(М) = Т(М)\м€>s и ограничена в замкнутой области Gy
то решение первой краевой задачи единственно.
Что касается задачи Неймана, то здесь также имеется доказательст¬
во единственности решения при наиболее общих предположениях,
накладываемых на краевые функции задачи (см.: К е л д ы ш М. В.
и Лаврентьев М. А. ДАН СССР, т. XVI, 1937; Смир¬
нов В. И. Курс высшей математики, т. IV. Физматгиз, 1958).
Для единственности решения внешних краевых задач стационар¬
ной теплопроводности от рассматриваемых решений нужно требовать
выполнения специальных условий на бесконечности. Действительно,
если решать первую внешнюю краевую задачу в пространстве, огра¬
ниченном изнутри сферой радиуса R с постоянным граничным условием
T(R) = T0y то, опуская условие равенства нулю решения на бесконеч¬
ности, можно получить серию различных решений Тг (г) = Т0\ Т2(г) =
= T0Rlr, решением является также и любая функция Т (r)=CiTi(r)+
Л-с2Т2 (г)у где Сх и с2 — произвольные постоянные; Ci+c,= l.
Приведем одну из теорем единственности решения внешних крае¬
вых задач.
Функцию Т (М), определенную в области G*, внешней по отно¬
шению к замкнутой поверхности S, ограничивающей область £/,
будем называть регулярной на бесконечности, если при стремлении
точки М к бесконечности сама она стремится к нулю как сх/гмм^
а ее частные производные первого порядка стремятся к нулю как
с2/г2мм0- Здесь сх и с2—некоторые постоянные величины, а гМм0—
расстояние от точки М до некоторой фиксированной точки
М0(гМм, = У(х—Х0)г + (у—Уо)г + (г—г0)г. Справедлива теорема (для
трехмерного пространства): решение внешней краевой задачи
AT(M) + (l/X)F(M) = 0, M€G»; (2.146)
р.ГаГ (М)/дл1—Р,Г(М) = — ф(М), М g S; lim Т(М) = 0, (2.147)
М -► 00
непрерывное в замкнутой области G * вместе с частными производными
первого порядка и регулярное на бесконечности, единственно.
Заметим, что для двумерных краевых задач достаточно потребовать,
чтобы искомое решение было ограниченным на бесконечности, а частные
производные первого порядка равномерно стремились к нулю, как
const/r^Av Условие (2.145) сохраняет свою силу и во внешней
задаче.
При доказательстве единственности первой краевой задачи ис¬
пользовался тот же прием, что и при доказательствах для второй и
третьей краевых задач. Это было вызвано целесообразностью единства
рассуждений. Однако в случае первой краевой задачи предполагалось
102
существование производных искомой функции на поверхности S,
что, вообще говоря, самой постановкой задачи не предусматривается.
Доказательство единственности решения первой краевой задачи, ос¬
нованное на принципе максимального значения [137], свободно от этих
недостатков. Заметим также следующее: рассматривая условия един¬
ственности решения краевых задач нестационарной и стационарной
теплопроводности, предполагалось, что эти решения существуют. До¬
казательство существования решений краевых задач теплопроводности
представляет собой весьма сложную математическую проблему, кото¬
рая требует развития специального математического аппарата, далеко
выходящего за рамки аналитических методов, которые обычно приме¬
няются при нахождении соответствующих температурных полей. Впро¬
чем, как отмечалось, одним из возможных приемов доказательства
существования решения краевой задачи является его непосредственное
нахождение. Отметим также, что аналитическая структура решений
краевых задач нестационарной теплопроводности такова, что эти
решения существуют, когда краевые функции задачи являются не
слишком гладкими; иными словами, в результате применения опреде¬
ленных операций в аналитическом решении задачи происходит сгла¬
живание разрывов краевых функций и сами решения оказываются
достаточно гладкими. В то же время для уравнения стационарной теп¬
лопроводности аналитические решения краевых задач существуют толь¬
ко тогда, когда краевые функции задачи являются достаточно глад¬
кими; это обстоятельство практически не является слишком ограничи¬
тельным при постановке краевых задач, так как любое граничное
условие процесса теплопроводности с определенным физическим смыс¬
лом можно аппроксимировать сколь угодно точно достаточно гладкими
функциями, и это приближение будет иметь тот же физический смысл,
что и исходное условие. При этом сами решения всегда оказываются
не менее гладкими (в смысле существования у них определенного числа
непрерывных производных), чем определяющие их краевые функции.
Обычно во внутренних точках области определения дифференциального
уравнения теплопроводности они даже дифференцируемьинеограничен-
ное число раз. Это свойство решений тесно связано с тем, что к крае¬
вым задачам уравнения Лапласа или Пуассона приводит изучение ус¬
тановившегося (стационарного) процесса теплопроводности — про¬
цесса равновесного, являющегося конечным результатом предшеству¬
ющего процесса выравнивания. Из физических соображений можно
заключить, что при этом не только решение задачи, но и граничные
функции, достаточно точно передающие природу явления, будут весьма
гладкими.'
Сформулируем далее несколько теорем, относящихся к свойствам
решений краевых задач нестационарной и стационарной теплопровод¬
ности.
Теорема I. Если в уравнении (2.122) функции /(М, 0^0, то
всякое решение этого уравнения, принадлежащее классу функций
С2(Q) р|С° (Q), достигает своего наибольшего значения либо в началь¬
ный момент времени (т. е. в точках области G), либо на боковой поверх¬
ности Sb (при 0<*</„).
103
Теорема II. Пусть f(M, t)^0. Тогда всякое решение уравне¬
ния (2.122), непрерывное в замкнутой области П, достигает своего на¬
именьшего значения или в начальный момент времени (т. е. в точках
области G+S), или в точках задания граничных условий задачи
(т. е. на границе S при 0
Нетрудно сформулировать физический смысл этой теоремы. Если
тело подогревается внутренними положительными источниками тепло¬
ты, то, естественно, оно должно иметь наименьшую температуру или
во внутренних его точках в начальный момент времени, или на его
границе во все последующие промежутки времени.
Теорема III (принцип максимального значения). Решение
однородного уравнения (2.122), непрерывное вплоть до границы в зам¬
кнутой цилиндрической или нецилиндрической области П, принимает
свои наибольшие и наименьшие значения или в основании этой облас¬
ти G (при /=0), или на боковой поверхности SB области Q (при
0</</0).
Переходя далее к теореме о максимуме и минимуме для уравнения
стационарной теплопроводности (1.35), напомним, что непрерывные
решения уравнения Лапласа (1.35) называются гармоническими функ¬
циями.
Теорема IV. Функция Т(х, уу z), гармоническая в конечной
области G, ограниченной замкнутой поверхностью S, и непрерывная
в G=G+S, не имеет внутри этой области ни максимумов, ни миниму¬
мов, достигая своих наибольшего и наименьшего значений на границе
S.
Для уравнения Пуассона (2.136) — уравнения стационарной теп¬
лопроводности с источником или стоком теплоты — имеет место сле¬
дующее общее свойство, которым обладают решения этого уравнения.
Теорема V. Если в уравнении (2.136) функция F (М) удовлет¬
воряет неравенству F(М)>0 (источник теплоты) всюду в области оп-
пределения этого уравнения G, то решение Т(М) уравнения (2.136)
не может достигать минимального значения во внутренних точках об¬
ласти G.
Аналогичным образом, если /ДМХО (сток теплоты) всюду в облас¬
ти G, то решение Т(М) уравнения (2.136) не может достигать макси¬
мального значения во внутренних точках в области G.
В более общей форме принцип максимального значения находит
свое выражение в оценках решения Т(М, t) и Т(М) через соответству¬
ющие оценки краевых функций задачи.
Эта часть качественной теории дифференциальных уравнений пара¬
болического типа имеет важное значение для практики (например,
для установления границ изменения термоупругих напряжений),
так как позволяет установить нижнюю и верхнюю границы изменения
температурного поля, не решая соответствующей краевой задачи
теплопроводности. Желающие могут ознакомиться с этими вопросами,
подробно изложенными в монографиях [81], [82] и работе [52].
В заключение остановимся на уравнении стационарной теплопро¬
водности в движущейся среде, имея в виду его многочисленные при¬
104
ложения и некоторые качественные особенности решений соответству¬
ющих краевых задач для этого уравнения.
Полученное в гл. I уравнение нестационарной теплопроводности в
движущейся среде (1.80) запишем в следующем виде:
Ф (дТ/dt + v grad Т) = ХАТ (М, t) + F (М, t). (2.148)
Для постоянных компонентов вектора скорости v это уравнение не¬
сложными подстановками приводится к виду (2.122) и поэтому вопросы
единственности решения краевых задач уравнения (2.148) можно рас¬
сматривать, как для уравнения (2.122). Что же касается уравнения
стационарной теплопроводности в движущейся среде
аАТ (М) — tfgrad Т + —F(M) = 0, (2.149)
ср
то здесь не удается с помощью какой-либо подстановки привести урав¬
нение (2.149) к виду (2.136). В то же время наличие второго слагаемого
в левой части уравнения (2.149) вносит свои существенные коррективы
в вопросы единственности решения соответствующих краевых задач,
которые следует иметь в виду при исходной постановке задачи.
Прежде всего преобразуем уравнение (2.149) с помощью подста¬
новки Т (M) = U (M)tx\)[{\l2a)(xvx-\-yvq +zvz), где vx, vyJ ^ — ком¬
поненты вектора скорости v, которые предполагаются постоянными.
Получим
AU (М) — c2U (М) = —0 (М), (2.150)
где с2 = + (1 /4а) | v |2; 0 (М) = (1/ф) /ДА^хехр [(—1/2a)rv]\ r = xi-\-
+ yj+zk.
Рассмотрим однородное уравнение
AU (М) — c2U (М) = 0, M$G. (2.151)
Для уравнения (2.151) или (2.150) краевые 'задачи ставятся так же,
как и для уравнения Лапласа (или уравнения Пуассона). Однако свой¬
ства решения уравнения (2.151) существенно зависят от того, какой
знак стоит в левой части перед функцией U. Для уравнения (2.151)
имеет место принцип максимального значения в следующей форме:
решение U(М) уравнения (2.151), определенное внутри области G
с границей S, не может достигнуть во внутренних точках этой облас¬
ти, в которых оно дважды непрерывно дифференцируемо, положитель¬
ных максимальных (и отрицательных минимальных) значений.
Действительно, предположив обратное, т. е. что максимальное
положительное значение принимается функцией U (М) во внутренней
точке Mi области G, получаем из (2.151):
AU(Mi)<^ 0, AU (MJ—OU (Мх)< 0,
а это противоречит тому, что в точке Л4г функция U (М) удовлетворяет
уравнению (2. 151).
Из принципа максимального значения вытекают следствия.
Следствие 1. Существует только одно решение первой внут¬
ренней краевой задачи для уравнения (2.150).
105
Следствие 2. Существует только одно решение первой внеш¬
ней краевой задачи для уравнения (2.150) при условии, что это решение
равно нулю в бесконечно удаленной точке.
Действительно, предположим и в первом и во втором случаях, что
существуют два решения U2(M) и их(М) с одинаковыми граничными
условиями. Тогда их разность W(M) = U2—Ни с одной стороны, будет
решением уравнения (2.151) с нулевыми граничными условиями, а с
другой — должна принимать положительное максимальное значение
во внутренней точке области, в которой эта разность дважды непрерыв¬
но дифференцируема. Но это противоречит принципу максимального
значения для уравнения (2.151), отсюда №(Л4)=0.
Для краевых задач уравнения (2.150) имеет место следующая теоре¬
ма *: решение второй и третьей внутренних краевых задач для урав¬
нения (2.150) в некоторой области G единственно в классе функций
С2+а (G).
Перейдем теперь к уравнению
MJ (M)+c2U{M) =0, (2.152)
которое внешне отличается от уравнения (2.151) только знаком при
c2U(M). Однако уравнение (2.152) отличается уже принципиально от
уравнения (2.151) как с точки зрения общих свойств решений, так и с
точки зрения постановки и единственности решения краевых задач для
этого уравнения. Для решений уранения (2.152) не имеет места ни прин¬
цип максимума, ни (в общем случае) единственность решения первой,
второй и третьей краевых задач. Об этом говорит следующий простой
пример. Рассмотрим первую краевую задачу следующего вида:
d2U/dx2+d2U/dy2+ (2n2/l2)U=0, 0<Х/, 0<у<1; (2.153)
U(0, £/) = ty(/, y) = U(x, 0) = U(x, 0=0. (2.154)
Нетрудно убедиться при непосредственной проверке, что решением
этой задачи является функция U(х, y)=s\n(nx/l) sin(ju//0, не равная
тождественно нулю. В то же время другим решением задачи (2.153) —
(2.154) является U(х, у)= 0, что следует непосредственно из постановки
этой задачи.
§ 6. РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ
В ВИДЕ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ
Довольно часто решение краевой задачи теплопроводности в двух- или
трехмерной областях можно записать в виде произведения решений
одномерных задач. Для этого начальная температура должна выражать¬
ся в виде произведения функций, каждая из которых зависит от
* Сравнить с теоремой единственности решения краевых задач (2.136)—(2.137).
Через С2+а (G) обозначено множество непрерывных в G функций по всем аргу¬
ментам до второго порядка включительно и удовлетворяющих по всем аргументам
условию Гельдера с показателем а(0<а<1) [функция f (х) удовлетворяет
условию Гельдера (непрерывна по Гельдеру) с показателем а в области X, если
для любых и к2^Х справедливо неравенство | / (лг2) — f (*i) | <С0 | х2 — х{ \*
(С0= const). Если а=1, то / (х) называется непрерывной по Липшицу на X].
106
одной пространственной переменной, а граничными условиями должны
служить условия либо нулевой температуры, либо нулевого потока,
либо теплообмена со средой нулевой температуры. Сказанное поясним
на решении следующей тепловой задачи: .
1 дТ _ дП дП д2Т
a dt дх\ + дх\ + дх\ ’
О <*,</„ t> 0, /=1, 2, 3; (2.155)
T(xt, х2, 0) = Ф10 (*,) Фа0 (хг) Ф30 (*3); (2.156)
(Pu|r-P«7’k-o“0.'l
) д£ , /=1,2,3. (2.157)
(Puf +&<T)xr_ir0 j
Здесь для краткости рассуждений назависимые переменные обо¬
значены через х1У х2, х3 (а не через х, //, г, как обычно).
Покажем, что решение краевой задачи (2.155) — (2.157) можно
выразить в виде произведения решений одномерных задач
Т (х1У х2, хЗУ t) = Tl(xl, t)-T2(x2> t)-T9(x„ 0» (2.158)
если Tt(x(y t) удовлетворяют условиям (t = l, 2, 3):
дTt!dt = a (d2Tt/dx\)y 0 < xt < /„ t > 0; (2.159)
Ti(x(, 0) = Ф/0(*/); ($цдТt/dx{ — fi2iTl)Xi=o = 0\
(Pi/ dT i/dxi + рг/7" t)xi=il = 0. (2.160)
Подставляя (2.158) в (2.159), получим
гр гр / дТj д2Т\\ * гр гр (дТ2 д2Т$\ . гр гр / дТ3 д*Т3\ л
так как выражения в скобках равны нулю [см. (2.159)]. При этом
очевидно, что удовлетворяются начальное и граничное условия
(2.156) —(2.157).
Рассмотрим далее так называемую однородную задачу на собст¬
венные значения и собственные функции для краевой задачи
(2.155) — (2.157). Однородная задача имеет вид
AY(xlf^f x,) + y1T = 0, <)<*,<■/, (/ = 1,2,3); (2.161)
\Ри№дХ')-РЛ.=о = 0; [К/(ат/а^)+рдаг//во. (2.i62)
Покажем, как и выше, что собственные функции можно предста¬
вить в виде произведения
^(*1, х„ х3) = (*1)-4'2(x2).'Fa(*g), (2.163)
если являются решениями следующих однородных задач:
d24Vd*r + YJV, (xt) = 0,
0 <*,</, (/=1, 2, 3); (2.164)
[pif(dY#/(bf,)-p2#Vf]rr0=0;
\Ри (d^t/dxt) + Р^,]^. = 0. (2.165)
107
Здесь собственные значения у2 равны сумме Y2==Yi + Y2 + Y3- Дейст¬
вительно, подставив произведение (2.163) и Y2 в виде суммы
в (2.161), получим
так как каждое из выражений в скобках равно нулю в силу (2.164).
При этом удовлетворяются и граничные условия (2.162).
Этот результат имеет,практическое значение, так как позволяет
при отыскании собственных функций в многомерных областях исполь¬
зовать более простые выражения для одномерных областей в комбина¬
циях (2.163).
Аналогичное положение остается справедливым и для случая комби¬
нированного радиального и осевого потоков в сплошном или полом ци¬
линдре:
Решение Т (лд, х2, t) может быть представлено в виде произведе¬
ния решений более простых задач: Т (xlt x2i t) = Ti(xil t)T2(x2> t),
где Ti и T2 удовлетворяют условиям:
При отыскании собственных значений и собственных функций
соответствующей однородной задачи
(Р^^ + РЛ..* =0; (p.; + (2.168)
ад (Wjdxl + Yi^) + ад (d'4Vd*S + Y^) +
+ ад (d2Y3/d^3+Y^) = o,
/г<*2</2; *>о;
Т (хи х-2, 0) = Ф10 (Х,)-Ф20 (*2);
(р,, дТldxi—PjjT)*, = R, = 0; (Р21 дТ[дхх + Р^)*,=R, = 0;
(р; дТ/дх2—р]'2Т')*;_/| = 0; (р;, дТ/дхг + рпТ)Хгы.. = 0.
можно записать
V(xlt AJ= y^xj Va(*e), Y4 = Yf + Yi.
108
где (Xj) и xF2 (*2) удовлетворяют условиям:
i!Ii4-_LiZi4-v2V -0 R ^ г ^ R
dx\ *1 djcj +V.V.-0. t<i<Xt<Ht,
d2^
■7^2 = 0. h<x2< /2;
(ft, dTydjc,= О, ф[, dTi/dx1-p{,Y1),,«/1 = 0;
Ф21 dTt/djCi+!№,.=*, = o, os, d4yd*2+pi.T,),,.,.=o.
ГЛАВА III
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
(МЕТОД ФУРЬЕ)
ВВЕДЕНИЕ
Изложение аналитических методов теории теплопроводности начинает¬
ся с метода разделения переменных, одного из наиболее эффективных
методов решения краевых задач для уравнений в частных производных.
Можно сказать, что этот метод лежит в основе почти всех аналитических
методов решения краевых задач теплопроводности (метода интеграль¬
ных преобразований, метода функции Грина, метода продолжений,
метода произведений, метода источников и стоков) и если решение зада¬
чи не удается получить методом разделения переменных, то другие
подходы также не дадут положительного результата. В литературе этот
метод часто встречается под названием метода Фурье или метода соб-
ственных функций.
Идея метода заключается в следующем: решение краевой задачи
для уравнения в частных производных (каким является
уравнение теплопроводности) сводится к решению вспомогательных
краевых задач специального типа для обыкновенных диф¬
ференциальных уравнений, методика решения которых
разработана достаточно хорошо. Затем для исходного уравнения в
частных производных строятся частные решения в виде про¬
изведения найденных решений вспомогательных краевых задач и берет¬
ся их линейная комбинация с постоянными коэффициентами в виде бес¬
конечного ряда, который дает общее решение исходной краевой задачи
(иногда этот метод называют также методом частных решений). Для
применимости метода существенным является: 1) линейность урав¬
нения в частных производных; 2) линейность краевых условий в ис¬
ходной задаче.
Типичными задачами теплопроводности, для решения которых на
практике применяется метод Фурье, являются краевые задачи
в ограниченных областях, хотя этот метод может быть
применен и в неограниченной, и в полуограниченной (совместно с мето¬
дом продолжений) областях, но с меньшим успехом.
В основу метода положено представление искомого решения теп¬
ловой задачи в виде ряда Фурье по некоторой системе ортогональных
109
функций, найденных при решении упомянутой нами вспомогательной
задачи для обыкновенного дифференциального уравнения (так назы¬
ваемой однородной задачи, или задачи Штурма — Лиувилля). В связи
с этим рассмотрим сначала (коротко, без доказательств, отсылая за
этим читателя к специальной литературе по дифференциальным урав¬
нениям математической физики [1; 2; 54; 114; 137]) некоторые формулы
и теоремы, которые служат вспомогательным аппаратом при изложе¬
нии метода Фурье.
§ 1. РЯДЫ ФУРЬЕ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ ФУНКЦИЙ
Пусть
<Pl (*), ф2 (*). Фз (*), . . . , Фп(х) • • • (З-1)
— бесконечная система непрерывных функций при л:6 [а, Ь], где
а—конечно или равно (—оо), b—конечно или равно (+ оо). Пусть
также задана на [а, Ъ] непрерывная функция г (*) > 0, называемая
весовой функцией, и ограниченный интеграл
ъ
J г (*) ф* (*) d* < + оо, 1.
а
Назовем систему функций (3.1) ортогональной относительно веса г (*)
на интервале [a, ft], если имеет место условие:
с ) 0, пфт,
5 г (X) Ф„ (х) фи (лг) djc = > > о п = m (3.2)
а '
а
Например, системы функций:
а) 1/2, cos л*//, cos 2л*//, ..., cosял*//, ... (п = 1, 2, 3 ...); (3.3)
б) sin л*//, sin 2л*//, ..., sin/гл*//, ... {п= 1, 2, 3, ...) (3.4)
ортогональны (каждая) на отрезке [0,/] относительно г (*) = 1.
Действительно, в случае (3.4) нетрудно проверить
\ sin nnx/l sin тлх/l d* = ) ?'*
о J //2, п = т.
Система функций <р„ (*) = cos р„*+(А/р„) sin цпх, где рп > О—
корни уравнения tg р/= 2pft/(jn2—ft2), ортогональна на [0, /] отно¬
сительно г (*) = 1. Можно показать, что при 1
+ /i2)/ + 2/i]/2p’, n = m.
Назовем нормой функций фп (х) неотрицательное число
1<РЛ| =
ио
- ь
\ Г (х) ф* (х) dx
1/2
(3.5)
и поставим задачу: представить некоторую функцию y=f(x), инте¬
грируемую на интервале [а, Ь], в виде суммы бесконечного ряда по
системе функций {ф„ (*)}
/(*) = 2 а«Ф.(*)■ (З-6)
me I
Найдем коэффициенты разложения (3.6). Для этого умножим
обе части равенства (3.6) на г (х) <рп (*) и проинтегрируем почленно
в пределах от а до Ь, предполагая, что это интегрирование бес¬
конечного ряда законно (позже это предположение должно быть
проверено), тогда получим
b оо b
5 г (*) / (ж) ф„ (х) dx = '2,ат\г (х) ф„ (х) фя (х) dx. (3.7)
а п—1 а
Все интегралы в правой части (3.7) при пфт обратятся в нуль
(кроме одного, при п = т) в силу условия ортогональности (3.2).
В результате, учитывая (3.5), получим
ь
an==|^|j-J''W/W9nWd^ (3-8)
а
Числа апУ определяемые по формуле (3.8), называются коэффи¬
циентами Фурье функции f(x) по ортогональной системе функций
{флМЬ а РЯД коэффициенты которого определяются по
S п
формуле (3.8), называется рядом Фурье функции f(x).
Итак, поставленная задача формально решена, так как в (3.6)
найдены коэффициенты разложения. Однако можно ли при этом
сохранить знак равенства в (3.6)? Известно, что интегрирование
бесконечного ряда далеко не всегда законно (см. [146], т. II). Отсюда,
если мы нашли для f(x) ее ряд Фурье, то это еще не значит, что мы
нашли ряд, сходящийся к f(x) (в [142], т. III показано на примерах,
что даже непрерывные функции могут иметь ряды Фурье, сходящиеся к
другим функциям или расходящиеся в бесконечном множестве точек на
[а, Ь]). Но тогда каков же смысл приведенных рассуждений (3.7) —
(3.8)? Их можно рассматривать лишь как формальный прием, достаточ¬
ный для построения ряда Фурье функции /(*), с тем чтобы затем
проверить, сходится ли этот ряд и притом именно к данной функции.
На практике для этой цели используются следующие теоремы.
Теорема I. Если ряд Фурье непрерывной функции f(x)
00
2 „ (X),
П* I
где
ь
ап = j г (х) I (*) Ф„ (*) dx, (3.9)
ill
сходится равномерно в промежутке [a, &], то его сумма равна f(x),
00
т. е. /(*)= 2 апф„(*).
Л = 1
Заметим следующее важное обстоятельство. При отыскании ко¬
эффициентов ап в (3.9) исходят из заданной функции / (х) и строят
для нее ряд Фурье. В приложении рядов Фурье к аналитической
теории теплопроводности дело осложняется еще и тем, что ищут
решение Т (M, t) тепловой задачи в виде ряда Фурье по специаль¬
ным системам ортогональных функций (отыскиваемых в ходе реше¬
ния задачи), не зная самого решения, а имея лишь информацию
о поведении решения в начальный момент времени / = 0 и на гра¬
нице области G при t^O. Иными словами, в равенстве Т (М, /) =
= 21ал(0Ф/|(М) известна только правая часть (в виде ряда) и не
имеется явного выражения для функции, представленной своим
рядом Фурье. И здесь также возникает серия вопросов, более серь¬
езных, чем в (3.9). Выше было сказано (см. § 3 гл. II), что реше¬
нием тепловой задачи является функция Т (М, t) класса С2 (Q) П С0 (Я)
(первая краевая задача) либо класса С2 (Я) п С0 (Й), grad мТ gC°(Q)
(вторая и третья краевые задачи). Но, следовательно, всеми этими
свойствами должен обладать и найденный ряд Фурье_для функции
Т {Му t)y т. е. он должен равномерно сходиться в Я, чтобы его
сумма была непрерывной функцией (при условии, конечно, если
все члены этого ряда—функции, непрерывные в Я), быть дважды
непрерывно дифференцируемым по пространственным координатам
при всех t > 0 и непрерывно дифференцируемым по времени * t для
всех t > 0 и удовлетворять всем условиям краевой задачи. Про¬
верка указанных свойств найденного ряда Фурье является одной
из труднейших задач аналитической теории теплопроводности.
Нам понадобится еще одно понятие при рассмотрении метода Фурье,
а именно понятие полноты системы ортогональных функций (3.1).
Система ортогональных функций (3.1) называется полной [с весом г(*)],
если для всякой функции }{х) выполняется равенство (равенство Парсе-
валя)
г 00
S г М /2 М dx = 2 а\ I Ф„ ||2 (3.10)
а п~ 1
при условии, что существуют все выражения, входящие в (3.10).
Здесь —коэффициенты Фурье функции f (х) (3.9).
В теории теплопроводности нам придется сталкиваться с орто¬
гональными функциями от двух переменных (х и у)} которые пред¬
ставляют собой произведения функций только от х на функции
только от у. Замечательным свойством таких систем является то,
что свойство их полноты вытекает из свойства полноты системы
* При определении класса функции С2 непрерывность Т (Mt f) вплоть до
вторых частных производных относилась ко всем переменным. Для уравнения
теплопроводности, строго говоря, непрерывными должны быть Г, Tt, Т'м, Т"м2-
112
функций одного переменного, из которых они образованы [114].
Укажем следующую полезную для приложений теорему о полноте
системы функций двух переменных.
Теорема II. Пусть {ф„(*)Ь (п^1)—полная система ортого¬
нальных функций на отрезке [а, Ь] с весом гх(х) и пусть каждая
из систем функций фп1{у)у фп2{у), ..., фпт(у), ... (п>1) —полная
и ортогональная на отрезке [<с, d] с весом г2(у). Тогда система
функций двух переменных {фЛ(л:)фпт(у)\ будет полной и ортого¬
нальной в замкнутом прямоугольнике A = {a^Zx^.b, c^.y^d\
с весом г {х, у) = г1(х)г2(у). В частности, функции фпт(у) могут и
не зависеть от п и можно говорить о системе функций ]ф„ (х) ф^ (у)).
Аналогичным образом можно сформулировать теорему о полноте
системы функций трех пространственных переменных.
В § 6 гл. II был рассмотрен метод произведения при решении мно¬
гомерной краевой задачи (2.155) — (2.157) с однородными граничными
условиями (2.157). Теорема II в последующих параграфах будет иметь
для нас в связи с этим важное значение, так как она явится обосновани¬
ем для построения многомерных полных и ортогональных систем соб¬
ственных функций, необходимых для решения линейных, плоских и
пространственных тепловых задач методом Фурье.
Ряды Фурье по полным системам ортогональных функций обладают
следующим замечательным свойством.
Теорема III. Если система ортогональных функций {фп(х)}
полна, то ряд Фурье для каждой функции f(x) с интегрируемым квад¬
ратом можно интегрировать почленно, независимо от того, сходится
он или нет, т. е.
где а 1 = 1, 2.
Были сформулированы необходимые теоремы для рядов Фурье,
представляющие суммы функций одного переменного. Все формулиров¬
ки могут быть перенесены и на ряды для функций двух и трех перемен¬
ных (двойные или тройные ряды). С этими случаями нам также придет¬
ся встретиться при решении плоских и пространственных задач теории
теплопроводности.
§ 2. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ КРАЕВЫХ
ЗАДАЧ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Переходя к изложению метода Фурье, заметим, что существенным
достоинством метода является возможность получать аналитические
решения и в неоднородных средах, а также с учетом наличия допол¬
нительных слагаемых в уравнении теплопроводности (характеризую¬
щих, например, движение среды, теплообмен через боковую поверх¬
ность и т. п.).
Вначале рассмотрим однородное уравнение теплопроводности и
однородные граничные условия, причем для полноты изложения в
(3.11)
ИЗ
(1.31) теплофизические коэффициенты будем считать переменными,
и, кроме того, введем в правую часть уравнения слагаемое, пропорцио¬
нальное температуре.
Итак, пусть требуется найти функцию Т.(М, /), удовлетворяю¬
щую в области Q = {M£G, t^0\ условиям (см. § 2 гл. II):
P(M)dT/di = d\v[k(M) \Т(М, t)]—q(M)T, MgQ, t > 0; (3.12)
Т(М, 0|/ = о=Ф0(М), M€G; (3.13)
[Pi(M)<^(M> 1)1дп-$2(М)Т(М, 0]м€5=0, 0. (3.14)
Здесь G— конечная область, ограниченная замкнутой кусочно¬
гладкой поверхностью S; функции Р(М) = С(М)р(М), Х(Л4), q (М),
Pi (М^ (i = 1, 2) непрерывны в G и Я (М) > 0, q (М) > 0, X (М) > 0,
Л1 g G. Для изотропного гомогенного тела эти функции постоянны
и вместо (3.12) имеем уравнение (1 /а)Т', = АТ(М, t)—с2Т и без
ограничения общности далее запишем:
±^ = АТ(М, (), MeG, (>0; (3.15)
Т(М, /)|,=о=Ф.(М), MgG; (3.16)
[МПМ, Г)!дп—№(М, r)]M€S = 0, <>0, (3.17)
так как уравнение (1/а)Т; = ДГ (Л4, t) — c2T подстановкой Т (УИ, t)=
=ехр (—c2at)U приводится к виду (3.15); краевые условия (3.16) —
(3.17) при этом не меняются.
Пусть 7\(М, /) и Т2(М, t)—две функции, удовлетворяющие
дифференциальному уравнению (3.12) и граничному условию (3.14),
но не обязательно удовлетворяющие начальному условию (3.13).
Так как уравнение (3.12) и граничное условие (3.14) линейные и
однородные, то линейная комбинация этих линейных функций
CLjTiW, t) +а2Т2(М, t) также будет удовлетворять (3.12) и (3.14).
Если удается найти бесконечное число таких функций ТК(М, t) —
частных решений указанного типа [т. е. удовлетворяющих уравне¬
нию (3.12) и граничному условию (3.14)], то составленный из них
бесконечный сходящийся ряд
ао
Т(М, t)= XaJAM, t) (3.18)
К= 1
также будет удовлетворять дифференциальному уравнению (3.12) и
граничному условию (3.14). Коэффициенты ак следует определить
таким образом, чтобы приведенный ряд (3.18) удовлетворил началь¬
ному условию (3.13)
Ф»(М)= ЪакТк(М, 0). (3.19)
К- 1
Тем самым поставленная задача о нахождении функции Т(М, t)
может быть решена до конца.
Однако в приведенной схеме решения задачи содержится несколько
грубых допущений, которые нуждаются в разъяснении. Во-первых,
114
записав решение Т (М, t) в виде бесконечного ряда част¬
ных решений ТК(М, /), мы тем самым предположили, что сумма
бесконечного числа непрерывных функций акТк(Му t) даст нам непре-
эывную функцию Т(М, t). Во-вторых, так как каждая из функций
ТК(М, t) удовлетворяет уравнению (3.12), то предположим далее, что
ряд (3.18) можно дважды дифференцировать по координатам точки М
и один раз по времени t. В-третьих, при нахождении неизвестных коэф¬
фициентов ак необходимо совершить операцию предельного перехода
в бесконечном ряду (3.18), чтобы получить ряд (3.19), с которым далее
опять пришлось бы работать также при определенных допущениях. Все
перечисленные операции безоговорочно справедливы только для
конечной суммы и в общем случае незаконны для бесконечного функ¬
ционального ряда. Поэтому после нахождения коэффициентов ан
и подстановки их в ряд (3.18) следует убедиться в том, что ряд (3.18)
обладает следующими свойствами: а) определяет в й непрерывную
функцию Т(М, /); б) во внутренних точках области Q является диф¬
ференцируемым и удовлетворяет дифференциальному уравнению
(3.12); в) удовлетворяет начальному условию (3.13) и граничному (3.14).
До тех пор, пока эти дополнительные исследования не проделаны,
найденный ряд не может считаться решением задачи (3.12) — (3.14),
хотя формально он и был найден по условиям этой задачи.
Систему функций ТК(М, t) можно определить следующим образом.
Будем искать нетривиальные (т. е. не равные тож¬
дественно нулю) частные решения уравнения (3.12), удовлет¬
воряющие граничному условию (3.14), в виде произведения двух функ¬
ций, одна из которых зависит только от пространственных координат
точки Af, а другая — только от времени /
Т(М, t) = V(M)-q>(t), (3.20)
где ¥ (М) непрерывна в G, а <р(/) непрерывна при 0^/ <оо.
Подставляя (3.20) в уравнение (3.12), получим
Р (М) V (М) ф'‘(О = ф (0 {div [k (М) (Af)] —</ (Af) Ч? (М)}
или
ф' (/)/ф (!) = {div [к (М) vT (Af)] — q (Af) ЧГ (М)}/[Р (М) ¥ (Af)]. (3.21)
В случае (3.15) имеем
ф' (0/яф (0 = ДО (М)/¥ (Af). (3.22)
Для того чтобы функция Т(М, 0 =ф (О^1* (А1) была решением урав¬
нения (3.12), равенство (3.21) должно соблюдаться при всех значениях
t>0 и во всех точках М £ G. Левая часть этого равенства зависит только
от переменной t и не может изменяться при изменении координат точки
М. Поэтому если зафиксировать t и менять координаты точки М, то
левая часть, а следовательно, и правая будут сохранять постоянное
значение. Рассуждая аналогично, установим, что правая часть, а следо¬
вательно, и левая не могут изменяться и при изменении t. Это будет
справедливо только в том случае, когда обе части равенства (3.21)
115
вообще не зависят ни от координат точки М, ни от времени /, т. е.
когда оба отношения и слева, и справа в (3.21) являются постоянными
величинами. В этом рассуждении ключ к методу разделения перемен¬
ных Фурье.
Обозначим теперь постоянную, которой должны быть равны и
левая и правая части равенства (3.21), через аы. Тогда уравнение
(3.21) распадается на два уравнения:
<р' (/)/ф (0 = ап; \
{div[^(Ai)v¥(M)] — <7(М)^(М)}/[Р (М)¥(М)]=ап. j (3-23)
Первое из них имеет общее решение ф (t) = С1ехр (ап/), где Ci —
постоянная величина. Поскольку ни в одной точке тела (т. е. ни
при каких фиксированных координатах точки М) температура
Т = Тг(М)*ф(/) не может неограниченно возрастать по абсолютной
величине при tоо, постоянная ап должна иметь отрицательное
значение. Положим ап = — у2, тогда ф(/) = С1ехр(—у2/). Второе
из уравнений (3.23) принимает вид
div [X (М) VY (Af) 1 — q{M) Y (Af) + у2Р (М) Y (М) = 0.
Так как мы ищем частные решения, удовлетворяющие гранич¬
ному условию (3.14), то при любом значении t^O должно соблю¬
даться равенство
■К0[Р.Й-РД('И)]„<5=0.
Если бы обращался в нуль первый множитель, то решение Т (М, t)
равнялось бы нулю при всех значениях t и во всех точках об¬
ласти G. Поэтому, чтобы отыскать решения, не равные тождест¬
венно нулю (а только такие нас и интересуют), мы должны счи¬
тать, что рх(д¥/дя)— p2Y = 0. Следовательно, в качестве функции
Y (Л4) надо брать решения задачи:
div [Я (Af) vY(Af)] — ?(М) Y(M) + y2P(M) Y(M) = 0, MgG; (3.24)
[Pi (Af) (54я (M)/dn) -pt (M) Y (М)]м es = 0. (3.25)
В случае (3.22) имеем
AY (Af) + y2Y (Af) = 0, Af € G; (3.26)
[p, (dY (Af)/an)-PaY (Af)]Mes = 0. (3.27)
Дифференциальное уравнение (3.23) называется уравнением Гельм¬
гольца. Задачу (3.24) — (3.25) или (3.26) — (3.27) называют (Однородной
задачей или задачей Штурма — Лиувилля. Она имеет нетривиальные
решения не при всех значениях у2.
Определение. Те значения у2, при которых задача (3.24) —
(3.25) имеет нетривиальные решения, называются собственными значе¬
ниями краевой задачи (3.24) — (3.25), а соответствующие им нетриви¬
альные решения 4я(М) уравнения (3.24)—собственными функциями
краевой задачи (3.24) — (3.25).
Сформулируем (без доказательства, см. [1]) необходимые для даль¬
116
нейшего некоторые теоремы о собственных функциях и собственных
значениях.
Теорема I. Существует бесконечное (счетное) множество соб¬
ственных значений {у*}, к=1, 2, 3..., и соответствующих им соб¬
ственных функций {Ч^(М)} краевой задачи (3.24) — (3.25).
В силу линейности и однородности уравнения (3.24) и условия
(3.25) очевидно, что если (М) — собственная функция, соответ¬
ствующая собственному значению у*, то и всякая функция d*4;*(M)
(где dK—произвольная постоянная) также является собственной
функцией для того же у£, и этим вполне исчерпывается класс соб¬
ственных функций (для того же yj.
Теорема II. Собственные значения у\ с возрастанием номера к
неограниченно возрастают, у* —> оо при к—+ оо.
Теорема III. Собственные функции 4^(714) и 4^(714), отве¬
чающие различным собственным значениям у%х и у^л(у^фу12) орто¬
гональны в области G с весом Р (7\4)
Замечание 1. Для уравнения (3.24) возможен случай, когда т — крат¬
ному собственному значению у? отвечает т линейно независимых собственных
функций Yi/ (М), ..., W„i (714), которые не обязаны быть попарно орто¬
гональными. Однако их можно заменить другими собственными функциями
’FiiJAf), (М), ...» Ч'пи (М), строящимися с помощью первых и являющимися
уже попарно-ортогональными (это построение излагается подробно в [1]). Для
уравнения (3.26) все собственные значения простые, т. е. у? < у\ < уз < .. *Ук< ••• •
Заметим также следующее: в (3.28) весовая функция Р (М) является одним из
коэффициентов в слагаемом у2Р (М) Y (М) уравнения (3.24). Для уравнения (3.26)
с условиями (3.27) собственные функции (Л4), отвечающие собственным значе¬
ниям у£, также обладают свойством, указанным в теореме III, но при Р(М) = 1
Квадрат нормы собственных функций однородной задачи (3.26) —(3.27) имеет
вид
Для задачи (3.24) —(3.25) также нетрудно записать аналогичное выражение,
используя (3.24) (сделайте это самостоятельно).
Заметим, что формулы (3.29) — (3.30) (которые будут использоваться чаще
всего) записаны в декартовой системе координат, так как всюду область G рас¬
сматривается в пространстве (х, у, г). Однако все рассуждения, проводимые для
уравнений (3.15) и (3.12) в декартовой системе координат, остаются справедли¬
выми и для любой другой ортогональной криволинейной системы, необходимо
лишь уметь записать эти формулы в соответствующей криволинейной системе
координат. Тогда в процессе перехода к этой системе координат под знаком ин¬
тегралов в (3.29) и (3.30) могут появиться весовые функции (отличные от еди¬
ницы), соответствующие конкретной системе собственных функций однородной
задачи (3.26) — (3.27) в тех или иных криволинейных координатах.
Теорема IV. Все собственные значения задачи (3.24)—(3.25)
вещественны и неотрицательны.
0, Кх^к,, (3.28)
>0, «х = Kj.
(3.29)
(3.30)
в
117
Замечание 2. Для первой и третьей краевых задач все собственные зна¬
чения строго положительны. Для второй краевой задачи (но при условии, что
q(M==0) значение 7 = 0 является собственным значением, а ЧГ(М)=1—соответ¬
ствующая ему собственная функция (действительно, нетрудно непосредственной
подстановкой 7 = 0, У=1 в (3.24) — (3.25) при <7 = 0,р2 = 0 убедиться, что все
условия задачи выполняются). В дальнейшем при решении второй краевой за¬
дачи учтем это замечание.
Теорема V. Система собственных функций краевой задачи
(3.24) — (3.25) полна.
Это очень важная теорема, которая вместе с теоремой III в § 1,
по существу, открывает путь к решению задачи (3.12) — (3.14).
Теорема разложимости (Стеклова) VI [1331.
Всякая непрерывная в G функция с кусочно-непрерывными частными
производными I и II порядков, удовлетворяющая краевым условиям
(3.25), разлагается в ряд Фурье по собственным функциям однородной
задачи (3.24) — (3.25), абсолютно и равномерно сходящийся в области
G.
Возвратимся к рассмотрению задачи (3.12) — (3.14) [или (3.15) —
(3.17)1 и построим аналитическое решение этой задачи методом Фурье
по следующей схеме:
1. Ищем частные решения вида Т(М, /)=Чг(Д4)ф(0, удовлетворя¬
ющие уравнению (3.12) и краевому условию (3.14). Разделяем пере¬
менные и переходим к однородной задаче (3.24) — (3.25) или (3.26) —
(3.27).
2. Находим собственные значения {у£} и собственные функции
{4^(M)} однородной задачи.
3. Для каждого собственного значения yl находим общее реше¬
ние уравнения ф'(0 + У*Ф (0 = 0 в виДе Ф*(0 = акехР(-“7«0-
4. Находим частные решения уравнения (3.12) TK(Mtt) =
= avexp(—уlt)x¥K(M) и берем сумму таких частных решений по
всем собственным функциям
00
Т (М, 0=2 а,е"# Ук (М). (3.31)
К — 1
5. Для нахождения коэффициентов ак удовлетворяем начальному
условию (3.13). Получаем разложение начальной функции Ф0(М)
в ряд Фурье по собственным функциям однородной задачи (3.24) —
(3.25)
ф» (Af) = 2 (Af). (3.32)
К- 1
Коэффициенты разложения ак находим по аналогии с (3.9)
= WjF Ш р (уИ) ф° (М) Ч'*m (3-33)
н G
где |Т,|» — квадрат нормы функций Ч;¥(М);
ITjp = div (3.34)
* G
118
6. Записываем окончательное выражение для Т (Л4, t)\
а) в случае краевой задачи (3.12) — (3.14)
00
Т w, t) = £ V,(M) e-v«' Щ Р (М) Ф0 (М) (М) dVм; (3.35)
б) в случае краевой задачи (3.15) — (3.17)
Т (М, о = £ pip V,(M) е(-К_в V2' Щ ф0 (m)Vk (М) dvM. (3.36)
к= 1 1 к G
Теперь покажем, что действительно найдено искомое выраже¬
ние, обладающее всеми свойствами решения рассматриваемой крае¬
вой задачи. Из теоремы разложимости VI следует, что полученные
ряды сходятся абсолютно и равномерно в каждой точке области Я,
так как представляют собой разложение функции Т (Л4, /) класса
С2 (Я) П С0 (Я) в ряд Фурье вида
т (м, о = 2 е. (О v, (М) (3.37)
к= 1
по собственным функциям соответутвуклцей однородной задачи.
Проверка остальных свойств этих рядов следует из теоремы VII,
доказанной в [1].
Теорема VII. Непрерывное в замкнутой области Q = {MgG,
t^0\ решение краевой задачи (3.12) — (3.14), принадлежащее классу
С2 (Я) П С0 (Я) при всяком фиксированном / ^ О, представляется
в виде ряда (3.35), абсолютно и равномерно сходящегося в области Я.
Полученные выражения (3.35) и (3.36) представляют собой общую
форму записи решения рассмотренных краевых задач и в зависи¬
мости от числа пространственных переменных в постановке задачи
принимают вид одно-, двух- или трехкратных рядов Фурье с пере¬
менными во времени коэффициентами разложения по собственным
функциям соответствующей однородной задачи. Следует всегда пом¬
нить: решения Т (М, t) краевых задач нестационарной теплопровод-
ности в конечной области MgG, 0, представляются, как пра¬
вило, в виде кратных рядов Фурье, причем кратность этих рядов
определяется числом независимых пространственных переменных
в температурной функции T(M, t) (по которым берется оператор
Лапласа Д71 (М, /)).
§ 3. МЕТОД ФУРЬЕ ПРИ РЕШЕНИИ НЕОДНОРОДНЫХ КРАЕВЫХ ЗАДАЧ
В большинстве практических задач граничные условия или диф¬
ференциальное уравнение неоднородны. Однако знание собственных
значений и собственных функций {Ч'ДМ)} соответствующей
однородной задачи позволяет решать и неоднородные задачи.
Рассмотрим (коротко) некоторые частные случаи неоднородных
краевых задач.
119
Найдем Т (М, t) — решение задачи
дТ /dt = акТ (Му t) + f{My t), MgG, t > 0; (3.38)
T (M, 0) = 0, [Мд77дл)—p2r]AieS==0# *>0. (3.39)
Искомое решение Т (Af, t) £ С2 (Q) П С0 (Q) и по теореме Стек-
лова VI может быть представлено в виде ряда Фурье (3.37) по соб¬
ственным функциям однородной задачи (3.26) — (3.27). Для вычисле¬
ния коэффициентов ©*, (/) этого ряда разложим заданную функцию
f(M, t)£C°(Q) в ряд Фурье по собственным функциям {¥у(УИ)}
f(M, 0 = ЗМО^ДМ),
к = 1
где
(3.40)
G *
Подставим теперь (3.37) и (3.40) в уравнение (3.38)
S 0, (0 Y, (М) = 2 а@к (t) AY.M) + 2 fK (t) ¥, (М). (3.41)
к = 1 к—1 к=1
Так как, согласно (3.26), A4fv(M) = —у£Ч^(М), то, сравнивая в
(3.41) слева и справа коэффициенты перед ^(М), получаем для
определения ©* (t) уравнение ©* (t) + (Vа ук) ®к (t) = fK (t) с началь¬
ным условием ©у(0) = 0 [так как Т (М, 0) = 0, то из (3.37) следует
2©*(0)Ч^(М) = 0 при условии, что все ©^(0) = 0]. Находим реше-
к
ние линейного неоднородного дифференциального уравнения первой
степени относительно QK(t):
t
€>* (/) = J exp [—{Va y> {t—x)] fe (x) dx
0
и далее искомое выражение для Т (М, t) в виде
Т(М, <)= it TnFjinexp[— (^«)2х
к~1 ОС?
х (/ — X)]/ (М, х) Wk (М) dx dVM- (3.42)
Заметим следующее: все операции, с помощью которых было найде¬
но решение (3.42), строго говоря, должны быть обоснованы. В то же
время очевидно, что в тех случаях, когда полученный ряд (3.42) после
почленного дифференцирования два раза по координатам точки М и
один раз по времени t равномерно сходится в Q, он представляет собой
решение задачи класса C2(Q)f|C°(Q). Строгая проверка всех диффе¬
ренциальных свойств ряда во многих случаях представляет техни¬
чески громоздкую задачу и зачастую опускается в аналитической тео¬
рии теплопроводности (в классических работах по дифференциальным
120
уравнениям математической физики этим вопросам, наоборот, уделя¬
ется большое внимание).
В случае неоднородного уравнения (3.38) и неоднородного началь¬
ного условия (3.16) этот случай нетрудно свести к уже рассмотренным
двум выше. Действительно, пусть Т(М, t) удовлетворяет уравнению
(3.38) и краевым условиям (3.16), (3.17). Будем искать решение задачи
в виде Т(М, t) = T1(M, /)+Т2(М, t), где функции Tt(M, t) (t = l, 2)
удовлетворяют условиям, полученным путем подстановки правой части
равенства в (3.38), (3.16) — (3.17):
dTjdt = abTt(M, О, t > 0;
дТJdt = а ДТ2(М, t) + f(M, t)% М g G, / > 0;
ГДМ, 0) = Фо(М), [pi(dri/an)-piT1]A(eS = 0;
Т,(М, о) = о, [МВД-И«55=о.
Каждая из этих задач уже решалась [см. (3.36) и (3.42)].
Пример. Дано начальное распределение температуры по толщине пластины
в виде некоторой функции Ф0 (*), а также распределение внутренних источников
теплоты в виде некоторой функции координат и времени / (х, t). В начальный
момент времени ограничивающие поверхности мгновенно охлаждаются до нулевой
температуры, которая поддерживается постоянной на протяжении всего процесса
охлаждения. Найти распределение температуры по толщине пластины.
Здесь Й = {х* 0*0 < х < /, t > 0), а 7 (х, t) удовлетворяет условиям:
dT/dt = a (d2T/dx2) + f(x, t), 0 < х < I, t > 0; (3.43)
T{xy 0) = Ф0 (jt), 0 <*</; 7(0, 0 = 7 (/, 0=0, ^0. (3.44)
Предполагается, что Ф0 (0) = Ф0 (/) = 0, так что 7(xt t)£C2 (Q)Г)С0 (Q).
Вначале найдем функцию Тг(х, 0, удовлетворяющую
dTi/dt = a (дЧфх2), 0 < * < /, t > 0; (3.45)
7j (х, 0) = Ф0 (*), 7(0, t) = T(l> 0 = 0, ^0. (3.46)
Полагая 7* (xt t) = W (х)-ф(0 и разделяя в уравнении (3.45) переменные
(1/е) (Ф' (0/ф (0) = У* MJV (х) = -
приходим к уравнению
ф' (0+( y)2 Ф (0 =0 (3*47)
и к однородной задаче (3.26) —(3.27)
V (х) + у*У (х) = 0, Ф“ (0) = Чг (/) =0. (3.48)
Общее решение уравнения (3.48) имеет вид У (х) = Ci sin ух-\-С2 cos ух.
Используя граничные условия, находим Cj sin 0 + С2 cos 0 = 0; Ci sin y^ +
4-C2cosy^ = 0. Первое уравнение дает C2 = 0, второе уравнение sin yl = 0, откуда
yl — пл, где n придаем неотрицательные значения (п = 0, 1, 2, 3, ...), поскольку
при отрицательных п будут получаться решения того же вида. Итак, собственные
значения Yn = (ял//)2, а собственные функции (х) = Сп sin (плх/l). Как видим,
каждому собственному значению у2п соответствует бесчисленное множество реше¬
ний Ч'л (х), отличающихся друг от друга постоянным множителем Сп. Можно
положить Сп — 1 и считать, таким образом, (х) = sin (плх/l). Каждому собст¬
венному значению у2 будет соответствовать своя функция ф„(х), определяемая
из (3.47) в виде фл (/)=ал ехр [— [У ауп)2 /], где ал — постоянная интегрирования.
121
Находим частные решения уравнения (3.45), удовлетворяющие граничным
условиям (3.46): Tln( х, t) =ап ехр [— (У~а уп)2 /] sin (плх/l). Составим далее ряд
Ti(x, fl=2 аУп^ 1 sin (ппх/l) (у„ = пл/0
П— 1
и найдем его коэффициенты* удовлетворяя в (3.44) начальному условию
CD
ф0 W = 2 ап sin (плх/1). (3.49)
п— 1
Получили разложение заданной начальной функции в тригонометрический
ряд по синусам [6]. По формуле (3.9) с учетом (3.4) находим коэффициенты раз¬
ложения
I
а„ = -j J ф° О sln (njll/0 d£.
О
I
так как || f = J sin2 (плх/l) dx = l/2.
о
Заметим, что в силу непрерывности начальной функции Ф0 (х) и выполнения
условий Ф0 (0) = Ф0 (/) = О ее ряд Фурье (3.49) сходится абсолютно и равномерно
в точках отрезка [0, /]; кроме того, из теории тригонометрических рядов [6]
00
известно, что ряд (3.49) в этом случае мажорируется рядом М0 2 ^п2» Ti е*
п= 1
довольно быстро сходится. Находим далее искомую функцию
Tl (х, 0 = f £ е-(лл V3/02 t sin яя* J ^ (B s.n пп|_ ^
ti— 1 О
Для нахождения функции Т2(х, /), удовлетворяющей условиям
dT2/dt = a (d*T/dx2) + f(x, t)9 0<х<
Т(х, 0) = Т(0, t) = T (I, 0 = 0,
вовсе нет необходимости повторять заново рассуждения (3.40) — (3.42). Для реше¬
ния этой задачи имеется готовая формула (3.42), которой и следует воспользо¬
ваться.‘В результате получим
t I .
nnl
U t > 0; |
sln-^-j^exp [—(< —
/(I, x)sin dTd£.
n=l 0 0
И (3'5I)
Искомое решение
Т (х, 0 = (дг, t) + T2(x, 0.
Преобразуем полученное выражение (3.50), поменяв местами порядок сумми¬
рования и интегрирования:
где
00
rt » л\ 2 Г -(rmV~a/l)2 t . ППХ , ПП^ /о сох
G(X, g, t) =—Zu е sin —j— sin —. (3.53)
n = 1
Изменение порядков суммирования и интегрирования всегда
законно при t > 0, так как в (3.52) ряд в фигурных скобках схо¬
дится равномерно по I при t > 0. Функция G (х, £, 0» определяе¬
мая рядом (3.53), называется функцией температурного влияния
мгновенного точечного источника теплоты. В [134] показано, что
функция G(x, £, 0 (функция источника) представляет собой рас¬
пределение температуры в стержне 0^*^/ в момент времени t > 0,
если температура в начальный момент / = 0 и в этот момент в точке
х = £ (0 < £ < /) мгновенно выделилось количество теплоты, равное
Q = cp (с—удельная теплоемкость, р—плотность вещества).
С учетом (3.53) можно теперь записать для решения задачи
(3.43)—(3.44)
/
Т(х, /) = $<D0(£)G(*, I, f)dl +
о
t I
+ S J / а, G (X, l, t-т) dt dx. (3.54)
0 0
Рассмотрим случай, когда функция Т (М, t) удовлетворяет урав¬
нению (3.38) и условиям!
Т(М9 0) = ФДЛ4), M€G;fa(dT/dn)—$2T=: — ф(М, t)9M$S9't>0.
(3.55)
Как указывалось, метод Фурье при неоднородном уравнении
и неоднородных граничных условиях формально неприменим, однако
можно преобразовать задачу (3.38), (3.55) таким образом, что при¬
менение метода разделения переменных станет возможным. Это
достигается- путем приведения граничных условий
к однородным. Для этого представим искомое решение Т (М, /)
в виде суммы Т (М, t) = W(M, t)-\-U (М, <)» гДе функция V (М, t)
подбирается так, чтобы она удовлетворяла только
граничным условиям, т. е. необходимо, чтобы [$Лди\дп) —
— P2^|m€S = — ф(Л4, 01^65. Подставляя в (3.38) и (3.55) вместо
Т (М, t) правую часть равенства, получим условия и для определе¬
ния W (М, t)\
dWldt==ahW (М, t) + fi(M, t), \
AfgG, t > 0; 1 (3.56)
W{M, о)=ф;(M), мео; [рцаг/ап)—p*r)MiS-ot t>o.J
Здесь Ф, (М)=Ф0 (Л4) — U (/И, 0); /,(М. t)=HM,l) — \U't—a\UW,t)].
Задача (3.56) знакома; ее решение имеет вид суммы выражений
(3.36) и (3.42).
123
Рассмотрим в качестве примера уравнение (3.43) с неоднородными граничными
условиями (всевозможные комбинации граничных условий)
[Pii(d7/dx)— Pi2^]*=o = —Ф1 (0; [Р21 (дТ/дх)-{-(>22Т]х-1 — У2 (0* ^ ^ 0- (3.57)
Функцию U (х, t) подберем следующим образом: ищем V (х, t) в виде U = Ci-^C2x
(при Р12 Ф 0 и р22 Ф 0) и подбираем константы Сг и С2 из удовлетворения усло¬
виям (3.57). Это дает систему двух алгебраических уравнений, решая которую
находим С/ (проделайте все расчеты самостоятельно). Окончательно получим
U (xt t) = {(Pii + Pi2*) ф2 (0 + [Р21 + Р22 (/— *)] Ф1 (0}/(Pi2p2i Р22Р11 “г Р22Р12О*
(3.58)
В случае второй краевой задачи (Р,‘2 = 0, t = l, 2) в качестве U (х, t) можно
выбрать, например,
и (х, о = [1/(2/021)1 *2ф2 (0 + [1/(2/Рп)] (/-X)2 ф1 (/). (3.59)
Применим указанные рассуждения к решению задачи
дТ/dt = а (д2Т/дх2), 0 < х < /, t > 0; (3.60)
7(х, 0) = 0, 7(0, /)=ф1(0, 7 (/, t) = ф2 (*), / ^ 0. (3.61)
Из (3.58) находим (при Pn = P2i = 0; р12 = р22 = 1): U (х, t) = Ф1 + (ф2—Ф1) х/1.
Функция W (х, t) определяется к^к решение задачи:
dW/dt = a(d2W/dя2) —[<pi (0 + (фа (0 —ф1 (0) x/l],
0 < х < /, t > 0; .
Г(*. 0) = — ф1 (0) + [<р2 (0) _ф1 (0)] ж//; ( У ■
Г(о, t) = W(i, о=о.
Решение этой задачи можно получить с помощью готовой формулы (3.54).
Находим после несложных вычислений для задачи (3.60) — (3.61):
т {X, 0={фх (0 + [ф2 (0-Ф1 (01 х/1}-(2/я) X
Г /пл. гШ\2
х
хЁ|[ф1(0)-(-1)»ф2(0)]ехр LfeiJCsY t
п= 1 -
ОО _ t _
Xsin (nnxjt)— (2/л) 2 e-(nny a/l) ' sin (ял*//) J е(плУ a/1)2 т у.
п= 1 о
X [ф( (т) -(-1)" ф2 (т)] dx. (3.63)
Это выражение, в котором первое слагаемое (в фигурных скобках) есть функция
U (х, 0, а оставшаяся часть — функция W (х, /), преобразуем, применяя к интег¬
ралу фюрмулу интегрирования по частям и используя суммы [20]
ао оо
2 V 1 I ППХ 1 Х 2 V / 1Чл 1 1 , ПЛХ Х /О СЛЧ
172- 7Г*1п—=1-Т: (3.64)
п-1 п=1
Окончательно получим
Т(х, nslti!!T§ е-{пя v*оА)2(<-[ф1 (т) — (— j)п ф2 (T)j dt. (3.65)
Л= 1
Замечание 1. В аналитической теории теплопроводности при работе
с решениями краевых задач в форме ряда Фурье часто возникают сомнения в пра¬
вильности найденного решения. Это сомнение появляется, когда
найденное решение пытаются проверить в точках гранич¬
ной поверхности 5, где должны выполняться граничные
условия задачи. Имеющиеся в нашем распоряжении примеры достаточно
наглядно поясняют сказанное.
124
Функции Ti (х, t) [задача (3.45) —(3.46)] и W (х, t) [задача (3.62)] удовле¬
творяют однородным граничным условиям и, как видно из найденных для них
выражений (3.50) и (3.63), этим условиям удовлетворяют и ряды (3.50) и (3.63).
Совсем иначе обстоит дело с решением Т (х, t) в виде выражения (3.65). Согласно
постановке задачи (3.60) — (3.61), функция Т (х, t) в точках х~0 и х—1 удовле¬
творяет неоднородным граничным условиям. Полученный же для Т (х, t) ряд в (3.65)
при формальной проверке не может удовлетворить неоднородным граничным усло¬
виям, так как отдельные члены этого ряда удовлетворяют однородным условиям.
В то же время весь ряд должен удовлетворять граничным условиям (3.61), иначе
Т (х, t) в виде (3.65) не было бы решением задачи (3.60) —(3.61).
Проверить же выполнение граничных условий в точках х = 0 и х = 1 нельзя,
так как формально при подстановке этих значений в (3.65) условия не выпол¬
няются. В действительности же это не так и все дело заключается в том, что
ряд (3.65) не является равномерно сходящимся при всей (сохраняя это
свойство только для внутренних точек промежутка [0, /]), и мы не имеем права
в (3.65) совершать предельный переход в точках * = 0 и х—1. Этим недостатком
не обладают ряды в выражении (3.63) для Т (.х, /), полученном путем решения
вспомогательной задачи (3.62). И это нетрудно объяснить.
Перейдя к функции W (х, /), мы перевели неоднородные граничные условия
в дифференциальное уравнение (3.62) и начальное условие, так что в новой задаче
граничные условия стали однородными и согласно теореме разложимости VI функ¬
ция W (х, t) должна иметь решение в виде ряда, абсолютно и равномерно схо¬
дящегося при всех х(;[0, /] и ^0. Такой переход был вынужденным, так как
решение задачи (3.60) — (3.61) мы пытались получить именно методом разделения
переменных, а для этого нужны были однородные граничные условия. Поэтому
первоначально получено выражение (3.63), а затем из него после преобразова¬
ний—(3.65).
Замечание 2. В этом параграфе показана принципиальная возможность
применения метода разделения переменных при решении краевых задач с неодно¬
родными граничными условиями и неоднородностью в уравнении теплопроводно¬
сти. Перевод неоднородных функций из граничных условий в начальное и урав¬
нение теплопроводности на практике применяются довольно редко; лишь в простей¬
ших случаях (линейный или радиальный поток) удается подобрать функцию
U (Mt t), удовлетворяющую неоднородным граничным условиям (для плоских
и пространственных задач это, как правило, не удается по техническим при¬
чинам). В следующем параграфе получим рабочие формулы записи решений крае¬
вых задач нестационарной теплопроводности с неоднородностями как в уравнении
теплопроводности, так и в граничных условиях задачи. Смысл этих важных
в прикладном отношении формул заключается в возможности автоматически
записать аналитическое решение исходной краевой задачи, если для нее известны
собственные значения и собственные функции соответствующей однородной задачи.
При этом будут рассмотрены пространственные, линейные и плоские задачи.
§ 4. РАБОЧИЕ ФОРМУЛЫ ЗАПИСИ АНАЛИТИЧЕСКОГО
РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ
Рассмотрим вначале пространственную задачу:
dTjdt —аАТ(М, () + /(М, t), (М, 0€G = (MeO, / > 0); (3.66)
Г (М. 0) = ФДМ), M6G; (3.67)
рпагдо, t)/dn]—PtT(M, 0 = — ф(М, t), M£S, />0. (3.68)
Здесь я—внешняя нормаль к S; Pf -f- р| >0.
Пусть yi и ^(М)—собственные значения и собственные функ¬
ции соответствующей однородной задачи
Д¥(М) + V2^(^) = 0; M£G-t [0,(дУ/дл)es = 0. (3.69)
125
Представим искомое решение Т (М, t) в виде формального ряда
Фурье по собственным функциям {^(М)} задачи (3.69)
г (М. 0= 2 ело'ММ), (3.70)
К— 1
где
или
0Л<)=та^ШГ(Л1, (з.71)
G
®к{t)=-viiv.pHfт{М' Т)л^(М)dVMt (3J2)
а
так как согласно (3.69) всюду в области G (Af) = (—1/у£) (/И).
Если воспользоваться далее формулой Грина для оператора Лап¬
ласа [см. (2.142)]
Ш<УАТ-Т4У)^ИКи£-7т)„.5*’. (3.73)
G S
в которой Т есть решение задачи (3.66)—(3.68), и положить U (М)=
z=:WK(M)t то (3.72) запишется в виде
*ю-г^ДО',*4ГЛ'«-
! CC(t*Zm.-v Ш) do
V.P JJ\ дп K^)Mtsao-
v*ll ..
S
Заменяя АТ (М, /) под знаком интеграла значением из уравнения
(3.66), получим
0‘ (0 =-(У~а укУ II V, р Ш Wk^X
G
х dVM + . __ ' СГГ/Т,dVM—
м (Г5ук)г11Щ12 JJJ м
—г—"—ГГ (т ^7г— d<r- (З-74)
YimpJJ \ дп дп J к ’
S
Из (3.71) находим
G
и, подставляя в (3.74), приходим к обыкновенному дифференциаль¬
ному уравнению относительно 0(/)
в. (/) + у,)* 0. (0 = IPCT [- Sj (г
(3.75)
126
Для его решения необходимо иметь начальные условия Ч;к (0).
Потребуем в (3.70) выполнения начального условия (3.67):
Т (М, 0) = Ф0 (М) = 2 ©« (0) Y, (М), (3.76)
к = 1
откуда, разлагая начальную функцию Ф0(М) в ряд . Фурье по
системе собственных функций (Ч'ДМ)}, найдем 0К(О)
©К (0) = Щ Ф. (М) (М) dVM. (3.77)
G
Решением уравнения (3.75) с начальным условием (3.77) являет¬
ся выражение
t
'г ат\
X
0S «
t
X da dt + J 5 5 J e-0^v«)V-T) f(M,x) (M) dt dK*].
0 G
После подстановки этого выражения в равенство (3.70) получим
(предположительно) основную интегральную формулу,
дающую представление решения уравнения нестационарной тепло¬
проводности (3.66) с'краевыми условиями (3.67) — (3.68):
т [М. I) = ± ЩФ„(М) »,(4dvu-a± ^ х
к=1 G к=1
ХШ [т (М, х) д-Ц£^]м gs dt da +
о S
t
+ £ TrfHHe"(K“V*)V"T>/(M’ ^(^dtd^. (3.78)
k=1 K 0 G
Действительно, в случае первой краевой задачи Pi = 0; Р2 = 1
T(M9t) = <p{M9t)9 M£St 0; 'Р,(М) = 0, M£S. (3.79)
Так как
0 S
t
Ш e"(r“VK)2<''T) [ф(М,т) —|^L€S dadt, (3.80)
0 S
127
то из (3.78) и (3.80) приходим к следующей формуле решения
первой краевой задачи:
X
т <"■')- £ fЯ'®. w<«> ■+ ■»£ тФлг
к=1 G к=1
[ ф(м. 4«^+i Ti^F х
fc = I
t
HHe'(^)V'T,/(M* T)Y«(M)dV*dT. (3.81)
t
X
6 ~s
t
X
6 ' G
В случае второй краевой задачи Р2 = 0; Рх = Х (к—теплопровод¬
ность):
— дТ (М, t)/dn= 1Дф (М, /), MeS, 0; dY*(M)/dtt|M6S = 0; (3.82)
аналогичным образом из (3.78) и (3.82) приходим к формуле
решения второй краевой задачи в виде
ПМ.П-± Ш'®- (Л)> +'“ t T^F x
к=1 G k= 0
t
e_(K"“v*)J('-T) [—[ф(м. T)4f*(M)]M€Sdordt +
0 5
+ Z Т^ИЯ e-(r~aVK)2{‘-x4(M, T) T,(A1) dx dV*. (3.83)
k=0 ' * 0 G
Здесь можно вести суммирование от нуля, имея в виду, что
уо = 0, Y0=l. В случае третьей краевой задачи [см. (2.10)] Рх=—
Р2 = а (а—коэффициент теплоотдачи)!
дТ(М, t)/dn + (a/K)T(M, 0 = (1А)ф(М, 0. f>0;
(M)/d/i + (a/Х) (M)]m e s - 0 (3.84)
и так как
t
ИГ(Т V. §)м ,/tdo-e-(^.,)V-»:х
0 5 0 5
X [— j<P(M. x)4;l((;Vl)]Ai6sdodT, (3.85)
128
то (3.78) и (3.85) дают решение третьей краевой задачи в
следующем виде:
Из (3.78) можно получить аналогичную формулу решения
краевой задачи со смешанными граничными усло¬
виями
где 1) вк(М, t)=—ф(М, t)dWK/dn на части граничной поверхности S,
где имеют место граничные условия первого рода (3.79); 2) @K(M, /) =
=[hF(1 /Л,)ф(М, /)]ЧГХ(УИ) на части граничной поверхности S, где име¬
ют место граничные условия второго (3.82) или третьего рода (3.84);
4^(714) — собственные функции соответствующей однородной задачи.
Выражения (3.81), (3.83), (3.86) содержат поверхностный и трой¬
ной интегралы. Эти интегралы необходимо вычислять при заданных
краевых функциях задачи в той или иной криволинейной (ортого¬
нальной) системе координат. В связи с этим приведем две полезные
формулы, используемые при вычислении интегралов, входящих в
полученные рабочие формулы.
Вначале рассмотрим формулу, сводящую поверхностный интеграл
после выбора определенной стороны поверхности к обыкновенному двой¬
ному.
Пусть в точках кусочно-гладкой поверхности S, ограниченной
некоторым кусочно-гладким контуром, определена некоторая функция
0(х, у, z) и пусть поверхность S задана параметрическими уравнения-
мих=ф 1(ui v)yy=y2(u, v), 2=ф3(и, и), где и, v изменяются вобласти А,
ограниченной некоторым кусочно-гладким контуром на плоскости
uv. При этом пусть между точками поверхности S и области А, также и
точками их контуров установлено взаимно однозначное соответствие.
Тогда имеет место следующая формула, связывающая поверхностный
интеграл с обыкновенным двойным:
х [|Ф(М, T)'MM)]jvigSdTda +
О 5
О 5
+ дм, T)Tv(M)dTd^. (3.86)
(С=1 ОС
X/(M,T)YK(M) dxdVV
(3.87)
5^ 0 (*. </. 2) da = $$ 0 [ф! (и, v), ф2(и, v),
S д
Ф3 {и, с)] У А'1В*С2 dиdt>,
(3.88)
5-339
129
где элемент площади поверхности do.в криволинейных координатах
(и, v) da = VА2 + В2 + С2 dи dv. Здесь
А =
(<Р2)и (фЛ
(ф2К (фзК
(ФзУи (фх)«
(фз)и (Фг)у
с =
(ф i)u (ф2К
(Фх)г (ф«К
(3.89)
В частном случае, если поверхность S задается явным уравнением
г = у¥п(х, у), где (х, у) изменяется в области D на плоскости (х, у),
то имеет место следующая формула:
55 © (*. Уу г) do = J J 0 (х, у, Wn (х, (/)) К 1 + (дУп/дх)2 + {d^Jdyfdx dy.
S D
(3.90)
Если поверхность S состоит из нескольких частей, каждая из кото¬
рых может быть представлена параметрическими уравнениями указан¬
ного типа, то для сведения поверхностного интеграла (взятого по такой
поверхности) к двойному можно воспользоваться тем, что поверхност¬
ный интеграл по S равен сумме интегралов, взятых по составляющим
эту поверхность частям, и затем применить формулу (3.88) к каждому
из этих частичных интегралов в ^отдельности.
Пусть далее в трехмерном пространстве (х, у, г) установлено
взаимно однозначное соответствие между декартовыми (х, у, г) и кри¬
волинейными координатами (qu q2t q9) с помощью соотношений:
х=ф!(?ь q2> ?з), У=Ф*(?ь Q2» ?з), *=фз(<7ь q2, <7з), где (pt непрерывны
вместе с частными производными первого порядка. Пусть при этом
имеет место взаимно однозначное соответствие между точками области
G [в которой определена некоторая функция 0(х, у, z)\ в системе
координат (х, у, z) и области А в системе координат (qu q2y q3)y а также
между точками кусочно-гладких поверхностей, ограничивающих эти
области. Имеет место следующая формула замены переменных в
тройном интеграле:
55 5 0 {X, у, г) dx dy dz = 5 5 $ © [<Pi (Я1. Як Яз), Фз (<7i> Яз, Яз), Фз (<?i. Яг
7*)]| Д</1. Яз, Яз) I d<7a dq3,
где
J (Як Яз< Яз) —
dyjdqi dtfjdqi d<p3/dqx
дф x/dq3 d(f>Jdq2 d<p3/dq2
d<pjdq, d(p2/dq3 d<p3/dq3
(3.91)
Элемент объема dK,, = dx Ay dz в криволинейных координатах
dVM = У (Як Яз> </з)М<71 dЯг dq3. (3.92)
Например, в цилиндрических координатах х —
<= г cos ф (ф! — г cos ф), у = г sin ф (фа = г sin ф), г — z (фа = г) вычисле¬
ния по формулам (3.91)—(3.92) дают dxd(/dz = r блбфбг; в сфе¬
рических координатах x = r«mpsin0, y = rsi^psin0,
z — г cos 0 формула (3.92) дает dV^ = гг sin Э dr d0 dф.
130
Перейдем к двумерным краевым задачам. Пусть D — конечная
область изменения двух переменных в плоскости (х, у); С — кусоч¬
но-гладкий контур, ограничивающий область D, причем кривую С
можно разбить на конечное число частей, на каждой из которых
координаты ее точек меняются монотонно; п—внешняя нормаль к С.
Требуется найти Т (х, у, t) — решение задачи:
Пусть у2к и У¥к(х,у)—собственные значения и собственные функ¬
ции соответствующей однородной задачи
Повторяя аналогичным образом предыдущие рассуждения, но
применительно к (3.93)—(3.95) и используя при этом формулу Гри¬
на для двумерного оператора Лапласа
получим основную интегральную формулу решения уравнения (3.93)
с начальным условием (3.94) в виде
Заметим, что во втором слагаемом при интегрировании по контуру
его обход совершается против часовой стрелки так, что ближайшая к
наблюдателю часть области, ограниченная контуром С, оказывается
лежащей слева от наблюдателя. Из (3.98) получаем рабочие формулы
записи решения плоских краевых задач нестационарной теплопроводнос¬
ти для различных видов граничных условий.
дТ/dt = atsT (х, у, t) + /(х, у, t), (xty)£Dt t > 0; -(3.93)
Т (х, у, 0|/=о = Ф0 (х> У)> У) € D; (3.94)
Pi [дТ(х,у9 t)/dn\—$2Т (х, у, t) = — Ф(х, у, t), (х,у)$С, />0. (3.95)
ДО (х, У) + ?2ТГ (*. У) = 0, (х, у) б D;
(3.96)
5 5 ('РДГ—TAY) dxdy=\ (VдТ/дп—Т дЧ/дп) d/, (3.97)
D
С
t
к = 1 0 D
131
Первая краевая задача:
Т {х, ty, t) — (p(x, у, t), (х, у) £ С, 0;
Чк(х,у) = 0, (х,у)<=С\
fix
Т(х, у, 0 = 21 Тч§Ге_(^к)2<
к=1 К D к-\ К'
х^е-(^)*«-о [_ф(х> у, т) 3L^]^)gcdTd/ + £ х
ОС к= I
t
X Je-^"“v*^(<-T)/(x, у, т)'^*, yJdrdP. (3.100)
О £>
Вторая краевая задача:
— 5Г (х, у, *)/д/г = (1А)ф(х, у, t),{x, у)£С, 0,
= 0.
(*, У) S С
(3.101)
(*^х
Т(*. «/, 0 = Ё7^е-(^*),'^Фв(дС> y)VK(x,y)dP+af^[
к = О D к = О
х^е-(^)а(/-х)[_|ф(х> у> x)yAXt dtdZ+^
О С к = О
*
Х Ш е"(1/“т*)а<('х)/(*» У> т) (*• У)dT dP- (3-102)
О D
Здесь суммирование ведется от нуля, имея в виду, что Yo = 0; ^=1.
Третья краевая задача:
~Ш+TT==T(f('x'y’ (Х’У)€С' {>0’
[-SJ^ + ?4'.(*, й]и.й.с“0: (3103)
Т(х, у. j,) V, (*, !/)^+aV
к=1 D к=1
х [ j e-('~^)s(/-t) ф (Хг у, г) Vg (х> у)^ y)6C dr d/ + £ х
О О К= 1
t
хЩе-^^'-^Дх, у, т) (х, г/) dt d/\ (3.104)
О о
132
Равенство (3.98) дает формулу решения и для краевых задан со сме¬
шанными граничными условиями:
Х$$фо(*> У)У«(х> </)dP + fl^
X Ук(х, у) dxdP,
(3.105)
где 1) &к(х, у у t) = — cp(jc, у, t)dWK/dn на части граничного кон¬
тура С, где имеют место граничные условия I рода (3.99);
2) ©*(*, У» 0 = (TlA) ф (х, у, 0^(*. У) на части граничного кон¬
тура С, где имеют место граничные условия II рода (3.101) или
III рода (3.103).
Выражения (3.100), (3.102), (3.104) содержат криволинейный
интеграл и двойной интеграл, подлежащие вычислению при задан¬
ных краевых функциях задачи. Приведем необходимые формулы
вычисления этих интегралов.
Пусть АВ—некоторая кривая, гладкая или кусочно-гладкая, и
пусть 0(jc, у)—функция, заданная на этой кривой. Кривая АВ
задана параметрическими уравнениями х = ср1ф), # = ф2(Р) Р0^
<P<Pj, причемcpi (Р) иф„ (р) непрерывны, a<pj (Р) и фа(Р) кусочно-не¬
прерывны и ограничены; ф|* (Р) + ф2* (Р) > 0- Тогда на АВ можно ввести
в качестве параметра длину дуги /, отсчитываемую от некоторой
фиксированной точки. Выберем при этом направление отсчета для
/ так, чтобы возрастанию параметра Р отвечало возрастание длины
дуги /. При этом дифференциал дуги d/
и криволинейный интеграл сводится к обыкновенному определен¬
ному интегралу
J 9 (дг, у) dl = $ © [ер, (Р), Ф2 (Р)] У ф;г (Р)+ф;* (Р) dp. (3.107)
Замечание к формулам (3.106) и (3.107). Следует запом¬
нить следующее: если положительное направление для отсчета дуги
^ (т. е. направление, .при котором / возрастает) в ходе решения
задачи выбрано не в сторону возрастания параметра р, а в сторону
его убывания, то в формулах (3.106) и (3.107) при вычислении диф¬
ференциала дуги необходимо поставить знак минус.
d I = Уц>[г (Р) + ф^1 (Р) dp
(3.106)
АВ
133
В частности, если кривая АВ задана явным уравнением у = ф0(л:),
x0^x^.xlt то формула (3.107) принимает вид
5 0 {*, у) dl = 5 0 (*, Фо (*)) у 1 + Фо* М d*. (3.108)
АВ х„
В полярной системе координат * = rcos<p, = г sin ф, если кри¬
вая АВ задана уравнением г = г(ф), ф0<ф<фх, выражение (3.107)
запишется в виде
ф!
5 в (х, у) dl = J ® (r cos Ф> г s^n Ф) г г2 (ф) + г * (ф) ^Ф- (3.109)
>45 Фо
Переходя к двойному интегралу, рассмотрим две плоскости
с декартовыми координатами (*, у) и (qlt q2) и предположим, что
в плоскости (ху у) выделена некоторая замкнутая ограниченная
область D с границей С, а в плоскости (qlt q2)—замкнутая огра¬
ниченная область Д. Пусть функции * = Ф1(<71, <72), # = ф2(<71» ?2)
определяют взаимно однозначное отображение этих областей друг
на друга; функция 0(jc, у) непрерывна в области D (включая гра¬
ницу) всюду или же ограничена в ней, а функции фх и ф2 (и обрат¬
ные для них) непрерывны вместе с частными производными первого
порядка. При этих условиях установлена следующая формула за¬
мены переменных в двойном интеграле:
5 5 0 (х, у) dP = 5 5 е [фх (ди <7,), ф, (qit д2)] \ J (gv gt) \ (3.110)
J (<7i> <7a)]
^ф1 ^ф2
'Iqi'dql
5фх дф2
dq2 dq2
; dP = dxdy = \J (glt gt)\ d^dft. (3.111)
Например, в полярных координатах х = г соэф, г/^гэтф имеем
qi = ry q2 = ф, ф1 = гсоэф, ф2 = гзтф;
cos ф sin ф I
— г sin ф г cos ф \Г
J (г, ф) =
и элемент площади. d* dy = г dr dq>.
Рассмотрим далее рабочую формулу записи аналитического ре¬
шения для одномерной краевой задачи нестационарной теплопро¬
водности (бесконечная пластина или стержень, теплоизолированный
с боковой поверхности):
dT/di = a(d*T/dx*) + f(x, t)y 0 < * </, *>0; (3.112)
Т (ху 0) = Ф0(х), (3.113)
(РпйГ/д*—Р12Т)„0 = — ф1 (0, t> 0; (3.114)
ФыдТ/дх + ?>22^)x=i = Фг (0» ^ 2^ 0» (3.115)
P<j>0; Р?х+Р?2> 0(1=1, 2), (/=1,2). (3.116)
134
Пусть Yk и ^(х)— собственные значения и собственные функции
соответствующей однородной задачи
d2'F*
d*2
• vi; ^Л*) = О, 0<х<1;
(3.117)
Рп
dT*
dx
РЛ)х=» = 0; (Рн^ + РЛ),= / = 0. (3.118)
Запишем решение задачи (3.112) —(3.116) в виде ряда Фурье по
системе функций {^(х)}:
т(Х, о=2 ©ловд.
к— I
где 0 (0 = J Т {х, 0 Ук (х) dx.
U
Используя уравнение (3.117), находим
(3.119)
"" Y2 ll^«
Здесь проведено дважды интегрирование по частям. Далее, как и
в (3.75), приходим к обыкновенному дифференциальному уравнению
относительно
ело + (К^т«)*^(0“у^г [(т
дТ\*-1 1
dx
-Y.
дх
dx
(3.120)
Как и в случае (3.76)—(3.77), начальное условие здесь имеет
вид
0ЛО)=то^ФЛ*)ВДс1х-
(3.121)
Находим из (3.120) —(3.121) функции ©*(/) и подставляем их
в (3.119). В результате приходим к следующей основной интеграль¬
ной формуле решения уравнения (3.112) с начальным условием
(3.113) и произвольными граничными условиями;
IX
к = 1
(х) dx + а £ j е'(^ О* х
[т(х, т)
dV„
dx
-УЛх)
дТ (х, т)
дх
1 dx —
J х=о
135
X
к= l
■^W
дТ (х, т)
дх
+ £^$Ие“'Г 0УкГ,“Т'Н*. x)¥KWdTd^. (3.122)
к — 1 * 0 0
Выпишем из (3.122) несколько решений.
Первая краевая задача. 1. Дано начальное распределение темпера¬
туры в точках стержня в виде некоторой функции Фо(*), а также распределе¬
ние внутренних нестационарных источников теплоты / (х, /); начиная с момента
времени t = 0 торцы стержня поддерживаются при переменной во времени тем¬
пературе ф1 (/) (при * = 0) и ф2 (0 (при * = /). Найти распределение температуры
в точках стержня в любой момент времени t. В (3.112) — (3.118):
Ри = Р21=0, У% = (кп/1)г, Wк (х) = sin (кпх/1),
Г(о, о=ф1 (0. г(/,о=ф*(<). <г&о;
Ч'*(0) = 'М')=0. (3.123)
Подставляя (3.123) в (3.122), находим решение первой краевой задачи:
\ 2
t I
*~(V °VK)2«-Т)
к — 1
. КЛХ л
sin —-— X
к= 1
Г ^ /tN • Knl . 2па . КЯХ
^ Фо (|) sin -у2- dg+-^- 2^ к sin —
Гф1 (т) — (—1)* ф2(т)] dx+
/ (I, т) sin dt d|.
(3.124)
хг
о « Л Л ( КЛ ^ V И Т)
к — 1 Об
Здесь для удобства переменную интегрирования обозначили через £.
2. Торцы стержня нагреваются с обеих сторон переменным во времени тепло¬
вым потоком (1/Я) ф1 (/) при х = 0 и (1Д)ф2 (0 при х = 1. Начальная температура
стержня представляет собой функцию Ф0 (х), мощность внутренних нестационар¬
ных источников теплоты */ (х, /). Найти распределение температуры в точках
стержня в любой момент времени t > 0.
Вторая краевая задача.
Pi2 = P22 = °; Рп = Р21 = Я.; ч1 = (кп11)*\ Ч'к{х) = со$(клх/[)
(см. § 7 гл. III):
дТ
дх
/А дТ I 1 /А
“-ХФПО.-^-^-уФ*^. ^0; -57-
/
х=о -—0;
х—1
1Y*P =
J cos2 (клх/l) dx = (//2), к > 0;
(3.125)
(3.126)
Jd * = /,
/с = 0.
КО
136
Подставив формулы (3.125) —(3.126) в формулу (3.122), найдем после несложных
вычислений решение второй краевой задачи в виде
<х _ ( КЛ У~а \2
г (г о- V cos (KWJf/0 V I J х
2- |т,к*
к s О
О к = 0
* _ fJB2d)2(/_T)
xje'1- ' / Т [ф1(т) + (-1)* 92(T)]dx+
О
оо ^ ^ { кл V~a \ ^
+2т0ЧК(-г')
к = 0 О О
Х/(|. T)cos-^dTd£, (3.127)
где || ||2 = //2 для к > 0; || ||а = /.
Совершенно аналогично могут быть рассмотрены и другие виды
граничных условий.
Формулы (3.78) и (3.98) справедливы как для задач на нагревание,
так и для задач на охлаждение. Впрочем, что касается задач на охлаж¬
дение, то их нетрудно свести к задачам на нагревание, особенно когда
начальная температура тела и температура его поверхности или тем¬
пература окружащей среды постоянны. Действительно, пусть Т0 —
начальная температура тела и в этот момент температура поверхности
тела мгновенно становится постоянной и равной ТС(ТС<Т0) или в на¬
чальный момент времени тело помещается в среду о постоянной
температурой поверхности Тс (Тс < Т0).
Имеем задачи на охлаждение: в первом случае
dTldt = аДГ (М, /), М <Е G, * > 0; \
Г(М, 0) = г0, меС; т(м, t)\M*s = Tcy />о; / (6АЩ
во втором случае
dT/dt = а&Т (М, t)9 M£G, t> 0, )
Т{М, О) = Г0, M^G; -k(dT/dn)\Mes = *(T\MeS-Tc), />0.1
(3.129)
Введем подстановку—безразмерную величину
е(м, (злз°)
i о * С
Получим задачи на нагревание, но уже относительно @(М, t):
дв/д( = аАв(М, 0. * > 0, (3.131)
0(М, 0) = 0, MgG;
а) в(М, t)\MiS = h t> 0; б) -X^^ = a(0-l)M€s; / > 0.
(3.132)
137
Замечание 1. Все рабочие формулы получены из предположения, что
G — конечная область, ограниченная замкнутой кусочно-гладкой поверхностью S.
Однако эти формулы в предельном случае могут быть использованы и для полу-
ограниченной области (а также и яля неограниченной) по той или иной прост¬
ранственной переменной. Необходимо лишь иметь в Еиду, что на части поверх¬
ности, уходящей в бесконечность, выражение (Т дЧ/дп — У дТ/дп) обращается
в нуль, так как, по предположению, решение Т таково, что как 7\ так и дТ/дп
ограничены, а У и дт/дп стремятся к нулю. В этом случае спектр собственных
значений (по данной пространственной переменной) становится непрерывным, из¬
меняясь для полуограниченной области 0 < у < оо (а для неограниченной области
— оо < у < + оо), и одна из сумм ряда Фурье заменяется на несобственный ин¬
теграл. Например, для первой краевой задачи в (3.93)— (3.95) при / = 0, <р = 0,
Pi =0, 0 < х < 1и 0 < у < /2 имеем
«ж оо f ( V~~a кп \2 ( V~~a тп \ 2"| ^
^ '« ' X
/l 1•
11 12 ' '
xjj<*o (x't y‘) sin sin ^ dx' d y\ (3.133)
Пусть теперь 0 < /2 < оо; тогда собственные значения и собственные функ¬
ции однородной задачи (по переменной у) будут slnyy, где 0 < у < оо. Полагая
в этом решении тл//2 = у» Так что ^7 ==(т+ 0 я//*—mnjt2 = n/l2t получим ин¬
тегральную сумму (по переменной у)
00
1 % sin у у sin уу' е~^ а Ду,
п “
m в 1
которая при m —*> оо (или Ду —► 0 при /$ —► оо) вырождается в интеграл, и окон¬
чательным решением первой краевой задачи в области 0 < х < llt у > 0 будет
выражение
Г(*. у, 0 = sln^e-^^'x
к— 1
00
Г (' . КПХ*
Xj J 0 (х * у )sln *“7Г~ *
О О
00
xJe-^^'slnyi/slnYI/' dV> (3.134)
о
которое можно существенно упростить, вычислив внутренний интеграл с помощью
таблиц [20].
Замечание 2. Относительно полученных основных формул (3.78), (3.98),
(3.122) следует сказать, что на правые части этих формул следует смотреть как
на ожидаемый результат решения соответствующей краевой задачи нестационар¬
ной теплопроводности, который нуждается в проверке. Дело в том, что эти фор¬
мулы получены в предположении, что решение задачи, записанное в виде ряда
(3.70) (как и собственные функции соответствующей однородной задачи), удовлет¬
воряет условиям применимости формулы Грина для оператора Лапласа в трехмер¬
ном и двумерном случаях и формуле (3.119) —в одномерном. А это связано с
непрерывностью решения вместе со своими первыми частными производными по
пространственным координатам точки М в замкнутой области G (D) и [0, /] и
138
непрерывностью вторых частных производных в области определения дифферен¬
циального уравнения теплопроводности (т. е. в G, D, (0, /), / > 0); кроме того,
во всех трех случаях предполагается существование и непрерывность частной
производной решения по времени t для любого t^t0 > 0.
Однако нам это заранее не известно, так как перечисленные условия не уча¬
ствуют ни в определении собственных функций, ни в определении решения соот¬
ветствующей краевой задачи. Таким образом, в каждом конкретном случае, для
того чтобы показать, что правая часть какой-либо из формул (3.78), (3.98), (3.122)
дает решение соответствующей краевой задачи теплопроводности, требуются до¬
полнительные исследования. В тех случаях, когда ряд (3.70) (для трех-, дву- и
одномерных задач), коэффициенты которого определяются путем формального
удовлетворения этого ряда всем условиям соответствующей краевой задачи после
почленного дифференцирования два раза по пространственным переменным и один
раз по времени t, равномерно сходится, он представляет собой решение задачи,
дважды непрерывно дифференцируемое по координатам точки М, непрерывно диф¬
ференцируемое по времени t во всех внутренних точках области Й = {Л4£(/,
t > 0} и непрерывное в замкнутой области й (если краевые функции задачи также
непрерывны в й). Эти дополнительные исследования, как правило, приводят к
положительному ответу, и, таким образом, вопрос о решении краевых задач не¬
стационарной теплопроводности с помощью полученных рабочих формул в суще¬
ственной своей части сводится к нахождению собственных значений и собствен¬
ных функций соответствующей однородной задачи. Если эту задачу удается
решить, то вопрос о решении исходной краевой задачи нестационарной тепло¬
проводности в принципе можно считать законченным.
Замечание 3. Формулы (3.78), (3.98), (3.122) выведены для уравнения
теплопроводности (3.66). Собственные функции в этих формулах при этом удов¬
летворяют уравнению (3.69) в трех-, дву- или одномерной задачах. Однако все
полученные формулы в одинаковой степени справедливы и для уравнения вида
(1 Ja)dT/dt = AT(M, t)—c2T(Mt t) + f(M, t). (3.135)
Но теперь собственные функции во всех рабочих формулах будут удовлетво¬
рять уравнению AH' (Л4)—с2хУ (Л4) + y21F (М) == 0 и соответствующим однородным
условиям. Заметим также, что уравнение (3.135) нетрудно привести к виду (3.66)
подстановкой: Т(М> t) = U(M, /Je”06** и в таком виде работать с ним дальше.
Рассмотрим несколько примеров полученных рабочих формул.
Пример 1. Найдем температурное поле области, имеющий вид прямоуголь¬
ника (х, y)£D = (0*^x ^ /ь 0^«/</2), нагреваемой при следующих условиях:
начальная температура — произвольная функция пространственных координат
Фо (*» У) \ внутри области действует нестационарный источник теплоты мощностью
/ (*. У> О! ограничивающие поверхности х = 0 и х = 1г нагреваются соответственно
переменными тепловыми потоками (pi(y, t) и <р2 (*Л •/); на границах у — 0 */ = /2
заданы переменные температуры соответственно <р3 (х, /) и <p4 (х, t). Имеем при
этих условиях задачу:
dT/dt = a(d2T/dx2 + d2T/dy2) + f(xt у, /), (3.136)
(x,y)£Dtt>Q\
Т (х, у, 0)=Фо (X, у), (X, y)€D;
~}i(dT/dx)jx=0 = <p1(y, t); b(dT/dx)\x=lt=(p2{y, I), 0<{/</2, 0; (3.137)
Т\у=0=Чз(х, t), T \y-ft — <Pi (*> 0. 0<дг</х, 0. (3.138)
В этой задаче задаются смешанные граничные условия, поэтому для записи
ее решения следует использовать формулу (3.98) или (3.105).
Вначале необходимо определить собственные значения и собственные функции
соответствующей однородной задачи
даЧ7дх2 + д2Ч'/&/+ у2хЕ = 0, 0 < х < /ь 0 <у<12, \
дЧ/дх |Л = 0=ЗУ/йдг |д = <4 =0; V |,= 0 = Г \у= 0. J- (3‘139>
139
Находим (см. § 7 гл. III) у2кт = [(асл//х)2 + (тл//2)2], где к = О, I, 2, ...; т =
«=1,2,3, ...; Ч^^х, y) = cos(K7ix!li)Xsln(mJiy/l2)'t
h It
ИЧ^ца — J ^ cos2 (K7ix/l{) sin2 (nrny/l2) dx dy = /j./2/4, к > 0, 1;
о о
ll^omll2= J ^ slfl2 (mjTl///2) dxdy = lik/21 k = 0, m^l. (3.140)
о о
Таким образом, устанавливаем, что в записи решения в виде двойных рядов
суммирование следует производить со значений к = 0 и m = 1. Распишем вначале
первое и третье слагаемые в формуле (3.105):
к= 1 * ' D
ОО 00 J
XdP = ^ ^ cos (кя*//!) sin {mny/I2)X
к=0 m=1
Хе”(>^7к/я)2/ ^ J Ф0 (х, у) cos {клх/li) sin (тлу/12) dx dt/;
о о
к= 1 О D
00 00
X (х, I/) dx dP = jj-qp—-jjjXcos (кпх/tj) sin (тпу/1г)X
K=Om=! (3I41)
» *1 *1
x) cos (клх/1{) sin (тлу/12) dx dx dy.
X
ooo
Распишем теперь второе слагаемое в фор¬
муле (3.105), учитывая, что интегрирование
по замкнутому контуру С (рис. 22) ведется
против часовой стрелки (для определенности
от начальной точки Е)\ при этом, согласно
(3.137) и (3.138), имеем
—дТ (дг, у, t)/dx |Е0 = (1 Д) ф! (у, 0; дТх
X (дг, у, t)/dx\AB = {l/X)<ft(y, 0;
Т(х, у, 0 |ол =Фа (лг. 0; Т(х, у, 0|ве =
= Ф4(ДГ, О
и далее
Рис 22 S = S + S + S + S •
кис* ** С ЕО ОА АВ BE
Рассмотрим отдельно каждый из этих интегралов. На контуре ЕО (уравнение
х = 0) имеем
в* (ДГ, у, <)=(— 1А)ф1 (у, О [COS (клдг//,)Х
Xsln (тя1///2)]д=о = (— 1А) Фх (м> 0 sln (mny/lt).
140
Согласно замечанию к формулам (3.106) — (3.107), дифференциал дуги на этом
контуре dl = У О2 + dу2 = —dу\ таким образом,
о
J ®к(х, У, т) d/ = + j у ф! {у, т) sin (mnyjlt) dу =
ЕО it
it
= (— 1Д)^ ф! (|у, т) sin (тлу/12) dу. (3.142)
о
На контуре О А (уравнение у = 0)
_ .. ,ч / д Г кпх . тпу "I \ тп . _ клх
ей*, 1/, 0=ф.(*. 0 \Fy [cos — sin j o=— ф3 (x, 0 c°s —;
направление внешней нормали к контуру ОА не совпадает с положительным
направлением оси у% dl=Y djc2 —|- О2 = d^c; имеем
Ц в*(*, У у V3(x’ flcos-^-djc. (3.143)
ОА 0
На контуре АВ (уравнение x = lx) dl=Y Q2-\-dy2 = dy,
п 1 / .ч Г KJlx 1 тпУ 1 / 1 / .ч , wm/
//, 0=у ф2 (*/, 0 [cos_7r" “7r~Jjc=i,:= хф2^’ )s “17";
о
^ в*(*. */, т) d/ = (—1)* (1/Я) J ф2 (у, т) sin dy. (3.144)
ав о
На контуре BE (уравнение у=12)
= (—l)m + 1 (тл//2) ф4 (х, t) cos —;
направление внешней нормали к контуру BE аналогично положительному направ¬
лению оси г/, т. е. д/дл = +ду%,
dl=Y d*2 + 02 = —d*;
о
P Л , ч л . (—l)m + irrm Г . _ кл*
\ 6*(*» у, t)d/ = + ^ }—^ j ф4 (*, 0 cos -j-— X
se 6
U
(_1)/Я + 2тяГ» кш
Xd*= \ ф4 (*, /)сos—j—d*. (3.145)
l2 J ч
• о
Используя теперь выражения (3.141) — (3.145), запишем окончательно реше¬
ние задачи (3.136) —(3'. 138) в следующем виде:
'г/. .. cos (KTixfk) sin (mny/li) w
(*, y, 0-2, 2- пет X
k= 0 m = 1
Л /.
x e - (^avif/я / ^ J (*» */) cos -j— sin —■dx dy +
о 0
ao oo
+xZI
cos (клх/li) sin (mny/l2)
гет
0 m= 1
141
xi J e_<V°"VKm)! *' T)[—ф1(у. t) + (—1)*ф2(</-, т)] sin (trmyHi) dtd{/+
■ о
+ £ £ WH»«pi,MWIJ
0 0
i (l
/Л/ \2 / #
к=0ш=1 " """ " О О
Х[ф3(*, т) + (— l)w ф4 (х, т)] cos (клх/1г)Х
Xdtck+У у „cos^/MsMmny/ZJ х
II * I)
к = 0 m = I
* (i /j
X
ООО
Здесь у2кт = (/сл//)2 + (тл/12)
4/(/i/2)* АС > 0; tn^z 1;
2/(/,/2), ас = 0, m^l.
* *1 *2
(J j j* e” (1/~^л?лг/7г)2 (/“x) f (x, у, т) cos {Knx,li) sin {mny/l2) dt dx dy. (3.146)
j
Пример 2. Дан неограниченный сплошной цилиндр 0<:г<;#, нагреваю¬
щийся по всей поверхности переменным (по времени) тепловым потоком, темпера¬
турное поле считается цилиндрическим. Постановка задачи следующая:
dT/dt = a[d2T/dr*+(\/r)dT/dr], 0<г<Я, / > 0; (3.147)
Т (л, 0) = Ф0 (л),
dT/dr\r=R = (\/X) ср (/), /^0; | Т (г, /) | < +оо, г^О. (3.148)
Решение этой задачи нетрудно записать с помощью формулы (З.Ю2), но в
полярной системе координат я^гсоэф, г/ = л sin ф. Прежде всего найдем собст¬
венные значения и собственные функции соответствующей однородной задачи
d21Ir/dr2 + (1 /г) d'F/d/’-b Y21^ (d=0, 0 </■</?;
d'F/dr |г_ ^ = 0; \V (r)\ < +*>, r^0. (3.149)
(Задача (3.149) рассмотрена в § 8 гл. III.)
Имеем
Тк=ак/Я2. ^«(r) = J0(aKr/R), к = 0, 1, 2...;
yl=al/R2 = 0; Ч'„(/-) = /0 (0) = 1,
где J0 (г) — функция Бесселя I рода нулевого порядка [54], ак ^ 0 — корни урав¬
нения Ji (а) =0.
Квадрат нормы функций
II ^|Р = ро (<V/*) dr= J * >0; (3.150)
В формуле (3.102) квадрат нормы ЦЧ^Ц2 записан в декартовой системе коор¬
динат 11^кИ2==5§ У)^Х(^У- Необходимо вычислить этот интеграл в поляр-
D
ной системе координат, используя формулу замены переменных в двойных интег¬
ралах (3.110). Подынтегральная функция в полярной системе координат уже
получена, т. е. Ч'- (х, у) = J20 {aKr/R)\ элемент площади dx dy = rdrdy\ таким об-
142
разом, испбльзуя (3.150), получим
R 2л
|Чг„Р=$$Ч'!2(*, j,)d*dif=J J rJl(aKr/R)X
D 0 0
R
X d/- ёф = 2л J rJ о (aKr/R) dr = 2л || 4^ ||J>.
о
Аналогичным образом можно записать в полярной системе координат и двой¬
ной интеграл (под знаком суммы) в первом слагаемом в формуле (3.102): так как
начальная функция Ф0(*, у) уже задана в полярной системе Ф0 (лт, ^/) = Фо(^)»
собственные функции известны W4 = J0 (aKr/R), элемент площади равен dЯ ==
= гdrdф, то имеем
2л R
y)dP=J J Ф0(г) JQ(aKr/R) rdrdy^
D 0 0
R
= 2л J гФ0 (г) JQ (aKr/R) dr.
о
Таким образом, первое слагаемое в формуле (3.102) в полярной системе
координат имеет вид
Я
Тг (г, <) = У -» е-111 ГгФ* (г)/„(«✓//?) <1^. (3.151)
" ||¥*||р о
где а* — корни уравнения J1(a) = 0t а Ц^^Цр дается выражением (3.150).
Перейдем далее к вычислению в полярной системе интеграла
t
/к =
„.С4""-
где подынтегральная функция рассматривается в точках контура С.
По условию (3.148), граничная функция (при r = R) равна (1Д)ф(дт, у, () =
= (1А)ф(0; в точках контура [У*]и| у)йС = l^« (a«//^)]rss r = Jo (aj. Вычис¬
лим дифференциал дуги dl: в нашей задаче граничный контур С представляет
собой окружность радиусом r = R с центром в начале координат, в точках кото¬
рой дт = г cos ф, г/ = /■ sin tp и интегрирование ведется против часовой стрелки от
горизонтального диаметра (соответствующего значению ф = 0). Г1о формуле (3.106)
находим
dl = У (-R sin ф)2 + (# cos ф)а dф = /?бф
и далее по формуле (З.Ю7)
j ^ф(д> т)Чг,(л, „)] сХ
о с
t 2я
Xdx d/ = y J (/~т) ф(т) dix J [/0 (a*'//?)],» R Я*1ф = Jo (a*) X
о о
t
w dXj
0
гле Т« = а*/Я.
143
Таким образом, второе слагаемое формулы (3.102) в полярной системе коор¬
динат имеет следующий вид:
Тг (г, 0 = a X
к= I
t
У)
IIVJI2
/« =
aR_y Jo (««) Jo (aKrlR)
X
k= 0
< j* exp [ — (y~~aaK/R)2 {t — т)] ф (т) dt.
(3.152)
Искомое решение задачи (3.147) — (3.148) представляется в виде суммы выраже¬
ний (3.151) и (3.152), т. е. Т (г, f) = 7^(r, t)-\-T2{r, t). Это решение нетрудно
записать в безразмерном виде, если йве£ти обозначения: z = r/R\ Fo = at/R2;
Фо (r)lT$\ фо (Fo) = /?ф {t)/(kT0)\
W\zjFb) = T(ry t)/TQy где Т0 — некоторое по¬
стоянное значение температуры, выбранное в
качестве масштаба. После несложных упроще¬
ний получим
ч /о (a *z) е“акр0
W (г, Fo) =
_ ^ Ли.
со
I V J0 (а*г) Г ^
j* гФ0 (г) /0 (а^г) dz+
о
Fo
'I е‘“5
-aj (Fo-т)
Ф (t) dt;
0. (3.153)
Рассмотрим частный случай, когда в (3.148)
начальная температура постоянна Г (г, 0) = 7,0,
а боковая поверхность нагревается равномерно
постоянным тепловым потоком ф (0 =qc = const.
В этом случае Ф0 (z) = 1; ф (Fo) =Rqc/XT0. В ре¬
шении (3.153) выделим нулевое слагаемое, имея в виду, что а„ = 0, /0 (0) = 1; кроме
1
того, учитывая формулы [15] J $J0 (aKz) dz = (1/a*) (av) = 0, (так как aK —
о
OO
корни уравнения /i(a) = 0), к > 1; 2 /° =-1- (z2 , получим из
KS1«kJo(<*k) 2 \ 2}
(3.153) после несложных вычислений
T{rCxTa = 2Fo -T(1 2гг/Яг) 2 X
J0 (aKr/R)
-ai Fo
a^o (a*)
(3.154)
Проведем краткий анализ решения (3.154). Ряд в (3.154) сходится достаточно
быстро из-за наличия множителя exp (— a*Fo), так как ак — величины большие
(см. [83]). Начиная с определенного значения Fo^Foi, этим рядом можно пре¬
небречь по сравнению с первыми двумя членами, т. е. записать:
[Т (г, t) — T0]/(Rqc/K) = 2Fo— (1 —2r2/R2)/4. (3.155)
В этом случае температура в любой точке цилиндра (когда г фиксировано) будет
линейной функцией времени, а распределение температуры — параболическим
(такой режим носит название квазистациопарного).
На рис. 23 приведены кривые безразмерной температуры 0 = (Т — T0)/(Rqc\-1)
для разных значений Fo [83]. Из рисунка видно, что начиная с Fo = 0,2 кривая,
144
характеризующая распределение 0 по относительной координате, равномерно
смещается вверх, т. е. начиная со значением Fo^0,2 может быть использована
формула (3.155).
§ 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
ДЛЯ НЕОГРАНИЧЕННЫХ ОБЛАСТЕЙ
Рассмотрим метод Фурье при решении тепловой задачи для бес¬
конечного стержня, теплоизолированного с боковой поверхности
(задача Коши); начальная температура стержня задана в виде функ¬
ции Ф0 (я):
dT/dt =а(д2Т/дх2, —оо<л:< + оо, / > 0; (3.156)
Т (*, 0) = Ф0 (ж), — оо<*< + оо;
\Т (х, t) < + °о, |*|< + оо. (3.157)
Здесь Ф0(*)— непрерывная и ограниченная функция.
Как обычно, находим сначала частные решения уравнения (3.156)
вида Т (х, /) = 0 (/) ¥ (х); подставляя правую часть этого равенства
в уравнение (3.156) и разделяя переменные, получаем
1 в'® Г(х) __ л
а 0 (0 W (х) 7 *
где у2—постоянная разделения, откуда имеем
©' (0 + (VayY © (0 = 0; ЧГ (*) + у*Ч (*) = 0.
Интегрируя эти уравнения, получаем
0 (0 = A exp [— {\fa у)2 /]; V (х) = В cos ух + С sin ух.
Частное решение уравнения (3.156) имеет вид
Т = (АВ cos ух AC sin ух) ехр [— (УНу)2 /],
или
Т = (a0cosvx + 60sin у*)ехр[—(VHy)2/], (3.158)
где а0 = АВ; Ь0 = АС.
Здесь А у By С — произвольные постоянные интегрирования, зна¬
чит, ,а0, Ь0—также произвольные постоянные.
Функция (3.158) при любом, фиксированном у удовлетворяет
уравнению (3.156) и можно для каждого значения у выбирать раз¬
личные постоянные а0 и Ь0. Это означает, что а0 и Ь0 могут быть
произвольными функциями от уУ так что окончательно имеем сле¬
дующее семейство частных решений уравнения (3.156):
т — [ао (Y) cos ух + b0 (у) sin y*] exp [— (Ka y)2 t\ (3.159)
Так как граничные условия в задаче отсутствуют, то параметр у
остается произвольным и может принимать все значения от —оо до
+ оо. Тем самым, как и выше, первая часть метода Фурье завершена.
Вторая часть метода Фурье заключается в суперпозиции полученных
частных решений. Для ограниченных областей суперпозиция частных
145
решений приводила к бесконечному ряду Фурье, суммирование которо¬
го происходило по индексу, пробегающему целые значения. Контину¬
альным аналогом ряда Фурье является интеграл Фурье: вместо сум¬
мирования по индексу, пробегающему целые значения, имеет место
интегрирование непрерывно изменяющейся переменной у в (3.159).
Таким образом, интегрируя (3.159) по параметру у» получаем также
решение уравнения (3.156)
+ 00
Т(х, t)= J [ай (у) cos ух + Ь0 (у) sin у*] ехр [— {У~ау)2 /] dy, (3.160)
— оо
если несобственный интеграл (3.160) равномерно сходится в обла¬
сти й = (|*|< + оо, £>0) и его можно дважды непрерывно диф¬
ференцировать по х и один раз по t (также под знаком интеграла).
Определим далее неизвестные функции a0(v) и ^o(y) так» чтобы
выполнялось и начальное условие (3.157), т. е.
+ QO
Т(х, 0) = Ф0(*)= ^ [До (?) cos ух + b0 (у) sin Y-c] dy.
— оо
Полученное равенство означает разложение начальной функции
Ф0(х) в интеграл Фурье.
Находим коэффициенты этого разложения по формулам:
+ 00
= i J <I>o(1)cosy£cI|; МY)=-
— оо
+ оо
= i (Б) sin YS dfi. (3.161)
— со
Напомним, что указанное разложение возможно, если функция
Ф0(*) кусочно-гладкая в любом конечном интервале и если интеграл
+ 00
I I Фо МI dx сходится (является конечной величиной). Оба эти усло-
— 00
вия выполняются в теории теплопроводности, первое в силу физи¬
ческого смысла функции Ф0 (х) [Ф0 (*)—начальное распределение тем-
+ оо
пературы], второе в силу того, что интеграл J | Ф0 (л:) | djc пропор-
— оо
ционален тепловой энергии стержня—конечной величине. Подстав¬
ляя (3.161) в (3.160), найдем
+ 00 +00
т (х, I) — -^ ^ exp [— (ay)21] dY J Ф, (£) cos y (1 — x) d* =
— oo — 00
ос + oc
exp[— iVay)'2 /JdY ^ Ф0 (I) cos y (S—x) di
0 — oo
146
Меняя порядок интегрирования, запишем
+ 00
00
Т (х, 0 = -^ { Ф0 (i) dg ^ е~<! а ^' cos y (£—х) dy.
— оо
О
Воспользовавшись далее формулой [20]
(3.162)
о
окончательно приходим к следующему выражению:
+ 00
Т(х, 0 = j (3163)
— 00
Непосредственной проверкой нетрудно убедиться, что функция
рассматриваемая как функция от х, t, удовлетворяет уравнению (3.156).
Функция (3.164) называется фундаментальным решением уравнения
теплопроводности (3.156).
Покажем далее, что формула (3.163), называемая интегралом
Пуассона, представляет при t > 0 для любой непрерывной ограни¬
ченной функции | Ф0 (х) | М0 ограниченное решение уравнения
теплопроводности (3.156), непрерывно примыкающее при /=0 к Ф0(*).
Для этого достаточно показать, что интеграл (3.163), а также интег¬
ралы, полученные его формальным дифференцированием (под знаком
интеграла) два раза по * и один раз по /, сходятся равномерно.
Дифференцируя (3.163) два раза по л: и один раз по/, получаем
сумму интегралов и нужно показать, что каждый из интегралов
равномерно сходится. Каждый из полученных интегралов, в том
числе и исходный, может быть записан в виде
где m = 0, 1, 2, ...; к > 0—некоторое число.
Произведем замену переменных (3 = (*—1)/2|/о7| (/>0) и пре¬
образуем интеграл (3.165) к виду
(3.164)
+ 00
— 00
/=(2 Ко/)" Г* Ф0 (х — 2\ral р)dp. (3.166)
147
Нетрудно видеть, что интеграл (3.166) сходится равномерно при
о > 0, так как мажорируется интегралом вида
Последний интеграл сходится, так как функция |Р|отехр(—реинтег¬
рируема в промежутке (— оо, + оо). При выводе неравенства использо¬
валось условие ограниченности функции Ф0(л:), т. е. неравенство
|ф0(*-21/^7р)|<М0. в частности, при т = 0 для исходного интег¬
рала (3.163) имеем
и так как интеграл (3.168) сходится равномерно относительно х
и /, а функция Ф0(*) непрерывна, то в (3.168) возможен предель¬
ный переход по t (при / —► 0) под знаком интеграла и под знаком
функции Ф0:
т. е. начальное условие (3.157) выполняется. Здесь был использо¬
ван известный из анализа интеграл (см. [146], т. II)
Для кусочно-непрерывной (и ограниченной) начальной функции
Ф0(*) предельный переход под знаком функции совершать нельзя,
поэтому для доказательства выполнимости начального условия (3.157)
следует применить другой прием. Об этом можно прочитать, например,
в [137]. Отметим, что условие (3.167) выполняется для любой ограни¬
ченной функции Ф0(х) во всех точках непрерывности этой функции.
При этом имеет место и единственность решения (3.163).
J Ф0(*—2Xrai§) Рст ехр(—Р2) dp ^
— 00
+ 00
< S |ФЛ*-2К5р)ИР1"ехр(-Р)^р<
<М0 J |Р|т ехр(—Р2) dp.
(3.167)
— 00
+ 00
Т(х, 0 = J ®e(E)e-<*-5>*/(««odS =
— 00
(3.168)
— 00
+ оо
+ 00
у=п j Фо(*)е-0Чр = Фо(*)-р^ j е-»Чр = Ф0(Д (3.169)
— О0
— 00
+ оо
00
(3.170)
148
Из (3.168) немедленно следует ограниченность решения Т(х> t)
для любой ограниченной функции Ф0(х)
+ 00
xdp<M0^ j* e-e‘d|3 = M0.
— 00
Итак, функция, определяемая формулой (3.162), непрерывна, имеет
непрерывные производные по х до второго порядка включительно
и непрерывную первую производную по t при />0, удовлетворяет
уравнению (3.156) при />0 и является ограниченным решением крае¬
вой задачи теплопроводности (3.156) — (3.157).
Если начальная функция Ф0(*) имеет конечное число точек разрыва,
то интеграл (3.163) представляет собой ограниченное решение уравнения
(3.156), непрерывное в Q всюду, кроме точек разрыва функции Ф0(х).
Отметим одно обстоятельство. Решение (3.163) в Q есть функция, непре¬
рывно дифференцируемая по х и t, т. е. сколько угодно число раз не¬
зависимо от того, дифференцируема функция Ф0 (х) или нет. Эта глад¬
кость решений существенно отличает уравнение теплопроводности —
уравнение параболического типа от уравнений в частных производных
других типов.
В (3.169) получен очень важный результат, который лежит в основе
метода исключения неоднородности в началь¬
ном условии для краевых задач нестационар¬
ной теплопроводности. Действительно, предположим,
что Т(х, t) есть решение задачи:
dT/dt=a(d2T/dx2), *>0, t > 0; (3.171)
Т(х, 0) = Ф0(л:), *>0; Г (0, 0 = ф(0.
|Т(х, /)1< + °°. *>° (З-172)
с ненулевым начальным условием, что создает некоторое неудобство
при ее решении методом, который предполагает наличие нулевого
начального условия [например, методом тепловых потенциалов
(см. гл. VIII) или операционным методом (см. гл. VI)].
Преобразуем задачу (3.171) — (3.172). Положим
+ со
W(x, t)=T (х, 0--тЦ Г (3-173)
2 у я at J
— 00
В соответствии с вышеполученными результатами имеем теперь для
функции W (х, t):
dW/dt — a (d2W/дх*), х > 0, < > 0; )
W (дг, 0) = 0, .v>0; W (0, <)=(Pi(0> | (3.174)
<>0; \W{x, ОК + оо, а>0. I
149
Если начальная функция Ф0 (х) не определена при отрицатель¬
ных ху то в (3.173) под знаком Интеграла можно взять функцию
Ф1(1)у совпадающую с ф0 (£) при |>0 и выбранную произвольно
при | < 0. Запомним этот результат, так как он достаточно часто
используется в аналитической теории теплопроводности.
Заметим далее следующее: требование ограниченности начальной
функции Ф0(*) при всех |je|<-f-oo является весьма ограничитель¬
ным для практических целей. Может случиться так, что начальная
функция на бесконечности является неограниченной, возрастая,
однако, по абсолютной величине не быстрее чем \x\pt т. е. |Фо(*Х
^M0|jc|p, где Р^Оу или |Ф0 (х) | ^М0ес1*!, где УИ, С, Р — посто-
Формулу (3.163) можно рассматривать в этом случае, как «обоб¬
щенное» решение задачи (3.156) — (3.157), так как невыполнимо раз¬
ложение такого рода начальных функций в интеграл Фурье (3.161).
Очевидно, и решение задачи Т (я, /), являясь ограниченным на
каждом конечном промежутке [—/, +/], будет вести себя при
х — =Ь оо так же, как и начальная функция Ф0(*)- Пусть, напри-
мер, Ф0(*) — Л0дг, найдем Т (л:, t) по формуле (3.163)
Выясним теперь физический смысл фундаментального решения
(3.164) и решения (3.163). Выделим около точки х0 малый элемент стер¬
жня х0—е, х0+е (где е>0 — сколь угодно малое число) и будем считать,
что начальное распределение температуры дается функцией Ф0(*)>
которая равна нулю вне промежутка х0—е, х0+г и имеет постоянное
знание Т0 внутри него
Начальное распределение температуры, удовлетворяющее условию
(3.175), называется физическим тепловым импульсом. Такое начальное
распределение температуры возникает, если в начальный момент вре¬
мени сообщить элементу стержня (х0—е, х0-Ке) количество теплоты
Q=2ecpT0, которое вызвало повышение температуры на Го в этом
участке стержня. При таком физическом тепловом импульсе темпера¬
тура в стержне в последующие моменты времени определяется форму¬
лой (3.163), которая в случае (3.175) принимает вид
янные.
+ 00
Т (х, () = - А= Г Ze-<x-W("t) d£=
2 у nat J
f (*—2l/Srp)e-0*dp = ;4,x.
V n J
если x0—e.< я < л:0 + е;
если \x—x0 \ > e.
(3.175)
От физического теплового импульса перейдем теперь к точечному
(идеальному) тепловому импульсу, физический смысл которого состоит
в следующем. Будем уменьшать в до нуля, считая, что то же количество
теплоты Q распределяется на все меньшем участке и в пределе сообща¬
ется стержню в точке х=х0. В этом случае придем к понятию мгновенного
точечного источника теплоты мощностью Q, действующего в точке
х=х0 в момент времени t—0 (точечный тепловой импульс). Температура
в стержне, соответствующая точечному тепловому импульсу, определя¬
ется по формуле
Т (.х, t) == lim
Q/cp
2 yUai
x0 + r
-H
e-(.v-e)V(4o<) <jg
Применяя теорему о среднем, получим
А'о + е
2е
где jf„—е < |0 < *0 + е. Так как |0
предел, окончательно найдем
Q 1
Т(х, t):
ф 2 УШ
х0 при е •
О, то, вычисляя
(3.176)
Предположим конкретно, что подведенное (выделенное) коли¬
чество теплоты Q = cp, тогда получим
Т(х, = *„ О, (ЗЛ77)
2 у nat
т. е. фундаментальное решение (3.164) при значении параметра
1 = х0. Таким образом, фундаментальное решение (3.164) или (3.177)
уравнения теплопроводности дает
распределение температуры в точке У
стержня х в момент времени t%
которое вызывается мгновенным
точечным источником теплоты
мощностью Q = ср, действующим
в точке х = 1 (или х = х0) в мо¬
мент времени t = 0.
Графики .фундаментального ре¬
шения G (.х, t) при фиксирован¬
ном I как функции от х для раз¬
личных моментов времени 0 < t1 <
< t2 < < • • • представлены на
рис. 24. Площадь под каждой из этих кривых равна
+ 00 + 00 _(х _£)2 +00
151
Это означает, что количество теплоты Q=cp в стержне остается
неизменным с течением времени. Кроме того, из рисунка видно, что
почти вся площадь, ограниченная кривой (3.164) и осью абсцисс, нахо¬
дится над промежутком ■(£—в, |+е), если только £>0 — достаточно
малое число. А так как количество теплоты в стержне равно произве¬
дению ф на всю площадь, то отсюда следует, что для малых значений
£>0 почти вся теплота сосредоточена в малой окрестности точки х—1\
устремляя t->0, приходим к выводу, что в начальный момент времени
t=0 вся теплота сосредоточена в точке x=ty т. е. имеем мгновенный
точечный источник теплоты.
Математически начальное распределение температуры при мгно¬
венном точечном источнике теплоты записывается с помощью так на¬
зываемой импульсной дельта-функции Дирака [21], [38], [103] 6(л:—х0),
представляющей как бы предел физического импульса Ф0е (х) при в-^0.
Дельта-функция определяется формально с помощью следующих
соотношений:
для всякой непрерывной в (а, Ь) функции ф(х). В частности, для
Ф (х) = 1 имеем
Дельта-функция является математическим выражением сосредото¬
ченных величин (точечный источник теплоты, точечная масса, точечный
заряд, сосредоточенный импульс и т. п.). Строгое определение дельта¬
функции как «предельного образа» может быть дано с помощью поня¬
тия «обобщенных функций» [21].
Нетрудно дать физическую интерпретацию формул (3.178) и (3.179).
В наших предположениях Q=cpt отсюда 2еТ0=1 и, устремляя е->0,
имеем Го-^+оо; это значит, что температура в точке х0 становится
равной бесконечности. Равенство (3.179) можно записать в виде
где е>0, это соответствует тому факту, что 2гГ0=1 при любом е;>0.
(3.178)
и
В случае, когда а =—оо, b=-f-oo,
+ СО
^ Ь(х—х0)с1л:=1.
(3.179)
— 00
х0 + н
152
Таким образом, можно сделать вывод, что фундаментальное реше¬
ние G(x, £, /) дает распределение температуры в бесконечном стержне
с теплоизолированной боковой поверхностью, начальная температура
которого равна Ф0(х)=б(л:—£). В справедливости этого вывода можно
убедиться непосредственно, если подставить в (3.163) вместо Ф„(х)
дельта-функцию.
Действительно, обозначив для удобства переменную интегрирова¬
ния через и учитывая (3.178), имеем
Формула (3.164) показывает, что во всякой точке х стержня температу¬
ра, создаваемая мгновенным точечным источником теплоты, действую¬
щим в точке х=1 в начальный момент времени /=0, отлична от нуля
для сколь угодно малых моментов времени. Это означает, что теплота
распространяется вдоль стержня с бесконечной скоростью. И хотя
это противоречит молекулярно-кинетическим представлениям о при¬
роде теплоты, но это противоречие логически объяснимо. В гл. I при
выводе дифференциального уравнения теплопроводности мы пользова¬
лись феноменологическими представлениями с распространении тепло¬
ты, не учитывающими инерционность процесса движения молекул.
Поэтому естественно ожидать проявление этого факта и в аналити¬
ческих решениях краевых задач уравнения теплопроводности.
Теперь нетрудно дать физическое толкование и решению (3.163).
Для того чтобы получить в точке х=\ стержня температуру Ф0(|)
в начальный момент, следует подвести к малому элементу стержня d|
около этой точки количество теплоты сК2=фФ0(£)с1£, или, что то же
самое, поместить в точке х=% мгновенный точечный источник теплоты
мощностью dQ. Температура, вызываемая этим источником, согласно
Общее же действие от начальной температуры Ф0 (£) во всех точках стер¬
жня суммируется из отдельных элементов, что и дает полученное выше
решение (3.163). Единственность этого решения для непрерывной функ¬
ции следует из теоремы, рассмотренной в § 5 гл. II.
В аналитической теории теплопроводности широко применяют инте¬
грал
(также часто встречаемый в теории вероятностей), который назы¬
вают функцией Лапласа или интегралом ошибок (или интегралом
+ оо
— ОО
X d|' = —^=- е- = G (я, I, t).
2 у nat
(3.176):
dQ 1
Ф 2 y~mt
ф0 ( S) d£ е - (* - £)*/( 4at)
2 \ГШ
2
(3.180)
153
вероятностей). Свойства этой функции и таблицы значений приве¬
дены, например, в книге [150]. Отметим некоторые из них: а)Ф(г)
монотонно возрастает, изменяясь в пределах —1, +1; б) Ф(—г) =
= —Ф(г), так что таблицы составлены только для положительных
значений аргумента; в) Ф(0) =
= 0; Ф (— оо) = —1; Ф (+ оо) =
= + 1; Ф (z ^ 2,7) ^ 1, так как
Ф(2,7) ^ 0,9999. В приложе¬
ниях часто используется обо¬
значение функции Лапласа в
виде Ф(г) = еН(г), а также
функция
ф* (г) = erfc (г) = 1 —erf (г) =
Рис. 25
= (2/К^) 5ехр(-рг)Ф- (3.181)
Графики этих функций приведены на рис. 25.
Пусть в постановке (3.156)—(3.157) начальная температура за¬
дана ступенчатой функцией
) 7\ при х > 0;
Ф0 М=?т (3182)
) * 2 при х < 0. '
Используя введенные функции (3.180)—(3.181) и формулу (3.163),
нетрудно получить решение задачи в виде
Г (х, 0 = (Т1 + Т2)/2 + [(7\ -Г2)/2] Ф [х/(2 VTt)}
или
[Т(х, t)—Тх]/(Тл—Т,) = (1/2) Ф* [xl{2V~ai)\. (3.183)
Настоятельно рекомендуем проделать все выкладки.
Из (3.183) видно, что в точке х=0 температура все время постоянна
и равна полусумме начальных значений справа и слева, так какФ(0) =
=0. Кроме того, полученные выражения зависят только от одного без¬
размерного параметра */(2)/"а/). Это позволяет сравнивать температуры
в различные моменты времени и в различных точках твердых тел,
обладающих различным коэффициентом температуропроводности.
Переходя к неоднородному уравнению, рассмотрим краевую задачу
вида
dT/dt =а(д2Т/дх2)-{- /(*, /), —oo<*<-foo, t > 0; (3.184)
Т (х, 0) = 0, |*| < +оо; \Т (*, t) | < +оо, |*| < +оо. (3.185)
Решение этой задачи можно получить аналогичным образом, как и в
случае (3.38) — (3.39).
Рассматривая уравнение (3.184) в ограниченной области с однород¬
ными краевыми условиями, раскладывают искомое решение в ряд
Фурье по собственным функциям соответствующей однородной задачи
(см. § 3 гл. III). Для неограниченной области следует искать решение
154
Т (ху t) задачи (3.184) — (3.185) в виде интеграла Фурье с переменными
во времени коэффициентами разложения
+ 00
Т (х, 0=5 И (v» Ocosy* + fl(Y, OsinY*]dY>
— оо
+ 00 +оо
где А (у, 0 = -^- j Т’ (i. OcosYldg; В (у, 0 = -^7 J т (1. Osinv^di,
— 00 — 00
и далее применить все рассуждения, изложенные в § 3. В резуль¬
тате придем к решению задачи в виде (проделайте все выкладки)
t + 00
Т(Х, 0 = 5 5 T)G^' S’ T)dTdi. (3.186)
О — оо
где G(Xy 5, t) — фундаментальное решение уравнения теплопровод¬
ности [см. (3.164)1.
Выражение (3.186) представляет собой непрерывную, ограничен¬
ную функцию от х и ty дважды непрерывно дифференцируемую поде
и непрерывно дифференцируемую по tt если функция /(л:, t)9 рассмат¬
риваемая как функция Ху удовлетворяет всем требованиям разложи¬
мости ее в интеграл Фурье.
Рассмотрен метод Фурье для одномерных тепловых задач в неог¬
раниченной области. Аналогичным образом можно получить решение
дву- и трехмерной задач.
Например, найдем температурное поле бесконечного пространства (*, уt z),
начальная температура которого задана в виде функции Ф0 (*, у у г); внутри про¬
странства действует нестационарный источник теплоты мощностью F (*, yt z, t).
Имеем при f (х, уу г, t) = F/cp
дТ (дЧ , дЧ , дЧ\ , Л Л
dt=a[-w+-w+'dF)+f(x'!l'z't)' -00 <*•*/<2 <+°°. <>°;
т (X, у, г, 0) = Ф0 (х, у, г), | Т (дг, у, г, <) 1 < +«, \х,у,г\< +оо. (3.187)
Решение Т (xf yt г, t) можно записать в виде
+ 00 + 0D + 00
т (X, у, г, 0= 5 5 5 Ф° ^ ° У’ *’ 1,1 4>р ^Х
— 00 — со —оо
t + OD +00 +00
Xd|dt)d(p+J 5 5 5 т'> 0 (х> t>> f’т) dT dS dtl d(P> (3.188)
О — 00 — 00 — OD
где
О (х, у, г, £, г|, (р, t—т) = , ' ехр Г_ fr-O’ + to-tiP+fr-q.)» 1
(2 У ка {t — т))у | 4а (t — т) J
(3.189)
— функция температурного влияния мгновенного точечного источника теплоты
мощностью Q = cpy действующего в точке * = £, у = г), г = ср в момент времени
t — Т.
155
Это решение можно получить, используя метод разложения функ¬
ции в тройной интеграл Фурье. Заметим, однако, что для дву- и трех¬
мерных задач этот метод технически менее удобен, чем, например,
метод интегральных преобразований Фурье для неограниченных
областей (см. гл. V).
§ 6. МЕТОД ПРОДОЛЖЕНИЙ ДЛЯ ПОЛУОГРАНИЧЕННОЙ
ОБЛАСТИ
Непосредственное применение метода разделения переменных к полу-
ограниченным областям (например, полуограниченная прямая, часть
координатной плоскости я > 0, у> 0 и др.) не приводит к цели *.
Однако наличие известного аналитического решения, полученного
методом разделения переменных для бесконечной области, позволяет
во многих случаях получить решение краевой задачи теплопровод¬
ности и для полуограниченнрй области.
Рассмотрим краевые задачи для полуограниченной прямой (полу-
бесконечный стержень) и покажем, как, используя решение для не¬
ограниченной прямой, получить решение исходной задачи. Как уже
отмечалось (см. гл. II), в тех случаях, когда интересуются распределе¬
нием температуры вблизи одного из концов стержня, а влияние другого
конца несущественно, можно считать, что стержень ограничен только
с одной стороны, а с другой простирается в бесконечность. Это приводит
к краевым задачам теплопроводности для полубесконечной прямой.
Рассмотрим некоторые из них:
1. Пусть Тг(х, t) есть решение задачи [см. (3.43) — (3.44)]:
dT1ldt = a(d2Tlldx2‘)1 х > 0, * > 0; (3.190)
Ti(x, 0) = Ф0 (х), *^0; Тг (0, 0=0, /^0;
\Тг(х9 01 <+оо, * > 0.
Функцию Т\ (х, 0 нетрудно найти, используя формулу (3.163). Для этого про¬
должим начальную функцию Ф0 (х) на отрицательную полуось нечетным образом,
иными словами, рассмотрим вспомогательную начальную функцию М* опре¬
деленную следующим образом:
<зт|
В чем смысл такого продолжения? Ясно, что и температурная функция 7'1(дг, t)
при условии (3.192) будет на всей числовой оси также нечетной, т. е. Ti (—х, t) =
= — Ti (х, 0» а Для такой функции граничное условие (3.191) при х = 0 всегда
имеет место: Г, (0, *)=—^(О, /), отсюда 2Т1(0, /) = 0 и 7\(0, /) = 0. Функцию
Тi (х, 0 запишем с помощью формулы (3.163), имея в виду (3.192)
Ti{x,0 = -y= C'V.e).e"U"0,/(4e<,dE. (3.193)
2 у nat J
* За исключением тех случаев, когда спектр собственных значений на полу-
бесконечных интервалах является дискретным.
156
Начальное условие при этом выполняется, так как, согласно (3.169), 7\ (х, 0) =
= 4% (*) = Ф0 (х) для х > 0. Преобразуем (3.193) следующим образом:
т'(х- 5F33- I
— оо 0
Если в первом интеграле заменить £ на (—|) и использовать (3.192), то
окончательно получим
* Г S)a (* + 6)»1
Тг(х, 0=—!= (Ф.® Le 4в< -е~ Ш J dg. (3.194)
2 у nat J
Заметим, что при х = 0 выражение, стоящее под знаком интеграла, обращается
в нуль. В частном случае, когда начальная функция в (3.191) постоянна Ф0 (*) =
= Т0, выражение (3.194) существенно упрощается и после несложных выкладок
принимает вид (проделайте эти выкладки самостоятельно)
Т (х, t)/T0 = <t>-lx/(2}rat)], (3.195)
где Ф(г) — функция Лапласа (3.180).
Итак, задача (3.190)— (3.191) решена.
2. Пусть теперь Т2(х, /) удовлетворяет условиям:
dT2/dt = a(d2T/dx2 + f(x, /), х > 0, t > 0; (3.196)
7^2 (дг, 0) = 0, 0; T2(09t)=0, t^z 0; \T2(xt t) | < +oo, х > 0. (3.197)
Используя формулу (3.186), можно получить решение и в этом случае. Для этого
следует продолжить функцию источника f (х, /), рассматриваемую для любого
t > 0 как функцию х на отрицательную полуось нечетным образом, введя вспо¬
могательную функцию
в (*. 0 = ( 1j*’ *4 ж > п’ (3.198)
\ —f(—x, t), х<0.
затем записать интеграл (3.186) с функцией 0 (ху t) и преобразовать его в соот¬
ветствии с (3.198). В результате получим
!00 Г -<*- £>* (*+1)ш 1
Т2(х, 0=—\=- 5 Г ■■ т) [e4fl (,'т)—е 40 ('"X)J dTdg. (3.199)
2 у an J J у t — т
г о о г
3. Более интересным является случай, когда при * = 0 имеет место неодно¬
родное граничное условие:
dT3/dt = a(d2T/dx2), х > 0, t > 0; (3.200)
T3(xt 0) = 0, х^0; Г3(0, /)=ф(0, ^0;
|Г3(х, 01 < +оо, х > 0.
Этот случай также может быть рассмотрен положительно. Действительно, введем
новую функцию W (х, t) = T3(x, 0— Ф (0 и преобразуем задачу (3.200) — (3.201).
Получим
dW/dt = а (d2W/дх2)—ф' (t), х > 0, / > 0; \
W{x, 0) = — ф (0), х^0; ИР(0, /)=0, 0: \ (3.202)
1 W (х, t) 1 < +оо, х >0. )
Функцию W (х, t) можно записать с помощью формул (3.194) и (3.199), имея
в виду, что W (*, t) = Ti(x, /) Т2 (.v, 0, если считать Ф0 (*) = --ф(0), / (*, I) =
157
= —ф' (/). Получим для W (ху t) и далее для Т3 (ху t):
-(*-£)» (х+ £)»
• Г (£+1>П 1
Г,(*,0 = Ф(0--^ С U 4а' -е" 4а< Jd* ‘ f-£JlLdTX
2yUai J 2/ал J \Tf~x
(0, *(-£=-)-
Х \ |_е4а (/-т)-е 4а<<‘
I
— ( ф' (т) Ф( — \ dx.
J \2 У а (t-т) )
После преобразования правой части равенства найдем
г*(‘’°-^11^гсп:'гг,л' фж)
Остановимся на полученном выражении, так как оно представляет опреде¬
ленный интерес для исследования. Согласно (3.201), функция Т3()с, t)—*0 при
t—*«0 и * > 0 и T3(Xyt)—*ф(0 при х—►О и t> 0 (вспомним, что краевые
условия понимаем в предельном смысле, как договорились в § 4 гл. II). Проверка
последнего условия наиболее важна, так как (на первый взгляд) из выражения
(3.203) следует, что при х—►О функция Т3(х, t) равна нулю благодаря множи¬
телю перед интегралом. В действительности же при * = 0 интеграл становится
расходящимся; это особенно ясно видно, если граничное условие—постоянная
функция ф (t) =ф0 = const). Действительно,
С dx 2
j (/_ytzrT
и при x = t правая часть превращается в оо. Таким образом, просто подставлять
значение х = 0 в выражение (3.203) нельзя, так как при х—- оо имеем неопре¬
деленность типа 0*оо. Эту неопределенность нетрудно раскрыть, преобразовав
(3.203) с помощью замены переменной
2/ЙТ^) ; dP 4/7(/-т)3'* :Т * 4ара-
Тогда
Г'(л0-Йг I ''('-ер)'""1*
x/(2Vrai)
Если ф (0 — непрерывная функция, то имеем
ОО CD
lim Г* (ж, t)=~^=r С Ф(0е-н^Р=<р (<)—£= С e-p,d(S=<p(0.
*—#-0 (/>0) у л J У л J
Здесь использовали интегралы (3.170).
Задача 1. Покажите, что в случае условия
гг //\ \ Фо> и < * < *о»
/ ф1. < > к
температурная функция Т3(Ху t), определенная формулой (3.203), имеет вид
Тз (х, 0=ф„Ф* L^/t2К^«7)] + СФХ — Фо) ®*[XI2V a
158
4. В случае, когда рассматривается вторая задача,
dT^ldx \х= о = 0; дТ2/дх |*=о =0; дТ3/дх |*= о = (1 /X) ф (/),
а все остальные краевые условия в (3.190) — (3.191), (3.196) — (3.197), (3.200) —
(3.201)' сохраняются, соответствующие решения Г,- (х, t) можно получить почти
дословным повторением всех рассуждений, приведенных при решении первой
краевой задачи. Разница заключается лишь в четном продолжении начальной
функции и функции источника на отрицательную полуось путем введения вспо¬
могательных функций ¥0 (х) и 0 (х, t):
При отыскании функции Г3(х, t) следует воспользоваться подстановкой
W (х, t) — Т3 (х, t) — (1Д)хф(/). Заметим, что при четном продолжении функций
Ф0 (х) и f (х, /) решения Т\ и Г2 также оказываются четными функциями
Ti(—x, t) = Ti(x, /); при этом автоматически выполняется условие дГ//дх |*= о = 0
(покажите, почему?).
5. Рассмотрим полезную подстановку при решении третьей краевой задачи
в полуограниченной области. Пусть функция Г (х, t) удовлетворяет уравнению
(3.190) и краевым условиям вида
Г (х, 0) = Г0 ( = const), х > 0; дТ (х, t)/dx |*=о =/гГ (0, /), t > 0; (3.204)
| Г (х, 01 <+оо, х > 0.
сведем третью краевую задачу (3.190), (3.204) к первой краевой задаче относи¬
тельно функции W (х, 0 (если это удается, то решение W (х, t) может быть за¬
писано по полученным выше формулам). Прежде всего покажем, что W (х, t)
удовлетворяет однородному уравнению теплопроводности. Для этого составим
разность W't — aW"xlt используя (3.205),
из (3.205) также следует, что W (0, /)=0. Таким образом, для W (х, t) имеем
Из (3.207) следует, что при х —► оо (/ > 0) функция W (х, t) имеет предел Г0
(так как Ф(+оо) = + 1). Теперь необходимо определить Г (х, t) — решение исход¬
ной задачи (3.190), (3.204). Для этого можно воспользоваться уравнением (3.205),
переписав его в виде
Общее решение этого уравнения, которое можно получить, например, мето¬
дом вариации произвольной постоянной, запишем в виде
С помощью подстановки
W (х, 0 = Г (х, 0 —(1/Л) дТ (х, t)/dx
(3,205)
dW_ dW
dt a дхг ~
выражения в скобках обращаются в нуль в силу уравнения (3.190).
Начальное условие для W найдем из (3.205)
Г (х, 0) = Т(х, 0)-±£[Т(х, 0)] = Г0_1^(Г0) = Г0;
Задача (3.206) уже рассмотрена выше [см. (3.194)]. Ее решением является
выражение
1Г(*, i) = To0[x/(2yrat)].
(3.207)
Т'х — hT = -hW.
ОО
Т(х, t)=Cehx+h ^ e~h^-x)W (£, /) d£.
X
159
где С — постоянная интегрирования. Эту постоянную можно определить, исполь¬
зуя условие ограниченности функции Т (.х, t) при х—* оо. Отсюда следует, что
С = 0. Следовательно,
00
Т (х, t)=h § e~h$W (* + Р, 0 dp. (3.208)
О
(Здесь положено £—* = Р*)
Учитывая (3.207), найдем
со
Т (X, t) =hTa J exp (—ЛР) Ф [(*-bP)/(2V'oO] dp. (3.209)
О
Задача 2. Покажите, что выражение (3.209) в результате применения
формулы интегрирования по частям может быть сведено к виду
Т(х, t)/T„ = Ф ( 2^L_ exp (hx + aft2/) Ф»(-\-hV~ai(3.210)
Определим температуру на торце стержня * = 0
Г (0, <)/7’о = ехР iflhH) Ф* (hY~ai). (3.211)
Если воспользоваться асимптотическим разложением функции Фо (г) [20]
Ф* (г) ~ л" 1/2 [exp (—г2)] (г_1—2“1-z“3 + 3»4“1»z-5—...)
для г> 1, то для (3.211) найдем
Т (0, t)/T0 = [\/(h\niai)] [1 — \/(2ah2t) + 3/(4a2h*t2) —...]
при h y/at^>\: Таким образом, через время f»(aA2)-1 после начала охлаждения
температуру на торце стержня можно считать равной Т (0, t)/T0 ~ {hY nat)"1 с
ошибкой, меньшей, чем (2ah2t)'~1.
В постановке задачи (3.190), (3.204) рассматриваются частные
значения краевых.функций. Это, однако, не ограничивает общности
приведенных рассуждений, справедливых и в более общем случае, т. е.
для переменных во времени и в пространстве краевых функций, вклю¬
чая неоднородность и в дифференциальном уравнении (3.190). При
этом только усложняются выкладки, которые в принципе можно довес¬
ти до конца. Однако в более общей постановке третьей краевой задачи
для полуограниченной области целесообразнее пользоваться либо ме¬
тодом функции Грина (см. гл. VII), либо методом интегральных преоб¬
разований (см. гл. V). К этой задаче вернемся позже в этих главах.
В заключение отметим, что для дву- и трехмерных областей метод
продолжения начальной функции и функции теплового источника
также приводит к цели и достаточно быстро, если граничные условия
задачи однородные или могут быть сведены к таковым. Однако метод
интегральйых преобразований или метод функции Грина в последнем
случае предпочтителен.
§ 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ
ОДНОРОДНОЙ ЗАДАЧИ В СЛУЧАЕ ЛИНЕЙНОГО
ТЕПЛОВОГО ПОТОКА
Знание собственных значений и собственных функций, по существу,
означает решение соответствующей краевой задачи теплопроводности,
если применить далее рабочие формулы записи аналитических реше-
160
ний, полученные в § 4 гл. III. Кроме того, согласно результатам § б
гл. II, собственные функции однородных задач с двумя или тремя неза¬
висимыми переменными можно представить в виде произведения
решений задач с одной переменной. Таким образом, для решения доста¬
точно большого числа краевых задач теплопроводности в дву- и трех¬
мерной областях необходимо рассмотреть однородные задачи с одной
независимой переменной. Так, в случае линейного потока теплоты,
имеющего место в неограниченной пластине или тонком стержне,
приходим к следующей однородной задаче на собственные значения и
собственные функции:
d*4/dx% + ytxP = 0, 0 <*</; (3.212)
(X.dW/dx-а^)х=0 = о; (М№ + аДЫ = 0, (3.213)
где Х{ ^ 0, at ^ О, X] -f а\ > 0, i = 1,2.
Записанные граничные условия (3.213) включают девять воз¬
можных комбинаций граничных условий соответствующих краевых
задач теплопроводности. Рас¬
смотрим все случаи. У
1. Граничные условия III
рода при х — 0 и х = I:
(dT' (x)/dx—h1{¥ (x)).r=0 = 0;
(dXY (x)/dx + h2W (x)x=i = 0)
(A, = a,A,). (3.214) _
Общее решение уравнения
(3.212) имеет вид
'Г (х) = Сх cos ух + С2 sin ух.
Удовлетворяя условиям Рис. 26
(3.214), приходим к однород¬
ной системе двух алгебраических уравнений относительно по¬
стоянных интегрирования С1 и С2:
h\Cx уС2 = 0,
(h2 cos у I—у sin у I) С\ + (у cos yl + h2 sin у I) С2 = 0.
Эта система имеет решения, отличные от нулевого (нас интере¬
суют только нетривиальные решения однородной задачи (3.212)—
(3.213), для которых должно быть CJ + C'2>0), если ее опреде¬
литель равен нулю. Это дает трансцендентное уравнение для
собственных значений
ctg yl = y/ (ht + А2) — ЛЛ/fY (^i + ^а)]* (3.216)
которое можно записать в следующем виде:
Р = р/(^ + ^0—4" Ла) р]» (3.217)
если положить р = у/. Это уравнение имеет бесчисленное множе¬
ство вещественных корней, в чем нетрудно убедиться, построив
графики кривых (рис. 26):
У = ctg р; У = р/(М + V) “ IAiV/^i + Ла)]/Р- (3.218)
| (3.215)
6-339
161
Из рисунка видно, что в каждом из интервалов (0, л), (л, 2л), ...
лежит положительный корень уравнения (3.217), а отрицатель¬
ные корни по абсолютной величине равны положительным. Ясно
также, что кратных корней нет.
Обозначим через р2, ..., \хк, ... положительные корни
уравнения (3.217). Тогда собственные значения равны
У 1 = \&П\ /с = 1, 2, 3, ... (3.219)
Каждому собственному значению соответствует собственная
функция
М = И* cos Vk (*/0 + М sin И* (*/0> (3.220)
определенная с точностью до постоянного множителя, который
положим равным единице. Согласно теоремам III и V см. § 3,
система собственных функций (3.220) ортогональна в области
[0, /] с весом р= 1 и полна. Найдем квадрат нормы собственных
функций. Так как d2X¥jdx2 + (р*//2) = 0, то
j Y2 (х) dx = ——2 j YK (x) d2y} dx.
0 0
Интегрируя по частям, получим
i i
J Y2 (*) dx-(H^f 5 (dY^/d*)2 d* =
= -(//^)2[YK(dYK/(d^))]S.
Ho Yt. (x) = \iK cos (x/l) + htl sin iiK (x/l) и
(//|xK) (dY^/dx) = — pK sin цк (x/l) + h,l cos (x/l).
Отсюда Y* + (//pj2 (dYK/d;t) = p* + h\, а также
i i
I Y2 dx + (//pj2 J (dYK/d*)2 d* = (p2 + h\) I.
0 0
Выражения (3.221) и (3.223) дают
i
2 S Y2 (x) dx = [pi + (hj)*] /-(/*/|i£)[Y, (dY^(Le)]*=i.
0
Согласно (3.214),
(d'Vjdx-h^^ = 0; (WK/dx + h2WK)x=l = 0,
отсюда следует, что
(/2/p2) [Y„ (dYK/dx)] = (hJViil) Y2 \ при лг = 0;
(/2/p2) [Y. (dYK/d.v)] = — (V2/p*) Y2 f при x = l.
Выражения (3.222) и (3.225) дают
Y2 (0) = ill Y2 (I) = ill (ill + hi I2) Kill + ft2/2)].
162
(3.221)
(3.222)
(3.223)
(3.224)
(3.225)
(3.226)
(3.227)
Таблица 1
Г раничные
значения
Собственные
значения
Собственные функции
<*>
при х — 0
при x — l
Vk
¥ = 0
dy/dx + W = 0
y£ = H*//2
М =Sin \lK x/l,
к=\, 2, 3, ...,
> 0 —корни уравнения
Ctg|Ll = --/z//jLl,
||Ч, р ./ (^ + Л*//2)+А/
11 * 2 (ц*+А*/*)
v = o
dV/d^O
Y“ = ^2.
H«=(2*-l)-j,
<e=l, 2, 3, ...
Ч'* (JC) = sin \хк xjlt
|]Щ12 = //2
v = o
У = 0
у% = (кщ О2,
к= 1, 2, 3, ...
*Fv = Sln [iKXjl (Ц* = КЛ),
|| Ужр = //2
dY/djf = 0
d'tr/dx + h'¥ = 0
Y 1=P?kIP>
к=1. 2, 3, ...
VW =cos р* x/lt
\хк > 0 — корни уравнения
ctgtu = n/(/z/),
/ (ц2+А*<*)+«
" *11- 2 (цЛ-АЧ!)
dV/dx = 0
d'¥/dx = 0
V2 = (кя//)*,
к = 0, 1, 2, ...
М =cos «ЯДС//,
II У, 11 = }//2, /С >0,
/, к = 0
d'F/djc—/z¥ = 0
y=o
Y 2 = ^/'2.
к = 1, 2, 3, ...
4,kW = M«cos ц„Х
Х*//+Л/sin u JC/i,
цк > 0 — корни уравнения
Ctg |LX =—Л//Ц,
|Тк||а = //2{[^ +
+(А/)*]+Л/}
dV/d* = 0
y=o
т2=»*;//*.
цк=(2к-1)-£,
/с= 1, 2, 3, ...
(*) = COS |,1 ы х/1,
|V,||*«=//2
163
Продолжение табл. 1
Граничные значения
Собственные
значения
dy¥/dx — hW = 0 d'F/d* = 0 VK (х) = \iK cos цк x/l -j-
AC = 1, 2, 3, ... + hi sin [iK x/l,
\xK > 0 — корни уравнения
ctg fi = ц/hl,
II^kII2— 2 {[l^« +
Из (3.226), (3.227) и (3.224) находим
2 J (x) dx = + h\P) I + V2 L(|iJ + hWKpl+hU*)] +
откуда после несложных преобразований окончательно получим
квадрат нормы собственных функций (3.220)
Другие случаи могут быть рассмотрены совершенно анало¬
гично, поэтому приводятся лишь окончательные результаты
в табл. 1.
Зная, таким образом, собственные значения и собственные функции
однородной задачи (3.212) — (3.213) для различных комбинаций гра¬
ничных условий при л;=0 и х=/, нетрудно выписать решение соответ¬
ствующей краевой задачи теплопроводности для стержня с помощью
соответствующей рабочей формулы § 4. И, более того, полученные
выражения дают возможность найти собственные значения и собствен¬
ные функции для прямоугольной области 0 ^ х ^ U, 0 у ^ /2
и для прямого параллелепипеда 0 ^ х ^ /*, 0 ^ ^ /2, 0 ^ z ^ /3
при любой комбинации граничных условий на граничных поверхно¬
стях этих областей. Для этого достаточно перемножить соответст¬
вующие решения для одномерных областей (см.§ 6 гл. II). Последнее
же, по существу, означает решение той или иной краевой задачи тепло¬
проводности, которое можно выписать по рабочим формулам § 4
гл. III.
В заключение заметим следующее. Обычно при рассмотрении тепло¬
вых задач для бесконечной пластины ограничиваются такими важными
величинами, как температура на поверхности пластины или в центре
центральной плоскости симметрии, если начало координат выбрано в
этой плоскости (тогда — /0 ^ х ^ /0 или с помощью подстановки
x'=x+/o можно перейти к случаю 0 < х' < /, где / = 2/0). Для реше¬
ния таких задач располагают множеством числовых данных в форме
о
u^r = S^)d*=4
о
1_ \12) [М + (Рк~Ь^2)] + М (н^ + ^а^2)
164
таблиц и графиков [83]. Удобнее начало координат выбирать в центре
исследуемой области, так как тогда яснее выявляется любая симмет¬
рия решения; в случае пластины — / < х < +/ приходят к области
О ^ х ^ /, в которой может отыскиваться четная функция. В первом
случае всегда (дТ/дх)х=0 =0, во втором всегда Т (0, t) = 0.
§ 8. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ
ОДНОРОДНОЙ ЗАДАЧИ ДЛЯ СПЛОШНОГО ЦИЛИНДРА
Приведем собственные значения и собственные функции однород¬
ной задачи для уравнения
dr2 ^ г дг ^ г2 d<p2 (3.228)
0<r < R, 0 < 2 < /
с граничными условиями любого рода на границах рассматриваемой
области. Имея собственные значения и собственные функции для каж¬
дого из случаев, с помощью рабочих формул § 4 гл. III можно вы¬
писать аналитические решения соответствующих краевых задач теп¬
лопроводности.
Уравнение (3.228) рассмотрим в несколько этапов, имея в виду боль¬
шую прикладную направленность этой задачи.
1. Радиальный поток теплоты в неограничен¬
ном сплошном цилиндре
TT+TlF+V^iM-O. 0<r<R; (3.229)
(MYj/dr + аДх)г= * = 0 | (г) | < + оо, г > 0. (3.230)
Вначале рассмотрим граничные условия / рода: (R) = 0. Уравне¬
ние (3.229) представляет собой дифференциальное уравнение Бесселя.
Его общее решение имеет вид
ЗД = ОгМУгГ) + C2Yq (Yir), (3.231)
где Joiys)— функция Бесселя I рода нулевого порядка; Y{i(y1r) —
функция Вебера.
Из физического смысла краевой задачи теплопроводности [в одно¬
родной задаче — это условие ограниченности в (3.230)] коэффициент
С2 должен равняться нулю, так как на оси цилиндра (при г = 0) тем¬
пература должна быть конечной и решение задачи не может содержать
бесселеву функцию II рода, которая при г 0 стремится к —оо.
Поэтому функция Х¥1 (г) в (3.231) выражается только через бесселеву
функцию I рода Wi (г)=ClJ0(ylr), Постоянную уг найдем из граничного
условия при г = R: J0(yiR) = 0; обозначив = р, придем к транс¬
цендентному уравнению
/о 0*) = 0. (3.232)
Таким образом, для отыскания собственных значений необходимо
найти корни р* (к = 1, 2, 3,. . .) бесселевой функции У0(р). Этих
корней счетное множество (рис. 27) и так как функция Л(р) четная
165
J0(\i)=J0(—|л) (см. [15]), то отсюда следует, что корни /0(р) будут
попарно одинаковыми по абсолютной величине и противоположными
по знаку; поэтому достаточно рассматривать только положительные
корни (которые приведены, например, в [150]). Зная корни (ы2,. . .
..., (ih,. . находим собственные значения по формуле yl = (x2K/R2 и
далее собственные функции (с точностью до числового множителя, кото¬
рый мы полагаем равным единице): ^(г) = Jo{\iKrlR). Остается вы¬
числить квадрат нормы собст¬
венных функций. Уравнение
(3.229) перепишем в виде, со¬
ответствующем уравнению (3.24),
d/d г [г (dVjdrfl + y'rV^O.
— Теперь видно, что Р(г) = г, и,
Л таким образом, собственные
функции T’l^r) ортогональны
Рис. 27 на [0, R] относительно весо¬
вой функции Р(г) = г. Исполь¬
зуя известные из теории бесселевых функций интегральные фор¬
мулы [15] [см. ниже (3.241)], найдем
R
1 %II2 = s rJl МЩ dг = (^2/2) Л (Ю. (3.233)
0
Другие виды граничных условий могут быть рассмотрены
аналогично, поэтому приведем лишь конечные результаты в табл. 2.
Таблица 2
Граничное
условие при
r=R
■ v*
Собственн e функции W1/c (л);
весовая функция Р (г)
d4j1/d/’ = 0
тг=(*5/л*.
к = 0, 1,2, 3, ...
^1* (r) — Jo {\^к'r /R)>
P(r) = r; fiK^0—корни уравнения
•Ми) = 0(164].
^0 = 0; Ч'10(г) = У0(0) = 1;
|Щ12 = («2/2)/5(рк), pKS=0,
dV,/dr +
+W1 = 0
2. H e о г p
k=1, 2, 3, ...
аниченный
(рк г/Я); Р(г) = г,
\хк > 0 — корни уравнения
р./, (р) — hRJ0(n) = 0,
|V,J» = (/?V2)io(p„)(l+/i2*V)
сплошной цилиндр, когда
температурное поле не является осесимметричным:
5+Т^+7^+^2 = 0, 0<г<Я; (3.234)
У.(г, Ф) = (г, ф + 2я); |V,<г. ф)|< -i оо, г>0. (3.235)
166
Граничные условия укажем позже. Решение этой задачи получим
методом разделения переменных. Полагая 47 (г, ср) = 47 (г) 0 (ср)
и подставляя в (3.234) вместо 47 правую часть указанного ра¬
венства, получим после разделения переменных
(r247 + rW[ + 77'2Ч7)/Ч7 = 070. (3.236)
Левая часть этого равенства не зависит от ср, а правая — от г.
Отсюда следует, что 070 = const. Для того чтобы 0 (<р) [а зна¬
чит, и 47 (г, ср)] была периодической функцией угла ср и не ме¬
нялась при изменении угла ср на 2л, необходимо и достаточно,
чтобы 070 = — т2, где т = 0, 1, 2, 3 ... . Тогда в качестве 0(ф),
удовлетворяющей уравнению 0" -f m20 = 0, можно взять семейства
функций:
cosmcp, m = 0, 1, 2, 3,
0(ф)= . 1 о Q л (3-237)
sm/лф, т= 1, 2, 3, 4, ... .
Уравнение (3.236) для 47 (г) оказывается уравнением Бесселя
следующего вида:
+7 IF + W' = °- (3'238>
Его общее решение имеет вид (см. [166])
Y, (г) = CtJm (ytr) + С2Ут (угг), (3.239)
где Jm{y2r)—функция Бесселя I рода порядка т\ Ym(y2r)—
функция Вебера.
Из условия ограниченности в (3.235) следует, что С2 = 0.
Граничные условия I рода. Пусть в (3.234) — (3.235) 4г2(/?)==0.
Находим из (3.239) (при С2 = 0): Jm(y2R) = 0 или ,/OT(pi) = 0, если
обозначить y2R = pi. Таким образом, собственные значения и соб¬
ственные функции первой краевой задачи для уравнения (3.238):
ylniK = VnJR*> т = 0, 1, 2, 3, ..., /с = 1, 2, 3, ...,
(r) = Jm (IW/Я)'
Отсюда и из (3.237) следует, что искомые собственные функции
состоят из двух семейств
} m = 0, 1, 2, 3, 4, ...;
J. tymKr/R) cos ту, \ . 9 „
2,!:<змо)
Sin т<р, к== ^ 2( 3
Уравнение (3.238) можно записать в виде (3.24)
зН'тМ'Ч’.-т'"’'1’.-0-
откуда Р(г) = гу и, значит, функции Jm(\^KmrlR) ортогональны
на [0, R] с весом Р(г) = г\ функции созтфиэттф ортогональны
167
на [0, 2л] с весом Р(ф)=1. Таким образом, согласно теореме II
о полноте системы функций двух переменных (см. § 1 л\л. III)
собственные функции (3.240) ортогональны на [0, /?], [0, 2л]
с весом Р = 1 - г = г.
Используя значение интеграла [51],
R
I гЦ^ПЯ) dr = (RV2) ./2+1 (ц). (3.241)
где р,—корень Jv(\i) = 0, найдем квадрат нормы собственных функ¬
ций (3.240)
2л R
S S rJm (VmJ/R) COS2 тф £(ф = лЯ 2/2/£+1(|хтк) /c^sl, т>0;
о о
л/?2/? (\10к), т = 0, ас>1,
2я я
S S (^дажг//?) sin2 mcp = яR2/2Jm+i ((А**),
о о
1, m > 0.
Другие виды граничных условий могут быть рассмотрены
аналогично, поэтому приведем лишь конечные результаты в табл. 3.
Таблица 3
|Y,„p =
Граничные
условие при
r = R
Собственные функции хУ‘2тк (г»
весовая функция Р (г, <р)
d^2/dr = 0
I та = 0, 1,
2, ..., к=0, 1, 2, ...;
JmfamKr/R) Sin Шф,
т= 1, 2, /с = 1, 2,
р 5= 0—корни /m+i(n)=0,
Цоо = 0> = 1;
(Ртк—М*)
2Я/лк
т > 0, к > 0;
яЛ2Уо(Цок)> м = 0, /с = 0, 1, 2, ...
Я (г, ф) = г
d'F2/dr+A4'2=0
ш = / Jm(VmKrlR) cos/лф. т^0,/с^1,
Sm* \ (яткГ/R) sln/лф, m3* 1, *3=1;
ц > 0—корни p/m+1 (р) —hRJm (р)=0[164),
‘ nRt (Я2^+^к- m2')j2m(amic),
№як||2=
2^к
т > 0, к
яЯ2
1
M-OiC
(w+tCc) '8 о**.).
\ т = 0, к ^ 1
168
Замечание. Собственные функции в каждом из трех случаев этого пункта
состоят из двух семейств. Значит, при решении соответствующих краевых задач
теплопроводности с помощью рабочих формул § 4 гл. III необходимо записывать
решение в виде суммы двух частей из двойных рядов Фурье так, что в первой
части под знаком двойной суммы будет содержаться Jm (Иткг/К) c°s тф, во вто¬
рой части под знаком двойной суммы —Jm (\imKr/R) sin m<p. Разумеется, каждая
из этих частей содержит определенное число слагаемых—двойных рядов Фурье,
соответственно заданию краевых функций в исходной постановке задачи.
3. Перейдем теперь к общему случаю
Положим ¥(/*, ф, z) = 4r1(z)4f2(r, ф) и подставим правую часть
в уравнение (3.242). Получим после разделения переменных
(X, дУ/дг + a^¥)r=R = 0; (Х2 dV/dz-а2У)г=0 = 0;
(Х3 dV/dz + а3ЧЪ=, = 0,
Y(r, Ф, г) = Т(/*,ф + 2л, г); | Т(г, Ф, г) | < + оо, 0. (3.245)
Подставляя = }¥1(z)y¥2(r, ф) в граничные условия (3.245),
Используя полученные результаты, можно записать для собст¬
венных значений и собственных чисел задачи (3.242), (3.245):
Этим самым завершается рассмотрение решений большого числа
краевых задач теплопроводности для конечного сплошного цилиндра,
бесконечного цилиндра с радиальным потоком теплоты, бесконечного
цилиндра, когда температурное поле не является осесимметричным,
конечного сплошного цилиндра с осесимметричным температурным
полем и,' наконец, для общего случая Г(г, ср, z, t).
В каждом из этих случаев (согласно виду граничных условий)
следует выписать собственные значения и собственные функции соот¬
ветствующей однородной задачи и записать аналитическое решение
краевой задачи теплопроводности по одной из рабочих формул § 4
гл. III в цилиндрической или полярной системах координат.
д2У
дг2 , V, , с/у \j с
’ 0<г<1.
■jpr -bYi’Ti — 0. 0 <*</,
(3 243)
(3.244)
где y* = Yi + Y2; Yi и y! — постоянные разделения.
Пусть далее для уравнения (3.242) заданы условия:
получим
(X, dVjdr + а^,),.,* = 0; (г, <р) = (г, ф + 2л);
1^2 (г, ф)| < + оо, г>0;
(3.246)
К (d^/dz-o.Y,).,, = 0; (Х3 d^/dz + а,*,),., = 0. (3.247)
ТкЛ'* Ф. г) = ЧГ,Д2)Чггя1К(Г, ф); Ym/cs = Yis + ylrmc- (3.248)
169
§ 9. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ ОДНОРОДНОЙ
ЗАДАЧИ ДЛЯ ПОЛОГО ЦИЛИНДРА
Переходя к краевым задачам теплопроводности для конечного полого
цилиндра, рассмотрим соответствующую однородную задачу для
уравнения
Как и выше, задачу рассматриваем в несколько этапов.
1. Радиальный поток тепл от ы в неограниченном
полом цилиндре
Запишем общее решение уравнения Бесселя (3.250) в виде
y¥l(r) = C1J0(y1r) + C2Y0(y1r). В отличие от предыдущих рассужде¬
ний здесь уже нельзя полагать С2 = 0, так как функция K0(Yir)
в промежутке [Rlt Т?2], не содержащем особой точки г = 0, имеет
конечное значение. Для нахождения собственных значений задачи
(3.250), (3.251) используем граничные условия (3.251):
Коэффициенты С1 и С2 не могут одновременно равняться нулю,
так как в противном случае решение Х¥1 (г) было бы тривиальным.
Система двух линейных однородных уравнений (3.252) относи¬
тельно неизвестных Сг и С2 имеет отличные от нуля решения только
в том случае, если определитель системы равен нулю:
Таким образом, если р^ р2, р3, ...—положительные корни транс¬
цендентного уравнения (3.253), то собственные значения задачи —
Yi* = Pk/#i- Что касается корней трансцендентного уравнения (3.253),
то имеет место следующая теорема (см. [22]), с. 107):
Теорема. Если v — вещественно, a bt и Ь2 > 0, то
является их однозначной четной функцией от р, все нули которой
вещественны и просты.
Из (3.252) найдем отношение Сг/С2 = — Y0 (р^)/70 (рД Можно
положить C1 = KJ(pJ, С2 — —*/0(pJ и подставить в выражение для
0 <Rt<r<R21 0 < г < /.
(3.24»)
(3.250)
(3.251)
о (Yi^i) + С2 К о (Yi*i) —
C17otYi^2) + Cayo(Y1/?2) = 0.
}
(3.252)
JAbWAvJi) _п
Jo(yiRz)Y0(ytRi) ~
или если ввести обозначение р = у,/?1, то
Jo ((*) Y, (\lR2/Rx) — Yt (ц) У о (pR*/Ri) = 0.
(3.253)
© (ц) = J. (&,ц) Y (6ац.) — У, (&,ц) J. (6ац)
170
Таблица 4
Граничные условия
2
Собственные функции (/■)
при rz=R1
при r— R2
Vik
V1== 0
d4Vdr = 0
•2
У\к =
= 1*kIR2»
k= 1,2,...
^1к = Уо (Мк) 'о (llKr/R) —
— h (Мк) x K0 ([\Kr/Ri),
0 — корни уравнения
Ко (M) Jl (\iR 2/R i) — Jo (m) Уi x
X (ft/?2/R1) = 0»
И \jr i| 2 2R\ [Уо (pv) J1 (uKR2/R1)]
^!=0
d4fi/dr +
+ ЛЧ'1=0
Y Ik =
/C = 1, 2, ...
К = Уо (Mv) Л (м Kr/R l) J D (|W '
X K0 (aKr/Rx) \iK > 0 корни уравнения
^0 (Н-к) Л) (M'K^2/#l)— }
Уо (^*) Ji {[^kR^IRi) —
Jo (M^) Уо (ИkRz/Ri) ,//;p v
-Jo(ViK)Yi(\iKRi/Ri)
n2\iK У \ h2R 1/
X У, (ЦкЯ2/Лг)] — lj.
d4fi/dr = 0
4^ = 0
Yik =
= tLilRl
k=\t 2, ...
j к — У\ (и к) Jo (И кг!R\) — J\ x
x (и*) Ко (HS/Ri), Ик > о—корни урав¬
нения
К1 (р^) J0 (м kR2/^1) J1 (и к) Уо х
X (|я^2//?1) = 0;
2Л![У?(ц«)-^(|1«Я2//?|)]
1,111 я*|&о (H«**/Ki>
d4r1/d/' = 0
dVl/dr = 0
Yik =
*=0,1,2...,
w0 = 0
ЧГ1К = Т1 (ц*)Л> —
— -Н (А*)^0(м*/-//?!) КЗ* 1, 4^0 = 1,
|Л*^=0— корни уравнения
У\ (v*)J 1 (\**R2/Ri)—Ji (м J у 1 х
X (,WK/?2/^l) =0,
/ 2y?i[y’i(jiK) — У? (Mv#2'#i)]
1-у(*'-*Я. *-о
dV1/dr = 0
dYi/dr —
-/1^ = 0
Yik =
= \i2K/RU
k = 1,2, ...
Т1к = г1 (цк) J0 —
— -Н (Ик) Т'о О'к''/^i) Н*>° —
—корни уравнения
171
Продолжение табл. 4
Г раничные
при r — Rt
условия
при r= Rt
V21K
Собственные функции Ф“1к ^
Yl (Mv) ^0 (^ic^2/^l)
УI 0*«с)Л (Ц^2 /?l)—
, -Л(И«)^в(М2Л) __ Цк
— Jl (^к) УI (M*f^2/^l) Л/?1*
>y-«4t^41+4i)x
*[ 4> (^K^/^l)—
(иЛ/Я!)]"*-!}
d^/d г —
—W i = 0
v1=.o
■2
Yik =
/с = 1, 2, ...
’Fi« = ^o 0^Ri/Ri) Jo (vs/R 1) —
— Jo (VkRo/Ri) Y0 (n*r//?])(
цк > 0 — корни уравнения
^oW^oWs/fii)-
^o(H«^s/y?i) У, (и,) —
, — ^о(М«)^о(Ц«Л*/Л1) p„
— Jo (PkRo/Ri) Yi (|i„) hRj
nV/c 1
X ('+^*) X f-/oW + (t*«/^x) X
x У1 (JU*)]-2}
d^/dr —
—=0
d'P1/d/- = 0
Yik =
= vi/Rl
k=\t 2, ...
<riK = J/l (цЛ/^i) Jo (И1//Л1) —
— (fi^/fti) K„ (pK/-//?i),
|nK > 0 — корни уравнения
*M^#2/tfi)-ММ—
^ 1 ^1 (Fk)
^ 1 (Fl^2/^l) У 0 (Млг) F к
— Ji (Mk^2/^i) Ki (f*) /г/^i
11 V.«Г2 = ^ ^ 1« <*i) W+A*/tf)]
d^/dr —
-^ = 0
dTt/dr +
+ ^2^1 =0
Y i* = М-к/
/с = 1, 2, ...
Vi«= po(M«) + ^A <»*«)] ^ X
X (]iKr/Ri)— [Ko(MK)+Qx«)] X
X j0 0а^//?1), f* > 0 —корни уравнения
172
Продолжение табл. 4
Граничные условия
при r=Rt
при r=Rt
Собственные функции
(г)
^0 Л (P*)J X
У о (Ц^г/^О— ^1 (И'к^а/^г)
Jo Ji №*R*/Ri)
х [K0(fiJ + ^Kx(^)]=0,
II ^ *f II 2 = 2 (я2ЛгЦл) ”1 X
Jo(v j]V+aI*!)
h\h~22
(г). В результате для собственных функций задачи имеем сле¬
дующее выражение:
Уи (г) = J* MR 1) П (Ю - -/о w П (iv/*i)- (З*254)
В предыдущем параграфе показано, что удовлетворяю¬
щие уравнению (3.250), ортогональны на [Rit /?2] с весом Р(г) = г.
Квадрат нормы собственных функций (3.254) вычислен в [104] и
равен
f rW[K (г) dr = . (3.255)
Ki
Аналогичным образом могут быть рассмотрены и другие виды
граничных условий: поэтому далее приведем лишь конечные резуль¬
таты в табл. 4. Во всех случаях следует считать Р(г) = г.
2. Радиальный поток теплоты в конечном полом
цилиндре
J^ + T?T + 5i + ^==0- Ri<r<Rt. 0<г<Ь (3.256)
(Xt дЩдг-а^гшк, = 0; (X, д%/дг + агЧ'2)г= *2 = 0; (3.257)
(МЧ'./дг-а.ЧГ,),.,; K^f/dz + at^tmi = 0. (3.258)
Решение этой задачи нетрудно получить, используя предыдущие
результаты. Действительно, положим ЧГ2 (г, г) = }i\ (л) (г) и под¬
173
ставим это значение в (3.256) —(3.257). Получим, разделяя пере¬
менные:
d2XF0
-Y?Y. = 0, 0<г<1- )
dz2 . ri-o ^ '-*• ( 3 259)
(^d^/dz-a3¥o),=o = 0; (X4d'Fe/dz + a4V,)iBl = 0; J
d24;i/drs + (l/r)d¥/dr + Y^4r1 = 0, Rt<r < R2; »
(^•1 d^Vdr—a1'F1)r=R, = 0; (XtdVjdr + a2W,)r=Л, = 0, I {^Щ
где Y2 = Yi + V3’ Vi и yl— постоянные разделения.
Задача (3.259) рассмотрена в § 7 гл. III, задача (3.260) — в этом
параграфе (п. 1). Используя полученные результаты, можно запи¬
сать для собственных значений и собственных функций однородной
задачи (3.256) —(3.258):
^2/С5 (^*» = ^lAT (О ^US (^)> V2KS = YlS Узк •
Этим самым завершается вопрос о решении краевых задач тепло¬
проводности для конечного полого цилиндра (температурное поле
осесимметричное) при различных комбинациях граничных условий
на граничных поверхностях цилиндра. Решение каждой из тепловых
задач может быть записано с помощью соответствующей рабочей
формулы § 4 гл. III.
3. Круговая область (неосесимметричное темпера¬
турное поле неограниченного полого цилиндр а). Со¬
ответствующие собственные функции удовлетворяют условиям:
^ + 7-lT + ;W + V^3 = 0, Ri<r<Rt; (3.261)
Ч’з (г, ф) = ¥3 (г, ф + 2л). (3.262)
Полагая ¥,(/■, ф) = 4^ (г) в (ф) и проводя рассуждения, аналогичные
рассуждениям, приведенным в п. 2 § 8, получим
\ П 1 О Q ^^1 . 1 d'Fx .( о /П2 \ ,Tf Л
в(ф)=Лсоз/жР’ т = 0'1’2- 3>--■-ЦТ+ТЧГ + 1г*-~ТГ' = 0’
) sln/rnp, m= 1, 2, 3, ...
(3.263)
Общее решение уравнения (3.263) имеет вид
хУг (г) = Cxjm (Y4Г) + СШУЯ (уЛ (3.264)
Граничные условия I рода при r = Rx и r = R2:
V) = V,(/?a,cp) = 0; У8(г, ф) = Чгз(г, ф+2л). (3.265)
Функция У3 (г,ф) в соответствии с (3.263) состоит из двух
семейств:
1 У1 (О cos mcp, m = 0, 1,2, ...;
^Ч чМОзштф, т =1,2,3 ^
Найдем Ух (О* общее выражение для которой есть (3.264). Функ¬
ция Ух (г), согласно (3.265), также удовлетворяет граничным усло¬
виям I рода: Ух (/?х) = Ух (R2) = 0. •
174
Используем эти условия для нахождения собственных значений
C1Jm(y,R1) + C2Ym(yiR1) = 0t *
с1^(тЛ) + с2уя(т4л,) = о. I
Условием существования нетривиальных решений системы (3.267)
будет равенство нулю определителя этой системы
К(У^г) Ут(У^)
Ym(y 4^2)
= 0,
или
Jm М Ут (^2/^1) — ^ М Jm №jRl) = 0. (3.268)
если обозначить \i = y4RУравнение (3.268) рассмотрено выше.
Пусть pml, рт2, . ...—положительные корни трансцендент¬
ного уравнения (3.268). Тогда собственные значения задач (3.261),
(3.265) будут y24mK = \i2mK/Rl
Отношение CjC2 определяется системой (3.267). Можно положить
Cl = Ym(yiRl)1 С2 = — Jmiy^Ri) и подставить эти значения в (3.264).
Окончательно получим для собственных функций следующие два
семейства;
ф) =
= —•/т(^*)УЯ.(^К''/^1)]сОЗтф,т = 0, 1,2...
Г[Ут(цякг/Л,)Гт(^тк) — т=1, 2, ...
(3.269)
Для нахождения квадрата нормы собственных функций можно
воспользоваться интегральной формулой, известной из теории бес¬
селевых функций (интеграл Ломелля [22])
(3.270,
Cl
где а (г) = Jm (а,*) Ym {rx) — Jm (rx) Ym (a.x).
Используя (3.270) и (3.268) после ряда выкладок (в силу чрез¬
мерной громоздкости эти выкладки не приводятся), найдем
■ т>0,к> 1;
|^зял2= УдТ
1г[^о(^0к) —^о(Цо^2/^1)]^о2(Цок^а/^1)> т = 0, К>1.
(3.271)
Собственные функции (3.269) ортогональны на [Ru /?а], [0, 2л]
с весом Р(гу ср) = г (см. § 8 гл. III). В табл. 5 приводятся лишь
конечные результаты.
175
Таблица б
Граничные условия при
г= Hi
r=R,
Собственные функции ^дтк(гФ)’ ^ (г*
^т*=}
дЧэ/дг^О
дЧя/дг = О
^4 тк
~ ^тк/^V
к = 0, 1,2,
т = 0,1,2,
7оо = °
®тк (r) COs тФ* ^^=0, К ^ 0;
0^* (л) sin тф, т^1, к^О,
® тк~ ^ т {\^ткг I ^\) ^/л (^йк)
^/л (M’mv'V^l) (№тк)> ^ * ф)==г*
^300 =1* 0 —корни * уравнения
dm (М) Ym (ИR2/R1) —(^^2/^1) X
ХГ>) = 0;
II У»** IIя-
2d,
{(-£)
_Л_£Л1;
*^т (М’стж)
3'пМ1ткК 2/^1)
2d(1
Wf’
f dl (Мок)
d 1 (М-ок^г/^1)
т— 0,
АЗгО,
dm«=R{lWtnK’ Н^Зоо Г = ^(^1 —^?)
а^а/аг-
—ЛУ3=о
а^3/аг+
+ /i'F3 = 0
2
74Ш« =
= »UIRV
т — 0,1,2,-
лс= 1, 2, ...
Ш _0 , Д cosm<p, т^0, ASsI;
и*~ J slnmq\ 1, feSs 1,
0/л '/) — Jт №ткг/Вl) ®1я> (рт*)
Тт (Ртк^/^l) 02т (Рт*)»
0,т(Р) = Гш(ц)—!^-Гт(р),
©2т 00 =-/тЫ-
Р
hRi
Jm GO,
Р(г, 9) = г>
11тк >0— корни уравнения
02т (Р) |Дт (P#2/#l) +
+ ^ Ут 0*/?./Лх)] -0im (р)Х
х [лДцЯ./^)+-^^т(цЯ2/Я1)] :
II Ш. 02 —
]-
-(
m2-Rjh*
Ртк
)Ь
т > 0, 1
Д-Ю+^)-
_(1+Я?А»/цв«)|. т = 0, feSsl,
4т* = (^/яЦт/с); 24,„ =/т (Р-т*)
тк Wm(P mJi
Вт = Jtn i^mK^2l^l) {hRll^mic) X
X d (Ц/л^*^2/^1)’
Здесь и всюду далее дифференцирование производится по всему аргументу.
4. Рассмотрим общий случай уравнения (3.249). Полагая
У (г, ф> г) = Ч'о (г) (г, ф) и подставляя это выражение в уравнение
(3.249), произведем (как и в п. 3 § 8) разделение переменных.
В результате получим
5^ +^„(2) = О, 0<г</: (З-272)
+ + = Rt<r<Rb. (3.273)
где у2 = 7^ + у4, yl и 74—постоянные разделения.
Каждое из этих уравнений (и соответствующая для него одно¬
родная задача) уже рассмотрены: уравнение (3.272)—в §7, уравне¬
ние (3.273)—в п. 3 § 9 гл. III.
Таким образом, для собственных значений и собственных функ¬
ций однородной задачи для уравнения (3.249) можно записать
У,Iks = yL + vLkI vegs(r, Ср, z) = ¥„,(z)¥w(r, ф), (3.274)
где y]s и 'Р'оЛ2)—собственные значения и собственные функции
однородной задачи, рассмотренной в § 7; у\тк и ф)—собст¬
венные значения и собственные функции однородной задачи, рассмот¬
ренной в данном параграфе.
Выражение (3.274) решает вопрос о построении аналитических
решений краевых задач теплопроводности для бесконечного и конеч¬
ного полого цилиндра с радиальным тепловым потоком, а также
для бесконечного и конечного цилиндра, температурное поле кото¬
рого не является осесимметричным. Каждое из этих решений может
быть записано с помощью соответствующей рабочей формулы § 4
гл. III.
§ 10. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ
ОДНОРОДНОЙ ЗАДАЧИ ДЛЯ СПЛОШНОГО И ПОЛОГО ШАРОВ
1. Вначале рассмотрим случай радиального теплового потока для
сплошного или полого шара. Собственные функции удовлетворяют
уравнению
^ + 7ТГ + ^ = 0’ (3.275)
которое приводится к виду Ч'Г + = 0 с помощью подстановки
Y* (г) = (г). Таким образом, однородная задача для сплошного
или полого шара сводится к соответствующей задаче для бесконеч¬
ной пластины (см. § 7 гл. III).
2. Рассмотрим теперь общий случай, когда температура сплош¬
ного шара зависит от всех координат (/*, ф, 0). Соответствующее
уравнение для собственных значений и собственных функций имеет
вид
дг2 + г дг + г2sin в (sin0 дв ) +
1 W + Ya^ = 0, 0<r<tf. (3.276)
г2 sin2 0 дф2
177
Полагая ¥(r, ср, 0) = Чг1(г)Чг2(ф, 0), подставим в уравнение
(3.276) это значение и произведем разделение переменных
Обозначая константу разделения через у\, получим для Ч^ (г) и
Рассмотрим вначале уравнение (3.278). Его решения будем искать
также по методу разделения переменных. Решения уравнения (3.278),
периодические по ф и конечные при всех значениях 0^0^ я,
называются сферическими функциями Лежандра. Полагая Ч^ (ф, 0) =
= Чг8 (0) Чг4 (ф), подставим произведение в (3.278) и произведем
разделение переменных:
Однозначные непрерывные на окружности решения Чг4 (ф), перио¬
дические с периодом 2л, получаются при целых значениях т.
Каждому такому значению т соответствуют два линейно-независимых
решения:
(ф) = cos т Ф; ^4Л(Ф) = 51п/лф, т = 0, 1, 2, ....
Для определения решений уравнения относительно Чг3(0) с помощью
подстановки z = cos0, —l^z^l, приведем его к виду
d/dz [(1 —г2) d4f5/de] + [у] — т2/(1 —г2)] Чгб = 0, — l<z<+ 1, (3.280)
где положено Чгб (г) = 4я3 (0).
При вычислении производной было использовано правило диффе¬
ренцирования сложной функции: Ч^ (0) = Ч;5 (г) г' (0). Если положить
в уравнении (3.280) т = 0, то получим
d/dz[(l-z2)d4Vdz] + Y?4'6 = 0, -1 <г< + 1, (3.281)
т. е. пришли к уравнению Лежандра: оно имеет особые точки г =
= — 1 и z = + 1.
В курсах математической физики рассматривается следующая
граничная задача: найти значения параметра у\, при которых в
Ч'Лф, 6)1
г2 + 2г ^ + (г2у2—у\) ЧГ1 = 0; (3.277)
^[з!п0ж(з1п0ж)] + ^'*f" + tfsin’0 = O.
Обозначая постоянную разделения через тг, получим
(Ф) + (ф) = 0.
(3.279)
178
промежутке [—1, +1] существует нетривиальное решение уравне¬
ния (3.281), ограниченное в особых точках г = ± 1. Собственными
функциями этой задачи являются полиномы Лежандра:
* = «• 1. 2. .... (3.282)
соответствующие собственным значениям Yik = k(/c+1). Формула
(3.282) называется формулой Родрига. Приведем нескблько первых
полиномов Лежандра, вычисляя их по формуле (3.282):
Рп(г)=и Pi(z) = z; Р2 (г) = (1/2) (Зг2 — 1); Р9 (г) = (1/2) (5г*-3г).
Полиномы Лежандра разных порядков ортогональны между собой
с весом Р (г) = 1:
(з-28з)
Возвращаясь теперь к уравнению (3.280), запишем
d/dz [(1 -z2) dYjdz] + [к(к + 1)—та/(1 -22)] Т,, = 0. (3.284)
Произведем в уравнении (3.284) подстановку ¥^=(1—za)m/2x
х?#к(г). Функция 4r„v (г) будет удовлетворять уравнению
(1 — 2s) [ (г)];.—2 (т + 1) iV*, (г) + (к—т) (к -f т + 1) ¥,к (г) = 0.
(3.285)
Чтобы найти его частные решения, продифференцируем уравнение
(3.284) при т = 0 [(1— г%)Р'к(г)\'г-\-к(к-\- 1)^ = 0 по г равно т раз.
Получим, применяя формулу Лейбница [19], m-кратной производной
для произведения
Ат +2р Am + ip dmP
(1 —г2) 'jprrf- —2 (m+ Ч 2 -згг+г—(«—'«) (« + rn +1) -^ = 0.
(3.286)
Сравнив это уравнение с уравнением (3.285), видим, что функции
1¥вкт (z) = drrPK (z)/dzm являются частными решениями уравнения
(3.286). Отсюда ясно, что функции
(*) = РТ (z) = (1 -z*)^d”PK (z)/dz'“ (3.287)
будут ограниченными на [—1, +1] частными решениями уравнения
(3.284).
Функция PT(z) называется присоединенной функцией Лежандра
m-го порядка. Очевидно, что Р™ (г) = Р„ (г); РТ(г)Ф 0 лишь при
т^к. Присоединенные функции Лежандра образуют ортогональную
систему функций с весом Р (z) = 1
+ 1 1 0, лс =5^= ас',
Возвращаясь к переменной 0, получим искомые частные решения
Функции PJ™ (cos 0) представляют собой непрерывные полиномы
от cos0, дифференцируемые неограниченное число раз. Таким обра¬
зом, для всякого к в уравнении (3.285) имеем (/с + 1) частных решений
этого уравнения, соответствующих значениям т = 0, 1, 2, ..., ky
/*°>(cos0), (cos0), ..., P^(cos0). Теперь нетрудно выписать
частные решения уравнения (3.278), удовлетворяющие условиям.
Так как ^(ф, 0) = 4^ (0) ¥4 (ф), то, комбинируя решения (3.289)
с решениями уравнения (3.279), получим (2/с+1) сферических функ¬
ций, являющихся частными решениями уравнения (3.278) [при у\ =
= к (к + 1)];
Эти (2/с+1) сферические функции линейно независимы, так как
линейно независимы множители cos/тгф, sin ту (т = 0, 1, 2, ..., /с).
Функции P„(cos0) получили название зональных, а функции
Р{кп) (cos 0) cos тф и ‘Pim) (cos 0) sin тф— тессеральных сферических
функций. Фундаментальное изложение теории сферических и эллип¬
соидальных функций дано в книге [32].
Сферические функции ортогональны между собой на сфере 2.
Интегрируя их произведение и пользуясь формулой (3.288), получим
Нам* осталось рассмотреть уравнение (3.277), которое следует
теперь записать в виде
Ч'зкт (0) = Рк1) (cos 0) = sin"2 0
Рк (cos 0)
d (cos S)m
, tn^K. (3.289)
¥,(Ф. 0) = ^2(Ф+2л, 0); | Y,(ф. 0)|< + oo; |Y,(q>, я)|< + оо.
(3.290)
т>1,к>0; (3.291)
/72 = 0.
2
(
1 o.
o,
m Ф m\
COS/Лф
sin rtifpr
J 2л-2/(2к + 1), m — m' = 0.
(3.292)
Таким образом, можно записать!
ц ,2 2яет (<с + т)1
I1 гкт ■! 2к+ 1 (к—т) 1 ’
е0 = 2; е,„ = 1; т > 0.
г* ddJ + 2г ЧГ + [r*V*- «(« + 1)] ^ = 0. (3.293)
180
С помощью подстановки W (г) =* (О уравнение (3.293)
можно привести к уравнению Бесселя Wrt-\-(\/r)W'r-{-[y2 +
+ (/c+ 1/2)2/г2] W = 0. Его ограниченным решением в области, содер¬
жащей начало координат, будет W (r) = JK+1/2(yr). Следовательно,
искомое ограниченное частное решение уравнения (3.293) есть
Ч^ (г) = (l/J/yr) «Лс+1/2 (Yr)- Ограниченность (г) при г — 0 нетрудно
доказать, если воспользоваться асимптотическим поведением функ¬
ции Бесселя Jv (z) при г —► 0, т. е. формулой
Jv (г) « ev/[2vr (1 + v)], г — 0. (3.294)
Таким образом, найдено (2/c-f-l) частных решений уравнения
(3.276), которое можно записать в виде
/ j
: Jk+i/2 (у/*)Ркт) (cos©) соэтф, 0<т</с, к^0\
ТмЛ'. Ф. ®) =
У~уг
—~=г JK+i/2 (yr) Pjcm)(cos 0)sin /лер, 0<т<к, /с^О.
. V уг
(3.295)
Значения у определяются из граничных условий.
Граничное условие I рода при r = R:'¥(R, ф, 0) = О,
| Чг(г, ф, 0) |< + оо, г>0, О<0< л. (3.296)
Имеем однородную задачу (3.276), (3.296). Из (3.295) и (3.296)
находим: ./*+1/2 (yR) = 0 или JK+l/2 (р) = 0, если обозначить р = у/?.
Собственные значения будут следующие: y£s = \i2KS/R2, где > 0 —
корни уравнения У*+1/2 (р) = 0, а собственные функции следующие!
^Kmsir, ф. ©) =
■Jk + i/2 (ц** £-) Я™ (cos 0) cos тф; ) /с>0, s>l,
]/ .„j
/
Jk+ 1/2 (i*KS i? ) nm) (cos 0) sin тф
|1"R
т^к.
(3.297)
Найдем || 4^J2, предварительно выяснив весовую функцию для
системы ортогональных функций |(ll]/~yr) 7*+1/2 ^p*s j . удовлет¬
воряющих уравнению (3.293). Запишем его в виде (3.24) (^)]r ~h
+ г2у2Чг1—/ф+ 1)ЧГ1 = 0. Теперь видно, что весовая функция
р (г) = г2. Используя известную из теории бесселевых функций
R
формулу (см. также (3.241)) J rJv (ar) dr = (RlV 2)2 [7'v (а/?)]2, где
о
а — корень Jv(aR) = 0, а также (3.292), получим
I t-.f = [-С* ■/. <*>..)]•. «>0, т»0. (3.298)
Здесь е0 = 2 и е,л = 1, m > 0.
181
Аналогично можно рассмотреть граничные условия II и III родов.
Приводим окончательные результаты в табл. 6.
Таблица б
Граничное
условие
при r= R
Собственные функции x^K/ns (/"ф, 0);
весовая функция Р (г, <р, 0)=г*
?=°
дг
V —
т Kms —
J/fiKSft
XP'k" (cos 9)cosm<p;
Jtc+I/2 ( IX
(3.299)
ХРГ (cos 9) sin тф,
s=l, 2, 3 k = 0, 1, 2, 3, ..., к
m = 0, 1, 2, 3, .... к,
корни уравнения
1
jk+ Ml
(И)—2j7^'t+1/a 0*) = °
и w i)2_ я/?3Л-н/:(Р^) («+"■)!
II KmJ - 1) (« — m)I p** m
«5* 0.
e0 = 2; em= 1, m > 0.
^ г
wat'. Ф. 0)=7T-slnNi-n - s>°;
Ф'ооо=1; Ро*ЗэО—корни уравнения tgp = p
ЦУосаГ^МгО+р;!*)], s>0;
|4foooll2 = «2/3
Собственные функции см. выше (3.299)
> 0 корни уравнения p/i+i/2 (и) +
1
+ ^(2W-1)7k+i/2(^) = 0,
f+w=°
Y/cs — •
R2
Н2 _ л/?3 (fe-j-m)I 7 /с 4-1 /2 (Mks)
H*msn- Micf(2№+1)(K —Я!)!
=[-!
em= 1, m > 0; e0 = 2 (m = 0).
Зная собственные значения и собственные функции каждой из
рассмотренных однородных задач, можно выписать аналитическое
решение соответствующей тепловой задачи для шара с помощью
рабочих формул § 4.
В качестве примера рассмотрим первую краевую задачу:
182
= (г, ф, в, /), 0<r < R, ( > 0; \
Т (г, ф, 0, 0) = Ф0(г, ф, в); T.\riaR=0; [
Т (г, ф, 0, t) — T (г, ф + 2л, 0, /); | Г (г, ф, 0, () | < + оо, г^ 0, 0 < 0 < л. )
(3.300)
Собственные значения и собственные функции получены выше [см. (3.297)].
Для записи аналитического решения задачи воспользуемся рабочей формулой
(3.81), которую запишем в сферических координатах x = г cos ф sin 0, у =
= т sin ф sin 0, z = rcos0; напомним, что элемент объема при этом равен
6V = r2 sin 0 dr бф d0 (см. § 4 гл. III). После перехода к сферическим координа¬
там в формуле (3.81) получим
Т(г, ф, в. /) = £ £
К= О S = 1 /71= О
iv^ll2
7 ехР
1/2
R 2п л
X
г3'*Ф0(г, ф, в)х
JK+U2 (Мк* If) (C0S в) |C°Sm<P
XJK+1/2 ркп> (COS 0) sin в cos тф Ar ctydej -f
Г R 2л я
-f" sin тф
R
II 1/-3/гфо('-. <P. в)/к+1/2 X
.0 0 0
P* (cos 0) sin 0 sin тф dr d0 dф
(3.301)
где || ^Ktns ||2 определена формулой (3.298). Заметим, что при i = 0 в правой части
(3.301) будет записано разложение начальной функции Фо (г, ф, 0) в ряд по соб¬
ственным функциям однородной задачи (3.276), (3.296).
§ 11. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ
ОДНОРОДНОЙ ЗАДАЧИ ДЛЯ КОЛЬЦЕВОГО СЕКТОРА
Рассмотрим кольцевой сектор 0^ф^ср0, температурное
поле которого может быть определено в результате решения одной
из соответствующих однородных задач для уравнения
d2XF . 1 dY . 1 d2VF 2Uf A л ^ n л /Q qao\
SF + Tir + 7*W + y ’ °^r<R' °<.(P<(Po- (3-302)
Граничное условие I рода при ф = 0 и ф = ф0:
(^5 + «^)гмЛ = 0; Y(r, 0)=¥(л, Ф0) = 0; |Т(г, Ф)|< + оо,г>0.
(3.303)
Полагая ¥ (л, ф)=Чг, (г) 0 (ф) и подставляя это значение в (3.302)—
(3.303), получим после разделения переменных (у?—постоянная
разделения):
с120/с!ф2 + у?0 = 0, 0 < ф < ф0;
0 (0) = 0 (ф0) = 0; (3.304)
dг* + г Ar 'г) 1 _ ^ 1 (3.305)
dVjdr -| аДх)г = н = 0; | (г) | < + оо, г > 0. J
183
Таблица 7
Граничные условия
при
V2
Собственные функции ^тк (г. Ф);
ф = 0
ф = Фо
"тк
весовая функция Р (г, ф)=г
[ 3|*
II
°
О ф
2 Цтк
Утк —
е0 = 2,
■ е/Я = 1 >
m > 0
(«1
bl ^
Мтк
;
:=«^тл/фо ^|Тлк COS/ПЛф/фо
^ 0, Xi^O), а* + х! > о
>olmS,°; а,=о\т>?*
/ к ^ 1, J к ^ 0,
Т«,= 1;
> 0 —корни (kiH/tf) J'mЛ/Фо 0i) +
4-aj/тл/фо (м-) — 0;
||ЗД2 =
= (фо^2/4) е^/тл/ФоСМ-т^Х
ч,Г| | h\R*—(тл/фо)2! .
L J
(ai >0, Л,1 > 0, т^О, к > 0);
(фо^2/4) 6/я^/;щ/фо+ 1 (Цтк)> Л*х = 0,
т ^ 0, 1;
(фо^2/4) етУ^л/ф0 (Цт/с) X
хГ^-^Н. («1-0.
L Пт* J
т^* 0, к^ 0)
У = 0
о
II
2 Нтлк
/?2
Oil 5
|^/п«
с = «^(2т-1) я/(2ф0> ^ М'/л/с ^ X
X sin (2т— 1) лф/(2ф0),
^ 0, ^i^O, a2+ ?i2 >0; 1, к ^ I
:> 0 —корни (^!fi//?)X
< J(2т-1) л/(2ф0) (ц) 4~а1^(2т- 1) л/(2фв) (Ц) = 0;
И^лк||2 =
(фо^2/4) ^(2т-1) л/2ф0; (М-тк)Х
*'[l | Л^2-(2"г->)2я»/(4фго) I
1 Цтк J
X-i > 0, ах > 0
(фо^2/4)/(2т-1)я/(2ф0)(р.тк)Х
Г , (2т— I)2 л2 1
X М 1 л 2 2 1 » а1 — 0,
L 4/хткф0 J
(фо^2/4) J(tm-1) л/(2ф0)+1(Цтк).
Xj-0.
184
Продолжение табл. 7
Граничные условия
при
Собственные функции (г, ф);
весовая функция Р (г, ф)=г
ф=0
ф = Фо
Утк
7(2m-D л/2ф0 X
6V
— = 0
<7ф
*5
II
О
2
2 Цтк
Утк у^2
Xcos (2т— 1) Яф /(2фо)»
^1^0, аг ^ 0, + ai > 0, т ^ 1,
1» Ртк > 0—корни уравнения
(A.ifl/7?) 7(2m-l) л/(2ф0) (р) +
+ ai7(2т-1) л/(2фо (Ц) = 0;
И'ГткЙ2 |см. уравнение (3.309))
Собственные значения и собственные функции однородной задачи
(3.304) будут vfm = («Mi/«p0)S 0я(ф) = sin (тлф/ф0); для задачи (3.305)
(см. § 8)—Y'f™ = Цт*/#2:
Лг)— ^тя/ф, (цтвк t т—1| 2, 3, ...
цгаК>0—корни уравнения
(К/R) |х/'т„/ф0 (р) + а,У
тл/фо
(р) = 0.
(3.306)
'(3.307)
Таким образом, для задачи (3.300) — (3.303) имеем
Утк == == 1» 2, 3, • • •, /с = 1, 2, 3. •., (при аг = 0, k ^0)*
*-? + а? > 0; (г, ф) Jтл/Фо (м*.* sin тлф/ф0.
Весовая функция /'(г, ф) = г, квадрат нормы
(3.308)
(фо^2/4) ^тл/ф,
(Urn*) [ 1
/ti#2 —(тп
M-m/c
= [ (Фо^2/4) 7;пл/ф0+, (ршЛ), Х,=0;
(М'л'с) |
(Фо«2/4) ^п/(Ро (Ю | ^-(Г/Фо>-! ] . «! = 0.
М г\
(3.309)
В табл. 7 рассматриваются различные случаи граничных условий
при ф = 0 и ф = ф0; при этом всюду (^'Р'г + atlF)r- д =’ 0.
Граничные условия III рода при ф = 0 и ф = ф0 в полярной сис¬
теме координат имеют вид [^2(1/г) + ==0; [А,3 (1/г) Ч/ф —
— а3Ч;]ф=фо = 0 и здесь может быть использован метод интеграль¬
ных преобразований по ф (см. гл. V) (метод Фурье здесь к цели
не приводит, так как граничные условия при а{=й=0 не разделяются).
В качестве примера рассмотрим температурное поле неограниченного сплош¬
ного цилиндра, в котором поверхность r=R и плоскости ф = 0 и ф = ф0 поддер¬
живаются при нулевой температуре; начальная температура Ф0 (г, ф). Для реше-
185
ния задачи
(3.310)
Т (г, ф, 0) = Ф0 (г, ф); Т (г, 0, t) = T(r, щ, t) = T(R, ф, 0=0;
I Т (г, ф, О | < + оо, г^ггО
используем результат (3.308), а также рабочую формулу (3.100), записанную
в полярной системе координат; получим
где Цшк— положительные корни уравнения /тл/ф0(р) = 0.
В § 8—11 нам приходилось иметь дело с корнями трансцен¬
дентных уровней достаточно сложного вида ax\iJ'x (р) -f a2Jx (р) =
= 0, а{ = const. К настоящему времени для многих из этих урав¬
нений составлены таблицы корней. Необходимые данные можно
найти, например, в работах [20], [164], [166] и др.
§ 12. НЕКОТОРЫЕ ЗАМЕЧАНИЯ, КАСАЮЩИЕСЯ МЕТОДА
РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
Метод разделения переменных — классический метод решения крае¬
вых задач теплопроводности — сводит подлежащее решению диффе¬
ренциальное уравнение в частных производных, каким является урав¬
нение теплопроводности, к системе двух или более обыкновенных
дифференциальных уравнений, общие решения которых хорошо изве¬
стны или могут быть найдены обычными методами интегрирования.
Строго говоря, не в любой системе координат дифференциальное урав-
ние теплопроводности имеет частное решение в форме произведения,
что с самого начала предполагается в методе разделения переменных.
Однако большинство ортогональных криволинейных систем координат,
с которыми обычно имеют дело на практике, допускает для уравнения
теплопроводности разделение переменных (см. ниже табл. 8). В то же
время непосредственное применение метода разделения переменных к
решению краевой задачи теплопроводности зависит не только от
возможности выполнения самого разделения переменных в уравнении
теплопроводности, но и от возможности согласовать решение, полу¬
чаемое в форме произведения с начальным и граничным условиями.
Мы видели, что для этого необходимо, чтобы граничные условия задачи
были однородными. Впрочем, при неоднородных граничных условиях с
помощью специальных подстановок эти условия в некоторых случаях
могут быть сведены к однородным (см. § 3 гл. III).
(3.311)
Я Фо
186
В § 4 гл. III были получены рабочие формулы записи аналити¬
ческих решений краевых задач нестационарной теплопроводности для
конечных областей. Как показывают эти формулы, основная трудность
при решении тепловых задач в ограниченной области состоит в нахож¬
дении собственных значений и собственных функций соответствующей
однородной задачи для данной области. Если эту задачу удается ре¬
шить, то тем самым практически находится аналитическое решение и
самой краевой задачи, которое может быть выписано с помощью рабо¬
чей формулы в той или иной криволинейной системе координат.
Независимо от геометрической формы тела, где изучается процесс
нестационарной теплопроводности, аналитические решения любой из
краевых задач имеют одинаковую конструкцию, т. е. представляют
собой сумму бесконечного ряда, члены которого расположены по экс¬
поненциальным функциям, быстро убывающим с течением времени /.
Таким образом, форма аналитического решения задачи, полученная
методом разделения переменных, удобна для исследования достаточно
развитой стадии процесса при больших временах U
При нагревании или охлаждении тел наблюдаются два этапа.
I. При малых значениях времени /от /=0 до t = tu
когда процесс охлаждения (нагревания) зависит еще от начальных
условий охлаждения (начальной температуры), от ряда случайных
факторов, не обусловленных условиями нагрева и охлаждения тела,
процесс носит характер неупорядочного режима. В этих условиях
распределение температуры в теле при однородных граничных усло¬
виях описывается выражением
Т (М, 0=2 A'V, (М) exp [- (1/^тк)9 *]. (3.312)
К= J
т. е. каждый член содержит экспоненту, причем, согласно теории
собственных значений (см. § 2), показатель экспоненты по абсолют¬
ной величине представляет собой ряд возрастающих чисел
(K^Yi)9 < Vs)2 < • • • < (K^Yk)2 < • • •
Множитель Ак имеет постоянное значение для каждого члена
ряда, не зависящее ни от координат, ни от времени. Множитель
^(М) является функцией только пространственных координат и
характеризует изменение температуры в пространстве. Например,
в случае .охлаждения бесконечной пластины начальная
температура которой TQt плоскость х = 0 теплоизолирована, а на
плоскости х = / происходит теплообмен с окружающей средой тем¬
пературы Гс; по закону Ньютона, аналитическое решение соответ¬
ствующей краевой задачи теплопроводности имеет вид
То-Тс
к= 1
у ^1я.Ц«со»|1.^еХрГ__/ь.У1уЛ> (3.313)
^ Utt + sinMtfCOSfi* rL \ I / J
где —положительные корни уравнения ctgp = p/2Bi — Bi/2p.
187
В выражении (3.313)
Ак = 2sin цДц, + sin рк cos цк); (М) = cos (х/1).
Становится очевидным, что при малых значениях времени t(t 1)
ряды (3.313) сходятся очень медленно и при числовых расчетах с ис¬
пользованием этих рядов приходится брать много первых членов,
чтобы избежать больших ошибок при вычислении. Следовательно,
для малых значений времени t желательно иметь другую форму ана¬
литического решения той же краевой задачи теплопроводности.
Такая форма решения, отличная от (3.312), может быть получена
несколькими путями.
1. Путем использования свойств тэта-функции Якоби. В теории
эллиптических функций встречается функция [20]
^ ! *=+00 _ О-*)2
{}(*, /) = 1 + 2 2^ е~* я / cos (2кпх\ = -7= 2* е 1 » (3.314)
к~ 1 У я t К= _ оо
называемая функцией Якоби. Первый ряд в (3.314) быстро сходится
при больших значениях t, второй ряд — при малых значениях t.
2. Операционным методом (см. гл. VI) путем разложения найден¬
ного решения задачи в классе изображений в ряд по отрицательным
степеням показательной функции.
3. С помощью следующей теоремы — формулы суммирования Пуас¬
сона. Пусть f(x) — четная функция х> которую можно разложить
так же, как и функцию f(x + 2kl)> в ряд Фурье по косинусам углов,
кратных углу nxtl. Тогда имеет место равенство [55]
К= + 00 ® 00 ® ,
f(x± 2к1) = — \/ (х) dx + —У cos^j/^cos^d*' (3.315)
к= - оо О к= 1 О
при условии, что интегралы и ряд сходятся.
В каждом из этих трех случаев аналитическое решение краевой
задачи теплопроводности имеет вид, отличный от (3.312), и вполне
может случиться так, что, имея заранее перед собой два различных
выражения, являющихся решением одной и той же краевой задачи,
можно предположить, что одно из них является неверным. В дейст¬
вительности же дело обстоит следующим образом.
Аналитическое решение одной и той же краевой задачи можно по¬
лучить в различных классах функций. Эти классы функций должны
обладать определенными свойствами: во-первых, быстро находиться,
во-вторых, обеспечивать хорошую сходимость процесса, чтобы можно
было делать требуемые в задаче заключения о свойствах найденного
решения. Форма же аналитического решения, иначе, класс функций,
его описывающий, зависит от метода дифференциальных уравнений
математической физики, который применяется для решения конкрет¬
ной краевой задачи теплопроводности. Применяя различные методы
для решения одной и той же задачи, можно получить различные формы
одного и того же аналитического решения, которые будут тождест¬
188
венны в смысле числа, но лишь в редких случаях путем эквивалентных
преобразований могут быть переведены одно в другое. И более того, в
рамках одного и того же метода возможно получить различные пред¬
ставления одного и того же решения, если на каком-то этапе его полу¬
чения возможны преобразования, имеющие принципиальное значение
для формы будущего решения. Особенно это характерно для операцион¬
ного метода, о чем будет сказано в гл. VI.
Рассмотрим пример. Пусть Т (х, t) — температурное поле бесконечной плас¬
тины ()<*</, начальная температура которой Ф0(*), а граничные плоскости
поддерживаются при нулевой температуре. Имеем (см. § 3 гл. III)
4\ 2 р | кпх ккх' —(t
(*, 0 = 73Ф°(*) X “Г "Т" е ' 1 '
dx',
(3.316)
При малых значениях времени t ряд в скобках сходится медленно. Преобра¬
зуем решение (3.316), используя формулу (3.314). Для этого предварительно
преобразуем произведение
. кпх кпх’ 1 Г кп , „ кп . ■ .. 1
sin-у-sin— = -j I cos —(x — x) — cos— (x + x')\,
что дает в соответствии с (3.314)
I ( к= + оо
f 0 Ч=- 00
Выражение (3.317) более удобно для числовых расчетов при малых
значениях /, так как ряд в скобках для малых t сходится достаточно
быстро.
II. На втором этапе начиная с некоторого момента вре¬
мени начальное состояние тела перестает влиять на изменение темпе¬
ратурного поля ц процесс охлаждения (нагревания) полностью опре¬
деляется только условиями охлаждения на границе тела и среды,
физическими свойствами тела, его геометрической формой и' размера¬
ми. Ряд (3.312) становится настолько быстро сходящимся, что начиная с
момента t > 0 первый, отличный от нуля член преобладает над суммой
остальных членов. Начиная с этого значения U (например, для пла¬
стины Foi > 0,3, для цилиндра F0i > 0,25), температурное поле в теле
описывается простой экспонентой
Т(М, t) ez АЧМ/И) exp t—CKaVi)-/].
(3.318)
189
Например, в случае (3.313) благодаря неравенству ц* < ц2 < Цз < ... ряд
быстро сходится и начиная с определенного значения F0i все члены ряда стано¬
вятся исчезающе малыми по сравнению с первым членом, так что ими можно
пренебречь. В [161] показано, что с точностью до 0,25% при (x/R) = 0 и Bi = 1
всеми членами ряда можно пренебречь начиная с Следовательно, при
Fo^Foi решение (3.313) значительно упрощается и имеет вид
г(*. 0-Тс 2sln ш cos х [_ /OilV/
То—Те Ц, + sin М-i cos Ц] I Р[ V I ) ■
Вторая стадия охлаждения называется регулярным режимом, и зависимость
между Т и t описывается уравнением (3.318).
Математическая теория регулярного теплового режима излагается
в работе [152].
Возвращаясь к методу разделения переменных, следует отметить
большие трудности при его применении для полуограниченных тел,
где необходимо одновременно использовать метод продолжений,
чтобы получить нужное решение (см. § 5 гл. III). Значительные
трудности возникают и при решении методом Фурье краевых задач
с граничными условиями сопряжения, а также, как неоднократно
отмечалось, и в случае неоднородных граничных условий, которые
вначале должны быть приведены к однородным. Несмотря на доста¬
точно ясную схему сведения неоднородных граничных условий к
однородным, изложенную в § 3 настоящей главы, тем не менее во
многих задачах при общем законе изменения граничных функций
(т. е. отличных от постоянных и зависящих от пространственных коор¬
динат и времени) подобные преобразования технически достаточно труд¬
ны. По-видимому, один из целесообразных подходов при использовании
метода разделения переменных для решения краевых задач нестацио-
парной теплопроводности (3.66) — (3.68) состоит в предварительном
нахождении собственных значений и собственных функций соответст¬
вующей однородной задачи (3.26) — (3.27) и записи искомого решения
тепловой задачи по одной из рабочих формул § 4 гл. III. При этом
предполагается, что свойства тела, в котором изучается процесс теп¬
лопроводности, не зависят от температуры и тело ограничено коорди¬
натными поверхностями некоторой подходящим образом выбранной
системы координат.
Что касается краевых задач стационарной теплопроводности, то
применение метода Фурье к этому классу задач вполне подробно из¬
ложено в § 7—11 гл. 3 при отыскании собственных значений и собст¬
венных функций однородных задач, описываемых в общем случае также
дифференциальными уравнениями в частных производных. Здесь, как
и выше, основная идея метода разделения переменных состоит в том,
чтобы свести уравнение стационарной теплопроводности к двум или
трем (в зависимости от числа пространственных независимых пере¬
менных) обыкновенным дифференциальным уравнениям, методика ре¬
шения которых к настоящему времени разработана достаточно хоро¬
шо. При этом в полной мере могут быть использованы результаты § 7—
11 гл. 3.
В табл. 8 приводятся ортогональные системы координат, в которых
возможно произвести разделение переменных в уравнении Гельмголь¬
ца (3.24).
190
Таблица 8
Система координат
Функции, входящие в решение уравнения
Гельмгольца
Прямоугольная декартовая
Экспоненциальные, тригонометрические, гипер¬
болические
Цилиндрическая
Экспоненциальные, Бесселя, тригонометриче¬
ские
Сферическая
Лежандра, степенные, тригонометрические
Параболическая цилиндри¬
Эрмита, тригонометрические
ческая
Параболическая (вращения)
Бесселя, тригонометрические
Параболоидальная
Бэра
Эллиптическая цилиндри¬
Матье, тригонометрические
ческая
Эллипсоидальная
Ламе
Вытянутая сфероидальная
Лежандра, тригонометрические
Сплюснутая сфероидальная
Лежандра, тригонометрические
Коническая
Ламе, степенная
К настоящему времени накоплен обширный материал по теории
решения однородных задач на собственные значения и собственные
функции в конечных, полубесконечных и бесконечных интервалах.
Здесь следует прежде всего указать на фундаментальные труды
[57, 87, 140]..Существующая обширная литература по теории специаль¬
ных функций (укажем некоторые работы [8, 9, 20, 22,88]) поможет в
отыскании собственных значений и собственных функций при решении
однородных задач в конкретных областях. Следует, однако, отметить,
что изучение процессов теплопроводности аналитическим путем (осо¬
бенно нестационарной) во многих из этих систем требует большой изоб¬
ретательности, хороших технических навыков и до сих пор представ¬
ляет собой открытые вопросы аналитической теории теплопроводно¬
сти. Имеющиеся в литературе результаты в основном посвящены
уравнению теплопроводности с граничными условиями I рода и на
этом пути, вероятно, еще могут быть получены весьма важные сведения
для теории теплопроводности твердых тел.
Задача. Пусть в (3.43) — (3.44) (первая краевая Задача для об¬
ласти 0^х^/, /^0) F(x, t) = 0, Ф0(х) = Г0, Г(0, *)= T(l, t)=Tx (Г0< Тх)
и решение задачи в безразмерных переменных z = x/l, Fo = at/I2
имеет вид
и/г ЕГ \ Т(х> 4 Д sin(2л + \ )nz
W(z, -Fo)=- ■■■—= у ехр[ —(2я + 1) л Fo].
-* 1 0 Пп=\ 2/2+1
Покажите, что это решение может быть представлено в виде:
_ Т, -Г. ,_L,„ \ 2 v'Fo ) \г JFo)'
/%
где Ф(г) = (2/у/к) exp(—y2/2)dy — функция Лапласа.
191
ГЛАВА IV
МЕТОД ДЮАМЕЛЯ ПРИ РЕШЕНИИ КРАЕВЫХ
ЗАДАЧ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Смысл метода Дюамеля заключается в следующем: решение краевой
задачи нестационарной теплопроводности с граничными условиями,
зависящими от времени, можно выразить через решение соответствую¬
щей задачи, в которой граничные условия не зависят от времени.
Решение общей задачи (3.66) — (3.68) с применением метода Дюа¬
меля разобьем на несколько этапов, каждый из которых может пред¬
ставлять и самостоятельный интерес.
1. Начальная температура равна нулю,
источники теплоты отсутствуют; гранич¬
ные функции являются заданными функциями
координат и времени ил и только времени:
dT/dt =аАТ (М, t), M£G, t > 0; (4.1)
Т(М, OI/-0 =0, MgG; (4.2)
A dTfn о=-ф(м. 0. m^s, о, (4.3)
где Р! + PI > 0 (Pi = const), 1=1, 2.
Решение этой задачи можно получить из решения задачи для по¬
стоянной (во времени) граничной функции ср, используя для этой цели
теорему Дюамеля (см. ссылку в [7]).
Пусть W(Mt /, т) есть температура твердого тела в точке М в мо¬
мент времени t, начальная температура которого равна нулю, а на по¬
верхности S задается либо температура ф(М, т) (Pi = 0, р2=1),
либо тепловой поток ф2 = 0, Рх = Я), либо происходит теплообмен со
средой, имеющей температуру (1/а)ф(М, т), фх=Я, р2=а). Тогда ре¬
шение задачи (4.1) —(4.3) в случае, когда начальная температура
равна нулю, а на поверхности S задается либо переменная во времени
температура ф(М, /),либо тепловой поток ф(М, 0, либо закон тепло¬
обмена со средой переменной во времени температуры (1/а)ф(М, t),
записывается в виде
t
Т(М, 0 = t—т, T)dT, I >0. (4.4)
о
Таким образом, согласно теореме Дюамеля, для решения задачи
(4.1) — (4.3) в виде (4.4) необходимо рассмотреть вспомогательную
задачу
dW!dt=at±W {М, t, т), M£G, / > 0; (15)
W(Mt 0, т) = 0, М £ G; ^dWldn— М7) = — ф(М, т),
MgS, *>0, (4.6)
где т — фиксированное число.
192
Докажем эту теорему. Пусть у2к и (М)—собственные значения и
собственные функции соответствующей однородной задачи (3.26) —
Используя рабочую формулу записи аналитического решения
краевой задачи нестационарной теплопроводности (3.86), запишем
функцию Т(М, /), удовлетворяющую (4.1) — (4.3), в следующем
виде:
Аналогичным образом, используя ту же формулу (3.86), запишем
функцию W (Му ty т), имея в виду стационарность граничной функ¬
ции ф(Л4, т) в условии (4.6):
£Щ<р(Л*, x)YK(Ai)]M€Sda. (4.8)
5
Ряд (4.9) (и его производная по t) сходится равномерно во внутрен¬
них точках области G при любом t — т ^ 0. Продифференцируем обе
части равенства (4.9) по /, а затем проинтегрируем почленно по т)
в промежутке от т=0 до т=t
ХИ1е’(,/Г^2</~г) Кф(м’ T)'MM)]AleidTda = :r(M)0 (4.10)
0 S
получим формулу (4.4).
Рассмотрим весьма важный частный случай граничной функции,
когда температура на поверхности S или тепловой поток, или темпе¬
ратура среды, с которой происходит теплообмен, не меняется от точки
к точке, а зависит только от времени
В этом случае теорема Дюамеля имеет следующую формулировку:
(3.27).
(4.7)
X
Отсюда находим
[1 —
(4.9)
_хаг^о|л^^ = а[Г(уи 0|Мб5_ф(0]( (41|)
7-339
193
если W(M, t, т) — температура твердого тела в точке М в мо¬
мент времени t, начальная температура которого равна нулю, а по¬
верхность поддерживается при температуре, равной единице, пли
тепловой поток на поверхности равен единице, ила происходит теп¬
лообмен с окружающей средой температуры, равной единице, то реше¬
ние задачи при условии, *тго поверхность поддерживается при пере¬
менной температуре ф (/) или на поверхности задан переменный тепло¬
вой поток ф(/), или происходит теплообмен со средой переменной тем¬
пературы ф(/), записывается в виде
t
Т(М, l) = ^(p(x)jtW(M, t—т)dx. (4.12)
О
Это соотношение следует из приведенного выше. Действительно,
пусть W (Mf t) удовлетворяет уравнению (4.5), начальному условию
(4.6) и граничному условию
|MeS = «F(M. 0IM6S-1]. 1> 0. (4.13)
Введем функцию 0(Л4, /, t) = W (М, /)ф(т), которая удовлетво¬
ряет уравнению (4.5), нулевому начальному условию и граничному
условию вида
— X (30/3п) \м б s = а [0 \м е s — ф (т)]. (4.14)
Таким образом, согласно общей теореме, можно записать
t t
Т(М, О = Ц[0(Л4, t-x, т)] dr = j" ф (т) ^ U7 (Af, t—т) dr.
о о
2. Переходя к общему случаю, рассмотрим краевую задачу
теплопроводности вида
dT/dt=a/XT(My t) + f(My t)y Me Gy t > 0; (4.15)
T (My 0) = ФД M)y MeG\ fa(dT/dn)-№=-<p(My t)y
MeSy о. (4.i6)
Пусть функция W (My t, т) служит решением той же задачи у
но при условии у что f(Mt t) и ф(Л4, t) заменены на f(Mt т) и
ф(Л4, т), т. е. значениями этих функций при t= т. Тогда решение
задачи (4.15) — (4.16) записывается в виде
t
T(M,t) = jt\W(M,t—T,x)6x. (4.17)
о
Таким образом, согласно этому утверждению, для решения за¬
дачи (4.15)—(4.16) в виде (4.17) необходимо решить вспомогатель¬
ную задачу, содержащую только стационарные неоднородности:
dW/dt =a&W (My ty т) + /(M, т), M € G, 0; (4.18)
W (Af, t, t)|/=o = <D0(Af), MdG- (4.19)
<3 W"' (/Vf, t, x )/дп—(Af, /, t)=—q>(Af, т), (4.20)
Af € S, t > 0.
194
Доказательство справедливости формулы (4.17) можно провести
аналогично, как и в случае (4.4), если воспользоваться рабочей
формулой (3.86).
3. Нам осталось рассмотреть, как сложную краевую задачу не¬
стационарной теплопроводности (4.15) — (4.16) свести к более про¬
стым, с тем чтобы, применяя теорему Дюамеля и метод разделения
переменных, получить до конца ее аналитическое решение.
Функцию Т (М, t) ищем в виде суммы Т (Л4, t) = Tl(M, 0 +
+ T2 (Mt t) + Tt (М, /), где Т.(уИ, /) — решения задач (при MgG,
t> 0):
dTjdt = а Д7\; \ dTjdt = abTt + f(M,t); ] dTjdt=aAT3‘
Tt(M, 0) = 0; I T2(Mf 0) = 0; I T3(Mt 0) = Ф0(М);
Pi (dTjdn) -p2T, = ( pt (дТ2/дп) -р2Г2 = 0, ( pt (dTjdn) - р2Г, =
= — ф(Л4, /), ] M£S J =0, Mg S.
Функции T-2 и Tg могут быть найдены методом разделения пе¬
ременных. Функция 7\(М, t) с неоднородным граничным условием
может быть найдена с помощью метода Дюамеля и метода разделе¬
ния переменных. Для этого предварительно ищем функцию
W (М, t, т), удовлетворяющую уравнению W’t = akW, начальному
условию W (Mf 0, т) = 0 и граничному условию
Pi (dW/dn)-$2W = -Ф (М, т), М € S, t > 0. (4.20')
Стационарную неоднородность ф(М, т) в граничном условии
нетрудно перевести в начальное условие, с тем чтобы получить та¬
кую форму задачи, где возможно непосредственно применить метод
разделения переменных. Для этого положим W (М, t% т)=
= ИРг(Л1, /, т)+И72(Л4, т), где Wt (i= 1, 2) удовлетворяют усло¬
виям:
dW1/dt=akWi(My /, т), М £ G, | AU72(jW, т) = 0, М £ G; ]
/>0; W1 (Mt 0, т) = Га(М, т); U, (dU7e/d/i)-PaU7f = [
Pi (pW^дп) —fi2W, |а* € s = 0. ] =-Ф(М, т), M£S. j
Каждая из функций И?! и 1Г2 может быть найдена методом Фурье, и
далее для отыскания 7\(М, t) следует использовать интеграл (4.4).
Теорема Дюамеля, справедливая при весьма общих краевых функ¬
циях задачи (в трехмерном, двухмерном и одномерном случаях), весьма
полезна при решении краевых задач нестационарной теплопровод¬
ности. Действительно, получить решение задачи для случая источника
и граничных функций, постоянных во времени, часто бывает значитель¬
но легче. Отметим также, что эта теорема справедлива и для краевых
задач с граничными условиями сопряжения, а также для полуогра-
ниченных областей с нестационарными функциями источника и гранич¬
ными функциями.
Рассмотрим пример. Найдем температурную функцию для бесконечной пла¬
стины 0<:*<;/ с заданным переменным тепловым потоком внутрь тела при
* = /; плоскость х = 0 теплоизолирована, начальная температура равна нулю.
195
Имеем
dT/dt = a (д2Т/дх2), О < х < I, / > Oj
7'(х,0)=0, 0 < х < /, дТ/дх U=0 = 0, / > 0| (4.21)
X (дТ/дх) \x_i = ф (/), / > 0.
Функцию Г (х, /) можно записать по теореме Дюамеля в виде
t
т (*> 0 = J ф (х) U7 (*, < —х) dx, (4.22)
О
где W (х, /)— решение вспомогательной, задачи, имеющей вид:
dW/dt=a (d2Wjdx2)t 0 < * < /, / > 0;
U7 (х, 0) =0, 0 < д; < /; dlF/d* \Xz=0 = 0, / > 0;
X(dW/dx)\x=l = \, /> 0. (4.23)
Эту задачу можно решить методом разделения переменных, если перевести
неоднородность из граничного условия при х = 1 в начальное условие и диффе¬
ренциальное уравнение. Это можно сделать с помощью подстановки (см. § 3
гл. III)
W(xf t) = U(x, t) + (3x2 — /2)/(6?0).
Переходя в (4.23) к функции U (х, /), находим
dU/dt =а (д2и/дх2)+\Цср1), 0 < * < /, / > 0;
(У (*, 0) = - (Зх2 — l2)/(6kl), 0 < х < /;
(a^)U=0 = (a^)U=i = 0, / > 0. (4.24)
В § 7 гл. III приведены собственные функции второй краевой задачи для
рассматриваемой области; в § 4 гл. III записана формула (3.127) для решения
второй краевой задачи. Используя эту формулу, находим U (х* /) и далее
W (х, /) в виде
(4.25)
TV7 / *\ t \ 1 /зх2—12 2 V (— 0х Г (кл У а У Л /слх\
W (х' t)=^i+l \-№—V-ехр г~) *\cos —/
Из (4.25) видно, что распределение температуры есть сумма линейной функ¬
ции времени //(ср/) и корректирующего фактора, который является функцией
времени и положения. График этого корректирующего члена приведен в [52].
Заметим также), что решение (4.25) удобно применять для больших значений кри¬
терия Fo = atjl2\ для малых значений Fo, например для Fo < 0,01 ряд (4.25)
сходится медленно. Функцию W (х, /) можно было бы получить и операционным
методом (и это сделать легче, чем методом Фурье), но уже не в форме ряда
Фурье, а в форме ряда с функциями ошибок или их интегралами, которые для
малых значений времени сходятся быстро. В этом случае получим (см. гл. VI)
(2/c + l) 1—х
2 У1й
+ 1Ф*
(2*~Н 1) 1-\-х
2 V~at
(4.26)
где 1'Ф* (х) = ^ Ф* (|) d\ = {\lY~n) е-*2—хФ* (х); Ф* (х) = 1—Ф (х).
X
Таким образом, имея два различных представления для функции W (х, /) в виде
(4.25) для больших значений времени /ив виде (4.26) для малых значений
времени /, с помощью интеграла (4.22) можно записать соответствующие пред¬
ставления и для искомого решения Т (х, /).
В заключение заметим следующее. При всей очевидности большого
значения метода Дюамеля для аналитической теории теплопровод¬
ности этот метод имеет и свои недостатки: 1) необходимо предваритель¬
196
но решить вспомогательную задачу с постоянными граничными усло¬
виями, если заранее не было известно соответствующее решение;
2) во многих случаях не удается получить эффективное решение при
переменных граничных функциях, так как это решение представляет
собой определенный интеграл, который не всегда вычисляется.
Поэтому в ряде случаев с самого начала предпочитают искать ре¬
шение исходной задачи с переменными граничными функциями, ис¬
пользуя для этих целей либо операционный метод (см. гл. VI), либо
метод интегральных преобразований (см. гл. V).
ГЛАВА V
МЕТОД ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
ВВЕДЕНИЕ
Метод интегральных преобразований математически эквивалентен
методу собственных функций, хотя исторически он возник позднее ме¬
тода разделения переменных, а метод конечных интегральных пре¬
образований появился лишь недавно (в середине 30-х годов).
Хотя в применении к уравнению теплопроводности класс задач,
разрешимых с помощью метода интегральных преобразований, не
выходит за пределы класса задач, решение которых в принципе может
быть найдено по методу Фурье, все же метод интегральных преобра¬
зований обладает рядом существенных преимуществ.
К числу этих преимуществ следует отнести возможность непосред¬
ственного применения метода как к однородным, так и неоднородным
краевым задачам, единообразие методики и значительное упрощение
выкладок в связи с более простой техникой вычисления, свойственной
именно интегральным методам. Наконец, при наличии таблиц, пря¬
мых и обратных для данного вида преобразований, техника решения
упрощается до применения стандартных рецептов, ведущих к решению
задачи коротким путем и в более простом виде, чем в методе разделе¬
ния переменных. Это чисто количественное преимущество переходит в
качественную особенность метода интегральных преобразований, так
как решения, получаемые методом разделения переменных, требуют
определенной изобретательности и большой затраты времени.
В то же время следует отметить, что для метода интегральных пре¬
образований характерны те же ограничения, что и для метода разде¬
ления переменных: он применим только к линейным дифференциаль¬
ным уравнениям с линейными граничными условиями, причем для
достаточно простых областей изменения пространственных перемен¬
ных. Кроме того, не всегда можно использовать рецептурные приемы
решения, особенно при решении новых задач, требующих тщательного
исследования. С этой точки зрения метод интегральных преобразова¬
ний не расширяет класса задач, для которого возможно получить ана¬
литическое решение, когда метод Фурье становится бессильным (или
ход решения задачи этим методом чрезвычайно усложняется). Однако
197
внутри этого класса применение метода интегральных преобразований
более целесообразно.
Сущность этого метода состоит в следующем.
Пусть требуется определить функцию Т(х, у, г, t ), удовлетворяю¬
щую в области £2 = (а < х < Ь> (у, г) С Glt t > 0) дифференциальному
уравнению теплопроводности (нестационарной или стационарной) с
заданными начальным и граничным условиями. Решение рассматри¬
ваемой задачи заметно упрощается, если вместо непосредственного
определения функции Т искать предварительно ее интегральное пре¬
образование, определяемое формулой
ь
Т (£. у, г, t) = ^T(x,.y, г, t) И (х, l)dx, (5.1)
а
где c<.l<d, К(х, I) — надлежаще выбранная функция, опреде¬
ленная в области (а < л; < Ьу с < £ < d) и называемая ядром ин¬
тегрального преобразования (5.1).
В результате интегрального преобразования получается некото¬
рая новая функция Т(\, у, z, t), уже не зависящая от х; функция
Т(1у у у Zy t) называется интегральной трансформантой у изображе¬
нием или образом функции Т(ху у у 2, t). Исходная функция T(xf у,
Zy t) называется оригиналом или прообразом функции Г(£, уу г, f);
переменная х называется переменной преобразования. Пределы а и Ь
(соответственно cud) могут быть как конечными, так и бесконечными.
В первом случае преобразование (5.1) называется интегральным пре¬
образованием с конечными пределамиу во втором — интегральным
преобразованием в бесконечных пределах.
Преобразованные функции обозначим тем же символом, что и
до преобразовайия, но с каким-либо значком над символом. Возможны
интегральные преобразования сразу по нескольким или по всем пере¬
менным последовательно. Последовательное применение преобразо¬
вания типа (5.1) эквивалентно некоторому преобразованию по не¬
скольким переменным :
ь
т (5,1). £, t) = J j J /Cl (*, у, г, I, Г], О Т (х, у, г, t) dx dy dz, (5.2)
a Gy
называемому кратным интегральным преобразованием.
Преобразование, которым функция Т (£, у, г, /) снова преобразу¬
ется в функцию Т(Ху у у Zy 0* называется обратным интегральному
преобразованию (5.1). Соответствующая формула, дающая переход от
изображений к оригиналам, называется формулой обраирния:
d
Т (Ху у у Zy t) = ^R (Ху I) Т (%у у у Zy t) dg. (5.3)
с
Интегральное преобразование определено, когда интеграл в правой
части (5.1) существует. Для практического применения интегрального
преобразования важно, чтобы существовало также и обратное преоб¬
198
разование (5.3), которое совместно с (5.1) устанавливало бы взаимно
однозначное соответствие между оригиналом и изображением. При
этом условии можно установить соответствие также и между уравне¬
ниями для функции оригинала и функции изображения и решение
задачи, заданной для оригинала, свести к задаче относительно изоб¬
ражения, которая может быть проще. Действительно, основная идея
применения интегрального преобразования (5.1) к задачам для диф¬
ференциальных уравнений в частных производных состоит в выборе
ядра К (х, £) таким образом, чтобы дифференциальные операции по
переменной преобразования в исходной задаче заменить алгебраиче¬
скими операциями в преобразованной задаче. При этом выбор ядра К
(.х, £) интегрального преобразования осуществляется в соответствии с
дифференциальным уравнением и граничными условиями задачи,
т. е. с учетом геометрической формы тела и законом его теплового
взаимодействия с окружающей средой.
После выбора ядра, применяя преобразование (5.1) к дифферен¬
циальному уравнению теплопроводности с п независимыми перемен¬
ными, переходим в пространстве изображений к уравнению с (п — 1)
независимыми переменными, что значительно облегчает решение рас¬
сматриваемой задачи. Последовательное применение интегральных
преобразований по независимым переменным сводит дифференциаль¬
ное уравнение в частных производных, каким является уравнение
теплопроводности, к обыкновенному дифференциальному уравнению,
теория решения которого разработана достаточно хорошо. Вообще
говоря, можно свести исходную задачу и к решению простого алгебраи¬
ческого уравнения, однако к этому следует прибегать в редких слу¬
чаях. После того как будет найдено решение преобразованной задачи,
с помощью обратного преобразования находится и решение исходной.
Интегральные преобразования, применяемые в аналитической
теории теплопроводности, можно разделить на два класса: интеграль¬
ные преобразования по времени t и интегральные преобразования по
пространственным переменным. Это условное разделение — следствие
той особой роли, которую время t играет в уравнении теплопровод¬
ности: во-первых, уравнение теплопроводности является уравнением
первого порядка относительно переменной /, тогда цак относительно
пространственных координат — это уравнение второго порядка; во-
вторых, время меняется в пределах от нуля до бесконечности (0 ^
^ < оо), что дает возможность применять по переменной t инте¬
гральное преобразование одного вида, независимо от геометрии рас¬
сматриваемого тела и вида граничных условий.
Таким образом, на практике применяют два класса интегральных
преобразований:
1) интегральное преобразование по врем е-
н и t\ этот класс преобразований составляет операционное исчисление
(изложение операционного исчисления дано в гл. VI). С точки зрения
(5.1) — это интегральное преобразование с бесконечными пределами
QD
т (М, р) = §е-г*Т(М, l)dt (/> = o + to>). (5.4)
О
199
Преобразование (5.4) называется преобразованием Лапласа в от¬
личие от преобразования Лапласа—Карсона
со
Т(М, р) = р Ц e~?f Т (М, t)dt (p = a+icо), (5.5)
о
отличающегося от преобразования Лапласа лишь множителем р перед
интегралом. Преобразование (5.4) иногда называют односторонним
преобразованием Лапласа в отличие от двустороннего преобразования
Лапласа
+ х
Т (М, р) = р Л e~ptT (М, t)dt (/? = a + ico), (5.6)
— 00
широко применяемого при решении краевых задач нестационарной
теплопроводности без начальных условий.
Применяя преобразование (5.4) к дифференциальному уравнению
теплопроводности, исключаем из уравнения частную производную по
/, заменяя ее линейным выражением относительно изображения иско¬
мой функции, так что преобразованное уравнение переходит в обык¬
новенное дифференциальное уравнение второго порядка (в случае одной
пространственной переменной) либо в уравнение типа Гельмгольца
(в случае двух или трех пространственных переменных).
Например, в случае первой краевой задачи для бесконечной пла¬
стины
dT/dt = а(д2Т/дх2)у 0 < х < /, t > 0; (5.7)
Т(ху 0)=0, 7(0, /) = Фi(0>
Г(/, 0 = ф.(0.' (5-8)
ищем вместо функции Т (х, t) ее изображение
OD
Т (xt p) = ^e~ptT (х, t)dt. (5.9)
о
Преобразуем задачу (5.7) —(5.8). Для этого вначале умножим
обе части уравнения (5.7) на ехр(—pt) и проинтегрируем по t от
О до оо:
Je_p'lrd/=aIe"/,(S-d/- (5Л0>
о о
предположив, что все интегралы существуют. Вычислим по частям
интеграл слева
00 оо
jje-P‘^dt = T (х, t) е-Р* |* + р J е~Р<Т (х, t) d/ =
= — Т (х, 0) + рТ(х, р) = рТ. (5.11)
200
Здесь было использовано начальное условие (5.8) и равенство
lim e~pfT = 0, справедливое в области сходимости интеграла Лап¬
ласа (5.9).
Преобразуем интеграл в правой части равенства (5.10)
о о
Здесь__частная производная пох переходит в обыкновенную от функ¬
ции Т (ху р)у зависящей только от одной независимой переменной х.
Таким образом, дифференциальное уравнение в частных производ¬
ных (5.7) относительно оригинала Т (ху t) в пространстве изобра¬
жений по Лапласу переходит в обыкновенное дифференциальное
уравнение
d2T/dx2 — (p/a) Т = 0, 0 <х<1, (5.12)
общее решение которого нетрудно записать в виде
Т (х9 р) = А%Щх1\/1а)У^] + В\сЩх1\га)УТ\ (5.13)
Применяя преобразование (5.9) к граничным условиям (5.8),
найдем
Т (0, р) = ф, (/?); Т (/, р) = ф2 (р),
где
Ф« (Р) = j е"^Фг (0 d/ (/=1,2). (5.14)
Находим из (5.13) — (5.14) постоянные интегрирования А и В и
вместе с этим операционное решение задачи (5.7)— (5.8) в виде
Т(х, р) = ф, (р)sh + ф2 (Р)sh . (5.15)
V Н) Yl sh (ну-?) Yip sh (llVT) VJ v ;
Используя далее формулу обращения для преобразования Лапласа,
можно определить оригинал (в гл. VI вернемся к этой задаче при вы¬
числении оригинала) Т(х, t). Заметим, что наибольшая трудность в
решении этой задачи операционным методом состоит в отыскании
оригинала по найденному изображению.
Предположим далее, что в постановке задачи (5.7) — (5.8) на¬
чальная температура отлична от нуля, т. е. Т (х, 0) = Ф0(х). Тогда
из (5.10) и (5.11) следует, что в пространстве изображений уравне¬
ние (5.7) имеет следующий вид:
d2T/dx- — (р!а) Т = —(1/а)Ф0(х), 0 < х < /. (5.16)
Общее решение неоднородного уравнения (5.16) можно получить,
например, методом вариации произвольных постоянных (см.:
Степанов В. В. Курс дифференциальных уравнений. М., Физ-
201
матгиз, 1958), причем в двух эквивалентных формах:
Т (х, р) — Ach -?==V~p + В sh + -7== ch -£= х
у а У а У ар У а
X I
xV~p |ф0(1) shp|=KT d£ + p==sh y^Vp j Ф„(£) Ch y^VJ d|=
I
x ^ Фц (I)exp ( V~p~) d| exp ( —/T)x
x ^Ji)exp(pj=l/p")d!j., (5.17)
где Ax=(A-\-B)l2; BX=(A—B)/2, причем Л, Б, Лх, Бх— величины
постоянные относительно х, но зависящие от р.
После определения произвольных постоянных Л и Б из граничных
условий (5Л4) задача сведется к определению оригинала по изобра¬
жению Т(х, р). Нетрудно сделать следующий вывод о недостатках
интегрального преобразования Лапласа (5.9).
Как показывает этот простой пример, при решении задачи в про¬
странстве изображений возникают трудности, когда начальное распре¬
деление температуры задано в виде функции пространственной коор¬
динаты. Трудности такого же порядка возникают и при решении
многомерных задач, так как после исключения из уравнения частной
производной по времени уравнение хотя и упростилось, но по-преж¬
нему остается уравнением в частных производных относительно про¬
странственных координат.
В этой связи были разработаны:
2) интегральные преобразования по про¬
странственным переменным в соответствии с
геометрической формой тела и граничным4 и
условиямизадачи.
С помощью этого класса интегральных преобразований из диффе¬
ренциального уравнения теплопроводности исключаются вторые част¬
ные производные по пространственным переменным путем замены ли¬
нейным выражением относительно изображения искомой функции и
граничными функциями задачи.
Последовательное применение интегральных преобразований по
всем пространственным переменным преобразует исходное дифферен¬
циальное уравнение в частных производных в обыкновенное линейное
дифференциальное уравнение первого порядка относительно перемен¬
ной t. Этот класс интегральных преобразований иногда называют пре¬
образованиями Фурье, так как построение теории преобразования
второго класса самым тесным образом связано с возможностью раз¬
ложения искомой функции Т(Mt t) в ряд Фурье по собственным функ¬
циям соответствующей однородной задачи (см. § 3 гл. V).
202
Поясним все сказанное с помощью конечного интегрального преобразования
синус-трансформанты Фурье, которое подробнее рассмотрим в § 3. В данном слу¬
чае найдем решение задачи (5.7) — (5.8) с помощью преобразования Фурье по
переменной х, полагая
/
Т (я, /) = ^ Т (х, t) sin (плх/l) dx (п= 1,2,3,...). (5.18)
о
Для этого умножим обе части уравнения (5.7) на ядро преобразования (5.18)
sin (ппх/l) и проинтегрируем по х от 0 до /:
I I
^ (dTjdt) sin (riTixJl) dx = a ^ (d2Tjdx2) sin (nnxjl) cl*. (5.19)
о о
В левой части равенства (5.19) дифференцирование и интегрирование ведутся
по разным независимым переменным, так что
i I
^ (dTjdt) sin (плх/l) dx = -^ Ц Т (х, /) sin (плх/t) d* = dT (n, t)/dt.
о о
В правой части равенства (5.19) вычислим интеграл, применяя дважды фор¬
мулу интегрирования по частям и используя граничные условия (5.8):
I l I
Г д2Т ппх , дТ ппх пл Г дТ
)мг51п-Гдх=-дГ81п- TJ
0*-х
б 0 0
плх , пл ~ плх
X cos —— ах = — Т cos ——
_(»«)■ J г ОХ (5.20)
0
. плх , ПЛ г , ,Ч„ , I пл\2тр ,
XSin-y-d*=-y- [ф1 — (— 1)"ф2] — (— J Т{п, t).
В этом последнем равенстве и заключается весь смысл интегрального преобразо¬
вания: вторая частная производная в пространстве изображений перешла в основ¬
ную (искомую) функцию и уравнение теплопроводности существенно упрощается*
так как переходит в обыкновенное, линейное неоднородное дифференциальное
уравнение первого порядка
M_+^nnV~ZyT=an(<)_(_1)П(р2 (/)] (521)
Если предположить, как и выше, что начальная температура Т (*, 0) = Ф0 (*),
то наряду с преобразованием уравнения (5.7) следует преобразовать и начальное
условие Т (я, 0) =Ф0 (п), где
I
Фо (п) = ^ ф0 (*) sin dx. (5.22)
о
Уравнение (5.21) в отличие от уравнения (5.16) решается более простым спо¬
собом. Его решение, удовлетворяющее условию (5.22), имеет вид
5>,
х $ “р[Г“~) (,_,)]*• W)dt- <5Я>
203
Формула обращения для преобразования (5.18) имеет вид (см. § 3)
оо
Т (х, t) = (2/1) 2 Т (я» 0 sin плх/1. (5.24)
п= 1
Подставляя в правую часть равенства (5.24) под знак суммы найденное изоб¬
ражение (5.23) и заменяя интегральную трансформанту Ф0 (п) интегралом (5.22),
придем к выражению (3.124), полученному в § 4 гл. IV методом разделения пе¬
ременных., но более длинным путем.
Следует заметить, что особенно эффективны преобразования Фурье
при решении краевых задач стационарной теплопроводности, описы¬
ваемые уравнениями Лапласа и Пуассона в области, имеющей вид бес¬
конечной полосы и полуполосы, неограниченного и полуограничен-
ного сплошного или полого цилиндра, в области, ограниченной изнутри
сферической или цилиндрической поверхностью, в краевых задачах с
граничными условиями сопряжения и др.
§ 1. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
Во введении определено интегральное преобразование /(£) функции
f(x) с помощью выражения
ь
Т(£) = S / (х) К (х, I) dx, (5.25)
а
где К(х, £) — известная функция х и £, называемая ядром интеграль¬
ного преобразования (5.25).
В качестве ядер преобразования.используются различные функции:
экспоненциальная, степенная, тригонометрические, функции Бесселя,
полиномы Лежандра, функции Вебера и Макдональда, сферические
функции и др., так что число интегральных преобразований может быть
увеличено за счет надлежаще выбранных новых ядер.
Рассмотрим интегральные преобразования (5.25), в которых а=
=0 (а=—оо), b = оо. Если искомая функция (5.1) удовлетворяет
дифференциальному уравнению в частных производных и некоторым
дополнительным условиям (краевым условиям), за исключением ус¬
ловия, относящегося к поведению функции при хоо, которое при¬
нимается во внимание при преобразовании уравнения, то с помощью
преобразования (5.1) эти краевые условия переводятся в соответствую¬
щие условия для изображения, а в дифференциальном уравнении в
частных производных временно исключается одна из независимых
переменных. Решение этого последнего уравнения является функцией
| и остальных переменных, и дальнейшая проблема сводится к задаче
обращения преобразования (5.1), т. е. к решению интегрального урав¬
нения (5.25) относительно оригинала f(x)\ функция /(Е) — изображе¬
ние f(x) теперь уже предполагается известной функцией.
204
В большинстве практически важных случаев это обращение может
быть дано в форме интеграла, симметричного с (5.25) вида, а именно:
00
/W=j/(P(x,5) dl, (5.26)
О
где R(x, |) — надлежаще выбранная функция, определенная в об¬
ласти 0^л;<оо, 0^|<оо и называемая ядром обратного преоб¬
разования.
Решение интегрального уравнения (5.25) в форме (5.26) может
быть получено формально с помощью интеграла Фурье для функ¬
ции /(*), имеющего, по определению [6], вид
+ 00 +00
/(*)=2^ j da j / (Р) cosa (Р—х) dp. (5.27)
— оо — оо
Здесь f(x)—функция, непрерывная на всей числовой оси, кусочно¬
гладкая на каждом конечном отрезке и абсолютно интегрируемая
на (—оо, -j-оо). Последнее означает, что сходится интеграл
+ 00 ,
J | / (л:) | бл: (есть конечная величина). (5.28)
— 00
Наиболее часто применяемые в аналитической теории теплопро¬
водности преобразования типа (5.25) следующие:
преобразование Лапласа (см. гл. VI)
00
Г(р) = §е~'х f(x) dx (р = о + ш); (5.29)
О
синус- и косинус-преобразования Фурье
00 ч sin \х
7(1)=К2м5/(х> } dx(0<£<«>); (5.30)
О 'cos 1х
экспоненциальное (комплексное) преобразование
Фурье
+ 00
Т{1)=и\/Г2п ^ e‘txf(x)dx (—оо<£<+оо); (5.31)
— 00
преобразование Ханкеля
со
Ы5) = $*/(*)-MW dx (v>—1/2, < оо), (5.32)
О
где yv —функция Бесселя I рода порядка v;
преобразование Меллина
00
J(s) = \f (х) Xs'1 dx (s = v + io>); (5.33)
О
205
преобразование Конторовича —Лебедева
0D
/(v)== J/W
О
оо
ИЛИ
= dx (0<T<oo), (5.34)
О
где /Cv(x) — функция Макдональда [51]; [Re v] < 60, где б0 — неко¬
торое положительное число, выбранное таким образом, чтобы обеспе¬
чить сходимость интеграла на нижнем пределе х=0;
преобразования Мелера — Фока
где Ру (х)—сферическая функция Лежандра первого рода [19],
Особенностью интегральных преобразований (5.29) — (5.35) яв¬
ляется наличие бесконечного верхнего предела, что, естественно, су¬
живает круг этих преобразований. Другими словами, интегральные
преобразования (5.29), (5.30), (5.32) — (5.35) успешно применяют
только к краевым задачам теплопроводности для тел полуограничен-
ной протяженности. При этом выбор соответствующего интегрального
преобразования при решении краевой задачи определяется видом
граничного условия при х=0 (предполагается, что х=0 — уравнение
граничной поверхности для рассматриваемого тела). Так, если на
поверхности тела заданы граничные условия II рода, необходимо
применить косинус-преобразование Фурье, в случае задания при
х=0 граничного условия III рода (<dT/dx)x==0 =h(Ty=0 —ф(0) можно
использовать интегральное преобразование следующего вида [121]:
Т (5, t) = \^2/n \Т(х, t) [(h sin cos E*)/(ft2 + £2)1/2] dx. (5.36)
Преобразование Ханкеля (5.32) применяется для тел, обладающих
осевой симметрией [134, 142]; преобразование Меллина (5.33) успешно
используется при решении стационарных краевых задач теплопро¬
водности в секториальных областях [142]; преобразование Конторо¬
вича — Лебедева и его различные модификации можно использовать
для областей, ограниченных поверхностью двугранного угла или ко¬
нуса [88, 144]; применение преобразования Мелера — Фока (5.35)
дает возможность решать тепловые задачи, связанные с интегрирова¬
нием уравнений Лапласа и Пуассона для области, ограниченной двумя
пересекающимися сферами, и областей, ограниченных одним или двумя
софокусными гиперболоидами вращения [40]. Практическое примене¬
ние названных интегральных преобразований существенно облегчает¬
ся наличием подробных таблиц прямых и обратных преобразований
(5.35)
о
206
Интегральные преобразования с бесконечными пределами
207
Продолжение табл.
-и
+
х
i4Л
1^
|K
IK
9-
-o
1^
IK
IM
9-
ТЭ
К
et
?-
ъЩ
X
"Ге
H,
К
X
£
sz
C/3
p
Э1
2
IK
X
+
X
£ -S
£ 2
и H
2 +
о X
й§
н
UJ)
?►
К
2
*
Л
i-Lft
I?
I
A\
8-
2
i
V»
4
IK
3
+
X
'&■
2
к
IK
8
+
V
н
8
+
V
н
Ml
о
X
*>?
I
к
X
8
V
н
M
208
различных функций, часто встречающихся в конкретных задачах [10,
41, 64].
В тех случаях, когда найденные изображения в таблицах отсутст¬
вуют, оригиналы этих изображений можно найти по формулам обра¬
щений для указанных преобразований. Вывод формул обращения
для указанных преобразований (5.29) — (5.36) не рассматривается
в данном пособии. Эти вопросы изложены в достаточно простой форме
в работах [41, 134, 141, 142]. Ниже, в табл. 9 приведена сводка формул
прямых и обратных преобразований (кроме преобразования Лапласа,
которому посвящена специальная глава), применяемых в аналитиче¬
ской теории теплопроводности.
Следует остановиться на условиях применимости записанных в
табл. 9 формул. В случае преобразований 1—5 функция f(x) должна
удовлетворять условиям Дирихле [6] в каком-либо из интервалов
(0, оо), (—оо, +оо) (что означает, что f(x) должна быть определена на
каком-либо из этих интервалов, иметь на каждом конечном сегменте
не более конечного числа точек разрыва и быть абсолютно интегрируе¬
мой). Последнее условие значительно ограничивает область примени¬
мости интегральных преобразований (5.29) — (5.36); они становятся
неприменимыми для f(x) — Т0 = const, f (x) = sin х (cos, х) и т. д.,
т. е. для функций, часто встречающихся в практике теплофизических
расчетов. Здесь можно поступать двояким образом и каждый из под¬
ходов, которые мы сейчас укажем, имеют большое значение в практике
конкретных расчетов.
1. Можно ввести так называемые обобщенные преобразования
Фурье (например, для косинуса- и синуса-преобразований) в виде
оо \ cos
7 (£) = Пт К 2/я J (х) > dx;
° о / sin £* /Г оуч
00 \ cos (O.tj/J
/(*)= lim |/2м(е-<"7(&) \ di.
а ■* 0 0 ) sin Ъх
В приложениях экспоненциального преобразования (5.31) (напри¬
мер, при решении задач теплопроводности с разнородными гранич¬
ными условиями на линии, см. гл. IX) рассматривается обо б ще н-
ное экспоненциальное преобразование. В случае, когда в (5.31)
/ (I) не существует, функции
оо
7+{l) = y^-§f{x)eil*dx, t*=u + iv;
° о (5.38)
7-(i)=yj=- j f(x)e‘t*dx, l = u + iv
— 00
могут существовать; /+(£)—для достаточно больших положитель¬
ных v (v^v0> 0), /_ (I) — при достаточно большой отрицательной
величине v (v^y0 <Q). Это обеспечит абсолютную сходимость
209
интегралов в (5.38) для любых ограниченных | f (х) | <1Л40. Дейст¬
вительно, рассмотрим /+ (Е) для точек £, лежащих на прямой Im£ =
*= va:
09
h (5) = j f (x) e_tvt e(ujr dx.
С*).
X > 0;
х < 0
I fix),
х> 0;
jo,
х< 0.
•Г'
х< 0;
1 fix).
*> 0.
\Г2л
Отсюда следует, что /+(£) есть преобразование функции, равной
/(*)ехр(—v0x) при *>0 и нулю при х < 0 и далее на основании
формулы 1 табл. 9 можно записать:
Г Т+ (I) z~iux d« = I 6
у1* Л j о,
или
+ 06»
у= j r+(S)e-<'(“+ft»' d« =
— оо
Аналогично,
+ оо
da-
—‘ 00
Полагая м = £— в интеграле, содержащем /+(£)» и и = \—iy0 в
интеграле, содержащем /_ (£), и складывая оба интеграла, получим
соответствующую формулу обращения для преобразования (5.38)
+ 00 + iv0 + ® + {у0
/(*) = -/!=- j 7+(E)e-‘*Sd6 + -^r j 7-(S)e-te*dg. (5.39)
-Ю+1У0 -®+i?0
Вычисление контурных интегралов в (5.39), сводящихся к интег¬
ралу Римана — Меллина (см. гл. VI), проводится с помощью теории
вычетов (см. гл. VI и [92]). Как и в формуле обращения для преоб¬
разования Лапласа, числа v0 и у0 связаны с особыми точками
функций /+(£) и 7- (£)> а именно: необходимо, чтобы v0 было больше
мнимых частей всех особых точек /+ (£)» а у0 было меньше мнимых
частей всех особых точек /_ (£).
2. Следует заметить, что более удобным при решении конкрет¬
ных тепловых задач является подход, связанный с введением (ус¬
ловно) переменных краевых функций для нахождения решения,
имеющего смысл обобщенного решения. Поясним сказанное на при¬
мере, достаточно наглядном и в то же время часто встречающемся
в практике решения следующей тепловой задачи;
dT/dt=a(d2T/dx2)-{-Q/(cp)y х > 0, t > О, Q = const; (5.40)
Т(х> 0) = ФД*), х^О; Г (0, 0 = 0, *>0, |Г(х, 1)\< + оо, х > 0.
(5.41)
210
Попытаемся получить решение этой задачи с помощью преобразования 2 в
табл. 9. Во введении к этой главе была частично показана методика применения
интегрального преобразования при решении тепловых задач нестационарной тепло¬
проводности. Она сводится к следующему: необходимо умножить уравнение (5.40)
и начальное условие (5.41) на ядро интегрального преобразования sin gx и
проинтегрировать по х от 0 до оо. Однако в данном случае возникает неожи¬
данное препятствие: в правой части уравнения (5.40) записана постоянная функ¬
ция источника Q/(cp), для которой преобразование синус-Фурье (5.30) непри¬
менимо. Это препятствие можно обойти следующим образом: введем вместо
Q/(cp) условно переменную функцию / (х), для которой будем считать возможным
применение преобразования (5.30)
дТ/dt = а (<d2T/dx*) + f (х), х > 0, t > 0. (5.42)
Все остальные условия в (5.41) сохраняются; при этом предполагается* что на¬
чальная функция Ф0 (х) также допускает применение преобразования (5.30).
Полагая далее
OD
Ts (£» 0 = У 2/л J Т (х, t) sin gx dx (5.43)
о
и применяя преобразование (5.43) к уравнению (5.42), получим
ОО 00
У 2/п J (дТ/dt) sin gx dх = а У 2/я J (д2Т/дх2)Х
о о
оо
Xsln gx dx+ У 2/я J / (х) sin gx dx. (5.44)
о
Если считать законной перестановку слева предельных операций, то левая
часть примет вид
V~2jn j (tдТ/dt) sin lx dx=-^- J T (x,t) sin \x dxj =
где Ts (g, t) зависит уже от одной независимой переменной t (5 понимается как
параметр).
В правой части (5.44) интегрируем по частям
00 00 00
У 2/л J (д2Т/дх2) sin lx dx = У 2/п (дТ/дх) sin gx —g У 2/п J (дТ/дх) cos gx dx.
о оо
Первое слагаемое в правой части этого равенства обращается в нуль на
нижнем пределе х = 0 из-за множителя sin gx>, если предположить, что (дТ/дх) —►О
при х—► оо, как это обычно бывает в задачах теплопроводности, то тогда пер¬
вое слагаемое обратится в нуль и на верхнем пределе х—► оо. При этом условии
после второго интегрирования по частям получим
00 р -1 X = 00
У 2/п ^ (д2Т/дх2) sin gx dx = — У 2/п g | Т (х, t) cosgx j —
OD
— 6* yifr$T(x, 0 singed*.
0
Предполагая далее, что T (х, t)—►О при х—► оо, и учитывая (5.41), полу¬
чим окончательно
со
\T2fr j (д*Т/дх*) sin lx dx = V'l/S I IT (0, t)}-141 (g, I) =- (g, 0. (5-45)
211
Приняв, что
00 0°
ф0 (|) = 1/~2М ^ Ф0 (^') sin ^д:' dx'; J Ц) = У~2/л [ f (х') sin %х'dx', (5.46)
J
О о
имеем для преобразованной задачи
dTJdtHsfal)2 f,=7®. ‘ > °; Т,а. 0)=Фо(1). (5.47)
откуда нетрудно получить
Тг(1, 0 = ФоШе-(1^£)>'+5е-^5)г(/-т)д|)(]т. (5.48)
О
Применяя далее формулу обращения для преобразования (5.43) и, кроме того,
заменяя изображения Ф0 (£), f(Q, соответствующими интегралами (5.46) и одно¬
временно изменяя порядок интегрирования, находим
00 00
Т (X, О = J Ф0 (*') dx' j е-(Г5 1 sin \х' sin d£ +
t CD оо
_l_ ? ^ dx j* f (*') dx:' ^ e “ ^ (/ ”T) sin sin \x d£.
о 0
По таблице интегралов [20] вычисляем внутренние интегралы. В результате
приходим к выражениям (3.194), (3.199), которые получены в § 6 гл. III методом
разделения переменных
* Г <*-*')* (*+*')» 1
Т{х9 /)= jL=r \ Ф0 (*') 1/* 4а/ -е“ 4а/ Jd*' +
2 у nat g
- *■
Наличие ядер экспоненты под знаком несобственных интегралов
в (5.49) обеспечивает сходимость этих интегралов для широкого
класса функций Ф0, /, в том числе и для их постоянных значений (и
именно в этом смысле решение (5.49) имеет смысл обобщенного решения,
так как для постоянных значений Ф0(х), f(x) преобразование (5.43)
неприменимо).
Заменим теперь в (5.49) f(x) = Q/ (ср), кроме того, положим Ф0(х) =
= Т0. После преобразования выражения (5.49) получим решение задачи
(5.40) — (5.41) (при Т(ху 0) = Т0) в виде
t
Т (х, t) = T0(b[xl(2\/~ai)] + Q/(cp) $ Ф[х/2 Va(t—т)] dr. (5.50)
о
В формуле обращения для преобразования Меллина (5.33) ин¬
тегрирование ведется вдоль любой прямой ReS^y0, где у0 > 0 —
некоторое число, находящееся в области сходимости интеграла (5.33)
00
(предполагается, что при у=у0> 0 интеграл \xv~l |/(x|dx ограничен).
о
212
Преобразование Конторовича—Лебедева (5.34) было введено
М. И. Конторовичем и Н. И. Лебедевым в 1938 г. и далее успешно
применялось при решении ряда интересных задач [88]. При приме¬
нении этого преобразования предполагается, что f (х) и */(*) абсо¬
лютно интегрируемы в промежутке (0, оо).
Как следует из п. 7 табл. 9, интеграл для J(t) должен сходиться
при всех 0^г<оо. Для этого необходимо предположить, что
/(*)—►О при х—* 0, что может и не иметь место в условиях той
или иной краевой задачи. На практике удается обойти это затруд¬
нение путем введения вместо f(x) новой искомой функции (х) =
= /(*)—[/ (*)*=<>] е“* и применить преобразование (5.34) к уравне¬
ниям относительно ¥(*).
В случае преобразования Мелера—Фока (5.35) предполагается,
что f(x) определена на (1, с») и при любом d> 1 выражение
/(*)(*—1)”3/4 абсолютно интегрируемо в промежутке (1, d), а вы¬
ражение f{x)x~lf2\gx—в промежутке (d, оо) [40].
В приложениях теории интегральных преобразований к решению
краевых задач теплопроводности необходимо уметь выразить
трансформанту Фурье функции d2f/dx2 через транс¬
форманту Фурье J(l) функции f(x), иными словами, найти
изображение производной d2//dLx2, входящей в заданное дифферен¬
циальное уравнение, причем выбор синус- или косинус-преобразо¬
вания определяется видом граничных условий на нижнем пределе
переменной, подлежащей исключению из дифференциального урав¬
нения.
Выше был рассмотрен случай, когда при х = 0 задано значение
функции f(x) и показано [см. (5.45)], что справедливо соотношение
К 2/я J (d2//d*2) sin lx dx = j/2/л I [/ (*)]*=о —I2/* (I)- (5.51)
Если при x = 0 задана производная функция f (х), т. е. d//dx = <p,
то, аналогично, интегрируя дважды по частям, получим
1/*2/л J (d2//dx2) cos lx dx= V~2/n [df (x)/dx]t = 0 — £2/c (£)» (5 52)
где /с(£) — косинус-трансформанта Фурье функции /(х), причем, как
и раньше, предполагается, что / и df/dx стремятся к нулю при
X —► оо.
Если при х = 0 задано граничное условие III рода, т. е. [df/dx—
— hf (x)]x=o =ф, то целесообразно воспользоваться интегральным
преобразованием (5.36), для которого аналогично (5.51) находим
00
О
оо
О
00
|/~2/я ^ (d2//d*2) [(/t sin lx +1 cos lx)l{№ +|2)1/2] d* =
о
(5.53)
213
Задача 1. Покажите, что для экспоненциального преобразования (5.31)
справедливо соотношение
+ 09
-р==- J (d*//d**) djc = - Е*Г(0, (5.54)
* CD
если предположить, что /(*) и df/dx стремятся к нулю при |х|—► оо.
В случае интегрального преобразования Ханкеля формула для трансфор¬
манты производной второго порядка имеет довольно сложный вид. Здесь более
целесообразно рассмотреть изображения оператора L (/)== d2//djt2+(l/*) df/dx —
— (v2/*2) /, имея в виду, что преобразование Ханкеля применяется при решении
тепловых задач, обладающих осесимметричным полем температур (дифференциаль¬
ное уравнение в этом случае содержит указанный оператор). Имеем по опреде¬
лению (5.32)
00 со
1 xL {f) J'(W dx=Ит S (* й) - 5']/ v ^ «Ь"
О О
оо оо
Jv(£*) d* —j -у AM£*) dx = — xf(x) {[/v(6*)*]"} +
0 0
если предположить, что xf (x) и x df/dx стремятся к нулю при х—►«.
Выражение, стоящее под знаком интеграла, можно преобразовать, используя
уравнение, которому удовлетворяет J\(%x)
или
Отсюда находим
7e[*ST?S]+(6,-5]-'-<W-0
00 00
j '(‘Зл^л'с!*-^ /)/v(£*)d*=— V ^xf(x)Jx(lx)dx=*— (5.55)
О о
В частном случае, полагая в (5.55) v = 0, получим
00
| * (-S■+7S) Уо {lx) d*=“(5-56)
Перейдем к преобразованию Меллина (5.33). Чаще всего это преобразование
используется для бесконечной области г^О, 0«^ф^2л или бесконечного клина
г^О, фо<Ф^ф1, температурное поле которого Г (г, ф) не обладает осевой
симметрией. В этом случае дифференциальное уравнение стационарной теплопро¬
водности вида
дЧ 1 дТ . 1 дЧ _л
в пространстве изображений по Меллину переходит в обыкновенное дифферен¬
циальное уравнение (5.59) (см. ниже).
Задача 2. Полагая
если предположить, что rs+1dT/dr, rsT стремятся к нулю при г—► оо.
Указание: необходимо обе части уравнения (5.57) умножить на rs+1, проин¬
тегрировать по г в промежутке (0, оо) и применить дважды формулу интегри¬
рования по частям.
В случае уравнения Пуассона ДТ (г, <р) + /(г, <р) = 0, умножая обе части его
на г*+1 и интегрируя по г в промежутке (0, оо) с учетом (5.59), можно получить
Разумеется функция f(r, <р) должна удовлетворять условию, чтобы интеграл
сходился
для некоторого у0 > 1 и любого 0<ср< 2ц (либо Фо<ф<Фг). Такими могут
быть функции /(/*, ф), убывающие при г—► оо равномерно относительно ф не
медленнее, чем | / (г, ф) | < М0е-*г (ас > 0), либо | / (г, ф) | < M0/(l +rv), М0 =*
= const, v > (Yo + 2).
Интегральное преобразование Конторовича—Лебедева (5.34) связано с рас¬
смотрением уравнений, содержащих оператор L (f) = x [(*/£)*—*/], где x = Rr
(г — расстояние до оси в цилиндрической системе, /?=const).
Действительно, рассмотрим уравнение
и найдем изображение левой части уравнения, применяя интегральное преобра¬
зование Конторовича — Лебедева:
предполагая, что это преобразование существует как для самой функции Г (г, ф),
так и для производной д2Т/ду2, причем этот дифференциальный оператор и опе¬
ратор L (f) коммутативны (перестановочны).
Уравнение (5.62) запишем в виде
и применим к нему преобразование (5.63). Для этого умножим обе
части уравнения на (1 /г) /Ctx* проинтегрируем по г от 0 до сю и
применим формулу интегрирования по частям; в процессе преобра¬
зования интеграла используем уравнение, которому удовлетворяет
00
(5.58)
о
покажите, что уравнение (5.57) переходит в следующее»
d2T / dy2sT = 0,
(5.59)
d27,/dф2 + s2Г = —f (s, ф), где
оо
(5.60)
f(s, ф)= J ri+1f(r, ф) dг.
о
J rvo+I I f(r, ф) I dr <+ oo
(5.61)
о
(5.62)
(5.63)
о
(5.64)
215
модифицированная функция Бесселя Кп(уг) [20]:
ИЛИ
гЬ[г^г\= - т2К,г. (5.65)
Получим
(л ?) ~yVT] к* (yr) dr+£? I ^TKi% (yr) dr=
о о
-[rfcg-r/?„r|; + |ir{ri[rigl]-TVK„}dr +
00
+^TTK*dr = -x2f+T>=0’
о
если предположить, что функция Т (г, ф) удовлетворяет условиям:
lim г (дТ/дг) In г = 0; lim Т = 0;
г —► 0 г—м.1
lim г1/2 (дТ/дг) = 0; lim г1/2 Т = 0. (5.66)
Г—► со г-* 00
Тогда, используя асимптотическое поведение функции Ki% (уг) при
г—*0иг—»оо и условия (5.66), получим: первое слагаемое в квад¬
ратных скобках в правой части исчезает на обоих пределах. Итак,
в пространстве изображений Конторовича—Лебедева уравнение (5.64)
переходит в следующее:
с1277(1фа—таГ = 0. (5.67)
В работе [145] построено интегральное преобразование, в неко¬
тором смысле обобщающее преобразование Конторовича—Лебедева.
Это преобразование связано с рассмотрением указанного выше опе¬
ратора L(/), но в конечной области Приведем это пре¬
образование^
Пусть Т (г, ф, г)— функци_я, заданная в области
0^2^/, Фх^ф^Фа- Если Т (т, ф, z) — изображение функции Г (г,
Ф, *)
R
Т (т, ф, г) = 5 Т (г, ф, г) ¥ (т, г) dг/г,
о
где ¥ = tf,T (R) /* (г) -/* (R) К 1х (г), (5.68)
то Т (г, ф, г) дается следующей формулой обращения!
00
Т (г, ф, г) = ^ j |- ;.;h(-”yp Т (т, ф, г) ¥ (т, г) dr. (5.69)
О
216
С помощью преобразования (5.68) — (5.69) могут быть рассмот¬
рены краевые задачи стационарной теплопроводности для уравнения
д2Т 1 дТ 1 д2Т д2Т __ п
дг2 * г дг ' г2 дф2 дг2 *
О < г < R, 0 < г < /, фх < Ф < Фа- (5.70)
Заметим, что при /?—► оо преобразование (5.68) переходит в пре¬
образования (5.63).
Интегральное преобразование Мелера — Фока (5.35) связано с опе¬
ратором вида
* <*<«>•
Задача 3. Используя дифференциальное уравнение для сферической функ-
ЦНЧ **_!/,+rtW
dP-1/d7‘t W ] + (т+Т°) Р-и» + * W=°- (5-71)
показать, что преобразование (5.35) переводит оператор Lx (f) в следующий:
5 МЛ М1/2 + ,т W - (V + ^J/(t). (5.72)
Заметим далее следующее.
Применяя построенное преобразование к решению краевых задач
теплопроводности, приходится предполагать законность перестановки
некоторых предельных операций (см. выше). Это приводит к тому,
что решения получаются недостаточно обоснованными. Строгое обос¬
нование решения, найденного методом интегральных преобразований,
по-видимому, возможно провести двумя путями.
Первый путь состоит в том, что искомое решение заранее подчи¬
няется условиям, которые обеспечивают законность всех операций
формального процесса решения и не являются ограничительными
с физической точки зрения. Далее с помощью какого-либо независимого
метода показывается существование и единственность решения рас¬
сматриваемого класса (см. гл. II). Тогда формула (5.3) дает это реше¬
ние.
Второй путь отличается от первого тем, что ограничения, необ¬
ходимые для обоснования формального процесса, не накладываются,
весь метод рассматривается как чисто эвристический и производится
непосредственная проверка найденного решения: действительно ли
полученное решение формально удовлетворяет заданному дифферен¬
циальному уравнению теплопроводности и краевым условиям задачи
(ср. с методом разделения переменных в гл. III).
Существенным преимуществом второго метода является отсутствие
необходимости отдельного доказательства существования ре¬
шения, что в большинстве случаев представляет большие трудности.
Кроме того, ограничения, необходимые для справедливости оконча¬
тельной формулы решения задачи, как правило, оказываются слабее
2 i 7
тех, которые требуются для обоснования законности всех промежу¬
точных этапов вычисления.
Таким образом, второй подход к решению этой проблемы предпоч¬
тительнее, так как обычно такого рода формальную проверку удается
осуществить, хотя в некоторых случаях это связано с кропотливыми
вычислениями.
Все результаты, полученные в этом параграфе, для удобства све¬
дены в табл. 9.
Перейдем к рассмотрению примеров, показывающих в действии
интегральные преобразования с бесконечными пределами.
I. Линейный поток теплоты в бесконечной области
dT/dt =я (д2Т/дх2) +/(*,/), -оо<*< + оо,*>0; (5.73)
Т(х, 0) = Ф0(*), | ж | < оо; | Т(х, /)| < + оо, \х\< со. (5.74)
Для решения этой задачи воспользуемся интегральным преобразованием (5.31),
полагая
Т а, 1) = J Т (х, 0 в'** d*. (5.75)
• 00
Умножим обе части уравнения (5.73) на (1 /]/ 2л) е^х и проинтегрируем по х
в области его определения, учитывая формулу^ (5.54). Получим обыкновенное
дифференциальное уравнение для определения Т (£, t)
dT/d/ + (g j/~£)2f=/(£, о,
T(t, 0) = Ф0 (£),
+ 00
где 7(1, /)= i__ J f(x, f) е‘&* dx;
— CO
+ 00
Ф,(0—-L=. С Ф, (*) o'** d*. (5.77)
V 2л J
— 00
Решение уравнения (5.76) имеет вид
t
fa, 0 = Ф„ (I) e“kV а>2 Ч *>* ('-т)7(1, т) dx. (5.78)
О
Применяя формулу обращения, запишем для оригинала
+ 00
Т(х, 0-у— j ®o(£)e-oJ,'-^d|+
— СО
/ + оо
+ -^=-J j е-а&*('-т)-‘'**Г(£, x)dxdg. (5.79)
' 0 - 00
Выражение (5.79), которое, по существу, является найденным
решением задачи (5.73) — (5.74), можно преобразовать, используя
так называемую теорему о свертке для преобразования (5.75). Сфор¬
218
(5.76)
мулируем эту теорему. Функция-
+ ®
= j* Мч)М*—Ч)ЙП (5.80)
— 00
называется сверткой функций fx и в интервале (—оо, + оо).
Если /\(£) и f2(l)—трансформанты Фурье соответственно функ¬
ций fx (х) и (х), то оригиналом произведения изображений /, (I) J2 (I)
является свертка т. е. [121]
+ 00 +00
у= f Ti (5) Ti (6) e- '6* d5 «. _J_ J ft (n) /, (x-ц) dt,. (5.81)
— 00 —00
Используем эту формулу для преобразования первого слагаемого в (5.78).
Оригиналом изображения Ф0 (£) является функция Ф0 (х); оригинал для ехр (— аа£а0
можно найти, вычислив по таблице интегралов [20] интеграл
+ •
_• Г е -<*«<- d g =-tL= е-х‘/ца() (5.82)
J \ГШ
— 00
Таким образом, для первого слагаемого имеем
+ 00 +00
— 00 — оо
Аналогичным образом может быть преобразовано и второе слагаемое в пра-
вой части (5.78). Окончательно находим
+ во
Т (X, fl = 2 ^ j* Ф0 (Л) e_u~ ”),/u‘,° dt) +
/ + 00
•яде
lLe-U-T»V[w<'-t)] dTd^. (5.83)
2У ла J J У t—т
о — во
Выше отмечалось формальность рассуждений, приводящих к вы¬
ражению (5.83). Поэтому, для того чтобы функция Т(х, /) в виде (5.83)
была действительно решением задачи (5.73) — (5.74), необходимо,
чтобы интегралы в (5.83), а также интегралы от ее производных схо¬
дились равномерно.
Выражение (5.83) можно записать в несколько иной форме, а имен¬
но в форме типа интеграла Фурье. Для этого воспользуемся известным
интегралом [см. (3.162)1
jV"4’ соз s (х т)) dtj = exp [—(5-84)
О
219
и перепишем выражение (5.83) в следующем виде:
+ 00 00
Т (х, t) = J Ф0 (ti) drj ^ е-а&' cos Е (д:— rj) d| +-
— оо О
t + 00 00
+-^J J/(ri, т) dridx ^е-°^('-т)соз^(л:—ri)di. (5.85)
О — 0D О
Выражение (5.85) более удобно для анализа решения, в частности
из него сразу следует: если Ф0(*) и f(x, t) абсолютно интегрируемы,
то при t-+0 функция, заданная выражением (5.85), в каждой точке
непрерывности имеет предел Ф0(х) (или предел. (1/2)[Ф0(х+0)+
+ Фо(*—0)], если х — точка разрыва первого рода) и сами интегралы в
(5.85) сходятся равномерно относительно х при любом t > 0. Нахож¬
дение условий, необходимых для двукратного дифференцирования
по х и однократного дифференцирования по t второго интеграла
в правой части равенства (5.85), представляет собой математически
интересную задачу и проделано в [81]. Заметим, что для этого функция
f(x, t) должна быть непрерывной по t и удовлетворять условию
Гельдера по переменной х (см. § 5 гл. II). В работе [141] рассмот¬
рены эти вопросы.
В практических задачах выражение (5.83) можно использовать
и при менее строгих условиях для функций Ф0(х) и f(x> t). Наличие
ядер экспоненты обеспечивает сходимость интегралов в (5.83) и в
том случае, когда функции Ф0(х) и/(х, t) являются неограниченными на
бесконечности, но растут не слишком быстро при |*|->-оо (не быстрее
ехр (сх2), с> 0). Кроме того, из (5.83) следует следующий практи¬
ческий интересный вывод. В § 5 гл. III рассмотрена задача Коши
для однородного уравнения теплопроводности, решением которой был
первый интеграл в (5.83). Отсюда следует, что второй интеграл в (5.83)
удовлетворяет неоднородному уравнению (5.73) и его можно исполь¬
зовать для снятия неоднородности в дифференциальном уравнении
теплопроводности при условии, если функция источника} (х, t) такова,
что этот интеграл сходится (см. § 5 гл. III).
Такие предварительные преобразования необходимы в тех задачах,
когда наличие неоднородности в дифференциальном уравнении тепло¬
проводности усложняет его решение выбранным методом (например, в
области с движущейся границей методом тепловых потенциалов см.
гл. VIII).
Задача 4. Показать, что если в (5.73) — (5.74) в начальный момент времени
область —/ < х <+/ имеет постоянную температуру Т0, а область | х | > I — ну¬
левую температуру и при t > 0 в единицу времени на единицу объема выде¬
ляется количество теплоты /(*, t) = Q/(ср) = const, то выражение (5.83) для этого
случая имеет вид
0-,7V2, ,, СШ,
где Ф (г)—функция Лапласа (3.181),
220
Задача 5. Используя методику решения задачи (5.40) — (5.41), с помощью
преобразования (5.43) показать, что решением тепловой задачи
Выражение (5.89) получено в § 6 гл. III методом продолжений для полу-
ограниченной области; там же проведено исследование этого выражения. Как
и выше, можно сделать вывод, что интегралы в (5.89) сходятся для достаточно
широкого класса краевых функций данной задачи и в этом смысле решение (5.89)
можно рассматривать как обобщенное решение. В частности, если начальная тем¬
пература постоянна и равна T0t а плоскость * = 0 поддерживается при темпера¬
туре Тс, то соотношение (5.89) можно упростить с помощью подстановок:
для первой части первого интеграла* (х-f-£)/(2а V~t) = Р для
второй части первого интеграла; х/(2а У t —т) =р для второго интеграла. После
преобразований получим
Если воспользоваться определением функции Ф* (z) = 1 — Ф (г), то выраже¬
ние (5.90) подлежит дальнейшему упрощению и окончательно имеем
Пусть Т0^> Тс\ определим потери теплоты на конце тела х = 0 при его охлаж¬
дении. Потери теплоты dQ за единицу времени через единицу площади поверхно¬
сти х = 0 равны
По формуле Лейбница [145] находим производную от функции Лапласа с пере¬
менным верхним пределом
Из (5.93) видно, что в первые моменты времени (начало охлаж¬
дения) скорость теплоотдачи бесконечно велика, а затем постепенно
уменьшается, оставаясь прямо пропорциональной разности темпера¬
тур Т0—Тс и некоторому термическому коэффициенту V^Ф (е= V^Ф—
коэффициент аккумуляции теплоты). Количество теплоты, отдавае¬
мое плоскостью х = 0 в течение конечного промежутка [0, /], най¬
дем, интегрируя (5.93) в пределах от 0 до t:
Q = -[2\n^lVH](Tu-Tc)V~ = — [2е (Г 0—Т С)/У1г] V~t. (5.94)
dT/dt = a (дЧ/дх2), х > 0, t > 0;
Т (х, 0) = Фо (*), *5=0; Т (0, 0 = ф (0>
| Т(х, 01 < + оо, * > 0
(5.88)
(5.87)
является выражение
(5.89)
о
Г (*, 0 = Т0ф [х!{2 VTt)] + ГсФ*[*/(2 \Г ai)}.
(5.90)
[Т(х, 0 — ТС]/(Т0 — Тс) = Ф [дс/(2 ]/~at)].
(5.91)
dQ = — Ь(дТ/дх)х=0 = — Х(Т0— Тс) {(5/0*) [Ф (х/2 V~at)]}x=0-
(5.92)
откуда для dQ имеем
dQ —— У7^р(Т0—Тс) (I/УШ).
(5.93)
221
Количество теплоты, отдаваемое плоскостью х = 0 с площади а
за время
Q = —2ео (Г0—Гс) yijyii.
II. Третья краевая задача для полуограниченного стерж¬
ня. В § 6 гл. III рассмотрена третья краевая задача (3.190), (3.204) для полу¬
ограниченного стержня с теплоизолированной боковой поверхностью и постоянной
начальной температурой Г0. Имея в виду практическую значимость этой задачи,
рассмотрим ее решение при произвольной начальной температуре, используя
интегральное преобразование (5.36)
дТjdt = а (д2Т1дх2), х > 0, t > 0; (5.95)
Т(х, 0) = Ф0(х), х^О; (дТ/дх—ЛГ)*=о = 0, />0;
| Г (х, 0 I < + °°» х>0. (5.96)
Полагая
со
Т (I, о = У~Щп^Т(х, t)[(h sin Ьс+1 cos tx)/(hl+V)' 2] d*.
0
переводим в пространство изображений уравнение (5.95), используя формулу
п. 4 табл. 9 для изображения второй частной производной
dr/d/+(^i)*F=0, <>0; га, 0) = Фо(£), (5.97)
где Ф0 (£) — изображение начальной функции Ф0 (х):
со
Фо (5) = 5 Фо (*') [(Л Sin Ъх' +1 cos £х')/(Л*+ Е2)2'2 ] d*'. (5.98)
о
Заметим, что в интеграле (5.98) переменную интегрирования следует обозна¬
чить буквой, отличающейся от х, с тем_чтобы не внести путаницы при вычисле¬
нии интеграла в общем выражении для Т (£, t). _
Находим решения уравнения (5.97) Т (£, /) = Ф0 (£) ехр (—а\Н) и далее по
формуле обращения искомый оригинал
0D
Т (х, о = V~2fr 5 Ф0 (а е-^< [(Л sln^+5 COS |х)/(А*+£•>»-21 dl. (5.99)
о
Выражение (5.99) зависит от изображения начальной функции. В случае
конкретного задания начальной функции интеграл в (5.99) может быть вычислен
с помощью таблиц [20]. В общем случае решение (5.99) можно преобразовать,
если вместо Ф0 (£) подставить интеграл (5.98), затем сменить пределы интегриро¬
вания и вычислить внутренние интегралы. В результате найдем
Tix л-2 fe-*,<*s,”£*+*C086*dEx
Т(Х’°~лJ (Л2 + 1)2)''2 S
о
С гт. , In £х' +£ cos Ёх/ , , 2 С
X j Фо (x ) ; ^2 i /2 “ j Ф (x ) dx X
0 о
v. Г .-avt (h s!n £x+£ cos £x) {>h sin £x'+£ COS £x') _
ху щф
* J Г (x+x')M
«-^Гф.соие" *a' +e‘ 4a' J"
2y Jial J
о
— h exp [h*ai -\-h (x-j-x')] Ф* + Л dx'. (5.100)
222
Выражение (5.100) используем позже для построения функции Грина третьей
краевой задачи для области х > 0, t > 0 (см. гл. VII). В частном случае, если
начальная температура постоянна O0(^) = ro, а температура окружающей сре¬
ды Тс, выражение (5.100) после вычисления интегралов дает (проверьте!)
T-(f-JlfcT-^ (гН)+ ехр(Л*+«Л*ОФ«(г^=+ЛГ57). (5.101)
III. Уравнение Лапласа с разнородными граничными
условиями. В качестве примера применения преобразования
Ханкеля рассмотрим стационарную задачу о температурном поле пространства
с постоянной температурой Т0 в плоскости г = 0 в точках области 0^r< 1.
Для решения этой задачи целесообразно выбрать цилиндрическую систему
координат (г, ф, г), начало которой поместим в центр круга г=1. Температур¬
ное поле Т является осесимметричным (т. е. зависит только от переменных гиг,
но не зависит от угла ф) и четным относительно переменной г. При этих усло¬
виях можно записать:
д2Т1дг2-\-(\/г) (дТ/дг)-\-д2Т/дг2 = 0, г^0, г > 0; (5.Ю2)
Т(г,г) |,ш0=Г0> 0<г<1;1
[дТ (г, z)/dz]z=о =0, г > 1; )
I Т ('» г) | < + оо, г^0, г > 0.
Второе условие в (5.ЮЗ) при г = 0 возникает вследствие симметрии температур¬
ного поля относительно плоскости z = 0.
Рассматриваемая задача содержит разнородные граничные условия в том
смысле, что при 0<r < 1 задано значение температуры Т0, при г > I — значение
дТ/дг = 0 (условие теплоизоляции).
Краевые задачи этого вида находят широкое применение в электродинамике
при определении поля^наэлектризованного диска [91], в микроэлектронике при
изготовлении полупроводниковых приборов с помощью селективной диффузии
примеси в полупроводник через окно в защитной маскеДПЗ] (подробнее см. гл. IX).
Для решения задачи воспользуемся интегральным преобразованием (5.32)
(при v = 0), полагая
00
Г (6, 2)=$/Т(л. г) J0 (I, г) dr. (5.104)
о
Используя формулу (5.56), получим для уравнения (5.Ю2) в пространстве изо¬
бражений _
tfT/dz2—£2f=0. (5.105)
Учитывая разнородность граничных условий, вначале целесообразно написать
общее решение уравнения (5.105), перейти по формуле обращения к оригиналу,
а затем воспользоваться граничными условиями для определения постоянных
интегрирования. Общее решение уравнения (5.105) имеет вид Т (£,’ z)=A (£) exp (£z)+
-f£(£)exp(—£z). Постоянная Л(£) = 0, так как функция Т (£, г) при г—► оо
должна быть ограниченной. Формула обращения для преобразования (5.104) дает
00
Г (г, г) = J В (g) I е-u J„ (gr) d£ (5.106)
о
Используя граничные условия (5.ЮЗ), получим интегральные уравнения для
определения В (£):
J S/o(S')S(Bd6=.7-et 0<г<1;
о
оо
$sV0(|r)B(|)dl = 0, г > 1,
(5.107)
223
Уравнения (5.107) называются дуальными интегральными уравнениями. Фор¬
мальное решение этих уравнений с помощью преобразования Меллина даноТитч-
маршем в его монографии по теории интегралов Фурье [141]. Однако решение
уравнений (5.107) может быть получено с применением хорошо известных интег¬
ралов, рассмотренных в монографии Ватсона [15]:
5 £-V0(£/-)sln £d£ = n/2, 0< г < 1; С ФО sin I d£ = 0, r> 1. (5.108)
0 0
Отсюда В (£) = [2/(л£2)] Г0 sin подставляя В (£) в (5.106) и вычисляя интеграл,
находим
оо
Т (г, г) = (2Т0/л) J I-1 е~ / (?г) sin | d£ =
о
= —roarcsin^ 2—/ =У (5.109)
л V V z2 + (r+l)2+ V22 + (r—\)2J
Другое решение этой задачи в сфероидальных координатах с помощью
конечного преобразования Лежандра приведено в [142].
В [88] получено решение первой краевой задачи стационарной
теплопроводности (задачи Дирихле) для области, ограниченной двумя
пересекающимися плоскостями с применением интегрального пре¬
образования Конторовича—Лебедева (5.34).
Задача 1. Применяя преобразование (5.34), получить решение краевой
задачи вида [88]:
д2Т 1 дТ 1 д2Т д2Т
-dr+7%-+-kw-+7?=0' г^°' м<+«.фкф<ф.; (злю)
Т(г, фъ (г, г); Г (г, <рг, г) =Ф'2 (л г); (5.111)
| Т (г, ф, г) | < -f оо, лёг 0, |г|< + оо. (5.112)
Здесь Т,*(г, г) — непрерывные функции, удовлетворяющие условию (5.112) истре-.
мящиеся при г —► 0 к общему пределу: ¥<> (2) = Т/ (г* *)•
г -*■ О
Задача 2. Пусть функция Т (г, <р, г), удовлетворяющая условиям (5.110)—
(5.112), не зависит от г (двумерная задача). Получите решение соответствующей
краевой задачи для рассматриваемой области с помощью интегрального преобра¬
зования Меллина [см. (5.58) — (5.59)].
С помощью преобразования Меллина в [16] получено решение тре¬
тьей краевой задачи стационарной теплопроводности- с постоянно
действующим непрерывно распределенным внутренним источником те¬
плоты. Там же приведена серия кривых по расчету температурного
поля в клине.
Другой класс краевых задач стационарной теплопроводности, ко¬
торый может быть рассмотрен с помощью интегрального преобразова¬
ния Мелера — Фока, составляют задачи Дирихле и Неймана для
областей, ограниченных одним или двумя софокусными гиперболои¬
дами вращения. Первоначальное решение указанных задач принадле¬
жит Мелеру (см. ссылку в [40]), который использовал метод частных
решений. Исследование ряда задач для этого вида областей произведено
Лебедевым [88].
В заключение параграфа заметим, что кроме рассмотренных имеет¬
ся еще ряд интегральных преобразований с бесконечными предела¬
224
ми, таких, как Мейера, Гильберта, Лагерра и др. В отличие от рас¬
смотренных выше интегральных преобразований применимость по¬
следних при решении краевых задач теплопроводности значительно
уже и они имеют больше теоретическое, чем практическое значение.
Теория этих преобразований изложена, например, в [40]. Мы не оста¬
навливаемся также на формулах Парсеваля для всех указанных ин¬
тегральных преобразований, учитывая их крайне редкое использова¬
ние в аналитической теории теплопроводности.
§ 2. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ С КОНЕЧНЫМИ
ПРЕДЕЛАМИ
Впервые идея метода конечных интегральных преобразований была
высказана Н. С. Котляковым [54], рассмотревшим преобразования с
синусоидальными и косинусоидальными ядрами. Наиболее полно тео¬
рия конечных интегральных преобразований была разработана
Г. А. Гринбергом [23], который дал обобщение этого метода на случай
скачкообразного изменения свойств среды в направлении той коорди¬
наты, по которой производится преобразование. Детальная разработка
интегральных преобразований с конечными пределами была проведе¬
на И. Снеддоном [134], К. Трантером [142]. Следует отметить работы
М. Д. Михайлова [104], который для одномерных задач дал обобщенное
интегральное преобразование Фурье — Ханкеля, объединяющее ко¬
нечные преобразования Фурье для бесконечной пластины, и преобра¬
зование Ханкеля для сплошного цилиндра (эта работа представляет
больше теоретический интерес), а также работу [64], посвященную
теории конечных интегральных преобразований.
С математической точки зрения метод конечных интегральных
преобразований эквивалентен методу собственных значений и соб¬
ственных функций. Это следует понимать в том смысле, что построе¬
ние конечного интегрального преобразования для данной области и
данного типа краевых задач основано на возможности разложения
искомого решения задачи в ряд Фурье или Фурье — Бесселя по орто¬
гональным функциям соответствующей однородной задачи.
Действительно, рассмотрим кратко теорию конечных интегральных
преобразований применительно к решению краевой задачи нестацио¬
нарной теплопроводности следующего вида:
1"1 = ДГ(М. + О, M6G, / > 0; (5.113)
Т(М, 0) = Фо(М), М £ G; = - Ф (М, t), M^S, 0.
(5.114)
Здесь fr2 = const, Р2 + Рг > 0» п — внешняя нормаль к S. Пусть уI
и 4^(M,yv)—собственные значения и собственные функции соответ¬
ствующей однородной задачи (см. § 2 гл. III)
7*)-^ + Л = 0, M6G;
8-339
225
Если собственные значения ук и собственные функции Ч'ДМ, yj
заранее известны или могут быть найдены в результате решения
задачи (5.115), то Ч'ДУИ, уД может быть принята в качестве ядра
интегрального преобразования температурной функции Т (М, /),т. е. *
Т (V,. О = s S S (М- у.)Т (м> 0 dVM. (5.116)
G
При этом нетрудно указать и формулу обращения для преобразо¬
вания (5.116), которая имеет следующий вид;
00
т m, t) = £ У-г(М' 2У,) т (Ук, t), (5.117)
к = 1 Il’PxlP
где ЦЧ^Ц2— квадрат нормы функции Ч^. Действительно, ряд Фурье
функции Т (М, t) по системе собственных функций Ч'ДМ, yj
имеет вид
Т(М, 0-2C,(0W т.). (5.118)
/г= 1
где коэффициенты Cu(t) согласно теории рядов Фурье равны (см.
гл. III):
с, (0 ’= -Д f f f v, (М. Y.) Т (М, t) dVM. (5.119)
Используя (5.117) — (5.119), запишем функцию T (М, t) в виде
Т(М, 0 = (5-120)
Кш1 Н'РгН
Отсюда, введя обозначение (5.116) как интегральное преобразо¬
вание функции Т (М, /), из (5.120) получаем для него формулу
обращения в виде (5.117). Найдем теперь решение задачи (5.113) —
(5.114) с помощью интегрального преобразования (5.116). Для этого
умножим обе части уравнения (5.119) на ядро преобразования
У к) и проинтегрируем по координатам точки М по области G,
предполагая, что преобразование (5.116) и преобразование произ¬
водной dT/dt существуют, причем дифференциальный оператор и
оператор (5.116) могут быть переставлены:
G G
* При записи формулы (5.116) в цилиндрической или сферической системе
координат под знаком интеграла появятся дополнительные множители — весовые
функции для соответствующей системы собственных функций.
226
Используя далее формулу Грина для оператора Лапласа (2.142)
и уравнение (5.115) для можно записать
G S
-b*T + ±F(yK, /) = -у^ + 1?(у„ О-
s
Таким образом,
тж+^-хМ^г^-т.^к^. (512"
S
Здесь F (ук% t)=[^ F (М, t)yVK(M, ук) dV м — изображение F (Му t).
“ G
В точках поверхности S выполняются граничные условия (5.114)
для функции Т и (5.115) для функции Используя эти условия,
преобразуем поверхностный интеграл в правой части (5.121), что
дает окончательно
7§ + «Г-Т?<^ T.)]„.sdo. (5.122)
S
Т (ук, 0) = Фо(7*).
где Ф„ (V,) = $ $ $ ф0 (М) 'Р* (М, ук) dVV
G
Итак, дифференциальное уравнение в частных производных (5.113)
с помощью интегрального преобразования (5.116) в пространстве
изображений свелось к обыкновенному линейному неоднородному
дифференциальному уравнению первого порядка с известным на¬
чальным условием.
Решение уравнения (5.122) с начальным условием Ф0(7*) нахо¬
дим по формуле
t
Т (ук, 0 = Ф0 (ук) exp (— aylt) + a $ e-(1/Tv*)2 <( _т) х
О
t
х (1/Х) F(ук, т) dt—a J e-^v^ (<-т) х
о s
X [£ Ф (М, т) W, (М. у»)] м 6S dx da.
По формуле обращения (5.117) найдем искомое решение; при
этом под знаком суммы вместо изображений Ф0 и F запишем соот¬
227
ветствующие интегралы:
Т(М, Q-t ^ e"(/rv/ ' Ш ^, V,)x
к=1 11 KU G
х Ф.(М) d VM + aj^ j j j e-(vTv/ (,-T) x
к- 1 * OS
[^ ф (M, T) (M, Y,)] M 6s dT.da+ £ *«’/*> x
t
хИИе"(^)г</"т,^/Г(м*т)Y*(M’^dTdi/*- (5Л23)
О G
Выражение (5.123) совпало с решением (3.86), полученным методом
разделения переменных (но только при Ь2 = 0; отсюда функции в
(3.86) и (5.123) не совпадают, но первые в (3.86) могут быть получены
из вторых в (5.123) при Ь2=0).
В конкретных тепловых задачах при их решении методом интеграль¬
ных преобразований исключение частных производных из дифференци¬
ального уравнения теплопроводности производится, как правило,
последовательно: вначале по одной переменной, затем по другой. При
этом важно еще раз подчеркнуть, что выбор соответствующего ядра
интегрального преобразования по той или иной пространственной
переменной определяется главным образом двумя факторами: а) об¬
ластью определения пространственной переменной; б) типом граничных
условий искомого решения по данной переменной в граничных точках
области. При этом полностью используются результаты § 7—11 гл. Ill
о собственных значениях и собственных функциях соответствующих
однородных задач.
Аналогичными рассуждениями можно получить аналитическое
решение и краевой задачи стационарной теплопроводности (см. § 7
гл. V, где рассмотрен общий случай), однако здесь появляются неко¬
торые особенности в применении интегральных преобразований, свя¬
занные именно со стационарностью процесса. В качестве существенно¬
го замечания для стационарных тепловых задач укажем следующее.
Предположим, что отыскивается решение уравнения
дгТ дЧ , д*Т , 1 ч п /с. 1ГМ.
+ + ~di*+TFУ' г) = 0> (5.124)
j/gG,, г€С,
при некоторых заданных граничных условиях в ограниченной области
G=Gi X С2 X G3. Наметим путь решения этого уравнения и по ходу
рассуждений сформулируем нужное замечание.
На первом этапе с помощью подходящего конечного интегрального
преобразования исключим из дифференциального уравнения (5.124)
производную д2Т/дх2, выразив ее через изображение Т искомого реше¬
ния (по переменной х).
228
На втором этапе проделаем аналогичные вычисления со второй
производной д2Т/ду2. В результате после второго этапа вместо диффе¬
ренциального уравнения в частных производных (5.124) получим в
пространстве двойного преобразования обыкновенное линейное неод¬
нородное дифференциальное уравнение второго порядка относительно
Т (по переменной z). Таким образом, можно и дальше продолжить
применение соответствующего интегрального преобразования к функ¬
ции 7\ исключить производную d2T/dz2 и свести задачу к решению
простого алгебраического уравнения. Однако к этому прибегать не
следует. Действительно, в первом случае, получив из обыкновенного
дифференциального уравнения функцию Г, следует дважды вернуться
в пространство оригиналов (Т -> Т Г), применяя соответствующую
формулу обращения, так что искомое решение в конечном счете будет
представлять собой двойной ряд Фур .ье. Во втором случае,
решив алгебраическое уравнение относительно Т, необходимо трижды
применять соответствующие формулы обращения (Т -+Т -+Т Т)
и конечный результат будет- представлять собой тройной ряд
Фурье. Суммирование одного из рядов редко удается осуществить
в практических задачах, и поэтому последняя форма решения при
числовых расчетах оказалась бы более сложной, чем в первом слу¬
чае. Если бы уравнение (5.124) было нестационарным dT/dt =
= аАТ(Ху у у Zy t) + (1 /k)Fy то для его решения методом конечных ин¬
тегральных преобразований пришлось бы исключать все простран¬
ственные переменные, что в конечном случае привело бы к уравне¬
нию (5.122).
§ 3. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ ДЛЯ ЛИНЕЙНОЙ
ОБЛАСТИ (СИНУС- И КОСИНУС-ТРАНСФОРМАНТЫ ФУРЬЕ)
1. Рассмотрим пример, на котором поясним изложенную выше теорию:
Ж==а(1^' + 1^') ’ °<x<li' °<У<‘г, t>0; (5.125)
Т (*, у, 0) = Ф0 (х, у); Т (0, у, 0=<pi (у, 0;
Т (h, у, 0 = фг (У. 0; ФТ/ду)у=,=|ф, (х, t);
Т (х, lt, i) = q>t(x, ()• (5.126)
Получим решение этой задачи методом конечных интегральных преобразова¬
ний, причем в процессе решения одновременно будем строить соответствующее
преобразование.
Вначале построим интегральное преобразование по переменной х, имея в виду,
.что и при х = 0 и х = /х заданы граничные условия I рода. Рассмотрим
для этого однородную задачу:
d24Vdr*+Y?'Fj = 0, 0 < дг < У, (0) = У, (/,) = 0. (5.127)
Эта задача решена в § 7 гл. III (см. табл. 1): Ч'* (х) = sin (кпх/l^; у® *■
= (кл//х)2; Ц VJ2 = /х/2. Таким образом, согласно (5.116), можно ввести следую-
229
щее интегральное преобразование по переменной х:
Т (kt yf t)=^T (х, yt 0 sin (клх/li) dx, k= 1,2, 3.,
(5.128)
о
с формулой обращения в виде (5.117)
Т С*» У, 0 = 2//i 2 т (к> У» 0 sln
(5.129)
Введенное таким образом интегральное преобразование (которое носит назва¬
ние синус-преобразование Фурье) позволяет исключить из дифференциального урав¬
нения (5.125) вторую частную производную д2Т/дх2, заменив ее в пространстве
изображений преобразованной функцией Т (к, у, /). Действительно, имеем (дваж¬
ды интегрируя по частям)
Здесь были использованы граничные условия для Т при * = 0 и х=/*, задан¬
ные в (5.126).
Выражение (5.130) показывает, что граничные условия относительно коорди¬
наты х,_по которой совершается преобразование, войдут в уравнение для изобра¬
жения Т. Это уравнение получим, если, как обычно, умножим обе части уравне¬
ния (5.125) на ядро интегрального преобразования (5.128) и проинтегрируем по х
в пределах (0, /х), используя формулу (5.130).
Предполагая возможным перестановку предельных операций, имеем
Далее к. уравнению (5.131) следует присоединить краевые условия (5.126),
но, конечно, в пространстве изображений. Для этого обе части равенств (5.126)
(начальное и граничные по переменной у) следует умножить на ядро sin (клх/lx),
проинтегрировать по х и поменять местами (там, где это необходимо) операции
дифференцирования и интегрирования, используя обозначение (5.128). Получим
Здесь Ф0 (к, у) и ф/ (/с, t) (1=3, 4)—соответствующие изображения краевых функ¬
ций, согласно определению (5.128).
На втором этапе из уравнения (5.131) подлежит исключению вторая частная
производная д2Т jdy2. Строим необходимое интегральное преобразование, учиты¬
вая, что при у = 0 задано граничное условие II рода, а при y = k—I рода. Соот¬
ветствующая однородная задача и имеет вид
d24rг/йу2+Ya'Pг = 0, 0 < у < /2; dVa/dy |„=0 = 0; V,(/J=0 (5.133)
и рассмотрена в § 7 гл. III. В результате решение задачи (5.133)
Ч^т (l/) = cos ytmy; у in = [(2т — 1) я/(2/2)]2,
11Ч'2я12 = /2/2.
о
/1
о
=™[<Pi(<0 0-(-!)* <Р.(1Л Т (к, у, 0. (5.130)
dTjdt = а (д2ТJdy*)—(у^а кл/li)* T+jKnjh) [ф1 (у, t)-(-l)K<ft {у, /)]>
0 < У < h, t > 0.
(5.131)
Т (к, у, 0) = Ф0 (к, у)] [дТ (к, у, t)/dy]y=0 = (1/Х) (р3 (к, t);
Т(к, 12, 0 = <Й(«. 0-
(5.132)
230
Таким образом, согласно (5.116), можно'ввести интегральное преобразование
по переменной у вида (косинус-преобразование Фурье)
Т (/с, т, /) = ^ Т (/с, у, 0 cos [(2т— 1) лу/(2/2)] dy, т= 1, 2, 3... (5.134)
о
с формулой обращения
00
т (К, У, О = (2//*) 2 т’ ^ cos [<2т_о лу/(2/2)]. (5.135)
т= 1
Совершенно аналогично, как и в случае (5.130), можно показать, что изобра¬
жением д2Т/ду2 является выражение
U —
С д2Т (2т—1)лу, (2т—1)я. ч А
J W C°S Яг (—1) ф4 (К' V-
О
-уфз(«. О-УгД (5.136)
т. е. преобразование (5.135) по переменной у£[0, /2] следует применять в том
случае, когда при у — 0 задано граничное условие II рода, а при у = /2 — I рода.
Поступая теперь обычным образом, т. е. умножая уравнение (5.131) на ядро
преобразования (5.134) и интегрируя по у в промежутке [0, /2], переводим крае¬
вую задачу (5.131) —(5.132) в пространство двойного изображения. В результате
находим
df/dt -\-{{У~акп,11^ -\-\У~а (2m— 1) я/(21г)]2\Т =
= (xn/k) [ф, (ш, 0 — (— 1)кфг (m, 0] + [(2m—1) л/(2/г)]Х
х(—I)™-1 ф4 («. О—ОА) фз («. 0; (5.137)
Т (к, т, 0) = Ф„ (к, т), (5.138)
где ф/(т, f) (i— 1, 2), Ф0 (к> т)—соответствующие изображения функций ф,- (у, I)
и Ф0 (х, у) по переменной у.
Находим решение Т (к, т, ():
Т (к, т, () = Ф„(к, т)ехр{—[(уТф11(),+(ГТугя)г1 <}+■
I
+ 5 ехр {—[(|/Тук)2 + (ГТу2и)*] ((—т)} {vi[<Pi(m, т) —
о
— (—!)* фа («. х)] + Уг (—l)m_1 ф4 (к, т) — (1/Х) фа (к, т)} dx. (5.139)
Здесь yix = (Kn/ll)\ vsm = (2m—1) я/(2/2).
Выражение (5.139) означает, по существу, решение задачи (5.125) —(5.126),
но в пространстве двойного изображения (по переменной х и по переменной у).
Теперь нужно возвратиться к оригиналам, дважды применяя формулу обраще¬
ния—вначале (5.135), затем (5.129) [по схеме: Т{к, m* t) —► Т(к, у, t) —►Г(х, у, t)];
кроме того, в процессе перехода к оригиналам все изображения от краевых функ¬
ций следует заменить соответствующими интегралами. В результате окончательно
231
найдем
k= 1 tn— 1
о о
-\-{\rayimY] (<—т)} [ф! (У. *) — (— 1)'СЧ>2(У. т)] cos угту dx dy+
4 °о оо t h
+тл'И 2Z.sln Yi,c^cosVamyA j exp{_f(^vx*)s+
к= 1 m- 1
0 0
+ (V~ay2m)2] t)} [(— I)771’1 Y2«<p4(*. *) — (1А)фз(дс, t)] sin yiiex dxdx- (5.140)
Рассмотрены в постановке задачи (5.125) — (5.126) при х = О
и х = U граничные условия I рода и с помощью несложных вычисле¬
ний в (5.130) найдено изображение второй частной производной
д2Т/дх2. Более сложными являются случаи комбинаций граничных ус¬
ловий I рода с граничными условиями II и III родов. Рассмотрим
одну из таких комбинаций, имея в виду лишь построение необходи¬
мого интегрального преобразования и дальнейшую с ним работу. Пред¬
положим, что при х — 0их = 11 в постановке (5.125) — (5.126) имеют
место граничные условия:
Для построения соответствующего интегрального преобразования необходимо
рассмотреть однородную задачу:
где [iiK — положительные корни уравнения ctgp^—Mi/Mi*
Таким образом, согласно (5.116), (5.117), можно ввести интегральное преоб-
т (0, у, o=<pi (у, 0;
дТ (х, у, t)
дх х=1,
= _А1[Г (lit у, 0 —Фг (У, <)]• (5.141)
d2'F1/d*2+v?4', = 0> 0<*</i: Ч'1(0)=0;
d^W/d* 1х=х1 = -ЛхЧ,х (hb
Ее решение получено в § 7 гл. III и имеет вид
(5.142)
Yne=^r I ’Pi* (*. Hi'*) =sin piu (x/li), к = 1, 2, 3...,
Т (Hi*. У, I) = jj Т (х, у, t) sin (pi Kx/lj) dx
(5.143)
о
с формулой обращения
т (X, У. fl = jr ||"y|j2 sln (1Ч*я//х) Т (1Чку, 0.
(5.144)
где квадрат нормы собственных функций есть
1 р = {IJ2) [(pu + h\li + Ах/J/(l& + hill)].
(5.145)
232
Введенное таким образом интегральное преобразование позволяет
исключить из дифференциального уравнения (5.125) вторую частную
производную д2Т/дх2> заменив ее в пространстве изображений пре¬
образованной функцией Т. Имеем, по определению (5.143),
С д2Т . iiiKx , дТ . ц1к*
\ -r-5- sin -т1- QX = -3— °,Г| -- -
h
J дх2
О
дх 1А
1 — с°5 (\х —
о U J дх 1Х
о
h
j Т (х, у, t)
X
л=0
V дх /, h
О
X sin '±fdx= Ctg щкг sinn,K + ^ T
-{тУТ{^'y'
Так как m*ctg plK = — hjit то далее имеем
о
Теперь можно использовать граничные условия (5.141). Окон¬
чательно получим
U а _
j^sin^dx = hl<pi(y, t)siniiil( + ^<?i(y, t) — (j^yT (5.146)
О
и далее следовало бы применить изложенную выше методику для на¬
хождения функции Т(х, у, t). Таким образом, как показывает резуль¬
тат (5.146), преобразование (5.143) по переменной xg[0, /J следует
применять в том случае, если при х = 0 заданы граничные условия
I рода, а при х — lx — III рода.
Остановимся на следующем важном замечании.
Замечание. Все конечные интегральные преобразования
(как было показано выше) и формулы обращения для них вытекают из
возможности разложения искомой функции Т в ряд Фурье (5.116)
(тригонометрический — в декартовой системе координат, Бесселя
или Дини — в полярной) по системе ортогональных функций, найден¬
ной в результате решения соответствующей однородной задачи (5.115)
методом Фурье. Поэтому решения, получаемые методом конечных
интегральных преобразований, имеют те же принципиальные недостат¬
ки, как и решения, получаемые классическим методом Фурье (см. заме¬
чание 1 в § 3 гл. III). Действительно, обратимся к формуле (5.140).
Искомое решение Т(х, у, t) после применения к равенствам (5.125) —
(5.126) последовательных преобразований (5.128) и (5.134) в оконча¬
тельном виде запишется двойным рядом Фурье
т (*. У> Q = ]j221 21 Т (к,
к= 1 /л= 1
0. кпх (2т—\)пу
Sin -г— COS оТ—-—- .
*1 **2
(5.146')
233
Из формулы (5.146') отчетливо видно, что отдельные члены двой¬
ного ряда удовлетворяют однородным граничным условиям, так как
sin = 0; It [cos ?т-1)лу]\ =0;
h |*=о, *=/, \ду L 21, ]}у=0
COS Р"1-1)"»! =0
21, \ymi, U-
Согласно же (5.126), ряд в целом должен удовлетворять неоднород¬
ным граничным условиям, что, вообще говоря, не удается проверить
формальной подстановкой в ряд граничных значений переменных х
и у. Все дело заключается в неравномерной сходимости ряда (5.146) на
границах интервалов изменения тех переменных, по которым произве¬
дены интегральные преобразования (или, иными словами, в области 0^
0<#</2). Вспомним, что, согласно теореме разложимости (Стек-
лова) (см. § 3 гл. III), абсолютная неравномерная сходимость ряда
Фурье (5.118) всюду в точках области G (в нашем случае в точках об¬
ласти 0 х ^ /ь 0 < г/ < /2) будет иметь место в том случае, если
функция Т удовлетворяет на границах этой области однородным гра¬
ничным условиям. Последнее же как раз отсутствует в общем случае
для рассматриваемых краевых задач, и ряды Фурье, которыми описы¬
ваются решения этих задач, являясь абсолютно и равномерно сходящи¬
мися во внутренних точках области G (при 0), не обладают этим
свойством в ее граничных точках. В силу этого мы не имеем права
совершать в граничных точках предельный переход по пространствен¬
ным переменным. Естественным выходом из этого положения является
улучшение сходимости рядов Фурье (5.117) до абсолютной и равномер¬
ной всюду в точках области G. Одним из способов улучшения сходимо¬
сти таких рядов, как отмечалось ранее (см. гл. III), является приведе¬
ние неоднородных граничных условий к однородным (о других спосо¬
бах см. § 7). В общем случае это не всегда удается сделать ввиду тех¬
нической сложности построения искомого функционального преобра¬
зования, но в некоторых частных случаях это удается: например, когда
граничные функции постоянные либо даются одной и той же функ¬
циональной зависимостью. Важно подчеркнуть, что решение (5.117)
или (5.146') следует рассматривать как формальное или как ожидае¬
мый результат, так как для его нахождения предположили, что ряд
(5.117) обладает необходимыми дифференциальными свойствами, что
заранее не известно. Таким образом, для того чтобы показать, что
правая часть формулы (5.117) дает решение соответствующей краевой
задачи теплопроводности, необходимо доказать равномерную сходи¬
мость полученного в дальнейшем ряда, его первой и второй производ¬
ных по пространственным координатам и первой производной по вре¬
мени (если процесс нестационарный). Эти дополнительные исследова¬
ния, как правило, приводят к положительным результатам.
Заметим, что для каждого из рассмотренных интегральных преоб¬
разований производная дТ/дп не выражается через изображение иско¬
мой функции. Это обстоятельство следует учесть при решении краевых
задач теплопроводности методом конечных преобразований Фурье, а
234
именно: если в дифференциальное уравнение входит частная производ¬
ная от температуры Т по координате, то следует предварительно,
применив подходящую подстановку, либо исключить частную произ¬
водную, либо выразить ее через искомую функцию. Например, от
уравнения стационарной теплопроводности ДГ(х, у> z) — b2T'z=0
следует перейти к уравнению &W(xt у> г) — (1/4)Ь2№=0, используя
подстановку r=tt^exp (bzl2), и далее применять по переменной z
преобразование к уравнению относительно W. В случае уравнения
нестационарной теплопроводности (см. § 7 гл. I)
dTldt=a (д2Т1дх2+д2Т/ду*+д2Т/дг2)—v (д Т/дг)
с помощью подстановки Т(х, у, 2, t) = exp [vzl(2a)—v4l(ba)]W
частная производная исключается из уравнения
dW/dt=a(d2W/dx2+d2W/dy*+d*W/dz2).
Разумеется, и в том и в другом случае следует преобразовать крае¬
вые условия задачи; кроме того, все сказанное относится к интеграль¬
ным преобразованиям с бесконечными пределами.
2. В качестве еще одного примера рассмотрим характерный случай. Вычис¬
лим температурное поле пластины 0 < х < /ь 0 < у < /а при следующих условиях:
д2Т/дх2 + д2Т/ду2 = 0, 0 < х <1и 0 < у < /2; (5.147)
дТ/ду\у=0 = дТ/ду\у = 17 = 0-, Т (0, y)=q(y), Т (/ь у)= 0. (5.148)
Здесь можно воспользоваться либо синус-преобразованием по переменной х, либо
косинус-преобразованием Фурье по переменной у. Синус-преобразование (5.128)
при вычислении изображения второй производной д2Т/дх2, согласно (5.130), пере¬
ведет граничную функцию ф («/) в правую часть обыкновенного дифференциаль¬
ного уравнения II порядка относительно функции Т (к, у), что затруднит его ре¬
шение. В то же время косинус-преобразование сохранит однородность дифферен¬
циального уравнения в пространстве изображений в силу нулевых граничных
условий. Предварительно нужно построить это преобразование, рассмотрев одно¬
родную задачу вида
d*Y/dif*+v1T = 0i 0 <у<12; d^/dy\y=0 = d^/dy\v=li = 0. (5.149)
Задача (5.149) рассмотрена в § 7 гл. Ill и имеет решение:
у1 = (кл/1г)г, Ч**(!/) = cos (клу/k), к = 0, 1, 2, ||У*f = 1г/2
при к > 0 и || 1|2 = /я. Итак, строим интегральное преобразование (косинус-
трансформанта Фурье)
Т(Х, к) = ^ Т (х, у) cos (клу/12) dy, к = 0, 1,2... (5.150)
о
с формулой обращения (в каждой точке непрерывности функции Т по ^£[0,/s|):
ао
т (X, у)=-т—Т (X, 0)+iVr (X, к) cos . (5.151)
*2 12 h
К= 1
Формулы (5.150) и (5.151) вытекают естественным образом из известной
в теории тригонометрических рядов теоремы о разложении функции в ряд Фурье
по косинусам [6]: пусть кусочно-непрерывная и кусочно-гладкая функция [(у)
задана на отрезке 0тогда в каждой точке непрерывности этой функ¬
235
ции имеет место разложение
оо h
f(y) = y£ а*cos ■где a* = ТУcos ~F~dy’ k^°- (5,152)
ac = 1 2 2 0 8
Другой подход при построении формул (5.150) —(5.151) —это использование
общей теории в виде формул (5.116) —(5.117), но для конкретных функций
^(M, ук) = cos (кпу/12) в области G = [0, /2], причем суммирование в (5.117)
нужно вести со значения к = 0 (см. замечание 2 к теореме IV в § 2 гл. Ill),
учитывая, что нулевое слагаемое имеет вид
(1/|| ||2) Ч^о (М, Уо)Пуо, 0 = 1/** ПО, о.
Именно этот подход был применен выше пру построении ряда конкретных интег¬
ральных преобразований. Переходя к решению задачи (5.147) —(5.148), переводим
в пространство изображений дифференциальное уравнение (5.147) и граничные
условия (5.148), используя формулу
^ д2Т/ду2 cos (кпу/12) dу = дТjdy cos кпу/12
о
— (асл//2)2 Т = — (/сл//2)2 Т,
получаем
d2T/dx2— (асл//2)2 Г = 0,Т (0, лс) = ф (лс); Т (1и ас) = 0. (5.153)
Здесь ф (к) — косинус-трансформанта Фурье функции ф (у).
Находим решение задачи (5.153) в виде
Т (х, лс) = ф (ас) [sh Acn(/i — x)/l2]/[sh (асл/х//2)] (5.154)
и далее по формуле обращения (5.151) искомый оригинал
во
Т{х,у) = ~Т(х, 0) +-Г-У]. ф (к) [sh кл (/j—Ai)/^]/[sh (Knljl2)] cos кпу/1г. (5.155)
l2 l2
K = I
При ас = 0 выражение (5.154) становится неопределенным; эту неопределен¬
ность можно раскрыть по правилу Лопиталя
Т (х, 0)= lim ф (ас) [sh асл (/х— х)/12\к/ [sh (асл/х//2)]к = Ф (0) (1 — x/l{).
•AC -► 0
h
Учитывая, что ф (ас) = J ф (у) cos (кпу/12) dy, окончательно находим,
о
h оо
Т(х, У)=у(1—J (P^db' + ‘^"Si {[shKn({i — x)/lt]/[sbKnl1/lt])x.
О к — 1
h
Xcos^.jj ф (у) cos-^ dy. (5.156)
Остальные виды интегральных преобразований, содержащие в качестве ядер
тригонометрические функции и применяемые в области х£[0, /] при любых гра¬
ничных условиях на поверхностях х = 0 и х = /, см. в табл. 11 интегральных
преобразований в § 8 гл. V.
236
§ 4. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ХАНКЕЛЯ
ДЛЯ СПЛОШНОГО И ПОЛОГО ЦИЛИНДРА
С ОСЕСИММЕТРИЧНЫМ ТЕМПЕРАТУРНЫМ ПОЛЕМ
Этот вид преобразований используется при решении уравнения
теплопроводности в цилиндрической или полярной системе коорди¬
нат. При построении соответствующей теории отчасти используются
результаты § 8 гл. III.
Рассмотрим краевую задачу
ж-а{т£ + т§)- <>0; (5.157)
Т (г, 0) = 0, T(R, /) = ф(0. *>0;
| Т(г, ОК + оо, г>0, (5.158)
для решения которой построим необходимое интегральное преобра¬
зование в соответствии с теоремой (5.116) — (5.117). Соответствую¬
щая однородная задача имеет вид
-^ + !-^- + 7г'Р = °. О¥(/?) = 0;
|Т(г)|< + оо, г>0. (5.159)
Эта задача рассмотрена в п. 1 § 8 гл. III уl = \i?K/R2\ }¥к (г) = */oOvAK),
II^р = (/г*/2) J] (ц*), где [хк > 0—корни уравнения J0(jlx) = 0; P(r)=r.
Отсюда следует интегральное преобразование вида
R
0 = S''T(r, t)JoM#)dг, к=1, 2, 3..., (5.160)
о
называемое преобразованием Ханкеля, и формула обращения для
него
г (Г, 0--£-£^^^(,,.0. (5.161)
Для практического использования преобразованием (5.160) сле¬
дует уметь исключать из дифференциального уравнения (5.157) опе¬
ратор L (Т) = д2Т/дг2+(1/г) дТ/дг. По определению (5.160) [ср. с (5.55)]
имеем
11 (r)rJ* ^r/R) dr = J г [т 1F (гтг)] х
о о
R
xJ0(iiKr/R)dr = ^ (г ^ J (iiKr/R) dr=
U
- ■r isr [ГГ'“Ir w У о MR)] dr
О
Первое слагаемое при г = R равно нулю, так как J0 (р) = 0, и равно
нулю при г = 0. Второе слагаемое после интегрирования по частям
преобразуем следующим образом, используя дифференциальное урав¬
нение Бесселя для функции J0(\iKr/R):
Здесь использована формула [*/0(lV'/#)lr =— (н*/#) Л OvV#)-
Таким образом, окончательно имеем
Уравнение (5.157) в пространстве изображений переходит в обык¬
новенное линейное неоднородное дифференциальное уравнение пер¬
вого порядка
Теперь следует вернуться в пространство оригиналов по теореме
обращения (5.161). Окончательно найдем
Совершенно аналогично могут быть рассмотрены преобразования
Ханкеля для второй и третьей краевых задач, описываемых уравнени¬
ем (5.161). Все необходимые для этого сведения изложены в п. 1 § 8
гл. III.
Рассмотрим интегральные преобразования для нахождения неосе¬
симметричных температурных полей. В отличие от выше рассмотрен¬
ных случаев здесь можно использовать также и теорию рядов Фурье —
Бесселя для построения соответствующих преобразований.
R
R
= /) + ^)2jrr(r, t)J,[iiKrlR)dr.
О
R
f 7 4г) MR), dr = Mi (M T(Я, 0— (■’2 Т (ц,, t).
(5.162)
i7+(i^)2r=aMi(M(P(0; г (iv 0) = о,
решение которого имеет вид
и
Т(г, /) = -
dx. (5.163)
238
В курсах по теории бесселевых функций (см., например, [54]) пока¬
зывается, что система функций lJv(\ikr^R)^ является ортогональной на
[О, R] относительно весовой функции Р(г) = г, т. е.
Здесь \iK > 0—корни уравнения УДц) = 0, расположенные в порядке
возрастания \it < р2 < ... < . ... Отсюда если f (г) — кусочно¬
непрерывная и кусочно-гладкая функция в промежутке [О, R], то
в каждой точке ее непрерывности можно записать ряд Фурье — Бес¬
селя вида
Из этой формулы следует следующее преобразование: если f(\iK)—
трансформанта Ханкеля функции /(г), кусочно-непрерывной и ку¬
сочно-гладкой в промежутке [О, R],
то в каждой внутренней точке интервала [0, /?], в которой функ¬
ция непрерывна, имеет место формула обращения
где > 0 —корни уравнения Jv(\i) = 0. При v = 0 имеем случай
(5.160) — (5.161), рассмотренный выше.
Другой более общий вид преобразования Ханкеля с конечными
пределами можно получить из теории рядов Фурье— Бесселя (ряды
Дини) по корням более сложного трансцендентного уравнения
\iJ'x(\i) + hRJv(\x) = 0. Для трансформанты этого типа классические
теоремы рядов Фурье—Дини (см. [15,]) дают следующее интеграль¬
ное преобразование и теорему обращения для него: если Дрк) —
трансформанта Ханкеля функции /(г), кусочно-непрерывной и ку¬
сочно-гладкой в промежутке [0, R],
то в каждой внутренней точке г этого промежутка, в которой / (г)
непрерывна, имеет место следующая формула обращения]
/ (') =-Jr Z j '/(') 'v Ov/Я) dr. (5.165)
К= 1 * г,
0
R
f(\xK) = \rf(r)Jv(vKr/R)dr,
(5.166)
о
ао
R
/ (И*) = S г/ (0^v (\iKr/R) dr,
(5.168)
о
У J, V
£ W+AW-v*)/?(|*«) nMt
(5.169)
239
где сумма берется по всем положительным корням уравнения
\iJ'v (р) + hRJv (р) = 0 (A/? + v > 0). (5.170)
Здесь также следует выделить случай v = 0, для которого имеем
R
T(K) = [rf(r) JA^r/R)dr,
о
'(г)-^| ,5171>
где \iH > 0—корни уравнения (5.170) при v = 0; Л/?У0(р) — \iJt (р)=0.
Все сказанное выше в замечании в § 3 сохраняет свою силу и
для преобразований Ханкеля и здесь уместно привести теорему
о разложении функции в ряд Фурье по функциям Бесселя, имею¬
щую, как и теорема Стеклова (см. § 2 гл. III), исключительно важ¬
ное значение в аналитической теории теплопроводности.
Теорема! если f (г)—непрерывна и дважды дифференцируема на
отрезке [0, R] и / (0) =/'(0) = 0, /'(/?) + hf (R)=> 0, то ее ряд Фурье
по функциям Jy (р///?), еде \iK > 0—корни уравнения (5.170), сходится
равномерно к f(r) всюду на отрезке [0, R],
Полагая в условиях этой теоремы l/ft = oo, получим аналогич¬
ную теорему для случая (5.165).
Указанные выше интегральные преобразования применяют при
решении краевых задач теплопроводности для сплошного цилиндра.
Практическое применение их связано с возможностью перевода
в пространство изображении оператора L (/) а= /" (г) + (11 г) /'—(v2/r2) /.
Совершенно аналогично, как и в случае (5.55) [кроме того,
см. (5.162)], можно показать, что применение преобразования (5.166)
дает
М5+7ЧГ-7^)^(lV7/?) ^ =
о
«-/?{/ (') 4 [J* (fV/tf )]}r=R ~{+У ТОО. (5.172)
Отсюда видно, что преобразование (5.166) необходимо применять
в тех случаях, когда на поверхности сплошного цилиндра заданы
граничные условия 1 рода. В частном случае преобразования (5.160)
(v = 0) формула (5.172) дает результат (5.162).
В случае преобразования (5.168) устанавливаем
Йда + 7Т—£ О <’*»"*>dr"
о
-WvW [4г- + А^г)]г-«“( (5Л73)
240
Здесь также следует рассмотреть случай v = 0 [преобразование
(5.171)], который дает
§ т + т w)^ “
О
= [ЁБГ+Л/и],=Л-(ж)*^- <5Л74>
Формулы (5.173)—(5.174) показывают, при каких обстоятельствах
следует пользоваться трансформантами Ханкеля, определяемыми
(5.169) и (5.171): очевидно, их следует применять в случае, когда
на поверхности сплошного цилиндра заданы граничные условия
III рода.
Задача 1, Методом интегральных преобразований, применяемым последо¬
вательно по пространственным переменным, найти решение тепловой задачи для
конечного сплошного цилиндра — / < z < /, 0</*</?, начальная температура
которого постоянна и равна Г0, а на граничных поверхностях осуществляется
теплообмен со средой постоянной температуры Тс > Г0. Внутри цилиндра дей¬
ствует источник теплоты удельной мощности Q = const. (Некоторые решения рас¬
сматриваемой задачи приведены в [55], [85], [161].)
Ш d2W 1 dW d2W
jro=^j^+w+Po=0i 0<р<1> 0<y<li‘ Fo>0: (5Л75)
1Г(р, у, 0)=1; dW/dp |рш/1=-В11Г| ; (5.176)
W/ду |j,= 0=0; dW/dy \y=h = -Bi W \y= t-
| W (p, y, Fo) | < -feo, pSsO. (5.177)
Здесь: p= r/R-, y=z/R; Fo=at/R2;li = l/R\ P0=R2Q/[b(T(l—7'c)]; W (p, y, Fo)=
= [T (r, z, i)—TC]/(T0^TC)\ так как распределение температуры симметрично
по у у то можно рассматривать */£[0, и при этом Wy = 0 при у — 0.
Задача 2. Показать, что при Q = 0 (Р0 = 0) решение задачи без источника
равно произведению решений частных задач: решения третьей краевой задачи для
неограниченного сплошного цилиндра и неограниченной пластины с граничными
условиями смешанного типа (см, § 6 гл, II).
Ответ'.
00
у, Fo) = ri(p, Ро)Я7а(у, Fo)=2Bi V 7,(рг р) е
m= 1 (И-2т+ Bi2) Jо (ц2т)
00
х2 V sln т«fc**+Bi2 **) CQS ^«Wli) *-^xFo- (5 178)
к= 1 [(^1к + в^ Ii) + Bi /J Pi*
где ргст >° — корни Bi /0 (^2) = li2/i (p2); Pi* > 0—корни ctg щ=т/(В\ 1±).
Что касается метода интегральных преобразований применительно
к решению тепловых задач в полом цилиндре 0 < Rt < г < R2> то
здесь также может быть построена соответствующая теория, причем
для граничных условий любого рода на поверхностях r = Rx и r = R2.
Для этого можно воспользоваться результатами § 9 гл. II, где по¬
лучены собственные значения и собственные функции однородной
задачи для полого цилиндра.
241
-<iFox
Задача 3. Показать, что решение краевой задачи
} (5.179)
Т (г, 0) = Ф0 (г), Rt<r<Rt; Т (Ru f) =Т (R2, t) =0 / > 0 )
можно получить с помощью интегрального преобразования вида
_ Rt
Т (Мк> 4=1 ГТ (г, QY,(m«, г) dr-,
(5.180)
00
где ^„(ц*, r) = /0(n«r/fli) ^о(Цк) — -^0 (|^к) (Mk^/^i); (i* > 0—корни уравнения
Задача 4. Пусть W {pr/Rd = У0 (ц) Jo (pr/Ri) — Jo (И-) Уо №/%{)• Обозначим
R2
f (jli) = ^ rf (г) Y (fir/Ri) dr. Покажите, что
Ri
В сводной табл. 11 интегральных преобразований приведены инте¬
гральные преобразования для полого цилиндра Rt < г < /?2 при
любых комбинациях граничных условий на его поверхностях r = Rt
(i = 1, 2) и указаны формулы перевода оператора L(f) = d2f/dr2 +
+ (l/r)d//dr в пространство изображений.
§ 5. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ХАНКЕЛЯ
ДЛЯ ПОЛОГОГО И СПЛОШНОГО ЦИЛИНДРОВ, ТЕМПЕРАТУРНОЕ
ПОЛЕ КОТОРЫХ НЕ ЯВЛЯЕТСЯ ОСЕСИММЕТРИЧНЫМ
Рассмотрим интегральные преобразования, которые позволяют исклю¬
чить из дифференциального уравнения теплопроводности оператор
вида
Z'i(7’) = l^" + 7 («—целое число), 0<Ях < л < tfs.
(5.183)
J0 (ц) Y„ (ц, RdRi)-yо (Ц) Jo (ц/?2/Лг>=0;
2RUjU»«)-JUi*kR2/Ri)] .
nVKJUv«Ri/Ri)
(5.181)
оо R
Ответ: Т (г, t) = £ ехР [ *] ] гФ° <г) r> dr<
(5.182)
242
С помощью построенных преобразований можно решать краевые
задачи для полого цилиндра (неограниченного, полуограниченного,
ограниченного), температурное поле которого не является осесиммет¬
ричным (т. е. зависит от угловой координаты ф).
Вначале рассмотрим полый цилиндр. Пусть функция Т(г, ср, z, t)
удовлетворяет дифференциальному уравнению
1 дТ д2Т . 1 дТ . 1 д2Т . д2Т /Е- 1Q/14
a dt “ дг2 + г дг + г2 дер2 + дг2 (0.184)
в области 0<;/?i< г <С R i, 0 ^ ф < 2 я, t > 0, z g G0 (линейные раз¬
меры области G0 указывать не будем).
Решение этого уравнения можно получить методом интегральных
преобразований. На первом этапе следует применить преобразование
по z, исключив из уравнения вторую частную производную д2Т1дг2.
На втором этапе можно исключить из уравнения угловую координату
Ф, при этом в уравнении появится оператор (5.183). Чтобы исключить
переменную ф, необходимо построить соответствующее интегральное
преобразование. Для этого воспользуемся тем обстоятельством, что
функция Г является периодической по ф с периодом 2л : Т(г, ф, z, t) =
=Т(г} ф + 2л, г, t) и, следовательно, может быть записана в виде
тригонометрического ряда Фурье в комплексной форме [6]
п- + 00
Т(г, ф, г, t) = -^ £ Спе1пч>,
где
Сп = J Т (г, ф, г, /)е-‘'!<Р(1ф. (5.185)
Отсюда следуют интегральное преобразование функции Т (г, ф, г, I)
по ф и формула обращения для него в виде
л
Т (г, п, г, 0 = \ т (г, ф, г, ()e-ln<fdф;
-Я
t\— + оо
Т(Г, ф, г, 0=4г L Т&*- (5.186)
2л
Л= - 00
Найдем теперь изображение д2Т[дсрг, пользуясь интегральным
преобразованием (5.186). Интегрируя дважды по частям, получим
л 'л
^-^е-‘п(Р(1ф = + (/ге’171ф^]ф-Яя—п* § Те-{п{*> бф = — п%Т.
-л -я
(5.187)
Выражение в квадратных скобках исчезает вследствие периодич¬
ности функции Т. Действительно, так как Т (г, ф, z, t) =
= Т (г, ф + 2л, z, /), то Т (г, ф—-л, z, t) = T (г, ф + л, z, /)> откуда
при ф = 0 для Т и dT/dcpi
Т (г, —л, z, t) — T(rf л, z, /); дТ (г, —л, г, t)/dcp=*
г=дГ(г, л, г, /)/<?ф; е±£пя = cos /гл.
243
Уравнение (5.184) после применения к нему преобразования
(5.186) имеет вид
1 дТ д2Т j [_ дТ^ п2 7р , д2Т n г Р 1 оо\
а dt ““ дг2 г дг г2 дг2 * ^ ^ ^§* (0.188)
Дальнейшие преобразования уравнения (5.188) связаны с исклю¬
чением оператора (5.183) относительно функции Т из данного урав¬
нения при любой комбинации граничных условий на поверхностях
r = /?j и г = /?2. Для сокращения выкладок введем безразмерную коор¬
динату р = г//?2» так что #0<р<1 (Ro = R1/R2)\ имеем слагаемое
вида
+ *.<Р<1. (5.189)
и предположим, что функция /(р) удовлетворяет условиям*
d//^|p=«.==fW*o)-0i]; d//dp |р=1 = —РЛ/d)—0J. (5.190)
Рассмотрим следующую схему построения интегрального преоб¬
разования (в отличие от рассуждений § 1 — это еще один подход при
построении соответствующих формул), с помощью которого можно
исключить из дифференциального уравнения теплопроводности сла¬
гаемое (5.189), выразив его через изображение искомой функции в
соответствии с граничными условиями (5.190). Для этого введем ин¬
тегральное преобразование вида
i
/>)= S/(P)tf(w>)dp; (5.191)
Ro
Ro Ro
+ (5.192)
Ro
Потребуем далее выполнения следующего равенства*
j 'U [рТр(7к <w»)]■-$к- (ИР)} --/‘‘Гм.
Ro
что дает с учетом (5.191)
[f {Ь &(Тк (w>)]+ (i‘’-?)к<w»}d<>-
далее .
Ф К ( ? К W ) ] + ( 9’ - Й X <ИР) -'»•
R
Полагаем далее .
244
Введя новую функцию
V(W>) = (l/p)/C(|ip), (5.193)
получим уравнение для определения ядра
Ш‘>?)1+(>‘,-£)'1'-0' <5-194>
С уравнением (5.194) мы неоднократно встречались. Это урав¬
нение Бесселя, общее решение которого имеет вид
Vn (М>) = A lnJ п (РР) + А2пУп (рр), (5.195)
где Jn и Yn—функции Бесселя соответственно I и II родов п-го
порядка; А1п и А2п—постоянные интегрирования. Эти постоянные
определяются из граничных условий для ^(рр), которые необхо¬
димо выбрать таким образом, чтобы первое слагаемое в правой части
равенства (5.192) выражалось через известные функции граничных
условий (5.190).
Учитывая (5.193) и (5.190), имеем для первого слагаемого в (5.192)
(м-р)—/рГр [ j к (ИР)] )v—/(1) О^п (IX)+№ 0*)]- .
- RJ (Ro) [№ (р/г.) ■(рЯ.)] +
+iW„ (и) + R#№. О*'/?*)- (5.196)
Здесь Т; (и) = d^/dw, так что (d/dp) [¥„ (рр)] = р¥; (рр).
Если теперь положить
№) + рТ, (Р) = 0,
№п № о) (Ibt/? 0) = 0»
то изображение L(f) в (5.192) будет выражаться через известные
граничные функции и изображение искомой функции /. В резуль¬
тате приведенных рассуждений пришли .к однородной задаче (5.194),
(5.197) на собственные значения р и собственные функции ^„(рр).
Прежде всего найдем коэффициенты А1п и А2п в (5.195), исполь¬
зуя (5.197). Это дает однородную систему линейных алгебраических
уравнений вида
л1лмлр)+р^Ир)]+л*драу,,(р)+рУ;.(р)]==о, )
Система (5.198) имеет решение, отличное от нулевого, если ее
определитель равен нулю, т. е.
[М* (р) + РЛ. ((0] №i^n (рЯ«) —V-Y’n (м-^о)] —
—\ptYa (р)+ру; (p)j pv „ (р/г.) - р./; (р/г.)]=о. (5.199)
Уравнение (5.199) является характеристическим, имеет бесконеч¬
ное множество положительных простых действительных корней
pnif (к=1, 2, 3, ...) — собственных значений однородной задачи
245
(5.197)
(5.194), (5.197). Постоянные А1пк и А2пк, соответствующие значению
р = рпк, находим из (5.198) с точностью до постоянного множителя.
Если положить
^lnK = Pl^n (^пКЯо) — РпкУ'п (КпЛ).
^гпк — [Рх^п (И'пк^о) ^пк*^п (Цпк^о)]'
то второе из уравнений (5.198) удовлетворяется автоматически, а
первое—в силу (5.199). Зная, таким образом, константы (5.200),
находим собственные функции ^¥пк однородной задачи (5.194), (5.197):
(ivp) = [Piy« (л«Я.)] X
Х^П(Ц„КР) —[Рх-^п^пЛ) —(5.201)
Согласно теореме III (§ 2 гл. III), система функции (рякр)}
ортогональна на промежутке [/?0, 1] относительно весовой функции
Я(р) = р. Запишем квадрат нормы (Ч^Ц2 (ввиду громоздкости вы¬
кладок приводим лишь окончательный результат):
1
IIТ*IIs = \ р^к(^пкР) dP=-V[ц*д;к(iij+(!*•« -п*)(Цпк)-
£ Щпк
° -tiKRlxK(рЛ)-(|« -п2) (рнк/?„). (5.202)
Здесь Yпк (рлк) = [Pi^n (Рлк^о) V'niXn (Рпк^о)! X
X J гг (И'пк) [Мл (Рлк^о) Рлк^л (РлЛ)] ^п (Рп*)*
Систематизируем теперь полученные результаты, записав их в окон¬
чательной форме.
Интегральное преобразование функции /(р) вводится формулой
вида
i
7 (lO = S р'Рл* (и„, р) / (Р) dp, (5.203)
Ro
где ядро преобразования (|ieifp) есть выражение (5.201).
Формула обращения для преобразования (5.203) может быть по¬
лучена при разложении функции /(р) в ряд Фурье—Бесселя по
системе функций (Ч^Др^р)} и имеет следующий вид:
СВ
f (р) = ^ II ¥ л К II2 ^ПК (РлкР) / (Рл*)» (5.204)
где ЦЧ^* дается выражением (5.202), а суммирование происходит по
всем положительным корням трансцендентного уравнения (5.199)
(вычисление корней такого рода уравнений см. в ссылках [166]).
Если функция /(р) удовлетворяет граничным условиям III рода
(5-190), то изображением выражения (5.189) является
R о
= М ,т „ GU + Р iK.Y», О^Я.) вх- |*Sj(|ie,). (5.205)
246
(5.200)
Возвращаясь теперь к уравнению (5.188), можно с помощью
преобразования (5.203) исключить из него слагаемое д2Т/дг2 +
+ (11г)дТ/дг— (п2/г2)Т (предварительно введя безразмерную перемен¬
ную р = r/R2), заменив правой частью выражения (5.205), если на по¬
верхностях цилиндров r=Ri и r=R2 заданы граничные условия III ро¬
да. Для других видов граничных условий соответствующие результаты
могут быть получены аналогичным образом. Запись основного интег¬
рального преобразования в виде (5.203) и формулы обращения для него
(5.204) всюду сохраняются, меняется лишь ядро преобразования в
зависимости от вида граничных условий. Все результаты по построе¬
нию соответствующих преобразований, формулы обращения для них и
формулы исключения оператора (5.189) приведены в табл. 11. Сформу¬
лированные в таблице результаты при п = 0 дают возможность рас¬
смотреть и случай осевой симметрии для полого цилиндра (температур¬
ное поле не зависит от угловой координаты) и, в частности, выписать
изображение слагаемого (d2//dp2+ (l/p)d//dp) при различных граничных
условиях на поверхности р=R0 и р=1. Что касается формул обращения
для этого случая, то здесь удобнее воспользоваться результатами
§ 9 гл. III.
Рассмотрим дифференциальное уравнение теплопроводности (5.184)
для сплошного цилиндра в области 0 ^ г < /?; 0 ^ <р <
< 2л; t > 0. Здесь также могут быть повторены предыдущие рассуж¬
дения, и необходимость построения соответствующей теории интег¬
ральных преобразований обусловлена исключением из преобразован¬
ного уравнения (5.188) слагаемого вида д2Т/дг2+ (1/г) дТд/г—
— (п2/г2)Т в области 0 г < R при любых граничных условиях его
на поверхности г = R. Здесь так же, как и выше, введем безразмерную
координату р = r/R, так что 0 ^ р ^ 1, и рассмотрим слагаемое
= W + £/’-0-SP<!. <5.206)
где функция /(р) удовлетворяет условиям:
d/(p)/dp|р=, = — Р[/(1) — 9]; |/(р) I < + оо, р>0. (5.207)
Соответствующие формулы для случая (5.206)—(5.207) можно
получить из предыдущих, если положить всюду /?„ = 0 и заменить
^Я(ИР) на У„(рр). Кроме того, в (5.195) следует положить А2п = 0,
так как функция К (рр) при р = 0 обращается в бесконечность, в то
время как в сплошном цилиндре решение всюду должно быть ко¬
нечным.
В результате приходим к следующим формулам: интегральное
преобразование функции /(р) и формула обращения для сплошного
цилиндра имеют вид
1 00
/(Ю = 5 Р/(Р) Jn (Ц„,Р) dp; /(Р) = Е TuNr Шпш). (5-208)
0 к=1 11
247
где цп„ > 0—корни уравнения: РУ„ (ji) + р/; (р) = 0; при этом
II I» =Т1г-Ф* + ОО, (5-209)
^ *М-лж
I р (тг+ j%-■£0 y«0w>) dp=ре/„ (IX..)- vtf(р„к). (5.210)
о
Все остальные виды граничных условий рассмотрены в табл. 11.
Заметим, что здесь, так же как и в случае полых цилиндров при
п = 0, приходим к интегральным преобразованиям Ханкеля для
сплошных цилиндров, температурное поле которых обладает осевой
симметрией. Соответствующие выражения для изображения da//dp2+
+ -^-d//dp нетрудно получить из приведенных в таблице формул,
полагая всюду п = 0.
В качестве примера рассмотрим общий метод решения осенесимметричного
дифференциального уравнения теплопроводности для полубесконечного сплошного
цилиндра, когда начальное распределение температуры задано в общем виде:
dW _d2W 1 dW 1 d2W d2W
d Fo dp2 p dp ** pa dtp2 ' *
0<p < 1, О^ф < 2л, г9 > 0, Fo > 0; (5.211)
W (p, ф, z\ 0) = Ф0(р, ф, z'); (5.212)
№(p, ф, 0, Fo) = 0; W(p, ф, z'Fo)=lF(p, ф + 2л, z', Fo); (5.213)
(dlF/dp+Bi W%»i = 0; | W (p, ф, z'f Fo)|< + oo, p^0, z > 0. (5.214)
Здесь p = r/R\ z9=z/R; Fo = at/R2\ B\=hR\ Ф0 (p, ф, г9) = Ф0(г, ф, г)/Т0;
W (р, ф, гг, Fo) = T(r, ф* z, t)/Tо, где Т0—некоторое начальное значение тем¬
пературы, фиксированное для определенной точки цилиндра.
Предполагаем, что функции W, Ф0 допускают вместе с соответствующими
частными производными интегральные преобразования по переменным р, ф, z'.
Наметим путь решения этой задачи.
На первом этапе из уравнения (5.'211) исключаем переменную г', применяя
для этих целей бесконечное синус-преобразование Фурье (5.30) (учитывая, что
при г9 — 0 задано граничное условие I рода). Выпишем все необходимые формулы:
00 -
W (р, ф, £, Fo) = У 2/л J W (р, ф, z', Fo) sin £zf dz';
о
00
W (p, ф, z', Fo) = У 2/л J W (p, Ф-, 6, Fo) sin £z' dg;
о
00
V~2in (j d2W/dz,z sin lz' dz' = - isr. (5.215)
0
На втором этапе с помощью комплексного преобразования (5.186) исключаем
из преобразованного уравнения теплопроводности переменную ф, используя фор-
мулу (5.187). Запишем все необходимые формулы:
я
W (р, п, I, Fo) = ^ IF (pf ф-, h Fo) exp (— Мф) 5ф;
-Я
П = + 00 Я
IF (р, Ф, £, Fo) = 2 ^ехр(шф); 'Ш/ду* e-in'i> dф = -я2lF (р, п, £, Fo).
-я
(5.216)
248
На третьем этапе исключаем из дважды преобразованного уравнения тепло¬
проводности переменную р, применяя преобразование Ханкеля (6.208). Запишем
необходимые формулы, используя (5.208) — (5.210):
После этого придем к обыкновенному линейному однородному дифференциаль¬
ному уравнению первого порядка относительно функции W я, £, Fo), решив
которое найдем W. Искомый оригинал W найдем, применив к найденной функции
W трижды формулы обращения W —► W —► W —► W. Итак, после третьего этапа
имеем
Здесь Ф0 — изображение начальной функции в результате применения к Ф0 трижды
указанных выше преобразований.
Находим решение
и далее, применяя к (5.219) формулы обращения (5.217), (5.216) и (5.215),— ис¬
комое решение задачи (5.211), (5.214) в виде
В выражение (5.220) входят изображения от начальной функции задачи.
В случае конкретной функции Ф0 ее изображения также представляют собой
конкретную функцию и в этом случае интеграл, входящий в решение, может
быть вычислен. Если начальная функция—функция общего вида, то следует от
изображения этой функции перейти к ее оригиналу, используя определение изо¬
бражения в виде соответствующего интеграла. При этом могут быть проведены
некоторые преобразования, ведущие к упрощению найденного решения. Действи¬
тельно, записав в (5.220) вместо Ф0 соответствующий интеграл (5.215), получим,
меняя пределы интегрирования и вычисляя внутренний интеграл [(см. (5.48) —
В7 (1W я. 5. F°) = 5 Pw (Р> я, I, Fo) Jn (цпкр) dp;
0
где цпк > 0—корни уравнения;
Bi /п(ц) + ц^(ц)=0;
о
г
dr/d Fo + fe+g») Г = 0; Г (ря<£, п> г, 0) = Ф0 (un>[i п, 0. (5.218)
W (рЛ1С, п, £, Fo) = Ф0 (Цл«» я,- £) exp [— (pjU+V) Fo] (5.219)
00 П* + OD
249
(5.49)]
09 —
J exp (— £2 Fo) Ф0 (ц„¥, n, £) sln %z' d£ = j/*2/nX
0
00 00
X J Фо (Мл*. n> P) dp ^ e_5‘Fo sln \z' sln £f) dg=-
о о
r <z'-Э)» (s' + P)1--!
==- С Фо (Мл*. n, P) Le 4Fo —e 4Fo]dP.
VTfS J
Возвращаясь далее от двойного изображения к оригиналу Ф0 п% f$) —►
—► Ф0 (рл*, ф> Р) —► ^0 (р> ф» Р) с помощью соответствующих интегралов можно
записать для W:
Г(р. ».Ро)-_' £ А^.<;..р)«-р w- AF°> х
2л |/jiFo (В12 + р„Л—n2)Jn (\inK)
00 я 1 Г (z'-fl)2 (z' + f3)M
XS S $P'A»(Mn*P')exp(—w«p') [e 4Fo—e 4 Fo J X
о -Я0
ХФ0(р'. ф'. P)dpdp'dq>'. (5.221)
Дальнейшие преобразования выражения (5.221) связаны с переходом от ряда
Фурье в комплексной форме к его тригонометрической форме. Здесь могут быть
использованы следующие полезные преобразования. Пусть дан ряд Фурье вида
п= + 00 jj
2 bnein(p \ А (ср') е”*Пф/ (1ф', где выполнено условие Ьп = Ь_п. Преобразуем
л = -а> _я
этот ряд следующим образом:
П = + оо ^ П = - 1 71
2 Ьпе‘п* V A (<p')e~tnlp df'= 2 *л J Л (ф')е1П(ф-<р’) dcp'-f-
7 = — ПО _ П г— СО
Л=-00 .я
я
+ 2 b" S Л(ф')е‘л(ф-ф'^ф' + 60 j 4(?W =
п~1 -Я -я
оо Я Я
= 2 2 ^ J Л (ф') cosn (ф—ф') с!ф' + 60 ^ Л(ф')ёф. (5.222)
п= 1 J
п= -1
Здесь ряд 2 заменой п на (—п) был преобразован в ряд 2 и Далее ис-
п = — 00 _ п — 1
пользовано равенство bn=b_n и формула Эйлера e*z = cos z + i sin z.
В выражении (5.221) имеем
ь Мяк-/п (МлкР) ех р (— цл/с Fo) , л л/ч
п~ (Ri2 I „2 г2 •/п(Мп»Р 1.
(Bi -f-pn/c Я / Jп (Рл*)
где р„*—положительные корни уравнения (р)— р*/А (р) = 0. При замене п на
(— п) последнее равенство не меняется, так как У_л (р) = (— 1)" Jn (р) (и это же
справедливо для j'n (р); следовательно, Рлк = Р-лк и отсюда b-n = bn.
250
Таким образом, преобразуя (5.221) в соответствии с (5.222), приходим окон¬
чательно к решению тепловой задачи (5.211) — (5.214) в следующем виде:
В выражение (5.223) на этот раз входят функции, заданные по ус¬
ловию задачи. Заметим, что наличие ядра экспоненты под знаком
несобственного интеграла обеспечивает сходимость этого интеграла
для широкого набора начальных функций задачи и в этом отношении
решения краевых задач довольно общего вида представляют опреде¬
ленный интерес для аналитической теории теплопроводности. Эти
решения можно рассматривать как общие
формулы, содержащие в себе достаточное ко¬
личество частных случаев. Ряд частных задач для осе¬
несимметричного цилиндра рассмотрены в известных монографиях
Карслоу и Егера [55], Лыкова и Михайлова [85], Лыкова [83], поэтому
в настоящем пособии они не рассматриваются.
Задача 1. Методом интегральных преобразований найдите решение первой
краевой задачи стационарной теплопроводности для круга
Задача 2. Используя соотношения (3.24) — (3.25), (5.116) — (5.120), полу¬
чите решение уравнения теплопроводности вида
*<Р.
ХФ0 (р', ф', Р) dp' dq>' dP; (60= 1; 6„ = 2, п > 0). (5.223)
т(г> ф)1г=я=^(ф); \т(г> Ф)1 <+°°»
в виде (интегральная формула Пуассона):
2л
с краевыми условиями
Т(х, 0) = Г„, 0<ж< 1;'—-jfi-ft | =0. Т (1, 0 = 0,00
ОХ \х— о
с помощью следующего обобщенного интегрального преобразования:
1
L {Г} = Т t) = J +1Т (х, 0 Jm (ц„дс) d*i
О
2т+1 дТ
х дх
251
• Здесь цп > 0—корни характеристического уравнения ^«(ц) = 0; т =—1/2
для бесконечной пластины, т = 0 для неограниченного сплошного цилиндра,
т = 1/2 для шара.
Ответ:
п = О
Задача 3. Получите указанное в задаче 2 интегральное преобразование.
Указание. Уравнение (3.26) для рассматриваемого случая
d2^ 2m+l dy
dx2 * x dx
eaпишем в виде
+ц2Ч' = 0
Sx (*2т+1 чг) **■х‘а+lv=°г
dx
откуда следует, что собственные функции (х) = (1/х)т Jm удовлетворяю¬
щие условиям (dY„/dx) = 0; YW(1) = 0 ортогональны в области *<J[0, 1] с весом
Р (х) = х2т+1. Здесь цп > 0—корни уравнения Jm (fi) = 0; Jm (z)—функция Бес¬
селя I рода m-го порядка
у
т ** к\ Г (к+m+l) ‘
к= О
Квадрат нормы собственных функций
1
II IP = J xJl (ц„х) dx=(l/2) J*m+, (цп).
§ 6. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ЛЕЖАНДРА
ДЛЯ ШАРОВЫХ ОБЛАСТЕЙ И НЕКОТОРЫХ ВИДОВ КРАЕВЫХ
ЗАДАЧ С РАЗНОРОДНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
Этот вид интегральных преобразований весьма полезен при решении
краевых задач стационарной теплопроводности для полого или
сплошного шаров, а также в случае разнородных граничных усло¬
вий. В § 10 гл. III были рассмотрены полиномы Лежандра Рк(х)
(3.282), удовлетворяющие дифференциальному уравнению (3.280).
В (3.283) показано, что Рк(х) ортогональны в интервале (—1, +1)
относительно веса Р(х)=1 и образуют замкнутую, полную систему
функций [122], по которой может быть разложена произвольная
непрерывная функция f (х):
00
/ м = 2 скрк{х),
к— О
где
+1
= vhr I f {х) Р‘(х) йх; 1 р*1,2 = 2^ТТ• (5-224)
* -I
252
Отсюда нетрудно ввести интегральное преобразование и формулу
обращения для преобразования следующим образом*
+ 1 00
7(«О = f / (*) Рк (X) dx; / (х) = Yi ~j~~ рн (х) / («)• (5.225)
_J, к=0
Преобразование (5.225), очевидно, применимо в том случае, когда
переменная х, подлежащая исключению, меняется в пределах (—1,
+ 1); оно позволяет исключить из дифференциального уравнения
слагаемое вида (d/djc) [(1—х2) f'x]. Действительно, интегрируя по
частям и используя при этом уравнение (3.280), находим
J й{1 ~х2) ъ]р* (*>d*= v-х2> € р« w С.-
-1
+ 1
"" 1 17 Рк (х) dx = W ^ —^ Р* \lV-i ~~
+ 1
—/с(/с+1) J f(x) Рк(х) dx = —■ /с(/с+ 1) /(/с). (5.226)
В практических задачах искомое температурное поле может быть
четной или нечетной функцией координаты х. В этом случае пола¬
гают 0 < х < 1, /'(*) *= о = 0, либо 0 < х < 1, / (0) = 0. Соответст¬
венно этому рассматривают:
а) четные преобразования Лежандра:
1 оо
7(2«) = $/(*) Pi.(X) dx\ /(*)=» s (4«+1)/(2/С) ягк (дс);
о *=°
1
|i[(l-^)-j7j^»d^=-PiK(0)/'MU=o-2/c(2/c+l)7(2/c); (5.227)
б) нечетные преобразования Лежандра:
/ (2/с + 1) = $ / (*) Я2к+1 (*) doc; / (дг) = 2 (4/с + 3) / (2« + 1) 1 (*);
о к=0
1
| й[<1 “**>ъ]Р^ W d* = <2/с + ^ (°) f <°> -
— (2л + 1) (2k + 2)J(2k + 1). (5.228)
Преобразование (5.225) может быть использовано при решении
тепловых задач для шаровых областей в случае, когда температурное
поле не является центрально-симметричным. Рассмотрим вначале
случай, когда функция Т = Т (г, 0, /), тогда уравнение теплопровод¬
253
ности (3.300) перепишется в виде
1 дт _д2т 2 дт 1 д ( йдт\
a dt дг2 ^ г дг “^sine дв \SlU^de ) 9
0 < 0 < я, Rt< г <R2t (Rt > 0), t > 0; (5.229)
IT(r, 0,0K + oo, 0<0<я.
Введем новую переменную т] = cos © (— 1 ^ т) ^ 1), а вместо функ¬
ции Т (г, 0, 0 — новую функцию W (г, г], 0- Так как
дТ/(50 = (<5№/<5т]) • (drj/d©) = (— dW/дгi) sin 0;
(1/sin 0) • (<5Г/(50) = — <51F/<5t],
то после преобразования уравнения (5.229) получим
±dW_^W_ 2_dW
a dt dr2 ' r dr ' г2 дт] [ ^ J *
Ri<r<R2, />0, —1 < n < 1;
I W(r, —1, OK + oo; |B7(r, +1, 0 | < + °°- (5.230)
Наметим путь решения уравнения (5.230), не выделяя специаль¬
ного конкретного типа краевой задачи. На первом этапе применения
интегральных преобразований положим
+ 1
¥(Г, К, 0= S w(r> л. 0Мч)*1- (5-231)
-1
Умножая далее обе части уравнения (5.230) на Pk (tj) и интегри¬
руя по г) в промежутке (—1; +1) получим, используя (5.226),
1 dW d2W . 2 dW 1 , , 1Ч ™
TW=l)??+7W-7rK(K+l)w>
Ri< r < Rv t > 0. (5.232)
Дальнейшие преобразования уравнения (5.232) основаны на
результатах предыдущего параграфа. Если ввести новую функцию
О (г, /с, t) = rl/2W (г, к, /), то уравнение (5.232) преобразуется к виду
1 дв _ д2в 1 де (к+1/2)2 -щ
a dt дг2 ' г дг г2
Rt<r<R2, />0, (Ri>0) (5.233)
и далее может быть полностью использована теория интегральных
преобразований, изложенная в § 5 для сплошного (Rt = 0) и полого
> 0) цилиндров при любых граничных условиях на поверхностях
r = R1 и r = R2 (в соответствующих формулах к нужно заменить
на (к+1/2). При переходе к функции 0, разумеется, необходимо
преобразовать и краевые условия задачи.
Заметим, что точки г] = ±1 являются особыми точками для диф¬
ференциального уравнения (5.230), и, отыскивая W (г, т], t) в виде
ряда Лежандра, получаем решение задачи, обладающее всеми необ¬
ходимыми свойствами гладкости во внутренних точках промежутка
254
— 1<т)<+1 и ограниченное в промежутке [—1, +1]. При этом
не затрагивается вопрос о сходимости ряда в концах промежутка;
в постановке краевой задачи требуется, чтобы в этих точках реше¬
ние было ограниченным и эти условия ограниченности используются
при исключении оператора L1(W) = [(1 —т]2) из уравнения (5.230).
Переходя к общему случаю (3.300), рассмотрим уравнение
дТ дЧ 2 дТ 1 д Г(] -vd74 , 1 дЧ /К OCMV
д¥о ~~ др2 "Г р др ~'г р2 &г\ 4 ' &г\ J “Гра(1—т)а) д<р2 •
где 0 < R0 < р < 1, — 1 < л < + 1» 0 < ф < 2л;
|Т (р, —1, ф, Fo) | < + оо, |Т (р, +1, ф, Fo)|< + oo; (5.235)
Т (г, г|, Ф, Fo) = T (г, г), ф + 2я, Fo). (5.236)
Условие (5.235) означает ограниченность решения при rj = ± 1;
условие (5.236) означает, что рассматривается периодическое реше¬
ние. Здесь, как и в случае (5.229), также можно свести дифферен¬
циальное уравнение (5.234) к обыкновенному линейному дифферен¬
циальному уравнению I порядка, содержащему лишь переменную Fo.
На первом этапе преобразования уравнения (5.234) можно
воспользоваться комплексным преобразованием (5.186), учитывая,
что функция Т периодическая по ф с периодом 2л. Полагая
л
Т (р, Г), m, Fo) = $ Т (р, Т], ф, Fo)e-im<^, (5.237)
-Л
исключаем из уравнения (5.234) переменную ф, используя фор¬
мулу (5.187):
дТ _ дЧ 2 дТ 1 д
dF0 др2 р др *’ р2 дг]
IТ (р, —1, т, Fo) | < + 5о,
;Т;
_ (1-Лг) ’ | (5.238)
Г (р, + F F°) | °°'
Чтобы построить интегральное преобразование, с помощью кото¬
рого можно было бы исключить из правой части уравнения (5.238)
выражение
д Г/i 2Ч дтЛ т2 7р
дт] дц J (1 —■Л2) ’
d
dt]
обратимся к § 10 гл. III. В этом параграфе было рассмотрено диф¬
ференциальное уравнение (3.284) относительно присоединенной
функции Лежандра Р(,ст)(Л):
(1 - V) ] + [*(К-+ 1)■-f^ji] РГ (ч) = о. (5.239)
Функция Лежандра Р^Чл). согласно (3.288), образует ортого¬
нальную систему функций с весом Р(т]) = 1. Отсюда введем интег¬
ральное преобразование вида
_ +1
Т (р, /с, ш, Fo) = ^ РТ]{Ц)Т (Р. Л» m, Fo) dr] (5.240)
-i
255
с формулой обращения
09
Г(р, Т|, т, Fo) = X. Р(Р- Kt т' F°)pT4r\)’> (5.241)
к= О
интегрируя дважды по частям и используя (5.239), находим
+ i
S, <Ч> [ (■ -Ч’) |] ~(ГЙ?> Г } d4 «(« +1) Г. (5.242)
Таким образом, уравнение (5.238) после применения к нему
преобразования (5.240) перейдет в следующее:
m=w+7 <5243>
Как видим, уравнение (5.243) совпадает с (5.233) и его решение
может быть получено по изложенной выше методике как для сплош¬
ного, так и для полого шаров, причем при любой комбинации
граничных условий на их поверхностях r = Rt и г = У?2(р = /?0,
Р = -1).
Более сложным является случай, когда рассматривается часть
шара, вырезаемая конусом 0 = 0О; при этом О^0<©о
и, учитывая подстановку r] = cos0, имеем Ло^Л^Л* Однако и
здесь возможно построить интегральные преобразования, с помощью
которых решение задачи можно было бы довести до конца, и такое
преобразование построено и указано в табл. 11.
Следует заметить, что в литературе имеется ограниченное число
сведений по этому классу задач и полученные результаты относятся
лишь к краевым условиям I рода [55].
Укажем методику решения уравнения (5.234) для этого случая,
т. е. для области 0^/?0^р^1, Ло ^ Л ^ 1, 0^ф<2л, Fo > 0.
В (5.235) сохраняется условие ограниченности при rj = 1 (при л = Ло
теперь необходимо задать граничное условие). На первом этапе
с помощью преобразования (5.237) из уравнения (5.234) исключаем
переменную ср; в результате приходим к уравнению (5.238). На вто¬
ром этапе применяем преобразование, называемое обобщенным преоб¬
разованием Лежандра:
1
Т (р, к, m, Fo) = 5 Р(к-тЧч)Т (р, Г], m, Fo) drj, (5.244)
“По
где Р(~т) (л)—обобщенная функция Лежандра, удовлетворяющая
уравнению (5.239) [8].
В функции Р(кт)(л)* к > —1/2 не является целым числом (чис¬
ловые значения этой функции см. в ссылках [52]). Формула обра¬
щения для преобразования (5.244) и исключаемый оператор приве¬
дены в табл. 11. После применения к уравнению (5.238) преобра¬
256
зования (5.244) получаем
Ло. m, Fo),
(5.245)
где функция Т (р, т]о» т, Fo) предполагается известной; к—корни
уравнения Р^т){г|0) = 0. _
Уравнение (5.245) с помощью подстановки Т = ]/r р W может быть
преобразовано аналогично, как и уравнение (5.232):
dW d2f 1 af (/c+l/2)2:p
aFo *“ aP2 p aP pa
+ (1—Ло)2^!Г'п)(Ло)1/Л"р^(р» Ло. tn, Fo) (5.246)
и далее может быть полностью использована теория интегральных
преобразований Ханкеля, развитая в § 5 для сплошного (R0 = 0) и
полого (R0>0) цилиндров при любых граничных условиях на поверх¬
ностях р = /?0* Р=1 (см- табл. 11 в § 8 гл. V, где в соответствую¬
щих формулах к нужно заменить на к +1/2).
Если рассматривается часть шара радиуса р = 1 (или 0 < R0 <
< р < 1), вырезанная конусом 0 = 0О и плоскостями ср = 0 и Ф = Ф0,
то здесь могут быть использованы преобразования Фурье с ядром
sin (гптсу/%) или cos(mmpAp0) и далее изложенная выше методика.
§ 7. УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ, ВХОДЯЩИХ
В АНАЛИТИЧЕСКИЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
ТЕПЛОПРОВОДНОСТИ
Существенный недостаток изучаемого в настоящей главе метода —
неравномерная сходимость ряда в решении задачи на границе интер¬
вала изменения той переменной, по которой произведено соответст¬
вующее интегральное преобразование. Причиной плохой сходимости
рядов, представляющих решения краевых задач нестационарной теп¬
лопроводности с неоднородными граничными условиями, является
то, что эти ряды не удовлетворяют неоднородным граничным условиям,
в то время как отдельные члены этих рядов удовлетворяют однород¬
ным условиям [см., например, (5.146')]. Поэтому в окрестности границ
указанного интервала полученные ряды сходятся неравномерно и най¬
денное решение нуждается в дополнительной доработке.
Одним из способов улучшения сходимости полученных рядов явля¬
ется переход от неоднородных граничных условий в исходной задаче
относительно функции Т (Mt t) к однородным условиям в преобразо¬
ванной задаче относительно новой функции W(M, t). Для этого необ¬
ходимо построить дважды непрерывно дифференцируемую по прост¬
ранственным координатам и непрерывно дифференцируемую по вре¬
мени t функцию 0 {М, t)f удовлетворяющую заданным граничным
условиям. В новой задаче функция W = Т (Mt t) — 0 (Л4, t) будет
удовлетворять однородным граничным условиям (см. 3 гл. III) и,
по теореме Стеклова (см. § 2 гл. III), ряд для W (М, f), полученный
9-339
257
методом конечных интегральных преобразований, будет сходиться аб¬
солютно и равномерно в области изменения пространственных перемен¬
ных при любом t > 0. Один из способов построения функции 0 (M, t)
предложен в [64]. Суть его сводится к решению дополнительной ква-
зистационарной задачи теплопроводности с соответствующими гра¬
ничными условиями. Действительно, рассмотрим краевую задачу (для
краткости полагаем функцию источника /=0)
1^ = ДГ(М, О M£G,t> 0; (5.247)
Т(М, 0) = Ф 0(М), МеО-, Эх раГ = — Ф (AJ, 0. t> 0,
(5.248)
где Р? + Р£>0; п — внешняя нормаль к S.
Пусть yl и Х¥К(М, ук)—собственные значения и собственные
функции соответствующей однородной задачи
Д¥(Л«) + Т*¥(М) = 0, М б G; [рж (Л1)] д, eS = 0. (5.249)
Если ввести интегральное преобразование (5.116) с формулой
обращения (5.117) и применить его к (5.247) — (5.248), то в резуль¬
тате найдем решение Т (М, t) в следующем виде (подробные выкладки
см. в § 2 гл. V):
г (Л1, о = L 7]$'гх) е" Шфо W) Т, (М, ук) dvM +
к=1 11 G
+ « t 'Щр.(И [- i ч> ■(«• Ч ■*, ■(Л у.)]х„г'™'X
* = 1 0S
X dt da. (5.250)
Ряды (5.250) сходятся абсолютно и равномерно во внутренних
точках области G_npH любом t > 0, но не обладают этим свойством
всюду в области G. Для улучшения сходимости этих рядов предста¬
вим искомое решение Т (М, t) как сумму решений нестационарной
и квазистационарной задач вида
Т(М, t) = W(M, t) + 6(M, 0. (5.251)
где
Д0(М, /) = 0, M£G; ^(дв/дп) — Р20 = — ф(Л1, /). М g 5; (5.252)
(Рг^О; при Р2 = 0 решение 0(M, t) может не существовать; этот
случай рассмотрен ниже на частном примере)
dW/dt =akW (М, о—в;(М, /), М £ G, / > 0; (5.253)
W(M, 0)=Фо(М) —0(М, 0), M£G;
t (Р, (dW/dn) —p2Г)м €s = 0, / > 0. (5.254)
Функция W (M, /) удовлетворяет однородным граничным усло¬
виям и может быть представлена в виде ряда Фурье по ортогона л ь-
258
ной системе функций [Ч^(М, yj], абсолютно и равномерно сходя¬
щегося всюду в области G при любом t > 0 (а вследствие выполнения
условий сопряжения в (5.254) начальной функции с граничным
условием и при 0).
Воспользуемся для W (М, t) выражением (5.123) [где следует
считать (\/cp)F(My t) = — ®t(M, /)] и запишем искомое решение
в виде, отличном от (5.250):
Т (Af, 0 = 0 (Af, 0 + £ е~ Ш [фо (М) -
-в (М. 0)]VK(M, yJdvM-
~ £ Ш е"(1/^к)2 ,,_Т) 0;(Л1> т> W*(M' V.)dx dvM- (5-255)
к~1 0 G
Это решение более удобно для числовых расчетов, так как ряды, вхо¬
дящие в (5.255), согласно теореме Стеклова (см. § 2 гл. III), сходятся
абсолютно и равномерно всюду в области G, причем коэффициенты
Фурье этих рядов убывают не медленнее чем 1/у£, в то время как
коэффициенты Фурье ряда (5.250) убывают лишь как \!yh [6].
Для практической реализации изложенной теории предложим
следующую расчетную схему, весьма стандартную и достаточно быстро
приводящую к конечной цели.
1. Строим функцию 0 (М, t), удовлетворяющую условиям (5.252)
и допускающую представление в замкнутом виде и в виде ряда Фурье
по собственным функциям WK (М, yh). Для получения последнего
находим решение задачи (5.252) с помощью интегрального преобразо¬
вания (5.116) у полагая
® (Yk> 0 = s J s (М, ук) 0 {М, t) dvM. (5.256)
G
Чтобы найти изображение А0, воспользуемся формулой Грина
для оператора Лапласа (2.142)
— (5.257)
G S
Находим отсюда, учитывая граничные условия в (5.249), (5.252) и
уравнение (5.249),
ЩдвТ„(1оя = -Т£в + ЭД [^Ф(М, ук) 1 eSdo. (5.258)
G S
И так как Д0 = О, то равенство (5.258) дает окончательно
0(7*. 0 = ^Ш1ГФ(/И* Y*)]m€s<10- (2’259>
Далее, по формуле обращения (5.117), находим
2. Из правой части выражения (5.250) (полученного при решении
исходной задачи) вычитается ряд (5.260) и одновременно прибав¬
ляется выражение для 0 (М, t) в замкнутой форме. Это дает иско¬
мый результат
Нетрудно убедиться в том, что правые части выражения (5.250)
и (5.261) тождественны, ибо переходят одна в другую с помощью
несложных преобразований, однако решение в форме (5.261) предпоч¬
тительнее, так как в конкретных задачах оно обладает большей просто¬
той (см. примеры ниже). Таким образом, задача об улучшении сходи¬
мости ряда (5.250) решена, так как ряд в правой части (5.261) удовлет¬
воряет однородным граничным условиям и равномерно сходится всюду
в точках области G.
Рассмотрим несколько примеров.
I. Улучшим сходимость (по изложенной схеме) ряда для третьей краевой
задачи
В табл. 11 построено интегральное преобразование для решения этой задачи;
применяя его, находим решение
X е-Р'4".)** JSS<D0 №Чв(М, У к) +
а
(5.261)
-^2 +/(*, 0. о < х < I, ( > 0;
Т (*> 0) = Ф#(дс); UL =0=Л [Г (0, 0-Г,];
(5.262)
(5.263)
t i
t i
о и
(5.264)
где \лп > 0 —корни уравнения ctg jj, = |я/(2/г/) —/z//(2fx).
260
Для улучшения сходимости ряда (5.264) необходимо рассмотреть задачу (5.252)
d20/dx2 = O, 0< х< /; d0/dx \x = 0 = h [0 (0) — ГД;
dB/dx \x = i = —h[Q(l) — Tc].
Находим решение этой задачи: 0 (х) = С1х + С2, граничные условия дают Сх —0,
С2 = Тс, таким образом 0(х) = 7\.. С другой стороны, найдем 0 (х), применяя
интегральное преобразование, как и при решении задачи (5.262) — (5.263):
I
0 ^ 0 (*) + cos ц„ Y+hl sin ц„ у) dx.
0
Это дает 0 (|Л„) = 2fi7"c/2/|LX/I и по формуле обращения (см. табл. 11) находим
оригинал
е ы=— V 2НТсР (Iх" cos Р-пх/! +hi Sin \inx/l)
1 2*. Vn (ц2+/Л2 + 2«)
rc= 1
Отнимая далее от правой части (5.264) 0 (х) в виде (5.266) и прибавляя 0 (х) = ТС1
находим улучшенное решение задачи (5.262) — (6.263)
Т(Х, D = Te+lf >*” C°/S e-<V/ « < X
1 (ц£+л2/2)+m
п. = 1
X | J Фо (I) (Цп COS Vnlll+hl sln n„g/0 d£-
. (5.267)
io
г i
+ ^ / (I. t) exp [(У~а ц„//)2 т] (p„ cos ц„|//+М $In ц„?//) dT dl
о о
2. Улучшим решение второй краевой задачи для бесконечной пластины
dT/dt = a (дЧ/дхг), 0 < х < I, t > 0; (5.268)
Т (х, 0) = Ф0 (х); дТ/дх |х=;0 = (1 A) фь /г 2fi94
дТ/дх \x=t = (\/X) ф2 (ф/ = const).
Для решения задачи применяем преобразование (5.150) (см. также табл. Ti). Это
дает
i
Т (X, t) = [a/m (ф2-ф1)/ + (1/0 J Ф0 (X) dx+
о
оо
+ (2/0 2 cos (плхМ ехР [~ пл/l)2 t] X
п= 1
X | J Фо W cos (плх/l) dx+ [12/(кп2л2)] [(— 1)” фа—фД [ехр (/“а пл/l)2 t — l] [ .
(5.270)
Улучшим сходимость ряда (5.270). При Р2 = 0 решение задачи (5.252) не су¬
ществует, так как не выполняется необходимое условие существования решения
задачи Неймана для области [0, /] (2.144). Поэтому будем считать* что в случав
р2 = 0 функция 0 (х* t) удовлетворяет неоднородному дифференциальному урав¬
нению второго порядка g некоторой правой частью (вид которой будет установ¬
лен) и условиям:
d26/dx* = Л (*), 0 < х </; d0/dx |**0 = (1/А.) фг, d0/dx |х=:* = (1 А) ф2. (5.271)
Выведем необходимое условие существования решения 0 (х, t) (в одномерном
случае), удовлетворяющего (5.271), В трехмерном (или двумерном) случае это
261
условие вытекает из формулы Грина для оператора Лапласа (2.142). В одномер¬
ном случае формула (2.142) имеет вид
о
Полагая в (5.272) У(х) = 1, U (х, /) = 0(х, t), находим, учитывая (5.271),
/ /
Г d20 Г 1 1
J 'd^“dx=j А (/) Лх=Т(ф2—’ф1)> откуда л ^=ТГ(ф2—ф1-1, (5,273)
о о
Таким образом, функция 0 (х, t) удовлетворяет условиям:
d20 Г 1 1
0< *<Ь
dB/dx U=0 = (1 А) ФГ, dS/dx \x=l = (1/Я) ф2. (5.274)
Однако условий (5.274) еще недостаточно, чтобы отыскать 0 (х). Потребуем, чтобы
^полнилось условие
0 (х, i)dx = 0. (5.275)
в случае второй краевой задачи выполнялось условие
i
S
С
Из (5.274) находим 0' (х) = [(ф2 — фО/АО! *+0 А) фц Отсюда, учитывая (5.275),
окончательно получим
0 (х, 0 = (I/2Я) ф2 [(х/t)2 —1/3] — (//2Я) ф1 [(1 —х//)2—1/3]. (5.276)
Далее, как и выше, найдем 0(х), применяя к (5.274) интегральное преобразова¬
ние косинус-трансфюрманту Фурье (5.150). При этом, так как в силу (5.275)
0(л)|п=о==О, то формула обращения не будет содержать нулевого слагаемого
(в случае невыполнения условия (5.275) нельзя было бы применить формулу
обращения для указанного преобразования). Иными словами, если
— г 00 _
0 (п) = \ 0 (х) cos (nnxjl) dx, то 0 (х) = (2//) 2 ® (п) cos (лях//), (5.277)
о "=1
Находим вторую форму функции
со
2/ 47 (—\)пФ* — CDi ппх
0(х)=—У iz^l2m£Lcos пт
w Ал2 Я2 со* ~
п= 1
и вместе с этим улучшенное решение задачи (5.268)— (5.269) в следующем виде '
[в отличие от выражения (5.270)]:
/
Т(х. 0 = [а!(Щ fo>2 - Ф,) *+|*Ф0 (*) <** + (//2А) срг [(х//)2 -1 /3] -
оо ®
— (//2Я) фх [(1—X//)2—1/3] + 2// 2 cos (плх/l) ехр [— (}/"а ппЦ)г t] X
п= 1
' /
J Ф0 (х) cos (nnx/l) dx—[/2/(я2л2Я)] [(—1)” фа — фх]
(5.278)
X
U
Ниже даете? табл. 10 функций Ь (x, t) , с помощью которой могут
быть улучшены решения краевых задач нестационарной теплопровод¬
ности для бесконечной пластины (0 < х < /) для различных сочетаний
граничных условий на ее поверхности х=0 и х=/* а также бесконеч¬
ного цилиндра (сплошного и полого и шара (сп¬
лошного O^p^R и полого Ri^p^Ri)-
262
. Декартова система координат: область о < х < I.
263
Продолжение табл. 10
264
. Сферическая система координат (область 0 £ г £ R; центральная симметрия)
265
Продолжение табл. 10
. Сферическая система координат (область Я, ^ г £ Л2; центральная симметрия)
267
Продолжение таЬл. 10
268
. Цилиндрическая система координат (область 0 ^ г ^ R; осевая симметрия)
/</, (w) - Bi /0 (и) = О (Bi = /iR).
. Цилиндрическая система координат (область Л, < г < Л2; осевая симметрия)
270
цп > С — корни уравнения
5. Цилиндрическая система координат (область Л, < г < R2\ осевая симметрия)
271
Продолжение табл. 10
272
>. Цилиндрическая система координат (область Л, < г < Л2; осевая симметрия)
273
у, 0<уя,) /0 00 - J, с«дг//г,) у0 О)
у, OV*,) Л О*) - С“«2/Л,) yi (“)
Продолжение табл. 10
274
I
II
&
к
3
*
VI
X
VI
I
II
s.
5
a
II
fel*
1
Ф
к
s
X
3
8.
2
X
X
Q)
3
8
S
<4
'S
О
II
X
X
£
о
II
:*-1 ♦
•Hi
О
II
s.
II
‘<
к
о
II
Я0
•HI
s.
«*|а
х|а<
о
II
is
s.
— h<
II
X
fe'
II
A
>
•HI
s.
о
II
9-
I
X,
к
275
fin > 0 — корни уравнения
Указанный прием можно использовать и при рассмотрении стацио¬
нарной теплопроводности, улучшая сходимость рядов в формулах
обращений для интегральных преобразований по тем или иным про¬
странственным переменным.
В заключение укажем на нелинейные преобразования Шенкса [58],
с помощью которых также можно ускорять сходимость рядов 2ГП.
Преобразование первого порядка переводит последовательность Тп
в Sn по формуле
= f (Тп) = Гп~1гп+2~ТТ+' ■ (5-279)
1 п ** л + 1 • п + 2
К последовательности S„, в свою очередь, можно применить пре¬
образование (5.279): Рп = f(Sn) = f2(Tn), еще более усилив сходи¬
мость ряда, и т. д. Особенно существенное сокращение объема вы¬
числений с помощью преобразования (5.279) достигается при решении
краевых задач в неоднородных средах и с двумя или тремя измерения¬
ми. Но отметим, что эти вопросы еще не нашли своего достаточного
развития в аналитической теории теплопроводности.
В [23] предложен другой способ улучшения сходимости рядов,
представляющих решения краевых задач с неоднородными граничными
условиями, основанный на построении функции Грина (обычной
или обобщенной) для соответствующего обыкновенного дифференциаль¬
ного уравнения; в [3] этот способ распространен на одномерные зада¬
чи нестационарной теплопроводности для бесконечной пластины.
§ 8. СПРАВОЧНАЯ ТАБЛИЦА ИНТЕГРАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
Систематизируем в виде табл. 11 конечные интегральные преобразова¬
ния, наиболее часто встречаемые на практике. При построении ука¬
занных в таблице преобразований использовалась методика, изложен¬
ная в предыдущих параграфах этой главы, а также результаты 7—11
гл. III о собственных значениях и собственных функциях соответст¬
вующих однородных задач для рассматриваемых областей.
Интегральные преобразования, изложенные в этой таблице, пред¬
ставляют определенный интерес для практики, так как позволяют до¬
статочно быстро получить аналитические решения для широкого
класса тепловых задач в декартовой, цилиндрической и сферической
системах координат.
ГМ. Интегральные преобразования Фурье-функции /(or) с конечными пределами в декартовой системе координат в области 0 £ х £ I
277
Продолжение табл. 11
;Rs
*
о.
+
с
54.
I
О
О
? ;
J.9-'
О ■«
Х' +
I
'У
&
i—,
I
Sr
ь
I
I**-»
X fV-v
*• ih
с v—"
I
О
>
+
О
ь
X
+
с
X
I <
o' +
v—' n с
- 5.
b
I
x
с
54.
3,
1^
I
о
+
3
ь
x
В
I
I
Cb
I**-*
о
I4*"*
3,
i**-.
5. x
8 WI I
ts I—, о
II A_
4.
2Ьч N«*C
С
& i +
" ^ S'S
•Wl'*i<4^' 2*
n +
S & Л
-. = -s
+
г* с
r*|—
II
L
о. x
!•
Ё
s
2
x
v
X
X
h
*
'h
&
XI—
X|-
Б
3.
v *
54.
с
и
3 С ж .—
^ 2 H
54. < SS<
5»
+
+
X|-
d + §
« xi- ё i
е
1
с
54.
4L *
s
u
O' J S
£ § о
с
^ U X 54.
+
54.
-’-.О ^ ,
II
И II о
-*Г
T О л П
54.
Зг 54. «
t
X
w
c
I-, *- ■*• Ы)
W Ъ
9>
=нс
5*.
*
x4
&
I4-»
XI--
и
■я |
"3 «>
? 5
hU*
*1^* >»
* 5
Js
3.
II
^ X
54. «
x *
T *
I ьр
I
&§
&чГ
b
&§
8.S
278
П.2. Интегральное преобразование Ханкеля функции Sip) с осесимметричным температурным полем
§
* -I*
8. +
е
8
S.g
I?
с S
§1
5-
>» и
8 *
£ ^
«в ^
у§ II
-S
1^.
IN К
5*.
I
3,
8
II
с
>s
о
г*-.
I
, * о
I II
О <34
Л
в о
VI
а
VI
о
о
I4-*
3
|**ч
8W!
о
•so
BQ
+
1 IN С
8
А
Ч-,
/—S
Q.
с
■ ’—* о I О
II I и
^ Al ,S
>»> К —
1^ ^
/•N
А
/■*4
К
vS
3
» "
i §,
0
1 о
а«
х о
о. ^
■??
1
'Л
о.
VI
о
VI
Q.
VI
о
279
Продолжение табл. 11
П.З. Интегральное преобразование Ханкеля функции /(/>, п) для сплошного цилиндра, температурное поле которого не является осесимметричным
а**»
8 +
•«к
3
а.
<8
I
о
е
А
гч-g
3L
I
Г:
А
A S
•Hi
А
I4».
«■8
з*.
I
К
А
I4-*
Q.
■8
А
■8
А
сч *:
I
гч-8
А
8
А
I4-*
«
+
1
А
Is-*
W
• Hi
CN
II
с4
А
с s
и
8
i 5 "
15 s'
j И
> А
А 5
■8
А
■8
А
г^>
I
VI
Q.
VI
1 8
8. 5
>* S-
1 I
is
in
Q.
■8
А
-’—> О О *_Г
N I О II II
* Л1 3 ° ° II
A " 8
1*^ 5. S .С Й ^
VI
VI
А
^ •
И
А
о
II
а
2 «
л *
!3
б. I
VI
Q.
VI
280
Продолжение табл. 11
П.4. Интегральные преобразования Ханкеля функции / (г) для полого цилиндра R\ < г ^ Яг с осесимметричным температурным полем
281
Продолжение табл. 11
282
Продолжение табл. 11
Продолжение табл. 11
И!
<Я 4.
|чП
*
зС
Зг
*|3
А
1 _ Г
i Jr
гЫ
х pf ht
^ I*
А
*-Г
+
А
ос; | ос; t
rf sT
< >
«|ог +
n
sflof
*V j 1
'в
A
I***»
of
X
&
8 W"
II
+
гч -w
A
-v
s
V
3,
1^4
4*
«*
• Wi
4
ПР
+
rs -*
X S
<N
V ^
4
X -Г
Q< I*
■*<
St.
3k
oi I *
«*
^|V
V
s
i
3
8
S*£
If.
e s
||
I*
&
Qt;
и
Q*
II
K\*
M
St.
-?
оГ|оГ
<S
Qt; I*
-V
5.
4*
■«
St.
A
I4-*
45
II
K\oc
м
St.
Qt; I*
*
St.
a ^
>> M
X &
X О
a.
oTlotT
sf
* >T
3>
oTR
-N
St.
*T
-*<
A
4* 4*
•X 4<
5- st.
45
3?
s
>T
■** X
3, s
Qt; \04
* 4* 3!
I
8.5
3,
1^
^3*
St.
s?
• S
+ 11
^ *
^ 1
о
>r
II
* I* «?[*
£ ^
1 >T
3, |~-
o St. Пч
*•» l-c
II
s
>T
J*
+
3
>?
q; \oz
St.
I'
S-5
284
3 I
2
a
5
в
2
X
5
»o
С
О С
;Го»
о.
1
-I
'в
06
VI
S £
2 g-
O &
§ as
§
'c'
A
2
So
a8!
*83
a4-
c X
§1
J3 ^
t VI 5
g >4 ^
VO VI II
— Q.
I t
* £
- ^
on с
06 5L
<:■
с w
sS ^
Э- ^
O ' ^
■w
4. t
f
О
h-.
■g J1
> =
&*
8 W"
ii
“S.
& Л
(4 О
't
Э* %
'ftf 3L
I
^ £* в
с
3 А *Ь
4)
II
-| (N
II
3
h-s
•3*
Is
s
3
2L * 1
- ^1
3^!
i <
& 'o
4 >? - ‘
^0? I
>.*%s ^
II 4 I ^
s'? X
Q *V
О 41 I
■» Ой в 1
О
- QC
VI
a *
VI II
O O
* *
+ -8
s 3
* *
^ I
'S О
"i -
> к
% ^
« с
5t &
+
о
*
3
о
-*
<4 С
i; =*
8 W"
и
<si С
3
c
з
>
*
Э*
Q.
о
II
w О
- i ^
% £ ^
* e ^
з a of
ii?
Mi
3- I ^
«© ->c
i л
о
«*5
^ 3
о <
06 ~ ^
н: •
о *
з
S?- ^
О w «Ч^в
■V —1 I
€Э
3L Э*
+
О
f*->
“i«i
i "к
э-
«И»
I
п в
+
(N
S
Э-
п о
\
14 с
§
S,
в
3
э-
Q.
I
О' w
^ . I
^ s
>■3» §.
V*
т
9 н 3 I
/-ч К О
^7 л
I
О о
II ^ ~
/—v ~ в О
3^3
X ^ 'Ъ
+
& 3 I
а Lc
Is
s. и
285
Продолжение табл. 11
8*1*
-I
8 +
5 4«J«4
■SI*
К
>5'-V
У*
f
?.
■j t 1
>%
ой
* 1
CQ
X ^
с 'Ъ
~ W
Ь а?
-W
с
А
О
I1
За?
I
S
с,
ъ
Л
I
О.
о
е
з
г**»
8 Гу^1
II
Л *■
А I
"8
чЬ
•«
O'
э-
«И!
~Ч
t %
% ~
-i А
ъЧ Т
В э-
7 „Л
с*>
I
3
II
1 ■*
5
IS
~ J
О
Б
9*
4 *
~o |
"б
9-
8W:
«■8
&
+
-|CN
«■8
&
I
rJ О
S
а
8о
S. .
с S
и
«в Е
г
vS
9?
Q.
*
I
%
Б
3
Б
>
А
> II
V
А
9?
5
5 «5
* 5 ^
? а*,*
I
5а
О ^
>’ I
’■'Ч §•
Jff.
* 1
а
*?
3
3
л
о»
I
Б
nS
•s*
о
■%
3
II
3
« к
^ X 3
* ш ^
^ S. Р? Н
^*38
^ 5 с $>
'Ъ х -» ^
\\
о I
>?
%
3
э?
Q.
I
3
с
3
с
*'»
о
%
3
х=
II
о "5
* t
3
в •'"Г4
n*. ;»
% 5 . . .
i & -
Б ^ "* О**,
^ о
Н ^
"3 * *
#ч? О.
%SX
3 I S
~в° *
л
■8*
s*.
I
3- I
€
и
<5.
ОС,
II
Q.
I
I
|3
& II
286
Изображение
dp1 Р dp р1’
1
~ 1
С /-Ч
\
А « 't 3.
1 1 -S 1->
/ v » N t
0с ■? >
* о*8 1
ь ^
X
X
•
« * ~ е4
*
^ 1 t ,ч*
^ ь* Г
Э8 S х
Ь
1
1
-С4 1 'S'
— ^ 3
V- о о
1*4*
*zy
?S 5
^ О
Ь t 5S
п* *-.
с О -
СЬ | »
•? 1
Формула обращения
1с4
i v
J= 1 Д
г 1'
3v % ч?
^ SL = Л. Ч.в *
t I j К *■ s
8 Hi L-S* $
II ffl
^ 11 Г
С4 I
3 ^ £
£ s "с
~ 1 -
% « * Jo Ъ
2 v * ^
^ а,е = ^Г4 «Ч* в
-g Ш t а ^ о
* ^ 1 Л"-»
"Hi ^ * 5
11 i « 2
/^ч Irvl в ч-^
с на- 1
vS II
Г*-» с с о „*в
^ = л *S «■* ■?«•*
^ J = t V 9-
М Э8 -£ ^ ^-N ^ ^
^ Э- мв ^ в
•Wi"
“ “|<ч- З."^
С4 II + 1 о
3 1
'*»»
Интегральное преобразование
функции /(/>, п)
t 1 «?
= % = I
0 й ^
1 3 & ^
j до^*е
t ^
^ to 1
«а. „ ^ * г-ч
t. 0 И w . о
и 04 ~ « 1 *
х. %-?<*&
К 1 Л *
* ^ 3t
1 J ос ®
^ * 5 1
Q XX V
§ <=■ % 5 «с
э- >.' -г §■ 1
b v
ч % ?*
1 £ 9- »■
^ ^ S ^ - 1
. Q? ^ Т g с>
§ 3 J 1 ^ 1 >1^*5 °
3 ^ ^
^ £_ /"о ^ ^ 1 « ^°
^ Н ^ .-- ^ “ 5. -S Д ' в
^ &•' 1 1 '15"Г +
i« £
Граничные условия
II
<5.
сз
I
CS
I
(N
Г4
s^
2- II
со м
2
о
•К
II
0.
|$
S- II
со •-
СО
1
СО
гм
§2-
& II
со ._-
03
ё Vi гГ
5vi »
° - о.
287
П.6. Интегральные преобразования функции f(r) для сплошного шара 0 < г < R температурное поле которого центрально-симметрично
Изображение
ii+ш
dP r dr
1
£Г £
В ~~.
7 1
1
S 3
Ч ХЧ
я 4IS
' Ък 1
X: |
X" X
* I «С!**
С -С -
‘я + 1
.ОС
Формула обращения
Sh
с
‘S3
11 s
£ ^
^ 8 pO H
«:
"IS
II
X
i
«Г»в * * &
II _ х
S *Wj
ч*"* Iм
"Is
+
X
14
С4 1
1 3
лг^з
W(S К
"S Я N « X
«W*
г*\ос
II
Интегральное преобразование
функции
1
1 * X
■w £ и
•v £
° *
II *
Об
S' .1
с 4.1 ш ^
X § 1"
- s
А *.* i | i
^ С И | 1
Ч Ч о »
ос *—» О £< Л1
11 х*
IX
S
X
1* . «
■в Ч* S
'Г 4* О. 7
л ? I 1 *3
а' 7Г w а 1
- £ 1 2 1
«К*—>о X * $
II > °
Л
К
4.
Граничное условие
I
о
II
©
II
О
II
=&!■&
о
II
*
II
к.
CJ
1
I
(N
3 рода
(А — относи¬
тельный коэф¬
фициент теп¬
лообмена)
Область
ОС
VI
VI
О
ос
VI
ь*
VI
о
ос
VI
•>»
VI
о
288
Продолжение табл. 11
х
* «I»*
ка
+ I
& *
&
с %
•S3 04
*
I
04
' £
N
04
I
*Д
з =*-
04 о
l 04
A
X I
£
f!
+
*
i
5.
•6
04
£
+
t
f*
04
?*
I
$
C4
I
A
* *
I l
£ £
•* +
M-
> л
■" X
7* X
* i
+ с
.4- *S3
Д X
X
*■*
= II
* *
X
04 СГ
W'
+ *
чгч в
ft
s.
ft
8PK|.
II
% X
§x ft; С
— С4 I I
04,
+
Д -
3, °4 r>
5 | eg
ajri
*5. os
* S J + *
i. ++ ^ '
S'S
N X .
1 x £ +
x
(V IM
7 &
<K
I
14
04,
+
N СЧ
$
2
§*jb
8-5
с и
8 I
5&
Q<
II
*
II
£
о
i *
I. £ *
'T g?
A £
r*-.
*
— *
• O X
* Г
I N
О X
О Л 9
V X
о
AI
А
К.
с
_ X
ос
т у
In I
04 ^
"£ *
“> I
ч^ь
^ X
\ !
X
I д S
гч Л I
0^ « 2
X g.
> л>*
■V J *М
't + ь
н ^
+
-IX
к
X
£9
-I •*
-~ *
1 X *.
I
Ос-
VI
VI
*
*1
I I
*&*
* *
I I
в О
Г А
1ч_
х5
•? !ч
35S
ter
¥ 1
1ч «?
*3
н w
х
290
Продолжение табл. 11
g.-ei-e
* "I*-
&
£
I
OC
I
rA
L S ^
& * i
at
? ~
!s 2,
X °t
Si
+ x
(4 с
5L
at "
+
£ -
l
О OS
at н
I ^
£ Sr
X4^
o-c
* I
c< ^
i es
X °i
S +
•< ^
+ X
w°£
Г4 С
5L
*
: I
£
e
+ +
о at -
О
f^-.
8
II
X ' ft;
7 N v2
+ ^rX
If;
- ~+- f *
il;
■a a
x +
Г*Ч X
ft; _ +
v м с J7^ '
* Sr
ъ - * л
‘So 1 ^
+0:5 £ •
+ I w ^T
xgis'o
*£■5 + ?
1 (yi - ^
£ 5 + X*
«i«f +
. ^-\ CJ
: .£*&
f "1
x
A
h-.
*
II
at
£ £
ft; о
HI
» t 5S
+ cr
*c7 ^
Nt ^
Л s
4"
'S
Г4 С
^cP
? ?
I I
* >N
f I
о ft;
£ e
+ +
cx>.
8.S
e s
11
at
II
ё
о
■s
-I *-
II
i*
S L
S.5S
>*o
S3
Ol. .
О +
* _
+ OH
Л
a
i
II
5*.
"V
?*->«
II
с
>S
T *
t£ X at
Lg*
а ж ft;
■ x
! If
fi i
if +
■s. ^ pj
|i I
IS*
* 5
8 &
1ч
S 1
=*.
X ьо
'V
II
>s
. II
s II *
X =t. c
0 $9 +
* ° О
1 -
1 ft;
O £
Л ***
A A
5L II
at 2
l ^
£ +
Se
_ £
t +
£
X
I
8.§
at
VI
VI
£
Is
I?
291
Продолжение табл. 11
П.8. Обобщенное интегральное преобразование функции /Ос) для бесконечной пластины, сплошного цилиндра и сплошного шара (область 0 < х < R)
а ®-
о ■ | fS
& I
с II
о *
g —
5 ^-3
* -
1+ к
■*| *5
I
S' '~к
$ А
А ^
♦ X
[■а ^
2
* i
+ 1^
=&j-S ?
>S I
s
s
I
(4
O.
'S
I
CL.
О
e
a
i^
~x
с
\
8 WI
Hk
5Ll
И с
О ^
II
■WI"*
+- —
: a
_ (4*.
cr ^
+ ?
11 i
si*
J
с
9>
■*
8 WI
Hk
II
h\*C
к
5*.
II
'T
i*
“■i
•i
Я4
sd
+
и
/e'
A
£1°
>s©
H\* 3
*
H
..s.
i
»о
о
II
%N
о
II
=&№
о
II
У-S
ОС
II
X
Is
a!
oc,
as
VI
VI
VI
X
X
X
VI
VI
VI
©
О
о
292
П.9. Интегральные преобразования Лежандра функции f(rj) для шаровых областей
П. 10. Интегральные преобразования функции /(х) для неограниченной и полуограниченной области
294
Его изображение
я
+
>■»
1^
— |^
+
ГЧ
1
1^
•4s
-14
Оператор L (/)
£|>
-ft
-|М
ъ\ъ
-ft
+ *£
Ъ X ,
|*Ъ 1
-I X
■^|Тз
1
■*w
•^r*
-ft
+
'bl X
<*> |ro
-IX
Формула обращения
Ьо
•JS
1
•V
8 8
+ т
Ъ Ъ
-IS
II
*
н,
X
&
JZ
i/i
1^ ^
»SeJ«
"П* X
II
X
N—'
xp(x) ■'♦*-</i*4M (»)// = 00/
QO
/-^4
1
Q.
X
0>
"tt"
H,
1^
8 8
JWi
« ■ e
II
X
V—✓
**>»
s.
1
< S
*«
S
X
2
8
*з
1
5
X
X О
*5
'h
1
&S
5: S
5
<4
-s 5
a
■f
2 ^
o.
X
u
с 1
v t
w
A 1
% Л
X v*
•*—>° и
^ *
x;
!*
!L *
8^0 *
II 'O'
8 '—» -
4*>
II
и
£7
и
H
s*
5*
1 ^
w w
l**%
S
l^v ^
£
1^
h
х 1
1
1
I
1
9 5
а >»
1
1
1
1
С—
Д
1
5
8 VI
8 VI
8
fe *
л
v S.
V
Э»
V
N V
Л
X VI
X VI
X
v S-
VO
о
yi
* VI
О о
VI ^
^ VI
О о
VI
s. vi
VI *
S.
О I
VI
VI
о
<
Э
Развитый подход может быть применен и в более сложных
случаях системы двух тел в условиях идеального теплового контак¬
та. Тепловые задачи такого вида связаны с чрезвычайно громозд¬
кими преобразованиями и лишь в отдельных простейших случаях
(например, при постоянных значениях краевых функций в постанов¬
ке задачи) можно выписать точное аналитическое решение задачи,
используя операционный метод как (практически) единственно воз¬
можный при решении указанного класса задач. Развитие теории
интегральных преобразований для такого рода усложненных моде¬
лей — открытая проблема аналитической теории теплопроводно¬
сти. Ее краткое изложение дается ниже.
Пусть Т((М, t), где М(х, у, z)eGi для /=1 и MgG2 для i— 2,—
решения задачи вида
дТ'
— = а (М)АТ, (М, 0+F, (М, /), MeGh t> 0; (5.280)
dt
Ti(M, OUo = ®«(AO. i'= i=2^MeG2, (5.281)
T\ (M, 0|«м. = T2 (M, t> 0, (5.282)
дТ{ (M, 0
dri
8T2(M, t)
MeS,, ’2 M
t> 0, (5.283)
AfeSa
^STdM, 0+pMMt t) = pn(PiiM> t), MeSi, t> 0. (5.284)
8rt
Здесь
Гд19 MgG1
a (M) =« w _
a2, MgG2
di = const, i= 1,2;
(Si + S0) — кусочно-гладкие поверхности, ограничивающие области
Gi (z = 1, 2); S0 — контактная поверхность областей Gx и G2, так что
‘So = G1QG2(Gi=Gi- -f5.-f50, z = 1, 2), при этом GjP)G2 = 0 (пустое
множество), п — внешняя нормаль к п' — общая нормаль к кон¬
тактной поверхности S0.
Пусть yl и (М, уп) — собственные значения и собственные
функции соответствующей однородной задачи
A4*in(M, >'„) + --?±-Чь{М9 уя) = 0, MeGh i= 1, 2, (5.285)
а (м)
296
(M, уп)|^0,
(5.286)
8Ч>1п(М, уп)
Л1
Sri
, (5.287)
MeSa Sn \MeS,
Г p.,8Ч>^ Уп)+pi24>m (M, y„)l = 0. (5.288)
L Sn _Us,
Обозначив
yif/fli = fin, Уп1а2 = m2j?2; m2 = a,/a2) (5.289)
перепишем (5.285) в виде
Д¥1л(Л/, Р^ + р^иМ, Р„)=0, MgGu (5.290)
Д^(М, рпНт2р^2п(М, Р„) = 0, MgG2. (5.291)
Условия (5.287), (5.288) остаются без изменения.
Зная /?„ и (Л/, /?„), можно ввести интегральное преобразование
вида
Т,(fin, о = ШЬ (M)Tj(М, 0 ¥и (М, p„)dVM, i= 1, 2, (5.292)
G
с формулой обращения вида
Т, (М, 0 = £ % (fin, t), 1=1, 2, (5.293)
л = 1 II * mil
вытекающей из возможности разложения искомой функции Г, (М, t)
в ряд Фурье по системе собственных функций {^„(Л/, /?„)}. Здесь
G = Gi + G2
h(M\ — MgG^
(M)-kla2, MeG2,
квадрат нормы собственных функций
цти||2=Я^(М)^2(м, pn)dv„=
= (;.,/а1)|Я^(М , p„)dV„+02ja2)\HVl(M, p„)dVM. (5.294)
G1 С2
297
Применим теперь преобразования (5.292) к (5.280), (5.281), пред¬
полагая, что дифференциальный оператор слева в (5.280) и оператор
(5.292) перестановочны и, кроме того, существуют все изображения,
выходящие по ходу действия. Получим
~=К JJJдг, (м, о (М, /?„) dvu+
+Я2 АТ2(М, t)42n{M, fodVM+F.Wn, t); t>0, (5.295)
■JJJ-
где
Ш, 0 = p„)dvu. (5.296)
G
Дальнейшие преобразования интегральных соотношений в
(5.295) основаны на использовании формулы Грина для операто¬
ра Лапласа, которая в случае системы двух сред имеет следующий
вид:
Л|аг,(м, ОЧ>„(М, ^)^=JJ|r(M, OAVbiM, P„)dvu+
G. G.
+
S<
S0
(5.297)
Преобразуя (5.295) с учетом (5.296) и граничных условий
(5.280) — (5.284), (5.286) — (5.288) найдем в пространстве изобра¬
жений
-ftf1
+-F [q>2 (M, t) ^ (M, pn)]M6S, da, t > 0, (5.298)
T,(fin, 01,-о=Фо(/и (5.299)
где Фц(Рл) — изображение начальной функции Фл (А/).
Находим решение задачи Коши (5.298) — (5.299) и возвращаем¬
ся в пространство оригиналов по формуле обращения (5.293), заме¬
няя все изображения краевых функций соответствующими интег¬
ралами вида (5.296). Получим решение исходной задачи (5.280) —
(5.284):
т /иж *\ V1 Л») г Го \2.vi
Ti (М, 0 = X ехр [ - у/a pn)2t)] х
Я-l ll“wl
х ГГГг>(А0Ф«(А0^(М, Рп)dvu+ £
JJJ л-1 ll^wll Pkl
G
I
x J|Jexp[-(V^P„)2(t-x)][<pk(M, х)Чы{М, P„)]^kdxda+
o Sk
0 G
xb(M)Fi(M, т)Ч?Ы(М9 Pn)dxdVM. (5.300)
Выражение (5.300) может служить рабочей формулой записи
аналитических решений задачи (5.280) — (5.284), если известно ре¬
шение существенно более простой однородной задачи (5.285) —
(5.288). Для случая /?*i = 0 {к — 1, 2) соответствующие выражения
выписываются из формулы Грина (5.297).
В качестве иллюстрации изложений теории найдем решение
следующей задачи:
dTi d2Tt
— = а(х)—, —A<x<0, i= 1; 0<х</2, /= 2; />0; (5.301)
dt дх2
Tt(x, OUo = 0, -l2<x<lu i= 1, 2; (5.302)
Tt(x, OU-у^Го, />0; (5.303)
299
Tiix, t)\x=0 — T2(x, OI*=o> *>0;
ST, (x, I)
dx
= A:
ST2(x, I)
x-0
dx
, />0;
a(x) =
T2(x, 0U-^=0, />0.
\au -l2<x<0;
[a2, 0<x<l2.
Решение соответствующей однородной задачи
d'Vm
dx2
dx1
+ #¥,„ = 0, -/,<*<0;
+т2^Ч/2л=0, 0 < x < /2;
^т(х, PX—it = 4u(x, P„)\x-,=0\
4'i„(*, WUo=4'2,(^ PX-o,
d¥i„(x, fin)
dx
= 1
<№гЛх, f>n)
x-0
dx
x-0
имеет вид
с cos (mp„l2)
'?in(x) = —— Sin P„ (x + Ъ);
cos (M)
^2n (x) = sin mp„ (x - /2);
0
(5.304)
(5.305)
(5.306)
mi2= Jb(x)4>i(x)dx=^j J4>Ux)dx+(^j Jn(*)</*=
-/1
sin 2mP„l2+aml2 sin2j9„/i
2 sin2 p„l.
'2,
o = ).2s/2,/(;., >/a2); m = /-; b(x)=<
v a2 I X2
— /x < jc <0;
, 0<-x</2,
/?Л>0 — корни уравнения tg(m/?/2) + cr tg(^/j) = 0. Полагая
300
и преобразуя (5.301) — (5.306) находим
(—\т0аптрп12
Ш, 0=- ' . {1 — ехр[—(л/д. /?„)2 ?]}
Pn^Pnh
и далее по формуле обращения (5.293) искомое решение:
Т,(х, 0-2Г. £ {l_exp[-(V^^t]) =
, Р„ (/i sin2 m/?„/2+tr/n/2 sin2 ft,/,)
7o(V2-22x) Д sin2mft,/2sinft, (x+/1) .
- . 2Г0 X Rn.lR,^ , exP [-(AW'l;
V2+M ft, (7i sin i»ft/2 + aml2sm2ft,/,)
_ , . OT, v sinft,/, sin mft,/2 sin mft, (/2 - x)
t) — Uo 2*i a n ^*2 Zo~i , 0 ; 4 X
n= 1
Pn M sin2 /nft,/2+aml2 sin2 ft,/,)
X {1 — exp [ — Ov/a, P„)2t] =
Wh-x)
X\l2+).2l\
£ sinftft sbmp„l2sinmp„(l2-x) , Г~ о \i л
-2T*L гтг-'!-», , . 2Д,чexP[-(vfliPn) t].
„=, Pn (Л sm2 mP„l2+aml2 sin2 ft,/,)
Задача. Покажите, что изображение вида (по Лапласу) 0(х, р) = (В/р)*
» _ _ .
* I — р.„+1 [е ,1"*—е >’2"J], где s=y/M2p2+p, у1я=х+2пх0, у2я=2(п + 1)х0~х
п = 0 +
имеет следующий оригинал:
e (X, г)= X f ехр (- ——) 1<р (у1п, тО - <р (Уь,, т')] dt';
-оni0 \ 2М /
</>&„■ 2')=/лГт' - л/у,„)+-— j ^ ^ 2 7i(2A/2 V*'2 y2^fn(y У m^)dy(i =1,2);
/„(*) = ( 1)"(5/Л/)exp^ МТ)^"(М
Ln(z) полином Лагерра; т/(т) единичная функция Хевисайда. К изображениям
такого вида приводится операционное решение уравнения гиперболического вида
в ограниченной области.
ГЛАВА VI
ОПЕРАЦИОННЫЙ МЕТОД И ЕГО ПРИМЕНЕНИЕ
К РЕШЕНИЮ КРАЕВЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ
ВВЕДЕНИЕ
Операционный метод является одним из самых эффективных аналити¬
ческих методов при решении краевых задач нестационарной теплопро¬
водности. Все задачи, для которых применим классический метод
разделения переменных, могут быть решены операционным методом.
Однако решения, получаемые методом разделения переменных, не
всегда удобны для практического использования. Например, иногда
необходимо иметь приближенные решения для начала процесса, кото¬
рые получить из классических решений трудно. С помощью же опера¬
ционного метода удается получить специальные решения для малых
и больших отрезков времени после начала процесса, что зачастую явля¬
ется главной задачей того или иного исследования.
Конечно, операционный метод, как и всякий другой метод, обладает
рядом недостатков; например: метод применим лишь для линейных
дифференциальных уравнений теплопроводности с линейными гра¬
ничными условиями, кроме того, возникают определенные технические
трудности, когда начальные условия в задаче заданы в виде функции
пространственных координат, или при решении многомерных задач,
или в областях достаточно сложной формы, когда найденное в простран¬
стве изображений по Лапласу решение задачи содержит специальные
функции, в индексы которых входит лапласова переменная.
Развитие операционного метода применительно к исследованию
процессов теплопроводности связано в первую очередь с работами
школы академика А. В. Лыкова [83], В. А. Диткина и А. П. Прудни¬
кова [41], а за рубежом — с именами Г. Карслоу и Д. Егера [55],
[56]. Число опубликованных монографий и статей, в которых излагается
метод применительно к конкретным задачам теплопроводности, чрез¬
вычайно велико, поэтому рассмотрим лишь основные идеи метода и
проиллюстрируем их на характерных задачах нестационарной тепло¬
проводности.
§ 1. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА
В основе операционного метода решения краевых задач теплопроводно¬
сти в соответствии с общим принципом интегральных преобразований
лежит следующая идея: вначале определяется не искомое решение
дифференциального уравнения, а функция, являющаяся результатом
некоторого преобразования искомого решения, причем это преобразо¬
вание выбирается с таким расчетом, чтобы преобразованное решение
можно было найти значительно проще; определив его, с помощью об¬
ратного преобразования находят искомое решение.
302
В качестве преобразования, позволяющего реализовать эту идею,
в операционном исчислении обычно применяют преобразование Лап¬
ласа, при котором функция f(t) преобразуется в функцию
f(p) = ]e-p4(t)dt,
(6.1)
О
где / — действительное переменное; р=а+ш — комплексное пе¬
ременное. _
Функция /(/) в (6.1) называется оригиналом, a f(p) — зображе-
нием; переход от оригинала к изображению с помощью преобразо¬
вания (6.1) обозначают символом /(От*/(р) [читается: функция
/(О переходит в f(pj] или /(/?) f (t) [функция f(p) является изо¬
бражением для /(0]; иногда применяют и такое обозначение
т. е. 1 \/р (1 переходит в 1//?);
2) если f(t) = t, то при а>0, интегрируя по частям, получим
В дальнейшем рассмотрим функции вещественной переменной О
удовлетворяющие следующим ограничениям:
1) функции f(t) являются кусочно-непрерывными и кусочно-глад¬
кими (т. е. /(0 и /'(/) на каждом конечном отрезке имеют не более
конечного числа точек разрыва и притом только первого рода);
2) понимая под / время, примем, что при / < 0 все рассматривае¬
мые функции от t обращаются в нуль, т. е. f(t) = 0 при t < 0;
3) с возрастанием t модуль функции /(/) растет не быстрее некоторой
показательной функции, т. е. существуют такие постоянные М0>0,
s > 0, что для всех t
Число s называется показателем роста функции / (/). Условие
(6.2) обеспечивает абсолютную сходимость интеграла (6.1) (как не¬
собственного) при a>s для всех точек р9 лежащих правее прямой
о
Например:
1) если /(0=1» то ПРИ <*>0
00
f(p)= j е-''d / = —
р ’
о
о
/(р) = р-2;
ао
3) если /(0 = eKt, то f(p) = ^ e~lP~K)i dt и при о > к получим
б
т. е. е"** -
р—к
|ИО|<М0е*
(6.2)
303
Rep > s (рис. 28). Действительно, если о > s, то
К е~Рг / (0 d/I < J е“а/1 / (/) | dt < Л40 J е“1а~5)* d/ = М0/(а—s).
оо о
Таким образом, в дальнейшем всюду предполагается, что о > s.
Отсюда следует, что отнюдь не всякая функция f(p) является изоб¬
ражением некоторой функции. Например, не существует оригинала
для функции tg р, так как полюсы тангенса расположены на всей
вещественной оси, а не слева от некоторой прямой a=s. Но можно
доказать, что если /(/?) является изображением, то соответствующий
оригинал является единственным в некотором смысле. Именно: две
кусочно-непрерывные и кусочно-гладкие функции /х (t) и /а(0» имею¬
щие одинаковые изображения, могут отличаться лишь в точках раз¬
рыва непрерывности, однако если f(p) является изображением некото¬
рой непрерывной функции /(/), то послед¬
няя определяется единственным образом.
Заметим далее следующее: если /(/)
ограничена во всем интервале 0 ^ / <С оо,
то, очевидно, достаточно выбрать о > 0;
если /(/) растет как tK (к > 0), то и в этом слу¬
чае достаточно выбрать a :> 0. Из (6.2)
следует, что функции вида е**2, tg Kt,
(/ — к)"1 (к > 0) не могут рассматриваться
в операционном исчислении, поскольку
для них это неравенство не может быть
выполнено для любого / > 0 ни при каких
постоянных М0 или s.
Вместе с тем ограничение (6.2) не являет¬
ся необходимым для существования изобра¬
жения; например, для функций/(/) = /“*/*
(или более общих: /(/) = tK, —1 < k <
< 0) условие (6.2) не выполняется для
всех /, но тем не менее интеграл Лапласа сходится и изображения
этих функций существуют при Re р > 0. С точки зрения физических
приложений условия 1) и 3) обычно выполняются для большинства
функций, описывающих физические процессы (t интерпретируется как
время). Условие 2), на первый взгляд, кажется искусственным. Однако
при решении физических задач нас обычно интересует протекание
процесса при / ^ 0, и для физики (в частности, теплопередачи) совер¬
шенно безразлично, как ведут себя искомые функции до начального
момента, принятого за момент t = 0, отсюда условие обращения функ¬
ций /(/) в нуль при t <. 0 физически вполне естественно. Необходимо
лишь иметь в виду, что под начальным значением /(0) функции /(/)
следует понимать предел
/ (0) = Нш / (/). (6.3)
/-*>0 +
Рис. 28
304
Изображение f (р) функции f(t) является аналитической функ¬
цией комплексной переменной р при Rеру s. Действительно, про-
00
изводная Т(р) существует, так как интеграл / (/?) =— J t е~Р* / (/) d/
О
абсолютно сходится при Rep>s. Заметим также, что из формулы
(6.1) следует
Т(р)—+ 0 при Re р = о—+ оо. (6.4)
В связи с этим приводим следующую теорему, полезную в практиче¬
ских применениях [42].
Все изображения f(p) обладают следующим общим свойством:
они стремятся к нулю, когда переменная ру пробегая вещественные
значения, стремится к +оо; это свойство сохраняется даже в том слу¬
чае, когда р + оо вдоль луча комплексной плоскости, образующего с
положительной вещественной осью угол, яо абсолютному значению
меньший я/2.
Сформулированная теорема дает необходимое условие, которому
должно удовлетворять каждое изображение; она позволяет установить
непосредственно, что та или иная функция / (/?) не может представлять
собой результат преобразований Лапласа какой-либо исходной функ¬
ции. Так, например, можно сразу сказать, что постоянная С или сте¬
пень рк (к > 0) не могут быть изображениями никаких функции
(имеются в виду функций, отличные от обобщенных, как, например,
6(0 1 [134]).
Однако условие /(/?)—► 0 при р + оо не является до¬
статочным, для того чтобы f(p) представляла собой изображение
некоторой функции; например, функция е“^ 0 при р + оо, но тем
не менее она не является изображением никакой исходной функции
[также имеются в виду функции, не принадлежащие классу обобщен¬
ных, так как е“^ 8(t—1)1 [40]; см. также (3.178).
Преобразование Лапласа (6.1) заменяет операции дифференциро¬
вания и интегрирования функции f(t) на соответствующие алгебраи¬
ческие операции над изображением этой функции f(p). В результате
этого оказывается возможным значительно упростить решение диф¬
ференциального уравнения теплопроводности (особенно в одномерном
случае), приведя его к стандартному методу, не зависящему от вида
уравнения.
Рассмотрим несколько основных свойств преобразования Лапласа.
I. Свойство линейности (теорема сложения).
Преобразование Лапласа является линейным, т. е. если ^ и с2 —
постоянные, то, по определению (6.1), можно написать
Cifi (0+cj„ (0 с,7, (р) + с£ (р),
или
т т
2ciM0->2 cj,(p), (6.5)
i=1 i*l
где с{ — произвольные постоянные.
305
II. Изображение производной. Пусть f(t)^f(p). Тогда
Г (0 “г* Pf (Р) — 1 (0)- в частности, если /(0) = 0, то дифференциро¬
вание оригинала сводится к умножению изображения на р:
]е-рЧ' U)<it = t~P4(t) +p]e-f,4(t)dt=pT-f(Q), (6.6)
Г, 0 0
так как при Re р = о > s lim ехр (—pt) I {() = 0.
(-►со
Аналогичным образом можно показать, что
f'(t)i+p4(p)-pf (0)-/' (0)
и вообще для любого конечного п= 1, 2, 3, ...
f{n) (о Рп Г(Р)-Р"-11 (0)-рп-* Г (0) /»-* (0). (6.7)
III. Изображение интеграла. Пусть /(0т^/(Р)- Тогда
интегрированию функции соответствует деление изображения на р
Щ. (6.8)
(/(х) dx -
Действительно, по определению (6.1) имеем
ОО Г / ~| 00 00 00
5 е”<Р* J / (т) И* — S f (т) \ e~pt ^ = — J е~рх f (т) dr = .
oLoJOt р о р
Здесь в процессе доказательства произведена перемена порядка ин¬
тегрирования.
IV. Теорема смещения. Пусть /(От^/(р)- Тогда
ек* /(От*Т(р —(6.9)
т. е. умножению оригинала / (*) на множитель ekt соответствует
в изображении замена переменной р на (р—к)
оо со
J e~Pl eKt f(t) dt = J е“^“'с)* / (/) dt = f(p—к).
о о
V Теорема запаздывания. Пусть /(От^Ар)* Тогда
/(* —*о)т*е-*'«7(р)| (6.Ю)
где постоянная /0 > 0.
Имеем
]е~Р* f(t — t„)df= J e-"<'--">/(T)dT =
о
О со
J х) / (т) dx -fe~pr° J e_pl / (т) dx = е~^°/ (р),
306
так как /(т) = 0 при — t0^T<0. Итак, сдвигу графика функции
/ (t) в направлении оси t на отрезок /0 соответствует умножение
изображения на e~pt°. Функция /(/ — /0) носит название функции
запаздывающего аргумента и обозначается как fto (t). При этом пред¬
полагается, что функция ft. (t) равна нулю при t < tQ и принимает
те же значения, что и функция / (/)• но на t0 единиц аргумента
«позднее».
VI. Теорема умножения изображений (теорема Бо¬
ре л я). _ _
Пусть /, (0 Л (р) и /2 (О -Г- f2 (р)- Тогда
/ /
Гх ср)Ъ (р) «н- ? и (т) т- х) dt=j /, (т) /, (t т) dr. (6.1 о
о о
оо
Выражение )М^—т)(1т, как отмечалось в гл. V, называется
о
сверткой функций fx(t) и /2(0- Отсюда соотношение (6.11) можно
сформулировать следующим образом: произведению из изображений
соответствует свертка из оригиналов этих функций. Формула (6.11)
имеет большое значение в практике применения операционного ис¬
числения. Имеем (меняя порядок интегрирования)
00 Г t '1 СО 00
§ е-*' 5/х(т)/,(/— x)d/ d/ = 5 /х (x)dT J e~Plft(t—x)dt =
0 Lo J о т
00 CO
= 5 e-pT/i (x)dt 5 e~pa Iг (и) du = 7t(p)J2(p). (6.12)
О о
VII. Теорема подобия. Если f (t) f (Р)> то
f(Kt)-^ (\/к)Г(р/к)(к > 0). (6.13)
Доказать соотношение (6.13) предоставляем читателю.
VIII. Теорема Эфроса. Эфрос доказал исключительно важ¬
ную теорему, с помощью которой можно находить оригинал для
изображений, представляющих собой суперпозицию элементарных
функций. Из теоремы Эфроса как частный случай вытекает теорема
Бореля.
Пусть f(p) есть изображение функции f(t), т. е. /(От*/(Р)-
Тогда оригинал изображения / [ф, (/?)] <ра (р) дается формулой
OD
Г[ф, (Л)] (р) *т S f (т) Ч (т- 0 dT» (6-14)
о
где ¥ (т, t)—оригинал функции 'ф2 (р) ехр [—тф, (/?)], т. е.
^(т> 0 "г* е_Х(^1 (р) Ф* (Р)- (6-15)
Для доказательства теоремы необходимо использовать формулу
обращения для преобразования Лапласа (см. ниже).
307
IX. Теоремы о предельном значении представ¬
ляют большой интерес для практики. В ряде случаев при решении
дифференциального уравнения теплопроводности достаточно огра¬
ничиться знанием температурного поля вблизи начального момента
времени (при очень малых t) или, наоборот, для моментов времени,
близких к установлению стационарного состояния процесса (для боль¬
ших /). Преобразование Лапласа в этом отношении обладает весьма
полезным свойством, состоящим в том, что по асимптотическому пове¬
дению изображения ~f(p) можно сделать соответствующий вывод об
асимптотическом поведении оригинала.
Имеют место следующие теоремы (приведем их без доказательства;
об этом см. [42]).
1. Теорема о начальном значении. Если lim f\t) существует, то
t-+ 0-h
Hm/(/) = lim/?/ (p). (6.16)
/—И' + 0-*OO
Формула (6.16) дает возможность по известному изображению /(/?)
определить начальное значение оригинала /( + 0), но только в том
случае, когда заранее известно, что /(0) существует. Например,
оригиналу /(/) = /_1/2 sin а/2/ (а > 0) соответствует изображение
f(p) = y~lipexр(—|/"а/?) sin Vар. Очевидно, что limpf(p) = 0, но
P-+GO
lim / (/) не существует. Теорема (6.16) особенно важна и в тех
t-+ и
случаях, когда изображение имеет очень сложный вид и соответст¬
вующий контурный интеграл не может быть вычислен, или, если
нас интересует оригинал в начале процесса. Тогда, разлагая /(/?)
в асимптотический ряд (для больших р) по формуле обращения
(6.26)г получим оригинал в виде ряда для малых значений I.
2. Теорема о конечном значении. Если lim / (/) существует, то
t-+ 00
lim /(/)== limp/ (р). (6.17)
t —► CD P-* 0
Здесь также без предварительной проверки существования ориги¬
нала при t—► оо могут быть допущены ошибки. Например, е*
1 /(/? — 1) и lim р/(р—1) = 0, в то же время lim exp (t) = оо.
0 t—► со.
В данном случае несоответствие произошло потому, что интеграл
Лапласа для функции ехр (/) существует лишь при Rep > 1 и,
отыскивая lim /?/(/?) при р—► 0, мы вышли за пределы области ре¬
гулярности функции f(p)=\/(p—1).
§ 2. ФОРМУЛА ОБРАЩЕНИЯ для ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Перейдем теперь к обратной задаче — задаче нахождения оригинала
функции по известному ее изображению. Очевидно, для решения
этой задачи необходимо уметь решать интегральное уравнение (6.1),
в котором следует теперь считать известной функцию/(р), а неизвест¬
ной функцию /(/). Рассмотрим не строгий, но зато конструктивный
вывод формулы обращения преобразования Лапласа (строгое дока¬
308
зательство этой формулы см. в курсах теории функций комплексного
переменного, например в [92]), используя для этой цели теорию ин¬
теграла Фурье.
Функция /(/) может не разлагаться в интеграл Фурье (если
сю
J|/(/)|cU расходится); возьмем вместо нее функцию
*> 0 (а>0),
о, \<о. <618>
Так как теперь fx(t) удовлетворяет условиям разложения ее в
интеграл Фурье и /,(*) = О при / < О, то можно записать, исполь¬
зуя комплексную формулу интеграла Фурье,
+ 00 00
S e'W, da) S /i(T)e"‘“TdT- (6‘19)
— oo 0
Подставляя (6.18) в (6.19), имеем
+ 00 00
Д/) = -^-е0/ J еШ( dco J /(т) e_(a+^)Tdt.
— oo О
Полагая в этой формуле р = а + но, так что dp = /dco, и исполь¬
зуя (6.1), получим формулу обращения для преобразования Лапла¬
са (формула Римана—Меллина)
G+ too
S eP(7(j»)d/7(o> s), (5.20)
0—1 оо
С + I оо
где символ J в правой части обозначает, что в качестве пути
О—Юо
интегрирования взята прямая Rep = a, параллельная мнимой оси.
Действительные числа а выбираются так, что все особые точки
подынтегральной функции в (6.20) лежали слева от прямой a = const
[иными словами, интегрирование в (6.20) должно происходить вдоль
прямой, лежащей в области сходимости интеграла Лапласа (6.1)].
Отметим при этом, что если: 1) функция f(p) регулярна в полу-
+ СО
плоскости Rep = a>s, 2) lim f(p) = 0, 3) интеграл J / (р) dp схо-
Р-*™ — оо
дится, то функция f(t), определяемая формулой (6.20), не зависит
от а и является оригиналом для изображения f(p). В то же время
эти условия являются лишь достаточными, но не необходимыми, при
которых функция f(p) является изображением оригинала f (t). По¬
этому если f(p) не удовлетворяет этим условиям или хотя бы одному
из них, то это еще не значит, что соответствующий интеграл Рима¬
на—Меллина не дает значение оригинала, отвечающего /(р). Мето¬
дика вычисления контурного интеграла (6.20) подробно изложена
в руководствах по теории функций комплексного переменного, по¬
309
этому ограничимся здесь лишь краткими сведениями в той мере,
в какой они понадобятся для дальнейшего изложения.
Большинство задач, рассматриваемых в теории теплопроводности,
распадается на два класса в зависимости от свойств функции f.(p)
(в наших задачах это будет функция Т (М, р) как функция р> где
р—лапласова переменная, М — пространственная точка):
1. Функция f(p) является однозначной функцией р со счетным
множеством полюсов, лежащих вдоль отрицательной вещественной
оси. В этом случае вычисление интеграла (6.20) производится с по¬
мощью теории вычетов по следующему правилу.
Контур интегрирования замыкается большой окружностью Г ра¬
диуса /?, не проходящей ни через один полюс подынтегральной
функции (рис. 29). Тогда, если f (р) удовлетворяет условиям
|Г(Р)| < С/?-\ когда p = Re^,
— л<<р<л, R>Rq> 0, (6.21)
где R0, С, к—постоянные и к > 0, то Je^f/(p)d/?, взятый вдоль
дуг ВВ'С и АА'С окружности, стремится к нулю при R—+ оо для
t > 0 (Лемма Жордано).
Поэтому при выполнении этого условия интегрирование вдоль
прямой АВ может быть заменено интегрированием по замкнутому
контуру ABC А при R —► оо и согласно теореме Коши [82], интег¬
рал в (6.20) в пределе равен сумме вычетов относительно полюсов
его подынтегральной функции
а + < оо
S e^/(0d/ = 2Resfe^/(p)j. (6.22)
а—i сю Р == Рк
Этот случай обычно встречается в задачах теплопроводности в
ограниченных областях. Практическая реализация формулы (6.22)
происходит %с помощью теорем разложения Ващенко—Захарченко
(см. ниже).
310
2. Функция f(p) имеет точки ветвления и только конечное число
полюсов. Пусть п—число полюсов, т—число точек ветвления;
построим около каждой такой точки контуры ск, как показано на
рис. 30. Тогда- внутри полученного замкнутого контура функция
ept I (р) однозначна и не имеет особенностей, а значит, по теореме
Коши можно записать:
а+ шп
_ а _ п тп
*2лГ J е*НР)*Р + Ш 2 Je^7(p)dp = 0.
о—шА ск ск
(6.23)
Если f(p) удовлетворяет условиям (6.21), то при R—+ оо ин¬
тегралы вдоль дуг BF и АС большой окружности Г стремятся к
нулю; первая сумма в (6.23) приводится к сумме вычетов функции
ept f (р) относительно полюсов, взятой с обратным знаком (из-за
отрицательного обхода окружностей у*), вторая сумма дает сумму
вещественных интегралов по «берегам» разрезов при обходе точек
ветвления и, возможно, будут слагаемые при интегрировании по
маленьким окружностям ук вокруг точек ветвления. Таким образом,
можно записать
п ] т С
fit) = 2 Re s»-p * [еЯ' f Ml—w 2 JePt I ip) 6p- (6-24)
K= 1 K= 1 cK
Заметим, что при рассмотрении полу ограниченных областей функ¬
ция Т (М, р) обычно имеет точку ветвления в начале координат
(Р = 0).
В конкретных задачах, где используется операционный метод,
нет необходимости каждый раз вычислять контурный интеграл
(6.20). Существуют таблицы интегральных преобразований, в част¬
ности для преобразования Лапласа, содержащие большое число
оригиналов и соответствующих им изображений [10], [37]. Лишь
в том случае, когда в таблицах отсутствует необходимый оригинал,
следует отыскивать его непосредственно, применяя формулу обра¬
щения (6.20).
Рассмотрим далее теоремы разложения Ващенко—Захарченко
для преобразования Лапласа (6.1).
Первая теорема разложения. Предположим, что изо-
00
бражение J(p) можно представить в виде ряда /(/?)= 2 /* (Р)» схо*
_ _ к = 0
дящегося в, полуплоскости Re/?>s, причем f{p) и fK(p) удовлетво¬
ряют указанным выше достаточным условиям, при которых они.
являются изображениями некоторых оригиналов. Тогда, согласно
(6.20),
/(0 = ir1
а—1 а,
311
Если почленное интегрирование этого ряда законно, то
оо o + icc
00 OfK*> да
/(0=2о2^г J e/’tfK(/?)dp= 20МО. (6.25)
a+ioo
где МО-^/ЛР)*
Пусть, в частности, f (р) для значений р, удовлетворяющих не¬
равенству 1/|р| <Р» разлагается в сходящийся к ней степенной ряд
по отрицательным степеням р
причем ряд справа в (6.26) не содержит постоянного слагаемого, так
как для него не существует оригинала. Если ряд в (6.26) сходится
равномерно при | \/р \ < р, то можно применить почленное обратное
преобразование и, согласно (6.25) и соотношению р{к+ h Л" О/я!) tK,
можно записать
Вторая теорема разложения и ее обобщение.
С помощью второй теоремы разложения строится оригинал в тех
случаях, когда изображение J(р) задано в виде отношения двух
многочленов
причем т < п. Случай т^п не может иметь места, так как при
наличии его оригинал /(/) будет содержать обобщенные функции
6*(0- Предполагая, что оригиналы, с которыми приходится иметь
дело, в теории теплопроводности не содержат таких функций, огра¬
ничимся случаем т < п. В соответствии с формулой (6.22) запишем
где рк—корни знаменателя /2 (/?) = 0 (полюсы функции e^/i (р)//2 (Р))•
При нахождении корней уравнения Т2{р) = 0 могут иметь место
два случая:
а) корни plt р21 ..., рп — различны; в этом случае воспользуемся
известной из теории функций комплексного переменного формулой
вычисления вычета функции JХ(р)/Т2(р) относительно простого по¬
люса р = рк
00
(6.26)
00
(6.27)
/ (Р) = f 1 (p)/f* (Р) = Фтра + + (6.28)
+ • • • Л-bxP + b^!(anpn + an-\Pn~l + • • • + axp + a0),
n
(6.29)
Это дает следующую теорему разложения!
п _
/(/) = £ (6.30)
* = 1 /2 (Рк)
б) корни рк многочлена /2 (р) = 0 имеют кратность гкУ т. е. ко¬
рень рх встречается гх раз, р2—г$ раз, ..., рк — гк раз (гх + г2 +...
... + гк = п). Если для этого случая воспользоваться известной фор¬
мулой вычета функции fi(p)/f2{p) относительно полюса р = рк крат¬
ности гк
то это дает следующую формулу для теоремы разложения!
/(0 = Е -jrznr lim —7-гг [(р ркУ*ер' у~т]• (6.31)
кт\ 1,1 Р-+иш dр * I Мр) J
Если среди корней знаменателя J2 (р) встречаются как простые,
так и кратные, то оригинал / (t) вычисляется соединением формул
(6.30) и (6.31). Вторая теорема разложения может быть обобщена
на случай, когда изображение J(p) представляет собой отношение
двух целых трансцендентных функций. Пусть эти функции таковы,
что изображение J (р) =* Ti/f2 имеет полюсы, вещественные части ко¬
торых ограничены и, следовательно, лежат левее прямой Re/? = s,
параллельной мнимой оси.
Пусть также f {р) =Ti(P)/f% (Р) имеет вид
Т (р) = /1 2 (Р) = (^o + ^iP + ^2P2+ ... + •• .)/(aiP+fl2p2+ • • •)» (0.32)
т. е. знаменатель f2(p) не имеет свободного члена. При этих усло¬
виях можно показать, что оригинал /(/) имеет вид
00 ' _
f(t) = Y, 4^L ер«<. (6.33)
к- I ^2 (Рк)
где предполагается, что все корни рк уравнения /2(/?) = 0 простые.
В противном случае оригинал может быть вычислен по обшей формуле
МО = 2 Re sp=D [е^7, (р)/7* (/>)]• (6.34)
К е= 1
Заметим, что теорема (6.33) получила наибольшее распространение
в аналитической теории теплопроводности.
В операционном исчислении иногда применяется вместо преобра-
0D
зования (6.1) несколько иное преобразование f(p)=p^e~ptf(t)dt,
о
так называемое преобразование Карсона — Хевисайда. Свойства преоб¬
разования Карсона — Хевисайда легко выводятся из свойств преоб-
313
Основные правила операционного исчисления
Таблица 12
№
п/п
но
00
7(р)= J e~pt /(/) d*
0
Примечание
1
o+i со
,(0“53 § eW7 (р) dp
0 — 1 ОО
Tip)
Формула об¬
ращения
2
т
2 (0 (с,= const)
i = 1
т
2 с<'Мр)
1= 1
Свойство ли¬
нейности
3
4
по
(0 (п 3* 0)
р7(р)—>Ф),
pnf (р)—рп~Ч (+0)—
-р"-2/'(+о)-
_/W-D (+0)
Изображение
производной
5
1
J /(т) dt
0
Интегрирова¬
ние оригинала
6
7
tf (0
<л/ (0(«^0)
-Г(р)
(-1)" /<п>(р)
| Дифференци-
<J рование изобра¬
жения
8
tw
СО
J Г(р') dp'
Р
Интегрирова¬
ние изображений
9
10
00
t
00
-^/V)dp'
Р
Р
lj/V)dp'
0
1 Интегриро¬
вание оригинала
И
е*Ч (/)
Т(р—ь)
Теорема сме¬
щения
12
/(/-<„); /(/) = 0, / < о
е-^оГ(р)
Теорема за¬
паздывания
13
t (к() (к > 0)
Т*(*)
Теорема по¬
добия
314
Продолжение табл. 12
№
п/п
Ш)
со
7(P)-J e~ptnt) it
0
Примечание
14
t
j /lW/i (<—T)dx
7l(p)7.(P)
Теорема ум¬
ножения изобра¬
жений
15
OD
J/(т)ЧЧт. 0 dT
*(T, 0
7 [ф1 (P)] фг (P).
е~тф,(‘,)ф> (P)
Теорема
Эфроса
16
v*i]*4t '(T)dT
Частный слу¬
чай теоремы
Эфроса
17
j) I/|X
x(3 K?)]/W*
y'1’,i/J(r)—функция Бессе¬
ля высших порядков [41]
Частный слу¬
чай теоремы
Эфроса
18
0 + f •
2^7 ^ 7\(<*)Tt(p—a) da
n — i со
Теорема Грин¬
берга об умноже¬
нии оригиналов
у fi(P«) cv
U (p) _ /l (p)
Теорема раз¬
ложения
19
Pt—корни уравнения
f2(p) = 0
/а (P) t-т . . .
И d«(p—P.)
x-l
разования Лапласа, так как изображение функции /(р), по Лапласу,
соответствует изображению J(p)/p по Карсону — Хевисайду. Послед¬
нее обстоятельство нужно иметь в виду при пользовании таблицами
по операционному исчислению, которые составлены как для преобра¬
зования Лапласа, так и для преобразования Карсона — Хевисайда.
Заметим далее, что и теоремы разложения, выведенные Хевисайдом
для преобразования Карсона — Хевисайда, также имеют иной вид
315
(в формулах Хевисайда появляется дополнительное слагаемое
/, (0)//2(0)).
В табл. 12 приведены основные правила операционного исчисления
(сюда включены также и правила, не рассмотренные выше).
§ 3. ОПЕРАЦИОННЫЙ МЕТОД ПРИ РЕШЕНИИ КРАЕВЫХ
ЗАДАЧ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
В этом параграфе на ряде задач покажем в действии аппарат опе¬
рационного исчисления. Задачи расположим по степени трудности,
рассмотрев при этом характерные случаи для преобразования Лап¬
ласа. Всюду предполагаем, что отыскиваемые функции принадле¬
жат классу функций, для которых применимо преобразование Лап¬
ласа по переменной t.
Найдем температурное поле полуограниченного стержня (*^0), теплоизоли¬
рованного с боковой поверхности, при нулевой начальной температуре; на торце
стержня х = 0 осуществляется теплообмен со средой переменной температуры
dT/dt=a (д2Т/дх2), х > 0, t > 0; (6.35)
Т (*, 0) = 0, * SS 0; 1 =Л [Г (0, /) — ф (<)], < & 0; (6.36)
ОХ \х = о
I Т(х, 01 < + », X > 0.
Положим
(6.38)
Т (дг, р) = j, e~ptT (X, t) dt (6.37)
о
и применим преобразование (6.37) к уравнению (6.35) и граничным условиям
(6.36). Для этого [поступая обычным образом, как подробно показано в гл. V,
см. (5.10) — (5.12)] умножим обе части (6.35) на ядро преобразования (6.37) и
проинтегрируем по / в промежутке (0, оо). Учитывая нулевое начальное условие
и формулу (6.6), а также предположив, что операции интегрирования и диффе¬
ренцирования справа в (6.35) перестановочны, находим для Т (х-, р):
^._£г = 0, * >0;
d х2 а
4т-1 =h[T (0, р) — ф(р)]; \Т{х, />)| < + оо, х > 0,
ах |*sso
где Ф (р) «Ч- ф (0-
Общее решение уравнения в (6.38) имеет вид
Т(х, p) = A(p)exp^yLr /~р^ + 8(/>)ехр^—
где~Я(р), В (р) — постоянные относительно х* но зависящие от р величины.
Постоянную А следует положить равной нулю, иначе не будет выполняться
условие ограниченности функции Т(х, р) при х—► оо (условие Т(х, р) < + оо).
Постоянную В найдем из граничного условия при * = 0 (6.38): B = <p(p)[l-f
-j- (/г Таким образом, решение задачи в пространстве изображений
имеет вид
Для нахождения оригинала в (6.39) воспользуемся теоремой Бореля (6.11).
Находим из таблиц изображения
= П(*. <) =
(6.40)
l~1[l + (hAriV~peXP(
=^гехр ^ехр \-xh+{]Г~а h)i erlc (jjhf+ }r^i)•
Кроме того, L”1 [ф(/?)] = Ф(0» отсюда
t
Т (х, 0=5 Ф (т) Т0 (х, t-x) dx. (6.41)
о
Рассмотрим некоторые частные случаи функции ф (/).
1. Если температура среды постоянна и равна ф (/) = Гс, то у (p) = Tjp и,
согласно (6.39), имеем
В таблице изображений находим
^[pd + ih Г~а)-'\П, еХР(_ф% V~P)\=a
t=Ф*(т?^‘)_exp(/,JC+a/,S0Ф*(yiЬг+/, (6-43)
Отсюда решение задачи можно записать в виде
* \_еЛ* + аЛП ф»/ 1_ + /) (6.44)
V, 2 / V, 2 /
Если коэффициент теплообмена а очень велик, то h—► оо. Тогда из гранич¬
ного условия (6.20) следует Т (0, /)==ф(/)* т. е температура конца стержня ста¬
новится равной температуре окружающей среды. Соответствующее температурное
поле можно найти из (6.44) предельным переходом при h—► оо, но проще это
сделать в изображении (6.39) или (6.42) при h—► оо. Это дает Т(х, р) =
= р"17’сехр (—х Y Р/Y а) и по таблице изображений находим (см. также (5.90)
при 7\> = 0)
Т (х, 0/7’с = Ф* [х/(2 v~ai)}. (6.45)
Температурные кривые* соответствующие решениям (6.44) и (6.45)* приведены
в монографии [83] А. В. Лыкова.
2. Пусть ф (/) =к/ (/с = const), h =оо. Так как t \/р2, то (6.39) дает (при
h —► оо) _
т (X, р) = (к/рг) ехр (— х У~р! У~а). (6 46)
Если ф (f)=Ktn/2t где п — любое положительное целое число и Л = оо, то из
(6.39) найдем при ф (р) = кГ (1 -\-n/2)/pn/'i + l
Т р) = КГехР х V~p!V~b)- (6-47)
Оригиналы (6.46) и (6.47) находим по таблице изображений, используя сле¬
дующую формулу:
L'l[y^7*~*У~Р] = МП/Чпф'(-^т)> п = °> *• 2* - ^48>
Это дает
Т (х, () = кГ (1 + л/2) (4/)"/2 1«ф* [х/(2 y~at)]. (6.49)
317
Здесь
)"Ф‘(г) = J 1"->Ф*.(0 dI, п = 2, 3, 4, ...
г
оо
\Ф* (Z) = 5 Ф* М*
(6.50)
(6.51)
Для случая л = 1, 2 (температура поверхности есть полином от / или /1/а)
решение (6.49) можно записать в виде табулированных функций по формулам:
*1ф» (г) = —J- e~“—гФ* (г),
У я
!*ф* (г) = 1 j^(l +2га) Ф* (г)-у= ге-г* j.
3. Рассмотрим интересный для практики случай периодической импульсно
меняющейся температуры среды (рис. 31). Прежде всего запишем аналитически
температуру окружающей среды. Для этого вос¬
пользуемся единичной функцией Хевисайда
?(*)
А
8
2t
Jt,
в -а
%
л (0
_\1. '
~/0, /<0.
(6.52)
Единичные импульсы АВ и CD длитель¬
ностью *о с амплитудой q0 можно записать с
помощью (6.52) соответственно в виде
(AB):q0 h (0-t| (*-«];
(CD):-?0 [т|(/_/в)—-n(/—2/0)].
Последовательность импульсов с периодом
2tQ выразится в виде бесконечной суммы сле¬
дующим образом:
Рис. 31
<Р(0 = 7о 2 [л (/—2к/о)—Л (#—#0—2«/о)] —
к=0
Яо 2 [Л (* — — 2ас/0) — r\ (t—2/0 — 2/с/0)].
к=0
(6.53)
Итак, температура среды, представляющая собой периодическое, импульсное
возмущение прямоугольной формы, аналитически записывается в виде (6.53).
Найдем изображение Лапласа функции (6.53):
00 00
?</»>-*£ J е-я»[л(< — 2/с/0)— т)(< —10 — 2Kt0)]dt—
к = 0 О
оо оо
-‘fo'Ei S e~pt [4 0-<o-2«g-T| (<-2<0-2кд] d/ =
к= 0 0
» Г 00 ОО 1 00 р ОО
= ^ e-z^df— J e-ptdt\ — ^ t~P4t —
к-0 \-2Kt0 (2/е + 1)t0 J к= О L(2\+l)
е-Р* dt
(2к + 2) tо
e~
=3o
P
V e—(2/c + l) e
^ U=o «=0
1)*0
oo oo
У* e-2Kf0P__^ e~(2/C+ 1) t0p
-K-Q к-0
~(2k+ 2) t0p _?o i—e~p/° _ q0
p i +e“pt° P
th£&L.
(6.54)
318
Таким образом, решение задачи (6.35) — (6.36) в пространстве изображений,
в случае когда температура окружающей среды есть функция (6.53), согласно
(6.39), имеет следующий вид:
Т(х, р)= ?oshy°/2) / * (6.55)
pch (р/0/2)[1+(Л Vl>] \ )
В таблице изображений отсутствует оригинал, соответствующий изображению
(6.55), поэтому воспользуемся формулой обращения для преобразования Лапласа
контурным интегралом (6.20) и запишем
0 + 1 ® х т/ —
'г (х а _ ?о С Wо/2) e V a dd (6 56)
Jiepch (p/0/2) [! + (/■ (' )
где Re p > 0 (показатель степени роста функции Хевисайда (6.52) равен s = 0 и
область сходимости интеграла Лапласа в (6.54) Rep = a>0).
Контурный интеграл (6.55) следует вычислить непосредственно (это очень
полезно, так как таблица изображений, естественно, не может охватить все слу¬
чаи, встречающиеся на практике).
Для подынтегральной функции в (6.55) начало координат (р = 0) является
точкой ветвления вследствие присутствия \Г~р в показателе экспоненты; кроме
того, знаменатель обращается в нуль в точках, определяемых из соотношения
ch(p/0/2) = 0 [множитель (l +(/ю)~1 У~р) в нуль не обращается]. Найдем корни
этого уравнения:
ch (pt0/2) = cos i (pt0/2) = 0; ipt0j2 = ± (я/2 + 2ля),
откуда
p„ = ± (2л +1) 7ii/t0t л = 0, 1, 2....(6.57)
Для вычисления интеграла (6.56) возьмем та¬
кой контур, внутри которого не содержится на¬
чало координат. Рассмотрим замкнутый контур
(рис. 32), где АВ параллельна мнимой оси и на¬
ходится на расстоянии о от нее. Окружность Г
радиуса R с центром в начале координат пересе¬
кает прямую Rep = o в точках /4 и В, мнимую
ось в точках А' и В'. Вдоль отрицательной ве¬
щественной оси проведен «разрез»; пусть е—ради¬
ус малой окружности с центром в начале координат.
Эта окружность открыта в DE, а окружность Г—в
CF. Если р = ре‘ф, то аргумент р равен (—я) на
CD и л на Ег. Таким образом, в области, огра¬
ниченной этим замкнутым контуром, подынтег¬
ральная функции однозначна и имеет простые
полюсы в точках ± (2я+1) Jii/t0. Если окружность Г имеет радиус R, равный
2nnift0, то она не будет проходить ни через один из полюсов подынтегральной
функции (причем, при л—► оо также и R—► оо).
Возьмем интеграл
1
2ш
§
д» sh (р<0/2)
pch(pt0/2) [l+(/i У~а)~1 V~p]
—4= +cl
l^e dp
(6.58)
по замкнутому контуру. Согласно__теореме Коши, интеграл (6.58) равен сумме
вычетов подынгегральной функции Т (х, р) относительно особых точек этой функ-
319
ции, находящихся внутри выбранного контура, т. е.
ы a +2М+2И+1И+
ABFEDCA
АВ
п
BF
FE
ED
(6.59)
DC СА к=1
Так как для подынтегральной функции справедливо неравенство
th (pt0/2)
X
~aV Р
h Y~a
< p312 "
на BF и AC, то условия леммы Жордано (6.21) выполнены; следовательно, интег¬
ралы вдоль дуг BF и АС стремятся к нулю, когда R—оо. Отсюда и из (6.59)
следует, что интеграл (6.58) равен сумме интегралов вдоль, EF, CD и вдоль
маленькой окружности, когда R—► со и е—>-0, сложенных с суммой вычетов
подынтегральной функции относительно всех особых точек подынтегральной функ¬
ции. В интегралах вдоль EF и CD положим соответственно р = ре1Я и р = ре”1Л;
при этом в первом случае J/ р= |/ реш/2 =/ У~р, а во втором У~~р= }/~ре*"ш/2 =
=—< У~р-
Интеграл вдоль EF
1 2т ^ ,
др th (р/р/2)
[\+i(h Vl>]
dp.
Интеграл вдоль CD
=_LC 1
г 2ni J p Г1 — t
<?„ tli (p<0/2)
+—-=.v P-PI
e V.a dp>
отсюда
Ti(x, t) =
+
, j <h sln cos exP dP- (6-60>
Для вычисления интеграла по малой окружности положим р=ее‘ф (—я<ф < я).
Имеем
= lim —L
3 е_*. о 2т
eiv ) ехр [(— е^е,<р) — -£= V ее1'4’72 1
V г , /-.i/- Va 1 <ее*Мф = 0.
J ее1ф [l + (h У^а) У^ё ехр (iq>/2)J J
Для вычисления вычетов в точках (6.57) воспользуемся обобщенной теоремой
разложения (6.33), которая в данном случае примет вид
Тг(х, 0 = У +Y, •(^^-ep«'i
^оЧЛРп) / Рп= (2ri+ 1) л(//0 +?0\ft(ptt) /рп = -(2ч +
где (6.55) записано в виде
<?о sh (Р<о/2) ехр — у= Г7)
pch (р/0/2) [l + (/i |/”а) 1К~р]
9oP-I[l + (ft F^)”1 l/~p]-1sh (р/0/2) ехр ( — F'~P>) -
\ V a / _/х(Р)
СП (/7/0/2)
Ыр)
320
Имеем
i [} ePnt I
\7i(Pn) f Pn -
(2n+ 1) ni/t0
(2w+l) л (2n +
2t„
(2/2 -j- 1) Л
[(2л + 1) ni/2] [ft »/"5 + + i у
| /l (Pn) Qpnt ) __
I/2 (Pn) f Pn = “(2Л+ 1) ni/t0
лГ~~1 J x т / (^n + 1) л t . [ x -| /~(2// -f-1) л
}f ahq0 exp ^ у— |/ __ + «|_ ]/ -
— [(2n+ l)nf/2] [/■ ^a+ |/ <2п+|)л
+^'li
■<v
(2n+ П л
2Л
— [(2л+ 1) m/2]
h\r-a+ у (2n+l)Jl-i ]/
(2/i + 1) л
2Z;
Складывая, находим после несложных преобразований
00
(27Г+1) >
г,(*,
п= О
Х“Р (-F? {(* Г:+
}■
(2/2+1) я , (2/2+ 1) л
(6.61)
*0 ‘о
Здесь были использованы соотношения:
ch z = cos iz\ sh г = — i sin iz\ V~£i = y~2/2 ± i V~2l2.
Искомое решение имеет вид Т (х, t) = Ti(xt t)-\-T2(x> t).
Заметим, что при скачкообразном температурном воздействии про¬
исходит аккумуляция теплоты полубесконечным телом [106]; аккуму¬
лированную теплоту, отнесенную к единице площади поверхности
jk = 0, можно определить по формуле
~~ о
Случаи скачкообразного температурного воздействия на стержень,
цилиндр и шар рассмотрены в работе [118].
Большое значение в практике операционного исчисления имеют
основные теоремы, с помощью которых можно подчас избежать гро¬
моздких выкладок. Обратимся вновь к решению (6.55) и перепишем
11-339 321
его следующим образом:
<7о S!1 (Р^а/-) ехР (— J/^a q°exp (~ 1_ ‘
Т (х, р) =
pc\\(ptal2)[\ + {hy~a) 1 V р\ p[l + (/:J/a) 1 У р] 1 + е“ pta
“i[H(»rir^l{ I + 2X 1).ехрJ. (6.62)
Воспользуемся далее теоремой запаздывания (6.10) и оригиналом
q0y¥0(xJ t) (6.40) для изображения множителя, стоящего перед скоб¬
ками в (6.62). Получим решение нашей задачи в несколько ином виде
Т (х, t) = ft'Fo (х, t) + 2<7о 2 (—1)"'Р0(дс, <—ft/0). (6.63)
1 < П < t/t0
4. Во введении к гл. V получено операционное решение (5.15) первой краевой
задачи (5.7) —(5.8) для бесконечной пластины О^х^/ с нулевой начальной
температурой и температурой <pi (0 при х = 0 и <р2 (/) при х = /. Перепишем это
решение в следующем виде:
Т (дг, р) = фх (р) Fx (х, р) + фа (р) Wt (х, р), (6.64)
где
тр /г -Ч_ sh[(/—X)/V~a\ |/“р. w . sh \_{xlV~a) У~р] „ „
,b[wrs>r-p ■ .ькнгигя '
Найдем оригинал T (x, /), используя теорему умножения (6.11). Оригиналы
изображений ф/ (р} нам известны, оригиналы изображений Wi (х, р) (/ = 1, 2) можно
найти либо^ по обобщенной теореме разложения (6.33), либо используя разложение
функций Wi (х, р) в ряд в виде бесконечно убывающей геометрической прогрессии.
В первом случае оригиналы UP/ (х, /) [а также и решение Т (.х, 01 будут иметь
вид ряда Фурье, удобного при расчетах для больших значений времен (эту форму
решения дает и метод конечного интегрального синус-преобразования Фурье);
во втором случае оригиналы Wi (х, /) будут иметь форму ряда, удобного для
малых значений времени t. После нахождения оригиналов W{ (х, 0 искомое реше¬
ние можно записать в виде
t t
Т (х, 0 = J ф1 (т) W1 (х, / —х) dx+ J ф2 (т) W2 (х, t — т) dx. (6.66)
о о
В выражениях (6.65) знаменатель sh [(//1/ а) |/ р] не содержит свободного
члена, следовательно, все условия теоремы разложения соблюдены и ее можно
использовать при переходе от изображений Wi (х, р) к оригиналам Wi (х, /). Най¬
дем корни функции sh[(//V^ a) Y р\'-
sh [(IIу/а) у[р] = — Г sln [; (I/ Y~a) у-р] = 0, откуда
i (ИУ~а) V~~p= ± пл,
рп = — (пл У^.П)2, п = О, 1, 2, ... (6.67)
322
Согласно (6.65),
L-1 [¥,(*, p)] = WM*, 0 =
= V jsh[(/-x) V~plV~a}^et\
n= 0 ’ [sh 1 V~~P/ У~о]’у > P = Pn--(яя v a(l)a
___ 2 1^q~ у (yTg nnifl) sh [i (/—x) пя/l] ^
/ “ ch in n
n= l
Xe-l™W/)V_^^JLslnl(1 _я//) e-(™ УГ //)*._
n= 1
П= 1
так как
i sh i (1 —x/l) nn = — sin [(1 — x/Z) nn) =
= (— 1)Л+1 sin (плх/t); ch мл = cos лл = (— 1)п, л = 1, 2, 3...
Аналогичным образом находим
/1= I
и далее решение Г (х, t) в виде (6.66) (ср. с (3.65) в § 3 гл. III). Для малых
значений Fo = at/l2 решение (6.66) малоудобно.
Операционный метод позволяет получить функцию Т (х, t)
в другой форме, наиболее пригодной для малых значе¬
ний Fo. С этой целью разложим функции №,-(х, р) в ряд
W/ -ч sh К(1—х)/У~а) ]/~р \ _
w'ix-*-—щ777771—
_ ехр[((1 —х)/Уа) Vр ]—ехр[— ((/ — х)!У~а) У~р] _
ехр [(//У~а) \Нр}—ехр[— (IIV a) Vp\
_ exp [— (дс/]/~а~) У~р\ — ехр[— ((21—х)1}Га) )/~р] _
1—ехр[— (21/уга) У~р
-(2<л + х) - (21п-х)
-2* п -2« ^ • <«•*>
п— 0 п—1
Здесь было использовано разложение:
т^=1+х + х»+... .
Воспользуемся табличной формулой
__ к е-лг/(40
2 /лР
(6.69)
323
Тогда оригинал W1 (jc, t) имеег следующий вид:
Wl(x, 0 = Е ^±4е-(2"' + Л,,;(40/)-
L2 In — X е_ (2/л1— х)г/\ at) __
, 2 )/1м73
п= 1
09 П= -1
е-(2/П + х)1/(4Д/) |_ ^ 2lri-\-X с-(2/n + X),/(4flO
“ 2 |Лш/а 2 ла/3
ПвО ' П = — оо
= 'yf ii«±i ехр [ - P^+i2!l. (6.70)
^ 2 / L 4а* J
В § 12 гл. Ill введена тэта-функция Якоби (3.314)
в(*. 0—4==Ш е-<-^ = -71тП=£ (6.71)
Нетрудно проверить, что выражение (6.70) представляет собой формулу вида
«~7 £•(*• Я’
Аналогичным образом находим, что
т . „ а д а ( 1—х at \
* (■*' I дх \ 21 ’ I* j'
Таким образом, решение Г (jc, 0 можно записать теперь в иной форме,
ь именно:
t
г(*; 0=—г 1ф1 (т) Ж 0 ("S7 ’ "F(<-т)) dT+
о
+*f Jфг (т)ж 0 (тг ■ Т*- ('_т))dT- (6-72)
Это решение удобно для малых значений Fo, так как ряд (6.71) быстро сходится
при малых значениях t. На этом конкретном примере видно большое преиму¬
щество операционного метода, который позволяет получить решение одной и той
же задачи в двух видах: одно удобное для расчетов при малых значениях Fo,
другое — при больших значениях Fo.
Наряду с операционным методом для этих целей может быть использована
также независимо функция Якоби (3.314). В случае когда непосредственное
использование этой функции для перевода полученного решения из одной формы
в другую затруднительно, следует найти операционное решение задачи и далее
переходить к оригиналам типа (6.72). В некоторых случаях решение такого вида
можно получить, не применяя операционный метод, используя лишь (3.314).
Например, в § 3 гл. III получено решение уравнения Т(=аТх +/(*> О»
О < jc < /, t > О с однородными начальными и граничными условиями I рода
324
в виде (3.51)
г <*. о - f 'Г {т £ «■‘ ("Л * 7">‘' (.«/О х
п = 1
X sin (/mg//) [ / (g, т) dT dg. (6.73)
о о
Преобразуем это решение следующим образом:
2 sin (nnxtt) sin (плЦ[) = cos (пл/l) (* — £) — cos (пл/l) (* + £),
откуда, согласно (3.314), имеем
со
2
21.
где
-у- ^ е“^пл ^ (/“т) sin (плх/l) sin (пл£//) =
гг = 1
| 1 + 2 2, e-(nn ^ ,)а (/-fl cos 2-^- (*-£) j-
1 + 2 L е ' ("Л ^ *'_Т) cos 217 <* + ] j “
__L Гй?*-6 а(<-тЛ *(*+ь
2/ [ \ 21 * /» J Ч“2Г ’ /* JJ’
— Т^) = V е-(*±1-гМ)*/(4ви-т)]
\2i г )
Таким образом, второй формой решения (6.73), удобной для малых времен /,
является следующая:
Г,, *-^)]**
О о
(6.74)
Выражение (6.74) можно получить и операционным методом, но
более длинным путем, учитывая неоднородность дифференциального
уравнения теплопроводности, которому удовлетворяет функция
Г (х, t).
5. В декартовой системе координат операционное решение задачи
содержит гиперболические функции, достаточно легко расклады¬
ваемые в ряды типа 2ехр[—Фа(л)1//7Г1- В полярной (или цилинд-
п
рической) системе координат операционное решение задачи содер¬
жит более сложные функции, которые непосредственно в такого
рода ряды не раскладываются. Точное решение задачи в этих слу¬
чаях принимает вид ряда Фурье—Бесселя, удобного для больших
времен (к этому виду решения приводит и метод интегральных
преобразований Ханкеля). Для получения решения, удобного при
малых временах, необходимо воспользоваться предельной теоре¬
мой (6.16), но речь может идти лишь о приближенном решении
с определенной степенью точности.
325
Рассмотрим один из таких характерных примеров—температурное поле полого
бесконечного цилиндра при заданной постоянной температуре на его боковых
поверхностях. Имеем:
lF=e (l75""*"7 57) • R' < ' < > 0 (д< > 1 (6.75)
Т (г, 0) = Го. Ri< Г < RT(Rt, 1) = Ти t > 0, /= 1, 2. J
Применяя преобразование (6.37), переходим в пространство изображений:
d*T 1 dr р т0 n".r.RA
dra + г dr аТ- a ’ Rl < < *2’ I (6.76)
T(Rhp) = Tllp, / = 1,2. J
Уравнение (6.76) представляет собой неоднородное уравнение Бесселя, общее
решение которого имеет вид [54]
Т(г,р) = А/0(г УТ/УТ) + В/С0(/■ У7/У7) + Т0/р. (6.77)
Постоянные интегрирования Л и В находим из преобразованных граничных
условий. В результате получим
[Г(г, p)-T0/p](Ti-Tt)-^ =
ГKq(Rq Vrplyra)-KARi УГр1У^')\1о(гУ71У^) +
" p[!o(Ri y~p/VT)Ko (RiVJ/VT)-i0(r2 yyiyH) KoiRt V1IY4))
+[/. (Rl VJ/V^)-K (Rl yitlY^)] Ко (r V7/}Ta) =
p[i, (Ri V~plVRo (R, V7IVT)-to (Ro Y1IV~Z) /Co (Ri V~pIV~^)}
= (6 78)
/.(/>)
Формула обращения для преобразования Лапласа (6.20) дает точное значение
оригинала в виде
С+/ во
С dp. (6.79)
J Ы ‘
a-/ ^ ' *
7 (г, 0-Г0 1 С Мр)
Т\— То 2л/ j f ч (р)
Выражение (6.79) является однозначной функцией р и представляет собой отно¬
шение двух полиномов бесконечного порядка, причем знаменатель не содержит
постоянной величины. Следовательно, для вычисления контурного интеграла
можно воспользоваться обобщенной теоремой разложения (6.33). Найдем корни
знаменателя /8 (р), для чего приравняем его к нулю
Т.
(yt •'') *■ (т= К?) J -л W-0.
где выражение в квадратных скобках обозначено через /8 (р).
Из этого равенства находим: 1) р = 0; 2) /3(р) = 0. Для нахождения корней
функции /з (р) преобразуем эту функцию, используя формулы, связывающие
модифицированные функции Бесселя !\(г) и К\ (г) с функциями J\(iz) и
Kv(«) [88]:
/у (z) = j-v/v («); /(, (z) = yie<,,v/2 Uv (u) +jTv(£z)]. (6.80)
326
Преобразуя по этим формулам выражение для /3 (р), находим
Если обозначить iRj }f~plY~a =\i, то придем к известному в теории бесселе¬
вых функций уравнению [88]
Известно, что корни этого уравнения все действительные и простые.
Пусть \лъ ц2» •••» Ил • • •—корни уравнения (6.81) (первые пять значений ц
Для вычисления первого слагаемого в правой части равенства необходимо исполь¬
зовать асимптотические формулы для функций Бесселя мнимого аргумента при
малых значениях аргумента
I Гг(Р) I liin 1п2 VJ/(R2 У~р)—In2 yUljRi V7)
ЧрТз (p)]p> p=0 о-«[in 2 V~a!{Ri V~p) — \n2}/~al(RiY~p)\
ft (Pn)=—2 (PnRi/Rt) J о (Vnr//Ri) —
— Jo (V-nRt/Rt) Ко (H„/7/?i)] — [K0 (n„) Jo (Vnr/Rt) — Jo (!‘n) Ко (Ц„г//?!)]}.
Последнее выражение можно упростить, имея в виду, что рп—корень уравне¬
ния (6.81). Так как из (6.81)
/1 (Pn) — ~2 Wo (Ил^2/^l) \Уо (Ил^г/Ri) X
х Jq (tLnr/Ri)lJo (ihtRt/RJ—yo (ИпГ/Ri)] —
[Уо (Ил) 'о WnrI^i) 'о (Ил) У о (Ил'/ ^i)]} —
== 2 (М'л) Wo (VnRzlRi) J0 (Ил)] Wo Wnr!Ri) X
X V о (Ил) У о (М'л^ / Ri) Jo (Мл)]-
(681)
приведены в монографии [83J), тогда подынтегральная функция имеет полюсы
в точках р = 0, рп =— apn/R\t п^\. Согласно теореме разложения, можно
записать
записать
; /о (0) = 1;
v>0
; /Со (z) « In 2/z;
(z -► 0)
(6.83)
v > О
находим
Используя далее (6.80), находим
Уо MlRi)W о (VnRi/Ri) = У о Wn)/J о (Ил). .
(6.84)
то получаем
327
Далее имеем
[р/э (Р)]рт рп =7а (Pn) + Pn [Т* (Р) ]р = рп = Рп [73 (р)]р= Р„.
так как /з(Рл) = 0* Используя (6.80) и (6,84), находим
^)к'(^^)~тр¥''(т7>гё)х
*«• (у**iw-'• (??:^) •*' (^'^)L
= И-Л [У0 (Мп^г/^l) У1 (Мл) Jl (Мл) Ко ^
X (Мл^2/^1)]+ i/?]4” ^ (H7X^2/^l)
— У о (М 1 (МлЯг/ЯО] = ~ Ил^о ОьЛ/ЛО х
v fv /„ | \ К0 (fin/?2//?i)-1 . nR2 /i„ v
X IК, (ц„)-у, (цп)Ta^T^rJ + -art
x Jo (Pn) [к,(PnR*/Ri)-JxOinRt/Ri)T^g-J] =
. J_ J о (Мя^г/^!)— У о (Мл)
2 У0(]О JofanRdRi)
2
Здесь использовано тождество JA [z)Yn(z) — К* (z) У0 (*) =—•
Окончательно находим Т (г, () в виде ряда Фурье—Бесселя:
^ ('» 0 — Tj -(Vaun/R<)2 t Jo (VnRi/RJVn (\lnr/Ri)
Ко - Тг “ ^ У О (Мл) + Уо Oi»*./*i) ’ 1
Л« I
где ¥п(цлг0/Я1) = У0(цп/-/Я,)У'0((1п) —/„(fi^VoOwVtfi); ц„—корни уравне-
ния (6.81).
Выражение (6.85) удобно для расчетов при больших значениях
критерия Fo, когда всеми членами ряда, кроме первого, можно
пренебречь (регулярный режим). Для значений Fo<^l эта форма
решения становится неудобной, так как приходится брать много
членов ряда (5.85). С уменьшением Fo число членов ряда, принад¬
лежащих учету, резко возрастает и при значениях Fo, близких
к нулю, пользоваться решением (6.85) не представляется возмож¬
ным (нет строгой оценки остатка ряда). Заметим также, что выра¬
жение (6.85) можно получить юраздо быстрее, используя конечное
328
интегральное преобразование Ханкеля по переменной г, причем,
имея таблицы интегральных преобразований (см. §8 гл. V, табл. II),
все расчеты становятся совершенно стандартными и достаточно быстро
приводят к конечной цели.
В этом отношении применять операционный метод нужно осмотрительно, так
как это далеко не самый быстрый способ получить аналитическое решение задачи,
особенно если речь идет о решении задачи в цилиндрической системе координат
(и в ограниченных областях). Однако операционный метод использован в решении
вадачи (6.75); имелось ввиду показать этот метод в действии. Кроме того, нас
интересовало решение Т (г, t), удобное для малых значений Fo, а для этого не¬
обходимо иметь предварительно операционное решение задачи, т. е. выражение
(6.78). Для нахождения другой формы решения Т (г, t) воспользуемся предель¬
ной теоремой\ (6.16), согласно которой большим значениям р в изображении
Т (г, р) соответствуют малые значения t в оригинале Г (г, t)..
В выражении (6.78) заменим модифицированные функции Бесселя их асимп¬
тотическими разложениями, используя формулы вида [20)
y0W=—7=i=-ez0(2), где 0(2) = 1+ 1
\ПЫг 1" А т8гт 12822
*,(*)= г » 1.
у 2г
(6.86)
После несложных преобразований получим, обозначив q=}^р/а:
fir D\ Г shq(R2 — r) Rt
Г (Г’ Р) р ~~ Р [ shq(Rt-Rx) V г Х
в(дг) sh д(г — Яг) Лр 0 (дг) ]
* 0 (?/?!) -Г shq (Я,-/?!) V — ~e~(qRi) J *
Заменив гиперболические функции показательными и разложив в ряд sh <7(Яа—£i)
[см. (6.68)], получим
Т„, ^|L|e,pl_(2„x
Х'(Л2—Rl) — (2R2—fli)+/0 17]—ехр [— ((2л —1) (fi2—/?i) + (г—/?,.)) <?] +
у ■ СО
+ /7 effa) X ^P[-^n(Ri-R1)-(Rt-2R1)-r)q\- (6.87)
П= 1
-ехр [- ((2/1-1) (/?,_/?,) +(г - Rx)) q\ I .
В выражении (6.86) для 0 (2) ограничимся тремя первыми членами; это дает
0 (qr)/S (qRi) = 1 + (Я,- — г)/{SqRtr) +
+ {9Rf—7r* — 2Rir)/(\28q*Rfr*) (1 = 1, 2). (6.88)
Подставим (6.88) в (6.87) и перейдем к оригиналам, используя таблицы изображе¬
ний. Полученное после преобразований, выражение запишем в безразмерном виде,
обозначив mi = R2/Ri, Fo — at/R^ (рекомендуем проделать все промежуточные
329
выкладки):
Т{Г, t)—T0 ^ i/£1 V Г^« / 2n («1— l)+l— r/Ri \
Г0_Г, V г £[ф 2 Fo Г
2n(mt— 1) + I— 2mt + r/fli ^ y^T ^ x
..Гф»/2я(лц— 0—■m + r/RA T>/2«(mi—1) + 2—пц—r/RAl .
I ^ 2 ]/~Fo J V 2}TfS /]
+l>^ /f (-T--1) t ['»•( s~)~
- <W 2^(mi-l)+l-2mt + r/ffi\j 1 ^ -l/Ж x
V 2 |/>o /J 4 r m,r
*[¥-')£ [“>*(*&=^+йй>)_я,х
m9>
/?■1f» (^Г ] £ [ w(-;l“!^—‘-) -
-~(»*-у^'»0М№Г«
xy Г;»ф»/2”(т1 — 1)—■mj+r/RjS. .,ф, / 2я (mi —1) + 2—mt—rjRt \~|
£] I { 2 ]УТо J V 2 KT3 / J •
Если ограничиться только членами, содержащими Ф*(г) = 1—Ф (г) [т. е. первыми
двумя рядами или полагая в (6.86) 0 (z) s 1], то получим
Г (г. 0-
Т,
X
■ о —7~1 .. Г^/ 2n(mt—1) + 1—2т! + т//?1 \
•_Г, К г 2* I ^ 2|ЛрБ )
_фрп(т,-1)+1-^1^+у^7^фх
r/Яг N ф/2л(т, —I)—mj+r/WA'
) \ )
2 УТо
(6.90)
Для весьма малых значений Fo можно ограничиться первым членом. Это дает
формулу
-4^^)]+>/vf4w)-4=ws)]- <6-91»
330
Следует заметить, что уточнение результата вычислений в (6.89)
и (6.90) не может идти за счет увеличения числа членов—слагае¬
мых ряда, как это имело бы место в решении (6.72) и (6.74) для
бесконечной пластины. Объясняется это тем, что использование
асимптотических формул разложения модифицированных функций
Бесселя (6.86) уже предполагает, что q = Ур/а должно быть доста¬
точно большим. Последнее же означает малые значения Fo в ориги¬
нале, поэтому для расчетов достаточно взять первые один или два
члена в разложении оригинала в ряд.
Укажем величину Фурье, при которой выражение (6.91) дает удов¬
летворительный результат для инженерных расчетов. На основании
сравнения точного решения задачи (6.85) с решением (6.91) точ¬
ность в четвертом десятичном знаке достигается уже при Foc=0,01.
Так, если r/R1 —1,25, R2 = 2Rif Fo = 0,013, то W = 0,8917,
где все знаки верны. Если r//?t = l,75, R2 = 2Rit Fo = 0,013, то
W = 0,8707 вместо W = 0,8706 по точной формуле. Таким образом,
формула (6.91) для Fo<;0,01 дает четыре верных знака [34].
Полученные решения (6.72) и (6.89)—(6.91) можно использовать
и для более сложных случаев, в частности для расчетов темпера¬
турного поля конечного полого цилиндра при малых значениях
Fo. Пусть Т (г, г, t) удовлетворяет условиям!
Так как уравнение (6.92) однородное (не содержит функцию
теплового источника), то решение Т (г, z, t) можно представить
в виде произведения решений для неограниченного полого цилиндра
и бесконечной пластины (см. § 6 гл. II):
Для каждой из этих функций известны решения для малых зна¬
чений Fo. Действительно, функция U (г; t) = {W2 — T0)/(Tl — T0)
удовлетворяет нулевому начальному условию, граничным условиям
и (0, t) = U (/, /)<=1 и поэтому может быть записана в виде (6.72);
функция f) — Г0]/(Г0 — Tj) имеет вид (6.89) —(6.91).
дТ (д*Т , 1 дТ , д*Т \ Л ^ ^ Л ЛОч
dt а \ дг* г дг + az* j ; (6.92)
dt ~~и\ дг* ^ г дг ^ дг* 1'
Т (г, г, 0) = Г0; Т (/?„ 2, 0 = Tt (I = 1, 2); Т (г, 0, t)=T(r, /, t) = Tt.
(6.93)
Г(г, z,t)-Tt [У, (г, 0 -ГЩУ, (г, t)-Tx\
То — Т\ (Го-74) (Го-Г!)
(6.94)
где t) и W2 (г, t) — решения задач:
331
Операционный метод дает возможность объединить аналитические
решения для пластины, цилиндра и шара. В работе [35] рассмот¬
рено дифференциальное уравнение вида Т'( = а + (8т/х) Т'х), где
6m = 2m+l; для пластины m = —1/2, для цилиндра пг = 0, для
шара пг = 1/2.
Имея операционное решение задачи, при любом виде граничных
условий можно получить соответствующее решение при малых зна¬
чениях времени для каждого из указанных тел, объединенных одним
общим выражением.
Задача 1. Применяя операционный метод, показать, что решением задачи
dW d*W . 2m+l dW Л , /л 1Ч _ л '
ТЕ”=“лтН — -л" » 0 < 2 < 1 0< г < 1 , Fo > 0;
dFo * дг v (695)
dW
W(z, 0) = Г0;
является выражение
W(x, Fo)-W0
= 0; W vl, Fo)=W{
,.-r. -~±Ш^аИ-КП)- ,6ЭД
n= 1
где \in — корни характеристического уравнения /Л(ц) = 0; Jm — функция Бесселя
I рода m-го порядка; т= —1/2 для бесконечной пластины; т = Ь для неограни¬
ченного сплошного цилиндра; т= 1/2 для шара (ср. с результатами § 5 гл. V).
Покажите, что решением второй краевой задачи
dW I dW I
W(zt 0) = JP0; +гЧ =°i ^JT-\
дг о дг |z=i *
для уравнения (6.95) является выражение вида:
W (г, Fo) = П7о + (?/2)^4 (т+1) Fo+z»-^±i-
п = 1 п J
Покажите, что в случае краевых условий
dW
dW
Г (г, 0) = г0; -+
„=°: “ЯГ = — Bi(lF |i=i — IFC)
2= 0 02 J г— 1
решение уравнения (6.95) запишется в виде
W(z, Fo)-r0_, oV Bi ( IV /т(ц„г) .-^Fo
Wc-Wv (Bi-2m)Bi+|i* \г
где \in — корни уравнения Jm (\i)/Jm + i (p) = H/Bi.
Покажите, что последнее решение стремиться к (6.96) при (1/Bi)—► 0.
Частные решения для пластины, цилиндра и шара получаются из приведен¬
ных решений для каждой из краевых задач при переборе значений т= —1/2;
0; 1/2. При этом следует иметь в виду связь бесселевых функций дробного по¬
рядка с тригонометрическими [20J
J -г/t (г) = V cos г; J 1/2 (г) = Y 2/(лг) sin г\
J3/2 (г)= ]/ 2/(лг) (sin г/г — cos г).
332
6. Операционный метод незаменим при рассмотрении задач нестационарной
теплопроводности на нагревание или охлаждение системы соприкасающихся тел
(слоистые среды), когда теплообмен между ними происходит по закону тепло¬
проводности и в постановке соответствующей краевой задачи имеют место гранич¬
ные условия сопряжения.
В качестве примера рассмотрим температурное поле двухслойной пластины,
нагреваемой поверхностным источником теплоты постоянной интенсивности:
ТГ=а1 dS>0<x<1’ ' > ^=а2 S - 1 < х < *• * > 0; ^97>
тих, о) = Г4(х, 0) = 0; -X,
дТ 1
дх L = o
— Яо'-
«• X дТ1 I -JL Щ
001 h~dT |«/“Xs'arL/.
(6.98)
Ti(i, 0;
Г,(х, 0—>-0, х-
Решение задачи ищем в классе функций, для которых применимо преобразование
OD
Лапласа по переменной t. Полагаем Г/ (х, р) = J ехр ( — pt) Ti (xt t) dt и переходим
о
в (6.97) — (6.98) в пространство изображений:
— Г, = 0, 0< х< /; ^Д £-Г, = 0, I < х< оо;
dx2 aj dx2 а2
TUI, />) = Г,(/, p)\ -h
_J7o .
дг= о p
Tt (x, p) —.0, x—► 00; X,
dr.
dr.
(6.99)
(6.100)
r 1 « 2
d* \x=/ d* |дг=/'
Общие решения уравнений (6.99) имеют вид
Т\ (*. p) = Ai$h (х V^p/yifi + B! ch (х У'р/У'а)-,
Тг (х, р) = At е* V~ilV~5+Bi е~* .
Постоянная интегрирования Л? = 0; так, согласно граничному условию (6.100),
функция T2(xt р) должна стремиться к нулю при х—► оо. Постоянные интегри¬
рования Ait Ви В2 находим из граничных условий (6.100). Это дает операцион¬
ное решение задачи в следующем виде:
ri(x, р) =
рУ Р [(ЫУ аг) sh (/ VhlYTJ+yktlVfi) ch (l У~ЦУ~ад\ '
Ял ехр
Т, (х, р)=-
(*-0
У~р\
)
P>7p[(^i/T_a:)sh (/ V~plV~a\) + (ytlV~a2) ch (/ V~i>IY~ad\
(6.101)
где l.'„ = KeTX,/KeTX, — критерий, характеризующий активность второй среды
по отношению к первой.
Знаменатели выражений (6.101) приведем к виду
у%-5117% ^ +Йch т= ^=t (Й+Й)х
где*-—
_ 1'-йехр(-ЙЙ]-(ЙЙ’
dQ— 1
^2 у/а\ + \/^2 ^1 ^0+1
(6. i 02 >
333
Разложим далее в ряд решения (6.101), используя при b > 0 разложение
ОО 2 In
——г-Чг—гv-t
'-’’'"‘(-Тт/П -
! оо
Если 6 < 0, разложение (6.103) примет вид 2 (— 1)"|&|я ехр (—2/л V^p/Yoi)»
л=0
Так как |6|<1, то ряд (6.103) быстро сходится. Решения (6.101)
перепишем следующим образом, учитывая (6.103), а также равенство
(Xi V^i)/2 K^ifl2==^i (1 +^о)/2
f, „= [£ ..-1= «р(-^±Д /?)-
-|;-77T-(-W+
По таблицам операционного исчисления находим искомые оригиналы
г,„. 6. ,Ф.(|±±£)_£ ». ,ф.(|г=£)j;
(6.104)
Т»(*> 0 =+7+4+У *n +=Н 7=-V (6Л05)
Ml+4.) + V 2\Г&/
Если термические свойства обоих тел одинаковы, т. е. а1=а2 = а, Xi = ^2, то
d0 = 1 и 6 = 0. Отсюда из (6.104) — (6.105) получаем такое же решение, как и для
одного полубесконечного стержня:
П(х, t) = Tt(x, 0 = Т(х, цVT1Ф*[jyYj =
|6-109
Задача 2. Показать, что решение задачи (6.97) — (6.98) в случае, когда
при х = 0 в (6.98) задано условие 7^(0, t) — Tc (остальные условия не меняются)
имеет вид:
Тг (*, 0
7\
^1=У w/ 2'"+iVy b"<r(2lnZ^ );
с _ П Ч 2 / + \ 2 j/’ajf /
Ti(Xj_J) __2_ ^ у.ф.ГРя + П/ . х-/ I j
7-с 1+4,+ 1 2 УЪ +2 УШУ )
(6.107)
где по-прежнему dQ = aiK2/[a2li),
334
Указание. При переходе от операционного решения задачи к оригиналам
воспользоваться разложением
ch -L- vj+d„ sh —t= vt=
V ai V fli
= i(i+d0)['l-6exp(--^L^)Jexp(-pL]^y (6.108)
В частности, как и выше было показано, если термические свойства тел одина¬
ковы (Xi = X2 = X), то d0=\, b = 0 и контактная задача превращается в первую
краевую задачу для полуограниченного стержня (jc > 0) с нулевой начальной
температурой и постоянной температурой на торце *;=0. Из (6.107) находим для
этого случая
Т(х, t)/Tc = Ф* (х/2 v~7t),
т. е. уже известное решение (6.45).
Применяя тот же способ решения, можно рассмотреть случаи ненулевой
(постоянной) начальной температуры, а также переменной граничной температуры
при jc = 0. Более сложным является случай, когда начальная температура — про¬
извольная функция пространственной координаты. Так, например, в случае раз¬
личных двухслойных одномерных тел имеем:
д]\
dt
= а1
дЧ\
дх2 '
Тi (х, 0) = Ф0,- (*), i=l, 2; X!
dt
д]\
дх
jc= 0 +
-1 ill
дх |jt= о — *
МО, 0 = М0, /); \Тг(х, 01 <+оо, х > 0;
\т2(х, 01 < + 00, х < 0.
(6.109)
(6.110)
Здесь можно указать два подхода при решении задачи. Можно ввести при Jt = 0
неизвестную функцию теплового потока, полагая
(6""
и разделить контактную задачу (6.109) — (6.ПО) на две самостоятельные. Решение
каждой из них может быть получено, например, методом интегральных преобра¬
зований с бесконечными пределами по пространственной переменной. Неизвестная
функция ф (t) может быть найдена как решение интегрального уравнения, полу¬
ченного из условия равенства решений Тх и Г2 при х = 0. Этот прием использован
в работе [148].
Возможен, однако, и другой подход, а именно с помощью преобразования
Лапласа по переменной t задача (6.109) — (6.110) сводится к системе обыкновен¬
ных линейных неоднородных дифференциальных уравнений второго порядка
и,далее решается обычным способом. Основная трудность при реше¬
нии этой системы уравнений состоит в правильном выборе
формы записи общего решения каждого из уравнений
в пространстве изображений. Общее решение необходимо записать
таким образом, чтобы после определения всех постоянных интегрирования можно
было вернуться в пространство оригиналов либо с помощью таблиц операцион¬
ного исчисления, либо вычисляя непосредственно контурный интеграл Римана —
Меллина (6.20). Поясним все сказанное на решении данной задачи операционным
со
методом. После применения преобразования Лапласа Г,-(*, р)~ f е~Р*Т((х, t) dx,
о
335
учитывая, что (Т/)/ рТ,• (х, р)— Ф0,-(х), получим
‘>0; Tif-i5'-—5Ф- <«>■»< »• I6"»
d7\ 1 ' d72
(6.113)
I Ti {x, p) I < + 00, x > 0; I T2(xt p) I < + oo, * < 0. (6.114)
Общее решение каждого из уравнений (6.112) запишем в следующем виде:
f, (X, p) = A1exV^lv°' + Ble-xV°'IV°:'-\-
+wH-W^b‘®dE+
х
X
+i?^M“i^’/7b,(E,dl('s0>’ ,6л'5,
О
Тг (х, р) = А2ех r^/vT‘ + Bit-xV7/v^‘ +
+T7S?l',p[w'^]'I,"®dE+
X
X
+ 2 f ехр V~P j Фо» (Э dg (х < 0). (6.116)
— СО
Согласно условию огранйченности решений (6.114) — постоянные интегриро¬
вания А\ = 0, Я2 = 0. Постоянные Вх и А2 находим из граничных условий (6.113)
и подставляем в (6.115) и (6.116). В результате получим
т,('’'”=кгг?+«.) 77 1“|“[-(тг-Т%),^]®",в,1Е+
— со
•I- ' J„рГ_ii+JLиг)ф„(£)6i+-/' х
2 V7 J L /«Г J 2/^KT
0
x i “p[~w ф-'® dE+Tp^?7x
-y^r j®0i a)di(x^O);
(.-I)
X j* exp J^-
T'<*тгI
— CO
CO
+ 7= 1 ~=Г Г exp Г — f -J= г4=Л V~P 1 Ф01 (£) dH +
/^7(1 +do) KT J L \ ]Г*% V^h J J
336
+^7т1'хр1т#,/7]Ф-®а£+
X
+wkv7 I
— «0
В интегралах, содержащих Ф02Ш» заменим £ на (—р). Кроме того, в выраже¬
нии для Т2 (*, р) заменой переменной х =—г преобразуем область —оо < лг^О
в область 0<2<+оо. Переходя затем с помощью таблиц к оригиналам, окон¬
чательно найдем решение задачи в форме, отличной от найденной
в работе [148]:
Т1 (дг, /) = __—Ё® — Г exp[ — 1 ф02 (— р) dp +
V^{i+d*)\nrt) L « J-
О
+ +1-*» — Г exp [-++] ®„(Bd6+
2 (1 + ^0) J L 4fli* J
0
00
+JT^i I "p [- ф,‘® d| 0)1
0
'’“ТТ^тЫ'"p [-Ф“,н”'"1+
0
00
+TF%5-j"p [-■‘w1] ^<-«^«*0,. . ,6.,,8)
0
Наличие ядер экспоненты под знаком несобственных интегралов
обеспечивает сходимость этих интегралов для широкого класса
начальных функций. Рассмотрим частный случай начального рас¬
пределения температуры, когда Ф01 (л:) = Т 01 = const, Фоа (л:) =
= 7,02 = const. Вычисляя интегралы в (6.117) и (6.118), после не¬
сложных преобразований находим:
Т (y Л T01-\-d0T02 - (T0i — Т02) d0 ф / х \ ^ rj.
П- 1+do + —d— ^^i-* ут)'
Г,(-г,0 = ГЛд:,0-+±^ + ^хФ(1гМг). *<0.
Если положить Т02 = 0, то получим решение, приведенное в ра¬
боте [83].
Решение более общих уравнений
дТ{ d*Ti , г , ■ , о
"ЗГ = а*“Жг+М*. О» * = 1.2,
337
причем как для полуограниченных тел, так и для ограниченных или
комбинации этих тел можно получить аналогичным методом или мето¬
дом функции Грина (см. гл. VII). Операционный метод дает положи¬
тельный результат и для краевых задач системы двух тел при наличии
несовершенного теплового контакта между соприкасающимися телами
(решение находится по той же схеме, как и в приведенной выше задаче),
а также в случае контакта с идеальным проводником или хорошо пере¬
мешиваемой жидкостью. Как отмечалось в § 2 гл. II, в этом случае
граничные условия сопряжения заменяются на другое условие (2.24)
и вместо контактной задачи для системы двух сред имеем задачу для
однородной среды, но с несколько своеобразным граничным условием.
Одна из таких задач для системы бесконечных составных труб стеклян¬
ной внутренней (R^ < г < R2) и металлической внешней (R2<.r<
< /?а) рассмотрена в [11].
Операционный метод является весьма эффективным при рассмот¬
рении краевых задач контактного типа в случае линейного или ради¬
ального потоков теплоты. Ряд решений для двухслойной пластины
и двухслойного полупространства при граничных условиях I и III
родов и при наличии источников теплоты получены в работах [50],
[119, 128], а также в монографиях [55, 83, 85]; теплопроводность
системы двух цилиндрических и сферических тел рассмотрена в [36,
84], а также в [55, 83, 85].
Более общие решения для системы двух сред, температурное поле
в которых многомерное, можно получить, используя одновременно
интегральные преобразования Фурье или Ханкеля с операционным
методом (либо интегральные преобразования с функцией Грина, см.
гл. VII). Этот подход использован для нахождения решений достаточно
общего вида в работах [59, 60]. Следует отметить ряд работ, в которых
рассматривается система сред, относящаяся к переносу теплоты и влаги
[85, 129]. Отметим также работу [107], в которой найдено нестационар¬
ное температурное поле двух тел, разделенных зазором; ряд решений
для описания нестационарного переноса в слоистых средах при пере¬
менных'коэффициентах даны в работах [153, 154].
Аналитические решения краевых задач теплопроводности и родст¬
венного типа для многослойных сред связаны с определенными мате¬
матическими трудностями. Здесь также используются интегральные
преобразования Фурье — Ханкеля с операционным методом либо ме¬
тодом функции Грина. В принципе методика решения такого класса
задач не отличается от методики решения задач для системы двух
сред, однако трудоемкость выполнения преобразований резко воз¬
растает с увеличением числа сред. Список имеющихся в настоящее
время решений для многослойных сред незначителен, укажем некото¬
рые из них [43, 76, 77].
В заключение отметим, что преобразование Лапласа может служить
методом, чтобы получить новые выражения для суммы некоторых бес¬
конечных рядов в виде конечных соотношений из элементарных функ¬
ций [142]. В большинстве случаев теории теплопроводности примене¬
ние операционного метода приводит к решениям в виде бесконечных
рядов (результат применения обобщенной теоремы разложения).
338
Поэтому свертывание таких рядов в конечные выражения имеет боль¬
шие перспективы в практике инженерных расчетов. Первые результа¬
ты такого рода имеются в работах [4, 46]. Следует также заметить, что
метод преобразования Лапласа является чисто формальным методом
получения решения, правильность которого необходимо проверять в
каждом отдельном случае. В предыдущих примерах нигде не проверя¬
лось, удовлетворяют ли полученные решения заданному дифференци¬
альному уравнению и краевым условиям. В некоторых случаях непо¬
средственная проверка не представляет трудностей. В других случаях
проще всего произвести проверку, рассматривая решение, полученное
в виде контурного интеграла (6.20). Эти дополнительные исследова¬
ния, как правило, приводят к положительному ответу и в практике
аналитической теории теплопроводности обычно не производятся.
С примерами на подобного рода расчеты можно ознакомиться в [56].
В этой главе не рассматривалось кратное преобразование Лапласа,
так называемое двумерное преобразование Лапласа [40]. Несмотря
на определенную стандартность рассуждений в процессе решения
задачи, метод двойного преобразования Лапласа требует высокой
техники в вычислениях и в этом отношении уступает методу интег¬
ральных преобразований Фурье с бесконечными пределами, обладаю¬
щему большей простотой и меньшей громоздкостью в промежуточных
расчетах. Кроме того, указанный метод вносит при решении задачи
неоправданные технические трудности, которых можно избежать, ис¬
пользуя опять-таки интегральные преобразования Фурье. В работе [60]
показано приложение метода двойного преобразования Лапласа к ре¬
шению краевых задач нестационарной теплопроводности; в [47] при¬
ведены температурные функции, полученные этим методом, и соот¬
ветствующие кривые для полубесконечного сплошного и полого ци¬
линдров при их охлаждении в жидкой среде.
Что касается преобразования (6.1), то в ряде случаев его можно применять
и по пространственной переменной х > 0, а не только по времени t > 0. Принци¬
пиальным при этом является выбор надлежащей формы записи решения преобра¬
зованной задачи в пространстве изображений по х. Проиллюстрируем указанный
подход рассмотрением полезной в методическом отношении задачи. Рассчитаем
температурное поле полуограииченного стержня (х^гО) теплоизолированного по
боковой поверхности, имеющего начальную температуру Т0\ на торце стержня
х = 0 осуществляется теплообмен со средой температуры Тс:
I
OT/dt — ад2Т/дх2, х > 0, / > 0;
Т (х, 0) = Т0, х > 0;
|дТ (х, i)/dx]x=0=h[T (0, t) — Гс|, I > 0;
T (x, 0/< + oo, x > 0, t > 0.
Введем безразмерные величины:
г=х/х0; Fo = al/xt', Bi =hx0;
IV[z,
339
где дг0 — выбранная единица масштаба. В новых переменных задача имеет вид
dWldPo = d*W/dz2, г > 0, Fo > 0; (6.119)
W (2, 0)=0, г > 0; (6.120)
[дйУ (г, Fo)/dz|*=0 = Bi(U7(0, Fo)—1], Fo > 0; (6.121)
| W(z, Fo)| < + oo, г > 0, Fo > 0. (6.122)
Положим
OO •
W (p, Fo) = ^ e~Pz\V (z, Fo) dz. (6.123)
о
Учитывая (6.7) в виде Wгг p2W — p(0, Fo) — (д1Г/дг)г_0 и граничное
условие (6.121) преобразуем уравнение (6.119) к виду
diF/dFo — p2W = — (р —J- Bi) W (0, Fo) + Bi, Fo > 0. (6.124)
Решение уравнения (6.124) следует записать в следующем виде:
W
(р, Fo) = — ^ ер,( Fo-T,[Bi — (p+Bi) W (0, т)1 dr. (6.125)
Выражение (6.125) под знаком интеграла содержит неизвестную функцию W (0, т),
для ее нахождения используем начальное условие (6.120), что дает
^ е“р,т [Bi—(p+Bi) W (0, x)]dT = 0,
о
или после вычисления интеграла
оо
(Je-p,TIF(0( T)dT = Bi/[p2(p+Bi)]. (6.126)
о
Записанное слева в (6.126) выражение можно рассматривать, как преобразование
Лапласа функции W (0, т) по переменной т с параметром преобразования р2.
Полагая
F(0, />*)=. Bi/[p*(/>+Bi)i
и заменяя р2 на р, находим
F (О, p) = Bi/[p(K7+Bi)]
и далее по таблицам изображений получаем искомую функцию W (0, т) в виде
W (0, т) = 1 — ехр (Ш2т)Ф*(Вц/т). (6.127)
Подставим найденное выражение (6.127) под знак интеграла в (6,125) и вычислим
интеграл
W(p, Fo) = -i [1 — ер’РоФ*(р|/То)]-
J |^Bi« Fo ,
P-
Возвращаясь с помощью таблиц операционного [39] исчисления в пространство
оригиналов и далее в систему координат (*, t), найдем решение исходной задачи
в виде
[е1И* Fo ф» (Bi/Fo)+ ер'РоФ* (pj/TU)].
Т 1\ Г° =Ф*( —£==.'\_е**+в*чФ»/ —±_ + /,у"Н7\
Тс — Т0 V 2|/^77 / ( 2|^о? )
С этим решением мы встречались в (6.44) при рассмотрении задачи (6.35)—(6.36),
решение которой было получено с помощью преобразования Лапласа (6,1), но по
переменной t > 0.
340
§ 4. Аналитические решения краевых задач теплопроводности
при переменных коэффициентах переноса
Отмечая выше возможности операционного исчисления при рас¬
смотрении различного рода «нестандартных» задач теплопровод¬
ности для уравнения (1.32), мы не затрагивали краевых задач при
переменных коэффициентах переноса. Речь идет об уравнении (1.31),
когда теплофизические характеристики среды зависят от координат
или от температуры; в последнем случае уравнение (1.31) становит¬
ся нелинейным и его решение связано с большими трудностями. Но
и в этих сложных ситуациях операционный метод приходит на
помощь и в ряде частных случаев позволяет выписать аналитичес¬
кие решения задач (точные или приближенные), представляющие
интерес для практического использования. К этому следует до¬
бавить, что многие задачи конвективной теплопроводности и диф¬
фузии, гидродинамики вязкой жидкости и другие рядом преоб¬
разований сводятся к уравнениям типа теплопроводности с пе¬
ременными коэффициентами. Таким образом, указанный класс за¬
дач представляет интерес для аналитической теории теплопровод¬
ности.
Полное изложение этой проблемы в рамках данной книги не
представляется возможным, тем более, что книга посвящена как раз
противоположному случаю, когда в (1.31) все коэффициенты посто¬
янны. Это возможно, если теплофизические свойства материала
меняются незначительно или самым беспорядочным образом.
В этих случаях соответствующие коэффициенты переноса принима¬
ются постоянными и равными средним (эффективным) их значени¬
ям. Тогда уравнение (1.31) переходит в (1.32) и для него ставятся
соответствующие краевые задачи. Однако в ряде случаев неодноро-
ность физических свойств среды оказывается значительной, а изме¬
нение свойств по координатам столь существенно, что в (1.31)
приходится учитывать зависимость коэффициентов переноса от
пространственных координат или от температуры, когда процесс
теплопроводности протекает в большом интервале изменения тем¬
пературы. В последнем случае поток тепла становится нелинейным
и для определения температурного поля необходимо решать кра¬
евые задачи для уравнения
с (Т)Р (Т) ~ = div [X (Т) grad Т\. (6.128)
8t
Решение таких задач связано с еще большими вычислительными
трудностями по сравнению с зависимостью коэффициентов в (6.128)
только от координат. Поэтому здесь широко используются различ¬
ные приближенные методы, обзор которых приведен в [83, 185, 186].
Ниже остановимся лишь на некоторых характерных случаях,
имея ввиду еще раз продемонстрировать операционный метод
в действии.
341
Уравнение нестационарной теплопроводности
с(х)р(х)
дТ(х, р= 3
dt дх
(6.129)
описывает процесс переноса тепла в неоднородных средах. В общем
случае задания коэффициентов переноса с(х), р(х), Л(х) общее
решение уравнения (6.129) записать не удается. Однако для ряда
частных зависимостей коэффициентов в (6.129) (наиболее распрост¬
раненных на практике) удается записать точное аналитическое ре¬
шение уравнения (6.129) при соответствующих краевых условиях.
1. Предварительно рассмотрим несколько полезных соотноше¬
ний для решения задач переноса в неоднородных средах.
Уравнение
где /v (z) и Ку (z) — модифицированные функции Бесселя. Действи¬
тельно, с помощью подстановок
и далее подстановкой А (£) = ^ 4х (<!;) к уравнению Бесселя
(6.130)
имеет общее решение
1 —а
~2~
у(х)=х
(6.131)
уравнение (6.130) сводится к виду
1 —а
d24> \<№
\<№ 4-/ (1-а)2/(2-Д):
(2 и? ¥
т=о
с известным общим решением.
Уравнение
d. 2-<xdy-[iyexр(ух) = 0 0?>0, у>0)
dxz dx
(6.132)
342
ijp
подстановкой <^= exp (ух/2); y(x) = x¥(^) сводится к виду
У
d2* (2/у) (а — у/2) (Р¥ у = 0
частному случаю (6.130). Отсюда, общее решение уравнения (6.132)
есть:
(2/у) (at—у/2) +1
= | -V. | 2 CXPpX((2/Y)(g~y/2)+1)"
'-И
|_ (2/у) (а —у/2)-И ^ у \2 J J
2
+ с2Л: (^^expf —
(2/у) («—у/2) + 1 \ у \ 2
(6.133)
2
2. Степенные зависимости коэффициентов переноса.
Рассмотрим в (6.129) случай
с (х) р (х) = с0ро=const')
Я(х) = 2оХП(«^2) J
так что а0=Хо/с0ро. В пространстве изображений по Лапласу
00
т(х, р)=Jexp (-pt) Т(х, 0 dt
О
(6.134)
задача о температурном нагреве
1 дТ д ( пдт\ л
~ —=—1х — , х>0, t>0, (6.135)
dQ dt дх\ дх)
Г(х, OUo = 0,JC>0, (6.136)
т(х, t)\xm0=Tc, t>0, (6.137)
\Т(х, f)|< +оо, х^О, t^O (6.138)
приводится к виду
d2f ndf ^/а°- л „ „
1 Т=0, х>0 (6.139)
dx2 xdx п
X
Т(х, p)\x=0=TJp; \Т(х,р)\< + со,х^О. (6.140)
343
относительно уравнения (6.130) с общим решением
1 —я
ф, ч 2 Г т (2\/р1аО (2-п)1г\
Т(х,р)=х с,/у1х 1 +
(6Ш)
Из (6.141) и (6.140) находим операционное решение исходной
задачи в виде:
г Ос, Р)=?Ъ—1 (г.]1 к,
(2-«)Y(v)^W \ 2“п
В пространстве оригиналов искомое решение имеет вид:
(2 — я) (1 4- v) — 1
(6Л42)
(2-п) r(v)aj^ \ /
. (2-»)/2 .
2х 1 —л
где у= ■=; v=-—.
(2-n)*Jao 2-n
Интеграл в (6.142) с помощью замены переменной z=y2/4т
можно преобразовать: в результате (6.142) запишется следующим
образом:
Пх, 0 1 Г V-. , . , г (v, У)
— = I z ехр(—z)dz=-
Тс Г(») J
Г(»)
2 —п
X
где Y= ; T(v, Y) — неполная гамма-функция.
(2-л)2 a0t
Случай п = 2 в (6.134) следует рассмотреть отдельно. Общее
решение уравнения
1 дТ=д (х28Т\ 0<х<1, />0 (6.143)
д0 dt 8х\ дх)
с начальным условием (6.136) в пространстве изображений по Лап¬
ласу имеет вид
344
f(x, p) = C,x(_l +Vl+ApMP + C2x"(1+'/l+4'w/2. (6.144)
Выражение (6.144) может быть использовано при решении соот¬
ветствующих краевых задач для уравнения (6.143).
Пусть теперь в (6.129)
с(х) = Сох"
Л(х)=V У (6.145)
р = const
и ао=Х01с0р. Операционное решение уравнения (6.129) с коэффициен¬
тами (6.145) и краевыми условиями (6.136) — (6.138) на основании
(6.130) — (6.131) имеет вид
(6.146)
Т‘ 2V_1r(v)AV
где v=(l — п)/2. Для вычисления оригинала (6.146) можно восполь¬
зоваться следующими формулами операционного исчисления
Д^)-
<»>■*'
-рГ(р) - ]/(т) а.
о
Рассмотрим далее в (6.129) случай:
с(х) = с0хт'у
Цх) = 1оХП; (6.147)
р (х) = р0 = const ^
Уравнение (6.129) с коэффициентами (6.147) и начальным усло¬
вием (6.136) в пространстве изображений по Лапласу приводится
к виду (6.130) с общим решением (6.131), где
Здесь также могут быть рассмотрены соответствующие краевые
с помощью подстановки £=1 +кх сводится к (6.147) — (6.148) и,
Здесь также можно воспользоваться известными формулами
операционного исчисления при переходе к оригиналам.
Приведем далее несколько полезных для практики подстановок,
полученных согласно (1.84) и (1.86) (см. гл. 1) для конкретных
значений коэффициентов уравнения (6.164).
2.1. Пусть с (z) p(z) = c0p0=const; X{z) — X^zn.
Уравнение
задачи.
Случай
(6.149)
таким образом, имеем для Т(х, р):
1 -л
f(x,p)=(l+kx) [«{^^+2)О + kxf” "+2)/2^+
(6.150)
(д0 — Ло/СоРо)
преобразованиями
;+i
2х0 1 2
х = —= ' Z , X = Xot
V«o"-2
л—1
при Л>2
п — 2 / 2хп \л—2
T(z,t) = k0aQ (-4 U{x,x)A
*0 1
х ==—= In
л/«о
z \ -1 /V^
Л/*0 V
T(z. o-w*.^ ')!
при п = 2
приводится соответственно к виду
ди д2и п \ди ,
—=—- + (п< 2);
Зт Зх2 2—пхдх
dU_d2U п 18U
Зт Зх2 л—2хЗх
(и >2);
ас/ a2t/
— =— (и=2).
Зт ду? к ’
Каждое из полученных уравнений может быть решено извест¬
ными методами
2.2. Пусть c(p)p(z) = c0poZn, l(z) = V"-
Уравнение
1 „ЗТ 8 „зт
— z— = — \z —
ао dt dz \ dz
подстановками
х=х0 --- -, т=x%t
Vа0
T(z, t) = kJt"]j2xlU{x, х)\
приводится к виду
ди д2и л SU
Зт дх2 х дх
347
2.3. Пусть
Уравнение
с (z) р (z)=Cop0zm\ X (z) = Xqz".
i zm8I=L(zndl\
oo dt dz у dz J
(flo — Ло/СоРо)
подстановками
*o 2
(m + 2) —л
2
JC = -
у^т-л + 2
, T = Xot
п+т n—1
при m + 2 > n
. I 2*0 Л/И + 2—л Л —(m + 2)
T(z, t) = kо —-—) a U(x, t)
\m + 2—л/ о
(/« + 2)—л
*0 2 2
X= Z
’ ^=k° (-
r(z:
x° 1
.x=—= In
2x0 V
Л+7Л
л — 1
при m + 2<n
n-(m+2)
(m+2)J о
■<A>
/— / z\“(m+1)
Г(z, /) = fc0\/flo I - I exp x
при
m + 2 = n
fy/ao(m + l) a0(/n + l)2\
4д^
приводится соответственно к виду
8U d2U т + п 1 8U
дх дх2 (т + 2) — п х дх
dU d2U т + п 1 dU
ёх ёх2 п — {т + 2)х ёх
(,т + 2>п);
(т + 2<п)\
348
Ъ=т? (m+2=“)-
3. Показательные зависимости коэффициентов переноса.
Пусть в (6.129)
с (х) р (х) = с0р0=const -j
Д(х) = Лоехр(—кх) j (6.151)
и ао=Хо/с0ро• В пространстве изображений по Лапласу уравнение
1дТ 5 Г . , чзг"|
с начальным условием (6.136) имеет вид
— — к———ехр(—кх) Т= 0. (6.153)
dx2 dx oq
Подстановка z=(2/к)у/pjao exp (кх/2); T(x, p)=W(z,,p) преобра¬
зует (6.153) в уравнение Бесселя
dz2 z dz
общее решение которого есть
W(z, р)=Cizli (z)+c2zK{ (z).
Возвращаясь к функции Т(х,р), общее решение уравнения (6.153)
запишем в виде
Г (*> Р)=\ у/Фо ехр ^ [с/, ^ у/фо exp
,(^ехр(^))
+
+ с2&\ ( 7 <
(6.154)
Постоянные интегрирования С\ и с2 находятся из граничных
условий задачи. Для области х^О переход к оригиналу не представ¬
ляет принципиальных технических трудностей. Более интересным
является случай ограниченной области O^x^l, 0. Пусть для
этого случая уравнение (6.152) имеет краевые условия
349
Т(х, 0)=0; 0<х</;
Т(0, /)=0, <>0; T(l, t)=Te, t>0,
а в пространстве изображений
f(0,p)=0,f(l,p)=Te/p. (6.155)
Находим из (6.155) постоянные С] и с2 в (6.154), а вместе с этим
и операционное решение исходной задачи:
Т(х, р) ехр [—(1—х)к12]
Тс ММ
[*i0 VpJaoj 1\ 0 л/фо X
х ехр (kx/2)j—1\ 0-у/р/^^ К\ 0 *JpJao ехр (b:/2)^J; (6.156)
А(р)=Кх 0V^)/i 0 V/>M>ехр(kl/l^j —
~ h 0 >/фо) ^ 0 VpM, ехр (W/2)). (6.157)
Для нахождения оригинала в (6.156) — (6.157) необходимо при¬
менить формулу обращения для преобразования Лапласа (6.20):
ff + JQO
T(x,t)=— f Т(х, р) ехр (pt) dp, (6.158)
2я/ J
o — ico
где интегрирование ведется вдоль прямой Rep = <x, параллельной
мнимой оси и проходящей правее всех особых точек подынтеграль¬
ной функции. Вычисляя контурный интеграл (6.158), находим:
Т(х, /) ехр (кх) —
Тс ехр (к!)
-1 Г кп л
---яехр --(/-*)
£ /i0i„V,[rt,exp(W/2)] Г Г fkx\
х ) < У, и„ ехр —"
11 Jl (Дп)-/,2 [Дпехр(кЦ2)] ( L V 2 /
X Г, (д„) - У, (д„) У, [* ехр 02^J| ехр ^ - --- 0 (6.159)
350
где fi„>0 — корни характеристического уравнения
Ji(jiexp(kl/2)) Yi (/1)-Yi (fiexp(kl/2))J\ <ji) = 0. (6.160)
Пусть далее в (6.129)
c(x) = c0exp(-A:ix)>|
X(x)=XoQxp(-к2х) V (6.161)
Р = Ро=const J
й kt<k2; oq=Хо/соро. Уравнение (6.129) с коэффициентами (6.161)
сводится к случаю (6.132) относительно Т(х, р) при
а= к2; у = к2- кх; р =р/ао. (6.162)
Общее решение для Г(х, р) имеет вид (6.133) с коэффициентами
(6.162). Если в (6.161) предполагается, что к2<кь то имеем на
основании (6.132) — (6.133):
Здесь также могут быть рассмотрены конкретные задачи тепло¬
проводности, для решения которых могут быть использованы при¬
веденные выше иллюстративные примеры.
4. Коэффициенты переноса — функции общего вида.
Рассмотренные частные зависимости коэффициентов в (6.129) не
исчерпывают проблемы. Ее дальнейшее развитие, по-видимому,
заключается в поиске новых законов изменения коэффициентов
в (6.129), допускающих точные аналитические решения соответству¬
ющих задач теплопроводности, и в развитии аналитических мето¬
дов, позволяющих рассмотреть в (6.129) произвольные зависимо¬
сти.
Одно из направлений исследований в общих чертах заключается
в следующем.
351
С помощью преобразований
х
’■= I—S Т(х, t) = W(z, О
J *00
Z-
0
уравнение (6.129) приводится к виду
1 d2W
dt q(z) dz2 9
q(z) = c(x)p(x)X(x),
S+2
допускающему подстановкой W(z, f)=^(^)exP(—У 0 переход
к спектральной задаче на собственные значения и собственные
функции для уравнения с переменными коэффициентами
~ + yS+2q(z)U=0. (6.163)
Ряд результатов (и соответствующие ограничения) при рассмот¬
рении уравнения (6.163) в области z^O получены в [83, 140].
Рассмотрим более подробно другой подход, позволяющий по¬
строить аналитическое решение задачи для уравнения (6.129) при
общих зависимостях коэффициентов. Попутно установим связь про¬
цессов теплопроводности в неоднородной среде и диффузии в поле
внешних сил.
В главе I было показано, что уравнение теплопроводности в не¬
однородной среде (1.83)
с(z) р 00^=4 \х(2)^1 0<2<L, t>О (6.164)
dt dz dz J
с помощью преобразований (1.84) — (1.86) сводится к виду (1.87)
dU d2U dU
-=—2 -/(*)-> 0<х<1> *>°- С6-165)
dz dx2 dx
Там же сформулированы ограничения на функции в преобразо¬
ваниях (1.84) — (1.86).
Рассмотрим теперь процесс диффузии в поле внешних сил.
В этом случае к диффузионному потоку — D grad С (М, t), вызван¬
ному осмотическим давлением, необходимо прибавить конвекцион¬
ный поток Cv с векторной скоростью v = Bf, где / — внешние силы,
В — подвижность молекулы растворенного вещества. Уравнение
диффузии будет иметь вид:
8С
—=div (Z) grad С—BCf)
dt
В частности, в одномерном случае
1 dC d
[dC В
dx D
f(x) С
d dt dx "
или
dU d2U dU
-=D — + Bf(x)-9 (6.166)
dt dx2 dx
(5=const, D = const),
где
x
с, /)=exp^-J
U(x, 0=exp| - (B/D)f(u)du
C(x, t).
Таким образом, уравнения (6.165) и (6.166) принадлежат к одно¬
му классу и имеют сходные решения.
Не ограничивая общности рассуждения, можно рассматривать
уравнение (6.165) с краевыми условиями
U(x, 0) = 0, O^x^l; (6.167)
U(0, т)=1, т>0; (6.168)
£/(/, т) = 0, т>0. (6.169)
В более общих случаях может быть использован интеграл Дю¬
амеля (см. гл. 4).
Задачу (6.165), (6.167) — (6.169) запишем в пространстве изоб¬
ражений по Карсону — Хевисайду, полагая
00
U(x, р)—р j* ехр(— рх) U(х, т)dx. (6.170)
о
Получим:
d2U dU
J2-/W 7-pU=0, О<X<1- (6.171)
dx dx
U(0,p)=l- (6.172)
0(1, p) = 0. (6.173)
Решение уравнения (6.167), удовлетворяющее условию (6.172), запи¬
шем в виде:
12-339 353
X I
U{x,p)=-p J ^ J U (tj, p) exp - J/(a) dr] +
о { t
X I
+ Ci(p) j*exp^-j*/(a)rfaj^ + l,
о {
где Ci ip) — постоянная интегрирования. Положим далее:
й(х, р)== А (х, р) с. О).
А (0, р)
Из (6.175) и (6.176) имеем
X I TJ
А (х, р) = -р J </£ J A (tj, р) ехр - J/(a) rfaj drj +
о { {
X I
- J exp - J/(a) dz J d£ + A (0, p).
+
о z
Так как согласно (6.179) A (I, p)=0, to
/ i
A(0, p)=p | d£ 11 (^, p) exp -1/(a) rfaj dr; -
о {
dZ
/(a) dx
o Z
и поэтому
/ I TJ
drj-
A{x,p)=p^d£, A(rj, p)expj^-J/(a)da
x ( {
н-i
f(a)d*\dZ.
(
354
(6.174)
(6.175)
(6.176)
Меняя порядок интегрирования в двойном интеграле и вводя
новую (известную) функцию
У У
fl(jc,y)=Jexp|^-|/(a)£fcJd?, (6.177)
окончательно приходим к интегральному уравнению Вольтерра
второго рода относительно А (х, р):
I
А (х, р)=р J* а (дг, ц) A (r\, p)dr\-a (дс, I). (6.178)
X
Решение уравнения (6.178) можно представить в виде ряда по степе¬
ням р, используя метод последовательных приблиижений
I i
-А(х,р)=а(х, 0+ Е / Jа(х, >7i)<*?i Jа(*1 и
х 4l
/ /
^rin-Odrjn-t J t)dr\„. (6.179)
Чп— 2 Чп—1
Тогда согласно (6.175) U (х, р) будет представлено в виде отношения
двух полиномов бесконечного порядка. Если предположить теперь,
что знаменатель А (0, р) имеет счетное множество простых корнеЁ
Ри р2,... р„, причем р=0 не есть корень знаменателя, то по второй
теореме разложения Хевисайда получим
ти \ a<JC> Ъ , V ( \
и(х’ Т) = ^Г^+ Е ~^ГГП—. ехр О* т)
a (О, I) ркАр{0, рк)
Согласно (6. 167) окончательно имеем:
U(х, т)= Е - *' Рк) [ехр (ркт) -1]. (6.180)
к= 1 РкА (0, рк)
Нетрудно показать равномерную сходимость ряда для А(х, рк)
(6.179) (и аналогично для А' (0, рк) относительно л:е[0, 1\ при любом
р=рк. Имеем
355
если f(x)>0 (при f(x)<О, но ограниченной, получим аналогичный
результат). Далее
Предложенный метод дает возможность получить решение уравне¬
ния (6.165) для широкого класса функций f(x).
Устремляя /-► + оо, нетрудно найти решение аналогичной задачи
для полуограниченной прямой. Однако, здесь функция f(x) должна
быть абсолютно интегрирована на [0, + оо).
Аналогичным образом может быть рассмотрена задача в цилин¬
дрической системе координат для радиального потока. Преобразо¬
ваниями
приводится к виду (6.165). Далее применимы все изложенные рас¬
суждения.
В случае центрально-симметричного поля
Поэтому, ряд (6.179) будет мажорироваться рядом
iii i
T(z, t)=k0[c(r)p(r)X(r)] 1/2г 'в(r, t),
х = х0
c(r)p(r)
Hr)
dr, в (r, t)=U (x, t), т = *ot
уравнение
приходим к уравнению (6.165) преобразованиями
Т (г, 0=к0 [с (г) р (г) X (г)] г 2в (г, t),
Х=Х° J /Г dr’ в^Г’ х = хо{-
5. Совместное использование преобразования Лапласа и метода
Бубнова — Галеркина.
Метод Бубнова — Галеркина (в литературе его иногда называ¬
ют методом Л. В. Канторовича) первоначально был разработан для
решения дифференциальных уравнений в частных производных эл¬
липтического типа, в частности краевых задач теории упругости.
Поскольку в нем только часть решения выбирается априорно, при
его реализации получаются более точные результаты, чем при
обычных прямых методах. Особенно эффективен этот метод при
решении краевых задач нестационарного переноса для уравнений
с переменными коэффициентами. Исходное уравнение теплопровод¬
ности (1.31) в пространстве изображений по Лапласу по временной
переменной сводится к уравнению эллиптического типа. Далее стро¬
ится приближенное решение этого уравнения по методу Бубнова —
Галеркина через так называемые координатные функции; точность
такого решения во многом зависит от удачного подбора этих
функций. Полученное в пространстве изображений приближенное
решение переводится в область оригиналов по правилам операцион¬
ного исчисления. Общей методики построения оптимальной систе¬
мы функций, при которой заданная точность достигается наимень¬
шим числом координатных функций, не существует. И тем не менее,
занимая промежуточное положение между точными и приближен¬
ными методами, метод Бубнова — Г алеркина обладает большой
общностью и может успешно применяться при решении одномер¬
ных и многомерных задач нестационарной теплопроводности для
уравнения (1.31).
Действительно, пусть Т(М, t) — решение задачи
с(М)р(М)8Т{М' ° = div [X (М) grad 7] + F(M, t), MeG, t > 0;
dl
(6.181)
T(M, 01/-о = Фо (M), MeG = G + S; (6.182)
p{{M)ST(M' l) + p2(M)T(M, t) = ip (M, t), M<=S, 0. (6.183)
dn
С помощью преобразования Лапласа
357
Т(М, р)=| exp (-pt) Т(М, 0 dt (6.184)
задача (6.181) — (6.183) переводится в пространство изображений
div [А (АО grad f(M, р)] -рс (М) р (М) f(M, р) +
+Фо(М)+Р(М,р)=0, MeG; (6.185)
A Т(М, р)=9(М, р), MeS, (6.186)
dn
где F(M, р) и ср(М, р) — изображения соответствующих функций.
Обозначим через Ь((Т) (/=1, 2) операторы:
U (7)=div [А (М) grad f(M, р)]-рс(М) р(М) f(M, р)+
+Ф0(М)+Р(М,р); (6.187)
Ь2(Т)=р1(М)^^+р2(М)ПМ,р), (6.188)
ап
так что задача (6.185) — (6.186) будет:
U [Т(М, р]=0, MeG-, (6.189)
La [f(M, p] = q> (M, p), MeS. (6.190)
Будем искать приближенное решение задачи (6.189) — (6.190)
в виде:
fn(M, р)=Ф(М, р)+ £ ак(р)Ч>к(М), (6.191)
к=\
где Ф (М, р) выбирается так, чтобы решение (6.191) удовлетворяло
граничному условию (6.190), т. е.
U [Ф (Л/, р)] = у (Л/, р), MeS; (6.192)
Ч*к(М) (к= 1, 2, ..., п) — система координатных функций, удовлет¬
воряющих однородным граничным условиям (6.190), т. е.
Ь2 [¥* (М)\ = 0, MeS. (6.193)
358
Напомним, что системой координатных функций называется
полная в области G система линейно-независимых функций
{Ч,к(М)}9 к— 1, 2, 3, п, ..., удовлетворяющих однородным гранич¬
ным условиям задачи. Функции '¥к(М) в (6.191) — первые п функ¬
ций некоторой системы координатных функций. В [186] разработа¬
ны рекомендации, облегчающие выбор системы координатных фун¬
кций. Входящие в (6.191) коэффициенты ак(р) неизвестны и подле¬
жат нахождению из следующих соображений.
Функция Тп(М, р) является точным решением уравнения (6.185),
когда L{ (f„) равняется нулю тождественно. Если считать, что Lx (Т„)
непрерывно в G, то это требование в методе Бубнова — Г алерки¬
на заменяется на требование ортогональности в G выражения L{ (fn)
ко всем функциям системы {'¥к(М)}, к= 1, 2, ..., п, то есть требова¬
нием
JJJ Lx[Tn{M,p)\'¥i(M)dvM= 0, f=l, 2, ..., л. <6.194)
G
Итак, в соответствии с (6.194) применяем к (6.191) оператор Lb
затем умножаем Ьх(Тп) на координатные функции x¥i(M) и интег¬
рируя по пространственным координатам по области G, приравни¬
ваем результат к нулю; п условий ортогональности дают систему
п алгебраических уравнений относительно ак(р):
£ (Aik+pBik)dk(p)=Di(p), i'=l, 2, п, (6.195)
к=\
где:
А*=Ш ^ (№ div V (АО grad ^ Ш dv*
G
в,к= - Я1 с (М) р (М) Ч>, (М) Чк (М) dvM
G
Д (Р) =Р Я! с(М)р(М)Ф (М, р) у, (М) dvu-
G
-Я! ЙМ, q>0(M)'¥i(M)dvM-
(6.196)
ЯЯ 'Р, (М) div [2 (М) grad Ф (Л/, p)]dvM
G
359
Решение системы (6.195) найдем по правилу Крамера. Определи¬
тель системы (6.195) есть:
А (р) =
Аи+рВц...А1к+рВ1к...А1п+рВ1л
А21 -\-рВ2\...А2к+рВ-1к—А2п+рВ2я
А„, +рВп1...Апк+рВпк...Ат+рВт
Определители неизвестных ак (р) имеют вид:
Л*(р) =
Ац +pBu---D 1 (р)...А\„+рВ\„
А21 +pB2l...D2(p).~A2„+pB2„
Ап 1 +pBnl...Dn(p)...Arm+pBm
= £ A(p)A/. kip), k= 1, 2, ... И,
1-1
где A, k (p) — алгебраические дополнения элементов к-то столбца.
Отсюда
IAWAuW „ д,- к(р)
Д^0)='~1 = Z —— Д(р).
А(Р) ,= i А(Р)
1, 2, ... 72.
(6.197)
Обозначим через /?2, ••• Рп корни уравнения А(р) = 0. Можно
показать, что эти корни простые и отрицательные [185]. Применив
к (6.197) теоремы разложения и умножения операционного исчисле¬
ния, найдем оригинал для ak(t):
п С п А,- к(рт)
а*(0=Ё j Ё ~77ГТ-
1=1 lm=l A (Рт) .
Д(т) exp [рт (t-x)]dx},
а вместе с этим и приближенное решение задачи (6.181) — (6.183)
в виде:
Т„(М, 1) = Ф(М, 0+1 ak{t)^k(M).
(6.198)
360
Приведенный подход можно распространить на более сложные
случаи, а именно — на краевые задачи для уравнения (6.128). Основ¬
ная идея метода ортогональности невязки ко всем координатным
функциям сохраняется, но в силу зависимости коэффициентов пере¬
носа от температуры перевод уравнения (6.128) в пространство
изображений по Лапласу осуществить не удается. Проиллюстриру¬
ем метод Бубнова — Галеркина на следующей задаче:
с(Т)р=div[X(7)grad 7] +F(M, t), MeG, t>0;
dt
(6.199)
T(M, 01|-о=Фо(АО, MeG=G+S; (6.200)
T(M, t)\MeS=Tc, t>0. (6.201)
Введем оператор
L(T) = c(T)p(T)div [X (7) grad T\.
Ot
Пусть Ф(А/, t) удовлетворяет граничному условию (6.201):
Ф(М, t)\MsS=Tc, t>0. (6.202)
Приближенное решение задачи (6.199) — (6.201) ищем в виде:
Т„СМ, 0 = ф(М, /)+£ ак(04>к(М), (6.203)
Ь= 1
где (как и выше) Ч*к(М) — первые п полной в области G линей¬
но-независимой системы функций {^(Af)}, к— 1, 2, п, ..., удов¬
летворяющих однородному граничному условию (6.201): ¥*(Л01л/е5=
= 0.
Составим невязку:
еп[аЛ0, a2(t), ... an(t)] = L[Tn(M, t)]-F(M, 0*0. (6.204)
Неизвестные коэффициенты ak(t) (к= 1, 2, ... п) в (6.203), при
которых получается наилучшее приближение для Т(М, t) [186],
определяются из условия ортогональности невязки (6.204) ко всем
координатным функциям:
snx¥i(M) dvM = 0, i= 1, 2, ... n. (6.205)
G
361
После интегрирования приходим к системе п обыкновенных
дифференциальных уравнений относительно ak(t) с начальными
условиями:
i а* (°) IIIЧк (М) М dv“=Ilf Фо (М) % (М) dvM -
G G
Ф (.М, 0) % (М) dvM. (6.206)
Пусть система координатных функций {¥* (А/)} ортогональна
в G, т.е<
\(М)%(М)(Ьи=Лпт н2
О,
||V*||2>0, k=i,
где ||'F*!!2 = HI4*1 (М) dvM — квадрат нормы системы функций
шщ.
Тогда выражение (6.206) упрощается и
at (0)=~ Ц|| Фо (АО % (М) dvu - HIФ (.М, 0) % (АО <**] •
G G
1=1, 2, ... п (6.207)
Рассмотрим в (6.199) — (6.201) задачу с линейным коэффициен¬
том теплопроводности Л(7) = Ло(1+ /?7) при с (Т) р(Г) = с0Ро = const,
так что Оо = 2о/^оРо и Т(х, t) удовлетворяют условиям:
м<а *>о; (6.208)
dt дх |_ дх J
Т(х, /)|,-о = Го, |х|</; (6.209)
Г(х, 0|х_±,= 7;, *>0. (6.210)
Если ввести безразмерные переменные z = x/l, Fo = aQt/l2, то зада¬
чу (6.208) — (6.210) можно записать в виде:
362
дТ д2Т „ д ( 8т\
1й=^+^Ы'0<г<1'ро>0: (6'2И)
Пг, Fo)|Fo.0 = r0,0<z<l; (6.212)
T(z, Fo)U-i = Те, Fo>0; (6.213)
8T(z, Fo)
i«o
=0, Fo>0. (6.214)
Согласно методу Бубнова — Галеркина приближенное решение
задачи (6.211) — (6.214) ищем в виде соотношения (6.203):
Т„(z, Fo) = Te+jPak(Fo)'F*(z), (6.215)
*=i
где коэффициенты ak (Fо) определяются из условия ортогональ¬
ности невязки (6.204) уравнения (6.211) к каждой из координатных
функций 'P*(z). Рассмотрим в (6.215) первое приближение (п = 1), для
которого примем:
Г, (z, Fo) = Тс+а, (Fo)(1 -z2). (6.216)
Согласно (6.202), (6.204), (6.205)
„ дт д2Т „г ( зт\
1
I
е, [в! (Fo)] = L [Тя (z, Fо)] Ф 0;
1
L[Tn(z, Fo)](1 —z2)dz=0,
О
или учитывая (6.216)
1
“ (1 - z2) + 2а, (Fo) + 2Ра, (Fo) -- [(Тс +
a Fo dz
+ а{ (Fo)(l — z2))z]j(l — z2)dz = 0.
363
Вычислив интеграл, получим нелинейное обыкновенное диффе¬
ренциальное уравнение первого порядка
da 1 (Fo) „
+ Н (Fo)+(5/2) (1 + рТс) a, (Fo)=0, Fo > О
dFo
общее решение которого имеет вид:
а\ (Fo)
— = с exp [ — 25Fo (1 + рте)]. (6.217)
(i+/?rc)+o,4M(Fo)
Постоянную интегрирования с найдем из условия (6.206), запи¬
санного в соответствии с (6.212) — (6.213), (6.216) в следующем
виде:
а, (0)
Сl-z2)2dz = T0
1 1
(1 -z2)dz-Tc
(1 —z2)dz,
откуда ах (0) = (5/4)(Г0 — Тс). Определив в (6.205) постоянную запи¬
шем окончательно решение задачи (6.211) — (6 214) в виде:
Tx(z, Fo)-Тс 1,25(1 +/?ГС)(1 — z2)exp[—2,5(1 -f/?rc)Fo]
Т0-Тс ” 1 + 0,5/? {Г0 + Гс - (Г0 - Гс) ехр [ - 2,5 (1 + /?ГС) Fo]} *
Построение последующих приближений в (6.215) связано с необ¬
ходимостью решения нелинейных систем обыкновенных дифферен¬
циальных уравнений в точной или приближенной форме.
В данном (кратком) изложении не рассматриваются слож¬
ные качественные вопросы, связанные с оценкой погрешности, до¬
пускаемой при выборе приближенного решения задачи в виде
(6.203), а также сходимость процесса приближения к точному ре¬
зультату. Ответ на эти вопросы можно найти в [185, 186]. Распро¬
странение изложенного подхода на линейные задачи теплопро¬
водности для областей канонического вида, а также на нестацио¬
нарные задачи теплопроводности для многослойных сред дано в
[186].
ГЛАВА Vll
МЕТОД ФУНКЦИЙ ГРИНА ПРИ РЕШЕНИИ
КРАЕВЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ
И СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
ВВЕДЕНИЕ
Этот метод, как и все предыдущие, применим к линейным уравнениям
теплопроводности с линейными краевыми условиями, но существенно
отличается от метода разделения переменных и метода интегральных
преобразований. Метод функций Грина весьма универсальный: его
можно применять для решения краевых задач при достаточно общей
постановке в одно- двух- и трехмерном случаях, в ограниченных,
полуограниченных и неограниченных областях, при неоднородных
начальном, граничных условиях и для неоднородных уравнений,
причем как для нестационарной, так и для стационарной теплопровод¬
ности.
Идея метода функций Грина достаточно проста: метод состоит в
том, что вначале находится специальное решение краевой задачи
теплопроводности того же типа (так называемая функция Грина G(M>
Р> t — т)), но более простой и через него дается интегральное пред¬
ставление решения исходной задачи.
При изложении метода функций Грина будем пользоваться реше¬
нием, соответствующим мгновенному точечному источнику теплоты
мощностью Q=cp в неограниченной области (л;, уу г). Такое решение
(для случая мгновенного точечного источника) в аналитической теории
теплопроводности называется фундаментальным; мы с ним встреча¬
лись в § 5 гл. III (поэтому рекомендуем предварительно прочитать
этот параграф). Выше было показано, что фундаментальное решение
уравнения теплопроводности T't=a&T(Xy у, z, t)(|х|, \у\, |г|) < +
+ оо, t > 0 дает распределение температуры в точке {х, у, г) неогра¬
ниченной области в момент времени t, вызванное мгновенным точечным
источником теплоты мощностью Q=cp, действующим в точке (х',
у'у г') в моменты времени t = 0.
Из формулы (7.1) видно, что функция G обладает свойством симмет¬
рии G(Xy Уу 2у х'у у'у г'у t) = G(x'y у\ г', х, у г, /), что является
выражением принципа взаимности: действие в точке М (х, у, г) источ¬
ника теплоты, находящегося в точке Р(х\ //', z'), равно действию в
точке Р(х'у у'у г') такого же источника, помещенного в точку М (xt
у у г). Однако относительно переменной t такая симметрия не наблю¬
дается, что является следствием необратимости тепловых процессов во
времени.
Нетрудно заметить, что функция (7.1) является б-образной функ¬
цией с параметром t по отношению к множеству функций, непрерыв-
G (*, у, г, х’, у’, г', /) =
(2/ал7)3
ехр [
(7.1)
365
ных и ограниченных в пространстве (*, у, z, t) [см. (3.178) — (3.179)1.
Действительно,
I °°
lim G(x, (/, z, х\ у\ z\t) = < в точке
/ -> о (и,
оо х = х , у=*у , г = г;
г = г';
-Г w -г w Т »
iiiG(x'у'г'х’'у>'Л od*d*d2=wWx
+ 0D - (х-х') -НУ-//)*+ (*-»*)*
X^Je ш dxdyd 2 =
"Йт f ''“'d“FTl t“- (3 |7°Я-
— 00 “ OD — 90
(7.2)
Математически, как отмечалось в § 5 гл. III, мгновенный то¬
чечный источник теплоты, действующий в момент времени / = 0,
записывается с помощью импульсной дельта-функции Дирака. При
этом можно указать две эквивалентные математические модели для
определения функции G(M, Р, /); в первой модели наличие мгно¬
венного точечного источника мощностью Q фиксируется в дифферен¬
циальном уравнении теплопроводности с нулевым начальным усло¬
вием, во второй—в начальном условии задачи при однородном
дифференциальном уравнении. Итак, имеем (при — с» < *, у, г <
< + оо / > 0; Q = ср):
W = + \ (73)
G(M, Р, /)|,=0 = 0; | G (М, Р, 01 < + оо, (|*|, |НИ)<+оо )
*
либо
dG _ / d*G дЮ . d2G \
dt ~й { дх* + ду* + дг* ) '
G(M, Р, OLo =»«(*-*') Ь(у-у')Ь(г-гУ, (7‘4>
|G(M, Р, О I < + °°> (|*|. М. |г|)< + оо.
Для решения каждой из задач (7.3) и (7.4) можно воспользо¬
ваться формулой (3.188), подставив в первом случае Ф0(М) = 0,
/ (Af, t). = o(x—х')Ь(у—у') б (z — z') б (t)f во втором случае Ф0(М) =
= б (х—х') б {у—у1) б (z—-z'), /(М, /) = 0 (см. § 5 гл. III.) Исполь¬
зуя затем свойство 6-функции (3.178), приходим и в первом и во
втором случаях к (7.1). Если выделенное количество теплоты
в точке (л:', у\ z')Q=^cp, то, согласно (3.176), распределение тем¬
• В (7.3) и (7.4) точнее было бы записать б (дс — х'* у —</'* z —г', /)» однако
по свойству расщепления 6-функции имеем: б (ж — х9, у—у91 г—z', t)=*
б (* — *') б {у—у*) б (г —г9) б (/).
366
пературы в неограниченной области дается выражением
*' ‘■'■У'-1’’ 'I- „,(2|ЛД). х
xexp I + j. (7.5>
которое может быть использовано для рассмотрения частных слу¬
чаев следующим образом.
Рассмотрим распределение мгновенных точечных источников
постоянной мощности Q&z’ вдоль линии (х = х\ у = у'), параллель¬
ной оси г. Температуру, вызванную действием всех этих источни¬
ков, определим, интегрируя (7.5) по переменной z'l
+ 00
G(x, у, х', у’, 0= S с.(*> У. 2, х\ у'-, г', t)Az'~
•ехр
(*--Q2+(y-
^] . (7.6)
ср(2УШ)2 г 1 Ш
Здесь Q—количество теплоты, выделяемое на единице длины этой
прямой. В частности, если Q = cp, то в (7.6) приходят к фундамен¬
тальному решению для двумерного уравнения теплопроводности
в неограниченной области |х|< + оо, |#|< + оо, t > 0.
Рассмотрим далее мгновенный плоский источник мощно¬
стью Q, действующий в момент времени / = 0, расположенный
в плоскости, параллельной плоскости х = 0 и проходящей через
точку jc'. Распределим линейные источники мощностью Q dy' вдоль
прямой х = х' и проинтегрируем (7.6) по у’\
+ 00
G{x, х\ 0 = $ G(x, У, х, у', t)dy' =
— оо
— Q е-(ДГ-АГ')г/(40/). (7.7)
ср2 У nat
Здесь Q—количество теплоты, выделяемое на единице площади
этой плоскости. При Q = cp приходим к фундаментальному решению
уравнения теплопроводности в одномерном случае [ср. с (3.177)].
Выражение (7.6) дает возможность рассмотреть случай мгно¬
венного цилиндрического источника мощностью Q
радиуса г\ действующего в момент времени / = 0;
ось источника совпадает с осью г. Пусть (г, ср) и (/*', <р')— поляр¬
ные координаты соответственно точек (jc, у) и (jc', у'). Распределим
линейные источники мощностью Qrf йц>' по окружности радиуса г'
и проинтегрируем (7.6), где jc = rcoscp, y = r sin ср, jc' = /'c.os<p',
y = r' sin ц/; суммируя действие всех источников, найдем темпера¬
туру в пространстве 0, / > 0:
2л
О- дф._
U
Q2nr'
’ ср4ла*
367
Здесь было использовано интегральное представление функции
Бесселя /о(г)[20]. В частности, если на единицу длины цилиндра
выделяется количество теплоты Q = cp/2rcr', то приходят к фунда¬
ментальному решению для уравнения теплопроводности T'f=ahT (г, t)
в пространстве г^О.
Аналогичным образом выражение (7.5) дает возможность рас¬
смотреть случай мгновенного сферического поверх¬
ностного источника мощностью Q и радиусом г',
действующего в момент времени / = 0. Фундаментальное
решение уравнения T't = a(T"2-\-(2/r)T'r) в пространстве г^О имеет
вид
Соответствующие выкладки приведены в [55]. Количество теплоты,
выделяемое на единицу площади поверхности шара, равно Q=cp/4nr,t
§ 1. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИЙ КРАЕВЫХ
ЗАДАЧ НЕСТАЦИОНАРНОЙ И СТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ
Покажем, что решение краевой задачи нестационарной теплопро¬
водности при достаточно общей ее постановке в конечном счете
может быть сведено к решению более простой задачи, а именно
к нахождению соответствующей функции Грина.
Пусть Т (Mt t)—температура некоторого тела, занимающего об¬
ласть G0-fS(S— граничная поверхность), которая должна быть най¬
дена в результате решения краевой задачи теплопроводности вида
dT/dt = ahT (Mt /) + /(М, /), M£G0, / > 0(Q = G0x* > 0);
где п — внешняя нормаль к S; |3;+ > 0, f (Му t) б С° (й), Ф0(М)€
€ С1 (G0)y ф (My t) £ С0 (S х t ^ 0), так что
Т (Му 0 6 С2 (Q) П С° (Й), VMT 6 С° (Й).
Рассмотрим распределение температуры в данной области й, выз¬
ванное действием мгновенного точечного источника теплоты мощностью
Q=cp, помещенного в точке P(x't у'у г') области G0 в момент времени
t=T (до этого момента времени температура тела равнялась нулю) при
некоторых температурных граничных условиях на поверхности S
(позже определим их вид). Из введения ясно, что выражение для тем¬
пературы, описываемой функцией Грина G(M, Ру t — т) (ниже будет
дано ее определение), в точке М области G0 для последующих моментов
Р, »Т (М. 0 = -ф(М, 0,
Т(М, 0) = Ф„ (М), M€G0;
(7.10)
(7.11)
(7.12)
368
времени (t > х) будет иметь следующий вид:
ощ, р, +М.Р.1-1.
(7.13)
Первое слагаемое правой части этого равенства, как было показано
выше, характеризует собой действие мгновенного точечного источника
теплоты мощностью Q=cp, действующего в точке Р(х', у\ z') в момент
времени t = т, но для бесконечной области. Для удовлетворения
соответствующих граничных условий на границей области G0, налагае¬
мых на G, необходимо добавить функцию q(M, Р, t — т), ограничен¬
ную в области G0 и определенную при t ^ т. Для того чтобы показать
зависимость функций G и q от точки действия источника, в обозна¬
чении этих функций фигурирует точка Р; ясно, что эти функции будут
зависеть также от (t — т), а именно от времени, прошедшего с момента
действия источника. Будем считать, что q как функция точки М и
времени t есть решение однородного уравнения теплопроводности в
области й, t > т, дважды непрерывно дифференцируема по координатам
точки Л4, непрерывно дифференцируема по времени t и непрерывна
в замкнутой области й, и, кроме того, при t=т обращается в нуль
в точках области G0.
lim q(M, Р, /—т) = 0, M$G0. (7.14)
/-►т+о
Таким образом, функция G удовлетворяет уравнению dG/dt = aAG,
М € G0, t > т. Так как t входит в форме (/—т), то отсюда непо¬
средственно следует
dG/dт =— aAG (Л4, Р, t—т), M£GU, т </. (7.15)
Предположим дополнительно, что функция G(M, Р, / — т), как и
первое слагаемое в (7.13), обладает отмеченным выше свойством сим¬
метрии относительно точек М и Р, т. е. G(M, Р, t — x)=G(P, М,
/ — т), что означает эквивалентность свойств этой функции по коорди¬
натам точек М и Р [это свойство может быть доказано строго после
формулировки краевой задачи для определения функции G с исполь¬
зованием формулы Грина для оператора Лапласа (2.142)].
Рассмотрим равенство
&\Т(М, х)G(M, Р, /_T)] = gG+rg = a(GAr-TAG) + G./.
(7.16)
Здесь использованы уравнения (7.10) и (7.15), оператор Лапласа
всюду берется по координатам точки М.
Проинтегрируем (7.16) по области G0 (по координатам точки М)
Ш | F*G]do« - а Щ (G AT-TAG) dvM + ЭД j G . / dvM. (7.17)
Go O0 G о
369
Используя далее формулу Грина для оператора Лапласа (2.142),
получим
ЯШ™]+
G о 5 (?0
(7.18)
Соотношение (7.18) справедливо при всех т < t и, следовательно,
его можно проинтегрировать по т для 0<т</—е, гдее>0 —
сколь угодно малое число. Получим
ОС?* OS
t-s
+ 5 nS0-fd'iv"-
О С? n
При 0 < т < t — е подынтегральная функция (слева) достаточно регу¬
лярна (так как исключена особенность у функции G в точке М=Р
при т = /), поэтому можно переменить порядок интегрирования
слева. Это дает
/-е
С?0 О
отсюда имеем
SSS (^'GjxsZ-e ^Vm — ^^^ (7,*G)T-0 dvM—
C?0 G0
°i I\{T
Перейдем в этом выражении к пределу при е—►О, учитывая (7.13),
(7.14); аналогично, как и в (3.169), найдем
Jim CCf (T-G)Xmt_edvM = lim \^T(xt у, г, /—e)x
e о J J J g->o
Go Go
Хт-^е" *oe dxdi/d2 = r(jt', </', г', 0,
(2 К яде)*
отсюда запишем
т(р. о - Ш ‘Г-°ь-dt>-—о ИКГ ^ -
С?* 0S
-GS)aleid‘d°« + IIHG-/dTd^- (7Л9)
о (?*
370
Выражение (7.19) справедливо для любой точки p£G0 при 0.
Заменим в этой формуле Р на М9 учитывая свойство симметрии
функции G, окончательно получим следующую основную интеграль¬
ную формулу для функции Т (М, t), дающую представление
произвольных решений уравнения теплопровод¬
ности (7.10) с начальным условием (7.11):
т (Л1> =Ш ф°{Р) G {М> р> °dVp+
Go
+а5^(а£-гШ)^'^+ <7М>
0 S
t
+ T)G(M, Р, t—i)dxdvp.
о а„
Из формулы (7.20) следует, что всякое решение уравнения теп¬
лопроводности (7.10), дважды непрерывно дифференцируемое по про¬
странственным координатам и непрерывно дифференцируемое по вре¬
мени t, будет аналитической функцией пространственных координат,
а по времени t иметь производную первого порядка (для одномерного
случая это показано в [114]).
Эта формула не дает решения краевой задачи (7.10) — (7.12), так
как для вычисления правой части нужно знать значение подынтеграль¬
ной функции на поверхности S во втором слагаемом — интеграле.
Потребуем теперь, чтобы функция G(Af, Р, t — т) на поверхности S
удовлетворяла граничным условиям того же типа, что и условия
(7.12):
kdG(Mjn' '~T)-PaG(M, Р, t-x)]M's = 0, <>т. (7.21)
Отсюда и из (7.20) аналогично, как и при выводе рабочих формул в § 4
гл. III, получаем явные формулы для решения Т(М, t)9 согласно
виду граничных условий. Не повторяя соответствующих рассуждений,
приведем основную формулу решения краевой задачи нестационарной
теплопроводности (7.10) — (7.12) со смешанными граничными усло¬
виями:
тш. /) = Щф„(/>)С(М, Р, t) dvP +
X
Go
t t
+ a^[S(M,P, t, T)]peSdxdOp + j /
OS 0 (?„
X (P, x)G(Af, P, t—T)ckcbp, (7.22)
где а) 0(Л4, P, /, т) = — cp(P, t) dG (M, P, t—т)/дпр на всей или
части граничной поверхности S, на которой в (7.12) имеют место
граничные условия I рода:
Т(М9 = М g S, 0; G Р, t—%)MeS = 0, t > т;
371
б) 0(М, Р, t, т) = ч= (1Д)ф(Р, т)G(M, Р, t—т) на всей или части
граничной поверхности S, на которой имеют место граничные
условия II рода:
— дТ (М, 1)/дп = (1/Цц>(М, t), M£S, I > 0;
дG(M, Р, t—x)/dn\M<iS = Q, t> т,
или III рода
д™±Л+«Т(М, П-{ф(М, I),
а°(<<'й.’ '~- + yOW р■ •)J».s-0, От.
Здесь всюду G(M, Р, t — т) — функция Грина соответствующей крае¬
вой задачи. Заметим, что д1дпр означает дифференцирование по коорди¬
натам точки Р в направлении внешней нормали к границе S и затем
производная функции G вычисляется (по Р) в точках границы S.
Таким образом, для каждой из краевых задач установлена интег¬
ральная формула решения и выяснено, каким условиям должна удов¬
летворять функция G(M, Р, t — т) в виде (7.13) для ее нахождения.
Сформулируем теперь следующее определение для этой функции.
Пусть q(Mt Р, t — т) как функция точки М и времени t есть
решение однородного уравнения теплопроводности (7.10); пусть она в
области й дважды непрерывно дифференцируема по координатам точки
М и непрерывно дифференцируема по времени t и непрерывна в замк¬
нутой области Й. Тогда если функция G{My Р, t — т) в виде (7.13) при
t т + 0 области G0 вне точки М = Р обращается в нуль, а на боко¬
вой поверхности Sa, области й удовлетворяет нулевым краевым усло¬
виям какой-либо из краевых задач для уравнения теплопроводности в
области й, то она называется функцией Грина соответствующй крае¬
вой задачи в области й. Из предыдущих рассуждений становится ясным
и физический смысл функции Грина G(M, Р, t — т), в каждой из
краевых задач она представляет собой температуру в точке М в момент
времени /, возникающую вследствие действия мгновенного точечного
источника теплоты мощностью Q = ф, действующего в точке Р в мо¬
мент времени т (до этого момента времени температура тела равнялась
нулю) при условии, что на границе рассматриваемого тела во все
последующие моменты времени t> т выполняются однородные усло¬
вия, соответствующие нулевым значениям граничных функций крае¬
вой задачи. Отсюда вполне оправдано второе наименование функции
G — функция влияния мгновенного точечного теплового источника.
Исходя из физического смысла функции Грина, запишем для G(7W,
Р, / — т) краевую задачу, соответствующую заданной (7.10) — (7.12):
dG/dt =a&G (М, Р, t—т), М £ G0, />т; \
G |<=т = 6 (М, Р), M€G0; 0)^-0. />т. ) (7-23>
Здесь 6(М, Р)—дельта-функция; 6(Л4, Р) = 8(х—х')8(у—у')х
хб(г—г')—функция в декартовых координатах; 6(М, Р) =
372
= -i-6(r—г') б(ср — ср')—функция в полярных координатах на пло¬
скости; 6(М, Р) = -^Ь(г— г') б (0 — 0') б (ф — ф')—функция в
сферических координатах.
Заметим, что для цилиндрического температурного
поля начальное значение соответствующей функции Грина
G (г, r'9 t—т) определяется равенством
с (г, г1, = 2^6 (/•-/•'); (7.24)
для сферического температурного поля имеем
С(г,г', 1-т)(=14бМ. (7.25)
Укажем теперь один из простейших методов нахождения функ¬
ции Грина, учитывая, что для этого имеются достаточно обширные
результаты, полученные в гл. III. В постановке задачи (7.23) гра¬
ничные условия однородные, начальное условие—заданная функция.
Решение этой задачи нетрудно получить методом разделения пере¬
менных (см. гл. III). Действительно, формальное применение метода
разделения переменных к нахождению решения задачи (7.23) дает
ряд
G (М,Р, t—x) = 2 «Д* (М) ехР [—V~ayk)V—*)]. (7.26)
fe=l
где yl и Ч^(М)—собственные значения и собственные функции
соответствующей однородной задачи (3.25)—(3.271).
Коэффициенты ряда (7.26) находим, используя начальное усло¬
вие для G, условие ортогональности собственных функций и свой¬
ство 6-функции (3.178)i
в.=РПгШ°(м» Р• 0)^K(M)d^ =
G0
= nTF III 6 ^ dt>M = '
G n
Таким образом, для краевых задач нестационарной теплопровод¬
ности в ограниченных областях функция Грина представляется ря¬
дом Фурье по собственным функциям однородной задачи
G(M,P, t—х) = X (7.27)
Нетрудно убедиться, что решение краевой задачи (7.10) — (7.12),
полученное методом функции Грина в виде (7.22) (в зависимости от
типа граничных условий), совпадает с соответствующими интеграль¬
ными представлениями в виде рабочих формул, полученных в § 4
гл. III. Используя результаты гл. III и формулу (7.27), нетрудно
записать функцию Грина соответствующей краевой задачи для соот¬
ветствующей области без решения краевой задачи для нее.
В других случаях для решения краевой задачи (7.23) может быть
использован и метод интегральных преобразований (см. гл. V), также
373
достаточно быстро приводящий к конечной цели. В сочетании с опе¬
рационным методом можно получить специальное решение краевой
задачи (7.23) для малых значений времени (см. § 3 гл. VI), а вместе с
этим (по соответствующей интегральной формуле) и решение исходной
тепловой задачи, удобное для малых значений t (см. пример ниже).
Следует также отметить, что после нахождения функции Грина
ее представление в виде (7.13) обнаруживается не сразу, а только после
определенных преобразований, в результате которых выделяется
фундаментальное решение уравнения теплопроводности и регулярная
составляющая q(My Я, t — т). В ряде случаев целесообразно с самого
начала отыскивать функцию влияния G в виде (7.13); в этом случае
ставится краевая задача относительно функции q(M, Я, t — т),
которая в области М С G0, t > т, удовлетворяет однородному уравне¬
нию теплопроводности, нулевому начальному условию (при t = т),
а на границе S — неоднородному граничному условию, содержащему
значения фундаментального решения и его нормальной производной
в точках граничной поверхности. Такой подход чаще всего использу¬
ется в области с движущейся границей (см. § 2 гл. VIII).
Формула (7.22) (и ее частные случаи) содержит кратные интегралы
по пространственным переменным. Эти интегралы в конкретных
областях необходимо уметь записать в виде повторных в той или иной
криволинейной ортогональной системе координат и затем вычислить
при заданных краевых функциях задачи. В § 4 гл. III приведены
для этих целей необходимые формулы (3.91) — (3.92).
При построении функций Грина G(M, Я, /—т) может быть
использована другая модель, эквивалентная (7.23), а именно:
SG/dt = aAG(M, Я, t-x) + 6(M, P)S(t-т), MeG0, t>0;
G(M, Я, /-t)U=0, MeG0, PeGQ; 0?idG/d/i-&GW=0, />0.
Перейдем к двумерным краевым задачам нестационарной теплопро¬
водности
дТ/dt = аАТ (х, у, t) + f(x, у, /), (х, y)£D, t > 0; (7.28)
Т(х, у, 0) = Ф0 (х, у), (х, у) 6 D; р, дГ/дп-&Т =
= -ф(*. У, 0. (*. У)€С, 0, (7.29)
где п — внешняя нормаль к контуру С, ограничивающему область D —
конечную область в плоскости (х, у).
Как и выше, функция Грина G(x, уу х\ у', t — т), определяемая
равенством (7.13) (но для двумерного случая), является решением со¬
ответствующей краевой задачи нестационарной теплопроводности:
dG/dt = aAG (х, у, х\ у\ t—т), (х, у) g D, t > т;
G\t=x = 8(x-x')6(y-y% (х, y)6D;
(р.^-Р2с)(^)бС = о.;>т.
Повторяя предыдущие рассуждения применительно к (7.28) —
(7.29) и используя при этом формулу Грина для двумерного опе¬
ратора Лапласа (3.97), а также (7.30), приходим к основной интег¬
ральной формуле решения уравнения (7.28) с начальным условием
374
(7.30)
Фо (X, у) в (7.29):
Т (х, у, I) = $ $ Ф0 (*', у') G (дс, у, х', у', t) dx' dy' +
Здесь д/дп' означает дифференцирование по координатам точки
(*', у') в направлении внешней нормали к контуру С; d/' указы¬
вает, что интегрирование проводится по координатам точки (*', у')
по контуру С, обход которого совершается против
часовойстрелки.
Учитывая теперь (7.29) и (7.30) конкретный вид граничных ус¬
ловий, приходим к следующему интегральному представлению ре¬
шения Т (х, yf t)i
Здесы а) 0 = — ср(х', у\ т) dG (х, у, х', yr, t—т)/дп' на всем или
части граничного контура С, где в (7.29) — (7.30) имеют место гра-
ничные условия I рода
б) 0 = Т (IA)^(jc', у\ %)G(x, уу х'у у'у t—т) на всем или части
граничного контура С, где в (7.29) — (7.30) имеют место гранич¬
ные уоловия II рода
D
ОС
t
•+S И f у'*т)G (*• у»х' у'*1 ix' dy'dT* ^,31^
0D
Т (X, у, I) 5 J Ф0 {х',у') G (х, у, х\у', 0 d*' dу' +
D
/
+ а J J [0 (х, у, х', у', t, т](^, У'Л еС dx dl' + (7.32)
+ Ш У’> х)G (*. У' *'» У' у т)dxdj<:' dy!.
0 D
т (,х, у, I) =я ср (х, у, 0. (*. У) € С, / > 0;
G{x,y, х', у', I—т) = 0, (х, у)&С, t > т;
или III рода
dT (л, £/, 0 _а
дп X
у, 0 = у- ср (дг, у, t), (х, у) € С, 0;
375
Формула (7.32) (и ее частные случаи) содержит криволинейный
и двойной интеграл по пространственным переменным. В §4 гл. III
приведены необходимые формулы (3.110)—(3.111) для вычисления этих
интегралов.
Что касается одномерного случая для области О^л:^/, 0 при
решении краевой задачи (3.112)—(3.116), то эта задача подробно
рассмотрена в § 4 гл. III, где указана рабочая формула (3.122) для ее
решения, а в §7 гл. III приведены собственные значения и собствен¬
ные функции однородных задач при любой комбинации граничных ус¬
ловий в области [0, /]; кроме того, в § 7 гл. V приведена табл. 10,
содержащая сведения, необходимые для улучшения сходимости лю¬
бого из полученных решений.
Запишем основную интегральную формулу представления произ¬
вольных решений уравнения теплопроводности (3.112) с начальным
условием (3.113)
i t
Т (X, о = 5 Ф0 (■*') С С*. 0 d*' + a S [с (X, х', t —т) т)—
о о L
—т (х!. т)90 (х’ *х:‘ т) ] ^ " dT—a J [ G (X, х', t— х)
дГ(х',х)
дх'
о
i I
— т (х\ т)dG (х’*х; ‘ т)1 ,=0 dt+ [[fix', т) G (х, х‘, t—т) dt dx'-. (7.33)
Х 0 0
Предлагаем читателю получить самостоятельно выражение (7.33),
используя формулу Грина для оператора Лапласа в одномерном
случае (5.272).
Функция Грина краевой^ задачи (3.112) — (3.116) для области
*€[0, /], f >0 является решением следующей задачи1
dG/dt = а (d2G/dx2)y 0 <х<1, t > т; (7.34)
G (ху х’у t — т) |/=х = S (jc—*'), 0 < а: < /; (7.35)
(Pug-PnG)x=0 = o, (р«§+№)хшГо, t>T. (7.36)
В качестве примера использования формулы (7.33) рассмотрим в (3.114) —
(3.115) граничные условия вида
дТ (.х, 0
дх
,= 0 = {ф1(0. Т(х, 0 и_/ = Ф» (0. О 0. (7.37)
Построим предварительно соответствующую функцию Грина G (х, х\ t—т) по
формуле (7.27), учитывая, что функция G удовлетворяет (7.34) —(7.36) при р12=0
(Зп = 1), &21=° (Р22=0- Находим по табл. 1 (см. § 7 гл. III): у% = (2к—\)2п2/
/4/2; vT„W = cos ук х\ Я ^ к II* = //2-
Отсюда в соответствии с (7.27) получаем
00
6 {х, х', t — т) = (2/7) V cos ук X cos {f~x) (7.38)
К=1
376
и далее по формуле (7.33) записываем интегральное представление решения зада¬
чи (3.112), (3.113), (7.38) в виде
I t
Т (дг, /) = J Ф0 (*') G (*, t) dx'— a f ср2(т) —
0 О
dt +
х'=1
t I
+ a J (1/Х) ф! (т) О (де, х’, <—J) $ /(•*'. *) G (*> *’> т) * d*'- (7-3^)
о оо
Рассмотрим случай малых значений времени t и построим* используя опера¬
ционный метод, соответствующую функцию Грина в форме, отличной от (7.38).
Для этого в соответствующей постановке (7.34) — (7.36) введем переменную tl=t—x
(так что теперь Г> 0) и положим
00
G (.х, р) = J e-zt'G (х, х'у t') d(7.40)
о
В пространстве изображений общее решение преобразованного уравнения (7.34)
и преобразованных граничных условий
^L.-2-G-. б (*-*'); 5 =0, G|x=/=0 (7.41)
дх а а ' дх *=о
запишем в виде, используя формулу (5.17)
G(x, x',p) = Ach —sh Y~p+-?=<& -£=. \Грх
У а У а У ар У а
х i
х f б (i-до sh --L- |Tpdg+-i- sh -L- V~p f б (g-jt') ch —L- r7di.
g К а К ар M d KO
(7.42)
В выражении (7.42) под знаком интеграла записана 6-функция и можно вос¬
пользоваться равенством (3.178) для вычисления интегралов, входящих в правую
часть (7.42). Однако здесь следует рассмотреть два случая положения точки х\
Пусть в первом случае 0 < *'< х, тогда имеем
X
С б ti—X') Sh -JL- V~-p dg = sh -±- V~P;
о V a V a
I
[b(\-x')ch-^V~pdl = Q.
J У a
x r
Если во втором случае x < *'< /, то получим
X I
С 6 <i—X')sh -7= /Tdg = 0; f 6 (£-*') ch -L- V~P d£ = ch V~P,
J V a J \a у a
Таким образом, из (7.42) находим
G(x,x',p)=Ach—L- ]/~р + В sh —?=-}Гр+—J=ch-£= /~psh -£= V~p,
У а У а У ар У а У a
0 <*'<*; (7.43)
G (x, x', p)=A ch-JL- j/“p+Bsh—1=- + sh -Д=- V~p ch —Z=- ]/~P,
у а У а У ар У а У a
x<x '</. (7.44)
377
Здесь постоянные интегрирования А и В не зависят от х, но являются функция¬
ми р. При их нахождении из граничных условий в (7.41) сле¬
дует проявлять особую внимательность.
Используя граничное условие при * = 0, следует воспользоваться выражением
(7.44); используя граничное условие при х = 1, следует применять выражение
(7.43). Находим А и Я, подставляем в (7.43) — (7.44) и после несложных преоб¬
разований приходим к выражению
ОК.,..,,), ',.<J. (7.(5)
yUp ch 1(//1/ a) t^l>\
Случай х'> х получается из (7.45) заменой х на х' и х' на х.
Дальнейшие рассуждения при переходе к оригиналам зависят от той формы
для функции G (х, x\t'), которую хотели бы получить. В § 3 гл. VI показано,
что если воспользоваться обобщенной теоремой разложения (6.33), то в оригинале
для G получим ряд типа Фурье, а именно ряд (7.38). Если же в (7.45) выразить
гиперболические функции через показательные и разложить' решения в ряд по
степеням ехр (—2 In У~р1ул'а), то придем к форме, удобной для малых времен.
Итак, находим
ch -£=- Y~P sh У~~р
1^ \^a \Га
У~а~р ch [(//j/~a) У~р]
-(Ч1п+х-х')У~р -(21п +х+х')У~р']
[-[2 (п+ 1) 1-х-х']У р —[2 (п+ 1) l-x + x’ ] V р 1 |
_ ^ +е ^ ]}.
п— 0
Переходя к оригиналам по таблицам изображений и объединяя ряды, по¬
лучим вторую форму для функции Грина G(x,x', t—т), отличную от (7.38) и
удобную при расчетах для малых значений времени:
I л= + ов Г - (21п-х+х')* —(21п + х+х')* "| Ч
G(xt х\ t—т)=—;■■■: - ■ I V (— \)п е 4-е 4fl(/—I) I
(7.46)
Выражение (7.46) может быть формально записано и через те-
та-функции (см. § 12 гл. III), но в более громоздкой форме. Кроме
того, приведенные выше рассуждения являются полезными как при¬
мер отыскания с помощью операционного метода функции Грина
соответствующей краевой задачи.
Рассмотрим наиболее простой и наиболее важный случай, когда
/(*, 0 = 0, Ф0 (х) = 0, Г(/, 0 = 7^
дТ (ху t)/dx\x~o = 0.
Подставляя эти частные значения краевых функций задачи в (7.39)
и используя (7.38) или (7.46), находим после несложных преобра¬
зований
t<^> = 1_± V JzdL coSB±i^ е-l-~TV~a]\ (1 47)
Т0 л 1) 21 е
* п = 0 '
378
или
2 (tt +!) + *//
~iуищ*
]■
(7.48)
Ряд (7.48) сходится довольно быстро для малых значений Fo =
= а///2; для больших значений Fo лучше сходится ряд (7.47); в
диапазоне средних значений Fo пригодным оказывается как выра¬
жение (7.47), так и (7.48), однако (7.48) пользоваться несколько
удобнее. Например, если at/l2= 1, то из (7.48) получим для х = 0;
Т (0, t)/T0 = Ф* (1/2) —Ф* (3/2) + Ф* (5/2) —... = 0,4795—0,0339+
В монографии [55] приведены температурные кривые, построен¬
ные по решению (7.47).
Замечание 1. В тех случаях, когда функция Грина той или иной крае¬
вой задачи найдена, на правые части интегральных формул (7.22), (7.32), (7.33)
следует смотреть как на предполагаемый результат решения соответствующей
краевой задачи. Это объясняется тем, что заранее не известно, что это решение
удовлетворяет всем условиям применимости интегральной формулы Грина (2.142),
как неизвестно и то, что функция Грина удовлетворяет этим условиям. Поэтому
этот предполагаемый результат каждый раз необходимо исследовать путем рас¬
смотрения предельных значений правых частей указанных выше интегральных
равенств. Эти дополнительные исследования, как правило, приводят к положи¬
тельному ответу, и, таким образом, вопрос о решении краевых задач в существен¬
ной своей части сводится к нахождению соответствующей функции Грина.
Замечание 2. При выводе интегральных соотношений (7.22), (7.32), (7.33)
(и их частных случаев) предполагалось, что G0—конечная область, ограниченная
замкнутой кусочно-гладкой поверхностью 5. Однако эти формулы в предельном
случае могут быть использованы и для полуогрдниченной области по той или
иной пространственной переменной; необходимо лишь иметь в виду, что на части
в нуль, так как по предположению решения Т таково, что как 7, так и дТ/дп
ограничены, a G и dG/dn стремятся к нулю.
Рассмотрим, например, интегральное представление решения
третьей краевой задачи для полубесконечного стержня,
теплоизолированного с боковой поверхности (одновременно укажем постановку
задачи и для соответствующей функции Грина):
+ 0,004—... =0,4460.
поверхности, уходящие в бесконечность, выражение
обращается
дГ=а t)' Х > °’ 1 > °;
Г(дс,0) = Ф0(х); d£\xm=hlT(o, о-ф(0);
|Г(дс, 01 < + », *> 0;
lim G (*, / — т) =0,
Х-+СО
379
Устремляя в (7.33) I—юо и учитывая граничное условие для Т (ж, 0 и О
при * = 0, находим интегральное представление для Т (ж, О
со L
т (ж, ^ Ф0 (*') G (*» *'0 dx' + ah J ф (т) G (ж, ж', / —х) |Х'=о dx +
0 о
t ОО
+ J J / (ж', т) G (ж, ж', / —х) dx <1ж\ (7.49)
о о
Функция Грина G (ж, ж', х) может быть найдена из решения задачи (5.95)--
(5.96), рассмотренной в § 1 гл. V, если в формулу (5.100) подставить вместо Ф0 (р)
функцию Ф0(Р) = бф—х ),
г -jx-x’)‘ -(*+*')■ 1
G (х. х\ t-т) = ■ ' = е +е J -
2 уПйГц—х)
—Лехр[аЛ2(/—т) + А (*+*')] Ф*( Г а т)\ (7-50)
\2уа(1—т) /
Что касается неограниченной области, то здесь функция Грина
совпадает с фундаментальным решением уравнения теплопровод¬
ности (7.1) и решение задачи Коши (3.184) — (3.185) записывается
через функцию Грина G в виде (3.186); постановка соответствующей
задачи для функции G дана в (7.4).
Замечание 3. В этом параграфе рассмотрены интегральные представления
решений уравнения Тt = aAT (M,t) + f(M,t) в трех-, дву- или одномерном случаях.
Однако все полученные выражения справедливы и для уравнения вида Т^аЛТх
Х(М,0—b2T-\-f(M, /)..В этом случае функция Грина G (М, Р, * — х) удовлет¬
воряет однородному уравнению вида Gt=akG (М, Р, t—х)—ЬЮ я соответствую¬
щим однородным граничным условиям.
Следует особо остановиться на краевых задачах уравнения теп¬
лопроводности в области с движущимися границами
(краевые задачи обобщенного типа).
Если П, — нецилиндрическая область и сечение области Г2, плос¬
костью / = const >0 представляет собой пространственную область
GQt с границей Sh зависящей от времени /, то в записи основных
интегральных формул типа (7.22), (7.32), (7.33) появятся особен¬
ности, вызванные наличием движущихся границ рассматриваемой
области. Кроме того, и в постановке краевой задачи относительно
функции Грина G(M, Р, /, т) также появятся свои особенности,
учитывая, что в нецилиндрических областях функция Грина не будет
обладать свойством симметрии: G(M, Р, /, t)=^G(P, М, t, т). меня¬
ется и запись граничных условий для функции Грина в некоторых
частных случаях, например в случае теплоизоляции боковой поверх¬
ности St (см. (2.76)). Все эти вопросы пока еще недостаточно изуче¬
ны в литературе и мы рассмотрим их в следующем параграфе.
Метод функции Грина широко применяется также и для решения
краевых задач стационарной теплопроводности; в этом случае этот
метод представляет собой часть хорошо разработанной теории, извест¬
ной в курсах математической физики как теория потенциала.
Рассмотрим краевые задачи стационарной теплопроводности (вну¬
380
тренние или внешние) вида
AT(M) + -J-F(Af) = 0, М € О0; (7.51)
Л
PtT(M) = -<p(M), M£S. (7.52)
Здесь п—внешняя нормаль к Sp^ + p^>Ot
<p(M)€0(S)f F(M)£C»(G0), r(M)€C*(G0)nC«(G0);
для внешних задач добавляется условие поведения искомого решения
на бесконечности.
Метод функции Грина, позволяющий получить интегральное пред¬
ставление решения таких задач, состоит в следующем. Вначале нахо¬
дится решение специальной задачи вида
ДС(М, P) = -6(M, Р), M€G0(P£G0); (7.53)
^ WL_p!C(M) /’)]M6S = 0. (7.54)
Функция G(M, P), удовлетворяющая (7.53)—(7.54), называется
функцией Грина краевой задачи (7.51)—(7.52).
Если функция Грина найдена, то с ее помощью нетрудно записать
интегральное представление решения задачи (7.51)—(7.52). Для
этого воспользуемся функцией Грина для оператора Лапласа (2.142),
записав ее в виде
J 5 J <C4r-T4Qd,« - -I J (7- *L_0 (7.55)
(?</ s
предполагая, что функция G удовлетворяет условиям применимости
этой формулы [для функции Т это следует из (7.51)—(7.52)]. Так как
в области G0 имеем ДТ=(—1 /X)F(M) и AG=—б(Af, Р), то из (7.55)
находим
т^—+
S
+ jif(M)G(M, P)dvM. (7.56)
Go
С помощью (7.55) можно убедиться, что функция G (М, Р) обладает
свойством симметрии, т.е. G (M, P) = G(P, М) [1]; отсюда, заменяя
в (7.56) Р на М, получим следующую основную интеграль¬
ную формулу для функции Г(М), дающую представление
произвольных решений уравнения ■ стационарной теплопроводности
(7.51):
7-(M) = jJ[0(M, Р)Ц£—7-(P)^2-]p,5tof +
S
+ (P)G(M’P)dyp- (757)
G о
381
Принимая теперь во внимание конкретный вид граничных условий
в (7.52) и соответственно в (7.54), окончательно находим
Здесь: а) 0(М, Р) = — <p(P)dG(M, Р)/дпр на всей или части гра¬
ничной поверхности S, где в (7.52) имеют место граничные
условия I рода
б) 0(М, P) = (=F 1А) (p(P)G(Af, Р) на всей или части граничной
поверхности S, где в (7.52) имеют место граничные условия
II рода
Область G0 может быть ограничена несколькими поверхностями,
на каждой из которых могут быть заданы граничные условия раз¬
личных типов. В этом случае в (7.58) поверхностный интеграл сле¬
дует брать по всем поверхностям, ограничивающим область G0.
Замечание 4. Относительно функции Грина второй краевой задачи ста¬
ционарной теплопроводности и, следовательно, относительно решения второй крае¬
вой задачи (7.51), (7.59) необходимо заметить следующее.
В § 5 гл. 11 показано, что для существования решения второй краевой зада¬
чи, непрерывного вместе с частными производными первого порядка в G0 = G0 + «S,
должно выполняться соотношение (2.143). Для случая конечных областей функция
Грина второй краевой задачи (7.53), (7.59) в указанном смысле не существует,
так как соотношение (2.143) для краевых функций задачи (7.53) и (7.59) прини¬
мает вид 0=1. Существование такой функции возможно для областей, не лежа¬
щих в конечной части пространства или плоскости. Поэтому, чтобы в случае
конечных областей формула (7.58) имела место для второй краевой задачи (7.51),
(7.59), необходимо несколько обобщить понятие функции Грина второй
краевой' задачи. Под обобщенной функцией Грина второй
краевой задачи для конечной пространственной области
G0 будем понимать функцию G(M, Р), если на поверхности 5, ограничивающей
область G0, она удовлетворяет нулевым граничным условиям (7.59) второй крае¬
вой задачи, в области G0 является дважды непрерывно дифференцируемым реше¬
нием уравнения AG = —б(Л4, Р) + р0, где р0 = 1/К(?0 (Кб0—объем области G0) и,
кроме того, выполняется условие нормировки в виде
Т(Л4) = ф(М), MgS; G (М, Р) = 0, M$S;
или III рода
-Lfn —+TG{M' Р) = 0’ M$S-
(7.60)
382
Нетрудно видеть, что соотношение (2.143) теперь соблюдается и, следователь¬
но, функция G(Af, Р) может существовать. Действительно, из (2.143) имеем
i s s-u а°—и s• ■<"• №"+t‘ in ■di'*"
S G0 G0
откуда Po =l/KGe.
Условию нормировки (7.60) также всегда можно удовлетворить, так как реше¬
ние внутренней задачи Неймана определяется с точностью до произвольного п)-
стоянного слагаемого (см. § 5 гл. II). Таким образом, найдя G (М, Р) как реше¬
ние задачи
AG(Af, Р)=—6(Af, Р)+1/Г<?0, MgG0;
dG (М, P)/dn\M€S = 0t (7.61)
можно по формуле (7.56) построить то из решений задачи Неймана (7.51), (7.59),
для которого произвольная постоянная равна нулю, а именно:
Г(Л*) = И [--ГФ(Р)0(Л1, P)]p6Sd0p+HIrf(P)G(;M’ Р)АУр- (7-
62)
Все остальные решения этой задачи могут быть получены прибавлением к
этому решению произвольной постоянной. Строго говоря, в случае (7.61) необхо¬
димо в качестве исходной взять формулу (7.55), тогда решение второй краевой
задачи по этой формуле имело бы вид (7.62) плюс в первой части этого равенст¬
ва интеграл (1 /У(?в) ш Т dVp. Данный интеграл представляет собой среднее
Go
значение неизвестной функции Т (Л4), вообще говоря, также неизвестное. Однако,
как уже говорилось, решения задачи Неймана определены лишь с точностью до
постоянного слагаемого, подбором которого среднему значению решения Т (М)
в области G0 можно придать любое наперед заданное значение. Следовательно,
указанный интеграл должен рассматриваться как произвольная постоянная, при¬
бавляемая к правой части (7.62).
Формула (7.58) и (ее частные случаи) содержит тройной и поверх¬
ностный интегралы и записана в декартовой системе координат (х, у,
г). Эти интегралы для конкретных областей в той или иной криволи¬
нейной ортогональной системе координат необходимо уметь записать
в виде повторных интегралов и затем вычислить при заданных краевых
функциях задачи. В § 4 гл. III приведены необходимые для этих целей
формулы (3.91)—(3.92).
В отношении распространения формулы (7.58) и ее частных случаев
на внешние задачи для уравнения Лапласа и Пуассона следует ска¬
зать следующее. Для уравнения Лапласа (F(M)=0) на внешние за¬
дачи она распространяется непосредственно *, а для уравнения Пуас¬
сона — при условии регулярности решения (см. § 5 гл. II) и сходимо¬
сти интеграла F(p)G(M, P)dvp. При этом внешняя задача Неймана
Со
(т. е. вторая краевая задача) не имеет каких-либо особенностей по
сравнению с первой или третьей внешней краевой задачей, так как
условие (2.143) не распространяется на функции, гармоничные в бес¬
конечной области, и решение ее в этом случае дается формулой (7.58).
* Это объясняется тем, что формула Грина для оператора Лапласа (7.55)
применима для неограниченной области (внешней и замкнутой поверхности)
к функциям, регулярным на бесконечности
383
Перейдем теперь к двумерным краевым задачам стационар¬
ной теплопроводности и одновременно укажем соответствующую крае¬
вую задачу для функции Грина G, исходя из ее определения (7.53)—
(7.54):
(х, У)+-%Р(х, у) = О,
(х, «/)€£>;
дТ (х, у)
Р.
дп
х
Х(х, у) = — Ф (х, у),
(х, у) € С\
ДС(лг, у, х', у') = —
— 6 (х—х')Ь(у—у'у,
(х, y)£D\
,.с = 0’
(7.63)
где D—конечная область в плоскости (.х, у); С—кусочно-гладкий
контур, ограничивающий конечную область; п—внешняя нормаль
к С» Pi ~Ь 6.
Повторяя предыдущие рассуждения, но применительно к плоско¬
му случаю, и используя при этом формулу Грина для двумерного
оператора Лапласа (3.97), приходим к основной интегральной фор¬
муле, дающей представление произвольных решений урав¬
нения теплопроводности (7.63):
т(х, у) = j [ -"а*-У~ G (х, у, х’, у’)—
-Т(ху')[
0G (х, у, у')
дп'
1 d/' +
J (х\ у')ес
+ y')G(xt у, х', y')dx'dy'. (7.64)
о
Здесь д/дп* и д/дГ имеют тот же смысл, что и в (7.31).
Учитывая теперь в (7.63) конкретный вид граничных условий,
получим следующее интегральное представление решений краевой
задачи (7.64):
Т (X, </)=$[© (X, У, х’, у')\(Х', S)ecdr +
С
IтF G у'х>'у^dx'dy
(7.65)
о \ гч / / /\ 3G (х, у, х', у')
Здесь: а) 0 = — ф(х , у)—-—*„/ ■■■■ 7 на всем или части граничного
контура С, где имеют место граничные условия I рода
Т (х, у) = ф(дг, у), (х, У)£С\ G(x, у, х’, у’) = 0, (х, у)£С;
б) 0 = =F (1/Я.)ф(х', y')G(xt у, х', у') на всем или части граничного
контура С, где имеют место граничные условия II рода
— дТ (х, у)/дп = ( 1Д)ф(х, у), (х, у)$С\
dG(x, у} х', у')/дп = 0, (х, у)£С, (7.66)
384
или III рода
дТ (х, у)/дп+(а/Х) Т (х, у) = (1Д) ф (х, у), (л:, #) € С;
dG(x, у, л:', y')/dn + (a/X)G (х, у, х', #') = 0 (х, */) 6 С.
В случае второй краевой задачи полностью справедливо заме¬
чание 4, сделанное выше. Под обобщенной функцией Грина второй
краевой задачи в плоском случае для конечной области понимает¬
ся функция G (х, у, х', у')} удовлетворяющая однородному гранич¬
ному условию (7.66) и уравнению AG =— 6 (х—х')8(у—y') + VsD
(где sD — площадь области D), а также условию нормировки в виде
(7.60) (но для области D). Отсюда формула (7.65) даст то из реше¬
ний задачи Неймана
т {х, t/) = j[ — Y<p(*\ y')G(x, IJ, х', /)](ж, ,)€С><
С
xd/' + J J у') G (х, у, х', y')dx’dy', (7.67)
D
среднее значение которого в области D равно нулю. Все остальные
решения задачи могут быть получены путем прибавления к правой
части равенства (7.67) произвольной постоянной.
Формула (7.65) (и ее частные случаи) содержит криволинейные и
двойной интегралы по пространственным переменным. Эти интегралы
в конкретных условиях задачи необходимо уметь записать соответст¬
венно через определенный и повторный. В § 4 гл. III приведены необ¬
ходимые для этих целей формулы (3.110)—(3.111). Формула (7.65)-
распространяется и на внешние задачи: для уравнения Лапласа непо¬
средственно, а для уравнения Пуассона при условии сходимости инте¬
грала ^(lM,)F*Gd/?. При этом для внешней задачи Неймана на плос-
D
кости остается в силе все сказанное относительно внутренней задачи
и при отыскании функции Грина второй внешней краевой задачи сле¬
дует пользоваться ее определением в виде (7.69) (см. ниже). Заметим
также, что для плоского случая остается справедливым замечание 3,
сделанное выше.
Как и для нестационарных задач, где функция G определялась
в виде (7.13), можно и для стационарного случая ввести аналогичное
определение функции G(M, Р).
Функцию 6 (М, Р) = 1/4лг, где г = V (х— х')2+ (у—у')2 + (z—z'f—
расстояние между точками М (х, у, г) и Р (xf, у', г'), будем назы¬
вать функцией точечного источника (в точке Р) для трехмерного
уравнения Лапласа ДТ (х, у, г) = 0. Аналогично, в плоском случае
функцию 6(М, Р) = (1/2л) In (1/г), где г = (х—х')2 + (у—у')2 —
расстояние между точками М (х, у) и Р(х\ у'), будем называть
функцией точечного источника (в точке Р) для двумерного уравне¬
ния Лапласа ДТ (х, у) = 0.
Непосредственной проверкой можно убедиться, что функции
1/(4л/*) и (1/2л) In (1/л) вне точки Р (х', у'} г') и соответственно вне
13-339
385
точки P{xfу у') являются дважды непрерывно дифференцируемыми
решениями уравнения Лапласа с тремя и соответственно с двумя
независимыми переменными. Эти функции называются также фунда¬
ментальными решениями уравнения Лапласа. Исходя из структуры
уравнения AG =— б (М, Р), которому удовлетворяет функция Гри¬
на G можно функцию G представить в виде
С(М, Р) = 1/(4яг) + ?(М, P) = V1+q(My Р) .(7.68)
в пространстве (Ху уу г) и
G(x, у, х', y') = (\/2n)\n(llr) + q(x, у, х\ y') = '¥i + q(x, у, х', у'),
(7.69)
где q—гармонична в G0 как функция точки М [в области D по
(х, у)]у а функция имеет особенность в точке Р (т. е. при г = 0
и должна удовлетворять уравнению АЧ*^—б(М, Я), АЧГ2 =—б (л:—
— х')Ь(у—у').
Таким образом, исходя из представления функции G (М> Р) в
виде (7.68) и (7.69) вопрос о построении функции Грина сводится
к нахождению ее регулярной части q(Mt Р), которая в соответст¬
вии с (7.53), (7.54) определяется как решение однородного уравне¬
ния со специальными граничными условиями:
Aq(My Р) = О, М £ G0,
§xdq!dn—р2<7 =
= —(1/4л) [0! (д/дп)х
х (1/г)-р. (1/г)],
MeS;
Aq(Xy уу х'у у') = 0(Ху y)£D;
^dqldn—$2q = (—1/2л) [f^x
х (д/дп) In (1/г) —Р2/1п (1/г)],
(Ху у) € С.
(7.70)
Она единственна для первой и третьей краевых задач.
Остановимся далее на физическом смысле функции Грина G.
Прежде всего покажем, что функция Т = <2/4лЯг характеризует со¬
бой стационарную температуру в неограниченном теле, обусловлен¬
ную действием точечного источника теплоты мощностью Q. Действи¬
тельно, если описать небольшую шаровую поверхность s радиуса г
вокруг точки Р(х'у у'у г'), в которой выделяется теплота, то при
г—>0 количество теплоты, проходящее в единицу времени через
шаровую поверхность, должно равняться мощности источника Q
й HS53i'Н “й ((Q/4n) i S -
S s
я 2л
= Нш [(Q/4n) J J ^ г1 sin edcpd0]=Q.
Таким образом (для первой краевой задачи), функция G(M, Р)
представляет собой температуру тела в точке А1, если температура
его поверхности равна нулю, а в точке Р помещен тепловой источ¬
ник мощностью Q = X. Отсюда понятно и второе наименование
функции Грина — как функции влияния температурного источника.
386
Аналогично может быть рассмотрен и плоский случай, где функ¬
ция T = (Q/2n^)ln(l/r) характеризует собой стационарную темпера¬
туру плоскости, обусловленную действием линейного источника мощ¬
ностью Q = X, расположенного на прямой, ^параллельной оси г и про¬
ходящей через точку (дг', у').
Следует особо подчеркнуть, что между определением функции
Грина в виде (7.53), (7.54) или в виде (7.68) и аналитическим ме¬
тодом, с помощью которого отыскивается функция G, существует
прямая связь. Если используется метод интегральных пре¬
образований, следует исходить из определения в виде (7.53)—
(7.54).
1. Действительно, пусть требуется найти стационарную температуру Т (х, у)
верхней полуплоскости 0, |*|<оо, граничная поверхность которой у = 0
имеет температуру ф (х).
Функция Грина G (х, у% х', у') первой краевой задачи для данной области
определяется как решение задачи
d2G/dx2-\-d2G/dy2 =— б (х —х') б {у—у')9 у > 0, — <е < х < + оо; 1
0(х, у, х', у')Ь-=о=°; |G(x, У> х\ у') \ < + оо, у > 0, |*| < со. J
Решение этой задачи получим с помощью бесконечного синус-преобразования
00
Фурье, полагая G (х, £, х', у') ^ G (х, у% x't y')sin£ydy (см. табл. 9
о
гл. V). В пространстве изображений имеем
~—6*G=— V~2iiib{x—*')sln \у'\ |G(x, g, x', /)|< + », |*|< + oo.
(7.72)
По формуле (5.17) (или с помощью метода вариации произвольных постоян¬
ных) общее решение уравнения (7.72) запишем в виде
G = Cie|j:+Cle-^-J-
sin ly'X
xjV'Je 6 (a—x') da + e & ^ e^a 6 (a—x') da^J.
Из условия ограниченности решения (7.72) в бесконечно удаленных точках сле¬
дует, что постоянные интегрирования должны быть равны нулю, т. е. 6^=0,
С2 = 0. Находим далее функцию G, рассматривая два случая положения точки х'
относительно х [см. (7.42)]:
О (х, х', у') =
1
sin 1у' exp [ — I (x—x')], x' < x;
sin ly' exp [—-I (x' — *)], x' > x.
(7.73)
Теперь нетрудно найти оригинал искомой функции G, используя формулу
обращения для синус-преобразования Фурье и таблицы определенных интегралов
387
{20]. Так, для х' < х имеем
о
_L’ln V (x-x,)» + Cv + y,)>
2л у (х—*'>*+(»—у')я ‘
(7.74)
Аналогичный результат имеет место и для х' > х. Искомое решение Г (дг,- г/) за¬
пишем, используя формулу (7.65)
Выражение (7.75) можно получить также и методом отражения (мето¬
дом источников), основанным на физической интерпрета¬
ции функции Грина. В этом случае следует пользоваться
ее определением в виде (7.68) или (7.69).
2. Построим функцию Грина второй краевой задачи для указанной выше
области. Пусть (х', у')— особая точка функции Грина. Так как
то задача сводится к отысканию функции qy гармоничной в рассматриваемой
области —оо <*< + оо, у> 0, и такой, чтобы обеспечить тепловую изоляцию
плоскости у = 0, т. е. чтобы имело место (dG/dy)y=.о=0. Это условие нетрудно
осуществить, если разместить вне плоскости у = 0 соответствующим образом по¬
добранный тепловой источник. В самом деле, поместим в точку Р* (х', —у')у
симметричную с точкой Р (*', у') относительно плоскости (/ = 0, тепловой источ¬
ник той же мощности Q = X. Результатом его действия будет температурное поле,
описываемое функцией G* (*, у, *', у') = (\/2п) In (1/V^(* — х')2 + (у — у')2 , кото¬
рая является гармонической в области \х | < оо, у > 0, и имеет нормальную про¬
изводную при у — 0, равную —(djdy) [(1/2л) In (1/г)]. Таким образом, искомая
функция Грина имеет вид
3. Наиболее трудной является следующая задача: методом отражения постро¬
ить функцию Грина первой краевой задачи для области дс^О, у^ 0.
Подберем такие источники теплоты, которые, с одной стороны, являются
гармоническими функциями в указанной области, а с другой — обеспечивают ну¬
левую температуру граничных поверхностей * = 0, у = 0. Пусть Р(х\ у') — особая
точка функции Грина [точка, в которой действует тепловой источник, создающий
температурное поле в плоскости (*, у)у б* = (1/2л) In (1/г)], Симметричных точке Р
относительно границ * = 0 и у = 0 будут две точки Pi (—*', у') и Р2 (*', —у')•
В этих точках поместим стоки теплоты (отрицательные источники). Однако, что¬
бы обеспечить нулевые температуры на плоскостях * = 0, у — 0, необходимо в
точку Ра (— *', —у')% симметричную точкам Pi и Р2 относительно этих плоско¬
стей, поместить источник теплоты той же мощности. Тогда функция Грина будет
иметь следующий вид:
где ri—У— у1)2; г2 = У (x—x')i+(y+y')i\ г3 = У\х+х')^-\-(у-\-у')г.
Нетрудно убедиться, что все условия, которым должна удовлетворять функ¬
ция Грина первой краевой задачи для области *^0, у^ 0, выполняются. Заме¬
+ оо
т (х. у) = j9<*o|p-L.e0d*' = 7rf *<*'>
— СО
— СО
G(x, у, х', у') = (1 /2л) In (]/r)-\-q(x, у, х\ у’)
Ог = у (х-х'У + (у-уГ),
G(x, у, х', у') = (1/2л) In (1 /У (х-х')*+(у-у')*) +
+ (1/2я) In (1/У (х-х')' + [у+у')*).
(7.76)
G (х, у, х’, {/') = (1/2я) In (1/г) —(1/2л) In (1/Гх) —
— (1/2я) In (1/гг) + (1/2я) In (1/г3),
(7.77)
388
тим, что результат (7.77) можно было бы получить и методом интегральных пре¬
образований по аналогии с п. 1.
4. Функцию Грина второй краевой задачи для указанной здесь
области можно получить аналогично, помещая в точке Рх, Р2 и Р9
тепловые источники. В результате найдем
з
G — (1/2я) [In (1/г) + 2 In 1/гк].
к = 1
Только что описанный метод источников (или метод отображений)
позволяет найти функции Грина первой и второй краевых задач для
целого ряда областей, обладающих специальными свойствами симмет¬
рии. Например, можно найти в явном виде функции Грина первой и
второй краевых задач для двугранного угла величиной л/п (п — целое
число) [114], первой краевой задачи для шара и полукруга [114],
для пространственного слоя, заключенного между двумя параллель¬
ными плоскостями |х|<Соо, |*/|<оо, [22], для полосы х<оо,
Ои полуполосы, х^О, и т. п. Здесь следует заметить,
что построить функцию Грина той или иной краевой задачи в явном
виде для наперед заданной области, как правило, не удается. Поэтому
каждый такой случай явного выражения функции влияния является
очень важным и ценным. Метод источников, который был использован
для отдельных областей, является очень ограниченным. Например,
этим методом нельзя найти функцию Грина второй краевой задачи для
шара и круга, да и вообще для всякой конечной области, так как в этом
случае функция q в (7.68)—(7.69) удовлетворяет не уравнению Лапла¬
са,^а уравнению Пуассона. Большие трудности возникают в результате
применения этого метода к третьим краевым задачам. Во всех этих
случаях можно применять метод интегральных преобразований, изло¬
женный в гл. V, как наиболее эффективный метод.
Следует также упомянуть о методе конформных отображений, кото¬
рый дает возможность построить функцию Грина первой краевой за¬
дачи для уравнения Лапласа на плоскости [55]. Этот метод в основном
применяется для областей сложной формы, которые не могут быть пред¬
ставлены в виде простейших областей. Однако здесь возникают серьез¬
ные трудности, связанные с построением аналитической функции,
преобразующей заданную область, например, на единичный круг
(т. е. на более простую область, хорошо изученную). Отсюда примене¬
ние этого метода в аналитической теории теплопроводности весьма
ограничено. В [22] приведены функции Грина краевых задач для ряда
практических областей: часть пространства, ограниченная внешним
образом цилиндром (r=R) или двумя пересекающимися плоскостями
(ср=0 и ф=ф(С>0), конечный сплошной цилиндр, часть пространства,
ограниченная двумя параллельными и двумя пересекающимися пло¬
скостями (2=0, z=C, ф=0, ф=ф0>0) или двумя пересекающимися
плоскостями и цилиндром (ф=0, ф=ф0, 7=/?), или двумя пересекаю¬
щимися плоскостями, двумя параллельными плоскостями и одним или
двумя цилиндрами. В работе [22] (в ссылках) приведены функции
Грина для областей, ограниченных сферами, конусами и пересекаю¬
389
щимися плоскостями. В [55] рассмотрены составные тела, а также об¬
ласти, ограниченные эллипсом или его частями.
В заключение заметим, что все сказанное о функциях Грина
G(M,P) автоматически переносится и на уравнение ДГ—Ь2Т +
+ (1/Х)Г = 0 с той лишь разницей, что теперь вместо (7.68) — (7.69)
имеем G = (l/4nr) exp (—br) + q(Mt Р) для трехмерного случая и
G = (1/2л) Ко (Ьг) + q (х, у, х\ у')—для двумерного (где К0 (г)—функ¬
ция Магдональда).
§ 2. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИЙ КРАЕВЫХ
ЗАДАЧ ТЕПЛОПРОВОДНОСТИ В ОБЛАСТИ
С ДВИЖУЩИМИСЯ ГРАНИЦАМИ
Ограничимся рассмотрением одномерного уравнения теплопроводно¬
сти, так как все изложенное ниже может быть перенесено на слу¬
чай многих переменных. Пусть задана краевая задача:
дТ/dt = а (д2Т/дх2), yt (t) < х < у2 (t), t > 0; (7.78)
T(xt t) |/-о =Ф0 (*)» yi(0)<x<ya(0); (7.79)
[ра<ЗГ (х, t)jdx—р12Г (х, t)]xmyi („ = — q>! (t) \ (7.80)
t)/dx + $itT (x, 0]x=ff,(/) = <Pt(0 Г ' (7.81)
Установим интегральное представление решений этой задачи
и соответствующую постановку краевой задачи для функции Грина
G(x, х\ ty т). Характерным для данной за¬
дачи является наличие движущихся границ
и, значит, что температурное поле, опи-
— F сываемое функцией G(x, х\ t, т) в силу ее
\ физического смысла (тепловой импульс мощ-
M(x,t) ) ^ ностью Q = cp), зависит не от разности
(t—т), а от / и т, так как определяющим
—д ^ j будет не только время действия (t—т),
но и момент т возникновения импульса.
Рис. 33 Пусть ABFE—область (рис. 33), ог¬
раниченная характеристиками А В (t = 0),
EF(t = const > 0) и кривыми * = */, (/) (для АЕ) и x = y2(t) (для BF).
Пусть М (.х, t) — некоторая фиксированная точка внутри области
ABFE, в которой определяется значение функции Г(х, t). Пред¬
ставим G (х, х\ /, т) в виде (7.13)
-(х-х')‘
G (ху х’у ty т) = — -е 4а(/~т) +
2 У па (t—т)
+ q(Xy х'у ty т) = G0 (Ху х'у ty %) + q(Xy xf, /, т), (7.82)
где Ge(*, х'у t—т)—фундаментальное решение уравнения теплопро¬
водности (7.78).
Функция G0 удовлетворяет уравнению (7.78) по переменным
(Ху t) и сопряженному уравнению по* переменным (*', т). Функцию
а выберем так, чтобы удовлетворялось уравнение (—dq/dт) =
390
= а(д^/дх'г) и начальное условие q(x,x’, t, т) |,_х = 0. Таким обра¬
зом, имеем для функции G(x, х\ t, т):
dG/дт + а {дЮ/дх’1) = 0, ух (т) < х’ < уг (т), (т < /); (7.83)
G(x, х', t, т)|т=/ = б(дс'— х), ух (0 < < уг (/). (7.84)
Рассмотрим равенство
^-[Г (*', т)G(x, х', t, x)] = g4£- +
+г£-«(°£-гЗ)- <^>
Проинтегрируем (7.85) по € |>х (т), */2(х)]:
"f
VxiТ) ух (т) 4 7
-Л{а^-тШ2- <78б>
Соотношение (7.86) справедливо при всех т < t и, следовательно,
его можно проинтегрировать по т для 0<т</—е, где е>0 —
сколь угодно малое число (при 0 < т < t—е подынтегральная функ¬
ция слева достаточно регулярна, так как исключена особенность у
функции G в точке х'=х при т =/). Получим
t-г у3 (х) t-г
J * J £<r.G)dV=o| (о£-
о (X) о
—T-^r) dx—a f (С£.-Г"Л dx. (7.87)
&К /х'=уг(т) J \ /Х'=Ух (X)
о
Вынося слева оператор (д/дт) за знак определенного интеграла,
найдем
Уг (t-г) уг( 0)
5 (Т-G)x=t-e dx’— J Т (х’, 0)G(jc, х\ t, 0)djc'-J-
у,(1-г) у,( 0)
+“Т[с-£-г(-§--4#°)],,,
0
о
Перейдем к пределу при е—* 0; учитывая (7.84) и равенство
Уг U-e)
lim J [Т (х\ t—e) G (х, х', t, х)]т,(_гdjc'=
0 Ух (/-в)
Уг (О
= 5 Т{х', 1)Ь {х—х') dx' = Г (*, /). (7.89)
i/1 (О
391
получим основную интегральную формулу
>Л°)
Т{х, /) = Т(х’’ °)G(X> х’’ ®)dx' +
>1(0)
+ а
^ ЭТ Ц5G 1 dy2 „
G Г -G
дх' \дх' a dx
dx-
* = Уг( t)
— а
Л
дТ 1
fdG
G Т\
G
J
дх' \
^дх'
a dx J
dx,
х'=уЛ*)
(7.90)
дающую интегральное представление произвольных решении урав¬
нения теплопроводности (7.78) через функцию Грина G(x, х', t, т).
Предположим теперь, что в (7.80) — (7.81) заданы граничные усло¬
вия: а) либо I рода рп = 0; f}a= 1; б) либо II рода /?п=(— 1)%; /?л = 0;
в) либо III рода /?/1 = Я,; /?д = а,. Если функцию G(x, xf, t, х) выбрать
так, чтобы по переменным (хг, т) удовлетворялись граничные усло¬
вия:
а) в случае первой краевой задачи
G(x, х’, t, т)|*_Л.(т) = 0, т</(/=1, 2);
б) в случае второй краевой задачи
(7.91)
8G _1^(?
ёх1 a dx
= 0, т<t (1=1, 2);
в) в случае третьей краевой задачи
8G IГ 1 1 dyi
.,+(—1)1 л,+(-1) -
сх |_ a dx
су =о,
я'=>/(*)
(7.92)
т </ (/г, = а,//,; /=1,2)
(7.93)
то из (7.90) получим искомые интегральные представления для
Т(х, /) в виде:
392
а) первая краевая задача
*<0)
Т(х, /) =
Т(х\ 0)G(x, х', Г, 0)Лс' + а
Г(*', т)
3G
дх!
dz —
Ух{ 0)
— а
8G
Т(х\ т)-
0У
Л;
(7.94)
*'=.ЫГ)
б) вторая краевая задача
*<Р)
Т(х, /) =
Т(х\ 0) G (*, f, 0) dx'
У i(0)
дТ(х\ т)(
дх!
dz +
х'=У i(t)
-Я!
+о||£^-с
^=>■2 to
(7.95)
в) третья краевая задача
>2<Р)
г(*, 0=
Г(х\ 0)G(JC, х\ и 0)dx'-
У i(0)
— а
<Щ.х\ т)
дх'
6?Т +
*'=>ito
+ я
гг(У’ ty ' чь-
+ A27\.x,t)G
сл: '
dz.
(7.96)
Из (7.90) могут быть выписаны интегральные представления
решений для смешанных граничных условий в (7.80) — (7.81) при
*= V, (0 и. x = y2(t). Если в (7.78) задано неоднородное уравнение
393
Tt=aT^+f(x, t), то к правой части интегральных формул (7.94) —
(7.96) следует прибавить слагаемое
/ У 2^)
| | f(x’, т) G (х, х’, t, т) dxdbt. (7.97)
0*(т)
Остановимся подробнее на рассмотрении функции Грина G (х, х\
/, т). Она определяется с помощью представления (7.82), по перемен¬
ным (х\ т) удовлетворяет уравнению (7.83), начальному условию
(7.84) и одному из трех видов граничных условий (7.91) — (7.93) (в
зависимости от типа краевой задачи в (7.78) — (7.81)). Как следует
из граничных условий (7.92) — (7.93), нахождение функции Грина
второй или третьей краевых задач для областей, границы которых
перемещаются по законам, отличным от линейного, связано с необ¬
ходимостью решения краевых задач с переменным во времени
dy
коэффициентом теплообмена вида h* (z) = h + y —. Точное решение
dx
%
краевых задач такого типа даже для цилиндрических областей
имеет достаточно сложный вид (см. гл. VIII, § 6), а наличие подви¬
жных границ еще более увеличивает его громоздкость и для боль¬
шинства практических случаев технически не реализуется. Впрочем,
из этой ситуации есть выход, так как оказывается, что для нахожде¬
ния функции Грина G(x, х\ t, т) следует использовать другую
модель, а именно соответствующую краевую задачу по переменным
(х, t). Чтобы показать это, рассмотрим функцию G(x, х\ t, т),
определяемую условиями:
8G/dt = ad2G/dx2, yl(t)<x<y2(t), t>z; (7.98)
G(x, x', t, т)|г=т = <5 (*-*'), >>i(t)<*'<}>2(t); (7.99)
(№G/dx + (-ljpaG)x=yi(t) = Q, t>z, (7.100)
где fin = 0, pi2=l в случае первой краевой задачи, fia = 0, fin = l
в случае второй и fin = 1, fin = hi(i= 1, 2) для третьей краевой задачи.
Покажем, что G(x, х', t, z) = G(x, х', t, т). Доказательство проведем
для второй краевой задачи; остальные случаи могут быть рассмот¬
рены аналогично.
Проинтегрируем выражение
394
по х" в интервале от у{ (0) до у2(0), где t>9>т. Получим, учитьшая
граничные условия (7.92) и (7.100) (при /?,2 = 0, fin = 1) для G и G:
У lift
д
дв
G * Gdx" = 0.
(7.101)
уЛВ)
Проинтегрируем далее (7.101) по промежутку [0, t — е], где
е>0 — сколь угодно малое число; повторяя предыдущие рассужде¬
ния (при выводе соотношения (7.90), найдем:
УгМ
Г G(x\ х', 0, т)G(x, х”, t, e)dx” =
Ух(в)
= f G(x", х', t-г, т)[G(x, х", t, &)]e=,_,dx".
Переходя к пределу при е->0, получим:
УМ
J G(x", х’, в, т) G (х, х", t, 6)dx" =
>,(0)
у Л 0
G{х\ х\ t, х)Ь{х” — x)dx" = G(x, х\ /, т). (7.102)
*(0
С другой стороны, интегрируя (7.101) по промежутку [т + е, 0],
находим:
G(x, x", t, x)b(x"-x')dx" =
(7.103)
•Mf+e)
G(x, x", t + e)[G(x", x', в, x)]e=:+cdx".
>l(T+£)
Устремляя e->0, приходим к выражению:
у2(в) уЛх)
G(x", х\ 9, t)G(x, х", t, 9)dx” =
Уг(0) >i(t)
= G(x, x', t, x).
Сравнение (7.102) и (7.103) показывает, что
G(x, х', t, x) = G(x, x', t, x).
Рассмотрим теперь в постановке краевой задачи (7.78) — (7.81)
следующие граничные условия:
I рода
Г(у,(0, /) = Ф.(0, t>0; T(y2(t), t) = (p2(t), t>0. (7.104)
Функция Грина G (х, х', t, х) определяется как решение задачи:
dG/8t=ad2G/dx2, yi(t)<x<y2(t), t>х; (7.105)
G(x, х', t, r)|,=t = <5 (*-*'), У\ (t)<jc'<>'2(т); (7.106)
Gb=>lW = G:|x=>](0 = 0, t>х. (7.107)
Интегральное представление решения первой краевой задачи
имеет вид (7.94)
II рода
гт(х, о
дх
1 дТ(х, 0
= (р, (Г), г>0; ■
Л СХ
= - cp2{t), /^0.(7.108)
х = У2( 0
Функция Грина G(x, х, t, т) второй краевой задачи удовлетворя¬
ет уравнению (7.105), начальному условию (7.106) и граничным
условиям
396
dG(x, x', t, т)
дх
dG(x, У, и т)
дх
= 0, t>x. (7.109)
Контрольное представление решения второй краевой задачи
имеет вид (7.95)
III рода
8Т(х, 0
дх
дт(х, о
= /г,[Г(д:, f)U_,lW-Pi (*)], '>0,
*=J4(0
ах
(7.110)
= - й2 [Т(х, t)\x=y,0 - <р2 (0], ^ 0. (7.111)
Функция Грина G(x, х', t, т) третьей краевой задачи является
решением уравнения (7.105) с начальным условием (7.106) и гранич¬
ными условиями
ас?(х, х7, /, т)
дх
dG(x, х!, I, т)
дх
=hxG(x, х\ t, t)U=>i(0, t>х, (7.112)
*=>i(0
= —h2G(x, x\ t, т)|х_л(0, t>x. (7.113)
х=У2(1)
Интегральное представление решения третьей краевой задачи
имеет вид (7.96).
Таким образом, функция G(x, х', t, т) может быть найдена как
решение эквивалентных задач (7.83), (7.84), (7.91) — (7.93) и (7.98) —
(7.100) и в области с движущимися границами не сохраняется эк¬
вивалентность в записи граничных условий в постановках задач по
(х, t) и (*', т) в отличие от областей цилиндрического типа. Всякий
случай нахождения функции Грина соответствующей краевой зада¬
чи в области с движущимися границами y\{t)^x^y2(t), t^0;
y(t)^x< +со, 0 имеет важное значение как для большого числа
практических приложений [172; 173], так и для аналитической те¬
ории теплопроводности, если учесть, что число таких случаев пока
крайне ограничено (см. гл. VIII).
Используя подходы [52; 126], можно доказать существование
и единственность решения задачи (7.98) — (7.100), если каждая кри¬
вая у,(/) (i= 1, 2) дифференцируема и производные dyJ3t удовлет¬
воряют условию Гельдера порядка У> ^
397
Задача. Используя развитые выше подходы, получите интеграль¬
ное представление аналитических решений для уравнения теплопро¬
водности гиперболического типа
дТ д2Т д2Т
— = а т* —+F(x, 0, 0<х<1, t>0 (7.114)
dt dx2dt2
через функцию Грина G(x, t, х\ т) в виде:
Т(х, t) =
Т(х', 0)G(x, t, х', 0)dx'~
I
- т* jjjr(x', т) ^ - G(x, t,x!, т) dx! -
— а
г
Т дв дТ~I
Т(х\ x)--G(x, t, х', х)— dx +
L г* 3yJ у=/
ГГ 8G ЗТ
■а I Т(х', х) — -G(x, t, х\ т)—
dx -Ь
+
/
t, х',
х)F(xf, x)dxdxf
о о
(7.115)
Замечание. Функция Грина G(x, t, т) по переменным (х, t)
удовлетворяет уравнению
8G 82G ^ 82G
= а т* 0<х<1, t>х
8t Sx2 8t2
и начальным условиям
G|,=r = 0, 0 < jc < /,
398
[SG/8t]t=z = (1 /т*) 5 (х — хг), 0 <х<1,
а по переменным (х\ т) — уравнению
d2G ^ d2G dG , ,
а—- — т —-Н— = 0, 0<jc </, т<г
5У2 5т2 дх
и начальным условиям
G|T=, = 0, 0<х'<1,
[3G/0r]t _, = - (1/т*) 5 (У - *), 0 < х? < I
Как нужно выбрать граничные условия для функции G (х, t, х\ т)
соответственно граничным условиям для Т(х, t) (см. гл. 2, § 3),
чтобы выписать из (7.115) искомые аналитические решения. Об¬
ратите особое внимание на граничные условия третьего рода (на¬
грев или охлаждение средой).
ГЛАВА VIII
АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ОБЛАСТИ
С ДВИЖУЩИМИСЯ ГРАНИЦАМИ
ВВЕДЕНИЕ
В этой главе рассмотрены аналитические методы решения одного из
труднейших классов краевых задач нестационарной теплопроводности,
относящихся к областям с движущимися границами.
Круг вопросов, при рассмотрении которых приходится сталки¬
ваться с необходимостью решения уравнения теплопроводности (а так¬
же диффузии, волновых и т. п.), для областей, форма которых изме¬
няется со временем, весьма широк и включает как случаи, когда дви¬
жение границ задано, так и более сложные, когда это движение тре¬
буется определить из дополнительных условий задачи (задача Сте¬
фана).
Подобные проблемы возникают при теоретическом изучении про¬
цессов переноса энергии или массы, связанных с изменением агрегат¬
ного состояния вещества, в некоторых вопросах теории хрупкого раз¬
рушения [67, 68], теории плотин, механики почв, термики нефтяных
пластов, некоторых электродинамических задачах, связанных с во¬
просами получения сверхсильных магнитных полей путем быстрого
сжатия магнитного потока, в задачах фильтрации, теории колебаний
* Последнее обстоятельство объясняет ошибочность результатов ряда работ,
в которых находятся функции Грина краевых задач обобщенного типа (см. об¬
зоры [63], [169], где эти работы перечислены).
399
(см. ссылки в [63]), тепловых задачах специального типа, например,
при изучении процесса передачи теплоты в тонком нагретом стержне,
если задано количество теплоты переменной части стержня, примыка¬
ющей к одному из его концов [52]. Наконец, решение диффузионных
задач для областей с движущимися границами лежит в основе теории
зонной очистки материалов, которая приобрела особенно важное зна¬
чение в связи с развитием электронной техники, потребовавшей раз¬
работки методов получения полупроводниковых материалов высокой
чистоты [63]; следует отметить задачи кинетической теории роста кри¬
сталлов, использующие аппарат аналитической теории теплопровод¬
ности для областей с границами, перемещающимися по определенному
закону (см. ссылки в [631).
С математической точки зрения краевые задачи теплопроводности
в области с движущейся границей [так называемые обобщенные крае¬
вые задачи (см. §3 гл. II)] принципиально отличны от классических
задач теплопроводности. Вследствие зависимости характеристического
размера области переноса теплоты от времени к этому типу задач в об¬
щем случае неприменимы классические методы разделения переменных
и интегральных преобразований Фурье, так как, оставаясь в рамках
классических методов математической физики, не удается согласовать
решение уравнения теплопроводности с движением границы области
теплопереноса. Попытки осуществить такое согласование приводили
уравнение теплопроводности в конечном счете к бесконечной системе
совокупных дифференциальных уравнений 1-го порядка с заданными
начальными условиями, что представляло определенное неудобство
в числовой реализации полученных решений, хотя сама идея разложе¬
ния искомых обобщенных температурных функций в ряды типа Фурье
по некоторым системам «мгновенных» собственных функций соответст¬
вующих решений классических температурных задач представляла
несомненный теоретический интерес и вскоре была эффективно ис¬
пользована при решении обобщенной задачи Стефана о промерзании
жидкости [26].
Решение этой проблемы до последнего времени шло, по-видимому,
следующим образом. С одной стороны, точные решения задач подоб¬
ного типа удавалось получить с помощью удачных догадок, искусст¬
венных приемов, причем для весьма ограниченного числа случаев дви¬
жения границы (линейного или параболического) и для частного вида
граничных условий (постоянных и Г рода [63]). С другой стороны, на
этих задачах при весьма их общей постановке отрабатывались класси¬
ческие методы решения дифференциальных уравнений математической
физики (и их модификации): тепловых потенциалов [69, 751, контур¬
ного интегрирования [78], продолжений [109], разложения искомой
функции в ряд [5, 61, 101], «мгновенных» собственных функций Грин¬
берга [25], а также методы, основанные на использовании интеграль¬
ных, интегродифференциальных или обыкновенных дифференциальных
уравнений, асимптотические и численные [65, 44, 79, 127]. При этом
точные решения аналитическим путем удалось получить лишь для
простейших законов движения границы, а именно для равномерного
и параболического (но для достаточно широкого класса краевых
400
функций задачи). Объясним был и тот факт, что для решения в общем
одного и того же класса тепловых задач применялись различные под¬
ходы. Это произошло главным образом по двум причинам. Во-первых,
применение известного аналитического метода к решению нового
класса задач означало дальнейшее развитие этого метода в новых ус¬
ловиях. Так, например, был усовершенствован метод тепловых потен¬
циалов при решении краевых задач теплопроводности обобщенного
типа в области с равномерно движущейся границей [69]. Во-вторых,
решение одной и той же тепловой задачи можно искать в различных
классах функций. Эти функции должны достаточно легко определять¬
ся и обеспечивать сходимость процесса настолько хорошо, чтобы можно
было сделать требуемые в задаче заключения об интегральных или диф¬
ференциальных свойствах полученного решения.
Представление одного и того же аналитического решения в различ¬
ных эквивалентных функциональных формах (тождественных в смысле
числа) имеет большую практическую ценность, так как позволяет варь¬
ировать решением в зависимости от постановки задачи, например
представление функции Грина первой краевой задачи для стержня
в форме ряда Фурье, удобной для больших времен, или в виде формулы
суммирования Пуассона, более подходящей для малых времен (см.
§ 12 гл. III).
Всякие попытки до последнего времени получить аналитическим
путем точное решение краевой задачи обобщенного типа в области
с границей, движущейся по произвольному закону, приводили к сис¬
теме интегральных уравнений Вольтерра II рода (или интегродиффе-
ренциальных), разрешить которую не удавалось вследствие сложности
ядер уравнения системы. Устанавливались лишь качественные ре¬
зультаты для такого рода системы, доказывались существование ре¬
шения и его единственность [137].
Решение этой проблемы значительно продвинулось вперед в 70-х
годах после выхода в свет серии фундаментальных работ чл.-корр. АН
СССР Г. А. Гринберга с сотрудниками [25—31]. Было получено функ¬
циональное преобразование, переводящее краевую задачу теплопро¬
водности обобщенного типа в подвижную систему координат, в кото¬
рой преобразованное уравнение теплопроводности допускало точное
решение классическим методом разделения переменных для весьма
широкого класса новых законов движения границы при соответствую¬
щих граничных условиях (см. §5 гл. VIII).
В дальнейшем в [66] было получено точное решение первой'обоб¬
щенной краевой задачи в конечной области с границей, движущейся
по произвольному закону в декартовой, цилиндрической и сферической
(радиальный случай) системах координат. Для полуограниченной об¬
ласти точное решение удалось получить при любом виде граничных
условий, включая и случай произвольной зависимости коэффициента
внешнего теплообмена от времени в законе Ньютона на границе, дви¬
жущейся также по произвольному (своему) закону [66].
К этому следует добавить, что решение второй и третьей краевых
задач обобщенного вида во многих случаях приводится в конечном
401
счете к классическим задачам, но с переменным во времени коэффици¬
ентом в граничном условии III рода. Этот класс задач рассмотрен в [13,
63, 102, 131, 132, 74].
§ 1. МЕТОД ТЕПЛОВЫХ ПОТЕНЦИАЛОВ (ОБЛАСТИ
оо), [0, l+vt\, [Л+М, К **0)
Изучение тепловых процессов в изотропной среде в области с дви¬
жущимися границами, в частности в полуограниченной области
[vt, + оо), началось с работы [160]. В этой работе делались по¬
пытки получить операционным методом решение первой краевой
задачи. Однако, как указал в своей критической статье [97] по
поводу работы [160] Любов, предлагаемый в [160] метод целиком
ошибочный. Любовым было указано на возможность сведения тепло¬
вой задачи обобщенного типа к интегральному уравнению Воль-
терра II рода (или системе уравнений, а вскоре было получено
точное решение системы этих уравнений для первой краевой за¬
дачи в областях [0, vt] и [;vt, оо] методом интегрального преобра¬
зования Карсона—Лапласа. Гринберг [24], рассматривая полуогра-
ниченную область [vt, + оо], указал на возможность решения в
квадратурах первой краевой задачи путем перехода в подвижную
систему координат. Позже были разработаны более общие подходы
при решении тепловых задач указанного класса. Один из таких
методов—метод тепловых потенциалов, который успешно применя¬
ется в декартовой и сферической (температурное поле—центрально
симметричное) системах координат для области с равномерно дви¬
жущейся границей.
Рассмотрим основы этого метода применительно к решению теп¬
ловых задач в областях с равномерно движущейся границей. Пусть
St—область, состоящая из концов х = 1 и x = y(t) отрезка [Uy(t)]y
где 0, y(t)—непрерывная функция.
Тепловым потенциалом простого слоя по прямой х = 1 и обобщен¬
ным тепловым потенциалом простого слоя по кривой x — y(t) назы¬
ваются соответственно интегралы:
<8')
где 4^(0 и ^(О — плотности тепловых потенциалов, представляю¬
щие собой функции, непрерывные в интервале (0, /).
Тепловые потенциалы (8.1) и (8.2) вне точек области St явля¬
ются решениями однородного уравнения теплопроводности T't ==
= аТхгу дважды непрерывно дифференцируемыми по пространствен¬
ной координате х и непрерывно дифференцируемыми по времени t,
и удовлетворяют нулевым начальным условиям. Это следует из того,
402
что производные этих функций вычисляются путем дифференциро¬
вания под знаком интеграла фундаментального решения уравнения
теплопроводности, так как подстановка, входящая при дифференци¬
ровании по /, равна нулю. Например,
-U-v (т)]«
= (т) G0 (дс, у(т), /, т) \tmx = О
2 У па (/—х)
.е 4а (/ — I)
t =т
в силу ТОГО, ЧТО хфу (т)=у (t) при t = т.
Таким образом, дифференцирование по х и t будет относиться к
функциям G0 (Ху у (т), ty т), которая, как отмечалось выше (см. гл. VII),.
является решением уравнения теплопроводности.
Рассмотрим поведение функций П1 (*. о и IL (х, t) в точках
х• области (*• = /; jc* = //(/). Имеют место следующие утверждения:
1. Тепловой потенциал простого слоя (8.1) и обобщенный теп¬
ловой потенциал простого слоя (8.2) в точках х* области St явля¬
ются непрерывными функциями точки х и времени ti
П/ (**■» 0— Пс (я* 0 U—-*+o — П/ С**» t).
(8.3)
где *• = / для i = 1 и х? = у (t) для i = 2.
Покажем это, например, для случая i = 2. Интеграл (8.2) — не¬
собственный, так как значение т = / является особым для подын¬
тегральной функции. Однако этот интеграл сходится равномерно
относительно х и t > 0. Действительно, по определению несобствен¬
ного интеграла второго рода [146], имеем
ГГ (х t) — lim ^-Т Уа(т) cxpf (дг~у(т)а1 dx
Ца I*, t) - urn 2 j ехр у 4а (<_т) j ах.
Записанный же под знаком предела интеграл сходится к своему
пределу Ц2(*» 0 при ц —►О равномерно относительно х и /, и это
нетрудно показать: пусть е > 0—произвольное, сколь угодно ма¬
лое число и функция ¥2(т) ограничена для всех т. е,
1%(T)|<M0 = c°nst; оценим по абсолютной величине разность
J =
Г-^ехр [-<!<
! IП\ J у t—x I 4а (I—х) J
' о '
"f -ехр Г (J:~j/(T))2l dx
2 УН 3 УИГг eXPL 4а (t—т) J
JTZ f ^exp[-£=f^ldx
2 Vn J *4 4a (1—x) J
*-n
< f Ё1 — м VaVn
^ 2VH 3 УТ=ГХ МоГаГЪ
t-4
403
Выберем б = г2!М1а, отсюда как только будет х] < 6, так У ^
^ MQV clV у\ < MQV aV б = е, т. е. неравенство J <е выполняется
одновременно для всех значений х и t, что и означает равномерную
сходимость интеграла (8.2). Отсюда следует непрерывность функции
П2 (ху t) в точке х — у (t) при любом ^ > 0.
2. Производная дП* (х, t)/dx теплового потенциала простого слоя
(8.2) при подходе к точкам х области St при t > 0 слева и справа
стремится к своим непрерывным предельным значениям и эти пре¬
дельные значения определяются соответственно равенствами:
<ЭП,и, о = ^{(0/2 + 311* (**, t)/dx\ \
дП^х, t)/dx\x^x* + 0 = — xVt(<t)/2 + dUt(x4^ О/5*» I
где dUt (jc*, t)/dx—результат формального дифференцирования П, (х, t)
в точке (jc*, t) под знаком интеграла (jc* = / при /=1 и x* = y(t)
при 1 = 2).
Покажем справедливость этого утверждения для /=1 в точке
= I:
дПг(х, Q_ 1 Р (т) (х /) Г (*-/)* 1 ,
дх ~ 4|^J (<_т)3/2 Р1 4а (£—т) J
Делая замену переменных z = (jc—/)/2 К а (/—т), находим
—FT i ^(--^expH^d,
(*-/)/2 Vа (/-х)
(при х > I)
Переходя к пределу при jc —* / + 0," получаем требуемое соотно¬
шение (см. также § 6, (3.203) гл. III)
ЗПП*. 0 (0 2 ? _ Wj(f)
дх дг —^ / + о 2 i/lJe 2
г о
Заметим, что дПД/, /)/<?jc = 0; случай i = 2 при jc* = г/ (^) рассмот¬
рен в [137].
Тепловые потенциалы являются .удобным аналитическим аппара¬
том для решения краевых задач теплопроводности в области с дви¬
жущейся границей, так как позволяют сводить решение дифферен¬
циального уравнения в частных производных, каким является урав¬
нение теплопроводности, к интегральному уравнению Вольтерра,
методика решения которого к настоящему времени разработана
достаточно хорошо [1]. Особенно удобен этот метод для законов
у (/) =/-|-и/, где возможно получить решение задачи в весьма ком¬
пактном виде.
Рассмотрим краевую задачу на определение температурного поля полубеско-
нечного стержня + оо), теплоизолированного с боковой поверхности; началь¬
ная температура стержня равна нулю, температура движущегося торца <р (f).
404
Имеем первую краевую задачу для области [l-\-vt, оо], t^O;
dTjdt = а (д2Т/дх2), х > l+vt, I > 0, (8.5)
Т (х, 0) = 0, x^l- Т (дг, 0 \Xml+vt = Ф (0,
|Г(*. /|< + оо,
Решение Т (*, t) ищем в виде обобщенного теплового потенциала простого слоя
по кривой x = l-{-vt
1 — (х — I — иг)2
т (X, 0 = -2QL С -Z (т) е 4а «'-« dr.
2VH J V7=4
(8,7)
Выражение (8.7) удовлетворяет уравнению (8.5) при х > ограничено на бес¬
конечности (при х —► оо), имеет нулевое начальное значение при любом выборе
Y (т). Для того чтобы оно было решением задачи, необходимо удовлетворить гра¬
ничному условию (8.6) при x = l-\-vt, из которого можно определить неизвестную
плотность потенциала
/— t -(vt-vx)*
2 У~п
= ат< (8.8)
2 V я J У I—т
где для упрощения обозначено: фх (0=ф (0 ехр[(и2/4а) /]; (0=Y (0 ехр [(а2/4а) /].
Уравнение (8.8) представляет собой интегральное уравнение Абеля (частный слу¬
чай уравнения Вольтерра), решение которого получим операционным методом.
В пространстве изображений можно записать (учитывая, что справа в (8.8) запи¬
сано выражение типа свертки)
Ф1 (р) = ,^Д (Р). откуда (/>) =—У~р фх (р) =—%= -РФ, (р).
2 К р V а V а V Р
(8.9)
Находим оригинал Yi (/), применяя теорему о свертке (6.11); так как
UV~P -f- UV~nt, Рфх (р) Ч- dqpi/di (ф1 (0) = 0), то
''■<'|-7т4?т=;^л' (810’
В этом выражении перейдем к функциям Y (/), ф (/) и подставим найденный
результат в (8.7) под знак интеграла. Окончательно решение задачи (8.5)—(8.6)
имеет следующий вид:
7T=;-Wft ivh Й+i »*]
е с
(8.11)
В литературе неоднократно отмечались сложность и громоздкость
метода тепловых потенциалов [86], хотя и указывалось, что этот
метод незаменим при решении краевых задач теплопроводности обоб¬
щенного типа. В [69] этот метод был модифицирован, благодаря
чему в значительной степени уменьшилась громоздкость в оконча-
405
тельной записи решения задачи. Действительно, пусть по-прежнему
решение задачи (8.5)—(8.6) отыскивается в виде (8.7). Найдем пред¬
варительно операционную форму Т (х, р) выражения (8.7)
Т (х, р) = ■ С e~pf At С -У ^ e 4fl (/”x) dx =
r о о f
® . (X-l-VT)2
= jQL f T (T)dx ( -pJLr e P <<-*> d/.
2 J w J
f 0 x r
Здес,ь был изменен порядок интегрирования. Произведя далее за¬
мену переменных y = V t—х и вычисляя внутренний интеграл, по¬
лучим
--&е l~° 'dt.
2/P J 1W
Окончательно находим
Г(^(fU2)
где (0 = ^ (0 ехр (и2//4а).
Теперь отчетливо видно, что неизвестную плотность потенциала
V (/) в пространстве изображений следует искать относительно того
вида, в каком она появилась в изображении решения Т (х, р) (8.12),
т. е. в виде некоторого выражения относительно функции ^ti[{V~p—
— v/2\^a)2]. Напомним, что согласно традиционному подходу неиз¬
вестная плотность потенциала определялась из решения интеграль¬
ного уравнения (8.8) относительно того вида, в каком она была
записана под знаком интеграла (8.7). Используя далее граничное
условие в (8.6), находим из (8.8) ^(р) в виде (8.9) и затем иско¬
мое выражение
Ч5, 1(Vp — vl2 Vй)2]= (2lVa) (V~p—vl2 v~a) ф, [{V~p—y/2 V~aY\
Таким образом, решение задачи (8.5) — (8.6) в операционной форме
имеет следующий вид:
Г(х’
х ехр[ ^~р\ • (8-13)
Переходим в класс оригиналов, используя теорему Эфроса (6.14)
(рекомендуем настоятельно проделать все необходимые выкладки).
406
09
(т) е~рт dx ^ <
(Х-1-1ГС)г
4 ау
”dу=>
Окончательно получим
Т(х- 177^ф(т)ех4~(м-~Т]dT' <8 И)
Нетрудно убедиться, что условия (8.5)—(8.6) удовлетворяются.
Сравнение выражений (8.11) и (8.14) (тождественных в смысле числа)
показывает, что последнее из них имеет очевидное преимущество
при численной обработке в конкретных условиях теплового режима
(см. ниже). Если на движущейся границе области [l + vt, оо], О,
задан теплообмен со средой
дТ (х, t)/dx \xmt+vt = h[T (jc, t) \XBl+vt—(f (/)], t > 0, (8.15)
то по-прежнему решение третьей краевой задачи для уравнения (8.5)
ищем в виде обобщенного теплового потенциала простого слоя (8.7),
операционная форма которого имеет вид (8.12). Удовлетворяя гра¬
ничному условию (8.15) и (8.7) и учитывая (8.4), приходим к инте¬
гральному уравнению относительно функции Yj (O—'F (/) ехр [иа//(4а)]
следующего вида!
(о+(rh+н (°-
Применяя преобразование Лапласа, получаем
Y, (р) + + h J/^) % (р) - 2 Аф, (р),
откуда
дг . . 2 \Hih\r~p -
* {Р) ~ V~a V~P+vl2+ ha Ф* (р)’ -
Подставляя полученное выражение в (8.12), находим операционное
решение задачи в виде
*-• *[(^-гттЯ
(8.16)
Переходя к оригиналу по теореме Эфроса (6.14) и используя при
этом таблицы операционного исчисления, найдем
t
— hVhikVh + vft v~a) Jcp(t) Ф* + h ]fa (i —т) ^ X
xexp [U—/ —vx)h + ah'1 (t— %)] dx. (8.17)
Рассмотрим частный случай граничной функции, когда <р(/) = !.
Вычисляя в (8.17) интегралы, и переходя к безразмерным перемен¬
407
ным г = х//, Bi=/i/, v0 = vl/a, Fo = a///2, найдем
п*. Ро) = 1ф-(^)+77в^_ф-х
X
z— 1
■v0 KFo) e1,0 Fo“u_t) t’°
г—1
'\exp[Bi2Fo+(z — 1) Bi]. (8.18)
t’o+2 Bi ф, /в; j/'pjj , ,
2(c-„ + Bi) w \Diy ro 1 2VT3 J
Заметим, что в случае равенства нулю скорости движения гра¬
ницы уо = 0 из (8.18) получим^уже известное нам решение (3.210).
■Va=0,7S; Fo = 1,m
-Vrl.O; Fo=1,0
■V0=1,5; Fo=0,B6B
■ V0-l,O', Fo=0,5
• V0=Z,5; Fo-0,lf
■Vo=3,33:Fo=0,3
■V„=.5,0;Fo=0,Z
lVo=6,66; Fo-0,15
^=10,0;Fo=0,1J’0 ^
Рис. 36
Выражение (8.18) описывает температурное поле в области z ^ 1+^Fo,
Fo^O, с нулевой начальной температурой. В случае, если началь¬
ная температура в исходной задаче не равна нулю, т. е. Т (х, t) =
408
='F0 = const, а на движущейся границе задан закон теплообмена
со средой постоянной температуры ТСУ то достаточно ввести безраз¬
мерную относительную температуру W = (Т — Т0)/(ТС — Т0), и мы при¬
дем к той же задаче с граничной функцией ф(/) = 1. Решение этой
задачи в безразмерных переменных дается правой частью равен¬
ства (8.18).
На рис. 34—36 приведены температурные кривые относительной
безразмерной температуры W (г, ¥о) = (Т — Т0)/(Тс—Т0), построен¬
ные по решению (8.18). Приведенные графики могут служить в ка¬
честве расчетных для указанных различных случаев.
Из (8.18) нетрудно получить частный случай, а именно решение
задачи (8.5)—(8.6), когда <р(/) = 1. Устремляя в (8.18) Bi —► оо и
используя при этом асимптотическое разложение функции Ф* (г) ^
^ (1/^Ляг)ехр (—z2), найдем
т(2,Ро)=1ф-Ш;) +
+ Тф* к0 KFo)exp[u?Fo —(г — !)»„]. (8.19)
Это выражение также описывает решение первой краевой задачи
в рассматриваемой области с начальной температурой Т (х, 0) = Т0
и граничным условием T(l-\-vt, t) = Tc, но для безразмерной тем¬
пературы W (z, Fo) = (Т—Т0)1(ТС—Г0). Следует заметить, что нали¬
чие неоднородности в дифференциальном уравнении теплопроводно¬
сти (8.5) затруднит применение тепловых потенциалов к нахождению
температурного поля в рассматриваемой области. Здесь целесообразно
перейти к отысканию функции Грина соответствующих краевых
задач [снятие неоднородности в уравнении не всегда целесообразно,
хотя и возможно (см. § 1 гл. V)].
Задача. С помощью теплового потенциала вида (8.7) получите
операционное решение тепловой задачи
dTld¥o = d2Tldz'2, z'> 1+PeFo, Fo>0,
T{z\ Fo)|Fo=o = 0, z'^1,
в случае температурного нагрева
T(z\ Fo)|Z'=1 + PeFo = ф(Fo), Fo>0,
теплового нагрева
[dT(z\ Fo)/dz']r __1+PcFo = -<p(Fo), Fo>0,
409
нагрева средой
[3T(z\ Fo)/3z']--=,+PcFo = Bi[T(z', Fo)1-=1+PcFo-(P(Fo)], Fo>0
|T(z’, Fo)|< + со, z>l+PeFo, Fo>0
в виде
где
f(z',p) = e(p)(l- exp [- (/ -1 )Vp] (pip-Pe-y/p)
ё(р) = -
температурньш нагрев;
тепловой нагрев;
' В i +yjр
Используя полученное операционное решение как базовое для
данного класса задач, выпишите частные решения (операционные
и в оригиналах) для различных граничных функций <p(Fo): постоян¬
ная; линейная; импульсная; пульсирующая и т. д.
§ 2. ФУНКЦИИ ГРИНА КРАЕВЫХ. ЗАДАЧ ДЛЯ ОБЛАСТЕЙ
С РАВНОМЕРНО ДВИЖУЩИМИСЯ ГРАНИЦАМИ
I. Рассмотрим вначале область \l-\-vt, оо), /^0. Учитывая необхо¬
димость нулевого начального условия при определении функции
Грина G (х, х', t, т) методом тепловых потенциалов, будем искать
функцию G в виде (7.82). Для рассматриваемой области, согласно
условиям (7.94), (7.97), (7.99) (берется только первое условие), имеем
при x — l + vt:G = 0 в случае первой краевой задачи, [(dG/dx) —
_.(/i + iVa)G] = 0 в случае второй (/г = 0) и третьей краевых задач
(всюду при t > т).
Рассмотрим подробно третью краевую задачу
dG/dt = a(d*Gidx*), х> l + vt, t> т; (8.20)
G|,=1 = 6(x—х'), x>l + vx\. [dG/dx—hG\x=l+vl = 0,
t>x\ |G|<H-oo, x>l-\-v т. (8-21)
410
Предварительно введем новые переменные t' — t — z, z=
= x — (l+vт), z'=x' — (l+vт). Имеем для функции q{z, z', t', т) (см.
7.82):
dq/dt' = a(.d2ql8z2), z>vt', t'>0; (8.22)
9l<=o=0, z>0; Iq(z, z', t)|< + co, z^vt', /'>0;
^+Abp[-^) <8и»
Решение этой задачи ищем в виде обобщенного теплового потен¬
циала простого слоя по кривой z=vtf
t'
q(z, z7, t', т)=——= [Д^ехрГ-^-^2]^'. (8.24)
2-у/я J yjt' — т! L ^)J
Операционная форма выражения (8.24) имеет вид [см. (8.12)]
ife /,,, t) = ^exp(-iv5)^[(vS~-)2_.
где vP,(/') = 'F0')exp[t;2/V(4a)].
Таким образом, неизвестную плотность потенциала Т' (/') в про¬
странстве изображений следует искать относительно функции
Т, [{s/p—v/2у/а)2]. Поэтому, опуская в данном случае подробные
выкладки (рекомендуем их проделать самостоятельно; это очень
полезно при изучении данного метода), приведем в окончательной
форме операционное решение задачи
у/а — (ylyja + h*ja) ["vz' (z + z/)
2y/ay/p(jp + hy/a)
[vz‘ (z + zf)
a yja
(8.25)
q(z, z', p, t)= ' _ ' —~rQXP\
2s/ay/p(y/p + hy/a) I
Переходим в класс оригиналов, предварительно разложив предэкс-
поненциальные множители на простые дроби вида А1/(А2-\-л/р)
(А( = const) и используя таблицы операционного исчисления:
G(x, xf, t, х)= ^ ехр
2у/ па (I - х)
Г_(* х'?~
4а (/ —т)_
+
Г (х+У-2(/+1-т))2 V ,
+ ехр гг ч + (а-(/+1.т))
|_ 4<з (f — т) а
411
-(h + v/2a)exp {[x+x'—2(l+vx)]h+h2a(t—x) + (v/a) [x'-(/+«т)]} x
x Ф* ГХ+У~2-^Т)+hyja (t - Л (8.26)
L 2 y/a(t-x) J
Полагая в (8.26) h = О, получим функцию Грина G(x, х\ t, т) второй
краевой задачи для области [l+vt, оо), /^0.
Задача 1. Полагая в (8.25) — (8.26) (1/А)—>0, получить функцию
Грина первой краевой задачи в виде
<?(*, X', г, =
1
2 у/па (/ — т)
Г (х + У-2(/+гт))2 V Л)
-ехр|.—+;(х-('+ст),Л' (827)
Задана 2. Исходя из постановки функции Грина G(x, х, t, т)
третьей краевой задачи в виде (7.83), (7.84), (7.93)
dG/dx+ad2G/dx'2 = 0, x’>l+vi, x<t;
G(x, x', t, t)|,=,=6(x'—x), x!>l+vt\
[dG/dx'-(h+v/a)G]x=i+vX = 0, x<t; \G(x, x!, t, t)|< +oo
получите для G (x, x', t, x) следующее выражение
nt < . \ 1 f Г (■, Г i.x + x'-2{l+vt))2
G(x,x',t, x)=-
— j h — I exp I (x -|- x' — 2 (/ -f- vtj) h -I-
^exp[i
hy/a + -'y) (t-x) + V(x'-(l+ «/))]Ф*ГХ+У-2(/-1,)+
2s! aj a J L 2ja(,-z)
+ (*V. + ^)vA-t}
Покажите тождественность полученного выражения и выражения
(8.26).
Выражения (8.26) — (8.27) дают возможность записать для об¬
ласти [l + vt, оо), 0 интегральное представление решения краевой
задачи (7.78) — (7.81) при общем виде краевых функций. Например,
решение краевой задачи
412
8T/8t=ad2T/8x2 +f(x, t), x>l+vt, f>0;
T(x, 0)=Ф0(х), |T(x, г)|< +00, x^l+vt, 0;
8Tjdx\x=,+v, = h[T\x=l+v! (p(/)], t^O
согласно (7.110), (7.111) (8.26) имеет вид
00
T(x, /)= O0(x')G(x,x',t,0)dx'-
00
Л
-ah \(p(x)G(x, x', t, t)\x:=,+„dx +
fix', x)G(x, x', t, t) dxdx!.
0
0 l+vz
11. Перейдем теперь к области [vt, l+vt], t^O. Для рассматрива¬
емой области функция Грина G (jc, jc', t, т) удовлетворяет уравнению
(8.20) с начальным условием в (8.21), а так же граничным условиям
(для первой, второй и третьей краевых задач):
Здесь также могут быть использованы тепловые потенциалы,
однако, в данном случае следует учитывать характер области, в
которой отыскивается функция G. Более целесообразным является
предварительный переход в подвижную систему координат, для
чего введем вместо переменных (jc, t) новые переменные — под¬
вижную систему z = x — vt(z' = x' — vr), t'=t — т, а вместо функции
G(jс, jc', /, т) — новую функцию W{z, z', t, т) с помощью со¬
отношения
G(jс, jc', t, т) = ехр
z /' ) W(z, z', t\ т). (8.28)
la 4 a J
413
В системе координат (г, /') имеем:
dW/dt' = a {d*W/dz2), 0 < г < /, t' > 0; (8.29)
ИН<'-о = ехр(£г)б(г-г'), 0 < г < /; (8.30)
3^/9г|,.0*-Р1Г|,ив, Г >0; dW!dz\tml = -^W\zmt, t' > 0, (8.31)
где 1/01 = 1/02 = 0 для первой краевой задачи, 0/ = (—l)i+1 v/2a
(/=1,2) для второй краевой задачи, 0/ = ft/ + (—ly+1 vjla (/ = 1,2)
для третьей краевой задачи.
Задача (8.29) — (8.31) уже рассматривалась в § 4 гл. III [см.
(3.112) — (3.116)] и для нее получено интегральное представление
решения в виде (3.122) для любой комбинации граничных условий
при г = 0 и 2 = /; начальной функцией в каждой из этих краевых
задач считается Ф0 (2) = ехр (vz!2a) 6 (г—г'), собственные значения и
собственные функции соответствующих однородных задач для об¬
ласти 0^2^/ указаны в § 7 гл. III.
Используя эти результаты, можно выписать для W выражение
в виде ряда типа Фурье, однако удобного лишь для больших зна¬
чений времени /' (для первой и второй краевых задач это сделано
в § 4 гл. III). Отсюда представляется целесообразным получить
операционное решение задачи (8.29) — (8.31), включающее в себя
все комбинации граничных условий в зависимости от значений
коэффициентов 0* и 02.
в (8.29) —(8.31) в пространство изображений
d2W/dz2 — (p/a) W = — (1/а) ехр (vz/2a) 6 (г—г'), 0 < г < /; (8.32)
dW/dzl^p.WU,,; dr/d2|,=, = -fJ,W|,=,. (8.33)
Общее решение уравнения (8.32) запишем по формуле (5.17)
[(см. также (7.41) — (7.44)] в виде:
Используя граничное условие (8.31) при 2 = 0 и выражение (8.35),
получим первое уравнение относительно постоянных интегрирова¬
ния Л и В; граничное условие (8.31) при г = / и выражение (8.34)
дадут второе уравнение для определения Л и В. Решая получен¬
ную систему, находим постоянные Л и В и подставляем их значе¬
ния в (8.34) и (8.35) (рекомендуем проделать самостоятельно эти
не сложные, но весьма полезные выкладки). В результате придем
оо
Полагая
о
х -jU rV sh -4= VJ e(u/2a) 0 < г' < г;
У а У а
(8.34)
W = А с h -^= VJ + В sh -L V7 +
У а У а
V~a V~p
а ур уа уа
}—= sh -?= V~p ch У^р e(v/2a) r , 2 < 2' < /.
(8.35)
414
к решению W в следующей форме при 0 < г' < г:
W (г, г', р, т) = ехр [vz' / {2а)] х
^(Pi + Pa)ch +-J)shyr,/^
(8.36)
Когда z < г' < /, решение имеет тот же вид, только гиг' меня¬
ются местами в дробном выражении.
Рассмотрим частные случаи выражения (8.36).
Для первой краевой задачи (8.29) — (8.31) необходимо в (8.36)
положить 1/Pi = l/P2 = 0; тогда получим
Для второй краевой задачи полагаем в (8.36): —pa = pi=|i
(где р = 3и/2я); находим
Дальнейший переход к оригиналу в выражениях (8.36) — (8.38)
связан с той формой оригинала, которую желают получить. Приме*
нение обобщенной теоремы разложения (6.33) дает оригинал в форме
ряда типа ряда Фурье, удобного при числовых расчетах для боль¬
ших времен. В то же время, разлагая выражения (8.37) и (8.38)
в бесконечный ряд по отрицательным степеням экспоненты, для
чего необходимо выразить гиперболические функции через показа¬
тельные и воспользоваться формулой
придем к оригиналу, имеющему вид, удобный при расчетах для
малых значений времени. Переходя, таким образом, к оригиналу
х
W (г, г', р, т) = ехр х
' sh [(г' У~р)!а 1/2] sh [(/ — г) У~р! а1/2]
У~а \Гр sh (l/a1/2) Y~p
(8.37)
W (г, г', p, т) = exp (vz'/2a) (p—a^2)-1 x
——-=-^=r = 2exp
sh (ayn) VIp
(8.39)
415
в (8.37) и возвратившись в систему координат (х, t) с учетом (8.28),
находим функцию Грина первой краевой задачи для рассматривае¬
мой области в виде следующих двух выражений:
С',) 1- 2 i'Jp-,)'ехр [- Ё- (х■-Т.) +
Г (2ln + x + x'-v(l+T))4\
0XPL 4^—i) J/-
= 7ехР \^(х'—х)+^(*—х)] 2. Sin пп {х ~1Ч) х
L П- 1
xsin^L(^exp[--(^^) (/—t)j. (8.40)
Аналогичным образом можно получить соответствующее выраже¬
ние и для функции Грина второй краевой задачи (мы не выписы¬
ваем оригинал, удобный для малых времен ввиду его громоздкости;
для больших значений t необходимое выражение приведем ниже).
Для выражения (8.36) простой ряд по отрицательным степеням
экспоненты написать не удается. Действительно, используя очевид¬
ное соотношение
v, Sh-^ V~p +Ъ ch-i=]/V =
у а У а
Г — /— 1
= У1±1?ехр (—УТ\ 1
2 eXp^KPJL* (Vi+Ya)e J’
запишем знаменатель Л в (8.36) в следующем виде
A=iexp(F7,/^)n ^+Kro~Pf) х
w Г1 (с1/гр1-У7)(а1/грг-К7) / 21 ^-\1
Х I (а-/%+^(а1/2ра + ^) *Ч\ГУЪУР)\- (84,)
Отсюда, раскладывая 1/А в ряд типа (8.39), столкнемся с необхо¬
димостью вычисления оригиналов от изображений вида
{УТЬ-У~р)п{УЫ*-]Гр)л г fin) кл п-о 1 2 3
(^tj1 + /7)"+1(K^ps + K/7)n+1 PL пп)У Pi’ n и’
где f (п) — некоторая положительная функция. (8.42)
Решение этой задачи связано с большими техническими труд-
ностями и в то же время представляет несомненный интерес для
аналитической теплопроводности ^предлагаем читателю^ подумать
над этой задачей. Воспользуйтесь формулой, приведенной в гл. 5 на
стр. 301).
Задача 2. Применяя обобщенную теорему разложения (6.33) для нахожде¬
ния оригинала (8.36), показать, что в системе координат (*, t) функция Грина
416
X
третьей краевой задачи для области \vt, l + vt], 0, имеет вид
2 Г v
G (х, х', *, т) =-уехр ^ (*'—*) +
и-x) 1 V (^+f&2)
4fl J ,1Г, to+P*f2)[P.J+to+tfi2)]+Pii(цЗ+РИ
X [fin COS (fl„//) (x—vt) cos (n„//) (*' — ot) +
+ (M2Sin (ц„/() (JC —oO Sin (ц„//) (*'—irt)-f
+ Hnpt/sln (,ЛС + ДС' — o(/ + x))]exp |^— ("n ((—t) . (8.43)
Здесь /?j = + v/2a; f$2 = h2 v/2a; |un > 0 —корни уравнения ctg jli =
= M/f(Pi -f- Рг) h — PiW/fM- (Pi + Pa)]-
Полагая в (8.43) 0, получим функцию Грина второй крае¬
вой задачи для рассматриваемой области. Заметим также, что в [138]
методом отражения получено решение третьей краевой задачи для об¬
ласти 10, /], ^0, в форме, удобной для вычисления при малых значе¬
ниях времени t. Однако знание оригинала (8.42) привело бы, по-ви¬
димому, к результату, отличному от полученного в [138].
Мы рассмотрели для уравнения (8.20) в области [vt> /+иЛ, t^O,
три вида граничных условий. Аналогичным образом можно рассмот¬
реть любую комбинацию граничных условий для этого уравнения,
так как исходная область сводится к области [0, /], ^0, достаточно
хорошо изученной в гл. III.
III. Область [0, l+vt\y ОЮ, и к ней сводящаяся [li+vj, l2+v2t]
являются наиболее трудными для построения функции Грина соот¬
ветствующих краевых задач. Достаточно сказать, что до настоящего
времени нет полной информации о функциях Грина всех краевых задач
(число которых, очевидно, равно 9), для рассматриваемой области
и даже полученные результаты нуждаются в уточнении (см. [63]
и §2 гл. VII).
Хотя граничные условия I рода являются наиболее простым слу¬
чаем среди всех остальных девяти, тем не менее построение функции
Грина первой краевой задачи для рассматриваемой области уже свя¬
зано с большими вычислительными трудностями. Вследствие громозд¬
кости выкладок рассмотрим лишь постановку задачи, укажем метод ее
решения и приведем конечный результат (все подробные выкладки
приведены в работе [69], и при необходимости читатель сможет с ними
познакомиться).
Исходим из определения (7.82) для функции G(xy х\ ty т), удовле¬
творяющей (7.103)—(7.104). Имеем для функции q(xt х'у /, т):
dq/dt' = a(d2q/iЭх2), 0 <x<l0 + vt\ t'> 0
(t'=t— т, /0 = / + ит); (8.44)
<71/'=о = 0; <7|x=0
1 - -
J р 4 at'.
2 VnaF
-(/0 + 1)Г-Л2
q I x=ia + vt' = 7ГГг—^тe ,at' (8-45)
14-339
417
Решение задачи (8.44) — (8.45) следует искать в виде суммы тепло¬
вого потенциала простого слоя (8.1) по прямой х = 0 и обобщенного
теплового потенциала простого слоя (8.2) по кривой x = l0-{-vt'i
Операционная форма функции q(xy х', р, т) имеет вид [см. (8.12)]
Дальнейшие рассуждения связаны с определением неизвестных
плотностей (О и 4^(0 в пространстве изображений в том виде,
в каком они появились в выражении (8.47) [исходя из граничных
условий (8.45)] и переходе в класс оригиналов. Окончательное выра¬
жение для функции G(xyx', /, т) следующее:
где /0 = / + irr, y = vl(2Vh).
Исследуя полученное решение, объединим экспоненты, содержа¬
щие в показателе множитель /г2. Тогда под знаком ряда появится
множитель ехр[—lQn2 (I+ vt)/[a(t—т)]. Отсюда видно, что ряд (8.48)
сходится и для отрицательных значений о, если т </< — l/v. Но
при t = — l/v (v < 0) заданная область исчезает. Следовательно,
решение (8.48) имеет силу для любых значений у, т. е. для отрезка
как с возрастающей длиной, так и с убывающей.
Из формулы (8.48) можно получить следующее следствие. Не¬
трудно убедиться, что ряд (8.48) сходится равномерно относительно
/^0 и в силу этого возможен предельный переход по / под знаком
суммы. Отсюда из (8.48) при 1—+0 можно получить функцию Грина
первой краевой задачи для области»[0, vt]y t^O:
Зная функцию влияния (8.49), нетрудно записать интегральное
представление решения первой краевой задачи (7.78), (7.102) в еле-
q (х. х'. я. г) = ^а . (п) ехп ( £_ |/7Г^ 4-
где Y, (Г) = Т2 (/') ехр [v2t'/(4a)].
G (Ху х'у ty т)
X
(ехр [
2 У па (/ — т)
(2 Ipn + x'—x)
4a (t — т)
G (х, х'у ty т)
х
(ехр[
2 У ла (t — т)
(2vTti-{- х' — х
4a (t — т)
418
W(z, Fo)=ip
1 0 1 С л
дующем виде [см. 7.105)]:
T(x,t) = a\ф1 (т) Ц dt-a jФг(т)gdt.
о о
В частном случае: пусть в области [0, l + vt], 0, начальное рас¬
пределение температуры есть Т (*, 0) = Т0, а на границах Т (О, /)=ТС,
t) = Tc. Для безразмерной относительной температуры
Г = [Г (*, 0 — ТС]/(Т0—Гс) по формуле (7.105) решение W t)
имеет вид
i
W (дг. О = J G (х, х\ /, 0) dx', (8.50)
О
где G (х, х', /, 0)—функция Грина (8.48) (но при т = 0).
После вычисления интеграла и приведения к безразмерным пере¬
менным z — x/l, v0 = vl/a, Fo = at IP найдем
T(x Л T I "V.® p Г zJ*2±S±^l
-e ,Fo №
(8.51)
На рис. 37 приведены графики изменения относительной темпера¬
туры (8.51) в зависимости от переменной длины стержня z для разных
значений критерия Фурье и скоро¬
сти iv Приведенные графики могут
служить в качестве номограммы
для практических расчетов.
Заметим, что решение первой
краевой- задачи для указанных об¬
ластей можно получить и в иной
аналитической форме, а именно в
форме ряда типа Фурье (пригодной
для больших значений времени t в
отличие от формы, определяемой
функциями Грина (8.48) и (8.49),
Удобной при расчетах для малых
времен), если воспользоваться функ¬
циональным преобраз о в а н и е м
Гринберга (см. §5 гл. VIII).
Что^ касается области
к+и2Л, ^0, то с помощью неслож¬
ных преобразований этот случай можно свести к предыдущему. Дейст¬
вительно, введем вместо независимой переменной х новую перемен¬
ную z — подвижную систему z=x—(l1+v1t), а вместо функции Т(х, Д,
Удовлетворяющей в этой области уравнению T't=aT"xt новую функ¬
цию W (z, t) с помощью соотношений Т(ху t) = W (г, /)ехр(—Viz/2a—
v\tlba)> тогда O^z^lo+vJ, где 10=12—к, v0=v2—vu a W(г, /) удов¬
летворяет уравнению того же типа, что и функция Т(х, t).
419
V0=tt,3;Fo*Ot03
Vo=25,0; Fo- 0,0b
Vo=16,6;'Fo=0,06
Vq-12,5i Fo-0,08
'o = 10,0;Fa = 0,f
V0-6,66; Fo-0,15
Vg*S; Fo-0,2
=J,JJ :Fo=0,3
Vq=2; Fo - 0,5
1 ; Vn=t
Используя полученные выражения (8.48), (8.49), нетрудно постро¬
ить функцию Грина первой краевой задачи для центрально-симмет¬
ричных областей с равномерно движущимися границами. Действи¬
тельно, пусть для шаровой области 0QsO, ставится задача:
определить функцию Грина первой краевой задачи
6G (дЮ ,2 dG\ Л ^ о \ 4 4 ^
dT==a(d7? + TW)' 0^r<R + vt, />т;
G(r,r0, t, T)|(„t = ^6(r—r0); G|re/?+t,( =0; |G[< + oo, r>O.j
(8.52)
В специальном решении этой задачи нет необходимости, так как
здесь можно воспользоваться формулами (8.48) и (7.95). Для этой
цели введем новую функцию W = rG, для которой, учитывая (8.52),
получим
dW/dt' = a(d2W/dr2), 0<г<Я0 + ^' (/' = / —т, л
/?0 = Я + эт); I (8 53)
«7|г=о=^6(г-г0); Г |г.0 = 0, W |r=/?t+t,r = 0. j
Задачу (8.53) можно рассматривать как первую краевую задачу для
области [0, Ro + vt']* t'^ 0, в декартовой системе координат (г,/').
Но для этого случая построили функцию Грина в виде выражения
(8.48) (где время t должно быть обозначено через время дейст¬
вия источника обозначим через т' во избежание путаницы).
Таким образом, для функции Грина С*(г, г', т') первой крае¬
вой задачи (8.53), согласно (8.48), можно записать
°‘(г’ Л V, = ??W=7) Д “К-5?х
.»И)
Зная функцию Грина G по формуле (7.105), находим решение за¬
дачи (8.53), а вместе с этим и искомую функцию G(r, г0, /, т)
G{r, г0, t, т) = -)- j -4^7-G*(r, г', t', 0)6(r'—r0) dr =
s ^-ir*expx
8nr,0j/T^O-T)nf?e Ч а я '\Кш1
х|_гй!дааг]). (MS)
Выражение (8.55), в свою очередь, по интегральной формуле (7.105)
позволяет записать решение первой краевой задачи для шаровой
области с равномерно движущейся границей.
* При изучении этих работ необходимо принять во внимание результаты
§ 2 гл. VII.
420
Заканчивав изложение метода тепловых потенциалов, заметим,
что для области x^l + vt, О, в качестве основного достаточно
использовать потенциал (8.1); для ограниченной области [0, l + vt],
t^O достаточно использовать потенциалы (8.1) и (8.2) при реше¬
нии краевых задач любого рода (мы не останавливались на тепло¬
вых потенциалах двойного слоя в одномерных областях, применение
которых нам не понадобилось [65, 114]).
Решение краевых задач для рассматриваемых здесь областей
целесообразно сводить к нахождению соответствующей функции
Грина. Это позволит в интегральной записи решения краевой задачи
через найденную функцию Грина значительно уменьшить громозд¬
кость полученного решения и сделает его более удобным для чис¬
ловых расчетов. Приведем в качестве справки сведения по найден¬
ным функциям Грина для областей с равномерно движущейся
границей*.
1. Область [0,/ + vt], / ^ 0: граничные условия I рода при
х=0 и II рода при x = vt (1 = 0); граничные условия I рода при
х = 0 и III рода при x — vt (/ = 0). 2. Область [vj, l + v2t], t ^ 0;
граничные условия I рода; граничные условия II 'рода; граничные
условия III рода. 3. Центрально-симметричная область [R1 + vt,
#2 + ^]» ^^0: граничные условия I рода (соответствующую лите¬
ратуру см. в ссылках в работе [63]).
Наряду с методом тепловых потенциалов для этого класса задач
может быть использован также метод контурного интегрирования,
основанный на операционном исчислении. Этот метод, развитый в
работе [78], здесь не рассматривается.
§ 3. МЕТОД РЯДОВ ДЛЯ ОБЛАСТЕЙ ВИДА [0, у V~2at], [у at, оо), t > 0
Систематическое изучение указанных областей началось с работы
Гринберга [24], в которой методом контурного интегрирования было
получено точное решение одномерной тепловой задачи для полуог-
раниченной области х > р 1/"7 при постоянной температуре на дви¬
жущейся границе. Развивая идеи Гринберга, автору работ [123, 124]
удалось получить замкнутое решение первой краевой задачи для
ограниченной области при постоянных начальном и граничном
условиях. В дальнейшем рассматривались случаи, когда граничные
функции были представлены в виде срi(t) — Aitn/2 (где п — неотри¬
цательное целое число), которые разлагаются в бесконечные ряды
Маклорена [5]. Метод, предложенный в работе [61], обобщил полу¬
ченные к этому времени результаты и дал дальнейшее развитие рас¬
сматриваемой проблемы. Этот метод назван методом рядов, так как
решение краевой задачи отыскивается в виде функционального ряда
специального типа, коэффициенты которого находятся из удовлет¬
ворения граничным условиям задачи.
* При изучении этих работ необходимо принять во внимание результаты
§ 2 гл. VII.
421
I. Область [0, у V 2 at], О (у—безразмерный коэффициент
пропорциональности). Рассмотрим первую краевую задачу. Темпе¬
ратура граничных поверхностей равна q>i(0 при х = 0 и (t) при
х = у V~2at. Несколько сложнее записать для данной области на¬
чальное условие. При / = 0 рассматриваемая область сосредоточи¬
вается в точке х = 0; поэтому в качестве начального условия для
функции Т (ху t) следует считать Т (х, 0) = фх(0). Имеем, таким
образом, для Т (х, /);
dT/dt = а (д*Т/дх*), 0 <х<у V~2at, t > 0; (8.56)
Т (0, t) = ф, (0, 0; Т (v V^at, t) = ф2 (/), t > 0. (8.57)
Введем вместо независимой переменной х новую переменную
I = i (х/У~2а1), i= |Л=Т, (8.58)
а вместо функции Т (х, t) — новую функцию 0 (£, /) = Г (х, t). Тогда,
учитывая правило дифференцирования сложной функции, получим
о, дб « дВ д2В Л t ^ ^ ^ л /о еп\
21 — £ gg- -^|2 » ^ > 0; (8.59)
© (0, t) = Ф1 (/), / > 0, © (iy, t) = ф2 (t), t > 0. (8.60)
Введем далее вместо функции 0 (£, t) новую функцию W (£, t)
©a = (6, <). (8.61)
Задача (8.56) — (8.57) примет вид
d*Wldt* + (l/2-l2/4)W + 2t(dW/dt) = 0, 0<l<iy, t > 0; (8.62)
ИР (0, О = q>i (0. ^ (iy) = ехр (уа/4) ф2 (/), 0. (8.63)
Из (8.58) следует* (—iQ= lim (х/2 Vat), откуда можно записать для
/->о
х-+0
W (g, t) следующее начальное условие: lim W(%, t)= lim W (£, t) =
/-►0+ (-*!)-► ° +
= lim фх(0 = ф1(0).
t -►O +
Предположим далее, что функции фх(0 и ф2(/) могут быть раз¬
ложены в абсолютно сходящиеся ряды вида
К= + оо к= + ео
Ф1 (0 = 2 bKlntK'n\ ф2(/)= 2 Ск/т/к/т, (8.64)
К= — со к — — со
где п и т—произвольные действительные числа.
Найдем решение W (£, t) задачи (8.62) — (8.63) в виде функцио¬
нального ряда
о = *2 NK/n{l)t^ + MK/m(l)t^, (8.65)
К — — СО
причем будем считать этот ряд равномерно сходящимся относитель¬
но | на любом конечном отрезке изменения переменной t (позже
это предположение будет проверено).
Выражение (8.65) удовлетворяет уравнению (8.62) и граничным
422
условиям (8.63), если выполняются следующие условия:
d'NK/n/dl* + (2к/п+ 1/2 — £2/4) Л/*п = О, 0 < I < iy; (8.66)
d2MK/m/d£a + (2/c/m -f 1/2—i2/4) Мк/т = U, 0< £< iy; (8.67)
(0) = bK/n* Л/к/п (/у) = 0; ^
(0) « 0, MK/m (iy) = exp (y2/4) cK/m. j <8-68)
Условие (8.66) — (8.68) получим, если подставим выражение (8.65)
в уравнение (8.62) и граничные условия (8.63) и приравняем
коэффициенты при одинаковых степенях t. Дифференциальные урав¬
нения (8.66) и (8.67) есть уравнения Вебера для функции
параболического цилиндра [8] и имеют соответственно независимые
решения
^2К/Л (^) И D _ 2К/Л— 1 ( /£)'» D2K/m (£) и D — 2к/т — \ (“Ф,
где Dp(z)—функция параболического цилиндра (ее определение см.
в [8]).
Следовательно, общее решение этих уравнений можно записать
как линейную комбинацию частных решений в виде
N к/п (I) = QiK/nDyc/n (i) + biK/nD _2к/л-1 (— /£)*, (8.69)
Мк/т (I) = Q2K/mD2K/m (I) + Ь2К(тР- 2к/т -1 (— *£)» (8.70)
где aiK/n, biK/n, а2К/т, &2*/m— постоянные интегрирования.
Используя граничные условия (8.68), составляем систему алгеб¬
раических уравнений, из которой находим постоянные:
QiK/n = йк/л^-2/с/л-1 (?)/Ai'» С12к/т = — &*,1Ск/тО-2к/т-\ (0)/Д2; )
biK/n = bK/nD2K/n(iy)/Ai\ b2K/m = €y2/*cK/mD2K/m (0)/Д2; j ^ ^
= ^2^ (*V) (0)» Pi==^/^'» p2 = KltTl.
Подставим найденные значения констант в общее решение (8.69)—
(8.70) и далее найдем функцию W (£, /) в виде (8.65)
W(l, /) = е5а/4 \*2? Ьк/пх
L/C = - оо
у, Р-2к1п-\ (у) Р%к1 n(l)—P2tcl n(iy) Р-2к> n-l( —1%) ±к/п , у»/л, у.
Х D^,n^(y)D2lc;n{0)-D2Kin{iy)D^Kln_l(^) ^ Ск/тХ
w ^2 к! т (Q) D-2к1 m-l ( *£) Р-2к1 т-1 (0) к/ т (£) ук/т
D — 2*1 т-l (У) D2l£/ т (0) D2te/т (ty) D_2*1 т-l (0)
Можно показать, что при этом удовлетворяется и начальное условие:
lim № (£, /) = lim ( 2 *W't//,)= Ит ф1(0 = Фг(0).
(-i|)-0+ (-.0+ \к=-оо / /-.0 +
Переходя в систему координат (х, /), находим искомую функцию
Т (х, t)y удовлетворяющую условиям сформулированной задачи
(8.56) —(8.57):
423
Т(х, /) = ехр ( —^7 ) х
К = + ОО
D-2к1п-\ (?) D2kiп ^ ~2к1п~1 ^y^ai)
^ Ьк/п Fi тгт—!—77v\ Гл 7ГТ~п 7т X
к = -
(8.72)
л^л ^ — 2к/п — 1 (y) DiKin (0) D2k1„ (iy) D_iKtn — 1 (0)
X tK/n + ev’/4cK/m x
Pj. (0) (0) P2Wm(<-p==)
D-2k! m-l (?) &2KI m (0)—^2 K! m (l?) ^ -2kI m-1 (0)
Можно показать, что для равномерной сходимости ряда (8.72)
достаточно, чтобы абсолютно сходились ряды (8.64), так как, оце¬
нивая по абсолютной величине найденное выражение (8.72), придем
к результату
\Т(х, 0 К 2 \bK/n\tK/n + ^ 2 \cK/m\tK/m.
к — — со к — — со
Для частных значений граничных функций в (8.57) решение (8.72)
может быть преобразовано в другую аналитическую форму.
Пусть, например, фЛО^о» ф2(0 —со- Тогда имеем:
^ 0, к > 0 к < 0; ^ 0, к > 0, к < 0;
Ьк/п = | VK/m = |
1 fo0, /с = 0; > с0, к = 0.
Из (8.72) находим соответствующее температурное поле
Т (х, /) = ехр (—gjy) A‘l(v){bo[0-i(Y)A(‘ ■D0(iy)D_}
х (74s)]+'w4d,(0,d- (гУ_1Чг ИЬУD-'(0)]};
A (y) = ^-х (Y) А> (0)—Ц> (ty) £>_, (0). (8.73)
Из теории специальных функций известны соотношения
D0 (г) = е_*!/4; 0_Ц2) = |/я/2 ег‘/<ф* (г/|/^). (8.74)
Принимая во внимание (8.74), из (8.73) находим решение Т (х, /),
приведенное в работах [24, 137]:
Т {X, t) = b0-(b0-c0) Ф (jy=%) | Ф (У/ ^)(Ф (г) = 1 -Ф*(г)).
Пусть далее граничные функции cp{(t) разлагаются в степенной ряд
Маклорена
Ti (о=L Щг1 ts> ф. (о=L 4й **• <8-75)
х
Sl sj
s= 0 s = 0
В этом случае
Ьк/п
) и, Ф(15) (0) ^ П. \ „ Ф(25) (0) *->()•
= ^ = -7Г-> к>°- ск/т= \с* =-5!— К>0- (8.76)
' 0, /с < 0; ) 0, к < 0.
424
Из (8.72) находим решение Т (х, t) с граничными условиями (8.76)
/ се
\ I
Г (х, 0 = ехр (~щ) { L ДГ: (Y) [ft, (Я-s,-i (Y) Я2*(-р==) —
— Ai, (l'Y)Ai-i( |/~2^)) + eV /4^
:(у=)-°-ь-.(0)A,(-p=r))]
- - \ у 'Ш j / ^
. _ . _ _ / Y \ _ _/
X<
a, (Y) = (Y) D2s (0) _DM (/Y) (0). (8.77)
Воспользуемся следующим известным соотношением для функций
параболического цилиндра [8]:
Dv (г) = Г (^tv) [e^/«D-v-, (iz) + e-v»'/2D_v_1 (_fc)], (8.78)
а также формулой, полученной на основе (8.78):
Я_„_, (г) =2S \Tnj2, erfc (z/K2), (8.79)
00
где f25 erfc г = J i2s~1erfcu du.
z
Заметим, что формула (8.79) может представлять самостоятельный
иттерес для теории специальных функций.
Преобразуя теперь выражение (8.77) с учетом (8.78) — (8.79),
приходим к решению, данному в работе [5]:
. Г , ^_ф<,(0)^егГсГ(=11^Х1
Tlx A-V V( IV 4 sl L_0_J_x
’ ’ 5=0 L= о ( } ^ erfc (y/V~2)-^ erfc (-Y/^2)
x its erfc
(-1)**
2 VTl
■W)s. (8.80)
Если граничные функции (8.57) степенные, т. е. ф, (/) = Л,/л,
Ф2(А = Лг/л, А, = const, п = 0, 1, 2, ..., то из (8.72) получим сле¬
дующее решение:
Т (ДГ, О - мр- ( i ) { v [ D.h., (V) D„ (-j^-)-
^2л (*Y) J ^ Х
ХО-Ь-1^^Т^)~^2л (у=-^-2л-1(0) j ^2eV/4| tn, (8.81)
An = D.Sn.f (Y) D2„ (0)—Din (iy) 0_|я_, (0).
Производя несложные преобразования выражения (8.81), с учетом
(8.78), (8.79) найдем температурное поле Т (х, /) в форме, получен-
425
ной в работе [124] (рис. 38, а, б, в):
Т(Г л = У ( \у-' w-Amir* trie [(—!)« yiv~2]
^ ^ ' i2n erfc {ylY~2) — i2n erfc (—у/У~2)
к = l
X
^рТ7=г]<4,)--
(8.82)
Задача 3. Применяя изложенный выше метод [по схеме (8.58), (8.61),
(8.64), (8.66), (8.67)], получите решение второй краевой задачи:
dT/di = о (д*Т/дхг), 0 < х < у У~2а1, t > 0;
дТ!дх и=„ = Фп(0 = (1/^091(0. t > 0;
дТ1дх\хшЧУй7 = Т2а(0 = (1/^1)фа(0. < > 0.
(8.83)
(8.84)
Кроме того, рассмотрите частные случаи граничных функций [61].
II. Переходя к области (у V 2at, оо), t 0, рассмотрим в ней пер¬
вую краевую задачу вида
dT/dt = а{д2Т/дх2)у х >yVHaty t > 0; (8.85)
Т (х, 0) = 0, х>0; Г (х, /) |Лву к-257 = Ф(0*
lim Т (х, /) = 0. (8.86)
д: -> оо
Наличие нулевого начального условия не ограничивает общности
задачи. В § 5 гл. III было показано, что с помощью интеграла
Пуассона всегда можно освободиться от ненулевого начального
условия с соответствующим изменением граничной функции (и при
этом тип граничного условия сохраняется). Переходим, как и выше,
с помощью подстановок (8.58), (8.61) в систему координат (?, /),
в которой задача (8.85) — (8.86) имеет следующий вид
d2W/dl2+(\/2-t2/4)W + 2t{dW/dt)=0, £ > iy, t> 0; (8.87)
W (ty, t) = exp (y2/4) ф (0» 0; lim W (£, /) = 0. (8.88)
(-i£) -►»
426
Пусть граничная функция ср(/) раскладывается в ряд вида
к= + оо
<р(/)= 2 Ck'ttS*1”1' где m—произвольное действительное число.
К— - СО
Решение задачи (8.87) — (8.88) ищем в виде функционального
ряда того же вида, но с неизвестными коэффициентами
^(1. 0= 2 MK/m© tK/m. (8.89)
К= - оо
Уравнение (8.87) с условиями (8.88) дает обыкновенное линейное
однородное дифференциальное уравнение второго порядка
dJMK/m/dia + (2«:/m+1/2 —i2/4)MK/m = 0, l> iy; (8.90)
MK/m(iy ) = eW4C)C/m; lim MK/m(l) = 0. (8.91)
(-Ф -* ®
Общее решение уравнения (8.90) запишем в виде (8.70). Из условия
(8.91) при (—i%) —► оо следует, что постоянная а2к/т должна рав¬
няться нулю, так как функция D2K/m(t) не ограничена при
(—«£)—>■<»■ Постоянную biK/m нетрудно найти из граничного усло¬
вия (8.91), которое дает
Ьгк/т — Ск/т СХр (у2/4) D_2K/m_j (у).
Запишем далее W (£, t) и перейдем в систему координат (х, /);
получим окончательное решение Т (х, t), удовлетворяющее условиям
задачи (8.85) — (8.86):
К~^\° ^ — чк/т— i ( . / „ ,)
Т (х, /) = е “ж2Л8в')+У’/4 £ Ск/т \ К 2atj {к/п1' ^8 92)
К= — оо — 2 к/ап — 1 \Y)
Для частных значений граничной функции <р (/) выражение (8.92)
принимает другую аналитическую форму. Например, при ф(/) = Г0
получим из (8.92) с учетом (8.79) решение, данное в работах Г124,
137]:
Т(х, t)lTa^{^y=)j^{ylV~2). (8.93)
Если <p(t) —T0t (Т0 = const), то аналогично найдем
1/Д (х _ )ф* ( —)—7±= e~x'liiat)
T(x,t) V 2\ 2 at) V 2 \TTt J \ГЫ (8.94)
То (1— у2)К я/2 Ф* (у/1/ 2) —у» ехр (—Т2/4)
Задача 4. Применяя изложенный выше метод, показать, что решение урав¬
нения теплопроводности (8.56) с граничным условием II рода на движущейся
границе (дТ/дх)х_ ^— = 4 (t) = q> (t)/Y~ti t > 0, имеет вид
Т(х, 0 = аГ2ех
X
\Л _ ^ - 2/c/m-1 {xIY~2ai) iK/ml у K/m
Kh„ Сф> Dl2K/m (V) - (7/2)0.^^., (V)' v . Л/т
(8.96)
427
Заметим, что в каждом из выражений в бесконечном ряду соответст¬
вующего решения Т(х, t) при числовых расчетах можно ограничиться
конечным числом членов и выразить функции параболического ци¬
линдра, например, через вырожденные гипергеометрические функции,
функции, широко табулированные и достаточно хорошо изученные.
Кроме того, как следует из изложенного, метод дает возможность для
частных значений граничных функций получать различные (эквива¬
лентные) формы решений, что имеет немаловажное значение при об¬
работке этих решений на ЭВМ; метод позволяет также рассмотреть
н слоистые тела (граничные условия сопряжения). Решение послед¬
ней задачи подробно разобрано в [61]. Полученные выражения вклю¬
чают в качестве частного случая автомодельные решения, рассмот¬
ренные для указанных областей в [63]. Термин «автомодельное реше¬
ние» связан с таким представлением искомого решения через безраз¬
мерные переменные, которое позволяет уменьшать число независимых
переменных в исходной постановке краевой задачи. Рассмотрим слу¬
чай двух независимых переменных, пространственной переменной х
и времени /, так, что автомодельность решения в данном случае будет
означать, что уравнение в частных производных (каким является урав¬
нение теплопроводности) может быть заменено обыкновенным диффе¬
ренциальным уравнением. Итак, пусть дано уравнение
дТ/dt = а [(д2Т/дх1) + (у/х) (дТ/дх)], (8.96)
где при v = 0—линейная задача; при v=l—температурное поле
цилиндрическое; при v = 2— температурное поле сферическое.
Найдем решение Т (х, /) уравнения (8.96) в виде Т (х, /) = /ц<р(г),
где z = x2/(at). Подставляя выражение для Т в уравнение (8.96) и
вычисляя частные производные функции Т по правилу дифферен¬
цирования сложной функции (например, Т\ = р/^_1ф (г) + (г) г
= р/ц"1ф(г) — (г)), после несложных преобразований по¬
лучим
4г (с12ф/с1г2) + (2 + 2v + г) (dq>/dz) — рф (г) = 0. х(8.97)
Общее решение этого уравнения можно записать через вырожден¬
ную гйпергеометрическую функцию Ф(а, у, г) = 1/г1(а, у, г) или
родственную ей функцию Уиттекера Wp(z):
ф (г) = 2-(1'4) (1+v> ехр (— г/8) \CXW 1 + 4цч.у v-i (г/4) +
4~ C2W1 ч- 4 ilx + v у -1 ( г/4)1 » (8.98)
4*4 J
где С, и С2—постоянные интегрирования.
Общее решение уравнения (8.97) при различных частных соче¬
таниях v и р можно найти в справочнике [57]. При v = 0 общее
автомодельное решение впервые было получено Рибадом (см. ссылку
в работе [63]).
Рассматривается случай, когда граница области движется по
закону Р Vt (Р = ]/"2 \Га у); для нахождения автомодельного реше¬
ния искомое решение Т (х, t) и его производная должны принимать
428
на движущейся границе значения
Т (*' 0|*=рК7=^ф(Р2/а);
дТ (х, t)/dx\x= р у- = (2|3/а) Ф' (Р*/а) ^-,/г. (8.99)
Эти свойства искомого решения и линейность уравнения (8.96)
позволяют решать весьма просто краевые задачи, в которых гранич¬
ные условия имеют вид полиномов. Рассмотрим пример.
Поверхность неограниченного цилиндра, радиус которого растет по закону
О< р 1ГТ, нагревается тепловым потоком q У~1. Требуется определить темпе¬
ратурное поле в цилиндре, если расширение происходит по закону р |/~7. Мате¬
матическая формулировка задачи имеет вид:
Решение задачи ищем в виде Т (х, /) = *ф (г) (jli = 1), z = x2/(at). Уравнение
(8.100) в соответствии с (8.97) примет вид
Здесь при частных значениях v = 1, |и = 1 функции Уиттекера в (8.98)
UP_6/4 о (z/4), ^5/4, о (— z/4) выражаются через степенную, показательную функ¬
цию и интегральную экспоненту Ei (— г/4).Приг—»► 0 функция Ei ( — г/4)—► — оо,
откуда следует, что должно быть С2 = 0; постоянную Сх найдем, используя гра¬
ничное условие (8.101), которое в новых переменных имеет вид ф' (г) |г=.р2/а =
Если уравнение теплопроводности неоднородно, т. е. имеет вид
T't = a[T"x, + (l/x)T'x] + f(x, t), то автомодельное решение указанного
вида возможно при условии, если функция теплового источника
задается выражением f(x> t) = f0(x)
Изложенный здесь метод автомодельных преобразований отно¬
сится, вообще говоря, к числу искусственных приемов, позволяю¬
щих получить точное решение задачи при специальном задании гра¬
ничных функций. Следует отметить, что в некоторых случаях соче¬
тание искусственных приемов (подстановок) с одним из интеграль¬
ных преобразований может привести к некоторому методу решения
краевых задач обобщенного типа. В качестве пояснения рассмотрим
кратко решение первой краевой задачи для области [Р0К U °°)>
*^0, когда граничная функция не представима в виде (8.64).
В безразмерных переменных имеем:
dTldt = a[{d2Tldx2) + {\lx) {dTjdx))y 0<* < Р }TJ, t > 0; (8.100)
Т(х, 0) = 0; дТ!дх\х у- = (1 A) q |/Т, / ^ 0; | Т (х, t)\ < + оо, *^0.(8.101)
4гф" (г)+ (4 +г) ф' (г)—ф (г) = 0, 0<г < Р2/а.
Общее решение уравнения (8.102) запишется в виде
Ф (г) = С, (г+4) + Сг |4е“г/4-(г+4) Ei (-г/4)].
(8.103)
(8.102)
Т(х, /)=.[/в?/(2ХР)][**/(вО + 4].
(8.104)
dW/d Fo = d*W/dx'\ х' > (3 УТБ, Fo > 0;
Г (*', 0)=0; WftVTo, Fo)= (p(Fo); \W (xr, Fo)| <+оо,д:,>0.
(8.105)
429
Применяем последовательно следующие функциональные преобразо¬
вания:
1. z = -k7P1/Fo, W(x', Fo) == А (г, Fo);
2. Fo = ехр (|32т), Л (2, Fo)=exp(—$2z2/8)B(z, т);
3. 5 = (Р/2) 2.
В новых переменных задача (8.105) имеет вид:
■^^=ж_(1+|2)В’?>р/2, -~<т+о°; (8-106)
Вф/2, т) = ¥(т); \В(Ъ, Т)| < + оо, |>р/2, |т|< + оо. (8.107)
Здесь ¥ (т) — новая (известная) функция.
Уравнение (8.106) можно привести к обыкновенному дифферен¬
циальному уравнению, если исключить переменную т е помощью
двустороннего преобразования Лапласа (см. (5.6) гл. V), полагая
+ 00
В (I, р)= § ехр(—Р*)В(1, т) бт. Так как изображением частной
— СО
производной В'х является функция рВ, то, применяя указанное пре¬
образование к уравнению (8.106), получим
if~(fp+1 + |2)5=0, |>р/2; (8Л08)
Вф/2, р) = Ч(р)\ |B(S. р)|< + 00, с > Р/2. (8.109)
Уравнение (8.108) представляет собой уравнение для функций
Эрмита 1571 I рода. Его общее решение
В(1, р) = с1ехр(-Р/2)// (±_ \(t) + c2exp&/2)H^_ (£),
Л Ра р+1/ р* р
где Яч,(г)—функция Эрмита I рода.
При | оо Н 2 (ig) —+ оо, отсюда и из условия ограниченности
решения (8.109) следует, что с2 = 0; постоянную находим из гра*
личного условия (8.109). Окончательно найдем
(~р+1)
Дальнейшие расчеты приводят к контурному интегрированию
специальной функции по индексу, т. е. к вычислению интеграла
вида
v+i°° н_(л_
\ ^ Р+' ’ e^dо (8 110)
Чш J РН . 2 v (Р/2) °Р- ^Л1и)
V-.oc, _("grp+1 )
Эти вопросы еще недостаточно хорошо изучены в операционном
исчислении, где, вероятно, могут быть получены интересные резуль¬
таты.
430
§ 4. МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ РЯДОВ ДЛЯ ОБЛАСТИ
ВИДА [0, у (f)], t^O
Излагаемый ниже метод можно назвать методом дифференциальных
рядов, так как его практическое использование предполагает вычис¬
ление производных любого порядка от выражений специального
вида в общем члене ряда. Метод дает возможность в области с произ¬
вольно движущейся границей получить аналитическое решение крае¬
вой задачи теплопроводности при любом виде граничных условий,
включая и случаи зависимости коэффициента относительного тепло¬
обмена от времени в граничных условиях III рода на границах
области. Следует особенно отметить эффективность метода при реше¬
нии так называемых обратных краевых задач для уравнения тепло¬
проводности стефановского типа (см. ниже) Первая формулировка
метода содержится, по-видимому, в работе Любова [98].
Для простоты изложения рассмотрим метод на примере решения
первой краевой задачи; позже приведем решения краевых задач
с граничными условиями другого вида.
Пусть Т (Ху t\ удовлетворяет условиям:
dT/dt = a(d*T/dx*)> 0 <x<y(t)9 t > 0 (у( 0) = 0); (8.111)
Т( 0,-/) = <Pi(0, t> 0; T(y(t), 0 = Ф.(0. *> 0. (8.112)
Здесь г/(0> 0—монотонная функция, непрерывно дифференцируе¬
мая любое число раз; ф2(/) — непрерывно дифференцируемая функ¬
ция с непрерывными производными любого порядка.
При / = 0 считается у(0), т. е. в начальный момент времени рас¬
сматриваемая область изменения переменной х сосредоточена в точке
а: = 0 и Ихмеет начальную температуру, равную нулю.
Будем искать температурное поле Т (х, t) в виде формального
ряда
со
Т(х, 0 = Х ъгТ„(х, 0. (8.113)
* = 0
предполагая, что этот ряд сходится и его можно почленно диф¬
ференцировать дважды по х и один раз по t (позже это предпо¬
ложение должно быть проверено). Подставим выражение (8.113)
в уравнение (8.111)
V 1 дТп ^ yi 1 д*Тп
2ш* а^п + 1) dt Zuan дх2
л = о л = 0
и заменим слева (я+1) на п. Получим
V - дТп-1 -V 1дЧп I а2Г°
an dt ап дх2 ' дх2 *
п-1 п=1
Полагая второе слагаемое справа равным нулю и приравнивая члены
при 1/а", придем к рекуррентным дифференциальным соотношениям
431
для функций Тп (х, t):
дгТ0/дхг = 0; ^1 = ^1, я>1. (8.114)
Для решения этих уравнений в форме, удобной для дальнейших
рассуждений, введем на движущейся границе функцию теплового
потока в случае граничных условий I и III родов в (8.112), запи¬
сав ее в виде
dT(x>t)/dx\x=y{i) = q(t)y />0, (8.115)
или температурную функцию Т (х, t) \х_у {t) = )F (/), если в (8.112)
задано граничное условие II рода. Потребуем далее, чтобы Тп(х, t)
удовлетворяли условиям:
= dT0(x,t)/dx\x=y{t) = q((yt (8.116)
Т п (*> 0 L=t/(O = 0» *>0, дТ п (х, t)/dx |x=sy {t) = 0, <>0(/i>l).
(8.117)
Тогда Т (ху t) в виде ряда (8.113) будет удовлетворять уравнению
(8.111) и граничным условиям (8.116), (8.112) (при x = y(t)). Нахо¬
дим нулевое приближение, удовлетворяющее уравнению (8.114) и
граничным условиям (8.116): Г0(х, t) ==ф2(/) + q(t) [х—y(t)\. Нахо¬
дим далее первое приближение, удовлетворяющее уравнению T'ot =
= Т'[Х1 и однородным условиям (8.117)
т\(*. 0 = + (8.118)
Для вычисления любого приближения Тп (х, t) запишем рекуррент¬
ное дифференциальное соотношение (8.114) в виде
у (О у И)
Тп(Х> 0 = 1 5 d6 I Т"-М' °dT1’ П>2‘ (8Л19)
* г
Подставив теперь (последовательно) в (8.119) 7\ (х, t) в виде (8.118),
затем вычисленное Т% (х, /), затем вычисленное Т8(х, t) и т. д., на¬
ходим
Л 0=si^j {^г [л—t' (0]Jn)+
+(кт-птда«)]■"')
Принимая далее во внимание (8.113) и выражение для Tv(x,t)9
можем записать Т (х, /) в следующем виде:
т (х, о = Ф2 (0 + ^ап (2п)\ 0/Й^Т [у (0““^]2”|
п = 1 '
(8-120)
л = 0
432
Формулу (8.119) можно назвать обобщенным рядом Коши для
уравнения теплопроводности (8.111), когда условия Коши задаются
на аналитической (бесконечно дифференцируемой) кривой x = y(t).
Выражение (8.120) зависит от .неизвестной функции q(t), которую
можно найти, используя граничное условие на неподвижной гра¬
нице х = 0 в (8.112). Полагая в (8.120) л; = 0, получим операторное
уравнение относительно q (t)
2- а" (2я+1)1 ^ lj2a+l ^ =
п = 0
-М0-фП0 + £^-^[*Ч“<(>]. (8.121)
п= 1
Укажем схему решения операторных уравнений такого типа.
00
Будем искать q(t) в виде функционального ряда <7(0= 2 <7Я(0.
т = 0
считая-этот ряд равномерно сходящимся на любом конечном про¬
межутке изменения переменной t (это предположение должно быть
проверено после вычисления коэффициентов qm(t)). Подставим
в (8.121) вместо q(t) ее выражение в виде ряда и применим к обеим
частям равенства преобразование Лапласа, считая, что существуют
все входящие по ходу действия преобразованные по Лапласу вели¬
чины:
M£5S£i&£«.<o}<«-
О VI = 0 т = 0 )
- L {<р, (0 •-<р. (0 + £ ’^1 [ф у- (0 J •
Здесь была использована формула (6.7) нахождения изображения
от производной п-го порядка функции <7± (t) = q (/) y2n+l (t) в виде
-> n~l __
<7im (0 T- PnPi (p)— 2 Pn~K~lq\K) Ф) = рпЙ1 (p),
к = 0
так как q[K> (0) = [<7 (t) ytn+l (/)](/”o = 0
в силу того, что у (0) = 0. Перемножив слева ряды по формуле
« СО 00 П
2 Я„ 2 Ьт = 2 2«А-*> получим
ш = 0 п = 0 Л = 0
!•-'•(£ £50’-«о}"-
о \п=0к=0 )
- l (ф, «)-Ф, (0+£ ^ ^ [ >" «>]' •
^ И = 1 /
433
Переходя в класс оригиналов, запишем
X | X ак (2/c+l)! d?* W ^
п—О \к=0
= ft <0 -ft «> + £ тгщ, ^ »“ Ml- (8Л 22)
Выделим в левой части (8.122) слагаемое, начинающееся со значе¬
ния п = 0, и члены, начинающиеся с 1; получим следующие
рекуррентные соотношения для коэффициентов qn(t) (я^О):
Яо (0 у (0 = ф2 (0—Ф1 (0;
: ! d”^1. [ ^$1 / А 1
а»(2я)! d^-1 [ dt у к}\
Т1
К= 1
(8.123)
Соотношения (8.123) дают возможность вычислить последова¬
тельно члены ряда для функции q(t)> которая может быть подстав¬
лена в выражение (8.120), чем и решается вопрос о нахождении
решения первой краевой задачи (8.111) — (8.112) для рассматривае¬
мой области. Аналогично можно рассмотреть граничные условия и
другого рода. Так, например, в случае второй краевой задачи
0T70*U-.“<MO. *>0; dT/dx\xmv(n = ^(t), />0 (8.124)
находим ® . Дп_1 f, ч
Т(х, t) = q(t) + £ ап (2п)1 (О-*]*")-
П— 1
п=0
где неизвестная температурная функция q(t) = T (*/(/), t) опреде¬
ляется из соотношений:
. JLу (0 (dq/dt) в?(0 = S (0 (q (0) = 0);
m = 0
^,(0 = ф*(0—Ф1 (0;
— X а* (2к +1)1 [У™ ^ ^п-к({)]-
К = 1
(8.125)
Рассмотрен (формально) метод нахождения аналитического реше¬
ния задачи (8.111)—(8.122) при различных граничных условиях в
(8.112). Исследование полученных рядов и их производных на сходи¬
мость при общем задании краевых функций задачи и закона движения
границы представляет собой достаточно сложную задачу, которая в
данной книге не рассматривается. Однако, как будет показано ниже,
434
для многих частных случаев эти ряды хорошо суммируются, что в не¬
котором смысле подтверждает их сходимость. Следует остановиться на
следующем важном обстоятельстве для рассматриваемого класса задач.
При нахождении функции теплового потока q(t), решая задачи (8.111)—
(8.112), пришли к операторному уравнению (8.121) через решение са¬
мой задачи, получив его в виде (8.120). Однако в предварительном
решении задачи вовсе нет необходимости и неизвестная функция q(t)
может быть найдена лишь из условий краевой задачи (8.111)—(8.112).
Задача 1. Используя уравнение (8.111), получить операторное уравнение
относительно функции дТ/дх при x = y(t) в виде [155]
QD .
4,1 ww*[Т^t)y2n w--
л = 0
_v ! £L[„*.+i(ft«I Л_
Z- a" (2/i + 1)1 dt" [y ( > dx x=y(i)\
n = 0
00
~Za"+i(2n+l)1 W" [у2П+1 {i) y'T (y (t)' W (8126)
л = 0
и привести выражение (8.126) к виду (8.121).
Указание. Умножить обе части уравнения (8.111) на независимую перемен¬
ную х и проинтегрировать полученное уравнение по х от х = 0 до x — y(t)
у U) y(t)
a J х{д2Т/дх2) dx = ^ x(dT/dt) dx. (8.127)
О о
Вычислить затем интеграл в левой части (8.127), а в правой части, применив
формулу производной определенного интеграла с переменным верхним пределом,
вычислить полученный интеграл пэ частям и повторить эти операции m раз,
после чего устремить m —► оо.
Задача 2. Пусть Т (rt t) — решение задачи
4i=aT*Tr(r*l!?)'(i<r<yV’ '>°(к = 1,2); (8-128)
T(y(t), 0 = ф2 (0, дТ/дг |г=0 = 0, ^0; у(0)=0.
Используя указанный выше прием (умножив предварительно обе части уравне¬
ния (8.128) на гк и проинтегрировав по г от г = 0 до r = y(t)), получить опера¬
торное уравнение для (дТ/дг)г_у (t) в виде [156]
1 d« Г ,и ^
п = 0
ап (2/г)!! (2п + к— 1)11 dtn
— Г У2п+К (t) — 1 =
t*ly {l)dr r-y(t) J
(2n)\\(2/» + /c+I)ll dt" [ It У2п+К+1 (0j- (8.129)
n- 0
Изложенным приемом можно воспользоваться и для отыскания
температурной функции Т (дс, /), удовлетворяющей неоднородному
дифференциальному уравнению
дТ/dt = а (<д2Т/дх2) + /(*,/). 0 <x<y{t), t> Q, (8.130)
435
Для этого заменим в уравнении (8.130) л: на £, умножим его на
(£—х) и проинтегрируем по I в пределах от х до y(t). В резуль¬
тате последовательного интегрирования по частям, как и в случае
(8.126), получим следующее выражение для Т (х, t):
Т (ху t) = T (у (t), /) + ^ ап (2л)! dtn~l х]2п Tt ^ (У
п= 1
1 дп
un{2n+l)\ dtn
п = 0
У(П
(2,+Dlfe ) <*-»>■"■/s. Oft (8.131)
П = 0 X
которое может быть использовано в качестве основной формулы при
решении краевых задач теплопроводности обобщенного типа методом
дифференциальных рядов.
Выражение (8.131) позволяет получить точное решение весьма
важного класса тепловых задач — обратных задач Стефана, когда
по известному закону движения границы поверхности фазового пере¬
хода и известным краевым функциям в граничных условиях на
движущейся границе отыскивается температура в среде, ее значение
на неподвижной границе и начальное распределение (последнее при
условии f/(0) = */0>0; выше считалось, что при /=0 также и х = 0,
так что Т (xt 0) = Т (0, 0) = 0). Итак, пусть Т (л:, t) удовлетворяет
условиям (см. § 3 гл. II):
dT/dt=a(d*T/dx*)y 0<x<y(t), t> 0; (у (0) = у0 > 0); (8.132)
Т(Ху 0) = Фо(х), 0 <х<Уо-у T(y(t)> /) = Г„; (8.133)
dT/dx\xmy{i) = y{dy/dt),
где у = ±ап(рА); —теплота перехода; р—плотность; причем
в выражении для у надо брать знак плюс или минус в зависимо¬
сти от того, охлаждается или нагревается среда с поверхности.
Начиная с момента / = 0 на поверхности х = 0 может быть задано
одно из трех граничных условий:
r = q>i(0; (5Г/(Зх=(1А)ф2(0; dT/dx = h[T-ф8(0]. (8.134)
В задаче (8.132) — (8.133) будем считать известными закон движе¬
ния границы y(t)x граничные функции в (8.133). Определим Т (ху /),
начальную температуру Ф0(х) и функции ф{(t) в (8.134). Для этого
используем основную формулу (8.131) (но при / — 0), из которой
найдем Т. (х, t)
т (X, t) = TK-y£lp±^£i{[y(t)-xrb 0 <x<y(t). (8.135)
Выражение (8.135) удовлетворяет уравнению (8.132) и гранич¬
ным условиям в (8.133) при x = y(t). При х = 0 из (8.135) найдем
граничную функцию ф/(£) в зависимости от типа граничного усло-
436
впя. Например, для ф! (/) имеем
(8.136)
Л = 1
К этому выражению следует добавить начальное условие, которое
вытекает из (8.133) и (8.135)
®. М - Т.-у ± ^ {£ [у . (8.137)
п= 1
В граничных условиях в (8.133) при x = y(t) рассматриваются
частные значения краевых функций, однако, как показывают рас¬
суждения, совершенно аналогично может быть рассмотрен и общий
случай, когда при x = y(t) заданы условия
T(y(t), / = ¥(/), t> 0; #r/dx\xmy{U = q(f), t> 0. (8.138)
В этом случае имеем обратную задачу для краевой задачи уравне¬
ния теплопроводности со свободной границей. Задачи такого рода
возникают при изучении фильтрации с учетом влияния связанной
воды (см. ссылки в [63]) и не всегда имеют решение. Например,
эта задача не имеет решения, когда Ф0 {х) = ¥ (/) = ср, (/) = const,
<7(/)=^0; не является очевидным и единственность решения рас¬
сматриваемой задачи; эти вопросы достаточно подробно освещены
в [81] и в данной книге не рассматриваются.
Рассмотрим сейчас различные частные случаи граничных функ¬
ций и законов движения границы, когда ряды (8.131) могут быть
просуммированы.
1. Область 0 < х < и/, /> 0 (v = const);
Т (vt, 0 = Ф (0* (dT/dx)x=vi = — (v/a)y(t).
Находим из (8.131) (при /=0)
00
Т (х, () = ф (/) exp [— (v/a) (х—ч/)] + 2 \(x—vtyn/an] х
п= I
X (dn(f/dtn) 0n [(я—vt) via]. (8.139)
Здесь
©„(?)= S(-lr[zm/(m + 2n)!]C^+n.
m — 0
Ряд для 0„(z) может быть просуммирован, например:
01 (г) = г'2 [1 + (г + 1) ехр (— г)];
02 (г) = г-4 [(2-1гг + 2г + 3) ехр (—г) + г — 3] и т. д.,
в частности при ср (/) = ф0 = const из (8.139) найдем
Т (х, /) = Ф0ехр[— %{х — у/)],
откуда Т (0, t) = фи ехр {vi/a).
437
2. При изучении влияния переохлаждения на границе раздела
фаз на скорость перемещения фронта кристаллизации в условиях
направленного теплоотвода [100] имеют место граничные условия:
Т(х, 0 \x=yit) = TK-D(dy/dt);
dT/dx\x=yit) = ydy/dt (у = апр/Х). (8.140)
В безразмерных переменных l = x/l, Fo = at/l2, z = y{t)!l> WK =
= TK/(ay)> p = D/(/y), W (£, Fo) = T (x> t)/(ay) (l—масштабная едини¬
ца) находим из (8.131) (при / = 0)
Г (|, Fo) - «7,-Ц dz/d Fo-p|^ №)-{]*■}-
-Е(551Гр?[г(Ро,-5!“ (8Л41)
п= 1
При 1 = 0 определяем ф(Ро) = №7(0, Fo)
ф1 (Fo) = WK—ф (Fo) = £ щг (р0)]" *
П— 1
+ рг' (Fo) + Р £ [г” (Fo) г2" (Fo)]<"-‘>. (8.142)
П= 1
Рассмотрим два случая: а) г (Fo)=y0J/To; б) г (Fo)=y0 J/ Fo + Р0—
— УоУТо-
Производя суммирование в (8.142), находим для этих случаев:
а) ф! (Fo)=(Kjt/2) v0ev“/'4 Ф (Yo/2)+[P/(2KFo)] [v0ev®/4—7^Ф (Уо 12)Ь .
б) ф1 (Fo)=p{[(l/2)Yoev®/4-(l/2)Y^F (х)]е-*'+(1/2) Y2e~v»/4F (Х)} х
X 1 /(|/Fb + p) - (K^Yo/2) ev »/4Ф (Х).
Здесь
% = у0^То/(2У^ТКУ,
а
F (а) = (1/"л/2) (1 /i) Ф (ia) = ех‘ dx.
о
3. При расчете температурного поля и скорости перемещения
фронта фазового перемещения в сферических телах имеет место за¬
дача [99]:
dT/dt =а [д2Т/дг2+ {2/г) {dT/dr)]t p(l) < г < R, t > 0; \
(Р(0 ) = /?) (8.143)
T(p(0, t) = TK; дТ/дг |г=р U) = ydp/ck, / > 0. J
Перейдем к новой функции U (г, t) — rT (г, t) и сведем рассмат¬
риваемую задачу- к виду, удобному для применения метода диффе-
438
ренциальных рядов
dU/д1 = а (d*U/dr2), р (t)<.r<R, t > 0;
U (г, 01г=р(О = Р(0 7'к; dU(r, /)/3r|,.p(ft = 7,e + W(/)(dp/d/).
Используя (8.131) (при f = 0), найдем U (г, I) и далее искомую
функцию Т (г, t)
Т (г, t) = Тк £ ал (2п + 1)1 dF { р ^ х ТТ [р (0 —rPn+11-
п = 0 V J
Из этого выражения получим формулу, описывающую соответ¬
ствующее изменение температуры поверхности шара <p (t) = T (R, t)
для двух законов движения границы: а) p(t) = R—р/, р > 0;
б) р (/) = /? —t > Р>0. Суммирование рядов для <р(/) дает для
этих случаев:
sqsbpii TF К* -М «“)"“)" т~1“+
+йг-»('+*-¥)«■"-'••
ф М = т. -i L гм5Г+ш £ К* -Р КТ> рда Ко] ф Кб-Ч _
п = 0
= ез*/<«»ф(_!=.) _рзеЭ./(4в,expKFJ.
4. Область [0„ Bf], t > 0; 7>(0, О-Г,; (dT/dx)x=y{t)=.
= (Л А) *п.
Задача 3. 1) Покажите, что в случае т = 0,5, я = — 0,5 выражение (8.131)
(при / = 0) в точках x=B6tm дает следующую формулу [45]:
T(Bl'/2S, 0 = 7'*—(К^/Я) A V~n exp [Ва/(4а)] (Ф [ВЦ 2 fa)]—Ф [бВДгК’а)]}.
2) При т=1, л = 0, A = qB
Т (ВЫ, 0 = 7’к-ИА)|ехр ^(i_fi)j_ij..
Задача 4. Распространите метод дифференциальных рядов на область
[0, /] / > 0.
Рассмотренные случаи достаточно наглядно показывают в действии
метод дифференциальных рядов. Следует заметить, что могут быть рас¬
смотрены и более сложные случаи законов движения границы, когда
возможно суммирование соответствующих рядов, и поиски таких слу¬
чаев продолжаются (см., например, в работе [157] случай y(t) =
At2+Bt+C в задаче (8.132)—(8.133)). Суммирование ряда (8.136)
приводит к выражению
1
Ф, (0 = Тш-± J ехр[г/ (/) у’ (/) (1/2)] х
о
х {ууЧ0 [1 ]/А (у/2)] + V~AyU [Е VA (у/2)]} &UVT-1,
439
где /0(z), /1 (z)—функции Бесселя мнимого аргумента, у (t) =
= У Al2+ Bt + C.
Здесь не рассматривался метод дифференциальных рядов в поляр¬
ных координатах применительно к случаю осевой симметрии. Частич¬
ные результаты, касающиеся применения этого метода к определению
температурного поля в кристаллизующемся слитке цилиндрической
формы, имеются в работе [139]. Пока это еще открытый вопрос аналити¬
ческой теории теплопроводности твердых тел.
§ 5. МЕТОД ФУНКЦИОНАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
(МЕТОД ПЕРЕВОДА КРАЕВОЙ ЗАДАЧИ ОБОБЩЕННОГО
ТИПА В КЛАССИЧЕСКУЮ)
Рассмотрим другой подход при решении краевых задач теплопровод¬
ности в области с произвольно движущейся границей. Этот подход,
с одной стороны, дает возможность значительно расширить число кон¬
кретных законов движения границы, для которых возможно получить
аналитическое решение задачи, и, с другой стороны, рассмотреть об¬
щий закон движения границы и соответствующее решение задачи в
форме, отличной от выражений, полученных методом дифференциаль¬
ных рядов.
Для краевых задач обобщенного типа можно построить функцио¬
нальное преобразование специального вида, основанное на введении
подвижной системы координат, в которой подвижная граница стано¬
вится неподвижной. При этом исходное уравнение теплопроводности
приводится к виду, допускающему в ряде случаев применение класси¬
ческого метода разделения переменных, и наряду с законами, указан¬
ными выше, могут быть рассмотрены новые конкретные законы, а так¬
же случаи движения границы достаточно общего характера.
I. Расширяющиеся или сжимающиеся обла¬
сти, форма которых меняется со временем с со¬
хранением подобия. Рассмотрим вначале одномерное урав¬
нение теплопроводности
дТ/д1 = а(д2Т/дхг) + ((х, t), 0 <x<y(t), t> 0; [у (0) = у0 > 0]
(8.144)
и с помощью подстановки
% = x/y(t), Т(х, о = в (S, 0 (8.145)
перейдем в подвижную систему координат, в которой подвижная
граница будет неподвижной. Преобразуем уравнение (8.144), исполь¬
зуя правило дифференцирования сложной функции: = + =
= 0*— Ъ{у'/у)®ъ> Tx = ®tl'x. Здесь и далее yf (t) = dy/dt\ предпола¬
гается, что функция y(t) — непрерывная с непрерывными первой и
второй производными.
Уравнение (8.144) в подвижной системе координат имеет вид
у2 (0 (дe/dt) = а (<Э20/<?£2) + 1у (0 у' (0 (дв/дЪ) +
+ 0. 0<6<1, <>0. (8.146)
440
Здесь производная по t берется уже при постоянном Е и гранич¬
ному условию на движущейся границе для функции Т (х, t) соот¬
ветствует условие для функции 0 (Е, t) при £=1. Что касается
начального условия Т (*, 0) =Ф0 (*), 0 ^х^.у0, то в случае у0 > 0
имеем для функции 0 (£, 0) =Ф0 (^0), если у0 = 0, то
в исходной постановке считается, что Т (.х, 0) = 0, следовательно, и
в подвижной системе также 0 (Е, 0) = 0, 0 ^ Е ^ 1.
Уравнение (8.146) содержит производную по I от искомой функ¬
ции с коэффициентом, зависящим в общем случае от координаты и
времени. Постараемся так преобразовать это уравнение, чтобы иск¬
лючить указанное слагаемое. Для этого положим 0(Е, t) =
= Ц (£> 0 w (£, /) и подставим правую часть равенства в уравне¬
ние (8.146)
у2 (0 (dW/dt) = a (<Э2\У/<?£*) + Ьл (g, t) (dW/dl) +
+ М6, OW + ff (07 (&(*). 0. (8-147)
где bi(l, t) = 2aq-1q’l + yy'\\ btd> 0 ^aq-'qit + lq-'q^yy'—q~lq'ty*-
Функцию (7(|, t) определим из условия равенства нулю коэффи¬
циента bx (£, /) при dW/dl. Это дает q(l, t) = у (t) exp [—yy'l2/(4a)]y
где функция у (t) выбирается таким образом, чтобы в выражении
для b2 (Е, t) исключить все члены, зависящие только от /. Получим
у (t) = y~l/2 (t) и вместе с этим искомое преобразование
0(1, 0 = у==-ехр t), (8.148)
которое переводит уравнение (8.147) [а стало быть, (8.144)] в сле¬
дующее)
у* (t) (dWjdt) = а (д’Г/д|2) + |12/(4а)] y\t) х
xy"(t)W + [y*(t)/qd, t)]fdy(t), t), 0 < i < 1, />0. (8.149)
Здесь q(t) — y~ |/2(0 exp {— [у (t) у' (/)/(4а)] Е2}.
Рассмотрим далее в этом пункте уравнение (8.144) в области
Ух (0 < * < (0* ^>0, где y{(t)—дважды непрерывно дифферен¬
цируемые и ограниченные функции времени (|ух (t) |; \у2 (t) |/ < » < °°).
Аналогично, с помощью функциональных преобразований:
а) ^=£^г- л (0=г/. (0—У» (0; Т(Х, о = в(Е, /);
б) в а, 0 = <7(1, 0W(i, 0;
9= l/kTj"exp I — (1/4a) (rjri'i2 + ^y\y'djу’* (t) dx
L 0
Уравнение (8.144) преобразуем к виду
т}2 (t) (dW/dt) = a (d*W/d¥) + [(1/4д) л3 (/) л" (/) £2 +
+ (1 /2а) л3 (0 y\ (t) l]W + [л2 (t)/q] f. (8.151)
Преобразования (8.145), (8.148) в одинаковой мере пригодны и
для случая радиальной и сферической симметрии, т. е. для урав-
(8.150)
441
нения Т;==а[Г*1 + Г/(лТ;)]-{-/(*, t) в области 0<#(/), />0
(Г = 1, 2). Что касается области yt (t) < х < ^ (/), ^ > 0 для пос¬
леднего уравнения, то для постоянства области в подвижной си¬
стеме координат и в силу наличия в уравнении члена Г/х для
второй границы x = y2(t) должно выполняться условие г/2 (/) = (/),
где р = const. Введем для этого случая преобразования:
a) t = x/yi(t), Т(х, /) = 0 (g, /);
б) q(l, t) = [yt (/)](Г“1,/2 ехр [— (12/Щ ух (t) уг (/)]; (8.152)
в) 0(1, t) = q(lt i) W (1, 0.
Исходное уравнение преобразуется к виду
2 /А dW ( d4V . Г dW\ . 3/А " /А vn , /А А
У\ (0 qi Яд ^^2 “Ь g J 4а ^ ^ ^ q ^ (&У1 (0»
(8.153)
где 0<1<Р, * >0.
Перейдем теперь к трехмерному случаю и для удобства
записи обозначим переменные х, у, г соответственно через xt, х2,
х8. Рассмотрим уравнение вида
dT/dt = al±T (х1? х2, х3, /), 0 < х, <y(t), t > 0 (/=1, 2, 3). (8.154)
Здесь можно повторить почти дословно все рассуждения, соответ¬
ствующие одномерному случаю. Применяя к уравнению (8.154) функ¬
циональные преобразования (в дальнейшем ограничимся в (8.154)
однородными уравнениями):
а) £< = *^(0. т (*1. *s> *s. 0 = ®(i,, £j, S3, 0; (
б) 0(ii. lt, 5з. t) = <7 (ii. ia. is. 0^(61. if. is. 0;'
где ^
<7 = y-'’/2(0exp|-[(l/(4a)]j/(/)i/'(0 2 5?}. (8.155)
получим в новых переменных для функции W
уг (/) dW/dt =a&W (it, 1г, |a, 0 +
+ [l/(4a)] y*(0/(0jSii^. 0< Е/ < 1. />0 (i = l, 2, 3). (8.156)
В формуле (8.155) нужно положить: п = 3, если рассматривается
пространственная задача, когда Т зависит от всех трех координат,
п = 2, если задача двумерная, и я=1, если она одномерная.
Если же ввести другое время х соотношением
t
t = $dt'/y‘(t'), W(llt i2, i3. t) = W(iu l2, 1„ t), (8.157)
o
то уравнение (8.156) примет вид
dWldx = abW(lu 12, £3, т) + [1/(4а)]//У'х
у 2 UW, 0 < S, < 1 (t = 1, 2, 3), / > 0; (8.158)
1 — 1
442
в такой форме оно отличается от исходного уравнения (8.154) только
наличием справа слагаемого [1/(4а)] у3у” 2 (и, конечно, тем, что
i
одно записано в переменных (х1У х2, х3, t)y другое — в переменных
(In !з» т)). Будем считать, что граничные условия в новых пе¬
ременных допускают разделение переменных (этот вопрос подробно
рассмотрим ниже). Тогда к уравнению (8.158) или (8.156) можно
применить метод Фурье в следующих частных случаях:
1. у" = 0, т. е. у (t) = At + B (Л, £ = const). Для этого закона
отличие уравнений (8.154) и (8.158) вообще исчезает. Отсюда сле¬
дует, что если умеем решать уравнение
dW/dx = abW(lly |2Л3, т), 0< Е, < 1, т>0 (1 = 1, 2, 3) (8.159)
для области, форма которой не меняется во времени, при извест¬
ном начальном распределении температуры и граничных условиях
I рода, содержащих граничные функции общего вида, то для урав¬
нения (8.154) можно решить аналогичную задачу для области,
имеющей такую же форму, но которая равномерно расширяется
или сжимается со временем, оставаясь подобной самой себе (неог¬
раниченная пластина, прямоугольный параллелепипед, конечный
цилиндр, сфера и т. п.).
2. Наряду с линейным законом y(t) = At + B особого внимания
заслуживает случай, когда в (8.156) y3{t)y"(t) = —P = const=^0,
откуда в общем случае у (t) = У"(At + В)2—Р/Л2 (Л, В = const); в
частном случае у (t) = V Mt + N (Р > О, М2 = 4Р), y(t) = At + B
(Р = 0). Уравнение (8.156) при этом обращается в следующее:
y'(t)(dWldt)=abW(l{, S2, ga. О-
-p/(4fl)] 2 W, 0 < I, < 1, t > 0 (8.160)
L= 1
и допускает разделение переменных в декартовых, цилиндрических
и сферических координатах для первой краевой задачи в указан¬
ных областях.
Рассмотрим теперь вопрос о функциях, входящих в уравнение
(8.160), при разделении переменных, причем ограничимся в декар¬
товых координатах одномерным случаем (п = 0), а в цилиндричес¬
ких и сферических—случаями радиальной (я = 1) или сферичес¬
кой симметрии (п = 2). Уравнение (8.160) принимает при этом вид
y*(t)(dW/dt) = a^[l«d^)-ll*W, 0 < £ < 1, t > 0. (8.161)
Полагая, как обычно в методе разделения переменных W =
= 'F(1 )0(О, и разделяя в (8.161) переменные, находим:
е' «> — *£««</);
^(Е-ТГ)+Й^Е’|,“0> (8Л62)
443
где у2 — постоянная разделения (заметим, что в декартовых коорди¬
натах при /1 = 0 придем к таким же уравнениям и в общем трех¬
мерном случае).
Рассмотрим второе из уравнений (8.162). При (3 = 0 его решение
хорошо известно и выражается через тригонометрические или бес¬
селевы функции (см. [57]). При Р=£0 введем новые переменные
z = К|3 £2/(2а); УР (г) = ф (z)e~2/2, преобразуем уравнение для 4я (z),
используя правило дифференцирования сложной функции:
z (d2<j>/dz2) + [(« + 1)/2 — z] d<p/dz — [(л + 1)/4—у7(8а |/р”)] ф = 0.
(8.163)
Пришли к уравнению вырожденной гипергеометрической функ¬
ции [88] y = F(b, с, z) с параметрами Ь = (1/4) [п+ 1 —у2/(2а [/р)],
с = (п+1)/2. Следовательно, для рассматриваемого закона движе¬
ния границы (у3у" = —Р) собственные функции однородной задачи
(см. § 2 гл. III) выражаются через известные, достаточно широко
протабулированные функции, а значит через них выражается и ре-
шение краевой задачи. Следует отметить особо случай у (t) =
Mt N\ при этом ////' = А1/2 и задача сразу упрощается после
введения подвижной системы координат £) = x/y(t). Действительно,
уже уравнение (8.146) при / = 0 становится уравнением с разделяю¬
щимися переменными и нет необходимости переходить в (8.148) к
функции W (£, t). Очевидно, что для такого движения границы мо¬
жет быть решена и вторая краевая задача для уравнения (8.144)
(третья краевая задача приводится к случаю переменного во вре¬
мени коэффициента в граничном условии III рода).
II. Расширяющиеся или сжимающиеся во вре¬
мени-области без сохранения подобия. Рассмотрим
теперь уравнение (8.154) в области 0 < xt <С yt (t), /> 0 (i= 1, 2,
3)» Уi (t) ф у2 (0 Ф Уз (0» гДе законы движения границы у( (t) дважды
непрерывно дифференцируемые и ограниченные по времени функ¬
ции для всех (/0 = const). Здесь также можно построить
функциональное преобразование, позволяющее свести уравнение
(8.154) к соответствующему уравнению, допускающему для ряда
законов у{ (t) разделение переменных. Построение такого преобра¬
зования фюрмально производится путем произведения трех рассмот¬
ренных преобразований для одномерного уравнения (8.144) (при
/ = 0) (имея в виду, что решение многомерного уравнения можно
представить в виде произведения решений одномерных уравнений).
Запишем формулы преобразований:
а) Е, = х/Ы0 0‘=1. 2. 3), Т(хи х„ ХЯУ 0 = 0(51, 5,. 5,. 0; (8-164)
б) e = qW(l,y Н2, б., 0,
з
1
г
»=1
где <7 = [</г(0'/»(ОЫО]“1/2ехр
444
Перейдем от уравнения (8.154) к уравнению вида
= 0<1‘<1' />0- <8Л65>
При y'i(() — 0 [yl(t) = Ait-srB{, At, Вi = const] уравнение (8.165)
примет вид
dWldt=a 2 (1 /iti(/))(d*r/dij), 0 < ?, < 1, * > 0. (8.166)
1= 1
В этом уравнении можно разделить переменные, если положить
W = ЧГ1 (tj) (S2) Yg (£3) © (/), подставить в правую часть в (8.166)
и произвести разделение переменных, подчинив функции Чг/ (|;) ус¬
ловиям: Ч^(?,)+ 7*4^ (?,) = (), у2— постоянные разделения. Для 0(0
при этом получается уравнение
(1/а) (de/dO + \y\fyl (t) + yl/yl (0 + Тз/^/з (0] ® = 0. , (8.167)
При другом подходе для решения уравнения (8.166) могут быть
использованы интегральные преобразования, учитывая, что в пра¬
вой части уравнения коэффициенты не зависят от пространственной
переменной и, следовательно, можно найти изображение d2W/d%fy
применяя соответствующие интегральные преобразования по прост¬
ранственным переменным (см. табл. 11, гл. V). При этом предпола¬
гается, что граничные условия для W линейные, с постоянными
коэффициентами.
Если y‘i(t) y’i (t) = — р, = const Ф 0, т. е. yt (t) = V (/!,/ +В,-)2—р,/Л?
(где А{у Bty — постоянные, зависящие от индекса /), то уравне¬
ние (8.165) принимает вид
0<5,<1, '>0, (i=,'2'3)'
(8.168)
В этом уравнении также разделяются переменные.
Таким образом, краевая задача для исходного уравнения (8.154)
полностью решается для параллелепипеда, расширяющегося или
сжимающегося без сохранения подобия.
Рассматривая уравнение (8.154) в цилиндрических координатах
Ui Ф. х2)
дТ_ (&Л+ 1 д2т | д*т
dt V дх\ *i dxi х\ ^Ф2 дх\
0<^1<Ух(0» ^>0, 0 < х2 < г/2(/), 0<ср<2л, (8.169)
приведем для него соответствующие формулы преобразования, ис¬
пользуя преобразования одномерного уравнения (8.144) в декарто¬
вой и цилиндрической (радиальный поток) системах координат:
a) li = xi/yi(t) (/=1,2), Т (х1У ф, ха, O = 0(£i, Ф, ?2, 0;
б) е = ?(51Э t)W(ti, ф, £2, о,
445
Уравнение (8.169) примет вид (относительно 1F)
1 8W Л 1 Г82W S2: , .. ,, .. _ '
-“г-Х тт; \ -^; + 7iy>®rf®w
а dt t\ yf (О L4a
+ 7i7 + i7T* (8Л7°)
Si d£i S? dtp2
(8.171)
где 0 < I, < 1, 0 < £s < 1, ф б [0, 2л], t > 0.
Здесь можно провести анализ совершенно аналогично, как и в
случае (8.158).
Задача 1. Распространите метод функциональных преобразований для
уравнений (8.154) на области [у\1) (/), (/)]. 0, i=l, 2, 3, и покажите,
что возможно точное решение первой краевой задачи, если для всех i одновре¬
менно выполняются условия [30]:
Ч?(0 (0 = — Pi1)== const; (t) y(iir (/) =pi2) = const.
к(0=г/?(0-«/Г’(0]-
Покажите, что в результате интегрирования имеет место один из трех следующих
законов движения границ рассматриваемой области:
1. Л« (0 = Р(3,= const (р:1> = 0); +M(t + Nc,
2. TU(0=»i<+B/(p!1,=0);
У? W=P!2> [2AHAit + Bt)]-xJ-Mit + N,i
з. л,-(0=)/М,-<+в/)2-Р11)М?
(Р/ > 0); y\l> (() = - [p;2,/p,(1)] T),- (t) + MД + N[.
Здесь Л/, B(t Mi, jV,- —постоянные, зависящие от индекса t.
Задача 2. Сформулируйте метод функциональных преобразований для
уравнения (8.169) в области x1^[y1(t)7^y1{t)]y х2^[у2 (t)t y3(t)]t t^0\ <pg[0, 2л]
Ф = const) и покажите возможность точного решения первой краевой задачи
в известных функциях, если одновременно имеют место условия:
VI (0 У\ (0 = — Ро = const; Г)3 (/) Г)" (t) = const;
Л3 (t) Уг (0 = const [т) {0—Уз (1)—Уз (01-
Какими законами при этом определяются функции y1{t), Уй((), ч (0?
Перейдем к полуограниченной области (сначала
одномерной) x^y(t)y / > 0, и рассмотрим в ней уравнение тепло¬
проводности (8.144). Предполагается, что y(t) — дважды непрерывно
дифференцируемая функция, ограниченная на любом конечном про¬
межутке изменения переменной t. Здесь также возможно построить
функциональное преобразование, приводящее к решению краевых
задач для уравнения (8.144).
Перейдем в подвижную систему координат по формулам:
a) 6 = *—1/(0. Т(Ху 0 = 9(6. 0- (8.172)
Преобразуем уравнение (8.144), учитывая, что 7') = 0)-f0t£’<,
Г; = 0&,
de/dt =а (д*9/д¥) + у' (t) (д@/д1) +
+ f(l + y(t), 0. ^>0. ^>0. (8.173)
Здесь производная по t берется уже при постоянном £.
Если у' (t) =1^ = const, т. е. J/(0 = IV + P2> то уравнение (8.173)
решается непосредственно (для этого достаточно ввести подстановку
0(£, t) = W (£, /)ехР[—Pii/(2a)—Pi//(4a)J, с помощью которой из
уравнения (8.173) исключается частная производная д0/<?£).
В общем случае произвольного закона y(t) введем вместо 0 (£, t)
новую функцию W (£, t) с помощью соотношения:
б) 0(6, 0 = ?(g, t)W & 0.
где
q(l, 0 = exp| — [l/(2a)j %у’ (0 + 0/2) J у'1 (т) dx |. (8.174)
Уравнение (8.173) преобразуется к виду
dW /dt = a (d'Wldt*) + [1/(2а)] у" (t) IW +
+ М6, t)lq, 6>0, t>0(ft = f). (8.175)
Из уравнения (8.175) следует: во-первых, что в случае равно¬
мерного движения, когда у" (t) = 0 (у (t) = At + B), решение краевой
задачи в области с подвижной границей сводится к решению ана¬
логичной задачи с неподвижной границей; во-вторых, если у" (/)=pt,
т. е. i/(/) = (Pl/2)/2 + P2/ + p3(Pi= const, /= 1, 2, 3), то однородное
уравнение* получаемое из (8.175) при — 0, допускает разделение
переменных в известных, хорошо изученных функциях.
Преобразование (8.172), (8.174) может быть обобщено и на про¬
странственное уравнение (8.154) для области АТ; > (/),
t > 0 (i=l, 2, 3). Для этого введем следующие формулы преобра¬
зований:
a) 6i = xf-yc(0f Т(хlf *а, 0 = 6(Si, Ез, 0*
б) 0 = H7(glt 1г, |8, 0 ехр |— [1/(2а)] х
х
2 ы (0 + (1/2) 5 2 у'- (т) dx] 1. (8.176)
<=1 о ‘=‘ J1
Уравнение (8.154) преобразуется в следующее:
OWtdt-aAW&i, lt, g„ /) + [№)]
li>0, t>0 (i=l, 2, 3) (8.177)
и допускает разделение переменных, если уН0=Р»,1>» т* е* Ui (0 =*
= (ft1}/2) ia + Pi2)/ + P!:,) (№У) = const, i, j = 1, 2, 3); при ftl) = 0 отли¬
447
чие уравнений (8.154), (8.177) вообще исчезает и краевая задача
для уравнения (8.177) решается одним из методов, изложенных
в предыдущих главах.
Остановимся теперь на вопросе о функциях, входящих в урав¬
нение (8.175) при разделении переменных (для / = 0) для основного
закона y(t), допускающего применение метода Фурье, например для
первой краевой задачи. Положим y"(t) = a2$ = const, т. e.y(t) =
= а2р/2/2 + (3^ + Р2 и запишем соответствующее однородное уравне¬
ние в (8.175) (при = 0):
(1/а) (dWldt) = {d*Wld¥) + $i2)tW, £>0, t > 0. (8.178)
Уравнение (8.178) имеет частные решения вида W = Ч;(£)ехр (аРу2//2),
где у2 — постоянная разделения, а (£) удовлетворяет уравнению
d2V/d¥+(l/2)ptf-y2)V = 0, 1>0(8.179)
Т(Е)кв0 = 0, Y(6)k„ = 0. (8.180)
Уравнение (8.179) интегрируется в бесселевых функциях порядка
одной трети [140] для Р > 0 и Р < 0. Остановимся на случае Р < 0,
полагая р = — со, где со > 0 [28]. Введем новую переменную т] =
= (со/2)1/3'(£—у2), считая Т (£) = Y (тр. Уравнение (8.179) преобра¬
зуется в Y" (rj)—TpF(r]) = 0; это уравнение известно [54]; его общее
решение имеет вид
V (л) = с, Vn /1/3 [(2/3) л3/2] + J/л К1/3 [(2/3) л3/2],
где с1 и с2—произвольные постоянные, /1/3, /Ci/3—модифицирован¬
ные функции Бесселя.
Вследствие условия (8.180) при £ —* оо (при этом также и г\ —► оо)
необходимо считать сх = 0. Переходя к переменной £, находим с
точностью до несущественно постоянного множителя решение урав¬
нения (8.179), удовлетворяющее второму из граничных условий (8.180)
V (I) = VJ=?K1/3 [(1/3) V~2a (S-у2)3'2] . (8.181)
Здесь функция У £—у2 при | > у2 берется вещественной и положи-
тельной (Kv (г) также принимает вещественные значения, ^если v
вещественно, a z положительно). Рассмотрим далее значения £ < у2,
так как собственные значения рассматриваемой однородной задачи
будут находиться из условий (S) =о = 0- Но для значений | < у2
функция V1—у2 становится мнимой и V\—у2 = *Куа— £, где i =
= V— 1—мнимая единица. Найдем для функции ¥(£) при \ < у2
выражение через функции вещественного аргумента, воспользовав¬
шись известными из теории бесселевых функций соотношениями
ATi/з (iz) = (ni/2) ехр (ш*/6) [Н{& (г) + з (г)];
М7» = (—1)я+1 * {V'Slty-1 [е(“ umni/3Ji/3 (г) — J-1/з (г)] (m = 1, 2).
(8.182)
448
Преобразуя по этим формулам выражение (8.181), найдем
V (I) = (л/Кз) {А/, [(1/3) К2со (у*— !)»/>] +
+ J.1/3 [(1 /3) (yj—i),/s]}.
(8.183)
Условие ¥ (£) = О дает уравнение для вычисления собственных
значений у2п
если обозначить \in = у% j/"2co/3, так что у2 = (9р„/2ю)1/3. Для урав¬
нения (8.184) существуют подробные таблицы (см. [15]. Найдя соб¬
ственные значения у2п и подставляя их в (8.181) и (8.183), опреде¬
лим собственные функции однородной задачи (8.179) — (8.180). Урав¬
нение (8.179) перепишется теперь в виде
d2Yn/d^_(1/2)(o(^T2)4fn = 0t 1>0 (/1в1> 2,3,...). (8.185)
Функции Vn(E) образуют ортогональную в промежутке (0, оо)
полную систему. Найдем квадрат нормы системы {¥„ (£)}: (I) ||а=
00
= 5 (£) d£. Прямое вычисление этого интеграла представляет
о
большие технические трудности, которые можно обойти, используя
следующий прием. Проинтегрируем по частям, учитывая условия
(8.180)
или
А/3 (v31/2©/3) + J-!/a (Yn V2Й/3)= 0
А/S (и-га) 4" *^-1/3 (м-я) = 0»
(8.184)
00
00
\ ^ (£) d£ = EVJ (I) |* -2 | |'F„ (£) d| =
О
О
оо
О
Из уравнения (8.185) находим
имеем далее:
00
оо
+ (2/«,)J^^dg + vi№v.(6)d6.
О о
449
Получили уравнение относительно интеграла. В результате найдем
II Vn Г = S ^ (D <11 = (2/со) (d¥n/d|)|=„.
о
Полученное выражение позволяет более простым методом вычислить
|| |2. Находим из (8.183) (при у2 = у^)
dYjdi |i_„ = — [nv„ [J_ 2/3 (ц„) — J2/3 (ц„)].
Окончательно имеем
I Vn II2 = (1/3) л V, [J- 2/3 (|хл) - Л/з ОО]1. (8.186)
Отсюда следует, что соответствующее разложение некоторой функ¬
ции F (I) в ряд по функциям ¥„(£) имеет вид [см. (3.9)]
F (Е) = Z тог^ (I). где сп=[ F(?) (?) d?. (8.187)
П = 1 " О
Не будем останавливаться на условиях разложимости F (5) в ряд
(8.178), об этом см. [141]. Используя формулы (8.187), нетрудно
найти точное решение первой краевой задачи для уравнения (8.175)
(при у* =— а2со):
(1/а) (dW/dt) = d2W/di* — (\/2)uW +
+ О/а) MS. 0. £>°> / > 0; (8.188)
W& 0) = 0, £>0; И^(0,0 = Ф(0. <>0;
|Г(£, 01 < + °°, S>0. (8.189)
Здесь f2 = fl/q\ для простоты начальная температура принята рав¬
ной нулю.
Формулы (8.187) позволяют построить интегральное преобразо¬
вание функции W (£, 0 по пространственной переменной | с фор¬
мулой обращения для этого преобразования. Действительно, из
(8.187) имеем
W(y„, 0 = S 0'*'„(£)<*?;
о
QD
^ СБ. 0 = Е то-w (V,.. 0. (8.190)
450
Найдем изображение правой части уравнения (8.188); для этого
используем (8.185), (8.180) и выражение для (d^/d^^o
— W
] (^—ft) ft) I*-
о
+ ]w (l, /)(^_|coiYn)di =
0
00
= W7-?LL=o-T^Itt7ft' 0T.(5)dS-
0
Ф (t) [J - S/» (Pn) •/-2/3 (M
ГП
Таким образом, в пространстве изображений задача (8.188) —
(8.189) имеет вид
о + едчо; W(Y„, 0) = 0. (8.191)
00
Здесь /2(yn, 0=S/2ft, O^dldl.
О
Находим решение уравнения (8.191)
t
w (Тп. О = j ехр [ — Д соу*а (t — т) j [ft (у„, т) + ав"» (т)] dt
О
и далее по формуле обращения искомое решение в следующем гиде:
t
X J exp [ — {шуг.а(1-т) J ф(т^т +
О
/
+ jjexp | —Дцуу;,а(/— т)] /а (Е, T)dxdlj>. (8.
О 0 '
192)
В (8.178) рассмотрен подробно случай Р < О, соответствующий
Дискретному спектру собственных значений однородной задачи
(8.179) — (8.180). При Р>0 спектр становится непрерывным; этот
случай рассмотрен в [62, 141].
Преобразования (8.164) и (8.183) позволяют рассмотреть также
и комбинацию областей с движущимися границами—ограниченные
области по одним пространственным переменным и полуограничен-
451
ные по другим. Здесь также можно указать некоторые частные слу¬
чаи разрешимости пространственных температурных задач в извест¬
ных функциях.
Действительно, пусть Т (хи х2, х3, t) удовлетворяет уравнению
Применяем по хх преобразование (8.176) и переходим к уравнению
(8.177) (*'=1). Пусть ух (/) =aV72 + P2/ + P3 (Р/ = const); тогда (8.177)
примет вид
Разделяем далее переменные, полагая Wx = ТГ (£х) 0 (х2, х9, t):
Здесь у2—переменная разделения.
Первое из уравнений рассмотрели выше, второе уравнение Можно
упростить с помощью подстановки © (х2, х3, t) = U (x2, х8, t) exp фхауг12)\
Далее, к (8.195) полностью применимы рассуждения (8.165)—(8.168).
В частности, если yt (t) = V A it*-{-2Blt +С, (Л/, Bh С{ — const), то,
переходя от уравнения (8.195) к уравнению (8.165) относительно
функции W2(l2t £3, /), находим
В этом уравнении переменные разделяются, если положить
где у}—постоянные разделения.
Для @/(0 получается при этом уравнении (8.167) (при Yi = 0).
Таким образом, из полученных выражений следует, что если
сечение области — прямоугольник, стороны которого, перпендикуляр¬
ные осям у и z, расширяются или сжимаются во времени по зако¬
нам yi (^) = А -j- 2Вit -j- Ci (i = 2, 3) соответственно, так что rpa-
dT/dt =а&Т (я„ хг, х3, t), *, > yt(t),
0 <x{<t/i(t) (i = 2, 3), />0.
(8.193)
i дв д*в aae
« di - dx* + a*!
V (Ex) + (Pi/2) (5, -Y2) v = 0, I, > 0;
Y + PiY2®. 0 <xt<y,(t) (( = 2,3), t>0.
■2 VX3
(8:196)
0 = 'МУ ^(is) @i(0 и подчинить функции Ч',(£,) усло¬
виям;
0 < < 1 (i = 2,3),
(8.197)
452
ничные значения относительных координат 12 и £3 не зависят от
времени, то, находя соответствующие собственные функции уравне¬
ний (8.197), отвечающие этим граничным значениям (но уже посто¬
янным!), можно по ним разложить решение исходной задачи. Заметим,
что с уравнениями (8.179) уже встречались в (8.162); их решения
выражаются через вырожденные гипергеометрические функции.
Если у2 (/) = ^/з (t) (однородное расширение или сжатие), то урав¬
нение (8.196) приобретает более простой вид
1 dW2
a dt
у\ (О
d*W2
d*W2
и в такой форме допускает разделение переменных не только в де¬
картовых координатах £2, £3, но и в соответствующих полярных.
При этом* задача расширяется в известных функциях и для сечений,
имеющих форму круга, кругового кольца и др.
Точные решения, которые могут быть найдены в каждом кон¬
кретном случае движения границы, могут служить также и для при¬
ближенного решения более общей задачи, когда движение границы
происходит по более сложному закону, но допускает поэтапную
аппроксимацию одним из изученных движений. Впрочем, и для
произвольного закона движения границы возможно получить ана¬
литическое решение задачи по достаточно простой схеме, применяя
указанные выше преобразования. Предоставляем читателю возмож¬
ность получить самостоятельно с помощью функциональных преобра¬
зований (8.145), (8.148), (8.157) решение первой краевой задачи
в декартовой и цилиндрической (радиальный поток) системах коор¬
динат'следующего вида:
дТт п (д2Тт I $т дТт \ . р / i\
^ = a[w- + T-dr) + f'»{x' 1)
( m = 1 —* б, = 0,. О <x<y(t) )
\ т = 2 —► 6 = 1, 0^x<!t(t)l > ;
тт(х, оС-Ф^х). 0<*<,(0); ! <8'198>
Тт (*> 0 и=у с» — Ф/я+i (0 ^ ^ 0;
Тг(х, ои=о = ф,(0. <>0; 01< +
x^sO (т = 1, 2).
Случай бт = 2 сводится к случаю St = 0.
Указание. Применяем преобразования:
а) l=xly((), Тт(х, t) = em(l, t);
б) ет (I. 0 = у~1/2 (0 ехр [- у (<) у’ (0 6»/4e] Wm (6, 0;
в) <' = $*-*(/) d/. Va (6, t) = Wm (Б, t'l
15*-339 453
Ответ.
tf
«^•(5. П = *«..(6. П + £ фуг jP fa)*! jp(T*) dr,...
n— 1 О 0
Tn-1 1 I
. • 5 P Ы dT„ J &(Gm (6, 6ь V, Tj) dSi J 6*0» (si, h. ть**) dft...
0 0 0
1 1
* * * 5 ^«-2» ^Л-i» ТЛ-2* 'fn-l) ^n-i j о (^ni Тл)Х
о 0
xG.ttn-i, 6„. тя-1, Trt)dE„. (8.199)
l
dx +
Здесь U^offi, 0=J Фот(Б')0«(5* Б', 0) d|' —
0
/' Л V
— ба-л0^ф(11’ <T)^L = 0dT—^^ ф‘и + 1
0 0
/' 1
+ JJ/«(6'. t)G-»(5. 6'. T)dxd6' (m = 1, 2);
0 0
6j=o; 6a = l; P(/')=?/3 (0 y"{t)\ P ; <n (5), <pm+i (*'); ф.ш(0.
к = \ y-*(t) d/
/m> (I» t')— новые (известные функции); Gm (£, t\ т)—функции Грина первой
краевой задачи для стержня (m = 1, 0 < £ < 1) и неограниченного сплошного
цилиндра (т = 2, 0<£ < 1).
Установите скорость сходимости ряда (8.199), наложив условие ограниченно¬
сти на функцию Р (О (| Р (/') | < М0.
Говоря о функциональных преобразованиях уравнения теплопро¬
водности, рассмотрим в этом же пункте обобщенное преобразование
Аппеля для одномерных уравнений (см. ссылку в [63]).
Преобразование инверсионного типа
z = VX7$+ci’ т = —rfir + c*; ^2’т) =
-(t+i>prme~x,IUit+mT^ о (8.200)
преобразует уравнение T't = T">-\-(v/x)T'x в уравнение того же типа
U'x = U? + (v/z) U'2. При v = 0 это преобразование найдено Аппелем
и использовано в работе Губера (см. ссылку в [63]), в которой
с помощью этого преобразования построено решение первой крае¬
вой задачи для области [0, R + vt], t^0. Найденное преобразова¬
ние позволяет область с равномерно движущимися границами пере¬
вести в соответствующую область с неподвижными границами.
В качестве примера рассмотрим тепловую задачу
М- = %Т + ±д1, 0^x<R + bFo(R^0, ЬФ 0), Fo > 0;
д Fo дх2 • х дх
Т (х, 0) = Ф0 (х); Т (R + b Fo, Fo) = 0;
| T (.л:, Fo)| < -j- оо, x^0.
454
(8.201)
Потребуем, чтобы т = 0 при Fo = 0; z = 0 при л; = 0; г = 1 при х =
= R + b Fo, получим fi = R/b, y = l/b. Если, кроме того, положить
а = сх = 0, с3 = Ь~19 то задача (8.201) примет вид
Ud/dx = d2U/dz2 + (l/z)dU/dzf т > 0, 0<z<l; \
и (г, 0) = R ехр [bz2!{AR)] Ф0 (zR)\ I (8.202)
U (\, х) = 0; \U (г, т)| < + оо, г> 0. J
Решение задачи (8.202) нетрудно записать, используя результаты
§4 гл. III, после чего, переходя к функции Т (х, Fo), получим
со
Т(х, Ро) = R(R + b Fo) ехр [ —4(/? + 6Fo)j Х^Г2(рп)х
П = 1
XJ° R + b Fo )еХр [— R (tf + 6Fo)] 1 ^Ф° ®
о
X Л,(ц„-|-)с1£, (8.203)
где р„—корни уравнения Уо(р) = 0.
Полагая теперь Ф0(х) = (2ях)-1б(х—л:'), найдем из (8.203) функ¬
цию Грина первой краевой задачи для неограниченного сплошного
цилиндра с равномерно расширяющейся боковой поверхностью
x^R + b Foi
G(x, л-', Fo, *)= n(R + bF[HK + bT)X
[bxa Г bxfZ I
— 4 (R+b Fo) eXP [4 (fl + 6x)J J~2(\1n)Jo'X
П = 1
x(^«T^)y"(Rn^T^)exp (8-204)
Полученный результат справедлив и при R = 0. Заметим далее,
что преобразование (8.200) следует из преобразования Гринберга
(8.145), (8.148), которое в этом смысле является преобразованием
более общего типа.
III. Преобразование граничных условий. Теоремы
разложения для преобразованных уравнений. Рас¬
смотрим теперь преобразование граничных условий для некоторых
видов функциональных преобразований предыдущего пункта. Пре¬
образования координат в (8.145), (8.148), (8.150), (8.172), (8.174)
и функция Т (.х, () — линейны и, следовательно, чтобы граничные
условия для W (£, t) были линейными, линейными должны быть гра¬
ничные условия для Т. Очевидно, что первая краевая задача для
функции Т переходит в соответствующую первую краевую задачу для
функции W и на пути могут быть получены точные решения для
всех указанных выше законов движения границы.
Преобразуем граничное условие II рода д77&*|г=фА по фор¬
мулам (8.145), (8.148) W^rf = [(2а; ~J yy'lW + А,"дф//2/?]*«г'. Отсюда
455
следует, что для постоянства коэффициента в граничном условии
задачи для W должно быть уу'= const, т. е. у (t) = Jf At + В.
Преобразования (8.150) дают для граничного условия II рода:
Wi=rf = [(2а)"1 (туп '% + r\y[) W + т]2ф/^]&=Г'; отсюда должно быть одно¬
временно (для обозначения этого понятия в гл. II введен знак П):
тщ' = const, г)у[ = const. При Г' Ф 0 одновременно выполняются:
(т] = VAt + В п у1 = С У^Аt + В, или r] = constn*/i = если
Г' = 0, то T]=const П yx=At-\-B, или т)=At-{-B п Уг=С1 In (t-\-B/A)+C2
реализуется случай С1 = 0)1 или г\ = У Mt2 + At + В Г\уг = Сх х
х!п(Л/ + Д + V~A t + В) -f С2 (реализуется случай С,=0), или
г\ = У At-\-B п у[ = С У (At + В)~1 (Г;—координата границы). В слу¬
чае преобразования (8.172), (8.174) имеем W'e=z0=(y'/2a)x
X W |4=0 + [ф/(^7) |б=о;• отсюда следует, что для линейности преобра¬
зованных условий II рода необходимо, чтобы у' = const, т. е. y(t) =
= At + B
Переходя к граничному условию III рода (7,* + ЛТ,)* = г = ф»
(h = const), преобразуем его по формулам (8.145), (8.148)
dW
dl
=r, + */(0{[/i-^t/'(0l] ^}4=г, = Уа(0(ф|<7)|=г'. (8.205)
Это выражение показывает, что для всех законов у (t) (Ф const)
в преобразованном граничном условии появляется переменный во
времени коэффициент «внешнего теплообмена», что вносит сущест¬
венные трудности в применение к преобразованной задаче класси¬
ческих аналитических методов решения. Можно, однако, отказаться
от требования постоянства коэффициентов h в граничном условии
исходной задачи и считать, что h = h(t), имея в виду наличие в
исходной постановке задачи движущейся границы и переменного во
времени коэффициента внешнего теплообмена. Но это даст возмож¬
ность получить точное решение преобразованной (а значит, и исход¬
ной) задачи при определенных соотношениях между этими законами,
Действительно, перепишем для этого случая условие (8.205) в виде
dW
dl
,г.+</(0 {[* m-is' (01] -г^Ч-г-Е e w. I).
Пусть граница перемещается по закону у (t) = V М/а + Nt -f С.
Тогда для разрешимости третьей краевой задачи необходимо, чтобы
на правом конце h (t) = hx (t) = \y' (t)/(2a)t на левом конце (£ = 0)
h (t) = h2 (t) = const/у (t).
Аналогичным образом могут быть рассмотрены и другие преобра¬
зования.
В заключение остановимся на теоремах разложения для преобра¬
зованных уравнений (частично этот вопрос был рассмотрен по ходу
изложения функциональных преобразований).
Задача, обобщающая все предыдущие случаи, сводится к инте-
456
грированию уравнения
1 dW 1т dW
a dt ~~ y\(t) £1 d£i
+%%■+№•&+ f&, 5,. S.. О
(8.206)
при произвольном начальном и линейными (с постоянными коэффи¬
циентами) граничными условиями.
Уравнения для собственных функций, порождаемые (8.206), имеют
следующий вид:
где (J, 6—заданные величины (6^0); у2 — постоянная разделения;
переменная £ принадлежит одной из трех областей: £g[0, со] либо
£g[o)i, со2], либо £g[co, оо] (со = const).
1. Разложение произвольных функций F (£) по собственным функ¬
циям уравнения (8.207) и условия, накладываемые при этом на /Ч£),
приведены для случаев: а) р < 0 — в работах Титчмарша [14Г
(с. 104, 174) для граничных условий I—II родов, Левитана [87
(с. 83), Гринберга [28] для граничных условий I рода; б) р>0 —
в работах Титчмарша [141] (с. 72, 106—107), Левитана [87] (с. 82—
83), в работе [62] для граничных условий I рода. Если р = 0, то
получается известное разложение в ряд или интеграл Фурье.
2. Уравнение (8.208) — вырожденное гипергеометрическое. Из¬
вестна обширная литература о разложении произвольной функции
в ряд Фурье по собственным функциям вырожденного ги пер геометри¬
ческого уравнения. Так, если: а) /л=р=6=0, то получается разложе¬
ние в ряд или интеграл Фурье; б) т= 1, 2, Р=0, 6>0, то разложение
по цилиндрическим функциям; в) т=0, 1,2,6>0: при Р>0, £g[0, со],
граничные условия I, II, III родов (см. Бухгольц [167], с. 187, 205—
207); при Р>0,1 € [со, оо] — собственные числа и собственные функции
для уравнения, имеющего самосопряженную форму с граничными
условиями I рода могут быть найдены с помощью [167]; при Р<0,
I 6 [0, со], граничные условия 1,11,111 родов; этот случай может быть
изучен аналогичным образом.
Все результаты по типам законов движения границы и виду гранич¬
ных условий, при которых возможно точное решение уравнения тепло¬
проводности для области, изменяющейся со временем, приведены
в табл. 13. В 1-й колонке таблицы приводится система координат, в
которой решается задача. Во 2-й колонке указываются область и за¬
коны движения ее границ, а в 3-й — сведения о преобразовании
координат, необходимом для решения исходной задачи. Вид граничных
условий и ограничения, накладываемые на коэффициенты граничных
условий и законов движения границ, даны в 4-й колонке.
Приведенная таблица основных законов движения границы яв¬
ляется хорошим материалом для постановки ряда студенческих курсо-
Ч'" + (Р£ + У2)Ч'=0;
ЧГ + (т/l) Г + (Р£а - б/g* + Y2) Т = 0,
(8.207)
(8.208)
457
Таблица 13
Система
коорди¬
нат
Область
Подвижная граница
Реализуются
граничные условия
(у4< + В)2 + С<* < оо
1
*
II
иь
I. и
± У (At + B)* + C*Z.x < со
i=x/i/</)
I Ш[А(/)* =
= у' (0/(2*)]
Р<*<(у4/ + В)2 + С
ь
х—У1 (0
у*(0—«в (0
I, И (Р=0)
5
f-
го
х
SC
ч
Р у (At + B)*+C<.x<
< К И<+в)*+с
II
III
У
I. Н(Р = 0)
P = 0f)A (0~
~{/-1 (!)
Р < 1ПЛ (0 =
= Р</ (0/2*
a
с
с
p(c± K^+s)<-f<c±
± У At+B
ь
_ *-л(0
I. II (р = 0)
X
ff
(С
с
ЫО—Ух (0
CL
ГО
ЬС
а>
fcj
(,4/+в)2+С«£*<
<(y4/ + B)2+C+D
ь
ТА
* ^
II
1
л.
1 1 Г t 1 С, у
ь
_ X — yt(t)
1
At + B 1 С2Г + С2<:*<
•» ^) / + Сз + В
Уг (0 Ух (0
Ci К (л<+а)2+с<*<
^ С4 (-/1/ —f— S)2 —j— С —}— Сд/ —{— СГд
t.
х~Ух (!)
I
ь
Уг СО — Vi (0
2
н
го
х
sc
r=l
р
у (Л/-)-В)2-|-С<г < 00
е = r/y(t)
I, in [Л(о =
=/(0/(2*)]
At + В «С г < оо
l=rly (/)
I, 111 [А (0 =
— у' (0/(2*)]
с
с
X
<+
к
и:
о
<и
ЕГ
Cl
р
X
Р 1/(Л! + В)2 + С<г<
<Z(/U + B)2 + C (0<8 < 1)
5 = Г/У (0
-J
I. II (Р = 0)
р=0(1 Л(/)~
(0
Р<Ь< 1 п
|ПЛ(0=|/'(0/(2*).
X
Г"
S
а
р(/П + В)</-< At + B
(0<8 < 1)
(-гШ
I, П(р = 0)
\ 8 = 0f|A(0~
111 1 ~V-1 (!)
0<р<1ПА(0 =
J =fV (0/(2*)
* h (О—коэффициент в граничном услоьин 111 рода на движущейся границе.
458
вых (и вообще научных) работ, так как предстоит еще большая работа
по конкретному описанию аналитической конструкции решения той
или иной краевой задачи обобщенного типа и расчету температурных
номограмм по найденному решению.
§ 6. МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ С ПЕРЕМЕННЫМ ВО ВРЕМЕНИ
КОЭФФИЦИЕНТОМ ТЕПЛООБМЕНА
Рассматриваемому классу задач в последнее время стало уделяться
большое внимание ввиду их практической важности.
В классической теории теплопроводности твердых тел относитель¬
ный коэффициент теплообмена h=а/к считается постоянным, не зави¬
сящим от температуры и одинаковым для всей поверхности тела. Это
дает возможность применять при решении соответствующих задач
метод разделения переменных и интегральных преобразований. Од¬
нако величина h зависит от пространственного распределения поверх¬
ностной температуры и ее предшествующей истории. Вид этой зави¬
симости определяется решением уравнений движения среды, окружаю¬
щей тело, при произвольном распределении температуры, по поверх¬
ности тела [83].
Существует особый класс задач нестационарной теплопроводности,
в которых h можно рассматривать зависящим больше от времени, чем
от температуры (или координат). Последнее наблюдается при форми¬
ровании теплового пограничного слоя в условиях нестационарного
обтекания твердых поверхностей охлаждающей средой, при нагреве
тел пульсирующим потоком, при рассмотрении температурного поля
баллистического тела, движущегося в среде с переменной плотностью
и температурой, при процессе теплообмена прокатываемого металла
с валками и окружающей средой [63]. Помимо технологических имеется
ряд других причин изменения коэффициента теплообмена во времени:
изменение физических характеристик теплоносителя (скорости движе¬
ния, степени черноты, плотности и т. п.) или изменение с течением вре¬
мени состояния поверхности нагреваемого тела (окисление, засорение
пылью, растрескивание и т. п.).
Кроме того, к этому классу задач приводят рассмотренные в пре¬
дыдущем параграфе функциональные преобразования, применяемые
при решении уравнения теплопроводности в области с движущимися
границами.
При произвольном законе изменения коэффициента h(t) искомая
температурная функция не выражается в квадратурах. Трудность ре¬
шения такого класса задач заключается в том, что, оставаясь в рамках
классических методов математической физики, невозможно согласо¬
вать решение линейного дифференциального уравнения T't=aAT(M, t)
с граничным условием вида дT/dn=h(t)[T(M, t)—Тс\, М g S. На прак¬
тике используются методы операционный или тепловых потенциалов,
которые сводят уравнение теплопроводности к интегральному уравне¬
нию Вольтерра II рода, так что в конечном счете решение задачи дает¬
ся в виде бесконечного ряда последовательных приближений. Чаше
459
всего эти методы применяют при переменных краевых функциях за¬
дачи. При их постоянных значениях можно воспользоваться с самого
начала классическим методом последовательных приближений, ап¬
проксимируя краевое условие задачи. Простота подхода здесь заклю¬
чается в том, что все приближения искомого решения сводятся к извест¬
ной задаче, методика решения которой отработана.
Итак, пусть Т (х, t) — решение задачи
dT/dt =ад2Т/дх2, х > 0, t > 0; (8.209)
Т (х, 0) = то, *>0; [дТ (х, t)/dx]x=0= |
= h(t)T(x, 0U=c *>0; I (8.210)
\Т(х, 0I<°°, *>0. j
Здесь h(t)—ограниченная функция.
Решение Т (х, t) ищем в виде ряда
т (х, 0=2^ (*. 0 = Т0 + 2 тп {х, 0. (8.211)
м=0 п=1
предполагая его равномерно сходящимся на любом конечном отрезке
изменения переменных х>0 и />0 (после определения Тп(х, /)
это предположение будет проверено).
Подставляя (8.211) в уравнение (8.209), потребуем для прибли¬
жений Тп(ху t) справедливость равенства
dTn/dt = ad2Tjdx\ *>0, t > 0; Тп(х, 0) = 0, *>0, л>1. (8.212)
Подставляя (8.211) в граничное условие (8.210) (при х = 0), по¬
лучим
L = 2>Wr>- 0U-.. (8-213)
п = 1 п- 0
В правой части равенства (8.213) заменим {п 1) на я', так что
при 0</г<оо будет 1<я'<оо; при этом Тп(х, /) = 7V-i(*, 0-
Возвращаясь для удобства рассуждений к старому обозначению
переменной суммирования и приравнивая общие члены ряда слева
и справа в (8.213), имеем
=h(t)Tn_1(x, 01,... <>0 (п> 1). (8.214)
ил 1х=о
Итак, в качестве первого приближения искомого решения сле¬
дует взять решение задачи:
дТ Jdt^ad^Tjdx2, х > 0, t > 0;
Tt(x, 0) = 0, *>0; d-w\x==b(t)TAx,t) U=.= 1 (8215)
= h{t)T0 = (f1 (t), t> 0; | T (x, 0l< + °°.
Функцию Tx (x, t) легко найти операционным путем. Пусть
OD
ТЛх, Р) = ^ехр(—pi) Тг{х, l)dt.
460
Операторное -уравнение для нахождения Тх(х, р) имеет вид
tfTjdx2 — {р/а)Т1 = 0 с условиями
(df’1/dx)x=0 = 91 (/?), |-7\(*, р)/< + оо, л: > 0.
Отсюда находим
Переходим к оригиналу, используя теорему о свертке [см. (6.11)]:
Первое приближение найдено. Совершенно аналогично находится
второе приближение как решение задачи
dTjdt = ад2Т2/дх2, х > 0, t > 0;
Это решение можно записать автоматически по формуле (8.216),
подставив вместо фх (t) функцию фа (t) = h (t) 7\ (0, /):
Теперь нетрудно записать искомое решение задачи по формуле
(8.211) в следующем виде:
Для того чтобы убедиться, что ряд (8.217) является решением
Уравнения (8.209) с условиями (8.210), нужно показать, что этот
ряд сходится равномерно при всех / >0 и х>0 в любом конеч¬
ном промежутке их изменения.
Так как по предположению функция h (t) ограничена на отрезке
[0, /], то можно записать \h{t)\^.MQ (М0 = const).
Т1 (*. Р) = — V а!р ф, (р)ехр — у= VР .
(8.216)
Тг(х, 0) = 0, х> 0; [дТ2(х, 0/<^L=o = W7\(0, 0 = <М0- t > 0;
01 < + °°. х> о.
{Xt t) = — LJL Г е-47(7^т) dx =
е 4а dx =
— Т
— 1 о
461
Оценим по абсолютной величине члены ряда (8.217)
|Т(х, /)|<Г
/ t Т, \П _ 2
„Г dT Р dtf Г dT8 Г dTn_x
J У t— Т # У 1 — *1 j у Т!—Та J V Т„_2 —Т„_Х
(8.218)
Общий член этого ряда можно вычислить. Действительно, имеем
1* "г,—~Тп~1 =2^; Г SL-с1т„_2 = \(тЯ73Г;
j К т„_2—Т„_, J к тл_8—т„_2 ^
j * dXn_9=j (у^у.
X К Тл-4— Тл_з d
Используя принцип математической индукции, можно показать,
что имеет место равенство [20]
"f* = Ти (УЧ^ГГ, (8.219)
q V ^n-m — 1 ^п — m
где коэффициенты ут пока неизвестны.
Для нахождения ут сделаем в интеграле (8.219) замену пере¬
менной по формуле тЛ-/я = тл_/я_1 sin2cp и преобразуем интеграл
л/2
Ут (V ^n-m-lT = 2 j S'0” Ф Йф-
о
Отсюда находим (используя таблицу интегралов [20])
я/2 ) 2 ■ если т = 2к—1, (к= 1, 2, 3...);
Тя> = 2 j sln-фЛр» [(ас_1)М
о J (2к)~11 п» если т = 2к•
(8.220)
Заметим, что из (8.220) следует —>0 при т—► оо; так как
n-й член ряда (8.218) содержит п интегралов, то он равен произве¬
дению (М0 У а/ я)пу1у2.. .уп (J/Т )п. Обозначим через dn = (M0Va/jx)nx
00
xYiV2-'-Yn- Тогда ряд (8.218) примет вид ^ dn(\/7)n и сходимость
П- 1
его для всех /> 0 можно проверить по признаку Даламбера. Но
отсюда следует, что ряд (8.218) для Т (х, t) (и аналогично
ряд для dT/dt, дТ/дх) сходится абсолютно и равномерно на
любом конечном отрезке изменения переменных х > 0, £ > 0,
и является решением рассмотренной задачи (8.209)—(8.210). Нера¬
венство (8.218) можно использовать для установления погреш¬
462
ности приближения. Действительно, ряд (8.217) знакопеременной
(если функция h (t) неотрицательна на отрезке [0, /]) и погреш¬
ность этого ряда при использовании конечного числа его членов-
приближений не превышает по абсолютной величине первого из
отброшенных членов. Чтобы оценить погрешность приближения,
необходимо вычислить коэффициенты dn. Это нетрудно сделать,
используя выражения (8.220); в результате получаем
— \ (Мп1/Т)пя~1/2 2Ш-+-~ , п = 2/с— 1;(8.221)
, fMoVH\n I п1]
\Г~^ ) | . г—\п2п/2
' ' I (M0Vh) -jjjy , п = 2к (к= 1, 2, 3, ...).
В качестве примера рассмотрим случай, представляющий инте¬
рес для процессов теплообмена прокатываемого металла с валками
и окружающей средой [102]. Пусть ft(Fo)=exp(— Fo), где Fo=
=atliо, /0 произвольно выбранная масштабная единица длины.
Используя (8.217), выпишем в безразмерных переменных г = л://0;
W (г, Fo) =
То-74*. 0
первые последовательные приближения реше¬
ния в виде
Fo
Wt{z, Fo) = 5 exp (—т) x (г, Fo—т) dr,
о .
Fo
IF, (г, Fo) = — £ exp (—2т) -j- Ф (i |ЛГ) x (z, Fo—t) dt;
Fo
Здесь
ника;
W3(z, Fo) = J 0(t)x(z, Fo—t) dx и т. д. (8.222)
о
X (2, Fo) = (I/J/'jiFo) exp (—г2/4Fo)—функция теплового источ-
т
0 (т)= J ехр (—Зр) ехр [ (т-р)] /0 (т-р)] dp, Ф (г) -
интеграл вероятности; /0 (г)—модифи- jv/Я,/з; г;
цированная функция Бесселя.
Анализируя выражения (8.222), мож- 0 ^
но убедиться в достаточно быстрой схо¬
димости процесса интеграций. На рис. 1
39 приведены значения приближений 0,1
температурной функции ty1 = Wi\ ф2= 0i
рассчитанной в зависимости от крите- 05
рия Fo для точек: a) z = 0,707; б) ’
г = 2. Из рисунка видно, что первое и
второе приближения берут в вилку 0,1
третье приближение; второе и третье q
приближения берут в вилку четвертое
приближение и т. д., что позволяет
5)
s==r?=g:
%
0,8
1,6
Рис. 39
463
с достаточной для практики точностью ограничиться третьим при¬
ближением.
В (8.210) рассмотрен случай постоянной начальной температуры
Т (х, 0) = Т0. Величину Т0 нетрудно перевести в граничное усло¬
вие с помощью подстановки W (х, t) = T (ху t) — Т0; тогда имеем:
W (х, 0) = 0 и (dW/dx)x=Q = h(t) [W (0, t) — (—Т0)], т. е. нулевое
начальное распределение температуры, а на границе—теплообмен
со средой температуры (— Т0).
Пусть теперь температура окружающей среды—переменная ве¬
личина, равная а начальная температура—по-прежнему ну¬
левая
Т (х, 0) = 0, х > 0,
[дТ(х, t)/dx\x=0 = h(t)[T(0, 0-<М0]. *>°. (8.223)
Найдем решение Т (х, t), удовлетворяющее (8.209), (8.223) и усло¬
вию ограниченности. Указанный выше подход аппроксимации гра¬
ничного условия при переменной температуре среды оказывается
для этого случая менее удобным, чем, например, операционный
метод, который и используем для решения этой задачи.
00
Полагаем, как обычно, Т (х, р)= ^ е~^Т (х, t)At\
о
00
Ф2 (р) = 5 е-я'ф2 (/) At [ф2 (0 = h (t) ф1 ([)]. (8.224)
о
Операционное решение уравнения (8.209) с учетом его ограни¬
ченности при х —■►оо имеет вид Т (х, р) = А (р) ехр (—х Vр!а)*
Переходим к оригиналу, используя формулу обращения (6.20) для
преобразования (8.224):
^ = Ш J (8.225)
а- too
Для определения постоянной интегрирования A (t) используем
граничное условие (8.223)
o+i оо o + i"eо
2^7 j ^~A(p)eptdp+h(t) 2^7 [ А(р)еР*др=cp2(t). (8.226)
а - ice cr- too
Обозначим V~p А (р) = В (р) и в равенстве (8.226) перейдем к ори¬
гиналам по теореме о свертке (6.11):
.— t
В ([) + А(0 Г -^М= di = Vr7h (t) ф4(0- (8-227)
у л J у / — т
Обозначим В (t)/h (t) =0 (tf) и перепишем уравнение (2.227)
в виде
/
0(O + 5=i{-^=0(T)dT = HTVl(O. (8.228)
у л J у t — X
464
уравнение (8.228) представляет собой интегральное уравнение
Вольтерра II рода относительно функции 0(0- Его решение будем
00
искать в виде степенного ряда ©(/)= 2 (Кя'/Кл;)'1 ©,,(/)» предпо-
п = О
лагая этот ряд для данного У'а'/Уп равномерно сходящимся на
любом отрезке изменения переменной t > 0 (позже это предполо¬
жение должно быть проверено для найденных ©„(0)- Подставляя
ряд в (8.228) и учитывая, что в силу сделанного предположения
знак суммы для ©(0 в левой части (8.228) может быть выведен за
знак интеграла, получим
в.«)+1 (Ц)' ®.«=^ <') - t (Щ | в-. м*.
Сравнивая коэффициенты при одинаковых степенях (Кя/Кя-)» на¬
ходим:
t
0о(О = Ко"ф1(О; ©п(0= — С (т) dx, 1. (8.229)
Нетрудно получить решение найденного рекуррентного соотно¬
шения, если последовательно расписать первые приближения:
t t
0, (0 = - j' 0О (т) dt = -КТ J ф, (х) dx; (8.230)
о о *
в*(0 = — i^=Q.('t)dx = l/a' C-^Ldx Г-Шкф, (Tj) dxf;
Jyt—т: J yt—т J Кт-tj
в,, (t)=(_i)»i/^c -4= dx 5 ~ш= dx,..
J V t — T J у т tx
... ]г-ьЛ(Тп-1] ■yi(T„-1)dx<,_1. (8.231)
V I».?-
о
___ Теперь можно и записать - искомую функцию Л (/). Находим
A(p) = B{p)lV~p и далее, переходя к оригиналам и заменяя
Я U) =h (t) 0 (/), запишем
Функция © (t) в виде ряда последовательных приближений
(8.230)—(8.231) уже найдена. Таким образом, окончательно можно
465
записать
*о-1<-'>-(ЯГ№*№х
М — п г пг пг 1
п=0 ' О
"Ci Тп-i
xdT.f^iM^dT,... f ^^(-Hdr„. (8.232)
Сходимость этого ряда (как и ряда для © (/)) исследуется совер¬
шенно аналогично случаю (8.217). Нам осталось записать искомое
решение рассматриваемо^ задачи (8.209), (8.223), операционная
форма которого имеет вид Т (х, р) = А (р) ехр (— х pl\f а). Переходя
к оригиналам по теореме о свертке, получим
<8-233>
где A(t) имеет вид (8.232).
В качестве примера использования полученного решения рас¬
смотрим случай, когда (дТ/дх)х=0 = h{itm [Т (0, t)—Tctr], t > 0, где
m, г—действительные числа.
Вычислим предварительно Л(/), имея в виду, что в (8.232) сле¬
дует подставить h(t) = h0tmy фi{t) = Tztrt Запишем A(t) в виде
Ж0= 2 (-1Н\Га1\Гп)п+гАЛ1)
л = О
и вычислим последовательно первые приближения
,4,0) = Г d, - А.Г, С dx -
J у t—T J V t т
1
= Л07с/",+'-+>/2 ^2m+/-(l—
0
Здесь была произведена замена переменной г = т//; преобразованный
интеграл можно выразить через функцию Бета
В(с; d) = J гс-Ц1 — z)d~ldz(c> 0; d> 0). (8.234)
о
Находим, используя (8.234),
Ло (0 = hQTс/г + (т+1/» В [г + 1/2 + (пг + 1/2); 1/2];
t
А х (/) = f А0 (•г) dx = [л + 1/2 + (т + 1/2); 1/2] х
а к /— т
о ^
t
-Г + 2ГП+ 1/2
/V Г + 2ЛП + 1 /Я
х ^-==- dx = TchUr+*m+1B [г + 1/2+ (m + 1/2); 1/2] х
J у t — т
х J 2г+2т+1/2 (1 _z)-i/2 (1г = Tchltr+^m + U2) В fr-f 1/2 + (m+ 1/2); 1/2] х
xfi[r+ 1/2 + 2 (m+ 1/2); 1/2].
466
Аналогичным образом можно показать, что
3
Л,(0 = 7\W'+3(m+1/2) II в [г + 1/2 + К (т + 1/2); 1/2]. (8.235)
Из (8.235) угадывается закон образования п-го приближения
4„(0 = 'W4'+l'1+l)(m+1/2,n Я[г + 1/2 + к(т+1/2); 1/2], (8.236)
в справедливости которого для всех п^О можно убедиться с по¬
мощью принципа математической индукции. Таким образом, окон¬
чательно находим следующее решение, если h (t) = h0tm; q>1(t)=Tctr:
Использование в (8.237) функции В (с, d) определяет и ограни¬
чения, накладываемые на числа т и г; необходимо, чтобы г+1/2+
+ /с(т+ 1/2) > 0 при /с= 1, 2, 3, ... . Рассмотрим случай, когда
относительный коэффициент теплообмена изменяется по закону h(t) =
= h0t-l/2(m = —1/2), а температура окружающей среды <Pt(0 по¬
стоянна и равна Т,с(г = 0).
Из формулы (8.237) находим для этого случая ([/i0] = cm_1c1 2):
Это выражение можно существенно упростить, если использовать
табличное значение функции -5(1/2, 1/2) = я и подстановкой г =
= х/2У~а (t—т) свести интеграл в (8.238) к специальной функции
В каждом из рассмотренных подходов получено точное решение
задачи в виде бесконечного ряда последовательных приближений.
Наряду с этим можно указать и приближенные способы расчета
температурного поля, правда для ограниченной области изменения
теплофизических параметров.
Рассмотрим температурное поле неограниченной пластины при
переменных коэффициенте теплообмена и температуре внешней среды.
к= 1
п+ 1
Т(х, t) = 1^j^ (-ly+'(±^)nU.B[r+l/2+K(m+l/2); 1/2]х
I у ал ля1 \ у л / к=1
п т^тщшт1/а/ г V» 1
X \ „ ехР - Ит. (8.237)
(8.238)
Ф* (г)
(8.239)
467
Задачу запишем в безразмерных переменных:
dW/д Fo = d2W/dz2, 0<z<l, Fo > 0;
W(2, 0) = Г0, 0<z<l; l
[dW(z, Fo)/dz]J=0 = 0; Fo > 0; )
[dW(z, Fo)/dz]z=I = — Bi (Fo) [Щ1, Fo)—0C (Fo)], Fo > 0. (8.241)
Здесь z = x/l; W0 = TG/Tocy где T0— начальная температура тела;
Tcc — начальная температура окружающей среды; Fo = at/l2,
Bi (Fo) = Л (/) /; ec(Fo) = rc (О/Гос; W(Z, Fo) = T(x, t)/Toc.
Решение этой задачи получим следующим образом. В равенстве
(8.241) правую часть обозначим через <7(Fo)
(dW/dz)z=l = q (Fo), где (Fo) =— Bi (Fo) [«7(1, Fo)—0c(Fo)]
и введем функцию W(z, Fo) = 0(z, Fo) + №0. Имеем для 0 (2, Fo):
<30/<3 Fo = 320/<3z2, 0 < z < 1, Fo > 0;
0(г, 0) = 0; [(30(г, Fo)/(3z]2=0 = 0; [30 (г, Fo)/<3z]2=1 = q (Fo). (8.242)
Решение 0(г, Fo) нетрудно получить методом интегрального
преобразования по переменной z (см. табл. И гл. V). Полагаем
1
0(n, Fo) = $0(z, Fo)cosmizdz (n = 0, 1, 2, 3, ...) (8.243)
о
и переходим в (8.242) в пространство изображений
<J0/d Ро4-(ял)20 = (—1)" ^ (Fo); 0(п, 0) = 0.
Решая уравнение, находим 0 (n, Fo)
Fo
в (л, Fo) = (—1)Л^ Q (т) exp [(— tin)2 (Fo—t) dt
о
и далее по формуле обращения для преобразования (8.243) искомое
решение
Fo *
0(2, Fo)=^ ^(x)dx +
б
оо Fo
+ 2^ (—l)ncosn л2 J <7(x)exp[—(nji)a(Fo—x)]dx. (8.244)
n — 1 0
Перейдем теперь в (8.244) к выражению для функции q (х):
Fo
W(z, Fo) = \F0-J Bi(T)[\F(l,T)-0c(T)]dT +
о
oo Fo
+ 2^Г (—l)n+1cosmiz J Bi(x)[lF(l, t) —
— 0C (T)] exp [—(пл)г (Fo—x)] dx. (8.245)
468
Выражение (8.245) дает формальное представление о темпера¬
туре в любой точке пластины через ее значение на поверхности.
Поэтому температура в произвольном сечении может быть опреде¬
лена только после того, как будет найдена функция №(1, Fo). Прежде
всего усилим сходимость ряда в (8.245); для этого применим фор¬
мулу интегрирования по частям к интегралу (другой подход см*
§ 7 гл. V);
Fo
^ Bi (т) [Щ1, т)—вс(х)]ехр[— (nn)s(Fo—x)]dx=
о
= [1 /(ля)2] Bi (Fo) [Г(1, Fo) —0С (Fo)] —(лл)-» Bi (0)х
Fo
X [117(1, 0)—©с (0)] ехр (—л2л2 Fo)—J {Bi (т) [U7(l, х) —
о
—0С (х)]}' ехр [— (ля)2 (Fo—т)] dx.
Учитывая также известное разложение в ряд Фурье
1—Зг2 0 v (-l)n+1
— “З^^^г-созляг.
П= 1
окончательно получим для функции W(zy Fo)
Fo
W(z, Fo) = W0— J Bi(x)[W7(l, T)-0c(T)]dT +
0
+ Izi3iJBi(Fo)[r(l, Fo)-0c(Fo)]-
2 £. ( ("£t" cos nnz {Bi (0) [^(1, 0)—0C (0)] x
П.— 1 '
Fo
Xexp(—n2n2Fo) + J [Bi(т) (и^(1, т)—0c(x))]{exp [—(nn)2(Fo—x)]dx[.
° (8.246)
Полагая 2=1, получим интегральное уравнение для 117(1, Fo)
Fo
1F(1, Fo) = H70— J Bi (t) [U7(l,x)-0c(x)]dx—(l/3)Bi (Fo)[lF(l, Fo)—
о
00
— 0C (Fo)]+2 £ да {Bi (°) iWV> °)-0c (0)] exP (—п2пг Fo) 4-
П= 1
Fo
4-^ [Bi (x) (1F(1, x) —0C (x))][exp [—(ял)2 (Fo—x)] dx}. (8.247)
0
Уравнение (8.247) может быть решено так же, как и (8.227),
т. е. методом последовательных приближений; при этом можно по¬
казать, что процесс последовательных приближений сходится. Сле¬
довательно, ближайшей задачей является отыскание наиболее удач¬
469
ного первого приближения. Как показал А. В. Лыков [83], при
нагреве тел переменным тепловым потоком [задача (8.242) как раз
и является таковой], начиная со значения Fo^0,4 тело вступает
в стадию квазистационарного режима. С точки зрения вычислитель¬
ной математики это означает несущественное влияние на поверх¬
ностную температуру суммы ряда в (8.247) при значениях Fo^0,4.
Таким образом, пренебрегая этим рядом при решении уравнения
(8.247), запишем уравнение в следующем виде:
Fo
[l + (l/3)Bi(Fo)]r(l, Fo) + J Bi(x)lF(l, T)dT = rt(T), (8.248)
0
где
Fo
(T) = + J Bi (Fo) ec (Fo) + J Bi (t) 0c (t) dx.
0
Продифференцируем обе части уравнения (8.248) по Fo и преобра¬
зуем полученное выражение, записав его следующим образом:
ИЛЬ Fo) + ^-g)+g')(Fo) W( 1, Fo) =
_ 3 Bi (Fo) ес (Fo) + [Bi (Fo) ec (Fo)]'
3+ Bi (Fo) ’ (О.^У)
Щ\, Fo)/Fo=o = [3^o + Bi(0)ec(0)][3 + Bi(0)]-». (8.250)
Начальное условие (8.250) определили из (8.248). Находим UP(1, Fo)
из (8.249)—(8.250):
31Г0 + В1 (0) вс (0)
Д7(] Fo) — схр Г С dx
I ’ ' е Р J 3+ Bi (х) 3 + Bi (0)
L о J v
+ 1 Э°'И6,,ТЖВ;„)8,„,Г ехр[| 3Byf+°;WdJdtl. (8.251)
о Lo J /
Подставив найденное выражение (8.251) в (8.246), можно полу¬
чить распределение температуры для произвольного сечения —1^
в любой момент времени Fo^ 0,4. В качестве числового
примера рассмотрим разогрев неограниченной пластины, когда кри¬
терий Bi (Fo) изменяется по закону Bi (Fo) = 0,5 ехр (Fo), а темпе¬
ратура внешней среды 0С (Fo) = 1 + 0,075 Fo; начальная темпера¬
тура Ц70 = 0,15 [131]. Для оценки погрешности б по полученным
формулам используются результаты численного интегрирования си¬
стемы (8.240) — (8.241) с помощью ЭВМ. Результаты расчета пред¬
ставлены в табл. 14.
Анализируя результаты таблицы, можно высказать утверждение
о регуляризации кинетики нагрева в условиях переменных температу¬
ры окружающей среды и относительного коэффициента теплообмена.
Заметим, что ряд плоских, цилиндрических и сферических задач
указанным методом решены в [132]. В задаче (8.209) — (8.210) рас-
470
Таблица 14
Температурное поле неограниченной пластины
в процессе нагрева при W> = 0,15
Fo
Температура поверхности
W( 1, Fo)
fit %
Температура центра
1Р<0, Fo)
в. J/,
ЭВМ
расч.
ЭВМ
расч.
0,4
0,48228
0,45768
5,1
0,28537
0,27483
3,6
0,5
0,53581
0,52282
2,42
0,33261
0,32562
2,15
0,6
0,57813
0,56714
1,89
0,36663
0,35992
1,87
0,7
0,62749
0,61785
1,54
0,41221
0,40633
1,44
0,8
0,66933
0,66100
1,2
0,44817
0,44391
0,96
0,9
0,71581
0,70883
0,97
0,49873
0,49475
0,81
1,0
0,75512
0,75101
0,545
0,52662
0,52382
0,535
1,1
0,81232
0,80817
0,513
0,60754
0,60611
0,236
1,2
0,84873
0,84623
0,295
0,64612
0,64612
+0,00
1,3
0,88637
0,88637
+0,00
0,69331
0,69331
+0,00
1,4
0,92243
0,92243
+0,00
0,74222
0,74222
+0,00
1,5
0,95561
0,95561
+0,00
0,77013
0,77013
+0,00
1,6
0,98031
0,98031
+0,00
0,79474
0,79474
+0,00
1,7
0,99984
0,99984
+0,00 *
0,82008
0,82008
+0,00
смотрен случай А(/) = Л0/“1/2, для которого решение соответствую¬
щей тепловой задачи имело достаточно простую форму (8.239).
Задача 1. Примените для решения задачи (8.209) — (8.210) следующий под¬
ход: с помощью замены переменной £ = x/i(/); Т(х, t)*=W (£, t) и преобразова¬
ния (8.148) задача (8.209) — (8.210) перейдет в следующую:
у2 (0 dWjdt = ad*Wldb* + (\Ha) у3 (/) / (/) l2W, I > 0, * > 0;
W (Б, 0) = Т0 /7(6) ехр [(1 /4а) у (0) у' (0) £2], £ > 0;
(dW/dt—W)^0 = 0, t> 0; | W (Б, /)| < + оо, £ > 0; [у* {t) = (()].
Рассмотрим два случая, допускающие точное решение:
а) У" (0 = 0 у (0 = At + В — h (t) = 1 /(At + В)
б) у* (t) у3 (0 =-Ра — у (0 = /(Л/ + р)2-ЛЯ2 —► Л (0 = 1/У (0.
Заметим, что доведение решения задачи до конца и построение соответствую¬
щих температурных номограмм было бы интересной студенческой работой, важ¬
ной для вопросов нестационарного охлаждения термоэлектрических элементов
(см. ссылки в [75]).
В этом параграфе показаны в основном аналитические методы реше¬
ния указанного класса задач. Вместе с тем существуют и приближен¬
ные методы их решения. Так, в ряде работ такие задачи решены для
пластины, шара и цилиндра в случае линейного потока теплоты при
произвольном законе изменения относительного коэффициента тепло¬
обмена и температуры окружающей среды. Из таких методов следует
отметить метод Кармана — Польгаузена, широко применяющийся для
решения задач динамического пограничного слоя. В применении к за¬
дачам теплопроводности метод Кармана — Польгаузена заключается
в введении термического слоя, характеризующегося тем, что за пре¬
делами этого слоя тело находится практически при начальной темпе¬
471
ратуре и теплообмена за его пределами не происходит. Дифференци¬
альное уравнение теплопроводности заменяется интегральным соот¬
ношением, полученным в результате усреднения исходного уравнения
по толщине термического слоя. Кроме того, известный профиль темпе¬
ратур в термическом слое заменяется некоторой полиноминальной
кривой, удовлетворяющей граничным и начальным условиям. Степень
интерполирующего многочлена выбирается в зависимости от числа
граничных условий. В результате неизвестной величиной, подлежащей
определению, является толщина термического слоя Д, причем метод
дает возможность свести уравнение в частных производных к нели¬
нейному обыкновенному дифференциальному уравнению первого по¬
рядка относительно А (см. ссылки в [63]).
В ряде случаев можно воспользоваться подстановкой W (х, /) =
= 1 пТ(х, t), приводящей уравнение (8.209) и .граничное условие
(8.210) при х=0 к виду a~1W,t = W',xt-\-{WxY\ (Wx)XaK0=h{t). Если рас¬
сматривать нагрев тонких тел, то в этом уравнении можно пренебречь
членом (Wx)2 [63].
Из других приближенных методов следует отметить метод осредне¬
ний функциональных поправок, метод сведения уравнения теплопро¬
водности к интегральному уравнению Фредгольма второго рода и да¬
лее к системе обыкновенных дифференциальных уравнений, метод не¬
определенных коэффициентов и др. [63]. Однако заметим, что примене¬
ние этих приближенных методов не намного облегчает техническую
возможность использования найденных решений, также достаточно
громоздких и требующих использования ЭВМ. В то же время (мы виде¬
ли на задачах этого параграфа) при использовании аналитического ре¬
шения задачи в виде бесконечного ряда последовательных приближе¬
ний можно остановиться уже на втором-третьем приближении с доста¬
точно высокой степенью точности в силу быстрой сходимости ряда —
решения.
Задача 2. Используя метод функциональных преобразований (8.172) и ме¬
тод функций Грина, получите решение задачи:
dT/dt =ад2Т/дх2, х > у (t), t > 0; (8.252)
Г (*, 0) = 0, х > у (0)^0;
[дТ(х, t)/dx]x=y{i) = h(t)[T(x, t)\x=y{t)-<p(i)), t> 0 (8.253)
Т (х, 01 < + 0°. * > У(0)-
§7. МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
СТЕФАНОВСКОГО ТИПА
В § 3 гл. II рассмотрены граничные условия (2.77) в краевых задачах
нестационарной теплопроводности о фазовых переходах (задачи Сте¬
фана). Остановимся на некоторых аналитических подходах при реше¬
нии задачи Стефана. Частично решение этой проблемы дано в § 3 гл.
VIII, где рассмотрено развитие метода дифференциальных рядов для
области [0, y{t)]y t>0. Указанный метод оказывается весьма эффектив¬
ным, если перейти от прямой задачи Стефана к обратной, т. е. если п)
известному закону движения границы раздела двух фаз и начальному
472
распределению температуры искать температуру на неподвижной гра¬
нице (краевое условие), а затем ее значение в среде. Существенно, что
физическое содержание задачи при этом в основном не меняется. Зато
система уравнений распадается на две подсистемы, каждая из которых
описывает процесс только в одной фазе, и, таким образом, сложная ис¬
ходная задача Стефана сводится к более простой — определению тем¬
пературного поля в двух областях с подвижными границами, закон дви¬
жения которых известен. Если эксперимент не позволяет установить
предполагаемый вид закона перемещения границы раздела фаз, задача
рассматривается в классической (прямой) постановке. Следует от¬
метить, что за последние годы проблеме Стефана уделено много
внимания и число публикаций в этой области непрерывно растет
(см. работы [12, 25—26, 31, 94—95, 98—100, 150, 155—159]).
Рассмотрим краевую задачу о перемещении фронта фазового пере¬
хода в среде, заполняющей с начального момента времени область
х>0, находящейся при температуре фазового перехода Тп=0 и ох¬
лаждаемой (или нагреваемой) с поверхности; будем считать, что процесс
одномерный и что обе фазы отделяются друг от друга плоскостью х=
=y(t). Имеем при этих условиях задачу:
дТ/dt = ад2Т/дх2, 0 < х < у (/),
*>0 (0(0) = 0); (8.254)
Г (О,/) = ф(0<0, *>0; (8.255)
Т(х, /)км/) = 0, 0; \
[дТ(х, t)/dx]A^{i) = Ady/dt9 1> 0, J
где /4=±Хпр/Л; — теплота перехода; р — плотность. Причем
знак плюс или минус соответствует процессу охлаждения или нагрева¬
ния среды с поверхности х=0. При х=0 может быть задана либо тем¬
пература, либо закон теплообмена со средой (закон Ньютона), либо
тепловой поток; ограничимся первым случаем. В указанной задаче
требуется определить закон движения поверхности раздела фаз y(t)
и температурное поле в среде Т(х, t). Используя выражения (8.131)
и (8.256), запишем
00
Т(х, 1) = -А £ \[у«)-х]"+'у' (0}. (8.257)
о v
откуда при х = 0 с учетом граничного условия (8.254) приходим
к операторному уравнению относительно закона движения границы
раздела фаз у (t):
00
= (8-258>
п = 1
Решение уравнения (8.258) можно получить различными прие¬
мами. При малых значениях t используется метод малого параметра,
развитый в работах [94—95, 98—100], при больших значениях t—
метод контурного интегрирования, развитый для этого класса задач
473
в [31, 158—159]. В этом случае выражение (8.258) переводится
в пространство изображений по Лапласу; для этого умножим левую
и правую части (8.258) на ехр(—apt) и проинтегрируем по t от
нуля до бесконечности [см. метод решения операторного уравнения
(8.121)], подразумевая при этом под р такое вещественное или комп¬
лексное число (р = о-fico) с Rep^P>0, при котором существуют
все входящие по ходу действия преобразованные по Лапласу вели¬
чины. Получим!
п= I О
(О
-МёФ
О 1_л=0
d< — — = — (I/аА) ф (ар),
ар
где ф (ар) = J ф (t) ехр (—apt) At. Суммируя ряд, запишем
О
оо
j е- ар< ch \у (t)V~p\ dt = (1/аА)у(ар). (8.259)
О
Выражение (8.259) [как и (8.258)] можно рассматривать как
интегральное уравнение для нахождения функции y(t). Если эта
функция будет найдена, то решение исходной задачи можно запи¬
сать в виде (8.257).
Мы остановимся на другом подходе, идеи которого могут быть
использованы для развития теории интегральных преобразований
в нецилиндрических областях (в областях с движущимися грани¬
цами). Пока это открытая проблема аналитической теории тепло¬
проводности, как и другая, не менее важная проблема — распро¬
странение метода дифференциальных рядов на область [у (/), оо), t > 0.
Указанные проблемы ждут своего решения и представляются весьма
важными в прикладном отношении; первые результаты в этом на¬
правлении получены в работах [25, 93—95, 150, 158—159].
Введем следующее преобразование:
У (О
^ (Р* 0= J Т (х, t) sh(xj/7?) dx, - (8.260)
о
где р = а + ((о — комплексное число с Rep^P >0 и -£<
< argj/"p< . Умножим обе части уравнения (8.254) на sh(xKp)
и проинтегрируем его по х от нуля до y(t):
у it) _ y(t)
J (dT/dt) sh (xVp) dx= a J (d2T/dx2) sh (xVp) dx. (8.261)
474
Интегрируя по частям, получим
У it)
^ j Т(х, t)sh(xV~p) dx—T(y(t), /)sh[y(0
0
у (t)
X ^ = a%^{xV~p)^n+aV~pT(xy t)ch(xV~p)
10
y(t)
+
0
T (*, /) sh {x\Tp) dx.
Учитывая краевые условия (8.255)—(8.256), а также (8.260), при¬
ходим к обыкновенному неоднородному линейному дифференциально¬
му уравнению первого порядка с начальным условием (задача Коши):
-J — apt = аА (dyldt)sh[y(t)V~p\+aVrp<?(t), t>0 1 (8 2б2)
Т(р, 0) = 0. j
Решение полученного уравнения запишем в виде
Т (/?, t) = [аА/]/^) еаР* {e~a^f ch [y(t) V~p\ —
' \. 1
— 1 +ap\ e_flpT ch[f/(x)Kr^] dxi A-aV^P $ еар(/_т)ф(т)(1т. (8.263)
о Jo
Будем искать T (x, t) в виде ряда типа Фурье, соответствующего
классическому решению задачи для #(/) = const:
_ rrw I2
Т(х, 0=2>„(0е У<° sin^ (8-264)
У(*)
предполагая этот ряд абсолютно и равномерно сходящимся при
любом 0 < х < y(t) и любом конечном / > 0. Подставляя ряд (8.264)
в (8.260) и производя интегрирование, получим следующее выражение:
^ (_l)n+l„.fln(0exp[-(i^p) -t y(t)T(p,{) (80б5)
£«, p+nV/vMO “ nsh[j/(0TT] 1
Левая часть соотношения (8.265) регулярна всюду, за исключением
полюсов, расположенных на отрицательной полуоси
Pn = — n2u4y*(t), n= 1, 2, 3, ... (8.266)
Проинтегрируем обе части равенства (8.256) по р последова¬
тельно по контурам у1( у2, у9, ..., у пХ ... (рис. 40). Контур уп
состоит из вертикали о > 0, полуокружности радиуса Rn =
= [л2/2*/2 (/)] (2п2 + 2п-\-Л) (контур уп пересекает ось х в средней
475
точке между рп и рп+1) с центром в начале координат и двух го¬
ризонтальных прямых У = ± [n2/2y2(t)] (2п2 + 2п-{-1). Тогда окруж¬
ность Rn не проходит ни через один из полюсов подынтегральной
функции и по теореме Коши [92] интеграл по контуру уп будет
равен произведению 2ш на сумму вычетов подынтегральной функ¬
ции относительно ее полюсов, находящихся внутри контура уп:
\ f (р) dp = 2ni^ res [/(/?); />*].
(8.267)
Уп
Так как в (8.265) полюса рп — простые, а подынтегральная
функция f(p) имеет вид fi(p)/f2(p), то при вычислении вычета функ¬
ции U(p)lf2(p) относительно простого
полюса р = рк можно воспользоваться
формулой (см. § 2 гл. VI)
Res [/, (p)/ft (ру, рк] = [/, (pK)/f:2 {р)]р=рк.
(8.268)
Проводя последовательное интегри¬
рование (8.265) по контурам у,, у2,
у3, ..., следует также учесть теорему:
если f (р)—аналитическая функция на
замкнутом контуре у и в односвязной
области, ограниченной этим конту¬
ром, то
Рис. 40
J/(/?)dP=0 (теорема Коши [92]).
(8 269)
С учетом сказанного, находим
°i«)exp[ — р + п2/у2 (i)'
dp
z па« w ехр \ -(w1 У111 f+a,
Чуа (0
= y(t) С Т(р, 0 dp
я J sh [y{t)V~T\
Так как Res[(p+n7t/2(/))'1; (—я7г/2(0]= 1. а $ [p+ninilyi{t)]~ldp=
v'
2), то находим:
«.W°»Wexp[(^),(j^rJ Ibmra ■ *8-270»
476
Проинтегрируем (8.265) по контуру у2
«.«>чр[-(^)’<П d"
р + п'Чу'1 (О
V*
-2а, (() ехр [-(£«*)•.<] f г+и
V*
+ £, (~:1)п+1«аЛОехр[— (*£§р) -<]х
п=3
V Г dp У(0РГ(Р. Qdp
J Р+"2я2/</2 (О Я J sh [у (0 |TpJ '
Отсюда находим, используя (8.267)—(8.270):
а.(0 = -^е*р[(1^р)1-ф
х f 'Г QdP 1 г т{Р, о dp \
( 2л‘ J sh [1/ (/) j/"pJ 2ju J Sh[i/ (/) f/~p} J '
Продолжая описанный процесс интегрирования, приходим к следую*
щему выражению:
[(*£)■/] х
(п> 2) _
( 1 С T(p,t)dp i_ г Т(р, 0 dp
Xn| 2яг J sh[(/(0|/^] 2ш’ J sh [*/ (/) Y~~p\ j * ^ ’ *
V ул v«-i J
где Т (/?, t) представлено соотношением (8.263). Запишем подробнее
подынтегральное выражение с учетом (8.263)
Т (р, t) = aAch[y(t)V~t>\ аА&Рt
sh [у (t) Гр] Y~P sh [У (0 V~P.I V~P sh [y (0 Yl>\
а2АУ~~р
sh L .
+ST^I'*"-’,»Wdb (8-272)
"l^|e"»:«-)ch[S(,)K7]dt+
sh [y (t) Y~p]
Анализируя подынтегральное выражение (8.272), видим, что
первые два слагаемые в (8.272) регулярны всюду, за исключением
простых полюсов /7 = 0 и р = рп (8.266). Если учесть, чго (см. § 3
477
гл. VI)
Res |У1сЬЫг)ГЯеар(<_тД
\ &[y(i)Vр] I Р— —п*л*/у* (/)
р=1-п*п*/уш (/)
I Г Т(р, о dp 1_ Г Т (р, t) dp n / T (p,t) . \
2я/ Jn sh[«/(0K7] 2я; vJ iSh[,(OI^] \sh[«/(Or^] |
sh [y(t)V~p\
то окончательно получим после вычисления интегралов (8.270)—
Таким образом, если предварительно найден закон движения
границы y(t) из интегрального уравнения (8.259) [или из (8.258)]
и затем вычислены коэффициенты an(t) по формуле (8.273), то ре¬
шение задачи (8.254)—(8.256) можно записать в виде (8.264), и это
еще одно из возможных аналитических представлений решения
указанной задачи наряду с приведенным выше (8.257). Приведенные
рассуждения показывают также, что в нецилиндрических областях
можно построить интегральное преобразование (8.260), однако его
формула обращения (8.264), (8.273) и методика применения специ¬
фичны и отличны от классических, изученных в гл. V данной книги.
Эти вопросы требуют своего дальнейшего изучения.
Рассмотрим приложение теории к конкретному случаю, когда
на границе х = 0 поддерживается постоянная температура ф(/) =
= Ф0 = const <0. Решение задачи (8.254)—(8.256) для этого случая
получим двумя различными подходами в двух различных функцио¬
нальных формах и затем докажем их эквивалентность.
Предварительно приведем полезные для приложений соотношения
о
о
(к> 0)
478
Полагая в (8.274) /с = 0, получим еще одно соотношение
(-L) „ £ . ф (г) = ^ jе- 8,(8.276)
m= О г о
Выражения (8.274)—(8.276) были получены путем последователь¬
ного интегрирования слева по частям при условии, что каждый
раз полагалось U = e±x\
Для решения задачи (8.254)—(8.256) при <р (/) = ф0 = const ис¬
пользуем вначале метод дифференциальных рядов, развитый в§4гл.8.
Находим из общего соотношения (8.131) [см. также (8.257)]
оо
Т(х, 0 = (8.277)
Удовлетворяя граничному условию при х = 0, получим
00
-Ф.М = £ [(/'-(Oll-const. ,8.278)
Последнее соотношение выполняется, если
I у2п+1 (/) dy/dt = yntn,
\ у(0) = 0.
Интегрируя, находим [y2(t)]n+l = 2yntn+1. Полагая 2уя = Р2("+1\ по¬
лучаем закон движения границы в виде y(t) = $\f /, где неизвест¬
ный коэффициент Р подлежит нахождению. Для этого подставим
y(t) = рК t в (8.278) и произведем суммирование, используя (8.276).
В результате получим трансцендентное уравнение
— 2%/А Wa = реР'/*"® (p/2 V~a), (8.279)
решение которого относительно р можно получить графическим пу¬
тем. Искомое решение, имеющее вид автомодельного, можно полу¬
чить из (8.277), если подставить y(t) = $)/~T и произвести суммиро¬
вание (настоятельно рекомендуем проделать все промежуточные
выкладки).
T{w^i)=:~ e'>(2n+i)iws[^^—^ ~рт] =
= -T^*eK2lb)-0(w)] =
= Фо + 4^^е9-^ф(г^). (8.280)
Используем теперь подход (8.264), (8.273).
В случае y(t) = $V~t интегральное уравнение (8.259) имеет вид
00
2 \ ге-а?! ch (Рг) с!г = -^ (1 —фjaA)
г а
479
и после вычисления известного интеграла [20]
00
2 j ze-aj! ch (Pz) dz = ^ ) -f i-
2f/~a J o.
0
приходим к выражению (8.279). Коэффициенты an(t) для указан¬
ного частного случая вычисляются по формуле (8.273) и имеют вид
/4\ 2дЛ
anu) = a =—
п \ / п пп
+ а J е0'соэрТЛ d/ + (ea"W — l) = const, n= 1, 2, 3, ...
0
Полагая t = z2 и применяя к интегралу в квадратных скобках
формулу интегрирования по частям, получим после несложных
преобразований
П711& о ( ЯЛ*Ла \
ап = j e«lsinpzdz + -^\e o’— l), 1,
0
откуда и из (8.264) приходим к следующей функциональной форме
для искомого решения Т (х> t):
л п л со , , f V а пп\^ пз1{&
т{,. J
xslnp2d2 + iS![l_e"(ilTi!)!]}Si„^ =
пл Р У t
оо
2, . tlTCX < .
a”sin7VT- (8-281)
п=1 рк {
Покажем, что решения (8.280) и (8.281) совпадают.
Разлагая в (8.281) sin|3e в ряд и применяя затем соотношение
(8.275), а также (8.279) и (8.276), найдем
ди1 тт2 оо ПЛ,/$
V (—1)ш (ап2тс2/$2)™ . Лр2 ^ Р2« ас !
х т=к+ 1 m 1 пл « =о а* (2«+1)! Х
V (— I)m (ап2я2/Р2)т _ Af>2 j v Р8**! | V Р2к«1
„“l ml _ пл \ к = о °к (2«+ 1)! ак (2лс —(-1)! Х
у (—1)*” (ап2я2/Р2)т 1 _ Лф2 ( у Р2* ас 1 , у (—1)* (а/12л2/р2)*
о "*! J ЛЯ I к = О аК (2/с + 0 ^ к = 0 **
X
^ Р2т т ! \ _ А В2 ^ (—1)к (ая2л2/р2)* ^ Р2/я m '
Х т=к а'л (2т + 1) 1 «I ат (2« + 1)1
480
Таким образом, решение задачи (8.254) — (8.256) для случая
ф(/) = Ф0 имеет вид
где коэффициенты Ьп находятся по формуле разложения функции
Т (x/2\^at) в ряд Фурье на отрезке 0<х<Р^7 (см. § 1 гл. III).
Отсюда находим
т. е. Ьп = ап и выражение (8.280) может быть представлено в экви¬
валентной аналитической форме (8.281) — (8.283).
В случае задания на неподвижной границе х = 0 плотности теп¬
лового потока (<?Т7дл:)л:=о = (1А)ф(0> ^^0» необходимо применить
преобразование вида
и далее остаются справедливыми все рассуждения, но применитель¬
но к преобразованию (8.285).
Преобразование (8.260) можно назвать обобщенным интеграль¬
ным преобразованием. Оно позволяет рассмотреть как области с
движущимися границами, так и классические (с неподвижными гра¬
ницами). Особенно эффективным является применение преобразова¬
ния (8.260) при решении более общих задач стефановского типа —
краевых задач для уравнения теплопроводности со свободной гра¬
ницей. Рассмотрим одну из таких задач в достаточно общей поста-
00
(8.283)
(8.282)
оо
Т (х/2 V~ai) = 2 bn sin , 0 < х < Э |
/7=1 р у t
(8.284)
-jfr-j + Ф(^)]х
ft
плх , 2 сро /1 ч . Л6 r—
xsin й'./т d.x=—(1 — cosnn) + — t/Зш еР8/4аФх
p V t nn пи
ЯУ1
nnx
T (p, t)= j T (x, t) ch (x Ур) d*
(8.285)
о
481
новке
ж = °<х<у(0. о
(8.286)
Т(х, t)\t=0 = f(x), 0<х<г/(0) = г/о>0; (8.287)
Т(х, 0|*=о = ФЛО. ^>0; Т (х, 01«чг(О = Ф.(0. ^>0; (8-288)
Требуется определить температурную функцию Т (.х, /) и закон
движения границы y(t).
Задачи подобного типа возникают при изучении фильтрации с
учетом влияния связанной воды. Частный случай —задача Стефа¬
на при ф2(/) = 0, Ч (t) = Ady/dt. Эта задача не всегда имеет реше¬
ние. Например, в случае, когда f{x) = (t) = ф2 (/) = const, W (t) =£ 0
решения нет. Характерной особенностью рассматриваемой задачи
является наличие невырожденного случая: */(0) = */0>0 (в отличие
от вырожденных, когда при t = 0 область [0, y(t)\ сосредоточивает¬
ся в точке jc =«/ (0) = 0). Вследствие этого метод дифференциальных
рядов (см. § 4 гл. VIII) для такого рода задач становится неэффек¬
тивным. Метод обобщенного интегрального преобразования (8.260)
обходит эту трудность и приводит к решению задачи. Учитывая,
что задача (8.286) — (8.289) имеет большое практическое значение
и ее точное решение в литературе, по-видимому, не получено, рас¬
смотрим схему ее решения. Прежде всего докажем теорему единст¬
венности решения.
Теорема. Решение задачи (2.286) — (2.289) такое, что функция
Т (х, /), дТ/дх, d2T/dx2y dT/dt удовлетворяет условию Липшица в
Qt = {*£[0, y(t)\, 0</</„}, функция у {t) дифференцируема при
dy/dt > ф'2 (t)p¥ (t) единственно, если:
1) функции фЛ(0. Фа(0* ^(0. Г (х) непрерывны;
2) ф!(0<0; ФПО<0; V(t)> 0; /'(*)< 0; Фг(0<Ф2(0.
Доказательство. Дифференцируя уравнение (8.286) по ty
получаем dq/dt = ad2q/dx2, где q = dT/dt. Имеем ? |/=о = а/" UX 0,
q\x=o = q>' (t) <0. Дифференцируя тождество Т (у (t), *) = ф2(/), по¬
лучаем ^ = Ф^_(/) —Ч1* (/) d£//d/ ^ 0. Следовательно, q = dT/dt =
= ad2T/dx2 ^0 в Qt. Но (dT/dx)x=y{t) = ХР (t) > 0, поэтому dT/dx>
> 0 в Qt.
Допустим, что существуют два решения задачи (8.286) — (8.289):
7\(*. t), yx(t) и Тг(х, t), уг (()• Пусть у (t) = min [yl (t), yt(t)\.
В области Q, функция U (x, t) = T1(x, t)—Тг(х, t) удовлетворяет
уравнению dUjdt^ad^U/dx1-, следовательно, величина | У | прини¬
мает максимальное значение на границе x — y(t), так как U |*=о =
= 0, t/|<=o = 0. Там, где y(t)=y1(t), имеем
[дТ (х, i)/dx]x=y{t) = ¥ (t), t > 0.
(8.289)
^|*-й(о = Ф.(0-Т,(Ух(0. = t)-
-т* (уI (0. 0 = (Уг (*)-Уг (0) дТг/дх> 0;
dU | \тг/^\ ^7^
дТ,
дТ,
482
Аналогично там, где у (t) = y2 (/), имеем U (у2 (/), t) О,
(dU/dx)x=y2{t)^0. Следовательно, функция U (х, /) не может достичь
ни положительного максимума, ни отрицательного минимума при
х = у (t). Итак, Т1 (х, t) = T2(x, /), yx(t)^y2(t). Рассмотрим далее
вывод интегрального уравнения для определения неизвестного за¬
кона движения границы y(t). Для этого применим преобразование
(8.260) к уравнению (8.286) и далее аналогично (8.261) придем к
задаче Коши:
df/d/— арТ = а'Р (/) sh [у (t) ]Гр\ — aV^p q2(t) х
xc\\[y(t)V~p] + aVl>4i(t)i t >0; /onnn
№ (8.290)
T (p, 0) = J / {x) sh (x V~p) dx
0
с решением в виде
t
Т (/?, t) е~аР' = 5 е~аРх Т (т) sh [у (т) V”p] dx +
о
t t
+ V~P 5 e~aPx ф, (x) dx— V~P 5 e~°Px ф, (x)
0 0
y°
sb о (t) yfp\+ (1 /a)Jsh (xdjc, (8.291)
0
где p = a-H‘cD с Rep^P>0. Так как при t—► oo Re (/?£)—* оо, как
бы мало Р > 0 ни было, и если предположить, что интеграл Т (х, р)
(8.260) ограничен *, то функция ехр (—apt)T (р, t) будет стремить¬
ся к нулю при /► оо. Поэтому, полагая в (8.291) t—+ оо получим
интегральное соотношение по определению закона y(t) через крае¬
вые функции задачи
оО 1
(l/a)J e~apx(Pi(х)[sh(y(*)s/p)j^ ajp *
° xch[y(T)v^]dT + |e-^'F(T)x
О
OD
х sh[t/(x) p\dx-\~Vp J e-apT фх(х) dx-f 1/ax
о
Vo
xjf (x) sh (x V~P) dx = 0. (8.292)
* В противном случае вывод уравнения относительно у (t) производится с
_ y{t)
помощью преобразования Т (pt t) = ^ Т {xt /) ехр (—х \^~р) cU.
о
483
Заметим, что в случае вырождения области [0, y(t)] (у (0) = 0)
при /(х) = 0, Ф2(0 = 0, Ч(t) = А -^-соотношение (8.292) приводится
к (8.259), являясь, таким образом, более общим интегральным урав¬
нением, определяющим закон перемещения границы y(t).
Что касается вида температурной функции Т (я, /), то далее
ограничимся схемой рассуждений, предоставляя читателю провести
самостоятельно все необходимые выкладки.
1. С помощью подстановки Т (х, t)=W (х, /) + ©(*, /), где
0 (*, t) = [х/у (/.)] ф2 (0 + [1 —х/у (0] фг (0 переходим в (8.286) —
(8.289) к функции W (,х, t) однородными граничными условиями I
рода при х = 0 и x = y(t).
2. С помощью преобразования (8.260) с формулой обращения
(8.264) находим искомое решение в виде
00 (У^пя\2
Т (X, t) = 0 (x,t) + Д ап (t) ' sin ; (8.293)
°»(0= ft + 'T?(T)sjn^MdT +
0 о
' (Гшт\2, УМ
Tdx J FJjc, T) sin dx, (8.294)
о о
где fl (*) = f(x)—Q(x, 0); Ft (л:, /) = —дв/dt; q (t) = ¥(/) —(дв/дх)х=!,{1)
Из (8.293) — (8.294) следует при //(/) = у„ — const > 0, t ^ 0, улуч-
шенное решение’первой краевой задачи для бесконечной пластины
в классической области *£[0, у0], t^0 (см. гл. V).
Мы не останавливаемся на методах решения интегральных урав¬
нений типа (8.292). Здесь могут быть использованы методы асимпто¬
тических оценок (асимптотические разложения; метод перевала; ме¬
тод производящих функций), а также различные искусственные при¬
емы, приводящие для частных случаев краевых функций достаточно
быстро к положительному результату.
Изложенный выше подход (8.260), (8.264) касался ограниченной
области [0, y(t)]y t^0. Что касается полуограниченной области
[y(t), оо), /^50, то здесь также удается ввести обобщенное интег¬
ральное преобразование типа (8.260) и получить решение задачи
Стефана на основе интегральных уравнений, вытекающих из кон¬
турных интегралов Лапласа (типа Лапласа). Эгот подход развит в
работе [158].
Рассмотрим решение задачи о росте изолированной капли, на¬
ходящейся в пространстве, заполненном перенасыщенным паром
вещества, из которого состоит сама капля. Будем предполагать, что
при росте капля все время остается сферической и плотность насы¬
щения q не зависит от ее радиуса; предположим также, что перво¬
начальная плотность пара на поверхности капли равна плотности
484
насыщения. Соответствующая задача имеет следующий вид:
дб д2в 2 дб / Л ,Q опгч
-^ = 172+7аГ. г>у(т), т>0; (8.295)
в (г, 0)=Ф„(/•), г > y (0) = у9 > 0; 0(г/(т), т) = 1, т > 0; (8.296)
а5в^т)| = ф(т) (8
дг \г=у(х) dx v 7
I® (п T) I < + °°» r^y(T)t т^О. (8.298)
Здесь у(т)— радиус капли; 0(г, т) = [С(г, т) — С0]/(^—С0) — плот¬
ность пара в точке г в момент т; С0(г) = С(г, 0) — начальная плот¬
ность: С0= limC0(r) (С0 Ф q)\ а = (q—С0)/(р — q) < 0, | а | < 1; т = Dt\
Г—► ОО
р — плотность капли; Ф0 (г) = [С0 (г)— C0]/{q— С0). Предполагается,
что на бесконечности функции г0(г, т) и (д/дг) [г0(г, т)] ограничены,
а следовательно, гФ0 (г), {д/дг) [гФ0 (г)] также ограничены при г—► оо.
Определить закон роста капли у{т).
С помощью подстановки W (г, т) = г0(г, т) перейдем к следую¬
щей задаче:
dWjd т = d*W/dr\ г>у (т), т > 0; (8.299)
W (г, 0) = гФо (0=Ф И. г > у0\ W [у (т), т] = у (т), т > 0; (8.300)
a [dW (г, т)/дг]г=у{т) = у{т)у' (т) + а, т > 0; (8.301)
I W {г, т)|< + оо, r^yot т>0, (8.302)
причем dW (г, т)/дг, ф(г) и ду(г)/дг при г —► оо будут ограничены.
Кроме того, потребуем, чтобы функция <р(г) была абсолютно интег-
00
рируема на [у0, оо), т. е. чтобы J | Ф (О |dr < оо. Умножим уравне-
г- Vo
ние (8.299) на ехр [—г у р], где р — комплексное число с Rер^
> 0, —л/4 < argj/^< л/4 и проинтегрируем по г от */(т) до оо:
</(т) у(т)
Интегрируя по частям слева и вынося оператор (д/дт) за знак
интеграла справа, получим
+ [f~pc-ry~pW
Ш -гУр
дг е
*/(*)
у(1)
+ р J W (Г, j)e~rV7 dr = ^- j № (Л, т)е"гКр 6г + у'(х)е~У(х)}^ х
& (X) 0 (Т)
xW(r, T)|r=//tx).
Вводя обозначение
W {р9 т)= J W7 (г, т)е г ^ dr (8.303)
У (X)
485
и учитывая граничные условия (при г = у(х)), получим уравнение
для W (р, т)
Ж—pW^ — [>(т)-1/' (т) (1 + 1/а) + У~ру (т) + 1]е т > О,
решение которого имеет вид
т
е-рт W {р, т) — W(p, 0) = — ^ [у (t) у’ (/) (1 + 1/а) +
О
+ y(t)V~p+ \}z-p<-ywv» At. (8.304)
со во
Здесь W (р, 0)= J W (г, 0) e~rVp dr — ^ ф (r)e_r Vp dr. Вычисляя
У (0) Уо
в (8.304) отдельные интегралы, получим
e-f>xW(p, т) — W(p, 0) = —(у0/Кр+1/д)е-<'»Ур’ +
X
+[y{t)lVp+ llp]e-^-y^v^—(l/a)l y(t)-y,(t)e~f>‘-v^v'pdt. (8.305)
о
В равенстве (8.305) перейдем к пределу при т —► оо. Так как
при т —► оо Rе(рт)—► оо, как бы мало р > 0 ни было, а интеграл
W (/?, т) всегда в нашем случае ограничен, то функция ехр(—рт)х
х W (/?, т) будет стремиться к нулю при т—► оо. Находим из (8.294)
при т —*оо:
00
(р/\аI) {,t)e-°f-y<t)V^dt=>
0
00
= 0/оКр+ 1 )e“^Vp —р J ф (г) e~r VpAr. (8.306)
Уо
Получено интегральное уравнение для определения закона движе¬
ния границы у(т). Используем это уравнение для нахождения
асимптотического значения функции у (т) при т—►оо. Для этого
перейдем в (8.306) к пределу при /? —► 0. Тогда из (8.306) следует,
что должно выполняться условие
ао
lim T?-r[y(t)-y'(t)z-<>‘-yWledl = \. (8.307)
р -+ О I а 1 J
486
Соотношение (8.307) непосредственно используется для опреде¬
ления у (t) при т—► оо. Разобьем интеграл в (8.307) на две части
во /V
-|£у j У (0-у' (0 е-"-* w *^d/ =-^j- j у (0-у' (/) е-р'-х') vp dl +
о о
N
во
xe-y„vT+j^|- j y(t)-у' (t)e-p‘-y<‘> ^dt, (8.308)
N
где N—достаточно большое фиксированное число, так что pN 0
при р —+ 0.
Тогда получаем, что должно быть
00
^■\y{i)-y' 1. — 0,
N
или, применяя формулу интегрирования по частям,
00
(N) у' (N) e-»N-yW Гр + ylj- J e“'f [у (/) у' (t) е-» «> ^ х
N
X d/ —► 1, —0. (8.309)
При достаточно малых а можно приближенно удовлетворить
соотношению (8.309), если положить, что при t^N выполняется
у{т)-у' (т)/|а|~ 1, (8.310)
откуда
у (т) ~ У"2/а/т (т^> 1). (8.311)
Теперь осталось убедиться в приближенном выполнении соотно¬
шения (8.309) при условии (8.310). Первое слагаемое слева в (8.309)
при р —► 0 стремится к единице, следовательно, необходимо пока¬
зать, что второе слагаемое в (8.309) при р —► 0 и достаточно малых а
стремится к нулю. Имеем при условии (8.310)
х t ———. e-p/-v* |а| fit J/ = — 1/ 2 I а I P Г - е_^,ЛР/+ 1 1“ l/2)s + |a 1/2 x
J 2 yt 1 IAJ 2 yT
N N
(8.312)
00
xd/ = —1/2 | a | elа ,/2 \ e“*2djc =— У'я \ a |/2 e*а x
V pA’ + Г | a|/2
X(K pN-]-y\a i/2)p^v л | a |/2 el “ l/2 Ф* (J/ | a |/2) -* 0. (a—* 0).
487
Соотношение (8.312) будет выполняться тем точнее, чем меньше а.
Поэтому можно считать, что
.'r.lw-'h0*'»-
где 0(1)—► О при а —* 0.
Задача 1. Используя изложенный подход (8.303), рассмотрите однофазную
задачу с цилиндрической симметрией:
д77дт = д277дг2 + (1/г) дТ/дг, г > у( т), т > 0;
Т(г, 0) = Ф о (г), г>у(0)=у0>0; (8.313)
Т[у(т), т] =0, т > 0;
а (дТ!дг)г~у (т> = t/' (т) — <р (т), т > 0,
где предполагается, что Т (г, т) и rdTjdr ограничены при г—► оо и ф (т) огра¬
ничена при т > 0.
Указание. Обе части уравнения (8.313) необходимо умножить на rKo(r р)
(Ко (г V7)—функция Магдональда) и проинтегрировать по г от у(т) до оо.
Задача 2. Рассмотрите аналогичную задачу для неоднородного уравне¬
ния вида
ik=irw'nd-sr+F*'^ '>*М.*>0.
где п = 0, 1, 2 соответственно в декартовой, цилиндрической и сферической
системах координат.
Задача 3. Распространите изложенные в § 7 подходы на конечную область
{0* */(01* ^ > 0 в декартовой (цилиндрической и сферической) системе координат
при решении уравнения dT/dt =ад2Т/дх2 для невырожденного случая у(0)=Уо > 0
с краевыми условиями:
Т (х, 0) = ф0 (.х), 0 < х < у (0) = у0 > 0;
(Pn-f-T+l^)„0“Ф*(0.
(P2f‘S'+p227')^(<)=(p2(0’
Указание. С помощью подстановки
j N (Рч^-Ри) . фг (/)
Р12Р21 — Р11Р22 4“ Р12P22V (0
перейдите к функции W (х, 0 с однородными граничными условиями.
Задача 4. Используя тепловые потенциалы (8.46), получите реше¬
ние краевой задачи
дТ д2Т
= а , 0<x<l+vt, t> 0; (8.314)
dt дх2
Т(х, 0) = 0, O^x^l; (8.315)
Т(х, /)U=o = <MO, Т(х, t)\x=i+t, = (p2(t), ОО (8.316)
488
в виде
T(x,t)= 1
2у/дял--оо% (f_T)3^2
[*+2л(/+гт)]2| ^
х + 2 n(/+v/) j v(/+vi)n2
ф! (т) ехр <
4а(/ —т) J 2у/алп*
[* + (2л +1) (/+w 0] ✓ ч
<р2(т)х
- 00 *
о
(г-т)3/2
j *(/+«)».(И + 1) [лМ-(2я + 1)(/+«)]*]
хехр< ></т. (8.317)
e 4e(<-t) j
Получите операционную форму решения (8.317) (по Лапласу)
в виде
Т(х, p) = 9i(p)exp(-xy/pja)+-L £ (\/р+2ул)ехр| —-^и2 )х
у/Рп=1 \ у/а J
х j^exp ^ Jp) “ ехр ^ Щ Ф> [(\/р+2?и)2] +
+~Т Е (V^+(2« +1 )У) ехр Г - 21УП (П+*} |ехрГ-(2п+1_/ * -
у/рп=о L Vfl Jl \/fl
-ехр [-2n+J-'+X V^]} Фз [(>/р+(2и+ 1)у)2], (8.318)
где фз (Г) = <^>2 (0 ехр(>)20; y = v/2^a.
Выражение (8.318) может служить рабочей формулой записи
аналитических решений в изображениях (а (8.317) — в оригиналах)
первой краевой задачи (8.314) — (8.316) для широкого класса
граничных функций <p,(/)'(z=l, 2): однородных, импульсных, пуль¬
сирующих, периодических и др. Из него можно получить соответст¬
вующее выражение в изображениях и для функции Грина G(x, х\
t, т) первой краевой задачи нестационарной теплопроводности, если
учесть, что в данном случае q>\(t) и cp2(t)— это известные функ¬
ции (8.45) (если использовать определение функции Грина в виде
(7.82)).
Задача 5. Получите оригинал (8.49) для функции Грина, исполь¬
зуя соотношения (7.82), (8.44) — (8.45) и рабочую формулу (8.318).
16-339 489
Покажите, что формулу (8.318) можно использовать для
нахождения функции Грина первой краевой задачи для области
XG[li+V\t, /2 + ^2*]» t^O.
Задача 6. Получите функцию Грина первой краевой задачи
нестационарной теплопроводности для области jcefil+vt], t^O
в виде:
G(x, х', t, т) = -■ -- ехр { — г- [(*-х')- (и/2) (г—т)]1 х
2yjna(t-т) (.2а )
п“ + с0 Г Г (2/л + х-х'-»(г-т))2"| Г (2/л + х+х'—г(/ + т))2~1]
\.U4—s™—J-Ч—lr
Ч*р14*— jc)+t~(f—T>1 Lsi°”lt(Jf. *°к
/ |_2a 4a J", / I
Задача 7. Рассмотрите в области хе[0, vf], 0 краевую задачу
нестационарной теплопроводности со смешанными граничными
условиями: первого рода при х=0 и второго рода при x—vt. Пока¬
жите, что соответствующая функция Грина имеет вид:
1 n=Lj;00 я ( v2n2x + vnx'
G{x,x’,t, т)= - £
2yjna(t — т) л= -оо \
S с-1)*“| [■
а
к
Х<£(-1Г
vn ^ (2mrr+Jc' + ( — 1)
+-ф =l=-
2а \ 2ja(t-t)
к-1 \ -|
X
Задача 8. Решение задачи
дТ д2Т
= а—х>2у/ау (t), />0;
dt Зх2 ^
Т(х, 0) = 0, х>0; \Т(х, /)|< + оо, х^О, 1^0;
ОС
| Т(х, t)dx=2s/ay(t), t>0 (8.319)
2v'ay(l)
490
может быть записано в виде обобщенного теплового потенциала
простого слоя
о
неизвестная плотность (t) которого находится из удовлетворения
(8.320) граничному условию (8.319) как решение интегрального ура¬
внения
1
f У 00 Ф*\У (01^01 dz=2у {i)ly/nt. (8.321)
J LV'(l-z)J
О
Рассмотрите в (8.321) случаи: у(t) = fit(/?=const) и y(t) = fiy/t. Пока¬
жите, что в первом случае
Ч (0 = (2^1 у/%) [\+p2t+(fi2t+\l2)<b(Pyft)+
+ 03/V") \/^ехр(-P2t);
во втором случае
ччо=/?/>АЯ
у = [1+Ф (/?)] [1 - у/% Р ехр (fi2) Ф* (/?)].
Здесь: Ф* (/?) = 1 — Ф (/?); Ф (/?) — функция Лапласа.
Замечание. Предложенная модель представляет собой одну
из сравнительно новых задач теплопроводности с интеграль¬
ным граничным условием (8.319) и встречается при моделировании
ряда процессов экологии, биологии, физики плазмы, термомеха¬
ники.
Задача 9. Построить функции Грина для области t^0.
Указание. При решении соответствующих краевых задач можно
воспользоваться следующим приемом. Так в случае первой краевой
задачи
dG d2G /
— а + S (х — х') 5 (/ — т), х > /у/1, 0;
dt дх2
G(x, х\ t, т)|/=о = 0, х^0; |G|< +оо, х>0 0
491
G(x, x!y t, т)|х=у%/, = 0, />0
преобразования
z=xjy/lat, /'=(1/2)In/; G(x, x', /, t) = Gi(z, x\ /', t)
совместно с экспоненциальным преобразованием Фурье по перемен¬
ной /'е(— оо, + оо) вида
+ 00
Gi (z, x', 1', т)ехр(— i£t')dt'
сводят исходную задачу к виду
d2Gi <Л7) - 1 — i£/2 S/. 4 , ПГ
—+z-—z£G, = =t 8(z-z0), z>yl^/2a
* dz 2y/nax
GiUy/V2S=G,|z=co = 0 {z0=x’ly/ax)
допускающему переход к следующей эквивалентной задаче
d'01 dOi - , /Г-
—+z i^Gi = 0, z>yls/2a
dz dz
^\\z = yjy/2a Gl |z= oo 0,
Gi\z = Zq-0— Gi|z=Zo+o,
dG{
dz
z=zQ-0
dG\
dz
-0/2)(i+ tf)
z=z0+o 2yJa%
Решение последней задачи выражается через функции параболичес¬
кого цилиндра.
ГЛАВА IX
аналитические методы решения краевых
ЗАДАЧ СТАЦИОНАРНОЙ И НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ С РАЗНОРОДНЫМИ
ГРАНИЧНЫМИ УСЛОВИЯМИ НА линиях
ВВЕДЕНИЕ
Сформулированный класс задач возник в результате исследований по
механике хрупкого разрушения, относящихся к телам, содержащим
трещины (прямолинейные, эллиптические, круговые, прямоугольные
и др.) [1111. Когда равномерный установившийся тепловой поток с
вектор-градиентом, лежащем в плоскости образца типа тонкой пласти¬
ны или цилиндрического вида, возмущается из-за присутствия гео¬
метрических неоднородностей (дефекты типа трещины или инородные
включения с острыми краями), появляются локальные возрастания
температурного градиента [135]. С этим связано значительное увели¬
чение температурных напряжений (см. §8, гл. I), которые часто при¬
водят к выходу из строя различные детали. Вследствие этого большое
практическое значение имеют исследования теплового потока и тем¬
пературы вблизи вершины трещины, учитывая, что соответствующие
им термоупругие поля расширения (как и их механические аналоги)
увеличивают интенсивность напряжений в вершине трещины, застав¬
ляя ее расти. Последнее приводит к разрушению образца. Таким об¬
разом, этот класс задач представляет большой практический интерес.
Вопрос о тепловом потоке в бесконечной области вокруг отверстий
различной формы и с системой трещин, ориентированных различным
образом, привлекал к себе значительное внимание. К. Трантер [168]
выразил распределение температуры вне эллиптического цилиндра че¬
рез функции Матье. В предельном случае его результат сводится к ре¬
шению Г. Карслоу и Д. Егера [55] для кругового цилиндра, которое
выражено через функции Бесселя. К. Коутс [53] получил решение
задачи о неустановившейся теплопередаче в бесконечной области вне
прямоугольника; Д. Си [135] дал распределение стационарной темпе¬
ратуры в бесконечной среде с системой конечных коллинеарных тре¬
щин; В. 3. Партон [120] и Н. М. Бородачев [14] — для бесконечного
пространства с круговой (осесимметричной трещиной), В. В. Панасюк
с сотрудниками [111] — для неограниченного тела с системой произ¬
вольно размещенных термоизолированных трещин при больших рас¬
стояниях между ними и т. д.
Тепловые задачи такого типа связаны со значительными математи¬
ческими трудностями; в частности, когда изучаемая область многоевя-
зана, классические методы теории потенциала 133] и интегральных
преобразований-(см. гл. V—VI) не приводят к аналитическому реше¬
нию задачи. В большей степени это касается краевых задач нестацио¬
нарной теплопроводности, для решения которых можно рекомендовать
методы тепловых потенциалов [114] и Винера — Хопфа [110]; приме¬
нение этих методов к конкретным задачам изложено ниже. Что касает¬
493
ся стационарных случаев для уравнения Лапласа (2.85), то они сводят¬
ся к линейной задаче сопряжения (задача Гильберта) из теории функ¬
ций комплексного переменного [105] или к дуальному интегральному
уравнению [143], аналитические методы решения их разработаны до¬
статочно полным образом. Эти случаи также будут рассмотрены в на¬
стоящей главе.
§ 1. МЕТОД СОПРЯЖЕНИЯ ПРИ РЕШЕНИИ КРАЕВЫХ ЗАДАЧ
СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Краевые задачи сопряжения, или задачи Гильберта, непосредственно
связаны с определением кусочно-голоморфных функций в двух до¬
полняющих друг друга до полной плоскости областях. Таким образом,
метод сопряжения может быть использован для решения уравнения
Лапласа на плоскости с разными граничными условиями на линии.
Пусть D = {(*, у): |*| < оо, \у\ < оо};
В = •[(*, у): у = 0, |*| < /}.
Обозначим через D\B дополнение В до D, т. е. совокупность
точек М (*, у) из D, которые не содержатся в В.
Рассмотрим вторую краевую задачу стационарной теплопровод¬
ности, когда функции, входящие в граничные условия задачи, имеют
разрывы на внутренней трещине |*|</, */=.0, в плоскости (*, у)
(математически трещина представляет собой разрез нулевой толщины):
U + |£=0, {x,y)dQ = D\B; (9.1)
(ж1+-о = (1/^^
(fr),~=o=(l/^w
.. дТ ( дТ\® дТ ( дТ\* .. 0.
дх * ( дх ) ’ —ду ~\ду) ■
Vx2 + y*-+ 00 4 ' V х* + ул -► со 4
Здесь знак « + » относится к верхнему краю трещины, знак
« — » —к нижнему; qt(x) (* = 1,2)—количество теплоты, выделяю¬
щееся на единице площади поверхности трещины за единицу вре¬
мени. Функции qt(x) удовлетворяют условию Гельдера (см. § 5 гл. II)
на трещине | *| < /.
Введем комплексную переменную z — x-{-iy и аналитическую
функцию F(z) = T(x, y) + iW(x, у), где W (х, у)— функция, сопря¬
женная с Т (*, у) и определяемая с точностью до произвольной
постоянной соотношением
w (X, у) = 5 {дТ/дп) ds, (9.4)
М0М
где М0М—произвольный путь, соединяющий некоторую (произволь¬
ную) постоянную точку А10 с переменной точкой М (*, у). Функции
\х\ </; (9.2)
494
f (x,y) и W (x,y) связаны между собой условиями Коши—Римана [92]
дТ/дх = dW/dy, дТ/ду = — dW/dx. (9.5)
Уравнение (9.1) с граничными условиями (9.2) — (9.3) можно
записать, используя одну аналитическую функцию. Действительно,
—^
из соотношения для вектора плотности теплового потока q= — Xgrad Т
и условий (9.5) имеем:
Л ( дТ , . dW \ Л dF
-Qx + Чу = * (-аг +1 ~дГ ) = Х ЧГ'
Если ввести функцию Ф (г) = (1/7(12 так, что F (г) = J Ф (г) dz, то
окончательно находим:
—<7* + % = ^ (*); (9-6)
Т (х, у) = Re [Е (2)] = Re [ 5 Ф (г) (1г] , (9.7)
где Re—действительная часть (например, Rez = x).
Соотношения (9.6) — (9.7) показывают, что решение краевой за¬
дачи (9.1) — (9.3) сводится к нахождению функции Ф (г), удовлетво¬
ряющей соответствующим граничным условиям согласно (9.2)—(9.3).
Прежде всего определим поведение функции Ф(г) при больших
| z | = Vх* + у2у учитывая согласно (9.3), что при | г | —* оо компо¬
ненты вектора градиента температуры принимают заданные значения.
За основу рассуждений возьмем характер поведения многозначной
функции F (z).
Из (9.7) следует, что Re[F(z)] однозначна, так как однозначна
левая часть равенства. Однако мнимая часть функции ^(г) (функ¬
ция W(x>y)), выражаемая интегралом (9.4)) в рассматриваемой
двухсвязной области й, не является функцией однозначной [105].
Последнее означает, что при однократном обходе (против часовой
стрелки) какого-либо замкнутого контура С, охватывающего тре¬
щину, функция W получит приращение, равное некоторой действи¬
тельной постоянной В0; соответственно этому функция F (z) получит
чисто мнимое приращение iBQ.
Вместо постоянной В0 для удобства дальнейших рассуждений
введем другую действительную постоянную А (точное значение ее
будет установлено), полагая В0 = 2яЛ. Представим далее функцию
^(г) в виде
F (z) = А In г + F* (z), (9.8)
где F*(z) — аналитическая и однозначная функция в области й;
так как In z при обходе по контуру С вокруг трещины (против
часовой стрелки) получает приращение 2ш, то функция F(z) получит
как раз приращение 2niA.
Установим физический смысл и значение постоянной А. Пусть
п(cos a, cosP)—единичный вектор внешней нормали к произвольному
контуру С, однократно обходящему (как указывалось) трещину,
a L — контур, состоящий из нижнего и верхнего краев трещины.
495
Имеем дТ/дп = (дТ/дх) cos а(дТ/ду) cosfi, но так как cosa = d///ds,
cosЭ = — dx/ds [105], а из (9.5) и (9.7) следует, что дТ/дх = Re [dF/dz],
дТ/ду= Re [/dF/dz],,то приходим к следующему равенству:
дТ/дп = Re [(dF/dz) (d^//ds) — i (dF/dz) (dx/dz)] =
= Re [(dF/dz) (d/ds) (y — ix)\ = Re [(— i) (dF/dz) (dz/ds)] =
= (d/d s) R e[—iF (z)];
отсюда dF/ds = dRe[—/F(z)]. (9.9)
Интегрируя обе части равенства (9.9) по контуру С (против часовой
стрелки), находим
J(дТ/дп) ds = Re {[— iF (г)]с}, (9.10)
С
где символ [ ]с обозначает приращение выражения, заключен!Юго
в квадратных скобках при однократном обходе по контуру С ука¬
занным образом. Стягивая далее контур С к контуру L и используя
при этом (9.2) и (9.8), получим
i
A=Ql(2n\)-, Q= J [qt (*)—qt (*)] d*. (9.11)
- /
Таким образом, постоянная А выражается через граничные
функции задачи. Функция F*(z) может быть представлена вне L
рядом Лорана
F*(z) = n~2 anz\ (9.12)
n= — 00
причем этот ряд равномерно сходится во всякой конечной области
вне L. С учетом (9.8), (9.11) — (9.12) имеем
п= + оо
F (г) = Q In г!(2пК) + 2 апгп. (9.13)
П— - ос
Отсюда
П= + оо
дТ/дх—idT/dy — dF/dz — 0(z) = Q/(2nXz)+ 2 папгп~г. (9.14)
п= — СО
Единственные члены, которые могут неограниченно расти вместе
с |z|, происходят от ряда
П— + * п- +ао
2 па„гп~1= 2 папгп~-1 ехр [(п—1)йр],
п= - оо п= - оо
где использована тригонометрическая форма числа z = rexp(/(p).
Отсюда для выполнения граничного условия (9.3) должно быть
ап = 0, 2. Таким образом, при больших |z| имеем:
dF*/dz = a, + а_ Jz'2 -f a_2/z3 + ...
Ф (z) = -j Q/(2nXz) h 0 (1/z2).
496
J (9.15)
Из (9.14) и (9.15) следует, что ах = (дТ/дх)00 — i(dTldy)°°. Окон¬
чательно находим для функции Ф(г) при больших \г\ следующее
представление:
Ф (г) = (dT/dx)°° — i (дТ/ду)00 + Q/{2nXz) + О (1/г2). (9.16)
Используем далее граничные условия (9.2). Из (9.6) имеем
0(z) = (dT/dx) — i (дТ/ду). Отсюда сопряженная с Ф(г) функция имеет
вид Ф (г) = (дТ/дх) + i (дТ/ду). В результате находим
Ф (г) —Ф (г) = —2i (дТ/ду). (9.17)
Равенство (9.17) на краях трещины имеет следующий вид:
Ф+ (х)—Ф+ (х) = —2/ (дТ/ду)+ о,
_ \\Х\<1. (9.18)
Ф" (х) —Ф” (*) = —2/ (дТ/ду)у=0 "
Обозначим через Ф (г) функцию, принимающую сопряженные
с Ф(г) значения в точках г
Ф(г)=Ф(г) (9.19)
(например, F(z) = T(x, —y)—iW(x, —у)).
Из (9.19) следует Ф(г)=Ф(г), так что
ф+ (х) = Ф“ (х); Ф~ (х) = Ф+ (х). (9.20)
Используя (9.18), (9.19) и (9.20), находим;
Ф+ (х)—Ф~ (х) = 2 (1/W) qt (х);
,,х|</. (9.21)
ф- (х)-Ф+(х) = 2(1А/)<72(х). ” '
Складывая и вычитая соответственно левые и правые части равенств
(9.21), приходим к следующим выражениям;
[Ф (х)—Ф (х)] + + [Ф(х)- Ф (х)]~ = 2/, (х), | х | < /; (9.22)
[Ф (х) + Ф (х)]+ — [Ф (х) + Ф (х)]" = 2/а (х), | х | < /, (9.23)
где M*) = (1AO[<7i(x) + <72(x)]; /, (х) = (1Д/) [qt (х)—q^x)].
Выражения (9.22) и (9.23) представляют собой граничные усло¬
вия задач линейного сопряжения [105, 135], суть которых заклю¬
чается в следующем: требуется определить кусочно-голоморфные
функции [Ф(г) — Ф(г)] и [Ф(г) + Ф(г)] по заданным скачкам на
на контуре (граничные условия (9.22) и (9.23) представляют собой
скачки названных функций на контуре L). Вначале запишем реше¬
ние задачи линейного сопряжения с граничным условием (9.23).
Для этого необходимо знать [Ф(оо) + Ф(оо)], которую находим
из (9.16)
Ф (оо) + Ф (оо) = 2 (дТ/дх)”. (9.24)
497
Решение задачи сопряжения с условиями (9.23) и (9.24) имеет
i
Ф(г) + Ф (z) = ± j ^ <И + 2 (дТ/дх)~. (9.25)
Неоднородные задачи сопряжения с условием (9.22) рассматри¬
вались Н. И. Мусхелишвили в связи с изучением задач упругого
деформирования [105]. Общее решение задачи с условием (9.22)
записывается в виде
,9 26)
Здесь Р (z) z=cQzJrcl—многочлен первой степени с неопредлен-
ными коэффициентами, подлежащими нахождению; X (г)—функция
Племеля
X(г) = V1^T\ (9.27)
Через Х+ (х) обозначено значение этой функции на верхнем краю
трещины. Заметим, что функция (9.27) является аналитической вне
контура L, многозначной в плоскости (х, у)> и в (9.26) выбрана та
ветвь X (г), которая при больших \ г\ имеет вид
X (г) = г (1 —/2/2г2 +...)• (9.28)
Сложение и вычитание равенств (9.25) и (9.26) дает;
Ф (z) = Ф0 (г) + Р (г)/Х (г) + (дТ1дх)~: (9.29)
Ф (г) = Ф0 (г)—Р (z)/X (г) + (дТ/дх)", (9.30)
где Ф0(г) и Ф0 {z) выражается через сингулярные интегралы:
<<»<>
<9-эд
- / -1
Выражения (9.31) и (9.32) записаны как сопряженные (проверьте
это утверждение), и это обстоятельство имеет важное значение для
определения постоянных с0 и сг. Здесь необходимо иметь в виду,
что X (г) = X (г) = X (г); Х+ (/) = — X + (t) (проверьте справедливость
этих равенств).
Из (9.29) и (9.30) следует, что правые части этих равенств
комплексно-сопряженные; отсюда коэффициенты с0 и ct должны
быть чисто мнимыми, т. е. c0 = ic'0, c1 = ic[ где с'0 и с[—действитель¬
ные постоянные. Из (9.26) и (9.28) находим при | г | —► оо
Ф(ОС)_Ф(ОО) = ( Шm (гНгпю -2*.
С другой стороны, из (9.16) следует, что Ф(оо)—Ф(оо) =
= (2/(,)(“^")°°‘ Таким образом, c0 = — i(dT/dyY°. Для определения
коэффициента используем условие однозначности температуры
498
f (x, у), согласно которому циклическое значение функции должно
равняться нулю. Более точно это условие заключается в требова¬
нии, чтобы величина Т (х> у) = Re [Z7 (2)] оставалась неизменной,
когда точка г опишет контур С (против часовой стрелки), окру¬
жающий трещину
Выражение (9.34) представляет собой, по существу, алгебраическое
уравнение относительно 6^ = ^. Функции OJ(jc) и Ф0~ (х) находятся
по формулам Сохоцкого—Племеля [105]:
Используя (9.34) — (9.36), а также значение интеграла [111]
находим, что Cj = 0 (проделайте подробно все выкладки). Оконча¬
тельно искомая функция Ф(г) имеет следующий вид:
Рассмотрим далее в (9.2) случай, когда граничные функции по¬
стоянные qx = const и <72 = const. Вычисляя по таблицам [20] интег¬
ралы, входящие в (9.37), и учитывая (9.7), находим решение задачи
Re ^Ф(г)бг =0.
(9.33)
с
Стягивая контур С к L, из (9.33) и (9.29) получим
(9.35)
фо М ~ х+ (ж) 2 W+2л( j
L -i
х+ (0 h (0
t—x ш
(9.36)
Ф(г) = -
УТ*-ТЦд 1 (<) + <?, (Q1
2я ХУ z*-P
t — z
(9.1) — (9.3):
Т (х, у) = Re {[(dT/dy)~-( 1/2Я) (q, + ?,)] (- i) +
+ [(<?! + 92)/(2(>-)] г + (дТ/дх)*‘г -— [ 1/(2jx>.)] (<7i — <7»)х
х [(г—/) In (г—/) — (г +1) In (г + /)]}. (9.38)
499
После выделения действительной части (рекомендуем проделать все
выкладки самостоятельно) окончательно приходим к следующему
выражению:
т {х'у) = утsign у [ {%)" ~(1/2^)^]х
х [V f + 2f (х2 +/2) + (х2—/2)2 + уг— (х2 — I2) Y/г —
- (1 /2пК) (gt - qt) [ ± (х -1) In (if + (x-l)2)-
—у (* + 0 1 n(y2 + (x+l)2)+y (arctg■jj-.—arctg^-y) j +
+ Л:('ду) +23L#(7i + fo)- (9.39)
Здесь sign у = j.
Выражение (9.39) содержит достаточно большое число частных
решений, которые нетрудно выписать, фиксируя значения гранич¬
ных функций, определяющих характер теплового режима на бере¬
гах трещины и на бесконечности.
Задача 1. Получите асимптотическое выражение для температуры в ок«
рестности вершины (правой х=1 и левой х= —/) трещины.
Ответ. Т{х, у) = 2Н^ъп (0/2), где Н^т^Щ^дТ/ду)™; т=\-(дТ/ду)°/(дТ/
/ду) (O^m^l). Здесь ql—q1 — q\ {г, 0) — полярные координаты с центром в вершине
трещины (г±/=гехр(/0)); (дТ/ду)+ = (дТ/ду)~ =(дТ/ду)°;
Задача 2. Используя изложенный метод, получите решение первой крае¬
вой задачи стационарной теплопроводности (задачи Дирихле) в плоскости с тре¬
щиной разрезом:
d2Tjdx2 + d2T/dy2 = 0, (х, y)£Q = D\B\ *
Г+(дс, 0) = Г1; ) I
T~ (x, 0) =7’2; | 1 1 ^ > (9.40)
lim T (x, y) = T°°. J
Ответ. T (x, y) = Re |Z^^№+Z^,n^+,-^+|(T1+r.2)}=,
_2Г°°-(7’1 + Гг) {(л:2+'/2)[(^-'2)г+У(^+^)+У4]1/2+(-^+‘/г)2-(-^-»2)^)1'2 |
2]Г2 У (x2 — l2)2 + 2y2(x2 + li) + yi
+z^(arctg7b--arctgFb)+I4z:2- (9-4i)
Задача 3. В условиях задачи 2 получите асимптотическое выражение для
температуры в окрестности вершины трещины.
Ответ. Т (х, у) = Н \Г~г cos 0/2 + 0 (rl/2), где Н = тТ°°У //2; т=1 — (ГХН-
Т2)/2Т°°\ (г, 0)—полярные координаты с центром в вершине трещины.
§ 2. МЕТОД ДУАЛЬНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
В ЗАДАЧАХ СТАЦИОНАРНОЙ И НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
В приложении теории интегральных преобразований Фурье (см.
гл. V) к решению краевых задач стационарной и нестационарной
теплопроводности на плоскости и в пространстве с разрывными
граничными условиями на линии часто удается свести задачу к
500
решению пары совместных уравнении:
со
(9.42)
ао
И1 - <7 (!) ] / (£) А- (Ю dl = ф (Г), о < Г < R-
О
оо
(9.43)
О
где ф(г) (а также и <7(6)) — известная функция, a f(Q — функция, под¬
лежащая определению. Уравнения типа (9.42)—(9.43) называются
дуальными интегральными уравнениями. Формальное решение урав¬
нений (9.42) с помощью теории преобразования Меллина дано Титч-
маршем в его книге по теории интегралов Фурье [141]. Что касается
уравнений (9.43), то Трантер [168] с помощью разложений в ряды Ней¬
мана свел некоторые частные случаи уравнений (9.43) к бесконечным
алгебраическим системам. Однако более эффективным оказался способ,
предложенный Куком [171] и Н. Н. Лебедевым [89], позволяющий
свести уравнения (9.43) к регулярному интегральному уравнению от¬
носительно некоторой вспомогательной функции. Помимо теории теп¬
лопроводности уравнения (9.42)—(9.43) нашли применение в задачах
электростатики, дифракции, гидродинамики идеальной жидкости, тео¬
рии упругости. В табл. 15 рассмотрены различные частные случаи
уравнений (9.42)—(9.43), наиболее часто встречающиеся в теории теп¬
лопроводности. Воспользуемся указанной таблицей при рассмотрении
конкретных задач стационарной и нестационарной теплопроводности.
Пусть Т (,х, у) есть решение задачи:
Учитывая, что функция Т (х, у) четная по х, достаточно рас¬
смотреть область х>0, у> 0, что позволяет применить к Т (х, у)
косинус-преобразование Фурье:
Решение преобразованного уравнения (9.44) (см. табл. 9) с уче¬
том выполнения условия (д77дх)х=0 = 0 запишем в виде
т (л. У) = с 01) ехР (— щ) (П > 0).
д2Т/дх2 + д2Т/ду2 = 0, | х | < оо, у > 0;
(дТ/ду)у=0 = — (1/А,) q, |*| </;
Т \у=а — О» I х I О
Т^дс, у)],* 1-.. = О, у> 0;
т (*> У) I- ~ = °> М<°°-
(9.44)
(9.45)
(9.46)
(9.47)
(9.48)
(9.49)
О
501
Таблица 15
Парные интегральные уравнения
Решения
Jf (5) Sin £п*£ = ф(г), 0 <г<Л
о
= г >Л
О
j / (£) sin 5rd* =-•= 2 апгП» 0 < r < Л
О п=0
Jlf IZ) sia= 0, г>Д
О
го
J / (5) cos = Ф (г), 0 < г < Л
о
со
j £~J/ (S) COS = 0, г > R
0
1 f (У ccs Irdl = 2 enr" ’ 0 < г < R
о n=0
]“*/(!;) cos £rd!; = 0, r > Д
о
0<г<д
0
f/l^v(^)^ = °- r>R
(a> 0)
f 5.“/(5.) /v (?r) d* = ф (г),0< r<i?
о
J f{f,)J4(tr)dt. = 0, r>R
° (— 2 < a < 0)
П1-
о
0<г<Д
lZf&)Jo{Zr)d*=0, r>R
/(0
/w
=yS«" ~к~т| $ ^ <гЛ*> ^
n "=» rUT2)e
2r f , , , , С Ф(РМР
=J ^/.(rj,)d^^==p-
/ (r) = j/" -y* OoR/i (rR) —
“ Г("2 + 2)с
— /2 Д 2 en ГлГ” \ g"Jl (гЛу> ^
«1 r(-2) o°
nr)^T:;./aga/1v^wx
1 (a/z) о
. „ . , V lv+1<p№)d<
X(^n)dnj (1_(1)i-a/it
,, ^2-<42rl-*llR™/l ^ fj irft^
f {r) Г (1 -г a/2) Г v+a/2 < Л> *
x j yv+1 (1 — ys)a г X ф (yR) dy + rRX
x ] riv+1 (1 — Л2) a'2 x j y2+a/2 X
о о
X Ф(етД)/у+1+а/2 (r^y)<ty]
H
/(r) = j У (y) cos rydy, где У (г) — реше-
о
нне интегрального уравнения У (г) —
4 R
— 1$ К (r,t)y (t)dt = F(r); здесь Я (г,
ло
ОО
t) = 2 j q (£) cos !;r cos Л (r) =
о
_ 2 dr У Ф (V) <*У
Jl dr J l/ ra — t/2
502
Таблица (продолжение)
Парные интегральные уравнения
Решения
И [!-?«)]/«) Л>Кг)<*$ = <Р(0.
О
0<r< R
J/(5)/.(^)« = 0, г > Л
j [1-9(5)]/'(5)/.(^)<^ = Ф(г).
О
0<г<Л;
Jf® ■?•&)<% =О, г>Л
10
11
i [l-9«)]/R)/v(W^-T(r)t
О
0<г<Я
00
$д/ d)Jv (lr)di =0, г > Л
j U1 — ? (£)] / К) л, Kr> ^ = v (г)-
о
О <г<Л
f/(5.) /v«r)« = 0, г>Л
/ (г) = J Y (у) sia rydy, где Y (г) — решение
о
интегрального уравнения ••
i R
fw-ij«(r,0 4'W* = f(1,
n 0
oo
здесь К (г, 0 = 2 J ? (£) sin £r sin
о
», v 2 г УФ (У) dy
F{r)=»>v^w
R
f (г) = г j ¥ (y) cos rydy, где ¥ (r) — pe-
o
шение интегрального уравнения
r (r)-if K(r,t)V[t) А-Г (г),
°
? У^У
здесь Л(г,1)-2 J ^__==Х
X J ^ (£) /о (Sy) cos ltdl\ F (г) =*
о
_ 2 Г У Ф (у) <*У
л" г /у1-'-8
R
f (г) = YЯГ/2 j / у Т (у) /v_l/t (гу) dy
О
где Т (г) — решение интегрального урав¬
нения R
V(r) — If K(r,t)'J'(t) А = r~vF(r),
71 О
оо
здесь Я (г, г) = я \[ rt j (£)/v_Vj X
о
X (£>■) J^i, (It)dl', F (г) = — gr X
Xj
/г2 — у2
dy
i (О = v^/211/у ^ (у) ^v+v« (гу)
0
где 'F (r) — решение интегрального
уравнения
1 R
'Y(r)-±lK(ryt)'F(t)dt = F(r)1
71 о ^
здесь К (г, t) = я^ rt J i;g (^)^Vl_i/t X
x (;r)/v+1/t =
= ir-vi
yVf4 (y) <*y
503
Таблица (продолжение)
Парные интегральные уравнения
12
J[l-»(«]/«) Л, (&■)<*-?(')
О
0<г<Я
ОО
J Ш/„ (W Я = О, г>д
13
5(^+Y*rV*/(5) /,(?г)<15 = ф(г),
О
О <г<Л
оо
J/(«/.(W<*5*=0, г>л
к
/(r) = r/j5T2J/Jy (y)Jv-t/t (гу) dy,
о
где ¥ (г) — решение интегрального
уравнения
4 R
¥(r)-±J*(r, t)4T(t)dt = F(r),
я J
здесь Л (г, f) = rv (2ж)'/* х f jd_^L= X
г |/ у» — г»
ОО
X j ^ ? (5) /v (5.v) /V.v> fcy) <15; Л (Г) =
О
= (2/п) гЧ+^ШЛУ
rl/y*-r>
Я
/(r) = r j У (у) cos (у /г»' + V*) dy,
О
где ¥ (г) — решение интегрального
уравнения
R
V (г) — J JT (г, ОЧ'(<)* = /■ (г),
О
оо
здесь Л-(г, t) = у J (r|t)n+'l• J х
п=0
X (yO (YO; /’(г) = |-^:х
х Г *Я>(») costyyA»—х» ) j_
О V*—X*
14
15
j / (T)^_,/i+it(cbl) dr = у (x), 0<x < 1
О
J т/ (т) th пт p.,/t+rt (ch x)dr = h (x),
0
x>l
I T/(T)/>.Vi+iT (chx) dx =* 9 (x),
о
0<x<J
oo
j 1 (T) th пт 1/t+iT (ch x) dr = A (x),
О
/ (*) = (V^/Ji) [ j C' (y) cos xydy -f
0
00
+ 1*1 (y) cos xydy],
1
„ „/ч ^ ^ (P) sh Pdp
здесь С (у) = Г — - i ;
^ V^chy —chp
Я(у) = $
h (P) sh Pdp
У j/"ch P ch у
i
1 (*) = (Vr2/ji)[ j С (y) sin xydy —
о
00
— (y)sinxydy];
1
„ , , “ g (P)sh Pdp
здесь С (у) = V -======;
о Vchy —chp
?MP)shpdp
, j/^ch p — ch у
504
Таблица (продолжение)
7*
Парные интегральные уравнения
16
17
5 зЬят/ (г) Р_1/|+1, (Chi) dt О,
0<*<1
ОО
j т ch ят / (т) Р_ |/>+1-т (ch х) dr =
о
= — 7(1 + ch, *>J
J/(t)[l + <V(t)]P_Vi+iT (ch*) dt =
= 9(x), 0<*<i
ft/ (t) thnt P_./>+>T (ch *) dt = 0,
0
*>1
18
19
]xf(r)P_l/t+ix(chx) dt = 0,
0 <*<!
J/ (t) thnt (1 + ЛГ (t)] P.,/i+iT X
0
X (chx) dx = q (x), x>J
J т/ (r) [1 + N (t) ] P!i/>+iT (Ch r) dt=
0
= ?(*), 0<x<J;
j / (t) th ят P™,/t+ix (ch i) dt = 0
0
(PTi/,+»t (chx) — присоединенные
сферические функции; =0,1,2...)
ch* j
где Y (x) — решение интегрального
уравнения
0 I
y(*)-£fJC(*, t)T(0dt = P(*).
здесь Р(*) = ?^Y 1 Г-_-х— 1;
яа dxLch(x/2)J
*Г/ .V Х “Ь * 1 1
= sh (х 4- г)/2 + sh(x —0/2
i
/СО- — ^(У) costydy,
о
где ¥ (у) — решение интегрального
уравнения
I
v (I/) + (2/n)J X (у, *)Y(t)dt =
,/? . V 9(0) ,? 9'(PMP 1
= _1?sh47^+J/3hF^pJ’
oo
здесь К (у, = $ N (т) соз т*соя tydt
/(т)= J TMsinrydy,
I
где Ч'’ (у) — решение интегрального
уравнения
¥ (V) т (2/.t)°j к (у, <) У (0 dt = Р (у),
I
p# 1 -сд. ■ d ? 9(Р)sh pdp
здесь Р (у) (/2/n)_j /chp_-W
ОО
К {ytt) = § N (т) sin ty sin тtdx
/(т)= jT(y) sin Tydy (T(0)-0),
0
где ¥ (у) — решение интегрального
уравнения
i
r (у) -f (l/я) f [* (t — V) — К (t + »)] X
X T(<)dt = P(y),
здесь К (*) •« ^ iV (t) cos txdt;
0
2 ^ ?(P)sh ftdfl
\f2 (ch у —-ch 0)
505
Таблица (продолжение)
Парные интегральные уравнения
Решения
20
^ / М Р\ых <сЬ *) I1 + N dx =
о
= ?(*). о<*<1
сс
^ т/ (т) th птР™1/,+(т (ch X) dx - О,
О
Х>1
= J ^cos ту dy'
0
где У {у) — решение интегрального урав¬
нения
1
Y (У) + — ^ [К (' + У) + к (< - »)] X
о
х*(ол = Г(у);
оо
здесь К (z) = \ N (т) cos xx dx; F (у) =
в 2_ £ Г
я dy )
Ф (х) sh х dx
]/2 (ch у — chx)
■, Ф (*) =
XX X
=§ S ■ ■ ■ §q {х) (Х* ~irm/2dxnv+
+
(Ь = ъЬх
= chx); постоянные ск нахо-
21
^ т*/ (т) sin xxdx — q (x)t 0 < x < I
0
oo
\^ / (t) cth nxsinixdi = Л (x), x>J
22
^ У (т) cos xx dx = q (x), 0<x< I
u
oo
x*f (t) cth пт cos xx dx = h (x), x > Z
№-±1)
дятся и? условий Ф(1) (Z) = 0, i = 0, 1, 2,...
... (m — 1)
I
1 (т) = T th ЛТ [ ij F, (p) P_1/i+iT (ch P) x
OO *»
X sh р<гр + \j f, (P) P_I/i+iT (ch P) sh pap j ,
здесь Fl (P) = iGL f — q'(y) dy ;
n J j/ ch P — ch у
F2 (P)_£Ef - ... ; Jfc = _ J:
я J ^ ch у — ch P
4iiv)=q'{y)\ k = + i:qi(y) =
X «
= — (/) dv‘ +c; ^ ^ / (т) dx
о 0
i
/ (t) = т th лт ^ Fl (P) F.,/i+it (ch P) X
0
X sh P dp + j Ft (P) P_,,i+iT (ch P) sh P dp j ,
здесь F, (P) = VT \? g (V) dV .
л J yA ch p — ch у
506
Таблица (продолжение;
Н Парные интегральные уравнения
23
24
25
jp (»»+1ы)\рп (*) = «(*).
п=0
-1 <ж<1
оо
£Л,Л(*) = М*). ,<;С<1-
П=0
Г(*) = _1_ -£1 (** — 1>Л — поли
\ 2 nl dx
номы Лежандра)
оо
jrw (*) = »(*>.
п*-0
оо
£(» + >/») i4nP„ (*) = />(*),
п—о
1<х<\
^(1-Рп) ^„(соз *) = ?(*),
п—о
О <*<«
оо
у1 (n + Va) (сое X) = О,
п-=0
J<X< Л
Рп (г) — подинолы Лежандра;
lim Рп = О
F% (Р) -
= V^2
(у) dy
к = — \:
71 g }f ch у — ch р
(у) = - h' (у); к = -f- 1 : ^ (у) =
оо оо
= — ^ л (у') dy' + с; с = jj / (т) dt
v о
arccrsI
An=)LL^ ^ cos (п+Чг) <fd<f J- X
и
X С _Ш*У + ? c03(n + i/t)x
J (у —СОЗфГ* J ,
совф arccos*
cos <p
х^ф С чШу Л
(cos ф — у) ''J
arccos I
An = iQ. £ ^ sin (n + >/«) ф<*ф X
0
x (
J (y — (
COS ф
я
— ^ sin (n + */«) ф<*ф Щ x
» Ф
f g (v) ]
J (COS Ф —
Ь (У) dy _
(y — COS ф)1/*
arccos *
cos ф
X
—l
I
An=§т (<) cos [(п^т)1 ] *•
0
где У (*) — решение интегрального урав¬
нения
i
Y(*)-(l/n) (j [А-(( + 1) + Я((-*)]Х
О
X4r{t)dt^F(z),
здесь Я (у) = pn cos (n +1/а) У\ F{x) =
П*=о
X
_ 2 d Р g (z) sin rdz
я dx j 2cos z — cos x
507
Таблица (продолжение)*
Парные интегральные уравнения
Решения
26
27
£ iinpn (««>■ в) - 9 (в). О < в < е.
п—О
^ (n + Vi) АпРп (С08 в) *=
п—о
еа<в<я
ОО
Л (л + т) ^пга(во*в)=°.
П—ТП
0<в<в,
ОО
£ <* - Р»МппЛ" (СОВ в) =/т(в)
п—т
во ^ в ^ Я
V (*) — присоединенные функции
Лежандра; т =0,1,2,. . Пт Рп=0
28
^ (я + Va)m^n sin (л + Va) ф = ? (ф),
>0
О < ф < р
оо
У, Ап sin (» + Va) ф = А (Ф),
Р<Ф<Л.
т = ± 1
508
__ а*
= J cos (п -Ь llt) * х
о
х ri.C-?(e)sipe<*e 1 ■>.
I dt J l/^COS в — cos t J
Л
/<«m=5 Ут<‘> *ь(я + у)<л.
вв
ГД0 W ~~ Решение интегрального урав¬
нения
л
(*(<-*)-* (< + *)] X
в.
Xrm(t)dt = F(x),
ОО
здесь ЛТ {„) = ^ pn cos (л + >/.) у; F(*)=.
П=з
£
л J
= р фш (сод в) sin в d8
: J |/ сов х — cos в
XX х
*mW = (-1)m ( ^ С £у(Х> **"+■
J J (1 _ x*)m/2
rv—1
-1 -1 -1
+ fm(X)=/m<0)- ^ = cos 0;.
*=0
постоянные akm находятся из условийг
V^>(e„) = Ot A = 0,1, 2,... (m — 1)
= ^n Г (f p
я/2" Lj n
(cos 0) sin 0 <Z0 x
X +
J (cos ф — cos 0),/f
- С (cos 0) sin 0 d0 \ ^ (фМф 1
J J ]/ COS 0 — COS ф J
здесь 'F (ф) ==
Я' (Ф), m =* — 1;
Ф ao
|-J* (ф') <V + ^ m = + 1; с = ^
Таблица (продолжение)
jsft Парные интегральные уравнения
Решения
29
30
31
32
оо
cos(n + -i)T = }<V),
п—О
о < ф < Р
оо
(" + Т ГАп cos(a + т)ч’=Л (ф)
п=О
Р<Ф<л; (т ± 1)
+
АП — ^ рп (cos е) sin 9 <*9 X
* о
е
х С д (ф) dtp [
J (cos ф — cos в)1^*
? я
\ Рп (cos в) sm9<i6 С 1М^£_1;
у J (СОЗв —СОЗф)'М '
Р о
—Л' (ф), т = — 1;
я
— ^ h (ф') Йф' 4- с, т = + 1;
здесь Y (ф) =
ОО
^Лпз1плф = ?(ф), 0<ф<р
П= 1
О»
^^п31плф = А(ф), р < ф < л
П=»1
ОО
- 1
И<Р
оо
^»псоз(л-|)г = 0,
П=» 1
Р<М<я
оо
У.КЧЛ (Pnr) = g(Q.
1<г<я
п=>1
v^ Va* рп>0 — корни
уравнения; /v (рД) = 0
п=о
9 (ф) sinn ф <*ф -f-
4--Ь[{
о
я
+ ^ Л (ф) sin п ф<*ф J
1
АП = 2 sin (Р/2) ^ (я, 1-л; 1; у» sin* р/2) ^
о
X У (v) dy,
Y(y) = 2ysin (P/2) X
у
Г g [2arcsin (д sin Р/2)]
J ]/7i/a-^2)(l-x»sin*p/2) *'
X
здесь F (n11 — n\ 1; y* sin* p/2) — гипер-
геометрпческая функция
, _21-^r(l-p/2)Pg/» ^
W}+i (Pn-R)
X J (Pn0
<F (0 Л,
где 'F (/) — решение интегрального урав¬
нения
4'(r)-^Lsia^L^ (t//-)V_p/2 X
X Я (r, /) >F(0 dt = F(r),
509
Таблица (окончание)
Nk
Парные интегральные уравнения
Решения
здесь
7 к. №)
K(r,t) J 1ч(Яу) 1у-"12 {Ги) /у-^2 х
0
X {ty)ydy\
2р^ d f ,zv+1q(z)dz
K } Г* (1 — я/2) dr ) (r.
о 7
* В соотношениях 7-12 предполагается lim <7 (1) *» 0.
fc-oo
** Решение интегрального уравнения Фредгольыа второго рода V (г^ — р j К (г, t)W (f) х
о
оо R
X dt=>F (г) имеет вид: V (г) = ^ где ^ = F ^r); = j*к dtl х
n^=0 (n > 1) О
X j К((„ ««....J К ((„-2- J К(! n-1. („>F<'n>d,n-
0 0 о
откуда по формуле обращения для преобразования (9.49) находим
— ®
т (*» У) = ]/"4 J ^ (Л) е"ПА'cos Л* (9.50)
о
Неизвестную функцию С (т|) найдем, удовлетворяя граничным
условиям (9.45) — (9.46), что приводит к следующей системе дуаль¬
ных интегральных уравнений:
00
S Чс (л) cos трс d»i = Vя/2 (q/X), 0 < х < /;
о
«D
J С (tj) cos r\x dr] = О, х>1,
или
оо
J 1УлС(11)] r\j~ 1/2 (трс) dr] = (q/X), 0 <x<i,
J [Vr\C(r\)]/_,/, (r)x) dri = 0,
. 0
(9.51)
510
если воспользоваться известным соотношением из теории бесселевых
функций: cost}X = V(п/2) r\xJ -ц2 (т]х).
По формуле 1 табл. 15 находим неизвестную функцию С (т])
в виде С (г|) = у (?/А) л”1 Л (лО» а вместе с этим и решение
исходной задачи (9.44) — (9.48)
00
Т (х, у) = {qim $ т]_1е- wJ, (i\l) cos i)x dt). (9.52)
0
Для вычисления интеграла в _(9.52) представим выражение
ехр (— т]у) cos цх в виде Re [ехр (— izt|)], где г = jк—iy, что дает
следующий результат:
оо
т (X, у) — (ql/X) Re J r\~lQ~sVt (r]I) dr] =»
0
= (q/>w) Re()/r/*—za— iz) = (q/X) Re(* z* —l* — iz). (9.53)
Поясним выделение действительной части в (9.53). Рассмотрим
Re 0 )/""г2 — /2), учитывая, что Re(—iz) =— у. Положим z — / =
ч 0 ^ = pi ехр (—itрО, где Pl = | Г—/1 =
^7 у = V(х—/)2 + у2, a cpj обозначает угол,
% образуемый с положительным нап¬
равлением оси Ох вектором, имеющим
начало в /, а конец в z (рис. 41),
причем угол ф| заключен в пределах
Рис‘ 41 (0, п) и отсчитывается от положи¬
тельного направления Ол: по часо¬
вой стрелке; аналогично, г+/=р2 ехр(—/ф2),где р2 = |г + /1 =
= У (х + 1)* +у*. Имеем
Re (i VI2 — /2) = Re|/ (cos [ sin2l+^ j j j =
= Vlhih sinSii^- = V PiP2/2 V1 —COS (<p, + Ф») =
= V P1P2/2 V 1 —cos фх cos ф2 + sin ф! sin ф2 =
Y 2 1Кг ' P1P2 P1P2
= (1/К2) [lV + 2(/2 (x4 + /а) + (x* - />)2 + </2-(x* - /»)]l/2. (9.54)
511
Здесь было учтено, что
X — / х-\-1 . и и
cos Ф1 = ; cos(p2 = —; sin ф,=-; sincp.2 = —.
Pi р2 1 Pi Т2 р2
Окончательно выражение (9.53) с учетом (9.54) можно записать
в следующем виде:
Задача 1. Используя указанный выше подход, найдите температурное
поле в полуплоскости | х | < оо, у > 0, если граничная линия у — 0 имеет темпе¬
ратуру ф (х) на отрезке \х\ < / и теплоизолирована вне его; кроме того, выпол¬
няются условия ограниченности температурной функции на бесконечности:
Перейдем далее к цилиндрической системе координат (г, ср, г)
и рассмотрим следующую задачу. В пространстве 0, г^О гра¬
ничная плоскость 2 = 0 имеет температуру Т0(г) внутри круга
0 ^ г </? и теплоизолирована вне его. Найти распределение тем¬
пературы в указанной области. Имеем:
С помощью преобразования Ханкеля по переменной г устанав¬
ливаем, что решение уравнения (9.56) может быть записано в виде
т С*. У) = (?А) [Г г/4 + 2 (*2 +12) г/2 + (хг—/г)2 +
(9.55)
дгТ/дх2-\-дгТ/ду* = 0, | дс f < оо, у > 0;
Т (*. У) |j,=o = <P (*). \x\<h
СО
где Ф W= 2<JnJtn-
ОО
Ответ. Т (х, у) = У2/п ^ ф (г|) е-ЛУ cos п jc dr|, где ф (тр = У n/2a0Uг (г\1) —
о
—V^ ап — р ' j a”^i Ша) ^а* Рассмотрите три случая: ф (jc) =а0 =
оо оо
= const; ф(*)= 2aKJc2K+' —нечетная функция; ф (х)= 2акх2к—четная функция.
(9.56)
(9.57)
(9.58)
(9.59)
(9.60)
Т (г, г)|^.=0, /•> 0.
Г (Г, г) = Sec (g) y,(Er)e-s*dg,
(9.61)
О
512
где неизвестная функция С (5) находится из удовлетворения гра¬
ничным условиям (9.57) — (9.58). Это дает следующую систему
дуальных интегральных уравнений:
(9.62)
5 I-1 [g*C (|)] J, (|r) d| = т0 (г), 0 < г < R,
О
оо
$tl*C(|)]7t(|r)d| = 0, r>R.
о
По формуле 2 табл. 15 находим
R х
с ®=А 5cos ^xF w dx> где F (x)=I (9-63)
о 0 ^ p
и далее решение исходной задачи в виде
Г (л, z) = ^Re(C—PW_d* (9.64)
где р(х) = х—iz (здесь z>0—аппликата, не путать с аналогичным
обозначением комплексного числа z = x-\-iy). Выделение действи¬
тельной части в (9.64) можно произвести аналогичным образом, как
и выше, однако здесь необходимо рассмотреть отдельно два случая:
0^r</?, z^O, и r>R, z^O. В результате найдем:
Т(г У? f Г ^ »* + 2»,(/-»+*,) + (г>-х«)1 + (г*-Ж«) + «*У/» w
(0<г<Л) “ я j w L **+2г* (/•*+**)+ ('■*-**)* J
г> 0 0
. , l/Ifp,, ч Г V V+2г2 (г2+хг) + (Jt*—Л2)2—(*2—г2) + 22~11 ■'* ,
л J z* + 2z2(/-z+*2) + (*2-/-2p J 1
Х<
л j L с--\-лс~
г
R
T(r, Z) = L1Jf'Wx
О
(г > Я, z>0)
w Г ]/’г4 + 2г2 (г2 + х2) + (г2 — *)2 + (г2—*2) + z2 ]1/2 ^
Л[ * + 2г*{Г* + Х*) + {г* — Х*)* J U*‘
В частном случае, когда температура внутри круга 0 ^ г < R
постоянна Т0(г) = Т0, выражения (9.61) и (9.63) приводят к сле¬
дующему решению задачи:
Т(г, г) = — arctg ^+lfp°sin *P/2t
д г + \Гро cos ф/2
где p2 = (r2 + z2— R2)2+ 4/?2z2; tg9=y2-_^2^^2 , допускающему также
иную функциональную форму, которую нетрудно получить из (9.64).
Задача 2. Используя выражение (9.61) и табл. 15, получите решение сле-
513
дующей задачи:
' ДТ (г, г) = 0, г > О, г > О;
^ (г. *) lz=o = о, /■>/?;
Г (г, г) |t^.e =Т (г, г) |г^ш =0.
R
Ответ. Т (r, г)= — Im
Гс .fw Д.
я (J V>-p*M j
dx*, где Im — мнимая часть комп¬
лексного выражения (например, Im z = y); F (х) = J ~====r df; p (x)=x—iz
о Vх*—$2
(z—аппликата).
После выделения мнимой части получите следующий результат:
.» -УЪ Г г™ Г V г* + 2г2(X2 + /•*) + (га-х2)2 + (x2-r2)-z2ll/2
foivjr “^rwL z4+222 (i2 + r2) + (r2-x2)2 J <*-
2>0
Гг,.лГ V^ + W (X2 + r2) + (x*~ r2)2 + (x2 - л2) - 22 ]1 /i!
Я J WL 2‘+222 (Х2 + Г2)-)-(Х2-/-2)2 J
X dx;
(г>Д, z>0) я J L
+ 2z2 (r2 + *2) + (ra—д:2)2— (г2 —x2)—22T/2 j
г* + 2г2 (x2 + г2) + (Z-2—x2)2 J
С помощью системы дуальных интегральных уравнений 9 табл. 15
могут быть рассмотрены более сложные случаи для уравнения (9.56)
в области г > 0, z > 0, когда в плоскости г = 0 имеют место раз¬
личные условия теплообмена со средой в к цуге 0 ^ г < R и вне его:
АТ (г, г) = 0, г > 0, г > 0; (9.65)
(,дТ/дг-^Т= - Тt (г), 0 < г < Я; (9.66)
(дТ/дг-кгТ)г=0 = - 7’, (г), г > Я; (9.67)
7>, г) = 0. г^О; (9.68)
Т (г, г) Iz-.» = 0, г>0. (9.69)
Решение уравнения (9.65) запишем в виде
Г (л, г)=}Л(!)7,(£г)е-е*(1Е,
(9.70)
где неизвестная функция А (£) находится из удовлетворения гранич¬
ным условиям (9.66)—(9.67). Это приводит к следующей системе
дуальных интегральных уравнений:
J (1 + К) А (|) У0 (lr) dt = Г, (г), 0 < г < Я;
О
оо
S(6 + *«MG)y.(£r)dS = ;r,(r), Л>Я,
(9.71)
514
которые могут быть сведены к случаю 9 табл. 15. Введем для этого
подстановки:
С(|) = (| + Л,)Л(&); <7(|) = (А,-Л1)/(| + А1) (9.72)
и преобразуем (9.71), учитывая (9.72):
оо
S 11 -Я Ш] С (I) У, (tr) d£ = Г, (л), 0 < л < R-
(9.73)
5С(|)У0(|л)б| = Г2(г), r>R.
О
Разложим далее функцию Т2(г) в интеграл Ханкеля
00
r.w-S&vujy.aods, (9-74)
о
доопределив ее каким-либо образом в промежутке (О, R)\ способ
доопределения в силу единственности решения не может влиять на
окончательное решение краевой задачи (9.65)—(9.69) и, следова¬
тельно, на значение величины С (£) = D (£) + ^ (£), где D(t) удов-
ле1воряет следующим парным интегральным уравнениям:
5 [1 -q{l)] D (|) /„ (lr) dg = Ф (л), 0 < л < R-
О
со
5D(|)yo(|r)d| = 0. r>R,
(9.75)
полученными на основе (9.73) — (9.74), если ввести обозначение
ca)-wa)=D(i).
00
Здесь Ф (г) = 7\ (л) — J £ [1 — ^7 (i)] Т(^) J0(lr) d£ —известная функ-
о
ция. Находим далее по формуле 9 табл. 15
* R
D (I) = £ j <р (у) cos Ъу йу = I Д J <р„ (у) cos \у dу, (9.76)
О л = О О
R
где ф0(г/) = -^-jp|p^=rdp; <р„(г/) (n> 1) — решение рекуррентного
41 я
уравнения ф„ ((/)=$ Z7 (у, а) ф„_, (а) da в виде
О
R R
Ф„ (У) = $ F (У, at) dax J F (at, аг) das...
515
• ••
0 0
Я 00
F(y,a) = 2 f —|-dP— f lq (I) J0 (10) cos la d|.
J J/ p у2 J
Из (9.72) и (9.76) находим
A (?) = V (?) + ^zpir I ч> (У)cos & dy
0
и далее искомое решение задачи из (9.70) в следующем виде:
оо
Г(Л *) = jI^'F(!)-U£r)e-&2dS +
О
Я оо
+ jq>(*)d* j j^j-J0(tr)e~iz cos| xdg, (9.77)
О U
где ф(х) и 4(1)— известные функции.
Задача 3. Рассмотрите тепловую задачу для уравнения (9.65) с условия¬
ми (9.68) — (9.69), когда внутри круга (г = 0, 0^r<R) задана температура,
а вне его происходит теплообмен со средой нулевой температуры по закону Нью¬
тона:
T(r, z)\2z=Q = T0(r), 0 <г</?;
(^дг Z)~hT{r' г))=°> '>*•'
Я ее
Ответ. Т (г, г) = J <р (у) dy J |(£+Л)-1 70(|/-) е~^ cos \у d|,
Ф(г/)=£^<РП(2/);
п=0 О r * v
R оо
<Гл (у) = У (у. «) Фл-1 (a) da (« Ss 0; F (у, а) = 2h j cos ?^°s ?a jg.
0 0
Задача 4. Рассмотрите случай, когда внутри круга z = 0, O^r < R про¬
исходит теплообмен со средой температуры TQ(r), а вне его температура равна
нулю
[дТ (r, z)jdz—hT (rf z)b=0 = — T0 (r)t 0< R;
т (r> 2) |z=0 = 0, г > R.
R оо /я \
Ответ. Т (г, г) = j (((х) dx Jyg (£cj e-J2 sin |x d|=— Im | J |.
u U Vo ^ и V ly
516
— 1
где р (х) ~x^iz (г > 0 —аппликата); <р (х)Фя W’*
п=о
ф°(*)=^|тЭДИ; флх)=
R
= §F(x, a)fn_!(a)da(n>l); F(x, a) = — h\n |*1”| •
О
Указанный подход сведения краевой задачи стационарной тепло¬
проводности к системе дуальных интегральных уравнений оказы¬
вается весьма эффективным и при рассмотрении более сложных слу¬
чаев, а именно, когда процесс теплопроводности нестационарный.
Здесь можно указать ряд задач, точное решение которых в литера¬
туре, по-видимому, не приведено.
Прежде всего рассмотрим задачу нестационарной теплопровод¬
ности для пространства 0, |z|<oo, с нулевой начальной тем¬
пературой и постоянной температурой Т0 в плоскости 2 = 0 в точках
круга 0^г</?. Учитывая симметрию температурной^ функции по
переменной z относительно плоскости 2 = 0, запишем:
дТ (д2Т , 1 дТ . д2Т \ . Л ^ Л /Л _0.
Ж==а{!?Г+Тд? + W)’ г>0’ z>0; (9,78)
Г(г, г, 01<-о = 0, г>0, г>0; (9.79)
Т (г, г, 01,-. = Т„ 0 < r < R, t > 0; (9.80)
[дТ(г, г, t)/dz]z= о = 0, r>R, t> 0; (9.81)
Т(г, г, 0lr—= 0, 2>0, 0; (9.82)
Т (г, г, /)|2_оо = 0, г > 0, ^>0. (9.83)
В § 1 гл. V отмечалось прикладное значение такого рода задач.
Применяя к Т (г, 2, t) последовательно преобразования Карсона —
Хевисайда по переменной t
00
Г (г, 2, р) = р\т (г, 2, t) e~pt d t (9.84)
о
и преобразование Ханкеля по переменной г (см. табл. 9 в гл. V)
со
7 (I, г, р) = 5 ^0 (Ъг) Т (Г, 2, />) dr, (9.85)
о
решение преобразованного уравнения (9.78)
d2f/d22 — (|2 + p/a)f = 0
с учетом граничного условия (9.83) запишем в виде: Т (£, 2, р) =
=С (|, р)ехр(—г l/~£2 -j- p/a) и далее в пространстве изображений
517
(9.84) получим для Т (г, z, р):
00
Т (г, г, р) = J 1C (g, р) У0 (gr) е~гУЪ‘+ро dg.
(9.86)
Здесь С (£, р) — неизвестная функция, подлежащая нахождению из
граничных условий (9.80) — (9.81) (но в пространстве изображений
Карсона — Хевисайда; напомним, что при этом изображением посто¬
янной величины Т0 является сама величина Т0). Удовлетворяя гра¬
ничным условиям (9.80) — (9.81), приходим к системе дуальных ин¬
тегральных уравнений:
1 00
$gC(g, p)JAlr)tl = T„ 0<г<Я
О
оо
5 i VI2 + р/а С (|, р) У0 (gr) dg = О, г > R,
о
которую можно записать в следующем виде:
J [\-q(t, р)] Л (g, р) yo(gr)dg = ro, 0<Я;
О
00
Sgl (g, р) У0 (gr) dg = 0, r>R,
(9.87)
если ввести подстановки
9(6. Р) = Г
Е
; Л (g, р) = С (g, р). (9.88)
V 12 + Р/а
Заметим, что при выборе подстановки для q(l, у?) всегда пред¬
полагается выполнение условия: <z(£, у?) —* 0 при £—*оо. По фор¬
муле 7 табл. 15 находим для А (£, р) в (9.87):
R оо
А (5. Р) = { Ф (У. Д) cos gу dy, где <р (у, р) = X, — ф (у, д);
И л=0 Л
Фо(у, p)=47’»i|p=p%=l7’o; *«<»• 0 =
я
= §F(y> а> P)<Pn-i(a> p)da(n> 1);
О
00
F(i/, a, p) = 2^q(t, р) cos gi/ cos ga dg =
0
^(.-^cosg^dg. (9.89)
518
Выражения (9.88) и (9.89) позволяют, записать решение исход¬
ной задачи в пространстве изображений Карсона — Хевисайда в сле¬
дующем виде:
00
Т (г, г, p) = V~a § £J4 (£, р)
—— Vp + al*
]а J0(lr)dl (9.90)
Переходя далее в (9.89) —(9.90) в пространство оригиналов, ис¬
пользуя для этого основные теоремы и формулы операционного
исчисления для преобразования Карсона—Хевисайда [41] (проде¬
лайте подробно все выкладки!), получим в окончательной
форме решение задачи (9.78) — (9.83):
Т (Г, г, t) = j уттг dT | T) e_aS,(<_T)y, (Sr) dl,
(9.91)
oo R
где Л(&, t) = ^rs\nlR+^ Дг (фл(Р. Ocos£PdP; Фл(P. 0 — решение
Яё „=1 «О ^
рекуррентного уравнения
t R
Ф»(Р. 0 = t-V'tn-xfr.WK п>1; ф0(Р, 0=-^;
00
F(p, к, 0 = 2^Ф*(т|Кв7) cos t|P cos г|Х dr) =
о
1 [p/1 1 3. (р+Х)*\ р( 1 ,.i з. №-».)* м
~ Ч 2 ’ ’ 2’ 2 ’ 4 at ) *г\2' * 2 ’ 2 * 4а/ JJ'
Здесь 2Р2 (а,, аг; р,, р,; г)—обобщенный гипергеометрический ряд [20].
Задача 5. Получите точное решение краевой задачи нестационарной тепло¬
проводности для бесконечной плоскости (дг, у) с внутренней прямолинейной тре¬
щиной | х | < /, у = О, поверхность которой имеет температуру Ч? (дс, /)> (где
¥ (дг, О —функция, четная по дг):
зт / а2г , а2г \ , , Л , Л
di ~~а ( дх2 ду* ) ’ Iх I <00 ’ у > ’ > ’
т (*. у> 0|,»о=°. 1*1 < у > 0;
Т[Х,.У, 0|„шд-ф(*. 0. 1*1 < 1,1> 0;
[ЗГ (ДС, у, 0/ЭД„-о = 0, |дг I > /, / > 0;
Т (х, у, /)||,|_«, =0, у > 0. / > 0;
Т (дг, (/, 01 .■-<* =0, I х I < оо, t > 0.
Ответ.
где В (£, /) — известная функция:
/
ВЦ, 0 = —Цт(У, О-М&Му—X т^г J ^УФл(У. f)h(\y)Ay;
О п= 1 О
, А 2 d f >(Р, О
Фо (г/, 0 = — т \ 1 dP‘»
Teu" я dr/J *,а_ра
/ R
4>п(у> = 1 dxjF<y> *—*, ч)фл-1 Ol. T)dri(rt^l);
00
f(y. <. T|) = nVr»iyJg®*(£|<Aa7)/l(^)yt(£»l)d6-
Замечание. Полученную в ходе решения задачи систему дуальных ин¬
тегральных уравнений
00
5 A Ц, р) COS £* d£= |^я72? (*, р), 0 < х < I;
О
00
5 V1*+р/аАЦ, р) cos £< d| = 0, х>1
сведите к формуле 10 табл. 15 с помощью подстановок:
Л=\ СЦ, Р) = -±=г\
1г+р/а V1
cos 1х = У л$х/2 J _ 1/г (|ж).
Я(1, Р) = 1 — -7=^ I С(Р) = —V 1г+р/аАЦ, р);
V 1*+р/а у 1
Приведем полезные для данного класса задан интегральные
соотношения, но-видимому, отсутствующие в известных справоч¬
ных руководствах [9, 20]
00
1
Ua (£0 sin £х ехр (- £у) <% =
= ~7-[х(х2-12+у2)у/р-(х2-12)+у2 +
VV
+у(х2 + 12+у2)л/р + (х2-12)-у2]; (2.31)
520
J\(Zl)cos txexp( — £,y)dc, = X\ \— ' f.Xs/p + (x2-l2)-y2_
{ 1 I Pwf2
-У\/'р-(х2-12+у2)\};
00
J
Jo (£/) cos £,x exp(-£j) d£,=—-= ^ p-{x2-l2)+y2.
pjl
Здесь p2 = (y2 + x2 — l2)2 + 4y2l2.
К этим соотношениям сводятся интегральные представления
искомых решений в виде (9.50), (9.61), (9.70) после решения парного
интегрального уравнения относительно Л(£) или С (г/).
§ 3. МЕТОД ТЕПЛОВЫХ ПОТЕНЦИАЛОВ ПРИ РЕШЕНИИ
КРАЕВЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
С одномерными тепловыми потенциалами мы встречались в гл. VIII
при рассмотрении областей с движущимися границами. Указанный
метод оказывается эффективным и при рассмотрении двумерного
уравнения нестационарной теплопроводности в плоскости, содержа¬
щей полубесконечные разрезы (трещины).
Прежде всего изучим свойства теплового потенциала для пло¬
ского случая.
Двумерным тепловым потенциалом простого слоя по прямой у= 0
называется интеграл
п<* »• *>-<9-92>
о о
где ф(х, 0 — плотность теплового потенциала, представляющая собой
функцию, непрерывную при |jc|<oo и /^0.
Пусть S—область, состоящая из точек |я|<оо, у = 0.
Тепловой потенциал (9.92) вне точек области S является реше¬
нием однородного уравнения теплопроводности Т\ = а&Т (х, у, t),
дважды непрерывно дифференцируемым по пространственным коор¬
17-339
521
динатам (х, у), непрерывно дифференцируемым по времени t и удо¬
влетворяющим нулевым начальным условиям. Это следует из того,
что производные функции П (х, уу t) вычисляются путем дифферен¬
цирования под знаком интеграла фундаментального решения дву¬
мерного уравнения теплопроводности (см. гл. VII), так как подста¬
новка, входящая при дифференцировании по /, равна нулю:
Т> Ала (i—) еХР[- JL, =
= [Ф (S. т) Go (X, у, /, Е, 0, т)]/=т = О,
в силу того, что уФ О при / = т. Таким образом, дифференцирова¬
ние будет относиться к функции G0(x, у, /, 0, т), удовлетворяю¬
щей уравнению теплопроводности в (7.30).
Имеют место следующие свойства функции П (х, у, t):
1. Тепловой потенциал (9.92) вне точек области S является непре¬
рывной функцией точки (х, у) и времени t.
Действительно, с помощью замены переменной
_ (X— 1)2 + у2 . . (X— 1)2 + у2
4а (t — т) ’ т ‘ 4аг
преобразуем потенциал (9.92) в интеграл следующего вида:
п<*-^ J ф(5. ^-(Д:~Е+у2)-7е~г(1г’ (9-93)
0 (х-Ъ)* + у*
4 at
являющийся непрерывной функцией точки (х, у) и времени t, что
устанавливается непосредственным рассмотрением приращений ин¬
теграла (9.93).
2. Нормальная производная теплового потенциала простого слоя
дП/ду при подходе вдоль нормали п к точкам области S изнутри
(г/ —► 0+) и извне (у —► 0—) стремится к своим непрерывным пре¬
дельным значениям и эти предельные значения представляются со¬
ответственно равенствами:
[дП (х, уу t)/dy]y-+o+ = — (1/2а)ф(х, О»
<?П(х, у, t)/dy]y-+o- = + (1/2а) ф (х, t).
Докажем это утверждение
= g_ Г ГФ(&^Е>ехрГ —(дс~l)3+y-ldTd£
ду 8яа» П (*-т)’еХР|. 4а (t— т) ]ата=*
Рассмотрим вначале для определенности значения х > 0. Запишем
для этого случая
t),\
)• )
(9.94)
ап у_ f (• ф(6, т) _Г (*-£)2+уа~
дг/ 8ла2
о
/ ао
Г Г ч»(6.
ехр[ — (JC4u f/iy ]dT dl = Jl (X, у, t) + jt{x, у, ().
522
Интегралы Jх и J2 преобразуем с помощью подстановок:
г = 0/2 V a (t—т); 0 =| *—£ 11 г \l\y\,
учитывая, что \г/у\ = г/у, \ х— 11 = (х—|) для У, и |х—|| = £ —х
для У2. Получим
(y>°') = lb ] e_z‘dz f ф(^-т* •*—E?)x
У х\г\
2V1 W\
xe‘P’dP-i j e-*id2Jq.(x—/-^je-P'dP;
v_ 0
2
1 e'2‘dz J ф(*—T-.i&-)e-p,dP-
У X \ z\
2 Vat I У I
“i J e-**d*Jq>(*—^r)e-P*dp.
У 0
2a VT
Переходя к пределу при у—+ + 0, получим требуемое соотноше¬
ние (9.94); аналогичным образом исследуется случай х < 0, для
которого \х—£| = Б — х и, например,
|г^>°) = —JST 5 е"г<1г 5 ф(Х-]T^-4&-)e'P'dP-
У -*l*l/lvl
2 Ко/
Тепловой потенциал (9.92) является удобным выражением для
записи общего решения двумерного уравнения нестационарной те¬
плопроводности на плоскости с разнородными граничными усло¬
виями на линии у = 0, так как позволяет сводить решение задачи
к интегральному уравнению Фредгольма; для решения последнего
могут быть использованы методы последовательных приближений,
Винера — Хопфа, интегральных преобразований Фурье и др. Осо¬
бенно удобным этот метод оказывается при рассмотрении плоскости
(или какой-либо ее части) с разнородными граничными условиями
на полубесконечной части действительной или мнимой оси.
Действительно, пусть Т (х, у, t) — неустановившееся температур¬
ное поле в верхней полуплоскости, удовлетворяющее условиям:
ж = а(5' + 'р') • М<°°. 0>О, />0; (9.95)
7" (лг, £/, /)|/=0 = 0, | jc| <оо, 0 > 0; (9.96)
Т(х, 0, <)|*=. = Г.. х>1, *>0; (9.97)
[дТ (х, у, t)/dy]l/=„ = 0, х < /, / > 0; (9.98)
1^ (*. 0- 01 < г °°. |*| <°°i 0^0, 0. (9.99)
523
Решение Т (х, у, () ищем в виде двумерного теплового потен¬
циала простого слоя по кривой у = 0 в виде, учитывающем наличие
разнородных граничных условий (9.97) — (9.98)
^ »■ (9Л00)
О о
Покажем прежде всего, что удовлетворяется граничное условие
(9.98)
= 1 т)схр[ (x-/-|)3+yaldTdE-
ду 8ла* J J (<-т)г Р| 4а (/-т) ■ Jат as
О о
если обозначить a = / + £. Введем далее следующие подстановки:
г = у1(2 V a(t— т)); р = | х — а | г/г/.
Для х</ и а >/ справедливо х < а, откуда P = (a—x)z/y. Пре¬
образуй (9.101), находим
Ъ{у> 0) = ~i J_e"^d2 J —fP.^—4&г)е“Э,йР-
у/2 Vat (I-X)zfy
откуда следует, что
')je“'dz) e-»-dp_0.
х < I n +00
Для нахождения неизвестной плотности ф(х, t) потенциала (9.100)
используем граничное условие (9.97), что приводит к следующему
интегральному уравнению:
ijJ^^exp[-i^5f-]dTd5==r0, х>1,
о о
записанному в пространстве изображений Карсона—'Хевисайда
ас
pj...-exp(—pt)dt в виде
о
со
[y(i,.p)K0(\x'-l\V7iddl = 2mT0, х’>0, (9.102)
о
гдех'=х—/, К0(г) — функция Магдональда. Уравнение (9.102) —
интегральное уравнение Фредгольма 1 рода, рассмотренное в книге
Б. Нобла «Метод Винера — Хопфа» (М., ИЛ, 1962). Приведем по¬
524
лезное соотношение для решений интегральных уравнений такого
типа.
Методом Винера — Хопфа можно показать, что интегральное
уравнение Фредгольма
00
^ha)Ku(y\x-l\)dl = f(x), х>0, (9.103)
О
имеет решение в виде
Выражение (9.104) позволяет получить решение уравнения (9.102),
если учесть, что f(Q = 2naT0, у = ]/ п/а. После ряда несложных вы¬
кладок (проделайте все выкладки самостоятельно) находим
Ф(х, р) = 2аТ0
У^Гаф(/ШП у-р) + -;7Л=:у-р':-<м °'У
¥ 7 V пх Y а
(9.105)
Для нахождения оригинала выражения (9.105) воспользуемся
следующей формулой операционного вычисления (для преобразова¬
ния Карсона — Хевисайда): если f (р) +~г f то
оо
T(}Tji)+*\f(y)e-№dy. (9.106)
VTt J
Применительно к (9.105) формула (9.106) приводит к следую¬
щему результату:
Ф(х, t) = 2T
V а/л , V xY а (* 1
т!
^ V ‘ Jv-a yVy-xlV~a
xexp(— if!At)&y+ u ' " - \ . 1 - -exp(— y*/4t)dy .
VTt J_ Vy-x/Гa f
(9.107)
Таким образом, решение исходной задачи (9.95)—(9.99) дается
выражением (9.100) с известной функцией ф(л\ /) в виде (9.107).
Однако это не единственная аналитическая форма искомого решения.
Можно не искать оригинал для изображения плотности ф(х, р)
в виде (9.105), а воспользоваться найденным выражением (9.105)
для записи изображения искомого решения Т (х, //, р). Действи¬
тельно, применяя преобразование Карсона—Хевисайда к (9.100),
найдем
Т(х, у,р) = 2^Ф(1, р)*,( j/lEIEIEEir^)d6f
0
525
откуда и из (9.105) получаем изображение решения
x(y^EEEE^,) d|.
(9.108)
Здесь не приводится оригинал для выражения (9.108). Предостав¬
ляется читателю получить этот оригинал самостоятельно; одновре¬
менно рекомендуется сравнить полученное при этом выражение для
Задача 6. Используя (9.108), показать, что температура на линии у = 0
дается выражением
Выражение (9.108) может служить базовым при рассмотрении ряда случаев,
сводящихся к (9.95)—(9.99). Действительно, пусть Т (дг, у, t) удовлетворяет урав¬
нению (9.95), начальному условию (9.96), условию ограниченности (9.97) и гра¬
ничным условиям вида:
в следующем виде: Т (х, у, t) = T1(x, у, t)-\-Ti(xl у, /). Если потребовать от
функций Тх и Т2 выполнения граничных условий
f (dTildy)y:=o = Ot х < /; Г (дТ21ду)у_ъ = 0, x<l-\-d\
\ Тг(х, 0, 0 = 7*0. *>l\ \ Тг{ху 0, t) = -T0, * > / + d,
то функция Т (х, (/, t) = Tx(x, у, О + Т'гС*! 0 будет удовлетворять условиям
(9.109)—(9.111). Функция Тх(ху у, f) найдена в виде (9.100), (9.107); функция
Т% (х, у, 0 находится из (9.100), (9.107) заменой Т0 на (— Т0), числа I — на
Задача 7. Покажите, что в случае (9.109)—(9.111)
§ 4. МЕТОД ВИНЕРА — ХОПФА
Метод Винера — Хопфа, впервые примененный к решению интеграль¬
ных уравнений, специального вида в одной из работ Н. Винера и
Э. Хопфа (см. ссылки в [ПО]), дает возможность преодолеть серь¬
езные аналитические трудности, возникающие при решении краевых
задач стационарной и нестационарной теплопроводности с разнород-
Т(х, у, 0 с (9.100), (9.107).
Т (х, 0, /) =
(дТ/ду)у=0 = 0, х < /;
(9.109)
(9.110)
(9.111)
Этот случай сведем к изученному, для чего представим искомую функцию
Г(х, 0, 0 =
\x-l-d\l
2 V~at
j Jd£, х<1
526
ными граничными условиями на линиях, в частности с различными
граничными условиями на полубесконечных границах. Указанный
метод расширяет класс задач теории теплопроводности (а также
теории электромагнитных волн, акустики, гидродинамики, теории
упругости, теории потенциала), которые можно решить с помощью
интегральных преобразований Фурье и Лапласа. При этом, как будет
показано, аналитическое решение одной и той же тепловой задачи
возможно получить в разных классах функций; указанное обстоя¬
тельство имеет важное прикладное значение, что неоднократно под¬
черкивалось на протяжении всей книги.
Суть метода заключается в следующем.
Предположим, что в области —оо < * < -{- оо, //>0, требуется
найти решение уравнения
S+w~k2T=0’ (9Л12)
удовлетворяющее при у = 0 граничным условиям
Т (х, 0) = / (х), *>0; 1
[дТ (х, у)/ду]и=0 = <р(х), х<0, )
а также условию ограниченности при | х| —► оо и у —*■ оо. То обстоя-
тельство, что х изменяется в интервале (—оо, +оо), подсказывает
применение к функции Т (.х, у) экспоненциального преобразова¬
ния (5.31):
+ 00
Г (g, у) = (Ц]Гъ1) 1^Т(х, y)dx, g = a + ip, Р = 0. (9.114)
— 00
Преобразуя уравнение (9.112) (см. табл. 9) к виду
d2T/dy2—у2Т = 0 (у2 = I2 + к2) (9.115)
и учитывая условие ограниченности функции Т (£, у) при у—*-оо,
решение уравнения (9.115) запишем в виде
Т (£, у) = А(1)гхр(—уу), (9.116)
где А (I)—пока произвольная функция, которая должна быть най¬
дена из граничного условия (9.113) при у = 0. С этой целью при¬
меняем в (9.113) преобразования (5.38) (см. гл. V), полагая:
00
Т+ (6, у) = (1 /|/Ш) J Т (.х, у) dx. Р > 0, (9.117)
о
о
т_ (I, у) = (1/|/~2я) 5 Т (X, у)е'&х dx, Р < 0, (9.118)
— оо
что дает
ао
Т+ (г, 0) = (11\ГЩ J / (X) dx; Ti (g, 0) =
О
= [ а7^]у=о = 7^1 cp(x)ei<xdx. (9.119)
— GO
527
Здесь Т+(£, 0) и Т1(£, 0) — известные функции. Выражения (9.116)—
(9.118) и граничные условия (9.119) приводят к следующей системе
функциональных уравнений:
ГДЕ, 0) + 7\ДЕ. 0) = Л(Е),
П (Б, 0) + г: (g, о) = -УА (I).
(9.120)
Исключив из этих уравнений А (Е), приходим к уравнению
7V (Е, 0) и Т_ (|, 0) неизвестны. Если удастся получить решение
уравнения (9.121), т. е. найти функции Г + и Г_, то постоянная
интегрирования А (Е) в (9.116) определится, например, из первого
уравнения (9.120), что и даст, в принципе, окончательное решение
задачи. Как будет показано далее, неизвестные функции в уравне¬
нии (9.121) можно найти, считая в преобразовании Фурье (9.114)
параметр Е комплексным и используя процесс аналитического про¬
должения и теорему Лиувилля. Этот метод называется методом
Винера — Хопфа; его основы изложены в [ПО].
Типичной задачей типа (9.121) является следующая: требуется
найти неизвестные функции Ф+(Б) и ¥_(£), удовлетворяющие функ¬
циональному уравнению
в полосе Pi < Р < Р2, — оо<а< + оо, в комплексной плоскости £,
причем Ф+ (Е) должна быть регулярна в полуплоскости р > рА,
a (Б) должна быть регулярна в полуплоскости Р < Р2 (функция
называется регулярной в области D, если она является аналитиче¬
ской в каждой точке этой области). Кроме того, эти функции
должны удовлетворять в соответствующих полуплоскостях опреде¬
ленным условиям на бесконечности, которые будут указаны ниже.
Функции Л (5), В (I) и С (Б) считаются заданными функциями Б,
регулярными в рассматриваемой полосе; при этом для простоты
предполагается, что А (|) и В (Е) не имеют в этой полосе нулей.
Основной шаг при решении уравнения (9.122) методом Викера —
Хопфа заключается в факторизации (иногда указанный метод
называют методом факторизации), т. е. в определении функции
F+(l)y регулярной и не имеющей нулей в полуплоскости Р > Pi, и
функции F_ (£), регулярной и не имеющей нулей в полуплоскости
Р < Р2, таких, что
Иногда функции F+ и F_ можно просто угадать, рассматривая
левую часть равенства (9.123); в более сложных случаях можно
воспользоваться приемами, указанными в [110]. Используя равен-
А (Б) Ф+ (Б) + В (Е).(Е) + С(Е) = 0 (Е = а+ /р) (9.122)
A(l)/B(l) = F+ (l)/F_ (£).
(9.123)
528
ство (9.123), запишем уравнение (9.122) в виде
F+ (I) Ф+ (?) + F_ (?) (?) + C(^-(S) =0. (9.124)
Представим слагаемое [С (?) /7_ (?)]/В (?) в виде
[С (?) F_ (?)]/£ (?) = С+ (?) + С. (?), (9 125)
где функция С+ (?) регулярна при Р>РП а функция С_(?) —при
р < Р2. В общем случае это можно сделать, применив следующую
теорему Коши [92]: пусть /(?)—аналитическая функция ? = а + /Р>
регулярная в полосе Pi < Р < Р2 и такая, что | / (а + Ф) | < М • | а | ~г,
г > 0 при |ос| —► оо, причем это неравенство выполняется равно¬
мерно для всех Р в полоса Pi + e^P^P2— е, е > 0. Тогда при
Pl<c<p<d<P2 функцию /(?) можно представить в виде суммы
двух функций: /(?) -Д (?) + /, (?), где
1*®-ш ] -r?Tdz’ мв-ет J <9126>
ic — оо id — со
Здесь функция /+(?) регулярна в полуплоскости Р>Р1} а функция
/_ (?)—в полуплоскости р < Р2.
Методика вычисления комплексных интегралов (9.126) изложена
в § 2 гл. VI.
Используя теперь равенство (9.125) перегруппируем слагаемые
в уравнении (9.124) и введем новую функцию 0 (?) равенствами
0 (?) = F+ (?) Ф+ (?) + С+ (?) = — F_ (?) 4L (?) — С_ (?), (9.127)
где функция 0(?) определена пока в полосе рг <р<р2. Однако
функция F+ (?) Ф+ (?) -f С+ (?) определена и регулярна в полупло¬
скости р > р!, а функция /7_(?)ЧГ_(?)— С_ (?) — в полуплоскости
Р<Р2. Таким образом, аналитическим продолжением функцию 0 (?)
можно определить на всей комплексной плоскости ?, причем © (?)
регулярна на всей плоскости ?. Предположим теперь, что имеют
место оценки:
Ц+(£)Ф+(£) + С+(?)|<|?|'-, Е-+0О, р>рх; )
\F.(l)^_(l) + C_(l)\<\l\r‘, l-оо, р<р2. Г
Тогда по обобщенной теореме Лиувилля [92] функция в(?) является
полиномом Р (?) степени не выше целой части min (гх, rt), т. е.
F+a)OAi)+c+a)=p(D- \
/7.(Е)Ф.(?)+С.(6) = Р(?)- I { }
Из этих уравнений функции Ф+ (?) и V. (?) определяются
с точностью до произвольного полинома Р(?), т. е. с точностью до
конечного числа произвольных постоянных, которые должны быть
определены иным способом.
Для рассматриваемого в настоящей главе класса задач теории
теплопроводности наиболее часто реализуется случай, когда левая
529
и правая части равенства (9.127) стремятся к нулю при % —^оо,
откуда следует, что 0 (£) является полиномом, тождественно равным
нулю. Для этого случая находим
ф+ (I)=-с+ (I)/f+ а) и а)=-с_ (1 )/f_ а).
Продемонстрируем изложенный метод при нахождении функции
Грина G(x,y,t—т, х\ у') для краевой задачи (9.95)—(9.99), рас¬
смотренной в § 3 данной главы. Аналитическое решение указанной
задачи получено методом тепловых потенциалов в форме (9.100),
(9.107). Функция Грина для этой задачи может иметь более простую
форму (особенно для малых времен t от начала процесса) и интег¬
ральное представление решения задачи (9.95) — (9.99) (см. гл. VII)
приведет нас к аналитическому выражению, отличному от (9.100),
(9.107).
В соответствии с определением функции Грина G (х> у, t—т, х\ у’)
для краевой задачи (9.95) — (9.99) (см. гл. VII) запишем:
dG (d2G . d2G \ . . , . Л ,, ^
~др- — а \ дг2 ду2 ) ' °° < 2 < °° ’ У > ’ ^ ’
G (z, уу t\ z', у’)\г=о = &(г — г')6(у—у')9 \г\ < оо, у> 0;
G(2, у% г', у’) |увО = 0, 2 > 0, /'>0;
[3G(2, у, 2', у )!ду]и=0 = 0, 2<0. *'>0;
G (г, у, г', */') | < + оо, | г | < оо, у > 0, > 0.
Здесь введены новые переменные: t' = t—т, z = x—/; 2' =х' — /.
Функцию G ищем в виде суммы фундаментального решения урав¬
нения теплопроводности (9.95) и регулярной функции q(z, у, Г, 2', г/')
(см. § 1 гл. VII, (7.13)):
0{г,у,Г,г\у')=-^е <г г^'У У) +Я(г, у, V, г’, у'), (9.131)
где функция q в соответствии с (9.130) — (9.131) должна удовлет¬
ворять уравнению *
dq/dt' = a (d2q/dz2 + d2q/dy2), — оо < z < + оо, у > 0, V > 0, (9.132)
и краевым условиям:
q(z, у, t\ г\ у') |r=0 = 0, |г| < оо, у > 0; (9.133)
<7 (г, у, г', fOI*-o = — 4^е . г > 0, *' > 0; (9.134)
[дд(г,у, (\г',у'/ду]у=0=—^е ^ ^ . г < 0, Г > 0; (9.135)
|<7(z, у, г', г/)| < + оо, | г | < оо, t/ > 0, t' > 0 (9.136)
530
и всем условиям, необходимым для применения преобразования
Лапласа (6.1) по переменной V и преобразования Фурье (5.31) по
переменной х. Для применения указанных преобразований правые
части равенств (9.134)—(9.135) удобнее записать в полярной системе
координат z = r cos ф, у = г sin ф (г' = г' cos ср', у' = г' sin ф'). Известно
на основании разложения Неймана [55], что в полярной системе
координат
G^z, у, t’, г', y') = j±Fe
п— + 00
= i S. C0Srt(<P—Ф') jiie_ert,Vn(^)^n(V)'dTjt
п— - со О
где (г, ф), (г', ф')—соответствующие координаты точки (z, у) и
источника (z', у') в полярной системе (г = Уг*-+ту*я9 ф = arctgy/z).
Если при этом учесть, что при
у = 0, z>0—^ф = 0, г = z, а при у = 0, z < 0 —> ф = л, r = — z
и
dG0 _ dG0 у | дО0 1 _1_
ду дг у г%+у2 1+*/2/*2 г *
так что (dGjdy)y^ = (\lz)dGjd^, то получаем для (9.134)—(9.135):
00 т»
q(z,y, t’, z', г/')|„=о = — 4" S. X
n— 1 0
oo
. хУ„(т]г) yn(tir')dn—(1/2л) ^т)е_в'',1'70 (t)z);
n= 1 0
■ IX
x J0 (y]z') drj, z>0, t’ > 0; (9.137)
Ш ®
[d<7 (z, I/. V, z', /) | <fy] v=„=^ £ n (—l)n+1 sin ncp' j t] x
n= 1 0
x e-ar^Jn (— r]z) /„ (t)/-') dr], z < 0, /'>0. (9.138)
Применим к (9.132) — (9.133), (9.137) — (9.138), (9.136) последова¬
тельно преобразование Лапласа и Фурье, полагая:
00
q (г, у, р) = j, e~p‘'q(z, у, t', z', y')dt', р = а + т, Rep > о0; (9.139)
О
4- со
<7(1, У, р) = (1/К/2л) 5 е(гЙ(г, У, />) dz, £ = ос + ф, р = 0, (9.МО)
— 00
531
что дает для функции q (£, у, р)
dJ<7/dуг—y2q = 0, */> 0; (9.141)
Oft
1
q+ (I, 0, p) = — —~ V cos пф'х
я у zji
со
п = 1
Лп + 1/п (лО dr)
Г л1-!2 (-<Б+/4е-6*)" (Р+оц*)
-| г — р^0 (9142)
^ J v ля—e*(p+«i*)
2я
qi(l,0,p) = —\г=- V (—l)nsinwp' Г Г*П+УП ^1'' — , Р<0;
2n 7?1 J (‘5+ У Л2—£2)л (р+ац2) (9.143)
|7(5. У,.Р)\< +«>, у>0. (9.144)
Здесь обозначено:
00
7+ (5. у. />) = (1/К2л) 5е'г|<7(2, 1/, p)dz, р>0;
О
о
q-(l, *Л р) = (1/1/л2л) J e‘*tq(z,y, р)йг, Р<0.
(9.145)
Для вычисления интегралов (9.145) при у = 0 от правых частей
(9.137) — (9.138) использовался табличный интеграл [20]
Гй-«/ (hr\Ar=—l bv Rev> i;
J Va*+b* (a+^5*+ft*)v ’ Re(a + ib)>0,
допускающий p>0 в случае (9.142) и P<0 в случае (9.143). В
уравнении (9.141) постоянная у2 = Е2-[-/с2, где обозначено к2 = р/а\
при этом к = Vpla = кх + ifc2 и выбрана одна из ветвей корня с
/с, > 0. Ограниченное при у—► оо, решение уравнения (9.141) имеет
вид =
q&> У, p) = C(t)exp(-yy) (Re у > 0), (9.146)
где С (|) должна определяться из граничных условий (9.142) —
(9.143). На основании (9.120) — (9.121) приходим к функциональ¬
ному уравнению
7+ (£> 0, р) + yq_ (|, 0, р) = — [7: (£, 0, p) + yq+ (I, 0, р)] (9.147)
относительно неизвестных функций q\ (£, 0, р) и q_ (£, 0, р). Срав¬
нивая (9.147) с (9.122) получаем,
A(l)_ 1 _ {jTf+IZ)-' _F+ (6)
в (£) у с/Ч-к2 У 1 — iK F- (I)
532
и проводим далее факторизацию уравнения (9.147) (сравнив с
(9.124)), что дает следующее выражение [125]:
+У1=Ткч_ (6, О, = о, /;).
У S-н* у I + W
(9.148)
В полученном соотношении функция <7+(!, 0, р)/УХ+Тк регу¬
лярна в верхней полуплоскости Р>0, а функция V l — iKq_ (!, О,
/?)— в нижней полуплоскости Р^О. Таким образом, оба слагаемых
в левой части (9.148) регулярны на линии р = 0. Здесь было учтено,
что функция V X ± *Vc = \^(а =р к2) -f i (Р ± кг) регулярна в любой об¬
ласти, не содержащей точки (!=Ы>с) = 0; в частности, функция
J/ !+i>c при /с, > 0 регулярна в верхней полуплоскости Р^О, функ¬
ция V I—Ск при «!> О — в нижней полуплоскости Р<0. Анало¬
гичным образом можно показать, что первое слагаемое правой
части (9.148) Oi(^) = ^l (!, 0, p)/V~l+iK регулярно в полосе —кх <
< Р ^ 0, второе слагаемое Ф2 (!) = V! — */of+ (!, 0, р) — в полосе 0 ^
^Р</с,. Согласно теореме Коши (9.126), функции Ф,(!) (i== 1, 2)
можно представить в виде: Ф1 (!) =Ф1+(!)+ Ф1-. (!), где Ф1+ (!) ре¬
гулярна при Р>— ки Ф1_(£) регулярна .при Р<0; Ф2(!) =
= Ф2+ © + ф2- (I). где Ф2+ (|) регулярна при р>0, Ф2_(!) — при
P^/q. Соответствующие выражения для Ф*±(!)(/=1, 2) находятся
путем вычисления интегралов (9.126) с учетом (9.142) — (9.143) ме¬
тодами, изложенными в § 2 гл. VI (рекомендуем проделать все вык¬
ладки подробным образом). Произведя, таким образом, расщепле¬
ние каждой функции Ф| (|) (t = l, 2) на сумму двух функций Фи (!)
и Ф£_ (!) из (9.148) после перегруппировки найдем:
+ ф1+ (|) + ф2+ (|) = - VT^c*. х
х (!, О, р)-Ф1в (!)—Ф2_ (I) = © (!). (9.149)
Левая часть (9.149) регулярна при Р^О, а правая — приР^О.
Следовательно, аналитическим продолжением функцию © (!) можно
определить на всей плоскости !. При ! —► оо левая и правая части
(9.149) стремятся к нулю, откуда по обобщенной теореме Лиувилля
заключаем, что ©(!) есть полином, тождественно равный нулю. От¬
сюда _ #
Я* (?. 0. Р) = — V l+iК [ф1+ (I) + ф2+ (£)]; 1 (9 150)
Я.(1, 0,^) = -(КЕ-*кГ1[Ф,-(5) + Ф,-(5)]. I
Согласно (9.120), постоянная С (!) в (9.146) равна С (!) = q+ (!, 0, р) +
+ (I, 0, р) или Vl—inC (|) = Ф2+ (|) + Ф2_ (|) + 1/~£ —»с Я- (£.
р), и из (9.150) находим С (£) = [Ф2+ (£) — Ф4_ (|)]/Ц| — in, а вместе
с этим и искомую функцию q (|, 0, р) в виде
q(l, 0, = ехр (—IV Р~+Р/о)- (9-151)
V
533
Переходя затем к оригиналу и возвращаясь к переменным (*, /),
получим искомую функцию Грина G (х, у, t—т, х', у') в виде (про¬
делайте все промежуточные преобразования самостоятельно):
G (х, у, t—т, х', у') =
1
ла (t — т)
=^7ехР
г2,-\-г'
4а (/— т)
^ (—1)" sin ф cos
2л+1 .
л = О
X
(ф' +у)^+т[2а(Т-т)]’
L 2а (/—т) J ’ (9.152)
гъ = (х—iy + у2; tg<p = y/(x—/); r'z = (x'—/)* + £/'*; tg ф' = у'/(х' — I).
Имея теперь функцию Грина в виде (9.152), можно записать
интегральное решение краевой задачи (9.95) — (9.99), используя для
этой цели основную интегральную формулу решения (7.31) (см. § 1
гл. VII) двумерного уравнения нестационарной теплопроводности
t 00
Т(х, у, t)-aT„ J J ду,
О I
dx dx'.
(9.153)
у'=0
Как видим, это выражение отлично ог (9.100), (9.107); оба
выражения тождественны в смысле числа, но получить с помощью
эквивалентных преобразований вторую аналитическую форму, имея
первую (или наоборот), технически достаточно трудно. Принци¬
пиальное значение для этих целей имеет выбор метода решения ис¬
ходной задачи, который в ряде случаев может дать соответствующую
аналитическую форму для искомого решения. Однако следует пом¬
нить, что это обстоятельство реализуется не всегда и применение
различных подходов может привести в ряде случаев к одной и той
же функциональной конструкции искомого решения.
Задача 8. Получите результат (9.152), используя метод тепловых потенциа¬
лов, изложенный в § 3 настоящей главы.
Задача 9. Пусть Т (х, у)—температурное поле в неограниченной пластине
толщиной б, вызывающее на плоскости у~0 на берегах полубесконечной теплоизо¬
лированной трещины однородный тепловой поток мощностью q= const (сис¬
тема координат выбрана в срединной плоскости пластины). Между пластиной и
окружающей средой происходит симметричный относительно срединной плоскости
теплообмен по закону Ньютона. Найдите функцию Т (х, у), удовлетворяющую ус¬
ловиям:
д2Т/дх2-\-д2Т 1ду2—т2Т = 0, | х j < оо, у > 0;
\дТ (дг, */)/di/]j,=o+ = — ) ^о-
[(дТ (х, 0)/d(/]„=o_ = — q/X, (
Т(х, у)|у=о = 0, дс< 0;
lim Т (х, у)= lim Т (х, у) = 0.
/дг I —► 00 у ^ 3D
Здесь та = 2а/(6Х) [см. (2.33)], где а —коэффициент теплообмена; А,—коэффициент
теплопроводности.
Пояснение. С помощью экспоненциального преобразования (5.31) по пере¬
менной х решение уравнения (9.154), удовлетворяющее условиям (9.156) —(9.157),
(9.154)
(9.155)
(9.156)
(9.157)
534
НОЧЕНИЕ
осесимметричными трещинами, а также с поверхностными прямо¬
линейными и криволинейными трещинами конечной длины); 4)
построение аналитических решений краевых задач для уравнения
(9.154) в областях с внутренними и поверхностными трещинами при
различной геометрии области, конфигурации трещины (и располо¬
жении ее в образце) и др. [189 — 191].
Разнообразные исследования могут быть выполнены для об¬
ластей с движущимися границами, представляющие большой ин¬
терес для многих областей народного хозяйства нашей страны [192].
Например, построение аналитических решений тепловых задач для
уравнения (8.5) для областей xe[0, l+vt\, 0; xe[0, at2 + flt+у], t^O
(девять случаев для каждой области), а также для областей с движу¬
щимися границами по законам в табл. 13; развитие метода диф¬
ференциальных рядов для области \y(t), оо), ^Оив цилиндричес¬
кой системе координат (осевая симметрия) (см. § 4 гл. VIII); ис¬
следование скорости сходимости рядов типа (8.131) (исключительно
важный вопрос для решения прямых и обратных задач Стефана
и типа Стефана для уравнений параболического типа со свободной
границей); построение теории «интегральных преобразований» для
областей с движущимися границами (см. § 7 гл. VIII) и др. Следует
подчеркнуть, что несмотря на кажущуюся простоту математических
моделей нестационарного переноса в областях с движущимися гра¬
ницами, приведенные в книге задачи являются далеко не тривиаль¬
ными для получения их точного аналитического решения. Прак¬
тически изучены простейшие законы движения границы (линейный,
параболический, квадратичный), но и для этих случаев аналитичес¬
кая теория теплопроводности находится лишь в начале своего
развития [192 — 200]. Что касается более сложных законов движе¬
ния границы, указанных в табл. 13 и допускающих точные аналити¬
ческие решения соответствующих краевых задач, то предстоит
большая работа по нахождению этих решений, изучению их свойств
и построению температурных номограмм. Как показано в книге,
при решении такого рода задач возникает большой круг проблем
вычислительной математики, в том числе и математической физики,
если говорить о развитии соответствующих методов при решении
краевых задач для дифференциальных уравнений в частных произ¬
водных. Как показывает материал § 5 гл. 8 в конечном счете речь
идет о необходимости решения спектральных задач для уравнения
1 ^ )-ha[y2-^(^)]vF(^) = 0, где q(£) — данная функция на
dl )
некотором интервале изменения переменной £, (например, q (£) = £;
с,2 и др.). Эти вопросы детально рассмотрены в известных моногра¬
фиях Титчмарша [140, 141]. По мере накопления результатов по
решению такого рода спектральных задач, по-видимому, возможно
появление и новых законов движения границы, то есть случаев,
536
допускающих точные аналитические решения соответствующих за¬
дач нестационарной теплопроводности в областях с движущимися
границами.
В координатных системах, отличных от указанных выше, дело
обстоит менее благополучно и каждая новая краевая задача анали¬
тической теории, рассмотренная в «нестандартной» криволинейной
системе координат, представляет большой интерес для теории теп¬
лопроводности. Вероятно, на этом пути следует ожидать интерес¬
ных результатов и для теории специальных функций, которые поро¬
ждаются естественным образом как решения обыкновенных диф¬
ференциальных уравнений, на которые распадается уравнение теп¬
лопроводности (1.32) при его интегрировании методами математи¬
ческий физики.
Большую практическую ценность имеет изучение уравнения те¬
плопроводности (1.110) в деформируемом твердом теле (имеются
ввиду соответствующие краевые задачи для этого уравнения)
[201 — 207]. Эффект связности поля деформации и температурного
поля, отраженный в уравнении (1.110), обычно мало влияет на
термическое возмущение и распределение тепловых напряжений
в стеклах, металлах и ряда пластмасс. Однако подобное положение
не сохраняется для новых полимерных материалов (например, по-
ливинилацетали, композиционные материалы). В этих материалах
при учете эффекта связности устанавливаются новые качественные
особенности распространения упругих волн, которые под влиянием
тепловых эффектов распространяются с затуханием и дисперсией.
Указанные случаи представляют собой практически не разрабо¬
танную область аналитической теории теплопроводности твердых
тел и теории термоупругости (включающей теорию теплопрово¬
дности как составную часть), если учесть, что подобного рода
исследования выполнены для простейших случаев, допускающих
возможность применения известных аналитических подходов (в ча¬
стности операционного метода). Например, уже простейший случай
для упругого полупространства z^/^0, t^O (упругой и упруго¬
вязкой области) открывает практически новое научное направление
для исследования в термомеханике на основе соотношений, при¬
веденных в § 8 гл. I. Круг вопросов, возникающих при изучении
моделей для уравнений (1.135) и (1.122), (1.135) и (1.126) (или
(1.127)) наряду с изучением термонапряженного состояния области,
включает такие проблемы, как: расчеты скачков напряжений на
фронте термоупругой, упруговязкой и тепловой волны через внеш¬
ние функции нагрева, что позволяет во многих случаях оценить
внутреннее состояние среды без необходимости заново решать за¬
дачу при измененных граничных функциях, характеризующих не¬
изотермическое воздействие на границу области [207]; эффект вли¬
яния возможного перемещения границы области z^l+vt, t^0 на
величину внутренних термических напряжений; эффект конечной
537
скорости распространения тепла; эффект конечной скорости нагрева
граничной поверхности области по закону (p(t)-—[(Tn—T0)/to][t —
— r}(t — t0)(t — to)], где rj(z) — функция Хевисайда, t0 — время дости¬
жения граничной поверхностью температуры Тп. Широкое поле
деятельности для исследования окрывают и среды с тепловой памя¬
тью на основе соотношений (1.130) и (1.131) в условиях температур¬
ного, теплового (тепловой поток однородный, импульсный, пуль¬
сирующий, периодический и т. д.) нагрева и нагрева средой, при
наличии и отсутствии внутренних источников теплоты, в областях
с постоянной геометрией и с движущимися границами и т. д.
Указанные вопросы представляют большой практический интерес
для развития теории неизотермического разрушения [189] не только
в рамках механики разрушения, но и в рамках обобщенной струк¬
турно-кинетической термофлуктуационной теории прочности, объ¬
единяющей кинетический, механический и термодинамический под¬
ходы [190, 191]. Малоизученной областью являются обратные зада¬
чи связанной и несвязанной термоупругости в динамическом, квази-
статическом и статическом случаях, которые заключаются в вос¬
становлении термонапряженного состояния в объеме тела по задан¬
ным на части границы температуре и смещениям. Обратные задачи
такого рода имеют практические приложения при исследовании
натурных конструкций в эксплуатационных режимах, когда, как
правило, измерения возможны лишь на части поверхности [80, 208,
209]. К сказанному можно присоединить обширный класс задач по
тепловому удару в терминах динамической термоупругости для
областей канонической формы с разрезами (прямолинейными, кру¬
говыми, криволинейными трещинами, поверхностными или внут¬
ренними). Можно ожидать интересных результатов и в качествен¬
ной теории для дифференциальных уравнений в частных производ¬
ных, приведенных в § 8 гл. 1, например, для интегродифференциаль-
ного уравнения (1.135): принцип максимума; теоремы существова¬
ния; априорные оценки; асимптотическое поведение решений и т. д.
Задача читателя — увидеть эти проблемы и понять необходимость
их изучения. Очевидна также и целесообразность нахождения точ¬
ных аналитических решений задач теплопроводности (и связанных
с ними термомеханики) во всех случаях, где это возможно. Точные
аналитические решения дают графические зависимости между пара¬
метрами исследуемых процессов более общие, наглядные и адекват¬
ные явлению в рамках принятой модели, чем зависимости, получен¬
ные численным решением исходной задачи или на основе ее прибли¬
женного решения. В последнем случае традиционно возникает се¬
рьезная проблема оценки погрешности полученного результата,
которая чаще всего остается неизвестной из-за трудностей вычис¬
лительного характера. Разумеется, в случаях, когда аналитические
методы оказываются бессильными, на помощь должны приходить
538
численные методы, обладающие неограниченными возможностями
[210].
Важно еще раз отметить, что полученные в литературе аналити¬
ческие решения касаются в основном тепловых задач на основе
классической феноменологии Фурье о распространении тепла в тве¬
рдых телах [83, 211—214], т. е. краевых задач для уравнений
параболического и эллиптического типов. Краевые функции в этих
задачах — гладкие функции (непрерывно дифференцируемые), для
которых существуют все преобразования, вытекающие по ходу
действия. Эти функции задаются практикой многочисленных прило¬
жений тепловых задач и соответствующие аналитические решения
задач теплопроводности принадлежат классу функций С2 (Q). В 30-х
годах С. JI. Соболев разработал теорию обобщенных решений для
уравнений в частных производных. В дальнейшем получили раз¬
витие качественная теория краевых задач для уравнений параболи¬
ческого типа в обобщенной постановке в пространствах Соболева
и других функциональных пространствах и теория этих пространств
для решения задач (теоремы вложения; теоремы о следах; компакт¬
ность вложения и теория усреднения и т. д.) [184]. Соответствующая
аналитическая теория теплопереноса для этих случаев представляет
собой обширное поле деятельности и ждет своего развития. Анало¬
гичная ситуация имеет место и для более сложных уравнений пере¬
носа на основе гипотезы Максвелла — Каттанео — Лыкова (урав¬
нения гиперболического типа (1.127), в средах с тепловой памятью
основе линеаризированной теории [215] в деформируемых средах
с учетом эффекта связанности поля температуры и деформации
в уравнении (1.110) и т. д.). Указанные случаи также представляют
собой практически не разработанную область аналитической тепло¬
проводности твердых тел. На этом пути, вероятно, возможны и ин¬
тересные физические результаты о влиянии, например, движения
границы тела и разрывов сплошности материала на процессы теп¬
лопереноса. Эти исследования — в XXI веке и автор желает чита¬
телям успехов на этом пути!
СПИСОК ЛИТЕРАТУРЫ
1. Арсенин В. Я- Методы математической физики и специальные функции. М.,
1974
2. Араманович И. Л, Левин В. И. Уравнения математической физики. М., 1969.
3. Айзен А. М., Редчиц И. С., Федоткин И. М. Об улучшении сходимости рядов,
входящих в решения уравнений теплопроводности.— Инж.-физ. журн., 1974, т. 26,
№4, с. 659—666.
4. Алексеева О. П. Замкнутое решение некоторых граничных задач математиче¬
ской физики.— Прикл. матем. и мех. 1953, N° 17, с. 627—630.
539
5. Антимиров М. В., Геллер 3. И. Решение тепловых задач при движении гра¬
ницы по закону t — Инж.-физ. журн., 1964, т. 7, № 9, с. 57—63.
6. Будак Б. М., Фомин С. В. Кратные интегралы и ряды. М., 1967.
7. Боли Уэйнер Д. Теория температурных напряжений. М., 1964.
8. Бейтмен Г. и Эрдейн А. Высшие трансцендентные функции. М., ч. I, 1973;
ч. 2, 1974.
9. Бейтмен Г. и Эрдейн А. Высшие трансцендентные функции. М., 1967, ч. 3.
10. Бейтмен Г. и Эрдейн А. Таблицы интегральных преобразований. М., 1969,
т. I; 1970, т. II.
11. Бартенев Г. М., Жорник А. И. Температурные напряжения в стеклянном
покрытии на металлических трубах.— Физика и химия обработки материалов,
1972, № 3, с. 100—108.
12. Борисов Б. Т., Любое Б. Д., Темкин Д. Е. О расчете кинетики, затвердева¬
ния металлического слитка при различных температурных условиях на его поверх¬
ности.—Докл. АН СССР, 1955, т. 104, №2, с. 223-226.
13. Бодрецова Л. Б. Решение одной задачи диффузии в условиях переменной
температуры.— Матем. сб., 1964, т. 64, № 2, с. 223—233.
14. Бородачев Н. М. Термоупругая задача для бесконечного тела с осесиммет¬
ричной трещиной.— Прикл. мех., 1966, № 2, с. 91—99.
15. Ватсон Г. Н. Теория бесселевых функций. 4.1. М., 1949, с. 799—890.
16. Васильев Б. А. Некоторые стационарные задачи теории теплопроводности для
клиновидных тел при граничных условиях III рода.— Инж.-физ. журн., 1966,
т. 11, № 2, с. 235—241.
17. Ваничев А. П. Приближенный метод решения задач теплопроводности при
переменных константах.— Изв. АН СССР, ОТН, 1946, № 12, с. 1767—1774.
18. Гребер Г., Эрк С., Григуль У. Основы учения о теплообмене. М., 1958.
19. Гухман А. А. Введение в теорию подобия. М., 1973.
20. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и про¬
изведений. М., 1963.
21. Гельфанд И. М., Шилов Е. Г. Обобщенные функции и действия над ними.
М., 1959.
22. Грей 3., Метьюз Г Б. Функции Басселя и их приложения к физике и меха¬
нике. М., 1953.
23. Гринберг Г А. Избранные вопросы математической теории электрических
и магнитных явлений. М., 1948.
24. Гринберг ГА. О статье В. Л. Шевелькова «Нахождение температурного
поля в изотропной среде перед фронтом движущегося источника тепла», напечатанной
в ЖТФ (16, 207, 1946), и о правильном решении поставленной в ней задачи.— Журн.
техн. физики., 1951, т. 21, № 3, с. 382—384.
25. Гринберг ГА. Об одном возможном методе подхода к рассмотрению задач
теории теплопроводности, диффузии, волновых и им подобных при наличии движу¬
щихся границ и о некоторых иных его приложениях.— Прикл. матем. и мех., 1967,
т. 31, № 2, с. 393—403.
26. Гринберг Г. А. О решении обобщенной задачи Стефана о промерзании жид¬
кости, а также родственных задач теплопроводности, диффузии и других.— Журн.
техн. физики, 1967, т. 37, №9, с. 1598—1606.
27. Гринберг Г А. О решении задач диффузионного типа для расширяющихся
или сжимающихся областей.— Прикл. матем. и мех. 1969, т. 33, № 2, с. 269—273.
28. Гринберг Г. А. О температурных или концентрационных полях, создаваемых
внутри бесконечной или конечной области движущимися поверхностями, на кото¬
рых задан временный ход температуры или концентрации.— Прикл. матем. и мех.,
1969, т. 33, № 6, с. 1051 — 1060.
29. Гринберг Г А., Косс В. А. О решении задач диффузионного типа для рас¬
ширяющихся или сжимающихся областей, форма которых меняется со временем без
соблюдения подобия.— Прикл. матем. и мех., 1969, т. 33, № 4, с. 755—756.
30. Г ринберг Г А., Косс В. А. О некоторых точных решениях уравнения Фурье,
для изменяющихся со временем областей.— Прикл. матем. и мех., 1971, т. 35, № 3,
с. 759—760.
31. Гринберг Г А.% Чекмарева О. М. О движении поверхности раздела фаз в
задачах стефановского типа.— Журн. техн. физики, 1970, т. 60, № 10, с. 2025—2031.
540
32. Гобсон Е. В. Теория сферических и эллипсоидальных функций. М., 1952.
33. Гюнтер Н. М. Теория потенциала и ее применение к основным задачам
математической физики. М., 1953.
34. Гейни, Р. Г. Температурное поле полого цилиндра при малых значениях кри¬
терия Фурье.— Инж.-физ. журн., 1965, т. 9, № 5, с. 674—679.
35. Гольдфарб Э. М. Объединение решений уравнения теплопроводности для
плиты, цилиндра и шара.— В кн.: Научные докл. высшей школы.— М., 1958, № 3,
с. 129—134.
36. Горелик А. Г. Теплопроводность полого цилиндра при граничных условиях
4-рода на внешней поверхности.— Инж.-физ. журн., 1968, т. 14, №5, с. 66—71.
37. Годунов С. К.у Рябенький В. С. Разностные схемы. М., 1973
38. Дирак П. А. Основы квантовой механики. М.—Л., 1937.
39. Диткин В. А., Прудников А. П. Справочник по операционному исчислению.
М., 1965.
40. Диткин В. А., Прудников А. П. Интегральные преобразования и операцион¬
ное исчисление М., 1974.
41. Диткин В. А., Прудников А. П. Операционное исчисление. М., 1975.
42. Деч Г Руководство к практическому применению преобразования Лапласа
и г-преобразования. М., 1971.
43. Дацев А. Б. Об охлаждении стержня из конечного числа однородных час¬
тей.—Докл. АН СССР, 1947, т. 56, №.4, с. 355—358.
44. Дорошенко А. П. Асимптотическое решение первой краевой задачи с подвиж¬
ной границей.— Изв. АН Казах. ССР, серия «Физ.-матем.»., 1970, № 5, с. 76—78.
45. Дубовис М. И. Плоская одномерная однофазная задача теплопроводности с
подвижной границей.— В кн.: Исследования по теплопроводности Минск, 1967,
с. 326-329.
46. Еругин Н. П. Замкнутое решение параболической граничной неоднородной
задачи.— Прикл. матем. и мех., 1950, т. 14, № 2, с. 215—217.
47. Жорник А. И., Карташов Э. М. Об одной задаче теплопроводности для полу-
бесконечного цилиндра.— Изв. вузов, серия «Авиационная техника», 1973, N° 3,
с. 128—132; Инж.-физ. журн., 1972, т. 22, №6, с. 1128—1129.
48. Жуковский В. С. Основы теории теплопередачи. М., 1969.
49. Исаченко В. Я., Осипова В. А., Сукомел А. С. Теплопередача. М., 1965.
50. Ильченко О. Т. Температурное поле двухслойной пластины при переменных
во времени граничных условиях теплообмена.— Инж.-физ. журн., 1970, т. 19, № 6,
с. 1094—1099.
51. Кутателадзе С. С. Основы теории теплообмена. Новосибирск, 1970.
52. Камынин Л. И. Теория тепловых потенциалов и ее приложения.— Дисс.
докт. физ.-мат. наук. М., 1967.
53. Коутс К. Теплопроводность в бесконечной области, окружающей тело пря¬
моугольного сечения.— В кн: Теплопередача (перевод Трудов Американского обще¬
ства инженеров-механиков), 1962, 84, № 4, с. 66—70.
54. Кошляков И. С., Глинер Э. Б.у Смирнов М. М. Уравнения в частных про¬
изводных математической физики. М., 1970.
55. Карслоу Л, Егер Д. Теплопроводность твердых тел. М., 1964.
56. Карслоу Г.у Егер Д. Операционные методы в прикладной математике. М., 1948.
57. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.,
1971.
58. Коган М. Г. Преобразование рядов и последовательностей в теории тепло¬
проводности.— ВИНИТИ, per. № 2271—74.
59. Карташов Э. М., Бартенев Г М., Разумовская И. В. Об одной задаче диф¬
фузии для систем двух сред.— Журн. вычисл. матем. и матем. физ., 1967, т. 7, № 6,
с. 1423—1429.
60. Карташов Э. М., Бартенев Г М., Сидоров А. Б. Об одной задаче тепло¬
проводности для системы цилиндрических труб.— Изв. вузов, серия «Физика»,
1967, № 12, с. 30—41.
61. Карташов Э. М., Любое Б. Д. Метод решения обобщенных тепловых задач
в области с границей, движущейся по параболическому закону.— Журн. тех. физики,
1971, т. 61, N°. 1, с. 3—16.
62. Карташов Э. М., Любое Б. Д., Бартенев Г. М. Об одной задаче диффузии
в области с подвижной границей. Изв. вузов, серия «Физика», 1970, № 12, с. 102—ПО.
541
63. Карташов Э. М., Любое Б. Я- Аналитические методы решения краевых
задач уравнения теплопроводности в области с движущимися грницами.— Изв.
АН СССР, серия «Энергетика и транспорт», 1974, № 6, с. 83—111.
64. Карташов Э. М. Метод интегральных преобразований в аналитической тео¬
рии теплопроводности.— Изв. АН СССР, серия «Энергетика и транспорт», 1976,
N° 4, с. 85—105.
65. Карташов Э. М. Об одной задаче диффузии в области с подвижной границей.
— Теплофизика высоких температур, 1967, N° 2, с. 308—316.
66. Карташов Э. М. Термокинетика процессов хрупкого разрушения полиме¬
ров в механических, температурных и диффузионных полях: Автор, дисс. на соиск.
уч. степ. док. физ.-мат. наук.— JI., ИВС АН СССР, 1982.— 54 с.
67. Карташов Э. М., Бартенев Г М. Процессы разрушения полимеров в хруп¬
ком и квазихрупком состояниях.— Высокомолек. соед., 1981, 23 (А), № 4, с. 914—912.
68. Карташов Э. УИ., Бартенев Г М. Временная зависимость прочности поли¬
мерных стекол в поверхностно-активной среде.— Высокомолек. соед., 1982, 24 (А),
N° 7, с. 1433—1439.
69. Карташов Э. М., Нечаев В. М. Метод функций Грина при решении краевых
задач уравнения теплопроводности в нецилиндрических областях-— Прикл. матем.
и мех. (ZAMM, ГДР), 1978, №58, с. 199—208.
70. Карташов Э. М. Метод функций Грина при решении краевых задач уравне¬
ния теплопроводности обобщенного типа.— Изв. АН СССР, «Энергетика и транспорт»,
1979, № 2, с. 108—116.
71. Карташов Э.М. Коэффициенты интенсивности напряжений в бесконечной
пластине с трещиной в неоднородном стационарном температурном поле.— Изв.
вузов, серия «Физика», 1979, № 3, с. 7—13.
72. Карташов Э. Л4., Тулинов Б. М., Нечаев В. М., Бартенев Г. М. О влиянии
инерционных эффектов на характер распределения термоупругих напряжений в
пространстве с движущейся границей.— Физика и химия обработки материалов, 1978,
№ 5, с. 38—41.
73. Карташов Э. М., Нечаев В. С., Бартенев Г. М. Термоупругая реакция бес¬
конечной среды со сферической нагреваемой полостью.— Физика и химия обработки
материалов 1981, №2, с. 26—34.
74. Карташов Э. М., Мосьяков В. Е. Об одном классе задач теплопроводности с
переменным во времени коэффициентом теплообмена.— Изв. вузов, серия «Авиацион¬
ная техника», 1973, № 1, с. 75—82.
75. Карташов Э. М. Аналитические методы в теплопроводности твердых тел.
М., 1979.
76. Кулик Л. М., Шаповалов Г. Е. Неустановившаяся теплопередача через
многослойную плоскую пластину.— Изв. АН СССР, серия «Энергетика и автоматика»,
1971, № 2, с. 72—77.
77. Коган М. Г. Нестационарная теплопроводность в слоистых средах.— Журн.
техн. физики, 1937, т. 27, №3, с. 522—531.
78. Квальвассер В. И., Рутнер Я- Ф• Метод нахождения функции Грина краевых
задач уравнения теплопроводности для отрезка прямой с равномерно движущимися
границами.— Докл. АН СССР, 1964, т. 156, №6, с. 1273—1276.
79. Коздоба Л. А. Электромоделирование температурных полей в деталях судо¬
вых энергетических установок. /С., 1964.
80. Коздоба Л. А., Круковский /7. Г. Методы решения обратных задач теплопере-
носа. Киев, 1982.
81. Ладырюенская О. А., Солонников В. А., Уральцева Н. Н. Линейные и квази¬
линейные уравнения параболического типа. М., 1967.
82. Ладыженская О. А., Уральцева Н. Н. Линейные и квазилинейные уравнения
эллиптического типа. М., 1973.
83. Лыков А. В. Теория теплопроводности. М., 1967.
84. Лыков А. В. Тепломассоперенос. Справочник. М., 1972.
85. Лыков А. В., Михайлов Ю. А. Теория тепло- и массопереноса. М.— Л., 1963.
86. Лыков А. В. Некоторые аналитические методы решения задач нестационарной
теплопроводности.— Изв. АН СССР, серия «Энергетика и транспорт», 1969, № 2,
с. 3—27
87. Левитан Б. М. Разложение по собственным функциям. М.— Л., 1950.
88. Лебедев Н. Н. Специальные функции и их приложения. М., 1963.
542
89. Лебедев Я. Я. Распределение электричества на тонком параболоидальном
сегменте.— Докл. АН СССР, 1957, т. 114, № 3, с. 513—516.
90. Лебедев Я. Я., Скальская И. П. Некоторые задачи теории теплопровод¬
ности для клиновидных тел.—Журн. техн. физики, 1964, т. 34, № 5, с. 801—808;
№9, с. 1558—1565.
91. Левин С. Я. Основы полупроводниковой микроэлектроники. М., 1966.
92. Лаврентьев М. А. и Шабат Б. В. Методы теории функций комплексного
переменного. М., 1965.
93. Любое Б. Я• Диффузионные процессы в неоднородных твердых средах. М.,
1981.
94. Любое Б. Я• Кинетическая теория фазовых превращений. М., 1969.
95. Любое Б. Д. Теория кристаллизации в больших объемах. М., 1976.
96. Любое Б. Я. Решение нестационарной одномерной задачи теплопроводности
для областей с равномерно движущейся границей.— Докл. АН СССР, 1947, т. 57,
№ 6, с. 551—554.
97. Любое Б, Я- О статье В. Л. Шевелькова «Нахождение температурного поля
в изотропной среде перед фронтом движущегося источника тепла».— Журн. техн фи¬
зики, 1948, т. 18, № 5, т. 713—716.
98. Любое Б. Я. Вычисление скорости затвердевания металлического слитка.—
Дока. АН СССР, 1949, т. 68, N° 5, с. 847—850.
99. Любое Б. Я•» Темкин Д. Е. Расчет температурного поля и скорости переме¬
щения фронта фазового превращения в сферических телах.— В кн.: Проблемы метал¬
ловедения и физики металлов. М., 1958, с. 311—316.
100. Любое Б. Я у Ройтбурд А. Л. О влиянии переохлаждения на границе раз¬
дела фаз на скорость перемещения фронта кристаллизации в условиях направленного
теплоотвода.— В кн.: Кристаллизация и фазовые переходы.— Минск, Изд. АН
БССР, 1962, с. 226—234.
101. Любое Б.Яч Карташов Э. М. Метод решения краевых задач диффузии
для области с границей, движущейся по произвольному закону.— Изв. вузов, серия
«Физика», 1970, №12, с. 97—101.
102. Любое Б. Я., Яловой Я. Я. Теплопроводность тела при переменном коэффи¬
циенте теплообмена.— Инж.-физ. журн., 1969, т. 17, № 4, с. 679—687.
103. Минусинский Ям Сикорский Р. Элементарная теория обобщенных функций.
М., 1963.
104. Михайлов М. Ф. Обобщенное конечное интегральное преобразование.—
Инж.-физ. журн., 1968, т. 14, №5, с. 826—831.
105. Мусхелишвили Я. Я. Некоторые основные задачи математической теории
упругости. М., 1966.
106. Милчев В. А., Михайлов М. Д., Тодаров Т. Т. Аккумуляция тепла полуог-
раниченным телом при скачкообразном температурном воздействии.— Инж.-физ.
журн., 1966, т. 10, №3, с. 348—351.
107. Микулин Е. Я. Температурное поле двух твердых тел, разделенных зазо¬
ром.— Инж.-физ. журн., 1961, т. 4, № 2, с. 52—57.
108. Меламед В. Г. О решении задачи Стефана сведением к системе обыкновенных
дифференциальных уравнений.— Докл. АН СССР, 1957, т. 116, с. 577—580.
109. Мартынов Г. А. О распространении тепла в двухфазной среде при заданном
законе движения границ фаз.— Журн. техн. физики, 1955, т. 25, № 10, с. 1754—1767.
110. Нобл. Б. Метод Винера — Хопфа. М., 1962.
111. Панасюк В. В., Саврук М. Я., Дацишин А. Я. Распределение напряжений
около трещин в пластинах и оболочках. Киев, 1976.
112. Подстригай Я- С. Влияние инородных макровключений на распределение
температурных полей и напряжений в упругих телах.— В кн.: Концентрация на¬
пряжений. Киев, вып. 1, 1965, с. 207—21о.
113. Пантелеев В. А.,* Урман П. Я., Скрябин Я. В. Распределение примеси в
случае селективной диффузии из круглого источника.— Изв. вузов, серия «Физика»,
1970, № 12, с. 146—149.
114. Положий Г. Я. Уравнения математической физики. М., 1964.
115. Прудников А. П. Брычков 10. А>, Маричее О. И. Интегралы и ряды. М.,
1981.
543
116. Петухов Б. С., Генин Л. Г. Теплообмен в ядерных энергетических установ¬
ках, М., 1974.
117. Петухов Б. С. Теплообмен и сопротивление при ламинарном течении жид¬
кости в трубах. М., 1967.
118. Пинчевский А. Д. Температурное поле тел в условиях импульсно-мсняю-
щихся температур.— Инж.-физ. журн., 1963, т. 6, № 12, с. 66—72.
119. Павловский Г. И. Теплопроводность в двухслойной пластине при граничных
условиях III рода.— Инж.-физ. журн., 1962, т. 5, № 4, с. 86—88.
120 Партон В. 3. Осесимметричная температурная зависимость для простран¬
ства с дискообразной трещиной.— Прикл. матем. и мех., 1972, № 1, т. 36, с. 117—124.
121. Равин В. С. Об эффективных граничных условиях в задачах стационарной
теплопроводности.— Инж.-физ. журн., 1967, т. 12, №4, с. 540—541.
122. Равин В С. Об одной задаче стационарной теплопроводности.— Докл.
АН СССР, 1967, т. 174, №5, с. 1041 — 1043.
123. Редозубов Д. В. О линейных тепловых задачах с одной движущейся грани¬
цей.— Журн. техн. физики, 1957, т. 27, №9, с. 2149—2157.
124. Редозубов Д. В. Решение некоторых типов линейных типовых задач в огра¬
ниченной и полубесконечных областях при движении границы по закону Yt.— Журн.
техн. физики, 1962, т. 32, № 5, с. 632—636.
125. Рутнер Я. Ф , Скрябина Л. П. Функция Грина уравнения теплопроводности
для полуплоскости при разнородных граничных условиях.— Волжский математ.
сборник. Изд. Казанского ун-та., 1966, с. 321—325.
126. Самарский А. А. Уравнения параболического типа с разрывными коэффи¬
циентами.— Докл. АН СССР, 1958, т. 121, № 2, с. 225—228.
127 Самарский А. А. Введение в теорию разностных схем. М., 1971.
128. Струнина Г М. Задача о сопряжении двух уравнений.— Инж.-физ.
журн., 1961, т. 4, №11, с. 99—104.
129. Смирнов М. С. Применение метода интегральных преобразований к реше¬
нию задач молекулярного переноса: Автореф. дисс. канд. техн. наук. М., 1955.
130. Седов Л. И. Методы подобия и размерности в механике. М., 1957.
131. Соломатов В. В., Гончаров Э. И. Температурное поле неограниченной
пластины при переменных значениях коэффициента теплообмена внешней среды.—
Инж.-физ. журн., 1968, т. 14, № 4, с. 743—745.
132. Соломатов В. В., Гончаров Э. И. Температурный режим тепловыделяющих
элементов при переменных значениях коэффициента теплообмена и температуры вне¬
шней среды.— Изв. АН СССР, серия «Энергетика и транспорт», 1967, № 4, с. 99—103.
133. Стеклов В. А. Основные задачи математической физики. М., т. 1, 1922.
134. Снеддон И. Преобразования Фурье М., 1955.
135. Си Д. С. Теплопроводность в бесконечной сфере с разрывными условиями
на линиях.— Теплопередача (перевод Трудов Американского общества инженеров-
механиков), 1965, т. 87, №2, с. 157—162.
136. Саврук М. П.у Ярема С. Я• Температурное поле в пластине с полубесконеч-
ной трещиной при наличии теплопередачи с боковых поверхностей.— Физ.-хнм.
мех. матер., 1971, т. 7, № 4, с. 92—93.
137. Тихонов А. Н. Самарский А. А. Уравнения математической физики. М.
1966.
138. Тихонов А. Н. О третьей краевой задаче для уравнения параболического
типа.— Изв. АН СССР, серия географическая и геофизическая, 1950, т. 14, № 3,
с. 193—198.
139. Темкин Д. Е. Температурное поле в кристаллизующемся слитке цилиндри¬
ческой формы. Инж.-физ. журн., 1962, т. 5, № 4, с. 89—92.
140. Титчмарш Э. Ч. Разложения по собственным функциям, связанные с
дифференциальными уравнениями второго порядка. М., т. 1, 1960; т. 2, 1961.
141. Титчмарш Э.Ч. Введение в теорию интегралов Фурье. М.— Л., 1948.
142. Трантер К. Д. Интегральные преобразования в математической физике.
М., 1956.
143. Уфлянд Я. С. Метод парных уравнений в задачах математической физики.
Л., 1977.
144. Уфлянд Я• С. Интегральные преобразования в задачах теории упругости.
Л., 1968.
145. Уфлянд Я. С., Юшкова Е. А. Решение задачи Дирихле для конечного клина
544
с помощью специального интегрального преобразования по цилиндрическим функ¬
циям.— Докл. АН СССР, 1965, т. 164, Ns 1, с. 70—72.
146. Фихтенгольц Г М. Курс дифференциального и интегрального исчисления.
М., 1969, т. 1, 2, 3.
147. Фридман А. Уравнения с частными производными параболического типа
М., 1968.
148. Цой Я. В. Теплообмен системы тел при нестационарном режиме.— Инж.-
физ. журн., 1961, т. 4, № 1, с. 120—123.
149. Цой Я. В. Об одном приближенном методе решения задач нестационарной
теплопроводности.— Теплофизика высоких температур, 1967, т. 5, № 6, с. 1048—
1062.
150. Цыбин А. М. К решению задачи Стефана.— Журн. техн. физики, 1974, т. 64,
с. 2441—2444.
151. Черский Ю. И. Краевые задачи теплопроводности с разнородными гранич¬
ными условиями.— Науч. труды Тбилисского матем. ин-та, 1962, т. 28, с. 209—249.
152. Черпаков В. П. Математическая теория регулярного теплового режима.—
Инж.-физ. журн., 1962, т. 5, № 4, с. 130—134.
153. Чудновский А. Ф. Теплообмен в дисперсных средах. М., 1954.
154. Чудновский А. Ф. Физика теплообмена в почве. М., 1948.
155. Чекмарева О. М. О перемещении фронта кристаллизации в затвердевающем
слитке при различных температурных условиях на его поверхности.— Журн. техн.
физики, 1970, т. 60, № 10, с. 2032—2034.
156. Чекмарева О. М. По поводу задачи Стефана в цилиндрической и сфериче¬
ской системах координат.— Журн. техн. физики, 1971, т. 61, №5, с. 1071 —1072.
157. Чекмарева О. М. Решение задачи Стефана, когда движение поверхности
фазового перехода происходит по закону у (т)= У Ат2-\~Вт+Н.— Журн. техн. фи¬
зики, 1974, т. 64, № 10, с. 2043—2050.
158. Чекмарева О. М. Некоторые интегральные уравнения нового типа для задач
с фазовыми переходами.—Журн. техн. физики, 1971, т. 61, №6, с. 1115—1121.
159. Чекмарева О. М. О движении поверхности фазового перехода при больших
временах в осесимметричной задаче Стефана.— Журн. техн. физики, 1975, т. 65, № 2,
с. 209—213.
160. Шевельков В. JI. Нахождение температурного поля в изотропной среде
перед фронтом движущегося источника тепла.— Журн. техн. физики, 1948, т. 18,
№5, с. 511—514.
161. Шнейдер П. Инженерные проблемы теплопроводности.— М., 1960.
162. Эккерт Э. Р. и Дрейк Р. М. Теория тепло- и Массообмена. М., 1961.
163. Юдаев Б. И. Теплопередача. М., 1973.
164. Юшков Я. Я. Функции Бесселя и их приложения к задачам об охлаждении
цилиндра. Минск, 1962.
165. Юшков Я. Я. Приближенное решение задач нестационарной теплопровод¬
ности методом конечных разностей. Минск, 1958, № 6, с. 3—158.
166. Днке £., Эмде Ф., Леш Ф. Специальные функции. М., 1978.
167. Buchholz Н. Die konfluente hypergeometrische Funktion. Springer — Verlag,
Berlin, 1953.
168. Tranter C. On some dual inteqral equations.—Quart. J. Math., 1951, 2,
N 5, p. 60—68.
169. Kartashov E. M. and Lyubov B. YA. Analytic Methods in Solving Boundary
Value Problems of Heat Conductionina Region with Moving Boundaries. Heat Trans¬
fer — Soviet Research, vol 8, N 2, 1976, pp. 1—39.
170. Bartenev G. M. und Kartaschov E. M. Festigkeit und Lebensdauer polymerer
Glaser. Acta Polymerica, 1981, 32, Heft 3, p. 123—130.
171. Cooke J. Asolution of Tranter’s dual inteqral equations problem. Quart.
J.Mecn. a. Appl. Math., 1956, v. 9, N 1, p. 103—109.
172. Карташов Э. М. Аналитические методы решения краевых задач теплопро¬
водности с разнородными граничными условиями на линиях (обзор). Изв. АН СССР,
Энергетика и транспорт, 1986, № 5, с. 125 150.
173. Карташов Э. М. Аналитические методы решения смешанных граничных
задач теории теплопроводности (обзор). Изв. АН СССР, Энергетика и транспорт,
1986, № 6, с. 116 129.
174. Карташов Э. М. Аналитические методы в теории теплопроводности твер¬
дых тел, М., 1985.
545
175. Карташов 3. М. Метод интегральных преобразований в аналитической
теории теплопроводности твердых тел. Изв. АН СССР, Энергетика, 1993, № 2, с.
99 — 127.
176. Карташов 3. М. Расчеты температурных полей в твердых телах на основе
улучшенной сходимости рядов Фурье — Ханкеля. Изв. АН СССР, Энергетика, 1993,
№ 3, с. 106 — 125.
177. Демирчан К С., Бутырин П. А. Моделирование и машинный расчет элект¬
рических цепей. М., 1988.
178. Зарубин В. С. Инженерные методы решения задач теплопроводности, М.,
1983.
179. Зайцев В. Ф., Полянин А. Д. Справочник по дифференциальным уравнениям
с частными производными. Точные решения. М., 1996.
180. Полянин А. Д., Вязьмин А. В., Журов А. И., Козенин Д. А. Справочник по
точным решениям уравнений тепло- и масс опере носа. М., 1998.
181. Ильин В. А. О равномерной сходимости разложений по собственным функ¬
циям во всей замкнутой области. Математический сборник, 1958, т. 45 (87), № 2, с.
195 — 232.
182. Ильин В. А. Спектральная теория дифференциальных операторов. Самосоп¬
ряженные дифференциальные операторы. М., 1991.
183. Садовничий В. А. Теория операторов. М., 1999.
184. Масленникова В. Н. Дифференциальные уравнения в частных производных.
М., 1997.
185. Рудобашта С. П., Карташов Э. М. Диффузия в химико-технологических
процессах. М., 1993.
186. Кудинов В. А., Карташов 3. М. и др. Тепломассоперенос и термоупругость
в многослойных конструкциях. М., 1997.
187. Маслов В. 77., Данилов В. Г., Волосов К. А. Математическое моделирование
процессов тепломассопереноса. Эволюция диссипативных структур. М., 1987.
188. Полежаев Ю. В., Юркевич Б. В. Тепловая зашита. М., 1976.
189. Карташов Э. М., Шевелев В. В., Валишин А. А. Временная зависимость
прочности хрупких полимеров при неизотермическом нагружении. Докл. АН РФ,
1996, т. 350, № 2, с. 216 — 219.
190. Цой Б., Карташов 3. М., Шевелев В. В. Прочность и разрушение полимер¬
ных пленок и волокон. М., 1999.
191. Карташов 3. М. Современные представления кинетической термофлукту-
ационной теории прочности полимеров (обзор). Итоги науки и техники, серия Химия
и технология высокомолекулярных соединений, 1991, т. 27, с. 3 — 112.
192. Карташов 3. М. Аналитические методы решения краевых задач нестаци¬
онарной теплопроводности в областях с движущимися границами (обзор). Изв. АН
РФ, Энергетика, 1999, № 5, с. 3 — 32.
193. Карташов Э. М. Метод обобщенного интегрального преобразования при
решении уравнения теплопроводности в области с движущейся границей. Инженер¬
но-физический журнал, 1990, т. 52, № 3, с. 495 -- 505.
194. Карташов 3. М. Метод функций Грина при решении уравнения нестаци¬
онарной теплопроводности в области с движущейся границей. Изв. АН СССР,
Энергетика и транспорт, 1989, № 3, с. 117 — 125.
195. Карташов 3. М., Стомахин И. В. Термическая реакция вязкоупругих тел на
тепловой удар на основе нового уравнения динамической термовязкоупругости.
Инженерно-физический журнал, 1990, т. 59, № 3, с. 409 — 419.
196. Карташов 3. М., Стомахин И. В. Метод обобщенного интегрального
преобразования при решении уравнения теплопроводности в области с движущейся
границей. Изв. АН РФ, Энергетика, 1992, № 5, с. 138 147.
197. Карташов 3. М. Новые интегральные представления аналитических реше¬
ний краевых задач нестационарного переноса в областях с движущимися границами.
Инженерно-физический журнал, 1999, т. 72, № 5, с. 826 836.
198. Карташов 3. М. Метод функций Грина при решении краевых задач для
уравнений параболического типа в нецилиндрических областях. Докл. АН РФ, 1996,
т. 351, № 1, с. 32 36.
199. Карташов 3. М. Новые интегральные соотношения для аналитических
решений уравнений параболического типа в нецилиндрических областях. Докл. АН
РФ, 2000, т. 374, № 2, с. 32 36.
546
200. Несененко Г. А. Пограничный слой в нелинейных температурных полях
многослойных тел с подвижными границами. М., 1993.
201. Карташов Э. М., Бартенев Г М. Динамические эффекты в твердых телах
в условиях взаимодействия с интенсивными потоками энергии (обзор). Итоги науки
и техники, серия Химия и технология высокомолекулярных соединений, 1988, т. 25,
с. 3 — 84.
202. Карташов Э. М., Хани А. М. Динамическая термоупругая реакция твердых
тел при конечной скорости изменения тепловых воздействий. Изв. АН СССР, Меха¬
ника твердого тела, 1989, № 4, с. 83 — 88.
203. Карташов Э. М., Партон В. 3. Динамическая термоупругость и проблемы
термического удара (обзор). Итоги науки и техники, серия Механика деформиру¬
емого твердого тела, 1991, т. 22, с. 55 — 127.
204. Карташов Э. М., Кунавина Н. А., Степанов Р. Д. Термоупругая реакция
поверхностных слоев твердого тела на тепловой удар. Поверхность. Физика, химия,
механика, 1991, № 12, с. 124 — 132.
205. Карташов Э. М., Рубин А. Г Проблемы теплового удара для области
с движущимися границами в моделях динамической термоупругости. Математичес¬
кое моделирование, 1995, т. 7, № 10, с. 3 — 11.
206. Карташов Э. М. Термическая реакция вязкоупругих тел на тепловой удар
на основе нового уравнения динамической термовязкоупругости. Докл. АН РФ, 1997,
т. 355, № 4, с. 479 — 483.
207. Карташов Э. М. Проблема теплового удара в области с движущейся
границей на основе новых интегральных соотношений. Изв. АН РФ, Энергетика,
1997, №4, с. 122 — 137.
208. Алифанов О. М. Обратные задачи теплообмена. М., 1988.
209. Темкин А. Г Обратные задачи теплопроводности. М., 1973.
210. Самарский А. А., Вабищевич 77. Н. Численные методы решения задач
конвекции — диффузии. М., 1999.
211. Леонтьев А., И. Теория тепломассопереноса. М., 1997.
212. Мартыненко О. Г., Березовский А. А., Соковишин Ю. А. Асимптотические
методы в теории свободно-конвективного теплообмена. Минск, 1979.
213. Павлюкевич Н. В., Горелик Г. Е., Левданский В. В., Лейцина В. Г., Рудин Г. И.
Физическая кинетика и процессы переноса при фазовых превращениях. Минск, 1980.
214. Карташов Э. М. Аналитические методы решения краевых задач нестаци¬
онарной теплопроводности в области с движущимися границами (обзор).— Ин¬
женерно-физический журнал, 2000, т. 74, № 2, с. 1 — 24.
215. Шашков А. Г., Бубнов В. Я., Яновский С. Ю. Волновые явления теплопрово¬
дности. Системно-структурный подход. Минск, 1993.
ОГЛАВЛЕНИЕ
Предисловие
Введение
Г лава I. Основы теории теплопроводности
§ 1. Общие вопросы теории теплообмена
§ 2. Температурное поле
§ 3. Температурный градиент
§ 4. Тепловой поток. Векторная и скалярная формы закона Фурье
§ 5. Дифференциальное уравнение теплопроводности
§ 6. Дифференциальное уравнение теплопроводности для анизотропных
твердых тел
§ 7. Дифференциальное уравнение теплопроводности в движущейся си¬
стеме координат и в движущейся среде
§ 8. Дифференциальное уравнение теплопроводности в деформируемом
твердом теле
Глава II. Математическая постановка краевых задач уравнения теплопровод¬
ности
§ 1. Условия однозначности
§ 2. Краевые условия
§ 3. Постановка краевых задач
§ 4. Безразмерные переменные
§ 5. Корректность постановок краевых задач
§ 6. Решения краевых задач теплопроводности в виде произведения функ¬
ций
Глава III. Метод разделения переменных (метод Фурье)
Введение
§ 1. Ряды Фурье по ортогональным системам функций
§ 2. Метод разделения переменных для краевых задач нестационарной
теплопроводности
§ 3. Метод Фурье при решении неоднородных краевых задач
§ 4. Рабочие формулы записи аналитического решения краевых задач
нестационарной теплопроводности
§ 5. Метод разделения переменных дтя неограниченных областей
§ 6. Метод продолжений для полуограниченной области
§ 7. Собственные значения и собственные функции однородной задачи
в случае линейного теплового потока
§ 8. Собственные значения и собственные функции однородной задачи
для сплошного цилиндра
§ 9. Собственные значения и собственные функции однородной задачи
для полого цилиндра
§ 10. Собственные значения и собственные функции однородной задачи
для сплошного и полого шаров
3
9
13
13
16
19
21
25
32
38
42
57
57
59
72
89
95
106
109
109
110
ИЗ
119
125
145
156
160
165
170
177
548
§ 11. Собственные значения и собственные функции однородной задачи
для кольцевого сектора 183
§ 12. Некоторые замечания, касающиеся метода разделения переменных 186
Глава IV. Метод Дюамеля при решении краевых задач нестационарной тепло¬
проводности 192
Глава V. Метод интегральных преобразований 197
Введение 197
§ 1. Интегральные преобразования с бесконечными пределами 204
§ 2. Интегральные преобразования с конечными пределами 225
§ 3. Интегральные преобразования Фурье в декартовой системе коор¬
динат для линейной области (синус- и косинус-трансформанты
Фурье) 229
§ 4. Интегральные преобразования Ханкеля для сплошного и полого
цилиндра с осесимметричным температурным полем 237
§ 5. Интегральные преобразования Ханкеля для полого и сплошного
цилиндров, температурное поле которых не является осесимметрич¬
ным 242
§ 6. Интегральные преобразования Лежандра для шаровых областей
и некоторых видов краевых задач с разнородными граничными
условиями 252
§ 7. Улучшение сходимости рядов, входящих в аналитические решения
краевых задач теплопроводности 257
§ 8. Справочная таблица интегральных преобразований 276
Глава VI. Операционный метод и его применение к решению краевых задач
нестационарной теплопроводности 302
Введение 302
§ 1. Преобразование Лапласа и его основные свойства 302
§ 2. Формула обращения для преобразования Лапласа 308
§ 3. Операционный метод при решении краевых задач нестационарной
теплопроводности 316
§ 4. Аналитические решения краевых задач теплопроводности при пе¬
ременных коэффициентах переноса 341
Г лава VII. Метод функций Грнна при решении краевых задач нестационарной и
стационарной теплопроводности 365
Введение 365
§ 1. Интегральные представления решений краевых задач нестационар¬
ной и стационарной теплопроводности 368
§ 2. Интегральные представления решений краевых задач теплопровод¬
ности в области с движущимися границами 390
Глава VIII. Аналитические методы решения краевых задач уравнения тепло¬
проводности в области с движущимися границами 399
Введение ... 399
§ 1. Метод тепловых потенциалов (области [l+vt, сю], [0, l+vt], [/j+ v{t,
+ [vf, l+vt], t^O) 402
§ 2. Функции Грина краевых задач для областей с равномерно движущи¬
мися границами 410
§ 3. Метод рядов для областей вида [0, y+2at], [y^2at, сю], />0 421
§ 4. Метод дифференциальных рядов для области вида [0, y(0L 1^0 431
§ 5. Метод функциональных преобразований (метод перевода краевой
задачи обобщенного типа в классическую) 440
§ 6. Методы решения краевых задач нестационарной теплопроводности
с переменным во времени коэффициентом теплообмена 459
§ 7. Методы решения краевых задач стефаноьлкого типа 472
549
Глава IX. Аналитические методы решения краевых задач стационарной и
нестационарной теплопроводности с разнородными граничными условиями
на линиях 493
Введение 493
§ 1. Метод сопряжения при решении краевых задач стационарной теп¬
лопроводности 494
§ 2. Метод дуальных интегральных уравнений в задачах стационарной
и нестационарной теплопроводности 500
§ 3. Метод тепловых потенциалов при решении краевых задач нестацио¬
нарной теплопроводности 521
§ 4. Метод Винера — Хопфа 526
Краткое заключение 535
Список литературы 539
Учебное издание
Карташов Эдуард Михайлович
АНАЛИТИЧЕСКИЕ МЕТОДЫ
В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ТЕЛ
Редактор Т. В. Высева
Художник К. Э. Семенков
Художественный редактор Ю. Э. Иванова
ЛР №010146 от 25.12.96. Изд. № Х/Е-240. Сдано в набор и
подп. в печать 12.07.01. Формат 60х 881/16. Бум. газета. Гарнитура «Таймс».
Печать офсетная. Объем 33,81 уел. печ. л. 33,81 уст. кр.-отт. 35,01 уч.-изд. л.
Тираж 5000 экз. Заказ № 339
ГУП «Издательство «Высшая школа», 127994, Москва, ГСП-4, Неглиыная ул., д. 29/14.
Факс: 200-03-01, 200-06-87
E-mail: V-Shkola@g23.relcom.ru http: // www.v-shkola.ru
Отпечатано в ОАО «Оригинал» 101990, Москва, Центр, Хохловский пер., 7.
Карташов Э. М.
К 27 Аналитические методы в теории теплопроводности твердых
тел: Учеб. пособие. — 3-е изд., перераб. и доп. — М.: Высш.
шк., 2001. — 550 с.: ил.
ISBN 5-06-004091-7
В пособии систематически изложены аналитические методы решения кра¬
евых задач теплопроводности твердых тел. Даны характеристика метода, его
особенности, область приложения, направления обобщения. Сформулирован
ряд проблемных вопросов аналитической теории.
В настоящем издании (2-е — 1985 г.) расширены таблицы интегральных
преобразований, дуальных интегральных уравнений и парных сумматерных
рядов; рассмотрена проблема теплового удара, уравнения переноса в средах
с тепловой памятью и с конечной скоростью распространения тепла.
Для студентов втузов. Может быть полезна специалистам в обмети
теплотехники, прикладной математики и физики.
УДК 536.2
ББК 22.37