Author: Москаленко Г.М.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника ракетодинамика
Year: 1974
Text
Г. М. МОСКАЛЕНКО
ИНЖЕНЕРНЫЕ
МЕТОДЫ
ПРОЕКТИРОВАНИЯ
В РАКЕТОДИНАМИКЕ
Москва
«Машиностроение»
1974
М82
УДК 629.76.001.2
Москаленко Г. М. Инженерные методы проектирования в ра-
кетодинамике. М., «Машиностроение», 1974, 392 с.
Книга посвящена общим вопросам выбора оптимальных пара¬
метров ракетных летательных аппаратов на начальном этапе про¬
ектирования. Рассмотрены экстремальные расчетные случаи для
элементов конструкции ракет. Описаны законы ракетодинамики
с учетом весового баланса для двух законов изменения
массы. Сформулирована общая теорема о делении точки пере¬
менной массы. Приведены аналитические решения, с помощью
которых найдены новые инженерные методы проектирования ле¬
тательных аппаратов. Изучены неустановившиеся и квазиустано-
вившиеся движения применительно к ракетным и ракетно-авиа¬
ционным системам однократного и многократного применения.
Книга содержит рабочие формулы, графики, таблицы и типовые
расчеты.
Книга рассчитана на инженеров-проектировщиков и специа¬
листов, работающих в области ракетно-космической и авиацион¬
ной техники. Она может быть также полезна студентам-диплом-
никам соответствующих учебных заведений.
Табл. 25, ил. 215, список лит. 95 назв.
Рецензент д-р техн. наук И. К. Бажинов.
М 31Э°?Т189. 189-73
038(01)—73
© Издательство «Машиностроение», 1974 г.
ПРЕДИСЛОВИЕ
Разработка новых ракетных летательных аппаратов (РЛА)
является сложным процессом, который определяется большим
числом различных факторов. Обычно этот процесс ведется в не¬
сколько этапов.
На первом этапе на основе анализа исходных данных, накоп¬
ленных сведений о характеристиках уже разработанных конст¬
рукций ракет, а также различных статистических данных, наме¬
чают область возможных или предполагаемых характеристик
проектируемого РЛА. Затем в этой области с помощью обычно
упрощенных методик проводят многопараметрические исследо¬
вания с целью:
а) определения конструктивно-силовой и компоновочной схе¬
мы РЛА, а также рационального выбора основных параметров
(таких как тип конструкции РЛА и его двигательной установки,
количество ступеней, тип используемого топлива и т. д.);
б) определениям первом приближении оптимальных значений
основных параметров (мес РЛА и его полезный груз, скорость
и дальность полета, распределение масс по ступеням, тяговые
характеристики и т. д.).
Этот этап иногда называют этапом баллистического проекти¬
рования, поскольку он связан с необходимостью совместного ис¬
следования весовых и баллистических зависимостей. Точность
получения характеристик проектируемого РЛА на этом этапе
зависит от точности используемых весовых зависимостей и
полноты учета действующих сил в уравнениях движения.
Следует отметить, что если уравнения движения ракеты в на¬
стоящее время уже достаточно хорошо исследованы и можно
достоверно оценивать погрешности благодаря тем или иным
упрощениям этих уравнений, то этого нельзя сказать относитель¬
но основных весовых зависимостей различных типов РЛА. Работ,
в которых исследуются вопросы установления весовых зависи¬
мостей для совместного анализа с уравнениями движения (раке-
тодинамики), известно очень мало и они далеко не полностью
отвечают на поставленные практикой вопросы.
На этапах разработки РЛА, следующих за баллистическим
проектированием, производят конкретную проектно-компоновоч-
3479 3
ную разработку, прочностные расчеты, уточнение весовых харак¬
теристик, аэродинамические расчеты, разработку систем управ¬
ления РЛА, уточненные баллистические расчеты. В процессе
этих работ могут производиться корректировки основных харак¬
теристик РЛА для более точного соответствия весовых характе¬
ристик исходным требованиям. Большинство известных в настоя¬
щее время работ содержат исследования по последним этапам
разработки РЛА.
Настоящая книга посвящена исследованиям на первых эта¬
пах разработки РЛА: установлению основных весовых зависимо¬
стей, анализу влияния весовых факторов на различные режимы
полета РЛА и разработке аналитической методики баллистиче¬
ского проектирования РЛА, т. е. определению оптимальных зна¬
чений основных параметров РЛА.
Учет весовых факторов в задачах прикладной ракетодинами-
ки существенно влияет на выбор оптимальных параметров РЛА.
По этой причине в работе уделено особое внимание разработке
аналитического метода весового расчета. Определены расчетные
случаи и экстремальные нагрузки на элементы конструкции
РЛА. Получены рабочие весовые формулы для различных отсе¬
ков, агрегатов, силовых элементов и систем. Исследована функ¬
циональная связь между основными проектными параметрами.
Записана основная весовая зависимость и показано существова¬
ние весового барьера, устанавливающего рациональные границы
по проектным характеристикам РЛА.
Рассмотрены некоторые положения механики полета, каса¬
ющиеся неустановившихся (вертикальных) и квазиустановив-
шихся (горизонтальных) режимов движения применительно к
задачам К. Э. Циолковского и А. А. Космодемьянского и най¬
дены новые решения.
Изучены режимы движения одноступенчатых РЛА в пустоте
с учетом уравнений весового баланса и с учетом влияния атмо¬
сферы при двух законах изменения массы и разработан метод
определения оптимальных значений основных параметров (осе¬
вых перегрузок, относительных весов полезных грузов, весовых
отдач по активным и пассивным массам, геометрических харак¬
теристик топливных емкостей и их отсеков).
Рассмотрено движение точки переменной массы применитель¬
но к движению многоступенчатой ракеты, для которой скорость
отброса массы может принимать различные значения, в том числе
(где I, II,..., п — индексы первого, второго и т. д. делений точки).
4
Сформулирована новая теорема, устанавливающая экстре¬
мальный закон деления точки (ракеты) в процессе ее движения
при учете массовых характеристик, гравитационных сил, траек¬
ториях данных, аэродинамического влияния среды и высотной
характеристики двигателя. Условия деления (распределения
масс) с учетом оптимальных перегрузок иллюстрированы инже¬
нерными методами расчета для линейного и показательного за¬
конов изменения массы. Показано, что известные в настоящее
время рекомендации по делению точки переменной массы явля¬
ются частными случаями полученной теоремы.
В настоящее время все больше уделяют внимания перспек¬
тивным РЛА многократного применения. В связи с этим в книге
рассмотрены маршевый и суборбитальный полет ракетоплана,
режимы входа возвращаемых ступеней РЛА в плотные слои
атмосферы (рикошетирующий, квазистационарное планирование
с положительной и отрицательной подъемными силами, пологая
баллистическая траектория) и переходные режимы (крутое вы¬
равнивание, нисходящий маневр, горка, вираж в горизонтальной
плоскости). Изучены также оптимальные условия маршевого
полета с учетом расхода топлива на участке выведения, влияние
маршевой скорости на дальность полета с учетом планирования,
а также активно-инерционный полет ракетоплана. Материал
этот взаимосвязан и дает возможность выполнять инженерные
расчеты по определению характеристик возвращаемых ступеней
РЛА многократного применения [12].
В книге рассмотрены локальные (в данной точке) и инте¬
гральные (в общем виде) свойства траекторий полета.
При написании книги автор стремился к наиболее простым
формам изложения и получению несложных зависимостей,
пригодных для выполнения проектных расчетов первого при¬
ближения. Графики, таблицы и примеры расчетов облегчают
понимание материала и способствуют приобретению началь¬
ных навыков к самостоятельному творчеству в этой области
знаний.
При изложении материала автор стремился к безразмерным
формам записи получаемых зависимостей. В связи с этим воз¬
никли некоторые трудности, относящиеся к вопросам терминоло¬
гии. Так, например, отношения скоростей (текущей к начальной)
названы безразмерными скоростями. Такая терминология явля¬
ется привычной для проектанта, в то время как с точки зрения
чистой механики такое определение не корректно. Имеет место,
например, несовместимость терминологии для двухрежимного
полета ракетоплана, осуществляющего взлет в режиме баллисти¬
ческой ракеты с последующим выходом на режим квазигоризон-
тального маршевого полета с постоянной скоростью. В первом
случае параметр n(t) (равный отношению тяги к весу J1A) опре¬
деляется как перегрузка, во втором случае — как тяговооружен-
ность. На стыке двух режимов движения, когда конечная ско¬
рость взлета становится скоростью маршевого полета, параметр
n(t) меняет свое определение.
Автор выражает благодарность кандидатам техн. наук
И. М. Ядунскому, И. Н. Моишееву, Г. Ю. Максимову, Н. М. Ива¬
нову, Г. А. Колегову, канд. физ.-мат. наук В. И. Киргетову, кото¬
рые сделали ряд полезных замечаний при просмотре рукописи,
а также д-ру техн. наук И. К. Бажинову, взявшему на себя труд
рецензирования книги.
Автор будет признателен всем читателям, которые пришлют
свои критические замечания по адресу: Москва, Б-78, 1-й Бас¬
манный пер., 3, изд-во «Машиностроение».
ВВЕДЕНИЕ
Современная ракетодинамика — раздел теоретической меха¬
ники, относящийся к механике реактивного полета. Приложения
теоретической механики в задачах динамики ракеты составляют
предмет ракетодинамики. Главной задачей этой науки является
определение основных характеристик, траекторных данных и
закономерностей, определяющих активные (при работающих
двигателях) и пассивные (при выключенных двигателях) режи¬
мы движения реактивных летательных аппаратов (ракет, ракет¬
ных самолетов, исскусственных спутников, межпланетных кораб¬
лей, гиперзвуковых объектов и т. д.). Научной основой ракето-
динамики является механика тел переменной массы, изучающая
законы движения материальных точек (систем точек) под дей¬
ствием сил с учетом расхода активных масс.
Под инженерными методами в ракетодинамике следует пони¬
мать те методы, которые относятся к вопросам проектирования
летательных аппаратов ракетного типа. Эта часть ракетодинами¬
ки (ее можно было бы назвать прикладной ракетодинамикой)
характерна результатами, получаемыми на базе учета конкрет¬
ных проектно-конструктивных факторов (экспериментальных
данных) и среди них прежде всего весовых факторов.
Как известно, развитие методов проектирования (например
в авиации) всегда сопровождалось развитием методов весового
анализа. В ракетной технике эти методы получили также боль¬
шое развитие благодаря возможности аналитического совмеще¬
ния уравнений ракетодинамики и уравнений весового баланса.
Все ракеты суть тела, масса которых изменяется во время
движения.
Основной закон динамики точки (тела) переменной массы
был открыт русским ученым, профессором Петербургского по¬
литехнического института И. В. Мещерским в 1897 г. и изложен
в его магистерской диссертации.
В соответствии с этим законом основное уравнение движения
точки переменной массы записывается в следующем виде:
m^-=p+f, (О
at
где р = w — реактивная сила (обусловленная истечением
массы), a F — равнодействующая всех остальных внешних сил.
7
Дифференциальный закон движения точки переменной мас¬
сы, описываемый уравнением (1), формулируется так:
для любого момента времени произведение массы М излу¬
чающего центра на его ускорение dVjdt равно геометрической.
сумме приложенных к нему внешних сил F и силы реактивной Р.
Давая высокую оценку научному наследию И. В. Мещерско¬
го, А. А. Космодемьянский в своей книге * пишет: «Полученное
И. В. Мещерским основное уравнение движения точки перемен¬
ной массы дало возможность установить количественные законо¬
мерности для различных частных задач. Мы не можем указать
работ иностранных авторов, которые по идейному богатству стоя¬
ли бы на одном уровне с этой «старой» работой И. В. Мещер¬
ского».
Ценный вклад в механику тел переменной массы внес знаме¬
нитый русский ученый К. Э. Циолковский. В своей работе «Ис¬
следование мировых пространств реактивными приборами»,,
опубликованной в 1903 г. **, К. Э. Циолковский впервые рас¬
смотрел ряд задач, относящихся к прямолинейному движению
тела (ракеты) переменной массы. При рассмотрении простей¬
ших случаев движения точки в среде без внешних сил К. Э. Ци¬
олковский впервые получил формулу для конечной скорости
ракеты
где Мт — масса топлива, расходуемого в полете; Мк — масса
ракеты без топлива (конечная масса).
Эта формула носит название формулы Циолковского. Лога¬
рифмический закон (2) был сформулирован К. Э. Циолковским
в 1914 г. в виде следующей теоремы***:
«Когда масса ракеты плюс масса взрывчатых веществ, име¬
ющихся в реактивном приборе, возрастает в геометрической про¬
грессии, то скорость ракеты увеличивается в прогрессии ариф¬
метической».
Действительно, если формулу Циолковского переписать
то увидим, что если задать
* К о с м о д е м ь я п с к и и А. А. Курс теоретической механики. М., Уч¬
педгиз, 1955.
** Работы К- Э. Циолковского по ракетной технике вошли во 2-й том его
собрания сочинений, Изд-во АН СССР, 1954.
*** Космодемьянский А. А. «К. Э. Циолковский — его жизнь и ра¬
боты по ракетной технике». М., Воениздат, 4960.
(2)
(4)
в виде геометрической прогрессии, то получим изменение ско¬
рости
In J^L = in т, 2 In m, 3 In m, 4 In m, 51nm, . . . (5)
в виде арифметической прогрессии (где m — любое число).
Формула Циолковского является фундаментальной для ис¬
следований в области ракетодинамики. В работе, посвященной
исследованиям динамики точки для двух законов изменения
массы, частных задач механики полета, а также различных
режимов движения ракетоплана, А. А. Космодемьянский впер¬
вые сформулировал новые задачи предмета теоретической меха¬
ники, выделив их в отдельную область знаний, названную раке-
тодинамикой *.
В книге, там где возможно, применен комплексный анализ
уравнений ракетодинамики на базе учета весовых факторов.
Обычно это выглядит так:
Кк=-1П (6)
щ
« * Т7 Ук
где т — полное время истечения активной массы; VK = — — без¬
размерная конечная скорость;
/('Г) = !Азл + (1-1Аэл)г + ^0- (7)
После приравнивания производной (dVK/dn0) нулю имеем
Ло = Я0[Рэл. 3(0,<). s, k\, (8)
где р:)Л — конструктивный параметр; п0 — коэффициент началь¬
ной (стартовой) перегрузки; сг(0к)—коэффициент, учитываю¬
щий гравитационные потери; е — коэффициент соотношения
масс; k — удельный измеритель двигательной установки.
С помощью уравнений весового баланса
Рк/ = Ые). = • • •
(где X — удлинение топливного отсека или корпуса ракеты) по-
«лучены результаты, трансформирующие выводы теоретической
ракетодинамики применительно к действительным условиям по¬
лета и работы элементов конструкции летательного аппарата.
Особенно важными для практики явились выводы по много¬
ступенчатым ракетам. Здесь получен общий закон распределе¬
ния масс по ступеням составных ракет с учетом комплекса ди¬
намических и массово-инерционных факторов. Сформулирована
* Выражение «Динамика точки переменной массы» применительно к ра¬
кетам может быть заменено как «динамика ракеты» или сокращенно «раке-
тодинамика».
9
новая теорема и введена безразмерная характеристика — пара¬
метр М как величина, зависящая от параметров, задаваемых при
проектировании (грузоподъемности, коэффициентов эффектив¬
ности конструкции, скорости истечения активной массы, грави¬
тационных потерь, количества ступеней и т. п.). Теорема, сфор¬
мулированная в самом общем виде, утверждает, что оптималь¬
ному делению соответствует постоянство характеристического
параметра М для всех ступеней. Знание этого нового закона ме¬
ханики полета является необходимым при выполнении научных
изысканий и при проведении проектных работ по выбору опти¬
мальных параметров ракетных летательных аппаратов различ¬
ных схем и назначений.
При составлении весовых формул, как это обычно делается,
введены дополнительные поправочные (конструктивно-техноло¬
гические) коэффициенты, величины которых определяются путем
сравнений теоретического веса с весом аналогичных реальных
конструкций. В книге значения самих коэффициентов (там где
они приведены) получены автором на базе обработки статисти¬
ческих данных. Анализ статистических данных для различных
схем ракет показывает, что элементы конструкции, близкие по
геометрии и нагрузкам, но разработанные разными проектными
организациями, могут значительно отличаться по весу. Это объ¬
ясняется различием в приемах проектирования, технологии про¬
изводства, квалификации кадров и т. п. Ориентируясь на стати¬
стические данные, взятые для одноименной группы ракет
и элементов их конструкции, мы тем самым имеем возможность
учесть сложную корреляцию, функциональное (параметрическое)
выражение которой известно. Следует также иметь в виду, что
некоторые формулы теории упругости, в том числе и формулы
Эйлера, взятые в качестве исходных уравнений, не учитывают
конкретных условий работы и дефектов конструкции, имеющих
место в производстве. По этой причине необходимо иметь в виду,
что зависимости, приведенные в гл. IV, могут быть использованы
только при условии обработки их статистическими данными и
введения поправочных коэффициентов.
Главной задачей, связанной с завершением полета спасаемых
ступеней многократно используемых космических систем, явля¬
ется безопасное возвращение к месту старта или какому-либо
другому району посадки. Здесь может быть осуществлено движе¬
ние в режиме квазистационарного планирования с положитель¬
ной или отрицательной подъемными силами, вход в плотные слои
атмосферы по баллистической траектории, полет с отражением
в атмосфере и другие режимы движения. Решение аналогичных
задач сводится к проблемам скорости, дальности, высоты и вре¬
мени полета, а также к проблеме действующих продольно-попе¬
речных перегрузок. Помимо этого, большое значение имеет зна¬
ние маневренных характеристик ступеней крылатых ракетно-
космических систем в вертикальной и горизонтальной
10
плоскостях. Вопросу таких многорежимных видов движений по¬
священы многие исследования советских и зарубежных авторов.
Как известно, полные дифференциальные уравнения неустановив-
шихся видов движений не решаются в конечном виде аналитичес¬
ки. Точное решение их может быть получено с применением элек¬
тронных вычислительных машин. Однако этот метод мало при¬
годен там, где решение должно быть получено не в виде иллю¬
стративных графиков, а в виде аналитических зависимостей, при¬
годных для выполнения массовых расчетов в минимальное время.
По этой причине при рассмотрении ряда задач в книге в каждом
конкретном случае приняты допущения, которые обеспечивают
аналитическое решение с точностью, приемлемой для проектных
расчетов.
В книге принят метод изложения от частного к общему, так
как он дает возможность более внимательно проследить после¬
довательность конструкторского мышления и получить соответ¬
ствующие навыки в этом направлении.
В настоящее время проектирование летательных аппаратов
производится с применением злектронновычислительных машин
(ЭВМ). Книга построена в основном на аналитическом материа¬
ле. Это очень важно в наши дни, когда успехи ЭВМ создали у
ряда исследователей иллюзию второстепенное™ и нисходящей
роли аналитических решений.
Ясная физическая интерпретация, отчетливый параметриче¬
ский прогноз, и что, пожалуй, самое главное, возможность вскры¬
тия и формулировки новых законов — вот преимущества анали¬
тического метода исследований. Мы полагаем, что при дальней¬
шем развитии прикладной ракетодинамики исследователи будут
стремиться к синтезу аналитических и вычислительных методов.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
а ^ = М (t) — текУщее УСК0Реиие точки переменной
массы;
(су/сх) — аэродинамическое качество;
Дм—диаметр по миделю (ракеты, топлив¬
ного бака и т. п.);
d — малый диаметр конического бака; диа¬
метр стержня; диаметр внутреннего
(телескопического) бака;
Е — модуль упругости (модуль Юнга);
Et—тангенциальный модуль (производная
напряжения по деформации);
V2
г = М —— — центробежная сила;
Н
fit)—непрерывная функция времени, выра¬
жающая определенный закон измене¬
ния массы;
/(0=1 — — линейный закон изменения массы;
/ (0 = е— ^ — показательный закон изменения массы;
G — вес летательного аппарата;
Gq — начальный (стартовый) вес;
GK — конечный вес;
GT — вес топлива, расходуемого в полете;
G^t — суммарный вес топлива всех ступеней
составной ракеты;
— вес составной ракеты без топлива (сум¬
марный конечный вес всех ступеней
вместе с полезным грузом);
Gr(t) — вес топлива в функции времени полета;:
G6 — вес бака;
Gc = ( — dG/dt) — секундный весовой расход топлива;
СЭл —вес элемента конструкции;
Gок — вес окислителя;
Gгор — вес горючего;
Gi — вес i-то элемента конструкции;
СЕ-фф ^ G0i — GST — ае “ Эффективный конечный вес составной ра¬
кеты (суммарный вес конструкции без
полезного груза);
12
___ <2(0 — текущий вес летательного аппарата;
GT = Gt/Gq — весовая отдача по топливу;
= <2St/Goi — весовая отдача составной ракеты
суммарному запасу топлива всех ступе*
ней;
q ^ ~ j^ —текущая весовая отдача по топливу;
g — ускорение сил земного тяготения на
данной высоте полета;
go — ускорение сил земного тяготения на
уровне моря;
<§0 (R3/R)2 — ускорение сил земного тяготения на
расстоянии R от центра Земли;
И — высота полета над уровнем моря;
Н — M/(W2/g) — безразмерная высота полета;
h — высота днища;
2Шп — момент инерции шпангоута;
i — количество элементов конструкции, вес
которых зависит от одинаковых пара¬
метров; i-я ступень;
^гор = <2ок/(/гор — весовое соотношение компонентов топ¬
лива (окислителя к горючему);
— коэффициент, равный отношению веса
верхнего компонента топлива к весу
нижнего компонента топлива;
£0с> Дн» Д —весовые коэффициенты;
£м = Дм Id — коэффициент конусности бака (корпуса
ракеты, обечайки и т. п.);
kg — обобщенный статистический коэффи¬
циент;
2*ф +1
Rfo — — параметр эллиптических днищ;
К
+ 1
= — параметр сферических днищ;
k — весовой коэффициент (удельный изме¬
ритель) двигательной установки; коэф¬
фициент местной потери устойчивости
па критическую силу;
k* = G*/GT — относительный вес верхнего компонента
топлива;
— G"/GT — относительный вес нижнего компонента
топлива;
k\, k2 — коэффициенты заделки на опорах;
Д — полная длина топливного бака (вместе
с днищами);
Mq — начальная (стартовая) масса;
М (t) —текущая масса;
13
мк -
конечная масса;
Л| ( dM\
Л1С ---.г I ——jj- I _ секундный расход активной массы;
М — число Маха;
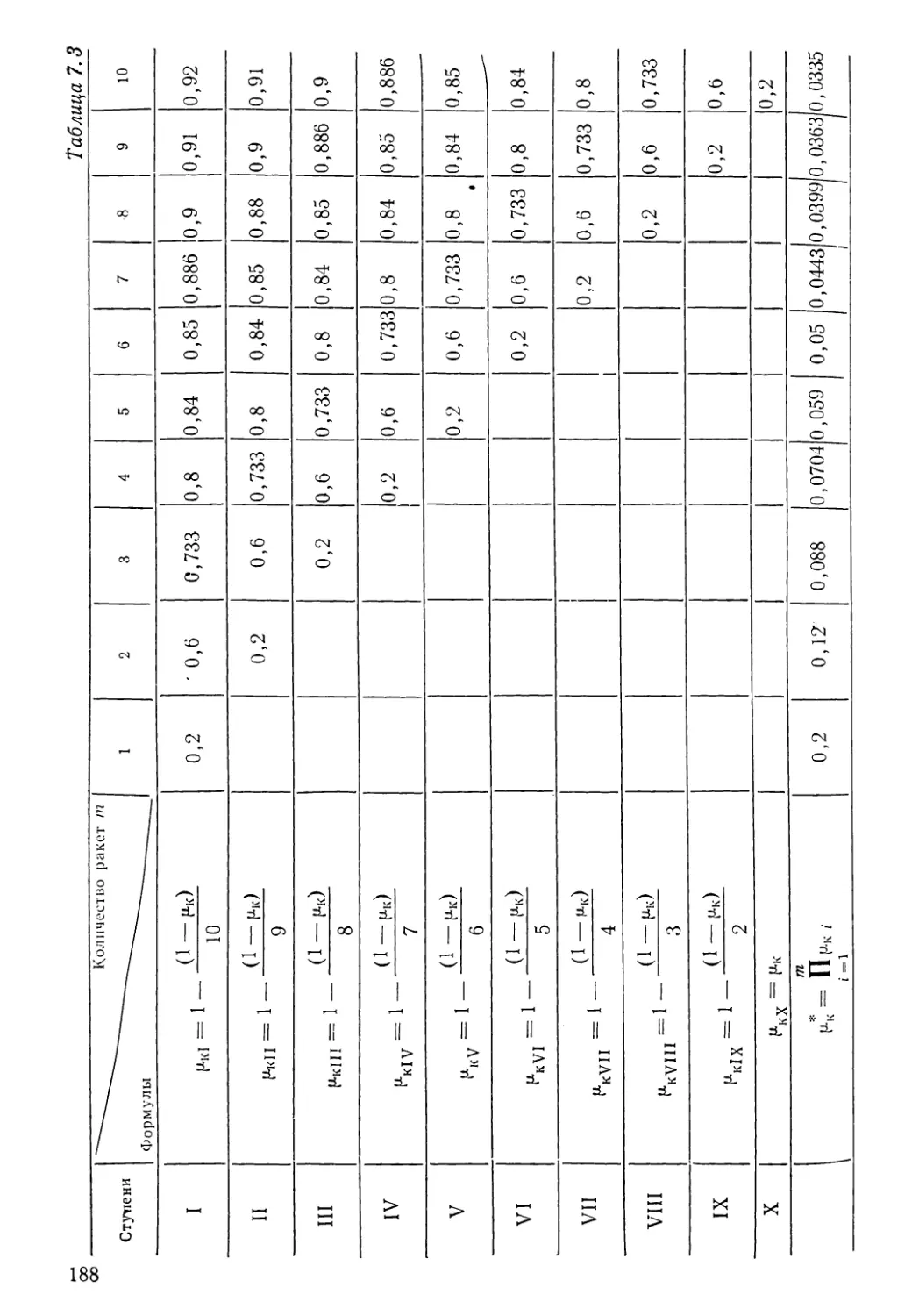
М — параметр распределения масс;
т — количество ракет в ракетном поезде;
Nx — осевая сжимающая сила;
Ar.v (0 — осевая сжимающая сила в функции
времени полета;
— осевая сила в сечении а—а\
п0 = «опт — оптимальная стартовая перегрузка;
(«о)тах — максимальная величина оптимальной
стартовой перегрузки;
/2о = Яо/Gq — стартовая перегрузка па уровне моря:
«шах = -Pq/Gk — конечная (максимальная) перегрузка
в пустоте;
/?q = P1q/Gq — стартовая перегрузка в пустоте;
п — количество ступеней составной ракеты;
Об
п = — параметр, характеризующим выпук-
2 п
лость днищ баков;
nK(t) = —(dV /dt) — осевая (продольная) перегрузка в
£'о
функции времени полета;
пу — коэффициент поперечной перегрузки;
Р — реактивная сила точки переменной мас¬
сы или тяга двигателя на марше;
Р0 — тяга двигателя на уровне моря;
Я'о — тяга двигателя в пустоте;
/?s — суммарное избыточное давление в баке;
/?дн — внутреннее давление на днище бака;
Go
^ — нагрузка от веса на единицу характер-
S
ной площади;
р и
Я1! = — удельная тяга двигателя в пустоте;
>л Gc
п Яо
ЯуД = — удельная тяга двигателя на уровне
Gc
моря;
р —удельная тяга точки переменной массы
или продуктов сгорания топлива при
маршевом движении ракетоплана;
Ризб — избыточное давление в баке;
/?ГИдр — гидростатическое давление в баке;
q _ погонная сила, растягивающая шпан¬
гоут; скоростной напор;
qN = NP/SU'K — удельная нагрузка па единицу площади
панели;
14
Np
iV x
Qk=—7Г-— погонная нагрузка на срезе корпуса;
jt DK
R3 — радиус Земли; *-:Г
R = R3 + И — расстояние от центра Земли до движу¬
щейся точки;
R—большой радиус торового бака;
г—малый радиус торового бака; радиус
виража;
S — характерная площадь;
SM — площадь миделя;
•Sii.k — площадь крепежной панели;
t — текущее время полета;
V — скорость полета;
vKp = VgR — первая космическая (круговая) ско¬
рость;
Vm—Vm/W — безразмерная маршевая скорость по¬
лета;
—безразмерная конечная скорость полета;
VK — конечная скорость полета (в конце ак¬
тивного участка траектории);
Vq,
^кр = ~W——безразмерная первая космическая (кру¬
говая) ско/рость;
v — объем (бака, обечайки, днища);
1
г/дн = — параметр эллиптических днищ;
3/г2 -f 1
н = — параметр сферических днищ;
12 пЧ\
W — скорость истечения точки переменной
массы; то же для продуктов сгорания
топлива при маршевом полете ракето¬
плана;
W11 — скорость истечения продуктов сгорания
топлива из камеры двигателя в пустоте;
Wq — скорость истечения продуктов сгорания
топлива из камеры двигателя на уров¬
не моря;
—
W i = — безразмерная скорость истечения L-й
W ]
ступени (отнесенная к скорости истече¬
ния первой ступени);
X (V) — сила лобового сопротивления в функции
скорости полета;
Y (V) — подъемная сила в функции скорости
полета;
Э = Мс/М0 — коэффициент расхода активной массы
(топлива);
15
YT = — средний удельный вес топлива (топлив-
1 _ 'С
Yrop Yok
пой пары);
Yrop — удельный вес горючего;
(Ym/[<j]) — величина, обратная удельной прочности;
Yok — удельный вес окислителя;
Ym — удельный вес материала конструкции;
ДЕ — суммарный вес грузов (полезный груз
вместе с оборудованием и другими ве¬
сами) ;
АР—статическая добавка тяги двигателя;
Д^шах — максимальная статическая добавка тя¬
ги в пустоте;
AV — потери в скорости за счет аэродинами¬
ческого сопротивления;
Ъ—толщина стенки (обечайки, днища, об¬
шивки корпуса);
°0(/+1)
е/ = — — коэффициент распределения масс;
Gqi
* Да
е = “— — коэффициент грузоподъемности;
°01
ек/ = — грузоподъемность, отнесенная к конеч-
GK
ному весу;
0 — угол, составленный вектором скорости
и местным горизонтом;
X — L/D — удлинение;
&ф + 1
Хо6 = Хб — — удлинение обечайки, выраженное через
2/гЛф
удлинение бака;
£ф "Г 1
Хб = Хоб + — удлинение бака, выраженное через
2/г/гф
удлинение обечайки;
^к.т (0 — текущее (в функции времени полета)
удлинение компонента топлива в баке;
fjLK = GK/G0 — весовая отдача по конечному весу;
{л2к = GSl./(70I — весовая отдача составной ракеты по
суммарному конечному весу ступеней
(вместе с полезным грузом);
Оэл
Р-эл = — безразмерный вес элемента конструк¬
ции;
ias эфф = эфф/С01 — коэффициент эффективности конструк¬
ции составной ракеты;
16
Иоб (^б)
Пдн (Л)
GK “ *z
jj-зфф = —коэффициент эффективности конструк-
Go — Aj,
ции одноступенчатой ракеты или ускори¬
телей составной ракеты;
п
— П р-кi — приведенная весовая отдача;
/ =1
р. — коэффициент Пуассона;
£ — коэффициент увеличения тяги двигателя
в пустоте ДЯщах/А); коэффициент за¬
полнения бака топливом vr/vQ\
[с] —допускаемое напряжение;
окр—критическое напряжение при сжатии;
от —предел текучести материала;
т
0 = 6*п ^ — параметр, учитывающий потери в ско-
0
рости на силы тяжести в зависимости
от выбранной программы полета (ко¬
нечного угла 0К);
а (0К)
а (вк) — — гравитационный параметр;
«о
т — полное время полета при работающем
двигателе;
М2
X = ш~£~ — характеристическим параметр нагруже¬
ния;
+ 1 / £ф + 1 \
= I Дб—~ ) — параметр, характеризующий величину
&ф \ 2п/гф /
поверхности обечайки;
тт / \ /l2 + ^
Пдн («) = — — параметр, характеризующим величину
/г2
поверхности днища, выполненного в ви¬
де шарового сегмента;
In (л+/«2 + 1)
= 1 + ; —— — параметр, характеризующий величину
п У п '2 — 1
поверхности днища, выполненного в ви¬
де эллипсоида вращения;
G0
Ц = —- — число Циолковского;
GK
п
ц*= П Ц/ — приведенное число Циолковского без
/ = 1
учета гравитационных потерь;
Цi = Ц/ — oi — приведенное число Циолковского для
i-й ступени с учетом гравитационных
потерь;
_ п
ц = П ЦI — приведенное число Циолковского для
/=1
составной ракеты с учетом гравитаци¬
онных потерь;
MV2
Э = —-— — кинетическая энергия.
17
Индексы и сокращения
акт — активный;
арм — арматура;
б — бак;
бал — балка; баллон;
в — верхнее;
газ — газ;
гар — гарантийный;
гор — горючее;
дет — деталь;
д. с — двигатель сухой;
дн — днище;
д. у — двигательная установка;
3 — земля;
изб — избыточное;
к — конечные условия полета; корпус;
каб — кабельная;
кр — критический; круговая;
м — мидель;
max — максимум;
мер — меридиональное;
min — минимум;
н — нижнее; высота; неучтенный;
ок — окислитель;
он — опорный; опора;
опт — оптимальный;
п -панель; пустота;
п. к — панель крепежная;
пл — планирование;
пр.н —продольный набор;
р — расчетный;
рам — рама;
с. дв —система двигательной установки;
ср — срез; среднее;
т — топливо;
т. н — топливо наддува;
т. о —топливный отсек;
шп — шпангоут;
шп. по — шпангоут промежуточный;
шп. ст — шпангоут стыковочный;
эк — экваториальное;
эл — элемент;
О —начальные (стартовые) условия полета;
I, II, III — порядковые номера ступеней;
2] — сумма; суммарное давление; суммарная нагрузка; суммарный
запас топлива;
F — центр давления; фокус;
Л А — летательный аппарат;
18
ЖРД — жидкостный ракетный двигатель;
ЯРД — ядерный ракетный двигатель;
ЭРД— электроракетный двигатель;
РПД — ракетно-прямоточный двигатель;
ПАД — пороховой аккумулятор давления;
ЖАД — жидкостный аккумулятор давления;
ИСЗ — искусственный спутник Земли;
ЗУР — зенитные управляемые ракеты;
В КС — воздушно-космический самолет;
PJIA — ракетные летательные аппараты;
КР — крылатая ракета;
РНМП — ракета-носитель ^многократного применения;
ЭВМ — электронновычислительная машина;
ст — ступень;
ТНА — турбонасосный агрегат;
НДМГ — несимметричный диметилгидразин;
С АС — система аварийного спасения;
УКВ — ультракороткие волны;
РЛС — радиолокационная система.
Глава I
КЛАССИФИКАЦИЯ РАКЕТНЫХ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Классификация ракетных летательных аппаратов различных
типов и назначений, приведенная в главе, имеет целью показать
главные направления их осуществления в прошлом и настоящем
и развития в будущем.
Поскольку в настоящее время уделяют большое внимание
исследованиям перспективных схем летательных аппаратов мно¬
гократного применения, поэтому они здесь также рассмотрены
(см. разд. 1.2).
1. 1. КЛАССИФИКАЦИЯ РАКЕТ
В настоящее время известно большое количество уже создан¬
ных и разрабатываемых разнообразных ракет. Некоторые из них
имеют между собой много общего по конструкции, двигательным
установкам, энергетическим системам, назначению и т. д. Это
дает возможность классифицировать ракеты, разделяя их на
группы по отдельным признакам, что, в свою очередь, существен¬
но облегчает процесс их изучения.
Классифицировать ракеты можно по различным признакам
(рис. 1):
— по многократности применения,
— по компоновочным схемам,
— по конструкции отсеков,
— по весу и габариту,
— по источнику энергии,
— по агрегатному состоянию топлив,
— по способу подачи топлива,
— по типу старта,
— по назначению,
— по боевому применению.
Классификация ракет по многократности применения
Различают ракеты однократного применения (не спасаемые)
и многократного применения (спасаемые).
20
1
ЗУР
ft
SJ
1
I
1
1
1
I
1
i
§
1
St
§
1
*
»
я
*0
1
5о
;s>
1
1
1
J
if
l
It
с ^
Э/9ЮЛН0НШ0СУ
it
I'll
T
5о
£>
$3
'v
t.
у
£
~j
1
*
1
I
t
а
• ■ *
с:
L
ti
it
j/qwjndcujd)
з/ чнройою P,
21
Рис. 1. Классификация ракет
Ракеты однократного применения не предназначены для по¬
вторного использования, и их конструкция разрушается во время
полета в заданных точках траектории.
Ракеты многократного применения приспособлены для по¬
вторного использования. Они имеют специальные устройства
(аэродинамические поверхности или несущий корпус), которые
дают возможность всей ракете или только части ее (частично
спасаемая ракета) вернуться на Землю без повреждений и быть
использованной повторно после относительно небольшого вос¬
становительного ремонта. В дальнейшем такие системы (пилоти¬
руемые или непилотируемые) будем называть многократно ис¬
пользуемыми космическими системами.
Орбитальный полет
г Выход
на орбиту
Г
баллистический полет
ускорителя
t
Маршевый полет
ускорителя
Расчет на посадку
Посадка ускорителя
. Сход с
орбиты
Разделение ступеней \\
Вход в плотные
слои атмосферы
Разворот на 161°
Расчет на
посадку
Посадка II ступени
Рис. 2. Схема полета двухступенчатой ракетной системы со спасаемыми
крылатыми ступенями (старт и посадка II ступени условно разнесены)
Ракеты с бортовыми средствами спасения (парашютной си¬
стемой, гибким крылом, авторотирующей системой, реактивной
системой торможения и другими) занимают особое место среди
ракетных летательных аппаратов (РЛА), поскольку они рассмат¬
риваются в основном как модифицированные варианты ракет-
носителей многократного применения.
Ракетная система может быть возвращена на Землю полно¬
стью и тогда такая система является полностью спасаемой. Схе¬
ма полета двухступенчатой ракетной системы со спасаемыми
крылатыми ступенями показана на рис. 2. Ракета может быть
возвращена на Землю не полностью, а только часть ее (напри¬
мер первая ступень), и тогда такая ракета является частично
спасаемой. Исследования с учетом стоимости показывают, что
для тяжелых ракет-носителей экономически выгодным является
22
спасение прежде всего первой (самой тяжелой) ступени. Однако
в тех случаях, когда ракета предназначается для пилотируемого
полета, ее спасаемой ступенью (или головной частью) может
быть именно последняя ступень, выполненная в виде пилотируе¬
мого космического корабля [12]. Ввиду большого разнообразия
возможных схем ракетно-космических летательных аппаратов
многократного применения (см. разд. 1.2) и неустановившейся
терминологии (воздушно-космический самолет, астроплан, кос¬
мический корабль, ракетный самолет и т. д.) таких летательных
аппаратов [12], в дальнейшем мы будем называть их ракетопла¬
нами. Поскольку системы многократного применения представ¬
ляют перспективный класс РЛА, им в дальнейшем (см. разд.
1.2) будет уделено особое внимание.
Классификация ракет по компоновочным признакам
К компоновочным признакам ракет относятся конструктивно¬
силовые схемы, характеризующие конструкцию летательного ап¬
парата в целом. По этим признакам ракеты могут быть разде¬
лены на одноступенчатые (одиночные) и составные (многосту¬
пенчатые) ракеты. Сюда относятся также и так называемые
непрерывные ракеты.
По классическому определению одноступенчатыми ракетами
называются такие, полет которых происходит за счет отброса
активных масс; многоступенчатыми — такие, полет которых про¬
исходит за счет отброса активных и пассивных масс. Активными
массами в ракете является топливо (горючее плюс окислитель
или рабочее тело ЯРД); пассивными массами — конструкция
ускорителей (баки, двигатели и т д.). Отделение (истечение)
активных масс происходит непрерывно в течение активного поле¬
та (при работающем двигателе), пассивных масс — дискретно,
после отделения активных масс.
Непрерывные ракеты являются как бы синтезом одноступен¬
чатых и составных ракет, полег которых происходит при непре¬
рывном истечении активных и пассивных масс.
Непрерывные ракеты не были построены из чисто конструк¬
тивных трудностей организации механического процесса подачи
топлива с пассивной (конструкцией) массой в камеру сгорания
двигателя. Типовая схема непрерывной ракеты на твердом топ¬
ливе может быть представлена, как показано на рис. 3.
У ракет последовательной схемы ступени расположены друг
за другом и их отделение происходит поочередно по мере выгора¬
ния топлива в младших (нижних) ступенях. Двигатели ступеней
таких ракет включаются в работу поочередно.
У ракет параллельной или как их называют «пакетной» схе¬
мы ускорители ступеней располагаются рядом (пакетом) и их
отделение происходит параллельно от крайних к средним. Все
23
двигатели пакетов работают одновременно с момента старта
ракеты.
Пакеты в свою очередь могут быть с переливом топлива и без
перелива. В первом случае по мере полета топливо переливается
{непрерывно или дискретно) из ускорителей младших (преды¬
дущих) ступеней в ускорители старших (последующих) ступе¬
ней; во втором случае двигатели сту¬
пеней расходуют топливо только своих
ступеней. Пакеты могут быть состав¬
лены из одинаковых (по конструкции,
размерам, топливу и т. д.) и неодина¬
ковых ракет.
Составные ракеты называются
«комбинированными», если они обра¬
зованы последовательной и пакетной
схемами.
На рис. 4 приведены схемы одно¬
ступенчатых баллистических снарядов
США и немецкого снаряда времен
Отечественной войны А-4, выполнен¬
ные в одинаковом масштабе:
Рис.. 3. Схема непрерывной твердотопливной
ракеты:
а—до выгорания топлива; б—после выгорания топ¬
лива; /—камера сгорания; 2—топливо; 3—полезный
груз
а — баллистический снаряд средней дальности ВВС США
«Юпитер» разрабатывался под руководством Редстоунского ар¬
сенала. Система наведения инерциальная фирмы Сперри-Рэнд:
силовая установка такая же, как у снаряда «Тор», но верньер¬
ный двигатель один, и снаряд перед запуском ориентируется по
азимуту.
На серийных снарядах может быть установлен другой носо¬
вой конус. Длина снаряда 17,7 м; диаметр корпуса 2,65 м; стар¬
товый вес 47,5 тс; максимальное число М около 12;
б — тактический баллистический снаряд «Редстоун» разрабо¬
тан для армии США Редстоунским арсеналом. Выпускается се¬
рийно. Система наведения инерциальная фирмы Сперри-Рэнд.
Для управления используются аэродинамические поверхности,
газовые рули и поверхности управления на отделяемой перед¬
ней части корпуса. Ракетный двигатель «Рокетдайн» с неподвиж¬
ной камерой сгорания развивает тягу 36 тс.
Длина снаряда 21 м (приводятся также цифры 18,9 м и
19,2 м), диаметр корпуса (у топливных баков) 1,77 м: старто¬
вый вес около 27 тс; расчетная дальность около 320 км; макси¬
мальное число А1 полета около пяти;
24
а) 6)
в — баллистический снаряд средней дальности ВВС СШЛ
Дуглас SM-75 «Тор». Инерциальная система наведения изго¬
товляется фирмой Спарк Плаг. Силовая установка состоит из
одного ЖРД «Рокетдайн» с камерой сгорания, установленной
на кардановом подвесе, с тягой 68—75 тс. Имеются два вернь¬
ерных двигателя для уточнения траектории полета.
а) ф гу
Рис. 4. Одноступенчатые баллистические ракеты
Длина снаряда 18,9 м; максимальный диаметр (без обтекате¬
лей) 2,4 м; стартовый вес около 50 тс; расчетная дальность су¬
ществующей модификации снаряда 2400 км; максимальное чис¬
ло М;
г — тактический баллистический снаряд Д-4 (V-2) разрабо¬
тан для немецкой армии в 1939—1944 гг. Ракетный двигатель с
неподвижной камерой сгорания и тягой 25 тс. Система наведе¬
ния снаряда состояла из автопилота и доплеровской радноси-
етемы, которая позднее заменена системой вычисляющих аксе¬
лерометров. Управление осуществлялось посредством аэродина¬
мических и газовых рулей. Боевая головка с зарядом амматола
весом 750 кгс.
Длина снаряда 14,3 м; диаметр корпуса 1,657 м; стартовый
вес 12870 кгс; расчетная дальность 350 км; максимальное число
М = 4,4.
25
Рис. 5. Двухступенчатая
ракета последовательной
схемы «Титан-2» (США)
26
Рис. 6. Трехступенчатая
ракета последовательной
схемы «Сатурн-5» (США)
Примером ракет последовательной схемы могут служить аме¬
риканские ракеты-носители «Титан-2» (двухступенчатая схема)
и «Сатурн-5» (трехступенчатая схема)
(рис. 5 и 6), а также англо-француз¬
ская трехступенчатая ракета-носитель
«Европа» (рис. 7).
Примером многоступенчатых ком¬
бинированных ракет могут служить
советская ракета-носитель «Восток» и
американская ракета-носитель «Титан-
3» (рис. 8 и 9).
Иногда советскую ракету «Восток»
(довольно условно) и американскую
ракету «Атлас» (в вариантах без пос¬
ледних ступеней) относят к так назы¬
ваемым ракетам полутораступенчатой
схемы. Это объясняется тем, что
у ракеты-носителя «Восток» сбрасыва¬
емые боковые блоки (ускорители) со¬
ставляют как бы часть первой ступени
(так как обладают недостаточной мощ¬
ностью), а у ракеты-носителя «Атлас»
еще меньшую часть первой ступени со¬
ставляют двигательные блоки, также
сбрасываемые в полете. Ракета «Атлас»
в полете приведена на рис. 10.
Ракеты чисто пакетной схемы бы¬
ли использованы в качестве носителей
1-го, 2-го и 3-го советских искусствен- ^
Рис. 7. Компоновочная схема ракеты-носителя
«Европа-1»:
/—отделяемый обтекатель; 2—спутник; 3—установоч¬
ное кольцо для размещения спутника; 4—топливный
бак; 5—кругова^ рама для восприятия сил тяги
н монтажа топливного бака; 6—бачки со сжатым
гелием; 7—верньерные двигатели, подвешенные на
кардановых подвесах; 8—основной двигатель III сту¬
пени; У—система наддува баков II ступени; 10—бак
с четырехокисыо азота; //—соединительная трубка
выравнивания давления; 12—бак с несимметричным
диметилгндразином; 13—сопла ракетного двигателя
II ступени; /4—антенна телеметрической аппарату¬
ры; /5—приборный отсек первой ступени; /б-люки
для доступа к приборному отсеку; /7—трубка над-
Дува бака с жидким кислородом; 18—бак с кисло¬
родом; 19—бак с углеводородным горючим; 20—кла¬
пан отсечки подачи горючего; 21—турбонасосный
агрегат подачи горючего; 22—бачки со сжатым азо¬
том; 23— выхлопная труба турбонасосного агрегата;
24—теплообменник азота; 25—теплообменник кисло¬
рода; 26—сопла двигателей I ступени
-17
ных спутников Земли. Использованная пакетная схема получила
название «простейшего пакета». Эту схему не совсем правильно
27
иногда относят к полутораступенчатым. Весовой анализ показы¬
вает, что несброшенная на 1-й ступени часть баков имеет неболь¬
шой вес и схема близка к оптимальной, что характерно для «па¬
кетов».
JV-
г5;
Рис. 8. Ракета-но¬
ситель космическо¬
го корабля «Во¬
сток» (СССР)
Рис. 10. Ракета полу-
тораступепчатой
схемы «Атлас» (США)
Рис. 9. Сбщий вид ком¬
бинированной ракеты с
ракетопланом:
1—ракетоплан; 2—централь¬
ная двухступенчатая раке¬
та последовательной схе¬
мы; 3—ускорители I сту¬
пени
На раннем этапе развития ракетной техники рассматрива¬
лись также ракеты с телескопическим расположением ступеней.
Однако такие ракеты не получили распространения из-за труд¬
ностей разделения ступеней в полете. На базе изучения их было
найдено инженерное решение, заменившее телескопический уско¬
ритель на ускоритель пакетной схемы.
28
Классификация ракет по конструкции отсеков
Современная одноступенчатая ракета состоит из головного,
промежуточного, приборного, топливного и двигательного отсеков.
Головной отсек обычно представляет тот полезный груз, ради
которого создается ракета. Его конструкция индивидуальна н
влияет на конструкцию ракеты
больше своими массово-инер¬
ционными характеристиками,
чем другими (например гео¬
метрической конфигурацией,
внутренним строением и т. д.).
Иногда головной отсек назы¬
вают «головной частью». В тех
случаях, когда головная часть
представляет собой самостоя¬
тельный летательный аппарат
типа «ракетопланер» (с боль¬
шой несущей поверхностью и
дестабилизирующим моментом
на участке полета в атмосфе¬
ре), в нижней части на корпусе
двигательного отсека распола¬
гаются аэродинамические ста¬
билизаторы. Последние имеют
также ракеты малой дально¬
сти (скорости) полета, когда
большая часть траектории про¬
ходит в присутствии аэродина¬
мических сил на участке атмо¬
сферы с большими значениями
скоростных напоров. Приме¬
ром оперенной ракеты неболь¬
шой дальности полета, как из¬
вестно, является ракета А-4.
Схема оперенной ракеты «Са¬
турн-1», приведена на рис. 11.
Промежуточные отсеки
(проставки и т. д.) являются
соединительными звеньями между другими отсеками и на общую
конструкцию ракеты практически не имеют влияния.
Приборные отсеки на ракетах располагают по-разному. Они
могут быть в верхней или нижней части ракеты или располо¬
жены в гаргроте вдоль по образующей двигательного и топлив¬
ного отсеков, как это имеет место на ракете «Атлас» (США).
На больших ракетах-носителях приборы, в-виду их малого отно¬
сительного веса и объема, не нуждаются в отдельном отсеке и
Рис. 11. Варианты ракеты «Сатурн-1»
с оперением и без оперения. Топлив¬
ные отсеки пакетной схемы (США)
29
располагаются в свободных местах верхней части топливных от¬
секов.
Топливные отсеки представляют собой большие емкости, пред¬
назначенные для размещения в них топливных компонентов.
Конструкция топливных отсеков, ввиду больших своих габари¬
тов, в значительной мере влияет на конструкцию ракеты в целом.
Двигательный отсек представ¬
ляет собой нижнюю, среднюю или
верхнюю часть ракеты (ступени),
в которой расположен ракетный
двигатель и связанные с ним
установки, системы и агрегаты.
Поскольку двигатель может на¬
ходиться вне корпуса ракеты или
наоборот может быть утоплен
в баке (зенитные ракеты), то
термин « д в и г а т е л ь н ы й отсек»,,
в дальнейшем оставим как услов¬
ный, при помощи которого удоб¬
но говорить о конструктивных
особенностях ракеты, связанных
с наличием различных типов дви¬
гательных установок, их крепле¬
нием, эксплуатацией, расположе¬
нием и т. д.
Независимо от ступенчатости различают ракеты с несущими,
подвесными и смешанной конструкции топливными отсеками
(топливными баками). Несущими баки (топливные отсеки) на¬
зываются потому, что они, будучи одновременно и корпусом ра¬
кеты, воспринимают (несут) общий комплекс нагрузок, дейст¬
вующих в полете. У ракет с подвесными баками эти нагрузки
(за исключением нагрузок от давления в баках) воспринимают¬
ся несущим корпусом.
Различают также ракеты с телескопическими топливными
баками (бак в баке). Из-за опасности взаимопроникновения,
компонентов через большую омываемую поверхность внутренне¬
го (центрального) бака, конструкция телескопических топлив¬
ных отсеков не нашла практического применения.
Конструкция топливных отсеков может быть выполнена в ви¬
де пакетов (набора) несущих топливных баков, как это имеет
место у американской ракеты «Сатурн-1» (см. рис. 11).
Конструкция топливных отсеков, состоящая из торовых ба¬
ков, обычно имеет место для последних ступеней составных ра¬
кет, однако, как показали проектно-конструкторские и научные
изыскания фирмы Боинг, выполненные для центра Эймс (США),
применение торовых отсеков для сверхмощных ракет также мо¬
жет быть успешным (рис. 12).
30
Рис. 12. Топливный отсек с под¬
весными торовыми баками (II сту¬
пень ракеты «Боинг», полезный
ГРУ3 As =1900 тс, США):
/—корпус; 2—бак жидкого кислорода;
3—бак жидкого водорода; 4—ЖРД:
5—тепловой экран
Ддигатепьны в отсека
№ дпнэжоиоиэщ
дпнэжоиоиэтзй
*3=3
Qj
Съ
3:
5-
ч <ъ
%
*
CU
J:
Qj
0Q
сЭ'
домэошо эпн эжои ои qv d
к
Р-.
CQ нЭ
к х:
Е" X1
С О
° Й
н о
к о
К с
г- ^
S о
Го
31
Возможные схемы топливных отсеков, по которым можно су¬
дить о конструктивных особенностях ракеты, приведены па схе¬
ме (рис. 13).
В зависимости от конструктивных особенностей двигатель¬
ного отсека различают ракеты с двигательными отсеками, рас¬
положенными в нижней части ракеты, в верхней части ракеты
и в средней ее части. Двигательные отсеки могут быть нагружен¬
ными (несущий корпус воспринимает нагрузки от реакции стар¬
тового стола) или ненагруженными (корпус является капотом
двигательной установки). Влияние двигательной установки па
конструктивно-силовую схему ракеты удобно проследить по схе¬
ме, представленной на рис. 14.
Классификация ракет по весу и габариту
На графике (рис. 15) представлены веса построенных и пер¬
спективных ракет в функции времени их осуществления. Из гра¬
фика видно, что большие веса характерны для космических ра¬
кет-носителей; малые — для
боевых ракет.
По имеющимся в литера¬
туре предварительным данным,
ракеты, габарит которых очень
мал, принято называть малы¬
ми ракетами.
Пример ракеты-носителя
больших размеров и весов по¬
казан на рис. 16.
Классификация ракет
по источнику энергии
.№5 50 55 60 65 70 75 1980 По ИСПОЛЬЗуеМОМу ИСТОЧ-
Годы нику энергии ракеты делят на
химические (термохимиче-
Рис. 15. Рост стартовых весов косми- ские), ядерные, электрические
ческих и военных ракет по годам и их возможные комбинации
(по ступеням).
В настоящее время наиболее распространенными являются
ракеты на химических топливах. Принцип устройства и действия
систем у таких ракет хорошо известен. При использовании
жидких ракетных топлив можно ожидать увеличения удельной
тяги до величины, равной 400—450 с на уровне моря. Для зна¬
чений удельной тяги более 450 с должны быть разработаны ядер¬
ные ракеты и более совершенные системы химического типа.
Исследование грузоподъемности химических ракет указыва¬
ет на то, что отношение массы полезной нагрузки к стартовой
массе ракеты не может превышать 0,01-1-0,02 для полетов, свя-
32
занных с выходом из гравитационного поля Земли, даже при
использовании наилучших комбинаций горючего и окислителя.
Рис. 16. Рисунок космической ракеты
по проекту фирмы Боинг (США) для
центра Эймса (NASA)
Основные данные
Вари
(анты:
од по¬
двух-
сту пен-
• сту цен¬
чатый
на ты й
Полезная нагру
зка, тс
454
1590
Стартовый вес,
тс
5800
30000
Перегрузка на
старте
1.25
1,37
Удлинение .
9 9
—
Коэффициент эффективно
сти конструкции
. 0,06
0,1
Стартовая тяга
на уровне
моря, тс ...
72СЮ
41000
Высота, м
48
—
Несмотря на малые величины отношения массы полезной нагруз¬
ки к стартовой массе ракеты, химические ракетные двигатели
остаются в настоящее время единст¬
венными двигателями, способными
обеспечить полет с посадкой на по¬
верхности планет солнечной системы.
Полеты ракет с экипажем к Луне
и запуск зондов к ближайшим плане¬
там осуществлены при помощи хими¬
ческих ракет, хотя они и являются не
экономичными с точки зрения массо¬
вого расхода компонентов топлива.
Полеты к звездам, а также межпла¬
нетные полеты космических кораблей
с экипажем потребуют применения
ядерных двигателей. К тому времени,
когда общее развитие космонавтики
достигнет этой стадии, вероятно уже
будут разработаны более усовершен¬
ствованные двигатели.
Рис. 17. Схемы ракет па химическом и ядерном
топливах:
/—-груз; 2—приборы управления; 3 - бак с окислите¬
лем; 4—бак с рабочим телом; 5—бак с горючим;
6—турбина; 7—насос; <?— пористая активная зона
с диспергированным сильно обогащенным U235
пли Рu239
Химические топлива используются также и в двигательных
Установках для осуществления полетов искусственных спутников.
2 3-179 33
Хотя в этом случае сами тяги невелики, двигатель должен рабо¬
тать в течение длительных периодов времени. При помощи хими¬
ческих ракетных двигателей можно осуществлять большую часть
предусматриваемых маневров, но продолжительность их работы,
вероятно, ограничивается — 100 ч вследствие чрезвычайно высо¬
кого расхода топлива.
Самым большим преимуществом химических ракет в настоя¬
щее время является то, что они уже существуют, работают и с
их помощью можно осуществить большинство космических по¬
летов ближайшего будущего. *
Большой перспективой обладают ядерные двигательные си¬
стемы. Они отличаются от химических двигательных систем тем,
что рабочее тело нагревается не за счет собственной химической
энергии, а за счет тепла, выделяющегося при ядерной реакции.
Сравнительные схемы ракет на ядерном и химическом топливах
показаны на рис. 17.
Ядерные теплообменные двигатели различаются активной зо¬
ной ядерного реактора, которая может быть твердой, жидкой
и газообразной. Наиболее высокие температуры нагрева, а
следовательно, и скорости истечения рабочего тела могут быть
достигнуты в ядерных реакторах с газообразной активной
зоной.
По американским данным, ядерные теплообменные двигатели
найдут применение на верхних ступенях больших ракет-носи¬
телей.
По некоторым проектам зарубежных специалистов в ядерных
двигательных системах для нагрева рабочего тела предполага¬
ется использовать атомные взрывы (пульсирующие ЯРД), тер¬
моядерный синтез, радиоактивный распад изотопов. Хотя при
этом могут быть достигнуты высокие температуры и большие
скорости истечения рабочего тела, тяга этих двигателей будет
мала. Такие двигатели малой тяги будут эффективны в качестве
маршевых двигателей.
Предполагают, что в ближайшем будущем удельная тяга
ЯРД с твердой активной зоной достигнет 800 с и будет возра¬
стать до предельного значения в 1000 с. ЯРД с газообразной ак¬
тивной зоной и пульсирующие ЯРД в будущем могут иметь
удельную тягу 2000 с с перспективой предельного увеличения до
3500 с [3].
На некоторых этапах развития механики полета главную
роль играют двигатели. Переход от одного класса двигателей к
качественно новому, более совершенному, позволяет осущест¬
вить скачок в развитии механики полета.
В развитии механики полета пилотируемых космических ап¬
паратов можно проследить некоторую аналогию с развитием
авиации.
34
В авиации переход от поршневого двигателя с винтом к ре¬
активному позволил преодолеть звуковой барьер и существенно
увеличить скорость полета.
В космонавтике пилотируемые скоростные межпланетные по¬
леты с приемлемой продолжительностью, не осуществимые в на¬
стоящее время с ЖРД, станут возможны с электроракетными
(ЭРД) и ядерными ракетными двигателями (ЯРД).
ЭРД будут иметь преимущество по сравнению с другими
типами двигателей для беспилотных полетов в пределах солнеч¬
ной системы.
Комбинированная силовая установка, состоящая из ЯРД и
ЗРД, обеспечит наилучшие характеристики корабля, предна¬
значенного для пилотируемого полета к Марсу.
Электрические двигательные системы объединяют типы дви¬
гателей, в которых разгон рабочего тела до определенной скоро¬
сти истечения производится электрическим или магнитным спо¬
собом. Необходимую электроэнергию дает ядерная (или солнеч¬
ная) электростанция, находящаяся на борту ракеты (космиче¬
ского летательного аппарата).
Вес ЯРД с твердой активной зоной и ЭРД .с ядерным источ¬
ником энергии определяется критической массой реактора.
В электрических двигателях рабочее тело нагревается до
очень высоких температур в электрической дуге с помощью на¬
гревательных элементов. Такие двигатели в принципе мало от¬
личаются от химических и ядерных теплообменных двигателей.
Комбинированные ракеты предполагают использование ком¬
бинированных силовых установок большой тяги. Из всех изве¬
стных комбинированных силовых установок наиболее перспек¬
тивной с точки зрения применения в ракетной технике является
ракетно-прямоточная (РИД), представляющая собой гибрид
ракетного и прямоточного двигателей [13].
Принцип работы РПД заключается в том, что продукты не¬
полного сгорания топлива, образующиеся при его сгорании в ка¬
мере ракетного двигателя, используются в качестве горючего для
прямоточного контура. Это горючее сжигается в воздухе, посту¬
пающем в камеру сгорания в полете, в основном благодаря
скоростному напору и частично эжектирующему действию высо¬
конапорного потока газов, вытекающих из сопла ракетной ка¬
меры, а па старте — целиком благодаря эжекции.
Особое место занимают ракетно-космические системы с плаз¬
менными двигателями. Ввиду малого ресурса и малой реактив¬
ной тяги их целесообразно применять в основном для коррек¬
ции орбит и осуществления управления летательным аппаратом
вокруг центра масс. Плазменный двигатель представляет собой
комбинированную термоэлектрическую систему. По принципу
работы и по характеристикам этот двигатель занимает промежу¬
точное положение между чисто тепловыми реактивными двигате¬
2* 35
лями (химическими или ядериыми) и чисто электрическими дви¬
гателями (ионными). Тяга плазменного двигателя создается бла¬
годаря расширению горячей плазмы, источником тепла для кото¬
рой является электрическая дуга. Максимально достижимая
удельная тяга плазменного двигателя составляет 2500 с, а отно¬
шение тяги к весу ~ 10_3 [3].
Большой перспективой обладают ионные космические раке¬
ты. Тяга ионного двигателя образуется вследствие ускоренного
движения заряженных частиц в электрическом поле. Напряже¬
ние и ток могут легко варьироваться, что позволяет изменять в
широких пределах тягу и удельную тягу одного и того же дви¬
гателя. Ионные ракеты являются перспективными для длитель¬
ных космических полетов с малыми отношениями тяги к весу
(10-4-М0-5) и высокими значениями удельных тяг (5 • 103—
25-103) с [3].
Классификация ракет по агрегатному состоянию топлив
Прежде всего различают жидкостные ракеты и ракеты на
твердом топливе (твердотопливные). Жидкостные ракеты содер¬
жат жидкие топливные компоненты; твердотопливные—твердые
компоненты (рис. 18). Жидкостные ракеты могут содержать уни¬
тарное топливо, топливо раздельной подачи и топливо с металли¬
ческими добавками. Твердое топливо является простейшим при¬
мером унитарного твердого топлива. Унитарные жидкие топлива
представляют собой одно вещество (или раствор нескольких
веществ), которое находится в подготовленном для сгорания
(или разложения) виде. Такие смеси можно назвать жидкими
порохами.
6)
Рис. 18. Схемы ракет на жидком {а),
твердом {б) и гибридном (в) топ¬
ливах:
а—жидкое топливо; /—ракетный двига¬
тель; 2—окислитель; 3—горючее; 4—полез¬
ная нагрузка; 5—топливные насосы; б—
твердое топливо; /—полезная нагрузка;
в—гибридное топливо; /—горючее (твердое); 2—окислитель (жидкий); 3—полезная
нагрузка
Жидкие топлива раздельной подачи, состоящие из горючего
и окислителя, подаются в камеру сгорания раздельно и смеши¬
ваются только в самой камере сгорания.
Задачи процессов распыла и смесеобразования у ракет этих
типов значительно различаются между собой.
36
У ракет, двигатели которых работают на унитарных топливах,
смешение компонентов, участвующих в реакции сгорания, про¬
изводится заранее, и в процессе распыления топливо должно
только возможно более равномерно распределяться по попереч¬
ному сечению камеры сгорания.
У ракет раздельной подачи в процессе распыления, кроме
того, должно происходить тщательное перемешивание частичек
горючего и окислителя, чтобы создавались наилучшие условия
для сгорания и для возможно более полного выделения химиче¬
ской энергии топлива.
У ракет, работающих на унитарных топливах, система пода¬
чи получается более Лростой, так как в ней используется один,
а не два бака и имеется также одна система коммуникаций
между баком и камерой сгорания.
Ракеты с раздельной подачей классифицируются более под¬
робно по типу применяемого окислителя, поскольку свойства то¬
го или иного окислителя в значительной мере определяют конст¬
руктивные особенности двигателя, а часто и возможность его ис¬
пользования на той или другой ракете. При классификации по
типу применяемого окислителя двигатели (ракеты) обычно полу¬
чают название по наименованию применяемого окислителя, на¬
пример, кислородный, азотнокислый и др. В настоящее время
наиболее распространены кислородные и азотнокислотные двига¬
тели.
Гибридными топливами называют такие, которые образова¬
ны жидкими и твердыми компонентами. Ракеты с гибридными
топливами устроены таким образом, что жидкие компоненты
находятся в баках топливного отсека, а твердые компоненты не¬
посредственно в камере сгорания двигателей (см. рис. 18). Гиб¬
ридные топлива могут быть двухкомпонентные и многокомпо¬
нентные.
В целях обеспечения более высокой удельной тяги в совре¬
менных ракетных двигателях применяются топлива с металли¬
ческими компонентами. При сгорании такого топлива образуют¬
ся окислы металлов либо твердой, либо жидкой конденсирован¬
ной фазы. Теплоотвод от конденсированной фазы в газовую по
тракту сопла позволяет снизить тепловые потери. Это объясняет¬
ся тем, что часть тепла конденсированной фазы, аккумулирован¬
ного ею в камере сгорания, благодаря межфазовому теплообме¬
ну восполняет затраты тепловой энергии газового потока на
разгон частиц конденсированной фазы.
Ракеты смешанной конструкции (комбинированные) могут
быть образованы твердотопливными ракетными ускорителями
(например первая ступень) и жидкостными ракетами (послед¬
них ступеней) по типу американской ракеты «Титан-3».
37
Классификация ракет по способу подачи компонентов топлива
Различают ракеты с насосной и вытеснительной системой по¬
дачи топливных компонентов.
При насосной подаче компоненты топлива из баков нагнета¬
ются в камеру сгорания насосами, которые требуют для своего
вращения какого-либо источника энергии. Для привода насосов
чаше всего используется газогенератор, работающий на одно¬
именных топливных компонентах либо на продуктах такого ра¬
бочего тела как перекись водорода.
Повышение давления в баках при вытеснительной подаче мо¬
жет осуществляться самыми разнообразными способами. Широ¬
ко распространена система подачи, в которой вытеснение ком¬
понентов осуществляется газом высокого давления.
Из баллона этот газ проходит через редуктор и затем посту¬
пает в баки, выдавливая компоненты топлива в камеру сгора¬
ния ЖРД. Такая система подачи носит название баллонной.
Более простая система вытеснения имеет место при исполь¬
зовании порохового аккумулятора давления (ПАД) или продук¬
тов сгорания жидких компонентов (так называемая подача
жидкостным аккумулятором давления ЖАД).
В этих системах вытеснительной подачи тяжелый баллон са
сжатым газом замещается более легким пороховым или жидко¬
стным аккумулятором; вес газа, вытесняющего компоненты,
уменьшается за счет более высокой температуры, при которой
газ поступает в топливные баки.
Классификация ракет по типу старта
Стартовые комплексы (оборудование, обеспечивающее подго¬
товку и пуск ракеты) бывают двух типов: подвижные и ста¬
ционарные. Атомные подводные лодки — один из наиболее из¬
вестных вариантов подвижных стартовых комплексов. Имея на
борту постоянно готовые к бою баллистические ракеты, они спо¬
собны занять позицию в любом районе Мирового океана и вне¬
запно атаковать противника из подводного положения.
Возможны и другие подвижные комплексы, в которых ракеты
могут быть размещены на железнодорожных платформах. Перед
пуском платформы опираются на гидравлические амортизаторы.
Аналогично могут быть также с успехом использованы и мощные
грузовые автомобили и гусеничные тягачи.
Старт ракет, предназначенных для изучения верхних слоев
атмосферы в различных районах околоземного пространства,
хорошо освоен со специально оборудованных кораблей морско¬
го флота.
При самолетном (горизонтальном) старте значительно увели¬
чивается досягаемость боевых ракет типа «воздух — земля»,
а также растет грузоподъемность тяжелых воздушно-космиче¬
ских систем.
38
Несмотря на то, что за подвижными пусковыми установками
противнику труднее следить, стационарные комплексы распро¬
странены больше. Их недостаток — не¬
подвижность — с лихвой окупается мощ¬
ной защитой. Если раньше ракеты и обо¬
рудование располагались на поверх¬
ности, то теперь все эти элементы стар¬
тового комплекса ушли глубоко под зем¬
лю.
Для космических ракет-носителей ос¬
тается по-прежнему старт с поверхности
Земли (ракетодрома).
Рис. 19. Общий вид зенитной
ракеты
Рис. 20. Общий вид антира¬
кеты «Ника-Зевс»:
7—боевая головка; 2— аэродина¬
мические рули III ступени;
3— II ступень; 4—топливный за-
РЯД РДТТ I ступени; 5—1 сту¬
пень
39
Классификация ракет по назначению
Ракеты могут быть разделены также на военные (стратеги-
ческие и тактические), ракеты-носители, а также ракеты-ускори¬
тели, предназначенные для увеличения стартовой перегрузки
(или скорости) различного типа самолетов и ракет.
Баллистическими ракетами обычно называют ракеты, полет
которых происходит по баллистической траектории.
В целом траектория полета баллистической ракеты состоит из
активного участка полета под действием силы тяги ракетного
двигателя, свободного полета в пустоте (по инерции — эллипти¬
ческий участок) и полета в плотных слоях атмосферы при ее
возвращении на Землю.
В зависимости от дальности полета различают также ракеты
дальнего действия (более 5000 км); ракеты средней дальности
(от 1000 до 5000 км) и ракеты малой дальности (до 1000 км) *.
На рис. 19 приведена фотография зенитной управляемой ра¬
кеты (ЗУР), а также общий вид антиракеты «Ника-Зевс»
(рис. 20). Их назначением является соответственно поражение
воздушных целей и головных частей баллистических ракет.
К ракетам-носителям относятся ракеты, являющиеся сред¬
ством для осуществления мирной программы космических ис¬
следований, изучения верхних слоев атмосферы Земли (метео¬
рологические ракеты) и совершенствования техники ракетного
полета (экспериментальные ракеты).
Разные ракеты включают в себя большое количество других
ракет, описание которых в настоящую классификацию не входит.
Классификация по боевому применению общеизвестна [2] и
мы здесь на ней более подробно, чем это показано на рис. К
останавливаться не будем.
1.2. КЛАССИФИКАЦИЯ РАКЕТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
МНОГОКРАТНОГО ПРИМЕНЕНИЯ
Общая классификация многократно используемых космиче¬
ских систем показана на рис. 21. На рис. 22 приведены общий
вид и траектория полета крылатого носителя многократного при¬
менения. Ракетные летательные аппараты такого типа после
выполнения задания могут возвращаться (полностью или ча¬
стично) к месту старта и могут быть использованы повторно.
Полностью возвращаемые ракетно-космические системы мо¬
гут осуществлять посадку в районе старта или в какой-либо точ¬
ке земной поверхности.
Многократно используемые космические системы, как и ра¬
кетные системы однократного применения, удобно разделять
* Латухин Л. Н. «Боевые управляемые ракеты», М., Воепиздат, 1968, 132 с.
40
Рокетные летательные аппараты
многократного применения
тчноиояпшбэд ,
LLidDUJJ г
отяилшночлбог
41
Рис. 21. Классификация ракетных летательных аппаратов многократного применения
Рис. 22. Траектория полета крылатого носителя многократного применения:
1—вертикальный взлет; 2— переход на баллистическую траекторию; 3— выгорание топ¬
лива п отделение носителя; #— баллистический полет к апогею; Л—вход в атмосферу на
гпперзвуковой скорости; Л—крейсерский полет в атмосфере, посадка
Рис. 23. Одноступенчатый ракетоплан (воздушно-космический самолет). Старт
горизонтальный. США. Фирма Мартин. Двигатель ЯРД работает на жидком
азоте, накапливаемом из атмосферы
Рис. 24. Составной двухступенчатый ракетоплан. Старт наклонный. Проект
«Астророкет» фирмы Мартин. США
42
прежде всего на одноступенчатые (рис. 23) и составные
(рис. 24). Как одноступенчатые, так и составные РЛА могут быть
выполнены по баллистической и крылатой схемам. В первом
случае посадка осуществляется путем повторного включения
двигателей на приземном участке вертикального спуска. Во вто¬
ром случае это происходит в режиме горизонтального полета
Рис. 25. Схемы крылатых ракет-носителей многократного применения:
параллельное соединение ступеней, отдельная нагрузка; б—последовательное
соединение ступеней
Рис. 26. Воздушно-космическая система горизон;
тальпого старта по проекту NASA (США)
(при выходе из планирования) как у обычных самолетов. Орби¬
тальные РЛА, выполненные по одноступенчатой схеме, могут
быть всегда возвращены самостоятельно к месту старта. Ступе¬
ни орбитальной ракеты-носителя многократного применения не
всегда (кроме последней) могут быть возвращены к месту стар¬
та, если для этой цели не резервирован специальный запас топ¬
лива для возвращения в режиме обратного баллистического по¬
лета или в режиме маршевого движения.
Многократно используемые крылатые космические системы
И спасаемые ракеты-носители могут быть выполнены по после¬
43
довательной (рис. 25), пакетной (параллельной) (рис. 26) и
комбинированной (рис. 27) схемам.
Спасаемые ракеты-носители могут быть оборудованы несу¬
щими поверхностями (жесткими, полужесткими и т. д.) или спе¬
циальными бортовыми системами спасения. Системами спасения
могут явиться парашюты, авто- ^
ротирующие устройства (рото¬
ры), тормозные ракетные двига¬
тели, парапланы и другие, как
показано в классификации (см.
рис. 21). Системы спасения,
в свою очередь, могут быть раз¬
делены на системы, не обеспечи¬
вающие возвращение ракеты
450-550 %,тс j
Рис. 27. Трехступенчатая ракетно-кос- Рис. 28. Влияние вида стар-
мическая система последовательпо-па- та на грузоподъемность ра-
р аллельной схемы кет пых аппаратов много¬
кратного применения:
/—вертикальный старт; 2—гори¬
зонтальный старт
к месту старта и системы, обеспечивающие возвращение ракеты
к месту старта. Обычно возвращение к месту старта (или на за¬
ранее запланированную площадку) возможно при условии, если
система обладает несущей способностью (аэродинамическим
качеством) или, например, достаточным запасом добавочного
топлива, для того чтобы осуществить поворот вектора скорости
в сторону возвращения.
Весьма существенным является деление многократно приме¬
няемых ракетно-космических летательных аппаратов на РЛА
вертикального и РЛА горизонтального старта. На рис. 28 пред¬
ставлена зависимость грузоподъемности от взлетного веса РЛА
горизонтального и вертикального стартов, полученная на базе
весового анализа. График показывает, что при малых старто¬
вых весах (G0<C450 тс) большей грузоподъемностью обладают
ракетопланы горизонтального старта; при больших стартовых
весах (G0>550 тс) большей грузоподъемностью обладают раке¬
топланы вертикального старта [12].
44
Для горизонтального старта необходима строго прямолиней¬
ная большей длины (несколько километров) горизонтальная
рельсовая дорожка (рис. 29). По такой дорожке скользят стар¬
товые салазки, несущие на себе разгоняемый ракетоплан
(рис. 30). Салазки разгоняются при помощи специальных ракет¬
ных ускорителей с автономным запасом топлива и развивающих
большую тягу при весьма невысоких скоростях истечения актив¬
ной массы (продуктов сгорания топлива).
Рис. 29. Горизонтальный старт составного ракетоплана с пред¬
варительным разгоном ракетным ускорителем по рельсовой
дорожке
Рис. 30. Многократно используемая космическая
система (составной ракетоплан) по проекту фир¬
мы JUNKERS и BOLKOW (ФРГ). Старт горизон¬
тальный с предварительным разгоном ракетным
ускорителем по рельсовой дорожке
Наклонный старт при помощи катапультирования ракетными
ускорителями (см. рис. 24) также позволяет заметно увеличить
как взлетную, так и конечную скорость ракетоплана. При таком
старте уменьшаются трудности, связанные с обеспечением безо¬
пасности взлета при высокой удельной нагрузке на единицу пло¬
щади крыла (до 1000 кгс/м2).
45
В ближайшее время можно ожидать быстрого развития кры¬
латых космических систем для многократных транспортных по¬
летов Земля — орбитальная станция — Земля и пилотируемых
космических кораблей с большим аэродинамическим качеством и
высокой маневренностью при полете >в атмосфере [12].
Ч.км
Ю2 10J 10 th 105 106 107 108 V^KM/Ч
Рис. 31. Области применения летательных аппаратов
(по Зепгеру)
На рис. 31 показано современное состояние механики полета
в координатах скорость — высота полета. Область до М = 3 зани¬
мает современная авиация, область, ограниченная первой и вто¬
рой космическими скоростями, принадлежит спутникам Земли;
область справа от кривой параболической скорости, принадле¬
жит межпланетным космическим аппаратам; область от М=5 до
М = 25 будет принадлежать гиперзвуковым самолетам и новому
46
типу летательных аппаратов для систематических транспортных
полетов Земля — орбитальная станция — Земля.
Как показывают исследования, переход от ракетных систем
однократного применения к ракетным системам многократного
применения обеспечит возможность проводить летные испытания
во всем диапазоне рабочих режимов (как это делается с опыт¬
ными самолетами), увеличить надежность бортовых систем,
а также существенно снизить стоимость стартовых операций и
доставки полезного груза на земную орбиту [12].
1.3. СХЕМА ОДНОСТУПЕНЧАТОЙ РАКЕТЫ
Тело, масса М которого непрерывно меняется с течением
времени вследствие истечения массы, называется телом пере¬
менной массы. Для тела переменной массы имеет место М~
=/(/), тле f(t)—непрерывная функция времени, выражающая
определенный закон изменения массы.
Классическим примером такого тела является одноступен¬
чатая ракета, масса которой во время полета непрерывно убы¬
вает вследствие расхода топлива.
Если при движении тела переменной массы его размерами
по сравнению с траекторными расстояниями можно пренебречь,
то такое тело можно рассматривать как мате¬
риальную точку переменной массы.
В дальнейшем в соответствии с рис. 32
будем представлять одноступенчатую ракету,
состоящую из активной (топливо), пассивной
(конструкция) и полезной (переносимый
груз) масс.
В начале движения активная, пассивная
и полезная массы составляют стартовую или
начальную массу М0. В конце движения, после
расхода активной массы, остаются пассивная
Рис. 32. Принципиальная схема одноступенчатой ракеты:
полезная масса (груз); 2—активная масса (топливо); 3— пас¬
сивная масса (конструкция)
и полезная массы, составляющие конечную массу М1{ одно¬
ступенчатой ракеты.
1.4. СХЕМА СОСТАВНОЙ РАКЕТЫ
На рис. 33, а представлена принципиальная схема составной
ракеты. По этой схеме ракета разбивается на ступени, а также
на полезный груз и ускорители.
Полезный груз ракеты предназначен для переброски на задан¬
ное расстояние на Земле или в космическое пространство с оп¬
47
ределенной скоростью и является задаваемой величиной при
проектировании.
Ступень ракеты представляет собой условную одноступенча¬
тую ракету, состоящую из ускорителя и условного полезного
груза в виде остальной (верхней) части ракеты. Каждая после¬
дующая (старшая) ступень ракеты образуется отделением ус¬
корителя предыдущей (младшей) ступени.
Рис. 33. Принципиальная схема составной
многоступенчатой ракеты:
«—по терминологии в СССР; б—по терминологии
в США
Рис. 34. Многоступенча¬
тая ракета последо¬
вательно-параллельной
схемы:
1— центральная ракета по¬
следовательной схемы; 2—
ракеты (ускорители), рас¬
положенные параллельно
Ускоритель составляет собственно ракетную часть ступени,
состоящую из ракетного двигателя, топлива, баков, систем по¬
дачи топлива, арматуры и других элементов конструкции, обес¬
печивающих полет данной ступени.
Во время полета ускорители отделяются поочередно после
выгорания в них топлива. Топливо является активной массой
ракеты; ускорители (их конструкция) — пассивной массой ра¬
кеты. Таким образом, полет составной ракеты происходит в ре¬
зультате отброса активных и пассивных масс. После такого от¬
броса (п раз) остается полезный груз, который получает необ¬
ходимую скорость для полета на заданное расстояние.
48
Как показано на рисунке, счет ступеней принято вести в вос¬
ходящем порядке — от основания ракеты к ее вершине.
Как мы уже говорили, различают последовательную и парал¬
лельную (пакетную) схемы ракет. В первом случае ракета со¬
ставлена последовательным соединением ракетных ускорителей;
во втором случае — рядом поставленных и сгруппированных по
ступеням ракетных ускорителей. Последние представляют собой
упрощенные схемы одноступенчатых ракет без полезного груза
и приборов управления. Последовательные ракеты в комбинации
с параллельно присоединенными ускорителями (бустерами) об¬
разуют последовательно-параллельную (или смешанную) схему
ракеты (рис. 34).
Мы говорили также, что двигатели последовательных ракет
включаются в работу поочередно по мере выгорания топлива и
отделения ускорителей младших ступеней. Двигатели парал¬
лельных или смешанных ракет могут работать одновременно,
начиная с первой ступени, облегчая при этом конечный вес уско¬
рителей младших ступеней. Примером такой ракеты является
также советская многоступенчатая ракета-носитель «Восток»,
впервые в мире осуществившая вывод на орбиту искусственно¬
го спутника Земли космического корабля, пилотируемого летчи-
ком-космонавтом Ю. А. Гагариным.
Для последовательных ракет представление ступеней в виде
одноступенчатых ракет особенно понятно, поскольку у них все
старшие ступени при неработающих двигателях действительно
составляют пассивную массу (полезный груз) для работающей
младшей ступени. Применительно к параллельным ракетам ука¬
занная условность остается в силе. Здесь следует только конеч¬
ный вес ускорителей младшей ступени (обычно первой) умень¬
шить на величину, обусловленную переносом части двигателей
с младшей ступени в старшую (обычно вторую).
В соответствии с американской терминологией составные
или многоступенчатые ракеты рассматриваются как совокуп¬
ность нескольких ступеней и субракет (рис. 33, б).
Ступень ракеты состоит из баков с топливом, расходуемым в
период работы двигателя данной ступени до ее отделения, дви¬
гателей, арматуры и приборов управления (если они имеются в
отделяющей ступени), а также из оболочки отсеков и несущей
силовой конструкции. Ступени отбрасываются в полете в опре¬
деленном порядке.
Субракетой называется такое сочетание полезного груза и
ступеней составной ракеты, в которой всегда одна или несколько
ступеней являются действующими, а остальные ступени, продол¬
жающие полет вместе с полезным грузом, составляют «полезную
нагрузку» для данной субракеты.
Ступени и субракеты нумеруются чаще всего по порядку их
работы, поэтому вся ракета одновременно называется 1-й суб¬
ракетой.
49
Полезный груз не включается в последнюю ступень, по вхо¬
дит в последнюю субракету.
Как легко видеть из сравнения рис. 33, а и 33,6, по приня¬
той терминологии в Советском Союзе и в США одинаковые смыс¬
ловые значения имеют: а) ускоритель (СССР) и ступень (США)
и б) ступень (СССР) и субракета (США).
1.5. ОСОБЕННОСТИ СХЕМ
ОДНОСТУПЕНЧАТЫХ И СОСТАВНЫХ РАКЕТОПЛАНОВ
Ракетопланы (ракетные самолеты) представляют собой кон¬
структивную комбинацию баллистической ракеты и гиперзвуко-
вого самолета. Ракетопланы состоят из отсеков и элементов кон¬
струкции, характерных как для ракет, так и для самолетов.
Фюзеляж ракетоплана состоит из передней части, в которой
располагается кабина пилота; средней части, предназначенной
для размещения топлива (горючего и окислителя), и кормовой
части, где располагается двигательная установка (ракетный дви¬
гатель с системой питания). Крыло, оперение и взлетно-посадоч¬
ные органы имеют расположение как и на самолетах обычных
схем. В зависимости от величины тяги двигателя ракетный само¬
лет может иметь горизонтальный, наклонный и вертикальный
старты. Взлетно-посадочными органами ракетного самолета,
50
Рис. 35. Общин вид состав¬
ного ракетоплана последо¬
вательной схемы
Рис. 36. Принципи¬
альная схема состав¬
ного ракетоплана ти¬
па «пакет»
независимо от характера взлета, могут быть обычное колесное
или лыжное шасси. Так же как и баллистические ракеты, ракет¬
ные самолеты могут быть одноступенчатыми и составными.
Рис. 37. Типовые траектории полета ракетоплана
и баллистической ракеты:
1—баллистическая ракета; 2—рикошетирующий ракето¬
план; .3—планирующий ракетоплан; 4—маршевый полет
ракетоплана
По аналогии многоступенчатых ракет составные ракетные са¬
молеты могут быть выполнены по последовательной и параллель¬
ной схемам. В первом случае (рис. 35) самолет второй ступени,
до разделения, является «полезным» грузом для первой ступени.
Двигатели по ступеням работают поочередно. Во втором случае
схема может быть образована как из одинаковых (рис. 36), так
и из неодинаковых (см. рис. 30) ракетных самолетов. Двигатели
по ступеням могут работать как одновременно, так и поочередно.
Все составные ракетные самолеты являются пилотируемыми ле¬
тательными аппаратами многократного применения.
Движение ракетоплана может происходить по баллистиче¬
ской, рикошетирующей, планирующей траекториям, а также в
режимах маршевого, суборбитального и космического (межпла¬
нетного) полетов (рис. 37).
Расчетные схемы ракетопланов и условные обозначения со¬
ставляющих элементов (ступеней, ускорителей и т. д.) те же, что
и для одноступенчатых и составных ракет.
1.6. ЭКСПЕРИМЕНТАЛЬНЫЕ РАКЕТОПЛАНЫ
Особое место среди летательных аппаратов многоразового ис¬
пользования в ракетно-авиационной технике занимают экспери¬
ментальные ракетопланы.
Основной целью создания этих ракетопланов является полу¬
чение данных, касающихся управляемых человеком аппаратов,
51
летающих с гиперзвуковыми скоростями и возвращающихся в
плотные слои атмосферы *.
5)
Рис. 38. Ракетный самолет Х-15 (США):
а—на смотровой площадке; б—выравнивание перед посадкой
Типовым и наиболее совершенным представителем экспери¬
ментального ракетного самолета является самолет американ¬
ской фирмы Норт-Америкен Х-15. Фотография и компоновочная
схема этого самолета представлены на рис. 38 и 39.
* Под гиперзвуковой скоростью понимают скорость, превышающую ско¬
рость звука более чем в 5 раз. Исследования в этой области оценивают физи¬
ческую границу чисто сверхзвуковой скорости полета примерно в 6000 км/ч.
После перехода через скорость звука (т. е. примерно 1200 км/ч у поверхности
Земли) ожидаются дальнейшие затруднения при скорости, примерно в 5 раз
превышающей скорость звука. При этой скорости наступает местное сжижение
воздуха под влиянием изменений давления при быстром полете аппарата в
атмосфере.
52
53
Самолет рассчитан на работу при высоких температурах и
имеет в основном монококовую или полумонококовую конст¬
рукцию.
Характеристика ракетного самолета Х-15
Размах крыла .
Длина самолета
Площадь крыла
Угол стреловидности крыла по 1/4 хорд
Относительная толщиная крыла
Удлинение .
Стартовый вес
Вес в момент прекращения работы двигателя
Вес расходуемого топлива
Максимальная скорость
Расчетная высота
Посадочная скорость ....
Тяга двигателя (на высоте 12200 м):
максимальная
минимальная
6,7 м
15,24- м
18.5 м2
25°
5%
2.5
14190 кгс
5880 кгс
8300 кгс
2000 м/с
(7200 км/ч)
76200 м
300 км/ч
25850 кгс
7700 кгс
В носовой части фюзеляжа находится герметизированный от¬
сек с двойной обшивкой, в котором размещаются летчик и обо¬
рудование. Там же распо¬
лагается передняя стойка
убирающегося колесного
шасси.
Центральная часть
фюзеляжа образована ба¬
ком для окислителя, рас¬
положенным впереди кры¬
ла, баком для горючего
и шпангоутами, к кото¬
рым крепится крыло.
К хвостовой части фю¬
зеляжа крепятся опере¬
ние, лыжное шасси и ра¬
кетный двигатель.
Для ракетного само¬
лета обеспечение безопас¬
ности является одним из
наиболее важных факто¬
ров при планировании
программы летных испы¬
таний и выработке тех¬
ники пилотирования. Не¬
обходимо проверить испытания новых систем на работоспособ¬
ность по определенному плану, обеспечивающему максимальную
уверенность в их исправности и безопасности.
54
Рис. 40. Схема полета эксперимен¬
тального ракетоплана Х-15
Полет самолета Х-15 происходит после сброса его с самоле¬
та-носителя, как это показано на рис. 40.
Во время полетов экспериментальных ракетопланов собира¬
ются данные о работе конструкции и систем самолета в сложном
многорежимном и высокотемпературном полете.
Полученная таким образом информация позволяет экстрапо¬
лировать ее на другие виды перспективных изысканий и созда¬
ния новой техники.
СПИСОК ЛИТЕРАТУРЫ
1. Г р о д з о в с к и й Г. Л., Иванов Ю. Н., Токарев В. В. Ме¬
ханика космического полета с малой тягой. М., «Наука», 1966, 679 с.
2. Е г о р о в П. Т. Реактивное оружие. М., Воениздат, 1960, 224 с.
3. Корлисс У. Ракетные двигатели для космических полетов. М.,
ИЛ, 1962, 489 с.
4. Королев С. П. О практическом значении научных и технических
предложений К. Э. Циолковского в области ракетной техники. «Из истории-
авиации и космонавтики», М., Изд-во АН СССР, 1966, вып. 4, 66 с.
5. К о ciM о д е м ь я иски й А. А. К. Э. Циолковский — его жизнь и
работа по ракетной технике. М., Воениздат, 1960, 187 с.
6. К и с л и к М. Д. Движение искусственного спутника в нормальном
гравитационном поле Земли. — В сб. «Искусственные спутники Земли»,
1960, вып. 4, 260 с.
7. П е т р о в Б. Н. Космические исследования в СССР. — «Вестник АН
СССР», 1967, № 11, с. 58—71.
8. С п р а в о ч н и к по космонавтике. Под общей ред. Н. Я. Кон¬
дратьева и В. А. Одинцова. .М., Воениздат, 1966, 325 с.
9. С. П. Королев — автор книги о ракетной технике. — «Авиация и кос¬
монавтика», 1966, № 5, с. 36—37.
10. Стволин скийЮ. и Ч у р и н Н. Ракеты Владимира Разумова.—
«Авиация и космонавтика», 1966, № 1, с. 30—35.
11. Тихонравов М. К. и др. Десять лет исследования космоса в
СССР. — «Космические исследования», М., Изд-во АН СССР, 1967, т. 5,
вып. 5, с. 643—679.
12. Ш у н е й к о И. И. Ракетостроение 1963—1965. Крылатые космиче¬
ские корабли. М., Изд. ВИНИТИ АН СССР, 1966, 263 с.
13. М i s s i 1 е s and Rockets, 1964, vol. lo, No 7.
Глава II
ДВИЖЕНИЕ РАКЕТЫ В ПУСТОТЕ
Прежде чем приступить к рассмотрению вопросов, связанных
€ выбором параметров ракетных летательных аппаратов, оста¬
новимся на выводе основных уравнений ракетодинамики.
Современная ракетодинамика — это наука о движении ракет
(или ракетных систем), представляемых в виде тел (или точек)
переменной массы. Ракетодинамика является разделом теорети¬
ческой механики.
В соответствии с этим в главе приведен вывод и дан анализ
уравнений, описывающих свободное движение точки переменной
массы, а также движение этой точки в поле сил земного тяго¬
тения. Полученные' выводы иллюстрированы графиками и пред¬
ставлены в виде, удобном для составления обобщенных уравне¬
ний ракетодинамики с учетом весовых факторов.
2. 1. СЕКУНДНЫЙ РАСХОД МАССЫ
Если к моменту времени t масса ракеты составляет M=f(t),
а к моменту времени — масса ее равна Mi=/(^i), то расход
массы АМ за время At = ti—t будет
AM = M1—M=f(t1)—f(t).
Средний за время At расход массы будет равен
Ш fjt,)- f(t)
At At
Переходя к пределу, находим мгновенное значение расхода
массы или ее секундный расход
Мс=-—. (2.1)
dt J
Знак минус в формуле (2. 1) означает, что происходит отде¬
ление (а неприсоединение) массы.
Секундный расход массы может быть постоянным и перемен¬
ным. В связи с этим различают два наиболее характерных зако¬
на изменения массы — линейный закон и показательный (экс-
56
поненциальный) закон. Ниже главное внимание будет уделено
линейному закону изменения массы, поскольку этот закон полу¬
чил широкое применение для подавляющего большинства совре¬
менных ракетных летательных аппаратов.
2.2. ИДЕАЛЬНАЯ ТЯГА
Понятие идеальной тяги имеет место для двигателя с иде¬
альным соплом, у которого давление истекающей струи газов
на срезе сопла дСр равно окружающему статическому-давлению
среды ра. Конструктивно такие сопла не всегда выполнимы, по¬
скольку по мере подъема ракеты на высоту их выходные сечения
должны менять площадь от величины Fср на уровне моря до ве-
личины FCv= °о в пустоте.
Для подсчета тяги, создаваемой ракетным двигателем в пу¬
стоте, применим (формально) второй закон Ньютона. В вектор¬
ной форме это запишется так:
Р = — d <МУ2, ; (2.2)
dt
где Р — сила тяги двигателя; MW — количество движения от¬
брасываемой струи в системе координат, связанной с ракетой.
Следует помнить, что это уравнение неприменимо к воздуш¬
но-реактивным двигателям типа, скажем, турбореактивного.
В этом случае должно быть учтено начальное количество дви¬
жения струи, заключенное в набегающем потоке. Поскольку ра¬
кетная система несет запас рабочего тела с собой, выражение
(2. 2) пригодно для наших целей.
Продифференцировав выражение (2. 2), получим
P = -W——m4¥-. (2.3)
dt dt
Для большинства реактивных двигателей последний член в
правой части уравнения (2.3) равен нулю, так как преоблада¬
ют системы с постоянной скоростью истечения. В результате мы
приходим к выражению
Р = (*-4>
или с учетом (2. 1)
P = MCW. (2.5)
Это и есть выражение для идеальной ракетной тяги. Как вид¬
но из формулы (2.5), величина ракетной тяги тем больше, чем
больше секундный расход массы и чем больше скорость истече¬
ния активной массы (продуктов сгорания топлива).
57
2.3. ЛИНЕЙНЫЙ ЗАКОН ИЗМЕНЕНИЯ МАССЫ
Для линейного закона изменения массы имеет место следую¬
щая зависимость:
M(t)=M0 — Mct, (2.6)
или
M(t) =М0(1 — р/), (2.7)
где M(t) —текущая масса; М0 — начальная масса; t — текущее
время полета; р = А1с/М0— коэффициент расхода массы.
Коэффициент расхода массы (3 характеризует ту часть на¬
чальной массы ракеты М0, которая расходуется каждую секун¬
ду для создания реактивной тяги. Поскольку величина коэффи¬
циента (3 остается постоянной в течение полета (p = const), то,
очевидно, что Мс = pM0 = const. При этом, как следует из выра¬
жения (2.5), тяга двигателя также остается постоянной и рав¬
ной Р = И7|ЗМо = const.
Для текущего ускорения, обусловленного действием силы тя¬
ги, получим следующее выражение:
w(-^\
М (О М (t)
или, принимая во внимание (2. 7),
«W = Y3^#C011st- (2.8)
Следовательно, при постоянной тяге (линейном законе изме¬
нения массы) движение происходит с переменным ускорением.
2.4. ПОКАЗАТЕЛЬНЫЙ ЗАКОН ИЗМЕНЕНИЯ МАССЫ
При показательном законе изменения массы имеет место сле¬
дующая зависимость:
M(t) = M0e-v, (2.9)
где, как и ранее (см. разд. 2. 3), коэффициент расхода |3 являет¬
ся постоянной величиной.
Продифференцировав выражение (2.9), найдем секундный
расход массы
(_^Д| = гШ0е-^ = Ш(0. (2.10)
Выражение (2. 10) показывает, что при показательном зако¬
не изменения массы, секундный расход топлива пропорционален
текущей массе ракеты.
58
Воспользовавшись формулой (2.4), получим следующее вы¬
ражение для тяги двигателя:
P(t) = W?M0e-v = ?WM(t). (2. 11)
Это означает, что показательный закон изменения массы со¬
ответствует движению с переменной тягой. При этом изменение
тяги пропорционально изменению массы ракеты. Такое движение
ракеты может быть осуществлено при наличии двигателя с регу¬
лируемой в полете тягой.
Ускорение, имеющее место на активном участке полета, бу¬
дет равно
а = — = riW = const. (2. 12)
м
Таким образом, если относительная скорость излучаемых ча¬
стиц (скорость истечения W) постоянная, то показательный за¬
кон изменения массы соответствует движению точки с постоян¬
ным реактивным ускорением.
Практическое применение показательного закона вытекает
из необходимости обеспечения в будущем постоянных перегру¬
зок nx(t)= const для многократно используемЪгх космических
систем, предназначенных для перевозки пассажиров и грузов на
дальние расстояния в пределах земного шара или для полетов
по трассе Земля — орбита — Земля.
Его применение особенно характерно для одноступенчатых
летательных аппаратов типа «Астроплан», полет которых проис¬
ходит без отброса пассивных масс и, следовательно, требующих
дросселирования тяги двигателей для уменьшения растущих в
полете продольных ускорений.
2.5. ТЯГА РАКЕТНОГО ДВИГАТЕЛЯ
Выше было рассмотрено образование ракетной тяги в иде¬
альных условиях (без учета влияния среды и конструктивных
особенностей самого двигателя).
Сила тяги ракетного двигателя в реальных условиях пред¬
ставляет собой осевую равнодействующую сил давления, рас¬
пределенных по всей его внешней и внутренней поверхности.
Воспользовавшись выражением для идеальной тяги (2.5),
а также учтя осевые составляющие внешнего статического дав¬
ления атмосферы (—/?н^ср) и давления истекающей массы га¬
зов на срезе сопла (рсpfcp), запишем полную тягу ракетного
Двигателя в следующем виде:
P = McW + Fcv(Pcv — Рн), (2. 13)
где Fcр — площадь среза сопла.
Равенство (2. 13) выражает текущее значение тяги двигате¬
ля, зависящее от высоты полета ракеты. Оно показывает, что
59
тяга двигателя возрастает по мере убывания давления среды,
т. е. по мере подъема ракеты на высоту, и достигает наиболь¬
шего значения в пустоте, когда рн = 0. При этом Р = Ртах-
Выражение (2. 13) можно переписать и в другом виде
P = MCW -\-Fcv (/?Ср — Ро)+^ср(Ро — Рн), (2. 14)
где /7,0, как и ранее, атмосферное давление на уровне моря.
Поскольку на уровне моря рн = ро, то стартовая тяга на уровне
моря Р0 будет равна
P0 = McW + Fcl)(pCv — ро). (2. 15)
Экспериментаторы называют эту тягу «стендовой» тягой, по¬
скольку она определяется замерами при стендовых испытаниях
двигателей.
Имея выражения (2. 14) и (2. 15), можно записать
^=е>+е:рл,!(1-^-). (2.16)
Последний член правой части выражения (2. 16) учитывает
увеличение тяги с высотой за счет уменьшения атмосферного
давления. Этот член называется барометрической добавкой тя¬
ги и его можно обозначить так:
ДЯ = /гср^о 1 ).
' Ро 1
(2. 17)
Это выражение является одновременно и высотной характе¬
ристикой двигателя, поскольку оно характеризует изменение
(прирост) тяги с высотой Н.
Легко видеть, что вели¬
чина барометрической до¬
бавки тяги тем больше, чем
Рис. 41. Изменение параметра
(1—рп/ро) в зависимости от вы¬
соты полета (по данным между¬
народной стандартной атмосферы)
Рис. 42. Характер изменения безраз¬
мерной тяги двигателя Р по времени
полета баллистической ракеты
60
менее плотная среда окружает двигатель, т. е. чем на большей
высоте происходит полет.
Изменение множителя (1—Рн/Ро) в стандартных условиях
по высоте Н приведено на графике рис. 41. Легко понять, что
максимальное значение барометрической добавки тяги в пусто¬
те при рн = 0 равно АР= (ДР)тах= 10300 Fcр.
Таким образом, тяга ракетного двигателя в пустотных усло¬
виях тем больше, чем больше площадь его выходного сечения.
Величина тяги, отнесенная к ее первоначальному стартовому
значению, записывается так:
P = f= 1+~- С2-18)
Характер изменения безразмерной тяги Р при полете балли¬
стической ракеты на активном участке траектории (в функции
времени /) представлен на рис. 42. Для жидкостных ракет уве¬
личение тяги с высотой составляет 12—18%.
2.6. УДЕЛЬНАЯ ТЯГА
Удельная тяга является одной из главных характеристик ра¬
кетных топлив и ракетных двигателей.
Удельной тягой называют тягу двигателя, отнесенную к се¬
кундному весовому расходу топлива, т. е.
, (2. 19)
Gc
где Gc = Mcg0 — секундный расход топлива, выраженный в кгс/с.
Ранее было показано (см. разд. 2.5), что тяга двигателя не
остается постоянной при изменении высоты полета. Ее величина
меняется от Р = Р0 (на уровне моря) до Р = Р+АЯ.тах=Лпах в
пустоте. В связи с этим различают удельную тягу «земную» (на
уровне моря Р}°ч ) и «пустотную» (в пустоте Р1^ ). Их выражения
соответственно имеют вид
Л°д = 7г- , (2.20)
Gc
+ . (2.21)
Gc
Легко понять, что увеличение удельной тяги с высотой является
следствием увеличения абсолютной тяги двигателя. При этом се¬
кундный расход топлива не меняется. Очевидно, что максималь¬
ное увеличение удельной тяги в пустоте составляет такой же про¬
цент, как и для самой тяги.
На величину удельной тяги влияет также давление в камере
сгорания pi, при котором происходит процесс образования газо-
61
образной активной массы. Такая зависимость для некоторых
топливных пар приведена на рис. 43. Из графика видно, что уве¬
личение удельной тяги благодаря pi особенно эффективно при
малых его значениях
(р;<100 кгс/см2).
Имея формулы (2.5) и
(2.19) легко показать, что
для двигателя с идеальным
соплом величина удельной
тяги равна Руд=№7/£'о- Оче¬
видно, что эта зависи¬
мость имеет место при
Рср = РII •
Удельная тяга опреде¬
ляется, следовательно, ско¬
ростью истечения продуктов
сгорания из сопла двигателя
и зависит от теплотворной
способности топлива. Кон¬
струкция двигателя влияет
на величину удельной тяги,
однако это влияние не имеет
первостепенного значения.-
Поэтому удельную тягу принято рассматривать главным обра¬
зом как характеристику топлива. Так например, при проектиро¬
вании ракет и при расчете их дальности, для двигательной уста¬
новки задают определенное значение удельной тяги, предпола¬
гая при этом, что конструкция двигателя является достаточно
рациональной.
2.7. ОСНОВНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ РАКЕТЫ
В классической механике масса точки (или системы точек)
всегда принимается постоянной. При изложении методов этой
механики исходят главным образом из 2-го закона движения
Ньютона, устанавливающего соотношение между силами, дейст¬
вующими на материальную точку, и ее ускорением (поступатель¬
ным движением).
Однако, если во время движения происходит истечение или
присоединение массы, то зависимость между действующими си¬
лами и ускорением точки должна быть сформулирована в более
общей форме.
Такая задача была решена русским ученым, профессором
Петербургского политехнического института И. В. Мещерским в
1897 г. [3].
Так как полет ракеты происходит в результате отброса актив¬
ных масс (горючего, окислителя), ее можно рассматривать как
материальную точку переменной массы. В таком движении на
62
Рис. 43. Зависимость удельной тя¬
ги РуЛ от давления в камере сго¬
рания для различных топлив (дав¬
ление на срезе сопла р ср =
= 1 кгс/см2):
1—кислород + керосин; 2—кислород +
+ сппрт; 3— 11ХОз+кероспн
нее действуют сила тяги, гравитационная сила и аэродинамиче¬
ские силы (сопротивление и подъемная сила).
Основное уравнение движения ракеты (уравнение Мещерско¬
го) записывается следующим образом:
MdV
(2-22)
dt
/=1
—> п
где clV/dt — вектор текущего ускорения точки (ракеты);
i = 1
сумма действующих во время полета сил, выраженная в вектор¬
ной форме.
Уравнение вида (2. 22) справедливо для большого класса за¬
дач, относящихся к современной ракетной технике, поскольку в
них допустимо считать относительную скорость излучаемых ча¬
стиц (скорость истечения продуктов горения топлива) посто¬
янной.
2.8. ПЕРВАЯ ЗАДАЧА ЦИОЛКОВСКОГО
Пусть точка переменной массы движется в--пустоте без внеш¬
них сил за счет отброса активной массы. Требуется определить
закон изменения скорости по мере расхода активной массы.
Эту задачу, относящуюся к частным задачам динамики точ¬
ки переменной массы, впервые поставленную и решенную
К. Э. Циолковским, называют первой задачей Циолковского.
м
w at
Рис. 44. Схема для вывода формулы Циолков¬
ского
Составим уравнение движения точки переменной массы, ис¬
пользуя ранее приведенное уравнение Мещерского (2.22). В на-
п
шем случае имеет место — Поскольку точка переменной
L = 1
массы имеет относительную скорость истечения частиц, посто¬
янную по величине и коллинеарную вектору скорости V
(рис. 44), то уравнение Мещерского дает
M — = — — W. (2.23)
dt dt
63
Принимая W = const, из уравнения (2.23), получим
yv=-w^,
откуда после интегрирования
V= — WlnM + C,
где С — постоянная интегрирования.
Принимая, что при / = 0, V=0 и М = М0, найдем С=
= W In М0.
При этом
V = w ln^-. (2.24)
М У
Полученное равенство называют формулой (или законом) Ци¬
олковского.
Из формулы Циолковского следуют важные выводы. Во-пер¬
вых, скорость ракеты непрерывно возрастает при увеличении от¬
ношения начальной массы ракеты к ее
конечной массе; во-вторых, скорость ра¬
кеты пропорциональна скорости истече¬
ния продуктов сгорания топлива; в-треть¬
их, увеличение скорости полета более
эффективно благодаря повышению ско¬
рости истечения, чем вследствие увеличе¬
ния относительного запаса топлива (т. е.
увеличения отношения начальной массы
к конечной массе); и, в-четвертых, наи¬
большая скорость в пустоте (к моменту
Рис. 45. Влияние скорости истечения и числа Ци¬
олковского на конечную скорость
полного расхода активной массы) в отсутствии сил земного тяго¬
тения (т. е. в идеальных условиях) не зависит от закона расхода
массы, а зависит только от ее относительного запаса (т. е. от
числа Циолковского).
Скорость в конце полета V=VU (конечная скорость) при пол¬
ном израсходовании активной массы, когда имеет место М = Ми
(конечная масса), будет равна
VK=W In Ц, (2.25)
где Ц = М0/МИ — число Циолковского.
Скорость истечения продуктов сгорания топлива характери¬
зует эффективность топлива как носителя энергии высокой кон-
64
центрации и является предметом исследований в области химии
и ракетных двигателей.
Число Циолковского, показывающее во сколько раз стартовый
вес ракеты больше ее конечного веса, характеризует совершен¬
ство конструкции ракеты в целом и является предметом иссле¬
дований в области проектирования ракет. Очевидно, что увели¬
чение скорости полета ракеты может быть достигнуто путем
одновременного увеличения скорости истечения продуктов сго¬
рания топлива и числа Циолковского (рис. 45).
Коэффициентом перегрузки или просто перегрузкой, действу¬
ющей вдоль продольной оси ракеты, называется число, показы¬
вающее во сколько раз тяга ракеты (за вычетом аэродинамиче¬
ских сил сопротивления) больше ее веса
где X(t) —сила лобового сопротивления (переменная по време¬
ни полета); G(t)—текущий вес ракеты в постоянном поле сил
земного тяготения.
В начальный момент времени (к моменту отрыва ракеты от
стартового стола) P = G0i Х = 0, G = G0 и тогда пх= 1.
Для удобства теоретических изысканий в ракетодинамике
принято условно, что тяга двигателя выходит на режим мгно¬
венно. При этом уже в начальный момент времени при / = 0 за¬
писывают значение тяги как Р = Р0. Очевидно, что выражение
для стартовой перегрузки п0, когда V/=0, и, следовательно Х = 0,
примет вид
Следует помнить, что под стартовой тягой подразумевается
та тяга, которая соответствует стартовым условиям на данной
высоте. Если старт ракеты (например 2-й ступени) происходит
в пустоте, то в этих условиях (t = О, Х = 0, G=G0, Ро = РоП) вы¬
ражение для начальной осевой перегрузки в пустоте запишется
так:
Пользуясь линейным законом изменения массы (2.7), легко
записать для пустотных условий
2.9. СТАРТОВАЯ ПЕРЕГРУЗКА
(2. 26)
(2. 27)
(2. 28)
«л-(О
1-
(2. 29)
3 3479
65
Как показывают расчеты, на участке пролета атмосферы си¬
лы лобового сопротивления в значительной мере компенсируют
высотную добавку тяги, благодаря чему с достаточной для весо¬
вых расчетов точностью можно записать для этого участка
(2. 30)
здесь / следует брать только на участке, где X — 0-ьХтах- Оче¬
видно, что на участке после Хтах следует ‘пользоваться форму-
лой (2. 29).
Общий характер изменения перегрузки в функции времени
полета nx(t), полученный по формулам (2.29) и (2.30) и мето¬
дом численного интегрирова¬
ния уравнений движения, пред¬
ставлен на рис. 46.
График содержит ряд ха¬
рактерных точек. Точка 1 ха¬
рактеризует период времени,
когда тяга двигателя еще на¬
ходится в пределах O^Po^G0.
При этом ракета испыты¬
вает реакцию со стороны стар¬
тового стола, равную ее на¬
чальному весу (действует как
бы фиктивная тяга P = G0).
Очевидно, что перегрузка
в этот момент времени равна
единице. Точке 2 соответст¬
вует теоретическое значение
перегрузки (подсчитанной по
формуле 2.30) для t = 0. Такая
перегрузка имела бы место,
если бы двигатель мгновенно
выходил на режим (полную
тягу).
В действительности, достижение полной тяги происходит не
сразу, а в течение некоторого (хотя и очень малого) времени At.
Этому случаю, вместо теоретической точки 2, соответствует слу¬
чай, отмеченный точкой 3. Расстояние между этими точками со¬
ставляет время порядка Д/=1,5-^-3 с. Ввиду малости расхода
топлива за время At, перегрузки в точках 2 и 3 практически оди¬
наковы. Несовпадение кривых на отдельных участках объясня¬
ется неучетом сил АР и X при построении зависимости nx(t) по
формуле (2.30). Точка 4 соответствует наибольшему значению
перегрузки, достигаемой ракетой в момент выключения двигате¬
ля. В этот момент времени t=т, а произведение |3<=|3т в фор-
66
Рис. 46. Изменение осевой перегруз¬
ки по времени полета ракеты:
а—по формуле; б—численным интегриро¬
ванием
муле (2. 29) будет равно
G-fio
Ос
или
■J
(2.31)
где gt = Gt/Gо — весовая отдача по топливу, равная отношению
веса топлив GT к стартовому весу G0; рк = GJG0— весовая отда¬
ча по конечному весу, равная отношению конечного веса (вме¬
сте с полезным грузом) к стартовому весу G0.
При этом максимальное значение осевой перегрузки запишет¬
ся так:
Для случая показательного закона изменения массы в соот¬
ветствии с определением перегрузки по формуле (2. 27) имеем
Это означает, что при показательном законе изменения мас¬
сы осевая перегрузка во время полета на работающем двигателе
остается постоянной и равной ее первоначальному значению,
т. е. nx(t) = п0.
Возвращаясь к выражению (2.26), запишем его в более об¬
щем виде через текущее ускорение ракеты и ускорение сил зем¬
ного тяготения g0. Тогда при X(t) =0 получим
n.(t)=—^—= M0)a(t) ==_giO_- (2. 34)
G (t) M (t) g0 g0
Это означает, что перегрузка n(t) характеризует число, по¬
казывающее во сколько раз текущее ускорение ракеты больше
земного ускорения на уровне моря.
Полное время работы двигателя т равно отношению веса топ¬
лива GT к его секундному расходу Gc, т. е. т =GT/GC.
Для линейного закона изменения массы имеет место Gc =
= const, что на основании выражения для идеальной тяги (2. 5)
Дает Gc = Po/pQ.{ . При этом легко получить
(2. 32)
nQ = W — = const.
go
(2. 33)
2. 10. ВРЕМЯ ПОЛЕТА
ПРИ РАБОТАЮЩЕМ ДВИГАТЕЛЕ
Полное время полета т, определяемое формулой (2.35), не
изменится, если в этой формуле произвести замену п0 на п0п и
Рул на Р£д.
Поскольку коэффициент расхода массы |3=GC/G0 можно
представить как р=п0/Р°я, то можно получить также
_ От 1-ик ^23б^
3 3
Для показательного закона изменения массы логарифмирова¬
нием выражения (2. 9) находим
/=_Lin_®0_, (2.37)
Р G(0 v
где G(t) — текущий вес ракеты.
Таким образом, время полета на активном участке (при по¬
казательном законе изменения массы) подчиняется логарифми¬
ческому закону (2.37). Его можно сформулировать следующим
образом:
если пассивная плюс активная массы возрастают в геомет¬
рической прогрессии, то скорость точки увеличивается в про¬
грессии арифметической.
В самом деле, формулу (2. 37), записанную для полного вре¬
мени полета t = т при Gt=т = GK, можно представить так:
3t = ln_^
GK
и, следовательно, если отношение G0/GK будет последовательно
принимать значения 2, 4, 8, 16, 32, . . ., то безразмерное время |3т
будет принимать значения рт = 1п2, 2(3т, 3|3т, 4|3т,...
Вспоминая теорему Циолковского, вытекающую из его пер¬
вого закона, легко видеть, что изменение параметров V^jW (при
линейном законе изменения массы) и |3т (при показательном за¬
коне изменения массы) происходит по одинаковому (логариф¬
мическому) закону.
Полное время полета, выраженное через число Циолковско¬
го, будет равно
т = Л-1пЦ. (2.38)
Разделив (2. 38) на (2. 36), получим
т=-^- = -^Д . (2.39)
Таин
Это означает, что при одинаковых коэффициентах расхода
массы время полета на активном участке при показательном
законе изменения массы тПОк больше в т раз по сравнению со
временем полета на активном участке при линейном законе из¬
менения массы Глин (см. разд. 10.4). Так, если весовая отдача
68
£т = 0,9, то увеличение времени полета при показательном за¬
коне изменения массы составит т~2,55 раза.
2. 11. ВТОРАЯ ЗАДАЧА ЦИОЛКОВСКОГО
ДЛЯ ЛИНЕЙНОГО ЗАКОНА ИЗМЕНЕНИЯ МАССЫ
Ранее (см. разд. 2. 8) была рассмотрена задача определения
скорости полета ракеты в пустоте при отсутствии сил земного
тяготения (первая задача Циолковского). Решение этой задачи
весьма полезно для сравнительного анализа летных характери¬
стик ракетных систем. В то же время эта задача, строго говоря,
неприменима для большинства ракет, полет которых происходит
в поле действия гравитационных сил, и особенно для ракет,
стартующих с поверхности Земли.
CLV
Рис. 47. Схема сил, действую¬
щих на ракету в гравитацион¬
ном поле тяготения
Во второй задаче ракетодинамики, решенной К. Э. Циолков¬
ским, исследуется прямолинейный вертикальный полет ракеты
с учетом силы тяжести.
Рассмотрим вторую задачу Циолковского в более общем ви¬
де для криволинейного движения ракеты (точки переменной мас¬
сы) в неоднородном поле сил тяжести, как показано на рис. 47.
Запишем уравнение Мещерского в следующем виде:
М
dV
dM
dt
dt
W-Mg?(dK),
(2. 40)
где go(0K)—средняя интегральная по времени величина уско¬
рения под действием местного гравитационного поля, умножен¬
ная на синус мгновенного угла наклона траектории полета (ме¬
тодика определения этой величины приведена ниже, разд. 10.2
и 12.6); 0 — угол, составленный вектором скорости и местным
горизонтом (мгновенный угол наклона траектории).
Закон изменения массы выразим в общем виде
M = M0f(t).
Запишем также 7
dM
Далее на основании уравнения (2. 40) получим
Поскольку
— = w—gzyj.
dt f(t) ь 1 w
/'(О d
f (О dt
In /(/),
TO «L=-W±-\nf(t)-g,{bK).
at dt
Интегрирование этого уравнения при условии, что М(==0=М^
и /(=0= 1, дает
V=-W\nf(t)-gt,{QK). (2.41)
Для линейного закона изменения массы имеем
/(*) =
Л40
и тогда
1/ = IF In —Г— — gh (0К). (2.42)
I pf
Как будет показано ниже (см. разд. 10. 2), для реальной кон¬
струкции ракеты существует оптимальное значение п0, которому
соответствует максимальная конечная скорость полета.
Если движение ракеты происходит строго вертикально (вы¬
сотный полет), когда 0 = 90°, то формула (2.42) принимает вид
V = w\ n— gt (2.43)
1
или для конечной скорости
VK = W (In- ^1. (2.44)
V р-к щ
Формула (2.44) определяет конечную скорость ракеты при
линейном законе изменения массы с учетом сил земного тяготе¬
ния и является решением второй задачи Циолковского. Как вид¬
но из формулы, скорость ракеты возрастает тем больше, чем с
большей перегрузкой стартует ракета. При увеличении пере¬
грузки происходит уменьшение потерь на силы тяжести (время
работы двигателя сокращается), в результате чего конечная ско¬
рость возрастает. Из формулы (2. 44) следует, что наибольшую
конечную скорость можно получить при перегрузке /г0, равной
бесконечности (п0= оо). При этом двигатель как бы мгновен¬
но сжигает топливо при тяге, равной бесконечности, исключая
потери во времени на преодоление сил земного тяготения.
70
Очевидно, что в этом случае скорость была бы такой, как и
при полете в отсутствии сил земного тяготения. Ранее получен¬
ная формула (2. 25) является, таким образом, частным случаем
формулы (2.44) при гц=оо. Описанное явление, однако, имеет
чисто теоретический интерес и характеризует влияние параметра
По без учета реальной конструкции ракеты.
2. 12. ВТОРАЯ ЗАДАЧА ЦИОЛКОВСКОГО
ДЛЯ ПОКАЗАТЕЛЬНОГО ЗАКОНА ИЗМЕНЕНИЯ МАССЫ
Для показательного закона изменения массы (2.9) имеет
место
При этом формула скорости полета (2.41) перепишется так:
Как и в случае линейного закона изменения массы, при по¬
казательном законе конечная скорость при движении в поле сил
земного тяготения тем больше, чем больше величина начальной
перегрузки п0 (постоянной во время полета), т. е. чем меньше
потери на преодоление сил тяжести. Весьма важно, что при
#о=оо потери на преодоление сил тяжести равны нулю и оба
закона (линейный и показательный) дают одинаковую конечную
скорость.
v=w&-gt'(BK)
ИЛИ
Поскольку
то
(2.45)
где текущее значение числа Ц равно Ц {t) = ^ .
Конечная скорость при t=т и \х = \\к запишется так
(2.46)
В случае вертикального полета при а(0) = 1 получим
(2. 47)
71
Таким образом, если тяга изменяется по показательному за¬
кону, при котором создаваемое ускорение постоянно, то в поле
гравитационных сил конечная скорость отличается от конечной
скорости, получаемой ракетой при линейном законе изменения
массы.
Это расхождение в скоростях обусловлено неодинаковым
временем полета при работающих двигателях, а следовательно,
и неодинаковыми потерями в скорости за счет силы тяжести.
Полет с постоянной перегрузкой создает наиболее приемле¬
мые условия пилотируемого полета по сравнению с условиями
полета при переменной перегрузке (непрерывно увеличивающей¬
ся по мере расхода топлива). Однако постоянная перегрузка
менее приемлема с чисто технической точки зрения, поскольку
показательный закон изменения массы требует непрерывного
дросселирования тяги двигателя. Такое дросселирование приво¬
дит к неполному использованию эксплуатационных возможностей
топливных насосов, трубопроводов, клапанов и самого двигателя
на протяжении всего активного участка полета, исключая корот¬
кое время после старта, где мощность двигателя форсируется
полностью. Если расход топлива подчиняется показательному
закону, время работы двигателя увеличивается, что, в свою оче¬
редь, требует увеличения ресурса при его создании. Несмотря
на это, практическое применение этого закона в будущем, как
мы уже говорили (см. разд. 2.4), диктуется пилотируемыми си¬
стемами типа ВКС (воздушно-космических самолетов).
Как и для линейного закона изменения массы, ниже будет
показано, что при показательном законе изменения массы для
реальной конструкции ракеты с учетом весовых, аэродинами¬
ческих и других факторов существует оптимальное значение
перегрузки, при которой скорость в конце полета достигает мак¬
симальной величины.
В разд. 1.4 мы ознакомились со схемой составной ракеты, ее
описанием и обозначениями. В соответствии с этим для каждой
/-й ступени можно записать
Если ракета состоит из п ступеней, то скорость полета в кон¬
це активного участка последней ступени будет равна сумме ско¬
ростей по ступеням, т. е.
2. 13. ФОРМУЛА ЦИОЛКОВСКОГО
ДЛЯ СОСТАВНОЙ РАКЕТЫ
VKl = W,ln
П
72
Если скорости истечения газа по ступеням одинаковы, т. е.
Wi = const,
то
п
i/K=ur Vm-L.
JmU Рк£
/ = 1
ИЛИ
VK = W\ п -Г, (2.48)
.ак
где
£= П (2-49)
/= 1
Формула (2.48) определяет идеальную скорость составной
ракеты (в пустоте без учета сил земного тяготения) и называет¬
ся формулой Циолковского для составных ракет.
Можно записать также
VK=W\nH*-, (2.50)
где
п
Ц* = п Ц:- — приведенное число Циолковского. (2.51)
/-1
Весовая отдача по конечному весу каждой ступени \iKi всег¬
да меньше единицы. При наличии п ступеней произведение
/I
Рк=Пу,к/ может оказаться достаточно малым, что соответству-
/=i
ет большой конечной скорости. Таким образом, принцип отброса
масс по Циолковскому делает реальным достижение весьма
больших скоростей полета, включая и космические скорости.
Формула Циолковского (2.48), полученная для идеальных
условий, дает верхний предел скорости. В действительных усло¬
виях полета, как и для одноступенчатых ракет, необходимо учи¬
тывать изменение скорости в результате действия сил земного
тяготения, сил лобового сопротивления, изменения удельной тя¬
ги с высотой и других факторов, связанных с выполнением про¬
граммы полета.
Пример 2. 1. Получить зависимость для текущей весовой отдачи по топ¬
ливу и конечному весу при линейном законе изменения массы.
Решение. Для линейного закона изменения массы имеет место
G т (t) = GT—Gct.
7.4
Поделив обе части этого равенства на С0, получим
Gr(t)=GT—fit,
а также
Пример 2. 2. По аналогии с примером 2. 1 записать выражения для теку¬
щих весовых отдач GT(t) и Цк(0 при показательном законе изменения массы.
Решение. Текущий вес топлива в баке (во время полета) можно выра¬
зить так
GT (t)=GT—Gc (t) t.
Поскольку для показательного закона изменения массы на основании
(2. 10) имеет место
Gc(0=PG0e_p<,
то предыдущее равенство перепишется так:
GT(<)=GT—pGgt~9<t
или __
GT(<)=GT—
М0=М-к + Р<е 9t.
Пример 2. 3. Доказать первый закон Циолковского для линейного закона
изменения массы, исходя из выражения для перегрузки
Пп
пх (0 = ‘
1-
Решение. Запишем выражение для текущего ускорения как
d^H пп
*«)=-ПГ = еоГ
Поскольку
t
dH Р щ
г<0« —==]«,НЬ«.
ТО
v (0 = go In ~1
Р 1- V
или
V(t)= —W In (1 — эо-
Пример 2. 4. Показать, что
Py*=Wlgo.
Решение. Тяга ракетного двигателя с идеально регулируемым сопломг
выраженная через скорость истечения, запишется как P=WMC. Поскольку
Мс W
удельная тяга равна PyA=P/Gc,. то получим PY l=W — .
GC -go
Ю есть удельная тяга численно составляет приблизительно десятую
часть от скорости истечения.
74
Пример 2. 5. Подсчитать, на каком расстоянии от Земли и Луны силы их
притяжения становятся уравновешенными.
Решение. Расстояние между Землей и Луной составляет 60 земных ра¬
диусов, а масса Земли в 81 раз больше массы Луны. В искомой точке х силы
притяжения массы М Землей и Луной одинаковы, т. е.
ММ мпм
V = V
*2 (60#3 — Х)2
«ли
_81 1
х2 “(60Я — X)2 ’
3
откуда
*=54/?3.
Таким образом, точка, в которой уравновешены силы притяжения Зем¬
ли и Луны, лежит на расстоянии 54 R3 от центра Земли. В решении через v
обозначен гравитационный параметр.
Пример 2.6. Сравнить по конечной скорости линейный и показательный
законы изменения массы при условии, что п0=оо.
Решение. Имея зависимости (2.44) и (2.47), находим, что при гс0=оо
в обоих случаях имеет место одинаковая конечная скорость, определяемая
формулой Циолковского Рк = №ЛпЦ.
Таким образом, конечная скорость точки переменной массы не зависит
от закона расхода этой массы (режима работы двигателя). Заданному чис¬
лу Циолковского в конце процесса отбрасывания соответствует вполне оп¬
ределенная скорость движения точки, независимо от того, быстро или мед¬
ленно происходило отбрасывание (сжигание) имеющегося запаса массы.
СПИСОК ЛИТЕРАТУРЫ
1. Горбате нко С. А. и др. Механика полета. М., «Машинострое¬
ние», 4969, 420 с.
2. Л е в а н т о в с к и й В. И. Механика космического полета. М., «На¬
ука», 1970, 491 с.
3'. Мещерский И. В. Динамика точки переменной массы. Спб., тип.
Имп. Акад. наук, 1897, 160 с.
4. С и н я р е в Г. Б., Добровольский М. В. Жидкостные ракет¬
ные двигатели. М., Оборонгиз, 1957, 580 с.
5. Ц а н д е р Ф. А. Проблема полета при помощи реактивных аппара¬
тов. Под ред. М. К- Тихонравова. [Сборник статей]. М., Оборонгиз,, 1961, 459 с.
6. Циолковский К. Э. Реактивные летательные аппараты. — Собр.
соч., т. 2. М., Изд-во АН СССР, 1954, 455 с.
Глава III
ЭКСТРЕМАЛЬНЫЕ РАСЧЕТНЫЕ СЛУЧАИ
НАГРУЖЕНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИИ РАКЕТ
При выполнении весовых расчетов необходимо знание толь¬
ко тех действующих на ракету сил, которые являются опреде¬
ляющими с точки зрения веса для данного элемента конст¬
рукции.
Существующие «нормы прочности» в силу своей приспособ¬
ленности к уже определившейся конструкции содержат не один,,
а ряд расчетных случаев (основных и поверочных), применить
которые при выполнении весовых расчетов на начальном этапе
проектирования нельзя, поскольку сами расчетные случаи, веса
и нагрузки являются искомыми.
Рис. 43. Схема деления ракет на отсеки. Приведены ракеты «Атлас-Эпбл» (а)
и «Атлас-Центавр» (б)
Таким образом, возникает необходимость в изучении каких-то
других зависимостей, соотношений или критериев, которые бы
указывали на доминирующие весовые нагрузки уже в самом
начале по параметрам, задаваемым при проектировании. Рас¬
четные случаи, указывающие на такие экстремальные нагрузки,
условимся называть «весовыми расчетными случаями».
Отыскание расчетных случаев будем производить, рассматри¬
вая осевые сжимающие силы Nx(t), являющиеся доминирующи¬
ми с точки зрения определения веса работающего элемента кон¬
струкции.
76
Нагрузки, определяемые в соответствии с весовыми расчет^
ными случаями, входят в аналитические весовые зависимости
(формулы) и являются единственными для расчета веса с уче¬
том динамических факторов.
Все рассмотренные в главе весовые расчетные случаи отно¬
сятся к линейному закону изменения массы.
При показательном законе изменения массы вследствие не¬
прерывного уменьшения тяги расчетные случаи для всех элемен¬
тов конструкции относятся к начальному времени полета, когда
^=0 (имеется в виду мгновенный выход двигателя на режим
начальной тяги).
Типовое деление ракеты на отсеки показано на примерах ра¬
кет «Атлас-Эйбл» и «Атлас-Центавр» (рис. 48).
3. 1. СИЛА ЛОБОВОГО СОПРОТИВЛЕНИЯ
Влияние атмосферы как сопротивляющейся среды на полет
ракеты происходит главным образом через силу лобового сопро¬
тивления, на преодоление которой расходуется определенное ко¬
личество энергии.
Полная величина силы лобового сопротивления, как извест¬
но, определяется по формуле
X = cx(IA)qSyl, (3. 1)
где с*(М) —коэффициент лобового сопротивления (задаваемый
oV'2
как функция числа М); = скоростной напор; q — плот¬
ность воздуха; 5М — площадь миделевого сечения; V — скорость
полета.
Величина и характер изменения сил лобового сопротивления
по траектории полета ракеты зависят от многих факторов. Од¬
нако при выполнении весовых расчетов обычно требуется знание
не текущих значений X = X(t), а максимальных сил лобового
сопротивления Х = Хтлх. На рис. 49 приведены типовые кривые
изменения сил лобового сопротивления по траектории полета
для различных значений начальных осевых перегрузок и удель¬
ных тяг. Кривые показывают, что силы лобового сопротивления
X = X(t), равно как и их максимумы Х = Хтах, пропорциональны
параметру п0 и обратно пропорциональны параметру Я';.,. Об
этом можно судить и по графику (рис. 50), построенному для
зависимости q = q(t). Такой характер указанных зависимостей
объясняется тем, что нарастание скорости в равные промежутки
времени происходит тем более, чем больше начальное ускоре¬
ние (т. е. по) и тем меньше, чем меньше секундный расход топ¬
лива (т. е. больше Я}°т). Последнее обстоятельство связано с
тем, что меньший секундный расход топлива замедляет измене¬
ние текущего веса ракеты, что вызывает уменьшение текущей
77
скорости V(t), а следовательно, и аэродинамического сопротив¬
ления.
Аппроксимация зависимостей Amax = ^max (^о> ^3°т) Дает сле~
дующую приближенную формулу для определения максималь¬
ных значений сил лобового сопротивления:
= £—SH, (3.2)
«а)
где kx — статический коэффициент; 5М — площадь миделя ра¬
кеты.
Рис. 49. Изменение сил лобового Рис. 50. Влияние стартовой перегруз-
сопротивления от параметров л о ки на величину скоростного напора
и РуД на активном участке полета
Формула (3. 2) является эмпирической. Вследствие этого под¬
бор в ней значений коэффициента kx и показателей степени а и
v необходимо производить на базе статистических данных для
конкретных схем ракет. Так, для одноступенчатых ракет с пара¬
метрами /1о=1,5-=-2 и Рут =200н-260 с можно принять kx =
= 4,1*103 кгс-с/м2, а= 1,0 и v= — .
4-
Следует помнить, что в тех случаях, когда осевая нагрузка
определяется не на всю ракету, а только на одно из ее сечений,
величину составляющей от максимальных сил лобового сопро¬
78
тивления следует брать как часть силы Атах, действующей на
рассматриваемое сечение. Имея аэродинамическую схему раке¬
ты, эту часть силы Armax легко подсчитать, пользуясь эпюрой
распределения давления по корпусу ракеты.
3.2. РАСЧЕТНЫЙ СЛУЧАЙ ДЛЯ ПОДВЕСНЫХ БАКОВ
Вес подвесных топливных баков определяется по суммарно¬
му внутреннему давлению , состоящему из избыточного дав¬
ления наддува ртб и гидростатического давления Дгидр, т. е.
Величина суммарного давления в подвесных баках опреде¬
ляется условиями работы топливных насосов без кавитации.
Рассмотрим случай, когда избыточное давление остается по¬
стоянным в течение (всего времени полета, т. е. рИЗб = const. Оче¬
видно, что в этом случае максимальное значение суммарного
давления будет соответствовать тому времени полета, когда гид¬
ростатическое давление достигнет наибольшего значения. При
этом достаточно проанализировать выраженйе для гидростати¬
ческого давления, записанное для случая полета в пустоте (без
учета аэродинамических сил сопротивления), «в виде
где 5М — площадь поперечного сечения цилиндрического бака;
kT — весовое соотношение компонента топлива (горючего, окис¬
лителя), равное отношению веса этого компонента к суммарному
весу горючего и окислителя.
Функция (3.4) не имеет экстремума. Наибольшее значение
гидростатического давления найдем, преобразуя эту функцию
к виду
Из этого выражения видно, что наибольшее значение гидро¬
статического давления имеет место в начале полета, когда / = 0
и пх (0 =п0. При этом
В конце полета имеет место [Зт = Ст, тогда ргиДР(/=Т) = 0.
В промежутке времени от t = 0 до t=т по мере расхода топ¬
лива гидростатическое давление, несмотря на увеличение пере¬
79
(3. 3)
или
(3.4)
грузки nx(t), непрерывно уменьшается. Следовательно, расчет¬
ным случаем для подвесных баков с постоянным избыточным
давлением наддува является начальный момент времени, когда
t = 0 и nx(t) =п0.
На рис. 51 представлены кривые гидростатического давления
двух компонентов топлива, построенные для случая полета ра¬
кеты в сопротивляющейся
среде. График показывает,
что и в этом случае макси¬
мальное гидростатическое
давление имеет место в на¬
чале полета, когда тяга дви¬
гателя достигает номиналь-
Рис. 51. Изменение гидростатиче¬
ского давления компонентов топ¬
лива в зависимости от времени
полета:
1—окислитель; 2—горючее
ного значения. На этом же графике нанесены кривые, построен¬
ные по формуле (3.4). Как и следовало ожидать, максимумы
этих кривых соответствуют начальному времени полета, когда
/ = 0 и nx(t) =п0.
Рис. 52. Гидростатическое давление, действующее
по отсекам топливных емкостей ракеты «Си Дре-
гон»:
Точка измерения
Гидравлические давле¬
ние, кгс/см2
1 — на днище бака с жидким
кислородом
2 — на днище бака с жидким во¬
дородом
3 — жидкий кислород перед кла¬
паном
4 — на днище бака с жидким
кислородом
5 — на днище бака с горючим
в — перед форсунками горючего
7 — перед форсунками жидкого
кислорода
Запуск
Перед
отделением
I ступени
2,39
5,47
0,42
0,98
8,4
19,4
5,83
0
2,46
0
3.53
2,95
9,8
9,2
При этом имеется в виду, что двигатель мгновенно выходит
на режим (теоретический случай). Максимум гидростатическо¬
го давления при ^=0 может иметь место в том случае, когда
срабатывание пироболтов, удерживающих ракеты на стартовом
столе (или отделяющуюся в полете ступень), происходит по
достижению тягой двигателя номинального значения. Кривые на
графике иллюстрируют хорошее совпадение гидростатического
давления в найденном расчетном случае. Расхождение в
Ргидр(0 на средних секундах полета обусловлено влиянием сил
аэродинамического сопротивления, которые уменьшают на этом
участке величину перегрузки nx(t). В пустотных условиях кри¬
вые, построенные по формуле (3. 4), совпадают на всех участках
с аналогичными кривыми, построенными по материалам числен¬
ного интегрирования уравнений движения ракеты.
Величины гидростатических давлений в баках можно просле¬
дить на примере составной ракеты «Си Дрегон» (рис. 52).
3.3. РАСЧЕТНЫЕ СЛУЧАИ ...
ДЛЯ ОПРЕДЕЛЕНИЯ ОСЕВЫХ НАГРУЗОК
Представим схему ракеты, составленную из постоянных и
переменных масс, как показано на рис. 53. Постоянные массы
составляют элементы конструкции, полезный груз, оборудова¬
ние и т. д.; переменные массы — компоненты топлива (горючее,
окислитель) и другие расходуемые массы. Полагаем, что полет
происходит в пустоте под действием постоянной тяги двигате¬
ля Р0. Составим выражение для текущей (в функции времени /)
по корпусу ракеты осевой нагрузки Nx(t) в произвольном сече¬
нии а — а. Тогда получим
Nx(t) =
j~ 1 J
(0,
или
^G,.+o0(ar-?/)
L / = 1
; = 1 J
(3.5)
где p — коэффициент расхода массы; k:
коэффициент,
показывающий, какую долю масса до сечения а — а составляет
от общего запаса переменной массы; i — индекс, обозначающий
постоянную массу; / — индекс, обозначающий переменную мас-
СУ; т — количество элементов в конструкции, относящееся к ка-
тегории постоянных масс; п — количество емкостей, содержащих
в себе (полностью или частично) переменную массу.
81
В верхней части ракеты до сечения а — а может оказаться
преобладание либо постоянной, либо переменной массы, и тогда
в первом случае с течением времени по
мере увеличения перегрузки nx(t) в этом
сечении нагрузка Nx(t) будет увеличи¬
ваться; во втором случае — уменьшаться.
Очевидно, что может оказаться и такое
соотношение постоянных и переменных
масс, когда нагрузка Nx(t) в сечении
а—а будет оставаться постоянной.
Функция (3.5) не имеет экстремума,
однако условие, при котором нагрузка
Nx(t) в сечении а—а остается постоян¬
ной в течение всего времени полета на
работающем двигателе, можно найти,
dN,{t)
приравняв нулю производную
Nx(t)
а
1
Тогда получим
dt
Рис. 53. Схема для определения осевых нагрузок:
/—переменные массы; 2— постоянные массы
(1-РО2
Г я
-(1_РООо2^+ S0l'+0o(5l“?0S
7-1 L/-1 7-1
(3.6)
Поскольку и (1 — (3/)^=0, то после сокращения на мно¬
житель (1 — Р0~2> уравнение (3. 6) дает
т
2«*
i=i
G,<
■±*'-
/=1
(3. 7)
где GK — конечный вес ракеты.
Подставив правую часть равенства (3.7) в уравнение (3.5),
легко убедиться, что величина нагрузки остается постоянной и
равной
лч=— Vo,.
/ = 1
(3. 8)
Полученное выражение показывает, что величина постоянной
нагрузки Nx равна весу всех постоянных грузов, лежащих выше
82
сечения а — а, умноженному на максимальную перегрузку
(в конце полета) nx(t) =/imax-
Очевидно, что при условии
2
; ^
/=1
(3.9)
нагрузка с течением времени увеличивается и принимает наи¬
большее значение в конце полета, когда t=% и nx(t)=nmах.
При выполнении условия
т
i=i
О К
<2*,
7 = 1
(3.10)
максимальное значение нагрузки соответствует начальному вре¬
мени полета, когда / = 0 и nx(t)=n0 (имеется в виду мгновен¬
ный выход тяги двигателя на
режим).
Левые части выражений (3.7),
(3.9) и (3.10) указывают на со¬
отношение постоянных масс до
рассматриваемого сечения а—а;
правые части — на соотношение
переменных масс до этого же се¬
чения. Таким образом, эти выра¬
жения являются условиями (кри¬
териями), указывающими на мак¬
симальные осевые нагрузки в ин¬
тересуемом поперечном сечении
по корпусу ракеты в зависимости
от соотношения постоянных и пе¬
ременных масс.
Максимальные значения нагру¬
зок определяются по уравнению
(3.5) путем подстановки в него
значений / = 0 или t — x в соответ¬
ствии с выполнением условий
(3.7), (3.9) и (3. 10).
Как показывает практика,
критерии (3.9) и (3.10) в боль¬
шинстве случаев остаются спра- Рис. 54> Изменение осевых сжима-
нсдливыми и для случая полета ющих сил Nx(t) в зависимости от
ракеты в сопротивляющейся времени полета
Среде ППОИГУОПИТ ПОТОМV Примечание. На графике вре-
t' ас. спи нрииелиди I llUiUAiy, мя отсчета ^=0 соответствует перегруз-
что в расчетных сечениях обычно ке пх=п0.
83
имеют место явно выраженные значения максимальных нагру¬
зок Nx(t) =Лгтах, при которых учет лобовых сил практически не
влияет на точность весовых расчетов. При выполнении условия
(3.7) к нагрузке Nx(t)=Nx,
определяемой по формуле
(3.8), необходимо добавить на¬
грузку от сил лобового сопро¬
тивления, действующую на
участке до рассматриваемого
сечения а—а. Характер кривых
Nx(t) для различных случаев
нагружения показан на рис. 54.
Кривые приведены для трех
сечений по корпусу ракеты,
обычно интересуемых при вы¬
полнении весовых расчетов
первого приближения. Пунк¬
тирные кривые, показанные на
графике, иллюстрируют харак¬
тер изменения Nx(t) с учетом
сил лобового сопротивления
X(t). Для баллистических ра¬
кет и тяжелых ракет-носителей
с оптимальными перегрузками
п0 (или близкими к ним), до¬
бавки сил X(t) невелики и
они, как видно из графика,
практически не влияют на изменение расчетных случаев.
Типовые кривые Nx = Nx(t), получаемые в результате числен¬
ного интегрирования уравнений движения одноступенчатых и
первых ступеней составных ракет, приведены на рис. 55.
3.4. РАСЧЕТНЫЕ СЛУЧАИ ДЛЯ НЕСУЩИХ БАКОВ
Вес несущих топливных баков, как и подвесных, является
функцией суммарного внутреннего давления, состоящего, как
мы уже видели (разд. 3.2), из избыточного и гидростатического
давлений. В отличие от подвесных баков, давление ру у кото¬
рых определяется условиями работы насосов без кавитации,
в несущих баках это давление зависит также и от сжимающих
сил, действующих со стороны головной части ракеты на оболоч¬
ку баков (рис. 56).
Запишем выражение для текущего суммарного давления не¬
сущих баков в предположении, что экваториальные напряжения
в обечайке равны нулю. Имея в виду расчетное сечение в ниж¬
нем стыке обечайки и днища, запишем
п т
О 20 40 60 80 t,c
Рис. 55. Характер кривых Nx(t) для
корпуса средней части ракеты, полу¬
чаемых численным интегрированием
уравнений движения:
/—условие (3.7); 2—условие (3.9)
Величины k^ = D6jd, £ф;- = —Ф + 1, (для /-го эллиптического*
З&ф
\ 7" + 1 / • * \
бака) или Аф;. = — (для /-го конического бака) в вы-
з*ф
ражении (3. 11) учитывают увеличение суммарного давления за
счет конусности баков. Поступая как и ранее (разд. 3.3), по¬
лучим
т
2<г«
i=i—(3.12)
GK кф}
j-1
Рис. 56. Первая ступень ракеты «Сатурн-5» с несущими топ¬
ливными баками, воспринимающими сжимающие осевые на¬
грузки со стороны головной части и двигательного отсека
Выражение (3. 12) является условием (или критерием) для
определения весовых расчетных случаев несущих топливных ба¬
ков. Эти случаи в зависимости от соотношения постоянных и
переменных масс до рассматриваемого нижнего сечения бака
могут иметь место как в начале, так и в конце полета. _
Для нижних цилиндрических баков имеет место ^=1 и
1. При этом условие (3. 12) принимает вид
2<*<
^—< 1.
(3.13}
Это означает, что расчетным случаем для нижних баков всег¬
да является начальный момент времени полета, когда /==0 и
nx(t) =nQ.
85
Сравнение условий (критериев) для определения максималь¬
ных нагрузок Nx(t) —NmSiX (3.7), (3.9), (3. 10) и условий (3. 12),
{3. 13) показывает, что верхние баки испытывают максимальную
осевую нагрузку в конце полета при t = т, а весовые расчетные
случаи у них могут быть как в конце (/ = т), так и в начале поле¬
та (/ = 0).
Для нижних баков имеет место обратное явление. У них мак¬
симальные осевые нагрузки могут быть как в начале (/=0), так
и в конце полета (t=т), в то время как весовой расчетный слу¬
чай всегда относится только к начальному времени полета, ког¬
да t=0 и nx(t) =п0.
Таким образом, расчетные случаи для элементов конструк¬
ции, содержащих в себе переменную массу, могут не совпадать
с расчетными случаями для определения действующих на них
осевых сжимающих сил.
Величина суммарного давления в баках определяется по урав¬
нению (3. 11) путем подстановки в него значений ^ = 0 или t=x
в соответствии с выполнением условий (3. 12) и (3. 13).
3.5. ОТСЕКИ ВЕРХНЕЙ ЧАСТИ РАКЕТЫ
В верхней части ракеты расположен полезный груз. В каче¬
стве полезного груза могут быть: старшая ступень у составных
ракет, отсек оборудования, космиче¬
ский корабль, контейнер с научной
аппаратурой, боевой груз и т. д. Харак¬
терным для этих отсеков является от¬
сутствие у них переменных масс, рас¬
ходуемых на активном участке полета.
В силу этого осевая нагрузка опреде¬
ляется инерционными силами только
от постоянных масс, расположенных
выше сечения а—а (рис. 57).
Рис. 57. Схема приборного отсека, расположен¬
ного в верхней части ракеты:
/—головная часть; 2—приборный отсек
Если расходуемая масса отсутствует, то (см. разд. 3.3)
2*,=о.
j-1
При этом на основании условия (3. 9) имеет место
Условие (3. 14) показывает, что максимальное значение осе¬
вой сжимающей силы на корпус верхней части ракеты всегда
имеет место в конце полета, когда t=x и nx(t) =птах. При этом
по уравнению (3. 5) имеем
Как отмечалось ранее, учет сил лобового сопротивления при
выполнении условия (3. 14) необязателен. При этом погрешность
величины ./Vmax для ракет минимальной дальности полета
(~300 км) составит не более 6—7%. Этот процент заметно
уменьшается при увеличении дальности полета и уже при L>
>600 км становится близким к нулю.
В отсеке средней части ракеты, или межбаковом отсеке, мо¬
гут располагаться оборудование, приборы управления, научная
аппаратура и другие постоянные по весу грузы. Иногда межба-
ковый отсек служит просто соединительным звеном между верх¬
ним и нижним баками и не содержит в себе каких-либо постоян¬
ных или переменных масс. Для межбакового отсека могут иметь
место все три условия (3.7), (3.9), (3.10).
В соответствии с ними осевая нагрузка на
корпус будет равна (рис. 58)
т
3.6. ОТСЕК СРЕДНЕЙ ЧАСТИ РАК1ЕТЫ
Рис. 58. Схема расположения межбакового отсека на
ракете с несущими топливными баками:
^—головная часть; 2—верхний несущий бак; 3—межбаковый
отсек
ИЛИ
при выполнении условия
т
т
(3. 15)
87
ори выполнении условия
2°*
/-1
>#,
Ок-
где G" — вес компонента топлива в верхнем баке;
^ 7 0Т
7 = 1
В первом случае максимальное значение осевой сжимающей
силы имеет место в начале полета, когда / = 0 и nx(t) =п0; во вто¬
ром случае — в конце полета, когда t=т и nx(t) =птах. Если по¬
лет ракеты происходит в пустоте (вторая ступень составной ра¬
кеты) и выполняется условие
SO*
/ =1
-kв
- гСу ,
то нагрузка на корпус может быть определена по любой из при¬
веденных формул. Для случая полета в сопротивляющейся среде,
т. е. для всех одноступенчатых и первых ступеней составных ра¬
кет, осевая нагрузка на корпус межбакового отсека определяет¬
ся с учетом сил лобового сопротивления.
3.7. ОТСЕКИ НИЖНЕЙ ЧАСТИ РАКЕТЫ
Отсеками нижней части ракеты могут быть двигательный от¬
сек или отсек оборудования и приборов управления как у ста¬
рых ракет (рис. 59). Характерным для этих отсеков является то,
что они расположены под главными расходуемыми массами
п
(горючим и окислителем). При этом всегда 2 1 и, следова-
7 = 1
тельно, имеет место условие (3.13). Это означает, что .осевая
нагрузка на корпус отсека от массовых сил всегда имеет место
в начале полета, когда /=0 и nx(t)=n0. Эта нагрузка уменьша¬
ется с течением времени и достигает минимального значения в
конце полета. Типовой характер зависимости Nx(t) для отсека,
расположенного в нижней части одноступенчатой ракеты, пред¬
ставлен на рис. 60. График показывает, что условие (3. 13) не
требует учета аэродинамических сил лобового сопротивления.
Выражение для осевой силы Nmax удобно записать, рассмат¬
ривая силы, приходящие к сечению а — а со стороны нижней
части ракеты. При этом получим
88
т
Nmax = P'i-n'^G^
/ = 1
(3. 16)
где сумма весов элементов от £=1 до т берется ниже сече*
ния а — а.
Формула (3. 16) записана для пустотных условий. Ее погреш¬
ность для первых ступеней ракет (без учета сил аэроди¬
намического сопротивления) составляет не более 2—3%.
\т
Рис. 59. Схема приборно¬
го отсека, расположен
ного в нижней части ра¬
кеты:
/—приборный отсек
О 20 40 60 80 t; с
Рис. 60. Изменение нагрузки на кор¬
пус приборного отсека, расположен¬
ного в нижней части ракеты
Формула (3. 16) справедлива также и для определения на¬
грузки на раму (или узлы) крепления ракетного двигателя.
В этом случае в сумму разгрузочных весов следует включать те
веса, которые крепятся непосредственно к раме, включая и вес
самого двигателя.
3.8. ТОПЛИВНЫЙ ОТСЕК С ПОДВЕСНЫМИ БАКАМИ
Конструкции ракет с подвесными топливными баками в на¬
стоящее время считаются устаревшими. Типичным представи¬
телем такой конструкции является немецкая ракета А-4. Од¬
нако, весовой анализ показывает, что в некоторых случаях, при
больших запасах топлива и стремлении уменьшить высоту тяже¬
лых ракет-носителей, может оказаться целесообразным примене¬
ние несущих корпусов с подвесными баками (см. например, аме¬
риканский проект ракеты «Космос» фирмы Дуглас).
89
примера, топливный отсек, приве-
Рассмотрим, в качестве
.денный на рис. 61.
В этом отсеке верхний бак подвешен тягами к верхней части
несущего корпуса, а нижний — опирается на стыковочное коль¬
цо отсека, которое является переходным
звеном к нижней части ракеты. Таким обра¬
зом, несущий корпус топливного отсека вос¬
принимает нагрузки только со стороны го¬
ловной части и верхнего бака. Головная
Рис. 61. Конструктивно¬
силовая схема топлив¬
ного отсека с подвесны¬
ми баками:
/—опорный узел; 2—фикса¬
тор; 3—подвеска; 4—бак го¬
рючего; 5—корпус топливно¬
го отсека; 6—бак окисли¬
теля; 7—изоляция
Рис. 62. Схема топливно¬
го отсека смешанной кон¬
струкции:
/—несущий бак; 2—изоля¬
ция; 3—подвесной бак; 4—
несущий корпус; 5—опорный
узел
часть и сам корпус представляют собой постоянные массы; топ¬
ливо верхнего бака — переменную массу. Легко видеть, что по¬
скольку в создании нагрузки на корпус Nx(t) принимает участие
не вся переменная масса, а только часть ее (£тв), то возможно
выполнение всех трех условий (3.7), (3.9) и (3.10)
т
/ = 1
kl
Следовательно, определение нагрузок необходимо вести, как
и для межбакового отсека, по формулам (3. 15) и (3.8).
90
График (см. рис. 55) показывает, что в случае выполнения
условия (3. 7) лобовые силы аэродинамического сопротивления
заметно влияют на величину нагрузки Nmax.
Необходимо заметить, что условия (3.7), (3.9) и (3.10) име¬
ют место и для топливных отсеков смешанной конструкции*
у которых верхний бак несущий, а нижний — подвесной (рис. 62).
Что касается нижних сечений топливных отсеков, то, как бы¬
ло показано ранее (3.4), независимо от их конструктивных осо¬
бенностей расчетный случай для определения нагрузки Nm
всегда имеет место в начале полета при / = 0 и nx(t)=nQ.
3. 9. УСЛОВИЕ ПОСТОЯНСТВА
ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
У ВХОДА В ТОПЛИВНЫЕ НАСОСЫ
Полагаем, что трубопроводы, соединяющие нижние днища
топливных баков с фланцами турбонасосов, всегда остаются за¬
полненными топливом. Удобно положить так¬
же, что моменту выключения двигателя соот¬
ветствует полное опорожнение топливных ба¬
ков. При этом переменное по времени t гидро¬
статическое давление компонента топлива
у входа в насос рГи.др(0 будет равно (рис. 63)
/7гилр(0 = ‘Ук.т/г(^) Р\<.т(0^б“Ь^грЬ (3* 17)
где ук.т — удельный вес компонента топлива;
^к.т(0 —«текущее удлинение» столба жидко¬
сти (компонента топлива) в баке; /тр — длина
трубопровода.
Рис. 63. Схема для определения условия постоянства
гидростатического давления у входа в топливные насосы
Off
<
Найдем выражение для параметра Як>т(/) как функцию вре¬
мени полета. Тогда запишем
Хк.т(0£>бУк.т =
GT — Gct
4 G0(Gr-?t)
nDl
откуда
ак.т(О=-|Ц0т-
гДе Аб — удлинение бака.
(3. 18)
91
Подставив найденное выражение (3. 18) в равенство (3. 17),
получим
Функция /7гидр = Ргидр(0 не содержит экстремальных решений.
Однако, дифференцируя равенство (3. 19) по t и приравнивая
нулю производную, можно получить
откуда условие постоянства гидростатического давления у входа
в насосы выразится так
где 1б — длина бака.
Очевидно, что при
(3.21)
L6 1 — fiK
давление у входа в насос по мере выгорания топлива будет уве¬
личиваться, а при
давление у входа в насос будет уменьшаться.
Для нижних баков обычно имеет место условие (3. 22). В этом
случае избыточное давление газа должно быть переменным с
компенсацией убывающего давления гидростатического столба
жидкости. Практически это осуществляется применением дрос¬
селей.
(3. 20)
(3. 22)
Пример 3. 1. Определить весовые
расчетные случаи по корпусу кры¬
латой ракеты-носителя (рис. 64). На
схеме цифры обозначают безразмер¬
ные веса и расстояния. Расчет про¬
извести для сечений а—a, b—b и с—с.
Распределение весов корпуса и топ¬
лива принять равномерным на еди¬
ницу длины Носителя.
Решение. Пользуясь схемой, под¬
считаем конечный вес ступени, опу¬
ская размерность. Тогда получим
GK = 13,6+1,6+15,6 + 0,9 + 3,4 + 3,3 =
Рис. 64. Схема расположения элемен¬
тов конструкции (весов) крылатой
ракеты (цифры означают безразмер-
ные веса и расстояния)
92
= 38.4. Принимая во внимание зависимости (3.9) и (3. 10), находим для каж¬
дого сечения (см. табл. 3. 1).
Таблица 3.1
Сечение
Численные значения критерия
Расчетные случаи
а—а
13,6+1,6+15,6 | о
38,4 ^ 32
Конец активного уча¬
стка t=x
b—b
62
13,6+1,6 + 15,6 —
90 16
38,4 > 32
(или 0,676 >0,5)
. Конец активного уча¬
стка t= X
с—с
13,6 + 1,6-
74
-15>б ™
90
29
<
38,4 32
(или 0,73 <0,907)
Начальный момент вре¬
мен^ полета ^=0
Пример 3.2. Пользуясь схемой (см. рис. 64) определить положение се¬
чения х от носка крылатой ракеты-носителя, где осевая сжимающая сила
Nx будет постоянной во время полета на активном участке траектории.
Решение. Имея в виду зависимость (3. 7)
т
21
/=1 .
; = i
запишем в соответствии с рис. 64
13,6+1,6 + 15,6
43
38,4
32
откуда
=65.
Пример 3.3. Доказать алгебраически условие (3.7), при котором на¬
грузка Nx(t) в сечении а—а (см. рис. 53) остается постоянной в течение
всего времени полета при работающем двигателе.
Решение. Выражение для текущей нагрузки Nx(t) в произвольном сече¬
нии а—а имеет вид
Nx (0 =
т
Я
jG, + G0 (GT-p
7=1 7=1
Р*
93
п
■s
Произведши замену
GT- = (1-30-tv
Тогда получим
т п
2 kj
Nx (t) = — J'=1 n0 + n0G0 ^ Ay. (3. 23)
; = i
Из этого выражения следует, что нагрузка Nx(t) будет постоянной, если
числитель первого члена правой части будет равен нулю, т. е.
т п
2 G/-Gft“K-2*y==0.
/=1 У=1
Отсюда следует, что
т
V Q. п
" V,
~sr-2ut'-
7 = 1
Величина нагрузки по критерию (3.7) в соответствии с выражением
(3.23) составит
ЛЪ = Л(А>2 (3-24)
7 = 1
СПИСОК ЛИТЕРАТУРЫ
1. Бессе р ер К. У. Инженерный справочник по управляемым снаря¬
дам. М., Воениздат, 1962, 624 с.
2. Г о ш е к И. Аэродинамика больших скоростей. М., ИЛ, 1954, 547 с.
3. Синярев Г. Б., Добровольский Д1. В. Жидкостные ракет¬
ные двигатели. М., Оборонгиз, 1955, 580 с.
4. Ф е о д о с ь е в В. И., Синярев Г. Б. Введение в ракетную тех¬
нику. М., Оборонгиз, 1960, 506 с.
5. Б е р е з и к о в В. В. и др. Конструкция управляемых баллистических
ракет. Под ред. проф. А. Д1. Сшшкова и доц. Н. И. Морозова. М., Воениздат,
1969, 444 с.
Глава IV
ФУНКЦИОНАЛЬНЫЙ ХАРАКТЕР
ВЕСОВЫХ ЗАВИСИМОСТЕЙ
Весовые расчеты в проектировании ракет и их систем зани¬
мают такое же положение, как и расчеты в области баллистики,
аэродинамики, прочности и других ведущих дисциплин.
Практика показывает, что успех проектирования в значитель¬
ной мере зависит от достоверности данных, получаемых в резуль¬
тате весовых расчетов. Более того, многочисленные примеры сви¬
детельствуют о доминирующем влиянии весовых расчетов и ис¬
следований в тех случаях, когда необходимо.выполнение боль
того и трудоемкого цикла работ по перспективным изысканиям
новых ракетных систем.
Важность весовых расчетов вытекает из их органической свя¬
зи с теми этапами работ, в результате которых рождается лета¬
тельный аппарат.
В силу этого разработка весовых формул представляет собой
весьма сложную и трудоемкую задачу. В окончательном виде
весовые формулы, как правило, содержат статистические коэф¬
фициенты. Эти коэффициенты приводят аналитические зависимо¬
сти в соответствии с данными статистики и эксперимента. Струк¬
турно статистические коэффициенты могут включать в себя такие
величины, как запас прочности, коэффициент безопасности и дру¬
гие величины, учитывающие расхождение между теоретическими
и действительными весами.
Пользованию весовыми формулами всегда должна предшест¬
вовать проверка их и уточнение статистическими данными. По
этой причине, а также учитывая текущую достоверность весовых
формул, значения статистических коэффициентов приведены в
главе не в полном объеме.
Главной целью приводимых ниже весовых формул является
вскрытие функциональной связи между основными весовыми и
проектными параметрами с тем, чтобы на базе этих формул мог¬
ли быть составлены упрощенные, но достаточно корректные за¬
висимости для включения их в обобщенные уравнения ракето¬
динамики по выбору оптимальных параметров ракет и их систем
с учетом весовых факторов.
Часть весовых зависимостей, представляющих определенный
интерес, приведены в сводной таблице в конце главы.
95
Обычно началу весовых расчетов предшествуют рекомендации
по делению ракеты на характерные весовые группы (ступени,
ускорители и т. д.), отсеки (топливный, дви¬
гательный и т. д.) и элементы конструкции
(баки, органы управления, оборудование
и т. д.), в соответствии с которыми и выпол¬
няются весовые расчеты.
Один из примеров весового состава совре¬
менной трехступенчатой ракеты может быть
представлен орбитальными носителями «Са¬
турн-1» и «Сатурн-5», как показано на
рис. 65 и 66.
4. 1. ТОПЛИВНЫЕ БАКИ
Вследствие большого запаса топлива на
ракете топливные баки составляют одну из
главных частей ее конструкции. Топливные
баки имеют разнообразную форму и конструк¬
цию. Чаще всего встречаются цилиндрические,
конические, сферические и торовые баки. Как
уже отмечалось ранее, существуют несущие и
подвесные баки. Топливные баки образуют
Рид. 65. Компоновочная схема и весовой состав по глав¬
ным элементам конструкции ракеты «Сатурн-1»:
/—баллоны с перскмсыо водорода системы управления; 2—при¬
боры ннерциальной системы управления; 3— бак горючего (во¬
дород); 4—бак окислителя (кислород); 5—два двигателя «Пратт-
Уитни^ Pv=13,6 тс; 6—тормозные двигатели для отделения от
S-V; 7—бак горючего (водород); 8— бак окислителя (кислород);
9— баллоны с гелием для наддува баков; 10—четыре двигателя
«Пратт-Уитни» /\=31.6 тс; //—двигатели для отделения от S-1;
12— контейнер с парашютом системы спасения S-1; 13—баллоны
из стекловолокна со сжатым азотом для наддува баков горю¬
чего; Ы— верхняя силовая рама; 15—центральный бак окисли¬
теля (кислород); /6'—нижняя силовая рама; /7—тормозные- дви¬
гатели системы спасения S-1; /#—восемь двигателей «Рокет-
дайн» Р =680 тс. Полный вес—375 (500) тс
ъ
Вес ускорителя II ступени—22,6 тс
Ьес III ступени—14,5 тс
Вес полезного груза—9 тс
топливные отсеки. Различают топливные баки высокого и низ¬
кого давлений. Во всех случаях, конструктивно, баки представ¬
ляют собой тонкостенные оболочки, гладкие или подкрепленные
продольно-поперечным набором для восприятия больших сжи¬
мающих сил. Большая несущая способность баков достигается
созданием внутреннего избыточного давления, при котором про¬
дольное сжатие заменяется полностью или частично эквато¬
риальными и меридиональными напряжениями растяжения. При
96
этом расчетным параметром для определения веса баков яв¬
ляется суммарное внутреннее давление. Оно остается расчетным
и в том случае, когда давление наддува выбирается из условий
работы обечайки на критическую силу.
Подвесные баки не воспринимают внешних нагрузок, однако
вес их также является функцией суммарного внутреннего дав¬
ления.
Для определения веса топливных баков и элементов их конст¬
рукции существуют разнообразные параметрические зависимо¬
сти, получаемые аналитическим путем. Ниже приведены некото¬
рые из них, наиболее часто употребляемые при выполнении весо¬
вых расчетов.
Вес бака в общем случае, состоящего из конической обечай¬
ки и т днищ, определяется выражением (рис. 67)
где i — индекс, означающий параметры данного (/-го) днища;
/7S —суммарное давление в баке (давление наддува плюс гид¬
ростатическое); рдц — давление (внутреннее) на днище.
В формуле (4. 1) величины k0б, £дн и /еб являются объединен¬
ными коэффициентами запасов прочности г], коэффициентов бе¬
зопасности /, статистических коэффициентов (учитывающих рас¬
хождение между теоретическими и действительными весами),
а также конструктивных факторов, связанных с наличием эле¬
ментов жесткости (продольно-поперечного набора), переменно¬
сти толщины или вафельной конструкции обечайки, деталей сбор¬
ки (анкерных труб, диафрагм, воронкогасителей) и т. д. Значе¬
ния этих коэффициентов берутся на основании обработки
статистических данных.
Остальными параметрами, входящими в формулу (4. 1), яв¬
ляются безразмерные множители, характеризующие поверхности
обечайки и днищ различных геометрических форм. Они равны
т
(4.1)
(4.2)
Для усеченных конусов и эллипсоидов вращения;
(4. 3)
4 3479
97
98862698 68
98
4*
для шарового сегмента и
П"(Я)=ЙГ1 + (4-4)
\ ч I
для эллипсоида вращения, рассеченного пополам плоскостью,
перпендикулярной малой полуоси.
Удлинение изолированной обечайки л0б = //^б, выраженное
через удлинение бака Kq = L/Dq равно
k(h “Г 1
55Г' (4'5)
Выпуклость верхнего и нижнего днищ характеризуется еди¬
ным параметром (см. рис. 67)
п=^- = —=-^—. (4.6)
2 А„ 2 Лв 2Лв*ф v ’
Рис. 66. Конструкция ракеты-носителя «Сатурн-5»:
/—двухкомпонентный ЖРД F-1; 2—карданов подвес; 3—привод кардаиова подвеса;
4—клапан окислителя; 5—клапан горючего; 6—насос окислителя; 7—насос горючего;
8—турбина (эффективная мощность 55 тыс. л. с.); теплообменник; 10—выхлопной па¬
трубок турбины; //—подмоторная рама; 12—теплозащита; /3—трубопровод подачи окис¬
лителя; 14—трубопровод подачи горючего; 15—предварительный клапан окислителя;
16—предварительный клапан горючего; /7—экран, предотвращающий вихреобразованне;
18—бак горючего (керосин); 19—бак окислителя; 20—гаситель колебаний; 21—датчик
отсечки топлива; 22— магистраль газообразного окислителя для наддува бака; 23—маги¬
страль наддува гелием; 24—баллоны с гелием; 25—тормозные РДТТ (8 шт.) тягой по
~39 тс каждый, время работы 0,66 с; 26— шпангоут разделения ступеней S-IC и S-II;
27—ЖРД J-2 Iягой пс ~ 102 тс каждый; 2#—трубопровод горючего (жидкий водород);
29—трубопровод окислителя (жидкий кислород); 30—ТНА горючего; 31—ТНА окислителя;
32—выхлопной трубопровод турбины; 33—теплообменник; 34—выхлопной патрубок тур¬
бины; 35—карданов подвес; 36—двигатели малой тяги; 37—бак горючего (жидкий водо¬
род), сотовое теплоизолирующее покрытие из фенольной пластмассы; 38—бак жидкого
окислителя; 30—предварительный клапан горючего; 40—предварительный клапан окис¬
лителя; 4/—дренажные клапаны; 42—трубопровод наддува; 43—заправочный штуцер;
44—дренажный трубопровод; 45—распределение газа (система наддува); 46—баллоны
с гелием системы наддува; 47—датчики уровня; 48—шпангоут разделения ступеней S-II
и S-IVB: 49—шпангоут отделения переходника; 50—тормозные РДТТ (4 шт.); 51—ЖРД
J-2 тягой ~ 102 тс; 52—бак жидкого водорода; 53—бак жидкого кислорода; 54— вспомога¬
тельная двигательная установка; 55—дренажная система; 55—дренаж с работающим
двигателем; 57—дренаж с выключенным двигателем; 58—отрывной разъем цепи назем¬
ного питания; 59—блоки электронного ообрудования и охлаждающие панели; 60—прибор¬
ный блок; 5/—крепление лунного корабля пироболтами; 62—основные амортизаторы
стоек шасси; 63—посадочная ступень; 64—возвращаемая на окололунную орбиту сту¬
пень с кабиной экипажа; 55—стыковочный лаз; 55—иллюминатор стыковки; 57—передний
лаз; 68—двигатели системы управления; 69—приборный отсек; 70—бак горючего (возвра¬
щаемая ступень); 7/—служебный отсек; 72—двигатель служебного отсека с кардановым
подвесом, тяга 9,3 тс; 73— бак горючего (50%-ная смесь гидразина и НДМГ); 74— бак
окислителя (четырехокись азота); 75—баки криогенного топлива (водород и кислород);
75—бак гелия; 77—горючее двигателей системы управления; 78—окислитель системы
управления; 79—топливные батареи; 80—насосные сопла системы аварийного спасения
(САС); 81—двигатель управления по тангажу; 82—двигатель отстрела опорного пилона
РДТТ САС; S3—РДТТ САС; 84—сопла; 85—защитный обтекатель (пробковая основа,
отражающая поверхность); 86—двигатели управления тангажем: 87—двигатели управле¬
ния креном; 88—двигатели управления рысканием; 89—отсек оборудования для призем¬
ления; 90—стыковочный лаз; 91—боковой иллюминатор; 92— иллюминатор стыковки;
93—боковой лаз; 94—крепежная рама отсека экипажа; 95—холодильники-излучатели си¬
стемы терморегулирования; 96—РАС обеспечения встречи; 97—поворотная антенна S-диа¬
пазона; 98— антенна УКВ; 99—холодильники-излучатели электроснабжения; 100—средства
радиосопровождеиия; 101—телеметрическая антенна; 102— антенна радиокомандной си¬
стемы управления; 103—контейнеры с приборным оборудованием; 104—обтекатель-пере¬
ходник лунной кабины (сбрасываемый)
100
Для конических топливных баков с двумя днищами, при
Лободы, /гФ=1 (для нижних днищ) и р = ря, выражение (4.1)
дает _
G6=k* ^l^jpzDlGM, (4.7)
где кг — обобщенный статистический коэффициент,
Об(лб)=^А0б+^ ЯПдн(я). (4.8)
У цилиндрических баков k$= 1 и для них
Q6=k*f(w)PzDPe0M' (4'9)
где
Об(Хб) = Х6-А+^_пдн(/г), (4.10)
если днища — усеченные эллипсоиды вращения, и
Об(Х6) = Хб-^+^Пди(д), (4.11)
если днища — шаровые сегменты.
Давление наддува баков или суммарное давление на обечай-
КУ и днища в формуле (4. 1) определяется в соответствии с рас¬
четными случаями (см. разд. 3.4). Значения коэффициентов кг
в формулах (4.7), (4.9) могут быть определены статистически
либо поверочным расчетом существующих аналогичных конст¬
рукций.
101
Вес обечайки G0e и днищ Одн определяется по формулам
Ооб=Ьоб f (^-) ^^бП,)6(л6); (4. 12}
Олн = Ки JL (g) P:iHDl Пдн (п), (4.13)
где для нижнего днища &ф= 1.
Другие параметрические зависимости веса баков и их эле¬
ментов конструкции приведены в сводной таблице (приложе¬
ние 2).
4.2. ШПАНГОУТЫ БАКОВ
Вес силовых шпангоутов, находящихся в стыке обечайки к
днищ, определяется по формуле
0= 0,ЗШи
(4.14)
а)
где kmTl — объединенный ста¬
тистический коэффициент
(обычно kum^ 1,5); ат — напря¬
жение предела текучести;,
ръ —суммарное избыточное
давление в баке.
Рис. 68. Схемы днищ:
а—сферическое днище; б—коническое
Множитель Gmil учитывает влияние формы днищ (рис. 68) на
вес шпангоута. Его величина равняется
для сферических днищ, и
Gmn = ctg а — 0,2
для конических днищ.
4.3. ИЗБЫТОЧНОЕ ДАВЛЕНИЕ НЕСУЩИХ БАКОВ
С УЧЕТОМ ЭКВАТОРИАЛЬНЫХ НАПРЯЖЕНИЙ
НА КРИТИЧЕСКУЮ СИЛУ
Как мы уже знаем, главной проблемой конструкции топлив¬
ных баков и их отсеков является сохранение формы (устойчиво¬
сти обечайки) при действии сил со стороны двигателя, инерцион-
102
яых сил, сил лобового сопротивления, перерезывающих сил и из¬
гибающих моментов, а также воздействие сил внутреннего избы¬
точного и гидростатического давлений.
Методы расчетов по определению необходимого давления га¬
за в несущих баках достаточно сложны и непригодны для весо¬
вых исследований.
Ниже приводится вывод упрощенной, но достаточно надеж¬
ной для весовых расчетов зависимости по определению избыточ¬
ного давления несущих баков с учетом
экваториальных напряжений со стороны
осевых сжимающих сил. Последние, как мы
видели (см. гл. III), являются наиболее
определяющими из общего комплекса дей¬
ствующих на ракету сил.
Несущую способность топливных баков
будем характеризовать максимальной осе¬
вой нагрузкой, которую может выдержать
обечайка бака, не теряя устойчивости при
определенном избыточном давлении. Избы¬
точное давление выберем такой величины,
при котором экваториальные напряжения ‘
в обечайке бака будут равны напряжениям
местной потери устойчивости.
Рис. 69. Схема для вывода формулы избыточного дав- ^
ления:
/—головной отсек; 2—несущий бак X1
Очевидно, что выбранное таким образом избыточное давле¬
ние будет соответствовать весу, близкому к минимальному весу
баков.
Для общности получаемых результатов будем рассматривать
изменение нагрузок, а следовательно, и изменение избыточного
или суммарного давлений в функции времени полета ракеты на
активном участке траектории от t=0 до t—%.
Рассмотрим схему нагружения баков, представленную на
рис. 69. В соответствии с этой схемой расчетным сечением яв¬
ляется нижнее сечение а — а. Разгрузка обечайки происходит в
сечении b—Ь, являющемся опорной поверхностью для нагрузок,
приходящих со стороны головной части ракеты. Условимся (как
и ранее) индексом «/» обозначать параметры, величина которых
меняется по времени полета.
В сечении а — а действует нагрузка, равная As nx(t) (где
Ал — суммарный вес элементов конструкции, лежащих выше се¬
чения а — a; nx(t) — текущее значение осевой перегрузки).
Разгрузочная сила в опорном сечении b — Ь будет S0Ilplv.^(t)
(где Son — площадь опорного сечения; /?ИЗб(0 — избыточное дав¬
ление в функции времени полета).
103
о
мер
Экваториальные напряжения в расчетном сечении а — а за¬
пишутся
/,\ ^ЯПЛ- (О ^ОпАкЗО (О ,л 1 -V
Зэкв(0 = ТгГТТл ’ (4-15)
л£>м0 (О
где б(/) —толщина обечайки, соответствующая нагрузкам в рас¬
сматриваемый момент времени полета.
Для меридиональных напряжений легко получить
(О = Ьги-Ф {t) Т Ршб (0] "7Т77Г > (4- 16)
2Ь (t)
где /7гидр(0 —гидростатическое давление компонента топлива в
баке.
Критическое напряжение местной потери устойчивости тон¬
костенных оболочек, не находящихся под внутренним давлением,
как известно, можно определить по формуле
А/7 25
aK?=kt — •
Согласно экспериментальным исследованиям эта формула в
известной мере может быть использована также и в тех случаях,
когда обечайки баков подвержены небольшому внутреннему дав:
лению, близкому к давлению у современных баллистических ра¬
кет на жидком топливе. При этом только коэффициент k прини¬
мает другое значение.
Выполняя условие сгЭкв(0 = сгкр (^), получим
Г(0]2-=^[<М0-л, з6(/)], (4.17)
где
0S (*) = /*, (0-^-. (4.18)
^оп
Для реальной конструкции бака всегда имеет место сгмер=1[сг]
(где [а] — допускаемое напряжение материала с учетом коэффи¬
циента безопасности).
Таким образом, из выражения (4. 16) можно получить также
+ (4.19)
Приравнивая правые части выражений (4. 17) и (4. 19) и раз¬
решая относительно /7Изб(0> получим
Ркзо (0"
104
/w
+
Га]2
где кф — коэффициент конусности бака; х = — характери-
kE
стический параметр нагружения.
Определение избыточного давления по формуле (4. 20) сле¬
дует вести в соответствии с расчетными случаями (см. разд.
3.4). Так, например, если бак цилиндрический £ф=1, а расчетный
случай при линейном законе изменений массы относится к ко¬
нечному времени полета, когда t=т, то
Для обеспечения устойчивости баков применяются следую¬
щие конструктивные решения:
а) гладкая оболочка с постоянным сечением, которая хотя
и проста по конструкции, рациональна только для небольших
ракет, где большая кривизна повышает напряжение устойчи¬
вости;
б) конструкция вафельного типа, имеющая преимущества по
сравнению с неподкрепленными оболочками с точки зрения кри¬
тического напряжения сжатия и не уступающая им по простоте
производства (для изготовления крупных панелей применяется
химическая или механическая обработка);
в) обычная самолетная конструкция — оболочка с продольно¬
поперечным набором стрингеров и шпангоутов;
г) слоистая конструкция.
Выбор той или иной конструкции определяется соображения¬
ми веса и сложностью производства.
Материалы, применяемые для изготовления топливных ба¬
ков, должны обладать большой удельной прочностью и жестко¬
стью, а также сохранять эти свойства в пределах широкого
Диапазона температур. Если, например, в качестве окислителя
используется жидкий кислород, то нижним пределом темпера-
тУрного диапазона будет —183° С, а верхний предел будет
/^гидР (0 Ргидр ( ^ ==т)
и формула (4. 20) принимает вид
•1/2
(4.21)
где
105
определяться аэродинамическим нагревом при прохождении ра¬
кеты через атмосферу. Кроме того, материалы должны противо¬
стоять химическому воздействию как горючего, так и окислителя
В каждом частном случае величина характеристического па¬
раметра нагружения % должна определяться на основании стати¬
стических и экспериментальных данных.
Заметим, что найденные ранее критерии для определения ве¬
совых расчетных случаев при экваториальных напряжениях, рав¬
ных нулю (аЭкв = 0), остаются справедливыми и в других слу¬
чаях, когда экваториальные напряжения не равны нулю
(ог)нв=7^0). Это легко показать, повторив выкладки разд. 3.4 на
базе полученного здесь выражения для избыточного давле¬
ния (4. 20).
Простой стержень представляет собой типовую круглую тру¬
бу, закрепленную шарнирно или с защемленными концами.
Для шарнирно закрепленного стержня допускаемое напря¬
жение общей потери устойчивости определяется по формуле Эн-
гессера [7]
где i — радиус инерции.
Эта формула может быть применена и к стержням с защем¬
ленными концами путем подстановки приведенной длины L0 вме¬
сто L.
Вес шарнирно закрепленного стержня с толщиной стенки 6
и средним диаметром cl определяется выражением
где &ст—статистический коэффициент; Е{ — тангенциальный мо¬
дуль (производная напряжения по деформации).
Отношение параметров d/б в формуле (4. 23) является зада¬
ваемой конструктивной величиной. Оптимальных значений эта
величина не имеет.
Уравнение для критического напряжения местной потери
устойчивости имеет вид
4.4. ПРОСТОЙ СТЕРЖЕНЬ
(4. 22}
(4. 23
(4. 24.
106
Величина коэффициента к в формуле (4. 24) определяется
экспериментальным путем. Обычно £ = 0,4. Эта величина счита¬
ется достаточно точной для выполнения весовых расчетов.
Совместное рассмотрение уравнений (4.22) и (4.24) для
стержня, допускаемое напряжение которого определяется удов¬
летворением условий общей и местной потери устойчивости, при¬
водит к следующей весовой формуле:
^ WVjvy- (4-25)
~Ъ Bt
где Et=— отношение модулей.
Е
Параметры Et и [а] в формуле (4. 25) определяются по эк¬
спериментальным кривым, построенным для различных материа¬
лов в виде функций Et = Et{[a\) и {a]==[a](Nx/L02). Величина
Nx/Lq2 является коэффициентом напряженности для случая раз¬
рушения стержня при сжатии от общей потери устойчивости.
Вместе со свойствами материала Е и параметром формы i2/F
(F — площадь поперечного сечения стержня) он определяет ве¬
личину допускаемого напряжения и, таким образом, позволяет
•оценить эффективность использования материала в данном эле¬
менте конструкции, т. е. конструктивную эффективность стержня.
Оптимальное отношение конструктивных параметров d/б, во¬
шедшее в неявном виде в формулу (4. 25), равно
--kE1/2 —
м
Формулы (4. 23) и (4. 25) применимы также для расчета ве¬
са многостержневых систем, таких как рама двигателя или фер¬
ма межбакового отсека.
4.5. ПАНЕЛИ
Панели являются составной частью таких элементов конст¬
рукции как гаргроты, обтекатели, люки отсеков и т. д.
Аналитические зависимости веса для панелей сложны. При¬
водимая ниже формула получена на основании приближенного
линейного закона изменения площади поперечного сечения, уста¬
новленного Ф. Р. Шэнли [7].
Формула имеет вид
Gl=klly,L^CM0 + ^), (4.26)
гДе £п — статистический коэффициент; ва — условное допускае¬
мое напряжение при сжатии (не для материала, а для
рассматриваемой панели в целом); b — ширина панели; Nx —
°севая сжимающая сила.
107
Величина ап рассматривается как постоянное допускаемое
напряжение при сжатии. Его величина оптимальна для данно¬
го материала (группы материалов) и типа конструкции, а не
произвольно определяется напряжением предела текучести при
сжатии.
Константа Са также зависит от материала и типа конструк¬
ции и имеет примерно одинаковое значение в довольно больших
интервалах значений коэффициента напряженности qlL0 (где q —
распределенная нагрузка на единицу ширины панели).
Для алюминиевых сплавов типа американских 24 S-Т и
75 S-Т, оптимальные значения константы С« и напряжения ва
равны соответственно С« =0,012, оа = 3430 кгс/см2 и Са =0,0015,
аа = 5180 кгс/см2.
Множитель в скобках формулы (4. 26) выражает площадь
работающего сечения панели. Часть этого выражения CabL0 мо¬
жет рассматриваться как площадь, необходимая для противодей¬
ствия потере устойчивости; вторая часть Nx/oa является обычным
выражением площади, необходимой для передачи нагрузки Л7*
при допускаемом напряжении а«.
Вес тонкостенной цилиндрической оболочки, находящейся
под действием осевой сжимающей силы Nx, равен
где &об 1 — статистический коэффициент; k — коэффициент
местной потери устойчивости.
Формула отражает функциональный характер изменения ве¬
са оболочки, критическое напряжение которой определяется ме¬
стной потерей устойчивости. Она применима для мало нагружен¬
ных корпусов, типа переходников для головных частей или не¬
больших межбаковых отсеков.
При действии на оболочку изгибающего момента Миз его
влияние на вес может быть учтено следующей зависимостью:
где /е0б 2 — статистический коэффициент.
Вес оболочки, выраженный через объем, записывается так:
где &обз — статистический коэффициент; v0c> — объем корпуса.
Формула (4. 29) наиболее удобна в применении ее к отсекам,
объем которых можно выразить в функции основных парамет-
108
4.6. ГЛАДКАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
(4. 27)
(4. 28)
(4. 29)
ров или задаваемых в расчете величин. Так, в применении к при¬
борному отсеку объем может быть найден по удельному измери¬
телю уПр, величина которого берется по статистическим данным
как отношение веса приборов к объему приборного отсека.
Обычно уПр~0>5 тс/м3.
Величина параметра D0б является либо задаваемой величи¬
ной, либо определяемой как оптимальный параметр на основании
весового анализа (см. разд. 5. 10, 5. 11, 10. 6).
Значение статистического коэффициента для дюралюминие¬
вых корпусов малого удлинения с учетом концевых шпангоутов
и небольших подкреплений колеблется в пределах &об з = 27ч-32.
Несущие корпусы-переходники служат обычно соединитель¬
ным звеном между грузом и верхним топливным баком. По¬
скольку объем таких корпусов не всегда удается выразить через
основные параметры ракеты, то для них определение веса мож¬
но вести по формуле
^ , As^ /8ЛМ1/2 (Л
G«6 — Kta '-осЛ’м (яА£) > (• )
о
где параметр удельной нагрузки на опорное сечение qs опреде¬
ляется по выражению (4. 18).
4.7. ТРЕХСЛОЙНЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
С РЕБРИСТЫМ ЗАПОЛНИТЕЛЕМ
Пользуясь приближенными зависимостями, выражающими
величины наибольших нормальных напряжений и минимальный
вес сжатых цилиндрических оболочек через действующие на¬
грузки, внешние размеры, характеристики материала конструк¬
ции и параметры, характеризующие форму поперечного сечения
подкрепляющих элементов, можно получить формулы для опре¬
деления веса трехслойных круговых цилиндрических оболочек с
тремя простейшими видами ребристого заполнителя:
— заполнитель в виде однослойного гофра (рис. 70);
■— заполнитель из швеллерных профилей (рис. 71);
— сотовый заполнитель (рис. 72).
В соответствии с рекомендациями А. А. Лебедева [5] запишем
весовые формулы для оболочек с одинаковой толщиной внеш¬
них слоев, изготовленных из одного материала.
Вес оболочки с заполнителем из швеллерных элементов
равен
/16,м3 у/5
О,)б=-0,935луАгАб (_у Ц)б) , (4.31)
где Миз — изгибающий момент; л0о — удлинение цилиндрической
оболочки.
109
В случае оболочки с гофровым заполнителем вес оболочки
выразится так:
'16 М„я \1/5
Go6 = k?nyJ.o6Dn6 (Шв D„f)j
где = 0,885 при
£■3 = 0,905 при
/гр = 0,910 при
= 52° 10';
= 45°;
= 60°;
$ — угол между гофром и внешним' слоем.
(4.32)
(4.33)
Рис. 70. Трехслойная оболочка с за- Рис. 71. Трехслойная оболочка с за¬
полнителем в виде гофра полнителем из швеллерных профилей
Рис. 72. Трехслойная обо¬
лочка с сотовым заполни¬
телем
Для оболочки с сотовым заполнителем весовая формула име¬
ет вид
п =1 1ях -V р3{-;(2Ум^из ^1/2
L/00 1 j 1 л/;00 Ум^об I ^
(4.34)
Числовые коэффициенты формул (4.31), (4.32) и (4.34)
найдены из условий обеспечения минимального веса конст¬
рукции.
4. 8. ПОДКРЕПЛЕННАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
Суммарный вес подкрепленной оболочки слагается из веса
шпангоутов, расположенных внутри оболочки по ее контуру, и
веса обшивки со стрингерами, составляющими конструкцию
панелей между шпангоутами.
110
Вес такой оболочки, находящейся под действием осевой сжи¬
мающей силы, определяется по формуле
0„б ^'o64Ym/4)6^(;6
яС'°б- Nxi2
шп
(4. 35)
где £0б4 — статистический коэффициент; 70г> — удлинение обо¬
лочки; Ащп — удлинение оболочки между шпангоутами; Nx —
осевая сжимающая сила.
Параметр А,Шп является устойчивой конструктивной величи¬
ной для подавляющего количества оболочек.
Выражение для G0e в формуле (4. 35) имеет вид
^=6глН,/2’ (4-36)
''Чии^шп /
где сши — безразмерный коэффициент, выбираемый из условий
сопротивления общей потере устойчивости; £Шп — модуль упру¬
гости материала шпангоута; ^u,n = JrL —безразмерный коэф-
F “
шп
фициент эффективности, характеризующий Жесткость попереч¬
ного сечения шпангоута на изгиб.
Параметр (4. 36) представляет собой критерий, подбором ко¬
торого можно предопределить тот или иной вид разрушения,
либо добиться оптимальных условий, когда разрушения от ме¬
стной и общей потери устойчивости наступают одновременно.
Величина допускаемого напряжения в формуле (4. 35) выби¬
рается по экспериментальным графикам вида [o] = [c](q/L0), по¬
строенных для различных материалов [7].
Формула (4. 35) применима для расчета веса нагруженных
корпусов и межбаковых отсеков ракет.
4.9. ЭЛЕМЕНТЫ КОНСТРУКЦИИ,
ВОСПРИНИМАЮЩИЕ ПОПЕРЕЧНЫЕ НАГРУЗКИ
К элементам конструкции, воспринимающим поперечные на¬
грузки, могут быть отнесены всевозможные балки, соединитель¬
ные звенья, элементы рамного крепления двигателя и т. д.
При определении веса балки, воспринимающей поперечную
нагрузку, предполагается, что поперечное сечение на длине бал¬
ки остается постоянным. В таком случае
°ба., = /гб^м5Са, (4.. 37)
где &б ! — статистический коэффициент; Миз — изгибающий мо¬
мент; Lqал — длина балки между опорами.
Параметр Gбач является оптимальной величиной отношения
F/М*£ и определяется по экспериментальным графикам, по¬
строенным для различных материалов и форм сечений балок как
ill
функция коэффициента напряженности M\['l h (где h — высота
сечения балки).
В случае сосредоточенной нагрузки вес балки определится
Ооал^о^ДЧа^М,, (4.38)
где коэффициент заделки на опорах &бз=1/4 для центрально
нагруженной балки со свободно опертыми концами и &оз= 1/8
для центрально нагруженной балки с неподвижно защемленны¬
ми концами. Статистический коэффициент k^2 формулы (4.38)
не равен статистическому коэффициенту &б1 формулы (4.37).
Если балка воспринимает погонную нагрузку q, ее вес будет
равен
^бал = ^64Ym^6o q^ ^бал, (4.39)
где 5=1/8 для свободно опертых концов и 5= 1/12 для непо¬
движно защемленных концов.
4. 10. конструкция,
ВЫПОЛНЕННАЯ В ВИДЕ ДИСКОПЛАНА
Конструкция, выполненная в виде дископлана, может быть
использована как топливная емкость верхней ступени ракеты
или как аэродинамически несущий корпус воздушно-космическо¬
го корабля (дископлана). Ее обводы могут быть образованы
Рис. 73. Дископлан, выпол¬
ненный соединением двух
шаровых сегментов
Рис. 74. Дископлан, выпол¬
ненный в виде эллипсоида
вращения
двумя шаровыми сегментами или представляют собой эллипсоид
вращения (см. рис. 65). В случае топливной емкости суммарное
внутреннее давление является, как известно (см. разд. 4. 1),
следствием наддува и гидростатического давления компонента
топлива. В случае дископлана внутреннее давление может быть
обусловлено спецификой корабля, осуществляющего челночные
операции по трассе Земля — орбита — Земля.
Для дископлана, образованного двумя шаровыми сегмента¬
ми (рис. 73), весовые зависимости, выраженные в функции диа-
112
метра D и объема пд, имеют (соответственно) вид
(4-40)
В формулах (4.40) и (4.41) n=D/'2h — параметр выпуклости
днищ.
Для дископлана, выполненного в виде эллипсоида вращения
(рис. 74), аналогичные весовые зависимости записываются так:
Q, = Пдн (п) ( npzD\ (4. 42)
01=АЛзпда(Л)(-^)№ (4.43)
Пдн(я) =
где
^ 1 | In (п -h jf 11* + 1)
п |/ п2 — 1
Вес эллипсоида вращения G3n_ может быть определен и по
формуле
°.<=^(т+ТМ-й-Н <4-44)
При этом толщина оболочки бэл будет равна
/2 D
0Э = /7а .
4 [а]
Формула (4.44) получена для наивыгодпейшего соотношения
параметров /i/D= ]/~2/4. Это соотношение обуславливает пред¬
отвращенные потери устойчивости оболочки от внутреннего дав¬
ления.
4. 11. ТОРОВЫЕ БАКИ
Схемы сечений торовых баков, выполненных с постоянной,
переменной и ступенчатой толщиной стенки, приведены на
рис. 75.
Существует следующая методика определения веса таких ба¬
ков. Определяется наименьшая толщина стенки в произвольном
Учении торового бака, находящегося под равномерным внутрен¬
ним давлением при Rjr^2-4-3. Эта толщина по безмоментной
теории оболочек равна (рис. 76)
8 = _^1/2/г±Г8Шу\+д8,
2 [а] \ R Г sin ср )
где Дб — допускаемое отклонение по толщине стенки
(4.45)
113
Поверхность кольцевого элемента бака равна
г-, я2г / z-ч , 180 sin т sin а \
П,= —а tf-j- — г ! ,
4о \ я а /
(4. 46)
где а подставляется в градусах.
Полная поверхность торового бака, равная сумме поверхно¬
стей отдельных элементов, выразится следующим образом:
т
П6 = 2П, = 4^,
/ = 1
где т — количество выделенных элементов бака.
Рис. 75. Схемы сечений торовых баков:
^—постоянная толщина стенки; б—переменная толщина стенки; в—-ступенча¬
тая толщина стенки
Вес произвольного элемента оболочки равен
0/=Ум»А,
(4. 47)
где параметры бг- и П; определяются выражением (4.45) и
(4.46).
Рис. 76. Схема для определе¬
ния поверхности и толщины
произвольного элемента торо-
вого бака
Полный (вес бака, равный сумме весов элементов, определится
следующим образом:
т.
®б = ^б.т2 Oi~\-^G6, (4.48)
/=1
где величина G2- определяется по формуле (4.47).
Параметр AGq учитывает вес оборудования, арматуры бака
и т. д. Для больших баков обычно AGg^50-M50 кгс.
114
Статистический коэффициент /гб.т формулы (4.48) учитывает
увеличение веса за счет сварки, местных утолщений под уста¬
новку арматуры и оборудования и т. д. Его величина может
быть принята равной /гб.т= 1,1 —1,3.
Для веса торового бака, имеющего одинаковую толщину обо¬
лочки, используем простую зависимость
Очевидно, что из возможных схем (см. рис. 75), торовые
баки с постоянной толщиной оболочки являются, наиболее тя¬
желыми.
Вес торового бака может быть определен также по фор¬
муле
Формула (4.50) получена с учетом наиболее встречающихся
соотношений большого и малого диаметров при постоянной
толщине оболочки.
4.12. ЭЛЕМЕНТЫ РАКЕТНО-АВИАЦИОННЫХ КОНСТРУКЦИЙ
Летательные аппараты типа «ракетоплан» состоят из эле¬
ментов конструкции, характерных как для самолетов (крыло,
фюзеляж и т. д.), так и для ракет (ракетный двигатель, топ¬
ливный отсек и т. д.).
Отличительной особенностью в работе ракетно-авиационных
конструкций по сравнению с чисто ракетными конструкциями
является действие на них больших изгибающих моментов, ха¬
рактерных для авиационных конструкций.
Приводимые ниже формулы составляют в целом метод весо-
вого расчета, разработанный И. С. Голубевым применительно к
Ракетно-авиационным конструкциям [3].
Цилиндрический корпус-монокок из однородного материала.
Такая схема предусматривает наличие двух элементов: обшив¬
ки и крайних шпангоутов. Все основные нагрузки (изгибающие
-h AS YMrA4-AGo- (4-49)
При этом толщина оболочки будет равна
(4. 50)
115
моменты, перерезывающие силы и крутящие моменты) воспри:
нимает обшивка. Шпангоуты выполняют роль соединительных
звеньев между отсеками. Вес единицы длины такой конструкции
определяется по формуле
^-=дУмШк, (4.51)
где
Выражение для 6 в формуле (4.51) справедливо при D/26^
Г.^70. При меньших значениях этого отношения толщину оболоч¬
ки следует подсчитывать по формуле
я £>к°т
(4. 52)
где ат — предел текучести материала корпуса.
Монококовые конструкции из однородного материала, вес ко¬
торых выражен формулой (4.51), применяются для корпусов
при Дк<400 мм.
Цилиндрический трехслойный монокок. Представляет собой
цилиндрическую конструкцию, у которой между внешней и внут¬
ренней оболочками находится заполнитель. Вес единицы длины
трехслойного монокока определяется по формуле
-^=5,98-Ю-6 ^+ 0,583-10-3Д;. (4.53)
7 к
Формула получена при допущении, что заполнитель и внут¬
ренняя обшивка не воспринимают сжимающих усилий. При этом
Узап = 0,1 гс/см3, 63ап~10 бцар, бВн = 0,6 мм (где индексы означа¬
ют: «зап» — заполнитель, «нар» — наружная, «вн» — внут¬
ренняя); допускаемое напряжение дюралюминиевых оболочек
принято [а] = 26 кгс/мм2.
Стрингерный корпус с неработающей обшивкой из дюраля.
Вес единицы длины стрингерного корпуса определяется по
формуле
— = 4,38-10"-6 -^- + 0,715- 10-3Ц.. (4.54)
L* £>к
Формула получена при допущении, что минимальная толщи¬
на обшивки составляет 6 = 0,8 мм, а допускаемое напряжение
[а] = 26 кгс/мм2.
116
Продольный набор. Вес продольного набора Gnp.н сильно на¬
груженного корпуса равен
Glip,=0,63^)iGX>^K, (4.55)
2а-'ет
где ов — временное сопротивление; <Ь=\ коэффици-
Go
енты уточнения начального веса G0; GneT — вес деталей, нахо¬
дящихся на внешней поверхности корпуса; /?р —: расчетное зна¬
чение поперечной перегрузки.
Вес продольного набора, выраженный через объем корпуса
будет равен
0„р.н = 0,63 (Щ Л- nlvf kT, (4. 56)
\ ав / 03ср
где г] — коэффициент использования объема корпуса (цилинд¬
рического по сравнению с действительной формой); соср — сред¬
ний удельный объем всех видов нагрузки.
Шпангоуты. Различают промежуточные, шпангоуты, распо¬
ложенные с определенным шагом по корпусу, и концевые шпан¬
гоуты, расположенные в стыках отсеков. Их веса определяются
по формулам
0Ш1[ = 0,06 (ТмТ _Л_ (4. 54)
V ав 1 03ср
для промежуточных шпангоутов и
0Ш|, = 0,22 ('^Д -Л- nvvf (4. 58)
\ J wcp
для концевых шпангоутов.
Обшивка. Вес части обшивки, не участвующей в работе вме¬
сте с продольно-поперечным набором, равен
^об.и = 3,64yм8П11пг'к/3>мУ3, (4. 59)
гДе 6min — минимальная, из технологических соображений, тол¬
щина обшивки.
Сумма весов продольного набора обшивки, промежуточных и
концевых шпангоутов составляет полный вес корпуса.
Несущий корпус. На этапе предварительных расчетов опре¬
деление веса несущего корпуса можно вести по формуле
Ок= 1,2(0,45- Ю-^Х + М^) . (4.60)
117
Топливные баки. Для баков высокого давления (рИзб>
>15 кгс/см2) весовая формула имеет вид
G6 = 90T 1 4~ °’Шб ■. (4.61)
, Yt ) ' И / 1 -г 3>-6
Вес баков низкого давления определяется зависимостью
К Y
и-бт6(у-
06 = 0,027 ( •—] : J - ■ (4.62)
б ' I I 1 р п'
Yt / I — 3/v6
Топливные отсеки. Вес нагруженных топливных отсеков оп¬
ределяется по формуле
От.о= 18?От » ^°’42Хт-0 . (4.63)
\[а] / Yt 1 | 3>.о
«если отсек высокого давления, и по формуле
К \1/2
, С + 3,2.104.Хт.оМ-1
От.0 = 0,054?GT (Щ , УЕ/ , (4.64)
V Yr / 1 -h Злт.о
если отсек малого давления.
В приведенных формулах коэффициенты р и q характеризу¬
ют особенности конструктивной схемы отсека. Обычно р = 1,04ч-
1,16 и д=1. Для отсеков с телескопическими баками
г
где do — диаметр внутреннего (телескопического) бака.
Крыло и оперение. Хорошее схождение с истинным весом
крыла дает формула Н. А. Фомина [6]
°кр=1QnVy ^Хкр5кр X
X
>(44,5 + 1^ -У) + —+14,6
+ 6,55кр, (4.65)
ЮОсо \ ч I лКр
где G — вес ракетоплана, соответствующий расчетному случаю
полета; ср — коэффициент разгрузки крыла; со — относительная
толщина корневого профиля; ц — сужение.
При определении веса стреловидных крыльев по этой форму-
1 I л ^кр /
ле следует иметь в виду, что /7 и ку = (где %—
cos у. ' COS2 X
угол стреловидности, измеренный по линии 1/4 хорд).
.118
Формула (4.65) применима для крыльев большого удлине¬
ния. Для крыльев малого удлинения можно рекомендовать ве¬
совую формулу В. П. Соколова [8]. Эта формула имеет вид
Окр=(^-)х/Ло„«№{х^ (0,1 + ^ + -^-)
\ ®В / / I . С \ Г\ COS 2 7,0.ж /
I
1+ °-3
C0S /.О.ж
-LU/2 (0,7 + Ы]\ + 2,8ум8т1п5К0Н, (4. 66)
где Out — временное сопротивление материала с учетом влияния
температуры; %t — коэффициент, учитывающий ' температурные
напряжения (х/=1,08—1,2); Хо.ж — угол стреловидности по оси
жесткости; ркон — нагрузка от веса на единицу площади консоли
крыла; Smin — минимальная (по технологическим соображениям)
толщина обшивки; = —коэффициент, учитывающий сниже-
ап
ние напряжений при малых с.
Все входящие в формулу (4.66) геометрические параметры
отнесены к площади консолей крыла. Формула дает удовлетво¬
рительную сходимость в следующем диапазоне геометрических
параметров: 2^r)Kori^oo; 0,5<^лКои <4; 0,02 <сКОн< 0,08 и 0<
^Хо.ж<60°.
Определение веса оперений производится по весовым форму¬
лам крыла. На начальном этапе прикидочных расчетов вес
крыла и оперения может быть определен по следующим эмпири¬
ческим формулам:
а) для крыльев больших удлинений
nvl V/2
пу1к р \
1000/?кр
где /кр — размах крыла, м; р1ф — нагрузка на крыло, кгс/м2;
б) для крыльев малых удлинений
GKP = G0^-l^- + 0,042), (4.68)
*^кр V Ркр /
где SKOn — площадь двух консолей;
в) для рулей (с учетом осей и рычажной системы)
GP = 0,2GKP; (4.69)
г) для стабилизаторов
GCT= 185ст, (4.70)
где SCT — суммарная площадь консолей стабилизаторов.
GKP = 4,5G0 , (4.67)
4. 13. ЗАПАС ТОПЛИВА
Полный запас топлива на ракете (бортовой запас) слагается
из веса расходуемого топлива и веса нерасходуемого топлива.
119
Расходуемое топливо идет на создание тяги двигателя и являет¬
ся активной массой ракеты. К нерасходуемой части топлива от¬
носится топливо, остающееся в баке (невырабатываемое топли¬
во) и в системе подачи (трубопроводах); топливо, идущее на
охлаждение различного вспомогательного оборудования; испа¬
ряющееся топливо в результате аэродинамического нагрева ба¬
ков; топливо, идущее на привод турбонасосов, а также топливо,
взятое на ракету как запас для компенсации возможных откло¬
нений параметров движения от расчетных (гарантийные запа¬
сы). Отклонения параметров движения могут быть вызваны та¬
кими факторами, как неточность расхода (соотношения) топ¬
ливных компонентов, связанная с изменением удельной тяги;
неточность изготовления конструкции ракеты и монтажа от¬
дельных ее агрегатов (например, двигателя), что вызывает до¬
полнительный расход энергии на компенсацию дестабилизирую¬
щих моментов; колебания состояния атмосферы, связанные с от¬
клонением параметров q(#), р{Н) и Р(Н) от расчетных; от¬
клонения действительных значений аэродинамических коэффици¬
ентов от принятых в расчете, а также другими факторами.
Нерасходуемое топливо является пассивной массой и относит¬
ся к составляющим конечного веса ракеты.
Вес расходуемого_топлива на ракете характеризуется весовой-
отдачей по топливу GT и определяется для одноступенчатой ра¬
кеты как Gt = GtGq.
Веса окислителя G0K и горючего Grop, отнесенные к общему
весу топлива, определяются по формулам
— G
оп. пк'
гор
От 1 + А?
гор
G
G
г°р п 1 I /Л
1 ! ^гор
(4.71)
г о Gnw
где krov= —— весовое соотношение компонентов топлива.
Gy op
Средний удельный вес топливной пары выражается через
удельный вес горючего уГор и удельный вес окислителя уок
1 4-
YT— (4.72)
1 гор
7 гор Уок
Зависимости для определения суммарного веса топлива и топ¬
лива по ступеням составных ракет приведены ниже (см. разд.
11.2).
120
4. 14. ПАССИВНЫЙ ГРУЗ
Пассивный груз состоит из полезного груза и оборудования
ракеты. Полезный груз является той частью ракеты, ради транс¬
портировки которого и создается сама ракета. В полезный груз
могут входить экипаж, кабина экипажа, научная аппаратура
и оборудование космического корабля, специальный груз, элемен¬
ты конструкции, обеспечивающие укрытие и крепление груза
и других предметов в корпусе ракеты. Оборудование ракеты со¬
ставляют бортовая система управления и наведения, средства
связи, источники электропитания и т. д.
Полезный груз, как правило, является задаваемой величиной
при проектировании. Оборудование определяется по составу и
весу и включается в пассивный груз уже в самом начале проек¬
тирования.
Как будет показано ниже (см. разд. 6.1; 11.2), величина полез¬
ного груза As (суммарный вес грузов) определяется по форму¬
ле As = G0e (где е — относительный вес груза или коэффициент
грузоподъемности).
4. 15. КОНЕЧНЫЙ ВЕС РАКЕТЫ
Конечный вес ракеты составляет та ее часть, которая остает¬
ся в конце активного участка полета после расхода топлива в мо¬
мент выключения двигателя. Сюда относятся: вся конструкция
ракеты, полезный груз, оборудование, нерасходуемое топливо (в
баках, топливных коммуникациях, рубашке двигателя, гарантий¬
ные запасы) и другие остающиеся на ракете массы (газ надду¬
ва, рабочее тело автоматики двигательной установки и т. д.).
В целом конечный вес является пассивной массой ракеты. Его
величина определяется через весовую отдачу как GK=G0pK.
Вес конструкции, т. е. конечный вес за вычетом полезного
груза (эффективный конечный вес G0(j)({}), для одноступенчатой
ракеты определяется выражением СЭфф = GK—As или
GocM) = G0 (Цк е)* (4.73)
Аналогичные зависимости для определения суммарного (с
грузом) и эффективного (без груза) конечного веса составной
ракеты приведены ниже (разд. 11.2).
4. 16. ПРОСТЕЙШИЕ ВЕСОВЫЕ ЗАВИСИМОСТИ
Приводимые ниже весовые зависимости построены на удель¬
ных измерителях и статистических коэффициентах. Пользование
такими упрощенными формулами возможно только на начальном
этапе прикидочных расчетов.
Топливные баки
О =(27-*-- 17) Ю“3— . (4.74)
Yt
121
Топливо наддува
GT.H = (9 --5-10) 10-3^ . (4.75)
Yt
Двигатель (сухой вес)
G.IiC = (20-:- 12,9) Ю_3Р0 (ЖРД Рг;д = 200-^300с); (4.76)
Ол.с = (25 -s- 14) Ю_3Р0 (фтор-(-водород РуД = 340-г-440 с); (4. 77)
О.(С = (Ю0 -т-20) 10—3 Р0 (аммиакЧ-водород Р"д=400-ь- 1000 с);
(4.78)
Ол с = (2^-20)Ро (цезий или рубидий P+=(5-*-20) 103 с). (4.79)
Рама двигателя (узлы подвески)
СРам=(0,8ж1,0)Ю-3Р0. (4.80)
Система двигательной установки
С0.дв=( 1.8Н-2,0)Ю-3Р0. (4.81)
Оборудование
Go6 = 120 + 0,9 • 10-3Go. (4.82)
Арматура топливных баков
Оарм = (0.4 н-0,6) ^ + 40. (4.83)
^уя
Гарантийные запасы
Огар = (1,1-^1,5)-^. (4.84)
иух
Кабельная сеть
Д<аб = (0.6 -ь 0,5) — . (4.85)
Yt
Крепежные узлы и детали
бдет= (0,754-1,0) Ю-3Я0. (4.86)
Неучтенные веса
GH= (1,64-0,2) 10_3G0. (4.87)
Капоты, обтекатели
Окап= (7—17) ПКап‘» (4.88)
Окап= 1,82-10"3(7ST, (4.89)
где Пкап — поверхность капота; GsT —суммарный вес топлива.
122
Элементы баллонной системы наддува:
а) рабочее тело (газ) наддува
= , (4.90)
RT '
где /?Газ — давление газа в топливном баке; v6 — объем топливно¬
го бака; R — газовая постоянная рабочего тела; Т — абсолютная
температура газа в топливном баке;
б) шаровой баллон
0ш = -^в/Ц^)Аш (4-91)
или
Ou-±RTQva3 (4-92)
где £ш = 4/3 — статистический коэффициент;
в) цилиндрический баллон со сферическими днищами
01(И1 = 30гаэ f liL >/^L±ixje (4.93)
,аз)м/ 2 +'3*хоб v
ИЛИ
(4-94!
где Я0б — удлинение обечайки баллона.
Вес арматуры баллонной системы подачи при малых запасах
рабочего тела составляет (20-У25) кгс.
Опоры
Gon = 0,l*10-3G0. (4.95)
Органы управления
Оо у = (180 230) + 0,75 • ю-3]/"р0. (4. 96)
Стабилизаторы
GCT = 0,7 • 10_3G0. (4.97)
Рабочее тело для клапанов ДУ (воздух)
0„.,з, = 0,036 (4.98)
PU
^ уд
Система наддува
ос.н=
Переходники (между баками)
Осн = (1,6 = 1,85) 10-3— + 20. (4.99)
Yt
^иер— 0,43 — Y 4s> (4.Ю0)
Яф
123
где
Чф s >
SM — опорный мидель груза.
Крепежные кольца на баках под фермы
GKp.K= (0,38-2,0) 10-зРо;
0^=1,13-10-3
<?ат
Корпус ДУ
Органы разделения
Ск.дв= 1,6 • Ю-3Р0.
Оразд = 2,5 • 10_3G0.
(4.101)
(4. 102)
(4.103)
(4.104)
Кабельная сеть
GKa6 = 0,6 • 10~3 —— . (4.105)
Yt
2,0
1,8
1,6
1,6-
1,2
1,0
0,8
0,5
0Л
0,5 0,6 0,7 0,8 5,850,0 0,95 W0Т
Рис. 77. График зависимости между Рис. 78. График зависимости между
Gq __ весовой отдачей по суммарному за-
параметрами ^ и ат при различ- пасу топлива трехступенчатой раке-
2 — ты Gj, и параметром Go/Дд
ных значениях VK „ллл
/—топливо и/ =3000 м/с; 2—ускоритель
с ДУ, использующий кислород атмосферы;
П ступень работает на химическом топ¬
ливе U711 = 4500 м/с; 3—ядериос «топливо»
W'11 -9100 м/с
Типовые зависимости, получаемые на базе весового анализа
по развернутым или упрощенным формулам, приведены на
рис. 77 и 78.
Пример 4. 1. Сравнить веса цилиндрической обечайки и сферического
бака при равных внутренних давлениях и объемах. Функциональную весо-
124
сую зависимость для обечайки вывести без учета влияния днищ, т. е. при
/г=°о.
Решение. Вес цилиндрической обечайки равен
G=Ga\)/Gоб, то на основании выражений (4. 106) и (4. 107) при v06=V6
получим С=3/4. Таким образом, вес сферического бака составляет 75% от
веса изолированной (без днищ) цилиндрической обечайки, если внутреннее
давление и объемы у них одинаковы.
Пример 4.2. Вывести зависимость для гидростатического давления
Ргидр в расчетном сечении обечайки с учетом осевой перегрузки nx(t) в функ¬
ции удлинения Хв и диаметра бака D5, выпуклости нижнего днища п и
удельного веса топлива у-г-
Решение. Для вывода этой зависимости воспользуемся формулой
Пример 4. 3. Исходя из условия постоянства объема на участке обечайки
Цилиндрического бака (u06=const), получить зависимость для суммарного
веса верхнего и нижнего днищ при постоянном избыточном давлении
(PH36=const). Полагать, что днища выполнены в виде эллипсоидов враще¬
ния и kv = \.
Решение. Суммарный вес эллипсоидных днищ цилиндрических баков при
Pn36=const и выполнении условия постоянства объема всего бака y6=const
определяется выражением
Выполняя условие постоянства объема только на участке обечайки, пе-
о
(4. 106)
то
где Voo — объем, заключенный обечайкой.
Вес сферического бака равен
(4. 107)
Если обозначить отношение веса сферического бака к весу обечайки как
Ргидр— {L—Ьц)утпх (t).
Поскольку L=XqD6 и hn=D/2ri, то
3/2
(4. 108)
°бходимо в формуле (4. 108) произвести замену ve=v06 и
Т°гда с учетом выражения (4.4) получим
125
^ 111 (n 4- Vn1 + 1) \ pn36V06
\ n I n- — 1 / '■'■' б
Пример 4. 4. Вывести зависимости для весов двух сферических днищ
конического и цилиндрического баков, внутреннее избыточное давление ко¬
торых выбирается из условий пулевых экваториальных напряжений. Ста¬
тистический коэффициент £дн принять равным единице.
Решение. Поверхность сферического днища (верхнего при k^\ и ниж¬
него при &ф = 1) равна
я о п2 -f 1
п'н“т°*^г
Аналогично толщина стенки определяется
nDo
Pv 130*
При нулевых экваториальных напряжениях в обечайке и при нагрузке
на бак, равной Аъпх (t)} избыточное давление выразится зависимостью
As/Ci- (О
Рпзб —
*р-6
«ф
С учетом полученных выражений суммарный вес двух днищ будет равен
2
a.vi = Т.м ®лн 2 Пд
-(Н
/=1
ИЛИ
для днищ конического бака и
Hw-)
для днищ цилиндрического бака.
Пример 4. 5. Показать во сколько раз вес бака, выполненного в виде
дископлана, больше веса цилиндрического бака со сферическими днищами
при п=5 и Я0б=6.
Решение. Возьмем для сравнения дископлан, образованный двумя шаро¬
выми сегментами. Тогда
г 3 / Тм \ ("2+1)2
°Д- 2_М[а]Гб 3«2 + Г*
Вес цилиндрического бака со сферическими днищами определяется пс
формуле
Разделив вес бака, выполненного в виде дископлана, па вес цилиндри¬
ческого бака, получим
Таким образом, сферический дископлан тяжелее цилиндрическою бака
со сферическими днищами в 6,85 раза. При этом имеется в виду, что для
обоих баков имеют место одинаковые значения параметров [о], ум» Рs и v6.
Пример 4. 6. Сравнить вес бака, выполненного в виде дископлана, и вес
R
торового бака при п=5, —=2,35. Для обеих емкостей принять одинаковы¬
ми [a], \\i, ps и Уб- Вес внутреннего набора (шпангоутов) не учитывать.
Решение. Напряжение в интересуемых точках торового бака опреде¬
ляется по формуле (см. рис. 76)
= (-
\ s
РъГ_
25
2R + г sin ср
(4. 109)
R -г г sin <р
Поскольку поверхность и объем тора равны соответственно П=4я2/?г и
2 R
v=2n2Rr2, то вес тора запишется так:
7 м
б
f- Г Sin ср
rsin ср
(4.110)
Разделив (4.41) на (4.110), найдем
3 (п2 + I)21— 4- sin cpj
\
2 (3/22 4- 1)1 4- sin ср J
G,,=
О д
Уменьшение веса торового бака по сравнению с баком, выполненным
в виде дископлана (при ф=270°), будет равно
_R_
3 (/22 4- 1)2 j г \ 3(52 + 1)2 j 2,35-1 \ _
1=4,9.
2-2,30—1 )
2(3/22+ 1)
2 R
г
— 1
2(3-52 + 1)
Таким образом, торовые баки меньше по весу баков, выполненных в ви¬
де дископланов.
На примерах 4. 5 и 4. 6 можно показать также, что торовые баки, в свою
очередь, тяжелее цилиндрических баков в 6,85/4,9=1,41 раза.
Пример 4. 7. Приняв за эталон вес шарового бака, получить зависимо¬
сти для относительных весов цилиндрического и торового баков, а также
Для бака, выполненного в виде дископлана. Найти экстремальные (не ана¬
литические) решения при Х0б^>1; (Rlr)^'l и /г^>'1. Сравнение весов произ-
127
вести при одинаковых значениях параметров ( /М~) > Рд, и kc, — \ (стати-
\ [°] /
стический коэффициент).
Имея весовые зависимости для шарового бака (4.107), ци¬
линдрического бака со сферическими днищами (4.94), торового
бака (4.110) и бака, образованного двумя шаровыми сегмента¬
ми (4.41), легко получить решения, представленные в табл. 4.1.
Таблица 4.1
Некоторые соотношения весов для баков различной геометрической формы
Отношение
пара метров
Уел о иные
рбозначенин
Аналитические
зависимости
Условия задачи
Предельные
отношения
весов
^б.ш
п
2А об + 1
4
3
и
©
3
2 05 + 1
^•об ©> 1
Сб.т
« <+)
2
/ R \ ,
4
О ш
©
3
V г /
W»1
~Г
б^д.Ш
02+ I)2
П > 1
/12
^б.Ш
©
\
3/2 2 + 1
3
СПИСОК ЛИТЕРАТУРЫ
Т. Астахов М. Ф. и др. Справочная книга по расчету самолета на
прочность. М., Оборонгиз, 1954, 702 с.
2. Б е р е з и к о в В. В. и др. Конструкция управляемых баллистических
ракет. М., Воениздат, 1969, 444 с.
3. Г о л у б е в И. С. Конструкция летательных аппаратов. [Труды МАИ]
М., 1964, 223 с.
4. К а н С. Н-, Свердлов И. А. Расчет самолета на прочность. М.,
Оборонгиз, 4958, 292 с.
5. J1 е б е д е в А. А., С т р а ж е в а И. В., Сахаров Г. И. Аэро¬
механика самолета. М., Оборонгиз, 1955, 472 с.
6. Фомин Ы. А. Проектирование самолетов. М., Оборонгиз, 1961, 362 с.
7. Шэнли Ф. Р. Анализ веса и прочности самолетных конструкции.
М., Оборонгиз, 1957, 408 с.
8. С о к о л о в Ф. А., Усов П. В. Техническая механика. М., «Выс¬
шая школа». 1965, 464 с.
Глава V
ВЛИЯНИЕ ДИАМЕТРА И УДЛИНЕНИЯ
НА ВЕСОВЫЕ ХАРАКТЕРИСТИКИ
ТОПЛИВНЫХ БАКОВ И ИХ ОТСЕКОВ
Ввиду большого запаса топлива, топливные баки и топлив¬
ные отсеки составляют наиболее важную конструктивную часть
ракеты. Несмотря на большие нагрузки, особенно у несущих
баков, их вес, отнесенный к внутреннему объему, невелик.
1
Рис. 79. Влияние диаметра кор¬
пуса ракеты па относительный
вес элементов топливного от¬
сека:
/—верхний
бак; 2—нижний бак;
3—отсек
Рис. 80. Влияние диаметра кор¬
пусу ракеты на весовую отда¬
чу Gг при двух значениях па¬
раметра Д2
На рис. 79 представлены кривые безразмерных (относитель¬
ных) весов баков и топливного отсека (составленного из этих
баков) в функции диаметра при постоянном внутреннем объ¬
еме. Кривые показывают, что, во-первых, существует экстремаль¬
ное решение, при котором вес топливных емкостей принимает
минимальное значение, и, во-вторых, отклонение от экстремума
функции (G6/G.r)= (^б) приводит к значительному увели¬
чению веса этих емкостей.
Весовой анализ показывает также, что изменение диаметра
заметно влияет на весовую_отдачу ракеты. Характер этого влия¬
ния представлен кривыми GT = GT(DM) на рис. 80 для двух зна¬
чений нагрузки Да. Из графика видно, что, несмотря на пологий
5 3479 129
вид максимума функции GT = GT(DMi) уменьшение весовой отда¬
чи (7Т на малых и больших диаметрах составляет большую ве¬
личину. Неправильный выбор диаметра (или удлинения) топлив¬
ного отсека пли корпуса ракеты приводит к существенному
уменьшению весовой отдачи Ст-
Таким образом, изучение весовых характеристик топливных
отсеков, топливных баков и их элементов конструкции (обечай¬
ка, днища, шпангоуты) является важной задачей при проектиро¬
вании ракет.
Оптимальные диаметры (удлинения) не всегда могут быть
выполнены практически. Помехой этому могут быть ряд причин
и, в частности, производственные ограничения, когда из условий
экономичности целесообразно сохранить имеющуюся оснастку
для производства баков уже освоенного диаметра. Весьма суще¬
ственными являются также ограничения, накладываемые усло¬
виями транспортировки по железной дороге, где габарит перево¬
зимого груза является строго обусловленным. Однако знание
оптимальных величин Лб, и в этих случаях необходимо, по¬
скольку такое знание является важным при выработке критери¬
ев оценки вынужденных отклонений параметров от оптимальных.
Изучение влияния геометрических параметров на весовые ха¬
рактеристики топливных отсеков, баков и их элементов конструк¬
ции представляет собой весьма трудоемкую задачу весового
анализа.
Приводимые ниже зависимости получены при определенных
допущениях и являются аналитическими. С их помощью в отчет¬
ливой форме вскрываются факторы, которые являются опреде¬
ляющими при выборе оптимального диаметра или удлинения
баков и их отсеков.
5.1. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ОБЕЧАЙКИ БАКА
ПРИ ПОСТОЯННОМ ВНУТРЕННЕМ ДАВЛЕНИИ
Оценку влияния геометрических параметров на вес элементов
конструкции бака удобно произвести при постоянном запасе
топлива (GT = const) или, что то же, при постоянном внутреннем
объеме бака
v6=— = const.
Yt
Для сохранения общности выводов и простоты получаемых
при этом результатов рассмотрим конический бак с днищами
(выпуклыми или вогнутыми), диаметр которого может быть вы¬
ражен
где /—индекс, обозначающий параметры г'-го днища; т — ко-
2к1 + 1
личестЕО днищ в баке; kf, = —^ параметр эллиптических днищ;
3*ф
параметр сферических днищ; vx
= 4fe2 ..upmup ^лн— я — з
6Нф опКф
4
v г,, 31
параметр эллиптических днищ; v —— = ——о— пара-
— D\ v2n%
метр сферических днищ.
Знаки в формуле (5.1) означают « + » — выпуклые и «—» —
вогнутые днища.
Под постоянным внутренним давлением будем понимать такое
давление, на выбор которого не влияют геометрические парамет¬
ры бака. Случай постоянного давления может иметь место для
подвесных баков, где это давление выбирается из условий работы
топливных насосов без кавитации или в системах без насосов
(например у зенитных ракет), где топливо в двигатель поступа¬
ет благодаря высокому давлению в баках (при этом величина
гидростатического давления сравнительно невелика).
При сделанных допущениях подстановка правой части равен¬
ства (5.1) в выражение (4.12) при k0^=\ дает
Ооб = (тт) ЧРп,б. (5. 2)
^•об^ф 4 ( i ^дн)/
/ = 1
где ризб = const — постоянное избыточное давление в баке.
Характер зависимости G0o = G06 (Лб) удобно проследить на
примере цилиндрического бака (йф=1) с двумя выпуклыми эл¬
липсоидными днищами, записав при этом в безразмерном виде
1
г Лб “ —
О. б ^ = . (5. 3)
2 рп - 1
1 м
ЩРизб f6 ' 0
3/1
Кривые безразмерного веса обечайки в функции удлинения
бака и выпуклости днищ £об = Соб(лс, п), построенные по фор¬
муле (5.3), приведены на рис. 81. Как видно из графика, влия¬
ние удлинения на вес обечайки при рИЗб = const сказывается при
малых его значениях, когда объемы днищ еще соизмеримы с объ¬
емом обечайки. По мере увеличения удлинения уменьшаются
объемы днищ, а следовательно, и их влияние на вес обечайки.
Положив в формуле (5.3) п= оо, уб = уоб и Аб = Х0б, получим
°""=const. (5.4)
5* 131
Это означает, что при постоянном внутреннем давлении вес
изолированной обечайки (без днищ) не зависит от ее удлинения
^об (^об) =COnst.
£0£ Граница предельного веса обечайки £
4
3
2
Рис. 81. График зависимости веса обе¬
чайки от удлинения бака, определяемый
множителем б0б(^б, я)
при постоянном избыточном давлении
О 2 4 6 8 А6
При п — оо выражение (5.3) дает G0б=1. Это означает также,
что вес обечайки при уменьшении объема днищ (п—*оо) и, сле¬
довательно, переливе топлива в ее объем, стремится к максималь¬
но предельной величине, определяемой выражением (5.4). Как
будет показано ниже (разд. 5.8), эта величина является одновре¬
менно характеристикой минимального веса баков при /?Изб = const
И /2=оо.
5.2. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ОБЕЧАЙКИ БАКА
ПРИ ПЕРЕМЕННОМ ГИДРОСТАТИЧЕСКОМ ДАВЛЕНИИ
Рассмотрим случай, когда с изменением удлинения меняется
высота гидростатического столба жидкости в баке и, следова¬
тельно, не остается постоянным его внутреннее давление, т. е.
Ргидр(Аоб) COnst.
Полагая сечение в стыке обечайки с нижним днищем расчет¬
ным, запишем выражение для гидростатического давления в этом
сечении с учетом выбранной перегрузки nx(t)
(5.5)
Имея зависимость для веса обечайки (5.2), после подстановки
в нее выражений (5.1) и (5.5) и преобразований при &об=1, по¬
лучим
-1/3
(t)
— — j Yt«v (0 поб (X)
_ т _ 14/3
^•об^ф "Ь ( i ^дн)/
/==1
(5.6)
Функциональный характер весовой зависимости по выраже¬
нию (5.6) для случая цилиндрической обечайки (&ф=1) пред-
132
ставлен на рис. 82 в виде безразмерной функции
G --
7об
и
(т
1/3
Yrпх (t) v£/3
(“-S-
4/3
(5.7)
Рис. 82. График зависимости веса обе¬
чайки от удлинения, определяемый мно¬
жителем Соб(Аг., п) при переменном гид¬
ростатическом давлении
,213
- ^об •
График показывает, что при переменном гидростатическом
давлении вес обечайки непрерывно увеличивается при увеличении
удлинения бака, стремясь к предельной величине при п = оо, оп¬
ределяемой выражением
б„в=
Это случай изолированной обечайки. Он означает, что при
переменном гидростатическом давлении изменение веса обечай¬
ки в функции; удлинения происходит по закону
5.3. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ДНИЩ БАКОВ
ПРИ ПОСТОЯННОМ ВНУТРЕННЕМ ДАВЛЕНИИ
Во избежание громоздких выкладок условимся, что избыточ¬
ное давление для верхнего, нижнего или совмещенного днищ, не¬
зависимо от их конструктивного выполнения (выпуклые или вог¬
нутые), определяется одним (общим для всех) расчетным
случаем. При этом допускаем также, что все сечения днищ ра¬
ботают на одно, одинаковое для всех постоянное избыточное
Давление /?Изб = const.
Имея выражения для веса днищ (4.13) и для диаметра бака
(5.1), легко записать в общем виде при кЩ1=1
G =
№
П
V
/=1
J з Вдн (и)
/гф
т
^об'^ф "Ь ( :Ь ^дн)/
/-1
ГДе как и ранее т — количество днищ в баке.
Ризб^б*
(5.8)
133
Характер изменения веса эллипсоидных днищ применительно
к цилиндрическим бакам (йф=1) в зависимости от удлинения Лб
и различных значений параметра выпуклости п представлен на
рис. 83 в виде безразмерной функции
G,
лПдн (п)
т(-
Риз-;.Щ
лб
1
(5.9;
3/2
Как видно из графика и выражения (5.8), при постоянном
давлении вес днища изменяется обратно пропорционально удли¬
нению бака.
Рис. 83. График зависимости веса днищ
от удлинения баков, определяемый мно¬
жителем б?лп(Лг,, п) при постоянном из¬
быточном давлении
5.4. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ДНИЩ БАКОВ
ПРИ ПЕРЕМЕННОМ ГИДРОСТАТИЧЕСКОМ ДАВЛЕНИИ
Весовую зависимость для днищ баков с учетом переменного
гидростатического давления получим подстановкой в формулу
(5.8) выражения для гидростатического давления (5.5) при за¬
мене в нем (Лб —) на Лб и выражения для диаметра (5.1), т. е.
2 п
G
--МтГ(м)х
т
Ч"х (о /Зп V
X
1 _
,3 Пл„ (/2)
4/3
^об-^ф г ^ ^
i -1
(5. 10}
Характер влияния параметра Лб на вес днищ цилиндрических
баков для различных значений параметра выпуклости п, опре¬
деляемый выражением (5.10) при кф=\, представлен па рис. 84
134
в виде безразмерной функции
От =
пх (О
1/3
Ym
-=«ПДН(«)-
2Х6
„4/3
/ 1 \ 4/3
(5.11)
Как видно из графика, уменьшение веса днищ с увеличением
параметра Хъ при переменном внутреннем давлении происходит
менее прогрессивно, чем при постоянном давлении. Причиной это¬
му является то обстоятельство, что с увеличением параметра Хб
днища работают соответственно на увеличенное гидростатиче¬
ское давление.
Рис. 84. График зависимости веса днищ
от удлинения баков^_ определяемый мно¬
жителем бди(^б, п)
при переменном гидростатическом дав¬
лении
8 Л6
5.5. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ОБЕЧАЙКИ
И ДНИЩ БАКОВ ПРИ ПЕРЕМЕННОМ
ИЗБЫТОЧНОМ ДАВЛЕНИИ
Если избыточное давление в баке выбирается из условий
компенсации нагрузок со стороны головной части ракеты (т. е
нулевых экваториальных напряжений в обечайке), то вместо вы¬
ражения (5.5) следует записать
Риэб k§tlx (t)
Ve
^об^ф
об,
(5.12)
£-1
где Да — суммарный вес грузов.
Выполнив подстановки и преобразования, аналогичные разд.
5-3 и 5.4, получим следующие зависимости:
О
об “
■(t)
поб (X)
Хоб^ф ~Ь ( i v№)i
i= 1
1/3
vF
(5.13)
135
для конической обечайки (/гф=?М),
G,,-
G*
1/3
п
(5.14)
для цилиндрической обечайки (£ф=1),
Q«=W (5.15)
для изолированной цилиндрической обечайки (йф=1, п = оо),
G ля= —
1 ( Ум
М
: (0 /гДа ^
i =1
1 Пл„ (/2)
^об^ф (Т^дн)/
/=1
для днищ конических баков {к^ФХ) и
-4^/3 (5.16)
1/3
о.
2/?Пш (/2)
т(-м
!-Г
° 3/2
(5. 17)
для днищ цилиндрических баков (&ф=1).
Анализ приведенных формул показывает, что функциональ¬
ный характер весов изолированных обечаек по параметру удли¬
нения одинаков и следует закону )2J£.
Для днищ аналогичные зависимости структурно не одинако¬
вы, что является следствием несовпадения расчетных случаев.
Так, изменение объема днищ влияет на изменение гидростатиче¬
ского давления в их полюсах, но не влияет на давление, выби¬
раемое из условий компенсации нагрузок со стороны головной
части ракеты. Однако для современных топливных баков с боль¬
шими Кб и п отмеченное расхождение в нагрузках невелико и
можно полагать, что изменение веса днищ в обоих случаях сле¬
дует закону л“об.
Сравнение зависимостей (5.6), (5.10) и (5.13), (5.16) показы¬
вает также, что при постоянной геометрии (Хб = const) веса обе-
4/3
чаек и днищ пропорциональны запасу топлива vd при рГидр =
= const и v\ 3 при ризб^ const.
136
5.6. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС
ШПАНГОУТОВ БАКОВ
Погонная сила, растягивающая шпангоут q, определяется из
уравнения
%i(2a), Х2(2а), %з(2а) — табличные функции; Fmn— площадь по¬
леречного сечения шпангоута; р— коэффициент Пуассона.
Согласно рекомендациям промышленности для типовых кон¬
струкций баков можно положить xi(2cc) =Х2(2а) =Хз(2а) = 1.
Тогда
Суммарное напряжение в оболочке бака, вызываемое напря¬
жениями растяжения и изгиба, равно
Подставляя в полученную формулу выражение для р и зная,
что из условий допустимых меридиональных напряжений
(5. 18)
/?ь(1 — ^—=0,
откуда
Ръ (1 — 0,5{л)
(5.19)
4 =
&м'0
(5. 20)
Так как
то
PyPб 6^2 (1 — 0.5м-)
Откуда
F
82р (4 [а] 5 - PSD6)
(5.21)
ШП
6ръ (1 — 0,5(л)
Рнзб^б
2 [а]
137
получим
где
/7шп=мз/2^,
, _ [12(l-[x2)]V4
(5.22)
6(1— 0,5р.)
Вес шпангоута равен Оши=л06умРшп или с учетом выраже¬
ния (5.22)
Применив также формулу для толщины оболочки бака, вес
шпангоута выразим в следующем виде:
( Рнзб \3/2
[°]
(5. 23)
Делая подстановки при помощи выражений (5.1), (5.5) и
(5.12), получим также
4byuv6
^об + 2 ( 4г^дн)/
i=l
( Ризб \3/2
\ 2 [a] J
ПрИ /7изб = COnst,
^ШН 'T^lxV м
АобМИОуб
\ 3/2
ПРИ ^гидр Ф COnst И
Ошп = л^у(
/=1
— 4 77 nx{t)
Л Ы
М
3/2
(5.24)
(5.25)
(5.26)
ПрИ Ризб Ф COnst.
Характер изменения веса шпангоутов от удлинения Хб удоб¬
но проследить, как и ранее, на примере цилиндрических баков
(£ф=1) по безразмерным параметрам
~q 1
дь / ^изб W2
^м1,б ( 2 [а]
при Д,зб = const,
О
2 [а
JT [а] \3/
лЛ’^Ум V 2угл v (0 v6
■)
1‘-5Г
1 \ 3/2
h —
п
h~ir
(5. 27)
(5. 28)
138
при А-идр Ф const И
ШГ1
' 2 , Д2
3/2
при РизбФconst.
Как видно из формул, вес шпангоутов меняется обратно
пропорционально удлинению бака при постоянном внутреннем
давлении и не зависит от удлинения при переменных гидроста¬
тическом и избыточном давлениях.
5.7. ОБЩИЕ ЗАМЕЧАНИЯ ПО ВЛИЯНИЮ УДЛИНЕНИЯ
НА ВЕСОВЫЕ ХАРАКТЕРИСТИКИ ЭЛЕМЕНТОВ
КОНСТРУКЦИИ БАКОВ
Если принять условие постоянства объема не всего бака, а
только на участке обечайки y06 = const (я = °°), то влияние уд*
линения на весовые характеристики бака можно представить
в наиболее удобном для запоминания виде. Функциональный
характер такого влияния представлен в табл. 5.1.
Таблипа 5.1
Функциональный характер влияния параметра Х0б на весовые
характеристики элементов конструкции бака
Случаи нагружении
Элементы
конструкции
Ризв = СОп5{
^ги -р- C0I1St
/7изб Ф const
Обечайка
Не влияет
Х2/3
Лоб
Днища
/-1/2
об
коб
кг/3
Шпангоуты
X-V2
Лоб
Не влияет
Не влияет
Как видно из таблицы, влияние удлинения на вес шпангоутов
при постоянном внутреннем давлении такое же, как и на вес
Днищ. В этом случае баки не имеют оптимального удлинения.
Их вес меньше, чем больше удлинение (см. рис. 85).
При переменном гидростатическом и избыточном давлениях
вес днищ не зависит от удлинения бака. Это означает, что отыс¬
кание оптимального удлинения (или диаметра) можно произво¬
дить в отдельных случаях по упрощенным зависимостям, без
Учета влияния шпангоутов.
139
5.8. ВЛИЯНИЕ УДЛИНЕНИЯ НА ВЕС ТОПЛИВНЫХ БАКОВ
ПРИ ПОСТОЯННОМ ВНУТРЕННЕМ ДАВЛЕНИИ
Имея зависимость веса бака в функции диаметра (4.7) и вы¬
ражение диаметра через его объем (5.1), можно получить
где
(5. 30)
4 kl
- лП ш (п)
(5.31:
^об^ф + ( _!_ ^дн)/
/=1
Формула (5.30) показывает, что вес баков при постоянном
внутреннем давлении находится в линейной зависимости от их
объемов.
&$,кгс
Рис. 85. Влияние удлинения и объе- Рис. 86. Влияние выпуклости днищ
ма на вес баков при постоянном внут- баков п на характер зависимости
рением давлении Gg = Gg(>,б) при ра = const
Графическая интерпретация зависимости (5.30) представлена
на рис. 85. Как видно из графика, увеличение удлинения вызы¬
вает уменьшение веса бака. Для гипотетического бака с плос¬
кими днищами (п = оо) и толщиной стенок как у сферических
днищ (п= 1) при Хб = Яоб = 00 величина множителя характе-
140
ризующего влияние удлинения на вес бака, принимает мини¬
мальное значение, равное
Н-
(5. 32)
К
Полученное выражение в известной мере характеризует и ре¬
альные баки, у которых объем днищ сравнительно невелик. Это
означает, что при малых выпуклостях днищ (больших значени¬
ях параметра п) и при увеличе¬
нии удлинения Лб вес бака стре¬
мится к своей минимальной
величине, равной весу изолиро¬
ванной обечайки.
Рис. 87. Влияние удлинения на вес
бака и его элементов конструкции
при ръ= const и п —4:
/—бак; 2—днище; 3—обечайка
О 2 4 6 8 Л,
Рис. 88. Влияние удлинения на вес
бака и его элементов конструкции
при р s = const и /г=1;
/—бак; 2—днища; 3—обечайка
Рассмотрим далее влияние параметра выпуклости днищ п
на вес баков. Для этого воспользуемся зависимостями (5.3) и
(5.9) применительно к цилиндрическим бакам (&ф=1) и, сложив
их, запишем
_L + 1
°.=2^—V ■ 15.33)
Кривые G6(Яб, /г), построенные по этой формуле, приведены
на рис. 86. График показывает, что в зависимости от значения
141
параметра п увеличение удлинения может вызывать не только
уменьшение, но и увеличение веса баков. В случае, представлен¬
ном на графике, увеличение удлинения вызывает уменьшение
веса баков при п = 4 и, наоборот,
увеличение веса баков при п= 1.
Аналогичные зависимости, но не
только для баков, а и для обечаек
и днищ, представлены на рис. 87
и 88.
Весьма любопытные кривые при¬
ведены также на рис. 89. Он по¬
строен по формуле (5.33), где пока¬
зано влияние на вес баков того же
параметра п, но при A,6 = const._JIer-
ко видеть, что функция G^ = G^{n)
имеет максимум, которому соответ¬
ствует наиболее тяжелый вес баков.
Такое влияние выпуклости днищ
на характер зависимости G^ = Ga(n)
объяснятся тем, что большие зна¬
чения параметра п вызывают более
высокие напряжения в днищах ба¬
ков, вследствие чего их вес оказы¬
вается доминирующим по сравнению
с весом ооечаики. при этом и характер изменения веса всего
бака по параметру_удлинения Хв остается близким к характеру
зависимости <?дн = <7дп(^б). При малых значениях параметра п
напряжения в днищах уменьшаются, вследствие чего домини¬
рующим весам оказывается вес обечайки. При этом характер за¬
висимости 5б = 6?б(Яо) сохраняется близким к зависимости
Gоб = Gоб (^б) •
Обратив внимание на формулу _(5.33), легко обнаружить, что
экстремальность зависимости Gb = Gs(ri) определяется влиянием
числителя во втором члене правой части этой формулы. Дейст¬
вительно, его величина принимает значения
—[-/г^ = со при п = сю;
— -\-п\=2 при п= 1.
л )
При значениях 1<я<оо этот член принимает всегда конечные
значения, в том числе и экстремальные. Это обстоятельство име¬
ет важное значение, поскольку оно определяет возможность отыс¬
кания оптимальных параметров не только баков, но и топливных
отсеков в целом. Исследования такого содержания следуют ниже
(см. разд. 5.10 и 5.11).
142
Рис. 89. Влияние выпуклости
днищ на вес баков при ръ =
= const
5.9. ОПТИМАЛЬНОЕ УДЛИНЕНИЕ НЕИЗОЛИРОВАННОЙ ОБЕЧАЙКИ
БАКА ПРИ ПЕРЕМЕННОМ ВНУТРЕННЕМ ДАВЛЕНИИ
Имея зависимости (5.7), (5.11), (5.14) и (5.17) и принимая
условие постоянства объема на участке обечайки, запишем
°o6 = /ixo63; (5.34)
Сдн-АСб173, (5.35)
где
Ум \
у.,лл.(/)г’б/3; (5.36)
JT у/6
\ т)
(—)
/, = -£«_ =k jy±Ly,!nAt)nU:iu{n)vr (5. 37)
0„ ^
При рги:[р ф const и
Л=^-=2 №-) Д^Я(0 ^б/3; (5.38)
Ооб V [с] /
/a==p^=-L(-M (5.39)
дн ^ \ /
При Ризб = const.
Суммарный вес бака на основании зависимостей (5.34) и
(5.35) будет равен
т
Сб = /Д3 + А0-61/32 fn. (5.40)
/« 1
Формула (5.40) показывает что вес бака (как сумма весов
обечайки и днищ) по параметру Л0б имеет экстремальное значе¬
ние. Изменение весов обечайки, днищ и всего бака в зависимо¬
сти от удлинения Л0б при pH36=^const показано на рис. 90. Как
видно из графика, вес бака в функции удлинения Л0б имеет ми¬
нимум.
Оптимальное удлинение обечайки, соответствующее весу
бака при 1>об = const, получим, приравняв нулю производную от
G6 по Лоб, т. е.
fl=(bL = 2kc6-
откуда
X
об •
2 ^2£‘
i=l
: 2/!
(5.41)
Для конических баков с двумя выпуклыми сферическими
днищами по формуле (5.41) можно получить
п2 4- 1
8/Г"
1-
*ф(*ф + 1) _
^дн
^об
при рГндр = const И
(5.42)
'Об '
/г2 + 1
8/2
^дн
^об
(5. 43)
при Ризб=^const.
Для цилиндрических баков в обоих случаях непостоянства
гидростатического и избыточного давлений формула (5.41) при
кф = 1 и равенстве статистических коэффициентов &дн = £0б дает
чоб"
_ /22 + 1
4/2
(5.44)
Таким образом, определяющим параметром при выборе удли¬
нения обечайки бака является выпуклость днищ п. При увели-
&б£дн£о6
Рис. 90. Влияние удлинения на вес ба¬
ков и их элементов конструкции при
рп ao^const:
1—бак; 2—обечайка; 3—днища
чении этого параметра оптимальное удлинение обечайки также
увеличивается.
Формулы (5.42) и (5.43) показывают еще, что при увеличе¬
нии конусности (£ф), оптимальное удлинение обечайки умень¬
шается.
0 2 ь ■ 6 8 \06
144
* 5. 10. ОПТИМАЛЬНЫЙ ДИАМЕТР МНОГОБАКОВОГО ОТСЕКА
ПРИ УЧЕТЕ ОСЕВЫХ СЖИМАЮЩИХ СИЛ
Рассмотрим случай нагружения топливных баков осевыми
силами, относящийся к конечному времени полета, когда t = т
и nx{t) =Ятах- При этом топливо в баках отсутствует, а осевые
сжимающие силы достигают наибольших значений. Полагаем,
что топливный отсек состоит из т§ баков, на каждый из которых
действует одинаковая нагрузка Nx = As ^max*
Вес топливного отсека, равный сумме весов всех его баков,
на основании формул (4.1) и (5.1) равен
тв
+S'
+
тПд,(й)Об-
/=1
(5.45)
/=1
где j — индекс, обозначающий параметры одного из баков.
Дифференцируя и приравнивая нулю производную
(dG^'o/dDb) при t>6 = const, получим
D6 = 2Х
(^ф + 1) ^ф
X
Ум
И
■Щ
kJi:
i=l
Ф«Ф
7-1
m т -1
V «п'.н('0 *ф +1 yv )>'■/'
2j 4*3ту-(± 4iH 1*4'
1/3
(5.46)
где k.
As
соотношение диаметров; D6 = Dq max — диаметр
наибольшего по габаритам бака.
Для отсека, состоящего из цилиндрических баков с двумя
сферическими днищами и выполненных из одинакового матери¬
ала при и kd=l, формула (5.46) дает
D6 = 2
4 2 "иы
7 = 1
7 = 1
1/3
(5.47)
где принято, что 7б^3~0.
145
Таким образом, главными параметрами, определяющими оп¬
тимальный диаметр многобакового отсека являются объемы
баков v^j и выпуклость днищ П). Как видно из формулы (5.47),
при увеличении параметра п и количества днищ в отсеке опти¬
мальный диаметр уменьшается.
Формулу (5.47) можно представить так
где GT— вес топлива на ракете; £ — коэффициент заполнения
баков топливом, равный отношению объема топлива к объему
бака.
В формуле (5.48) принято, что для всех баков имеет место
fij — п — const. Эта формула, равно как и формула (5.47), дает
любопытный результат. Во-первых, при п = оо (плоские днища)
оптимальный диаметр становится равным нулю £>б = 0; во-вто¬
рых, при п= 1 (днища представляют собой выпуклые полусфе¬
ры) оптимальный диаметр должен быть равным бесконечности.
Физически это означает, что плоские днища с бесконечно боль¬
шими напряжениями неприемлемы, применяются другие днища,
геометрическая форма которых близка к форме полусферы.
5. 11. ОПТИМАЛЬНЫЙ ДИАМЕТР МНОГОБАКОВОГО ОТСЕКА
ПРИ УЧЕТЕ СИЛ ВНУТРЕННЕГО
ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
В отличие от рассмотренного в предыдущем параграфе слу¬
чая учтем действие на топливные баки не только осевых сжи¬
мающих сил, но и сил гидростатического давления компонен¬
тов топлива. Будем полагать также, что постоянство объемов
сохраняется только на участках обечаек. Для реальных конст¬
рукций баков, у которых топливо в днищах составляет неболь¬
шой процент по отношению к общему запасу топлива, это допу¬
щение вполне приемлемо. При этом (т. е. при a06j = const) реше¬
ние задачи существенно упрощается.
На основании выражений (5.1), (5.5) и (5.12) вес топливно¬
го отсека GT.0 с тб баками запишется
Or
1/3
4
£Ут
(5.48)
ou
Or =
Ут'*0^б .
я
’
"Г
^ф
тп
V
п
2и
i = 1
. К
^cb "i_ 1 ’ v -
ал = —7 1 ^ss.
Я
-пдн(«)
Nx = tntix(t).
После дифференцирования выражения (5.49) ' по диаметру,
приравнивая нулю производной и преобразований, получим
V [а{ (а2 -f а3) а4]у
тб
У [а!(а2 + а3)а5]у
1/3
(5. 50)
Если расчетный случай относится к начальному времени по¬
лета / = 0, пх(1)=По, а осевые нагрузки отсутствуют (подвесные
баки) Nх = 0, то для цилиндрических баков с двумя сферически¬
ми днищами, выполненных из одинакового материала при k^ —
= 1, &ф=1 и пjг— п, формула (5.50) дает
-1/3
D6 = 2
4 2 (4 Yr)y
; = i
(5.51)
я2 - 1
Л
7 = 1
(^бУт)у
Сравнение полученного выражения с формулой (5.47) приме¬
нительно к однобаковому отсеку или отсеку с одинаковыми ба¬
ками (V(yj = V()9 Ут] = Ут) показывает, что, несмотря на различие
расчетных случаев, оптимальные диаметры определяются в ос¬
новном объемом и геометрией баков. Перестановка местами ба¬
ков в отсеке, если при этом не меняются нагрузки, на оптималь¬
ный диаметр не влияет. Изменение самих нагрузок (расчетных
случаев) влияет на выбор оптимального диаметра, однако это
влияние не существенно.
Пример 5. 1. Объем цилиндрической обечайки № 1 заполнен топливом
веса GT. Обечайка № 2 равного объема, но без топлива нагружена силами
внутреннего избыточного давления ризб, величина которого выбирается из
Условий компенсации осевых напряжений от груза ДЕ. Показать, каков ха¬
рактер зависимости веса обеих обечаек от параметров Х0б и D0б, а также
Чему равно соотношение их весов. Учет осевой перегрузки nx(t) не произво¬
дить.
147
Решение. Вес обечайки равен G0б —• я£^б5А0б7м. Поскольку 5 —
A [aj
Goo о D'0ftPVlзб ( Г_1 ) Лоб*
2
Имеем также = ^°n . Следовательно,
Goo ^об-РцЗб ^ j- ^ j • ^2)
Гидростатическое давление в баке № 1 меняется по закону ргпдр=
=Л0б^обУт. Следовательно,
G0:"i “ ^Vo6'f o6^o6^T ^ ^ »
или
Go6 = 2GT(-^ Ao6Do6. (5.53)
Давление газа в баке № 2 запишется так:
А я
Р\ 13 б —
— D2-
4 00
Воспользовавшись выражением (5.52), получим
GT / Дд \ Тм
G06 = 2-
Поскольку
7т I jLrf- !
4 ^о6 /
— ^об^ооТт»
— D2
4 ''
об
ТО
М
\
J
Go6 = 2is I -pv I Ao6£>o5. (5. 54)
Формулы (5.53) и (5.54) показывают, что веса обечаек № 1 и № 2
находятся в линейной зависимости от параметров Я0о и D0g. Отношение
веса обечайки № 2 к весу обечайки № 1 составит величину G=
= (G0Q)mJ(G06)№i=As/GT.npH этом видно также, что характер изменения
гидростатического давления и давления газа по параметру Х0б у обоих баков
одинаков.
Пример 5.2. Произвести сравнение весов цилиндрических и сфериче¬
ских топливных баков по параметру Ко5 при одинаковых значениях ръ ^б, Тм,
[а]. Днища цилиндрических баков принять полусферическими. Сравнение про¬
извести без учета веса впутренших подкреплении (шпангоутов).
148
Решение. Толщина обечайки цилиндрического бака равна
5 = — —. (о. 55>
н л 2 [а]
Для сферы имеем также
лА>
Slt,7[-r. (0.0 о
Объемы цилиндрического и сферического баков равны соответственно
я Di
^ЦИЛ . О"/ -}- JT
пЗ (К'О 1 \ .
— = я/)в(— -YJ: (0-о7>
VC<P = ““ D\. (5.Т8>
Поверхность сферического бака равна ПСф=я/)^, а его вес ССф =
—-бСфПсфу.м или
«б-*»
и на основании (5. 58)
^сф — 2 Pivo ^ j » (5- 60)’
где 1>б=^сф. Вес обечайки цилиндрического бака равен Соб=л£>^б6Лос,у.м.
или на основании (5. 55)
0.6- 2
(5.61)
Суммарный вес бака, равный сумме весов обечайки и двух сферических
днищ, на основании выражений (5.60) и (5.61) запишется так:
с,„, - с„+О „=f ».«£<;» (+-f рА (Jb.)
2 +TJ- (5-62)
Делая подстановку при помощи выражения (5.57), получим окончательно.
1
A n п “7“ _
{ ^
^ЦИЛ ( Г 1 ) Т^цил - ,
\ LaJ / об 1
2 3
(5. 63>
Сравнение весов произведем при помощи величины G, равной отношение
веса сферических баков к весу баков цилиндрических. При этом на основа¬
нии выражений (5.60) и (5.63) получим
/I ^ '
а = ^ = А' ^
0\П!, 2
V
1
А°5 + 2
(5. 64)-
149
Характер отношения весов баков G в функции параметра X0s удобно
представить, как показано на рис. 91. Из графика видно, что соотношение
весов в пользу сферических баков (их более легкого веса) тем больше, чем
'больше удлинение цилиндрических баков. При этом, если Х0в = °°, величина
— — — 3
<5 достигает минимального значения и равняется G=Gm-1п= . Если ^Об=0,
цилиндрические баки вырождаются_ в_сферические, и величина G достигает
максимального значения, равного С=б?тах=1.
Рис. 91. Влияние удлинения обечайки на
весовое соотношение сферического и ци¬
линдрического баков при =const
Пример 5.3. Найти выражение для оптимального диаметра бака, избы¬
точное давление которого выбирается из условий компенсации нагрузок со
•стороны головной части ракеты. Принять бак цилиндрическим; днища —
сферическими.
Решение. При k% = \ вес бака определяется
г п пя( 7м \Л ,п2 + 1
6 = ~2~ Ркз6 6 (~jyj~) ( 6 4/г
Удлинение оболочки бака, выраженное через его объем, равно
V& 3п2 -!- 1
л
D:
,з
6 п3
Поскольку при нулевых экваториальных напряжениях избыточное дав¬
ление наддува равно
(О
Ризб -
то вес бака выразится формулой
п2 4- 1N
Для определения экстремума приравняем нулю' производную
При допущении, что 1/6 п3~0, условие экстремума дает
п2 — 1 8г/б
dG б
4/г
яО:
з ’
откуда
41/л
/22 — 1
1/3
(5. 65 >
Таким образом, главными параметрами, определяющими оп¬
тимальный диаметр топливного бака, являются его объем Vq и;
выпуклость днищ п.
СПИСОК ЛИТЕРАТУРЫ
1. Б а с с а р д Р. и Де-Лауэр Р. Ракета с атомным двигателем..
М., ИЛ, 1960, 416 с.
2. Конструкция управляемых баллистических ракеТ. Под ред. проф.
А. М. Синюкова и доц. Н. И. Морозова. М., Воениздат, 1969, 444 с.
3. Ч е р н ы й Г. Г. Течение газа с большой сверхзвуковой скоростью*.
М., Физматгиз, 1959, 220 с
Глава VI
ОСНОВНАЯ ВЕСОВАЯ ЗАВИСИМОСТЬ
И ЕЕ ПРИЛОЖЕНИЯ
Процесс проектирования летательного аппарата, будь то ра¬
кеты или ракетоплана, представляет по существу комплекс пов¬
торных работ, последовательно приближающих окончательный
выбор и назначение проектных параметров в соответствии с
предъявляемыми техническими требованиями.
В таком процессе приближений представляется возможным
первые шаги по выбору основных параметров (G0, цк, п0у е, V)
производить не по развернутым формулам весового анализа, а по
упрощенным весовым зависимостям, получаемым обработкой
(при определенных допущениях) весовых уравнений. При этом
выделяются только те параметры, изучение которых представ¬
ляет интерес в данном исследовании. Такие упрощенные зависи¬
мости устанавливают функциональную взаимосвязь между ос¬
новными параметрами и их мы будем называть «основными ве¬
совыми зависимостями».
6. 1. ВЫВОД ОСНОВНОЙ ВЕСОВОЙ ЗАВИСИМОСТИ
Для типовой схемы одноступенчатой ракетной конструкции
можно составить весовое уравнение следующего вида:
т N L
0к=2 (°т)+2 Oi (ок)+2 (°о)+
i=1 /=1 /=1
+ Gl(^—W —-f- Gl (G0 — Да) Д-... -f As, (6. 1)
/=i /=i
где правая часть представляет собой сумму весов элементов
конструкции и полезного груза (пассивных масс), зависящих
функционально от веса топлива (первый член), конечного веса
(второй член), стартового веса (третий член), тяги двигателя
(четвертый член), веса ускорителя (G0—As) (пятый член)
и т. д. Параметры ту Ny L, v, j означают количество элементов
конструкции, вес которых выражается одинаковой функциональ¬
ной зависимостью. В общем виде подстановка функций GZ(GK)
152
и так далее приводит к нелинейному уравнению относительна
параметра GK.
Исследование уравнения (6.1) путем массовых расчетов по
развернутым весовым зависимостям показывает, что его можно
линеаризировать и привести к виду
G =G,
+W
т l
^i + °K^i + G0^i +
i=1 /= 1 /=1
^•+(С0-Де)^ + ... + ДЕ, (6.2)
/=1 /=1
\ dt
где рг — постоянные коэффициенты, величина, которых зависит
от большого количества параметров, «замораживаемых» в дан¬
ном исследовании.
Разделив обе части уравнения (6.2) на G0j после преобразо¬
ваний получим
!\ = а+7г-4-£/г0,
(6.3),
где
(6.4)
т L j
2 2 2 V'i + • • •
а=—— — — ;
т N
1 + 2 — 2 + • • *
/=1 ;=i
i-2n
у= 4) ;
т N
1 -г 2 ~ 2 .а‘ + • • •
г=i ;=1
2 N
k= ,
т Л
1+2-2 ^ + ••■
х-1 /=1
п0 = ~^~ = ——стартовая (начальная) перегрузка;
G0 go
As
e = коэффициент грузоподъемности (грузоподъемность).
G0
В применении к составным ракетам параметр е выражает со¬
отношение масс по ступеням как ei = G0i+i/G0i и называется ко¬
эффициентом распределения (соотношения) масс.
153
Выражение (6.3) является основной весовой зависимостью.
Пользуясь ею, можно изучить влияние различных факторов на
характеристики проектируемого летательного аппарата, не при¬
бегая к трудоемким расчетам по развернутым аналитическим
весовым зависимостям. При этом очевидно, что ее функциональ¬
ная запись может видоизменяться в зависимости от постановки
задачи, не исключая возможность сохранения нелинеаризирован-
ных членов, как это имеет место для оперенных или крылатых
ракет. В силу функционального характера коэффициентов (6.4)
основная весовая зависимость может быть трансформирована
для изучения факторов, связанных не только с основными пара¬
метрами (цк, По, е), но и с параметрами внутренних конструкций
и системы ракеты (ум, Ут> М, /?а, Яб, W, ць SM и т. д.).
Особенно большое применение основная весовая зависимость
получила в теоретических и проектно-конструкторских изыска¬
ниях по определению параметров ракет с учетом динамических
факторов.
6.2. ВАРИАНТЫ ОСНОВНОЙ ВЕСОВОЙ ЗАВИСИМОСТИ
В простейшем случае, когда весовые зависимости для эле¬
ментов конструкции неизвестны, уравнение (6.3) можно записать
Ок = (Оо-Да)1> + Д>,
и затем получить
— ^эфф + П — ^эфф) г> (6-5)
где
G о wT д2
(АЭфф= = ^ : ,
Jmk О0 —Д J, 1— <
/ =1
:у (б>б)
Коэффициент эффективности конструкции цэфф является на¬
дежным статистическим коэффициентом и легко определяется
как весовая отдача цк = Цэфф изолированного ускорителя.
При пользовании уравнением (6.5) следует помнить, что ко¬
эффициент эффективности конструкции может быть принят по¬
стоянным только для определенного класса ракет как по их кон¬
струкции, так и по начальному весу, поскольку для него имеет
место зависимость Рэфф = Цэфф(£0). Характер такой зависимости
представлен на рис. 92. Как видно из графика, величина коэф¬
фициента цэфф уменьшается по мере увеличения стартового
веса системы. Обычно такие кривые получают либо статистиче¬
ским путем, либо проектно-конструкторскими проработками на
базе весового анализа.
154
Если обработка статистических данных производится с уче¬
том параметра я0, то для этого случая основную весовую зави¬
симость можно получить из выражения
__ — кР _ — £ — кщ
Gq — д2 1 — £
ИЛИ
с^к ==r ~Ь ( ^ (6.7’)
где коэффициент k имеет такое же происхождение, как и в вы*
ражении (6.3). Параметр р является величиной, показывающей,
какую долю от веса изолированного ускорителя составляет ко¬
нечный вес без учета тех элементов конструкции, вес которых за¬
висит от тяги.
Рис. 92. Значения коэффициента эф¬
фективности конструкции для некото¬
рых типов ракет в пересчете па
Y г = 1 тс/м3
Преобразование уравнения (6.5) в уравнение (6.7) произво¬
дится подстановкой
Рэфф^-
кпо
Весовая отдача рк может быть выражена и через конечную
грузоподъемность ек, равную отношению груза к конечному весу
ракеты. Воспользовавшись основной весовой зависимостью (6.5),
запишем
Аэфф "К 1 — ^Эфф)
О,/-
откуда
где
G,c
-‘•эфф
Р« = Т-а- » '
1 О М'Эфф) £к
конечная грузоподъемность.
(6 .8)
155
Между начальной и конечной грузоподъемностью существу¬
ет очевидная зависимость — =jv Эта зависимость будет приме¬
р-
пена для упрощения некоторых выражений, описывающих рас¬
пределение масс по ступеням составных ракет (см. гл. XI).
В дальнейшем в целях упрощения записи и получения наибо¬
лее общих результатов в решениях по выбору оптимальных па¬
раметров различных схем одноступенчатых и составных ракетных
летательных апппаратов (ракет, рекатопланов и т. д.) мы будем
пользоваться вместо основных весовых зависимостей (6.3) и
(6.5) зависимостями вида
Рк = Р,л+Ал<»
где
И
где \,= 1 Цэфф-
Выражение (6.9) удобно использовать, когда исследуемым
параметром является стартовая перегрузка п0.
Выражение (6.10) удобно применять, когда исследуемыми па¬
раметрами являются грузоподъемность е*, распределение масс
в г, весовые отдачи рКг и другие параметры, изучение которых
может происходить при замороженных (заданных) коэффици¬
ентах /2 о г’.
6.3. ВЛИЯНИЕ УДЕЛЬНОГО ВЕСА ТОПЛИВА
НА ВЕСОВУЮ ОТДАЧУ
Рассмотрим влияние удельного веса топлива на весовую от¬
дачу по топливу GT. Это удобно проследить по основной весовой
зависимости вида GT = GT(yT). Для получения такой зависимости
составим весовое уравнение
т
<1> О,л ^ ДуУэл/ +6-Г+ Дз, (6.11)
/=1
где — вес элементов конструкции, функционально не завися¬
щих от веса топлива; т — количество элементов конструкции,
вес которых зависит от веса и объема топлива; уЭлг — статисти¬
ческий коэффициент для i-го элемента конструкции, показываю¬
щий сколько единиц веса конструкции приходится на единицу
объема топлива; vT — объем топлива (либо топливного бака).
156
(6.9)
(6. Ю)
Преобразование уравнения (6.11) дает
От = — . (6-12)
J ^Эл
Ут
_* G31 + As
От = 1 — • (6.13)
Параметр GT*, определяемый выражением (6.13), указывает
на весовую отдачу по топливу без учета топливных емкостей и
других элементов конструкции,
вес которых зависит от веса &т
топлива.
Выражение (6. 12) является
основной весовой зависимостью,
связывающей функционально меж¬
ду собой весовую отдачу Ст и удель- о,95
ный вес топлива ут.
Рис. 93. Влияние удельного веса топли¬
ва па весовую отдачу бт л п/_
0 0,5 1,0 1,5 %т; тс/м7
На рис. 93 представлены кривые GT = GT(yT), построенные по
формуле (6.12) для различных значений параметра уэл при
GT*=1. Как видно из графика, увеличение параметра уэл при¬
водит к уменьшению весовой отдачи £т, в то время как увеличе¬
ние параметра ут приводит к увеличению весовой отдачи GT.
Поскольку параметр уэл характеризует относительный вес эле¬
ментов конструкции, функционально зависящий от удельного
веса топлива, то это означает, что эффект увеличения весовой
отдачи (7Т вследствие увеличения удельного веса топлива тем
больше, чем менее совершенными по конструкции (тяжелыми
по весу) оказываются топливные баки, система питания, система
наддува п другие элементы конструкции. В то же время влияние
Yt оказывается тем меньше, чем больше относительный вес эле¬
ментов конструкции, функционально не зависящий от веса топ¬
лива. Это видно из основной весовой зависимости, где пара¬
метр GT* играет роль как бы масштабного фактора в оценке
весовой отдачи, если при этом уЭл = const.
Изменение удельного веса топлива вызывает изменение веса
только тех элементов конструкции, проектные характеристики
Которых зависят от веса топлива и его объема.
157
тп
где Уэл 2 ^элп
/=i
Из графика видно, что для топливных пар, средний удель¬
ный вес которых лежит в диапазоне от ут^1,0*103 кгс/м2 (на¬
пример, 75% спирт +кислород) до ут^1,5*103 кгс/м3 (гидра¬
зин -Ьтрифторид хлора), изменение весовой отдачи при уэл =
= 60 кгс/м3 и GT* = 1 составляет не более 2—3%. В то же время
уменьшение среднего удельного веса топлива от ут~1 • Ю3 кгс/м:?
до ут^0,26*103 кгс/м3 (например, водород + кислород) вызыва¬
ет уменьшение весовой отдачи Ст на 4—6%. Очевидно, что
в случае криогенных топлив необходимо совершенствование кою
струкции не только баков (корпусов ракет), но и всех топливных
коммуникаций до приемлемых значений конструктивного коэф¬
фициента уэл- Такая задача относится к оценке эффективности
ракетных топлив и, как будет показано ниже, решается учетом
двух факторов — удельного веса и скорости истечения продуктов
сгорания топлива.
Формула (6.12) получена безотносительно к конкретному
типу ракеты и может быть использована для самого широкого
класса реактивных систем.
6.4. ОЦЕНКА ЭФФЕКТИВНОСТИ РАКЕТНЫХ ТОПЛИВ
Оценку эффективности ракетных топлив удобно производить
по формуле Циолковского, поскольку эта формула связывает,
конечную скорость ракеты с параметрами, величины которых
зависят от характеристик топлив. Такими параметрами, как бы¬
ло показано ранее (см. гл. 2), являются скорость истечения W
и весовая отдача (ик.
Скорость истечения является следствием физико-химических
свойств топлива и характеризует его как носителя энергии вы-
сокой концентрации. Весовая отдача рк характеризует совер'
шенство конструктивной схемы ракеты и, как мы видели выше
(6.12), является функцией удельного веса топлива. Таким обра¬
зом, главными параметрами для оценки эффективности ракет¬
ных топлив являются скорость истечения и удельный вес топ¬
лива.
Имея формулы (2.25) п (6.12), легко записать
1 1^2-
l 'K U In —L , (6.14)
* , Y э л
Ю .
к Yr
где
Рк =-■ 1 — G г.
Очевидно, что выгодность того или иного топлива может
быть определена по формуле (6.14) путем сравнения конечных
скоростей VK. Такое сравнение приведено па рис. 94 путем по-
158
Vk,km/c
строения кривых Vk=Vk(yt) Для двух топлив с неодинаковыми
скоростями истечения W.
Предполагается, что топливо с большей скоростью истечения
располагается в ракете с более тяжелыми топливными емкостя-
ми и, следовательно, большим зна¬
чением конструктивного коэффи¬
циента 7а л.
Как видно из графика, кривые
Кк=Ук(7т) имеют точку пересе¬
чения.
Это означает, что преимущества
ракетных топлив не могут быть оце-
2,0
Рис. 94. К оценке эффективности ракетных
топлив:
/—топливо А; '’—топливо Б
1,0
0,5
!
-t\
£ !
ч.
-
0,5 1,0 1,5 уг, ус/м3
нены однозначно ни по параметру W, ни по параметру уэл, по¬
скольку влияние этих параметров на конечную скорость ракеты
в свою очередь зависит от параметра ут.
Оценка ракетных топлив может быть произведена и по дру¬
гим зависимостям. Простейшей из них является произведение
удельной тяги на удельный вес топлива, т. е.
РудУт- (6.15)
По своему физическому смыслу, это произведение означает
величину импульса тяги, получаемой двигательной установкой
с секундного объема расходуемого топлива. Будучи простой, эта
зависимость, однако, дает весьма приближенное представление
о выгодности топлива, поскольку произведение двух параметров
составлены без учета весовых факторов. Последнее обстоятель¬
ство, как мы уже видели, является весьма важным, поскольку
неучет его может дать неправильное представление об основных
характеристиках (например конечной скорости) проектируемо¬
го летательного аппарата.
Среди других зависимостей можно привести также следую¬
щую:
_ L
ут Giq (°к)
Vv = W
ln-
Уэл
Ут
1 +
Уэл
По
(6.16)
Эта зависимость составлена с учетом потерь в конечной ско¬
рости на преодоление сил тяжести. Некоторая громоздкость
зависимости (6. 16) окупается большей ее точностью.
В тех случаях, когда выбор топлива является одним из глав¬
ных вопросов в определении схемы ракеты, точность зависимо-
159
Таблица 6.1
Некоторые ракетные топлива для ЖРД и их характеристики
Компоненты топлива
Теплотвор¬
ность,
ккал/к гс
Удельный вес,
к г с/л
о -
Л с
X Е
О 5 >
v5 5 5
о ^
Молекулярный
вес
Температура
сгорания*
Удельная
тяга, с
Окислитель
Горючее
Азотная кис¬
лота 98%-ная
Керосин
1460
1,36
1990
26
2980
230—313
Тонка 250
1490
1,32
1970
26
3000
235—310
Анилин (80%)
+ФурФурил°“
вый спирт
(20%)
1420
1,39
1980
26
3050
225—313
Тетранитро¬
метан
Керосин
1590
1,47
2340
26
3200
245—360
Четырех-
окись азота
Керосин
1550
1,38
2140
25
3300
240—331
Перекись во¬
дорода 80%-на я
Метиловый
спирт (50%) +
+ гидразингид-
рат (50%)
1020
1,30
1330
20
2600
215—280
Керосин
2200
1,00
2200
24
3600
275
Жидкий кис¬
лород
Этиловый
спирт
93,5%-ный
2020
0,99
2000
23
3300
255—247
Диме тил гид¬
разин
2200
1,02
2240
22
3350
285—291
Аммиак
1650
0,89
1470
19
3000
285-254
Жидкий фтор
Г идразим
2230
1,32
2940
20
4650
345—455
Аммиак
2315
1,18
2730
20
4650
345—410
* Значения температуры сгорания и удельной тяги ориентировочные (для
средних по своим данным ЖРД) при отношении давлений в камере и на срезе
сопла, равном 40: 1.
160
Таблица 6.2
Расчетные характеристики некоторых ракетных топлив
Горючее
Окислитель
гор
t, °с
^ср
гр
п =
с V
тс/м3
руд’с
Этилсиликат
1,6
3150
26
1,21'
1,05
243
75%-ный этило¬
вый спирт
1,3
2840
23
1,22 •
0,99
247
Метиловый спирт
1,2
2890
22
1,21
0,95
250
Нитроэтан
0,65
3080
23
1,23
1,09
252
92%-ный этило¬
вый спирт
1,5
2700
23
1,21
0,98
252
Нитропропан
0,9
2830
23
1,23
1,06
258
Изопропиловый
спирт
Кислород
1,7
3070
22
1,22
0,98
260
Пропиленоксид
1,6
3260
23
1,23
1,00
262
69,5% этилено-
ксид + 30,5% про¬
пиленоксид
1,5
3260
23
1,23
1,00
264
Этиленоксид
1,1
3180
22
1,24
0,99
266
Скипидар
2,4
3250
22
1,23
1,04
267
Аммиак
1,3
2750
19
1,23
0,88
268
6 3479 15!
Продолжение
Г о;>ючсе
Окислитель
гор
t, °с
!\:р
п= —
т.г,
тс/м3
Несимметричный
диметилгидразин
Кислород
1,4
3012
20
1,24
0,96
277
Г идразпн
0,75
2960
18
1,25
1,06
278
Водород
3,5
2480
9,0
1,26
0,26
365
Аммиак
Красная ды¬
мящаяся азот¬
ная кислота
(22% N02)
2,15
2330
21
1,24
1,12
237
Скипидар
4,2
2980
26
1,22
1,36
237
Полиэтилен
4,5
2960
25
1,22
1,4
237
Несимметричный
диметилгидразин
2,6
2870
22
1,23
1,23
250
Гидразин
Четырехокись
азота
1,1
2730
19
1,26
1,20
265
92,5%-пый этило¬
вый спирт
99,6% -ная
перекись водо¬
рода
4,0
2540
23
1,20
1,24
240
Г идразин
1,7
2590
19
1,22
1,24
265
Скипидар
100 %-ная
азотная кислота
4,4
2730
25
1,22
1,32
235
Г идразин
Тегранитро- ! 1,4
метан |
2900
20
1,27
1,29
263
Аммиак
Трифторид
хлора
3,0
2750
22
1,32
1,26
240
Г идразин
2,5
3320
23
1,33
1,46
258
162
Продолжение
Горючее
О к целитель
*°
гор
/, °с
р-
' ер
п = —
сг/
1 т>
тс/м3
яуГ с
Аммиак
3,0
4020
19
1,33
1,16
310
Диборан
Фтор
5,0
4370
21
1,30
1,07
315
Г идразин
2,0
4290
19
1,33
1,30
320
Водород
4,5
2760
8,9
1,33
0,32
375
Гидразин
М
3530
18
1,29
1 ,23
295
Аммиак
Дпфторид
кислорода
1 ,9
3340
18
1,33
1,07
290
Нормальный
октан
3,8
4060
20
1,20
1,22
302
В таблице обозначено: Руд—теоретическая удельная тяга, с; /фор=
=С/окД7гор — весовое соотношение компонентов топлива (окислителя к горюче¬
му); t—теоретическая температура сгорания, °С; n~cpfcv—показатель полит¬
ропы; 1лср—средний молекулярный вес продуктов сгорания топлива; ут—сред¬
ний удельный вес топлива, тс/м3.
стей (6.14) и (6.16) становится недостаточной, и оценку эффек¬
тивности сравниваемых топлив следует производить на основа¬
нии комплексных (весовых и баллистических) расчетов.
При оценке эффективности ракетных топлив следует учиты¬
вать также, что топливо должно обеспечивать хорошие термо¬
динамические свойства продуктов сгорания в камере двигателя.
Характеристики некоторых ракетных топлив для ЖРД приве¬
дены в табл. 6.1 и 6.2.
6.5. ВЛИЯНИЕ ГАРАНТИЙНЫХ ЗАПАСОВ ТОПЛИВА
НА ВЕЛИЧИНУ ПОЛЕЗНОГО ГРУЗА
СОСТАВНОЙ РАКЕТЫ
Для компенсации ошибок в скорости полета каждая ступень
составной ракеты содержит определенный гарантийный запас
топлива. Рассмотрим случай, когда компенсация ошибок в скоро¬
сти производится не всеми, а только последней ступенью благо¬
даря увеличенному гарантийному запасу топлива в ней. При
6* 163
этом на всех младших ступенях гарантийные запасы топлива
отсутствуют. Для простоты и наглядности получаемых результа¬
тов будем полагать, что полет происходит в пустоте ib отсутствии
сил земного тяготения, а распределение масс по п ступеням вы¬
полнено по закону геометрической прогрессии (см. разд. 11.2).
Ошибка в конечной скорости ДУК, накапливаемая всеми сту¬
пенями ракеты, может быть выражена так:
aV=w
ln-
- — 1п-
(6. 17)
где W — скорость истечения одинаковая для всех ступеней; п —
количество ступеней; At— дополнительное время работы двига¬
теля, необходимое для компенсации ошибок (одинаковых по ско¬
рости на каждой ступени).
Если гарантийные запасы топлива расположены только на по¬
следней ступени, то для компенсации ошибок в скорости AVK ве¬
совая отдача этой ступени должна быть улучшена на величину
рд/п. При этом
!\-л = !Лк (6-18)
где Atn — дополнительное время работы двигателя последней
ступени, необходимое для компенсации ошибок в скорости всех
ступеней.
Суммарная скорость изолированной последней ступени Vn,
равная скорости без гарантийных остатков Е=К(рк) плюс
ошибка в скорости AVU = AVn, составит
:VPln—+U?
Ук
ln-
■ —ln-
1
(yK + тп
Принимая во внимание, что
V„ = Wln-
Ук
из равенства (6.19) находим
\Ук + / J
(6. 19)
(6. 20)
(6.21)
Поскольку все младшие ступени не расходуют топлива на
компенсацию ошибок в скорости, их весовые отдачи цк и коэф¬
фициенты е остаются неизменными. На последней же ступени
эти параметры принимают другие значения. Так, на основании
выражений (6. 18) и (6. 21), получим
164
(6. 22)
Пользуясь основной весовой зависимостью (6. 10), перепишем
равенство (6. 18) в следующем виде:
Н-ЭффТ ( 1 - ^эфф} гя = И-эфф + ('1 - ^эфф) £ - РМп
ИЛИ
s„ = s-pAV, * , (6.23)
(^ ^Эфф)
где Еп — новый множитель в основной весовой зависимости для
последней ступени вместо знаменателя геометрической прогрес¬
сии г.
Развернутое выражение для коэффициента гп легко получить
подстановкой выражения (6.21) в равенство (6.23), т. е.
1 —
(1-^эфф) L W + рД*
Грузоподъемность системы составит
С* — с/1-1~
" "Л
ИЛИ
(6.24)
- сЛ-1 J с
1 -
М-к
[Хк + рА t
(6. 25)
(1 (^Эфф)
Если гарантийные запасы топлива имеются на каждой сту¬
пени в равных относительных величинах (W, то весовая отдача
i-и ступени с новым коэффициентом г* запишется так:
!\; = !-1эфф-г(1 — ^эфф) +
Условие сохранения конечной скорости требует, чтобы
= (6.26)
или
^эфф + ( 1 ^эфф) 3 — ^эффН~ (1 ~^эфф) +
откуда
e, = s——. (6.27)
(^ М-эфф)
Очевидно, что при этом величина относительного веса груза
£* будет равна
Относительное изменение переносимого ракетой груза е* =
= e*/el с учетом зависимости (6.6) составит величину
1
Кривые е* = е* ((ЗА/, п), построенные по формуле (6.29),
представлены на рис. 95. Как видно из графика, перенос гаран¬
тийных запасов топлива в последнюю ступень ракеты увеличи¬
вает ее грузоподъемность. Это увеличение пропорционально ве¬
личине гарантийных запасов (ЗА/ и количеству ступеней п.
Рис. 95. Увеличение грузоподъемности
составной ракеты при расположении га¬
рантийных запасов в последней ступени
по сравнению с ракетой, имеющей рав¬
номерное распределение этих запасов по
ступеням
6.6. «ВЕСОВОЙ БАРЬЕР» РАКЕТНО-АВИАЦИОННЫХ КОНСТРУКЦИЙ
Рассмотрим влияние размеров ракеты на весовую отдачу по
топливу GT.
Стартовый вес современных ракет на жидком топливе, име¬
ющих малые значения коэффициентов эффективности конструк¬
ции Цэфф, в значительной мере определяется весом содержимого
в них топлива. При этом можно заключить, что:
а) стартовый вес пропорционален кубу линейных размеров,
т. е. G0~L3 (где L — масштаб измерения линейных размеров);
б) толщина рабочих элементов конструкции пропорциональ¬
на квадрату масштаба линейных размеров, т. е. 6i~L2\
в) напряжения в стенках топливных баков от сил внутрен¬
него давления не зависят от масштаба ракеты;
г) напряжения в элементах конструкции, воспринимающих
аэродинамические нагрузки, не зависят от масштаба ракеты;
д) напряжения в элементах конструкции, работающих на
сжимающие силы, линейно пропорциональны масштабу ракеты,
/66
О 0.005 0,010 0,015 0,020J3At,С
~ i-Рг-Г
(6. 29}
При помощи эмпирических методов можно показать, что вес
двигательной установки пропорционален Р*и. Поскольку при
этом тяга пропорциональна G0~L3, то вес двигателя изменяет¬
ся как L3’75. Вес остаточного топлива приближенно пропорцио¬
нален L3.
Веса других элементов конструкции, являющиеся функцией
начального или конечного веса, а также связанные с наземный
ми нагрузками, подчиняются тем же законам, что-и элементы
конструкции, воспринимающие тягу двигателя, т. е. их вес про¬
порционален ZA
//
са элементов конструкции G3n/G0:
/—двигательная установка; 2—топливо,
остающееся в баках и двигателе; >3—
конструкция; 4—суммарный вес с уче¬
том технологии
На рис. 96 приведены безразмерные веса перечисленных эле¬
ментов конструкции в функции масштабного фактора L~ УG0.
При уменьшении размеров ракеты рабочие сечения элементов
конструкции не могут быть беспредельно уменьшены. Условия
производства и эксплуатации определяют практические пределы
минимально допустимых толщин. Это означает, что уменьшение
размеров ракеты после достижения минимально допустимых
толщин должно сопровождаться увеличением веса конструкции.
На графике верхняя кривая построена с учетом указанных фак¬
торов. Эта кривая показывает, что ракета имеет экстремальный
вес G0=G0*, которому соответствует минимальный вес конст¬
рукции. На рис. 97 представлена аналогичная кривая для числа
i I
Q 2000 -'tOOO 6000 8000 80,тс
Рис. 96. Влияние масштаба раке¬
ты L~p Gq на безразмерные ве-
Рис. 97. Типовой характер «весового
барьера» по числу Ц
167
Циолковского Ц, построенная в функции того же начального
веса G0. Экстремум такой зависимости был получен путем мас¬
совых расчетов по развернутым весовым зависимостям с учетом
нарастания нагрузок от собственного веса ракеты. Кривая пока¬
зывает, что реальная конструкция ракет содержит ограничения,
в силу которых число Циолковского не может быть увеличено
сверх определенной величины путем увеличения стартового веса
ракеты. Таким, образом, существует как бы «барьер» на пути
увеличения числа Циолковского или условно «весовой барьер»*
преодоление которого путем увеличения стартового веса ракеты
не представляется возможным. Увеличение веса свыше его
экстремального значения приводит не к увеличению, а наоборот,
к уменьшению числа Ц.
Изучение поэлементных весовых зависимостей для крылатых
ракетных систем возвращения показывает, что относительный
конечный вес ракетоплана цк может быть выражен основной ве¬
совой зависимостью вида
pK = aK + ?KGj/2 + YK(^-) , (6.30)
где
т L v
2 ,“/ + 2 + по 2 'х‘
т N
1 + 2 i*< ~ 2
г-1 <•-1
2 ч,-
„ ; } (6-31)
i=1 i=l
i-2 ^
т 1-1 у '
1 + 2 ы ~ 2
£=1 £ =1
Остальные параметры, входящие в зависимость (6.30), име¬
ют такое же происхождение, как и у основной весовой зависи¬
мости (6. 3).
В каждом конкретном случае при рассмотрении той или иной
конструктивно-силовой схемы ракеты возвращения (с аэродина¬
мическими поверхностями, несущий корпус, вертикальный старт,
горизонтальный старт), а также учете характера движения к
месту старта (гиперзвуковое планирование или маршевый полет
168
в присутствии реактивной тяги) зависимость (6. 30) может ви¬
доизменяться по количеству членов правой части и значениям,
входящим в нее весовых коэффициентов.
Легко видеть, что относительный вес элементов, определяе¬
мых вторым членом правой части зависимости (6.30), является
возрастающей функцией параметра G0 (влияние крыла, опере¬
ния), в то время как относительный вес постоянных грузов As
является убывающей функцией того же параметра G0. Указан¬
ные противоположно действующие факторы определяют экстре¬
мум, лежащий в точке
(GoW-(^ дф/3. (6.32)
Выражение (6. 32) указывает на вес G0, которому соответ¬
ствует максимальное значение весовой отдачи по топливу GT =
= (5т)пк.х- Этот вес является в то же время максимально допу¬
стимым весом, поскольку даль¬
нейшее его увеличение приво¬
дит не к увеличению запаса
топлива, а наоборот, к умень¬
шению этого запаса. Очевидно,
что при прочих равных усло-
0 Ш0 8000 12000 16000 00,тс
Рис. 98. «Весовой барьер» для двух
•случаев старта ракетоплана (РНМП):
■/—вертикальный старт; 2—горизонтальный
старт
Рис. 99. Влияние стартового веса и
полезного груза на весовую отдачу
маршевого ракетоплана (РНМП)
виях (удельных расходах топлива, весовых характеристиках эле¬
ментов конструкции, аэродинамических характеристиках и т. д.)
это означает ограничение дальности полета в соответствии с гра¬
ничным весом, определяемым выражением (6.32).
Кривые |ik = Pk(G0), иллюстрирующие явление весового
'барьера для ракетно-авиационных конструкций различного на-
169
значения и режимов полета, приведены на рис. 98 и 99. Как вид¬
но из графиков, вертикально стартующие ракетопланы имеют
значительно больший диапазон по стартовому весу и весовой от¬
даче по сравнению с ракетопланами, стартующими горизонталь¬
но. Влияние весового барьера сказывается тем быстрее, чем
больший относительный вес имеют элементы конструкции, отно¬
сящиеся к аэродинамическим и взлетно-посадочным устройст¬
вам (шасси, пневматики и т. д.). Уменьшение весовой отдачи
GT при увеличении груза Да (см. рис. 99) не может быть ком¬
пенсировано увеличением стартового веса G0. Это свидетельст¬
вует о том, что параметр G0 не является доминирующим факто¬
ром в достижении максимальных весовых отдач GT.
Таким образом, наличие весового барьера является крае¬
угольным камнем в оценке баллистических возможностей и лет¬
ных характеристик ракетно-космических систем. Изыскание пу¬
тей к преодолению весового барьера составляет одну из главных
задач при проектировании этих систем.
Пример 6.1. Составить основную весовую зависимость вида p,K = jJiK(e, п0)
для первой ступени составной ракеты, если неизвестны весовые зависимости
для несущих корпусов отсеков (работающих на осевые сжимающие силы),
а также данные по весу двигательной установки. Известными в задаче яв¬
ляются: весовая отдача рк=0,25; перегрузка первой ступени п0т= 1,25; вес
топлива первой ступени GTi=2500 тс; вес топливного бака Go=50 тс; вес;
деталей сборки G,1CT=30 тс; вес гарантийных запасов топлива Grap=25 тс;
конечный вес ступени GK =1175 тс.
Решение. Составим весовое уравнение вида
где последний член выражает неизвестный нам суммарный вес отсеков и
двигателя. Выполняя преобразования и подстановку заданных значений,
будем иметь
После разрешения относительно параметра k и подстановки остальных
значений для G0n, G0i и п0, получим
Таким образом, основная весовая зависимость принимает вид рк=
GK — Gg + G д е т + Grap + Goil + kP0,
GT -г Gon 4- kP0
или
и затем
или
Gn i г
=0.0301 -И .005 —^+0,023 /20.
При мер 6.2. Составить основную весовую зависимость вида
- * °гар, G0. п0, ут) для ракеты, имеющей следующие весовые
характеристики по элементам конструкции: топливные баки, арматура топ-
г °'2т.
ливпых оаков, система наддува О,-> = уi , двигательная установка, рама
Yt
двигателя, узлы крепления Сд.у—угРо; органы управления, монтажные узлы
и элементы жесткости б0.у=уз^о; гарантийные запасы компонентов топлива
СГар==Угар^2т* Значения коэффициентов у i принять следующими: Yi =
=5,9-Ю-2 тс/м3; у2=2,4-10-2; уз=1,510-2.
Решение. Составим весовое уравнение
С:к = Сб + Сд.у + Со.у+СГар + А^
«ли GK — Yi ч + Y2P0 + УзРо + YrapGST +
Yt
откуда
1 f Yi , , ,
— “ Yrap + V‘2n0 т Y3 — n
1 ■ Л. . , L Yr Gf)
1 ■ Yrap
Yt
Подставляя заданные значения коэффициентов уо получим окончательно
1
Рк = 7-Z X
о,9
1 + Ю" 2 + Yrap
Yt
5,9
X
■10“2 4- Yrap 4-2,4-10—2лг0 + 1,5-10-2 + —
L Yt 11 U Go
Пример 6.3. Вывести основную весовую зависимость вида рк=|Лк(е, п0)
для ракетоплана, имеющего следующие весовые характеристики по элемен¬
там конструкции: крыло GKY)—qKpSKV, фюзеляж Сгф =0,06 GT, оперение
Gon=0,014G0, шасси Gin=0,03 G0, органы управления G0.>- = 0,015 G0, двига¬
тельная установка G;i.>-=0,0i3 Ро, топливная система GT.C=0,022 G0, оборудо¬
вание G(i,-, =0,03 G0, экипаж G;)K=200 кгс.
Решение. Составим весовое уравнение для конечного веса ракетоплана
GK = GKp + Сф -f G0M + GUI +Goy т G ,>у 4- Gr>c 4- Go6 4- G3K 4- As
«ли
GK = ^KpSKp 4- 0,06GT -f 0,014G0 4- 0,03G0 4- 0,015G0 4-
4- 0,03P0 + 0,022G0 4- 0,03G0 4- Дa, ^ (6.33)
где -(0,2 + А) тс.
G0
После подстановки выражений SK[) и P0=G0n0 в уравнение (6.33),
Ркр
деления обеих частей на G0 и решения относительно tuK получим
1_ / _А_\
‘а,; ~ 1,06 \ pKV + Go /
+ 0,161 + 0,283/Jo,
Ркр U0
где qKj, — вес единицы поверхности крыла; ркр — нагрузка на единицу пло¬
щади крыла от начального веса ракетоплана.
СПИСОК ЛИТЕРАТУРЫ
1. Бонни Е. А., Цукров М. Д., Бессерер К. У. Аэродинами¬
ка. Теория реактивных двигателей. Конструкция и практика проектирования.
М., Воениздат, 1960, 672 с.
2. Т и х о и р а в о в Д1. К. Ракетная техника. М., ОНТИ, 1935, 78 с.
Глава VII
ХАРАКТЕРИСТИКИ РЕЖИМОВ ВЕРТИКАЛЬНОГО ПОЛЕТА
РАКЕТЫ В ПУСТОТЕ
С УЧЕТОМ ВЕСОВЫХ ФАКТОРОВ
В главе рассмотрены вопросы, касающиеся режимов верти¬
кального полета ракеты на активном и пассивном участках в
пустоте при двух законах изменения массы.
Дан анализ влияния стартовой перегрузки на режимы дви¬
жения без учета и с учетом весовых факторов. Показано, что
учет последних существенно меняет представления о критериях
оптимальности, получаемых методами теоретической ракетоди-
намики. Глава имеет целью показать важность учета весовых
факторов в теоретических исследованиях механики полета.
Глава содержит также исследования, касающиеся теорети¬
ческих основ космического поезда Циолковского. Этот материал
помещен безотносительно к характеру траектории полета и име¬
ет целью решение практических задач ракетодинамики.
В последнем разделе главы рассмотрен вертикальный по¬
лет ракеты на пассивном участке траектории с учетом сопро¬
тивления среды.
Рассмотрим движение в пустоте при W=const и g = const.
Поскольку
то на основании уравнения (2.41) при а(0к) = 1 получим
Таким образом, чтобы найти высоту подъема на активном
участке полета необходимо знать закон изменения массы f(t).
Для линейного закона изменения массы (2.7) имеет место-
зависимость
7.1. ВЫСОТА ВЕРТИКАЛЬНОГО ПОДЪЕМА
НА РАБОТАЮЩЕМ ДВИГАТЕЛЕ
ПРИ ДВУХ ЗАКОНАХ ИЗМЕНЕНИЯ МАССЫ
dt ’
(7.1)
172
тогда
H{t)= — W^\n{\ — $)dt—ZL.. (7.2)
Интегрирование (7.2) с учетом того, что Я<=0 = 0, дает
Ж0=//акТ=у[(1-^)1п(1-;«)+М—1^-. (7.3)
где индекс «акт» означает полет на активном участке траек¬
тории.
Формула (7. 3) выражает текущую высоту подъема в функ¬
ции времени работы двигателя t.
Рис. 100. Характер кривых #акх =
= //акт(ло) для двух законов изме¬
нения массы:
/—показательный закон; 2—линейный за¬
кон
Полное время работы двигателя при линейном законе изме¬
нения массы и 7^= Руд в соответствии с формулой (2.35) за¬
пишется так
* = —РуЛ-
Щ
При этом высота подъема на активном участке, на основа¬
нии выражения (7. 3), будет равна
W 2
g'4)
О,
т( 1 2^) —IX In —
\ 2пп I к U,
(7.4)
Характер кривой На1{Т = Н(п0) у построенной по формуле (7.4),
представлен на рис. 100. Как видно из графика, высота актив¬
ного участка по перегрузке п0 имеет максимум. Приравняв ну¬
лю производную dHimi:/dno и решив полученное уравнение от¬
носительно п0, найдем
я« = =-
(1-р-к)2
•С7т-р.к1пЦ
(7.5)
173
Выражение (7. 5) определяет перегрузку, которой соответст¬
вует максимальная высота активного участка Яакт= (Яант)тах.
Подставив выражение (7.5) в равенство (7.4), получим
(//,KTU=-^(i—|-1»ц)2. (7.6)
Это максимальная высота подъема на активном участке при
оптимальной перегрузке для линейного закона изменения массы.
Для показательного закона изменения массы на основании
(2. 9) имеет место соотношение
, , ,4 М rjf
и тогда по аналогии (7. 2)
н (/) = ;w j tdt - -J- . (7. 7)
После интегрирования выражения (7. 7) получим
* H{t) = QW-g)^. (7.8)
Поскольку
о "О
Ру,
то
= = (7.9)
В конце активного участка полета имеет место
РУ ' 1
In— ,
п0 Вк
и тогда
Яакт = ^(я„-1)(^1п — I. (7.10)
2 \ п0 \хк!
Зависимость Яакт = Яакт(/20), как и для случая линейного за¬
кона изменения массы, имеет экстремальный характер (см.
рис. 100). Приравняв нулю производную dHai{T/dn0, находим, что
п0 = 2. При этом в соответствии с формулой (7. 10) максималь¬
ная высота полета Яакт= (Яакт)тах определяется так
(И \ —W2 ( lnLt Г (7 1 1 л
( акт)тах 2° \ 2 / *
_ W2 ( 1м Ц \2
\ * акт 'max
174
Таким образом, с точки зрения чистой механики режим дви¬
жения при показательном законе изменения массы реализуется
тогда, когда ускорение, сообщаемое реактивной силой, не зави¬
сит от весовой отдачи и ровно в два раза больше ускорения
силы тяжести.
7.2. ВЫСОТА ВЕРТИКАЛЬНОГО ПОДЪЕМА
НА ПАССИВНОМ УЧАСТКЕ ТРАЕКТОРИИ
На пассивном участке траектории полета, после выгорания
топлива, ракету следует рассматривать как точку постоянной
массы, движущуюся в поле сил земного тяготения.
Для случая вертикального полета при движении точки в гра¬
витационном поле Земли дифференциальное уравнение для еди¬
ницы массы принимает вид
dv _ I R3
al Н*)' (7Л2)
где R = R з +Н.
Знак минус показывает, что действие сил тяжести происхо¬
дит в направлении, обратном движению.
Умножив обе части уравнения (7. 12) на clR и заменив в нем
V=dRfdt, получим
VdV=-g0^jdR.
Интегрирование этого выражения от Ик (конечной скорости)
до У и RK (конечного радиуса) до R дает
По мере подъема на высоту скорость полета уменьшается и
при # = #тах становится равной нулю. Положив при этом RK=
= R з, получим
"ma*= 17.14)
о„. _К_
Полученное выражение определяет высоту подъема ракеты
в поле переменных сил земного тяготения. Если имеет место
(VKZ/R3) <^2g0l то получим известную формулу Галилея для
случая полета в поле постоянных гравитационных сил
В дальнейшем мы будем пользоваться формулой (7. 15) при
рассмотрении задач, связанных с определением оптимальных па-
0 2^68 Vh,km/c
раметров полной высоты подъема
ракеты при двух законах изме¬
нения массы.
Зависимость высоты подъема
на пассивном участке от конеч¬
ной скорости VK представлена на
рис. 101. Интересно заметить, что
подъему на высоту, равную од¬
ному радиусу Земли (/?3~
— 6378 км), соответствует скорость
спутника на уровне моря, равная
Рис. 101. Зависимость высоты вертикаль¬
ного подъема ракеты на пассивном уча¬
стке траектории от конечной скорости
Любопытно также, что в поле постоянных сил земного тяго-
тения эта величина по формуле (7. 15) составила бы только по¬
ловину радиуса Земли, т. е. Ятах = /?з /2.
7.3. ВЛИЯНИЕ ПЕРЕГРУЗКИ НА ВЫСОТУ ВЕРТИКАЛЬНОГО ПОДЪЕМА
НА АКТИВНОМ УЧАСТКЕ ПРИ ДВУХ ЗАКОНАХ
ИЗМЕНЕНИЯ МАССЫ
Перепишем формулу для высоты вертикального полета раке¬
ты на активном участке траектории при линейном законе изме¬
нения массы (7. 4) в следующем безразмерном виде:
^r = 4f-=— (7Л6)
wPyл по \ GT Рк 2/10)
где имеется в виду, что п^ = п^.
Учет весовых факторов произведем при помощи зависимости
(6.9). После подстановки выражения для рк по этой зависимо¬
сти в формулу (7. 16) получим
/_/ 1 — (рэл кщ)
11 а кт
1 + . 7' : ■*? 71п ^ + кПо} ~
1 — (м-э.1 + kn0)
1 — (^эл + кп0)
(7- 17)
2 п0
Кривая ЯакТ = ^акт(рк)» построенная по уравнению (7. 17) с
учетом влияния параметра п0, представлена на рис. 102. Как
176
видно из графика, функция #ант = #акт(п0) имеет максимум. Для
отыскания этого максимума приравняем нулю производную от
Яакт по "о- Тогда получим
rftfaKT
dn-л
= nik In Ц - [Gt (k - 1) 4- J*K In Ц] По - (1 - цк)а = 0,
откуда оптимальная перегрузка выразится так:
Р \2 | (1-м-к)2
2 / k In Ц
Л»-—§-+[(i
1/2
(7. 18)
где
'“'г-
In Ц
\Ы
Рис. 102. Влияние стартовой перегрузки на высоту
вертикального полета ракеты при линейном и показа¬
тельном законах изменения массы:
/—линейный закон; 2—показательный закон
Воспользовавшись формулой высоты полета на активном уча¬
стке для случая показательного закона изменения массы (7.10)
с учетом весовой зависимости (6. 9) и поступая аналогично, по¬
лучим также
Формулы (7. 18) и (7. 19) выражают оптимальные стартовые
перегрузки /г0=(/г0)опт в функции параметров рн и /г, которым
соответствуют максимальные высоты подъема ракеты на актив¬
ном участке траектории при линейном к показательном законах
изменения массы.
Кривые оптимальных перегрузок я0 = ц0(рк), построенные для
двух законов изменения массы по формулам (7. 18) и (7. 19),
представлены на том же графике (см. рис. 102). Там же для на¬
глядности приведена зависимость Цо = ^0(рк), построенная по
формуле (6.9). Кривые на графике иллюстрируют оптимальную
перегрузку в точке Л, которой соответствует максимум высоты
Яакт= (Яакт)тах в точке Б. Величина перегрузки в точке С сов¬
падает с оптимальной перегрузкой в точке А. Как видно из гра¬
фика, функция п0 = п0(цк) в свою очередь имеет максимум для
обоих законов изменения массы, что является также следствием
влияния весовых факторов.
7.4. ПОЛНАЯ ВЫСОТА ПОДЪЕМА
ПРИ ДВУХ ЗАКОНАХ ИЗМЕНЕНИЯ МАССЫ
Полная высота вертикального полета ракеты Я а будет скла¬
дываться из высоты полета на активном участке Яакт и высоты
полета на пассивном участке Япас- При этом
//а //акт —j— У /пас.
0,2
И1
/
Мк=0,5
Пакт
Рис. 103. Влияние перегрузки на высоту
полета при линейном законе изменения
массы без учета весовых факторов
8 п0
Имея зависимости (7.4) и (7. 15), а также воспользовавшись
формулой Циолковского для линейного закона изменения массы
(2. 44), запишем в безразмерном виде
Н у
©
По
|у , —1п Ц-
2/1о
1пЦ —
дД2
По
[7.20)
Как видно из формулы (7.20) и кривых на рис. 103, постро¬
енных по этой формуле, несмотря на экстремальный характер
зависимости Яакт = Яакт( /г0), увеличение перегрузки п0 вызыва¬
ет непрерывное увеличение суммарной высоты полета Я а .
Поступая аналогично для случая показательного закона из¬
менения массы с учетом зависимостей для высоты подъема на
178
активном участке (/. 10), пассивном участке (7.15) и скорости в
конце активного участка (2. 47), получим
Ну
Из формулы (7.21) и графика (рис. 104), построенного по
этой формуле, следует, что максимальная высота подъема Н%
будет при /го=оо. Значение п0=оо соответствует мгновенному
сгоранию имеющегося запаса топлива (т. е. такому случаю, ког¬
да весь имеющийся запас топлива выбрасывается ■ в начале
движения с относительной скоростью истечения W). Макси¬
мальная высота подъема в этом случае, как легко видеть из
формул (7.20) и (7.21) не зависит от закона расхода активной
массы и равна
Я1!11М = ^-(1пЦ)а. (7.22)
7tf
■— (1пЦУ-.
«о
(7.21)
Рис. 104. Влияние перегрузки на высоту
полета при показательном законе изме¬
нения массы без учета весовых факторов
Таким образом с точки зрения чистой механики, в однород¬
ном поле силы тяжести в тех случаях, когда силами сопротив¬
ления можно пренебречь, для достижения максимальных высот
подъема выгодно как можно быстрее израсходовать заданный
запас топлива.
Скорость в конце активного участка полета при показатель¬
ном законе изменения массы определяется по формуле (2.47).
Переписав ее в безразмерном виде и подставив значение пере¬
грузки /20 = 2, получим
Ук = ±ых. ,(7.23)
Подсчитаем теперь суммарную высоту подъема в режиме
перегрузки п0 = 2. При этом, воспользовавшись формулой (7.21),
получим
//2=-^-(1пЦ)3. (7.24)
Чг
Сравнивая выражения (7.22) и (7.24), видно, что при мгно¬
венном отбрасывании данного запаса массы высота подъема ра¬
кеты в два раза больше, чем при медленном горении, когда мы
Желаем получить максимальный активный участок.
179
Воспользовавшись формулами (7.10) и (7.21), найдем от¬
ношение суммарной высоты подъема к высоте подъема на ак¬
тивном участке траектории. Тогда получим
(7.25
То есть, полная высота подъема при показательном законе
изменения массы по сравнению с высотой на активном участке
больше в п0 раз. При оптимальной перегрузке п0 = 2, высота
подъема на активном и пассивном участках одинакова.
Полученные здесь выводы являются результатом рассмотре¬
ния задач методами чистой механики. Как будет показано ни¬
же, учет весовых факторов существенно меняет представление
об оптимальности аналогичных режимов движения.
7.5. ВЛИЯНИЕ ПЕРЕГРУЗКИ НА ПОЛНУЮ ВЫСОТУ
ПОДЪЕМА ПРИ ДВУХ ЗАКОНАХ ИЗМЕНЕНИЯ МАССЫ
Влияние перегрузки п0 на полную высоту полета Нs учтем,
как и ранее (см. разд. 7.3), при помощи основной весовой за¬
висимости (6. 9).
Для линейного закона изменения массы формула полной вы¬
соты полета (7.20) с учетом (6. 9) дает сложную зависимость
//s = Нъ (я0), отыскание оптимальной перегрузки по которой
следует производить численно.
Для показательного закона изменения массы, имея формулу
(7. 21), легко записать
——- = (1 - —) ('In ! )2 . (7. 26}
(W2_\ I «о А Иэл+W
\ 2 g )
Приравняв нулю производную dHs /dn0 и решив получен¬
ное уравнение относительно п0, найдем
Оптимальная перегрузка, определяемая формулой (7.27),
в свою очередь имеет экстремальное значение по параметру цк.
Приравняв нулю производную dn0/d\iKi получим In Ц= 1 и затем
Рк= 1/е.
При этом максимальное значение оптимальной перегрузки
составит
(7. 27)
П0 max
(7. 28)
180
Если принять в формуле /г = 0,02, то максимальное значение
оптимальной перегрузки будет n0max = 3,57.
7.6. КОСМИЧЕСКИЙ РАКЕТНЫЙ ПОЕЗД ЦИОЛКОВСКОГО.
КОНЕЧНАЯ СКОРОСТЬ РАКЕТНОГО ПОЕЗДА
Космический ракетный поезд, как новая идея ракетодинами-
ки, был впервые сформулирован и обоснован К. Э. Циолковским
в его одноименной работе, изданной в Калуге коллективом Ка¬
лужской секции научных работников в 1929 г.
нп
cfy Отделение заправщика I ст.
Одозначе н и я
А Ракета с полным запасом
топлива
А Ракета с частично израс¬
ходованным топливом
Д Пустая ракета в свободном
полете
НП - Направление полета
Рис. 105. Схема полета ракетного поезда по Циолковскому:
/—конец активного участка I ступени. Топливо израсходовано на 1/4.
Отделяющийся заправщик переливает топливо в остающиеся ракеты;
2—конец активного участка II ступени. Топливо израсходовано на 1/3.
Отделяющийся заправщик переливает топливо в остающиеся ракеты;
3—конец активного участка III ступени. Топливо израсходовано на 1/2.
Отделяющийся заправщик переливает топливо в остающуюся ракету;
4—конец активного участка последней ступени. Топливо полностью
израсходовано
ч ст.
181
Под ракетным поездом Циолковский подразумевал соедине¬
ние определенного количества ракет, стартующих одновременно
для получения необходимой конечной скорости (рис. 105).
Рассмотрим движение ракетного поезда, составленного из
т одинаковых ракет.
Все ракеты имеют одинаковые начальные веса G0 и весовые
отдачи GT. Полет ракетного поезда происходит за счет перелива
топлива из ракет предыдущей ступени в ракеты последующих
ступеней. Каждая последующая ступень ракетного поезда обра¬
зуется путем отброса ракет-заправщиков предыдущей ступени,
которые после израсходования у них топлива составляют уже
пассивную массу поезда. Ракета последней ступени не выполняет
функции заправщика и несет груз, предназначенный для сооб¬
щения ему необходимой конечной скорости.
Движение каждой ступени поезда будем рассматривать как
движение одноступенчатой ракеты, состоящей из активной и
пассивной масс. Активную массу составляет расходуемое топ¬
ливо; пассивную массу — конструкция поезда.
Если число ракет-заправщиков первой (данной) ступени рав¬
но /П;3 (где индекс «з» означает «заправщик»), то весовая отда¬
ча по топливу на этой ступени будет равна
/?2 3tGt тз1 ^
и т1 — — — и т,
mCiQ т
где GT — вес топлива одной ракеты.
После отделения тя\ ракет-заправщиков первой ступени на
второй ступени остается (т — тя i) ракет и весовая отдача при
/773 п ракет-заправщиков будет равна
П ^зИ П
игц— их.
т - т3]
Для г-й ступени можно записать
, = = ^ F О,
['«з!+■
- т
или
G ■ = ^ G
1' L L —1
Весовая отдача последней ступени не меняется и остается
равной GTn = GT2 (где индекс «/» означает любую из составляю¬
щих ракет поезда).
182
Переходя к весовой отдаче по конечному весу цк ?, запишем
!\i = 1
о,;
т
™зн
Оа
ftdll — ^
т — т3\
тз\и
т — (m3j -h тзи)
о,;
■On
• (7. 29)
— Отл= 1 — От,
где индекс «п» означает последнюю ступень поезда.
При этом, как и ранее (2.49), величина коэффициента рк"
для ракетного поезда будет равна
П
Ракетные поезда, движение которых обеспечивается непре-
рывным (поочередным) отбросом по одной ракете в каждой сту¬
пени (m3 i = m3 h = W3(?i-i)= 1), называются непрерывными ра¬
кетными поездами. Для таких поездов формулы (7. 29) еще бо¬
лее упрощаются и принимают вид
^1=1-
От .
G...
т— 1
От .
т — 2
/ = 1 —
G-
т — (/ — 1)
(7. 30)
Ркя=1-От.
Термин «непрерывные поезда» является чисто условным и
употребляется по аналогии «непрерывных ракет» Ф. А. Цанде¬
ра, у которых отброс пассивных масс (конструкции) происходит
также непрерывно, как и отброс активной массы (топлива) [3].
18а
Полет ракетного поезда, составленного из одинаковых ракет,
происходит не при оптимальных условиях с точки зрения мини¬
мального веса всей системы. Однако в силу одинаковости ра¬
кет, такое соединение имеет определенный практический инте¬
рес. Действительно, не прибегая к созданию новой ракетной систе¬
мы, ракетный поезд обеспечивает получение той или иной
дальности полета путем соединения существующих ракет в ра¬
кетный поезд. Неизбежное ухудшение при этом характеристик
используемых ракет (в результате доработок) вполне окупает¬
ся большими преимуществами многоступенчатого полета ракет¬
ного поезда. Зависимости = Для различных вариантов
ступенчатого и непрерывного поездов приведены на рис. 106. Из
графика видно, что непрерывные поезда имеют преимущества
перед поездами ступенчатыми. Это объясняется тем, что непре¬
рывные поезда более часто производят отброс пассивных масс
(пустых ракет-заправщиков).
Трехступект- Иепрерыдныа
поезо крь/ли¬
тый. поезд кры¬
латых ракет
тых ракет
1ст.
Ист.
Шст.
А
А
/ст.
Ест.
Шст.
Шст.
Ест.
. Шст.
Рис. 106. Зависимость = Мк* (Щ 0 для непрерывного и сту¬
пенчатого ракетных поездов:
/—трехступенчатый поезд; 2— непрерывный поезд
Необходимо заметить, что чисто теоретически непрерывная
схема ракетного поезда при условии большого числа заправщи¬
ков (га—^оо) является наиболее оптимальной. Это видно из си¬
стемы (7.29), где весовая отдача непрерывно уменьшается
при увеличении параметра га. Аналогичная зависимость для
р* = ^.(га) приведена на рис. 107.
Схемы образования ступеней у различных типов поездов на
графике (см. рис. 106) приведены применительно к крылатым
ракетам многоразового действия. Такие поезда с возвращением
184
заправщиков к месту старта имеют наибольший практический
интерес.
Рис. 107. Влияние «непрерывности» (ко¬
личества ракет) на величину приведенной
весовой отдачи ракетного поезда Циол¬
ковского
0 2 4 6 8 т
Безусловно, ракетные поезда могут быть составлены и из не¬
одинаковых ракет. При расчете весовых отдач таких поездов
зависимости (7.29) должны быть соответственно скорректиро¬
ваны.
7.7. ВЕРТИКАЛЬНЫЙ ПОДЪЕМ РАКЕТЫ
НА ПАССИВНОМ УЧАСТКЕ ТРАЕКТОРИИ
С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
Для вертикального полета угол, составляемый вектором ско¬
рости и горизонта, равен 0 = я/2. Кроме того, из уравнения дви¬
жения в проекции на нормаль к траектории полета следует, что
L = 0. Уравнения движения принимают вид
M-=-X(V)-Q;
dt
**L=v
dt
Исключая время,
получим
dV _ __
dH ~
X{V)
G
+1]
(7.31)
(7. 32)
В общем виде интегрирование этого дифференциального урав¬
нения возможно выполнить с помощью приближенных методов.
Однако, если коэффициент аэродинамического сопротивления
принять постоянным, то при условии экспоненциального закона
изменения плотности среды можно получить аналитическое реше-
185
ние. Оно будет
v=vl exp [_2Х(е“рЯв-е-р")]-
— 2g-exp(2/.e_?//) [R(H) — R(H0)\, (7.33)
где Но — высота начала пассивного полета (в момент выключе¬
ния двигателя). В формуле (7. 33) имеют также место
V*x =
'2G/SM \i/2.
'Hvxf ’
R (Я) = - 4- [ - W - 2Xe”?" + (- 2Xe_?")2 —
? L 2-
2!
+ (-2Хе-?")
3-3!
Если 2A,<Cl, то решение существенно упрощается, так как
тогда при любом Н>Н0>0 ехр 1 -\-2ке-^н°и R(H)~H.
Обращаясь к системе дифференциальных уравнений (7.31),
легко заметить, что она описывает случай восходящего движения
геликостата при действии силы, направленной против вектора
скорости. Таким образом, между вертикальным полетом ракеты
на пассивном участке и подъемом геликостата в режиме замед¬
ления (тяга двигателей выполняет роль гравитационных сил-,
если она по величине равна весу корабля) существует траектор-
но-параметрическая аналогия.
Пример 7. 1. Во время свободного падения тела для сохранения средней
высоты полета к нему прикладывается реактивная сила, создающая компен-
Таблица 7. /
Ступе¬
ни
LL . =UL
' К 1 ‘К
0
0,1
0,2
0,3
0,4
0,5
0.6
0,7
0,8
0,9
1,0
I
Ук 1 = 1 —
3
— — (1— Ук)
О
—
0,55
0,6
0,65
0,7
0,75
0,8
0,85
0,9
0,95
1,0
II
Ук 11 = 1 —
-у (1—fXK)
—
0,4
0,466
0,533
0,6
0,667
0,733
0,8
0,867
0,933
1 ,о
III
Ук 111 =
= Ук/ = У к
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
*
Ук
0
0,022
0,056
0,104
0,168
0,25
0,352
0,475
0,624
0,798
1,0
186
Таблица 7. 2
188
сирующее ускорение а. Определить, во сколько раз это ускорение должно
быть больше ускорения гравитационных сил q. Принять время свободного
полета (со снижением) равным t, а время действия на тело реактивной силы,
равным т-
Решение. Во время свободного падения тело проходит путь s=qt2/2.
Аналогично при действии ускорения тело набирает высоту, равную И=
=ат2/2. Для сохранения средней высоты полета необходимо, чтобы высота
падения и высота подъема были одинаковыми. Следовательно, необходимо
приравнять правые части выражений s(t) и Н(т). При этом получим
(тМтГ
Таким образом, отношение ускорений равно квадрату обратного' отно¬
шения времен действия этих ускорений.
Пример 7. 2. Построить кривые приведенных весовых отдач рк = цк (р.к t-)
для трехступенчатого и непрерывного поездов Циолковского, составленных
из шести (т=6) одинаковых ракет. Отделение ракет в трехступенчатом
поезде принять по схеме:
на первой ступени — три ракеты (т3i=3);
на второй ступени — две ракеты (тзП=2).
Решение. Воспользовавшись формулами (7.29), перепишем их примени¬
тельно для трехступенчатого поезда и произведем вычисления для различных
значений весовых отдач при р,Кг=Рк. Значения приведенных весовых отдач
определим по формуле
п
Р-К = П p-к i »
i =1
где п — число ступеней.
Результаты вычислений сводим в табл. 7. 1.
Для непрерывного поезда Циолковского поступим аналогично, восполь¬
зовавшись формулами (7. 30) при т=6. Вычисления сводим в табл. 7. 2.
Обе кривые, построенные по данным этих таблиц, приведены на графике
(см. рис. 106).
Пример 7.3. Показать влияние «непрерывности» (количества ракет т)
на величину приведенной весовой отдачи ракетного поезда Циолковского.
Расчет произвести для двух случаев, когда весовые отдачи составляющих
ракет равны
Ркг = Рк = 0,2
и
Ркг = Рк=0,6.
Решение. Для определения влияния «непрерывности» иа величину при¬
веденной весовой отдачи рк следует воспользоваться формулами (7.30) и
(2.49) и выполнить расчеты по формулам, приведенным в табл. 7.3.
По данным таблицы для pKi=0,6 построен график (см. рис. 107).
СПИСОК ЛИТЕРАТУРЫ
1. Зенгер Е. Техника ракетного полета. М., Оборонгиз, 1947.
2. Циолковский К. Э. Труды по ракетной технике. М., «Машино¬
строение», 1967, 376 с.
3. Ц а н д е р Ф. А. Проблемы полета при помощи реактивных аппара¬
тов. М., Оборонгиз, 1964, 459 с.
Глава VIII
ОПТИМАЛЬНЫЕ РЕЖИМЫ В ПРОСТЕЙШИХ СЛУЧАЯХ
ДВИЖЕНИЯ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ
Материал главы представлен в виде трех задач Космодемьян¬
ского, первая из которых посвящена прямолинейному движению
точки переменной массы в среде с квадратическим законом со¬
противления среды; вторая — движению точки переменной мас¬
сы в среде, сила сопротивления которой изменяется по линей¬
ному закону; третья — горизонтальному движению ракетоплана
при равновесии вертикальных сил.
Эти задачи исследованы с учетом уравнений весового балан¬
са, вследствие чего получены новые данные, касающиеся экст¬
ремальных движений точки переменной массы.
Применение к точке (или телу) переменной массы законов
весового анализа также правомерно, как правомерно примене¬
ние к ней законов аэро- и гидродинамики. Получаемый при этом,
результат существенно расширяет область исследований, важ¬
ных для практики, и является полезным с точки зрения инженер¬
ной интерпретации основ практической ракетодинамики.
В первой задаче проф. А. А. Космодемьянского рассматри¬
вается случай прямолинейного движения точки переменной мас¬
сы в сопротивляющейся среде; принимается квадратический за¬
кон аэродинамического сопротивления при постоянном секунд¬
ном расходе массы, т. е.
Таким образом, рассматривается движение точки перемен¬
ной массы по абсолютно гладкой горизонтальной плоскости,
когда вес точки уравновешивается нормальной реакцией этой
плоскости. Решение, полученное при рассматриваемом условии,
полезно с точки зрения изучения неустановившегося горизонталь¬
ного полета ракетного самолета.
Дифференциальное уравнение движения точки запишем в
следующем виде:
где X(V)—сила аэродинамического сопротивления в функции
скорости полета.
190
8. 1. ПЕРВАЯ ЗАДАЧА КОСМОДЕМЬЯНСКОГО
= const.
(8.1)
При постоянной тяге имеет место линейный закон изменения
q — плотность среды на данной высоте полета; S — харак¬
терная площадь, к которой отнесены аэродинамические коэффи¬
циенты.
Разделяя переменные в уравнении (8. 2) и интегрируя при
условии, что Vt=o = 0, получим
где WX = W/V*X.
Безразмерная конечная скорость при t=x и (Зт=GT будет
равна
На рис. 108 представлена зависимость безразмерной конеч¬
ной скорости (l/K V'x) от весовой отдачи рк, построенная по
формуле (8.4). Эта зависимость показывает, что конечная ско¬
рость ракетоплана заметно возрастает по мере уменьшения па¬
раметра pic и увеличения безразмерной скорости истечения Wх-
При увеличении стартовой перегрузки п0 скорость полета непре¬
рывно увеличивается (рис. 109).
Этот результат имеет чисто теоретический интерес. Ниже бу¬
дет показано, что с учетом реальной конструкции перегрузка
имеет свое оптимальное значение.
массы М = М0( 1 — (5/). При этом
—) = (Ш0 и, следовательно,
dt
(8.2)
где
const;
1 + (1 — v"°
(8.3)
(8.4)
191
Найдем далее закон изменения пути. Исходя из форму¬
лы (8. 3), запишем
<IL=«± , (8.5)
dt df dt 0 9
1 -f / VTo
где/=1—pt. Поскольку (df/dt)= — p,
TO
/ _
w
и затем
A_ V* I f Yn0 __ .
L = Vn0-* \ -Д= -<//,
° 3 1 J
1 I 2 A
/ ]/"° + 1
£=v4^(/-i)+v4^2 Г—(8-6)
§ 3
№'
XI
/ По
Рис. 108. Влияние параметров
и Wх на конечную скорость движе¬
ния точки переменной массы в пер¬
вой задаче Космодемьянского без
учета весовых факторов
0,6
(
m,~o,s
^ в
О 2 4 6 8 п0
Рис. 109. Влияние перегрузки nG
на конечную скорость движения
точки переменной массы в первой
задаче Космодемьянского без уче¬
та весовых факторов
W
При любых значениях 2 Л ,интеграл не может быть выра-
V по
жен в квадратурах. Поэтому представим подынтегральную функ-
192
цию в виде
-1—^1 ^//Л“ .
2
1 + /
/л0
При этом приближенное значение искомого интеграла будет
равно
df
7 1+/
V По
'=2^/«0
2 1
I L f Vno
!rf/ =
= 2-f (1 -/)-
* V4V1-/
21Г,
/л0
Расстояние, проходимое точкой переменной массы, выразит¬
ся формулой
L{t) = Vx Vn0
t /яр
l 2Г*р
/г; I
(8.7)
Очевидно, что полученная зависимость справедлива в том
случае, если сделанное выше допущение обеспечивает доста-
Wx
точную точность при данных значениях параметра 2 —-=■
У п0
Формула (8.7) выражает расстояние в функции времени
движения точки. Расстояние в конце движения при t=% и |к=
= GT будет равно
v
р^РуЛ 1-Ю
Yn о
1
1 — и ^п° J Г—
h /«о
2W х (1 — (хк)
Можно показать, что зависимость L=L(nо) является моно¬
тонно убывающей функцией параметра п0. Действительно, возь¬
мем производную от L по п0.
Тогда получим
dL
dn0
vxPy*
' 2nf
he
V По
In
(1 —P-к)
+ 1/(1 — (Ак).
Знак минус показывает, что при всех значениях перегрузки в
интервале от п0=0 до п0= оо, производная dL/йщ отрицатель-
7 3479 193
на. Из этого следует, что если прямолинейное движение точки
переменной массы происходит под действием только двух сил:
реактивной и силы сопротивления среды, то наивыгоднейшее зна¬
чение перегрузки должно быть бесконечно малым для получе¬
ния максимальной дальности полета.
С практической точки зрения полученный результат показы¬
вает, что чем большее значение в общем балансе внешних сил
имеют силы сопротивления среды, тем меньше оптимальный
расход топлива, обеспечивающий максимальный пройденный
путь прямолинейного движения.
Ниже будет показано, что с учетом весовых факторов стау
товая перегрузка имеет конечное оптимальное значение, кото¬
рому соответствует наибольший проходимый путь и наибольшая
скорость полета.
Воспользовавшись основной весовой зависимостью (6.9) и
формулой для конечной скорости точки переменной массы (8. 4Л,
после выполнения несложных преобразований получим
Кривые FK = FK(/Zo), построенные по формуле (8.8) для раз¬
личных значений параметра Wх, приведены на рис. 110. Как
видно из графика, функция 7к = 7к(п0) имеет максимум. Таким
образом, в отличие от предыдущего случая (см. разд. 8. 1) мак¬
симальная скорость полета достигается не при максимальной
перегрузке, а при перегрузке, имеющей свое оптимальное значе¬
ние tiQ= (fio)опт- Это результат учета весовых факторов. Физи¬
чески это понятно, поскольку непрерывное увеличение перегруз¬
ки привело бы в конечном счете к превращению точки перемен¬
ной массы в точку постоянной массы, для которой имело бы ме¬
сто |Лк=1. Применительно к ракетоплану это означало бы, что
для большого двигателя (по весу, тяге и габаритам), заполнив¬
шего всю конструкцию летательного аппарата, не осталось бор¬
тового запаса топлива.
График (см. рис. 110) показывает также, что увеличение ско¬
рости истечения Wx вызывает смещение оптимальных перегру¬
зок в сторону их более высоких значений. Это происходит пото¬
му, что при большей скорости истечения имеет место понижен¬
ный расход топлива, вследствие чего текущая скорость умень¬
шается. Для сохранения скорости (при завышенной текущей
массе), когда имеет место оптимальный баланс сил, в том чис¬
8. 2. УЧЕТ ВЕСОВЫХ ФАКТОРОВ
В ПЕРВОЙ ЗАДАЧЕ КОСМОДЕМЬЯНСКОГО
1 + (Рэл + kn0) Vn°
(8.8)
194
ле и аэродинамических, перегрузка по—(п^)опт должна быть
увеличена.
Выражение для оптимальной перегрузки найдем, приравняв
нулю производную dV-^/drio. Тогда получим
/ .?л-\
О 10 20 30 40 П0
Рис. ПО. Влияние стартовой
перегрузки и параметра Wx на
конечную скорость точки пере¬
менной массы с учетом весовых
факторов в первой задаче Кос¬
модемьянского
Рис. 111. Влияние весовой отда¬
чи на оптимальную перегрузку
при учете весовых факторов в
первой задаче Космодемьян¬
ского
Характер изменения оптимальной перегрузки п0= (ясОопт по
параметру цк, полученный по уравнению (8. 9) при Wх—0,25
и £=0,02, показан на рис. 111. Как видно из графика, оптималь¬
ная перегрузка уменьшается по мере уменьшения запаса пере¬
менной массы. Это является результатом учета сил сопротивле¬
ния, меньшее значение которых особенно желательно при малых
запасах топлива. Очевидно, что наши выводы справедливы без
учета вертикальных сил, когда в рассмотрении задачи отсутст¬
вуют гравитационные факторы.
8.3. ВТОРАЯ ЗАДАЧА КОСМОДЕМЬЯНСКОГО
Вторая задача проф. А. А. Космодемьянского рассматривает
случай движения точки переменной массы в среде, сила сопро¬
тивления которой изменяется по линейному закону.
7* 195
Пусть точка движется прямолинейно по горизонтальной аб¬
солютно гладкой плоскости, причем масса точки изменяется по
линейному закону.
Запишем уравнение движения в следующем виде:
м— =(—^7) w—kxV,
(8. 10)
dt \ dt)
где kx — коэффициент сопротивления.
Интегрирование обыкновенного линейного неоднородного
дифференциального уравнения первого порядка (8.10) дает
V
-1-1
Мп
dt
/
С
~*У-7
ехр
где С — постоянная интегрирования;
М
У М0
При i=0 скорость V=0 и /= 1, тогда
i/=с/Ш+Ш~м0
X
'[Ух.
J Щ
dt
1dt
С—%-М„
Rx
Скорость движения точки будет равна
*Х
(8.11)
Интегрируя (8. И) при условии, что при t—0 и L = 0, полу¬
чим формулу для расстояния, проходимого точкой за время /,
W
(-
Uo ,
1 +
t —
i — (1 -ю
т0
Р +
(8. 12)
В конце движения t =т и тогда формулы (8. 11) и (8. 12)
перепишутся так:
Кривые Кк=Кк(ио) И Хакт = Ьакт(«о), построенные по форму¬
лам (8. 13) и (8. 14) с учетом весовой зависимости (6.9), пред¬
ставлены на рис. 112.
Рис. 112. Влияние стартовой пере¬
грузки на скорость VK и дальность
полета Laкт во второй задаче Космо¬
демьянского при учете весовых фак¬
торов:
/—скорость; 2—дальность
Как видно из графика, при движении точки в среде, сила
сопротивления которой изменяется по линейному закону, суще¬
ствуют оптимальные перегрузки, которым соответствуют макси¬
мальная конечная скорость движения VK и максимальная даль¬
ность полета LaKT при работающем двигателе.
Без учета весовых факторов максимальное расстояние,
пройденное точкой, имеет место при п0=0. В соответствии с
формулой (8. 14) это означает, что
Спах = ОоХ^1-!*к). (8Л5)
X
Как показал проф. А. А. Космодемьянский, результат (8. 15)
означает, что если в среде с линейным законом сопротивления
точка получает некоторую конечную кинетическую энергию, то
она проходит вполне определенный конечный путь.
8.4. ТРЕТЬЯ ЗАДАЧА КОСМОДЕМЬЯНСКОГО
Третья задача проф. Космодемьянского посвящена горизон¬
тальному движению ракетоплана при равновесии вертикальных
сил.
Изучается движение самолета с жидкостным ракетным дви¬
гателем, когда изменение массы на активном участке полета
происходит только за счет истечения продуктов сгорания топ¬
лива. Предполагается, что W—const, а сила сопротивления и
подъемная сила пропорциональны квадрату скорости. Имея в
виду, что вектор тяги совпадает с вектором скорости, запишем
уравнение движения в следующем виде:
dV
М-
dt
—) w—x,
dt j
(8. 16
где X — сила аэродинамического сопротивления.
Условие равновесия вертикальных сил при постоянном аэро¬
динамическом качестве дает
или
где
Х = Мп
■te)
X
m
(8. 17)
Поступая далее как и в случае вывода второго закона Циол¬
ковского для двух законов изменения массы (см. разд. 2. 11 и-
2. 12), получим в окончательном виде
VK = W
1пЦ
Су_
СХ
по
для линейного закона изменения массы и
1
VK = W
1-
По
In Ц
(8.18)
(8. 19)
для показательного закона изменения массы.
Легко видеть, что формулы (8. 18) и (8. 19) аналогичны вы¬
ражениям для конечной скорости ракеты при двух законах изме¬
нения массы (2. 44) и (2. 47). В них только влияние сил тяжести
уменьшено в Раз-
Опуская выкладки, аналогичные выкладкам при выводе фор¬
мул (7.4) и (7. 10), дальность полета при равновесии вертикаль¬
ных сил и постоянном аэродинамическом качестве запишем сле¬
дующими выражениями:
W 2 ,
2(tb
(8.20-
198
для линейного закона изменения массы и
(In Ц)2
(8.21)
для показательного закона изменения массы.
При (— )=1 формулы (8.20), (8.21) и (7.4), (7.10)
идентичны.
Имея (8.20), приравнивая нулю производную dLK!dn0 и раз¬
решая затем полученное выражение относительно Яо=(^о)опт.
получим
Поступая аналогично для случая показательного закона из¬
менения массы, на основании (8.21) получим также
Как видно из формул (8.22) и (8.23), оптимальная пере¬
грузка горизонтально летящего ракетоплана обратно пропор-
циональна величине аэродинамического качества.
Формула (8. 23) аналогична ранее полученному решению для
вертикального подъема ракеты (см. разд. 7. 1). В ней только
гравитационные потери уменьшены величиной аэродинамическо¬
го качества (су/сх).
Рассмотрим далее, какое влияние оказывает на выбор пере¬
грузки при линейном и показательном законах изменения мас¬
сы учет весовых факторов.
8.5. УЧЕТ ВЕСОВЫХ ФАКТОРОВ В ТРЕТЬЕЙ ЗАДАЧЕ
КОСМОДЕМЬЯНСКОГО ПРИМЕНИТЕЛЬНО К ДВУМ ЗАКОНАМ
ИЗМЕНЕНИЯ МАССЫ
Рассмотрим влияние стартовой перегрузки на дальность го¬
ризонтального полета ракетоплана при линейном и показатель¬
ном законах изменения массы.
Пользуясь формулами горизонтальной дальности полета для
двух законов изменения массы (8.20) и (8.21) и выполняя дей¬
ствия, аналогичные разд. 7. 3, получим в окончательном виде
(8. 22)
2
(8. 23)
для линейного закона изменения массы и
Р-к
•f+ш
k (Су/Сх)
где
In Ц
1/2 , (8. 25)
/?1 = — 1пЦ L_
2k {Су/сх)
для показательного закона изменения массы.
Если в формулах (8. 24) и (8. 25) исключить влияние на пере¬
грузку сил тяжести, положив при этом (су/сх)= оо, то получим
Яю=0. Это означает, что в отсутствии сил земного тяготения
главенствующую роль в достижении скорости или дальности
полета играет число Циолковского, величина которого согласно
формулам (разд. 2. 8 и 6. 1) тем больше, чем меньше стартовая
перегрузка Последнее обстоятельство, как мы уже знаем,
объясняется в возможности облегчения конструкции в результа¬
те постановки более легкого (меньшей тяги) двигателя, а сле¬
довательно, и получения более совершенной конструкции с ее
минимальной весовой отдачей цк.
8.6. ВЕРТИКАЛЬНОЕ ДВИЖЕНИЕ ЛЕТАТЕЛЬНОГО АППАРАТА
В ПРИСУТСТВИИ ТОРМОЗЯЩЕЙ РЕАКТИВНОЙ ТЯГИ
Рассмотрим вертикальное движение точки постоянной мас¬
сы в несопротивляющейся среде под действием гравитационных
сил и тормозной силы реактивной тяги. Этот случай имеет место
для летательных аппаратов, осуществляющих вертикальную по¬
садку на ракетном двигателе, когда можно пренебречь сопротив¬
лением среды (ввиду малой скорости) и расходом активной
массы.
Считал положительным направление в сторону действия
гравитационных сил, запишем уравнение движения Мещерского
в следующем виде:
M—=Q-P, (8.26)
dt
откуда
V ~—gt(no — t) +С,
где С — постоянная интегрирования.
При й=0 (т. е. к началу торможения) скорость движения
равна V= Vtopm и тогда С=Уторм. При этом
V=—gt(n о—1)+^торм. (8.27)
Формула (8.27) описывает изменение скорости снижения в
зависимости от параметров t и п0 при скорости, имевшей к на¬
чалу торможения V=Vtopm.
Воспользовавшись выражением (8.27), легко записать
— — — 1) + ^орм.
и затем получить
H=—g -^(«о-^ + ^торм^-^торм.
торм’
(8.28)
где знак минус при Нтот определяется выбранным в нашем слу¬
чае положительным направлением движения.
Поскольку в конце движения (в момент посадки) имеют ме¬
сто условия V= О, Н = 0 и t=x, то очевидно, что формулы (8. 27)
и (8. 28) удобно записать так:
где l/торм и Ят0Рм — параметры в начале торможения.
Найдем далее выражение для весовой отдачи GT, обеспечи¬
вающей движение на участке торможения в .соответствии с вы¬
ражениями (8.29) и (8.30). Для этого, имея в виду линейный
закон изменения массы (т. е. движение при постоянной тяге),
воспользуемся выражением для полного времени полета (2.35),
подставив его в формулу (8.29). Тогда получим
где ТтоРм=(1/торм/^) —безразмерная скорость торможения.
Как видно из формулы (8.31), потребный запас топлива на
торможение уменьшается при увеличении перегрузки п0 и дости¬
гает минимального значения при п0= оо. При этом
Однако практически величину параметра п0 следует выби¬
рать с учетом весовых факторов. Воспользовавшись весовой за¬
висимостью (6.9), подставим ее в выражение (8.31). Тогда по¬
лучим
Экстремум функции (8. 33) найдем приравняв нулю производ¬
ную dVTOm/dn0. При этом получим следующее выражение для
оптимальной перегрузки в период торможения:
'/торм=(«о- !)£*;
^тоРМ=К-
(8. 29)
(8.30)
(8.31)
Gт — Gт mln — V’.
торм-
(8. 32)
V.
торм
(1-Н-эл-ЛЛо)-
"о
(8.33)
(8.34)
201
Легко понять, что если торможение осуществляется всеми уже
имеющимися на борту летательного аппарата двигателями при
перегрузке большей оптимальной, то это только лучше (меньше
израсходуется топлива), поскольку увеличение перегрузки при
этом происходит без увеличения веса двигательной установки.
Найдем далее выражение для высоты начала торможения
ЯТОрМ. Для этого, как и ранее, воспользуемся выражением
(2. 35), подставив его в формулу (8.30). После преобразований
и разрешения относительно параметра GT получим
О 2И . (8.35)
Рул У g(no~l)
У
Приравнивание правых частей выражений (8.35) и (8.31)
дает
/2
XI
2g(n0— 1)
^торм= „:,торм. (8.36)
Время торможения после подстановки выражения (8.35) в
формулу (2.35) определится так:
1/2
(8. 37)
/ 2Нгот
Х = (
\g(n 0— 1)
где Я = ЯТОрМ — высота начала торможения (включения двига¬
теля) .
Пример 8. 1. Определить минимальное значение удельной тяги, при ко¬
торой горизонтальная посадка на крыльях эквивалентна (в весовом отно¬
шении) вертикальной посадке на двигателях. Значения параметров принять
следующими:
k = 0,02, Vторм = 100 м/с,
р.эл = 0,20, W = 4000 м/с,
(Gkp/Gi.oc) = 0,15,
где GKр — вес крыла; Gnос — посадочный вес.
Решение. По формуле (8.34) находим значение оптимальной перегрузки
Щ
У k у 0,02
Воспользовавшись формулой (8.31), получим
Кторм = GT (l-—).
где по условию задачи необходимо принять GT = (GKp/Gnoc). Поскольку
установка двигателя, обеспечивающего найденную перегрузку п0=3,\6 умень¬
шит запас топлива на величину knQ=0y02 • 3,16=0,0632, то
^торм = [GT — *п0] ^1 —““) = (0,15 —;0,0632) ^1 — J^) = 0,0594.
202
Величину удельной тяги найдем по выражению
W ^торм 100
Руг, = — = —= = = 172 с.
У g ^торм 9,81-0,0594
Примечание. Если бы в нашей задаче летательный аппарат уже
имел двигатель, обеспечивающий перегрузку, например /г0=6, то величина
удельной тяги потребовалась бы равной всего
^торм ^торм 100
Рул = —= = = 81,0 с.
gVro рм 9,81-0,15^1 —-1-)
СПИСОК ЛИТЕРАТУРЫ
1. Лебедев А. А., Стражева И. В., Сахаров Г. И. Аэро¬
механика самолета. М., Оборонгиз, 1955, 472 с.
2. С о к о л о в Ф. А., Усов П. В. Техническая механика, М., «Выс¬
шая школа», 1965, 464 с.
Глава IX
ЛЕТНЫЕ ХАРАКТЕРИСТИКИ РАКЕТОПЛАНА
В настоящее время в ряде зарубежных стран усиленное вни¬
мание уделяется вопросам разработки ракет-носителей, а та.кже
космических аппаратов многократного применения. Это обуслов¬
лено рядом преимуществ (экономичность, надежность и т. д.), о
которых мы говорили ранее (см. разд. 1.2). В связи с отсутстви¬
ем установившейся терминологии мы условились (см. разд. 1.1)
возвращаемые ступени ракетно-космических систем, имеющие
несущие аэродинамические поверхности или обладающие несу¬
щим корпусом, называть ракетопланами. Ракетопланы относятся
к многорежимным ракетным летательным аппаратам. Как ука¬
зывалось ранее (см. разд. 1.5), движение ракетоплана может
происходить по баллистической, рикошетирующей и планирую¬
щей траекториям, а также в режимах орбитального, квазигори-
зонтального и суборбитального полетов.
В настоящей главе мы остановимся на изучении маршевого
(квазигоризонтального), планирующего (с положительной и от¬
рицательной подъемными силами) и активно-инерционного ви¬
дов движений. Маршевый полет ракетоплана происходит в гори¬
зонтальной плоскости при непрерывно работающем двигателе.
Такой вид движения наиболее применим к крылатым летатель¬
ным аппаратам, обладающим аэродинамическим качеством, и
силовой установкой которых является сверхзвуковой прямоточ¬
ный воздушно-реактивный двигатель (СПВРД). В этом случае
выведение ракетоплана в режим маршевого полета происходит
при помощи ракетных ускорителей, являющихся как бы первой
ступенью РЛА. В многократно используемой ракетно-авиацион¬
ной системе маршевый полет возможен после прохождения бал¬
листического участка траектории и последующего выхода на
траекторию горизонтального полета. Как будет показано в гла¬
ве, все виды маршевого полета на дальность при непрерывно
работающем ракетном двигателе (ЖРД) являются невыгодны¬
ми вследствие больших расходов ракетного топлива. Их приме¬
нение может быть оправдано только в случае вынужденного (по
каким-либо причинам) выполнения многорежимного маневрен¬
ного полета, включающего в себя планирующий или активно¬
инерционный виды движений. Исключением является суборби-
204
тальный вид движения, где в силу больших скоростей и высот
полета, связанных с высокими значениями эффективного аэро¬
динамического качества и малой плотностью среды, расход ра¬
кетного топлива не достигает больших величин. Изучение мар¬
шевого полета ракетоплана с ЖРД является важным для пони¬
мания законов ракетного движения в сопротивляющейся среде
и установления рациональных границ применимости такого ви¬
да движения для многократно используемых космических сис¬
тем.
Квазистационарный режим планирования с положительной и
отрицательной подъемными силами представляет собой пассив¬
ный вид движения (двигатели не работают). Используя его, воз¬
вращаемая ступень многократно применяемой ракетно-авиацион¬
ной системы может войти в плотные слои атмосферы с первой
космической скоростью или превышающей ее и достигнуть
места старта или другой предназначенной для этой цели поса¬
дочной площадки. Рассмотрение такого вида движения включе¬
но в настоящую главу из соображений удобства изучения сов¬
мещенных режимов активного и пассивного полетов. По этой же
причине в главу включен активно-инерционный полет. Послед¬
ний представляет собой чередующийся двухрёжимный полет с
дискретным расходом топлива на активном участке и последую¬
щим планированием.
Экстремальные режимы движения показаны без учета и с
учетом весовых факторов. В первом случае это решения чистой
механики, во втором — прикладной ракетодинамики.
9. 1. КВАЗИГОРИЗОНТАЛЬНОЕ ДВИЖЕНИЕ РАКЕТОПЛАНА
С МАЛОЙ ПОСТОЯННОЙ СКОРОСТЬЮ
Рассмотрим простейший случай квазигоризонтального поле¬
та ракетоплана с малой постоянной скоростью, когда центробеж¬
ными силами можно пренебречь. В таком движении набор высо¬
ты по мере расхода топлива происходит при малых углах атаки,
когда можно положить а^О и принять также постоянным аэро¬
динамическое качество (су/сх) = const.
Выполняя условие равенства тяги силе лобового сопротивле¬
ния, запишем дифференциальное уравнение движения ракето¬
плана в следующей форме:
^W+.MS =0, (9.1)
dt (су/сх)
где M = M(t) —текущая масса ракетоплана.
Интегрируя уравнение (9.1) при условии, что М = М0 при
t = 0, получим
'=-(т7)яуД 1п0-ео. (9-2)
где (3 — коэффициент расхода топлива.
205
Полное время полета при t = x и рт=1—рк будет равно
t = fe)Py>U' (9.3)
Поскольку движение ракетоплана происходит с постоянной
скоростью, дальность полета, равная произведению скорости на
время, будет равна
£» = (—')КмЯуд1пЦ, (9.4)
\ СХ /
где индекс «м» означает параметры маршевого участка полета.
Очевидно, что дальность, выраженная через время маршевого
полета, запишется так:
ImW==“&) (9-5)
Поскольку вывод формул (9.3) и (9.4) произведен без учета
центробежных сил, то их применение ограничено скоростями
полета в пределах 3—5 чисел М.
Из формул (9.4) и (9.5) следует, что пройденный ракетопла¬
ном путь будет тем больше, чем больше будет скорость марше¬
вого полета.
Покажем далее влияние тяговооруженности п0 на дальность
полета ракетоплана без учета центробежных сил.
Применив в общем виде степенной закон сопротивления сре¬
ды, можно записать
Х = Р = Х1/м (9.6)
и затем получить
(9.7)
где Х=Х(сх, q, SKp) —приведенный параметр аэродинамическо¬
го сопротивления; т — показатель степени.
Подстановка выражения (9.7) в формулу (9.4) дает
LM = [^)Py^)M < 1пЦ. (9.8)
Выражение (9.8) показывает, что при любом законе сопро¬
тивления среды дальность полета пропорциональна тяговоору-
женности /гсГ .
Настоящий вывод получен без учета влияния весовых фактот
ров (увеличения веса двигательной установки при увеличении
тяговооруженности м0) и имеет практическое применение только
206
для уже построенных конструкций. Например баллистический
ракетоплан, рассчитанный на перегрузки п0> 1, может быть ис¬
пользован в маршевом полете и тогда для него увеличение даль¬
ности будет следовать закону LM = LM(n™ ) (9.8), поскольку
при этом увеличение тяги не вызовет утяжеления конструкции,
а1 следовательно, и уменьшения дальности LM.
В тех случаях, когда маршевый полет является единствен¬
ным расчетным режимом (например в-схеме ракетоплана со стар¬
товыми ускорителями), выбор перегрузки связан с учетом весо¬
вых факторов через параметр цк. При зтом, как будет показано
ниже, стартовая тяговооруженность на марше имеет оптималь¬
ное значение.
9.2. ВЛИЯНИЕ СТАРТОВОЙ ТЯГОВООРУЖЕННОСТИ
НА ДАЛЬНОСТЬ МАРШЕВОГО ПОЛЕТА РАКЕТОПЛАНА
С МАЛОЙ ПОСТОЯННОЙ СКОРОСТЬЮ
Рассмотрим случай, когда бортовой запас топлива ракето¬
плана расходуется только на участке маршевогов полета, вслед¬
ствие чего этот участок является расчетным для выбора старто¬
вой тяговооруженности.
Влияние стартовой тяговооруженности на дальность полета
ракетоплана с малой постоянной скоростью учтем при помощи
основной весовой зависимости (6.9). Имея в виду случай малой
скорости полета, а также степенной закон сопротивления среды,
после подстановки в формулу (9.8) зависимости (6.9) получим
j_
£МЮ= — По 1п(!*эл-Н/г0), (9.9)
где
4 («о) = 1м(По) ± • (9- Ю)
(tMff
Влияние тяговооруженности п0 на безразмерную дальность
полета представлено на рис. 113. Как видно из графика, функ¬
ция Lm = LM(n0) имеет максимум. Выражение для оптимальной
тяговооруженности п0пт найдем, приравняв нулю производную
dLM(no)/dn0. Тогда получим
«О = «опт = -^1ПЦ. (9.11)
km
Зависимость оптимальной тяговооруженности от весовой от¬
дачи представлена на том же графике в виде функции
Ят[Т = -^—= — {J-kIh^k-
Из графика видно, что оптимальная тяговооруженность, в
свою очередь, имеет максимум по параметру рк. Приравняв ну¬
лю производную от АХопт п0 М'К, найдем
откуда
-(^L) = 1+ln^K = °.
(9.12)
Рис. 113. Зависимость опти¬
мальной тяговооруженности
от весовой отдачи при мар¬
шевом полете ракетоплана
с малой скоростью
Таким образом, каждому значению весовой отдачи соответ¬
ствует определенная оптимальная стартовая тяговооруженность
п0пт- Ее величина не зависит от аэродинамического качества и
удельной тяги двигательной установки. Подставив величину
(9.12) в формулу (9.11), найдем, что максимальное значение
оптимальной стартовой тяговооруженности равно
'‘'опт
шах
km е
Для квадратического закона сопротивления
(9.11) и (9.13) при т = 2 дают
пп
2k
1пЦ;
п
опт О hr.
max ^ke
(9.13)
среды формулы
(9.14)
(9. 15)
Как видно из формулы (9.15), максимальное значение опти¬
мальной тяговооруженности является функцией весового пара¬
метра k. При уменьшении этого параметра (т. е. уменьшении
удельного веса двигательной установки) стартовая тяговоору-
208
женность увеличивается. Если принять & = 0,213, то максималь¬
ное значение оптимальной тяговооруженности составит величи¬
ну, равную п =0,866. При этом, как мы уже видели (9.12),
J опт
шах
весовая отдача должна быть равной рк = 0,368.
9. 3. КВАЗ И ГОРИЗОНТАЛЬНОЕ ДВИЖЕНИЕ РАКЕТОПЛАНА
С БОЛЬШОЙ ПОСТОЯННОЙ СКОРОСТЬЮ
Теория маршевого полета с большой постоянной скоростью
применима как к ракетоплану, так и к самолету, силовой уста¬
новкой которого является, например, прямоточный воздушно-
реактивный двигатель.
В квазигоризонтальном полете на ракетный самолет действу¬
ют силы, как показано на рис. 114. Рассмотрим движение с по¬
стоянной маршевой скоростью VM = const при дросселируемой
тяге двигателя и постоянном угле атаки а = const. В соответст¬
вии с рисунком проекции сил в скоростной системе координат
дают
Я cos а — Х = 0;
Р sin a-{-Y— G = 0,
(9.16)
где F--
MVl
центробежная сила; R=R3 + H—радиус тра¬
ектории полета; M = M(t) — текущая масса.
Рис. 114. Схема сил, действующих при квазигори¬
зонтальном движении ракетоплана (РНМП)
209
Совместным решением уравнений (9.16) с учетом (2.4) легко
получить
G1- —
(Су\
— cos а — sin а
V сх
Разделив переменные и проинтегрировав при условии, что
M*=0 = Mo, получим
t = Pyx <c»/^)cosct2+ sma,lnLt< щ
1--^-
gR
Поскольку полет происходит с постоянной скоростью, то
Lu = pyjyu ^,;cos atsin_a }пЦ> ^ lg)
Выражение qR в формуле (9.18) имеет размерность квадра¬
та скорости и представляет энергию поля на данном расстоянии
R. Поэтому скорость, соответствующую этой энергии, может
иметь только материальное тело, которое не сходит с эквипотен¬
циальной поверхности радиуса R. Таким образом, движение
этого тела должно происходить по большому кругу эквипотен¬
циальной сферической поверхности диаметра 2R, причем пло¬
скость большого круга по определению проходит через центр
сферы. Поэтому эта скорость называется круговой скоростью и
обозначается как 1/Кр = Уя^- Эту скорость называют еще первой
космической скоростью и обозначают как l/Kp=V'i.
Маршевый полет при больших скоростях происходит на ма¬
лых углах атаки, для которых можно положить cosa^l и
sina~0. При этом получим обобщенную формулу, описывающую
дальность полета,
(Су/Сх)
Лч'Р
При этом полное время полета будет равно
LM = PvyM In Ц. (9. 19)
уд м I-GVV'kp)2
Х = Р (суРх) 1пЦ (9. 20)
уд I-(W^kp)2
Формула (9.19) показывает, что главными параметрами, оп¬
ределяющими дальность маршевого полета ракетоплана, явля¬
ются удельная тяга, аэродинамическое качество, число Циолков-
210
ского и скорость VM. Действие последней сказывается также
через величину так называемого эффективного аэродинамическо¬
го качества (су/сх)эфф, равного
f СУ \ (су/сх) /д 2,1)
\сх)эфф~ 1-(VJVKP)2 * 1 '
При достижении круговой скорости VM=VKV эффективное
аэродинамическое качество становится равным бесконечности
(Су/сх)эфф = о°, что означает полную разгрузку веса центробеж¬
ными силами. При этом ракетный самолет переходит в режим
движения спутника. Положив VM/VKV = 0, легко убедиться, что
полученная ранее формула дальности без учета центробежных
сил (9.4), является частным случаем формулы. (9.19). Характер
дросселирования тяги по трассе полета легко определить по
следующей зависимости:
V2
P = X = qcx —
* 2 cos а
где 5 — характерная площадь (для ракетоплана S = SKp). Это
означает, что тяга двигателя дросселируется в‘соответствии с
изменением плотности воздуха при подъеме ракетного самолета
по мере выгорания топлива.
Высота маршевого полета также легко определяется совмест¬
ным решением уравнений (9.16), которые дают
1 - (Vm/Vkv)2
r=Q(t)-
откуда
Q(//) = 2
а
1 + — —~
(сУ/сх)
i-GVV^p)2 / р(о
, . \°уу1
(9. 22)
(Су/Сх)
где GJS — удельная нагрузка на крыло (несущую поверхность)
от стартового веса G0; |х(^) = ^-^—коэффициент текущего (по
мере выгорания топлива) веса ракетоплана.
При этом высота полета Н определяется по таблице стандар¬
тной атмосферы как H = H(q).
Для экспоненциального закона изменения плотности по вы¬
соте Н формула (9.22) принимает вид
я—‘"<W I, (9.23)
211
Р i\ VM / tga
('Cy/Cx)
(3 — показатель экспоненты.
Таким образом, высота полета является функцией текущего
уменьшения (веса \i(t) и маршевой скорости VM. Высота полета
тем меньше, чем больше вес ракетоплана и тем больше, чем
больше маршевая скорость VM.
Высота маршевого полета ракетоплана мала по сравнению с
радиусом Земли. На этой высоте ускорение сил земного тяго¬
тения немногим отличается от ускорения на уровне моря. Вслед¬
ствие этого при пользовании формулами (9.22) и (9.23) целесо¬
образно принимать R=R3, g = go. При этом также круговая ско¬
рость будет равна ее значению на уровне моря ^кр = "Кё’о^з-
Необходимо отметить, что ввиду больших расходов топлива
ракетным двигателем маршевые полеты ракетопланов возможны
только на больших высотах и больших гиперзвуковых скоростях
с малой тягой. Ниже (см. разд. 9.4) будет показано, что величи¬
на маршевой скорости с учетом весовых факторов имеет свое
оптимальное значение.
9.4. ВЛИЯНИЕ СТАРТОВОЙ ТЯГОВООРУЖЕННОСТИ
НА ДАЛЬНОСТЬ МАРШЕВОГО ПОЛЕТА РАКЕТОПЛАНА
С БОЛЬШОЙ ПОСТОЯННОЙ СКОРОСТЬЮ
Рассмотрим сначала случай, когда изменение тяговооружен¬
ности не вызывает изменения весовых характеристик ракето¬
плана.
Воспользовавшись выражением (9.7) для случая квадратиче¬
ского закона сопротивления среды, подставим его в формулу
(9.19). Тогда получим
Из формулы (9. 24) видно, что увеличение тяговооруженности
вызывает значительное увеличение дальности маршевого поле¬
та. Это увеличение обусловлено влиянием эффективного каче¬
ства, величина которого в функции тяговооруженности п0 опре¬
деляется выражением (9.21).
Полученные выводы справедливы только в том случае,- когда
увеличение тяги не связано с увеличением конечного веса раке¬
топлана (случай полета на максимальной тяге).
2
1п ц
(9.24)
где
212
Для учета весовых факторов воспользуемся формулами
(9.24) и (6.9), записав для квадратического закона сопротивле¬
ния среды
1
L, («о)
£м (Ло)
1П (Р*эл (9- 25)
(Су/Сх) РудVX ^ (ух/у*?Упо
Из формулы (9.26) видно, что эффект действия центробеж¬
ных сил заметно сказывается (как и в случае, когда весовые
факторы ие учитываются) на увеличении максимальной дально¬
сти полета.
Приравняв нулю производную dL^(n0)/dn$ и решив полу¬
ченное выражение относительно параметра я0= (по)опт, найдем
Яп = -
1
(^кр)2
-пп
у т
(Vx!v*p)2
(9.26)
где поит = — In Ц — оптимальная перегрузка без. учета центробеж-
2k
ных сил (9. 14).
Рис. 115. Оптимальная тяговоору-
женность с учетом и без учета
центробежных сил:
/—с учетом центробежных сил; 2—без
учета центробежных сил
(Що)
40
30
20
10
1 /TV
V 1
1,3501 .у*
/ 1,085
/1,000) V
[по)опт
max
г
! ;
!
/а
п i
/ 1
/^!
!/
"j
4.1
. . 1
О 0,2 0,4 0,6 0,8
Кривая По = По(\1к) представлена на рис. 115. Как и в случае
неучета центробежных сил, кривая п0 = По(\хк) имеет максимум.
Дифференцируя п0 по рк и приравнивая нулю производную, по¬
лучим
dll о пт
1
> о. 2
1
1
I
L п™\
{Vx/V*»Y
d\L к
2
1
^ОП'Г
2 Яопт
г
.**
to
1
iYxlVкр)2|
213
Поскольку множитель в скобках не равен нулю, то очевид¬
но, что
d\LK d^.K
Как было показано ранее (см. разд. 9.2), это имеет место
при рк=1/е. Таким образом, максимум оптимальной перегрузки
в случаях с учетом и без учета центробежных сил достигается
при одинаковых значениях весовой отдачи рк- Поскольку при этом
__1_
~2&е
то после подстановки его в формулу (9.26) получим
П0 шах
{Ух!у кр)2 2*е
1 1 1 11
2 1
4 [ 1/к;02 2*е
2*е {V*x V',,)2
Сравнение оптимальных перегрузок с учетом и без учета
центробежных сил показано на графике (см. рис. 115). Кривые
«о = Ло(|Ык) построены по формулам (9.14) и (9.26). График по¬
казывает, что, несмотря на совпадение максимумов при рк=1/е,
течение кривых /г0 = /го(цк) для случаев большой и малой марше¬
вой скорости Км неодинаково.
Найденные решения для оптимальных стартовых перегрузок
имеют место для случая, когда выведение ракетоплана в режим
маршевого полета происходит не из-за расхода бортового запа¬
са топлива, а благодаря специальным стартовым (разгонным)
ускорителям. При этом топливо, имеющееся на борту ракетопла¬
на, используется только в режиме маршевого полета для дости¬
жения максимальной дальности.
9.5. ОПТИМАЛЬНАЯ СКОРОСТЬ МАРШЕВОГО ПОЛЕТА РАКЕТОПЛАНА
С УЧЕТОМ РАСХОДА ТОПЛИВА НА УЧАСТКЕ ВЫВЕДЕНИЯ
Рассмотрим случай, когда выведение на режим маршевого
полета и полет на марше происходят исключительно в результа¬
те расхода бортового запаса топлива одноступенчатого ракето¬
плана. Будем иметь в виду также, что ракетоплан многорежим¬
ный и его основные параметры, такие как стартовая перегрузка
или весовая отдача, уже выбраны применительно к одному из
наиболее главных его режимов движения. В этом случае рас¬
смотрение задачи можно вести без учета весовых факторов.
214
Дальность на участке выведения и планирования после выклю¬
чения двигателя учитывать не будем.
Конечная скорость выведения (она же и маршевая скорость)
тем больше, чем больше израсходовано топлива на этом участ¬
ке. Однако при этом уменьшается та часть топлива, которая ос¬
тается для расхода ее на марше. Следовательно, существует оп¬
тимальная скорость выведения, при которой пройденное
расстояние на марше будет максимальным. Такие зависимости
в координатах «дальность—скорость» приведены на рис. 116 и
117 для различных значений весовых отдач рк и удельных тяг
Р уд-
(Щ
К 0x1 1200
[CZX1 км
800
т
Руд ~ 300 с
н“
<
/ А
//Я=4А
®)"
8000
6000
ШО
2000
1
Руд ‘
-500с
Л
/
//>
у
У
У\
О 2 0-6 Vm^km/c
Рис. 116. Оптимальная скорость дви¬
жения ракетоплана (РНМП) на мар¬
ше (влияние весовой отдачи)
С >км
(ЕУ)
800
ООО
200
Т’км
Ф
8000
6000
0000
2000
4 Kf,™/c
Мк
= 0,1
м
I
/ i
У
0 2 0 6 Ум,км/с
Рис. 117. Оптимальная скорость дви¬
жения ракетоплана (РНМП) на мар¬
ше (влияние удельной тяги)
Полагая, что режим взлета и выведения происходит при пос¬
тоянной тяге, а режим маршевого полета при постоянной скоро¬
сти, воспользуемся формулами (2.25) и (9.19), переписав их в
следующем виде:
(Гм + дГа)=-1пр.к1; (9-2В)
215
где Vu = ^- — безразмерная марш'евая скорость (или конечная
скорость выведения); AVz = -^~ —суммарные потери в окорости
вследствие влияния среды и полета в поле гравитационных сил,
отнесенные к скорости истечения W; ркь рш — потребные весо¬
вые отдачи для осуществления полета на первом (выведение) и
втором (маршевом) участках полета.
Поскольку приведенная весовая отдача ракетоплана равна
Pk* = UkiPkii, то на основании формулы (9.28) легко получить
Делая подстановку выражения (9.30) в уравнение (9.29),
получим
где FKp=VKp/Wn — безразмерная круговая скорость (отнесен¬
ная к скорости истечения в пустоте).
Для отыскания оптимальной_скорости Им=(Им)опт приравня¬
ем нулю производную от LM по FM. Тогда получим
В частном случае, без учета центробежных сил (FM/FKp = 0)
и потерь в скорости вследствие влияния среды и полета в поле
гравитационных сил AV ъ =0, уравнение (9.32) упрощается к
виду
Из этой формулы следует, что для достижения максимальной
дальности маршевого полета необходимо, чтобы скорость выве¬
дения составляла половину от располагаемой конечной скорости
ракетоплана.
(9.30)
L
м
dV „
= (^-УОпь + Д^) + 2Км+(1пнС + АК.) = 0, (9.32)
\Хкр /
откуда
21/м + 1п^ = 0,
откуда
(П,)опт=^1ПЦ*-
(9.34)
216
9.6. ВРЕМЯ, СКОРОСТЬ, ДАЛЬНОСТЬ И ВЫСОТА
КВАЗИСТАЦИОНАРНОГО ПЛАНИРОВАНИЯ
ПРИ ПОЛОЖИТЕЛЬНОЙ ПОДЪЕМНОЙ СИЛЕ
Движение ракетоплана в режиме квазистационарного плани¬
рования при положительной подъемной силе происходит на ско¬
рости, при которой силы инерции значительно увеличивают даль¬
ность полета.
Разгон до /необходимой начальной скорости планирования
может быть осуществлен либо бортовым ракетным двигателем,
либо специальным стартовым ускорителем ракетного типа.
В первом случае дальность достигается благодаря расходу топ¬
лива, находящегося в ракетоплане; во втором — благодаря топ¬
ливу, находящемуся в ускорителе.
Рис. 118. Траектории выведения и гиперзвукового планирования:
/—участок выведения; 2—баллистический участок; 3—участок планирования
Преобразование кинетической энергии в работу сил сопротив¬
ления планирующего полета может происходить как непосред¬
ственно по достижении необходимой высоты планирования (рис.
118, а), так и после предварительного участка баллистического
полета (заброса) со скоростью, близкой к скорости в конце уча¬
стка выведения (рис. 118, б).
В режиме гиперзвукового планирования при V<zVlw на ра¬
кетоплан действуют силы, показанные на рис. 119. Там обозна¬
чено:
X — сила лобового сопротивления; Y—подъемная сила:
F = MV2/R — центробежная сила; G — вес; 0 —угол пла¬
нирования, составленный вектором скорости и линией горизонта.
При гиперзвуковом планировании угол 0 невелик и можно
положить 0 ^0, cos 0«1, sin 0=0. Принимая во внимание сде¬
ланные допущения, запишем
М-=-Х;
dt I (9.35)
G = Y + F
и затем
dV 1
(£-,). С.*,
dt (су/сх)
где R = R3 + H^R3; g — ускорение сил земного тяготения на
данной высоте полета.
217
Разделим переменные и проинтегрируем. Тогда получим
V
Гкр
1
V
(Су/Сх)
Ygt+c,
vKP
где 1^Кр=у^ — круговая (первая космическая) скорость на
данной высоте полета.
Рис. 119. Схема сил, действующих на ракетоплан
(РНМП) при планировании
Постоянную интегрирования найдем из начальных условий
/ = 0 и V = Vo, т. е.
При этом
1 + ■
-YR In
Vo
Vkp
Va
VKp
1 +■
■)
- Y in ^IS . (9.37)
2VKP
(1_ vj (1+ VKp)
Формула (9.37) выражает время планирования в функции
аэродинамического качества, начальной и конечной скоростей
218
планирования. Формула (9.37) дает также
V'Q \ 2V,
кр
1-
VKp 1 Vy/cx)R
1 +-
v=v
кр
кр
Vo
2V,
кр
(9.38)
1 +
Ккр 1 «УЫ*
1 +
Vo
кр
Зависимость между временем, начальной и конечной скоро¬
стями планирования показана на рис. 120 в виде кривых
Vq VK
t (—тгЧ . где t =
\ *Kp
' кр ^кр
(Су/Сх)
Рис. 120. Зависимость времени
планирования t от начальной и ко*
нечной скоростей
Дальность планирования найдем по выражению (9.38), за¬
менив в нем V=dL/dt. После интегрирования получим
-tVKV-(f]R In
■ +
кр
ZLe<*v/cx>*
1
кр
-т-С.
Поскольку при t = 0 имеет место 0, то постоянная интег¬
рирования определится как
Су \ о 1/ 2
С= f —) R In
Сл
Vn
219
При этом
Ln„=tVKp-^Rln
2
, (9.39)
где время t определяется по формуле (9.37).
Область гиперзвукового планирования располагается в диа¬
пазоне высот от Н^100 км до Нж 40 км. На этом участке, как
и в случае маршевого полета, можно положить R=R3 и g=go.
Имея зависимости (9.37) и (9.39), легко получить формулу
дальности 1Пл, выраженную через текущую скорость планиро¬
вания:
где Vo ■—начальная скорость планирования; V — текущая ско¬
рость планирования.
Если планирование происходит до полной потери скорости
Е = 0, то формула (9.40) еще более упрощается
Кривые, характеризующие влияние скорости на дальность
планирования (в безразмерных единицах), показаны на рис. 121.
График показывает, что величина конечной скорости V=VK су¬
щественно влияет на дальность квазистационарного планирова¬
ния.
Перегрузки, действующие на ракетоплан во время планиро¬
вания, будут равны
(9. 40)
(9.41)
Y
V \2
Как следует из формул (9.42) и (9.43), при равновесном пла¬
нировании максимума перегрузки не наблюдается. В процессе
торможения перегрузки пу и пх растут асимптотически, прибли¬
жаясь К Пу = 1 и пх = (Су/Сх)-К
Высота квазистационарного планирования определится из
второго уравнения системы (9.35). При этом
г=°-р=о['-Ш]'
где G = const.
Рис. 121. Влияние начальной К) Рис. 122. Зависимость
и конечной VK скоростей на высоты от скорости пла-
дальность планирования раке- нирования
топлана (РНМП)
Для экспоненциального закона изменения плотности среды
высота квазистационарного планирования Исt(V) определится
так:
(9. 44)
где
VI
/ 2G/S У/2
\ суЯо )
Типовая траектория планирования в координатах «ско¬
рость—высота» показана на рис. 122. Из графика хорошо видно,
что главными параметрами, определяющими высоту планирова¬
ния, являются скорость V и удельная нагрузка на единицу несу¬
щей площади от веса ракетоплана G/S.
221
9.7. ВЛИЯНИЕ МАРШЕВОЙ СКОРОСТИ НА ДАЛЬНОСТЬ ПОЛЕТА
РАКЕТОПЛАНА С УЧЕТОМ ПЛАНИРОВАНИЯ
Ранее было показано (9.5), что если выведение на маршевый
режим происходит вследствие расхода бортового запаса топли¬
ва, то скорость маршевого полета имеет
оптимальное значение с точки зрения до¬
стижения максимальной дальности. Такая
кривая представлена на рис. 123. Там же
приведена кривая суммарной дальности
полета на марше и при планировании, по¬
строенная с учетом формул (9.31) и
(9.41) по уравнению Lz=LM + LUJl, т. е.
L7km
4800
4200
3200
2400
1600
800
,
/
1
/руд=М0
С
/
s~^2
!
\
\
1
(Су]СХ) у,
4%км/с'
-KtM'-(£)]• <••«>
Рис. 123. Дальность полета ракетоплана
(РНМП) на марше и планировании:
/—полная дальность полета; 2—дальность полета на
марше
Как видно из графика, функция Lz = Lv(VM) монотонно
возрастает. Это можно показать также аналитически, взяв про¬
изводную от Le по Vm. Тогда получим
dLv.
dV м
VK?WPу л
2V
кр
£,) +<|п1‘:+д1/)(£',)-
Л^-ОпК + йУ)-
где
VKpWPy
V =Х«_- у =3^.
м W ’ кр W
(9.46;
Как легко убедиться, при всех _ значениях параметра
(V м/ К Кр)== 0—!— 1 производная dL^jd Vu положительна, что
свидетельствует о непрерывном увеличении рассматриваемой
функции. Таким образом, увеличение маршевой скорости вызы¬
вает увеличение суммарной дальности полета. Чем меньше мар-
222
шевый участок, тем больше суммарная дальность полета. Мак¬
симальная дальность полета достигается при полном расходе
топлива на участке выведения, когда развивается максимальная
конечная скорость. При этом ракетоплан как бы вырождается в
планирующий летательный аппарат (ракетопланер), достижение
дальности которым осуществляется исключительно в режиме
планирования.
9. 8. АКТИВНО-ИНЕРЦИОННЫЙ ПОЛЕТ РАКЕТОПЛАНА
Активно-инерционный полет ракетоплана может происходить
путем периодического включения и выключения, бортового ра¬
кетного двигателя. При этом траектория полета делится на пе¬
риоды, состоящие из активных и пассивных участков полета
(рис. 124).
Рис. 124. Схема активно-инерционного полета ракетоплана
(РНМП):
а—периоды одинаковы; б—периоды неодинаковы; /—активный
участок; 2—планирование
Активные участки представляют собой обычные участки вы¬
ведения; пассивные участки — режим планирования на даль¬
ность. Периоды могут быть одинаковыми и неодинаковыми как
по режиму, так и по дальности полета. Топливо, расходуемое
по периодам, составляет в делом общий запас топлива на раке¬
топлане. Рассмотрим, как влияет количество (частота) перио¬
дов на дальность и другие параметры полета одноступенчатого
ракетоплана.
Если весовая отдача ракетоплана равна периоды одина¬
ковы и количество их равно п, то очевидно, что располагаемая
223
(9.47
весовая отдача одного периода |дКп составит
где индекс «п» означает период.
Воспользовавшись формулой дальности планирования (9.41)
и полагая для простоты, что скорость разгона на каждом перио¬
де может быть выражена формулой (2.25), запишем
Ly\ =
п
S
Li = n\
>(£jl
V с х
In
_/ In Ц1/л^
\ I
(9.48)
где Т^1ф=^кр/^*
В этом уравнении число Циолковского определяется с уче¬
том потерь на силы тяжести и силы аэродинамического сопро¬
тивления по приведенной конечной скорости Ущшв (см. разд.
10.9).
L.km
Из уравнения (9.48) видно, что при увеличении параметра п
суммарная дальность полета уменьшается. Эта дальность мак¬
симальная при п=1 и равна нулю при п = оо.
Некоторые кривые, характеризующие активно-инерционный
полет ракетоплана, представлены на рис. 125. Кривые построе¬
ны на основании уравнения (9.48), формулы Циолковского и
формулы для определения квазистационарной высоты планиро¬
вания (9.44). Как видно из графика, характеристики активно¬
инерционного движения имеют явно выраженный экспоненци¬
альный характер и значительно уступают по параметру суммар¬
ной дальности Ьл исходным характеристикам ракетоплана.
Сравнительное уменьшение дальности такого полета по количе¬
ству периодов легко выразить зависимостью вида
224
7 Lt In [ 1— (in u}lnjvкр)2]
Ls = = п —
In [1 - (In Ц/Укр)2]
(9.49)
Кривые L = L(n, Ц), построенные по этой зависимости, пред¬
ставлены на рис. 126. Как видно из графика, активно-инерцион¬
ный вид движения особенно ,невыгоден при больших числах Ци¬
олковского. Это объясняется тем,
что при делении больших скоростей
на малые по периодам, потеря эф¬
фекта действия центробежных сил
в режиме планированйя оказывает¬
ся наиболее ощутимой.
Активно-инерционный полет при¬
меним как маневренный вид движе¬
ния, но он не выгоден с точки зре¬
ния получения максимальной даль¬
ности. Последняя, как было пока-
Рис. 126. Влияние количества периодов па
дальность активпо-ииерциопного полета
(РНМП)
зано ранее (см. разд. 9.7) и как это следует из равенства (9.45),
может быть достигнута при обычном разгоне ракетоплана до
максимальной конечной скорости на участке выведения и после¬
дующем полете в режиме планирования или рикошетирования.
9.9. ВРЕМЯ, СКОРОСТЬ, ДАЛЬНОСТЬ И ВЫСОТА
КВАЗИСТАЦИОНАРНОГО ПЛАНИРОВАНИЯ
ПРИ ОТРИЦАТЕЛЬНОЙ ПОДЪЕМНОЙ СИЛЕ
Обобщая законы равновесного планирования в присутствии
положительной подъемной силы (см. разд. 9.6), можно также
изучить и аналогичные законы при использовании ракетопланом
отрицательной подъемной силы для случая глубокого касания
атмосферы, когда скорость входа в атмосферу планеты превы¬
шает первую космическую скорость V0>ygR.
Уравнения движения, при условии, что 0^0, cos 0 ^ 1 и
sin 0 » 1, имеют вид
М — =— X; |
dt (9.50)
F — G-\-Y. J
Решение такой системы уравнений по аналогии разд. 9.6 да¬
ет следующие зависимости для определения параметров движе¬
ния ракетоплана:
( V \ / Кп \
Полученные зависимости параметрически аналогичны зави¬
симостям разд. 9.6.
Формула (9.54) показывает, что в отличие от случая планиро¬
вания с положительной подъемной силой, при ее отрицательном
значении по мере уменьшения скорости происходит не уменьше¬
ние высоты планирования, а наоборот, увеличение этой высоты,
при которой имеет место V = ygR.
По мере планирования и уменьшения скорости от V>^gR до
перегрузки пу и пх падают, достигая минимальных зна¬
чений (теоретически равных нулю при l/ = yg7?).
Рассмотрим далее соотношение текущих скоростей битраек-
торного планирования при V'^^gR. В обоих случаях будем по¬
лагать постоянным и одинаковым параметр аэродинамического
качества (су/сх) = const. Другими словами, мы рассмотрим два
режима движения, выполняемых одним ракетопланом.
Выполняя условие равенства высот планирования, приравня¬
ем правые части выражений (9.44) и (9.54). Тогда, после не¬
сложных преобразований, получим
или
(9.58)
где индексы I и II относятся к режимам планирования при
Vi <С V~gR и V n^>V gK соответственно.
Формулы (9.57) и (9.58) идентичны. Они устанавливают
связь (соотношение) между скоростями Vi и.Vn, при которых
высоты планирования остаются одинаковыми, несмотря на не¬
равенство на этих высотах скоростей полета Vi^Vn.
Рис. 127. Параметры квазистационарного битраекторно-
го планирования
Существует единственное решение, при котором, в соответст-
ствии с формулами (9.57) и (9.58), имеет место V\ = Vu = VgR-
Это означает, что при входе в атмосферу со скоростью, превы¬
шающей первую космическую скорость, максимальная высота
будет тогда, когда скорость планирования упадет до величины,
равной первой комической скорости. Эта точка в свою очередь
является общей для начальной высоты планирования при поло¬
жительной подъемной силе.
Если в формуле (9.58) положить равным нулю знаменатель,
то получим
Н7км 1 ,—. ,
Область Область
О
4 6
8
—■ 1—Ч,
10 12 V^km/c
(9. 59)
227
Это означает, что при скорости входа, равной бесконечности
(К0П = оо), существует предельно малая высота входа (началь¬
ного планирования) #о = Я0тт, при которой обеспечивается за¬
хват ЛА атмосферой планеты и требуемый режим планирования
с отрицательной подъемной силой. Этой минимальной высоте
входа соответствует скорость на нисходящем участке планиро;
вания (при положительной подъемной силе), составляющая по
величине 71% от первой космической скорости.
Общий характер кривых H = H(V) для квазистационарного
битраекторного планирования, построенных по формулам (9.44)
и (9.54) для различных значений удельной нагрузки G/5, пред¬
ставлен на рис. 127. Как видно из графика, влияние удельной
нагрузки G/S на высоту планирования одинаков для двух уча¬
стков при Очевидно, что поворот вектора аэродина¬
мической подъемной силы Y(V) при переходе с восходящего на
нисходящий участок планирования происходит в точке, где име¬
ет место V~YgR.
Пример 9. 1. Определить дальность активно-инерционного планирования
если дано: скорость истечения 117=4000 м/с, весовая отдача рк=0,27, циклов
п= 1=4, аэродинамическое качество (су/сх) =4,5, стартовая перегрузка
п0=1,5, коэффициент гравитационных потерь а(9к) = 1. Силами сопротивле¬
ния воздуха на участке выведения пренебречь.
Решение. Весовая отдача, скорость выведения и дальность полета по пе¬
риодам определяются выражениями
C.-rf”, V.-W (|ПЦ-.<ЛК>У),
Вычисления по этим формулам сводим в таблицу.
Количество периодов п
1 |
2
3
4
Весовая от ача и.к
0,27
0,52
0,615
0,72
Число Ц
3,7
1,925
1,55
1,39
Величина In Ц
1,31
0,65
0,44
0,33
Величина Ол./п0
0,49
0,32
0,24
0,19
Скорость выведения VK, м/с
3280
1320
800
520
Величина (ИК/НК1,)2
0,16
0,0174
0,01
0,0042
Величина 1— {VK/VKl))2
0,84
0,983
0,99
0,9958
Величина In
1- (V'kA'kp)2
0,18
0,03
0,01
0,004-
Дальность одного ' периода 7/, км
2600
430
144
58
Суммарная дальность, L^nLj, км
2600
860
430
230
228
Как видно из таблицы, дальность одного периода больше дальности че¬
тырех периодов в 2600/230—11 раз.
Пример 9. 2. Составить аналитическую зависимость и определить по ней
разность пути, отнесенного к величине
при движении ракето¬
плана в режиме гиперзвукового планирования, а также при четырех перио¬
дах активно-инерционного полета. Решение выполнить в безразмерных еди¬
ницах при Ц—6, VK]
кр •
W
— 2,3 и а (0К) = 0.
Решение. Дальность гиперзвукового планирования определяется по фор¬
муле
—теМ-СУ
где VK — конечная скорость выведения (или все равно, что начальная ско¬
рость планирования).
Разность пути, пройденного в режимах одного и п периодов, составит
Ln=-1 Ln— -
су
In
1-1^
V,
кр
R IСу 11
n — — ln
2 u
.-iV
V^KP
где Vn и VKn—скорости в конце активного участка при, одном и п периодах
полета, отнесенные к скорости истечения W.
Поскольку а(0к)=О имеют место VK=ln Ц и Vk„ — In (Ц1^), то
М =
Ln = 1 Ln
_R_ fcy_
2 V cx
1 —
ln Ц \2
+ n In
1- -=e
In Ц \2
nVKP
M = In
In U \2
ln Ц \2
V
кр
Подстановка в полученную формулу значений параметров, указанных в
условиях примера, дает следующую разность относительной дальности:
\L = In
[1 — (In 6/4-2,ЗЯ
-0,77.
При
1 — (In 6/2,3)2
аэродинамическом качестве, взятом, например
= 6,
.£"Л=1
Cx /
это означало бы, что превышение дальности одного периода планирования
по сравнению с суммарной дальностью шести периодов планирования состав¬
ляет величину, равную
iZ — (—) = 0,77 (/?3/2) 4 яг 1000 км.
2 \ сх )
Пример 9.3. Найти соотношение между начальной скоростью входа
V'on Д> 1/~ gR и конечной скоростью планирования при котором
229
время битраекторного полета будет одинаково на-восходящем и нисходящем
участках.
Решение. Время, выраженное через текущую скорость по участкам би¬
траекторного планирования, определяется формулами (9.37), (9.51). При¬
равняв правые части этих выражений, после несложных преобразований по¬
лучим
^оц1Л=Укр- (9-60)
Таким образом, скорость в конце планирования gR указывает
на вполне определенную скорость входа V^n > j/£'£5 если время движе¬
ния по восходящему и нисходящему участкам должно быть одинаково.
Если скорость входа равна второй космической скорости Е0ц = у 2gR, то
формула (9.60) дает V\=j/gR/2. Любопытно заметить, что в этом
частном случае характер изменения скорости по участкам битраекторного
планирования следует закону геометрической прогрессии со знаменателем
l/-|/2. При этом: VQU = y2gR (при входе), Vi = Уц = у gR (в точке
восходящего и начала нисходящего участков планирования) и V\\~VsR/2
(в конце планирования).
СПИСОК ЛИТЕРАТУРЫ
1. Дубошин Г. Н. Небесная механика. М., Физматгиз, 1963, 586с.
2. Исследования по динамике полета. Под ред. д-ра техн. наук
проф. И. В. Остославского. [Сборник статей]. М., «Машиностроение», 1965,
вып. 1, 355 с.
3. Мартин Д ж. Вход в атмосферу. Введение в теорию и практику.
Под ред. канд. техн. наук Н. А. Анфимова. М., «Мир», '1969, 320 с.
4. Орлов Б. В. и др. Основы проектирования ракетно-прямоточных дви¬
гателей для беспилотных летательных аппаратов. Под ред. д-ра техн. наук
проф. Б. В. Орлова. М., «Машиностроение», 1967, 424 с.
5. Рабинович Б. И. Вариационные режимы полета крылатых лета¬
тельных аппаратов. М., «Машиностроение», 1966, 182 с.
6. Р у п п е Г. Введение в астронавтику, т. I. М., «Наука», 1970, 612 с.
7. Ш к а д о в Л. М. и др. Механика оптимального пространственного дви¬
жения летательных аппаратов в атмосфере. М., «Маншностроение», 1972, 240 с.
■8. Штерн Т. Е. Введение в небесную механику. М., «Мир», 1964, 242 с.
9. Э л ь я с б е р г П. Е. Введение в теорию полета искусственных спутни¬
ков Земли. М., «Наука», 1965, 540 с.
10. Эрике К. Космический полет, т. 1. М., Физматгиз, 1963, 586с.
11. Ярошевский В. А. Приближенный расчет траекторий входа
в атмосферу. — «Космические исследования», 1964, т. 2, вып. 4, с. 507—531,
вып. 5, с. 579—696.
42. Becker J. V. Re-Entry From Space, Scientific American, January,
1961, p. 10—59.
13. Cazley C. Atmospheric Entry. The RAHD Corp., Rep., P-2052,
July, 1960.
Глава X
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ
ОДНОСТУПЕНЧАТЫХ РАКЕТ
Проектирование летательного аппарата, в том числе и раке¬
ты, будь то одноступенчатой или составной, баллистической или
носителя космических кораблей, по существу, имеет целью вы¬
бор и назначение таких параметров, которые наивыгоднейшим
образом отвечали бы предъявляемым техническим требованиям.
Уже на первых этапах проектно-конструкторских изысканий
(например при подготовке аванпроекта) является важным наз¬
начить такие значения основных параметров (начальный вес,
весовую отдачу, перегрузку, закон расхода постоянных и пере¬
менных масс и т. д.), которые в последующем, претерпевая из¬
менения, в основном отвечали бы ожидаемым характеристикам
ракеты.
Разработка методики выбора оптимальных параметров свя¬
зана с учетом многих факторов и прежде всего весовых факто¬
ров. Опыт проектирования показывает, что достоверность полу¬
чаемых результатов в значительной мере зависит от точности
вводимых весовых данных.
Действительно, без учета весовых факторов и, в частности,
влияния перегрузки на весовую отдачу, второй закон Циолков¬
ского (2.44) запишется так:
где полагаем, что величина параметра рк не зависит от пере¬
грузки п0у т. е.
Изучение этого выражения показывает, что для достижения мак¬
симальной конечной скорости необходимо, чтобы п0= оо.
Этот чисто академический вывод не имеет практического
смысла. При увеличении тяги увеличивается вес реальной конст¬
рукции, что приводит к увеличению коэффициента цк= цЦпо).
Таким образом, варьирование перегрузкой п0 вызывает измене¬
ние весовой отдачи по конечному весу, влияние которой на ско¬
рость Vl{ требует отыскания наиболее выгодного (оптимального)
значения перегрузки п0. Зависимость Цк = цк(п0) учитывает вли-
Рк = рк(/г0) = const.
231
яние весовых факторов и, как мы уже видели (гл. VI), составля¬
ется на базе трудоемких работ весового анализа. Учет весовых
факторов потому и дает наиболее достоверные результаты при
проектировании, что сам по себе весовой расчет является наибо¬
лее адэкватным сложному и многогранному процессу создания
ракетного летательного аппарата.
В дальнейшем по мере углубления проектных работ (напри¬
мер на этапе эскизного проекта) первоначально установленные
значения параметров уточняются. При этом в зависимости от
специфики задания, конструктивных, технологических и других
требований, отдельные значения параметров могут быть приняты
не равными оптимальным. В этом случае знание оптимальных
параметров .необходимо для оценки и установления возможных
(допустимых) пределов их отклонений.
Определение оптимальных значений основных параметров
будем производить на базе совместного решения обобщенных
весовых уравнений (основных весовых зависимостей) и уравне¬
ний ракетодинамики, исходя из максимума конечной скорости
при постоянном весе ракеты.
10. 1. ОСНОВНЫЕ ПАРАМЕТРЫ
ОДНОСТУПЕНЧАТЫХ РАКЕТ
К основным параметрам одноступенчатых ракет относятся:
— весовая отдача по топливу GT;
— весовая отдача по конечному весу рк;
— число Циолковского Ц;
— коэффициент грузоподъемности е;
— стартовая перегрузка п0;
—-коэффициент расхода активной массы (топлива) (3;
— коэффициент эффективности конструкции |л0фф;
—-скорость истечения активной массы (топлива) W\
— удельная тяга Руд.
Эти параметры, кроме последних двух, являются конструк¬
тивными характеристиками ракеты. Скорость истечения и удель¬
ная тяга являются характеристиками энергетических свойств
топлива, а также совершенства процессов, осуществляемых дан¬
ной конструкцией ракетного двигателя для получения тяги.
Функциональная взаимосвязь между основными параметра*
ми имеет следующий вид (см. гл. II, VI):
Ц=1/.ЛК, W = gPy„ !*к = !Аэ, + £Яо> ftc + От
е = Д1/О0, /г0 = ^=?Я¥Д, р
Lf0 - 1 — г
а — ц . . \’г
■ •• эфф I • •
(10.1)
Как будет показано в главе, две последние зависимости яв¬
ляются основными при учете весовых факторов в поисках
по выбору оптимальных параметров.
232
10.2. СТАРТОВАЯ ПЕРЕГРУЗКА В ПУСТОТЕ
ПРИ ЛИНЕЙНОМ ЗАКОНЕ ИЗМЕНЕНИЯ МАССЫ
Оптимальность стартовой перегрузки для случая полета ра¬
кеты в пустоте определяется двумя противоположно действую¬
щими факторами. С одной стороны, желание уменьшить потери
на преодоление силы тяжести указывает на необходимость уве¬
личения перегрузки /г0; с другой — увеличение перегрузки п0
связано с понижением весовой отдачи GT, что вызывает умень¬
шение конечной скорости Vu. Последнее обстоятельство связано
с действием весовых факторов, учет которых произведем, вос¬
пользовавшись основной весовой зависимостью вида
Кс^эл+Н'-
Параметр цэл не связан функционально с перегрузкой и яв¬
ляется постоянной величиной. Коэффициент k при параметре л о ,
как было показано ранее (см.
разд. 6. 1.), учитывает изменение ко¬
нечного веса ракеты в связи с из¬
менением тяги двигателя (или все
равно, что перегрузки п0и). Напом¬
ним также, что на величину коэф¬
фициента k влияют и те элементы
конструкции, вес которых зависит
от тяги. Сюда можно отнести арма¬
туру двигательного отсека, несущие
корпусы, частично баки и крепеж¬
ные детали.
Рис. 12S. Влияние перегрузки /ф на конеч¬
ную скорость полета в пустоте при линей¬
ном законе изменения массы
Воспользовавшись вторым законом Циолковского, запишем
7к = 1п-Ь_з(0к)±=^, (Ю.2)
Р-к п0
77 W
где V к-—±- —конечная скорость, отнесенная к скорости ис¬
течения в пустоте.
Параметр а(6к) в формуле (10.2) учитывает потери на силы
тяжести в зависимости от выбранной программы полета (см. за¬
висимость 10.8).
Подстановка выражения (6.9) в уравнение (10.2) дает
FK = ln Ц -iM [1 _ (,**,+ **«)] . (10.3)
[хэл + kn0 п0
233
Равенство (10.3) устанавливает зависимость безразмерной
конечной скорости FH от параметров, характеризуемых учетом
динамических и весовых факторов.
Характер зависимости VK= VK (/zo) для различных значе¬
ний параметра сг(0к), построенной по уравнению (10.3), пред¬
ставлен ;на рис. 128. Как видно из графика, при значениях
о(0 к) >0, функция \7к = V^K (/го) имеет максимумы, которым
соответствуют наивыгоднейшие (оптимальные) значения пере¬
грузок
Из графика видно также, что эти перегрузки тем меньше, чем
меньше гравитационные потери. Если последние отсутствуют,
т. е. сг(Ок)=0, то функция VK = VK(nlo) не имеет экстремума
и теоретически максимальная скорость достигается при значени¬
ях по =0. Этот вывод имеет смысл для космических летатель¬
ных аппаратов, где действующие перегрузки могут быть пре¬
дельно малы (ttJJ <С1).
Поскольку в выражении (6.9) имеет место е = const, то оче¬
видно, что отыскание экстремума функции ^к = 1/к(яо) воз¬
можно при постоянном весе полезного груза As=const и посто¬
янном стартовом весе ракеты G0 = G0i = const. При этом, прирав¬
нивая нулю производную dVJdnjj, получим
k (nlf - 3 (0К) |ХЭЛ (1 — - 3 (0J (1 - jxJ knl = Q, (10.4)
откуда оптимальная перегрузка ^о = /гопт будет равна
1/2
(10.5)
Выражение (10.5) определяет оптимальное значение старто¬
вой перегрузки /г£ит в функции параметров, задаваемых при
проектировании.
Выражение (10.5) может быть представлено и в другом виде.
Для этого разрешим уравнение (10.4) относительно параметра
Яо после подстановки в него выражения рэл = рк— kti™.
Тогда получим
0 (0к) „ 1 Г / а (0к) \2 1 а (0к) П
,; + [(^ *)г + ^А]Л (Ю.6)
где GT=(1—Цк)—весовая отдача по топливу.
График оптимальных перегрузок, построенный по формуле
(10.6) для различных значений параметра а = а(6к), представ¬
лен на рис. 129. Характерным для кривых на графике является
наличие максимума функции ^Jj = «jj(pK) для оптимальных
значений параметра по = по0ю' Этот максимум указывает
на необходимость уменьшения оптимальных перегрузок
234
/7и = /г'' как па малых, так и па больших значениях пара¬
то оопт
метра цк. Физическое объяснение такого явления заключается в
следующем.
При движении (на графике) от больших к средним значени¬
ям весовой отдачи рк увеличение перегрузки необходимо для
уменьшения потерь на силы тяжести, которые в противном слу¬
чае были бы велики ввиду увеличе¬
ния параметра GT, а следовательно, по
и увеличения времени полета т. з,5
Ухудшение при этом весовой отда¬
чи рк (увеличение этого параметра) з,о
не оказывает доминирующего влия¬
ния на конечную скорость, посколь- 2,5
ку относительный вес двигательной
установки в общем весе конструк- 20
ции (конечном весе ракеты) неве¬
лик. При движении от средних к ма- 15
лым значениям параметра рк умень- 7
1,0
Рис. 129. Влияние на оптимальную пере- 0,5,
грузку пQ параметров tuK и сг(вк) при ли¬
нейном законе изменения массы q
шение оптимальной перегрузки связано с возрастанием относи¬
тельного веса двигательной установки. Выигрыш в весовой от¬
даче при уменьшении параметра рк здесь является доминирую¬
щим фактором, хотя при этом возрастают и без того большие
потери на силы тяжести.
Другими словами, при малых значениях параметра цк отно¬
сительный вес двигательной установки велик, вследствие чего,
несмотря на большое время полета (а следовательно, и большие
потери на силы тяжести), оптимальная перегрузка п"ит (а сле¬
довательно, и относительный вес двигательной установки) дол¬
жна быть уменьшена.
При больших значениях параметра рк относительный вес
двигательной установки невелик, однако при этом слишком ма¬
ла скорость по Циолковскому, которую можно увеличить только
вследствие уменьшения параметра рк, а следовательно, благода¬
ря уменьшению перегрузки п0. График показывает также, что
оптимальные перегрузки пропорциональны гравитационным по¬
терям, характеризуемым параметром а(0к).
Из формулы (10.6) видно, что при рк=1, оптимальная пере¬
грузка в пустоте равна по =а(0к). Если а(0к) = 1 и рк=1, то
^oirr^l- Это случай стоянки на стартовом столе гипотети¬
ческой ракеты, у которой отсутствует топливо. При рк = 0 и всех
235
значениях параметра а(Ок) величина оптимальной перегрузки
равна нулю. Это чисто теоретический случай, при котором вся
ракета должна состоять из расходуемой в полете активной
массы.
Крайние области по параметру цк> где /zjj<4, не имеют
практического смысла для одноступенчатых и первых ступеней
составных ракет, стартующих вертикально, поскольку для отры ¬
ва от стартового стола всегда необходима перегрузка больше
единицы п0> 1. Однако график не нуждается в перестройке,
поскольку эти области применимы к космическим кораблям и
старшим ступеням составных ракет, у которых имеет место
а(9к) < 1 и По ^1.
Выражение для параметра рк, при котором имеет место мак¬
симум функции Л011Т = Л011Т(^к) нетрудно
ражению (10.6), приравняв нулю производную
этом
получить по вы-
dn"!d\±K. При
IV
4 а(0К) k
1
11/2
4 а (0К) k
4 а (0К) k
(10. 7)
*'Л)
Рис. 130. Зависимость парамет- Рис. 131. Зависимость дальности, вы-
ра гравитационных потерь соты, времени и угла 0К от конечной
о(0к) от конечного угла 0К для скорости ракеты
одноступенчатых ракет
Если пренебречь малыми значениями произведений а(0н)&
(обычно меньших 0,023 для ЖРД), т. е. положив а(0к)* = О, то
получим цкя^1/2. Это означает, что наибольшие значения опти¬
мальных стартовых перегрузок (Ло)01ГГ имеют место для ракет
с половинной весовой отдачей.
Значения параметра сг(6к), рассчитанные для оптимальных
траекторий одноступенчатых ракет, приведены на рис. 130. Гра-
236
фик построен по данным численного интегрирования уравнений
движения как
X
з(6к) = -Г- ^ sin0d*, (10.8)
о
где 0 —угол наклона траектории к местному горизонту; т —
полное время полета.
Рис. 132. Зависимость основных параметров движения ра¬
кеты от дальности при полете по баллистической траекто¬
рии (без учета дальности активного участка)
Таблица 10.1
Параметры баллистической траектории
2?
К
L, км
V , км/с
т
Н, км
15°
41°15'
1667
3772
1047,4"
495
30°
37°30'
3333
5033
16'09,0"
827
45°
33°45'
5000
5839
20'18,6"
1093
60°
30*00'
6666
6408
25'29,8"
1286
75°
26°15'
8333
6828
29'27,5"
1402
90°
22°30'
10000
7144
32'59,7"
1441
105°
18°45/
11667
7383
36'И,8"
1402
120°
15°00'
13333
7562
38'37,4"
1286
135°
11°15'
15000
7692
40'38,2"
1093
150°
7°30'
16667
7780
42'04,6"
827
165°
3°45'
18333
7832
42'56,1"
495
180°
0°00'
20000
7849
43'13,1"
100
Примечание. 2(1—центральный угол, 0К—конечный угол (в момент вык¬
лючения двигателя), VK—конечная скорость, L, Т, Н—соответственно даль¬
ность, время и высота баллистического полета.
237
Другие траекторные данные, связанные с конечным углом О к
различными параметрическими зависимостями, приведены в таб¬
лице 10.1 и на рис. 131 и 132.
Таблица составлена для оптимальных углов Ок=(0к)опт [4].
Эти данные необходимы также для отыскания значений
а(0к) при вычислениях оптимальных перегрузок и других па¬
раметров ракет, в том числе и многоступенчатых (см. гл. XII).
10.3. СТАРТОВАЯ ПЕРЕГРУЗКА В ПУСТОТЕ
ПРИ ПОКАЗАТЕЛЬНОМ ЗАКОНЕ ИЗМЕНЕНИЯ МАССЫ
Изучение оптимальности параметра по при показательном
законе изменения массы произведем как и в предыдущем пара¬
графе, воспользовавшись весовой зависимостью (6.9). После
подстановки этой зависимости в формулу (2.47) получим
VK= -
1
°(0к)'
[^эл +кп0].
(10. 9)
Равенство (10.9) связывает
между собой основные пара¬
метры движения и параметры,
характеризующие влияние на
конечную скорость весовых
факторов.
б(вк)
8 ппп
Рис. 133. Влияние перегрузки
п0п на конечную скорость по¬
лета в пустоте при показатель¬
ном законе изменения массы
Рис. 134. Зависимость оптимальных
значений стартовой перегрузки от ве¬
совой отдачи для случая полета в
пустоте при показательном законе
изменения массы
238
На рис. 133 представлены кривые VK=zV* построен¬
ные по уравнению (10.9) для различных значений параметра
гравитационных потерь а(0к). Как и в случае линейного закона
изменения массы, при показательном законе функция
Ук= VK (яо)имеет максимум, определяемый влиянием весовых
факторов. Уменьшение гравитационных потерь также уменьша¬
ет оптимальную перегрузку, которая, как и при линейном зако¬
не изменения массы, становится равной нулю при сг(0к) =0.
Экстремальное значение функции VK — VK (/го)' по уравне¬
нию (10.9) найдем, приравняв нулю производную dVJdrio.
При этом, поступая как и ранее (см. разд. 10.2), получим
Кривые оптимальных значений = построенные по
формуле (10.10) для различных значений параметра а(6к), при¬
ведены на рис. 134.
Как видно из графика, для случая показательного расхода
массы так же, как и в случае линейного расхода массы, функция
оптимальной перегрузки /г^г = /г” (!^к) имеет максимум. Как
и ранее (см. разд. 10.2), этот максимум характеризует влияние
на оптимальные перегрузки весовых факторов. По сравнению с
линейным законом, максимумы кривых (р*ка (6К)
при показательном законе сдвинуты в сторону малых значений
коэффициента цк. Это свидетельствуете несколько меньшем вли¬
янии весового фактора на величину /zjj = /^nT и объясняется
тем, что конструкция ракеты работает не на максимальные (ко¬
нечные) перегрузки, а на минимальные, равные начальным осе¬
вым перегрузкам п".
Увеличение абсолютных значений параметра /г^1, по сравне¬
нию с линейным законом, обусловлено необходимостью значи¬
тельного уменьшения потерь на силы тяжести, поскольку при
показательном законе изменения массы время полета на актив¬
ном участке траектории (время работы двигателя) значительно
больше, чем для линейного закона изменения массы.
Значение коэффициента рк, при котором имеет место макси¬
мум функции /г" = /г^1 (i^K) для оптимальных значений /г^1, как
и ранее, найдено по выражению (10.10), приравняв нулю произ¬
водную dn"d\bK. Тогда получим ptK= 1/е~0,36-8. Таким обра¬
зом, необходимость уменьшения гравитационных потерь сдвига-
ет (яоит)шах в сторону малых значений параметра рк по срав¬
нению с линейным законом на величину Дрк~0,132.
По формуле (10.10) имеем также = ^ ПРИ = 0 и /го =
= <т(0к) при Рк=1.
(10. 10)
239
Как и при линейном законе изменения массы, график (см.
рис. 134) не нуждается в коррекции крайних областей по пара¬
метру Цк, поскольку такое построение функции п" — п" (;хк)
приемлемо для космических систем и старших ступеней состав¬
ных ракет.
10.4. СРАВНЕНИЕ ЛИНЕЙНОГО И ПОКАЗАТЕЛЬНОГО ЗАКОНОВ
ИЗМЕНЕНИЯ МАССЫ
На рис. 135 представлены кривые оптимальных значений на¬
чальных осевых перегрузок в функции параметра рк для ли¬
нейного и показательного законов изменения массы. График по¬
казывает, что большие значения оптимальных перегрузок для
показательного закона изменения массы по сравнению с линей¬
ным законом имеют место на всем участке 0<р,к<1, причем
расхождение в значениях тем больше, чем меньше величи¬
на параметра цк. Указанное явление имеет место для любых
траекторий, характеризуемых параметром гравитационных по¬
терь а (О к). Расхождение в оптимальных перегрузках, как отме¬
чалось ранее (см. разд. 10.3), связано с неодинаковым временем
работы двигателей при разных законах расхода топлива, что в
свою очередь связано с неодинаковыми потерями на преодоле¬
ние сил тяжести на активном участке полета. При прочих рав¬
ных условиях оптимальное значение стартовой перегрузки тем
больше, чем больше время полета т.
Пользуясь формулами (2.36) и (2.38), найдем относитель¬
ное увеличение времени полета при показательном законе изме¬
нения массы по сравнению с линейным законом. Оно составит
где индексы «пок» и «лип» означают параметры, относящиеся к
показательному и линейному законам изменения массы.
Для случая одинаковых перегрузок (/го);1иН = (,го)П(ж выра¬
жение (10.11) принимает вид
Кривые т^=т(цк) для одинаковых и оптимальных значений
перегрузок по , построенные по выражениям (10.11) и (10.12),
приведены на рис. 136. График показывает, что увеличение вре¬
мени работы двигателя при показательном законе изменения
массы особенно заметно при малых значениях параметра рк- Из
графика видно также, что оптимальные перегрузки заметно
уменьшают это время, что и способствует уменьшению гравита¬
ционных потерь. Для большей иллюстрации сказанного на рис.
240
("о) lnU
У U/лин
(10.11)
In Ц
Х=
1 — Ик
(10. 12)
137 представлены кривые г,. = К1;(|л1;), построенные по формулам
(102) и (10.9) при одинаковых значениях перегрузок п о . Гра¬
фик показывает, что ракеты с расходом массы, подчиняющимся
показательному закону, значительно проигрывают в конечной
скорости ракетам с расходом массы, подчиняющимся линейно¬
му закону, если значения перегрузок в одном и другом случаях
одинаковы. На другом рис. 138 приведены аналогичные кривые
у =j7|.(l(].)> но построенные с учетом оптимальных перегрузок.
Как видно из графика, оптимальные перегрузки значительно
Рис. 13-'). Сравнение оптимальных
перегрузок п q для линейного и по¬
казательного законов изменения
массы:
j—линейный закон; 2—показательный закон
О 0,2 ОА 0,6 0t8 JJ,с
Рис. 137. Сравнение_ безразмерных
конечных скоростей VK для линейно
го и показательного законов измене¬
ния массы при постоянной перегрузке
л о = const:
1—линейный закон; 2— показательный закон
Рис. 136. Зависимость относительного
увеличения времени полета ракеты на
активном участке траектории для по¬
казательного закона изменения массы
по сравнению с линейным законом:
п
7—при одинаковых tiQ\ 2—при оптималь-
п
ных по
Рис. 138. Сравнение безразмерных ко¬
нечных скоростей VK для линейного
и показательного законов изменения
массы при оптимальных перегрузках
по ~ (/?0^о.гг •
1—линейный закон; 2—показательный закон
241
уменьшают потери в скорости на преодоление сил тяжести при
показательном законе изменения массы, вследствие чего рас¬
хождение в конечных скоростях, даже на малых рк, составляют
небольшую величину.
10.5. СТАРТОВАЯ ПЕРЕГРУЗКА
С УЧЕТОМ ВЛИЯНИЯ АТМОСФЕРЫ
Влияние атмосферы на конечную скорость ракеты сказывает¬
ся через аэродинамические силы лобового сопротивления и баро¬
метрическую добавку тяги ракетного двигателя АР. Аэродинами¬
ческие силы лобового сопротивления замедляют движение,
вследствие чего происходит уменьшение конечной скорости ра¬
кеты; статическая добавка тяги увеличивает суммарный им¬
пульс двигательной установки, вследствие чего конечная скорость
возрастает.
Если в пустотных условиях оптимальность стартовой пере¬
грузки определяется двумя противоположно действующими фак¬
торами (гравитационными и весовыми), то в сопротивляющейся
среде к этим факторам добавляется еще один фактор, учитыва¬
ющий потери скорости от аэродинамических сил лобового сопро¬
тивления AVX- Величина этих потерь может быть оценена изу¬
чением кривых AVx = AVx{no, О к), построенных интегрированием
выражения вида
"0ЛЗ)
о
где X(t) —текущая сила лобового сопротивления; M(t)—теку¬
щая масса ракеты.
Кривые AVx = AVx(no, О к) показывают, что потери скорости
пропорциональны стартовой перегрузке п0 и обратно пропорцио¬
нальны углу 0 к. Такой характер этих кривых объясняется тем,
что при увеличении перегрузки возрастает скорость полета, а
следовательно, и сопротивление X(i) на участке атмосферы; при
увеличении угла 0К уменьшается общий путь, проходимый раке¬
той в сопротивляющейся среде, что уменьшает интегральные по¬
тери скорости AVX.
Изучение экстремума функции FK = FK(/20) произведем при¬
менительно к линейному закону изменения массы.
Представляя полет в атмосфере с пустотными характеристи¬
ками двигателя и воспользовавшись вторым законом Циолков¬
ского, запишем
Кк = Wu In -L - a (0K)gT- де. - А1Д, (10.14)
где в правой части первый член определяет идеальную скорость
в пустоте по Циолковскому; второй член — потери в скорости на
242
преодоление сил тяжести; третий член — потери в скорости
вследствие того, что на участке атмосферы полет происходит не
при пустотных характеристиках двигателя, а при других, опре¬
деляемых увеличение тяги от стартовой Pq до пустотной Ро ;
четвертый член — потери в скорости на аэродинамические силы
лобового сопротивления
Пользуясь данными численного интегрирования уравнений
движения, можно путем аппроксимации получить
где a, v, г), Ь, с — коэффициенты аппроксимации.
Зависимости (10.15) и (10.16) с удовлетворительной для па¬
раметрических изысканий точностью остаются справедливыми в
пределах всех значений G к, имеющих место для жидкостных ра¬
кет с высокими энергетическими и конструктивными характери¬
стиками.
Подстановка выражений (10.15) и (10.16) в равенство (10.14)
и затем его преобразование дает
Коэффициенты аппроксимации 6, с и т, имеющие место в
уравнении (10.17), из дальнейшего рассмотрения выпадают.
Учет весовых факторов произведем, как и ранее, по зависи¬
мости (6.9). Для решения уравнения (10.17) на экстремум необ¬
ходимо произвести дифференцирование по параметру п0 и при¬
равнять нулю производную. Выполнив эти действия, получим
Безразмерный параметр т]0 учитывает влияние атмосферы на
величину оптимальной перегрузки п0. Характер кривых цо =
= r]o(Wo, О к) представлен на рис. 139. Как видно из графика, ве¬
личина т]о в значительной мере зависит от конечного угла 0К, что
в свою очередь является определяющим и для перегрузки п0. Из
графика видно тарке, что увеличение скорости истечения пони¬
жает величину т]о, что сказывается на некотором увеличении оп¬
тимальной перегрузки.
д1/п = Г;-1)(аГ0 + г/г0);
kV х —^1 T ci
(10.15)
(10.16)
о—и-к) — ^m+v(5— 1)]—
Wq
(10. 17)
0.5a (6K)fe
S/г
(10. 18)
243
Зависимость оптимальной перегрузки от весовой отдачи для
различных значений а(0к), построенная по формуле (10.18),
представлена на рис. 140. Как видно из графика, характер
кривых Яо = Ло[|Дк, ст (О I?) ] остается таким же, как и для случая
полета в пустоте. При этом сами значения перегрузок на всем
диапазоне весовых отдач jlik = 0-f-1 уменьшены, что является
следствием влияния атмосферы. Как и в случае полета в пусто¬
те, величина перегрузки поит тем больше, чем больше гравитаци¬
онные потери. Области на графике, где я0пт^1, практического
смысла не имеют, поскольку при вертикальном старте с поверх¬
ности земли всегда имеет место По>1.
Рис. 139. Характер зависимости Рис. 140. Изменение начальной осе-
параметра г|0 от конечного угла вой перегрузки п0 в зависимости от
0к и скорости истечения W0 весовой отдачи с учетом влияния ат¬
мосферы
При г|о = 0 и £=1 формула (10.18) дает выражение (10.6).
Таким образом, пустотная перегрузка является как бы частным
случаем перегрузки, выбираемой с учетом влияния атмосферы.
Результаты вычислений по формуле (10.18) хорошо согласу¬
ются с данными, полученными на базе расчетов траекторий дви¬
жения с учетом весовых факторов.
10. 6. ОПТИМАЛЬНЫЙ ДИАМЕТР КОРПУСА РАКЕТЫ
С УЧЕТОМ ВЛИЯНИЯ АТМОСФЕРЫ
Получение простой зависимости рк = цкфо) чисто аналитиче¬
ским путем не представляется возможным. Наиболее целесооб-
244
разным здесь является метод, основанный на аппроксимации-
кривых весового анализа, представленных на рис. 141. Такие
кривые удовлетворительно аппроксимируются зависимостью
вида
(10.19)
где значения р0 и Do соответствуют экстремальным точкам кри¬
вых Цк = p-к (-^м) при d[xK/dDyi = 0.
Воспользовавшись формулой (2.44) и учитывая потери в ско¬
рости за счет аэродинамического сопротивления Д1/X(DM), за¬
пишем
[МЦ,)]'
По
Do
где параметр определяется статистически на базе весового
анализа по аналогии определения параметра &VX (10.16).
Рис. 141. Влияние диаметра и гру¬
зоподъемности на весовую отда¬
чу Ик
Рис. 142. Изменение отношения
А
в зависимости от весовой отда¬
ло _
чи GT для различных значений диа¬
метра D
Приравнивая нулю производную
dVK/d (Dm/Dq) ,
получим
V (0кГ,
2vxDl(DJD^
О ("о
2 по
-(DJD0)
а (8к)
2лп
1*0 = 0,
М_у
'о )
(10. 20)
245
Решение этого уравнения для случая переменной нагрузка
на мидель <7m = ?m(Gt) (по данным весового анализа или зависи¬
мостей разд. 5.11) представлено на рис. 142. Как видно из гра¬
фика, влияние сопротивления воздуха на уменьшение диаметра
корпуса ракеты одинаково уменьшается при малых и боль¬
ших значениях весовых отдач GT- При малых значениях пара¬
метра GT это происходит вследствие уменьшения потерь AVX =
= VX(GT) (активный участок не полностью проходит атмосфе¬
ру), при больших значениях GT — вследствие увеличения на¬
грузки на мидель q^ = q^i(GT). Из графика видно также, что ве¬
личина (DM/£)0) пропорциональна параметру qu.
Рис. 143. Зависимость соотно- Рис. 144. Влияние параметра qм
шеиия диаметров DM/D0 от па- на соотношение диаметров
раметра GT при различных при различных значени-
значепиях нагрузки на ми- ях перегрузки п0
дель qyl
Представление о влиянии параметра qM на величину
(D^/Dq) дает график (рис. 143), построенный по тому же урав¬
нению при различных значениях параметра qyi = const.
Из графика видно, что влияние сопротивления воздуха на
диаметр ракеты особенно сказывается при малых нагрузках на
мидель. Из графика_ видно также, что величина DM/D0 на участ¬
ке весовых отдач GT = 0,6-f-l остается практически постоянной.
Это позволяет положить в уравнении (10.20) ро = 0 и после ре-
246
щения относительно Dyi/D0 получить
1/2
(10.21)
где
d= Я*Уо
2AVX
Кривые =f—(<7м) Для различных значений - пара-
\ А> / \ А) /
метра По> построенные по формуле (10.21), приведены на рис.
144. График показывает, что параметр qyi является доминирую¬
щим в выборе диаметра ракеты. При увеличении нагрузки на
мидель возрастает величина DM/D0, что указывает на прибли¬
жение диаметра ракеты к значениям, близким при полете в пус¬
тоте. Увеличение перегрузки также вызывает увеличение отно¬
шения DM/D0.
Напомним, что в пустотных условиях диаметр корпуса раке¬
ты D0 определяется либо по развернутым формулам весового
анализа, либо по приближенным зависимостям. (см. разд. 5.10,.
5.11). При этом, если обозначить (DM/D0) =г\х, то оптимальный
диаметр корпуса ракеты с учетом аэродинамического сопротив¬
ления определится как DM = r|ADo.
10. 7. ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ
ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ОСНОВНЫХ ПАРАМЕТРОВ
Воспользовавшись основной весовой зависимостью (6.3),,
можно нанести семейство линий цк(е, п0) с шагом е и угловом
коэффициентом k на кривые оптимальных перегрузок nQ —
= ^о[рк, су (0 к)] (см. рис. 129) и /гоп = Яо11[р,к, а(0к)] (см. рис. 140),
как показано на рис. 145 и 146. Таким построением совмещаются
потребные и располагаемые значения параметров п0 = /20(рк)•
Искомые значения оптимальных параметров п0 (или я0п) и цк
находятся в точках пересечения двух семейств цк(б, п0) и п0 =
а (О к)]. Порядок определения оптимальных параметров
по этим графикам (номограммам) следующий:
а) по заданному грузу Де и весу ракеты Go определяют вели¬
чину е=-Д s/G0;
б) по найденному значению е и предполагаемой величине
а(0к) (см. рис. 130), по графикам (см. рис. 145 или 146) опреде¬
ляются значения параметров рк и п0 (или п0п).
Задача выбора параметров может быть поставлена и по дру¬
гому, когда вместо начального веса задается дальность (или ко¬
нечная скорость) полета. Тогда прежде всего необходимо опре¬
делить (по графикам или расчетным путем) потребное значение
весовой отдачи pK=|iK(l/K). Зная цк и а(0к), находим по гра-
247
Рм.
Do
1
V(l
■+d
фикам (см. рис. 145 или 146) оптимальную перегрузку п0 (или
л0п) и грузоподъемность в. По найденной грузоподъемности стар¬
товый вес ракеты устанавливается в зависимости от веса полез¬
ного груза как G0 = Aа/г. Если задан вес ракеты, то груз опре¬
деляется как А2 = О0г.
Типовой график для определения чисел Ц в зависимости от
скорости и дальности полета приведен на рис. 147.
'0,05 0,15 0,25 0,35 0;Ь5
О 0,10 0,20 0J0 ОМ 0,50
U,05 0,f5Q,25 QJSQfiP
О | 0,101 0,20 0,30\ ОМ 0,50
Рис. 145. Номограмма для определе¬
ния основных параметров односту¬
пенчатых ракет с учетом влияния ат¬
мосферы
Рис. 146. Номограмма для определе¬
ния основных параметров одноступен¬
чатых ракет без учета влияния атмо¬
сферы
10.8. ВЫБОР СТАРТОВОЙ ПЕРЕГРУЗКИ ПО КРИТЕРИЮ
МАКСИМАЛЬНОЙ НАГРУЗКИ НАТЯГУ
Представим себе ракету (одноступенчатую или составную),
стартовый вес которой меняется благодаря весу топлива, топ¬
ливных емкостей и их коммуникаций. Тяга двигателя и вес
двигательной установки остаются постоянными. Ставится задача
об отыскании такого веса ракеты G0 или все равно, что старто¬
вой перегрузки п0 (поскольку Ро=const), при которых величина
As, приходящаяся на единицу тяги, достигла бы максималь-
;248
ного значения. Очевидно, что при этом ставится условие
A = (Ai) • (10.22)
Р0 Ро Апах
Аналогичные задачи имеют место, когда ставится вопрос о
преимущественном использовании двигательной установки дан¬
ной тяги, как наиболее дорогостоящего конструктивного элемен¬
та ракеты, с целью получения Дх = д1тах ценой завышенного
стартового веса ракеты.
Рис. 147. Типовой характер
кривых Щ(Ц) и L{Ц) для оп¬
ределения потребных значении
чисел Ц
Рис. 148. Выбор перегрузок п0 по крите¬
риям ■
Av
А у
О |
О max
Для рассмотрения этого вопроса обратимся к основной весо¬
вой зависимости (6.3), сделав в ней подстановку
А, А,
>'=— = —По.
Тогда получим
Р о
Av
о
■kjn0.
(10. 23)
Приравняв нулю производную dVJdn0 при P0 = const, най¬
дем в случае линейного закона изменения массы
уе ч 2 —11/2
| (Дт Р Y£) а (®к)
(У - ? —
И-г,-
ki (Ок) —5
f*K
2 ho
11
H-K
•'to +
il
f4
(10. 24)
249
При полете в пустотных условиях (|=1, г|о=:0) получим
также
0 (°к) — V
2/г
° (Вк) М — У
(10. 25)
для линейного закона изменения массы и
с(Вк)£ — У£ I Г I °(ЙК
^-(уз + !хк1пЦ)11/2 (10.26)
k
для показательного закона изменения массы.
Характер зависимости /Zq1 = /zj] (^1С), построенной по формуле
(10.25), представлен на ри*с. 148. Там же для сравнения приве¬
дена аналогичная кривая, но для случая (критерия) (As/G0)max-
Как видно из графика, стартовая перегрузка значительно пони¬
жается для случая (As/P0)max.
Выбор перегрузки по критерию максимальной нагрузки на
тягу (10.22) представляет особый интерес для тяжелых ракет-
носителей, у которых сравнительно большие значения е = £г оп¬
ределяют заметное увеличение грузоподъемности.
Если обозначить в равенстве (10. 23)
то определение оптимальной перегрузки можно вести по уже из¬
вестным формулам (10.6) или (10. 10), заменив в них k на /г0.
При этом только грузоподъемность в будет не задаваемой вели¬
чиной, как это имеет место в равенстве (10.25), а определяемой
по выражению (10.27) как
где п0— (п0)опт — оптимальная перегрузка.
10.9. ОПРЕДЕЛЕНИЕ ПОТРЕБНОЙ ВЕСОВОЙ ОТДАЧИ
ПО ПРИВЕДЕННОЙ КОНЕЧНОЙ СКОРОСТИ
Наибольшей популярностью у проектантов зачастую пользу¬
ются простейшие зависимости, расчеты по которым сводятся к
элементарным действиям. При этом имеющиеся статистические
материалы или специально построенные графики позволяют
свести к приемлемому минимуму ошибки вычислений.
Введем понятие приведенной конечной скорости УПр, которой
должна обладать ракета для того, чтобы обеспечить скорость
по Циолковскому и преодолеть потери на гравитацию и силы
250
(10.27)
аэродинамического сопротивления. Тогда можно записать
И11Р = Иц + дКгра11 + ДИа9Р, (10.28)
где Vn —скорость по Циолковскому; ДУГрав — гравитационные
потери; ДКаЭр— потери на аэродинамическое сопротивление.
Все составляющие правой части
уравнения (10.28) обычно являют¬
ся хорошо известными величинами
и определяются либо по графикам
типа (рис. 149), либо по графикам:
Рис. 149. Влияние стартовой пере¬
грузки на величину потерь ДРаор
и ДТграв при полете на орбиту
ИСЗ высотой Н0ро — 300 км
о
Рис. 150. Дальность и конечная:
скорость в зависимости от при¬
веденной скорости
типа (рис. 150). Поскольку нас интересует потребное значение
весовой отдачи рк, то перепишем уравнение (10.28) в следую¬
щем виде:
W 1П = ^грав аэр»
Р-к
откуда потребное значение рк найдется так:
'^ц
Рк=ехр
г pan + Д^аэр
W
)]
(10.29)
Формула (10.29) имеет одинаковую силу как для односту¬
пенчатых, так и для составных ракет. В последнем случае толь¬
ко необходимо произвести замену рк на Цн*.
Пример 10.1. Определить оптимальную перегрузку по критерию (As/Po)max>
если известно, что VK=KKl/U^=l,08,
Решение. Составим выражение для относительной конечной скорости
— G (Ок)
yr _in _L±L(i_ )
По
■где
Кк=-1п(о,08 + ^-л0)-— (о,92-^-
V Ро ) по \ Ро
— по=~'
^0
0,10
«
0,08
ОМ
1
Г
Ч
■К
X
VK=t,08
О
пд
Рис. 151. Графическое решение при- Рис. 152. Графическое решение при-
VK = 1/к
151).
мера 10. 1 мера 10. 1
составленным равенством, строим
Воспользовавшись
А*
кривую
По
9 Рп
для произвольно задаваемых параметров п0 и (рис.
Далее строим кривую (Д2/Рд) ;
о
(л0) для rK=l,08=const (рис.
152).
ство кривых (As/P0) = \ — j (По)
Очевидно, что для различных значений VK может быть построено семей-
о
По полученному графику (см. рис. 152) находим, что значение оптимальной
перегрузки составляет п0—л0Пт = 1,4.
Пример 10.2. Выразить оптимальную перегрузку для двух законов из¬
менения массы с учетом и без учета влияния атмосферы через критерий
максимальной нагрузки на тягу (X/,iDo)max. Показать влияние этого крите¬
рия на величину параметра /г0 при линейном законе изменения массы при
<Т(0К)=1 И ,113,7=0,06.
Решение. С учетом критерия максимальной нагрузки на тягу основная
весовая зависимость принимает вид
!Ч- = Р-эл “i" hno >
Имея выражения (10.6), (10. 10) и (10.18), можно получить
°(fll<)*0 , ff а(йк)£о
О ( _1_ N \ о( <
2 ^r ^1/2
a(0K)GT
'По + '
Рк
(10.30)
для линейного закона изменения массы с учетом влияния атмосферы,
(0к)
Рк +
f[:
(Як)
2
+ , G-rP-K
для линейного закона изменения массы при полете в пустоте и
п 0 (9'<) , I г
пшя = — НктД
° (.Як)
+ а (0К) 1.1 Ц
1/2
(10.31)
(10.32)
Рис. 153. Влияние параметра k0 на
величину оптимальной перегрузки
^0= (^о) опт
для показательного закона изменения массы при полете в пустоте.
Влияние критерия (-W^o)max на перегрузку удобно проследить по па¬
раметру &о ~/го (-Ч/^о). Воспользовавшись приведенной выше зависимостью
/7о=/?о(^о> P-к) Для линейного закона изменения массы (10.31), строим
график (рис. 153). График показывает, что переход от одноступенчатого но¬
сителя (^о=0,05) к тяжелым составным носителям (k0=0,25) снижает опти¬
мальную перегрузку с /2q = 1,62 до njj = 1,14 соответственно.
СПИСОК ЛИТЕРАТУРЫ
1. А п п а з о в Р. Ф., Лавров С. С., М и ш и н В. П. Баллистика управ¬
ляемых ракет дальнего действия. М., «Наука», 1966, 307 с.
2. Д м и т р и е в с к и й А. А. Внешняя баллистика. М., «Машиностроение»,
1972, 583 с.
3. К о о й И. и Ютенбогарт И. Динамика ракет. М., Оборонгиз,
1950, 328 с.
4. Э и о - П е л ь т р и Робер. Космические полеты. М., Оборонгиз, 1950,
148 с.
5. Э р и к е К. Космический полет, т. 2, ч. 1. М., «Наука», 1969, 571 с.
6. Э р и к е К. Космический полет, т. 2, ч. 2, М., «Наука», 1970, 744 с.
Глава XI
ЧАСТНЫЕ СЛУЧАИ РАСПРЕДЕЛЕНИЯ МАСС
ПО СТУПЕНЯМ МНОГОСТУПЕНЧАТЫХ РАКЕТ
Дальность полета ракеты, как известно, определяется в ос¬
новном величиной и направленйем вектора скорости в конце ак¬
тивного участка полета. Стремление к увеличению конечной ско¬
рости составляет главный предмет работ по выбору параметров
ракет, в том числе и составных. На рис. 154 представлена зави¬
симость конечной скорости от числа Циолковского для различ¬
ных значений скоростей истечения Wn. Из графика видно, что
при данном значении параметра Wn число Ц является оп¬
ределяющим в достижении максимальной скорости, а сле¬
довательно, и дальности полета.
Весовой барьер, как было показано в гл. VI, ограничивает
получение потребных чисел Циолковского для одноступенчатых
У,, км/с
Рис. 1.54. Влияние числа Ц и скорости истечения на конечную
скорость полета
254
ракет, вследствие чего перспектива достижения ими больших
скоростей полета зависит полностью от прогресса в создании но¬
вых ракетных двигателей, работающих на высококалорийных
топливах.
Влияние весового барьера заметно уменьшается, если при¬
менить принцип составных ракет по Циолковскому. Простейшим
примером этого является ракетный поезд, у которого теоретиче¬
ски нет границ к достижению сколь угодно больших чисел Циол¬
ковского. Это, как мы видели (см. разд. 7.6), достигается путем
введения в ракетную систему требуемого количества односту¬
пенчатых ракет-заправщиков, безотносительно к их барьерным
характеристикам.
На приведенном графике показаны другие области, ограни¬
ченные числами Циолковского для двухступенчатых ракет с ко¬
личеством ступеней п = 3 и более. Границы этих областей также
обусловлены влиянием весового барьера. Однако, как видно из
графика, это влияние по мере увеличения ступенчатости умень¬
шается, что приводит к увеличению чисел Ц, а следовательно,
и к достижению больших скоростей полета, включая первую
и вторую космические скорости.
Проследить количественную сторону этого явления можно на
примере сравнения ДЕух ракет путем отыскания соотношения
Go, как частного от деления барьерного веса составной ракеты
(Gq)coct на барьерный вес одноступенчатой ракеты G*.
Напомним, что барьерным весом был назван такой старто¬
вый вес ракеты (см. разд. 6.6), при котором достигается мак¬
симальное значение числа Ц.
Воспользовавшись выражением (6. 32) применительно к срав¬
ниваемым схемам ракет, запишем
где обозначено (G0)max = G*.
Поскольку старшие ступени можно рассматривать как по¬
лезный груз младших ступеней, то выражение для груза I сту¬
пени Avi запишется так:
где в — коэффициент распределения масс.
После подстановки выражения (11.2) в равенство (И. 1) по¬
лучим
(ил)
As, = O(III = G01s,
(11.2)
Go
£
(11.3)
д.
255
Для случая распределения масс по закону геометрической
прогрессии, как будет показано ниже (см. разд. 11.2), имеет
место равенство
/=1
где
; ■ = ■ 2 — const.
O0i
При этом выражение (11.3) принимает вид
Полученное выражение показывает, что барьерный вес со¬
ставной ракеты значительно превосходит барьерный вес одно¬
ступенчатой ракеты. Так, если принять е = 0,25, то уже для
двухступенчатой ракеты диапа¬
зон «безбарьерных» стартовых
весов увеличивается в 8 раз, а
для трехступенчатой ракеты —
в 64 раза.
Таким образом, принципи-
а л ь н ы м конструкт и в и ы м отл и-
чием составных ракет от одно
ступенчатых является возмож¬
ность преодоления ими весово¬
го барьера путем наращивания
ступеней и, следовательно, зна¬
чительного увеличения чисел Ц
Рис. 155. Влияние числа Ц и скорости
истечения на дальность полета
В дополнение к графику (см. рис. 154) на рис. 155 приведены
кривые потребных чисел Циолковского в зависимости от даль¬
ности полета при различных значениях скоростей истечения Wn.
Аналогичные графики, построенные в приемлемом для пользо¬
вания масштабе, являются настольными при выполнении работ
по выбору параметров различных схем ракет.
В целях доступности материала более широкому кругу спе¬
циалистов, а также удобства объяснения физических явлений на
256
(11.4)
(11.5)
примерах частных следствий, в главе принят последовательный
метод изложения от частного к общему.
Всем случаям распределения масс, рассмотренным в настоя¬
щей главе, соответствуют условия полета в отсутствии сил зем¬
ного тяготения. При этом полученные зависимости (рабочие
формулы) являются одинаково справедливыми как для линей¬
ного, так и для показательного законов изменения массы.
В заключение следует отметить, что читатель, который по¬
желает ознакомиться с другими работами по аналогичной тема¬
тике, может прочесть содержательные исследования советских
авторов Л. М. Воробьева [1] и В. А. Космодемьянского [3], а так¬
же зарубежных авторов М. Фертрегта [7] и А. Миеле [4].
11. 1. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТАВНЫХ РАКЕГ
К основным параметрам составных ракет относятся:
— приведенное число Циолковского, равное произведению
чисел Ц по ступеням
ц*=П и/;
/ = 1
— приведенная весовая отдача по конечному весу, равная
произведению весовых отдач по ступеням
П К
i = l
— коэффициент грузоподъемности, равный произведению ко¬
эффициентов распределения масс по ступеням. Он также равен
отношению веса полезного груза к стартовому весу ракеты
П <п-6>
Л)1
1=1
— коэффициент распределения масс, равный отношению ве¬
са старшей ступени к весу младшей ступени
Gn
0( / 4-1)
Ч—
— стартовые перегрузки ступеней /ген;
— коэффициенты расхода масс ступеней (V,
— скорости истечения активных масс ступеней Wi (или
удельные тяги ступеней РУш).
Как и у одноступенчатых ракет, эти параметры являются
конструктивными и энергетическими характеристиками ступеней
и составной ракеты в целом.
9 3479 257
Таблица 11. 1
Некоторые соотношения между основными параметрами многоступенчатых ракет при распределении масс по закону
геометрической прогрессии
258
Основные параметры составных ракет, вместе с другими па¬
раметрами (не основными, по также являющимися конструк¬
тивными и энергетическими характеристиками отдельных эле¬
ментов ступеней, траекторные данные, данные силовых устано¬
вок, закон расхода активной массы, гравитационный параметр и
т> п.) находятся между собой в определенной функциональной
зависимости. Наиболее важные из них, выраженные безразмер¬
ными соотношениями, приведены в табл. 11. 1.
11.2. ПРОСТЕЙШИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ МАСС
Как мы уже видели, скорость многоступенчатой ракеты скла¬
дывается из скоростей, получаемых каждой ступенью. Чем боль¬
шую скорость обеспечивает каждая ступень, тем больше будет
конечная скорость составной ракеты.
Одним из главных параметров, определяющих скорость по¬
лета ступеней, является весовая отдача по конечному весу цКг-
В соответствии с основной весовой зависимостью (6. 5) параметр
цнг является функцией коэффициента распределения масс
(11.4).
Изменение соотношения весов по ступеням вызывает измене¬
ние весовой отдачи ркн а следовательно, и конечной скорости
полета каждой i-и ступени.
При заданном начальном весе составной ракеты чрезмерное
увеличение коэффициента е* приводит к ухудшению весовых от¬
дач |ыКг по всем ступеням, кроме последней ступени (рис. 156);
При очень малых значениях коэффициента е?; имеет место также
ухудшения весовых отдач цкг-, кроме первой ступени. В том и
другом случаях параметр (ик* (2. 49) не достигает желаемых ми¬
нимальных значений. Очевидно, существует такое соотношение
масс (величина коэффициента в*), при котором произведение ко¬
эффициентов рк i по ступеням определяет минимальное значение
параметра цк*.
На рис. 157 представлены кривые изменения параметра цк:?:
в зависимости от коэффициента Вг = е, построенные для случая
многоступенчатой ракеты с учетом зависимости (6. 5) при д0ффг =
= Дэфф = const и е* = const по формуле
=[ ^эфф Ч- (1 — ^эфф) Кфф+С-^эффМ"-1-
Как видно из графика, функция д* = |л*(г) имеет минимум.
Там же показано, что одноступенчатая ракета с тем же полез¬
ным грузом имеет значительно худшую характеристику по весо¬
вой отдаче рк по сравнению с многоступенчатой ракетой того
же начального веса.
Остановимся на простейшем случае распределения масс, ког¬
да полет происходит в пустоте в отсутствии сил земного тяготе¬
ния при одинаковых скоростях истечения активной массы сту-
9* 259
пеней. Полагаем также, что все ступени выполнены по одинако¬
вой конструктивно-силовой схеме и для каждой из них имеет
место известная уже нам зависимость (6. 5).
/V
а)
И
ff)
Ш
в)
Рис. 156. Схема для выбора
коэффициента распределения
масс:
а—большое значение е^; б—малое
значение е^; в—оптимальное значе¬
ние е-
Рис. 157. Зависимость приве¬
денной весовой отдачи jnK* от
коэффициента распределения
масс е
/—одноступенчатая ракета; 2—со¬
ставная ракета
Экстремальное значение параметра е* будем искать по мак¬
симуму конечной скорости при постоянном начальном весе ра¬
кеты. Пользуясь формулой (2.48), запишем
^к=“2 [^эфф + О —^эфф) e/]i (11*7)
/=1
где Vек = VzJW — безразмерная суммарная скорость ступеней сос¬
тавной ракеты.
Для решения задачи воспользуемся методом неопределенных
множителей Лагранжа. Уравнение свкзи будет иметь вид
($1> гп> £Ш’ • • • > ej — £* = 0. (11.8)
Обозначим равенство (11.7) через f(ei, ец, ещ, ..еп), а вы¬
ражение (11.8) через F (еъ ец, еш,.. ., еп), и составим уравнение
Ф (-11 £П> £1П’ • • • 1 Sn) = f (еИ £П’ £1П’ • • • * £л) +
-\~kF (£j, 6П, £1П, . . . , £,.),
где Х=const — неопределенный множитель.
260
Далее легко получить в общем виде
дФ 1—н-эфф . с*
Н-эфф (1 [-‘‘Эфф) £ / \ е * /
Последнее выражение справедливо, если имеет место посто¬
янство коэффициента распределения масс, т. е. Si = e = const.
На основании выражения (11.4) находим
где п — количество ступеней.
Легко видеть, что распределение масс по ступеням состав¬
ных ракет следует закону геометрической прогрессии. Знамена- •
тель прогрессии в соответствии с выражением (11. И) равен
где параметр е* определяется выражением (11.6).
Таким образом, знаменатель геометрической прогрессии, оп¬
ределяемый выражением (11. 12), является ничем иным, как ко¬
эффициентом оптимального распределения масс. Этот коэффи¬
циент показывает, что при оптимальном распределении масс вес
ступеней тем больше, чем больше полезный груз Да.
На основании зависимости (6. 5) и принимая во внимание,
что в нашем случае цЭффг = const и 8i = const, получим
Таким образом, распределение масс по закону геометрической
прогрессии соответствует одинаковым весовым отдачам по сту¬
пеням. Это означает также, что скорости, наращиваемые каждой
ступенью также одинаковы. Если при этом задаваемым пара¬
^0П = ^01£>
^ОШ ~^0И£=^01£2»
^0IV=^0III£ = ^0I£3»
(11.9)
G0n = Go{n-i)Z = Golzn-1
J
или
G0/ = G0Je^
(11.10)
и для полезного груза
(11.11)
(е*)л= const,
(11.12)
р.к/ = const.
(11.13)
261
метром является приведенная весовая отдача (2.49), то очевид¬
но, что
/ *\п (11.14)
Формулу (11. 12) можно представить и по другому. Для это¬
го введем параметр распределения масс по конечному весу eKiy
равный отношению стартового веса старшей ступени к конечно¬
му весу младшей ступени, т. е.
Сп
■' к I '
Применительно к последней ступени этот параметр прини¬
мает вид
As
ск п Д •
п
В связи с введением параметра вКг параметр грузоподъемно¬
сти по начальному весу в* следует также заменить параметром
грузоподъемности по конечному весу вк*. Его величина будет
равна
К=П £К;• (П-16)-
х = 1
Имея в виду, что
^/ = -^7^- = —, (П.17)
Г-^О/Дк i H-ic i
выражение для грузоподъемности по конечному весу преобра¬
зуется к виду
£/
У-к i
:=П
х = 1
и затем
S* = — . (И. 18)
Н-к
Делая подстановку выражений для параметров в* и в* в фор¬
мулу (11. 12), будем иметь
г_
£К Х^К X = (£к[Ак) »
или зная, что в простейшем случае распределения масс имеет
место рк г= const, получим
i_
sKi. = (s:)n=const. (11.19)
262
Таким образом, при распределении масс по закону геомет¬
рической прогрессии конечные веса ступеней также распределя¬
ются по закону геометрической прогрессии.
Несмотря на предельную простоту формул (11. 12) и (11. 19),
выбор параметров по ним может быть затруднен, если требуется
найти распределение масс не по одному, а одновременно по двум
заданным параметрам рк* и е*.
В этом случае целесообразно
прибегнуть к построению кривых
Цк* = Цк*(8*)> ег = 8г(е*), ^i =
= М-кг(е*)> как показано на
рис. 158. Такие совмещенные кри¬
вые представляют свободу выбо¬
ра интересуемых параметров |лк и
бг и 8* с одновременным удовле¬
творением требований дальности
и грузоподъемности.
Рис. 158. График оптимального рас¬
пределения масс по закону геометри¬
ческой прогрессии
Для весовой отдачи по суммарному весу топлива GvT можно
записать
и затем
; = i
/-1
0Иг=2-°т<П ег (11.20)
/=1 / = 1
В частном случае, при распределении масс по закону геомет¬
рической прогрессии, когда рКг = Цк и ег = е, формула (11.20)
принимает вид
QzT=Qr 2
(11.21)
/= 1
Выражение, стоящее под знаком суммы, представляет собой
геометрическую прогрессию со знаменателем е. По известному
свойству, сумма п первых членов равна
г/-1-
1-ВЯ
1 — е
/= 1
263
При этом
Oa=0-Llil. (11.22'
Г 1 1— £
С помощью формулы (11.22) в зависимости (6.5) можно
получить
03т = (1-Рэфф)(1-£*)'- (11-23)
Таким образом, между параметрами GsT и е* существует
функциональная взаимосвязь. При этом одинаковому запасу
топлива на двух ракетах одинакового стартового веса соответ¬
ствуют одинаковые веса полезных грузов.
Формула (11.23) дает возможность производить сравнение
ракет по параметрам или е*, если при этом м,Эфф=рЭфф г =
= const. На практике чаще всего сравнение ракет производит¬
ся по грузоподъемности.
Суммарный конечный вес ракеты вместе с полезным грузом
равен (?ак = (/01 —(?2т или
hK = Gol
1 — 1 GTl +C?TlI£i + GT
(11.24;
Вес конструкции всех ступеней без полезного груза (эффек¬
тивный суммарный вес) С2эфф запишется как Gs зфф — G0I G%T д т
или
1 Еэфф — О01
1 — (0-ri-ЬО-rnSi+GTlII2IsII-)-...-\-Qrn- j —.-] .
(11.25;
В случае распределения масс по закону геометрической про¬
грессии формулы (11.24) и (11.25) при Gt; = Gt и 8г = е дают
Gsk ^1-а,.1-^-'; (11.26
_2ДФФ=(1 _г*)^—: . (11.27)
Goi 1 — s
Другие соотношения основных параметров применительно к
простейшему случаю распределения масс приведены в
табл. 11.1.
Распределение масс по закону геометрической прогрессии со
знаменателем е является первым приближением оптимальности
деления ступеней. Отыскание точного закона распределения
масс представляет сложную задачу. Здесь необходимо учитывать
характер траектории, влияние сил земного тяготения, сопротив¬
ление среды, изменение тяги с высотой, разность удельных тяг и
перегрузок по ступеням, а также непостоянство коэффициента
эффективности конструкции.
264
При пользовании простейшим законом распределения масс
необходимо в величину полезного груза включать все пассив¬
ные грузы, находящиеся на борту последней ступени ракеты.
В тех случаях, когда в самом начале проектирования еще не
известны веса пассивных грузов (например, веса вспомогатель¬
ного оборудования и т. д.), величину коэффициента в необходи¬
мо увеличить на 15—20%.
11.3. ЧАСТНЫЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
ДЛЯ ДВУХСТУПЕНЧАТЫХ РАКЕТ
В соответствии с определением ступеней (см. разд. 1.4) и ос¬
новной весовой зависимостью (6.5) запишем для двухступен¬
чатой ракеты
где Bi=G0n/Goi —коэффициент распределения масс.
Рассмотрим случай полета в пустоте без учета сил земного
тяготения [a(0K)]i = [o(0iO]n = O, а также при условии, что конст¬
руктивные коэффициенты и скорости истечения по ступеням
имеют неодинаковые значения, т. е. Рэфф^Щэффи и Wi¥=Wn.
Воспользовавшись формулой (2.25), запишем
где Wn^WnlWf
Кривые безразмерной конечной скорости vK=VK[Wi, постро¬
енные по уравнению (11.28) в функции коэффициента распреде¬
ления масс Bi для различных значений параметра Wu, приведе¬
ны на рис. 159. Там же показана кривая ц*(е) =рК1!Ык11. Как
видно из графика, увеличение скорости истечения второй ступе¬
ни приводит к смещению максимальных значений безразмерной
конечной скорости в сторону больших значений^коэффициента bi.
Для отыскания экстремума функций FK = FK(ei) необходимо
приравнять нулю производную dVjdei. При этом после преобра¬
зований получим
'Хк1 1%фф1 Т“ (1 Iхэфф!) ~ I ’
^KlI 1Хэфф11 ~Ь ( 1 ^эфф! I) q
гоп
FK = VJWX = - 1п [|хэфф1 + (1 - (,эфф1) ?1] -
(1 М-эффО
(1 1аЭффп) ^ 2
М-эфф! (1 Г'Эфф!) £1
265
откуда
ч-
(l)2+vr„
(1 — Н-эффп) Н-э^фф1
(1 — ^эффО У-эффН
(11.29;
- {Wn — 1) * С1 —н-эффп) .
где в== ~— £ ;
2 Р-эффП
в*— Ад — коэффициент грузоподъемности.
Gqi
Рис. 159. Влияние параметра Wn на Рис. 160. Влияние грузоподъемности
экстремальное значение VK=VK(e\) е* и скорости истечения U7n на ко
для двухступенчатой ракеты эффициент распределения масс
Формула (11.29) выражает закон оптимального распределе¬
ния масс по ступеням двухступенчатых ракет с учетом неодина¬
ковых скоростей истечения и коэффициентов эффективности кон¬
струкции. Как видно из формулы, величина параметра ei тем
больше, чем больше отношения величин
Wj
1 'J
эффП
Н-эфф!
1 ■
' Р-эфф1 Р-эффП
Это означает, что при оптимальном распределении масс уве¬
личение веса второй ступени следует за увеличением скорости
истечения второй ступени Wn и уменьшением коэффициента эф¬
фективности конструкции этой же ступени цЭффи.
Если коэффициенты эффективности конструкции обеих ступе¬
ней одинаковы (цэфф i= Цэфф и) , то формула (11.29) еще более
упрощается и принимает вид
sI = r+[(i)2 + U/llS*]\
(11.30)
266
где параметр е имеет такое же выражение, как и в форму¬
ле (11- 29) при Рэфф I= Рофф и j-Ыфф*
Кривые влияния скорости истечения и грузоподъемности на
коэффициент распределения масс, построенные по формуле
(11.30), приведены на рис. 160. Из графика видно, что вес 2-й
ступени тем больше, чем больше переносимый груз и более со¬
вершенной является ступень в конструктивном и энергетическом
отношениях.
При одинаковых скоростях истечения W\ = Wn и неодинако¬
вых значениях коэффициентов эффективности конструкции
*хэфф1^,ноффн формула (11.30) принимает вид
(1 каэффн) / 1аэфф1 \ *
1 L (1- !аэфф1) Х^эффП /
Легко видеть, что при равенстве коэффициентов эффективно¬
сти конструкции Цэфф I= М'эфф п формула (11.31) дает распреде¬
ление масс по закону геометрической прогрессии (11. 12).
1/2
(11.31)
11.4. ЧАСТНЫЙ СЛУЧАЙ УСЛОВИЯ ОПТИМАЛЬНОСТИ ПРИ а(0н)=О
В дополнение к уже имеющемуся рис. 33 примем расчетную
схему многоступенчатой ракеты и обозначения, как показано на
рис. 161.
Весовые отдачи по ступеням р.к * запишем в следующем виде
КII ‘
+Yim;
'эФФп + 'Уц-п;
эфф1
ц
(11.32)
\хк (п-1) = JJ-эфф (п-1) +
I^k/z ^эфф п Н"- YгГп'
где yi = 1 M-эфф г*
Параметры ei, ец, . . ., е?г обозначают соотношения масс меж¬
ду двумя смежными ступенями; параметр еп определяет соотно¬
шение масс между грузом н последней ступенью.
Вес каждой ступени в функции составляющих ее элементов
(конструкции, топлива и полезного груза) выразится так:
<?01 — ^Эфф1 "Т 0Т1 Т~ О.
Ооц = 0Эффц +От11-
1 Гг
эффП ~Т~ *-*т11
-.. .+0.
эфф п ~
• • I w эфф
■ Отп-г As;
со
со
Оол Оэфф n-\-Grn , As,
где йЭфф — конечный (эффективный) вес ускорителя (конструк¬
ции без топлива); GT — вес топлива.
267
Для коэффициентов распределения масс получим также
^эфф11 + Gti i + • • • + ^эфф п "г GT п +
^эфф! + GTI + СЭффп + <?т11 + • • • + ^эффл -г^тЛ + д2
^11 —
ея_1
^эффш + GTlII 4- ... 4- 0Эффп + GTп + As
б* эфф II + ^т11 + • • • + ^эфф л + ^тл +
Оэфф л + От п “Ь
(.л-1) + GT (л-1) +
эфф (л 1 )
^эффл + Отл + As
tv — #
Оэфф л + От л + Аа
со
И
10
щж
Рассмотрим случай полета многоступенчатой ракеты в пу¬
стоте без учета потерь в скорости на
Ах преодоление сил тяжести.
GTn Воспользовавшись формулой Циол-
6э<рфп ковского, составим уравнение для без¬
размерной конечной скорости в сле¬
дующем виде:
V?K = ^=-ln!xKl-rulnfxKlI-...
... - Wn^ In jlK („_!) - Wn In [*K
(11.35
где
^л-1
;
"bT(n-1)
' ^Эфф(л-Г)
-Gr III
-L Эфф III
.GT
II
Wx=\\ wx
U-Эфф II
7 T I
U Эфф I
=JTll • w _ =:
IF, ’ " 1
Wn=^~.
w,
Рис. 161. Схема многоступенчатой ра¬
кеты:
7—1 ступень; 2—II ступень; 3— III ступень;
4—предпоследняя ступень; 5—последняя сту¬
пень; 6—ускоритель последней ступени; 7—
ускоритель предпоследней ступени; 8—ускори¬
тель III ступени; 9—ускоритель II ступени;
10—ускоритель I ступени
Принимая во внимание выражения (11.32) и (11.34), пере¬
пишем уравнение (11. 35) в следующем виде:
VK =
К— 1П ^эл1 +
| ^ ^Эфф11 + б?тц + . . . + б?Эфф п -f- GTmn + As
б?эфф1 + GTl + СЭффл + GTu + . . . + аэфф п 4- GT п 4- А2
268
W? In/,, I „ °ЭФФ"' + °fni + • • • + °эфф,1 4-
— W nln И-элц-r Yu
^эффп + G-r\i + • • • + 0ЭффЛ + GT„ + Aj,
y(_ In ( Рэл (л-1) + Yn-l'
-W'nX
^эфф n + G r n + -Ц
^эфф (л—l) + G-cn—i + • • • + 0Эфф „ + Grn + As
-wn 1пиэ,1Л+Тл-
Уэфф n '
G, П "T“
(11.36)
Оптимальное распределение масс будем искать исходя из
максимума безразмерной конечной скорости Vu при постоянном
начальном весе составной ракеты. Для решения этой задачи вос¬
пользуемся методом неопределенных множителей Лагранжа.
Обозначим равенство (11.36) через f(GTh GTn, ..., GT п) и со¬
ставим уравнение связи
^эфф1 + ^т1 + ^эффП + ^т11 + * • •+Оэффл4"^тлН"Д2”^01==0>
(11.37)
которое обозначим через F(GTjy Gth, . . ., GTn). При этом
Ф(От„ От11, . . . , 0.г „)=/ (От1, 0,,„ . . (?.,„) +
-fX/- (Qtl, От11, . . С.[П),
где X— неопределенный множитель
Полагая
dФ
dG.r]
= 0,
дФ
dG
= 0, . .
дФ
■гП
dG-m-l
= 0,
dф
dG.T
= 0,
получим п уравнений, которые вместе с уравнением связи (11. 37)
определяют условие FK=(FK)max и величину неопределенного
множителя X. Частные производные дают
дУК | } dF
dG,, ‘
дУК
dG,u
дат1
dF
J0l — ^011
P-к I^o I
- a = 0;
dGTl i
Yi ■
Gnr — G,
on
+ Yii
Wu G<
M-Ki^oi
-X = 0;
dVK
} dF = i
dG,m 1 dGrIII ^1
G0i — Gpn л, {^7 Gqtt — Qqui
iu'kII^oii
-YnVFn
+ YinlFin
-a = 0;
(11.38)
269
I
oo
CO
+ynw
Решением системы уравнений (11.38) получим следующие
рекуррентные соотношения:
Соотношения (11.39) являются условиями оптимальности
Они показывают, что для каждой пары смежных ступеней су¬
ществует определенное функциональное соотношение одноимен¬
ных параметров, при котором, и только при котором, обеспечи
вается оптимальное распределение масс этих ступеней. Посколь¬
ку «смежность» непрерывна и связывает между собой все сту¬
пени, то установленные соотношения одноименных параметров
распространяются непрерывно на все деления ракеты. Таким
образом, можно сформулировать следующую теорему: массы по
ступеням многоступенчатой ракеты распределены оптимально,
если эта оптимальность соблюдена для каждой, наперед задан¬
ной пары смежных ступеней.
Теорема имеет важное практическое приложение. Из нее
следует, что каждая готовая многоступенчатая ракета, если она
оптимальна, может быть увеличена или уменьшена по количест¬
ву ступеней без нарушения исходной оптимальности.
Необходимо заметить, что в соответствии с определением сту¬
пеней ракетная система не может быть образована комбинаци¬
ей не смежных ступеней.
Л-Ylyri =-!!!_ Y„urn;
B-Kl M-к 11
(11.39)
BkII BkIII
270
Поскольку условия оптимальности (11. 39) получены для слу¬
чая [а(0к)]г = О, они остаются справедливыми и для показатель¬
ного закона изменения массы.
11.5. ЧАСТНЫЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
ПРИ ЗАДАННОМ ПАРАМЕТРЕ е*
Рассмотрим частный случай распределения масс при задан-
ной грузоподъемности е*, если |ыЭфф\фconst, [o(0K)]; = O и Wi =
= const. Тогда на основании формулы (11.31) и принимая во
внимание, что Wn= 1 и e* = eien, можно записать
Перемножая левую и правую части равенства (11.41), по¬
лучим
Подстановка выражения (11.42) в равенство (11.41) дает
Формула (11.43) удобна для применения, если заданы ко¬
эффициенты эффективности конструкции Цэффг и грузоподъем¬
ность 8*.
Легко видеть, что при одинаковом конструктивном совершен¬
стве ступеней y2 = const и р,ЭЛг = const формула (11.43) указы¬
вает на распределение масс по закону геометрической про¬
грессии.
Как будет показано ниже (см. разд. 12.5), формула (11.43)
без учета сил тяжести справедлива и для показательного зако¬
на изменения массы.
^эфф! у j j
(11.40)
М-эффП У\
Из теоремы оптимальности следует, что
„ Н-эфф/ ул „
л,
Y / {^эфф п
(11.42)
где
П
П
У"=П Y,-; ^фф=П ^фф/-
/ =1
(11.43)
271
11.6. ЧАСТНЫЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
ПРИ ЗАДАННОМ ПАРАМЕТРЕ
Рассмотрим случай распределения масс, аналогичный рас¬
смотренному в предыдущем параграфе при yi^const, рэффг^
const, [а(0к)]г = О и PPi = const, но когда задаваемой величиной
является ие грузоподъемность е*, а приведенная весовая отдача
^к = П !*.</•
i = 1
На основании условий оптимальности (11.39) запишем
е/У/ £f + iY/+i
Н-к/ ‘ак(/ + 1)
Поскольку
то очевидно,что
!J-K / ^эфф I (/ + 1) *цэфф (/ + 1)
Р-К L 1ак (/ +1)
ИЛИ
Р”Эфф i ‘аэфф (/ -Ы)
P-к i
Запишем далее
п
П
(11.44)
М-эфф i
/= 1
/ М-эфф (/+ 1) V
\ **«(/ + !) /
П f*K i
i= 1
и затем
/ * Х1/^
^эфф (i +1) j ^эфф \
И-к (Z + 1) I /
(11.45)
После подстановки выражения (11.45) в равенство (11.44)
получим
(11.46)
\ ^эфф J
Формула (11.46) известна в литературе как формула Ферт-
регта [7]. Этой формулой удобно пользоваться, когда задаваемой
величиной является приведенная весовая отдача рк *.
Формула (11.46) может быть записана и через приведенное
число Ц *
ц/=-]— ((4нД*)1/л- (п-47)
^эфф i
272
Очевидно, что формулы (11.46) и (11.47) идентичны.
При одинаковом конструктивном совершенстве ступеней, т. е.
при рэл i = const, формулы (11.46) и (11.47) дают известное рас¬
пределение масс по закону геометрической прогрессии. Формулы
(11.46) и (11.47) справедливы и для показательного закона
изменения массы.
11.7. ЧАСТНЫЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
ПРИ ЗАДАННОМ ПАРАМЕТРЕ М
В случае выполнения условий (11.39) при рЭфф i^const,
p^=/=const и [о(0к)]г —0 можно записать
После подстановки в полученное равенство выражения для
егУг, взятого из основной весовой зависимости (6. 10), получим
Как видно из выражения (11.49), параметр М является
функцией параметров, задаваемых при проектировании.
Для коэффициента распределения масс 8г формула (11.49)
принимает вид
п
i=l
и затем
(11.48)
где
П
Wi=
/ \ m
i ’^эфф i / ттг?
откуда
^эфф /
(11.49)
1
м
W,
где
(11.50)
(11.51)
273
Аналогично для числа Ц получим
М
и,—1—(И-52)
^эфф i
Параметр М в формулах (11.49) и (11.51) не может быть
задан сколь угодно большим. Его максимальная величина, как
следует из формулы (11.49) при рКг=1> равна
Mmaxi = #i(l — Н'эффг)- (11.53)
Рис. 162. График оптимального распределения масс
по параметру М при [ог(0к)]* = О
Расчет по формулам (11.51) и (11.52) удобно производить
построением совмещенных графиков Цг(М), еДМ), Ц*(М) и
е*(М), как показано на рис. 162. Расчет и выбор параметров
производится по очень простой схеме. По формуле (11.53) вы¬
числяются параметры Mmax* и величина наибольшего из них
(обычно первой ступени) наносится на ось абсцисс; дальнейшие
вычисления производятся в пределах 0-ьМтах. По формулам
(11.51) и (11.52) рассчитываются кривые еЦМ*) и ЦЦМ*) и за¬
тем В*(Мг) И Ц:?:(Мг*).
Когда график построен, пользование им сводится к определе¬
нию параметра в*, если задаваемой величиной является приве¬
денное число Ц* или параметра Ц*, если задана величина гру¬
зоподъемности 8*.
Потребные значения приведенных весовых отдач рк* или чи¬
сел Циолковского Ц* в зависимости от скорости или дальности
274
полета, как и для одноступенчатых ракет, могут быть найдены
по типовым графикам 14—pi (VK, W'1) или [iK = u.K(Z,, \Vn).
11.8. ЧАСТНЫЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
ПРИ ЗАДАННОМ ПАРАМЕТРЕ ек*
Воспользовавшись ранее полученным выражением для ко¬
эффициента распределения конечных масс (11. 17), выполним
следующую подстановку:
еД, = гк1. = -^. (11.54)
<4l
Полученное равенство позволяет переписать условия опти¬
мальности (11. 39) в следующем виде:
eK/Y^ = sK(,+1)Y/+1WW (П.55)
Делая преобразования как и ранее (см. разд. 11.6), получим
=K,=-^«VirT, (11.56)
где
i =1
Расчеты по формуле (11.56) выполняются обычным поряд¬
ком, как и по формуле (11.43), с той лишь разницей, что зада¬
ваемой величиной вместо грузоподъемности по начальному весу
е* является грузоподъемность по конечному весу ек- При этом
весовые отдачи ступеней определяются по формуле (6.8).
По количеству учитываемых факторов формула (11. 56) инва¬
риантна формуле (11. 51). Расчеты по ней наиболее просты, если
в работе отдается предпочтение параметрам ек и ек и цк(вк)
вместо обычных е2, е* и цк(е).
Формула (11. 56) одинаково справедлива для линейного и по¬
казательного законов изменения массы.
11.9. ОПТИМАЛЬНОЕ КОЛИЧЕСТВО СТУПЕНЕЙ
Помимо выбора оптимального соотношения масс по ступеням
составных ракет, когда количество ступеней может быть задан¬
ным, немаловажное значение имеют работы по выбору оптималь¬
ного числа ступеней. Правильно выбранное соотношение масс
само по себе еще не всегда означает, что ракета обладает мак¬
симальной конечной скоростью при заданном стартовом весе,
275
если количество ступеней в ней не оптимально. На рис. 163 пред¬
ставлена зависимость ^к = 1хк(^) (п — количество ступеней) дли
частного случая распределения масс по закону геометрической
прогрессии. Из графика видно, что, несмотря на оптимальное
распределение масс, величина параметра р.к (характеризующая
дальность полета) имеет также экстремальное значение по числу
ступеней, определяемое зависимостью
Рк = (14фф+ ¥£)''. (11.57)
Коэффициент распределения масс е является функцией коли¬
чества ступеней. При этом на основании формулы (11. 12) выра¬
жение (11. 57) следует переписать как
11к=({Аэфф-Ь У Vе» (11.58;
где имеет место (для рассматриваемого случая) рЭфф i = const.
Экстремум функции р,к = [А*(/г) найдем по выражению
(11.58). Дифференцирование сложной показательной функции
(11.58) по параметру п и приравнивание нулю производной
d\iK*/dn, дает
10^7-^111^=0
и затем
/ 1 Л
* In £* \ V J ’
'К
откуда
е*
1п—
(11.59)
Полученная формула определяет оптимальное количество сту¬
пеней в зависимости от параметров р-к, г* и конструктивного
коэффициента у. Величины их должны быть назначены или подо¬
браны расчетом таким образом, чтобы удовлетворялось условие
V Рк^эфф-И*-
Влияние параметров s* и «л на ступенчатость ракеты, опре¬
деляемое формулой (11.59), представлено на рис. 164. Как вид¬
но из графика, количество ступеней должно быть тем больше, чем
больше конечная скорость полета ракеты и чем меньше перено¬
симый ею груз.
276
П--
1п
V In Е*
При выборе параметров и назначении количества ступеней
следует хорошо знать, что нерационально применять п ступеней
там, где задача может быть решена применением (п—1) сту¬
пеней не только потому, что это усложнит конструкцию, но и
потому, что чрезмерное увеличение количества ступеней может
привести не к увеличению, а наоборот, к уменьшению конечной
скорости полета составной ракеты. Происходит это потому, что
наряду с эффектом отброса масс при увеличении числа ступеней,
12 3 4 5 п
Рис. 163. Влияние количества ступе¬
ней на величину параметра цк*
Рис. 164. Влияние грузоподъемности
е* и параметра цк* на оптимальное
количество ступеней
0,001 0,01 0,1 е*
происходит уменьшение общего запаса топлива на ракете вслед¬
ствие присоединения конструктивных элементов (двигателей, топ¬
ливных баков, органов управления и т. д.) новых ступеней. Гра¬
фически условно это можно представить, как показано на
рис. 165.. Ясно, что при /г = оо мы имели бы крайний неприем¬
лемый случай, когда ракета состояла бы только из пассивной
массы (конструктивных элементов), отброс которой в отсутст¬
вии топлива (активной массы) не имел бы смысла, поскольку ее
скорость равнялась бы нулю.
Приведенные в главе частные случаи распределения масс
(исключая случай расчета по параметру М, разд. 11.7) не ука¬
зывают на оптимальное количество ступеней, выбор которых про¬
изводится путем сравнения получаемых чисел Ц для различных
(варьируемых в расчете) значений параметра п.
Существенное отличие метода определения параметров по за¬
данному параметру М (см. разд. 11.7) заключается в том, что
выбранные оптимальные параметры ступеней указывают одно¬
временно и на оптимальное количество ступеней.
277
Пример 11. 1. Показать, что в случае распределения масс составной ра¬
кеты по закону геометрической прогрессии имеет место соотношение
' ^ 1аэфф) 0 £ ‘) •
Решение. Полный вес топлива составной ракеты GsT равен сумме весов
топлив на каждом t-м ускорителе. Имея в виду, что Цэфф* — М^эфф, можно
записать
п п
^Ет ^ 2 1 ~ 1азфф) (Go/ *^Е/ )•
/=1 / = 1
Поскольку As. =G0(.+1), то
п
2 (^0i’ = Gq Ajj.
i =1
Рис. 165. Диаграмма влияния ступенчатости на конечную ско¬
рость ракеты
При этом
GSt = (1 — р-эфф) (G0 — Аа). (11.60)
После деления обеих частей равенства (11.60) на G0, получим заданное
для доказательства соотношение. Поскольку при распределении масс по за¬
кону геометрической прогрессии е* = еп, то очевидно, что имеет место также
зависимость
0£Т = (1-Нэфф)(1-*Л)-
Пример 11.2. Показать аналитически, что в простейшем случае распре¬
деления масс по закону геометрической прогрессии при бг = е и р,Эффг=М<эфф
коэффициент эффективности конструкции составной ракеты в целом Р-Еэфф
равен коэффициенту эффективности конструкции i-й ступени.
Решение. Запишем выражение для коэффициента эффективности конст¬
рукции всех ступеней составной ракеты в следующем виде:
Gn — — А. 1 — — е*
Поскольку Gst = (1 — ,аЭфф) (1 — е*), то
1-0-(Цфф)(1 —«*)-«*
^2зфф— j_e
И затем
1аэфф {^эфф£
M'S эфф ~ ^ g = М'-эфф •
Пример 11.3. Доказать справедливость зависимости для я-ступеичатой
ракеты
1 М*эфф
1 ■
' М'зфф
(11.62)
При выводе зависимости полагать 8г=е, |Шкг=|Лк и [хЭффг=^эфф.
Решение. Для получения указанной зависимости воспользуемся выраже¬
нием для суммарной весовой отдачи по топливу
GSt = (1 — (J-эфф) (1 — г*).
Решая это выражение относительно е*, получим
1
1
■ М-зфф
Поскольку е^'^е71, то после несложных преобразований получим иско¬
мое равенство (11.62).
Пример 11.4. Показать, что для составной ракеты при распределении
масс по закону геометрической прогрессии имеет место
1 М-эфф \
-- — • (П.63)
1 М-?фф /
Решение. Запишем выражение для коэффициента эффективности конст¬
рукции применительно к одноступенчатой ракете в следующем виде:
Ок
р4фф= С0-Да •
Поделив числитель и знаменатель правой части записанного выражения па
G0 и решив его относительно е, получим
м-к М-эфф ^ 1 — р.3фф — GT
1 М-зфф 1 Р-эфф
Поскольку в простейшем случае распределения масс имеет место для
всех ступеней бг=е, (.1Кг=Рк и |Лэфф* = |Аэфф, то очевидно, что возведением в
степень п (по числу ступеней) левой и правой частей этого равенства полу¬
чим формулу (11.63).
Пример 11.5. Получить условие оптимальности для двух смежных сту¬
пеней составной ракеты, записав весовые отдачи для них в функции времени
полета тг-. Полагать, что полет происходит в пустоте и в поле гравитацион¬
ных сил, потери в скорости на которые характеризуются параметром сг(Ок).
Задачу решить для линейного закона изменения массы.
279
Решение. Запишем весовые отдачи ступеней
И-к i ~ 1агфф / "I- (1 *аэфф /) £/>
iaK (i -г 1) ‘азфф( Н-1) О 1и'э4>ф (/ +1)) £ [ ; 1 •
Поскольку £г-И = е*/ег> то
(11.64)
Н-К(/ + 1) —‘аэфф(/-!-1) + О ^эфф( / +1))
откуда
1 — и..
■эфф(/ + 1)
(11.65)
Р*к(/4-1) М-эфф(/ + 1)
Подстановка (11.65) в (11.64) дает
, (1 + рЭфф;) (1 — Н-ЭФФС/ + 1)) „
Н-к i ~ Р-.фф i + н __ м £ •
^К(/ + 1) ^эфф(/+1)
Можно также записать
Н'к (/ + 1) = ^ 3/+1Т/Т»
Т/_!_ 1
где т = ——; pi + i—коэффициент расхода массы старшей ступени,
т -•
Принимая во внимание зависимость (11.67), перепишем выражение (11.66)
(1 Рэфф/)(1 — М-эфф(г+1))
(11.66)
(11.67)
Рк/ — ^Эфф/+ ,0. ,т.т_м *’*
1 Pi-rlT<T ^эфф ( £+1 )
Воспользовавшись формулой (2.44) запишем
(1 — М-эфф () (1 ^эффс /-4-1))
е
1 — Эг - 1т/т Р'Эфф(/Ч-1)
Wi+x 111 (l — Э/ + 1Т/Т) — [а (0к)]г X
(1 Р?фф i) (1 1хзфф(<-И))
(11.68)
FK= - In
^эфф i
W[-
X
‘ 1аэфф i'
1 1аэфф(/4-1) ~ ?/-ЫТ/Т
[о (0к)](/+1) ; A+iH-п
Wi-
где
_ W i — DFVm
WY W J
Для отыскания экстремума скорости, приравняем нулю производную
dVK/dx. Тогда получим
(! — М-эфф /) (1 — Р-эфф(Л-1))Э/+ lxiWi Р/х!Тх-
— П ^ =Т2 е*Н-1Г/+1 +
^к/(1 >аэфф(/ +1) И-к (/ 4-1)
+ [° (вк)]/(1 —У-эфф /) (1 — 1Аэфф(/-ь1))^'+1Т^/ — 1-а (^к)]г + 1^'-Ы?/-Ыт/ “ О»
откуда в общем виде
■Д/<1 = в/мЦ/+1(1 -(хэфф:(.+1))Г/+1.
280
Пример 11.6. Произвести расчет параметров ег-, Ць е* и Ц* для двухсту¬
пенчатой ракеты если известно, что
^эфф 1=0»08; р-эфф II = 0,10; W{ ~ Y, Wu — 2 и [а (0К)]; = 0.
Влиянием сопротивления воздуха и изменением тяги с высотой прене¬
бречь.
Определить также коэффициенты распределения масс ei, еп и числа
Ць Цц, принимая грузоподъемность равной е*=0,0258.
Решение. Имеем случай полета в пустоте без учета сил земного тяготения.
При этом следует воспользоваться зависимостями
1 _ w/Wi
ц« =
{^эфф i
^эффг / m/Wj \
г,’ = 1-^эфФЛ 1 -м/Г,-/.’
а также Ц*=Ц1Цп и e* = eien. Расчет удобно свести в таблицы. В табл. 11.2
определим граничные значения чисел Mj=Mmax i по формуле (1-1.53).
В табл. 11.3 определим значения параметров Ць Цц, Ц*, еь бц и е*.
Таблица 11. 2
Ступени
^эфф i
^зфф /
1 1^эфф i
wi
Мшах/
= Wi О-^эфф i)
I
0,08
0,087
1
0,92
V II
0,10
0,111
2
0,80
Таблица 11.3
I ступень (wj = l)
II ступень ( \V j j = Г)
м
ui
M/U7j
M
1-J5-
Цц
м /wu
Ц*
e*
U7I
(i-m/vFj)
£i
wu
wn
1-м/^и
2ii
0,92
0,08
1,0
11,5
1
0,46
0,54
5,4
0,85
0,0945
5,4
0,0945
0,80
0,20
2,5
4,0
0,348
0,40
0,60
6,0
0,667
0,074
15
0,0258
0,60
0,40
5,0
1,5
0,13
0,30
0,70
7,0
0,43
0,0478
35
0,0062
0,40
0,60
7,5
0,667
0,058
0,20
0,80
8,0
0,25
0,0278
60
0,00161
0,20
0,80
10
0,25
0,0217
0,10
0,90
9,0
0,111
0,0123
90
0,00027
0
1,00
12,5
0
0
0
1,0
10
0
0
125
0
Кривые еЦМ), ЦЦМ), е*(М) и Ц*(М), построенные по полученным
данным, приведены на рис. 166. Как следует из графика, решением примера
для е*=0,0258 являются следующие значения параметров: Ui=2,5, ei=0,348,
Цц—6,0 и ец=0,074.
Пример 11.7. Произвести выбор количества ступеней составной ракеты,,
если известно, что e*=G,07, р*=0,10 и у=0»95. Распределение масс принять
281
по закону геометрической прогрессии. Определить также потребное значение
параметра рЭфф в основной весовой зависимости (6.10).
Решение. По формуле (11.59) находим
In —
Рк
In
0,07
1 0,10
,п(_1п^\ 1п /—1П0Л0
\Y 1 п е* / V 0,9о In 0,
шть п=5. Значение
9)
П* П/—
У Н = ^эфф + Y V е
= 4,8.
Целесообразно принять п=5. Значение параметра рЭфф найдем по вы¬
ражению (см. разд. 11. 9)
Рис. 166. Определение опти¬
мальных параметров двухсту¬
пенчатой ракеты по числу М
(к решению примера 11.6)
откуда
Р-эфф = У^Р-К — Y >/"£* = >/0,10 — 0,95 /0,07 = 0,07.
Пример 11.8. Произвести пересчет и составить новую таблицу весовых
характеристик спасаемых ракет-носителей типа «Сатурн», приведенных в
соответствии с американской разбивкой ступеней в приложении 6, Б
(стр. 376). Рассчитать также параметры ег-, е*, рКг, р.* и рЭффг.
Решение. Поскольку в американской системе ступенями названы уско¬
рители (без полезных грузов и головных частей или старших ступеней), пе¬
ресчет производим по формулам:
G0II = G0 уск II -г As; G0I = GoycK I + G01l’>
i — Goi GT i и Сэфф i = GK yCK i = GoyCK i GT i.
При этом также имеют место зависимости
Результаты расчетов сводим в табл. 11.4.
Таблица 11.4
Параметры
Взлет гор и з о н та л ь н ы й
Взлет вертикальный
I ступень
II ступень
I ступень
II ступень
GojrcK. тс
578,8
142,2
851,4
156,5
Дв. тс
155,8
13,6
170,1
13,6
Gr, тс
346,3
105,5
566,1
116,-6
Оэфф = GK уск, тс
232,5
36,7
285,3
39,3
GK1 тс
388,3
50,3
455,4
53,5
G0, тс
734,6
155,8
1021,5
170,1
Р-эфф
0,42
0,258
0,335
0,255
е
0,212
0,087
0,1665
0,08
Рк
0,53
0,323
0,445
0,315
*
Рк
0,171
0,1435
е*
0,01845
0,0133
Пример 11.9. Определить вес топлива III ступени и суммарный вес топ*
лива на всех ступенях четырехступенчатой ракеты, если дано G0i=100 тс„
GT = GTi=0,35 И £=£г=013.
Решение. Вес топлива III ступени в соответствии с формулой (11.10)
будет равен
G,.m=G0iGTe(:j-1)=100 • 0,35- ■ 0,32 = 3,15 тс.
Суммарный вес топлива согласно формуле (Г1.22) определится так:
- 1—£AZ . 1—0,34 _
Gv.r = GoiGT = 100-0,35 = 49,о тс.
ш 1 — Е 1—0,3
Пример 11. 10. Определить пассивный вес вместе с полезным грузом, а:
также суммарный вес конструкции без полезного груза для трехступенчатой
ракеты, у которой G0i=100 тс, GT = GTi=0,5, е = £;=0,3.
Решение. Подсчитаем грузоподъемность. Тогда на основании (11.6) по*
лучим £* — £п =0,33;=0,027.
Пассивный вес вместе с полезным грузом GSk = Griac определим па
формуле (11.26), т. е.
- 1— £л\ / 1 — 0,027 \
Gnac = G0I (l-GT ^—) =100(1-°'5 ! _0,3 j ТС'
Вес конструкции всех ступеней без полезного груза в соответствии с фор*
мулой (L1.27) составит
С2эфф = О01(1-е”) -^5^= 100 (1 -0,027)0’5о~°’3^27,8 тс.
Решение правильно, поскольку G0ie* — GIiac— 62эфф = 2,7 тс*
283
Пример 11.11. Составить выражение для приведенной весовой отдачи
вида [лк = jjlk (е, е*) и показать, что в простейшем случае движения состав¬
ной ракеты (в пустоте без учета гравитационных сил и при постоянных зна¬
чениях конструктивного коэффициента p3(i)<j>i=const) распределение масс по
ступеням следует закону геометрической прогрессии.
Решение. Предположим, что при делении ракеты на ступени имеет место
Bi=8, ец=е,. .en_i = e и еп = е*/е, что обеспечит поиск наивыгоднейшего со¬
отношения масс при постоянных значениях стартового веса G0=Goi=const,
полезного груза Aa=const и коэффициента грузоподъемности е* = const.
Весовые зависимости будут иметь вид
Р*К ^ Р”Эфф т (1 P-Эфф) е
для всех ступеней, кроме последней, и
I е*
Р*К п ~ М'Эфф ~г (1 ^эфф) ~
для последней ступени.
п
Приведенная весовая отдача, равная р.* = П рк/> запишется как
/ = 1
М'к = [рЭфф -Г (1 рЭфф) с] ^рЭфф “Ь (1 рЭфф) п — \ 1 *
В простейшем случае на основании формулы (2.50) можно записать
VK =—Infv Это означает, что максимум конечной скорости VK = (Кк)тах
может быть найден по минимуму параметра р* = (p*)min- Приравнивание нулю
производной dupde по уравнению (11.69) дает
е* е*
[рэфф -г (1 — рЭфф) £] ~ = Рэфф + (1 — Р-Эфф) С11* 70)
Равенство (11.70) справедливо при условии, что е£-= е = const. При этом
СПИСОК ЛИТЕРАТУРЫ
1. Воробьев Л. М. К теории полета ракет. М., «Машиностроение»,
1970, 223 с.
2. Космическая техника. Под ред. Г. Сейферта. М., «Наука», 1964, 727 с.
3. Космодемьянский В. А. Об одном типе вариационных задач. —
«Прикладная математика и механика», 1963, т. 27, вып. 6, с. 1111 —1116.
4. М и е л е А. Механика полета. М., «Наука», 1965, 407 с.
5. По ловко А. М. Основы теории надежности. М., «Наука», 1964, 446 с.
6. Фан Ля н ь-Ц энь, Вань У у-С е н, Дискретный принцип максимума,
М., «Мир», 1967, 180 с.
7. Фертрегт М. Основы космонавтики. М., «Просвещение», 1969, 301 с.
8. С г а у J. S. and Alexander R. V. Cost and weight optimisation for
multistage rockets. Journal of Spacecraft, 1965, vol. 2, No. 1, pp. 80—86.
Глава XII
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ
МНОГОСТУПЕНЧАТЫХ РАКЕТ
Когда речь идет о выборе параметров составных ракет, име¬
ется в виду прежде всего выбор соотношения масс по ступеням
этих ракет. От того как распределены массы, в каком соотноше¬
нии они находятся между собой и какое количество ступеней
приемлемо для данной схемы, существенно зависит грузоподъ¬
емность ракеты, скорость и дальность ее полета.
Отысканию этих законов, а также других экстремальных ре¬
шений и посвящена настоящая глава.
В главе сформулирована новая теорема об оптимальном де¬
лении ступеней ракет. Введена новая безразмерная характери¬
стика — число М, как величина, зависящая от отношения на¬
чальных масс делящихся частей, веса полезной массы, конст¬
руктивно-весовой характеристики, скорости истечения активной
массы, числа делений и т. п.
Теорема, сформулированная в самом общем виде, утверждает,
что оптимальному делению соответствует постоянство характе¬
ристического параметра М для всех отделяемых масс. Этот ре¬
зультат имеет применение в научных исследованиях и проведе¬
нии проектных расчетов.
Глава иллюстрирована графическим материалом, что облег¬
чает понимание физических следствий и дает представление о
характере и объеме аналогичных проектно-изыскательских
работ.
12. 1. ОБЩИЙ СЛУЧАЙ УСЛОВИЙ ОПТИМАЛЬНОСТИ
Имея выражение (10.2), запишем уравнение для конечной
скорости /i-ступенчатой ракеты в следующем виде
п
п
\^1пЦ,- (12.1)
Si
i= 1
где —- — относительная (безразмерная) скорость ис-
W{
течения активной массы i-и ступени;
285
рп.
с/ = — коэффициент увеличения тяги в пустоте
P{)i
i-й ступени;
[s(8K)]f-= —параметр гравитационных потерь.
n0i
Параметры AFni и AFai, учитывающие поправку в конечной
скорости на высотную характеристику двигателя и сопротив¬
лению среды при полете первой ступени (обозначено индек¬
сом I), имеют такое же происхождение, как и параметры
AFn и AFa в уравнении (10.14).
Будем искать максимум конечной скорости при постоянном
грузе As = const и начальном весе составной ракеты G0 = const.
Поскольку при этом величина грузоподъемности также является
постоянной величиной, то задача заключается в том, чтобы оты¬
скать такое распределение коэффициентов ei, ец, ещ,..., еп и 1ць.
Лоп, Яопр_. . .,/гол, при котором величина безразмерной конечной
скорости FK была бы максимальной.
Для решения этой задачи воспользуемся методом неопреде¬
ленных множителей Лагранжа. Уравнение связи будет иметь
вид
(s„ £Ш, . . . , гп) s* = 0. (12.2;.
Обозначим равенство (12. 1) через /($,, ?-п> $ш, . . . п01,
п'т, «опь • •/гол), а выражение (12.2) через/7(г,, su, гш, ..., г„,
/г01, /гоп, Яош, по„) и составим уравнение
Ф(е1> £Ц’ £Ш’ • • • ’ г/р л01> ^оп, Лсш, • • • ? Лол) — f (£i? £Пг
е1Ц) • • ч гп'> Л01, Лоп, Лопь • • ч Ло«) i'F (Д, - X19 • • ч
Л01, Лоп, Лопь . • ч Ло'л), (12.3)
где A, = const— неопределенный множитель.
Полагая
0, ii-=0, -^-=0,. . -^=0,
(?£ji дгп
И
* =0, -^-=0, . ., -^- = 0,
(12.4}
^п°1 ^/?оп ^/7оп1 driQn )
получим 2/2 уравнений, которые вместе с уравнением связи
(12. 2) _определяют величину максимальной безразмерной ско¬
рости FK и величину неопределенного множителя %.
Частные производные дают следующую систему уравнений
286
дФ
де\
дФ
Yi
> (0k)]i
Yi+>-
P-kI £ eI
Yu
= 0,
0ец
дФ
deni
дФ
M^ii “1“ [3 (®k)]iiYii^ii
<^kII eII
: ^-Wni-(- [(a (0k)]iiiYiiiV^Iii + ^ =0,
(%III £III
Y n
n
Wn+[3(B — = 0,
дФ
dnoi
дФ
—+(От I+h п01 ^ - 0,
P-kI
£Л(Н
e
d/ion
дФ
d^oni
Wnf
+(0,m+*„,,).= o,
№11 (л||ш)-
(12.5)
дФ
дп0п
+ (GT л + =О,
<*» «)
где, как и ранее (см. разд. 10.5),
W,
Решив систему уравнений (12.5), получим следующие рекур¬
рентные соотношения
eiUIYiV^1 = SlIUIIYIIV^n,
£iiLXi iYiiV^h = £hiUiiiYii mi.
г^п-^п-^п-г = ьЛпЧп&п,
а также зависимости
(12.6)
0.5 И6К)]1 , Г /0.5а[(9к)]1\ 2 , GTi[g(6K)]i 1
I £ Шп I Ek\
+ Vo
/7
0,5 [a(0K)]!
'^01 -
S
JJ-kI k\
nn -
M0k)]ii tr
on
" 2
_ [a (Or)] 111 )JL
"oill
I J_ + Л I J^L
-VkI ki J (J-kI
1/2
2 | [a (Упл
k\\
o^Y
I Г/[а(6к)]ш \2 I [а(0к)]ш fi- I1/2
!XKIII I P'kIII j \ — ^TlII^KlIlj
c4
287
В общем .виде это запишется так
(12.8)
\ 2
Рк L "И ki L V 1 ki / ^
где
Ц, = Ц,-№)]/■
(12. 10)
^ sin Oidti. (12. 11)
о
Равенство (12.8) представляет собой известное уже нам
условие оптимальности, но записанное в самом общем виде
с учетом гравитационных потерь, высотной характеристики дви¬
гателя и аэродинамического сопротивления среды.
Знакомое уже нам другое выражение (12.9) показывает, что
оптимальные перегрузки по ступеням составных ракет опреде¬
ляются такими же зависимостями, как и для одноступенчатых
ракет. Этот вывод имеет важное значение для разработки про¬
стейших методов определения оптимальных значений основных
параметров многоступенчатых ракет.
Воспользовавшись условиями оптимальности (12.8) и основ¬
ной весовой зависимостью (6. 10) можно записать для каждой
пары смежных ступеней
12.2. ОБЩИЙ СЛУЧАЙ РАСПРЕДЕЛЕНИЯ МАСС
МЕТОДОМ СМЕЖНЫХ СТУПЕНЕЙ
Wl ’ " 111 W, ’ " ' ’ " n W\
Решение каждого из уравнений системы (12.12) имеет вид
(f)
2
1/2
— 4i
(12. 13)
где
Pi =
1 [а (°к)]/-Ь1 (^эфф (/ + 1)~
[« (9к)h
5
Y/ И9к)Е
Н (0к)]Л У/
Все параметры, входящие в систему уравнений (12.12),
кроме параметров ei, ец, ещ,..., гп, являются задаваемыми ве¬
личинами при проектировании. Определение коэффициента рас¬
пределения масс £ц следует вести, задавшись произвольным
значением коэффициента ei или определив его, например, по
закону геометрической прогрессии. Тогда, подсчитав значение
Ui = LJj l— [a (0K)]j, определим величину ец решением первого
Уравнения системы (12.12) по формуле (12.13) как для двух¬
ступенчатой ракеты со ступенями I и II. Если перегрузка n0i
не задана, ее следует уточнить на оптимальность по формуле
(12.9) и расчет по определению ец повторить. Найденное зна¬
чение коэффициента ец является входным значением во второе
Уравнение системы (12.12) для определения коэффициента вш
по той же формуле (12. 13) как для двухступенчатой ракеты, но
уже со ступенями II и III. Этот расчет следует также повторить,
10 3479 289
если перегрузка второй ступени п"и не задана постоянной вели¬
чиной. Таким образом каждый найденный коэффициент в,- яв¬
ляется входным в формулу (12.13) для определения коэффи¬
циента ег-+ь Если количество ступеней задано, расчет прекра¬
щается после определения коэффициента гп.
Решение системы уравнений (12.12) целесообразно произво¬
дить для ряда задаваемых значений коэффициента рт
с последующим построением графиков, как показано на рис. 167
и 168. Оптимальные значения параметров определяются либо
по заданной грузоподъемности в*, либо по заданной конечной
скорости FK.
Как видно из приведенных графиков одинаковой грузоподъ¬
емности в* соответствуют два решения Вг+ь Обычно параметры р,
выбираются по левому участку кривых b*(bi), где на графике
имеет место (вг+Ошах- При этом распределение масс обес¬
печивает большую конечную скорость FK, чем на участке
Сг+1> (Вг+1) max-
Пользуясь условиями оптимальности (12.8), а также основ¬
ной весовой зависимостью (6. 10), можно показать еще, что
Ц2- —
^/+1
'(0JL
/+1 '
+
. Ц;-И9к)]/, ,
1 — (jiK i — Н-эфф;)
Wi-^i
• ^эфф(/ + 1)
[°(6к)]< + 1 _Q
Ц/
i + 1"
(12. 14)
Н'эффО'-Н)
Очевидно, что уравнения (12.12) и (12.14) идентичны. Типо¬
вые расчеты параметров распределения масс методом смежных
ступеней иллюстрированы примерами в конце главы.
12.3. ВЫБОР ПАРАМЕТРОВ МЕТОДОМ M = const
Имея условия оптимальности (12.8), легко записать выра¬
жение
откуда
где
а также
(4UiylWl)n = e*lX*y*W*,
t
еД,уЖ = Л1,
М= (£*Ц*7*И^*)1/'Л = const,
ц=п Д/, у*= П То 1Г*=П Щ.
/-1 г=1 г-i
(12.15)
(12. 16)
290
l>^ N-^ C\l К й
10*
291
Рис. 167. Параметры оптимального Рис. 168. Параметры оптимального Рис. 169. Оптимальное распределение
распределения масс для двухступеп- распределения масс для трехступен- параметров е*, Ц* и ег- для двухсту-
чатого носителя чатого носителя пенчатой ракеты по числу М
<М
’"ч
О
S'
3
VO
0)
*
(4
O.
О
H
X
c3
u
Л
г
s
s
X
s
о
X
A
4
cd
s
X
HI
11 [M
[(»)£]
«)£]
s
c3
o.
ed
X
CO
5 e о :S
3 1“ 5 °
“ u >iX
^ о н
3
О
to
о
о
о
•lO
CM
ю
CN
О
Ю
CM
о
Ю
CM
b-
o
о
о
о
о
о
о
о
о
о
ю
(М
о
ю
см
!>•
о
ю
см
о
о
о
о
%
СО
ю
О)
СО
о
о
о
о
ю
о
о
о
см
о
о
о
о
Si
и
т1<
ю
о
<Э
о
о
со
СО
о
о
о
о
о
О я
О к
О о
- с;
О «
Равенство (12.15) пока¬
зывает, что оптимальное
распределение масс по сту ¬
пеням составных ракет со¬
ответствует закону постоян¬
ства параметра М для каж¬
дой ступени. Как видно из
выражения (12.16), пара¬
метр М является задаваемой
величиной и подсчитывает¬
ся в соответствии с потреб¬
ными значениями грузо¬
подъемности е*, приведен¬
ного числа Циолковского
Ц*, количества ступеней /?,
а также располагаемыми
значениями приведенных
параметров у* и W*. По¬
скольку параметр М непре¬
рывно корректируется по
мере уточнения схемы ра¬
кеты, его величину удобно
задавать в некотором диа¬
пазоне чисел, при котором
графическое изображение
искомых параметров 8* =
= 6г(М) И Цг = Цг(М) ОХВЭ-
тывало бы вероятное их из¬
менение по мере уточнения
входных данных. Выполняя
■ преобразования выражения
(12.15) при помощи основ¬
ной весовой зависимости
(6. 10), получим
я
СО
Pi
2
[Г
(-*-эфф /
3 К
3 н
то tqj
S s w
£ °i и
сь
О <D ji
Й 5 -
Н (0к)]/У/ \ Wi
м
1/2
где
, (12.17
м
1 [с (0к)]/ (^Эфф /
VV I
Pi = = •
[®(0K)]iY.-
Типовые кривые е* =
= е*(М), Ц* = Ц*(М) и
292
Si ** Ei
(M)> построенные по формуле (12.17), представлены на
рис
169.
Примеры распределения масс для некоторых схем составных
ракет по различным параметрам приведены в табл. 12.1.
Число М не может быть задано сколь угодно большим. Его
максимальное значение может быть найдено из равенства нулю
выражения в квадратных скобках в формуле (12.17). При этом
[а (®к)] / М-эфф i"
м
Wt
2[а(0к)]/У/
^эфф i / М
Йвк)](У?
откуда
При этом
или
а также
(12. 18)
Pi
2
М
— [а (®к)1 i М-эфф i — -ZT-
Wj
2[a(0K)]/Y/
1
V/
^эфф i
Г«(вк)]/
1/2
P*эфф i
г^эфф i \1/2
Й(0к)]//
;i2.19)
(12.20)
Ha практике максимальные значения М, егтах и Цкгтах
обычно определяются по параметрам первой ступени, поскольку
числа м
г max У старших ступеней, как правило, больше чем
у всех предыдущих ступеней из-за убывающих значений грави¬
тационных потерь [а(0к)]г+ь
Если в равенство (12.15) подставить выражения ег = 8г(|1к)
и Ц = Цг-(рк), взятые по основной весовой зависимости (6.10),
то после преобразований получим
11/2
!Аэфф i
где
[® (®к)]г
(12.21)
М
Г,
wi — ^эфф < Н ~
Не¬
очевидно, что формулы (12.17) и (12.21) идентичны. Расчет
оптимальных перегрузок производится обычным порядком по
формуле (12.9).
293
Метод М = const является самым общим и, как показала
практика, минимально трудоемким. Его применение также
аффективно при выполнении контрольно-вычислительных работ
по уже спроектированным и построенным ракетным системам.
12. 4. ТЕОРЕМА М = const В ОБЩЕМ ВИДЕ
С точки зрения чистой механики, составная ракета представ¬
ляет собой совокупность точек переменной массы. Условимся
такую совокупность точек называть системой точек (или тел)
переменной массы. Будем‘предполагать, что положение или дви¬
жение каждой точки системы зависит от положения и движения
всех остальных точек. Система материальна и дискретна.
В силу такого строения система оказывается делимой и в про¬
цессе ее движения происходит отброс как активных, так и пас¬
сивных масс. В частном случае деление системы может не про¬
исходить и тогда движение осуществляется аналогично движе¬
нию точки переменной массы вследствие отброса только
активных масс (случай одноступенчатой ракеты).
Деление материальной системы точек переменной массы про¬
исходит путем отброса пассивной массы после расхода на дан¬
ном участке деления активной массы. Движение на i-м участке
осуществляется аналогично движению изолированной точки
переменной массы с полезной массой, равной сумме пассивных
и активных масс на участках (i+1) делений. Если число делений
равно п, то после отброса активной и пассивной масс на послед¬
нем участке i = n остается нерасходуемая полезная масса Ми.
Выразим закон изменения массы системы точек в общем виде
как
М i = M-Qi fi (ti) , (12.22)
где Mi — текущая масса на i-м участке деления; М0{ — началь¬
ная (стартовая) масса на i-м участке деления; fi — функция,
указывающая на закон изменения активной массы; ti — время
движения на i-м участке деления при непрерывном истечении
активной массы.
Если для точки переменной массы безразмерная конечная
скорость по уравнению (2.41) может быть представлена таким
образом
i^=-^=-ln/(T)-gta(0K), (12.23)
то для системы точек переменной массы, состоящей из п делений,
уравнение для безразмерной конечной скорости принимает вид
У* = -2 ^[1пЛ-(М + [Д0к)]Л + дПо/], (12.24)
/=1
294
где xi==~^ безразмерное время движения на i-м участке де-
©,
ления; AVQi=—{AVxi-\-AVni)— потери безразмерной скорости
вследствие влияния среды (аэродинамического сопротивления
и высотной характеристики двигателя).
Параметры AV х% и AVni имеют такое же происхождение, как
и аналогичные параметры в уравнении (10. 14).
Будем искать максимум конечной скорости системы при по¬
стоянных значениях полезной Мп и начальной М0 масс. По¬
скольку при этом величина безразмерной полезной массы
постоянна
п
£* = ^п_=П e/ = COnst,
м0 11
i= 1
то задача заключается в том, чтобы отыскать такое соотношение
оптимизируемых параметров е2, цк и (Wgo)oi при заданных
коэффициентах Цэффг, у и &г, [ст (0К) ]г, Wiy которые обеспечат мак¬
симальное значение безразмерной конечной скЬрости Vu. Для
решения этой задачи следует воспользоваться методом неопреде¬
ленных множителей Лагранжа.
Уравнение связи имеет вид
jf[et-s* = 0. (12.25)
i = l
Обозначим правую часть равенства (12.33) через
а также выражение (12.25) как
и составим уравнение
295
где ^ = const—неопределенный множитель; 0, п — индексы,
обозначающие начальные и пустотные движения системы соот¬
ветственно.
Положив
дб! де; деп
дФ
дФ
дФ
-О,
д(~) *(-)" *{-)"
\ go /01 V go JOi \ go Jon
получим 2n уравнений, которые вместе с уравнением связи
(12.25) определяют величину максимальной безразмерной ско¬
рости FK и величину неопределенного множителя X. Частные
производные дают следующую систему уравнений:
л. 1
д
L^77r + [’M'?j
/1 (Tj) deiJ
-=-wt
дч
д
— fi (Ti)
дв[
fi (тг)
■[«(вк)]/^
dei
-j-X — — О,
дФ
дЪ
■ч fn(?n) л“
^7—+ №)L^
L f n i^n) сгп
+ь—=о,
дФ
k\
1
[Уо/<
f I (Tl) Si
01
0 /01
81
\ go /01
дФ
ki
ш:
f i (Л‘) £/
1 Г°(6к)Ь-77гЬг+Т- =
K/Ji ( V
d
\ go /0i
—) aCT
go /01 V go JOi,
дФ
kn
V\n fn(xn) in
>(-)
\Vo Jon
1 г /л \1 ^T/2 I j_ ^ p.
а(®к)]л f, vii I - / .и ’ ‘
„(Лу aCT
\ go /0/1 V go /0л
(12.26)
где | — коэффициент увеличения скорости истечения активной
массы в отсутствии влияния среды.
296
Решая первые п уравнений попарно для каждого из смежных
делений, получим
s.VT,
Г д
J~fl <Ti>
L^TTT + t^U.f11
/1 (Ti) <?е, J
= Хе*
-
’•w‘ LXtt +l°
L Ji (T/)
(0Jb
dr i
дЧ-
= Хв
£ W
n n
г d
V fn (Гщ) -r—
Д£а1 I 1 n
/ It \ I” l (®)к]л -ч
fnifn) OBn.
= Xe*
или
X
(T;) X,
T- + [3(0K)]4-
fi (Ti) os i
1
'//+1 (*<+l)
//+1(^+1)
+ K&
= e i+1Wi+lX
n ^/ h I
JJ1+1 .
C£i+ 1
(12.27)
где /=1, 2, 3,., n.
Рекуррентное соотношение (12.27) является условием опти¬
мальности, выполнение которого обеспечивает оптимальное соот¬
ношение масс по частям делимой системы, а следовательно
и максимум конечной скорости при заданных значениях пара¬
метров М0 и Мп.
Решение последних п уравнений системы (12.26) дает выра¬
жения для подсчета начальных (безразмерных ускорений) на
всех участках деления.
Имея условия оптимальности (12.27), легко записать для п
делимой системы
— //(*/) v-
. /; (Т,) dsi J
:e*U7
п
t -1
Г д
7 f i (т/)
д_Ч [_
f i (т,0 1
[=» (0к)]/
dXj
d&i
297
откуда
ЖУЬг* = М, = М, (12.28)
d*i J
где
Также очевидно, что М = const.
Выражение (12.28) является математической записью тео¬
ремы о делении системы точек переменной массы, которая форму¬
лируется так: массы по частям делимой системы распределены
оптимально, если для каждой массы сохранено постоянство
параметра М.
Теорема имеет большое практическое применение. Покажем
далее некоторые ее частные случаи.
12.5. ПРАКТИЧЕСКИЕ СЛЕДСТВИЯ ТЕОРЕМЫ M = const
Для нзвестных'и практически применимых в настоящее время
линейного и показательного законов изменения массы имеет
место
При этом рассмотрение теоремы применительно к каждому из
законов изменения массы необходимо производить раздельно.
Полное время движения системы на i-м участке при линей¬
ном законе изменения массы равно
~/i (Ti) = Y(-
de;
(12.30)
(12.31)
А. Линейный закон изменения массы
т,.= ——Wt= Yf(1 ■ Е<- W'
(12.32)
и, следовательно,
При этом
(12.33)
£'0 /оL
После подстановки выражений (12.30), (12.31) и (12.33) в ле¬
вую часть равенства (12.28) получим известное уже нам равен¬
ство (12. 15)
При подсчете числа М. и других параметров системы точек
переменной массы следует помнить, что
Равенство (12.15) выражает собой теорему M = const для
случая линейного закона изменения массы.
Решение задачи имеет смысл для параметров М^Мг-тах-
Максимальные значения параметров Мгшах, вгшах, М^нгшах опре¬
деляются, как и ранее, по выражениям (12.18), (12.19)
и (12.20).
Для линейного закона изменения массы, в соответствии с по¬
следними п уравнениями системы (12.26) и основной весовой
зависимостью (6.3), имеет место также
где на основании выражения (12.29)
п
п
w* = П Y* = П Уп U/ = Ui-[3(0K)]„
П
(12.34)
и затем
(12.35)
299
При этом
•^- + И0к)]г
Н-к/
GT, + ki(—)
' go hi
go hi 1 Wv0h
\go 0 i
откуда, как и в случае (12.7), получим
Д\ _ 0,5 [° (Вк)],-
<§■0 Jot ii_ + !1од
IJ-Ki ki
0,5 [g (9К)]/
i ki
H~)
\ go hi
Ивк)]/От/
4~+f)
Vh-k i ki!
:0,
где, как и ранее (см. разд. 10.5),
d(WQ)i
"По
V go 'оi
1/2
Б. Показательный закон изменения массы
При показательном законе изменения массы полное
движения системы на i-м участке деления равно
go / о/
или с учетом зависимости (6. 10)
*/=-■
Wi
«ьО
При этом
(-)
\golo
1п(1*эфф/ + У/гг).
1
v_
go /о/
1п(^эфф/+'Ур/).
На основании этого выражения имеем также
-г л 1
0Х{ de-t
Те~ =
У/
(-) (-)
V go Jot ' go /Oi
Как и ранее, после подстановки выражений (12.30),
и (12.39) в равенство (12.28), получим
Е,.Ц(.у,-(1-Й8к)]г)^ = М,
300
(12.36)
время
(12.37)
(12.38)
(12.39)
(12.31)
(12.40)
где
а также
М = [s*U*y* (1 - [з (0,<)];)* W*]'/”,
(1-ЙУ,'Г=П (1-ЙМД
'12.41:
Ц* = П Ц/. /=1,2,3,..., п.
i= 1
Равенство (12.40) представляет собой математическое выра¬
жение теоремы М = const для показательного закона изменения
массы. Эта теорема дает
[^эфф i М
(12.42)
Решение задачи имеет смысл для параметров М, равных или
меньших тах, т. е. М^Мгтах. При этом на основании (12.42)
iVl/max = V/(l-b(eK)lZ)^..
(12.43)
Для показательного закона изменения массы в соответствии
с зависимостью (6. 3) можно записать
Т; =
Wi
V
so /о/
In
a/ + Y/£/ + ^;(—
go hi
(12.44)
и затем
дх,-
1
“i-) (-
?0 hi \£о /о/
ki
In i
[4 i
-) s
/0/ J
(12.45)
При этом
ki [о(0к)]< L
(V/<?o)o/
ki
(-) :
\ go о i
0,5 irL
In H-k /
(V/gt!)oi
_J L
4)i
+7,
=0,
-Ц'П
ki — — [% i
Zi
_L
I
0,5^/
^ (Ok)]/
'Чо/
ki — — [4 i
С/
J-
i(6K)]/
5/
(4c i I11 Ц/
*40/
ki — — 4 i
?/
1/2
(12.46)
301
Следует помнить, что параметр г\0 для случаев показатель¬
ного и линейного законов изменения массы имеет неодинаковые
значения и определяется в результате аппроксимации расчетных
данных траекторий движения как Ло = Л°(^п, 0К) (см. разд.
10.5).
Воспользовавшись выражениями (12.15) и (12.40), можно
убедиться, что в пустоте во всех случаях при [а(0к)]г- = О, распре¬
деление масс по ступеням составных ракет при линейном и по¬
казательном законах изменения массы одинаковы. При этом
в обоих случаях расхода массы имеет место равенство (11.50).
Рис. 170. К выбору оптимальных пара¬
метров составных ракет при показатель¬
ном законе изменения массы (р-эфф! =
= 0,07; р-эффп = 0,08; р.Эффш = 0,09;
Й0К)]1=О,3; [а(0к)]п=О,^ [а(0к)]ш=
=0; W\ = 1; №п=1,2; W\n = 1,5)
0 0,2 0,4 0,5 М
Полученный результат является чрезвычайно важным. Он
указывает на то, что без учета потерь на преодоление сил тяже¬
сти, распределение масс по ступеням ракет не зависит от закона
расхода массы. Таким образом все зависимости, полученные
нами для линейного закона изменения массы при сг(Ок)г = 0,
одинаково справедливы и для показательного закона расхода
массы.
При задании (или выборе) стартового в$са следует помнить,
что коэффициент эффективности конструкции цэфф должен соот¬
ветствовать (по данным статистики) задаваемому весу G0. По¬
строение графиков, аналогичных (рис. 168), выполняется с уче¬
том формулы (12.46), если значения перегрузок noi и п0гп най¬
дены оптимальными. Время интерраций при этом минимально.
Выбор ступенчатости (количества ступеней) производится
п л + 1
сравнением значений Ц = П и s*= П ПРП Ц* = const.
/=1 /=1
Типовой график для определения оптимальных параметров
в случае показательного закона изменения массы, приведен на
рис. 170.
302
12.6 ЗАМЕЧАНИЯ К УЧЕТУ ПРОГРАММЫ ПОЛЕТА ПО УГЛУ 0
При выполнении расчетов по выбору оптимальных парамет¬
ров составных ракет на этапе аванпроекта нет необходимости
в задании точной программы изменения угла 0 с целью получе¬
ния данных по учету потерь на силы тяжести. Как показывают
расчеты, в этом случае достаточно принять
0 = 0 (/). При этом
линеиныи закон
-(во—вк)— . (12-47)
т
где 0о — начальный угол наклона траектории.
Выражение для коэффициента гравитационных потерь ст(0к)
с учетом зависимости (12.47) запишется как
т
(0К) = — f sin [б0— (0О—0 )—’
т j L т
dt.
К,
т
о
Выполнив интегрирование, получим
о(ек)= ,cos . (12.48)
°0 — 0к
Формула (12.48) справедлива для одноступенчатых и состав¬
ных ракет в предположении линейного закона изменения
угла 0(/).
В случае вертикального старта 0о = я/2 и тогда
*(0к)
— — 0к
2
Если полет заканчивается при 0 = 0К = 0 (например выведе¬
ние на круговую орбиту), то
о(8к)= cos0o . (12.49)
60
Кривые, построенные по формулам (12.48) и (12.49), приве¬
дены на рис. 171. Сравнение этого графика с графиком (см.
рис. 130) показывает, что при линейном законе изменения угла 0
величина параметра гравитационных потерь несколько завы¬
шена. Очевидно, что при определении параметра а(0к) для одно¬
ступенчатых и первых ступеней составных ракет следует пользо¬
ваться графиком (см. рис. 130). Во всех остальных случаях, осо¬
бенно при свободном выборе углов 0О и 0К, величину о(0к)
с достаточной для предварительных расчетов точностью можно
определять по формуле (12.48).
Иногда в целях модификации существующей ракеты рас¬
сматриваются траекторные варианты ступеней, с тем чтобы
303
поварьировав углами 0К* (например первой ступени), получить
максимальную грузоподъемность всей ракеты. При этом, как
видно из рис. 172, функция ц*=\ь*(дк1) имеет максимум, который
и отвечает условию получения Д2 = Д2тах путем догружения
всех ступеней ракеты или только последней из них.
Выполнение аналогичных изысканий требует особо коррект¬
ного отношения к выбору параметра гравитационных по¬
терь а(0к).
Рис. 171. Характер зависимости а(0к) Рис. 172. Характер зависимости
при линейном законе изменения угла рк*=|Тк*(0ki) при п> 1 и Hovr> =
.0=0(7) = const
Значения параметра сг(0к), полученные по данным числен¬
ного интегрирования уравнений движения для некоторых вариан¬
тов составных ракет, приведены в табл. 12.2.
Среди существующих методов расчета основных параметров
многоступенчатых ракет мы привели здесь (гл. XI и гл. XII)
наиболее достоверные и практически апробированные методы.
Эти методы просты и не требуют большого объема вычислитель¬
ных работ. В силу математической корректности и достоверности
аналитического метода весового расМета они удовлетворяют
требованиям точности и рационального применения на этапах
предварительных проектно-конструкторских и научных поисков
и обеспечивают получение падежных данных на всех этапах
создания предэскизного проекта.
Пример 12. 1. Воспользовавшись весовой зависимостью (6.3) произвести
сравнение двухступенчатой и трехступенчатой ракеты по грузоподъемности
е* методом смежных ступеней (см. разд. 12.2), если заданы следующие
значения параметров: «1=0,074; «ц=0,09; сцп=0,1;
h\ = k\\ = =— 0,02; azqj = 1,3; ^оп = ^ош ~ 1 = 4200 м/с;
304
Таблица 12.2
Значения параметра о(0 к) для некоторых вариантов составных ракет
-—
Варианты ракет
Изменение
ПО числу
ступеней
по назначению
Ступени
угла 0 от 0о
Л.о ок, град
° («к)
Баллистическая
I
90—22
0,65
II
22—17
0,27
я = 2
Выведение на низкую ор¬
биту ИСЗ
I
II
90—22 -
22—0
0,65
0,174
■Т* 'Г’-'У ф
п = Ъ
Выведение на низкую ор¬
биту ИСЗ
I
II
90—25
25—4
0,743
0,225
III
4—0
0,03
Примечание. 0О, 0к—начальный и конечный (соответственно) углы наклона тра¬
ектории к местному горизонту
<«- М
sin Qdt.
Y, = Yn = Yni =0,965; [a(tK)]{ = 0,743;
[a(0K)]„=O,226; [a (0k)],!! = 0,174; Ик=10,9км/с.
Решение. В соответствии с постановкой задачи, сравнение грузоподъем¬
ности е* произведем по параметру Ук=1/к/И7п=,10,9/4,2=2,6, одинаковому
для обеих ракет. Введем обозначения и в соответствии с формулой (6. 3)
подсчитаем для каждой ступени:
Р-эфф! = ai + ^oi = 0,074 + 0,02-1,3 = 0,1;
Нэффп =ац -Ь Л/igii =0,09 4-0,02.1 = 0,П;
Р-эффш = аш -г ^ош =0,1 4-0,02-1 =.-0,12.
При этом pKi=0,1+0,965 ei; pKii=0,l1 +0,965 ец; p,i<ni=0, 12+0,965 еш.
Параметры гравитационных потерь, определяемых формулой
Г~/о МУ];
La (9к)]/ = »
n0i
будут равны: [a(0K)]i=O,57; [сг(0 к)]н=0,226; [a(0K)]iii=0, 174. Расчет сводим
в табл. 12. 3 (А и Б) раздельно для каждой из ракет, воспользовавшись фор¬
мулой (12. 13), имеющей вид
_Р±_ ГI Pi V _11/2
£,'‘1 2
11 3479 305
А. Расчет параметров двухступенчатой ракеты
см
у
к
—
1^
+
1^
05
ю
см
оо
со
3
сО
ОО
о
ю
1^
см
г_'
Д
5
05
оо
о
Sj
ю
со
СО
05
н
lr*1
1^
ю
см
см
д
"ф
05
СО
t"-
СО
г-
СО
оо
1
ю
о
о
о
о
о
ч
±
-
*2
а
05
IO
ю
см
СО
05
оо
СО
с
1—1
т—1
1—1
1—1
1—1
JZ
II
Ь£
1^
'j2
ю
со
о
см
г-
00
см
05
СО
см
СО
см
см
t-.
оо
L
о
о
о
о
о
F-
ю
t^-
*
1^
1,183
0,593
0,302
0,122
0,012
сГ
1
-1
±
F-*
ю
о
оо
о
0,61
0,418
0,225
0,032
с
7
’btf
1^
"" 1 dT
С
СО
0,94
0,54
0,25
0,03
ш
*
о
ю
ю
о
ю
см
оо
о
оо
о
см
t*-
о
о
о
о
о
о
о
со
оо
ю
СО
см
оо
о
о
о
о
о
о
LO
О
1
оо
С4)
см
о
со
05
см
to
см
05
о
см
L
ОС
о
о
о
о
о
:=г
о
1
см
0
1
CSI
ch
ю
00
о
со
о
1,26
с
э*
— СМ
S. 1
СО
см
ю
05
ю
со
05
см
см
со
--Г
о
о
—Г
i-Г
LO
o'
1
гГ
/—ч
Г"
иГ Ю
Ю 0~
СО ,
05 |
о" i-T
0,437
0,577
0,555
0,486
0,4
—
ОС
- -
ю
со
05
о
см
o'
-0,57)
СО
Ю
05
05
ю
см
о-
со
LO
1"
05
1
3
г""1
о
о
1
||_
d.
ю
СО
05
05
со
см
оо
IO
ю
г-.
о-
00
со
05
С
о
о
о
о
о
со
1-0
05
(0
о
о
о~
о
о
0>
*
л
о.
ЭЯ
о
с
>>
3
О.
н
СО
О
О.
5
S
ей
о.
ed
ed
О.
U3
и
+
I©
IO
—со
д S
=. I
Ю 05
О ОО СО
05 О ■—| С4!
. £« со ю
N О) ^ 1Q ач
00 ^ ^ ос
о о о о о"
СО —• со
С4! СМ ^ -
• СО ^ LQ
f0 О 00 ^ (М
1—1 со СМ СМ —'
о о о о о
ю
о » о а>
Д ^ Tf о
О О —< —I
О —< О О
о о о о о
ю
О О) N СО
о о о о о
СО С4)
СО СМ —I СО ю
со^ ^ СО О
о о о о о
^ 05 CD
Ю ^ Ю i—•
СО
см ь-
^
(N N Ю ^ OI
СО 05 t"- О
'Tf Ю Ю Ю О
о о о о о
CD N О! со
О 00 со СМ 00
см см см см оо
о о о о о
со Ю
О ОО со СМ оо
о о о о о
306
Поскольку полет происходит в пустоте, то в соответствии с формулой
Циолковского (2.44), имеем также:
VKl = _ lnN-0,57GTl;
Vkh = — In [xKlI — 0,226(хгП;
V'k-iii = — ln P-kiii — 0,174GTIII.
В соответствии с методом смежных ступеней, найденные параметры двух¬
ступенчатой ракеты ец (табл. 12.3. А) являются входными для расчета па¬
раметров 8ш трехступенчатой ракеты (табл. 12.3. Б). Результаты расчетов
наносим на графики (см. рис. 167) и (см. рис. 168) в виде кривых
ег=е; (ei), е*=е* (ei) и VK=VK (ei).
В дальнейшем задача сводится к определению грузоподъемности е* по
заданной безразмерной скорости Ук=2,6. Это дает е*=0,01 для двухступен¬
чатой ракеты (см. рис. 167) и е*=0,012 для трехступенчатой ракеты (см.
рис. 168). Таким образом мы получили, что грузоподъемность трехступенча¬
той ракеты больше грузоподъемности двухступенчатой ракеты.
Пример 12. 2. Суммарная скорость, необходимая для полета по маршруту
Земля—Луна—Земля, составляет (с учетом потерь на преодоление сил тя¬
жести и сопротивления воздуха) Т/к=16,9 км/с. Определить начальный
(стартовый) вес и разбивку масс по ступеням трехступенчатого носителя,
если Да=6,8 тс, и Wn = 4200 м/с. Расчет произвести по данным примера 12. 1
а графика (см. рис. 168).
Решение. Потребное значение безразмерной конечной, скорости носителя
при U7n=4200 м/с равно
- 16,9
VK =, — = 4,03.
" 4,2
При этом по графику (см. рис. 168) находим 8* = ^“ =0,003, а также
Goi
81=0,143; 611=0,138; em=0,162.
Вес ступеней определится так
6,8
G0] = = —:— = 2270 тс,
01 в* 0,003
О0ц = G0i3i =, 2270-0,143 = 325 тс,
С?0ш = О'011еп = 325-0,138 = 45 тс.
Пример 12.3. Сравнить одноступенчатую и оптимальную двухступенча¬
тую ракеты по приведенной весовой отдаче рк, если для каждой из них
имеет место
Рк / = 0,1 -1-0,98^
G01 = 100 тс; = 1 тс; а (6К) = 0.
Решение. Весовая отдача одноступенчатой ракеты составит
1
Рк — 0,1 4-0,9 —— = 0,1 4-0,9— = 0,109.
G0I 100
Оптимальное распределение масс двухступенчатой ракеты найдем по
закону
Г ^ -11/2 г 1 -.1/2
- Gqj J I 100J ~0,1'
Весовая отдача ступеней найдется как р,к1=и.к11=0,14- 0,9еi=0,1 +
+ 0,9-0,1=0,19. При этом рк = pjj; =0,192=0,0361. Таким образом, обладая
11* 307
одинаковой грузоподъемностью, двухступенчатая ракета заметно превосхо¬
дит одноступенчатую ракету по приведенной весовой отдаче ^к-
Пример 12.4. Найти соотношение масс ег-, грузоподъемность е* и числа
Цг по ступеням двухступенчатой ракеты для случая M = Mimax, если
известно, что
^хк1 = 0,08 + 0,95ег, = 0,10 + 0,95ец , W™ = 3000 м/с,
1Г“=4400 м/с, [s(0K)h = 0,6, [с (0к)]ц =0,25,
л01 = 1,31, 71^ = 1,58, ^ = 1,18.
Решение. Подсчитаем значения входных параметров формулы (12. 17).
При этом допуская, что —Нэффг), будем иметь
Р*эфф1 = 0*08; Р-эффп — 0,10; yI=yII = 0,95; 1ГД = 1;
_ - Га (0k)1i
wu = Wu/W, = 4400/3000 = 1,467; [а (0К)], = 1 , кЛ1 • = , , ’ ■ =
?Л01 1,1о*1,31
— [g (0к)1 Iт 0,25
= 0.387; [а (8к)]п — JL=T+ = 0,155.
«он ]’°8
Найдем значение M=Mimax.
Mlmax = ^1 [l + [(a (0k)]i Р-эфф1 ~ 2 Y [a (0K)]l М-эфф^ =
= 1 [l + 0,387• 0,08 — 2 /0,387• 0,08] = 0,6688.
При этом
1_
EImax —
Yi
1 / .аэфф1 1 Г, /^0.08 1
У “«IV
Величину коэффициента ец найдем по формуле (12.17). Она будет рав¬
на 8ц=0,095. Грузоподъемность определится как e*=eien=0,386 • 0,095 =
=0,0367.
Основные весовые зависимости по ступеням дают: jlxki=0,08Ч-0,95ei
= 0,08+0,95*0,386=0,447; ркн^ОД + 0,95ец=0,1 +0,95 • 0,095=0,19. При этом
числа Циолковского будут равны: Ui=2,24 и Цц=5,27.
Пример 12.5. В стыке ступеней двухступенчатой ракеты необходимо
произвести доработки, связанные с утяжелением одной из ступеней на
ДС=1 тс. Определить, в каком случае потери в конечной скорости будут
минимальными — при доработке первой или доработке второй ступени?
Произвести расчет величины р* при следующих исходных данных: G0=100tc,
Pki = M'kii=0,3; ei=0,25.
Решение. Найдем вес второй ступени. Он будет равен
G0ii=6iGoi=0,25 • 100=25 тс.
Если утяжеление произошло в результате доработки первой ступени, то
A G 1
jjlkI =0,3 + =0,3 + = 0,3099.
^ G0I + AG 100 + 1
При этом р.* = р.К!{хкп = 0,309*0,3 = 0,0927.
Если же утяжеление произошло при доработке второй ступени, то
A G 1
Сравнение величин в первом (р,*=0,0927) и втором (рк=0,105) слу-
_ях показывает, что минимальные потери в конечной скорости будет иметь
ракета, доработки с утяжелением веса которой произведены на первой сту-
Пример 12.6. Рассчитать и построить кривые ец=ец (ei), е* = е* (ei) и
= VlK (ej) для двухступенчатой ракеты при следующих значениях за¬
данных параметров:
рэфф1=0>077’ Р-эффн = 0,11, Yi = Yu = 0,965, и = 1,3, у1ф(1— р-эффг),
[о (0k)]i = 0,65, [а (0К)] ц=0,174, /Zqj = 1,3, Z2gj| = 1,0, AVх = 0, £ = 1,0.
Определить веса первой G0i и второй G0n ступеней для случаев:
а) = 130 тс, VlK = 8 км/с, WJ1 = 3200 м/с и
б) = 6,8 тс, 1/Бк=10,5 км/с, 1^ = 3200 м/с.
Решение. Воспользуемся методом смежных ступеней и запишем формулу
(12. 13) в следующем виде:
l 2
Pi
£п 2
[(tr-4
где
0,981 —0,743=:, (Ц, — 0,5) 0,0845(Ц, — 0,5)
Л = 7T7IZ > ЧI =
0,168 ’ 0,108
Вычисления сводим в табл. 12.4, задаваясь величиной параметра ei. При
этом Цк1 = 0,077+0,965 Ei; Ui= 1/|xki и [о(0h)]i =0,5. Продолжая вычисления,
находим также e* = eien и затем
^Ек “ ^К1 + Ук11 = ln — [а (0k)]i ^tI -f- w Ilf In — [а (0к)]ц С?т1Л ,
P-kI \ P-KlI /
где
aKlI =0,11 + 0,965e„ и [a(0K)]„ =0,174.
По полученным данным строим кривые (рис. 173)
£п = еп (£i). £* = £* (£i) и ^ек = (£i)-
8
В первом случае потребная безразмерная скорость равна уЪк = —— =2,5.
о, Z
Этой скорости соответствуют значения (по графику) параметров е* =0,034
и ei = 0,28.
Следовательно
As 130
Got = = = 3820 тс,
11 е* 0,034
G0n=Goisi = 3820-0,28 = 1070 тс.
Во втором случае потребная безразмерная скорость определится как
- 10>5
К2к = = 3,28. Этой скорости соответствуют значения (по графику)
3,2
6,8
параметров е* = 0,01 и £i = 0,ll. Следовательно = = 680 тс и Gon =
= 680-0,11=75 тс. Найденные значения ei = 0,28 и ei = 0,11 являются оптималь-
11* 3479 309
ными, поскольку они не превышают максимально допустимом величины, равной
€1 шах — ‘
Yi
/~ ^ФФ1 1 Г, /~0,077
V [а (0К)]Г _ ^эфф1_ = 0,965 L V 0,5 '
-0,077
= 0,332.
Пример 12. 7. Доказать теорему M=const, исходя из мощности, развивае¬
мой многоступенчатой ракетой на единицу полезного груза.
Таблица 12.4
*1
«VI
н(1Ч-°>5)
Р\
еп
Е*
2
0,1
0,1735
0,527
1,76
0,263
0,08
0,008
0,3
0,367
0,669
1,44
0,334
0,12
0,036
0,5
0,559
0,645
1,49
0,322
0,11
0,055
0,7
0,752
0,581
1,63
0,29
0,09
0,063
0,9
0,947
0,504
1,81
0,252
0,07
0,063
Продолжение
*1
а т т
• к11
GtII
^•1
^к11
V*K- Кк1 +
+ ^к11
0,1
0,1872 .
0,8265
0,813
1,337
2,0
3,337
0,3
0,226
0,633
0, /74
0,695
1,76
2,455
0,5
0,216
0,441
0,784
0,36
1,82
2,18
0,7
0,1968
0,248
0,803
0,156
1,94
2,096
0,9
0,1775
0,053
0,223
0,024
2,07
2,094
Решение. Мощность, сообщаемая одноступенчатой ракетой полезному
грузу в конце активного участка полета может быть выражена как
ДЯУК = ASW [ In -J- - о (6К) (1 - цк)]
или
= £[1п7"_°(1Ш1_,ик)] ’ (12,50)
кг V'< -
где Nд = £ —— — оезразмерная мощность. *
w
Соотношение параметров в точке Na=Na max найдем по выражению
(12.50), приравняв нулю производную от N а по е. Принимая во внимание
весовую зависимость (6. 10), получим
VK =-^--увЦ, (12.51)
где Ц = Ц— о (0К).
Полученное выражение описывает условие, при котором обеспечивается
максимальный выход мощности одноступенчатой ракеты, приходящейся на
единицу полезного груза.
310
Запишем условие (12.51) применительно к двухступенчатой ракете. Тогда,
воспользовавшись формулой (2.44), получим
ИЛИ
Укл = Ик1 + VkU = Yi£iUi + ^iiYii£ii Uii
_ _ __ £*ц*
V'SK = YIMUI+Wrir
£iUi
(12. 52)
.* .
L 7 £ff
Рис. 173. К решению примера 12. 6
Рис. 174. Влияние коэффициента рас¬
пределения масс (грузоподъемности)
е на мощность, развиваемую ракетой
в конце активного участка
Если произведение параметров EiUi характеризует максимальный выход
мощности ТУд;, то очевидно, что можно найти и его оптимальное распреде¬
ление по ступеням, при котором будет сохранено условие VSK = (V’SK)max*
Очевидно, что для этого необходимо приравнять нулю производную
dV$K/d.(&iUi). Имея равенство (12.52), получим
, ... И/2
£1Ц1 ""
или
где
_ м
eiUi = —.
Yi
(12.53)
Легко видеть, что выражение (12.53) может быть преобразовано
к виду (12. 15).
Таким образом оптимальное распределение масс по закону М = const ха¬
рактеризует максимальный выход мощности, приходящийся на полезный груз
многоступенчатой ракеты.
11** 311
Пример 12.8. Пользуясь условием оптимальности примера 12.7 (12.51)
доказать справедливость выражений ,uK * шах (12.20) и е* max (12.19), выте¬
кающих из теоремы М = const.
Решение. Условие оптимальности (12.51) применительно к многоступен¬
чатой ракете запишется так
VK / = *Д/У/^/. (12-54)
где VKi и Wi отнесены к скорости истечения первой ступени W\.
С учетом весовой зависимости (6.10) равенство (12.54) принимает вид
VKi
у iWi
1 [о (вк)],
Р-эфф + Vе/
(12.55)
Кривые, построенные по выражению (12.55) для различных значений па¬
раметра гравитационных потерь [о (Эк)]; показаны на рис. 174. Как видно из
графика, оптимальные скорости VK г в свою очередь имеют максимумы по па¬
раметру ег-. Приравняв нулю производную d(e;U;)/de;, после'Преобразований
получим (12.20)
Н-эфф i \ ^
Р-к i max — I _
[«(вк)]/
е/ max — (M-к i max (^эфф /)•
Y/
Пример 12. 9. Найти закон распределения масс для двухступенчатого ра-.
кетного самолета, если маршевые скорости KMi, KMii, коэффициенты эффек¬
тивности конструкции (лЭфф1, Цэффц, удельные тяги ЯУД1, Яудп и аэродина¬
мические качества (су/сх) i, (су/сх)п по ступеням неодинаковы.
Решение. Дальность маршевого полета каждой ступени ракетоплана опре¬
деляется по формуле (9. 19)
(Су/С,) ,пц
1 — (^м/^кр) УД
где Ккр — круговая скорость.
Учет весовых факторов произведем при помощи основной весовой зави¬
симости (6.5)
Р-к ~ Р'Эфф (1 М-эфф) £ •
Суммарная дальность маршевого полета обеих ступеней составит
•^Бм = ^М1 [Р-эфф1 Р-эффО el] ^м11 [Р*эфф11 "Ь (1 Р*эффп) eI i] »
где
Т/* _ (gl//Сх)\Ум\ D л Т Т* _ (°у!р
Ml 1 /Т / /т/ \о уд!’ Mil 1 /т / /т / \о Уд1ь
1 — \Уи\/ук\)Г 1 — (^мп/^крГ
I, II — индексы, означающие первую и вторую ступени.
Поскольку en = e*/ei, то
^2м = ~ I'm. 1,1 Гм-эфф! + (1 — (АэффО el] — п >4
312
£
Р-эффП + (i — Р-эффп) ^
Дифференцируя это выражение по 8i и приравнивая производную пулю,
получим
1/2
<4 = — Ч 4-
■п2 +
^эффШ М"Эфф1) ^м11
е*
Р-эффП (1 — р-эффц) 1/*
м!
(12.56)
где
1 —
Р-эффП
Р-эфф!
Mil
V
м!
Су
Если параметры Руд, ,иЭфф, Км и ^ J одинаковы по ступеням, то
£j = Уе*. Следовательно, распределение масс по ступеням составных ракето¬
планов в простейшем случае, как и для составных ракет, подчинено закону
геометрической прогрессии. Из формулы (12.56) можно сделать вывод, что
увеличение веса 2-й ступени пропорционально удельной тяге Рудп, маршевой
скорости Ума и аэродинамическому качеству (су/сх)и.
СПИСОК ЛИТЕРАТУРЫ
1. Воробьев Л. М. Астрономическая навигация летательных аппаратов.
М., «Машиностроение», 1968, 208 с.
2. Исследование оптимальных режимов движения ракет. [Сборник пере¬
водных статей]. Под ред. канд. техн. наук И. Н. Садовского. М., Оборонгиз,
1959, 293 с.
3. Кар а годин В. М. Теоретические основы механики тела переменного
состава. М., Оборонгиз, 1963, 178 с.
4. Космодемьянский В. А. Об одном типе вариационных задач.—
«Прикладная математика и механика», 1963, т. 27, вып. 6, с. 1111 —1116.
5. Основы теории полета космических аппаратов. Под ред. д-ра физ.-мат.
наук, проф. Г. С. Нариманова и д-ра техн. наук, проф. М. К- Тихоиравова.
М., «Машиностроение», 1972, 607 с.
Глава XIII
РЕЖИМЫ ДВИЖЕНИИ РАКЕТНО-КОСМИЧЕСКИХ
СИСТЕМ МНОГОКРАТНОГО ПРИМЕНЕНИЯ
В главе рассмотрены различные виды движений, которые мо¬
гут быть применены для возвращаемых ступеней многократно
используемых космических систем. Сюда отнесены рикошети¬
рующий полет, полет по пологой баллистической траектории,
суборбитальный полет, а также переходные режимы движений
высокоманевренного ракетоплана в вертикальной и горизонталь¬
ной плоскостях.
Рис. 175. Схема сил, действующих на
летательный аппарат при входе в ат¬
мосферу (плоское движение)
Движение летательного аппарата в пустоте (перед входом
в плотные слои атмосферы) происходит по законам небесной
механики. При этом на летательный аппарат действуют инерци¬
онные и гравитационные силы. Движение летательного аппарата
в атмосфере происходит под действием многих сил. Сюда входят
(рис. 175) сила тяжести, аэродинамическая сила лобового сопро¬
тивления, аэродинамическая подъемная сила и центробежная
сила.
Изменение различных параметров вдоль траектории спуска
в атмосфере представлено на рис. 176. Как видно из графика,
скоростной напор, перегрузка и тепловой поток имеют экстре¬
мальные точки. Это является следствием противоположно дейст¬
вующих факторов: уменьшением скорости летательного аппарата
и увеличением плотности воздуха по мере прохождения плотных
слоев атмосферы. Аэродинамические силы, равно как и вызы-
314
раемые ими перегрузки, изменяются пропорционально qV2; теп¬
ловой поток — пропорционально qI/3 (работа сил сопротивления,
приходящаяся на единицу поверхности).
Рис. 176. Изменение различных параметров по траек¬
тории спуска в атмосфере
Характер траекторий входа и движения в плотных слоях
атмосферы определяется в основном аэродинамическими харак¬
теристиками. В связи с этим различают баллистические, плани¬
рующие и рикошетирующие траектории спуска (рис. 177). В пер¬
вом случае полет происходит
без участия подъемной силы;
во втором и третьем случаях
полет происходит в присутст¬
вии подъемной силы. Условия
входа в атмосферу со второй
космической скоростью значи¬
тельно сложнее, чем при сходе
с орбиты искусственного спут¬
ника Земли. При возвращении
из космического пространства
особо важное значение приоб¬
ретает точность входа. Здесь
чрезмерно крутой вход приво¬
дит к разрушению летатель¬
ного аппарата вследствие вы¬
соких перегрузок и температур
нагрева; чрезмерно пологий
вход может привести к безвозвратному уходу аппарата в косми¬
ческое пространство. Коридор входа по Чепмену (применительно
к Земле или Венере) [13] показан на рис. 178. Там видно (в мас¬
штабе рисунка), что коридор входа, в границах которого воз¬
можно сохранение и наведение в заданную зону космического
корабля, является очень узким [5].
Термин «плотные слои атмосферы» перешел в ракетодина-
мику из астрономии, где граница плотных воздушных слоев
Земли оценивается высотой 120—150 км — высотой вспышки
315
баллистический
оход \
Рикошетиро
j дание
Планирование
' малом
' (су/сх)
°Р$ита
Рис. 177. Траектории спуска в атмо¬
сфере с круговой орбиты
метеоритов, входящих в атмосферу с огромными скоростями. На
высотах около 100 км начинается сильный разогрев космических
аппаратов, возвращающихся на Землю. Эти слои плотные лишь
для тел, летящих с очень большими скоростями.
На рис. 179 представлена схема спуска с многократным вхо¬
дом летательного аппарата в верхние слои атмосферы и после¬
дующим выходом на чередующиеся эллиптические орбиты
в космическое пространство. Такой метод дискретного торможе-
Рис. 178. Коридор входа Рис. 179. Спуск с многократны v;
входом в атмосферу
ния требует большой точности определения и коррекции траек¬
тории. Современная техника не обеспечивает таких точностей.
В будущем такой метод может быть приемлем для ракетно-кос¬
мических систем, у которых минимальный расход топлива
остается доминирующим фактором.
Возможность рикошетирующего вида движения была впер¬
вые обнаружена и теоретически ^обоснована Е. Зенгером
и И. Бредтом в их работе [3].
Траектория рикошетирующего ракетоплана представляет со¬
бой чередующуюся последовательность баллистических и ри¬
кошетных фаз. В баллистической фазе ракетоплан находится
в квазипустотной окружающей среде, из которой он затем попа¬
дает в атмосферу.
В рикошетной фазе, как будет показано в главе, ракетоплан
входит в атмосферу, совершает поворот вектора скорости и
затем отражается от атмосферы.
Режим движения по пологой баллистической траектории,
рассмотренный в главе, может быть применен спасаемой сту¬
пенью многократно используемой ракетной системы после окон¬
чания активного участка траектории полета, а также является со-
316
ставной частью (чередующейся фазой) рикошетирующего
полета.
Летательный аппарат, находящийся в режиме суборбиталь-
ного полета, должен перемещаться под действием небольшой
силы тяги. Большая скорость полета и малая величина потреб¬
ной тяги обусловливают полет на протяжении значительного
количества оборотов. Суборбитальный ракетоплан может дви¬
гаться по круговой орбите на различных высотах в широком
диапазоне скоростей VKP gR. Полет со скоростью, превы¬
шающей первую космическую скорость, может происходить при
отрицательной подъемной силе, направленной к центру -Земли
(см. рис. 192). В главе приведены некоторые характеристики
суборбитального полета ракетоплана по тяге, расходу топлива,,
дальности и времени полета.
К переходным режимам движения отнесены различные виды
движений в вертикальной и горизонтальной плоскостях (крутое
выравнивание, вираж и т. д.), которые являются связующими
между другими режимами движений (например выход из бал*
листической траектории). Эти виды движений могут иметь ме¬
сто для возвращаемых ступеней многократно используемых
ракетно-космических систем в зависимости от характера балли¬
стического участка траектории, параметров орбитального или
суборбитального движений, района предполагаемой посадки,,
а также в случае аварийной ситуации.
Материал главы дополняет также раздел, посвященный вер*
тикальному снижению ракетоплана с больших высот.
13.1. ДВИЖЕНИЕ РАКЕТОПЛАНА В РЕЖИМЕ РИКОШЕТИРОВАНИЯ
Рассмотрим случай, когда траектория полета гиперзвукового
ракетоплана состоит из ряда баллистических участков, соединен¬
ных между собой фазами рико-
шетирования, где ракетоплан Н,км
входит в сравнительно плот¬
ные слои атмосферы, совер¬
шает поворот вектора скорости 100
и затем снова рикошетирует
на баллистическую траекто¬
рию (рис. 180).
Рис. 180. Типовая траектория полета
с отражением
Чередующаяся последовательность баллистических и рико*
шетных фаз определяет нестационарность режима рикошетиро-
317
вания. Минимальная высота рикошетирования всегда остается
меньше высоты квазистационарного планирования.
Уравнения движения ракетоплана в рикошетной фазе могут
быть записаны в следующем виде
где 0 — угол наклона траектории к местному горизонту;
М — масса ракетоплана (постоянная в полете).
Расстояния, проходимые ракетопланом в рикошетной фазе
сравнительно невелики и составляют порядка 4* 102 км. По этой
причине в наших исследованиях можно принять Землю плоской.
Кроме того, на участках отражения гравитационные силы зна¬
чительно уступают аэродинамическим силам и, следовательно,
имеет место Gsin0<C^ и Gcos0<cK В режиме рикошетирова¬
ния обычно 0<1О°. При этом можно положить также sin 0 = 0
и cos 0 = 1.
При сделанных допущениях уравнения движения (13. 1) упро¬
щаются и принимают вид
Как показывает интегрирование уравнений (13. 1) численным
методом, изменение скорости на участке рикошетирования не
превышает ~8%. Это означает, что интегрирование уравнений
(13.2) можно выполнить при допущении K=const. Поскольку
при больших гиперзвуковых скоростях полета зависимость аэро¬
dt
(13.1)
-— = V cos 0,
dt
(13.2)
dt
dt
где
318
динамических коэффициентов от скорости V невелика, полагаем
«также сх = const и су = const. Везде имеется в виду, что вели¬
чина g отнесена к условиям на средних высотах отражения.
Однако, принимая во внимание малые высоты отражения
(tfmin<100 км), при выполнении практических расчетов целесо¬
образно положить g = go-
Найдем распределение углов в рикошетной фазе траекто¬
рии. На основании предпоследнего уравнения системы (13.2)
имеем
После подстановки во второе уравнение той же системы получим
Интегрирование при выполнении начальных условий H = HQ
и замены dH/dt=VQo дает
Если положить в формуле (13.5) Н = Ни = Н0, то получим
0К =—0К. Это означает, что при постоянном угле атаки а, углы
входа и выхода в рикошетной фазе траектории одинаковы по
абсолютной величине и противоположны по знаку.
Минимальную высоту отражения Н = Нтin найдем, положив
в формуле (13.5) 0 = 0. При этом
Как видно из полученной формулы, минимальная высота отра¬
жения тем меньше, чем больше угол входа 0О и тем больше, чем
больше величина коэффициента подъемной силы су. Из фор¬
мулы (13.6) видно также, что при увеличении нагрузки на еди¬
ницу характерной площади (площади крыла G/SKp), высота
отражения уменьшается.
Время рикошетирования найдем, переписав выражение
(13.5) для левого участка отражения (0О<0<0) в следующем
виде:
(13.4)
(13.5)
откуда
(13.7)
319
Введем обозначения для текущих f( Ш ) и начальных /(ЭЛЦ )
условий отражения
/(а») =
уж —
ал
-2-^
Р
I
СП.
1
<D
<м
1/2
V ЭЛ - 0
уш +
ал-
1/2
У Ш. + е
/ал —
/т0=
ш,-
V \2
Р \К,
■2 — /-/V е~^н°
/ЭЛ +
Ы = ^- = В1
V2
т-
л
р
У \2 пн’
—~\ е“^я°
1/2
/*й-
У шг +1
?(УгУ
.е-№о ,
(13.9)
После интегрирования и определения постоянной интегриро¬
вания при условии, что Н = Н0 и f( ЯЛ ) =/( Щ ), выражение
(13.7) дает
р/ЗЛ
■In
/(9й)
/т0)
(13. 10)
Заменив знак «минус» на «плюс» в выражении (13.7) приме-
нительно к правому участку отражения (0О>0>0), легко убе¬
диться в справедливости выражения (13.10) и на этом участке
полета.
Полное время полета т'при отражении получим, положив
в формуле (13. 10) 0 = —0о. Обозначив индексом «к» параметры
конца отражения и принимая во внимание, что
Шк _/Vk\2
\Vq) ’
получим
Шо
1+^ -
__^_1П/юг
/ № / т -- 00 ’
(13.11)
Легко видеть, что время отражения тем больше, чем больше
угол входа 0о и чем меньше конечная скорость торможения VK.
Текущую высоту на участке рикошетирования, выраженную
в функции времени полета H = H(t), легко определить по фор¬
муле (13. 10), решив ее относительно параметра Н. Тогда, с уче¬
том обозначений (13.9), получим
320
я=—
— In
э
ЭЯ
/ (Ш?о)
- /(Щ,)е(р У' W
а- I у
2—1 —
э [Vy
. (13. 12)
Характер зависимости H = H(t), построенной по формуле
(13.12), представлен на рис. 181. Из графика видно, что траек¬
тория отражения симметрична относительно минимальной вы¬
соты // = tfmin. Последняя, как мы уже видели, определяется по
формуле (13.6).
Угол наклона траектории в функции
найдем из выражения (13.10), решив его
метра 0. При этом найдем
времени отражения
относительно пара-
1 + /(%)
(13.13)
Зависимость 0 = 0(/) представлена на рис. 182. Как видно из
графика, в процессе полета траекторные углы 0(/) распределены
симметрично относительно половинного времени отражения.
Время, при котором угол наклона траектории становится рав¬
ным нулю (половинное отражение), найдем по формуле (13.13),
положив в ней 0 = 0. Тогда получим
0=0 =
L in^-00
(13.14)
Этому же времени полета соответствует минимальная высота
отражения. В этом легко убедиться по формуле (13. 12), прирав¬
няв нулю производную dH/dt.
Имея выражения (13.11) и (13.14), найдем
0=0
1 +
Ко.
VK
(13.15)
Поскольку Vo«VK> то о/т~ 1/2. Таким образом время до¬
стижения минимальной высоты отражения составляет примерно
половину общего времени полета в рикошетной фазе.
Найдем далее распределение скоростей на участке рикошета.
Тогда сделав замену dt = dH/VQ в первом уравнении системы
(13. 2), получим
V (КУ
e-WdH.
(13. 16)
321
Перепишем затем формулу (13.5) в следующем виде
т-
НКГ
1/2
(13.17)
Обозначим
и запишем
dH--
х2 = У1-
Л е-8 Я
dx.
р (КГ
(13.18)
е-?я
в, град
(КГ
Подставляя выражения (13.17) и
(13. 18) в уравнение (13. 16), получим
dV dx
V
i Kj_
\
Н,км
6
4
2
О
-2
-4
-6
-8
-10
!
i
1 /
!
КГ-
1
\
/
!
!\
!
/
1
i
/
О 10 20 30 tfO t,c
Рис. 181. Зависимость H = H(t)
О 10 20 30 kO tjC
Рис. 182. Зависимость 0 = 0(0
Интегрирование этого выражения с учетом начальных усло¬
вий V=V0 и Н = Но дает
V
—=ехр
V7)
1-
(13.19}
Скорость полета в конце отражения (ее относительное изме¬
нение при 0 = —0О) будет равна
X*.
Vn
=ехр
/ Су
\ Сх
(13.20)
Изменение скорости в функции времени полета при отраже¬
нии показано на рис. 183. Как видно из графика, рикошетная
фаза осуществляется с потерей кинетической энергии, причем
величина этой потери возрастает с увеличением угла входа
322
й уменьшением аэродинамического качества. Ввиду малых углов
входа, эти потери невелики и, как мы уже говорили ранее, со¬
ставляют порядка 8%.
Поперечная перегрузка, равная отношению подъемной силы
к силе тяжести, запишется так:
Vy
или с учетом (13.17) и (13. 19)
б2)| ехр
-2-
су
1- —
(13.21)
(1.3.22)
Характер зависимости перегрузки от времени полета показан
на рис. 184. Как видно из графика, поперечная перегрузка при
Рис. 184. Зависимость пу —
= nv(t)
Рис. 183. Изменение скорости
V \
по времени полета t
10
в
%
V
0,9
0,8
1
- II
И
•JS
О 10 20 30 90 t,c f
л
ГМ
/
\: |
/
г
\
\
t
1
1
!
1
1
\
1
f
!
\
\
\
\/
10 29 30 90 t,C
отражении достигает значительных величин. Формула (13.22)
показывает, что главными параметрами, определяющими вели¬
чину пу, являются скорость 1/0 и угол входа 0Q.
На минимальной высоте отражения, где 0 = 0, перегрузка
равна
—2 •
Пу{ о=0)
Оо
й
(13.23)
Как видно из графика (см. рис. 184), перегрузка, определяе¬
мая выражением (13.23), близка к максимальной путах. Значе-
323
ние последней легко определить по формуле (13.22), если изве¬
стен угол 0 = 0„йтах. При КОТОрОМ ИМевТ место Пу = Пу шах- Для
нахождения этого угла продифференцируем по 0 выражение
(13.22) и приравняем нулю производную (dny/dQ). При этом
получим
02 +
0 — ЗЛ = 0,
откуда
Л
max'
т©+[т£
i+af*.
(13. 24)
Рис. 185. Максимальная перегрузка
рикошетирующего полета в зависимо¬
сти от дальности
Рис. 186. Максимальная перегрузка в
зависимости от дальности при входе
в плотные слои атмосферы по балли¬
стической траектории
Формула (13.24) показывает, что поперечная перегрузка до¬
стигает максимального значения несколько раньше, чем насту¬
пает 0 =0.
Для ракетопланов, имеющих аэродинамическое качество
( —)>1, угол 0П щах можно считать практически равным нулю.
V СХ ) ^
При зтом для определения путах с достаточной точностью можно
пользоваться формулой (13.23).
Необходимо отметить, что при движении в режиме рикоше-
тирования возможны перегрузки порядка пу = 20—30, что яв¬
ляется весьма серьезным обстоятельством с точки зрения проч¬
ности и веса конструкции, а также с физиологической точки зре¬
ния, если ставится задача обеспечения необходимых условий для
полета экипажа.
Величины максимальных перегрузок гсутах для различных
случаев полета приведены на рис. 185 и 186.
324
Для определения горизонтальной дальности рикошетирова-
нИя найдем из последних двух уравнений системы (13.2)
1 = ^. (13.25)
Делая подстановку при помощи выражения (13. 17) и выпол¬
няя интегрирование, находим
L=—±=ln /(т . (13.26)
p/ж /т)
В конце отражения 0 = —во, Н = Н0 и следовательно
£ = —3=1п + 6° ■. (13.27)
р V ж V шг — 0О
Условной границей, разделяющей полет ракетоплана в ква-
зипустотной среде по баллистической траектории и в режиме
отражения, целесообразно принять квазистационарную высоту
планирования. Поскольку в режиме квазистационарного плани¬
рования имеет место dQ/dt = 0, то из второго уравнения системы
(13.2) легко получить
откуда при V=Vo
т-Ш!1//)]!- <13-28)
Как видно из полученной формулы, высота условной границы
начала отражения определяется главным образом параметрами
1/, су и G/S. При этом увеличение скорости входа и коэффи¬
циента подъемной силы увеличивает начальную высоту отраже¬
ния, а увеличение нагрузки на единицу площади крыла умень¬
шает эту высоту.
Обычно рикошетирующее движение сравнивается с квазиста-
ционарным и баллистическим режимами спуска. Главными пара¬
метрами сравнения являются дальность, температура и пере¬
грузка. На рикошетной фазе возникают высокие температуры
и перегрузки, чего нет при гиперзвуковом планировании. В то
же время дальность рикошетирующего полета превышает сум¬
марную дальность баллистических и рикошетных фаз примерно
на 12%- Что касается тепла, то его интегральная величина ока¬
зывается наименьшей при баллистическом спуске [5]. Таким
образом использование рикошетирующих траекторий для воз¬
вращения ступеней, обладающих подъемной силой и охлаждае¬
мых излучением, представляется менее перспективным, чем
325
спуск по траекториям планирования, и требует применения си¬
стемы охлаждения с поглощением тепла, уступая в этом отно¬
шении траекториям баллистического спуска.
13.2. ПРИБЛИЖЕННЫЕ ЗАВИСИМОСТИ ДЛЯ ПОЛОГОЙ
БАЛЛИСТИЧЕСКОЙ ТРАЕКТОРИИ
Рассмотрим теперь пологую баллистическую траекторию,
когда возвращаемая ступень ракетной системы многократного
применения, выйдя из рикошетной фазы, попадает в квазипу-
стотпую среду и затем снова входит в атмосферу. Вследствие
малых углов отражения, для пологой баллистической траекто¬
рии справедливы допущения cos 0 — 1, sin 0^0 и V = const. Диф¬
ференциальные уравнения движения для таких траекторий при¬
нимают вид
dV
V
dl
dt
dt
==-g
dH
dt
0,
1-
1/0.
yj .
Делением
получить
откуда
почленно уравнений (13.30) и
(13.29)
(13.30)
(13.31)
(13.31) легко
Ш
— \Х~(—)
V2 L V Ркр)
dH,
92
~2
V2
1-
— |2"|/У+С,
Ркр / 1
1
где С — постоянная интегрирования.
Для восходящего участка траектории начальные условия
равны G = 0о и Я = Я0. При этом
ДТ)2|(Я-/У0)11/2, (13.32)
Укр / I J
где Я о — начальная высота баллистического полета.
На максимальной высоте полета (в апогее) имеет место 0 = 0.
При этом формула (13.32) дает
(W
6 = Ш-2^
где Яшах
326
н И -L
11 щах — 11 0 I
высота апогея.
) J
(13.33)
Обращаясь к формуле (13.32), легко заметить, что текущие
значения углов 0 на одинаковых высотах Я = Я0 восходящего
и нисходящего участков траектории одинаковы и противопо¬
ложны по знакам. Это означает, что баллистическая траектория
полета симметрична относительно вертикали, соединяющей
точку максимального удаления с центром Земли.
Для определения времени полета воспользуемся равенством
(13.31), подставив в него выражение для текущего угла 0 при
О 0 = 0 для нисходящей ветви траектории.
Тогда получим
dH
dt
и затем
dt= —
dH
\~(^-
. \vKV
1/2
[2^(ЯП
Я)]1/2
где знак минус означает отрицательные углы 0 на нисходящем
участке траектории.
После интегрирования получим
С
2 (Ятах - Я)
£Л
; 13.34)
В конце полета имеет место Я = Я0, и тогда полное время по¬
лета по баллистической траектории, равное удвоенному времени
полета на нисходящем участке, будет равно
2 (Ятах Я о)
Т = 2
\ VKf )
или на основании выражения (13.32)
т= ^ -
V
кр
(13.35)
(13.36)
где V — скорость, сообщаемая летательному аппарату к началу
его полета по баллистической траектории.
Найдем теперь дальность при снижении летательного аппа¬
рата по пологой баллистической траектории в квазипустотной
среде. Для этого запишем
Поскольку для участка снижения при 0о=О текущий угол на
основании формулы (13.22) равен
то после подстановки этого выражения в (13.37) получим
VdH
L=-
(Ятах-Я)
Рис. 187. Характеристика полета в ре- Рис. 188. Стационарная и динамиче-
жиме рикошетирования: ская высоты в функции скорости
1—осевая перегрузка; 2—угол 0; 3—ско¬
рость; 4—динамическая высота
полета:
/—стационарная; 2—динамическая
Интегрирование с учетом начальных условий L = 0 и Я = Ятах
дает
или на основании формулы (13.32)
328
L 2УЩ-,
~Л'-(кП
(13.38)
В справедливости полученной формулы легко убедиться
также на основании выражения (13.36), вспомнив, что наши вы¬
кладки выполнены при допущении V = const.
Высоту снижения по параметру времени t получим из фор¬
мулы (13.34)
Формула (13.39) показывает, что при V=VKV происходит
орбитальный полет на высоте Я = Ятах.
На рис. 187 и 188 показаны типовые характеристики по чере¬
дующимся фазам рикошетирующего полета.
13.3. ВХОД РАКЕТОПЛАНА В ПЛОТНЫЕ СЛОИ АТМОСФЕРЫ
ПО БАЛЛИСТИЧЕСКОЙ ТРАЕКТОРИИ
Участок движения ракетоплана в плотных слоях атмосферы
относительно невелик, вследствие чего при изучении этого уча¬
стка можно считать землю плоской. Баллистические траектории
входа иногда называют траекториями «столкновения», имея при
этом в виду, что при движении по ним ракетоплан, в случае
отсутствия атмосферы, неминуемо столкнется с поверхностью
планеты [13]. В случае полета ракетоплана в атмосфере, харак¬
тер движения обусловлен в основном действием больших аэро¬
динамических сил сопротивления, а траектория на большом
участке остается приблизительно прямолинейной. При этом для
больших скоростей и сравнительно крутых траекторий полное
изменение угла наклона траектории мало, что значительно упро¬
щает задачу интегрирования. В этом случае можно пренебречь
действием силы тяжести и, положив постоянным коэффициент
лобового сопротивления, записать следующие уравнения дви¬
жения
где 0 — угол входа.
После подстановки второго уравнения системы (13.40) в пер¬
вое, разделения переменных и интегрирования при условии,что
Я = Я0 и V=V0, получим
(13.39)
(13.40)
dH т/ . д
= — V sin 0,
dt
V
g(e-W_e-Wo -
Р sin 0 (V^f
(13.41)
12 3179
329
Осевая перегрузка, действующая на ракетоплан по траект0
рии спуска, на основании первого уравнения системы (13.40]
и формулы (13.41) будет равна
я„ =
е-РЯеХр
2g(e-P"-e-P"o)'
Э Sin 0 (V* )2
(13.42)
Кривые V=V($H) и пх = пх($Н), построенные по формулам
(13.41) и (13.42) для трех значений параметра G/S, представ-
0,2
ол
0,6 0,8 V/y
Рис. 189. Изменение безразмерной Рис. 190. Влияние нагрузки G/S
скорости V/Vo по высоте полета на характер зависимости пх =
РЯ при входе JIA в атмосферу по =пх($Н) при входе JIA в атмо-
баллистической траектории сферу по баллистической траек¬
тории
лены на рис. 189 и 190. Как видно из графиков, уменьшение ско¬
рости происходит непрерывно по мере снижения ракетоплапз
в плотные слои атмосферы, а функция пх = пх($Н) имеет мак¬
симум.
Найдем высоту H = Hnxm3iyi, на которой перегрузка дости¬
гает максимального значения пх = пХт&х- Для этого продиффе¬
ренцируем выражение (13.42) по параметру Н и приравняем
нулю производную. Тогда получим
Я =_^1п|>(1/х)2 — I • (13.43)
"Л* max а \ 2g \
330
формула для максимальной перегрузки, на основании вьшя-
жений (13.42) и (13.43), будет иметь вид
шах
(13.44а)
При больших высотах входа можно положить ехр(—рЯ0) =0
и тогда формулы (13.41), (13.42) и (13.44) принимают вид
где Н — текущая высота входа; 0 — угол входа, постоянный
во время полета.
Подстановка (13.43) в (13.446) дает
Это означает, что максимум осевой перегрузки достигается
при скорости, равной приблизительно 61% от скорости входа.
Обращаясь снова к графику (см. рис. 190), легко видеть, что
с увеличением нагрузки от веса ЛА на единицу характерной
площади G/S, кривые пх = пх($Н) смещаются на малые высоты,
включая = 0 (уровень моря). При этом скорость и пере¬
грузка, определяемые не аналитическим экстремумом по форму¬
лам (13.446) и (13. 44в) при р# = 0, будут равны
Полученные в главе зависимости применимы для расчетов
параметров движения ЛА многократного использования, типа
космического корабля «JANUS» (США). Конструкция такого
корабля состоит из контейнера (спускаемого аппарата), внутри
которого находится ЛА. После входа в плотные слои атмосферы
и торможения до дозвуковой скорости на малой высоте
12* 331
(1.3.446)
(13. 44»)
(13. 44г)
п max
0,61.
о —
(~15 км) контейнер (имеющий гиперзвуковые обводы) сбра¬
сывается и приземляется на парашютах, a ЛА (имеющий дозву¬
ковые обводы) производит дальнейший полет и посадку.
Оценка ошибки, допускаемой в аналогичных задачах без
учета энергии положения GH, может быть выполнена по выра¬
жению
GH 2 Н
M\rf~ R3 + Н ’
2
где имеется в виду скорость входа, равная первой космической
скорости VKP= V gR- Для высоты //=100 км ошибка составляет
-3,1%.
Любопытно отметить, что зависимости (13.41) и (13.42) при
sin 0=1 описывают нисходящее движение аэростатического ле¬
тательного аппарата в отсутствии активных сил. Примером
такого движения может служить движение геликостата на пас¬
сивном участке после выключения двигателей вертикального
маневра, работавших в режиме отрицательной тяги.
Такая аналогия для космических и аэростатических лета¬
тельных аппаратов (КЛА и АЛА) имеет место потому, что
в обоих случаях движение происходит как бы в отсутствии сил
тяжести и в среде с одинаковыми законом изменения плотности
по высоте Н (имеется в виду общий случай полета в атмосфере
планет, например в атмосфере Венеры). Для КЛА эффект отсут¬
ствия сил тяжести обусловлен большой скоростью входа в плот¬
ные слои атмосферы, когда силы тяжести становятся пренебре¬
жимо малы по сравнению с аэродинамическими силами сопро¬
тивления: для АЛА этот зффект обусловлен присутствием аэро
статических сил, полностью уравновешивающих вес ЛА.
13.4. ВЕРТИКАЛЬНОЕ СНИЖЕНИЕ С БОЛЬШИХ ВЫСОТ
Рассмотрим случай вертикального входа тела в плотные слои
атмосферы с начальной скоростью 1/0- Исследование проведем
с учетом влияния веса. Пользуясь обозначениями, сделанными
ранее (см. разд. 13.1), запишем уравнения движения в следую¬
щем виде
dV
dt
dH
dt
= v,
43.45)
где, как и ранее, предполагается, что cx = const.
Решение системы уравнений (13.45) имеет следующий вид
интегральной показательной функции
332
1/2=ехр
^\|^+уехр
Hvx)
2 g
Hvxf
X
■e~^(Ei(x)-Ei(xо))
где
ч
—зя
Ei{x)-Ei{x0) = ^
(13.46)
Разложением в ряд подынтегральной функции (13.46) легко
получить
(* е* 1 , VI хп
\т=|"* + 2^П"
п = 1
(13.47)
В нашем случае можно отбросить члены второго порядка.
Тогда получим
2 g
?кг
-р я
Ei (х) — Ei (х0) = (In л;+х)
е-Р^о
ЦХ)2
= ?(Н0-И) + - -;с ■ -2 Де-Р"- е-Р"»).
Р (X)2
При этом
I/2 ехр
2 g
HV'xf
е-ря
X
X
ННо-Н) +-^(е-Ря_е-РЯо)
(13.48)
Без учета энергии положения формула (13.48) при Н = Н0
и при sin 0=1 дает выражение (13.41). Для случая свободного
падения в пустоте при Уо = 0 и q = 0 формула (13.48) дает из¬
вестную зависимость
V = V‘2
333
Очевидно, что расчет скорости снижения по формуле (13.48)
следует начинать с высоты, где замедление движения от сопро¬
тивления атмосферы становится заметным.
Формулу для осевой перегрузки запишем в следующем виде
J о 20 W 60 80 100 Н,км
где V определяется по фор¬
муле (13.48).
Характер кривых V ~-
= V(H) и пх = пх(Н), опре¬
деляемый формулами
(13.48) и (13.49), показан
на рис. 191. Как видно из
Рис. 191. Влияние сопротивления
атмосферы на скорость V(H) и
перегрузку пх(Н) при вертикаль¬
ном снижении
графика, кривая V=V(H) имеет максимум, что объясняется
влиянием гравитационных сил на всем участке снижения.
Как и в предыдущем случае (см. разд. 13.3), здесь имеет,
место траекторно-параметрическая аналогия с АЛА, осущест¬
вляющего нисходящее движение под действием тяги двигателей
вертикального маневра. При этом только в формуле (13.48) вза¬
мен параметра g будет иметь место ускорение, вызываемое си¬
лой тяги, направленной по вектору скорости АЛА.
13.5. СУБОРБИТАЛЬНОЕ ДВИЖЕНИЕ РАКЕТОПЛАНА
После выхода на орбиту возвращаемой ступени ракетно-кос¬
мической системы многократного применения может возникнуть
ситуация, при которой ракетоплан (возвращаемая ступень) дол¬
жен понизить высоту полета и выйти в режим маршевого движе¬
ния в верхних (сильно разреженных) слоях атмосферы. Такой
режим суборбитального полета может быть вызван необходи¬
мостью проведения длительного научного эксперимента на ма¬
лых высотах (80—130 км) [16], осуществления скоростных ма¬
невров с поворотом вектора скорости (вследствие действия
аэродинамических сил) при поисках в космосе интересуемых
объектов, а также выполнения других маневров, связанных с ра¬
счетом на посадку в заданном районе земной поверхности
(рис. 192).
Рассмотрим случай маршевого полета ракетоплана по круго¬
вой орбите с постоянной скоростью V=const в присутствии подъ¬
емной силы У = const и тяги Р = const, направленной под углом а
334
к линии местного горизонта. Ввиду малого расхода топлива вес
ракетоплана примем постоянным G = const. Полагая также, что
установочный угол крыла равен нулю, а вектор тяги совпадает
с продольной осью ракетоплана, можно записать
р cos а = X, (13.50)
Psina= — Y-\-0 ^1 ”^г) ’ (13.51)
Совместное решение (13.50) и (13.51) дает
P = {(,c_rSf + [0(l , 113.52)
o(H)V2
где q= * - ; скоростной напор на данной высоте полета.
Рис. 192. Виды движений суб-
орбитального ракетоплана
При движении с круговой скоростью V2 = gR в отсутствии
подъемной силы су = 0 формула (13.52) определяет равенство
P = Pi*i> = cxqS9 (13.53)
где Ркр — маршевая тяга при круговой скорости полета.
Рассмотрим далее влияние скорости суборбиталы-юго полета
на величину тяги двигателя при постоянном радиусе траектории
R = const. Для этого разделим (13.52) на (13.53), т. е.
На рис. 193 представлены кривые изменения безразмерной
тяги Р/РЩ1 в зависимости от безразмерной скорости V/VKp для
случая полета ракетоплана на двух высотах при G/S =
= 300 кгс/м2. Как видно из графика, уменьшение скорости мар¬
шевого полета ракетоплана вызывает сильное увеличение по¬
требной тяги двигателя, причем, это увеличение тем больше, чем
больше высота суборбиталы-юго полета. Так уменьшение скоро¬
сти на 5% вызывает увеличение тяги в 10 раз на высоте Н =
= 100 км и в 100 раз на высоте #=130 км.
335
Однако такое увеличение тяги не вызывает больших практи¬
ческих затруднений, поскольку выбором соответствующей вы¬
соты полета маршевая тяга ракетоплана может быть установ¬
лена достаточно малой величины. Действительно, из формулы
(13.53) легко получить
■J = M' ОЗ. 55)
Кривые изменения удельной нагрузки от тяги Р/S в завнси-
мости от высоты полета для случая сх= 1, построенные по фор-
Рис. 193. Изменение маршевой
тяги в зависимости от скорости
для двух высот суборбитально-
го полета
Рис. 194. Изменение удельной
нагрузки на мидель от тяги в
зависимости от высоты полета
муле (13.55), приведены на рис. 194. Как видно из графика, по¬
требные значения тяг на высотах более ста километров весьма
невелики.
Секундный расход топлива Gc (отнесенный к характерной
площади S) на основании зависимости (13.52) будет равен
при движении с околокруговой скоростью и
°с _ дсх
S Рул
при движении с круговой скоростью.
336
V2
gR
(qcy)J (13.561
(13.57':
Если время полного оборота вокруг Земли т равно
т = 2я *3 + Н , (13.58)
^кр
то полный расход топлива одного оборота, приходящийся на
единицу площади S в круговом полете, составит
— = 2я ^3 + Я qc . (13.59)
5 РулУкр 4 х У
Кривые изменения секундного и полного расходов топлива
(отнесенных к площади 5) в зависимости от высоты полета для
различных значений удельных тяг при сх= 1, построенные по
формулам (13.57) и (13.59), приведены на рис. 195 и 196. Гра¬
фики показывают, что выбором высоты полета расходы топлива
Gc/S и GT/S могут быть установлены достаточно малой вели¬
чины. При этом главное влияние на уменьшение расходов ока¬
зывает не удельная тяга, а суборбитальная высота полета. Пос¬
леднее обстоятельство является весьма важным, поскольку
ракетоплан может быть снабжен двигателями малой тяги упро¬
щенной схемы.
Полная дальность полета ракетоплана в режиме круговой
скорости при V= V gR и су = 0 будет равна
Z = IV = Gt—V'kp (13.60)
п0
0\Р:
L=Q, l^L)-rxVKp. (13.61)
ИЛИ
5 Jcxq
Как видно из формулы (13.61), дальность полета ракето¬
плана тем больше, чем больше удельная тяга и меньше величина
скоростного напора q.
Потребное значение весовых отдач в круговом полете при
V = VgR и су = 0 легко подсчитать, решив уравнение (13.61)
относительно параметра GT. Тогда получим
0=—^ . (13.62)
г VKpG/SPy:i
Кривые изменения весовых отдач (рк=1—GT) в зависимости
от высоты полета для различных значений удельных тяг при
L = 40-103 км, построенные по формуле (13.62), представлены
на рис. 197. Как видно из графика, влияние удельной тяги на ве¬
совую отдачу сказывается тем меньше, чем больше высота по¬
лета. Потребные значения весовых отдач не превышают 5—6°/0
по топливу на высоте Я^ПО км и становятся близки к нулю на
высотах Я>140 км. Аналогичные зависимости можно получить
и для режима полета при V < воспользовавшись фор-
337
МУЛОЙ (13.56). Очевидно, что в этом случае на величину расхода
топлива будет влиять, помимо удельной тяги, и величина аэро-
( Су\
динамического качества •
Легко понять, что дальность длительного суборбитального
полета, когда расходом топлива уже нельзя пренебречь и следо-
Рис. 195. Зависимость секундного Рис. 196. Изменение расхода топлива
расхода топлива от высоты полета на единицу площади GT/S за один
оборот в зависимости от высоты по¬
лета
вательно G (t) ф const, будет определяться известной уже нам
зависимостью (9. 19). При этом потребное значение числа LL
определится так
(13.63)
Таким образом суборбитальный полет в присутствии аэро¬
динамического качества уменьшает потребный запас расходуе¬
мого топлива.
Ц = ехр
vPy* (—
338
13.6. ПЕРЕХОДНЫЕ РЕЖИМЫ ДВИЖЕНИЯ РАКЕТОПЛАНА
В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
К переходным режимам движения ракетоплана в вертикаль¬
ной плоскости отнесем крутое выравнивание, восходящий
маневр, нисходящий маневр и горку (рис. 198).
В общем случае уравнения переходных режимов движения
можно решить методами численного интегрирования. Прибли¬
женные решения можно получить при некоторых допущениях,
упрощающих задачу. Будем полагать, что вследствие аэродина¬
мической механизации (тормозные щитки, поворотные несущие
поверхности), а также наличия ракетных двигателей (обеспечи¬
вающих регулирование продольной и поперечной тяги), силы
сопротивления и подъемные силы при выполнении переходных
режимов остаются постоянными. Мы рассмотрим также, в по¬
рядке частных случаев, режимы полета, у которых сила аэро¬
динамического сопротивления полностью компенсируется тягой
ракетного двигателя. Вследствие малого расхода топлива вес
примем постоянной величиной G = const. Действием сил, вызы-
339
ваемых кривизной земли, пренебрегаем вследствие малых траек-
торных расстояний.
Крутое выравнивание представляет по существу глубокий
вираж в вертикальной плоскости, когда ракетоплан из режима,
близкого к пикированию, выходит в горизонтальный полет.
Уравнения движения имеют вид
M — =-X + G sine, (13.64)
dt
MV — = r-Gcos0. (13.65)
dt
Чтобы получить соотношение между скоростью полета V
и углом наклона траектории к горизонту 0, следует разделить
почленно первое уравнение (13.64) на второе (13.65). Тогда
получим
1 dV tix — sin 0
V dd ny — cos 1
(13.66)
где nx и ny — соответственно продольная и поперечная пере¬
грузки.
Интегрирование этого уравнения при пх = const и % = const
в пределах от У0 и 0 до некоторой скорости У и 0 = 0 (горизон¬
тальный полет в конце выравнивания) дает
V Пу — cos 0
Vq tly— 1
(13.67)
где
(13'68)
если п2у )> 1 и
К 1 - ^ tg — + («г/+ 1)
v = —■——== In 1 , (13.69)
У{~П1 Vl-n] tg^- —(Пу+ 1)
если п2 <! 1.
При включенном двигателе пх = 0 и тогда
—= ny-cos& ш (13.70)
V0 пу — 1
Формула (13.70) показывает, что при включенном двигателе
скорость полета в режиме выравнивания непрерывно возрастает.
340
При полном выравнивании (0 = 90°) увеличение скорости при
пх = 0 составит
—=—. (13.71)
Г0 пу — 1
Если пу^> 1 и пхф0, то выражение (13.67) дает
>г ——
L Й).
Наибольшая потеря скорости при выравнивании
будет равна
V
—=ехр
(13.72)
_У_
Vo
= ехр
;i3.73)
v I
vo
1,0
Характер изменения скорости в функции угла 0 вдоль тра¬
ектории выравнивания показан
на рис. 199. График показывает,
что наибольшее снижение скоро¬
сти выравнивания происходит
при/гх^>1 и tiy^ 1, что характери¬
зует полет в отсутствии сил тя¬
готения.
Найдем далее выражение для
высоты А#, теряемой ракетопла¬
ном во время выравнивания. Для
этого запишем уравнение баланса
vf1
У
_ Общ
ий случай пу-2
1^/
Ф=2
20 0-0 60 в, град
Рис. 199. Характер изменения безраз¬
мерной скорости по углу 0 при полете
в режиме кругового выравнивания
энергии в начале и в конце выравнивания. Сумма кинетической
и потенциальной энергий ракетоплана в конце выравнивания
отличается от суммы этих энергий в начале выравнивания на ве¬
личину работы внешних сил на пути, пройденном ракетопла¬
ном, т. е.
MV2 MVq
<ЗШ
Xds,
(13.74)
где ds — элемент пути.
В первом приближении можно считать, что радиус кривизны
траектории постоянен. Тогда путь, пройденный ракетопланом
341
в процессе выравнивания, будет равен s = 0r (где г — радцус
кривизны траектории). Поскольку АН = г(\—cos0), то
0АЯ ,1Q
(13./о)
1 — COS
Ранее мы приняли, что во время переходных режимов имеет
место пх = const и J = const. При этом равенство (13.74) с уче¬
том формулы (13.67) дает
, Пу— COS 6 _ \2
/2 \ 1 — — :— е
1 — COS 0
где параметр v определяется выражениями (13.68) и (13.69).
Длина участка выравнивания будет равна L = rsin0 или,
принимая во внимание, что АЯ = г(1—cos0),
L = lH- sin-— , (13.77!
1 — COS 0
где АН определяется по формуле (13.76).
Время полета в режиме выравнивания при включенном дви¬
гателе найдем, проинтегрировав уравнение (13.65) с учетом,
зависимости (13.70). Тогда получим
/ = ^ . (13.78)
g(ny— 1)
Как следует из формулы (13.78), время полета в режиме
выравнивания при пх = 0 существенно зависит от поперечной
перегрузки пу.
Траектория восходящего маневра представляет собой как бы
отраженный вид траектории выравнивания. Такой вид маневра
может применить спасаемая ступень в аварийной ситуации, на¬
ходясь в точке апогея эллиптической траектории.
Уравнения движения имеют.вид
M — =-X~Gsme, (13.79)
dt
MV —=K-Gcos9. (13.80)
dt
Поступая, как и ранее, легко получить
V пу — \
V(J Пу — COS 0
где параметр v определяется выражением (13.68) и (13.69).
(13.81)
3 V2
При v = 0, т. е. когда тяга равна силе лобового сопротивления
(пх = 0), формула (13.81) дает
V пу— 1
К0 Пу-
(13. 82)
Таким образом по мере движения в режиме восходящего ма¬
невра скорость ракетоплана непрерывно уменьшается, несмотря
на действие тяги работающего двигателя, полностью компенси¬
рующего силу лобового сопротивления.
Если tiy1, то формула (13.81) дает известную уже нам за¬
висимость (13.72). Следовательно, уменьшение скорости при
больших перегрузках в режиме выравнивания и восходящего
маневра примерно одинаково.
Кривые 1/ = V(0) представлены на рис. 200. Как видно из
графика, на восходящем маневре происходит понижение скоро¬
сти во всех случаях, включая полет ракетоплана при работаю¬
щем двигателе. Заметим, что кривая, построенная по формуле
(13.81), занимает там наиболее низкое положение. Это свиде¬
тельствует о дополнительных потерях кинетической энергии на
преодоление гравитационных сил.
На выводе зависимостей для времени, высоты и дальности
полета мы останавливаться не будем. Их легко получить, повто¬
рив выкладки, аналогичные режиму крутого выравнивания.
Нисходящим режимом движения мы назвали такой вид ви¬
ража в вертикальной плоскости, при котором поворот вектора
скорости и понижение высоты полета происходит при отрица¬
тельных углах атаки или положении ракетоплана «вверх коле¬
сами». Такой маневр возможен при отделении спасаемой ступени
космической системы многоразового применения с последующим
разворотом ее в сторону старта.
Уравнения движения имеют следующий вид
М— =-.Y + Gsin 6, (13.83)
dt
MV — = — Y — G cos 0. (13.84)
dt
Решение этой системы дает
V Пу ч~ 1
и затем при пх = 0
Vq Пу + COS 0
V Пу + 1
К) пУ
(13.85)
(13.86)
Как и в предыдущих режимах, при нисходящем маневре по¬
тери в скорости при пу^> 1 и пхФ0 определяются зависимостью
(13.72). Кривые т/= 1/(0) показаны на рис. 201. Как следует из
343
графика, качественная картина изменения скорости в режиме
нисходящего маневра близка к режиму выравнивания.
Горкой называют маневр ракетоплана в вертикальной плоско¬
сти с целью набора высоты. В нашем случае горка является как
бы отраженным видом траектории нисходящего маневра, выпол¬
няемого также при положении пилота «вниз головой». Горка
может быть выполнена спасаемой
ступенью ракетной системы мно¬
гократного применения с целью
выхода из режима полета в конце
ветви баллистической траекто¬
рии.
Ф
о
ф
0,5
■<*
v_
^уЛ9
- 1
%0
0,5
'>/
/
случай
4
1 II
■=2
Ф=2
Lx
V*
V
20
40
60 в, град
20
40
60 в7 град
Рис. 200. Характер изменения безраз¬
мерной скорости по углу 0 при поле¬
те в режиме восходящего маневра
Рис. 201. Характер изменения безраз¬
мерной скорости по углу 0 при поле
те в режиме нисходящего маневра
Уравнения движения ракетоплана при выполнении горки
записываются в следующем виде
dV
М
dt
db
— X — G sin
M — —-Y — G cos (
dt
При этом легко получить
V Пу 4- cos 0
Гп
и далее при пх = 0
V_
Vn
пу 4- 1
пу 4- cos
Пу -Г 1
(13.87)
(13.88)
(13.89)
(13.90)
344
При tiy ^>1 и пхФ0, как и ранее, имеет место зависимость
(13.72).
Таким образом потеря скорости при больших поперечных
перегрузках во всех переходных видах движения примерно оди¬
накова, что является следствием исключения влияния сил грави¬
тации на параметры движения.
Рис. 202. Характер изменения безраз- Рис. 203. Влияние аэродинамического
мерной скорости по углу 0 при поле- качества на изменение безразмерной
те в режиме горки скорости при полете в режиме горки
Характер кривых V=V(Q) показан на рис. 202. Как видно
из графика, характер этих кривых близок к режиму восходя¬
щего маневра. Это имеет место потому, что в обоих случаях рас¬
ходуется энергия на преодоление сил тяготения, в то время как
на нисходящем маневре и выравнивании силы тяжести замед¬
ляют падение скорости.
Влияние аэродинамического качества на изменение скорости
показано на рис. 203. Из графика хорошо видно, что увеличение
аэродинамического качества уменьшает потери в скорости на
переходных режимах движения ракетоплана.
13.7. ПОТЕРИ СКОРОСТИ ПРИ ВИРАЖЕ
В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
Рассмотрим движение ракетоплана в режиме разворота при
неработающем двигателе и G = const. В процессе выполнения
разворота понижаются скорость и высота полета. Таким обра¬
зом вираж ракетоплана с выключенным двигателем происходит
по траектории, напоминающей движение по спирали, наклон вит¬
ков которой меняется в соответствии е изменением скорости ви¬
ража. При оценке изменения скорости пренебрежем изменением
высоты полета.
345
Проектируя силы, действующие на ракетоплан при вираже,
на оси координат (рис. 204), будем иметь
м—=-х,
dt
Y cos y = G,
„ . MV2
Y sin у — ,
(13.91)
(13.92)
(13.93)
где r — радиус кривизны траектории.
Выражение для радиуса виража
можно получить, если
в уравнение (13.93) подста¬
вить выражение подъемной
силы, взятое из равенства
(13.92). Тогда получим г =
= V2/'g tg у. Или поскольку
tgY = V я„2—1, то
V2
Рис. 204. К выводу уравнений движе¬
ния ракетоплана на вираже в горизон¬
тальной плоскости
г
(13.94)
Запишем далее уравнение
баланса энергии в начале и я
конце виража, исходя из того, что сумма кинетической и потен¬
циальной энергий ракетоплана в конце выхода из разворота отли¬
чается от суммы кинетической и потенциальной энергий в начале
входа на величину работы внешних сил на пути, пройденном
ракетопланом, т. е.
.Vi
V2
13.95)
где Vo и V — скорость в начале и в конце разворота соответст¬
венно; X — сила лобового сопротивления; ds — элемент пути,
проходимый ракетопланом во время разворота.
Принимая приближенно j* Xds = Xyr (где ср — угол
$
виража в горизонтальной плоскости), получим
М — = УИ — Х'й 1/2 < 13. 96)
2 2 Д/4-1
зю
откуда
Если riy^ 1, то
V_
г0
V
Vo
i +
2гсд-
-1/2
1 + -
2cr л
(?)
-1/2
(13.97)
(13.98)
График уменьшения скорости по углу разворота, построен¬
ный по формуле (13.98), пред¬
ставлен на рис. 205. (¥-)
Уравнения (13.91) и 0
(13.92) npHX = const дают сле¬
дующее выражение для вре- W
мени выполнения виража
t =■¥*-( 1 - —) , (13.99) 0,6
gnx \ Г0 /
где величина V/Vq определяет-
ся по выражению (13.97).
Рис. 205. Потеря безразмерной скоро¬
сти на вираже в зависимости от угла
разворота ф
160 (р
Пример 13.1. В соответствии с формулой (13.41) безразмерная скорость
вертикального входа в плотные слои атмосферы при sin 0=1 определится как
V
V,
= ехр
р та2
(е-Р" - е-
(Э/М
Показать справедливость этой формулы, исходя из равенства кинетиче¬
ской энергии работе внешних сил. Энергией положения пренебречь.
Решение. Изменение кинетической энергии тела, движущегося в сопро¬
тивляющийся среде, равно работе внешних сил на рассматриваемом участке
снижения ДЯ. Переходя к пределу, запишем
d3 = XdH,
(13.100)
\/2
где Э = Л1 -
Поскольку
X = G
V \2
т)'
-ря
d3 = MVdV,
то равенство (13. 100) перепишется так
dV g — ря
V ~
(ПТ
dH.
347
Интегрирование полученного выражения при условии, что начальная вы¬
сота и скорость входа равны Н = Н0 и V = V0, дает заданную формулу (13.446).
Пример 13.2. Определить допустимую скорость входа пилотируемого
ракетоплана в плотные слои атмосферы при условии, что максимальная осе¬
вая перегрузка не должна превышать величины пх mах = 11 - Скорость входа
рассчитать для углов входа от 0=0 до 0 = 90°.
Рис. 206. Допустимые скорости в за¬
висимости от угла входа пилотируемо¬
го ракетоплана (РНМП) в плотные
слои атмосферы при птах=П
О 20 40 60 80' в} град
Решение. При входе в плотные слои атмосферы осевая перегрузка может
быть подсчитана по формуле (13. 44г)
i^L sin 9
2^е
• — 2,63V: sin 0,
где Vo—Vbx-
Разрешая это выражение относительно интересуемой нас допустимой
скорости входа Vbx, найдем
V*
Поскольку ПО условию задачи Лжтах=П, ТО
V*
Расчеты по формуле (13. 101) сводим в таблицу
/пх max
2,63 sin 0 ’
ЧИ Пх тах= И, ТО
= 2,05 \/ —
V sin
(13. 101)
0, град
90
80
70
60
50
40
30
20
10
0
sin 0
\/ sin 0
1
0,98
0,94
0,87
0,77
0,64
0,5
0,34
0,174
0
1
1,01
1,03
1,07
1,14
1,25
1,41
1,71
2,4
оо
VBX, KM/C
2,05
2,07
2,12
2,2
2,34
2,57
2,9
3,5
4,9
сю
348
Из таблицы видно, что допустимые скорости входа при постоянной пере¬
грузке тем больше, чем меньше углы входа 0. Данные таблицы хорошо также
иллюстрируются графиком (рис. '206).
СПИСОК1 ЛИТЕРАТУРЫ
1. Авдуевский В. С. и др. Основы теплопередачи в авиационной и ра¬
кетной технике. М., Оборонгиз, 1960, 389 с.
2. Динамика полета. Под ред. д-ра техн. наук, проф. А. М. Мхитаряна,
М., «Машиностроение», 1971, 368 с.
3. Зенгер Е. иБредтИ. Дальний бомбардировщик с ракетным дви¬
гателем. Под ред. ген.-майора инж.-авиац. службы В. Ф. Болховитинова. М.,
Воениздат, 1946, 248 с.
4. К и н г-Х или Д. Теория орбит искусственных спутников в атмосфере.
М., «Мир», 1966, 189 с.
5. Лох У. Динамика и термодинамика спуска в атмосферах планет. М.,
«Мир», 1966, 276 с.
6. Механика космического полета. Под ред. д-ра физ.-мат. наук, проф.
В. В. Добронравова. [Сборник статей]. М., «Машиностроение», 1969, 288 с.
7. Миеле А. Механика полета. М., «Наука», 1965, 407с.
8. Остославский И. В. Аэродинамика самолета. М., Оборонгиз, 1957.
560 с.
9. О с т о с л а в с к и й И. В., С т р а ж е в а И. В. Динамика полета. М.,
«Машиностроение», 1969, 499 с.
10. Петерсен Н. В. Продолжительность полета спутников по почти
круговым и эллиптическим орбитам. — «Вопросы РТ», 1957, № 1, с. 3—27.
11. Погорелов Д. А. Теория кеплеровых движений летательных аппа¬
ратов. М., Физматгиз, 1961, 107 с.
12. Тихо нравов М. К- и др. Основы теории полета и элементы проек¬
тирования искусственных спутников Земли. М., «Машиностроение», 1967, 295 с.
13. Чепмен Д. Р. Приближенный аналитический метод исследования
входа в атмосферы планет. Под ред. канд. техн. наук Э. Э. Шпильрайна. М.,
ИЛ, 1962, 114 с.
14. Шкадов Л. М. и др. Механика оптимального пространственного
движения летательных аппаратов в атмосфере. М., «Машиностроение», 1972.
240 с.
15. Е g g е г s A. J., Jr., Allen Н. J. and N е i с е S. Е. A Comparative
Analysis of the Performance of Long-Range Hypervelocity Vehicles. NASA,
TN 4046, 1957, 20 p.
16. Ehricke K. A. The Satelloid. Astronautica Acta, 1956, vol. 11, No. 2,
52, p.
17. Turnacliffand R. D., Hazthett J. P. Generalized Trajectories
for Free Falling Bodies of High Drag, Jet Propulsion, 1958, No. 4, p. 263—266.
Приложение \
Функциональный характер основных параметров
для двух законов изменения массы
Наименование параметров
Закон
линейный
показательный
Число .Циолковского
Ц 1 — GT =
1
Рк
Коэффициент расхода
?(GC, G)
—— = const
G0
Gc (0
_ — const
G(t)
?(ло. / у .)
—— = const
Py,
= const
/>ул
Весовая отдача
а) Gr (ij.k)
б) <*к (GT)
1 — 1% 1 _
1 — Gj = 1
Текущее значение весовой отдачи
a) GT(p, t)
GT — $t
Gr —
б) |*к(Э, t)
рк +
рк + e
Весовая отдача в конце полета
а) От(?т)
0
0
б) (?т)
1
1
Реактивное ускорение, м/с2
Ф const
1 —?t
w
а) текущее a (t)
б) начальное £(/=0)
• pur = const
в) конечное a (jjlk)
Рк
Удельная тяга, с
а) Яуд(Р, Gc)
Рул ~
P
Gc
б) рУ,т
Py д =
W
go
Секундный расход топлива, кг/с
o
p(t)
ф const
Py,
a) Gc (Р, Руд)
г
= const
Pyx
б) уИс (р, М)
(Ш0 = const
$M (t) = const
350
/7родолжение прилож. 1
Наименование параметров
Закон
линейный
показательный
Полное время активного полета, с
а) т(&г, п0, Руд)
б) т(От, (3)
GT
Щ
От
р
In Ц
Л[)£о
т1п ц
в) r(GT) Gc)
Or
Gc
—
Приближенная зависимость для конеч¬
ной скорости ракеты при оптимальной
траектории выведения
VK AV
1Г-1пЦ-1V'
где
АУ=1200 м/с (гра¬
витационные поте¬
ри 900 м/с; AVx =
—300 м/с)
Перегрузка — текущая п (t)
а) стартовая п^(=0^ = п0
б) конечная = ~ «шах
n(f)~ "°
w 1 — ^
Ро/О0
п(т\- Л°
1 P(t)/G(0=
= P(J G0=const
1 — ог
Произведение рт
Or
GT
Величина (1 — рт)
у-к
;лк
Коэффициент грузоподъемности е
VGo
AE/a0
Скорость истечения W, м/с
щ
iToy
/70
"°y
Удельная тяга Рул, с
|о
Л±
э
Приложение 2
СВОДКА ПАРАМЕТРИЧЕСКИХ ЗАВИСИМОСТЕЙ ПО ТОПЛИВНЫМ
БАКАМ РАЗЛИЧНЫХ СХЕМ ПРИ £а=£об=£Д11=1
Первая колонка содержит формулы для баков, у которых
обечайка и днища выполнены в виде эллипсоидов вращения;
вторая колонка — для баков, у которых обечайки представляют
собой усеченные конусы, а днища — шаровые сегменты.
351
А. Топливные баки с двумя выпуклыми днищами
1. Обозначения
‘Диаметр бака D6
Л./\
4 I 06 3kl
Ф
_4 + i
3nk\
1/3
jt I 1 ( 3n2 + 1
3 ki
\2rfikl
1/3
:ф А^1/гф
Удлинение конической обечайки %0ь = Х0в(^б, я)
^Ф +1
2/2 к,
:Ф
^Ф + 1
2nk.
’Ф
Удлинение цилиндрической обечайки
Лоб = Х0б (Хб, fl)
к-—
п
Л< —■
14
Параметр Пдн (я)
In (/2 + -/"л2 + 1)
/2 у'п2 — 1 )
Отношение радиуса днища к радиусу обечайки
*ii*)
/2 2 1
2/2
Параметр П0б
1+1^'
V 2Хоб/?ф /
1/2
1+
\2Хоб£ф/
1/2
'Ink*,
Высота днища
Об
о6
2nk
;Ф
(При Зэк1! = Зкр)
Удлинение конической обечайки А,0б = А,0б(Уб, 2?б)
Ж
2^+1
4 + 1
Jt о
Т 6
3 пкь
3*ф
*ф+V
Щ
3/22+1
12/23А?
352
Удлинение цилиндрической обечайки
^Об = ^Об (^б> Dб)
Di
3/2
3/22
ГА
12/23
2. Поверхности
Обечайка коническая
яDV4+l
2k*
^Об “f
I \
\ 2nk*
1/2
ИЛИ
2k,
ф
\>б
14-л2 п
при допущении у—- - ) ^О
Чб
*Ф-1
2k*
11/2
или
при допущении
*ф—1
2А*
Обечайка цилиндрическая
nDle^-o
я220б/.об
— dS
^ _l_ In (п + У^Я2 + 1)
n]/^2Zri
Днище
Ф
4 ^6 n2k{
п2 -г 1
Ф
3. Объемы
Обечайка коническая
я Г)3Х 12кФ + 1
«к»
ЗАф
Обечайка цилиндрическая
ти‘(х«-т)
Д н и щ е
я ,>.3 3/22 -I- 1
г>ь-
48 ~ n^k*
353
. /2*ф + 1 \ , kl+l
'o6\ 3$ r Znkl
Бак конический
з
x
/ i- 1 \
\ 3^ Г I2n% ~
Бак цилиндрический
■JL/jsA J_ + 3n2-M_
4 \ n 6 ri&
P%Pб у 2
M *ф4
PsD6
2[o]
p2 D6«
4 [®] /гф
(при 0ЭКВ = 5К]
кр/
4. Толщина стенок
Обечайка
Днище
РцР б
2 И
Р^бп
4 [а] *ф
5. Напряжения
Экваториальное критическое в днище
2£ 5 q ^ 2£ о
£б /3(1-Р2)'~ ’ ~~D^ ~
Экваториальное в стыке с обечайкой
Ръ® б //22-}-1'
2 — п2) '
45 V
Меридиональное в полюсе
6/2
P'sPб /л2 -f- 1
354
6. Давление в баке
X
— *фМОХ
V6
j +1 f йф + 1
об 7^2
Наддув при стэкв = О
Л
3fe
•ф
ЗлЛф
X
— (О X
V6
4 + 6ф + 1 , ЗП'2 + 1
3 ki
' 12«34
Гидростатическое (в нижнем сечении обечайки)
('■б-—)(0
Гидростатическое (в полюсе днища)
\6y,nx{t)D6 | K6\,nx(t)D6
Критическое для днища.
I 5 \2
(2 —л2)/3(1 —(J.2)
т »*(■£)
7. Вес элементов конструкции в функции
внутреннего давления и диаметра бака
^эл = ^эл(Рз» -^б)
Обечайка коническая
&ф -г 1
[о] ) 06 V 2*ф 1 Пнб
п - П? / Ym ) 1 / /гФ “г 1 1 J-J
— ръ1Л — Кб V
2 U«] ) V 2*ф
об
Обечайка цилиндрическая
f I
Днище (верхнее или нижнее)
_Л_ ( Ум \ '
16 I [о] > 4
пПдн (/г) /7s £>б
я / Ум
16 I [а]
355
Два днища цилиндрического бака
f (^)*п>),.ог j
Бак конический
х
кф Hr 1
X
4 + 1
'■об —— Поб+ 3 ■ иПдн(/г)
*Ф 4*ф
Л п /)3 / Ум
т',,£Ч"м
X
X
х *ф + 1п i”2 + 1f^ + 1)
Х°6 *ф П»б+ 4п
Бак цилиндрический
X
Я „ А')3 / Ум
2 6 ( [а]
1 ■ /I2 +
п 2/7
8. Вес обечайки при ризo=const
Коническая (u6 = const)
/гф -г 1 ^
/ Ум \
\ [о] / 2бф+1 йф + 1
Лоб Q, 2 "Г "5 ПГ
З^ф 3/7&ф
^■об
з ~ 7 ^бЯизб
&ф + 1
£ф
об
Ум \
[°] / £ф+#ф+1 3/72+1
Х°б +ПпЧ1
^бРиЗб
Цилиндрическая (^6 = const)
2 (—)
\М /
х«--
^бРизб
3/7
2(й-)
ХЛ--
/7
1 _ 3/72 + 1
^б — + ю о
/7 12/73
‘У б Р изб
356
Коническая (а0б = const)
(—)
V [о] I
\ кф + 1
кф
^обЯизб
Ум А +■1
7Y —— ^обЯизб
М /
Цилиндрическая (y06 = const)
21 "Й"1 ®об/7няб
2 ( I «„бАов
9. Вес обечайки при рги;;р^сопз*
Коническая (i>6 = const)
10. Вес обечайки при рИзo^const
Коническая (vq = const)
358
Два днища конического бака (и^ = const)
359
Два днища конического бака (х;б = const)
360
S/Л 1+F5
13
3479
361
Одно днище (верхнее или н и ж н е е, v0q = const)
362
14. Вес изолированной обечайки в функции
различных параметров (u06=const)
Коническая
О06 {pv Doo)
Цилиндрическая
Ооб ^об)
Коническая
G,)6(As, Do6)
Цилиндрическая
^об(^а’ ^об)
Коническая
Ооб (/^ГИДР’ ^об)
Цилиндрическая
Соб (/^ГИДР’ -^об)
Коническая
С0б(^0б, Ps)
Цилиндрическая
Go6(vоб, /?а)
" 1 УЛ psD^lJ-^П^
[«]
2*ф
(“■) дЛ.(0>-,ЛМ*Ф+ 1)Поб
«АЛ
об об1Аоб
2 \М
-i- 1 —
об
2£ф
П
об
Б. Топливные баки, выполненные в виде дископланов
1. Объем и(/)д)
б п
Jt 3/2 ^
24 Л
/23
2. Поверхность П(/г, £д)
, П2
■ГС
2 Д /22
3. Радиус сферы г(/)д, п)
П2 + 1
D.
4/2
4. Толщина стенки 6(/?а, £д)
PyPx
4 [а]
3 / /У \ /22 + 1
6 [о] / /2
13*
363
5. Вес в функции диаметра £д(Од)
6. Вес в функции объема (7д(ул)
где Дд — диаметр диско-плана; h — половинная высота дископла¬
на; n^D^I2h — параметр выпуклости днищ; иЛ — объем диско¬
плана.
В. Топливные баки, выполненные в виде дископланов
(случай наивыгоднейшего соотношения h/D}l=y 2/4)
1. Толщина оболочки 6(ps, /)д)
Примечание. Соотношение /г/£)д = у"2/4 обусловливает предотвраще¬
ние потери устойчивости оболочки от внутреннего давления.
Приложение 3
ОПТИМАЛЬНАЯ СКОРОСТЬ СНИЖЕНИЯ ГРУЗА НА ПАРАШЮТНО¬
РЕАКТИВНОЙ СИСТЕМЕ
Под парашютно-реактивной системой будем понимать систе¬
му, состоящую из парашюта и ракетных двигателей. Парашют
предназначен для уменьшения скорости снижения груза; реак¬
тивные двигатели обеспечивают приземление груза с минималь¬
ной (теоретически нулевой) вертикальной скоростью. В зависи¬
мости от веса спускаемого груза (космический корабль, ступень
ракеты и т. д.) парашют может быть одноступенчатым (одноку¬
польным) или составным (многокупольным). Реактивное устрой¬
ство может быть 'выполнено в виде отдельного агрегата, состоя¬
щего из тормозных пороховых двигателей, либо на базе уже име¬
ющихся маршевых двигателей спускаемого аппарата (например
ракетный ускоритель с ЖРД), тормозной импульс которых со¬
здается благодаря расходу бортового запаса топлива.
На рис. 207 приведены безразмерные веса систем спасения
в зависимости от обеспечиваемой ими скорости снижения, по¬
строенные на основании расчетов этих систем применительно к
американской ракете «Космос» (проект).
/2 Од
, ^ тт
2. Вес бд(/?21> уд)
Из графика хорошо видно, что парашютная и реактивные си¬
стемы имеют явно противоположный характер изменения веса по
параметру скорости снижения Уси. Это означает, что суммарный
вес парашютно-реактивной системы имеет экстремальное значе¬
ние по скорости снижения.
Для определения этого экстремума составим весовое уравне¬
ние следующего вида
= + Gn.y "Г Д°гр + ДОд + Оцар + Ор.у,
где Gs— полный вес снижающейся системы «груз—
реактивное устройство»;
As — вес спасаемого груза
(отработавшая ступень раке¬
ты и т. д.); Gn.y — вес поса¬
дочных устройств (шасси,
опорные пяты, амортизация
и т. д.); AGrp — добавочный
вес (оборудование, система
стабилизации и т. д.);АОл—
утяжеление спасаемого гру¬
за в связи с возможными
(и
Рис. 207. Оптимальные весовые ха¬
рактеристики парашютов и тор¬
мозных реактивных устройств:.
/—суммарный все: 2—реактивное уст¬
ройство; 3—парашют
60 V , М/С
его доработками (усиление конструкции и т. д.); Gnap — вес па¬
рашютной системы; Gp.y — вес тормозной реактивной установки.
Вес парашютной системы выразим зависимостью следующего
вида
^пар Ynap^M ~Г ^^нар» (^)
где
п
Yuap oci (^)
/= 1
п — количество парашютов (вытяжной, тормозной, стабилизи¬
рующий и т. д.); \i — удельный весовой измеритель для i-го па¬
рашюта; \*г — статистический коэффициент для уточнения габа¬
ритов /-го парашюта; voc — удельный весовой измеритель для
основного парашюта; AGnap — добавочный вес, связанный с уточ¬
нением параметров малой парашютной системы.
365
Поскольку при вертикальном снижении на парашюте имеет
место равенство
I/2
G* = cxQSM-f-,
ТО
о 2Gs
(4)
Подстановка выражения (4) в формулу (2) дает
V
сн
где
Л 2уиар
а* =
<Л,ар = а* -%+ДОйар. (5)
Полагая, что во время реактивного торможения масса систе¬
мы практически не меняется, запишем весовую отдачу по топли¬
ву для реактивного устройства в виде
При этом вес топлива составит
QT = G* -jJL'- . (7)
По
Если выразить вес конструкции тормозной реактивной уста¬
новки (ее сухой вес без топлива) как
GkoiI = PGT
(где (3— удельный измеритель), то вес реактивной установки
запишется так
Gp. у= GT + pGT
или на основании выражения (7)
Gp.y = G.r(l -j-p) = $vGsV, (8)
где
о* l + ft
W
366
(-i)
Далее имеет место
0„.jr = Y,f. yOs,
ДОд = У;(Л£,
(9)
где угг. у и уд — весовые удельные измерители.
После подстановки выражений (5), (8) и (9) в уравнение (1)
и разрешения относительного параметра Gs получим
Легко видеть, что общий вес системы имеет экстремум по ско¬
рости снижения Усп. Для отыскания этого экстремума прирав¬
няем нулю производную dGs /dVcu.
Тогда после решения относительно параметра Vcu и преоб¬
разований получим
где W — скорость истечения активной массы реактивного устрой¬
ства; п0 — перегрузка, создаваемая реактивным устройством при
торможении.
Если принять упар = 0,35 кге/м2; (3 = 0,11; п0 = 5; q —
= 0,125 кгс-с2/м4; с* = 0,75 и 1V=2500 м/с, то скорость сниже¬
ния получится равной
Так как проблемы раскрытия парашютов, скорости сноса и
колебаний спасаемой ступени упрощаются при меньшем числе
парашютов, обычно выбирается скорость снижения в пределах
от 30 до 38 м/с, которая обеспечивается группой из трех (и не
более пяти) парашютов.
УСЛОВИЯ ВОЗВРАЩЕНИЯ РАКЕТОПЛАНА К МЕСТУ СТАРТА
ПРИ МАЛЫХ СКОРОСТЯХ ПОЛЕТА
Рассмотрим условия возвращения ракетоплана к месту стар¬
та после выполнения им баллистического полета и разворота в
вертикальной и горизонтальной плоскостях на 180°. Схема тако¬
го полета применительно к возвращаемой ступени ракеты-носи¬
теля приведена на рис. 208.
1 — Yu. у — Э^сн
(10)
сн
(И)
1/3
4.0,35-2500 ^1 ——
= 30 м/с.
L 0,75-0,125(1 4- 0,11)
Приложение 4
3 67
При малой конечной скорости Vu баллистическая дальность
полета тела, брошенного под углом 0К к горизонту, определяет¬
ся по формуле
= 20,,.
Формулу (12) легко преобразовать
L6a* = 2/?3 Sin 26к,
(12)
(13)
Рис. ,208. Характеристика режимов
возвращения ракетоплана к месту
старта
/—дальность планирующего полета
(после разворота в двух плоскостях);
2—баллистическая дальность; .'/—даль¬
ность при внутреннем выравнивании
где 1/1ф — круговая скорость (в центральном поле гравитацион¬
ных сил); Rз — радиус Земли.
Известно также, что дальность планирования (без учета цен¬
тробежных сил) выражается зависимостью *
(-)
(14)
где ^ — J — аэродинамическое качество; VnjI = Vo — скорость на¬
чала планирования.
Уменьшение скорости после эволюций в вертикальной и гори¬
зонтальной плоскостях (при развороте на 180°) учтем коэффи¬
циентом равным отношению скоростей
(15)
vK
* Ее можно получить разложением в ряд логарифмического множителя в
формуле (9.41).
368
С учетом этого коэффициента формулу (14) можно перепи*
сать
(16)
Очевидно, что формула (16) содержит допущение равенства
скоростей на концах баллистической ветви траектории.
Поскольку по условию задачи дальность планирования долж¬
на быть равной баллистической дальности (дальностью полета
на активном участке пренебрегаем), то, приравняв правые части
выражений (13) и (16), получим
Формула (17) выражает зависимость потребного аэродина¬
мического качества от параметров £ и 0К, при которых обеспе¬
чивается возвращение планирующего ракетоплана к месту
старта.
При оптимальном угле бросания, равном в нашем случае
6К = 45°, потребное аэродинамическое качество, составит макси¬
мальную величину, определяемую выражением
Если скорости и дальности полета достаточно велики, реше¬
ние аналогичной задачи следует искать, пользуясь выражениями
для дальности квазистационарного планирования.
Расчет условий возвращения ракетоплана к месту старта
удобно проследить на примерах.
Пример 1. Определить диапазоны углов тангажа, при которых не обес¬
печивается возвращение ракетоплана к месту старта. Расчет произвести для
значений аэродинамического качества 4, 5 и б при Ек=2500 м/с. После разво¬
рота в вертикальной плоскости (выхода из пикирования 0 = 0ц) ракетоплан
осуществляет разворот на 0=180° в горизонтальной плоскости для возвраще¬
ния к месту старта. Припять /гу> 1.
(17)
(18)
для баллистической дальности и
369
Решение. По формуле (13) строим кривую баллистической дальности
£бал(0к) при FK = 2500 M/c = const.
0, град
0
15
30
45
60
75
90
£бал, км
0
320
554
640
554
320
0
Потери в скорости при выходе из пикирования и развороте на 180° най¬
дем по формулам (см. разд. 13.6 и 13.7)
V
5В= ~— = е \сх)—в вертикальной плоскости,
g V
1 +
2ср
Су_\
Сг /
-1/2
— в горизонтальной плоскости.
Расчет по этим формулам сведем в таблицу, обозначив
£—г — суммарные потери в вертикальной и горизонтальной плоскостях.
Траектория
О,
град
15
30
45
60
75
90
180
* „
В вертикальной
плоскости
0,935
0,8780,82 0,77
0,95
0,905
1 0,955 0,91
0,72
0,677
0,86
0,81
0,£
0,84
0,77
0,73
0,8 0,77
В горизонтальной
плоскости
0,39
0,444
0,49 6
В вертикальной и
горизонтальной
плоскостях
62
1 0,341
0,301
0,262 0,232
0,401
0,368
0,448
0,407
0,329
0,203
0,179
0,29
0,264
0,237
0,38
0,345
0,314
0,29
370
Дальность планирующего полета (к месту старта) подсчитаем по фор¬
муле (14)
0, град
0
15
30
45
60
75
90
(t)
1280
436
385
335
297
260
229
4
£нл» км
1600
642
590
526
467
423
380
5
1920
860
780
730
662
602
557
6
Данные расчетов нанесены на график (см. рис. 208). Из графика видно,
что возвращение ракетоплана к месту старта не представляется возможным
при
0= (21—78°) если =4
И
0=(33—68°) если =5.
При — =6 ракетоплан возвращается к месту старта на всех
\ сх ;
углах 0к = 0.
При внутреннем выравнивании мы имели бы пунктирные кривые (на гра¬
фике), построенные по формуле (13.72).
При этом потребное значение аэродинамического качества для возвра¬
щения ракетоплана к месту старта (по сравнению с предыдущим случаем)
может быть несколько меньшим.
Приложение 5
СРАВНИТЕЛЬНЫЙ АНАЛИЗ БАЛЛИСТИЧЕСКИХ И КРЫЛАТЫХ
РАКЕТ-НОСИТЕЛЕЙ МНОГОКРАТНОГО ПРИМЕНЕНИЯ
Ракеты-носители с очень большой полезной нагрузкой (по¬
рядка нескольких тысяч тонн) имеют такой большой возвра¬
щаемый (конечный) вес, что единственным практически возмож¬
ным способом их возвращения представляется баллистический с
вертикальной посадкой, а не способ с использованием большого
371
аэродинамического качества и горизонтальной посадкой. Недав¬
ние исследования * показали, однако, что возвращаемые ракеты -
носители с вертикальным взлетом и вертикальной посадкой
VTOLV с низкой маневренностью (гиперзвуковое аэродинами¬
ческое качество су/сх = 0,5) могут вполне конкурировать с кры¬
латыми аппаратами или аппаратами с несущим корпусом и в
области малых полезных нагрузок.
Сравнительный анализ выполнен по стоимости, эксплуатаци¬
онным данным, весовым параметрам и основным характеристи¬
кам трех вариантов летательных аппаратов многоразового дей¬
ствия, схемы которых приведены на стр. 374.
Приведенные материалы исследований позволяют сделать
следующее заключение.
Крылатые системы многократного применения могут наилуч¬
шим образом решить, проблемы входа, благодаря их высокой
маневренности, возможности управления перегрузкой, увеличе¬
ния дальности полета в атмосфере и осуществления обычной го¬
ризонтальной посадки в заданном районе. Однако чрезмерное
увеличение веса конструкции, связанное с наличием крыльев, де¬
лает невозможным вывод на орбиту полезной нагрузки только
одной ступенью даже при использовании наиболее эффективных
жидких топлив, известных в настоящее время. Результаты мно¬
гочисленных исследований NASA и ВВС США показывают, что
для этого требуются по крайней мере две (часто три) ступени.
Хотя внешне крылатая двухступенчатая система больше напо¬
минает современный самолет, чем одноступенчатый баллистиче¬
ский аппарат, режим его подъема совершенно не похож на само¬
летный. Более того, разделение соединенных крыльев (поверхно¬
стей) при параллельном расположении ступеней в условиях
больших скоростных напоров, которые могут иметь место при
аварийном прекращении полета, представляет собой не решен¬
ную с точки зрения безопасности проблему.
К этому следует добавить проблему статической устойчиво¬
сти, связанную с задним расположением реактивного двигателя;
центр масс пустого аппарата оказывается позади центра давле¬
ния.
С другой стороны, решение проблемы входа КК «Джемини» и
«Аполлон» и накопленный опыт могут быть успешно использо¬
ваны при проектировании одноступенчатых возвращаемых ап¬
паратов (пилотируемых или непилотируемых) баллистического
типа. Небольшое аэродинамическое качество таких аппаратов
Senator F. Е. «Reuse Concepts Technology Test Vehicles». Dougles
Report No. DAC-56423, November 14, 1966.
Gordon T. J., Bono P. and Senator F. E. «Navigation and Guidance
System Requirements for a Conceptual Single-Stage-to-Orbit Rensable Launch
System». Douglas Report No. DAC-56496, November, 1966.
372
(порядка 0,5) может быть обеспечено путем смещения центра
тяжести относительно оси симметрии. Исследования показали,
что располагаемое аэродинамическое качество су/сх = 0,42 и уп¬
равление креном дают возможность уменьшить максимальную
перегрузку до 2,5, так что возможные пассажиры будут испыты¬
вать перегрузку, превышающую двухкратную, не более 1,5 мин.
су/схж 0,5 обеспечит маневренность аппарата ~ 1480 км по про¬
дольной дальности и порядка 222 км по боковой дальности, что
более чем достаточно для компенсации прогнозируемого разбро¬
са точек посадки, представление о котором дает возвращение
чисто баллистического аппарата типа «Меркурий» после 24 ча¬
сов полета по орбите ожидания. Кроме того, точность приземле¬
ния может быть еще более увеличена благодаря управлению на
конечном участке и ручному управлению на режиме висения. По¬
садка может совершаться на неподготовленную поверхность
вблизи пускового комплекса. При решении проблем посадки на
сушу могут быть использованы методика и средства, разработан¬
ные для посадки на Луну лунного корабля по программе «Апол¬
лон». Одноступенчатый баллистический аппарат может быть
использован для прямой доставки грузов с Земли на Луну с
дозаправкой на геоцентрической орбите. Такая задача для кры¬
латой системы была бы исключительно трудной ввиду отсутст¬
вия на Луне атмосферы.
Вертикальная посадка на Землю возвращаемого аппарата
имеет большие преимущества в условиях возможных поврежде¬
ний аэродромов (посадочных дорожек). Простота в эксплуата¬
ции одноступенчатого аппарата значительно сокращает время
использования стартовой площадки по сравнению с двухступен¬
чатой системой, и тем самым, приводит к уменьшению числа ап¬
паратов, необходимых для обеспечения заданной частоты за¬
пусков.
Исследования* по снабжению обитаемой* космической стан¬
ции на 370-километровой круговой орбите показали, что аппарат
с несущим корпусом, рассчитанный на 6 человек, будет весить на
4800 кгс больше, чем соответствующий аппарат баллистической
конфигурации типа «Аполлон». Если на баллистический аппарат
установить систему ракетодинамического маневрирования при
спуске того же веса 4800 кгс, то боковая маневренность балли¬
стического аппарата будет на 40% больше по сравнению с аппа¬
ратом с несущим корпусом. Иначе, при той же маневренности,
которую имеет пустой аппарат с несущим корпусом, баллистиче¬
ский аппарат может доставить с орбиты полезную нагрузку с
относительным весом 25% от веса пустого аппарата.
* R о о t М. В. «Ап Evaluation of the National Space Jewentory for
Logistics». Donglas Aircraft Company, Jnc., AIAA Paper No. 66-866 presented
to AIAA Third Annual Meeting, Boston, November 31, 1966.
373
Общие данные
V TOY L*
VTOHL**
VTOHL
Стартовый вес G0, тс .
98
119
183
Тяга двигателя Р0, тс .
122
—
—
Стартовая перегрузка п0
1,25
1,3
1,31
Эффективный вес конст¬
рукции Сэфф, тс . . . .
6,7
—
—
Грузоподъемность е*, %
3,75
3,1
3,4
Вес полезного груза А2, тс
3,68
3,68
6,22
Коэффициент эффективно¬
сти конструкции |Ыэфф . •
0,071
—
—
Вес груза без вспомога¬
тельных устройств А, тс
2,81
2,08
2,83
Грузоподъемность по Д,
е, %
2,89
1,75
—
Конечная скорость поле¬
та. VK
^кр
^кр
V'kp
Тормозной импульс скоро¬
сти ДК, м/с
109
102
102
Вес конструкции без обо¬
рудования и ДУ, тс
4
8,3
4
11,8
6,37
Посадочный вес без полез¬
ного груза, тс
8,5
14,5
6,08
20,5
9,2
Удельная тяга РуД/РуД, с
367/464
390/416
455
390/416
455
Соотношение компонентов
(окислитель/горючее) . . .
6:1
7:1
7:1
7:1
7:1
Аэродинамическое качест¬
во на гиперзвуке . . .
0,5
2,0
1,2
2,0
1,95
Компоненты топлива
О2+Н2
О2+Н2
О2+Н2
Стоимость проектирова¬
ния, млрд долларов . . .
1,1
1,8
2,4
1
374
Продолжение
Общие данные
VTOVL*
VTOHL**
VTOHL
Стоимость летного экзем¬
пляра, млрд долларов . . .
а) 1 шт.
25,8
71,2
102,2
б) 10 шт
24,1
66,6
95,6
в) 50 шт. . . .
16,1
44,5
63,9
Число ступеней
1
2
' 2
Примечание. Размеры на схемах JIA даны в метрах.
* VTOVL — vertical — takeoff (вертикальный старт,
vertical — Landing вертикальная посадка)
** VTOHL — vertical — takeoff (вертикальный старт,
horisontal — Landing горизонтальная посадка)
Приложение 6
ВЕСОВЫЕ ХАРАКТЕРИСТИКИ НЕКОТОРЫХ РАКЕТНЫХ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ И ИХ СИСТЕМ
А. Весовые характеристики типовой ракеты-носителя*
Элементы ступени
Вес, кгс
Нагрузка (вес второй ступени)
74100
Запас расходуемого топлива
139100
Запас перасходуемого топлива .
5600
Турбонасос
910
Вспомогательные элементы
520
Трубопроводы топливной системы
630
Система наддува .
350
Конструкция .
3750
Общий вес ступени
226800
Отношение веса топлива ракеты к стартовому весу
0,613
Отношение веса топлива ступени к общему весу ступени
0,914
Скорость полета ступени VK, м/с .
3300
Начальная перегрузка п0
1,13
Время работы двигателя т, с
182,4
* Astronautics, I, 1963
375
Б. Весовые характеристики спасаемых ракет-носителей
типа „Сатурн**
Вес, тс
Весовой состав
взлет гори¬
зонтальный
взлет
вертикальный
Нагрузка (полезный груз)
13,6
13,6
II ступень
Корпус .
12,9
15,6
Крыло . . .
3,2
3,3
Посадочные приспособления .
1,4
1,4
Силовая установка
3,2
3,4
Оборудование ...
1,6
1,6
Невыработанное топливо .
0,9
0,9
Общий вес:
сохраняемый ...
23,2
26,3
в конце активного участка .
36,7
39,9
топлива
105,5
116,6
стартовый
142,2
156,5
I ступень
Корпус
32,7
48,1
Крыло .
15,0
19,0
Посадочные приспособления
4,1
5,7
Силовая установка:
ЖРД
12,7
19,1
ТРД .
10,4
15,2
Оборудование .
1,4
1,4
Невыработанное топливо .
5,0
7,3
Топливо для ТРД .
9,1
13,1
Общий вес:
сохраняемый .
90,4
128,9
в конце активного участка
232,5
285,3
топлива
стартовый
346,3
578,8
566,1
851,4
* Astronautics, I, 1963
Примем а и и я. 1. Оба варианта носителей, по возвращению к месту
старта, осуществляют горизонтальную посадку.
2. Под первой ступенью здесь понимают полностью заправленный уско¬
ритель без полезного груза и второй ступени; под второй ступенью — часть
ракеты без ускорителя I ступени и полезного груза.
376
В. Вес и удельная тяга систем ориентации для различных топлив и импульса
2270 кгс*с *
Рабочее тело
S
>,
и
Удельная тяга,
сх
S
« а
я <->
2J л
Водяной пар . . .
90%-на я перекись
водорода
Г идразин+азотная
кислота
Сжатый азот . . .
21,8
18,6
10,4
39,9
6.3
1.4
1.4
24
0,7
0,5
нет
нет
нет
2.7
6.8
9.1
3.2
30.8
27.9
21,7
67,1
130
152
270
71
104
121
216
57
Зависимости веса систем ориентации от потребного импульса для раз¬
личных топлив (рабочих тел) приведены на рис. 209.
* Space Aeronautics, IV, 1963, vol. 39, pp. 116—119.
Рис. 209. Зависимость веса систе¬
мы ориентации от потребного им¬
пульса (удельная тяга от теорети¬
ческой составляет 80%; степень
расширения 50):
/—90%-ная перекись водорода; 2—сжа¬
тый воздух; 3—пары воды; 4—гидра¬
зин -газотная кислота
т 800 1200 1600 кге-
Полный, импульс
Г. Проектные данные ракеты-носителя «Сатурн-5» (США) *
Стартовый вес
Общая длина (с кораблем «Аполлон»)
Максимальный диаметр (без килей) .
2735 тс
106 м
10 м
По материалам иностранной печати на 31 декабря 1965 г.
377
I ступень
Силовая установка .
Тяга
Время работы
Топливо
Удельная тяга
Длина ступени (ускорителя)
Диаметр
Сухой вес ступени . .
II ступень
Силовая установка .
Тяга ....
Время работы
Топливо .
Удельная тяга .
Длина ступени .
Диаметр
Сухой вес ступени .
5 ЖРД Рокетдайн F-1
(680X5) тс
до 150 с
RP1 +жидкий кислород
260 (на уровне моря)
~42 м
~ 10 м
~140 тс
5 ЖРД Рокетдайн
(90,7X5) тс
390 с
жидкий водород +
-жидкий кислород
420 с (в пустоте)
25 м
10 м
37 тс
J-2
III ступень
Силовая установка
Тяга
Время работы
Топливо
Удельная тяга
Длина ступени
Диаметр .
Сухой вес ступени
ЖРД Рокетдайн J-2
90,7 тс
до 500 с
. жидкий водород+
+жидкий кислород
420 с (в пустоте)
21 м
6,5 м
14 тс
Ракета рассчитана для запуска полезного груза весом до 120 тс на орбиту
высотой 480 км и сообщения второй космической скорости нагрузке весом
43 тс
Д. Проектные данные ракеты-носителя «Титан-ЗС» (США) *
Стартовый вес .
Общая длина .
Максимальный диаметр
I ступень
Силовая установка
Тяга
Топливо
Удельная тяга .
Длина .
Диаметр .
Стартовый вес
* По материалам иностранной
635 тс
37,7 м
9,1 м
два РДТТ Юнайтед
Тек нол оджи
(544X2) тс
. полибутадиенакрило-
вая кислота (акрилонит-
рил с присадками алю¬
миния) +перхлорат
амоиия
. 245 с
. 23 м
. 3,0 м
. (227X2) тс
на 1965 г.
378
II с т у п е н ь
Силовая установка
Тяга
Время работы
Топливо
Длина .
Диаметр
модифицированный
ЖРД
Эрджет Дженерал
XLR-87-AJ-5
195 тс (225 тс
в пустоте)
150 с
аэрозин 50 + четырех-
окись азота
20 м
3,0 м
III ступень
Силовая установка
Тяга
Время работы
Топливо
Длина .
Диаметр
. модифицированный
ЖРД
Эрджет Дженерал
XLR-91-AJ-5
45 тс
150 с
. аэрозин 50 + четырех-
окись азота
8,2, м
3,0 м
IV ступень
Силовая установка
Тяга
Время работы
Топливо
Длина
Диаметр .
Стартовый вес
. ЖРД Эрджет
Дженерал
многократного
включения
7,2 тс
до 500 с
. аэрозин 50 + четырех-
окись азота
5 м
3,0 м
13 тс
Ракета-носитель «Титан-ЗС» обеспечивает вывод нагрузки весом 11,8 тс
на орбиту высотой 480 км и вторую космическую скорость нагрузке весом
2,3 тс.
379
Е. Весовой состав крылатых ракет-носителей многократного
применения с горизонтальным и вертикальным стартом*
Вес, кгс
Весовой состав
горизонтальный
старт
вертикальным
старт
Полезная нагрузка
13608
13608
II ступень:
конструкция
12873
15603
крыло
3175
3311
шасси
1361
1361
Силовая установка
3231
3402
Оборудование .
1588
1588
Невырабатываемое топливо
907
1043
Возвращаемая ступень
23125
26308
Вес в конце активного участка:
топливо
105505
116573
общий
142238
156489
I ступень:
конструкция
32659
48100
крыло
14970
19051
шасси
4082
5670
Силовая установка:
ракетная
12700
19051
турбореактивная .
10450
15195
Оборудование
1361
1361
Невырабатываемое топливо
4990
7257
Горючее для ТРД возврата
9072
13150
Возвращаемая ступень
90284
128840
Вес в конце активного участка:
топливо
346217
566091
общий
578839
851420
* Шунейко И. И. Ракетостроение. Крылатые
Изд. ВИНИТИ АН СССР, 1966.
космические
корабли. М.,
Приложение 7
МОДИФИЦИРОВАННЫЕ РАКЕТЫ-НОСИТЕЛИ
Особое место среди возможных схем ракет-носителей зани¬
мают тяжелые ракеты, получаемые в результате модификации
(усовершенствования) уже имеющихся ракет. Они могут быть
380
образованы заменой отдельных ступеней из арсенала уже дейст¬
вующих аналогичных ракет или
называемых «нулевых ступеней»
ускорителей первой ступени).
Подбор ступеней в первом слу¬
чае обычно происходит среди
жидкостных ракет; во втором
случае как среди жидкостных
ракет, так и путем изготовления
специальных твердотопливных
ускорителей.
Работы по модификации ра¬
кет-носителей чрезвычайно вы¬
годны, выполнимы в минималь¬
ные сроки и, как следствие, целе-
Рис. 210. Схемы модификаций существу¬
ющей PH «Сатурн-5» грузоподъемностью
от 182 до 318 тс
простейшим добавлением так
(параллельно присоединенных
А
А
Щ
А
Щ
шш
А
А
сообразны при условии, что эти работы предусмотрены уже
в начале проектирования основного (исходного для будущей
модернизации) носителя. Примеры таких работ иллюстриро-
I'4
§? О?
^ ^ ,
А
4+'
С::_/
Рис. 211. Варианты установки подвесных РДТТ на моди¬
фикациях PH со ступенью 5-11, запускаемой на старте
ваны двумя схемами ракет (рис. 210 и 211), а также таб¬
лицей некоторых характеристик.
381
Модификации PH, являющиеся комбинацией ступени S-II,
запускаемой с Земли, с РДТТ „Минитмен"
ю
см
05
СО
о
00
1,25
867
410,9
00
75,7
33,7
ю
см
О)
t"-
00
СО
о
о
оо
ОС
00
см
-f
ю
см
05
О)
см
со
со
см
со
00
ю
ь-
t"-
С"-
см
ю
см
оо
см
см
СО
*
•>
,—1
со
,—1
со
г--
О)
см
00
см
тг
1,25
577
236,7
"ф
73
00
ю
см
LQ
со
см
о
со
1—<
ь-
ь-
СО
см
ю
»-
О"
см
ю
см
см
t"-
ео
см
см
см
(М
1—1
t-~
о
сО
со
оо
см
ю
см
см
о
о
,
00
00
ю
см
оо
СО
—
S
о.
с
lO
см
см
см
00
о-
СО
со
см
ю
см
ь-
СО
см
см
СО
см
,—1
см
со
ь-
со
СО
см
•&
S
о
£
S
Cl
С
е
о
Он
о
f-
ffl
к
CL
С
к
m
CQ
>
c
>,
H
о
CCS
CQ
S
c
PQ IT cd IT CQ
>»
Cl
tr
s
H
e
382
Примечание. В седьмой модификации имеется 2 РДТТ для третьего запуска.
Приложение 8
ЦЕНТРОВОЧНЫЕ РАСЧЕТЫ ПО ВЫБОРУ КОМПОНОВОЧНОЙ
СХЕМЫ САМОЛЕТА С РАКЕТНЫМИ УСКОРИТЕЛЯМИ
Характер течения фокуса при изменении скорости ракетного
полета xF = xF(N[) налагает особые условия на выбор компоно¬
вочной схемы системы, состоящей из крылатой ракеты (КР) и
ракетных ускорителей.
В зависимости от взаимного расположения ракетной системы
(параллельной схемы) «крылатая ракета + ускорители», а также
xi+1(t; xn(t)
t г ■ *1 h ■■
i: ; ;
III! 1 1
III i II
I li
J-n , -с ^rt ^
САХ
с ,
® Ц.Т. (ус ко-
I ригпеля) (
A i+i
* Ц.Т.) у с к
а* :
jC^ZZr' _у
^Шсамопета) (ХцХ)к„
Рис. 212. Схема расположения постоянных и пере¬
менных масс системы «крылатая ракета + ускорители»
(пакетная схема)
характера центровочных кривых хц. т. = *ц. T.(GycH) для изолиро¬
ванных ускорителей, центровочные кривые системы яц. т.(0 при¬
нимают самый разнообразный характер. Этот характер опреде¬
ляется как конструктивной схемой ускорителей (удлинением,
расположением компонентов топлива, наличием объемов, не за¬
пятых переменной массой и т. д.), так и порядком расхода топ¬
лива в них.
На рис. 212 изображена схема расположения топливных ем¬
костей и центра тяжести пустого ускорителя, а также центра
тяжести полностью заправленной крылатой ракеты (расходом
топлива у которой на участке работы ускорителя пренебрегаем).
Согласно этому рисунку положение центра тяжести, в функции
времени полета (по мере выгорания топлива) xlh т (t) системы,
состоящей из п баков, запишется в общем виде как
п.
Х».Л (О = Q0_^_Q t — + (+1_ Ocit)-\-
° 1=1
+ (Ок)уск t+.+CK ++'о')кр (+.+ )> (19)
где xi{t) = — li\
X
383
G0 — начальный (стартовый) вес системы «крылатая раке-
та + ускорители»; U — длина i-го бака; Gc — секундный расход
топлива всех ускорителей; GT{ — вес топлива в i-м баке; Gci —
секундный расход топлива в t-м баке; (GK)yCK — конечный вес
всех ускорителей; (хц, т.)уск — координата центра тяжести всех
ускорителей без топлива; (G0)Kp — стартовый вес крылатой ра¬
кеты (КР); (хц. т.)Кр — координата центра тяжести заправлен¬
ной КР.
fi W
Рис. 213. Характер движения центра тяжести и фо¬
куса крылатой ракеты в функции текущего веса уско
рителей
После преобразования выражения (19) получим
(Hr (1 “ т) + Li J ~7^рГ к*} +
/-1
, (н-K £) ('^Ц.т)уск “Ь е (^u.t)kp
1 — р t
(20)
Q
где kTi = ——коэффициент веса топлива в i-м баке; Get — ве-
совая отдача по суммарному весу топлива всех баков; $ = — —
G0
коэффициент расхода топлива; |аг = —11—весовая отдача по конеч¬
но
ному весу системы; GK— конечный (без топлива) вес системы; е =
(^о)кр
— коэффициент распределения масс.
°о
Кривые, построенные по формуле (20), имеют вид как пока¬
зано на рис. 213. Там же нанесена кривая движения фокуса си¬
стемы «КР +ускорители», в зависимости от текущего веса систе¬
384
мы G(t) или, все равно что от текущей скорости на активном уча¬
стке работы ускорителей.
Легко видеть, что такое наложение кривых однозначно ука¬
зывает на наиболее целесообразную компоновку (расположение
ускорителей относительно КР) в соответствии с требуемым рас¬
положением кривых Хц, т. = *ц. т. (G) и xf = xf(G) .
В частном случае для изолированных (без второй ступени)
ускорителей при е = 0 зависимость (20) принимает вид
(НгГ-тН*'
2 V ^
;=1
^Ет 1 \ , Р*к (-^и.т)уск
fer.Ui^u-T,ycK-. (21)
1 — $t ' 1-^
Зависимостями (20) и (21) удобно пользоваться при выпол¬
нении массовых центровочных расчетов ракетных систем пакет¬
ного типа.
Приложение 9
МАКСИМАЛЬНО ДОПУСТИМЫЙ ВЕС РАКЕТОПЛАНЕРА
Возможности весового анализа, особенно применением крат¬
ких аналитических зависимостей, поистине неограничены в позна¬
нии новых весовых закономерностей.
Среди многочисленных задач, выпадающих на долю весового
анализа, встречаются и такие, которые носят более академиче¬
ский, чем практический характер, однако, в силу новизны вскры¬
ваемых явлений и получаемых при этом теоретических выводов
они являются полезными для проектанта. Примером таких задач
и является задача о максимально допустимом весе планера.
Имеется в виду гиперзвуковой планер, выполненный по схеме
«летающее крыло» *.
Будем полагать, что бортовой запас переменной массы пла¬
нера невелик и для него можно положить цк= 1. Условимся так¬
же, что вес планера Gnjl составляют весовые группы крыла GKP
и полезного груза As . Группа крыла включает в себя крыло, опе¬
рение и другие элементы конструкции, вес которых связан функ¬
ционально с весом крыла. Группа полезного груза состоит из
полезного груза, оборудования, внутренних систем и других по¬
стоянных грузов. При сделанных допущениях весовое уравнение
планера запишется в простом виде как
Дл = 0кр + Дз. (22)
Анализ весовых зависимостей, полученных для крыльев раз¬
личных конструктивно-силовых схем, показывает, что вес крыла
может быть выражен зависимостью вида
0KP = aKp0M.S-p, (23)
где т — показатель степени.
* Понятие «ракетопланер» впервые введено И. Н. Моишеевым в 1949 г.
385
Коэффициент акр в формуле (23) является функцией боль¬
шого количества параметров таких как удлинение 7кр, допускае¬
мое напряжение материала конструкции |[а], удельный вес мате¬
риала конструкции ум, относительная толщина профиля крыла
с, расчетная перегрузка пР, сужение крыла г|. Таким образом
(+> ЯР,
Коэффициент акр учитывает также разгрузку крыла от соб¬
ственного веса и от расположенных в нем грузов.
После подстановки выражения (23) в равенство (22) и пре¬
образований получим
°**=—«V м
1 икр°кр
и затем
Р*р= s (l—a Sm) ’
где pKp = Gnn/5Kp — нагрузка на единицу площади крыла от ве¬
са ракетопланера.
Для отыскания экстремума приравняем нулю производную
dpKv/dSKp. Тогда после преобразований получим
— акр (т + 1) S™
Де = 0.
[SKp (1 — акр5кф)]2
Поскольку знаменатель не равен нулю, это выражение дает
5КФ = КР(т + 1)]-1/,я. (26)
Формула (26) выражает площадь крыла, при которой имеет
место РиР= (Ркр)тт- После подстановки выражения (26) в форму¬
лу (24) и преобразований получим
/72 + 1
‘ ил ^ ил max "
Формула (27) показывает, что максимально допустимый вес
планера бил max, соответствующий условию минимальной нагруз¬
ки на единицу площади крыла, не зависит от конструктивных
параметров Якр, [а], ум, пР и так далее и определяется величиной
переносимого груза As. Как показывает .весовой анализ (Крыла,
обычно т= 1/2. При этом
Сплтах = ЗДа. (28)
Очевидно, что увеличение 1веса ракетопланера свыше утроен¬
ного веса груза бессмысленно, поскольку при этом возрастает
также и нагрузка на единицу площади крыла.
386
Кривые, иллюстрирующие существование экстремума функ¬
ции рКр = Ркр(5Кр) при т= 1/2, приведены на рис. 214 и 215.
Как видно из графиков, поперечная перегрузка крыла
функцией которой является конструктивный коэффициент акр(лр)»
оказывает влияние только на величину параметра Ркр = Рьртт.
^12
8
4
A^Wtc
Граница Jутроенного
беса
A1
плат
?pa^
2
\
\
О 100 200 300 SHp,M2 Q 100 200 300 SKp1MZ
Рис. 214. Зависимость веса планера от Рис. 215. Зависимость нагрузки от
площади крыла площади крыла
Примечал и с. Точкам 1 и 2 соответствуют минимальные значения пара¬
метра 011Л/5кр.
В соответствии с выражениями (25) и (26) минимальное
значение нагрузки на крыло определится как
( I 1 \ m+1
ЛрЫп=ау--^±11 - Д2=[акР(т + 1)]>/-ОПЛтах. (29)
Формула (29) показывает, что величина минимальной нагруз¬
ки на крыло от веса ракетопланера определяется не только гру¬
зом As, но и конструктивным параметром акр.
Таким образом независимо от действующих нагрузок, темпе¬
ратурных условий полета, материала конструкции и других фак¬
торов, определяемых конструктивным коэффициентом акр, вес
планера не должен превосходить величины, определяемой выра¬
жением (28).
СПИСОК ЛИТЕРАТУРЫ
1. Flug-Revue, 1956, No. 1, pp. 37—40.
2. Missiles Space Daily, 1965, v. 11, No. 7, pp. 48—49.
3. SAE Special Publications, 1964, No. 257, pp. 63—85.
4. Aviation Week and Space Technology, 1963, vol. 79, No. 1, pp. 54—55;
59—61; 63—65.
5. Missiles and Rockets, 1966, vol. 18, No. 22, pp. 50—52—54
6. Spaceflight, 1966, vol. 18, No. 4, pp. 14—16.
7. SAE Journal, 1967, vol. 75, No. 1, pp. 84—88.
ОГЛАВЛЕНИЕ
Стр.
Предисловие 3
Введение * » . . . 7
Условные обозначения 12
Глава I. Классификация ракетных летательных аппаратов 20
1.1. Классификация ракет 20
1.2. Классификация ракетных летательных аппаратов многократ¬
ного применения . 40
1.3. Схема одноступенчатой ракеты 47
1.4. Схема составной ракеты 47
1.5. Особенности схем одноступенчатых и составных ракетопланов 50
1.6. Экспериментальные ракетопланы 51
Список литературы 55
Глава II. Движение ракеты в пустоте 56
2. 1. Секундный расход массы 56
2.2. Идеальная тяга ...... 57
2. 3. Линейный закон изменения массы . . 58
2.4. Показательный закон изменения массы 58
2.5. Тяга ракетного двигателя .... 59
2.6. Удельная тяга 61
2.7. Основное уравнение движения ракеты . 62
2.8. Первая задача Циолковского . . . 63
2.9. Стартовая перегрузка 65
2. 10. Время полета при работающем двигателе 67
2. 11. Вторая задача Циолковского для линейного закона измене¬
ния массы 69
2. 12. Вторая задача Циолковского для показательного закона из¬
менения массы 71
2. 13. Формула Циолковского для составной ракеты . 72
Список литературы . . 75
Глава III. Экстремальные расчетные случаи нагружения элементов кон¬
струкции ракет 76
3. 1. Сила лобового сопротивления .... 77
3.2. Расчетный случай для подвесных баков 79
3. 3. Расчетные случаи для определения осевых нагрузок ... 80
3.4. Расчетные случаи для несущих баков . 84
3.5. Отсеки верхней части ракеты . . 86
3.6. Отсек средней части ракеты . . 87
3.7. Отсеки нижней части ракеты 89
3. 8. Топливный отсек с подвесными баками 89
3.9. Условие постоянства гидростатического давления у входа
в топливные насосы 91
Список литературы . 94
388
Стр.
Глава IV. Функциональный характер весовых зависимостей 95
4. 1. Топливные баки . 96
4. 2. Шпангоуты баков 102
4. 3. Избыточное давление несущих баков с учетом экваториальных
напряжений на критическую силу . . 102
4.4. Простой стержень ... 106
4.5. Панели 107
4. 6. Гладкая цилиндрическая оболочка 108
4. 7. Трехслойные цилиндрические оболочки с ребристым заполни¬
телем 109
4.8. Подкрепленная цилиндрическая оболочка • . . . 110
4.9. Элементы конструкции, воспринимающие поперечные нагрузки. 111
4.10. Конструкция, выполненная в виде дископлана . ... 112
4.11. Торовые баки . . 113
4. 12. Элементы ракетно-авиационных конструкций ‘. 115
4.13. Запас топлива .... 119
4.14. Пассивный груз 121
4. 15. Конечный вес ракеты . . 121
4. 16. Простейшие весовые зависимости . 121
Список литературы . 128
Глава V. Влияние диаметра и удлинения на весовые характеристики
топливных баков и их отсеков 129
5. 1. Влияние удлинения на вес обечайки бака при постоянном
внутреннем давлении ^ 130
5. 2. Влияние удлинения на вес обечайки бака при переменном гид¬
ростатическом давлении 132
5. 3. Влияние удлинения на вес днищ баков при постоянном внут¬
реннем давлении 133
5. 4. Влияние удлинения на вес днищ баков при переменном гидро¬
статическом давлении 134
5. 5. Влияние удлинения на вес обечайки и днищ баков при пере¬
менном избыточном давлении 135
5. 6. Влияние удлинения на вес шпангоутов баков 137
5. 7. Общие замечания по влиянию удлинения на весовые характе¬
ристики элементов конструкции баков 139
5. 8. Влияние удлинения на вес топливных баков при постоянном
внутреннем давлении 140
5.9. Оптимальное удлинение неизолированной обечайки бака при
переменном внутреннем давлении 143
5. 10. Оптимальный диаметр многобакового отсека при учете осевых
сжимающих сил 145
5.11. Оптимальный диаметр многобакового отсека при учете сил
внутреннего гидростатического давления . .... 146
Список литературы 151
Глава VI. Основная весовая зависимость и ее приложения . . . 152
6. 1. Вывод основной весовой зависимости . . 152
6.2. Варианты основной весовой зависимости 154
6. 3. Влияние удельного веса топлива на весовую отдачу .... 156
6. 4. Оценка эффективности ракетных топлив 158
6. 5. Влияние гарантийных запасов топлива на величину полезного
груза составной ракеты 163
6.6. «Весовой барьер» ракетно-авиационных конструкций . 166
Список литературы . 171
Глава VII. Характеристики режимов вертикального полета ракеты в пу¬
стоте с учетом весовых факторов 172
389
Стр.
7. 1. Высота вертикального подъема на работающем двигателе при
двух законах изменения массы 172
7.2. Высота вертикального подъема на пассивном участке траек¬
тории 175
7. 3. Влияние перегрузки на высоту вертикального подъема на ак¬
тивном участке при двух законах изменения массы .... 176
7.4. Полная высота подъема при двух законах изменения массы . . 178
7. 5. Влияние перегрузки на полную высоту подъема при двух за¬
конах изменения массы 180
7. 6. Космический ракетный поезд Циолковского. Конечная скорость
ракетного поезда 181
7.7. Вертикальный подъем ракеты на пассивном участке траекто¬
рии с учетом сопротивления среды 185
Список литературы 189
Глава VIII. Оптимальные режимы в простейших случаях движения
точки переменной массы 190
8. 1. Первая задача Космодемьянского 190
8. 2. Учет весовых факторов в первой задаче Космодемьянского . 194
8.3. Вторая задача Космодемьянского . 195
8. 4. Третья задача Космодемьянского 197
8.5. Учет весовых факторов в третьей задаче Космодемьянского
применительно к двум законам изменения массы 199
8. 6. Вертикальное движение летательного аппарата в присутствии
тормозящей реактивной тяги 200
Список литературы 203
Глава IX. Летные характеристики ракетоплана 204
9. 1. Квазигоризонталыюе движение ракетоплана с малой постоян¬
ной скоростью 205
9.2. Влияние стартовой тяговооруженности на дальность марше¬
вого полета ракетоплана с малой постоянной скоростью . . . 207
9.3. Квазигоризонтальное движение ракетоплана с большой по¬
стоянной скоростью 209
9.4. Влияние стартовой тяговооруженности на дальность марше¬
вого полета ракетоплана с большой постоянной скоростью 212
9.5. Оптимальная скорость маршевого полета ракетоплана с уче¬
том расхода топлива на участке выведения 214
9. 6. Время, скорость, дальность и высота квазистационарного пла¬
нирования при положительной подъемной силе 217
9. 7. Влияние маршевой скорости на дальность полета ракетоплана
с учетом планирования 222
9. 8. Активно-инерционный полет ракетоплана 223
9. 9. Время, скорость, дальность и высота квазистационарного пла¬
нирования при отрицательной подъемной силе . . . 225
Список литературы 230
Глава X. Оптимальные параметры одноступенчатых ракет 231
10. 1. Основные параметры одноступенчатых ракет 232
10.2. Стартовая перегрузка в пустоте при линейном законе измене¬
ния массы 233
10.3. Стартовая перегрузка в пустоте при показательном законе
изменения массы 238
10.4. Сравнение линейного и показательного законов изменения
массы 240
10. 5. Стартовая перегрузка с учетом влияния атмосферы 242
10.6. Оптимальный диаметр корпуса ракеты с учетом влияния атмо¬
сферы . 244
390
Стр.
10.7. Графический метод определения оптимальных значений основ¬
ных параметров 247
10.8. Выбор стартовой перегрузки по критерию максимальной на¬
грузки на тягу . . 248
10.9. Определение потребной весовой отдачи по приведенной конеч¬
ной скорости . . . 250
Список литературы 253
Глава XI. Частные случаи распределения масс по ступеням многосту¬
пенчатых ракет 254
11. 1. Основные параметры составных ракет . . . 257
11.2. Простейший закон распределения масс 259
11.3. Частный случай распределения масс для двухступенчатых
ракет 265
11.4. Частный случай условия оптимальности при сг(0к) = 0 .... 267
11.5. Частный случай распределения масс при заданном пара¬
метре е* . . 271
11.6. Частный случай распределения масс при заданном пара¬
метре (Ык* 272
11.7. Частный случай распределения масс при заданном пара¬
метре М 273
11.8. Частный случай распределения масс при заданном пара¬
метре ек* 275
11.9. Оптимальное количество ступеней . . 275
Список литературы 284
Глава XII. Оптимальные параметры многоступенчатых ракет 285
12. 1. Общий случай условий оптимальности 285
12.2. Общий случай распределения масс методом смежных ступеней 288
12.3. Выбор параметров методом M = const . 290
12.4. Теорема M = const в общем виде .... 294
12.5. Практические следствия теоремы M = const ... .... 298
12.6. Замечания к учету программы полета по углу 0 ... 303
Список литературы . 313
Глава XIII. Режимы движений ракетно-космических систем многократ¬
ного применения 314
13. 1. Движение ракетоплана в режиме рикошетирования 317
13.2. Приближенные зависимости для пологой баллистической траек¬
тории 326
13.3. Вход ракетоплана в плотные слои атмосферы по баллистиче¬
ской траектории , . . . 329
13.4. Вертикальное снижение с больших высот 332
13.5. Суборбитальное движение ракетоплана 334
13.6.• Переходные режимы движения ракетоплана в вертикальной
плоскости . , , 339
13. 7. Потери скорости при вираже в горизонтальной плоскости . 345
Список литературы 349
Приложения.
1. Функциональный характер основных параметров для двух за¬
конов изменения массы ' . . . 350
2. Сводка параметрических зависимостей по топливным бакам раз¬
личных схем при kYi=koo = k^u= 1 351
3. Оптимальная скорость снижения груза на парашютно-реактив¬
ной системе 364
4. Условия возвращения ракетоплана к месту старта при малых
скоростях полета . . 367
391
Стр.
5. Сравнительный анализ баллистических и крылатых ракет-носи¬
телей многократного применения 371
6. Весовые характеристики некоторых ракетных летательных аппа¬
ратов и-их систем 375
7. Модифицированные ракеты-носители 380
8. Центровочные расчеты по выбору компоновочной схемы само¬
лета с ракетными ускорителями 383
9. Максимально допустимый вес ракетопланера . . ... 385
Список литературы 388
Григорий Макарович МОСКАЛЕНКО
ИНЖЕНЕРНЫЕ МЕТОДЫ ПРОЕКТИРОВАНИЯ В РАКЕТОДИНАМИКЕ
Редактор издательства В. Г. Гатагогу Технический редактор Л. А. Макарова
Переплет художника А. /О. Литвиненко Корректор Е. П. Карнаух
Сдано в набор 31/V-1973 г. Подписано к печати 5/1-1974 г. Т-02844
Формат 60 X 90/16 Бумага № 2 Печ. л. 24,5 Уч.-изд. л. 22,9
Тираж 2700 экз. Изд. зак. 3911 Цена 1 р. 39 к.
Издательство «МАШИНОСТРОЕНИЕ», 107885, Москва, Б-78, 1-й Басманный пер., 3.
Московская типография № 8 «Союзполиграфпрома»
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли,
Хохловский пер., 7. Тип. зак. 3479