А. А. ЯБЛОНСКИЙ, В. М. НИКИФОРОВА
КУРС
ТЕОРЕТИЧЕСКОЙ
МЕХАНИКИ
ЧАСТЬ I
СТАТИКА. КИНЕМАТИКА
Издание третье,
исправленное
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебника для студентов
машиностроительных, механических, приборостроительных,
электротехнических и строительных
специальностей высших технических учебных заведений
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МОСКВА —1966

Рецензенту.
Кафедра теоретической механика
Московского авиационного института
Профессор И. М. Воронков
2-4-2

ПРЕДИСЛОВИЕ
Настоящий учебник составлен в полном соответствии с програм-
программой курса теоретической механики для высших технических учебных
заведений и содержит материал, который является основной частью
рабочих программ этого курса всех специальностей.
Учебник рассчитан на студентов очной и заочной систем обу-
обучения
Наряду с изложением теоретического материала в учебнике
имеется подробное решение задач основных типов и даны вопросы
для самоконтроля.
Решение всех примеров выполнено в единицах системы МКС.
Первая часть учебника содержит курс статики и кинематики,
вторая -часть — курс динамики.
При переиздании учебника учтены многие пожелания и замечания
читателей, которым авторы выражают признательность.
Отзывы о книге и пожелания, направленные на улучшение этого
издания, следует посылать в адрес издательства «Высшая школа».
Авторы

Из истории развития механики
Механика является одной из древнейших наук, которая своим
возникновением и развитием обязана потребностям практики.
Энгельс отмечает, что развитие механики тесно связано с раз-
развитием земледелия (подниманием воды для орошения в Египте), с рос-
ростом городов, возведением крупных построек, развитием ремесла и
мореплавания. Известно, например, что при постройке египетских
пирамид применялись некоторые простейшие механические приспо-
приспособления: рычаги, блоки, наклонная плоскость. Таким образом, еще
в древние времена человечество обладало некоторыми эмпирическими
знаниями по механике, но потребовался длительный период времени
для того, чтобы установить основные законы механики и заложить
фундамент этой науки.
В древности не существовало деления науки по отраслям знаний,
а поэтому механика, наряду с философией, естествознанием и дру-
другими естественными науками, являлась составной частью единой науки
о природе и обществе.
Лишь после Аристотеля C84—322 гг. до н. э.) начинается
процесс выделения отдельных частных наук из общего естество-
естествознания.
На первой стадии развития механики, от древнего мира до эпохи
Возрождения A4—16 вв.), в результате изучения простейших машин
создается учение о силах.
Основоположником механики как науки является знаменитый
ученый древности Архимед B87—212 гг. до н. э.) Архимед дал
точное решение задачи о равновесии сил, приложенных к рычагу,
и создал учение о центре тяжести, тел. Кроме этого, Архимед открыл
и сформулировал закон о гидростатическом давлении жидкости на
погруженное в нее тело, который носит его имя.
Быстрое и успешное развитие механики начинается лишь с эпохи
Возрождения, когда создаются условия для развития науки и
техники.
В эпоху Возрождения, как отмечает Энгельс, «... были заложены
основы для позднейшей мировой торговли и для перехода ремесла

в мануфактуру, которая, в свою очередь, послужила исходным пунк-
пунктом для современной крупной промышленности. Духовная диктатура
церкви была сломлена».
«Это был величайший прогрессивный переворот из всех пере-
пережитых до того времени человечеством, эпоха, которая нуждалась
в титанах и которая породила титанов по силе мысли, страсти и
характеру, по многосторонности и учености» *.
С эпохи Возрождения начинается следующий период развития
механики. Для решения практических задач требуются исследования
движений тел. На основе накопленного за четыре столетия опыта
к концу XVLI в. создаются основы динамики — науки об общих зако-
законах движения материальных тел.
Блестящим представителем эпохи Возрождения является знамени-
знаменитый итальянский художник, физик, механик и инженер — Леонардо
да Винчи A451—1519). На основании своих исследований в области
механики Леонардо да Винчи установил, что сила трения скольжения
не' зависит от величины поверхности соприкасания трущихся тел.
Кроме того, Леонардо да Винчи занимался изучением движения па-
падающего тела, движения тела по наклонной плоскости и ввел в меха-
механику понятие момента силы.
Зарождение небесной механики — науки о движении небесных
тел — связано с великим открытием Николая КоперникаA473—1543)—
созданием гелиоцентрической системы мира, сменившей геоцентри-
геоцентрическую систему Птоломея.
Это открытие произвело переворот в научном миросозерцании
той эпохи — освободило естествознание от теологии. На основании
учения Коперника и астрономических наблюдений Кеплер A571—1630)
сформулировал три закона движения планет, которые впоследствии
Привели к открытию Ньютоном закона всемирного тяготения.
Создание основ динамики принадлежит великим ученым — италь-
итальянцу Галилео Галилею A564—1642) и англичанину Исааку Нью-
Ньютону A643—1727).
В своем знаменитом сочинении «Математические начала натураль-
натуральной философии», изданном в 1867 г., Ньютон в систематическом
виде изложил основные законы так называемой классической меха-
иики. Эти законы, установленные на основании наблюдений и опы-
опытов Ньютона и его предшественников, являются объективными зако-
заколами природы.
XVIII в. характеризовался разработкой общих принципов класси-
классической механики и важнейшими исследованиями по механике твердого
тела, гидродинамике и небесной механике.
Наиболее крупными зарубежными учеными XVIII и XIX вв. в области
механики являются Иван Бернулли A667—1748), Даниил Бернулли
A700—1782), Даламбер A717—1783), Лагранж A736—1813), Шаль
A793—1880). В работах французских ученых Вариньона A654—1722)
* Ф. Энгельс. Диалектика природы. Госполитиздат, 1950, стр. 4.
5

и Пуансо A777—1859) наряду с динамикой дальнейшее развитие
получила и статика. Вариньон решил задачи сложения сил, прило-
приложенных к одной точке, и параллельных сил; он установил условия
равновесия этих сил и доказал теорему о моменте равнодействующей.
Вариньону принадлежит создание основ графостатики (построение
силового и веревочного многоугольников).
Развитие науки в России связано с образованием по инициативе
Петра I в 1725 г. в Петербурге Российской Академии наук. Боль-
Большое влияние на развитие механики оказали труды гениального рус-
русского ученого, основателя Московского университета, акад. М. В. Ло-
Ломоносова A711—1765) и знаменитого математика, астронома и физика
Леонарда Эйлера A707—1783).
За 30 лет работы в Российской Академии наук Эйлер создал
большое количество работ по математике, механике твердого и
упругого тела, гидромеханике и небесной механике.
Огромное значение для дальнейшего развития механики имеют
работы выдающихся-отечественных ученых XIX и XX вв.: М. В. Остро-
градскесо 1*1801—1861), П. Л. Чебышева A821 — 1894), С. В. Кова-
Ковалевской (.1850—1891), А. М. Ляпунова A857—1918), И. В. Ме-
Мещерского A859—1935), К. Э. Циолковского A857—1935),
А. Н. Крылова A863—1945), Н. Е. Жуковского A847—1921),
С А. Чаплыгина A869—1942) и ряда других ученых.
Деятельность русских ученых, несмотря на крайне тяжелые усло-
условия развития науки в дореволюционной России, значительно способ-
способствовала развитию как общей теоретической механики, так и спе-
специальных механических дисциплин.
Великая Октябрьская социалистическая революция создала исклю-
исключительно благоприятные условия для развития науки в нашей стране.
Благодаря этому советские ученые в области механики освоили
богатое наследие русской дореволюционной науки и своими работами
обогатили сокровищницу мировой науки.
В многочисленных научно-исследовательских институтах и вузаЬс
Советского Союза в настоящее время ведется большая работа по
дальнейшему развитию механики.
Тесная связь науки и практики в СССР обеспечивает прогресс
механики, при помощи которой решаются многочисленные задачи,
выдвигаемые практикой социалистического строительства.

РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
ГЛАВА I
ВВЕДЕНИЕ
§ 1. Основные понятия статики
Теоретическая механика — это наука, в которой изучаются
общие законы механического движения и механического взаимодей-
взаимодействия материальных тел.
Механическим движением называется перемещение тела по от-
отношению к другому телу, происходящее в пространстве и во вре-
времени.
Курс теоретической механики делится на три раздела: статику,
кинематику и динамику.
Статикой называется раздел механики, в котором изучаются
методы преобразования систем сил в эквивалентные системы и уста-
устанавливаются условия равновесия сил, приложенных к твердому телу.
Кинематикой называется раздел механики, в котором изучается
движение материальных тел в пространстве с геометрической точки
зрения, вне связи с силами, определяющими это движение.
Динамикой называется раздел механики, в котором изучается
движение материальных тел в пространстве в зависимости от дей-
действующих на них сил.
Приступая к изучению статики, следует определить основные по-
понятия механики, встречающиеся в этом разделе.
Материальное тело, размеры которого в рассматриваемых кон-
конкретных условиях можно не учитывать, называют материальной
точкой. Материальная точка обладает массой и способностью взаимо-
взаимодействовать с другими телами. Например, при изучениии движения
планет солнечной системы вокруг Солнца их размерами -по сравне-
сравнению с их расстояниями от Солнца пренебрегают и рассматривают
эти планеты как материальные точки.
Системой материальных точек, или механической систе-
системой, называется такая совокупность материальных точек.

в которой положение и движение каждой точки зависят от
положения и движения других точек этой системы.
В теоретической механике часто рассматриваются такие тела, рас-
расстояния между любыми точками которых остаются неизменными.
Такие тела называются абсолютно твердыми телами.
Полагая тела абсолютно твердыми, не учитывают деформаций,
которые возникают в реальных телах. Это значительно упрощает
изучение действия сил на тело и условий, при которых эти силы
уравновешиваются.
Условия равновесия сил, приложенных к абсолютно твердому телу,
используются при изучении действия сил на деформируемое тело.
Твердое тело может находиться в состоянии покоя или некоторого
движения. Каждое из этих состояний условимся называть кинема-
кинематическим состоянием тела.
Важнейшим понятием теоретической механики является понятие
силы. Взаимодействие двух тел, способное изменить их кинематиче-
кинематическое состояние, называется механическим взаимодействием.
Сила — это мера механического взаимодействия тел, определяю-
определяющая интенсивность и направление этого взаимодействия.
Сила определяется тремя элементами: числовым значением
{модулем), направлением и точкой приложения. Сила изобра-
изображается вектором (рис. 1). Прямая, по которой направлена данная сила,
Рис. 1,
называется линией действия силы. За единицу силы в Междуна-
Международной системе единиц измерения СИ (в механике система МКС)
принимается ньютон («). Совокупность нескольких сил, действующих
на данное тело или систему тел, называется системой сил.
Системы сил, под действием каждой из которых твердое тело
находится в одинаковом кинематическом состоянии, называются экви-
эквивалентными.
Сила, эквивалентная некоторой системе сил, называется равно-
равнодействующей.
Система сил, которая, будучи приложена к твердому телу, нахо-
находящемуся в покое, не выводит его из этого состояния, называется
системой взаимно уравновешивающихся сил.
8

Силы, действующие на механическую систему, делят на две
группы: внешние и внутренние силы.
Внешними называют силы, действующие на материальные точки
(тела) данной системы со стороны материальных точек (тел), не
принадлежащих этой системе.
Внутренними называют силы взаимодействия между материаль-
материальными точками рассматриваемой системы.
Основной задачей статики является исследование условий равно-
равновесия внешних сил, приложенных к абсолютно твердому телу.
§ 2. Аксиомы статики
Приступая к изучению курса статики твердого тела, рассмотрим
аксиомы, лежащие в основе этого курса. Эти аксиомы сформулиро-
сформулированы на основе наблюдений и изучения окружающих нас явлений
реального мира. Некоторые основные законы механики Галилея —
Ньютона являются одновременно и аксиомами статики.
1. Аксиома инерции
Под действием взаимно уравновешивающихся сил материаль-
материальная точка (тело) или находится в состоянии покоя, или
движется прямолинейно и равно-
равномерно.
Аксиома инерции выражает установ-
ленный Галилеем закон инерции.
2.	Аксиома
равновесия двух сил
Лее силы, приложенные к твер-
твердому телу, взаимно уравновеша-
еаются только в том случае, если	Рис. 2.
их модули равны и они направлены
по одной прямой в противоположные стороны (рис. 2).
3.	Аксиома присоединения и исключения
уравновешивающихся сил
Если к твердому телу, находящемуся под действием неко-
некоторой системы сил, приложить уравновешивающуюся систему
или исключить такую систему сил, то получится система сил,
эквивалентная заданной системе.
Пусть, например, к твердому телу приложены силы Plf P2, Р3
и Р4, под действием которых тело находится в покое или совер-
совершает какое-то движение (рис. 3). Приложим к телу две равные

противоположно направленные силы Qj и Q2. которые взаимно уравно-
уравновешиваются
Если тело в покое, то оно сохранит его; если тело в движении,
то оно будет двигаться под действием новой системы сил Qp Q2>
Pv Р2> Р3. Р4 так же- как П°Д действием сил Pv P2. Р3. P-i- т- е*
новая система сил эквивалентна прежней.
Это же произойдет, если из заданной системы сил, приложенных
к твердому телу, исключить взаимно уравновешивающиеся силы, вхо-
входящие в ее состав.
Р"
Рис. 3.
Рис. 4.
Следствие. Не изменяя кинематического состояния абсолютно
твердого тела, силу можно переносить вдоль линии ее дей-
действия, сохраняя неизменными ее модуль и направление.
Предположим, что к твердому телу в точке А приложена
сила Р (рис. 4). Приложим в точке В две силы Р' и Р", равные
по модулю силе Р и направленные по ее линии действия в проти-
противоположные стороны. Затем отбросим силы Р и Р" как взаимно
уравновешивающиеся. Тогда к телу
в точке В будет приложена сила Р'=Р,
эквивалентная силе Р .в точке А.
Таким образом, силу можно пе-
переносить в любую точку по линии
действия, не изменяя ее модуля и на-
направления. Поэтому в статике твер-
тверда Р»	/ дого тела с и л а рассматривается как
скользящий вектор.
4. Аксиома параллелограмма сил
рис< 5.	Равнодействующая двух пе-
пересекающихся сил приложена в
точке их пересечения и изображается диагональю параллело-
параллелограмма, построенного на этих силах (рис. 5).
Это положение, хорошо известное из элементарного курса физики,
выражается следующим геометрическим равенством:
ю

Модуль равнодействующей силы определяется по следующей фор-
формуле:
R = VW+ Р| + 2РгР2 cos cp,	B.1)
где <р — угол между направлениями сил Рг и Р2.
5. Аксиома равенства действия и противодействия
Всякому действию соответствует равное и противоположно
направленное противодействие.
Эта аксиома утверждает, что силы действия друг на друга
двух тел равны по модулю и направлены по одной прямой в проти-
противоположные стороны. Таким образом, в природе не существует
одностороннего действия силы.
Аксиома действия и противодействия установлена Ньютоном
н известна как один из основных законов классической механики.
6. Аксиома сохранения равновесия сил,
приложенных к деформирующемуся телу,
при его затвердевании
Равновесие сил, приложенных к деформирующемуся телу,
сохраняется при его затвердевании.
Из этой аксиомы следует, что условия равновесия сил, прило-
приложенных к абсолютно твердому телу, должны выполняться и для
сил, приложенных к деформирую-
деформирующемуся телу. Однако в случае де- а]
формирующегося тела эти условия а А	В р
необходимы, но недостаточны. { г.	- 1 ¦ ¦ *¦
Так, например, условие равнове-
равновесия двух сил, приложенных к у\
твердому стержню на его концах, ' .	В п
состоит в том, что силы равны по ^г г_ .	-	| ж 2
модулю и направлены по одной
прямой в противоположные сто-	Рис. 6.
роны (рис. 6,й и б).
Две уравновешивающиеся силы, приложенные к нити, удовле-
удовлетворяют этому условию, но при наличии добавочного условия — силы
должны только растягивать, а не сжимать нить (рис. 6,а).
§ 3. Несвободное твердое тело. Связи.
Реакции связей
Твердое тело называется свободным, если оно может переме-
перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела,
является по отношению к нему связью.
11

Твердое тело, свобода движения которого ограничена связями,
называется несвободным.
Все силы, действующие на несвободное твердое тело, наряду
с делением на внешние и внутренние силы, можно также разделить
на задаваемые силы и реакции связей.
Задаваемые силы выражают действие на твердое тело других
тел, вызывающих или способных вызвать изменение его кинематиче-
кинематического состояния.
Реакцией связи называется сила или система сил, выражающая
механическое действие связи на тело
Одним из основных положений механики является принцип осво-
бождаемости твердых тел от связей, согласно которому не-
несвободное твердое тело можно рассматривать как свободное, на ко-
которое, кроме задаваемых сил, действуют реакции связей.
Рис 7.
в
J:
Пусть, например, на гладкой неподвижной горизонтальной
плоскости покоится шар (рис. 7, а). Плоскость, ограничивая движе-
движение шара, является для него связью. Если мысленно освободить шар
от связи (рис. 7, б), то для удержания его в покое к нему в точке
касания с плоскостью нужно приложи 1ь
силу N, равную весу шара G по модулю
и противоположную ему по направлению.
Сила N и будет реакцией плоскости.
Тогда шар, освобожденный от связи, бу-
будет свободным телом, на которое дей-
действует заданная сила Q и реакция пло-
плоскости N.
Гладкая плоскость не противодействует
Т ^	J q перемещению тела вдоль плоскости под
рис g_	действием задаваемых сил (рис. 7, в), но
не допускает его перемещения в направле-
направлении, перпендикулярном к плоскости. Поэтому действие плоскости на
тело выражается нормальной реакцией N (рис. 7, г).
Реакция гладкой плоскости направлена перпендикулярно
к плоскости.
Если к концу В нити АВ, прикрепленной в точке А, подвесить
груз весом О (рис. 8, а), то реакция S ниги будет приложена
12

к грузу в точке В, равна по модулю его весу G и направлена вер-
вертикально вверх (рис. 8, б). Реакция нити направлена вдоль нити.
Пусть балка весом G в точке В опирается на гладкую поверх-
поверхность, а в точках А и D—на гладкие горизонтальную и верти-
вертикальную плоскости (рис. 9) Тогда реакции опорной поверхности и
опорных плоскостей будут
иметь указанные на рис. 9 на-
направления.
Определение модулей этих
реакций показано после уста-
установления условий равновесия
сил, произвольно расположен-
расположенных на плоскости (§ 25).
Для определения каждой
реакции нужно знать три ее	Рис 9
элемента: модуль, направление
и точку приложения. Точка приложения реакции, как правило, бы-
бывает известна. Направление же реакций известно лишь для некоторых
типов связей Если существуют два взаимно перпендикулярных на-
направления на плоскости, в одном из которых связь препятствует
перемещению тела, а в другом нет, то направление ее реакции
противоположно первому направлению.
Так, например, гладкая горизонтальная плоскость препятствует
перемещению шара вертикально вниз и не препятствует его горизон-
горизонтальному перемещению. В этом случае реакция плоскости направлена
вверх (рис. 7, б). Так же определяется направление реакции нити
(рис. 8).
Гладкая поверхность, на которую опирается балка точкой В
(рис. 9), препятствует перемещению балки по нормали к поверх-
поверхности вниз и не препятствует пере-
перемещению вдоль оси балки. Поэтому
реакция этой поверхности напра-
направлена по нормали к поверхности
вверх.
Аналогично, если балка опи-
опирается на ребро в точке D (точечная
опора), то реакция в точке D на-
направлена перпендикулярно к оси
балки (рис. 10)
Рис ю	Рассмотрим два основных типа
опор балок и их реакции.
На рис. 11 изображена шарнирно-неподвижная опора, которая
препятствует любому поступательному движению балки, но дает ей
возможность свободно поворачиваться вокруг оси шарнира. По своей
конструкции такая шарнирная опора состоит из двух обойм, из ко-
которых одна закреплена на балке, а другая — на неподвижной поверх-
поверхности. Эти обоймы соединяются при помощи цилиндрического
1R-,
13

валика (на рис. 11 показано среднее сечение конструкции). В зави-
зависимости от действующих сил, валик может прижиматься к различ-,
ным точкам обоймы. Реакция R такой опоры проходит через центр
шарнира О и точку соприкасания А (рис. 12а, б). Линия действия
реакции этой опоры всегда проходит
через центр шарнира, но модуль и на-
направление реакции не известны.
Обоими
Обойма
Рис. И.
Рис. 12.
Шарнирно-подвижная опора, нижняя обойма которой
поставлена на катки, не препятствует перемещению балки парал*
лельно опорной плоскости (рис. 13). Если не учитывать трения кат-
катков, то линию действия реакции такой опоры следует считать про-
проходящей через центр шарнира перпендикулярно к опорной плоскости.
Таким образом, не известен лишь мо-
модуль этой реакции.
В курсе теоретической механики
обычно рассматривают только действие
внешних сил на абсолютно твердое
р,
р,
А
А
_j
и
D
$2 П
•*¦—1—
s,
В
	Г"
В
Pi
Р?
Рис. 13.
Рис. 14.
тело. Однако при расчете различных конструкций бывает необхо-
необходимо определять внутренние силы, возникающие в растянутых
и сжатых стержнях. Для определения внутренних усилий в стержнях
воспользуемся так называемым методом сечения, дающим возмож-
возможность переводить интересующие нас внутренние силы в разряд внеш-
внешних сил. Рассмотрим сущность этого метода.
Пусть стержень АВ, весом которого пренебрегаем, растягивается
двумя равными по модулю силами Pt и Р2, приложенными
к его концам (рис. 14). Рассечем мысленно стержень, разде-
разделив его на две произвольные части AD и DB. На часть AD
14

действуют две уравновешивающиеся силы: внешняя сила Pt и вну-
внутреннее усилие Si, заменяющее действие отброшенной части стержня.
Из второй аксиомы следует, что внутреннее усилие Si направлено
по оси стержня и равно по модулю силе Р1# Внутреннее усилие Si,
выражающее действие отброшенной части DB на рассматриваемую AD,
является по отношению к рассматриваемой части стержня внешней силой.
а>р,
'р,
А
-А
S,
Рис.
15
Si
Si
в
в
р?
д,
Если стержень АВ растягивается (рис. 15, а) или сжимается
(рис. 15, б) силами Рх и Р2> то^ на тела, вызывающие его растяжение
или сжатие, со стороны стержня действуют реакции St и S2.
При этом реакции растянутого стержня равны, по модулю
задаваемым силам а направлены по оси стержня от его концов.
Реакции сжатого стержня равны по модулю заданным си-
силам и направлены по оси стержня к его концам. Так как
реакции и внутренние усилия по модулю равны, то для определения
усилия в стержне достаточно определить его реакцию.
ГЛАВА II
СИСТЕМА СХОДЯЩИХСЯ СИЛ НА ПЛОСКОСТИ
§ 4. Сложение двух сходящихся сил.
Параллелограмм и треугольник сил
Сходящимися называются силы, линии действия которых
пересекаются в одной точке.
Если к телу приложены две силы, линии действия которых пере-
пересекаются в одной точке, то, как указывалось в аксиоме параллело-
параллелограмма сил, их равнодействующая приложена в точке А пересечения
линий действия сил; она изображается диагональю параллелограмма,
построенного на этих силах (рис. 16). Построение параллелограмма
сил можно заменить построением треугольника сил ABD (рис. 17).
Направление равнодействующей силы R по контуру силового тре-
треугольника противоположно направлению обхода контура треуголь-
треугольника, определяемому слагаемыми силами.
При помощи параллелограмма или треугольника сил можно ре-
решить и обратную задачу — разложить силу Р на две составляющие
Pi и Р2, приложенные в той же точке и направленные по заданным
линиям действия KL и DE (рис. 18 и 19).
15

Используя известные формулы тригонометрии (теорему синусов),
Л =- 3.-^ . р
Sin P Sin a sin A80° — ер) "
Рис. 16.
Рис. 18.
Так как ср = а-{- р, то
Рис. 19.
sln
sin (« + (*)'
§ 5. Многоугольник сил. Условие равновесия
сходящихся сил
Пусть к твердому телу в точках Av A2. As, At, Аь приложеЕ1ьг
сходящиеся силы Р,, Р2, Р3, Р4 и Р5 (рис. 20). Все эти силы можно
перенести в точку О пересечения их линий действия и, строя тре-
треугольники сил, последовательно сложить. Тогда равнодействующая
этих сил изобразится замыкающей стороной многоугольника сил.
Таким образом, равнодействующая R сходящихся сил приложена
в точке пересечения линий действия сил и равна их геометрической
сумме:
16

Следует учитывать то, что направление равнодействующей по
контуру силового многоугольника противоположно направлению об-
обхода контура этого многоугольника, определяемому направлением
первой силы.
Сходящиеся силы уравновешиваются в том случае, если их рав-
равнодействующая равна нулю, т. е. многоугольник сил замкнут (рис. 21):
или
2Р4=0.
В замкнутом много-
многоугольнике сил все силы
А
Рис. 20.
Рис. 21.
направлены по контуру многоугольника в одну сторону.
Частный случай. Три сходящиеся силы уравновеши-
уравновешиваются, если треугольник этих сил замкнут.
Все задачи на равновесие сил, приложенных к некоторому телу
(точке) решаем по следующему плану:
1.	Показываем действующие на тело задаваемые силы
2.	Мысленно освобождаем тело от связей, заменяя их действие
¦соответствующими силами — реакциями связей.
3.	К полученной системе сил применяем условия равновесия, со-
соответствующие этой системе.
4.	Определяем искомые величины.
§ 6. Примеры на построение замкнутого
треугольника сил
Пример 1.,На гладкой наклонной плоскости АВ, образующей
с горизонтом угол а = 30°, при помощи веревки DE, параллельной
плоскости АВ, удерживается однцридный шар tfettm G = 4 н Опре-
Определить давление шара на плоскдогЩ i	f
2 А А Яблонский
17

Решение. Решаем задачу по изложенному плану, рассматривая
равновесие сил, приложенных к шару.
1.	Показываем действующую на шар, задаваемую силу—вес шара G,
приложенный в центре шара (рис. 22,6).
2.	Мысленно освобождаем шар от связей, заменяя действие свя-
связей их реакциями. Связями для шара являются наклонная плоскость АВ,
реакция которой приложена в точке соприкасания К и направлена пер-
перпендикулярно к плоскости, и веревка DE, реакция которой на-
направлена вдоль веревки.
<*)
Рис. 22.
3.	К шару приложены три сходящиеся силы: вес шара G, реак-
реакция N плоскости АВ и реакция Т веревки DE. К этой системе сил
применяем условие равновесия трех сходящихся сил, т. е. строим
замкнутый треугольник этих сил. Для этого откладываем заданную
силу Q (рис. 22,в). Из конца b силы G следует провести прямую,
параллельную линии действия либо реакции Т, либо реакции N.
Проведем из конца Ъ силы G прямую, параллельную реакции Т.
тогда из начала а силы G должна быть проведена прямая, парал-
параллельная другой реакции N (рис. 22,в). Точка пересечения с проведен-
проведенных прямых является третьей вершиной треугольника сил. Сторо-
Стороны треугольника должны иметь такое направление, чтобы все
силы G, Т и N были направлены в одну сторону по обходу кон-
контура треугольника.
4.	Из треугольника сил, определив его углы, находим модули
искомых реакций:
7 = О sin 30° =4--i-=2«; N =
cos 30° =
:3,46 «.
Найденные реакции Т и N прикладываем к шару (рис. 22,6).
Давление шара на плоскость и сила, растягивающая веревку, по
модулям равны найденным реакциям, направлены противоположно
им и приложены в точках D и К к плоскости и к веревке
(на рисунке эти силы не указаны).
18

Примечание. Условие равновесия всегда применяется к системе
сил, действующей на одно тело. Поэтому всегда определяются не давления
тела на опоры, а реакции опор, которые вместе с задаваемыми силами дей-
действуют на рассматриваемое тело.
В примере 1 условие равновесия применялось к силам, действующим
на шар, а потому определялись приложенные к шару реакции опор, а не
давления шара на опоры.
Пример 2. Кран состоит из цепи АВ= 1,2 м и подкоса
СВ= 1,6 м, прикрепленных к вертикальной стойке в точках А к С,
причем АС = 2А м. В точке В подвешен груз весом О = 30 кн.
Определить усилия S1 в цепи и S2 в подкосе (рис. 23,д).
Рис. 23.
Решение. Решаем задачу по общему плану, не выделяя его
отдельных пунктов. Рассматриваем равновесие трех сил, прило-
приложенных к. узлу В: заданной силы G и реакций цепи и под-
подкоса Si и S2, линии действия которых совпадают с отрезками АВ
и СВ (рис. 23,<Г>. Строим замкнутый треугольник abc этих сил
(рис. 23,в). По треугольнику сил определяем направления реакций Sx
и S2. Приложив найденные реакции к узлу В (рис. 23,0), устана-
устанавливаем, что растянута только цепь, а подкос сжат. Так как стороны
треугольника сил и треугольника ABC соответственно параллельны,
то эти треугольники подобны. Из подобия следует:
G Sy St
Из этих равенств определяем искомые усилия:
— О —— 30 ——15 «• S —G СВ
¦ 24 кн.
в точке D к ка-
с горизонталью
канат привязан
Пример 3. Груз весом 0 = 518 « подвешен
нату ADE, участок которого AD составляет
угол 30°, а участок DE — угол 45°. В точке А	р
к вертикальному столбу АВ, поддерживаемому подкосом АС, на-
наклоненным к горизонтали под углом 60°. Определить натяжение ка-
каната на участках AD и DE и усилия в столбе и подкосе (рис. 24а).
Решение. В этой задаче следует рассматривать отдельно рав-
равновесие сил, приложенных к каждому из узлов D и А. На узел D
2*
19

действуют заданная сила G и реакции Tj и Т2 частей каната DE
и AD, а на узел А — реакция Тг каната AD, а также реакции
столба и подкоса S! и S2 (рис. 24,6). Прикладываем к узлу D за-
заданную силу О и строим замкнутый
треугольник сил G, Tv Т2, дейст-
действующих на этот узел (рис. 24,в).
Определив углы треугольника сил,
по теореме синусов находим:
G	Т2	Т,
sin 15°
откуда
sin 45°
sin 120°
sin 45°
= 518
Рис. 24й.
sin 15°
= 1414 Я,
= 1732 «.
0,707
0,259
0,866
0,259
Затем строим треугольник сил Т2, Si, S2, приложенных к узлу А>
откладывая прежде всего реакцию Тг каната AD, которая по модулю
равна реакции Т2, приложенной к узлу D, а по направлению противо-
противоположна ей (рис. 24,г). Из равнобедренного треугольника сил находим:
откуда
[ = T2= 1414 H,
_S2	К
" sin 30°'
0,8C6
sin 120°
sin 120°
= 2449 и.
Приложив все найденные силы к узлам D и А (рис. 24,б), уста-
устанавливаем, что столб АВ сжат, а подкос ЛС растянут.
20

§ 7. Теорема о равновесии трех непараллельных сил
Линии действия трех непараллельных, взаимно уравно-
уравновешивающихся сил пересекаются в одной точке.
Пусть к твердому телу в точ-
точках Аг, А2 и Аг приложены три
непараллельные взаимно уравно-
уравновешивающиеся силы Pj, Р2, Рз
(рис. 25). Так как силы Рх и Р2
расположены в одной плоскости,
то эти силы можно перенести
в точку О пересечения их линий
действия и определить их равно-
равнодействующую R, которая будет
приложена в этой же точке. Так	рис_ 25.
как по условию силы Pj, P2 и Р3,
уравновешиваются, то силы Р3 и R должны быть равны по модулю
и направлены по одной прямой в противоположные стороны. Следо-
Следовательно, линия действия силы Р3 проходит через точку О, что и
требовалось доказать.
Примечание. Если две заданные силы Р, и Р2 параллельны, то, как
известно из элементарного курса физики, линия действия уравновешивающей
силы Р3 параллельна линиям действия заданных сил и находится от линий
действия этих сил на расстояниях, обратно пропорциональных модулям сил.
В
§ 8. Примеры на применение теоремы о равновесии
тр?х непараллельных сил
Пример 4. Рама АВ весом 0 = 1,5 кн может вращаться во-
вокруг оси шарнира А. Центр тяжести рамы С определяется по усло-
условию АС = 2СВ. Рама удержи-
удерживается под углом а = 45° к гори-
горизонтали веревкой BDE, к концу Е
которой подвешен груз Р. Уча-
Участок BD горизонтален. Опреде-
Определить вес груза Р и реакцию
шарнира А при равновесии сил,
пренебрегая трением на блоке
(рис. 26, а).
Решение. Решаем задачу
по изложенному выше плану, рас-
Рис. 26а.	сматривая равновесие сил, прило-
приложенных к раме АВ (рис. 26, б).
1.	Показываем действующую на раму заданную силу — вес
рамы G, прикладывая его в центре тяжести С.
2.	Мысленно освобождаем раму АВ от связей, заменяя их дей-
действие соответствующими реакциями. Реакция веревки Т приложена
Е
ршт
21

в точке В и направлена по прямой BD, реакция шарнира RA при-
приложена в точке А, но линия действия ее не известна.
3. К системе трех уравновешивающихся сил G, T, R4, приложенных
к раме, применяем теорему о равновесии трех непарал-
непараллельных сил.
Линии действия сил G, T, R^ должны пересекаться в одной
точке. Находим точку К пересечения линий действия сил G и Т;
через эту же точку должна пройти линия действия реакции Ид;
определяем эту линию, соединяя точки А и К. Строим замкнутый
треугольник трех сил, -сходящихся в точке К (рис. 26,в).
	i-
Рис. 26,<?, в, г.
4. Определяем искомые величины, т. е. реакции Т и R^ следую-
следующим образом. На рис. 26,6' строим треугольник ALK, стороны ко-
которого соответственно параллельны сторонам треугольника сил.
Определяем стороны треугольника ALK-
Обозначаем AL = /. Так как а = 45°, то
, = AL = l\ ACKBoo&CLA;
¦отсюда имеем:
КС
~ст
KL =
АК =
СВ
КС
АС ' CL
~ТСВ~' Kb — j^L — jl,
~2
¦+-KL* =
1/2__ ?13 z
Треугольник сил abc подобен треугольнику AKL.
Стороны треугольников пропорциональны.
Т
о
Ж"
АК ' I

Определяем модули искомых реакций опор:
УТз
3
= -|О=1 кн;
/?Л = ^-13-О = 0,5/13«1,8
кн.
Прикладываем к раме все действующие на нее взаимно уравно-
уравновешивающиеся силы: заданную силу О, реакцию веревки Т и реак-
реакцию шарнира RA (рис. 26г).
При отсутствии трения на блоке D натяжение веревки на участках б?>
и DE должно быть одинаково и равно весу груза Р. Таким образом,
вес груза определяется:
р = Т=\ кн.
Пример б. Определить реакции шарниров А и В трехшарнирной
арки АСВ, изображенной на рис. 27а, вызванные горизонтальной
силой Р = 40 кн.
р
>
1
1 \
0 \
/
Им
¦ч-
В
\
Рис. 27а.
Решение. Трехшарнирная арка представляет собой систему
двух тел, соединенных между собой ключевым шарниром С и при-
прикрепленных к земле шарнирами А и В. На арку действуют три
уравновешивающиеся внешние силы: заданная сила Р и реакции шар-
шарниров R^ и Кв, линии действия которых не известны. Так как не
известны линии действия двух сил, то определить эти силы по тео-
теореме о равновесии трех непараллельных сил Р, ЯЛ и RB невозможно.
Но арка представляет собой систему двух тел. Расчленяем ее и
рассматриваем равновесие сил, приложенных к каждой части
арки.
К правой части арки (рис. 27,в) приложены две силы: давление
левой части в точке С и реакция шарнира В. Эти две силы уравно-
уравновешиваются, следовательно, они направлены по одной прямой в про-
противоположные стороны и равны по модулю. Находим их линии
действия, соединяя точки В и С.
К левой части арки (рис. 27,6) приложены три силы: заданная сила Р,
реакция шарнира А, линия действия которой не известна, и давление
правой части в точке С, действующее по прямой ВС, так как
га

согласно аксиоме действия и противодействия взаимное давление
частей в точке С равно по модулю и противоположно по напра-
направлению. К системе трех сил Р, Rc, RA применяем теорему о равно-
Рис. 276, в, г. д.
весии трех непараллельных сил. Находим точку К пересечения линий
действия сил Р и Rc и через эту точку проводим линию действия
реакции RA (рис. 27,6"). Строим замкнутый треугольник этих сил
(рис. 27г).
24

Треугольник сил abc подобен треугольнику АКБ. Определяем
стороны треугольника АКБ Так как СО = ОБ, то / KBD =. 45а
и DB = KD =
= AB — DB = Q м,
АК =
=/4 + 4 = 2 /2 м;
= /36+~Т = 2
Определяем модули искомых сил:
#д Р Rc
АК
АВ ~~ KB
Р-АК 40-2/16
АВ
Р-КВ
АВ
8
40-2/2
¦=10/10 =31,6 кн,
= 10/2" =14,1 кн.
К левой части арки (рис. 27,д) прикладываем действующие на нее
силы Р, Ял. Rc- К правой части прикладываем действующие на нее
силы Rc и Rb. При этом по аксиоме равенства действия и противо-
противодействия имеем —Rc = Rc, т. е. по модулю Rc — Rc= 14,1 кн,
а по направлению Rc противоположно Rc.
По аксиоме равновесия двух сил имеем RB = — Rc, т. е. RB = Rc =
= 14,1 кн, а направление RB противоположно направлению Rc.
§ 9. Проекции силы на две
взаимно перпендикулярные оси на плоскости
Взяв две взаимно перпендикулярные оси х и у. силу Р можно
разложить на две составляющие силы Рх и Ру, направленные парал-
параллельно этим осям (рис. 28).
Силы Рх и
Р
Ру называются компонен-
компонентами силы Р по осям х и у.
Обозначив i и j — единичные векторы,
направленные по осям х и у, а Л" и К —
проекции силы на эти оси, получим
Поэтому
p = iX + jY.	(9.1)
Это равенство представляет собой
формулу разложения силы на составляю-	Рис. 28.
щие по осям координат.
Из прямоугольных треугольников Aad и Add имеем:
i); F = Pcos(P, j),	(9 2)
РУ
А
i
¦ »х
X
d
25

где (Р, f) и (P, j) — углы, заключенные между направлением силы Р
и направлениями осей х и у (единичными векторами i и j).
Угол отсчитывается от оси по направлению движения часовой
•стрелки или против, чтобы величина его не превышала 180°
любом направлении силы.
при
X
Рис. 29.
Выражения (9.2) показывают, что проекция силы на ось опре-
определяется произведением модуля силы на косинус угла между
направлениями оси и силы.
При вычислении проекции силы на ось возможны следующие
частные случаи (рис. 29):
1. Проекция положительна:
= Pcosa..
2.	Проекция равна нулю:
/_а = 90°; X =
3.	Проекция отрицательна:
/_а>90°; X==Pcoscc==—Pcosp,
где Р — острый угол между линией действия силы и осью.
При решении задач рекомендуется вычислять абсолютное зна-
'чение проекции силы как произведение модуля силы на косинус
острого угла между линией действия силы и осью, определяя знак
проекции непосредственно по чертежу.
Если известны проекции силы на две взаимно перпендикулярные
оси х и у, то модуль и направление силы Р определяются по
следующим формулам:
cos(P, i) = 4; cos(P, j) = -?.
(9.3)

§ 10. Аналитический способ определения
равнодействующей сходящихся сил на плоскости.
Уравнения равновесия сил
Равнодействующая R сходящихся сил Р5, Р2. .... Р„ равна гео-
геометрической сумме сил (рис. 30):
Из векторной алгебры известно, что проекция геометрической:
суммы векторов на любую ось равна алгебраической сумме проекций
составляющих векторов на ту же ось. Таким образом, проекции К
и Y равнодействующей силы R определяются по формулам:
где
1,	i);
2,	i);
Xn=pncos(Pn, i);
K, = P,cos(P,. j);
F2 = P2cos(P2, j);
Кп = Р„'соз(Р„', j).
Формулам A0.1) можно придать вид
X=^iXi, K=2V/. (Ю.2)
A
i
й/
\
*2
X
*3 '
Рис. 30.
где 2— знак суммирования, а ?=1, 2, ..., га.
Вычислив проекции равнодействующей X и Y, найдем модуль иг
направление равнодействующей по формулам (9.3):
cos(R, i) = -f; cos(R, j)=-?.
Если сходящиеся силы уравновешиваются, то
-(-К2 =0, т. е. Х = 0 и К = 0.
В этом случае имеем два следующих уравнения равновесия сил:
2г' = о|	A°'3>
При помощи этих уравнений можно решать задачи на равновесие
27

1 V х
J&l	J
~C ~B
Рис. 31.
•сходящихся сил, если число неизвестных величин в задаче равно
двум. Такой метод решения этих задач называется аналитическим.
Если в задаче на равновесие сходящихся сил число неизвестных
превышает два, то ее нельзя решить методами статики твердого
тела. Методы решения таких задач изла-
излагаются в курсе сопротивления мате-
материалов.
Пример 6. Решить пример 3 (рис. 24а)
аналитическим способом [при помощи
уравнений равновесия A0.3)].
i jf . i i Решение. Воспользуемся уравне-
AJf^-	 | ниями равновесия сходящихся сил, при-
приложенных к каждому из узлов D и А.
Покажем на схеме (рис. 31) все силы,
приложенные к этим узлам, как извест-
известные, так и неизвестные. Направления
реакций столба АВ и подкоса АС не
известны. Условимся эти стержни счи-
считать растянутыми и направим их реакции
St и S2 от узла. Ответ со знаком минус укажет, что соответствую-
соответствующий стержень не растянут, а сжат.
Проведем оси координат, направив их по горизонтали и верти-
вертикали. Составим суммы проекций всех сил, приложенных к узлу D,
да оси х и у и приравняем эти суммы нулю:
2^ = 0; 7\cos45° — T2cos30° = 0.
]&Yi=0; 7\cos45° — T2 cos 60е — G = 0.
Вычитая второе уравнение из первого, найдем:
— Т2 cos 30° -f- T2 cos 60° -f- О = 0,
G	518
откуда
2 ~~ cos 30° — cos 60° 0,866 — 0,5
= 1414 н.
Из первого уравнения определим Ту
Т2 cos 30° _ 1414 ¦ 0,866
cos 45°
0,707
= 1732 «.
Составим уравнения равновесия сил, приложенных к узлу А,
учитывая, что 7*2 = 7"г = 1414 «:
2 Х{ = 0; — S2 cos 60° + Т2 cos 30° = 0.
2 Y( = 0; — S2 cos 30° — Sj + T2 cos 60° = 0.
Из первого уравнения:
T2 cos 30° 1414 • 0,866
cos 60°
0,5
-=2449 «.
28

Из второго уравнения
S1 = — S2 cos 30°+ Т'2 cos 60° =
= — 2449-0,866+1414-0,5 = —1414 к.
Так как S2 —+ 2449 н- то условно принятое направление
силы S2 совпадает с действительным, т. е. подкос АС растянут.
Ответ S] =—1414 « показывает, что условно принятое направление
силы Sj противоположно действительному, т. е. столб АВ не растя-
растянут, а сжат.
Примечание. Схема, по которой составлены уравнения равновесия
(рис. 31) не изменяется, хотя направления некоторых сил на ней и противо-
противоположны действительным (Si). Числовые значения полученных из уравнений
равновесия величин определяют модули сил, а их знаки — их направления.
Истинное направление сил определяют по схеме и по знаку ответа.
§ 11. Определение усилий в стержнях плоских ферм
по способу вырезания узлов.
Леммы о нулевых стержнях
Фермой называется геометрически неизменяемая шарнирно-стерж-
невая конструкция (рис. 32).
Верхм/й пояс
II
II
\
\
/
±~ Нижний пояс 4
Пролет фермы
|
1
Рис. 32.
Если оси всех стержней фермы лежат в одной плоскости, то ее
называют плоской фермой. Точки, в которых сходятся оси стерж-
стержней, называются узлами фермы, а те узлы, которыми ферма опи-
опирается на основание, называются опорными узлами.
Стержни плоской фермы, расположенные по верхнему контуру,
образуют верхний пояс, а расположенные по нижнему контуру —
нижний пояс фермы.
Вертикальные стержни называются стойками, а наклонные— рас-
раскосами. На рис. 33, 34 и 35 изображены стержневые опоры фермы.
Реакция каждого из опорных стержней, очевидно, направлена по оси
этого стержня.
Если шарниры, соединяющие стержни фермы, предполагаются
идеальными, т. е. без трения, а все внешние силы — приложенными
29

Опорный стержень
к узлам фермы, то все стержни испытывают лишь растяжение или
сжатие, так как к каждому стержню приложены силы только на его
концах *
Реальные фермы не имеют идеальных шарниров, однако такое
допущение облегчает вычисление усилий в стержнях фермы, а резуль-
результаты вычислений при этом допущении
вполне пригодны для практики.
Рассмотрим определение усилий
в стержнях фермы по способу вы-
вырезания узлов
Этот способ состоит в том, что
мысленно вырезают узлы фермы, при-
прикладывают к ним соответствующие
внешние силы и реакции стержней и
составляют по два уравнения равнове-
равновесия сил, приложенных к каждому узлу.
Так как в начале расчета фермы не известно, какие стержни фермы
растянуты и какие сжаты, то условно предполагают, что все стержни
растянуты (реакции стержней направлены от узлов)
Если в результате вычислений получают ответ со знаком минус,
то соответствующий стержень сжат
Рис 33
Рис -34
Рис 35
Найденные реакции стержней равны по модулю внутренним уси-
усилиям в стержнях (§ 3).
Последовательность рассмотрения узлов определяется обычно 1ем,
чтобы число неизвестных сил, приложенных к узлу, не превышало
двух. Тогда эти неизвестные определяются сразу из двух уравнений
равновесия сил, действующих на этот узел.
Чтобы убедиться в правильности произведенных вычислений, для
сил, приложенных к каждому узлу, можно построить многоугольник,
который должен быть замкнут.
Определим по способу вырезания узлов усилия в стержнях
фермы, изображенной на рис. 36, а. Если сила Р = 60 кн, приложен-
*) Веса стержней достаточно малы по сравнению с силами, приложен-
приложенными в узлах фермы, поэтому ими обычно пренебрегают.
30

ная к узлу Е фермы, вертикальна и реакция шарнирно-подвижной
опоры В, перпендикулярная к опорной плоскости, тоже вертикальна,
то линия действия реакции шарнирно-неподвижной опоры А должна
быть им параллельна, т. е. должна быть тоже вертикальна (приме-
(примечание к § 7).
С
Рис 36а.
Из элементарного курса физики известно, что силу Р можно
разложить на две, параллельные ей составляющие силы, приложен-
приложенные в точках А и В Модули этих составляющих сил обратно про-
пропорциональны расстояниям АЕ и BE, а сумма их равна модулю
силы Р Этим силам, представляющим собой давление фермы на
Узел А
УзелЕ
Рис. 36,<Т, в.
опоры, соответствует равное по модулю противодействие в виде
реакций опор, которые определятся по следующим формулам:
RA-\-RB = P = 60 кнг / = ^ =
АЕ
откуда
= 40 кн и Rb =
Составим по два уравнения равновесия сил, приложенных
к каждому из узлов фермы (рис. 36,б) и для проверки правильности
произведенных вычислений построим многоугольники сил, которые
31

должны быть замкнутыми. При построении многоугольников все
силы отложим в некотором масштабе по их истинным направлениям,
соответствующим растяжению или сжатию, руководствуясь резуль-
результатами вычислений (рис. 36,в).
Расчет начнем с узла А, к которому приложены лишь две неиз-
неизвестные силы Sj4 и S2.
Узел А
2^ = 0; S2-f Si cos 30° = 0;
S1 = — cos ?QO = — 80 кн; S2 = — 5j cos 30° = 69,2 кн.
Узел С
2 Y.t =0; —S'i cos 60° — 53 = 0;
— S[ cos 60° = 40 кн; S4 = 5{ cos 30° = — 69,2 кн.
Узел Е
2 *, = <>; — 52+56 + S5 cos 30° = 0;
2^=0; S3 —
cos 60°
= 40 кн; S6 = S2 — Ss cos 30° = 34,6 ш.
Узел /="
Узел
• = — 40 кн •
Таблица 1
№ стержня
5 (кн)
1
-80
2
69,2
Таблица
3
40
4
—69,2
усилий
5
40
6
34,6
7
0
8
34,6
9
—40
Приведенная таблица показывает, что верхний пояс фермы сжат,
нижний — растянут.
32

Усилия в отдельных стержнях загруженной фермы могут ока-
оказаться равными нулю. Такие стрежни фермы принято называть нуле-
нулевыми стержнями. Рассмотрим леммы, пользуясь которыми можно
определить нулевые стержни, не производя расчета фермы.
Лемма 1. Если в незагруженном
узле фермы сходятся два стержня, то
усилия в этих стержнях равны нулю
(рис. 37).
= 0; S1 cos (90° — a) == 0;
Sl = 0 и 52 = 0.
Рис. 37.
Лемма 2. Если в незагруженном узле фермы сходятся три
стержня, из которых два расположены на одной прямой, то
усилие в третьем стержне равно
нулю. Усилия в первых двух стерж-
стержнях равны, между собой (рис. 38).
2 Y. = 0; S3 cos (90° — a) = 0;
1== S2.
, = U и
Рис. 38
Лемма З. Если в узле фермы
сходятся два стержня и к узлу
приложена внешняя сила, линия
действия которой совпадает с осью одного из стержней, то
усилие в этом стержне равно по модулю приложенной силе,
а усилие в другом стержне равно нулю (рис. 39).
2 Xt =
cos a = 0; S1 =
S2 = -~P.
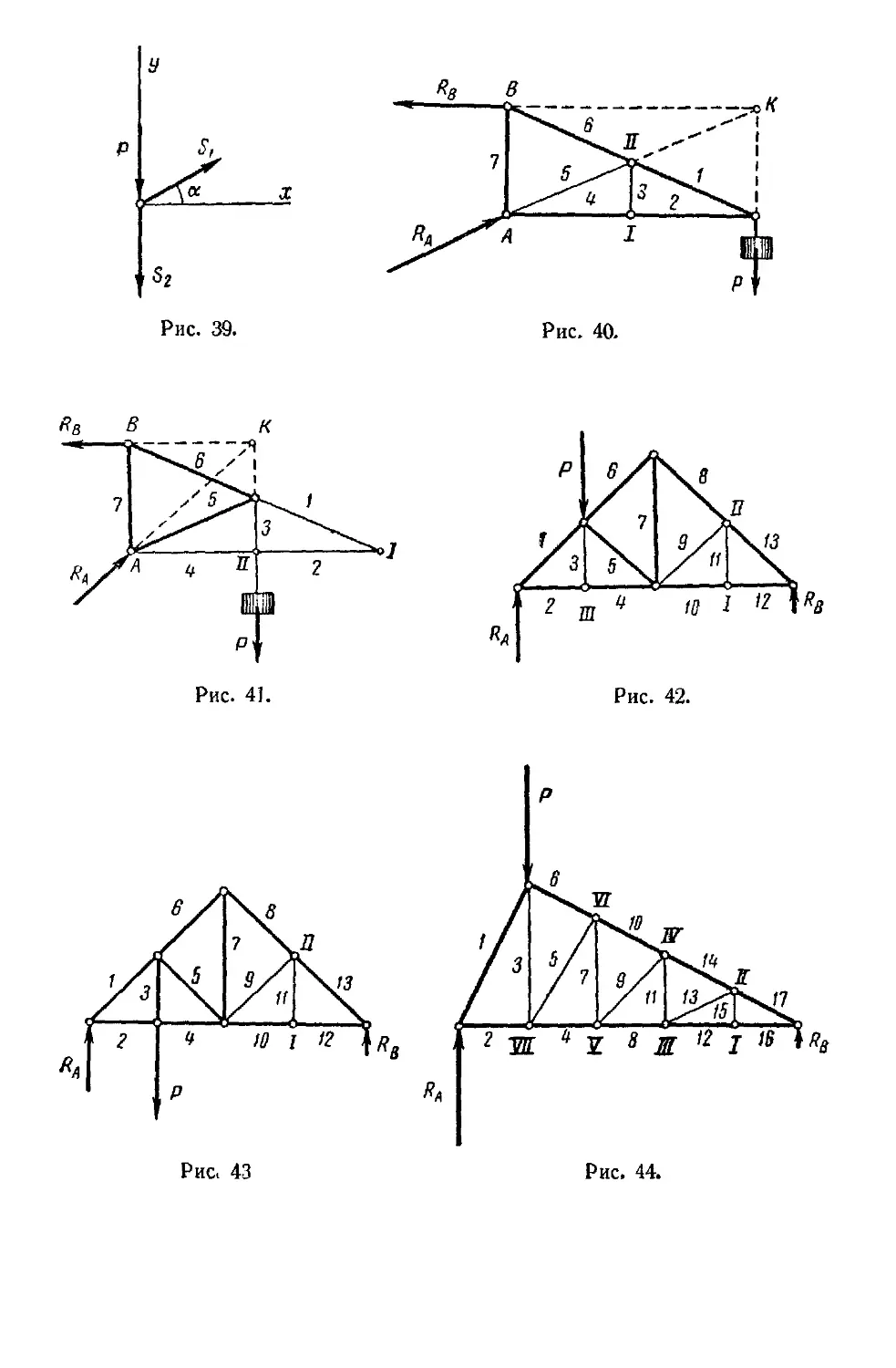
Пример 7. Применить леммы о нулевых стержнях к определению
незагруженных стержней ферм, изображенных вместе с действую-
действующими на них внешними силами и реакциями опор (рис. 40—44).
Применяя лемму 2 к узлу / фермы, изображенной на рис. 40,
устанавливаем, что S3 = 0. Далее, мысленно отбрасывая стержень 3,
применяем эту же лемму к узлу // и находим, что S5 = 0.
Рассматривая ферму, изображенную на рис. 41, применяем лемму 1
к узлу / и заключаем, 4To5j=0 и S2 = 0. Затем применяем лемму 3
к узлу // и устанавливаем, что S4 = 0.
На рис. 42 рассматриваем узлы /, //, /// и находим: 5п = 0,
59 = 0, 53 = 0.
Рассматривая узлы lull (рис. 43), можно заключить, что Sn = 0
и S9 = 0.
3 А. А. Яблонский
33

s,
\<x	X
S2
Рис. 39.
Рис. 40.
W I 12 |/f
Рис. 42.
Рис. 43
Рис. 44.

Рассматривая последовательно узлы 1—VII фермы, изображенной
на рис. 44, находим:
Вопросы для самоконтроля
1. Что называется связью? В чем заключается принцип освобождаемости
от связей?
2У Перечислите основные типы опор, для которых линии действия реак-
щ известны.
3.	Как направлена реакция опорного шарнира, если твердое тело соеди-
соединено с опорой при помощи стержня, имеющего на концах шарниры?
4.	Как определяется направление равнодействующей системы сходящихся
сил при построении силового многоугольника?
5.	Каковы условия и уравнения равновесия плоской системы сходящихся
сил?
6.	Как формулируется план решения задач статики на равновесие сил?
7.	При каком условии три непараллельные силы, приложенные к твер-
твердому телу, уравновешиваются?
8.	В чем заключается сущность способа вырезания узлов?
9.	Каковы леммы о нулевых стержнях?
ГЛАВА III
ТЕОРИЯ tlAP СИЛ, ЛЕЖАЩИХ В ОДНОЙ ПЛОСКОСТИ
§ 12. Момент силы относительно точки на плоскости
Моментом силы относительно некоторой точки на плоскости
называется произведение модуля силы на ее плечо относительно
этой точки, взятое со знаком плюс или минус (рис. 45):
M0=±Pd.	A2.1)
Плечом силы Р относительно точки О называют длину перпенди-
перпендикуляра, опущенного из точки О на линию действия силы; точка О
называется центром момента.
Момент силы относительно точки будем считать положительным,
если сила Р стремится повернуть плоскость чертежа вокруг точки О
в сторону, противоположную движению часовой стрелки, и отрица-
отрицательным — в обратном случае.
Момент силы Р относительно точки О численно равен удвоенной
площади треугольника АОВ
Мо = ± 2А АОВ,
где А и В — начало и конец силы, а О — центр момента.
Если линия действия силы проходит через точку, т. е. d = 0, то
момент силы относительно этой точки равен нулю.
Единица момента равна произведению единицы силы на единицу
длины.
3*	35

Если сила выражена в ньютонах, а плечо в метрах, то момент
силы выражается в ньютон-метрах (н • м).
В том случае, если к телу приложено несколько сил, лежащих
в одной плоскости, можно вычислить сумму моментов этих сил от-
относительно какой-либо точки О в этой же плоскости (рис. 46):
и т. д.
Рис. 45.
Рис. 46.
Момент Мо, равный алгебраической сумме моментов данной си-
системы сил относительно какой-либо точки в той же плоскости, на-
называют главным моментом системы сил относительно этой точки:
о 1ог 2о* '¦¦ ' по
§13. Пара сил. Теорема о моменте пары
Из элементарного курса физики известно, что равнодействующая R
двух параллельных сил Р1 и Р2 одного направления (рис. 47,а) имеет
Рис. 47.
такое же направление, а ее модуль равен сумме модулей слагаемых
сил.
Точка С приложения равнодействующей делит отрезок между
точками приложения сил Л и В на части, обратно пропорциональ-
36

ные модулям сил, т. е.
АС
ВС
A3.1)
Отсюда по известному свойству пропорции можно получить:
АС ВС
или
АС
ВС АВ
R
A3.2)
Равнодействующая R двух параллельных сил Рх и Р2 противо-
противоположного направления (рис. 47, б) имеет направление большей по
модулю силы и модуль, равный разности модулей этих сил. Точка С
приложения равнодействующей лежит на продолжении отрезка АВ
за точкой приложения большей силы, нэ расстояниях от точек А и В,
обратно пропорциональных модулям приложенных в них сил, т. е.
АС
ВС
АС
ВС
Pi
АВ
R
A3.3)
Система двух равных по модулю, параллельных и противоположно
направленных сил Pj и Р2 называется парой сил.
Пара сил не имеет равнодействующей, однако силы пары, не лежа-
лежащие на одной линии, не уравновешиваются, а стремятся произвести
вращение тела, к которому они приложены, в направлении движения
часовой стрелки (рис. 48, а) или противоположно ему (рис. 48, б).
Рис. 48.
Пара сил, не имея равнодействующей, очевидно, не может быть
уравновешена силой.
Расстояние d между линиями действия сил, составляющих пару
сил, называется плечом пары. Понятие пары сил введено в механику
Пуансо.
37

Теорема. Сумма моментов сил, составляющих пару, отно-
относительно любого центра в плоскости действия пары не зависит
от выбора этого центра а равна взятому со знаком плюс
или минус произведению модуля силы на плечо пары.
Момент силы Рх, приложенной
в точке А, относительно произволь-
произвольной точки О (рис. 49)
М1(} = Р^Оа= Pi {Ob + d).
Момент силы Р2, приложенной
в точке В, относительно точки О
Сумма моментов сил пары отно-
относительно произвольно выбранней на
плоскости точки О равна:
Рис 49	° ° '
Эта сумма, не зависящая от положения центра и равная произве-
произведению модуля силы на плечо пары, определяет момент пары сил.
Момент пары положителен, если пара стремится повернуть пло-
плоскость чертежа против движения часовой стрелки, и отрицателен —
в обратном случае.
Таким образом, моментом пары сил называется взятое
со знаком плюс или минус произведение модуля силы на плечо
пары-
M—±Pd.	A3 4)
§ 14. Теорема о возможности перемещения пары сил
в плоскости ее действия
Пара сил, полученная путем перемещения заданной пары
в любое положение в плоскости ее действия, эквивалентна
заданной паре сил
Пусть к твердому тему приложена пара сил Р, Р' с плечом АВ
(рис. 50). Покажем, что не изменяя кинематического состояния тела,
пару можно перенести в плоскости ее действия, совместив ее плечо
с произвольно расположенным отрезком CD, где CD = АВ
Для этого в точках С и D восставим перпендикуляры к ог-
резку CD и продолжим их д© пересечения с линиями действия сил
заданной пары в точках К, Е, L, f — вершинах ромба. Перенесем
силы пары в вершины К и L и приложим в этих точках по две
противоположно направленные силы Р,, Р2, Р3, Р4~. равные п»
модулю Р и направленные по прямым, перпендикулярным к от-
отрезку CD. Построим в точке К на силах Р и Р2 и в точке L на
силах Р' и Р3 параллелограммы равных по модулю сил, т. е. ромбы.
38

Полученные равнодействующие Rj и R2 взаимно уравновеши-
уравновешиваются, так как они равны по модулю и направлены до диагонали
ромба KELI в противоположные стороны. Перенеся оставшиеся
силы Pj и Р4 по их линиям действия в точки С и D, получим пару
Рнс. 50.
сил в требуемом положении. Полученная пара сил эквивалентна за-
заданной, так как при доказательстве теоремы системы сил заменялись
только эквивалентными системами.
§ 15. Теорема об условии эквивалентности пар
Пары сил, моменты которых численно равны и одинаковы
по знаку, эквивалентны.
Рис. 51.
Пусть даны пары сил Р, Р' с плечом АВ, равным dv и Q, Q
с плечом CD, равным d2, моменты
наковы по знаку (рис. 51).
которых численно равны и оди-
39

Так как
M1=Pdv M2 = Qd2 и М1 — М2,
то
Pd^Qd, „ли -? = !?-.	A5.1)
Продолжим отрезок АВ и от точки В отложим отрезок BE =
= CD = d9. Приложим в точке Е взаимно уравновешивающиеся силы
Qi и Q2> по модулю равные Q и направленные перпендикулярно
к прямой BE. Сложив силу Р, приложенную в точке А, с силой Q2,
приложенной в точке Е, получим параллельную им равнодействую-
равнодействующую R (см. § 13), равную по модулю P-j-Q2, приложенную в точке В,
так как по условию A5.1) именно эта точка делит отрезок АЕ на
части, обратно пропорциональные модулям сил Р и Q2:
BE do. P
АВ ~~ di Q '
Тогда в точке В будут приложены две силы R и Р', направленные
по одной прямой в противоположные стороны. Равнодействующая
этих сил Q'2 по модулю равна их разности и направлена в сто-
сторону R. Сила Q'2 в точке В составит с силой Qt в точке Е пару
сил, которую, согласно § 14, можно перенести, совместив ее плечо
с отрезком CD.
Таким образом, рассматриваемая пара Р, Р' с плечом АВ будет
заменена эквивалентной ей парой Q, Q' с плечом CD, имеющей момент
той же величины и того же знака, как и момент пары Р, Р'.
Примечание. Основным параметром пары сил является ее момент.
Силы пары, приложенной к твердому телу, можно изменить, изменив одно-
одновременно ее плечо так, чтобы величина момента не изменилась; полученная
пара будет эквивалентна заданной.
§ 16. Теорема о сложении пар на плоскости
Момент пари сил, эквивалентной рассматриваемой системе
пар на плоскости, равен алгебраической сумме моментов
составляющих пар.
Пусть на твердое тело одновременно действуют несколько пар:
Pi, Pi", P2. Р2; Рз> Рз. плечи которых равны dv d2, d3.
Возьмем на плоскости произвольный отрезок длиной d (рис. 52)
и заменим заданные пары эквивалентными парами Qv Qj; Q2, Q^;
Q3, Qg с общим плечом d. Найдем модули сил эквивалентных пар
из соотношений:
40

Сложив силы, приложенные к каждому из концов отрезка АВ,
найдем модуль их равнодействующей:
Равнодействующие R, R' составляют пару сил, эквивалентную
системе заданных пар. Вычислим момент этой пары.
М = Rd = (Q, + Q2 — Qj) d = Qyd + Q2d —
Mx +
Из-
Извели к твердому телу приложены п пар, то момент эквивалент-
эквивалентной им пары определится по формуле
М = Му-\-М2-\- ... -\-Ма или M = '%Mi, A6.1)
т. е. момент эквивалентной пары равен алгебраической сумме мо-
моментов составляющих пар.
Рис. 52.
В случае равновесия системы пар на плоскости момент равно-
равнодействующей пары равняется нулю.
Условие равновесия пар на плоскости формулируется так:
Пары на плоскости уравновешиваются в том случае, если
алгебраическая сумма их моментов равна нулю
2мг = 0.	A6.2)
§ 17. Примеры на применение условия равновесия
пар на плоскости
Пример 8. Груз весом G = 50 н подвешен к канату, намотан-
намотанному на барабан радиусом г =10 см. Барабан удерживается парой
сил, приложенных к концам рукоятки длиной /= 1,25 м, скрепленной
41

с барабаном и лежащей в одной плоскости с веревкой. Определить
реакцию оси О барабана и "силы пары Р, Р', если они перпенди-
перпендикулярны к рукоятке (рис. 53а).
Решение. Рассмотрим равновесие сил, приложенных к барабану:
заданной вертикальной силы веса G, пары, составленной силами Р
и Р', и реакции Ro цилиндрического шарнира О, модуль и линия
действия которой не известны. Так как пару сил может уравновесить
только пара, то силы G и Ro должны составлять пару сил, уравно-
Линия действия силы G известна, реакцию Ro
шарнира О направим параллельно силе G
в противоположную ей сторону (рис. ЪЪб).
Модули сил должны быть равны, т. е.
R0 = G = 50 и.
Алгебраическая сумма моментов двух
пар сил, приложенных к барабану, должна
быть равна нулю:
вешиваемую парой Р, Р'
где / — плечо пары Р, Р', г
пары G, Ro.
Находим модули сил Р и Р'\
плечо
Рис. 53а.
Рис. 536.
50 • ОД
1,25
= 4 «.
Рис. 54э.
Пример 9. Балка длиной АВ = 10 м имеет шарнирно-неподвиж-
ную опору А и шарнирно-подвижную опору В с наклонной опорной
плоскостью, составляющей с горизон-
горизонтом угол а = 30°. На балку действуют
три пары сил, абсолютные величины
моментов которых равны jATj]=8 кн-м\
|.М2| —10 кн ¦ м; |Ж3| = 7 кн ¦ м.
Определить реакции опор (рис. 54а).
Решение. Рассмотрим равновесие
сил, приложенных к балке АВ: трех
заданных пар сил, реакции опоры RB,
направленной перпендикулярно к опор-
опорной плоскости, и реакции опоры R^,
линия действия которой не известна.
Так как заданная нагрузка состоит
только из пар сил, то реакции опор
RA и RB должны составить пару сил,
уравновешивающую заданные "пары.
Направим реакцию RA параллельно
реакции RB, чтобы силы RA и RB составили пару, направленную
в сторону, обратную движению часовой стрелки (рис. 546).
Рис. 546.
42

Воспользуемся условием равновесия четырех пар сил, приложен-
приложенных к балке:
Отсюда находим:
АВ cos 30°
= 0, где h =
8—10 + 7 1 „ со
, ——¦	'	— . . 	 	 I] 1-iV If LI
———	.			 ~		 \J fKJKJ fXtt/t
10-
Знак плюс в ответе указывает, что принятое направление реак-
реакций опор RA и RB совпадает с истинным.
R, = RR = 0,58 кн.
ГЛАВА IV
СИСТЕМА СИЛ, ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
§ 18. Приведение силы к заданному центру
Для сложения сил, произвольно расположенных на плоскости,
следует применять метод, предложенный французским ученым Пуансо,
заключающийся в приведении сил к заданному центру. Рассмотрим
сущность этого метода.
Рис. 55.
Дана сила Р, приложенная в точке А (рис. 55,а). Опустим из
центра О перпендикуляр на линию действия силы Р и определим ее
момент относительно этой точки:
Мо = Pd.
Приложим в точке О взаимно уравновешивающиеся силы Р' и Р",
параллельные силе Р и равные ей по модулю (рис. 55,6). Тогда по-
получим силу Р", геометрически равную силе Р, приложенную в центре
приведения, и пару сил, составленную силами Р и Р', момент
которой М = Pd равен моменту силы Р относительно центра
43

приведения О. Таким образом, метод Пуансо заключается в замене
силы Р эквивалентной ей совокупностью — геометрически равной ей
силой Р", приложенной в центре приведения, и парой сил с моментом,
равным моменту силы относительно центра приведения (рис. 55,в).
§ 19. Приведение системы сил, произвольно расположенных
на плоскости, к силе и паре. Главный вектор и главный момент
Применим метод приведения силы к заданному центру к сложе-
сложению сил, произвольно расположенных на плоскости (рис. 56). Пусть
даны силы Рх, Р2 и Р3, приложенные в точках Av А2 и А3. Примем
за центр приведения произвольную точку О и приведем все силы
Рис. 56.
к этому центру. Складывая силы Pi, Р
ника, получим их равнодействующую
сумме сил Pj, P2, Р3:
, Рз по правилу многоуголь-
многоугольR*, равную геометрической
Геометрическая сумма всех
вектором системы сил.
Складывая пары сил Pi, Р
равны моментам сил Pj, P2, Р3
сил системы называется главным
Рг, Рг; Рз. Рз. моменты которых
относительно центра приведения О,
получим эквивалентную им пару сил. Момент этой пары:
где
44

Как видно, момент пары сил, эквивалентной системе пар, появив-
появившихся в результате приведения сил к центру О, равен главному
моменту рассматриваемой системы сил относительно центра приве-
приведения. Распространяя полученные результаты приведения данной
системы сил на п сил, имеем:
.. +рп, или R* = 2p,;
М = Мп = М, +Ж2 + ... -\-Мп , или M = J^iMl .
° 'о о	"о	о
Таким образом, силы, произвольно расположенные на пло-
плоскости, можно привести к одной силе, приложенной в центре
приведения, равной главному вектору данной системы сил, а
к паре сил с моментом, равным главному моменту этой
системы сил относительно центра приведения.
Выбор центра приведения не отражается на модуле и направле-
направлении главного вектора, но влияет на величину и знак главного момента.
Модуль и направление главного вектора плоской системы сил
определяются по способу проекций так же, как определяется модуль
и направление равнодействующей сходящихся сил (см. § 10):
х = ^х- к = 2 к,,
cos (R*. i) = -?-; cos (R*. j) = -^.
§ 20. Возможные случаи приведения сил, произвольно
расположенных на плоскости
Рассмотрим возможные случаи приведения сил, произвольно рас-
расположенных на плоскости.
Случай I. R* = 0; M = 0.
В этом случае силы взаимно уравновешиваются.
Случай II. R* = 0; МФО.
В этом случае заданная система сил приводится к паре сил, мо-
момент которой равен главному моменту сил относительно центра при-
приведения. Если система сил приводится к паре сил, то главные
моменты данной системы сил относительно всех точек плоскости
равны по величине и совпадают по знаку.
Случай HI. R*^=0; Л1 = 0.
В этом случае заданная система сил приводится к равнодействую-
равнодействующей силе, равной главному вектору сил, линия действия которой
проходит через центр приведения. Действительно, если сила R*. рав-
равная главному вектору, при отсутствии пары эквивалентна данной
системе сил, то она является равнодействующей этой системы сил.
Случай IV. Я*ФО; МФО.
Покажем, что в этом случае заданная система сил также приво-
приводится к одной силе — равнодействующей данной системы сил.
45

Пусть, например, данная система сил приведена к силе R* = 2'V
приложенной в центре приведения О и к паре сил с моментом
М = 2-М/0 (Рис- 57'а>-
Выберем силы пары R*, R равными по модулю R*. Тогда плечо
этой пары следует взять равным
Одну из сил пары R* приложим в точке О, направив ее противо-
противоположно главному вектору R* (рис. 57 ,б), тогда как другую силу
Линия дейстЗия
равнодействующей
Рис. 57.
пары R приложим в точке К на отрезке OK = d, отложенном пер-
перпендикулярно к линии действия силы R* в ту сторону, чтобы пара
Rj, R стремилась вращать плоскость чертежа против движения часо-
часовой стрелки. Силы R* и R*, приложенные в центре приведения О,
как равные и противоположно направленные, уравновешиваются, и
рассматриваемая система сил приводится к одной силе R, равной
главному вектору сил и приложенной в точке К- Эта сила является
равнодействующей данной системы сил (рис. 57,е).
На основе рассмотренных выше случаев приведения можно сде-
сделать следующий вывод.
Если силы, произвольно расположенные на плоскости, не
уравновешиваются, то их можно привести или к одной силе
или к паре сил.
Теорема Вариньона о моменте равнодействующей плоской
системы сил. Момент равнодействующей силы относительно
любой точки на плоскости равен алгебраической сумме мо-
моментов составляющих сил относительно той же точки.
Определим момент равнодействующей силы R, приложенной
в точке К< относительно произвольно выбранного центра приведе-
приведения О (рис. 57,в).
Мо (R) = Rd,
46

но
Тогда
^f? и d =
м
что и требовалось доказать.
§ 21. Уравнения равновесия системы сил, произвольно
расположенных на плоскости
Для сил, произвольно расположенных на плоскости, имеются два
условия равновесия:
B1.1)
Из второго условия B1.1) следует, что X='^iXl=Q и К=2 К4=0.
Таким образом, два условия равновесия сил, произвольно располо-
расположенных на плоскости, можно выразить в виде системы трех уравнений:
B1.2)
Эти уравнения называются основными уравнениями равновесия
плоской системы сил A система уравнений). Центр моментов и на-
направление координатных осей для этой системы уравнений можно
выбирать произвольно.
Существуют и две другие системы трех уравнений равновесия
сил (II и III системы):
111.
B1.4)
При этом в системе II ось и не должна быть перпендикулярна
прямой, проходящей через точки А и В, а в системе III точки А, В а С
не должны лежать на одной прямой. Покажем, что при этих усло-
условиях системы II и III являются уравнениями равновесия плоской
системы сил.
47

Пусть дана система сил, произвольно расположенных на плоско-
плоскости, Pj, Р2	Рп (рис. 58), удовлетворяющая трем уравнениям B1.3):
причем ось и не перпендикулярна прямой АВ.
Известно, что неуравновешивающиеся силы, произвольно распо-
расположенные на плоскости, приводятся или к паре сил или к равнодей-
равнодействующей (см. § 20).
Так как главные моменты системы сил относительно двух центров
равны нулю, то рассматриваемая система сил не приводится к паре
сил. При наличии пары
главные моменты системы
сил относительно всех то-
точек плоскости одинаковы и
равны моменту этой пары
(см. теорему о моменте пары
сил § 13).
Если силы приводятся
к равнодействующей силе,
то ее линия действия должна
проходить через точки А
и В, так как на основании
теоремы Вариньона
MA(R) = 2M, =0;
Рис. 58.	Но проекция равнодействую-
равнодействующей на любую ось равна
сумме проекций составляющих сил, т. е. /?cosa = 2 Ut = Q, где
cosa=fcO, следовательно, предполагаемая равнодействующая R=:Q.
Таким образом, II система уравнений показывает, что данная
система сил не приводится ни к паре, ни к равнодействующей, сле-
следовательно, она уравновешивается. В случае, если ось и перпенди-
перпендикулярна прямой АВ, то II система уравнений справедлива и при нали-
наличии равнодействующей, для которой АВ является линией действия.
Пусть плоская система сил удовлетворяет трем уравнениям:
48

причем точки А, В и С не лежат на одной прямой. В этом случае
силы не приводятся к паре сил, так как главные моменты этих сил
относительно трех центров равны нулю. Силы не приводятся и
к равнодействующей силе, так как если она существует, то линия
ее действия не может пройти через три точки, не лежащие на одной
прямой. Следовательно, рассматриваемая система сил уравновеши-
уравновешивается и III система уравнений является системой уравнений равно-
равновесия плоской системы сил.
Итак, установлено, что число уравнений равновесия плоской
системы сил равно трем. При помощи этих уравнений можно решать
задачи статики на плоскости, в которых число неизвестных не пре-
превышает трех.
§ 22. Сложение параллельных сил на плоскости.
Уравнения равновесия параллельных сил.
Положим, что даны параллельные силы Pv Р2, ..., Р„, распо-
расположенные на плоскости и приложенные в точках Av А2, ..., Ап.
Приведем силы к произвольному центру О. Получим в этом
центре силу R*, равную главному вектору, и пару сил с моментом М.
Вычислим проекции главного вектора на координатные оси х, у,
направив ось у параллельно силам:
где Yl=-\-Pi, если направление силы Рг совпадает с направлением
оси у, и Yt = — Pt, если направления силы Pf и оси у противопо-
противоположны. Так как X = 0, то главный вектор R направлен по оси у.
При К =2 — -^г > 0 направление глав-
главного вектора R* совпадает с направлением
оси у, а при Y—'2i±. Pt<i0 направле-
направление R* противоположно направлению оси.
Таким образом, имеем:
т. е. главный вектор системы параллель-
параллельных сил параллелен силам, его модуль
равен абсолютному значению алгебра-
алгебраической суммы проекций сил на ось, па-
параллельную силам, а его направление	_ ._
определяется знаком этой суммы.
Момент пары сил, эквивалентной системе пар, появившихся в ре-
результате приведения, равен главному моменту параллельных сил отно-
относительно центра приведения:
или
4 А. А. Яблонский
49

/////
Для параллельных сил на плоскости возможны все те же случаи
приведения, что и для сил, произвольно расположенных на плоскости
(§ 20). Параллельные силы, если они не уравновешиваются, можно
привести или одной силе, или к паре сил.
Для системы параллельных сил на плоскости имеем два усло-
условия равновесия:
Для получения уравнений равновесия одну из осей координат;
например ось у, направляют параллельно силам. Тогда все силы
проектируются на ось у, а проекция каждой силы на ось х равна
нулю. Два условия равновесия системы параллельных сил на плоскости
можно выразить в виде двух уравнений:
Эти уравнения называются основ-
основными уравнениями равновесия парал-
параллельных сил на плоскости (I система
уравнений). Центр моментов для этой
системы уравнений можно выбирать
А3°	"•»•	произвольно.
4t»f	Существует и другая система двух
\ уравнений равновесия параллельных сил-
Рис 60	Н- 2Ж ==0;
При этом прямая АВ не должна быть параллельна силам. II си-
система уравнений показывает, что силы не приводятся к паре сит
(рис. 60) и к равнодействующей силе, так как линия ее действия,
параллельная силам, не может пройти через точки А и В.
§ 23. Статически определенные и статически
неопределенные задачи. Определение реакций
внешних и внутренних связей
системы взаимосвязанных тел
Статически определенными называют задачи, которые можно
решать методами статики твердого тела, т. е. задачи, в которых
число неизвестных не превышает числа уравнений равновесия сил.
Статически неопределенными называют задачи с числом не-
неизвестных, превышающим число уравнений равновесия сил, т. е.
задачи, которые нельзя решать методами статики твердого тела и
для решения которых нужно учитывать деформации тела, обусло-
обусловленные внешними нагрузками.
50

Для решения задач на равновесие сил, приложенных к твердому
телу и лежащих в одной плоскости, можно пользоваться тремя урав-
уравнениями равновесия сил. Такая задача статически определенна, если
число неизвестных не больше трех. Если к телу приложена система
параллельных сил, то можно воспользоваться только двумя уравне-
уравнениями равновесия с«л. Эта задача статически определенна, если число
неизвестных в ней не превышает двух.
Для параллельных сил, приложенных к системе п тел, можно
составить по два уравнения равновесия для сил, приложенных
к каждому из этих тел, т. е. всего 2й уравнений равновесия. Если же
на эту систему действуют силы, произвольно расположенные на пло-
плоскости, то общее число уравнений равновесия сил, приложенных
к системе п тел, равно Зге.
Рассмотрим некоторые У
статически определенные
и статически неопреде- у,,
ленные задачи, в которых
по заданным силам тре-
требуется определить реак-
реакции опор.
На рис. 61а изобра-	Рис 61а.
жена балка на двух опо-
опорах, находящаяся под действием двух заданных непараллельных сил
Р и Q. Так как опора А неподвижна и линия действия ее реакции не
известна, то реакция должна быть разложена на две составляющие
по осям х и у. Если будут найдены эти составляющие Хд и YA,
то модуль и направление реакции RA определятся согласно § 9.
Реакция опоры В как шарнирной опоры на катках направлена пер-
перпендикулярно к опорной плоскости и необходимо определить лишь
ее модуль. Общее число неизвестных величин равно трем, т. е. числу
уравнений равновесия сил.
Эта задача статически
(определенна.
D	I р	На рис. 616 изобра-
g I х8 х жена балка с двумя непо-
У 1'
У
движными опорами, на-
находящаяся под действием
Р 616	сил Р и Q-
Реакцию каждой из
этих опор можно опреде-
определить только по двум ее составляющим по осям х и у. В этой задаче
имеем 4 неизвестных и 3 уравнения равновесия сил. Следовательно,
задача является статически неопределенной.
На рис. 62 изображена двухшарнирная арочная ферма, нагру-
нагруженная силами Р и Q. Пяты арки шарнирно прикреплены к непод-
неподвижным опорам А и В. Реакции этих опор определяются по двум
составляющим по осям х а у. Задача содержит 4 неизвестных,
4*	51

а число уравнений, в которые входят неизвестные, равно трем, т. е.
она статически неопределенна.
Применяются конструкции, представляющие собой систему от-
отдельных твердых тел, связанных между собой. Примером такой
конструкции является трехшарнирная арка (рис. 63). В такой кон-
конструкции связи, соединяющие ее отдельные части, называются внут-
внутренними (на рис. 63 шарнир С), а связи, соединяющие ее с телами,
Рис. 62.
в нее не входящими (опорами), называются внешними (на рис. 63
шарниры А и В).
Для определения реакций связей такую конструкцию мысленно
расчленяют на отдельные тела и каждое тело рассматривают как
Рис. 63.
свободное, находящееся под действием задаваемых сил и реакций
внешних и внутренних связей.
Для сил, приложенных к каждому телу, составляют уравнения
равновесия. Если число неизвестных сил не превышает числа урав-
уравнений равновесия, то задача статически определенна.
52

Так, на левую полуарку системы, изображенной на рис. 63, дей-
действуют: задаваемая сила Р, реакция внешней связи — шарнира А
в виде составляющих ХА, УА и реакция внутренней связи шарнира С
в виде составляющих Хс и Yc. Соответственно на правую полуарку
действуют силы Q, X?, Yc, X^., Y^. При этом реакции внутренних
связей попарно равны по модулю и противоположны по направлению,
т. е. X ~^=^ X q.
Составив по три уравнения равновесия сил, приложенных к каждой
полуарке, получим шесть уравнений, содержащих шесть неизвестных
величин ХА, YА, Xв, Y в, Хс, Ус, т. е. данная задача статически
определенна. Так решены примеры 12 и 15.
Однако, реакции опор трехшарнирной арки (рис. 63) удобнее
определять так, как это сделано в примере 16.
Рассматривая арку как одно твердое тело, составляют три урав-
уравнения равновесия действующих на нее задаваемых сил Р и Q и
реакций внешних связей ХА, \А, Хв и YB. Затем, расчленив ее,
составляют три уравнения равновесия сил, приложенных к одной
части, например, левой — Р, ХЛ, YA, Xc, Yc.
В этом случае система уравнений решается проще и реакции
внутренних связей определяются в последнюю очередь.
§ 24. Примеры на равновесие параллельных
сил на плоскости
Пример 10. Однородная горизонтальная балка АВ, весом E=2 кн,
опирается на стену в точках В и D. Вес подвешенного груза Р = 1 кн.
Размеры: ЛВ = 4л, DB = 0,5 м.
Определить реакции опор D и В
(рис. 64а).
Решение. Руководствуемся
изложенным выше планом реше-
решения ,задач статики, рассматривая
равновесие сил, приложенных
к балке АВ.	а	С
г i	. —
Рис. 64а.
Рис. 646
1.	Показываем действующие на балку заданные силы: вес груза Р
в точке А и вес балки G в середине балки С (рис. 646).
2.	Освобождаем балку от связей, заменяя их действие реакциями
опор RB и RD, направленными перпендикулярно к поверхности балки.
53

3. К полученной системе вертикальных сил Р, О, RD, Ra, дей-
действующих на балку АВ, применяем условия равновесия сил в виде
двух уравнений равновесия параллельных сил на плоскости:
При составлении алгебраической суммы моментов сил относительно
точки пользуемся правилом знаков, изложенным в § 12. При этом
сумму моментов сил составляем относительно точки, в которой при-
приложена одна из неизвестных сил. В этом случае сила, приложенная
в этой точке не имеет момента относительно нее и уравнение
,, содержит только одну неизвестную вели-
3 чину.
R'd Составляем сумму моментов сил относи-
относительно точки В:
2Л1, =0, Р-ВА-\-О- ВС— RD.BD = 0.
При составлении алгебраической суммы
вертикальных сил условимся силы, напра-
направленные вверх, брать со знаком плюс,
а направленные вниз — со знаком минус:
т
4. Из первого уравнения определяем мо-
модуль реакции опоры RD:
Рис. 64в.
BD
0,5
Определив RD, находим из второго уравнения модуль реакции
опоры Яв:
А	С
_)-88 = 76 кн-
Рис. 64г.
Проведем анализ полученных результатов.
Значение обеих реакций получено со знаком
плюс потому, что на расчетной схеме (рис. 646) указано действи-
действительное направление этих реакций: вверх для реакции RD и вниз
для реакции RB. Воздействие двух опор D и В на балку можно
представить в следующем виде. Разбиваем реакцию RD на две силы
Ц'о и Rd такого же направления, имеющие модули (рис. 64в):
R'D = RB=7Q кн;
= Rd — Rb=\2 кн.
Силы
и Rb составляют пару сил с моментом
I м I == R'd ¦ DB = 76 • 0,5 = 38 кн ¦ м.
54

Кроме пары сил, имеется вертикальная реакция Ro [Rd— 12 кн),
приложенная в точке D и направленная вверх (рис. 64г).
Пример 11. Горизонтальная балка АВ, длиной I =1,2 м, под-
поддерживающая балкон, заделана в стену. На балку действует равно-
равномерно распределенная нагрузка интенсивностью ^ = 1,25 кн/м. Опре-
Определить реакции заделки (рис. 65а).
Решение. Рассматриваем равновесие сил, приложенных
к балке АВ. Равномерно распределенную нагрузку можно заменить
сосредоточенной силой Q — равнодействующей системы равных парал-
ч
/~
lilllllllllllllllflUIIIIIHIIIIIIIIIIU
1
IIIIIIIIIIHIII
в
1
1
Рис. 65а.
Рис
лельвых сил, приложенной в середине загруженного участка АВ.
Модуль этой силы определяется:
Q = ql = 1,25 кн/м ¦ 1,2 м = 1,5 «й.
Реакции заделки представляют собой силы, распределенные по
всей опорной площади, причем на нижнюю поверхность балки дей-
действуют силы, направленные вверх, а на верхнюю—силы, направленные
вниз. Из этой системы сил образуется вертикальная реакция опоры
(если все заданные силы вертикальны) и реактивная пара сил, пре-
препятствующая вращению балки вокруг закрепленного конца (см. при-
пример 10). Момент этой пары сил называется опорным моментом.
Показываем на схеме (рис. 656) реакцию заделки R^ и реактивную
пару с моментом М. Условимся направлять реакцию опоры вверх,
а реактивную пару против движения часовой стрелки. Истинное их
направление определим по знаку ответа.
Составляем два уравнения равновесия параллельных сил на пло-
плоскости. При этом сумму моментов всех сил составляем относительно
точки В, так как в этой точке приложена неизвестная реакция
опоры Rjj. Сумму моментов сил реактивной пары относительно
точки В включаем в уравнение в виде момента пары М, согласно § 13.
=—1>5> 0>6==~0>9
Момент получен со знаком минус, следовательно, реактивная
пара сил имеет направление, противоположное принятому на рас-
55

четной схеме, т. е. пара направлена в сторону движения часовой
стрелки.
II. Ц/>, = ();
RB = Q=l,5 кн.
Знак плюс показывает, что реакция RB направлена так, как при-
принято на расчетной схеме, т. е. вверх.
Пример 12. Балка моста состоит из двух частей AD и DC,
соединенных между собой шарниром D. Собственный вес погонного
метра моста qx= 10 кн/м, вес погонного метра поезда #2 = 20 кн/м.
Определить реакции опор балки при условии, что поезд находится
на участке АЕ (рис. 66а).
28м
Юм
20м
20м
Рис. бба.
Решение. Рассматриваем равновесие сил, приложенных
к балке АС: равномерно распределенной нагрузки от собственного
веса балки, веса поезда и реакций опор R4, RB и Rc. Так как
реакции опор А и В и равномерно распределенная нагрузка вер-
вертикальны, то уравновешивающая их реакция неподвижной шарнирной
опоры С должна быть тоже вертикальна.
20 м
At
9,
10м
15м
«в
В
30м
1 Qi
% г
Е
20м
25м
Рис. 666.
Рис. 66в.
Таким образом, имеются три неизвестные вертикальные реакции
опор, RA, RB и Rc. Определить их модули из двух уравнений равно-
равновесия параллельных сил, приложенных к балке АС, невозможно. Так
как балка АС представляет собой систему двух тел, соединенных
шарниром D, то расчленяем ее на части AD и DC и рассматриваем
равновесие сил, приложенных к каждой части (рис. 66 б,в).
56

Заменяем равномерно распределенную нагрузку сосредоточенными
силами. Нагрузка на участке AD
Q1 = Dl + q2) AD = 30 • 20 = 600 кн.
Нагрузка на участке DC от собственного веса
<22 = qi ¦ DC = 10 • 50 = 500 кн.
Нагрузка на участке DE от веса поезда
<23 = q2. DE = 20 • 30 —. 600 кн.
Каждая из сил Qv Q2, Q3 приложена в середине соответствующего
участка. На балку AD, кроме заданной силы Qv действуют реакция
опоры RA и реакция RD правой балки в точке D. Очевидно, что
обе реакции направлены вверх. На балку DC, кроме заданных сил
Q2 и Q3, действуют реакции RB и Rc и реакция HD левой балки
в точке D, которая равна по модулю силе RD и направлена про-
противоположно ей, т. е. вниз. Реакции RB и Rc условно направляем
вверх.
К балке AD приложены две неизвестные силы R4 и Ro,
к балке DC — три неизвестные силы Ro, Rs, Rc. Поэтому составим
сначала два уравнения равновесия параллельных сил, действующих
на балку AD:
RA = Q1 — RD = 600— 300 = 300 кн.
Сила Ro, приложенная к балке DC в точке D, равна по модулю
силе Rfl, т. е. RD = RD = 300 кн.
Таким образом, из сил, приложенных к балке DC, остались не-
неизвестными только реакции опор RB и Rc. Определяем их модули
из двух уравнений равновесия сил, приложенных к балке DC.
Центр моментов берем в точке приложения одной из неизвестных
сил, например В:
= 187.5 «я.
2^ = 0; R'D- 10-Q3-5-Q2
— R' ¦ 10 + Q3 • 5+ Q2 ¦ 15 —300 • 10+600 ¦ 5+500 • 15
40	=	40
' B — Q3 — Q2 + Rc = Q;
300 + 600-+500—187,5= 1212,5 кн.
Так как величины всех сил получены со знаком плюс, то их на-
направления указанные на схеме (рис. 666, в), совпадают с действи-
действительными.
57

§ 25. Примеры на равновесие
плоской системы сил
Пример 13. Определить реакции опор консольной балки АВ,
¦весом 0=15 кн, находящейся под действием сил Рг=40 кн, Pi= 30 кн,
и пары с моментом |уИ|'=30 кн- м. Известны размеры: Ли = 9 м,
АС = 1,5 м, CD = 6 м СЕ = 2 м, (рис. 67а).
Л В
>
Рис. 67а.
Решение. Решаем задачу согласно общему плану решения за-
задач статики, рассматривая равновесие плоской системы сил, дейст-
действующей на балку АВ.
1. Показываем действующие на балку заданные силы: "Pv P2,
пару сил М, а также вес балки G, который прикладываем в сере-
середине О длины АВ, считая балку однородной (рис. 676).
U 0
С Хс
тс
Рис. 676.
2. Мысленно отбрасываем связи: неподвижную шарнирную опору С
и шарнирную опору на катках D, заменяя их действие соответствую-
соответствующими реакциями. Реакция опоры RD направлена перпендикулярно
к опорной плоскости, т. е. вертикально. Линия действия реакции
опоры С не известна. Если на рассматриваемое тело действуют силы,
произвольно расположенные на плоскости, то необходимо провести
оси координат и разложить реакцию неизвестного направления на две
составляющие, направленные вдоль осей координат. Оси могут иметь
любое направление, выбор их направления обусловлен характером
задачи. В рассматриваемой задаче направляем ось х вдоль горизон-
горизонтальной оси балки вправо, а ось у вертикально вверх. Направления

составляющих Хс и Yc реакции опоры С принимаем совпадающими-
с направлениями осей координат. В случае, когда принятое направ-
направление не совпадает с действительным, ответ, полученный для соот-
соответствующей силы при решении задачи, имеет знак минус. Когда
будут найдены величины Хс и Кс, модуль и направление реакции
опоры С определим согласно § 9.
3. Для плоской системы сил Pj, P2, G, Xc, Yc, Ro и пары сил
с моментом М, действующих на балку, составляем три уравнения
равновесия:
Цл1,0 = о. 23** = о. 2к, = о.
Из трех уравнений можно найти три неизвестные величины Хс,
Yc, RD. Необходимо помнить, что до составления уравнений равно-
равновесия сил на расчетной схеме должны быть показаны все силы,
действующие на рассматриваемое тело, как известные, так и неиз-
неизвестные, как это выполнено на рис. 676. Эта расчетная схема не изме-
изменяется ни в процессе решения задачи, ни после него, так как урав-
уравнения равновесия сил составляются именно по этой схеме и только
ей соответствуют. При составлении первого уравнения за центр
моментов принимается, как правило, точка, относительно которой
моменты наибольшего числа неизвестных сил равны нулю, т. е.
в данной задаче точка С, в которой приложены две неизвестные
силы Хс и Yc.
Составим уравнения равновесия:
2 М1С = 0; Р1 ¦ СК — Р2 ¦ СЕ — О - СО -\- RD • CD — \ М | = 0;
2К, = О; — /Vos30°+Kc — P2 —
Здесь СК — перпендикуляр, опущенный из центра моментов С
на линию действия силы Р,, длина которого равна плечу силы Pt
относительно С
СК — AC sin 60° = 1,5 • 0,866 = 1,3 м.
4. Из трех уравнений равновесия сил определяем искомые реак-
реакции. Так как неизвестные силы Хс и Yc не имеют момента отно-
относительно точки С, то из первого уравнения определяется RD:
— 40-1,34-30.2+15-3 + 30 83 1OO
Из второго уравнения находим
ХС = Р cos 60° = 40 • 0,5 = 20 кн.
59

Из третьего уравнения получаем
G — RD=40 ¦ 0,866-4-30+15—13,8 = 65,8кн.
Все три ответа имеют знак плюс, следовательно, принятые на-
направления сил Хс, Yc и RD совпадают с действительными.
Найдем модуль и направление реакции опоры С (рис. 67в):
:==l/202+65,82 = 68,8
20
: 0.291;
Yr 65,8
= -/r- = soo =0,956;
cos(Rc, /) = -p^- =
cos(Rc,
/_(RC, *)«73°, 21 (Rc. Л «17°.
В дальнейшем условимся заканчивать решение
задачи определением модулей и направлений соста-
составляющих X и Y реакции опоры.
Примечание. Если в рассматриваемую систему сил входит пара
сил, то при составлении уравнений проекций следует помнить, что сумма
проекций сил, составляющих пару, hi
любую ось равна нулю (рис. 68).
Пример 14. Однородный бру-
брусок АВ весом G—16« опирается
концом А на гладкий горизон-
горизонтальный пол и промежуточной точ-
ГУ	i
i i	i
i i	i
i i	i
Рис. 68.
Рис. 69а.
кой D — на ребро. Брусок удерживается под углом а = 60° к гори-
горизонтали веревкой EF, перпендикулярной к оси бруска, причем
Определить натяжение веревки EF и реакции опор А и D
(рис. 69а).
Решение. Рассматриваем равновесие сил, приложенных
к бруску АВ. Прикладываем к бруску в середине его длины О
заданную силу—вес бруска О (рис. 696). Освобождая брусок от
трех связей, прикладываем к бруску их реакции: реакцию пола RA,
реакцию S нити EF и реакцию ребра RD. Направления всех трех
60

реакций известны, а их модули можно определить из трех уравне-
уравнений равновесия плоской системы сил, действующей на брусок.
В двух первых примерах сумма моментов сил составлена отно-
относительно точки приложения двух неизвестных сил. Из каждого
уравнения равновесия определена одна из неизвестных сил и не
требуется совместного решения системы уравнений с несколькими
неизвестными. В рассматриваемом примере такой точки нет, так как
три неизвестные реакции приложены к бруску в различных точках.
Найдем точку пересечения линий действия двух неизвестных сил,
например S и КА и примем ее за центр моментов. Тогда силы S и RA
не будут иметь моментов относительно этой точки К. Плечи силы RD и
силы G найдем, опустив перпендикуляры из точки К на линии действия
этих сил. Обозначим длину бруска I, тогда:
Оси координат проведем, как указано
на рис. 696.
Уравнения равновесия сил имеют вид:
1. 2M,7c = 0; G ~ cos 60° — RD ~ = 0.
Сокращая обе части уравнения на Z, оп-
определяем RD:
Отсюда
1
о V у 	|
О. / I / ; ¦	 У
= G = l6 к.
2,	RAzos60° — S —
— Gcos60°+/?D = 0.
Так как RA = G, то — S-\-RD =
2
Рис. 696.
= /?o=12 и.
o
Проанализировав результаты, увидим, что силы G и R^ состав-
составляют пару сил, а силы RB и S — другую пару. Нетрудно убедиться
в том, что моменты этих пар равны по величине и противоположны
по знаку.
Примечание. Иногда трудно определить моменты сил относительно
точки пересечения линий действия двух неизвестных сил. Тогда за центр
моментов принимают точку приложения одной неизвестной силы и уравне-
уравнение моментов, содержащее две неизвестные величины, решается совместно
с уравнениями проекций.
Пример 15. Груз весом G — 280 н подвешен в точке Е к гори-
горизонтальной балке АВ весом О1=160н. Балка АВ укреплена при
помощи шарнира А и свободно опирается концом В на балку CD
весом G2= 120 н. Балка CD имеет шарнир С и концом D опирается
61

на гладкую вертикальную стену; балки однородные, поверхность их
гладкая. Расстояния АЕ = -^АВ, CB = -^CD, Определить реакции
опор А, С и D (рис. 70а).
Решение. Неизвестные по направлению реакции шарниров А
и С разложим на составляющие ХА, YA, Хс, Yc. Реакция стены R^
направлена перпендикулярно к стене. Пять неизвестных величин X А,
YА, Хс, Yc и RD нельзя определить из трех уравнений равновесия
сил, приложенных к системе двух балок. Произведем расчленение
балок, т. е. рассмотрим отдельно равновесие сил, приложенных
к каждой из балок.
Рис. 70а.
На балку АВ действуют заданные силы G и Qv составляю-
составляющие ХА, \А реакции шарнира А и реакция RB балки CD, направ-
направленная по нормали к ее поверхности (рис. 706).
На балку CD действуют вес балки G2> приложенный в сере-
середине CD, реакция RB балки АВ, равная по модулю реакции RB и
направленная противоположно ей, составляющие Хс, Yc реакции
шарнира С и реакция стены Ro (рис. 706). В- число внешних сил,
приложенных к каждой балке, входят силы Ив — — Rb. выражаю-
выражающие взаимодействие балок. Эти силы для системы балок являются
внутренними.
Составим по три уравнения равновесия сил, действующих на
каждую балку, и определим шесть неизвестных величин XА. YA, Xc,
Для сил, приложенных к балке, АВ, получим:
1.
а = 0; — GjAB — G^ AB-\-RBABsin30° = 0;
, = 0; ХА — RB cos 30° = 0;
, = 0; YA — G — O1-f-/?
62

Для сил, приложенных к балке CD, получим:
II. ^ М1с = 0; — R'B 1 CD — G2 1 CD cos 60° + /?OCD sin 60° = 0;
ZiY i — u> 'с
Из системы I уравнений найдем:
1 - ¦ Х
Rr == —
^.280+1-160
= 300 я;
sin 30" ~~	0,5
ХА = RB cos 30° = 300 • 0,866 = 260 «;
YA == G +- Gx — RB cos 60° = 280 H- 160 — 300 - 0,5 = 290 «.
Учитывая, что Rs = —R^, т. е. Яд = /?в = 300 «, из системы II
уравнений найдем:
1-300 + 1-120-0.5
0^866
= 150 к;
Arc = — R'bcos 30°+-RD = — 300-0,866+ 150 = —ПО к;
Yc = /?^ cos 60° -+ G2 = 300 • 0,5 + ^20 = 27'0 «.
Знаки ответов показывают, что сила Хс направлена влево, а дей-
действительные направления остальных сил совпадают с указанными на
схеме.
Пример 16. Мост состоит из двух частей, связанных между собой
шарниром С и прикрепленных к береговым уетоям шарнирами А и В.
5м
\2м
"г.
1,5м
e
tfi»
Ъ %
Рис. 71а.
Вес каждой части моста Gx = G2 = 130 кн, их центры тяжести D и Е.
На мосту находятся два груза Ql= 10 кн и Q2 = 40 кн. Все размеры
указаны на рис. 71а. Определить давление в шарнире С и реакции
шарниров А и В.
63

Решение. Так как реакции шарниров А и В не известны по
направлению, то они должны быть разложены на составляющие Хд,
\А, Хв, \в- Эти четыре неизвестные силы нельзя определить из трех
уравнений равновесия плоской системы сил, приложенной к мосту,
рассматриваемому как одно тело (рис. 716). Так как мост пред-
представляет собой совокупность двух тел, соединенных шарниром С, то
можно произвести его расчленение и рассмотреть равновесие сил.
	X
Рис.
приложенных к каждой части моста. В число внешних сил, действующих
на каждую часть моста, войдут реакции отброшенной части Хс = — Х'с
и Yc — — Y^,, приложенные в точке С, которые для всего моста
являются внутренними силами (рис. 71 в).
A
У
у
/
X
"?' 'f—-¦
С •
v'
\
Рис. 71в.
Для плоских систем сил, приложенных к каждой части моста,
можно составить по три уравнения равновесия и из шести уравнений
определить шесть неизвестных величин: ХА, YА, Xв, YB, Xc, Yс.
Однако в этой задаче система шести уравнений получается проще,
если составить сначала три уравнения равновесия сил, приложенных
ко всему мосту, рассматриваемому как одно тело, а потом — три
уравнения равновесия сил, приложенных к одной части.
Рассматриваем равновесие сил, приложенных к мосту, как к одному
телу. Прикладываем к мосту заданные силы Qv G2, Qi и Q2 (рис, 716).
Заменяем действие связей — шарниров А и В — соответствующими
64

реакциями ХА, YA, Хв, YB. Составляем три уравнения равновесия
плоской системы сил, приложенной к мосту:
= 0; — О,- 1,5 — Qr5 — Q2. 11— О2 • 12,5+ YB- 14 = 0;
V —
130- 1,5+ 10-5 + 40-11 + 130-12,5 2310
_	и		.—-д-
г = 0; YA~ Q, — <?,— 02-О2+Кя = 0;
Третье уравнение содержит две неизвестные и на этом этапе
решения не используется.
Рассматриваем равновесие сил, приложенных к левой части
моста. Прикладываем к левой части моста заданные силы Gj и Qt
и реакции связей Хл, YA, Хс и Yc, где Хс, Yc — реакции отбро-
отброшенной правой части моста. К правой части будут приложены
силы Gv Qy XB, YB, X'c, Y'c, где Х^, Y^, — реакции левой части
моста (рис. 71 в).
Составляем три уравнения равновесия сил, приложенных к левой,
части моста:
YA.7 — Q1.2—GV5,5 145-7 —10-2 —130-5,5 280 _
XА =	^	=	^	= -|- = 70 кн.
2Г( = 0; YA-Ol-Q1 + Yc = 0;
Yc~G1-JrQ1 — YA= 130+-10— 145 = — 5 кн.
Знаки минус при величинах Хс и Кс показывают, что истинные
направления сил Хс и Yc, приложенных в точке С к левой части
моста, противоположны показанным на схеме. Следовательно, истин-
истинные направления сил Х'с и Y'c, приложенных к правой части, тоже
противоположны направлениям, показанным на схеме.
Из третьего уравнения первой системы находим
Хв~ — Хд = — 70/ся.
Таким образом, горизонтальная составляющая Хв реакции шар-
шарнира В направлена не вправо, а влево.
5 А. А. Яблонский	C5

§ 26. Определение усилий в стержнях ферм по способу Риттера
Применим метод сечений к определению усилий в стержнях пло-
плоских ферм. Рассмотрим ферму, изображенную на рис. 72 а. На ферму
действуют вертикальные внешние силы: заданная сила Р = 60к« и
реакции опор /?д = 40 кн и RB — 20 кн.
А <
1 у
Ч
f >
2
а
\з
1
/ 8 /
V
р
л*
1 Яд
Рис. 72а.
При определении усилий все стержни фермы условимся считать
растянутыми, знак минус в тответе будет означать то, что стержень
сжат. Пусть требуется определить усилие в стержне 6 фермы. Для
этого проводим сечение /— /, рассекая не более трех стержней,
в том числе стержень 6, усилие в котором определяется. Мысленно
отбрасываем левую часть фермы,
заменяя ее действие на оставшуюся
правую часть усилиями S6, S7 и S8,
приложенными в соответствующих
сечениях стержней и направлен-
направленными в сторону отброшенной части
(рис. 726).
Чтобы определить усилие 56
независимо от усилий S7 и S8, со-
составляем уравнение моментов сил, действующих на правую часть
фермы, относительно точки К, в которой пересекаются линии дей-
действия сил S7 и Sg. Эту точку называют точкой Риттера:
Так как h = 0,5 а, то
В
Рис. 726.
Воспользуемся тем же сечением /—/ для определения уси-
усилия S7 независимо от усилий 56 и 58. Спроектируем все силы,
действующие на правую часть фермы, на вертикальную ось у, так
66

как проекции сил S6 и S8 на эту ось равны нулю:
^в
cos 45е
¦ = — 28,3 кн.
Для определения усилия 58 составим уравнение моментов этих же
сил относительно точки Риттера L, в которой пересекаются линии
действия сил S6 и S7:
Se =-**-? = -40 кн.
Знаки полученных ответов показывают, что стержень 6 растянут,
а стержни 7 и 8 сжаты.
Изложенный способ определения усилий в стержнях фермы пред-
предложен Риттером и носит название способа Риттера.
Для определения усилий в стержнях рассмотренной фермы по
способу Риттера использована II система уравнений равновесия пло-
плоской системы сил.
А
1 /
/
/
к.
>
3
Т Za
6у
/
\
ч
\
«
/
7
у/
р.
ft
/
а
А
i/4'з
X
\
/г
а
рг
V
Рис. 73а.
Пример 17. Определить усилия в стержнях 8, 9 и 10 фермы, изо-
изображенной на рис. 73а, если Р. = 40 кн, Ро = 80 км, Q, = О, = Ю кн
Q2 = 2O кн. АВ = Аа; KD = 2a.
Решение. Прежде всего определим реакции опор фермы Хл,
^а- ^в (рис. 7Ъб). Для этого составим три уравнения равновесия
5*	67

сил, действующих на ферму:
J? Л1 ,д = 0; — Pfia — Р2Ъа + RB4a — Q2a /2 — Q32a /2 = 0;
32 /2 = 94 л км
—Q1cos45° —Q2cos45°_—Q3cos45° = 0;
cos 45° = 40 ¦ -^- = 28,3 кн.
^ = 0; уА—Рх—Рг-{- RB-Q1 cos 45°-Q2 cos 45°-Q3 cos 45° = 0;
Для определения усилий в стержнях 8, 9 п 10 проведем сече-
сечение /—/. Мысленно отбросим левую часть фермы, заменив ее дей-
действие на оставшуюся часть реакциями разрезанных стержней S8, S9
и S10, направив stsi силы в сторону отброшенной части (рис. 73в).
Рис 736.
Рис. 73в.
Чтобы определить каждое усилие независимо от двух других, при-
применим' III систему уравнений равновесия (§ 21).
Составим уравнения моментов сил, действующих на правую часть
фермы, относительно точек Риттера К, В и L, в которых пересе-
пересекаются по две линии действия усилий:
^~m'5 KH-
|) = -76,6 кн.
= 80 кн.
68

§ 27. Условие равновесия сил, приложенных к рычагу.
Устойчивость при опрокидывании. Коэффициент устойчивости
Рычагом называется твердое тело, имеющее неподвижную
ось вращения и находящееся под действием сил, лежащих
в плоскости, перпендикулярной к этой оси.
Положим, что к рычагу в точках Av Л2	Ап приложены
задаваемые силы Р1( Р2, . .., Р„, лежащие в плоскости чертежа, а ось
рычага пересекает эту плоскость в точке О, которую назовем опорной
точкой (рис. 74).
Рис. 74
Реакция R оси рычага, уравновешивая задаваемые силы, лежит
в их плоскости, но направление ее не известно.
Разложим реакцию оси на две составляющие R,. и Ry и выведем
уравнения равновесия сил, действующих на рычаг. На основании
уравнений равновесия плоской системы сил имеем:
Л,
2*1=0;
B7.1)
¦ 0.
B7.2)
B7.3)
Здесь У\ X, и 2 Yi— суммы проекций задаваемых сил, прило-
женных к рычагу, на оси х и у; Rx и Ry — проекции реакции оси
л
рычага на эти оси;
2
t=i
. — сумма моментов задаваемых сил отно-
сительно опорной точки.
69

Р
С
а
А
Третье уравнение, не содержащее реакции оси рычага, и выражает
условие, которому удовлетворяют задаваемые силы, уравновешиваемые
реакцией оси рычага.
Это условие формулируется так: при равновесии сил, приложен-
приложенных к рычагу, алгебраическая сумма моментов всех задаваемых
сил, действующих на рычаг, относи-
относительно опорной точки равна нулю
Из уравнений B7.1) и B7.2) опре-
определяется реакция оси рычага.
Из условия равновесия сил дей-
действующих на рычаг, -получим условие
устойчивости тел при опрокидывании.
Положим, что к прямоугольному парал-
параллелепипеду (рис. 75) весом О на вы-
высоте d приложена горизонтальная сила Р,
которая может не только сдвинуть тело, но и опрокинуть его враще-
вращением вокруг ребра А. Считая, что сила Р недостаточно велика,
чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие
(см. § 29). Обозначим а расстояние от точки А, изображающей
на чертеже ось вращения рычага, до линии действия силы О, которая
препятствует опрокидыванию.
Составим сумму моментов задаваемых сил Р и G относительно
опорной точки А:
2i Mt —Q; Ga— Pd — О, откуда Ga=Pd.
Назовем абсолютные величины моментов сил О и Р относительно
точки А удерживающим и опрокидывающим моментами:
Ga = Жуд; Pd = Жопр.
Тогда на границе устойчивости получим:
Рис. 75
При устойчивом состоянии тела:
М
ул
~М
опр.
Устойчивость при опрокидывании в технике принято определять
отношением величины удерживающего момента к величине опрокиды-
опрокидывающего момента:
¦д
'уд
опр
70

действием
можно и
силы Р или
графическим
Это отношение называют коэффициентом устойчивости.
Очевидно, что в случае предельной устойчивости коэффициент
устойчивости равен единице, а в случае устойчивого состояния
Определить, опрокинется ли тело под
будет находиться в устойчивом состоянии
путем. Для этого продолжим линии дей-
действия сил G и Р до их пересечения
в точке К, перенесем силы в эту точку и
найдем их равнодействующую R (рис. 76).
Продолжая линию действия равнодей-
равнодействующей силы, найдем точку ее пере-
пересечения с опорной плоскостью.
В рассмотренном примере возможны
три случая:
1.	Если эта точка лежит слева от
ребра А, то состояние тела устой-
устойчиво.
2.	Если линия действия равнодействующей пересекает ребро А,
то состояние тела предельно устойчиво.
3.	Если эта точка лежит справа от ребра А, то тело опрокинется.
§ 28. Примеры на применение условия равновесия сил,
приложенных к рычагу
Пример 18. Определить вес противовеса Gj, обеспечивающий
коэффициент устойчивости нагруженного крана при опрокидывании,
1,25 м .	2м
Рис. 77.
равный 1,5, если вес крана О2 = 50 кн, вес груза G3 = 40 кн. Раз-
Размеры указаны на рис. 77.
Решение. Предполагаемое опрокидывание крана под действием
веса груза G3 является вращением вокруг оси О, совпадающей с пра-
71

вым рельсом. Силами, препятствующими опрокидыванию, являются
вес крана G2 и вес противовеса Gj. Определим опрокидывающий
момент как абсолютную величину момента силы G3 относительно
точки О:
Жопр = G3 • 1,25 = 40 • 1,25 = 50 кн ¦ м.
Определим удерживающий момент как сумму абсолютных величин
моментов сил G, и G2 относительно точки О:
MyA = Gx- 2 +02-0,75 = 0!-2 +50-0,75 = B0!+ 37,5) кн ¦ м.
Воспользуемся коэффициентом устойчивости тела при опроки-
опрокидывании
Муд
Отсюда
ЛГуд = kMonp,
2GX +37,5 =1,5- 50;
G,= 18,75 кн.
Пример 19. Определить минимальную ширину а бетонной пло-
плотины прямоугольного сечения по условию устойчивости при опроки-
опрокидывании, если высота плотины
0	Л = 3,5 м, вес 1 мг бетона
•у = 22,5 khjm3, горизонтальное
давление воды на 1 м длины
плотины со стороны верхнего
бьефа Рх = 45 кн, со стороны
нижнего бьефа Р2= 11,25 кн.
Расстояния от точек приложе-
приложения сил Pj и Р2 до основания:
hx = 1 м, п2 = 0,5 м (рис. 78).
Решение. Рассмотрим
бетонный массив в форме пря-
прямоугольного параллелепипеда,
измерения которого равны Л,
а и 1 л в направлении длины
плотины.
Л2, возможным опрокидыванием
р,
-сГ
-С
—
\1
\1
1
1
1
1
1
\
\
\
\
G

0 Р2 -с"
\-
Рис. 78.
Вследствие того, что Рх> Р2и hY
плотины будет ее вращение вокруг ребра О.
Силой, вызывающей опрокидывание, является сила Рх, направлен-
направленная относительно точки О в сторону движения часовой стрелки.
Силами, препятствующими опрокидыванию, являются G и Р2, на-
направленные относительно точки О в сторону, обратную движению
часовой стрелки.
Определим опрокидывающий момент:
Жоир = Pxhx = 45 • 1 = 45 кн • м.
72

Определим удерживающий момент:
Вес массива, т. е. одного метра длины плотины определяется:
где ha • 1 —объем массива.
Тогда
Мул~чНа- 1 ~-\-P2h2 =
-+11,25 ¦ 0,5 = C9,4а2 + 5,6) кн ¦ м.
Минимальной ширине плотины соответствует коэффициент устой-
устойчивости k — 1.
Тогда будем иметь:
Afonp
_	__
§ 29. Сцепление и трение скольжения
Исследованием явления трения впервые занимался Лео-
Леонардо да Винчи. В конце XVII в. французский физик Амонтон
A663—1705) обнаружил независимость силы трения от вели-
величины поверхности соприкасания тел. Законы трения были сфор-
сформулированы французским физиком Кулоном A736—1806).
Если к твердому телу, покоящемуся на шероховатой горизонталь-
горизонтальной плоскости (рис. 79а), приложить горизонтальную силу S, то дей-
действие этой силы вызовет появление силы сцепления Fcu = — S, пред-
представляющей собой силу противодей-
противодействия плоскости смещению тела.
Благодаря сцеплению, тело остается
в покое при изменении модуля силы S
от нуля до некоторого значения 5 .
\
/V
Это значит, что модуль силы сце-	F
пления тоже изменяется от Fca = 0
до Fcn = F™% в момент начала дви-
движения.
Модуль максимальной силы сце-	Рис. 79а.
пления, как показывает опыт, про-
пропорционален нормальному давлению N тела на плоскость. В рас-
рассматриваемом случае N = G.
F™x=fcaN-	B9.1)
ртлх
Коэффициент пропорциональности /сц = ~-^т- является отвлечен-
отвлеченным числом и называется коэффициентом сцепления.
73

Коэффициент сцепления зависит от материала и физического
состояния соприкасающихся тел и определяется экспериментально.
Его величина для материалов, используемых в технике, обычно меньше
единицы. Так как максимальное значение силы сцепления равно /СЦЛЛ
то модуль силы сцепления всегда удовлетво-
/V	ряет условию
M.	B9.2)
---*- Направление силы сцепления противопо-
^гй^^^йШ^Ш ложно направлению того движения, которое воз-
F	никло бы под действием приложенных к телу
сил при отсутствии сцепления.
При скольжении тела по шероховатой
Рис. 796.	поверхности к нему приложена сила трения
скольжения. Направление этой силы, противо-
противодействующей скольжению, противоположно направлению скорости
тела (рис. 79, б).
Модуль силы трения скольжения пропорционален нормальному
давлению N:
F = fN.	B9.3)
Коэффициент пропорциональности / называется коэффициентом
трения скольжения и определяется опытным путем.
Коэффициент трения скольжения является отвлеченной величиной
и зависит от материала и физического состояния трущихся по-
поверхностей, а также от скорости движения тела и удельного дав-
давления.
Однако, в элементарных расчетах зависимость коэффициента тре-
трения скольжения от скорости и удельного давления часто не учиты-
учитывается.
Экспериментально установлено, что
/ < /сц-
Реакция R реальной (шероховатой) поверхности, fi отличие от реак-
реакции идеальной (гладкой) поверхности, имеет две составляющие: нор-
нормальную реакцию N и силу сцепления Fcu. (или силу трения F при
движении тела).
Угол фсц, образованный реакцией шероховатой поверхности
с нормалью к поверхности в предельном состоянии покоя при
Fm = F™x, называется углом сцепления (рис. 80).
Тангенс угла сцепления равен коэффициенту сцепления:
ртах
4„,„ 	 СЦ 	 f
ИЛИ
cpclI = arctg/cu.	B9.4)
74

Угол, тангенс которого равен коэффициенту трения скольжения,
называется углом трения.
Угол сцепления можно определить опытным путем. Прибор для
определения угла сцепления очень прост. Он представляет собой
наклонную плоскость, угол наклона которой а можно изменять
(рис. 81, а).
Зафиксируем угол наклона а
плоскости О А, при котором по-
помещенное на ней тело находится
в предельном состоянии покоя и
сила сцепления достигает максималь-
максимального значения. Построим замкнутый
треугольник сил, действующих на
тело, и определим угол а (рис. 81, <?):
А1
¦пах
w
\
с-max
N
Smax
G
_	Рис. 80.
т. е. угол наклона плоскости а, при котором тело находится
в предельном состоянии покоя, равен углу сцепления фсц.
Величину коэффициента сцепления для соответствующих мате-
материалов (тело — плоскость) можно определить по таблице тангенсов
углов, так как /сц = *&фсц.
mat
'СИ
<%%йй%%йй%9Л%йй5й<йй
Рис. 81.
Конус с вершиной в точке касания тел, образующая которого
составляет угол сцепления с нормалью к поверхностям тел, называется
конусом сцепления (рис. 82). Поверхность конуса сцепления пред-
представляет собой геометрическое место максимальных реакций опорной
поверхности. Действительно, максимальная реакция поверхности
может занимать различные положения на поверхности этого конуса,
зависящие от направления силы S, стремящейся сдвинуть тело (рис, 80).
Пространство внутри конуса представляет собой совокупность воз-
возможных положений реакций опорной поверхности в состоянии покоя.
Пусть к покоящемуся телу приложены силы (в том числе вес
тела), линия действия равнодействующей Р которых лежит внутри
75

конуса сцепления (рис. 82). Эти силы не приведут тело в движение,
так как сила Р будет уравновешена реакцией поверхности.
Рассмотрим равновесие сил, действующих на тяжелый брусок,
опирающийся на две шероховатые плоскости (рис. 83). В точках
А и В возникают реакции опор,
линии действия которых не выхо-
выходят за пределы конусов сцепления.
Проведя линии А— I, А — //,
В — /// и В — IV, составляющие
углы сцепления ф1сц и ф2сц с пер-
перпендикулярами к опорным пло-
плоскостям, восставленным в точках
А и В, получаем границы кону-
сов сцепления. Четырехугольник
р „2
klmn, образованный этими ли-
линиями, внутри которого могут
пересекаться линии действия реакций опор А и В, называется
областью равновесия.
Брусок АВ находится под действием трех сил: его веса G и
двух реакций опор R^ и R5. При равновесии линии действия этих
трех сил пересекутся в одной
точке.
Так как любая точка пло-
площадки klmn может являться точ-
точкой пересечения линий действия
реакций опор Л и В, то бру-
брусок находится в состоянии покоя, б |
если линия действия силы веса
бруска пересекает область равно-
равновесия.
В случае, если линия действия
силы веса проходит через точку k
области равновесия, брусок на-
находится в предельном состоянии
покоя.
Брусок не может удержаться в указанном на рисунке положении,
если линия действия силы веса проходит вне области равновесия.
Если на брусок действует несколько задаваемых сил и они при-
приводятся к равнодействующей силе, установленным условиям должна
удовлетворять эта равнодействующая.
§ 30. Примеры на равновесие сил,
приложенных к твердому телу при наличии сил сцепления
Пример 20. Определить величину груза Р, удерживающего тело
весом О на шероховатой наклонной плоскости с углом наклона а,
который больше угла сцепления фсц (рис. 84а).
Рис. 83.
76

Решение. Необходимо иметь в виду, что направление силы
сцепления FCQ зависит от величины груза Р. При максимальной воз-
возможной величине этого груза Ртах сила сцепления направлена вниз
по наклонной плоскости, так как под
действием реакции нити груз стремится
перемещаться вверх по наклонной пло-
плоскости (рис. 846). При минимальной ве-
величине груза Ят1п сила сцепления на-
направлена вверх по наклонной плоскости
(рис. 84в).
Составим уравнения равновесия сходя-	рис- §4а.
щихся сил, действующих на тело, когда
оно удерживается в предельном состоянии покоя максимальным гру-
грузом Ртах (рис. 846):
2^ = 0; N — Gcosa = 0.
Отсюда A/ = Gcosa. .
« '	Ртах
Рис. 846.
nwt
Рис. 84в.
Так как F™x = fc N, из первого уравнения получаем
Лпах = /
Так как
sin a = /CIlG cos a -)- G sin a.
_ sinycu
COS '
то имеем
	р COS а Sin срсц -f- Sin a COS <рсц 	q sin (a -f- 9са)
mdx	cos 9СЦ	cos 9СЦ
Аналогично определяем Pmin (рис. 84в):
р —g sln(g —Ум)
Таким образом, условие равновесия сил, приложенных к телу,
покоящемуся на шероховатой наклонной плоскости, имеет вид:
q sin (а — усц) ^p^Q sin (а -f- Усц)
cos 9сц ^ "^ cos feu
77

Это неравенство показывает, что величина груза Р, который
удерживает тело на наклонной плоскости, изменяется в пределах от
¦^rnin до ^тз.х- Эти пределы соответствуют изменению модуля и
направления силы сцепления от F™*, направленной вверх по пло-
плоскости, до F™x, направленной вниз.
Таким образом, задачи на равновесие сил при наличии сил сце-
сцепления имеют совокупность решений, границами которых служат
решения, полученные в условиях предельного состояния покоя.
Пример 21. Однородный брус АВ весом О = 10 гн удержи-
удерживается веревкой BD под углом а к шероховатой вертикальной стене,
причем AD = АВ.
Определить в предельном состоянии покоя угол а, натяжение
веревки и нормальную реакцию стены, если коэффициент сцепления
между брусом и стеной /сц = 0,5 (рис. 85а).
Решение. Рассмотрим равновесие трех сил, приложенных
к брусу: заданной силы О, реакции S веревки BD и реакции RA
Рис. 85а.
Рис. 856.
шероховатой стены в точке А (рис. 856). Линии действия трех
взаимно уравновешивающихся сил пересекаются в одной точке (см. § 7).
Найдем точку К пересечения линий действия сил G и S; соединив
эту точку с точкой А, получим линию действия реакции 9.д. По-
Построим замкнутый треугольник этих сил. Рассмотрим Д ABD.
Отрезок СК, проходящий через середину стороны АВ параллельно
стороне AD, является средней линией Д ABD, т. е. точка К делит
сторону BD пополам. В равнобедренном треугольнике ABD (по
условию задачи AD — AB) медиана АК является и высотой, т. е.
АК A_BD.
Угол КАп, составленный реакцией R^ с перпендикуляром An
к стене, в предельном состоянии покоя, равен углу сцепления,
г. е.
78

где
сц = Лц = 0,5; ?сц = arctg 0,5 = 26° 34'.
Но 1_КАп = l^KDA, так как стороны этих углов взаимно пер-
перпендикулярны.
Таким образом,
Из Д ABD определяем угол а:
а = /. KDA + /_ KB A = 2<рсц = 2-26° 34' = 53° 08'.
Модули сил S и RA найдем из треугольника сил, определив его
углы:
S=Gcoscpcu,
где	со =
/5 '
4/50,5 = 2/5=:4,47 гк.
Разложив реакцию Ил на нормальную реакцию N и силу сцепле-
сцепления F™uax, определим Л/:
4 гн.
Пример 22. Однородный тонкий брусок АВ весом G опирается
концом А на вертикальную стену и точкой D на ребро. На конце В
подвешен груз весом О3 — -=-. Известны расстояния по горизонтали
и вертикали: АЕ = 2а и DE=a, а также коэффициенты сцепления
между бруском и стеной /сц (л) = 0,3 и между бруском и ребром
/«.№> = 0.2.
Определить наименьшую длину бруска АВ, при которой конец А
не скользит вниз, а также нормальные реакции опор А и D (рис. 86а).
Решение. Рассмотрим систему сил, приложенных к бруску АВ,
находящемуся в предельном состоянии покоя. На брусок действуют
заданные силы О и Gv нормальные реакции N^ и No в точках А
и D и максимальные силы сцепления в этих же точках F™uaf^> и
F^fn)» направленные противоположно направлению возможного
скольжения этих точек бруска (рис. 866).
Модули этих сил сцепления выражаются:
ртах — . w ртах , д,
' сц (А) — Jen (A)'4 A' cu(D) Jcu(D)' D'
Обозначим длину бруска: АВ=1,
79

Определим расстояние AD, cos а. и sin a:
АЕ 2а 2 . ED a	1
Составим три уравнения равновесия плоской системы сил, при
ложенкых к бруску:
—A/Dcos(90° —a
— 0; A)
)r=0; B)
''-a)-Oi = 0. C)
Эти уравнения содержат три неизвестные величины: /, NА и ND,
так как зависимость сил сцепления от нормальных реакций известна.
Рис. 86а.
Рис. 866.
Выразим в уравнениях проекций силы сцепления через нормаль-
нормальные реакции:
NA — ND Si0 a + feu. (D)ND C0S « = 0.
/сд (л)^л— G + Wccos
-?=о.
Определим из этих уравнений NA и ND. Из первого урав-
уравнения:
NA = WD (Sin a — /сц (D) C0S а)"
Подставив это выражение во второе уравнение, найдем ND:
,sina— -?=0,
/сц (А) + /сц (D)) Si" a + С1 — /сц (а/сц (D^ COS л "

Подставив значения коэффициентов сцепления и функций угла а,
получим
— G
2
@,3 + 0,2) у=- + A - 0,3 • 0,2) •
Определим NA:
NA = 0,63 Vb 0[—L- — 0,2 ¦ ~) = 0,380.
А	У 1/5	У 5/
2
Подставив найденное значение - ND и cos а = —^ в уравнение
моментов A), определим искомую длину бруска:
— О - -L + 0,63 УЪ Ga 1/5 — - / -jL = 0,
откуда I =1,575 а У5, т. е. AB—\,575AD.
Найдем длину участка DB:
= AB — ADr= 0.575AD.
Вопросы для самоконтроля
1.	Относительно каких точек плоскости момент данной силы имеет одно
и то же значение?
2.	Сформулируйте теоремы о парах сил на плоскости.
3.	Чем можно уравновесить пару сил?
4.	Как направлены реакции опор балки, нагруженной парой сил и ле-
лежащей на двух опорах, из которых одна — шарнирно-неподвижная, а дру-
другая— на катках?
5.	Зависит ли главный вектор и главный момент заданной системы сил
от выбора центра приведения?
6.	Каковы возможные случаи приведения сил, расположенных произ-
произвольно на плоскости?
7.	К какому простейшему виду можно привести систему сил, если из-
известно, что главный момент этих сил относительно различных точек на пло-
плоскости:
а)	имеет различную величину;
б)	имеет постоянное значение, не равное нулю;
в)	равен нулю.
8.	При каком условии сила, равная главному вектору плоской системы
¦сил, является равнодействующей этой системы?
9.	Перечислите системы уравнений равновесия сил, произвольно рас-
расположенных на плоскости?
10.	Какие задачи статики называют статически определенными и ка-
какие — статически неопределенными?
11.	В чем состоит условие равновесия сил, приложенных к рычагу?
12.	Что называют коэффициентом устойчивости?
13.	В чем заключается сущность способа Риттера?
14.	В чем заключается разница между силой сцепления и силой трения?
15.	Что называют конусом сцепления?
16.	Каковы возможные направления реакции шероховатой поверхности?
17.	Что представляет собой область равновесия и каковы условия равно-
равновесия сил, приложенных к бруску, опирающемуся на две шероховатые
плоскости?
6 А. А. Яблонский	81

ГЛАВА V
ГРАФИЧЕСКАЯ СТАТИКА
§ 31. Многоугольник сил и веревочный многоугольник.
Графическое определение равнодействующей плоской
системы сил
Рассмотрим графический прием сложения сил, произвольно рас-
расположенных на плоскости, называемый способом веревочного много-
многоугольника.
Как известно из § 20, в результате приведения плоской системы
сил к любому центру можно получить либо равнодействующую, либо
пару сил или установить, что силы уравновешиваются. Каждому из
Линия действия
равнодейстЗующей
этих трех случаев приведения сил соответствует определенный вид
веревочного многоугольника.
Рассмотрим сначала случай, когда многоугольник данных сил Pj,
Р2 и Р3, приложенных в точках Ах, А2 и А3 (рис. 87, а), не замкнут,
т. е. главный вектор сил не равен нулю. В этом случае силы при-
приводятся к равнодействующей силе.
Построив в любом месте плоскости многоугольник данных сил,
найдем главный вектор этих сил R*, который определит модуль и
направление равнодействующей силы (рис. 87, б). Остается опреде-
определить лишь одну из точек линии действия равнодействующей силы.
Для этого и производят построение веревочного многоугольника.
82

Возьмем произвольную точку О — полюс — и соединим ее с вер-
вершинами многоугольника сил лучами, число которых всегда
на единицу больше числа сил. Так, например, при сложе-
сложении трех сил число лучей равно четырем. Очень удобно давать лу-
лучам двойные обозначения. Так, луч, проведенный из точки О к вер-
вершине многоугольника сил, в которой сходятся силы Pj и Р2, обо-
обозначим /—2 (или Р1—Р2), луч, проведенный из точки О к вершине
многоугольника сил, в которой сходятся силы Р2 и Р3, обозначим
2—3 (или Р2—Р3) и т. д. Первый луг обозначим 0—/ (или 0 — PJ,
а последний 3—0 (или Р3 — 0). Проведем из произвольной точки L
плоскости прямую (рис. 87, а), параллельную лучу 0—/, до пересе-
пересечения с линией действия силы Р1 в точке Ку Из точки Кх проведем
прямую, параллельную лучу /—2 до пересечения с линией действия
силы Р2 в точке К2 и т. д. Из точки /С3 проведем прямую KZN,
параллельную лучу 3—0.
Ломаная линия LKiKJi^N, стороны которой параллельны соот-
соответствующим лучам, а вершины лежат на линиях действия сил, на-
называется веревочным многоугольником.
Обозначения сторон веревочного . многоугольника соответствуют
обозначениям сил, между линиями действия которых расположены
эти стороны.
Продолжим первую и последнюю стороны веревочного много-
многоугольника до их пересечения в точке К и покажем, что эта точка
принадлежит линии действия равнодействующей силы. Для этого
перенесем все силы по линиям их действия в вершины веревочного
многоугольника Kv Kv Л"з и разложим их на составляющие, на-
направленные по соответствующим сторонам веревочного многоуголь-
многоугольника. Так, сила Рх разложится на составляющие So_1 и Si_2, сила
Р2—на Si'_2 и S2-3 и сила Р3 — на S2-3 и вз-о-
Сопоставляя параллелограммы сил, построенные в точках К.х,
K<i и К3, с треугольниками аОЬ, ЬОс и cOd, устанавливаем:
Ос = S2-3; cO = S2-3; Od = S3-0.
Силы Si-2 и Si_2. приложенные в точках Кх и К2> равны по
модулю длине одного и того же луча Ob и противоположно напра-
направлены, а потому они взаимно уравновешиваются. Аналогично уравно-
уравновешиваются силы S2-3 и S2-3. приложенные в точках К2 и К3-
Остающиеся в действии силы S0_l и S3_o переносим в точку их
пересечения К и, построив на этих силах параллелограмм, находим
их равнодействующую R, т. е. равнодействующую данных сил Рг,
Р2 и Р3. Сравнивая построенный параллелограмм и \aOd, видим,
что R = R*. Таким образом, точка пересечения первой и последней
сторон веревочного многоугольника представляет собой одну из точек
линии действия равнодействующей силы. Выбор полюса О и точки
L — начала построения веревочного многоугольника — не отражается
6*	83

на результатах построения. При изменении положения точек О и L
пересечение первой и последней сторон веревочного многоугольника
произойдет в другой точке, также принадлежащей линии действия!
равнодействующей силы.
§ 32. Случай замкнутого многоугольника сил.
Графическое определение момента
результирующей пары сил
Пусть дана система сил Рг Р2 и Р3, приложенных в точках Л1(.
А2 и Аг, треугольник которых замкнут, а линии действия не пере-
пересекаются в одной точке (рис. 88, а). Эти силы не приводятся к равно-
равнодействующей, так как их главный вектор равен нулю, и не уравно-
уравновешиваются, так как их линии действия не пересекаются в одной.
Рис. 88,
точке. Следовательно, они приводятся к паре сил. Определим момент
этой пары построением веревочного многоугольника. Выбрав полюс О,
проводим лучи к вершинам многоугольника сил и заключаем, что
первый луч 0—1 и последний 3—0 совпадают (рис. 88, б).
Построим веревочный многоугольник LKiK2K5N; его параллельные
крайние стороны 0—/ и 3—0 не совпадают, т. е. веревочный много-
многоугольник является не замкнутым. Перенесем заданные силы в точки
Л",, К2' и К3- Разложив силы Pv P2 и Р3 на составляющие, напра-
направленные по сторонам веревочного многоугольника, устанавливаем,
что силы Si_2 и Si—2. приложенные в точках К\ и /С2. a также силы
S2-3 и S2-3. приложенные в точках К2 и /С3, взаимно уравновеши-
84

ваются. Остающиеся в действии силы S0_i = аО и Sz-o — Oa, при-
приложенные в точках Ki и АГ3. равны и параллельны, но направлены
в противоположные стороны, т. е. образуют пару сил. Момент этой:
пары определяется: М = — S0_jd, где SQ_-l — длина отрезка, соот-
соответствующего совпавшим лучам, определенная по масштабу сил,
d— расстояние между крайними сторонами веревочного многоуголь-
многоугольника, определенное по масштабу длин. Момент пары в данном
случае имеет знак минус, так как пара сил So_1, S3_o стремите»
вращать плоскость чертежа по движению часовой стрелки.
§ 33. Графические условия равновесия плоской
системы сил
Рассмотрим систему сил Pj, Р2 и Р3, приложенных в точках А1Г
А2 и Л3, треугольник которых замкнут и линии действия которых,
пересекаются в одной точке (рис. 89, а). Такие силы взаимно уравно-
уравновешиваются.
Рис. 89.
Покажем, что веревочный многоугольник этих сил также будет1
замкнут, т. е. его крайние стороны будут лежать на одной прямой.
Выбрав за полюс точку О, проведем из этой точки лучи 0— ]г
J — 2, 2— ЗиЗ — 0, причем луч 3 — 0 совпадет с лучом 0 — /
(рис. 89, б). Построив веревочный многоугольник, перенесем все-
силы по их линиям действия в вершины веревочного многоуголь-
многоугольника К\, К2 и К3 и разложим эти силы на составляющие по напра-
направлениям сторон веревочного многоугольника. Из треугольников аОЬ,-
ЬОс и cOd установим:
Si_2 = — S1-2; S2_3 = — S2-3; вз-о^ — So-i-
Действительно, последняя сторона веревочного многоугольника
3 — 0 должна совпасть с первой стороной 0 — /, так как только-
в этом случае силы, направленные по сторонам веревочного много-
85-

угольника, уравновешиваются. Замкнутость веревочного многоуголь-
многоугольника, т. е. совпадение последней и первой его сторон, имеется
и при равновесии любого числа сил на плоскости.
Основываясь на полученных результатах, сформулируем графиче-
графические условия равновесия системы сил, произвольно расположенных
на плоскости: силы, произвольно расположенные на плоскости,
находятся в равновесии, если силовой и веревочный многоуголь-
многоугольники замкнуты.
§ 34. Примеры применения веревочного многоугольника
Пример 23. Определить путем построения веревочного много-
многоугольника равнодействующую вертикальных нагрузок Pj = 60 кн,
Р2=80 кн и Я3 —40 кн, приложенных к балке АВ в точках D,
Е и F. Известно, что АВ — 8 м, AD — 2 м, DE = 3 м и BF = 2 м.
Решение. Решая задачи при помощи веревочного многоуголь-
многоугольника, необходимо выбрать масштабы длин и сил. В выбранном
масштабе длин вычерчивается схема с изображением точек прило-
Рис. 90.
жения и линий действия сил. В выбранном масштабе сил строят
многоугольник сил.
В рассматриваемом примере балка АВ с точками D, Е и F
изображена в масштабе длин, показанном на рис. 90. Равнодействую-
Равнодействующая данных параллельных сил (/? = Рх -\- Р2 -j- Рз = 180 кн) направлена
вниз по вертикали. Для определения линии действия равнодействую-
равнодействующей силы строим многоугольник сил и веревочный многоугольник.
Находим точку пересечения первой и последней сторон веревочного
многоугольника К, которая принадлежит линии действия равнодей-
равнодействующей силы. Проведя через точку К вертикаль, определяем
линию действия равнодействующей силы, а, следовательно, и точку
ее приложения L к балке АВ. По масштабу длин определяем Л/<=4,2 м.

Пример 24. К балке АВ, лежащей на двух опорах А и В,
в точках D и Е приложены вертикальные силы Рх = 60 кн и Р2 = 40 кн.
Опора А — шарнирно-неподвижная, опора В — на катках. Определить
построением веревочного многоугольника реакции опор балки, если
известно, что ЛВ=10 м, AD = Z м, BE = 2 м.
Решение. На балку АВ действуют четыре взаимно уравнове-
уравновешивающиеся силы: заданные силы Pv Р2 и реакции опор А и В.
Линия действия реакции RB шарнирной опоры на катках направлена
вертикально, силы Pj и Р2 также вертикальны. Из этого следует,
что и реакция неподвижной шарнирной опоры RA направлена по-
вертикали.
Изобразим балку АВ в некотором масштабе длин, приложим
к ней заданные силы Р1 и Р2 и проведем вертикальные линии дей-
действия неизвестных реакций опор R^ и RB (рис. 91).
Рис. 91.
Многоугольник сил и веревочный многоугольник взаимно уравно-
уравновешивающихся сил Pj, P2, R^ и RB должны быть замкнуты. Выбрав
масштаб сил, построим часть замкнутого многоугольника сил, отло-
отложив две заданные силы Pt и Р2. Выберем полюс и проведем три
луча. Условимся, что в замкнутом многоугольнике четырех сил Pj,
Р2, RB и RA с концом силы Р2 совпадает начало реакции RB, а с кон-
концом RB совпадет начало реакции RA, конец которой совпадет с на-
началом отложенной силы Pv Три проведенных луча обозначимг
RA-PV Рг — Р2 и Pa — RB.
Чтобы определить модули неизвестных реакций опор RA и RB,
построим веревочный многоугольник из любой точки а линии дей-
действия реакции опоры RA. Из этой точки проведем сторону, парал-
параллельную первому лучу RA — Рх (между линиями действия сил RA
и Pi), далее из точки d — сторону, параллельную второму лучу
87

Pl — P2, и из точки е — сторону, параллельную третьему лучу Р2 — RB
до пересечения с линией действия реакции Rfl в точке Ь. Соединив
точки а и b отрезком прямой, получим четвертую сторону замкну-
замкнутого веревочного многоугольника RB — RA. Этой стороне веревоч-
веревочного многоугольника соответствует параллельный ей луч RB— RA,
который проводится из полюса О. На этом луче должна лежать
вершина многоугольника сил, соответствующая концу реакции RB
и началу реакции R^. Таким образом, из конца силы Р2 проводим
вертикальную реакцию R5 до луча RB — RA. Из полученной точки
проводим реакцию R4 до начала силы Рг Получаем замкнутый
многоугольник четырех сил Pv Р2, RB и RA, все стороны которого
вертикальны. Пользуясь масштабом сил, находим числовые значения
реакций опор /?Д = А!В —50 кн. Найденные реакции опор приклады-
прикладываем к балке в точках А и В.
Пример 25. Определить построением веревочного многоуголь-
многоугольника реакции шарнирно-неподвижной опоры А и шарнирной опоры
на катках В балки АВ. В точке D на балку действует вертикальная
сила Р=40 кн, а в точке Е — сила Q==60««, направление которой
составляет с направлением В А угол 45°. Известно, что AB—W м.
Рис. 92.
Решение. Изобразим балку в масштабе длин (рис. 92). При-
Приложим к балке в точках D и Е заданные силы Р и Q и проведем
линию действия реакции RB шарнирной опоры на катках. Выберем
масштаб сил и построим часть замкнутого многоугольника четырех
сил Р, Q, R^, R^ отложив заданные силы Р и Q.
Если известна линия действия только одной из двух реакций
опор, то в многоугольнике сил реакцию с известной линией дей-
действия удобно помещать за последней отложенной заданной
силой. В этом примере из конца силы Q проведем прямую, парал-
параллельную линии действия реакции опоры RB. Затем, проведем три
луча, обозначив их RA — Р, Р — Q и Q — RB.

Реакция неподвижной шарнирной опоры А, линия действия кото-
которой не известна, приложена в центре шарнира А. Так как сторону
RA — Р веревочного многоугольника нужно провести между линиями
действия реакции опоры R^ и силы Р, то построение веревочного
многоугольника следует начать в центре шарнира А, единственной
известной точке линии действия реакции ЦЛ.
Построив веревочный многоугольник и определив положение
его стороны RB— RA, проведем из полюса О луч RB — RA, парал-
параллельный этой стороне веревочного многоугольника. Тогда точка
пересечения этого луча с прямой, проведенной из конца Q парал-
параллельно RB, будет концом реакции Rfl и началом реакции RA. Сое-
Соединив эту точку с началом силы РР получим реакцию опоры RA.
При этом направление реакций определяется направлением сил
в замкнутом многоугольнике. Измерив соответствующие стороны
многоугольника сил, получим:
= 37 кн\ /?л =
кн.
Кроме модулей реакций опор, определено также и направление
реакции RA неподвижной шарнирной опоры А. Приложим к балке
в точках Л и В найденные реакции опор RA и RB. Установим сле-
следующее правило построения веревочного многоугольника.
Если линия действия одной из двух реакций опор не известна,
то построение веревочного многоугольника для определения реак-
реакций опор следует начинать в точке приложения реакции
с неизвестной линией действия.
Пример 26. Определить построением веревочного многоугольника
реакции опор навесной фермы, изображенной на рис. 93а, если,
известно, что Q, —Q5=10 кн; Q2 = Q3 = Q4 — 20 кн.
Рис. 93а=
Решение. Линия действия реакции шарнирно-стержневой опоры В
направлена по оси стержня. Линия действия реакции неподвижной
шарнирной опоры А проходит через центр шарнира, но направление
ее не известно. Поэтому построение веревочного многоугольника
89

начинаем в центре неподвижной опоры А (рис 936). Так как линия
действия силы QY проходит через центр шарнира А, то сторона
веревочного многоугольника RA— Qr обращается в точку, а поэтому
построение веревочного многоугольника начинаем в точке А, про-
проведя через эту точку прямую, параллельную лучу Qx — Q2 до пере-
пересечения с линией действия силы Q2. Затем проводим стороны вере-
вереQ Q	Q % С
2
вочного многоугольника Q2 — Q3, Q3
Q R
— ^5 и Qs —
Сто-
Сто3 & i5
рону Q5 — RB проводим до пересечения с линией действия реакции
опоры В в точке Ь и, соединяя эту точку с точкой А — началом
лостроения веревочного многоугольника, получаем его сторону RB—RA.
Рис. 936.
Проводим из полюса О луч, параллельный стороне RB — RA,
до пересечения с прямой, параллельной линии действия реакции
опоры RB, проведенной из конца силы Q5. Реакция опоры RB заклю-
заключена между лучами Q5 — Rg и RB—RA и направлена по обходу
контура многоугольника сил в одну сторону с силами Q1( Q2	Q5.
Реакция опоры R4, заключенная между лучами RB — RA и RA — Qv
замыкает многоугольник сил, т. е. имеет по обходу контура много-
многоугольника такое же направление, как и остальные силы. Определив
реакции опор, прикладываем их к ферме в точках А и В.
90

§ 35. Диаграмма Максвелла — Кремоны и примеры
ее построения
В 1864 г. известный английский физик Дж. Максвелл A831—1879>
и независимо от него в 1872 г. итальянский математик Л. Кремона
A830—1903) предложили графический метод определения усилий
в стержнях фермы, получивший название диаграммы Максвелла —
Кремоны.
Порядок построения диаграммы Максвелла — Кремоны
Для построения диаграммы Максвелла — Кремоны необходимо-
знать модули и направления реакций опор, которые определяются
аналитически или путем построения веревочного многоугольника.
При построении диаграммы Максвелла — Кремоны необходимо
придерживаться следующего порядка:
а)	начертить схему фермы в выбранном масштабе Алин с указа-
указанием приложенных к узлам заданных сил и реакций опор, распола-
располагая их вне контура фермы;
б)	обозначить буквами внешние области, ограниченные внешним
контуром -фермы и линиями действия внешних сил, и внутренние
области, ограниченные только стержнями фермы;
в)	построить многоугольник внешних сил в выбранном масштабе
сил, откладывая силы в такой последовательности, в какой они рас-
расположены по контуру фермы в направлении, обратном движению
часовой стрелки;
г)	на базе многоугольника внешних сил построить для каждого
узла фермы замкнутый многоугольник сил, откладывая силы в такой
последовательности, в какой они встречаются при обходе узла
в направлении, обратном движению часовой стрелки. Узлы выбирать
так, чтобы в них было не известно не более двух сил;
д)	установить, какие стержни фермы растянуты и какие сжаты,
определяя направления реакций стержней по диаграмме;
е)	определить модули усилий измерением отрезков диаграммы.
Рассмотрим построение диаграммы Максвелла — Кремоны для
стропильной фермы, изображенной на рис. 94,а'вместе с действую-
действующими на нее заданной вертикальной силой и соответствующими
реакциями шарнирно-неподвижной опоры и опоры на катках с на-
наклонной опорной плоскостью.
Обозначим А, В, С внешние области—-части плоскости, огра-
ограниченные внешним контуром фермы и линиями действия внешних
сил, a F, E, D — внутренние области — части плоскости, ограни-
ограниченные только стержнями фермы. Это даст возможность каждую
внешнюю силу и усилие в стержне обозначить двумя буквами, соот-
соответствующими названиям прилегающих областей. Буквы будем ставить
в таком порядке, в каком эти области расположены по контуру
фермы или узла фермы в направлении, обратном движению часовой
стрелки. Например, согласно обходу контура фермы в указанном
9L

направлении, силу, приложенную к верхнему узлу фермы, обозна-
обозначим АВ, реакцию левой опоры — ВС, а реакцию правой опоры — С А.
Построим в масштабе сил замкнутый треугольник внешних
¦сил АВСА, откладывая силы в такой последовательности, в которой
они расположены по контуру фермы в направлении, обратном дви-
движению часовой стрелки, а затем перейдем к построению замкнутых
многоугольников сил, действующих на каждый из узлов фермы
(рис. 94, б). Построение многоугольников сил, действующих на узлы
•фермы, следует начинать с того узла, к которому приложены две
неизвестные силы.
а)
Рис. 94.
Начнем построение с левого опорного узла /, на который дей-
действуют известная реакция опоры ВС и две неизвестные реакции
стержней CF и FB.
Проводим из точки С диаграммы прямую, параллельную
стержню CF, а из точки В диаграммы — прямую, параллельную
стержню FB. Точка F пересечения этих прямых определит третью
вершину замкнутого треугольника BCFB сил, действующих на узел /.
Отрезки CF и FB, изображают в принятом масштабе сил реакции
стержней CF и FB, приложенные к рассматриваемому узлу /.
Согласно § 3, модули этих реакций равны модулям усилий
в этих стержнях. При этом, если реакция стержня направлена
от узла, то стержень растянут, а если реакция направлена к узлу —
стержень сжат.
В замкнутом треугольнике сил BCFB реакция опоры ВС напра-
направлена от В к С (В—начало силы, С — конец). В ту же сторону
по контуру треугольника должны быть направлены реакции стерж-
яей, т. е. реакция CF направлена от С к F (С—-начало силы, F — ко-
конец), а реакция FB направлена от F к В (F — начало силы, В —
конец).
Приложив силы указанного направления к узлу /, установим,
что реакция CF направлена от узла, а реакция FB — к узлу.
Из этого следует, что стержень CF растянут, а стержень FB сжат.
92

Приложим реакцию растянутого стержня FC к узлу // (для узла //:
/" — начало силы, С — конец) и реакцию сжатого стержня BF к узлу IV
{В — начало силы, F— конец). Тогда из сил, действующих на узел //,
¦будут не известны только две: реакция стержня СЕ и реакция
стержня EF.
Построим замкнутый треугольник FCEF сил, действующих на
узел //, проведя из точки С диаграммы прямую, параллельную
•стержню СЕ, а из точки F — прямую, параллельную стержню EF,
до взаимного пересечения в точке Е.
Приложив к узлу // найденные на диаграмме реакции стержней
СЕ и EF, установим, что оба эти стержня растянуты. Реакции
этих же стержней приложим к узлам /// и IV. Далее рассмотрим
узел /// и, зная реакцию стержня ЕС, построим замкнутый треуголь-
треугольник ECDE, из которого определим модули и направления реакций
CD и DE. После этого остается неизвестным лишь усилие в стержне DA.
Так как в построенной диаграмме уже имеются точки А и D, то,
соединяя эти точки отрезком прямой, получаем усилие AD. Этот
стержень сжат, так как его реакции—DA, действующая на узел IV,
и AD, действующая на узел V, —направлены к узлам.
Параллельность отрезка, соединяющего в данном примере точки Л
и D диаграммы, оси стержня AD служит критерием качества построе-
построения диаграммы. Если отрезок AD параллелен оси стержня AD, по-
построение диаграммы выполнено правильно, если же он не параллелен,
то в построении диаграммы допущена ошибка. Только точное по-
построение диаграммы Максвелла — Кремоны при помощи чертежных
инструментов обеспечивает параллельность последнего отрезка диа-
диаграммы оси соответствующего стержня, а следовательно, точность
графического определения усилий в стержнях фермы. Модули
усилий во всех стержнях фермы определяются измерением соответ-
соответствующих отрезков диаграммы. Значения усилий заносятся в таблицу,
причем усилие в растянутом стержне считается положительным,
а в сжатом — отрицательным.
Пример 27. Построить диаграмму Максвелла — Кремоны для фермы,
изображенной на рис. 95, а, вместе с действующими на нее верти-
вертикальными заданными силами: ОЛ —40' кн, ВС— 120 кн и верти-
вертикальными реакциями опор Л2?=100 кн и CD = 60 кн.
Решение. Построение диаграммы начинаем с построения замкну-
замкнутого многоугольника внешних сил DABCD. Затем последовательно
рассматриваем узлы /, //, ///, IV, V и строим многоугольники сил, дей-
действующих на эти узлы: АВЕА, AEFA, FEBCKF, DAFKLD, LKCML,
т. е. получаем последовательно точки Е, F, К, L, М (рис. 95, б).
Правильность построения диаграммы Максвелла — Кремоны под-
подтверждается параллельностью отрезка диаграммы DM оси стержня DM.
Направления реакций стержней фермы определены по диаграмме
(рис. 95, б) и показаны на рис. 95, а.
Пример 28. Построить диаграмму Максвелла — Кремоны для
фермы, изображенной на рис. 96, а в масштабе длин вместе с дей-
93

ствующими на нее вертикальными заданными силами DA = 40 кн >
ВС = 80 кн и вертикальными реакциями опор АВ = 70 кн а
CD = 50 кн.
Решение. Прежде всего строим замкнутый многоугольник,
внешних сил, который в рассматриваемом случае представляет собой
Рис. 95.
вертикальный отрезок DABCD. Затем, рассматривая последовательно
узлы /, //,..., VI, строим многоугольники действующих на них
сил АВЕА, EBCFE, AEFKA, AKLA, LKFCML, MCNM, т. е.
получаем последовательно точки Е, F, К, L, М, N (рис. 96, б).
Рис. 96.
Построение диаграммы Максвелла — Кремоны заканчивается сое-
соединением точек D и N диаграммы.
Так как отрезок DN диаграммы параллелен оси стержня DM,
то диаграмма Максвелла — Кремоны построена правильно. Точки М

я N диаграммы совпали, следовательно, усилие в стержне NM равно
нулю. Направления реакций стержней фермы определены по диаграмме
{рис. 96, б) и показаны на рис. 96, а.
Вопросы для самоконтроля
1.	Какие виды многоугольника сил и веревочного многоугольника соот-
соответствуют каждому случаю приведения плоской системы сил?
2.	Каковы графические и аналитические условия равновесия системы
-сил, произвольно расположенных на плоскости?
3.	Из какой точки следует начинать построение веревочного многоуголь-
многоугольника при определении реакций опор в случае, если известна линия действия
лишь одной из реакций опор?
4.	Сформулируйте правило построения диаграммы Максвелла — Кремоны.
ГЛАВА VI
СИСТЕМА СХОДЯЩИХСЯ СИЛ В ПРОСТРАНСТВЕ
§ 36. Многоугольник сил. Параллелепипед сил
Положим, что к твердому телу приложены силы Р^ Р2, Р3, и Р4,
линии действия которых не лежат в одной плоскости, но пересе-
пересекаются в одной точке О.
Рис. 97.
Перенося силы по их линиям действия в точку О, строим про-
пространственный многоугольник этих сил. Замыкающая сторона много-
многоугольника сил определяет равнодействующую силу (рис. 97). При
этом направление равнодействующей по контуру многоугольника
обратно направлению составляющих сил.
95

Таким образом, равнодействующая пространственной си-
системы сходящихся сил приложена в точке пересечения линий
действия сил и равна геометрической сумме данных сил
R^Pi + Ps-j- ... +Р„.
Таким же способом определяется равнодействующая плоской
системы сходящихся сил.
Если к телу приложены три сходящиеся силы, не лежащие
в одной плоскости, то их равнодействующая приложена в точке
пересечения линий действия сил
и изображается диагональю па-
параллелепипеда, построенного на
этих силах (рис. 98).
Действительно, диагональ па-
параллелепипеда Ос является замы-
замыкающей стороной многоугольника
сил Oabc, т. е.
Рис- 98-	R^Pi + Рз + Рз.
Изложенное правило сложения трех сходящихся сил в простран-
пространстве называется правилом параллелепипеда сил.
Сходящиеся силы в пространстве взаимно уравновешиваются,
если многоугольник этих сил замкнут, т. е. их геометрическая сумма
равна нулю
2
Как видно, условие равновесия сходящихся сил на плоскости
и в пространстве одно и то же.
Однакр, решение задач на равновесие сходящихся сил в простран-
пространстве путем построения замкнутого многоугольника сил весьма сложно,
так как стороны этого многоугольника не лежат в одной плоскости.
Поэтому для решения этих задач графический метод не применяют,
а пользуются аналитическим методом, т. е. составляют уравнения
равновесия этих сил.
§ 37. Проекции силы на оси декартовых
координат
Взяв правую систему неподвижных осей декартовых координат х,
у и г, разложим силу Р по правилу параллелепипеда на три соста-
составляющие силы Р^., Ру и Рг, направленные параллельно этим осям
(рис. 99).
Силы Рх, Ру, и Рг называются компонентами силы по осям лг,
у a z.
Алгебраические значения длин направленных отрезков Аа, АЬ
и Ас называются проекциями силы на оси х, у и г.
96

Обозначив i, j и к — единичные векторы, направленные по осям х,
у м z, a X, К и Z — проекции силы на эти оси, получим
Р— Р -+-Р -4-Р
НО
поэтому
р = |АГ-4~ jK + kZ.	C7.1)
Равенство C7.1) представляет собой формулу разложения силы
на составляющие по осям координат.
у
в
/
р
/
/г
Рис 99.
Проекция силы на каждую координатную ось определяется произ-
произведением модуля силы на косинус угла между направлениями оси и силы:
X = Pcos(P, i); Y — Pcos(P, j); Z = Pcos(P, k),
где (P, i), (P, j) и (P, k) — углы, заключенные между направлением
силы Р и направлениями осей х, у и z.
Если известны проекции силы на три взаимно перпендикулярные
оси х, у и z, то модуль и направление силы определяются по сле-
следующим формулам:
P = yr^2 + K2+Z2,	C7.2)
cos(P, i) = -p-; cos(P, j) = -p-; cos(P, k) = -^-. C7.3)
§ 38. Аналитический способ определения
равнодействующей системы сходящихся сил в пространстве.
Уравнения равновесия сил
Равнодействующая сходящихся сил Pv P2, ..., Р„ (рис. 100)
равна геометрической сумме этих сил:
7 А. А. Яблонский
97

Проекция равнодействующей на каждую из координатных осей
равна алгебраической сумме проекций всех составляющих:
C8.1)
n = Pncos(Р„, j);
Zn = Pn cos (Р„, k).
где проекции сил вычисляются по формулам:
*, = />, cos (Р„ I); *2 = P2cos(P2, I); ...; *„ = Я„ cos (Ря, i);
K1 = P1cos(P1. j); F2 = P2cos(P2, j); ..
Zx = Pj cos (Pj. k); Z2 = P2 cos (P2, k); ..
Формулам C8.1) можно придать вид:
X = IiXi-> V = '?Yl; Z = ^iZi,	C8.2)
причем i=\, 2, .... «.
Вычислив проекции равнодействующей X, Y и Z, найдем модуль
и направление равнодействующей по формулам C7.2) и C7.3):
cos(R, 0 = -|: COS(R> J)=7r; C0S(R-k)=^-.
В случае, если силы взаимно уравновешиваются, их равнодей-
равнодействующая R равна нулю.
Так как R = jAY2 + К2 + Z2, то ^ = 0; К = 0 и Z = 0.
J
Рис. 100.
Таким образом, для сходящихся сил в пространстве имеем сле-
следующих три уравнения равновесия:
КП =0 или
=0 или
=0.
C8.5)
98

При помощи уравнений C8.3) можно решать задачи на равно-
равновесие сходящихся сил, если число неизвестных величин в задаче
не превышает трех.
§ 39. Примеры на равновесие сходящихся сил
Пример 29. Груз А весом О = 20 « привязан к веревке, за-
закрепленной в точке В, и удерживается на шероховатой наклонной
плоскости BCDE силой Q, на-
направленной по линии наиболь-
наибольшего ската этой плоскости.
Определить наименьшее зна-
значение этой силы, если коэф-
коэффициент сцепления между те-
телом и плоскостью /сц = 0,2,
угол наклона плоскости к го-
горизонту а =45° и угол, со-
составленный веревкой АВ
и горизонтальной прямой ВС,
р = 30° (рис. 101а).
Решение. Рассматриваем
равновесие сил, приложенных
к грузу Л: заданных сил — ве-
веса О, силы Q, а также реакций	рис \<у\я.
связей — реакции веревки S,
нормальной реакции плоскости N и максимальной силы сцепле-
сцепления F™uax, направленной
противоположно напра-
направлению возможного сколь-
скольжения груза. Возможное
Рис. 1016.
Рис. 101в.
движение груза при недостаточной величине силы Q должно происхо-
происходить по дуге окружности с центром в точке В, а сила сцепления
99

должна быть направлена по касательной к этой окружности, т. е.
перпендикулярно к радиусу ВА (рис. 1016).
В момент предельного состояния покоя F?" = fca.N. Три не-
неизвестные величины Q, N и S можно определить из трех уравнений
равновесия сходящихся сил C8.5).
Проводим оси координат, как показано на рис. 1016, в и соста-
составляем уравнения равновесия сил:
2 Zi =0;, N — О cos а = 0.	C)
Из уравнения C) определяем ЛА:
TV
О cos a = 20 ^~ = 10
14,14 и.
Из уравнения A) находим S:
2У6
= 1,63 «.
Из уравнения B) определяем Q:
Q = — /СЦЛ/ cos p — 5 sin p + О sin a =
= -0,2- 10/2 Ц—
20 -^-=10,87 «.
Пример 30. Горизонтальный провод АЕ, натяжение которого
равно 300 «, подвешен к вертикальному столбу АВ, укрепленному
оттяжками АС и AD, расположенными симметрично относительно пло-
плоскости ВАЕ. Известно: Л5=6 м,
Определить натяжение оттяжек и усилие в столбе (рис. 102, а).
Решение. Рассмотрим равновесие сил, приложенных к узлу А:
заданной силы — реакции Т провода АЕ, реакции S столба АВ и
реакций Т1 и Т2 оттяжек АС и AD. Три неизвестные силы S, 'Т1
100

и Т2 определим из трех уравнений равновесия этой системы схо-
сходящихся сил:
Для этого проведем оси координат из точки В, направив ось z
вдоль В А, ось у — параллельно АЕ и ось х — перпендикулярно
к осям у и г (рис. 102, б). Приложим к узлу А все действующие
на него силы, направив их от узла, т. е. предположив, что все эле-
элементы растянуты. При проектировании сил Tj и Т2 на оси х и у
применим двойное проектирование, так как углы, составленные этими
силами с осями х и у, не даны. Спроектируем сначала каждую
из этих сил на плоскость хВу и полученную проекцию спроекти-
спроектируем на соответствующую ось.
Вычислим предварительно:
СВ	4,5	. с
cos а =	= ,	= 0,6.
С А 	' " "
В А	6	„ о
Sina =	=		— О,ft.
СА V&2+ 4,52
Составим уравнения равновесия:
2^ = 0;	7\ cos a cos 30° — Т2 cos a cos 30° = 0; A)
2 К, =0; — 7\cosacos600— Г2 cos a cos 60° + Г = 0; B)
^iZi =0; — 7\cos(90o — a) — 72cos(90°— a) — S = 0. C)
Из уравнения A) получим
Ti = T2.
Из уравнения B) найдем эти силы:
— 2Т1 cos a cos 60° ¦+- Т = 0.
Т	300
T	= 50° М"
Tl == 2 cos « cos 60° = 2 • 0,6 ¦ 0,5
= 7^!== 500 и (натяжение симметричных оттяжек одинаково).
Из уравнения C) определим 5:
— 27\sina — S — 0.
= — 2- 500-0,8 = —800 «.
Вертикальный столб АВ сжат.
Пример 81. Определить усилия в стержнях фермы, изображенной
на рис. 103а, если на узел В фермы действует вертикальная сила
Р1==40 кн, на узел С — горизонтальная сила Р2 = 20 кн, направлен-
направленная вдоль стержня CD. Размеры указаны на рисунке.
Решение. Для определения усилий в стержнях фермы восполь-
Вуемся способом вырезания узлов. Так как силы, действующие
на каждый из узлов фермы, взаимно уравновешиваются то. вырезая
отдельные узлы фермы, составляем по три уравнения равновесия
сил, действующих на каждый узел.
101

Узлы фермы вырезаем в такой последовательности, чтобы число
неизвестных сил в рассматриваемом узле не превышало трех. Так же,
как и при определении усилий в стержнях плоских ферм, все стержни
фермы условимся считать растянутыми; знак минус у вычисленной
реакции стержня означает то, что
стержень сжат.
Для определения усилий в стерж-
стержнях рассматриваемой фермы будем
вырезать последовательно узлы А,
В, С и D (рис. 1036). В точках
Е, F, К, L показаны составляю-
составляющие реакции опор R^,, Rf2, Ri, Rf,,
Rfj Rav Rav уравновешивающие
реакции стержней. Как показано
ниже, усилия во многих стержнях
рассматриваемой фермы равны нулю.
Рис. 103а.	Поэтому не будем определять пред-
предварительно всех косинусов углов,
составленных силами с осями координат, и проекции некоторых
сил запишем в уравнения равновесия в общем виде, не определяя по
чертежу знака проекций.
Рис. 1036.
Очевидно, что и составляющие реакций опор, направленные вдоль
стержней с нулевыми усилиями, будут равны нулю.
Узел А
(. =0;
102

Так как узел А не загружен внешней силой, а силы Sv S2 и S6
не лежащие в одной плоскости, не могут уравновешиваться, то они
равны нулю.
Узел В
2*( = 0; — 53+55cos(S5, I) = 0;	A)
2 Y, = 0; — 52 + 55 cos (S5, j) = 0;	B)
2j^\ =—-v'i 	/j	O^2=0j ^\2 ===	*\==	 ^ KH. (o)
Из уравнения B) находим
55 cos (S5, j) = 5г = 0; 55 = 0.
Из уравнения A) находим
53 = 55 cos (Sv j) = 0, 54 = 0.
Узел С
2v 	п* С' I С лЛС (с з\	п*	/1 \
Л j	U, Оз ~Г~ *^П ^*-*S ^Эц» '/ •— V/»	(.-I/
V1 К 	П* 	 С 	Р 	П- С 	 Р 	 ОП jt^t/.	/ол
^^j Г . — - VJ ^ ^^^ *^4 * О ~~ "* **) *^4 •*""' ~"^ х 2 ™ ¦¦ iU /viX')	V J
X1 7 	П-	С I С гло /'С ^	• П	/ЧЛ
>^ ij? 	 V» ~~~ Оjq |— *^Ц ^Uo ^Oii) Л^ 	 U.	\t-V
Из уравнения A) находим:
5ц cos (Sn, i) = — S3 = 0; Sn = 0.
Из уравнения C) находим:
510 = Sn cos (Su, k) = 0; 510 = 0.
Узел D
2*t = 0; 5i + 55Cos(S5, i) + 57cos(s7, i) = 0; A)
2 Yt = 0; 54+S'5 cos (si- J*)+59 cos (S9. j) = Q; B)
2 Zt = 0; — 58 + 57 cos (S7, k) + 59 cos (S9, k) = 0. C)
Из уравнения A) находим:
57cos(S7, 0 = — 5i — 55Cos(S5, i) = 0; 57 = 0.
Из уравнения B) находим:
9 _-S;-^cos(S5, j)
^ — cos (S,, j)
Так как
55 = 0 и 54 = — 20 kh,
&
4
to
Si	20
103

Из уравнения C) находим
Так как
7, k)-hSgcos(S0. к).
cos(S9, k) = —-
- = — 0,6;
то
2-f-42
= 59cos(S9, k) = — 25.0,6 = — 15 кн.
Таблица усилий
Таблица 2
Стержни
Усилие S, кн
1
0
2
0
3
0
4
—20
5
0
6
0
7
0
8
—15
9
25
10
0
11
0
12
—40
Основываясь на результатах расчета, можно установить следующее:
1.	Если в незагруженном узле фермы сходятся три стержня,
не лежащих в одной плоскости, то усилия в каждом из этих стерж-
стержней равны нулю (узел Л, стержни 1, 2 и 6).
2.	Если в некотором узле фермы все внешние силы и все стержни,
кроме одного, лежат в одной плоскости, то усилие в стержне,
не лежащем в этой плоскости, равно нулю (узел С, стержень 11
при 5з= О).
Эти соображения, дающие возможность определить без вычисле-
вычислений стержни с нулевыми усилиями, значительно упрощают опреде-
определение усилий в стержнях пространственных ферм.
ГЛАВА VII
ТЕОРИЯ ПАР СИЛ В ПРОСТРАНСТВЕ
§ 40. Момент пары сил
Числовое значение момента пары сил на плоскости равно произ-
произведению одной из сил пары на ее плечо, а знак момента опреде-
определяется направлением, в котором пара сил стремится вращать плоскость.
В пространстве направление вращения, вызываемого парой сил
в плоскости ее действия, не характеризуется знаком ее момента, так
как смотря на плоскость действия пары сил с различных ее сторон,
можно видеть одну и ту же пару стремящейся вращать плоскость
в различных направлениях. Момент пары сил в пространстве рас-
рассматривают как вектор (рис. 104а и б), направленный по перпенди-
перпендикуляру к плоскости заданной пары сил в такую сторону, чтобы, смотря
104

навстречу этому вектору, видеть пару стремящейся вращать пло-
плоскость против движения часовой стрелки. Этот вектор может быть
приложен в любой точке плоскости действия пары, так как пару
в этой плоскости можно переносить.
_^1Х	/ /
Рис. 104а.
Модуль вектора момента равен произведению одной из сил пары
на ее плечо:
Таким образом, вектор момента определяет не только числовое
значение момента, а также плоскость действия пары сил и направле-
направление, в котором пара стремится вращать эту плоскость.
§ 41. Теорема о возможности переноса пары сил в любую
плоскость, параллельную плоскости действия пары
Заданную пару сил, не изменяя ее действия на твердое тело,
можно перенести в любую плоскость, параллельную плоскости
действия этой пары.
Положим, что к некоторому твердому телу приложена пара сил
Р, Р' с плечом АВ, распо-
расположенная в плоскости /.
Проведем плоскость //,
параллельную поскости /, и
возьмем в этой плоскости от-
отрезок DC, равный и парал-
параллельный отрезку АВ, и при-
приложим к концам этого отрез-
отрезка по две взаимно уравно-
уравновешивающиеся силы, равные
по модулю и параллельные
силам рассматриваемой пары
(рис. 105а):
Ч-*
п
f
к.
P1=P2 — Pi=:pi = p.	Рис. 105а.
Сложим силу Р, приложенную в точке А, с силой Р2, прило-
приложенной в точке С. Их равнодействующая Rl = P-)-P2, приложена
в точке /С, делящей отрезок АС пополам, т. е. в точке пересечения
105

диагоналей параллелограмма ABCD. Сложив силу Р', прило-
приложенную в точке В, с силой Р3, приложенной в точке D, получим
их равнодействующую /?2 = ^' +^з- которая также приложена
в точке К-
Силы Rt и R2> как равные по модулю и направленные по одной
прямой в противоположные стороны, взаимно уравновешиваются.
Остаются силы Рх и Р4, составляющие пару сил с плечом DC, рас-
расположенную в плоскости //, параллельной плоскости /. Эта пара
сил, эквивалентная заданной паре сил, стремится вращать плоскость //
в том же направлении, в котором стремится вращать плоскость /
заданная пара сил, а момент эквивалентной пары сил численно равен
моменту заданной пары сил:
Таким образом,, пару сил можно переносить из одной плоскости
в другую, параллельную ей плоскость.
§ 42. Теорема об эквивалентных парах
Пары сил эквивалентны, если их моменты геометрически
равны.
Положим, что даны две пары сил, лежащие в различных пло-
плоскостях и имеющие геометрические равные моменты Mj = M2. Дока-
Докажем, что эти пары эквивалентны.
Рис. 1056.
Так как моменты М1 и М2 пар Р, Р' и Q, Q' геометрически
равны, т. е. не только равны по модулю, но и совпадают по напра-
направлению, то плоскость / действия пары Р, Р' и плоскость // дей-
действия пары Q, Q' параллельны, и направления, в которых пары сил
стремятся вращать эти плоскости, совпадают (рис. 1056). Согласно
предыдущей теореме, пару сил Р, Р' с плечом АВ в плоскости /
106

можно заменить эквивалентной ей такой же парой сил Р, Р' с пле-
плечом C'D' = AB в плоскости // с моментом
М2== Mi.
Согласно § 15, полученная пара сил эквивалентна паре Q, Q'
в той же плоскости //, так как
М2 = Mi = М2.
Таким образом, пара Р,~Р' в плоскости/ эквивалентна паре Q, Q'
в плрвкости //.
Из доказанной теоремы следует, что момент пары сил яв-
является свободным вектором, т. е. его можно переносить в любую
точку пространства, не изменяя его модуля и направления.
§ 43. Сложение пар сил в пространстве.
Условие равновесия пар
Рассмотрим сложение двух пар, расположенных в пересекающихся
плоскостях и докажем следующую теорему:
Геометрическая сумма моментов составляющих пар равна
моменту эквивалентной им пары сил.
F
Рис. 106.
Пусть требуется сложить две пары сил, расположенные в пересе-
пересекающихся плоскостях / и //, имеющие моменты Мх и М2 (рис. 106).
Выбрав силы этих пар равными по модулю
определим плечи этих пар:
М2
Расположим эти пары таким образом, чтобы силы Рх и Р3 были
направлены по линии пересечения плоскостей KL в противополож-
противоположные стороны и уравновешивались.
107

Оставшиеся силы Р2 и Р4 образуют пару сил, эквивалентную
данным двум парам. Эта пара сил имеет плечо BC — d а момент,
перпендикулярный к плоскости пары, равный по модулю M — Pd.
Покажем, что геометрическая сумма моментов составляющих пар
равна моменту эквивалентной пары. Так как момент пары сил яв-
является свободным вектором, перенесем моменты составляющих пар
М, и М2 в точку В и сложим их, построив на этих моментах парал-
параллелограмм.
Докажем, что его диагональ Z?F = M1-r-M2 представляет собой
момент эквивалентной пары сил Р2, Р4- Для этого необходимо до-
доказать, что:
1)	BF = Pd;
2)	отрезок BF перпендикулярен к плоскости действия эквива-
эквивалентной пары Р2, Р4;
3)	смотря навстречу вектору BF, можно видеть пару Р2, Р4.
стремящейся вращать плоскость, в которой она расположена, в сто-
сторону, противоположную движению часовой стрелки.
Доказательство
1. Треугольники ВАС и BDF подобны, так как
T' e"
BD вл
М2 ~~ d2 '	DF ~~ AC
и /__ BDF = 1_ ВАС, как углы со взаимно перпендикулярными сто-
сторонами.
Из подобия этих треугольников следует, что
BF _ ВС	BF _ d
откуда
BF^M,±- = Pdx± = Pd.
2.	Так как вектор момента каждой пары сил перпендикулярен
к плоскости действия этой пары, то:
MX_LP2 и M2_LP2.
а потому плоскость параллелограмма BDFE перпендикулярна к силе
пары Р2 и ~BF J_P2.
Кроме того, /. ОВЛ=90° и /. СВА^^ FBD, откуда /. CBF=90°,
т. е. BF±BC.
Так как диагональ параллелограмма BF перпендикулярна к силе
пары Р2 и к плечу пары ВС, то можно утверждать, что она пер-
перпендикулярна к плоскости действия эквивалентной пары Р2, Р4.
3.	Выполнение третьего условия показано на рисунке 106. Смотря
навстречу вектору BF, можно видеть пару Р2, Р4 стремящейся вра-
вращать плоскость, в которой она расположена, против движения
часовой стрелки.
108

Из вышеизложенного следует, что вектор BF — М, т. е. гео-
геометрическая сумма моментов составляющих пар равна моменту
эквивалентной пары:
M + M
Установленное правило сложения моментов пар называется пра~
билом параллелограмма моментов.
Построение параллелограмма моментов можно заменить построе-
построением треугольника моментов. Применяя построение параллелограмма
или треугольника моментов, можно решить и обратную задачу, т. е.
разложить любую пару сил на две составляющие пары.
Пусть требуется сложить несколько пар, расположенных произ-
произвольно в пространстве (рис. 107). Определив моменты этих пар,
Рис. 107.
согласно § 42, их можно перенести в любую точку О простран-
пространства. Складывая последовательно моменты этих пар, можно построить
многоугольник моментов пар, замыкающая сторона которого опре-
определит момент эквивалентной им пары сил.
На рис. 107 показано построение многоугольника моментов при
сложении трех пар.
Момент пары сил, эквивалентной данной системе пар
в пространстве, равен геометрической сумме моментов соста-
составляющих пар.
+-...+№„ или М = 2МГ D3.1)
109

Если" момент эквивалентной пары сил равен нулю, то пары урав-
уравновешиваются
М = 2Мг = 0.	D3.2)
Таким образом, условие равновесия пар сил, расположенных
произвольно в пространстве, можно сформулировать так:
Пары сил, расположенные произвольно в пространстве,
уравновешиваются в том случае, если геометрическая сумма
их моментов равна нулю.
ГЛАВА VIII
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО» ТОЧКИ И ОТНОСИТЕЛЬНО ОСИ
§ 44. Момент силы относительно точки как векторное
произведение
Момент силы относительно точки в пространстве изображается
вектором, модуль которого равен произведению модуля силы на ее
плечо относительно этой точки (центра момента):
Мо = Pd.
Вектор момента силы направляется перпендикулярно к плоско-
плоскости, проходящей через точку О и силу Р, в такую сторону, чтобы,
смотря навстречу этому вектору,
видеть силу Р, стремящейся вра-
вращать эту плоскость вокруг точки О
против движения часовой стрелки
(рис. 108).
Модуль момента силы отно-
относительно точки может быть также
выражен удвоенной площадью
треугольника АОВ:
Рис. 108.
Мо = 2 /\АОВ.
Момент силы относительно точки равен нулю в том случае,
если линия действия силы проходит через эту точку, т. е. d = 0.
Если из центра О в точку приложения силы провести радиус-
вектор г (рис. 107), то вектор момента силы можно выразить сле-
следующим векторным произведением: М0 = гХР-
Как известно из векторной алгебры, вектор, равный векторному
произведению г X Р. направлен по перпендикуляру к плоскости век-
векторов— сомножителей, т. е. к плоскости Д АОВ, в такую сторону,
чтобы, смотря ему навстречу, видеть совмещение первого множи-
множителя г со вторым множителем Р (отложенным из той же точки О)
в виде поворота на угол, меньший 180°, против движения часовой
стрелки, т. е. направление векторного произведения г X Р
дает с направлением момента Мо.
ПО

Покажем, что и модуль этого векторного произведения равен
модулю момента силы Р относительно точки О. Как известно из
векторной алгебры, модуль векторного произведения равен:
\rXP\==rPsln(r, Р),
но
а потому
/•sfn(r,
rP sin(r,
Таким образом, вектор момента силы Мо относительно
точки можно рассматривать как векторное произведение
радиуса вектора г, проведенного из центра моментов в точку
приложения силы, на вектор силы Р.
§ 45. Момент силы относительно оси
Кроме момента силы относительно точки, при операциях с силами
в пространстве широко применяют момент силы относительно оси.
Чтобы вычислить момент силы Р относительно оси z, следует
спроектировать эту силу на плоскость /, перпендикулярную к оси,
а затем вычислить момент этой
проекции Р1 относительно точки
О пересечения оси с плоскостью
(рис. 109).
Таким образом, моментом
силы Р относительно оси г на-
называется взятое со знаком
плюс или минус произведение
модуля проекции Рг силы Р на
плоскость, перпендикулярную
к оси, на ее плечо d± относи-
относительно точки О пересечения
оси с плоскостью:
Момент силы относительно оси	Рис< 10^'
считается положительным, если,
смотря навстречу оси z, можно видеть проекцию силы Р, стремя-
стремящейся вращать плоскость / вокруг оси z против движения часовой
стрелки.
Момент силы относительно оси изображается отрезком, отложен-
отложенным по оси z от точки О в положительном направлении, если
Mz > 0, и в отрицательном, если Мг < 0.
Значение момента силы относительно оси может быть также вы-
выражено удвоенной площадью треугольника АХОВ{.
M2=±2J\Al0Bl.
Ill

Момент силы относительно оси равен нулю в двух случаях
П если Я =0 т. е. линия действия силы параллельна оси,
2) если й\= 0,' т. е. линия действия силы пересекает ось.
§ 46. Зависимость между моментом силы °™о«тельно
точки и моментом силы относительно оси, проходящей
через эту точку
Установим зависимость между моментом ^лы относительно точки
и моментом силы относительно оси, проходящей через эту точку
(рис. 110).
В § 44 и 45 установлено:
МО = 2/\АОВ
Так как треугольник AfiB, является п
на плоскость Л перпендикулярную к оси г, то его
Рис. И0.
площади треугольника АОВ, умноженной на косинус угла между
ЭТИИ3вест°ноОСчто'угол между плоскостью треугольника АОВ и пло-
скостью / рав^н ?глу между перпендикулярами к этим плоскостям,
т. е. углу между моментом Мо и осью z.
Поэтому
l1AOB-=/
Умножив обе части этого равенства на два, получим
ИЛИ
Мх = Мо cos i = MQ cos (Мо, к).
D5.0
112

Проекция момента силы относительно точки на ось, про-
проходящую через ату точку, равна моменту силы относительно
оси.
Если сила расположена в плоскости, перпендикулярной к оси,
то
cos f = ± 1 и М2 = ± Мо.
§ 47. Аналитические выражения моментов силы
относительно координатных осей
Возьмем три взаимно перпендикулярные координатные оси х, у,
Z, которым соответствуют орты i, j, k.
Момент Мо силы Р относительно начала координат, как известно
из § 44, выражается формулой:
где г — радиус-вектор точки А приложения силы относительно на-
начала координат (рис. 111).
А
/
/
Л. 1
I /
I /Х-
РИС 111.
Разложим вектор Мо на составляющие по осям координат:
где Мх, Му, Мг — проекции Мо на оси координат.
Из векторной алгебры известно, что векторное произведение
г X Р можно представить определителем:
i j k
-f У z
X Y Z
где x, у, z — проекции вектора г, а X, У, Z — проекции вектора Р
на оси координат.
8 А. А. Яблонский
ИЗ

Приравнивая значения Мо и определителя, разложенного по эле-
элементам первой строки, получим
— yX).
Сопоставляя левые и правые части этого равенства, находим
проекции момента Мо на оси координат, равные, согласно § 46,
моментам силы Р относительно этих осей.
D7.1)
iz =r= XY — ул .
Формулы D7.1) называются аналитическими выражениями
моментов силы относительно координатных осей.
§ 48. Главные моменты системы сил относительно точки
и относительно оси
Если имеется система сил Рх, Р2, ..., Рп, произвольно распо-
расположенных в пространстве, то можно определить моменты всех сил
относительно произвольной точки О:
Рис. 112.
Рис. 113.
Построив в точке О многоугольник этих моментов, можно найти
их геометрическую сумму.
Момент, равный геометрической сумме моментов всех
заданных сил относительно точки О, называется главным мо-
114

ментом системы сил относительно этой точки:
Mo-M1q + M2o+ ...Mv	D8.1)
На рис. 112 показано определение главного момента трех сил
Рг Р2 и Р3 относительно точки О.
Если заданы силы Pv P2	Р„, произвольно расположенные
в пространстве (рис. 113), то можно определить моменты всех этих
сил относительно произвольной оси z:
Mlz, М2г	Mnz.
Момент, равный алгебраической сумме моментов всех
заданных сил относительно оси г, называется главным мо-
моментом системы сил относительно оси z:
Mz = Mlz+M2z + ... + МЯ2.	D8.2)
Главный момент системы сил относительно оси изображается от-
отрезком, отложенным по оси z от любой ее точки О в положитель-
положительном направлении, если Мг > 0, и в отрицательном, если Мг < 0.
§ 49. Зависимость между главными моментами системы сил
относительно точки и оси, проходящей через эту точку
На рис. 112 изображен многоугольник моментов сил Plt P2 и Р3
относительно точки О.
Проведем через эту точку произвольную ось z и спроектируем
на эту ось главный момент Мо, а также моменты Щ , М2 , М3 ;
получим
Mocos(Mo> 2) = M,ocos(Mio> 2)+M2ocos(M2o, 2) + M3ocos(M3o, z).
Согласно § 46
MlQ cos (MlQ. z) = Mu; M2q cos (M2o> z) = M2z;
Af3ocos(M3o, z) = MZz.
Тогда
Mocos(Mo, г)=*Ми+Мъ + МЬж = Мг.
Распространяя эту зависимость на любое число сил, получаем
Мо cos (Mo, z) = 2 Ми = Мг.	D9.1)
Таким образом, проекция главного момента системы сил
относительно некоторой точки на ось, проходящую через эту
точку, равна главному моменту заданной системы сил отно-
относительно этой оси.
8*	U5

Вопросы для самоконтроля
1- Возможно ли равновесие трех сходящихся сил, не лежащих в одной
плоскости?
2.	Перечислите теоремы о парах сил в пространстве.
3.	Каким свойством обладает момент пары сил в пространстве?
4.	Чем различаются условия равновесия пар сил на плоскости и в про-
пространстве?
5.	Какой третьей парой сил можно уравновесить две пары сил, лежа-
лежащих в пересекающихся плоскостях?
6.	Покажите, что момент силы относительно точки можно рассматри-
рассматривать как векторное произведение радиуса-вектора точки приложения силы
на вектор силы.
7.	Как вкч 1сляется момент силы относительно оси и в каких случаях,
он равен нулю?
8.	Выразите моменты силы относительно координатных осей через
проекции силы на эти оси.
9.	Какая зависимость существует между моментами силы относительно»
точки и оси, проходящей через эту точку?
10.	При каких условиях модуль момента силы относительно точки
равен моменту силы относительно оси, проходящей через эту точку?
11.	Как должна быть направлена сила, приложенная в заданной точке
пространства, чтобы величина ее момента относительно заданной оси была
наибольшей?
12.	Чему равна проекция главного момента системы сил относительно
точки на ось, проходящую через эту точку?
ГЛАВА IX
СИСТЕМА СИЛ, ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ
В ПРОСТРАНСТВЕ
§ 50. Приведение силы к заданному центру
При сложении сил, произвольно расположенных в пространстве,
так же как и в плоскости, пользуются методом приведения сил
к заданному центру, предложенным Пуансо.
Пусть задана сила Р, приложенная в точке Л, и произвольная
точка О, принятая за центр приведения (рис. 114).
Приложим в точке О две уравновешивающиеся силы Р' и Р",
равные и параллельные силе Р, не изменяющие кинематического-
состояния тела. Полученную систему трех сил можно рассматривать
как совокупность силы Р", приложенной в центре приведения Ок
и присоединенной пары сил Р, Р'.
Опустив из точки О перпендикуляр на линию действия силы Р»
получим плечо этой пары и найдем модуль ее момента
M = Pd.
Вектор момента присоединенной пары направлен перпендику-
перпендикулярно к плоскости пары Р, Р', проходящей через точку О и за-
заданную силу Р, в ту сторону, с которой пара представляется стре-
стремящейся вращать плоскость против движения часовой стрелки.
116

Момент пары сил является свободным вектором и может быть,
приложен в любой точке пространства. Приложив его в центре при-
приведения О, убедимся в том, что
вектор момента присоединенной
пары сил совпадает по направле-
направлению с вектором момента силы Р
относительно центра приведения
и равен ему по модулю, т. е.
Из изложенного следует, что
при приведении силы Р к неко-
некоторому центру О получаем в этом
центре силу Р", геометрически
равную заданной силе Р, и при-
присоединенную пару сил с моментом, геометрически
этой силы относительно центра приведения.
Рис. 114.
равным моменту
§ 51. Сложение сил, произвольно расположенных
в пространстве
Для сложения системы сил Pv P2 и Р3, произвольно располо-
расположенных в пространстве, воспользуемся методом приведения сил
к заданному центру.
Z
Рис. 115а.
Приведя все силы к некоторому центру О, получим три силы
Рь Рг и Рз, приложенные в точке О, и три присоединенные пары
Рь Pi, P2. Р2 и Рз, Рз (рис. 115а).
117

Складывая силы Pi, P2 и Р3, приложенные к точке О, полу-
получаем их равнодействующую R*, которая приложена в точке О
и равна главному вектору заданной системы сил:
Складывая присоединенные пары, находим эквивалентную пару
сил.
Момент каждой присоединенной пары равен моменту соответ-
соответствующей силы относительно центра приведения, т. е.
Момент пары сил, эквивалентной трем присоединенным парам,
равен геометрической сумме моментов этих пар:
т. е. момент полученной пары равен главному моменту трех задан-
заданных сил относительно центра приведения. Распространяя полученные
результаты на любое число сил, произвольно расположенных в про-
пространстве, получим:
Полученный результат можно сформулировать следующим обра-
образом: силы, произвольно расположенные в пространстве, всегда
могут бить приведены к одной силе, равной их главному век-
вектору, приложенной в центре приведения, и к паре сил с момен-
моментом, равным главному моменту всех сил относительно центра
приведения.
§ 52. Вычисление главного вектора
и главного момента
Для вычисления главного вектора R* и главного момента Мо
воспользуемся методом проекций (рис. 1156).
Известно, что R* = Pl-j-P2-f- ... +РЛ.
Обозначив X, Y и Z, проекции главного вектора на оси коор-
координат, получим:
+ ... +*„.
где Хх, Х2, ..., Хп, У7! У2	 Yn, Zv Z2	Zn — проекции
¦сил Pt, Р2	Р„ соответственно на оси х, у, z.
118

Модуль и направление главного вектора R* определяются по
формулам:
cos(R*, i) = ^*: cos(R*. j) = ~; cos(R*. k) = -|^. E2.1)
Главный момент системы сил:
Его проекции Мх, Му, Мг на оси х, у, z, проведенные череа
точку О, равны главным моментам системы сил относительно этих
осей (§ 49):
^х=М\х + М2х + •¦¦ +Мпх>
My = Miy-\~M2y-\- ... -\-Мпу,
Модуль и направление главного
момента Мо определяются по фор-
формулам:
E2.2)
Рис. 1156.
можно вычислить непосредственно или
cos(Mo, 0 =
М
My
cos(Mo, j) = -
cos(Mo, k) = -
Момент каждой силы
по формулам § 47:
Аналогично главные моменты Мх, Му, М2 можно определить-
по формулам:
E2.3),
§ 53. Условия и уравнения равновесия сил, произвольно
расположенных в пространстве
Случаю равновесия сил, произвольно расположенных в про-
пространстве, соответствуют два условия равновесия:
М = Мо = 0 и R* = 0.
119

Модули главного момента Мо и главного вектора R* рассматри
ваемой системы сил определяются по формулам E2.1) и E2.2):
= 0 или
= 0 или
+ ... +Mnz = Q или
+ •¦• +хп =0 или
+...+К„ =0 или
=0 или
¦Они обращаются в нуль только при следующих условиях:
которым соответствуют шесть уравнений равновесия сил, располо-
расположенных произвольно в пространстве:
E3.1)
Первые три уравнения называются уравнениями моментов сил отно-
относительно осей координат, а последние — уравнениями проекций сил
на оси.
При помощи формул E2.3) можно представить уравнения момен-
моментов в «иде:
E3.2)
где xt, yi3 zt — координаты точки приложения силы Pt, a Xt, Yt, Zi —
проекции этой силы на оси координат. Оси координат могут иметь
любое направление. Их направления выбирают обычно так, чтобы
каждая конкретная задача имела наиболее рациональное решение.
Таким образом, задача на равновесие сил, произвольно располо-
расположенных в пространстве и приложенных к одному телу, статически
определенна, если число неизвестных в ней не больше шести. Для
системы сил, приложенных к совокупности двух тел, задача стати-
статически определенна при числе неизвестных не больше двенадцати
и т. д.
§ 54. Приведение системы сил к паре сил
В том случае, когда главный вектор R* системы сил оказывается
равным нулю, а главный момент Мо не равен нулю, силы приводятся
к паре сил.
Момент этой пары сил равен главному моменту заданных сил
относительно центра приведения:
м=мо = м1о+м2о+ ... +м„0.
120

Следует учесть, что если силы приводятся к паре сил, то глав-
главный момент заданной системы сил относительно любой точки про-
пространства будет неизменным как по модулю, так и по направлению.
Постоянство значения главного момента некоторой системы сил
относительно произвольно выбранных точек пространства является
признаком того, что эта система сил приводится к паре сил*.
§ 55. Приведение системы сил к равнодействующей силе
если главный вектор системы сил R* не равен
момент Мо или равен нулю, или направлен пер-
заданная система сил приводится
В том случае,
нулю, а главный
пендикулярно к главному вектору
к равнодействующей силе.
Рассмотрим каждый из этих случаев от-
отдельно,
В первом случае, когда R* Ф 0, а Мо = О,
силы приводятся к равнодействующей силе,
линия действия которой проходит через
центр приведения О.
Действительно, в этом случае сила R*
заменяет собой заданную систему сил, т. е.
является ее равнодействующей.
Рассмотрим второй случай, когда R*=?0,
Мо Ф О и M0J_R (Рис- 116)- Пусть после
приведения системы сил к центру О полу-
получена сила R*, приложенная в этом центре и
равная главному вектору сил, и пара сил,
момент которой М равен главном}' моменту
Мо всех сил относительно центра приведе-
приведения, причем Мо J_R*.
Выберем силы этой пары R' и R равными
по модулю главному вектору JR*. т. е.
R~R' — R*. Тогда плечо этой пары сле-
следует взять равным OK = -~* •
К
ИС'
Проведем через точку О плоскость /, перпендикулярную к мо-
моменту пары сил М. Пара сил R', R должна находиться в этой пло-
плоскости. Расположим эту пару так, чтобы одна из сил пары R' была
приложена в точке О и направлена противоположно силе R*. Вос-
Восставим в плоскости / в точке О перпендикуляр к линии действия
силы R*, и в точке К на расстоянии ОК = -^- от точки О прило-
приложим вторую силу пары R.
Отрезок ОК откладываем в такую сторону от точки О, чтобы,
смотря навстречу вектору момента М, видеть пару стремящейся
Это следует из формулы E8.2), § 58.
121

•вращать свою плоскость против движения часовой стрелки. Тогда силы
R* и R', приложенные в точке О, уравновесятся, а сила R пары,
приложенная в точке К, заменит собой заданную систему сил, т. е.
будет ее равнодействующей.
Прямая, совпадающая с линией действия этой силы, является
линией действия равнодействующей силы.
Рис. 116 показывает различие между равнодействующей силой R
и силой R*, полученной при приведении сил к центру О.
Равнодействующая R системы сил, приложенная в точке К, имею-
имеющая определенную линию действия, эквивалентна заданной системе
сил, т. е. заменяет собой эту систему.
Сила же R* в точке О заменяет заданную систему сил только
в совокупности с парой сил с моментом М = М0.
Силу R* можно приложить в любой точке тела, к которой приве-
приведены силы. От положения этой точки зависит только модуль и
направление главного момента Мо.
§ 56. Теорема о моменте равнодействующей силы
(теорема Вариньона)
Зависимость между моментами равнодействующей и составляющих
сил устанавливается следующей теоремой:
Момент равнодействующей относительно любой точки равен
геометрической сумме моментов составляющих сил относи-
относительно этой точки, а момент равнодействующей силы относи-
относительно любой оси равен алгебраической сумме моментов соста-
составляющих сил относительно этой оси.
Установим сначала зависимость между моментом равнодействую-
равнодействующей и моментами составляющих сил относительно какой-либо точки.
Определим модуль момента M0(R) равнодействующей силы, при-
приложенной в точке К и расположенной в плоскости /, относительно
.центра приведения О (рис. 117), который является произвольной точкой.
it	S\IS	M	п	г,*,
Учитывая, что O/C = -q*- и И = н*, имеем:
П & *	AM	% Я
т. е. момент равнодействующей равен по модулю главному моменту
¦системы сил.
Направление момента равнодействующей Мо (R), перпендикулярное
к плоскости /, очевидно, совпадает с направлением главного момента
сил Мо относительно центра приведения О.
Следовательно, момент равнодействующей силы M0(R) геометри-
геометрически равен главному моменту Мо, а поэтому
Мо (R) = Мо = М,о -f- М2о + ... + М„о,	E6.1)
122

т. е. момент равнодействующей относительно произвольного центра
приведения равен геометрической сумме моментов составляющих сил
относительно этого же центра.
Установим теперь зависимость между моментом равнодействующей
силы и моментами составляющих сил относительно некоторой оси.
Проведем через центр приведения О произвольную ось z и опре-
определим момент равнодействующей
силы MZ(R) относительно оси z
как проекцию ее момента M0(R)
относительно точки О на эту ось	^^ /I
(рис. 117).
Согласно § 46, получим:
где f — угол между осью z и на-
направлением вектора M0(R).
В этом выражении M0(R) за-
заменим геометрически равным ему
главным моментом Мо, проекция
которого на ось г, проходящую
через точку О, равна главному мо-
моменту сил относительно этой оси
(§ 49); тогда получим:
Известно, что главный момент
системы сил Мг относительно
оси z равен алгебраической сумме моментов составляющих сил отно-
относительно этой оси, а поэтому
^2 W — "'г — ™12 + ™2г Т ••• ~T'"'nz'	E6.2)"
т. е. момент равнодействующей силы относительно произвольной
оси z равен алгебраической сумме моментов составляющих сил от-
относительно этой оси.
Рис. 117.
§ 57. Приведение произвольной системы сил к двум
скрещивающимся силам или к силовому винту (динаме)
В том случае, если главный вектор системы сил R* и ее главный
момент Мо относительно центра приведения О не равны нулю и не
перпендикулярны между собой, т. е. R* Ф О, Мо ф О и R* не пер-
перпендикулярно Мо, заданную систему сил можно привести или к двум
скрещивающимся силам или к силовому винту (динаме).
Рассмотрим сначала приведение системы сил к двум скрещиваю-
скрещивающимся силам (рис. 118). Пусть после приведения системы сил к не-
некоторому центру О получена сила R*. равная главному вектору.
123

Рис. 118.
приложенная в этом центре, и пара сил, момент которой М = Мо
не перпендикулярен R*.
Проведем плоскость //, перпендикулярную к моменту пары сил М,
и выбрав плечо пары d, а силы пары Q==Q' = —-, расположим
в этой плоскости пару сил
,р*	Q, Q', эквивалентную си-
" м	стеме присоединенных пар.
Приложим одну из сил па-
пары Q' в точке О, а другую
силу Q — на конце отрез-
отрезка ОК, проведенного из
точки О перпендикулярно
к силе Q'. Сложив прило-
приложенные в точке О силы R*
и Q', получим новую си-
силу Р, которая вместе с си-
силой Q, приложенной в точ-
точке К, представляет собой совокупность двух скрещивающихся сил.
Покажем, что в этом случае рассматриваемую систему сил можно
также привести к силовому винту — динаме, представляющей собой
совокупность силы и пары сил, распо-
расположенной в плоскости, перпендикуляр-
перпендикулярной к линии действия этой силы.
Допустим, что в результате приве-
приведения заданной системы сил к центру О,
получена в этом центре сила R* и
пара сил, момент которой М, равный
главному моменту системы сил Мо, не
перпендикулярен R* (рис. 119).
Известно, что пару сил можно за-
заменить двумя парами. Для этого разло-
разложим момент пары сил М на два соста-
составляющих момента: М*, направленный
по R*, и М', направленный перпенди-
перпендикулярно к R*:
М = М* + М'.	E7.1)
Изобразим в плоскости / пару сил,
имеющую момент ЛГ. Силы этоЧ пары	рис, ид.
возьмем равными по модулю R* и
одну из сил пары R' приложим в точке О и направим противопо-
противоположно главному вектору. Плечо этой пары сил
d =
М'
R*
E7.2)
124

Отложим плечо d = ОС в плоскости / от точки О по направле-
направлению, перпендикулярному векторам R* и М' в такую сторону,
чтобы, смотря навстречу вектору момента пары М', видеть пару сил
стремящейся вращать плоскость / против движения часовой стрелки.
Две силы R* и R', приложенные в точке О, взаимно уравно-
уравновешиваются. Остается сила R*, приложенная в точке С, и пара сил
с моментом М*, параллельным R*, который как свободный вектор
переносим из точки О в точку С.
Прямая CL, вдоль которой на-
направлены R* и М*, называется цен-
центральной осью системы сил.
Совокупность силы R* и пары
сил Р, Р' с моментом М*, распо-
расположенной в плоскости, перпенди-
перпендикулярной линии действия этой
силы, называют силовым винтом,
или динамой (рис. 120).
Полученную совокупность силы
R* в точке С и пары сил с момен-
моментом М* можно рассматривать как
результат приведения заданной си-
системы сил к центру С, лежащему на
центральной оси. Следовательно,
момент пары сил М* равен глав-
главному моменту Мс заданной системы
сил относительно точки С, лежа-
лежащей на центральной оси. Совокуп-	Рис- 120-
ность силы R* и момента пары М* можно перенести в любую точку
центральной оси, так как эта ось является линией действия силы R*,
а момент пары М* является свободным вектором.
Отсюда следует, что главные моменты системы сил относительно
всех точек центральной оси равны М*.
Рассмотрим изменение главного момента Мо системы сил относи-
относительно произвольной точки О при изменении положения этой точки
по отношению к центральной оси.
Согласно формуле E7.1), имеем (рис. 119):
где, согласно формуле E7.2), М' = R*d.
Модуль главного момента Мо определится:
Мо = V М*2 + М'2 = Ум*2 + Я* V.	E7.3)
где d — расстояние от точки О до центральной оси.
Направление Мо определится углом, образованным Мо и главным
вектором R*:
cos(Mo, R*) = ^==-7=t=r.	E7.4)
125

I
Очевидно, что cos (Мо, R*) > 0 при М* > 0, тогда /_ (Мо, R*) < 90"
и направление М* совпадает с направлением R* (рис. 119). При
cos(Mo, R*)<0: имеем Ж*<0 тогда /_(M0, R*) > 90°, т. е. направле-
направления М* и R* противоположны. В формулах E7.3) и E7.4) переменной
величиной для заданной си-
/	стемы сил является только
расстояние d.
R*	Эти формулы показыва-
показывают, что при увеличении рас-
ж стояния d от точки О до
мс*М центральной оси модуль глав-
главного момента Мо увеличи-
увеличивается, ъ.?_ (Мо, R*) прибли-
р жается к прямому углу (рис.
121). Для любой точки С,
^ лежащей на центральной оси,
5 d = 0, а потому
|	cos(Mc> R*)= ± 1 и
т. е. ^(Мс, R*)—0 или it.
Рис. 121.	Полученные результаты
показывают, что главный
момент рассматриваемой системы сил относительно любой точки
центральной оси направлен вдоль этой оси в ту или другую сто-
сторону и имеет наименьший для
этой системы сил модуль,
равный М*. Таким образом,
центральная ось системы
сил представляет собой гео-
геометрическое место точек
пространства, относитель-
относительно которых главные момен-
моменты заданной системы сил
имеют наименьший модуль
Mmln — |М*| к направлены
вдоль этой оси.
Рассмотрим точки, нахо-
находящиеся на одинаковом рас-
расстоянии от центральной оси,
т. е. лежащие на поверхности
кругового цилиндра, осью ко-
которого является центральная	Рис. 122.
ось системы сил.
Согласно формулам E7.3) и E7.4), главные моменты системы
сил относительно этих точек равны по модулю и составляют с обра-
вующей цилиндра одинаковый угол а (рис. 122).
126-

Установим формулу для вычисления алгебраического значения
наименьшего главного момента заданной системы сил.
Наименьший главный момент системы сил М* равен проекции
главного момента рассматриваемой системы сил Мо на направление
главного вектора R* (рис. 119):
ЛГ= Mocos(Mo, Г).	E7.5)
Умножив обе части равенства E7.5) на R*, получим
R*M* = R*M0 cos (M.o, R*).	E7.6)
Правая часть равенства E7.6) представляет собой величину ска-
скалярного произведения R* и Мо, т. е.
R*MO cos (Mo, R*) = R* • Мо.	E7.7)
Выражая скалярное произведение E7.7) через проекции векторов
сомножителей на координатные оси. из формулы E7.6) получим
R* . М* = R* • Мо = X Мх -Ь УМу + ZMZ,
откуда
XMx + YMy + ZMz
М* =	х^ ^у^	г-.	E7.8)
Формула E7.8) выражает алгебраическое значение наименьшего
главного момента М* через проекции R* и Мо на координатные оси.
Установим при помощи формулы E7.8) аналитическое условие,
при котором пространственная система сил приводится к равнодей-
равнодействующей.
Заданную систему сил можно привести к равнодействующей
в двух случаях (§ 54): а) если R*=5tO, а Мо = 0 и б) если R* Ф О,
Мо^0 и M0J_R.
В обоих случаях М* = Мо cos (Mo, R*) = 0. Поэтому, если система
сил приводится к равнодействующей, то выполняются условия:
E7.9)
Соотношения E7.9) являются аналитическими условиями при-
приведения системы сил к равнодействующей силе.
§ 68. Влияние положения центра на результаты
приведения к этому центру системы сил в пространстве.
Инварианты системы сил
Положим, что задана система сил Рг, Р2, .... Р„, произвольно
расположенных в пространстве. Выберем в пространстве два раз-
различных центра приведения Ох и О2 (рис. 123).
127

Полученные нри приведении к этим центрам силы R* и R* равны
главному вектору заданных сил:
т. е. r;=r2=
или
R* = const.
E8.1)
Модуль и направление силы, равной главному вектору заданных
сил R* и получаемой при приведении системы сил к некоторому
центру, не зависят от положе-
положения этого центра, т. е. главный
вектор данной системы сил
инвариантен по отношению
к центру приведения.
Установим зависимость ме-
9 •» жду главными моментами си-
I стемы сил относительно центров
'Р3 приведения О, и О2.
Найдем эти главные моменты
(см. § 48):
Рис. 123.	М =2Г- X Р-.
здесь rt —радиус-вектор точки приложения силы Р1 относительно
центра приведения Ох\
г; — радиус-вектор точки приложения силы Pi относительно
центра приведения О2.
Проведем из центра приведения Ох в центр О2 радиус-вектор d.
Тогда
Подставив значение г 1 в выражение, определяющее Мо, получим
откуда
Mo, — d X
E8.2)
Согласно зависимости E8.2), на рис. 123 главный момент си-
системы сил относительно первого центра Мо, представлен как сумма
векторов d X R2 и ^о • ^Ри этом вектоР d X R2 представляет собой
момент силы R*, приложенной в центре 02, относительно центра Оу
Этот вектор направлен перпендикулярно плоскости, в которой
лежат векторы d и R*, в такую сторону, чтобы, смотря навстречу
128

этому вектору, видеть силу R*, направленной по отношению
к центру О1 против движения часовой стрелки.
Зависимость E8.2) можно сформулировать следующим образом:
Главный момент системы сил относительно второго центра
приведения О2 равен разности главного момента этих сил от-
относительно первого центра приведения О± и момента силы, рав-
равной главному вектору этой системы сил, приложенной во вто-
втором центре приведения, относительно первого центра.
Из формулы E8.2) следует, что при перемещении Центра при-
приведения по прямой, имеющей направление главного вектора,
главный момент заданной системы сил остается неизменным
как по модулю, так и по направлению.
Действительно, если центры Ох и О2 лежат на прямой, парал-
параллельной главному вектору, то ОХО2 = d и R* являются параллель-
параллельными векторами, а потому
dXR* = 0 и М0=М02.
8	случае, если главные моменты заданной системы сил от-
относительно произвольно выбранных центров приведения геоме-
геометрически равны между собой, то рассматриваемая система
сил приводится к паре сил.
Действительно, при Мо1=Мо2=. • .=Мо имеем d X R*=0. Так как
векторное произведение d X R* равно нулю при любых значениях d,
то R* = 0 при Л1о=?0, т. е. силы приводятся к паре сил (§ 54).
Умножив скалярно обе части равенства E8.2) на главный вектор
R* = R* = R*, получим:
R«.Mo^R;.MOi-R;-(dXR2>
Но
R* • (d X К) = °- так как К -L (d X Щ),
поэтому Щ • Мо = R* ¦ Мо , т. е.
R*.M0 = const.	E8.3)
Полученный результат показывает, что скалярное произведение
главного вектора на главный момент данной системы сил
инвариантно по отношению к центру приведения.
Выразив скалярное произведение E8.3) через проекции перемно-
перемножаемых векторов на координатные оси, получим
ХМх-\- YMy -)- ZMZ = const.
Итак, для любой системы сил имеются два основных инварианта,
т. е. две величины, не зависящие от положения центра приведения.
Первым {векторным) инвариантом системы сил является
главный вектор системы сил, а вторым {скалярным) инвариан-
инвариантом является скалярное произведение главного вектора на
главный момент этой системы.
9	А. А. Яблонский	129

Выше получена формула E7.8) для вычисления наименьшего
главного момента:
•" — R*
Так как числитель и знаменатель этой дроби инвариантны по
отношению к центру приведения, то наименьший главный момент
системы сил М* тоже инвариантен по отношению к центру при-
приведения. Это означает, что проекция главного момента рассма'
триваемой системы сил относительно любого центра на напра'
вление главного вектора есть величина постоянная, не завися-
зависящая от положения этого центра (рис. 121).
При приведении системы сил к одной из точек центральной оси
получаются две инвариантные величины R* и М*. совокупность ко-
которых представляет собой динаму.
§ 59. Уравнения центральной оси системы сил и линии
действия равнодействующей
Через произвольный центр О, после приведения к которому по-
получены сила R* и пара сил с моментом М = Мо, проведем оси коор-
координат х, у, z (рис. 124).
Рис. 124.
Возьмем какую-либо точку А(х, у, z) на центральной оси си-
системы сил. Как известно, главный момент относительно этой точки
МА — М* направлен по линии действия силы R*. равной главному
вектору заданных сил.
130

Положение центральной ос^ (прямой линии) в пространстве опре-
определяется двумя уравнениями с тремя переменными координатами х,
у, г.
Для получения этих уравнений воспользуемся результатами, полу-
полученными в § 58.
Примем за первый центр начало координат О, а за второй
центр — точку А, принадлежащую центральной оси; тогда по фор-
формуле E8.2):
М* М dR*
Спроектируем векторы обеих частей этого равенства на коорди-
координатные оси х, у, z.
Так как произведение d X R* представляет собой момент силы R*,
приложенной в точке А, относительно точки О, то проекции его на
оси координат представляют собой моменты этой же силы относи-
относительно координатных осей, которые можно выразить аналитически,
согласно § 47. Спроектировав, получим:
Так как М* и R* направлены по одной прямой, то одноименные
их проекции пропорциональны:
Мх Л!* Мч, М*
X ~ Y ~~~ Z ~~ R*
или
Мх - (yZ - zY) _Му~ (гХ-xZ) _MZ~ (xY-yX) __ M*
¦ у —	у	—	2	~~Rr' {b Л)
Здесь постоянными величинами являются: главный вектор R* задан-
заданной системы сил и его проекции на оси X, Y, Z, проекции Мх,
Му, Mz главного момента Мо относительно начала координат,
а также наименьший главный момент М*. Переменными величинами
являются текущие координаты точек центральной оси х, у, г. Два
уравнения центральной оси можно получить, приравняв друг другу
любые два отношения из четырех.
Уравнения имеют более простой вид, если приравнивается одно
из первых трех отношений последнему, не содержащему переменных
координат.
Координаты точек пересечения центральной оси с координатными
плоскостями получаются путем приравнивания нулю соответствующих
координат. Так, в точке Ах пересечения центральной оси с пло-
плоскостью yOz имеем х1 = 0, в точке А2 z2 = 0, а в точке Л3 у$ — 0
(рис. 125).
9й	131

Если силы приводятся к равнодействующей, то М* = 0исила R*
является равнодействующей силой R. В этом случае центральная
Рис. 125.
ось системы сил становится линией действия равнодействующей силы,
уравнения которой будут:
Mz — (xY—yX)
X
= 0
или
= yZ — zY,
= zX — xZ,
= xY — zX.
E9.2)
Здесь X, Y, Z — проекции равнодействующей силы на координат-
координатные оси;
[у, Мг — главные моменты заданной системы сил относи-
относительно координатных осей.
Из трех уравнений E9.2) независимыми будут только два.
Мх,
§ 60. Сложение параллельных сил в пространстве. Условия и
уравнения равновесия параллельных сил
Для сложения параллельных сил Pv P2	Р„, приложенных
в точках Alt А2. .... Ап выберем произвольный центр приве-
приведения О.
132

После приведения системы сил к этому центру получим силу,
приложенную в центре приведения и равную главному вектору за-
заданных сил R*, и пару сил с моментом М, равным главному мо-
моменту Мо всех сил относительно центра приведения О.
Проведем через центр приведения О три взаимно перпендикуляр-
перпендикулярные оси х, у, z, направив ось z параллельно рассматриваемым си-
силам (рис. 126).
Вычислим проекциии главного вектора сил на оси координат:
где Z, = -f- Pt, если направление силы Р{ совпадает с направлением
оси z; Z; — — Pt, если направления силы Pt и оси z противопо-
гР»
Ми I
Рз
С
Аз
R"
Рис. 126.
ложны. Так как X = 0 и Y = 0, то главный вектор R* направлен
по оси г, а его модуль равен абсолютному значению его проекции Z:
(бол)
При Z = 2i^>(>0 направление главного вектора R* совпадает
с направлением оси z, а при Z = 2i + Pl<0 направление R* про-
противоположно направлению оси.
Вычислим проекции главного момента Мо относительно начала
координат на оси х, у, z как главные моменты сил относительно
этих осей:
133

Так как заданные силы параллельны оси z, то Мг = 0 и глав-
главный момент Мо рассматриваемой системы сил лежит в плоскости хОуг
т. е. направлен перпендикулярно главному вектору R*.
Модуль главного момента Мо равен:
При приведении системы параллельных сил в пространстве воз-
возможны следующие случаи:
1.	Главный вектор R* и главный момент Мо равны нулю. В этом
случае силы взаимно уравновешиваются.
2.	Главный вектор R* равен нулю, а главный момент Мо не ра-
равен нулю. В этом случае силы приводятся к паре сил с моментом М,
равным главному моменту Мо этих сил относительно центра при-
приведения.
3.	Главный вектор R* не равен нулю, а главный момент Мо или
равен нулю или не равен нулю.
Если Мо — 0, то силы приводятся к равнодействующей силе R,
линия действия которой проходит через центр приведения О.
Если Моф0, то, как указывалось выше, MOJ_R*. В этом слу-
случае силы приводятся к равнодействующей силе R, линия действия
которой проходит через точку К (рис. 126).
Из рассмотренных случаев следует, что параллельные силы не
приводятся к динаме.
Для системы параллельных сил в пространстве имеются два
условия равновесия сил:
Если взаимно уравновешивающиеся силы параллельны оси z, то
получим
т. е.
а также
Таким образом, для системы сил, параллельных оси г, имеем
три уравнения равновесия:
2 *.
F0.2)
Задача на равновесие параллельных сил, не лежащих в гдной
плоскости и приложенных к одному твердому телу, статически ©пре-
134

деленна в том случае, если количество неизвестных в ней не пре-
превышает трех.
Для системы параллельных сил, приложенной к совокупности
двух тел, задача статически определенна при числе неизвестных не
больше шести и т. д.
§ 61. Примеры на приведение системы сил к простейшему виду
Пример 32. К вершинам прямоугольного параллелепипеда, ребра
которого имеют длину а == 20 см, Ь = 40 см и с = 30 см, прило-
приложены указанные на рис. 127 силы Р1 = 5н, P2 = 8w, P3=2«,
Р,
Рис. 127.
Р4=10и, Р5=г3к, Я6 = б«(рис. 127), Требуется привести эту
систему сил к простейшему виду.
Решение. Предварительно находим:
since = -
Определяем модуль и направление главного вектора системы сил
по ег* проекциям на координатные оси:
Х = Р1—Р3 — Р5 = 5— 2 — 3 = 0,
Y — P2 — P4cosa = 8— 10- 0,8 = 0,
Z=P4sina —P6 = 10- 0,6 — 6 = 0,
R* = yx2-\-Y2-{-Z2 = 0.
Определяем модуль и направление главного момента системы сил
относительно начала координат по его проекциям на координатные
135

Мх = — Р2с
оси, равным главным моментам сил относительно этих осей:
& sin а — Рф —
— — 8- 30+10- 40-0,6 — 6 ¦ 40 = — 240 я- см;
а = 5- 30 — 3-30 + 6- 20 = 180 и- см,
Mz = Р2а + Рф = 8 • 20 + 3 - 40 = 280 « • см;
VmI+a.
М
¦ Ml=V(— 240J+ 1802+2802 = 410 я см;
COS(MO, !)___ —^- — О,
Mv
180
cos(Mo,j) = -^= 410=0,439;
C0S(M0, к) = -|j =-|^ = 0,683.
Полученные результаты показывают, что заданная система сил
приводится к паре сил. Модуль момента пары Ж = Жо = 410м • см.
Направление момента составляет
с координатными осями углы,
определяемые найденными коси-
косинусами.
Пример 33. К вершинам пря-
прямоугольного параллелепипеда,
ребра которого имеют длину
а = 20 см, Ь = 30см, с = 40 си,
приложены указанные на рис. 128
силы Рх — 4н, Р2=10м, и
Р3 = 5н. Требуется привести
эту систему сил к простейшему
виду.
Решение. Определяем мо-
модуль и направление главного век-
вектора системы сил по его проек-
Рис. 128.
циям на координатные оси:
= yu\= 11,87 я.
cos(R*. 1) = — = 0.337, cos(R*. j) = ~ = 0,842.
cos(R*. k) = -Jr = — 0.421.
136

Вычисляем главные моменты данной системы сил относительно
координатных осей
Мх = — Рф = — 150 н-см, Му = Рхс = 160 я-см,
Mz = Р2а = 20Q и • см
Очевидно, главный момент системы сил относительно начала ко-
координат Мо = У Мх -\-М2у-\-М2г не равен нулю Чтобы установить,
к чему приводится: система сил — к равнодействующей или к динаме,
определяем наименьший главный момент системы сил
XMx+YMy + ZMz —4.150+10.160 — 5-200
М* =	^s	=	ПТ87	~0-
Равенство числителя нулю есть аналитическое условие существо-
существования равнодействующей.
Поэтому рассматриваемая система сил приводится к равнодей-
равнодействующей силе: /? = /?* =11,87 и. Определяем ее линию действия
по уравнениям E9 2), пользуясь найденными проекциями равнодей-
равнодействующей X, Y, Z и главными моментами системы сил относительно
осей координат Мх, Му, Mz:
Mx = yZ — zY, —150 = — Ъу — Юг; у + 2г = 30; A)
My = zX — xZ, 160 = 4z-(-5x; 5x + 4z = 160, B)
Mz = xY — yX; 200=10x — 4y; 5x —^2y=100. C)
Так как линии в пространстве соответствуют два уравнения с тремя
переменными координатами, то из трех уравнений независимыми
являются только два
Действительно, вычитая уравнение C) из уравнения B) и деля
полученное уравнение на два, получаем уравнение A).
Координаты точки Av пересечения линии действия равнодей-
равнодействующей с плоскостью zOx, определяем из уравнений C) и A) при
* = 0:
У1 = 0, х1 = 20 см, zx— 15 см.
Координаты точки Л2, пересечения линии действия равнодей-
равнодействующей с плоскостью хОу, определяем из уравнений B) и A) при
z2 = 0.
22 = 0, д:2 = 32 см, у2 = ЗО см.
Линия действия равнодействующей силы показана на рис. 129.
Сила R направлена по этой линии соответственно найденным
выше косинусам углов.
Пример 34. В вершинах пирамиды, ребра которой О А = 63 см,
ОВ = 45 см и OD = 60 см взаимно перпендикулярны, приложены
силы Рг = 21 н, Р2 = 29 «, Р3=25 к и Я4=15 и (рис. 130).
Требуется привести эту систему сил к простейшему виду.
137

Рис. 130,
Рис. 129.

Решение. Предварительно находим:
0А 63 Ю 21- --- =/1=^ = 2;
cosa==Dl =
в_од _
45
87 = 29; 51Па:
45 3 . .
/бО2 + 452 75 5 '
'29'
 '
Определяем модуль и направление главного вектора системы сил
это его проекциям на координатные оси:
X = Р3 cos
4 = 25.-^ — 15== О,
21
= —PI —P2cosa = —21—29-=^ = —42«.
90	4
= P2sina —P3sin р = 29 • g — 25 •-^- = 0,
откуда /?* =
cos(R*.
=:42 «;
; cos(R*, J)==— 1; cos(R*. k) = 0.
1L
м*Центральная ось
системы сип
__	. ..	fM
Рис. 131.
Прикладываем к точке О главный вектор R*, направляя его про-
противоположно оси у (рис. 131). Определяем главные моменты задан-
заданной системы сил относительно координатных осей:
20
Mr = P2d2 = P2- GMsina = 29-63.^=1260 к • см;
= 25- 45 •-^ = 900
Так как Жг = 0, то главный момент Мо заданных сил относи-
относительно начала координат лежит в плоскости хОу и не перпенди-
перпендикулярен главному вектору R*, лежащему на оси у. Следовательно,
заданные силы приводятся к динаме.
139

Откладывая на осях х и у проекции Мх и Му главного мо-
момента Мо, получаем его компоненты М* и М' по направлениям глав-
главного вектора и перпендикуляра к нему (§ 57). Модули этих компо-
компонентов равны:
| М* | = | Му | = 900 н-см;
\М.'\ = \МХ\— 1260 м- см.
Находим плечо пары R*, R' с моментом ЛГ:
* = ос = ? = .!*» = зо с*.
Прикладываем силы пары R* и R' в точках О и С плоскости yOz.
Исключая уравновешивающиеся силы R* и R' в точке О и пе-
перенося М* из точки О в точку С, получаем R* и М*, т. е. динаму,
в точке С.
Пример 35. Привести к простейшему виду систему сил, изобра-
изображенных на рис. 132, если Рх = 2 н, Р2 = 5 н, Р3=14 «, а раз-
размеры прямоугольного параллелепипеда д = 2 см, й = 4 см, с = 3 см.
\2
Рис. 132.
Если силы приводятся к динаме, то найти уравнения центральной
оси и координаты точек пересечения ее с плоскостями zOx и хОу.
Решение. Определяем модуль и направление главного вектора
системы сил по его проекциям на координатные оси:
Х~Р2 = Ъ я; К = — -Р И Z P
!= |^52 4-142 4-22= 15 и;
cos(R*, 0 = ^ = 1 = 1; cos(R*, j)= Г";
15
cos(R*. к) = 4=Д.
15'
Так как R* Ф 0, то силы приводятся к равнодействующей или
к динаме.
140

Вычисляем главные моменты сил относительно координатных осей:
Му = Р2с = 5 • 3= 15 я ¦ см;
Mz = — Р2о — Р3а— — 5 ¦ 4 — 14-2== — 48 н • см.
Чтобы узнать, к чему приводятся силы, находим наименьший
главный момент:
—14-15 — 2-48 306 _
R*
0
/
/^
2-JLJL——^ '. /иенграпыая ось
/I2BjJ, зм, 0} У система сип
Рис. 133.
Так как М* Ф 0, то силы приводятся к динаме.
Определяем положение центральной оси в пространстве двумя
уравнениями E9.1):
1)
откуда
2)
откуда
Mx-(yZ — zY) _ М* — 2у — Иг _ 20,4
	х	"Ж'	5 ~~ 15
— (zX — xZ)
2х
z = 4,04.
Координаты точки А.х пересечения центральной осью плоскости zOx
находим при У]—0 из этих уравнений:
у1==0; jCj = 3,23 см; ^ = 0,486 см.
Координаты точки А2 пересечения центральной осью плоскости хОу
находим из этих уравнений при z2 = 0:
Так как М* < 0, то наименьший главный момент рассматриваемой
системы сил М* направлен по центральной оси противоположно
главному вектору R* (рис. 133), направление которого установлено
найденными выше косинусами углов.
141

§ 62. Условия равновесия сил, приложенных
к несвободному твердому телу.
Определение реакций опор
Согласно принципу освобождаемое™ от связей, несвободное твер-
твердое тело можно рассматривать как свободное, находящееся под
действием задаваемых сил и реакций связей.
Для системы взаимно уравновешивающихся задаваемых сил и
реакций связей, приложенных к твердому телу и произвольно рас-
расположенных в пространстве, можно составить шесть уравнений равно-
равновесия. Из этих уравнений определяются реакции опор и устанавли-
устанавливаются условия равновесия задаваемых сил, приложенных к несвобод-
несвободному твердому телу.
Так как оси координат могут иметь любые направления, то сле-
следует проводить их так, чтобы они пересекали возможно большее
числе неизвестных сил или были перпендикулярны к ним, т. е. чтобы
каждое из уравнений равновесия содержало возможно меньшее число
неизвестных величин.
1. Твердое тело с одной закрепленной точкой
Допустим, что на твердое тело с неподвижно закрепленной точ-
точкой А действует система задаваемых сил Р^ Р2	Р„ (рис. 134).
Заменим действие связи в точке А (сферического шарнира) реак-
реакцией R^, направление которой неизвестно. Проведем оси коорди-
координат х, у, z из точки А и разложим эту реакцию на три соста-
составляющие ХА, YA, ZA, направленные по осям координат.
Если силы, приложенные к твердому телу, уравновешиваются, то
для этих сил можно составить шесть уравнений равновесия.
Составляющие реакции связи не имеют моментов относительно
осей координат и не входят в уравнения моментов.
Уравнения равновесия имеют вид
2
»=1
i-l
142

Здесь Xt, Yh Zt — проекции задаваемой силы Р, на оси х, у, z.
Mix, M!y, Miz — моменты силы Р^ относительно тех же осей.
Три уравнения моментов, не содержащие реакций опор, и выра-
выражают те условия, которым удовлетворяют задаваемые силы, действую-
действующие на это тело, при равно-
равновесии приложенных к нему сил.
Таким образом, если силы,
приложенные к твердому
телу с одной закрепленной
точкой, уравновешиваются,
то суммы моментов всех
действующих на тело зада-
задаваемых сил относительно
трех координатных осей,
проведенных через закреп-
закрепленную точку, равны нулю.
Из этих трех условий сле-
следует, что главный момент МЛ
системы задаваемых сил отно-
относительно закрепленной точки
равен нулю, т. е. система за-
задаваемых сил приводится к
равнодействующей R, линия
действия которой проходит че-	Рис- 134'
рез точку А.
Из трех уравнений проекции определяются величины составляю-
составляющих реакций связи:
откуда
cos (RA,
2
RA
гл=-.
X,	Y,
i=-Br-; cos(RA, j)=-^
Л,
V
Zl.
Реакция связи RA уравновешивает равнодействующую задаваемых
сил R, т. е. эти силы равны по модулю и противоположно напра-
направлены; RA — — R.
2. Твердое тело с двумя закрепленными точками
Рассмотрим твердое тело с двумя неподвижно закрепленными
точками А к В. Допустим, что на это тело действует система зада-
задаваемых сил Рг Р2. ..., Р„ (рис. 135).
143

Расстояние между точками А и В обозначим I. Заменим действие
связей в точках А и В реакциями Яд и RB, направления которых
не известны. Начало координат поместим в одну из закрепленных
точек, например А, и одну из осей проврдем через вторую закре-
закрепленную точку В.
Рис. 135.
Разложим каждую из реакций R^ и RB на три составляющие по
осям координат: ХА, YA, ZA, XB, YB, ZB.
Составим шесть уравнений равновесия для сил, действующих
на тело:
п
Здесь Xv Y(, Zt — проекции задаваемой силы Рг на оси х, у, z,
a Mlx, Mfy, Mlz — моменты силы Р. относительно тех же осей.
Из шести составленных уравнений равновесия только одно урав-
п
нение 2 М,„ = 0 не содержит реакций опор. Это уравнение и
144

выражает то условие, которому удовлетворяют задаваемые силы,
действующие на это тело при равновесии приложенных к нему сил.
Таким образом, если силы, приложенные к твердому телу
с двумя закрепленными точками, уравновешиваются, то сумма
моментов всех действующих на тело задаваемых сил отно-
относительно оси, проходящей через точки закрепления, равна
нулю.
Остальные пять уравнений равновесия используются для опреде-
определения составляющих реакций связей:
я
Mix'<
l = ,
п
42
я	л
¦ iV ж. -
Последнее уравнение показывает, что величины составляющих
реакций YA и YB вдоль оси, проходящей через точки закрепления,
определить невозможно. Поэтому для YA и YB рассматриваемая
задача статически неопределенна.
Если предположить, что точка А закреплена неподвижно,
а в точке В имеется подшипник, тогда продольная реакция Yв = О,
л
a YА = — 2 Уi (CM- пример 36).
1-Х
При этом условии задача становится статически определенной.
§ 63. Примеры на равновесие сил, произвольно расположенных
в пространстве
Пример 36. Дверь ABDE весом G = 240 н удерживается откры-
открытой на угол FBD= 120° двумя веревками. К веревке DFK, пере-
перекинутой через блок F, подвешен груз весом Q = 60 к; веревка EL,
протянутая перпендикулярно двери, закреплена в точке L пола.
Размеры двери: АВ — 2 м, Л? = 0,8 м.
Определить реакции подпятника А и подшипника В и натяжение
веревки EL (рис. 136а).
10 А. А. Яблонский	145

Реш-ение. Рассматриваем равновесие сил, приложенных к двери.
Для этой системы составляем шесть уравнений равновесия сил,
расположенных как угодно в пространстве. Проводим оси коор-
координат, как показано на рис. 1366. Дверь имеет одну закреплен-
закрепленную точку — подпятник А я
другую точку — подшипник В.
Для упрощения уравнений рав-
равновесия, начало координат по-
помещаем в одну из этих точек
(А) и одну из осей координат
(z) проводим через обе точки.
Прикладываем к двери зада-
задаваемые силы: ее вес G, дей-
действующий по вертикальной оси
симметрии, и реакцию Т1 ве-
веревки DF, равную по модулю
весу груза Q. Освобождая
дверь от связей, прикладываем
ве-
Рис. 136а.
их реакции. Реакция Т2
ревки EL направлена вдоль
веревки. Подшипник В схематически представляет собой кольцо,
сквозь которое проходит ось, скрепленная с дверью. Подшипник
не препятствует перемещению двери вдоль его оси, т. е. вдоль оси z,
а препятствует перемещению в плоскости, перпендикулярной к этой
оси. Согласно § 3, реакция
подшипника не имеет со-
составляющей по оси z. Раз-
Разложим эту реакцию на со-
составляющие XB и \в, напра-
направив их по осям хну.
Подпятник А схемати-
схематически представляет собой
совокупность такого же
кольца и опорной плоскости.
Благодаря наличию кольца,
реакция подпятника имеет —«е.:
составляющие Хл и YA, a
благодаря опорной плоско-
плоскости — составляющую ЪА.
Направим и эти силы по
'г Е
YB, T2, определятся
х
Рис. 1366.
осям координат.
Шесть неизвестных сил ХА, YA, ZA, XB,
из шести уравнений равновесия сил.
Обозначим размеры двери: ЛВ = Л, АЕ = а.
При определении реакций опор тела, имеющего две опорные
точки, в первую очередь составляются уравнения моментов, так как
они содержат меньше неизвестных сил. При составлении уравнений
146

¦моментов следует учитывать, что если линия действия силы парал-
параллельна оси или пересекает ось, то момент этой силы относительно
оси равен нулю.
Если же момент не равен нулю, то силу следует спроектировать
иа плоскость, перпендикулярную к оси, и вычислить момент получен-
полученной проекции относительно точки пересечения оси с плоскостью.
Чтобы облегчить вычисление моментов сил относительно осей коор-
координат, проектируем систему сил на три плоскости, каждая из кото-
которых перпендикулярна одной из координатных осей (рис. 136в, г, д).
r2cos60°X
Рис. 136в.
Рис. 136г.
По рис. 136в, г, д вычисляем моменты полученных проекций сил
относительно точки А, в которой оси координат пересекают пло-
плоскости проекций.
Сначала составляем уравнение 2 Mlt = 0, так как ось z прохо-
проходит через точки А и В и моменты неизвестных реакций в этих
точках относительно оси z равны нулю.
1. 2М(г = 0 (рис. 136<Э); Т^автЗО0— Т2а = 0, откуда имеем:
Т2 = Тх sin 30° = 60 • 0,5 = 30 я.
10*
147-

2. 2^ = 0 (рис. 136в)"> ~YBh~Ti cos 30°ft-\-Ga co*™ = 0.
откуда находим Y в:
Ув = — 7\cos 30° + О ~~ = — 60 • 0,866 + 240 М^ = _28«.
3.	^Л1„ = 0 (рис. 136г); Л-дй-7tcos60°й + G gС°2^ ^0-
откуда определяем А"в:
^ = Т1со.6О'-О^ВГ^ = 60. 0.5-240 ^^ = -11.6 и.
Для определения проекций сил А"/1, Y A, ZA, не вошедших в урав-
уравнения моментов, составляем три уравнения проекций, пользуясь
рис. 1366.
4.	^Xi = Q; XA-{-XB — T1cos60° — T2cos60°~0, откуда
ХА = — Хв + G\ + r2)'cos 60° = 11,6 -j-F0-f- 30) ¦ 0,5 = 56,6 н.
5.	2К< = °; KA + KB4-^iCOs30° —72cos30° = 0, откуда:
YA = — YB — {T1 — T2)cos 30° = 28 — F0 — 30) • 0,866 = 2 и.
6.	2Zf = °; ZA — O = 0, откуда
ZA = О = 240 «.
Знаки ответов показывают, что силы ХА, YA, ZA направлены так,
как показано на схемах, т. е. в сторону осей координат, а1 напра-
направления сил Хв, YB противоположны указанным, т. е. противоположны
направлениям осей х и у.
Принятая последовательность составления уравнений равновесия
сил позволила определить из каждого уравнения одну неизвестную
величину, не решая системы уравнений.
Пример 37. На рис. 137а и б изображен коленчатый вал дви-
двигателя. При вертикальном положении средней плоскости колена
давление шатуна на середину шейки вала составляет Р=\2 кн и
направлено в плоскости, перпендикулярной оси вала, под углом 15а
к горизонтали.
На оси вала в точке С закреплен маховик весом 0=12 кн.
В точке Е укреплен шкив диаметром D = 80 см с ремнем, передаю-
передающим момент на вал рабочей машины. Ветви ремня лежат в плоскости
шкива и составляют с горизонталью угол, равный 30°. Отношение
натяжений ведущей и ведомой ветвей
-L-2
Расстояние от оси шейки колена до оси вала г—\Ьсм. Рас-
Расстояния по оси вала указаны на рис. 137а в сантиметрах. Опреде-
Определить величины натяжения ветвей ремня Г и Mi реакции подшипни-
подшипников А и В при равномерном вращении вала и при заданном его
148

положении. (Весом шкива и вала по сравнению с весом маховика?
можно пренебречь.)
Решение. При равномерном вращении правильно сконструиро-
сконструированного вала приложенные к нему силы должны удовлетворять усло-
условиям их равновесия.
Прикладываем к валу задаваемые силы: вес маховика Q, давле-
давление шатуна на шейку вала Р и реакции ветвей ремня Т и t, напра-
направленные по касательной к окружности обода шкива. Отбрасывая
связи (подшипники), приклады-
прикладываем к валу их реакции, раз-
разложенные на составляющие Y^.
гА, \в, гв (рис. 137в).
Выбрав оси координат, как
показано на рис. 137в, соста-
составляем уравнения равновесия*
Рис. 137а.
Рис. 1376.
сил, произвольно расположенных в пространстве. Вал имеет две-
точки опоры А и В; первым составляем уравнение моментов относи-
относительно оси х, проходящей через эти точки. Пользуемся, рис. 137г,
так как на нем изображены только силы, моменты которых относи-
относительно оси х не равны нулю.
^ = 0; t~~ Т-^- + Pr cos \5° = 0.
Так как T==2t, то модули сил t и Т можно, определить:
откуда
2Pr cos 15°
t — '
D
"ТГ ~ 2t "Т
2 • 12 • 15 • 0,966
~ 80
r cos 15°=
= 4,347 кн,
= 8,694 кн.
Затем составляем следующие уравнения моментов по рис. 137в.
При вычислении моментов сил Т, t и Р относительно оси у проектируем
149»

Рис. 137в.
Рис. 137г.

каждую из этих сил на плоскость, проходящую через точку прило-
приложения силы перпендикулярно оси у.
Полученные проекции 7sin30°, ?sin30°, Psinl5° параллельны-
оси z.
2. 2^ = 0; Psin 15° • 50 + ZB-85 —G • 115 + Tsin30°. 155+
+ fsin30°- 155 = 0, откуда находим ZB:
7 __ — Psin 15° -50+0-115 — (Г+ t) sin 30° -155 _
zB_	gg	¦ _
— 12-0,259-50+12-115 —13,04-0,5-155 214 „ _o
=	gg	=-gg-_2,W KH.
Аналогично при составлении уравнения 2-^iz —0 находим
проекции сил Т, t и Р на плоскости, перпендикулярные оси z.
Эти проекции параллельны оси у и соответственно имеют абсолют-
абсолютные величины: Т cos 30°, *cos30°, Pcosl5°.
3- 2Л1/г = 0, Pcos 15° • 50 — KB-85 + rcos30°- 155 +
+ ^cos30°- 155 = 0.
Определяем YB:
V — P cos 15° • 50 + (Г + Q cos 30° • 155 _
_ 12 - 0,966 -504-13,04.0,866 ¦ 155 __ 2330 _ 07 .
— 		gg	-Щ- — ЛЛУ KH.
Составляем уравнения проекций на оси у и z (все действующие
силы перпендикулярны оси х и уравнение ^jXi = 0 обращается
в тождество 0 = 0).
4.	2К? = 0; Ка —Pcos15°+Kb —74os30° —*cos30° = 0.
Находим YA:
YA = P cos 15°—Ye-lriT-^t) cos 30° =
= 12 • 0,966 — 27,41 + 13, 04 • 0,866 =—4,53 кн.
5.	2Z, = 0; ZA-\-Psin\5°-\-ZB — G + Tsin 30°-\-tsin30° = 0.
Определяем ZA:
ZA — — Psin 15°— ZB-\-G — {T +1)sin 30° =
= — 12 - 0,259 — 2,52+12— 13,04 • 0,5 = —0,15 кн.
Пример 38. Тонкая горизонтальная плита ABDE весом G = 2,4 кк
поддерживается шестью стержнями, расположенными вдоль диагона-
диагоналей граней или вдоль ребер прямоугольного параллелепипеда.
Определить усилия в стержнях, если а= I м, Ь=1,& м, с = 2Лм
(рис. 138а).
Решение. Рассматриваем равновесие сил, приложенных к плите-
Прикладываем к плите в центре симметрии прямоугольника ABDE'
151.

задаваемую силу —вес плиты G. Заменяем действие связей, т. е.
шести стержней, их реакциями. Считаем стержни, как это принято,
растянутыми и направляем их реакции от узлов (рис. 1386). Для
сил, действующих на плиту, составляем шесть уравнений равновесия
сил, расположенных как угодно в пространстве. Начало координат
\В
Рис. 138а.
Рис. 1386.
помещаем в точку О пересечения линий действия трех неизвестных
реакций Sj, S2. S3. чтобы исключить эти реакции из уравнений
.моментов:
lx = Q; — О |-—-S4fr — Ss sinp.fr = 0;
- а — О;
• Ь —
53cosa —
, = 0; — О
— S2
S3sina — 54 —
¦ S5 sin p — 5e sin a = 0.
A)
B)
C)
D)
E)
F)
По заданным размерам вычисляем синусы и косинусы углов а и Р;
¦sina =
2,4
-=—; cos a =1/1—sima ——
5	Y	5
Sin
2,4
_12_
13
_5_
13
152

Из уравнения B) находим
а
	 G 	 2,4 	 . f.
— ¦ <>о1„„ — 4" — КИ"
2,4
Из уравнения C)
'-'s —^6
Из уравнения A)
Из уравнения D)
Из уравнения E)
2
a cos a
'•»4
= —1,3 ки.
Sj^ — Ss= 1,3 кн.
Sz = — 56 = 1,5 кн.
Из уравнения F)
2 = — G — SjSinfl —53sina — Si —
— 56sina =
= — 2,4 — 1,3 • 44 — 1.5 • 4 — 0 + 1,3 • 4t+ 1,5 • 4- = — 2,4 кн.
Величины сил, приложенных к плите, помещаем в табл. 3.
Таблица 3
Силы
Величина силы, кн
G
2,4
5,
1,3
S2
—2,4
s3
1,5
0
55
-1,3
s.
—1,5
Из табл. 3 следует, что стержни /, 3 растянуты, стержни 2, 5, &
сжаты, а стержень 4 не работает.
Силы, приложенные к плите, образуют три взаимно уравновеши-
уравновешивающиеся пары сил, лежащие в различных плоскостях:
1)	О, S2;
2)	Sp S5;
о) S3* Sg.
Пример 39. При повреждении одной из двух петель прямоуголь-
прямоугольной парниковой рамы ABDE ее удерживают в горизонтальном поло-
положении двумя вертикальными стержнями FJ и KL.
Вес рамы G=180«.
Расстояния: BF = BD ND	^
Определить реакцию шарового шарнира (петли) А и усилия
в стержнях FJ и KL (рис. 139а).
153

Решение. Рассматриваем равновесие сил, приложенных к раме.
Прикладываем к раме в центре тяжести С задаваемую силу — вес
рамы G (рис. 139E). Отбрасывая связи, прикладываем к раме их
реакции. Реакции сжатых стержней Rp и R^-, равные усилиям
в стержнях, направляем вертикально вверх. Реакция шарового шар-
шарнира RA может иметь любое направление, но при условии, что
Рис. 1396.
остальные силы G,
приложенные к раме, вертикальны,
реакция R^ тоже имеет вертикальное направление.
Для полученной системы вертикальных сил, из которых три силы
не известны, составляем три уравнения равновесия параллельных сил
в пространстве. Начало координат помещаем в одну из опорных
154

точек А, ось z направляем параллельно силам, оси х и у проводим"
по краям рамы.
Уравнения равновесия сил имеют вид:
4	1
В уравнение B) подставляем BN =-?- BD, BF = -т BD и, сокра-
сокращая, получаем:
= о.	C)
Подставив значение G —180 м. решаем систему двух первых
уравнений и находим RK и RF:
)
д	1	i или ifi
Вычитая из одного уравнения другое, находим:
^ RK = 270; Яд- = 100 м; Я^ = 40 к.
Из уравнения C) определяем RA:
RA = G — /?д- — RF = 180 — 100 — 40 = 40 «.
Вопросы для самоконтроля
1.	Каковы возможные случаи приведения произвольно расположенных;
и параллельных сил в пространстве?
2.	К какому простейшему виду можно привести систему сил, если
известно, что главный момент этих сил относительно различных точек про-
пространства:
а)	имеет одно и то же значение, не равное нулю;
б)	равен нулю;
в)	имеет различные значения и перпендикулярен к главному вектору;
г)	имеет различные значения и не перпендикулярен к главному вектору?
3.	Каковы условия и уравнения равновесия пространственной системы
сходящихся, параллельных и произвольно расположенных сил и чем они
отличаются от условий и уравнений равновесия такого же вида сил на
плоскости?
4. Каковы геометрическое и аналитическое условия приведения прост-
пространственной системы сил к равнодействующей?
155

5.	Сформулируйте теорему о моменте равнодействующей пространст-
пространственной системы сил относительно точки и оси.
6.	Составьте уравнения линии действия равнодействующей.
7.	Какую прямую в пространстве называют центральной осью системы
¦сил?
8.	Выведите уравнения центральной оси системы сил.
9.	Покажите, что две скрещивающиеся силы можно привести к сило-
силовому винту.
10.	По какой формуле вычисляют наименьший главный момент заданной
системы сил?
11.	Какова зависимость главного момента системы сил в пространстве
от расстояния центра приведения до Центральной оси этой системы сил?
12.	Относительно каких точек пространства главные моменты заданной
системы сил имеют один и тот же модуль и составляют с главным векто-
вектором один и тот же угол?
13.	Относительно каких точек пространства главные моменты системы
-сил геометрически равны между собой?
14.	Каковы инварианты системы сил?
15.	В чем состоит особенность условий равновесия сил, приложенных
к твердому телу, имеющему одну или две закрепленные точки?
ГЛАВА X
ЦЕНТР ТЯЖЕСТИ
§ 64. Последовательное сложение параллельных сил.
Центр параллельных сил
Допустим, что к твердому телу в точках ¦ Л,, Л2, .... А5 при-
приложены параллельные силы Pv Р2, .... Р5, из которых силы Рг,
Р2, Р3 направлены в одну сторону, а силы Р4, Р5 — в противопо-
противоположную сторону (рис. 140).
Складывая силы Р1 и Р2 по правилу сложения двух параллель-
параллельных сил, направленных в одну сторону, получаем
А1В1 _ Р2
Определив модуль равнодействующей силы Rj и точку приложе-
приложения ее Bv складываем Rj с силой Р3 и получаем:
Аналогично определяем равнодействующую сил Р4 и Р5:
В результате последовательного сложения заданных параллельных
сил получены две противоположно направленные параллельные силы
R2 и R3 в точках В2 и Вг.
156

В зависимости от модулей и точек приложения этих сил воз-
возможны следующие случаи:
1. Силы R2 и R3 не равны по модулю. Предположим, что в рас-
рассматриваемом случае (рис. 140) /?2 > /?3. Тогда равнодействующая R
заданных сил имеет модуль R = /?2 — /?3 и направлена в сторону
•большей силы R2.
Точка С, в которой приложена равнодействующая сила R, нахо-
находится на продолжении отрезка В2В3, за точкой приложения большей
силы, причем
В2С
~ЩС
А
?ис. 140.
Точка С называется центром
параллельных сил.
Через эту точку обязательно
проходит линия действия равно-
равнодействующей заданной системы
параллельных сил, если, не изме-
изменяя модулей сил, поворачивать
линии действия сил вокруг точек
их приложения на один и тот же
угол в одну и ту же сторону
{рис. 140).
Действительно, все приведен-
приведенные равенства, определяющие мо-
модули и точки приложения равно-
равнодействующих сил Rj, R2> R3, R, при повороте сил остаются справед-
справедливыми.
2.	Силы R2 и R3 равны по модулю, но их линии действия
не совпадают.
В этом случае заданные силы приводятся к паре сил.
3.	Силы R2 и R3 равны по модулю и их линии действия
¦совпадают.
В этом случае заданные силы взаимно уравновешиваются.
Система параллельных сил, направленных в одну сторону, не
может уравновешиваться или приводиться к паре сил. Эта система
всегда имеет равнодействующую.
§ 65. Формулы радиуса вектора и координат центра
параллельных сил
Рассмотрим систему параллельных сил Рг, Р2, ..., Рп, приложен-
приложенных в точках Av A2> .... Ап, приводящуюся к равнодействующей R,
приложенной в точке С (рис. 141).
Положение центра параллельных сил С определится его радиу-
радиусом-вектором гс относительно начала координат О или тремя коорди-
координатами хс, ус, zc.
157

Положение точки приложения каждой силы Рг определяется радиу-
радиусом-вектором г,- или координатами xit yt, zt, где i=l, 2, ..., я.
На основании теоремы Вариньона о моменте равнодействующей
относительно любого центра (§ 56) приравниваем момент равнодей-
равнодействующей относительно центра О геометрической сумме моментов,
составляющих сил относительно этого центра:
или согласно § 44
Рис. 141.
Введем единичный вектор и, параллельный линиям действия сил.
Тогда получим
Р; = иЯ?,
где Рг—алгебраическое значение силы.
Подставив значения Р, и R в выражения моментов, будем иметь
Переместим скалярные множители в векторных произведениях:
или
Вектор и может иметь любое направление, так как, согласно-
свойству центра параллельных сил, линии действия сил можно пово-
поворачивать. Следовательно,
ГсХР; — SrjP; = 0.
158

Из этого равенства получим формулу, определяющую радиус-
вектор центра параллельных сил:
F5.1)
Спроектировав векторы левой, и правой частей равенства F5.1)
на оси координат, получим формулы для вычисления координат
центра параллельных сил:
F5.2)
В формулах F5.2) числителем и знаменателем каждой дроби
является алгебраическая сумма. Координаты точки приложения ка-
каждой силы имеют тот или другой знак, и параллельные силы, на-
направленные в одну сторону, считаются положительными, а напра-
направленные противоположи© — отрицательными. Таким образом, коор-
координаты xt, yt, zt и значения сил Pt в этих формулах являются
алгебраическими величинами.
Выбор направления, вдоль которого параллельные силы считаются
положительными, произволен и на результатах вычисления коорди-
координат по формулам F5.2) не отражается.
§ 66. Центр тяжести твердого тела
Силы притяжения отдельных частиц тела к Земле направлены
приблизительно к центру Земли. Так как размеры рассматриваемых
тел малы пэ сравнению с радиусом Земли, то эти силы можно счи-
считать параллельными. Равнодействующая этих параллельных сил.
равная их сумме, есть вес тела, а центр этой системы параллельных
сил, в котором приложен вес тела, называется центром тяжести
тела.
В твердом теле центр тяжести занимает вполне определенное
положение, которое не зависит от расположения рассматриваемого
тела в пространстве.
Обозначим силы притяжения отдельных элементарных частиц
тела к Земле AGj, AO2	 kGn, вес тела G, координаты его
центра тяжести хс, ус, zc, а координаты любой частицы твердого
тела — хр yt, zl (рис. 142). Координаты центра тяжести твердого
тела можно определить как координаты центра параллельных сил.
159

Для центра тяжести формулы F5.1) примут вид:
2*'д0*
G
Ус =
G
F6.1)
где суммирования распространены на все частицы твердого тела.
В этих формулах алгебраическими величинами являются только коор-
координаты точек, а значения Двг всегда положительны, так как все силы
направлены в одну сторону.
По формулам F6.1) можно также вычислять координаты центра
тяжести тела, разбивая его не на элементарные частицы, а на от-
z
i
Рис. 142.
дельные части веса Ot, координаты xit yt, z-t центров тяжести
которых известны.
Определим положение центра тяжести однородного тела.
Вес однородного тела определяется формулой О = ~(V, где V —
объем тела, f— вес единицы объема.
Аналогично вес каждой частицы определяется по формуле
ДО,- = ~[^vi> гДе bwl — объем элементарной частицы Mt тела.
Обозначим xL, у;, zt координаты центра тяжести этой частицы.
Подставив эти значения, получим
хг —
¦fV
или
аналогично получим
160
zc
F6.2)

Центр тяжести однородного тела, заполняющего некоторый объем,
называется центром тяжести этого объема.
§ 67. Центр тяжести плоской фигуры. Статический момент
площади плоской фигуры относительно оси
Однородное тело, имеющее форму тонкой пластинки, можно
рассматривать как материальную плоскую фигуру. Положение центра
тяжести плоской фигуры определяется двумя координатами хс и ус
(рис. 143).
Вес однородной пластинки выразим формулой О = ш/\ где
F — площадь плоской фигуры, со — вес единицы ее площади.
Разобьем площадь фигуры на элементарные площадки. Вес каждой
площадки Mi определится по формуле \Gt — соД/7;, где AFt — ее
площадь. Обозначим xt, у1 координаты центра тяжести элементарной
площадки ML. Тогда координаты центра тяжести фигуры опреде-
определятся при помощи формулы F6.1)
Xr
у
G
Таким образом,
2 *i
Хг ¦
F
F7.1)
i	I
Рис. 143.
где суммирования распространены
на все элементы площади.
Эти формулы показывают, что координаты хс и ус центра тя-
тяжести однородной пластинки не зависят от постоянной ш, характе-
характеризующей вещество пластинки.
Центр тяжести однородной пластинки называют центром тяжести
площади этой пластинки.
Сумма произведений элементарных площадей, входящих в состав
площади фигуры, на алгебраические значения их расстояний до не-
некоторой оси, называется статическим моментом площади плоской
фигуры относительно этой оси.
Обозначая Sx и S статические моменты площади плоской
фигуры относительно осей х и у, на основании F7.1) имеем
F7.2)
Таким образом, статический момент площади плоской фигуры
относительно оси равен произведению площади фигуры на алге-
алгебраическое значение расстояния от центра тяжести до этой оси.
Статический момент площади плоской фигуры относительно оси
измеряется в см3.
= 2 «ДО =
11 А. А. Яблонский
161

Если известны статические моменты площади плоской фигуры
относительно координатных осей, то координаты ее центра тяжести
можно определить по формулам:
хс = ~г и Ус = ~г-	F7-3)
Очевидно, что статический момент площади плоской фигуры отно-
относительно оси, проходящей через центр тяжести фигуры, равен нулю.
§ 68. Центр тяжести линии
Определим положение центров тяжести однородных тел, имею-
имеющих большую протяженность при сравнительно малой площади
поперечного сечения. Рассмотрим, например, кусок однородной
тонкой проволоки постоянного
сечения, ось которой распо-
расположена по дуге кривой A3
(рис. 144). Вес проволоки вы-
выразим формулой G =р?, где
L — длина линии АВ, р — вес
единицы длины проволоки.
Разобьем линию АВ на эле-
элементарные участки Mi дли-
длиной Д/г. Вес каждого участка
определится по формуле:
Рис. 144.
Координаты центра тяжести
элементарного участка обо-
обозначим xt, yit zt. Тогда координаты центра тяжести С рассматри-
рассматриваемого куска проволоки определятся по формулам F6.1):
G
ИЛИ
L
IS уi
F8.1)
где суммирования распространены на все элементы проволоки.
Формулы F8.1) показывают, что координаты центра тяжести не
зависят от постоянной р, характеризующей вещество проволоки.
162

Центр тяжести однородной тонкой проволоки постоянного се-
сечения, ось которой совпадает с некоторой линией, называется цент-
центром тяжести этой линии.
§ 69. Вспомогательные теоремы для
определения положения центра тяжести
При вычислении координат центров тяжести пользуются различ-
различными приемами, позволяющими упростить вычисления. Рассмотрим
четыре вспомогательные теоремы, упрощающие в некоторых слу-
случаях нахождение центров тяжести.
Теорема 1. Если однородное тело имеет ось симметрии, то
центр тяжести тела находится на этой оси.
Рассмотрим однородное тело, имеющее ось симметрии (рис. 145).
Совместим с осью симметрии одну из осей координат, например
ось z, и определим две коорди-
координаты центра тяжести однород-	Z
ного тела по формулам F6.2):
п
Рис. 145.
ус— v
Возьмем в этом теле любые
две точки М( и М'г расположен-
расположенные симметрично относительно
оси z. Выделим около них равные
элементарные объемы Дг»г. Точки
М. и M't лежат на одном перпен-
перпендикуляре к оси z, на равных
расстояниях от этой оси, т. е.
MlNi = M'lNl (рис. 145). Следовательно, координаты хь и уг этих
точек равны по величине и противоположны по знаку.
Разбив все тело на пары симметрично расположенных и равных
элементарных объемов, составляем произведения х(-Д»(- и суммируем
их. Сумма слагаемых, относящихся к одной паре, равна нулю, так
как объемы Дг»(- равны, а координаты хх равны по величине, но имеют
противоположные знаки.
Из этого следует, что равна нулю и сумма, содержащая все
элементарные объемы тела, т. е. 2 xi b/Vi = О и аналогично
Подставив эти значения в формулы F6.2), получим:
хс —
V
11*
163

Так как хс = 0 и ус — О, то центр тяжести тела лежит на оси г,
являющейся осью симметрии тела, и его положение на этой оси
определяется лишь одной координатой:
V
Применяя эту теорему к плоской фигуре или линии, легко уста-
установить, что если плоская фигура или линия имеет ось симмет-
симметрии, то ее центр тяжести лежат на этой оси.
Теорема 2. Если однородное тело имеет плоскость симмет-
симметрии, то его центр тяжести находится в этой плоскости.
Рис. 146.
На рис. 146 изображено тело, имеющее плоскость симметрии;
сечение тела этой плоскостью заштриховано. Расположим оси х и у
в плоскости симметрии, а ось z перпендикулярно к ней. Возьмем
в этом теле две точки М. и ЛГ, симметрично расположенные отно-
относительно плоскости хОу. Выделим около них равные элементарные
объемы Дг»г Точки М1 и M'i лежат на одном перпендикуляре к пло-
плоскости хОу, на равных расстояниях от этой плоскости, т. е.
M.N( = M'iNl (рис. 146). Следовательно, координаты zt этих точек
равны по величине и противоположны по знаку.
Суммируя произведения 2(Дг»г, получим
= 0, где сум-
суммирование распространено на все элементарные объемы.
Вычислим координату zr центра тяжести рассматриваемого одно-
однородного тела по формуле F6.2):
= 0
Полученный результат показывает, что центр тяжести рассмат-
рассматриваемого тела находится в плоскости симметрии.
На основе рассмотренных теорем можно определить положения
центров тяжести некоторых симметричных линий, фигур и тел:
164

1)	центр тяжести отрезка прямой лежит в его середине;
2)	центры тяжести окружности, площади круга, поверхности и
объема шара находятся в их геометрических центрах;
3)	центры тяжести периметра и площади параллелограмма, ромба,
прямоугольника и квадрата лежат в точках пересечения их диаго-
диагоналей;
4)	центр тяжести периметра и площади правильного многоуголь-
многоугольника находится в центре вписанного (или описанного) круга.
Теорема 3. Объем тела вращения, полученного вращением пло-
плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не
пересекающей ее, равен произведению площади фигуры на длину
окружности, описанной ее центром тяжести*.
Пусть плоская фигура площадью F вращается вокруг оси у,
лежащей в плоскости фигуры и не пересекающей ее. При вращении
вокруг оси у контур этой фигуры описывает некоторую замкнутую
поверхность, называемую поверхностью вращения. Тело, ограничен-
ограниченное этой поверхностью, называется телом вращения (рис. 147).
У
XII
0
X
Рис. 147.
Объем этого тела вращения определим, как сумму бесконечно боль-
большого числа объемов элементарных круговых колец, образованных
вращением вокруг оси у бесконечно малых площадок AFt. Радиус
каждого кольца равен расстоянию этой площадки от оси у, т. е.
координате xt.
Объем элементарного кольца
Объем тела вращения
V = 2 А^ = 2* 2 *, Д^г-
Здесь суммирование распространено на все площадки, входящие
в состав данной плащади F.
* Эта и последующая теоремы выведены математиком IV столетия
Паппом, а в XV11 столетии они вновь были применены в работах Гюльдена
о центре тяжести.
165

Сумму 2 •*< A^i можно определить из формулы F7.1):
хс—
y
2
-х F
— хсг-
у
Подставив это значение в выражение, определяющее объем тела
вращения, получим:
V = 2kxcF,	F9.1)
где 2ъхс— длина окружности, описанной центром тяжести фигуры.
Теорема 4. Площадь поверхности вращения, полученной вра-
вращением плоской кривой вокруг оси, лежащей в плоскости этой
кривой, но ее не пересекающей, равна произведению длины, этой
кривой на длину окружности, опи~
санной ее центром тяжести.
Пусть кривая АВ длиной L
вращается вокруг оси у, лежащей
в плоскости этой кривой, но не
пересекающей ее. При вращении
вокруг оси у эта кривая опишет
некоторую поверхность вращения
(рис. 148).
Разобьем кривую на бесчислен-
бесчисленное множество бесконечно малых
элементов длиной Д/(. Поверхность,
описанную каждым элементом, мож-
но принять за поверхность усечен-
усеченного конуса.
Как известно из геометрии, площадь боковой поверхности усе-
усеченного конуса равна произведению-длины окружности среднего сече-
сечения на длину образующей. Поэтому площадь поверхности, образован-
образованной вращением элемента кривой Д/г можно определить по формуле
Рис- 148-
где xt — радиус окружности, равный расстоянию середины элемента
от оси у.
Площадь поверхности вращения
здесь суммирование распространено на все элементы Д/^ кривой АВ.
Сумму ^x^li определим из формулы F8.1):
2 xt Mi „ _
Подставив это значение в выражение, определяющее площадь по-
поверхности вращения, получим
:.	F9.2)
166

§ 70. Определение положения центра тяжести
плоской фигуры по центрам тяжести ее частей.
Способ отрицательных площадей
Пусть требуется определить положение центра тяжести неко-
некоторой плоской фигуры, состоящей из трех частей, положение цен-
центров тяжести которых известно (рис. 149).
Положим, что площади частей фигуры соответственно равны Fv
F2, Fv а координаты их центров тяжести Cv С2 и С3 будут xv
-1hnc'
О
Рис. 149.
Рис. 150.
уг, х2, у2 и х3. Уз- Статические моменты площади плоской фигуры
относительно осей координат равны суммам статических моментов
площадей отдельных ее частей, которые можно определить по
формулам F7.2):
Определив статические моменты Sy и Sx плоской фигуры, можно
найти координаты ее центра тяжести С по формулам F7.3):
Sv
и
Л.
F
Подставив значения статических моментов, получаем:
G0.1)
при определении положения
которой вырезана некоторая
Этот способ удобно применять и
центра тяжести плоской фигуры, из
часть (рис. 150).
Зная величину Fx площади фигуры с контуром А и координаты
х1 и ^! ее центра тяжести Cv а также площадь F2 части, выре-
вырезанной по контуру В, и координаты х2 и у2 ее центра тяжести С2,
можно вычислить координаты центра тяжести оставшейся части
фигуры по формулам, аналогичным формулам G0.1). При этом
площадь оставшейся части должна быть равна разности площадей
167

Fx и F2, а ее статические моменты — разности статических момен-
моментов площадей фигур А и В. Тогда
Этот способ определения центра тяжести плоской фигуры, из
которой вырезана некоторая часть, называется способом отрица-
отрицательных площадей.
Аналогичный прием, называемый способом отрицательных
объемов, применяется при вычислении координат центра тяжести
однородного тела, полученного вырезанием из тела объемом vx,
с центром тяжести Cx(xv yx, zx), части объемом v2, с центром тя-
тяжести С2(х2, у2, 22). Тогда
*с=-1:гУ2- Gо.з)
' Ус = v\ _
§ 71. Определение положения центра тяжести плоской фигуры
путем применения веревочного многоугольника
Если плоскую фигуру можно разбить на несколько частей, по-
положения центров тяжести которых известны, то положение центра
S)
Рис. 151.
тяжести этой фигуры можно найти графически, по методу веревоч-
веревочного многоугольника.
На рис. 151, а показана плоская фигура, которую можно разбить
на три прямоугольника с центрами тяжести Cv C2 и С3. В центрах
168

тяжести прямоугольников приложим параллельные силы Fv F2 и F3.
модули которых пропорциональны соответствующим площадям. Оп-
Определим центр этих параллельных сил. Этот центр лежит на линии
действия равнодействующих заданных сил.
Построим линию действия / — /равнодействующей сил Fj, F2 и F3
при помощи веревочного многоугольника. Воспользуемся тем, что поло-
положение центра параллельных сил не изменяется при повороте всех сил на
один и тот же угол. Повернем все силы на угол 90°. Многоугольник сил,
соответствующий новому положению сил Fp F2 и F3. строить не
будем. Проведем стороны веревочного многоугольника 0' — V,
Г—-2', 2'— 3', 3'— 0' не параллельно, а перпендикулярно лучам
О—/, / — 2,2— 3,3 — 0 (рис. 151, а, б) и найдем линию действия
равнодействующей повернутых сил // — //. Точка С пересечения
линий / — / и // — // является искомым центром тяжести заданной
плоской фигуры.
§ 72. Центры тяжести некоторых линий, плоских фигур и тел
1. Центр тяжести площади треугольника
Разбивая площадь треугольника на ряд узких полосок, парал-
параллельных одной из сторон треугольника, убеждаемся, что центры
тяжести всех этих полосок лежат
на медиане треугольника(рис. 152).
Из этого следует, что центр тя-
тяжести С площади треугольника
находится на этой медиане, а сле-
следовательно, и на других медиа- ^^^^^^^^^^^^gv^
нах, т. е. в точке "пересечения Л	к
его медиан и СК = -^ВК ¦	Рис. 152.
2. Центр тяжести площади трапеции
Обозначим параллельные стороны трапеции АЕ = а, BD = b,
а высоту трапеции h (рис. 153). Центр тяжести площади трапеции
должен лежать на прямой FK, соединяющей середины параллельных
сторон трапеции. Эта прямая является линией центров тяжести поло-
полосок бесконечно малой ширины, параллельных основаниям трапеции,
на которые можно разбить площадь трапеции.
Для определения координаты центра тяжести площади трапеции
разобьем трапецию на два треугольника ABE и EBD, площади и
координаты центров тяжести которых соответственно равны:
„ ah	„ bh	h	2 ,
f1 = ___ и F2 = -y; yi = -j и y2 = jh.
Центр тяжести площади трапеции дблжен находиться на прямой СХС2>
соединяющей центры тяжести рассматриваемых треугольников. Из
169

этого следует, что центр тяжести площади трапеции находится
в точке пересечения прямых FK и СхСг.
Координату центра тяжести площади трапеции определяем по
формуле G0.1):
ah h_>bh_ 2^ .
_Fly,+F2y2 2 + 2 
2
bh
2
G2.1)
Центр тяжести площади трапеции можно построить и графиче-
графическим способом. Для этого отложим на продолжении стороны BD
отрезок DL = a и на продолжении стороны АЕ отрезок AN = b
(рис. 154). Соединим точки N и L прямой. Покажем, что точка С
В г	п_
пересечения прямых NL и FK является центром тяжести площади
трапеции. Опустим из точки С на прямую АЕ перпендикуляр CJ и
определим его длину.
Действительно,
откуда
CJ _
h ~~
CJ=h
СК
FK '
СК
-ж-
Из подобия треугольников NCK и LCF имеем
СК CF
170

По свойству пропорции:
СК _ CK+CF
~ з , з ,
откуда
или
Полученный результат показывает, что точка С действительно
является центром тяжести площади трапеции.
3. Центр тяжести дуги окружности
Возьмем дугу АВ окружности радиусом R с центральным углом 2а
(рис. 155). Так как ось х является осью симметрии этой дуги, то
центр тяжести дуги лежит на этой оси и положение его опреде-
определяется только координатой хс.
_
хс—
Длина дуги L — R2a, где 2а — центральный угол в радианах.
Разбиваем всю дугу на бесконечно малые элементы длиной Д/(-
и вычисляем координату хс:
у	 ^ у- Д/ ——	, ^ 	*¦ Д/ f*i"ic го — —
с L Ы ' ' i j-J cos ср- ' '
n 2^sina
Окончательно получаем
xc=R^,	G2.2)
где а — половина центрального угла в радианах.
Так как sin a < а, то центр тяжести дуги лежит внутри сек-
сектора АОВ.
4. Центр тяжести площади сектора круга
Разбиваем сектор круга, соответствующий центральному углу 2а,
на бесчисленное множество элементарных секторов (рис. 156).
171

Каждый элементарный сектор можно рассматривать как треуголь-
треугольник высотой R и основанием R Aip, центр тяжести которого нахо-
находится на расстоянии -^ R от центра круга.
В
Рис. 155.
Рис. 156.
Очевидно, что центр тяжести площади сектора АОВ совпадает
2
с центром тяжести дуги окружности радиусом г = -=- R.
о
По формуле G2.2), получим
sin а
: Г 	 ИЛИ
	 2 „ since
3 а
G2.3)
5. Центр тяжести объема четырехгранной
пирамиды
>.Z7 Разобьем пирамиду плоскостями, па-
параллельными основанию ABD, на бесчи-
бесчисленное множество тонких треугольных
пластинок (рис. 157). Центры тяжести
этих пластинок лежат на прямой ЕК,
соединяющей вершину Е пирамиды с
центром тяжести К ее основания. Оче-
Очевидно, что центр тяжести объема пира-
пирамиды должен лежать на этой же прямой.
Аналогично, центр тяжести объема пирамиды должен лежать и
на прямой AL, соединяющей вершину А пирамиды с центром тяже-
тяжести L грани BED.
Следовательно, центр тяжести объема пирамиды находится
в точке С пересечения прямых ЕК и AL.
Так как KF = ±-AF и LF = \-EF, то КЦАЕ и KL = \-AE.
172

Из этого следует, что &ACEoo&KCL< а потому
/^ U	IS 1	1
откуда
Таким образом, центр тяжести объема четырехгранной пира-
пирамиды лежит на отрезке, соединяющем вершину пирамиды с цен-
центром тяжестиЪснования, на расстоянии одной четверти длины
этого отрезка от центра
тяжести основания.
Если из центра тяжести
объема пирамиды опустить
перпендикуляр на основание,
то длина его составит одну
четверть высоты пирамиды.
Рис. 158.
Рис 159.
Полученный результат можно применить и к многогранной пира-
пирамиде (рис. 158), так как ее можно разбить на четырехгранные пира-
пирамиды, разбив многоугольник ее основания на треугольники.
Так как конус представляет собой предел многогранной пирамиды,
то расстояние от центра тяжести его объема до основания составляет
одну четверть его высоты (рис. 159).
§ 73. Примеры на определение положения центра тяжести
Пример 40. Навес представляет собой жесткую прямоугольную
плиту ABDE, поддерживаемую шестью брусками постоянного сече-
сечения, расположенными вдоль ребер и диагоналей граней прямоуголь-
прямоугольного параллелепипеда.
Вес плиты G7 = 4 кн; веса брусков: O1^=G5=Q,5 кн; G3 = 0,3 кн;
G2 = G6 = 0,4 кн; О4 = 0,6 кн.
173

Расстояния: а = Ь м; b = 4 м; c = 'S м.
Определить положение центра тяжести всей конструкции
(рис. 160а).
В	Л
Рис. 160а.
Решение. Определяем координаты центра тяжести конструкции
по формулам F6.1):
Ус — '
с	G	¦***	О	*-	G
Проводим оси координат и указываем на схеме (рис. 160tf) задан-
заданную систему сил тяжести, прикладывая веса брусков постоянного
сечения в их серединах, а вес плиты, конструкция которой предпо-
предполагается симметричной, в точке пересечения диагоналей прямоуголь-
прямоугольника ABDE. Выписываем значения каждой силы тяжести и координат
ее точки приложения (Ог выражены в кн\ xt, у,, zt — в м):
G^O.5, Xj = O,	у1 = Ь = 4, zx — %> = 1,5;
KJcy •— U»T"t Xq — "» 3^2 — "о" —" *^2 "~= "o^ — ^ »*^»
/•> 	П Ч v ' 0	\t i. n	^ 	 	1 1ч•
/7 	4 r __ Sl	Q \i	9 * 	r	Я
174

Для вычисления координат центра тяжести конструкции соста-
составляем таблицу (табл. 4).
Вписываем в таблицу веса элементов GL и координаты xv у,, zL
точек приложения этих сил, а затем вычисляем произведения G,X;,
O,yi и OfZ,.
Таблица 4
Номер
эле-
элемента
1
1
2
3
4
5
6
7
) а
Вес
элемента,
кн
Gi
0,5
0,4
0,3
0,6
0,5
0,4
4
6,7
Координаты центра
тяжести элемента,
м
XI
0
0
0
3
6
6
3
—
У1
4
2
0
0
0
2
2
—
1,5
1,5
1,5
1,5
1,5
1,5
3
—
Произведения веса элемента
на координаты,
кн- м
оЛ
0
0
0
1,8
3
2,4
12
19,2
2
0,80
0
0
0
0,80
8
11,6
0,75
0,60
0,45
0,90
0,75
0,60
12
16,05
Рис. 1606.
Суммируя числа соответствующих столбцов таблицы, находим
числитель и знаменатель выражений, определяющих координаты
175

центра тяжести системы:
2<3( — 6,7 к«,	20,л;(= 19,2 кн ¦ м,
^iGiy[= 11.6 кн ¦ м,	^lGizl = IQ.05 Kfl ш м-
Вычисляем координаты центра	тяжести системы:
16,05
м.
По найденным координатам строим центр тяжести конструкции
на рис. 1606.
Пример 41. Определить положение центра тяжести тела, состоя-
состоящего из колонны и фундамента с общей осью симметрии, изго-
изготовленных из одного материала.
Высота колонны Н =Л м, глубина
фундамента h = 2 м. Диаметр ко-
колонны D — Q,5 м, ширина квадрат-
квадратного в плане фундамента а = 1 м
(рис. 161а).
Решение. Центр тяжести од-
,нородного тела, имеющего ось сим-
симметрии, лежит на этой оси. Прини-
Принимаем эту ось за ось z, начало
координат выбираем в точке пе-
пересечения диагоналей основания
(рис. 1616). Разбиваем тело на две
части: прямоугольный параллелепи-
параллелепипед и цилиндр. Центры тяжести этих
частей С1 и С2 совпадают с середи-
серединами высот этих тел. Определяем
координату центра тяжести одно-
однородного тела по формуле F6.2):
Рис. 161а.
Рис. 1616.
Zr = -
«1 +
Объем прямоугольного параллелепипеда г», = «2Л; координата его
h
центра тяжести z1 = -к ¦
Объем цилиндра v2 = . Н; координата его центра тяжести
176

Вычисляем координату zc:
„, h , tcD2
4B + 2)
= 1,85 м.
По найденной координате строим центр тяжести тела С, нахо-
находящийся внутри объема параллелепипеда.
Пример 42. Найти координаты центра тяжести однородной пла-
пластинки, изображенной на рис. 162, если известны размеры: АВ =
= 20 см; BD — 24: см; ED= 10 см; AN = 2 см; NL= 18 см;
L/C =20 см; FK = 8 см.
А
F Е
1
хс
1
8
Рис. 162.
Решение. Для нахождения центра тяжести площади пластинки
разбиваем ее на три прямоугольника и отмечаем центры тяжести
каждого из них Су, С2 и С3. Все результаты вычисления помещаем
в таблицу (табл. 5), пользуясь формулами G0.1).
Таблица 5
Номер
элемента i
1
2
3
см2
40
40
20
100
XI,
см
1
12
23
—
Уь
см
10
1
5
—
S/y = Fixh
см3
40
480
460
980
Six = р1Уь
см3
400
40
100
540
12 А. А. Яблонский
177

Каждому прямоугольнику соответствует одна строка таблицы. В эту
строку помещаем значения его площади F\ и координат его центра
тяжести xt и уг Умножая Ft на х{ и Ft на yL, находим его стати-
статические моменты относительно осей координат Siy и Six.
Суммированием определяем площадь и статические моменты всей-
заданной фигуры.
Площадь заданной фигуры: F = 100 см2. Ее статические моменты:
см3;
= 540 см3
Координаты центра тяжести пластинки:
Sv 980
v	у_	.	Q ft r и •
хс—-р- — тоо" — у>й см>
100
= 5,4 см.
По вычисленным координатам центра тяжести пластинки строим-
центр ее тяжести С (рис. 162).
Пример 43. Определить положение центра тяжести однородного-
диска радиусом г, с круглым отверстием радиусом л2 = -^-(рис. 163).
Решение. Решаем задачу по способу отрицательных площадей
(§ 70). Принимаем за ось д: ось симметрии рассматриваемой
плоской фигуры. Центр тяжести фигуры находится на этой оси,.
т. е. ус = 0. Координату хс опре-
определяем по формуле G0.2):
Здесь
Тогда
/="¦> = кг*
Хг =
6
Рис. 163.
Строим центр тяжести Су	^-, 0\
(рис. 163).
Пример 44. Определить положение центра тяжести С площади
сегмента круга ADB радиусом АО — 50 см, если угол АОВ = 90°
(рис. 164).
Решение. Воспользуемся способом отрицательных площадей.
Площадь сегмента круга представляет собой разность площадей сек-
сектора круга АОВ и треугольника АОВ. Примем за ось х биссек-
биссектрису угла АОВ, т. е. ось симметрии сегмента. Положение центра
178

тяжести площади сегмента круга на этой оси определится форму-
формулой G0.2):
хс— р—
Площадь сектора круга АОВ: Fx = R2a; площадь треуголь-
треугольника АОВ: F2 = R2 sin a cos а. Координаты центров тяжести сектора
и треугольника:
	 2_ R sin а
1 3 а
х2 = -g- R cos а.
й
Подставив эти значения в фор-
формулу 'G0.2), получим:
2	2
-5- R3 Sin а. — -^ R3 Sin a COS8 a
о	о
с	А|2а — R2 sin a COS а
_ 2	Sin3 a
3 a — Sin a COS a
При R—50 см и а = 45а
найдем
2 -п К2
¦*с — з 0U 4 @,785—0,5)'
- = 41,3 см.
Рис. 164.
Пример 45. Определить по-
положение центров тяжести полу-
полукруга и полуокружности.
Решение. Положение центра тяжести полукруга определим
по теореме Паппа — Гюльдена об объеме тела вращения, пользуясь
формулой F9.1):
Совместим ось у с диаметром полукруга, а ось х — с его осью
симметрии (рис. 165). При вращении полукруга вокруг оси у полу-
получится шар, объем которого известен:
Зная площадь полукруга F = -^ кг2, можно определить коорди-
координату хс его центра тяжести, лежащего на оси х:
V 3 '"	4
2-r.F о 1 , ~~ Зге
2ге -j яг2
0,4244г.
Положение центра тяжести полуокружности определим по тео-
теореме Паппа — Гюльдена о поверхности вращения, пользуясь форму-
формулой F9.2):
F =2kxcL.
12*
179

Совместим ось у с диаметром, соединяющим концы полуокруж-
полуокружности, а ось х — с ее осью симметрии (рис. 166). Центр тяжести С
полуокружности лежит на оси х.
При вращении полуокружности вокруг оси у получится поверх-
поверхность шара, площадь которой известна: F = 4ят2.
У
Рис. 165.
Зная длину полуокружности L = ¦
нату хс ее центра тяжести:
Рис. 166.
можно определить коорди-
с 2kL 2-nnr тс
Вопросы для самоконтроля
1.	Каким свойством обладает центр параллельных сил?
2.	По каким формулам вычисляются координаты центра параллельных
сил?
3.	По каким формулам вычисляются координаты центров тяжести одно-
однородных тел, плоских фигур и линий?
4.	Что называется статическим моментом площади плоской фигуры от-
относительно оси, как он вычисляется и какую размерность имеет?
5.	Какими способами можно определить положение центра тяжести пло-
площади в случае, если известны положения центров тяжести отдельных ее
частей?
6.	Какими вспомогательными теоремами пользуются при определении
положения центра тяжести?

РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
ГЛАВА XI
КИНЕМАТИЧЕСКИЕ СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
§ 74. Введение в кинематику
Кинематикой называется раздел механики, в котором изучается'
движение материальных тел в пространстве с геометрической точки
зрения, вне связи с силами, определяющими это движение.
Слово^кинематика происходит от греческого слова «кинема», что»
значит движение.
«Движение, рассматриваемое в самом общем смысле слова, т. е-
понимаемое как форма бытия материи, как внутренне присущий мате-
материи атрибут, обнимает собою все происходящие во вселенной изме-
изменения и процессы, начиная от простого перемещения и кончая мышле-
мышлением» х.
«Материя без движения так же немыслима, как движение без
материи» 2.
«В мире нет ничего, кроме движущейся материи, и движущаяся
материя не может двигаться иначе, как в пространстве и во вре-
времени» 3.
Таким образом, всякое движение происходит в пространстве и-
во времени, т. е. пространство и время представляют собой формы
существования материи. Они так же объективно реальны, как ш
материя.
Движение и материя существуют вечно и не могут быть ни со-
созданы, ни уничтожены.
В теоретической механике изучается простейшая форма дви-
движения материи — механическое движение, т. е. происходящее во-
1	Энгельс. Диалектика природы, 1952, стр. 44.
2	Энгельс. Анти-Дюринг, 1951, стр. 57.
3	В. И. Ленин. Материализм и эмпириокритицизм, 1948, стр. 158.
18k

времени изменение положения одного тела относительно другого тела,
с которым связана система координат, называемая системой отсче-
отсчета. Систему отсчета можно связать с любым телом. Эта система
может быть как движущейся, так и условно неподвижной.
При изучении движений на Земле за условно неподвижную систему
отсчета обычно принимают систему осей, неизменно связанных с Землей.
Тело, положение которого по отношению к выбранной системе
отсчета не изменяется, находится в состоянии относительного покоя
(по отношению к этой системе).
Время в классической механике предполагается во всех системах
отсчета одинаковым и не зависящим от движения одной системы по
отношению к другой. Оно рассматривается как непрерывно изменяю-
изменяющаяся величина и обозначается буквой t. За единицу времени при-
принимается 1 сек, равная „. „„- средних солнечных суток *.
Представления древнего мира о движении ограничивались равно-
равномерным движением и его скоростью как отношением пути, пройден-
пройденного телом, ко времени, в течение которого пройден этот путь.
Понятие ускорения введено Галилеем A564—1642) и обобщено
для случая криволинейного движения голландским физиком Гюйген-
Гюйгенсом A629—1695). Гюйгенс первый применил разложение ускорения
на касательную и нормальную составляющие.
Развитие кинематики в XVIII в. связано с работами Леонарда
Эйлера A707—1783). Эйлер заложил основы кинематики твердого
тела, создал аналитические методы решения задач механики.
Быстрое развитие техники в начале XIX в., в частности ма-
машиностроения, потребовало исследования геометрических свойств
движения тел. Кинематика выделилась в самостоятельный раздел,
причем особое значение приобрела кинематика механизмов.
Крупные исследования в области кинематики механизмов и машин
принадлежат французским ученым Понселе A788—1876), Шалю
A793—1880), Кориолису A792—1843) и русским ученым: осново-
основоположнику русской школы теории механизмов и машин акад. П. Л. Че-
¦бышеву A821 — 1894), проф. Л. В. Ассуру A878—1920), Н. И. Мер-
цалову A866—1948), А. П. Котельникову A865—1944) и др.
В разделе „Кинематика" изучается движение материальных иди
геометрических точек какого-либо тела. Описание движения тех и
других точек одинаково, поэтому будем употреблять термин „точка",
•без пояснения „материальная" или „геометрическая".
§ 75. Естественный способ задания движения точки
Движущаяся точка описывает в пространстве некоторую линию.
Зта линия, представляющая собой геометрическое место последова-
* Точнее, согласно ГОСТу, 1 сек = 1/31556925,9747 части тропического
года, т. е. времени между двумя последовательными прохождениями Солнца
через одну и ту же точку на небесной сфере.
182

тельных положений движущейся точки в рассматриваемой системе
отсчета, называется траекторией точка.
По виду траектории все движения точки делятся на прямо-
прямолинейные и криволинейные.
Изучение движения точки заключается в определении основных
характеристик этого движения: положения точки в выбранной системе
отсчета, а также ее скорости и ускорения в любой момент времени.
Эта задача решается различными способами.
Существуют три способа задания движения точки: естествен-
естественный, векторный и координатный.
Рассмотрим естественный способ задания движения точки, при-
применяемый в случае, когда траектория точки заранее известна.
Траекторией может быть как
прямая, так и кривая линия —0+	ffi	у*
(рис. 167).
Выберем на траектории непо-
неподвижную точку О, которую на-
назовем началом отсчета дуговой
координаты. Положение движу-
движущейся точки М на траектории бу-		 \Jo
дем определять дуговой коорди-
натой, т. е. расстоянием ОМ = s,
отложенным по траектории от	Рис. 167.
начала отсчета О.
Расстояния, отложенные в одну сторону от точки О, будем счи-
считать положительными, а в противоположную — отрицательными, т. е.
установим направление отсчета дуговой координаты.
При движении точки М расстояние s от этой точки до непод-
неподвижной точки О изменяется с течением времени, т. е. дуговая коор-
координата 5 является функцией времени:
s = f(t).	G5.1>
Эта зависимость называется уравнением движения точки.
Если вид функции f (t) известен, то для каждого значения t
можно найти значение s, отложить соответствующее расстояние па
траектории и указать, где находится движущаяся точка М в этот
момент времени.
Таким образом, движение точки определено, если известны сле-
следующие элементы: траектория точки, начало и направление отсчета
дуговой координаты и уравнение движения s = f(t).
Дуговую координату точки не следует смешивать с длиной пути о,
пройденного движущейся точкой. Дуговая координата s точки М
в некоторый момент времени t может равняться пути <з, пройденному
точкой за промежуток времени [0, t] только в том случае, если дви-
движение точки начинается из точки О и совершается в положитель-
положительном направлении.

Если в начальный момент времени t0 точка занимала положе-
положение Мо, а в момент времени t занимает положение М (рис. 167),
то пройденный ею путь за промежуток [0, t] при движении точки
в одном направлении определяется по формуле
о=:М0М = ОМ — OM0 = s — s0.	G5.2)
Изменение дуговой координаты s за элементарный промежуток
¦времени dt равно дифференциалу дуги
ds = f'{t)dt;
при движении точки в сторону возрастания дуг ds > 0; при движе-
движении точки в противоположную сторону ds < 0.
Приращение пути da (элементарное перемещение точки) всегда
положительно, т. е. do —| ds\ = \f (t)\ dt.
Путь, пройденный точкой за некоторый промежуток времени
JO, t], определяется как предел суммы элементарных перемещений
точки за этот промежуток времени:
t
f'(t)\dt.	G5.3)
Расстояние 5 и путь о выражаются в метрах.
§ 76. Векторный способ задания движения точки
Положение точки в пространстве однозначно определяется зада-
заданием радиуса вектора г, проведенного из некоторого неподвижного
центра О в данную точку М
(рис. 168).
Для определения движения
точки нужно знать, как изменяется
с течением времени радиус-век-
радиус-вектор г, т. е. должна быть задана
вектор-функция г аргумента t:
А/г,
г = г (t).
G6.1)
рис
Траектория точки является
геометрическим местом концов
радиуса-вектора г движущейся
точки.
Линия, образованная концами
переменного вектора, начало кото-
которого находится в определенной точке пространства, называется годо-
годографом этого вектора. Следовательно, траектория точки М
является годографом ее радиуса-вектора г.
Векторный способ определения движения материальной точки или
-системы материальных точек широко используется и в кинематике.
184

и в динамике, так как он значительно упрощает многие выводы и
иногда подчеркивает физическую сущность явлений.
От векторных формул легко перейти к аналитическим выраже-
выражениям, обычно более удобным для вычислений.
§ 77. Координатный способ задания движения точки.
Уравнения движения точки в декартовых координатах
Положение точки М в системе отсчета Oxyz определяется тремя1
декартовыми координатами точки х, у, z (рис. 169). При движении-
точки М ее координаты изменяются с течением времени. Следова-
Следовательно, координаты х, у, z движущейся точки М являются функ-
функциями времени t:
у = /2 С).
G7.1)
Эти уравнения называются уравнениями движения точки в декар-
декартовых координатах.
Уравнениями G7.1) определяется движение точки.
Действительно, имея эти уравнения, можно для каждого момента
времени t найти соответствующие координаты х, у, z и по ним
определить положение точки
в пространстве в этот момент
времени.
Рис. 170.
Движение точки М в одной плоскости определяется	двумя ура-
уравнениями движения (рис. 170):
„	 е с/\ .,	 f /f\	/77 О\,
X — Jj уь)* У — J 2 х**)•	\' ' ••^/
Прямолинейное движение точки М (рис. 171) определяется одним
уравнением движения:
* = /(*).	G7.3)
185.

Б этом случае координатный способ задания движения точки сво-
сводится к естественному.
Уравнения движения, определяющие координаты точки в любой
момент времени, можно рассматривать как параметрические урав-
уравнения траектории точки. При исключении параметра t из урав-
уравнений движения
О X	М
Рис. 171.
получаются уравнения траектории точки в координатной форме.
Пусть уравнения движения точки М имеют вид
Решив первое уравнение относительно t, получим
Подставив полученное для t выражение в два других уравнения,
найдем уравнения траектории точки в координатной форме
}	G7'4)
Как известно из аналитической геометрии, линии в пространстве
соответствуют два уравнения с тремя координатами.
Пусть движение точки М в плоскости задано уравнениями
Исключив параметр t, получим уравнение траектории точки
в координатной форме:
У = 1ъ\ф(х)\-	G7.5)
Помимо декартовых координат для определения положения точки
на плоскости и в пространстве, применяют и другие системы коор-
координат (полярные, цилиндрические, сферические и др.).
Пример 46. Концы линейки АВ движутся по двум взаимно пер-
перпендикулярным прямым L'L и N'N, причем угол ОВА = (р изме-
186

няется пропорционально времени, т. е. tp = atf. Составить уравнения
движения точки М, находящейся от концов линейки на расстояниях
AM —а и ВМ~Ь, и определить ее траекторию (рис. 172а).
Рис. 172а.
Рис. 1726.
Решение. Прямые UL и N'N примем за оси координат
(рис. 1726). Из точки М опустим на оси перпендикуляры MD и ME.
Тогда из треугольников AMD и МВЕ получим:
х = DM = AM cos у,
у = EM — BM sin <p.
Подставляя значения AM = a,
нения движения точки М:
= b, y — mt, получаем урав-
уравл = ac&s u>t,
у = bsinuat.
187

Для определения траектории точки М исключаем из этих урав-
уравнений время t:
х	v
— = cos(o?; -4~ —sinw^;
а	Ь
X2	V2
—5- = cos2 a>t; -г?- = sin2 ait;
а2	Ьг
a2 "r" a* ~ ' •
Полученное уравнение траектории точки М является уравнением
эллипса с полуосями а и Ь и с центром в начале координат
{рис. 1726).
При изменении положения точки М на линейке изменится форма
эллипса. На этом принципе основано устройство эллипсографа —
прибора для вычерчивания эллипсов.
Вопроси для самоконтроля
1.	Какие кинематические способы задания движения точки существуют
и в чем состоит каждый из этих способов?
2.	При каких условиях значение дуговой координаты точки в некоторый
момент времени равно пути, пройденному точкой за промежуток времени
от начального до данного момента времени?
3.	Чем является траектория точки при векторном способе задания дви-
движения точки?
4.	Как по уравнениям движения точки в координатной форме опреде-
определить ее траекторию?
ГЛАВА XII
СКОРОСТЬ ТОЧКИ
§ 78. Определение скорости точки при задании ее движения
векторным способом. Вектор скорости точки
Скорость — это векторная величина, характеризующая
•быстроту и направление движения точки в данной системе
отсчета.
При векторном способе задания движения положение движущейся
точки в каждый момент времени определяется радиусом-вектором г,
который является функцией времени г = г (t). Пусть в момент вре-
времени t точка занимает положение М, определяемое радиусом-векто-
радиусом-вектором г, а в момент ti = t-\-l^t — положение Мх, определяемое ра-
радиусом вектором гх (рис. 173).
Из треугольника ОММХ имеем:
188

При перемещении точки ее радиус-вектор получает приращение,
т. е.
Из двух последних равенств следует, что вектор перемещения
точки ММг является приращением радиуса-вектора точки Дг за про-
промежуток времени Д?.
Отношение вектора перемещения Дг к промежутку времени Д^,
в течение которого произошло это перемещение, представляет собой
U
М
Рис. 173.
вектор средней скорости vcp воображаемого движения точки по
хорде ММХ
Vcp-^--	G8.1)
Направление вектора vcp совпадает с направлением Дг. При
уменьшении промежутка времени At и приближении его к нулю
вектор Дг также стремится к нулю, а вектор vcp = -т-т — к неко-
некоторому пределу. Этот предел является вектором скорости точки
в момент t:
v=lim — •	G8.2)
д<о al
Так как Д^— приращение скалярного аргумента t, а Дг — при-
приращение вектора-функции г, то предел отношения -гт- при kt —>0
является векторной производной от г по t:
lim .*?.= *	G8.3^
д;->о Ы dt
Из равенств G8.2) и G8.3) получаем
Таким образом, вектор скорости точки в данный момент
равен производной, от радиуса-вектора точки по времени.
189

Вектор vcp направлен по хорде ММХ в сторону движения точки.
Когда Д^ стремится к нулю, точка Мх стремится к точке М, т. е.
предельным положением секущей ММ^ является касательная.
Из этого следует, что вектор скорости точки v направлен по-
касательной к траектории в сторону движения точки.
Рис. 174.
При движении точки по криволинейной траектории направление
вектора скорости непрерывно изменяется (рис. 174)-
Установив, что скорость точки является вектором, усло-
условимся вместо термина „вектор скорости" употреблять термин
„скорость".
Примечание. Из векторного исчисления известно, что векторная
производная от некоторого вектора по любому скалярному аргументу пред-
представляет собой вектор, направленный по касательной к годографу диффе-
дифференцируемого вектора. Так, вектор скорости \ = -— направлен по касатель-
касательной к траектории, т. е. по касательной к годографу радиуса-вектора г.
Модуль векторной производной определяется обычно способами,
изложенными в § 79 и 80.
§ 79. Определение скорости точки при задании ее движения
естественным способом. Проекция скорости
на касательную к траектории
Определим скорость точки в случае, когда ее движение задано
естественным способом, т. е. известны: ее траектория АВ, начало
и направление отсчета дуговой координаты и уравнение движения
точки s=/@ (рис. 175).
Пусть в момент времени t точка занимает положение Ж, а в мо-
момент tx — t-\-Lt — положение Mv Дуговые координаты этих точек
имеют следующие значения:
Приращение дуговой координаты
Проведем из произвольного центра О' в точку М радиус-вектор г
и определим скорость точки в момент t по формуле G8.4):
dt
190

Введем в качестве промежуточной переменной дуговую координату 5,
от которой зависит радиус-вектор г движущейся точки. Действи-
Действительно, каждому значению s соответствует определенное значение г,
т. е. г можно рассматривать не только как функцию t, но и как
функцию s, полагая г = г ($)
(рис. 176); тогда получим
v =
ds
ds
Здесь
— lim
Вектор
Дг
-г-
АГ
направлен так
Рис. 175.
же, как вектор Дг (рис. 176).
При As->0 его направление
стремится к направлению каса-
касательной, проведенной в точке М в сторону увеличения дуговой
координаты s. Модуль этого вектора стремится к единице:
lim
Is
——¦ llill
; 	> 1 ¦
Таким образом, вектор —г- имеет модуль, равный единице и на-
направлен по касательной к кривой в сторону увеличения дуговой
Рис. 176.
dr
координаты (см. примечание § 78). Вектор -г- является ортом этого
направления. Обозначим этот орт х:
ds'
Пользуясь G9.1), получаем вектор скорости в виде
_ iL
dt "
G9.1)
G9.2)
191

ds
Производная —гт в выражгнии G9.2) представляет собой проек-
проекцию скорости v на касательную, т. е. определяет алгебраическую
величину скорости.
Условимся алгебраическую величину скорости обозначать симво-
символом v, а модуль скорости буквой v.
Тогда:
*=%.	G9-3)
а
v =
dt
G9.4)
т. е. модуль скорости равен абсолютному значению производ-
производной от дуговой коор-
координаты точки по
времени.
Орт касательной т
всегда направлен в сто-
сторону увеличения дуго-
дуговой координаты.
Если в некото-
некоторый момент времени
ds . п
-тг > О, ТО В ЭТОТ
момент функция s воз-
Рис. 177.	растает, т. е. точка
движения в сторону
увеличения s и направление скорости v совпадает с направлением
орта 1 (рис. 177, а).
Если —тт <0, то в этот момент функция s убывает и направле-
ние скорости v противоположно направлению орта ч (рис. 177, б).
ds
Если в некоторый момент времени — = 0 и изменяет знак, то
дуговая координата s в этот момент достигает максимального или
минимального значения, а точка изменяет направление движения.
Таким образом, знак v — -тт указывает направление движения
точки по траектории.
При движении точки только в сторону возрастания дуговой
ds
координаты во все моменты времени -тт- > 0, т. е.
ds_
dt
ds_
dt '
В этом случае формуле G9.4), определяющей модуль скорости,
можно придать вид
ds
V =
dt '
G9.5)
192

Пример 47. Точка движется по окружности радиусом /? = 150 см
согласно уравнению
где t выражено в сек, s — в см.
Определить:
1) среднюю скорость точки за первые шесть секунд и вторые
шесть секунд, отсчитанные от начального момента;
точки в конце шестой и в конце
двенадцатой
2) скорость
секунды;
3)дуговую коорди-
координату точки, при кото-
которой скорость точки
равна 10 см/сек.
Решение 1. Опре-
Определяем среднюю ско-
скорость точки. Для опре-
определения средней скоро-
скорости точки за проме-
промежутки времени @—6) и
F—12) сек требуется
найти пути, пройден-
пройденные точкой за эти про-
промежутки времени.
Из уравнения дви-
движения видно, что при
увеличении t дуговая
координата 5 монотон-	Рис j7g_
но возрастает, т. е.
точка движется, удаляясь от начала отсчета в положительном направле-
направлении. В этом случае пройденные точкой пути можно найти как прираще-
приращения дуговой координаты. По уравнению движения находим значения ду-
дуговой координаты, соответствующие моментам времени t = 0, 6, 12 сек.
При t = 0	s0 = 50 см;
при ? = 6 сек sfi = 50 + 6 • 6 + -^ • 63= 104 см;
1
при ?=12 сек s12 = 50-|-6 • \2-\-^х • V2a = 2t>t> см.
Пройденные пути определяются (рис. 178):
o0j6 = M0M6 =s6 —s0=104 — 50 =54 см,
о6) 12 = М6М12 = s12 — s6 = 266 — 104 = 162 см.
Средние скорости за эти промежутки времени по шесты секунд
находим делением пути на величину промежутка времени:
vcp = —4— = -д- = 9 см/сек,
^р*» = -
6
, 162
'- = -г- = 27 см/сек:
13 А. А. Яблонский
193

2.	Определяем скорость точки в данный момент. Прежде всего
по формуле G9.5) определим модуль скорости точки в любой
момент времени:
«=4Н6+т'2-	G9-6>
По формуле G9.6) вычислим модули скорости точки в моменты
времени 6 и 12 сек:
а)	при t = Q сек
©6 = 6 + -f-36= 15 см/сек;
б)	при t = 12 сек
г/12 = 6 + j • 144 = 42 см/сек.
Как указано выше, точка движется в положительном направле-
направлении отсчета дуговой координаты, поэтому скорости точки v6 и vv2
направлены так же, как орты т.
Примечание. Средняя скорость точки vcp = 27 см/сек за про-
промежуток времени от 6 до 12 сек не совпадает с полусуммой модулей
начальной и конечной скоростей этого промежутка --6~^—— = ¦—i— _
= 28,5 см/сек, так как движение точки не является равнопеременным.
3.	Определяем дуговую координату точки, соответствующую за-
даннвй скорости. По формуле G9.6) можно определить момент
времени, когда точка обладает скоростью 10 см/сек:
-t% tz = lb; t = 4 сек.
По уравнению движения определится значение дуговой коорди-
координаты в этот момент времени:
1
при t = 4 сек	s, = 50 -4- 6 • 4 -)- -^я- • 43 = 79,3 см.
§ 80. Определение скорости точки при задании ее движения
координатным способом. Проекции скорости точки на
неподвижные оси декартовых координат
Определим модуль и направление скорости точки по уравнениям
ее движения в декартовых координатах.
Пусть заданы уравнения движения точки (рис. 179):
У =/2 С).
194

Обозначим орты осей координат i, j, k. Проведем из начала
координат О в движущуюся точку М радиус-вектор г. Согласно
рис. 179 имеем:
ОМ = О А -[- АВ + ВМ
или
Скорость точки равна производной от радиуса-вектора по вре-
времени G8.4). Найдем эту производную,' учитывая, что орты i, j, k
имеют неизменные модули и направления, т. е. постоянны и могут
быть вынесены за знак про-
производной:
dx
_ dt _; dx | j аУ I
/If	Hi \ * Hi I
dt
dt
dt
Построив прямоуголь-
прямоугольный параллелепипед, ребра
которого параллельны осям
координат, а диагональ сов-
совпадает со скоростью v,
получим проекции ско-
скорости v на оси координат
равные алгеб-
vx, vy, vz,
Рис. 179.
раическим величинам отрез-
ков Ma, Mb, Me.
Тогда разложение скорости на компоненты по осям координат
примет вид
i
Сопоставляя обе формулы, определяющие скорость, находим
dx	dy	dz
dt ' Vy~ dt
(80.1)
Следовательно, проекции скорости точки на неподвижные оси
декартовых координат равны первым производным от соответ-
соответствующих координат точки по времени.
Пользуясь принятым обозначением производных по времени,
можно написать
vx — х; vy = у, vz = z.
Вычислив проекции скорости на оси декартовых координат, можно
определить модуль и направление скорости точки по следующим
формулам.:
13*
cos(v, i) = — > cos(v, j) = — ! cos(v, k) = — • (80 2)
195

Движение точки в плоскости хОу (рис. 180) задается двумя
уравнениями движения:
Модуль и направление скорости точки в этом случае опреде-
определяются
cos(v, i)=—; cos(v, J)=
(80.3)
Прямолинейное движение точки задается одним уравнением:
* = /(*).
В этом случае модуль скорости
точки равен абсолютной величине
проекции скорости на ось х:
dx
dt
(80.4)
Рис. 180.
Рис. 181.
При vx > 0 точка движется по направлению оси х (рис. 181),
при vx < 0 — противоположно направлению оси.
§ 81. Годограф скорости точки и его уравнения
Скорость точки при неравномерном криволинейном движении
изменяется как по модулю, так и по направлению.
Отметим ряд положений движущейся точки на траектории Mv
М2, Мъ, Mi и покажем скорости точки в этих положениях vP v2.
v3, v4 (рис. 182,a).
Выбрав в пространстве некоторую неподвижную точку Ov отло-
отложим от этой точки векторы, геометрически равные скоростям vv v2,
v3, v4 (рис. 182,6).
Если от точки Ох отложить скорости, соответствующие всем
положениям точки М на кривой АВ и соединить концы этих векто-
векторов, то получится линия CD, являющаяся годографом скорости.
Таким образом, годограф скорости представляет собой гео-
метрическое место концов векторов скорости движущейся
точки, отложенных от одной и той же произвольной точки
пространства.
196

Изобразим на рис. 183,а траекторию точки АВ и ее скорость v
в произвольный момент времени t, а на рис. 183,<5" — годограф ско-
скорости CD этой точки.
Проведем через точку Ог оси координат X, Y, Z, параллель-
параллельные основным осям х, у, z.
а)
В
Рис. 182.
а)
Рис. 183.
Тогда радиусом-вектором любой точки N годографа скорости CD
будет скорость v, а координаты точек годографа X, Y, Z будут
равны проекциям скорости на оси координат, т. е.
Z = vz = z.
(81.1)
Эти уравнения являются параметрическими уравнениями годо-
годографа скорости.
197

Пример 48. Построить годограф скорости точки М линейки
эллипсографа, рассмотренной в примере 46.
Решение. Уравнения движения точки М линейки имеют вид
(см. пример 46. рис. 172а, б):
х = a cos at,
Траекторией точки М является эллипс, имеющий уравнение
¦^ -\--T2 = !• Эллипс построен на рис. 184а. Находим параметри-
Рис. 184а.
ческие уравнения годографа скорости точки по формулам (81 1), т. е.
дифференцируя уравнения движения точки:
X = vx = х — — wa sin <at.
Y = vy = у = mb cos mt.
Исключая время t из этих
уравнений, получаем уравнение
годографа скорости
«в
э
2 aid
Рис. 1846.	Годограф скорости является
эллипсом с полуосями шс и <ob,
пропорциональными полуосями эллиптической траектории (рис. 184<Г),
при этом длины этих полуосей выражены в единицах скорости
Так, если скорости движущейся точки в положениях Mv M, Мг,
М3, МА (рис. 184а; изобразим на рис. 1846, то получим векторы \v
198

v, v2, v3, v4, начала которых находятся в начале координат, а концы
на эллипсе — годографе скорости.
Очевидно, что при движении точки из Мх в М2 скорость ее
возрастает по модулю от г», до v2 и наибольшие значения ско-
скорости соответствуют нахождению точки на концах малой оси, а наи-
наименьшие— на концах большой оси.
Вопроси для самоконтроля
1.	Чему равен вектор скорости точки в данный момент и какое напра-
направление он имеет?
2.	Как связан орт касательной к кривой с радиусом-вектором движу-
движущейся точки?
3.	Чему равна проекция скорости точки на касательную к ее траектории
и модуль ее скорости?
4„ Как определяются проекции скорости точки на неподвижные оси
декартовых координат?
5.	Что представляет собой годограф скорости и каковы его параметри-
параметрические уравнения?
6.	Какой вид имеет годограф скорости прямолинейного неравномерного
движения и равномерного движения по кривой, не лежащей в одной пло-
плоскости?
ГЛАВА Xfff
УСКОРЕНИЕ ТОЧКИ
§ 82. Определение ускорения точки при задании ее движения
векторным способом. Вектор ускорения точки
При неравномерном криволинейном движении точки изменяются
модуль и направление ее скорости. Ускорение точки характеризует
быстроту изменения модуля и направления скорости точки.
Допустим, что в момент времени t точка занимает положение М
и имеет скорость v, а в момент времени ^, = ^-|-Д^ она занимает
положение Мх и имеет скорость \х (рис 185,а)
Найдем приращение скорости за промежуток времени Д^.
Для этого отложим, от точки М скорость Vj и построим при
этой точке параллелограмм, одной из сторон которого будет ско-
скорость v, а диагональю — скорость \у Тогда вторая сторона парал-
параллелограмма будет приращением скорости &v, так как
V, = v-f-Av.
Разделив приращение скорости Av на промежуток времени At,
получим вектор среднего ускорения точки за этот промежуток:
__ Ду
W°P~ At '
Этот вектор имеет направление Ду и, следовательно, направлен
в сторону вогнутости кривой.
199

Построив годограф скорости CD (рис. 185,tf). отложим там же
скорости v и vv приращение скорости Ду, а также вектор сред-
среднего ускорения wcp, направленный по хорде AWj годографа ско-
скорости.
О,
~Vlcp
Рис. 185.
Предел, к которому стремится вектор среднего ускорения wcp,
когда At стремится к нулю, является вектором ускорения точки w
в данный момент времени t:
w= lim -r^.
Учитывая, что скорость является вектором-функцией от времени,
т. е. v = v (t) и что v = —тг, имеем
dt
dv
dt
dt'
(82.1)
Следовательно, вектор ускорения точка равен первой производ-
производной от скорости или второй производной от радиуса-вектора-
точки по времени.
Установим направление вектора ускорения.
Вектор среднего ускорения wcp направлен по хорде NNX годо-
годографа скорости. Когда Д^ стремится к нулю, точка Nx стремится
к точке N и секущая NNX в пределе превращается в касательную
к годографу скорости. Из этого следует, что вектор ускорения
точка имеет направление касательной к годографу скорости
(см. примечание § 78).
Выясним расположение вектора ускорения точки по отношению
к ее траектории, если траектория не является плоской кри-
кривой. Вектор wcp находится в плоскости, проходящей через каса-
касательную к траектории в точке М и прямую, параллельную каса-
касательной в точке Мх (рис. 185,а). Предельное положение этой пло-
200

скости при стремлении точки Мх к точке М называется соприкасаю-
соприкасающейся плоскостью.
Из этого следует, что вектор ускорения точки w расположен
в соприкасающейся плоскости и направлен в сторону вогнутости
кривой.
Если кривая плоская, то соприкасающейся плоскостью является
плоскость кривой и вектор ускорения лежит в этой плоскости.
Установив, что ускорение точки является вектором, усло-
условимся вместо термина „вектор ускорения" употреблять термин
„ускорение".
§ 83. Определение ускорения точки при задании ее движения
координатным способом. Проекции ускорения точки на
неподвижные оси декартовых координат
Определим модуль и направление ускорения точки по уравне-
уравнениям ее движения в декартовых координатах.
Рис. 186.
Пусть заданы уравнения движения точки (рис. 186):
Радиус-вектор г движущейся точки М представим в виде:
r — ix-\-jy-\-kz,
Так как ускорение точки равно второй производной от радиуса-
вектора по времени, а векторы i, j, k постоянны, то имеем:
d2y
w —
df'
dt*
201

Разлагаем ускорение w на составляющие по осям координат:
w = iwx -f- \wy + кюг,
где wx, wy, wz — проекции ускорения w на оси х, у, z.
Сопоставляя обе формулы, определяющие ускорение, получаем:
= ^r='z- (83
Так как первые производные от координат точки по времени
равны проекциям скорости на соответствующие оси, т. е. —гг = vx,
dy	dz
у	и ~df:=lVy' ~dT = Vz' T0 пР°екчии
ускорения точки можно представить
еще так:
dvx
dvy
-4T
dv,.
Таким образом, проекции уско-
ускорения точки на неподвижные оси
декартовых координат равны вто-
вторым производным от соответст-
соответствующих координат точки по вре-
времени или первым производным по времени от проекций ско-
скорости на соответствующие оси.
Вычислив проекции ускорения на координатные оси, можно опре-
определить модуль и направление ускорения точки по следующим фор-
формулам:
Рис. 187.
Wr.	Wv W,
cos(w, l) = —;	cos(w, j)=~; cos(w, k) = —. (83.3)
Движение точки в	плоскости хОу задается двумя уравнениями
движения:
Модуль и направление ускорения точки в этом случае (рис. 187)
определяются:
-«?;
wx
cos(w, 0 = —; cos(w, j) = —
(83.4)
202

Прямолинейное движение точки задается одним уравнением
* = /(*)•
В этом случае модуль ускорения w равен абсолютному значе-
значению его проекции на ось х, т. е.
ч2/ ^ I ш „ I = I X1 ¦	loo D)
Ускорение w направлено в сторону оси х, если wx > 0 (рис. 188)
и противоположно оси х, если <тх < 0.
0	М UT
Рис. 188.
Пример 49. Определить ускорения точки М линейки эллипсо-
эллипсографа АВ, рассмотренной в примере 46, в моменты нахождения
точки М на осях координат.
У
М
Я\
Рис. 189.
Решение. Уравнения движения точки М имеют вид (см. при-
пример 46, рис. 172а, б):
х = acosmt,
Траекторией точки М является эллипс, имеющий уравнение
•? + ?=1 (Рис- 189).
Модуль и направление ускорения точки М определим по фор-
формулам (83.4), определив предварительно его проекции на оси коор-
203

динат по формулам (83.1):
wx = x = — <Лг cos at = — а>2х;
wy=: у = — aPb sin at — — <?>2y;
, .. wx
cos(w, i) = —— = —
= — cos a;
(83.6)
COS (W, j) = 	 =
Полученные выражения показывают, что модуль ускорения да
пропорционален расстоянию OM = Yх2Л-У2 от точки М до начала
координат О, а направление w составляет с осями Ох и Оу углы
180° — а и 180° — р, т. е. вектор ускорения w направлен к началу
координат.
Модули ускорений в положениях М1(а, 0), М2{0, Ь), М3(—а, 0)г
Л14@, —Ь) определяются по формуле (83.6) путем подстановки зна-
значений соответствующих координат:
¦и*] —ю2а; ¦к>2 = ю26; w3 = ttJa; •до4 = (о2й.
§ 84. Естественные координатные оси. Вектор кривизны
Проведем в точке М кривой АВ соприкасающуюся плоскость,
нормальную плоскость, перпендикулярную к касательной, и спря-
Нормальная
плоскость'
ГлаВная
Солрикасаю-/ нормаль
щаяся
'плоскость
Рис. 190.
мляющую плоскость, перпендикулярную соприкасающейся и нор-
нормальной плоскостям, образующую с этими плоскостями естествен-
естественный трехгранник (рис. 190).
Линия пересечения соприкасающейся и нормальной плоскостей на-
называется главной нормалью кривой.
204

•ср
Линия пересечения нормальной и спрямляющей плоскостей назы-
называется бинормалью кривой.
Естественными координатными осями называются три
взаимно перпендикулярные оси: касательная, направленная в сто-
сторону возрастания дуговой координаты, главная нормаль, направлен-
направленная в сторону вогнутости кривой и бинормаль, направленная по
отношению к касательной и главной нормали так же, как ось Oz
направлена по отношению к осям Ох и Оу в правой системе коор-
координатных, осей. Единичные векторы-орты этих осей обозначаются
соответственно х, п и Ь.
Естественные координатные
оси имеют начало в точке М
кривой и при движении точки М
по этой кривой перемещаются
вместе с ней, оставаясь взаимно
перпендикулярными, но изменяя
свое направление в простран-
пространстве.
Возьмем на кривой АВ две
точки М и Мх, соответствующие
дуговым координатам ОМ = 5
и ОМХ — s-\- As. Покажем
орты касательной х и Xj в этих
точках (рис. 191). Модуль
орта х, равный единице, по-
постоянен, но направление орта изменяется при перемещении точки по
кривой, т. е. орт х является переменным вектором.
Определим приращение орта х на участке MMl = As. Для этого
отложим от точки М орт Xj и построим при этой точке парал-
параллелограмм, одной из сторон которого будет орт х, а диагональю —
орт Xj. Тогда другая сторона параллелограмма будет приращением
орта Ах, так как Xi = x-j-Ax.
Разделим приращение орта Ах на приращение дуговой коорди-
координаты As. Вектор Кср = -д~> характеризующий поворот касательной
к кривой на участке MMV называется вектором средней кривизны
кривой на участке ММХ. Этот вектор имеет направление вектора Ах,
т. е. направлен в сторону вогнутости кривой.
Предел К, к которому стремится вектор средней кривизны кри-
кривой Кср, когда As стремится к нулю, называется вектором кри-
кривизны кривой в данной точке:
К— lim —.—.
Д*->0 As
Орт касательной к кривой является вектором-функцией дуговой
координаты s, так как его направление зависит от положения точки
на кривой, т. е.
Рис. 191.
205

Тогда
dz
(84.1)
Следовательно, вектор кривизны кривой в данной точке равен
производной от орта касательной к кривой по дуговой коор-
координате.
Для определения модуля этого - вектора рассмотрим равно-
равнобедренный треугольник, образованный т, tj и Дт (рис. 191).
Угол е между направлениями касательных в двух точках кри-
кривой М и Мг называется углом смежности. При малом расстоя-
расстоянии As угол смежности тоже мал.
Модуль |At| найдем как длину основания равнобедренного
треугольника с малым углом е при вершине и боковыми сторонами,
равными единице.
Тогда
Модуль вектора кривизны К определяется по формуле
К= lim
= lim -т—•
As
At
As
Из дифференциальной геометрии известно, что предел отношения
угла смежности е к приращению дуговой координаты As, при
стремлении As к нулю, равен кри-
кривизне кривой —, где р — радиус кри-
кривизны кривой в точке А\.
Таким образом, получим модуль
вектора кривизны
J_
Р "
р
•-Iltn-ЕГ —
Установим также направление век-
вектора кривизны.
Вектор средней кривизны Кср на-
находится в плоскости треугольника, со-
составленного векторами t, т, и At,
предельным положением которого является соприкасающаяся пло-
плоскость. Следовательно, вектор кривизны К расположен в соприка-
соприкасающейся плоскости.
Рассмотрим угол C, составленный вектором Кср с касательной
в точке М (рис. 191).
20$

При приближении точки Мх к .М угол смежности е стремится
к нулю, а потому
limp = 90°.
Так как вектор кривизны К расположен в соприкасающейся
плоскости и перпендикулярен орту т, то он направлен по главной
нормали к центру кривизны кривой (рис. 192).
Представим вектор К в виде произведения орта на модуль этого
вектора
К = п|,	(84.2)
где р = МС — радиус кривизны кривой в данной точке М.
§ 85. Определение ускорения точки при задании ее движения
естественным способом. Касательное и нормальное
ускорения точки
Определим проекции ускорения точки на естественные коорди-
координатные оси. Для этого представим вектор скорости точки по фор-
формуле G9.2):
ds
v = xrfP
Определим ускорение точки по формуле (82.1), продифференци-
продифференцировав по t произведение двух переменных величин:
	 dv 	 dx_ ds_ , d?s_	 cH_ ds_d±i <Ps_
W ~~ dt ~ dt <й ~T"x dt* ~ ds ~di dt^ dt* '
По формулам (84.1) и (84.2) получим
ds	p
Так как проекция скорости на касательную v =t —гг может отли-
отличаться от модуля скорости v только знаком, то
Подставив эти выражения, получим вектор ускорения в виде
Ускорение точки равно геометрической сумме двух векторов,
один из которых направлен по главной нормали и называется нор-
нормальным ускорение^, а другой направлен по касательной и назы-
называется касательным ускорением точки (рис. 193):
w = W;i + wT,	(85.2)
207

где нормальное ускорение точки
I/2
а касательное ускорение точки на основании формул (85.1) и G9.3):
dv
и/ 	«г .		т
т~ dt2 ~~
dt
dv
(85.3)
G9.3):
(85.4)
Скалярные множители — и -ш~ = —тг в выражениях (85.3)
и (85.4), определяющих нормальное и касательное ускорения точки,
представляют собой проекции ускорения точки на главную нормаль
и касательную.
Проекция ускорения точки
на бинормаль оказалась равной
нулю, так как вектор ускоре-
ускорения расположен в соприкасаю-
соприкасающейся плоскости (см. § 82).
Согласно формуле (85.3)
имеем:
VJ
Рис. 193.
„ = ^-, (85.5)
т. е. проекция ускорения
точки на главную нормаль
равна квадрату модуля скорости точки, деленному на радиус
кривизны траектории в соответствующей точке. Эта проекция
всегда положительна.
Из этого следует, что нормальное ускорение точки всегда на-
направлено к центру кривизны траектории и равно по модулю этой
проекции.
Условимся алгебраическую величину касательного ускорения обо-
обозначать w,, а его модуль хох.
Согласно формуле (85.4) имеем:
dv
dt
(85.6)
т. е. проекция ускорения точки на касательную равна второй
производной от дуговой координаты точки по времени или
первой производной от алгебраической величины скорости точки
по времени.
Эта проекция имеет знак плюс, если направления касательного
ускорения точки wx и орта %, совпадают, и знак минус, если они
противоположны.
Очевидно, что ад, = | w^\ =
d2s
dv
dt
Таким образом, в случае естественного способа, задания движения,
когда известны траектория точки, а следовательно, ее радиус кри-
208

визны р в любой точке и уравнение движения s = f(t), можно найти
проекции ускорения точки на естественные оси и по ним определить
модуль и направление ускорения точки:
w=ywl-\-w2n,	(85.7)
cos (w, t) = —- ; cos (w, n) = —-»
где (w, t) и (w, n) — углы, образованные направлением ускорения
с принятыми направлениями касательной и главной нормали в дан-
данной точке.
Если проекции скорости v и касательного ускорения wT на каса-
касательную v =—тг и wT=~^7r имеют одинаковые знаки, то и напра-
направления этих векторов совпадают, т. е. точка движется ускоренно.
„	ds	d2s
Если же их проекции ©=—- и wiz=~h~n имеют различные
знаки, то и направления v и wT противоположны, т. е. точка дви-
движется замедленно.
При движении точки только в сторону возрастания дуговой коор-
координаты, согласно формулам G9.5) и (85.6), имеем:
__ ds
dv	(85.8)
dt
где v — модуль скорости точки.
При этом, если —тт > 0, т. е. модуль скорости возрастает, точка
ах
движется ускоренно, а если —пг<.0 — замедленно.
При прямолинейном движении точки радиус кривизны траекто-
траектории р = со и, следовательно,
¦ш = — = 0.
" Р
Нормальное ускорение существует лишь при криволинейном
движении точки и характеризует изменение направления ско-
скорости.
При равномерном движении точки v = const и, следовательно,
dv
dt
= 0.
Касательное ускорение точки существует лишь при неравно-
неравномерном движении точки и характеризует изменение модуля
скорости.
Пример 50. По условию примера 47 определить ускорение точки
в моменты времени 6 и 12 сек.
14 А. А. Яблонский	209

Решение. В примере 47 получена формула G9 6) для опре-
определения скорости точки в любой момент времени:
и также значения р6=15 см\сек и г>12 = 42 см/сек. Радиус окруж-
окружности— траектории точки R =150 см. Определим касательное и
нормальное ускорения точки по формулам (85.5) и (85.8) и полно&
ускорение точки по формуле (85.7):
dv
dt
— 2 t,
v2
где R — радиус окружности,
Вычислим да,, wn и w в заданные моменты времени:
a) t — 6 сек:
=j'6 = 3 см/сек2,
==^=l,5 см/сек2,
-1,52 = 3,35 см\сек2*
б) * =12 «w:
= 6 см/сек2,
1
422
w"" = 150 = 11'7 6 см1сек2>
да12=-)/б2+11,762 =
Рис. 194.	=13,2 см/сек2.
Так как -^ = -н- ^ > 0 при всех значениях Л то точка движется
ускоренно и направление ее касательного ускорения wT во всех точках.
совпадает с направлением v.
Нормальное ускорение wn в каждой точке направлено к центру-
окружности (рис. 194).
§ 86. Классификация движений точки по ускорениям ее
движения
Выясним зависимость характера движения точки от значений ее
нормального и касательного ускорений.
Случай I: wB = 0; w, = 0. Если в течение некоторого проме-
промежутка времени нормальное и касательное ускорения точки равны
210

нулю, то в течение этого промежутка не изменяется ни направление,
ни модуль скорости, т. е. точка движется прямолинейно, равно-
равномерно и ее ускорение w = 0.
Случай II: wn Ф 0; wT = 0. Если в течение некоторого про-
промежутка времени не равно нулю нормальное ускорение и равно
нулю касательное ускорение, то происходит изменение направления
скорости без изменения ее модуля, т. е.
точка движется криволинейно равномерно
V2
и модуль ее ускорения w = wn = •
(рис. 195).
Если wx =
dv
dt
Р
= 0 в отдельный момент
Рис. 195.
времени, то точка не движется равномерно,
а в этот момент времени модуль ее ско-
скорости имеет максимум, минимум или наи-
наименьшую быстроту монотонного изменения.
Случай HI: wn = 0; wt ф 0. Если в течение некоторого про-
промежутка времени равно нулю нормальное ускорение точки и не равно
нулю касательное, то не изменяется направление скорости, а изме-
-0 +
М Ш-
V
-0 +
ш--
м
V
Рис. 196а, б.
няется ее модуль, т. е. точка движется по прямой неравномерно.
Модуль ускорения точки в этом случае
W =
dt1
Рис 196в
При этом, если направления векторов v
f и w = wT совпадают, то движение точки
ускоренное (рис. 196,а). Если направле-
ния вектоРов v и w = wT противопо-
противоположны, то движение точки замедленное
(рис. 196,G). Если wn = — = 0 в некоторый момент времени, то
точка не движется прямолинейно, а проходит точку перегиба траек-
траектории (р = со) (рис. 196в) или модуль ее скорости обращается
в нуль (например, при изменении направления движения точки ^ = 0).
Случай IV: wrt Ф 0, wT ф 0. Если в течение некоторого про-
промежутка времени ни нормальное, ни касательное ускорения точки не
14*
211

равны нулю, то изменяется как направление, так и модуль ее ско-
скорости, т. е. точка совершает криволинейное неравномерное движе-
движение. Модуль ускорения точки
W
= V W* -4- w2.
r z ' п
При этом, если направления векторов v и wT совпадают, то движе-
движение ускоренное (рис. 197а), а если они противоположны, то движе-
движение замедленное (рис. 1976).
М
(L
щ
Рис. 197а.
Рис. 1976.
Если модуль касательного ускорения постоянен, т. е. wz = const,
то модуль скорости точки изменяется пропорционально времени, т. е.
точка совершает равнопеременное движение.
Составим уравнение равнопеременного движения точки, полагая»
что в начальный момент ^0 = 0, начальная скорость точки равна г>0,
а начальное значение дуговой координаты OM0 = s0 (рис. 198).
-ЭЮ
Рис. 198.
Воспользовавшись формулой (85.6) получим:
dv
dt
¦ = wx = const; dv = wx dt.
Проинтегрируем уравнение в пределах, соответствующих точ-
точкам Л10 и М:
V	t
I dv = wx I dt, v — v0 = wxt,
v = vo+wxt.
(86.1)
Выражение (86.1) является формулой скорости равноперемен-
равнопеременного движения точки.
212

Воспользовавшись формулой G9.3), получим
ds = vadt-\- wxt dt.
Проинтегрируем уравнение в пределах, соответствующих точкам
и М:
s	t	/
fds = vofdt-\-wx f tdt,
	 ~ f | Wj.2
S — Sq — VqC —I	g— .
(86
Выражение (86.2) является уравнением равнопеременного дви-
движения точки.
Если v0 > 0, то при ускоренном движении чях > 0 (рис. 198),
а при замедленном движении wx < 0.
§ 87. Примеры определения скорости и ускорения точки
при задании ее движения естественным способом
Пример 51. Поезд движется равнозамедленно по закруглению
радиусом R = 1 км. В начале участка длиной 560 м поезд имеег
скорость tH=36 км/час и ускорение tiyo = 0,125 м/сек2. Определить
скорость и ускорение поезда в конце участка.
Решение. Рассмотрим движение одной из точек поезда, напри-
например его центра тяжести. Чтобы написать уравнение движения точки,
необходимо выбрать начало отсчета дуговой координаты. Совместим
начало отсчета О с начальным положением точки Мо и направление
движения примем за положительное направление (рис. 199). Тогда
so = O.
При равнозамедленном движении точки уравнение движения и
формула скорости точки, полученные в § 86, будут иметь вид
s = vQt-^f-,	A)
v = v0 — vi)xt,	B)
где vdx — модуль касательного ускорения.
По условию задачи известны: дуговая координата движущейся
точки Ж в конце участка, равная длине участка, т. е. s = 560 м,
213

скорость и ускорение точки в начале участка т»0 = 36 км/яас = 10 м/сек
и wo = 0,125 м/сек2, а также радиус кривизны траектории во всех
ее точках /? = 1000 м.
tfo
Рис. 199.
Модуль нормального ускорения точки М в начале участка опре-
определим по формуле (85.5):
vi 100
(Г/%1		 .	..
«о~ R ~ 1000
= 0.1
Зная модуль полного ускорения точки М в начале участка wu,
определяем модуль касательного ускорения точки wx, являющегося
ускорением ее равнопеременного движения:
^	^	М(сек2.
Подставляем в уравнения A) и B) все известные величины:
v= 10 — 0,075);.
Из этих уравнений находим время движения t:
0,07 5*2 — 20* -h 1120 = 0,
10 ± KlOO—1120-0,075 10 ± 4
i —
0,075
0,075 '
Значение большего корня превышает момент остановки
= rriyf= сек, который-определяется из уравнения B) при v = 0. По-
214

этому берем меньший корень:
6
= 80 сек.
~~ 0,075
Из уравнения B) находим скорость в конце участка:
Vea = 10 — 0,075 • 80 = 4 м1 сек.
Модуль нормального ускорения точки М в конце участка:
Модуль полного ускорения точки М в конце участка:
ww = Yw2nto-i-w* = ^0,0162-f-0,0752 = 0,0767 м/сек2.
При равнозамедленном движении точки по окружности модуль-
касательного ускорения не изменяется, а модуль полного ускорения
убывает за счет уменьшения модуля нормального ускорения (см.
рис. 199).
Пример Б2. Уравнение движения шарика математического маят-
маятника имеет вид
5 = 5sin7/,
где t выражено в сек, s — в см. Длина нити маятника / = 20 см~
Определить закон изменения полного ускорения шарика, а также
его скорость и ускорение в среднем н в крайних положениях.
Решение. 1. Определяем моменты времени, соответствующие
крайним и среднему положениям шарика. Крайним положениям ша-
шарика М1 и Мь (рис. 200,а) соответствуют наибольшие значения дуго-
дуговой координаты |s|ma][ = 5 см.
Для положения Mj принято: Sj = 5 см при sin7^=1, т. е.
при 7t = 2kn-\-~, где k — целое число.
Наименьшее значение t, соответствующее положению Мх, имеет
место при k = 0, т. е.
7t-JL. t	^__ЗЛ1_0225се/,
"¦1— 2' *i~2-7~ 14 ~ ""J сел"
Для положения М3 принято: s3 = — 5 см при sin7? = —1,
т. е. при 7t = 2Air—j—^- it. Наименьшее значение / при k — 0:
7/3 = f«; *3 = tJ = 0-675 сек.
В среднем положении: s = 0; sin7/ = 0; 7t = kt:. В этом
положении находится точка при ^ = 0. Момент прохождения шариком
215

среднего положения t2, следующий за начальным, будет при k — l,
т. е.
или
я 3,14 . ._
—-— = —=—=0,45 сек.
Следующий момент tA будет при k = 2, т. е.
Проследим движение точки в промежутке времени [0; 0,9] сек
(рис. 200,а). При ? = 0 точка находится в начале отсчета О; при
Рис. 200.
i1 = 0,225 сек она занимает положение Mv при ?2 = 0,45 сек — по-
положение М2 @), при t3 = 0,675 сек—положение М3, при tA = 0,9 сек —
положение Ж4@). Затем этот цикл повторяется, т. е. точка совер-
совершает периодическое колебательное движение с периодом Т — 0,9 сек.
2. Модуль и направление скорости определяем, пользуясь форму-
формулой G9.3):
v = ~ = 35 cos It {cMJceK).
В крайних положениях Мх и Мъ имеем:
sin ltXt з = ± 1; cos 7th з = 0; vh3 = 0.
В среднем положении .О(Ж2. Ж4) имеем 7ti=^iz и 7^4 = 2it.
При 7^2 = %
рг\с лг — — ,^__ 1 • tft '¦ ' - \ ^ р it Inpif
216

Знак минус у проекции скорости на касательную показывает, что
точка движется в сторону отрицательных координат (влево).
При 7^4 = 2т:,
cos2ir—1; 1L=35 см/сек,
т. е. точка движется в положительном направлении (вправо).
3. Определяем ускорение шарика. Алгебраическую величину
касательного ускорения получаем по формуле (85.6):
wz = -^f- == —245 sin It (см/сек2).
Модуль нормального ускорения получаем на основании фор-
формулы (85.5):
v2 C5 cos ItI „, „- ,., . , ,.
wn = -^=-—2Q-^-= 61,25cos27t (см/сек2).
Составляем требуемую по условию задачи формулу, определяю-
определяющую модуль полного ускорения шарика в любой момент времени
(рис. 200,6):
w = Vw\-\-w\ = /(—245 sin 7jfJ + F1,25 cos27fJ (см/сек2).
Определяем конкретные значения ускорения в заданных положе-
положениях шарика (рис. 200,а).
Для положения Мг:
w^ —— 245 см/сек2,
знак минус у проекции ускорения на касательную указывает, что
вектор wT направлен в сторону уменьшения дуговых координат s,
т. е. влево:
<а;Я1 = 0; te>i = дат, =245 см/сек2.
Для положения М3:
/3=-Й-; 7^3 = Y7c; sin'2c = —!; cos-g-те = 0; wt9 = 245 см/сек2;
знак плюс указывает, что вектор wTa направлен в сторону увеличе-
увеличения дуговых координат s, т. е. вправо;
¦вуЯ8=0; ^3 = ^, =245 см/сек2.
Для положения М2, М4@):
t2 = -y'' 7t2 = iz; sin те = 0; cos те = —I;
*4 = -у-". 7^= 2т:; sin2w = 0; cos2«=l;
w^ =0; «оП24 = 61,25 см/сек2.
Вектор Wa направлен всегда к центру кривизны траектории:
W2,4 = wn =61,25 см/сек2.
217

§ 88. Примеры определения траектории, скорости и ускорения
точки при задании ее движения координатным способом
Пример 63. Составить уравнение движения ползуна В криво-
кривошипного механизма, изображенного на рис. 201а, если известно, что
кривошип ОА длиной г вращается равномерно, т. е. угол <р, обра-
образованный кривошипом с осью цилиндра, изменяется пропорционально
времени cp = atf, а длина шатуна АВ = 1. Определить также скорость
к ускорение ползуна.
Рис. 201а.
Решение. 1. Составление уравнения движения.
Примем за ось х ось цилиндра и поместим начало координат в точке О,
тогда ОВ — х. Чтобы получить уравнение движения ползуна В, сле-
следует выразить х как функцию времени t.
Опустив из точки А перпендикуляр АК на ось х, получаем:
х = ОК+ KB,
OK = О A cos <р = г cos tp,
KB — АВ cos р = / cos р.
Подставляя значения ОК и KB, получаем
х = г cos «р + / cos
х = r cos <р —|— i cos p.
Чтобы представить координату х как функцию времени t,
дует выразить cos p через функцию угла ср.
Из треугольника ОАВ имеем
еле-
sin ft
sin<p
sin p =
sin ср.
Обозначая -т- = X, имеем:
= 1Л — sin2 g =
X2 sin2ср.
Применяя к выражению cosp=]/l—X2sin2cp формулу бинома
Ньютона, получаем
218

Отбрасывая третье и последующие слагаемые как малые вели-
величины высших порядков |X = -g-; g" ^4 = ttwt). приближенно полу-
получаем
cosB=l—-^-
, 1-19 1
—1-т
X3
X1
Подставляем значение cos [3 в выражение, определяющее х и учи-
учитывая, что Х==-—, находим
Так как ср = ш^, окончательно получаем следующее уравнение
движения ползуна В
= Г (
COS V>
COS 2@
П -(- /	~ .
По этому уравнению можно вычислить значение х, соответствующее
заданному моменту времени t и указать, где находится ползун.
X
Рис. 2016.
2. Определение скорости ползуна.
Проекцию скорости прямолинейного движения ползуна получаем!
согласно § 80, дифференцируя уравнение движения:
vx = --?- = — rcofsin о)/—}- -g- sin 2шЛ.
По этой формуле можно вычислить проекцию скорости для.
любого момента времени. Например, при ср = mt — -?-, т. е. при
t — -=— . получаем
vx = — га) (sin — + -jj- sin ul := — rw < 0.
Вектор v направлен противоположно оси д; (рис. 2016).
2Ш

3. Определение ускорения ползуна.
Ускорение ползуна В получим, согласно § 83, по его проекции
на ось х:
—пг
= — гоJ (cos Ы -f- A cos 2u>t).
По этой формуле можно вычислить проекцию ускорения
ось х для любого момента времени. Например, при <р = ш?
получаем
Wx = 	ГОJ (COS -7Г ~Ь^ COS тс) =	Г(О2(	Х) = ГОJ у = -^-(й2.
на
Так как
Направление вектора w совпадает с направлением оси х (рис. 2016).
Направления w и v противоположны; в данный момент ползун
движется замедленно.
Пример 54. Движение точки определяется уравнениями:
х = г cos kt.
= rsinkt.
1.
Рис. 202a.
ние траектории точки
точки параметр t (см. § 77):
Найти уравнение траектории
точки и построить траекторию.
2.	Найти уравнение годографа
скорости точки и построить годо-
годограф.
3.	Определить ускорение точки.
4.	Получить закон изменения
дуговой координаты, отсчитываемой
по траектории от начального поло-
положения точки.
Решение. 1. Определение
тр аектории. Чтобы найти уравне-
исключаем из заданных уравнений движения
Траектория точки определяется по уравнению х2-\-у2 = г2, т. е.
точка движется по окружности радиусом г, центр которой совпадает
с началом координат (рис. 202а).
2. Определение годографа скорости. Найдем пара-
параметрические уравнения годографа скорости (см. § 81):
X — vx = х = — kr sin kt.
Y = vy = у = kr cos kt.
220

Исключая из этих уравнений параметр t, получаем:
X2 = k2r2sm2kt,
os2^). т. е. X2-{-Y2 — k2r2.
Полученное уравнение показывает, что годограф скорости также
представляет собой окружность с центром в начале координат и
радиусом, равным kr (рис. 2026). Отсюда следует, что модуль ско-
скорости точки не изменяется
при ее движении, т. е. точка
движется равномерно.
V
М
Рис. 202в.
Модуль скорости точки определяем по проекциям скорости на оси
координат (§ 80):
v —
v* = У (kr sin ktf + (kr cos ktJ =
= kr У sin2 kt -j- cos2 kt = kr = const.
3. Определение ускорения. Модуль полного ускорения
точки находим по проекциям ускорения на оси координат (§ 83):
да, = -4т- =? —k?r cos kt,
<wy = —~ = — k2r sin kt,
w = Yw2x + w2 = У (— &V cos A^J+(— ft2r sin *O2 =
= ^ у sin2 й^ + cos2W = k2r = const.
Так как модуль скорости постоянен, то касательное ускорение
точки равно нулю:
dv
~dt
Таким образом, полное ускорение точки является нормальным уско-
ускорением и направлено к центру окружности (рис. 202в).
221

4. Определение закона изменения дуговой коор-
координаты. По уравнениям движения
х — rcoskt, y = rsinkt
определяем начальное положение точки. При / = 0 имеем
Начальное положение точки М0(г, 0) принимаем за начало отсчета
дуговой координаты, тогда so = O.
Из уравнений движения следует, что при увеличении t от нуля
координата х уменьшается, а у увеличивается, т. е. точка движется
по окружности из Мо противоположно движению часовой стрелки.
Это направление принимаем за положительное (рис. 202в).
Представим дуговую координату s = MQM как функцию времени.
Так как точка движется по окружности в одном направлении (по-
(положительном), то пользуемся формулой G9.5):
ds
v = -dT'
откуда
ds = vdt.
При модуле скорости v = kr имеем
ds = krdt.
Проинтегрируем это уравнение в пределах, соответствующих на-
начальному моменту fo = O, когда so = O, и произвольному моменту t,
когда дуговая координата равна s:
s	t
j ds = J krdt,
о
о
s — krt.
Полученное выражение есть уравнение равномерного движения
точки со скоростью v = kr.
Пример 55. Уравнения движения груза, сброшенного с самолета
на высоте Л = 320 м, имеют вид
х = 60Л
у = 5*2.
где х, у выражены в м, t — в сек и направления осей координат
указаны на рис. 203а.
Определить:
1)	траекторию груза,
2)	расстояние по горизонтали между точками сброса и падения,
3)	годограф скорости груза,
222

4)	скорость и ускорение груза в точке падения,
5)	радиус кривизны траектории в точке падения груза.
Решение. 1. Определяем траекторию. Из двух уравнений дви-
движения груза исключаем время t подстановкой во второе уравнение
значения t, полученного из первого уравнения
х
W
= 5 "fin или У =
1
720
Полученное уравнение является уравнением параболы
с вершиной в начале координат, симметричной относительно оси у.
Рис. 203а.
Часть этой параболы, являющаяся траекторией груза, изображена
на рис. ,203а.
2. -Определяем расстояние по горизонтали между точками сброса
и падения. В точке падения Мх известна координата yj=/z. Требуется
найти координату х1=^1 (рис. 202,6).
Воспользуемся не уравнением траектории, а уравнениями движения,
чтобы одновременно найти момент падения:
л: = 60*, 1 = х1 = 60tl = 60 • 8 = 480 м.
3. Определяем годограф скорости согласно § 81:
223

Первое уравнение, не содержащее t, соответствует прямой,
параллельной оеи Y и отсекающей на оси X отрезок 60 м/сек
(рис. 203,в). Отрезок этой прямой, заключенный между концами на-
начальной скорости vQ и конечной скорости vv является годографом
скорости груза.
Годограф скорости показывает, что при падении груза горизон-
горизонтальная составляющая его скорости остается равной начальной ско-
скорости о0 —60лг/шг, а вертикальная составляющая возрастает.
Рис. 2036, в.
4. Определяем скорость и ускорение груза в точке падения. При
движении точки по траектории в одном направлении это направление
принимается за положительное, а модуль скорости точки определяется
по найденным выше проекциям ее скорости на оси координат (80.3):
v =
= /602 4- A0/J = 10 /36 +1
В точке падения имеем
/х = 8 сек; vx = 10 у 36 + 64 = 100м\сек.
Модуль и направление ускорения точки определяем по его проек-
проекциям на оси координат (§ 83):
dvx _	dv-,.
¦w =
^ == Юм(сек2
224

Проекции ускорения груза не зависят от времени, т. е. модуль
и направление ускорения груза постоянны. Так как wx = 0, awy> 0,
то вектор ускорения w направлен параллельно оси у по направлению
этой оси во всех точках траектории. Это ускорение является уско-
ускорением свободного падения ? = 9,8 л/сек2«10 м/сек2 (рис. 203г).
Рис. 203г.
5. Определяем касательное и нормальное ускорения и радиус
кривизны траектории. В зависимости от радиуса кривизны траекто-
траектории р по формуле (85.5) определяется нормальное ускорение точки
" р
Отсюда можно определить р, зная v и wn. Формула скорости
получена выше: v = 10 "^36-j-Я.
Для определения нормального ускорения по формуле (85.8) найдем
касательное ускорение:
VU
«L =
dt
10
2"У36+^2
По полному ускорению w =10 м/сек2 и касательному ускоре-
ускорению wx найдем нормальное ускорение:
9	9 ! .2
12) — *Ш —!— w
"СУ = l/ISp'	liP' = l/
15 А. А. Яблонский
100-
1Ш2
60
225

Нормальное и касательное ускорения зависят от времени, т. е.
движение груза не является равнопеременным, при котором wr = const.
Разложение постоянного полного ускорения на касательное и нор-
нормальное в различных точках траек-
траектории показано на рис. 203г.
Определяем радиус кривизны
в любой точке траектории:
_ v* _ 100C6 + <»)
60 ~
Рис. 204.
В точке падения М1 имеем
= 8 сек; Pi=-g- C6+64J =
= -|- 1000=1667 л.
Пример 56. Уравнения движе-
движения точки имеют вид
х = г cost2,
y = rsint2,
z = at2.
Определить касательное и нормальное ускорения точки и радиус
кривизны траектории в любой момент времени.
Решение. 1. Определяем траекторию. Исключая время t из двух
первых уравнений движения точки, получаем
т. е. уравнение окружности в плоскости хОу, по которвй движется
проекция N точки М на эту плоскость. Следовательно, точка М
движется по поверхности круглого цилиндра с образующей, парал-
параллельной оси z. Если обозначить t2 = ср, то получим (рис. 204):
х = r coscp,
у — г sin<p,
Так как координата z точки М пропорциональна углу поворота f
радиуса, проведенного в точку N. то траекторией точки М является
винтовая линия.
22в

2. Определяем скорость. Скорость точки определяем по ее проек-
проекциям на оси координат (§ 80):
vx = х = — г sin t2 ¦ 2t,
vy = у = г cos t2 ¦ 2t,
— 'z — 2at,
3. Определяем ускорение. Полное ускорение точки определяем
по его проекциям на оси координат, дифференцируя проекции ско-
скорости как произведения функций t (§ 83):
w
— Y^r2 Di4 cos212-\- At2 cos t2 ¦ sin t2-\-sm2t2)-+-
+4/-2D*4sin2^—4^sin^cosi?2+cos2^)+4a2 =
4. Определяем касательное и нормальное ускорения и радиус
кривизны траектории. Касательное ускорение определяем по фор-
формуле (85.8):
dv_
dt
Точка движется равноускоренно, так как wx — const и —тг > 0.
Нормальное ускорение точки определяем по полному и касатель-
касательному ускорениям:
Это ускорение совпадает с нормальным ускорением движения проек-
проекции ./V по окружности, вычисляемым по формуле
Радиус кривизны траектории точки Ж определяем из формулы
та. = —:
" Р
Величина р не зависит от времени, так как кривизна винтовой
линии во всех точках одинакова.
15*	227

Известно, что главная нормаль, вдоль которой направлен век-
вектор wn, в каждой точке М винтовой линии параллельна радиусу ON
(рис. 204).
Откладывая по этому направлению МС = р, получаем центр кри-
кривизны. Параллелограмм ускорений расположен, как известно, в сопри-
соприкасающейся плоскости.
Вопросы для самоконтроля
1.	Чему равен вектор ускорения точки и как он направлен по отноше-
отношению к годографу скорости?
2.	Как направлены естественные координатные оси в каждой точке
кривой?
3.	Каковы величина и направление вектора кривизны кривой в данной
точке?
4.	В какой плоскости расположено ускорение точки и чему равны его
проекции на естественные координатные оси?
5.	Что характеризуют собой касательное и нормальное ускорения точки?
6.	При каком движении точки равно нулю касательное ускорение и при
каком — нормальное ускорение?
7.	Как классифицируются движения точки по ускорениям?
8.	В какие моменты времени нормальное ускорение в криволинейном
движении может обратиться в нуль?
9.	В какие моменты времени касательное ускорение в неравномерном
движении может обратиться в нуль?
§ 89. Графики движения, пути, скорости и касательного
ускорения точки
При движении точки по заданной траектории ее дуговая коорди-
координата s = OM, пройденный ею путь а, а также скорость v и уско-
ускорение w изменяются с течением времени, т. е. являются функциями
времени (рис. 205). Наглядное
представление о характере
движения точки дают графики
зависимости этих величин от
времени.
Для построения таких гра-
графиков по оси абсцисс откла-
откладывают последовательные зна-
значения времени t, а по оси
ординат — соответствующие им
значения дуговой координаты, пути, алгебраических величин скорости
и касательного ускорения, в определенном масштабе.
Графиком движения точки называется график зависимости ее
дуговой координаты s от времени t.
График движения, изображенный на рис. 206, показывает, что
в течение промежутка времени [0, tt] дуговая координата s возрастала
от 0 до sv т. е. точка двигалась от начала отсчета О в положитель-
положительном направлении до точки с координатой sv а затем в течение про-
Рис. 205.
228

межутка времени [iv t2] дуговая координата убывала до нуля, т. е.
точка двигалась в обратном направлении до начала отсчета.
График пути можно построить по графику движения.
Путь, пройденный точкой за некоторый промежуток времени,
представляет собой сумму абсолютных значений элементарных пере-
перемещений точки за данный промежуток времени, т. е. линия этого
графика непрерывно поднимается вверх независимо от направления
движения точки, и только при остановках точки превращается в пря-
прямую, параллельную оси времени t.
На рис. 207 изображен график
пути, построенный по графику ?
¦е о
Рис. 206.
Рис. 207.
движения, показанному на рис. 206. На рис. 207 расстояния, пройден-
пройденные точкой в промежуток времени [tv t2], суммируются с путем ^ = 5!,
пройденным к моменту времени tv
Путь, пройденный точкой к мо- S
менту времени t2
о2 = 2sv
Графики движения и пути изо-
изображаются одной и той же линией
лишь при условии движения точки
из начала отсчета в положительном
направлении, т. е. в промежутке вре- S.
мени [0, fj (рис. 206 и 207).
Положим, что известен график
движения точки (рис. 208).
Определим алгебраическую вели-
величину средней скорости движущейся
точки за промежуток времени [tv t2]
как отнэшение приращения дуговой координаты к промежутку вре-
времени (рис. 208):
НО
Следовательно, wCp:=tga1, т. е. средняя скорость точки за этот
промежуток времени равна тангенсу угла наклона секущей ЛгА2 гра-
графика движения к оси времени t.
229

Определим по этому же графику (рис. 209) алгебраическую
величину скорости точки в некоторый момент времени t:
ds
(89.1)
Таким образом, для определения скорости точки в любой момент
времени следует провести касательную к графику движения в соот-
соответствующей точке А и опреде-
определить угол а наклона этой каса-
касательной к оси t.
Тангенс угла а равен алгеб-
алгебраической величине скорости точ-
точки в этот момент времени.
График скорости изображает
зависимость алгебраической вели-
величины скорости точки v от вре-
времени t (рис. 210).
По графику скорости опре-
определяется алгебраическая величина
касательного ускорения точки:
w,=~ — \g^. (89.2)
Для определения касательного
ускорения точки следует провести
касательную к графику скорости в соответствующей точке В и найти
угол {5 наклона этой касательной к оси t. Тангенс угла р определяет
алгебраическую величину касательного ускорения точки в этот момент.
V
t
Рис. 210.
Рис. 211.
График касательного ускорения изображает зависимость алгебраи-
алгебраической величины касательного ускорения wz от времени (рис. 211).
В случае неравномерного криволинейного движения точки для по-
построения графиков нормального и полного ускорений точки числовые
значения <wn и w для различных моментов времени определяют рас-
расчетом по соответствующим формулам,
230
пользуясь значениями v и w%

определенными по соответствующим графикам; значения же радиуса
кривизны р определяются по заданной траектории точки.
На осях графиков скорости и касательного ускорения алгебраи-
ческие значения этих величин обозначены не v и wT, a v и wx, как
это принято при построении графиков.
1. Графики равномерного движения и его скорости
Уравнение равномерного движения точки имеет вид
Линейной зависимости s от: t соответствует график движения
в виде прямой линии (рис.212,а). Постоянную скорость равномерного
движения точки можно определить из уравнения движения
s — s0
v =
но
следовательно.
v = iga. Графиком постоянной ско- а)
ростии = г» является прямая, парал-
параллельная оси t (рис. 2\2,б).
2. Графики равнопеременного
движения, его скорости и
касательного ускорения
Уравнение равнопеременного дви-
движения точки имеет вид
Этой зависимости s от t соот-
соответствует график движения в виде
параболы (рис. 213,о, рис. 214, о).
Скорость этого движения опре-
определяется по формуле	'	pHCi 212.
v = vo-\-wxt.
Графиком скорости является прямая (рис. 213,6" и рис 214,6').
При равнопеременном движении алгебраическая величина касатель-
касательного ускорения остается постоянной:
wr = const.
Графиком ее является прямая, параллельная оси t (рис. 213,в,
« 214,в). Графики на рис. 213 соответствуют равноускоренному
движению точки, когда wz > 0. Графики на рис. 214 соответствуют
231

случаю wx < 0, т. е. равнозамедленному движению точки, кончаю-
кончающемуся остановкой в момент времени Т.
в)
ог
Рис. 213.
Рис. 214.
В этом случае при t > Т дуговая координата точки s больше
не изменяется, скорость ^ = 0, касательное ускорение ^ = 0.
3. Графики гармонического колебательного движения точки,
его скорости и ускорения
Прямолинейное движение точки, заданное уравнением
(89.3)
называется гармоническим колебательным движением. Такое дви-
движение является основным типом колебательного движения точки.
Так как синус является периодической функцией, принимающей
все значения промежутка [—1, 1], то координата х движущейся точки
изменяется периодически, принимая значения промежутка [—а, а],
т. е. точка М отклоняется последовательно в ту и другую сторону
на величину а от начала координат О (рис. 215).
232

Периодом колебаний Т называется промежуток времени между
двумя последовательными прохождениями точки через одно и то же
положение в одном и том же направлении.
Постоянная а, равная величине наибольшего отклонения колеблю-
колеблющейся точки от ее среднего положения, называется амплитудой
колебаний точки.
Расстояние между крайними положениями точки, равное удвоен-
удвоенной амплитуде, называется размахом колебаний.
Аргумент синуса kt-\-§ называют фазой колебаний точки,
а величину р— начальной фазой.
О	М
—х
а
Рис. 215.
Постоянная k называется круговой или циклической частотой
колебаний.
Татг как период синуса равен 2гс, то увеличение аргумента синуса
на 2тс должно произойти за промежуток времени, равный периоду
колебаний точки, т. е.
й*-Н + 2* = А('+Г) + Р-
откуда
2* = kT
или
г— 2п
Число колебаний точки в одну секунду или частота колебаний
определяется как величина, обратная периоду колебаний:
1 __ k
v — Т ~ 2т- '
За единицу частоты колебаний принимается один герц (гц), т. е.
частота, равная одному периоду в секунду.
Из последней формулы находим: А = 2™, т. е. циклическая
частота k равна по величине числу колебаний в 2тс секунд.
Определим алгебраические значения скорости и ускорения точки,
совершающей гармоническое колебательное движение согласно
уравнению (89.3) х — a sin {kt -f- P):
S = -»,. = i = eft cos (M-ЬР),	(89-4)
w = да^ = ж = — eft2 sin {kt + P) == — k2x.	(89.5)
Последнее выражение показывает, что при гармоническом колеба-
колебательном движении точки модуль ускорения точки пропорционален
отклонению точки от среднего положения О, а знак противоположен
знаку координаты.
233

Наибольший модуль ускорения соответствует крайним положе-
положениям точки: w юак = k2a. В среднем положении ж» = 0.
Вектор ускорения точки направлен всегда к началу координат О,
т. е. к среднему положению точки, так как при х > 0 алгебраиче-
алгебраическая величина ускорения w < 0 и вектор w направлен противо-
противоположно оси х, а при х < 0 величина w > 0 и вектор w направлен
в сторону оси (рис. 216).
Гт °
Xi.0
л
3
Ш
а
_ад,ах.
Рис. 216.
Из этого следует, что при движении точки к центру О напра-
направление ее ускорения совпадает с направлением скорости, а при дви-
движении ее от центра направление ускорения противоположно напра-
направлению скорости, т. е. приближение к центру происходит ускоренно,
т
i
Рис. 217.
а удаление от него — замедленно. Наибольший модуль скорости v
соответствует среднему положению точки (л: = 0); в крайних поло-
положениях v = 0.
Изменение скорости и ускорения точки можно проследить по графи-
графикам движения, скорости и ускорения, лостроенным согласно уравнениям:
(рис. 217).
234
v — ka cos (kt + P),
¦ш = — #*a sin Ш -4- B)

4. Построение графиков скорости и касательного ускорения
по графику движения точки
В ряде практических задач не удается найти аналитическую за-
зависимость s = f(t) для некоторых точек механизма, но по данным
автоматов-самописцев, связанных с соответствующей частью меха-
механизма, можно получить график движения точки (рис. 218,о).
График скорости точки в этом случае строят следующим образом.
Откладывают от начала осей координат vOxt (рис. 2\Ь,б) отре-
отрезок Oj/C], равный единице времени в принятом масштабе, и из точки Кх
проводят прямые, параллельные касательным к графику движения
в точках О, Av А2, ... Отрезки, отсекаемые этими прямыми на
оси OjV, дадут в соответствующем масштабе алгебраические величины
скоростей точки в моменты О, tv t2, ... Действительно, на рис. 218,а
имеем:
При Oj/Cj = 1 получаем (рис. 218,б)
°ivo = °i^i % ао = Ч ао> О А = tg ар O,V2 = iga2 ...
Восставив перпендикуляры к оси t в точках tv t2, tz, ... и
к оси v — в точках vv v2, v3, .... получим точки Bv В2, В3 ...
графика скорости.
График касательного ускорения строят аналогично.
Отложив от начала осей "W^O2t отрезок О2К%, равный единице
времени в принятом масштабе (рис. 218,в), проводим из точки К2
прямые, параллельные касательным к графику скорости в точках
Bv В2, В3, ...
Отрезки, отсекаемые этими прямыми на оси O2w^, определяют
в соответствующем масштабе алгебраические величины касательных
ускорений точки в моменты О, tv t2, t3, ...
Восставив перпендикуляры к оси t в точках tv t2, tv ... и к оси
ie>z — в точках wx, шт, w^, .... получим точки Сх, С2, Съ ... гра-
графика касательного ускорения.
Построение графиков скорости и касательного ускорения по за-
~ ds
данному графику движения, основанное на зависимостях v = —tt и
дат = —jr-, является методом графического дифференцирования.
Вопросы для самоконтроля
1.	Чем отличается график пути от графика движения точки?
2.	Как по графику движения определить алгебраическую величину ско-
скорости точки в любой момент времени?
3.	В каком направлении и с какой скоростью движется точка," график
движения которой изображен на рис. 219?
4.	Как по графику скорости прямолинейного движения точки определить
алгебраическую величину ускорения точки в любой момент времени?
235

— с
Рис. 218.

5. Какое движение точки называется гармоническим колебательным
движением и какие величины характеризуют это движение?
t	ft
i	CO
Рис. 219.
6. Как направлено ускорение гармонического колебательного движения?
В какие промежутки времени это движение происходит ускоренно и в какие
замедленно ?
ГЛАВА XIV
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 90. Поступательное движение твердого тела
Различают пять видов движения твердого тела:
1)	поступательное движение;
2)	вращательное движение;
3)	плоское или плоскопараллельное движение;
4)	сферическое движение;
5)	общий случай движения твердого тела. -
Приступая к изучению движения твердого тела, нужно прежде
всего установить, к какому из указанных выше видов движения оно
относится.
Поступательное и вращательное движения являются про-
простейшими движениями твердого тела.
Рассмотрим в первую очередь поступательное движение тве'рдого
тела.
Поступательным движением твердого тела называется
такое движение, при котором любая прямая, соединяющая
две точки тела, движется параллельно самой себе.
Теорема. Все точки твердого тела, движущегося поступа-
поступательно, описывают тождественные и параллельные между собой
траектории и в каждый момент времени имеют геометри-
геометрически равные скорости и ускорения.
Для доказательства теоремы выберем две произвольные точки
твердого тела А и В и проведем из точки А в точку В радиус-век-
радиус-вектор гАВ (рис. 220).
237

Так как тело движется поступательно, то во время его движения
отрезок АВ остается параллельным своему начальному положению,
а потому значения радиуса-вектора тАВ в любые моменты времени t
и tx геометрически равны, т. е.
=rAlBl = const.
Проведем из произвольного неподвижного полюса О в точки А,
В, Av Вх радиусы-векторы гА, тв, тА ¦ тв ¦
Из Д ОАВ устанавливаем равенство
которое будет справедливым во асе время движения.
Это равенство показывает, что любому положению точки А со-
соответствует определенное положение точки В, отстоящее от А по
направлению гАВ на расстоянии АВ.
Рис. 220.
Поэтому, если траекторию точки А переместить по направле-
направлению гАВ на расстояние АВ, то она совпадет с траекторией точки В,
т. е. траектории точек А и В тождественны и параллельны.
Определим вектор скорости точки В как производную от радиуса-
вектОра этой точки по времени по формуле G8.4):
dt
dt
в
dt
dt
но
На
dt
¦ = Vi
а ~1Г~[
Поэтому vB = vA, т. е. скорости точек А и В геометрически равны.
Определив ускорения точек Л и В тела согласно (82.1), получим
На
dt
'A' WB
т. е. ускорения точек А и В геометрически равны.
Так как точки А к В произвольны, то полученные соотношения
относятся ко всем точкам тела.
Установленные свойства поступательного движения позволяют
свести изучение поступательного движения твердого тела к изучению
238

движения отдельной точки этого тела, т. е. к задаче кинематики
точки.
Общие для всех точек твердого тела, движущегося поступательно,
скорость v и ускорение w называют скоростью и ускорением по-
поступательного движения твердого тела.
При любом другом движении твердого тела точки тела двужутся
с различными скоростями и ускорениями.
Уравнениями поступательного движения твердого тела являются
уравнения движения любой точки этого тела — обычно уравнения
движения его центра тяжести С:
Ус-=/»(').
(90.1)
Точки твердого тела, движущегося поступательно, могут описывать
любые траектории, в том числе и прямые.
Примером поступательного движения твердого тела является дви-
движение' спарника АВ, соединяющего пальцы равных кривошипов ОХА
и Оф (рис. 221). Все точки спарника описывают окружности ра-
радиусом, равным длине кривошипа, и имеют геометрически равные
скорости и ускорения.
§ 91. Вращательное движение твердого тела.
Уравнение вращательного движения.
Угловая скорость и угловое ускорение тела
Вращательным называется такое движение твердого тела,
при котором остаются неподвижными все его точки, лежа-
лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоско-
плоскостях, перпендикулярных оси вращения, и описывают окружности,
центры которых лежат на этой оси.
239

Для осуществления этого движения следует неподвижно закрепить
две некоторые точки твердого тела А и В. Тогда прямая АВ будет
осью вращения тела и все точки, лежащие на этой прямой во все
время движения будут оставаться неподвижными (рис. 222).
Определим положение вращающегося тела следующим образом.
Зададимся направлением оси вращения z. Проведем через эту ось две
полуплоскости: неподвижную полуплоскость Я и подвижную полу-
полуплоскость Q, связанную с твердым
2	телом и вращающуюся вместе с ним.
Двугранный угол ф между этими
полуплоскостями, отсчитываемый от
неподвижной полуплоскости Р к под-
подвижной полуплоскости Q, называется
углом поворота тела.
Условимся считать угол поворота
положительным, если, смотря навстречу
оси вращения, можно увидеть его от-
отложенным против движения часовой
стрелки. Числовые значения угла по-
поворота выражаются в радианах.
Радианом, как известно из гео-
геометрии, называется центральный угол,
длина дуги которого равна радиусу.
Числовое значение угла в радианах
равно отношению длины дуги к ра-
радиусу, т. е. оно— отвлеченное число.
Угол, равный 360°, содержит 2л ра-
радиан. Один радиан составляет
Рис. 222
360°
2л
= 57° 17'44,8".
Угол поворота часто выражают числом оборотов N. Тогда угол <р
в радианах, соответствующий N оборотам, определяется:
= 2nN.
(91.1)
Угол ф, определяя положение подвижной полуплоскости, опре-
определяет также положение всего вращающегося тела. Поэтому его можно
рассматривать Karf угловую координату тела.
При вращении тела угол поворота ф изменяется в зависимости
от времени, т. е. является функцией времени t:
Ф =
(91.2)
Уравнение (91.2) называется уравнением вращательного дви-
движения тела. Оно полностью определяет положение тела в любой
момент времени,
240

Угловая скорость и угловое ускорение тела
Величина, характеризующая быстроту изменения угла поворота ср
с течением времени, называется угловой скоростью тела.
Условимся абсолютное значение угловой скорости обозначать ш,
а алгебраическую величину угловой скорости символом ш. Очевидно,
что | со | = ш.
Если в моменты времени t и t-\-M вращающаяся полуплоскость
занимает положения Q и Qv т. е. угол поворота ср за время Д^ по-
лучает приращение Дер, то отношение -jj- определяет алгебраическую
величину средней угловой скорости вращающегося тела за время М:
~ Ду
Шср = ~КГ '
При стремлении Д/ к нулю получаем алгебраическую величину
угловой скорости тела в момент t:
,. ~ ,. A? d<9
S=-g=?.	(91.3)
dtp
Если -—¦ > 0, то угол поворота ср увеличивается, т, е. вращение
тела происходит в положительном направлении отсчета угла поворота.
Если —~- < 0, то угол поворота ср уменьшается, т. е. тело вра-
вращается в обратную сторону.
d<&
Если в некоторый момент времени -~ = 0 и изменяет знак, то
угол поворота ср в этот момент достигает максимального или мини-
минимального значения, а тело изменяет направление вращения.
Таким образом, знак производной —^- указывает направление вра-
вращения тела, а ее абсолютное значение равно угловой скорости тела, т. е.
¦&I	<•¦¦<>
Если вращение тела происходит в одном направлении, которое
принимается за положительное, то и = -jf > 0, т. е.
формул! (91.4) принимает вид
гг
dt
~dt
и
Величина, характеризующая быстроту изменения угловой скорости
с течением времени, называется угловым ускорением тела.
Условимся абсолютное значение углового ускорения обозначать е,
а алгебраическую величину углового ускорения е.
Очевидно, что | е | = е.
16 А А Яблонский	241

Если за промежуток времени At приращение угловой	скорости
равно Дш, то отношение -?- определяет алгебраическую	величину
среднего углового ускорения вращающегося тела за время	Д?:
~ Д (о
При стремлении Д? к нулю получаем алгебраическую	величину
углового ускорения в момент t
т. е.	___
?=-? = ?.	(91.6)
Из формулы (91.3) следует:
Знак е = -ф- также дает возможность установить, является ли
вращение тела в данный момент ускоренным или замедленным.
Если знаки w и е одинаковы, тело вращается ускоренно, а если
их знаки различны — замедленно.
Абсолютное значение углового ускорения
dt
dt*
При вращении тела в одном направлении, когда w = ш, имеем
e =z
If
= <o.	(91.8)
dm
Если —гт- > 0, то угловая скорость о> увеличивается, т. е. тело
вращается ускоренно. Если -гг < 0, то ш уменьшается, т. е. враще-
вращение происходит замедленно.
Уравнение равномерного вращения тела
Вращение тела с постоянной угловой скоростью называется
равномерным. Составим уравнение равномерного вращения тела
с угловой скоростью ш, принимая направление этого вращения за
положительное направление отсчета угла поворота ср.
Положим, что в начальный момент te = 0 угол поворота имеет
значение <р0. По формуле (91.5) получим -^~ = ш — const; dcp = wutf.
Проинтегрируем уравнение в пределах, соответствующих началь-
начальному моменту tQ = Q и произвольному моменту времени t:
9	t
f dcp = (o I dt; cp — cpo =
-p.
242

откуда	(р = <р0 -f- a>/.	(91.9)
Выражение (91.9) является уравнением равномерного враще-
вращения тела.
Если в начальный момент времени подвижная полуплоскость Q
-совпадает с неподвижной полуплоскостью Р, т. е. сро = О, то урав-
уравнение равномерного вращения тела (91.9) принимает вид
Из уравнения равномерного вращения тела при %ф 0 находим
«о = -!=*-.
т. е. угловая скорость равномерного вращения тела равна
отношению приращения угла поворота за некоторый проме-
промежуток времени к величине этого промежутка времени.
Если за единицу угла принять 1 радиан, а за единицу времени —
1 секунду, то единицей угловой скорости будет 1 сек~х.
Обычно угловая скорость измеряется числом оборотов в минуту
и обозначается п. Так как один оборот равен 2гс рад, то зависимость
между угловой скоростью ш сек~1 и п об\мин имеет вид
w==tlW или Ш:==Ж	(91.10)
и
«=¦^¦0».	(91.11)
Например, угловая скорость турбины, совершающей 4000 off/мин,
выраженная в сек~1, равна:
4000ix ..„„л _«
ш = —5пг— = 418,88 сек \
Угловая скорость вращения Земли вокруг ее оси, выраженная в сек~1,
" = -нД^ = 0,0000727
Уравнение равнопеременного вращения тела ^ $
Вращение тела, при котором угловое ускорение постоянно, на-
называют равнопеременным вращением. При этом, если абсолютная
величина угловой скорости увеличивается, вращение называют равно-
равноускоренным, а если уменьшается—равнозамедленным.
Составим уравнение равнопеременного вращения, полагая, что
в начальный момент ?0 = 0 начальная угловая скорость равна и>0, на-
начальное значение угла поворота равно у0:
— = е== const; d<a = edt.
16*	243

Проинтегрируем уравнение в пределах, соответствующих началь-
начальному моменту /0 = 0 и произвольному моменту времени t:
w	t
I йш = е I dt, о) — u>0 — et,
Z	(91.12)
Проинтегрировав это уравнение в соответствующих пределах,
получим
t
То
9 — ?о =	g	2
Уравнение (91.13) является уравнением равнопеременного вра-
вращения тела.
Так как равнопеременное вращение происходит обычно в одной
направлении, то со = а>, а е = ± е, где з^ак плюс соответствует уско-
ускоренному вращению, а знак минус — замедленному. Учитывая это,
формулам (91.12) и (91.13) можно придать более удобный для реше-
решения задач вид:
ш = (о0 ± tt,	(91.12*)
<р = сро+шог±^.	(91.13*)
Из формулы угловой скорости находим е = " ~~ ю° , т. е. при.
равнопеременном вращении абсолютное значение углового уско-
ускорения тела равно отношению изменения угловой скорости тела
за некоторый промежуток времени к величине этого проме-
промежутка.
Если за единицу угла принять 1 радиан, а за единицу времени —
1 секунду, то единицей углового ускорения будет 1 сек~2. Если за
единицу угла принять 1 оборот, а за единицу времени 1 минуту,
то единицей углового ускорения будет 1 об/мин2.
Покажем на примерах переход от одних единиц углового уско-
ускорения к другим. Выразим, например, в сек~2 угловое ускорение
е = 15 об/мин2:
? = 15 об/мин2 = 15 тр- сек~2~ТШ сек~2.
Рассмотрим и обратный переход. Выразим угловое ускорение
s = 5тс сек~2 в об/мин2;
? = 5гс сек~2 — 5п^- o6jmuh2 — 9000 об (мин2.
244

Пример 57. Вал начинает вращаться равноускоренно из состоя-
состояния покоя; в первые 20 сек он совершает 100 оборотов. Каковы его
угловые скорость и ускорение по истечении 20 сек?
Решение. Так как вал начинает вращаться из состояния покоя,
то шо = О. В этом случае уравнения (91.12) и (91.13) при <ро = О
имеют вид
Ф = -2-,
ID =zst.
(б)
Из уравнения (а) находим е = -т|-,
где
Подставляя числовые значения, находим:
2 •
100
202
¦ = и сек
'2,
= е • 20 = 20-гс сек'1.
§ 92. Скорости и ускорения точек твердого тела,
вращающегося вокруг неподвижной оси
На рис. 223 изображена окружность, представляющая собой
траекторию произвольной точки М тела; расстояние точки М
от оси вращения, равное радиусу этой окружности, обозначим /?.
Если ОС — радиус, лежащий в неподвижной полуплоскости Р,
a NC — радиус, лежащий в подвижной полуплоскости Q и вращаю-
вращающийся вместе с ней, то /_OCN = cp = f(t).
Величина угла NCM=n при вращении его сторон NC и МС
вместе с телом не изменяется, т. е.
а = const.
Неподвижную точку О примем за начало отсчета дуговой коорди-
координаты s точки М, направление движения точки за — положительное.
Тогда получим
где углы <р и а выражены в радианах.
Определим модуль скорости точ-
точки М, называемой вращательной, или
окружной, скоростью этой точки:
ds
v =
dt
_
dt
= /?u>. (92.1)
Модуль вращательной скорости
точки твердого тела равен произве-	Рис- 223.
дению расстояния от точки до оси вращения на угловую ско-
скорость тела.
Так как угол <р выражается в радианах, то угловая скорость и>
в этой формуле должна выражаться в сек~1.
245

Из формулы (92.1) следует, что модули вращательных скоро-
скоростей различных точек вращающегося тела пропорциональны
расстояниям от этих точек до оси вращения (рис. 224).
Если соединить отрезком прямой конец скорости, например, точки А
вращающегося диска, с центром вращения С, то концы скоростей
точек В, D и Е диска будут лежать на этой прямой. Это очевидно из
подобия образовавшихся треугольников, высоты
которых vE, vD, vB, vA пропорциональны их осно-
основаниям СЕ, CD, CB, С А.
Ускорение точки М определим по его со-
составляющим: касательному ускорению, направлен-
направленному по касательной к окружности, и нормаль-
нормальному ускорению, направленному к центру С.
Эти ускорения точек вращающегося тела на-
называют вращательным и центростремительным
ускорениями и обозначают wB и w" (рис. 223):
«в = ^*= -зг =Л sr =Яе. (92.2)
Рис. 224.
Модуль вращательного ускорения точки тела равен произ-
произведению расстояния от точки до оси вращения на абсолютное
значение углового ускорения тела.
По формуле (85.5) найдем:
wa = wn = ~ = I*—- — ЯоЛ	(92.3)
Модуль центростремительного ускорения точки равен про-
произведению расстояния от точки до оси вращения на квадрат
угловой скорости тела.
Модуль полного ускорения
точки определяется по формуле
= /?Уе2+иL. (92.4)
Тангенс угла р, составлен»
ного ускорением w с радиусом
.окружности СМ, определится
по формуле
1g В = -!Ц-= -1^ = 4.(92.5)
Эта формула показывает,
что угол, составленный ускоре-
ускорением точки вращающегося тела с отрезком, соединяющим точку с цен-
центром окружности, не зависит от положения точки в теле.
В формулах для вычисления w9, та»ц и ti> угловая скорость ш а
угловое ускорение е должны быть выражены в сек'1 и сек~2.
Из формул (92.2), (92.3) и (92.4) следует, что модули враща-
вращательных, центростремительных и полных ускорений точек
Рис. 225.
246

вращающегося тела пропорциональны расстояниям от этих
точек до оси вращения. Поэтому по ускорению какой-либо точки А
вращающегося диска (рис. 225) можно определить графически уско-
ускорение любой другой точки В этого диска, лежащей на радиусе АС.
При равномерном вращении тела
,	da
to = const, e =
dt
= 0,
а поэтому •wB — Re = Q.
Таким образом, при равномерном вращении ускорение точки
является центростремительным, а его модуль равен:
¦W = W» = Rw2.
В этом случае ускорение w точки М направлено к центу С
окружности, описываемой этой точной.
§ 93. Примеры на вращательное движение
Пример 58. Вращение маховика в период пуска машины опре-
определяется уравнением
1
где t — в сек, <р— в рад. Определить модуль и направление ускоре-
ускорения точки, отстоящей от оси врещения на расстоянии 50 см, в тот
момент, когда ее скорость равна 8 м[сек.
Решение. По уравнению вращения маховика находим его угло-
угловые скорость и ускорение согласно формулам (91.5) и (91.8):
Ё =
dt2
= 2*.
(а)
(б)
Пользуясь формулой (92.1), находим
момент времени tv когда скорость
точки М равна 8 м/сек:
По этому значению w из (а) находим
t1 = У~ю1 = У^б = 4 сек.
По уравнению (б) вычисляем е, а затем
по формулам (92.2), (92.3) и (92.4)—	Рис.226,
модули вращательного, центростремительного и полного ускорений
точки М в этот момент времени:
?j = 2 -4 = 8 сек~2;
= 0,5-8 = 4 м(сек2;
= 0,5- 162=128 м/сек2;
», = /(*•)¦+ («*)*=¦
w\ =
1282 = 128,06 м/сек2.
247

Как видно, модуль полного ускорения точки весьма мало отли-
отличается от модуля центростремительного ускорения точки (рис. 226).
Направление ускорения точки определяется углом [3, образован-
образованным ускорением и радиусом СМ:
tgp1 = 4- = -V = —; Pi = l°48'.
ы\ 162 32 г
Пример 59. Груз А, подвешенный к нити АВ, намотанной на
барабан, опускается равноускоренно из состояния покоя, приводя
во вращение барабан. За первые 3 сек барабан совершает 9 обо-
оборотов. Определить в конце	(
5-й сек скорость и ускорение
точки обода барабана, а также
груза А, если диаметр барабана
?> = 30 см (рис. 227а).
В
Рис. 227а.
Рис. 2276.
Решение. Барабан вращается равноускоренно согласно урав-
уравнению (91.13*):
Формула угловой скорости имеет вид (91.12*):
со = ш0 -f-еЛ
Для того, чтобы начальное значение угла поворота ср0 обратилось
в нуль, следует неподвижную полуплоскость поместить в начальном
положении подвижной полуплоскости, вращающейся с барабаном
(см. § 91). Выполним это и получим ср0 = 0. При вращении из со-
состояния покоя начальная угловая скорость барабана равна нулю со0=:0.
При этих условиях формулы (91,12*) и (91.13*) принимают вид
(О =г St.
(а)
(б)
248

Так как ср = 9 оборотов при t — Ъ сек, то из уравнения (а) опре-
определим одинаковое для всех моментов времени угловое ускорение е;
2ф 2-9 о ,, , .	„
е = -г?- = -™— = 2 об/сек1 = 4тс сек~2.
Из уравнения (б) найдем угловую скорость барабана в конце
5-й сек:
t — § сек, ш5 = 4тс • 5 = 20т: сек'1.
Определим в точке В обода барабана (рис. 2276) модули враща-
вращательной скорости, вращательного и центростремительного ускорений
в этот же момент времени по формулам (92.1), (92.2), (92.3):
¦у5 = /?ш5 = 0,15- 20тс = 3- 3,14 = 9,42 м/сек,
wl — wB — Rs = 0,15 ¦ 4тс = 0,6 • 3,14= 1,88 м/сек2
(модуль вращательного ускорения точки тела при равнопеременном
вращении одинаков для всех моментов времени),
<а>« = /?и>2 = 0,15 • 400u2 = 60 • 9,86 = 591,6 м/сек2.
Модуль полного ускорения точки обода барабана определяется по
формуле (92.4):
,62 « 591,6 м[сек2.
Вследствие незначительной величины модуля вращательного уско-
ускорения по сравнению с модулем центростремительного ускорения, пол-
полное ускорение приближенно равно центростремительному.
Скорость груза равна скорости точки обода барабана:
vrps — v5 — 9A2 м/сек.
Ускорение груза (рис. 2276) равно вращательному ускорению
точки обода, т. е.
tiyrp = TOB= 1,88 м/сек2.
§ 94. Векторные выражения вращательной скорости,
вращательного и центростремительного ускорений
Введем понятия векторов угловой скорости ю и углового ускоре-
ускорения s.
Условимся откладывать вектор угловой скорости тела м от любой
точки оси вращения, направляя его по этой оси так, чтобы смотря
навстречу этому вектору, видеть вращение тела происходящим против
движения часовой стрелки (рис. 228, а и б). Модуль этого вектора дол-
Жен равняться абсолютному значению угловой скорости, ш = —jt- •
(IT
Принятое правило обусловлено применением правой системы осей
координат, которой соответствует положительное направление вра-
вращения, противоположное направлению движения часовой стрелки. При
Пользовании левой системой вектор to следует направить так, чтобы,
смотря ему навстречу, видеть вращение тела происходящим в на-
направлении движения часовой стрелки.
249-

Векторы, направления которых зависят от принятой системы коор-
координат, называются псевдовекторами. Примерами псевдовекторов,
кроме угловой скорости, могут служить также момент силы относи-
относительно точки и момент пары сил. При сложении псевдовекторов
.действительны правила параллелограмма и многоугольника (§ 129).
Л-V/vV1
Рис. 228.
Рис. 229.
Вектор углового ускорения е характеризует изменение вектора
угловой скорости со в зависимости от времени, т. е«. он должен быть
2	равен производной от вектора угловой скорости по
времени
.-¦?.	<и.1)
Направление векторной производной совпадает
с предельным направлением приращения дифферен-
дифференцируемого вектора (см. примечание. § 78, стр. 190).
Так как вектор w имеет постоянное направление,
то направление его приращения Да> совпадает с на-
направлением самого вектора w при ускоренном вра-
вращении и противоположно ему — при замедленном.
Таким образом, направление вектора e = -j~ сов-
совпадает с направлением вектора о> при ускоренном
вращении и противоположно ему при замедленном
(рис. 229, а и б).
Модуль вектора е равен абсолютному значению углового уско-
Г
Рис. 230.
-рения, е= |
Так как точкой приложения векторов и» и е может быть любая
точка оси вращения, то векторы о> и е являются скользящими.
Пользуясь понятием вектора угловой скорости ш, легко получить
векторное выражение вращательной скорости.
-250

Изобразим (рис. 230) вектор угловой скорости е>, радиус-вектор г
точки М тела относительно произвольной точки О оси вращения и
вращательную скорость этой точки v. Модуль вращательной скоростиг
v = R& = cor sin а, где а — угол между радиусом-вектором г и век-
вектором угловой скорости ш.
Модуль векторного произведения йХт:
|«* X г| = (о^ • sin а.
Сопоставляя значения v и 1 « X г |, устанавливаем, что модуль вра-
вращательной скорости v равен модулю векторного произведения « X г.
Вращательная скорость v направлена перпендикулярно к пло-
плоскости треугольника4 СОМ, т. е. плоскости векторов сомножите-
сомножителей «иг; если смотреть навстречу v, можно видеть поворот век-
вектора в) к вектору г на угол а, совершающимся4 против движения
часовой стрелки, т. е. направление вращательной скорости v совпа-
совпадает с направлением вектор-
векторного произведения »Хг.
Следовательно, векторы
v и йХг имеют равные
модули и одинаковое на-
направление, т. е. они равны
между собой:
v = «Xr. (94.2)
Таким образом, враща-
вращательная скорость точки
твердого тела, вращаю-
вращающегося вокруг неподвиж-
неподвижной оси, равна вектор-
векторному произведению век-
вектора угловой скорости
тела на радиус-вектор
этой точки относительно
любой точки оси ера-	Рис. 231.
щения.
Выражение (94.2) является одним из основных соотношений ки-
кинематики твердого тела.
Если известны проекции и>х, <ву, <oz вектора угловой скорости, на-
направленного по оси вращения тела О А, на оси координат (рис. 231}
и координаты некоторой точки М тела х, у, z, то вращательную
скорость этой точки можно найти при помощи определителя вектор-
векторного произведения:
I i к
X
х
(By
У
К* —
— ах).
251

Отсюда определяются проекции вращательной скорости точки на оси
координат:
(94.3)
х.
Эти формулы получены Эйлером в 1765 г. и называются фор-
формулами Эйлера.
В случае, если ось вращения тела совпадает с одной из осей
координат, например, с осью г, имеем: и>х = 0, шу = 0, <ог = ш,
откуда vx = — ffiy. vy = &x, vz = 0.
Для получения векторных формул вращательного и центростре-
центростремительного ускорений продифференцируем по времени выражение
v = w X г;
тогда получим
dt
dt
n	dm
Здесь -^ == i
dr
dt
dt '
= v =
= »Xr.
Подставляя эти значения,
получим
Рис. 232.
или
= e X
X v
Покажем, что первое слагаемое е X г есть вращательное ускоре-
ускорение, а второе слагаемое о) X v — центростремительное ускорение.
На рис. 232, а показаны направления вращательного ускорения wB
и центростремительного ускорения w" для случая ускоренного вра-
вращения, а на рис. 2%2,б—направления тех же ускорений для случая
замедленного вращения.
Модуль вращательного ускорения (рис. 232, а)
wB = eR =er sin а,
где а — угол между радиусом-вектором г и вектором углового уско-
ускорения е.
Модуль векторного произведения е X г;
|е X т | =er sin а.
Сопоставляя значения модулей taB и | е X г |, устанавливаем:
дав == I в X г I.
252

Вращательное ускорение wB направлено перпендикулярно пло-
плоскости треугольника СОМ, г. е. плоскости векторов сомножите-
сомножителей s и г; если смотреть навстречу wB, то можно видеть поворот
вектора е к вектору г на угол а (рис. 232, а) или на угол 180 — а
(рис. 232,6), совершающимся против движения часовой стрелки, т. е.
направление вращательного ускорения wB совпадает с направлением
векторного произведения е X г.
Следовательно,
wB = eXr.	(94.4)
Таким образом, вращательное ускорение точки твердого
тела, вращающегося вокруг неподвижной оси, равно вектор-
ному произведению вектора углового ускорения тела на радиус-
вектор этой точки относительно любой точки оси вращения.
Модуль центростремительного ускорения
Модуль векторного произведения <о X vt
j » X v | = mv sin (to, v) = (S)V,
так как sin(o>, v)=l при (vj_w).
Сопоставляя значения модулей wa и | to X v |, устанавливаем:
wn =r | ю X v |.
Если мысленно перенести вектор угловой скорости в точку М
(рис. 232), то, смотря навстречу центростремительному ускоре-
ускорению wu. перпендикулярному плоскости векторов сомножителей ы
и v, можно видеть поворот вектора ы к вектору v на угол 90°,
совершающимся против движения часовой стрелки, т. е. направление
центростремительного ускорения wu совпадает с направлением век-
векторного произведения w X v. Следовательно,
wu = wXv.	(94 5)
Таким образом, центростремительное ускорение точки твер-
твердого тела, вращающегося вокруг неподвижной^оси, равно век-
векторному произведению вектора угловой скорости тела на
вращательную скорость этой точки.
§ 95. Передаточные механизмы
Передаточные механизмы предназначены для передачи вращения
от одного вала, называемого ведущим, к другому, называемому
ведомым.
Если оси ведущего и ведомого валов параллельны или пересе-
пересекаются, то вращение можно передать при помощи фрикционной или
зубчатой передач (рис. 233а, б, в).
253

Во фрикционной передаче вращение передается вследствие дей-
действия силы сцепления на поверхности соприкасающихся колес, в зуб-
зубчатой передаче — от зацепления зубьев.
Рис. 233а.
Вращательная скорость v в точке соприкасания колес относится
к точкам обоих колес, т. е. ее модуль определяется
откуда
(95.1)
Таким образом, угловые скорости колес фрикционной или зубча-
зубчатой передачи обратно пропорциональны радиусам колес.
Отношение угловой скорости ведущего колеса к угловой
скорости ведомого колеса называется передаточным числом.
а>2
(95.2)
Передаточное число можно вычислить как обратное отношение
радиусов колес
/ = -?-.	(95.3)
254

Так как числа зубьев пропорциональны длинам окружностей и,
следовательно, радиусам, то передаточное число определяется и по
числу зубьев:
/ = ?!. (95.4)
При внешнем зацеплении
(рис. 233а) направление вращения
ведущего и ведомого колес про-
противоположное, а при внутреннем
{рис. 2336) — одинаковое.
Кроме фрикционной и зубча-
зубчатой передач, существует передача
на расстоянии при помощи гиб-
гибкой связи (ремня, троса, цепи)
(рис. 234).
Так как скорости всех* точек
ремня одинаковы и ремень не
скользит по поверхности шкива,
то к ременной передаче относятся
те же соотношения:
Применяются также серии ко-1
лес с неподвижными осями вра-
вращения в виде последовательного
ряда с паразитными колесами
{рис. 235а) и последовательного ряда с кратным зацеплением
{рис. 2356), называемые рядовыми соединениями колес.
Рис 2336
Рис. 233в.
Определим передаточное число фрикционной передачи в виде
рядового соединения с паразитными колесами.
Для колес /—2
СО] __ Г2
255

Для колес 2—3
Перемножая левые и правые части, получаем
Для зубчатых колес
'" ' ... — 	 л- - t
<а3 Г,
Передаточное число рядового соединения с паразитными
колесами равно отношению радиусов (чисел зубьев) ведомого и
ведущего колес и не зависит
от радиусов (чисел зубьев)
паразитных колес.
Рис 234.
Рис. 235а.
Определим передаточное число рядового соединения с кратным
зацеплением.
Частное передаточное число для колес 1—2
Частное передаточное число для колес 3—4
Так как колеса 2—3 соединены жестко, т. е. а2 = а3, то общее
передаточное число t = — равно произведению передаточных чисел:
или
Для зубчатых колес
«Л
(95.5)
Таким образом, общее передаточное число рядового соедине-
соединения колес с кратным зацеплением равно произведению чисел
256

зубьев ведомых колес, деленному на произведение чисел зубьев
ведущих колес.
В рассмотренных выше передачах при равномерном вращении
ведущего вала ведомый
вал вращается тоже рав-
равномерно.
Для получения пере-
переменной угловой скорости
ведомого вала применя-
применяются передачи, в которых
расстояние от точки со-
соприкасания колес до оси
одного из валов или
обоих валов изменяется.
Во фрикционной пе-
передаче, изображенной на
рис. 236, колесо / пере-
перемещается вдоль его оси
и отношение угловых ско-
скоростей зависит от пере-
переменного расстояния х
«2
Рис. 2356.
На рис. 237 изображены эллиптические колеса, оси вращения
которых находятся в фокусах эллипсов. Отношение угловых скоро-
Рис. 236.
Рис. 237.
стей зависит от переменных расстояний х1==О1М и
xi~\- х2 = 2а,
«о, _ х2
ОJ
17 А. А. Яблонский
j = 02M, где
(95.7)
257

§ 96. Примеры на преобразование вращательного
движения
Пример 60. Ведущий шкив ременной передачи, обладающий угло-
угловой скоростью п/о = 60 об/мин, останавливается через 10 сек. Ра-
Радиусы шкивов: г{ = 25 см, г;/ = 50 см.
Рис. 238а.
Считая вращение шкивов перед остановкой равнозамедленным,
определить число оборотов ведомого шкива до остановки, а также
модули скорости, вращательного и центростремительного ускорений его
точки М (О2Ж = 20 см) в конце 5-й сек (рис. 238а).
г
Рис. 2386.
Решение. При решении задач положительным всегда считается
направление происходящего вращения (в данном примере направле-
направление движения часовой стрелки) (рис. 238 6).
258

Формула (91.12*), определяющая угловую скорость равнозамедлен-
ного вращения шкива /, имеет вид
При t= 10 сек шкив останавливается, т. е. ш, =0.
МО
Начальная угловая скорость шкива в сек~1 определяется по
формуле
71П,	ТС ¦ 60
Подставляя эти значения в формулу, имеем
0 = 2тс — е; • 10; е, = 0,2те сек~2.
Поэтому
Определяем характеристики вращения шкива //. Угловые скорости
шкивов передачи обратно пропорциональны их радиусам. По усло-
условию (95.1) получаем формулу, определяющую угловую скорость
ведомого шкива //:
25
Г
Отсюда находим уравнение вращения шкива // и его угловое
ускорение
d<fn
,, = о)., == it — 0,lit?,
dt и
VII	t
[Т//= f (it —0,1 itf )<**•, ?„ = «* — 0,05it^,
= 0,1 it сек-2.
0
dt
— 0,
lit
Определяем требуемые условием величины. Угол поворота шкива //
в момент остановки при ?=10 сек
ш„ =те- 10 — 0.05те. 102 = 5тт;
'0
соответствующее число оборотов за 10 сек
NH = 1йГ = 1тТ = 2l5 o6°Pomoe
Определив модули угловой скорости, вращательной скорости цен-
17*	259

тростремительного и вращательного ускорений точки М при t = 5 сек
(рис. 238<Г) находим по формулам (92.1). (92.2) и (92.3):
mUs = к — 0,1ж • 5 = 0,5тс сек~1,
vB = Ru>n5 — 20 ¦0,5ir=10it = 31,4 см/сек,
w« — Riojh = 20 @,5icJ = 5ic2 = 49,3 cMJceK2,
wB = Re{1 = 20 • 0, lie = 2* = 6,3 см/сек2.
Модуль вращательного ускорения при любом значении / постоянен.
Направление чяв .при замедленном вращении противоположно напра-
направлению V.
Пример 61. Редуктор скоростей, изображенный на рис. 239, а, б,
обеспечивает вращение валов / и //, имеющих общую геометрическую
Рис. 239.
ось, с различными угловыми скоростями. Определить угловую скорость
вала //, соответствующую угловой скорости вала / п{ = 800 об/мин,
если числа зубьев шестерен соответственно равны: z1=12, 22 = 60,
23 = 20, 24 = 80.
Решение. Передаточное число редуктора равно отношению
угловой скорости ведущего вала к угловой скорости ведомого, т. е.
"п
— I.
При этом угловые скорости ведущего и ведомого валов равны угло-
угловым скоростям жестко соединенных с ними шестерен, т. е.
260

Для получения зависимости между угловыми скоростями шесте-
шестерен 1 л 4 следует определить передаточное число передачи, состоя-
состоящей из двух пар колес (рис. 239, б"):
t — l .1 -Zl I±.— m 80-20
Пользуясь угловыми скоростями, выраженными в об/мин, будем
иметь:
-^ = *
пп '
откуда
п. 800
пП = -f- = -w = 40 об/мин.
Вопросы для самоконтроля
1.	Перечислите основные виды движений твердого тела.
2.	Какое движение твердого тела называется поступательным и какими
свойствами оно обладает?
3.	Какое движение твердого тела называется вращением вокруг непо-
неподвижной оси и как оно осуществляется?
4.	По каким формулам определяются модули угловой скорости и угло-
углового ускорения вращающегося твердого тела?
5.	Как направлены векторы угловой скорости и углового ускорения при
вращении тела вокруг неподвижной оси?
6.	Выведите формулы модулей скорости и ускорения точек твердого
тела, вращающегося вокруг неподвижной оси.
7.	При каких условиях ускорение точки вращающегося тела составляет
с отрезком, соединяющим точку с центром описываемой ею окружности,
углы 0, 45°, 90°?
8.	Ускорения каких точек вращающегося тела:
а)	равны по модулю,
б)	совпадают по направлению,
в)	равны по модулю и совпадают по направлению?
9.	Каковы -векторные выражения вращательной скорости, вращатель-
вращательного и центростремительного ускорений?
10. Выведите формулы Эйлера для проекций вращательной скорости
точки на координатные оси.
11. Что представляет собой передаточное число передачи и как опре-
определяется передаточное число сложной передачи?
ГЛАВА XV
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 97. Свойства плоского движения твердого тела.
Движение плоской фигуры в ее плоскости
Плоским ала плоско-параллельным движением твердого тела
называется такое движение, при котором каждая точка тела
движется в плоскости, параллельной некоторой неподвижной
плоскости.
261

Плоская фигура, образованная сечением тела этой неподвижной
плоскостью Q, во все время движения остается в этой плоскости
(рис. 240).
Рассмотрим движение точек тела, расположенных на одном перпенди-
перпендикуляре к неподвижной плоскости Q. Точка Мг движется в плоскости Qv
а точка М2 — в плоскости Q2;
обе плоскости параллельны не-
неподвижной плоскости Q.
При движении тела отре-
отрезок МгМ2 остается перпенди-
перпендикулярным к плоскости Q, т. е.
остается параллельным своему
начальному положению. Это
значит, что все точки этого
перпендикуляра аналогично точ-
кам тела, движущегося посту-
поступательно, описывают тождест-
тождественные и параллельные между
собой траектории и в каждый
момент времени имеют геоме-
Рис 240.	трически равные скорости и
ускорения, т. е. траектории
AtBv А2В2, АВ точек тела Mv M2, M тождественны и параллельны,
их скорости равны v1 = v2 = v и ускорения также равны wx = w2 = w.
Таким образом, движение каждой точки плоской фигуры в непо-
неподвижной плоскости Q определяет собой движение всех точек твердого
тела, расположенных на перпендикуляре к плоскости Q, восстановлен-
восстановленном в этой точке. Это позволяет свести изучение плоского движения
твердого тела к изучению движения плоской фигуры в ее плоскости.
Так как положение плоской фигуры на плоскости вполне опре-
определяется положением двух ее точек или положением отрезка, соединя-
соединяющего две точки этой фигуры (рис. 241), то движение плоской
Рис. 241.
фигуры в ее плоскости можно изучать как движение прямолинейного
отрезка в этой плоскости.
Будем считать, что движение плоской фигуры происходит в пло-
плоскости рисунка и, следовательно, рисунок является натуральным
изображением фигуры.
262

§ 98. Разложение движения плоской фигуры
на поступательное движение вместе с полюсом
и вращение вокруг полюса. Уравнения
движения плоской фигуры
Предположим, что плоская фигура переместилась на плоскости
из положения / в положение // (рис. 242). Отметим два положения
отрезка АВ, принадлежащего фигуре.
Покажем, что перемещение фигуры можно осуществить совокуп-
совокупностью двух перемещений: поступательного перемещения и поворота.
Первый вариант. Переместим фигуру поступательно, из поло-
положения АВ в положение АХВ'', т. е. так, чтобы точка А переместилась
в новое положение Ах, а точка В
описала траекторию, тождествен-
тождественную траектории точки А. Затем
повернем фигуру вокруг точки Аг
на угол cpj так, чтобы точка В'
заняла тоже свое положение Bv
Второй вариант. Переме-
Переместим фигуру поступательно из по-
положения АВ в положение A'BV
а затем повернем ее вокруг точ-
точки Вх на угол <р2 так, чтобы точ-	Рис. 242.
ка А' совпала с точкой Ах.
Вариантов перемещений может быть столько, сколько точек пло-
плоской фигуры, т. е. бесчисленное множество.
Как видно, поступательное перемещение плоской фигуры различно
в различных вариантах, а величина угла поворота и направление
поворота одинаковы, т. е.
<Pl = ?2-	(98-1)
Из этого следует, что всякое непоступательное перемещение
плоской фигуры в ее плоскости можно рассматривать как со-
совокупность двух перемещений: поступательного перемещения
плоской фигуры вместе с произвольной точкой, называемой по-
полюсом, и поворота вокруг полюса.
При этом поступательное перемещение зависит
от выбора полюса, а величина угла поворота и на-
направление поворота от выбора полюса не зависят.
Из вышеизложенного следует, что действительное движение пло-
плоской фигуры в ее плоскости в каждый момент времени можно рас-
рассматривать как совокупность поступательного движения и вращения.
Поступательная часть движения фигуры зависит от выбора полюса
и определяется его движением.
Приняв за полюс некоторую точку О и обозначив х0, у0 ее коор-
координаты в неподвижной системе хОу (рис. 243), можно определить
движение полюса О, а следовательно, и поступательное движение
всей фигуры уравнениями xo — fl(t) и уо = /2@-
263

Для получения угла, характеризующего вращательную часть дви-
движения плоской фигуры, проведем через полюс О две полупрямые Оа
и Ob, из которых Оа не принадлежит плоской фигуре и движется
поступательно- вместе с полюсом О, а ОЬ принадлежит этой фигуре
и вместе с ней вращается вокруг полюса О.
X
Рис. 243.
Обозначив 1_аОЬ=-у, можно определить вращательное движение
фигуры уравнением вращения ср = /3(?)- Таким образом, движение
плоской фигуры в ее плоскости, а следовательно, и движение всего
тела определяется тремя уравнениями, называемыми уравнениями
плоского движения твердого тела:
х0 = /х (t),
(98.2)
Покажем, что вид уравнения ср = /3(/) не зависит от выбора полюса.
Рассмотрим плоскую фигуру, движущуюся в плоскости чертежа
(рис. 244). Возьмем за полюсы точки Ог и О2 этой фигуры, описы-
описывающие при ее движении траектории А1В1 и А2В2 и укажем соответ-
соответствующие им углы поворота плоской фигуры <рх и ср2. Для этого
проведем в точках Ог и О2 две параллельные между собой полу-
полупрямые Огау и О2а2, которые предположим движущимися поступа-
поступательно вместе с полюсами, т. е. остающимися параллельными между
собой во все время движения.
Проведем также на плоской фигуре две параллельные между
собою полупрямые Oxb± и О2Ь2, которые, очевидно, в любом поло-
положении этой фигуры останутся параллельными. Тогда угол <рх между
полупрямыми Охйх и Ох&! и угол ср2 между полупрямыми О2а2 и
во все время движения будут равны между собой, т. е.
ср1==ср2
или
264

Это равенство показывает, что вид уравнения, определяющего враща-
вращательную часть движения плоской фигуры, не зависит от выбора полюса.
Рис. 244.
Рис 245.
Обозначая алгебраические величины угловых скоростей и угло-
угловых ускорений плоской фигуры в ее вращении вокруг полюсов Ох и О2
соответственно wv ег и со2, s2, имеем:
~ 	 d?i 	 d<?t 	~
1 dt dt ~Ш2'
~W
е,.
Эти равенства показывают, что
угловая скорость и угловое ускоре-
ускорение плоской фигуры в ее вращении
вокруг произвольно выбранного по-
полюса также не зависят от выбора
полюса. Следовательно, угловая ско-
скорость (й и угловое ускорение е явля-
являются общими для всех полюсов и
называются угловой скоростью и
угловым ускорением плоской фи-
фигуры. Они определяются по следую-
следующим формулам:
rfcp
~df
(98.3)
(й = -
3
Рис. 246.
dt ~~ dt* '
Векторы о) и s, согласно § 91, направлены по оси, проходящей
через полюс, перпендикулярно плоскости фигуры.
265

Если направления whs совпадают, то вращение плоской фигуры
происходит ускоренно (рис. 245, а), а если они противоположны, то
замедленно (рис. 246, а).
Так как векторы о> и е перпендикулярны к плоскости чертежа,
то направления угловой скорости и углового ускорения плоской фи-
фигуры условимся обозначать так, как показано на рис. 245, б и
246, б, используя эти обозначения для указания направления враще-
вращения плоской фигуры (й>) и направления е.
§ 99. Теорема о скоростях точек плоской фигуры
и ее следствия
Зависимость между скоростями точек плоской фигуры устанавли-
устанавливается по следующей теореме:
Скорость любой точки плоской фигуры равна геометриче-
геометрической сумме скорости полюса и вращательной скорости этой,
точки вокруг полюса.
Точку О, скорость которой равна v0, примем за полюс. Опреде-
Определим скорость любой другой точки плоской фигуры, например,
точки А (рис. 247). Для этого проведем из неподвижной точки пло-
плоскости Ох в точки О и Л радиусы-векторы р0 и рА. Проведем также
радиус-вектор т0А из полюса О в точку Л.
Так как этот радиус-вектор соединяет две точки плоской фигуры,
то за все время движения он вращается вокруг полюса с угловой
V0A^	^	скоростью плоской фигуры о», не изменяясь
по модулю.
-^ /^~- у-*» v-^ За все время движения между радиуса-
* ><1 УЧ\ \ ми-векторами сохраняется зависимость
где
r0A = const.
Определим отсюда скорость точки А:
v - dPA _ d?O ¦ dTOA
v
V^— dt ~ dt ~*~ dt '
Рис. 247.	d
где -^- = \0 — скорость полюса О.
Так как при движении плоской фигуры модуль радиуса-вектора год
остается неизменным, а направление его при повороте фигуры изме-
dr,..
няется, то производная " представляет собой вращательную ско-
скорость точки А вокруг полюса О, которую обозначим \0А:
Согласно § 94, вращательную скорость v0A можно представить
в виде векторного произведения вектора угловой скорости плоской
266

фигуры 0) на радиус-вектор г0А:
Вращательная скорость \0А направлена перпендикулярно от-
отрезку ОАу. в сторону вращения фигуры, и имеет модуль
v0A = О А • (в.
После подстановки получаем
vA = v0 + v0A	(99.1)
или
vA = v0 + «Xr0A.	(99.2)
Скорость точки А изображается диагональю параллелограмма,
построенного при точке А на скорости полюса О, перенесенной
в точку А, и вращательной скорости точки А вокруг полюса О
(рис. 247).
Следствие 1. Проекции скоростей точек плоской фигуры на
ось, проходящую через эти точки, равны.
Положим, что в данный момент времени известна скорость v^
точки А плоской фигуры, направление ее вращения и модуль угло-
угловой скорости фигуры ш (рис. 248). Приняв точку А за полюс, оп-
Рис. 248.
ределим скорости точек В и D плоской фигуры, лежащих на одной
прямой с точкой А:
причем вращательные скорости этих точек вокруг полюса А:
\АВ = ЬХВХ и vAD = dlDl направлены перпендикулярно отрезкам АВ
и AD в сторону вращения фигуры.
Проведем ось д; через точки A, D и В и спроектируем скорости
этих точек на ось х; тогда получим
vDx = '
JABX<
UADX>
267

но vABX = 0 и vADX — 0, так как векторы vAB и vAD перпендику-
перпендикулярны оси х.
Поэтому
vdx~vax>
или
т. е. проекции скоростей всех точек отрезка АВ на ось х, напра-
направленную вдоль этого отрезка, равны по величине.
Следствие 2. Концы скоростей точек неизменяемого отрезка
лежат на одной прямой и делят эту прямую на части, про-
пропорциональные расстояниям между соответствующими точ~
нами отрезка.
Рассматривая рис. 248, устанавливаем, что
blBl = vAB — АВ • ш; dxDx = vAD = AD • ы,
откуда
d,D, AD
АВ "
Так как Axdx = AD и Axbx = АВ как противоположные стороны
параллелограммов, то имеем
d,D, _ A,d,
Это соотношение показывает, что AXDXBX — отрезок прямой. Из
подобия треугольников AxdxDx и АХЬХВХ имеем
Л,?>, _ Axdx	A{D, _ AD AtDt _ AD
Л,В, ~ Л,6,	AiBi ~~ АВ И D,B{ — DB '
т. е. расстояния между концами скоростей пропорциональны рас-
расстояниям между соответствующими точками.
§ 100. Примеры на применение теоремы о скоростях точек
плоской фигуры
При решении примеров с помощью теоремы о скоростях точек пло-
плоской фигуры используют следствия этой теоремы. Обычно в таких
случаях применяют графический метод, который требует построения
схем в масштабе длин, а скоростей — в масштабе скоростей в их
истинном направлении.
Пример 62. По заданной скорости одной точки плоской фигуры
построить годограф возможных скоростей другой точки этой фигуры.
Решение. Пусть известна скорость точки А, требуется опре-
определить возможные скорости точки В плоской фигуры (рис. 249). Про-
268

ведем через точки А и В ось х и найдем проекцию Аа скоро-
скорости Уд на эту ось. По первому следствию теоремы о скоростях
точек плоской фигуры проекции скоростей точек Л и В на эту ось
равны. Отложим по оси х от точки В проекцию ВЬ, равную по
величине проекции Аа и совпадающую с ней по направлению.
В точке b восставим перпендикуляр к оси х. Только на этой
прямой и может находиться конец скорости vfl точки В. Эта пря-
прямая является годографом возмож-
возможных скоростей точки В.
Пример 63. Зная скорости
ползунов А и В, определить ско-
скорость шарнира С механизма, изо-
изображенного на рис. 250 а, в ука-
указанном положении.
Решение. Так как шарнир С
соединяет стержни АС и ВС
механизма, то точка С одновре-
одновременно принадлежит каждому из	рис< 249.
этих стержней. Поэтому проек-
проекция неизвестной скорости шарнира С на ось стержня АС равна
проекции скорости ползуна А на эту ось и имеет такое же напра-
Рис. 2506.
вление, а проекция скорости шарнира С на ось стержня ВС равна
проекции скорости шарнира В на эту же ось (рис. 2506).
269

Находим проекцию Аа скорости v^ на ось АС и откладываем
по этой оси из точки С отрезок Ссх = Аа. Аналогично находим
проекцию ВЬ и откладываем отрезок Сс2 = ВЬ. Затем восставляем
в точках сх и с2 перпендикуляры к направлениям этих осей.
Точка К пересечения этих перпендикуляров определит собой конец
скорости шарнира С, т. е. \С — СК-
Пример 64. Зная модуль и направление скорости vA одного
конца отрезка и прямую, по которой направлена скорость vs дру-
другого конца, определить модуль скорости vB, а также модуль
и направление скорости
w
/
/
/
Рис. 251а.
середины отрезка С
(рис. 251а).
Решение. Находим
проекцию Аа заданной
скорости уд на ось. на-
правленную по АВ
(рис. 2516). Откладываем
по этой оси от точки В
проекцию ВЬ = Аа иско-
искомой скорости vB и в точ-
ке b восставляем перпен-
дикуляр к АВ. Точка Вх
пересечения этого пер-
перпендикуляра с прямой, по
которой направлена ско-
скорость vB, является кон-
концом скорости точки В.
Отрезок ВВХ геоме-
геометрически равен скоро-
'8 сти Уд.
Согласно второму
следствию теоремы о ско-
скоростях точек плоской фи-
фигуры соединяем концы известных скоростей vA и vB и делим отре-
отрезок А1В1 пополам. Соединяя середину отрезка АВ с серединой от-
отрезка АХВХ, получаем отрезок ССХ, геометрически равный скорости vc
середины отрезка С.
Таким образом, для определения скоростей всех точек отрезка
необходимо знать модуль и направление скорости одной его точки
и прямую, по .которой направлена скорость другой точки.
Пример 66. Зная скорости концов неизменяемого отрезка, опре-
определить скорость любой точки этого отрезка.
Решение. Соединяя концы заданных скоростей vA и \в концов
Л и В отрезка АВ, получаем отрезок АХВТ—геометрическое место
концов скоростей точек этого отрезка (рис. 252а и б). Находим
проекцию скорости какого-либо конца, например Av на направление
отрезка АВ, т. е. Аа,
270

Для графического определения скорости какой-либо точки от-
отрезка, например D, откладываем от точки D вдоль отрезка АВ
проекцию скорости этой точки Dd = Aa.
?,.
Л,
fi,
Рис 2526.
Рис. 253.
В точке d восставляем перпендикуляр к направлению отрезка
АВ, который продолжаем до пересечения с отрезком AiB1 в точке Dy
Соединяя точки D и Dv получаем отрезок DDV геометрически рав-
равный искомой скорости точки ?>. т. е. DDX = vD. Скорость любой
271

другой точки отрезка, например, точки Е, определяем аналогичным
построением.
Пример 66. Зная скорости концов отрезка, определить точку
этого отрезка, скорость которой в данный момент времени напра-
направлена вдоль этого отрезка (рис. 253).
Решение. Соединяя концы заданных скоростей точек А и В
отрезка АВ, получаем отрезок А1В1 — геометрическое место концов
скоростей точек этого отрезка.
Конец D, скорости искомой точки D, направленной вдоль АВ,
должен быть в точке d пересечения отрезка AXBX с отрезком АВ.
Начало скорости, т. е. точку D, определяем из равенства проек-
проекций скоростей: Dd = Аа — ВЬ.
§ 101. План скоростей
Зависимость между скоростями точек плоской фигуры (99.1) поз-
позволяет он1с4елять скорости точек этой фигуры простым и нагляд-
наглядным построением, называемым планом скоростей.
Доп^ыим, что нам известны скорости точек А, В, С и D пло-
плоской флгуры, изображенной на рис. 254, а. Отложим из произвольной
точки О по направлению скоростей точек А, В, С, D отрезки Оа,
Ob, Ос, Od, равные скоростям этих точек, и соединим точки а, Ь,
с, d отрезками прямых (рис. 254, б).
1С
Рис. 254.
Выполненное построение называется планом скоростей; отрезки
Оа, Ob, Ос, Od называются лучами, а точки а, Ь, с, d — вер-
вершинами плана скоростей.
Из треугольника аОЬ имеем
= Oa-{-ab
или
По формуле (99.1) имеем
(а)
(б)
272

Сопоставляя равенства (а) и (б), устанавливаем, что ab = vAB;
аналогично be = \вс; cd = vco и т. д.
Следовательно, каждый из отрезков, соединяющих вершины
плана скоростей, геометрически равен вращательной скорости
соответствующей точки фигуры вокруг другой точки как вокруг
полюса.
Поэтому имеем:
ab = АВ ¦ со и ab _]_ АВ,
be = ВС -ш и Ьс±ВС,
cd — CD-ш и cd ± CD
и т. д. Отсюда следует, что многоугольник abed подобен много-
многоугольнику ABCD и повернут относительно последнего на 90° в сто-
сторону вращения движущейся плоской фигуры.
Построение плана скоростей
Для построения плана скоростей точек плоской фигуры необхо-
необходимо знать модуль и направление скорости одной из точек этой
фигуры и прямую, по которой направлена скорость какой-либо
другой точки фигуры.
Допустим, что известны модуль и направление скорости точки А
треугольной пластинки ABC, движущейся в плоскости чертежа, и
прямая, по которой напра-
направлена скорость точки В
этой пластинки (рис. 255, а).
Требуется определить ско-
скорости точек В и С путем
построения плана скоростей.
Проведем из произволь-
произвольной точки О отрезок Оа — \А
и прямую, параллельную #	—</
прямой, по которой на-	Рис. 255.
правлена скорость vB
{рис. 255, б). Известно, что отрезки, соединяющие вершины плана
•скоростей, перпендикулярны отрезкам, соединяющим соответствую-
соответствующие точки фигуры.
Чтобы определить вершину b плана скоростей, проведем из вер-
вершины а прямую, перпендикулярную АВ; точка пересечения ее
¦с прямой, по которой направлена скорость точки В, и будет
вершиной Ь, а отрезок Ob определит скорость точки В, т. е.
Чтобы получить вершину с плана скоростей, следует провести
из вершин а и b прямые, перпендикулярные сторонам треуголь-
иика АС и ВС. Точка пересечения этих прямых будет вершиной с,
& отрезок Ос определит скорость точки С.
18 А. А Яблонский	273

Аналогичным построением можно определить скорость любой
точки плоской фигуры, соединив ее с двумя точками, скорости кото-
которых уже известны.
Рассмотрим, например, построение плана скоростей для точек А*
В, С и D механизма, изображенного на рис. 256, а.
Зная модуль и направление скорости vA точки А и прямую,
по которой направлена скорость точки В, строим план скоростей
для шатуна АВ.
Из произвольной точки О откладываем отрезок Оа, изображаю-
изображающий по модулю и направлению скорость vA. После этого проводим
6)
а
Рис. 256.
из точки О прямую ОЬ. параллельную ОХВ, а из точки а — прямую
ab, перпендикулярную АВ.
Эти прямые продолжаем до их пересечения в точке Ь, являю-
являющейся вершиной плана скоростей. Отрезок ОЬ изображает по модулю
и направлению скорость vB.
Для определения модуля и направления скорости точки С ша-
шатуна АВ делим отрезок аЪ в отношении АС: ВС, находим точку с
и проводим луч Ос, определяющий собой модуль и направление
скорости точки С.
План скоростей для стержня CD строим на основе плана скоро-
скоростей шатуна АВ. Проведем из точки О прямую Od, параллельную
прямой, по которой направлена скорость точки D, т. е. пря-
прямую, перпендикулярную O2D, а из точки с прямую ей, перпенди-
перпендикулярную CD. Эти прямые продолжаем до их пересечения в точке d,
являющейся вершиной плана скоростей.
Отрезок Od изображает по модулю и направлению скорость vD.
Лучи Оа, ОЬ, Ос, Od (рис. 256, б) определяют модули и направле-
направления скоростей всех заданных точек плоского механизма.
Остановимся на случае, когда заданная скорость точки плоской
фигуры параллельна прямой, по которой направлена скорость другой
точки этой фигуры. Для построения плана скоростей требуется
знать модуль скорости второй точки.
Например, если скорости точек А и В плоской фигуры перпен-
перпендикулярны отрезку АВ (рис. 257, а) и известен только модуль ско-
274

рости vA, то определить положение вершины Ъ плана скоростей невоз-
невозможно, так как на плане скоростей перпендикуляр к АВ сливается
с прямой, по которой, направлена скорость \в (рис. 257, б).
Необходимо знать модуль vB, чтобы, отложив Ob = \в, полу-
получить точку Ь плана скоростей.
Определение скоростей остальных точек, например С, производится
как и в предыдущих примерах: ас J_ AC, be _|_ ВС.
Рис. 257.
Пример 67. Определить путем построения плана скоростей ско-
скорости точек механизма, изображенного на рис. 258, а, в положении,
когда ср = 135°, если угловая скорость ведущего кривошипа ОХА
равна шс^л- Положение неподвижных точек Ov О2 и О3 определяется
расстояниями lv 12, /3 и 14.
Решение. Механизм, изображенный на рис. 258, а, состоит из
шарнирного четырехзвенника ОХАВО2, к шатуну которого в точке С
присоединено шарнирно звено CDE, соединяющее шатун АВ с ба-
балансиром O3D и шатуном EF. Механизм имеет три звена Oj^A, O2B
и О3?>, которые поворачиваются вокруг неподвижных центров Ov
О2 и О3, три звена АВ, CDE и EF, совершающие плоское движе-
движение, и ползунок F, движущийся поступательно. Механизм служит
для преобразования вращательного движения ведущего кривошипа
О1А в поступательное движение ползунка F. Известны траектории,
а следовательно, и прямые, по которым направлены скорости точек
А, В, D, движущихся по окружностям, а также точки F, движу-
движущейся по оси направляющих.
Изобразим механизм в выбранном масштабе и заданном положе-
положении (рис. 258, б). По заданной угловой скорости ведущего кривошипа
вычисляем скорость точки А:
Va = о>о,л ¦ О\А.
Скорость Уд перпендикулярна отрезку ОХА. Для построения
плана скоростей (рис. 258, в) выбираем масштаб скоростей и в этом
масштабе откладываем луч Оа = v^.
Для определения скорости точки В из точки О плана скоростей
проводим прямую, по которой направлена скорость vfl, перпендику-
18*	275

a-
о*

лярную 02В, а из вершины а прямую, перпендикулярную шатуну АВ.
Получаем луч Ob = \в. Для определения скорости точки С делим
отрезок ab на части:
ас АС	, АС
ac ab
Проведя из точки О в точку с луч, получаем Ос = \с.
Для звена CDE известны модуль и направление скорости vc и
прямая, по которой направлена скорость \D, перпендикулярная
O3D. Проводим из точки О прямую, перпендикулярную ОЪЬ, а из
вершины с прямую, перпендикулярную CD. Пересечение этих прямых
определяет вершину й и луч Od — vD.
Зная скорости vc и \D двух точек звена CDE, можно опреде-
определить скорость точки Е, хотя прямая, по которой направлена ско-
скорость точки Е, не известна. Вершину е плана скоростей опреде-
определяем как точку пересечения прямых, проведенных из вершин end
перпендикулярно отрезкам СЕ и DE. Проведя из точки О в вер-
вершину е луч, получаем Ое — \Е. Для звена EF известны модуль и
направление скорости \Е и прямая, по которой направлена ско-
скорость v^.
Для определения скорости точки F из точки О проводим пря-
прямую, параллельную траектории точки F, а из вершины е — прямую,
перпендикулярную шатуну EF. Пересечение этих прямых опреде-
определяет вершину / и луч O/ = vF.
Измеряя в соответствующем масштабе лучи Ob, Ос, Od, Oe~
и Of, определяем скорости точек В, С, D, Е и F, которые
изображены на рис. 258, б.
§ 102. Мгновенный центр скоростей
1. Доказательство существования мгновенного центра скоростей
Пользуясь теоремой о скоростях точек плоской фигуры, покажем,
что в каждый момент времени существует точка, неизменно связан-
связанная с плоской фигурой, скорость которой в этот момент равна
нулю. Эту точку называют мгновенным центром скоростей.
Допустим, что известна скорость некоторой точки О плоской
фигуры v0 (рис. 259) и угловая скорость фигуры ш в некоторый
момент времени. Примем точку О за полюс. Тогда скорость любой
точки фигуры будет равна геометрической сумме скорости полюса vo
и вращательной скорости точки вокруг этого полюса (99.1). Вос-
Восставим в точке О перпендикуляр к направлению скорости v0 так,
чтобы направление поворота скорости v0 к этому перпендикуляру
совпадало с направлением вращения фигуры.
Вращательные скорости всех точек этого перпендикуляра вокруг
полюса О направлены противоположно скорости полюса.
277

Найдем такую точку Р, вращательная скорость которой v0P
¦равна по модулю скорости полюса v0, т. е. vop = vo.
Так как направления этих ско-
скоростей противоположны, то имеем
Скорость точки Р:
Следовательно, точка Р в рас-
рассматриваемый момент времени
является мгновенным центром
скоростей.
Определим положение точки Р.
Вычислив вращательную скорость
точки Р вокруг полюса О и прирав-
приравняв ее скорости полюса, получим
vOp — OP • u) = v0.
откуда
Рис. 259.
Следовательно, мгновенный центр скоростей плоской фигуры на-
находится на перпендикуляре к направлению скорости полюса, на рас-
расстоянии от полюса, равном
"о
2. Определение скоростей точек плоской фигуры при помощи
мгновенного центра скоростей
Определим скорости точек А, В и К плоской фигуры (рис. 260),
приняв за полюс мгновенный центр скоростей Р. По формуле (99.1)
получим:
Но скорость точки Рв данный момент равна нулю, т. е. Vp =
Тогда скорости точек определяются по формулам:
*А — *РА'
У в = vpb-
Vat = vPjr.
т. е. скорость любой точки плоской фигуры в данный момент вре-
времени представляет собой вращательную скорость этой точки вокруг
278

мгновенного центра скоростей; поэтому
vK =
vB±PB;
т. е. скорость любой точки плоской фигуры в каждый момент
времени имеет модуль, равный произведению угловой скорости
фигуры на длину отрезка, соединяющего точку с мгновенным
центром скоростей, и направлена
перпендикулярно этому отрезку в
сторону вращения фигуры.
Найдем зависимость между скоро-
скоростями точек плоской фигуры в рассма-
рассматриваемый момент времени:
v PB f PK
——=-гПГ' —^ = -г7Т И Т. Д.,
vA PA vA PA
т. е. модули скоростей точек пло~
ской фигуры в каждый момент вре-
времени пропорциональны расстоя-
расстояниям от этих точек до мгновенного	Рис. 260.
центра скоростей.
Чтобы определить скорости точек плоской фигуры при помощи
мгновенного центра скоростей, необходимо знать положение мгно-
мгновенного центра скоростей и угловую-
скорость фигуры.
3. Различные случаи определения
положения мгновенного центра
скоростей
1. Допустим, что известны пря-
прямые, по которым направлены скорости
двух точек плоской фигуры А и В'
(рис. 261). Тогда мгновенный центр
скоростей фигуры определится как
точка пересечения перпендикуляров
к этим прямым, восставленных в точ-
точках А и В. Зная модуль скорости
точки А и определив расстояние этой
точки от мгновенного центра скоростей РА, находим угловую ско-
скорость плоской фигуры
Рис. 261.
ш~~ РА'
Модуль скорости точки В можно определить из пропорциональ-
пропорциональности скоростей точек их расстояниям от мгновенного центра

•скоростей:
откуда
PA '
РВ
или при помощи угловой скорости фигуры
vB = PB ¦ to.
Скорость любой другой точки плоской фигуры определяется ана-
аналогично.
S)
Рис. 262а, б.
2. Если скорости точек А к В плоской фи-
фигуры параллельны между собой и перпендику-
перпендикулярны АВ, то для определения положения
мгновенного центра скоростей должны быть
известны модули скоростей обеих точек А и В
(рис. 262, а, б).
Известно, что модули скоростей точек фи-
фигуры пропорциональны их расстояниям от
мгновенного центра скоростей, т. е.
PA'
Рис. 262в.
Следовательно, концы скоростей точек А к В
лежат на прямой, проходящей через мгновенный
•-центр скоростей. Пересечение этой прямой с прямой АВ определяет
мгновенный центр скоростей фигуры.
Если скорости точек А и В плоской фигуры равны, па-
параллельны между собой и перпендикулярны АВ (рис. 262в), то
280

мгновенный центр скоростей находится в бесконечности (АР = со),
а угловая скорость вращения фигуры
3. Если известно, что скорости двух точек А и В плоской фи-
фигуры параллельны и они не перпендикулярны АВ (рис. 263), то мгно-
мгновенный центр скоростей находится в бесконеч-
бесконечности (ЛР = оо). Очевидно, что и в этом случае
АР оо
Расстояния от всех точек плоской фигуры
до мгновенного центра скоростей в этом случае
равны между собой, т. е.
— ... =оо.
Поэтому скорости точек плоской фигуры в
рассматриваемый момент геометрически равны:
Рис. 263.
Следует учесть то, что при поступательном движении плоской фи-
фигуры скорости всех ее точек в каждый момент также геометрически
равны и мгновенный центр скоростей этой
фигуры находится в бесконечности.
Если условие vA = vB остается спра-
справедливым в течение некоторого промежутка
времени, а не только в отдельный момент,
то движение плоской фигуры является по-
поступательным.
Если же \д = хв только в некоторый
момент времени, то утверждать, что плоская
фигура движется поступательно, нельзя
(рис. 268г).
4. На практике часто происходит дви-
движение плоской фигуры, при котором она
катится без скольжения по некоторой не-
неподвижной кривой (рис. 264). В этом случае мгновенный центр ско-
скоростей плоской фигуры находится в точке ее соприкасания с кривой.
Действительно, при отсутствии скольжения скорость точки сопри-
соприкасания плоской фигуры по отношению, к неподвижной кривой
равна нулю, т. е. эта точка в данный момент является мгновенным
центром скоростей.
§ 103. Примеры на применение мгновенного центра скоростей
Пример 68. Колесо радиусом ^? катится без скольжения по пря-
прямому рельсу. Скорость центра колеса в рассматриваемый момент
времени vc — 2 м/сек.
Рис. 264.
281

Определить скорости точек А, В, D и Е колеса, расположенных
на концах взаимно перпендикулярных диаметров (рис. 265, а).
Решение. 1-й вариант. Примем за полюс центр колеса С
(рис. 265, б). Тогда скорость любой точки колеса будет равна гео-
геометрической сумме скорости полюса и скорости вращения этой точки
вокруг полюса (99.1). Так как колесо катится без скольжения, то
скорость точки А касания колеса с рельсом равна нулю г»А = 0.
<0 А.
Рис. 265.
Точка А является мгновенным центром скоростей. В этой точке
скорость вращения вокруг полюса vCA и скорость полюса vc равны
по модулю и противоположны по направлению, т. е.
Расстояния от точек А, В, D, Е до полюса С равны. Следова-
Следовательно, и вращательные скорости точек вокруг полюса тоже равны,
т. е.
•°св = vCD = vCE = vCA = vc.
Откладывая в каждой точке скорость полюса vc и вращательную
скорость, перпендикулярную соответствующему радиусу колеса, на-
находим:
= vc
v
= vc
= 2vc = 4
vE = y-vl -J- v%B = Yv\ -I-v% = vc
= 2 у2 =2,82 м/сек;
= 2 /2 = 2,82 м/сек.
2-й вариант. Примем мгновенный центр скоростей колеса за
полюс. Тогда скорости всех точек колеса определятся как враща-
вращательные скорости вокруг мгновенного центра скоростей. Модули
скоростей всех точек найдутся по пропорциональности скоростей их
расстояниям от мгновенного центра скоростей:
PD	п л ,
<uD = vc-ртг^=vc-2 = A м/сек.
582

Так как PB =
• = rY2, to
PB
PE
— 2,82 м\сек;
РЕ	г—
Vc—- = Vc у 2 = 2,82 м/сек.
Найденные скорости точек направлены перпендикулярно соответ-
соответствующим отрезкам в сторону вращения колеса (рис. 265, в).
Аналогичное распределение скоростей имеет место при качении
колеса без скольжения по любой поверхности.
Пример 69. Кривошип ОС вращается вокруг оси О с угловой
скоростью шос = 5 сек~1 и приводит в движение подвижную шесте-
шестеренку радиусом г2 = 8 см, насаженную свободно на его конце С.
Подвижная шестеренка катится без скольжения внутри неподвижной
Рис. 266а.
шестеренки радиусом г1 = 24 см. Определить модули и направления
скоростей точек А, В, D и Е подвижной шестеренки, если BE _|_ AD,
а также ее угловую скорость (рис. 266а).
Решение. Вторая шестеренка катится по внутренней поверх-
поверхности первой неподвижной шестеренки без скольжения и мгновенный
центр скоростей второй шестеренки находится в точке их соприка-
соприкасания. Поэтому vA = 0 (рис. 2666).
Зная угловую скорость кривошипа ОС, определим скорость,
центра второй шестеренки:
vc = ОС • шос = (г j — г2) соос = 16 • 5 = 80 см/сек.
Соединяя точки В и Е с мгновенным центром скоростей, на-
находим
Зная скорость центра второй шестеренки vc = 80 см/сек и рас-
расстояния от точек В, D и Е до мгновенного центра скоростей, опреде-
283.

ляем их скорости:
vB = vc-p? — vc Y<1 = 113,12 см[сек;
PD
vD = vc -p? = vc • 2 = 160 см\сек;
PF	r—
c? = pc^=tic/2 = 113,12 см[сек.
Найденные скорости точек направлены перпендикулярно соот-
соответствующим отрезкам РВ, PD, РЕ в сторону вращения шестеренки
вокруг ее мгновенного центра.
Скорость любой точки фигуры равна произведению угловой ско-
скорости фигуры на ее расстояние от мгновенного центра скоростей,
например,
vc = PC ¦ ш.
Отсюда определяем угловую скорость второй шестеренки:
vr vr 80
Пример 70. Две параллельные рейки движутся в противополож-
противоположные стороны с постоянными скоростями Vj и v2. Между рейками
зажат диск радиусом R, катящийся по рейкам без скольжения
{рис. 267, а). Найти угловую скорость диска и скорость его центра.
Решение. Так как диск катится по рейкам без скольжения, то
скорости точек диска Мг и М2 равны скоростям движения реек.
а)	$)
	М,			/V/
Мг
Рис. 267.
Для определения положения мгновенного центра скоростей диска
соединяем концы скоростей точек Мл и М2 (рис. 267, (У). Точка пере-
пересечения этого отрезка с диаметром диска М1М2 является мгновенным
центром скоростей диска в рассматриваемый момент.
Определим расстояние от мгновенного центра скоростей Р до центра
диска О.
Полагая ОР = х, имеем:
284

откуда
у—
Вычисляем угловую скорость диска:
i + «2
Подставляя значение /? -\- x, получаем
Скорость центра диска определяем по формуле
При v1 = v2 центр диска остается неподвижным и диск вращается
вокруг него.
Пример 71. Кривошип О А кривошипного механизма вращается
вокруг оси О с угловой скоростью ш0А. Принимая ОА = г и АВ — 1,
й
О
Рис. 268а.
7777777
Рис. 2686.
определить угловую скорость шатуна АВ и скорость ползуна В
механизма в тот момент, когда кривошип ОА составляет с осью
направляющих ползунка угол <р (рис. 268а).
Решение. Зная угловую скорость кривошипа и его длину,
определим скорость пальца кривошипа А:
A	шол = rw0A.
Скорость пальца кривошипа А направлена перпендикулярно ОА.
а скорость ползунка В — по прямой ОВ (рис. 268, <?).
285

Восставляем в точках А и В перпендикуляры к направлениям их
скоростей. Точка пересечения этих перпендикуляров определяет поло-
положение мгновенного центра скоростей шатуна РАВ-
Вычислим расстояние от точки А до мгновенного центра скоростей.
Р А-
но
— АК2 = Yl2 — г2 sin2 <p.
Подставляя значение AL, получаем
р л— V Р — г2 sln2 У
Ав	cos q>
Угловая скорость шатуна АВ
со
Для определения скорости ползуна В найдем РАВВ:
ВВ = PABL -\- LB = РАВА sin ср —|— АК = V"/2—/ sii
Тогда скорость ползуна В будет равна:
= (/^2 - г2 sin* ер tg у + г sin
F/2-/-2sln2<p/ УЛ
Скорость любой точки шатуна АВ можно определить как вра-
вращательную скорость вокруг мгновенного центра скоростей Р'лв.
Однако вычисление расстояний от точек до мгновенного центра скоро-
скоростей приводит к громоздким вычислениям.
Рис. 268в.
Поэтому в практических расчетах расстояния от точек до мгно-
мгновенного центра скоростей обычно определяют графически по чертежу
механизма, выполненному в масштабе.
При ср = О мгновенный центр скоростей шатуна совпадает с точ-
точкой В и скорости всех точек шатуна являются вращательными
вокруг точки В (рис. 268в).
286

Угловая скорость шатуна
_ A
°АВ — Та
Скорость точки В
При ср = 90° скорости пальца кривошипа Л и ползунка В парал-
параллельны, поэтому мгновенный центр скоростей шатуна АВ находится
в бесконечности (рис. 268г). В этот у
момент все точки шатуна АВ имеют
одинаковые скорости, равные \А,
а шАВ = 0.
Пример 72. Кривошип ОА вра-
вращается вокруг оси О равномерно
с угловой скоростью п = 60 об/мин
и приводит в движение шатун АВ,
соединенный жестко с колесом //.
Колесо // приводит во вращение колесо /, не соединенное
с кривошипом, но вращающееся вокруг той же оси О.
Радиусы колес: г, = 50 см, гп = 20 см.
Длина шатуна: ЛЛ=130 см.
Определить скорость ползунка В, угловую скорость шатуна АВ
и угловую скорость колеса / в моменты времени, когда кривошип
параллелен и перпендикулярен траектории ползунка В (рис. 269а).
Рис. 268г.
Рис. 269а.
Решение. Механизм имеет четыре звена, совершающих раз-
различные движения. Кривошип О А и колесо / вращаются вокруг
центра О с различными угловыми скоростями; ползунок В движется
поступательно, а шатун АВ вместе с колесом // совершают пло-
плоское движение.
а) Кривошип ОА параллелен траектории ползунка В
(рис. 269, б). Вычисляем вращательную скорость пальца кривошипа vA
287

по угловой скорости кривошипа и направляем ее перпендикулярно
к кривошипу ОА в сторону его вращения:
%П	7с60 п
шол = -до*= ~W =2*
vA = шол • О А = 2тс • 30
п CMJceK = 188,5 см/сек.
Находим мгновенный центр скоростей шатуна АВ как точку пере-
пересечения перпендикуляра к скорости ползунка В и перпендикуляра
к скорости точки А, являющегося продолжением отрезка ОА.
Рис. 269E".
Определяем расстояния от точек А, В и С до мгновенного центра
скоростей РАВ:
АВВ = г, = 50 см;
РАВА =
АВ'
— РАВВ* = У1302 — 502~= 120
-ЛС= 120 — 20 = 100 см.
Скорости всех точек шатуна являются вращательными вокруг
мгновенного центра скоростей. Скорость каждой точки равна про-
произведению угловой скорости шатуна на ее расстояние от мгновен-
мгновенного центра скоростей:
"Ол = «>ав • рлвА>
*>В = «>ЛЛ ¦ РАВВ>
VC = ШАВ • РАВС-
Определяем угловую скорость шатуна АВ по известной скорости
точки А:
v,
60™ я
= 120" = 2" сек~1'
288

Тсгда скорости точек В и С определяются:
vB = ~ ¦ 50 = 25тг с-и/сек = 78,55 см/сек;
¦ус — у • 100 = 50тг см\сек— 157,1 см\сек.
Скорость г>с является не только скоростоЮ точки С шатуна, но
и вращательной скоростью точки обода колеса /, т. е.
vc = «у,,
откуда
б) Кривошип ОА перпендикулярен траектории ползунка В
(рис. 269в).
*///;
Рис. 269в.
Перпендикуляры в точках А я В к скоростям этих точек парал-
параллельны. Следовательно, мгновенный центр скоростей шатуна нахо-
находится в бесконечности, угловая скорость шатуна равна нулю, а ско-
скорости всех точек геометрически равны:
°АВ
	 г\
vc — vB = vA = 60л см/сек =188,5 см/сек.
Угловая скорость колеса /
-50-=5* сек-
19 А. А Яблонский
289

§ 104. Теорема о центре поворота для конечного перемещения
плоской фигуры (теорема Шаля).
Мгновенный центр вращения фигуры
ЛСгновенный центр скоростей характеризует распределение ско-
скоростей точек плоской фигуры в данный момент времени.
Докажем теорему, предложенную французским геометром Шалем
A793—1880), о конечном перемещении плоской фигуры:
Плоскую фигуру можно переместить из одного положения
в любое другое положение на плоскости одним поворотом этой
фигуры вокруг некоторого неподвижного центра.
Положим, что отрезок, соединяющий точки А а В плоской фи-
фигуры, занимает на плоскости в два различных момента времени по-
положения АВ и АхВг (рис. 270). Сое-
Соединим точки А и Av В и В1 и разде-
разделим отрезки АА1 и ВВХ пополам. Из
середин этих отрезков D и Е восста-
восставим перпендикуляры к отрезкам и про-
продолжим их до пересечения в точке С.
Покажем, что эта точка неподвижной
плоскости является центром поворота
для данного конечного перемещения
плоской фигуры.
Соединяя точку С с концами отрез-
отрезков АВ и А1В1, получаем два тре-
треугольника АСВ и AjCBv Эти треуголь-
треугольники равны согласно равенству трех
сторон: А1В1 — АВ как отрезки, сое-
соединяющие две точки неизменяемой
фигуры; АХС — АС и ВуС — ВС как
расстояния от точек перпендикуляров, восставленных в серединах
отрезков до концов этих отрезков.
Из равенства треугольников следует, что
или
Отняв от обеих частей этого равенства /_ АгСВ, получим
?, АСВ — /_ АуСВ = 1_ АХСВХ — ? АгСВ
/_ АСАХ = /. ВСВ1 = ср.
где ср — абсолютная величина рассматриваемого угла.
Таким образом, перемещения двух точек фигуры, а следовательно,
и всей плоской фигуры из первого положения во второе, можно
осуществить поворотом на угол <р вокруг центра поворота С.
Очевидно, что поворот плоской фигуры вокруг найденного центра
не отображает действительного движения плоской фигуры, а лишь
290

позволяет переместить эту фигуру из первого положения во
второе.
Если перпендикуляры, восставленные в серединах отрезков ААХ
и ВВу сливаются (рис. 271), то центр поворота лежит на пересе-
пересечении продолжений отрезков АВ и АХВХ.
Рис. 271.
Рис. 272.
На рис. 272 изображено поступательное перемещение плоской
фигуры. В этом случае перпендикуляры к отрезкам ААХ и ВВг
параллельны и центр поворота находится
в бесконечности.
Каждым двум положениям плоской
фигуры на плоскости соответствует свой
центр поворота.
Покажем, что предельным положе-
положением центра поворота при стремлении
времени перемещения плоской фигуры
№ к нулю является точка неподвиж-
неподвижной плоскости, с которой в данный мо-
момент времени совпадает мгновенный
центр скоростей плоской фигуры.
Для этого рассмотрим какое-либо
перемещение точки А плоской фигуры
(рис. 273).
Отметим на траектории этой точки положения А и Av зани-
занимаемые точкой в моменты времени t и t-\-td. Соединив точки А
и Лг с центром поворота С, получим равнобедренный треуголь-
треугольник АСАХ с углом при вершине С, равным Дер. Длина хорды
ААХ = 2 AC sin-^-.
Найдем модуль скорости v' воображаемого равномерного движе-
движения точки А по хорде ААХ:
Рис. 273.
v
1С A sin Щ-
cp
19*
291

Для определения истинной скорости точки находим предел v'
I sin —-~- д
Обозначим С* предельное положение центра поворота С при
Имеем
Да
sin 2
lllTl 	г	= 1
lim -~г = ш.
Модуль скорости точки Л в момент ?
© = С*А ¦ (о.
Определим также угол, составленный скоростью v^ с отрез-
отрезком СА, и его предельное значение
L. ? — Z. ^И^1 = -g" 2~ *
При Дср->0 и С—>С* получим
4f->0	^
Этот результат показывает, что скорость v точки А, направлен-
направленная по касательной к траектории, образует с направлением С*А пря-
прямой угол.
Кроме того, модуль скорости v точки А равен:
т. е. она является вращательной скоростью этой точки вокруг
точки С*.
Из этого следует, что точка С* есть точка неподвижной плос-
плоскости, с которой в данный момент времени совпадает мгновенный
центр скоростей Р. Эту точку называют мгновенным центром
вращения фигуры.
§ 105. Неподвижная и подвижная центроиды. Теорема
о качении подвижной центроиды по неподвижной
Отметим на неподвижной плоскости положения АХВ1% А2В2,
А3В%, .., отрезка АВ, определяющего положение плоской фигуры
в моменты времени t. t-\-kt, t-\-2At, t-\-3At, ... и т. д.
(рис. 274).
292

Определим путем построения, указанного в § 104, точки непо-
неподвижной плоскости Сь С2, С3 и т. д., поворотом вокруг которых
можно переместить отрезок АВ из одного положения в другое.
Так, из первого положения во второе отрезок АВ можно пере-
переместить поворотом на угол Аф1 вокруг точки Сх, из второго поло-
положения в третье — поворотом на угол Дф2 вокруг точки С2, из третьего
положения в четвертое — поворотом на угол Дф3 вокруг точки С3 и т. д.
Соединив последовательно точки Сх, С2, С3, С4 и т. д. отрез-
отрезками, получим ломаную линию С1С2СЪСА . ..—линию центров пово-
поворота на неподвижной плоскости. Определим путем построения точки
движущейся плоской фигуры, которые при последовательных ее
поворотах совпадают с точками Сь С2, С3, ... неподвижной пло-
плоскости (на рис. 274 рассматриваемая плоская фигура с принадле-
принадлежащим ей отрезком А1В1 заштрихована).
Рис. 274
Для определения точки плоской фигуры С2, которая после пер-
первого поворота вокруг С1 совпадает с центром следующего пово-
поворота С2 неподвижной плоскости, построим отрезок C\Ci = С\Сч под
углом Дф! к отрезку СХС2, отложенным от отрезка СгС2 в напра-
направлении, обратном направлению поворота фигуры вокруг центра Cv
Для определения точки плоской фигуры С3, которая после вто-
второго поворота вокруг центра Сг совпадает с центром следующего
293

поворота С3 на неподвижной плоскости, отложим ^/, C\Cid — ?. С1С2С3
и построим отрезок С'ъСъ — СгСз под углом Д<р2 к прямой C^d,
отложенным от прямой C2d в направлении, обратном направлению
поворота фигуры вокруг центра С3.
Путем*аналогичного построения найдем точки С4, С$, ... на движу-
движущейся плоской фигуре, которые после третьего, четвертого и т. д.
поворотов совпадут с точками С4, С5, ... неподвижной плоскости.
Ломаная линия С1С2С3С4 . .. является линией центров поворота
на движущейся плоской фигуре. Эта линия, как показано на
рис. 274, неизменно связана с отрезком АВ и движется вместе
с ним. Ее вершины последовательно являются центрами поворота
при перемещениях отрезка из одного положения в другое. Движе-
Движение плоской фигуры в виде ряда последовательных поворотов этой
фигуры вокруг соответствующих центров поворота Cv С2, С3.
С4 . .. сопровождается качением линии CjdCsCi по неподвижной
линии С1С2С3С4. Так как длины линий С1С2С3С4 и CfoCsCi равны,
то это качение происходит без-
скольжения.
Предельными положениями
центров поворота Cv C2, С3, ...
Рис. 275.
р
Рис. 276.
являются мгновенные центры вращения плоской фигуры. Поэтому
в пределе ломаная линия С1С2С3СА ... обращается в кривую. Эта
кривая представляет собой геометрическое место мгновенных цент-
центров вращения на неподвижной плоскости и называется неподвиж-
неподвижной центроид ой.
Линия С1С2С3С4 также обращается в кривую, представляющую
собой геометрическое место мгновенных центров скоростей на
движущейся фигуре. Эта кривая неизменно связана с плоской фигу-
фигурой (с отрезком АВ) и движется вместе с ней. Она называется под-
подвижной центроидой.
Таким образом, при движении плоской фигуры в ее плоскости
подвижная центроида MN катится без скольжения по неподвижной
центроиде KL (рис, 275). Точка соприкасания подвижной цен-
центроиды с неподвижной центроидой является в данный момент вре-
времени мгновенным центром скоростей. Это положение представляет
собой теорему Пуансо о качении подвижной центроиды по непод-
неподвижной, которая имеет следующую формулировку:
294

При действительном движении плоской фигуры подвижная
центроида катится без скольжения по неподвижной центроиде.
Теорема Пуансо иллюстрируется качением колеса по рельсу без
скольжения (рис. 276). В этом случае мгновенный центр скоростей
находится в точке соприкасания колеса и рельса; неподвижной цен-
троидой является прямая KL, а подвижной — окружность.
Рассмотрим диск радиусом R, катящийся без скольжения между
двумя параллельными рейками, которые движутся в противополож-
противоположные стороны со скоростями у1иу2(рис. 277, а). Неподвижной цен-
троидой диска является прямая KL, параллельная рейкам и отстоя-
отстоящая от центра диска на расстоянии OP = •t>1 ~V* R (пример 70),
а подвижной центроидой является окружность такого же радиуса.
о) 	м, у,	6)
УГ2.
Рис. 277.
Заданное движение диска можно осуществить качением без сколь-
скольжения валика радиусом ОР по неподвижной горизонтальной ли-
линейке KL (рис. 277, б).
Теорию центроид можно использовать для получения эквивалент-
эквивалентного движения плоской фигуры при другом устройстве механизма,
практически более удобном.
§ 106. Уравнения неподвижной и подвижной центроид
Неподвижная центроида является геометрическим местом мгновен-
мгновенных центров вращения на неподвижной плоскости. Поэтому для
получения уравнений неподвижной центроиды в неподвижной си-
системе осей ?С\т] следует найти выражения проекций скорости
точки плоской фигуры на оси ? и -ц и приравнять их нулю
(рис. 278).
Скорость любой точки М плоской фигуры определяется выра-
выражением (99.2)	у
где v0 — скорость полюса О;
w — угловая скорость плоской фигуры;
г — радиус-вектор точки М относительно полюса О.
Проведем через полюс О систему подвижных осей х и у, не-
неизменно связанных с движущейся плоской фигурой. Обозначим
295

координаты точки М плоской фигуры в неподвижной системе осей
S и t], а в подвижной системе—х и у.
Угол, характеризующий вращательную часть движения плоской
фигуры, ^обозначим ср, а координаты полюса О в неподвижной
системе осей ?0 и ~ц0.
Проекции радиуса-вектора г на оси ? и т) соответственно равны
\ — \0 и т) — 7]0. Вектор угловой скорости вращения плоской фи-
фигуры ш перпендикулярен плоскости этой фигуры; поэтому опре-
определитель векторного произведения «Хг, выраженный через проек-
Рис. 278.
ции векторов сомножителей на неподвижные оси, имеет вид
О
О
= i, [— й G, — %)] + J, [й (| — У],
A03.1)
где iv jj, kj—орты неподвижной системы осей ?, t\. С, а &—ал!е-
браическая величина угловой скорости плоской фигуры.
Проекции скорости любой точки М плоской фигуры на непо-
неподвижные оси на основании (99.2) и A06.1) определятся так:
= vol — С7) — 'По)& = -fi- — С7) — "По)
A06.2)
Обозначив Ер и т}я, координаты мгновенного центра скоростей
в неподвижной системе осей, являющиеся в то же время коор-
координатами мгновенного центра вращения плоской фигуры, определим
проекции его скорости на оси ; и tj и приравняем их нулю;
296

На основании A06.2) получим
di0
откуда найдем
(О
1
A06 3)
J
Уравнения A06.3) являются уравнениями неподвижной центро-
центроиды в параметрической форме в неподвижной системе осей ко-
координат.
Для получения уравнений подвижной центроиды в подвижной
системе осей хОу следует найти выражение проекций скорости
точки плоской фигуры на оси х и у и приравнять их нулю.
Разложив вектор скорости полюса v0 по направлениям непо-
неподвижных осей на две составляющие vo= и vOi), представим вектор
скорости точки М в следующем виде:
v = voe+v0l)-fcoXr.	A06.4)
Так как проекции радиуса-вектора г на оси х и у соответственно
равны х и у, а вектор угловой скорости вращения плоской фигуры
перпендикулярен плоскости этой фигуры, то определитель вектор-
векторного произведения со X г, выраженный через проекции векторов
сомножителей на неподвижные оси, имеет вид
со X
О 0 ш
х у 0
A06.5)
где i, j, к — орты подвижной системы осей х, у, z.
Тогда проекции скорости точки М на подвижные оси на осно-
основании A06.4) и A06.5) определятся так:	v
i.cos 9 + von sin 9
votsin 9 + % c°s 9 +
ux, /
A06.6)
где
= "# и vc
dt
Обозначив координаты мгновенного центра скоростей в подвиж-
подвижной системе осей хр и ур, определим проекции скорости мгно-
мгновенного центра скоростей на оси х и у и приравняем их нулю:
г)о„=:0 и vp., = 0.
297

На оснований A06.6) получим:
— йур==0;
-?- sin 9 + -jf- cos <p -j- <Ьхр = 0,
откуда найдем:
-sincp
].
A06.7)
Уравнения A06.7) являются уравнениями подвижной центроиды
в параметрической форме в подвижной системе осей, неизменно
связанной с движущейся плоской фигурой.
§ 107. Примеры нахождения центроид
Пример 73. Рассмотрим центроиды линейки эллипсографа
(рис. 279).
Линейка АВ скользит своими концами по двум взаимно пер-
перпендикулярным прямым EF и KN. Мгновенный центр скоростей
этой линейки находится в точке Р
пересечения перпендикуляров, вос-
восставленных в точках А и В к на-
направлениям скоростей этих точек,
т. е. к направлениям прямых EF и KN.
Так как ОР = АВ при всех по-
положениях линейки, т. е. расстояние
от мгновенного центра скоростей да
точки О постоянно, то неподвижной
центроидой является окружность,
описанная из точки О, радиусом,
равным длине линейки.
По отношению к подвижной
плоскости точка Р всегда будет
в вершине прямого угла АРВУ
опирающегося на линейку АВ. Так
как геометрическим местом вершин прямых углов, опирающихся на
отрезок, является окружность, построенная на этом отрезке как на
диаметре, то подвижной центроидой линейки АВ является окруж-
окружность, диаметром которой является отрезок АВ.
Таким образом, радиус окружности, представляющей подвиж-
подвижную центроиду, вдвое меньше радиуса окружности, представляющей
неподвижную центроиду.
298

Центроиды линейки эллипсографа были установлены итальянским
математиком Карданом, по имени которого они называются карда-
новыми окружностями.
Следовательно, движение линейки эллипсографа можно получить
как движение диаметра круга, катящегося без скольжения внутри
другого .круга, радиус которого в два раза больше (рис. 280).
При этом точки А и В малой кардановой окружности движутся
по диаметрам большой кардановой окружности, т. е. так же, как
двигались точки линейки АВ.
Любая другая точка, лежащая на малой кардановой окружности,
например точка D, также движется по соответствующему диаметру
большой кардановой окружности. Любая точка М катящегося круга
описывает эллипс с полуосями ^	X/
а — ВМ и b = AM, а точка С
описывает окружность радиу-
радиусом ОС.
Рис. 280.
Рис. 281.
Это движение можно осуществить при помощи рукоятки ОС,
соединенной шарнирно с центром катящегося колеса.
Найдем уравнения неподвижной и подвижной центроид эллипсо-
эллипсографа. За неподвижные оси примем оси ? и -ц, по которым скользят
концы отрезка О А = 21. Приняв точку О за начало координат под-
подвижной системы, направим ось х перпендикулярно отрезку АО,
а ось у — вдоль него (рис. 281).
Уравнения неподвижной центроиды в неподвижной системе осей
имеют вид A06.3):
l
= «О
dt
dt
В рассматриваемом примере имеем:
?о = 0; тH = О A cos cp = 21 cos ср.
Tt
о—О-
dt
= — 21 sin cp ¦ ~ = — 21 sin cp • оз.
299

Подставляя эти значения в уравнения A06.3), находим:
т)р = 2/cos ср.
Исключая ср, получаем выражение
которое является уравнением окружности радиусом R = 21 с центром
в начале координат, т. е. в точке Ох. Уравнения подвижной цен-
центроиды A06.7) имеют вид
Чо-	%
Хр — -sr 	— Sin Ср	 COS
Р ш\ dt Y dt
d4 rfij
Подставляя в эти уравнения значения -~^- и - ¦, получаем:
хр — 2/ sin ср cos ср = / sin 2cp,
ур = — 21 sin2 <f = — / A — cos 2cp)
или
Исключая из этих уравнений ср, получаем
Это выражение есть уравнение окружности радиусом г =1 с цен-
центром в точке С, координаты которой
Пример 74. Найти неподвижную и подвижную центроиды
звена ВС антипараллелограмма, поставленного на менъшее звено AD,
полагая AB=DC = 2a, ВС = AD —2c и а> с (рис. 282, а).
Решение. Звено АВ вращается вокруг точки А, ско-
[~о:ть vB точки В перпендикулярна АВ. Звено DC вращается
вокруг точки D, скорость vc точки С перпендикулярна к DC
(рис. 282, б). Мгновенный центр скоростей звена ВС лежит на пере-
пересечении перпендикуляров к скоростям точек В и С, т. е. в точке Р.
Соединяя точки А и С, устанавливаем, что
Д ABC = Д ADC,
а следовательно,
l_ ABC = /_ ADC.
300

Кроме того, имеем: ?_ APD = /_ ВРС (вертикальные углы) и
AD = ВС (по условию).
Поэтому
Д APD == Д ВРС,
откуда следует, что
следовательно,
= РС и
= PB,
= 2я,	A)
= 2а.	B)
Равенство A) показывает, что сумма расстояний до мгновен-
мгновенного центра Р от двух неподвижных точек А и D есть постоян-
постоянная величина.
а)
Рис. 282.
Это означает, что неподвижной центроидой звена ВС антипарал-
антипараллелограмма является эллипс с фокусами в точках А и D, с большой
полуосью а и малой Ъ = У а2 — с2.
Сумма расстояний до мгновенного центра скоростей от двух точек
плоской фигуры (звена ВС), как видно из равенства B) есть тоже
постоянная величина. Поэтому подвижной центроидой является также
эллипс с полуосями той же величины и фокусами в точках В и С.
§ 108. Теорема об ускорениях точек плоской фигуры
и ее следствия
В § 98 показано, что движение плоской фигуры в ее плоскости
можно рассматривать как совокупность двух движений: поступатель-
поступательного движения фигуры вместе с полюсом и ее вращения вокруг по-
полюса.
Ускорения точек плоской фигуры определяются следующей тео-
теоремой:
301

Ускорение любой точки плоской фигуры равно геометри-
геометрической сумме ускорения полюса и ускорения этой точки во
вращательном движении вокруг полюса.
Для установления этой зависимости допустим, что известно уско-
ускорение w0 некоторой точки О плоской фигуры и алгебраические ве«
личины угловой скорости и углового ускорения плоской фигуры <о
и е, т. е. кроме модулей ш и е известны направление вращения
плоской фигуры в данный момент времени и характер ее вращения
(ускоренное вращение или замедленное).
Рис. 283.
Положим, что в данный момент времени фигура вращается
ускоренно в сторону, противоположную движению часовой стрелки
(рис. 283). Так как вращение фигуры ускоренное, то направим г
в сторону и (рис. 245).
Определим ускорение любой точки А фигуры, приняв точку О
за полюс.
Воспользуемся теоремой о скоростях точек плоской фигуры; на
основании (99.2) имеем
Ускорение точки А найдем как векторную производную по вре-
времени от скорости этой точки:
dv . dv~ . dm	,	drn.
dt '
Так как
dw
йт„
имеем
302
= wo + s X
lOA'
a) X Vqa-

Здесь е X т0А = \ч°)Д — вращательное ускорение точки А во вра-
вращении вокруг полюса О,
wXvOA = wJ^ — центростремительное ускорение точки А
во вращении вокруг полюса О.
Поэтому
.	A08.1)
Но геометрическая сумма вращательного и центростремитель-
центростремительного ускорений w^A и ш?л является полным ускорением точки А
во вращении вокруг полюса О
Ка
Окончательно получаем
wA = w0-{-w0A.	A08.2)
По формулам § 92 имеем
Ка
WOA
= ОА
+ ?
Ч
¦ S,
<)в% -
г R
i V
да"
1==ол
Е
ОJ '
• оJ;
При ускоренном вращении вращательное ускорение \у^д напра-
направлено по отношению к полюсу в сторону вращения плоской фигуры,
а при замедленном вращении — противоположно, т. е. направление wj^
по отношению к полюсу всегда соответствует направлению углового
ускорения е.
Ускорение точки А плоской фигуры определяется путем построе-
построения многоугольника ускорений. На рис. 283 построен прямоугольник,
определяющий ускорение точки Л в ее вращательном движении
вокруг полюса О:
WOA WOA < WOA'
а затем находится ускорение точки w^ как диагональ параллело-
параллелограмма ускорений, сторонами которого служат ускорение полюса w^
и ускорение точки во вращательном движении вокруг полюса w0A.
Следствие 1. Проекция ускорения любой точки плоской фи-
фигуры на ось, проведенную из произвольного полюса через эту
точку, не может быть больше проекции ускорения полюса на
ту же ось.
Если известно ускорение полюса О, ускорение точки А плоской
фигуры определяется по формуле A08.1):
303

Сложим w0, w^A и w^A по правилу многоугольника, тогда w^
будет замыкающей стороной многоугольника ускорений (рис. 284).
	к	-*—*¦- S-	Л-х
Рис. 284.
Проведем из полюса О через точку А ось х и спроектируем
все эти векторы на эту ось:
*Ч = W°x + W°Ax + W°Ax
Проекция центростремительного ускорения \у?л на ось х всегда
отрицательна, так как это ускорение направлено от точки А к по-
полюсу О, т. е. противоположно направлению оси х:
Проекция вращательного ускорения w^ на ось х равна нулю,
так как это ускорение всегда перпендикулярно оси х:
= 0.
ОА,
На этом основании находим
т. е.
В этом заключается первое следствие теоремы об ускорениях то-
точек плоской фигуры.
Примечание. Проекции ускорений на ось, направленную из по
люса, могут иметь знаки плюс и минус.
304

Из следствия вытекает, что алгебраическая величина
проекции Wа меньше "Wq . а абсолютное значение | Wa может и
превышать \wo при большой величине центростремительного уско-
ускорения Л,. Проекции ускорений точки А и полюса О на ось х
равны в том случае, если w^A= О А ¦ ш2 = 0, т. е. при ш —0.
Проведем через конец ускорения полюса w0, отложенного
в точке А, прямую, перпендикулярную оси х. Эта прямая пред-
представляет собой годограф возможных ускорений точек плоской фи-
гуры при та" — 0, т. е. при
0 и является границей, за кото-
которую не могут выходить концы возможных ускорений точки А.
Действительно, если и»ОЛ = 0, то конец ускорения wA обязательно
находится на этой прямой, а если -w^A Ф 0, то конец ускорения wA
находится с той стороны этой прямой, где расположен полюс.
Следствие 2. Концы ускорений точек неизменяемого от-
отрезка лежат на одной прямой и делят эту прямую на части,
пропорциональные рас-
расстояниям между этими
точками.
Зная ускорение шд точки
А отрезка АВ, алгебраи-
алгебраические величины угловой
скорости со и углового уско-
ускорения s, определим ускоре- ^
ние точки В отрезка, приняв А
точку А за полюс:
vab-
ы ?
Рис. 285.
Построим в точке В уско-
ускорение полюса wA (рис. 285).
Положим, что отрезок вращается ускоренно в направлении обрат-
обратном направлению движения часовой стрелки. Из конца ускорения w4
отложим ускорение wAB под углом $ = arctg-\ к отрезку Аф,
равному и параллельному отрезку АВ. Соединив точку В с кон-
концом w4B, получаем ускорение точки В.
Для определения ускорения какой-либо другой точки отрезка,
например точки D, выполним аналогичное построение.
Очевидно, что ускорение wAD составляет с отрезком Аф тот же
угол р.
Ускорения точек В и D отрезка в их вращательном движении
вокруг полюса А пропорциональны расстояниям этих точек от
полюса:
dD1 = <wAD = AD
ЬВХ = wAB = АВ
20 А. А Яблонский
305

Поэтому -To— = -та-¦ но AD = Axd и АВ = АХЪ как противополож-
противоположные стор.оны параллелограммов. Тогда
<Ш, _ Aid
bBi ~ Avb '
Таким образом, Д AxDxd со Д АХВХЬ. Из подобия треугольников
следует, что:
1) концы ускорений — точки Av Dx и Вх лежат на одной
прямой;
Л.Р, _ Atd	Л,Р, _ AD Л,Р, _ AD
г>'А~^; — ~Аф ИЛИ 'А^' — 'Ш И D1BI — ~DB •
Последнее соотношение показывает, что концы ускорений точек-
неизменяемого отрезка делят прямую, соединяющую эти концы, на
части, пропорциональные расстояниям
между соответствующими точками.
Поэтому, зная ускорения w^ и wB
концов отрезка АВ, можно определить
графически ускорение любой точки
этого отрезка.
Допустим, что требуется опреде-
определить ускорения точек D, С и Е, деля-
делящих отрезок на четыре равные части
(рис. 286). Соединяем концы ускоре-
Рис. 286.	НИЙ точек Л и В, отложенных в мас-
масштабе, отрезком прямой АХВХ и делим
этот отрезок точками Dv Cx и Ех на четыре равные части. Соеди-
Соединяя точки D и Dx, С и С,, ? и Ех, получаем ускорения этих
точек wD, wc и w?. Пользуясь масштабом, находим их модули и
по чертежу чпределяем их направления.
Пример 76. Концы бруска АВ длиной 1=1 м, движущегося
в вертикальной плоскости, скользят по горизонтальной и наклонной
плоскостям, образующим угол, равный 120°. В момент, когда ось
бруска образует с горизонталью угол <р=30°, конец В имеет ско-
скорость vB = 50 см/сек и ускорение wB = 20 см/сек2, направленные
по наклонной плоскости вверх.
Определить в этот момент скорость и ускорение конца А,.
а также угловое ускорение е бруска АВ (рис. 287, а).
Решение. Конец А бруска движется по прямой, следовательно*
его ускорение направлено по этой прямой. Таким образом, в за-
задаче известны:
1)	модуль и направление ускорения одной точки отрезка В;
2)	прямая, по которой направлено ускорение другой ег&
точки А. Кроме того, по заданной скорости точки В можно опре-
определить угловую скорость ш отрезка, найдя его мгновенный центр-
скоростей.
Находим мгновенный центр скоростей Р отрезка, восставляя
в точках А и В перпендикуляры к направлениям скоростей этих.
306

точек (рис. 287, б); получаем равносторонний треугольник АРВ, где
РА = РВ = АВ = 100 ел.
Так как РА=гРВ, то г>д = ©в = 50 см/сею.
Определим угловую скорость отрезка:
v 50
051
Точку В, ускорение которой известно, следует принять за по-
полюс, и ускорение точки А определить по формуле A08.l)i
а)
Г "ВА-
Модуль центростремительного ускорения точки А во вращении
вокруг полюса В можно вычислить, зная угловую скорость ш:
wBA =ж со2 • В А = 0,52 • 100 = 25 см/сек2.
Для вращательного ускорения w^ точки А во вращении вокруг
полюса В известна лишь прямая, по которой направлено это ускорение,
перпендикулярная ВА. Мо-
Модуль ускорения не известен,
так как не известен модуль
углового ускорения от-
отрезка е.
Для построения много-
многоугольника ускорений, опре-
определяющего АУЛ, можно вос-
воспользоваться тем, что пря-
прямая, но которой направлено
ускорение vfA, известна. От-
Отложим из точки А ускоре-
ускорение полюса wB по его на-
направлению; из его конца
отложим центростремитель-
центростремительное ускорение "WBA во вра-
вращении точки А вокруг полю-
полюса В, направленное парал-
параллельно оси стержня ВА от
\\\\\\\\\\чд\
Рис. 287.
точки А к полюсу В, а из
его конца проведем прямую,
лерпендикулярную ВА, т. е.
параллельную неизвестному
вращательному ускорению
wBBA, ДО пересечения с прямой, по которой направлено уско-
ускорение №д. Чтобы вычислить при помощи построенного многоугольника
ускорение wA, следует спроектировать левую и правую части
20*
307

векторного равенства wA = wB-f- w-f-wBBA на ось х, проходя-
проходящую через точки А к В.
Проектируя, получаем:
w . cos 30° = w „ cos 30° + oft ,,
-Д	?f	iS A
- = 20
откуда
¦шл = 49 CMJcen2.
Проектируя эти векторы на ось у, можно определить wBA и за-
затем найти угловое ускорение е бруска АВ:
— w. cos 60° = wo cos 60° — а»» ..
откуда
wba ~ {wa + ^в)cos 60° ~ D9 + 20) • 0,5 == 34,5 см/сек2.
twBA — &-BA; отсюда определяется е:
wBRA 34,5
s==	^iL —	= 0,345 сек~2.
Направление s определяется по направлению ускорения w^, при-
приложенного в точке Л, по отношению к полюсу В. В решенном
примере угловое ускорение е направлено противоположно направлению
движения часовой стрелки, т. е. в сторону вращения бруска. Следо-
Следовательно, брусок в данный момент вращается ускоренно.
§ 109. Мгновенный центр ускорений
Ускорение любой точки плоской фигуры определяется как гео-
геометрическая сумма ускорения полюса и ускорения точки во враща-
вращательном движении вокруг полюса. Покажем, что в каждый момент
времени существует точка плоской фигуры, ускорение которой в этот
момент равно нулю.
Положим, что в данный момент времени ускорение некоторой
точки О плоской фигуры равно w0, фигура вращается ускоренно
в направлении, противоположном направлению движения часовой
стрелки, а модули угловой скорости и углового ускорения плоской
фигуры равны to и s. ¦
Определим угол а:
a = arctg^j-.	A09.1)
где ? — модуль вектора е.
308

Тогда tga = -^->0. Соответствующий этому тангенсу угол-
находится в пределах от 0 до 90°. Отложим угол а от ускорения w0
по направлению углового ускорения е (в данном случае по направле-
направлению, противоположному направлению
движения часовой стрелки).
На проведенной полупрямой отло-
отложим отрезок
а»
A09.2)
Определим ускорение построенной
точки Q, приняв точку О за полюс,
по формуле A08.2):
Ускорение точки Q во вращатель- •
ном движении вокруг полюса О со-
состоит из центростремительного ускорения и вращательного, кото-
которое направлено по отношению к полюсу в сторону углового уско-
ускорения е:
рЙС
Ускорение w0Q образует с отрезком OQ угол {J, который'
определяется из следующего равенства:
«•
woq OQ'W<1 щ2
Так как углы аир лежат в пределах от 0 до 90°, то
Из этого следует, что ускорения w0Q и w0 равны по модулю,
но противоположны по направлению:
Точка Q, ускорение которой в данный момент равно нулю, назы-
называется мгновенным центром ускорений.
Таким образом, установлено, что мгновенный центр ускорений
находится на отрезке, составляющем с ускорением полюса w0 угол
?
а = arctg—, который откладывается от ускорения полюса в сто-
сторону углового ускорения е, на расстоянии от полюса, равном
309'

Если мгновенный центр ускорений принять за полюс, то ускоре-
ускорение любой точки плоской фигуры в данный момент определится как
ускорение этой точки во вращательном движении вокруг мгновен-
мгновенного центра ускорений.
Действительно, приняв за полюс мгновенный центр ускорений Q
<рис. 289), получим
Так как
то
Аналогично
wQ=0,
VQB>
Из этих соотношений следует, что
"Поэтому
I
В
_t —
A
QB
~ QA1
?fiye2
wK
WA
-feu4.
QK
--QA-
A09.3)
A09 4)
Таким образом, модули ускорений точек плоской фигуры
s каждый момент времени пропорциональны расстояниям
от этих точек до мгновенного центра ускорений, а векторы
ускорений составляют с отрезками, соединяющими эти
точки с мгновенным центром ускорений, один и тот же угол
Если угол а отсчитывать от ускорения точки к отрезку, соеди-
соединяющему ее с мгновенным центром ускорений, то направление от-
хчета угла совпадает с направлением углового ускорения е
Иначе, в каждый момент ускорения точек плоской фигуры
таковы, как будто плоская фигура совершает вращение вокруг не-
неподвижной точки — мгновенного центра ускорений Q, различным
моментам времени соответствуют различные положения мгновенного
дентра ускорений
Мгновенный центр скоростей Р и мгновенный центр ускоре-
ускорений Q являются различными точками плоской фигуры (рис 290)
Соединим точку М плоской фигуры с мгновенным центром ско-
скоростей Р и мгновенным центром ускорений Q отрезками РМ и QM,
я затем разложим ускорение точки w на составляющие: один раз на
касательное ускорение wT и нормальное ускорение wn, а другой раз
на вращательное ускорение w^ и центростремительное ускоре-
ускорение w" во вращении точки вокруг мгновенного центра ускорений Q.
310

Касательное ускорение wt и нормальное ускорение wn направлены по
касательной и главной нормали к траектории точки М, т. е. пер-
перпендикулярно отрезку РМ и вдоль
этого отрезка.
S уГ	х.	Вращательное ускорение v/qm и.
центростремительное ускорение
Рис. 289.
Рис. 290.
направлены перпендикулярно отрезку QM, соединяющему точку М
с мгновенным центром ускорений и вдоль этого отрезка.
Таким образом, Wqaj и v^qm не следует смешивать с истинными
касательным и нормальным ускорениями точки wT и wn.
§ 110. Способы определения положения мгновенного
центра ускорений
Все задачи на определение положения мгновенного центра уско-
ускорений плоской фигуры можно свести к трем указанным ниже основ-
основным случаям, каждому из которых, очевидно, соответствует ряд част-
частных случаев, зависящих от характера движения плоской фигуры.
Случай I. По условию задачи известна точка плоской
фигуры, ускорение которой в данный момент равно нулю. Эта
точка и является мгновенным центром ускорений.
Рассмотрим, например, качение без скольжения колеса по прямо-
прямолинейному рельсу с постоянной скоростью центра vc (рис. 291).
Мгновенный центр скоростей Р находится в точке соприкасания
колеса с рельсом. Поэтому
vc — PC ¦ со = /?ш,
где R — радиус колеса.
Угловая скорость вращения колеса ш = —&- = const.
311

Центр колеса движется равномерно по прямой, следовательно,
его ускорение равно нулю:
т. е. центр колеса является мгновенным центром ускорений.
Так как колесо вращается равномерно, то ускорения всех точек
колеса равны центростремительным ускорениям этих точек в их вра-
вращательном движении вокруг
мгновенного центра ускорений.
Например, ускорения точек
обода определяются:
А	В О * *
= wp =r Rio2 = ~~.
Ускорение каждой точки
колеса направлено к мгновен-
мгновенному центру ускорений.
В рассмотренном примере
наглядно видно, что мгновен-
мгновенный центр скоростей Р и мгно-
мгновенный центр ускорений Q
являются различными точками
плоской фигуры.
Мгновенный центр скоростей, не имея в данный момент скорости,
имеет ускорение wP, а мгновенный центр ускорений, не имея в дан-
данный момент ускорения, имеет скорость vc.
Случай II. Известны модуль и направление ускорения
какой-либо точки плоской фигуры, алгебраическая величина
угловой скорости со и алгебраическая величина углового уско-
ускорения е.
Пусть, например, задано ускорение точки А плоской фигуры wA.
Рассмотрим частные случаи определения положения мгновенного
¦центра ускорений, зависящие от ш и е
1. Неравномерное вращение: шфО, е=?0. В этом слу-
случае мгновенный центр ускорений находится на отрезке, составляю-
составляющем с направлением ускорения wA угол а = arctg-^-. который отло-
отложен от ускорения точки в сторону е, на расстоянии от точки Л,
равном
w.
На рис. 292 показан случай ускоренного вращения плоской фи-
фигуры, а на рис. 293—случай замедленною вращения.
Ускорение любой другой точки плоской фигуры можно опре-
определить по формулам A09.3) или A09.4). Как видно, направление
312

вращения на построение угла а не влияет и угол а всегда от-
откладывается от направления ускорения в сторону е (§ 109).
2. Равномерное вращение: ш=?0, е = 0 (также момент
обращения е в нуль при неравномерном вращении) (рис. 294).
В этом случае
га = -^ = О
a = 0,
т. е. ускорения всех точек направлены к мгновенному центру уско-
ускорений.
Рис. 292.
Рис. 293.
Рис. 294.
Расстояние от точки до мгновенного центра ускорений опре-
определяется по формуле
3. Момент обращения угловой скорости в нуль:
= 0, гфО. В этом случае
У/
a == 90°,
т. е. ускорения всех точек направлены перпен-
перпендикулярно отрезкам, соединяющим эти точки
с мгновенным центром ускорений (рис. 295).
Расстояние от точки до мгновенного центра
ускорений определяется по формуле
w.
AQ±
Рис. 295.
Угловая скорость фигуры обычно обращается в нуль при изме-
изменении направления вращения фигуры.
4. Момент обращения угловой скорости и угло-
углового ускорения в нуль при непоступательном дви-
движении w = 0, е = 0.
313

В этом случае ускорения всех точек плоской фигуры в данный
¦мо*мент геометрически равны, так как ускорение любой точки равно
ускорению полюса (рис. 296):
= wB = wD =
0
Случай III. Известны модули и направления ускорений
двух точек плоской фигуры. Допустим, что известны ускорения
-точек А и В плоской фигуры vtA и wB (рис. 297).
Примем точку А за полюс, тогда на основании A08.2)
Построим при точке В параллелограмм ускорений по заданной
.диагонали wB и одной из сторон wA Другая сторона параллело-
Рис 296
Рис 297.
грамма определит ускорение wAB во вращении точки В вокруг по-
полюса А.
Ускорение wAB составляет угол а = arcrg —%¦ с отрезком АВ, со-
соединяющим точку В с полюсом А.
Отсчитывая полученный угол а от ускорения wAB к отрезку АВ,
получаем направление е, в данном случае противоположное направле-
направлению движения часовой стрелки. Определив угол а и направление е,
отложим этот угол от ускорений точек Л и В по направлению в. Две
полученные полупрямые продолжим до пересечения в точке Q, кото-
которая и будет мгновенным центром ускорений.
Этот способ определения положения мгновенного центра ускоре-
ускорений не требует определения угла а путем вычислений. Если положе-
положение мгновенного центра ускорений по этому способу определяется
графически, то ускорения точек должны быть отложены в масштабе
по их истинным направлениям
Рассмотрим случаи, когда ускорения точек плоской фигуры парал-
параллельны. Положение мгновенного центра ускорений в этом случае
определяется на основании того, что:
314

1) модули ускорений точек пропорциональны длинам отрезков, сое-
соединяющих точки с мгновенным центром ускорений, т. е.
wB - QB •
2) ускорения точек составляют с отрезками, соединяющими точки.
с мгновенным центром ускорений, один и тот же угол (§ 109>
Рис. 298.
Рис. 299.
Рис. 300.
Рис. 301.
Рис. 302.
На рис. 298 и 299 выполнено построение для случая
0<а<90°, т. е. ш^О, е=^0.
Рис. 300 и рис. 301 соответствуют случаю а = 90°,
На рис. 302 и рис. 303 построен мгновенный центр ускорений
для случая:
<х = 0, tga = -^- = 0, е = 0, ш^0.
31S

В случае wA = wB (рис. 304) мгновенный центр ускорений нахо-
находится в бесконечности, а ускорения всех точек плоской фигуры
геометрически равны.
Рис. 303.
Действительно: игв =
Рис. 304.
но wB = wA, а потому
При АВфО; е = 0; <й =
и AQ =
	 ™А
' е2 + и4
= оо.
§111. Примеры на применение теоремы об ускорениях
точек плоской фигуры и на определение
положения мгновенного центра ускорений
Пример 76. Цилиндр радиусом г = 40 см катится по плоскости
без скольжения. Скорость и ускорение точек его оси в данный
момент:
vc — 0,4 м/сек, wc = 0,2 м/сек2.
Диск радиусом R = 50 см жестко соединен с цилиндром в сече-
сечении, где плоскость не препятствует его движению. Определить в дан-
данный момент времени ускорения концов
двух диаметров диска: параллельного
неподвижной плоскости и перпендику-
перпендикулярного к ней. Определить также по-
положение мгновенного центра ускоре-
ускорений диска (рис. 305а).
Решение. По условию данной
задачи можно определить угловую ско-
скорость а и угловое ускорение е диска.
Тогда ускорения точек Mv M2. М3,
М4 диска определятся согласно тео-
теореме об ускорениях точек плоской
фигуры (§ 108) по ускорению цент-
центра wc, угловой скорости со и угловому
ускорению 8 диска.
а) Определяем о и е. Мгновенный центр скоростей диска Р
находится в точке соприкосновения поперечного сечения цилиндра
с неподвижной плоскостью (рис. 3056).
Рис. 305а
316

Угловую скорость диска определяем согласно § 102:
vc vc 0,4
ш=~рс~ = ~г==ш
1 сек'1.
Расстояние от центра диска С до Р при движении не изменяется,
а потому по формуле (91.8) получим
rfco
dt
d
~dt
v
1 dv^
dt
Подставляя числовые значения, находим
w 0,2
=-+- = -qj = 0,5 сек.

Так как вращение диска ускоренное, то е имеет такое же на-
направление как и (о.
б) Определяем ускорения точек. Принимаем за полюс
центр диска С, ускорение которого известно, и определяем ускорение
каждой из четырех точек М по
формуле A08.2):
™м = wc -т- w^ + w'см-
Модуль вращательного ускоре-
ускорения точек М во вращении вокруг
полюса С определяется по формуле:
Рис. 3056.
= 0,5-0,5 = 0,25 м/сек2.
Модуль центростремительного
ускорения точек М во вращении
вокруг полюса С
"Ц ; == UJ • СМ = ОJ • R =
= 12-0,5 = 0,5 м/сек2.
Откладываем (рис. 3056) в каждой точке М векторы wc,
wcm' складывая одновременно векторы, направленные по одной
прямой. Вектор wc откладываем в каждой точке по его направле-
направлению; wBCM направляем перпендикулярно отрезкам СМ в сто-
сторону е, т. е. по направлению движения часовой стрелки; wi^
направляем к полюсу С.
Ускорение каждой точки определяется диагональю прямоуголь-
прямоугольника, сторонами которого являются сумма двух векторов, оказавшихся
на одной прямой, и третий вектор, перпендикулярный к ним:
w = 1/ (vd„ —(- tw'i Y* —I— tw?,2., = V @,2 —I
1 ' \ С ' CAi/ ' CM < ^ '
wcm'
= 0,74 м/сек2;
Ц2ж = уг@,2
—дасK
та«^=/@,25—O
,25J+ 0,52 = 0,67 м/сек2;
Щ2 == Oi39 л/сел:2.
JTS2» 0,50 л/сек2.
317

в) Определяем положение мгновенного центра
ускорений. Приняв точку С за полюс, находим согласно § 109
угол а и расстояние CQ:
CQ — -
0,2
: = 0,179 М.
'/////Л
V 0,5+!
Откладываем угол а от ускорения wc по направлению е, т. е.
по направлению движения часовой стрелки. На построенной полу-
полупрямой откладываем отрезок CQ и
получаем мгновенный центр ускоре-
ускорений Q (рис. 305в).
Если соединить точки Mv M2,
Мъ и М4 с точкой Q, то ускорения
этих точек составят с отрезками QM
один и тот же угол а == 26°34'.
Направление отсчета угла а от уско-
ускорения w к отрезку QM совпадает
с направлением е. Ускорения точек
пропорциональны расстояниям QM,
что видно по рис. 305в, на кото-
котором ускорения точек Mv уИ2, М3,
Мц, С отложены в масштабе по их
истинным направлениям. Определив
отрезки QM, можно было бы вычислить ускорения точек по форму-
формулам § 109, но в рассмотренном примере этот способ решения тре-
требует бдльших вычислений, чем выполненное решение.
Необходимо отметить, что при определении ускорений точек пло-
плоской фигуры пользоваться мгновенным центром ускорений целесооб-
целесообразно только в том случае, когда положение мгновенного центра
ускорений находится легко, т. е. тогда, когда его применение при-
приводит к упрощению (рис. 291), а не к усложнению вычислений.
Пример 77. Кривошип О А вращается вокруг оси О и приводит
в движение колесо //, соединенное с ним в точке А шарнирно.
Колесо // катится без скольжения внутри неподвижного колеса /.
Радиусы колес: г; = 50 см, г;/ = 20 см. Модули угловой скорости
и углового ускорения кривошипа в некоторый момент времени равны:
Рис. 305в.
и),
ОА
— 1 сек
~1
?од = 0,5 сек~2.
Определить ускорения точек Mv M2, Мг, М4 колеса II в этот
момент (рис. 306а).
318

Решение. Так как заданы шол и г0А кривошипа, то можно
определить скорость и ускорение точки А и при нахождении уско-
ускорений точек Mv Мг> Мя, Ж4 принять точку А колеса // за полюс.
Рис. 306а.
Рис. 3066.
а) Определение скорости и ускорения точки А и
угловой скорости и углового ускорения колеса П.
Точка А движется ускоренно по окружности с центром О и радиу-
радиусом г, — гц. Модуль ее вращательной скорости
vA — щол (г, — гп) — 1 • 30 = 30 см/сек;
ее ускорение (рис. 3066)
wa = woa (ri — rii) = I2 • 30 = 30 см/сек2.
Зная, что мгновенный центр скоростей колеса // находится в точке
М2 (АР = АМ2), определяем его угловую скорость в рассматриваемый
момент времени:
А 	 О А
-г
II'	 1 С fan.
	 nj\— —~" А , v С с/V
Получаем формулу для вычисления еи, пользуясь формулой (91.8):
*//=
ап
dt
d
Ж
ги
г, —г
II
da)
ОА
dt
г, —г
II
41
Модуль углового ускорения колеса // в рассматриваемый мо-
момент времени
г. — г..	т
г-2
Г1 ~ ГП
п
воа
= 0-75 сек
Направление ги совпадает с направлением <з>и, так как вращение
ускоренное.
319

б) Определение ускорений точек /ИР М2, Mv М4.
Согласно A08.1), приняв точку А за полюс, получим
Здесь ускорение полюса имеет две следующие составляющие:
Тогда ускорение точек М
W = WB —г- \УЦ -4- WB -4— Wa
Определим вращательное и центростремительное ускорения
точек М во вращении вокруг полюса А:
= 0,75-20=15 см/сек2;
AM // //
= 1,52. 20 = 45 CMJcetc2.
Откладываем в каждой из то-
точек Mv M2, Мг, М4 все состав-
составляющие ускорения (рис. ЗОбв).
В каждой точке прежде всего от-
откладываем составляющие ускоре-
ускорения полюса wA и w^.
Вращательные ускорения viBAM
точек во вращении вокруг полю-
полюса А направляем перпендикулярно
радиусам AM в сторону угло-
углового ускорения ея.
Центростремительные ускорения м/АМ точек во вращении вокруг
полюса направляем к полюсу А.
Ускорения точек Mv УЙ3> М4 определяем как диагонали прямо-
прямоугольников:
Рис. ЗОбв.
= /C0+15J +A5+ 45J = 75 CMjceKit

/C0 — 15J+ D5 — 15J = 33,5 см/сек2;
w
AMf
= /A5+ 15J + D5 — 30J = 33,5 см/сек2;
Так как в точке М2 w^M = — wA, то сумма этих векторов
равна нулю:
w2 = wА + wAM — 30 + 45 = 75 CMJceK2.
320

6)
Пример 78. Модули ускорений точек А и В — концов отрезка АВ
в данный момент времени равны w f~w в-=-\^> см/сек2, а их направле-
направления указаны на рис. 307, а. Определить положение мгновенного
центра ускорений, а также модули угловой скорости ш и углового
ускорения s отрезка, если aj
длина отрезка АВ = 20 см.
Решение. Построим
мгновенный центр ускорений а шл
согласно случаю III (§ ПО), с
приняв за полюс точку А.
Построив при точке В па-
параллелограмм, соответствую-
соответствующий равенству wB = wj4-}-w/t5,
определим его углы (рис. 307, б).
Так как wB = wA, то парал-
параллелограмм состоит из двух
равносторонних треугольников. ,
Известно, что угол а отсчи- /
тывается от ускорения «гдв X
в направлении к отрезку АВ. / о\
В рассматриваемом примере а
а = 60° и откладывается в на-
направлении, обратном направле- ^
нию движения часовой стрелки.
Откладывая по этому же
направлению углы а = 60° от л,
ускорений vA и wB, получаем "¦;
мгновенный центр ускорений
отрезка Q в вершине равно-
/ \
щ,
Рис- 307.
стороннего треугольника ABQ. Чтобы найти т и е, разложим уско-
ускорение \удв во вращении точки В вокруг полюса А на вращательное
и центростремительное ускорения (рис. 307, в):
где
wab = AB-z; wAB = АВ • <о2.
Из прямоугольника ускорений находим:
= 8,66 см/сек2;
wAB = tmAB cos 60° = 10 • -и- = 5 см/сек2.
Определим <о и е:
wAB 8,66
= -x5- = -ojr = (J,4d сек
5I
АВ
20
—— \Jt*J LC/v ¦
21 К А. Яблонский
321

777777Z
Направление углового- ускорения в совпадает с направлением
углал, направление ш определить невозможно.
Пример 79. Кривошип ОА нецентрального кривошипно-шатунного
механизма, изображенного на рис. 308, а, вращается с постоянной
угловой скоростью <Д=Ю сек~1.
Определить ускорения пальца кри-
кривошипа А, ползунка В, середины С
шатуна и угловое ускорение ша-
шатуна АВ в тот момент, когда кри-
кривошип ОА перпендикулярен траек-
траектории движения ползунка, если
ОЛ=25 см. OD=5cm, АВ=Ь0 см
(рис. 308, а).
Решение. Кривошип О А вра-
вращается равномерно с угловой ско-
скоростью шод=10 сек~1, а потому
(рис. 308, б, в):
vA=OA ¦ шод=25 • 10=250 см/сек2;
w. = ?сн = О А • wl . =
= 25- 100 = 2500 см/сек2.
В заданном положении механизма
мгновенный центр скоростей шату-
шатуна АВ находится в бесконечности,
а потому скорости всех точек ша-
шатуна АВ в этот момент геометри-
геометрически равны (рис. 308, б): \А~
Угловая скорость шатуна АВ
равна нулю:
Ускорения точек В и С шатуна
определим при помощи мгновенного
центра ускорений шатуна QAB.
Для определения положения мгно-
мгновенного центра ускорений находим
величину угла а:
Рис. 308.
tga=-~-==оо
а =90°.
"АВ
Так как ползунок В движется по прямой, то ускорение точки В
направлено по этой прямой, а центростремительное ускорение пальца
кривошипа А направлено по АО (рис. 308, в).
Точка пересечения перпендикуляров к направлениям ускорений
точек А и В шатуна будет мгновенным центром ускорений QAB.
322

Модули ускорений точек В к С определяются из соотношений:
30
в,
w,
<?.«С
w.
= 2500 • -jjr = 1875 см/сек2;
Q'arC
25
-q—j ; wc = wA- q A = 2500 • -щ = 1562 см/сек2.
^АВ	^АВ
Модуль углового ускорения шатуна
w, 2500
Направление е указано на рис. 308, в.
§ 112. Определение ускорений точек и угловых ускорений
звеньев плоского механизма
Для определения ускорений точек и угловых ускорений звеньев
плоского механизма применяется теорема об ускорениях точек плоской
фигуры и ее следствия. Имеются два основных случая определения
План
Скоростей
а
Рис. 309а, б.
ускорения точки звена механизма по ускорению другой точки этого
звена, принимаемой за полюс.
Случай I. Пусть, например, требуется найти ускорение пол-
ползунка В кривошипно-шатунного механизма и угловое ускорение ша-
шатуна АВ этого механизма (рис. 309, а), если известно, что кривошип О А
вращается равномерно с угловой скоростью ш в направлении, про-
противоположном направлению движения часовой стрелки.
Для решения этой задачи используются следующие данные:
1) модуль и направление ускорения W^ пальца кривошипа А
w. = w\ = О А • ш2;
21*
323

2)	прямая, по которой направлено ускорение ползунка В, дви-
движущегося прямолинейно;
3)	угловая скорость <*>АВ шатуна АВ, которую легко определить
по плану скоростей или применением мгновенного центра скоростей.
Зная скорость пальца А кривошипа vA, модуль которой равен
vA = О А ¦ ш,
определим скорость vB ползунка В по плану скоростей или при по-
помощи мгновенного центра скоростей. После этого вычислим модуль
угловой скорости шатуна АВ:
ab	v. О А ¦ (о
Приняв точку А шатуна за полюс, определим ускорение точки В
по формуле A08.1):
Центростремительное ускорение точки В, в ее вращательном дви-
движении вокруг лолюса А, направлено по оси шатуна от точки В
к точке А, а его модуль равен
да" = АВ*-ш2
АВ	АВ
или
Отложив в точке В в соответствующем масштабе ускорение по-
полюса \/А и приложив к его концу центростремительное ускорение
точки' В во вращательном движении вокруг полюса А, направленное
параллельно ВА от В к А, проведем из конца w^B прямую, перпен-
перпендикулярную ВА, т. е. прямую, параллельную вращательному уско-
ускорению w^B.
Точка пересечения этой прямой с прямой, по которой направлено
ускорение ползунка В, определит недостающую вершину многоуголь-
многоугольника ускорений. Это позволит определить графически модули
ускорений wB и 1®ВАВ-
Так как wAB = АВ • едд, то, определив wAB, найдем модуль угло-
углового ускорения звена АВ по формуле:
WAB
*АВ— АВ ¦
Если отложить найденное ускорение v/BAB из точки В, то его на-
направление по отношению к полюсу А укажет направление углового
ускорения шатуна гАВ. На рис. 309, а направления гАВ и iaAB противо-
противоположны, т. е. шатун в данный момент вращается замедленно. Зная
ускорения концов шатуна АВ (рир. 309. б), можно определить графи-
графически ускорение любой точки шатуна.
324

Так, например, для определения ускорения точки С, середины
шатуна, соединим концы ускорений точек А а В отрезком АХВХ и
разделим его пополам точкой Сх. Соединив точки С и Cv получим
ускорение середины шатуна wc.
Когда кривошип и шатун находятся на одной прямой (рис. ЗОЭв),
то мгновенный центр скоростей шатуна РАВ совпадает с точкой В.
План
скоростей
Рис. ЗОЭв.
план скоростей шатуна АВ получает вид отрезка прямой и много-
многоугольник ускорений в точке В обращается в отрезок прямой, так как
направления ускорений vtA и w^B совпадают.
В этом случае
Случай II. Пусть, например, требуется определить ускорение
точки В шатуна АВ шарнирного четырехзвенника ОХАВО2, если
известно, что кривошип ОХА вращается с постоянной угловой ско-
скоростью (о в направлении, противоположном направлению движения
часовой стрелки (рис. 310, а). В этом случае прямая, по которой на-
направлено ускорение точки В, не известна. -
Для решения этой задачи используются следующие данные:
1)	модуль и направление ускорения w^ точки А
•w . = <аЛ = О А ¦ (в2;
л А
2)	угловая скорость шАВ шатуна АВ;
3)	угловая скорость ш0 в балансира О2В;
4)	траектория точки В.
Угловые скорости шАВ и со0 в определяются по плану скоростей
или при помощи мгновенного центра скоростей. Их модули равны:
аЪ	vA О А ¦ со
^ л п === г"гГ ИЛИ О) - п == —fz ; - ~r» i~ »
"АВ —
Ob	V
325

Так как точка В одновременно принадлежит шатуну АВ и ба-
балансиру О2В, то ускорение этой точки можно определить совокуп-
совокупностью двух построений.
План
скоростей
а
Рассматривая точку В как точку шатуна АВ и принимая точку Л
за полюс, на основании A08.1) имеем:
АВ
Центростремительное ускорение точки В в ее вращательном движе-
движении вокруг полюса А направлено по оси шатуна от точки В к точке А,
а его модуль равен
или
Отложив в точке В в соответствующем масштабе ускорение по-
полюса wA и приложив к его концу центростремительное ускорение
точки В во вращательном движении вокруг полюса А, направленное
326

параллельно ВА or В к А, проводим из конца wAB прямую, перпен-
перпендикулярную ВА, т. е. прямую, параллельную вращательному уско-
ускорению w^B. Определить модули вращательного ускорения wBAB и
ускорения wB точки В из этого построения невозможно, так как на-
направление ускорения точки В не известно.
Чтобы определить ускорение точки В, выполняем дополнительное
построение, рассматривая точку В как точку балансира ОгВ, вра-
вращающегося вокруг оси О2. Тогда
Модуль центростремительного ускорения точки В в ее вращатель-
вращательном движении с балансиром Оф вокруг оси О2 равен:
w$ = O2B.wliB или «S = -§iT-
Отложив в точке В в том же масштабе центростремительное
ускорение точки В в ее вращательном движении вокруг оси О2 П0
направлению ВО2 от В к О2, проводим из конца wB прямую, пер-
перпендикулярную к О2В, т. е. прямую, параллельную вращательному
ускорению ч/д.
Точка пересечения этой прямой с прямой, проведенной из конца wAB
перпендикулярно направлению ВА, определит конец ускорения wa.
а также позволит определить w^B и wB графически.
Так как wAB—AB • едд, awB=O2B ¦ eQ в, то, определив графически
\/А и w^, находим модули угловых ускорений шатуна АВ и балан-
балансира О2В по следующим формулам:
Направления ускорения w^B по отношению к точке А и ускоре-
ускорения wB по отношению к центру О2 указывают направления гАВ
и е0 д. Ускорение середины шатуна определяется по ускорениям кон-
концов'л и В согласно § 108: если АС=СВ, то А1С1=С1В1 (рис. 310, б).
При наличии большого числа звеньев механизма последовательное
определение ускорений его точек и угловых ускорений звеньев гра-
графоаналитическим методом производится на основе двух рассмотрен-
рассмотренных случаев.
Вопросы для самоконтроля
1.	Какве движение твердого тела называется плоским?
2.	Зависят ли поступательное перемещение плоской фигуры и ее пово-
поворот от выбора полюса?
3.	Как определяется скорость любой точки плоской фигуры?
4.	Покажите, что проекции скоростей точек неизменяемого отрезка на
ось, совпадающую с этим отрезком, равны между собой.
5.	Что представляет собой отрезок, соединяющий две вершины плана
скоростей?
327

6.	Какие минимальные данные необходимы для построения плана ско-
скоростей?
7.	Какую точку плоской фигуры называют мгновенным центром скоро-
скоростей и каковы основные случаи определения его положения?
8.	Что представляет собой распределение скоростей точек плоской фи-
фигуры в данный момент?
9.	Как построить центр поворота плоской фигуры, зная ее начальное и
конечное положения?
10.	Что представляют собой неподвижная и подвижная центроиды и что
происходит с центроидами при действительном движении плоской фигуры?
И. Как определяется ускорение любой точки плоской фигуры?
12.	Почему проекция ускорения любой точки плоской фигуры на ось,
проходящую через эту точку и полюс, не может быть больше проекции
ускорения полюса на эту ось?
13.	Какую точку плоской фигуры называют мгновенным центром уско-
ускорений и может ли мгновенный центр ускорений совпадать с мгновенным
центром скоростей?
14.	Перечислите известные Вам способы определения положения мгно-
мгновенного центра ускорений.
15.	Что представляет собой картина распределения ускорений точек
плоской фигуры в данный момент времени в трех случаях:
2)
3) <й =
16. Как производят определение ускорений точек н угловых ускоре-
ускорений звеньев плоского механизма?
ГЛАВА XV/
СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 113. Эйлеровы углы. Уравнения сферического движения
твердого тела.
Рассмотрим движение твердого тела, одна из точек которого во
все время движения остается неподвижной. При таком движении все
остальные точки тела движутся по сферическим поверхностям, центры
которых совпадают с неподвижной точкой. По этой причине рас-
рассматриваемое движение тела называют сферическим движением твер-
твердого тела.
Примером сферического движения твердого тела может служить
движение волчка, имеющего неподвижную точку О (рис. 311).
Для определения положения тела в каждый номент времени вос-
воспользуемся двумя системами осей координат: неподвижной систе-
системой Oxyz с началом в неподвижной точке О и подвижной систе-
системой Oi-TjC, неизменно связанной с твердым телом, с началом в той же
неподвижной точке О.
Обозначим OJ линию пересечения неподвижной плоскости хОу
и подвижной плоскости %Of\, называемую линией узлов.
Отметим углы:
328

Угол ф лежит в плоскости хОу, перпендикулярной оси г.
Плоскость угла 6 перпендикулярна оси OJ. которая перпендику-
перпендикулярна одновременно осям z и С. Плоскость угла ср перпендику-
перпендикулярна оси С. Условимся считать углы <|), б, ср положительными в слу-
случае, если, смотря навстречу осям z, J, С, перпендикулярным
плоскостям этих углов, можно видеть эти углы отложенными от
осей х, z, J в направлении,
противоположном направ-
направлению движения часовой
стрелки.
Заданием углов ф, 9, ср
однозначно определяется по-
положение подвижной системы
осей ?, i\, С, неизменно
связанной с твердым телом,
а потому и положение са-
самого тела.
Действительно, зная углы
ф, 9, <р, положение подвиж-
подвижной системы O?,rf, получаем
следующим образом. Отло-
Отложив от оси х угол if, нахо-
находим линию узлов. Отложив
в перпендикулярной к ней
плоскости от оси z угол 9,
Рис. 311.
получаем ось С. В плоскости, проходящей через линию узлов перпен-
перпендикулярно оси С. откладываем от линии узлов OJ угол <р и на-
находим ось ?.
Ось i\ строим под прямым углом к оси ?, отложенным в сто-
сторону, противоположную движению часовой стрелки, если смотреть
навстречу оси С.
Углы ф, 6, <р называются эйлеровыми углами; угол ф — угол пре-
прецессии, угол 9 — угол нутации, угол ср — угол собственного вра-
вращения. Названия этих углов заимствованы из астрономии.
Так как положение твердого тела, имеющего одну неподвижную
точку, определяется тремя эйлеровыми углами, т. е. тремя параме-
параметрами, то оно имеет три степени свободы.
При движении твердого тела, одна из точек которого остается
неподвижной, углы ф, 9, ср непрерывно изменяются во времени,
являясь функциями времени t:
? = /»(').
Эти уравнения, однозначно определяющие сферическое движение
тела, называются уравнениями сферического движения твердого
тела.
329

§ 114. TeopejMa о перемещении твердого тела, имеющего одну
неподвижную точку. Угловая скорость тела
Положение твердого тела в пространстве определяется положе-
положением трех его точек, не лежащих на одной прямой. Действительно,
две точки определяют некоторую ось, а третья точка — положение
тела по отношению к этой оси. Следовательно, положение твердого
тела, имеющего одну неподвижную точку, можно определить поло-
положением двух его точек, не лежащих на одной прямой с неподвиж-
неподвижной точкой.
Докажем следующую теорему Эйлера — Даламбера:
Твердое тело, имеющее одну неподвижную точку, можно
переместить из одного положения в любое другое поворотом
вокруг некоторой оси, преходящей
через неподвижную точку.
Для доказательства теоремы про-
проведем сферическую поверхность с
центром в неподвижной точке О
(рис. 312).
Отметим положения двух точек тела
Ах и Вх на этой поверхности, которые
после перемещения тела займут поло-
положения А2 и В2 на той же поверхности.
Выполним на проведенной поверхности
ряд построений.
Проведем через эти точки дуги
больших кругов АХВХ и А2В2 (дуги
окружностей, полученных пересече-
пересечением сферической поверхности пло-
плоскостями, проходящими через ее центр). Тогда положение тела
в некоторый момент tx определится точками Ах и Вх. т. е. ду-
дугой АХВХ, а его положение в момент t2 той же дугой в новом по-
положении А2В2. Проведем далее дуги больших кругов АХА2 и ВХВ2.
Разделим эти дуги точками D и Е пополам и проведем из
этих точек дуги больших кругов, перпендикулярные дугам АХА2
и ВХВ2, продолжав их до их пересечения в точке С. Соединяем
точку С поверхности с ее центром О. Покажем, что тело можно
переместить из первого положения во второе поворотом вокруг этой
прямой. Соединим точку С с точками Ах, Вх, А2 и В2 дугами боль-
больших кругов АХС, ВХС, А2С, В2С. Получившиеся сферические тре-
треугольники АХСВХ и А2СВ2 равны по равенству трех сторон: АХС == А2С
и ВХС = В2С, как стороны равнобедренных сферических треуголь-
треугольников АХСА2 и ВХСВ2, а АХВХ = А2В2, как два положения одной и
той же дуги.
Из равенства этих треугольников имеем
/А2СВ2 = /тА1СВх.	(П4.1)
Рис. 312.
336

Следует отметить, что угол сферического треугольника опре-
определяется углом между касательными, проведенными в вершине угла
к дугам, образующим этот угол (рис. 313).
Прибавляя к обеим частям равенства A14 1) 1_А?В2, получаем:
?, А2СВ2 + ?_ АХСВ2 = L AlCBl
А?В2
или
а.
Этот результат показывает, что сферический отрезок А1В1 можно
переместить в положение А2В2 поворотом вокруг неподвижной оси ОС,
т. е. что перемещение тела из первого положения во второе можно
осуществить одним поворотом вокруг этой оси.
Рассмотрим малый промежуток времени t2—t1 — At, которому
соответствует поворот тела на угол Ла. Уменьшая величину про-
промежутка времени At, т. е. приближая дугу А2В2 к дуге AXBV
получим ряд положений оси ОС. Предельное положение этой оси 2
Рис. 313
Рис 314
при At->0 называется мгновенной осью вращения тела для данного
момента t (рис. 314).
Предел, к которому стремится отношение -гт-, когда At стре-
стремится к нулю, называется угловой скоростью твердого тела в момент t:
	 До
Д<-»0 Д* '
В случае сферического движения вектор угловой скорости тела
в данный момен w откладывается от неподвижной точки О по мгно-
мгновенной оси в такую сторону, чтобы, смотря навстречу этому
331

вектору, видеть вращение тела происходящим против движения часо-
часовой стрелки.
Мгновенная ось представляет собой геометрическое место
точек тела, скорости которых в данный момент равны нулю.
§ 115. Угловое ускорение тела при сферическом
движении
При сферическом движении тела положение мгновенной оси вра-
вращения со временем изменяется, а следовательно, изменяется не только
модуль, но и направление вектора угло-
угловой скорости тела.
Допустим, что моменту времени t
соответствует вектор угловой скорости <а,
а моменту t-\-ht—вектор угловой ско-
скорости A>! (рис. 315). Тогда вектор Дш
представит собой приращение вектора
угловой скорости за время Д^.
Отношение приращения вектора угло-
угловой скорости Да) к времени At опреде-
определяет вектор среднего углового ускорения:
Рис.315.	B..=4t.
Направление вектора еср совпадает с направлением До).
Предел этого отношения при Д^ —>0 называется угловым ускоре-
ускорением тела в момент t:
e=lim
Дш
"дГ
Предел отношения приращения пере-
переменного вектора к соответствующему
приращению скалярного аргумента есть
векторная производная от этого вектора:
8 =
d»
dt
A15.1)
т. е. вектор углового ускорения равен
производной от вектора угловой ско-	Рис. 316.
роста по времени.
Откладывая от неподвижной точки О векторы угловой скорости,
соответствующие ряду' последовательных моментов времени, и соеди-
соединяя концы этих векторов, получим в пределе кривую, представляю-
представляющую собой годограф вектора угловой скорости (рис. 316).
Определим скорость и движения точки А — конца вектора угло-
угловой-скорости ю — по годографу в момент времени t. Радиусом-векто-
332

ром этой точки является вектор w, а скорость точки равна произ-
производной от радиуса-вектора по времени:
и =
dto
~dt
Так как векторы ей» геометрически равны одной и той же
величине, то они равны между собой:
е = и,	A15.2)
т. е. угловое ускорение тела геометрически равно линейной
скорости конца вектора угловой скорости.
Вектор углового ускорения г, геометрически равный скорости и,
откладывается от неподвижной точки.
Прямая, по которой направлен вектор углового ускорения, назы-
называется осью углового ускорения и обозначается Е.
Правило определения направления е при вращении тела вокруг
неподвижной оси (§ 94) является частным случаем общего правила,
соответствующего сферическому движению. При вращении тела вокруг
неподвижной оси годографом угловой скорости является прямая,
совпадающая с осью вращения. При ускоренном вращении линейная
скорость и конца вектора to направлена по этой оси так же, как и
вектор о), при замедленном — противоположно о>. Направление век-
вектора е совпадает с направлением скорости и.
Рис. 317.
Я
§ 116. Скорости точек твердого тела при сферическом движении.
Проекции скорости точки тела на оси декартовых координат
Скорости точек твердого тела, совершающего сферическое дви-
движение, в каждый момент времени определяются как их вращательные
скорости при вращении вокруг мгновенной
оси 02 (рис. 317).
Мгновенная ось вращения представляет
собой геометрическое место точек тела,
скорости которых в данный момент равны
нулю. Для определения мгновенной оси до-
достаточно найти какую-либо точку С твердого
тела, скорость которой в данный момент
равна нулю. Тогда прямая, проходящая через
точку С и неподвижную точку О, будет
мгновенной осью вращения тела 2, а угловая
скорость вращения о> будет направлена вдоль
этой оси.
Зная положение мгновенной оси враще-
вращения и угловую скорость тела, можно опре-
определить скорость любой точки тела М как скорость этой точки
во вращательном движении вокруг мгновенной оси по известной
333

формуле (94.2):
где г — радиус-вектор точки, проведенный из неподвижной точки О.
Модуль скорости точки определяется:
v =
sin 7 =
где hs — расстояние точки от мгновенной оси вращения.
Таким образом, распределение скоростей точек тела в данный
момент времени t при сферическом движении по отношению к мгно-
мгновенной оси вращения не отличается от_распределения скоростей при
вращении тела вокруг неподвижной оси.
Рис. 318.
Проекции скорости точки на неподвижные оси декартовых коор-
координат определяются по формулам Эйлера (94.3):
/J?	vx = myz— wzy,
Проекции скорости на подвижные оси декар-
декартовых координат определяются по аналогичным
формулам (рис. 318):
Рис. 319.	г»с = <»^ — ш^.
Формулы для вычисления проекций угловой скорости тела на
неподвижные и подвижные оси декартовых координат по уравне-
уравнениям сферического движения твердого тела получены в § 130.
334

Если положение мгновенной оси 2 уже установлено, то для
нахождения угловой скорости w достаточно знать скорость vA какой-
либо точки А, не лежащей на мгновенной оси (рис. 319).
Тогда, опустив из этой точки перпендикуляр АК на мгновенную
ось 2, получим vA = АК • <о, откуда
-—лк
т. е. для определения модуля угловой скорости тела ш следует
модуль скорости точки vA разделить на расстояние от точки А до
мгновенной оси вращения.
Пример 80. Угловая скорость вращения тела, совершающего
сферическое движение, равна 14 сек-1, а мгновенная ось в этот
момент времени составляет с неподвижными осями декартовых коор-
координат следующие углы: а = arccos -=-; р = arccos =- ; 7 = arccos -=¦.
Для точки с координатами х:=10 см; у = 0; z = 20 см найти
модуль скорости v и ее проекции на оси vx, vy, vz, а также рас-
расстояние Ла от этой точки до мгновенной оси.
Решение. Проекции угловой скорости тела ы на неподвижные
оси равны:
= 14--|==6 сек-1;
шу = о) cos р = 14 • -=-= 12 сек'1;
2
wz = m cos y = 14 • у = 4 сек~х.
Проекции скорости точки М на неподвижные оси вычисляем
по формулам Эйлера (94.3):
vx = wyz — согу = 12 • 20 = 240 см/сек;
vy = согг — (о,.* = 4 • 10 — 6 ¦ 20 = — 80 см/сек;
vz=mxy — (оух = —12-10 = —120 см/сек.
Модуль скорости точки
v — yv*x -|_ х,2 J^JF = ]/2402 +802-]-1202 _ 280 см/сек.
Расстояние от точки М до мгновенной оси:
. v 280 ОЛ
^	2Qcm
§ 117. Аксоиды мгновенных осей
При сферическом движении твердого тела положение мгновенной
оси со временем непрерывно изменяется и процесс движения тела
можно рассматривать к*ак непрерывный ряд вращений тела вокруг
последовательно перемещающейся мгновенной оси, проходящей через
335

неподвижную точку О. Перемещаясь в неподвижном пространстве,
мгновенная ось описывает некоторую коническую поверхность с вер-
вершиной в неподвижной точке О. Коническая поверхность / с верши-
вершиной в неподвижной точке, представляющая собой геометрическое
место мгновенных осей в неподвижном про-
пространстве, называется неподвижным аксои-
дом (рис. 320).
В движущемся теле можно установить
геометрическое место тех прямых, которые
будут последовательно совпадать с мгно-
мгновенными осями вращения. Коническая по-
поверхность // с вершиной в точке О, пред-
представляющая собой геометрическое место
мгновенных осей в движущемся теле, назы-
называется подвижным аксоидом.
Подвижной и неподвижный аксоиды в любой момент времени
касаются друг друга по прямой, которая является мгновенной осью
вращения тела в этот момент.
При сферическом движении тела подвижной аксоид катится
без скольжения по неподвижному а/ссоиду. Например, при качении
конуса по неподвижной плоскости без скольжения его вершина О
остается неподвижной, следовательно, конус совершает сферическое
движение (рис. 321). Мгновенная ось совпадает с образующей 02,
Рис. 320.
Рис. 321.
по которой конус соприкасается с плоскостью, так как скорости
точек этой образующей в данный момент равны скоростям точек
плоскости, т. е. равны нулю. При движении конуса мгновенная ось
перемещается по неподвижной плоскости, т. е. эта плоскость является
неподвижным аксоидом.
С мгновенными осями последовательно совпадают все образую-
образующие конуса, например OQ[ совпадает с О2ь OQ'2 с О2г и т. д.,
т. е. боковая поверхность катящегося конуса является его подвиж-
подвижным аксоидом.
Приравнивая нулю проекции скорости точки на неподвижные и
подвижные оси декартовых координат E 116), получаем уравнения
336

мгновенной оси, отнесенные к неподвижной системе осей Oxyz и
к подвижной системе Obf-
Уравнения мгновенной оси в неподвижной системе осей:
ш.х — mxz = 0, или — = Х —-?..	(П7.1)
шх шу иг
¦*	У
Здесь л, у, z — координаты точек мгновенной оси.
Уравнения мгновенной оси в подвижной системе осей:
Ие?-«? = 0. или -L=X=JL.	(Ц7.2)
(Й?7) 	 (I) Е = 0 '
Здесь ?, Y), С — координаты точек мгновенной оси.
Исключая время из уравнения A17.1), получаем уравнение непо-
неподвижного аксоида, а исключая время из уравнения A17.2), получаем
уравнение подвижного аксоида.
§ 118. Ускорения точек твердого тела при сферическом
движении
Для вычисления ускорения какой-либо точки тела при сфериче-
сферическом движении воспользуемся векторным выражением скорости этой
точки (§ 116):
Тогда
w __ dv <*» w _ i .. ч, Л-
но
w =
di»
Ж
~ dt —
= 8, a
dt ¦
dt
dt
Подставляя эти значения, получаем
w = eXr + wXv,	A18.1)
или
w = !Xr+MX(«Xr).	A18.2)
Здесь 8Xf = *?—вращательное ускорение точки.
(о X v == w?c — осестремительное (центростремительное) ускоре-
ускорение точки.
Таким образом,
w~w«-fw»c.	A18 3)
22 А, А Яблонский	337

Это равенство выражает теорему Ривальса об ускорении точки-
тела, совершающего сферическое движение, которая формули-
формулируется так:
Ускорение любой точки твердого тела при сферическом
движении определяется как геометрическая сумма ее враща-
вращательного и осестремительного ускорений (рис. 322).
Вектор вращательного ускорения точки w^, = eXr направлен
перпендикулярно плоскости, , проходящей через вектор углового
ускорения е и радиус-вектор точки г, в ту сторону, откуда поворот
вектора е к вектору г на наимень-
наименьший угол виден происходящим про-
против движения часовой стрелки.
Модуль вращательного уско-
ускорения
где hE = MKi — расстояние от точ-
точки М до оси углового ускорения Е.
Вектор осестремительного уско-
ускорения w" = »Xv направлен пер-
перпендикулярно векторам угловой ско-
скорости « и линейной скорости:
точки v, т. е. по перпендикуляру»
Рис. 322.	опущенному из точки М на мгно-
мгновенную ось Q, в ту сторону, откуда
поворот вектора ь>, условно отложенного в точке М к вектору V
на наименьший угол, виден происходящим против движения часовой
стрелки.
Модуль осестремительного ускорения
v) = <Df='
A18.5)
где Ла = МКч — расстояние от точки М до мгновенной оси Q.
Модуль ускорения точки как диагонали параллелограмма ускоре-
ускорений можно определить по формуле:
или
¦w —
w=
w«c cos (w|, w°c)
Aseu>2Cos(w|,
A18.6)
Из этого выражения можно получить формулу ускорения точки
тела, вращающегося вокруг неподвижной оси (92.4).
При вращении тела вокруг неподвижной оси векторы whs на-
направлены вдоль оси вращения, а потому й?= hs — R; wB_J_wu; тогда
338

При сферическом движении тела, так же как и при вращении
вокруг неподвижной оси, осестремительное ускорение точки w?c
направлено по перпендикуляру, опущенному из точки на ось враще-
вращения (мгновенную ось 2).
Вращательное ускорение точки при сферическом движении тела Wg
определяется относительно оси углового ускорения Е и направлено
перпендикулярно плоскости, проходящей через вектор углового уско-
ускорения е и радиус-вектор г (перпендикулярно hE), т. е. w?j_e и
w^J_A?- Следовательно, направление w? не совпадает с направ-
направлением скорости точки v.
Вращательное и осестремительное ускорения точки wE и Wgc
при сферическом движении не следует смешивать с ее касательным
и нормальным ускорениями wt и wn.
Пример 81. Конус с углом при вершине 2а = 60° и радиусом
основания г = 20 см катится по неподвижной горизонтальной пло-
плоскости без скольжения. Скорость центра основания vc = 60 см/сек
постоянна.
Определить:
1)	угловую скорость конуса ю;
2)	угловое ускорение конуса е;
3)	скорости наинизшей и наивысшей точек основания vA и vB,
4)	ускорения этих же точек wA и wB (рис. 323, а).
Рис. 323а, б.
Решение. 1. Определение угловой скорости тела.
Движение1 катящегося конуса является сферическим, так как его
вершина О остается неподвижной. Это движение в каждый момент
времени представляет собой вращение вокруг мгновенной оси.
Мгновенная ось конуса 2 совпадает с образующей О А, по кото-
которой конус соприкасается с неподвижной плоскостью, так как ско-
скорости точек этой образующей равны нулю (рис. 323, б и в).
Модуль угловой скорости вращения конуса вокруг мгновенной
оси определяем по заданной скорости точки С. Находим расстояние
от точки С до мгновенной оси (рис. 323в):
СК = С A cos 30° = г cos 30° = 20 • -?~~ =17.32 см.
22*
339

Вычисляем угловую скорость:
v	60
Руководствуясь направлением скорости vc, откладываем от точки О
по мгновенной оси Q вектор угловой скорости ы так, чтобы смотря
ему навстречу, видеть вращение конуса вокруг этой оси происхо-
происходящим против движения часовой стрелки.
2. Определение углового ускорения тела. Для
определения углового ускорения е необходимо построить годограф
угловой скорости W. При качении конуса по горизонтальной плоскости
вектор to перемещается в этой плоскости, поворачиваясь вокруг вер-
вертикальной оси z. Так как модуль его не изменяется, то конец,
вектора ш описывает окружность в горизонтальной плоскости.
^Вектор s геометрически равен скорости и конца вектора со A15.2).
В данном случае скорость и является вращательной вокруг оси z.
Угловая скорость этого вращения Wj определяется как угловая ско-
скорость вращения оси конуса ОС вокруг оси z. Чтобы определить ее
модуль, находим расстояние от точки С до оси z:
CL = ОС cos 30° = О A cos 30° cos 30° = 2r cos2 30° = 40 • ~ = 30 см.
Определяем Mji
!—" CL 30
Скорость и находим как вращательную скорость точки — конца:
вектора угловой скорости «о, при вращении вокруг оси Oz:
=:6,93 сек~2.
Скорость и направлена по касательной к годографу ю в точке*
совпадающей с концом ы в рассматриваемый момент времени.
Угловое ускорение е = и. Его модуль е = а = 6,93 сек~2.
Вектор 8 отложен от неподвижной точки по направлению ско-
скорости и, т. е. он лежит в горизонтальной плоскости и перпендику-
перпендикулярен со (рис. 323, б).
3. Определение скоростей точек тела. Скорость-
точки Л, лежащей на мгновенной оси вращения, равна нулю:
Скорость точки В определяем как вращательную вокруг мгно-
мгновенной оси (§ 116):
BKl = 2CK = 20 УЪ см,
20/3 = 120 см\сек (-^.= -^-=
340

Скорость vB, так же как и vc, направлена перпендикулярно»
плоскости QOz.
4. Определение ускорений точек тела. Ускорение-
точки тела определяем как геометрическую сумму осестремитель-
ного ускорения wgc во вращении тела вокруг мгновенной оси Q и
вращательного ускорения 1нЕ относительно оси углового ускорения Е
по формуле A18.3):
w — woc -I- wB •
w В S? ' Ев'
2. ВКг = B УЪ~J ¦ 20 Уъ = 415,7 см/сек2.
woc .
зв
Wqc направлено по перпендикуляру ВКХ, опущенному из точки на.
3
мгновенную ось 2 (рис. 323в).
Для определения wE опускаем
из точки В перпендикуляр на ось
Е углового ускорения, который со-
совпадает с отрезком ВО = 2г.
= е
= 4
¦ 40 = 277,1 см/сек2.
Направляем w^ перпендикуляр-	" ш~ к, к да
но ОВ в плоскости, перпендику-	Рис 323в.
лярной е (QOz) так, чтобы, смотря
навстречу е, видеть w^. , направленным противоположно движению-
часовой стрелки (рис. 323в).
Определяем модуль wB как длину диагонали параллелограмма:
у -f- (
= |/ 1602.3-4- 2402-3 — 2-160-240-3-1 = 80
= 366 см/сек2.,
•В точке А, лежащей на мгновенной оси вращения, осестреми-
0
тельное ускорение равно нулю:
щательного ускорения точки А:
wBE — е • АО = 4 У~Ъ
р
==0. Определяем модуль вра-
вра40 = 277,1 см/сек2.
Направляем w^ перпендикулярно ОА в плоскости QOz в со-
соответствующую сторону (рис. 323в):
wa~we =277'1 см/сек2.
Вопроси для самоконтроля
1. Какими параметрами определяется положение твердого тела, одна из.
точек которого неподвижна?
34L

2.	Как формулируется теорема Эйлера-Даламбера о перемещении твер-
твердого тела, имеющего одну неподвижную точку?
3.	Что называют мгновенной осью вращения твердого тела с одной
неподвижной точкой и каковы уравнения мгновенной оси в неподвижной
и подвижной системах осей декартовых координат?
4.	Что представляют собой неподвижный и подвижной аксоиды мгно-
мгновенных осей при сферическом движении и что происходит с аксоидами при
действительном движении тела?
5.	Как определяются модуль и направление углового ускорения тела
при сферическом движении?
6 Почему направления векторов углового ускорения и угловой скорости
тела при сферическом движении не совпадают?
7.	Как определяются скорости точек тела при сферическом движении?
8.	Какие модули и направления имеют составляющие ускорения точки
тела при сферическом движении?
9.	Почему направления векторов вращательной скорости и вращатель-
вращательного ускорения при сферическом движении тела не совпадают?
ГЛАВА XVII
ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 119. Разложение движения свободного твердого тела
на поступательное движение вместе с полюсом
и сферическое движение вокруг полюса. Уравнения
движения свободного твердого тела
Положение свободного твердого тела в пространстве однозначно
определяется положением трех его точек, не лежащих на одной прямой.
Соединяя эти точки между собой прямыми, получаем треугольник.
Движение твердого тела в пространстве можно изучить как дви-
движение треугольника, определяющего его положение
Предположим, что треугольник ABC определяет положение не-
некоторого тела. Рассмотрим перемещение треугольника ABC в новое
положение Afifi^.
Осуществим это перемещение как совокупность двух перемеще-
перемещений. Для этого соединим одну из вершин, например А, с ее новым
положением Av Затем проведем отрезки ВВ' и СС, равные и парал-
параллельные отрезку ААХ (рис. 324, а).
Соединив между собой прямыми точки Аъ В', С, получим тре-
треугольник АХВ'С', стороны которого равны и параллельны сторонам
треугольника ABC как противоположные стороны параллелограммов.
Треугольник АХВ'С представляет собой новое положение треуголь-
треугольника ABC после его поступательного перемещения вместе с точкой А,
принятой за полюс.
Согласно теореме Эйлера — Даламбера для перемещения треуголь-
треугольника из положения А^В'С в положение AiB]Cl произведем поворот
треугольника на некоторый угол вокруг оси, проходящей через
точку Ах, которая не участвует в перемещении.
Таким образом, установлено, что всякое перемещение свободного
твердого тела из одного положения в другое можно осуществить
342

совокупностью двух перемещений: поступательного вместе с точкой,,
принятой за полюс, и поворота тела вокруг некоторой оси, прохо-
проходящей через полюс.
На рис. 324, а и б показано, что результирующее перемещение
тела не зависит от последовательности, в которой осуществляются
составляющие перемещения. Перемещение треугольника из положе-
положения ABC в положение А1В1С1 (рис. 324, б) можно осуществить путем
а)
Рис. 324.
поворота его вокруг оси, проходящей через точку А, до положе-
положения АВ'С, в первую очередь, и поступательного перемещения вместе
с полюсом А из положения
АВ'С в положение А1В1С1 —
во вторую очередь.
Очевидно, что совокупность
этих двух перемещений не
отображает действительного
движения твердого тела, а по-
позволяет лишь осуществить пе-
перемещение твердого тела из
первого положения во второе.
При действительном дви-
движении свободного твердого
тела составляющие движения
этого тела совершаются одно-
одновременно, т. е. движение сво-
свободного твердого тела можно	Рис. 325.
рассматривать как сложное,
состоящее из поступательного движения вместе с некоторой точ-
точкой тела, принятой за полюс, и сферического движения вокруг этого
полюса.
Выберем произвольную точку О за полюс и покажем траекторию
полюса АВ (рис. 325). Поступательная часть движения твердого тела
определяется движением полюса О.
34а

Обозначив координаты полюса О в неподвижной системе осей
.декартовых координат х0, у0, z0, напишем уравнения движения
полюса О:
Сферическое движение твердого тела можно определить заданием
-эйлеровых углов как функций времени. Для определения эйлеровых
углов проведем три взаимно перпендикулярные оси а, Ь, с, движу-
движущиеся поступательно вместе с точкой О и остающиеся параллель-
параллельными неподвижным осям х, у, z, а также взаимно перпендикуляр-
перпендикулярные оси ?, i\, С. связанные с телом.
Рис. 326.
Определив при помощи этих осей эйлеровы углы ф, 6 и ср, на-
шишем три уравнения сферического движения тела вокруг полюса О:
Таким образом, движение свободного твердого тела определяется
шестью уравнениями, называемыми уравнениями движения свобод-
344

ного твердого тела:
A19.1)
Положение свободного твердого тела определяется заданием шести
независимых величин я0, у0, 20, ф, 6, ср; следовательно, свобод-
свободное твердое тело имеет шесть степеней свободы.
Вид первых трех уравнений, определяющих поступательную часть
движения твердого тела, зависит от выбора полюса, так как коор-
координаты различных точек тела различны (рис. 326).
Вид остальных трех уравнений, определяющих сферическое движе-
движение твердого тела вокруг полюса, от выбора полюса не зависит.
Действительно, если связать с телом две системы O^jTjjCj в
О^т^Ча. ос^ которых соответственно параллельны, то эта параллель-
параллельность сохранится при движении тела и эйлеровы углы при полюсах Ох
и О2 будут одинаковы.
§ 120. Теорема о скоростях точек свободного твердого
тела и ее следствия
Движение свободного твердого тела в общем случае предста-
представляет собой сложное движение, которое можно рассматривать как
состоящее из поступатель-
поступательного движения вместе с по-
полюсом и сферического дви-
движения вокруг полюса.
Докажем теорему о ско-
скоростях точек свободного
тела.
Скорость любой точка
свободного твердого тела
равна геометрической
сумме скорости полюса
и скорости этой точки
в ее сферическом движе-
движении вокруг полюса.
Для доказательства тео-
теоремы определим скорость
точки М, приняв за полюс
точку О, скорость кото-
рой v0 известна.
Проведем радиусы-векторы р0 и р в точки О и Ж из начала
неподвижной системы осей, а также радиус-вектор г из полюса О
в точку М (рис. 327).
рис
345

Во все время движения тела между этими радиусами-векторами
сохраняется зависимость:
где г = const, как расстояние между точками, принадлежащими
твердому телу.
Определим скорость точки М как векторную производную по
времени от радиуса-вектора р:
dp dan dt
V ~ dt ~
dt
где
vo
dt
= v0 — скорость полюса О.
Так как при движении твердого тела модуль радиуса-вектора г
остается неизменным, а направление его при вращении тела вокруг
полюса О изменяется, то производная —?? представляет собой вра-
вращательную скорость точки М в ее сферическом движении вокруг
полюса О, т. е. вращательную скорость точки вокруг мгновенной
оси, проходящей через полюс.
Тогда
Поэтому
или
v = vo + «Xr.	A20.2)
Следствие 1. Проекции скоростей точек свободного твердого
тела на ось, проходящую через эти точки, равны.
Рис. 328.
Приняв за полюс точку А, определим скорости точек В и С.
лежащих на прямой, проходящей через точку А (рис. 328):
346

скорости на ось х, проходящую через точки*
Спроектируем эти
В и С:
Вращательные скорости точек vAB и vAC направлены перпендику-
перпендикулярно отрезку АС, вдоль которого направлена ось х.
Следовательно,
Поэтому
= 0 и vACx =
— vCjc~vAx или Bb = Cc —
Следствие 2. Концы скоростей точек свободного твердого-
тела, расположенных на отрезке прямой, лежат на одной:
прямой и делят эту прямую на
части, пропорциональные расстоя-
расстояниям между этими точками.
Так как вращательные скорости vAB
и vAC пропорциональны расстояниям
точек В и С от мгновенной оси вра-
вращения Q, а следовательно, и отрезкам
АВ и АС, то точки A, bv cl распо-
расположены на прямой.
Кроме? того, по построению
1 — Ь1В1 = с1С1 и AAl\\b1B1
Следовательно,
c1Cv
= АЬ1 и
AiCl — Acl и AlCl\\Acv
Рис.329.
Поэтому точки Av Вг и Сх лежат на одной прямой. Из подобиш
треугольников АСсх и АВЬХ имеем
AC
АВ
или
Л,С, ... АС В{С, __ ВС
АВ
-*|В|
т. е. точка Вх делит отрезок АгСг на части, пропорциональные рас-
расстояниям между соответствующими точками тела.
Следствие 3. Скорости точек свободного твердого тела*
расположенных на прямой, параллельной мгновенной оси,
геометрически равны.
Проведем прямую, параллельную мгновенной оси вращения тела,
проходящей через полюс О, и определим скорости точек А и 3
тела, лежащих на этой прямой (рис. 329):
34Х

Вращательные скорости v0A и v0B равны и параллельны, так
как равны и параллельны перпендикуляры АК и BL, опущенные из
точек А и В на мгновенную ось.
Стороны параллелограммов, определяющих скорости точек А
и В, соответственно равны и параллельны, следовательно, скорости
точек А и В геометрически равны, т. е. vB = vA.
§ 121. Независимость векторов угловой скорости
и углового ускорения тела от выбора полюса
Для того, чтобы установить независимость вектора угловой ско-
скорости твердого тела от выбора полюса, примем за полюсы две раз-
различные точки тела О, и О2.
Обозначим ад1 и щ векторы угловых скоростей вращения тела
вокруг мгновенных осей, проходящих через эти полюсы.
Проведем радиусы-векторы г, и г2 в произвольную точку М тела
яз этих полюсов (рис. 330). Определим скорость точки М в зависи-
зависимости от скорости каждого полюса:
v=vo, + a»1Xr1;	(a)
V = VO2+W2Xr2.	(б)
Выразим скорость второго полю-
полюса v0 через скорость первого по-
полюса:
Рис.330.	Здесь г0 — радиус-вектор полюса О2
относительно полюса Ох.
Используя эту зависимость и приравнивая два выражения (а) и (б)
скорости v, получаем
«ли
vo, + »,Xr1 = v()+M1Xro +
Так как rv — г0 = г2, то имеем
X r2
или
w2)X r2 = 0.
Это равенство имеет место при любом значении г2, т. е. для
любой точки тела, а потому
о).— ft>z = 0, т. e. w1 = w2.	A21.1)

Таким образом, вектор угловой скорости твердого тела не
зависит от выбора полюса.
Дифференцируя по времени равенство A21.1), получаем
^	,^,	A21.2)
т. е. вектор углового ускорения твердого тела не зависит от
выбора полюса.
Общие для всех полюсов угловую скорость w и угловое ускоре-
ускорение $ называют угловой скоростью и угловым ускорением тела.
Направление мгновенной оси вращения тела в данный момент
времени вполне определенно и одинаково для всех полюсов.
При перемене полюса изменяется только скорость составляющего
поступательного движения.
§ 122. Теорема об ускорениях точек свободного
твердого тела
Докажем теорему об ускорениях точек свободного твердого тела.
Ускорение точки свободного твердого тела равно геощмри-
ческой сумме ускорения полюса, осестремительного ускорения
точка и ее вращательного ускорения, определенных относи-
относительно мгновенной оси и оси углового ускорения, проходящих
через полюс.
Пусть известны ускорение w0 точки О, которую примем за полюс,
угловая скорость w тела вокруг мгновенной оси и его угловое уско-
ускорение е (рис. 331).
Чтобы доказать теорему, называемую теоремой Ривальса для сво-
свободного твердого тела, определим ускорение произвольной точки М
тела. Для этого воспользуемся выражением скорости точки М сво-
свободного тела A20.2):
v = vo+h>X г.
Определим ускорение точки М как производную по времени от
скорости v:
dx dxQ d»	dt
w = ~dt= ~dT ~^~dT X r + ы X ~dt •
Здесь ""jT^—wo —ускорение полюса О;
dt*
dt*
Xr = «Xr = w^ — вращательное ускорение точки М относи-
относительно оси углового ускорения Е, прохо-
проходящей через полюс О;
349

шх^-=«х
Поэтому
5= ft) X (ю X г) = wSc — осестремительное уско-
ускорение точки М относительно мгновенной оси
вращения 2, проходящей через полюс О.
A22.1)
Таким образом, ускорение любой точки свободного твердого
тела определяется построением многоугольника ускорений.
Вращательное ускорение точки тела w| направлено перпендику-
перпендикулярно плоскости, проходящей через ось углового ускорения Е и
данную точку М тела в такую сторону, чтобы, смотря навстречу
ускорению wj, видеть поворот угло-
углового ускорения в к радиусу-вектору г
на наименьший угол против движения
часовой стрелки.
Модуль вращательного ускорения
точки тела равен произведению мо-
модуля углового ускорения тела е на
hE = МКХ — расстояние точки от оси
углового ускорения Е:
Осестремительное ускорение точки
тела w°e направлено по перпендику-
перпендикуляру МК2> опущенному из точки М на
р с зз1	мгновенную ось вращения 2.
Модуль осестремительного ускоре-
ускорения точки тела равен произведению
квадрата модуля угловой скорости тела на h& = МКъ— расстояние
от точки до мгновенной оси вращения 2, проходящей через полюс:
Вопросы для самоконтроля
1.	На какие составляющие движения можно разложить движение свобод-
свободного твердого тела в общем случае и как они зависят от выбора полюса?
2.	Как определяют скорости точек свободного твердого тела?
3.	Как связаны между собой скорости точек свободного тела, располо-
расположенных на отрезке произвольного направления, и на отрезке, параллельном
мгновенной оси?
4.	Покажите, что векторы угловой скорости и углового ускорения сво-
свободного тела не зависят от выбора полюса.
5.	Как определяют ускорения точек свободного твердого тела?
350

ГЛАВА XVlfl
СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 123. Относительное, переносное и абсолютное
движения точки
Составное движение точки (тела)—это такое движение, при кото-
котором точка (тело) одновременно участвует в двух или нескольких
движениях. Например, составное движение совершает лодка, пере-
переплывающая реку, пассажир, перемещающийся в вагоне движущегося
поезда или по палубе плывущего парохода, а также человек, пере-
перемещающийся по лестнице движущегося эскалатора. Составным
является и движение шаров С и D центробежного регулятора Уатта
<рис. 332), вращающегося вокруг вертикальной оси, когда при изме-
изменении нагрузки машины шары удаляются от этой оси или прибли-
приближаются к ней, вращаясь со стержнями АС и BD вокруг шарниров
А и В.
Рассмотрим движущееся тело А (рис. 333) и точку М, не при-
принадлежащую этому телу, а совершающую по отношению к нему
Рис. 333.
некоторое движение. Через произвольную точку О движущегося тела
проведем неизменно связанные с этим телом оси jc, у, z. Систему
осей Oxyz называют подвижной системой отсчета.
Неподвижной системой отсчета называют систему осей O^ff.,
связанную с некоторым условно неподвижным телом, обычно
с Землей*.
Движение "точки М по отношению к неподвижной системе отсчета
называют абсолютным движением точки.
* При выводе формул скорости и ускорения составного движения
точки пользуются координатами точки в подвижной системе отсчета. В связи
с этим в отличие от принятого в § 113 и 119 обозначения осей, здесь удоб-
удобнее неподвижные оси обозначать ?, ij, С, а подвижные оси х, у, г.
351

Скорость и ускорение точки в абсолютном движении называют
абсолютной скоростью и абсолютным ускорением точки и обо-
обозначают v и w.
Движение точки М по отношению к подвижной системе отсчета
называют относительным движением точки.
Скорость и ускорение точки в относительном движении называют
относительной скоростью ,и относительным ускорением точки
и обозначают vr и wr-
Движение подвижной системы отсчета Oxyz и неизменно связан-
связанного с ней тела А по отношению к неподвижной системе отсчета О]|г]?
является для точки М переносным движением. Точки тела А,
совершая различные движения, имеют в данный момент различные
скорости и ускорения.
Скорость и ускорение точки тела А, связанного с подвижной
системой отсчета, совпадающей в данный момент с движущейся
точкой, называют переносной скоростью и
переносным ускорением точки М и обозна-
обозначают ve и we.
Например, если человек идет вдоль радиуса
' вращающейся платформы (рис. 334), то с плат-
платформой можно связать подвижную систему
отсчета, а с поверхностью Земли — неподвиж-
неподвижную. Тогда движение платформы является пе-
переносным, движение человека по отношению
к ней — относительным, а движение человека
ло отношению к Земле — абсолютным. Пере-
Рис. 334.	носной скоростью человека \е и его пере-
переносным ускорением we являются скорость и
ускорение той точки платформы, где находится в данный момент
человек.
Движение точки М (рис. 333) по отношению к неподвижной
системе отсчета, которое названо абсолютным движением, является
составным, состоящим из относительного и переносного движений
точки.
Основная задача изучения составного движения состоит в устано-
установлении зависимостей между скоростями и ускорениями относительного,
переносного и абсолютного движений точки.
Положение точки М относительно неподвижной системы отсчета
определяется радиусом-вектором р, проведенным в точку М из начала
этой системы Ох. Изменение радиуса-вектора р характеризует абсо-
абсолютное движение точки. Положение точки М относительно подвиж-
подвижной системы отсчета определяется радиусом-вектором г, проведен-
проведенным в точку М из начала этой системы О, или тремя координатами
х, у, z в этой системе.
Согласно § 80, имеем
г =
352

Изменение радиуса-вектора г или координат х, у, z точки М
характеризует относительное движение точки. Таким образом, урав-
уравнения относительного движения точки имеют вид
A23.1)
Изменение радиуса-вектора р0, проведенного из начала неподвиж-
неподвижной системы координат Oj в полюс О, характеризует абсолютное
движение полюса.
§ 124. Теорема о сложении скоростей
Докажем теорему о сложении скоростей для составного движения
точки, состоящего из относительного движения по отношению к под-
подвижной системе отсчета Oxyz и переносного движения вместе с этой
системой в случае, когда подвижная система отсчета связана с твер-
твердым телом, совершающим
произвольное движение в
пространстве (рис. 335).
Согласно § 119, движе-
движение свободного твердого
тела в общем случае со-
состоит из поступательного
движения вместе с некото-
некоторым полюсом и сфериче-
сферического движения вокруг этого
полюса.
Таким образом, само
переносное движение явля-
является сложным, представляю-
представляющим собой совокупность
поступательного движения
подвижной системы вместе
с точкой О (полюсом) и
сферического движения во-
вокруг этого полюса. Это сфе-
сферическое движение в каждый момент можно рассматривать как вра-
вращение подвижной системы с угловой скоростью ше вокруг мгновен-
мгновенной оси Qe, проходящей через полюс О.
Во все время движения точки радиусы-векторы р, р0 и г связаны
зависимостью
A24.1)
рис_ 335.
Вектор абсолютной скорости точки М
dp
V =
dt
23 А. А Яблонский
353

Дифференцируя выражение A24.1) и учитывая, что орты J, j, к
подвижной системы Oxyz, оставаясь неизменными по модулю, вра-
вращаются вокруг мгновенной оси с угловой скоростью юе, получаем
d?n ld\ d\ . dk
Рис. 336.
A24.2)
Производная от каждого орта
по времени представляет собой
линейную скорость точки, для кото-
которой этот орт является радиусом-
вектором (рис. 336)
dk
dt A"
Но каждый орт вращается вокруг мгновенной оси Qe, и враща-
вращательная скорость его конца определяется согласно (94.2) векторным
произведением, т. е.
Следовательно,
Таким образом, будем иметь
dk
dt
: 0)e X к.
A24.3)
Подставляя A24.3) в A24.2), получаем
Здесь
— vo—скорость полюса О;
рость точки М.
Поэтому
-~-
— vr — относительная ско-
скоA24.4)
Переносная скорость точки, как указывалось в § 123, предста-
представляет собой скорость точки, связанной с подвижной системой отсчета
и совпадающей в данный момент с движущейся точкой М. В рас-
рассматриваемом случае такой точкой является точка М свободного
твердого тела. Скорость этой точки на основании A20.2) состоит из
354

скорости полюса О и вращательной скорости точки вокруг мгновен-
мгновенной оси Qe, т. е.
ve = v0-r-«eXr.	A24.5)
На этом основании формула A24.4) принимает вид
v = ve+vr.	A24.6)
Это равенство выражает теорему о сложении скоростей, кото-
которая формулируется так:
Абсолютная скорость точки равна геометрической сумме
ее переносной и относительной скоростей.
Эту теорему называют правилом параллелограмма или тре-
треугольника скоростей.
Как видно, в рассматриваемом случае составного переносного дви-
движения переносная скорость точки ve сама определяется как диагональ
параллелограмма, построенного на скорости полюса v0, и вращатель-
вращательной скорости точки «е X г вокруг мгновенной оси Qe (рис. 335).
В случае поступательного переносного движения скорости всех
точек, неизменно связанных с подвижной системой отсчета, в каждый
момент геометрически равны. Поэтому переносная скорость точки М
равна скорости полюса \0 и формула A24.5) принимает вид
Очевидно, что в этом случае абсолютная скорость точки М также
определяется по формуле A24.6).
Так как абсолютная скорость точки v определяется диагональю
параллелограмма, построенного на переносной скорости ve и относи-
относительной скорости vr, то ее модуль можно вычислить по формуле:
v =Vvl + v1 + 2vevrzos{\e, vr).	A24.7)
§ 125. Теорема о сложении ускорений
(теорема Корполиса)
Для определения абсолютного ускорения точки в случае непосту-
гательного переносного движения, описанного в § 124, восполь-
воспользуемся выражением абсолютной скорости точки в этом движении
A24.2):
'<Я d) dk \ I dx
'— dt
Абсолютное ускорение точки М
_d\
23*	355

Дифференцируя выражение,	определяющее v, и приводя подоб-
подобные члены, получаем
_ dx _ <Рр0 Id4 d>) d>k
W~~dT~~dF* i~[dt2 X~f- dt2	У-t- dt2
tl _ ki\ __ o(di dx d) dy_ dk dz
dt* ^"K dt*)~T~z\~d7 "rff1" dt dt "t~ dt 'idt
A25Л)
На основании A24.3) имеем
Аналогично
Рассмотрим отдельные слагаемые выражения, определяющего w:
1) -^r=wo — ускорение полюса О;
X j + «>e X (», X J)] У + [«. Хк + ае X
= s, X (I* + Jy + kz)+w, X »е X
= е,Хг+»,Х(и,Хг);
d^x rf2v rf2^
3) l ~W 'Jri1F^rk~dF = Ыгх + №тУ + к^гг = wr — относи-
относительное ускорение точки;
= toe X (i»rjr + jwry 4- кг-гг) = we X vr.
Подставляя эти выражения в формулу A25.1), получаем
w = wo + eeXr + II)eX((i)eXr)+wf + 2(M,Xvr). A25.2)
Переносное ускорение точки, как указывалось в § 123, предста-
представляет собой ускорение точки, связанной с подвижной системой
отсчета и совпадающей в данный момент с движущейся точкой М.
В рассматриваемом случае такой точкой является точка М свобод-
свободного твердого тела, ускорение которой состоит из ускорения полюса w0,
вращательного ускорения ¦yv^ = sgX г и ее осестремительного ускорения
w°c = tae X («><, X г), определенных относительно осей Ее и Qe, про-
проходящих через полюс О:
», = »о + «.Хг + »,Х(»,Хг).	A25.2)
356

Таким образом, первые три слагаемых выражения, определяю-
определяющего w, представляют собой переносное ускорение точки. Учитывая
это, окончательно получаем
Здесь 2 (те X vr) = wc — поворотное ускорение точки (ускорение
Кориолиса).
Следовательно, установлено, что
w = w^ + wr + wc.	A25.3)
Это равенство выражает теорему Кориолиса A792—1843) о сло-
сложении ускорений в случае непоступательного переносного движения,
которая формулируется так:
В случае непоступательного переносного движения абсолют-
абсолютное ускорение точки равно геометрической сумме переносного,
относительного и поворотного ускорений.
Таким образом, абсолютное ускорение определяется замыкающей
стороной многоугольника ускорений.
В случае поступательного переносного движения «в = 0, &е = 0,
а ускорения всех точек, неизменно связанных с подвижной системой
отсчета, в каждый момент геометрически равны.
Поэтому переносное ускорение точки М равно ускорению полюса,
т. е. we = w0. Так как в этом случае wc = 2(toe X vr) = 0, то в слу-
случае поступательного переносного движения формула A25.3) прини-
принимает вид
A25.4)
Полученный результат является следствием теоремы Кориолиса и
формулируется так:
В случае поступательного переносного движения абсолют-
абсолютное ускорение точки равно геометрической, сумме ее перенос-
переносного и относительного ускорений.
Таким образом, в случае поступательного переносного движения
абсолютное ускорение точки w определяется диагональю параллело-
параллелограмма, построенного на двух составляющих ускорениях: перенос-
переносном wff и относительном wr.
Модуль абсолютного ускорения точки в этом случае можно вы-
вычислить по формуле
w = V w^ -4- vifi-\— 1w w cos fw . w \.	A25.5^
r e i wr i e т V ^ Г/	\*-«-v ^y
Относительное ускорение wr расположено в соприкасающейся
плоскости траектории относительного движения; переносное ускоре-
ускорение we<—в плоскости, которая параллельна соприкасающейся пло-
плоскости траектории полюса О.
357

§ 126. Модуль и направление поворотного ускорения
(ускорения Кориолиса)
Поворотным ускорением (ускорением Кориолиса) называется соста-
составляющая абсолютного ускорения точки в составном движении, равная
удвоенному векторному произведению угловой
скорости переносного вращения на относитель-
относительную скорость точки:
wc = 2(«eXvr).	A26.1)
Появление поворотного ускорения обусло-
обусловливается двумя причинами:
1) вследствие относительного движения
точки, перемещающейся по отношению к под-
подвижной системе отсчета, изменяется перенос-
переносная скорость точки;
Рис. 337.
2) вследствие вращательного переносного движения дополнительно
изменяется направление относительной скорости по отношению к не-
неподвижной системе отсчета.
Например, если человек идет равномерно вдоль радиуса равно-
равномерно вращающейся платформы, то его относительной скоростью
является скорость его движения вдоль радиуса, а пе-
переносной— скорость той точки платформы, где он на-
находится в данный момент (рис. 337).
Пусть в момент времени t человек занимает положе-
положение М, а в момент t-\-ht— положение Mv
Так как относительное движение равномерное и
прямолинейное, то относительное ускорение человека
wr = 0. Однако за время kt относительная скорость
изменяется по направлению от vr до v^ благодаря вра-
вращению подвижной системы (платформы).
За время kt происходит изменение модуля перенос-
переносной скорости от ©е = ше • ОМ до <о'е = те • ОМХ, благо-
благодаря относительному перемещению человека из точки М
в точку Мх.
Указанные изменения vr и \е вызывают появление
поворотного ускорения.
Модуль поворотного ускорения определяется как модуль вектор-
векторного произведения A26.1):
we = 2wevT sin (<ле, vr).	A26 2)
Поворотное ускорение равно нулю в трех случаях:
1)	если *>в = 0, т.. е. в случае поступательного переносного дви-
движения или в моменты обращения в нуль угловой скорости непосту-
непоступательного переносного движения,
2)	если vr = 0, т. е. в случае относительного покоя точки или в мо-
моменты обращения в куль относительной скорости движущейся точки;
Рис. 338.
358

S) если sin(«>,,, vr) —0, т. е. в случае, когда Z.(»g. vr) = O
или /.(оL. vr)==« и относительная скорость точки параллельна оси
переносного вращения, как например, при движении точки М вдоль
образующей цилиндра, вращающегося вокруг своей оси (рис. 338).
Направление поворотного ускорения определяется по правилу
векторного произведения.
Пусть точка М движется со скоростью vr по отношению к телу,
вращающемуся вокруг оси 2, с угловой скоростью <ле (рис. 339).
Рис. 339.
Рис. 340.
Построив условно вектор юв в точке М, направляем поворотное
ускорение wc по перпендикуляру к плоскости векторов те и vr в ту
сторону, откуда поворот вектора we к скорости v, на наименьший
угол виден происходящим против движения часо-
часовой стрелки.
Для определения направления поворотного уско-
ускорения удобно пользоваться правилом Жуковского:
Чтобы найти направление поворотного
ускорения, следует спроектировать относи-
относительную скорость точки на плоскость, перпен-
перпендикулярную оси переносного вращения, и повер-
повернуть эту проекцию в той же плоскости
на 90°, в сторону переносного вращения
(рис. 340).
Действительно, полученное направление wc (рис. 340) перпенди-
перпендикулярно плоскости треугольника, образованного скоростью vr и ее
проекцией v^, а эта плоскость совпадает с плоскостью векторов ые
и v, (рис. 339).
359
Рис. 341.

Если <ае _]_ vr, то sin(we, vr)=l, тогда wc = 2mevr
В этом случае три вектора \г, ые и wc взаимно перпендикулярны
(рис. 341).
Этот случай определения направления поворотного ускорения
возможен при относительном движении точки в плоскости, перпен-
перпендикулярной оси переносного вращения.
Для иллюстрации правила Жуковского рассмотрим несколько при-
примеров определения модуля и направления поворотного ускорения.
Предположим, например, что диск вращается вокруг оси, перпенди-
перпендикулярной его плоскости, против движения часовой стрелки с угло-
угловой скоростью ше, а по хорде диска KL дви-
движется точка М (рис. 342).
Определим модуль и направление поворотного
ускорения точки М в положении, указанном на
рисунке, если относительная скорость точки
в этот момент равна мт.
Так как точка движется в плоскости дис-
диска, перпендикулярной его оси вращения, то
sin(ws, vr)=l и модуль поворотного ускорения
равен
Рис.342.	™е = 2«Л.
Направление поворотного ускорения we получаем, повернув
в плоскости диска вектор \т против движения часовой стрелки на
угол 90°.
Определим теперь модуль и направление поворотного ускорения
точки М, движущейся с относительной скоростью vr по образующей
кругового конуса под углом МО А — а. от
его вершины к основанию (рис. 343). Ко-
Конус вращается вокруг своей оси с угло-
угловой скоростью ые в направлении, указан-
указанном на рисунке.
Отложив вектор угловой скорости tae
переносного вращения по оси этого вра-
вращения, находим:
/_(ые, vr)=180° — a.
Определяем модуль поворотного уско-
ускорения точки М:
wc = 2юег>г sin A80° — а) — 2<nevr sin а.
Чтобы найти направление поворотного
ускорения, проектируем относительную
скорость точки на плоскость, перпендикулярную оси вращения ко-
конуса. Проекция относительной скорости v^ направлена по прямой СК,
совпадающей с радиусом СМ. Повернув эту проекцию на угол 90э
по направлению вращения конуса, установим, что поворотное уско-
360

рение wc направлено по касательной к окружности радиусом СМ
в сторону вращения конуса.
Поворотным ускорением обладают точки (тела), движущиеся по
поверхности Земли, например, частицы воды в реках, поезда, авто-
автомобили и т. д.
Для тел, движущихся по поверхности Земли, ее вращение вокруг
оси является переносным движением.
Определим, пользуясь правилом Жуковского, поворотные ускоре-
ускорения точек Mv M2, Mz, Ж4, М5, движущихся по поверхности Земли
в направлениях, указанных
на рис. 344.	\N
Так как точки М1 и М2	ЦЗ
движутся в плоскостях, пер-
перпендикулярных к оси вра-
вращения Земли, то модули
их поворотных ускорений
определяем по формулам:
Направления этих ускорений
получаем путем поворота от-
относительных скоростей этих
точек в сторону вращения
Земли. Относительная ско-
скорость точки Мг, движу-
движущейся по меридиану, в мо-
момент прохождения через
экватор, параллельна оси
вращения Земли. В этот мо-
момент sin(we, v3r) = 0, а по-
потому W3<, = 0. Модули поворотных ускорений точек М4 и М5,
движущихся по меридианам^ находим по формулам:
Здесь sin(n>e, vr) = sin<f» где ср — широта точки Земли. Направления
этих ускорений определяем по правилу Жуковского.
§ 127. Примеры на применение теорем о сложении скоростей
и о сложении ускорений при поступательном
переносном движении
Пример 82. Вертикальный подъем вертолета происходит согласно
уравнению ,г = 0,25?2, где t выражено в сек, z — в м. При этом
уравнение вращения винта имеет вид ср = ЪР, где t — в сек, ср — в рад.
Определить абсолютные скорость и ускорение точки винта, отстоя-
361

щей на расстоянии /? = 0,5 м от вертикальной оси вращения, в конце
5-й сек.
Решение. Свяжем подвижную систему отсчета с корпусом верто-
вертолета, неподвижную — с Землей.
Абсолютное движение точки винта вертолета составное: оно состоит
из движения с винтом, вращающимся вокруг вертикальной оси, и
движения в вертикальном направлении вместе с корпусом вертолета.
Вращение винта вокруг его оси является относительным движе-
движением (это движение наблюдает пассажир вертолета, связанный с по-
подвижной системой отсчета).
Переносным движением является поступательное движение кор-
корпуса вертолета вертикально вверх.
Применяем теорему о сложении скоростей (рис. 345, а):
v = v,-bvr.
Переносная скорость точки М винта равна скорости той точки
корпуса, которая совпадает в данный момент с точкой винта. При
Рис. 345.
поступательном движении корпуса скорости всех его точек одинаковы.
Их модули определяются по уравнению его вертикального посту-
поступательного движения z = 0,25t2;—по формуле G9.5), соответст-
соответствующей движению точки по траектории в одном и том же направ-
направлении:
При ( = 5 сек
ve = 0,5 • 5 = 2,5 м/сек.
Для определения относительной скорости точки находим угловую
скорость винта по формуле (91.5), соответствующей также враще-
вращению тела в одном и том же направлении.
г = tp = 6t.
362

При t — 5 сек	шг = 6-5 = 30 сек'1.
Относительная скорость точки определяется как вращательная
скорость (92.1); ее модуль равен:
vT = /?<ог ==0,5 ¦ 30= 15 м/сек.
Так как переносная и относительная скорости взаимно перпенди-
перпендикулярны, то абсолютная скорость точки изображается диагональю
построенного на них прямоугольника. Ее модуль равен:
52= 15,21 м/сек.
Применяем теорему о сложении ускорений (рис. 345, б):
w = w^-j-w,.
Переносное ускорение точки М винта равно ускорению точки
корпуса, совпадающей в данный момент с точкой винта. Ускорения
всех точек корпуса одинаковы и определяются по уравнению его
движения. Модуль переносного ускорения любой течки корпуса
согласно формуле (85.8) равен:
^| = 0,5 м/сек2.
Относительное ускорение точки М винта определяется как уско-
ускорение точки вращающегося тела по формулам (92.2) и (92.3):
J = 0,5 • 302 = 450 м/сек2;
du>r
=6 сек
~2'
wb =z 0,5 • 6 = 3 м/сек2.
Абсолютное ускорение точки равно геометрической сумме трех
ускорений: переносного ускорения wg, вращательного ускорения
в относительном движении wj! и центростремительного ускорения
в относительном движении wf.
Так как эти векторы взаимно перпендикулярны, то абсолютное
ускорение изображается диагональю прямоугольного параллелепипеда,
построенного на этих векторах. Его модуль определяется:
f = V,52+ 32+ 4502 = 450,01 MjceK2,
Как видно, модуль абсолютного ускорения точки мало отличается
от модуля ее центростремительного ускорения в относительном дви-
движении wf.
363

Пример 83. Решить пример 82 для горизонтального поступатель-
поступательного движения вертолета с постоянной скоростью 40 м/сек при
равномерном вращении винта с угловой скоростью 60 сек'1.
Решение. Переносная скорость точки М винта, равная скорости
горизонтального движения вертолета, постоянна:
ve = 40 м/сек (const).
Относительная скорость точки М винта тоже постоянна:
vr = Яш, = 0,5 • 60 = 30 — (const).
т г	сек v '
В те моменты времени, когда относительная скорость перпенди-
перпендикулярна переносной (на рис. 346 положения М2 и М4), модуль
абсолютной скорости определяется по формуле
v2 = v4 = Vv]-{-v2r = ]ЛЮ2+ 302 = 50 м/сек.
В моменты времени, когда направления переносной и относитель-
ной скоростей совпадают, модуль абсолютной скорости равен сумме
Рис. 346.
модулей составляющих скоростей, а направление совпадает с их на-
направлением (положение MJ:
г»1 = г»е-г-г»,. = 40+30 = 70 м/сек.
В моменты времени, когда направления переносной и относитель-
относительной скоростей противоположны, модуль абсолютной скорости равен
разности модулей составляющих скоростей, а направление совпадает
с направлением большей скорости (положение М3)
©3 = ve — trr = 40 —30=10 м/сек.
Переносное ускорение we = 0, так как все точки корпуса верто-
вертолета движутся равномерно и прямолинейно.
В равномерном относительном движении отсутствует вращательное
ускорение, т. е.
<wв = Rb = 0
г	т
И
wr = «»« = /?о>2 = 0,5 • 602 = 1800 м/сек2.
364

Таким образом, в любой момент времени абсолютное ускорение
точки М винта равно центростремительному ускорению в относи-
относительном движении и направлено по радиусу окружности от точки М
винта к центру окружности О.
Пример 84. Центр тяжести однородного стержня длиной 11 — 50 см,
сброшенного с некоторой высоты, движется в вертикальной плоско-
плоскости согласно уравнениям:
где t — в сек, хс и ус—в м (направление осей указано на рис. 347, а).
При падении стержень равномерно вращается вокруг центра тяжести
о)
—г*-Ч&с
Рис. 347.
И
в плоскости хОу с угловой скоростью со = -г- об/сек. В начальный
момент стержень находился в вертикальном положении.
Определить в момент t = 2 сек скорость и ускорение конца М,
находившегося в начальный момент наверху.
Решение 1. Разложение движения точки М на
составляющие движения. Определим положение стержня
в заданный момент времени.
При t — 2 сек
хс — 15 • 2 = 30 м, ус = 5 • 22 = 20 м.
365

Угловое перемещение за 2 сек <р = tat = -g- • 2 = 7 -g- об1. Положение
стержня указано на рис. 347, б. В качестве подвижной системы отсчета
возьмем систему осей Схх и Cyv проведенных через точку С парал-
параллельно неподвижным осям Ох и Оу, и пусть эта система движется
поступательно, т. е. направление осей не изменяется. По отношению
к этой системе движение стержня является равномерным вращением
вокруг точки С.
Относительная скорость точки М представляет собой вращатель-
вращательную скорость, перпендикулярную к радиусу окружности СМ
(рис. 347, в), имеющую модуль
vT = /?w = /o) = 0,25 •-^¦ = 5,76 м/сек.
Относительное ускорение точки М представляет собой центро-
центростремительное ускорение, направленное к центру вращения (рис. 347, г),
а его модуль равен:
wr = wf = to2 = 0,25 (-^-J == 132,56 м/сек2,
так как при равномерном вращении w* = 0.
Переносное движение стержня является поступательным движением
вместе с подвижной системой отсчета. В этом движении скорости и
ускорения всех точек стержня одинаковы и равны скорости и уско-
ускорению центра тяжести, уравнения которого заданы.
2. Определение абсолютной скорости точки. По
теореме о сложении скоростей абсолютная скорость точки равна гео-
геометрической сумме ее переносной и относительной скоростей:
Следовательно, проекция абсолютной скорости на любую ось
равна алгебраической сумме проекций переносной и относитель-
относительной скоростей на ту же ось:
Vx = Vex + Vrx'> «, = «., 4-«V
Находим vex и vey по уравнениям движения точки С;
vex = vCx = xc = l5 м/сек:
vey — vCy=yc=lQt; при t = 2 сек г/^ = 10 • 2 = 20 м/сек;
vrx и vry находим непосредственно по рис. 347, в, так как модуль
и направление vT известны:
•»ГЛ. = — vr cos 60° = — 5,76 • 0,5== —2,88 .м/сек;
vry = vr cos 30° = 5,76 • 0,866 = 4,99 м/сек,
Проекции абсолютной скорости:
^=15 — 2,88=12,12 м/сек;
vy = 20 + 4,99 = 24,99 м/сек.
366

Модуль абсолютной скорости
Ц 1Л2.122_|_ 24,992 = 27,77 м/сек.
Абсолютная скорость изображается диагональю параллелограмма,
построенного на ve и vr
3. Определение абсолютного ускорения точки.
По теореме о сложении ускорений
w = we + wf.
Отсюда следует, что проекция абсолютного ускорения точки на
любую ось равна алгебраической сумме проекций переносного и
относительного ускорений на эту же ось:
Находим wex и wey по найденным выше проекциям переносной
скорости:
dvex	dvey
w'* ~ ~5Г = 0: Wgy — ~ЗГ — l ° М1сек2-
Так как wejr = 0, a wey > 0, то переносное ускорение we напра-
направлено параллельно оси у по этой оси (рис. 347, г).
Проекции относительного ускорения w,. находим непосредственно
по рис. 347,г, учитывая, что wr = w|?:
wrJc—— <o>»cos30° = —132,56 -0,866 = —114,80 jn/сея:2;
<0ry = — «? cos 60° = —132.56 .0,5 = — 66,28 м/сек2.
Проекции абсолютного ускорения
«»Л = —114,80 м/сек2;
¦wy == 10 — 66,28 = — 56,28 м1сек>.
Модуль абсолютного ускорения
¦w = У «? + «? = /(—114.80J-+- (—56,28J == 127,9 м/сек2.
Абсолютное ускорение изображается диагональю параллелограмма,
построенного на we и wr (рис. 347, г).
Пример 86. Кривошип ОА кривошипно-кулисного механизма
вращается вокруг оси О, перпендикулярной плоскости механизма.
Конец А кривошипа соединен шарнирно с ползунком, который пере-
перемещается в прорези кулисы ВС и сообщает кулисе поступательное
движение. Определить скорость и ускорение поступательного движе-
движения кулисы, а также скорость и ускорение движения ползунка по
отношению к кулисе и их максимальные значения, если кривошип
367

вращается с постоянной угловой скоростью п =120 off (мин и имеет
длину ОА = 1—30 см (рис. 348, а).
Решение 1. Определение скорости и ускорения
ползунка А. Угловая скорость кривошипа в сек'1
те-120 .	, . ,.
¦ = 4тс сек~1 (const).
ЯП
0
30
Положение механизма определяется углом поворота кривошипа
<р = <at = 4v:t.
Условимся отсчитывать угол ср от оси кулисы DE (рис. 348, б).
Конец А кривошипа движется по окружности равномерно. Его ско-
Рис. 348.
рость v направлена по касательной к окружности, т. е. перпендику-
перпендикулярно радиусу ОА, а ее модуль равен:
1) = wR = ш1 = 4тс • 30 =
377 см/сек = 3,77 м\сек.
Вращательное ускорение wB = 0, так как вращение кривошипа
равномерное. Поэтому модуль ускорения w точки А равен:
— w« = co2Z= 16тс2- 30 ж 4733
м/сек2.
Ускорение точки А, равное центростремительному ускорению,
направлено к центру окружности О.
368

2. Разложение движения ползунка А на состав-
составляющие движения. Сравнивая крайнее положение кулисы ВХСХ
с рассматриваемым положением ВС, видим, что перемещение АХА
точки А можно рассматривать как совокупность перемещения ползун-
ползунка А вдоль кулисы АгА' и перемещения его вместе с кулисой А'А.
Таким образом, движение точки А можно разложить на два
прямолинейных составляющих движения: движение по отношению
к кулисе (по прямой ВС) и движение с кулисой (перпендикулярно
ВС). Если подвижную систему отсчета (оси хну) связать с кули-
кулисой, то первое движение будет относительным, а второе — переносным,
при этом переносное движение будет поступательным.
Применяем теорему о сложении скоростей:
Раскладываем абсолютную скорость v точки А на переносную и
относительную скорости, направленные по соответствующим прямо-
прямолинейным траекториям этих движений.
Определяем модуль переносной скорости v^ точки А, т. е. ско-
скорости точки кулисы, совпадающей с ползунком А в любой момент
времени:
ve = 1 v sin ср | = | 3,77 sin 4itf | (м/сек).
Определяем модуль относительной скорости vr точки А, т. е.
скорости движения ползунка вдоль кулисы:
vT = \vcoscp| = | 3,77cos 4itf| (м/сек).
Применяем теорему, о сложении ускорений:
w = we + wr.
Раскладываем абсолютное ускорение точки А на переносное и
относительное ускорения, направленные по тем же прямолинейным
траекториям, и определяем модули этих ускорений:
we = |teicos<j> | = | 47,33 cos 4nt | (м/сек2),
¦wr — | w sin cp | — D7,33 sin 4izt | (м/сек2).
В рассматриваемом положении кулиса движется ускоренно, так
как направления ve и we совпадают, а ползунок движется вдоль
кулисы замедленно, так как направления vr и wr противоположны.
При <pt = Ant = 0 имеем (рис. 348, е):
ve = 0; wr = 3,77 м/сек;
we = 47,33 м/сек2; wr = 0.
При ср=4т^ = -^ имеем:
ve = 3J7 м/сек; vr = 0.;
we = 0; wr = 47,33 м/сек2.
24 А. А. Яблонский	369

Нетрудно установить, что движение кулисы и относительное дви-
движение ползунка являются гармоническими колебательными движениями,
а следовательно, изменение скорости и ускорения каждого движения
происходит в соответствии с § 89.
§ 128. Примеры на применение теорем о сложении
скоростей и о сложении ускорений в случае, когда переносное
движение — вращение вокруг неподвижной оси
Абсолютное ускорение точки в составном движении определяется
как геометрическая сумма трех ее ускорений: переносного we
относительного wr и поворотного w^., т. е.
Если точка движется по свободному твердому телу, совершаю-
совершающему сложное движение, то ее переносное ускорение we опреде-
определяется по формуле A25.2):
w* = woН- ее X г-4- <ае X (»е X г)
или
w = w -4- wB -I- vioc
При неравномерном криволинейном относительном движении
относительное ускорение точки wr состоит из касательного и нор-
нормального ускорений:
Таким образом, абсолютное ускорение точки можно представить
в виде
w = wo4-w|+w°cH-wf. + wrn4-w<;.	A28.1)
Таким выражением абсолютного ускорения удобно пользоваться при
решении задач.
В каждой конкретной задаче следует вычислить все составляющие
абсолютного ускорения и установить их направления. Вид формул,
по которым производят это выздсление, зависит от того, как заданы
составляющие движения. Затем определяют модуль и направление
абсолютного ускорения точки по способу проекций или другим путем,
в зависимости от того, сколько составляющих требуется сложить и
как они расположены по отношению друг к другу.
Наибольший практический интерес представляет случай, когда пере-
переносное движение является вращением вокруг неподвижной оси. В этом
случае переносное ускорение точки состоит из вращательного и
центростремительного ускорений во вращении вокруг этой оси,
а ускорение полюса равно нулю, т. е.
370

Тогда выражение, определяющее абсолютное ускорение, приобре-
приобретает вид
+ wrn + wc.	A28.2)
Модули составляющих переносного ускорения в этом случае
определяют обычно по формулам (92.2) и (92.3):
Модули составляющих относительного ускорения определяют
обычно по формулам кинематики точки (85.6) или (85.8) и (85.5):
dt*
или wrl =
dvf
dt
где p — радиус кривизны траектории относительного движения в соот-
соответствующей точке.
Если же относительное движение совершает точка вращающегося
тела, находящаяся от оси вращения на расстоянии г, то модули
составляющих относительного ускорения можно вычислять как модули
вращательного и центростремительного ускорений:
Модуль поворотного ускорения вычисляют по формуле A26.2):
, vr).
Пример. 86. Диск радиусом СМ = R = 50 см вращается из
состояния покоя с постоянным угловым ускорением е = 0,2 сек~2
в направлении, обратном направлению движения часовой стрелки.
По ободу диска в направлении, обратном его вращению, движется
точка М с постоянной относительной скоростью vr = 50 см/сек
(рис. 349,а). Определить абсолютную скорость и абсолютное уско-
ускорение точки М в конце 5-й секунды.
Решение. Свяжем подвижную систему отсчета с вращающимся
диском, а неподвижную — с Землей; движение точки М вместе
с диском будет переносным движением, а ее движение по отноше-
отношению к диску — относительным.
Абсолютное движение точки М состоит из этих двух движе-
движений. Так как диск вращается равноускоренно, его угловая скорость
определяется выражением (91.12*):
24*	371

Учитывая, что диск вращается из состояния покоя, т. е ше0 = О,
находим его угловую скорость в конце 5-й сек:
1. Определение абсолютной скорости точки М. Абсо-
Абсолютная скорость точки М определяется как геометрическая сумма
двух скоростей: переносной скорости точки, равной скорости точки
обода диска и относительной
скорости точки A24.6):
Вычислим модуль переноской
скорости точки в конце 5-й сек:
ч)е = Rd>es = 50 • 1 =50 CMJceK.
Эта скорость направлена
по касательной к окружности
обода в сторону вращения
диска, т. е. противоположно
относительной скорости vr
(рис. 349,0)-
В конце 5-й сек:
ve% s= 50 см/сек = vr;
Рис. 349.
Модуль относительной скорости постоянен, а модуль пере-
переносной скорости возрастает равномерно от нуля. Следовательно, при
5
t < 5 сек ve < vr,
совпадает
>5 сек ve
с направлением vr
направление v
направление v
при t — 5 сек ve = vr, v = 0; при ?
совпадает с направлением \е.
2. Определение абсолютного ускорения точки Ж*
Абсолютное ускорение точки при вращательном переносном дви-
движении определяется по формуле A28.2):
w = wj
wjf
Условимся называть траекторией переносного движения точки
для данного момента времени траекторию точки, неизменно связан-
связанной с подвижной системой отсчета и совпадающей в данный момент
с движущейся точкой.
В рассматриваемой задаче траекторией переносного движения
является траектория точки обода диска, т. е. траектория nepeHocHorc*
движения совпадает с траекторией относительного движения точки.
Следовательно, эта же окружность является и траекторией абсолют-
абсолютного движения точки.
372

Вычислим модули пяти составляющих абсолютного ускорения
точки М и изобразим эти ускорения на схеме (рис. 349,в).
Переносное вращательное ускорение точки w^ направлено по каса-
касательной к траектории переносного движения, а его модуль равен:
w\ = ге • R = 0,2 • 50 = 10 см\сек2.
Переносное центростремительное ускорение точки w? направлено
по радиусу МС к центру С окружности — траектории переносного
движения точки, а его модуль равен:
¦дап = аJ • R = 1 • 50 = 50 см/сек2.
Так как относительное движение точки — движение равномерное*
то относительное касательное ускорение равно нулю:
= 0.
dt
Относительное нормальное ускорение точки \/гп направлено по
радиусу МС к центру кривизны траектории относительного движе-
движения, а его модуль равен:
vl 502
™гп = -R = "go"
Модуль поворотного ускорения точки М вычисляем по фор-
формуле A26.2):
wc = 2<uevfs\n(v>e, vr) = 2 • 1 • 50 • 1 = 100 см/сек2.
Так как относительное движение происходит в плоскости, пер-
перпендикулярной оси переносного вращения, то направление пово-
поворотного ускорения wc определяется поворотом относительной ско-
скорости точки vr на угол 90° в сторону вращения диска.
Из четырех составляющих ускорений три направлены по одной
прямой.
При этом 1^=100 см/сек2 и w*-\-wfn=\№ см/сек2, т. е.
w + w
Поэтому w —w|, т. е. абсолютное ускорение точки М совпадает
по направлению с переносным вращательным ускорением и имеет
одинаковый с ним модуль, т. е. to =10 см/сек2.
Пример 87. Кривошип О А вращается вокруг оси О с постоянной
угловой скоростью и>0; на палец А свободно надето колесо //
радиусом г, катящееся без скольжения по неподвижному колесу
того же радиуса и с центром в точке О (рис. 350,а). Найти ско-
скорости и ускорения точек К и L колеса //, лежащих на концах
взаимно перпендикулярных диаметров, один из которых совпадает
с кривошипом.
Решение. Если подвижную систему отсчета связать с криво-
кривошипом, то движение точек колеса // будет состоять из переносного
37а

«ращения вместе с кривошипом вокруг оси О с постоянной угловой
скоростью <ое = (о0 и относительного движения — вращения вокруг
оси А этого колеса Угловую скорость относительного вращения шг
¦следует определить.
Рис. 350.
Так как колесо // катится по колесу / без скольжения, то точка М
тих соприкасания является мгновенным центром скоростей (рис. 350,6).
Поэтому
Vjm = v* + v,. = 0; ve = — vr,
-здесь ve — переносная вращательная скорость точки М колеса // во-
вокруг оси О;
vr — относительная вращательная скорость этой точки колеса
вокруг его оси А.
ve = ОМ ¦ we, vr = AM • шг ОМ • шв = AM ¦ шг
«ли гше == пог откуда шг = ше = соо = const. Так как ее =
= 0,
то и ег = 0-
Направление скорости vf указывает, что относительное вращение
происходит против движения часовой стрелки.
-374

1. Определение абсолютных скоростей точек К
и L. Абсолютная скорость каждой точки определяется как геоме-
геометрическая сумма ее переносной и относительной скоростей:
Переносные скорости точек колеса // являются вращательными
вокруг оси О, относительные скорости — вращательными вокруг оси А
(рис. 350,<У).
В точке К
ve = OK • o>e = Згш0; ve X OK;
vt = АК • шг = rm0; v, J_ AK.
Направления ve и vr совпадают:
Vk = Ve + vr —
В точке Z.	_
ve = OL ¦ we = г У 5ш0; ve X ОЛ;
г»г = Л^. • шг = гш0; vr X Л^'»
cos(ve, vr) = cos [_ AlO = -7=- •
V 5
Абсолютная скорость точки L определится диагональю парал-
параллелограмма, а потому ее модуль A24.7)
vr cos (ve> vr) =
2. Определение абсолютных ускорений точек К
и L. Так как переносное и относительное движения являются враща-
вращательными движениями, то ускорение каждой точки колеса // равное
w = w° 4- w? + w° -f- w^ + w,.
Но оба составляющих движения происходят равномерно, а потому
вращательные ускорения точек в этих движениях равны нулю.
Поэтому
w = w« 4- wj? + wc.
Траектории переносного движения точек колеса // представляют
собой окружности с центром О, траектории относительного движе-
движения— окружности с центром А.
350)
« направлено к центру О);
« направлено к центру А};
Vr) =r 2шЛ — 2цHГ-
375
В точке
е
tip- =
так как
К (рис.
: ОК • Ш»
:АК-«?
W =
350в):
= 2(o^rsin
sin

Направление v/c получаем поворотом vr на 90° в сторону пере-
переносного вращения.
Так как направления переносного, относительного и поворотного
ускорений совпадают, то ускорение точки w^ направлено к точке О.
а его модуль равен:
wK = вд« + w«+ wc = Зг@о"+" Г@о"+" 2гц)о = 6гшо-
В точке L (рис. 350,г):
и»ц = OL • ш2 = г У~Ъ оJ (w« — направлено к центру О);
wf = AL ¦ <а2г — гвJ	(wjf — направлено к центру А\,
w = 2ю v sin С<й„, v,1) = 2<о « = 2оJг.
Направление wc получаем путем поворота vr на 90°.
Абсолютное ускорение точки Z, определяется как диагональ
параллелограмма со сторонами (w^-\-w^ и w*. т. е. его модуль
равен:
где cos a =
(L() + (^r^)	a,
1
= —^=г .
/5
Подставляя значения всех величин, получаем
г2 + 6 V 5
Примечание. Ускорения точек колеса // можно определять и как
ускорения точек плоской фигуры (§ 108), разлагая движение колеса на п о-
ступательное движение вместе с полюсом и вращение вокруг
полюса. В таком случае переносное движение является поступательным,
а относительное — вращением с угловой скоростью, равной сумме угловых
скоростей ше и м,..
Выполненное в примере 87 решение основано на разложении движения
колеса //на два составляющих вращения.
Пример 88. Определить скорость и ускорение точки М, для
которой известны уравнения движения в полярных координатах:
г=3=/1@;ф = Л@(рис 351,a).
Решение. Если движение точки М задано в полярных коор-
координатах, то для определения скорости и ускорения этой точки можно
воспользоваться теоремами о сложении скоростей и ускорений. Про-
Продолжим полярный радиус точки М в сторону возрастания г и про-
проведем через эту точку прямую, перпендикулярную полярному
радиусу г, которую направим в сторону возрастания у (рис. 351,(Г).
Проведенные в точке М оси Mr и Мер называют осями поляр-
полярных координат; при движении точки М направления этих осей из-
изменяются.
376

Разложим абсолютное движение точки М на два движения: от-
относительное движение вдоль полярного радиуса, т. е. вдоль оси Or,
и переносное вращение вместе с осью Or вокруг центра О. Относи-
Относительная скорость точки vr, направленная вдоль полярного радиуса,
называется радиальной скоростью; она равна скорости прямолиней-
прямолинейного движения вдоль этого радиуса.
Рис. 351.
Поэтому ее алгебраическая величина
г dt
Переносная скорость ve, называемая трансверсальной скоростью,
как вращательная скорость точки М оси Or направлена перпенди-
перпендикулярно оси Or и имеет алгебраическую величину:
ve = /-ш = rep
Тогда модуль абсолютной скорости точки
Абсолютное ускорение точки определяется по четырем составляю-
составляющим, указанным на рис. 351,в:
w =
wr
Алгебраические величины составляющих ускорений:
__ rs __
так как при прямолинейном относительном движении u>rn =
Здесь формула A26.2) принимает вид
Для определения модуля абсолютного ускорения найдем его
проекции на оси полярных координат:
l = wr — w^ = г ¦
= тюв -\- w = гер -)- 2(р г.
377

Тогда
cos (w, r) = —-; cos (w,
Пример 89. Точка М, находящаяся в начальный момент в вер-
вершине кругового конуса, движется равномерно по образующей конуса
к основанию, с относительной скоростью г»г = 24 см/сек. Конус
вращается вокруг своей оси в указанном на рис. 352,а направлении,
согласно уравнению ср = О, 125/2. Определить абсолютные скорость и
ускорение точки в конце 4-й сек, если ?
Решение. Подвижную систему отсчета свяжем с вращаю-
вращающимся конусом. Движение точки М по отношению к конусу вдоль
«го образующей является относительным, а движение точки М вместе
<; конусом, вращающимся вокруг оси Az, — переносным.
Траектория относительного движения точки М — образующая
конуса, по которой движется эта точка. Траектория переносного
движения точки М в данный момент — окружность, которую описы-
описывает точка конуса, совпадающая в этот момент с точкой М (рис. 352,<f).
Определим положение точки М в конце 4-й сек:
0^=^ = 24.4 = 96 см;
МК = 0М sin 30° = 96- 0,5 = 48 см.
Определим переносную угловую скорость и переносное угловое
ускорение по формулам (91.2) и (91.3)
~dt
= 0,25*;
при t — 4 сек.
=l сек
-1.
"Ж
= 0.25 сек~2.
.378

Векторы tae и ее направлены по оси вращения конуса вверх (§ 94),
1. Определение абсолютной скорости точки М.
Абсолютная скорость точки М в конце 4-й сек определяется как
геометрическая сумма двух скоростей:
Переносная скорость vg направлена по касательной к траектории
переносного движения, а ее модуль равен:
ve s= MK ¦ ше = 48 • 1=48 CMJceK.
Относительная скорость vr направлена вдоль прямолинейной траекто-
траектории относительного движения, т. е. вдоль образующей конуса, а ее-
модуль vr = 24 CMJceK.
Так как составляющие скорости взаимно перпендикулярны, то
имеем (рис. 352,6)
v = УфГ&т — l/482-f-242 = 53,64 сж\сек.
1. Определение абсолютного ускорения точки М.
Абсолютное ускорение точек М при вращательном переносном
движении определяется:
W = W° -j- W^ + W>T -f- Vf,n -f WC.
Определим составляющие абсолютного ускорения точки М
(рис. 352;в).
Переносное вращательное ускорение wD направлено по касатель-
касательной к траектории переносного движения точки в соответствии с на-
направлением углового ускорения ее, а его модуль равен:
-дав __ д|д-. eg = 48 • 0,25 = 12 см/сек2.
Переносное центростремительное ускорение w? направлено
к центру кривизны К траектории переносного движения, а его модуль
равен:
•ия = МК ¦ оJ = 48 • 1 = 48 см/сек2.
Относительное движение точки равномерное, а потому
~W
= 0.
Так как относительное движение точки — движение прямолиней-
прямолинейное, то
v2T vl
¦wrn = — = -^- = 0.
Направление поворотного ускорения wc определяем по правилу
Жуковского; оно совпадает с направлением w«, а его модуль равен:
wc = 2 • <ое • vr • sin a = 2 • 1 • 24 • 0,5 = 24 см/сек2.
Проектируя все составляющие абсолютного ускорения на оси х
и у, направленные по касательной и нормали траектории переносного
379

движения, получаем:
wx — wBe-\-wc=\2-{-24 — 36 см/сек2;
<w = те»и — 48 см/сек2;
w = yw1 -J- w2 = у 362 —j- 482 = 60 см/сек2.
Направление абсолютного ускорения точки М определяем по
косинусам углов:
cos(w, i) = -^p = 0,6;
cos (w, j) = —- = 0,8.
Пример 90. Диск вращается с постоянной угловой скоростью
о) = 3 сек~1 вокруг оси, совпадающей с его вертикальным диаметром.
По диаметру диска, перпендикулярному оси его вращения, дви-
движется точка согласно уравнению х = 20 sin -g-1. Определить абсо-
абсолютные скорость и ускорение точки в конце 3-й и 4-й сек (рис. 353,а).
Рис. 353.
Решение. Переносным движением точки М является движение
точки вместе с диском, т. е. вращение с угловой скоростью
ое = и = 3 сек~1, а относительным — колебательное движение точки
вдоль оси х. Траекторией переносного движения точки в рассматри-
рассматриваемый момент времени является окружность в плоскости, перпенди-
перпендикулярной оси вращения Oz, с центром О и радиусом, равным
абсолютной величине координаты х (рис. 353Д).
380

Траектория относительного движения точки совпадает с осью х.
1. Определение абсолютной скорости точки. По
теореме о сложении скоростей
Переносная вращательная скорость ve точки М в любой момент
времени направлена перпендикулярно плоскости диска, а ее модуль
равен:
ve = Rme.
Относительная скорость vr точки М является скоростью ее колеба-
колебательного движения по диаметру диска, перпендикулярному оси его
вращения.
При колебательном движении определяется обычно алгебраическая
величина скорости:
Ъг = vrx — ~ == Ют: cos — t {см/сек).
При t = 3 сек
#3 = 20sin-|. 3 = 20(— 1) = —20 см;
Д3 = | х31 = 20 см; ve3 = 20 ¦ 3 = 60 см/сек;
vr3— Юте cos -5-З = 0, так как cos-2-tc = 0;
г»3 = veZ = 60 CMJcetc.
Направление абсолютной скорости точки v3 совпадает с напра-
направлением ее переносной скорости ve3, которая направлена по каса-
касательной к траектории переносного движения в сторону вращения
диска.
При t = A сек
xi = 20 sin-я- • 4 = 0, так как sin2ic = 0;
R4 = 0; vei == 0;
wr4= IOtccos w • 4= 10tc = 31,4 см/сек.
Относительная скорость vr4 направлена по направлению оси х,
так как ее проекция на ось х, найденная по уравнению движения,
в этот момент положительна. Очевидно, что
v4 = vr4 и «4 = ©rt = 31,4 см1сек,
т. е. направление абсолютной скорости совпадает с направлением
относительной скорости, и их модули равны.
2. Определение абсолютного ускорения точки.
По теореме о сложении ускорений при вращательном переносном
движении:
381

Переносное движение является равномерным вращением. Поэтому
в любой момент времени w*e = Q.
Относительное движение точки — прямолинейное, колебательное
движение, поэтому «>,.„ —О, а алгебраическую величину касательного
ускорения находим по формуле (85.6);
¦и»Гт =-5j? = — 5u2sin|-* (си/сек2).
Определим модули и направления составляющих абсолютного уско-
ускорения в заданные моменты времени (рис. 353,6).
При t — 3 сек. Переносное центростремительное ускорение w%
направлено к центру О траектории переносного движения точки,
а его модуль равен
w% = /?3 • 0J = 20 ¦ З2 == 180 см/сек2.
Относительное касательное ускорение w^ направлено по прямо-
прямолинейной траектории относительного движения точки и его алгебра-
алгебраическая величина равна:
wrx = — 5я2sin-| • 3 = 49,3 см!сек2>0.
Так как wrz > 0, то ускорение wrT3 имеет направление оси х.
Поворотное ускорение wc3 точки М в этот момент равно нулю,
так как vr3 = 0.
Таким образом, при ? = 3 сек только два составляющих абсолют-
абсолютного ускорения w«3 и w,3 не равны нулю и направлены по одной
прямой в одну сторону.
Направление абсолютного ускорения w3 точки М в конце 3 сек
совпадает с направлением этих составляющих, а его модуль равен:
wz~^й+^ггз— 180 + 49,3 = 229,3 см/сек2.
При t = 4 сек. В этот момент /?4 = 0, а потому wj*4 = 0.
Относительное касательное ускорение в этот момент
•wrvt= —5%2sin-^ -4 = 0.
Направление поворотное ускорение w^ получается поворотом ско-
скорости вг4 на 90° в сторону переносного вращения
W(,4 = 2a)et»rsin~ = 2- 3.31,4- 1 = 188,4 см\сек*.
Таким образом, при t = 4 сек только одно составляющее уско-
ускорение wc4 не равно нулю. Поэтому w4 = wc4. т. е. направление абсо-
абсолютного ускорения точки М в конце 4 сек совпадает с направлением
поворотного ускорения, а его модуль равен модулю поворотного
ускорения:
w4 = we4= 188,4 см/сек2.
382

Пример 91. Шары центробежного регулятора Уатта, вращаю-
вращающегося вокруг вертикальной оси, благодаря изменению нагрузки
машины, отходят от этой оси. Найти абсолютную скорость и абсолют-
абсолютное ускорение центров этих шаров, если в рассматриваемый момент
регулятор вращается с угловой скоростью о> = 4 сек~] и угловым
ускорением е==0,8 сек~2, а угловая скорость расхождения шаров
1	2
~1
! = 2 сек~1 и угловое ускорение 6j = 0,2 сек~2. Длина стержней
/ = 40 см, расстояние между осями их привеса 2е=10 см, а углы,
образованные стержнями с осью регулятора а = 30° (рис. 354,а).
а)
Рис. 354.
Решение. Подвижную систему отсчета связываем с частями
регулятора, вращающимися вокруг его оси.
Переносным движением шаров является их вращение вокруг верти-
вертикальной оси с угловой скоростью о>е = ш = 4 сек~х и угловым
ускорением ee = s-=0,8 сек~2, а относительным — вращение стерж-
стержней с шарами вокруг осей их привеса с угловой скоростью
383

о), = u>j = 2 сек 1 и угловым ускорением ?r = el = 0,2 сек~2. Векторы
юе, ее, ыг, §г изображены на рис. 354,в.
Траекторией переносного движения центра каждого шара является
горизонтальная окружность с центром на оси регулятора, прохо-
проходящая через центр шара. Траектория относительного движения—-это
дуга окружности радиусом I, лежащей в плоскости регулятора,
с центром на оси привеса стержня.
Радиус окружности, являющейся в рассматриваемый момент вре-
времени траекторией переносного движения шара
0-0,5 = 25 см.
1. Определение абсолютной скорости центра шара.
Абсолютная скорость центра каждого из шаров определяется как
геометрическая сумма его переносной и относительной скоростей
(рис. 354,6):
v = ve+vr.
Переносная скорость центра шара \е направлена по касательной
к траектории переносного движения, а её модуль равен:
ve = R ¦ те = 25 • 4=100 см/сек.
Относительная скорость центра шара v, направлена по касатель-
касательной к траектории относительного движения, т. е. перпендикулярно
к стержню, а ее модуль равен:
vT = I ¦ шг = 40 • 2 = 80 см/сек.
Скорости ve и vr взаимно перпендикулярны.
Модуль абсолютной скорости
02=128 см/сек.
2. Определение абсолютного ускорения центра
шара.
Абсолютное ускорение центра каждого шара при вращательных
составляющих движениях равно:
W = \Уг + W" + W, + W"H- Wc.
Найдем модули и направления составляющих ускорений (рис. 354а).
Переносное вращательное ускорение w« направлено по касатель-
касательной к траектории переносного движения в соответствии с направле-
направлением se, а его модуль равен:
wae — R • ее = 25 • 0,8 = 20 см/сек2.
Переносное центростремительное ускорение w? направлено
к центру окружности, являющейся траекторией переносного движе-
движения центра шара, а его модуль равен:
да" = R ¦ ш2е = 25 ¦ 16 = 400 CMJceic2.
384

Относительное вращательное ускорение центра шара w' напра-
направлено по касательной к траектории относительного движения, т. е.
перпендикулярно стержню, в соответствии с направлением ег, а его
модуль равен:
w* = I • ег = 40 ¦ 0,2 = 8 см/сек2.
Относительное центростремительное ускорение центра шара w"
направлено к центру траектории относительного движения, лежащему
на оси привеса стержня, а его модуль равен:
дай = I • оJ = 40 • 4 = 160 CMJceK2.
Поворотное ускорение центра шара wc имеет направление, опре-
определяемое по правилу Жуковского, а его модуль равен:
wc = 2wevr sin (ioe, vr) = 2 • 4 • 80 • 0,866 = 554 cMJcetc2.
Здесь /_{ые, vr) = 60°, siii(«oe, vr) = 0,866 (рис. 354, e).
Абсолютное ускорение точки, равное геометрической сумме пяти
слагаемых, находим по способу проекций. Проводим оси координат
с началом в точке М, направляя ось х по касательной к траектории
переносного движения, ось у— вдоль ее радиуса, ось z— параллельно
оси регулятора.
Ускорения wj, wJS w* располагаются в плоскости yMz, ускоре-
ускорения wBe и wc — на оси х.
Вычисляем проекции абсолютного ускорения на оси координат
как суммы проекций составляющих ускорений на эти оси:
wx — — wc — wBe — ~ 554 — 20 = — 574 см/сек2;
wy = <w* cos 30° — w* cos 60° — w* —
= 8-0,866—160-0,5 —400 = —473 см/сек2;
«iz = «;»cos60o + w«cos30o = 8 • 0,5+160 • 0,866= 142 см/сек2.
Тогда модуль абсолютного ускорения
w = Ywx + w2y-\-w\ = /(—574J + (—473J + A42J = 869 CMJcen2.
Вопросы для самоконтроля
1.	Дайте определение относительного, переносного и абсолютного движе-
движений точки, а также скоростей и ускорений этих движений.
2.	Как определяют абсолютную скорость точки в составном движении?
3.	Как определяют абсолютное ускорение точки при непоступателыюм
переносном движении и при поступательном переносном движении?
4.	Каковы причины появления поворотного ускорения?
5.	Каковы модуль и направление поворотного ускорения и при каких
условиях поворотное ускорение точки равно нулю?
6.	Какой вид имеет выражение абсолютно о ускорения точки в случае,
когда переносное движение представляет собой свободное движение твердого
тела, и в случае, когда переносное движение является вращением вокруг
неподвижной оси?
25 А. А. Яблонский	385

и,
ГЛАВА XIX
СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 129. Сложение вращений твердого тела вокруг
пересекающихся осей. Параллелограмм и многоугольник
угловых скоростей
Угловая скорость вращения твердого тела вокруг неподвижной
оси согласно § 94 рассматривается как скользящий вектор, напра-
направленный вдоль оси вращения в такую сторону,
к	чтобы, смотря ему навстречу, видеть вращение
тела, происходящим противоположно движению
часовой стрелки.
Ось вращения, положение которой в про-
пространстве изменяется со временем, называют
мгновенной осью вращения тела.
Как указывалось выше, мгновенная ось вра-
вращения представляет собой геометрическое место
точек тела, скорости которых в данный момент
равны нулю.
J,UU	Вектор угловой скорости тела в этом случае
рассматривается так же, как скользящий вектор.
Рис. 355.	направленный вдоль мгновенной оси вращения
тела.
Рассмотрим составное движение тела, представляющее собой сово-
совокупность двух вращательных движений тела вокруг осей, пересекаю-
пересекающихся в одной точке. Примером такого движения является совокуп-
совокупность вращения диска вокруг оси OL
с угловой скоростью со2 и его вращения
вместе с осью OL вокруг неподвижной
оси ОК с угловой скоростью щ (рис 355).
Вращение диска вместе с осью OL
вокруг оси ОК представляет собой пере-
переносное вращение, а его вращение вокруг
оси OL— его относительное вращение.
Определим абсолютное движение тела,
получающееся при сложении двух враща-
вращательных движений вокруг пересекающихся
осей. Пусть твердое тело одновременно
вращается вокруг двух мгновенных осей,
пересекающихся в точке О (рис. 356), при-
причем его вращение вокруг оси ОК является переносным, а вокруг оси
OL—относительным вращением. Предположим, что угловая скорость
переносного.вращения тела равна 0)е, а относительного вращения—tor.
Скользящие векторы угловых скоростей ые и wr перенесем
в точку О пересечения мгновенных осей и построим на этих векто-
векторах параллелограмм ОАСВ.
Рис. 356
386

Покажем, что диагональ ОС этого параллелограмма представляет
собой угловую скорость результирующего вращения тела, которое
происходит вокруг оси ON.
Для этого прежде всего установим, что ось ON является мгно-
мгновенной осью абсолютного вращения тела, т. е. абсолютные скорости
точек тела, расположенных на прямой ON, равны нулю.
Точка О расположена одновременно на двух мгновенных осях вра-
вращения ОК и OL, поэтому ее абсолютная скорость равна нулю v0 = 0.
Покажем, что скорость вершины С параллелограмма ОАСВ также
равна нулю.
Точка С принадлежит твердому 1елу и поэтому она одновременно
участвует в его вращениях вокруг осей ОК и OL.
Переносная вращательная скорость ve направлена перпендикулярно
плоскости ОАСВ от читателя, а ее модуль равен:
ve — DC-we = 2 пл. /\ОАС
Относительная вращательная скорость vr направлена перпендику-
перпендикулярно плоскости ОАСВ к читателю, а ее модуль равен:
vr = EC-ar = 2 пл. Д ОВС.
Так как ДОЛС = ДОВС, то ме = — vr.
По теореме о сложении скоростей получим
Установив, что скорости точек О и С твердого тела в рассматри-
рассматриваемый момент равны нулю, можно утверждать, что прямая ON,
проходящая через эти точки, в этот момент является мгновенной осью
абсолютного вращения тела.
Покажем теперь, что геометрическая сумма векторов <ое и <аг,
т. е. вектор ОС, равен вектору угловой скорости абсолютного
вращения тела ю. Для этого проведем из точки О в какую-либо
точку М тела радиус-вектор г и определим скорость этой точки:
Абсолютная скорость точки равна произведению неизвестного по
модулю вектора ю, направленного по оси ON, на радиус-вектор
точки:
v = «j X г-
Вращательные скорости составляющих движений
Подставляя выражения скоростей, получаем
ю X г = о>в X г + м, X г = (ю, + о>г) X г-
откуда находим, что
ft) = w,-|-wr.	A29.1)
25*	387

Таким образом, угловая скорость абсолютного вращения тела
равна геометрической сумме угловых скоростей составляющих
вращений.
Установленное соотношение называют правилом параллело-
параллелограмма угловых скоростей.
Если твердое тело одновременно совершает вращения вокруг
нескольких мгновенных осей, пересекающихся в одной точке, то
угловая скорость w абсолютного вращения тела равна геометрической
сумме угловых скоростей ы1% ю2, .... ып составляющих вращений:
w = to1 + w2+ ... -f юи.	A29.2)
Это соотношение называют правилом многоугольника угловых
скоростей. Оно показывает, что абсолютную угловую скорость со
можно найти как замыкающую сто-
сторону многоугольника угловых скоро-
скоростей (рис. 361). Рассмотрим несколько
примеров на построение параллело-
параллелограмма угловых скоростей.
Допустим, например, что конус //
катится без скольжения по неподвиж-
неподвижному конусу / (рис. 357). Так как
при отсутствии скольжения точки со-
соприкасания конуса // с неподвижным
конусом / имеют скорости, равные
нулю, то линия соприкасания конусов
является мгновенной осью Q абсолют-
абсолютного вращения конуса //._
При качении конуса // его обра-
образующие поочередно становятся линиями
касания с неподвижным конусом, т. е.
мгновенными осями абсолютного вращения конуса //. Ось конуса //
не остается неподвижней, а вращается вокруг оси неподвижного
конуса. Следовательно, абсолютное вращение конуса // вокруг
мгновенной оси Q представляет собой совокупность его относитель-
относительного вращения вокруг оси Qr, являющейся его осью, и переносного
вращения вокруг оси Qe, совпадающей с осью неподвижного конуса.
Угловые скорости этих вращений связаны зависимостью
Рис. 357.
Зная одну из трех угловых скоростей и положение всех трех
осей вращения, молено построить параллелограмм угловых скоростей
и определить две другие угловые скорости.
На рис. 358 пог.азан параллелограмм угловых скоростей для
случая качения без скольжения конуса // по внутренней поверхности
неподвижного конуса /, а на рис. 359—для случая качения без
скольжения конуса // по неподвижной плоскости /. По рисунку легко
убедиться в том, что смотря навстречу соответствующему вектору

угловой скорости, можно видеть каждое из трех вращений проис-
происходящим против движения часовой стрелки.
Покажем применение параллелограмма угловых скоростей на сле-
Рис. 359.
дующем примере (рис. 360). Допустим, что конус // обегает непо-
неподвижный конус / за минуту 15 раз. Определим угловую скорость
вращения конуса // вокруг своей оси, его абсолютную угловую
26 А. А. Яблонский
389

скорость и его угловое ускорение. Для этого представим абсолют-
абсолютное вращение конуса // вокруг мгновенной оси Q состоящим из
относительного вращения вокруг его оси Qr и переносного вращения
вместе с этой осью вокруг оси неподвижного конуса Qe.
Модуль угловой скорости переносного вращения
ше = —^— = 0,5тс=: 1,57 сек \
Задавшись направлением переносного вращения (против движения
часовой стрелки, если смотреть сверху), откладываем вектор ые и
строим параллелограмм угло-
угловых скоростей. Из параллело-
параллелограмма находим модули угло-
угловых скоростей абсолютного и
относительного вращений ко-
конуса //:

sin 30°
= гс=3,14 сек
'1;
I
r = we ctg 30° =
= 0,5*
= 2,72 сек
~1
Рис. 360.
Движение конуса // явля-
является сферическим, так как его
вершина О остается неподвижной. Для определения углового уско-
ускорения конуса е следует построить годограф угловой скорости ы и
определить линейную скорость и конца вектора а) (§ 115).
Годографом о) является окружность, параллельная основанию
неподвижного конуса. Зная модули угловой скорости переносного
вращения юе и относительного вращения <ог конуса //, определим
модуль вращательной скорости и:
и = оуог = 0,5тг • 0,5я Уъ = 0,25и2 yli = 4,23 сек'2;
е = ц; е = н = 0.251с2
Вектор s перпендикулярен плоскости параллелограмма угловых
скоростей.
§ 130. Проекции угловой скорости и углового ускорения
твердого тела, совершающего сферическое движение,
на неподвижные и подвижные оси декартовых координат
Пусть сферическое движение тела задано уравнениями A13.1):
= Л
390

Быстроту изменения эйлеровых углов характеризуют алгебраи-
алгебраические величины соответствующих угловых скоростей:
di/ :
а>1 = -^-==ф — угловой скорости прецессии, т. е. вращения тела
вокруг оси z, перпендикулярной плоскости угла ф;
^—"ТГ^ ® —угловой скорости нутации, т. е. вращения тела вокруг
линии узлов, перпендикулярной плоскости угла 6;
й3=-^- = ср—угловой скорости собственного вращения, происходя-
происходящего вокруг оси С, которая перпендикулярна пло-
плоскости угла ср.
Сферическое движение тела в каждый момент времени может
рассматриваться как вращение вокруг мгновенной оси, проходящей
чгрез неподвижную точку О.
Разложим это вращение на три составляющих вращения вокруг
осей z, J, С, проходящих через эту же точку (§ 113).
Тогда вектор «о. угловой скорости вращения тела вокруг мгно-
мгновенной оси Q будет равен сумме угловых скоростей tav w3, w2, на*
правленных вдоль осей	g-
z, С, J, т. е. определится
как замыкающая сто-
сторона многоугольника ?>
угловых скоростей:
Модуль угловой
скорости о) можно
определить непосред-
непосредственно из многоуголь-
многоугольника угловых скоро-
скоростей (рис. 361) и по
способу проекций.
Определяя w при
помощи многоуголь-
многоугольника угловых скоро-
скоростей, найдем сначала
GO — сумму двух угловых скоростей ©j и ю3, как диагональ парал-
параллелограмма, построенного на этих векторах. Учитывая, что угол
между ы>] и ц>3 равен 9, имеем
О)*	 о)? —1— (О? —{— Зш.О),, COS О.
Найденный вектор w/ расположен в плоскости zOL а вектор о>2
направлен по линии узлов 0J, перпендикулярной к этой плоскости,
т. е. угол между векторами to/ и ш2 равен 90°, а потому
Рис. 361.
П2 = 1
).
26*
391

Подставляя в это выражение ю2, получаем
(IJ = ОJ -\- AJ _]_ 0J -j-
2o>1oKcos9
ИЛИ
COS0.
A30.1)
По этой формуле определяем модуль угловой скорости враще-
вращения тела вокруг мгновенной оси.
Модуль и направление угловой скорости to можно определить
в	также по ее проекциям на непо-
неподвижные оси декартовых коор-
координат х, у, z или на подвиж-
подвижные оси I, у), С. Проекция ю
на каждую ось определяется
как сумма проекций составляю-
составляющих угловых скоростей о>г
2 И Ю3.
Найдем сначала проекции w
на неподвижные координатные
оси х, у, z.
Проекции о>! и ft>2 нахо-
находим непосредственно. Чтобы
получить проекции w3 на все
три оси, разложим эту угловую
скорость на две составляющие,
из которых одна направлена
по оси z, а другая лежит
в плоскости хОу (рис. 362).
Первая составляющая имеет алгебраическую величину o>3cos6,
вторая <a3sine. Вторая составляющая направлена по прямой Oj,
лежащей в плоскости хОу и перпендикулярной прямой OJ. Прямая Oj
образует с осями х и у углы, равные 90°—ф и 180°—ф.
Проектируя угловые скорости на неподвижные оси, получаем:
0)^. = aJcos(j>-f-oKsin 6 sin ф;
— «Ksin9 cos ф;
Рис. 362.
Подставляя значения <av ш2 и ш3, находим:
шх = 0 cos ф + <р sin б sin ф,
си — 9 sintj) — ср sin 9 cos ф,
A30.2)
При вычислении проекций о> на подвижные оси %, т;, % (рис. 363)
проекции оJ и ю3 определяем непосредственно.
392

Чтобы получить проекции Wj на все три оси, разложим эту угло-
угловую скорость на две составляющие: направленную по оси С и лежа-
лежащую в плоскости ?От|. Их алгебраические величины равны u)t cos б и
o>j sin S. Вторая составляющая направлена по прямой Ои, лежащей
в плоскости %Оу\ и перпендикулярной прямой OJ. Прямая Ои
образует с осями \ и т; углы,
равные 90° — <р и ср.
Проектируя угловые скорости
на подвижные оси, получаем:
(D, COS в
sin cp —j— uJ coscp;
or = u)j sin G cos cp — oJ s'n ?!
шс = a)x cos
Подставляя значения <Oj, io2
и io3, находим:
u)S = <j» sin 8 sin cp—J—© cos cp,
to =ф sin 6 coscp—Osincp, A30.3)
со,. = ф cos 0 —j— cp.
Легко убедиться в том, что при вычислении модуля ш по ее
проекциям на неподвижные или подвижные оси получается значение,
определяемое формулой A30.1), т. е.
Рис. 363.
ш = Уш1+ ш2-|- <¦>! = У^\+ «>'-г- <о?
Модуль и направление углового ускорения е также можно опре-
определить по его проекциям на неподвижные или подвижные оси декар-
декартовых координат.
Определим проекции углового ускорения на неподвижные оси
координат.
Разлагая векторы угловой скорости w и углового ускорения 8
по ортам неподвижных осей, имеем:
,	A30.4)
A30.5)
Вектор углового ускорения равен производной по времени от
вектора угловой скорости A15.1):
do>r
dt
¦+k
IF
A30.6)
Сопоставляя выражения A30.5) и A30.6), определяющие е,
находим
da>r	da>.,	du>,
С 	; .
У
dt
dt
A30.7)
393

т. е. проекции углового ускорения на неподвижные оси декар-
декартовых координат равны производным по времени от проекций
угловой скорости на соответствующие оси.
Таким образом, выражения проекций углового ускорения на не-
неподвижные оси содержат эйлеровы углы и их производные.
Определим проекции углового ускорения и на подвижные оси
декартовых координат, связанные с твердым телом.
Обозначим единичные векторы подвижных осей ilt jj, kv Эти
орты, неизменные по модулю, вращаются вместе с телом вокруг
мгновенной оси с угловой скоростью «в.
Поэтому производные от этих ортов по времени как вращатель-
вращательные скорости концов этих векторов определятся по формулам A24.3):
-§- = »Х11. -4b- = «XJi. ^- = 4>Xkv A30.8)
Разлагая векторы угловой скорости о> и углового ускорения е
по ортам подвижных осей, поЯучаем
c>	A30.9)
A30.10}
da>^ du>	d<
Преобраауем первое слагаемое правой части этого равенства,
пользуясь значениями производных от ортов:
ш+ % + Щ
= ы X (IiU)e+iim4+Me) = » X о) = 0.
Угловое ускорение
fifw,	da	das
A30Л1>
fifw,	da	das
Сопоставляя выражения A30.10) и A30.11), определяющие е,
находим проекции вектора е на оси ?, т]. С:
dnnr	dm	rfo)
т. е. проекции углового ускорения тела на подвижные оси декар-
декартовых координат равны производным по времени от проекций
угловой скорости на соответствующие подвижные оси.
§ 131. Проекции ускорения точки твердого тела,
совершающего сферическое движение, на неподвижные
и подвижные оси декартовых координат
Пользуясь проекциями угловой скорости и углового ускорения
тела на оси координат, можно определять проекции ускорения точки
тела при сферическом движении на неподвижные или подвижные оси
394

декартовых координат. Вектор ускорения точки при сферическом
движении A18.2)
Из векторной алгебры известно выражение двойного векторного
произведения
А X (В-Х С) = В (А • С) — С (А ¦ В).
Преобразуя по этой формуле двойное векторное произведение
«> X (** X г), получаем
w = е X г + (о (о> • г) — г (w • ш)
или
Проектируя левую и правую части этого векторного равенства
на неподвижные оси декартовых координат, получаем
wх = еу2Г — ггу -\- шх (<ахх -{- (оуу + wzz) — ш2х, )
wy = e.zx — exz + «у (ш^л: + соуу -f- t»zz)—ш2у, | A31.2)
В проекциях на подвижные оси декартовых координат получаем
A31.3)
Ускорение точки определяется по его проекциям на оси:
или w =
2 -f- да2
Применим полученные формулы к определению характеристик
сферического движения тела.
Пример 92. Сферическое движение тела задано уравнениями
Определить модуль угловой скорости сферического движения
тела, мгновенную ось вращения тела, неподвижный и подвижный
аксоиды, а также модуль и направление вектора углового ускорения.
Решение. Проекции угловой скорости на неподвижные оси
декартовых координат вычисляем по формулам A30.2):
<ох— 6 cos t|> + <p sin б sin t]>;
wy — 6 sin ф — <р sin 0 cos (|i;
(в2 = ф —J— <p cos 9.
395

При ф = ге, о = 0, <f = 2k получаем:
u>r = 2k sin -J- sin nt = k sin «^:
•*	о
= — 2& sin -щ cos ra^ = — k cos л^;
Проекции угловой скорости на подвижные оси декартовых коор-
координат вычисляем по формулам A30.3):
о)? = ф sin 6 sin cp —(— 9 cos cp;
ш = ф sin б cos 9 — 6 sin cp;
ш( = ф cos б-{-ср.
Подставляя значения ф, ср и 6, получаем:
ш^ = п sin -г- sin 2^f = 0,5и sin 2W;
ш^ = п sin -^ cos 2kt = 0,5n cos 2A/;
ш,. = я cos ^- -(- 2A = J-s— « + 2k.
Модуль угловой скорости ш постоянен и равен:
Так как и2 = 0, то направление угловой скорости совпадает
с диагональю параллелограмма, построенного на угловых скоростях
«J и w3 (рис. 364). Мгновенная ось вращения тела Q направлена
по этой диагонали.
Согласно формулам A17.1) и A17.2), уравнения мгновенной оси
имеют вид:
в неподвижной системе координат Oxyz
х _ у _ г
°>х <°>. «г
или
х 	 у 	 г
k sin nt — k cos nt n-\- ylf k
в подвижной системе координат O\tf,
или
4	Tj
0,5л sin 2kt 0,5л cos 1
396

В каждой системе координат мгновенную ось, т. е. прямую линию,,
определяют два уравнения. Исключая из двух уравнений время t,
получаем одно уравнение, определяющее геометрическое место мгно-
мгновенных осей, соответствующих различным моментам времени, т. е
поверхность, называемую аксоидом.
Уравнение неподвижного аксоида:
kf
• = 0;
уравнение подвижного аксоида:
0,25п2
= 0.
Полученные уравнения показывают, что аксоиды представляют-
собой поверхности круговых конусов.
Рис. 364.
При движении тела подвижный аксоид-конус, ось которого сов-
совпадает с осью С, катится без скольжения по неподвижному аксоиду-
конусу с осью, совпадающей с осью z (рис. 365).
Модуль и направление вектора углового ускорения определим
по формулам A30.7) и A30-12):
da
?(: = ¦
е ^ = ——- = kn cos nt,
dt
•-=-#=«
- = kn sin nt,
или
¦?¦•
din
sn == Г ~ — ^n sin 2liil
~dT
= 0.
397

Модуль угловогр ускорения е постоянен и равен:
Направление вектора углового ускорения определяется косинусами
углов, составленных им с направлениями координатных осей:
cos (e, i) = — = cos nt — cos <|>;
cos (e, j) = — = sin nt = sin ф;
cos (e, k) = -^ = 0;
cos (e, ix) = —- — cos 2kt = cos <p;
Рис. 365.
cos (e, jx) = — = — sin 2kt = — sin <p;
cos(s, k1) = -^- = 0.
Полученные значения косинусов углов показывают, что вектор
углового ускорения в направлен по линии узлов (рис. 364).
Рассмотренное сферическое движение твердого тела представляет
собой совокупность двух вращений: вращения с постоянной угловой
скоростью ш3 = ср = Ik вокруг оси ОС и вращения вместе с осью С
вокруг оси z с постоянной угловой скоростью со1 = ф = ге.
Такое сферическое движение тела называется регулярной пре-
прецессией.
§ 132. Сложение вращений твердого тела вокруг
параллельных осей
Случай I. Переносное и относительное вращения напра-
направлены в одну сторону.
Допустим, что плоская фигура // движется в неподвижной пло-
плоскости /, а плоская фигура /// совершает движение в этой же пло-
плоскости по отношению к фигуре // (рис. 366,а). Тогда движение
фигуры /// по отношению к неподвижной плоскости /, т. е. ее абсо-
абсолютное движение, является составным. Оно состоит из ее относи-
относительного движения по отношению к фигуре //, с которой связана
подвижная система отсчета и переносного движения вместе с фигу-
фигурой //, т. е. вместе с подвижной системой отсчета. Точку Ре пло-
плоской фигуры ///, переносная скорость которой в данный момент
равна нулю, назовем мгновенным центром скоростей ее переносного
движения.
398

Очевидно, переносное движение является вращательным движением
вокруг центра Ре, т. е. вокруг оси йе, перпендикулярной рассматри-
рассматриваемым фигурам. Точку Рт плоской фигуры ///, относительная ско-
скорость которой в данный момент равна нулю, назовем мгновенным
центром скоростей ее относительного движения. Относительное дви-
движение фигуры /// является вращением вокруг Центра Рг т. е. во-
вокруг оси Qr.
Предположим, что модули угловых скоростей we и и>г этих вра-
вращений известны. Определим абсолютное движение фигуры ///, рас-
рассматривая сначала случай, когда переносное и относительное вра-
вращения происходят в одном направлении, т. е. когда векторы юе и ti>r
направлены в одну сторону.
Рис. 366.
Абсолютная скорость любой точки плоской фигуры ///, совер-
совершающей составное движение, равна геометрической сумме ее отно-
относительной и переносной скоростей:
Так как переносная скорость мгновенного центра скоростей Ре
равна нулю, то его абсолютная скорость vp равна относительной
скорости, которая определяется как вращательная скорость вокруг
центра Рг. Скорость vP направлена перпендикулярно отрезку РтРе
в сторону относительного вращения, а ее модуль равен:
Так как относительная скорость мгновенного центра скоростей Рт
равна нулю, то его абсолютная скорость vPr равна переносной
скорости, представляющей собой вращательную скорость вокруг
центра Ре. Скорость vp направлена перпендикулярно отрезку РеРг
в сторону переносного вращения, а ее модуль равен
Изобразив абсолютные скорости точек Ре и Рг (рис. 366,15),
найдем мгновенный центр скоростей Р абсолютного движения
399

плоской фигуры /// как точку пересечения отрезка, соединяющего
концы скоростей \р и \р с отрезком РеРг (§ 102).
Пользуясь пропорциональностью скоростей точек их расстояниям
от мгновенного центра скоростей Р абсолютного движения, опре-
определим расстояния от точки Р до точек Ре и Р/.
Р Р VD Р Р -со Р Р со
рр — vD — рр .и ' рр—~^-- u^.i;
г	Рг	гее	г	е
Мгновенная ось абсолютного вращения Q проходит через мгно-
мгновенный центр скоростей Р.
Таким образом, мгновенная ось абсолютного вращения пло-
плоской фигуры лежит в плоскости, проходящей через оси пере-
переносного и относительного вращений, и, будучи параллельной
им, делит расстояние между этими осями на части, обратно
пропорциональные угловым скоростям.
Для определения угловой скорости ш абсолютного вращения
плоской фигуры /// воспользуемся скоростью точки РТ — мгновен-
мгновенного центра скоростей относительного движения.
Так как относительная скорость точки Рт равна нулю, то абсо-
абсолютная и переносная скорость этой точки равны между собой.
Модуль абсолютной скорости точки Рг, как вращательной вокруг
центра Р, равен произведению модуля неизвестной угловой скорости «>
на расстояние РРТ этой точки от мгновенной оси абсолютного вра-
вращения плоской фигуры.
Модуль переносной скорости этой точки равен произведению
модуля угловой скорости <ае на расстояние РеРт от точки до мгно-
мгновенной оси переносного вращения плоской фигуры.
Приравнивая эти значения, получаем
РРт . с = РеРг . а)е == (РеР 4- РРГ) ¦ и>е = РеР ¦ ше + РРТ ¦ ше.
Из условия A32.1) следует
Подставляя это значение, находим
РРт . ш = РГР ¦ и>г + г е
откуда
u) = cor-j-u)e>	A32.2)
m. e. модуль абсолютной угловой скорости равен сумме моду-
модулей угловых скоростей составляющих вращений.
Рис. 366,E позволяет установить, что абсолютное вращение
плоской фигуры направлено против движения часовой стрелки,
т. е. в сторону составляющих вращений.
Направляем вектор абсолютной угловой скорости ы по оси 2
(рис. 366,а) так же, как направлены векторы ые и ыг.
Случай II. Переносное и относительное вращения напра-
направлены в разные стороны, а модули их угловых скоростей не равны.
400

Определим абсолютное движение плоской фигуры /// в случае,
когда переносное вращение вокруг оси Йе и относительное враще-
вращение вокруг оси Qr имеют противоположные направления и модули
угловых скоростей ше и шг не равны между собой (рис 367,а). Усло-
Условимся при выполнении построений считать,-что шг > ше.
Так как переносная скорость мгновенного центра скоростей Ре
равна нулю, то его абсолютная скорость равна относительной ско-
скорости — вращательной скорости вокруг центра Р/.
;
Аналогично абсолютная скорость мгновенного центра скоростей Рг
равна его переносной скорости — вращательной скорости вокруг
центра Ре:
Показав абсолютные скорости точек Ре и Рг (рис. 367,б), най-
найдем мгновенный центр скоростей Р абсолютного движения плоской
Рис. 367.
фигуры /// как точку пересечения прямой, проведенной через концы
скоростей хр и хр с продолжением отрезка РеРг (§ 102).
Определим расстояния от точки Р до точек Ре и Р/.
Р Р
е
РгРе
Р Р
Р Р
е
A32.3)
Мгновенная ось абсолютного вращения Q проходит через мгно-
мгновенный центр скоростей Р.
Таким образом, мгновенная ось абсолютного вращения плоской
фигуры параллельна осям переносного и относительного враще-
вращений а лежит в плоскости, проходящей через эти оси, со сто~
роны той оси, угловая скорость вращения вокруг которой больше.
Расстояния между осью абсолютного вращения и осями
переносного и относительного вращений обратно пропорцио-
пропорциональны угловым скоростям.
401

Для определения угловой скорости абсолютного вращения пло-
плоской фигуры /// воспользуемся скоростью точки Рт.
Приравниваем модули абсолютной скорости точки Рт— враща-
вращательной вокруг центра Р и переносной скорости этой точки — вра-
вращательной вокруг центра Ре:
РРГ ¦ *> = РеРт ¦ ше = (РеР-Рг
Из условия A32.3) следует, что
РеР-ше =
Подставляя это значение, находим
РРГ • со = Pf . <»Г
откуда
ш = шг — ше,	A32.4)
т. е. модуль абсолютной угловой скорости равен разности
модулей угловых скоростей составляющих вращений.
Рис. 367,6" показывает, что абсолютное вращение плоской фи-
фигуры направлено против движения часовой стрелки, т. е.
в сторону относительного вращения, угловая скорость которого
по модулю больше угловой скорости переносного вращения.
Откладываем (рис. 367,а) по оси Q вектор угловой скорости со
абсолютного вращения, направляя его так же, как направлен век-
вектор юг.
Необходимо отметить, что три мгновенных центра скоростей
переносного, относительного и абсолютного движений плоской
фигуры всегда лежат на одной прямой.
Рассмотренное составное движение плоской фигуры в ее пло-
плоскости представляет собой сложение плоских движений твердого тела,
происходящих параллельно одной и той же плоскости или сложение
вращений твердого тела вокруг параллельных осей.
Результаты рассмотренных случаев показывают, что сложение
параллельных векторов угловых скоростей осуществляется по извест-
известному правилу сложения параллельных скользящих векторов, т. е.
так же, как и сложение параллельных сил.
Случай III. Переносное и относительное вращения на-
направлены в разные стороны, а модули их угловых скоростей
равны.
Определим абсолютное движение плоской фигуры /// в случае,
когда переносное вращение вокруг оси 2е и относительное враще-
вращение вокруг оси Qr направлены в разные стороны (рис. 368,а), а мо-
модули их угловых скоростей равны, т. е.
Покажем, что в этом случае абсолютные скорости всех точек
фигуры /// геометрически равны. Фигура /// совершает составное
движение, а потому абсолютная скорость любой точки этой фигуры
402

равна геометрической сумме ее переносной и относительной ско-
скоростей:
Переносная скорость \е точки М фигуры /// (рис. 386,tf) пер-
перпендикулярна отрезку РеМ, а ее модуль равен:
vt=:PtM.tae.
Относительная скорость vr этой точки перпендикулярна от-
отрезку РГМ, а ее модуль равен:
Строим параллелограмм скоростей и находим абсолютную ско-
скорость V-
Рис. 368.
Треугольники Мае и РеМРт подобны, так как стороны Ma = ve
и ac = vr пропорциональны сторонам РеМ и РГМ, а ?_Мас =
= ?,РеМРт как углы со взаимно перпендикулярными сторонами.
Из подобия этих треугольников находим:
РеМ
¦ ргм
или v —
Так как две стороны Ма и ас треугольника Мае перпендику-
перпендикулярны двум сторонам РеМ и РТМ треугольника РеМРг, то и
третьи стороны этих треугольников должны быть взаимно перпен-
перпендикулярны, т. е. скорость абсолютного движения точки v направлена
перпендикулярно отрезку PJPr-
Так как точка М выбрана произвольно, то абсолютная скорость
любой точки плоской фигуры /// направлена перпендикулярно от-
отрезку PfP,, а ее модуль равен произведению расстояния между
мгновенными центрами скоростей переносного и относительного дви-
движений на модуль угловой скорости одного из составляющих враще-
вращений (рис. 368,а и б). Следовательно, скорости всех точек фигуры ///
геометрически равны, т. е. мгновенный центр скоростей абсолют-
абсолютного движения этой фигуры Р находится в бесконечности, а угло-
угловая скорость ее абсолютного вращения равна нулю (§ 102, рис. 262,в).
403

Если за все время движения направления составляющих вра-
вращений остаются взаимно противоположными, а угловые скорости
равными по модулю, то фигура /// совершает поступательное дви-
¦жение. Совокупность двух вращений тела, направленных в противопо-
противоположные стороны и имеющих равные мо-
модули угловых скоростей, называют парой
вращений.
Так как фигура /// представляет собой
сечение некоторого тела плоскостью,
можно считать установленным, что в слу-
случае, если в течение некоторого проме-
промежутка времени тело участвует в двух
противоположно направленных вращениях
вокруг параллельных осей с равными по
МОДУЛЮ УГЛОВЫМИ СКОРОСТЯМИ @j = Ш2 = «О,
то его движение поступательное (рис. 369).
Модуль скорости этого движения равен
произведению модуля угловой скорости <о
на расстояние между осями вращений:
v= cud.
Рис. 369.
Вектор скорости v направлен перпендикулярно плоскости пары
угловых скоростей со1, оJ в ту же сторону, в какую направлен
вектор момента пары сил М по отношению к паре сил Р, Р' (§ 40).
Следовательно, вектор скорости поступательного движения тела
представляет собой момент пары угловых скоростей.
Таким образом, сложение векторов угловых скоростей как пере-
пересекающихся, так и параллельных, производится так же, как и сло-
сложение сил; это закономерно,
так как векторы угловых
скоростей и сил являются
скользящими векторами.
Случай пары угловых ско-
скоростей аналогичен случаю
пары сил.
Так же, как и момент
пары сил, вектор скорости
поступательного движения—
вектор свободный, так как
он относится к любой точке
-тела.
Примером пары враще-
Рис. 370.
ний является движение вело-
велосипедной педали АВ относительно рамы велосипеда (рис. 370).
Это движение представляет собой совокупность переносного враще-
вращения вместе с кривошипом Ofi^ вокруг оси Ог и относительного
вращения педали по отношению к кривошипу вокруг оси О2.
404

Педаль АВ за все время движения остается параллельной своему
первоначальному положению, т. е. совершает поступательное движе-
движение, вследствие того, что угловые скорости составляющих вра-
вращений 0)г И
влению.
ео2 равны по модулю и противоположны по напра-
§ 133. Примеры на сложение вращений твердого тела
вокруг параллельных и пересекающихся осей
Пример 93. Кривошип ОА эпициклического механизма равно-
равномерно вращается с угловой скоростью % против движения часовой
стрелки и приводит в движение колесо /У. Зная радиусы колес г^
и г2. вычислить абсолютную угловую
скорость ю2 колеса // и его относи- а)
тельную угловую скорость аг по отно-
отношению к кривошипу ОА (рис. 371, а)
Решение. Абсолютное движение
колеса II представляет собой враще-
вращение вокруг мгновенной оси, проходя-
проходящей через мгновенный центр скоростей
колеса — точку Р соприкасания колес
(рис. 371, б). Это вращение можно раз-
разложить на два составляющих враще-
вращения: переносное вращение вместе
с кривошипом с угловой скоростью
сае = и0 вокруг оси О (Ре) и относи-
относительное вращение по отношению
к кривошипу вокруг оси, проходящей
через ось колеса А (Рт) с угловой ско-
скоростью сог. Действительно, двигаясь
с кривошипом, видим движение коле-
колеса II как вращение вокруг оси А.
Так как абсолютный мгновенный
центр скоростей Р находится между
переносным и относительным мгновен-
мгновенными центрами скоростей, то абсо-
абсолютное вращение направлено в сторо-
сторону составляющих вращений, т. е. про-	Рис. 371.
тив движения часовой стрелки, а
модуль абсолютной угловой скорости равен сумме модулей относи-
относительной и переносной угловых скоростей:
Определим юг, пользуясь соотношением A32Л):
РТР
405

Определив wr, найдем модуль абсолютной угловой скорости ш2 колеса /Л
Ш2 = ше + "V = ш0 Н- ш0 7Г- '
откуда
Пример 94. Линейка Ли эллипсографа приводится в движение
кривошипом ОС который вращается с угловой скоростью со0 вокруг
оси О в сторону, обратную движению часовой стрелки.
ОС = АС = ВС.
Определить относительную угловую скорость линейки по отно-
отношению к кривошипу и ее абсолютную угловую скорость (рис. 372,а).
Решение. Построим абсолютный мгновенный центр скоростей
линейки как точку пересечения перпендикуляров к траекториям
точек А и В (рис. 372,6).
Разложим абсолютное вращение
линейки вокруг точки Р на два
составляющих вращения: пере-
переносное вращение вместе с кри-
кривошипом ОС вокруг оси О (Ре)
с угловой скоростью а>/? = ш0 и
относительное вращение по отно-
отношению к кривошипу с угловой
скоростью шг. Центром этоговра-
щения Рг является ось шарнира С,
так как точка С является общей
для линейки и кривошипа и в от-
относительном движении по отно-
отношению к кривошипу не участ-
участвует. ' Если двигаться вместе
с кривошипом, то можно видеть
движение линейки как вращение
вокруг точки С.
Так как точка Р лежит вне
отрезка РеРг то направление
относительного вращения противоположно направлению переносного
и модуль абсолютной угловой скорости равен разности модулей
угловых скоростей сог и ы>е. При таком положении точки Р напра-
направление абсолютного вращения совпадает с направлением относитель-
относительного вращения.
Определяем модули относительной и абсолютной угловых скоро-
скоростей линейки:
^- = ^4 = ^=2: со, = 2.,^;
Рис. 372.
РГР
ОС
406

Пример 95. Определить относительную угловую скорость ведо
мого колеса // передачи по отношению к ведущему колес} / и абсо-
абсолютную угловую скорость колеса //, если известны радиусы ко-
колес гх и г2 и угловая скорость
ведущего колеса <аг (рис. 373,а).
Решение. Разложим абсолют-
абсолютное вращение колеса // вокруг его
центра (рис. 373,tf) на переносное
вращение вместе с колесом / во-
вокруг его центра Ре с угловой
скоростью сое = ш1 и относительное
вращение по отношению к колесу /
с угловой скоростью шг. Мгновенным
центром относительного вращения Рт
является точка соприкасания колес:
эта точка колеса // не участвует
в движении по отношению к ко-
колесу /. Если двигаться вместе
с колесом /, то можно увидеть
движение колеса // как качение
по колесу /, т. е. как вращение
вокруг точки Рг. По расположе-
расположению точек Ре, Pr, P (второй слу-
случай) показываем направление относительного и абсолютного враще-
вращений колеса // и определяем модули их угловых скоростей:
Рис. 373.
PrP	«1	Гг	Г	]
	 	 	 rK-\-r2
r2
Пример 96. Кривошип ОА, вращаясь вокруг оси О с угловой
скоростью ш0 по направлению движения часовой стрелки, приводит
в движение зубчатое колесо //, катящееся внутри неподвижного ко-
колеса ///. Колесо // приводит в движение колесо /, находящееся
с ним в зацеплении и вращающееся вокруг оси О (рис. 374,а).
Определить угловую скорость колеса /, если числа зубьев колес /
и // соответственно равны zl и z2-
Решение. Разложим абсолютное вращение каждого колеса на
два составляющих вращения: переносное вращение вместе с криво-
кривошипом вокруг оси О с угловой скоростью ш^ = ш0 и относительное
вращение по отношению к кривошипу с угловой скоростью и>(Г.
Двигаясь вместе с кривошипом, видим движение каждого
колеса как вращение вокруг его центра. Следовательно, относи-
относительное вращение каждого колеса происходит вокруг его центра
и относительные угловые скорости колес обратно пропорциональны
радиусам колес или их числам зубьев.
407

В первую очередь устанавливаем относительную угловую скорость
Неподвижного колеса. Двигаясь вместе с кривошипом, видим непо-
неподвижное колесо вращающимся в направлении, обратном направле-
направлению вращения кривошипа, причем модуль его угловой скорости
шзг = % (Рис- 374,<5).
Колеса // и /// образуют внутреннее зацепление, а поэтому
направления их относительных вращений совпадают. Направления
Ш
Рис. 374.
относительных вращений колес I и II противоположны, так как их
зацепление внешнее.
Пользуемся зависимостью между модулями относительных угло-
угловых скоростей:
ШЗГ
Перемножая части равенств, получаем
2-t	Z<k
: —-, откуда ш1г = —- oK = -
Z\	Zi
Так как направление относительного вращения колеса / совпа-
совпадает с направлением переносного вращения, то модуль его абсолют-
абсолютной угловой скорости равен сумме модулей угловых скоростей пере-
переносного и относительного вращений:
Ш1 = <°е + Ш1г = ШО + -~ ШО = ШО ' Jt ' •
По чертежу (рис. 374,а) находим:
Числа зубьев пропорциональны радиусам колес, т. е.
Тогда имеем
408

Пример 97. Шестерня 4 планетарного зубчатого механизма, изо-
изображенного на рис 375, а, свободно насажена на конце рукоятки О А,
которая вращается вокруг оси О неподвижной шестерни / с по-
постоянной угловой скоростью <о0 против движения часовой стрелки.
Ось двойной шестерни 2—3, соединенной с рукояткой О А, нахо-
находится в зацеплении с шестернями 1 и 4; числа зубьев шестерен
соответственно равны zv z2, zz, ^.Опре-
^.Определить, угловую скорость шестерни 4.
Решение. Примем вращение ру-
рукоятки ОА вокруг оси О за перенос-
переносное вращение и найдем угловые ско-
скорости относительных вращений шестерен
по отношению к рукоятке (рис. 375,6).
Относительное вращение неподвижной
шестерни 1 происходит вокруг оси О
навстречу вращению рукоятки с угло-
угловой скоростью, модуль которой равен
модулю угловой скорости рукоятки:
<olf = (й0.
Направление относительных враще-
вращений двойной шестерни 2—3 и шестер-	Рис. 375.
ни 4 показаны на рис. 375,E".
Модули относительных угловых скоростей шестерен обратно про-
пропорциональны числам их зубьев, т. е.
- = f (а);
= 2±. (б).
Шестерни 2—3 связаны между собой жестко, а поэтому
Ш2г =
Перемножая (а) и (б), получаем
откуда
Так как переносное и относительное вращения шестерни 4 на-
направлены противоположно, то, полагая ие > шг, найдем ш4 как раз-
разность модулей ее переносной и относительной угловых скоростей:
откуда
27 А. А. Яблонский
409

На рис. 375,6" абсолютное вращение шестерни 4 направлено в сто-
сторону переносного вращения, так как положено тв > шг, т. е.
В случае 1 < -j-~ направление абсолютного вращения шестерни 4
противоположно указанному.
Пример 98. Редуктор скоростей, изображенный на рис. 376,а, б,
служит для передачи вращения от ведущего вала / ведомому валу //,
ось которого совпадает с осью вала /. Редуктор имеет два ведущих
элемента: вал /, вращающийся с угловой скоростью пх = 800 об/мин.
Рис. 376.
и колесо /, вращающееся в противоположную сторону с угловой
скоростью ях = 200 об/мин. Ведущие элементы приводят в дви-
движение спаренные между собой шестерни 2—3, свободно насаженные
на концах Ау и Л2 рукоятки, заклиненной на ведущем валу. При
этом шестерни 2 находятся в зацеплении с ведущим колесом 1,
а шестерни 3 — с колесом 4, заклиненным на ведомом валу //. От
шестерен 3 получает движение колесо 4, а следовательно, и ведо-
410

мый вал //. Радиусы колес соответственно равны: гх = 30 см;
г2 = 15 см; г3 = 30 см; г4 = 75 см. Определить угловую скорость
ведомого вала // и шестерен 2—3.
Решение. I способ. Применяем теорию сложения вращений
тела вокруг параллельных осей. Предположим, что вращение веду-
ведущего вала с угловой скоростью аO происходит по движению часовой
стрелки, а вращение колеса 1 с угловой скоростью ш1 — в противо-
противоположную сторону (рис. 376,б). Разложим движение каждого элемента
редуктора на два составляющих вращения: переносное враще-
вращение с валом, на котором заклинена рукоятка, несущая оси шесте-
шестерен (в данной задаче вместе с ведущим валом /), и относитель-
относительное вращение по отношению к этому валу.
Вращение, принятое за переносное, происходит вокруг оси О
с известной угловой скоростью <ае — (о7. Относительные вращения
колес 1 а 4 происходят вокруг оси О, а колес 2—3 — вокруг
осей Ах и Л2. т. е. относительные вращения всех колес происходят
вокруг осей, проходящих через их центры, и, следовательно, модули
их угловых скоростей обратно пропорциональны радиусам или числам
зубьев колес (см. § 95). Определим модули угловых скоростей и на-
направления относительных вращений всех колес, пользуясь модулем
заданной абсолютной угловой скорости Wj колеса 1.
Так как колесо 1 вращается навстречу валу /, то его относи-
относительное вращение происходит в ту же сторону и модуль относительной
угловой скорости оIг равен сумме модулей угловых скоростей <о7
и cdj, т. е.
a)ir = 0)/ + '°r	(а)
Относительное вращение шестерни 2, образующей с колесом 1
внешнее зацепление, направлено противоположно относительному вра-
вращению колеса /, т. е. по движению часовой стрелки. Шестерня 3,
спаренная с шестерней 2, совершает это же движение. Колесо 4,
образующее с шестерней 3 внутреннее зацепление, вращается в сто-
сторону вращения шестерни 3, т. е. по движению часовой стрелки.
Модули угловых скоростей этих вращений определяются по формулам:
7	(б)
Так как о>2г = со3г, то, перемножив пропорции (б) и (в), получим
откуда со4г = со1г
Подставив значение ю1г определяемое формулой (а), получим
Так как направления относительного и переносного вращений
колеса 4 совпадают, то модуль его абсолютной угловой скорости
27*	411

равен сумме модулей переносной и относительной угловых скоростей:
Ш4 = ше + Ш4г = ш1 -Н«/+ «О ~--	(Г)
'2Г4
Угловая скорость ведомого вала // равна угловой скорости закли-
заклиненного на нем колеса 4. Вычислим ее модуль по формуле (г) в об{ман'.
Пц = «4 =
= 800 + (S00 + 200) j^ = 1600 обIмин.
Абсолютное вращение колеса 4 с ведомым валом // происходит
в сторону составляющих вращений, т. е. по движению часовой стрелки.
Для определения движения шестерен 2—3 найдем модуль их от-
относительной угловой скорости из пропорции (б):
Ш2г = №ir 77 — О/+ ^i) 77'
Так как направления относительного и переносного вращений
шестерен 2—3 совпадают, то модуль их абсолютной угловой скорости
равен сумме модулей относительной и переносной угловых скоростей:
+ °>)
Вычисляя в o6jmuh, получаем
л2 = W/+(й; -f «!> -^- = 800 + (800 + 200) -^г- = 2800 об/мин.
Абсолютное вращение шестерен 2—3 происходит в сторону
составляющих вращений, т. е. по движению часовой стрелки.
II способ. Применяем теорию плоского движения твердого тела.
По модулям угловых скоростей ведущих элементов найдем модули
вращательной скорости точки Ах оси спаренных шестерен и враща-
вращательной скорости точки В касания колес / и 2 (рис. 376,в):
кп. л-800 80
теп, я-200 20
Ш1 ~ "Ж" ~~ 30 ~ Т % СвК '
80
vAi — (в7 {гх -\- г2) = -к- тс - 45 = 1200тс см{сек\
20
vB = шхгх = -д- тс . 30 = 200ic см/сек.
Отложим векторы \А и vB по их истинным направлениям.
Зная скорости точек Ахж В плоской фигуры, построим мгновен-
мгновенный центр скоростей шестерен 2—3 (§ 102) и определим его
положение:
200*

Так как
то
Определим модуль скорости точки С:
300
vr Р9 ЧС ~ 10	10 10
-?- = 7±±г='=~; г»с = тг»д, = ^-12ООи = 4ООО«
7
По модулю скорости одной из точек находим модуль угловой
скорости шестерен 2—3:
ьл 1200л; 280
сек~и,
30 280
По модулю скорости точки С, принадлежащей также и колесу^ 4,
находим модуль его угловой скорости:
160*
= 1600 об мин,
пп = п4 — 1600 об/мин.
На рис. 376,в показаны истинные направления вращений всех
элементов редуктора.
Пример 99. Рукоятка ОА вращается вокруг оси О неподвижной
шестерни радиусом г =10 см в направлении, противоположном на-
направлению движения часовой стрелки, с постоянной угловой скоростью
<во = 2 сея;" и соединена с осями трех других шестерен того же
радиуса (рис. 377,а). Найти скорость и ускорение точки В
шестерни 4, лежащей в данный момент на конце диаметра, перпен-
перпендикулярного оси рукоятки.
Решение. Определим прежде всего абсолютную угловую ско-
скорость а>4 шестерни 4. Для этого примем вращение рукоятки ОА
вокруг оси О за переносное вращение и найдем угловые скорости
относительных вращений шестерен по отношению к рукоятке
(рис. 377,6"). Относительное вращение неподвижной шестерни / про-
происходит вокруг оси О навстречу вращению рукоятки с угловой
скоростью, равной по модулю угловой скорости рукоятки, т. е.
(о1г = ш0.
413

Направления относительных вращений шестерен /, 2, 3, 4, обра-
образующих рядовое зацепление, показано на рис. 377,6. Относительная
угловая скорость шестерни 4 определяется (см. § 95) по формуле!
Переносное и относительное вращения шестерни 4 происходят
против движения часовой стрелки. Следовательно, ее абсолютное
вращение направлено в ту же сторону, а модуль абсолютной угловой
скорости равен:
ш4 = ше -j- w4r = 2ш0 = 4 сек~г-
Для определения скорости и ускорения точки В удобнее разло-
разложить плоское движение шестерни 4 не на два составляющих вра-
вращения, а на поступательное движение с полюсом А и вращение
с угловой скоростью 1»4 вокруг этого полюса.
а)
Рис. 377.
Тогда скорость точки В определится как геометрическая сумма
скорости полюса А и вращательной скорости точки В вокруг
полюса А (рис. 377,6).
Модуль скорости полюса А
©л = ОЛш0 = 6по0 = 6 ¦ 10-2=120 см/сек.
Модуль вращательной скорости точки В во вращении шесте-
шестерни 4 вокруг полюса А
vAB = АВ ¦ ш4 = 10 • 4 = 40 см/сек.
Модуль абсолютной скорости точки В
* 126 см\сек.
Ускорение точки В определится как геометрическая сумма уско-
ускорения полюса А и ускорения точки В во вращении вокруг полюса А
414

(рис. 377,8). При равномерном вращении рукоятки ускорение полюса
вычисляется как центростремительное:
wA = «И» = О А • cog — 6ГШ2 = 60 • 4 = 240 см/сен?.
При равномерном вращении рукоятки шестерня 4 вращается равно-
равномерно и ускорение точки В во вращении шестерни 4 вокруг по-
полюса А тоже является центростремительным:
wab~
>2 = /-а>2= ю. 16 = 160 см/сек2.
Модуль абсолютного ускорения точки В
; = У2402Ч-1602= 288,5 см/сек2.
wB =
Пример 100. На рис. 378,а изображен механизм, называемый
двойным дифференциалом. На кривошип ///, вращающийся вокруг
неподвижной оси АВ, свободно насажен сателлит IV, состоящий
о)
б)
Рис. 378.
из двух наглухо скрепленных между собой конических зубчатых
колес радиусами /-j —6 см, и г2 = 3 см. Колеса сателлита сопри-
соприкасаются с двумя коническими зубчатыми колесами / и // радиу-
радиусами Rx = 12 см и /?2 = 6 см, вращающимися вокруг оси АВ, но
с кривошипом не связанными. Модули угловых скоростей колес /
и //, вращающихся в одном направлении, соответственно равны:
(й; = 4 сек'1 и <в7/ =
Определить угловую скорость кривошипа /// и угловую скорость
сателлита IV по отношению к кривошипу.
Решение. Сателлит IV участвует в двух вращениях вокруг
пересекающихся осей: в относительном вращении по отношению
к кривошипу ///, т. е. вокруг своей оси, и в переносном вращении
вместе с кривошипом III вокруг оси АВ. По условию задачи тре-
требуется определить угловые скорости этих вращений шг и и>е.
415

Так как известны модули угловых скоростей колес / и //, то
можно найти модули абсолютных скоростей точек М1 и М2 сопри-
соприкасания сателлита с этими колесами:
vx = /?j. Ш/ — 12 • 4 = 48 см/сек;
v2 = R2 • шп = 6 ¦ 8 = 48 см/сек.
Пусть колеса I и II вращаются против движения часовой-
стрелки, если смотреть сверху. Тогда, если смотреть справа, векторы
Vj и v2 будут направлены так, как показано на рис. 378,<>.
Переносные и относительные скорости точек Мг и М2 парал-
параллельны их абсолютным скоростям. Зададимся такими направлениями
переносного и относительного вращений, чтобы в результате сло-
сложения переносной и относительной скоростей каждой из точек Mt
и М2 получились абсолютные скорости vt и v2.
Предположим, что переносное вращение сателлита IV вокруг
оси АВ, если смотреть сверху, происходит против направления движе-
движения часовой стрелки, а его относительное вращение вокруг своей оси,
если смотреть справа, — по направлению движения часовой стрелки.
Тогда переносные и относительные скорости точек Му и М2
будут иметь направления, показанные на рис. 378,б. Уравнения,
выражающие теорему о сложении скоростей, примут вид:
ve, — Vr, — Vv Ve, + «г, = V2.
Здесь
Подставив эти значения, будем иметь
Подставив числовые значения, получим
12шв — 6о), = 48, \ 2we — шг = 8,
) ИЛИ
Решив систему уравнений, найдем
№е = 6 сек'1, <ог = 4 сек~х.
Положительные ответы указывают, что принятые направления
относительного и переносного вращений сателлита совпадают с дей-
действительными.
§ 134. Общий случай сложения движений твердого тела.
Аналогии со статикой
В § 129 и 132 рассмотрено сложение вращений твердого тела
векруг пересекающихся и параллельных осей и установлено, что
сложение параллельных и пересекающихся векторов угловых ско-
416

ростей производится по тем же правилам, как сложение векторов
сил в статике.
Рассмотрим общий случай сложения движений твердого тела,
одновременно участвующего в нескольких вращательных движениях
вокруг произвольно расположенных мгновенных осей и в нескольких
поступательных движениях. Покажем, что к системе угловых ско-
скоростей можно применить метод приведения к произвольно выбран-
выбранному центру, аналогичный методу Пуансо, применяемому в статике
к системе сил.
Вектор угловой скорости, так же как и вектор силы, является
скользящим вектором потому, что его можно отложить от любой
точки оси вращения тела. Вектор угловой скорости так же как и
вектор силы, нельзя просто перенести с одной оси на другую парал-
параллельную ей ось; это означало бы замену
вращения вокруг одной оси не эквивалент-
эквивалентным ему вращением вокруг другой оси.
Применим к вектору угловой скорости
приведение к заданному центру, анало-
аналогичное приведению силы. Предположим,
что дан вектор угловой скорости в>, при-
приложенный в точке А, и требуется при-
привести его к заданному центру О (рис. 379).
Приложим в точке О два вектора
ft)" = ft) и <»>' =	(J).
Вектор ю в точке А и вектор ft>'
в точке О образуют пару угловых ско-	рис> 379.
ростей.
Вектор момента этой пары v, согласно § 132, равен вектору поступа-
поступательной скорости v0. Проведем из центра приведения О в точку А ра-
радиус-вектор г и определим момент полученной пары угловых скоростей:
Кроме вектора поступательной скорости v0, имеется вектор угло-
угловой скорости ю", равный вектору «о, но приложенный в центре
приведения О.
Таким образом, вектор угловой скорости можно перенести
Параллельно его первоначальному положению в любой центр
приведения, присоединив вектор поступательной скорости,
равный моменту заданной угловой скорости относительно
атого центра.
Это означает, что вращению вокруг оси, проходящей через
точку А, с угловой скоростью w, эквивалентно вращение вокруг
параллельной оси, проходящей через точку О, с угловой скоростью
и" = о) в совокупности с поступательным движением со скоростью Vq.
Модуль и направление момента v пары угловых скоростей ft), <й'
определяются так же, как в статике определялись модуль и напра-
направление момента М пары сил Р, Р'.
417

При этом
v = v0 = to ¦ d,
где v0 — скорость поступательного движения, соответствующего
приведенной паре угловых скоростей.
Предположим теперь, что в некоторый момент времени дана си-
система угловых скоростей Wj, ta2, .... е>л, приложенных в точках Alt
А2	Ап, и система поступательных скоростей щ, щ, ..., ил,
характеризующих движение твердого тела (рис. 380). Выберем произ-
произвольный центр .' приведения О и приведем все векторы Юр щ, ..., <ап
к ьтому центру. •
Приведенные векторы, согласно § 129, можно заменить одним
вектором <й, равным их геометрической сумме:
При переносе векторов ь>1, to2, . .,, м„ в точку О образовалось я
пар угловых скоростей.
Момент каждой присоединенной пары угловых скоростей равен
соответствующей поступатель-
поступательной скорости:
где Г! =
Так как поступательные
скорости являются свободными
векторами, то их можно пере-
перенести в центр приведения.
Результирующую поступа-
Рис. 380.	тельную скорость v0 найдем
как геометрическую сумму по-
поступательных скоростей v10, v20, .. ., vn0, соответствующих парам
угловых скоростей, и скоростей заданных поступательных движений
твердого тела щ, и2, ..., и„:
Таким образом, в результате приведения заданная совокупность
движений твердого тела оказалась замененной одним вращением
вокруг мгновенной оси 2, проходящей через точку О, с угловой
скоростью w и поступательным движением со скоростью \0.
Эта замена движений эквивалентными движениями аналогична
замене заданной системы сил и пар в статике одной силой, равной
418

главному вектору R*, и одной парой с моментом, равным главному
моменту сил относительно центра приведения М = М0.
Рассмотрим возможные случаи приведения аналогично тому, как
это проводилось в разделе „Статика".
Случай I: ю = 0 и vo = 0. Тело находится в состоянии покоя*.
В статике аналогичным является случай, когда R* = 0 и Мо = 0,
при котором силы уравновешиваются.
Случай II! ю = 0, v0 Ф 0. Тело движется поступательно.
Скорость этого движения v0 можно рассматривать как момент
пары угловых скоростей (рис. 381), модуль которого
v0 = v = wd.
В статике этому случаю соответ-
соответствует пара сил, момент которой
M = Pd (рис. 382).
Рис. 381.
Рис. 382.
Рис. 383.
Рис. 384.
Случай III: u> Ф 0, vo = 0. Тело совершает сферическое движе-
движение вокруг точки О с угловой скоростью о) (рис. 383), а в случае
неизменности направления и> вращается вокруг неподвижной оси,
проходящей через точку О. В статике этому случаю соответствует
приведение сил к равнодействующей силе R, линия действия которой
проходит через центр приведения (рис. 384).
* Здесь и ниже имеется в виду, что указанные условия в отношении »
и \Q сохраняются в течение некоторого промежутка времени.
419

Случай IV: » Ф О, \0 Ф О и v,jj_w. Тело совершает плоское
движение. Пусть после приведения угловых и поступательных ско-
скоростей к центру О получен вектор w и вектор v0, перпендикуляр-
перпендикулярный w (рис. 385).
Заменим поступательную скорость v0 парой угловых скоростей
с моментом v = v0, лежащей в плоскости, перпендикулярной v,
выбрав угловые скорости рав-
равными по модулю ю и определив
плечо d = -?-. Поместим один из
векторов угловой скорости пары
I
Рис. 385.
Рис. 386.
вращений »' в точку О, а другой, равный w, в точку К на расстоя-
расстоянии OK = d, отложенном перпендикулярно ю в такую сторону,
чтобы по отношению к паре угловых скоростей вектор скорости
поступательного движения \о
был расположен так же, как
по отношению к паре сил
расположен ее момент М
(рис. 385 и 386).
Тогда равные и противо-
противоположно направленные век-
векторы ы и ю' в точке О
можно отбросить, так как
соответствующие им враще-
вращения взаимно компенсируются.
Остается только вектор «*,
приложенный в точке К-
Рис. 387.
Тело в этом случае вращается с угловой скоростью ю вокруг
мгновенной оси Q, лежащей в плоскости, перпендикулярной посту-
поступательной скорости v0 на расстоянии ОК =— от центра приве-
420

дения. В статике этому случаю соответствует приведение сил к равно-
равнодействующей силе, линия действия которой находится в плоскости,
перпендикулярной главному моменту Мо на расстоянии OK = ~s-
от центра приведения (рис. 386).
Случай V: о> Ф О, чоф0 и v0 не J_ w — общий случай движе-
движения свободного твердого тела. Пусть после приведения угло-
угловых и поступательных скоростей к центру О получены векторы ы
и v0 (рис. 387). Заменим поступательную скорость v0 парой угло-
угловых скоростей произвольной величины taj и Wj с моментом v = v0
и плечом OK = d = —.
Сложив по правилу параллело-
параллелограмма векторы угловых скоростей
w и й)| в точке О, получим
Движение тела сводится к двум
вращениям вокруг скрещиваю-
скрещивающихся мгновенных осей Qn и 2,,
проходящих через точки О и К,	Рис. 388.
С УГЛОВЫМИ СКОРОСТЯМИ б)]] И 0)j.
В статике этому случаю соответствует приведение сил к двум
скрещивающимся силам Р и Q (рис. 388).
Л.
Рис. 389.
Рис. 390.
Рассмотрим другое представление этого же случая. Пусть после
приведения угловых и поступательных скоростей к центру О полу-
421

чены вектор ft) и вектор поступательной скорости vo = v, не пер-
перпендикулярный о) (рис. 389). Разложим поступательную скорость
на две скорости: v*, направленную вдоль вектора to, и v', перпен-
перпендикулярную to. Поступательную скорость v' заменим парой угло-
вых скоростей о>7 и о> с плечом ОС = d = —.
Векторы о) и о)' в точке О как равные по модулю и противопо-
противоположно направленные отбросим, а момент пары вращений v* как сво-
свободный вектор перенесем из точки О в точку С.
Тогда векторы w и v* будут направлены вдоль одной прямой,
проходящей через точку С.
Таким образом, движение свободного твердого тела можно рассмат-
рассматривать как совокупность его вращения с угловой скоростью ю во-
вокруг мгновенной оси 2в и поступательного движения вдоль этой
оси со скоростью v*.
Совокупность этих движений называется мгновенным винтовым
движением, а мгновенная ось Qe называется мгновенной винтовой
осью. Так как точки мгновенной винтовой
оси не участвуют во вращении, то их ско-
скорости геометрически равны v*.
Таким образом, мгновенная винтовая
ось представляет собой геометрическое
место точек тела, скорости которых
равны по модулю и направлены вдоль
этой оси.
В статике этому случаю соответствует
приведение сил к динаме (рис. 390).
Общий случай движения свободного твер-
твердого тела можно представить в виде^мгно-
венного винтового движения или в виде двух
мгновенных вращений вокруг скрещиваю-
скрещивающихся осей. Если принять за полюс какую-
либо точку С мгновенной винтовой оси, то скорость любой точки
тела М определится как диагональ прямоугольника, построенного на
скорости полюса v* и вращательной скорости точки М вокруг мгно-
мгновенной винтовой оси (рис. 391):
Рис. 391.
Здесь v' — со • hse, где Пяв — перпендикуляр, опущенный из
точки М на мгновенную винтовую ось.
При увеличении расстояния hag точки от мгновенной винтовой
оси увеличивается ее вращательная скорость г»', а следовательно,
и абсолютная скорость точки vM.
Положение мгновенной винтовой оси как в неподвижном про-
пространстве, так и в движущемся теле с течением времени изменяется.
Линейчатая поверхность, представляющая собой геометри-
геометрическое место мгновенных винтовых осей в неподвижном про-
422

странстве, называется неподвижным аксоидом мгновенных
винтовых осей.
Линейчатая поверхность, представляющая собой геометри-
геометрическое место мгновенных винтовых осей в движущемся теле,
называется подвижным аксоидом мгновенных винтовых осей.
В каждый момент времени эти аксоиды соприкасаются по общей
производящей, являющейся мгновенной винтовой осью для данного
момента времени, и одновременно подвижной аксоид перемещается
относительно неподвижного со скоростью v*, направленнрй по линии
их соприкасания.
Таким образом, при действительном движении свободного твер-
твердого тела подвижной аксоид мгновенных винтовых осей катится по
Рис. 392.
Рис. 393.
неподвижному аксоиду и в то же время скользит вдоль линии их
соприкасания.
В статике установлена следующая зависимость между главным
моментом сил относительно центра приведения Мо, наименьшим
главным моментом системы сил М* и главным вектором R*:
где d — радиус-вектор произвольной точки центральной оси системы
сил относительно центра приведения (рис. 392).
В кинематике существует аналогичная зависимость между резуль-
результирующим вектором поступательных скоростей v0, наименьшей
поступательной скоростью v* и результирующим вектором угловых
скоростей ш:
где d — радиус-вектор произвольной точки мгновенной винтовой
оси относительно центра приведения (начала координат) (рис. 393).
28*
423

Выражая эту зависимость в проекциях на неподвижные оси декар-
декартовых координат х, у, г, получаем:
где л:, у, г — текущие координаты точек мгновенной винтовой оси.
Так как векторы v* и ю параллельны, то их одноименные про-
проекции пропорциональны.
Пользуясь этим, получим уравнения мгновенной винтовой оси:
•
ИЛИ
ух — {ущ2 — га>у) Ру — (гю ж — лга>г) Vг — (ха>у —
а>х	й)у	<лг	а>
Эти уравнения аналогичны уравнениям центральной оси системы
сил.
В статике установлены два инварианта системы сил:
R* = const, X24-K2-f-Z2 = const; I
R* • Л10 = ХМХ -f УМу -f- ZMt = const. /
В кинематике также имеются два инварианта, т. е. две величины,
не зависящие от положения центра приведения:
(о = const; (o^. -f- «»2 -f~ ш| = const; \
•» • vo=»Лг+ Vb + «Л = const. I
Минимальная поступательная скорость vm[n = v* направлена вдоль
мгновенной винтовой оси и ее алгебраическая величина равна:
v«Aa==v =00 COS (в), Vo);
с» • \ <t>xv!( Н~ "у^у "Г" "•«t'z
(I)	СО
Отношение минимальной поступательной скорости г»т1п к угло-
угловой скорости результирующего вращения тела ш называется пара-
параметром кинематического винта
•^ГОШ	r Ч	* * i У У 1 * *
" ш	се2	со2
Вопроси для самоконтроля
1.	Что представляет собой абсолютное движение тела, участвующего
в нескольких вращениях вокруг сходящихся мгновенных осей?
2.	Как по уравнениям сферического движения твердого тела опреде-
определяют его угловую скорость?
424

3.	Каковы проекции углового ускорения тела при сферическом движе-
движении на неподвижные и подвижные координатные оси?
4.	Как определяют угловую скорость твердого тела, вращающегося
вокруг двух параллельных осей в одну и в разные стороны?
5.	Что называют парой вращений и при каком условии пара вращений
эквивалентна поступательному движению? Чему равна скорость этого посту-
поступательного движения?
6.	Какие понятия статики аналогичны угловой скорости вращения тела
и поступательной скорости?
7.	В чем заключается правило приведения вектора угловой скорости
к заданному центру?
8.	Что представляет собой движение твердого тела, участвующего
в нескольких вращениях вокруг произвольных осей и в нескольких посту-
поступательных движениях?
9.	Сравните все возможные случаи приведения угловых и поступатель-
поступательных скоростей к заданному центру с аналогичными случаями приведения
системы сил в статике.
10.	Что называется мгновенной винтовой осью вращения твердого тела
и каковы ее уравнения?
11.	В каком виде при помощи мгновенной винтовой оси может быть
представлен общий случай движения свободного твердого тела?
12.	Что называют подвижным и неподвижным аксоидом мгновенных
винтовых осей и как перемещается подвижной аксоид при движении свобод-
свободного твердого тела?
13.	Укажите распределение скоростей точек свободного твердого
тела?
14.	Скорости каких точек свободного твердого тела являются наимень-
наименьшими?
15.	Скорости каких точек свободного твердого тела равны между собой
по модулю?
16.	Какие характеристики движения свободного твердого тела не зависят
от выбора центра приведения?
17.	Что называют параметром кинематического винта?

Физическая величина
название
Длина
Масса
Время
Сила
Вес
Плоский угол ....
Угловая скорость . .
Угловое ускорение . .
обозна-
обозначение
1
т
t
Р
а
. t
ш
е
Механические величины и единицы их
Формулы размерностей
в системе
LMT
(МКС и СГС)
в системе
LPT
(МКГСС)
1
М
L~l РТ3
Г
LMT~2
Р
1
r-s
измерения
Система единиц МКС
единица измерения
метр
килограмм
секунда
ньютон
(килограмм-метр
на секунду в квад-
квадрате)
радиан
радиан в секунду
радиан на секунду
в квадрате
сокращенное
обозначение
ж
кг
сек
н
(кг ¦м/сек?1)
•рад
сек~х
сек~2
Скорость
Ускорение
v \ LT~X
w
LT~2
метр в секунду " | ж/сек
метр на секунду
в квадрате
м/сек1
Площадь
L*
квадратный метр
Объем
Удельный вес ....
Плотность
Механическое напря-
напряжение, давление . .
Лмпульс силы ....
Количество движения
Момент силы
Момент инерции (ди-
(динамический) ....
Момент количества
движения
Работа
Энергия
V 1 I»
Г
р
Р
S
К
м
J
L
А
Е
N
L-*MT-*
L~3M
L~XMT-2
LMT~l
12МТ~г
L'M
l*mt-1
L2MT~2
L2Mr~3
l~3P
L'*PT2
L~*P
PT
LP
LPT'
LPT
LP
LPT~l
кубический метр
ньютон на кубиче-
кубический метр
килограмм на куби-
кубический метр
ньютон на квадрат-
квадратный метр
ньютон-секунда
килограмм-метр
в секунду
ньютон-метр
килограмм-метр
в квадрате
килограмм-метр
в квадрате в секунду
джоуль
ватт
м>
н/м*
(кг/мг'Секг)
кг/м*
н/м1
(кг/л ¦ сек1)
«.•сек
(кг-м!сек)
кг-м/сек
н-я
(кг-л2/сел2)
кг-мг
кг-м'/сек
дж
(кг-м'/сек')
em
(кг-м*1сек')
426

ПРИЛОЖЕНИЕ
Таблица 1
в системах СИ (МКС), СГС и МКГСС
Система единиц СГС	Система единиц МКГСС
сокращенное	сокращенное
единица измерения	обозначение	единица измерения	обозначение
сантиметр	см	метр	м
грамм	г	техническая единица массы (ки- т. е. м.
лограмм-сила-секунда в квад- ^сгс^сек'/м)
	рате на метр)
секунда	сек	секунда	сек
дина (грамм-сантиметр на	дин	килограмм-сила	кгс
секунду в квадрате)	(г-см/сек2)
радиан	• рад	радиан	рад
радиан в секунду	сек~	радиан в секунду	сек~
| радиан на секунду в квадрате сек~г радиан на секунду в квадрате	сек~
I сантиметр в секунду	| см/сек \ метр в секунду	| м/сек
сантиметр на секунду в квад- см/сек2 метр на секунду в квадрате м/сек2
	рате
I квадратный сантиметр	I	см*	| квадратный метр	|	м'
t кубический сантиметр	I	см^	| кубический метр	|	м^
| дина на кубический сантиметр дан/см' килограмм-сила на кубический кгс/м3
1	(гкм'-сек1) метр
! грамм на кубический санти- г/см" килограмм-сила-секунда в квад- кгс-сек21м*
метр рате на метр в четвертой
	степени
дина на квадратный санти- дан/см2 килограмм-сила-на квадратный кгс\м>
	метр	(г/си ¦ сек2)	метр
! дина-секунда диЯ'сек килограмм-сила-секунда
_'	(г-см/сек)		_	 кгсст
грамм-сантиметр в секунду	г-см/сек т. е. м. -метр в секунду
дина-сантиметр диН'СМ килограмм-сила-метр кгс-м
I	(г'См?1сек?)
1 грачм-сантичет) в квадрате г^см2 килограмм-сила-метр-се кгС'М-сек*
	кунда в квадрате
грамм-сантиметр в квадрате г-см2/сек килограмм-сила-четр-се-	кгс-М'Сек
	в секунду	кунда
I
эрг	(г-см^/сек1) килограмм-сила-метр	кгс-м
эрг в секунду	эрг/сек килограмм-сила-метр в се-	кгс-м/сек
(г-см'/сек3) кунду
28*
427

Таблица 2
Соотношения между единицами механических величин
Название
механической
величины
Масса
Сила
Работа
Мощность
Основные единицы измерения и соотношения
между единицами различных систем
1 килограмм (кг) = 0,102 т. е. м.
1 техническая единица массы (т. е. м.) == 9,81 кг
1 ньютон (к) = 105 дин = 0,102 кгс
1 килограмм-сила (кгс) = 9,81 н
1 джоуль (дж) = Ю7 эргов (эрг) = 0,102 кгс-м
1 килограмм-сила-метр (кгс ¦ м) = 9,81 дж
1 ватт-час (em • ч) = 3600 вт ¦ сек ¦=¦ 3600 дж
1 киловатт-час (кет ¦ ч) = 36 • 105 док
1 ватт (em) = 1 дж/сек = W эрг/сек = 0,102 кгс • м/сек
1 кгс ¦ м/сек == 9,81 вт
1 киловатт (кет) — 103 вт = 102 кгс ¦ м/сек = 1,36 л, с.
1 лошадиная сила (л. с.) = 75 кгс • м/сек = 736 вт = 0,736 кем

ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиомы статики 9
Аксоид
—	винтовых осей неподвижный 422
—	винтовых осей подвижный 423
—	мгновенных осей неподвижный
336
—	мгновенных осей подвижный 336
Амонтон 73
Амплитуда колебаний 233
Аналогии кинематики со статикой
416
Аристотель 4
Арка
—	двухшарнирная 62
—	трехшарнирная 23, 52, 63
Архимед 4
Ассур 182
Балка 13, 56, 58
Бернулли Д. 5
Бернулли И. 5
Бинормаль кривой 204
Вариньон 5, 6
Вектор
—	главный системы сил 44, 118
—	единичный 25, 95
—	кривизны 205
—	момента пары сил 105
—	момента силы ПО
—	свободный 107
¦— скользящий 10
—	скорости 189
¦— угловой скорости 250
—	углового ускорения 250
¦— ускорения 200
—	функция 184
Веревочный многоугольник 82
Взаимодействие механическое 8
Вращение
—	равномерное 242
—	равнопеременное 243
Время 182
Галилей 5, 9
Годограф
—	радиуса вектора 184
—	скорости 196
График
—	движения 228
—	касательного ускорения 230
—	пути 229
—	скорости 229
График гармонического колебатель-
колебательного движения точки 232
Графическая статика 82
Гюйгенс 182
Даламбер 330
Движение
—	абсолютное 351
—	вращательное 239
—	криволинейное 183
—	механическое 7, 181
—	неравномерное 199
—	относительное 352
—	переносное 352
—	плоское 261
—	плоской фигуры 262
—	поступательное 237
—	прямолинейное 183
—	равномерное 211
—	равнопеременное 212
—	составное 351
429

Движение свободного твердого тела
342
—	сферическое 328
Диаграмма Максвелла — Кремоны
91
Динама 124
Динамика 7
Естественные координатные оси 204
Жуковский Н. Е. 6, 359
Задача
—	статически неопределенная 50
—	статически определенная 50
Заделка жесткая 55
Зацепление
—	внешнее 255
—	внутреннее 255
Изменение центра приведения 128
Инварианты статической системы
сил 129
Кардан 299
Кеплер 5
Кинематика 7
—	твердого тела 237
—	точки 181
.Кинематического винта параметр 424
Кинематическое состояние тела 8
Классификация движений точки 210
Ковалевская С. В. 6
Колеса эллиптические 257
Компоненты силы 25
Конус сцепления 70
Координата
—	угловая вращающегося тела 240
—	дуговая 183
Координаты полярные 376
—	центра тяжести 160
Коперник 5
Кориолис 182, 357
Коэффициент
—	скольжения 74
—	сцепления 73
—	устойчивости 69
Кривизна кривой 206
Кремона Л. 91
Крылов А. Н. 6
Кулон Ш. 73
Лагранж 5
Леммы о нулевых стержнях 33
Ленин В. И. 8
Леонардо-да-Винчи 5
Линия
—	действия силы 8
—	узлов 328
Ломоносов М. В. 6
Ляпунов А. М. 6
Максвелл Дж. 91
Масса 7
Материальная точка 7
Мгновенное винтовое движение 422
Мгновенный центр
—	вращения 292
—	скоростей 277
—	ускорений 308
Мерцалов Н. И. 182
Метод
—	Пуансо 43, 116
—	сечения 14, 66
Механика 4
—	теоретическая 7
Механизм кривошипный 218, 286,323
Механическая система 7
Мещерский И. В. 6
Многоугольник
—	моментов сил 114
—	моментов пар сил 109
—	силовой 16, 95
—	сид замкнутый 17, 96
—	угловых скоростей 388
Момент
—	главный системы сил 36, 114
—	главный относительно оси 115
—	пары сил 38, 104
—	силы относительно оси 111
—	силы относительно центра 35, 110
—	статический площади 161
—	эквивалентной пары сил 109
Направление силы 8
Нормаль главная 204
Ньютон 5
Область равновесия 76
Опора
—	шарнирно-неподвижная 13
—	шарнирно-подвижная 14
Орт
—	касательной 204
—	главной нормали 204
—	бинормали 204
Орты координатных осей 25, 97
Оси
—	декартовых координат 96
—	естественные 204
—	полярных координат 376
430

Остроградский М. В. 6
Ось
—	вращения 222
—	мгновенная 332
—	мгновенная винтовая 422
—	углового ускорения 333
—	центральная системы сил 125
Паппа — Гульдена теоремы 165, 166
Пара
—	вращений 404
—	сил 36, 104
—	присоединенная 43, 117
Пары эквивалентные 39, 106
Параллелограмм
—	сил 10
—	скоростей 355
—	угловых скоростей 386
—	ускорений 357
Передаточные механизмы 253
Передаточное число 254
Период колебаний 233
План скоростей 272
Плечо
—	пары сил 37
—	силы относительно центра (точ-
(точки) 35, 116
Плоскость
—	действия пары сил 104
—	нормальная 304
—	соприкасающаяся 204
—	спрямляющая 204
Покой тела 8, 9
Понселе 182
Правило
—	Жуковского 359
—	параллелограмма сил 10
—	параллелепипеда сил 96
Прецессия регулярная 398
Приведение системы сил
—	к данному центру 43, 116
—	к простейшему виду 45, 135
Принцип освобождаемое™ твердых
тел от связей 12
Производная векторная 189
Проекции на оси
—	декартовых координат вектора
угловой скорости 251
—	главного вектора 45, 49, 118,
133
—	равнодействующей 27, 98
—	силы 25, 96
—	скорости 194
—	ускорения 201
Проекции ускорения на естественные
оси 208
Птолемей 5
Пуансо 6, 43, 116, 295
Равнодействующая 8
—	двух параллельных сил 37
—	плоской системы сил 46
—	произвольной системы сил 121
—	системы параллельных сил 157
—	сходящихся сил 16, 96
Радиан 240
Разложение силы на составляющие
15
Размах колебаний 233
Реакция связи 12
Риттера способ 66
Рычаг 69
Связи И
Сила 8
—	трения скольжения 74
—	сцепления 73
Силы
—	внешние 9
—	внутренние 9
—	задаваемые 12, 17, 69, 142, 145
—	параллельные 49, 133
—	скрещивающиеся 124
—	сходящиеся 15, 95
Силовой винт (динама| 123
Система
—	материальных точек 7
—	сил 8
—	сил параллельных 49, 133
—	сил произвольно расположенных:
в пространстве 116
—	сил произвольно расположенных
на плоскости 43
—	сил сходящихся 15, 95
—	сил взаимно уравновешивающих^
ся 15, 95
—	сил эквивалентная 8
Скорость точки 188
—	абсолютная 352
—	относительная 352
¦— переносная 352
—	радиальная 377
—	средняя 189, 193
Скорость 188
—	трансверсальная 377
—	полюса 266, 345
—	тела угловая 241
Сложение вращений твердого тела
—	вокруг параллельных осей 398
—	вокруг пересекающихся осей 386Т
Сложение
—	пар сил 41, 107
—	скоростей 35Э
—	ускорений 355
Способ вырезания узлов 30
Способы определения движения точ-
точки 182, 184, 185
43L

Статика 7
•Стержень
—	опорный 30
—	растянутый 15
—	сжатый 15
Сцепление 73
Тело
—	абсолютно твердое 8
—	несвободное 12
—	свободное 11
Теорема
—	Вариньона 46, 122
—	Кориолиса 355
—	Пуансо 294
—	Ривальса 338, 349
—	Шаля 290
—	Эйлера — Даламбера 330
Траектория точки 183
Трение скольжения 73
Треугольник сил 15
Угол
—	нутации 329
—	поворота 240
—	прецессии 329
—	собственного вращения 329
—	сцепления 75
—	трения 75
Узел фермы 29
Уравнение вращательного движения
тела 240
Уравнения движения точки
—	в векторной форме 184
—	в координатной форме 185
—	в полярных координатах 376
Уравнения
—	линии действия равнодействую-
равнодействующей силы 132
—	плоского движения твердого тела
264
•— поступательного движения твер-
твердого тела 239
—	свободного
тела 345
движения твердого
—	сферического движения твердого
тела 329
—	равновесия сил 27, 47, 50, 98, 120,
134
Уравнения
—	траектории точки в координат-
координатной форме 186
—	траектории точки в параметриче-
параметрической форме 186
—	центральной оси системы сил 131
—	центроид 295
Усиление внутреннее 14
Ускорение 199
—	абсолютное 352
—	вращательное 246
—	касательное 208
—	нормальное 208
—	осестремительное 338
—	относительное 352
—	переносное 352
—	поворотное (кориолисово| 358
—	полюса 302, 350
—	угловое 250
—	центростремительное 246
Устойчивость при опрокидывании 70
Фаза колебаний 233
—	колебаний начальная 233
Ферма 29, 66, 67
Формулы Эйлера 252
Центральная ось системы сил 130
Центр
—	кривизны кривой 206
—	паралелльных сил 157
—	приведения 44, 117
—	тяжести 159, 161, 162
Центроида
—	неподвижная 294
—	подвижная 294
Циолковский К.. Э. 6
Чаплыгин С. А. 6
Частота колебаний циклическая 233
Чебышев П. Л. 6
Число степеней свободы 345
Шаль 5
Шарниры идеальные 29
Эйлер 6, 336
Эйлеровы углы 328
Энгельс 4, 181

Оглавление
Стр-
Преднсловие 	 3-
Из истории развития механики	 4-
РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
Глава I. Введение
§ 1. Основные понятия статики	 7
§ 2. Аксиомы статики 	 &
§ 3. Несвободное твердое тело. Связи. Реакции связей	 11
Глава П. Система сходящихся сил на плоскости
§ 4. Сложение двух сходящихся сил. Параллелограмм и треуголь-
треугольник сил	 15
§ 5. Многоугольник сил. Условие равновесия сходящихся сил . . 16
§ 6. Примеры на построение замкнутого треугольника сил ... 17
§ 7. Теорема о равновесии трех непараллельных сил	 21
§ 8. Примеры на применение теоремы о равновесии трех непарал-
непараллельных сил 	 21
§ 9. Проекции силы на две взаимно перпендикулярные оси на пло-
плоскости 	 2&
§ 10. Аналитический способ определения равнодействующей сходя-
сходящихся сил на плоскости. Уравнения равновесия сил .... 27
§ 11. Определение усилий в стержнях плоских ферм по способу вы-
вырезания узлов. Леммы о нулевых стержнях	 29
Вопросы для самоконтроля	 35
Глава III. Теория пар сил, лежащих в одной плоскости
§ 12. Момент силы относительно точки на плоскости		35
§ 13. Пара сил. Теорема о моменте пары		36
§ 14. Теорема о возможности перемещения пары сил в плоскости ее
действия 		38
433.

Cm p.
¦§ 15. Теорема об условии эквивалентности пар	 39
¦§ 16. Теорема о сложении пар на плоскости	 40
§ 17. Примеры на применение условия равновесия пар на плоскости 41
Глава IV. Система сил, произвольно расположенных
на плоскости
¦§ 18. Приведение силы к заданному центру .	 43
§ 19. Приведение системы сил, произвольно расположенных на пло-
плоскости, к силе и паре. Главный вектор и главный момент . . 44
¦§ 20. Возможные случаи приведения сил, произвольно расположен-
расположенных на плоскости 	 45
$ 21. Уравнения равновесия системы сил, произвольно расположен-
расположенных на плоскости	 47
¦§ 22. Сложение параллельных сил на плоскости. Уравнения равно-
равновесия параллельных сил	 49
§ 23. Статически определенные и статически неопределенные задачи.
Определение реакций внешних и внутренних связей системы
взаимосвязанных тел	 50
§ 24. Примеры на равновесие параллельных сил на плоскости . . 53
§ 25. Примеры на равновесие плоской системы сил	 58
§ 26. Определение усилий в стержнях ферм по способу Риттера . . 66
§ 27. Условие равновесия сил, приложенных к рычагу. Устойчивость
при опрокидывании. Коэффициент устойчивости	 69
§ 28. Примеры на применение условия равновесия сил, приложен-
приложенных к рычагу	 71
§ 29. Сцепление и трение скольжения 	 73
§ 30. Примеры на равновесие сил, приложенных к твердому телу при
наличии сил сцепления 	 76
Вопросы для самоконтроля	 81
Глава V. Графическая статика
¦§ 31. Многоугольник сил и веревочный многоугольник. Графическое
определение равнодействующей плоской системы сил . . .	82
¦§ 32. Случай замкнутого многоугольника сил. Графическое определе-
определение момента результирующей пары сил		84
§ 33. Графические условия равновесия плоской системы сил ...	85
§ 34. Примеры применения веревочного многоугольника		86
$ 35. Диаграмма Максвелла — Кремоны и примеры ее построения .	91
Вопросы для самоконтроля 		95
Глава VI. Система сходящихся сил в пространстве
§ 36. Многоугольник сил. Параллелепипед сил		95
§ 37. Проекции силы на оси декартовых координат		96
§ 38. Аналитический способ определения равнодействующей системы
сходящихся сил в пространстве. Уравнения равновесия сил .	97
§ 39. Примеры на равновесие сходящихся сил		99
Глава VII. Теория пар сил в пространстве
§ 40. Момент пары сил	 .	104
§ 41. Теорема о возможности переноса пары сил в любую плоскость,
параллельную плоскости действия пары		105
§ 42. Теорема об эквивалентных парах .		106
§ 43. Сложение пар сил в пространстве. Условие равновесия пар .	107
434

Стр.
Глава VIII. Момент силы относительно точки
и относительно оси
§ 44. Момент силы относительно точки как векторное произведение ПО1
§ 45. Момент силы относительно оси	 111
§ 46. Зависимость между моментом силы относительно точки и мо-
моментом силы относительно оси, проходящей через эту точку . 112"
§ 47. Аналитические выражения моментов силы относительно коор-
координатных осей	 ИЗ'
§ 48. Главные моменты системы сил относительно точки и относи-
относительно оси	 114
§ 49. Зависимость между главными моментами системы сил относи-
относительно точки и оси, проходящей через эту точку	 115-
Вопросы для самоконтроля	 116»
Глава IX. Система сил, произвольно расположенных
в пространстве
§ 50. Приведение силы к заданному центру	 116
§ 51. Сложение сил, произвольно расположенных в пространстве . 117
§ 52. Вычисление главного вектора и главного момента ..... 118
§ 53. Условия и уравнения равновесия сил, произвольно располо-
расположенных в пространстве 	 119
§ 54. Приведение системы сил к паре сил	 1204
§ 55. Приведение системы сил к равнодействующей силе .... 121
§ 56. Теорема о моменте равнодействующей силы (теорема Ва-
риньона)^	 	 122'
§ 57. Приведение произвольной системы сил к двум скрещивающим-
скрещивающимся силам или к силовому винту (динаме)	 123-
§ 58. Влияние положения центра на результаты приведения к этому '
центру системы сил в пространстве. Инварианты системы сил 127
§ 59. Уравнения центральной оси системы сил и линии действия
равнодействующей . . 	 130'
§ 60. Сложение параллельных сил в пространстве. Условия и урав-
уравнения равновесия параллельных сил	 132'
§ 61. Примеры на приведение системы сил к простейшему виду . . 135-
§ 62. Условия равновесия сил, приложенных к несвободному твер-
твердому телу. Определение реакций опор	 142
§ 63. Примеры на равновесие сил, произвольно расположенных в
пространстве 	 	 145-
Вопросы для самоконтроля . 	 15&
Глава X. Центр тяжести
§ 64. Последовательное сложение параллельных сил. Центр парал-
параллельных, сил . . :	 15&
§ 65. Формулы радиуса вектора и координат центра параллельных
сил 	-	 157
§ 66. Центр тяжести твердого тела	 15&
§ 67. Центр тяжести плоской фигуры. Статический момент площади
плоской фигуры относительно оси	 161
§ 68. Центр тяжести линии	 162
§ 69. Вспомогательные теоремы для определения положения центра
тяжести 	 163
§ 70. Определение положения центра тяжести плоской фигуры по
центрам тяжести ее частей. Способ отрицательных площадей . 167
§ 71. Определение положения центра тяжести плоской фигуры пу-
путем применения веревочного многоугольника	 168
435

Стр.
¦§ 72. Центр тяжести некоторых линий, плоских фигур и тел . . . 169
:§ 73. Примеры на определение положения центра тяжести .... 173
Вопросы для самоконтроля	 180
РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
Глава XI. Кинематические способы задания движения точки
•§ 74. Введение в кинематику		181
§ 75. Естественный способ задания движения точки		182
§ 76. Векторный способ задания движения точки		184
§ 77. Координатный способ задания движения точки. Уравнения дви-
движения точки в декартовых координатах		185
Вопросы для самоконтроля		188
Глава XII. Скорость точки
§ 78. Определение скорости точки при задании ее движения вектор-
векторным способом. Вектор скорости точки 	 188
§ 79. Определение скорости точки при задании ее движения есте-
естественным способом. Проекция скорости на касательную к
траектории 	 190
§ 80. Определение скорости точки при задании ее движения коорди-
координатным способом. Проекции скорости точки на неподвижные
оси декартовых координат	\.	 194
§ 81. Годограф скорости точки и его уравнения	 196
Вопросы для самоконтроля	 199
Глава XII. Ускорение точки
¦§ 82. Определение ускорения точки при задании ее движения век-
векторным способом. Вектор ускорения точки 	 199
§ 83. Определение ускорения точки при задании ее движения коорди-
координатным способом. Проекции ускорения точки на неподвижные
оси декартовых координат	 201
§ 84. Естественные координатные оси. Вектор кривизны	 204
§ 85. Определение ускорения точки при задании ее движения есте-
естественным способом. Касательное и нормальное ускорения точки 207
§ 86. Классификация движений точки по ускорениям ее движения . 210
§ 87. Примеры определения скорости и ускорения точки при зада-
задании ее движения естественным способом . 	 213
§ 88. Примеры определения траектории, скорости и ускорения точки
при задании ее движения координатным способом	 218
Вопросы для самоконтроля	 228
§ 89. Графики движения, пути, скорости и касательного ускорения
точки 	 ,228
Вопросы для самоконтроля .... 	 235
Глава XIV. Простейшие движения твердого тела
§ 90. Поступательное движение твердого тела . .	. .	237
§ 91. Вращательное движение твердого тела. Уравнение вращатель-
вращательного движения. Угловая скорость и угловое ускорение тела .	239
§ 92. Скорости и ускорения точек твердого тела, вращающегося во-
вокруг неподвижной оси		245
§ 93. Примеры на вращательное движение		247
436

Стр.
§ 94. Векторные выражения вращательной скорости, вращательного
и центростремительного ускорений		IO „.q
§ 95. Передаточные механизмы 	¦ • . . /4У
§ 96. Примеры на преобразование вращательного движения ' ' ' окя
Вопросы для самоконтроля	 ' ' 261
Глава XV. Плоское движение твердого тела
§ 97. Свойства плоского движения твердого тела. Движение пло-
плоской фигуры в ее плоскости	 " «ai
¦§ 98. Разложение движения плоской фигуры на поступательное дви-
движение вместе с полюсом и вращение вокруг полюса. Уравне-
Уравнения движения плоской фигуры	¦ .	263
§ 99. Теорема о скоростях точек плоской фигуры и ее следствия [ 266
§ 100. Примеры на применение теоремы о скоростях точек плоской
Ф
- |п, ФУР • •		268
§ 101. План скоростей 		272
§ 102. Мгновенный центр скоростей		277
§ 103. Примеры на применение мгновенного центра скоростей . . .	281
§ 104. Теорема о центре поворота для конечного перемещения пло-
плоской фигуры (теорема Шаля). Мгновенный центр вращения
фигуры 		290
§ 105. Неподвижная и подвижная центроиды. Теорема о качении по-
подвижной центроидй по неподвижной		292
§ 106. Уравнения неподвижной и подвижной центроид		295
§ 107. Примеры нахождения центроид		298
§ 108. Теорема об ускорениях точек плоской фигуры и ее следствия	301
§ 109. Мгновенный центр ускорений		308
§ 110. Способы определения положения мгновенного центра ускоре-
ускорений 		ЗП
§ 111. Примеры на применение теоремы об ускорениях точек плоской
фигуры и на определение положения мгновенного центра уско-
ускорений 		316
§ 112. Определение ускорений точек и угловых ускорений звеньев
плоского механизма 		323
Вопросы для самоконтроля 		327
Глава XVI. Сферическое движение твердого тела
§ 113. Эйлеровы углы. Уравнения сферического движения твердого
тела 		328
§ 114. Теорема о перемещении твердого тела, имеющего одну непо-
неподвижную точку. Угловая скорость тела		330
§ 115. Угловое ускорение тела при сферическом движении ....	332
§ 116. Скорости точек твердого тела при сферическом движении.
Проекции скорости точки тела на оси декартовых координат . .	333
§ 117. Аксоиды мгновенных осей , . ¦ • • . .	. .	335
§ 118. Ускорения точек твердого тела при сферическом движении . .	337
Вопросы для самоконтроля • • ¦ • 		341
Глава XVII. Общий случай движения твердого тела
§ 119. Разложение движения свободного твердого тела на поступа-
поступательное движение вместе с полюсом и сферическое движение
вокруг полюса. Уравнения движения свободного твердого тела 342
§ 120. Теорема о скоростях точек свободного твердого тела и ее
следствия	 345
437

Стр.
§ 121. Независимость векторов угловой скорости и углового ускоре-
ускорения тела от выбора полюса		348
§ 122. Теорема об ускорениях точек свободного твердого тела . . .	349
Вопросы для самоконтроля		350
Глава XVIII. Составное движение точки
§ 123. Относительное, переносное и абсолютное движения точки , . 351
§ 124. Теорема о сложении скоростей	 353
§ 125. Теорема о сложении ускорений (теорема Кориолиса) .... 355
§ 126. Модуль и направление поворотного ускорения (ускорения Ко-
Кориолиса) 	 358
§ 127. Примеры на применение теорем о сложении скоростей и о сло-
сложении ускорений при поступательном переносном движении . 361
§ 128. Примеры на применение теорем о сложении скоростей и о сло-
сложении ускорений в случае, когда переносное движение — вра-
вращение вокруг неподвижной оси	'.	 370
Вопросы для самоконтроля	 385
Глава XIX. Составное движение твердого тела
§ 129. Сложение вращений твердого тела вокруг пересекающихся
осей. Параллелограмм и многоугольник угловых скоростей . 386
§ 130. Проекции угловой скорости и углового ускорения твердого те-
тела, совершающего сферическое движение, на неподвижные и
подвижные оси декартовых координат	 390
§ 131. Проекции ускорения точки твердого тела, совершающего сфе-
сферическое движение, на неподвижные и подвижные оси декар-
декартовых координат 	 . 394
§ 132. Сложение вращений твердого тела вокруг параллельных осей 398
§ 133. Примеры на сложение вращений твердого тела вокруг парал-
параллельных и пересекающихся осей . 	 405
§ 134. Общий случай сложения движений твердого тела. Аналогии со
статикой 	 416
Вопросы для самоконтроля	 424
Приложение
Таблица 1. Механические величины и единицы их измере-
измерения в системах СИ (МКС)\ СГС и МКГСС	 426
Таблица 2. Соотношения между единицами некоторых меха-
механических величин 	 428
Именной и предметный указатель	 429

Александр Александрович Яблонский
Валентина Михайловна Никифорова
КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
Редактор 3. Г. Овсянникова
Технический редактор С. С. Горохова
Корректор И С. Шмелева
Т-15816. Печать с матриц. Подписано к пе-
печати 2/XII-65 г. Бумага бОхЭО'/щ. 27,5 печ. л.
25,18 уч.-изд. л. Тираж в пер. № 7 — 10 000 экз.,
цена 91 коп.; в пер. J* 5 — 90 000 экз., цена 84 коп.
Изд. № ОТ — 31/65 г. Заказ 2114.
Тематический план издательства
«Высшая школа» (вузы и техникумы) на 1956 г.
Позиция № 108.
Издательство «Высшая школа»
Москва И-51, Неглинная, 29/14
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Комитета по печати при Совете Министров
СССР. Измайловский проспект, 29.